А. Т. Фоменко
НАГЛЯДНАЯ
ГЕОМЕТРИЯ
И ТОПОЛОГИЯ
МАТЕМАТИЧЕСКИЕ
ОБРАЗЫ
В РЕАЛЬНОМ
МИРЕ
2-е издание
Издательство
Московского
университета
Издательство "ЧеРо"
1998

УДК 514+515.1
ББК 22.15
Ф76
Фоменко А. Т. Наглядная геометрия и топология: Математические образы в реальном
мире. — 2-е изд. — Mj Изд-во Моск.ун-та, Изд-во "ЧеРо", 1998. — 416 с.
Эта книга A-е издание — 1992 г.) — необычное явление в отечественной и зарубежной
научной литературе.
Основное внимание в ней уделяется графическому, наглядному изображению основных
понятий и объектов современной геометрии и топологии.
Все иллюстрации в книге, а они занимают в книге приблизительно 50% ее объема,
выполнены автором — доктором физико-математических наук, академиком РАН, профессором
МГУ А. Т. Фоменко. Графические листы А. Т. Фоменко уже давно привлекают к себе внимание
своей необычностью, художественной выразительностью, математической точностью стоящих
за ними образов.
Для математиков, физиков, будет интересна широкому кругу читателей.
Рисунки А. Т. Фоменко
Рецензенты:
академик Укр. АН Б. В. Гнеденко,
академик РАН В. А. Садовничий
Печатается по постановлению
Редакционно-издательского совета
Московского университета
Научно-художественное издание
Фоменко Анатолий Тимофеевич
НАГЛЯДНАЯ ГЕОМЕТРИЯ И ТОПОЛОГИЯ:
МАТЕМАТИЧЕСКИЕ ОБРАЗЫ В РЕАЛЬНОМ МИРЕ
Зав. редакцией Л. А. Николова. Художественный редактор Ю. М. Добрянская. Обложка
художника А. М. Ясинского. Технический редактор Г. Д. Колоскова. Корректор Н. В. Иванова.
Изд. лиц. № 040414 от 18.04.97. Подписано в печать 29.08.96. Формат 70x100/16.
Бумага офс. № 1. Офсетная печать. Гарнитура литературная. Усл. печ. л 33,8. Уч.-изд л. 38,79.
Тираж 5000 экз. Заказ «5 . Изд. № 6192.
Ордена "Знак Почета" изд-во Московского университета. 103009, Москва, ул. Б. Никитская,
5/7. ТОО "ЧеРо". Воробьевы горы, МГУ, главное здание, Д-4. тел.938-2481, 939-3381
Отпечатано в Московской типографии № 6
Министерства печати и информации РФ.
109088, Москва, Ж-88, Южнопортовая ул. 24.
ISBN 5-211-03631-Х
© А. Т. Фоменко, 1998

ПРЕДИСЛОВИЕ
Современная геометрия и топология
занимают особое место в математике
благодаря наглядности многих образов,
с которыми они имеют дело. В то же
время эта наглядность сегодня успешно
подвергается формализации и далеко
идущему абстрагированию, что
обусловило замечательные успехи,
достигнутые современной геометрической
наукой и ее многочисленными
приложениями. Д. Гильберт писал в 1932 г.:
«Что касается геометрии, то в ней
тенденция к абстракции привела к
грандиозным систематическим
построениям алгебраической геометрии, рима-
новой геометрии и топологии, в
которых находят широкое применение
методы абстрактныхрассуждений,
символики и анализа. Тем не менее и ныне
наглядное понимание играет
первенствующую роль в геометрии, и притом
не только как обладающее большой
доказательной силой при исследовании,
но и для понимания и оценки
результатов исследования» [3, с. б].
Многие геометрические понятия
рождались из конкретных задач механики,
физики и т. д. Мы отмечаем в
настоящей книге некоторые из этих связей.
Сегодня в математическую жизнь
смело входит компьютерная геометрия,
позволяющая, в частности,
визуализировать сложные математические
объекты, являющиеся результатом
длительных вычислительных экспериментов и
геометрический характер которых
заранее трудно предсказуем. Здесь следует
назвать, в частности, работы Банхоффа
[67], исследования Мандельброта [20],
Фрэнсиса [66], Пенроуза [76], Постона
и Стыоарта [77], Пеитгена и Рихтера
[80]. С некоторыми геометрическими
аспектами теории вероятностей и
математической статистики читатель может
познакомиться в трудах А. Н.
Колмогорова [54], Б. В. Гнеденко [55],
А. Н. Ширяева [43], Н. Н. Ченцова [90].
Некоторые из этих идей отражены
нами в разделе «Наглядный материал».
В настоящей книге отобраны лишь те
фрагменты геометрических знаний,
которые особенно наглядны и тесно
связаны с приложениями. См., в
частности, главу 3, посвященную
некоторым современным наглядным аспектам
симплектической топологии и гамиль-
тоновой механики, а также работы
В. П. Маслова [40], Д. В. Аносова
[27], И. М. Гельфанда [62], Ю. И. Ма-
нина [481, [49], А. Д. Фаддеева, В. Е.
Захарова [51], В. В. Козлова [47], С. В.
Матвеева [44], А. В. Болотова [38].
Главная цель настоящей книги
—рассказать на доступном и достаточно
наглядном языке о некоторых
классических и современных достижениях
геометрии, связанных как с внутренними
математическими задачами, так и с
приложениями. Мы не ограничиваемся
классикой и затрагиваем актуальные
проблемы, бурно развивающиеся
сегодня. При этом мы делаем упор на
наглядном объяснении постановок задач,
методов их решения и полученных
результатов, стремясь как можно быстрее
ввести читателя в круг геометрических
идей, игнорируя пока
абстрактно-логическую сторону вычислений,
рассуждений и т.п. Заинтересованный читатель
после прочтения книги сможет уже
самостоятельно углубиться в более
формальное изложение затронутых здесь
вопросов в специальной литературе.
Многие современные разделы
математики допускают такое наглядное
изложение, не претендующее, конечно, на
полную логическую строгость, но зато
быстро дающее представление о
существе предмета. В связи с этим,
например, мы поместили в главе 1
краткое изложение классической
теории полиэдров -и симплициальных
гомологии, поскольку эти идеи сегодня

Предисловие
Л
широко используются в математике,
физике и т.д., однако в современном
виде их логическое упрощение и
совершенствование часто достигаются за
счет большего уровня абстракции. В
этом отношении геометрический
подход к теории гомологии, восходящий
еще к А. Пуанкаре, возможно, более
громоздок (в области теоретического
обоснования), зато существенно проще
и нагляднее (а потому понятнее на
первых этапах знакомства с предметом).
Геометрическая интуиция играет
огромную роль в современных алгебро-
топологических и геометрических
исследованиях. Во многих глубоких
научных математических работах,
посвященных многомерной геометрии, активно
используется «наглядный жаргон»,
выработанный при исследовании двумерных и
трехмерных образов, вроде «разрежем
поверхность», «склеим листы»,
«приклеим цилиндр», «вывернем сферу
наизнанку» и пр. Такая терминология —
не прихоть математиков, а
«производственная необходимость», поскольку ее
употребление и само математическое
мышление авторов в терминах этих
образов оказываются совершенно
необходимыми при доказательстве многих
технически невероятно трудных
результатов. Довольно часто доказательство
того или иного математического факта
удается сначала "увидеть", а лишь
затем (следуя этой наглядной идее)
оформить в виде логически
непротиворечивого текста, что иногда
оказывается весьма трудной задачей, требующей
серьезных затрат интеллектуальной
энергии. Однако целесообразность таких
затрат психологически оправдывается
наглядной и красивой картиной, уже
сложившейся в голове исследователя и
убеждающей его в правильности
избранного пути. Таким образом, часто
критерий красоты того или иного
геометрического образа служит компасом для
выбора оптимального пути дальнейшего
формально-логического доказательства.
На эту тему см., например, глубокие
работы Ю. И. Манина [48, 49].
Мы не задавались целью
систематически изложить отдельные области
геометрии, а отправились в путешествие
по этому богатому миру,
«фотографируя» по пути те его фрагменты,
которые показались нам особенно
интересными. Поскольку наглядный и научно-
актуальный материал очень обилен, то
не может быть и речи о полноте или
систематичности изложения. Перед
читателем — краткий «дневник», попытка
рассказать широкому кругу
математиков, механиков, физиков о
разносторонности методов и приложений
современной геометрии, помочь увидеть за
сложными абстракциями реально
существующие геометрические, физические
объекты. Каждая глава книги написана
по возможности автономно от других,
чтобы читатель мог быстро войти в
круг идей каждого раздела,
самостоятельно выбирая порядок чтения глав.
Автор выражает благодарность
A. А. Зенкину, С. В. Матвееву,
Я. В. Татаринову, А. В. Чернавскому,
B. В. Федорчуку, любезно
предоставившим некоторые материалы по
наглядной геометрии и топологии.
У каждого математика имеется
свой комплекс представлений о
внутренней геометрии своего (известного
ему) математического мира и о
наглядных образах, с которыми
ассоциируются те или иные абстрактные
математические понятия (в том
числе в алгебре, теории чисел, анализе
и т. д.). Интересно, что у разных
математиков одни и те же абстракции
рождают иногда примерно
одинаковые наглядные представления,
которые, однако, в большинстве случаев
чрезвычайно трудно изобразить,
«нарисовать». Все рисунки в книге
выполнены автором. Часть
графического наглядного материала,
содержащегося в настоящей книге, —
это попытка «сфотографировать
изнутри» сложный, своеобразный
математический мир, богато
населенный образами и понятиями,
составляющими предмет современной
геометрии. Эти графические листы
собраны в разделе "Наглядный ма-

Предисловие
J_
териал». Каждый рисунок из этого
раздела снабжен отдельным
комментарием в тексте. Некоторые рисунки
дополняют содержание глав
понятиями, не отраженными в основном тексте
книги. В комментариях мы указываем
на это обстоятельство, приводя ссылки
на соответствующую литературу. Наши
графические листы либо основаны на
конкретных геометрических
конструкциях, идеях, теоремах, изображают
реальные математические объекты и
процессы, либо отражают различные
приемы восприятия тех или иных
математических понятий, например
бесконечности, непрерывности, гомотопии и
т. п. Первым опытом в этом
направлении была книга, написанная автором
совместно с Д. Б. фуксом и В. Л. Гу-
тенмархером «Гомотопическая
топология» [5]. Эта тема была развита далее в
книгах А. Т. Фоменко и Д. Б. Фукса
«Курс гомотопической топологии» [89]
и А. Т. Fomenko «Mathematical
Impressions» [21].
Разные разделы книги предполагают
различный уровень математической
подготовки читателя, однако большая
часть материала написана в расчете на
читателя, уровень подготовки которого
обеспечивается стандартными курсами
1 — 2-го годов обучения на
факультетах математических и физических
специальностей.
В книгу включены некоторые
наглядные аспекты результатов в области
современной компьютерной геометрии,
полученные в рамках научной темы
«Компьютерная геометрия» (механико-
математический ф-т МГУ, научный
руководитель А. Т. Фоменко). В книге
также отражены некоторые
направления, развиваемые в лаборатории
«Компьютерные методы в естественных
и гуманитарных науках» под
руководством д. ф.-м. н. А. В. Балашова (при
кафедре дифференциальной геометрии
и приложений).
Книга рассчитана на лиц,
интересующихся приложениями современной
геометрии и топологии, а также
студентов естественно-научных
специальностей (начиная с первого курса),
аспирантов.
Автор благодарит А. В. Балашова за
ценные замечания, способствовавшие
улучшению книги.

Полиэдры. Симплициальные
комплексы. Гомологии
§ 1. Полиэдры
1.1. Вводные замечания
Геометрия и топология чаще всего
имеют дело с геометрическими фигурами,
объектами, реализованными в виде
множеств точек в евклидовом
пространстве (быть может, большого числа
измерений). Полезно рассматривать эти
объекты не как жесткие (твердые) тела,
а как фигуры, допускающие
непрерывную деформацию, сохраняющую
некоторые качественные свойства объекта.
Напомним, что отображение какого-то
объекта на другой объект считается не-
гферыбным, если оно может быть
задано при помощи непрерывных функций
в какой-либо декартовой системе
координат в пространстве. Отображение
одной фигуры на другую называется
гомеоморфизмом, если оно
взаимно-однозначно и непрерывно в обе стороны,
т.е. устанавливает взаимно-однозначное
и взаимно-непрерывное соответствие
между точками обеих фигур. Тогда
существует обратное отображение с
такими же свойствами, а исходное
отображение (как и ему обратное)
называется гомеоморфизмом. Например,
прямолинейный отрезок и непрерывная
дуга (без самопересечений) на плоскости
гомеоморфны (рис. 1). Гомеоморфны
квадрат и круг (рис. 1), куб и тетраэдр
(иногда называемый симплексом) (рис.
1), плоскость и сфера с одной
выколотой (выброшенной) точкой (рис. 1). В
последнем случае гомеоморфизм
можно установить при помощи так
называемой стереографической
проекции (рис. 2). Для этого нужно
положить стандартную сферу на плоскость,
взять точку касания за южный полюс,
самую верхнюю ее точку — за
северный полюс N. Затем проведем луч из
северного полюса через произвольную
точку х на сфере и продолжим его до
пересечения с горизонтальной плоско-
Рис. I

}1. Полиэдры
7
стью. Полученную при этом точку
обозначим через f(x/. Отображение
x->f(x) и задает гомеоморфизм сферы
без точки с евклидовой плоскостью.
Понятие гомеоморфизма оказывается
удобным для выявления важных
свойств фигур, не меняющихся при
таких деформациях. Эти свойства иногда
называются топологическими, в
отличие от метрических, которые обычно
связывают с расстояниями между
точками, углами между линиями, ребрами
фигуры и т. п. С метрической точки
зрения куб и тетраэдр (рис. 1),
конечно, различны, хотя в то же время они
гомеоморфны. Для многих задач
"тонкие" метрические свойства фигуры
часто несущественны, поэтому
представляет интерес обнаружение ее более
"грубых" топологических свойств
(обычно замаскированных).
Рис.2
Иногда гомеоморфность двух фигур
сразу не очевидна. Простейший
пример: обычная плоская окружность У в
трехмерном евклидовом пространстве
К и заузленная окружность (рис. 3).
Конечно, они гомеоморфны. Для
установления этого факта достаточно
разрезать каждую из этих кривых в одной
точке и наложить друг на друга два
получившихся отрезка. Наглядное
изображение этих фигур в пространстве кажется
различным лишь благодаря тому, что
здесь окружность по-разному (двумя
Рис.3
способами) вложена в В . В трехмерном
пространстве нельзя непрерывно и без
самопересечений продеформкровать
нетривиальный узел в плоскую
окружность. Однако в четырехмерном
пространстве это уже можно сделать.
Точно так же гомеоморфны обычная лента
(кольцо) и лента, два раза закрученная
в трехмерном пространстве (рис 3).
Впрочем, не следует думать, что
любая закрутка ленты (на любое число
оборотов) приводит к гомеоморфной
фигуре. Рассмотрим, например, ленту,
закрученную один раз (рис. 3). Можно
проверить, что такая лента уже не
гомеоморфна плоскому кольцу
(обычной ленте). Лента, закрученная
один раз, называется лентой Мебиуса
(или листом Мебиуса). Вопрос: что
произойдет с лентой, если мы закрутим
ее любое четное или нечетное число
раз? Будет ли она гомеоморфна
плоскому кольцу или листу Мебиуса?
Назовем простой дугой множество
точек, гомеоморфное прямолинейному
отрезку. На простой дуге есть две
выделенные точки — ее концы. Иногда их
называют вершинами дуги. При

8
I. Полиэдры. Симплициальные комплексы. Гомологии
гомеоморфизмах простой дуги на себя
ее вершины переходят сами в себя или
друг в друга. Остальные точки простой
дуги (так называемые внутренние
точки) равноправны между собой в том
смысле, что для любой пары х и у
внутренних точек дуги всегда
существует гомеоморфизм дуги на себя,
переводящий точку х в точку у. Наглядное
доказательство см. на ри с. 4. Здесь
отображение отрезка на себя задано в
виде графика. Ясно, что в одном из
двух изображенных случаев концы дуги
меняются местами, а в другом —
переходят сами в себя, т. е. остаются на месте.
Рис. 4
Нульмерным симплициальньш
комплексом (нульмерным полиэдром)
называется конечная система точек (его
"вершин"). Одномерным комплексом,
или графом (одномерным графом),
называется система, состоящая из
конечного числа щ точек ("вершин") и
конечного "числа оц простых дуг (его
"ребер/'). При этом требуется
выполнение следующих двух свойств.
1) Любые два ребра или не имеют
общих точек, или пересекаются только
своими вершинами (концами). Каждая
вершина или не принадлежит ни
одному ребру (такие вершины мы назовем
"изолированными"), или служит
концом одного или нескольких ребер.
Число таких ребер называется
степенью, или индексом, вершины.
2) Оба конца каждого ребра входят в
число вершин графа (рис. 5).
Граф называется связным, если его
нельзя разбить на два подграфа без
общих вершин и ребер. В противном
случае граф несвязен и распадается на
несколько связных подграфов, которые
называются его компонентами
(компонентами связности).
Мы начали с понятия графа, чтобы
уже в начале главы 1 наглядно
продемонстрировать основные понятия,
которые ниже будут развиты в более
общем случае произвольных полиэдров.
Если из графа Г удалить одно ребро,
не удаляя ни одной вершины (в том
числе и концов этого ребра), то
возникает подграф Г'. Эта операция,
очевидно , может менять число компонент
связности в графе. Число компонент у
графа Г' будет прежнее (что и у графа
Г), если выброшенное ребро соединяло
вершины одной и той же компоненты
Г' (рис. 5). Напротив, число компонент
у графа Г' увеличится на единицу, если
выброшенное ребро соединяло
вершины из разных компонент графа Г'.
Рис. 5

§1. Полиэдры
9
Порядком связности графа .назовем
максимальное число ребер, которые
можно удалить из него, не меняя числа
компонент гр-^фа.
Простым циклом называется связный
граф, у которого все вершины имеют
индекс 2. Он изображается
окружностью. Более точно, такой граф го-
меоморфен окружности (рис. 6).
Рис.6
Далеко не каждый граф можно
реализовать в виде множества точек на
плоскости.
Вскоре мы познакомимся с общим
понятием гомологии. Здесь мы обсудим
пока простейший вариант этого
понятия. Рассмотрим произвольный граф Г
и выберем на каждом его ребре
произвольное направление, которое
фиксируем. Ребро, снабженное направлением
(стрелкой), назовем ориентированным
ребром и обозначим его буквой Л,-, где
номер * пробегает числа от 1 до щ (см.
выше, где о^ — число ребер в графе).
То же самое ребро, но снабженное
противоположной ориентацией,
обозначим через —А,-. Каждый простой
цикл на графе с выбранным на нем
направлением обхода запишем
формально в виде алгебраической суммы
составляющих его ребер, беря каждое
ребро со знаком «+» или «—» в
зависимости от того, совпадает его
направление с направлением на цикле или
противоположно ему. Если некоторое ребро
графа не вошло в цикл, то будем считать,
что в эту алгебраическую сумму оно
вошло с нулевым коэффициентом.
Следовательно, каждый простой цикл z
запишется в виде суммы z — гг Aj-k..
...+8дАд, где числовые коэффициенты е,
равны +1, —1 или 0. Рассмотрим
всевозможные линейные комбинации
таких линейных форм, т.е. простых
циклов , записанных на алгебраическом
языке. Такие общие формы уже не
будут, вообще говоря, отвечать
простым циклам. Назовем их циклами
(без прилагательного «простой»).
Такой общий цикл после «приведения
подобных членов» превратится в
линейную форму вида a!A i+...+a*A k, где
коэффициенты а, являются некоторыми
целыми числами, вообще говоря, уже
отличными от +1, -1, 0. В то же время
ясно, что получившиеся числовые
коэффициенты а, не совсем произвольны:
они удовлетворяют некоторым
линейным соотношениям. Можно было бы
рассмотреть произвольные линейные
комбинации вида Хх А fk..+Х* А*, где
коэффициенты к, — уже произвольные
целые числа. Такие линейные
комбинации называются цепями. Ясно, что
простой цикл и цикл являются
частными случаями цепей. Но не всякая цепь
является циклом. Цикл является
линейной комбинацией простых циклов.
Теперь можно дать алгебраическое
определение порядка связности графа:
порядок связности графа равен
алгебраическому числу линейно независимых
циклов в графе. Предоставляем
читателю проверить, что новое опреление
порядка связности графа совпадает с
прежним, геометрическим.
На этом примере мы видим, что
некоторые геометрические понятия можно
превратить в алгебраические путем
введения довольно простых и
естественных объектов
алгебро-геометрического характера (циклы, цепи

10
1. Полиэдры. Симплициальные комплексы. Гомологии
и т. п.). Оказывается, этот прием
чрезвычайно полезен в первую очередь тем,
что позволяет применить для
исследования геометрических свойств фигур
мощные методы алгебры.
В частности, мы получаем
возможность вычислять те или иные
качественные топологические
характеристики фигур, сравнивать их между собой.
Перейдем теперь к изложению
простейших понятий комбинаторной геометрии
полиэдров.
1.2. Понятие n-мерного симплекса.
Барицентрические координаты
Пусть в евклидовом пространстве R^1
заданы п +1 линейно независимых точек
Л), ..., Ац Мы считаем точки
независимыми, если независимы п+\ векторов,
идущих из начала координат в эти точки
(рис. 7). Поместим в каждую точку А,
неотрицательную массу щ (т. е. будем
считать А, материальной точкой),
причем потребуем, чтобы суммарная масса
всех точек равнялась единице. Это
означает, что выполнено равенство
*яь+...-ии^=1. Центром тяжести этих
масс (точек) является точка А,
являющаяся концом вектора О А, который
Рис. 7
имеет вид следующей линейной
комбинации: ОА—тоОАо +...+^,ОД,
векторов OAj, соединяющих начало
координат О с точками А,-. Числа п^^.^щ,
называются барицентрическими
координатами точки А. Они связаны
соотношениями: w,^0, ***>+... Л-Шн = 1.
Меняя массы т0> ...,т„ мы заставляем
точку А менять свое положение. В
результате она пробегает некоторое
множество Д*, которое и называется п-
мерным симплексом. Другими словами,
симплекс А" является Выпуклой
линейной оболочкой точек Ао, ...Дя.
Поэтому он иногда называется
прямолинейным (или евклидовым) симплексом.
На рис. 7 показаны простейшие
примеры. Нульмерный симплекс
изображается точкой. Одномерный симплекс
изображается отрезком на плоскости.
Двумерный симплекс изображается
треугольником в трехмерном
пространстве. Трехмерный симплекс можно
реализовать как заполненный тетраэдр в
трехмерном пространстве. Точки Ао,
..., Ап называются вершинами симплекса.
Ясно, что прямолинейный симплекс
полностью определяется, если заданы все его
вершины. Поэтому иногда симплекс
обозначается просто набором своих вершин.
Рассмотрим теперь множество точек
п-мерного симплекса, i-я
барицентрическая координата которых равна
нулю, т. е. т, = 0. Исходя из определения
симплекса, сразу видим, что это
множество в свою очередь является (п-\)~
мерным симплексом. Кроме того, этот
симплекс (который мы обозначим через
А" ) вложен в исходный симплекс Л и
противоположен его вершине А, (рис. 8).
Симплекс Д/*~ называется i-й (п-\у
мерной гранью симплекса Дя. Таким
образом, п-мерный симплекс имеет п
+1 граней размерности и-1.
Далее, k-мерной гранью симплекса
Дя называется множество точек п-
мерного симплекса Дя, для которых
какие-то n-k барицентрических
координат равны нулю, а остальные k?\

$ 1. Полиэдры
11
барицентрических координат
изменяются так, что соответствующие
массы (координаты) неотрицательны и их
сумма равна единице. Ясно, что Л-мер-
ная грань симплекса А" сама
является ^-мерным симплексом.
Рис. н
Одномерные грани, симплекса
обычно называются его ребрами. Сколько
/е-мерных граней имеет л-мерный
симплекс? Каждая грань однозначно
определяется своими k-\-\ вершинами,
которые являются в то же время
частью вершин исходного симплекса
Лл. Следовательно, полное число /г-мер-
ных граней в симплексе Дл равно
CnVu т. е. числу сочетаний из п -\-1
по k+ 1.
Согласно определению, л- мерный
прямолинейный симплекс является
выпуклым множеством, т. е. для
любых двух его точек соединяющий их
отрезок целиком содержится в
симплексе.
Геометрической границей л-мерного
симплекса называется объединение всех
его (л — 1) -мерных граней. Каждый
симплекс имеет однозначно
определенный центр, т. е. точку,
барицентрические координаты которой равны
между собой. Это означает, что
т0= . - . = Шп = ^рт • На Рис- 8
изображены центры одномерного,
двумерного и трехмерного симплексов.
В дальнейшем нам будет удобно
работать с ориентированными
симплексами. Будем говорить, что симплекс
ориентирован, если задан некоторый
определенный порядок его вершин.
Будем считать, что два порядка
вершин симплекса, отличающиеся четной
перестановкой, определяют одну и ту
же ориентацию симплекса. Если
порядки вершин отличаются на нечетную
перестановку, то они определяют
противоположные ориентации симплекса.
Например, меняя местами две
соседние вершины симплекса (в данном
упорядочивании), мы м'еняем
ориентацию (рис. 8). Иногда мы будем
обозначать ориентированный симплекс
знаком +ДП, а симплекс с
противоположной ориентацией —
символом— Дп.
Здесь усматривается связь с
линейной алгеброй. Данное выше
определение ориентации связано с тем,
что линейное отображение л-мерного
симплекса на себя, определенное
какой-либо перестановкой его вершин,
имеет положительный или
отрицательный определитель (детерминант) в
зависимости от того, является ли эта
перестановка четной или нечетной.
В связи с этим иногда будем говорить
о положительной или отрицательной
ориентации симплекса. Здесь следует
напомнить, что любая перестановка
вершин симплекса может быть
получена как композиция элементарных
перестановок, где под элементарной
перестановкой понимается перестановка
двух его соседних вершин. В то же
время линейное отображение
симплекса на себя, задаваемое перестановкой
двух соседних вершин, имеет
отрицательный определитель.
В дальнейшем мы будет
рассматривать не только сами прямолиней-

12
1. Полиэдры. Снмплицнальные комплексы. Гомологии
ные (евклидовы) симплексы, но и их
всевозможные гомеоморфные образы,
т. е. образы прямолинейного симплекса
при гомеоморфизмах. Такие
гомеоморфные образы симплекса называются
топологическими, или криволинейными
симплексами. Например, рассмотрим
стандартный тетраэдр, вписанный в
сферу, т. е. расположенный внутри
сферы так, что все его вершины
лежат на сфере. Тогда центр
тетраэдра совпадает с центром сферы.
Проектируя ребра тетраэдра из центра
сферы на сферу, получаем на ней
криволинейные треугольники — образы
равносторонних граней тетраэдра
(рис. 9). Следовательно, сфера
разбивается в объединение четырех
криволинейных треугольников — гоме-
оморфных образов равносторонних
прямолинейных треугольников. На
Рис. 9
рис. 9 показан процесс превращения
прямолинейного треугольника в
криволинейный. Здесь также изображены
криволинейные одномерный,
двумерный и трехмерный симплексы. Таким
образом, на каждом криволинейном
симплексе имеются вершины,
криволинейные грани и ребра. Из
криволинейных симплексов можно
составлять значительно больший запас
объектов, чем из прямолинейных
выпуклых симплексов. Понятие выпуклости
для криволинейного симплекса, вообще
говоря, уже не имеет столь
содержательного смысла, как для евклидова.
В то же время каждый
криволинейный симплекс «помнит» свое
происхождение из прямолинейного
симплекса. Для этого можно было бы
фиксировать какой-нибудь конкретный
гомеоморфизм прямолинейного
симплекса на криволинейный. Отсюда
легко понять, как естественно определить
линейное отображение двух
топологических, криволинейных симплексов.
Это—топологическое отображение, при
котором прообразы точек
криволинейных симплексов (принадлежащие
прямолинейным симплексам) переводятся
друг в друга линейным отображением
соответствующих прямолинейных
симплексов.
1.3. Полиэдры. Снмплицнальные подразделения
полиэдров. Снмплицнальные комплексы
Из симплексов можно составлять
более сложные объекты, фигуры. Пусть
некоторое множество X точек
евклидова пространства (или, более общо,
так называемое «топологическое
пространство») представлено в виде
объединения конечного или счетного
числа криволинейных симплексов
размерностей от нуля до некоторого п.
Другими словами, множество X
«склеено» из криволинейных симплексов.
В дальнейшем полезно представлять
себе топологический
(криволинейный) симплекс как пару,
состоящую из прямолинейного симплекса
и некоторого его топологического
отображения в некоторое множество точек

§1. Полиэдры
13
евклидова пространства. К множеству
симплексов, покрывающих X, должны
принадлежать все грани этих
симплексов. Для простоты будем считать в
дальнейшем, что число симплексов,
покрывающих множество Ху конечно.
Наложим теперь простые и
естественные ограничения на указанное
разбиение.
Будем говорить, что криволинейные
симплексы образуют конечное симпли-
циальное разбиение множества X, если
выполнены два условия:
1) симплексов конечное число и
каждая точка множества X попадает в
некоторый симплекс (покрыта
некоторым симплексом);
2) два симплекса либо вообще не
пересекаются (не имеют общих точек),
либо один из них является гранью
другого, либо они имеют общую грань,
являющуюся пересечением этих симплексов-.
Вместе с каждым симплексом в X
содержатся и его грани.
Рис. 10
На рис. 10 показаны все варианты
взаимного расположения двумерных
симплексов. На рис. 11 изображены
некоторые "запрещенные" ситуации.
Как уже отмечалось, с каждым
криволинейным симплексом естественно
связывается некоторое
соответствующее топологическое отображение на
него прямолинейного симплекса. В
этом случае нужно четко представлять
себе условие, что два симплекса имеют,
например, общую грань. Требуется,
чтобы при склейке двух симплексов по
общей грани в одну и ту же точку
множества X переходили такие точки
граней прямолинейных симплексов,
которые отнесены друг другу при линей-
нон отображении одной грани на
другую. Другими словами, склейке
топологических симплексов (граней) должна
отвечать склейка соответствующих
прямолинейных симплексов (граней) по
некоторому их линейному отображению.
Если некоторое множество точек
евклидова пространства (более общб,
топологическое пространство) разбито
на симплексы так, что выполнены
указанные условия 1 и 2, то такое
множество назовем полиэдром. Одно и то же
множество точек можно пофазному
разбить в объединение симплексов,
удовлетворяющих условиям 1 и 2. Если
фиксировано какое-то одно такое
разбиение , то будем говорить, что нам
дано симплициальное разбиеАие
данного полиэдра или дан симплищшльный
комплекс. Другими словами, симплипи-
альный комплекс — это множество
всех симплексов (и их граней) данного
разбиения полиэдра, причем указано,
как именно склеены эти симплексы. У
одного и того же полиэдра может быть
много различных симплипиальных
разбиений, т. е. один и тот же полиэдр
можно разными способами представить
в виде симплипиального комплекса.
Рис. 11
Для упрощения вычислений, мы будем
иногда рассматривать разбиения
пространства на симплексы, которым
разрешается иметь несколько общих
граней (в том числе, вершин). Более того,
для вычисления групп симплипиальных
гомологии можно пользоваться клет-

14
$1. Полиэдры. Симплициальные комплексы- Гомологии
ками (их точное определение см. ниже).
В частности, можно разрешать склейку
нескольких вершин симплекса в одну
точку. Таким образом, при покрытии
пространства симплексами можно
ослаблять условие 2. Это не влияет на
подсчет групп гомологии.
Не составляет труда определить
полиэдры, склеенные из счетного числа
симплексов (бесконечные полиэдры).
Для этого нужно потребовать, чтобы
каждая точка данного множества X
была покрыта лишь конечным числом
симплексов, причем окрестность
каждой точки в множестве X должна
получаться как результат объединения
окрестностей этой точки в каждом из
симплексов, которым она принадлежит.
Однако в дальнейшем нас будут
интересовать в основном лишь конечные
полиэдры.
Два симплекса симплициального
комплекса X называются инцидентными,
если один из них является гранью
другого. Симплициальный комплекс (и
соответствующий ему полиэдр)
называется п-мерным, если он содержит по
крайней мере один п- мерный симплекс
и не содержит симплексов более
высоких размерностей.
Подведем некоторые итоги.
1) Полиэдр — множество точек,
которое можно правильным образом
разбить на симплексы.
2) Симплициальный комплекс — это
множество симплексов и их граней,
составляющих это разбиение.
3) Определенные выше полиэдры
естественно назвать криволинейными,
или топологическими.
4) Евклидовым полиэдром иногда
называется множество точек евклидова
пространства, являющегося суммой
некоторого конечного или счетного числа
прямолинейных симплексов,
удовлетворяющих перечисленным выше условиям.
Из предыдущего ясно, что
топологический полиэдр можно определить
абстрактно, безотносительно к его
вложению в некоторое евклидово
пространство. Однако это расширение
общности нас не будет здесь
интересовать, так как в действительности можно
доказать (мы не будем здесь этого
делать), что всякий конечный
топологический полиэдр гомеоморфен
некоторому евклидову полиэдру, т. е. может
быть вложен в евклидово пространство
(быть может, достаточно большой
размерности).
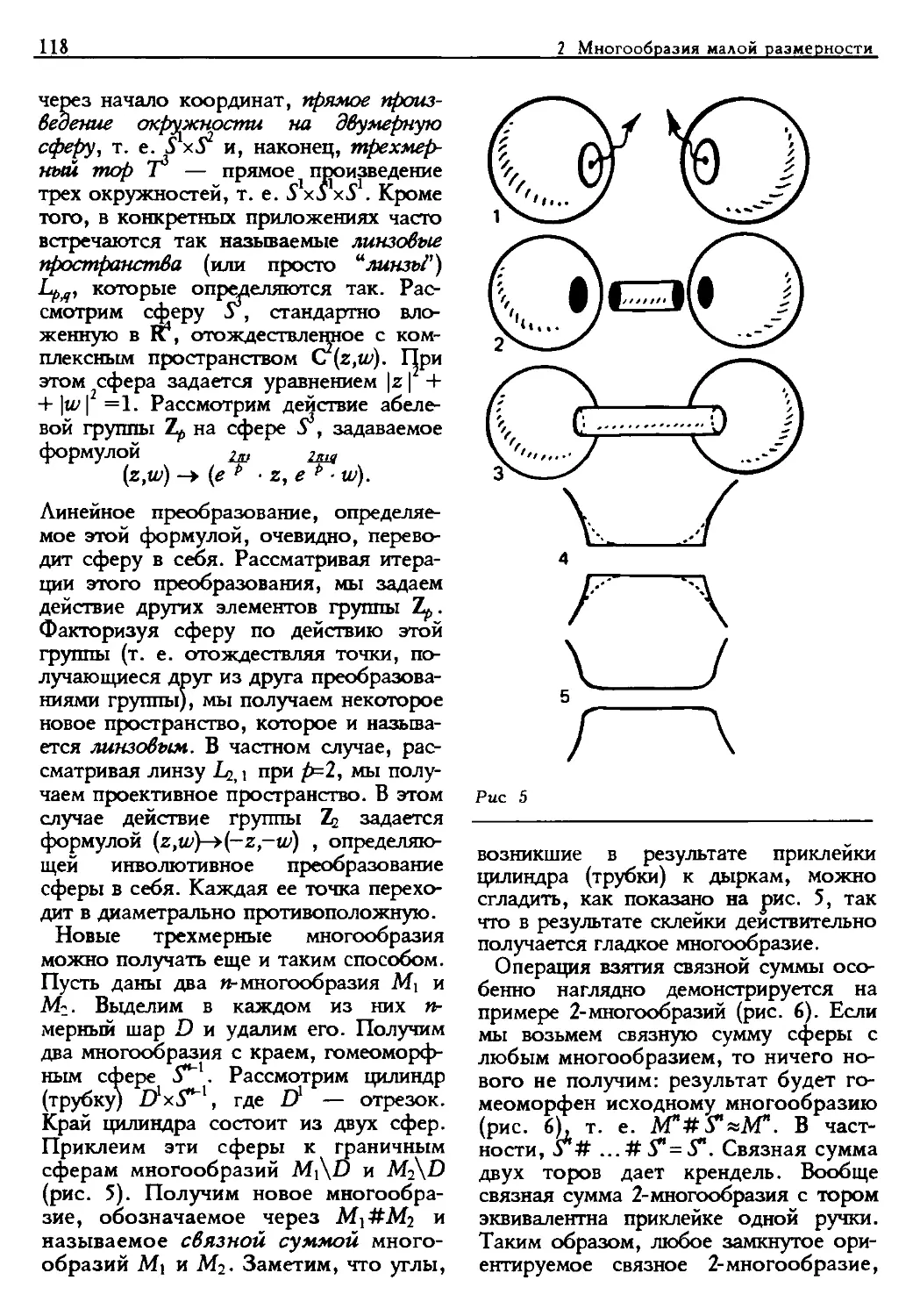
1.4. Примеры полиэдров
Из предыдущего пункта видно, что
полиэдр можно представлять себе как
результат склейки некоторого
(конечного или бесконечного) числа
симплексов по некоторым общим граням. Под
склейкой мы понимаем следующее.
Берем два симплекса, выделяем в них по
одной грани (одинаковых
размерностей) и отождествляем эти грани при
помощи некоторого линейного
отображения (в случае прямолинейных
симплексов) или при помощи
соответствующего топологического отображения
(в случае криволинейных симплексов)
(рис. 12). В результате получается
более сложный объект, составленный из
двух симплексов, склеенных по одной
общей грани. Это простое замечание
открывает большие возможности для
наглядного конструирования
конкретных полиэдров, поскольку процесс
склейки разных симплексов можно
продолжать неограниченно.
Рис. 12

§ 1. Полиэдры
15
Пример. 1. Евклидово пространство
является бесконечным полиэдром.
Например, плоскость можно . замостить
равносторонними треугольниками.
Такие и аналогичные замощения
плоскости изображены на многих
графических работах известного художника
М. К- Эшера. Трехмерное пространство
можно замостить тетраэдрами
(рис. 13). На рис. 13 показан один
из многих способов разбиения
трехмерного стандартного куба в
объединение симплексов (тетраэдров). Эти
тетраэдры не являются
равносторонними. Покрывая все пространство
кубами (что легко сделать) и
разбивая каждый из них по указанному
рецепту, мы и получаем разбиение
пространства на симплексы, что и
требовалось. Плоское кольцо и цилиндр
гомеоморфны и "являются полиэдрами
(рис. 13). Беря прямоугольник и
отождествляя его противоположные
стороны с изменением ориентации,
получаем лист Мебиуса (рис. 13), также
являющийся полиэдром. Естественно,
что отдельный симплекс также
является (простейшим) полиэдром.
Пример. 2. Окружность и
двумерная сфера являются конечными
полиэдрами. Для окружности этот факт
очевиден, а для двумерной сферы S
мы уже построили ее симплициаль-
ное разбиение на рис. 9. Простым
обобщением этой конструкции легко
доказать, что л-мерная сфера Sn
также является конечным полиэдром
(докажите!). Напомним, что сфера Sn
задается как множество точек в
.евклидовом пространстве R"+l,
удовлетворяющих уравнению (х'J+ . ..+
+ V+')W2, где *',...,
х"+|-декартовы координаты точки х. Число
- называется радиусом сферы.
Ясно, что сфера гомеоморфна
границе трехмерного куба. Чтобы
убедиться в этом, достаточно вписать сферу
в куб так, чтобы ее центр совпал
с центром куба (рис. 14), после чего
спроектировать сферу из ее центра
на границу куба. Легко убедиться,
что эта проекция задает
гомеоморфизм. Следовательно, в некоторых
случаях удобно рассматривать сферу
как двумерный полиэдр, являющийся
границей стандартного куба. Так как
квадрат можно представить в виде
склейки двух треугольников (т. е. дву-
Рис. 13

16 31. п
мерных симплексов) (рис. 14), то,
разбивая все грани куоа на пары
треугольников, мы получаем еще одно
представление двумерной сферы в виде
полиэдра. Здесь число двумерных
симплексов, составляющих сферу; равно,
очевидно, 12.
Рис. 14
Напомним, что сфера — граница
стандартного шара. Высверлим в шаре
несколько дырок, как показано на рис.
15. В результате получается трехмерное
множество точек, граница которого
двумерна. Оказывается, это двумерное
множество также допускает структуру
полиэдра.
Пример 3. Двумерные сферы с
некоторым числом "ручек". Начнем с
простейшего случая. Представим сферу в
виде полиэдра, как показано на рис. 15,
т. е. в виде границы плиты. Чтобы не
загромождать рисунок, не будем
изображать разбиение боковых граней
плиты на треугольники. Мы помним, что
любой квадрат можно
триангулировать , т. е. разбить на треугольники.
эдры. Симпдициальные комплексы. Гомологии
Затем высверлим из плиты квадратную
дыру, как показано на рис. 16. Ясно,
что мы получим новый полиэдр. В
самом деле, двумерная граница плиты с
дырой" состоит из нескольких
многоугольников, каждый из которых можно
разбить на несколько треугольников.
Рассматривая получившийся двумерный
полиэдр с точностью до
гомеоморфизма, легко увидеть, что он эквивалентен
"бублику" (рис. 16). Этот полиэдр
называется тором (двумерным тором).
Применяя еще один гомеоморфизм,
легко превратить тор в сферу, к
которой приклеена одна "ручка (рис. 16).
Следовательно, можно сказать, что
тор — это сфера с одной ручкой. Тор
также можно склеить из квадрата,
отождествив его противоположные
стороны, как показано на рис. 16. (Мы
будем разрешать разным треугольникам
триангуляции иметь несколько общих
граней, в том числе вершин).
Рис. 15

f 1. Полиэдры
17
Рис. 16
Теперь рассмотрим плиту, из
которой высверлены две дырки (рис. 17).
Ясно, что снова получается
двумерный полиэдр, составленный из
прямоугольников, каждый из которых
можно разбить на симплексы. Применяя
подходящий гомеоморфизм, можно
превратить «плиту с двумя дырками»
в объект, изображенный на рис. 17
и называемый на математическом
жаргоне «кренделем*. Продолжая
превращения этой фигуры, мы можем
представить ее в виде сферы с двумя
ручками, как показано на рис. 17.
Описанный процесс высверливания
дырок из плиты можно продолжить.
Ясно, что в плите можно
просверлить произвольное конечное число
квадратных дырок (рис. 18). Применяя
Рис. 17
подходящие гомеоморфизмы, получаем
сферы с произвольным количеством
ручек. Следовательно, мы обнаружили
Рис. 18

18
1. Полиэдры. Симплнцналыше комплексы. Гомологии
бесконечную серию двумерных
полиэдров— сферы с g ручками. Число g
называется родом поверхности.
Пример 4. Проективная плоскость.
Напомним, что полиэдры можно
получать, склеивая симплексы по их
общим граням. На рис. 19 показан
пример полиэдра, полученного
склеиванием восьми треугольников,
составляющих разбиение квадрата.
Одинаковыми*:. 19
ми буквами показаны те стороны
треугольников, которые следует склеить,
причем направления стрелок
показывают, с какой ориентацией нужно
склеить соответствующие стороны
(отрезки). Если отвлечься от системы
треугольников и рассмотреть весь
квадрат, то очевидно, что интересующий
нас полиэдр получится, если на
сторонах квадрата отождествить пару
сторон а и а (с учетом стрелок) и
пару сторон р и р (также с
учетом стрелок) (рис. 19).
Получившийся полиэдр называется
проективной плоскостью, или двумерным
проективным пространством. Позднее мы
еще неоднократно будем встречаться
с этим полиэдром и более подробно
познакомимся с его разнообразными
интересными свойствами.
Пример 5. Бутылка Клейна. Снова
возьмем квадрат, разбитый на восемь
треугольников, однако изменим (по
сравнению с примером 4) правило
склейки сторон квадрата в
соответствии с рис. 20. Получившийся полиэд
называется бутылкой Клейна. Удобн
изобразить его в трехмерном прост
ранстве следующим образом. Склеивая
сначала две стороны E и |3,
получаем цилиндр (рис. 20), на
граничных окружностях которого поставлены
стрелки а и а. Для того чтобы отож-
Рис. 20
дествить эти окружности (так, чтобы
совпали направления стрелок), нужно,
к сожалению, «проткнуть» поверхность,
что приведет к самопересечению.
Среди множества всех полиэдров
выделен важный класс полиэдров,
называемых многообразиями
(топологическими многообразиями). Полиэдр
размерности п называется п-мерным
многообразием (или п-многообразием),
если каждая его точка имеет
окрестность (в полиэдре), которую можно
гомеоморфно отобразить на
внутренность стандартного л-мерного шара
D". Напомним, что стандартным
открытым шаром называется
множество точек х в евклидовом
пространстве R\ удовлетворяющих
неравенству (*')* + . . . + (х"J<1.
Замкнутым шаром (или шаром с границей)

$ 1. Полиэдры
Ю
называется множество точек,
удовлетворяющих неравенству (х'J+. . . +
+ (хлJ^1. Ясно, что замкнутый шар
получается из открытого
присоединением граничной сферы.
М
Рис. 21
Перечисленные примеры полиэдров
(евклидово пространство, сфера,
сфера с ручками, проективная плоскость,
бутылка Клейна) являются в
действительности многообразиями. На рис. 21
показаны два примера полиэдров
(одномерный и двумерный), не
являющихся многообразиями. В обоих
случаях точка 0 не имеет окрестности
(в полиэдре), гомеоморфной соответ
ственно одномерному диску (т. е.
интервалу) и двумерному диску.
Рис. 22
Пример 6. «Дом Бингаъ. Этот дву
мерный полиэдр полезен при
изучении задач трехмерной топологии, о чем
мы подробнее расскажем в
следующих главах. Строится он так.
Рассмотрим куб, разобьем его на две
части экваториальной горизонтальной
плоскостью (рис. 22). На верхней
грани куба начнем «выедать»
вертикальную дыру вниз. Доходим до
экваториальной плоскости, «проедаем» ее,
выходим в нижнюю камеру и
«выедаем» ее всю, за исключением
фигуры В, которая образована
аналогичной конструкцией, начинающейся
с нижней грани куба. Аналогично
«врезаемся» в куб снизу, «проедаем»
дырку внутри В, пробиваем
экваториальную плоскость, выходим в
верхнюю камеру и «выедаем» ее
внутренность, за исключением стенок
конструкции А.
1.5. Барицентрическое подразделение
Как мы отмечали, каждый полиэдр
можно многими способами представить
в виде симплициального комплекса,
т. е. разбить на симплексы. Таких
способов бесконечно много. Оказывается,
для более глубокого изучения
полиэдров полезно выделить специальный
класс симплициальных разбиений,
которые называются барицентрическими
подразделениями (данного
симплициального разбиения). Вообще говоря,
операция подразделения
(измельчения) симплициального комплекса
заключается в том, что каждый
симплекс разбивается на меньшие (более
мелкие) симплексы таким образом,
чтобы в результате снова получился
симплициальный комплекс. Ясно, что
при этой операции полиэдр не
изменится. Изменится симплициальный
комплекс, носителем, «телом» которого
является данный полиэдр. В
дальнейшем полезно представлять себе
полиэдр как множество точек, а
симплициальный комплекс — как некоторую
«схему» этого множества,
возникающую, когда мы представили множество
в виде объединения симплексов. И

20
1. Полиэдры. Симплициальные комплексы. Гомологии
опять, можно многими способами
измельчать симплекс. Для нас
представляет интерес некоторый
специальный способ этого измельчения.
Перейдем к его точному описанию.
Рассмотрим все вершины, данного
симплициального комплекса. Их мы
менять не будем (нельзя разбить
точку на более мелкие части). Затем
рассмотрим все одномерные ребра,
т. е. одномерные симплексы. Введем
(добавим) новые вершины, взяв
середины (центры) одномерных
симплексов. Каждое ребро распадается на
два одномерных симплекса. Затем
возьмем все двумерные симплексы и
назовем новыми вершинами центры этих
симплексов. Мы считаем, что понятие
центра криволинейного симплекса
корректно определено, так как все наши
симплексы всегда являются
топологическими образами прямолинейных
симплексов, у которых центр (центр
тяжести) определен однозначно
(рис. 23). Из центра двумерного
Рис. 23
симплекса проектируем (при помощи
прямых линий на прямолинейном
симплексе) уже подразделенные
одномерные границы (т.е. ребра).
Другими словами, проводим в треугольнике
медианы. Они пересекаются в его
центре тяжести (рис. 23). Итак,
каждый одномерный симплекс
разбился на два одномерных симплекса.
Каждый двумерный симплекс разбился
на 6 двумерных симплексов. Берем
трехмерные симплексы. В каждом из
них выделяем центр и проектируем
из него уже подразделенные
двумерные грани этого симплекса. В
результате разбиваем трехмерный
симплекс на 6-4 = 24 более мелких
трехмерных симплексов. Ясно, что этот
процесс можно продолжить и на
высшие размерности. В результате мы
получаем новый симплициальный
комплекс, который называется
барицентрическим подразделением исходного.
Процесс барицентрического
подразделения можно повторить, т. е. можно
рассмотреть двухкратное, трехкратное,
m-кратное барицентрические
подразделения. Интуитивно ясно, что,
увеличивая /л, мы сможем разбить
исходный симплициальный комплекс на мел-
Рис. 24
кие симплексы сколь угодно малого
размера. Таким образом, измельчая
исходное симплициальное разбиение,
мы покрываем исходный полиэдр все
более мелкими симплексами, размеры
которых одновременно и равномерно
уменьшаются. С наглядной точки
зрения этот процесс приводит к
следующему. Если полиэдр разбит на
малое число симплексов, то он
является достаточно жестким телом, если

§ 1. Полиэдры
21
каждый симплекс рассматривать как
твердое тело и разрешать вращать
симплексы вокруг их общих граней.
Увеличивая число симплексов, мы
вводим большее число ребер, вокруг
которых могут вращаться соседние
симплексы. В результате полиэдр
становится более «мягким», податливым, его
можно деформировать большим числом
способов.
Пусть О — некоторая вершина сим-
плициального комплекса. Рассмотрим
все симплексы, инцидентные с этой
вершиной. Их объединение называется
симплициальной звездой данной
вершины. Ясно, что она является
окрестностью данной вершины в
полиэдре (рис. 24).
1.6. Комментарий к наглядному материалу
Цель этого пункта — дать наглядное
представление о полиэдрах на
примере геометрических конструкций. На
рис. 25 показан пример полиэдра
довольно сложного вида. Он покрыт
квадратами, каждый из которых
можно разбить на пару треугольников,
т. е. фактически на рис. 25
изображена триангуляция полиэдра.
Аналогичная конструкция (без
триангуляции) изображена на рис. 26. На
рис. 27 показан пример бесконечного
полиэдра, имеющего вид веретена. Он
состоит из «раковин», причем отверстие
/-Й раковины стыкуется с завитком
(/—1)-й раковины. Этот полиэдр
содержит две предельные точки, в
окрестности которых скапливается
бесконечное число раковин. Он полезен при
изучении так называемых локальных
гомологии и гомологической
размерности. К этому рисунку полезно
обратиться еще раз после прочтения § 2.
С точки зрения одномерных групп
гомологии этот полиэдр весьма
любопытен. Рассмотрим две его
концевые точки. На рис. 27 хорошо видна
точка, ближайшая к зрителю.
Вторая точка отнесена назад, в
бесконечность. Любая сколь угодно малая
окрестность концевой точки имеет
ненулевую группу одномерных гомологии.
Ясно, что, отсекай часть полиэдра,
мы обязательно разрежем трубку
какой-нибудь раковины. Следовательно,
ее горловина станет циклом,
негомологичным нулю. Это происходит в
любой окрестности концевых точек,
так как раковины уменьшаются в
размерах и число их бесконечно
внутри любой окрестности концевой точки.
Бесконечный полиэдр более простого
вида показан на рис. 28. Он
состоит из блоков, каждый из которых
допускает простую триангуляцию. На
рис. 29 показан первый этап
построения известного бесконечного
полиэдра— сферы Александера. Сама эта
«рогатая сфера* изображена на рис. 30.
Для ее построения нужно «вырастить»
из обычной сферы два «рога»,
направленные навстречу друг другу, но
не склеивать их. Затем из основания
каждого рога нужно вырастить свою
пару новых рогов, которые также
вытянуты по направлению друг к другу,
но не касаются друг друга и
образуют в пространстве «почти
зацепленную» систему (рис. 29). Затем процесс
нужно продолжить до бесконечности,
выращивая на каждом шаге новые
пары уменьшающихся в " размерах
рогов на основаниях прежних.
Несколько шагов показаны на рис. 30,
из которого более или менее ясно
общее устройство получающегося в
пределе полиэдра. Основным его
свойством является то, что в результате
получается (как это ни странно)
вложение сферы S2 в R3. Однако
оно не является локально плоским
в бесконечном множестве точек и
разбивает R3 на шар и неодносвяз-
ную область. Если же гладко
вложить сферу S2 в RJ, то она
разбивает R3 на две области, каждая
из которых односвязна (это шар и
внешность шара), т.е. любой
замкнутый путь непрерывно стягивается в
точку по области. В случае сферы
Александера можно найти такой путь,
который не стягивается в точку
внутри области. На рис. 31 изображен
симплициальный комплекс, составлен-

22
1. Полиэдры. Симплициальные комплексы. Гомологии
ный из большого числа трехмерных
симплексов. Центральная его часть
является звездой вершины,
расположенной в центре площадки. Вся
конструкция предназначена для того,
чтобы по мере возможности наглядно
представить структуру особых точек
полиэдров, не являющихся
многообразиями. Симплициальные звезды
показаны также и на рис. 32. Они
изображены «сбоку». На рис. 33
изображены сложные полиэдры, разбитые
в объединение кубов,
параллелепипедов. Как мы знаем, все эти объекты
могут быть в свою очередь
триангулированы, что и даст нам
триангуляцию полиэдров. Но, оказывается,
можно рассматривать кубические
разбиения полиэдров, т. е. взяв за
элементарный объект не симплекс, а куб.
Эта теория имеет свои преимущества
(как и недостатки). На ее основе
можно определить так называемые
кубические гомологии (сравните с
материалом следующего $ 2).
Аналогичная мысль (в более прямолинейном
варианте) выражена на рис. 34.
Вообще в целях наглядности удобно
представлять себе полиэдры (даже в
том случае, когда они являются
гладкими многообразиями) в виде
конструкций, составленных (склеенных)
из кубов, параллелепипедов. Этот
образ, вероятно, более психологически
удобен, чем образ, составленный из
тетраэдров. На рис. 35 изображен
«кубический полиэдр» с разрезом. Этот
образ вскоре будет полезен нам при
обсуждении понятия цепей и того
важного алгебро-геометрического
факта, что суммирование цепей
приводит иногда к взаимному
уничтожению общих кусков границы.
«Заклеивая» трещину в полиэдре на рис. 35,
мы тем самым, очевидно, уменьшаем
его границу: границы трещины
взаимно уничтожаются. Похожий
процесс показан и на рис. 36. Здесь
«трещина» разъединяет симплициаль-
ную цепь (полиэдр) на две части с
«большими границами», однако,
заклеивая трещину, мы уменьшаем общую
границу цепи, т.е. д(А+В) = дЛ-\-
-j-dB— (дА()дВ). Кроме того, на рис.
36 изображены призмы и начальный
момент их триангуляции. Этот
процесс нужен при доказательстве
независимости гомологии от выбора
триангуляции. Рис. 37 посвящен
наглядному изображению процесса
вычисления гомотопических групп полиэдров.
Эти группы состоят из
гомотопических классов отображений сфер в
полиэдры. Внутри полиэдра «плавают»
сфероиды (образы сфер), их можно
складывать, вычитать, что и
порождает гомотопическую группу п*{Х)
полиэдра X, где i—размерность сфер
(рис. 37). Плавающая сфера —
наглядный образ сфероида,
подвергающегося гомотопии. На рис. 38
показаны призмы, в объединение которых
распадается прямое произведение
полиэдра на отрезок. На рис. 39 см.
кубические полиэдры.
Некоторые из математических
рисунков, использованных в настоящей
книге, содержат кроме своего
первого, основного математического
направления, также другое неформальное,
ассоциативное направление.
Перечисляемые ниже графические работы были
в свое время предназначены как для
иллюстрации математических понятий,
так и для использования в издании
замечательного романа М. А.
Булгакова «Мастер и Маргарита»: рисунки
к гл. 1, § 1: 32—36, 38, 39; гл. 1, § 2:
21,27 — 30; гл. 1,§ 3: 9, 11, 12, 16—18;
гл. 2, § 4: 25; гл. 2, § 5: 44, 45, 48,
49; гл. 3, § 1: 13; гл. 3, § 3: 18, 20;
гл. 4, § 1: 9.

§ 2. Группы симплициальных гомологии полиэдров
23
§ 2. Группы симплициальных гомологии
симплнцнальных комплексов (полиэдров)
2.1. Симплициальные цепи
Язык полиэдров и симплициальных
групп гомологии (см. ниже) является
весьма наглядным и удобным для
первого знакомства с важными
понятиями геометрии. Он достаточно
первичен, основан на небольшом числе
понятий, хотя при конкретных
вычислениях иногда достаточно
громоздок. В современной геометрии
вычисление групп гомологии выполняется
обычно в других, более гибких
терминах, например в терминах так
называемых клеточных гомологии.
Однако относительная простота
вычислений клеточных гомологии опирается
на достаточно сложную процедуру
самого определения групп клеточных
гомологии. Можно составить
следующую таблицу, показывающую
преимущества и недостатки разных
определений групп гомологии.
Отсюда видны преимущества
клеточных гомологии, поскольку в
конкретных исследованиях полезно иметь
дело с легко вычислимым объектом
(пусть и сложно определяемым).
Однако мы предпочли познакомить
читателя именно с симплициальными го-
мологиями (и соответственно
полиэдрами)', так как поставили на первое
место наглядность и элементарность.
Знакомство с симплициальными го-
мологиями позволяет очень быстро
усвоить саму идею гомологии,
играющую важную роль в современной
геометрии, механике, физике. Эта же
общая идея лежит и в основе
понятия клеточных гомологии, поэтому
с нашей точки зрения язык
полиэдров и симплициальных комплексов
полезен именно на первых стадиях
изучения основ топологии. После
этого переход к клеточным гомологиям
не составляет труда.
Рассмотрим полиэдр X и
фиксируем какое-либо его симшшциальное
разбиение. Для простоты будем в
дальнейшем обозначать той же
буквой X соответствующий симпли-
циальный комплекс. Рассмотрим
множество всех fc-мерных симплексов
полиэдра Ху занумеруем их в
каком-то (произвольном) порядке и
припишем каждому симплексу (также
произвольным образом) ориентацию.
Будем обозначать эти симплексы
символами А* где i указывает'
порядковый номер, a k — это размерность
симплекса. Номер i может
изменяться от 1 до бесконечности. В
дальнейшем будем считать, что нумерация
и ориентации симплексов фиксированы.
Рассмотрим какую-либо абелеву
группу G, например группу целых чисел Z,
или группу вещественных чисел R,
или конечную группу Zp вычетов
по модулю р. Перечисленные
группы— наиболее употребительные в
топологии. Для определенности
сосредоточимся пока на случае, когда G= Z.
Перенос всех дальнейших конструкций
на случай произвольной абелевой
группы делается автоматически и не
добавляет никаких новых
принципиальных моментов.
Рассмотрим линейные комбинации
вида с = 2,- о/А* где а, — целые числа
(положительные или отрицательные),
а А*— ^-мерные симплексы, причем
будем предполагать, что в этой сум-
Симплициальные
гомологии
Клеточные гомологии
Легко определяются
Достаточно сложно
определяются
Сложно доказывается ин-
ва риа нтность гомологии
Легко доказывается
инвариантность гомологии
Достаточно сложно
проводить конкретные вычисления
Вычисляются существенно
легче, чем симплициальные

24
§1. Полиэдры. Сммплициальные комплексы. Гомологии
ме лишь конечное число чисел щ
отлично от нуля. Такие линейные
комбинации называются целочисленными к-
мерными цепями (или симплициальны-
ми целочисленными к-мерными
цепями). Каждую такую цепь можно
трактовать как функцию с целочисленными
значениями, определенную на
множестве всех ^-мерных симплексов, т. е.
с : А, -» а, для всех *. При этом
предполагается, что эта функция отлична
от нуля лишь на конечном числе
симплексов и что она нечетная, т. е.
с(-&?)=-а=-с(А;), где через -Д,
обозначен симплекс Д, с обратной
ориентацией'. В дальнейшем, работая с
цепями, мы будем пользоваться в основном
языком линейных форм, поскольку он
удобен для вычислений.
Простейшими примерами цепей
являются цепи вида 1 Д, и (-1) *Д, ,
которые иногда называются
элементарными. Цепи можно складывать как
обыкновенные линейные формы. А именно
суммой й+<2? двух цепей С1=?^,Д, и
С2 — ZA-Д,, называется цепь С\+С2=
— T,t(a&bi)&i • Следовательно,
множество всех ^-мерных целочисленных
цепей образует абелеву группу, которую
мы обозначим через Ск(Х).
Образующими этой группы являются
элементарные цепи вида 1 Д, и (-1) Д, .
Определение. Группа Ск(Х)
называется группой k-мерных симплиииальных
целочисленных гленей полиэдра X
(симплициального комплекса X).
Отсюда видно, как можно определить
цепи с коэффициентами из
произвольной абелевой группы. Для этого нужно
рассматривать линейные формы вида
Z, gi Д, , где коэффициенты g
принадлежат абелевой группе G.
Возникающую при этом аоелеву группу цепей
с коэффициентами в группе G мы
будем обозначать через С/XX, G). В этих
обозначениях определенная выше
группа Ск(Х) целочисленных цепей
запишется как Ск(Х, Z). Эта группа
является свободной абелевой группой, т. е.
представляется в виде прямой суммы
некоторого числа бесконечных
циклических групп Z.
Если полиэдр X — конечный, то
группа его к- мерных целочисленных цепей
является группой с конечным числом
образующих (конечно-порожденной
абелевой группой).
Итак, мы сопоставили каждому
полиэдру X (симплициальному комплексу
X) набор абелевых групп Со(Х),
С\(Х),..., Сп(Х). Ясно, что при Л<0 и
k>n группы цепей не определены, так
как нет симплексов, у которых
размерность k меньше нуля либо больше
w=dim X. Иногда, впрочем, удобно
считать (по определению), что все
группы Ск(Х), где к>п, являются нулевыми.
2JZ. Граница цепи
Рассмотрим элементарную
целочисленную цепь 1-Д (которую обозначим для
простоты через Д^ и определим ее
алгебраическую границу как некоторую
(к -1 у мерную целочисленную цепь,
которую мы сейчас зададим явной
формулой. Предварительно обсудим
понятие ориенпшцци, индуцированной
на i-й грани Д, симплекса Д .
Напомним, что ориентация симплекса Д
предполагается заданной и
фиксированной. Симплекс Д задается набором
своих вершин Ао, А\, ..., Ak (см. § Д].
Ясно, что (k—\У мерные грани Д,-
симплекса Д получаются
последовательным вычеркиванием его вершин,
т. е. Д, " =(А), ..., Ан, А.-+1, ..., Ак).
Будем считать, что ориентация грани
Д, (с номером ?'), индуцированная
на ней ориентацией симплекса Д ,
определяется знаком (-1)'.
Рассмотрим примеры. Одномерный
симплекс (отрезок) Д задается своими
двумя вершинами Ао и А\ (рис. 1).
Тогда его грани — это пара точек Ао и А\,
взятых со знаками: точка Ао со знаком
"-", а точка А\ со знаком "+". В самом
де^е, дЦАэ.Д), $={-\)%=Ах;
Д] = (-1) Ао= -Ао .. Геометрически
различие в знаках объясняется тем, что в
точке Ао (рис. 1) стрелка, указывающая
ориентацию симплекса, смотрит внутрь
симплекса, а в точке А\ эта же стрелка
смотрит наружу симплекса. Таким

S2. Группы симплициальных гомологии полиэдров
25
образом, двигаясь по прямой, на
которой лежит отрезок, мы сначала входим
в отрезок (знак "-а), а затем выходим
из него (знак "+"). Следовательно,
введенное выше понятие ориентации
граней соответствует интуитивному
представлению о ней. Рассмотрим
следующий пример.
Рис. 1
Двумерный симплекс задается тремя
вершинами А2=(Д>, Аь А2) (рис. 1). У
симплекса — три одномерные грани
(стороны треугольника), а именно:
ребро До'= (-lN(Ai, А2) = (А„ А2),
ребро А* = (-lftAo, А2) = -Ио, А2) = (Аъ
Д,), ребро A? = (-lftAo, Л!) = (Д,, А,).
На рис. 1 расставлены стрелки на
одномерных гранях симплекса,
показывающие индуцированную на них
ориентацию. Подчеркнем, что ребра (А\, А2)
и (Aq , А\) получили положительную
ориентацию, а ребро (Д>, А2) —
отрицательную. Поэтому мы заменили
ребро — (Ао, А2) на эквивалентное
ему ребро (Л2 , Л>). Из рис. 1 видно,
что данное выше формальное
определение индуцированной ориентации
прекрасно согласуется с
геометрической интуицией. В самом деле,
в результате вычислений мы
обнаружили, что граничные ребра,
снабженные индущрованной ориентацией у
задают одно и то же направление
вращения на треугольнике. Обходя его
границу по часовой стрелке, естественно
было бы ожидать, что проходимые
ребра снабжены стрелками,
указывающими то же направление движения.
Именно этот факт мы и получили,
опираясь на алгебраическое определение
индуцированной ориентации. Теперь
мы можем определить важное понятие
алгебраической границы симплекса.
Определение. Границей ЗА
ориентированного симплекса А называется
сумма всех его (k-Yyмерных граней,
взятых с индуцированной ориентацией.
Запишем границу симплекса на языке
алгебры. Получим 5А = Zj=(j(-1)'A; =
ДК~1 А К~1 ¦ А ДС~1 ¦ A /f""l Т>
о ~Ai +А2 — ...±Д* . 13 терминах
вершин эта же формула запишется так:
д(А> Л^Е*=ю(-1)'(Л),...,Ам, А*и
..., Ак).
Другими словами, мы
последовательно вычеркиваем вершины симплекса,
получаем соответствующие грани (на
единицу меньшей размерности) и суммируем
их (в виде формальной линейной ком-
Рис. 2
бинации), беря со знаком (-1)', где г —
номер вычеркнутой вершины. Поясним,
что \k-Л\-мерный симплекс А, '
получающийся при вычеркивании вершины
А,, геометрически изображается как
грань, противоположная (в симплексе
А ) вершине А, (рис. 2).
Естественность такого
алгебраического определения границы симплекса (ал-
гебраичность проявляется в учете знака —
ориентации) теперь для нас очевидна. В

26
Полиэдры. Симплициальные комплексы. Гомологии
самом деле, границей одномерного
симплекса является сумма его вершин
вида 9А1=9(Д), Ai^Ai-Д). Границей
двумерного симплекса является сумма
его реоер :
ал2-Э1Ло,1А1|Аа)-(Ао1А1) +
+(Л,,А2)+(А2,А)).
Все эти три ребра задают одно и то же
вращение по часовой стрелке, т. е.
именно ту ориентацию, которая
индуцируется на границе треугольника, если
задать внутри его вращение по
часовой стрелке.
Теперь мы можем определить границу
произвольной цепи. Пусть агАг +... +
+qjAq — симплициальная
целочисленная цепь.
Определение. Границей k-мерной г^епи
с называется (к—Ту мерная
целочисленная симплициальная цепь дс,
задаваемая следующей явной формулой: Зс=
= щдАу +... + ctfpAq .
При этом мы считаем, что смысл
выражения ЗДу был определен выше.
Другими словами, задав оператор 3 на
элементарных цепях 1 Д; , мы затем
продолжаем его "по линейности" на
произвольные линейные комбинации
элементарных цепей, получая тем
самым корректно определенный оператор
на всей абелевой группе цепей С^Х).
Он называется граничным оператором,
или оператором границы, или
оператором взятия границы.
2Л. Простейшие свойства оператора
границы. Циклы. Границы
1) Оператор 3 линеен. Это означает,
что для любых &-мерных цепей сх, Ох и
для любых целых коэффициентов а, Ь
выполняется тождество д(аС}+Ыь)=
—a dc\+bdoi. Другими словами,
оператор 3 задает гомоморфизм абелевой
группы к- мерных цепей 6*(-Ю в абелеву
группу (к-1)-мерных цепей С^Х).
Иногда будем обозначать этот
оператор через dkt явно указывая
размерность цепей, на которых он определен.
Следовательно, в предыдущем пункте
мы определили фактически целое
семейство операторов ф>, Эь ... , dkt... ,
дп, где n=dimX (т. е. размерность
комплекса X). Итак, дк : Ск(Х) -> Cfc./W.
2) Квадрат граничного оператора д
тождественно равен нулю.
Доказательство. Так как оператор 3
линеен, то утверждение достаточно
доказать лишь для элементарных цепей,
т. е. для одного ^-мерного симплекса
А . Иногда удобно записывать оператор
границы в виде:
5А* = Е*1Ч,(-1)'(Д),...Л,...,А*),
где знак « А » (крышка) означает, что
символ, стоящий под ним, пропущен,
выброшен. Мы должны доказать, что
сг А = 0. Применяя оператор 3 второй
раз, мы получаем длинную сумму, в
которую обязательно входят следук)-
щие два слагаемых: (—1)* (—1/(Аэ, ...»А,-,
.Л.,Д>Л..,А,), и (-1У(-1Г(Ао,...,
Aj, ..., А ,, ... , Ак). Без ограничения
общности можно считать, что j< г. В
первом слагаемом вершина Аг была
вычеркнута при первом применении
оператора 3, т. е. раньше, чем была
вычеркнута вершина А; (уже при
втором применении оператора 3). Во
втором слагаемом картина иная. Здесь
раньше была вычеркнута вершина Лу
(при первом применении 3), а лишь
затем была вычеркнута вершина А,- (при
втором применении 3). Следовательно,
при вычеркивании вершины А,- для
учета знака мы должны подсчитать число
вершин, стоящих левее ее. Ясно, что
левее ее расположено /-1 вершин,
так как вершина А; была уже
вычеркнута на предыдущем шаге. Так
как знаки (-1)**и (-1)*г/
противоположны, то выделенные нами два
слагаемых входят в общую сумму с разными
знаками, поэтому взаимно
уничтожаются. Утверждение доказано.
Геометрический смысл его
абсолютно ясен: граница симплекса сама не
имеет границы*
3) Если д(ас) = 0 и а * 0, то дс =
= 0. Это утверждение очевидно, так
как мы рассматриваем целочис-

§ 2. Группы симплицнальных гомологии полиэдров
27
ленные цепи и из равенства д(ас)=0,
где афО, вытекает, что адс = Оу т.е.
а(дс) = 0 и 3с = 0 (на коэффициент
афО можно сократить).
Определение. Цепь z называется
циклом, если ее граница равна нулю,
т. е. dz = 0. Цепь Ь называется
границей, если она представима в виде
b = dh, т.е. в виде границы некоторой
цепи h на единицу большей
размерности.
Ясно, что все эти объекты
(оператор границы, циклы, границы)
можно определить и для произвольной
абелевой группы коэффициентов. Мы
не будем здесь повторять
соответствующие определения, предоставляя
читателю продумать этот вопрос
самостоятельно.
4) Множество циклов образует
абелеву подгруппу в группе цепей.
Эта подгруппа обозначается через
Z* (X). Множество границ образует
абелеву подгруппу в группе цепей.
Эта подгруппа обозначается через
Вь(Х). Каждая граница является
циклом. Это означает, что подгруппа
Bk (X) всегда содержится в
подгруппе Zk(X). Эти утверждения следуют
из линейности оператора д и из
доказанного выше равенства д2 = 0.
Цикл не обязан быть границей.
Это означает, что в общем случае
группа Zk(X) может быть больше,
чем ее подгруппа Bk(X). Итак, dk:
Ck(X)^Bk-^{X)\ дк: Zk(X)-+0\ dk-i:
fl*_i(X)+0.
2.4. Примеры вычисления оператора границы
Будем считать, по определению, что
граница любой нульмерной цепи равна
нулю (так как нет ненулевых цепей
отрицательной размерности).
Поскольку любая нульмерная цепь — это
линейная комбинация точек (вершин
полиэдра) с целыми коэффициентами, то
принятое нами соглашение наглядно
очевидно: точка не имеет границы
(т. е. граница точки равна нулю).
Следовательно, любая нульмерная
цепь является циклом.
Рассмотрим двумерный симплекс
Л2 как элементарную цепь. Тогда его
граница дА2 имеет вид C1+C2 + C3
(рис. 3). Следовательно, одномерная
цепь с = С\-\-С2 + Сз является границей.
В то же время она, очевидно,
является одномерным циклом.
Рис. з
Рассмотрим квадрат, разбитый на
четыре двумерных симплекса (рис. 3),
на каждом из которых зададим
вращение по часовой стрелке.
Возьмем цепь, являющуюся суммой этих
четырех симплексов с
коэффициентами 1, и вычислим ее границу.
Для этого нужно вычислить границы
всех четырех симплексов, после чего
сложить эти границы. При этом
произойдет следующее. Каждое
одномерное ребро, лежащее внутри квадрата,
войдет в эту сумму дважды, причем
с разными знаками: Дело в том, что
ориентации, индуцируемые на ребре
двумя прилежащими треугольниками,
противоположны. Следовательно, все
ребра р, q, г, s сократятся и в
окончательную сумму не войдут. В то же
время одномерные ребра а, Ь, с, d

п
Полиэдры. Симплициальные комплексы. Гомологии
войдут в сумму по одному разу, и,
следовательно, граница квадрата,
рассматриваемого как двумерная цепь,
совпадает с его геометрической границей —
суммой четырех ориентированных
ребер а+Ь+ с +d.
Рассмотрим квадрат с дыркой,
показанный на рис. 3, разбитый на 8
треугольников. Снабдим каждый из них
ориентацией (вращение по часовой
стрелке) и возьмем двумерную цепь ?,
являющуюся суммой всех этих
треугольников с коэффициентами 1.
Поступая как и в предыдущем случае, мы
видим, что все внутренние одномерные
ребра взаимно уничтожаются. В итоге
граница цепи будет состоять из двух
сумм: a +b +с +d (со знаком "+") и
т+пчН-А (со знаком "-"). Итак,
алгебраическая граница квадрата с дыркой
совпадает с его геометрической
границей, причем внешняя часть границы
берется со знаком "+", а внутренняя — со
знаком "-": dc=a+b+c+ d-m -п-
-h - /. Так как квадрат с дыркой
гомеоморфен кольцу, то
алгебраическая граница кольца состоит из
внешней окружности (со знаком "+") и
внутренней окружности (со знаком "-").
Поэтому с наглядной точки зрения
цикл можно представлять себе как
"замкнутую поверхность", т. е.
поверхность без границы. Граница
цепи — это ее геометрическая граница,
Рис. 4
если все симплексы, составляющие
цепь, взяты с коэффициентом 1 (рис. 4).
В предыдущем пункте мы отмечали,
что цикл не обязан быть границей.
Например, если мы триангулируем
двумерную сферу и возьмем цепь,
являющуюся суммой всех получившихся
треугольников с коэффициентами 1, то
получим, очевидно, двумерный цикл. В
то же время его нельзя представить в
виде границы некоторой трехмерной
цепи по той простой причине, что наш
комплекс вообще не имеет ни одной
ненулевой трехмерной цепи
(размерность сферы равна двум). Можно
привести и более тонкие примеры (вскоре
мы с ними познакомимся), когда циклы
не являются границами.
2Л Грутшы симплициальньк гомологии
Пусть z — некоторый k -мерньвд цикл,
т. е. dz =0. Будем говорить, что он
гомологичен нулю, если он является
границей, т. е. z=dh для некоторой
(к +1)-мерной цепи h. Кстати, цепь h
определяется в таком случае, вообще
говоря, неоднозначно. Если z=dh для
некоторой цепи h, то также имеет
место равенство z =d(h +/ ), где / —
любой (&+1)-мерный цикл, т. е. 01 = 0.
Два &¦ мерных цикла Z\ и 2% назовем
гомологичными 1 если их разность Z\-Zq_
гомологична нулю, т. е. Z\~Z2=dh для
некоторой (k?\)rмерной цепи h. Тот
факт, что цикл z гомологичен нулю,
иногда записывается так: z~0. Тогда
гомологичность двух ЦИКЛОВ Z\ И Z2
записывается так: Z\-Zz ~0 или Z\ ~ 22
Соотношение Z\-~z% иногда называют
гомологией* Если цикл Z\ гомологичен
циклу ^2 то он отличается от него на
некоторую границу, т. е. имеет место
равенство Z\=Z2~fd h.
Отношение гомологичности
определено не только для циклов, но и для
цепей. Две цепи С\ и с2 называются
гомологичными (c\~Gz), если они
отличаются на некоторую границу, т.е.
С\ = fy+dh или С\-С2~4).
Вернемся к циклам. Пусть X —
произвольный полиэдр, Zk(X) — группа

$2. Группы Симплициальных гомологии полиэдров
2Э
его &-мерных циклов, Вк(Х) —
группа его к- мерных границ. Так
как группа Вк(Х) всегда содержится
в группе Zk(X) и обе группы абеле-
вы, то корректно определена фак-
тоо-группа Hk(X)=Zk(X) / Вк(Х).
Определение. Группа Нк(Х)
называется группой к-мерных
целочисленных симплигщальных гомологии
полиэдра X, Она является абелебой группой.
Если бы мы рассмотрели цепи с
коэффициентами в произвольной абеле-
вои группе G, то, повторяя
практически дословно все предыдущие
конструкции, мы получили бы определение
tpymt гомологии полиэдра X с
коэффициентами 6 группе G. Эти группы
обозначаются Нк(Х, G), т. е. указывается
группа коэффициентов. В этих
обозначениях группы целочисленных
гомологии Нк(Х) запишутся так: Нк(Х, Z). Мы
будем пользоваться обоими
обозначениями в зависимости от контекста.
Обсудим понятие группы гомологии в
терминах гомологичных циклов.
Рассмотрим группу циклов Zk(X). Любая
линейная комбинация циклов,
гомологичных нулю, снова есть цикл,
гомологичный нулю. Это и означает, что Вк(Х)
является подгруппой в Zk(X). Поэтому
для каждого цикла z можно
рассмотреть его класс смежности по подгруппе
ок(Х), т. е. рассмотреть множество
циклов вида я+dh, где h пробегает все
(к +1)-мерные цепи. Получающийся
класс смежности можно обозначить
через {z }. Тогда ясно, что два класса {z\}
и {j2& } либо совпадают, либо не
пересекаются. Ясно, что корректно
определена линейная комбинация классов {z\} и
{jBfc}, а именно a{z\) 4- h{z^ = {azx+bzz}.
Таким образом, группа Нк(Х)
интерпретируется как группа классов вида
{t}. Однако в дальнейшем, говоря об
элементах группы Нк(Х), мы часто
будем иметь в виду сами циклы —
какие-либо представители класса {z }.
Отметим важное свойство группы
гомологии Нк(Х). Из того что цикл mz
гомологичен нулю (где т — некоторое
целое число) отнюдь не вытекает в
общем случае, что сам цикл z
гомологичен
нулю. Другими
словами,
гомологии нельзя делить". С точки
зрения группы Нк(Х) это означает, что
могут существовать такие ненулевые
элементы {z} из группы Нк(Х), что
некоторое их целое кратное m\z} равно
нулю (в группе Нк)9 т. е. mz ~ О, хотя
z ч* 0. Следовательно, такие элементы
являются элементами конечною
порядка в группе Нк(Х). Отсюда следует, что
группы гомологии Нк не являются,
вообще говоря, свободными абелевыми.
Они могут содержать подгруппы,
состоящие из элементов конечного
порядка. Таким образом, каждую группу Нк
можно представить в виде прямой
суммы двух ее подгрупп Ak и Вк где Ак —
свободная абелева группа (прямая
сумма некоторого числа экземпляров
группы Z), а Вк — конечная абелева группа.
Группа Ак однозначно характеризуется
числом р* экземпляров группы Z, ее
составляющих. На языке алгебры число
Р* является рангом группы Ак, т. е.
минимальным числом образующих в
этой группе. В то. же время ясно, что
число р* является также рангом всей
группы Нк , т. е. (в данном случае)
минимальным числом свободных
образующих (образующих бесконечного порядка).
Определение. Число р* называется
к-мерным числом Бетти полиэдра X.
Подведем некоторые итоги. Каждому
«-мерному полиэдру X мы сопоставили
набор абелевых групп Но(Х), ..., НН(Х)
(группы гомологии). Группы гомологии
Нк(Х) равны нулю во всех
размерностях к, превышающих п (размерность
полиэдра). Эти группы были вычислены
для какого- то симплициального
разбиения полиэдра. Если симплициальное
разбиение фиксировано, то с ним
связывается следующая
последовательность свободных абелевых групп Ск(Х)
(групп цепей) и гомоморфизмов дк
(граничных операторов):
о -> с„(Х) 4 с^(ХK ..."% ск(Х) *->
4 ...±>с0(Х)±>о.

30
1. ПОЛИЭДРЫ. Симплициальные комплексы. Гомологии
Эта последовательность называется
цепным комплексом (данного симпли-
циального комплекса).
Однако, как мы знаем, один и тот же
полиэдр можно разными способами
представить в виде симплициального
комплекса, т. е. по-разному
триангулировать. Но разным симплициальным
комплексам отвечают, вообще говоря,
и разные цепные комплексы. Поэтому
можно было бы ожидать, что группы
симплициальных гомологии Н^Х)
зависят от выбора триангуляции полиэдра.
Однако это не так. Оказывается,
группы симплициальных гомологии
определяются только самим полиэдром и не
зависят от его триангуляции.
Теорема. Группы симплищшльных
гомологии полиэдра не зависят от
способа представления полиэдра в виде
симплициального комплекса.
Это обстоятельство резко повышает
ценность групп гомологии, превращая
их в алгебраические объекты,
характеризующие сам полиэдр, а не способ его
задания (представления). В дальнейшем
мы будем рассматривать в основном
лишь конечные полиэдры. В этом
случае все группы гомологии Н^Х)
конечно порождены. Каждая группа Нк(Х)
представляется в виде прямой суммы:
HdX)r Z Ф». © Z Ф Z* Ф- Ф
•А
SS
ч.
р*
где р* — ранг (число Бетти), a Z^. —
конечные циклические абелевы группы
порядков р,, причем каждое число Д
можно считать делителем предыдущего
при 2 < ; < s. Числа pi t..., ps иногда
называются коэффициентами кручения
симплициального комплекса X в
размерности k.
2& Примеры вычисления групп гомологии.
Гомологии двумерных поверхностей
1) Группы нульмерных гомологии..
Начнем с вычисления нульмерной группы
гомологии Н0(Х) линейно связного
полиэдра X. Полиэдр (симплициальный
комплекс) называется линейно
связным, если любая пара его точек может
быть соединена непрерывной кривой,
целиком лежащей в полиэдре. Мы
утверждаем, что нульмерная группа
гомологии линейно связного
симплициального комплекса изоморфна
группе Z. Если же симплициальный
комплекс несвязен, то ею нульмерная
группа гомологии изоморфна прямой
сумме Z®... ®Z=2*, где число
слагаемых q равно числу компонент
линейной связности комплекса X.
Как мы уже знаем, группа
нульмерных циклов совпадает с группой
нульмерных цепей, т. е. Cq(X)=Zo(X).
Нульмерный цикл — это линейная
комбинация вершин симплициального
комплекса с произвольными целыми
коэффициентами. Фиксируем произвольную
вершину а комплекса X, рассмотрим ее
как элементарную нульмерную цепь
(цикл). Докажем, что любая другая
нульмерная цепь гомологична цепи та,
где т — некоторое целое число.
Докажем, что элементарные нульмерные щ-
пи, отвечаюгцие любым двум
вершинам аир комплекса X, гомологичны.
Поскольку комплекс X линейно
связен, то всегда можно построить
непрерывный путь у, состоящий из одномерных
ребер симплексов, начинающийся в
вершине а и заканчивающийся в вершине
р (рис. 5). Этот путь можно
рассмотреть как одномерную цепь. Для
этого достаточно задать на каждом
Рис. 5

$ 2. Группы симплициальных гомологии полиэдров
31
его звене ориентацию (например,
зададим ее стрелками, идущими от
вершины а по направлению к
вершине р) и затем приписать каждому
звену, т. е. каждому одномерному
симплексу, целое число, равное 1.
В результате получим цепь у = Д| +
4- . . . + Д*. где N — число ребер,
составляющих путь. Найдем границу этой
цепи. Рассмотрим какую-нибудь
внутреннюю вершину а, пути, т. е.
являющуюся концом некоторого ребра
Д/ и началом следующего ребра Д,+1
(рис. 5). Тогда имеем дД,'=а,- —a,-_w
дД,-+1 = а<+1 — Ш- Поэтому д(у) =
= д(А\+ . . . +ДИ = . . - +а( . . .
— а,. . . . Следовательно, каждая
внутренняя вершина войдет в сумму
два раза: один раз со знаком «-)-»,
другой раз со знаком « —».
Следовательно, эти два слагаемых
взаимно погасят друг друга. Этого не
произойдет только для двух граничных
вершин a=ao и fi = aN, т.е. для
начальной и конечной точек пути у.
Итак, dy=aN — ao=p — а. Это
означает, что нульмерная цепь р — а
гомологична нулю (она представлена
как граница некоторой одномерной
цепи у). Отсюда следует наше
утверждение. В самом деле, так как
любая нульмерная вершина (с
коэффициентом 1) гомологична выбранной
нами вершине а, следовательно,
любая нульмерная цепь 2?=iaA°=c
гомологична нульмерной цепи ma= (Zf=i
Ot)a. Таким образом, для вычисления
нульмерной группы Но(Х) достаточно
рассмотреть только одну вершину а.
Отсюда получаем, что группа Но (X)
у связного комплекса X такая же,
как и у комплекса, состоящего из
одной точки а. Но последняя группа
изоморфна Z, поскольку все циклы
имеют здесь вид ma, где т —
произвольное целое число (а ненулевых
границ нет).
Из приведенного рассуждения сразу
видно, как доказать, что группа
Но(Х) несвязного комплекса X
изоморфна Z9, где q — число компонент
линейной связности. Предоставляем это
сделать читателю.
2) Гомологии окружности.
Рассмотрим какое-либо симплициальное
разбиение окружности 5'. Ясно, что оно
задается набором вершин oto, . . . , а^
и одномерными симплексами у,-,
заключенными между соседними вершинами.
Ориентируем все эти одномерные
ребра по часовой стрелке (рис. 6).
Группа нульмерных гомологии Но (S )
нам уже известна — она изоморфна Z.
Группы //,(S'), где />1, равны нулю,
так как комплекс S1 одномерен.
Рис. 6
Осталось вычислить только группу
tfi(S'). Мы утверждаем, что Hi (S ) =
= Z. Произвольная одномерная цепь
имеет вид с = а0у0 + . . . +aNyN, где
а, — целые числа. В каком случае
такая цепь является циклом?
Вычисляя границу цепи, получаем
дс = ао(а\—ао) +а\ (а2 — он) + . . .
+ aN(ao — а*).
Раскроем скобки и приведем
подобные члены. В результате получим
следующую нульмерную цепь:
дс= ( — a0 + aJV)ao+ (a0 — ai)ai+ . . .
+ (aN_x — aN)aN.
Таким образом, одномерная цепь с
является циклом в том и только в
том случае, когда дс=0, т.е. когда
коэффициенты а, удовлетворяют
следующей системе уравнений: — ао + ад/=
= 0, а0 — ai = 0, . . . , aN_]—aN=0,
откуда получаем ao = ai= . . . =aA/_,=
= aN. Итак, цепь с является циклом
в том и только в том случае, когда

32
1. Полиэдры. Симплициальные комплексы. Гомологии
все коэффициенты равны между собой.
Другими словами, мы описали все од-
номерные циклы. Они имеют вид z =
= д(уо+-..+Улг)> где а — произвольное
целое число. Группа одномерных границ
Bi(S) равна нулю, так как нет цепей
размерности два. Следовательно,
группа одномерных гомологии H\(Sl)
совпадает с группой одномерных циклов
Z\(S). Так как все одномерные циклы
имеют вид а(?уক), где а е Z,
следовательно, группа одномерных гомологии
изоморфна Z. Итак, для окружности мы
имеем Ho^Z, Hf= Z, Н,— 0 при i # О, 1.
3) Группы двумерных гомологии
двумерных полиэдров, являющихся
многообразиями без границы. Будем
говорить , что двумерное
топологическое многообразие не имеет
границы, если каждая его точка имеет
окрестность , гомеоморфную открытому
двумерному диску (точка является
центром этого диска). Любое
двумерное топологическое многообразие
является полиэдром. Будем, для
простоты, рассматривать лишь те
многообразия, которые являются конечными
полиэдрами. Например, сфера, тор,
сферы с ручками являются
многообразиями без края (без границы).
Чтобы нагляднее пояснить данное
определение, на рис. 7 приведены
примеры многообразий с границей (с краем).
Точки, лежащие на краю (граничные
точки), отличаются от внутренних
точек тем, что они обладают
окрестностью, гомеоморфной половинке
диска, причем сама точка лежит на
диаметре этой половинки диска. В
многообразии без границы таких точек нет.
Итак, пусть дан конечный полиэдр,
являющийся многообразием без
границы. Тогда его триангуляция обладает
следующим важным свойством: каждое
одномерное ребро (одномерный
симплекс) инцидентно двум и только
двум смежным треугольникам.
Другими словами, каждое ребро входит в
состав ровно двух треугольников
(склееных по нему) (рис. 8).
Рис. 8
Рис. 7
Ясно, что здесь мы существенно
используем отсутствие границы у
многообразия. Если бы многообразие имело
границу, то нашлось бы ребро,
лежащее на границе и инцидентное только с
одним треугольником (подходящим к
нему изнутри многообразия) (рис. 8).
Назовем 2-многообразие
ориентируемым, если каждый двумерный
симплекс его триангуляции можно
ориентировать так, что любые смежные
треугольники, инцидентные по ребру
(имеющие общее ребро), индуцируют
на нем противоположные
ориентации (рис. 8). В противном случае
многообразие назовем неориентируе-
мым. Оно характеризуется тем,

$ 2. Группы симплициальных гомологии полиэдров
33
что при любом способе ориентации
треугольников найдется хотя бы одно
ребро, на котором смежные
треугольники индуцируют одну и ту же
ориентацию.
Теорема. Группа двумерных
гомологии Я2 (М) связного двумерного
конечного полиэдра, являющегося
ориентированным многообразием без
границы, изоморфна группе целых
чисел Z. Если же многообразие нео-
риентируемо, то группа //2(М) равна
нулю.
Доказательство. Пусть сначала
многообразие ориентируемо.
Рассмотрим его триангуляцию и ориентируем
все треугольники А? так, чтобы на
каждом ребре смежные с ним
треугольники задавали противоположные
ориентации. Произвольная двумерная
цепь имеет вид с = 2/L [ а,-А/. Наша
цель: описать все двумерные циклы.
Вычисляя границу цепи с, получаем
dc=Haid\f. В результате мы
получили некоторую одномерную цепь. Цепь
с будет циклом в том и только
в том случае, когда одномерная цепь
дс равна нулю на каждом
одномерном симплексе (ребре
триангуляции). Берем произвольное ребро А1.
Оно инцидентно только с двумя
треугольниками А,2 и А2, являясь их
общим ребром. По условию, оба
треугольника индуцируют на ребре
А1 противоположные ориентации
(рис. 9). Следовательно, ребро А1
войдет в сумму дс (после
приведения подобных членов) с коэффициентом
Ъ — а,, где а, и а,- — значения
двумерной цепи с на треугольниках А?
и А2 соответственно. Так как <?с = 0,
то ai=aj. Итак, мы доказали, что
двумерная цепь с является циклом в
том и только в том случае, когда
она принимает одинаковые значения
на любых двух смежных
треугольниках. Но так как многообразие связно,
то любые два треугольника /их
можно соединить цепочкой смежных
треугольников (рис. 9).
Следовательно, цепь с принимает одно и то же
значение на всех треугольниках
триангуляции. Итак, с = а*B/Д,2). Итак,
Рис. 9
мы полностью описали все циклы в
размерности 2. Оказалось, что
группа Z2(M) изоморфна группе Z,

<*4
1. Полиэдры. Снмплициальные комплексы. Гомологии
так как коэффициент а может
принимать произвольные целые значения.
Поскольку многообразие двумерно, то
у него нет ненулевых трехмерных
цепей, следовательно, группа границ
Лг(М) равна нулю. Отсюда сразу
следует, что группа гомологии Яг(М)
равна Z. В первом случае теорема
доказана.
Пусть теперь многообразие неори-
ентируемо. Фиксируем ориентации
всех треугольников триангуляции.
Снова запишем двумерный цикл с в виде
2*L,a,-A?. Повторяя предыдущие
рассуждения, мы видим, что если два
смежных треугольника А? и А2
индуцируют на их общей стороне разные
ориентации, то at = a}, а если они
индуцируют одну и ту же
ориентацию, то cti=—dj. Следовательно, в
силу связности многообразия все
коэффициенты а, равны друг другу по
модулю, т. е. | а,-1 = | а/ | при любых
/, j. Берем два смежных
треугольника A?, Af и ориентируем их так,
что они индуцируют разные
ориентации на общем ребре. Тогда at = aj.
Последовательно берем треугольники,
смежные к двум предыдущим и также
ориентируем их согласованно (до тех
пор, пока это возможно). Тогда цикл
с будем принимать на всех этих
треугольниках значение, равное
первоначальному а,. Но в силу
неориентируемости многообразия
обязательно наступит момент, когда
встретятся два -смежных треугольника,
индуцирующие на их общем ребре одну
и ту же ориентацию (рис. 9). При
этом цикл z принимает на обоих
треугольниках одно и то же значение щ.
С другой стороны, должно выполняться
равенство a, + a, = 0. Отсюда получаем,
что а, —0. Следовательно, любой
двумерный цикл на неориентированном
многообразии равен нулю. Теорема
полностью доказана.
Приведем примеры ориентируемых
и неориентируемых многообразий.
Плоскость, квадрат, сфера, тор,
кольцо, цилиндр, сферы с ручками — ори-
ентируемые многообразия. Лист
Мебиуса, проективная плоскость, бутылка
Клейна — неориентируемые
многообразия. Проверку предоставляем
читателю.
Итак, если полиэдр является
двумерным замкнутым многообразием, то
мы вычислили его нульмерную и
двумерную группы гомологии. Осталось
вычислить одномерную группу
гомологии. Здесь рассуждения будут
сложнее, хотя в своей основе они также
элементарны.
Определим полезное для
дальнейшего понятие носителя цикла. Пусть
z—некоторый /е-мерный цикл. Его но-
сителем назовем объединение всех k-
мерных симплексов, на которых цикл
z принимает ненулевые значения.
4) Вспомогательная лемма о
деформации одномерных циклов.
Лемма. 1) Пусть в некотором
полиэдре имеется одномерный цикл
z, принимающий значения a, Ь, с
соответственно на ориентированных
ребрах /, т, р (рис. 10), являющихся
сторонами двумерного симплекса
(треугольника) А2. Тогда цикл z
гомологичен другому циклу z', который
принимает на ребрах t, т, р
следующие значения (соответственно ):
О, Ь-\-а, с-\-а. При этом значения
циклов z и zf совпадают на всех
остальных ребрах триангуляции
(рис. 10). Образно выражаясь, цикл
z можно снять с ребра t.
2) Пусть в полиэдре имеется
одномерный цикл z, принимающий
значения а, 6, с соответственно на
ориентированных ребрах t, т, р (рис. 10),
являющихся сторонами треугольника
А2. Пусть цикл z равен нулю на всех
остальных ребрах триангуляции,
инцидентных с вершиной А треугольника
А2 и отличных от ребер тир. Тогда
обязательно Ь = с и цикл z
гомологичен другому циклу z', который
принимает на ребрах /, т, р следующие
значения (соответственно): а-\-Ь, О, 0.
При этом значения циклов z и z'
совпадают на всех остальных ребрах
триангуляции. Другими словами, цикл
z можно снять с суммы ребер тир
и направить его значение b по реб-
РУ t.

$2. Группы симплициальных гомологии полиэдр
г г
Рис. 10
3) Пусть в полиэдре имеется
одномерный цикл z, принимаюгций
некоторое значение а ни ребре tt одна из
вершин которою инцидентна лишь с
такими ребрами полиэдра, на которых щкл
z равен нулю (рис. 10). Тогда д=0 и
ребро t не входит в состав носителя
цикла z.
Доказательство. Пусть ребра
ориентированы так, как показано на рис. 10.
Подсчитаем разность z - z' циклов z и
z' Из рис. 11 видно, что в результате
получается цикл, принимающий
значения: а на /, -а на т, -а на р.
Рассмотрим двумерную цепь с, принимающую
35
значения а на треугольнике Л и равную
нулю на всех остальных треугольниках
триангуляции. Подсчитаем ее границу дс.
Ясно, что получаем одномерную цепь ,
равную нулю на всех ребрах
триангуляции, отличных от /, т, р, а на этих
ребрах она принимает значения а,
-я, -а соответственно.
Рис. 11
Здесь мы используем тот факт, что
ориентированная граница треугольника
А состоит из ребер t, -р, -т, (рис. 11),
поэтому (dc/(t) = -fa, (дс)(-р) = Ч-я,
(dc)(-^z) =+а. Итак, циклы z и z/
гомологичны, так как z -z/= дс.
Доказательство второй и третьей частей
леммы проводится аналогично (см. рис.
10, 11). Мы не будем на этом
останавливаться. Отметим только, что
равенство Ь = с в пункте 2 и равенство а = 0
в пункте 3 вытекают из условия dz = 0.
Здесь мы опираемся на то, что вершина
А инцидентна только с двумя ребрами
триангуляции, на которых цикл
принимает ненулевое значение, а именно с т и
р. Остальные ребра, инцидентные с А,
дают нулевой вклад в нульмерную цепь
dz. Лемма доказана.
Этой лемме можно придать
прозрачный геометрический смысл.
Оказывается, мы можем деформировать

36
1. Полиэдры.Симплициальные комплексы. Гомологии
исходный цикл z, перемещая его
носитель по поверхности. Мы заменяем его
ребро, входящее в некоторый
треугольник, на сумму двух других ребер
этого треугольника, причем значение а,
ранее приписанное ребру t,
«переходит» на эти ребра и добавляется к
прежним значениям цикла на этих ребрах.
В результате цикл z заменяется на ему
гомологичный, а ребро / можно вынер-
киуть из его состава, так как на нем
цикл z* принимает значение нуль.
Аналогично если некоторый треугольник
имеет «свободную» вершину, т. е.
такую, с которой не инцидентны
больше никакие ненулевые ребра
цикла (кроме двух сторон
треугольника), то цикл можно снять с
треугольника, про деформировав сумму
двух сторон на третью сторону (рис.
12). Другими словами, мы можем
непрерывно деформировать
одномерные циклы по полиэдру, скользя
по двумерным симплексам (не меняя
класса гомологии цикла). На рис. 12
наглядно показаны процессы
выдавливания цикла вдоль треугольника и
замена его суммой двух других
сторон треугольника. Применим эту
простую, но полезную лемму для
вычисления одномерных гомологии
двумерных многообразий. Полезно
представлять себе одномерный цикл
в виде резиновой замкнутой нити,
расположенной на многообразии.
Мы деформируем цикл, натягивая
или сокращая эту нить без разрывов
(склейки допускаются). В результате
мы можем существенно упростить
цикл, расположив его на
поверхности оптимальным образом.
Все эти операции наглядно
интерпретируются в терминах носителя
одномерного цикла z. Согласно лемме
мы можем подвергать носитель
следующим операциям (перестройкам):
1) любое ребро носителя, входящее
в состав двумерного симплекса,
можно заменить суммой двух других
ребер этого симплекса (рис. 12) с
соответствующим изменением
числовых значений цикла;
2) некоторые пары ребер, сходя-
» -.
слепил
Рис.12
щихся в свободной вершине
треугольника , можно заменять одним
ребром (рис. 12);
3) ребро носителя, торчащее в
сторону и имеющее свободный конец,
можно убрать (рис. 12).
Эти операции можно назвать ком-
бинаторной разборкой (упрощением)
цикла.

$2. Группы симплициальных гомологии полиэдров
37
Если отвлечься от триангуляции и
рассмотреть носитель как одномерное
множество, состоящее из отрезков ло-
маных на многообразии, то введенные
нами операции упрощения носителя
интерпретируются еще одним образом.
Если несколько ломаных в какой-то
области идут достаточно близко и
параллельно друг другу (но, возможно, по-
разному ориентированы), то эту
систему можно заменить одной дугой (рис.
12), склеив вместе все предыдущие
ломаные. При этом нужно
просуммировать (с учетом знаков) все числа,
стоявшие на прежних ломаных, и
получившийся результат приписать новому
отрезку. Можно упрощать цикл, отрезая
от него (или стягивая на него) "ветви",
т. е. ломаные, имеющие свободные
концы, выходящие из некоторой точки
цикла и больше на него не
возвращающиеся. Итак, систему резиновых нитей,
изображающих цикл, можно
непрерывно деформировать по многообразию,
склеивая нити и упрощая носитель
цикла. Например, замкнутую кривую,
нарисованную на торе и два раза
обходящую его вдоль параллели (и, очевидно,
изображающую одномерный цикл),
можно непрерывно продеформировать
в кривую, являющуюся параллелью, но
взятую с коэффициентом 2 (т. е. в
параллель, пройденную дважды).
5) Гомологии сферы. Рассмотрим
произвольную конечную триангуляцию
двумерной сферы (рис. 13). Пусть z —
произвольный одномерный цикл. Мы
утверждаем, что он гомологичен
нулевому циклу, т. е. циклу, тождественно
равному нулю на всех ребрах
триангуляции. На рис. 9 представлена
триангуляция сферы. Рассмотрим
произвольный одномерный цикл z на сфере. Из
леммы о деформации циклов следует,
что цикл z гомологичен циклу вида
т(а + Ь) + п(с + d), где тип —
некоторые целые числа, а ребра af b, ct d
показаны на рис. 9. Но так как а +Ь
циклом не является (концы ребра
а +Ь не отождествляются) и так как
с Л-d — тоже циклом не является (по
такой же причине), и так как начало
ребра а и конец ребра d — это тоже
разные точки на сфере (см. рис. 9),
следовательно, линейная комбинация
т(а + Ь) + п(с 4- d) может быть цик-
лом^только если т =п =0.
Таким образом, на сфере нет
ненулевых 1-циклов.
К >"! *-71
\ + у7
+ /О <Т\
3 / \ а
— ^-*-« ~ »*»
}
/V
,
а
C
р
i
а
-*-
Рис. 13
Рис. 14

38
i. Полиэдры. Симплициальные комплексы. Гомологии
Мы доказали, что группа одномерных
гомологии сферы тривиальна (равна
нулю). Итак, Щ?) = Z, Нх($) = О,
Н2{у) = Z. Предоставляем читателю
доказать, что группы гомологии п-
мерной сферы имеют вид H${S*) = Z,
ЯДУ1) = 0при1<* <п-1,Ня(Г) =Z.
Попутно читателю придется доказать
многомерный аналог леммы о
деформации цикла. Из доказательства
нашей леммы видно, что аналогичным
образом можно деформировать и
носители многомерных циклов,
выдавливая их внутрь многомерного
симплекса и заменяя одну грань симплекса
суммой остальных его граней (с
измененными числовыми значениями).
6) Гомологии тора. Представим тор
в виде квадрата с отождествленными
сторонами (рис. 14). Рассмотрим
триангуляцию тора, показанную на
рис. 14. Мы специально расставили
ориентации всех симплексов, чтобы
показать, что тор — ориентируемое
многообразие. Видно, что все
ориентации согласованы, т.е. смежные
треугольники индуцируют на общих
сторонах разные ориентации. Пусть
задан некоторый одномерный цикл z
на торе. Докажем, что он
гомологичен циклу вида wcx+яр, где а и Р —
два цикла, показанные на рис. 14, а
тип — некоторые целые числа.
Более точно, цикл а равен а+6, где а
и b — ориентированные ребра (рис.
14), а цикл р равен c+d. Применяем
описанные выше три операции
упрощения (деформации) цикла.
В результате (рис. 14) мы можем
снять носитель цикла z со всех
внутренних ребер триангуляции, исходя-
гцих из центра квадрата. Получится
цикл z', носитель которого состоит
только из граничных ребер квадрата.
Видно, что а = а+Ь и р = c+d.
Осталось доказать, что цикл z' =
m(a+by\- n(c-f-d) гомологичен нулю в
том и только в том случае, когда
коэффициенты тип равны нулю. В
самом деле, допустим, что хотя бы одно
из чисел т или п отлично от нуля и что
существует некоторая двумерная цепь
qt такая, что dq =z'. Так как цикл г'
равен нулю на всех внутренних ребрах
триангуляции (инцидентных с центром
квадрата), то цепь q обязана принимать
одинаковые значения на всех смежных
(по общему ребру) треугольниках.
Следовательно, цепь q принимает одно и
то же значение X на всех
треугольниках триангуляции. Дело в том, что
любая пара треугольников соединяется
цепочкой треугольников, смежных по
некоторому общему ребру. Но в таком
случае граница dq цепи q принимает
нулевые значения на всех ребрах а, Ь, с,
d. В самом деле, например, два
экземпляра стороны а (на противоположных
сторонах квадрата), очевидно,
индуцируют противоположные ориентации
квадрата, поэтому, будучи взяты с
одинаковыми по модулю
коэффициентами, но с разными знаками, взаимно
уничтожат друг друга в границе цепи q.
Аналогичные рассуждения применимы
и для остальных ребер b, с, d. В
результате мы получаем, что dq — 0. Но
так как dt^z', то z—0. Следовательно,
m(cH-b)+n(c+d)=0. Осталось убедиться в
том, что циклы а = а+b и р = c+d
линейно независимы. Но это
очевидно, поскольку цикл а равен нулю на
ребрах с, d, а цикл р, напротив, равен
нулю на ребрах а, Ь. Отсюда получаем,
что т = п — 0. При этом следует иметь
в виду, что все четыре вершины А], А2,
Аз, А< квадрата изображают в
действительности одну и ту же вершину
полиэдра. Этот факт диктуется правилом
отождествления сторон квадрата в
случае тора. Утверждение доказано.
Итак, каждый одномерный цикл
гомологичен циклу вида та+ф,
причем циклы а и р линейно независимы.
Следовательно, группа одномерных
гомологии тора Н2 {j ) изоморфна
прямой сумме Z ® Z двух
экземпляров группы Z.
Возвращаясь к модели тора в виде
«бублика» (рис. 14), мы видим, что

$ 2. Группы симплициальных гомологии полиэдров
39
образующая а соответствует параллели
тора, а образующая р— его меридиану.
Как мы доказали выше, любой другой
цикл на торе является линейной
комбинацией параллели и меридиана,
взятых с некоторыми целыми
коэффициентами.
Рис. 15
7) Гомологии сферы с g ручками.
Теперь понятно, как вычислить
одномерную группу гомологии сферы с
произвольным количеством ручек.
Напомним, что тор — это сфера с одной
ручкой. Сферу с g ручками удобно
представлять так, как изображено
на рис. 15. Видно, что в
значительной степени рассуждения сводятся
к многократному повторению
конструкции, реализованной нами на торе. Для
этого построим удобную триангуляцию
сферы с g ручками. Разрежем
поверхность по кривым, как показано
на рис. 15. В результате получится
плоский многоугольник с 4g
сторонами. Обозначим на ручке с номером
i ее параллель через а,, а ее меридиан
через pi. Тогда стороны
получившегося многоугольника занумерованы
следующим образом (мы выписываем
буквы в порядке их появления при
обходе границы по часовой стрелке):
а^аГ'РГ1 • - - agpgaf'Р^1-
Триангулируем многоугольник (и тем самым
поверхность) так, как показано на рис. 16.
Ясно, что теперь применимы
рассуждения, аналогичные проведенным выше
для тора. Сначала мы доказываем, что
каждый цикл z гомологичен циклу z',
имеющему вид
z' = miai + rtipi+ . . . +mgag +
+ng$g=m\(ai+bi) +nl(c\+di) +
+ . . . +mg(ag + bg) +ng(cg + dg).
Здесь m,, n, — некоторые целые
числа. Далее, как и в случае тора,
доказывается, что все циклы a, = a,H-
+ bi и р, = с, + dh где 1 < |\ / < g,
линейно независимы. Следовательно,
мы в явном виде указываем базис
Рис. 16

40
1. Полиэдры. Симплициальные комплексы. Гомологии
в группе H\(MgO где Mg — сфера с g
ручками. А именно базис состоит из
циклов оц, ...,ag, pi, ...,P». Таким
образом, Hi(M.) = ^® ... ®Z Bg раз),
т. е. H\(Mg) =Zg. Собирая вместе
полученные выше результаты,
Рис. 17
мы можем сформулировать следующую
теорему.
Теорема. Группы целочисленных
гомологии сферы с g ручками, где g —
щлое неотрицательное число, имеют
вид Hq= Z, Щ= Z2*, Н2= Z.
8)Гомологии проективной плоскости
RP\ Рассмотрим триангуляцию
проективной плоскости, показанную на рис.
17. Видно ее отличие от триангуляции
тора. Хотя в обоих случаях, мы
триангулируем квадрат, но склейки на его
сторонах устроены по-разному. При
этом мы специально задали ориентацию
на двумерных симплексах, как и на
триангуляции тора, чтобы отчетливо
была видна неориентируемость
проективной плоскости, В самом деле, на
границе квадрата, на сторонах а, Ь, с, d
индуцируются одинаковые ориентации.
Это обстоятельство отмечено на рис. 17
знаками "+". Поступая по аналогии с
тором, мы получаем, что любой
одномерный цикл z гомологичен циклу z\
носитель которого состоит из
граничных ребер квадрата. Другими словами,
z ~ тх+ф = m(a+by\-n\c+d) =?, где т,
п — некоторые целые числа. Здесь а и
р (по отдельности) циклами не
являются, так как да = Аг — А\ ^0, Щ = А3 -
-А2^0. В случае тора аир, напротив,
являются циклами, так как на торе мы
имеем Ax=Aj=Ay=AA. Однако в случае
проективной плоскости здесь имеется
дополнительное обстоятельство,
отличающее дальнейшие вычисления от
случая тора. В самом делеу вычислим
границу цикла z'. С одной стороны,
она является нульмерной цепью вида
dz' = д(тшН-яр) = d(ma+mb±nc+nd) =
— т{А2-А-^угп(Аъ-А2). Но из правила
отождествления сторон квадрата
видно, что из четырех вершин Аи Аъ А3,
АА (рис. 17) различны лишь две
вершины, так как А1=Аз, А2=А4.
Следовательно, 0 = dz' = (т-п]А2+ (п-т)А\. Так
как А\Ф Ах, то т = п. Итак, мы
доказали, что на проективной плоскости
любой одномерный цикл гомологичен циклу
z' вида q(a-ifi) = qy, где у = <х+Р, а q —
произвольное целое число. Далее, мы
утверждаем, что цикл у, взятый
дважды, гомологичен нулю, т. е. 2у — 0. В
самом деле, рассмотрим двумерную
цепь х, принимающую значение 1 на
каждом ориентированном треугольнике
нашей триангуляции. Вычисляя ее
границу, очевидно, получаем из рис. 17
соотношение дт =2a+2lrt-2c+2d=2f, что
и требовалось доказать. Следовательно,
мы доказали, что группа ff^RP;
изоморфна группе Zqi образующей
которой является цикл у, изображенный на
рис. 17, т. е. у =а +b +с + d.
Теорема. Группы целочисленных
гомологии проективной плоскости
имеют вид Но —Ъ, Н \ —Ъ 2, Hi =0.
9) Гомологии бутылки Клейна.
Рассмотрим триангуляцию бутылки
Клейна К, показанную на рис. 18.
Видно, что это многообразие неори-
ентируемо. Как и в предыдущих
случаях, сразу получаем, что любой
одномерный цикл z гомологичен циклу

f 2. Группы симплициальных гомологии полиэдров
41
г' вида z' = ma-|-rtp, где т и п —
некоторые целые числа, а а и E — циклы,
причем a=a-\-b, $ = c-\-d. Имеем да=
= d[J=0, так как все четыре
вершины квадрата изображают в
действительности одну вершину на бутылке
Клейна, т. е. i4i = Л 2 =-4 3 = ^4 (как и на
торе). Рассмотрим двумерную цепь т,
принимающую значение 1 на всех
ориентированных треугольниках (рис. 18).
Вычисляя ее границу, получаем дт =
= а+Р — а+Р = 2В. Следовательно,
удвоенный циклр гомологичен нулю.Та-
ким образом, одномерная группа
гомологии изоморфна прямой сумме двух
абелевых групп Z © Z2, где
подгруппа Z порождена образующей а (цикл
бесконечного порядка), а подгруппа Z2
порождена образующей р (цикл
порядка два, т. е. 2р — 0).
— /V
Рис. 18
Теорема. Группы целочисленных
гомологии бутылки Клейна имеют вид
//0=z, //, = ze z2? #2=0.
10) Гомологии неориентируемых
двумерных замкнутых поверхностей.
Рассмотрим многоугольник на
рис. 19. Он является естественным
Обобщением многоугольника,
задающего проективную плоскость (рис. 17).
Предоставим читателю проверить, что,
отождествляя ребра на границе
многоугольника в соответствии с
расставленными на них буквами и
стрелками, мы получим некоторое
двумерное замкнутое компактное
многообразие. Кроме того, это многообразие
будет неориентируемым. Опуская
детали вычислений, которые мы уже
неоднократно демонстрировали,
получаем, что любой одномерный цикл z
гомологичен циклу г', составленному
из ребер — циклов cti, . . . , а*, взятых
с произвольными целыми
коэффициентами, т.е. z' = micti + . . . -\-m,kOk.
При этом цикл 2(оы+ . . . +а*)
гомологичен нулю, так как он является
границей двумерной цепи,
принимающей значение 1 на каждом
ориентированном треугольнике.
Следовательно, в качестве образующих в группе
одномерных гомологии можно взять
следующие циклы: ai, . . . , a*_i, h,
где /i = ai+. . .+aft_i + а*. Тогда
2/i~0, а циклы ai, . . . , a*_i
являются свободными. В результате
группа гомологии И\ изоморфна прямой
сумме Zfc_I ф Z2.
Теорема. Группы целочисленных
гомологии неориентируемой двумерной
замкнутой поверхности имеют вид
//0=Z, //, = Z*-1 0 Z2, //2 = 0.
До сих пор мы вычисляли це-
Рис. 19

42
1. Полиэдры. Симплицнальные комплексы. Гомологии
лочисленные гомологии полиэдров. В
качестве полезного (и простого)
упражнения советуем читателю
вычислить гомологии всех перечисленных
полиэдров с коэффициентами в
группе Z2 или, более общо, в группе Zp
для произвольного простого р.
Приведем здесь лишь ответ, не
углубляясь в детали доказательства (хотя
в действительности весь необходимый
материал мы уже изложили).
Группы гомологии двумерного
многообразия М с коэффициентами в
группе Z2 имеют следующий вид.
1) В случае сферы с g ручками
имеем //0=Z2, //i = Z2 ф . . . © Z2
Bg pa3)=Zi*, tf2 = Z2.
2) В случае неориентируемого
многообразия имеем #o=Z2, #i = Z2®...
0 Z2 (k раз)=г2, //2=Z2.
Подчеркнем следующее: если
группа двумерных целочисленных
гомологии неориентируемого многообразия
была равна нулю, то группа
двумерных гомологии этого же
многообразия, но с коэффициентами в группе
Z2 отлична от нуля и равна Z2.
2.7. Комментарий к наглядному материалу
На рис. 20 иллюстрируется операция
суммирования цепей, имеющих общие
куски границы. Если ориентации на
встречающихся частях границы
противоположны (и значения цепей по
модулю совпадают), то эти части
взаимно уничтожаются. Обратный процесс —
появление дополнительных участков
границы — происходит при разрезании
полиэдров (цепей). Такой процесс
разрезания показан на рис. 20. Другой
вариант этой поцедуры см. на рис. 21.
Слева — исходный полиэдр, справа — он
же после разреза (граница
увеличилась). На рис. 22 показан
бесконечный полиэдр, составленный из
трехмерных симплексов (тетраэдров).
Похожая картина получится, если
развернуть шар, триангулированный так,
что симплексы имеют основания на
границе шара (на сфере), а одну из
вершин — в его центре. На рис. 23
показано разбиение двумерной
поверхности на симплексы и квадраты, в
результате чего получается двумерная
цепь с границей (в центре и левом
нижнем углу рисунка). На рис. 24
изображена бесконечная симплициаль-
ная цепь с границей (т. е. не
являющаяся циклом), на рис. 25 (внизу) —
цепь без границы, т. е. цикл,
замощенный «брусчаткой». См., также
материал главы 4, § 2, пункт 2.1, где
обсуждается понятие топологической
размерности и сформулирована так
называемая «теорема о мостовых»
(Лебег, Брауэр). Она утверждает, что
двумерный полиэдр можно замостить
замкнутыми множествами,
пересекающимися не более чем по три, т. е.
пересечений по четыре можно
избежать. На рис. 25 показано
замощение плоскости, в котором каждая
точка покрыта не более чем тремя
«кирпичами». В трехмерном случае
эта теорема проиллюстрирована на
рис. 26. Трехмерность пространства
означает, что его можно замостить
сколь угодно мелким покрытием, в
котором элементы покрытия («кирпичи»)
пересекаются не более чем по
четыре, т. е. пересечений по пять и выше
можно избежать. На рис. 27, 28, 29
показаны полиэдры, кубические цепи
и наглядно проиллюстрирована
операция вычисления границы (склейка
кубов по общим граням уменьшает
их суммарную границу). На рис. 30
показана цепь, составленная из
квадратов, снабженных числовыми
коэффициентами (числа условно
изображены разными фигурами). Условие,
что цепь является циклом, означает,
что все эти числа равны, т. е. все
фигурки одинаковы. Если фигурки
различны, то цепь не является циклом.
Как наглядно изобразить общую идею
вероятности? На рис. 3! реализована
идея, подсказанная автору А. Н.
Ширяевым. Рассмотрим игральную кость,
на каждой грани которой помещена
фигурка, в руках которой — следующая
игральная кость. Итого на каждой
кости «первого уровня» получается
шесть костей «второго уровня». Затем
на каждой кости 2-го уровня распо-

} 3. Свойства групп симплнциальных гомологии
43
лагаем снова по фигурке. В руках
этих фигурок 3-го уровня — снова кости
C-го уровня) и так далее до
бесконечности. Затем каждая фигурка
начинает подбрасывать свою кость, причем
разные фигурки делают это
независимо друг от друга. В результате все
кости приходят в движение и
начинают хаотически (и независимо друг
от друга) вращаться. Конечно,
буквально изобразить эту схему
невозможно, поэтому на рис. 31 кости
оснащенные шестью соседними
костями, помещены лишь в узлы
трехмерной кубической решетки (для
простоты изображения). В глубине
пространства (на заднем плане) еще
видна исходная, «неиспорченная»
структура кубической решетки. Но на
переднем плане эта упорядоченная
структура уже разрушается под влиянием
хаотических вращений,
осуществляемых фигурками, разбросанными по
решетке. Кроме того, разметка
самих костей также случайна — сумма
чисел на противоположных гранях
не является постоянной. См. также
рис. 32, 33.
§ 3. Общие свойства групп симплнциальных гомологии.
Некоторые методы вычисления групп гомологии
3.1. Матрицы инциденций
Рассмотрим произвольный полиэдр X
и некоторую его триангуляцию.
Занумеруем все его ориентированные
симплексы символами А* где k
указывает размерность симплекса, a i —
его порядковый номер (в своей
размерности), т.е. l^i'^cz*. Здесь а*—
число /е-мерных симплексов в
полиэдре. Кроме того, 1</е<п, n=dimX,
т.е. п — это размерность полиэдра.
Будем, для простоты, считать, что
полиэдр конечен, тогда а*<;оо. Из
дальнейшего рассказа будет ясно, как
перенести большинство конструкций и
на случай бесконечных полиэдров.
Рассмотрим оператор границы д. Тогда
для каждого симплекса Af+1 мы
получаем соотношение dAf+^Z^af/A* где
aff—некоторые целые числа. При этом
l^/<a*+u 1</<а*. Число ац равно
либо +1, либо —1 в зависимости
от того, с какой ориентацией симплекс
Д? входит в границу симплекса А/+1.
Другими словами, а* равно +1,
если ориентация, заданная на А*
совпадает с ориентацией,
индуцированной на нем симплексом А/, и а*
равно —1 в противном случае. Число
off называется коэффициентом
инцидентности симплекса А,- и симплекса
А*+|. Если же симплексы А? и Af'+l не
инцидентны (т. е. симплекс А? не
является гранью симплекса А*+'), то
положим, по определению, а,* = 0.
Ясно, что числа ац естественно
организуются в прямоугольную матрицу,
которую мы обозначим через Ek.
Удобно записать ее так:
Д?+1
*+|
Ek=
А?
А?
Эта матрица имеет а* строк и a*+i
столбцов. Она называется k-мерной
матрицей инциденций. Таким образом,
с каждой триангуляцией полиэдра
связывается набор матриц инциденций
?°,..., Е
П—\
где n= dimX.
Рассмотрим простейшие примеры.
На рис. 1 показаны два полиэдра:
отрезок и треугольник. В случае
отрезка мы имеем одну матрицу
инциденций ?°, которая имеет вид
Е°= А?
-1
+ 1

44
1. Полиэдры. Симплициальные комплексы. Гомологии
а
а
а*+1
* + 1
Аг-1
:*-1
а.
Рис. 1
а
*-i
Для треугольника мы имеем две
матрицы инциденций Е° и Ех, а именно
?° =
А?
А?
AS
А!
0
— 1
+ 1
А!
-1
0
+1
AJ
— 1
+ 1
0
Е] =
А!
ДА
+ 1
-1
+ 1
Читатель может, в качестве
упражнения, составить три матрицы
инциденций, отвечающих стандартной
триангуляции трехмерного симплекса (тетраэдра).
3.2. Метод вычисления групп гомологии
при помощи матриц инциденций
Какова роль матриц инциденций?
Оказывается, симплициальный комплекс
(соответапвующий данной триангуля-
ции полиэдра) полностью (и однозначно)
определяется матрицами инциденций.
Действительно, зная эт^и матрицы и беря
какой-то симплекс Д,, мы однозначно
восстанавливаем, с какими симплексами
размерности п-\ он инцидентен.
Продолжая этот процесс вниз по
размерности, мы, в конце концов,
реставрируем всю схему симплициального
комплекса, т. е. выясняем, какие его
симплексы инцидентны, а какие — нет.
Следовательно, бее свойства симплициально-
ю комплекса заложены в его матрицах
инциденций и должны вычисляться, ее-
ли эти матрицы известны (заданы).
Это относится и к группам симплици-
альных гомологии комплекса. Другими
словами, зная матрицы инциденций
симплициального комплекса (отвечаю-
гцего данной триангуляции полиэдра),
мы можем вычислить все ею группы го-
мологий. Покажем, как это можно
сделать. Это и даст нам один из способов
алгоритмического вычисления групп сим-
плициальных гомологии. Другими
словами, этот прием позволяет написать
программу для ЭВМ и затем, подавая
на ее "Вход" конкретные матрицы
инциденций полиэдров, алгоритмически
(т. е. по единой программе, не
зависящей от конкретного вида полиэдра)
вычислять все группы гомологии полиэдра.
Как мы уже знаем, дважды взятый
оператор границы дает нуль, т. е. о=0.
Отсюда получаем следующую систему
уравнений на матрицы инциденций
соседних размерностей:
L.T-VH) *-чг*\ uqt <*Я
к-\
= 1??Ы&)Ь =0-
k-l
Так как симплексы Aq линейно
независимы (как элементарные цепи), то
равенство нулю их линейной комбинации с
какими-то коэффициентами означает,
что все эти коэффициенты равны нулю.
Следовательно, получаем систему
уравнений Е ?* Or/ aqJ =0, W 1 ^ У^
? a^j, 1 < q < <х.ь-\. Ясно, что эта
система при фиксированном к
эквивалентна одному матричному
уравнению, а именно: ЕГ~ \с =0. Здесь
индекс к пробегает значения от 0 до

I 3. Свойства групп симплициальных гомологии
45
I — 1. На рис. 1 показано, что,
гмножая матрицу ?*-1 размера a*~iX
<a* на матрицу Ек размера afeXaft+i,
ш получаем новую матрицу размера
U-1X а*+1, целиком состоящую из
{улей.
Полученная нами система матрич-
1ЫХ уравнений записывает на языке
1атриц инциденций тот факт, что
свадрат оператора границы д равен
|улю. Предположим, что мы вместо
избранных выше элементарных цепей
1ерешли к другому базису в
пространстве цепей при помощи какого-то
1евырожденного линейного преобра-
ювания. Тогда матрицы инциденций
:\ конечно, преобразуются и
превратятся в некоторые новые матрицы
:*. Однако легко видеть, что матриц-
toe уравнение Ек~1Ек = 0 не изменится,
'. е. по-прежнему будет выполняться
юждество ?*"'?* = 0. В самом деле,
¦ереход к другому базису в
пространнее цепей не меняет того геометри-
1еского факта, что квадрат операто-
>а границы равен нулю.
Это простое наблюдение открывает
шм путь к упрощению матриц
инциденций путем замен базиса в
пространствах цепей. Мы хотим привести
>ти матрицы к наиболее простой,
санонической форме, чтобы затем
быстро вычислить группы гомологии.
1аши преобразования будут состоять
13 последовательности шагов, причем
\г каждом шаге мы будем менять
голько один элемент базиса (в группе
4епей) в одной определенной размер-
юсти. Эти простейшие преобразования
ды назовем элементарными (здесь воз-
жкает аналогия с языком алгебры),
i заключаются они в следующем.
1) Симплекс Д* можно заменять
:имплициальной цепью Д?+ Д* где
Ф1.
2) Симплекс Д? можно заменять
1епью —Д*
Здесь мы рассматриваем каждый
:имплекс как элементарную цепь. Что
фоисходит с матрицами инциденций
фи элементарных преобразованиях?
Лемма. /) При .преобразованиях
типа 1 матрица Ek~' получается из
матрицы ? ' путем добавления к
i-му столбцу матрицы Ek~' ее t-го
столбца. Матрица Ек получается из матрицы
Ек вычитанием i-й строки из ее t-й
строки. 2) При преобразованиях типа 2 i-u
столбец матрицы Ek~' и i-я строка
матрицы Ek умножаются на — 1 (т. е.
все элементы, стоящие в этих столбце
и строке, меняют знак). 3) При
перенумерации симплексов (i-^j и
j^-i) соответствующие строки
(столбцы) меняются местами.
Доказательство этой леммы
элементарно, сводится к простому
вычислению, которое мы предоставляем
читателю как полезное упражнение,
опирающееся на стандартный материал
линейной алгебры.
Отсюда следует, что при помощи
элементарных преобразований в
пространстве цепей можно осуществлять
элементарные преобразования матриц
инциденций, а именно: складывать
строки, складывать столбцы, умножать
строку на —1, умножать столбец на
— 1, переставлять между собой строки
(столбцы). Эти операции хорошо
известны в линейной алгебре. Далее
мы сошлемся на известную теорему
из алгебры, утверждающую, что
любая целочисленная матрица может быть
путем применения перечисленных
элементарных преобразований приведена
к канонической форме. Эта форма
имеет следующий вид: на главной
диагонали матрицы (выходящей из
левого верхнего угла матрицы) стоят
ненулевые инвариантные множители
матрицы, число которых равно ее рангу.
Все остальные элементы матрицы
равны нулю. Напомним, что
получившиеся диагональные элементы
(инвариантные множители) упорядочены так, что
каждый из них является делителем
следующего за ним. Инвариантные
множители однозначно определяются
матрицей и могут быть вычислены в
терминах ее миноров. Поскольку их
явный вид нам здесь не потребуется,
эти формулы мы опустим, отметив
лишь, что сам факт их
существования позволяет вычислять все ин-

46
1. Полиэдры. Симплициальные комплексы. Гомологии
вариантные множители алгоритмически.
Теперь мы немного изменим
каноническую форму и нормализуем матрицы
инпиденций. При этом полезно
понимать, что здесь нам неважно, что
матрицы ?г, ..., Е*~ являются матрицами
инпиденций некоторого симплициаль-
ного комплекса. Нам важно лишь то,
что они удовлетворяют уравнениям
Е ~*Е =0. В остальном эти матрицы
произвольны.
Начнем для простоты, с матрицы
Приведем ее к каноническому виду.
Затем, применяя элементарные
преобразования, переставим инвариантные
множители матрицы Е* так, чтобы они
отсекали правый верхний угол матрицы
i? (рис. 2). Пусть у0—ранг матрицы ??.
В* &
S
а.
<>i-Yo
Рис. 2
Так как матрицы Е и Е
связаны уравнением Е Е =0, то, преобразуя
матрицу ?°к виду Н , мы
автоматически преобразуем и матрицу Е . Так как
Е°Е =0, то последние у0 строк
преобразованной матрицы Е 1 должны
состоять сплошь из нулей. В противном
случае мы получили бы ненулевые
элементы, умножая на ненулевые
инвариантные множители.
Теперь начнем преобразовывать
верхние ai — у0 строк матрицы Е ].
Эти преобразования индуцируют
преобразования первых а] — у0 столбгрв
матрицы ?°, а так как эти столбцы
состоят сплошь из нулей, то
соответствующие коэффициенты
инцидентности a^j не изменятся. Измениться
в
.*-1
--
—
!
i
\
S
1 •
1 '
1 <
1 1
4 cs.
ylg*.1c*.1
в*
Hk-\
Vi
В
Ук
Л-i
Рис. 3
могут лишь одномерные базисные цепи.
При этом матрица Е примет свою
окончательную, нормальную форму,
которую мы и обозначим через Н
Далее, выполняя преобразования
столбцов матрицы Е1 (которые уже не
меняют матрицы Н ), мы приведем
матрицу Е1 к нормальной форме Н , в
которой инвариантные множители
занимают такое же положение, как и в
матрице Н° (отсекают верхний правый
угол матрицы). Этот процесс можно
продолжить вверх по размерности. В
результате мы приведем все матрицы
инпиденций к нормальной форме.
Опишем подробнее полученную нами
нормальную форму матриц.
Приведенная к нормальной форме FT
матрица инпиденций Е устроена так,
что все ее элементы равны нулю, за
исключением тех, которые
расположены на диагональном отрезке,
отсекающем верхний правый угол матрицы
(рис. 3). На этой диагонали сначала
стоят р* отличных от единицы чисел
е 1, •••t^Pk, каждое из которых является
делителем предыдущего. Остальные
числа диагонали равны единице. Их
количество равно у*- р^. Оказывается, такая
форма матриц инциденций
позволяет сразу вычислять группы
целочисленных гомологии. Представим
группу гомологии Hk(X) в виде
прямой суммы свободной абелевой
группы F и конечной группы Т.
Группа F = Z однозначно
характеризуется своим рангом fik (числом

ф 3. Свойства групп симплициальных гомологии
47
свободных образующих, т. е.
образующих бесконечного порядка). Группа
Г может быть разложена в прямую
сумму своих конечных подгрупп
Z,f ® . . . 0 2ск порядков с*, . . . , Cyk
соответственно, причем (как известно
из алгебры) всегда можно считать,
что порядок cf является делителем
Предыдущего. Числа с*, . . . , c?ft
называются иногда k-мерными
коэффициентами кручения. Таким образом,
группа k-мерных гомологии Hk(X)
однозначно определяется своим рангом и
Своими коэффициентами кручения.
Оказывается, все эти числа можно
вычислять, зная нормализованные матрицы
инциденций. Имеет место следующая
важная теорема.
Теорема. Пусть ak-число k-мерных
симплексов симплициального
комплекса X (отвечающего некоторой
триангуляции полиэдра X) и пусть y* —
ранг матрицы инциденций Ек. Тогда
k-мерное число Бетти р*. т. е. ранг
группы целочисленных гомологии
Йь(Х)у равно а* —у* —7*-1- При этом
мы считаем, что y-1 = Y« = О- Далее,
k-мерными коэффициентами кручения
группы Hk(X) являются отличные от
единицы инвариантные множители
матрицы инциденций Ек. При k = n эти
коэффициенты кручения отсутствуют,
Т.е. группа Ип(Х), где n=dimX,
всегда свободна (не имеет элементов
конечного порядка).
В терминах предыдущих
обозначений мы имеем тождества ef=cf, . . . ,
е?А = с?*> гДе Р*=ф*; Р* = а* —Y* —Y*-i-
Приведем схему доказательства этой
теоремы. Рассмотрим k-мерные цепи
комплекса X и разобьем их базис
на три группы. Цепи каждой
группы обозначим соответственно через
Аку Z?\ Ск. Любая 6-мерная цепь
представляется в виде их линейной
комбинации. Указанные три группы
выберем в соответствии с видом
матриц Нк~х и Ик (рис. 3). Число
цепей вида Ск равно y*-i- &се они
имеют отличную от нуля границу,
Т. е. не являются циклами. В самом
деле, граница каждой цепи вида Ск
получается умножением некоторой
цепи вида Ak~] на отличный от нуля
инвариантный множитель матрицы
Нк~х (рис. 3). Запишем введенные выше
три группы цепей в явном виде,
указывая их количество. Имеем
Л*: Л?,... , Akk; Вк:Вк ВкРк;
С ft . r*k r*k
Все эти обозначения мы расставили
для удобства читателя на рис. 3
на матрицах Ик~1 и Нк.
Вычислим границы цепей вида Ак
и Вк. Из вида матрицы Нк~{ ясно,
что все эти цепи являются /г-мерными
циклами, так как все столбцы
матрицы, соответствующие цепям вида Ак
и Вк, состоят сплошь из нулей. Итак,
дАк=0, дВк=0. Далее, из
нормализованных матриц инциденций
извлекается следующая система соотношений:
e*A$=dCi+\ где е*—ненулевые числа,
стоящие на жирной диагонали
матрицы Нк на рис. 3 (т. е.
инвариантные множители). Следовательно, все
циклы вида Af являются элементами
конечного порядка, причем порядок
этот равен числу е* т. е.
соответствующему инвариантному множителю.
Таким образом, циклы Ак, . . . , Akk
являются образующими конечных
подгрупп в группе гомологии Hk(X),
причем порядок этих образующих
(соответственно порожденных
элементами Ак циклических подгрупп)
равен е*
Рассмотрим теперь оставшиеся
циклы вида Вк. Их количество, очевидно,
равно a* — Y* — Y*-i (Рис- 3). Все
эти циклы замечательны тем, что
никакая их линейная комбинация с
отличными от нуля коэффициентами
не является циклом, гомологичным
нулю. Это отчетливо видно из
матрицы Ик, где горизонтальная полоса,
составленная из строк вида Вкч
состоит сплошь из нулей. Это и
означает, что границы всех (k -\- 1)
-мерных цепей (при нашей нормализации
матрицы инциденций) расположены
«вне» цепей Вк и их линейных
комбинаций. Следовательно, все циклы

48 1. П
Bj являются свободными образующими
в группе гомологии. Теорема доказана.
Подведем итоги. Базис в группе k-
мерных щпей можно разбить на три
части, т. е, на г^епи вида А , п, С .
Цепи вида С циклами не являются и
поэтому не интересуют нас с тонки
зрения вычисления k-мерной группы,
гомологии Нк(Х). Цепи вида А и В
являются циклами. При этом щклы
Bj являются свободными
образующими, а щклы Aj — образующими
конечною порядка, причем этот порядок
равен соответствующему инвариантному
множителю матрицы инциденций.
В то же время следует отчетливо
понимать , что практическое вычисление
гомологии при помощи матриц
инциденций достаточно громоздко, так как
триангуляция даже достаточно простых
поверхностей (тор и т. п.) содержит
довольно много симплексов. Приведение
больших целочисленных матриц к
каноническому (и нормальному) виду —
тяжелая работа, хотя теоретически она
всегда выполнима, в частности при
помощи ЭВМ. Поэтому актуальна
задача более быстрого получения ответа.
В полном объеме такое упрощение
достигается применением языка
клеточных гомологии, о которых мы не
имеем возможности подробно
рассказать в настоящей книге. Детальное
изложение см., например, в [1, 2, 5].
Однако оказывается, «следы»
клеточных гомологии хорошо видны и могут
быть объяснены внутри симплициаль-
ных гомологии. Продемонстрируем это
в следующем пункте.
3.3. «Следы» клеточных гомологии внутри
симплициальных
Вычислительные трудности,
возникающие при попытке реального вычисления
симплициальных групп гомологии,
коренятся в их определении, а именно в
том обстоятельстве, что цепи являются
суммой симплексов взятых с какими-то
коэффициентами. Хотя симплекс —
простой объект, но симплексов
довольно много, поэтому работать с такими
1Иэдры.Симплициальные комплексы. Гомологии
цепями довольно трудно. Однако
можно попытаться (и эта попытка,
оказывается, увенчивается успехом)
объединять симплексы в более крупные
объекты (блоки), которые мы назовем
клетками, а соответствующие цепи —
клеточными симплищальными цепями.
Затем будем работать с этими
крупными блоками так, как будто они
являются отдельными «симплексами», т.
е. по прежним правилам. В результате
процесс вычисления гомологии резко
сокращается. Именно на развитии
этого пути и можно определить клеточные
группы гомологии (через клеточные
цепи). Мы не будем здесь делать этого
подробно, отсылая заинтересованного
читателя к [1, 2, 11].
Итак, выберем (внутри комплекса X)
в размерности k конечное число
симплициальных комплексов QT, ..., QMi,
таких,что Int Qv (т. е. множество
внутренних точек Qj ) гомеоморфно
открытому &-диску и j и таких, что они
линейно независимы, т. е. из равенства
t\ Qi + ...+ tMkQMt = 0 следует, что все
числовые коэффициенты f,- равны нулю.
Это условие будет, например,
выполнено, если никакие два из этих
комплексов не имеют общих ^-мерных
симплексов. Линейную комбинацию таких
комплексов назовем клеточной симплищ-
альной цепью. Ясно, что мы можем
говорить о границе клеточной симплици-
альной цепи, о циклах и т. п. Будем
считать, что граница (k+1)- мерной
клеточной симплициальной цепи
является &-мерной клеточной
симплициальной цепью. Для этого достаточно
потребовать, чтобы граница каждого сим-
плициального комплекса вида Q,
была бы линейной комбинацией
симплициальных комплексов вида Q;.
Далее нужно потребовать, чтобы для
каждого ^-мерного симплгщиального цикла (в
прежнем смысле) существовал
гомологичный ему клеточный симплици-
альный цикл. Наконец, нужно
потребовать , что если k- мерный
клеточный симплициальный цикл гомоло-
^гичен нулю (в обычном смысле), т. е.

$3. Свойства групп симплициальных гомологии
49
является границей некоторой (k+l}~
мерной симплициальной цепи,
то он является также границей
некоторой (&+1)-мерной клеточной
симплициальной цени.
Легко видеть, что в каждом симпли-
циальном комплексе всегда можно
найти систему комплексов вида Q,,
удовлетворяющих всем перечисленным
условиям. Теперь можно начать
вычисление групп гомологии, пользуясь не
прежними мелкими симплексами, а более
крупными кусками — клеточными сим-
плициальными цепями, блоками. Все
вычисление нужно выполнять по
прежним рецептам. Единственная разница
заключается в том, что исходным
пунктом вычислений будут уже не прежние
матрицы инциденций исходного сим-
плициального комплекса, а новые
матрицы клеточных симплициальных
инциденций, определяемых
граничными соотношениями для клеточных
симплициальных цепей. В остальном
алгоритм приведения матриц
инциденций к канонической форме
сохраняется. Мы не будем здесь
углубляться в теоретические детали этой
процедуры, предоставляя заинтересованному
читателю самостоятельно продумать
всю эту геометрически совершенно
прозрачную и наглядную схему. Вместо
абстрактно-формальных выкладок мы
предпочтем наглядно
продемонстрировать идею на простых примерах.
Для сокращения формулировок будем
называть клеточные симплициальные
цепи просто клеточными г^епями, а
базисные комплексы — просто
клетками. Таким образом, клеточные цепи
являются линейными комбинациями
клеток (с числовыми коэффициентами).
Рассмотрим тор, изображенный на
рис. 4, как квадрат с
отождествленными противоположными сторонами.
В качестве базиса клеточных цепей
можно взять, например, следующие
объекты:
1) одна нульмерная клетка, т. е.
нульмерная базисная клеточная цепь
0°
а
0°
Рис. 4
р
о2
р
а°
>
а
о°
?°
1
а
п0.-^-
Gi*
'V
р
о2
Р
a
о2
°°
а
;'с°
• и2
^ и
Q0, являющаяся единственной
вершиной. Она представлена на рис. 4
четырьмя вершинами квадрата. Ясно, что
все они отождествляются в одну точку
на поверхности вследствие заданных на
сторонах квадрата склеек ;
2) две одномерные клетки, т. е. две
базисные одномерные клеточные цепи
аир ;
3) одна двумерная клетка, т. е.
базисная клеточная двумерная цепь Q2 —
сам квадрат.
Вычислим клеточные группы
гомологии. Ясно, что нульмерная группа Но
изоморфна Z, так как мы имеем
единственную нульмерную клетку Q0 (она
же — единственный нульмерный цикл).
Далее, любой одномерный клеточный
цикл z является линейной комбинацией
двух клеточных циклов а и р, т. е.
z =тх+п р. Найдем одномерные циклы,
являющиеся границами. У нас есть
единственная двумерная клетка —
квадрат Q , следовательно,
произвольная двумерная клетка — квадрат Q2,
следовательно, произвольная двумерная
клеточная цепь записывается в виде
/Q2, где р — целое число. Имеем
дф= а+р-а-р = 0, т. е. д{$$) = О при
любом р. Следовательно, имеется лишь
один одномерный цикл, являющийся
границей, — это нулевой цикл. Итак,
одномерная группа гомологии
изоморфна Z©Z, причем образующими в
ней являются клетки-циклы аир.
Заодно мы уже нашли и группу
двумерных гомологии, так как все
двумерные клеточные цепи в нашем

50
1. Полиэдры. Симплициальные комплексы. Гомологии
примере являются циклами. Отсюда
/?=Z, так как любая двумерная цепь-
цикл имеет вид рф, где р — целое число.
Таким образом, мы нашли группы
гомологии тора существенно быстрее,
чем раньше, когда опирались на
обычные симплициальные цепи и циклы.
Приведем еще один пример:
проективная плоскость (рис. 4).
Запишем действие граничного
оператора: dy=Qb-Q°=0f aQ2=2/.
Следовательно, группы целочисленных
гомологии таковы: Но =Z, H\=Z2> Н2- 0. Если
же использовать группу коэффициентов
Z^, то появится ненулевой двумерный
цикл— это клетка (jf. Ее граница равна
2у, т. е. равна нулю по модулю группы
Ъ Итак, ШКР2,^ Ъ, HWF, 1г)=
=Ъг, Н2(Ш>\ Ъг)=гг.
Вычислим в качестве простого
упражнения группы гомологии во всех
случаях, которые были разобраны в
предыдущем параграфе, и убедимся, что
использование языка клеточных сим-
плициальных цепей существенно
ускоряет процедуру вычислений.
На рис. 5 изображены
симплициальные комплексы, задающие бутылку
Клейна, сферу с g ручками, неориенти-
руемую поверхность типа к. Во всех
перечисленных случаях все вершины
соответствующего многоугольника
склеиваются в одну точку (следуя
отождествлениям, указанным на сторонах
многоугольника), следовательно,
изображают единственную вершину Q . Таким
образом, каждая из сторон
многоугольника (взятая по отдельности)
изображает собой одномерный цикл на
поверхности . Осталось найти границу
двумерных цепей. Единственная клетка
размерности два — это сам
многоугольник Q . Вычислим границу этой
клетки. В случае бутылки Клейна имеем
dQ*= а+р-а+р =28 * 0; для сферы с g
ручками имеем dQ = щ + р! - щ - р] +
+ ...-kxyf Pg-ot^— pg= 0; для неориен-
тируемой поверхности типа к имеем
dQ =2<Xi + ...+2а^0. Следовательно,
Рис. 5
гомологии бутылки Клейна имеют вид
Но =1, Нх =Z(a)©Z2(p), Н2= 0, где через
Z(a) и Z2(fl) обозначены абелевы
циклические группы, порожденные
образующими аир соответственно.
Гомологии сферы с g ручками имеют вид
Но = Z, Я, = Z(a,) в Z(p0 © ... ©
© Z(ag) © Z(p4) = Z2*, H2 = Z.
Гомологии неориентируемой поверхности типа
к имеют вид Но = Z, Н\= Z(oci) ©
© ... © Z(abl)© %l{al+...+ak), /?= 0.
3.4. Цепная гомотопия. Независимость
симплициальных гомологии полиэдра от
выбора триангуляции
Как мы отмечали, важность групп
гомологии основывается на том, что они
не зависят от способа триангуляции
полиэдра.
Теорема. Пусть X — конечный
полиэдр и К\ j К2 — симплициальные
комплексы, отвечающие двум ezo
произвольным, триангуляциям. Тогда
группы симплициальных гомологии Н^(К\)
и ЩК2) изоморфны и совпадают (по
определению) с группами гомологии
полиэдра Hi(X).
Мы не будем доказывать эту теорему,
так как доказательство технически
громоздко. Дадим здесь лишь краткую

f 3. Свойства групп снмплнцнальных гомологии
51
схему доказательства, вскрывающую
его геометрический наглядный смысл.
Пусть X—полиэдр, на котором
фиксирована некоторая триангуляция,
порождающая симплициальный комплекс
К. Мы ввели ранее группы
снмплнцнальных цепей Ci(K) и граничные
операторы д<. Собирая эти группы
вместе,, мы можем организовать их
в последовательность групп и
гомоморфизмов следующего вида:
о+ся(/о-*...-^с,(/0^с1-|(/о+...
...-*С,(Ю-*СоA0-*2-*0.
Эта последовательность называется
цепным комплексом (комплексом
цепей). Гомоморфизм е устроен так:
e(I/a/A?) = 2!/a/6Z. Кроме того,
напомним, всегда выполнено тождество
dtdi+i =0 для любого /. Напомним,
что Kerdi=Zi(K) (циклы), Imd,+i =
= В>(К) (границы), //,(*)= Кегй/
lmdi+i.
Пусть даны два симплициальных
комплекса /С и L. Отображение
f:K-+L называется симплициальным,
если оно непрерывно и линейно
отображает каждый симплекс из К
на некоторый симплекс из L
(следовательно, на симплекс той же или
меньшей размерности). В частности,
при симплициальном отображении
вершины переходят в вершины.
Рассмотрим симплициальный комплекс
К и его прямое произведение /(X/ на
единичный отрезок /. В результате
получим «призму» (рис. 6). Мы
утверждаем, что прямое произведение
можно превратить в симплициальный
комплекс, т.е. что /СХ/ можно
триангулировать (вообще говоря, многими
способами). Укажем один такой
способ. Ясно, что достаточно научиться
триангулировать прямое
произведение Д'Х/ одного симплекса А* на
отрезок /. Процесс триангуляции
показан на рис. 6 для одномерного
и двумерного симплексов Л1 и Л2.
Совершенно ясно, как продолжить
этот процесс на высшие размерности.
Рис. 6
При этом мы построили и будем
рассматривать в дальнейшем лишь
такие триангуляции призмы /СХ/,
которые совпадают на основаниях
призмы (т.е. -на /СХО и /СХ 1) с
ранее заданной триангуляцией /С,
причем триангулированная призма /СХ/
распадается в объединение призм
Д'ХЛ где А1 пробегает все симплексы
комплекса /С. Мы не будем далее
каждый раз повторять эти условия,
а будем просто говорить о
триангуляции призмы /СХ/, согласованной
с исходной триангуляцией /С.
Определение. Два симплициальных
отображения /, g: K~*-L комплекса
/С в комплекс L называются симпли-
циально гомотопными, если существу-

52
1. Полиэдры. Симплициальные комплексы. Гомологии
ет симплициальное отображение F
прямого произведения К xl
(рассматриваемого как симплициальный комплекс,
причем триангулировать Kxl можно
произвольным согласованным
способом, не обязательно тем, какой был
показан на рис. 6) в комплекс Ь такое,
что на основаниях призмы Kxl
отображение F совпадает с /и g> т. е.
F(x, 0) =f(x), F(x, 1) =g(x).
Пусть f : К —> L — симплициальное
отображение двух симплициальных
комплексов. Так как оно переводит
каждый симплекс в симплекс, то очевидно,
определено отображение ?
симплициальных цепей Cj(K) комплекса К в
симплициальные цепи С,{Ь) комплекса
Ь . Все отображения fj являются
гомоморфизмами. Удобно изобразить эту
систему гомоморфизмов и групп в виде
таблицы (диаграммы), где через е
обозначено тождественное отображение Z -> Z:
...^d(K) Д C,-i</() -*...
u и*-.
_.. —G(M -+ Ci-x(L) -*...
+ C,(L) Д Co(M iZ-^0.
Из определения граничного оператора
следует, что эта диаграмма
коммутативна, т. е. fi-idi—d-fij ?8 = е%.
Система отображений {/, } называется
цепным отображением.
Из коммутативности диаграммы сразу
следует, что гомоморфизмы fi
индуцируют некоторые гомоморфизмы f^: Ker dj
/Im Э;+1-> Ker 3',/lm d'i+l , т. е.
гомоморфизмы групп гомологии цепных
комплексов ? : ЩК) -»• ЩЬ). Иногда
вместо Д будем писать ft. Легко
проверить выполнение следующих свойств.
1) Bcmf:K->L ng:L->N
—симплициальные отображения
симплициальных комплексов К, L, N, то {gf)=gft-
2) Если lj^ — тождественное
отображение комплекса К на себя (оно,
очевидно^ симплициальное), то (lj^)^:
ЩК) ->ЩК) — тождественный
гомоморфизм (для любого / ).
Теорема. Пусть ftg:K->L — сим-
плициально гомотопные друг другу два
симплициальных отображения
комплекса К в комплекс Ь. Тогда индугщ-
робанные гомоморфизмы f* и g* групп
гомологии ЩК) в группы гомологии
ЩЬ) совпадают при всех г.
Для доказательства нам потребуется
понятие цепной гомотопии. Пусть
С ={С,} и СЩС$— два цепных
комплекса, т. е. Ci=Ci(K)t C;=C/L).
Пусть ф и ц/— два отображения С в С,
т. е. ср={фЛ» УЧЧ^Ь где Ф* и Ч>* —
гомоморфизмы С, —> С/. Будем
говорить, что задана г^епная гомотопия D
между отображениями (ри \|/ цепного
комплекса С в цепной комплекс С',
если задана совокупность D={D,}
гомоморфизмов Dj : Cj ~^> C/+i , таких,
что для каждого / выполнено равенство
D^idj+ 9/+1Д- = ф, - ф,. Это можно
записать в виде диаграммы:
Естественно назвать такие два
отображения ф и v|/ цепных комплексов С и
С' ценно гомотопными.
Ценно гомотопные отображения
цепных комплексов индугафуют
одинаковые отображения групп гомологии.
Другими словами, если ф цепно
гомотопно ф, то все гомоморфизмы ф*,
vj/* : ЩК) -> ЩЬ) совпадают.
В самом а^я^у если цепь z еС/Х)
является циклом,, т. е. д&=0, то из
определения цепной гомотопии имеем
<p,fz) - w.-W- D^diizy, aViAW-
= д'мфМ)= 9'm(W)f т.е. образы
цикла z при отображениях ф,- и ф,-
отличаются на цепь-границу, поэтому
гомологичны. Это завершает
доказательство.
Лемма. Если два симплициальных
отображения ftg: К -» Ь симплигашльно
гомотопны, то индуцированные ими

§3. Свойства групп симплициальных гомологии
53
отображения цепей <р={/5} и Ч*={&)
ценно гомотопны.
Следствие. Если два симплициальных
отображения f9 g: К-> L комплекса К
в комплекс L симплициально
гомотопны, то они индуцируют одинаковые
отображения групп симплициальных
гомологии ЩК) ~-> ЩЬ) для всех и
Доказательство следствия сразу
вытекает из леммы и из свойств цепной
гомотопии. Осталось доказать лемму.
Так как отображения / и g симплици-
ально гомотопны, то существует сим-
плициальное отображение призмы Kxl
в L, причем призма триангулирована
согласованным образом (ее
триангуляция на ее основаниях совпадает с
исходной триангуляцией комплекса К).
Нужно построить цепную гомотопию
комплекса цепей С,{К) в комплекс
цепей Сг{Ь). Достаточно определить ее
лишь на отдельных симплексах
комплекса К. Итак, пусть А* —
произвольный симплекс в К. Так как
триангуляция призмы Kxl согласована с
триангуляцией К, то над А1 "висит" призма
Ах/, вложенная в призму Kxl.
Призма Д'х/ как-то триангулирована (как
именно, для нас неважно).
Следовательно, она сама является симплици-
альным комплексом. Рассмотрим все
(* +1) -мерные симплексы, на которые
разбита призма A'xl, возьмем их
сумму, обозначим ее через Д (А*) и
сопоставим ее исходному симплексу в
основании призмы. Так как каждому
симплексу А' мы сопоставили некоторую
цепь Д(А*Ъ, то возникает
гомоморфизм Д: С,\К)->С&х(Ь). В самом деле,
достаточно взять теперь образ
призмы Д{А') при симплициальном
отображении F. В результате получится
некоторая (/+1)-мерная симплициальная
цепь в комплексе L,. которую мы и
обозначим через Dj(A'). Осталось
проверить основное свойство цепной
гомотопии, а именно что Д^д^Ч- д'^Д =
=f$~&- Перепишем это равенство так:
д'т1%= fc-Di-idi-gi. Ясно, что это
соотношение следует из геометрически
очевидного факта, что полная граница
призмы A'xl слагается из трех
компонент: 1) нижнего основания, 2) боковой
стенки призмы (являющейся
цилиндром), 3) верхнего основания, взятого
со знаком минус, чтобы учесть
ориентацию. Это замечание и завершает
доказательство леммы. Мы доказали
теорему о том, что симплициально
гомотопные отображения комплексов
индуцируют одинаковые отображения
фут симплициальных гомологии.
В действительности верно более
сильное (и более просто формулируемое)
утверждение. Для этого напомним
понятие непрерыбной гомотопии (уже
не обязательно симплициальном).
Два отображения / и g полиэдра X в
полиэдр У называются гомотопными,
если существует семейство
непрерывных отображений <р*: X->Y
(непрерывно зависящих от точки хеХ и
параметра /) такое, что 0 й t <1 и <ptf=/,
Фг=?. Другими словами, отображение /
непрерывно деформируется в
отображение g. Гомотопность отображений /
и g обозначается так: f~g.
Оказывается, любое непрерывное отображение
симплициальных комплексов можно
аппроксимировать симплициальным.
Теорема о симплициальной
аппроксимации. Пусть f\K-*L —
непрерывное отображение конечного симплици-
ального комплекса К в конечный симг
плициальный комплекс L. Тойа
существует такое измельчение К'
комплекса К (пи е. симплициальный
комплекс К\ полученный из К делением
каждого симплекса на более мелкие
симплексы, например при помощи
последовательных барицентрических
подразделений) и такое отображение
f'.K'^tL, которое гомотопно исход-
ному отображению и является
симплициальным.
Итак, измельчая достаточно мелко
(нужное число раз) исходный комплекс,
можно всегда продеформировать
непрерывное отображение в симплициальное.
Этот "мостик" между непрерывными
и симшшциальными отображениями иг-

54
1. Полиэдры. Снмплициальные комплексы. Гомологии
рает важную роль в изучении свойств
групп симплициальных гомологии.
Доказывать эту теорему мы здесь не будем.
См., например, [5].
Ясно, что понятие непрерывной го-
мотопии можно сформулировать на
языке отображения цилиндра
(призмы). Отображения / и g гомотопны, если
существует непрерывное отображение
F.XXI^Y такое, что F{0,x) = f(x) и
F(\y x) = g(x). Ясно, что в качестве
отображений yt'.X-^Y достаточно взять
отображения ф/(х) = Д/, х), 0</<1.
Оказывается, во всех
сформулированных и доказанных выше
утверждениях можно всюду заменить слова «сим-
плициальное отображение» на
«непрерывное отображение». В частности,
непрерывно гомотопные отображения f,
g:/C-*-L индуцируют одинаковые
гомоморфизмы групп гомологии Hi(K)-*-
Утверждение. Пусть К — симплици-
альный комплекс, отвечающий какой-то
фиксированной триангуляции
полиэдра X. Пусть р'/( — симплициальный ком-
плекс, получающийся при j-кратном
барицентрическом подразделении
исходной триангуляции (комплекса К).
Тогда группы гомологии комплекса К и
его j-кратного барицентрического
подразделения совпадают (изоморфны).
Доказательство (которое мы здесь
опускаем) следует из свойств цепной
гомотопии, рис. 7 и теоремы о симпли-
циальной аппроксимации.
Итак, возвращаясь к теореме о
независимости групп гомологии от выбора
триангуляции, можно отметить
следующее. Измельчая одну
триангуляцию, мы, с одной стороны, не меняем
группы гомологии (см. выше). С другой
стороны, мы покрываем комплекс все
более мелкими симплексами. Начиная
с другой триангуляции, мы также, не
меняя групп гомологии, покрываем
полиэдр очень мелкими симплексами.
Можно доказать, что измельченные
циклы первой триангуляции можно
поставить в соответствие с некоторыми
другими циклами, соединяющими
черты симплициальных и клеточных цепей.
То же можно сделать и с другой три-
Рис. 7
ангуляцией. Отсюда и выводится
изоморфизм групп гомологии.
Два полиэдра X и У называются
гомотопически эквивалентными, если
существуют непрерывные отображения
f\X-+Y и g:Y-*-X такие, что их
композиции fg и gf гомотопны
соответственно тождественным отображениям 1Y и
\х на себя. Из свойств групп гомологии
сразу следует, что гомотопически
эквивалентные полиэдры имеют
одинаковые группы гомологии. В самом деле,
(fe)* = U,)• = /* (*/). = A*). = «* т.е.
гомоморфизмы f*:Hi(X)-*~Hi(Y)-и g*:
:Hi(Y)-*Hi(X) взаимно обратны, а
потому каждый из них является
изоморфизмом.
3.5. Комментарий к наглядному материалу
На рис. 8 условно изображена главная
геометрическая идея теоремы о сим-
плициальной аппроксимации; см. пункт
3.4. настоящего параграфа. Исходное
непрерывное отображение полиэдров
подвергается малой непрерывной
деформации (гомотопии), в результате
которой отображение локально
выглаживается» и становится
кусочно-линейным. Этот процесс распространяется
затем на весь полиэдр. В несколько
ином виде эта же идея реализована
на рис. 9. Исходное непрерывное
отображение задавалось полиномом
высокой степени (см. график в центре
рисунка). Затем график
триангулировался, что давало возможность считать
отображение локально линейным (на
каждом симплексе) после подходящей
малой деформации. Видно, что в точках,

}3. Свойства групп симплициальных гомологии
55
где производная отображения
достаточно велика (эти точки расположены
на тонких "усах" поверхности),
требуется особенно мелкое измельчение
поверхности. Чем больше модуль
производной, тем меньше симплексы. Для
простоты, изображено разбиение на
квадраты. Замена непрерывных
изображении кусочно-линейными условно
показана также на рис. 10. В нижней
его части см. также триангуляции
призм. На рис. 11 изображены
графические математические вариации на
тему возникновения клеточных
гомологии "внутри" симплициальных.
Достаточно мелкие симплексы могут
организовываться в сложные и более крупные
фигуры, которые сами могут играть
роль элементарных объектов-циклов.
Рис. 12 показывает триангуляцию
призмы, и, следовательно, показана
цепная гомотопия; см. теорему о
независимости групп гомологии от
триангуляции. На нижнем основании призмы
здесь задано некоторое непрерывное
отображение, а на верхнем —
тождественное. Рис. 13 условно изображает
идею объединения мелких симплексов в
более крупные блоки, что дает
возможность перейти к клеточным (или
кубическим) гомологиям. В верхней
части рис. 14 показана аппроксимация
непрерывного отображения симплици-
альным; в центре — разрезание
полиэдра и появление нетривиальной
границы. Две фигурки раздвигают берега
разреза. Этот прием будет применен
далее при доказательстве теоремы
классификации двумерных
поверхностей. Поверхность разрезается на
треугольники, из которых затем
склеивается плоский много-угольник. На
рис. 15 условно изображена
последовательность матриц инциденций
(прямоугольные таблицы-плиты)
полиэдра. См. пункт 3.1 в § 3.
Произведение любой пары расположенных
рядом матриц равно нулю. На рис. 16
показано пространство, заполненное
прозрачными трехмерными
симплексами, что приводит к сложным
преломлениям света. Рис. 17 и 18
изображают разные виды призм цепной
гомотопии и разные способы их
разбиения на элементарные куски.
Определение. Если Щ(Х) —
целочисленные гомологии, то число
xW = 22e(-l)'A, W Д — числа
Бетти, называется эйлеровой
характеристикой пространства X; здесь
п =dim X.
Если Hi (X, F) — группы гомологии
с коэффициентами в поле F, то число
Z?o(-l) dim Н,(Х, F) называется
эйлеровой характеристикой над полем F.
Так как гомотопически
эквивалентные пространства X и У имеют
изоморфные группы гомологии, то, в
частности, у таких пространств:
Нетрудно показать, что %(Х) можно
подсчитать и по такой формуле:
XiX^ZUi-lYpattrCifX)* где через
ранг С;(Х) обозначено число
образующих в свободной абелевой группе
Ci(X1 Z), или, (что то же самое) число
/-мерных симплексов в триангуляции
пространства X.

2
Многообразия малой размерности
§ 1. Некоторые основные понятия дифференциальной геометрии
1.1. Координаты в области. Преобразования
криволинейных координат
Современная дифференциальная
геометрия является самостоятельной
научной дисциплиной» чрезвычайно
разветвленной и связанной с
многочисленными приложениями. В выстроенном
сегодня здании дифференциальной
геометрии выделяются два основных слоя.
Первый, оформившийся исторически
первым, условно можно назвать
локальной дифференциальной
геометрией, развивающейся обычно в области
евклидова пространства. Это
фундамент и первые этажи всего здания.
Затем появились следующие этажи,
исторически сложившиеся позднее. Они
объединяются названием «глобальная
дифференциальная геометрия». Здесь
локальные понятия тесно
переплетаются с глобальными, топологическими.
Позвоночным столбом всего здания
является теория гладких многообразий.
Начинаясь на первых этажах, она
первоначально локальна, т.е. события пока
развиваются в достаточно малой
области многообразия. При подъеме вверх в
теории возникают глобальные аспекты,
и, наконец, на вершине современная
геометрия оперирует с существенно
нелокальными эффектами.
Начнем с локальных понятий.
Рассмотрим евклидово пространство R",
снабженное обычным декартовым
(евклидовым) скалярным произведением и
отнесенное к евклидовому базису,
состоящему из единичных и попарно
ортогональных векторов С\у ... , ен* Идея
задавать точку пространства Вя при
помощи набора вещественных чисел хи
... , хя. являющихся ее координатами
относительно базиса еъ ... , епУ в
окончательном виде принадлежит Р.
Декарту A596—1650), хотя в менее четкой
форме эта мысль присутствует race в
работах Виета A540—1603) и П.Ферма
A601—1665). Впрочем, понятия широты
и долготы на плоскости (аналог абсцисс
и ординат) для построения графиков
использовал еще в XIV в. Орезм (N.
Oresme, 1323—1382). Плодотворность
этой идеи была окончательно осознана
с появлением понятия криволинейных
координат. Прежде чем переходить к
их обсуждению, задержимся на
понятии декартовых координат. Их роль в
первую очередь определяется тем, что
они позволяют алгебраически задавать
и изучать кривые у в R". Характерным
свойством декартовых координат
является их жесткая связь с евклидовым
скалярным произведением -< , >~
векторов а и Ь, записывающимся так:
-< a, b >• = Zf-i Q*b\ где а' и Ь* —
декартовы координаты векторов а и Ь.
Понятие криволинейных координат
оформилось под давлением конкретных
механических и физических задач,
требовавших более утонченного аппарата,
чем обычная теория декартовых
координат. Во многих прикладных задачах
встречаются траектории движения
материальных точек в поле каких-либо
сил, явная запись которых в
декартовых координатах затруднительна или
слишком громоздка. Укажем простой
пример. Пусть материальная точка А с
массой, равной 1, движется в
плоскости в центральном поле сил. Пусть
центр притяжения находится в точке О.

jl. Некоторые понятия дифференциальной геометрии
57
Введем на плоскости полярные
координаты г и ф, где г — расстояние от
переменной точки А до точки О, а ф —
угол, образуемый радиус-вектором а
этой точки с осью Ох (рис. 1). Так
как точка А движется, то г и ф
являются функциями времени /. Рассмотрим
в точке А единичный вектор ег. Он на-
фт„ „— А ;
Рис. 1
правлен вдоль радиус-вектора, и а =ге^
.Дифференцирование по t обозначим
точкой. Тогда движение материальной
точки в центральном поле сил
определяется дифференциальным уравнением
lhf(r)ert где / — некоторая гладкая
функция от г при г >0 и r(t}= \a(tjif где
\а | — евклидова длина вектора а.
Рассмотрим случай поля, в котором сила
притяжения обратно пропорциональна
г , т. е. ньютоновское поле тяготения.
Тогда финитными (компактными)
траекториями движения точки являются
эллипсы, уравнения которых имеют вид
l+e cos ф — р/r, где р и е — параметр
и эксцентриситет, орбиты, причем
$ < 1 для финитных движений. Центр
притяжения находится в одном из
фокусов эллипса. Здесь полярные
координаты существенно облегчают изучение
траектории точки, и их введение
оправдано. Аналогично при решении
конкретных задач механики и физики
появлялись и другие удобные
криволинейные системы координат:
сферические (например, при изучении движения
твердого тела с закрепленной точкой в
поле силы тяжести), цилиндрические
(при изучении устойчивости столба
жидкости и сил поверхностного
натяжения) и т. п.
Анализ всех таких систем координат
позволяет обнаружить, что в их основе
лежит некоторая общая идея,
допускающая простую и самостоятельную
формулировку.
Рассмотрим в IT с декартовыми
координатами ж\ ...,У произвольную
открытую область С. Сопоставляя
каждой точке Р из С набор п вещественных
чисел УСР),...|У(Р)| мы определяем п
функций на области С. В терминах
этих функций мы и будем задавать
криволинейные координаты. Так как
положение точки можно однозначно задать
ее декартовыми координатами, то
введенные выше функции записываются
так: У- У(*\ ...^),..МУ- /(*> *")•
Определение 1. Непрерывной
системой координат в области С называется
система функций У = У (я*, ... ,х"),
задающих взаимно-однозначное и
непрерывное в обе стороны отображение
/области С на некоторую область А в
другом экземпляре евклидова
пространства. Другими словами, /является
гомеоморфизмом области С на область Л.
Особый интерес для приложений
представляет случай, когда
отображение / является гладким, т. е. все
функции У (я7, ...,**) гладко зависят от
аргументов. Под термином "гладкость"
мы понимаем следующее. Будем
требовать, чтобы функции имели столько
непрерывных производных, сколько это
требуется по условию задачи. Для
простоты можно считать, что мы берем
функции из класса С°° (бесконечное
число непрерывных производных).
Определение 2. Матрицей Якобы
отображения f: С -> А
называется функциональная матрица
дух ду"
дх1 дх1
«=(!) =
дхп
дх'
Ее определитель называется якобианом
отображения/ и обозначается через J(f)
Определение 3. Регулярной
криволинейной системой координат в области
С называется система гладких функций
У(**, •••»**)> задающих взаимно-одно-

58
2. Многообразия малой размерности
значное отображение С на область А в
R", причем якобиан отображения f
отличен от нуля во всех точках области.
Из теоремы о неявных функциях
следует, что тогда отображение /~',
обратное к f, также является гладким.
Итак, регулярная криволинейная
система координат задается гладким
взаимно-однозначным отображением,
устанавливающим, в частности,
гомеоморфизм между областями С и А. Такие
отображения называются
диффеоморфизмами. Предположим, что в области
задан некоторый набор гладких
функций у\Р),...,уп(Р). Как узнать, задает
ли он регулярную систему координат
в области?
Лемма 1. Предположим, что якобиан
системы гладких функций у\Р),---,уп{Р)
отличен от нуля во всех точках области.
Тогда для каждой точки существует
открытая окрестность, в которой эти
функции задают регулярную
(локальную) систему координат.
В то же время этот набор функций
может не определять глобальные
криволинейные координаты во всей области.
Доказательство первого
утверждения следует из теоремы о неявных
функциях. Второе утверждение
означает, что отображение /_1 области А на
С может не существовать. Приведем
простой пример. Рассмотрим в качестве
С и Л плоскость R2 с выколотым
начатые. 2
лом координат. Положение точки Р на
С зададим комплексным числом z — re14.
Отображение / зададим так: /(z) = z2
(рис. 2). Ясно, что якобиан этого
отображения отличен от нуля (на всей
области), но / не является
взаимнооднозначным отображением, поэтому не
имеет обратного однозначного
отображения.
Определим регулярную замену
координат. Пусть в С заданы две
регулярные системы координат, т. е.
фиксированы два диффеоморфизма f:C—*-
^c=RV yn)ng:C^BczRn(z\...,
zn). Поскольку эти отображения
взаимно-однозначны, то корректно
определение. 3
но отображение, сопоставляющее
координатам tf(P) точки Р ее координаты
zl{P). Возникает отображение gf~] =
= q:A-*B (рис. 3). В результате мы
получаем функции г' = г\у1,...,уп)у
задающие это преобразование. Его мы и
назовем регулярной заменой координат
в области. При этом мы опираемся на
следующее утверждение.
Лемма 2. Отображение zl = z\y\...,
уп) является взаимно-однозначным и
гладким в обе стороны отображением
области А на область В с ненулевым
якобианом.
Доказательство следует из свойств
матрицы Якоби. Напомним, что
матрица Якоби композиции отображений
распадается в произведение матриц Якоби
этих отображений.
Система криволинейных регулярных
координат у1 уп в области С
определяет в ней семейства координатных
линий. А именно i-я координатная линия,
проходящая через точку Ро, — это глад-

I I. Некоторые понятия дифференциальной геометрии
59
кая траектория, задаваемая системой
уравнений: у*(Р) = с', j^i и 1</<п,
где с' —некоторые фиксированные
постоянные, а именно с*=у>(Ро). Другими
словами, вдоль *-й координатной линии
изменяется только координата i/\ а
остальные координаты фиксированы.
Итак, из каждой точки выходит п
различных координатных линий (рис. 4).
Рис. 4
Приведем примеры классических
криволинейных координат на плоскости и в
R'\ Зададим на плоскости декартовы
координаты х, у. Взяв в качестве
области С плоскость с выброшенным лучом
U^O, </ = 0), мы можем задать на ней
функции <p=arctg-^-, r=Vx2-(-i/2- ^та
пшена координат задается также
формулами x=rcos<p, i/=rsin<p.
Прямоугольная сетка декартовых координат
превращается в полярную сетку
координатных линий (рис. 5).
(.2т?
О
Рис. 5
Цилиндрические координаты г, <р, /
к R3 корректно определены, например,
в области, получающейся
выбрасыванием из трехмерного пространства
полуплоскости (х^О, !/=0). Формулы
замены следующие: x=rcosq>, */—rsinq>,
z=t (рис. 6).
Рис. 6
Сферические координаты г, 0, <р в R3
корректно определены, например, в
области, получающейся выбрасыванием
из пространства той же полуплоскости,
что н в предыдущем примере. Формулы
замены следующие: x=rsin6cos«p, i/=
= rsin6sinq>, z=rcos8 (рис. 7).
Рис. 7
1.2. Понятие многообразия. Гладкие
многообразия н способы яж задания. Многообразия с краем.
Касательное нространстно в касательное
расслоение
Сегодня существует несколько способов
построения карты поверхности земного
шара или отдельных его регионов. Все
они так или иначе сводятся к одной
и той же процедуре: к проекции
выпуклой сферической поверхности
глобуса (или ее Частей) на плоскость.
Более или менее очевидно, что построить
взаимно-однозначное непрерывное
проектирование всей сферы на какую-либо
область в плоскости (или на всю
плоскость) невозможно. Это утверждение
можно точно математически доказать.
Однако это принципиальное
обстоятельство было осознано средневековыми
картографами не сразу. Первичный
опыт наблюдателя приводит к гипотезе,
что земная поверхность—плоская.
Возникло представление о плоской земле,
ограниченной «границей мира>. В соот-

60
2. Многообразия малой размерности
ветствии с этим первые средневековые
карты мира изображались на плоскости
в виде диска или прямоугольника, куда
и помещался весь известный в то время
мир. См., например, средневековые
карты, традиционно датируемые X и V вв.
(рис. 8). Таковы также, например.
Cosmas Indicopieustes
Рас. 8
карты X—XV вв. Такова известная
всемирная карта 1527 г., составленная
португальцем Diogo Ribeiro [16].
После открытия шарообразности
Земли, после путешествий Христофора
Колумба A492), Васко да Гама
A497—1498), Магеллана A515—1522)
была, наконец, осознана необходимость
создания карт, учитывающих
сферичность поверхности земного шара.
Первоначальные попытки сводились к тому,
что на плоском рисунке просто
изображали шар, глобус, повернутый к
зрителю какой-то одной своей (наиболее
важной для картографа) стороной.
На ней изображались соответствующие
регионы, постепенно искажавшиеся,
однако, по мере приближения к видимой
границе шара. Такова, например,
всемирная карта Стабиуса-Дюрера A515)
[16]. В то же время такой способ
изображения не удовлетворял
картографов, поскольку невидимая часть
шара все равно нуждалась в отдельном
изображении и, кроме того, трудности
изображения на плоском рисунке
выпуклой поверхности глобуса требовали
чрезвычайного искусства гравера,
рисовальщика. Поэтому уже в XVI в. были
изобретены различные способы
проектирования больших участков земной
поверхности на плоскость,
позволяющие учитывать возникающие при этом
(неизбежные) искажения. Разработке
теории проектирования и ее
приложениям (к картографированию и к
живописи, графике) большое внимание
уделял, в частности, А. Дюрер A471 —
1528). Таким образом, начиная с XVI в.
картографы прибегают к различным
ухищрениям, сводящимся в основном
к тому, что сфера разрезается на
несколько кусков и каждый из них
отдельно проектируется на часть плоскости.
Исходная сфера (глобус)
реставрируется из них путем обратной склейки в
соответствии с правилами, указанными
на плоской карте. Наиболее часто
использующийся прием состоит в том, что
поверхность глобуса покрывается двумя
областями, каждая из которых чуть
больше полусферы, и затем отдельно
проектируется на плоскость (рис. 9).
Склеивая обратно два получившихся
диска по их общей части (по узкому
кольцу), мы можем восстановить
исходную картину на глобусе. Карту
земного шара можно склеить из
нескольких кусков (рис. 9). Таким образом,
здесь достаточно сложный объект
(сфера) получается из нескольких более
простых объектов (двух или более

t I. Некоторые понятия дифференциальной геометрии
61
Рис. 9
дисков) путем их склейки по некоторой
общей части. •
Эта идея и лежит в основе
построения широкого класса геометрических
объектов, называемых многообразиями.
В наиболее четком виде понятие
многообразия оформилось в работах
К. Гаусса A777—1855) во время его
исследований в области геодезии и
картографирования земной
поверхности. При практическом построении карт
достаточно больших участков земной
поверхности они разбиваются на более
мелкие, частично перекрывающиеся
области, в каждой из которых работает
своя группа специалистов. Они создают
карту каждой отдельной области,
снабженную опорными точками
(названиями населенных пунктов, рек и т.п.).
При построении общего атласа эти
отдельные карты затем сшиваются, склей-
и а юте я по тем их участкам, которые
перекрывались, и тем самым отражены
н нескольких локальных картах.
Привязывание друг к другу отдельных
локальных карт осуществляется путем
сопоставления и наложения друг на
друга их общих опорных точек.
Именно эта идея и легла в основу
современного понятия многообразия.
Сам термин «многообразие» был введен
н математику Б. Риманом A826—1866)
в его известной лекции «О гипотезах,
лежащих в основании геометрии».
Грубо говоря, многообразия — это
геометрические объекты, получающиеся
склейкой открытых дисков (шаров)
наподобие того, как изготовляется
папье-маше склейкой небольших
лоскутков бумаги. Для этого сначала
изготовляется глиняная или
пластилиновая фигура, которая покрывается
несколькими слоями наклеенных друг
на друга клочков бумаги. После
удаления пластилина остается двумерная
поверхность. Дадим теперь
математическое определение.
Определение 4. Топологическое ха-
усдорфово пространство М называется
п-мерным топологическим
многообразием, если оно представлено в виде
объединения своих открытых
подмножеств ?/j, причем для каждого из
этих подмножеств фиксирован
гомеоморфизм yt:Ui->Dnt отображающий С/,
на стандартный открытый диск в
евклидовом пространстве R".
Гомеоморфизм <р< называется координатным
отображением, пара (Uif <р,-) называется
картой (или локальной картой),
объединение карт {(?/,-, ф,)) называется
атласом на многообразии М. Число п
называется размерностью
многообразия. Многообразие называется
компактным или некомпактным в зависимости
от того, является ли соответствующее
топологическое пространство
компактным или некомпактным.
Каждое координатное отображение
задает координаты на множестве (Л,
так как это отображение определяет
на карте набор непрерывных функций
х\Р)9...ухя(Р), которые можно
рассматривать как координаты переменной
точки Р (рис. 10). С каждым атласом
на многообразии естественно связано
понятие функций перехода. Рассмотрим
две произвольные карты Uiy U\ и их
пересечение UiflUj. На нем определены
два координатных отображения ф,:?/,П
{]Uj^^(Ui(]Ui)czDa и *,:1/,П1//-*
-+q>i(Ui(}Ui)c:Dn (рис. 10). Поскольку
композиция гомеоморфизмов является
гомеоморфизмом, то на открытом
подмножестве yt(Ui()Ujy в диске D" кор-

62
2. Многообразия малой размерности
Рис. 20
ректно определен гомеоморфизм ср|; —
= ф, ф, отображающий множество
Ф,- (U; П Uj) на множество ф; (С/, П U}).
Определение 5. Гомеоморфизмы ф;;
назьшаются фунщиями склейки, или
функциями перехода (в данном атласе).
Задание функций перехода позволяет
восстановить все многообразие, если
уже заданы отдельные карты и
координатные отображения. Функции склейки
могут принадлежать к разным
функциональным классам, что позволяет
выделять внутри класса топологических
многообразии более узкие классы
гладких, аналитических и тому подобных
MHoroo6pac.Jf. Введем на диске LP
стандартные декартовы координаты. Тогда
гомеоморфизм ф^ можно записать в виде
набора функций у —f*j (х1,... , ха).
Определение 6. Многообразие М
называется гладким, класса Сг или
аналитическим, если все функции /,;
являются соответственно гладкими,
класса Сг или аналитическими.
Аналогично определяются кусочно-
гладкие, литиицевы и другие типы
многообразий.
Два топологических многообразия
называются гомеоморфньши, если го-
меоморфны соответствующие им
топологические пространства. Гладкие
многообразия назьшаются диффеоморф-
ными, если они гомеоморфны, и
гомеоморфизмы f и f~l являются
гладкими отображениями.
Простейшие примеры многообразий:
открытые области в евклидовом
пространстве , графики гладких функций
вида х9^ =f(x , ...,**) в R*4. Одним из
важных способов задания
многообразий является следующий. Рассмотрим в
R* систему гладких функций &{хх, ...,
хн), 1 < i < k< п. Тогда совместная
поверхность уровня этих функций, в
каждой точке которой ранг матрицы Яко-
би ( д4~х ) этой системы равен k, т. е.
максимален, является гладким
многообразием размерности n-k. Это следует
из теоремы о неявных функциях.
Таким образом, многообразия можно
задавать как множества решений
систем уравнений g(*\ ..., хп) = 0 в R*.
При k-l мы получаем
гиперповерхность. Гладкими многообразиями
являются, например, стандартные сферы
5", вещественные и комплексные
проективные пространства ЛР*к СР", группы
ортогональных матриц SO(n)t
унитарных матриц U(N), специальных
унитарных матриц SU(n), симплектических
матриц Sp(n) и т. п.
Здесь мы естественно подошли к
понятию подмногообразия. В дальнейшем мы
будем в основном иметь дело с
гладкими многообразиями, поэтому иногда не
будем повторять условие гладкости.
Определение 7. Подмножество V в
многообразии М* называется гладким
подмногообразием размерности п -k,
если для каждой точки Р е V существует
открытая окрестность U(P ) с
локальными координатами х , ..., хп и набор k
гладких функций gi, ...,&,
определенных на и(Р ) таких, что ранг ( -&z)=k и
VnU(P) = { хеЩР ): &(дг>=0, 1 < ; < k}.
Другими словами, пересечение V с
окрестностью U(P ) должно совпадать с
совместной нулевой поверхностью
уровня функций#,..., &.
Условие на ранг матрицы Якоби
означает, что все функции gi,...,gt функ-
гщонально независимы в
рассматриваемой окрестности.

jfl. Некоторые понятия дифференциальной геометрии
63
Определение 8. Подмножество V в
многообразии М" называется гладким
подмногообразием размерности n-kt
если для каждой точки Р eV
существует открытая окрестность ЩР ), в
которой можно ввести локальные
криволинейные координаты х1,..., Xя такие, что
Vt)U(P )={хеЩР ) : х'=0,1й /<S *},
Предложение 1. Определения 7 и 8
эквивалентны.
Однако данное определение
многообразия не охватывает ряд естественных
объектов, например »-мерный
замкнутый диск. Дело в том, что для точек,
расположенных на границе диска, не
существует открытой окрестности,
гомеоморфной открытому диску в R*.
Эта категория объектов охватывается
понятием многообразия с краем.
Определение 9. Пусть f(x) — гладкая
функция, заданная на гладком
многообразии М* (ц смысле определений 4 и
6). Замкнутое подмножество V,
определяемое неравенством • f(x) < 0 (или
f(xJ.Q), называется п-мерным
гладким многообразием с краем (с
границей), если его край (граница) 3V,
задаваемый уравнением /(х)=0, является
неособым гладким подмногообразием
размерности и-1 в Л1*, т. е. df* О во
всех точках дУ (рис. 11). Компактное
многообразие, не имеющее края,
называется замкнутым.
Рис. II
Точки многообразия с непустым краем
разбиваются на два класса: внутренние
точки (центры окрестностей, гомео-
морфных открытому диску) и
граничные тачки, имеющие окрестность, го-
меоморфную половине диска, причем
граничная точка лежит на
экваториальном сечении диска (рис. 12).
С каждой точкой х на гладком
многообразии ЛГ естественно связано
линейное я-мерное пространство,
называемое касательным.
Рис. 12
Определение 10. Будем говорить, что
в точке хеМ задан касательный вектор
а, если в каждой локальной регулярной
системе координат задан набор чисел а1,
... ,а* (координат вектора),
преобразующихся при замене координат
х->(х') по следующему закону:
а'= Z, %i а\ где %?— коэффициенты
матрицы Якоби замены координат.
Определение 11. Будем говорить, что в
точке хеМ задан касательный вектор
а, если задана линейная,
дифференциальная операция D =Z,a' §р первого
порядка с постоянными
коэффициентами, определенная на функциях,
заданных в окрестности точки х
Эти оба определения эквивалентны.
Соответствие между ними
устанавливается так. Если в какой-то системе
координат в точке Xq задан касательный
вектор а ={а ,..., *г)> то однозначно
определено дифференцирование гладких
функций /по направлению этого
вектора, а именно
Предложение 2. Совокупность всех
векторов, касательных к многообразию
ЛГ в некоторой точке х, образует
линейное пространство размерности п.
Это пространство называется каса-
тельным пространством к многообразию
в данной точке и обозначается ТХМ.
Если в окрестности данной точки
фиксирована система координат х1, ... , х",

64
2. Многообразия малой размерности
то в этой точке естественно возникают
п линейно независимых касательных
векторов 6i = -тр (т. е.
дифференциальных операторов). Они соответствуют
дифференцированиям вдоль
координатных линий, проходящих через точку х.
Из регулярности локальных координат
следует, что эти векторы образуют
базис в касательном пространстве ТХМ.
Так как касательное пространство
определено в каждой точке
многообразия, то возникает естественный
геометрический объект, являющийся
многообразием размерности 2п.
Определение 12. Касательным
расслоением Т#М называется совокупность
всех пар вида (х, а), где х—точка
многообразия М, а а — касательный
вектор в этой точке к многообразию.
Для проверки того, что Т+М
является 2гс-мерным гладким многообразием,
достаточно ввести регулярные
локальные координаты на Т*М. Пусть х1,...,
хп—координаты в области U на М.
Тогда в каждой точке x^U возникает
базис в ТХМ из векторов ^-,-, и каждый
касательный вектор а^ТхМ
разлагается по этому базису: a=S,a'^-j. Пары
вида (х, а), где jte?/, образуют область
W в Т*М. Локальные координаты в
W имеют вид jtl,...,jc", а',...,ал.
Непосредственно проверяется, что функции
перехода являются гладкими, что и
доказывает требуемое утверждение.
1.3. Ориентируемость и неориентируемость.
Дифференциал отображения. Регулярные и
правильные точки. Вложения н погружения многообразий.
Критические точки гладких функций на
многообразиях. Индекс невырожденных критических
точек и функции Морса
Определение 13. Многообразие М
называется ориентируемым, если на нем
существует атлас (?/,-, <р,-) такой, что
якобианы всех функций перехода <pi;
от карты к карте положительны для
всех пересекающихся пар областей.
Многообразие называется
ориентированным, если такой атлас на нем задан
и фиксирован. Многообразия, не
удовлетворяющие указанному свойству,
называются неориентируемыми. Это
означает, что всегда существует пара карт,
на пересечении которых якобиан
функции перехода отрицателен.
Существует и другой вариант
определения ориентируемости. Рассмотрим
на многообразии М произвольную точку
х и фиксируем в касательной плоскости
ТХМ репер е(х)у являющийся базисом.
Пусть y(t)— произвольный гладкий
замкнутый путь, содержащийся в
многообразии, начинающийся и
кончающийся в точке х (т.е. петля).
Напомним, что гладкий путь — это
гладкое отображение у отрезка [0,1 ] в
многообразие, причем вектор скорости
y(t) кривой y(t) отличен от нуля во
всех точках кривой. Так как каждая
точка у пути у покрыта какой-то картой
в М, то всегда можно определить
непрерывную невырожденную
деформацию любого репера, заданного в этой
точке, в близкую точку вдоль пути у.
Для этого достаточно перенести точку
у и путь у в евклидов диск, используя
координатное отображение, и
осуществить любую непрерывную
невырожденную деформацию репера вдоль пути в
шаре, что уже не составляет труда.
Ясно, что непрерывная деформация
репера вдоль пути определена
неоднозначно. Пусть гG@) —РепеР»
полученный невырожденной деформацией
репера е(х) вдоль пути у из точки х в
точку y(t) (рис. 13).
Рис. 13
Определение 14. Будем говорить,
что многообразие М ориентируемо,
если для любого замкнутого пути уу
начинающегося и кончающегося в точке
х, любая непрерывная невырожденная
деформация репера е(х) вдоль пути у
переводит его в репер е'{х) в касатель-

Ф I. Некоторые понятия дифференциальной геометрии
65
ной плоскости ТХМ, имеющий ту же
ориентацию, что и исходный репер. Это
означает, что эти два репера отличаются
друг от друга на преобразование с
положительным определителем. В
противном случае многообразие называется
неориентируемым. Это означает, что
существует такой замкнутый путь,
начинающийся и кончающийся в точке х, и
такая непрерывная невырожденная
деформация репера вдоль пути, что репер
возвращается в точку х с
противоположной ориентацией.
Предложение 3. Определения 13 к 14
эквивалентны.
Лемма 3. Касательное расслоение
любого гладкого многообразия
является ориентируемым многообразием.
Различия в свойствах
ориентируемых и неориентируемых многообразий
легко увидеть в двумерном случае.
Рис. 14
Двумерные многообразия допускают
простую классификацию. Для
формулировки результата напомним две опера
ции: а) приклейку ручки, б) приклейку
пленки Мебиуса. Ручка—это прямое
произведение отрезка на окружность,
т. е. кольцо, цилиндр (рис. 14, а).
Чтобы приклеить ручку к двумерному
многообразию, нужно поступить так.
Следует выбросить из многообразия два
достаточно малых непересекающихся
диска (рис. 14) и приклеить к двум
образовавшийся дыркам цилиндр,
отождествив его края с границами
дырок. Для определения второй
операции нам потребуется лист Мебиуса
(рис. 14,6), получающийся из
прямоугольника отождествлением его
противоположных сторон с изменением
ориентации (рис. 14). Лист Мебиуса
можно получить также из обычного
плоского кольца, отождествив
диаметрально противоположные точки на
одной из его граничных окружностей.
Затем выбросим из многообразия
достаточно малый диск и отождествим
границу получившейся дырки с
границей листа Мебиуса.
Теорема 1. (Теорема классификации
двумерных замкнутых поверхностей.)
Любое двумерное гладкое компактное
Рис. 15
связное замкнутое многообразие гомео-
морфно (и диффеоморфно) одному из
следующих многообразий: а)
двумерная сфера с g ручками (рис. 15), где
g—неотрицательное целое число (род
поверхности), б) двумерной сфере с
k пленками Мебиуса, где
k—положительное целое число. Многообразия 1-го
типа ориентируемы, а 2-го типа не-
ориентируемы. Многообразия 1-го и
2-го типов не гомеоморфны.
Многообразия внутри каждой из этих двух серий,
отвечающие разным g или разным &,
также не гомеоморфны.
Неориентируемость многообразий
серии б) видна на рис. 16. Путь у,
один раз проходящий по пленке
Мебиуса вдоль ее оси, обладает тем свойством,
что двумерный репер, непрерывно де-

66
2. Многообразия малой размерности
Рис. 16
формирующийся вдоль пути,
возвращается в исходную точку с
противоположной ориентацией.
Большую роль в геометрии играет
понятие дифференциала гладкого
отображения одного многообразия на
другое.
Определение 15. Пусть f:Mn^Np —
гладкое отображение гладких
многообразий. Дифференциалом df
отображения f в точке х^М называется
линейное отображение касательного
пространства ТХМ в касательное
пространство TyN, где y = f(x), определяемое в
локальных координатах х',...,хя на М и
у\...уур на N матрицей Якоби
отображения /, т. е.
Дифференциал отображения
допускает несколько разных
интерпретаций. Приведем здесь интерпретацию,
особенно полезную для дальнейшего.
Рассмотрим на М гладкую кривую
y(t)> проходящую через точку х. Пусть
х = у@)- В локальных координатах х1,...,
х" кривая задается набором функций
х1(/),...,хл(*). Для любого вектора а,
касательного к М в точке х, всегда
существует гладкая кривая у, имеющая
вектор а = (а1,...,ал) своим вектором
скорости в точке х, т. е. у@) = а. Здесь и
далее мы обозначаем точкой
дифференцирование по времени. При
отображении / кривая у отображается в
некоторую гладкую кривую g(t) =f(y(t))
в многообразии N, проходящую через
точку y = f(x). Эта кривая имеет в точке
у некоторый вектор скорости b = g(Q).
Лемма 4. Имеет место равенство
b = df(a).
Доказательство сразу следует из
правила дифференцирования сложных
функций.
Таким образом, дифференциал
отображения можно определить еще и
так. Берем касательный вектор а в точке
хеМ, берем любую гладкую кривую уу
имеющую а своим вектором скорости
в точке х. Рассматриваем ее образ в
многообразии N и вычисляем вектор
скорости кривой fy в точке y = f(x).
Получившийся вектор и являемся, как
мы видели, образом вектора а при
отображении df:TxM-^TyN (рис. 17).
Рис. 17
Определение 16. Пусть f:M-+N —
гладкое отображение многообразий.
Тогда xeAf называется регулярной
точкой отображения /\ если
дифференциал df в точке х является
эпиморфизмом, т. е. если он отображает
пространство ТХМ на все пространство TyN> где
у=/(х). Точка y^N называется
правильной точкой отображения / (или
относительно отображения /), если все
ее прообразы являются регулярными
точками в М. Если f~\y) = 0, то точку
у также будем считать (по
определению) правильной точкой.
Свойство точки быть регулярной или
правильной не зависит от выбора
локальных координат на М и N.
Предложение 4. Пусть f:M-*N —
гладкое отображение многообразий,
У^М — правильная точка отображения
{. Тогда ее прообраз P = f~\y) (в том

§1. Некоторые понятия дифференциальной геометрии
67
случае, когда он непуст) является
сладким подмногообразием в М
размерности dim М — dim N.
Определение 17. Пусть f': М —» N —
гладкое отображение. Оно называется
погружением, если в каждой точке
хеМ "дифференциал df является
мономорфизмом, т. е. имеет нулевое ядро.
Если, кроме того, отображение / го-
меоморфно отображает многообразие
М на его образ f(M) в N, и f(M) —
замкнутое подмножество в N, то
отображение / называется вложением. Для
топологических многообразий М
понятие вложения определяется как
гомеоморфизм многообразия М на
замкнутое подмножество в N.
Образ гладкого многообразия М при
вложении его в N является гладким
подмногообразием в N в смысле
определений 7, 8. Роль погружений и
вложений в геометрии можно пояснить на
таком примере.
Выше мы определили понятие
гладкого многообразия на языке карт и
атласов, безотносительно к его реализации
в виде какой-либо поверхности в
некотором евклидовом пространстве. С другой
стороны, для изучения многих свойств
многообразий полезно представлять их в
виде поверхностей в КЗ.
Оказывается, класс подмногообразий в
конечномерных евклидовых пространствах
совпадает с классом абстрактно
заданных многообразий.
Теорема 2. Любое конечномерное
многообразие М класса гладкости С\
еде 1йгй *», как компактное, так и
некомпактное, допускает вложение
класса (? в некоторое конечномерное
евклидово пространство достаточно
большой размерности.
В действительности верны более
сильные утверждения.
Теорема 3 (Уитни). Всякое Пгмерное
многообразие класса гладкости С', где
1 < г < оо t как компактное, так и
некомпактное, дотекает при п^-1
вложение кмцяй СГ в евклидово
пространство я, а при п>2 допускает
погружение класса U в евклидово
пространство .К3*.
Доказательство этого факта достаточно
нетривиально1 (теорема 2, напротив,
доказывается достаточно просто с
использованием разбиения единицы). См.
подробности и литературу, например, в
[1, 6]. Более просто, на основе теоремы
Сарда, устанавливается более слабая
теорема, а именно что любое п~мерное
многообразие, как компактное, так и
некомпактное (снова класса С, где
1^г<"), допускает вложение класса
(TbR и погружение в R . Это так
называемая слабая теорема Уитни, в
отличие от сильной теоремы Уитни
(теорема 3). В некоторых частных
случаях теорема 3 может быть усилена.
Например, если п положительно и не
является степенью двойки, то всякое
гладкое многообразие т допускает
гладкое вложение в R .С другой
стороны, для любого п вида 2?, где q ^0,
существуют замкнутые гладкие п~
мерные многообразия, не допускающие не
только гладкого, но и топологического
вложения в R " . Это относится,
например, к вещественному проективному
пространству RP", где п-Ъ. Например,
проективная плоскость RP2 даже
топологически не вкладывается в R\ но
погружается в него. Всякое «-мерное
гладкое многообразие, не имеющее
замкнутых компонент, допускает гладкое
вложение в R^ . Всякое ориентируемое
гладкое многообразие М" при w*l, 4
допускает гладкое вложение в R .
Подробности см., например, в [6].
Поэтому в дальнейшем без
ограничения общности можно рассматривать
гладкие многообразия реализованными
в виде гладких поверхностей в
конечномерном евклидовом пространстве.
Пусть /: Af1—>N"— гладкое
отображение . Будем говорить, что точка
х еМ является критической для
отображения f если дифференциал df:
7yVf-> Tflx)N имеет ранг, меньший чем
m=d\mN. В этом случае точку y=f(x)
будем называть критическим значением
отображения f Согласно теореме Сарда
(см., например, [I]), множество всех
критических значений гладкого
отображения f: М ~>N всегда имеет меру нуль
в многообразии N. Рассмотрим частный

68
2. Многообразия малой размерности
случай, когда N=R — вещественная
прямая. Так как dimTf^N=lf то точка
х является критической для / тогда и
только тогда, когда df |.=0.
Критические точки х гладкой скалярной
функции /на М находятся из системы
уравнений -fc= 0, 1 <, i <* п, т. е. gradf=0.
Будем говорить, что критическая точка
х гладкой функции / называется
невырожденной, если матрица второго
дифференциала ( $^ ) невырождена в
этой точке. Поскольку gradflx^=0, то
это определение корректно, т. е. не
зависит от выбора локальных координат.
Функция /на многообразии М
называется функцией Морса, если все ее
критические точки невырождены. Второй
дифференциал d2f можно трактовать
как симметричную билинейную форму
на касательном пространстве Tja.
Пусть а, ЬеТхМ. Включим векторы а и
b в гладкие локальные векторные поля
А и В соответственно и положим
d2f(at b) =A(B(f))L Ясно, что так
определенная форма оусимметрична и ее
матрица относительно базиса j^ имеет
вид $#$~х>- Эта форма называется
гессианом функции. Индексом
невырожденной критической точки х для
функции / называется максимальная
размерность подпространства Vc ТхМ, на
котором гессиан a f отрицательно
определен. Другими словами, индекс —
это число отрицательных квадратов
после приведения формы af к
диагональному виду. Оказывается, в
окрестности невырожденной критической
точки индекса X всегда существуют такие
локальные регулярные координаты х ,
..., х", что " этих координатах функция
/запишется в окрестности в следующем
виде' (так называемая лемма Морса,
см., например, [7]):
f(x) = const-(х1/ - ,..-(ххJ+
Таким образом, функция приводится к
каноническому виду не только в одной
точке, но сразу в целой окрестности.
Существуют ли на многообразиях
функции Морса? Ответ дается следующей
теоремой (см., например, [7]).
1) На любом гладком компактном
многообразии существуют функции Морса
2) Функции Морса всюду плотны в
пространстве всех гладких функций на
многообразии.
3) Каждая функция Морса имеет на
компактном многообразии только
конечное число критических точек.
4) Существует всюду плотное
подмножество S в множестве всех
функций Морса такое, что у любой
функции feS каждому ее критическому
значению отвечает только одна
критическая точка
В этом смысле функции Морса "ти-
пичньГ (являются функциями общего
положения") в пространстве всех
гладких функции.
1.4. Векторные и юшекгорные поля
Интегральные траектории. Коммутатор векторных полей.
Алгебра Ли векторных нолей на многообразии
Многие физические, химические
процессы задаются векторными полями на
некоторых многообразиях. Например,
поток идеальной несжимаемой
жидкости моделируется бездивергентным
векторным полем.
Определение 18. Будем говорить, что
на гладком многообразии М задано
гладкое векторное поле, если в каждой
точке хеМ задан касательный вектор
а Ос), гладко зависящий от точки.
Если х, ..., х" — локальные
координаты, то векторное поле в окрестности
некоторой точки может быть записано в виде
набора функций, т. е. координат вектора а,
а именно а (х , ..., х")9 ... , а"(х , ..., хп).
Каждое векторное поле
взаимнооднозначно определяет систему
обыкновенных дифференциальных
уравнений первого порядка на многообразии, а
именно х=аг(х ,..., хя), \<гй и.
Наряду с касательным пространством
7yVf в каждой точке гладкого
многообразия определено кокасатель-
ное пространство Т*М, являющееся
дуальным (сопряженным) пространством
к TfM. Элементами кокасательного
пространства (которые мы будем иногда
называть ковекторами) являются ли-

§1. Некоторые понятия дифференциальной геометрии
69
нейные функционалы, определенные на
TJ4. Ясно, что касательное и кокаса-
тельное пространства линейно
изоморфны, имеют поэтому одинаковую
размерность. По аналогии с
определением 18 будем говорить, что на М
задано гладкое ковекторное поле, если в
каждой точке х задан ковектор §(х),
гладко зависящий от точки. По аналогии
с касательным расслоением строится
кокасательное расслоение 7*М, точками
которого являются пары (х, ?), где хеМ,
?еТхМ. Пространство ТМ является
гладким Ъьмерным многообразием, го
меоморфным многообразию 71М.
Определение 19. Траектория y(t) на
многообразии М называется
интегральной траекторией векторного поля
а(х) в том и только в том случае, когда
ее вектор скорости в каждой точке
совпадает с вектором поля а, т. е.
y('MyO)-
Интегральные траектории поля а
являются решениями системы
дифференциальных уравнений х (t) —a(x(t)).
Каждое векторное поле а можно
рассматривать как линейный
дифференциальный оператор с переменными
коэффициентами на многообразии. В
самом деле, если а — поле и у — его
интегральная траектория (напомним,
что при достаточно малых / уравнение
х (t) = a(x(t)) всегда имеет решение
при гладкой правой части), то для
любой гладкой функции / на
многообразии можно определить ее
производную вдоль векторного поля а. Для
этого нужно рассмотреть в каждой
точке следующее выражение: a(f)= '™
; , где х ~ fyJfj т. е. у —
интегральная траектория поля, выходящая
из точки х. Иногда вместо a(f)
используется обозначение -&-. Ясно, что
функция a(f) может быть записана в виде
<*(f) = Z jf ТГ = & h)f- Итак,
каждое векторное поле а, будучи записано
относительно базиса ?,— ??, может
интерпретироваться как линейный
дифференциальный оператор.
Определение 20. Пусть а и Ь — два
векторных поля. Тогда однозначно
определено векторное поле [а, Ь\ =аЬ~
-Ьа, называемое коммутатором (или
скобкой) полей а и Ь. Здесь ab и Ьа —
композиции дифференциальных
операторов an Ь.
В локальных координатах х1,..., хп
поле [а, Я имеет следующие
компоненты: [a, *J=Z,V-f?f ~ V -?• Хотя ди<Ъ-
ференциальные операторы ab и Ьа
имеют порядок два, однако их разность
является оператором первого порядка,
что и означает, что пространство всех
гладких векторных полей на
многообразии замкнуто относительно опера-
гфш коммутирования (коммутатор
векторных полей снова является
векторным полем). Дадим геометрическую
интерпретацию коммутатора векторных
полей. Пусть а и Ь — векторные поля,
определенные в окрестности точки х.
Оказывается, можно построить кривую
у на М, вектор скорости которой в
точке х = у@) совпадает со значением
поля [а, Ь] в точке х. Пусть t —
достаточно малое число и у\ — интегральная
кривая поля а, выходящая из точки х.
Пусть уг — интегральная кривая поля Ъ,
выходящая из точки yi(f); затем уз —
интегральная кривая поля -а,
выходящая из точки уг(/); наконец, у4 —
интегральная кривая поля -Ь, выходящая из
точки уз(*). Определим теперь кривую
у, выходящую из точки х, равенством
y(t2) = у4(/). Тогда можно проверить,
что [a, b]f(x) = -ДО)/* для любой гладкой
функции / Итак, коммутатор
векторных полей геометрически измеряет
степень разомкнутости
четырехугольника, получающегося при
последовательном смещении на одну и ту же
величину вдоль полей а, Ь, -а, -Ь. Если
поля а и Ь коммутируют, то этот
четырехугольник замкнут. В
частности, для коммутирующих полей а к b
смещения из точки х на величину б по
направлению поля а, а затем на
величину ц по направлению поля Ь
приводят нас в ту же точку, что и
при смещении на величину ц по

/и
2. Многообразия малой размерности
направлению Ь, а затем на величину
е по направлению а.
Предложение 5. Если два векторных
поля а и Ь касаются некоторого
гладкого подмногообразия V в каждой его
точке, то их коммутатор также касается
этого подмногообразия.
С множеством векторных полей на
многообразии естественно связано одно
из важнейших понятий
дифференциальной геометрии — понятие алгебры
Ли.
Определение 21. Говорят, что
линейное пространство G (конечномерное или
бесконечномерное) является алгеброй
Ли, если в нем задана билинейная
операция [,], называемая
коммутатором и удовлетворяющая требованиям:
1) операция кососимметрична, т. е.
[а, Ь] = — [Ь, а] для любых векторов
а, /?^G, 2) операция удовлетворяет
тождеству Якоби [а, [Ь, с\ ] -(-
+ [с, [а, Ь] ] + [/?, [с, а] ] = 0 для любых
а, by ceG.
С каждой алгеброй Ли естественно
связана важная операция, называемая
присоединенным представлением
алгебры Ли. Для каждого a^G положим,
по определению, adaF)= [а, 6]. Ясно,
что ada — линейный оператор на алгебре
Ли.
Лемма 5. Оператор ad а является
дифференцированием алгебры Ли, т. е.
удовлетворяет формуле Лейбница
adQ[6, с] = [ada6, с] -\- [b,adac\.
Приведем простейшие примеры
алгебр Ли. Алгебра всех линейных
операторов линейного пространства
является алгеброй Ли относительно
операции коммутирования, задаваемого
формулой [А, В] =АВ — ВА. Алгеброй Ли
является и пространство всех
квадратных матриц порядка п. Для разных
приложений большую роль играет
следующая бесконечномерная алгебра Ли.
Предложение 6. Линейное
пространство всех векторных полей в области
многообразия М является
бесконечномерной алгеброй Ли относительно
коммутатора векторных полей [а, Ь\ =
= ab — ba.
Из предложения 5 вытекает, что
линейное пространство всех векторных
полей, касающихся гладкого
подмногообразия, является подалгеброй
Ли в алгебре Ли всех векторных полей
на многообразии.
1.5. Комментарий к наглядному материалу
На рис. 18 показан простой, но важный
объект — декартова координатная сетка
на плоскости. При помощи координат
можно задавать положения точек и
описывать более сложные объекты.
Например, на рис. 18 изображена так
называемая звездная диаграмма Херц-
шпрунга, отнесенная к декартовым
координатам (показывающая
распределение звезд по некоторым их
характеристикам). На рис. 19 показана схема
локально-тривиального расслоения.
Вверх уходят слои (каждый из которых
гомеоморфен некоторому стандартному
слою, условно показанному в виде
некоторой фигуры в центре). Слои
опираются на базу — изогнутую дугу на
рисунке. На рис. 20 показана схема
векторного расслоения — каждый слой
имеет линейную структуру (векторного
пространства). Слои по-прежнему
«опираются» на базу. На рис. 21 изображена
часть касательного расслоения к
окружности. Это расслоение гомеоморфно
двумерному цилиндру, слоем которого
(расслоения) является прямая.
Окружность изображена на рис. 21 с угловой
точкой (вдали). Этот объект встретится
нам в главе 3, § 2. Так как в угловой
точке касательная не определена, то на
рис. 21 слои изображены
«сжимающимися» по мере их приближения к особой
точке. На рис. 22, 23, 24 показаны
некоторые элементы алгебро-геометри-
ческой конструкции, предназначаемой
для алгоритмического вычисления
групп гомологии (и когомологий)
расслоений. Этот метод называется
методом спектральных последовательностей.
Идея его заключается в том, что
вводится весьма усовершенствованный
аналог матриц (таблиц) инциденций,
но не отдельных симплексов, а более
крупных блоков, порожденных так
называемой фильтрацией расслоения.
Получающиеся таблицы последова-

J I Некоторые понятия дифференциальной геометрии
71
ггльно нумеруются Ео, Е\, Еа, ..., Ent
после чего они начинают приводиться к
каноническому виду (по аналогии с
гсм, как приводятся к каноническому, а
¦штем и нормализованному виду обыч-
иые матрицы инциденции). Зная
гомологии базы и слоя, можно (в
принципе) вычислить "предельную" таблицу
К, Она содержит в себе много ин-
<[юрмации о гомологиях пространства
расслоения. Поэтому можно (очень
грубо) сказать, что теория
спектральных последовательностей — это далеко
идущий аналог теории приведения
системы целочисленных матриц (матриц
инциденции) к нормализованному виду.
Понимание этого факта полезно при
изучении спектральных
последовательностей. Последовательность таблиц и
«ами таблицы условно показаны на рис.
22, 24. На рис. 22 условно показана
схема так называемых "убивающих
11ространств" (см. [5]), позволяющая
i юследовательно вычислять гомото-
нические группы топологических
пространств. На рис. 25 изображена схема
гак называемой ортогональной
периодичности Ботта. Эта замечательная
теорема утверждает, что гомотопические
группы ортогональной группы 0(N)
(где число N очень велико) периодичны
с периодом 8. Метод доказательства
(>снован на построении восьми
пространств, каждое из которых является
11 ространством петель предыдущего.
Первые 4 этапа построения этой
последовательности объектов условно
изображены на рис. 25. Сплюснутое
тело — это группа ортогональных матриц
ЮA6г). Белые ребра — это
многообразия Грассмана и т. д. На рис. 26
представлена фантазия на темы известной
проблемы гомотопической топологии —
вычисления гомотопических групп
сфер, т. е. групп я?($*). Интерес к ней
объясняется тем, что к проблеме
подсчета гомотопических групп сфер
сводятся многие вычислительные вопросы
современной топологии. Недавно
В. А. Смирнов открыл алгоритм
вычисления этих групп. На рис. 27
изображена идея метода "убивающих
пространств" и спектральных
последовательностей. Свободное место в первом
ряду соответствует моменту
использования теоремы Туревича. На рис. 28
изображен график гладкой функции на
двумерной области ее определения.
Отчетливо видны критические точки
функции (максимумы, перевалы, т. е.
седла, седловые точки). Теория
критических точек функций — одна из важных
ветвей современной геометрии (см.
пункт 1.3 в § 1). Изображенный на
рисунке горный рельеф может быть
достаточно сложен, но если
предположить, что все внутренние (т. е. не
расположенные на берегу острова)
критические точки изолированы и вычислить
число А максимумов, число С
минимумов и число В седел, то из этих чисел
можно построить число А -В+С,
которое, оказывается, всегда равно
единице для острова, гомеоморфного
кругу. Горный рельеф (или языки огня,
которые также можно рассматривать как
рельеф, границу раздела двух сред)
более сложной структуры показан на рис.
29. На рис. 30, 31, 32 изображены (в
разных вариантах) критические точки
гладких функций на трехмерных
многообразиях и локальная структура
клеточного разложения многообразия в
окрестности этих точек. На рис. 30
показана окрестность точки индекса два.
Вниз спускается двумерный сепаратрис-
ный диск, вверх поднимается
одномерный сепаратрисный диск. Получается
объект, похожий на колокол. Вдали
изображено большое число других
критических точек функции. На рис. 31
более наглядно показаны "сепаратрис-
ные усы" сепаратрисной диаграммы и
отдельные сепаратрисные траектории,
заполняющие сепаратрисный диск. На
рис. 32 изображен "сепаратрисный
колокол" , отвечающий невырожденной
критической точке индекса 2. Меняя
знак у функции, мы видим, что те же
сепаратрисные диаграммы будут
отвечать критическим точкам индекса два.
На рис. 33 изображена очень важная в
вариационном исчислении операция
"опускания цикла" вдоль интегральньгх
траекторий градиента функции (или
общего функционала). При этом скольже-

11
2. Многообразия малой размерности
нии вниз цикл рано или поздно
зацепится за критические точки функции
(функционала) и повиснет на них. Это
обстоятельство лежит в основе
известной теории Морса и ее многих
современных обобщений. На рис. 33
изображен цикл, повисший на двух
критических точках. Они условно показаны в
виде двух штырей, вбитых в "тело"
многообразия. На рис. 34 показана
алгебраическая поверхность, задаваемая
как поверхность уровня сложной
алгебраической функции f. Точки, в
которых градиент функции / равен нулю,
являются особыми, в них поверхность
теряет свою локальную евклидову
структуру. Эти особые точки могут иметь
весьма сложную структуру. На рис. 34
отчетливо видны разные листы
поверхности, которые иногда пересекаются,
ветвятся и т. п. Эта поверхность дает
наглядное представление об объектах,
реально встречающихся в задачах га-
мильтоновои механики, где такие
функции / появляются как интегралы
гамильтоновых систем. На рис. 35
изображена структура трехмерного
многообразия с краем в окрестности
граничной точки. Такая точка всегда
является центром экваториального
сечения шара, причем окрестность точки
состоит из половинки этого шара. На
2.1. Изотопии, оснащения
Напомним определение многообразия.
Множество точек М в некотором
евклидовом пространстве называется
«-мерным многообразием, или просто
»-многообразием, если каждая его
точка имеет окрестность, гомеоморф-
ную евклидову пространству В".
Другими словами, многообразие —
это локально-евклидово
пространство. Пространство R" гомеоморфно
открытому »-шару, поэтому
топологическое пространство является
многообразием, если каждая его точка
имеет шаровую окрестность. Чтобы
избежать патологических примеров,
переднем плане показаны обычные
шары — окрестности внутренних точек
многообразия. Эти точки расположены
в центрах шаров. Рис. 36 является
математической вариацией-фантазией на
темы известной "математической"
гравюры А. Дюрера, на которой, в
частности, был изображен магический квадрат
(вверху справа). На рис. 36, однако,
вместо магического квадрата в таблице
справа помещен более современный и
актуальный объект — десятичное
разложение числа е, записанное по
квадратной спирали, раскручивающейся из
центра (от числа 2) против часовой
стрелки. Изображен 121 знак этого
десятичного разложения. Такие
последовательности цифр используются в
современных исследованиях на ЭВМ как
датчики случайных чисел. Дело в том,
что последовательность цифр в
разложении е может считаться (в некотором
точном смысле, который мы здесь не
будем уточнять) случайной
последовательностью. Здесь же на рис. 36
изображена сепаратрисная диаграмма
критической точки в виде колокола с
языком-сепаратрисой. Небо вдали
представлено в виде фрактального объекта (о
фракталах мы вкратце расскажем в
главе 4, § 2).
обычно накладывают два
дополнительных условия. Во- первых,
требуется, чтобы многообразие было
хаусдорфобым топологическим
пространством. Это означает, что любые
две его точки должны иметь
открытые , непустые непересекающиеся
окрестности, т. е. требуется, чтобы
каждую из этих точек можно было
окружить "своим шаром" так, что эти
шары не пересекаются. Для
подмножеств евклидова пространства это
условие автоматически выполнено.
Во-вторых, требуется, чтобы
многообразие можно было покрыть не
более чем счетным числом шаровых
окрестностей. В дальнейшем мы
§ 2. Наглядные свойства одномерных многообразий

$ 2. Наглядные свойства одномерных многообразий
73
будем рассматривать только такие
многообразия, не оговаривая каждый
раз специально.
Имеется только два связных
одномерных многообразия—окружность S1
и прямая R1. На рис. 1 хорошо видно,
что каждая точка окружности или
прямой имеет окрестность, гомеоморф -
ную открытому 1-шару (т.е.
интервалу).
о/
Рис. /
Как мы уже знаем, каждое гладкое
многообразие, в том числе и
одномерное, можно гладко вложить (или
погрузить) в некоторое евклидово
пространство. Вкладывая многообразие в
R , мы тем самым наглядно изображаем
его в виде некоторой гладкой
поверхности в евклидовом пространстве. Такая
наглядность часто оказывается
полезной при решении многих практических
задач. В то же время ясно, что одно
и то же многообразие можно, вообще
говоря, вложить в одно и то же
евклидово пространство многими разными
способами. Возникает естественный
вопрос: сколькими «существенно
разными» (не эквивалентными) способами
можно вложить данное многообразие
в фиксированное евклидово
пространство (или, более общо, в какое-то другое
Фиксированное гладкое многообразие) ?
тветы на такие вопросы дают теория
вложений и теория погружений
многообразий, созданные в современной
топологии. Мы не можем здесь
вдаваться в какое-либо систематическое
изложение этих интересных и в то же время
достаточно сложных проблем, поэтому
ограничимся лишь некоторыми
наглядными примерами.
Начнем с простейшего случая
одномерных многообразий. Как мы уже
знаем, согласно теореме Уитни, любое
одномерное многообразие можно
гладко вложить в двумерную евклидову
плоскость. В самом деле, не составляет
никакого труда построить такие
вложения. Они уже фактически построены
на рис. 1. Следующий вопрос: сколько
имеется разных вложений окружности
и прямой в плоскость? Для ответа на
вопрос следует сначала определить,
какие вложения мы будем считать
одинаковыми, т. е. эквивалентными, а
какие—разными, т.е.
неэквивалентными. Сначала напомним понятие гомо-
топии.
Определение 1. Пусть X и
Y—топологические пространства и
/—единичный отрезок. Отображения f;X-*~Y и
g:X-*~Y называются гомотопными (f~
~g), если существует непрерывное
отображение F прямого произведения
F-.XXI-+Y такое, что на основаниях
цилиндра XXI оно совпадает с
отображениями / и g. Если X и Y—гладкие
многообразия, а /, gt F—гладкие
отображения, то F называется гладкой
гомотопией. При этом отображения f и g
называются гладко гомотопными. Два
пространства X и Y называются гомо-
топинески эквивалентными, если
существуют непрерывные отображения
Рис. 2

74
2. Многообразия малой размерности
/: X-^>Y и g : Y—>Х такие, что gf
гомотопно тождественному отображению X
на себя, т. е. 1Х9 afg гомотопно 1Y (рис- 2).
Определение можно
переформулировать. Отображения fug гомотопны,
если существует семейство
непрерывных отображении ф, JC—>Y (непрерывно
зависящих от / и хеХ), "соединяющее"
отображения / и g, т. е. в начальный
момент деформации / =0 мы имеем
(ро=/, а в конечный момент деформации
/=1 имеем (pi=g. Достаточно положить
(pt(x)= F(x, t). См. рис. 3. Все непре-
Рис. 3
рьшные отображения, гомотопные
данному отображению, образуют класс
попарно гомотопных отображений (или
гомотопический класс данного
отображения). Пусть даны два вложения /и
g многообразия X в многообразие У.
Определение 2. Два гладких вложения
ftg:X—>Y называются изотопными
(или гладко изотопными), если
существует гладкая гомотопия F: X х / —> Y
между отображениями fug такая, что
отображение <р,: X —>Y, определенное
по формуле F(xt t) = ф, (х), является для
каждого *е[0,1] гладким вложением.
Другими словами, два вложения
изотопны, если их можно продеформиро-
вать друг в друга в классе вложений,
т. е. чтобы в процессе деформации
многообразие <ptM оставалось гладко
вложенным в N.
Аналогично два погружения
многообразия М в многообразие N называются
эквивалентными, если их можно гладко
продеформировать друг в друга в классе
погружений, т. е. если существует
гладкая гомотопия ф,: M->N такая, что
каждое ф,, 0 < t < 1, является погружением.
Возвращаясь к вопросу,
поставленному в начале параграфа, мы будем
считать два вложения данного
гладкого многообразия М в многообразие N
эквивалентными, "одинаковыми", если
эти вложения изотопны. В противном
«MS1)
Рис. 4
случае два вложения будем считать
неэквивалентными, "различными".
Легко видеть, что любые два гладких
вложения прямой в плоскость
изотопны. Также образы любых двух гладких
вложений окружности в плоскость
изотопны. Итак, одномерное
многообразие М можно лишь единственным
образом (с точностью до изотопии)
вложить в плоскость. Этот факт можно
проиллюстрировать так. Пусть fug —
два вложения прямой R в плоскость
R2. Рассмотрим в R3 две параллельные
плоскости Д) и П] и в каждой из них

{1 Наглядные свойства одномерных многообразий
75
рассмотрим образ прямой R при
вложениях fug (рис. 4). Рассмотрим
переменную плоскость Ц, где 0?&1,
параллельную плоскостям Ц, Ци при
изменении / от 0 до 1 движущуюся от
Ц)кД. Помещая в плоскость Ц
кривую ф/М] и меняя t, мы получаем
цилиндр (двумерную поверхность),
основания которого совпадают с двумя
ладанными вложениями многообразия
М в плоскость.
В то же время существует мною
(шных, неэквивалентных погружений
окружности в плоскость. Рассмотрим,
Ооо
Гис. 5
например, два погружения на рис. 5.
Интуитивно ясно, что, оставаясь в
классе погружении, нельзя продефор-
мировать стандартно вложенную
окружность в восьмерку. Любая попытка
построить такую деформацию
обязательно наткнется на препятствие, также
изображенное на рис. 5. Видно, что
обязательно возникает уменьшающаяся
петая, которая в конце концов
вырождается в острый клюв. В вершине этого клюва
гладкое отображение окружности в
плоскость не является положением
(проверьте вычислением!). Поэтому классов
[ югружений окружности в плоскость
больше, чем классов ее вложении.
Рассмотрим более тонкие свойства
пложенных многообразий. Пусть Ж —
гладкое подмногообразие в евклидовом
пространстве R* . Пусть в каждой
точке х из т задан рейер т(#),
нормальный (ортогональный) к
подмногообразию т , причем репер гладко
зависит от точки. Репер х(х) состоит из
независимых векторов е\ (х),..., еп (х),
ортогональных подмногообразию М (рис.
6). В таком случае будем говорить, что
вдоль подмногообразия т задано п-
реперное поле т. задающее оснащение
многообразия т. Иногда многообразие
М называют в таком случае оснащенным
многообразием, а поле т — оснащением,
Если фиксировано подмногообразие
М* в R* , то его можно разными
способами снабдить оснащением (т. е.
превратить в оснащенное подмногооб-
Af = S'
Рис. б
разие). Рассмотрим простейший случай
вложения окружности в плоскость.
Здесь, с интуитивной точки зрения,
имеется ровно два разных способа
снабдить окружность оснащением. Для
этого нужно направить нормальное поле
либо наружу окружности, либо внутрь
окружности (рис. 7). Однако, чтобы
Рис.7
можно было говорить о разных
оснащениях, нужно сначала определить,
что такое одинаковые или эквивалент-

76
2. Многообразия малой размерности
ные оснащения. Остановимся на
следующем естественном определении.
Скажем, что два оснащения т и т] одного
и того же подмногообразия Мк в Rrt+A
эквивалентны, если существует гладкая
деформация подмногообразия Мк в
R"^fe в классе погружений,
переводящая реперное поле т в нормальное
Рис. 8
реперное поле т|. При этом требуется
чтобы поле ф/т— результат гладкой
деформации исходного поля т — было
нормально к погруженному
подмногообразию ф/М, т. е. чтобы ф,т было
оснащением многообразия ф/М при
каждом /, изменяющемся от 0 до 1.
Снова рассмотрим два оснащения
окружности, показанные на рис. 8,
т. е. нормальное поле наружу и
нормальное поле внутрь. Вопрос:
эквивалентны ли эти два оснащения?
Другими словами, можно ли вывернуть
окружность наизнанку, т. е. сделать ее
«внутреннюю сторону» внешней и
наоборот? Можно доказать, что эти
оснащения не эквивалентны в смысле
данного выше определения. Интуитивно
это следует из рис. 8, на котором
показана попытка продеформировать
оснащение т в оснащение ц. Вдавливая
навстречу друг другу две
противоположные дуги окружности, мы можем
добиться того, чтобы большая часть
нормального наружного векторного
поля была направлена внутрь
получившейся кривой. Однако очевидно, что при
этом обязательно возникают и остаются
маленькие петли, на которых поле по-
прежнему направлено наружу. Эти
петли, уменьшаясь в размерах, вынуждены
в конце концов выродиться в острые
клювы» которые запрещены нашими
правилами, поскольку в вершине
каждого такого клюва гладкое отображение
окружности уже не является
погружением (излом кривой).
2.2. Комментарий к наглядному материалу
На рис. 9 изображены две человеческие
фигуры, напоминающие композицию в
центре картины Рембрандта
«Возвращение блудного сына». Однако этот
образ угадывается далеко не сразу,
поскольку вся композиция подвергнута
гомеоморфизму, исказившему
первоначальную картину до неузнаваемости.
В этом важное свойство
гомеоморфизма— менять метрические
(следовательно, легко узнаваемые) свойства
объекта, но сохранять его
топологические (не столь легко распознаваемые)
свойства. На заднем плане, за
горизонтом, изображены оснащенные
окружности. На рис. 10 изображено
человеческое лицо с деталями,
воспроизводимыми на любой фотографии. Однако в
то же время известно, что текстовая
(и зрительная) информация часто
избыточна. Например, из литературного
связного текста можно удалить
фрагменты многих слов, а иногда и целые
слова, встречающиеся внутри
устойчивых, привычных словосочений, без
утраты смысла текста. Точно так же из
зрительного образа можно удалить
многие фрагменты, и тем не менее объект
будет узнаваем. Конечно, желательно

$3. Наглядные свойства двумерных многообразий
удалять лишь малосущественные детали,
сохраняя главное. Именно это и делают
гомеоморфизмы и гомотопии. Они
позволяют выявить самое существенное в
геометрическом объекте, очистить его от
массы второстепенных, ненужных
деталей, часто мешающих распознавать
главные инвариантные свойства объекта. На
рис. 11 изображен другой женский
портрет, лишенный некоторых привычных
деталей, и тем не менее он, оказывается,
сохраняет самые существенные,
характерные черты оригинала. Отсюда видно,
насколько устойчиво зрительное
восприятие к "белому шуму помех. Причина
этого коренится л глубоких свойствах
восприятия, фиксирующих, по-видимому, в
первую очередь инвариантные, основные
свойства объекта, а лишь затем
дополняющие их более мелкими деталями
метрического характера. Эта мысль
позволяет более глубоко проникнуть в
математическую природу гомеоморфизма и
гомотопической эквивалентности. На рис.
12 показан еще один "портрет", черты
которого подверглись еще большему
"стиранию". См. также рис. 13.
Подчеркнем, что на этом принципиальном
§ 3. Наглядные свойства
3.1. Двумерные многообразия с краем
Как мы видели, 1-многообразий мало:
все они являются объединениями
окружностей и прямых. 2-многообразий
гораздо больше. Например, любое от-
крьггое подмножество плоскости
является 2-многообразием (рис. 1).
Приведем примеры компактных
2-многообразий: сфера J2, тор Т?=У х,5 (рис. 2).
Сферами тор Т^2 -Г"*
Г.являются примерами компактных
»-многообразий. Другие примеры
многомерных многообразий можно
построить, заметив, что прямое произведение
многообразий размерностей тип есть
многообразие размерности т+п. Как
мы видели, очень удобно расширить об-
77
факте узнавания объекта лишь по
отдельным штрихам основаны многие
современные статистические методы
распознавания образов. Главной проблемой в
разработке соответствующих методик
является обнаружение главных
инвариантных характеристик объекта. Решение
этой задачи чаще всего нетривиально. Эту
же идею мы попытались
проиллюстрировать при помощи математической
фантазии на рис. 14, основанной на анализе
некоторых палеонтологических мотивов.
Уместно напомнить о науке
восстановления первоначального образа живых
организмов (ныне не существующих),
развитой современной палеонтологией.
Специалисты вынуждены восстанавливать
образ существа, располагая часто лишь
фрагментами скелета или даже
отдельными костями животных, случайно
сохранившимися до нашего времени. Мотив
распознавания образов по частичной
информации о них широко применяется в
современном искусстве, в том числе и в
балете, например в так называемом
"скульптурном театре". См. рис. 15,
являющийся одновременно символом
зодиакального созвездия Скорпиона.
двумерных многообразий
шее понятие многообразия, включив в
него понятие многообразия с краем.
Рис. 1

78
Многообразия малой размерности
Рис. 2
Напомним, что хаусдорфово
топологическое пространство называется п-
многообразием с краем, если каждая его
точка имеет окрестность, гомеоморфную
либо пространству R* (т. е. шаровую
окрестность), либо замкнутому
полупространству К*}, (т. е. полушаровую
окрестность). Объединение точек
многообразия М, не имеющих окрестности
первого типа, называется его краем дМ.
Теорема 1. Если край п-мноюобразия
не пуст, то он является (п-1)-
многообразием без края.
Все точки на граничной
гиперплоскости пространства R*+ равноправны и
имеют в ней (**-1)-шаровые
окрестности. С другой стороны, интуитивно
очевидное существование хотя бы одного
многообразия с непустым краем
является с формально-логической точки
зрения нетривиальным фактом, так как
априори неясно, почему
полупространство К+ (с выделенной точкой на краю)
не гомеоморфно пространству R (с
выделенноГ: точкой внутри). На самом
деле, это является прямым следствием
теоремы Брауэра об инвариантности
области (см. [17, т. 1]). Следуя нашему
принципу, в настоящей книге мы не
вникаем в формально строгие
изыскания с целью обоснования интуитивно
очевидных (и верных) фактов. Следует,
впрочем, иметь в виду, что существуют
вроде бы очевидные, однако заведомо
неверные (!) математические факты.
Мы будем всякий раз сообщать
читателю, какие "геометрически очевидные"
факты верны, а какие — нет.
Приведем примеры многообразий с
краем: полуинтервал (некомпактное
многообразие^, отрезок (компактное
многообразие). Это — одномерные
многообразия. Далее: диск D , кольцо
S х/, лист Мебиуса (двумерные
многообразия), см. рис. 3. Их края состоят
из точки, двух точек, окружности, двух
окружностей, окружности
соответственно.
Рис. 3
Рассмотрим трехмерный шар, т. е,
множество точек, ограниченное в R
стандартной сферой. Назовем
трехмерной ручкой прямое произведение
диска на отрезок, т. е. заполненный
цилиндр. Ясно, что такую ручку можно
приклеить к шару по двум основаниям
ручки, т. е. по двум дискам. В
результате получится шар с ручкой. Можно
приклеить несколько таких ручек. В
результате получится трехмерное тело,
которое называется полным кренделем,
или заполненным кренделем, причем
родом кренделя называется число
ручек. Итак, примером 3-многообразия с
краем может служить полный крендель
Кр рода р (шар с р ручками, см. рис. 4).
Для любого п «-мерный iuap DH и
полупространство R+ являются
примерами п-многообразий с краем.
Прямое произведение многообразий
размерности типе краем является
многообразием размерности т-Нг с
краем. При этом справедлива
формула а(МхАГ) = дМх NU М х ON,
напоминающая формулу
дифференцирования произведения функций.

f 3» Наглядные свойства двумерных многообразий
79
шар
.шар
с ручкой
Рис.4
Пусть М\ и Мг — «-многообразия с го-
меоморфными краями и h; дМг+dMj —
гомеоморфизм. Если склеить
многообразия М] и М2 по гомеоморфизму /г,
т. е. отождествить каждую точку
хедМу с точкой h(x)edM2t то получится
^многообразие М без края.
Действительно, каждая точка хедМх имеет в Mi
полушаровую окрестность, точка h (х)
Рис.5
имеет полушаровую окрестность в М2.
Эти полушаровые окрестности
склеиваются и дают шаровую окрестность
соответствующей точки в М (рис. 5).
Например, если из сферы удалить открьпъга
диск и вклеить лист Мебиуса по
некоторому гомеоморфизму их краев
(окружностей), то получится новое 2-мвогообра-
эие, называемое проективной
плоскостью и обозначаемое через RP2
(рис. 6). Проективная плоскость не
Рис. 6
вкладывается в В?. Можно склеивать п-
многообразия и по подмногообразиям
их краев, получая при этом п-
многообразия с краем. Например,
полный крендель К2 рода 2 можно
получить склеиванием двух полных
кренделей рода 1 (полных торов, гкхлноторий)
по некоторому гомеоморфизму дисков
на их краях (рис. 6).
Х2. Примеры двумерных многообразий
Простейшее замкнутое 2-многообра-
зие — сфера. Кроме того, мы уже
знакомы с тором. Мы уже говорили,
что процесс построения
многообразий в какой-то степени напоминает
изготовление бумажных фигур,
папье-маше, когда глиняная заготовка
обклеивается мелкими кусочками
бумаги в несколько слоев, так как
кусочки достаточно малы, то с их помощью
можно воспроизводить довольно
сложные глиняные модели. Помня об
этой аналогии, ограничимся, для
простоты, пока одним клочком бумаги,
который возьмем в виде квадрата.

80
2. Многообразия малой размерности
Вопрос: какие двумерные многообразия
можно получить из него склейкой
граничных ребер, сторон квадрата'* Для
удобства описания склеек фиксируем
на квадрате ориентацию (направление
вращения, например по часовой
стрелке), припишем каждому ребру на
границе букву и снабдим ребро
ориентацией (поставим стрелку). Эта ориента-
ъ г^ч
i
г
а а
i
b о
RP2
л
Рис. 7
ция может совпадать, но может и не
совпадать с направлением движения,
индуцированным на ребре ориентацией
квадрата. Выберем какую-либо вершину
квадрата (например, левую нижнюю) и,
двигаясь по часовой стрелке, будем
последовательно выписывать
встречающиеся буквы а?м Ь? в степенях е=±1,
указывая степенью е=+1 факт совпадения
стрелки на ребре с направлением
нашего движения, а степенью е=-1 факт
противоположного направления стрелки. В
результате получится некоторое слово
W, составленное из букв. Примеры см.
на рис. 7. Соответствующие слова W
имеют вид: 1) abb^a1, 2) aba1^1, 3) abab,
4) аЬаБ . Что за многообразия мы
получили? На рис. 8 видно, что
результатом склейки квадрата в соответствии с
требованиями, указанными в записи
слова 1), является обычная сфера У.
Рис. 8
При этом, для удобства, мы заменили
исходный квадрат на гомеоморфный
ему объект: сферу, из которой
вырезана четырехугольная дырка, на сторонах
которой расставлены те же буквы и
стрелки (рис. 8). Словесное описание
деталей склейки мы опустим, заменив
его известной формулой средневековых
геометров: "смотри".
Второе слово на рис. 7 задает нам
процесс склейки, наглядно
изображенный на рис. 9. Получился двумерный
тор (бублик). Итак, в первых двух
случаях мы получили двумерные
ориентируемые многообразия, гладко
вложенные в R3. Их ориентируемость
легко следует из определения (это
упражнение мы предоставляем читателю).
Третье слово на рис. 7 задает
проективную плоскость RP . Чтобы убедиться в
этом, вспомним классическое
определение проективной плоскости. Ее точками
являются всевозможные прямые / в л,
проходящие через фиксированную
точку, например через начало координат
(рис. 10). Эквивалентная модель строится
так. Рассмотрим стандартную сферу с
центром в начале координат. Тогда
каждая прямая из нашего пучка однозначно

I 3. Наглядные свойств» двумерных многообразий
81
Рис. 9
определяется точками ее пересечения со
сферой. Таких \ точек ровно две. Они
диаметрально противоположны на
сфере. Условно обозначим эту вару точек
гик: (х, — х). Итак, проективная
плоскость может быть задана как
совокупность пар/ вида (х, —х), где х
пробегает/ сферу. Эквивалентная
модель: проективная плоскость
получается из сферы S2 отождествлением ее
диаметрально противоположных точек.
Условно это записывают так: RP2=
— S2/Z2. Дело в том, что на сфере
можно задать гладкое действие группы
Za, состоящей из двух элементов:
единицы и инволюции а, т. е.
преобразования, квадрат которого равен
единице (тождественному преобразованию).
Инволюция задается формулой о(х) =
— —х. Факторизуя сферу по действию
••той группы (т. е. отождествляя точки
* и а(х)), мы и получаем проективную
плоскость.
Следующая эквивалентная модель
проективной плоскости: рассмотрим
верхнюю (или нижнюю) полусферу
¦Sa+ и отождествим на ее границе, т. е.
на граничной окружности, диаметральг
но противоположные точки (рис. 10).
Эквивалентность этой подали
предыдущим очевидна. Достаточно разрезать.
сферу плоскостью, проходящей через
центр сферы. Отбрасывая нижнюю
полусферу, мы обнаруживаем, что для
построения RP* вполне можно обойтись
лишь верхней полусферой,, но при этом
следует отождествить диаметрально
противоположные точки на экваторе.
Эта модель может быть переформу-
Рис. 10
лирована так. Применяя гомеоморфизм
(считая, что сфера сделана из тонкой
резины, которую можно растягивать без
разрывов н склеек), продеформнруем
полусферу в большую сферу, нэ< которой
выброшен маленький диск, причем
затем на границе получившейся дырки
отождествлены диаметрально
противоположные точки (рис. 10). Наконец,
опишем последнюю модель. Ту же
полусферу можно гомеоморфно п род
сформировать в плоский двумерный диск,
на границе которого отождествлены
противоположные хочки (рис. 11).
Диск гомеоморфен плоскому квадрату.
Чтобы описать отождествление точек
на граншде квадрата, симметричных
относительно его центра, достаточно
расставить на сторонах буквы1 а и Ь,
как показано на рис. 11. Е результате
получается слово* ababy указанное выше
как адин т кодов* проективной
плоскости.

82
2. Многообразия малой размерности
Вопрос о моделировании (а более
точно, о гладком погружении)
проективной плоскости в R: мы обсудим позже.
Перейдем к последнему, четвертому
слову^коду на рис. 7. Поверхность,
получающаяся из квадрата при его
Рис. 11
склейке в соответствии с этим кодом,
называется бутылкой Клейна К2 и (как
и проективная плоскость) является не-
ориентируемым замкнутым
2-многообразием. Построение К аналогично
склейке тора из квадрата, но в конце
построения появляется важное
отличие: теперь мы не можем склеить
основания цилиндра в к без
самопересечения поверхности. На рис. 12 наглядно
показано, как именно нужно
выполнить последнюю склейку. Итак, нам
удалось смоделировать бутылку Клейна
г виде замкнутой поверхности в R3.
Правда, ра^-лоложена она с
самопересечением, но в то же время ясно, что
мы построили погружение К в R .
Как доказать, что проективную
плоскость и бутылку Клейна нельзя гладко
вложить в R ? Можно убедиться, что
каждая замкнутая двумерная
поверхность, гладко вложенная в R3,
обязательно разбивает R; на внутреннюю и
внешнюю части, каждая из которых
является трехмерным многообразием с
краем. Каждое из этих многообразий
ориентируемо, и поскольку события
происходят в R3, то на их краю
однозначно определено понятие внешней и
внутренней нормали к поверхности.
Это означает, что исходная двумерная
поверхность ориентируема.
Рис. 12
3.3. Моделирование проективной
плоскости в трехмерном пространстве
Вернемся к задаче погружения
проективной плоскости в R\ Сначала
попытаемся "хотя бы грубо" смоделировать
RK в виде поверхности в R . Берем
квадрат, отвечающий слову-коду 3 на
рис. 7, т. е. abab. Считая квадрат
изготовленным из тонкой резины,
продавливаем его вниз, за плоскость
книжного листа и получаем сферу, из которой
вырезан маленький квадрат с
указанными склейками на его сторонах.
Дальнейшие события показаны на рис. 13
(" смотри!"). В результате получается
довольно сложная поверхность с
самопересечением. Для наглядности на рис. 13
показаны ее сечения плоскостями,
ортогональными сингулярному отрезку в
верхней части фигуры (и тем самым
плоскости книжного листа). Ясно, что
построенное нами отображение f
проективной плоскости в R не только не
является вложением, но даже не
является погружением. Мешают
концы сингулярного отрезка АВ, на
котором пересекаются два листа
поверхности , причем пересекаются они
так, что в точках А л В возникает
сложная структура, отличная от
пересечения нескольких локально евклидо-

I S. Наглядные свойства двумерных многообразий
83
Рис. 13
¦ых дисков. Тем не менее построенная
модель позволила «взглянуть» на
некоторое (пусть не очень «хорошее»)
изображение проективной плоскости в
трехмерном пространстве. На рис. 14
изображена эволюция сечений
построенной нами фигуры и ее
предпоследнего этапа D на рис. 13)
плоскостями, ортогональными сингулярному
ребру ЛВ. Эту поверхность можно
задать в R3 алгебраическим
уравнением: (e*4»*W+lf+r)-
Конечно, мы не хотим на этом
останавливаться и сейчас построим
погружение RP* в R3. Предварительно
опишем несколько простых фактов
наглядной топологии, полезных для
дальнейшего.
Рассмотрим лист Мебиуса ц на рис.
15. Он получается склейкой противо-
Рис. Г4
положных сторон квадрата с
изменением ориентации. Оказывается,
склеивая его с диском, мы получим
проективную плоскость.
а-
j
Рис. /5
Лемма 1. Проективная плоскость
гомеоморфна многообразию,
получающемуся склейкой листа Мебиуса с
обычным диском по их общей границе.
Другими словами, выбрасывая из RP2
двумерный диск, мы получаем лист
Мебиуса. Условно этот факт запишем
так: RP^ji + D2.
Доказательство. На рис. 16
показана модель проективной плоскости в виде
квадрата со склейками abab.
Докажем, что, выбрасывая диск из RP2,
мы получаем лист Мебиуса. Так .как
RP2—гладкое замкнутое многообразие,
то все равно, где брать центр
выбрасываемого диска, В данный момент
все точки проективной плоскости
равноправны. Выберем точку на середине
стороны а. Диск с центром в этой
точке изобразится двумя своими
полудисками (показаны черным на рис. 16),
склеенными по диаметру. Выбрасывая
этот диск, мы получаем после
распрямления оставшихся углов квадрат,

84
2. Многообразия малой размерности
Рис. 16
две противоположные стороны которого
склеены с изменением ориентации.
Лемма доказана.
При классическом (обычном)
вложении листа Мебиуса в R3 его граница,
т. е. окружность, вложена так, что она
два раза обходит вокруг вертикальной
оси (рис. 17). Попытаемся продеформи-
ровать лист Мебиуса в R3 так, чтобы
Рис. 17
упростить вложение его границы.
А именно добьемся, чтобы граница
листа Мебиуса изображалась обычной
плоской окружностью, т. е.
расположенной в некоторой плоскости. За это нам
придется заплатить усложнением
изображения самого листа Мебиуса. Как
именно он расположится? Оказывается,
ответ дается рис. 17. Фигура,
изображенная здесь, очевидно получается
из модели проективной плоскости на
рис. 13 отсечением от нее нижней
чашечки плоскостью, ортогональной
плоскости книжного листа. Отрезая
чашечку, мы фактически выбрасываем
диск из проективной плоскости.
Оставшаяся часть (с самопересечением)
иногда называется скрещенным колпаком.
Итак, скрещенный колпак — это просто
лист Мебиуса, расположенный в R так,
что его граница — стандартная плоская
окружность.
Лемма 2. Бутылка Клейна
получается склейкой двух листов Мебиуса по
их границе. Другими словами, разрезая
бутылку Клейна по подходящей
окружности, мы получаем два листа Мебииса.
Рис. 18

I 3. Наглядные свойства двумерных многообразий
85
Условно этот факт запишем так:
Доказательство. Берем квадрат со
склейками abqb~\ изображающий
бутылку Клейна. На середине стороны
а отметим точку 1/2 и соединим ее с
вершинами квадрата так, как показано
на рис. 18. Затем разрежем квадрат по
ггим двум линиям. В результате
получим параллелограмм и два
треугольника. Параллелограмм, очевидно,
является листом Мебиуса. Склеивая два
треугольника по их общей стороне Ь,
получаем второй лист Мебиуса. Лемма
доказана.
Как изобразить эту линию разреза
на бутылке Клейна, погруженной в R3
(рис. 12)? Предоставляем читателю
внимательно проследить по рис. 18 и
12 движение линии разреза. Итак,
разрезая бутылку Клейна, как показано
на рис. 19, получаем два листа
Мебиуса. Каждый из них погружен в R3
(с самопересечением). Следовательно,
•та модель листа Мебиуса—более
регулярная (более «хорошая»), чем в виде
скрещенного колпака, который,
напомним, не является погружением
листа Мебиуса. Отметим, что
обнаруженное нами погружение листа
Мебиуса замечательно тем, что его
граница погружена в плоскость, т. е. его
граница является плоской кривой (с
самопересечениями).
Согласно лемме 1 проективная
плоскость получается заклейкой листа Ме-
Рис. W
биуса двумерным диском. Доказав
лемму 2, мы построили погружение
листа Мебиуса такое, что его граница —
плоская окружность. Воспользуемся
этим погружением, чтобы продолжить
его до погружения всей проективной
плоскости. Будем считать, что этот лист
Мебиуса, погруженный в R3, является
частью проективной плоскости. Чтобы
погрузить всю проективную плоскость,
I Г ч f f
i
Рис. 19
Рис. 21

86
2. Многообразия малой размерности
достаточно добавить диск, т. е. заклеить
плоскую границу листа Мебиуса
погруженным диском. Итак, мы приходим
к следующей задаче. Дана плоская
кривая 7о. показанная на рис. 20 и
являющаяся погружением окружности
в плоскость. Как заклеить ее
погруженным диском? Пусть Rq —
плоскость, содержащая границу листа
Мебиуса (рис. 21). Начнем перемещать
эту плоскость, поднимая ее вверх
параллельно самой себе. Получим
семейство плоскостей R* зависящих от
параметра /, где O^f^l.
Одновременно с подъемом плоскости начнем
гладко деформировать в ней исходную
плоскую кривую 7о. Получим семейство
кривых yt. С изменением t эти кривые
образуют некоторую двумерную
поверхность (заметают поверхность). Опишем
процесс деформации кривой уо в кривые
Рис. 22
yt. Он показан на рис. 22. Эта плавная
деформация приводит к тому, что
кривая сползает с себя и получается
кривая уже без самопересечения, т. е.
окружность, стандартно вложенная в
плоскость. Как мы отмечали, при
подъеме плоскости эта
деформирующаяся кривая заметает некоторую
поверхность. В тот момент, когда кривая
превратилась в окружность, мы
заклеиваем ее гладким диском. Итак, мы
заклеили лист Мебиуса диском, т. е.
получили модель проективной
плоскости. В то же время мы, очевидно,
построили погружение ее в R3. Как
устроено множество точек
самопересечения этого погружения? Из рис. 22
следует, что это множество состоит
из трех окружностей, склеенных в одной
точке. В результате мы получили
некоторую поверхность в пространстве,
изображающую погруженную
проективную плоскость. Эта реализация
проективной плоскости называется
поверхностью Боя. Можно нарисовать ее в
R3. Для этого представим проективную
плоскость как результат
отождествления противоположных точек на* границе
Рис. 23

f 3. Наглядные свойства двумерных многообразий
87
правильного шестиугольника (а не
квадрата, как Мы делали ранее).
См. рис. 23; Соответствующий код
выглядит так: abcabc. Ясно, что
шестиугольник с такими отождествлениями
эквивалентен диску, на границе
которого отождествлены противоположные
точки. Как и раньше, превратим
шестиугольник в сферу, из которой вырезан
шестиугольник (рис. 23). На сторонах
шестиугольника расставлены буквы и
стрелки, задающие склейку. Разрежем
сферу на три дольки меридианами
</, d, р (рис. 23). В результате сфера
развалится на три конгруэнтных куска,
т. е. совмещающихся друг с другом при
подходящем повороте. Возьмем один из
них, например заключенный между
меридианами q и d (рис. 24). Обратим
внимание на три острия,
поднимающиеся вверх. Склеим их . в одной точке,
которую обозначим через N (аналог
северного полюса сферы). Отметим, что
*та склейка не требуется с точки
зрения топологии проективной
плоскости, однако, как далее будет видно,
мы вынуждены склеивать указанные
точки, поскольку пытаемся реализовать
проективную плоскость в трехмерном
пространстве. Результат см. на рис. 24,
шаг 2.
Рис. 24A)
Рис. 24 (И )
Теперь фиксируем два меридиана
9, d, а петлю а поднимаем вверх, как
показано на рнс. 24, шаг 3. Следующие
шаги см. на рис. 24 (III): 5,6.
Аналогичные деформации мы выполним и для
двух остальных долек первоначальной
поверхности. В результате мы получаем
три конгруэнтные фигуры. Возьмем
вторую дольку. Пусть соответствующие
буквы на ней помечены штрихом.
Совместим часть границы первой дольки
с частью границы второй дольки.

88
Для этого совместим дугу df с цл причем
так, чтобы точка S' совпала с S, а
точка N'—с точкой N. Следовательно,
петля а' совпадет с петлей с. Какова
граница получившейся поверхности,
т. е. склейки двух долек? Ясно, что
граница состоит из дуг q*, а, с7, d.
Чтобы этот процесс стал более
наглядным, обратимся к исходному
шестиугольнику, на котором отметим все
Рис. 25
участвующие в склейках разрезы (рис.
25). Три ребра этого шестиугольника,
исходящие из его центра, снабжены
парой букв, что показывает, какие
ребра склеиваются при восстановлении
проективной плоскости из трех долек.
На рис. 24, шаг 6 показана
вертикальная пунктирная ось симметрии
третьего порядка. Это означает, что при
повороте фигуры вокруг этой оси на
угол 2л/3 ребро d совпадет с q, а
петля а — с петлей с. Итак, добавляем
к двум уже склеенным долькам
последнюю третью дольку в соответствии
со склейками, задаваемыми
шестиугольником на рис. 25. В результате
получается поверхность Боя (рис.
26 (I)). Отчетливо видно, что мы
построили погруженную поверхность,
т. е. при изменении точки по
поверхности касательная плоскость в этой
точке меняется непрерывно (и гладко).
Поверхность не имеет никаких изломов
и других особых точек. Она имеет
только несколько линий
самопересечения, которые организованы в три петли.
В окрестности каждой точки на этих
петлях, отличных от точки N (центра
2. Многообразия малой размерности
Рис. 26A)
Рис. 26(//>

t 3. Наглядиме свЫктм двумерных многообразий ^ 89
фигуры), пересекаются два листа
поверхности. На рис. 26 (II) показана
поверхность Боя с четырьмя «окнами».
М. Дм ссрян
•браэий
двуигринг замкцутых
В предыдущих пунктах мы обсудили
свойства поверхностей, получающихся
в результате склеек сторон квадрата.
тор (см. выше). Эта аналогия с
алгебраическими объектами не
исчерпывается внешним сходством, а является
следствием глубоких связей слова-кода
W с фундаментальной группой
многообразия. Выполним все склейки,
требуемые словом-кодом W (рис. 27).
Полученное многообразие называется
кренделем рода 2, или просто кренделем.
Ямс. 27
Т'псрь рассмотрим более сложный
Плоский многоугольник, например
восьмиугольник, на сторонах которого
расставим буквы и стрелки в
соответствии с кодом abarxb'xcdc~xd~\
С алгебраической точки зрения мы
пара множили два коммутатора [а, Ь\ —
• оЬо*1* и [c,d]=cdc-ld-\
Напомним, что один коммутатор [а, 6] задает
Оно допускает другое представление,
описываемое ниже. Сначала напомним
операцию приклейки ручки. Ручка—это
обычный цилиндр (рис 28). Его край—
две окружности. Выбросим из
двумерного многообразия два
непересекающихся диска, получим многообразие с
краем (две окружности). Приклеим
цилиндр к этому многообразию, отож-

90
2. Многообразия малой размерности
Рис. 29
дествив его граничные окружности с
краями дырок в многообразии. Эту
операцию, дающую нам некоторое новое
многообразие, назовем приклейкой
ручки.
Лемма 3. Тор получается из сферы
приклейкой одной ручки. Крендель го-
меоморфен сфере с двумя ручками.
Доказательство показано на рис.
29. Условно будем обозначать
приклейку ручки так: тор= 72=S2 + r;
крендель = S2 + 2r, где г обозначает
ручку. Ясно, что теперь можно
построить бесконечную серию
многообразий, приклеивая к сфере произвольное
количество ручек (рис. 30). Получаем
первую серию двумерных многообразий
М =S2 + gr. Целое неотрицательное
число g называется родом поверхности.
Эти многообразия можно представить
как результат склейки
многоугольников по аналогии с тем, как это было
продемонстрировано выше для тора и
кренделя. Рассмотрим 4^-угольник на
плоскости, на сторонах которого
расставлены буквы в соответствии с кодом:
Wg = a\biarlbrl ¦¦¦ QgbgaJxbjs =
= [ai, b\\ Х- X [ае,Ье],
Рис. 28
Лемма 4. Многообразие, полученное
склейкой сторон Ag-угольника в
соответствии с указанным кодом Wg,
гомеоморфно сфере с g ручками.
Итак, число коммутаторов в слове-
коде Wg совпадает с родом
поверхности. Представляем читателю простую
проверку следующего утверждения: все
многообразия М2 ориентируемы и
замкнуты.
Укажем вторую бесконечную серию
т. е. перемножим g коммутаторов.
Рис. 30

I 3. Наглядные свойства двумерны» многообразий
91
2-многообразнй. Сначала
переформулируем леммы 1 и 2. Определим операцию
приклейки листа Мебиуса (или пленки
Мебиуса). Выбросим из
многообразия диск, затем вклеим лист Мебиуса
по некоторому гомеоморфизму его
границы и границы получившейся дырки
(рис. 31).
Рис.31
Лемма 5. Проективная плоскость
гомеоморфна сфере с одной пленкой
Мебиуса* Бутылка Клейна гомеоморфна
сфере с двумя пленками Мебиуса.
Доказательство сразу следует из
лемм 1 и 2 и определения операции
приклейки пленки Мебиуса. Приклейку к
сфере k пленок Мебиуса р. будем
условно обозначать так: S2+fe|i, где
*>0. Все эти многообразия неориентн-
руемы. В самом деле, воспользуемся
определением ориентируемости в тер*
минах ориентации репера, переносимого:
вдоль замкнутого пути на
многообразии. Возьмем на многообразии 54+
+*Ц» где k>0f замкнутый путь у,
проходящий ровно по одному листу
Мебиуса (рис. 32). Мы утверждаем, что при
движений касательного репера вдоль
Рис.32
пути ориентация репера после
возвращения в начальную точку заменится
на противоположную. Этот факт
показан на рис. 32.
Итак, мы обнаружили две
бесконечные серии 2-многообразий: S2+
+gr (сферы с ручками, g>0), SS+*K*
(сферы с пленками Мебиуса, А>0).
Многообразия 1-й серии ориентируемы,
а 2-Й—неориентируемы. Поэтому
многообразия из разных серий не гомео-
морфны, так как
ориентируемость—инвариант гомеоморфизма.

92
2. Многообразия малой размерности
Возникает естественный вопрос:
почему мы до сих пор не говорили здесь
о смешанной серии многообразий, когда
к сфере приклеиваются одновременно и
ручки и пленки Мебиуса? Оказывается,
такая смешанная приклейка ничего
нового не дает: получаются многообразия
из 2-й серии.
Лемма 6. Многообразие вида S2-\-
+ ?Г + Лц, т.е. полученное из сферы
приклейкой g ручек и k пленок Мебиуса
(где fc;>0), гомеоморфно многообразию
S2 + Bg + fc)p,, т.е. одному из
многообразий 2-й неориентируемой серии.
Рис. зз
Доказательство. Рассмотрим
бутылку Клейна и продеформируем ее в
трехмерном пространстве, как показано
на рис. 33. Таким образом, ее можно
представить как сферу, к которой
приклеена ручка, но приклейка эта — не
такая, как было определено выше на
рис. 28, а «вывернутая:», т. е. мы
приклеили к сфере вывернутую ручку.
При такой операции одна подошва
ручки приклеивается к сфере снаружи,
а другая — изнутри. В результате мы
получаем поверхность с
самопересечением, так как в трехмерном
пространстве невозможно попасть снаружи сферы
внутрь, не пересекая при этом сферы.
Это вызвано лишь трехмерностью
пространства. Если бы мы вышли
в четырехмерное пространство, то в нем
приклейку вывернутой ручки можно
было бы осуществить без
самопересечения поверхности. В частности,
бутылку Клейна можно гладко вложить
(т. е. без самопересечений) в R4. Это,
впрочем, гарантируется и теоремой
Уитни. Итак, бутылка Клейна гоме-
оморфна сфере с вывернутой ручкой.
С другой стороны (см. выше), бутылка
Клейна гомеоморфна сфере с двумя
пленками Мебиуса. Сопоставляя эти
факты, получаем утверждение:
приклейка к поверхности одной вывернутой
ручки эквивалентна приклейке к
поверхности двух пленок Мебиуса.
Рассмотрим теперь сферу, к которой
приклеены как ручки, так и пленки
Рис. 34
Мебиуса. Для простоты ограничимся
случаем, когда имеется одна ручка и
одна пленка Мебиуса (рис. 34).
Рассмотрим на поверхности замкнутый путь
Y, начинающийся на одной из подошв
ручки, проходящий затем по оси пленки
Мебиуса и возвращающийся в
исходную точку. Осуществим следующую
деформацию (гомеоморфизм)
поверхности.
Начнем перемещать подошву ручки
вдоль пути у, предварительно фикси-

I 3. Наглядные свойства двумериых многообразий
93
ровав первую подошву. Из рис. 34
видно, что ручка начнет
деформироваться, если одна из. ее подошв
подойдет к листу Мебиуса, выйдет на него,
пройдет вдоль его оси и, сойдя с листа
Мебиуса, перевернется, т. е. ручка
вывернется (!). При дальнейшем
движении подошвы вдоль пути у мы вернем
ее на прежнее место. Но теперь ручка
вывернулась. Этот процесс можно
продемонстрировать на другом, более
наглядном чертеже (рис. 35). Ясно, что
при движении подошвы вдоль оси листа
Мебиуса направление нормали к листу
Рис. 35
Мебиуса заменится на
противоположное, что вызовет выворачивание ручки.»
Но так как вывернутая ручка
эквивалентна двум листам Мебиуса, то мы
можем теперь заменить ручку и лист
Мебиуса тремя листами Мебиуса (не
меняя поверхности). Итак, каждая
ручка в присутствии хотя бы одного листа
Мебиуса превращается в два листа
Мебиуса. Отсюда, очевидно, следует
лемма 6.
Выше было показано, что все
ориентируемые замкнутые 2-многообра-
зня (т. е. серии S2+gr) гладко
вкладываются в R3. Докажем, что все
многообразия неориентируемой серии
S2+k\jL могут быть гладко погружены
в R3 (но не вложены!). Мы доказали,
что RP25=S2+|*, следовательно, любое
многообразие вида S2+&P представи-
мо в виде, показанном на рис. 36.
Как мы видим, многообразие
распадается в сумму сферы с k дырками я к
экземпляров проективной плоскости,
из которой выброшен диск. Каждое
из этих слагаемых допускает погруже-

94
2. Многообразия малой размерности
ние в R3. Сфера с к дырками, очевидно,
вкладывается в R3, а проективная
плоскость с дыркой погружается в R3
(см. выше). Следовательно, все
многообразие S -\-k\i погружается в R3.
Перечисленные две серии
поверхностей исчерпывают список всех
двумерных компактных замкнутых связных
многообразий. Кроме того,
многообразия S2 + gr и S2 + sr не гомеоморфны,
если g=^=s, и многообразия 52 + /ец и
S2 + l\i не гомеоморфны, если k ФI.
В заключение сформулируем
несколько наглядных задач. Рассмотрим
Рис. 37
ось листа Мебиуса (показана
пунктиром на рис. 37). Разрежем его по этой
окружности. Какое многообразие
получится (ориентируемое или неориенти-
руемое)? (Получится ориентируемая
лента, закрученная на 2л.) Рассмотрим
закрученную ленту предыдущей задачи
и разрежем ее вдоль оси. Докажите,
что получатся две ленты (выясните, на
какой угол они закручены),
зацепленные в R3 так, как условно показано
на рис. 37. Продолжим процесс и будем
разрезать каждую из этих лент по оси
и т. д. Получится набор новых лент.
Докажите, что в этом наборе каждая
лента зацеплена с любой другой.
3.5. Классификация замкнутых 2-многообразий
Из сказанного выше извлекаются две
серии замкнутых (= компактных без
края) 2-многообразий: поверхности
(края) кренделей Kg, g>0, и сферы
с k^l выброшенными открытыми
дисками, вместо которых вклеены k листов
Мебиуса. Оказывается, других
замкнутых связных 2-многообразий не
существует.
Теорема 2. Любое связное замкнутое
2-многообразие гомеоморфно либо
поверхности полного кренделя некоторого
рода, т. е. сфере с ручками, либо сфере
с несколькими листами Мебиуса.
Приведем схему доказательства.
а) Любое 2-многообразие можно
триангулировать, т. е. разбить на
криволинейные треугольники так, чтобы
любые два треугольника либо не имели
общих точек, либо пересекались по
одной вершине или по одному ребру
(рис. 38). Этот факт кажется
интуитивно очевидным (и он верен).
Рис. 38
Действительно, многообразие
покрывается евклидовыми окрестностями,:
каждая из которых, разумеется,
допускает триангуляцию. Таким образом,,
задача сводится к согласованию
триангуляции окрестностей. В случае
размерности 2 это удается сделать с
помощью теоремы Жордана либо
опираясь на свойства геодезических (если
предварительно ввести на многообразии

I 3. Наглядные свойства двумерных многообразна
95
какую-нибудь риманову метрику, что
всегда можно сделать). На рис. 39
изображена минимальная
триангуляция тора Г2, представленного в виде
прямоугольника с отождествленными
противоположными сторонами.
Разбиение тора на треугольники на рис. 40
не является триангуляцией, так как
некоторые пары треугольников
(например, треугольники А и В)
пересекаются по двум вершинам.
Рис. 39
Рис. 40
б) Вместо каждой вершины
триангуляции возьмем диск, вместо каждого
ребра—полоску (ленту). См. рис. 41,
на котором буквами D обозначены
диски, буквами L—ленты, а буквами Z—
оставшиеся части, которые удобно
назвать заплатами. Отметим, что каждая
лента топологически представляет
собой прямоугольник, приклееный к
объединению дисков по двум
противоположным сторонам, а каждая
заплата—круг, который заклеивает
окружность на крае объединения дисков и
лент. Таким образом*, каждое замкнутое
2-многообразие можно получить так:
Рис. 41
взять k дисков, приклеить к ним m
лент и каждую из п окружностей,
получившихся на крае 2-многообразия,
заклеить заплатой. В этом случае
будем говорить, что 2-многообразие
имеет тип (й, т, п).
в) Докажем, что каждое замкнутое
2-многообразие имеет тип A, т, 1).
Для этого нужно научиться уменьшать
число дисков и заплат. Сделать это
легко. Если число дисков больше 1, то
найдутся два диска D\ и D2»
соединенные лентой L.. Тогда нужно их
объединение объявить новым диском.
В результате число дисков и лент
уменьшается, а число заплат остается
прежним (рис. 42). Уменьшение числа
заплат производится с помощью
двойственного рассуждения: две заплаты, к
которым своими свободными боковыми
сторонами примыкает одна из лент,
можно объединить с ней и объявить
новой заплатой.
г) Пусть замкнутое 2-многообразие
имеет тип A, т, 1), т.е. получается
из диска D приклеиванием m лент и
одной заплаты. Прямоугольник можно
Рис. 42

96
2. Многообразия малой размерности
Рис. 43
приклеить к диску D двумя способами:
так, чтобы его одинаково направленные
боковые стороны задавали одно и то
же направление на окружности 3D, и
так, чтобь" они задавали различные
направления на окружности 3D.
Получающуюся ленту будем называть
соответственно неориентируемой или
ориентируемой. Лента 1 на рис. 43
Рис. 44
ориентируема, а ленты 2, 3 и 4 —
нет. Допустим, что все ленты
ориентируемы. Пусть L\ — одна из них.
Тогда обязательно должна найтись
лента La, которая соединяет две дуги,
на которые окружность 3D
разбивается основанием ленты L\ (рис. 44),
так как в противном случае
потребовались бы по крайней мере две
заплаты. Отметим, что основание каждой
следующей ленты можно изотопно
двигать по краю объединения диска
D с предыдущими лентами (рис. 45).
Многообразие при этом не меняет-
Рис. 45
Рис. 41
ся. С помощью этой операции можно
освободить от оснований лент
выделенные на рис. 44 участки, отделив
тем самым так называемую пару
скрещенных лент. Повторяя это
рассуждение, получаем, что в случае
только ориентируемых лент
многообразие получается из диска
приклеиванием нескольких (пусть k)
отдельных пар скрещенных лент и одной
заплаты (рис. 46). Легко проверить,
что тогда многообразие гомеоморф-
но поверхности кренделя рода к.

I 3. Наглядные свойства двумерных многообразна
У/
Допустим теперь, что имеется
хотя бы одна неориентируемая лента
L. Тогда, как и выше, выделенный на
рис. 47 участок окружности 3D можно
освободить от оснований других лент,
отделив тем самым ленту L от
остальных.
В результате подобных
преобразований мы придем к случаю нескольких
отдельных неориентируемых лент и
нескольких отдельных пар скрещенных
лент. На рис. 48 видно, как (в случае
наличия неориентируемой ленты)
можно пару скрещенных лент заменить
на пару отдельных неориентируемых
лент.
Таким образом, многообразие
получается из диска D приклеиванием
нескольких (пусть k) отдельных
неориентируемых лент с последующей
приклейкой заплаты. Легко видеть, что
в этом случае многообразие гомеоморф-
но сфере с к листами Мебиуса. Это
завершает доказательство теоремы 2.
риантом гомеоморфизма. Внутри одной
серии многообразия различаются с
помощью эйлеровых характеристик:
X@/C«)=2 — 2л и х(Л*«)=2—л, где
Кн—полный крендель рода л и Мп—
сфера с л листами Мебиуса.
Из теоремы 2 можно получить также
теорему классификации компактных
2-миогообразий с краем: каждое такое
многообразие М получается удалением
нескольких открытых дисков либо из
поверхности кренделя некоторого рода,
либо из сферы с несколькими листами
Мебиуса. Действительно, если
компоненты края многообразия М заклеить
дисками, то получится' замкнутое
многообразие М i, т. е. поверхность
кренделя или сфера с листами Мебиуса.
Обратно, М получается из Mi
удалением приклеенных дисков.
Стоит отметить еще один
употребляемый способ задания 2-многообразий.
Возьмем несколько многоугольников» их
ребра разобьем на пары и склеим ребра
• . .. . • • . •
• ¦ • ¦ - *
• » » * •
• *•.»•• • •
• ¦ • ¦ *
• •••¦•_ •
Рис. 48
Отметим, что все 2-многообразия,
указанные в теореме 2, различны.
Действительно, многообразия первой
серии ориентируемы (т. е. не содержат
листов Мебиуса), а второй серии—
неориентируемы (т. е. содержат листы
Мебиуса). Это отличает многообразия
первой серии от многообразий второй
серии, так как свойство «многообразие
содержит лист Мебиуса» является инва-
каждой пары одним из двух возможных
способов. В результате получится
замкнутое 2-многообразие. Любое замкнутое
2-многообразие можно получить таким
способом.
3.6. Выворачивание двумерной сферы наизнанку
В $ 2 мы обсудили задачу
выворачивания наизнанку окружности в
плоскости. Эта задача неразрешима в классе

98
гладких погружений. Оказывается, при
повышении размерности ситуация
меняется: двумерную сфФу можно
вывернуть наизнанку S Iv (в классе гладких
погружений). Впрочем, не следует
думать, дальнейшее повышение
размерности сохраняет этот эффект.
Трехмерную сферу снова нельзя вывернуть
наизнанку в К*. Нельзя сделать этого
и со сферой & в R и со сферой $ в R?.
Однако сферу З6 снова можно
вывернуть наизнанку в R7. И это —
последняя размерность, в которой операция
выворачивания сферы выполнима [65].
Все остальные саЪеры (больших
размерностей , w. е. при п> 7) нельзя
вывернуть наизнанку в К**1 (С. Смейл).
Итак, сфера 5" выворачивается
наизнанку в К* 1 лишь при n=2j 6.
Наглядное выворачивание Д в л было
построено Арнольдом Шапиро.
Выворачивание сферы S в к
достаточно нетривиально. См. работы С. Смей-
ла, Н. Кюйпера, Б. Морина. Здесь же
мы лишь в нескольких .словах опишем
идею этой деформации.
Оказывается^ существует гладкая
деформация сферы в классе погружений,
переводящая ее в окрестность
погруженной проективной плоскости в R% а
именно в окрестность поверхности Боя,
построенной выше в пункте 3.3.
Именно этот процесс (самая сложная часть
всей конструкции) и показан нами на
рис. 53 в пункте 3.7. В результате
сфера S располагается в tv таким
образом (как погруженная поверхность),
что она является границей нормальной
трубчатой окрестности поверхности
Боя (т. е. погруженной RP2). Это
означает, что нормальный отрезок,
восстановленный в произвольной точке из
RP", встречает погруженную сферу в
двух близких точках (по одну и по
другую сторону от листа RP2). Возьмем
эти две точки и начнем двигать их по
отрезку навстречу друг другу. Тогда
они встретятся на проективной
плоскости (в центре нормального отрезка),
после чего пройдут друг друга насквозь
и, следовательно, поменяются местами,
т. е. при дальнейшем движении 1-я точ-
2. Многообразия малой размерности
ка займет положение 2-й точки и
наоборот. В результате этой гладкой
деформации сферы ее точки поменяются
местами: наружная точка займет
положение внутренней и наоборот. Таким
образом, мы устроили деформацию
погруженной сферы (вблизи поверхности
Боя), в результате которой наружная
сторона сферы поменялась с ее
внутренней стороной, т. е. сфера
вывернулась наизнанку. Теперь осталось
применить процесс, обратный
первоначальному, который переводил сферу из
ее стандартного положения в
окрестность поверхности Боя. В результате
мы вернемся к прежнему стандартному
вложению сферы, но теперь ее
внешность и внутренность поменялись
местами. Если наружная сторона сферы
была закрашена белой краской, а
внутренняя — черной, то теперь мы получим
черную сферу с белой внутренностью.
3.7. Комментарий к наглядному материалу
Выше мы обсуждали гомеоморфизмы
сферы. На рис. 49 показан один из
гомеоморфизмов сферы (довольно
произвольный), чтобы
продемонстрировать, насколько неузнаваем может
быть этот образ. Вообще говоря,
распознать, что данное многообразие
является сферой, всегда можно,
используя описанные выше
алгоритмические методы. Бесконечная
последовательность сфер, подвергшихся
гомеоморфизмам, изображена на рис.
50. Если представлять себе сферу,
изготовленную из мягкой резины, то
ее можно мять руками, растягивать,
сжимать (как показано на рис. 50), не
меняя ее основного топологического
свойства, а именно односвязности.
Это означает, что любой замкнутый
путь (петля) стягивается по сфере в
точку. Никакое другое 2-
многообразие (замкнутое) таким свойством
не обладает. На рис. 51 показана
гибкая (гладкая) деформация листов
книги ("Книги и ураган"). Изгибание
правых листов наглядно показывает

|3. Наглядные свойства двумерных многообразий
99
события, происходящие со сферой,
когда мы пытаемся вывернуть ее
наизнанку тривиальным образом,
проталкивая навстречу друг другу два
противоположных диска, лежащих на
сфере. Тогда рано или поздно возникнет
излом сферы (см. излом листа на рис.
51), запрещенный условием, что мы
должны деформировать сферу,
оставаясь в классе гладких погружений. Итак,
пытаясь вывернуть сферу, мы должны
поступить более аккуратно и не столь
прямолинейно, как в описанной выше
попытке. На рис. 52 показан один из
моментов выворачивания сферы,
описанного в пункте 3.6. Если считать, что
параметр деформации меняется от 0 до
1, то на рис. 52 изображена картина,
отвечающая моменту 1/2. Более
наглядная схема изображена на подробном
рис. 53. Справа внизу под номером I
показано стандартное вложение сферы.
Двигаясь вверх, мы видим
последовательные стадии ее деформации,
занумерованные римскими цифрами от I до
IX. Описывать процесс деформации
словами здесь чрезвычайно трудно.
Поэтому снова вспомним средневековых
геометров, которые иногда вместо
логического доказательства говорили:
исмотри". Конечно, в современной
научной и более популярной современной
математической литературе существуют
очень детальные изображения процесса
этой деформации (в частности, такие,
где показаны сечения сферы
плоскостями, чтобы можно было разобраться в
происходящих событиях). Но мы
решили ограничиться лишь изображенным
на рис. 53 качественным (и отнюдь не
подробным) описанием, чтобы
показать то положение сферы, которое
она займет. Это — положение IX на
рис. 53. Здесь видно, что
погруженная сфера приобрела вид довольно
симметричного объекта. Далее,
применяя процесс встречного
проталкивания листов сферы, описанный в
пункте 3.6, мы меняем местами ее
внутренность и внешность. В
результате погруженная сфера IX остается
прежней как геометрическое
множество точек, но вывернется: черные и бе"
лые зоны на ней поменяются местами.
Здесь поясним, что в положении IX
часть видимой зрителю поверхности
сферы раскрашена как белым, так и
черным, т. е. здесь внутренность сферы
и ее внешность уже довольно сложно
перемешаны. После выворачивания
меняется лишь раскраска этих зон (белая —
в черную и черная — в белую). Затем
начинаем обратный процесс, двигаясь
от положения IX к положению VIII и
т. д. вплоть да положения I. В результате
мы возвращаемся к стандартно
вложенной сфере, но теперь она вывернулась.
На рис. 54 показано несколько
двумерных полиэдров. В центре
изображена процедура, естественно
продолжающая предыдущий рассказ о
выворачивании сферы. Рассмотрим двумерный тор
в R7, проделаем в торе дырку (рис. 54,
центр). Для реального эксперимента
можно взять, например, велосипедную
камеру, в которой уже имеется дырка
(для накачивания воздуха). Что
получится, если тор вывернуть наизнанку
через эту дырку? Легко сообразить, что
снова получится тор с дыркой. Однако
меридиан и параллель тора теперь
поменяются местами. Если сначала мы
имели тонкую трубу — велосипедную
камеру, то получим толстую
трубку-бублик с маленьким отверстием в центре.
Это наглядно показано на рис. 54.
Далее, здесь изображен 2-адический
соленоид, о котором мы еще будем
говорить в разделе гамильтоновой
механики (на рис. 54 см. тор, вложенный
в большой тор и два раза намотанный
вдоль его оси). Справа показан
полиэдр, уже обсуждавшийся выше и
составленный из бесконечного числа
раковин (локально гомологически
несвязный полиэдр). На рис. 54 показано,
как этот полиэдр распадается на
свои составные элементы. Слева
внизу показан еще один тип соленоида,
а также изображена известная
минимальная поверхность (пример

100
2. Многообразия малой размерности
Дж. Ф. Адамса), получающаяся
склейкой обычного листа Мебиуса и тройного
листа Мебиуса. Последний получается,
если вдоль обычной окружности
провернуть трилистник (составленный из
трех отрезков, исходящих чз одной
точки под углами 2л/3), нормальный
к окружности. Причем нужно
потребовать, чтобы после полного оборота
три отрезка этой фигуры (одинаковой
длины и выходящие под равными
углами из точки на окружности)
повернулись на угол 2л/3. Далее, на рис. 54
двое лесорубов распиливают этот
полиэдр как раз в том месте, где
обычный лист Мебиуса склеивается с
тройным. На рис. 55 показаны
проективные плоскости и скрещенные
колпаки, изображающие листы Мебиуса,
помещенные в R3 так, что их граница
является плоской окружностью. Грубо
говоря, если расположить лист Мебиуса
в R3 так, что его граница будет
плоской, то получится «папоротник»,
изображенный на рис. 55. Вдали
изображен крендель — сфера с двумя
ручками. На рис. 56 изображены листы
Мебиуса с плоской границей
(скрещенные колпаки), проективные плоскости,
двумерные сферы с большим числом
ручек, сферы с тремя
отождествленными точками, тор. На рис. 57 показана
деформация, знакомая нам по
конструкции рогатой сферы Александера. На
рис. 58—60 представлены деформа-
Как мы видели, 2-многообразия
разбиваются на две серии: сферы с ручками
(ориентируемые) и сферы с пленками
Мебиуса (неориентируемые). Так как
гомеоморфные многообразия
одновременно ориентируемы или нет, то сфера
с ручками не может быть гомеоморфна
сфере с пленками Мебиуса. Итак,
многообразия из разных серий
отличаются с4оей ориентацией. Теперь
р- ссмотрим многообразия одной серии,
например сферы с ручками. Оказывает-
ции двумерных поверхностей при
помощи различных гомеоморфизмов. Для
наглядности использованы привычные
образы, чтобы подчеркнуть характер
(и возможности) таких деформаций.
Гомеоморфизмы на рис. 59 не меняют
топологии поверхности и мало меняют
ее площадь, хотя существенно меняют
метрические свойства объекта.
«Выращивание» из поверхности длинных и
тонких трубок-отростков может,
например, привести к тому, что
последовательность замкнутых поверхностей,
площадь которых стремится к
минимуму (например, в данном классе
гомологии), может тем не менее заметать
все объемлющее пространство за счет
тонких усов, не влияющих на
сходимость площади к минимуму, но
влияющих на свойства предельной
поверхности. В качестве «предела» можно
получить все многообразие* вмещающее
в себя деформирующиеся циклы. На
рис. 61 изображена двумерная
поверхность бесконечной связности, т. е. сфера
с бесконечным числом ручек. Ручки
уменьшаются в размере и
накапливаются к некоторой предельной точке,
никогда ее не достигая, так что
получается вложение поверхности R3. На
рис. 62 показано, в частности,
разложение бутылки Клейна в сумму двух
листов Мебиуса. На рис. 63, 64
изображены различные двумерные
поверхности.
ся, сферы с разным количеством ручек
не гомеоморфны и даже гомотопически
не эквивалентны. Как это доказать?
Почему, например, тор не гомеоморфен
и гомотопически не эквивалентен сфере !
или, скажем, кренделю?
Ответить на этот вопрос непросто.
Ведь мы должны найти какие-Yo.
характеристические свойства,
отличающие тор от кренделя, т. е. обнаружить
какие-то инварианты 2-многообразий,
различные для тора и кренделя. Эти
§ 4. Чем отличаются друг от друга разные двумерные
многообразия? Группы когомологий и дифференциальные формы

I 4, Чем отличаются двумерные многообразия
101
инварианты должны сохраняться при
гомотопической эквивалентности. Как
ММ уже знаем, такие инварианты
|'уществуют—это группы гомологии
полиэдров. В случае многообразий можно
указать другой подход к определению
групп гомологии, который мы сейчас
акратце опишем.
4.1. Дифференциальные 1-формы на гладком
многообразии
Пусть Мп—гладкое многообразие и
* хп —локальные регулярные
координаты на нем. Обозначим через
dx' dxn дифференциалы этих
координат. Пусть в каждой системе координат
задана следующая сумма,
дифференциальное выражение co=Pidxl + ...
+ Pndxnt где А=Р|(х,,...,У1) —
гладкие функции от координат х\...,хп.
Теперь потребуем, чтобы это
дифференциальное выражение ^=IiPidxt
оставалось инвариантным при произвольной
регулярной замене координат, т. е.
потребуем, чтобы при переходе от
координат х1,...,х" к координатам V ,—,*я
выполнялось следующее тождество:
XtPidxi'=,LPidxi. Ясно, что это
требование накладывает некоторые условия
на закон преобразования функций
1\~+Ру при замене координат. В самом
деле! из правила' дифференцирования
«¦ложных функций мы получаем
Так как дифференциалы dxv\...,dx*'
независимы, то, приравнивая
коэффициенты перед ними, получаем равен-
дх1
ства Pt, — 2,Р,—jr, Таким образом,
мы вывели закон преобразования
коэффициентов Р( в сумме о>,
обеспечивающий инвариантность
дифференциального выражения ш = 2 РДх? при
заменах координат.
Определение 1. Дифференциальное
выражение о>=2Р^, где
коэффициенты Р|,...,Я« преобразуются при
заменах координат указанным выше
образом, называется дифференциальной
1-формой, или внешней 1-формой. •
Рассмотрим важный пример
дифференциальных 1-форм. Пусть
/—гладкая функция на л-мерном
многообразии. Рассмотрим ее полный
дифференциал df. В локальных координатах
хх,...,хп он запишется в явном виде
так: df=X—p-rfx'. При заменах
координат (*)->-(*') мы имеем Ре=^-Л-^
= *171F=*PS' те- пол'ный
дифференциал df является
дифференциальной 1-формой в смысле
предыдущего определения. Ясно, что в
данном случае закон преобразования
коэффициентов Pi=-^r обеспечивает нам
ОЯТ
хорошо известную инвариантность
первого дифференциала относительно
замен координат.
Определение 2. Дифференциальные
1-формы о вида df называются
точными формами.
4.2. Замкнутые и точные формы на двумерном
многообразии
Оказывается, на множестве
дифференциальных 1 -форм можно определить
естественную операцию, называемую
внешним дифференцированием и
обозначаемую тем же символом d, что и
обычный дифференциал гладкой
функции. Мы не будем давать здесь общее
определение операции d, а ограничимся
лишь обсуждением понятия замкнутых
форм, которые определяются как
формы, внешний дифференциал которых
тождественно равен нулю. Конкретное
выражение этого условия дается
следующим определением.
Определение 3. Дифференциальная
1-форма a> = 2P,dxi называется
замкнутой, если для всех *, / выполняются
dPt dk>,
тождества
дх'
©V

<102
2. Многообразия малой размерности
Читатель, знакомый с общим
понятием внешнего дифференцирования d
(например, по [1]), сразу увидит, что
эти условия эквивалентны равенству
Ао = 0.
Предложение. Каждая точная
форма является замкнутой.
В самом деле, точная 1-форма
имеет вид полного дифференциала
некоторой функции, т.е. о)=2—-^d*'. Тогда
P = JL дР> = d2f = d2f = дР<
dxL ' дх1 дх'дх' дх'дх1 дх' '
что и требовалось. Мы
воспользовались известным фактом, что частные
дифференцирования —- и —- всегда
дх1 дх1
коммутируют для гладких функций.
Рассмотрим гладкое многообразие
М и на нем все замкнутые и точные
1 -формы. Ясно, что они образуют
линейные пространства: линейные
комбинации (с постоянными
коэффициентами) точных форм дают снова
точные формы. Аналогичным свойством
обладают и замкнутые формы.
Обозначим линейное пространство всех
замкнутых форм через Z\M), а линейное
пространство всех точных форм — через
В\М). Так как каждая точная форма
замкнута, то, очевидно, имеем
включение B'(Af)c=Z'(M). Эти пространства
можно рассматривать как абелевы
группы (по сложению), следовательно,
можно естественно определить
факторгруппу Z'/B' (или
фактор-пространство).
Определение 4. Фактор-группа
Z{ /В{ обозначается через //'(Af, R) и
называется группой одномерных
вещественных когомологий
многообразия М.
Здесь буква R указывает, что
рассматриваются формы с вещественными
коэффициентами. Иногда замкнутые
формы называются коциклами, а
точные формы — кограницами. Опуская
обозначение R поля вещественных
чисел, иногда будем писать просто
Н\М).
В действительности по такой же
схеме можно определить и группы
^-мерных когомологий многообразия,
однако сейчас они нам не потребуются,
и мы не будем на них останавливаться.
4.3. Важное свойство групп когомологий
Итак, с каждым многообразием М
естественно связана его группа
одномерных когомологий Н\М). Отметим,
что при определении этой группы
мы могли рассматривать и
многообразия с краем, а не только замкнутые.
Рассмотрим теперь произвольную
непрерывную деформацию многообразия.
Более точно —рассмотрим
многообразие ЛГ, гомотопически эквивалентное
многообразию М. Эти многообразия
могут внешне значительно отличаться
друг от друга. Например, плоское
кольцо гомотопически эквивалентно
окружности. Кольцо стягивается на свою,
например, внутреннюю границу,
являющуюся окружностью (рис. 1). Здесь
Рис. 1
гомотопически эквивалентные
многообразия имеют разную размерность.
Далее, лист Мебиуса также
гомотопически эквивалентен окружности (рис.
1). Следовательно, плоское кольцо
гомотопически эквивалентно листу
Мебиуса. При этом кольцо —
ориентируемое многообразие, а лист Мебиуса —
неориентируемое. Следовательно, при
гомотопической эквивалентности
некоторые важные свойства многообразия

f 4. Чем отличаются двумерные многообразия?
103
(размерность, ориентируемость или
неориентируемость) могут разрушаться.
При гомеоморфизме с размерностью и
ориентацией многообразии таких собы-
'пт не происходит. Следовательно» мы
убедились, -.то два многообразия могут
быть гомотопически эквивалентны, но
не гомеоморфны.
И тем не менее плоское кольцо и лист
Мебиуса имеют "нечто общее": они
непрерывно стягиваются (без разрывов)
на одну и ту же окружность.
Оказывается, "нечто общее; заключается и в
одинаковых группах когомологий и
гомологии.
Теорема 1. Пусть М и М'—
гомотопически эквивалентные многообразия
(в частности гомеоморфные). Тогда
их фута* одномерных когомологий
изоморфны, пи е. tf(Nfy=lt(M).
Это свойство иногда называют
гомотопической инвариантностью групп
когомологий. Теорема 1 верна также и
для групп когомологий любой
размерности. Мы не будем здесь доказывать
теорему 1 ввиду ее нетривиальности.
Ограничимся лишь комментариями и
некоторыми ее следствиями.
Подчеркнем важность теоремы 1. Она
укалывает нам инварианты многообразий,
т. е. объекты, которые сохраняются
при непрерывных деформациях —
гомотопической эквивалентности. В чем
важность этих (и подобных им)
инвариантов? Они позволяют, например,
доказывать, что два многообразия
"различны", например гомотопически
не эквивалентны (а следовательно, и не
гомеоморфны). В самом деле, если
группы когомологий двух многообразий
не изоморфны, то в силу теоремы 1
эти многообразия гомотопически не
эквивалентны. Ниже на конкретных
примерах мы убедимся в
эффективности этого критерия.
Для многообразий имеет место
важная теорема: группы вещественных
когомологий (в терминах форм)
изоморфны группам вещественных
гомологии. Последние группы вычисляются
как в общем случае полиэдров (с
коэффициентами в группе вещественных
чисел). Поэтому гомотопическую
инвариантность групп когомологий можно
извлекать из соответствующей теоремы для
гомологии полиэдров. Важность групп
когомологий объясняется также тем, что
иногда их легче вычислить, чем группы
гомологии многообразия (в терминах
симплексов и т. п.). кроме того, они
описывают некоторые свойства
дифференциальных уравнений на многообразиях.
4.4. Прямое вычисление групп одномерных
когомологий одномерных многообразия
Рассмотрим 1-мяогообразие.
Таких многообразий всего два:
окружность и прямая.
Теорема 2. Группа одномерных
когомологий для окружности изоморфна
группе вещественных чисел R, а для
прямой группа когомологий — нулевая,
me.lt(F)=R\lt(lt)=Q.
Доказательство. Начнем с более
простого случая прямой. Согласно
определению №=2?/о. Следовательно,
нужно вычислить группы Z и 2?. Из
определения дифференциальных форм
сразу следует, что 1-форма на прямой
записывается так: g(x)ax — со, где х —
декартова координата на прямой, a g —
произвольная гладкая функция.
Обращаясь к определению замкнутой 1-
формы, видим, что любая такая 1-
форма на прямой замкнута, поскольку
здесь имеется лишь одна координата х,
поэтому -$*-= -&- для любой функции
g. Итак, любая 1-форма a>=g(x)dx на
прямой замкнута. Оказывается, любая
1-форма на прямой является точной. В
самом деле, для любой гладкой
функции g имеем следующее тождество ю=
=g(x)dx=d( f0g(tjdt), т. е. ю = df, где
fjx) = j» g(t) at. Известно, что
интеграл гладко зависит от своего верхнего
предела, поэтому/— гладкая функция.
Тем самым мы доказали, что на
прямой любая замкнутая 1-форма
точна, поэтому ^—В1^ а
следовательно, группа п — нулевая- В
случае прямой теорема доказана.

104
2. Многообразия малой размерности
Перейдет к окружности. Введем
на ней стандартную угловую
координату ф, где 0^ф^2л. Тогда функции g
на окружности — это такие функции от
параметра ф, что ?(ф) = ?(ф + 2л), т. е.
периодические по ф функции. Следова-
тельио, общий вид 1-формы на
окружности такой: о) = ?(ф)^ф, где g@) =
= gBn) (т.е. g—периодическая
функция по ф). Как и в случае прямой,
сразу получаем, что любая гладкая
1 -форма на окружности является
замкнутой. Осталось вычислить группу
точных форм. Рассмотрим следующее
линейное отображение к пространства
Z1 замкнутых 1-форм в группу R
вещественных чисел, где Я.(о>) =
= Х(?(-ф)<*ф) = $оЛ?(ф)<*Ф- Другими
словами, сопоставляем форме на
окружности ее интеграл вдоль всей
окружности (т. е. от 0 до 2я). Ясно, что к
линейно в силу аддитивности интеграла.
Поэтому ф—гомоморфизм
пространства Z1 в вещественную прямую R1.
Лемма 1. Отображение к является
эпиморфизмом, т. е. отображением
«на»,'его образ покрывает всю прямую.
Доказательство. Расемотрим
простейшую ]-форму taa окружности, а
именно a> = d<p. Ясно, что ярл
отображении к она отобразится в число
2л, так как k(dy) = \l*dy = 2n. Итак,
Х(а4ф)=5лл, где a = const.
Следовательно, вся прямая в1 принадлежит
образу отображения, так как,
произвольно меняя а, мы заставляем 2ла
пробегать все вещественные числа.
Из элементарной алгебры известно,
что если к:В-*А — эпиморфизм абе-
левых групп (например, линейных
пространств), то всегда имеем
изоморфизм Л = В/КегХ, где КегА,— ядро
гомоморфизма А,, т. е. совокупность всех
элементов Ь^В, для которых к(Ь) = 0),
а В/КегА, обозначает фактор-группу
(фактор-пространство). В нашем
случае получаем, что Zl/KerA,= Rl.
Осталось вычислить ядро отображения к.
Лемма 2. Ядро отображения к
совпадает ? подпространством В1 всех
точных 1-форм на окружности.
Доказательство. Докажем сначала,
что КегТИэВ'1. Пусть (*> = dfy где /—
гладкая функция на окружности (т. е.
2л—периодическая функция от ф;
Д0) = Д2л)). Тогда *.(«>) = М(ф) =
= Д2л) — f@) = 0, т.е. *(<й) = 0, т.е.
о) принадлежит ядру отображения.
Докажем обратное включение, а именно
что KerA.czВ1. Пусть о) =
?(ф)с?ф—некоторая 1-форма на окружности,
причем А,((о) = 0, т.е. \ол#(ф)^ф = 0.
Определим на окружности функцию /(ф) =
= \lg(t)dt. Проверим, является ли она
корректно определенной функцией на
окружности, т. е. будет ли она 2л-пери-
одической. Имеем fBn) = \lng(t)dt =
= 0 = /@). Здесь мы использовали тот
факт, что 1-форма ш принадлежит ядру
к. Следовательно, мы указали на
окружности 2л-периодическую
функцию /(ф) такую, что <u = df, так как
df=d(\lg(t)dt) = g{y)d(<p) Итак, В' =
= КегА,. Следовательно, Z jB =R , т. е.
Hl = Rl, что и требовалось.
Из теоремы 1 сразу получаем, что
окружность и прямая гомотопически
не эквивалентны. Впрочем, это легко
усмотреть и из других соображений.
Отметим, что прямая гомотопически
эквивалентна точке (рис. 2),
стягивается по себе в точку. Следовательно,
окружность гомотопически не
эквивалентна точке.
Рис. 2
4.5. Прямое вычисление групп одномерных
когомологиЙ плоскости, двумерной сферы и тора
Перейдем к 2-многообразиям.
Теорема 3. Группы одномерных кого-
мологий плоскости и сферы нулевые
(тривиальны), а в случае тора Т2
имеем H\T2)=R2.
Для начала вычислим одномерные
когомологии плоскости. Найдем общий
вид замкнутой 1-формы на плоскости.
Имеем для общей 1-формы выражение
<u = Pdx + QdyJ где Р(х, у) и Q(x,y) —
гладкие функции декартовых координат
хну. Форма замкнута в том и только

I 4. Чем отлинаются двумерные многообразия?
105
дР дО ,
н том случае, когда — — ^-? (см. выше
определение замкнутости формы).
Лемма 3. Любая замкнутая глад-
лип /-форма на плоскости тонна.
Доказательство. Мы должны
предъявить функцию / на плоскости такую,
что выполняется тождество co = d/, т.е.
Pdx + Qdy = df(x,y) - -?dx +^dy.
Отсюда получаем следующие
уравнения на функцию f: ~-?-=Р, -L=Q9 где
-р к —2-. Проинтегрируем первое из
них. В результате получим / (х, у) =
*m\aP(x*y)dx+g(y)f где ?(#) —некото-
рмя гладкая функция от одной
переменной у. Требуется найти эту
функцию. Для этого продифференцируем
предыдущее соотношение по у. Полу-
дх " ду
ag(y)
дх
Xdx +
dy
-Я{0.У) + *Р

т.е.-Q(xfу)-Ниоткуда *W* —
-Q@.y). т.е. *(у)НЮ(О.*0«*у + С.
где С — произвольная постоянная.
Итак, мы получаем явное
выражение для искомой функции f (х, у) =¦
- \1 Р (х, у) dx + \1Р @, у) dy + С. Тем
самым мы предъявили функцию / такую,
что <u = df, следовательно, доказали
лемму 3.
В силу симметрии проведенных
рассуждений относительно замены х на у
мы получаем также второе
выражение для той же функции /(х, (/) =
-\lQ(x,y)dy + SxoP{x,0)dx + C. Для
что го надо лишь начать интегрирование
с уравнения -j- = Q- Так как Zl=B\
то //1=0, что и требовалось. В случае
плоскости теорема 3 доказана.
Поскольку мы рассматриваем
плоскость в декартовых координатах,
то 1-форму со можно интерпретировать
как векторное поле v с компонентами
Р и Q, т.е. v = {Pt Q). Тогда лемма 3
переформулируется так: любая
замкнутая 1-форма <D=Pdx + Qdy на
плоскости определяет векторное поле и =
(Р, Q), являющееся градиентом
некоторой функции /, т. е. u = grad/,
P—jiy Q—j- Такая функция
называется потенциалом, а поле
v—потенциальным. Следовательно (в декартовых
координатах), замкнутость 1-формы со
на плоскости эквивалентна
потенциальности векторного поля у = (Р, Q) (и
точности 1-формы со).
Для дальнейшего полезно обсудить
еще одну интерпретацию потенциала /,
связанного с замкнутой 1-формой на
плоскости. Для этого напомним понятие
интеграла 1-формы вдоль кривой у.
Рис. $
Зададим кривую у так: y(t) = (x(t), y\t))>
где t—параметр (время) вдоль кривой
(рис. 3). Если на плоскости задана
1-форма Pdx-\-Qdy> то можно
определить ее интеграл вдоль кривой у
(например, от некоторой точки А на
кривой до точки В на кривой):
\BA<*=]';p(x(t),y(t))dx(t) +
+ Q(x{t), y(t)) dy{t) = \?,(Рх + Qy)dt,
где A = y(t% В=у(П i-jjj. У=%
Этот же интеграл можно более
компактно записать так: $1w = ]<zv9y>dtf где
у = (Р, Q), y=(x, у)—два векторных
поля вдоль кривой (рис. 4). При этом поле
Рис. 4

106
2. Многообразия малой размерности
v изображает форму о>, поле у является
полем векторов скоростей кривой, а
<u,Y> обозначает их евклидово
скалярное произведение.
В этих терминах явную формулу
для потенциала замкнутой 1-формы на
плоскости можно переписать более
наглядно. Рассмотрим на плоскости
кусочно-гладкий путь yi (рис. 5), сос-
V
Уу
<0,к!
п
<*,к)
Y2
В
о
Рис. 5
<х,0)
тоящий из двух отрезков: вверх по оси
?/, затем направо, параллельно оси х.
Этот путь идет из точки 0 (начала
координат) в точку (х, у). Тогда первая
формула для потенциала / перепишется
так: /=5Т1ш. ибо f = \yQQ{0.y)dy +
+ \x0P(x,y)dx = \Ао Pdx + Qdy +
+ \%Pdx+Qdy = \yiPdx + Qdy. Здесь
мы считаем, для простоты, что Д0,0) =
= 0, а, кроме того, dx=0 вдоль отрезка
О А кривой yi и dy = 0 вдоль отрезка АС
кривой yi-
Совершенно аналогично получаем,
для потенциала f имеется еще одно
представление: / = $?2о), где путь у2
составлен из следующих двух отрезков:
отрезок ОВ по оси х, затем отрезок
ВС параллельно оси у (рис. 5). Итак,
для вычисления значения потенциала f
в какой-то точке (х, у) нужно
проинтегрировать форму (о по ломаному
пути, начинающемуся в точке 0
(например, в начале координат) и
кончающемуся в точке (х,у).
Лемма 4. Результат интегрирования
замкнутой 1-формы вдоль пути на
плоскости зависит лишь от положения
начальной и конечной точек пути
интегрирования и не зависит от выбора
кусочно-гладкого пути, соединяющего
эти точки. В частности, интеграл от
замкнутой 1-формы не меняется при
непрерывной деформации пути,
сохраняющей его начальную и конечную точки.
Следствие. Интеграл $тш от
замкнутой 1-формы ш по любому замкнутому
пути (т. е. по петле) на плоскости равен
нулю.
Доказательство следствия очевидно.
Обратно, если известно, что интеграл
от замкнутой 1 -формы по любому
замкнутому пути равен нулю, то
результат интегрирования этой формы вдоль
разомкнутого пути (т. е. вдоль пути
с несовпадающими начальной и
конечной точками) не зависит от вида
пути, а зависит лишь от начала и
конца пути.
Доказательство леммы 4 вытекает из
того, что JYla) = $Y2(o для двух путей,
показанных на рис. 5, и из того, что
любой кусочно-гладкий путь,
соединяющий точки @, 0) и (х, у), можно
аппроксимировать кусочно-гладким
ступенчатым путем (рис. 6), составленным из
сторон прямоугольников, как на рис. 5.
Рис. 6
Меняя начальную точку (начало
пути интегрирования), мы меняем
потенциал f на некоторую постоянную С
(см. выше явные формулы для
потенциала). Из рис. 7 видно, что / = $Yw =
= $T + Y'a) = $r(D-r-$Y<a)= const+ /', где
const = Sxfc).
Рис. 7

14. Чем отличаются двумерные многообразия?
107
Итак, 1-форма Pdx+Qdy замкнута па
плоскости в тон и только в том
случае, когда соответствующее
векторное поле v=(P, Q) потенциально, пи е.
psgradf. Укажем полезную
гидродинамическую интерпретацию условия
.«амкнутости 1-формы со на плоскости.
Векторнсч. поле на многообразии
можно интерпретировать как поле
скоростей потока жидкости, текущей по
многообразию. При этом нужно
считать, что касательный вектор v,
прикрепленный к точке х многообразия,
изображает вектор скорости частицы
жидкости, находящейся в данный
момент в точке х. Такая интерпретация
полезна со многих точек зрения.
Определение 5. Поток жидкости
(векторное поле) гЦР, Q) на плоскости
называется безвихревым, если jy = fi .
Ясно, что это условие эквивалентно
замкнутости формы со. Собирая
воедино все полученные нами факты,
сформулируем следующую теорему.
Теорема 4. Следующие условия
эквивалентны: 1) дифференциальная 1-
форма w=P<hc+Qdy на плоскости
замкнута, 2) соответствующее
векторное поле v =(Pt Q) безвихревое, 3)
векторное поле v=(P, Q)
потенциально, т. е. v =gradf, 4) форма а>
точна, т. е. является полным
дифференциалом функции f.
Перейдем к вычислению одномерных
когомологий сферы. Этот случай
сводится к случаю плоскости. Фиксируем
на сфере какую-нибудь начальную
точку 0, и пусть задана замкнутая 1-
форма со. Рассмотрим произвольную
точку С на сфере и соединим ее с
точкой 0 каким-нибудь кусочно-гладким
путем у. Мы утверждаем, что на сфере
любая замкнутая 1-форма тонна.
Предъявим в явном виде функцию /на
сфере такую, что &=df. Положим, по
определению, jyCo ¦=/, т. е. будем
действовать по схеме, разобранной нами
выше. Требуется лишь доказать, что
это определение функции / корректно,
т. е. не зависит от выбора пути,
идущего из точки 0 в точку С. В самом
деле, пусть у' — другой такой путь
(рис. 8). Если пути у и у' пересекаются
лишь в начальной и конечной точках,
то можно считать, что между этими
путями заключен двумерный диск.
Напомним, что на сфере такие пути
гомотопны. Объединение путей образует
границу диска. Если пути пересекаются
(рис. 8), то нужно рассмотреть не один
диск, а несколько. Схема рассуждений
останется прежней, как и в лемме 4.
Рис.8
Tax как пущ кусочно-гладкие, то диск не
покрывает всю сферу. Мы доказали, что
интеграл замкнутой формы по любому
замкнутому пути на сфере равен нулю.
Итак, функция (потенциал) / корректао
определена на сфере. Мы использовали
здесь то обстоягельегао, что на сфере
любые два пути с совпадающими началом
и концом можно нецрерывн» ттродефор-
мировапь друг в друга (не смещая их
концы). С другой стороны ясно, что
&=df. Мы предъявили гладкий
однозначный (на сфере) потенциал, доказали
точность формы. Игах, 1т(УУ=0.
Рассмотрим тор. Удобно снова
представить его в виде квадрата с
отождествленными сторонами (рис. 9).
Введем на нем декартовы координаты х9 у
и зададим две 1-формы a>\=dxf &f=dy (с
постоянными коэффициентами). Их
можно изобразить (следуя описанному

108
2. Многообразия малой размерности
выше принципу сопоставления 1-форме
векторного поля) полями вида v\ =
= A,0), У2 —@, 1). Оба поля показаны
на рис. 9. Они изображают потоки
жидкости, текущие вдоль осей х и у
соответственно с постоянными
скоростями, равными 1.
Рис. 9
Пусть Z1 —линейное пространство
замкнутых 1-форм на торе. Рассмотрим
линейное отображение (гомоморфизм)
X группы Z1 в абелеву группу R2, т. е.
в евклидову плоскость: Х(ш) = (а, Р), где
а=$аа>, р = \ьы — два числа,
являющиеся соответственно интегралами 1-
формы to по двум окружностям а и Ь
на торе, а именно по меридиану а и по
параллели Ь. При склеивании тора из
квадрата сторона а квадрата
превращается в окружность-меридиан, а
сторона Ь — в окружность-параллель. В
явном виде к запишется так. Общий вид
1-формы на торе следующий: Pdx-\-
+ Qdy, где Р и Q—двоякопериодиче-
ские функции на плоскости (т. е.
периодические по х и у). Тогда k(Pdx-\-
+ Qdy) = (\i0P(x,0)dx, \loQ@,y)dy).
Мы утверждаем, что к является
отображением на всю плоскость, т. е.
к — эпиморфизм. В самом деле, если в
качестве 1-формы со взять wi = dx,
то получим k{dx) = (\, 0). Взяв в
качестве со форму a>2 = d[/, получаем k(dy) =
= @, 1). Так как векторы A,0) и @, 1)
образуют базис на плоскости, то к—
эпиморфизм, что и требовалось. При
этом обе формы dx и dy замкнуты на
торе, т. е. принадлежат пространству Z1.
Следовательно, из общих
алгебраических соображений следует (как и в
случае плоскости, сферы), что
Z'/KerA,= R2. Осталось доказать, что
КегХ=В\ т.е. что ядро А, совпадает
с пространством точных 1-форм. Если
форма точна, т. е. to = df, где / —
функция, определенная на всем торе, то
\adf = 0 и \bdf=0, так как а и b —
замкнутые пути (циклы).
Следовательно, В'сгКегА,. Обратно, докажем, что
В'=>КегХ. Пусть замкнутая 1-форма о>
такова, что ее интегралы по меридиану
и параллели на торе равны нулю.
Нужно доказать, что она точна, т. е.
что существует потенциал / на торе
такой, что to = df. Предъявим его в
явном виде. Положим, по определению,
/ = $уО), где у—любой кусочно-гладкий
путь, идущий из фиксированной точки
0 на торе в переменную точку (х, у)
на торе. Нужно снова доказать, что это
определение не зависит от выбора пути,
идущего из точки @,0) в точку (лс, у).
Как мы знаем, этот факт будет вытекать
из того, что интеграл от данной
замкнутой формы по любому замкнутому пути
(петле) равен нулю. Пусть у—любой
такой путь на торе. Как мы уже знаем,
при непрерывной деформации пути
интеграл от замкнутой 1-формы по этому
пути не меняется. Далее, геометрически
очевидно, что путь всегда можно про-
деформировать в путь, движущийся
лишь по некоторой параллели и по
некоторому меридиану тора (в
произвольном порядке). Например, путь
пройдет вдоль параллели, потом
несколько раз вдоль меридиана, затем
снова вдоль параллели и т.д.
Следовательно, исходный интеграл 1-формы
по пути у равен интегралу от этой
же формы, но вдоль нового,
описанного выше пути, составленного из
нескольких экземпляров параллели и
нескольких экземпляров меридиана
(причем, может быть, с разными ориента-
циями). В силу аддитивности интеграла
исходный интеграл \уш представляется
в виде суммы интегралов от формы
to по параллели и по меридиану,
причем каждый из этих интегралов

I 4. Чем отличаются двумерные многообразия?
109
берется, вообще говоря, несколько раз,
в зависимости от того, сколько раз путь
Y обернулся вдоль параллели и сколько
раз — вдоль меридиана (с учетом
направления обхода). Но так как каждый
из этих интегралов равен нулю, то
равен нулю и исходный интеграл.
Мы доказали, что функция /=J7to
корректно определена на всем торе. Далее,
как и в случае плоскости, получаем,
что <a = df. Следовательно, замкнутая
I -форма с нулевыми интегралами вдоль
параллели и меридиана тора является
тонной формой. Итак, #* = KerA,.
Отсюда имеем tf'G*2)=R2.
Таким образом, мы начинаем
обнаруживать следующую
закономерность. Сфера—замкнутое многообразие
без ручек, имеет нулевую группу
//'. Тор—это сфера с одной ручкой
и имеет ненулевую группу //',
изоморфную R2. Таким образом,
приклеивая к сфере одну ручку, мы
увеличиваем группу одномерных когомологий
на группу R . Естественно
предположить, что если мы приклеим к сфере еще
одну ручку (т. е. получим крендель,
сферу с двумя ручками), то группа
когомологий снова увеличится на R2, и в
результате группа одномерных
когомологий кренделя будет изоморфна R4.
В частности, мы фактически
доказали теорему: на торе замкнутая 1-форма
точна в том и только в том случае,
когда ее интегралы по двум
замкнутым окружностям—параллели и
меридиану—равны нулю. Обобщение этого
критерия для сферы с произвольным
количеством ручек мы получим в
следующем пункте.
4.6. Прямое вычисление групп одномерных
когомологий ориентированных поверхностей, т. е.
сфер с ручками
Теорема 5. Пусть М2—замкнутое
компактное связное ориентируемое 2-мно-
гообразие, т. е. сфера с g ручками.
Тогда его группа одномерных
когомологий //' изоморфна R2*.
Доказательство проведем по схеме,
уже разработанной для плоскости,
сферы и тора. Главное в этой
конструкции—предъявить в явном виде
достаточно большой набор независимых
замкнутых 1-форм.
Рассмотрим поверхность рода g ь
представим ее в виде выпуклого
плоского 4g-угольника со сторонам*
а,, 6„ где 1 </<?, причем код W имеет
вид а\Ь\аТхЬ\~х...agbgagXbg{. (рис. 10).
Построим на поверхности замкнутые
Рис. 10
1-формы о»,...,<*>? и xi,...,Tg. Если на
поверхности задан замкнутый путь
(такие пути иногда называются циклами),
то интеграл формы вдоль пути
называется ее периодом вдоль цикла.
Выделим на поверхности циклы аь...,а? и
b],...ybgy которые назовем базисными
(по соображениям, которые вскоре
опишем). Каждый из них изображается
окружностью на поверхности. На
каждую ручку приходится ровно два таких
цикла: о, и 6„ где i—номер ручки
(рис. 10). Для каждой из форм о/ и т;-
(которые мы сейчас построим)
определен ее период по базисным циклам.
Вычисляя периоды, получаем
квадратную матрицу, называемую матрицей
периодов. Мы хотим так построить
1-формы щ и т/, чтобы матрица
периодов была единичной, т. е. имела
следующий вид:
<*\ ¦ • eg bj ... bg
1.
•
0
0
0
ч
0
*
0
0
'1

по
2. Многообразия малой размерности
Построим форму ©1. Выделим четыре
ребра многоугольника W,
соответствующие начальным буквам кода W, а
именно коммутатору aJb\a^T\ . На
ребре ах выберем последовательные три
точки: С, В, А, затем рассмотрим
соответствующие им точки Су В\ А на
ребре a~i (рис. 10). Соединим отрезками
соответствующие точки, т. е. построим
отрезки АЛ', ВВ', СС. При
склеивании поверхности М из
фундаментального многоугольника W отрезок СА
отождествится с отрезком С 'А'.
Теперь построим на многоугольнике
функцию /следующим образом:
1) положим ?0 вне четырехугольника
САЛС ' (покрыт точками на рис. 10);
2) положим ^1 на четырехугольнике
ВАЛ В (заштрихован на рис. 10);
3) в четырехугольнике СВВ'С' в
качестве / возьмем гладкую функцию,
равную нулю на стороне СС, равную 1
на стороне ВВ' и гладкую внутри
четырехугольника, в том числе и на двух
его сторонах СВ и С'В'. При этом
ограничение функции на сторону СВ
совпадает с ее ограничением на
сторону С'В\ и после склейки сторон СВ и
С'В' мы получаем гладкую функцию.
Подчеркнем, что построенная нами
функция на многоугольнике W
разрывна! Линия ее разрыва — это отрезок
АЛ. По одну сторону от него функция
равна 1, а по другую — нулю. В
качестве 1- формы со i возьмем форму df.
Она корректно определяет 1-форму
всюду на многоугольнике, кроме отрезка
АЛ. На отрезке АЛ положим, по
определению се>1=0. В результате мы получаем
гладкую форму на всем многоугольнике и
мл всей поверхности, получающейся
склейкой сторон многоугольника.
Гладкость формы следует из конструкции и
¦тго обстоятельства, что функция / по-
1*тх>янна в некоторой окрестности справа
и слева от отрезка АЛ, т. е. df=Q в этой
t »к|*стности. Доопределяя форму щ
мумгм на отрезке АЛ, мы и получаем
<|к»рму, гладкую уже во всех точках по-
wpMKTM. Построенная форма замкну-
frt I) самом А^ле, условие замкнутости,
т. е. условие dbi—0, вне
четырехугольника СВВ'С очевидно в силу того
обстоятельства, что здесь форма равна
нулю. В четырехугольнике СВВ'С
форма имеет вид dft следовательно
«й=йг/=0, что и требовалось.
Совершенно аналогично, взяв теперь
за основу другие два ребра: ^ и Ь\, мы
строим вторую 1-форму тг на
поверхности. Рассматривая остальные
коммутаторы ait bit a'i bi мы строим другие
формы со, и т,. В результате мы
предъявляем на поверхности рода g набор
замкнутых 1-форм в количестве 2g,
вида со\, Tj, ©2» х2 >... ®g*xg* Вскоре мы
увидим, что все они не являются
точными. Хотя в их построении участвовала
функция fi, тем не менее эта функция не
может быть продолжена до гладкой
функции на всей поверхности. В нашем
построении эта функция была разрывна.
Обозначим через Z линейное
пространство всех замкнутых 1-форм на
поверхности и построим отображение X
этого пространства в пространство
(группу) R по следующей формуле:
M©Walfpb ... <vpj), где аг4щЩ,
PrnbPi. Здесь со, и т, — построенные
выше формы. Мы утверждаем, что
отображение X является
эпиморфизмом. В самом деле, вычислим все
периоды форм со, и г,. Возьмем,
например, форму со!. Ее период вдоль
окружности flj paBeHiai<0i=\c@i=f(B)~
-ДС)=1-0=1. В то же время период
этой же формы по любому другому из
базисных циклов, отличных от аи
очевидно, равен нулю. Дело в том, что эта
форма равна нулю на всех остальных
оазисных циклах. Следовательно,
имеем А.(©!^A, 0, 0, ...,0).
Совершенно аналогично проверяется,
что X(Ti)^@, 1,0, ...,0). В итоге мы
получаем, что матрица периодов форм
©ьт1> ... ®&>х$ вдоль циклов аъЬъ ...
Ogt bg является единичной, что и
требовалось . Рассматривая в
пространстве R2* стандартный базис,
состоящий из векторов, все координаты
которых — нулевые, за исключением
одной (равной 1) мы, очевидно, и получа-

44. Чем отличаются двумерные многообразия?
111
ем» что все эти базисные векторы
попадают в образ отображения X.
Следовательно, образ отображения Я,
накрывает все пространстве* R . Как и ранее,
докажем, что JLerX=n , т. е. замкнутая
1-форма на поверхности точна в том
и только в том случае, когда все ее
периоды по базисным циклам равны
нулю. Докажем лемму, справедливую
для любого гладкого многообразия.
Лемма 5. Если 1-форма © имеет вид
df, где f — гладкая функция,
определенная на всем многообразии, то инте-
$рал формы по любому замкнутому
циклу у равен нулю.
В самом деле, Jy®4r^,/fr(l))~
-ffyiO^O, так как путь у замкнут,
поэтому у@)=7A).
Отсюда вытекает, что tfcfcA.
Докажем обратное включение.
Лемма 6. Пусть®— некоторая
замкнутая 1-форма на М, все периооы которой
вдоль базисных циклов на поверхности
Равны нулю. Тогда эта форма точна.
Построим,в явном виде потенциал /,
т. е. такую функцию, что o=df.
Фиксируем на поверхности произвольную
точку 0 ("начало координат"), возьмем
произвольную точку Р и соединим ее
на поверхности кусочно-гладким путем
у с точкой 0. Положим по определению
f(P)=tyo. Требуется доказать, что эта
функция корректно определена, т. е. не
зависит от выбора пути. Это будет,
очевидно, вытекать из следующего факта:
период замкнутой 1-формы га по любому
замкнутому пути (циклу ) у равен нулю (в
наших предположениях). Возьмем
произвольный кусочно-гладкий замкнутый путь
и подвергнем его непрерывной
деформации. Тогда интеграл У/д не изменится. В
самом деле, любую непрерывную
деформацию пути можно представить как
последовательность следующих
простейших (элементарных) деформаций
у-»у' (рис. 11). С другой стороны,
можно считать, что разность путей у-у'
(рис. 11) является границей двумерного
диска. Следовательно, можно
применить лемму 4, откуда получаем, что при
непрерывной деформации искомый
интеграл не меняется. Далее, непрерывно
деформируя произвольный замкнутый
путь на замкнутой 2-поверхности гг. е.
на сфере с ручками), можно
добиться, чтобы он превратился в путь,
составленный из нескольких экземпля-
Рис. 11
с
в элементарных путей-циклов аь
, ..., ag, bg (рис. 10), взятых с
некоторыми кратностями (т. е. по одной и той
же петле можно проходить несколько
раз, причем в разных направлениях).
Эти пути могут проходиться в
произвольном порядке. В результате
искомый интеграл |усо превращается в сумму
интегралов от 1-формы га по петлям д,
и bit проходимых, быть может, по
нескольку раз. Но эти отдельные
интегралы равны нулю в силу предположения:
все периоды формы вдоль базисных
циклов — нулевые. Следовательно, равен
нулю и интеграл формы по любому
замкнутому циклу. Лемма 6 доказана.
Поскольку ra=rf/, где / —построенная
выше функция, то мы доказали
точность любой замкнутой 1-формы с
нулевыми периодами по базисным
циклам. Следовательно, КегА^В1 и 1Г(т^
=R . Теорема 5 доказана.
Следствие. Двумерные замкнутые
многообразия розною рода не юмеоморфны и
зомотопически не эквивалентны.
В самом деле, мы имеем rf=R2*, где
g — род. Если ptq, то абелевы группы
пр и В» не изоморфны.
Следовательно, сфера с р ручками и сфера с q
ручками имеют разные группы когомологий. В
силу теоремы 1 эти многообразия гомо-
топически не эквивалентны. Этот факт
мы вывели ранее и из
гомотопической инвариантности групп гомологии.

112
2. Многообразия малой размерности
4.7. Алгоритм распознавания двумерных '
многообразий.
Элементы компьютерной двумерной геометрии
Рассмотрим множество замкнутых
связных компактных 2-многообразий.
Зададимся вопросом, который на
первый взгляд элементарен и ответ на
который вроде бы очевиден: что
означают слова «рассмотрим множество всех
двумерных многообразий»? Что
означает фраза «задать многообразие»?
С одним из вариантов ответа мы
знакомы. Задавая слово-код W и
соответствующий ему фундаментальный
многоугольник, мы задаем 2-многообразие,
склеивая стороны многоугольника.
Здесь мы задали многообразие его
кодом W. Однако если многообразие
задано каким-либо другим способом,
например алгебраическими
уравнениями, то выяснить, какой
фундаментальный многоугольник ему
соответствует,— сложная задача. Возникает
вопрос: как распознать двумерное
многообразие (например, сферу) среди
множества всех многообразий,
закодированных каким-то способом (вообще
говоря, отличным от описанного)? Как
мы знаем из главы 1, удобным
способом задания (кодирования)
2-многообразий является предъявление их
триангуляции. Напомним, что любое
гладкое многообразие можно
триангулировать. Занумеруем все треугольники,
ребра и вершины триангуляции и
укажем, по каким ребрам или по каким
вершинам склеены треугольники.
Например, запишем, что треугольники 5
и 15 склеены по ребру 9, а ребра
8 и 15 склеены по вершине 578.
В результате получим некоторую
таблицу. В главе 1 мы знакомились с
одним из ее вариантов — с матрицами
инциденций. Обозначим эту суммарную
таблицу через Т(М). Очевидно, она
позволяет однозначно восстановить 2-
многообразие. Итак, таблица Т(М)
может играть роль кода многообразия.
Мы можем задавать многообразия
такими таблицами. Этот способ удобен,
поскольку опирается на простой
принцип: мы указываем, «что с чем склеено».
Этот способ применим в значительно
более общей ситуации, чем способ
кодирования 2-многообразий при помощи
их фундаментальных многоугольников.
Дело в том, что если поверхность задана
уравнениями (или каким-то
геометрическим правилом), то обычно
поверхность всегда можно эффективно
разбить на достаточно мелкие
треугольники, начиная этот процесс с какой-то
точки и постепенно распространяя его на
всю поверхность. Иногда придется
возвращаться назад и подразделять
некоторые из уже построенных
треугольников на более мелкие (т. е. измельчать
разбиение), чтобы согласовать
триангуляцию на разных кусках поверхности.
Если поверхность компактна, то рано
или поздно процесс завершится. Важно,
что при этом на каждом шаге мы
работаем лишь на малом куске
поверхности.
Рис. 12
Пусть 2-многообразие реализовано в
пространстве как гладкая поверхность,
и на нее «высажен» маленький
геодезист с заданием составить точную
карту поверхности и установить ее
топологический тип. Он не видит всю
поверхность сразу, целиком, и ему трудно
ответить на вопрос: на каком именно
многообразии он оказался (рис. 12)?
Существует ли алгоритм, позволяющий
распознать поверхность, т. е. сказать,
ориентируема она или нет, сколько у нее
ручек или листов Мебиуса. Если
читатель серьезно вдумается в задачу, он
убедится, что ответ на вопрос
достаточно сложен. Простой обход поверхности
ничего на дает: непонятно, как
обнаружить ручки, как их пересчитать. Ин-

§4. Чем отличаются двумерные многообразия?
113
туитивно ясно, что выяснить, какой у
этой поверхности фундаментальный
многоугольник, просто разглядывая ее,
практически невозможно. Формальное
знание (которым геодезист
располагает) того факта, что у поверхности
существует какой-то фундаментальный
многоугольник, здесь бесполезно.
Однако, как мы уже знаем, у
геодезиста есть способ решить задачу, не
покидая поверхности. Опишем этот
метод еще раз. За конечное время
геодезист может нарисовать на
поверхности набор треугольников, чтобы
получить триангуляцию. ?>га работа
может оказаться трудоемкой, однако,
непрерывно двигаясь по поверхности,
иногда возвращаясь назад, можно
согласовать все треугольники. При этом
геодезист последовательно нумерует
(без повторов) все треугольники, ребра,
вершины. Результатом этой
картографической съемки будет таблица Т(М).
Конечно, процесс разбиения
многообразия на треугольники неоднозначен. Если,
ьапример, стереть уже построенную
триангуляцию и предложить геодезисту
повторить процесс, то через некоторое
• ^— оооо^роОо
I* *- ОоЯ?о<С>0<?0
?* *- ^О4Эр90Ф?9''—-
2* *~ ОСРООо^О
о
|Ь +~гъръ<РЬЪ?><о
* коды многообразий
Рис. 13
время он снова триангулирует
поверхность, и эта триангуляция почти навер-
>1яка будет отличаться от
первоначальной. Тем самым одному и тому же
многообразию можно сопоставить
бесконечное число таблиц Т(М),
кодирующих данную поверхность (рис. 13).
Итак, мы можем построить алгоритм
перечисления всех 2-многообразий и
получить в результате их список. Он
избыточен в том смысле, что одно и то
же многообразие представлено в
списке бесконечное число раз, т. е.
приобретает бесконечное число кодов.
Возникает проблема: как распознать по двум
кодам из списка, задают ли они одно и то
же многообразие или нет? Такой
алгоритм распознавания существует.
4.8. Вычисление эйлеровой
характеристики поверхности при помощи триангуляции
Здесь следует обратиться к материалу
главы 1. Напомним, что эйлерову
характеристику ^М) (см. выше) можно
вычислить по формуле: %(МУ=Ц)~Щ +
+щ , где щ — число вершин
триангуляции, П\ — число ребер, щ — число
треугольников. Поскольку геодезист уже
триангулировал исследуемую им
поверхность, он легко находит х№) и,
следовательно, ее топологический тип.
Ориентируемость или
неориентируемость поверхности он определяет
описанным ранее методом.
Составив матрицы инцидентности, можно
вычислять гомологии симплициальных
пространств, не являющихся многообразиями.
Эти матрицы фактически уже
известны геодезисту, если он составил
таблицу T(M)f отвечающую данной
триангуляции. Геодезист должен вычислить
все операторы границы (рис. 14), найти
Рис. 14
все циклы и границы (рис. 15). Затем,
пользуясь компьютером, он мажет
привести матрицы инциденций к нор-

114
2. Многообразия малой размерности
Рис. 15
мальной форме и вычислить группы
гомологии.
4.9. Комментарий к наглядному материалу
В § 4 описаны лишь простейшие методы
вычисления гомологии и когомологий.
Кроме них часто применяется метод
спектральных последовательностей.
См., например, [1, 5]. На рис. 16 — 19
изображены различные идеи, лежащие
в основе метода спектральных
последовательностей. В значительной мере этот
метод обобщает изложенный в главе 1
процесс нормализации
последовательности целочисленных матриц инциден-
ций (рис. 16 настоящего пункта). В
топологии часто встречается
пространство ОХ петель полиэдра X (рис. 20).
Он состоит из всевозможных
непрерывных отображений окружности (с
отмеченной точкой) в полиэдр X,
причем отмеченная точка окружности
всегда переходит в одну и ту же точку
полиэдра. Гомотопические группы
пространства петель ОХ совпадают с
гомотопическими группами полиэдра X
со сдвигом размерности на 1, т. е.
7t,(J?)=7tj-i(?lX). На рис. 20 показана
схема построения пространства Е(Х)
путей полиэдра X. Для этого нужно
рассмотреть все непрерывные
отображения отрезка I в X такие, что начало
отрезка отображается в одну и ту же
точку из X. Тогда возникает
расслоение ЕХ—>Х со слоем ОХ.
Пространство ЕХ стягиваемо (по себе в точку).
На рис. 21 предлагается еще один
взгляд на идею гомотопии — стекание
жидкости, аморфность и потеря
метрических свойств объекта. На рис. 22
изображен начальный этап
триангуляции двумерной поверхности,
необходимый для алгоритмического
выяснения топологической структуры
объекта, на котором находится геодезист
(см. пункт 4.7). При помощи "газовых
горелок" можно разрезать
поверхность на треугольники, после чего
склеить из них плоский
фундаментальный многоугольник — код
поверхности. На рис. 23 изображен
человек, деформирующий сферу с
дыркой, в результате чего получается
"раковина". На рис. 24 показана
бесконечная последовательность сфер,
на заднем плане — сфера,
подвергшаяся гомеоморфизму. На рис. 25
показаны гомеоморфные
преобразования двумерных поверхностей. На
рис. 26 изображена триангуляция
полиэдра, затем процесс его разрезания
на элементарные куски, блоки. В
результате полиэдр превращается в
хаотическое скопление симплексов
(или параллелепипедов), каждый
из которых, однако, помнит своих
соседей, поскольку матрицы ин-
циденций полностью восстанавлмг
вают полиэдр. Поэтому в случае
необходимости все блоки могут снова
собраться вместе и образовать
единый полиэдр. При этом необходимый
объем памяти отдельного блока
(симплекса) очень мал: он должен
помнить лишь своих
непосредственных соседей, с которыми он
инцидентен . Таким образом, сложную
систему можно эффективно
сконструировать из большого числа отдельных
элементов со сравнительно малой
памятью. На рис. 27, 28 показаны
двумерные поверхности, сферы с
ручками, отражена схема
деятельности геодезиста, составляющего
матрицу инциденций 2-многообразия,
на котором он находится. На рис. 29,
30 показаны "рогатые многообразия".

|5. Наглядные свойства трехмерных многообразий
115
§ 5. Наглядные свойства трехмерных многообразий
5.1. Разбиение (или диаграммы) Хегора
Задача классификации 3-многообразий
гораздо сложнее классификации
2-многообразий и до сих пор полностью не
решена, даже в случае замкнутых 3-
многообразий. Решение задачи
классификации состоит в построении двух
алгоритмов: алгоритма перечисления
многообразий (повторения допускаются) и
алгоритма распознавания
многообразий, который по каждым двум
многообразиям (их кодам) выясняет,
различны многообразия или нет. Имеется
несколько хороших алгоритмов
перечисления замкнутых 3-многообразий.
Полного алгоритма распознавания
3-многообразий до сих пор не построено.
Лишь недавно был открыт
замечательный алгоритм распознавания
стандартной сферы У (А. Томпсон, [50], [44]).
Хотя частичные алгоритмы, например в
классе так называемых 3-многообразий
рода 2, существовали давно.
Например, в 1973 г. Бирман и Хилден
в работе [84] свели задачу
распознавания стандартной сферы в классе
диаграмм Хегора рода 2 к известному
алгоритму Хауча распознавания
тривиального узла. Однако алгоритм Хакена
достаточно сложен и его фактическая
реализация на ЭВМ, по-видимому, пока
невозможна. Поэтому задача
эффективного распознавания стандартной
сферы при помощи простого и
наглядного алгоритма (допускающего
простую реализацию на компьютере) по-
прежнему оставалась актуальной.
Такой алгоритм (для рода 2) был
предложен и экспериментально
^разработан И. А. Володиным и А. Т.
Фоменко в 1974 г., реализован на ЭВМ
совместно с В. Е. Кузнецовым (см. [18]).
Окончательное обоснование
эффективности этого алгоритма было затем дано
в работе Хомма, Очая, Такахаши [19] в
1980 г. Подробное и наглядное
изложение алгоритма дано в книгах [2, 12].
Здесь мы этот материал опустим.
Одним из наиболее употребительных
классических способов задания 3-
многообразий являются разбиение Хегора
и их модификации (диаграммы Хегора,
сети, специальные разбиения). Для
сокращения дальнейших формулировок
будем называть сферу с g ручками
кренделем (рода g). Вложив такой
крендель в В , можно рассмотреть
ограниченное им трехмерное многообразие
(тело), называемое полным (или
заполненным) кренделем рода g.
Пусть имеются два экземпляра Kg, К'
полного кренделя рода g и некоторый
гомеоморфизм h: dKg-+ dK'g их краев.
Склеив крендели по этому
гомеоморфизму, получим замкнутое ^многообразие
М. Отметим, что многообразие М
представляется в виде объединения двух
лежащих в нем полных кренделей (образов
кренделей Kg и К. при склейке).
Определение 1. Разбиением Хеюра
замкнутого ориентируемого 3-многооб-
разия М называется его представление
в виде объединения двух лежащих в
нем полных кренделей с общим краем.
Так как края кренделей совпадают, то
их род одинаков. Он называется рейдом
разбиения Хегора.
Теорема 1. Любое замкнутое
ориентируемое 3~многообразие дотекает
разбиение Хеюра некоторого рода.
Доказательство теоремы проводится
теми же приемами, что и
доказательство теоремы классификации
двумерных поверхностей. Предварительно
введем очень важное понятие ручки.
Нусгь__М является м-многообразием
и h: Sx xD*"A-> дМ некоторое
вложение. Тогда говорят, что
многообразие Mf=MUh{DAxD ^получено из
многообразия М приклеиванием пг
мерной ручки индекса X. Образ
многообразия D xD *~ в многообразии
Mi при склейке называется ручкой,
многообразие h{Sх xD ""*) —

116
2. Многообразия малой размерности
ее основанием. Диск, лента и заплата
из доказательства теоремы 2 § 3
являются двумерными ручками индексов
О, 1 и 2 соответственно. Приклеивание
ручки индекса 0 к л-многообразию
состоит в добавлении отдельно
взятого л-шара; приклеивание ручки
индекса л — в заклеивании сферической
компоненты края л-шаром. Примеры
трехмерных ручек индексов 1 и 2
изображены на рис. 1.
Рис. 1
Говорят, что л-многообразие
разбито на ручки, если оно получено из
шара последовательным приклеиванием
ручек различных индексов. Здесь имеет-
' ся следующая двойственность: любую
ручку индекса К приклеенную к
объединению предыдущих ручек, можно
рассматривать как ручку индекса п — К
приклеенную к объединению
оставшихся ручек.
Доказательство теоремы 1
проводится по следующей схеме. Сначала
доказывается, что произвольное 3-много-
образие можно триангулировать, т. е.
разбить на криволинейные тетраэдры
так, чтобы два любых тетраэдра либо
не пересекались, либо пересекались по
вершине, ребру или грани. Для этого
нужно уметь согласовывать
триангуляции евклидовых окрестностей точек.
Как доказал Мойс, в размерности 3
это всегда удается сделать. Нужно
отметить, что в старших размерностях
такого согласования, вообще говоря,
добиться нельзя.
Потом вершины, ребра,
треугольники заменяются на ручки индексов 0, 1, 2
соответственно. Оставшиеся «средние»
части тетраэдров являются ручками
индекса 3 (рис. 2).
Если две ручки индекса 0
соединяются ручкой индекса 1, то их
объединение можно объявить новой
ручкой индекса 0, уменьшив тем самым
общее число ручек. Двойственным
образом две ручки индекса 3, к которым
свободными сторонами примыкает
ручка индекса 2, можно объединить с
ней и объявить новой ручкой индекса
3. Повторяя это рассуждение, мы
придем к случаю одной ручки индекса О
и одной ручки индекса 3. Тогда
объединение ручки индекса 0 и ручек
индекса 1 является шаром с ручками, т. е.
полным кренделем. Его дополнение —
это объединение ручек индекса 2 и
ручки индекса 3, т. е. с двойственной
точки зрения объединение ручек
индекса 1 и ручки индекса 0, что также
является полным кренделем. В
результате получаем разбиение Хегора.
Очевидно, что единственное 3-мно-
гообразие рода 0 (т. е. получающееся
склеиванием двух шаров) есть сфера.
Сфера обладает также разбиением Хе-
Рис. 2

} 5. Наглядные свойства трехмерных многообразий
117
гора рода 1 (как, впрочем, и
разбиением Хегора любого большего рода).
Проще всего это можно увидеть из
формулы «дифференцирования»: S3 =
- 6{D2 XD*) = dD2 XD2[)D2X dD2t
где 3D2 X D2 и D2 X dD2 — крендели
рода 1 (полные торы). Если
отождествить симметричные относительно
иуля точки сферы d(D2 X D2), то
получится трехмерное проективное
пространство RP5. При отождествлении
Рис. 3
точек каждого из полных торов
получаются также полные торы. Таким
образом, мы построили пример
разбиения Хегора рода 1 многообразия RP3.
Построенные разбиения Хегора сферы и
проективного пространства можно
увидеть на рис. 3 и 4. Сфера S3 на
Вис. 3 представлена как пространство
:3, компактифицированное
«бесконечно удаленной» точкой. Один из торов
разбиения получается вращением круга
А вокруг оси /, которая вместе с
бесконечно удаленной точкой
составляет окружность. Дополнение к нему
разбивается на диски, каждый из
которых пересекает ось / ровно в одной
точке и получается вращением
соответствующей «соленоидальной» дуги.
Поэтому дополнение также является
полным тором. Отметим, что меридианы
р, Кур! 02
Рис. 4
и параллели полноторий при склейке
меняются местами: меридиан
становится параллелью, а параллель —
меридианом.
На рис. 4 пространство RP3
представлено как пространство R3 с
добавленными несобственными точками,
по одной для каждого направления
(класса параллельных прямых).
Изображенный однополостный гиперболоид
разбивает RP3 на два полных тора.
Меридиональный диск одного тора
совпадает с диском, натянутым на
горловое сечение гиперболоида,
меридиональный диск другого — составлен из
частей pi, {Ь плоскости, проходящей
через ось гиперболоида. В качестве
параллели обоих торов можно взять
прямолинейную образующую
гиперболоида.
5.2. Примеры трехмерных
многообразен
С простейшими трехмерными
многообразиями мы уже знакомы: это
стандартная сфера S3, задаваемая
уравнением (х1J + (х2J + (х3J +
+ (х4J з= 1 в евклидовом пространстве
R4, трехмерное проективное
пространство RP3, точками которого являются,
например, прямые в R\ проходящие

118
2. Многообразия малой размерности
через начало координат, прямое
произведение окружности на двумерную
сферу, т. е. S хУ и, наконец,
трехмерный тор i — прямое произведение
трех окружностей, т. е. S хЛ xS . Кроме
того, в конкретных приложениях часто
встречаются так называемые линзовые
пространства (или просто "линзы")
Lpq, которые определяются так.
Рассмотрим сферу У, стандартно
вложенную в FT, отождествленное с
комплексным пространством (J(zfw). При
этом сфера задается уравнением \z\ +
+ |w| =1. Рассмотрим действие абеле-
вой группы Ър на сфере У, задаваемое
формулой ы 2mg
(ztw) -> (е р • z, е р • w).
Линейное преобразование,
определяемое этой формулой, очевидно,
переводит сферу в себя. Рассматривая
итерации этого преобразования, мы задаем
действие других элементов группы Ър.
Факторизуя сферу по действию этой
группы (т. е. отождествляя точки,
получающиеся друг из друга
преобразованиями группы), мы получаем некоторое
новое пространство, которое и
называется линзовым. В частном случае,
рассматривая линзу Lzt\ при /*=2, мы
получаем проективное пространство. В этом
случае действие группы 7% задается
формулой (ztu>)—>(— zy—w) ,
определяющей инволютивное преобразование
сферы в себя. Каждая ее точка
переходит в диаметрально противоположную.
Новые трехмерные многообразия
можно получать еще и таким способом.
Пусть даны два «-многообразия М} и
М2. Выделим в каждом из них п-
мерный шар D и удалим его. Получим
два многообразия с краем, гомеоморф-
ным сфере 5й. Рассмотрим цилиндр
(трубку) $х$*~х, где .D1 — отрезок.
Край цилиндра состоит из двух сфер.
Приклеим эти сферы к граничным
сферам многообразий M\\D и M^\D
(рис. 5). Получим новое
многообразие, обозначаемое через М\ #Мг и
называемое связной суммой
многообразий М\ и М2. Заметим, что углы,
I*. * f
Li* *iJ
4
\ /
5
) V
Рис. 5
возникшие в результате приклейки
цилиндра (трубки) к дыркам, можно
сгладить, как показано на рис. 5, так
что в результате склейки действительно
получается гладкое многообразие.
Операция взятия связной суммы
особенно наглядно демонстрируется на
примере 2-многообразий (рис. 6). Если
мы возьмем связную сумму сферы с
любым многообразием, то ничего
нового не получим: результат будет го-
меоморфен исходному многообразию
(рис. 6), т. е. ЛГ^УаМ*. В
частности, У*# ...#5"= 5". Связная сумма
двух торов дает крендель. Вообще
связная сумма 2-многообразия с тором
эквивалентна приклейке одной ручки.
Таким образом, любое замкнутое
ориентируемое связное 2- многообразие,

§5. Наглядные свойства трехмерных многообразий
119
т. е. сфера с ручками, получается в
результате взятия связной суммы
соответствующего числа торов. В этом
смысле "независимыми"
многообразиями являются сфера S и тор i (в
классе ориентируемых многообразий!.
Остальные ориентируемые
многообразия разлагаются в связные суммы
Рис. 6
этих многообразии. На этом основании
можно дать следующее естественное
определение. Многообразие М
называется неприводимым (в топологическом
смысле), если любая двумерная сфера в
нем ограничивает трехмерный шар.
Неприводимое многообразие нельзя
представить в виде связной суммы двух
многообразий Mi и Мг, отличных от
стандартной сферы, т. е. M*Mi#M2.
Остальные многообразия называются
приводимыми. Следовательно,
многообразие М приводимо, если М=М]#М2, где
М,аз , г=\;2. Единственное
исключение — многообразие Ух5 (и косое
произведение У на S в неориентируе-
мом случае), которое приводимо, но не
распадается в нетривиальную связную
сумму. При этом стандартная сфера
считается неприводимым многообразием
(хотя распадается в связную сумму
произвольного числа сфер).
5.3. Эквивалентность разбиений Хегора
Два разбиения Хегора 3-многообразия
М называются эквивалентными, если
существует гомеоморфизм
многообразия М на себя, переводящий
поверхность Хегора (т. е. общий край
кренделей) одного разбиения в поверхность
Хегора второго разбиения. По этому
поводу имеется следующая информация.
1) Любые два разбиения Хегора сферы
одинаковою рода эквивалентны
(результат Вальдхаузена).
2) Любые два разбиения рода
1 многообразия рода 1 эквивалентны.
3) Существуют не эквивалентные
разбиения рода 2 связной суммы двух
линзовых пространств.
4) Любые два разбиения Хегора одною
и тою же многообразия стабильно
эквивалентны, т, е. становятся
эквивалентными после применения к каждому из
них нескольких операций стабилиза-
ifuu — локального добавления к кренделю
разбиения тривиальной ручки (рис. 7).
Отметим, что ни один из этих фактов
не является тривиальным. Первый до-
Рис. 7 ^И^^
пускает красивую переформулировку
на языке гомеоморфизмов поверхности
кренделя. Обозначим через ср
гомеоморфизм поверхности стандартного
кренделя, переводящий его меридианы
в параллели. Тогда юмеоморфизм
h задает сферу тогда и только тогда,
когда h имеет вид a q>b, где
гомеоморфизмы а и b продолжаются
-на внутренность полною кренделя.
Структура группы гомеоморфизмов по-

120
2. Многообразия малой размерности
верхности кренделя хорошо известна.
Ликориш нашел образующие, Вэйн-
риб — соотношения (см., например,
РЖ- 1984. 4А597). Структура группы
гомеоморфизмов полного кренделя
также хорошо известна. См. обзор этих
результатов, например, в [12].
Задача алгоритмического распознавания
сферы сводится к задаче
распознавания двусторонних классов смежности
известной группы по известной
подгруппе.
Из второго факта легко получается
топологическая классификация
линзовых пространств (без использования
кручения Радемайстера).
С помощью четвертого факта
задача классификации всех 3-многообразий
сводится к задаче классификации
двусторонних классов смежности
стабилизированной группы гомеоморфизмов
поверхности кренделя по
стабилизированной группе гомеоморфизмов полного
кренделя.
Пусть М3 представлено в виде
объединения двух полных кренделей
Kg, Kg с общим краем Hg = dKg = dKg.
Меридианы кренделей Kg, Kg образуют
систему кривых на 2-многообразии Hgy
которое можно считать стандартным.
Эта система кривых называется
диаграммой Хегора многообразия М3. Для
того чтобы кривые о, Сг,. - -, cgy с\у
с'2, . . . ,c'g на Hg образовали диаграмму
Хегора некоторого многообразия М ,
необходимо и достаточно, чтобы
выполнялись условия: 1) кривые с, не
пересекались, и после разреза по ним
получалась связная поверхность, 2) то
же самое, для кривых с'. Иногда
диаграммой Хегора называют систему
кривых [с!\ на крае Кв (или систему
кривых {с,} на крае Kg).
Соответствующее 3-многообразие получается
приклеиванием g ручек индекса 2 (толстых
дисков) к К8 по кривым {с!\ и одной
ручки индекса 3 (шара).
5.4. Спайны
Понятие спайна (от англ. spine —
хребет, костяк, остов; не путать со
«сплайном») служит удобным способом
задания 3-многообразий и основано на
идее сведения изучения 3-многообразий
к изучению полиэдров размерности 2.
Кодирование 3-многообразий спай-
нами удачно с точки зрения
последовательного перечисления
многообразий по мере возрастания их
«сложности» (см. об этом ниже). Теория
спайное и ее приложений к задачам
трехмерной топологии (в том числе и
компьютерной геометрии) получила
глубокое развитие в работах С. В.
Матвеева. Некоторые из его результатов,
допускающие особенно наглядную
интерпретацию, мы изложим в настоящем
параграфе. Подробности см. в [34, 52].
Определение 2. Полиэдр Р cz М
называется спайном п-многообразия М
с краем, если М — Р « дМ X @, 1 ].
Полиэдр Р называется спайном
замкнутого п-многообразия, если Р
является спайном многообразия М — IntD",
где IntD" — открытый я-шар в М.
Рис. 8
Пример спайна многообразия, гоме-
оморфного диску, изображен на рис. 8.
На рис. 9 видно, что любое
дерево (граф без циклов) в шаре или
сфере любой размерности является

I 5. Наглядные свойства трехмерных многообразий
121
спайном шара или сферы. Окружность
является естественным спайном кольца
S1 X / и листа Мебиуса. Для любого
М с непустым краем многообразие М—
О (дМ), где О (JVf) —«воротник» края,
является спайном М,
Рис. 9
Рис. 10
симплициальный комплекс (например,
триангулированное многообразие), а"—
его главный открытый симплекс, т. е.
симплекс, не являющийся гранью
никакого симплекса из /С, и пусть Ья~1 —
его свободная грань, т. е. грань, не
являющаяся гранью никакого другого
симплекса из /С. Тогда операция от-
брасыванйя от комплекса /С симплексов
а и б называется элементарным кол-
лапсированием (стягиванием). На
рис. 10 изображены коллапсирования
размерности 1, 2 и 3. Коллапсиро-
ванием называется последовательность
элементарных коллапсирований. Под
коллапсированием полиэдра
понимается коллапсирование какой-нибудь его
триангуляции. В этом случае
элементарные коллапсирования можно укрупнить:
можно включить в их число
отбрасывания п-клеток вместе с их
свободными (п — 1)-гранями (рис. 11).
Оказывается, понятие
коллапсирования н понятие спайна очень тесно
связаны между собой.
'червяк выел яблоко'
Рис. tt
Вряд ли имеет смысл рассматривать
все возможные спайны многообразия.
Удобно ограничиться так называемыми
неколлапсируемыми (или
несжимаемыми, замкнутыми, неуменьшаемыми
и т.д.) спайнами. Напомним
определение коллапсирования. Пусть К —
Теорема 2. Если Р — спайн
многообразия М и Р коллапсируется на Q,
то Q — спайн многообразия М.
Доказательство этой теоремы
состоит в том, что структуру прямого
произведения М — Р « дМ X @, 1]
можно локально (в окрестности
рассматриваемых симплексов) изменить
так, чтобы получить структуру прямого
произведения на М — Q. Возможность
такого изменения достаточно проверить
для стандартного симплекса в
евклидовом пространстве (рис. 12),
поскольку все симплексы в многообразии

122
2. Многообразия малой размерности
Рис. 12
расположены стандартно с точностью
до гомеоморфизма»
Назовем спайн неколлапсируемым,
если его нельзя сколлапсировать на
меньший спайн. Из приведенных выше
примеров спайнов только окружность
(спайн кольца и листа Мебиуса) и
точка (спайн шара или сферы) некол-
лапсируемы — по причине «отсутствия
начала», т. е. свободных граней, с
которых можно было бы начинать кол-
лапсирование. Нетрудно доказать, что
точка — единственный неколлапсируе-
мый спайн двумерной сферы
(двумерного диска). Действительно, некол-
лапсируемый спайн 2-диска не может
содержать 2-симплексов, так как тогда
нашелся бы 2-симплекс со свободной
гранью. Поэтому он должен быть
полиэдром размерности, не превосходящей
единицы, причем гомотопически
стягиваемым полиэдром, т. е. деревом.
Единственное дерево без свободных
вершин — это точка. Первая часть этого
рассуждения проходит для любой
размерности.
Теорема 3. Любой спайн п-много-
образия коллапсируется на полиэдр
размерности, не превышающей л — 1.
В частности, любое п -многообразие
имеет спайн размерности < п — 1.
Вторая часть рассуждения,
показывающая, что все одномерные спайны
диска коллапсируемы в точку, не
проходит уже в размерности три: есть
примеры неколлапсируемых двумерных
спайнов сферы S3. Одним из таких
примеров является так называемый ¦
«дом Бинга» с двумя комнатами,
изображенный на рис. 13 и знакомый
нам по материалу главы 1. Коллап-
Рис. 13
сирование шара на него происходит
так. Сначала мы через верхний диск
по трубке проникаем внутрь нижней
комнаты и исчерпываем ее вплоть до
перепонки между трубкой и стенкой.
Потом через нижний диск по трубке
проникаем внутрь верхней комнаты и
исчерпываем ее вплоть до перепонки
между вехней трубкой и стенкой.
Другой пример неколлапсируемого
двумерного спайна шара — «шутовской
колпак», изображенный на рис. 14.
Он получается из треугольника
отождествлением сторон. И «дом Бинга», и
«шутовской колпак» неколлапсируемы
по причине «отсутствия начала» кол-
лапсирования. Эти примеры
показывают, что одно и то же многообразие

§5. Наглядные свойства трехмерных многообразий
1ZJ
Рис. 14
Рис. 25
может иметь несколько различных
спайное. Другая неоднозначность,
которая имеется в этом вопросе, состоит
в том, «по различные многообразия
могут иметь яжеоморфные
(одинаковые) спайны. Другими словами,
полиэдр может утолщаться до
многообразия несколькими способами, если хотя
бы одно утолщение существует. На рис.
15 изображены примеры двух утолщений
окружности с диаметром до
многообразия размерности два. Это — "настоящая
пряжка", т. е. диск с двумя дырками,
и "пиратская пряжка" — т. е. тор
с дырой. На рис. 16 аналогичные
Рис. 16
примеры приведены для многообразий
размерности 3: полный тор с двумя
удаленными шарами и многообразие
ЗгхЗ1 с двумя удаленными шарами имеют
один и тот же двумерный спаян —
поверхность тора с двумя дисками,
приклеенными по меридиональным кривым.
5.5. Специальные спаЙшы
Понятие сющмьного спаина вводится
для того, чтобы ликвидировать вторую
неоднозначность — возможность
существования нескольких различных утолщений.
Определение 3. Двумерный полиэдр Р
называется егшрюлггным, если
выполнены следующие условия:
1) каждая его точка имеет замкнутую
окрестность, гомеоморфную либо
диску, либо конусу над окружностью с
двумя или тремя радиусами ( рис. 17);
2) каждая компонента связности
неособых точек (т. е. точек, имеющих
окрестность первого типа) является 2-диском.
Множество особых точек
специального полиэдра представляет собой
регулярный граф степени 4, т. е. граф, из
каждой вершины которого исходит
ровно 4 ребра. Отметим, что особен-

124
2. Многообразия малой размерности
Рис. 17
ности именно указанных выше типов
наблюдаются у мыльных пленок
(принципы Плато). См. об этом в книге
А. Т. Фоменко [12].
Спайн 3-многообразия называется
специальным, если он является
специальным полиэдром. Ясно, что каждый
специальный спайн неколлапсируем.
Примером специального спайна 3-сфе-
ры является «дом Бинга>. Он имеет
ровно 2 вершины (точки третьего типа),
три 2-компоненты (компоненты
связности неособых точек), а множество
его особых точек имеет вид,
показанный на рис. 18.
ооо
Рис. 18
Теорема 4. Любое 3-многообразие
имеет специальный спайн.
Идея доказательства следующая.
Разобьем многообразие М на ручки:
по одной ручке индекса 0 для вершин,
по одной ручке индекса 1 для ребер
и по одной ручке индекса 2 для 2-
симплексов какой-нибудь его
триангуляции. Ручки индексаг 3 отвечают 3-
симплексам (рис. 19). Объединение Р0
краев этих ручек представляет собой
специальный полиэдр (это видно
непосредственно). Обозначим через Мо
многообразие, получающееся
удалением открытого шара из внутренности
каждой ручки. Тогда ясно, что Р0
является специальным спайном
многообразия Мо. Из него можно получить
спайн Р многообразия Af, протыкая его
2-компоненты и соединяя тем самым
удаленные шары в один шар. Если
край многообразия М не пуст, то и его
нужно проткнуть в одном месте. Спайн
Рис. 19
Р будет иметь свободные ребра,
возникшие на краях пробитых дыр,
поэтому допускает коллапсирование и не
приводит, вообще говоря, к
специальному спайну. Однако если
протыкания сделать аккуратно, чтобы
свободных ребер не возникло, то
получится специальный спайн. Такое
аккуратное протыкание с помощью так
называемых арок изображено на рис. 20.
Это же рассуждение показывает, что
любое 3-многообразие имеет
бесконечное число различных специальных спай-
нов.
Преимуществом специальных спай-
нов является возможность
однозначного восстановления 3-многообразия по
его специальному спайну. Это
означает, что специальный спайн несет в
себе всю информацию о топологической
структуре многообразия.
Теорема 5 (см. [64]). Если два
3-многообразия имеют гомеоморфные
специальные спайны, то они гомеомор-
фны.
Идея доказательства состоит в
следующем. Так как окружность с тремя

f 5. Наглядные свойства трехмерных многообразий
125
Рис. 20
радиусами вкладывается в двумерную
сферу единственным с точностью до
гомеоморфизма образом, то окрестности
вершин специального полиэдра
утолщаются до шаров единственным образом.
Это утолщение единственным образом
продолжается до утолщения ребер
специального полиэдра. Остается
доказать, что возникшее при этом
утолщение окрестности границы каждой
2-компоненты, т. е. прямое
произведение этой окрестности на отрезок,
продолжается до утолщения (т. е. прямого
произведения на отрезок) самой
2-компоненты единственным образом. Это
легко следует из того, что все
2-компоненты являются клетками — именно
лпя этого и накладывалось это условие.
Аналогичное рассуждение показы-.
вает, что окрестность множества
особых точек любого специального
полиэдра (не обязательно спайна
какого-нибудь 3-многообразия) утолщается
до 3-многообразия. Продолжению этого
утолщения до утолщения 2-компонент
может мешать нетривиальность
расслоения на отрезки, возникающего в
окрестности границы. Такая помеха
встречается реально: пусть специальный
полиэдр получен приклеиванием диска к
проективной плоскости по проективной
прямой. Тогда он не вкладывается ни
в какое 3-многообразие именно по
указанной причине. Таким образом, не все
специальные полиэдры являются спай-
нами 3-многообразий, т. е. утолщаются.
Но если уж специальный полиэдр
утолщается, то утолщается однозначно!
5.6. Фильтрация 3-многообразий
¦о сложности
Из теоремы 5 следует, что задана
перечисления 3-многообразий сводится
к задаче перечисления утолщаемых
специальных полиэдров.
Важное обстоятельство: для
каждого числа k существует, только конечное
число различных 3-многообразий,
имеющих специальные спайны с k
вершинами. Перечисление всех специальных
полиэдров с k вершинами можно
произвести так. Сначала нужно построить
все регулярные графы степени 4 с k
вершинами. Это сделать нетрудно.
Потом для каждого такого графа Г
нужно перебрать все специальные
полиэдры, множество особых точек
которых гомеоморфно графу Г. Для этого
нужно поступить так. Вложим граф Г
в R3 и заменим каждую его
вершину на так называемую «деталь», го-
меоморфную конусу над окружностью
с тремя радиусами (рис. 21).
Окрестности тройных точек границы
детали — триоды (на рис. 21 они
выделены) — должны соответствовать
ребрам графа, исходящим из данной
вершины. Для каждых двух триодов,
отвечающих одному и тому же ребру
графа Г, выберем гомеоморфизм одного
из них на другой и склеим детали
по выбранным гомеоморфизмам. Край
получившегося полиэдра Ро (т. е.
множество точек свободных ребер какой-
нибудь его триангуляции) состоит из
нескольких окружностей. Заклеив эти
окружности 2-дисками, получим
специальный полиэдр, множество особых
точек которого совпадает с графом Г.
Ясно, что любой специальный полиэдр
с графом Г в качестве множества
особых точек можно получить таким

126
2. Многообразия малой размерности
Рис. 21
способом. Проанализируем произвол,
допущенный при построении. Он
заключается в выборе гомеоморфизмов,
по которым склеиваются триоды. Для
каждых двух триодов имеется 6
способов их отождествления, из которых 3
реализуемы внутри пространства
(будем называть их четными), а 3 не
реализуемы в R3 (будем называть их
нечетными). См. рис. 22.
1 1
/123
U 23
/123
\2 3 1
/123
\31 2
Рис. 22
А А
1 23
2 1 3
1 23
1 32
1 2 3
32 1
Таким образом, имеется ровно 6
возможностей, где k — число вершин, 1к —
число ребер. Перебрав все эти
возможности, получим все специальные
полиэдры, отвечающие графу Г. Задача
выделения утолщаемых полиэдров не
вызывает? затруднений: полиэдр Р утолщаем
тогда и только тогда, когда при обходе
каждой окружности на границе полиэдра
Pq нечетные склейки встречаются четное
число раз. Можно показать, что
существует не более т~1** утолщаемых до
ориентируемого 3-многообразия
специальных полиэдров, отвечающих графу Г.
Отметим связь описанной конструкции
с диаграммами Хегора, см. конец пункта
5.3. Пусть замкнутое ориентируемое 3-
многообразие М имеет специальный
спайн Р, полученный приклеиванием
дисков к склеенному из деталей полиэдру Pq.
Рис. 23
Утолстим каждую деталь так, как это
изображено на рис, 23.
Топологически утолщенная деталь
представляет собой 3-шар с четырьмя
выделенными дисками на его крае, каждые
два из которых соединены выделен-

{ Б. Наглядные свойства трехмерных многообразий
127
ной дугой. После склеивания
утолщенных деталей получается полный
крендель. Из выделенных дуг склеятся
простые замкнутые кривые на его
поверхности, которые образуют диаграмму
Хегора многообразия М. Таким
образом, любое замкнутое ориентируемое
многообразие М имеет диаграмму
Хегора очень специального вида, склеенную
из стандартных кусков (утолщенных
деталей). Для любого числа к имеется
только конечное число специальных
диаграмм рода k — это обстоятельство
выгодно отличает их от обычных
диаграмм (которых бесконечно много).
Конечность числа многообразий,
имеющих специальные спайны с < k
вершинами, приводит к естественной
мысли взять в качестве сложности 3-
многообраэия М число вершин в его
минимальном (по числу вершин)
специальном спайне. Эта характеристика
хороша тем, что имеется только
конечное число 3-многообразий сложности Л.
Однако у нее есть недостатки:
во-первых, сложность сферы оказывается
равной 1, в то время как сложность
многообразия Lza оказывается равной
нулю. На рис 24 изображена окрест-
Рис. 24
ность особого графа минимального
специального спанна сферы, на рис. 25 —
окрестность особого графа
минимального спайна линзы L3,i, который
представляет собой треугольник с
отождествленными согласованно
ориентированными ребрами (будем называть его
«мебнусовым колпаком»).
Во-вторых, сложность связной
суммы двух многообразий не равна,
вообще говоря, сумме их сложностей.
Появление этих двух недостатков выз-
Рис. 25
вано одной и той же причиной: не-
коллапснруемый подполиэдр
специального полиэдра не обязан быть
специальным. Введем понятие почти
специального полиэдра, свободное от этого
недостатка.
Определение 4. Неколлапсируемый
полиэдр Р называется почти
специальным, если каждая его точка имеет
окрестность, гомеоморфную либо
полиэдру размерности <1, либо объеди-
Рис. 26
нению такого (может быть, пустого)
полиэдра с конусом над окружностью,
окружностью с двумя или тремя ради-
усами.
Точки, в любую окрестность которых
входит конус над окружностью с 3
радиусами, называются вершинами
почти специального полиэдра. Каждый
почти специальный полиэдр
представляет собой объединение одномерного
полиэдра и двумерного полиэдра,
который отличается от специального тем,

128
2. Многообразия малой размерности
что может иметь не гомеоморфные
диску 2- компоненты. Пример почти
специального полиэдра изображен на
рис. 26. Свойство полиэдра быть почти
специальным сохраняется при переходе
к неколлапсируемому подполиэдру. Это
легко следует из определения.
Определение 5. Сложность 3-много-
образия равна к, если оно имеет почти
специальный спайн с к вершинами и не
имеет почти специальных спайнов с
меньшим числом вершин.
Многообразия У,52х5 , RP\ L^
имеют сложность нуль. Их минимашг
ными почти специальными спайнами
являются точка, букет сферы и
окружности, проективная плоскость и меоиу-
сов колпак соответственно. Связные
суммы этих многообразий также имеют
сложность 0. Оказывается, других
замкнутых ориентируемых
многообразий сложности 0 не существует.
Теорема 6 (С. В. Матвеев). Пусть
сложность замкнутого ориентируемою
3-многообразия М равна k Тогда М=#Ж,
где каждое М; гомеоморфно 52х5 , RP^,
L3]l или имеет спеьашлънъш. спайн Рг,
число вершин которою совпадает со
сложностью к+ многообразия М,. При
этом справедливо равенство k=Xi к, •
Идея доказательства такова. Если
минимальный почти специальный спайн
Р многообразия М содержит точки с
одномерными окрестностями, то он
содержит главное ребро, т. е. ребро, к
которому не примыкает двумерная
часть полиэдра Р. После разрезания
этого ребра спайн Р либо распадается
на две части, что отвечает разложению
многообразия в связную сумму, либо
не распадается, что отвечает
выделению слагаемого S xS . Если какая-
нибудь 2-компонента полиэдра Р
содержит не ограничивающую диск
простую замкнутую кривую, то нужно
разрезать полиэдр Р по ней и заклеить
одну из возникших после разрезания
окружностей диском. При этом
многообразие распадается в связную сумму
двух многообразий с более простыми
спайнами. Если же спайн Р не
содержит главных ребер и все простые
замкнутые кривые в его 2-компонентах
ограничивают диски, то он либо
является специальным полиэдром, либо го-
меоморфен Ю*, что отвечает случаю
проективного пространства.
Доказательство неравенства ?kj>k очевидно, так
как если соединить минимальные почти
спайны многообразий М, дугами, то
получится почти специальный спайн
многообразия М. Доказательство
обратного неравенства 2j kj<k производится при
помощи теории нормальных
поверхностей Хакена и довольно громоздко.
Из этой теоремы вытекает
упоминавшийся выше результат о замкнутых
ориентируемых многообразиях
сложности 0, так как единственным
специальным спайном с 0 вершин является
мебиусов колпак. Из теоремы
получается, что с точностью до связных сумм
с многообразиями S х5 , RP% Z^i
существует только конечное число
замкнутых многообразий сложности к.
Другими словами, если ограничиться
замкнутыми ориентируемыми
многообразиями , не содержащими неразби-
вающих сфер, проективных плоскостей
и мебиусовых колпаков, то имеется
лишь конечное число таких
многообразий сложности к, причем минимальный
почти специальный спайн такого
многообразия является специальным.
5.7. Упрощение специальных спайнов
Как отмечалось выше, 3-многообразие
может иметь бесконечное число
различных специальных спайнов. Как
связаны различные специальные спайны
одного и того же 3-многообразия? Как
описать множество всех его
специальных спайнов, как среди них выделить
минимальный? Опишем прием,
называемый перекладкой 2-компоненты,
который позволяет из одного специального
спайна получать другие. Для простоты
ограничимся случаем замкнутых
3-многообразий. Пусть Р — специальный
спайн замкнутого 3-многообразия М и
пусть Da М — такой, не имеющий с Р
общих внутренних точек, диск в М, что
кривая dD лежит в Р и находится

13. Наглядные свойства трехмерных многообразий
129
в общем положении к его особому
графу Г. Это означает, что кривая ди
не проходит через вершины графа Г и
пересекает его ребра трансверсалыю.
Диск D разбивает открытый шар М —
Р на два шара Vj и 1^. Важный и легко
проверяемый (исходя из структуры
особых точек полиэдра Р) факт: пересе-
Оказывается, что даже этих
простейших перекладок достаточно, чтобы
перевести один специальный спайн 3-
многообразия в любой другой его
специальный спайн.
Теорема 7 (С. В. Матвеев)., Два
специальных полиэдра тогда и только тогда
являются специальными стйнами од-
Рис. 27
чение К замыканий шаров V\ и %, т. е.
их общая граница, является замкнутым
2-многообразием, целиком состоящим
из 2-компонент полиэдра Р UD,
Полиэдр Р UD является специальным
спайном многообразия М с двумя
удаленными шарами. Если мы проткнем диск
D, то вернемся к спайну Р
многообразия М с одним удаленным шаром, т. е.
просто к спайну многообразия М.
Однако если мы проткнем одну из 2-
компонент на поверхности К, то после
коллапсирования получим другой
специальный (или почти специальный)
спайн Pi многообразия М. На рис. 27
изображены две простейшие
перекладки 7t и Тч, которые производятся в
окрестности вершины или ребра
полиэдра Р. Обратные преобразования 77
и i 2 также являются перекладками.
ною и того же 3-многообразия, когда
их молено соединить цепочкой
преобразований Т^\ Т^\
Доказательство этой теоремы
основано на том, что любые две триангуляции
3-многообразия имеют общее
подразделение.
Отметим, что сложность (число
вершин) специального полиэдра при
преобразовании Ti возрастает на 2, а при
преобразовании 7*2 — на 1. Проанализируем,
как изменяется сложность специального
полиэдра при произвольной перекладке.
Пусть кривая oD пересекает граф Г в к
точках и пусть граница протыкаемой 2-
компонеяты а поверхности К содержит
m вершин. При приклеивании к
полиэдру Р диска D число его вершин
увеличивается на к, при протыкании 2-
компоненты а и коллапсировании —

130
2. Многообразия малой размерности
уменьшается не менее чем на т.
Поэтому сложность fj(P\) получившегося в
результате перекладки специального
полиэдра Р\ не превосходит р(Р}±к-т ,
где //(Р) — сложность полиэдра Р.
Будем называть перекладку упрощающей,
если /4Р\ )< /i(P), и уравновешенной,
если /л(Р\}= М.Р)- Число к будем называть
степенью перекладки. Некоторый опыт
работы со спайнами показывает, что
особенно важны перекладки степени <6.
Гипотеза. Любой специальный спайн
3-многообразия сводится к любому
минимальному (в смысле числа вер-
гиин) с помощью упрощающих и урав-
новегиенныл перекладок степени <б.
Отметим, что из положительною ре-
тения этой гипотезы вытекала бы
возможность алгоритмического
распознавания юмеоморфных 3-многообра-
зий. Это следует из конечности числа
специальных полиэдров фиксированной
сложности и из того, что перекладки
фиксированной степени можно
применить к данному специальному полиэдру
также конечным числом способов.
Пусть Р\ и Р2 — специальные спайны
многообразий М\, М2. Будем применять к
ним упрощающие и уравновешенные
перекладки до тех пор, пока это
возможно. Если два получившихся конечных
множества специальных спайнов
пересекаются, то Mi и М2 гомеоморфны, если
нет, то Mi и Ы2 различны.
Обоснованием справедливости
гипотезы служат следующие соображения:
1) гипотеза справедлива для всех
многообразий сложности <6. На самом деле,
здесь достаточно перекладок степени ^4;
2) гипотеза справедлива для серии
специальных спайнов сферы, которые
строятся каноническим образом по
диаграммам Хегора сферы, упрощаемьк методом
"волны" Володина — Фоменко [12];
3) гипотеза справедлива для специальных
спайнов сферы, полученных описанной
при доказательстве теоремы 4
конструкцией из "комбинаторно разбираемых" (т. е.
после удаления 3-симплекса коллапсируе-
мых в точку) триангуляции сферы.
Вьаделим наиболее простые и поэтому
легко применимые на практике частные
случаи упрощающих перекладок —
упрощение по противоходу и по короткой
граничной кривой. Напомним, что
любой специальный полиэдр получается
из некоторого регулярного графа
степени 4 приклеиванием нескольких 2-
дисков по некоторым отображениям их
граничных окружностей.
Соответствующие этим отображениям кривые в
графе будем называть граничными
кривыми 2-компонент. Скажем, что
граничная кривая имеет противоход, если
она проходит по одному из ребер
графа два раза в противоположных
направлениях. Скажем, что граничная кривая
короткая, если она проходит не более
чем по трем вершинам графа, причем
по каждой из них не более одного раза.
Рис. 28
Теорема 8. Если спещшльньал спайн
замкнутою 3-мноюобразия имеет
граничную кривую с противоходом или
короткую граничную кривую, то он не
минимален.
Доказательство. Пусть в специальном
спайне Р замкнутого S-многообразия М
есть граничная кривая с противоходом.
Тогда в М найдется не имеющий с
полиэдром Р общих внутренних точек диск D,
край которого содержит ровно одну
особую точку и лежит в 2-компоненте с
противоходом на границе (рис. 28).
Операция перекладки, состоящая в
добавлении к спайну Р диска Оив протыкании
одной из боковых стенок (как на рис. 28),

J5. Наглядные свойства трехмерных многообразий
131
шляется упрощающей. Действительно}
при протыкании и коллапсировании
исчезнут, по крайней мере, как
добавленная вершина, так и начинающиеся в ней
особые ребра вместе с другими
вершинами (их концами).
добавленный протыкание
диск
Рис. 29
*«1
добавленный
диск
Рис.30
протыкание
Пусть теперь в специальном спайне Р
замкнутого 3-многообразия М есть 2-
компонента а с короткой граничной
кривой, проходящей через fe3
различные вершины. Если внутри
многообразия приклеить к Р диск, параллельный
компоненте а, и проткнуть боковую
стенку получившегося цилиндра, то
после коллапсирования получится
почти специальный полиэдр с меньшим
числом вершин. Действительно,
добавляются к вершин, а исчезают по
крайней мере 2 при k=l и 4 при к=2, 3 (рис.
29,30)Г
Отметим, что указанные приемы
упрощения легко произвести реально и
фактически построить почти
специальный спайн с меньшим числом вершин.
Дом Бинта имеет как короткую
гранитную кривую, так и противоход. С
помощью любого из этих приемов он
упрощается до точки. Отметим, что в
случае граничной кривой длины 4 такая
перекладка является уравновешенной.
5Л. Применение ЭВМ в трехмерной
топологии. Перечисление многообразий в
порядке возрастания сложности
Результаты пунктов 5.6 и 5.7
позволяют организовать перебор всех
замкнутых ориентируемых многообразий (не
содержащих нераэбивающих сфер,
проективных плоскостей и мебиусовых
колпаков) с помощью ЭВМ. Такой
перебор многообразий сложности <5 был
произведен в 1972 г. С. В. Матвеевым и
В. В. Савватеевым и в расширенном
варианте (с захватом некоторых
многообразий сложности 6) повторен С. В.
Матвеевым в 1984 г. В 1986 г. С. В.
Матвеев перечислил все многообразия
сложности 6. В 1987 г. в работе С. В.
Матвеева и А. Т. Фоменко [74]
компьютер был использован при решении одной
из задач трехмерной топологии —
оценки наименьшего объема компактного
гиперболического многообразия.
Остановка на сложности 6 вызвана
как недостатком машинного времени
(каждый граф с 5 — 6 вершинами
обсчитывался 5 — 8 ч, в зависимости от
его типа), так и трудностью ручной
идентификации выданных машиной
многообразий. Принцип работы
программы таков. Вручную (в 1972 г.) или с
помощью ЭВМ (в 1984 г.) перебираются
регулярные графы степени 4 с данным
числом вершин. Затем каждый граф
вводится в машину, которая перебирает
все возможные склеивания триодов (см.
пункт 5.6) и граничные кривые
получившегося специального полиэдра

132
2. Многообразия малой размерности
подвергает следующим проверкам.
1) Есть ли граничная кривая длины
?3?
2) Есть ли противоход^
3) Получается ли при .склеивании
утолщенных деталей диаграмма Хегора
ориентируемого многообразия?
При положительном ответе на один
из первых двух вопросов или при
отрицательном ответе на третий вопрос
машина браковала выбор склеивания
триодов и переходила к следующему
варианту. В противном случае она
вычисляла одномерную группу гомологии
многообразия и результат выдавала на
печать вместе с системой склеек
триодов. Результаты машинного расчета
приведены в табл. 1-9. Таблицы
включают в себя все многообразия
сложности < 5 и многообразия сложности <
6, смоделированные на одномерном
остове октаэдра, длинной восьмерке и
замкнутой цепочке. Рядом с рисунком
графа стоят замкнутые ориентируемые
3- многообразия, смоделированные на
нем и выдерживающие проверку по
признакам 1, 2, 3. Здесь Lp4 обозначает
линзовое пространство с параметрами
Р* 41 j/G— мнообразие с конечной
фундаментальной группой,
универсальным накрывающим пространством
которого служит сфера У, другими
словами , фактор сферы по некоторому
свободному действию группы G.
Группы эти таковы:
1) Q* = {*, у; х2 = (хуJ « /},
где п>1\
2) Рм, Рщ, Р120 - {*, у; х2 = (ху? -
У\ *=1}, где п— 3, 4, 5 соответственно;
3) А*<2*и) = {** У! х2 = 1, у**1 = 1,
ху*'1 = У l)9TAfikZ 3, nZ 1;
4),Р«" {x'J> z; x% " Wi - у2»
«уг = лу, zxz = у, z = 1}.
Но всех случаях индекс внизу показы-
мт порядок групы;
5) прямые произведения
перечисленных выше групп на циклическую группу
гмимно простого порядка.
Известно, что эти группы могут
свободно и линейно действовать на сфере
У (Дж. Милнор). В частности, группы
Qinf ^24t Р* 1*/>1» являются
подгруппами группы У ( кватернионов
единичной длины). При двукратном накрыти-
ии j -> RP^ = 50C) эти подгруппы
двукратно накрывают группы
сохраняющих ориентацию симметрии
правильной я-угольной призмы (диэдра),
тетраэдра, октаэдра и додекаэдра
соответственно. Через 1 х I / (ас d) обозна-
начается 3-многообразие, получаещееся
склеиванием оснований прямого
произведения тора на отрезок по
гомеоморфизму, задающемуся указанной
матрицей. Через ( Й$,')\7*х//(§$|) обо-
значается многообразие, получающееся
отождествлением точек одного
основания прямого произведения Г х/по
инволюции с матрицей ( с\ d\), второго —
с матрицей (c22d22)-
Для каждого из многообразий,
подчеркнутых в табл. 1-3,в табл. 4-9
приведен рисунок окрестности графа его
минимального специального спайна.
Выбор этих многообразий произведен
по принципу первого появления в табл.
1-3. Исключение сделано для линзовых
пространств, минимальные специальные
спайны которых смоделированы на
длинных восьмерках и выглядят
однотипно. Поэтому мы ограничиваемся
одним произвольно взятым примером
каждой сложности.
Приведем список всех неприводимых
замкнутых ориентируемых
3-многообразий сложности ^ 5 с
некоммутативной фундаментальной группой.
Многообразия с коммутативной
фундаментальной группой сложности <, 5 имеют
род Хегора <, 1. Итак, SYQ8, S*/Q24,
Jj/Pa, У/ D2A,//Q*x Z3, f/ Qw,
J/ *». #P«. #/Ph r/Dnf/Q&Zb
fjQn \ 23, 53/ QgxZ,, y/Q12xZ5,
f/D+f/P&Zbf/Qn.

S • Наглядные свойства трехмерных многообразий
133
Таблица 1
л = 0
/7*1
л = 2
о
оо
3.1
4,1 ' иь,г
оооо
ООО:
6,1 ' L9,2' *-io,3 ' ^ 11,:
*2,5' ^13,5
5.1
7.2
SVQ
12
л*3
""i^YYYY^ Чл*L"'2* 'i33'i,M/
VA^VAAJ ^1М. ^.7, Ц„. *1„.
^19.7/ ^21.8
^•12.5' S/Q12'
s3/o24, s3/qb X z3

134
2. Многообразия малой размерности
л-5
Таблица 2
LB,4' *Н3.2' ^16.3' LW.2' LW.A' Чо.Э' ^22,5'
L23.5 ' ^23.7' ^24.7' ^25.7' L2S.S' ^26.7 '
L21.*' L29,B* L29.12/ '¦ЗО.П' *1,2' ^34,13
**10.3 ' *-11,3'
s3/^, s3/^2
S3/Q,6, S3/DAQ
3 tr\ v т c»3i
5J/016XZ3/ SJ/Q20XZ3
i16.7, s3/a,6, s3/°4o. s3/°48,
S3/Q8XZ5 , S3/Q12 X Z5
^ 11.2' ^16,7' ^17,5' LV$.T S lP2A' S /DA8'
s2ip'12, s3/o8xz5/ s3/o12xz5, s3//>24xz5
GO

% :> Наглядные свойства трехмерных многообразий
135
л = 6
Таблица 3
*"9.1 ' ^15.2' *9.3' ^20.3' 21,4' *3.4 ' ^24,5'
^24,11' ^27,5' ^28.5' *" 29,9 ' 30.7' *-31.7 ' ^31.11'
^32,7' *3.7' *3,10' **34,9' *5,8' **36.11 ' 37.8'
*7,10' *9,14' *9.16' ^40,11' ^41,11' ^41,16' 43,12'
** 44,13' ^45,19' ^46.12' 46.17' ** 47,13' ^49,18'
50
.19' *5.
21
т2*>/[-\-\). Ы& о). *"/A1).
С 1V»/li -4, (i-lV*i/l-i ?).
S2/Q
24

136
2. Многообразия малой размерности,
Таблица 4

I А Наглядные свойства трехмерных многообразий
137
Таблица 5

138
2. Многообразия малой размерности
Таблица 6

$ 5. Наглядные свойства трехмерных многообразий
139
Таблица 7

140
2. Многообразия малой размерно
Таблица 8

§ 5. Наглядные свойства трехмерных многообразий
141
Таблица 9
(l-SlW/ttJi)
U-S)W(-i?)

142
1. Многообразия малой размерности
5.9. Сложность 3-многообразий и
склеивания симплексов
Выше отмечалось, что если взять
несколько треугольников, разбить их ребра
на пары и склеить ребра каждой пары, то
получится замкнутое 2-многообразие.
При этом любое замкнутое 2-много-
образие получается таким способом.
Посмотрим, что происходит в размерности 3.
Возьмем несколько ориентированных
тетраэдров, разобьем их грани на пары
и склеим грани каждой пары по одному
из трех возможных меняющих
ориентацию гомеоморфизмов. В результате
получится некоторое топологическое
пространство (клеточный комплекс,
полиэдр) X. Попытаемся доказать, что X
является замкнутым ориентируемым 3-
многообразием. Если точка хеХ
отвечает внутренней точке одного из
тетраэдров, то она имеет в X шаровую
окрестность, так как такая шаровая
окрестность имелась в тетраэдре. Если
точка х отвечает паре точек внутри
двух граней тетраэдров, то ее шаровая
окрестность склеивается из двух полу-
шаровых окрестностей (рис. 31). Пусть
Рис. 31
точка х отвечает точкам а,\, fy, ..., ам на
ребрах. Каждая точка на ребре имеет в
своем тетраэдре окрестность типа
"ломтика арбуза". Из них склеивается
шаровая окрестность точки х (рис. 32).
Пусть точка х получается
склеиванием вершин. Каждая вершина имеет в
содержащем ее тетраэдре окрестность
типа конуса над треугольником. Такие
конические окрестности при склеивании
дают окрестность точки #, гомеоморф-
Рис. 32
ную конусу над некоторой
ориентируемой замкнутой поверхностью.
Итак, пространство X является 3-
многообразием с особенностями типа
конуса над поверхностью. Если все
поверхности являются 2-сферами, toZ —
замкнутое 3- многообразие. Имеется
простой способ выяснения этого факта.
Теорема 9. Пространство X,
получающееся склеиванием граней
тетраэдров, является 3-многоооразием тогда
и только тогда, когда ею эйлерова
характеристика равна 0.
Необходимость равенства %(Х)=0
следует из того, что эйлерова характеристика
любого замкнутого 3- многообразия равна
0, что в свою очередь можно вывести из
существования разбиения Хегора.
Действительно, если К„ и К?п — полные
крендели разбиения Хегора рода », то
х\Х) = х(?) + Х(х;) - Х(к*пк;>= 1-
- и+ 1 - я- B- 2») = 0, где КгПК^ —
их общая поверхность.
Достаточность равенства %(Х)=0
получается с помощью следующих
соображений. Пусть X имеет особенности в
точках 0\9 Ог, .,
поверхностями F\9 F2,
ая типа конусов над
, Fn. Удаление
открытой конической окрестности
точки а, приводит к уменьшению
эйлеровой характеристики на число l-%(Ft)9
так как при этом удаляется одна
вершина (точка а^) и столько ребер,
треугольников , тетраэдров, сколько
вершин, ребер и треугольников имеет

13. Наглядные свойства трехмерных многообразий
143
поверхность F,. После удаления
открытых конических окрестностей всех
особых точек получается 3-многообразие
Y с краем и характеристикой
X(l>*(*M?i (ИС№ С другой сто-
роны, с помощью рассмотрения
удвоения многообразия Y легко получается
формула хОт= т?мХ№)«
Сопоставление этих равенств приводит к равенству
Х^тЕм B^с№ Так как харакге-
ристика любой поверхности не
превосходит 2, то в случае %(Х)=0 получается,
что %(Ft)=2f т. е. что все Ff — сферы.
Оказывается, существует тесная связь
между сложностью 3-многообразия и
числом тетраэдров, необходимых для
его склеивания.
Удалим также окрестности типа
прямого произведения кругового сектора на
отрезок оставшихся частей ребер (рис.
33). Легко видел», что получится
утолщенная деталь со стандартной деталью
(см. пункт 5.6) внутри. Пусть сложность
многообразия М равна к. Тогда М имеет
почти специальный спайн с к вершинами.
Так как М неприводимо, то по теореме 6
этот спайн специален. Окрестность в М
его особого графа получается
склеиванием утолщенных деталей, т. е. тетраэдров с
удаленными окрестностями вершин и
ребер. Добавление к ней окрестностей 2-
компоненг эквивалентно добавлению к
тетраэдрам удаленных окрестностей
ребер и приводит кМ без шара. Добавление
Рис.33
Теорема 10. Если сложность
замкнутого ориентируемою неприводимого 3-
многообразия отлична от 0, то она
совпадает с минимальным числом
тетраэдров, необходимых для
склеивания этого многообразия.
Доказательство этой теоремы основано
на следующем замечании. Возьмем
тетраэдр и в нем конус с вершиной в центре
тетраэдра над объединением коротких
отрезков всех медиан всех его граней.
Срежем у тетраэдра уголки, т. е. удалим
конические окрестности вершин.
этого шара эквивалентно
добавлению к тетраэдрам срезанных уголков и
приводит к искомому склеиванию
многообразия М из к тетраэдров. Обратно,
если М получается склеиванием к
тетраэдров, то конусы над их медианами
склеиваются в специальный спайн с к
вершинами многообразия М с
несколькими удаленными шарами. Их число
совпадает с числом точек,
получающихся склеиванием вершин
тетраэдров. После объединения этих
шаров в один шар путем протыка-

144
2. Многообразия малой размерности
Рис. 34а
осхххэ
Рис. 346
L
^~V
Рис. 34в
ния стенок между ними и коллапсиро-
вания получается почти специальный
спайн многообразия М с<к вершинами.
Приведем пример применения этого
результата. Какие многообразия можно
получить склеиванием граней одного
октаэдра? В своем известном препринте
"Геометрия и топология 3-многообразий"
Тёрстон приводит грубую опенку их
числа 8505 (т. е. = 8! ТГ D!)Г). На самом
деле, замкнутых многообразий такого
типа гораздо меньше. Их можно все
перечислить. Действительно, октаэдр
склеивается из 4 тетраэдров (рис. 34, а), и,
следовательно, неприводимое многообразие
такого типа должно иметь сложность <4.
Все такие многообразия перечислены в
табл. 1, причем многообразия,
отвечающие графу на рис. 34, 5, получиться не
могут, так как в октаэдре тетраэдры уже
частично склеены по схеме рис. 34, 6,
которая отсутствует в длинной восьмерке.
Например, приклеивание каждой грани
октаэдра к противоположной по
суперпозиции параллельного переноса и
поворота на угол 6СР приводит к
многообразию У/Pw Опрокидывание каждой
верхней грани на нижнюю дает сферу.
Если при этом две несмежные верхние
грани подкрутить на угол 120^ то
получится связная сумма двух
экземпляров линзы L^i (рис. 35).
Рис. 35

$ 5. Наглядные свойства трехмерных многообразий
145
5.10. Комментарий к наглядному материалу
На рис. 36 изображено одно из
наиболее известных представлений
стандартной трехмерной сферы в виде
склейки двух полноторий (заполненных
торов). При этом их границы
склеиваются так, что параллели и
меридианы меняются местами. Если изобразить
эту диаграмму Хегора в R3, то нужно
нарисовать полноторие (на рис. 36—
горизонтальное полноторие), тогда
дополнение к нему будет вторым полно-
торием (на рис. 36— вертикальная
фигура). На рис. 37 изображен другой
тип трехмерных многообразий —
линзовые пространства. Они получаются
факторизацией сферы S3 по действию
какой-либо дискретной группы.
Например, проективное пространство RP* —
линза (фактор S3 по действию Z2).
На рис. 38—40 изображено (в разных
вариантах) действие фундаментальной
группы полиэдра ni(X) на высших
гомотопических группах пя(Х). При этом
к каждому многомерному сфероиду
добавляется тонкая трубка, вырастающая
из некоторой его точки (вырастает
тонкий длинный «ус») и идущая вдоль
петли, представляющей выбранный
элемент фундаментальной группы. В
результате к первоначальному сфероиду
добавляется тонкая замкнутая трубка,
что дает в итоге некоторый, вообще
говоря, другой сфероид. Если полиэдр
односвязен (т. е. п\(Х) = 0), то тогда
описанное выше действие тривиально.
Но может случиться и так, что группа
ni(X) отлична от нуля, но ее действие
на всех группах пп(Х) сводится к
тождественному преобразованию. На
рис. 40 описанное действие условно
изображено как перенос сфероида «на
другое место». На рис. 41 изображен
конкретный узел в R3, т.е. вложение
окружности, отличное от стандартного
(плоского). Узел называется нетри-
зиальным, если путем деформации
в классе вложении его нельзя привести
к стандартно вложенной окружности.
Изображенный на рис. 41 узел
нетривиален (проверьте!). При помощи узлов
можно также задавать (кодировать)
3-многообразия. Этот способ их
кодирования часто используется в топологии
наравне с диаграммами Хегора и с
сетями [12}. Вообще говоря, проверка
нетривиальности конкретного узла —
достаточно сложное дело. На серии рис.
42—46 проиллюстрирована схема
кодирования трехмерных многообразий при
помощи спайнов. Для этого нужно
сначала разрезать многообразие (рис. 42),
удалить из него, например, одну
трехмерную клетку (шар). В результате
получится 3-многообразие с краем (рис.
43). На рис. 42,43 операция разрезания
показана «буквально» — кат
разрезание ножом трехмерного тела (объема).
Затем многообразие с краем начинает
* стягиваться к своему специальному
двумерному остову (спайну)г описанному
выше в $ 5. Снайны можно
представлять себе как кусочно-линейные
полиэдры, как это показана на рис. 44.
Здесь гибкие, аморфные клетки
гладкого 3-многообразия постепенно
стягиваются на прямолинейные остовы
(рис. 44) и застывают в таком виде
как «код многообразия». При этом
каждому многообразию можно приписать
«сложность» — число вершин в
специальном спайне. В результате коды всех
3-многообразий выстраиваются в
бесконечную цепочку (последовательность)
по степени возрастания ях сложности.
Такое упорядочение (фильтрация)
условно показано на рис. 47. Чем
дальше мы уходим вдоль этой цепочки,
тем сложнее коды многообразий.
Стягивание 3-многообразия на его спайн
условно показано также на рис. 48,
где в виде изогнутых, достаточно
аморфных объектов показаны гибкие
клетки многообразия, а в виде
прямолинейных (кубических)
конструкций — спайн многообразия. Постепенно
все клетки «оседают» на спайн, и код
многообразия превращается в
двумерный евклидов полиэдр.

3
Наглядная симплектическая
топология и механика
§1. Некоторые понятия гамильтоновой геометрии
1.1. Гаиильтоновы системы на симплекти-
ческих многообразиях
Рассмотрим векторное поле v на
гладком многообразии. Вводя локальные
координаты ж^ ...,, У, можно записать
его в виде ^%-=v'(x1t ..., хп), где 1<г<я,
a v'(x*j..., хп) — гладкие функции,
являющиеся компонентами поля v.
Таким образом, каждое векторное поле
интерпретируется как система
обыкновенных дифференциальных уравнении
на многообразии. Верно и обратное,
каждая система обыкновенных
дифференциальных уравнений может быть
изображена в виде векторного поля на
соответствующем многообразии. Среди
множества механических и физических
систем выделен важный класс систем,
описываемых при помощи так
называемых гамильтоновых уравнений. Эти
системы могут реализоваться лишь на
гетномерных многообразиях.
Многообразие М называется симплек-
тическиму если на нем задана кососим-
метрическая, гладкая, невырожденная,
замкнутая дифференциальная 2-форма
<&=Zij G>ij а*х'лах> т. е. detffi^^M) и dcr=0.
Это означает, что в каждой
касательной плоскости 7yVf к многообразию М в
точке х задана невырожденная кососим-
метрическая форма (а, Ь) (на
касательных векторах а и Ъ к
многообразию), замкнутая и гладко зависящая
от точки. Эту форму можно
трактовать как кососимметрическое скалярное
произведение векторов а и Ьу т. е. (а, ?)=
Пример: евклидово пространство к ,
отнесенное к декартовым координатам
//, ..., /Г, q1,..., q* и снабженное
билинейной формой, матрица которой
имеет вид _ ? о I» где ^ — единичная
матрица размера пхп.
Оказывается, в окрестности любой
точки на произвольном симплектичес-
ком гладком многообразии можно
всегда выбрать такие локальные
координаты/I, ..., р", 4 у •¦¦> € (уже не °°Я"
зательно локально евклидовы),
относительно которых матрица формы (а, Ь)
запишется в виде Г_ ? о > пРичем эта
запись не зависит от точки (в данной
окрестности). Другими словами, если
записать форму (а, Ь) в явном виде
Y*G>ij&%V» где fi^=-o»jj и Q=(fl^) — косо-
симметрическая матрица формы (а, Ь)9
то существует такая замена координат
в целой окрестности данной точки, что
в каждой точке этой окрестности
матрица формы примет вид
Г-? 0 1 (теорему Дарбу). Такие
координаты называют симплектическими.
Определение 1. Пусть v — гладкое
векторное поле (система
дифференциальных уравнений) на четномерном
симплектическом многообразии Мп.
Эта система называется
гамильтоновой у если на многообразии существует
гладкая функция Н (называемая
гамильтонианом или функцией
Гамильтона) такая, что в локальных
симплектических координатах />\ ...,
р", q1, ..., q* (которые, как мы знаем,
всегда существуют в окрестности
любой точки многообразия) эта
система v запишется в следующем (так
называемом гамилътоновом) виде:

41. Некоторые понятия гамильтоновом геометрии
147
w = тр. §у isL= т_р, 9)
dt Фщ* * dt ~2р >
Иногда для краткости будем
обозначать df/dt через /. Таким образом,
гамильтонова система в подходящих
координатах записывается как
векторное поле f/=@\ ..., /J", q\ ..., q") с
компонентами вида:
Р - ц > 9 "" ~ВрГ>
Многие фундаментальные физические
уравнения имеют именно такой вид
(при правильном выборе координат).
Этим и объясняется повышенный
интерес к гамильтоновым уравнениям как
математиков, так и физиков.
Напомним, что функция / на
многообразии называется интегралом
векторного поля (системы) г/, если ее
производная вдоль этого поля (т. е.
функция v(f)rL v*Ц#) тождественно равна
нулю. Эквивалентное определение:
функция / является интегралом поля v
в том и только в том случае, когда она
постоянна на всех интегральных
траекториях системы. Интегральной
траекторией системы называется гладкая
кривая, вектор скорости которой в
каждой ее точке совпадает с вектором
поля v (в этой точке).
Легко видеть, что гамильтониан
всегда является интегралом гамильтонова
поля, В самом деле
, ж ЛГ_Л
+ -JpT' Т^я °-
Если функция / является интегралом
поля vt то это поле касается
поверхностей уровня функции /(см. определение
интеграла). Следовательно, каждое
гамильтоново поле всегда касается
поверхностей уровня своего
гамильтониана Н (интеграла энергии). Другими
словами, гиперповерхности, задаваемые
уравнением /*=const (если они неооо-
бые, то их размерность равна,
очевидно, 2я-1), инвариантны относительно
поля и, т. е. интегральные траектории
поля заполняют эти поверхности и не
покидают их (рис. 1).
Таким образом, любое гамильтоново
поле всегда имеет по крайней мере
один интеграл. Если поле — не
гамильтоново, то такой теоремы, конечно,
нет. Допустим, что поле v имеет два
функционально независимых интеграла
ли /. Напомним, что две функции
называются функционально независимы^
ми на многообразии, если их градиенты
grad Н и grad / линейно независимы
почти всюду (т. е. на открытом
множестве точек, всюду плотном в
многообразии). Тогда поле v касается как
поверхностей №=constt так и
поверхностей /=const, следовательно, оно
касается Bя^2)-мерных поверхностей,
являющихся пересечениями B»-1)-мерных
поверхностей ff=const и ^=const (рис. 2).
Рис. 2

148
3. Симплектическая топология и механика
И так далее. Если система обладает к
функционально независимыми
интегралами H=fi, f, ...^, то она сохраняет
все поверхности уровня ^=const,
1<г <kt и все их пересечения,
следовательно, интегральные траектории
системы "укладываются" на Bп-к)-мерные
поверхности, являющиеся совместными
поверхностями уровня всех интегралов
/\г..&. Эти совместные поверхности
задаются системой уравнении /J=constr..,
/t=const. Следовательно, чем больше
найдено интегралов у системы, тем
больше понижается ее порядок. Этим
обстоятельством объясняется
стремление специалистов, исследующих ту или
иную систему уравнений, найти как
можно больше ее независимых интегралов.
1.2. Инволютивные интегралы и торы
Лиувилля
Предыдущие рассуждения применимы к
любому векторному полю. В случае га-
мильтоновых полей имеется важное
специфическое обстоятельство,
позволяющее в некоторых случаях, грубо
говоря, понижать каждый раз порядок
системы не на единицу, а на две
единицы, т. е. каждый интеграл как бы "за-
считьшается за два интеграла". Это
происходит в тех случаях, когда
система обладает интегралами,
находящимися в инволюции (инволютивными
интегралами). Напомним определение скобки
Пуассона двух функций. Пусть /и g —
гладкие функции на симплектическом
многообразии М. Выберем локальные
симплектические координаты />', ..., р",
а1, ..., 4* на М2п. Скобкой Пуассона
{/, g} функций f и g называется
функция, задаваемая формулой
if а \ — Vя di д* - Д— я*
Определение 2. Говорят, что функции
fug находятся в инволюции
(коммутируют) , если их скобка Пуассона
тождественно равна нулю.
В механике и физике встречаются
ситуации, когда гамильтонова система v
на симплектическом многообразии М3*
имеет п независимых интегралов H=f\,
ft ... tfM t находящихся в инволюции.
Оказывается, в этом случае можно
довольно много сказать о поведении
решений системы (т. е. ее интегральных
траекторий). Такие системы называются
интегрируемыми по Лиувиллю или
вполне интегрируемыми системами.
Рассмотрим совместную поверхность
уровня 1 всех п интегралов, т. е.
задаваемую уравнениями f\=cu ..., fn~cH (где
Cj — некоторые постоянные).
Предположим, для простоты, что эта
поверхность связна, компактна, и пусть
интегралы независимы на этой поверхности.
Тогда, оказывается, эта поверхность
диффеоморфна n-мерному тору Т*, пи е.
прямому произведению п окружностей
{теорема Лиувилля). Эти торы иногда
называют торами Лиувилля. Далее,
исходная система оставляет эти торы
Рис. 3
инвариантными, т. е. интегральные
траектории (решения) системы лежат на
торах и целиком заполняют их. Более
того, на торе Лиувилля и в некоторой
его окрестности всегда можно выбрать
такие координаты, что относительно
них система v запишется как система с
постоянными (!) коэффициентами.
Следовательно, в этих координатах
интегральные траектории будут задавать
прямолинейную обмотку тора. Например,
если тор двумерен, то его можно
представить в виде склейки квадрата (рис. 3).
Тогда (в подходящих координатах)
интегральные траектории поля изобразятся
прямыми (рис. 3). При этом возможны
два случая: а) все интегральные
траектории (прямые) замкнуты на торе; б) все

11. Некоторые понятия гамильтоновой геометрии
149
они незамкнуты, т. е. бесконечно долго
и без самопересечений наматываются
на тор. В первом случае все
интегральные траектории гомеоморфны
окружности (периодические решения
системы). Во втором случае все они
гомеоморфны прямой. Говорят, что во
втором случае система определяет
условно-периодическое движение (и
периодическое — в первом случае). В модели
тора на квадрате легко объяснить,
когда реализуется случай **а ", а когда —
случай ". Рассмотрим угол а,
образуемый прямой с осью х на рис. 3.
Если тангенс угла а рационален, то
интегральная траектория рано или
поздно замкнется на торе. Дело в том,
что прямая на плоскости рано или
поздно попадет в точку с
целочисленными координатами (ш, я), где взаимно
простые числа тип таковы, что
tga^m/w. Если же тангенс угла а
иррационален, то прямая проходит мимо
всех целых точек (т, п) на плоскости
(за исключением своей начальной точки
(О, 0)), и, следовательно, после
сворачивания плоскости в тор траектория не
может замкнуться. В частности, она
никогда не вернется в начальную точку
и начинает бесконечно наматываться на
тор, покрывая его все более плотно.
Можно показать, что получающаяся
обмотка тора будет всюду плотной, т.
е. если мы фиксируем произвольную
точку тора и произвольно малое число
&'>0, то обязательно наступит момент,
когда наша траектория пройдет вблизи
выбранной точки на расстоянии, не
превышающем числа е. Другими
словами, с течением времени такая
траектория пройдет сколь угодно близко от
любой наперед заданной точки тора.
Правда, этого события, может быть,
придется ждать очень долго.
Если же мы рассмотрим замыкание
иррациональной траектории, то
получим весь тор. В этом случае тор Лиу-
вилля представляет собой то
множество точек, которые сколь угодно
близко аппроксимируются точками данной
интегральной траектории. Из механики
известно, что описанный выше случай
для аналитических, нерезонансных в
целом, систем является случаем общего
положения, т. е. если мы выберем "на-
yra/f начальную точку, выпустим из
точки траекторию, продолжим ее до
бесконечности и рассмотрим
замыкание, то получится весь тор Лиувилля.
Случаи, когда интегральная траектория
вернется в прежнюю точку (т. е. будет
гомеоморфна окружности),
"чрезвычайно редки", они соответствуют так
называемым случаям резонанса. В
системах общего вида такие резонансные
точки заполняют множество нулевой
меры, т. е. очень "тощее" множество.
Назовем интегрируемую систему
нерезонансной, если почти все ее торы
Лиувилля иррациональны. Здесь мы
будем рассматривать только такие
системы. Оказывается, точки симплектичес-
кого многообразия (в механике оно
называется фазовым пространством
механической системы), на котором
задана вполне интегрируемая система,
разбиваются на точки трех типов. Тачки 1-
ю пата характеризуются тем, что
выпущенная из них интегральная
траектория никогда не возвращается в эту же
точку, а начинает наматываться на
некоторый тор Лиувилля, который
является ее замыканием (рис. 4). Тонки 2-го
типа характеризуются тем, что
выпущенная из них интегральная траектория
движется по тору Лиувилля и через
некоторое время возвращается обратно,
т. е. траектория замыкается. Течки 3-ю
типа — это все остальные. Здесь мы не
будем уточнять поведение |*нггегралыюй
траектории для точек 3-го типа, так как
оно может быть достаточно сложным.
Оказывается, для аналитических, нереэо-
нансных в целом, систем тонки 1-ю
типа являются типичными, точками
общею положения, их —
"большинство". Танки 2<о и 3-ю типов
заполняют тощее подмножество меры нуль.

150
3. Симплектическая топология и механика
Рис. 4
Рассмотрим точку х первого типа в
фазовом пространстве Мп и через
i(x) обозначим тор Лиувилля,
являющийся замыканием интегральной
траектории, выпущенной из точки х. При
изменении точки х тор 7*(х) тоже
будет как-то меняться. Двигаясь по
фазовому пространству, он может в
некоторый момент выродиться, например, в
окружность. Таким образом, торы
Лиувилля могут деформироваться
внутри фазового пространства, как-то
перестраиваясь, распадаясь в
объединение других торов Лиувилля, сливаясь с
торами, вырождаясь и т. п. Эти
события с торами Лиувилля важны для
понимания геометрии данной
механической системы, так как они
показывают нам, что происходит с
решениями гамилътоновой системы уравнений
при изменении начальных данных.
Другими словами, топологические
деформации и перестройки торов Лиувилля
наглядно показывают нам качественный
характер зависимости решений
гамилътоновой системы от начальных данных.
Для читателя, знакомого с механикой,
поясним дополнительно, что точка
фазового пространства задается двумя
наборами из п чисел: п координатами и
п импульсами. Таким образом, мы
приходим к следующей естественной
задаче: дать wtaccuqbuxatfwo
топологических перестроек торов Лиувилля,
возникающих внутри фазовою
пространства, В следующем параграфе
мы уточним постановку задачи.
Следует подробнее описать механизм,
заставляющий тор Лиувилля дрейфовать
по фазовому многообразию. В физике
и механике особый интерес
представляют деформации торов Лиувилля,
вызванные изменением значения энергии.
Пусть v — интегрируемая гамильтоно-
ва нерезонансная система на М2п, Пусть
Н — ее гамильтониан, а ^, ..., fn —
дополнительные независимые гладкие
интегралы, находящиеся в инволюции
(в том числе и с гамильтонианом).
Рассмотрим произвольный тор Лиувилля.
Мы утверждаем, что он определяется
только гамильтонианом H=f\ и самим
фактом существования других
дополнительных интегралов fa, ..., fnt т, е.
тор Лиувилля общею положения не
зависит от конкретного выбора
(конкретного вида) интегралов f2, ...,
fn. Другими словами, если вместо
первоначально заданных интегралов ^, ..., fH
взять какие-либо другие интегралы Д,
..., fn (но по-прежнему независимые с
Н и находящиеся с ним в инволюции),
то торы Лиувилля не изменятся. Это
простое, но важное обстоятельство
объясняется тем, что в случае общею
положения тор Лиувилля совпадает с
замыканием интегральной
траектории, выпущенной из произвольной тон-
ки этого тора и образующей на нем
иррациональную обмотку. Сама же
интегральная траектория, т. е. решение
системы, полностью определяется
начальной точкой и гамильтонианом Н и
абсолютно нечувствительна к выбору
конкретного вида остальных интегралов
fa, ..., f„ (лишь бы они существовали).
Из самого факта существования
дополнительных интегралов вытекает, что траек-

ДI. Некоторые понятия гамильтоновой геомет|
тория намотается на некоторый тор.
Поясним здесь, что дополнительные
интегралы системы определяются,
вообще говоря, неоднозначно. Функции ?,
..., fn можто заменить на другие,
например на функционально зависящие
от них и от л. Так, например, вместо
набора интегралов^, ...,Д можно взять/5=
Рис. 5
13. Отображение момента интегрируемой
системы
Пусть v — интегрируемая система с
набором независимых инволютивных
интегралов №= f\j fi> ...» fn . Тогда с ней
естественно связано важное
отображение, называемое отображением момента.
Определяется оно так. Положим F(x)=
«(/!Й,..., fH(x))* т. е. мы сопоставляем
каждой точке симплектического
(фазового) многообразия набор чисел —
значения интегралов в этой точке. В
результате возникает гладкое
отображение многообразия в евклидово
пространство R" (рис. 5). Задав некоторую
точку аеВ?, мы тем самым задаем
совместную поверхность уровня Та всех
интегралов f\} ?9 ..., Д. Она
определяется уравнениями f\(x)=a*t «чЛ(*НЛ
где <*=(«, -..^0» т. е. числа а — это
компоненты вектора (точки) а в
пространстве R*. Из теоремы о неявных
151
функциях известно, что поверхность
уровня будет .многообразием, если на
ней все интегралы независимы. Как
проверять независимость интегралов?
Для этого сначала нужно вычислить их
градиенты в точках рассматриваемой
поверхности. Тогда функции f\, fa, ...,
fn независимы в окрестности точки х,
если в этой точке линейно независимы
их градиенты grad)J, .„, grad?.
Напомним, что grad/= TO,...t3>)-B
каждой точке х многообразия Аг
определен дифференциал drx отображения
F. Напомним, что точка х называется
критической для отображения Ft если
в этой точке ранг дифференциала dF
меньше л, т. е. меньше размерности
пространства R", в которое
отображается многообразие. Образ F(x)
критической точки назовем критическим
значением отображения момента. Через X
обозначим множество всех критических
значений. Иногда оно называется
бифуркационным множеством
(бифуркационной диаграммой). Таким образом,
если N — множество всех критических
точек отображения F (в многообразии
А^), то E=F(N). Известно, что
множество ? является множеством меры
нуль в пространстве К (если М —
компактно, то дополнение к Г
открыто и всюду плотно в R").
1.4. Перестройка торов Лиувнлля при
критических значениях энергии
Точки а из R*, не являющиеся
критическими значениями, назовем
регулярными (или правильными). Пусть r(q) —
полный прообраз точки q при
отображении F. Если а — регулярная точка и
прообраз F*{a) компактен, то,
согласно теореме Лиувилля, он состоит из
торов Аиувилля (рис. 5). Если точка а
движется вдоль какой-то гладкой
кривой у в пространстве R", оставаясь
при этом регулярной точкой для
отображения момента, то ее прообразы
гладко деформируются в
многообразии. Другими словами, каждый из
торов Лиувилля 7* гладко деформируй

152
3. Симплектическая топология и механика
ется внутри многообразия М2",
оставаясь при этом тором Лиувилля. Однако
события резко меняются, когда точка а
приближается к диаграмме Е и в
некоторый момент времени протыкает ее.
Предположим, что Е является
многообразием с особенностями. Пусть с —
точка встречи пути у с множеством Е.
Так как с является критическим
значением отображения момента, то ее
прообраз может не быть тором (или
объединением торов). Другими словами,
именно в этот момент происходят
перестройки (бифуркации) торов. На рис. 5
условно изображены перестройки
торов в тот момент, когда путь у
протыкает бифуркационное множество Е.
Следует выделить два типа множеств
I. Множества первою типа
характеризуются тем, что их размерность
равна п-\. Множества второго типа
таковы, что их размерность строго
меньше, чем п-\. Отметим, что так как F —
гладкое отображение, то всегда
выполнено неравенство dim Е < п -1.
Рис. 6
Предположим, что для данной
интегрируемой системы dimE< w-1 и
— связно. В этом случае
прообразы Fx(a) и F~l(b) любых двух
регулярных точек а и о из В? "одинаковы" в
том смысле, что они состоят из
одного и того же числа торов Лиувилля,
причем многообразие F1 (а) диффеомор-
фно многообразию F~x(b). Для
доказательства достаточно соединить точки а
и Ъ гладким путем у, который не
пересекается с ? и лежит в образе F(M").
Это можно сделать, так как согласно
предположению мы имеем dim Е <, п -2
(рис. 6). Следовательно, по теореме о
неявных функциях при движении точки
y(t) по пути у от точки а до Ь ее полный
прообраз деформируется в многообразии
М при помощи диффеоморфизма. В
результате мы получаем, что каждьш из
торов Лиувилля заметает цилиндр uxl",
причем га4линдры, отвечающие разным
торам, не пересекаются. Это и
доказывает сформулированное утверждение.
В этом смысле гаммльтоновы
системы, у которых dimE< и-2, устроены
довольно просто (с топологической
точки зрения): любые два набора торов
Лиувилля вида F (а) и F~l (о) могут
быть гладко продеформированы друг в
друга в классе торов Лиувилля. В
самом AUict рассмотрим точки а и Ь,
соединим их непрерывным путем у,
лежащим в л- мерном F(m"). Вообще
говоря, он может пересечься с
бифуркационным множеством Е. Но так как
dimE< w-2, а путь у одномерен, то
при помощи малой деформации можно
снять путь у с множества Е. Мы
получим путь в F(M2h), соединяющий а с b и
не пересекающийся с Е. Тогда
применимо описанное выше рассуждение. В этом
смысле при "большинстве" деформаций
торов Лиувилля в многообразии Лг
никаких перестроек торов Лиувилля не
происходит (а если даже они случайно
появились, то путем малого "шевеления"
эти перестройки можно устранить).
Совсем другая картина возникает в
случае, когда dim Z — п — 1. Здесь
множество Е, вообще говоря,
разбивает образ F(M) на отдельные
изолированные "камеры" (рис. 7). Дело в
том, что здесь Е состоит из кусков
гладких гиперповерхностей (быть мо-

41. Некоторые понятия гамильтоновой геометрии
153
Рис. 7
жет, с особенностями). Поэтому ?
разделяет F(M). Выбирая точки а и ft в
разных камерах, мы видим, что любой
гладкий путь, соединяющий эти точки,
обязательно проткнет множество I в
некоторой точке с (или в нескольких
таких точках). Следовательно, двигаясь
вдоль этого пути, тор Лиувилля (в
многообразии М) обязательно наткнется на
множество N критических точек и
может подвергнуться серьезной
топологической перестройке. Более того, как бы
мы ни пытались перевести тор из F~l(a)
в тор F*{b)9 мы обязательно будем
вынуждены в какой-то момент
подвергнуть этот тор качественной перестройке.
Таким образом, если dim ? = п-\, то
каждая камера (т. е. связная
компонента множества F(M)\Z) характеризуется,
вообще говоря, своим уникальным
набором торов Лиувилля. Число этих
торов для каждой камеры может быть
свое. Эта ситуация наиболее часто
встречается в конкретных
интегрируемых системах физики и механики.
Поэтому мы остановимся подробнее на
случае, когда dim Т, = л-1.
Обсудим конкретный механизм,
вызывающий дрейф реальных торов
Лиувилля по симплектическому (фазовому)
многообразию. Рассмотрим следующий
простой пример — яму, профиль
которой показан на рис. 8. Пусть по стенке
ямы начинает падать шарик, причем
предположим, что пока трение
отсутствует. Тогда движение шарика полностью
определяется его начальным положением
(высотой), т. е. его потенциальной
энергией в вертикальном поле силы тяжести.
В отсутствие трения шарик будет каждый
раз подниматься на прежнюю высоту,
снова падать в яму и т. д. до
бесконечности. Теперь "включим" силы трения.
Пусть трение очень мало. Тогда в первом
приближении можно считать, что
движение шарика практически не изменилось и,
рассматривая достаточно малые отрезки
времени, мы можем сказать, что система
ведет себя, как и раньше. Но на больших
интервалах времени действие малого
трения начинает заметно сказываться.
Ясно, что с течением времени шарик
будет подниматься на все меньшую
высоту вследствие потери энергии (диссипации
энергии). Наконец, наступит момент
качественной перестройки движения ша-
Рис. 8
рика: он навсегда останется либо в левой,
либо в правой яме (рис. 8). Эта
перестройка происходит в тот момент, когда
уровень подъема шарика коснется седла
А. Если выше точки А линия уровня го-
меоморфна окружности, то в момент
касания седла А (критический уровень
энергии) линия уровня превратится в
восьмерку, а затем при дальнейшем уменьшении
энергии линия уровня распадается на две
отдельные окружности, которые будут
опускаться вниз, пока, наконец, не
превратятся в точки минимума

154
3. Симплектическая топология и механика
Таким образом, здесь изменение
поведения системы вызывалось
уменьшением энергии шарика. В общем случае
эта ситуация описывается так.
Рассмотрим интегрируемую систему с
интегралами Я= fi, ?,..., fn. Зафиксируем
значения всех интегралов, кроме одного,
а именно пусть значения функций^,...,,?
фиксированы, а значение интеграла
энергии (т. е. Я) меняется. Начинается дрейф
торов Лиувилля по многообразию,
вызванный изменением значения Я. При
этом тор будет заметать некоторую (пЛ)-
мерную поверхность, которую мы
обозначим через Jl . Ясно, что она является
совместной поверхностью уровня
интегралов^, ...,/, (за исключением/J). См.
рис. 9. Можно считать, что
поверхность X* является прообразом прямой
линии, лежащей в R* и проходящей
через точку а параллельно
координатной оси Я. Следовательно, поверхность
X можно рассмотреть вне
многообразия М. Тогда Я превращается в
гладкую функцию на поверхности, т. е. Я
можно рассматривать как отображение
X в вещественную прямую. Тор или торы
Лиувилля, отвечающие значению энергии
а, начинают деформироваться по X при
увеличении значения энергии. Затем
при некотором критическом значении
энергии с тор подвергается
перестройке, например распадается на несколько
торов, после чего эти торы
продолжают свое движение, увлекаемые ростом
энергии (рис. 9).
Вопрос: как классифицируются
перестройки торов Лиувилляг Ответ мы
дадим в следующем параграфе для
достаточно большого класса систем.
1.5. Комментарий к наглядному материалу
Гамильтоновы системы возникают во
многих задачах механики, физики. На
рис. 10 показано движение твердого
тела в идеальной несжимаемой
жидкости по инерции. Динамика такой
системы описывается гамильтоновыми
уравнениями. Это позволяет использовать
при изучении топологии таких систем
методы алгебры, анализа, теории групп. В
случае 2-многообразий гамильтоново
поле изображается потоком несжимаемой
жидкости, текущей по поверхности. В
данном случае несжимаемость
эквивалентна сохранению площадей фигур на
поверхности, увлекаемых потоком
жидкости (рис. 11, 12). Жидкость может
стекать при этом довольно причудливо,
однако в каждой неособой точке потока на
многообразии дивергенция потока равна
нулю. На рис. 11 и 12 изображены линии
фронтов движущихся потоков. На рис. 13
представлены математические вариации
на близкие темы оптических
эффектов, каустик, теории особенностей
Рис. 9

61. Некоторые понятия гаиильтоновой геометрии
155
[38]. Эти вопросы связаны также с
теорией лагранжевых многообразии
[40]. См. работы В. П. Маслова. На
рис. 14 изображены уровни интеграла
энергии, являющиеся двумерными
поверхностями (если фиксирован второй
интеграл). Тор Лиувилля при своем
движении "пробивает" эти уровни,
преобразуясь. Это движение тора
(снизу вверх) и показано в виде
взрывного процесса на рис. 14. На рис. 15
показана перестройка общего
положения тора Лиувилля, описанная ниже в §
2 как перестройка типа 3. На рис. 15
показана последовательность полното-
рий, внешняя граница которых
постепенно стягивается на два внутренних
тора. В центре рисунка показан
результат перестройки — два тора. В более
сложной ситуации похожая
деформация изображена на рис. 16. Здесь
алгебраическая поверхность гомеоморфна
тору и представлена в виде двух сфер,
соединенных двумя трубками (что и
дает тор). Затем нижняя сфера
раздувается, а верхняя — сжимается. Этот
процесс реально происходит в
двумерном комплексном пространстве С с ри-
мановыми поверхностями
алгебраических функций, когда простые корни
соответствующего алгебраического
уравнения стремятся к кратным корням и
сливаются. На рис. 16 верхняя и нижняя
сферы разрезаны, чтобы можно было
наблюдать их внутренность, где
происходит деформация. Эти геометрические
образы возникают в теории
эллиптических кривых. См., например, книги Н.
Коблитца [41], а также [42]. На рис. 17
показана другая перестройка общего
положения тора Лиувилля, описанная
ниже в § 2 как перестройка типа 4.
Здесь внешняя граница полнотория (го-
меоморфная тору) постепенно
превращается в два раза намотанный тор (см.
центр рис. 17). Эта перестройка тесно
связана с процессом построения 2-ади-
ческого соленоида, изображенного на
рис. 18. В большой тор нужно вложить
более тонкий тор, два раза намотанный
вдоль оси первого тора. Затем внутрь
второго тора нужно вложить третий
тор, два раза намотанный вдоль оси
второго тора (т. е. четыре раза
намотанный вдоль оси первого тора). Затем
внутрь третьего тора нужно вложить
четвертый тор, два раза намотанный
вдоль оси предыдущего, и т. д. В
результате получится бесконечная
последовательность вложенных торов,
каждый из которых намотан два раза вдоль
оси предыдущего и, следовательно, 2*
раз намотан вдоль оси исходного,
первого тора. На рис. 18 изображено 6
этапов в построении соленоида. Для
наглядности торы вскрыты (разрезаны),
чтобы можно было наблюдать
события, происходящие внутри них. На рис.
19 изображена перестройка общего
положения тора Лиувилля, описанная
ниже в § 2 как перестройка типа 5.
Отчетливо видно, как тор — гранила
трубчатой окрестности бутылки Клейна
— сжимается на бутылку Клейна,
двулистно накрывая ее в последний момент
времени. Стрелками показано
направление движения точек тора. В одну
точку на бутылке Клейна всегда
переходят ровно две точки тора. На рис. 20
показано покрытие многообразия
непересекающимися шарами таким
образом, чтобы дополнение к объединению
шаров имело меру нуль (нулевой
объем). Этот процесс нужен для
построения полного инволютивного набора
функций на любом гладком
многообразии. Строя такие функции на
каждом шаре отдельно и сшивая затем их
воедино, мы получаем искомые
функции на всем многообразии.
Аналогичные процессы возникают в
теории фракталов, вкратце затронутой
нами в главе 4 (см. также книгу Б.
Мандельброта [20]). С этой точки
зрения фракталом является "белое
множество" на рис. 20, т. е.
дополнение к объединению черных шаров
(дисков). Некоторые предельные
процессы показаны на рис. 21, 22.

156
3. Симплектическая топология и механика
§ 2. Качественные вопросы геометрического интегрирования
некоторых дифференциальных уравнений. Классификация простых
перестроек торов Лиувилля интегрируемых систем
с морс-боттовскими интегралами
2.1. Морс-боттовские интегралы но представлять себе следующим об-
В" этом параграфе мы, в частое™, Р33™" Предположим, для простоты,
изложим наиболее наглядные аспекты т часть «"Ч™™ V, <яобР'
теории перестроек торов Лиувилля, по- %**>Щ**<* функцией / в отрезок \а,
сгроешойЧработах автора[21, 22]. *]' J^c""* Т™ тРехмеРным
¦л *^ r-L » j многооооазием. Аля этого достаточ-
Рассмотрим, для простоты, случаи че- "««"«««ул» w™ «
тырехмертого симш{екп«еского (фазо- но потребовать, чтобы градиент Я
boi^) многообразия с интегрируемой был отличен от "У™ на этои части по"
системой на нем. Хотя практически все
перечисляемые ниже факты остаются \ ' ! / R
справедливыми и в произвольном мно- V^»T>| [^у, _^/,
гомерном случае, однако в целях на- V—?\ ) ^/
глядности изложения ограничимся \ "О4^- -fy- лс
лишь случаем размерности 4. \ '- § I ^.
Здесь интегрируемая система обладает ~ з \^ Jl f
двумя независимыми интегралами Ни XL^^l^l ~ma
/, из которых один — это гамильтониан ; J
(интеграл энергии), а второй — допол- ;
нительный, находящийся в инволюции с Puc.l
Н и независимый. Отображение момен-
та F отображает многообразие М* в верхности Q. Тогда функция /является
евклидову плоскость К% в качестве ко- гладкой функцией на многообразии Q.
ординат на которой вотш зтачения ин- Вне отрезка [«, Ь] поверхность Q нас
тегралов Я и/, т. е. Г{хЩЩх)9Дх)). С сейчас не интересует. При этом с яв-
точки зрения нашей задачи интегралы ляется крггическим значением функции
Я и /равноправны, поскольку они на- / та многообразии Q, т. е. на мно-
ходятся в инволюции. Поэтому Ни/ жестве уровня Q,-{*€ Q: fo^*\-r(c)
можно менял» местами в зависимости от имеются критические точки функции /
того, изучение какой из этих функций (в которых grad Я>). Рассмотрим слу-
1тедставляетпервсочереднои интерес. 4BUf ттдл функция / имеет типичные
Итак, рассмотрим трехмерную по- «Нев14южде11ныея счюбенности. Это об-
верхность Q% накоторои гамильтониан стоятельство уточняется так. Будем го-
Н постоянен. Ограничивая интеграл / ворить, что гладкая функция /является
на эту поверхность, мы получаем на функцией Морса—Бета на многообра-
неи Аункцию, которую обозначим той 3m Qf e^ критические точки функции
же буквой, чтобы не вводить новых /образуют невырожденные критические
обозначений. Так как мы хотим клас- многообразия.
сифицировать перестройки торов Лиу- Распшфруем это определение. Рас-
вилля, то предположим, что при изме- смотрим множество критических точек
нении уровня /=coret от значения а до функции/. Требуется, чтобы сию явля-
значения Ь (где <кЬ) (при фиксирован- лось гладким подмногообразием в мно-
яом значении гамильтониана) тор гообразии Q, причем не обязательно
Лиувилля подвергся перестройке при связным. Кроме того, требуется, чтобы
некотором промежуточном значении гессиане/функции/(второй дкффе-
энергии с (рис. 1). Эту картину удоб- ренциал) шл невырожден на

2. Геометрическое интегрирование дифференциальных уравнений
157
плоскостях, ортогональных* к
подмногообразию критических точек (рис. 2).
Другими словами, рассмотрим матрицу
'" V дх*дх? /» где х — локальные
координаты. Тогда требуется, чтобы ее
ядро совпадало с касательной
плоскостью к критическому подмногообра-
Рис.2
зию, а на ортогональном дополнении к
нему матрица должна быть
невырожденной, это означает, что ограничение
функции /на каждый нормальный диск
малого радиуса с центром в точке на
критическом подмногообразии является
функцией Морса. Такие функции были
введены еще М. Морсом и затем
изучались в работах Р. Ботта. Мы будем
называть их функциями Морса-Ботта
или морс-боттовскими функциями.
Итак, пусть интеграл f является
морс-боттовской функцией на
поверхности Q в окрестности интересующей
нас перестройки тора Лиувилля, тл. в
окрестности критического значения
энергии. Интегрируемую гамильтонову
систему назовем невырожденной, если:
1) ее интеграл f является функцией
Морса-Ботта на регуярном 3-уровне
Q= (Я= const),
2) она нерезонансна на Q,
3) она устойчива на Q.
Устойчивость означает, что при
малом изменении энергии Н топология
слоения Q на торе Лиувилля не
меняется.
Рассмотрим бифуркационное
множество отображения момента. Из § 1
следует, что особо интересен случай,
когда Z одномерно, т.е. состоит из
отрезков гладких дуг на плоскости.
Они могут склеиваться, т.е. множество
Z имеет,вообще говоря, особенности.
Перестройки торов Лиувилля
происходят в тот момент, когда точка, двигаясь
по кривой на плоскости, протыкает (в
точке с) бифуркационную диаграмму
(рис. 3). Ясно, что мы получаем
трехмерную поверхность Q (см. выше). Так
как нас интересует случай общего
положения, то можно считать, что
гладкий отрезок у протыкает кривую ? в
ее неособой точке (рис. 3) и трансвер-
сально к кривой, причем протыкает ее
с ненулевой скоростью. Любой отрезок
можно всегда малым шевелением
превратить в такой «типичный отрезок».
Рис.3
12. Классм1ипшция простыв; вги.вроптупшд
перестроек торов Лмувмлля
Оказывается, типичные перестройки
торов Лиувилля можно эффективно и
наглядно описать. Рассмотрим
следующие три топологические перестройки
двумерного тора.
1) Рассмотрим полноторие,
стандартно вложенное в В (т.е. полный тор,
прямое произведение окружности на
диск) (рис. 4). Внутри его рассмотрим
ось, т.е. окружность. Граница полно-
тория — это тор. Рассмотрим
следующую его деформацию. Тор ежи-

158
3. Симплектическая топология и механика уравнений
мается внутрь полнотория и
превращается в осевую окружность. Условно
обозначим эту перестройку так: i -»
2) Высверлим из полнотория
концентрическое ему тонкое полноторие, т.е.
рассмотрим в R стандартно
вложенный утолщенный тор — прямое
произведение тора ня отрезок (рис.
^.Рассмотрим «срединный» тор в этом утолщенном
торе. Можно построить деформацию,
стягивающую границу утолщенного
тора (т.е. внутренний и внешний торы)
на срединный тор (рис. 4).
чим эту перестройку так:
0.
3) Высверлим из стандартно
вложенного в R полнотория два
полнотория так, как показано на рис. 4.
Каждое из внутренних полноториев
обходит один раз вдоль оси большого
полнотория. Получается трехмерное
многообразие, край которого состоит
из трех торов. Теперь рассмотрим
деформацию внешнего тора. Он
стягивается на два расположенных
внутри него тонких тора (рис. 4). В
некоторый критический момент внешний
Рис. 4
Два тора движутся навстречу друг
другу (один, уменьшаясь в размере,
другой — увеличиваясь) и, наконец,
встречаются в середине утолщенного тора,
сливаясь в один тор. Условно обозна-
тор превращается в поверхность,
ортогональное сечение которой
(плоскостью, ортогональной оси тора) является
восьмеркой. Затем восьмерка
разрывается и распадается в две окружности.

§2. Геометрическое интегрирование дифференциальных уравнений
159
Это соответствует разрыванию
внешнего тора на два тора, после чего каждый
из них сжимается на свеж внутренний
тонкий тор. Обозначим эту
перестройку так: 7^ -* 27^. Обращая стрелки,
получим три обратные перестройки.
Оказывается,. эти три перестройки
реализуются как бифуркации торов
Лиувилля в интегрируемых невырож-
де;лых системах. Перестройки 1 и 2
отвечают некоторым минимаксным
значениям /, а перестройка 3 описывает
простые бифуркации, отвечающие
некоторым седловым значениям /.
Рис.5
Рассмотрим критическую поверхность
уровня, т.е. поверхность / — с в
^-многообразии Q (рис. 5). Рассмотрим
события с двумерным тором Лиувилля,
который начинает двигаться
(увлекаемый изменением значения /) по
направлению к этой критической
поверхности. Тогда возможны следущие
события с этим тором.
1) Тор наталкивается на критическую
поверхность / = с и «гаснет» на ней,
превращаясь (вырождаясь) в
окружность (рис. 5).
2) Тор движется к критической
поверхности, ударяется о нее и
отражается. Затем тор снова погружается вниз,
в область меньших значений /.
3) Тор приближается к критической
поверхности, пробивает ее и
распадается на два тора, которые уже
самостоятельно продолжают свое
движение вверх (уже в зоне бвлыпнх
значений/).
Обращая стрелки (см. также рис. 5),
получаем три обратных процесса.
Рассмотрим критическую
поверхность /, и пусть на ней находится
ровно одно связное критическое
многообразие морс-боттовского
интеграла /*. Тогда тор Лиувилля,
пересекая эту критическую поверхность,
подвергнется некоторой перестройке.
Назовем такую перестройку простой.
Нижеследующая теорема 1 дает
полное описание всех возможных
простых перестроек. Прежде чем
формулировать ее, предъявим еще две
перестройки тора.
4) Рассмотрим стандартно
вложенное в R3 полноторие и высверлим из
него тонкое полноторие, как
показано на рис. 6, т.е. обойдя два раза

160
3. Симплектическая топология и механика
вдоль оси бо/шиюго полнотория. В
результате получится 3-многообразие А , краем
которого являются 2 тора: внешний и
внутренний. Опишем процесс
превращения наружного тора во внутренний. На
рис. 6 показана деформация внешнего
тора (в нормальном сечении полнотория,
Рис. 6
т. е. на диске с двумя дырками). Он
стягивается внутрь полнотория, затем
превращается в тор, два раза
намотанный вдоль своей оси и касающийся сам
себя по окружности (рис. 7). Эта
поверхность получается так. Нужно взять
стандартную плоскую окружность,
рассмотреть ортогональную ей
восьмерку , петл:. которой занумерованы
цифрами 1 и 2, а затем начать
перемещать восьмерку вдоль окружности,
оставляя восьмерку ортогональной
основной окружности, но вращая ее
так, чтобы после полного оборота
восьмерка вернулась в прежнее
положение, но ее петли 1 и 2 поменялись
местами. Поверхность, заметаемая
восьмеркой при таком движении, и
будет срединным положением внешнего
тора, который стремится превратиться
в тонкий, два раза намотанный вдоль
своей оси тор. Эту перестройку мы
обозначим так: Т ->Т . Она означает
следующее. Тор подходит к
критической поверхности (рис. 7), пробивает
ее и, преобразовавшись снова в один
тор, продолжает движение уже в зоне
больших значений /. Преобразование
тора в тор заключается в его двойной
намотке на самого себя.
5) Рассмотрим погруженную в
бутылку Клейна К (рис. 8). Хотя это
погружение имеет окружность
самопересечения, но с точки зрения
интересующего нас вопроса" это
несущественно. Рассмотрим трубчатую
окрестность этого погруженного подмно-
Рис. 7
гообразия. Это означает, что в каждой
точке х бутылки Клейна мы берем
маленький отрезок с центром в точке х и
ортогональный поверхности.
Объединяя все эти отрезки, т. е. заставляя
точку х пробегать всю бутылку Клейна,
получаем некоторое 3- многообразие
К , погруженное в R . Оно содержит
внутри себя бутылку Клейна и,
очевидно, стягивается на нее. Для
стягивания достаточно заставить точки р и q

42. Геометрическое интегрирование дифференциальных уравнений
161
(концы отрезка с центром в точке х,
см. рис. 8) двигаться навстречу друг
другу по направлению к точке х. В
результате многообразие К*
стягивается на 2-поверхность — бутылку
Клейна. Рассмотрим границу
многообразия .К3. Легко видеть, что она
диффеоморфна двумерному тору. Он
погружен в R3 и при указанном выше
9Q
R-
¦\\\
Рис. 8
стягивании "накрывает" бутылку
Клейна. При этом в одну точку переходит
ровно две точки тора. А именно в
точку х переходят точки р и q. Попытка
изобразить эту картину предпринята
автором книги на рис. 19 предыдущего
§ 1. В топологии такое преобразование
тора в бутылку Клейна назьшается
двулистным накрытием. Обозначим эту
перестройку тора следующим образом:
i -> Кг—> 0. Здесь тор Лиувилля
приближается к критической поверхности,
не пробивает ее и "гаснет4,
превращаясь в бутылку Клейна, лежащую на
поверхности /= с.
Теорема 1 (А. Т. Фоменко [21, 22]).
Любая простая перестройка тора
Лиувилля (общего положения)
совпадает с одной из перечисленных выше
пяти элементарных перестроек 1, 2,
h 4, *•
Теорема 2 (Т. 3. Нгуен). Пусть га-
мильтонова интегрируемая система
является невырожденной на Q*=
=Gf=const; в М4. Тогда сколь угодно
малым возмущением гамильтониана Н
и симплектической 2-формы ш можно
добиться того, что возмущенная
система останется интегрируемой, не-
вырожденной, и станет простой на Q7.
Напомним, что мы рассматриваем
здесь лишь нерезонансные системы.
-Y -Н
¦т
-А-'.1 ~&:\1
3+3
л
V
Рис. 9

162
3. Симплектическая топология и механика
Для дальнейшего удобно ввести
наглядную символику. На рис. 9
показано, как мы будем изображать
перестройки 1 — 5 торов Лиувилля. Это
будет также полезно при изучении
топологического строения
поверхностей постоянной энергии.
Итак, перестройка 1 (рис. 9) означает,
что тор вырождается в свою осевую
окружность. Перестройка 2 (рис. 9)
изображает слияние двух торов в один.
Перестройка 3 (рис. 9) изображает
превращение одного тора в два.
Перестройка 4 (рис. 9) показывает
превращение одного тора в один тор, два раза
намотанный на него. Перестройка 5
(рис. 9) означает превращение тора в
бутылку Клейна (путем ее двулистного
накрытия). На рис. 9 показаны и
обратные перестройки.
Конечно, в интегрируемых системах
часто встречаются перестройки, когда на
одном критическом уровне / лежит
несколько критических подмногообразий.
Назовем возникающие при этом
перестройки торов Лиувилля сложными.
Полная классификация всех сложных
перестроек получена А. В. Болотовым,
С. В. Матвеевым и А. Т. Фоменко в [91].
Этот материал мы здесь опустим.
В настоящей книге мы будем
обозначать сложные перестройки более
сложными графами, как например внизу на
рис. 9.
Ясно, что из элементарных графов на
рис. 9 можно составлять более
сложные графы Г, склеивая концы ребер.
При этом внутренняя (не особая) точка
на ребре графа условно изображает
неособый тор Лиувилля. При
скольжении точки по ребру тор движется
внутри поверхности Q, заметая некоторую
ее часть. В тех точках, где ребра графа
сливаются или заканчиваются
вершиной, происходят соответствующие
перестройки торов. Итак, строя
одномерный граф Г, мы наглядно
изображаем совокупность всех перестроек
торов Лиувилля на 3-поверхности,
задаваемой постоянным значением
энергии Н.
2.3. Топологическая структура
критических уровней
Рассмотрим какой-либо критический
уровень ^const на многообразии Q ,
т. е. при условии, что фиксировано
значение энергии Н.
Вопрос: как топологически устроен
этот уровень? Сначала перечислим,
какие могут быть критические
подмногообразия интеграла /.
Теорема 3 (см. [21, 22]).
Критические точки гладкого интеграла f,
являющеюся морс-боттовской функ-
цией на компактном неособом
многообразии Q3=(H=const), заполняют
либо изолированные критические
окружности, либо двумерные торы,
либо бутылки Клейна.
Назовем интеграл / простым, если
любой его критический уровень
содержит ровно одно связное
критическое многообразие.
Теорема 4 (см. [21, 22]). Пусть v —
невырожденная интегрируемая
система и f — морс-боттовский
простой интеграл на компактной
неособой поверхности Q =(H=const).
Тогда каждая критическая
поверхность уровня f на Q, являющаяся
гладким многообразием, обязательно
диффеоморфна либо тору, либо
окружности, либо бутылке Клейна.
Каждая критическая поверхность
уровня f на Q3, не являюгцаяся
многообразием, либо получается
склейкой двух двумерных торов Tj и Т2 по
не стягиваемым циклам
(окружностям)^ и у2у расположенным
соответственно в торах Tj и T2l либо
является погруженной бутылкой
Клейна, показанной на рис. 7.
Теорема 4 проиллюстрирована на
рис. 10. Берем, например, два
экземпляра тора, на каждом из которых
нарисована стандартная (нестягивае-
мая) параллель. Склеивая два тора по
этой параллели, мы получаем
поверхность, сечение которой показано на
рис. 10.

Ц. Геометрическое интегрирование дифференциальных уравнений
163
описываемой теоремой Лиувилля на
неособом торе.
Рис. 10
Другой пример. Берем два тора, на
каждом из которых нарисован
стандартный (нестягиваемый) меридиан.
Склеивая торы по этому меридиану,
получаем поверхность, показанную на
рис. 10, причем один из торов
изображен пунктиром, так как при
реализации в В3 он обязательно находится
внутри внешнего тора и касается его
изнутри по меридиану. На рис. 11
показано поведение интегральных
траекторий интегрируемой системы на
особой 2-поверхности уровня второго
интеграла. На каждом из двух торов
(рис. 10) имеется "запирающий цикл",
на который справа и слева бесконечно
наматывается интегральная траектория.
Этот цикл препятствует траектории
совершать обороты вдоль параллели
(для конкретного случая, показанного
на рис. 11). Видно, что картина резко
отличается от прямолинейной обмотки,
Рис. II
2.4. Примеры из механики. Уравнения
движения твердого тела. Сфера Пуассона.
Геометрическое истолкование
механических систем
Начиная с этого момента и до конца
настоящего параграфа 2, мы
продемонстрируем плодотворность методов
наглядной геометрии при анализе
конкретных механических систем. Будем
опираться на новый язык,
разработанный выше и позволяющий, в частности
при помощи графов Г наглядно
изложить некоторые известные ранее
результаты, полученные М. П.
Харламовым [30, 32], Т. И. Погосяном и
М. П. Харламовым [31], Я. 6. Татари-
новым [33J и др. Ниже мы, в частности,
изложим результаты М. П. Харламова.
Будем считать, что твердое тело с
закрепленной точкой находится в поле
осесимметричных потенциальных сил.
Конфигурацией твердою тела назовем
движение В3, переводящее некоторый
ортонормированный репер в
фиксированный ортонормированный репер (еи
ег, еъ). Таким образом,
конфигурационное пространство твердого тела —
это группа 50C), т. е. группа
собственных вращений трехмерного
пространства. Рассмотрим однопараметрическую
группу 5*, действующую на
конфигурационном пространстве А^= 50C) еле-

164
3. Симплектическая топология и механика
дующим образом: 57={\|/т; xeR}, где
преобразования \j/x определяются
формулами
Г1 ° ° Л
\\fz (Q)= f 0 cos т -sin x j • Q,
V 0 sinx cosx J
rjitQe 50C).
Это действие определяет группу
вращении вокруг вертикали. Мы считаем,
что вектор е\ направлен вертикально.
Определим отображение р г
1
Очевидно, что Vj+ V2+ vy=l, а значит,
отображение р переводит группу 50C)
в сферу 5*, назьшаемую сферой
Пуассона. Прообраз любой точки veS* (т. е.
vi+ v2+ Vj=l) при отображении р есть
в точности орбита действия группы 51.
Следовательно, сфера Пуассона
допускает представление 1?=50Cу51. Так как
потенциал П симметричен
относительно вертикальной оси, то можно
записать, что П=П(У], V2, v3). Можно
показать, что преобразования, касательные
к преобразованиям группы 51,
сохраняют векторное поле на 7**50C)=
~50C)xR , задающее динамику
твердого тела. Поэтому определена
динамическая система на r,50C)/51=52xR3={v'+
+ v2+ V3=l }x{coeR3}, где со — угловая
скорость.
Для осесимметричного потенциала П
эту систему определяют уравнения
Эйлера — Пуассона
А а> + со х Асо = у х grad П,
где А — диагональная матрица (тензор
инерции), veS*={vi+ v24- Vj=l} задает
положение твердого тела с точностью
до вращений вокруг вертикали, х —
векторное умножение,
У этой системы уравнений всегда
существуют два интеграла. Это H(v,
©)= j<Aa>, юУ + П( v), — интеграл
энергии и G(v, со) = <Аа>, у>
интеграл площадей, где -< 9 >- —
евклидово скалярное произведение векторов.
Можно показать, что если существует
интеграл K=Kfy, ю), независимый с
интегралами G и Н, то связная
компонента неособой поверхности 1^ ± =
={* е S2 х RJ | HfoHi, G(-x>=g,
iTfx^A} диффеоморфна тору 7е и
движение на нем условно-
периодическое.
Множество критических значений
отображения / =HxGxK: ,?хВ?-Л? есть
бифуркационная диаграмма ZczR3. Для
исследования фазовой топологии
механической системы необходимо: 1)
построить бифуркационное множество Е,
2) указать число торов 7й, отвечающих
каждой из компонент Iv\S, 3)
исследовать критические интегральные
поверхности для точек ?.
Областью возможности движения
(ОВД), соответствующей (h, g, &)eR3,
называется множество U^ gt 1=рA}1 ^)а
czS29 где S2 — сфера Пуассона,
обобщенной границей ОВД Uh^ называется
множество критических значений
отображения p=p\i^.k: Ih,g,k->uh,g,k-
Вектор со е R такой, что (v, coJeJ/^*,
называется допустимой скоростью в
точке v е S1 для ОВД tV*> •
Классификация типов ОВД с
указанием множества допустимых скоростей в
каждой точке называется
геометрическим анализом механической системы
[30-32].
2.5. Пример исследования механической
системы. Система Лиувилля на плоскости
Конфигурационное пространство в
данной задаче — это л(х\, л^).
Система определяется функцией Аагранжа
Ь= 4 (Л\(х\)+ Ыхг))(<*\(х\)% +
, / , .2 , wto^wW
^а2\х2/х2/ М<*(Шх^ '
гдеА^Хг)* Л2(х2)#0, ах(хх)>0,
а2(х2)>0.

jl, Геометрическое интегрирование дифференциальных уравнений 165
У ггой системы есть два интеграла:
«- hih+ЬК ai*+ <*г$)+ -ЗЙГ .
ЛГ- 7(Лх?Лг)(&1<Х\х1-&\агх1)+
+ Х\ + хг •
Рассмотрим проекцию />: ГД2-»!!2,
#*н *2* А> *i /= (*ь *гЛ Здесь
вместо сферы Пуассона берется
конфигурационное пространство В2. Из
условий, что H=hy K=kt легко вычислить
.> *»- Ajh+t-t)'*) . - -
Следовательно, Ць.л-Л'АлНС*!* *г)е
с 1Г|Л,^0 ; /==1, 2}, где ЛД*,>=^-
- А.#Л +(-1) л Таким образом, наиболее
типичный вариант имеет вид Uhjrf/h»
М х \Рг> *г] с R2 (рис- 12). Для
внутренних точек прямоугольника мы
имеем 4 допустимые скорости, на
сторонах — две и в вершинах — одну
(нулевую). Траектории в
прямоугольнике (проекции фазовых траектории)
подобны фигурам Аиссажу (сумма
независимых колебании по горизонтали
и вертикали). Прообраз Ih.klrf'^hjth
тор с условно-периодическим
движением. Можно показать, что тип ОВД
Рис. 13
Рис. 14
Рис. 12
идее Ihjt есть прямое произведение
восьмерки на окружность (рис. 14). Его
средняя линия — предельный цикл для
остальных фазовых (интегральных)
траекторий. Для систем Лиувилля
изменение типа ОВД происходит только
при (h, к)ё?. В общем случае
изменение типа ОВД может происходить и
при (h, к), не являющихся
критическими значениями отображения момента
1=НхК.
2.6. Система Лиувилля на сфере
изменяется при переходе через такие
(h, к), когда A\(xi) или Л2(х2) имеют
кратный корень. Пусть х] — кратный
корень Лх на отрезке [а\, Ь\\ (рис. 13).
На рис. 13 цифрами обозначено число
допустимых скоростей. Соответствую-
Пусть твердое тело закреплено в
центре масс и находится в
центральном ньютоновском поле. Здесь Il(v)=
= , и кроме интеграла энергии и
площадей имеется интеграл K(v, ®)=

166
3. Симплектическая топология и механика
— j(Ao), Асо)- ^Л V, Av). Этот интег-
рал указан Клебшем для задачи о
движении твердого тела в жидкости.
Рис. 16
Рассмотрим случай G = 0. Имеем
7VS4(v, о>) е У х R3|G(v, о>)=0}.
Теперь i?= Hlr.s2 и ?= JClr,^ — это
интегралы системы на ТтУ.
Бифуркационная диаграмма отображения
момента имеет
/>ыс. /7
Рис. /S
вид, показанный на рис. 15.
Бифуркационное множество Г состоит из трех
лучей и отрезка параболы,
касающегося двух из них. Множество Е разбивает
плоскость на 5 областей. Для областей
I, И, III I^ji=Zi , для области IV имеем
Ihjr^* * для остальных точек, не
лежащих на X, /^^=0. Для отрезков ?,
помеченных цифрой 1, имеем //^25 , аля
отрезка 2 /^^=45*, для отрезков 3 имеем
Ihrk=Rx$ (рте. 16). Для отрезков 4 /м=
двум экземплярам (SrvS )xS (рис. 14).
Далее, ОВД для I имеет вид: два квадрата
на противоположных сторонах сферы
Пуассона (рис. 17). Проекции фазовых
траекторий заполняют квадраты подобно
фигурам Лиссажу. Далее, ОВД для типа
II имеет вид — кольцо (pic. 18), а для
типа Ш — другое кольцо (рис 19). По
кольцу в обе стороны (так как это образ двух
торов) идет траектория, касаясь пооче-

f 2. Геометрическое интегрирование дифференциальных уравнений
167
редно его границ. Далее, ОВД для
типа IV — это два кольца (рис. 20).
По каждому кольцу в обе стороны
идут траектории. Перестройка при
переходе из области I в область II
показана на рис. 21. При этом ква-
Рис. 19
Рис. 20
л*
Рис. 21
драты (ОВД для области I)
склеиваются боковыми сторонами и
образуют «горизонтальное» кольцо (ОВД
для области II). Перестройка при
переходе из области II -в область III
показана на рис. 21. При этом
горизонтальное кольцо (ОВД для II)
склеивается по отрезкам сечения v2 =0,
лежащим между точками Р\у Р2 и Р3, Ра
и разрывается по отрезкам РгРг и
Р*Ри где Pi, Р2, Рз, Ра — точки на
Av3
V 4 3
Рис. 22
Рис. 23
Рис. 24
сечении v2 = 0 (рис. 22). Здесь для
критической поверхности /*, * ОВД есть
вся сфера Пуассона.
Перестройка при переходе из
области III в область IV показана на рис.
23. «Вертикальное» кольцо (ОВД для
III) разрывается по средней линии.
Переход из области I в область IV
вызывает преобразования торов Лиу-
вилля, показанные на рис. 23. При этом
на сфере Пуассона происходят
события, показанные на рис. 24. Таким
образом, верхние и нижние стороны
квадрата складываются вдвое и
склеиваются, а по отрезку Р\Ра происходит
разрыв. Получается одно из колец
ОВД IV (рис. 24).

168
3. Снмплектическая топология и механика
2.7. Движение гиростата по инерции
Здесь уравнения Эйлера — Пуассона
выглядят так:
Лш + о) X (Аш + к) = О, v = v X со,
где к — некоторый постоянный вектор
в R3. Интегралы имеют вид
И = i- <Ло),о)>;С = <(Лш + *),v>;
/С= <(Ло) + ЩЛш + А,)>;
/ = И X С X К: S2 X R3 — R3.
1) Пусть Я| • А.2 • Хз =^= 0.
Бифуркационное множество 2g = 2 П (Я —
= const) показано на рис. 25. Здесь 2
Рис. 25
IV
III
II
IV
Рис. 26
разбивает пространство R3 на 4
области: для области I имеем h.g.k = Т2,
для областей II и III Ih,g,k = 2Т2,
для области IV /л, g, * = 0.
Перестройки торов Лиувилля, возникающие вдоль
прямой А, показаны на рис. 26.
Отсюда легко описать структуру /*, g, *
для точек из множества 2. Для
точек возврата имеем Ih,g,k = Sl XSl,
где Si — окружность с угловой точкой
(рис. 27).
Рис. 27
Рис. 28
Рис. 29
2) Пусть к\ = А.2 = кз = 0. Это
случай Эйлера для обычного твердого
тела. При этом Sg вырождаются
таким образом, как показано на рис. 28.
Если исключить тривиальный случай
g = h = k = 0t когда /ft> gi k = S2 —
сфера Пуассона, заполненная непод-

t 2. Геометрическое интегрирование дифференциальных уравнений
169
Рис. 30
Рис. 31
вижными точками, то непустые
множества //,, g. k получаются при k > 0.
Тогда можно ввести параметры е =
= g2/k и а = 2h/k и спроектировать
множество 2 на плоскость (е,о).
Получим картину, показанную на рис. 29.
Здесь тип ОВД меняется не только при
переходе через точки (Л, g, k\ е 2,
как это имело место для систем Лиу-
вилля в предыдущих примерах. Всего
получается 25 типов ОВД,
соответствующих 25 областям, на которые разбит
образ на плоскости (е,а). При этом
получаются три основных типа образов
тора Лиувилля на сфере Пуассона
(рис. 30, случаи а, 6", в). При этом
случаи а, б, в на рис. 30
распределены на плоскости (е,а) так, как
показано на рис. 31. Эти образы
торов устойчивы в смысле устойчивости
гладких отображений. Возможны также
два типа неустойчивых образов ,
реализующиеся на кривых, разделяющих
области а, б, е.
2.8. Случай Чаплыгина — Сретенского
Здесь A i = А2 = 4Лз, ку = к2 = 0, кз =
= к, FI(v) = ^vi. Кроме интегралов
энергии И и площадей G есть
частный интеграл К = 2(о>3 — А,)(о>? + о>2)+
к а) Л = 0
1* 6H<Л2<4/3 I* в)Л2-4/3
V
vo
е) А2>4
Рис. 32

170
3. Симплектнческая топология и механика
Рис. 35
+2o)iV3 на множестве (G = 0).
Рассмотрим отображение / = И X К :
:TmS2->S2. Бифуркационное
множество 2(b) изображено на рис. 32.
Пунктирные линии не принадлежат S.
Случай «а» — это случай Горячева —
Чаплыгина движения твердого тела.
Множество ЩХ) разбивает R3= R2(M)XR'
(X) на 7 областей. Рассмотрим наиболее
богатый случай 4/3 < К2 <4 (рис. 32,
г). Здесь плоскость R2(M) разбита на 7
областей, являющихся сечениями
соответствующих 7 областей в
пространстве R3(MA) (рис. 33). Перестройки
торов Лиувилля вдоль стрелок
показаны на рис. 34. Здесь перестройка
(//) имеет вид композиции двух
перестроек типа (С), когда обе
критические окружности лежат на одном
уровне. Критическая поверхность
уровня есть прямое произведение
окружности на кривую, получающуюся
склейкой в двух точках трех экземпляров
окружностей.
Рис. 36
Рассмотрим случай Горячева —
Чаплыгина (Х_=0). Бифуркационная
диаграмма показана на рис. 35. На рис. 36
изображено разбиение множества
KM); *>0}czR2(M) на 10 областей,
каждой из которых соответствует свой
тип ОВД. Пунктирные линии не
являются разделяющими. На рис. 37
изображены ОВД для шести случаев
1(a) — 1(e) (см.. также рис. 36). Это
образы одного тора Лиувилля.
Изображены стереографические проекции
из полюса ( — 1,0,0). Римские цифры
указывают число допустимых
скоростей. На рис. 38 показаны ОВД для
четырех областей II (а) — II (г). Это образ
двух торов Лиувилля. Проекция
каждого из торов на сферу Пуассона в этом
случае симметрична относительно
плоскости V3 = 0. Поэтому изображена
лишь полусфера v3 >0. Узкая полоса
около границы круга на рис. 38 является
образом одного из торов, который
целиком лежит в образе другого тора.

$ 2. Геометрическое интегрирование дифференциальных уравнений
171
Рис. 37
Рис. 38
2.9. Случай Ковалевской
Здесь А\ = А2 = 2Аг\ X = 0; П(у) =
= —vi. Дополнительный интеграл
имеет вид К = ( — со? — G>2 + v1J+Bo>ia>2 +
+ V2J. Рассмотрим отображение / =
= Н X G X К : S2 X R3 -* R3. Сечения
бифуркационной диаграммы 2в
изображены на рис. 40.
а) ? = 0, б) 0<g2<-p
/>мс. 39
ж) ^2= J, з) #2>1.
В области I имеем h g * = Т2,
в областях II, III, IV /а.*.* = 2Г2,
в области V /А^,* = 47*2. Перестройки,
например, для случая 0 < g2 < -^
см. на рис. 39.

172 3. .Снмплектическая топология и механика
Рис. 40

43. Геометрия изоэнергетических поверхностей
173
2.10. Комментарий к наглядному
материалу
На рис. 41 изображено вращение
различных волчков, отличающихся друг от
друга своими моментами инерции, т. е.,
грубо говоря, формой. Детская
игрушка юла — один из таких волчков.
Быстро раскрученные волчки — одна из
основных частей таких
распространенных приборов, как гироскопов. При их
изготовлении предъявляются высокие
требования к симметрии и точности
центровки волчков. Если волчок
несимметричен, то он может разорваться на
куски, когда наберет большое число
оборотов (рис. 42). Гироскопы
используются для ориентации различных
аппаратов (самолеты, корабли и пр.). В
современной механике неголономных
систем значительное внимание
уделяется изучению качения твердых тел по
двумерным поверхностям (рис. 43, 44),
а также скольжению разнообразных
"коньков" или остро заточенной
пластинки (бритвы) по льду или
аналогичной поверхности. Интегрирование
таких уравнений движения —
увлекательная, но трудная задача. На рис. 45
изображена сфера Пуассона, на которую
3.1. Одномерный граф как диаграмма
гамильтониана
Рассмотрим поверхности Q=Q3
постоянной энергии (иногда их называют
изоэнергетическими поверхностями),
т. е. задаваемые уравнением #=const.
Будем изучать неособые изоэнергети-
ческие поверхности, т. е. на которых
функция Н не имеет критических
точек, т. е. grad H*Q всюду на Q. Из
теоремы о неявных функциях
следует, что в таком случае Q3 является
гладким 3-многообразием в М\ Так
как М4 всегда ориентируемо (как
симплектическое многообразие), то
3-поверхности Q также всегда
ориентируемы Не следует здесь путать
(при отображении, описанном в пункте
2.4) отображается трехмерное
многообразие и содержащиеся в нем торы
Лиувилля интегрируемой гамильтоно-
вой системы. Свойства
бифуркационной диаграммы отображения момента
можно изучать, следя за поведением
образов тора Лиувилля на сфере
Пуассона. На рис. 45 эти образы заполняют
экваториальные полосы. Аналогичные
события изображены на рис. 46 — 48.
Образы торов могут изображаться
довольно экзотическими множествами.
Кроме того, на рис. 47, 48 показаны
вихревые движения в потоках
жидкости, перестройки поверхностей уровня
интегралов гамильтоновых систем.
Движение твердого тела по инерции в
идеальной несжимаемой жидкости
описывается гамильтоновыми уравнениями.
Однако возникновение турбулентности
сразу искажает и резко усложняет
картину линий тока. Различные
геометрические образы, связанные с такими
потоками жидкости (особые точки
потоков, вихри, сепаратрисы потоков и пр.),
изображены на серии pic. 49 — 52.
Превращение ламинарного потока в
турбулентный см. на рис. 51, 52.
термин "поверхность" с двумерными
поверхностями, изучавшимися выше.
Из механики известно, что
положения равновесия гамильтоновой
системы задаются критическими точками
гамильтониана (т. е. такими точками,
где gradH= 0). Следовательно,
рассматривая неособые (некритические)
поверхности постоянной энергии, мы
предполагаем тем самым, что на них
нет положений равновесия системы.
Будем в дальнейшем предполагать
также, что Q3 — компактное
замкнутое многообразие. Ограничим второй
интеграл / на поверхность Q и
обозначим получившуюся при этом
функцию той же буквой /*, чтобы не
§3. Трехмерные многообразия и наглядная геометрия
изоэнергетических поверхностей интегрируемых систем

174
3. Симплектическая топология и механика
вводить новых обозначений. Двумерные
неособые поверхности уровня
интеграла / на многообразии ^г являются,
очевидно, торами Лиувилля. Меняя
значение /, мы заставляем эти торы
дрейфовать вдоль многообразия ^г.
Будем считать, что интеграл
/является морс-боттовским на Q .
Предположим, для простоты, что на
каждой критической поверхности
уровня интеграла / (в многообразии Q3)
лежит ровно одно связное критическое
подмногообразие интеграла /. Такие
интегралы /будем называть простыми.
Остальные интегралы назовем
сложными. Излагаемые ниже конструкции
легко переносятся и на случай
произвольных сложных интегралов, но для
упрощения изложения мы ограничимся
рассмотрением лишь простых
интегралов. Общую теорию см. в книге [85].
Таким образом, мы уже довольно
много знаем о поведении интеграла / на
изоэнергетической поверхности.
Удобно задавать это поведение (а заодно и
топологию многообразия Q) при
помощи одномерного графа, который
обозначим через Г(<Э, л и назовем
диаграммой интеграла /, или диаграммой
интегрируемою гамильтониана Н на
поверхности Q =(if=const).
Интеграл / можно рассматривать как
гладкое отображение многообразия Q в
вещественную прямую R1. Если а —
регулярное значение в R1, то прообраз
точки а при отображении / состоит из
конечного числа двумерных торов.
Изобразим каждый тор точкой. Меняя
значение а, мы заставляем эти точки
перемещаться. В результате они
заметают ребра некоторого графа. Если
значение а стало критическим, то ребра
могут сливаться или, напротив,
распадаться на несколько ребер, втыкаться в
вершину. Следовательно, мы получаем
некоторый граф Г (Q, /), который
назовем диаграммой простого интеграла
f на Q (рис. 1). Ясно, что этот граф
наглядно показывает нам не только
топологическое строение многообразия
Q, но и основные детали, поведения
интеграла на Q, так как слияния,
распад ребер и другие особые точки
(вершины) графа соответствуют
различным критическим многообразиям
функции /на Q.
ПО) =
Рис. I
Сформулированные в § 2 теоремы
позволяют нам многое сказать о
геометрии графа Г. Дело в том, что мы
фактически описали структуру всех
критических подмногообразий морс-
боттовского простого интеграла /, а
следовательно, мы уже знаем все виды
распада, слияния ребер графа и все
типы вершин графа.
Теорема 1 (см. [21, 22]). Пусть Q3 —
компактная неособая изоэнергетиче-
ская поверхность невырожденной
интегрируемой системы с
морс-боттовским простым интегралом f. Тогда
все возможные типы вершин графа Г
(Q, f) и все возможные типы
взаимодействия ею ребер перечислены

|1 Геометрия кзоэнергетических поверхностей
175
на рис. 2. В частности, вершины графа
Разбиваются на пять типов. Все
указанные типы вершин и
взаимодействий ребер действительно
реализуются в реальных механических и
физических интегрируемых системах.
Вершины типов 1, 2, 5 изображают
критические многообразия интеграла /
на Q, являющиеся минимумами или
максимумами интеграла. Такие
вершины и соответствующие им
подмногообразия назовем минимаксными.
Вершины типов 3 и 4 изображают седловые
критические подмногообразия
интеграла. Следовательно, мы будем
называть их седловыми вершинами. Более
того, можно точно сказать, какие
именно критические многообразия
изображаются теми или иными
вершинами графа.
1) Черные минимаксные вершины
графа — это минимаксные окружности
интеграла.
2) Белые минимаксные вершины фа-
фа — это минимаксные двумерные торы.
3) Треножники (см. тип 3) — это
критические седловые окружности
интеграла, обладающие тем
свойством, что при прохождении через
них тор Лиувилля распадается на два
тора (или, наоборот, два тора
сливаются в один при изменении
направления движения).
4) Звездочка с одним входящим и
одним исходящим ребрами графа —
это критическая седловая окружность
интеграла; при прохождении через
которую тор Лиувилля
перерабатывается снова в один тор. Это
преобразование заключается в его
двухкратной намотке на тор.
5) Белые с точкой внутри
минимаксные вершины графа — это
минимаксные бутылки Клейна.
Мы видим, что в случаях 1, 2, 5 тор
Лиувилля не пробивает критический
уровень интеграла /по той причине,
что этот уровень является
максимальным или минимальным. "Выше"
г... . ••*..* .. -.т., •
гт- ... Ж. . • •. Д • •
V* -«г- * ."•• I'-"
V\ " -|V "-Т."
I I •¦- jrv
I •. 4- • */~\ (if
— •'I-"¦• V ^T7'
G) •' "ft-'" 5 --'A'"
W I ."I.* '
Рис. 2
максимума и "ниже" минимума вообще
нет точек многообразия Q, поэтому
тору некуда двигаться. Это приводит к
тому, что в случае 1 тор превращается
в минимаксную окружность и
останавливается, в случае 5 — в бутылку
Клейна и останавливается. В случае 2
два тора сливаются вместе,
превращаются в минимаксный тор и
останавливаются. Или можно считать, что
тор поднимается из многообразия,
ударяется о минимаксный уровень
интеграла и, отразившись, снова уходит в
глубь многообразия. Проходя уровень
типа 3, тор разваливается на два (либо
два тора сливаются в один) и
продолжает движение в том же направлении.
В случае 4 тор, претерпев
преобразование, также продолжает движение в
том же направлении. На рис. 3 мы
условно изобразили граф T(Q, /)
общего вида, в котором представлены

176
3. Симплектическая топология и механика
общий вид
Рис. 3
все типы простых вершин. С точки
зрения интересующих нас задач можно
считать, что все минимумы функции /
находятся на одном уровне (например,
/= 0). Аналогично можно считать, что все
максимумы функции / также находятся
на одном уровне, например/=1 (рис. 3).
3.2. Какие известные многообразия
встречаются среди изоэнергетических поверхностей?
Рассмотрим замкнутую ориентируемую
2-поверхность Mg, т. е. сферу с g
ручками. Предположим, что по ней
движется тяжелая материальная точка.
Возникает механическая система, кон-
фигурацмонным пространством
которой (т. е. пространством положений)
является поверхность М1. Фазовым
пространством является 4-многообразие
ТМ2** ТМ2. Его точками являются пары
(х, 4)» где х — точка поверхности, а ?—
касательный вектор к поверхности в
точке х (рис. 4). В дальнейшем будем
иногда отождествлять ТМ с кокаса-
тельным расслоением 7*М, фиксируя
для этого какую-либо риманову
метрику на М. При помощи метрики можно
отождествить касательное
пространство с двойственным ему кокасатель-
ным. Важным примером гамильтоновой
системы на пространстве ТМ является
геодезический поток какой-либо
метрики. Чтобы задать эту систему, нужно
ввести на поверхности М риманову
метрику g».
Рис. 5
Рис. 4
На поверхности возникают
геодезические линии, т. е. линии,
минимизирующие расстояние между любыми двумя
своими достаточно близкими точками.
Например, на евклидовой плоскости
такими кратчайшими будут прямые
линии. На сфере, стандартно вложенной
в R3, геодезическими являются
всевозможные экваторы, т. е. центральные
плоские сечения сферы (рис. 5).
Геодезический поток — это векторное поле
на пространстве ТМ, определяемое
так. Рассмотрим точку (х, \) на ТМ.
Она определяет точку х на М и
касательный вектор 5 кМв этой точке.
Известно, что из любой точки
многообразия по любому направлению
всегда можно выпустить единственную
геодезическую у(/). Рассмотрим точку
y(t) с вектором скорости y(t). Получаем
кривую oc(f}=( у(/), у(/)) в пространстве
ТМ. При этом мы считаем, что х=*((Р),
Ф=7 ((|- Итак, получаем семейство кри-
вых о(*Н*М, «')) =М'), 7«) на ТМ.
Рассматривая их векторы скоростей,
получаем гладкое векторное поле на

3. Геометрия изоэнергетических поверхностей
177
ТМ. Оно и называется
геодезическим потоком данной метрики.
Оказывается, на пространстве ТМ можно
естественным субразом ввести симплек-
тическую структуру и превратить ТМ в
симплектическое многообразие. При
ртом геодезический поток оказывается
гамильтонозым полем. Он всегда имеет
интеграл энергии #, записываемый так:
Н(ху |^ g$W&"i т. е. он совпадает со
скалярным квадратом касательного
вектора ? в точке х, измеренным
относительно заданной на многообразии
римановой метрики. С точки зрения
механики функция Н(х, ?)
интерпретируется как кинетическая энергия точки,
движущейся по поверхности. При
движении материальной точки без трения по
поверхности в отсутствие внешних сил ее
кинетическая энергия сохраняется. При
движении вдоль геодезических длина
вектора скорости геодезической
сохраняется, следовательно, функция H(xf ?)
сохраняется вдоль интегральных
траекторий геодезического потока на
пространстве ТМ. Это и означает, что
Я(х, с]) является интегралом.
Итак, любой геодезический поток всегда
имеет первый интеграл энергии Я(х, §).
Рассмотрим простейший пример
геодезического потока. Если в качестве
многообразия М взять одномерную евклидову
прямую В1 с метрикой оГ=Жг, где х —
евклидова координата, то фазовое
пространство ТМ естественно
отождествляется с плоскостью В2, на
которой введены декартовы координаты х и
?. Тогда геодезический поток евклидовой
метрики на прямой изобразится
векторным полем на плоскости Вт,
задаваемым так: Xs ?, | =-0. См. рис. б.
Интегральными траекториями этого
потока явллются прямые,
параллельные оси х.
Если взять в качестве М
окружность в евклидовой плоскости, то
фазовое пространство 731
отождествляется с прямым круговым цилиндром.
Координатами на нем служат переменная <р.
Рис. б
(изменяющаяся вдоль окружности, т. е.
угол) и переменная ? (вдоль
вертикальной образующей цилиндра). См. рис. 6.
Рассмотрим на окружности локально
евклидову метрику a?=dqt. Тогда
геодезический поток этой метрики
изобразится векторным полем на циливдре
(рис. 6).
Рассмотрим геодезический поток
римановой метрики &j на поверхности Mg.
Как мы знаем, он всегда имеет
интеграл энергии Я(х, с}). Следовательно,
можно рассмотреть иэоонергетическую
поверхность этой гамильтоновои системы
как множество точек (х, ?),
удовлетворяющих условию Н(х9 |)=4r=:comt*0.
Как геометрически изобразится
поверхность постоянной энерпиг Вспомним, что
#(х, ?) задает нам квадрат длины
вектора ?, касающегося поверхности в точке х.
Следовательно, если точка х
фиксирована, то уравнение №=с? определяет (при
подходящем выборе координат) окпуж-
вость в касательной плоскости Т/Л к
поверхности М в точке х (рис. 7).
Обозначим эту окружность через 5L . Ее
уравнение запишется так; g?x%g**d.
Так как, вообще говоря, функ-

178
3. Симплектическая топология и механика
ции gq{x) изменяются от точки к точке,
то радиус окружности Sx будет,
вообще говоря, различным в разных точках.
Здесь использован тот факт, что
кинетическая энергия материальной точки
записывается как положительно определенная
невырожденная билинейная форма на
касательных векторах к поверхности.
Отсюда, в частности, следует, что
радиус окружности Sx всегда отличен от
нуля во всех точках поверхности.
Рис. 7
Итак, изоэнергетическая 3-поверхность
Q является в данном примере
компактным 3-многообразием, задаваемым
уравнением Н(х, ?)=с? в пространстве ТМ.
Что можно сказать о его топологии?
Главное свойство этой поверхности
заключается в том, что имеется
естественное отображение (проекция) я
многообразия (Jr на многообразие М . А
именно я: Q -> М, л(х, ?)=.*. Ясно, что
эта проекция накрывает всю
поверхность М. Какие точки из Q переходят в
одну точку х из М? Ясно, что эти
точки образуют окружность Sx (рис. 7). В
таком случае говорят, что отображение
л определяет расслоение с базой М и
со слоем окружность. Многообразие Q
расслаивается над поверхностью М со
слоем окружность. Итак, можно
сформулировать следующую теорему.
Теорема 1. Изоэнергетинеские
поверхности Q3 геодезического потока
римановой метрики на двумерной
компактной замкнутой поверхности М2
являются трехмерными
компактными многообразиями,
расслаивающимися над М со слоем окружность.
Какие из перечисленных выше
геодезических потоков интегрируемы, а
какие — нет? В -нашем случае
геодезический поток изображается полем на
фазовом 4-многообразии ТМ. Он всегда
имеет один интеграл — гамильтониан
Щх, ?). Следовательно, для полной
интегрируемости недостает еще одного
интеграла /*, независимого с Н и
находящегося с ним в инволюции. Если такой
дополнительный интеграл есть, то
интегральные траектории геодезического
потока "укладываются" на двумерные
торы Лиувилля. Проблеме
существования второго интеграла сегодня
посвящена чрезвычайно большая литература.
Интуитивно ясно, что ответ может
зависеть от свойств римановой метрики
и от топологии многообразия М. В
настоящее время в геометрии и
механике существенно прояснилась картина
интегрируемости и неинтегрируемости,
которую мы отразим в следующей
таблице. Детали см., например, в [1, 2,
26, 47], а также в работах Дж. Д. Бир-
кгофа, А. Пуанкаре, В. В. Козлова,
С. Л. Зиглина, В. Н. Колокольцова,
Я. В. Татаринова, С. В. Болотина,
И. А. Тайманова и др.
Из таблицы видно, что препятствием
к интегрируемости аналитического
геодезического потока может, во
всяком случае, служить топология
многообразия: если ручек много, то
интеграла нет (В. В. Козлов) [26, 47]. Если
же ручек мало (сфера, тор), то главную
роль начинают играть аналитические
свойства метрики. В одних случаях
интеграл есть, в других — нет.
Нас сейчас интересует вопрос
каковы изоэнергетические
поверхности, возникающие в интегрируемых
системах? Ответив на вопрос, мы поймем,

ij, Гаометрия изоэнергетическиж поверхностей
179
Иаковы топологические препятствия к
интегрируемости. Например, если нам
у9астся более или менее эффективно
описать класс изоэнергетических по-
ёерхностей интегрируемых систем,
то, обнаружив, что в какой-то
конкретной механической системе исследу-
Фмая изоэнергетическая поверхность не
Принадлежит этому классу, мы сможем
сразу заявить, что Ванная система не-
интегрируема (по крайней мере на
данной иэоэнергетинеской поверхности).
Доказательство. Каждой паре (х, §), где
I ?| =1 (можно считать без ограничения
общности, что а=1), сопоставим орто-
репер в В? следующим образом. Будем
считать радиус сферы единичным,
перенесем касательный вектор ? параллельно
самому себе в центр сферы и дополним
пару векторов х и ? третьим вектором у
так, чтобы получился репер е(х, ?>) той
же ориентации, которая заранее
фиксирована в Вт (рис. 8). Каждой паре (х,
§) мы сопоставили репер е(хг ?). Верно
Таблица
Топология
Простые римановы
метрики, ntupnaeep,
обладающие большой
группой симметрии
Простые многообразия:
сфера и тор
Чаще всего система интегрируема
Сложные многообразия:
сферы с двумя и более ручками
Если метрика аналитическая, то
система всегда неинтегрируема, т. е. второго
независимого инволютивного
интеграла нет
Сложные римановы
метрики
В некоторых случаях интеграл есть,
а в некоторых — нет. Существуют
критерии (правда, не всегда
эффективные), позволяющие выяснять,
когда существует второй интеграл
Если метрика аналитическая, то
система всегда неинтегрируема
Как видно из таблицы, для получения
конкретных примеров следует
рассмотреть простые метрики на простых
многообразиях — сфере и торе. Начнем со
сферы, снабженной стандартной
метрикой, инвариантной при вращениях.
Гамильтониан Н задается здесь так:
И(ху ^(евклидовой длине вектора §,
касательного к сфере в точке х).
Известно, что геодезический поток такой
стандартной метрики на сфере вполне
интегрируем, т. е. существует второй
интеграл. Изоэнергетические
поверхности Q3 имеют в данном случае вид
Q «={(*, ?), где |^|-tf=const?0}.
Следовательно, Q образовано точками вида
(х, ?), где % — касательный вектор
длины а в точке хе S (рис.8).
Лемма 1. Изоэнергетические
поверхности Q3 интегрируемого
геодезического потока стандартной метрики на
сфере диффеоморфны трехмерному
проективному пространству YS?.
и обратное: каждый орторепер
однозначно определяет некоторую пару
вида (х, ?). Итак, мы доказали, что
многообразие Q гомеоморфно
множеству всех ортореперов (с началом в
0) в трехмерном пространстве. Оста-
Рис.8

180
лось доказать, что каждый орторепер
однозначно определяется точкой
проективного пространства RP3. Из
линейной алгебры известно, что множество
ортореперов фиксированной
ориентации в № идентично множеству
ортогональных собственных преобразований
IT, т. е. группе ортогональных матриц
50C). Докажем, что группа 50C) го-
меоморфна RP3. Каждое ортогональное
преобразование А: л —> Е? однозначно
определяется некоторой неподвижной
осью /, вокруг которой происходит
поворот на некоторый угол (р (рис. 8).
Откладывая на прямой / величину угла
поворота, получаем точку (/, ф) в №.
Если ф меньше я, точка однозначно
определяет исходное ортогональное
преобразование. Если же угол поворота
равен iji, то получаем одно и то же
ортогональное преобразование R5, хотя
две изображающие его точки (/, +л) и (/,
-п) различны в Вт. Следовательно, нужно
склеить эти точки, т. е. считать (/, -Mi) и
(/, -п) одной точкой. Итак, множество
всех ортогональных (собственных) матриц
гомеоморфно следующему объекту.
Нужно взять в R3 трехмерный шар,
ограниченный сферой радиуса л, и склеить на
его границе (т. е. на сфере) диаметрально
противоположные точки. Это —
проективное пространство. Лемма доказана.
Обозначим класс всех компактных
изоэнергетических поверхностей
интегрируемых гамильтоновых систем
(при помощи морс- боттовского
интеграла) через (Н). Множество (класс)
всех компактных замкнутых
ориентируемых 3- многообразий обозначим
через (М). Ясно, что (Н) с (М).
Из леммы 1 следует, что проективное
пространство RP принадлежит классу
(Я). Рассмотрим тор Iй и снабдим его
локально евклидовой (плоской)
метрикой. Это можно сделать, так как тор
представляется в виде фактора
евклидовой плоскости по действию группы
Z®Z. Известно, что геодезический
поток плоской метрики па торе
вполне интегрируем. Поступая как и в
предыдущем случае, видим, что изоэнерге-
тическая поверхность Q гомеоморфна
3. Симплектическая топология и механщ
здесь множеству пар вида (х, ?), где х —
точка на торе, а ? — касательный
вектор длины 1 (в этой точке).
Лемма 2. Изоэнергетические поверх*
ности Q3 интегрируемого геодезически
го потока стандартной плоской мет*
рики на торе диффеоморфны
трехмерному тору Т3.
Рис. 9
Доказательство. Рассмотрим тор как
квадрат с отождествленными
сторонами (рис. 9). В каждой точке квадрата
рассмотрим касательную окружность
на плоскости (радиуса 1). Ясно, что их
ориентации на склеиваемых сторонах
квадрата правильно согласованы.
Отсюда следует, что Q гомеоморфно
прямому произведению тора на
окружность, что и требовалось доказать, так
как 1— 5x5.
Итак, трехмерный тор также
принадлежит классу (л).
В механике хорошо известны примеры
интегрируемых систем, гамильтониан
которых Н достигает на симплектическом
(фазовом) пространстве m
изолированного минимума или максимума в
некоторой точке. Рассмотрим такую
точку минимакса гамильтониана, т. е.
положение равновесия системы.
Пусть Н, например, равно нулю в
точке Хо минимума. Рассмотрим поверх-

II Геометрия изоэнергетических поверхностей
1S1
иость Q постоянной энергии, зада-
•ммую уравнением й= е >0, где 8
достаточно мало. Так как H(xq)=0 и
точка До — изолированный минимум, то
уравнение Я(*)=€ определяет
трехмерную сферу с центром в точке ль- Итак,
стандартная трехмерная сфера 53
принадлежит классу (Я).
Наконец, в механике известны
примеры интегрируемых гамильтоновых
систем на многообразиях М4,
гамильтониан которых достигает минимума или
максимума на окружности 3*. Таковы,
например, некоторые системы,
описывающие динамику трехмерного тяжелого
твердого тела (закрепленного в одной
точке). Снова, как и в предыдущем
примере, рассмотрим поверхность уровня
гамильтониана Я, близкую к минимаксной
окружности. Ясно, что она гомеомор-
фна прямому произведению
окружности на сферу з2. Дело в том, что в
каждой точке х критической
окружности нормальный к окружности диск
является ^многообразием. Следовательно,
уравнение ff=const определяет в нем 2-
сферу. Перемещая точку по окружности,
получаем искомое прямое произведение.
Итак, классу (Я) пшнадлежит также
многообразие .Ух У. Подведем итоги.
Предложение 1. Классу (Н) иэо&нерге-
тических поверхностей интегрируемых
невырожденных гамильтоновых систем
принадлежат, в частости* следующие
многообразия: У, RP3, Г, SVS\
' Что объединяет эти многообразия с
топологической точки зрения' Пока
ответ дать трудно, поскольку неясно, в
каких терминах его формулировать.
Оказывается (и к объяснению этого мы
сейчас перейдем), все эти многообразия
представляются в виде склейки простых
элементарных "кирпичей". Таким
образом, возникают некоторые
элементарные многообразия, которые можно
склеивать затем в произвольном
порядке, конструируя новые 3-многообразия.
Оказывается (это — нетривиальная
теорема, см. [21, 22, 81]) ,что все
3-многообразия, полученные склейками этих
кирпичей, принадлежат классу (Я), и,
более того, никаких других
многообразий класс (Я) не содержит. Перейдем
к изучению элементарных кирпичей,из
которых сконструированы изоэнергетиче-
ские поверхности интегрируемых систем.
^Предложение 2. Многообразия у,
Rr, ?ху получаются склейкой двух
полноторий (по некоторым
диффеоморфизмам их границ, являющихся торами).
Доказательство. Рассмотрим два пол-
нотория Рь Р2, и пусть T\t Т2 — их
границы, гомеоморфные тору. Пусть
рТ\->Тг — произвольный
диффеоморфизм тора на тор. Зададим на
каждом из торов стандартные параллели и
меридианы, обозначив их
соответственно щ, Pi и аз, Рг (рис. 10).
Диффеоморфизм отображает кривые оц и pi в
некоторые гладкие кривые Доц) и /(pi) на
торе Т2. В предыдущей главе мы
познакомились с деформацией замкнутых
кривых на торе. Напомним, что,
непрерывно деформируя кривые/(cxi) и flp\)f
мы можем добиться, чтобы они
превратились в композиции базисных
кривых аа и Рг. Например, кривая^
/од) всегда гомотопна кривой вида <t2
Р2, т. е. нужно Ъ раз обойти меридиан
р2, а затем а раз обойти параллель
Оа. Аналогично кривую /ф\) можно
продеформировать в кривую вида а2$2 •
Возникает квадратная целочисленная
матрица/^ = ( а » ). Если
рассматривать лишь диффеоморфизмы,
сохраняющие ориентацию торов (которые
заранее фиксированы), то эта матрица

182
3. Симплектическая топология и механи
Я|
унимодулярна, т. е. имеет единичный тические
определитель, ad~bc=\. Итак, мы
сопоставляем каждому диффеоморфизму /
торов матрицу ?. Обратно, по каждой
унимодулярной целочисленной матрице
А можно построить такой
диффеоморфизм торов /, что fm совпадает с
матрицей А. Склеивая два полнотория
по диффеоморфизму / их граничных
торов, получаем некоторое замкнутое
компактно** 3-многообразие. Так как
поверхности получаютсв
склейкой двух экземпляров одного
элементарного кирпича — полнотория
(по диффеоморфизму краев).
3.3. Простейшие изоэнергетические
поверхности (с краем)
Рассмотрим следующие 5 трехмерных
многообразий с краем.
Тип I. Полнопюрие—прямое произведение
А =5 xD . Его край — один тор (рис. 11).
Рис. 11
диффеоморфизм задается матрицей, то
каждой унимодулярной целочисленной
матрице А сопоставляется некоторое 3-
многообразие М=М(А). Рассмотрим в
качестве примера следующие матрицы:
(_iq), ( л 1 ). Склеивая с их
помощью полнотория, легко убедиться, что
получаются сеютвегственно сфера 53 и
многообразие Sxy. Предоставляем
читателю в качестве упражнения
построить матрицу, порождающую RP .
Итак, перечисленные выше изоэнерге-
Тип II. Прямое произведение ixD
назовем гщлиндром. Его край — два
тора (рис. 11). Цилиндр можно
реализовать как область в R (рис. 11).
Нужно из полнотория высверлить тонкое
полноторие, ему концентрическое.
Тип III. Прямое произведение п —
=АГх5 назовем "штанами", или ори-
ентированным седлом, где — диск
с двумя дырками (рис. 11). Чтобы
реализовать NxS в Бг, нужно высверлить
из полнотория два тонких полнотория.
Край l\xS состоит из трех торов.

|1 Геометрия иэоэнергетических поверхностей
1S3
Тип IV. Рассмотрим в В полното-
рие и высверлим из него тонкое пол-
ноторие, два раза обходящее вокруг
оси первого (рис. 11). Получится 3-
многообразие А , край которого
состоит из двух торов. Назовем его
неориентированным седлом
(неориентированными штанами).
Тип V. Возьмем в В погруженную
бутылку Клейна л (рис 11) и рассмотрим
ее трубчатую окрестность 1С. Как мы уже
выясняли, граница этой окрестности —
Лемма 3 (см. [21. 22J). Из перечислен-
ных пяты многообразий лишь два
топологически ппмйшгшш, Многообразия
II, IV и V являются склейками
многообразий типов I и IIL А именно:
формально можно записать, что 2V=
=1+111, a V=I+IV% m§^2 MIL
Это означает» что А пояушется
склейкой полнотория со штатами, а
К получается склейкой двух полното-
рий со штанами. Наконец, Ib*t?llL
Здесь знак «сшаро указывает склейку
Рис. 12
тор, погруженный в В . Трубчатая
окрестность образована маленькими
отрезками, ортогональными к бутылке
Клейна и имеющими центр в ее точках.
Получается. 3-многообразие X,
погруженное в В . Чтобы устранить его
самопересечения, достаточно перейти от
В к В . За счет появления еще одной
размерности можно малым шевелением
убрать самопересечения бутылки
Клейна (напомним, что множество ее точек
самопересечения образует
окружность) и, следовательно, устранить
самопересечения и 3-многообразия
К . Итак, К можно гладко вложить
в В . Назовем К — неориентируе-
мым цилиндром.
элементарных кирпичей по некоторым
диффеоморфизмам их граничных
торов. Докажем, например, первое
соотношение. Рассмотрим многообразие IV,
реализованное в В . Рассмотрим центр
2-диска (с двумя дырками) и
окружность h, проходящую через этот центр
и являющуюся осью большого
полнотория (из которого высверлено тонкое
полноторме, два раза обходящее вдоль
оси). Выбросим из большого
полнотория маленькую трубчатую окрестность
окружности h, т. е. высверлим тонкое
полноторие, концентрическое
большому полноторию. Расслоим
оставшуюся часть К на окружности,
показанные пунктиром на рис. 12 и два раза об-

184
3. Симплектическая топология и механика
ходящие вдоль оси большого полного-
рия. Нарисуем на диске два радиуса,
занумеруем их буквами а со стрелками
(рис. 12). Легко видеть, что R
превращается в прямое произведение диска с
двумя дырками на окружность, т. е.
является штанами.
Аналогичные рассуждения нужно
провести и для многообразия типа V.
Можно показать, что все
перечисленные пять многообразий реализуются
как куски некоторых изоэнергетических
поверхностей классических
механических интегрируемых систем. Поэтому
мы их назвали изоэнергетическими
поверхностями с краем.
3.4. Любая изоэнергетическая поверхность
интегрируемой морс-боттовской системы
распадается в сумму элементарных
кирпичей пяти (или двух) типов
Теорема 2 (А. Т. Фоменко, см. [21,
22]). Пусть М4 — гладкое симплекти-
ческое (фазовое) многообразие
(компактное или некомпактное) и о —
невырожденная гамильтонова система с
гамильтонианом Н, интегрируемая по
Аиу биллю на какой-то одной неособой
компактной трехмерной изоэнергети-
ческой поверхности Q при помощи
морс-боттовского интеграла f
(простого или сложного, — все равно). Тогда
критические подмногообразия интеграла
/на Q могут быть только следующими:
1) минимаксные окружности, 2)
минимаксные двумерные торы, 3) седловые
окружности с ориентируемой сепарат-
рисной диаграммой, 4) седловые
окружности с неориентируемой сепаратрисной
диаграммой, 5) минимаксные двумерные
бутылки Клейна, Пусть т, р, q, s, г —
соответственно количество этих
критических многообразий. Тогда
многообразие Q представляется в виде склейки (по
некоторым диффеоморфизмам
граничных торов) следующих элементарных
кирпичей: Q= ml + pll 4- qlll +
+$W +rV, где элементарные 3-мно-
гообразия I, II, III, IV, V описаны выше.
Эта теорема дает наглядную
топологическую классификацию
изоэнергетических поверхностей интегрируемых
морс-боттовских систем. Числа т, р, q,
s, г имеют четкую интерпретацию —
они указывают, сколько критических
многообразий каждого типа имеет
интеграл/на Q.
Если же на время забыть о
конкретном виде интеграла и поставить вопрос
о наиболее простом топологическом
представлении изоэнергетической
поверхности , то ответ дает следующая
теорема.
Теорема 3 (см. [21, 22]). Пусть Q —
компактная неособая
изоэнергетическая поверхность гамильтоновой
системы, интегрируемой при помогай
некоторого морс-боттовского интеграла
f Тогда Q представляется в виде
Q =ml -\-qlII , где т', q' —
неотрицательные ирлые числа, связанные с
числами из теоремы 2 следующими
формулами: m—m+s±2r\-p, q*=q + s +r + p.
Итак, каждая изоэнергетическая
поверхность интегрируемой системы
допускает два разложения: гамильтоново
(в сумму кирпичей пяти типов) и
топологическое (в сумму кирпичей двух
типов). Первое разложение — более
"подробное , оно помнит структуру и
количество критических многообразий
интеграла /. Топологическое
разложение — более грубое, хотя и более
простое (по записи). Оно игнорирует
тонкие свойства интеграла. Ясно, что
гамильтоново разложение однозначно
восстанавливается по диаграмме T(Q, f)
простого интеграла /".
Рассмотрим всевозможные замкнутые
компактные 3-многообразия,
получающиеся склейками элементарных
кирпичей типов I, III. Обозначим этот класс
3-многообразий через (Q).
Сформулированные выше теоремы показывают, что
(H)cz(Q). Верно и обратное включение.
Оказывается (А. В. Браилов, А. Т.
Фоменко [81]),что классы (Н) и (Q)
совпадают, т. е. любое 3-многообразие,
полученное склейкой полноторий и штанов,
можно реализовать в виде компактной
изоэнергетической поверхности
некоторой невырожденной интегрируемой

$3. Геометрия изоэнергетмческих поверхностей
185
гамильтоновой системы на
подходящем симплектическом многообразии
М4 (быт» может, некомпактном).
3.5. Новые топологические свойства класса
изоэнергетическмх поверхностей
Напомним, что многообразие М3
называется топологически приводимым,
если оно представляется в виде связной
суммы М=Мг#М2, где Mi и М: не
гомеоморфны стандартной сфере j . В
противном случае многообразие
называется неприводимым. Связная сумма
определяется так. Из многообразий М\
и М2 выбрасывается по шару.
Получаются многообразия с краем 2-сфера.
Склеивая эти две сферы по
тождественному диффеоморфизму, получаем
новое многообразие, обозначаемое
Мх# М2 (рис. 13).
А#,#**2
Рос. 13
Теорема 4 (А. Т. Фоменко, X. Ци-
шанг). Пуст» Qj uQ2 — изоэнергети-
ческие поверхности из класса (H)=(Q).
Тогда их связная сумма Q/#<& снова
принадлежит этому классу. Обратно,
если изоэнереетическая поверхность Q
из класса
(HHQ) представлена в виде
связной суммы QjttQ2 некоторых
многообразий Qi и Q2, то каждое из них
обязательно принадлежит этому же
классу (HMQ).
Итак, класс иэоэнергетических
поверхностей интегрируемых
невырожденных систем замкнут относительно
операции взятия связной суммы.
Теперь мы подготовлены к ответу на
вопрос: существуют ли чисто
топологические препятствия к
интегрируемости гамильтоновой системы на
отдельной изоэнергетической
поверхности? Поскольку мы рассматриваем
гладкие системы, то не исключены
ситуации, когда на одной
изоэнергетической поверхности система
интегрируема, а на другой — нет. Хотелось бы
иметь инварианты, запрещающие (или
разрешающие) существование морс-
боттовского интеграла, лишь на
одной изолированной
изоэнергетической поверхности независимо от
поведения системы на других (в том
числе и на близких)
изоэнергетических поверхностях. Оказывается,
такие топологические препятствия
существуют. Здесь мы не будем
вдаваться в детали (см. подробности
в [21, 22]), а ограничимся наглядной
геометрической интерпретацией.
Теорема 5 (см. [21, 22]). Класс
изоэнергетических поверхностей
невырожденных интегрируемых систем не
совпадает с классом всех трехмерных
компактных замкнутых
ориентируемых многообразий.
Следствие. 3-многообразия из класса
(М)\(Н) не могут являться изоэнер-
гетическйми поверхностями
невырожденных интегрируемых систем, т. е.
имеются топологические
препятствия, запрещающие гамильрюновой
системе быть интегрируемой, если
данная изоэнереетическая поверхность
не принадлежит классу (H)^Q).
Чтобы эффективно решать вопрос,
интегрируема ли гамильтонова система
на данной изоэнергетической
поверхности, нужно уметь эффективно
вычислять топологические препятствия,
кратко описанные выше. Для этого полезно
знать как можно больше о топологии

186
3. Симплектическая топология и механика
класса интегрируемых изоэнергетиче-
ских поверхностей. Опишем некоторые
их любопытные свойства.
Пусть гладкая 2-поверхность М го-
меоморфна сфере и снабжена гладкой
римановой метрикой общею положения,
пи е. на поверхности нет ни одной
устойчивой замкнутой геодезической.
Тогда соответствующий этой метрике
геодезический поток неинтегрируем на
каждой отдельной неособой изо-
энергетической 3-поверхности в классе
морс-боттовских интегралов [21, 22].
Рис. 14
Обсудим понятие устойчивости
периодического решения системы v на
изоэнергетической 3- поверхности.
Периодическое решение изображается
замкнутой интегральной траекторией у
(рис. 14). Рассмотрим трубчатую
окрестность траектории, т. е. полноторие,
краем которого является 2-тор с осью
у. Скажем, что траектория у
устойчива, если полноторие целиком (без
"щелей") расслаивается на концентрические
2-торы, общей осью которых является
окружность у, причем все эти торы
инвариантны относительно системы о.
Это означает, что все интегральные
траектории системы, близкие к у,
"укладываются" на указанные 2-торы.
Оказывается, свойство системы иметь
устойчивые периодические решения
тесно связано с ее интегрируемостью.
Имеет место следующее утверждение:
если система имеет на данной
изоэнергетической поверхности не более
одного устойчивого периодическою решения
и если, кроме того, группа одномерных
щлонисленных гомологии Hi(Q, Z)
является конечной гфяслической (т. е.
имеет вид lq), то данная система не-
интегрируема на этой
изоэнергетической поверхности (у нее не может
быть гладкою морс-боттовскою
интеграла). Грубо говоря, если на
изоэнергетической поверхности мало ненулевых
г^иклов и мало устойчивых
периодических решений, то система обязательно
неинтегрируема.
Сам факт существования у системы
могх>боттовского интеграла /
накладывает сильные ограничения на
топологию изоэнергетических поверхностей.
Сохранятся ли эти ограничения, если
ослабить требования на интеграл?
Например, потребуем от функции
/"меньше", чем в предьщущих пунктах.
Рассмотрим класс E) 3-многообразий,
обладающих тем свойством, что на них
существует гладкая функция, все
критические точки которой организованы в
невырожденные критические
окружности, а все неособые поверхности
уровня функции являются объединениями
2-торов. Другими словами,
многообразие принадлежит (S), если и только
если на нем есть морс-боттовская
функция, все критические многообразия
которой — окружности, а все неособые
поверхности уровня — торы. При этом
функция уже не обязана быть
интегралом какой-либо интегрируемой
системы. Оказывается тем не менее, что
класс (S) совпадает с классом (Q) (СВ.
Матвеев). Итак, если на
3-многообразии М есть морс-боттовская функция,
критические многообразия которой —
окружности, а некритические
поверхности уровня состоят из торов, то на
нем обязательно существует некоторый
интеграл / некоторой интегрируемой
гамильтоновой системы. При этом
многообразие реализуется как ее изоэнер-
гетическая поверхность.
В некоторых ситуациях требования на
функцию / можно еще больше
ослабить. Рассмотрим класс (R) 3-
многообразий, на которых существует гладкая
морс-боттовская функция h9 все
критические многообразия которой —
окружности. В отличие от многообразий
класса (S) не требуется, чтобы неособые

$3. Геометрия иэоэнергетических поверхностей
1S7
поверхности уровня функции были
торами. Такие функции называются в
литературе круглыми функциями
Морса (Тёрстон, Азимов и др.). См. также
работу С. В. Матвеева, А. Т. Фоменко,
В. В. Шарко [87].
Ясно, что (К) з(Н), т. е. любая иэоэнер-
гегическая поверхность интегрируемой
системы допускает круглую функцию
Морса. Можно доказать, что класс (R)
строго больше класса (Я), т. е.
существуют многообразия, допускающие круглую
функцию Морса, но не реализующиеся
как изоэнереетические поверхности.
Различие между классами (R) и (Я)
обусловлено их разным поведением по
отношению к операции взятия связной
суммы многообразий. Согласно [28]
если М — любое 3-многообразие (мы
не оговариваем каждый раз, что
работаем в классе компактных связных
замкнутых ориентируемых
многообразий), то, рассматривая его связную
сумму с достаточным числом
экземпляров многообразия Sxyf мы в конце
концов обязательно попадем в класс
(R). Другими словами, при достаточно
большом т имеем М#(#*! Sxy)e(R).
Как уже отмечалось, класс (Н)
обладает замечательным свойством: если М=
=М\ # Мз)е(Н), то многообразия М\ и
Mi обязательно принадлежат (Я). В
терминах класса (S) это свойство было
доказано С. В. Матвеевым. Отсюда
сразу следует, что класс (R) строго
больше класса (Н). В самом деле,
достаточно взять многообразие М0, не
принадлежащее классу Ш) (такие, как
мы знаем, существуют). Беря его
связную сумму с достаточно большим
числом экземпляров Sxy, мы попадаем в
класс (R). Однако полученное
многообразие Мне лежит в (Я), так как в
противном случае исходное
многообразие М0 принадлежало бы классу (Щ9
что противоречит выбору М0. Итак, М
e(R), но не принадлежит (if).
Картина резко меняется, если мы
ограничимся рассмотрением лишь класса
неприводимых 3-многообразий.
Оказывается, внутри класса неприводимых
многообразий имеет место
замечательное тождество (i?)=(Q)=(S^(R).
Это означает, что если взять
неприводимое 3-многообразие с круглой
функцией Морса h на нем, то утверждается,
что на этом же многообразии
обязательно имеется и морс-боттовский
интеграл некоторой подходящей
интегрируемой гамильтоновой системы.
При этом многообразие будет
некоторой изоэнергетической поверхностью
этой системы.
3.6. Об одной применении компьютеров в
симплектнческой топологии
Мы познакомились с замечательным
классом (Н) изоэнергетических" 3-мно-
гообразий интегрируемых
невырожденных гамильтоновых систем. Согласно
главе 2 (см. § 5) 3-многообразия можно
упорядочить по мере возрастания их
сложности, причем многообразий (и их
кодов) данной сложности будет лишь
конечное число. Этот факт позволяет
применить компьютеры для изучения
топологии "достаточно простых" 3-мно-
гообразий. Развивая исследования автора
[21, 22), С. В. Матвеев получил
следующий результат.
Теорема. Все замкнутые
3-многообразия сложности, не превосходящей 8,
принадлежат классу (Н), пи е.
являются изоэнергетическими
поверхностями интегрируемых невырожденных
гамильтоновых систем.
Этот факт был доказан с
использованием ЭВМ, опирается на результаты
главы 2 и на теорему классификации
иэоэнергетических поверхностей
интегрируемых систем, доказанную в [21, 22].
Остановимся подробнее на
принадлежности всех замкнутых
многообразий сложности й 8 к классу (Н).
I) 3-многообразие М назовем ториче-
скиМу если его край состоит из
нескольких торов или пуст. Пусть М —
торическое 3-многообразие сложности
k, т. е. пусть М имеет почти
специальный спайн с к вершинами. С
помощью техники упрощения (см. [34])
можно доказать, что найдутся такие

188
3. Симплектическая топология и механика
торические многообразия М„ что:
1. Af, имеет специальный спайн с <к
вершинами;
2. М получается из М,- с помощью
следующих операций: приклеиванием
штанов Лгх5 , взятием связных сумм
друг с другом и с ErxS , л х5 или RP5.
Упомянутые операции не выводят за
пределы класса (Я). Поэтому, если все
торические многообразия со
специальными спайнами с <к вершинами лежат в
(Н), то все торические многообразия
сложности <к лежат в (Н).
II) Все торические многообразия,
имеющие специальные спайны с 0 или
одной вершиной, лежат в (Н). Их всего
3 штуки. Из [34] следует, что все
торические многообразия сложности ?1
лежат в (Н). Отметим, что существует
торическое многообразие сложности 2,
не лежащее в (Я).
Ш) Пусть Р — специальный спайн
замкнутого 3-многообразия М и а —
одна из его 2-компонент. Проткнем ее,
т. е. удалим из нее открытый 2-дяск.
После коллапсирования получится
почти специальный спайн Pj торическо-
го многообразия Mlt из которого М
получается приклеиванием полнотория.
Число вершин кг спайна Рх меньше
числа вершин к спайна Р, так как при
коллапсировании исчезают вершины на
границе компоненты а и, может быть,
другие вершины. Например, если а
дважды примыкает к ребру, то исчезает
еще одна 2-компонента, примыкающая
к этому ребру. Назовем 2-компоненту
а большой, если к{<,1 .
IV) Просмотр всех выданных ЭВМ
специальных спайнов с ^5 вершинами
показывает, что во всех есть большая
2-компонента. Специальные спайны с 6
вершинами просчитаны не все. Однако
те, которые просчитаны, также имеют
большие 2-компоненты. Наличие
большой 2-компоненты гарантирует
принадлежность многообразия классу (л), так
как оно получается приклеиванием
полнотория к многообразию из (Я).
Подведем итоги этого компьютерного
эксперимента.
Имеется естественная фильтрация 3-
многообразий по сложности — числу
вершин в минимальном почти
специальном спайне [34]. Для каждого к
существует лишь конечное число
неприводимых 3- многообразий сложности
йк. Анализ результатов перебора 3-
многообразий сложности ?5,
произведенного С. В. Матвеевым и В. В. Сав-
ватеевым с помощью ЭВМ (см. [34]) и
затем С. В. Матвеевым для сложности
<10, показывает, .что все замкнутые
ориентируемые 3-многообразия
сложности йо лежат в классе (Н).
Замкнутые ориентируемые 3-многообразия, не
принадлежащие классу (Н), впервые
появляются в сложности 9.
3.7. Комментарий к наглядному материалу
На рис. 15 изображены
3-многообразия, являющиеся изоэнергетическими
поверхностями интегрируемых систем.
Как доказано в [21, 22] эти
многообразия распадаются в объединение
элементарных многообразий двух типов. На
рис. 15 показаны перестройки
двумерных торов при их подъеме вверх по
изоэнергетической поверхности (вслед
за изменением значения второго
интеграла). Именно эти перестройки и
определяют топологию изоэнергетических
поверхностей. На переднем плане (в
основании ствола дерева) показана
перестройка типа I — рождение тора из
критической минимальной окружности.
Выше, около развилки дерева —
перестройка типа 3, т. е. распад тора на два
тора, каждый из которых начинает
затем самостоятельное движение вверх.
Слева внизу у основания другого
дерева — перестройка типа 5 — рождение
тора из бутылки Клейна (на которой
интеграл достигает минимума). Вдали
слева показано рождение двух торов из
одного минимального тора у основания
дерева. На рис. 15 изоэнергетические
поверхности специально изображены в
виде деревьев, так как это точно
отвечает математическому содержанию (см.
пункт 3.1). Этот наглядный образ
существенно помогает при исследовании

§ 3. Геометрия нзоэнергетическнх поверхностей
симплектической топологии
конкретных интегрируемых систем.
На рис. 16 отдельно показана изо-
энергетическая поверхность (более
условно, чем на рис. 15), отвечающая
перестройке тора типа 3. При
наглядном изображении эта перестройка
порождает седло (вверху справа на
рис. 16). Снизу поднимается тор
(изображаемый окружностью), который
распадается на два тора.
На рис. 17 показано разложение
изоэнергетической поверхности в сумму
элементарных кирпичей пяти типов.
Элементарные многообразия условно
показаны на рис. 17 как трехмерные
тела, свободно плавающие в
пространстве. На рис. 18 изображена
перестройка тора, когда он, увлекаемый
изменением значения интеграла, пересекает
критический уровень. На рис. 18 видна
внешняя (белая) часть этого тора —
белое полукольцо. Один из элементов
на рис. 19 изображает ориентированную
сепаратрисную диаграмму критической
окружности морс-боттовского
интеграла. Она образована отрезками
интегральных траекторий,
втыкающихся в окружность. Возможно два
варианта: диаграмма гомеоморфна кольцу,
разрезанному вдоль его оси
критической окружностью (рис. 19), либо
листу Мебиуса.
Эти два кольца (ленты) затем
раздвигаются и движутся по многообразию
(вверх и вниз). На рис. 20 показан
процесс перестройки тора, опускающе-
189
гося ниже критического уровня энергии.
Сравните с рис. 18, где тор еще
находится в основном выше этого уровня.
На рис. 21 показано разложение
изоэнергетической поверхности в сумму
элементарных многообразий. Разрезая
ее на куски, мы можем построить ее
код в виде одномерного графа (см.
пункт 3.1)чРис. 21 достаточно сложен,
поскольку "является попыткой
изобразить «изнутри> чрезвычайно сложную
структуру трехмерных объектов,
естественно возникающих в симплектической
топологии. На рис. 22 трехмерные
многообразия склеиваются из трехмерных
шаров путем отождествления
некоторых их частей. Рис. 23 и 24
нацелены в основном на передачу
психологического ощущения геометрической
бесконечности. На рис. 25 слева показан
спайн трехмерного замкнутого
гиперболического многообразия возможно
наименьшего объема,
обнаруженного Дж. Виксом, С. В. Матвеевым и
А. Т. Фоменко [81]. Справа см. спайн
многообразия Тёрстона (его объем
оказался не минимальным).
Отметим еще одно важное свойство
класса (Н) всех компактных гладких
изоэнергетических 3-поверхностей
интегрируемых невырожденных систем.
Оказывается, он в точности совпадает
с классом так называемых
граф-многообразий, открытых Вальдхаузеном в
трехмерной топологии вне всякой
связи с задачами гамильтоновой
механики и симплектической геометрии.

4
Наглядные образы в некоторых
других областях геометрии и
ее приложений
§ 1. Наглядная геометрия мыльных пленок.
Минимальные поверхности
1.1. Границы раздела физических сред и
минимальные поверхности
Пусть в К3 имеется несколько
соприкасающихся, но не
перемешивающихся физических сред, например в
большой сосуд налито несколько несме-
шивающихся жидкостей.
Предположим, что вся эта система находится
в равновесии. Так как среды не
смешиваются, то определены границы
раздела сред. Их можно представлять
себе (в первом приближении) как
двумерные кусочно-гладкие поверхности,
отделяющие друг от друга
соприкасающиеся среды. Рассмотрим, для
простоты, случай двух сред, которые условно
обозначим через А\ и Л2. Пусть
давления в средах равны ру и р2
соответственно. Оказывается, условие
равновесия сред накладывает сильное
ограничение на геометрию их поверхности
раздела. Чтобы сформулировать это
ограничение, нам потребуется важное
понятие из локальной дифференциальной
геометрии, а именно понятие средней
кривизны поверхности.
Пусть Р — точка на гладкой
двумерной поверхности М2 в К3.
Рассмотрим в точке Р единичную нормаль и,
т. е. вектор единичной длины,
ортогональный касательной плоскости к
поверхности в точке Р (рис. 1).
Проведем через эту нормаль плоскость П.
Она рассечет поверхность по некоторой
гладкой кривой у. Здесь мы
интересуемся лишь малой окрестностью точки
Р. Итак, мы получаем плоскую кривую,
лежащую в плоскости П. Известно, что
в каждой точке кривой можно
вычислить ее кривизну. Геометрически
кривизна выражается как величина,
обратная радиусу так называемой
соприкасающейся окружности, т. е.
окружности, касающейся кривой в
рассматриваемой точке и аппроксимирующей
кривую с точностью до малых второго
порядка (касание второго порядка).
Кривизну можно трактовать и с точки
зрения механики. Пустим по кривой мате
риальную точку единичной массы с пос
тоянной по модулю скоростью. Будем

$ 1. Геометрия мыльных пленок
191
считать, что длина вектора скорости
равна 1 (т. е. на кривой введен
натуральный параметр). Тем самым мы
получаем механическую систему,
состояние которой определяется формой
кривой. Материальная точка, двигаясь по
кривой, вынуждена менять направление
движения и вследствие этого
испытывает ускорение. Оно изображается
вектором, ортогональным к кривой (точнее к
касательной к кривой в данной точке).
Величина ускорения и является
кривизной кривой (в данной точке). От точки
к точке кривизна (ускорение) может
меняться. Получаем гладкую функцию,
называемую функцией кривизны
плоской кривой. Аналогично определяется
кривизна и пространственной кривой.
Кривизна прямой линии
тождественно равна нулю: материальная точка
движется по прямой равномерно и
прямолинейно, не испытывая ускорения.
Кривизна окружности радиуса R равна
\/R. Здесь ускорение постоянно по
величине.
Вернемся к поверхности М.
Каждому положению плоскости П
(проходящей через нормаль к поверхности)
отвечает своя кривая пересечения у,
а следовательно, свое значение
кривизны k(y) этой кривой в точке Р.
Вращая плоскость П (вокруг нормали), мы,
вообще говоря, изменяем значение
k(y). Рассмотрим максимальное
значение А.| этой кривизны и ее
минимальное значение Х.2. Получаем два числа.
Они, в частности, могут совпадать. Из
их определения видно, что кривизна
k(y) в этом случае будет постоянна,
т. е. не зависит от угла поворота
плоскости. Рассмотрим общий случай.
Числа к i и Х.2 называются главными
кривизнами поверхности в данной точке.
От точки к точке эти числа меняются,
т. е. к\ и А.2 являются функциями точки.
Полусумма главных кривизн, т. е.
выражение (Х1+Х2)/2, называется
средней кривизной Н(Р) поверхности
в данной точке.
Теорема Пуассона. Пусть М —
двумерная поверхность раздела двух сред
в R3, находящихся в равновесии. Пусть
Р\ и р2— давления в средах. Тогда
в каждой регулярной точке Р
поверхности М средняя кривизна Н(Р)
имеет вид у.(Р\-рг)> где ^.-некоторая
постоянная, не зависящая от точки, а
Р\—рч — разность давлений в
соприкасающихся средах. В частности,
средняя кривизна поверхности раздела
постоянна (во всех регулярных точках).
Постоянная х имеет важный
физический смысл. Число 1/х называется
коэффициентом поверхностного
натяжения (на границе) раздела; он
характеризует свойства сред. Итак, средняя
кривизна границы раздела постоянна.
Рассмотрим два случая: 1) средняя
кривизна равна нулю (это происходит в том
и только в том, случае, когда
давления в соседних средах равны); 2)
средняя кривизна отлична от нуля; тогда
можно считать, что она строго
положительна (изменения знака можно
добиться, заменяя нормаль к поверхности
на противоположную).
Оба случая хорошо моделируются
в физическом опыте, известном
каждому читателю. Это опыты с мыльными
пленками. Рассмотрим водный мыльный
раствор, опустим в него замкнутый
проволочный контур и извлечем его
обратно. Тогда на контуре повиснет
радужная мыльная пленка. Ее можно
трактовать как границу раздела двух
соприкасающихся газовых сред. В самом
деле, по каждую сторону от пленки
находится воздух, причем здесь давления
р\ и р2 равны, так как пленка
незамкнута, поэтому обе газовые среды вдали
от пленки соприкасаются, переходят
друг в друга. Итак, мы реализовали
случай 1 (см. выше).
Случай 2 реализуется так. Опустим
в мыльный раствор тонкую трубку и
выдуем затем через нее мыльный
пузырь. Он оторвется от трубки и начнет
плавно падать, приобретая форму
сферы. Здесь мы имеем две среды:
внутренний объем воздуха с давлением р\
и внешний объем воздуха с давлением
Р2. Ясно, что pi>p2, и система
находится в равновесии только благодаря
тому, что силы поверхностного
натяжения на мыльной пленке
компенсируют избыток внутреннего давления по

192
4. Наглядные образы в приложениях геометрии
Итак, здесь
а строго положительна
(и постоянна).
Сконцентрируем внимание на первом
случае, т. е. на мыльных пленках с
границей. Для таких пленок средняя
кривизна нулевая.
Можно показать, что этот класс
поверхностей допускает другое
эквивалентное описание. А именно средняя
кривизна двумерной поверхности равна
нулю тогда и только тогда, когда она
локально минимальна, т. е. когда
любое достаточно малое возмущение
поверхности (сосредоточенное в малой
окрестности произвольной тонки) не
уменьшает ее площади. На этом
основании мыльные пленки первого типа (т.
е. с нулевой средней кривизной)
называются минимальными поверхностями.
Итак, равновесная граница раздела двух
физических сред с равными давлениями
всегда является минимальной
поверхностью.
Поскольку теория минимальных
поверхностей теснейшим образом
связана с границами раздела физических
сред, с оптимальными формами
мембран и пр., то она находится в центре
постоянного внимания огромного числа
современных исследований, ведущих
свое начало от работ XVII —XVIII вв.
Обзор некоторых из этих направлений
см. в [11, 12]. Эти исследования
образуют один из важнейших разделов
вариационного исчисления.
Здесь мы ограничимся лишь
демонстрацией некоторых наглядных свойств
Каков геометрический смысл
равенства нулю средней кривизны? Из ее
определения сразу следует, что в точке,
где средняя кривизна нулевая, обе
главные кривизны равны по модулю и
противоположны по знаку, так как Я.]+л.^=
—0. Из определения чисел ^ и ^ видно,
что локально, около точки Р,
поверхность устроена наподобие седла, если
Л.1*0 (рис. 2). В одном направлении
поверхность поднимается вверх
(относительно нормали). Это направление отвечает
положительной главной кривизне,
например Х2. В другом направлении
(можно доказать, что оно всегда
ортогонально первому) поверхность
опускается вниз. Это направление отвечает
отрицательной главной кривизне A-i-
12. Некоторые примеры и
Приведем некоторые классические
примеры минимальных поверхностей,
изучавшиеся математиками и физиками
(с разных точек зрения), начиная со
времен Лапласа, Лагранжа, Плато.
1) Катеноид (рис. 3). Он образован
вращением вокруг оси кривой,
задаваемой графиком у=а.с\\-*т, где а =
=const. Эта кривая называется также
цепной линией, поскольку совпадает с

Я. Геометрия мыльных пленок
и(ввер-
Л -
ной в двух точках. Границей катеноида на
рис. 3 являются две соосные окружности
(вообще говоря, разных радиусов).
2) Геликоид (рис. 4). Он образован
равномерным вращением прямой линии
I, пересекающей вертикальную ось Oz и
равномерно поднимающейся вверх, так
что каждая точка прямой / прочерчива-
Рис.4
3) Поверхность Шварца (рис. 5). Она
получается, если в качестве граничного
контура взять четыре ребра
правильного тетраэдра. Тогда поверхность
Шварца является седловой поверхностью,
ограниченной четырьмя
прямолинейными отрезками.
Поверхность Шварца интересна не
только сама по себе, но и потому, что
позволяет строить новые минимальные
поверхности. Здесь уместно
сформулировать следующие принципы, которым удо-
верхность имеет свободную границу у,
нои поверхности М в
ная поверхность пересекается с
поверхностью М по кривой у и под прямым
углом к поверхности.
2 свойство. Три гладких куска
минимальных поверхностей, образующих
вместе устойчивую минимальную
поверхность (с особенностями) и
пересекающиеся по общей гладкой кривой,
обязательно образуют друг с другом равные
углы в 2ц/3=Ш\ Только четыре таких
сингулярных ребра (вдоль каждого из
которых пересекаются три листа
минимальной поверхности) могут встречаться в
одной изолированной особой точке. В
этой точке углы между любыми двумя
сходящимися в ней сингулярными
ребрами равны примерно 1QBP28W.
f свойство. Если
нимальной поверхности М содержится
в некоторой прямой линии, то
отражение поверхности М с
М и М
образует гладкую минимальную
поверхность без излома на
прямолинейном участке т\
4 свойство.
границы.
>. Если мин
я поверх-
М встречает плоскость под
прямым углом, то ее зеркальное отражение
М относительно этой плоскости также

I Наглядные образы в приложениях геометрии
является минимальной поверхностью и
объединение М с Af образует гладкую
минимальную поверхность.
Применяя свойства 3 и 4 к
поверхности Шварца, можно построить
новые, так называемые периодические
минимальные поверхности. Это
обстоятельство сегодня широко
используется в архитектуре. Например,
известный олимпийский стадион в Мюнхене
(построенный в 1972 г.) был создан с
ностей. Его гибкая крыша, поднятая на
ж штанги, образовала
неблизкую
ность. На рис. 9 изображена разбитая
на квадраты минимальная поверхность
(часть плоскости). При малом
возмущении, сосредоточенном в малой области
(т. е. при возмущении с малым
носителем), площадь поверхности может
только увеличиться. Это отчетливо
видно на рис. 9. Возмущение изображается
точки зрения площади и устойчивости.
4) Поверхность Эннепера задается в
В3 при помощи радиус-вектора а(г, 0^=
=(rcos9 - (//3) cos 39, -г sm9 -
- (f/i) sin 39, / cos 29). Попробуйте
построить ее график.
5) Поверхность Шерка
задается уравнением ^1п с" 2?~ z> гДе
«=const; или еи= ^ %. Постройте ее
график.
На рис. 6 изображена сфера —
поверхность постоянной средней
кривизны, образованная мыльной пленкой (т.
е. мыльный пузырь). Эта система
устойчива (пока вода не испарится),
однако при быстром прокалывании
пузыря он мгновенно разрушается,
лопается, что и показано на рис. 6. На рис. 7
изображена целая система таких
мыльных пузырей, выдуваемых из кратера.
Такого рода системы пузырей возника-
___ _ - пене ^^ взбивании
». При этом на одном
юре могут (устойчиво)
встречаться лишь три листа пленки под
равными углами (один из принципов
Плато). Если пузырь прокалывать
очень осторожно (и медленно) тонкой
проволокой, то его можно
раствора. ]
ом ребре
. е разрушая пузыря (см. рис.
7 справа и слева). На рис. 8 i
множество сфер, заполняющих поверх-
Если же возмущение мало по
амплитуде, но имеет большой носитель, то в
некоторых случаях оно может строго
уменьшить площадь минимальной
поверхности. Так происходит, например,
с двумерным экватором в трехмерной
стандартной сфере. Возмущение
поверхности с большим носителем,
похожее на концентрически расходящиеся
волны (от источника возмущения),
показано на рис. 10. Здесь множество
точек, в которых возмущение отлично от
нуля, может быть достаточно велико,
например совпадать со всей
поверхностью. На рис. 11 показано вихревое
движение, часто возникающее на
границе раздела двух сред, когда система
не находится в равновесии. В данном
случае это — вихри в атмосфере,
возникающие вблизи земной поверхности.
Границы раздела нескольких сред
показаны также на рис. 12. Вихреобразное
движение жидкости (водоворот),
приводящее к образованию мыльной пены,
изображено на рис. 13. Около центра
водоворота (слева на рисунке) движение
жидкости не образует пены. Она
возникает лишь на периферии вихря.
Справа изображены трехмерный
евклидов полиэдр и часть диаграммы Хегора.
На рис. 14 изображены объекты, тесно
связанные с теорией поверхностного
натяжения жидкости. Это капилляры,
наполненные жидкостью, и капли,
отрывающиеся от смоченной
поверхности под действием силы тяжести.
Теория движения жидкости в
капиллярах, теория формы мениска и капли —
одна из интереснейших областей
приложения понятий дифференциальной
геометрии. В рамках этой теории уда-

f 2. Фрактальная геометрия и размерность
195
ется описать не только процесс отрыва
капли, но и процесс превращения
неустойчивого цилиндрического столба
жидкости в набор отдельных капель,
например, нанизанных на общую
горизонтальную нить — ось
первоначального жидкого цилиндра. На рис. 15 и 16
показаны границы раздела сред, вихре-
2.1. Различные понятия размерности
В предыдущих главах мы имели дело в
основном с симплициальными
комплексами, полиэдрами и гладкими
многообразиями, для которых понятие
размерности интуитивно ясно и математически
легко определяется естественным
путем, поскольку сводится к
представлению о размерности евклидова
пространства. Понятие размерности R" мы
считаем известным из элементарной
геометрии и линейной алгебры.
Размерность ктогообразия — это
размерность евклидовых шаров (областей), из
которых склеено многообразие.
Размерность полиэдра — это
максимальная размерность симплексов, входящих
в его состав. Однако в математике,
механике, физике встречаются
множества, для которых понятие
'размерности нуждается в специальном
обсуждении и, более того, для которых
можно естественным путем определить не
одну, а несколько различных
размерностей. При этом эти размерности могут
не совпадать. Интуитивно ясно, что
речь идет о множествах, устроенных
локально "существенно хуже1, чем
открытые области в евклидовом
пространстве. Строго говоря, разные
понятия размерности можно определить
для произвольного топологического
пространства. Но для "хороших
пространств", к которым относятся
многообразия, конечные полиэдры, все эти
числа (размерности) совпадают. Однако
как только мы переходим к
рассмотрению более сложных, экзотических (а
иногда в некотором смысле
"патологических") объектов, разные понятия
вые движения в атмосфере и в
пограничном слое жидкости или газа. На
рис. 17 изображены некоторые
интересные эффекты, обусловливаемые
поверхностным натяжением жидкости
(в частности, механизм образования
капель).
размерности приводят нас, вообще
говоря, к разным числам. Раньше
считалось, что это происходит в основном
для класса пространств, редко
встречающихся на практике, например в
физике и т. д. Однако не так давно
выяснилось (и стало уже
общеизвестным), что такие аномальные с
точки зрения размерности объекты
встречаются в классических областях
математики, связанных с конкретными
физическими приложениями, например в
теории дифференциальных уравнений,
динамических систем (так называемые
"странные аттракторы") и т. п. В связи
с этим вновь оживился интерес, в
частности, к анализу разных понятий
размерности. Были выработаны понятия
"фрактала" и "фрактальной геометрии"
(см. известную книгу Б. Мандельброта
[20]). В рамках этого научного
направления изучается целый комплекс
вопросов, возникающих при изучении
"локально сложных" объектов. Мы
лишь вкратце коснемся этой богатой
темы. Начнем обсуждение с понятия
размерности.
Напомним, что система подмножеств
U/ топологического пространства X
называется покрытием (пространства
X), если каждая точка * из X
принадлежит какому-то множеству UJ.
Открытое покрытие состоит из открытых
множеств Ut. Замкнутое покрытие
состоит из замкнутых множеств. Будем
рассматривать сейчас лишь конечные
покрытия. Кратностмо покрытия
называется наибольшее из таких целых
чисел я, что существует п элементов
покрытия (т. е. множеств) Uit
имеющих непустое пересечение.
§ 2. Фрактальная геометрия и размерность

196
4. Наглядные образы в приложениях геометрии
Система множеств V, называется
вписанной в систему множеств U; , если
каждый элемент системы Vj содержится
хотя бы в одном элементе системы Ui.
Сейчас мы сформулируем понятие
топологической размерности,
восходящее к работам Брауэра, Лебега, Мен-
гера, Урысона. Подробности см.,
например, в [20, 37]. Рассмотрим, для
простоты, класс компактов
(компактных множеств), т. е. таких, что из
любого открытого их покрытия всегда
можно выбрать конечное покрытие.
Определение. Топологической
размерностью dim X компакта X называется
наименьшее из таких целых чисел я,
что во всякое открытое покрытие
пространства X можно вписать замкнутое
покрытие кратности <, я+1.
Если таких чисел п нет, то
размерность полагается равной
бесконечности. Наглядный смысл этого
определения предельно прост. Например, при
п=2 оно утверждает, что всякая
двумерная "площадка" (компакт) может
быть вымощена сколь угодно мелкими
камнями (замкнутыми множествами)
так, что камни примыкают друг к другу
не более чем по три. В то же время эта
площадка не может быть вымощена
сколь угодно мелкими камнями так,
чтобы были только примыкания по два.
Поэтому утверждение, что, например,
квадрат имеет размерность два, иногда
называется "теоремой о мостовых" —
при замощении улиц и площадей
брусчаткой всегда бывают примыкания
камней по три, а примыкания по четыре
могут быть избегнуты. При заполнении
некоторого трехмерного объема
достаточно мелкими камнями (например, при
заполнении большой полости
кирпичной кладкой) необходимо возникают
уже примыкания по четыре.
Большим достижением
математической мысли было обнаружение того
факта, что в этом числе примыканий (в
кратности покрытий) и заключается
естественное содержание понятия
размерности. Это достижение принадлежит
Лебегу A911). На рис. 1 показано мелкое
покрытие кратности два одномерного
отрезка замкнутыми множествами.
Рис. 1
Здесь же показано покрытие кратности
три двумерного квадрата. Оно
характеризуется тем, что в каждом узле
сходятся ровно три одномерных ребра,
объединение которых составляет
границу элементов покрытия.
Другим подходом к понятию
размерности является идея Хаусдорфа A919),
позднее развитая Безиковичем.
Фактически эта идея впервые зародилась в
работах Каратеодори A914). Чтобы
сформулировать это понятие
размерности, нам потребуется сферическая мера
Хаусдорфа. Пусть X — некоторое
компактное подмножество в метрическом
пространстве, например в римановом
многообразии или в евклидовом
пространстве. Рассмотрим конечное
покрытие этого компакта w-мерными
шарами D"(e,) радиусов е,. Пусть ум —
m-мерный объем стандартного
единичного m-мерного шара (в евклидовом
пространстве Вт). Число ут можно
вычислить явно, но эта формула здесь
нам не потребуется. Тогда объем шара
радиуса е* запишется так: ymef .
Начиная с этого момента, мы не будем
заранее предполагать, что число т целое.
Пусть т ?0 — произвольное
неотрицательное вещественное число. Подсчитаем
сумму Е,7шеГ- Беря другое покрытие
компакта X шарами, мы будем получать и
другое значение для этой суммы, рассмотрим
всевозможные покрытия компакта X
шарами с радиусами, не превосходящими
фиксированного числа р, и вычислим

S 2 Фрактальная геометрия и размерность
197
А,, = inf 2у<ие™ где inf берется по всем
таким покрытиям. Если устремить р
к нулю, то этот inf может лишь
увеличиваться. Следовательно, всегда
существует предел Игл Ар. Это число
всегда неотрицательно (оно может быть
конечным или бесконечным) и
называется т-мерной сферической мерой
Хаусдорфа множества X. Будем
обозначать ее через \хт(Х). Теперь можно
перейти к понятию размерности. Еще
раз отметим, что в определении меры
Хаусдорфа число т отнюдь не
предполагалось целым.
Пусть X — компакт в метрическом
пространстве. Безикович показал, что
для каждого X всегда существует
вещественное число D такое, что
/«-мерная мера Хаусдорфа компакта X
бесконечна при т < D и, напротив, равна
нулю при m>D.
Определение. Число D называется
хаусдорфовой размерностью компакта
X (или размерностью Хаусдорфа — Бе-
В указанном выше смысле число
J) — D(X) является критической
размерностью. В отличие от
топологической размерности dim X размерность
О(Х) не обязана быть целым числом.
В частности, эти две размерности могут
не совпадать. Они связаны
неравенством D^dim, т.е. D(X)^dimX для
любого X. Для <хороших пространств>
эти размерности совпадают. В то же
время можно привести примеры
сложных пространств, для которых D > dim.
Определение (см. [20]). Фрактал —
это множество, для которого D>dim.
В частности, любое множество, для
которого размерность не является
целым числом, — это фрактал.
2.2. Фракталы
Рассмотрим так называемое канторово
множество (названное по имени Георга
Кантора). Его простейший вариант
строится так. Рассмотрим единичный
отрезок на вещественной оси от 0 до 1.
Разобьем его на три равные части,
после чего выбросим среднюю треть —
открытый интервал от 1/3 до 2/3
¦
*
¦
Рис. 2
(рис. 2). Оставшиеся две трети также
разобьем (каждую из них) на три
равные части, после чего выбросим их
средние (открытые) части. И так далее до
бесконечности, В результате получится
некоторое замкнутое множество К на
единичном отрезке. Интуитивно ясно
(и можно доказать точно), что dim К =
= 0. В то же время хаусдорфова
размерность канторова множества строго
положительна и равна D(AC) = log2/
log 3 ж 0,6309. Можно так
видоизменить процесс построения канторова
множества (предоставляем читателю
сообразить, как именно), что его
хаусдорфова размерность будет равняться
любому наперед заданному числу X,
заключенному между 0 и 1. При этом
по-прежнему будет выполняться
равенство dim К = 0. Итак, канторово
множество — фрактал. Примером
фрактала является также так называемый
ковер Серпинского — замкнутое
множество на евклидовой плоскости. Оно
строится практически по тому же
рецепту, что и канторово множество, но
нужно начинать с плоского квадрата,
юследовательно выбрасывая из него
все более мелкие квадраты.
Фракталы естественно возникают
также в теории комплексных
преобразований плоскости. Введем на
плоскости комплексную переменную z = х -\-
-\-iy и рассмотрим комплексный
полином f(z) степени k. Его можно
трактовать как комплексное преобразование
плоскости, как отображение /: С -*¦ С,
задаваемое формулой w = f(z). Это
отображение можно итерировать,
рассматривая бесконечную
последовательность его степеней /„ = f, где fn (z) =

198
4. Наглядные образы в приложениях геометрии
-ПиММЯ..§г)))(п V^h
Например fi(zj= ftz), Hz)= f(f(z)) и
т. д. Пусть z — произвольная точка
плоскости. Применяя к ней
бесконечную последовательность
преобразований f, мы получаем бесконечную
последовательность точек z, f(z), f (z),
...,f*(z), ... . Другими словами, мы
рассматриваем орбиту точки z при
действии на нее итерациями
отображения /. Удобно рассматривать
комплексную пополненную плоскость как
двумерную сферу. Для этого нужно
добавить к евклидовой плоскости
бесконечно удаленную точку. Тогда бесконечная
последовательность точек f(z)
обязательно имеет предельные точки на
сфере. Мы скажем, что некоторое
подмножество Q на сфере (или плоскости)
инвариантно относительно отображения
/, если оно переходит в себя при
действии всех итераций/", ж=1, 2,....
Оказывается, такие множества часто
являются фракталами [20]. Впервые такие
объекты возникли в известных работах
П. Фату A878—1929) и Г. Жулиа
A893- 1978). Так как / —
комплексный полином, то отображение w=f(z)
всегда имеет неподвижные точки. Они
определяются как корни уравнения
f(zf=z, т. е. j{z)-z=Q^ Если степень
полинома / равна к, то это уравнение
имеет к корней. Некоторые из них
могут совпадать, т. е. могут быть
кратными корнями. Корни изображаются
точками Z\, ....zk на пополненной
плоскости "С =R U оо . Пусть в какой-
то из этих точек z, выполнено
неравенство гагЛ'х*Л<1. Т°гда отображение f
является сжимающим4 в этой точке, т.
е. корень 2, является точкой
притяжения некоторых других точек плоскости.
Можно далее рассмотреть на
плоскости область притяжения корня z,-,
т. е. совокупность точек z, для которых
LlSi/"^)-2»-Оказывается, такие
множества также часто являются
фракталами. Они могут иметь исключительно
сложную и в то же время красивую
форму [20]. Можно также
рассмотреть следующее множество-точек:
{z : Jim|/¦<*)¦!-~Ь
т. е. область притяжения бесконечно
удаленной точки. Эти множества
также часто оказываются фракталами.
Некоторые примеры фракталов
показаны на рис. 3.
2Л. Комментарий к наглядному материалу
Фракталы естественно возникают при
моделировании броуновского
движения, при построении множеств,
похожих на канторово, при изучении
случайных процессов. Примерами
случайных последовательностей чисел
являются десятичные разложения,
например, чисел пне (рис. 6). Разложение
числа я дано на передней стороне
призмы, разложение е — на боковой
справа. Число черных пятен (кругов) в
квадрате обозначает соответствующий
знак десятичного разложения, которое
выписывается по горизонтали, затем
перескакивает в начало следующей
строки и т. д. Наверху призмы
показаны примеры фракталов,
конструируемых наподобие канторова множества
или ковра Серпинского. На рис. 7
также изображены (в ином ракурсе)
десятичные разложения я И е. На рис. 8
показаны последовательности падающих
(из центра, удаленного на
бесконечность) случайно ориентированных
параллелепипедов (балок). Встречая на
своем пути препятствия (плоские
площадки), они начинают образовывать
холмы и горы, напоминающие
нормальное распределение. Начальная стадия
этого процесса показана на рис. 9.
Вдали, за горизонтом, видны горы,
образованные в результате длительного
падения таких объектов. Десятичное
разложение я (но только закодированное
другим способом) показано на рис. 10.
На рис. 11 показаны типичные
картины, возникающие во фрактальной
геометрии при изучении комплексной
динамики (см. [20]) комплексных
преобразований плоскости. Фракталы возникают
в динамических системах при изучении
преобразований сдвига вдоль траекторий
системы. Часто полезно представ-

лять себе структуру фундаментальных
областей данного действия группы (рис.
12). Различные элементы фрактальной
геометрии показаны на рис. 13 — 17.
На рис. 13 можно видеть хаотические
всплески, возникающие на поверхности
жидкости при высокочастотном
возбуждении границы раздела. На рис. 15
(слева) видчы образования, похожие на
области притяжения корней
комплексных преобразований плоскости. Они
напоминают звезды с бесконечным
числом лучей, исходящих из нескольких
центров. На рис. 16 ("От хаоса к
порядку'), перекликающемся с идеями
книги А. Н. Ширяева [43], в
абстрагированном виде показана идея теории
вероятностей и статистической
фрактальной геометрии — постепенное
обнаружение гармонии и порядка в
кажущемся первоначально хаотическом
нагромождении образов. На рис. 18
предпринята попытка передать идею
математической (геометрической)
бесконечности, тесно связанной с идеей
фракталов. Бесконечные вариации и
разнообразие одного и того же
привычного оС^лза напоминают искажение
фундаментальной области при
дискретном действии бесконечной группы. Рис.
19 — 21 посвящены попытке
современного геометрического преломления
некоторых научных идеи, волновавших
еще средневековых ученых и
художников (в частности, Босха, Брейгеля,
Дюрера и др.). Все они интересовались
и теорией перспективы,
принципы правильного
изображения объектов, впервые нащу-
механизмы оп-
. п. Творчество
авторов тех времен находилось,
естественно, под влиянием специфического
(и очень интересного) научного
мировоззрения, которое отражалось и в
графике, живописи той эпохи. Такова,
например, известная гравюра Брейгеля
"Алхимики". Рис. 19 можно
рассматривать как математическую
вариацию на эту тему, главным
содержанием которой является наглядное
моделирование идеи математической
бесконечности, так живо интересовавшей и
глубоко волновавшей многих ученых,
начиная с эпохи Возрождения. В этом
смысле рис. 19 — 21 являются
попыткой представить себе, как
средневековые графики и геометры изобразили бы
волновавшие их идеи, легенды и пр.,
если бы они владели понятием
математической бесконечности в том объеме,
который известен современному
математику. Конечно, многие научные
представления авторов средних веков
сейчас потеряли свою актуальность и
воспринимаются современным
читателем и зрителем как весьма странные,
однако многие довременные
геометрические идеи органично выросли из
удобренной ими почвы. Поэтому нам
показалось любопытным синтезировать
в нескольких графических работах
немного странные средневековые
образы и современные математические
концепции бесконечности, деформации,
непрерывности. На рис. 19 — 21
изображены как многие символы и образы
средневековой науки (геометрические и
астрономические приборы, химические
принадлежности и пр.), так и сугубо
еяные предметы (оптические
аппаратура и т. п.). Однако эта
смесь — не механическая, а
наследственная, поскольку рассматривается
глазами современного зрителя,
чувствующего связь между глубокими
математическими исследованиями нашего
времени, и тем своеобразным научным
мышлением, которое населяло
тогдашний окружающий мир странными
фантастическими образами. Рис. 22 — 25
иллюстрируют идею гомеоморфизма.
§ 3. Наглядная компьютерная геометрия
в теории чисел
На первый взгляд теория чисел лишена действительности это не так. А при со-
какой-либо геометричности. Однако в временном развитии компьютеров поя-

§3. Наглядная компьютерная геометрия в
вилась возможность объяснить
широкому кругу читателей, что наглядная
геометрия помогает не только
иллюстрировать те или иные абстрактные
положения из теории чисел, но и
помогает иногда решать новые задачи.
Наглядная компьютерная геометрия
помогает нащупывать математическое
утверждение, после чего следует этап его
логического доказательства. В такой
сложной теории, каковой является
теория чисел, иногда трудно даже
сформулировать правдоподобную
гипотезу. Современные вычислительные
средства позволяют правильно выбрать
гипотезу в результате обработки
большого экспериментального материала и
его изображения в наглядном виде.
Многое зависит от способа
изображения информации. Нужно так удачно
закодировать ее наглядными образами,
чтобы возникающие на экране
компьютера картины помогали исследователю
угадывать правильное направление ис-
Условимся помечать те натуральные
числа, которые непредставимы в виде
A), черным цветом, а представимые —
белым. Теперь рассмотрим один из
возможных способов изображения
натурального ряда на экране компьютера.
Возьмем бесконечную ленту и
разметим ее на одинаковые квадратики, в
которые последовательно впишем
натуральные числа (рис. 1). Фиксируем
целое число d и разобьем эту
бесконечную ленту на куски длины а. Это число
назовем модулем изображения.
Вспомним, как формируется изображение на
экране телевизора. Электронный луч
пробегает 1-ю горизонтальную строку,
перескакивает в начало 2-й строки,
пробегает ее и т. д. В результате луч
заметает весь квадратный экран,
создавая на нем некоторое изображение. Мы
поступим так же. Первый отрезок дли-
Рассмотрим задачу о представлении
натуральных чисел »?l в виде сумм
п=п[+г!г + + nrs, A)
где все числа' щ; 1 <, i < s—
неотрицательные целые.
Фиксируем произвольные значения
г>2 и &>1. В таком случае все
натуральные числа разбиваются на два класса. К
одному классу относятся все те
натуральные числа, которые
представляются в виде A), а ко второму классу —
числа, которые нельзя при данных
параметрах rws представить в виде A).
Возникает общая задача (обобщенная
проблема Варинга): как описать
каждый из указанных выше классов?
Задача эта чрезвычайно сложна. Мы
вкратце опишем как известные ранее
результаты, так и недавно полученные.
Особое внимание мы уделим здесь
результатам, первоначально
"нащупанным" при помощи компьютерной
графики (после чего они были доказаны
математически).
Эта работа выполнена А. А. Зенки-
ным. Некоторые из этих результатов
«(см. [20, [25]).
¦Н'М'М'1
Рис. 1
ны d укладываем на первую строку
экрана, второй отрезок ленты — на
вторую строку и т. д. Тогда экран
заполнится натуральными числами от 1
до некоторого N, определяемого
размером экрана.
Поскольку основное интересующее нас
сейчас свойство натуральных чисел —
это "представимость или непредстави-
мость" (в виде A)), то абсолютная
величина чисел нам не нужна. При желании
эту информацию можно восстановить,
подсчитывая число квадратиков на
экране. Итак, отмечая черным
непредставимые числа, а белым — представимые,
мы получаем на экране компьютера
некоторый пятнистый черно-белый ковер,
состоящий из черных и белых
квадратиков (при заданных г, s, d). Ковер
этот может быть чрезвычайно сложен.
Фиксируем г=2 и начнем увеличивать
параметр^!, 2, 3,.... Величину d
фиксируем. Итак, мы изучаем вопрос о предста-

202
вимости чисел в виде: а) квадрата
некоторого числа, б) суммы двух квадратов,
в) суммы трех квадратов и т. д.
Посмотрим на характер изменения
картины на экране (рис. 2). Сначала
(при s=l) почти весь экран — черный.
Кое-где видны белые квадратики.
Видно, насколько мало чисел, являющихся
квадратами. При увеличении s экран
s = 3 (Ф.Гаусс)
Рис. г
Наглядные образы в приложениях геометрии
начинает "белеть". Наконец, при s=4
весь экран вспыхивает белым цветом.
Черные квадратики исчезли. При 5=5
картина уже не меняется: экран
остается белым. Ясно, что мы "увидели"
некоторую закономерность.
Компьютерная гипотеза 1. Суммы
четырех квадратов (пи е. s =4)
достаточно, чтобы представить в виде A)
1-2 (Л. Эйлер)
n Q Q.
q
1« 4 (Л. Лагранж)

§ 3. Наглядная компьютерная геометрия я теории чисел
203
любое натуральное число.
Оказывается, мы увидели на экране
известную теорему Лагранжа,
доказанную им в 1740 г.
Теорема Лагранжа. Любое
натуральное число представшю в виде
суммы четырех квадратов.
Каждый математик знает и может
привести много примеров из своей
научной практики, когда почувствовать,
«увидеть» правильную гипотезу
оказывается иногда гораздо сложнее, чем по-
Рис.З
том ее доказать. Особенно часто
наглядными образами пользуются в геометрии и
топологии, где приходится работать с
многомерными объектами, ' иногда в
принципе не допускающими изображения
в трехмерном пространстве.
Рисунком 2 комьютер сообщил нечто
большее. Ковер при 5=2 явно
содержит простую структуру: отчетливо видны
б вертикальных черных столбцов, т.е.
целиком состоящих из черных квадратов.
Это — тоже известная теорема.
Теорема Эйлера A749). Пуст»
натуральное число п имеет вид и н 3. 6, 7
(mod 8). Тогда все числа видап- К , где
k = 0, 1, 2,..., непредставимы в виде
A) для г = 5= 2 , тх. п ¦ 4* * и/ч-я/.
Мы так удачно выбрали модуль d,
что указанные в теореме Эйлера числа,
непредставимые в виде A),
расположились точно друг под другом на экране,
в результате чего и образовались
черные столбцы. Но это еще не все. На
рис. 2 при s =3 черных квадратов
осталось уже немного. Остальное белое
поле явно организовано в несколько
наклонных полос, концентрирующихся
вдоль белых отрезков, имеющих
одинаковый наклон.
Ясно, что это снова не случайно.
Однако пока ковер на рис. 2 при s = 3 еще
недостаточно выразителен. Попробуем
слегка изменить изображение, стремясь
сделать его более «завершенным». Будем
менять модуль d. Результаты см. на рис.3,
где изображены картины при d = 22-24.
Совершенно ясно, что при а = 24 картина
приобрела «окончательный» вид.
Столбцы стали вертикальными. Конечно, вне
столбцов есть черные квадраты, но сейчас
для нас основной интерес представляют
черные столбцы. Это — не менее
известная теорема Гаусса.
Теорема Гаусса A801). Суммой трех
квадратов непредставимы те и только
те натуральные числа, которые имеют
вид п = 8/Ы-7, k = 0, 1, 2,... (т.е.
я = 7(mod 8)), и те числа, которые полу-
mod 22 mod 23 mod 24
(Ф. Гаусс)

4. Наглядные образы в приложения! геометрии
з них умножением на любукг-
степень числа 4, т. е. числа вида п-4,
где 1=1,2,3,....
Все нюансы теоремы Гаусса отчетливо
видны на экране (рис. 3). Отметим, что
в любом k-м столбце на экране (по
модулю d) стоят числа вида п ш ?(mod d),
т. е. дающие при делении на а один и
тот же остаток k. На рис. 3 визуально
выделяется главная серия столбцов
(сплошь черных). Следовательно, в них
стоят числа, которые при делении на 8
дают в остатке 7 (числа s7(mod 8)), т. е.
числа вида я=8лН-7, Ы), 1, 2, ....
Используя процедуру выметаниЯт которая
в любом множестве чисел находит все
подпоследовательности типа арифмети-
ющии ответ.
Теорема Т. Райли A825, затем
Ричмонд, 1930). Любое рациональное
число а представимо в виде сумм трех
кубов рациональных чисел, а именно
"Кйй-йг**) +(iv+&$) +(яЗ+Я+зО •
Перейдем теперь к классической
проблеме Варинга. Фиксируем г=3 и будем
менять s, т. е. изучать вопрос о
представимости чисел п в виде суммы s
кубов: п=щ +...+П, . Снова выведем
информацию на экран в виде "ковра".
На рис. 4 показаны картины (для 5=1,
7, 8), последовательно
ческих и геометрических прогрессии,
легко убедиться, что все остальные
черные квадраты изображения на рис.
3 при а=24 являются элементами гео-
гаеских прогрессий вида п-4, t=l,
метрическ
2, 3, ....
элемент одного из
столбцов главной серии.
Перейдем к следующей по сложности
задаче — о представимости чисел в
виде суммы кубов. Если бы мы имели
дело не с целыми, а с рациональными
числами, то этот вопрос имел бы следу-
при увеличении 5=1, 2, 3, 4, 5, 6, 7, 8, 9.
Вообще этот материал было бы удобнее
иллюстрировать мультфильмом, кадры
которого можно было бы снимать
прямо с экрана компьютера. Итак, первые
— почти сплошь черные, затем
белое поле начинает увеличиваться.
Наконец, при 5=8 на белом фоне экрг
остается лишь 2 черных квадрата.
5=9 исчезают и они. Итак,
экрана
а. При

§3. Наглядная компьютерная геометрия в теории ч>
5=9 весь экран — белый! Кстати, два
последних черных квадрата на 8-м
кадре — это числа 23 и 239.
Компьютерная гипотеза 2. Любое
натуральное число представимо в виде
суммы девяти кубов.
Это — известная теорема немецкого
математика А. Вифериха, доказанная
им в 1909 г.
Компьютерная гипотеза 3. Сначала (при
малых s) черного цвета очень мною (и,
по-видимому, множество черных
квадратов бесконечно), потом черного ста-
Л
0
-?*¦
12 3... Gir)..
Рис.5
новится гораздо меньше (и,
по-видимому, здесь множество черных квадратов
стало конечным).. И наконец, черный
цвет пропадает совсем (по-видимому,
здесь множество черных квадратов
пусто).
Из полученных картин можно
сформировать гипотезу, что такая ситуация
верна и для других степеней 7^4, 5,
6, .... Графическое изображение
гипотезы см. на рис. 5. Здесь s — число
слагаемых в сумме A), г ?2 —
фиксированный показатель степени, N —
количество натуральных чисел черного
цвета (т. е. непредставимых). Пусть г
фиксировано. Поскольку число
слагаемых s монотонно возрастает (рис.
5), то существует некоторое значение
s=G(r) (зависящее, конечно, от г) такое,
что при s<G(r) черное множество
бесконечно, а при s?d(r) черное
множество конечно. Другими словами, G(r) —
число слагаемых в
с:
суммах A), при котором черное
множество впервые становится конечным.
Аналогичная граница возникает при
дальнейшем возрастании s, т. е. при
переходе числа элементов черного
множества от конечного к нулю. Эту вто-
границу мы обозначим через g(r).
g(r) — это наименьшее число
слагаемых в сумме A), при котором
черное множество впервые оказывается
пустым.
Другими словами, при s>G(r) лишь
конечное число натуральных чисел не
разлагается в сумму nT\?..A-ns, а при
s?g(r) все натуральные числа предста-
вимы в виде nrf?...+nrt.
Эти две функции G(r) и g(r)
называются гильбертовскими. Мы привели
соображения, подсказанные
компьютерной графикой, в пользу гипотезы о
том, что число g(r) конечно. Из его
определения это, конечно, не вытекает.
Гипотеза Варинга. Для любой степени
т&2 существует (т. е. конечно)
наименьшее число слагаемых ф) такое,
что при всех &g(r) множество
натуральных чисел, непредставимых в виде
n'i+...+п,, пусто. Здесь я, —
неотрицательные целые числа.
Варинг сформулировал эту гипотезу в
1770 г., опираясь на теорему Лагранжа
и эмпирические предположения своих
предшественников, что всякое
натуральное число представимо суммой
девяти кубов и девятнадцати четвертых
степеней. Теоремы Вифериха A909) он,
конечно, не знал, но соответствующая
эмпирическая гипотеза о суммах кубов
существовала уже в то время.
Известно, что gB)=4, gC)=9, gD)=19.
Как видно, функция g(r) быстро растет,
поэтому априори не исключено, что для
некоторого Го она окажется равной
бесконечности. Это означало бы, что при
любом сколь угодно большом числе
слагаемых s найдется такое достаточно
большое натуральное я, которое
непредставимо в виде суммы пг[+...+пг?.
В результате значительных усилий
многих математиков гипотеза Варинга
была, наконец, доказана в 1909 г.

4.Наглядные образы в приложениях геометрии
Д. Гильбертам, и с тех пор носит
название теоремы Гильберта-Варинга. •
Классическая гипотеза Варинга
обобщалась затем по разным направлениям.
Здесь мы не будем вдаваться в эти обоб-
" зовем лишь имена некоторых
», получивших здесь дальней-
таты: И. М. Виноградов A938,
Гольдбаха-Варинга), Хуа
"", Хуа Ло-ген и Р. Хастон
т A934), Б. И. Сегал A933},
Ло-ген A937), Хуа Ло-ген и Р. Хастон
A938), Е. Райт
К. Рот A951), В. И/Нечаев A953), А. А.
Карацуба A962) и др.
Имеется, впрочем, одно естественное
обобщение, которого мы здесь
коснемся. Во время экспериментов с ЭВМ
(А. А. Зенкин) по классической
проблеме Варинга неожиданно вскрылось
следующее обстоятельство. Если в-
суммах A) условие «я,- —
неотрицательные целые» заменить на условие
«я,- — натуральные (т.е.
положительные целые)», то ситуация меняется.
Интересно, что первоначально
компьютер сделал эту подмену условий
самостоятельно, поняв желание
экспериментатора сэкономить его память, как всегда,
слишком буквально. Компьютер начал
отбрасывать малоинформативные с его
точки зрения нулевые слагаемые, т.е.
случаи, когда я = 0. Оказалось, уже
в простейшем случае теоремы Лагранжа,
т.е. при г = 2, s= 5 и 6, вместо теоремы
Лагранжа получился следующий
мультфильм,показанный на рис. 6. Отличие в
том, что с ростом числа слагаемых s
черное поле убывает до значения 5=6,
но дальше с ростом s количество
черных квадратов не меняется! Остается
сухой остаток из 7 чисел вида J+{1, 2,
4, 5, 7, 10, 13} при всех * ? 6. Этот
визуально-эмпирический результат
(обнаруженный в результате случайно
возникшего недопонимания между
экспериментатором и компьютером) позволил
сформулировать гипотезу.
Компьютерная гипотеза 4. При г =2 и
для всех 5^6 любое натуральное число
я ? 1 представимо суммами A) с
ограничением я,? 1, кроме чисел 1, 2,..., 5-1
и чисел вида s?z, где z является одним из
чисел{1,2,4, 5, 7,10,13}.
Дополнительный анализ научной
литературы вскоре обнаружил теорему
американского математика Г. Полла,
доказанную им еще в 1933 г. и которая
дословно совпадает с компьютерной
естественный вопрос: что за
странное множество выделил
компьютер вслед за Поллом? Было решено с
помощью компьютера просмотреть со-

§ 3. Наглядная компьютерная геометрия в теории чисел
¦а О"

208
4.Наглядные образы в приложениях геометрии
ответствуюший мультфильм для кубов,
т.е. при г = 3, т.е. аналог теоремы
Вифериха, но с ограничением на
слагаемые в суммах A) вида я, S 1.
Результат см. на рис. 7. Снова остается сухой
Компьютерная гипотеза 5. При г =3
и для всех 5 ^ 14 любое натуральное
число п гфьЭстабюю суммой A), где
все ъ ? 1, за исключением
натуральных чисел: 1, 2,..., ?-1, м 5+74 чисел
вида *fz, где z является элементами
«странного» множества: {1-6, 8-13,
15-20, 22-25, 27, 29-32, 34, 36-39, 41,
43-46, 50, 51, 53, 55, 57, 58, 60, 62, 64,
65, 67, 69, 71, 72, 74, 76, 79, 81, 83,
86, 88, 90, 93, 95, 97,100,102, 107, 109,
114, 116,121, 123, 128, 135, 142, 149}.
Как видим, и здесь появляется
странное множество, которое (и ему
подобные) Дж. Лагариус назвал
исключительными множествами.
Компьютерная гипотеза 5 была затем
строго математически доказана в [24].
Это — новый математический
результат. Мы имеем пример успешного
использования компьютерной графики
для формирования правильной
математической гипотезы. Затем с помощью
компьютеров были исследованы многие
интересные свойства таких множеств, в
частности, удалось сформулировать, а
потом строго доказать гипотезу их
конечности.

Литература
1. Дувром Б. А, Нем» С О, Фоменко А. Т.
Современная геометрия. Части 1, 2. М.: Наука,
1979; Часть 3. М.: Наука, 1984.
2. Фомевжо А. Т. Дифференциальная геометрия и
топология. Дополнительные главы. М.: Иэд-во
МГУ, 1983.
3. Гильберт Д., Ков-Фоссея С. Наглядная
геометрия. М.: Наука, 1981.
4. Земферт Г., Трельфалль В. Топология. М. — Л.:
ГОНГИ, 1938.
V Фуке Д. Б., Фоменко А. Т., Гутенмахер В. А.
Гомотопическая .пологая. М.: Изд-ао МГУ, 1969.
6. Рохлин Б. А., Фукс Д. Б. Начальный курс
топологии. М.. Наука, 1977.
7. Ммлиор Дж. Теория Морса. М.: Мир, 1965.
8. Погорело* А. В. Дифференциальная геометрия.
М., Наука, 1974.
9. Александров А. Д. Внутренняя геометрия
выпуклых поверхностей. М. — Л.: Гостехиздат,1948.
10. Погорело» А. В. Внешняя геометрия выпуклых
поверхностей. М.: Наука, 1969.
П. Фоменко А. Т. Вариационные методы в
топологии. М.: Наука, 1982.
12. Фомевжо А. Т. Топологические вариационные
задачи. М.: Иэд-во МГУ, 1984.
13. Зейферт Г., Трельфалль В. Вариационное
исчисление в целом. М.: ИЛ, 1947.
14. Де Рам Ж. Дифференцируемые многообразия.
М.: ИЛ, 1956.
15. Понтряпш А. С. Непрерывные группы. М.:
Наука, 1973.
16. Ebergard Schroder. DQrer Kunst und Geometric.
Ber&n: Akademie - Veriag, 1980.
17. Математическая энциклопедия. Т. 1 — 4, M.,
1977 —1984.
18. Володин И А., Кузнецов В. Е., Фоменко А. Т. О
проблеме алгоритмического распознавания
стандартной трехмерной сферы // УМН. 1974. Т. 24,
№ 5. С. 71 -168.
19. Homma Т., OcMai М, ТакаЬавЫ М. An algorithm
for recognizing S3 in ^manifolds with Heegard spittings
of genus two// Osaka J. Math. 1980.17. P. 625 — 648.
20. Mandelbrot В. B. The fractal geometry of nature.
New York: W. H. Freeman and Company, 1977.
21. A. T. Fomenko. Mathematical Impressions. —
American Math. Society, USA, Providence, 1990.
22. Фоменко А. Т. Топология поверхностей
постоянной энергии интегрируемых систем и препятствия
к интегрируемости // Известия АН СССР. 1986. Т.
50, № 6. С. 1276 — 1307.
23. Татаривов Я. В. Лекции по классической
механике. М.: Изд-во МГУ! 1К4-
24. Зеякш А. А. Обобщение теоремы Вифернха на
случай натуральных слагаемых // ДАН СССР.
1982. Т. 264, №2. С. 282 - 285.
25. Зеякмв А. А. Обобщение теоремы Гильберта —
Варинга// Вести. Моск. ун-та. Сер. 1. Математика,
механика. 1983. № 2. С. 11 - 19.
26. Козлов В. В. Методы качественного анализа в
динамике твердого тела. М.: Изд-во МГУ, 1980.
27. Аносов Д. В. Грубые системы //Труды
МИАН.- Т. 16971985.
28. Morgan J. Non-sinnilar Morse — Smale flows on
3-dimenBonal manifolds // Topology. 1979. 18. N 1.
P. 41 - 54.
29. Ефремович В. А., Чернявский А. В. Элементы
топологии. Ярославль: Изд-во Ярославского ун-та.
1977.
30. Харламов М. П. Метод интегральных
отображений в задачах динамики твердого тела //
Методы исследования стационарных движений
механических систем. М.: Иэд-во МГУ, 1980. С. 17 -18.
31. Погосан Т. И., Харламов М. П. Области
возможности движения в некоторых механических
системах // Прикладная математика и механика.
1981. Т. 45, вып. 4. С. 605 — 610.
32. Харламов М. П. Симметрия в гироскопических
системах // Механика твердого тела. 1983. Вып. 15.
С. 87 - 93.
33. Татаривов Я В. Глобальный взгляд на динамику
твердого тела. Описание конфигурации // Вести.
Моск. ун-та. Сер. 1. Математика, механика. 1978,
№ 4. С. 101 - 109.
34. Матвеев С В., Савватеев В. В. Трехмерные
многообразия, имеющие простые специальные
остовы // Coboqubn Mathematicum. 1974. V. 32,
F. 1. Р. 83 - 97.
35. Матвеев С В., Бурмистром А. Б. Структура S-
функций на ориентируемых 3-многообразиях //
Тезисы XI Всесоюзной школы по теории
операторов в функциональных пространствах. Т. I.
Челябинск. 1986. С. 70.
36. HUdebrandt S., Tromba A. Mathematics and
optimal form. Sdentinc American Library. N. Y.:
Scientific American Boob Inc., 1985.
37. Александров П. С Комбинаторная топология.
ОГИЗ: Гостехиздат. 1947.
38. Болсинов А. В. Гладкая траекторная
классификация интегрируемых гамильтоновых систем с
двумя степенями свободы. // Матем. сборник. 1995.
Т. 186, вып. 1, С. 3-28.

210
Литература
39. Новиков С. П. Гамильтонов формализм и
многозначный аналог теории Морса // УМН. 1982.
Т. 37, № 5. С. 3 — 49.
40. Масло* В. П. Теория возмущений и
асимптотические методы. М.: Изд-во МГУ, 1965.
41. КоЬКгх N. Introduction to Effiptic Curves and
Modular Form. N. Y.: Springer-Verlag, 1984.
42. Kobfitz N. P-adic Numers, p-adic Analysis, and
Zeta-Functionj. N. Y.: Springer-Verlag, 1977.
43. Shiryaev A. N. Probability. N. Y.: Springer-
Verlag, 1984.
44. Матвеев С. В. Алгоритм распознавания
трехмерной сферы (по А. Томпсон). // Матем. сборник.
1995. Т. 186, вып. 5, С. 69 -84.
45. Черкавскмй А. В. Локальная стягиваемость
группы гомеоморфизмов многообразий //Матем.
сборник. 1969. Т. 79. С. 307 — 356.
46. ЕгЬу R, Stable homeomorphisms and die annuhs
conjecture // Annals of Math. 1969. V. 89. P. 575 -
582.
47. Козлов В. В. Интегрируемость и неинтегрируе-
мость в гамильтоновой механике // УМН. 1983. Т.
38, вып. 1. С. 3 - 67.
48. Машп Yu. I. A Course of Mathematical Logic.
N. Y.: Springer-Verlag. 1977.
49. Маян Ю. И. Математика и физика. М.:
Знание, 1979.
50. Thompson A. Thin position and the recoqnMon
problem for S3 // Preprint, 1994.
51. Захаров В. E., Фаддеев А. Д. Уравнение Корте-
вега — де Фриза — вполне интегрируемая гамиль-
тонова система // Фуккц. анализ и его
приложения. 1971. Т. 5, № 4, С. 18 - 27.
52. Матвеев С. В. Один способ задания 3-
многообраэий // Вести. Моск. ун-та. Сер. 1.
Математика, механика. 1975. № 3. С. 11 — 20.
53. Fomenko А. Т. Symmetries of soap films // Сотр.
Math, with Appl. 1986. V. 12 B. N 3/4. P. 825 — 834.
54. Колмогоров A. H. Основные понятия теории
вероятностей. 2-е изд. М.: Наука, 1974.
55. Гвкдеяко Б. В. Курс теории вероятностей. 4-е
изд. М.: Наука, 1965.
56. Wakfcaueen F. Erne Basse von 3-dimensional
MariBg&Wgkehen. I. // Invent Math. 1967. V. 3, №. 4.
P. 308-333.
57. Zeschang H. Finite groups of mapping classes of
surfaces. N. Y.: Springer-Verlag, 1981.
58. Rubinstein H. The solution to the recognition
problem for J3. - Lectures, Haib, Israel, May 1.
59. Федррчук В. В. Метод развертываемых
спектров и вполне замкнутых отображений в обшей
топологии// УМН. 1980. Т. 35, вып. З.С.Ш-121.
60. Татаринов Я. В. Построение компактных
инвариантных многообразий, отличных от торов, в
одной интегрируемой неголономной системе
(тезисы докл.)//УМН. 1985.Т. 40, вып. 5, С. 216.
61. Thurston W. P. Three dimensional manufolds,
Klernian groups and hyperboEc geometry // Bull.
Amer. Math. See. 1982. V. 6. P. 357 - 381.
62. Смейд С. Топология и механика // УМН. 1972.
Т. 15, вып. 2. С. 77 - 123.
63. Гельфаяд И. М., Черешок И. В. Абстрактный
гамильтонов формализм для классических пучков
Янга - Баксгера // УМН. 1979. Т. 38, вып. 3.
С. 3-21.
64. Casler В. С. An embedding theorem for connected
3-manifolds with boundary // Pros. Amer. Math. Soc.
1965. V. 16, N 4. P. 559 - 566.
65. Smale S. The classification of immersions of the
Spheres in EucBdean spaces // Am. Math. Ser. 2.
1959. V. 69, N 2. P. 327 — 344.
66. George K. Francis. A Topological Picturebook.
N. Y.: Springer-Verlag, 1987.
67. Banchoff Thomas and diaries Strauss. Complex
Function Graphs, Dupin Cycldes, Gauss Map, and
Veronese Surface // Computer Geometry Films.
Brown University, Providence, 1977.
68. Birman Joan. Braids, Links and Mapping Class
Groups. Princeton: Princeton Univ. Press, 1983.
69. Boy Werner. Ober die Curvatura Integra und die
Topologie geschbstener Fbchen. Dissertation
Gotnngen. 1901 // Math. Am. 1903. 57. P. 151 -184.
70. Francis George K.~and Bernard Morin. Arnold
Shapiro's eversion of the sphere // Math. Inteffigencer.
1979. V. 2. P. 200-203.
71. Freedman Michael The topology of four-
dimensional manifolds // J. Off. Geometry. 1982.
V. 17. P. 357 — 452.
72. Hatcher Allan and William Thurston. A
presentation for the mapping class group of a closed
orientable surbce// Topology. 1980. V. 19. P. 221 -
237.
73. Дао Чонг Тхи, Фоменко А Т. Минимальные
поверхности и проблема Плато. М.: Наука, 1987.
74.*Матвеев С. В., Фоменко А. Т. Иэоэнергетиче-
ские поверхности гамильтоновых систем,
перечисление трехмерных многообразий в порядке
возрастания их сложности и вычисление объемов
замкнутых гиперболических многообразий // УМН. 1988.
Т. 43, вып. I. С. 5-22.
75. Nhsche J. Vorlesungen Qber Mfaimalftachen.
N. Y.: Springer-Verlag, 1975.
76. Penrose L. S. and Penrose R. Impossible objects: a
special type of illusion// Brit. J. Psychol. 1958. V. 31.
P. 31-,33.
77. Poston Tim and Stewart Ian. Catastrophe Theory
and its AppBcations. London: Pitman Boob Inc., 1978.
78. Thurston William. Hyperbolic structures on 3-
marifoke// Am. of Math. 1986. V. 124. P, 203 - 246.

Литература
211
79. Zeeman Е. С. Catastrophe Theory. Selected
Papers 1972 — 1977. Mass. Addeon - Wesley,
Reading, 1977.
80. Peitgen HO., Richter P. H. The beauty of
fractals. Images of complex dynamical systems. N. Y.:
Springer-Verlag, 1985.
81. Браилов А. В., Фоменко А. Т. Топология
интегральных многообразий вполне интефируемых
гамильтоновых систем // Математический сборник.
1987. Т. 133, № 3. С. 375 — 385.
82. Новиков С. П., Фоменко А. Т. Элементы
дифференциальной геометрии и топологии. М.: Наука,
1987.
83. Фоменко А. Т., Цишанг X. О топологии
трехмерных многообразий, возникающих в гамильтоно-
•ой механике //ДАН СССР. 1987. Т. 294, № 2.
С. 283-287.
84. Birman S., Hflden М. The hcmeomorphism
problem for S* // Bull. Amer. Math. Soc 1973. V. 79,
N 5. P. 1006 -1010.
85. Фоменко А. Т. Симплектическая геометрия.
Методы и приложения. М.: Изд-во МГУ. 1988.
86. Фоменко А. Т., Цишанг X. О типичных
топологических свойствах интефируемых гамильтоновых
систем// Известия АН СССР. 1988. Т. 52, № 2.
С. 378 - 407.
87. Матвеев С. В., Фоменко А. Т., Шарко В. В.
Круглые функции Морса и иэоэнергетические
поверхности интефируемых гамильтоновых систем
// Математический сборник. 1988. Т. 135, № 3.
С. 325-345.
88. Fomenko А. Т., Tronmov V. V. Integrable
systems on Lie algebras and symmetric spaces. London:
Gordon and Breach. 1988.
89. Фоменко А. Т., Фукс Д. Б. Курс
гомотопической топологии. М.: Наука, 1989.
90. Ченюв Н. Н. Статистические решающие прааи-
91. Болотов А. В., Матвеев С. В., Фоменко А. Т.
Топологическая классификация интефируемых
гамильтоновых систем с двумя степенями свободы.
Список систем малой сложности. — УМН, 1990,
Т. 45, вып. 2. С. 49 -77.
92. Weeks J. R. Hyperbolic structures on three-
manifolds. — A dissertation presented to the Faculty of
Princeton Univ., Dept. of Math., 1985.