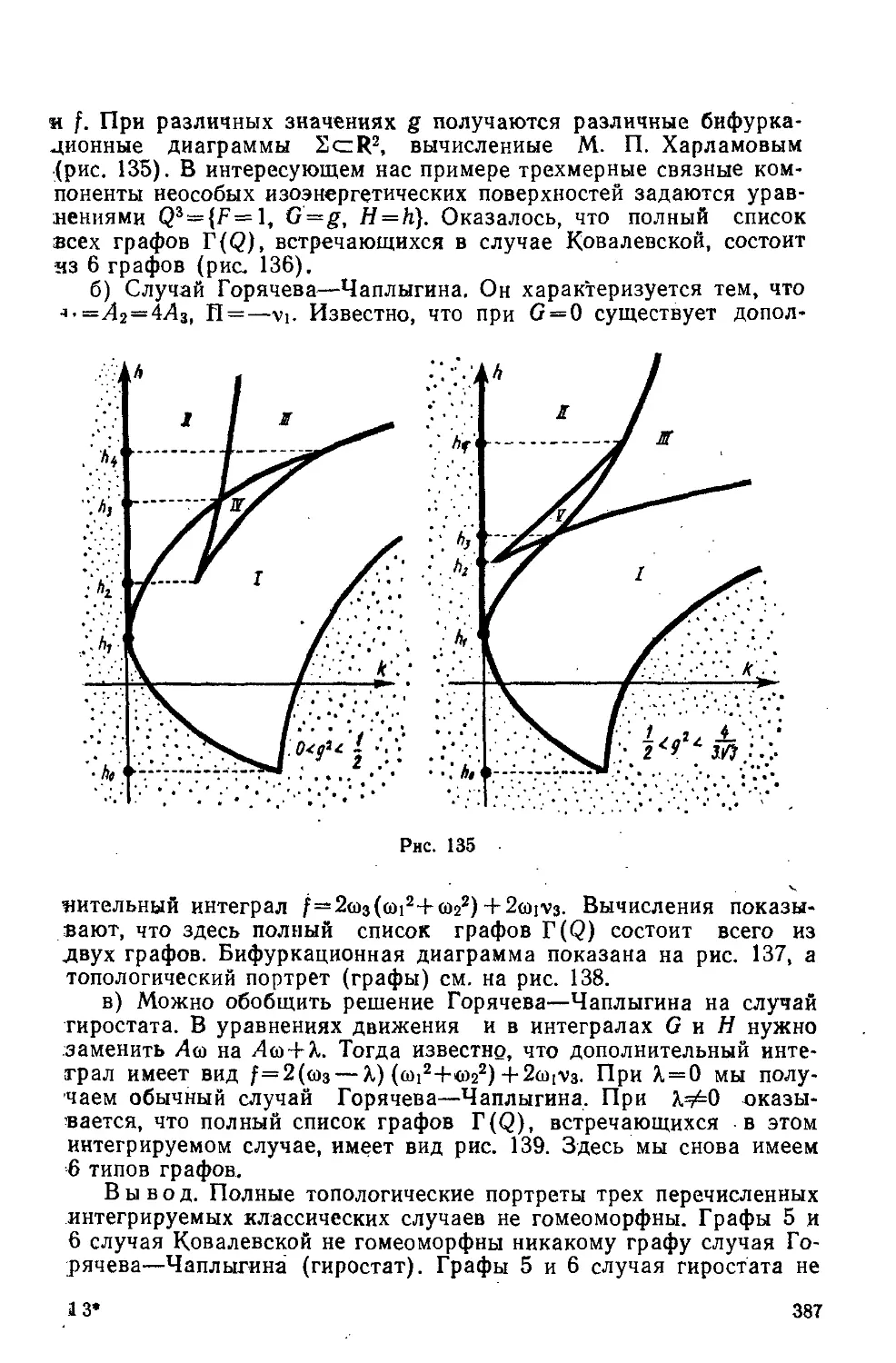
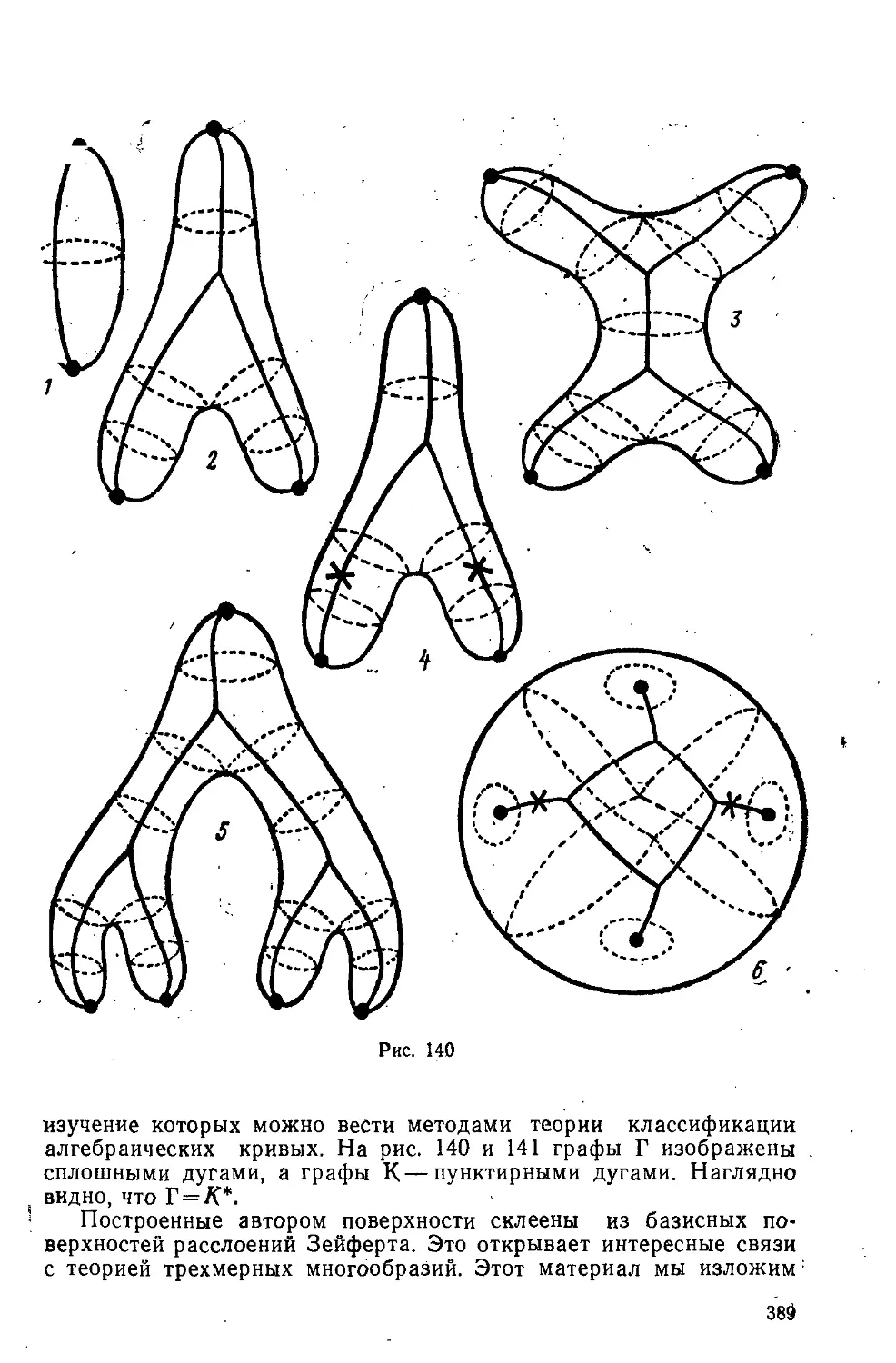
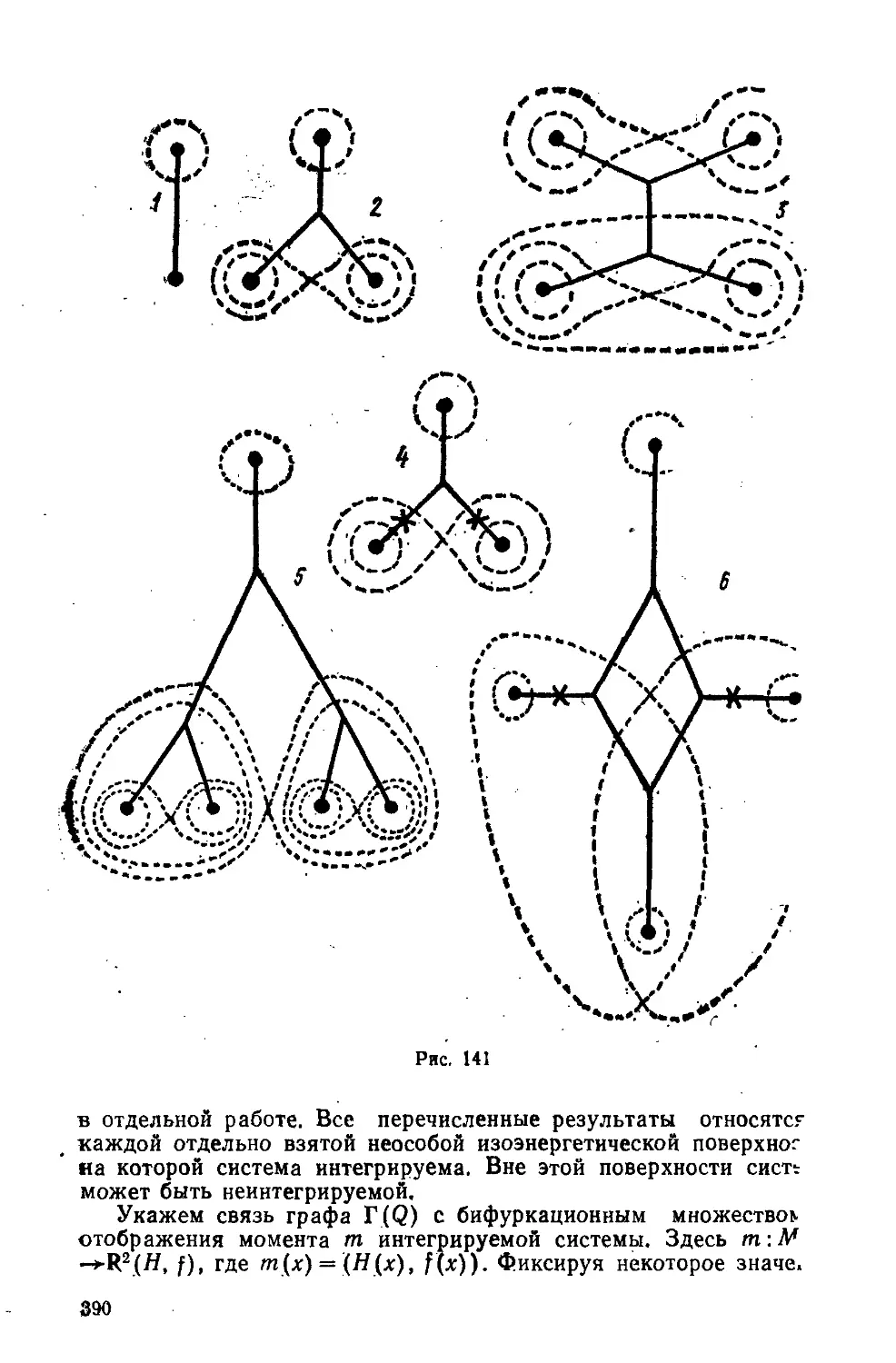
Text
А. Т. Фоменко
СИМПЛЕКТИЧЕСКАЯ
ГЕОМЕТРИЯ
Методы и приложения
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособия для студентов
-вузов, обучающихся по специальности «Математика»
ИЗДАТЕЛЬСТВО МОСКОВСКОГО УНИВЕРСИТЕТА
1988
B18fc».151
Ф76
УДК 513.83
Заставки к главам и рисунки в тексте выполнены л. i. фом1_
Рецензенты: академик В. П. Маслов,
кафедра алгебры и топологических методов ана;
Воронежского государственного университета
им. Ленинского комсомола
Фоменко А. Т.
Ф76 Симплектическая геометрия. Методы и приложения
Изд-во Моск. ун-та, 1988. — 413 с.
ISBN 5—211—00083—8.
Учебное пособие, в основу которого положен курс лекций, ч
ся автором на механико-математическом факультете, посвящено f
находящимся иа стыке классической механики, теории гамильтоь
стем и симплектической геометрии. Основное внимание сосредот
анализе вполне интегрируемых гамильтоновых систем, алгебро--
ческих методах их интегрирования, а .также иа анализе топол
и геометрических препятствий к полной интегрируемости. Разо
вопросов специального характера: уравнения Эйлера на алге
свойства интегралов гамильтоновых систем и др.
1702040000D309000000)—083 „„
ф §3—88 - Б;
077@2)—88
© Издательство Мо
ISBN 5—211—00083—8 универостета, .19..
ОГЛАВЛЕНИЕ
1родисловие '". '"'''. ' .'" , . . '."
чраткая историческая справка . . . . ■
Глава I. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ В ЕВКЛИДОВОМ
ПРОСТРАНСТВЕ . i
j § 1. Некоторые необходимые сведения из теории матричных групп 1
1.1. Группы и алгебры Ли. — 1.2. Полные линейные группы GL(n,
R), GL(n, С) и их алгебры Ли. — 1.3. Специальные линейные груп-
группы SL(n, R) и SL(n, С). — 1.4. Ортогональная группа О(п) и спе-
специальная ортогональная группа SO(n). — 1.5. Унитарная группа
0{п) и специальная унитарная группа SU(n). —1.6. Компоненты
связности матричных групп. — 1.7. Операция овеществления и ком-
. плексные структуры.
• § 2. Группы симплектических преобразований линейного пространства 3|
2.1. Симплектические линейные преобразования. — 2.2. Некомпакт- •
ные группы Sp(n, R) и Sp(n, С). — 2.3. Компактная группа Sp(n).—
2.4. Связь симнлектических групп с другими матричными группами.
| § 3. Лягрянжева геометрня и лагранжевы многообразия .... 47
3.1. Вещественные1 лагранжевы многообразия в симплектическом ли-
линейном, проаранпне. •■- 3.2. Лагранжевы комплексные грассмаиовы
многопбря.'ши. -•• 3.3. Лагранжевы вещественные грассмановы много-
многообразия.
"лава 2. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ НА ГЛАДКИХ МНО-
МНОГООБРАЗИЯХ. ИНТЕГРИРУЕМЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ГА-
МИЛЬТОНОВЫ УРАВНЕНИЯ 63
1§ I. Симплектические многообразия 63
1.1. Симплектическая структура на гладком многообразии. —
1.2. Гамильтоиовы, локально гамильтоновы векторные поля и скобка
Пуассона. — 1.3. Интегралы гамильтоновых полей. — 1.4. Теорема
Лиувилля.
1§ 2. Геометрические свойства скобки Пуассона 81
2.1. Первичность понятия скобки Пуассона. — 2.2. Теорема Дарбу.
i 3. Вложения симплектическнх многообразий. Примеры симплекти-
симплектических многообразий 86
Глава 3. НЕКОТОРЫЕ КЛАССИЧЕСКИЕ УРАВНЕНИЯ МЕХАНИКИ,
И ИХ ГАМИЛЬТОНОВОСТЬ . . . 97
1§ I. Классические уравнения движения трехмерного твердого тела . 97
1.1. Уравнения Эйлера—Пуассона, описывающие движение тяжелого
твердого тела вокруг неподвижной точки. — 1.2. Интегрируемые слу-
случаи Энлерп, Лаграижа и Ковалевской. — 1.3. Общие уравнения дви-
движения трехмерного твердого тела.
| § 2. Гамильтоновость уравнений движения трехмерного твердого тела 108
У § 3. Некоторые сведения ^_о группах и алгебрах Ли, необходимые
для гЯмильтоново.й геометрий". - ";"".' 111
3.1. Присоединенное и коприсоединенное представления, полупростота,
система корней и простых корней, орбиты, каноническая симплекти-
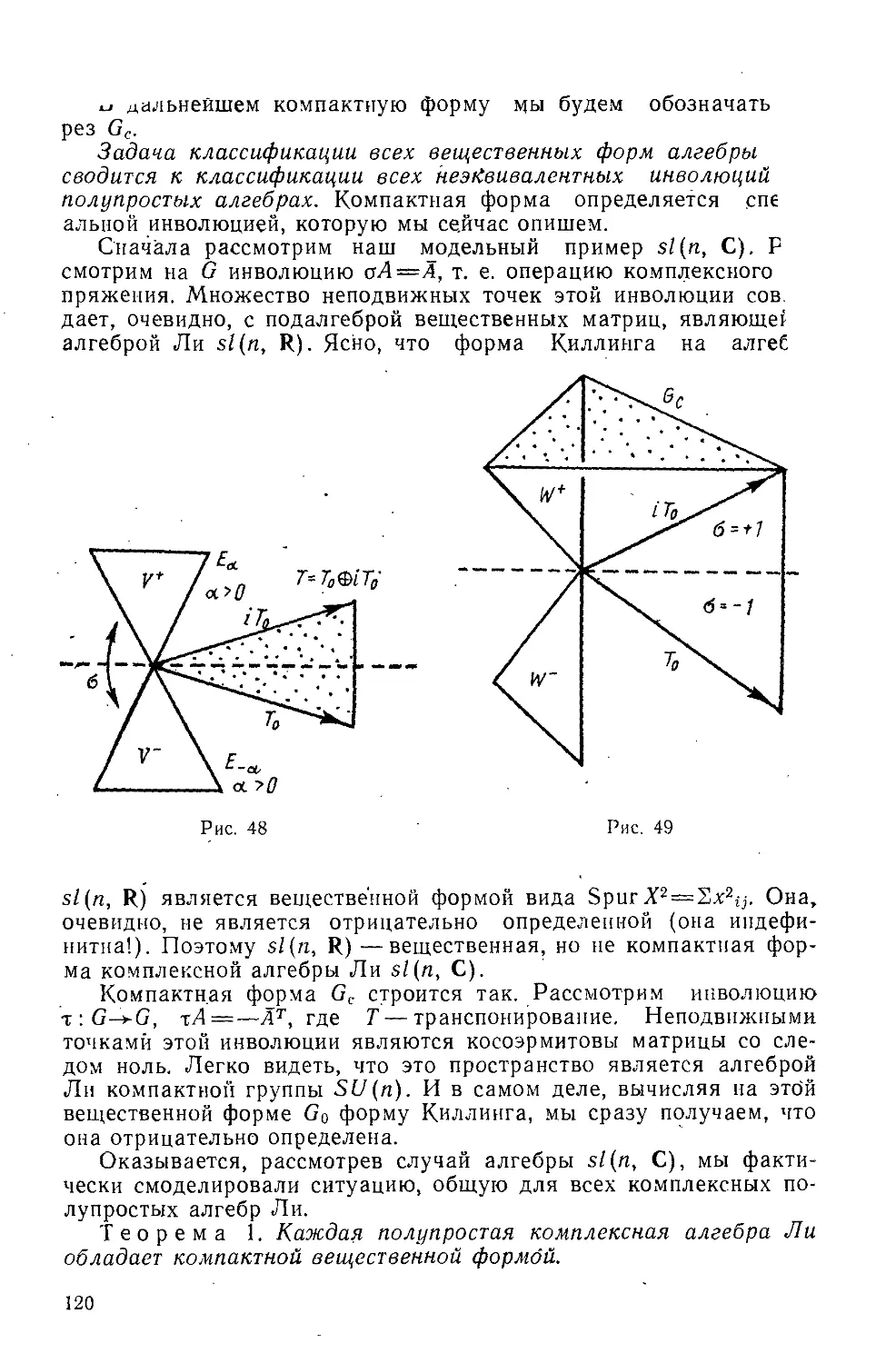
симплектическая структура. — 3.2. Модельный пример: SL(n, С) и sl(n, С).—
3.3. Вещественные, компактные и нормальные подалгебры.
. 3
.. ава 4. ЭЛЕМЕНТЫ СИМПЛЕКТИЧЕСКОИ ТОПОЛОГИИ. КАЧЕ-
КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ ИНТЕГРИРУЕМЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ НА СИМПЛЕКТИЧЕСКИХ
МНОГООБРАЗИЯХ 129
§ 1. Классификация трехмерных поверхностей постоянной энергии
интегрируемых уравнений. Оценка* количества устойчивых периодиче-
периодических решений на поверхности постоянной энергии. Препятствия к
гладкой интегрируемости уравнений на сцмплектических многообразиях 129i
1.1. Случай четырехмерных симнлектических многообразий. — 1.2.
Краткая сводка необходимых сведений из классической теории Морса
гладких функций. —■ 1.3. Топологические перестройки торов Лиувилля
интегрируемой системы при изменении значения второго интеграла. —
1.4. Сепаратрисные диаграммы высекают нетривиальные циклы на
неособых торах Лиувилля.— 1.5. И'зоэнергетические поверхности зада-
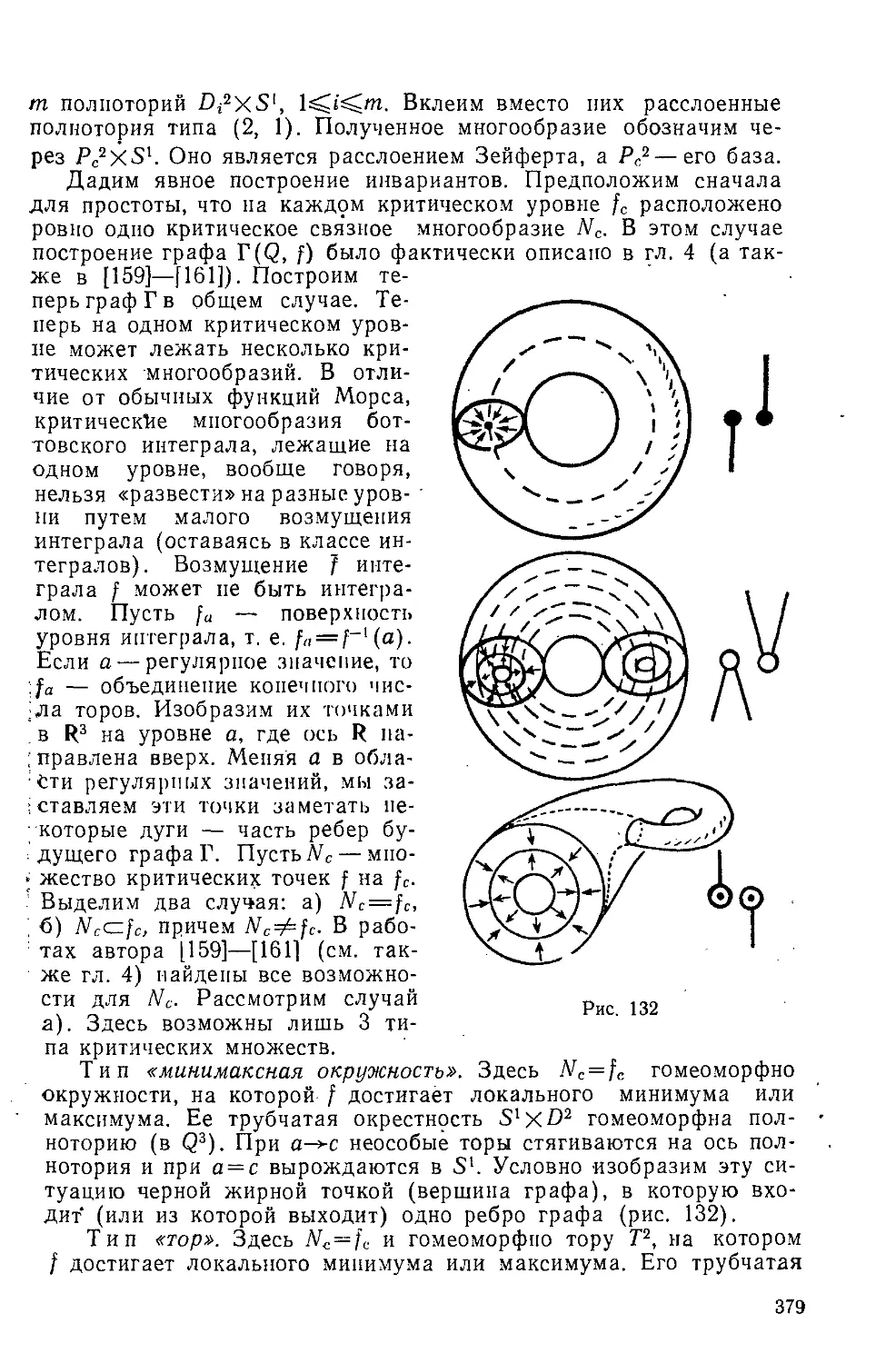
задаются одномерными графами, вершины которых разбиваются на пять
канонических типов, — 1.6. Любая поверхность постоянной энергии
интегрируемой системы представляется в виде склейки простейших
трехмерных многообразий трех типов. — 1.7. Двулистные накрытия
над изоэнергетическими интегрируемыми поверхностями всегда обла-
обладают ориентированным интегралом.— 1.8. Нижние оценки на число
устойчивых периодических решений системы. — 1.9. Топологические
препятствия к гладкой интегрируемости. Далеко не каждое трехмер-
трехмерное многообразие может реализовываться как .нзоэнергетическая по-
поверхность интегрируемой системы. — 1.10. «Достаточно большие»
трехмерные изоэпергетичеекпе поверхности полностью определяются
pH фундаментальными группами.
2. Классификация перестроек'торов Лиувилля па многомерных сим-
лектическнх многообразиях в окрестности бифуркационной диаграм-
диаграммы отображения момента 180
2.1. Бифуркационная диаграмма отображения момента интегрируе-
интегрируемой системы. Перестройки общего положения. — 2.2. Классификация
бифуркаций торов Лиувплля. — 2.3. Торические ручки. Сепаратрис-
ная диаграмма всегда приклеивается к неособому тору Лиувилля по
нетривиальному 'циклу. '
А§ 3. Свойства разложения изоэнергетических поверхностей интегри-
уых систем в сумму простейших многообразий 194
3.1. Фундаментальное разложение Q = mI-\-pIl+qllI+slV+rV и
структура особых слоев. — 3.2. Гомологические свойства изоэпергети-
ческих поверхностей.
"лава 5. СИМПЛЕКТИЧЕСКИЕ ДЕЙСТВИЯ КОММУТАТИВНЫХ И
НЕКОММУТАТИВНЫХ ГРУПП ЛИ НА • СИМПЛЕКТИЧЕСКИХ
МНОГООБРАЗИЯХ. ГАМИЛЬТОНОВЫ УРАВНЕНИЯ С СИММЕТ-
РИЯМИ 209
I § 1. Полные инволютивные наборы функций и максимальные лнней-
' ные коммутативные подалгебры в алгебре функций на симплектиче-
ском многообразии 209
{ § 2. Гамильтонова система уравнений интегрируема, дели ее гамиль-
гамильтониан включается в достаточно большую алгебру Ли функций. . 215
\ § 3. Общие свойства инвариантных подмногообразий гамильтоиорых
систем дифференциальных уравнений 222
3.1. Редукция системы на одной изолированной поверхности уров-
уровня. — 3.2. Некоммутативное интегрирование в тех случаях, когда
набор интегралов не образует алгебры. — 3.3. Некоторые дальнейшие
обобщения метода некоммутативного интегрирования. — 3.4. Канони-
Канонический вид скобки Пуассона в окрестности особой топки. Случай
вырожденных скобок Пуассона.
§ 4. Системы уравнений, вполне интегрируемые в некоммутативном
' смысле, часто вполне интегрируемы по Лиувиллю в обычном смысле. 236
4.1. Формулировка общей гипотезы эквивалентности и ее справедли-
справедливость для компактных многообразий. — 4.2. Некоммутативная интег-
интегрируемость и ее связь с каноническими подмногообразиями и изо-
изотропными торами. — 4.3. Свойства отображения момента системы,
интегрируемой в некоммутативном смысле. — 4.4. Теорема существо-
существования и явная конструкция максимальных. линейных коммутативных
алгебр функций на орбитах в полупростых и редуктивных алгебрах
Ли. — 4.5. Доказательство гипотезы эквивалентности для случая
компактных многообразий. — 4.6. Отображение момента систем, ин-
интегрируемых в некоммутативном смысле при помощи избыточного
набора интегралов. — 4.7. Достаточные условия компактности алгеб-
аы Ли интегралов гамильтоновой системы.
^5. Динамические системы и .симплектические структуры, порождае-
порождаемые секционными операторами 258
5.1. Общая схема построения секционных операторов. — 5.2. Секцион-
Секционные операторы на ■ симметрических пространствах. — 5.3. Тензор
римановой кривизны и порождаемые им симплектические структуры.
Глава 6. ГЕОДЕЗИЧЕСКИЕ ПОТОКИ НА ДВУМЕРНЫХ РИМАНО-
ВЫХ МНОГООБРАЗИЯХ . .".■./.. 271
f § 1. Топологические препятствия к аналитической полной интегрируе-
интегрируемости 271
1.1. Неинтеррируеность уравнений движения натуральных механиче-
механических систем с двумя степенями свободы. наг поверхностях большого
рода. - ■ i.2. Jk'iiirrripiipyt'Morn, геодезических потоков на римановых
поверхностях большого рода с иыпуклым краем. — 1.3. Неинтегри-
Неинтегрируемость задачи п rpanurnpymiiiiix центров при я>2. — 1.4. Неинтег-
Неинтегрируемость некоторых гироскопических систем.
j § 2. Топологические препятствия к аналитической интегрируемости
геодезических- потоков на многомерных неоднюевязных многообразиях. 277
I % 3. Интегрируемость и неннтегрируёмость геодезических потоков на
двумерных поверхностях, на сфере и торе . . ' 279
3.1. Голоморфная 1-форма полиномиального по импульсам интеграла
геодезического потока и случай рода g>l. ■— 3.2. Случай сферы и
тора. — 3.3. Свойства геодезических интегрируемых потоков на
сфере. . ,
Глава 7. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КОНКРЕТНЫХ ГА-
МИЛЬТОНОВЫХ СИСТЕМ УРАВНЕНИИ В ГЕОМЕТРИИ Ц МЕ-
МЕХАНИКЕ, МЕТОДЫ И. ПРИЛОЖЕНИЯ- .■,...-.-... 291
|§ 1. Алгебры- Ли и механика. Вложения динамических систем в ал-
I гебры Ли на канонические симплектические многообразия . . . 291
I § 2. Левоинвариантные гамильтоновы системы на группах Ли и урав-
уравнения Эйлера на алгебрах Ли . 293
2.1. Симплектическая структура и левоинвариантные гамильтониа-
гамильтонианы. — 2.2. Квадратичные гамильтонианы, порожденные методом сдвига
аргумента. — 2.3. Свойства общих уравнений Эйлера.
I § 3. Секционные операторы в случае полупростых алгебр Ли и со-
соответствующие им левоинвариантные твердотельные метрики . . . 303
3.1. Секционное разложение полупростой алгебры Ли совпадает с
картаповским разложением. — 3.2. Различные виды секционных опе-
операторов (твердотельных метрик). Комплексная серия. Нормальная
нильпотентная серия. Нормальная разрешимая серия. — 3.3. Ком-
Компактная серия операторов (твердотельных метрик). — 3.4. Нормаль-
Нормальная серия операторов (твердотельных метрик).
(■ § 4. Явное построение интегралов уравнений Эйлера, отвечающих
' комплексной, компактной и нормальной сериям операторов (лево-
инвариантных твердотельных метрик) 312
4.1. Интегралы комплексной серии. — 4.2. Интегралы компактной
серии. — 4.3. Интегралы нормальной серии. — 4.4. Инволютивиость
•^построенных интегралов.
/ § 5. Случаи полной интегрируемости уравнений Эйлера на полупрос-
■^—тых алгебрах Ли 319
5.1. Комплексная серия твердотельных метрик. — 5.2. Компактная
серия твердотельных метрик. — 5.3. Нормальная серия твердотель-
твердотельных метрик. — 5.4. Интегрируемость уравнений Эйлера на сингуляр-.
/-ных орбитах.
( § 6. Список обнаруженных максимальных линейных коммутативных
^-алгебр функций на орбитах1 коприсоедииениых представлении
групп Ли ' 332
Приложение 1. Геометрические свойства твердотельных инвариантных
метрик на однородных пространствах ..,...,,, 343
Приложение 2. Уравнения Эйлера на алгебре Ли soD.) , , , , , 345
Приложение 3. Выпуклость отображения момента при пуассоновом дей-
действии тора 357
Приложение 4. Любая композиция'элементарных бифуркаций (трех ти-
типов) торов Лиувилля реализуется для некоторой интегрируемой сис-
системы на подходящем симплектическом многообразии. Классификация
неориеитируемых критических подмногообразий боттовских интегра-
интегралов ...... 358
Приложение 5. Некоторые другие методы построения интегралов диффе-
дифференциальных уравнений иа алгебрах Ли 366
Приложение 6. Критерий полноты набора интегралов, получаемых мето-
методом, сдвига аргумента .....,, 371
Приложение 7. Новый топологический инвариант гамильтоиовых систем
дифференциальных уравнений, интегрируемых по Лиувиллю. Инва-
Инвариантный портрет интегрируемых гамильтонианов ....... 375
Приложение 8. Теория типа Морса для гамильтоновых систем, интегри-
интегрируемых при помощи неботтовских интегралов ....... 393
1екоторые обозначения . ,,..........< 400
Дополнение. О рисунках , , .,.,.,...».. 400
Титература .,,.......,.•..... 402
Дополнительный список литературы . . ......... 412
ПРЕДИСЛОВИЕ
В последние годы сформировалось новое научное направле-
направление, органично выросшее из недр классической механики, мате-
математической физики,- теории гамильтоновых систем, симплектиче-
ской и лагранжевой геометрий. Это направление можно услов*
но очертить так: новые методы интегрирования гамильтоновых
дифференциальных уравнений на симплектических многообрази-
многообразиях. Определяющим фактором здесь являются, в частности, дости-
достижения математических школ, созданных С. П. Новиковым,
И. М. Гельфандом, В. П. Масловым, Л. Д. Фаддеевым, В. И. Ар-
Арнольдом.
Были обнаружены новые глубокие связи между эффектом ин-
интегрируемости систем и их скрытыми алгебраическими свойства-
свойствами, из которых на первое место следует поставить «симметрии
систем», понимаемые не просто как группы их инвариантности,
а более общо — как совокупность алгебраических свойств систе-
системы дифференциальных уравнений, позволяющих естественно свя-
связать с системой некоторую алгебру (группу) Ли, орбиты кото-
которой инвариантны относительно данной системы. Оказалось, что
такого рода механизмы управляют интегралами многих интерес-
интересных гамильтоновых систем в геометрии, механике, физике.
Известно, что поиск интегралов конкретной системы уравне-
уравнений — трудная задача. Более того, дифференциальные уравне-
уравнения «общего положения» обычно вообще не имеют достаточного
числа интегралов (позволяющих проинтегрировать систему). По-
Поэтому задача отыскания редких интегрируемых случаев в без-
безбрежном океане всех гамильтоновых систем («большинство» из
которых неинтегрируемы) требует эффективных методов поиска
интегралов.
Одна из целей настоящей книги заключается в том, чтобы дать
читателю представление о некоторых алгоритмах поиска интег-
интегралов. Особое внимание мы сосредоточим на алгоритмах, позво-
позволяющих предъявлять интегралы (в тех случаях, когда их удается
найти) в явном виде, например в виде полиномов. Поскольку мы
не в состоянии осветить здесь все такие методы, известные на
сегодня, то мы сосредоточили внимание в основном на методе
«сдвига аргумента». Список литературы может служить путево-
путеводителемпо другим важным методам, оставшимся за рамками на-
нашего изложения.
Понятно, что мы не можем пройти мимо обсуждения общих
механизмов, лежащих в основе эффекта неинтегрируемости урав-
уравнений общего положения. Поэтому мы уделяем внимание неко-
некоторым проблемам неинтегрируемости. При этом останавливаемся
на качественной стороне обсужденных эффектов, оставляя в сто-
стороне вычислительные аспекты и заменяя их точными ссылками
.~ ^июси;шующую литературу. Для удобства читателя при-
зодим необходимые сведения из смежных областей: из теории
групп Ли, топологии и т. д. ^_____ —-_.
В книге затронуты следующи^^сновные темы: 1) некоторые
механические системы и соответствующие им гамильтоновы урав-
уравнения; 2) основы симплектической геометрии; 3) элементы симп-
аектической топологии; новая качественная топологическая тео-
теория интегрируемых дифференциальных уравнений; новый тополо-
топологический инвариант интегрируемых * уравнений (позволяющий
классифицировать их по топологическому типу); 3) классифика-
классификация перестроек торов Лиувилля в момент пересечения критиче-
:ких уровней энергии; 5) коммутативное >и некоммутативное4
интегрирование гамильтоновых уравнений; приложения; 6) ин-
интегрирование некоторых конкретных динамических систем; мето-
методы и приложения; 7) некоторые механизмы иеинтегрируемости
гамильтоновых дифференциальных уравнений.
Материал книги разбивается на три части, предъявляющие к
читателю различные требования. Первая часть (главы 1, 2) до-
достаточно элементарна и доступна студентам младших курсов ме-
механико-математических факультетов. Вторая часть (главы 3, 4)
доступна для студентов, уже знакомых с простейшими элемента-
элементами дифференциальной геометрии и топологии. Д'ля чтения этих
глав полезно владеть такими понятиями, как дифференциальные
формы, гладкие функции на многообразиях, группы и алгебры
Ли. Эта часть фактически является дополнением к обязательному
курсу «Дифференциальная геометрия и топология».
Третья часть (главы 5, 6, 7)__может служить основой для спе-
специальных курсов и предназначена для студентов старших кур-
курсов, аспирантов, специализирующихся в области симплектической
геометрии и ее приложений. Здесь, в частности, развиваются идеи,
высказанные С. П. Новиковым.
В книге также отражены результаты, полученные автором, в
частности теория топологических перестроек торов Лиувилля и
полная классификация изоэнергетических поверхностей гамиль-
гоновых уравнений, интегрируемых при помощи интегралов об-
общего положения. В рамках этой теории обнаружена глубокая
:вязь между свойствами интегрируемых уравнений и топологией
трехмерных многообразий, обнаружен топологический инвариант
интегрируемых уравнений общего положения. В книге освещают-
освещаются также результаты, полученные участниками научно-исследова-
научно-исследовательского семинара «Современные геометрические методы», дей-
действующего под руководством автора на механико-математичес-
сом факультете МГУ.
Основой книги послужил спецкурс, читавшийся автором сту-
1ентам — математикам и механикам механико-математического
эакультета МГУ.
Книга рассчитана на широкий круг читателей, интересующих-
я приложениями современной геометрии к гамильтоновой меха-
ике, теории интегрирования уравнений на многообразиях.
Автор выражает благодарность рецензентам В. П. Маслову,
Ю. Г. Борисовичу, В. В. Козлову и В. В. Федорчуку, сделавшим
ряд полезных замечаний.
КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА
В. этой книге будут часто встречаться; в частности, следующие
термины: функция Гамильтона (гамильтониан), скобка Пуассо-
Пуассона, теорема Лиувилля, лиувиллевы координаты, три случая ин-
интегрируемости уравнений движения твердого тела, открытые Ла-
гранжем, Эйлером, Ковалевской. В современной специальной на-
научной литературе эта терминология чаще всего живет в отрыве
от личностей упомянутых математиков. Нам представляется
уместным хотя бы вкратце осветить некоторые аспекты их дея-
деятельности, чтобы подчеркнуть преемственность научных идей, со-
сохраняющих актуальность до настоящего времени.
1) Гамильтон Вильям Роуан (William Rowan Hamilton, 1805—
1865) — английский математик и астроном. Родился в ирланд-
ирландской семье в Дублине, где провел всю жизнь. В 1827 г. поступил
в Триппти колледж (Trinity college), в двадцать один .год стал
королевским астрономом Ирландии и занимал этот пост до са-
самой смерти. Один нз гл.чвпых его трудов «Общий метод динами-
динамики» (General Method in Dynamics) был- опубликован в 1834—
1835 гг. Руководящей идеей Гамильтона было внедрение вариа-
вариационных принципов в оптику и^динамику. В современную науку
прочно вошла мысль Гамильтона о выводе законов физики и ме-
механики путем варьирования соответствующих функционалов (ин-
(интегралов). В этом Гамильтон следовал, конечно, идеям Эйлера.
Гамильтон впервые записал уравнения динамики в- следующем
дН дН ~ .
каноническом виде: q = , р= . Эта форма записи се-
др dq
годня носит название^гамильтрновой, соответствующие уравнения
называются гамильтоновыми, а функция Н — гамильтонианом.
В 1835—1843 гг. Гамильтон отходит от задач механики и оп-
оптики и целиком обращается к алгебре. Как и Гаусс (вероятно,
независимо от него), Гамильтон строит теорию комплексных чи-
чисел как «теорию пар вещественных чисел», чему посвящен его
трактат «Теория алгебраических пар» (Theory of Algebraic Coup-
Couples, 1835).
Естественно, что следующим шагом Гамильтона была попытка
построения соответствующей теории троек вещественных чисел,
четверок чисел и т. д. Результатом этих исследований было от-
открытие в 1843 г. кватернионов (о которых мы будем говорить в
связи с симплектической геометрией). Известное изящество, ко-
которым обладает алгебра кватернионов, ее глубокие свойства не
могли не вызвать восхищения' в среде математиков того време-
времени. Д. Я. Стройк отмечал: «Во времена Гамильтона и долгое
иремя спустя кватернионы сами по себе были предметом чрез-
мерного восхищения. Некоторые британские математики видели
в исчислении- кватернионов нечто вроде «универсальной арифме-
арифметики» Лейбница, что, конечно, вызвало оппозицию (Хевнсайд
против Тета), и из-за этого слава кватернионов значительно по-
потускнела» [129, с. 240]. Дальнейшее развитие алгебры (в частно-
частности, работы Пирса, Штуди, Фробениуса, Кдртана по гнперком-
плексным числам) и особенно развитие теории групп отвело ква-
кватернионам существенно более скромное (хотя и важное), место.
Тем не менее, вплоть до первой мировой войны, активно функ-
функционировала «Международная ассоциация для содействия изу-
изучению кватернионов и родственных математических систем». Де-
Детали этих бурных споров см., например, в [129, 213].
2) Пуассон Симеон Дени (Simeon Denis Poisson, 1781—1840).
Сын солдата, получивший первоначальное математическое обра-
образование в Фонтебло, после чего в 1798 г. явился в Париж для
поступления в знаменитую Политехническую школу. Здесь он об-
обратил на себя внимание Лагранжа, который читал математичес-
математический анализ. Диапазон подготовки воспитанников Политехничес-
Политехнической школы был чрезвычайно широк: математика, топография,
теория мостов и дорог, теория артиллерии, горное дело и пр. Этим
объясняется, в частности, широкий спектр интересов Пуассона
(как и многих других знаменитых воспитанников Политехниче-
Политехнической школы). Например, в 1825 г. Пуассон разрабатывает тео-
теорию действия выстрела орудия на его лафет. Использующаяся
в симплектической геометрии и гамильтоновой механике скобка
Пуассона является видоизменением скобки Лагранжа, введенной
Лагранжем при анализе задач небесной механики ■ ([60], с. 292—
293). Пуассон понял роль этой операции в аналитической меха-
механике и плодотворно эксплуатировал ее при решении многих фи-
физических задач. Дальнейшее развитие скобки Пуассона получили
в работе Гамильтона «Second essay on a general- method of dy-
dynamics» (Philos. Trans. Roy. Soc. 1835. T. 1. P. 95—144). Имя
Пуассона закрепилось во многих математических областях: ши-
широко известны интеграл Пуассона и уравнение Пуассона в тео-
теории потенциала, закон Пуассона в теории вероятностей и т. д.
3) Лиувилль Жозеф (Joseph Liouviile, 1809—1882). Один из
ведущих математиков Франции того времени, профессор Фран-
Французского колледжа в Париже, организатор и издатель в течение
многих лет известного французского «Журнала чистой и при-
прикладной математики» (Journal de Mathematiques pures et appli-
quees). В частности, именно Лиувилль в своем журнале в 1846 г.
напечатал большую часть работ Галуа, что послужило толчком
к развитию теории Галуа. Лиувиллю принадлежат работы по
арифметической теории квадратичных форм; он доказал сущест-
существование трансцендентных чисел и, в частности, в 1844 г. то, что
числа е и е2 не могут являться "корнями квадратного уравнения
с рациональными коэффициентами.
В статистической механике известна «теорема Лиувилля». Он
интересовался дифференциальной геометрией кривых и поверх-
10
постей, изучил так называемые «поверхности Лиувилля», для ко-
которых геодезические могут быть найдены при помощи квадратург
Он нашел все поверхности вращения постоянной кривизны, до-
дополнив результаты Миндинга. Лиувилль доказал, что гладкие
конформные преобразования в пространстве являются компози-
композициями преобразований инверсии, подобия (растяжения) и конгру-
конгруэнции (т. е. сдвига). Важной (в том числе и для настоящей кни-
книги) задаче интегрирования дифференциальных уравнений посвя-
посвящена работа Лиувилля «Memoire sur l'ihtegration des equations ,
differentielles du mouvement d'un nombre quelconque de points
materieles» (J. Math. 1849. T. XIV. P. 257—299).
4) Эйлер Леонард {Leonard Euler, 1707—1783). Уроженец Ба-
Базеля, один из наиболее знаменитых математиков XVIII в. Его
продуктивность поразительна; даже ослепнув, он, пользуясь сво-
своей феноменальной, памятью, продолжал диктовать свои открытия.
При жизни Эйлер опубликовал 530 статей и книг-, полное же их
число составляет 886 (часть работ опубликована посмертно)
[129, с. 162—163]. Сделанные Эйлером открытия в самых разных
областях математики и приложений послужили основой его гро-
громадного авторитета; во время своей деятельности в Берлинской
и Петербургской академиях Эйлер основал крупные математиче-
математические школы. Гаусс писал: «Изучение работ Эйлера остается наи-
наилучшем iiiKOJiDi'l и р.титчиых областях математики, и ничто дру-
другое не может что заменить».
Работы Эйлера настолько разнообразны, что в рамках крат-
краткого замечания невозможно остановиться на всем, что достойно
нппмаиия. Для нас здесь особый интерес представляют исследо-
исследования Эйлера по механике. Он занимался астрономией, теорией
движения Луны, задачей трех тел. Эйлера интересовала задача
притяжения эллипсоидов и т. д. Эта сторона деятельности Эй-,
лера нашла отражение в его трактате «Теория движения планет
п комет» (Theoria motus planetarum et cometarum, 1774). В на-
настоящей книге мы познакомимся с важным частным случаем в
динамике тяжелого твердого тела (случай Эйлера), когда тело
закреплено в центре масс. Эти уравнения (называемые сегодня
уравнениями Эйлера) изучены им в «Теории движения твердых
тел» A765 г.). Соответствующая система уравнений была проин-
проинтегрирована Эйлером. Ему принадлежат работы по теории чи-
чисел, по математическому анализу, гидравлике, кораблестроению/
артиллерии, оптике, музыке, философии.
5) Лагранж Жозеф Луи (Joseph Louis Lagrange, 1736—
1813). Лагранж родился в Турине в итало-французской семье.
В возрасте 19 лет он стал профессором математики туринской
артиллерийской школы. В 1766 г. Фридрих II пригласил Лагран-
Лагранжа в Берлин, поскольку (как было сказано в приглашении) «не-
«необходимо, чтобы величайший геометр Европы проживал вблизи
величайшего из королей». После смерти Фридриха Лаграпж пе-
переехал в Париж. Берлинский период творчества Лагранжа харак-
характеризуется его повышенным интересом к астрономии, небесной
11
If"
механике, сферической тригонометрии. Из 5000 страниц семи то-
томов, где собраны мемуары Лагранжа, около 2000 страниц посвя-
посвящено астрономическим темам [150, с. 27].
Особое место в развитии естествознания XVIII—XIX вв.
занимает трактат Лагранжа «Аналитическая механика» A788).
Современный термин «лагранжева механика» обязан своим про-
происхождением именно этому трактату. Лагранж анализирует с
единой точки зрения механику материальной точки, абсолютно
твердого тела, механику системы материальных точей со связя-
связями, гидромеханику, механику упругих тел и пр.
В нашей книге мы коснемся результатов Лагранжа о движе-
движении тяжелого твердого тела. Еще раньше Эйлер пришел к этой
задаче, рассматривая астрономические проблемы и вопрос о ко-
колебательном движении корабля. Задача об устойчивости корабля
была сформулирована Петербургской академией наук как важная
проблема. Изучая ее, Эйлер столкнулся с необходимостью по-
построения общей теории вращения твердого тела. В книге «Ко-
«Корабельная наука» A748) Эйлер вводит понятие центра инерции,
строит теорию распределения масс в твердом теле и выводит
уравнения движения. Ему удалось проинтегрировать уравнения
лишь в частном случае, а именно в случае отсутствия силы тя-
тяжести (без действия внешних сил). Найти решение в общем слу-
случае Эйлер не. смог. Объективные препятствия мы объясним в
нашей книге. Лагранж продолжил исследования на эту тему.
В 1775 г. он дал несколько усовершенствованное уравнение Эй-
Эйлера в случае Эйлера (без действия внешних сил). Излагая ре-
результаты Эйлера и Даламбера, Лагранж довел их до квадратур,
после чего перешел к изучению второго случая интегрируемости
уравнений, получившего впоследствии имя Лагранжа. В этом
случае твердое тело имеет ось симметрии (волчок Лагранжа) и
точка опоры находится на оси симметрии. Лагранж дал полное
решение задачи в этом случае.
Лагранж также детально исследовал проблемы гидромехани-
гидромеханики, гидродинамики сжимаемых и упругих жидкостей, занимался
вопросом о форме колонн под нагрузкой и т. д. Один лишь спи-
список полученных им результатов занимает несколько страниц.
6) Ковалевская Софья Васильевна A850—1891). Первая в
мире женщина — профессор математики. Так как в России дос-
доступ в университеты для женщин был закрыт, то для получения
образования она выезжает за границу, в 1869 г. прибывает в
Германию и начинает работать под руководством К. Венерштрас-
са. Уже в 1874 г. Вейерштрасс направляет в университет Геттин
гена три работы Ковалевской: «К теории ур-авпепий в частных
производных», «О форме кольца Сатурна», «О приведении одно-
одного класса абелевых интегралов третьего рода к интегралам эл-
эллиптическим».
В 1884 г. Ковалевская становится профессором математики
в Швеции, в Стокгольмском университете, где она начинает чи-
читать лекции. В 1888 г. за обнаружение третьего случая интегри-
32
})уемости уравнений движения тяжелого твердого тела она полу-
получает премию Парижской академии наук. Этот новый случай ин-
интегрируемости (случай Ковалевской) существенно отличается от
двух известных ранее случаев Эйлера и Лагранжа. В частности,
в случае Ковалевской интегрирование уравнений движения тре-
требует более тонких аналитических средств. Благодаря усилиям
Чебышева, Буняковского и Имшенецкого, в 1889 г. Ковалевская
была избрана членом-корреспондентом Петербургской академии
наук. Ковалевская умерла в 1891 г. в расцвете творческих сил
и похоронена в Стокгольме. Интерес к ее работам и ее жизни не
иссякает как в нашей стране, так и за рубежом. Недавно появи-
появились новые интересные исследования творческой биографии Ко-
валевской (см., например, книгу Э. Коблитц [215]).
7) Анри Пуанкаре (Henri Poincare, 1854—1912). Один из круп-
крупнейших математиков XX в., родился в Нанси (Лотарингия) в
семье, которая уже дала Франции нескольких знаменитых людей.
Сам Пуанкаре считал, что, математические способности он унасле-
унаследовал от бабушки со стороны матери. У дяди Пуанкаре (гене-
(генерального инспектора мостов и дорог) было два сына: Раймон —
Президент Французской Республики и Председатель Совета Ми-
Министров, и Люсьен — известный физик, впоследствии ректор Па-
Парижского университета.
Имя I ly.'iiiKfipc тесно связано с современной гамильтоповой
геометрией п механикой. В частности, созданный им метод иссле-
исследования гамильтоиовых систем, близких к интегрируемым, и се-
сегодня остается одним из самых эффективных приемов. Имя Пуан-
Пуанкаре связано со многим^ фундаментальными открытиями в обла-
области математики и приложений. Его универсализм поражал совре-
современников. В частности, в многочисленных курсах, которые он чи-
читал в Сорбонне по небесной- механике; находят свое отражение
все новые и новые его открытия (например, интегральные инва-
инварианты и т. д.). Вот некоторые из названий его курсов (и соответ-
соответствующих им книг, написанных Пуанкаре): Новые методы небес-
' ной механики, Лекции о фигурах равновесия жидкой массы, Лек-
Лекции о космогонических гипотезах, Теория вероятностей, Термоди-
Термодинамика, Электричество, Оптика, Теория упругости, Теория света,
Электромагнитные колебания. От .исследования дифференциаль-
дифференциальных уравнений и периодических решений Пуанкаре естественно
перешел к фундаментальным исследованиям по топологии. Этот
цикл его работ по праву позволяет считать Пуанкаре одним из ос-
основоположников топологии (в ее современном понимании). Кро-
Кроме глубоких научных исследований Пуанкаре обращался к вопро-
вопросам философии науки. Он является автором нескольких известных
работ, объединенных в четырех книгах: Наука и гипотеза, Цен-
Ценность науки, Наука и метод, Последние мысли. Всего Пуанкаре
написал более 500 мемуаров и книг. С 1886 г. до самой смерти
Пуанкаре возглавлял кафедру математической астрономии и не-
небесной механики, с 1893 г. занял пост члена Бюро долгот, с
1902 г. заведовал кафедрой теории электричества Высшей школы
13
ведомства связи. В 1887 г. был избран членом Академии наук по
отделению геометрии, которое он возглавил в 1906 г. В 1908 г.
Пуанкаре был избран членом Французской Академии.
Огромное внимание Пуанкаре уделял философским проблемам
науки в целом, стремясь осмыслить истинное место науки в жиз-
жизни общества. Некоторое представление о позиции Пуанкаре в
этом вопросе может дать заключительный параграф, которым Пу-
Пуанкаре завершает свою известную книгу «Ценность науки»
(А. Пуанкаре. О науке. М.: Наука, 1983, с. 281—282).
«Мы не можем познать все факты; необходимо выбирать те,
которые достойны быть познанными. Если верить Толстому, уче-
ученые делают этот выбор наудачу вместо того, чтобы делать его,
имея в виду практические применения, что было бы благоразум-
благоразумно. В действительности это не так: ученые считают определенные
факты более интересными в сравнении с другими, потому что они
дополняют незаконченную гармонию или потому, что они позво-
позволяют предвидеть большое число других фактов. Если ученые-
ошибаются, если эта неявно предполагаемая ими иерархия фак-
фактов есть лишь пустая иллюзия, то не могло бы существовать на-
науки для науки и, следовательно, не могло бы быть науки... Уро-
Уровень цивилизации зависит от науки и искусства. Формула «наука
для науки» возбуждала удивление; а между тем это, конечно,
стоит «жизни для жизни», если жизнь не жалка и ничтожна, и
даже «счастья для счастья», если не держаться того взгляда, что-
все удовольствия равноценны, если не считать, что цель цивили-
цивилизации состоит в том, чтобы доставлять алкоголь охотникам до
вьшивки.
Всякое действие должно иметь цель. Мы должны страдать,
должны трудиться, должны платить за наше место в спектакле,
чтобы видеть, или, по крайней мере, чтобы другие увидели свет...
Геологическая история показывает нам, что жизнь есть лишь бег-
беглый эпизод между двумя вечностями смерти и что в этом эпизоде
прошедшая и будущая длительность сознательной мысли — не бо-
более, как мгновение. Мысль — только вспышка света посреди дол-
долгой ночи.
Но эта вспышка — всё» (А. Пуанкаре).
ШЖЖ
штт
ГЛАВА 1
СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
§ 1. Некоторые необходимые сведения из теории матричных
групп
1Л. Группы и алгебры Ли. В геометрии часто возникают при-
меры групп, оказывающихся в то же время топологическими про-
пространствами и снабженных структурой гладких многообразий. На
первых порах основной интерес для нас будут представлять мат-
ричные группы преобразований, т. е. группы, реализующиеся как
подгруппы в группе невырожденных матриц. При этом топология
в группе матриц (а следовательно, и на вложенных в нее под-
группах) определяется следующим естественным образом: матри-
матрицы считаются близкими, если они близки поэлементно. Дадим те-
теперь общее определение группы Ли.
О nj еделение 1. Гладкое многообразие М
Ной Люесли на. нем заданы два гладких отображения f
-*-М (называется умножением) и v:M-*-M (называемое взятием
обратного элемента), обозначаемые обычно так: f(x, у)=х-уу
\(х)=х~\ а также существует отмеченная (выделенная) точка
ееМ, удовлетворяющая вместе с отображениями f и v следую-
следующим алгебраическим соотношениям (аксиомам группы):
1) x(yz) — (xy)z (ассоциативность), 2) ех=хе=х, хх~]=х]х—е.
В дальнейшем будем обычно обозначать группу Ли через ©.
. Определение 2. Множество элементов g группы Ли @,
которые можно соединить непрерывным путем с единицей группы,
называется связной компонентой единицы и обозначается че-
через ©„.
Предоставляем читателю в качестве полезного и простого
упражнения убедиться в том, что множество @0 является подгруп-
подгруппой в группе @ и, кроме того, &0 является нормальным делите-
делителем в @. В частности, всегда корректно определена фактор-груп-
фактор-группа ©/Фо, число элементов в которой равно, следовательно, коли-
количеству компонент линейной связности группы &.
■ Определение 3. Линейное пространство V, на котором
задана кососимметричная билинейная операция [,] (называемая
обычно коммутатором), называется алгеброй Ли, если для любых
X Y ZV ется~следующ
р ,
трех элементов X, Y, ZeV выполняется~следующее тождество, на-
навиваемое тождеством Якоби: [X, [Y, Z]]+[Z, [X, Y]]+[Y,[Z,X]]=0.
17
Для любого X^V можно определить линейное отображение
aux'-V-^-V, полагая aux(Y)=[X, У]. Тождество Якоби, которому
удовлетворяет операция коммутирования, с использованием опе-
оператора ad может быть переписано в следующем виде: adxl^, %\—
=[adx У, -2]+[У, adx-Z]. Следовательно, оператор ad* можно рас-
рассматривать как дифференцирование алгебры Ли V. Приведем
пример важной алгебры Ли.
Лемма 1. Линейное пространство gt(n, R) (или gl(n, С))
всех матриц порядка п с вещественными (или комплексными)
элементами является алгеброй Ли относительно коммутатора
[X, Y\=XY—YX, где XY и YX обозначают обычные произведения
матриц.
Доказательство сводится к элементарной проверке тождест-
тождества Якоби. Косая симметрия операции XY—YX очевидна.
Существует тесная связь между конечномерными группами и
алгебрами Ли (в бесконечномерном случае эта связь существенно
-сложнее). Имеет место классическая теорема, доказательство ко-
которой мы здесь опускаем (см., например, [165]).1М " i.*m
Предложение 1. Пусть C — группа Ли и G=Te © — каса-
касательное пространство к группе & в ее единице е. Тогда линейное
пространство G естественно снабжается структурой алгебры Ли,
операция коммутирования в которой является дифференциалом
преобразования, индуцированного на G операцией (g\, £г)—>-
—*-g\g2grl в группе ©. Если © — матричная группа Ли, то ком-
коммутатор в ее алгебре Ли G задается явной формулой [X, У]=
=XY—YX, где XY и YX — обычное произведение матриц.
Рассмотрим основные примеры матричных групп и алгебр Ли.
1.2. Полные линейные группы GL(n, R), GL(n, С) и их алгеб-
алгебры Ли. Рассмотрим евклидово пространство R" и совокупность
всех невырожденных линейных преобразований R" в себя, остав-
оставляющих на месте начало координат. Они могут быть записаны в
виде квадратных невырожденных матриц (пХп) с вещественны-
вещественными коэффициентами. Множество таких матриц обозначается через
GL(n, R). Совершенно аналогично определяется совокупность
матриц GL(n, С) над полем С.
Лемма 2. Множества GL(n, R) и GL(n, С) являются неком-
некомпактными группами Ли размерностей п2 и 2п2 соответственно. Ал-
Алгеброй Ли группы GL(n,. R) является линейное пространство
gl(n, R), состоящее из матриц размером (пхп) с вещественными
коэффициентами. Аналогично алгеброй Ли группы GL(n, С) яв-
является линейное пространство матриц gl(n, С).
Доказательство. 'Ясно, что группа GL(n, R) может быть
представлена в виде Rn2\(detg=O), где R''2 отождествлено с про-
пространством всех матриц размером (пХп) с вещественными коэф-
коэффициентами, a (detg=O) обозначает Множество матриц с нулевым
определителем, задаваемое одним полиномиальным уравнением в
R. Отсюда следует, что GL\n, R) является гладким некомпакт-
некомпактным многообразием размерности п2 (рис. 1). Совершенно анало-
аналогично рассматривается случай группы GL(n, C)=C"!\(detg'=O).
18
I от факт, что групповые алгебраические операции в GL(n, R) к
<il.(n, С) являются гладкими, очевиден. Осталось вычислить ал-
м'бры Ли указанных матричных групп. Поскольку алгебра Ли G
■пипадает с касательным пространством Те®, то достаточно изу-
изучить матрицы, бесконечна близкие к единице группы.
Рассмотрим для определенности группу GL(n, R). Касатель-
Касательное пространство ТХМ в точке х к гладкому многообразию М со-
состоит из всех векторов у@), являющихся векторами скоростей
гладких кривых y(t), лежащих в Л! и проходящих через точку ху
т. е. ^@)=^:. В нашем случае очевидно, что пространство, каса-
касательное к GL(n, R) в точке Е, совпадает с пространством всех
матриц размером (пхп), так как группа GL(n, R) получена вы-
выбрасыванием из этого пространства R гиперповерхности, за-
Рис. 1
Рис. 2
даваемой уравнением detg=O, причем точка Е не лежит на этой
поверхности (рис. 1). Таким образом, группа GL(n, R) вложена
в свою алгебру Ли gt(n, R) в виде открытой области. В частно-
частности, достаточно малая окрестность единицы в группе GL(n, R>
совпадает ,с соответствующей окрестностью в алгебре Ли. Рас-
Рассуждения в комплексном случае аналогичны. Лемма доказана.
1.3. Специальные линейные группы SL(n, R) и SL(n, С).
Группа SL(n, R) определяется как подмножество в полной линей-
линейной группе G'L(n, R), задаваемое одним полиномиальным уравне-
уравнением detg=l. Аналогично определяется и группа SL(n,'C).
Лемма 3. Множества SL(nt R) и SL(n, С) являются неком-
некомпактными группами Ли размерностей п2—Х и 2п2—2 соответствен-
соответственно. Алгеброй Ли группы SL(n, R) является линейное простран-
пространство sl(n, R), состоящее из всех вещественных матриц X разме-
размером (пХп) с нулевым следом, т. е. SpurX = 0. Аналогично алгеб-
алгеброй Ли группы SL(n, С) является линейное пространство sl(n, С)
■ всех комплексных матриц с нулевым следом.
Доказательство. Рассмотрим на пространстве R"' функ-
функцию f(g)=uetg. Прямое вычисление показывает, что gradf отли-
отличен от нуля во всех точках поверхности (detg=l). Например,
при п=2 имеем g= (° *), f(g)=ad~bc, gradf=(.d, -с, -b, a).
Если grad/=O, то возникающая система уравнений, связывающая
элементы а, Ь, с, d матрицы g, показывает, что g=0, что противо-
противоречит выбору g. Таким образом, в силу теоремы о неявных функ-
функциях поверхность уровня f(g) = \ является гладким (п2—^-мер-
(п2—^-мерным подмногообразием в пространстве Rn\ Аналогично проверя-
проверяется, что и в комплексном случае поверхность уровня J(g) = \ яв-
является гладким подмногообразием1 размерности 2п2—2. В этом
■случае одно, комплексное уравнение detg=l эквивалентно двум
вещественным уравнениям.
Найдем алгебры Ли указанных групп. Для этого достаточно
вычислить касательную плоскость в единице группы. Найдем
множество всех векторов скоростей гладких кривых y(t), прохо-
проходящих в группе SL(n, R) через единицу Е, т. е. у@)=Е,
<dpty(t) = l. Если параметр t мал, то матрицу y(t) можно пред-
представить (с точностью до бесконечно малых высших порядков) в
виде y(t)=E+tX+..., где Х=^@) — матрица размером (пХп),
являющаяся вектором скорости траектории у в точке Е. Ясно, qfo
dely(t) = 1 + /-Spur X+ ... . Отсюда мы получаем, что SpurJ = 0.
Итак, вектор скорости каждой кривой, проходящей через единицу
(вычисленный в единице), изображается матрицей с нулевым сле-
следом. Докажем обратное, а именно, что каждая матрица X с ну-
нулевым следом является вектором некоторой кривой, проходящей
через единицу. Рассмотрим семейство матриц y(t) вида
— Хорошо известно, что этот ряд сходится,
2Г=о
поэтому определение семейства матриц у(() корректно. Из опреде-
определения экспоненты следует, что X— ехр^Х|(_^о. Из курса ал-
dt
гебры известно, что det exp tX+exp Spur tX. Так как SpurJ = 0,
то" dety(£) = l, что и завершает доказательство. Случай группы \
SL(n, С) рассматривается совершенно аналогично. <
1.4. Ортогональная группа О(п).и специальная ортогональная Д
труппа SO(n). Рассмотрим пространство R" с билинейной поло-
положительно определенной формой {a,b)='2lf_laibi, задающей ев-
евклидово скалярное произведение. Вещественная (полная) ортого-
ортогональная группа О(п) определяется как группа вещественных
"матриц g порядка п, сохраняющих это скалярное произведение,
т. е. (ga, gb}=(a, b> для любых векторов a, freR". Аналогичным
образом определяется и комплексная ортогональная группа
О(п, С) как группа матриц из GL(nt С), оставляющих инвариант-
инвариантной квадратичную форму Zi2-h ..+zn2 в комплексном пространст-
пространстве Сп(ги .-., zn). Ясно, что detg=±l, если g^O(n).
Группа О (п) содержит подгруппу, обозначаемую SO(n) и на-
называемую специальной ортогональной группой. Она образована
ортогональными унимодулярными преобразованиями, которые, в
частности, не меняют ориентации R". Аналогично SO(n, C)=»*
=О(п, C)[)SL(n, С).
20
Лемма 4. Множество SO(n) является компактной группой
hi размерности п(п—1)/2. Алгеброй Ли группы SO(n) является
in не иное пространство so(n), состоящее из всех вещественных ко-
i асимметрических матриц размером (пХп).
Прежде чем доказывать лемму 4, опишем удобное для многих
приложений представление группы О(п) в виде замкнутого под-
подмножества в R"\ определяемого системой квадратичных уравнений
figT=E. Здесь Rn* отождествляется с линейным пространством
матриц g порядка п, а Т обозначает транспонирование. Рассмот-
Рассмотрим в R билинейную форму <gb g2>=Spur g\g2T- Ясно, что она
определяет евклидово скалярное произведение в базисе, состоя-
состоящем из элементарных матриц <?,■/, рассматриваемых как векторы
из R. Все элементы матрицы е,-,- равны нулю, за исключением
одного элемента, равного 1 и расположенного в Ч'-й строке и
/-м столбце. В самом деле, если g1 = Zaiiei/, g2--=I,bijeij, то (glt
g2) ---SpurgjgJ —2a,-;-bf;-, что, очевидно, совпадает со скалярным
евклидовым произведением. Отождествляя каждую матрицу
£еО(я) с вектором, мы можем сопоставить ей евклидо-
евклидову длину вектора g, где | g]2=Spur ggT. Напомним, что группа
О (п) реализована как подмножество в R"\ удовлетворяющее мат-
матричному уравнению ggT = E. Следовательно, для g^O(n) мы
имеем \g\ =Уя, т. е. группа О(п) лежит как подмножество в стан-
стандартной сфере S"'-1 радиуса Уп (рис. 2).
Доказательство леммы 4. Докажем, что множество
О(п) является гладким многообразием размерности п(п—1)/2.
В действительности, достаточно доказать это утверждение для
окрестности единицы в О(п). В самом деле, отображение La'.g—>-
-*-ag, где а, geO(n), можно рассматривать как линейное, а по-
потому гладкое преобразование объемлющего пространства Rn\
поскольку оно определено не только на подмножестве О(п), но и
на множестве всех матриц. Преобразование La'.X-+.aX называет-
называется левым сдвигом. Ясно,.что левым сдвигом можно совместить
любШе' бее точки на группе О(п), в частности, перевести любую
точку из О (п) в единицу .группы. Следовательно, если О(п) ока-
• жется многообразием в окрестности единицы, то это же будет
верно и для любой точки из О(л).
Рассмотрим множество всех гладких кривых g{t), лежащих
в SO(n) и проходящих через единицу Е. Вектор скорости каждой
такой кривой в единице группы является кососимметрической
матрицей, т. е. g@)=X, где Хт=—X. В самом деле, в силу орто-
ортогональности всех преобразований вида g(t) мы имеем
(S(t)a, g(t)b}=(a, b} для любых векторов a.freR". Дифференци-
Дифференцируя по t и полагая /=0 (напомним, что g@)=£), получаем
(Ха,Ьу+(а, ХЬУ — О, что эквивалентно кососимметричности матри-
матрицы X. Докажем теперь обратное, а именно, что любая веществен-
вещественная кососимметрическая матрица X порядка п является вектором
скорости некоторой гладкой кривой g(t), проходящей через Е и
целиком -лежащей в множестве SO(n).
21
Рассмотрим семейство матриц вида
Пегко проверить, что этот ряд сходится, поэтому матрицы g(t)
корректно определены и, кроме того, g@)—X. Так как Хт=—Х,
го g(t)~1==g(t)T при любом t, т. е. кривая g(t) целиком лежит в
множестве ортогональных матриц и имеет в единице вектор ско--
эости, равный X, что и требовалось. В частности, мы доказали,
по множество всех векторов скоростей кривых, проходящих через
гдиницу в SO(n), образует линейное пространство so(n) размер-
размерности п(п—1)/2, состоящее из всех кососимметрических матриц
порядка п. Напомним, что каждая кососимметрическая веществен-
вещественная матрица X=(xi,) однозначно определяется элементами хц,
где £</.
Рассмотрим теперь систему из — п(п+1) квадратичных урав-
уравнений, определяющих множество О(п). В матричном виде эти
уравнения записываются так: ggT=E. Мы должны доказать, что
зсе градиенты функций ft/ = 2iLia0ia/fe~~fii7» где t</, g=(a«p),
линейно независимы в единице группы. Группа О(п) задается в
пространстве всех матриц g — (aap) как решение системы уравне-
уравнений /ij = 0, t^/. Уравнения fa —0 означают, что скалярные квад-
квадраты столбцов матрицы равны единице, а уравнения fu = O, i<jr
означают, что скалярные произведения разных столбцов равны
f-const f S°in)
Рис. 3 ' Рис. 4
(условия ортогональности).
Из курса геометрии известно, что градиент гладкой функции
!сегда ортогонален поверхности уровня (если градиент отличен or
1уля) (рис. 3). В единице группы рассмотрим линейное по'дпро-
:транство N, состоящее из векторов, ортогональных всем гради-
градиентам grad/i/, t</. Мы утверждаем, что подпространство N сов-
гадает с пространством всех кососимметрических матриц. В самом
1,еле, если вектор X принадлежит N, то он ортогонален одновре-
4енно всем градиентам и, следовательно, касается совместной по-
уровня всех функций /;/=0, i*ij. Но мы знаем, что-
via поверхность уровня совпадает с группой О(п) (согласно ее
определению). Следовательно, согласно доказанному выше вектор
А' изображается кососимметрическои матрицей.
Таким образом, Ncso(n). Обратное включение нами фактиче-
фактически доказано выше, так как каждая кососимметрическая матрица,
рассматриваемая как вектор скорости кривой, лежащей в SO (n),
касается совместной поверхности уровня функции f,,-, £</', и по-
поэтому ортогональна пространству градиентов. Для доказательст-
доказательства линейной независимости всех градиентов grad /,/, '^Л доста-
достаточно доказать, что размерность порожденного ими линейного под-
подпространства L в точности равна п(п+1)/2. Ясно, что прямая
сумма плоскостей L и N дает все пространство R (рис. 4).
Следовательно, dimL=n2—n(n— l)/2=n(n+l)/2. Таким образом,
функции fi/, i<j, функционально независимы в окрестности еди-
единицы группы и по теореме о неявных функциях их совместная по-
поверхность уровня является гладким подмногообразием размерно-
размерности л (л—1)/2.
1.5. Унитарная группа U(n) и специальная унитарная группа
SU(n). Рассмотрим комплексное пространство C"Bi, ..., zn) с
эрмитовым скалярным произведением (a, 6) = Re2"=ia£A-, по-
порожденным билинейной комплекснозначной формой X?=iai^'-
Через U(л) обозначим группу всех линейных операторов в С", со-
сохраняющих это скалярное произведение и переводящих в себя на-
начало координат. Другими словами, U (л) — это группа комплекс-
комплексных матриц g порядка л, обладающих тем свойствам, что <а, Ь}—
—iga, gb} для любых a, be С. Следовательно, унитарные матри-
матрицы задаются матричным уравнением ggT=E, где «черта» обозна-
обозначает комплексное сопряжение. Если get/(л), то получаем, что
detg=ei(f. В группе U(л) содержится подгруппа SU(n), состоя-
состоящая из всех унитарных матриц с определителем единица.
Лемма 5. Множество U(n) является компактной группой Ли
размерности л2, a SU(n) является компактной группой Ли размер-
размерности л2—1. Алгеброй Ли и(п) группы U(n) является пространст-
пространство всех косоэрмитовых комплексных матриц, а алгеброй Ли su(n)
группы SU(n) является пространство всех косоэрмитовых ком-
комплексных матриц со следом ноль.
Доказательство проводится по схеме доказательства лем-
леммы 4, и поэтому мы предоставляем его читателю.
Мы определили U(п) как группу матриц, сохраняющих веще-
•ствеппозначпое скалярное произведение <a,/;>=Re 2a;5,-. Однако
наряду с ним в С" имеется ассоциированная комплексибзначная
форма (a, b)' = 2"=i аА'< а потому естественно возникает груп-
группа матриц И{п)', сохраняющих комплекснозначную форму. По-
Поставим естественный вопрос: совпадают ли группы U(п) и U(n)'?
Оказывается эти группы совпадают. В самом деле, поскольку
группа U(n)' сохраняет форму <а, ЬУ, то она сохраняет по от-
отдельности ее вещественную и мнимую части. Следовательно,
U(n)'aU^n). Обратно, пусть задана матрица g^U(n), т. е.
23
я, b~}=(_ga, gby для любых а и Ь. Это тождество верно также и
ля векторов вида ia и Ь, поэтому Re<ia, b>'=Re<g(ia), g(&)>'.
ак как оператор g — комплексный, то g(ia)=ig(a) и Im<a, Ь>'=
= lm{ga, gb)', поскольку Re(iz) = Im(z). Таким образом, преобра-
ование g сохраняет не только вещественную часть формы <,>',
о и ее мнимую часть, а следовательно, сохраняет всю форму, что-
означает включение U(n)czU(n)'.
Поэтому в дальнейшем мы не будем различать группы инва-
иантиости эрмитовой формы и ее вещественной части. Легко до-
:азать, что группа U (п) гомеоморфна прямому произведению
руппы SU(п) на окружность. Как и в случае 0(п), группу U(n)
[ногда удобно представлять как замкнутое подмногообразие, вло-
кенное в R2n' и определяемое в нем системой -квадратичных
■равнений ggT=E. Здесь R2"* = C отождествлено с пространством
icex комплексных матриц порядка п. Рассмотрим в R2 скаляр-
юе произведение ReSpurg/ir и выделим R2 базис, состоящий
(з всех матриц вида A), (i), все элементы которых равны нулю,
а исключением одного, расположенного в k-u етолбце и в
-й строке и равного 1 или i. Если g—(aa), n—(^ii), то
?е Spur ghT=:Zaijbij, что совпадет с эрмитовым скалярным про-
(зведением в С. Отождествляя каждую матрицу g с вектором и
:опоставляя ей евклидову длину вектора |g|2=ReSpurggr, г^олу-
(аем, что группа U (п) вложена в сферу S2n'~l радиуса У п.
1.6. Компоненты связности матричных групп. Из скольких
хвязных кусков» состоят перечисленные группы? Чтобы ответить
m этот вопрос, докажем три леммы.
Лемма 6. Группа SO(n) линейно связна и совпадает с ком*
гонентой единицы в группе О(п). Группа О(п) состоит из двух
'вязных компонент.
Доказательство. Из курса алгебры известно, что для лю-
>ой ортогональной матрицы go^SO(n) существует ортогональная
O() xa имеет вид
рица g€
COS фх
—sin ф1
=O(n), такая,
sin^
СО5ф1
что
1
матрица ^
0
Г
О
ри четном п = 2k и
cos cpj sin cpj
sin cp,
cos
ри нечетном n=2k+l.
кпчестве непрерывного пути y> соединяющего матрицу g0 с еди-
цей группы, можно рассмотреть семейство матриц (
"H'la(t)g, где
a(t) = \
Таким образом, группа SO(n) связна (рис. 5).' Поскольку она
гомеоморфна также множеству ортогональных матриц с определи-
определителем — 1, то группа О(п) со-
состоит из двух компонент связно-
связности. На одной из них delg= + l,
на другой detg = — 1. Лемма до-
доказана.
Лемма 7. Группы U(n) и
SU(n) линейно связны.
Доказательство. Из
курса алгебры известно, что для
любой матрицы go^SU(n) суще-
r(t)
Рис. 5
Рис. 6
ствует унитарное преобразование g такое, что матрица a = ggog~l
является диагональной:
а =
О
Рассмотрим непрерывный путь y(t), соединяющий матрицу
единицей Е и имеющий вид y{i)=g~xCL(t)g, где
25
• a{t)J
Ясно, что у@)=Е и y(l)=go- Связность U(n) доказывается ана-
аналогично. Лемма доказана.
Лемма 8. Группа GL(n, R) состоит из двух связных компо-
компонент. Группы GL(n, С) и SL(n, С) линейно связны.
Доказательство. Группа GL(nt R) распадается в объеди-
объединение двух, непересекающихся подмножеств Go и Gb где Go=
= {g : detg>0}, Gi = {g : detg<0} (рис. 6). Ясно, что множества GO
и Gi гомеоморфны и этот гомеоморфизм задается отображением
g->~ag, где матрица а имеет вид I \ I. Осталось до-
1° '-J
казать связность Go. Так как каждая матрица g^G0 интерпрети-
интерпретируется как некоторый базис в R", то, применяя известный процесс
ортогонализации базиса, получаем, что матрица g представима в
виде ар, где aeSO(n), ар — верхнетреугольная невырожденная
матрица с положительными диагональными элементами. Затем
можно непрерывно продеформировать матрицу р в Е и, следова-
следовательно, матрицу g в матрицу а. При этом мы воспользуемся тем,
что множество указанных верхнетреугольных матриц связно. В яв-
явном виде эту деформацию можно задать, например, так:
Р@ = | - '-. Ь гДе все Р.>°-
Поскольку группа SO(n) связна, то для случая GL(n, R) лем-
лемма доказана. Рассмотрим теперь группу GL(n, С). Построим глад-
гладкое отображение f:GL(n, C)->S', положив f(g)=detg. Ясно, что
образом / является вся окружность; при этом прообразом едини-
единицы на окружности является подгруппа матриц с определителем
единица, т. е. подгруппа SL(n, С) (рис. 7). Поскольку окружность
связна, то достаточно доказать связность группы SL(n, С). При-
Применяя процесс ортогонализации, приводящий от произвольного
унимодулярного комплексного базиса- к эрмитовому, мы сводим
вопрос о связности группы SL(n, С) к вопросу о связности груп-
группы SU(n). Но группа SU (п) связна по лемме 7. Лемма доказана.
Связность группы GL{n, С) объясняется тем, что эта группа
получается из пространства С"г выбрасыванием комплексной ги-
гиперповерхности, задаваемой уравнением detg=0. Так как ее ве-
вещественная коразмерность равна двум, то поверхность detg=O
26
iff разбивает С" на два куска (рис. 8). В вещественном же слу-
<ис поверхность detg = O имеет вещественную коразмерность один
i разбивает R на два связных куска, поэтому GL(n, R) со-
состоит из двух связных компонент.
1.7. Операция овеществления и комплексные структуры. One-
щция овеществления позволяет отождествить пространство С" с
lin. Выберем в С" эрмитов базис в\, ..., еп\ каждый вектор as
-^О допускает однозначное разложение вида
2"=1г/А> Где zk = xk + ii/k, а хк и
iu. вещественны. Рассмотрим попарно ортогональные векторы
't. ..., еп, iei, ..., ien. Каждый вектор а записывается в виде а==
JL(rijC.
GL(n,C)
Рис. 7
. Рис. 8
() Отображение ф:С"-^-^п, задаваемое формулой
т>'(а) — (хи ..., хп, Уи ■■■, У"), будем называть оператором овеще-
явления. При этом О отождествляется с R2ra.~4i0 ггуиисхидИг с
эрмитовой формой <a, by после овеществления ф? Ясно, что
=YJа
Y
k=\
*. e. (a, b) = Re (a, b)' ->-~Zxkck + </ftdft. Это означает, что эрмитово
скалярное произведение С" после овеществления переходит в
обычное скалярное произведение в R2".
Обратно, как задать комплексную структуру в четномериом
-•вклидовом пространстве? Снова рассмотрев овеществление
D:O-^R2ra, в R2n получим ортобазис е\, ..., еп, ie\, ..., ien, причем
12n=Rn(BiRn=Cn. Поэтому в R2" возникает линейный оператор /,
юйствующий по формуле Ix=ix. Ясно, что 12 = —Е и Iiek=—ek-
'ледователыю, относительно указанного ортобазиса матрица /
где Е — единичная матрица поряд-
собственные числа Х\—
шисывается так:
[Е О
i п. Этот оператор, очевидно, имеет
27
= .. ,=xn—i, Лл+1=.. . = Я2л=—i. Ясно также, что оператор / орто-
ортогонален, т. е. /eS0Bn). Эти свойства мы и положим в основу
следующего определения.
Определение 4. Будем говорить, что ортогональный опе-
оператор A^SOBn) такой, что А?=—Е, определяет комплексную
структуру в R2n. Иногда комплексной структурой называется сам
оператор А.
Условие ортогональности в определении 4 можно было бы
опустить, но для простоты мы будем рассматривать в дальнейшем
именно ортогональные комплексные структуры. Предъявим теперь
отождествление R2n с С", используя этот оператор А. Поскольку
он ортогонален, то подходящим ортогональным преобразованием
базиса можно привести матрицу А к каноническому виду
cos ф1 sin cp1 \
О
-sin cpt cos
о
\f
Так как Л2 = —£, то yk = ^— + nlk, /fce Z. Делаем еще одну за-
замену базиса (перестановки векторов) и приводим оператор к ви-
виду 1 — {р j?y. Итак, возникает некоторый ортобазис еи ..., еп,
t\, ..., tn такой, что lek=tk, Itk = —ek. Натягивая на векторы
еи ..., еп подпространство R™, получаем разложение R2"=
= R"(e)©R«@ такое, что /:R»(e)->Rn(f), /:R"(/)^Rn(e). Следо-
Следовательно, любой вектор aeR2" допускает однозначное разложение
а=х+1у, где x,(/eR"(e). Так как 12=—Е, то можно отождествить
R2" с С", рассмотрев все комплексные линейные комбинации век-
векторов {ек}.
Возникает естественный вопрос: сколько комплексных структур
можно задать в R2n? Другими словами, как описать, все такие ор-
ортогональные матрицы А, что А2——Е. Так как А~х = —А, А~Х=АТУ
то Ат=—А, т. е. оператор А является комплексной структурой тог-
тогда и только тогда, когда он кососимметричен. Рассмотрим овеще-
овеществление ср:OWR2", и пусть n2fcczR2n — произвольная 2й-мерная
вещественная плоскость. Возникает вопрос: когда она является
комплексной плоскостью, т. е. когда Y\2k является образом неко-
некоторого комплексного подпространства после овеществления? Ока-
Оказывается, пло.скость П является комплексной тогда и только тогда,
когда она инвариантна относительно действия оператора j4:R2"->~
->R2n. Доказательство предоставляем читателю.
Для дальнейшего полезно представлять себе, как устроено
множество всех комплексных структур в R2", т. е. множество всех
различных (ортогональных) комплексификаций R2"., превращаю-
превращающих его в С". Рассмотрим группу SOBn) и ее алгебру Ли как
подмножества в пространстве всех вещественных матриц пор'яд-
ка 2п.
Лемма 9. Множество всех ортогональных комплексных струк-
28
,/i n R2" совпадает с пересечением группы SO Bn) с ее алгеброй
in ao{2n) (рис. 9).
Доказательство сразу следует из обнаруженного нами
"Mine факта кососимметричности ортогональной матрицы, являю-
пся в то же время комплексной структурой. Полезно помнить,
каждая ортогональная комплексная структура А имеет вид
ц1ц~\ где g^SOBn). Следовательно, множество всех комплекс-
комплексных структур в R2" естественно
отождествляется с множеством
м.тгриц вида glg~\ где матрица vC- " • •'• ">ч. <nf
ц пробегает всю группу SOBn). /\'\'-\'У.:Р\г '
Определение 5. Линейное
отображение g^SO Bn) назы-
нпстся комплексным, если оно
коммутирует с оператором / ум-
умножения на мнимую единицу,
т. е. если gl = lg.
Если рассмотреть отождеств-
отождествление R2" с С", т. е. R"©(R"=R2n,
то условие комплексности матри- рис 9
цы g означает, что g(iz)=ig(z),
где zeC" = R2". Таким образом,
определение 5 в точности соответствует стандартному представ-
представлению о комплексных операторах. Как устроено множество всех
комплексных ортогональных преобразований? Какие события про-
происходят с унитарной группой U(n) после овеществления
ip : C"-^R2"?
Пусть g^U(n). Так как этот оператор сохраняет эрмитову
форму, то после овеществления он превратится в оператор фь-,
действующий в R2" и сохраняющий евклидову форму, так как эр-
эрмитово скалярное произведение превращается при овеществлении
в евклидово скалярное произведение. Так как оператор ц>е сохра-
сохраняет евклидово скалярное произведение, то он является элемен-
элементом группы SOBn). Найдем явный вид вложения' ф:£/(л)->-
-*£ОBп).
Предложение 2. Мономорфизм ф:С/(n)-»-SOBn), возни-
возникающий при овеществлении ф*. O-^-R2", явно записывается так:
еде матрицы С и В имеют порядок п и вещественны. Кроме того,
выполняется равенство xpU(n)=SOBn)f\<pGL(n, С).
Доказательство. Пусть е\,...,еп — эрмитов базис в С". •
Тогда при овеществлении он переходит в ортобазис " еи ..., ел,
tei ien. Поэтому (C+iB)ek=Cek+B(iek), (C+iB)iek = -Bek+
д °\. Прямое вычисле-
вычисление показывает, что det cpg= | det g\2, т. е. det9§>0. Докажем те-
теперь, что SOBn)n<pGL(n, С)=ф[/(п). Пусть ф^еф[/(п), тогда, с
пдной стороны, (fg^SO Bn), а с другой стороны, оператор ф£ по-
29
лучен овеществлением комплексного невырожденного оператора,
т." е. q>U(n)<=SdBn)(](pGL(n, С). Обратно, пусть g<=SOBn) и
GL(n, С). Это означает равенство g(iz)=igz, из которого еле-
1С /?
( ) ()
1С /? \
дует, что (fg имеет вид I ^ р,), т. е. g^q>U(n), что и требова-
требовалось доказать.
Предложение 3. Множество всех ортогональных комплекс-
комплексных структур в R2" является гладким многообразием и гомеоморф-
но компактному однородному пространству SOBn)jV (п), где под-
подгруппа U (п) стандартным образом вложена в группу S0Bn)
(см. предложение 2).
Доказательство. Как мы уже знаем, множество М всех
комплексных ортогональных структур в R2" отождествляется с
множеством матриц вида glg~\ где g пробегает SOBn). Следо-
Следовательно, M—SOBri)jH, где через Я обозначена подгруппа тех
матриц, которые коммутируют с матрицей /. Эта подгруппа иног-
иногда называется централизатором элемента I^SOBn). Через
S0Bn)IH обозначено множество левых классов смежности по
подгруппе Н. Условие коммутирования h с /, очевидно, эквива-
эквивалентно равенству I = hlh~\ которое означает, что Я — это множе-
множество всех преобразований, коммутирующих с умножением на мни-
мнимую единицу. Отсюда получаем, что Я совпадает с множеством
всех комплексных ортогональных операторов, т. е. H=U(n), что
и требовалось доказать.
Итак, SOBri)[\soBn)=SO{2n)IU(n). Множество всех ком-
комплексных структур оказалось вложенным в группу SOBn) в ви-
виде гладкого компактного подмногообразия SO Bn)/U(п). Оказы-
Оказывается, это вложение обладает и другими интересными метричес-
метрическими свойствами. Напомним в связи с этим определение вполне
геодезических подмногообразий.
Определение 6. Подмногообразие риманова многообразия
называется вполне геодезическим, если каждая геодезическая в
подмногообразии (с точки зрения индуцированной на нем римано-
вой метрики) остается геодезической и в объемлющем многооб-
многообразии.
Предложение 4. Множество SOBn)/U(n) всех комплекс-
комплексных ортогональных структур является вполне геодезическим под-
подмногообразием в группе SOBn).
Доказательство. Напомним, что гладкая кривая в группе
Ли является геодезической тогда и только тогда, когда она полу-
получена левым или правым сдвигом из некоторой однопараметриче-
ской подгруппы, проходящей через единицу группы. Поскольку
нас интересует группа SOBn)t то любая однопараметрическая
подгруппа имеет вид exp tY, где Y — некоторая кососимметриче-
ская матрица. С-ледовательно, каждая ортогональная матрица,
близкая к единице, однозначно представляется в виде ехр X, где
кососимметрическая матрица X имеет малые коэффициенты.
Пусть g — произвольная комплексная структура. В силу
предыдущего замечания любая другая близкая к ней комплексная
30
структура может быть однозначно записана в виде gexpX, где
X ~ некоторая малая кососимметрическая матрица. Таким обра-
лом, мы описали структуру малой окрестности каждой точки g в
подмногообразии SOBn)/U(n).
Докажем следующее вспомогательное утверждение: матрица
ЦехрХ является комплексной структурой тогда и только тогда,
когда X антикоммутирует с g, т. е. когда gX+Xg=0. В самом де-
деле, если матрицы X и g антикоммутируют и g2——E, то —X—
= g~lXg, следовательно, ехр(—X) =g~l (expJ)g =—g(expX)g. От-
Отсюда получаем равенство (g ехр ХJ=—Е, которое означает, что
оператор gexpX является комплексной структурой. Обратно, если
(gexpXJ=—E, то, выполняя предыдущие вычисления в обратной
порядке, получаем exp{g~:Xg)exp Х=Е. Так как матрица X ма-
мала, то g~:Xg=—X, что и означает антикоммутирование g и X. Та-'
ким образом, мы доказали, что малая окрестность точки g в под-
подмногообразии SUBn)IU(n) состоит из всех матриц вида gexpX,
где X пробегает все матрицы из некоторого линейного подпро--
странства в алгебре Ли soBn). Это подпространство состоит из:
матриц, антикоммутирующих с g. Следовательно, малая окрест-
окрестность точки g в подмногообразии SOBn)IU(n) заполнена траек-
траекториями, исходящими из g и являющимися образами однопара-
метрических подгрупп при их левом сдвиге из единицы в точку g.
Таким образом, SOBn)IU(n) — вполне геодезическое подмного-
подмногообразие в группе SOBn), что и требовалось доказать.
Множество комплексных структур допускает еще одну инте-
интересную геометрическую характеристику, которую мы приведем
здесь без доказательства. Оказывается, если в группе 50 Bл) рас-
рассмотреть множество всех кратчайших геодезических, соединяющих
единицу Е с точкой —Е, то каждая такая геодезическая ровно в-
одной точке пересекается с подмногообразием S0Bn)IU(n), вло-.
женным в S0Bn). Эта точка расположена на середине геодезиче-
геодезической. Следовательно, множество комплексных структур гомео-
морфно множеству всех минимальных геодезических в группе
S0Bn), соединяющих Е с —Е. Кроме групп GL(n, R), GL(n, С),
U(n), SU(n), 0(n), SO(n) в геометрии естественно возникают
группы симплектических преобразований, к изучению которых мы
теперь переходим.
§ 2. Группы симплектических преобразований линейного
пространства
2.1. Симплектические линейные преобразования. Известно, что
свойства евклидовой геометрии определяются свойствами симмет-
симметричного невырожденного положительно определенного скалярного
произведения <,>, превращающего линейное вещественное «-мер-
«-мерное пространство в евклидово пространство R". Параллельно этой
Теории строится симплектическая геометрия, свойства которой
Определяются свойствами кососимметрического невырожденного
вк.члярного произведения (,), превращающего линейное вещест-
iP четномерное пространство в симплектическое пространст-
31
во L2n. Наряду с многими общими чертами евклидова и симплек-
тическая геометрии обладают принципиальными различиями.
Удобно моделировать симплектическое пространство L2" на ев-
евклидовом пространстве R2n. . ^ • ■— *
Будем говорить, что в R2" задана (линейная симплектическая_
структура, если задано билинейное кос^йм"м^трйчёс'кое""Т1евырож-~
денТюёТкалярное произведение (,), т. е. (а, Ь) = — (Ь, а) для лю-
любых двух векторов fl,beR2" и (а, Ь)=0 для любого ceR2" в том
и .только в том случае, когда Ь = 0. Пространство R2™ с такой до-
дополнительной структурой называется симплектическим линейным
пространством. Если в R2™ фиксировать какой-либо базис еи ....
..., в2п, то скалярное произведение (а, Ь) можно записать в явном
виде так: (а, ^) = Е^и;/аг^/-) где а,- и Ь; — координаты векторов а
и b относительно выбранного базиса, а Й= (©,•/) — невырожденная
кососимметрическая матрица, со;,=—со/;. Коэффициенты со;,- пока
будем считать постоянными числами, не зависящими от точки
пространства R2". При невырожденном линейном преобразовании
базиса матрица Q также меняется, но остается кососимметриче-
ской. Приведем пример простейшей симплектической • линейной
структуры. Для этого введем в R2re координаты р\, ..., рп, q\, ...
..., qn и зададим симплектическую структуру формулой (а, й) =
=^Piqi'—pi'qi, где a=(ph ..., qn), b={px', ..., qn'). Ясно, что мат-
матрица Q, записанная относительно базиса, соответствующего этим
координатам, имеет вид J=\F ^ ), где через Е обозначена еди-
единичная матрица размером (пХп). Оператор / уже знаком нам как
оператор, задающий комплексную структуру в R2". Если же ко-
координаты занумеровать в другом порядке, а именно: р\, qu p2,
<72 рп, qn, то матрица Q запишется в следующем блочно-диа-
гональном виде:
О 1
— 1 О
О
о
О 1
-1 О
Этот пример является в некотором смысле универсальным. Де-
Дело в том, что если Q — произвольная невырожденная кососиммет-
кососимметрическая матрица размером B/гХ2«), то, как известно из курса
линейной алгебры, всегда существует такая невырожденная ли-
линейная замена координат в R2", что матрица Q приведется к ка-
каноническому виду, указанному выше. Поэтому всегда можно счи-
считать, что если Q — матрица симплектической линейной структуры
в R2n, то всегда можно выбрать такие координаты, относительно
которых эта структура принимает простейший вид, описанный вы-
выше. Базис из 2л векторов ai, ..., ап, fh, ..., р«, в котором струк-
32
Iура Q принимает канонический вид /, будем в дальнейшем назы-
иать симплектическим. Ясно, что матрица попарных кососкаляр-
пых произведений базисных векторов имеет в этом случае вид
_£ о)'
при 1Ф\.
Отметим, что скалярный квадрат каждого вектора равен ну-
нулю, т. е. все векторы в симплектическом пространстве изотропны.
Векторы m и р; будем называть сопряженными, так как (a*, р\) =
-1. По аналогии с симметричным скалярным произведением будем
говорить, что два вектора а и Ь, косоортогональны, если их косо-
скалярное произведение равно нулю, т. е. если (а, Ь)—0. В част-
частности, в симплектическом пространстве каждый вектор сам себе
косоортогонален. Несмотря на эти различия, между евклидовым и
симплектическим скалярными произведениями имеется много объ-
объединяющих их черт. Перечислим некоторые из них, нужные для
дальнейшего.
Множество всех векторов, косоортогоиальных всем векторам
н.ч некоторой плоскости П* в R2", называется косоортогональным
дополнением к плоскости П* в R2". В частности, косоортогональ-
ное дополнение к одному вектору а является Bя—1) -мерной ги-
гиперплоскостью в R2", содержащей вектор а (рис. 10). Это утверж-
Рис. 10
Рис. 11
депие следует из невырожденности симплектическои структуры,
поскольку ненулевой вектор о не может быть косоортогоналеи все-
всему пространству R2". Ясно также, что если Т — косоортогональ-
imc дополнение к плоскости Ylk в R2", то размерность Т равна
Чц-k. Подпространство в R2" будем называть симплектическим,
пели ограничение на него симплектическои структуры невырож-
чено.
Как мы уже видели, из линейной алгебры следует, что в каж-
|"м симплектическом пространстве всегда существует симплек-
■ гкий базис. Таких базисов много, и, кроме того, в качестве
• иго вектора симплектического базиса можно взять любой не-
1 ной вектор aeR2re. Докажем это последнее утверждение ин-
'■ : "ной по п. При п=1 в качестве вектора ег, дополняющего век-
t Фоменко
33
тор в\=а до симплектического базиса в R2, достаточно взять век-
вектор, не являющийся косоортогональным к а в R2, и подобрать»
его длину так, чтобы {Ь, а) = 1. Такой вектор b существует в силу
невырожденности формы (,).
Пусть теперь п> 1 и а=е\Ф0. Как и на первом шаге, выберем-
вектор e2eR2fl так, чтобы (е2, ei) = l. Рассмотрим натянутую на
них двумерную плоскость П2, и пусть К — косоортогоналыюе до-
дополнение к П2 в R2™. Ясно, что размерность К равна 2п—2 и, кро-
кроме того, П2|"|/( = 0 и оба вектора в\ и е2 не лежат в К (рис. 11).
В самом деле, если бы, например, в\ лежал в К, то в\ был бы ко-
соортогонален к е2, что невозможно в силу выбора е2.
Покажем теперь, что Bя—2) -мерная плоскость К является
симплектическим подпространством в R2n, т. е. что ограничение:
симплектической структуры на К невырождено. В самом деле, д<-
пустим противное: пусть некоторый вектор h^K косоортогонален
всей плоскости К. Но в таком случае он косоортогонален всемт
пространству R2re, поскольку плоскость К косоортогональна плос-
плоскости П2, а сумма К и П2 дает R2™. Так как по предположении
индукции в симплектическом пространстве К2"^2 можно выбратг.
симплектический базис, то, дополняя его двумя векторами е2 и е,_
мы и получаем симплектический базис во всем пространстве R2r.
что и доказывает утверждение.
Определение 1. Будем говорить, что плоскость П* в сиь-
плектическом пространстве R2" является -издтузопной^ если она се-
себе косоортогональна, т. е. кососкалярное произведение любых двуг
векторов плоскости равно, нулю. Если k=n (т. е. равно половину
размерности R2n), то изотропную плоскость и а з ов е м(^шгранже eoR.
Поскольку симплектическая структура моделируется намй~ДЛ?
удобства на евклидовом пространстве R2", это позволяет задать
кососимметрическое скалярное произведение в несколько иног
форме. Если {а, Ь) = ^Р1р\ + Я1Я'Р где а={ри ..., qn), Ь=
= {Р\, ..., qn') в R2", то кососкалярное произведение (а, Ь) мо>ь-
но переписать так: {a, 6)=<Qa, b}, где оператор Q:R2"-vR2" за-
задает некоторое линейное невырожденное преобразование. Яснс.
что этот оператор кососимметричен относительно выбранного н?-
ми ортогонального базиса.
Будем в дальнейшем считать для удобства, что симплектичь-
ская и евклидова структуры в R2" согласованы в том смысле, чт<
векторы симплектического базиса си, ..., а^, рь ..., рп ортоног-
мированы, т. е. взаимно ортогональны и имеют евклидову длин^
равную единице. В симплектическом ортонормированном базиса
оператор Q, очевидно, задается канонической матрицей. /=
= [ |, в частности Q2=—Ein. С геометрической точкг
зрения действие оператора Q сводится к следующему: в каждор
из п двумерных плоскостей, натянутых на векторы ш, р;, проис
ходит поворот на угол я/2. Описанная связь между евклидовой г
симплектической структурами, вообще говоря, разрушается прр
34
■произвольном линейном невырожденном преобразовании R2". Од-
иадо при фиксации описанного выше базиса из, этой связи извле-
извлекаются полезные следствия.
Лемма 1. Плоскость П в симплектическом пространстве яв-
является изотропной в том и только в том случае; когда плоскости
П и QFI взаимно ортогональны (в обычном евклидовом смысле).
Доказательство. В силу согласованности симплектической
и евклидовой структур мы имеем (a, b) = (iia, b) для любых век-
векторов а, йеП. Следовательно, (а, й)=0 тогда и только тогда, ког-
когда <Qa, fr>=0, что и доказывает лемму.
Лемма 2. Размерность изотропной плоскости Ylk в симплек'
тическом пространстве R2" всегда не превосходит числа п.
Доказательство. В силу леммы 1 плоскости П и QFI вза-
взаимно ортогональны, что эквивалентно изотропности П. Так как
оператор Q невырожден, то размерности плоскостей П и QF1 оди-
одинаковы. Следовательно, &+&<2п, т. е. &<п.
2.2. Некомпактные группы Sp(n, R) и Sp(n, С). Рассмотрим
в симплектическом пространстве структуру (,).
Определение 2. Линейное преобразование g:R2"-^R2"
симплектического пространства в себя называется симплектиче-
ским в том и только в том случае, когда оно сохраняет сим- -
плектическую структуру, т. е. сохраняет кососимметрическое ска-
скалярное произведение: (ga, gb) = (a, b) для любых a, fteR2". Со-
Совокупность всех симплектических преобразований R2", оставляю-
оставляющих на месте начало координат, образует группу, которая назы-
называется вещественной симплектической (некомпактной) группой и
обозначается Sp(n, R).
Мы должны проверить корректность определения 2, а именно
доказать, что симплектические преобразования действительно об-
образуют группу. Тот факт, что композиция (произведение) сим-
симплектических преобразований снова является симплектическим
преобразованием, очевиден. Докажем, что линейные симплектиче-
i'kiip преобразования невырождены'. Для этого напомним связь
между кососймметрическими скалярными произведениями и внеш-
внешними (дифференциальными) 2-формами. Рассмотрим дифферен-
дифференциальную форму юB> =^j=]dpi/\dqi. Ясно, что она определяет
кпеосимметрическое скалярное произведение (a, b) = '%j=\piqi — piq{
при естественном отождествлении R2re с касательным к нему про-
пространством TR2n. Другими словами, произведение двух векторов
n-=(plf ... , qn) и b — (p'v ... , q'n) может быть записано в виде
{а, Ь)'=(й(а, Ь), так как dpi(a)=pi, dqi(a)=qi, dpt(b)=p\, dqt(b) =
•*sq\ H(dpt/\dqt)(a, b)=piq'.—p'fli. Определение и простейшие свой-
свойства внешних дифференциальных форм см., например, в- учебни-
учебнике E3].
Поскольку кососкалярное произведение двух векторов равно
шичению, которое 2-форма со принимает на этих векторах, то в
дальнейшем мы можем пользоваться некоторыми простейшими
Ойопгтвами внешних форм.
Лемма 3. Определитель любого линейного симплеКРШескогсг
преобразования равен единице.
Доказательство. В силу описанной выше связи между
кососкалярным произведением и внешними 2-формами линейное
отображение g-:R2"->R2" симплектического пространства, отнесен-
отнесенного к стандартным симплектическим координатам р\, ..., рп,
q\, ..., qn, является симплектическим тогда и только тогда, когда
оно сохраняет соответствующую внешнюю 2-форму. Этой харак-
характеристикой симплектических преобразований мы часто будем
пользоваться в дальнейшем.
Рассмотрим п-ю внешнюю степень 2-формы со и положим тBп>=
= иЛ---Дш (п раз). Из общих свойств внешних форм следует,
что форма х степени 2л имеет вид i=X(x) -йхх/\.. .f\dx2n, где
%{х) — некоторая гладкая функция от коэффициентов формы со=
"=Sce,7a;b/, а в конечном итоге — функция от координат хи ..., хгп
в R2". Мы утверждаем, что X^j/det (col7) = ]/detQ , где Q=
= (@i/) — матрица коэффициентов формы. Если А — произвольная
невырожденная линейная замена координат, то Q=AQ'AT, где
£У — матрица формы со в новой системе координат. Следователь-
Следовательно, det Q'■ (detЛJ = det Q. Если координаты выбраны так, как это
было сделано выше, т. е. матрица Q' принимает в них канониче-
канонический вид, то очевидно, что detQ'=l и detQ=(detАJ. В то же
время при замене координат (х)-^-(р, q) форма т преобразуется
по следующему закону: т= (detЛ) ■%'=&<&A-dxxf\.. ./\йх2п- Так
как det А —- V^det Q, то ^ = ]/detQ, что и требовалось доказать.
В частности, если координаты Xi'...,X2n совпадают с канониче-
каноническими р\, ..., qn, то det Й=1 и Х=1.
Итак, форма т = (оЛ---Л« (п раз) интерпретируется как форг
ма 2«-мерного объема в R2", причем мы в явном виде вычислили
коэффициент К. Таким образом, симплектическое преобразование,
сохраняя форму со, автоматически сохраняет и ее п-ю внешнюю
степень, т. е. форму т, и, следовательно, сохраняет форму 2п-мер-
ного объема в R2". Отсюда следует, что преобразование унимоду-
лярно, что и требовалось доказать.
В частности, мы доказали также следующее утверждение.
Следствие 1. Кососимжетрическое произведение и (а, Ь) =
= {а, Ъ) невырождено в точке ^eR2" тогда и только тогда, когда
. форма т=соЛ- ■ -Л(о (я раз) отлична от нуля в этой точке.
Из леммы 3 вытекает, что совокупность симплектических пре-
преобразований действительно образует группу, так как преобразова-
преобразование, обратное к симплектическому, также невырожденное и сим-
симплектическое. Из доказанного выше следует также, что симплек-
симплектическое преобразование переводит любой симплектичёский базис
снова в симплектичёский. Верно и обратное: если некоторое ли-
линейное преобразование переводит некоторый симплектичёский ба-
базис в сиплектический, то преобразование является симплектиче-
симплектическим. Следовательно, любые два симплектических базиса могут
быть совмещены симплектическим преобразованием. В этом смыс-
36
ле свойства симплектической группы сходны со свойствами, на-
например, ортогональной группы. Однако имеются и различия, неко-
некоторые из которых мы сейчас опишем.
В евклидовом пространстве все плоскости.одинаковой размер-
размерности равноправны в том смысле, что любую из них можно пе-
перевести в любую другую при помощи некоторой изометрии R2",
т. е. при помощи трансляции (параллельного переноса) и орто-
ортогонального преобразования. В симплектическом пространстве это
не так.
Выше мы доказали, что любой ненулевой вектор симплектиче-
симплектического пространства можно взять за первый вектор симплектиче-
ского базиса. Следовательно, любой ненулевой вектор симплекти-
ческого пространства, можно перевести в любой другой ненулевой
вектор симплектическим преобразованием. Другими словами, сим-
плектическая группа Sp(n, R) транзитивна на множестве всех не-
ненулевых векторов симплектического пространства, выходящих из
начала координат. Однако уже для двумерных плоскостей это
свойство не выполняется. Существуют такие пары, двумерных
плоскостей, которые не могут быть совмещены друг с другом сим-
симплектическим преобразованием. Чтобы убедиться в этом, нам по-
потребуется следующее утверждение.
Лемма 4. Симплектическое преобразование переводит любую
изотропную плоскость снова о изотропную. В частности, образ лаг-
/шнжевой плоскости при симплектическом преобразовании снова
чиляетси лагранжеаой плоскостью.
Д о к и i и т с л ь с т п о. Согласно определению симплектического
ii|H4iO|Ht.infijiHii»i оно сохраняет кососкалярпое произведение любой
пары iM'iwnpon. Следошптлыт, плоскость, в которой произведение
.'iiofloft пиры лекторов равно нулю, переходит в плоскость с тем
же eimlicTHoM. Поскольку при симплектическом преобразовании
размерность плоскости не меняется, то лемма доказана.
Отсюда следует, что, например, изотропная и неизотропная
Овумерные плоскости не могут быть совмещены симплектическим
преобразованием. В качестве примера можно взять изотропную
плоскость, натянутую на векторы аг-, -а,-, где 1ф\ (см. выше матри-
матрицу попарных произведений базисных векторов), и иеизотропную
плоскость, натянутую на пару векторов а«, C,-. В качестве задачи
предоставим читателю доказать, что группа Sp(n, R) транзитив-
транзитивна на множестве всех неизотропных двумерных плоскостей в R2",
проходящих через начало координат, т. е. любые две неизотроп-
неизотропные двумерные плоскости могут быть совмещены симплектическим
преобразованием. Отметим также, что параллельные переносы в
R2" также являются симплектическими преобразованиями.
Фиксируем в R2'.' канонический симплектический ортопормиро-
ванный базис. Тогда матрица оператора Q, соответствующего
симплектической структуре (см. выше), записывается в этом бази-
/ 0 Е\
се в виде матрицы / = ( . Ясно, что оператор / является
Е 0 /
37
симплектическим и Р——Е. Рассмотрим более подробно свойства
группы Sp{\, R). Согласно определению эта группа состоит из ли-
линейных преобразований, оставляющих на месте начало координат
на двумерной плоскости R2 и сохраняющих кососимметрическую
форму (a, b)=alb2 — a2bh где а= {аи а2), b=(bit b2) — координат-
координатная запись векторов относительно канонического сймплектического
базиса еи е2, являющегося в то же время ортонормированным от-
относительно евклидового скалярного произведения.
Лемма 5. Группа Sp(l, R) изоморфна группе вещественных
матриц порядка два с определителем 1, т. е. группе SLB, R).
С топологической точки зрения эта группа матриц некомпактна,
имеет размерность 3 и гомеоморфна прямому произведению ок-
окружности на двумерную плоскость. В частности, группа Sp(l, R)
неодносвязна и ее фундаментальная группа изоморфна группе це-
целых чисел Z.
Доказательство. Ясно, что кососкалярное произведение
пары векторов a, b равно площади параллелограмма, натянутого
IP Q"
на а и Ь. С другой стороны, известно, что если g =
\r s
произвольное линейное однородное преобразование плоскости, то
площадь параллелограмма, натянутого на векторы g(a) и g{b),
получается из первоначальной площади умножением на определи-
определитель преобразования g. Следовательно, преобразование g сохра-
сохраняет кососкалярные произведения векторов в том и только в том
случае, когда оно унимодулярно. Как известно из линейной ал-
алгебры, каждое унимодулярное преобразование плоскости можно
однозначно представить в виде композиции двух преобразований:
ортогонального поворота плоскости и преобразования, задающе-
задающегося верхнетреугольной матрицей. Получаем топологическое раз-
разложение группы матриц SLB, R) в прямое произведение окруж-
окружности 50B) и множества матриц вида ( ], где а>0. Ясно,
\ 0 1/а /
что указанная группа верхнетреугольных матриц гомеоморфна от-
открытой полуплоскости R+2={(a, b), a>0, b — произвольное}. Лем-
Лемма доказана.
Группы Sp(n, R) при п>\ имеют более сложную структуру,
которую мы частично опишем ниже. Наряду с группой Sp(n, R)
нам потребуется также группа Sp(n, С) симплектических преоб-
преобразований комплексного линейного пространства. Рассмотрим эр-
эрмитово пространство С2", отнесенное к стандартному базису
е\,..-.,е2п. Положение точки в С2™ будем задавать набором ком-
комплексных чисел BЬ .._., 22п). Эрмитова форма в С2" задается фор-
формулой (a, b} = '£2i!Liaib(, где знак «черта» означает комплексное
сопряжение. Симплектическую структуру в С2" зададим так:
(a, b) = 2H^\aibn+i—an+ibi.
Определение 3. Невырожденное комплексное линейное пре-
преобразование g:Q2n->Cln называется симплектическим^ если оно
сохраняет симплектическую структуру в Cire, т. ёГсохргшяет внеш-
38
нюю 2-форму dZ\f\dzn+\+. • .+dzn/\dzin (форма записана на язы-
языке координат в С2"), Совокупность всех симплектических преобра-
преобразований С2", оставляющих на месте начало координат, образует
группу, которая называется комплексной симплектической группой
II обозначается через Sp(n, С).
Корректность определения 3 проверяется, как и в случае опре-
определения 2. Ясно, что группа Sp(n, R) содержится в группе Sp(n,
С) как подгруппа вещественных симплектических преобразований.
Изучим подробнее алгебраическую структуру комплексных и ве-
вещественных симплектических преобразований. Рассмотрим сим-
плектические преобразования, близкие к тождественному, т. е.
записывающиеся в виде матриц Е+еХ, где Е — единичная матри-
матрица, е — бесконечно малый параметр, а X— некоторая матрица.
Здесь удобно пользоваться понятием алгебры Ли, соответствую-
соответствующей данной группе Ли. Напомним, что если @ — группа Ли, а
G = Te<3 — касательное пространство к группе в единице, то G
естественным образом превращается в алгебру Ли. В следующей
лемме мы дадим описание алгебр Ли вещественной и комплекс-
комплексной симплектических групп. Для дальнейшего полезно также пом-
помнить, что каждая из этих групп определяется матричным уравне-
уравнением gIgT—I, где /=[ ), а матрица ~g порядка 2п яв-
ляется вещественной для случая Sp(n, R) и комплексной для слу-
чмя Sp{n, С).
Лемма 6. Группа Sp(n, С) является некомпактной группой
1и вещественной размерности 2пBп+\). Алгебра Ли sp(n, С)
>ТОЛ группы состоит мя комплексных матриц вида
где Zj — произвольная комплексная матрица порядка п, а ком-
комплексные матрицы Z2 и Z3 симметричны.
Группа Sp(n, R) является некомпактной группой Ли размерно-
размерности пBп+1). Алгебра Ли spin, R) этой группы состоит из веще-
(Хх Х2\
ственных матриц вида ( |, где Х\ — произвольная ее-
(Хх
\х3
щестаенная матрица порядка п, а матрицы Х2 и Х$ имеют порядок
п и симметричны.
Д о к а л а тел ьство. Проверка того, что перечисленные груп-
группы являются гладкими многообразиями, проводится по схеме, из-
изложенной нами в § 1 для случая ортогональной группы. Изучим
теперь структуру алгебры Ли группы Sp(n, С). Матрица g при-
принадлежит Sp(n, С) и том и только в том случае, когда она удов-
удовлетворяет матричному уравнению gIgT=I. В трм случае, когда
элемент g близок к единице, его можно представить в виде g=
= exptZ, где t—бесконечно малый параметр. Следовательно,
39
g-\ т. е. exp(//-'Zr/)=exp(—tZ), так как Л(ехрХ)Х
i = exp(AXA-i). Поскольку для элементов, близких к едини-
единице, представление в виде exp tZ однозначно, мы получаем, что Ze
^sp(n, С) в ton; и только в том случае, когда /~'Zr/=—Z, т. е.
когда ZT/+/Z = 0. Записывая матрицу Z в виде
zz
U3
где Z, — комплексные матрицы порядка п, мы получаем, что ука-
указанное выше условие эквивалентно равенствам ZiT + Z4 = 0, Z2=
=Z2r, Z3 = Z3r. Тем самым лемма доказана для случая Sp(n, С).
Ясно, что рассуждения дли случая Sp(n, R) полностью аналогич-
аналогичны, поэтому мы их опускаем. Лемма доказана.
Можно доказать, что группы Sp(n, R) и Sp(n, С) линейно
связны. Доказательство мы предоставляем читателю.
Мы уже отметили связь между симплектической и комплекс-
комплексной структурами в R2n. Обе они порождаются одним и тем же
оператором ^= ), но разными способами. В частности,
множество всех комплексных структур SOBn)IU(n) является ор-
орбитой, порожденной элементом / при действии на него группой
SOBn), а группа симплектических преобразований является груп-
группой, сохраняющей форму с матрицей /. Выше мы видели, что
эрмитово скалярное произведение представляется в виде (а, Ь) +
+ i(a, b), где вещественная часть {а, Ь) совпадает с симметрич-
симметричным евклидовым скалярным произведением, а мнимая часть (а,
Ь) совпадает с кососкалярным произведением. Ниже мы более
подробно опишем взаимные включения и пересечения симплекти-
симплектических групп с другими основными матричными группами.
Отметим еще одно важное свойство симплектических преобра-
преобразований. -
Предложение 1. Характеристический полином !(%) =
= det(g — КЕ) симплектического вещественного преобразования
g^Sp(n, R) обладает свойством f {i) =Х2п/AД), что означает
симметричность его коэффициентов: ak — ain-h, zdef(K)~2л=оЯ*Л*.
В частности, если X — собственное число симплектического
преобразования, то 1/л, также собственное число.
"Доказательство. Из определения симплектического преобра-
преобразования следует, что gIgT = I, т. е. g — —Ig~iT/, так как /2 = —Е.
Отсюда /^) = det(g— X£)=det(—Ig~XTI— X£)=--det(—£-1Г + Щ =
=det (—E + Xg), так как det g — det gT = 1. Окончательно det (—
\ - X2nf{l!K), что и требовалось.
— -j-E\
Полезно также и_меть в виду, что если X — собственное (комп-
(комплексное) число, то X — также собственное число. Это вытекает из
вещественности характеристического полинома /(л). Таким обра-
образом, в случае общего положения собственные числа вещественного
40 .
снмплектического преобразования разбиваются на-четверки вида
X, К, l/k, 1/K, т. е. собственные числа расположены симметрично
относительно вещественной оси и относительно единичной окруж-
окружности. Это обстоятельство полезно при изучении устойчивости
симплектических преобразований [5].
2.3. Компактная группа Sp(n). Мы познакомились с двумя
группами симплектических преобразований: комплексной группой
Sp(n, С) и ее «вещественной формой» Sp(n, R), Оказывается,
группа Sp'(n, С) содержит еще одну под-
подгруппу, обозначаемую через Sp(n) и на-
называемую «компактной формой», Эта
группа играет важную роль в современ-
современной геометрии. Удобно определить груп-
группу Sp(n) при 'помощи алгебры кватер-
кватернионов Q. Напомним ее определение.
Рассмотрим евклидово пространство R4,
фиксируем в нем ортонормированный
базис векторов, которые обозначим 1,
f, /', k (рис. 12). Следовательно, каж-
каждый вектор q из R4 однозначно' за-
записывается в виде линейной комбинации <7=/
i r,\k, где числа rt вещественны. Определим" затем умножение век-
трон (точек) в R4, задай его сначала на векторах базиса 1, £, /,
I,-, и затем продолжив по линейности па опальные векторы. Таб-
Таблице умножения базисных векторов 1, I, \, k имеет вид
Рис. 12
1
i
/
k
i
1
i
' J
k
i
i
— i
—k
i
i
i
k
i
— i
k
k
£"
j
Это умножение ассоциативно и косокоммутативно на обра-
образующих. Например, ij = —ji. Вектор 1 играет роль единицы. Оче-
Очевидно, возникает четырехмерная вещественная алгебра с едини-
единицей, снабженная ассоциативным умножением (некоммутативным).
Эта алгебра п намывается алгеброй кватернионов Q. Векторы q
из Q называются кватернионами. В алгебре кватернионов естест-
естественно определена операция сопряжения, переводящая кватернион
ц в кватернион <7 = го1—rxi — r2j — г3&. Векторы i, j, k называются
мнимыми единицами, компонента rol кватерниона q называется
его вещественной частью и обозначается Re q, а составляющая
rii + r2j + r3k называется мнимой частью и обозначается Iraq. Сле-
Следовательно, каждый кватернион допускает однозначное разложе-
41
ние q=Req+Imq. Ясно, что q=Req— Imq. Легко проверить,
что ЯхЯг — Я&х- Кватернионы с нулевой вещественной частью на-
называются мнимыми. Из определения умножения следует, что про-
произведение двух мнимых кватернионов косокоммутативно, т. е.
\mqlq2=—1т^2<?ь если Re<7i = Re<72=0. В алгебре Q можно
определить вещественнозначное симметричное скалярное произве-
произведение (<7ь q2)=Reqiq2. Если qi = r\-l + r2i+r3j + r4k, q2 — U-\ +
+ t2i + t3j+tik, то (<7ь q2)~=riti + r2t2+rztz+r4t4, т. е. это скаляр-
скалярное произведение совпадает с обычным евклидовым произведе-
произведением в R4. Можно определить норму (длину) \q\ кватерниона,
положив |<?|2=(<7. q), т. е. |<7|2=Re<7<7=£ri2. Это число совпа-
совпадает с обычной евклидовой длиной вектора q в R4. Очевидно, что
алгебра Q распадается в прямую сумму двух ортогональных под-
подпространств, а именно R'®RS=Q, где R1 — прямая, состоящая из
вещественных кватернионов, a R3 — ортогональная трехмерная
плоскость, состоящая из мнимых кватернионов. В алгебре Q есте-
естественно определяется понятие обратного элемента <?"' для каждо-
каждого <7=И=0, а именно q~l=ql\q\si. Ясно, что qq-l=='q~lq=l.
Рассмотрим п-мерное линейное кватернионное пространство
Qn с базисом ех еп. Каждый вектор a<=Qn допускает одно'
эначную запись вида а=2пг=1а*еь где a^eQ. Рассмотрим в Qrt
вещественнозначное невырожденное скалярное произведение {а,
b) = Re2"=i aipi. Оно симметрично. Число п называется кватерни-
онной размерностью Qn. Эта форма является вещественной
частью следующей кватернионнозначной формы (а, &)' = 2?=1а,-6{.
где аи &i<=Q. Ясно, что Q' = Q.
Определение 4. Симплектической компактной группой
Sp(n) называется множествоТсёх линёМых~кватернионных пре-
преобразований g пространства Qn, оставляющих на месте точку О и
сохраняющих вещественнозначное скалярное произведение в Qn:
: (a, b) = Re2ai5i, т. е. (ga, gb) = (a, b).
Как и в комплексном случае, наряду с группой Sp (n) опреде-
определена группа Sp(n)r инвариантности кватернионнозначной формь
(а, Ъ)'. Имеет место следующее утверждение: группьь Sp(n) i
Sp{n)' совпадают. Доказательство проводится по схеме доказа
тельства § 1 для комплексного случая.
Кватернионное пространство Q" можно канонически отождест
вить с комплексным пространством С2п. Начнем с п=\, тогдг
Q':=Q. Запишем <?eQ в виде q^=rol + rii+r2}+rzk. Использу!
таблицу умножения, можно переписать кватернион q в виде q=
■=(го+г11)+}(г2 — Ы)=г1 + ]г2, где zi = ro+/-i£, Z2=i\+tzi-
комплексные числа. Выполняя эту операцию вдоль каждой ква
тернионной координаты в Qn, мы и получаем отождествление Q
с С2п. Обозначим эту операцию через ф: Qn^C2n. Что происходи
при этой операции с кватернионнозначной формой (а, Ь)'? Поле
■ф
жим п=\, тогда <a, _6>'->(p + jq) (c+jd)= (p + jq) {c — dj) =
= (pc — jqdj) — {pdj — jqc) =\pc+ qd) + (~pd + qc)j. Здесь ipa=
=p + /<7, tyb = c+jd. Выше мы воспользовались тем, что jq=qj,
j2 = — 1, ab = 5a. Следовательно, при произвольном п кватерни-
онная форма (а, Ь)' переходит в форму I,nk=ipkCk + qkdk +
d{){ j i~)b
(h7hft pkh)j,P£{u1){p jq iq)
— {bu...,bn)->~(Ci + jdi,...,cn+jdn). Указывая в явном виде ко-
коэффициенты форм, получаем
ф : (а, ьуц-+{а, Ь)'с + (а, Ь) с, ,
где (а, Ь)'с =2pfeCfe + <7fedfe, (a, b)c =2<7ьС/: — phdh.
Форма {a, b)fc эрмитова, а форма (а, Ь) с кососимметрична.
Лемма 6. Множество Sp (n) является связной компактной
группой Ли вещественной размерности пBп+1). При отождест-
отождествлении Q" с С2п группа Sp(n) вкладывается как подгруппа в
группу £/Bп). При этом вложении алгебра Ли sp(n) группы
S() состоит из комплексных матриц порядка In следующего
1 z z\
V-z2 zj
1 zi z*\
вида: I _ _ I, где Z\ — комплексная косоэрмитова матри'
ца порядка п, a Z2 — комплексная симметрическая матрица по-
порядка п. Если матрицы из группы UBn) представить в виде
А В \
\, г<)е Л. В, С, D — комплексные матрицы, то подгруппа
w LJ
Sp(n) it UBп) состоит it:i унитарных матриц вида
( А В\
I _ _ I.
\-В А
( А П\
При птои матрица I _ _ I является унитарной в том и толь-
\-Д А)
лп п том случае, когда комплексные матрицы А и В удовлетво-
удовлетворяют уравнениям ААТ + ВЁТ=Е, ВАТ=АВТ.
Доказательство. Проверка того факта, что множество
Sp(n) является связным гладким подмногообразием, в линейном
пространстве матриц, проводится по схеме, изложенной в § 1, по-
полому здесь мы его опустим. Каждое кватернионное преобразова-
преобразование g^Sp(n) сохраняет кватернионную форму (а, Ь)'о и, следо-
следовательно, сохраняет эрмитову комплексную форму (а, Ь)'с и ко-
сосимметрическую комплексную форму (а, Ь)с. Таким образом,
кватериионный оператор g в Q" является унитарным оператором
в C2"-<-Qn.
Ht.'ik, мы получили вложение группы Sp(n) в группу UBn).
В частости, снмплектические операторы — это в точности унитар-
унитарные операторы, сохраняющие кососимметрическую форму в С2и.
Рассмотрим более подробно вложение Sp(n) в U.{2ri), Представляя
матрицу g&Sp (п) в виде g = ( ) и записывая условия ее симп-
лектичности и унитарности, получаем gIgT = I, gT = g~l, т. е. gl =
= /g, откуда
43
IA BX /О -Е\
\С D) \Е о)
Следовательно, В =—С, A = D, т. е. g=4 _ _ ). Условие уни-
{ - -У
\-В А)
тарности оператора g дает искомые уравнения на матрицы Л и Б, а
именно: ААТ + ВВТ = Е, ВАТ = АВТ. Если матрица g близка к; еди-
единичной, т. е. если
то легко проверяется, что полученные выше уравнения для А и В
означают: Z^=^ZX, Z3 = —Za, Z\ = -r-Z1( Zl = Z.%, что и требовалось
доказать.
/ 7 7 \
Итак, g — E + e\ _ _ I-f ... , где Zx—косоэрмитова, a Za—
V-2a zj
симметричная матрицы.
Эти утверждения можно получить еще и так. Рассмотрим про-
произвольный кватернионный оператор X из алгебры Ли sp(n) и за-
запишем его в виде X = A + Bj, где А и В — комплексные матрицы
порядка п, а в качестве образующих поля комплексных чисел
взяты элементы 1 и i в алгебре кватернионов. Выполненное нами
выше вычисление показывает, что при отождествлении Qn с С2п
матрица X переходит в матрицу порядка 2п вида
Накладывая на эту матрицу условие косоэрмитовости (т. е. при-
принадлежности алгебре Ли иBп)), получаем, что А — косоэрмитова,
а В — симметричная матрицы. Лемма доказана.
2.4. Связь симплектических групп с другими матричными груп-
группами.
Предложение 2. Рассмотрим стандартные вложения групп,
описанные выше: O(n)czU(n), U (n) <=:SO Bn), Sp(n)<=U Bn).
Тогда имеют место следующие соотношения:
- 1) SOBn)[\Sp(n)=U(n); здесь группы SOBn) и Sp{n) <pac-
сматриваются как подгруппы в одной группе UBn);
. 2) Sp(n, C)(]UBn)=Sp(n);
3) Sp(n, R)(]GLBn, C)=t/(n);
4) t/(n)=Sp(n, ЮПЩ2л).
Доказательство. Соотношение 2 фактически уже доказа-
доказано выше (см. лемму 6), так как симплектические операторы — это
в точности унитарные операторы, сохраняющие, кроме того, косо-
симметрическую форму в С2п. Операторы, сохраняющие кососим-
метрическую форму в С2п, образуют группу Sp(n, С). Докажем
соотношение 1.
44
Ясно, что каждая матрица g из Sp(n) имеет определитель,
•равный единице. Следовательно, условие принадлежности матри-
матрицы g пересечению SOBn)f\Sp(n) эквивалентно следующей систе-
системе равенств: ggT — E (принадлежность SOBn)); ggT=E (при-
(принадлежность UBn)), т. е. g=g; glgr = l (принадлежность
Sp(n)). Записывая матрицу g в виде I У, где А, В, С,
\С D)
D — вещественные матрицы, получаем
A = D, B = — С, АТВ + ВТА^=О, АтА + ВтВ=гЕ.
Рассмотрим матрицу A + iB и запишем условие ее унитарности:
;{A + iB) (Ar— iBT)=E. Раскрывая скобки, мы, очевидно,
получаем последние два условия из четырех приведенных выше.
Эти условия эквивалентны унитарности оператора A + iB, что и
требовалось доказать. Равенства 3 и 4 проверяются аналогичными
рассуждениями. Лемма доказана.
Изучим топологическую структуру группы Sp(n).
Предложение 3. Группы. Ли SUB) и Sp(l) изоморфны
\{в алгебраическом смысле) и обе гомеоморфны трехмерной сфере
S3. Факторгруппа группы SUB) по подгруппе Z2, состоящей из
ideyx элементов Е, —Е, изоморфна группе S0C) и гомеоморфна
трехмерному проективном;/ пространству RP3.
Доказательств). Грунпл >S"pA) действует в пространстве
'Qi:=Q как умножение на «скллмр»— кпнтсрпноп, т. е. каждое
Преобразование tf:Q-*-Q, где f><~Sp(\), имеет вид gq=qa, где
<$prrQ, aCwQ, Здесь элемент а фиксирован и полностью задает пре-
«ОрН'ШИйИКг Ц. Тик кик киптерпнонная форма {q\, <?2)'=<7i92 co-
Хрйингтси при действии преобразования g, то qiq2=q[uaq2=:
щ' I'M'Vi'/iii т. е. |я|2=*1, |а| = 1. Так как для любых кватернио-
Нон а II 1> иыполпепо тождество \а-Ь\ = \а\ ■ \Ь\, то группа Sp{l)
изоморфна группе всех кватернионов а таких, что |а| = 1. Все та-
такие кватернионы единичной длины образуют сферу 53 в R4, так
как , |а|2 = 2f=or;, где a=ro\ + rxi+r2] + rzk. Единицей группы
Sp(\) является точка 1 = A, О, О, 0). Рассмотрим описанное выше
вложение Зр(п)-»-£/Bп). При п=\ это вложение имеет вид
(I, где [р|2+|9|2=1, р и q—комплексные числа. Дру-
гимн словами, множество таких матриц образует в группе VB)
подгруппу, изоморфную $рA). В самом деле, действие кватерни-
оппого оператора g:r-+ra после отождествления Q1 с С2 прини-
принимает ипд
= (ар + $q) + $p
Отсюда следует, что матрица оператора правого сдвига на
(Р —Я\
элемент а записывается в пространстве С2 так: I _ _ I. После
р
(Р —Я\
: I _ _ I.
\Я PJ
45
I р <?\
замены q-*-—q мы получаем матрицу - - г Осталось заме-
\ — q p i
тить, что каждый кватернионный оператор geSp(l) задает изо-
метрию R4, так как он сохраняет евклидово скалярное произведе-
произведение (см. выше). Следовательно, этот оператор сохраняет форму
объема, а потому определитель преобразования равен единице,,
что и означает, что |р|2+ |^|2=1. В частности, так как (га, га) =
= (г, г), то |г|2 = гаа7= |а|2|г|2, т. е. |а|=1.
Итак, мы доказали, что группа 5рA) изоморфна группе мат-
где \р\2+ \q\z=l. В частности, группа Sp(l) го-
мебморфна стандартной трехмерной сфере. Поскольку группа
Sp(l) изоморфна трехмерной подгруппе унимрдулярных матриц в.
группе U[2), т. е. Sp(l)<^:SUB), то мы получаем, что в действи-
действительности Sp(l)=SUB), так как размерность SUB) также рав-
равна трем; В частности, мы доказали, что матрицы из группы SUB},
( Р Я\
всегда могут быть записаны в виде I _ _ ), |р12+|<?|2=1-
V—ч р)
Впрочем, этот факт легко усмотреть непосредственно из опре-
определения группы SU B), не обращаясь к анализу группы Sp(l)
(докажите!). Осталось найти связь между группой SpA) и груп-
группой SOC) собственных вращений в R3. Докажем существование
эпиморфизма f :Sp(l)-vSQC) с ядром Z2. Реализуем группу
Sp(l) как группу единичных кватернионов в пространстве Q=R4
и положим f(a)r—ara, где aeS3=Sp(l), |а|=1, r<=Q и Rer=
= 0, т. е. группа преобразований вида f(a) действует на мнимых
кватернионах, образующих гиперплоскость R3 в R4, ортогональ-
ортогональную вектору 1. Ясно,_что отображение f задает гомоморфизм, так
как f(a1a2)r = ala2ra^i1 = f(a1)f(a2)r. Преобразование f(a) перево-
переводит в себя трехмерное подпространство мнимых кватернионов и
является его изометрией, так как \ara\2 = araarq— |r|2.
Итак, f(a) является собственным ортогональным преобразова-
преобразованием, т. е. f(a)<=SOC). В силу связности сферы образ fE3) ле-
лежит именно в SOC). Найдем ядро /. Коммутирование а се всеми
мнимыми кватернионами означает, что мнимая часть а равна ну-
нулю, поэтому а=а~\ т. е. а=±1. Если ага = г при любом г, где
Rer=0, то аг=га. Так как эпиморфность отображения f очевид-
очевидна, то из Kerf= (±£)=Z2 следует 50C) =SpA)/Z2. Предложе-
Предложение доказано.
Можно доказать, что группа Sp B) изоморфна группе Spin E),
являющейся универсальным накрытием над группой SO E). На-
Напомним, что при п^З односвязная группа Spin(n), дважды на-
накрывающая группу SO(n), называется спинорной группой. Все
остальные группы Sp(n), n>2, уже не сводятся к унитарным и
ортогональным группам.
46
Можно проверить, что группа Sp(n) является максимальной-
компактной подгруппой в группе Sp(n, С). На этом основании
группа Sp(n) называется компактной формой комплексной груп-
группы Sp(n, С). Группа Sp(n) односвязна, что можно проверить ис-
исходя из точной гомотопической последовательности расслоения
Sp(n) ■sp<*-|>_>.s4"~1. Подробнее доказательство см., например,
в [53].
§ 3. Лагранжева геометрия и лагранжевы многообразия
3.1. Вещественные лагранжевы многообразия в симплектиче-
■ском линейном. пространстве. Пусть R2™— симплектическое про-
пространство, моделью которого является евклидово пространство с
симплектической структурой (,). Мы уже знакомы с понятием
л.агр_анжевых плоскостей.
Определение 1. Подмногообразие М в „сдшлектическом
пространстве R2n назыъаетсяСлагранжевым многообразие^, если
все его касательные плоскости являются лагранжевыми плоско-
плоскостями в R2". В частности, размерность лагранжева многообразия
равна п.
Важнейшим примером лагранжевых подмногообразий явля-
является так называемые торы Лиувилля (лагранжевы торы), кото-
которые возникают в так называемых вполне интегрируемых гамиль-
тоновых системах. Эти объекты появятся у нас позже. Здесь же
мы познакомимся с общими свойствами лагранжевых многооб-
многообразий.
Как мы уже знаем, симплектическая структура в R2n может
•быть задана внешней дифференциальной 2-формой (u==2dpjA^</t,
где Pi,...,pn, <?ь• • • >Яп — канонические координаты в R2n.
Лемма 1. Подмногообразие Мп в симплектическом простран-
пространстве R2n является лагранжевым в том и только в том случае, ко-
когда ограничение на него дифференциальной формы ^]=\dpt/\dqi
тождественно равно нулю.
Доказательство. Кососкалярное произведение в R2n сле-
следующим образом связано с формой ю: (а, Ь)=а(а, Ь). Отсюда
следует, что касательная плоскость изотропна тогда и только то-
тогда, когда ограничение формы тождественно равно нулю.
Рассмотрим примеры лаграижевых многообразий. Ясно, что
кнждля изотропная плоскость Пп в R2" является лагранжевым
Mi[()i'()of)|)ii:iiieM. Следующий пример особенно важен потому, что в
некотором гочмом смысле позволяет описать локальную структуру
произнолмюш ллгрпнжепа многообразия.
Окааьикюгси, е.рафик градиента гладкой функции S(qi,,..,qn)
всегда является лагранжевым многообразием. Дадим необходи-
необходимые пояснения. Пусть plt...,pn, qu...,qn — канонические сим-
плектические координаты в R2n и пусть S(qi qn) — гладкая
-функция, зависящая только от переменных qi,...,qn и определен-
определенная в некоторой области U координатной плоскости Rn(q\,...,qn).
47
Пусть рс =
dS(qi, ... , qn)
dqi
n, задает гладкое отображение
P—p(Q) области U в координатную плоскость R"(/?b... ,р„). Так
как R2" распадается в прямую сумму координатных плоскостей
R2n(p, a) = Rn(p)®Rn(<7), то в R2n можно построить график это-
„■ / aS (q) \
го отображения, рассмотрев множество М точек вида I—-—, q\
|(рис. 13). Здесь для сокращения записи мы использовали собира-,
тельные символы р и q вместо plt... ,рп и qu... ,qn. \
Рис. 13
Рис. 14
Предложение 1. Для любой гладкой функции S(q) график
' • as ()
является лагранжевым мно-
. . as (а)
p=p(q\ ее градиента р — -21
dq
q
гообразием в симплектическом пространстве R2n(p> q). Функция-
S называется при этом производящей функцией.
Доказательство. Рассмотрим в R2n стандартную 2-форму
2,dpi/\dqi и ограничим ее на подмногообразие Мп, задаваемое
, as , ^. ^ „
графиком pi — , l^i^n. В координатах <7i.---.9n получим
oqi
да.доь
dqk/\dqt =
(ввиду косой симметрии внешнего умножения). Итак, ограничение
симплектической 2-формы dp/\dq на подмногообразие М триви-
тривиально, что и требовалось доказать.
Обратно, оказывается, любое гладкое лагранжево многообра-
многообразие Ml1 в R2n можно локально представить в виде графика гради-
градиента некоторой гладкой функции S. Докажем это утверждение.
Предложение 2. Пусть Мп —произвольное гладкое ла-
лагранжево подмногообразие в симплектическом пространстве R2n.
Тогда подмногообразие Мп в окрестности каждой своей точки мо-
может быть взаимно однозначно спроектировано на некоторую ла~
48
гранжеву координатную плоскость размерности п в R2" и пред--
ставлено в виде графика градиента гладкой функции, определен-
определенной на некоторой области в этой координатной плоскости. В част-
частности, если лагранжево многообразие взаимно однозначно проек-
проектируется на координатную плоскость Rn(q), т. е. является гладким
графиком в R2n (p, q), то это многообразие в действительности за-
задается некоторой производящей функцией S(q) no формуле
р= *Ш (рис.14).
dq
Для разных точек на М локальное представление многообра-
многообразия в виде графика градиента некоторой функции будет, вообще-
говоря, различным, поскольку при изменении точки будет ме-
меняться и та координатная плоскость, проекция на которую опреде-
определяет искомую производящую функцию. Для доказательства нам
потребуется следующая алгебраическая лемма.
Лемма 2. Пусть Пп.— произвольная лагранжева плоскость в
симплектическом пространстве R2n. Тогда всегда существует та-'
кая координатная п-мерная лагранжева плоскость, которая пере-
пересекается с плоскостью Пи только в одной точке.
Замечание. Две л-мериые плоскости, пересекающиеся лишь
в одной точке, называются иногда трансверсальными.
До к n :t л те л ь ст в о. Пусть Р —лагранжева координатная
плоскость'pi /»„. Рассмотрим се пересечение с лагранжевой
плоскостью 11. В результате получим плоскость Т1' размерности k,
где О^/г^я. В линейном л-мерпом пространстве Р всегда можно-
иыбрнть такую (л — k) -мерную координатную плоскость N, кото-
ран тршк'иерсальпа плоскости Т. Предположим, что эта коорди-
натнян плоскость N порождена координатами р,;, ,..., р,-„_А. Обо--
яннчим набор индексов i\,...,in-k сокращенно через /, соответ-
соответствующий набор координат — через pi. Итак, мы имеем N(&T =
= /*, N[}T—0. Дополним координатную (л — k)-мерную коорди-
координатную плоскость ./V до л-мерной координатной лагранжевой плос-
плоскости X. Для этого рассмотрим л-мерную плоскость X, порожден-
порожденную координатами р,-„ ... , pin_k, q,\, ... , qjk, или в наших со-
сокращенных обозначениях р7, qj, где набор индексов /=(ii,....
...,in-h) является дополните^чьпым к набору индексов /—(/i,...
...,jh). Так как ни один из индексов набора / не встречается в.
наборе /, то кососкалярное произведение любых двух векторов в
плоскости X равно нулю; следовательно, X — лагранжева коорди-
координатная плоскость.
Докажем теперь, что плоскости Хп и Пп — дополнительные в
R2", т. е. что Xf|ll = 0. Так как Тс=П, то плоскость Т косоортого-
нальпа плоскости II. Так как ./VczX, то плоскость ТУ косоортого-
нальна плоскости X. Следовательно, сумма N®T косоортогональ-
ня пересечению Х[\Х\ (рис. 15). Но так как N(&T=P, то плоскость
Р косоортогональна плоскости ХПП. Но Р является лаграпжевой
плоскостью, поэтому любой вектор, косоортогональный плоскости
Р, ей принадлежит. В противном случае мы получили бы изотроп-
изотропную плоскость размерности большей, чем п, что невозможно (см.
§ 2). Следовательно, ХППс=Р. Отсюда Xf\U={XpiP)(](Uf]P)=Tf]
0^=0. Лемма доказана.
Рассмотрим теперь лагранжево многообразие М в R2" и пусть
М — произвольная точка. Через ТтМ обозначим касательную
лагранжеву плоскость к М в точке т. Рассмотрим два дополни-
дополнительных набора индексов /= (£i,...,tn-fe) и /=(/,,... ,/й) и пред-
представим пространство -R2n (р, q) в виде прямой суммы двух под-
подпространств Rn(pi, qj)®Rn(pj, qi), порожденных координатами
Pi, qj и pJt qi соответственно. Так как наборы / и / дополнитель-
дополнительны, то оба указанных выше подпространства являются лагранже-
выми плоскостями в R2n.
Л е м м а 3. Для любой лагранжевой плоскости ТтМ, касатель-
касательной к лагранжевому многообразию М, всегда существует такой
набор индексов I, что естественная проекция плоскости ТтМ на
рп
ТтМ
Рис. 15
Рис. 16
координатную лагранжеву плоскость Rn(pj, qi) (вдоль дополни-
тельной плоскости Rn(Pi, qj)) является линейным изоморфизмом.
В частности, координаты pj, qi задают локальную систему коор-
координат в некоторой окрестности точки m на многообразии М
(рис. 16).
Доказательство. Обозначим касательную плоскость ТтМ
через П. Так как П — лагранжева плоскость, то в силу леммы 2
существует такая координатная лагранжева n-мерная плоскость
X, которая трансверсальна плоскости П. При этом в обозначениях,
использованных при доказательстве леммы 2, можно представить
эту координатную плоскость X в виде Rn(pi, qj), где / и / — не-
некоторые дополнительные наборы индексов.
Рассмотрим плоскость Rn(p/, <?/), ортогональную плоскости
Rn(P/. Qj) (iH0 He косоортогональную). Рассмотрим естественную
■проекцию h всего пространства R2n (p, q) на плоскость R" (pj, qi)
вдоль дополнительной плоскости Rn(P/, qj). Мы утверждаем, что
эта проекция является искомой. В самом деле, мы должны дока-
доказать, что отображение h :II-»-Rn(pj-, qi) является линейным изо-
изоморфизмом. Так.как обе плоскости имеют размерность п, то до-
достаточно доказать, что ядро проекции h пересекается с плоскостью
П только в одной точке. Другими словами, ядро проекции h -дол-
50
жно быть трансверсально плоскости П. Но ядро проекции h со-
совпадает с плоскостью R"(pi, qj)- Следовательно, нужно убедиться?
в том, что плоскости Rn(pi, qj) и П трансверсальны. Но это усло-
условие ^выполнено в силу выбора плоскости X—Rn(pi, qj), ^порож-
^порожденной набором индексов /. Из теоремы о неявных функциях сле-
следует, что для подмногообразия М в R2n координаты pJt qi за-
задают локальную криволинейную регулярную систему координат в.
окрестности точки т^М в том и только в том случае, когда про-
проекция h: TmM-yRn(pj, qt) является изоморфизмом. Таким обра-
образом, утверждение леммы вытекает из теоремы о неявных функ-
функциях, поскольку нужное свойство h уже доказано.
Определение 2. Пусть т — произвольная точка на лагран-
жевом многообразии М в R2n. Тогда будем говорить, что коорди-
координаты pj, Ци существование которых доказано в лемме 3, задают
локальную _Kaf±22^iecKUto систему координат в окрестности точ-
точки т."
Утверждение леммы 3 можно переформулировать следующим
образом. Для любой точки т&М нам удалось найти такую от-
открытую окрестность U, в которой многообразие М можно пред-
представить в виде графика некоторого гладкого отображения f:(pj,,
qi)-*~{pi, qj). Другими словами, f отображает некоторую область
из R"(p./, qi) в область из Rn(pj, qj). Таким образом, на поверх-
поверхности М координаты р, и qj являются гладкими функциями от ко-
координат pJt qx. Запишем эту зависимость в виде Pi = Pi(Pj, 97).
4j — 4j{Pj* qi)- Открытая карта U на многообразии М, в кото-
которой локальными координатами являются координаты pj, q,, на-
называется иногда канонической картой. Таким образом, утвержде-
утверждение Леммы 3 можно переформулировать еще и так: на любом ла-
гранжевом многообразии всегда существует атлас канонических
карт. Оказывается, утверждение леммы 3 можно существенно уси-
усилить. Мы доказали пока лишь тот факт, что поверхность М в
окрестности каждой своей точки является графиком некоторого
гладкого отображения. В действительности это отображение мож-
можно задать в виде градиента некоторой гладкой функции, которая
и будет искомой производящей функцией, существование которой
утверждается в предложении 2.
Доказательство предложения 2. Рассмотрим произ-
произвольную точку пг на М и каноническую карту U с координатами
Pj, q,. Запишем 2-форму 2dpi/\dqi с учетом найденного нами
разбиения координат р, q на группы pIt qJt pJt qi. Ясно, что фор-
форма примет вид u>=dpI/\dqI — dqj/\dpj. Для того чтобы форма о»
приняла стандартный вид, когда мы вместо прежних базисных
координат q— (qh... ,qn) возьмем новый набор координат pj, qu
нужно переписать ее в виде i>-) — d{—qj)/\dpJ-Jrdpif\dqJ. Следова-
Следовательно, форма о» принимает канонический вид в координатах — qJt
Pj и pi, qt. Другими словами, нужно изменить знак у коорди-
координат qj.
Поскольку мы хотим представить поверхность М локально в
виде графика градиента некоторой функции S=S{pj, <?/), то мы
51
> „ dS " dS л
должны решить систему уравнении -*—— Pi, д = —Qj- Функ-
Функция S является решением такой системы в том и только в том
случае, когда она удовлетворяет следующему уравнению, запи-
записанному на языке дифференциальных- форм: dS = Pidqt— qjdpJt
так как dS~ ,"- dq,-\ -5—dp.j. Напомним, что употребляемые
I J
нами обозначения расшифровываются так:
Для того чтобы дифференциальное уравнение указанного вида
было разрешимо, достаточно, чтобы одномерная форма Pidq, —
— djdpj — a была бы замкнутой на карте U в многообразии М.
Проверим условие замкнутости. Ясно, что
Итак, da—to. Поскольку нас интересует разрешимость уравне-
уравнения a=dS на поверхности М в R2", то мы должны ограничить
уравнение da — ы на многообразие М. Но поскольку М лагранже-
лагранжево, то ограничение формы ы на М является тождественным нулем.
Это* означает, что в окрестности U на многообразии М форма a
замкнута, т. е. da—О. Так как мы всегда можем- считать, что
окрестность U гомеоморфна открытому я-мерному диску на М, то
замкнутость формы означает ее точность. Следовательно, в
окрестности U существует функция S = S(pj, qi) такая, что dS =
=p,dq, — qjdpj. Таким образом, уравнение dS = a разрешимо в
достаточно малой окрестности точки т и многообразие М пред-
ставимо в виде графика градиента некоторой гладкой функции S.
Предложение 2 доказано.
3.2. Лагранжевы комплексные грассмановы многообразия. Мы
видели, что лагранжевы плоскости играют важную роль при изу-
изучении лаграпжевых многообразий, естественно возникающих во
многих математических и физических задачах [5], [48], [42].
Ясно, что свойство плоскости быть лагранжевой не является
«свойством общего положения». Другими словами, для любой ла-
лагранжевой плоскости в симплектическом пространстве R2n всегда
существует линейное преобразование, задаваемое матрицей,
сколь угодно близкой к тождественной (единичной), которое пере-
переводит лагранжеву плоскость в плоскость, не являющуюся лагран-
лагранжевой. Это означает, что подходящим малым линейным шевеле-
шевелением плоскости можно всегда разрушить ее лагранжевость. Сле-
Следовательно, множество лагранжевых плоскостей имеет «меру
ноль» в множестве всех «-мерных плоскостей в пространстве R2™.
Если мы будем деформировать лагранжево подмногообразие в
R2n, то деформация общего вида разрушает, вообще говоря, его
лагранжевость. Значит, для того чтобы деформируемое многооб-
разие< оставалось лагранжевым, следует рассматривать лишь до:
52,
сгаточно узкий класс деформаций. В связи с этим полезно пред-
представлять себе структуру множества всех вещественных лагранже-
вых плоскостей в симплектическом пространстве. Обозначим это
множество через LG*. Оказывается, это топологическое про-
пространство является гладким многообразием. Обычно оно назы-
называется вещественным лагранжевым грассмановым многообразием.
Его роль в симплектической геометрии обусловлена тем простым,
но важным обстоятельством, что любое лагранжево многообразие
естественно отображается в LGn. В самом деле, если М — глад-
гладкое лагранжево многообразие в R2n, то, сопоставляя каждой точ-
точке пг из М касательную плоскость ТтМ в точке т (и перенося ее
параллельно в начало координат), мы и получаем гладкое отобра-
отображение f:M->~LG*. Эта конструкция копирует соответствующую
схему, часто использующуюся при изучении вещественных подмно-
подмногообразий в евклидовом пространстве R^. В связи с этим напом-
напомним некоторые определения.
Рассмотрим в пространстве R^ пучок ft-мерных плоскостей IP,
проходящих через начало координат. Вводя естественным образом
топологию в этом множестве, "мы получаем гладкое многообразие,
которое обозначается через G%,k и называется вещественным
фшсмановым многообразием. Тот факт, что Gu.k является мно-
многообразием, следует ил представления этого множества в виде од-
однородного пространепш SO(N)/S(O(k)xO(N — k)). В самом де-
деле, любые две Л-мерпыс плоскости u R^ можно совместить соб-
собственным ортогональным преобразованием. При этом плоскость
IP переходит в себя при преобразованиях вида [„ !;), где А —
вращение и плоскости II'1, а В — вращение в ортогональной к ней
плоскости размерности N — k. При этом det ЛВ = 1. Через
S[O(k)xO(N — k)) мы и обозначили подгруппу ортогональных
матриц вида(|? „], где detAB—l. Следовательно, G%,k гомео-
морфно множеству классов смежности группы SO(N) по подгруп-
подгруппе S(О(к) XО{N — к)).
Наряду с многообразием неориентируемых плоскостей, опи-
описанным выше, в геометрии часто рассматривается грассманово
многообразие ориентируемых k-мерных плоскостей, обозначаемое
через GNfk. Точками этого пространства являются ориентируемые
Л-мерные плоскости в RN. Ясно, что пространство G^ допускает
представление в виде однородного пространства SO{N)/SO(k)X
XSO(N — k). Сопоставляя каждой ориентируемой плоскости со-
соответствующую ей неориентируемую плоскость (т. е. просто «за-
«забывая» ориентацию на плоскости), мы получаем естественную
проекцию- многообразия G^.fe на многообразие G^j k. Ясно, что это
отображение является двулистным накрытием. Можно убедиться
в том, что многообразие Грассмана ti%,k ориентированных плос-
плоскостей односвязно, а многообразие Грассмдна !v,fe неориентиро-
55
иных плоскостей имеет фундаментальную группу, изоморфную
. ЯСНО, ЧТО G*>k = GN,N-k-
Аналогичным образом определяются комплексные грассмано-
i многообразия. Рассмотрим множество всех fe-мерных комплекс-
комплексах плоскостей, проходящих через начало координат з CN. Это
южество также естественно снабжается структурой гладкого
югообразия, допускающего представление в виде однородного
остранства G%.k = U (N)/U (k)XU (JV— k) = SU (N)/S(U (k)xUt(N~
k)). Здесь через S(U(k)U.U(N— k)) обозначена подгруппа
1триц вида (А °в\, где A<=U(k), B<=U{N — k}
По такой же схеме определяются и кватернионные грассмано-
\ многообразия, допускающие представление в виде однородных
остранств Sp(N)/Sp(k)xSp{N — k).
Напомним, что множество всех ортогональных комплексных
руктур g, где g2——Е, совпадает с однородным пространством
)Bя)/£/(«) и допускает представление в виде пересечения груп-
. SOBи) с ее алгеброй Ли soBn). Аналогичным свойством об-
обдают и комплексные грассмановы многообразия.
Лемма 4. Рассмотрим группу U(N) и ее алгебру Ли u(N)
к подмножество в пространстве матриц. Тогда пересечение
уппы с ее алгеброй, т. е. U(N)f\u(N), совпадает с несвязным
ъединением всех комплексных грассмановых многообразий, об-
зованных комплексными плоскостями всех размерностей от I
[N/2] в комплексном пространстве CN. Другими словами, U(N) f)
1 (М) — U fi%,k- При этом пересечение U(N)[)u(N) совпадает с
'.ожеством унитарных матриц g таких, что g2=—Е.
Доказательство. Пересечение группы U(N) с ее алгеброй
ггоит из матриц g таких, что gT — g~\ gT ——g, т. е. g2=—£.
ждая комплексная косоэц^/штова матрица g может быть приве-
на подходящим унитарным преобразованием а к диагоналыю-
виду, т. е. agfa-I=j Q '• J. Так как gz=— E, то (г"фаJ =
\ 'Щп1
— 1, т. е. фа=±1. Таким образом, каждое унитарное преобра-
«ание g такое, что g2=—Е, взаимно однозначно определяется
ксимальной fe-мерной инвариантной плоскостью, на которой
i преобразование равно —it. Другими словами, это число k
зно количеству собственных чисел преобразования g, равных
. Множество матриц g, у которых кратность собственного чис-
—i равна k, образует тем самым грассманово многообразие
;х fe-мерных комплексных плоскостей в пространстве CjV. Лемма
сазана.
Следует иметь в виду, что пересечение группы U(N) с ее ал-
рой Дп u(N) несвязно и отдельные компоненты связности име-
разные размерности.
Таким образом, .определение лаграижева вещественного грас-
■сманова многообразия LG* полностью аналогично приведенным
примерам классических однородных пространств.
Определим также лагранжево комплексное грассманово мно-
многообразие. Рассмотрим эрмитово пространство С2ЛГ и зададим в
нем симплектическую структуру, т. е. кососимметрическую ком-
плекснозпачную билинейную форму (а, Ь), определяющуюся в
стандартном базисе матрицей / = Ip ^|. Как мы уже знаем,
группа комплексных симплектических преобразований Sp{n, С)
может быть определена как группа инвариантности этой формы,
т. е. как группа матриц g, удовлетворяющих матричному уравне-
нию gIgT-=L Как и в вещественном случае, назовем комплексное
подпространство П" в С2п лагранжевой плоскостью, если ее раз-
размерность равна п и ограничение формы (а, Ь) на эту плоскость
тождественно равно нулю, т. е. кососкалярное произведение лю-
любых двух векторов из П" равно нулю. Совокупность всех лагран-
жевых плоскостей, проходящих через начало координат в С2п,
обозначим через LGn и назовем лагранжевым комплексным
грассмановым многообразием. Как мы вскоре увидим, это множе-
множество действительно является гладким многообразием. Оба много-
многообразия Щ* и IXh\ допускают представление в виде однородных ■
пространств. Рассмотрим сначала комплексный случай.
Легко проверить, что любое комплексное симплектическое пре-
преобразование переводит лагранжеву плоскость снова в лагранже-
ву. Оказывается, комплексная симплектическая группа транзитив-
на на множестве всех комплексных лагранжевых плоскостей.
Предложение 3. Любые две комплексные лагранжевы
плоскости могут быть совмещены друг с другом при помощи под-
подходящего симплектического преобразования.
Доказательство. В качестве примера, лагранжевой плос-
плоскости возьмем координатную «-мерную изотропную плоскость О,
порожденную первыми « координатами ги...,гп. Докажем, что
"для любой лагранжевой плоскости П в С2п существует симплекти-
симплектическое преобразование g такое, что оно переводит С" в П, т. е.
n=gO. Фиксируем в С2п стандартный базис el,...,e2n; тогда
получим, что плоскость С" натянута на первые п векторов этого
базиса. Так как П является комплексным n-мерным подпростран-
подпространством в С", то в П всегда можно выбрать ортонормированный
комплексный базис из векторов аи...,ап. Разложим эти векторы
по базису еи...,егх, т. е. ak = ^=1 akpep + ^=1 bkpen+P. Выписывая
координаты векторов аи...,а„ относительно базиса еи...,е2п,
мы получаем прямоугольную комплексную матрицу X из п строк
и 2п столбцов вида (Л, 5), где A = (akp), B= (bkp) —матрицы
порядка п. Построим теперь матрицу порядка 2я, положив по
определению g— I ). Оказывается, матрицы Л и В не
\ — В AJ
могут быть произвольны. Они связаны простыми соотношениями.
55
Лемма 5. Матрицы А и В, образующие матрицу g, удовле-
>пяют уравнению ААт+ ВБ=Е.
Доказательство. Векторы а.\,...,ап образуют ортонорми-
ванный базис в комплексной плоскости П, поэтому скалярный
здрат каждого из них равен единице, а попарные их произве-
произведя (относительно эрмитовой формы) равны нулю. Очевидно,
i условия в точности эквивалентны уравнению АА + ВВТ = Е.
Лемма 6. Матрицы"А и В, образующие матрицу g, удовлет-
ыют уравнению АВТ = ВАТ. (
Доказательство. Плоскость П является лагранжевой
оскостью, что накладывает дополнительные ограничения на
трицы А и В. Лагранжевость плоскости П означает, что по-
рные кососкалярные произведения всех векторов баз«са ей,..*
,ап тождественно равны нулю. Следовательно, мы должны за-
задать равенство нулю попарных произведений векторов относи-
пьно кососимметрической формы, задаваемой матрицей {Я, £),
но, что это условие принимает вид Х1Хт-= О, где Х=
(А, В). Отсюда (А,В)(°Р ~Е) (j.TT) = 0, что эквивалентна
авнению АВТ = ВАТ. Лемма доказана.
Доказательство предложения 3. Из условия ортб-
1альности базиса.аи...,а„ в плоскости П мы получили соотно-
ние ААТ + ВВ —Е, а из условия лагранжевости плоскости П:
отношение АВТ — ВАТ. Оказывается, отсюда уже вытекает, что
трица ё—\ — — ) является комплексной симплектической.
самом деле, мы должны проверить выполнение тождества g
?г=/. Подставляя сюда явную формулу для g и используя
лмы 5 и 6, получаем
ВТ \ВАт—АВт) \Е О
> и требовалось доказать.
В частнрсти, любая лагранжева плоскость может быть пред-
влена в виде gCn, где g<^Sp(n, С) и С" — координатная ла-
шжева плоскость, натянутая на первую половину базиса.
Построим естественное отображение f:Sp(ii, C)->LGnc, no-
кив f(g)=gCn. Предлож.елие 3 означает, что f является*Ьтоб-
кением «на». Пусть И—подгруппа симплвктической группы,
тоящая из всех преобразований, переводящих в себя лагранже-
плоскость Cn = O(ei,...,е„).
Предложение 4. Лагранжево комплексное грасснаново
вообразив LGn допускает представление в виде однородного
'странства Sp(n, С)/Я, где стационарная подгруппа Н состоит
натриц вида "g= № Л-м)' ^ 'А<=<Щп,С) и АВТ=ВАТ.
- Достаточно найти стационарную подгруппу Н, т. е. подгруппу
симплектических преобразований, переводящих в себя плоскость
О(£],-•• |£п). Симплектическое преобразование можно предста-
представить в виде ё~[р о)> где gIgT — L Следовательно, матрицы
А, В, С, D удовлетворяют соотношениям ВАТ = АВТ, ВСТ—ADT' =
= —Е, DCT — CDT. Накладывая на g условие инвариантности
плоскости Cn(ei,...,en), получаем С=0. Отсюда ВАТ = АВТ и
ADT—E. В качестве матрицы А можно брать произвольную невы-
невырожденную комплексную матрицу. Предложение доказано.
Наряду с представлением, описанным в предложении 4, мно-
многообразие LGn допускает и другое представление в виде однород-
однородного пространства.
Предложение 5. Лагранжево комплексное грассманово
многообразие LGn диффеоморфно однородному пространству
Sp(n)/U(n), где группа U(n) вложена в компактную группу
Sp(n) как подгруппа матриц вида („ /»_1чГ], Л е У (я).
Доказательство. Пусть П — произвольная комплексная
лагранжева плоскость. Выше было доказано, что П можно пред-
представить в виде Il=gCn, где g — комплексное симплектическое
преобразование, ge?.Sp(n, С). В действительности мы доказали
более сильное утверждение, а именно: можно всегда считать, что
преобразование ц но только симплектическое, по и унитарное,
т. e..geUBn). В самом деле, из лемм 5 и G следует, что преобра-
преобразование g допускает представление в виде! _ _ J, где АВТ — ВАТ,
\ — В А /
ААТ -\- ВВТ ---£. Но эти два условия эквивалентны унитарно-
унитарности матрицы g, так как унитарность матрицы g записывается
/ А В\ 1АТ —Вт\ (Е 0\ ^
уравнением I 2 _ I _r = I ■ Очевидно, что эти
две системы уравнений совпадают. В силу предложения 2 из
п. 2.4 получаем, что совокупность таких преобразований обра-
образует компактную группу Sp(n), так как Sp{n, C)f]UBn)=Sp(n).
Таким образом, компактная симплектическая группа транзитивна
на множестве всех лагранжевых комплексных плоскостей.
Осталось найти стационарную подгруппу, т. е. подгруппу, тех
преобразований, которые переводят в себя плоскость Cn(ei,...
,..,е„). В силу предложения 4 достаточно вычислить пересечение
Hf\UBn). Так как матрицы из подгруппы Я имеют вид
'& — [ п< л—\\т ). т0 условие унитарности означает ggT = E, откуда
\ и v1 ) /
получаем В = 0. Предложение доказано.
3.3. Лагранжевы вещественные грассмановы многообразия.
В вещественном случае многообразие LG* также можно представ
вить в виде однородного пространства. При этом можно было бы
повторить вычисления предыдущего пункта. Но мы сократим рас-
57
рдении, используя полученную информацию о структуре много-
)азия LGn •
Предложение 6. Лагранжево вещественное грассманово
эгообразие LGn диффеоморфно однородному пространству
пIО(п), где группа О(п) естественно вложена в группу U (га)
с подгруппа вещественных матриц.
Для доказательства нам потребуется установить естественную
[зь между комплексными и вещественными лагранжевыми
эскостями. Рассмотрим в С2п вещественное 2я-мерное подпро-
•анство R2n, порожденное линейными комбинациями базисных
сторов е\,...,е2п с вещественными коэффициентами. Ясно, что
1 является «вещественной частью» С2п. Ограничение формы
) с С2п на подпространство R2n задает на нем кососимметриче-
гю вещественнозначную форму, которую мы обозначим для
эстоты тем же символом. Ясно, что R2n является симплектиче-
ш пространством с формой (,). Рассмотрим в С2™ операцию
мплексного-сопряжения, т. е. переводящую вектор a=2fc=iflA
зектор a = 2f=i afeefc. Ясно, что это отображение о: а-+а яв-
гтся антикомплексной инволюцией, т. е. cr2=id (тождественное
гобразование) и a(Xa)=ho(a). При этом подпространство R2"
:тоит в точности из всех неподвижных точек этой инволюции,
е. aR2"=R2n.
Лемма 7. Операция комплексного сопряжения а: С2п->С2г>
оеводит любую лагранжеву комплексную плоскость снова в ла-
гнжеву плоскость.
Доказательство. Пусть П — произвольная лагранжева
эскость. Тогда для любых двух векторов а, &еП имеем (а, Ь) — >
0. В то же время (ста, аЪ) = (а, Б) = (а, Ь)=0. Таким образом,
эскость all также лагранжева.
Определение 3. Лагранжева плоскость П в С2п называется
явственной лагранжевой плоскостью, если она инвариантна от-
•.ительно операции комплексного сопряжения.
Лемма 8. Пусть П — произвольная вещественная лагранжева
плоскость в С2". Тогда
Re С
2n
Рис. 17
1) nnR2"=n<T, где через
Па обозначено подпространст-
подпространство неподвижных векторов пре-
преобразования а;
2) плоскость nflR2™ являет-
является лагранжевой (веществен-
(вещественной) плоскостью в веществен-
вещественном симплектическом прост-
пространстве R2"= (C2n)a =ReC2n;
пг. е. П = ИеПф1тП (рис. 17)'.
Доказательство. Пер-
Первый пункт следует из того, что
подпространство R2" в С2" состоит в точности из неподвижных век
торов преобразования а. Далее, так как плоскость П изотропна в
С2", то любое его подпространство также изотропно, поэтому для
доказательства утверждения 2 достаточно проверить, что
dim (nnR2n)=«. Для этого нам потребуется сначала доказать
п. 3. .. .
Рассмотрим более подробно действие антикомплексной инво-
инволюции а в С2я. Если aena=nnR2n, то ш^Па, так как ia=ia=
=—ia. Следовательно, Па(\Ша=0. В то же время для любого
вектора оеП можно однозначно определить векторы х — — (а +
+ а)еП°, i/ = —(a-a)e№. Ясно, что a=x+iy, где х, уеП".
Таким образом, мы представили плоскость П в виде прямой сум-
суммы Па©Щст, что и доказывает п. 3. Поскольку умножение на чис-
число i определяет обратимое линейное преобразование С2", то
dimRn^ + dimRiTI01, откуда dimRn = 2 dimRna = 2штсП = 2я. Таким
образом, dimcn = /t. Лемма доказана.
Таким образом, существует взаимно однозначное соответствие
между вещественными лагранжевыми плоскостями (комплексной
размерности п) в пространстве С2п и лагранжевыми (веществен-
(вещественными) плоскостями вещественной размерности п в пространстве
R2". Следует обратить нннманне на несколько различное употреб-
употребление здесь термина «нещестиенный». Особенно наглядно это раз-
различие видно на рис. 17, где «настоящая вещественная» плоскость
до в R2n определяет плоскость ПаФШ°, инвариантную относитель-
относительно сопряжения a: C2n->C2n. Ясно, что вещественная плоскость
Пс0Шп в С2" отнюдь не содержится в множестве неподвижных
точек о. Другими словами, мы доказали, что каждая веществен-
вещественная лагранжева плоскость П в С2п получается комплексификацией
вещественной лагранжевой плоскости Пст, лежащей в R2nc:C2n.
Лемма 8 важна для установления соответствия между вещест-
вещественным и комплексным лагранжевыми грассмановыми многообра-
многообразиями.
Доказательство предложения 6. В лемме 8 мы фак-
фактически доказали, что вещественное лагранжево грассманово мно-
многообразие LG* диффеоморфно множеству Pfn всех веществен-
вещественных лаг'ранжевых плоскостей (комплексной размерности п) в С2™.
Ясно, что Рта LGn . Рассмотрим в С2п стандартное действие ор-
ортогональной группы ОBп). Напомним, что эта группа вложена в
группу UBп) как подгруппа вещественных матриц. Рассмотрим
в С2" стандартную лагранжеву вещественную плоскость (С2п)а=
= R2". Пусть /: Sp (п) -*• LGn —естественное отображение, по-
построенное нами при доказательстве предложения 4 и сопостав-
сопоставляющее каждому симплектическому преобразованию g^.Sp(n)
плоскость gCn~, являющуюся образом стандартной лагранжевой
плоскости С"(еь... ,еп) в С2п. Так как / — отображение «на», то
Р'2п содержится в образе f. Рассмотрим в Sp(n) подгруппу орто-
• 59
ильных преобразований в С2п, т. е. пересечение G=Sp(n)f|
>Bгс). Здесь ОBп)—группа ортогональных преобразований в
зисе е\,...,в2П. Мы утверждаем, что /(G) — P?n. Это следует из
го, что группа ОBп) транзитивна на множестве всех 2«-мерных
ад R) вещественных плоскостей в С2п. Значит, Р*п ;= G/H, где
-стационарная подгруппа, т. е. подгруппа преобразований, пе-
водящих в себя какую-то фиксированную вещественную лагран-
:ву плоскость. Мы утверждаем, что G = U(n). Пусть g— вещест-
нное симплектическое преобразование из G, т. е. g^Sp(n) и
= ОBп). Симилектичность g означает, 4roglgr = /. Так как ge
ОBл), то gT = g~i. Отсюда следует, что gl = Ig. Поэтому каж-
е преобразование geG задает ортогональное преобразование
щественного пространства R2n, коммутирующее с преобразова-
преобразовали /. Но, как мы знаем, преобразование / позволяет определить
R2n комплексную структуру; при этом операторы, коммутирую-
ие с /, оказываются комплексными. Следовательно, каждое пре-
разование g^G оказывается унитарным преобразованием из
(п). Таким образом, GcU(n).
Верно и обратное. Пусть geU (п) -^ произвольное унитарное
>еобразование R2", т. е. оператор, коммутирующий с /. Тогда
1лучаем, что g^0Bn) и gl — Ig. Отсюда gIgT — I, что и озна-
ет симплектичность преобразования. Тем самым G = U(n),
гталось найти преобразования из U(n), переводящие в себя ка-
'ю-то фиксированную вещественную лагранжеву плоскость. Ясно,
о вещественные унитарные преобразования из группы U (п) об-
обдуют группу 0(п). Предложение доказано.
Как и в случае вещественных грассмановых многообразий, на-
ду с многообразием LGn рассматриваются лагранжевы вещест-
нные грассмановы многообразия LG^, состоящие из ориентиро-
нных лагранжевых плоскостей. Ясно, что имеется двулистное
крытие LGn -*■ LGa . Общая теория лаграпжевых многообразий
строена в работах В. И. Арнольда и В. П. Маслова.
ГЛАВА 2
СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ГЛАДКИХ МНОГООБРАЗИЯХ.
ИНТЕГРИРУЕМЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
ГАМИЛЬТОНОВЫ УРАВНЕНИЯ
§ 1. Симплектические многообразия
1.1. Симплектическая структура на гладком многообразии. Вы-
Выше мы ввели фактически симплектическую линейную структуру
в касательном пространстве ТхМ2п к четномерному гладкому мно-
многообразию. В некоторых случаях на всем многообразии М2п можно
задать симплектическую структуру, гладко зависящую от точки*
Другими словами, может случиться, что на М2п определено глад-
гладкое косодимметрическое тензорное поле со;/ второго ранга, невы-
невырожденное в каждой точке многообразия М и удовлетворяющее
некоторому условию «замкнутости». В этом случае М называется
симплвктичсским многообразием. Можно показать, что далеко не
на каждом чстпоморном гладком многообразии можно задать та-
такую структуру.
Определение 1. Гладкое четшшерное многообразие М2п
называется симплектическим] если на нем задана внешняя диффе-
дифференциальная 2-форма (т. е. степени два) со = V a>ijdxif\dxj, об-
'</
ладающая следующими свойствами:
1) Эта форма невырождена, т. е. матрица ее коэффициентов.
п{х) = (со;/ (х)) невырождена в каждой точке многообразия.
2) Эта форма замкнута, т. е. ее внешний дифференциал раве»
нулю: ёау^О. Такая форма называется симплектической структу-
структурой на М.
Здесь хи. ..,хчп— локальные регулярные координаты на М2п..
Такая 2-форма, очевидно, определяет в каждой точке х^М ли-
линейную симплектическую структуру <а(а, Ь)—(а, Ъ) ^Заща^Ь/, где
а, Ь^ТхМ. Для любой фиксированной точки х форма со опреде-
определяет линейную симплектическую структуру в ТХМ.
Напомним, что с каждой точкой х^М естественно связано не
только касательное пространство ТХМ, но и кокасательное прост-
пространство ТХ*М, сопряженное к ТХМ. Пространство ТХ*М состоит из
всех ковекторов, т. е. линейных форм (линейных функционалов)
на касательном пространстве. Вообще говоря, в случае произволь-
произвольного гладкого многообразия линейные пространства ТХМ и ТХ*М
нельзя отождествить так, чтобы это отождествление было инва-
инвариантно относительно замен координат, т. е. чтобы оно носило-
тензорный характер. Однако если на многообразии задано, на-
пример, невырожденное тензорное поле второго ранга qif, то такое
отождествление можно сделать. Для этого зададим отображение
.q : ТхМ-*-Тх*М, положив (q{a)){ = 2jU Qiflh гДе а== (аь • • • - а«)<=
^ТХМ. Так как матрица (с/,-,) обратима, то можно задать обрат-
обратное линейное отображение. Следовательно, q задает изоморфизм
между Тх и Тх*, инвариантный при заменах координат.
Операция канонического отождествления касательного и кока-
кокасательного пространств особенно важна в случае, когда qn — gn
задает риманову метрику кг. М, или в случае, когда qij = <Hij задает
на М симплектическую структуру. Рассмотрим на М гладкую
функцию f(x). Ее градиент gradf(x) является в каждой точке х
ковектором, т. е. элементом пространства ТХ*М. Ецли многообра-
многообразие М риманово, то, используя отождествление касательного и
кокасательного пространств при помощи метрики gn, можно рас-
рассматривать градиент функции как векторное поле на М, которое
обозначим для простоты тем же символом grad/(x). Если же
М — симплектическое многообразие, то при отождествлении ка-
карательного и кокасательного пространств при помощи симплекти-
ческой структуры со ковекторное поле gradf превращается в век-
векторное поле, которое мы обозначим через sgrad f и которое, ко-
конечно,'отличается от векторного поля gradf.
Ясно, что векторное поле grad/ однозначно определяется ра-
равенством (v, grad/) = u(f), где v пробегает все векторные поля
на M,'v(f) — производная функции / вдоль поля v, а (,} — ска-
скалярное произведение, соответствующее римановой метрике.
Определение 2. Пусть / — гладкая функция на М2п и « —
^симпд^ктическая структура. Кососимметрическим градиентом
"'sgrad / функции f (косым градиентом) называется гладкое вектор-
~~«©е~Поле на М, однозначно определяемое соотношением со (и,
sgrad/) =v(f), где v пробегает множество всех гладких векторных
полей на М, a v(f) — значение поля v на функции / (т. е. произ-
производная функции f по направлению поля и).
Видно, что определение sgrad/ фактически копирует определе-
определение grad/. Отличие заключается .в том, что вместо симметричного
тензора gn рассматривается кососимметрический тензор <лц.
Как мы отмечали, риманова метрика всегда может быть при-
приведена в одной точке к каноническому диагональному виду б,-/ вы-
выбором подходящих локальных координат на многообразии. Точно
так же и симплектическая структура (со,-/) может быть всегда
.приведена в одной точке к каноническому виду ( р п)" ^Ри
доказательстве этого мы опираемся на сведения из алгебры, изло-
изложенные в гл. 1. Таким образом, в этом отношении риманова и
■симплектическая структуры похожи.
Однако при переходе к рассмотрению не одной изолированной
точки (и отдельного касательного пространства), а целой откры-
открытой окрестности данной точки сразу же обнаруживается карди-
кардинальное различие между риманавой метрикой и симплектической
структурой.
■Ы
Хорошо известно, что риманова метрика в общем случае не
приводится локальной заменой координат к диагональному виду-
сразу в целой окрестности точки. Этому может воспрепятствовать
отличие от нуля тензора кривизны Римана. А именно если в дан-
данной точке отлична от нуля хотя бы одна его компонента, то ни-
никакими локальными заменами координат нельзя привести метрику
к диагональному (единичному) виду сразу во всех точках любой,
сколь угодно малой открытой окрестности данной точки.
Симплектическая структура ведет себя совсем по-иному. Ока-
Оказывается, подходящей заменой координат она всегда может быть
/ О F\
приведена к каноническому виду р п сразу во всех точ-
ках некоторой (быть может малой) окрестности любой точки на
симплектическом многообразии. Этот факт составляет содержание
известной теоремы Дарбу, аналога которой (в указанном смысле)
нет в римановой геометрии.
Теорема 1 (Дарбу). Пусть со,-,- — симплектическая струк-
структура на М2п. Тогда для любой точки хеМ всегда существует ок-
окрестность с локальными регулярными координатами Р\,...,рп,
qi,...,qn такими, что в них форма со записывается в простейшем
каноническом виде Tdpi/\dqit т. е. в каждой точке этой окрестное
сти матрица (t<>,,) имеет вид ( р ~i).
О и jn' дс л о и и I1 '.I. Локальные координаты р\,...,рп, q\,...,qn
на симплектическом многообразии, в которых форма со записыва-
записывается K.iионическим образом, называются симплектическими.
Итак, для каждой точки можно указать открытуит^окрестность
с симилектическнмп координатами. Покрывая многообразие та-
такими окрестностями, мы получаем симплектический атлас. Дока-
Доказательство теоремы Дарбу мы здесь опускаем.
Пусть в окрестности некоторой точки з-адана симплектическая
система координат. Как запишется в них векторное поле sgrad/?
Так как матрица формы имеет вид [ F о) и так как гРа"
/ df df \ , ,
диент имеет вид ——, ... ,—— I—gradf, то косой градиент
\ dpi dqn-J
записывается так ' .
, / df " df df df
К ' \ dqL ' '' ' ' dqn dpt' dpn
Пример симплектического многообразия ^""евклидово простран-
пространство К2"(р\,... ,q,i), на котором задана невырожденная замкнутая
2-форма n) = ^dpi/\dqi. Другой пример — гладкие двумерные ори-
ориентируемые римаповы многообразия. Симплектическая структура
задается здесь 2-формой риман'ова объема (площади). Более об-
общий пример: кокасательное расслоение Т*Мп произвольного глад-
гладкого многообразия Мп. Это — 2л-мер'ное многообразие, на кото-
котором имеется естественно определенная замкнутая и невырожден-
невырожденная 2-форма.
3 А. Т. Фоменко 65
1.2. Гамильтоновы, локально гамильтоновы векторные поля и
скобка Пуассона. Обозначим через V(M) бесконечномерное ли*
нейное пространство всех гладких векторных полей на многообра-
многообразии М. Если М2п — симплектическое многообразие, то в V(М)
выделяется' линейное подпространство Н\0С(М) векторных полей"
специального вида, называемых локально гамильтоновыми поля-
полями, а в Н\ис(М) в свою очередь содержится еще одно линейное
подпространство Н(М), состоящее из так называемых гамильто-
новых полей. Итак, 1/(Л1)гэЯ!ос(Ж)^эЯ(М) (рис. 18).
Рис. 18
Рис. 19
Определение 4.. Гладкое .векторное поле v на симплектич£=_
ском многообразии М, имеющее вид u = sgrad/:, напвается £га;...
мильтоновым на М, если гладкая функция F определена на всем
■многообразии. При этом функция /; называется гамильтонианом.
Итак, гамильтоновы поля — это в некотором смысле аналоги--
градиеитиых (или потенциальных) полей y = grad/, играющих
важную роль в механике и геометрии. Не менее фундаментальную-
роль играют гамильтоновы поля в симплектической геометрии и
механике. Отметим, что в современной геометрии и механике
встречаются случаи, когда гамильтониан, не является однозначной
функцией на многообразии (многозначен). См., например, работу
С. П. Новикова [104]. Поэтому следующее определение является
■содержательным.
Определение о. Гладкое векторное поле v на симплектлче-
•ском многообразии называется локально гамильтоновым, если для
любой точки х^М существуют такая открытая окрестность U(х)
точки х и такая -гладкая функция Fu, определенная на этой окре-
окрестности, что y = sgrad Fu, т. е. поле v гамильтоново в окрестности
U с локальным гамильтонианом Fu.
Ясно, что локально гамильтоновы поля образуют линейное под-
подпространство НЬс(М) в V(M) и что Hinc(M)^H(M), так как
любое гамильтоново поле, очевидно, — локально гамильтоново.
Обратное неверно. Это означает, что существуют поля, допус-
допускающие в окрестности каждой точки представление в виде
sgrad/-'у, однако не допускающие единого представления в виде
o = sgradf, где F — однозначная функция, определенная на всем
М. Другими словами, локальные гамильтонианы, определенные на
66
отдельных окрестностях, нельзя «сшить» в одну гладкую однознач-
однозначную функцию, заданную на всем многообразии.
Простейший пример: рассмотрим на евклидовой плоскости с
выброшенным началом координат векторное поле
v,
где х, у — декартовы координаты. Это поле является полем ско-
скоростей потока жидкости, вытекающего из начала координат по
радиальным лучам (рис. 19). Легко видеть, что оно локально
гамильтоново на симплектическом многообразии R2\0, снаб-
снабженном 2-формой dx/\dy. В качестве локального гамильто-
гамильтониана Fu достаточно взять функцию полярного угла ф =arctg-;—,
являющуюся гладкой функцией в достаточно малой окрестности
любой точки {х, у)^@,0) и определенную с точностью до посто-
постоянной. Ее обычный градиент имеет вид
к* 4
Тик кик еимилсктичеекаи структура dx/\dy на R2\0 выбрана
Ними кйшшичвской, то иектор s^iailf получается из вектора
grad/--(/j,, /„) тик: sgrnd/- (—fu, /,). Отсюда
Однпко .что поле не является глобально гамильтоновым, так
Кйк полярный угол ср(х, у) — многозначная функция на плоскос-
плоскости без точки и указанные выше локальные гамильтонианы нельзя
«сшить» в единую гладкую однозначную функцию. В данном слу-
случае этот эффект коренится в неодносвязности многообразия
R2\0 (рис. 20).
Рис. 20
Рис. 21
Вернемся к гамильтоновым полям. Они могут быть также опи-
описаны на языке порожденных ими однопараметрических групп диф-
диффеоморфизмов многообразия. Пусть v — гамильтоново поле и
<9" — одномерная группа диффеоморфизмов М, представленная
на М сдвигами вдоль интегральных траекторий поля у. Это озна-
означает, что группа ®v состоит из гладких преобразований gt, дей-
действующих так: gt(x)=y, где х = у@), y = y{t), и у — интеграль-
интегральная кривая поля v, проходящая через точку х при < = 0. Другими
словами, диффеоморфизм gt сдвигает каждую точку х на время
/ вдоль траектории \{t) (рис. 21). Так как 2-форма со, задающая
симплектическую структуру, переводится диффеоморфизмом gt в
некоторую новую форму gt*(o (определяемую так: (gt*®) {x) =
= <>}{gt(x))), то корректно определена производная day/dt формы
diti(x) d / * ч, »„
w вдоль векторного поля v, т. е. —L-i- -- (g,^)\t=o- Можно
dt dt '
проверить, что симплектическая структура инвариантна относи-
относительно группы диффеоморфизмов, порожденной гамильтоновым
полем "у. Мы докажем здесь более общее утверждение.
Теорема 2. Гладкое векторное поле v на симплектическом
многообразии с симплектической структурой со является локально-
гамильтоновым тогда и только тогда, когда оно сохраняет сим-
симплектическую структуру, т. е. когда производная формы со по нап-
направлению поля v тождественно равна нулю, или, другими слова-
словами, когда g(w==co при всех t.
Доказательство. В силу теоремы Дарбу (см. теорему 1)
достаточно доказать это утверждение лишь для случая, когда М
является простейшим симплектическим многообразием R2" с кано-
канонической структурой a = 1.dpi/\dqi. Пусть форма и сохраняется
однопараметрической группой gt, т.-е. a>(y(t)) — O, где y(t) —
dt
интегральные траектории поля v=(Xi, Yi). Имеем
] + dPiAdYi = V I-^L + ^ ) dpkAdqt +
fJ \ dPk dqi )
\- У (fL_.%*.) dptAdPk--0.
*J \ dpk [dpi )
Отсюда следует, что равны нулю коэффициенты перед незави-
независимыми мономами, т. е.
dXt _ dYk "dXj _ dXk dYj __ dYk
dPk . дЯс ' dqk dqi ' dpk dpi ' . ,
Рассмотрим дифференциальную форму <x — 'Z — Yidpi+Xidql. Она
замкнута. В самом деле,
da „ 2 ^- dqkAdPi- -^p-dqkAdPl + ^- dpkAdqt +
dpk dqk dpk
68
Что обнаруживается после приведения подобных членов и исполь-
использования полученных выше условий на частные производные ком-
компонент векторного поля и.
Замкнутость формы а на R2" означает ее точность (в силу так
называемой леммы Пуанкаре), т. е. существует гладкая функция
Н такая, что a = dH. Отсюда получаем, что
ИЛИ
II
a = 2^-dpt + -^-dqi= 2-Ytdpt + Xtdqt,
dpi дщ
V _ дН Y _ дН
dpi dpi
т. е. y = sgrad#, что и требовалось доказать. Обратное утвержде-
утверждение получается повторением предыдущих рассуждений в обрат-
обратном порядке. Теорема доказана.
В случае двумерного риманова многообразия с римановой мет-
метрикой М2 и с формой римановой площади со = У (let [gii)dx/\dy
в качертве симплектической структуры условие сохранения формы
«и группой &а диффеоморфизмов gt эквивалентно сохранению пло-
тадей областей на поверхности М2 при сдвигах этих областей
шффеоморфизмами gt. Итак, сдвиги вдоль интегральных траек-
и||)цй гамильтонова поля им двумерном симплектическом много-
О|)азии сохраняют площади областей.
Аналогичное утверждение порно и в многомерном случае. Пусть
о» — симплектпчеекаи структура на многообразии М2п. Тогда п-я
инешння степень 2-фо|)МЫ м может' рассматриваться как форма
piiMUttiMin об'Ы'МН II.I M'in, так как форма т = (оЛ—Л<* (« Раз)
iip»'nfipii;iyeri'M и точности так же, как преобразуется форма ри-
м а нона объема (домножается на определитель матрицы Якоби
(амеиы координат). Так как локально гамильтоново поле сохра-
сохраняет форму и, то оно же сохраняет и внешнюю 2л-форму т, т. е.
сохраняет объемы областей на многообразии.
В случае двумерного симплектического. многообразия условие
локальной гамильтоновости поля допускает другую наглядную
геометрическую интерпретацию. Пусть g,,- — риманова метрика на
М2 и co = VrdeT(g7/)" dx /\dy — форма римановой площади.
В силу теоремы Дарбу всегда можно выбрать такие локальные
координаты р и <7,' чт0 в них форма запишется каноническим об-
образом dp/\dq. Здесь р и ? — некоторые функции от х и у (и на-
наоборот).. Пусть v — локально гамильтоново поле v=(P(x, у),
Q(x, У.)), где Р и Q — координаты (компоненты) этого поля в
системе координат р и q. Будем трактовать пбле v как поле ско-
скоростей потока жидкости постоянной плотности (равной единице)
на поверхности М2. Изучим изменение массы жидкости, находя-
находящейся в бесконечно малом прямоугольнике на поверхности при
его сдвиге вдоль интегральных траекторий поля. Ясно, что масса
этой жидкости равна площади прямоугольника. Отсюда следует,
что Масса жидкости, заключенной в "ограниченной (достаточно
69
"■ ■'' t
малой) области на М2, равна площади области. Пусть D — огра-
ограниченная область с кусочно гладкой границей в М2 и D(t) — об-
область, полученная из области D ее сдвигом на время t вдоль ин-
интегральных траекторий поля (рис. 22).
Другими словами, D(t) =
—gt(D), т. е. D(t) является об-
образом области D при диффеомор- .""
физме gt: M-rM. Обозначим через
дР
dp
—
dq
дивергенцию поля v и пусть5 (t) —
площадь области D(t), т. е. масса
заключенной в ней жидкости.
Рис. 22
Рис. 23
Предложение 1. Для любой ограниченной области D(t)
на поверхности М2 выполнено соотношение
Поток жидкости называется несжимаемым, если изменение
массы жидкости в любой области равно нулю. Из предложения 1
вытекает следующее полезное утверждение.
. Следствие 1. Поток v жидкости постоянной плотности на
поверхности М2 является несжимаемым тогда и только тогда, ког-
когда div(y) =0.
Доказательство предложения 1. Достаточно дока-
доказать утверждение для области D, имеющей вид бесконечно малого
прямоугольника. Хорошо известно (см., например; [53]), что из-
изменение его площади при сдвиге измеряется определителем мат-
матрицы Якоби преобразования. Итак, достаточно вычислить указан-
указанный определитель для бесконечно малого преобразования \p,q)-*-
-+(р + еР(р, q), q + zQ(p, <?)), где 8 — бесконечно малый пара-
параметр. Ясно, что матрица Якоби имеет вид
70
. , дР
1 + е—-
др.
— i - ь
dp
Ее определитель (с точностью до е2) имеет вид 1 -f e div (и) =
, , / дР . dQ \ ■ .
— l-j-Ё 1 . 1аким образом, искажение площади беско-
\ dp dq I
нечно малой области измеряется дивергенцией поля, что и дока-
доказывает предложение 1.
Итак, в случае двумерного симплектического многообразия ЛО'
кально гамильтоновы векторные поля — это в точности потоки не-
несжимаемой жидкости, т. е. поля с нулевой дивергенцией. Иными
■словами, условие лекальной гамильтоновости поля v в двумерном
случае эквивалентно равенству div(y)=0.
Выше мы привели пример локально гамильтонава векторного
поля на R2\0, не являющегося гамильтоновым. Здесь симплекти-
ческое многообразие было некомпактным. Однако примеры такого
рода можно строить и на компактных замкнутых (т. е. не имею-
имеющих края) многообразиях. Возьмем, например, обычный плоский
тор Г', снабженный евклидовой метрикой. Тогда 2-форма площади
лпппшетси в декартовых координатах х, у (па торе) как dx/\dy,
т. v. будет канонической.
Рассмотрим на торе векторное поле и=- A, 0), задающееся рав-
равномерным движением жидкости идоль его плрлллелей (рис. 23).
Интегральными траекториями поля являются параллели тора. До-
КВЖем, чти sto иоле негамнльтоцово на всем торе (хотя и локаль-
локально гйМНЛЬТонннн, что очоишдпо). В самом деле, допустим сущест-
RiiHNinii* глпдкчП одио.-шачиой функции f(x,'y), определенной на
торс, т. с. дноикопориодической на плоскости R2(x, у), а именно:
f(x[m, у | n)=f(x, у) для любых целых m, n и такой, что
o-sgracl/, т. е. A, 0) = (—fy, fx). Тогда f* = 0, fy= — 1. Отсюда
следует, что векторное поле да=@, —1) на торе является потен-
потенциальным, т. е. w = gradf. Это поле сопряжено полю v, т. е. их
интегральные траектории взаимно ортогональны. Следовательно, ■
интегральные траектории поля w являются меридианами тора
(рис. 23). В частности, все они замкнуты.
Осталось напомнить, 'что если гладкое векторное поле w на
многообразии М имеет хотя бы одну замкнутую траекторию \
Cw;i особых точек поля w, то это поле не может быть потенциаль-
потенциальным. II самом деле, допустим существование потенциала /, т. е.
такой функции, что выполнено равенство a> = gradf. Параметри-
Параметризуем траекторию у параметром t так, чтобы v@) =v(l)• Проин-
Проинтегрируем 1-форму df вдоль замкнутой траектории Y- Получим
= ^dxt{t)=f{l)-f(O) Ф 0,
71
так как функция монотонно возрастает вдоль траектории у. Итак,
/ не может быть однозначной функцией.
Полученное противоречие доказывает отсутствие неособых зам-
замкнутых траекторий у потенциальных полей. Таким образом, поле
w на торе не потенциально, а следовательно, исходное поле v не
гамильтоново на всем торе, что и требовалось доказать.
Напомним, что многообразие называется односвязным, если
каждый замкнутый путь (петля) стягивается по нему ib точку.
Дифференциальная /г-форма т называется замкнутой на М, если
dx=0, и форма называется точной, если x=dp для некоторой
(k—1)-мерной формы р. Любая точная форма замкнута. Обрат-
Обратное, вообще говоря, неверно.
Отчетливо видно препятствие, мешающее произвольному ло-
локально гамильтонову полю быть гамильтоновым. Это — неодно-
неодносвязность многообразия. В первом нашем примере многообразие
R2\0 неодносвязно за счет- выкалывания точки из плоскости.
Замкнутый путь, обходящий эту точку, не стягивается в точку по
R2\0. Во втором примере неодносвязным является тор Т2. Его па-
параллель -и меридиан задают образующие в ненулевой фундамен-
фундаментальной группе Я\(Т2) =Z©Z.
Из доказательства теоремы 2 видно, что локальная гамильто-
новость поля v=(Xi, У,-) эквивалентна замкнутости дифференци»
альной 1-формы а = 2—Ytdpi + Xidqi на многообразии М. Для гло-
глобальной гамильтоновости достаточно, чтобы эта форма была точ-
точной. Например, так всегда будет на R2" (лемма Пуанкаре). Одна-
Однако если симплектическое многообразие неодноавязно, то на нем
могут существовать замкнутые, но не точные 1-формы. Так будет,
если группа одномерных когомологий Hl(M, R) отлична от нуля.
В обоих наших примерах мы имеем ненулевую группу когомоло-
когомологий, а именно: Hl(R2\0, R)=R и Я1 (Г2, R) = R®R=R2. В частно-
частности, замкнутые 1-формы a = dp и a' = dq на торе не являются
точными.
Предложение 2. Пусть симплектическое многообразие М
имеет нулевую группу вещественных когомологий Я1 (М, R) {на-
{например, так будет всегда, когда многообразие односвязно). Тогда
любое локально гамильтоново векторное поле на многообразии
будет в то же время и глобально гамильтоновым.
Если многообразие односвязно, то всегда Н[(М, R)=0. Обрат-
Обратное, вообще говоря, неверно. Существуют неодносвязные много-
многообразия, для которых Hl(Mu R)=0. Правда, в этих случаях фун-
фундаментальная группа П](М) 'многообразия М «не очень велика» в
том смысле, что ее фактор по коммутанту, т. е. группа nil[n\,n\]
(совпадающая с одномерной группой целочисленных гомологии
H-i(M, Z)), не .имеет элементов бесконечного порядка.
Перейдем к описанию важной операции вычисления скобки
Пуассона двух функций на симплектическом многообразии.
Определение 6. Скобкой Пуассона гладких функций / и
g на симплектическом многообразии М с формой со называется
72 ~
функция {/, g}, задаваемая формулой
п {/. ё) = «(sgrad /, sgrad g) = 2 юг/ (sgrad /);'(sgrad g)p
Здесь (u = H(uljdxif\dx1 и sgrad/ = ((sgrad/)lt ... , (sgrad /J„). Та-
Таким образом, скобка Пуассона функций fug — это кососиммет-
рическое скалярное произведение (относительно формы со) их ко-
косых градиентов. Если через со'7 обозначить коэффициенты матри-
матрицы, обратной к матрице (со,;), то скобку Пуассона можно записать
в локальных координатах Xi,...,X2n на М так:
f -fk
Мы опираемся здесь на тот факт, что градиент функции и ее
косой градиент связаны соотношением
(sgrad/) ,-=
Ткким ибрйяом, скобка Пуассона вычисляется, если известны гра-
ЛН0Н1Ы функций I \\ ц.
Лги формула момч>т выть принята .ш определение скобки Пуас-J
юна. При чтом формула может бит. распространена и на тот
олучйй, когда митрицв Ы") яилиеп-н вырожденной. В некотором
точном смысле скобка Пуассона является более первичным и об-
общим тшптШ'М, чем симплектическая структура. Конечно, задание
ШМ1Ш«К1 нчеокой структуры (в ее классическом понимании) поз-
иолиег корректно (и. однозначно) определить операцию взятия
скобки Пуассона. Однако скобку Пуассона можно определить в
существенно более широком классе случаев, когда соответствую»
щпя структура ю вырождена. Однако пока мы будем, придержи-
паться определения скобки Пуассона через форму ш.
Скобка Пуассона имеет простую интерпретацию. Имеет место
ьажпое соотношение (f, g}= (sgrad f)g, т. е. скобка Пуассона сов-
совпадает с производной функции g no направлению векторного поля
sgrad/. В силу косой симметрии формы о) справедливо также ра-
нспстио {/, g}=—(sgrad^)/. Это сразу вытекает из определения
«Kracl j?, а именно
(v, щпн\ g)
где v — произвольное гладкое поле на М.
Предложение 3. Операция взятия скобки Пуассона f,g->
-*■{}, g} удовлетворяет следующим свойствам:
1) билинейность, т. е. {af+$g, h} = a{f, h} + fi{g, h), где аир —
постоянные числа;
2) кососимметричность, т. е. {f, g}=—{g, /};
3) справедливо тождество Якоби, т. е. {h, {f, g}} + {g, {h,f}} +
+ {f,{g,ft}}=0 для любых гладких функций f,g и h на М;
4) скобка Пуассона, рассматриваемая как дифференциальная
операция, удовлетворяет тождеству Лейбница, т. е. {h, fg} = {h,
f)g + f{h, g}, где fg — произведение функций fug.
Доказательство. Свойства 1 и 2, очевидно, следуют из
определения скобки Пуассона. Проверка свойства 3 нуждается в
некотором вычислении. Ясно, что
JL J!L- Jl +
dxj dxi dxp dxq дхс дх/дхр dxq
EL .*«
dxi дхр dxjdxq
"Циклически переставляя h, f, g и суммируя получающиеся выра-
выражения, мы обнаруживаем, что первая сумма обращается в ноль
за счет того, что форма to замкнута, т. е.
^- dxa/\dxt/\dxj = 0.
Вторая и третья суммы обратятся в ноль за счет симмет-
симметрии вторых частных производных и того обстоятельства, что ком-
коммутатор двух векторных полей есть снова векторное поле, т. е.
дифференциальный оператор первого (а не второго) порядка. На-
Наконец, свойство 4 следует из того, что {/г, fg}= (sgrad/г) (fg) =
= ((sgrad h)f)g + f (sgrad h)g, что и требовалось доказать.
Из предложения 3 вытекает важное следствие, аналога которо-
которому нет в римаповой геометрии, основанной на понятии симмет-
симметричного скалярного произведения.
Предложение 4. Линейное бесконечномерное пространство
СХ(М) гладких функций f на симплектическом многообразии М,
снабженное операцией взятия скобки Пуассона f, g-*~{f, g}, естест-
естественно превращается в некоторую бесконечномерную алгебру Ли
(над полем R). Роль коммутатора играет скобка Пуассона.
Напомним, что алгебра Ли — это линейное пространство, снаб-
снабженное билинейной кососимметричной операцией, удовлетворяю-
удовлетворяющей тождеству Якоби. Подчеркнем, что появление структуры ал-
алгебры Ли в пространстве функций на симплектическом много-
многообразии целиком обязано наличию симплектической структуры
(скобки Пуассона). Легко убедиться, что операция /-э-gradf, з'а-
даваемая симметричным (т. е. римановым) скалярным произве-
произведением, не порождает в пространстве функций естественной струк-
структуры алгебры Ли. В этом важное различие римановой (симмет-
(симметричной) и симплектической (кососимметричной) геометрий на мно
гообразии.
Имеется тесная связь алгебры Ли С°°(М) (с операцией —
скобка Пуассона) с алгеброй Ли V(M) всех гладких векторньп
полей на многообразии (с операцией — обычный коммутатор век
торных полей). Построим естественное отображение а простран
iisd функции 1_,--^ш; в пространство векторных полей V(M), за-
задав его формулой a(/)=sgradf.
Предложение 5. 1) Отображение oc:/->sgradf задает го-
гомоморфизм алгебры Ли С°°(М) в алгебру Ли V{M), т. е. sgrad{/,
g}= [sgrad f, sgradg]. Другими словами, скобка Пуассона {f, gj
при отображении а переходит в обычный коммутатор векторных
полей sgrad/, sgrad gf.
2) Образом алгебры 'Ли С°°(М) при гомоморфизме а является
подалгебра Н(М), состоящая из всех гамильтоновых векторных
полей.
3) Если многообразие связно, то имеет место изоморфизм
H(M)=C°°(M)/Rl, где через R1 обозначен идеал в С°°(М), состоя-
состоящий из постоянных функций на М (т. е. из констант).
4) Локально гамильтоновы поля образуют подалгебру Ли
Н\0С(М) в алгебре Ли V(M) всех векторных полей.
5) Гамильтоновы поля образуют идеал в-алгебре Ли локально
гамильтоновых векторных полей.
Доказательство. Из определения операции sgrad получаем
(sgrad {/, g}) h = {{/, g), h) = (в силу тождества Якоби) = ~{{h, /}, g}~
-{{tf.A},/} = {/.{ff.A}}-{g.{f.A}}-(sgrad/)(sgradg)A-(sgradg) X
X (ицгнс1/)А [sgr.-id/, sgrad#]/i, что и доказывает п. 1. Для дока-
амтслы'гии II. 2 дистнточио происрить, что обычный коммутатор
Дйук niMHJHiiuiionwx нолей мцпн1 / и sRrarig снова является га-
мнльпшопым 11ол«М, Это срезу следует им п. 1, так как [sgrad f,
sgrid^j—sgrttd ((/, и), В частности, гамильтониан коммутатора
Гймильтономых нолей иилистся скобкой Пуассона гамильтонианов
«тих полей, Таким обрияом, пространство гамильтоновых полей —
ЯГ» notiuAevflpa « пространстве всех векторных полей на много-
многообразии, Докажем и. 3. Пусть f — гладкая функция на связном
мипкшбрп.'иш и такая, что sgrad f = 0. Так как форма ш невырож-
Д«чк1, то grad/ = O. Так как многообразие связно, то f постоянна
на всем М, что и требовалось доказать.
Докажем п. 4. Пусть vl и У2 = локально 'гампльтоновы поля. Это
означает, что для любой точки на многообразии существует такая до-
достаточно малая ее окрестность U, в которой v1 = sgrad /f7, v2--- sgrad f\j.
Тогда коммутатор [и1;и2] в этой окрестности допускает представление
[Vl,v2] = [sgrad /у, sgrad %]= sgrad{ ft, %}; {/^/2у} = ш (sgrad/f, sgrad
fV) = w(v1,vi).
Таким образом, коммутатор [и]; Уг] является глобально опре-
определенным гамильтоновым полем, так. как гладкая функция <i>(i>i,
v2) корректно определена на всем многообразии (и не зависит от
выбора окрестностей U).
Итак, мы сразу доказали не только п. 4, но и п. 5. В самом
деле, как выяснилось, коммутатор двух локально гамильтоновых
полей V] и v2 является настоящим гамильтоновым полем. Поэтому
гамильтоновы поля образуют идеал в пространстве локально га-
гамильтоновых полей. Теорема доказана.
75
Отметим, что подалгебры Ли Н(М) и Н\ОС{М) зависят от вы-
выбора формы ш на М. При изменении симплектической структуры
эти подалгебры будут, вообще говоря, меняться в алгебре Ли всех
функций.
Для приложений полезно знать явное выражение для скобки
Пуассона двух функций в канонических симплектических коорди-
координатах. Пусть pi,...,pn, q\,...,qn — канонические координаты в
R2". Тогда
dg df
{f, g} = o, (sgrad /, sgrad g) = V f~ f-- f- -f
LJ dpi idqt dpi dqi
1=1
Здесь мы воспользовались тем, что форма to имеет матрицу
/ 0 £\ ' -
\-EOj-
1.3. Интегралы гамильтоновых полей. Напомним, что гладкая
функция f на многообразии М назьявается интегралом векторного
поля v, если она постоянна вдоль поля и(/)=0. Это эквивалентно
тому, что функция / постоянна на всех интегральных траекториях
поля v (рис. 24). Хорошо известно, что наличие интеграла у поля
v(x) = (vi(x),..., vN(x)), отвечающего системе обыкновенных диф-
дифф () l^i^N MN
ференциальных уравнений Xi = Vi(xi,...,x»r),
д дй
на MN, поз-
позфр ур i i(i,,), ^, ,
воляет понизить порядок исходной системы на единицу. Дело в
Рис. 25
том, что интегральные траектории системы.лежат на поверхностях
уровня интеграла f. Эти поверхности'являются (в точках общего
положения) гладкими гиперповерхностями в М. Если известно
несколько интегралов flt...,fr поля (уравнения) v и если они
функционально независимы на какой-то открытой области в мно-
многообразии, это позволяет понизить порядок системы- (в этой об-
области) на г единиц (рис. 25).
Таким образом, .поиск максимально возможного числа незави-
независимых интегралов векторного поля — важная задача. Длягамиль-
76
тоновых систем поиск интегралов иногда облегчается за счет спе-
специфики таких систем.
Теорема 3. 1) Пусть u = sgrad/ — гамильтоново поле с га-
гамильтонианом f на с'имплектическом многообразии М. Тогда функ-
функция g на М является интегралом поля v тогда и только тогда,
когда ее скобка Пуассона с гамильтонианом f тождественно рав-
равна нулю, т. е. {/, g}=0.
. 2) Гамильтониан f всегда является интегралом гамильтонова
поля t/ = sgradf.
3) Если hug — два интеграла поля u = sgradf, то их скобка
Пуассона {h, g) также является интегралом этого поля. Этот ин-
интеграл может, впрочем, оказаться зависимым с интегралами h
и g (выражаться через них).
Доказательство. Функция g является интегралом поля
-sgradf = u тогда и только тогда, когда v(g)=0, т. е. когда
{sgrad f)g = {f, g} = 0, что и доказывает п. 1.
Есл.и g = f, то в силу косой симметрии скобки Пуассона полу-
получаем {/, f} = 0, что и доказывает п. 2. Если h и g — два интеграла,
то из тождества Якоби получаем {{h, g}, f}+{{/, h), g}+{{g,f), ft} = 0
и так как {f, h} = {g,f} = 0 (функции hug — интегралы), то
{{h, ё), f}=0. т. e. {h, g) — интеграл. Теорема доказана.
Итак, зная некоторый запас интегралов гамильтонова поля,
можно строить серию других интегралов, вычисляя попарные
скобки Пуассона исходных интегралов. Не все получающиеся при
чтом пп'ктралы будут существенно -новыми, т. е. независимыми
от предыдущих. Дело <ц том, что на 2п-мерном с'имплектическом
MHOtoofipii-itiii не может существовать более чем п функционально
Ht>aanU(intit\ (на открытых областях) функций. Однако в некото-
некоторых случиич (iiiiicttiiiifiii процедура действительно дает новые инте--
грйЛЫ, lll'lliniU'llMUl' ОТ ИСХОДНЫХ.
Рнгсмотрим поле y = sgradf на М. Гамильтониан f можно рас-
смптринать как элемент алгебры Ли С°°(М) гладких функций на
М. Можно рассмотреть линейное подпространство G(f) всех функ-
функций g&C°°(M), коммутирующих с элементом f относительно скоб-
скобки Пуассона, т. е. удовлетворяющих уравнению {f, g}=0. Ясно,
что подпространство G(f) является совокупностью всех интегралов
гамильтонова поля f = sgradf. Очевидно, что feG(f) (рис. 26).
Таким образом, каждый гамильто-
гамильтониан f однозначно определяет не-
киторог подпространство G(f) ком-
коммутирующих с ним функций, т. е.
пространство всех интегралов по-
поля si — strati /, Ии теоремы 3 сразу
следует, что прск-трипстмо G(f)
всех иптегрнлои янлнется подал-
подалгеброй в алгебре Ли О(М) функ-
функций на М. Подпространство G(f)
сможет иметь бесконечную размер-
яость, однако в нем можно выбрать . . Рис. 26
77
не более чем п различных коммутирующих функционально неза-
независимых интегралов поля sgradf на 2я-мерном многообразии
М. Остальные элементы пространства G(f) будут функциональ-
функционально выражаться через эти независимые интегралы, если G (f) ком-
коммутативна.
Приведем полезную теорему, обобщающую результат Э. Нётер.
Теорема 4. Пусть на симплектическом многообразии М дана
гамильтоново поле y = sgrad/. Пусть гамильтониан f инвариантен
относительно однопараметрической группы @х преобразований
gt: М-э-М, порожденных некоторым другим гамильтоновым полем
T = sgradg. Тогда гамильтониан g является интегралом поля v.
Доказательство. Так как гамильтониан f сохраняется
преобразованиями gt, то -r(f)=O, или (sgradg)f = O, т. е. {g, f} = 0,
что и требовалось доказать.
Существуют и другие обобщения теоремы Нётер. Пусть дано
гамильтоново поле u = sgradf и другое гамильтоново поле w —
= sgradg, коммутирующее с v. Это означает, что [v, ку]=0. На-
Напомним, что это эквивалентно тому, что две соответствующие од-
иопараметрические группы преобразований @" и <3W коммутируют
как диффеоморфизмы многообразия М. Из коммутирования полей
v и w следует 0=[и, w] = [sgrad[, sgradg] =sgrad{f, g).
Из предложения 5 следует, что скобка Пуассона {f, g} являет-
является локально постоянной функцией, а если многообразие М связно,
то эта функция постоянна «а всем М. Итак, мы доказали, что два
гамильтоновых поля v и w коммутируют (как векторные поля) ■&
том и только в том случае, когда скобка Пуассона их гамильто-
гамильтонианов {f, g) локально постоянна (в случае связного многообра-
многообразия '— постоянна.
1.4. Теорема Лиувилля. Если для поля v на многообразии Мн
удалось найти г независимых (почти всюду) интегралов fi, •••,)>,
то порядок соответствующей системы дифференциальных уравне-
уравнений понижается на г единиц. Геометрически это означает, что ин-
интегральные траектории системы v движутся по .совместным по-
поверхностям уровня интегралов f\,...,fr, которые (в случае общего
положения) являются (N—г)-мерными гладкими подмногообра-
подмногообразиями в М. Поэтому для полного интегрирования системы нужно
иметь ./V—1 независимых интегралов. Тогда их совместные поверх-
поверхности уровня будут одномерны и совпадут с интегральными тра-
ркториями системы. Однако такой идеальный случай встречается
редко. Чаще всего найти полный, запас интегралов не удается
(или его вообще нет). Поэтому приходится довольствоваться раз-
различными версиями «.частичной интегрируемости». При этом жела-
желательно, чтобы частичная интегрируемость выглядела примерно
так.
Требуется найти набор независимых (почти всюду) интегралов
fi,...,fr таких, чтобы их совместные поверхности уровня были дос-
достаточно простыми, например, чтобы все они (в случае общего по-
положения) были диффеоморфны какому-то одному и тому же
простому многообразию. Кроме того, хотелось бы, чтобы исходная
78
система, будучи ограничена на эту совместную поверхность уров-
уровня, превращалась бы на ней в «просто устроенную» систему, что-
чтобы интегральные траектории допускали простое описание.
Замечательно, что эта программа во многих случаях может
быть реализована. Для некоторых гамильтоновых систем имеет
место чрезвычайно полезная частичная интегрируемость, когда
совместная поверхность уровня интегралов оказывается тором и
ограничение- на него исходной системы задает условно периодиче-
периодическое движение по тору.
Остановимся подробнее на этой ситуации, которую условно на*
зовем случаем коммутативной интегрируемости гамильтоновой
системы.
Будем говорить, что две функции f и g находятся в инволюции
на симплектическом многообразии М2п, если их скобка Пуассона
равна нулю (тождественно). Оказывается, чтобы более или менее
полно описать картину движения интегральных траекторий га-
гамильтоновых систем, достаточно найти лишь п независимых интег-
интегралов, находящихся в инволюции. В этом случае каждый интег-
интеграл «засчитывается за два- интеграла». Более точно каждый такой
интеграл позволяет понижать порядок системы не на единицу, как
и общем случае, а сразу на две единицы. Мы приведем здесь из-
(«Остпую теорему Лнувилля, решающую эту задачу интегрирова-
интегрировании | П |.
Теорема fl Пусть на симплектическом многообразии-М2п
шОан набор п гладких функций /, /„, находящихся в инволю-
инволюции, Обозначим через /И6 совместную поверхность уровня, зада-
п'п-мун) системой уравнений f\ (х) =\\,... ,fn(x) =|n. Предположим,
•'(к нц ней пес функции fi функционально независимы (т. е. гра-
функций или их косые градиенты линейно независимы в
точке на поверхности уровня). Тогда выполняются следу-
следующие утверждения:
1) Поверхность уровня Мъ является гладким п-мерным под-
подмногообразием, инвариантным относительно каждого векторного
поля y, = sgrad fi, т. е. все эти поля касаются поверхности уров-
уровня Mi.
2) Если поверхность уровня Мъ связна и компактна, то она
диффеоморфна п-мерному тору Тп. В общем случае если М% связ-
связно (но не обязательно компактно), и если все векторные поля
я паяются полными на поверхности уровня, то Мъ диффеоморфно
некоторому «цилиндру», т. е. фактору евклидова пространства R"
tlo некоторой решетке (ранг которой не превосходит п).
'Л) Пели поверхность уровня Мъ связка и компактна (тогда она
является тором Тп), то в некоторой ее открытой окрестности мож-
можно ввести регулярные криволинейные координаты su...,sn;
<pi,... ,ср„, называемые «действие — угол», с такими свойствами:
а) Функции Si(x),... ,sn(x) задают координаты в направле-
направлениях, трансверсальных (нормальных) тору Тп., и функционально
выражаются через интегралы fi,...,fn. В этих координатах урав-
уравнение тора задается так: Si = ...^=sn=0.
79
• б) Функции ф] (х),..., <р„ (х) задают угловые координаты на
торе Тп (и, следовательно, на близких к нему торах, являющихся
поверхностями уровня интегралов fi,...,fn). Другими словами,
ф,- изменяются от 0 до 2л и задают представление тора Тп в виде
стандартного прямого, произведения п окружностей, где ф,- — уг-
угловая координата на 1-й окружности.
в) Симплектическая структура ш, будучи записана в окрестно-
окрестности тора Тп в координатах «действие—угол», приобретает канони-
канонический вид co = 2ds<A^<P;- Это эквивалентно тому, что попарные
скобки Пуассона координат «действие—угол» имеют простейший
вид: {5£,5/} = {ф()ф;} = 0, {si,^j}—б(/.
г) Каждое векторное поле u = sgradf, где f — любая функция
из набора f],...,fn или любая функция, функционально выража-
выражающаяся через функции fi,...,fn (поле касается тора), будучи за-
записано в координатах «.действие—угол», приобретает простой
вид: (fi = e{(si = O,... ,sn = O) = const. Здесь уравнения s, = 0 экви-
эквивалентны уравнениям U — Ъ, где %\,...,%,п— постоянные, опреде-
определяющие тор Тп как поверхность уровня fi = sb ... ,fn = ln. Таким
образом, поле и имеет на торе Тп (в координатах '(pu...,<fn) про-
простейший вид: его компоненты постоянны и интегральные траекто-
траектории поля задают прямолинейную обмотку тора, т. е. условно пе-
периодическое движение по тору. В каждой точке тора векторы vt =
= sgrad/j образуют базис в касательной плоскости к тору.
д) Функции qu...,qn из предыдущего пункта определены и в
.некоторой окрестности данного тора. Поэтому на поверхностях
уровня, близких к тору (и также являющихся торами), мы также
имеем (fi = qi(sl°,.. .,sn°), где уравнения sx = st°,..., sn = Sn° задают
близкую поверхность уровня. Таким образом, исходная система
u = sgradf записывается в окрестности тора в координатах «дей-
«действие—угол» так: sj = O,.. .,sn = 0, (pi = qi(su.. ■ ,sn), l<i^n. ■
Торы, указанные в теореме, иногда называются торами Лиу-
Лиувилля. Ясно, что все они являются лагранжевыми подмногообра-
подмногообразиями.
Итак, если интегралы f\,...,fn независимы, то неособые ком-
компактные совместные поверхности уровня являются объединениями
торов. Вложение каждого из этих торов в объемлющее многооб-
многообразие может быть достаточно сложным. Оно задается функциями
f\,...,fn и тем сложнее, чем сложнее эти функции. Тем не менее,
зная функции f\,...,fn, можно многое сказать о характере распо-
расположения тора в многообразии. На торе исследуемое поле sg'radf
устроено максимально просто. В координатах ф[,. .., <р„ оно ста-
становится полем с постоянными компонентами, т. е. полностью опре-
определяется заданием вектора скорости в какой-то одной точке то-
тора. Все остальные Лекторы скоростей -получаются из него парал-
параллельным переносом в координатах cpi,...,tpn (рис. 27).
Теорема Лиувилля приобрела большое значение в современной
геометрии и механике, физике благодаря тому, что, как оказа-
оказалось, многие физические системы (и их геометрические многомер-
многомерные аналоги) обладают набором интегралов в инволюции, позво-
80
Рис. 27
ляющим проинтегрировать систему в указанном смысле. Будем
говорить, что гамильтонова система u = sgrad/ на симплектическом
многообразии М2п вполне интегри-
интегрируема по Лиувиллю (или допускает
полное коммутативное интегриро-
интегрирование), если для нее существует на-
набор из п функций fi,..., fn, нахо-
находящихся в инволюции и* пезависи-.
мых, причем f\ = f и функции
/],...,/„ удовлетворяют условиям
теоремы Лиувилля. Набор функ-
функций /ь ..., fn будем называть пол-
полным коммутативным (инволютив-
ным) набором функций.
Задача интегрирования данной
системы по Лиувиллю означает
включение ее гамильтониана f в
семейство функций, находящихся
в инволюции и таких, что из них
можно выбрать п независимых
функций, где п — половина раз-
размерности объемлющего многообра-
многообразия. Если такой набор функций
удается найти, то (в предположе-
предположениях теоремы 5) траектории системы движутся по торам половин-
половинной размерности, задавая на них условно периодическое движение
в подходящих координатах.
С точки зрения алгебры Ли С°°(М) функций на М2п, задача
интегрирования гамильтоновой системы эквивалентна поиску ком-
коммутативной подалгебры G(f), содержащей гамильтониан f данной
системы и обладающей тем свойством, что в G(f) можно выбрать
аддитивный базис из п независимых (функционально) функций.
. § 2. Геометрические свойства скобки Пуассона
2.1. Первичность понятия скобки Пуассона. При изучении сим-
плектических многообразий иногда чрезвычайно удобно класть в
основу определения пшплоктпчноети на внешнюю 2-форму со, а
операцию вычислении скобки Пуассона. Свойства скобки Пуассо-
iiii могут быть определены аксиоматически. При этом понятие
скобки Пуассона и некотором смысле 'более гибкое, чем понятие
каноническом симнлектичеекон структуры, порожденной невырож-
невырожденном формой о). Во многих палачах механики можно успешна
полышипты'И вырожденной скобкой Пуассона. Однако пока мы
сосредоточим внимание ни пены.рожденной скобке Пуассона.
Определенно I, Ьудем считать, что иа гладком многообра-
многообразии задана кммоничеаищ структура (скобки Пуассона)^ если на
пространстве С°° (М)~гл1П1Ких функций "на М определена операция
{,}, сопоставляющая каждой паре функций fug новую функцию
{f, g} со следующими свойствамл:
81
1) {f-&}=—{&- f} {косая симметрия);
2) {f\ + fi, g} = {f\, g} + {f2, g} (билинейность);
3) {fg, h} = f{g, h} + g{f, h} {правило Лейбница);
4) {f,{g, h}} + {h,{f, g}} + {g,{h,f}} = ® (тождество Якоби);
5) если в некоторой точке *<=Л1 имеем df^O, то существует
такая функция g, что в этой же точке {f, g}фO. Это свойство озна-
означает невырожденность операции (скобки Пуассона). ,
Пусть- F = (fu...,fi), G=(gu...,gm) — два набора гладких
функций на симплектическом многообразии М. Рассмотрим мат-
матрицу Пуассона {F, G}, составленную из попарных скобок Пуассона
функций наборов F и G, т. е. {F, G}= ({/,-, gj}). Тогда многие
свойства скобки Пуассона можно переформулировать на языке
матрицы {F, G}.
- Лемма 1. Пусть в некоторой открытой области на многообра-
многообразии М функции наборов F и G функционально выражаются через
какие-то другие функции Z— (z\,..., zk). Тогда в этой области мы
.имеем равенство {F,G} = A{Z,Z}BT, где А и В — матрицы Якоби:
°П \ п_._ dg _/ dgj
дг \ дгр / дг \ dzp
Здесь fi = fi(zu...,zk), gj = gi(zu...,zk).
. Доказательство вытекает из определения матрицы {F, G}
и простых вычислений, которые мы предоставляем читателю.
Отсюда следует, что если S — некоторое пространство функ-
функций, функционально порожденных функциями r\,...,rs, то для за-
задания скобки Пуассона на всем пространстве S достаточно задать
ее лишь на функциях r\,...,rs, а затем продолжить на все про-
пространство в соответствии с формулами леммы, 2. Ясно, что все
предыдущие рассуждения можно провести для функций, опреде-
определенных п-е на всем многообразии, а лишь на какой-то открытой
его области.
Следствие 1. Пусть х= (х\,... ,xN) — локальные координа-
координаты на гладком многообразии MN. Рассматривая эти координаты
как функции, определенные на некоторой открытой карте в М, мы
можем построить соответствующую им матрицу Пуассона J = {x,
х}= ({xi, х/}). Тогда матрица J кососимметрична и невырождена, в
частности Ат = 2я. Если F и G — два произвольных набора глад-
гладких функций, определенных на М, то выполняются тождества
к ' дх дх
Доказательство. Достаточно в качестве функций zu ... ,zk
из леммы 2 взять локальные координаты х\,...,хы, а в качестве
■А и В — матрицы Якоби
dft
дх \ дхр I дх \ дхр
Если задать скобку Пуассона равенством {F, G} = —— J
дх дх
то условия 1, 2, 3 из определения 1 выполняются автоматически.
Условие 5 эквивалентно условию det 1фО, т. е. невырожденности
J=(Ja») в классическом смысле. Условие 4 (тождество Якоби)
приобретает следующий вид (см. работу Я. В. Татаринова [133]):.
. dJva r
•> p; — "Г Jyp
dx
Г Jyp
dxt dxp
Для дальнейшего нам будут полезны некоторые простые свой-
свойства ранга матрицы {F, G}. Пусть rk С обозначает ранг матрицы.
С. Напомним известные неравенства для ранга произведения двух
матриц. Если имеется матрица А размером lXk и матрица В раз-,
мером kXm, то гкЛ^/, k; гк B^k, m и для ранга их произведения
АВ выполняются неравенства гкЛ + гкБ—/г<тк ЛВ^гк Л, гк В.
Обозначим через гк F ранг матрицы dfjdz, где F=(fu ..., /;),.
Z=(zu ..., zk) и fi=fi(zu ..., zk). Тогда для общего равенства
{F,G} = ——{Z,Z}—^-, считая для простоты, что rkZ=k', полу-
получаем rkf + rkG + rk{Z, Z}—2k^rk{F, G}<rk F, rk G, rk{Z, Z).
В частном случае, когда в качестве функций набора Z взяты
локальные координаты х\, ..., х%п на многообразии, т. е. когда
k = 2n, для соотношения {F,G\ — —— J —^— получаем следующие
дх ох
неравенства для рангов: rk^ + rkG—2/z^Crk{.F, GJ^Crk F, rk G. При
этом мы использовали равенство rki = 2n. Будем понимать под
независимостью функций их функциональную независимость.
Лемма 2. Пусть (F, G}——— J —— , где х=(хи ..., х2п) —
дх дх
локальные координаты на многообразии. Если ранг матрицы
{/•', G} максимален (пусть для простоты он равен l^m), то хотя бы
в одном из наборов функций F, G составляющие его функции неза-
независимы (соответственно rk F = l). Если в каждом из наборов F, G
составляющие их функции независимы и {F, G} = 0, то l + m^.2n.
Доказательство сразу следует из приведенных выше
неравенств для рангов матриц.
Определение 2. Будем говорить, что функции набора F
находятся в инволюции с функциями набора G (в одной точке
или и области), если {F, G} = 0, т. е. {/,-, g,} = 0 для всех i, j. Если
/•'— (!, то будем говорить, что функции набора F находятся в инво-
инволюции (инполютивный набор).
Вообще (а особенно в алгебраических ситуациях) будем гово-
говорить, что функции, находящиеся в инволюции, образуют инволю-
тивный набор функций. Ясно, что если набор F находится ,в инво^
люции с набором G, то и набор G находится в инволюции с набо-
набором F. Поскольку, как мы знаем, операция взятия скобки Пуассо-
Пуассона превращает пространство гладких функций в алгебру Ли, то
83-
только тогда, когда они коммутируют (в смысле алгебры Ли
-функций). На многообразии М2п, снабженном невырожденной
£кобкой Пуассона, не может быть больше • чем п независимых
функций в инволюции. В самом деле, напомним, что если функции
f[, ..., ft независимы, то в точках общего положения независимы
их градиенты. Следовательно, линейно независимы их косые гра-
градиенты. Плоскость, натянутая па косые градиенты, является,
«очевидно, изотропной плоскостью в пространстве, касательном
к многообразию. Из гл. 1 следует, что в невырожденном случае
размерность изотропной плоскости не превосходит п, что и требо-
требовалось доказать.
Рассмотрим на М2п симплектическую структуру о и порожден-
порожденную ею скобку Пуассона. Ясно, что локальная система координат
Z==(pi, ...,_р„, q , qn) является симплектической в том и
только в том случае, когда матрица Пуассона этих функций имеет
канонический вид J = {Z,Z}~ [p ^)=/. В этих канонических
\ /
симплектических координатах скобка Пуассона принимает клас-
классе п\ V* dF dG , dF д<3
сическии вид {F,G}= \ 1 .
Ami dpi dqc dqi dpi
■ i
2.2. Теорема Дарбу. Эта теорема утверждает, что если симп-
лектическая структура на М2п невырождена, то для любой точки
существует открытая окрестность с локальными координатами
р\, ..., рп, q\, ■■■, qn такими, что форма ы записывается в кано-
каноническом виде 'Ldpi/\dqi.
Существует много разных доказательств этой теоремы. См., на-
-пример, [5], [133], [42]. Следуя работе Я. В. Татаринова [133],
мы приведем доказательство,, опирающееся на'свойства матрицы
Пуассона.
Лемма 3. Пусть на многообразии М2п в- окрестности некото-
некоторой точки заданы п независимых функций р„ находящихся в ин-
инволюции. Тогда существует набор из п независимых функций ц„
также находящихся в инволюции и таких, что полный набор не-
независимых функций р\, ..., рп, q\, ..., qn задает симплектические
координаты в окрестности данной точки.
Доказательство. Обозначим набор функций ри ..., рп
через Р. Рассмотрим векторные поля sgradp;, отвечающие функ-
функциям pt. Так как {pi, p/}= [sgradp,-, sgradp,] и так как функции
Pi находятся в инволюции, то поля sgradp, коммутируют. Из кур-
курса дифференциальной геометрии известно, что если заданы k ли-
линейно независимых векторных полей у,- таких, что все их попарные
коммутаторы равны нулю в окрестности некоторой точки, то су-
существует локальная регулярная система координат х\, ..., л>,
JCk+i- ■■■, хп такая, что в ней и,-= , 1<(<^. Другими словами,
0X1 •
любые k коммутирующих независимых векторных полей могут
■быть локально представлены как поля скоростей k координатных
«4 '
sgrad p, существует система координат xu- ■-, xn, У и • ••, Уп такая,
чт© sgradPi = . Поэтому равенства {р;, p.) = (sgradрЛ р, = —f-L = О
dxi dxi
означают, что функции pj не зависят от координат х\,...,хп,
"т. е. pi = Pj(yu .... уп).
Далее {*,-, Р/} = (—sgrad pj) xL = — —^- = — 6{/. Следовательно,
OX j
матрица Пуассона набора функций xhpf невырождена и все дальней-
дальнейшие рассуждения можно вести в системе координат ху, . .. ,хп,р1,...
... ,рп. Заметим, что {хь х,} = %{,- (р1?... ,р„) = Ц-(Р), так как -~L =
= sgrad ра (к:/) = (sgrad ра){хг, л:,-} = {ра, {г,-, а:/}} = {^-, {ра, ^£}} -f {x£, {х,-,
Ра}} = 0 И .{P(,JC/} = const. Будем искать координаты (функции) qf в
виде qj = Xj—fj(P)- Мы получаем тождества {pi,qj)=—8i;- и уравне-
уравнения на функция /.-, а именно: {<?,-, <7/} = ^,-;Н—-——— = 0. Здесь мы
— ■ dpi dpi
использовали общее равенство: ,
В нашем случае
Для того чтобы полученная выше система имела решение,
необходимо и достаточно, чтобы выполнялось тождество
дру дрр ^Ра
которое действительно выполнено в силу тождества Якоби, так как
{{*«. ^р}. ^v} = {^Р> xv) = т^ • Лемма доказана.
Легко проверить, что если qx> ... ,qn—какие-то другие координа-
координаты, дополняющие координаты р\,...,рп, ю они связаны с коорди-
иитамп A),..\,A„ соотношениями (/( г/Н- -—-, где <р = <р(Р).
apt
Д ox ti i ;i л v л ьс:т но т е о р е м м Дарбу. В силу леммы 3
допятчип покипит)», что в окрестноеги любой точки существуют
п iKMtiHiifiiMMX функций и нниолюции. В действительности спра-
ведлино более сильное ипд^уктпппое утверждение, а именно, если
имеется к неэппигимых функций р\, ..., pt, находящихся в инво-^
люции, где к<п, то всегда существует независимая от них функ-"
ция"р*+1, такая, чго {Рн+i, Р,}~0, 1<г<й. В самом деле, следуя
доказательству леммы 3, получаем, что в некоторых координатах
85
\-to' "" PI) PJ-
= —££-, из которых следует, что Pi=--pi(y\, .... Уъп-ь). Так как
2л—k>k, то существует новая функция Рк+\(у), независимая с
функциями Pi(y), ..-, Рк(у). Тогда {р*.ц. Pi} = ^- = 0,что
и требовалось доказать.
Теорему Дарбу можно рассматривать как теорему о существо-
существовании локального вложения окрестности любой точки симплек-
симплектического многообразия М2" в симплектическое пространство R2"
с каноническими координатами, причем исходная 2-форма, задан-
заданная на М2п в окрестности точки, индуцируется стандартной фор-
формой 2 dpi/\dqi из R2". Мы естественно приходим к следующему-
вопросу: для любого ли симплектического многообразия М2п
с точкой симплектической 2-формой существует глобальное вложе-
вложение в некоторое конечномерное симплектическое пространство R2N,
при котором каноническая 2-форма R2yv~индуцирует на М2п исход-
исходную 2-форму? Решению этого вопроса посвящен следующий па-
параграф.
§ 3. Вложения CHMiMeKTHHetKHx многообразий. Примеры
симплектических многообразий
Хорошо известно, что каждое компактное гладкое замкнутое
многообразие Мт можно вложить в некоторое конечномерное евк-
евклидово пространство R^ch-", где т — размерность многообразия, а
s — число открытых шаров, образующих покрытие М. Известные
теоремы Уитни позволяют существенно понизить размерность
вложения, однако мы не будем здесь на этом останавливаться.
Пусть теперь М2п — симплектическое многообразие. Можно ли
вложить его в некоторое пространство R2N таким образом, чтобы
симплектическая структура со на М2п индуцировалась бы стандарт-
стандартной симплектической структурой Q па R2/V, т. е. чтобы ш = /*Й,
где / : M->-R2N — вложение? Можно рассматривать как компакт-
компактные, так и некомпактные многообразия.
Определение 1. Пусть даны два симплектических много-
многообразия (М, toi) и (N, ©г). Отображение f : M-+N назовем симп-
лектическим, если /*(сог) =ыь т. е. симплектическая форма toi на
многообразии М является прообразом симплектической формы ы2.
Рассмотрим симплектические многообразия М и N одинаковой
размерности. Согласно теореме Дарбу для любой точки х^М и
для любой точки y^.N существует симплектический диффеомор-
диффеоморфизм некоторой окрестности U (х) точки х на некоторую окрест-
окрестность V(у) точки у. Таким образом, локально вопрос о вложении
симплектических многообразий тривиален.
Что касается вложения симплектического многообразия М
в целом в другое симплектическое многообразие N, то может не
существовать даже симплектического отображения / : A1-WV'. В са-
самом деле, отображение / порождает гомоморфизм групп когомо-
86
логий f*:H2(N, R)-*IP{M, R). Класс когомологий [ол]е
^Н2(М, R), определяемый 2-формой соь может не принадлежать
образу группы H2(N, R) ни при каком гомоморфизме
j*:H2(N, R)-+H2(M, R).
Итак, необходимым условием существования симплектического
отображения из многообразия (М, coi) в многообразие (R2V,
Hdpi/\dqi) является точность формы ом, т. е. возможность ее
записи в виде a\~da, где a — некоторая 1-форма. Отсюда, в ча-
частности, следует, что компактное замкнутое симплектическое мно-
многообразие (М2п, Ш() нельзя симплектически вложить ни в какое
симплектическое пространство (R2N, Й).
Существование такого вложения противоречило бы невырож-
невырожденности симплектической формы coi на М. Дело в гом, что точная
2-форма ом па компактном замкнутом ориентируемом многообра-
многообразии не может быть невырожденной. В самом деле, если мы допус-
допустим существование точной невырожденной фо_рмы, то, с одной
•стороны, ее п-я внешняя степень дает 2п-мерную форму ы\п рима-
нова объема на многообразии. Следовательно, jMwi" = vol М^---0.
С другой стороны, форма ы\п точна, так как w\=da и ом" —
=d{af\daf\.. ./\da) (n—1 раз). По формуле Стокса интеграл
по замкнутому компактному многообразию М2п от точной формы
<oi" равен нулю. Полученное противоречие доказывает отсутствие
•симплектических вложений М2п в R2/V для компактного случая.
В частности, мы доказали, что па компактном симплектическом
- многообразии форма coi всегда иекогомологична нулю, т. е. опре-
определяет ненулевой элемент в группе когомологий Н2(М, R). В част-
частности, всегда Н2{М, R)=/=0.
В силу невырожденности симплектической формы а>\ на много-
многообразии М всякое симплектическое отображение f;M-*-N, coi =
= /*(со2), будет погружением. Доказательство предоставляем чи-
читателю. Необходимым условием существования симплектического
погружения симплектического многообразия (М, coi) в симплекти-
симплектическое многообразие (N, шг) является существование такого отоб-
отображения f : M-+N, что индуцированный им гомоморфизм групп
когомологий f* : H2(N, R)-^№(M, R) переводит класс когомоло-
когомологий формы со2 в класс когомологий формы (oi, т. е. /* : [u^j—^lwi].
Согласно М. Л. Громову, это условие является и достаточным
для существования симплектического погружения М в N в случае,
4>сли dim N^2d\mM (см. [270]). Приведем точную формулировку
•тих результатов.
Обозначим через /'(Л1, /V) многообразие 1-струй отображений
из М и N. Тогда Jl(M, N) является расслоением над М, слой ко-
которого есть объединение над х^М по всем y^N пространств ли-
линейных отображений TxM-*-TyN. Обозначим это пространство
L(TXM, TyN). Пусть QczJl(M, N) — подрасслоение расслоения
Jl(M, N), состоящее из таких отображений h^.L(TxM, TyN), что
для любых X, Y^TXM имеем coi(X, Y)=ix>2{hX, hY). Обозначим
через B = BS(Q), s = 0, l,...,oo, пространство О-сечений M-^Qcz
<zJl(M, N), а через A=As+l(Q) пространство С-с-отображений
87
v : M-*-N, струи которых /Tv : M-^Jl(M, N) переводят М в Q. Кро-
™е того, потребуем, чтобы В состояло из иммерсий с допустимьши
гомоморфизмами, т. е. для любого у^В имеем у* ( [со2]) = [coi].
Рассмотрим естественное вложение / : А~*~В, J : y-^Jyl.
Теорема 1. Отображение I индуцирует изоморфизмы /*:
т(А)-+тц(В), s = 0, 1, ..., всех гомотопических групп пространств
А и В, если сНтЛГ>2сНт./И.
Рассмотрим вопрос о вложении симплектических многообразий
в комплексные проективные пространства.
Рассмотрим канонический гомоморфизм e:Hk(M, Z)-*-
-+Hk{M, R), отображающий группы целочисленных когомологий
многообразия М в группы его вещественных когомологий. Этот
гомоморфизм возникает, когда мы стандартно вкладываем Z в R
и рассматриваем каждую целочисленную -коцепь как веществен-
вещественную. Напомним, что замкнутая внешняя /е-форма на многообразий
~М называется целочисленной, если ее класс когомологий является
образом некоторого целочисленного класса когомологий при гомо-
гомоморфизме 8. Удобно работать также со следующей формой этого
определения. Замкнутая й-форма щ многообразии М называется
целочисленной, если ее интеграл по любому замкнутому ^-мерному
целочисленному циклу в М является целым числом. Эти интегра-
интегралы называются периодами формы.
Пространство CPN снабжается естественной кэлеровой струк-
структурой, которой соответствует каноническая симплектическая струк-
структура на СР^, задаваемая 2-формой йо. Легко проверить, что эта
2-форма представляет образующую в группе H2(CPN, R), являю-
являющуюся образом образующей группы Н2(СР№, Z) при гомоморфиз-
гомоморфизме 8. Следовательно, Qo является целочисленной формой. Ясно,
что необходимым условием существования симплектического вло-
вложения симплектического многообразия (М2п, coi) в (CPN, Qo) яв-
является условие целочисленпости формы соь Оказывается, это усло-
условие достаточно в случае замкнутого многообразия. В работе
VI. Л. Громова содержится следующее следствие.
Следствие I. Если симплектическалг форма на М2п имеет
целочисленные периоды, то ее можно индуцировать из стандартной
'-формы в СР2п (cdimRCP2n = 4n = 2dimAl).
Это означает, что всегда существует симплектическое погруже-
ие многообразия М2п в СР2п. Что можно сказать о существовании
имплектического вложения? Следствие 1 имеет еще и такую-
юрму.
Следствие 2. Если М2п — замкнутое симплектическое мно-
эобразие (компактное) и он — симплектическая структура на
\2п, являющаяся целочисленной 2-формой, то всегда существует
гмплектическое вложение М2п в CP-V для некоторого достаточно
эльшого числа N.
Следствие 2 было отмечено Тишлером как простая комбинация
;зультата Громова с известной теоремой Мозера о стабильности,
риведем здесь эту полезную теорему.
Теорема 2. (Мозер [271]). Пусть Мт — замкнутое многооб-
многообразие и mt (O^C^l) — гладкое семейство невырожденных 2-форм
(или пг-форм) из одного класса когомологий. Тогда существует
семейство диффеоморфизмов Ft:M-^M, 0</<l, такое, что
Эта теорема Мозера-позволяет аппроксимировать построенное
симплектическое погружение симплектическим вложением (в неко-
некоторых случаях, указанных выше).
Существование симплектического погружения М2п в CPN при
условии целочисленности симплектической формы со сформулиро-
сформулировано Громовым в [270]. Как мы отметили, существование симп-
симплектического вложения следует из этого результата, скомбиниро-
скомбинированного с теоремой Мозера. В самом деле (см. [253]), пусть g —
симплектическое погружение М в CPN' при достаточно большом N.
Можем считать, что N достаточно велико для того, чтобы погру-
погружение g можно было сколь угодно близко аппроксимировать вло-
вложением /. Выберем вложение /: М-^СР" так, чтобы форма /*Q0-
была близка к форме ом. По теореме Мозера существует диффео-
диффеоморфизм h многообразия М на себя такой, что h*(f*Q0) — W|. Сле-
Следовательно, r=fh — искомое симплектическое вложение.
Эти результаты были .обобщены Тишлером в [253] в следую-
следующей форме. Оказывается, в некоторых случаях можно ослабить
требования на форму coi, а именно: достаточно потребовать лишь
ее замкнутости и целочисленности (т. е. отказаться от условия
невырожденности).
Теорема 3 (Тишлер). Пусть М — замкнутое компактное
многообразие и со — целочисленная замкнутая 2-форма на много-
многообразии (необязательно невырожденная). Тогда для достаточно
большого N существует симплектическое отображение f : M-^CPN,
такое, что f*(Qo)=cu, где Qo — стандартная симплсктическая
форма на CPN.
Стандартная 2-форма на CPN в однородных координатах
(г0: Z\ : ...: zN) имеет вид
N N
Ц, - { [(TV,) (\\dzkAdzl
N
у » ичфсме 3 не предполагается невырожденность
формы, то ут1Нфждп(ччям еущестпование не вложения, а всего лишь
отображении мишппЛразим "» проективное пространство. Напом-
Напомним еще раз, что люГша симплектическое отображение симплек-
симплектического многообразия является погружением.
Приведем идею доказательства теоремы Тишлера. Искомое
отображение / строится в несколько этапов; /-й этап обознача-
89
ется через ft, 0</<p (p — некоторое число, зависящее от числа
элементов некоторого открытого покрытия компактного многооб-
многообразия М). Выберем fQ:M^~CPn таким, что /o*Qo и ш лежат в од-
одном классе когомологий. Это можно сделать, так как СРп явля-
является 2п-остовом комплекса Эйлеиберга—Маклейна типа /((Z, 2).
Обозначим через da точную форму da = (o— /o*Qo. Для каждой
точки х^М найдем такую ее окрестность Wx, что множество
/о(И^а)с:СР" покрывается симплектической картой на СРп доста-
достаточно малых размеров. Существование симплектического атласа
следует из теоремы Дарбу и явно строится на СР" Тишлером.
Выберем конечное подпокрытие W\, ..., Wp этого покрытия. Тогда
существует набор вещественных функций /;*, 1и, 1^/г^р, носите-
носители которых содержатся в одном из элементов покрытия {№",} и
такие, что
11dhAdt da
Для каждого /, 1^/^р, предположим выполненным индуктив-
индуктивное предположение: существует отображение /,--i : ДО-»-СРя+'-;,.
такое, что
/!_, Q-г/-. =/;q» + ± 2i~;l dhkf\dtk.
Заметим, что отображение fp было бы искомым. Остается про-
провести шаг индукции, т. е. построить отображение // исходя нз ото-
отображения fj_i. На M\Wj положим fj = ifj-U где i: CPn+J "]->-
~*-СРп~!' — естественное включение. Существует симплектическая
карта на СРЯ+/ со значениями в шаре радиуса 1, B"+iR2
Обозначим через ai проекцию шара Bn+i(\) .на шар
dR2<-n+i А\ а через лг проекцию шара В'н/A) на шар
Пусть фх : DX~^BNA) — карта. Определим отображение
gi : Wt-*-Bn+i(\), положив Л1^, = фх//-ь no,q, = hj+\:—П/, и отоб-
отображение fi = (fx~lgi. Через фх обозначено симплектическое коорди-
координатное отображение ц>х: Dx-*-BN (\), DxaCPN (для любого N).
Теорема Мозера о стабильности симплектических форм позво--
ляет аппроксимировать построенное симплектическое погружение
/ : M~*-CPN сийплектическим вложением g : M-*-CPN. Чтобы полу-
получить симплектическое вложение g замкнутого симплектического
многообразия М с целочисленной симплектической формой о>
в CPN, исходя из имеющегося симплектического погружения
I: M~^CPN, аппроксимируем / вложением g0: M-^CPN таким, что
все формы A — t)a + tgo*£~ioN = wi, 0</<1, невырождены. Тогда
по теореме Мозера существует диффеоморфизм /•": М-*-М такой,
что /г*со1 = ыо, т. е. /7*^о*Оол' = ш. Вложение gF : M-*CPN будет
искомым. Теорема доказана. ч.
Приведем еще несколько результатов о симплектических отоб-
отображениях некомпактных многообразий, полученных В. А. Попо-
Поповым (теоремы 4, 5, 6).
Теорема 4. Пусть (М, ы) — произвольное симплектическое
многообразие размерности m = In с точной симплектической формой
90
•w — da. Тогда существует собственное симплекгическое отображе-
отображение (погружение) f : M^-R2N, /*B£Li dP(Ad<7,) = со, где Л: =
' Теорема 5. Пусть (М, со) — произвольное симплектическое
многообразие с целочисленной симплектической формой со. Тогда
существует симплектическое погружение f :M-+CPN, N — m3,
4imM — m = 2n. Существует симплектическое погружение g : AJ->
-*-<СР*"+1, образ которого g(M) содержится в V2n+1 = {Bq, ..., Zn,
Zn+\, ..., z2n+\), существует k^.N, гкФ0} и отображение g:M^-
-+V2N+l — собственное. Тогда g гомотопно вложению.
Доказательство получается некоторой модификацией тео-
теоремы Тишлёра, и мы его здесь опустим. Далее оказывается, что-
справедливо обобщение теоремы Мозера на случай некомпактного
многообразия; это обобщение позволяет строить симплектическое
вложение, исходя из собственного симплектического отображения
(погружения) (В. А. Попов).
Приведем примеры симплектических многообразий.
Теорема 6 (С. В. Матвеев, А. Т. Фоменко). Пусть МА — лю-
любое глпдкое компактное замкнутое ориентируемое трехмерное
многообразие, Р\ — отрезок. Тог-
ди примое произведение M3XD|
MliJltlt'lCII lllMIUU'KrilMl'l'KIIM MIIO-
rtjonini.'uieM, н чш'тностн, любое
KOMiuiKTHoe ориентируемое грех-
Мерное многообразие является
нэокморгетпческой поверхностью
(Т. е, многообразием постоянной
чнерпш) некоторой гладкой га-
мильтоповой системы.
Как мы отмечали, простей-
простейшим примером являются гладкие
двумерные ориентируемые замк-
замкнутые римановы многообразия,
т. е. двумерные сферы с ручками
(рис. 28). В качестве снмплекти-
ческой структуры можно взять
стандартную 2-форму римановой
площади.
Более сложный пример — ко-
касательные расслоения к глад-
гладким многообразиям. Эти расслоения возникают в классической
механике как фазовые пространству механических систем. Если
М — конфигурационное пространство механической системы (ко-
(которое отождествим с некоторым многообразием М, простран-
пространством положений системы), то ее фазовое пространство совпа-
совпадает с кокасательным расслоением Т*М к М. Определим на Т*М
естественную симплектическую структуру. Точкой Т*М является
пара (х, I), где х^М, 1^ТХ*М, т. е. 5 — ковектор в точке х. Про-
Рис. 28
екция p:T*M^f-M определяется так: р(х, |)=х. Слоем проекции
над точкой х является кокасательное пространство ТХ*М.
Построим на Т*М гладкую 1-фор'му а. Пусть а<=Ту(Т*М) —
вектор, касательный к кокасателыюму расслоению Т*М в точке
у^Тх*М. Дифференциал отображения р: Т*М^-М переводит
вектор а в вектор р\а, касательный к М в точке х = р(у) =р(х, £
(рис. 29). Определив 1-форму а равенством а{а)=у{р„а), получь
Of.
i/гпЫ
Рис. 29
ем, что значение формы а равно значению ковектора у ни
р*а. В качестве искомой 2-формы возьмем w = da. . Легко
рить, что эта 2-форма замкнута и невырождена. Следов^.
Т*М превращается в симплектическое многообразие.
Следующий пример — кэлеровы многообразия. Пуст- .
комплексное многообразие, на котором задано эрмитово скалку-
произведение {а, Ь). Рассмотрим co(a, b) =Im(a, Ъ). Тогда
кососимметрическая невырожденная 2-форма. Кэлеровы многоии-
разия задаются тем условием, что м.нимая часть со скалярного
произведения {а, Ь) является замкнутой дифференциальной фор-
формой. Следовательно, каждое кэлерово многообразие является сим-
плектическим (обратное — неверно). Таковы, например, комплекс-
комплексные проективные пространства (см. выше).
Четвертый пример симплектических многообразий особенно
важен здесь для нас, поскольку связан с алгебрами Ли. Это —
орбиты коприсоединенного действия групп Ли. Пусть G — алгебра
Ли некоторой группы Ли @. Напомним, что присоединенным пред-
представлением группы Ли ® на алгебре Ли G называется действие,
AdX Xl @ XG М
ру р
задаваемое формулой AdgX = gXg~l, где
Л й
д
X<=G. Мы счита-
считафру
ем, что группа Ли является матричной группой, поэтому символ
gXg имеет смысл как произведение матриц g, X, g~l. Присоеди-
Присоединенное представление группы индуцирует присоединенное пред-
представление алгебры Ли, а именно: adA- Y= [X, Y).
Для нужд гамильтоновой механики особый интерес представ-
представляет другое представление алгебры Ли, называемое коприсоеди-
ненным. Пусть G* —. пространство, дуальное (сопряженное)
к пространству G, т. е. пространство ковекторов (линейных функ-
ционалов) на алгебре G. Определим коприсоединенное представ'
ление Ad* группы C на G* так: (Adg%)X — £,{Adg—iX). Диффе-
Дифференциал этого представления в единице группы называется ко-
присоединенным представлением алгебры Ли, , а именно:
(ad*xZ)Y=Z([X, У]), где X, YzeG, £e=G*.
Особый интерес для нас будут представлять орбиты коприсо-
единенного представления группы @ на G*..Оказывается, на этих,
орбитах имеется естественная симплектическая структура, в ре-1
зультате чего каждая орбита оказывается симплектическим мно-
многообразием. Отметим, что в случае произвольной алгебры Ли ор-
орбиты представлений Ad* и Ad, вообще говоря, различны (неэкви-
(неэквивалентны). Однако, если на алгебре Ли существует невырожден-
невырожденное скалярное произведение {X, У) такое, что (AdgX, AdgY) = (X, У>
для любого ge @, то присоединенное и коприсоединенное пред-
представления эквивалентны; в частности, они имеют одинаковые ор-
орбиты (при отождествлении G с G*).
Все так называемые полупростые алгебры Ли удовлетворяют
этому условию. Билинейная форма {X, y> = Spur ad.? ady называ-
называется формой Киллинга на алгебре G. Полупростые алгебры Ли
характеризуются тем свойством, что форма Киллинга Невырож-
Невырождена на алгебре G.
Перейдем теперь к построению симплектической структуры на
орбитах коприсоединенного представления. Пусть $^G* — про-
произвольный ковектор. Через О(|) обозначим орбиту этого элемента
при действии группы ©, т. е. O(g)={Adg*g; ge@ } (рис. 30).
Лемма 1. Касательное пространство в точке | к орбите О(|)
состоит из всех векторов вида adx* |, где X пробегает G.
Доказательство. Любой касательный вектор к орбите
О(|) в точке | имеет вид
dt
для некоторого X^G. Пусть в\, ..., еп — базис в G, а е1, ..., еп —
'базис в G*, сопряженный к базису ei, т. е. е'(е/) =б/'. Если
то £ = 2|»е', где & — линейная функция на G*. Получаем v = ]
где
что и требовалось докипать.
Определение 2. Пусть о, ЬеГ^О(^) -т два касательных
вектора к орбите 0A) в точке |. Тогда в силу леммы 1 можно
считать, что векторы а и Ь допускают представление (неоднознач-
(неоднозначное) в виде a — ad*Oil, р = аё^|, где аь b,^G. Положим.
<i){(a, b)=|([ai, bi]). Кососимметрическая 2-форма ш оказывается
замкнутой и невырожденной на орбитах 0A) и называется стан-
стандартной симплектической структурой (формой Кириллова) на ор-
орбитах. Можно проверить корректность этого определения, см.,
например, [5]. Поскольку форма со задает симилектическую струк-
структуру на каждой орбите, то все орбиты коприсоединенного пред-
представления четномерны. Из определения формы легко следует, что
она инвариантна относительно коприсоединенного представления.
ГЛАВА 3
НЕКОТОРЫЕ КЛАССИЧЕСКИЕ УРАВНЕНИЯ
МЕХАНИКИ И ИХ ГАМИЛЬТОНОВОСТЬ
§ 1. Классические уравнения движения трехмерного
твердого тела
1.1. Уравнения Эйлера—Пуассона, описывающие движение тя-
тяжелого твердого тела вокруг неподвижной точки. Рассмотрим
твердое тело, находящееся в поле силы тяжести и движущееся во-
вокруг неподвижной точки О. Для описания движения удобно поль- -
зовать'ся двумя системами декартовых координат. Первая из них бе-
берется неподвижной в объемлющем трехмерном евклидовом прост-
пространстве R3; координаты точки относительно нее обозначаются
х\, у\, Z\. Вторая, подвижная система координат, жестко связана
с твердым телом («вморожена в'него»); координаты точки относи-
относительно нее обозначим х, у, z. Удобно считать, что оси подвижной
(вмороженной в тело) системы координат направлены по главным
осям инерции тела для точки О.
Рассмотрим единичным помор с, направленный но оси zx
неподвижной в проем ранстне < uruwii.i координат. Пусть его коор-
координаты относительно подвижном ечктсмы координат (вращающей-
(вращающейся имеете с телом) (>\ iyr u, |i, у. Ясно, что эти координаты явля-
являются функциями иремони / (рис. 31). Через Р обозначим центр
масс шердого тема и пусть х0, Уо, z0 — его координаты относи-
относительно подвижной системы координат. Так как эта система жестко
связана с телом, то числа х0, у0, z0 от времени не зависят (центр
масс не меняет своего положения в теле относительно вморожен-
вмороженных в него координатных осей). Пусть т — масса твердого тела
И Л, В, С — главные моменты инерции тела относительно точки О.
В силу выбора подвижной системы координат тензор инерции
твердого тела можно записать в виде квадратной диагональной
/А О 0\
матрицы I о В 0 )• Диагональный вид этой матрицы объяс-
\о о с)
няется тем, что оси вмороженной системы координат направлены
по главным осям инерции тела.
Пусть со — вектор мгновенной угловой скорости тела, коорди-
координаты которого относительно подвижной системы координат обо-
обозначим р, q, г. Ясно, что р, д, г являются функциями, времени.
Итак, движение твердого тела описывается шестью функциямиу
Р@. <?@> Г(Й> а@> Р@> т@- Через g обозначим ускорение силы
тяжести. Ясно, что если d — вектор силы тяжести, приложенный
1 Л. Т. Фоменко ■ 97
в центре масс тела, то он направлен вертикально вниз (вдоль оси
Ozi) и имеет вид d ——mge.
Из классической механики известно, что если К — это кине*-
тический момент тела относительно точки О, а М — момент внеш-
внешних сил (в нашем случае — силы тяжести d), то согласно теореме
об изменении кинетического момента имеет место соотношение
dK ,, . „
—— = УИ, выписанное относительно неподвижной системы kooi-
dt
динат хи уи г,. Величины К и М можно вычислить явно. Эти вь
числения мы здесь опустим. Проектируя указанное вектошю^
х
Рис. 31
Рис. 32
уравнение на оси подвижной системы координат х, у, г, получао.
следующие три скалярных уравнения, называемых обычно динп-
мическими уравнениями Эйлера:
A-%- + (C—B)qr = mg(zop—yoy),
С — -rlB-
dt ~^~
Эти уравнения содержат шесть неизвестных функций времен!
р, q, г, а, р, у и шесть постоянных величин А, В, С, хо, Уо, Zo, ■x?
рактеризующих распределение массы тела относительно главны;
осей инерции для точки О. Чтобы замкнуть систему уравнение
к ним следует добавить еще три уравнения, выражающих тсг
факт, что скорость конца единичного вектора е в неподвижно!
системе координат xi, y\, Z\ равна нулю (этот вектор неподвижен,
Проектируя получающееся векторное уравнение на оси подвиг
ной системы координат, получаем три недостающих скалярны
уравнения: ___
da
— qy,
dt
dt
98
Эти уравнения называются уравнениями Пуассона. Полная си-
система всех шести дифференциальных уравнении называется урав-.
нениями Эйлера—Пуассона. Задача их интегрирования весьма
нетривиальна.
Положение твердого тела в R3 в каждый момент времени од-
однозначно определяется положением подвижной системы координат
А", у, z, вмороженной в тело, относительно неподвижной системы.
Чтобы задать это положение, достаточно задать так называемые
углы Эйлера 8, ф, ф (рис. 32). При этом 8 обычно называется
углом нутации, a ty — углом прецессии. Углы Эйлера можно вы-
выразить через введенные выше функции р, q, r, а, р, у. Непосредст-
Непосредственным вычислением устанавливается, что
0=arccosY, 9 = arctg-^-, ty =
pa-,-
«2 -Ь р2
Отсюда видно, что если тем или иным способом найдены ре-
решения уравнений Эйлера—Пуассона p(i), q(t), r(t), a(t), Щ/),
•у@, то приведенные выше формулы задают нам законы измене-
изменения углов нутации 0(t) и собственного вращения ф(/) твердого
тела. Закон же изменения угла прецессии ty(t) определяется квад-
квадратурой из последней формулы (см. выше). Итак, для- описания 1
движения тяжелого твердого тела следует решить уравнения Эй-\
лера—Пуассона. Из теории дифференциальных уравнений извест-
известно, что обнаружение первого интеграла системы позволяет пони-
понизить ее порядок на единицу. Если же обнаружено k функциональ-
функционально независимых интегр.члоп, это позволяет понизить порядок сис-
системы па к единиц. Полому одной из важнейших задач в теории
движения тяжелого твердого тела является поиск достаточного
числа независимых интегралов. Для полного интегрирования
уравнений Эйлера—Пуассона достаточно найти пять независимых
первых интегралов, не содержащих времени, и затем выполнить
еще одну простую квадратуру. Поскольку эта последняя операция
принципиальных затруднений не вызывает, то задача сводится
в основном к поиску пяти независимых интегралов. Оказывается
три из них легко указать:
1) Так как функции a(t), p(tf), у(t) являются координатами
единичного вектора е, то очевидно, что с^+рМ-у2 — 1.
2) Интеграл энергии Ap2 + Bq2+Cr2+2mg(xoa+yo$ + zoy) =
= const.
3) Интеграл площадей Apa+Bqfi + Czy — const.
Эти интегралы выписаны в координатах подвижной системы.
Следовательно, для полного интегрирования уравнений Эйлера—
Пуассона достаточно найти еще два независимых первых интег-
интеграла.
В действительности достаточно указать еще всего лишь один
независимый (четвертый) интеграл (не зависящий от времени),
после чего система может быть полностью проинтегрирована. Ос-
Остановимся подробнее на этом важном обстоятельстве.
4* 99
Напомним известную тео£емц_^Якоби- из теории дифференци-
дифференциальных уравнений. Пусть^задано дифференциальное уравнение
£; — ^ которое можно переписать так: X2dxi—
Х1 (*,, x.t) Хг(хи х2)
—X^dx2 = 0. Хорошо известно, что для нахождения первого интег-
интеграла этого уравнения следует найти такую функцию (так назы-
называемый множитель Якоби) М(хи х2), умножение на которую (на-
(нашего уравнения) обращало бы его левую часть й полный диффе-
дифференциал некоторой функции f(x\, х2), т. е. чтобы выполнялось ра-
равенство М (X2dx\—X\dx2)=df.
В самом деле, если такой множитель существует, то d/ = O
в силу нашего дифференциального уравнения, т. е. /(хь x2)=const
и есть искомый интеграл. Интегрирующий множитель {множитель
Якоби) может быть найден путем решения некоторого дифферен-
дифференциального уравнения.
В самом деле, поскольку df = ——dx. -\ —dx2, то из определе-
dxj dx-i
ния М следует, что —— = МХ„ и —'— = —MX,. Отсюда и из тож-
дхх дхг
дества / = / следует, что ——(МХ1)+—— (УИХ2)=0.
oxidxi дхгдхх dxi дх2
Если множитель М известен заранее, то первый интеграл находится:
по формуле
f (Xj, х2) = \ М {xt, хг) Ха (xv х2) dxt—^ М (h, x.2) Xt (h, x2)dx2 — c
h h
Отсюда следует, что для нахождения первого интеграла / = const
исходного уравнения достаточно решить уравнение -■■. (МХ,) +
д dXl
~\ (МХ2)=0 относительно интегрирующего множителя, причем
дхц
достаточно найти любое частное решение М этого уравнения.
Аналогичная конструкция' проходит и для системы п уравнений
первого порядка —— = X,- (xv ... , хп), 1 ^ I ^ п. Представим эту сис-
систему в виде —~— ... --—'—. Последним (интегрирующим) множи-
Xi Хп
телем Якоби для этой системы будем называть функцию М(хх, ... ,хп)г
являющуюся одним из решений уравнения
Теорема Якоби. Если для системы дифференциальных
уравнений -*-1- — ... = —~ известны последний множитель
■ х1 хп
М(х{, ..., хп) и п—2 первых интеграла системы, т. е. {з(х\, ..
..., xn)=const, ..., fn(X[, .... x,,)=const, то заменой переменных
У\=хи У2—х2, yz=h, •••> Уп=]п исходная система уравнений при
100
водится к уравнениям
—— =
= —^2- известным интегрирую-
щим множителем М(у\, ..., уп), который алгоритмически выра-
выражается через известные п—2 первых интеграла /з, ..., fn и функ-
функцию М.
Поскольку это явное выражение нам в дальнейшем не потре-
потребуется, то мы его здесь опустим. Таким образом, общий случай
сводится к случаю уравнения для двух переменных, который ин-
интегрируется описанным выше приемом. Вернемся теперь к ана-
анализу уравнений Эйлера—Пуассона. Интегрирование этих уравне-
уравнений, очевидно, эквивалентно интегрированию системы
dp
dq
dr
, da , dp _fi, dy
где
q'=-±-(mg(xoy-zoa)-(A-C)rp),
a
r' -
a'=r-r$—qy, p'--=pv— ro, y' = qa—pp.
Эту систему можно представить,в следующем каноническом
ниде:
dp dq _j_ dr _ da dp dy _
~~Г~~~~~"~Г~~~~~~
,,
Как было указано выше, эта система всегда обладает тремя неза-
независимыми первыми интегралами:
Ар2 + Bq% + Сг* + 2mg (хоа + у0Р + гоУ) = ^ (= const),
Ара + 5<7Р + Cry = с2 ( — const),
Составим теперь уравнение для последнего интегрирующего
множителя М:.
dp
dq
op
dy
dr
да
101.
Из явных формул, задающих функции р', q', г', а', {5', у' (см.
выше) как функции от переменных р, q, r, а, р, у, легко получаем
dp' dq' дг' ■ da' д[У ду' п
— _ — — .._ —. у
dp dq дг да dfi dy
Поэтому уравнение для М заведомо удовлетворяется, если поло-
положить Л1==1. Итак, мы нашли одно частное решение этого уравне-
уравнения и можно считать, что М=\ и есть последний множитель урав-
уравнений Эйлера—Пуассона.
Следовательно, по теореме Якоби, для сведения этих уравнений
к квадратурам достаточно знать лишь четыре (из пяти) первых
интегралов, т. е. нужно добавить к трем уже известным квадра-
квадратичным интегралам еще один дополнительный четвертый интеграл.
Поискам этого четвертого интеграла посвящено много работ
крупных математиков. Хотя в общем случае он не найден, однако
многие его свойства (в тех случаях, когда его существование
можно ожидать) удается выяснить. В некоторых случаях (для
специальных форм твердого тела) четвертый интеграл можно
указать явно. При этом четвертый интеграл можно искать в раз-
разных классах функций: аналитических, гладких и т. п.
Частные случаи, когда четвертый интеграл можно указать, ха-
характеризуются ограничениями на форму твердого тела, т. е. на
постоянные А, В, С (моменты, инерции) и Хо, у0, zQ (координаты
центра масс тела). Перечислим некоторые из этих частных слу-
случаев.
1.2. Интегрируемые случаи Эйлера, Лагранжа и Ковалевской.
1) Случай Эйлера. Он характеризуется тем, что тело произ-
произвольной формы предполагается закрепленным в его центре масс,
т. е. Хо = г/о = Zo = 0 (рис. 33). В этом случае уравнения Эйлера
принимают вид
+ (CB)qr Q, B%
at at
Умножая их соответственно на Ар, Bq, Cr и складывая, получаем,
очевидно, искомый четвертый интеграл A2p2+B2q2 + C2r2 =
= с4( = const). Уравнения Эйлера интерпретируются как гладкое
векторное поле в евклидовом пространстве R3 переменных р, q, r.
Так как р, q, r — это координаты вектора со мгновенной угловой
скорости в теле, то интегральные траектории уравнений Эйлера
описывают нам эволюцию вектора угловой скорости со временем
(относительно системы координат, вмороженной в тело).
Уравнения Эйлера имеют два первых интеграла: Ap2 + Bq2 +
+ Cr2 = const и А2р2+B2q2+ C2r2 = const. Для исследования траек-
траекторий системы удобно перейти к рассмотрению вектора кинетичес-
кинетического момента К, связанного с вектором со угловой скорости прос-
102
(л и и \
О В О I — оператор
О О С/
инерции, т. е. диагональная матрица, собственные числа которой
совпадают с моментами инерции. Тогда уравнения Эйлера могут
быть записаны в терминах кинетического момента следующим
образом: -- [К, со], где К = Н(ы) и через [,] обозначено век-
векторное произведение векторов в R3. Указанное дифференциальное
уравнение можно рассматривать, конечно, и как уравнение отно-
Рис. 33
Рис. 34
ительно вектора угловой скорости со, так как оператор h обратим
в случае общего положения, когда все три главных момента
1нерции тела отличны от нуля). Так как <o = fo~1(/(), то /г(со) =
- | /г (со), со], или (a = h-l[h((a), to].
Если декартовы координаты вектора кинетического момента К
шозначить через (ku k2, k3), то уравнения Эйлера примут вид
где
—В
ВС
. Тогда указанные" выше два первых
' * СА '
квадратичных
штеграла уравнений Эйл>ера запишутся так:
—i-
-i
-
+ —— — const и k\
k2 -!- k\ -- const.
Первый из них означает закон сохранения энергии, а второй —
:акон сохранения момента. Таким образом, вектор кинетического
ломента K(t), двигаясь вдоль интегральных траекторий вектор-
103
ного поля, изображающего уравнения Эйлера, движется в дейст-
действительности по траекториям, получающимся как пересечения сфе-
сферы и эллипсоида (рис. 34),
Для определенности можно фиксировать эллипсоид и менять
радиус сферы. Качественная картина траекторий показана на
рис. 34. Среди них следует отметить шесть точек — концы шести
полуосей эллипсоида. Это отдельные траектории уравнений Эйле-
Эйлера. Этим шести положениям вектора .кинетического момента со-
соответствует постоянное значение вектора угловой скорости, на-
направленного вдоль одной из осей инерции тела, причем угловая
скорость со при этом остается все время коллинеарной вектору
кинетического момента. Таким образом, здесь тело вращается
с постоянной угловой скоростью вокруг неподвижной в прост-
пространстве оси инерции тела. Движение тела, при котором вектор
угловой скорости постоянен, в классической механике называется
стационарным вращением. Таким образом, из существования двух
указанных выше первых интегралов следует такой результат:
твердое тело, закрепленное в своем центре масс, всегда допуска-
допускает стационарное вращение вокруг любой из трех своих осей
инерции.
Эти вращения отличаются друг от друга с точки зрения их ус-
устойчивости. Можно проверить, что стационарные решения K(i),
соответствующие большей и меньшей осям инерции (в том слу-
случае, когда все моменты инерции попарно различны), устойчивы по
Ляпунову, а решение K(t), соответствующее средней оси, неустой-
неустойчиво.
В самом деле, как видно из рис. 34, при малом возмущении
начальных данных около большой, и малой осей интегральная
траектория уравнений Эйлера остается малой замкнутой кривой
(окружностью), следовательно, стационарное решение устойчиво.
В случае средней оси малое возмущение стационарного решения
заставляет конец вектора кинетического момента двигаться по
замкнутой траектории «большого диаметра», в результате чего
вектор К(t) быстро удаляется от средней оси эллипсоида
(рис. 34).
Таким образом, в случае Эйлера мы получаем довольно полное
описание движения твердого тела вокруг закрепленного центра
масс. Сделаем полезное для дальнейшего замечание. Твердое тело
в случае Эйлера является механической системой, конфигурацион-
конфигурационным пространством которой является группа ортогональных соб-
собственных вращений пространства R3, т. е. группа SOC). Как мы
увидим далее, эта ситуация является частным случаем более об-
общих «групповых систем», являющихся многомерными аналогами
уравнений Эйлера и также допускающих полное интегрирование
2) Случай Лагранжа. Он характеризуется тем, что А — Б
и хо = уо = О. Это означает, что мы имеем дело с.осссиммстричным
твердым телом {волчком), поэтому обычно говорят, что случай
Лагранжа — это случай симметричного волчка. Другими словами
■симметричный волчок (или волчок Лагранжа) -~- это твердое тело
104
чллипсоид инерции которого является эллипсоидом вращения,
центр тяжести лежит на оси вращения (рис. 35).
В этом случае последнее из уравнений Эйлера приобретает вид
г = 0. Следовательно, четвертый искомый интеграл устроен особен-
особенно просто и имеет вид r = const. Движение волчка Лагранжа мо-
может быть описано весьма детально, например, в терминах углов
Эйлера Э, ф, г|л. В частности, наклон 0 оси волчка Лагранжа ме-
меняется периодически по времени между двумя предельными зна-
значениями Gmin и Этах (рис. 36). Если рассмотреть две параллели,
Рис. ;)Г)
Рис. 36
отвечающие углам бпи,, и Этах, то между ними возникает полоса,
в которой и движется ось волчка. Периодическое изменение "угла
О называется нутацией. Изменение угла <р называется прецессией.
Следовательно, окончательное движение волчка Лагранжа состоит
из вращения вокруг собственной оси, нутации и прецессии. Геомет-
Геометрические свойства этих движений см., например, в [5].
3) Случай Ковалевской. Этот важный случай интег-
интегрируемости, как и случай Эйлера и Лагранжа, приобрел в послед-
последние годы особое значение, поскольку были обнаружены многомер-
многомерные аналоги (см., в частности, обзор С. П. Новикова [104], ра-
работы А. М. Переломова).
Случай Ковалевской характеризуется тем, что А=В = 2С и
//о== zo = O. Уравнения Эйлера приобретают в этом случае вид
cy', r = —cp,
где постоянная с имеет вид с=-—mgxQ, где С — третий момент
инерции. Умножая второе уравнение на i и складывая его с пер-
105
вым, получаем 2 (p + i</) =—ir(p + iq) +icy. Рассмотрим те-
dt
перь два первых уравнения Пуассона: a — rfi—qy, |3 = ру—Га- ^м"
ножая второе уравнение на i и складывая с первым, получаем
(а + Ф) = —ir(a-\-i$)-riy(p + iq). Исключим из двух полу-
dt
ченных нами комплексных уравнений величину у..Для этого умно-
умножим первое уравнение на p+iq, а второе — на —с, "после чего
сложим. В результате получаем
[(p
dt
Это уравнение, очевидно, переписывается в следующем виде:
JL In [(р + iqf-c (a + Щ = - ir.
Аналогичным образом, только заменив умножение на i умноже-
умножением на —I, получаем уравнение lii[(/?—iqJ—c(a—ф)] — ir.
Складывая эти два последних уравнения, получаем тождество
at
*
Следовательно, мы получили четвертый интеграл, который можно
записать так: {(p + iqJ — c(a + i$] ■ [(р — iqJ — c(a — ip)]=const,
или (p2—q2—caJ+ Bpq—c$J = const.
Во Всех трех указанных случаях (Эйлера, Лаграпжа, Кова-
Ковалевской) задача сводится к квадратурам. Общее решение урав-
уравнений Эйлера—Пуассона выражается в случаях Эйлера и Лаг-
ранжа в эллиптических функциях, а в случае Ковалевской — в ги
перэллиптических функциях (см., например, [8]).
К интегрируемым случаям относится также так называемьн
случай Горячева—Чаплыгина, хотя здесь интегрируемость имев'
место лишь на одной поверхности уровня.
1.3. Общие уравнения движения трехмерного твердого тела
• Движение твердого тела в R3 под действием различных сил опи
сывается во многих задачах классической механики следующим;
общими уравнениями: К= [К, а] + [е, и], ё.— [е, го], где /( -
кинетический момент тела, ы — угловая скорость тела, а вектор!
е и и определяют физическое содержание задачи и зависят о
,г - ' д}
условии движения твердого тела. Удооно считать, что со = —
д]
и « — , где Я (К, е) — некоторая известная функция наев1
де
лидовом пространстве R6 = R3(K) XR3(e). Здесь каждый из вект(
ров Кие меняется в трехмерном пространстве R3(/() и R3(£
соответственно. Как ча-стный случай, получаем уже рассмотреннь
нами выше уравнения движения твердого тела с закрепление
.106 .
точкой в поле силы тяжести. В самом деле, пусть е — единичный
нсктор, направленный по вертикальной оси z, a u = mr — произ-
произведение массы тела пг на радиус-вектор г центра масс. Полная
энергия, т. е. функция Н, имеет тогда следующий вид:
Н = — (К, /г1 (/С)} +т (г, е). Здесь {,) — обычное евклидово
скалярное произведение в R3, a hrx — положительно определенный
самосопряженный оператор. Уравнения движения тела запишутся
теперь так: h (ш) = [h (ш), ш]+ш[е, г], ё=\е, со]. Сравнивая их
с уравнениями" п. 1.1, мы видим, что это в точности уравнения
Эйлера—Пуассона движения тяжелого твердого тела с закреплен-
закрепленной точкой. Так как h — самосопряженный оператор, то в некото-
некотором орторепере, связанном с вращающимся телом, он приводится
к диагональному виду и тогда его матрица приобретает вид
К
0
0
0
К
0
0
0
А.
Собственные направления матрицы h называются осями инерции
тела, а собственные значения hu h2, /г3 — главными моментами
инерции тела. В этом случае уравнения движения содержат шесть
параметров: hu h2, hz и mx0, my0, mz0, где r= (x0, yQj z0) — радиус-
вектор центра масс тела.
Приведем еще один важный пример. Возьмем в качестве функ-
функции Н следующую положительно определенную квадратичную
форму на шестимерном прострннстве Rw — R:i(K) XR3(e):
II (К, .-) -j(AK, K)-\ (/Ж,' е) + ±-(Се,е).
Тогда выписанные выше общие уравнения превращаются в так
называемые #£08Н£нця Кирхгофа^ описывающие движение твер-
твердого тела в идеальной безграничной жидкости. При этом векторы
дн , . „
с и и = обыч1ю называются импульсивной силой и импуль-
импульде
сивным моментом соответственно. Так'как матрицы А, В, С сим-
симметричны, то, не ограничивая общности, можно считать, что
матрица А уже приведена к диагональному виду, т. е.
А =
При этом, конечно, остальные матрицы В и С отнюдь не обязаны
диагопализироваться. * ' -
Следовательно, в общем случае квадратичная форма Н (пол-
пая энергия тела) зависит от 15 вещественных параметров —
коэффициентов матриц А, В, С. Если накладывать па тело различ-
различные ограничения (типа симметрии тела и т. п.), то число пара-
107
cl
0
0
0
C2
0
0
0
с.
15тров будет, конечно, уменьшаться. Например, если тело имеет
язи взаимно ортогональные плоскости симметрии (таким свойст-
свойством обладает, например, трехосный эллипсоид), то 6 = 0,
С =
§ 2. Гамильтоновость уравнений движения тришерного
твердого тела
Напомним, что движение твердого тела в RJ описывается урав-
уравнениями К= [К, со] + [е, и]', ё= [е, со], где К. — кинетический мо-
момент тела, со — угловая скорость тела, а векторы е и и опреде-
определяются физическим содержанием задачи, описывают взаимодей-
взаимодействие внешних сил. Указанные общие уравнения имеют следующие
три интеграла: /i = //, где полная энергия Н имеет вид
H=-j-(K, h-1 (К)) + ш (г, е) (см. § 1, п. 1.3), затем f2 = (K, е)
и }з = (е, е). Рассмотрим, например, задачи о движении тяжелого
твердого тела вокруг неподвиокной точки. Тогда е — единичный
вектор, направленный, по вертикальной оси z, и, следовательно,
третий интеграл /з имеет вид 1ъ — (е, е)=1.
Общие уравнения движения твердого тела задают векторное
поле на шестимерном пространстве R6 = R3(/() XR3(e). Оказывает-
Оказывается, это поле гамильтоново на совместной поверхности уровня двух
интегралов /2 = с2 = const и /з = с3 = const относительно некоторой
естественной скобки Пуассона (С. П. Новиков). Это позволяет
применить к этой системе богатый аппарат исследования общих
гамильтоновых систем.
Рассмотрим, следуя [67], совместную поверхность уровня М2з
двух интегралов f2 и /з, т. е. Л42з={/2 = С2, /з = с3>0}. Эта поверх-
поверхность является четырехмерным подмногообразием в R6. Более то-
того, ее топологическая структура легко описывается.
Лемма I. Поверхность уровня М2з диффеоморфна (ко)ка-
(ко)касательному расслоению двумерной сферы.
Доказательство. Запишем в R5{K, e) два квадратичных
уравнения: (е, e) = c3=const>0 и (К, e) = c2 = const. Так как
вектор е меняется в R3(e), то первое уравнение означает, что его
конец пробегает все точки стандартной двумерной сферы радиуса
Ус3. Второе уравнение можно интерпретировать так. Отождествим
R3(K) с R3(e), тогда уравнение (К, е) = с2 превращается при
каждом фиксированном е в уравнение двумерной евклидовой
плоскости, ортогональной вектору е и удаленной от начала коор-
координат на одну и ту же величину (не зависящую от направления
вектора е), см. рис. 37. Меняя е, мы получаем множество плоско-
плоскостей, касательных к двумерной сфере фиксированного радиуса.
Следовательно, два вектора К, е, удовлетворяющих указанным
108
уравнениям, однозначно определяют некоторый вектор, касатель-
касательный к двумерной сфере, что и доказывает лемму, так как каса-
касательное расслоение к сфере S2 определяется как четырехмерное
многообразие, точками которого являются пары вида (е, |), где
е — точка на сфере, а | — произвольный вектор, касающийся сфе-
сферы в точке е (рис.38). _ -
Рис. 37
Рис. 38
Определим теперь на пространстве R6(/(, е) некоторую опера-
операцию {,} (из которой впоследствии мы изготовим скобку Пуассона
на поверхности уровня М2з). По определению будем считать, что
если К— (ki, k2, h) и е—(ёи е2, ег), то
{ku ех} = {к2, e2} = {h, e3} = 0, {ки еи} = —е3.
('.(Kiiiii'TC1!чующая квадратная таблица, задающая операцию
(,} па ofipji tyioimix ki и еи имеет вид
1 *l
к
кг
*з
ч
е3
0
0
«3
-,2
^2
-*з
0
*i
-в.
0
*
кК
кг
-к,
0
е2
0
0
е3
-Ь
0
0
0
ег 1 ез
-,з
0
0
0
0
«2
—е1
0
0
0
0
Легко видеть, что эта операция задает на пространстве Я6(/С,_
е) структуру алгебры Ли, причем эта алгебра изоморфна алгебре
Ли группы движений трехмерного пространства R3. Другими ело-'
вами, она изоморфна полупрямой сумме двух подалгебр Ли: трех-
109
мерной подалгебры Ли R3(/(), изоморфной алгебре Ли группы
SOC) вращений R3, и трехмерной абелевой подалгебры Ли R3(e),
изоморфной алгебре Ли группы сдвигов (трансляций) в R3. При
этом подалгебра Ли-R3(/(). представлена на подалгебре R3(e)
стандартным образом.
Считая теперь операцию {,} билинейной, косрсимметрической
и удовлетворяющей правилу Лейбница дифференцирования про-
произведений функций, мы можем распространить ее на пространство
всех гладких функций, заданных на R6(K, e). Можно проверить,
.что так определенная операция удовлетворяет тождеству Якоби.
Итак, теперь мы можем вычислять «скобку Пуассона» любой па-
пары функций па R6(K, e). Можно проверить (см. [67]), что урав-
уравнения движения твердого тела представляются теперь в виде «,=
= {*,,//}, ei = {eitH}, i= 1,2,3.
Однако построенная выше операция обладает одним сущест-
существенным недостатком: она вырождена. Действительно, функции
(интегралы) /2 и fa коммутируют (в смысле нашей скобки) с лю-
любой гладкой функцией g(K, e). Для того чтобы убедиться в этом,
достаточно проверить, что функции f2=(K, е)=Е^г^г и !з = (е,
e) = Ze,-2 коммутируют со всеми образующими k,, а. Подсчитаем,
например, скобку {/2, k^}=-'L{kiei, k1} = 2 {kL, k^e^ +fe£ {eit k^} —
= k3e2—k2e3+k2e3—k3e2 = 0. Аналогично проверяется, что {f2, k2} =
= {/2, *8} = 0.
Далее вычислим {/2, el}^2{kiei, e1}=2{ki, e^ei + 2 ki{et, et}=
= 2{ki, e1}e£=e3<?2—e2ea = 0. Аналогично {/2, е2}~{/2, е3} = 0. Кроме
того, {/„ e;} = 2{e?, e,) =0, {/3, *1} = 2{e?, *x> - 2e^8-2вле2 - 0 и
аналогично {/3, k2}--={fa, ka} — 0.
Следовательно, построенную выше вырожденную скобку Пуас-
Пуассона можно сузить (ограничить) на совместную поверхность уров-
уровня М2з интегралов /2 и f3. Можно убедиться, что в результате на
пространстве функций, определенных на многообразии М2з, воз-
возникает уже невырожденная скобка Пуассона {,}'.
Вычисление этой скобки можно описать еще и так. Пусть f и
g — гладкие функции на поверхности уровня Af23. Продолжим их
гладким образом до функций /' и g', заданных на всем простран-
пространстве R6(K, e). Положим по определению {/", g}'(x)={f, g'}(x), где
х^М2з- Такое определение скобки {,}' корректно, т. е. не зависит
от способа продолжения функций / и g до,функций f и g'. Итак,
скобка Пуассона {,}' задает на поверхности Л42з структуру сим-
плектического многообразия.
Теорема 1. (С. П. Новиков, И.-Шмельцер [105]). Уравнения
движения твердого тела R= \K, со] + [е, и], ё=[е, со] можно
представить на совместной поверхности уровня M2i двух интегра-
интегралов f2 и /з в гамильтоновом виде f = {f, h}', где h — сужение функ-
функции Н на поверхность М2з-
В том случае, когда второй интеграл f2 равен нулю, эта кон-
конструкция принимает более простой вид, т. е. на поверхности
Л4°2з— (/2=0, f3=const). Мы опишем ее здесь, следуя работе
В. В. Козлова [67].
НО
Пусть /2=0 и К= [р, е]. Если /з>0 и fe={K, e) = 0, то вектор
р существует и определен однозначно, с точностью до сдвигов
вдоль вектора е. Положим далее М(р, е)=Н([р, е], е).
Теорема 2 ([67]). Функции pit) и e(t) удовлетворяют ка-
г дМ • дМ
ноническим и равнениям Гамильтона р = , е = .
де др
Векторы е, р, К допускают простую интерпретацию, а именно:
е — радиус-вектор точки в R3, р — ее импульс, К — кинетический
момент (взятый с противоположным знаком). В случае /2=7^=0 за-
замену переменных {К, е)-*-(р, е) следует производить более дели-
деликатно (см. работу Новикова, Шмельцера).
„ о т, „ • дМ дН дК
Доказательство теоремы 2. паидеме= = . =
др дК др
= [е, о]. Поскольку К = [р, е], то
е] = - [^-, е]+[р, [е, о,]),
= +.и + 1<а,Р1
де де дК де L И1
Отсюда
К=-[и, е]+[е, К р]]+[р, [е, <о]] = [К, со] + [е, и],
что и завершает доказательство.
Гамильтоиовость уравнении дпижеиия твердого тела на по-
поверхности уровня Мгз интегралов /'., н f;) имеет глубокий алгебраи-
алгебраический смысл. В дальнейших глпипх мы увидим, что этот факт
справедлив и для различных многомерных аналогов уравнений
движении тверд(I'о тела и именно благодаря ему удается проин-
тегриронать по Лиуииллю соответствующие многомерные уравне-
уравнения движения. /
§ 3. Некоторые сведения о группах и алгебрах Ли,
необходимые для гамильтоновои геометрии
В этом параграфе систематизируем уже известные (и некото-
некоторые другие)-классические факты из теории групп и алгебр Ли.
Как мы увидим дальше, в современных вопросах гамильтоно-
гамильтоновои механики и геометрии часто возникают системы, обладающие
теми или иными, вообще говоря, некоммутативными группами
симметрии: Поэтому нам потребуются некоторые понятия, которые
для удобства читателя мы собрали вместе в настоящем парагра-
параграфе. Доказательства мы опускаем, отсылая читателя к учебной ли-
литературе, например [53].
3.1. Присоединенное и коприсоединенное представления, полу-
полупростота, система корней и простых корней, орбиты, каноническая
симплектическая структура. Пусть @ —группа Ли и иеТе @—
вектор, касательный в единице. Разнесем вектор v с помощью ле-
■вых сдвигов по всей группе © . Получим векторное поле на груп-
111
пе. Более точно, для каждого aeS положим La(g)—ag. По-
Поскольку La^1 = La-s то левый сдвиг является диффеоморфизмом
группы. Положим £a= (dLa)rv. Построенное векторное поле яв-
является левоинвариантным, т. е. 1аь= {dLa)bb,b для любых а, £>е@.
Линейное пространство всех левоинвариантных векторных по-
полей, очевидно, отождествляется с алгеброй Ли G данной группы
Ли. Операцией здесь является коммутатор векторных полей.
Если | — левоинвариантиое векторное поле на группе, то оно
порождает некоторую глобально определенную группу диффеомор-
диффеоморфизмов. Однопараметрической подгруппой в группе Ли назы-
называется гладкий гомоморфизм g : R1—>-<§. Легко проверить, что ле~
воинвариантное поле | порождает однопараметрическую под-
подгруппу.
Итак, алгебру Ли группы Ли можно определить одним из че-
четырех эквивалентных способов: 1) множество однопараметриче-
ских подгрупп, 2) множество касательных векторов в единице
группы, 3) множество левоинвариантиых векторных полей, 4) мно-
множество левоинвариантных R'-действий.
Можно определить отображение . exp:G-v@, при котором
exp(tX) : R'-vjp, задает однопараметрическую подгруппу с векто-
вектором скорости Jf в единице группы.
Определение 1. Группа & действует еама на себе посред-
посредством сопряжения (a, b)-+abcrl. Это действие индуцирует линей-
линейное действие группы на ее алгебре Ли Ad :@-vGL(G), которое
называется прцг.пр.диненным представлением группы. При этом
AA ' '
g(g)
Присоединенное представление труппы индуцирует присоеди-
присоединенное представление ее алгебры Ли, а именно ad = d(Ad)e: G-v
-vHom G. Имеет место равенство ad* Y= [X, Y], где [, ]-—ком-
]-—коммутатор в алгебре Ли. Для нужд гамильтоновой механики нужно
другое представление. Пусть G* — пространство, дуальное к G,
т. е. пространство линейных отображений /:G-vR. Определим
коприсоединенное представление Ad* : @ -+GL(G*), (Adg* f)X=
= f(Adg—iX). Дифференциал этого представления называется ко-
присоединенным представлением алгебры Ли: ad* : G->Hom G*.
Имеет место равенство: (ad** f)Y=}( [X, У]), X, Y<eeG, G*
Иногда adx*/ будем обозначать через {X, /}. Здесь X^G,
(Не путайте со скобкой Пуассона!)
Мы будем интересоваться орбитами коприсоединенного пред-
представления. Как мы уже отмечали, на них имеется естественная
симплектическая структура и любое однородное симплектическое
многообразие с инвариантной 2-формой можно реализовать в виде
орбиты коприсоедииенного представления в некоторой алгебре Ли.
Заметим, что орбиты присоединенного и коприсоединенного пред-
представлений в общем случае различны. Приведем простейший пример,
иллюстрирующий это явление. Пусть О—группа афинных преобразо-
преобразований вещественной прямой х -*■ ах + Ъ, афО, а, Ъ eR. Эта группа
/ о, Ь \ г,
допускает матричную реализацию: . Легко проверяется, что
112
о o
cue,—
*н?
2
О
o o
Из явного вида присоединен-
то Ada E =
.0 0
ного представления имеем |i = tii, Ц2=Ъ^1— Ъаь Следовательно,
орбиты устроены так, как показано на рис. 39. Исследуем теперь
орбиты коприсоединенного представления. В алгебре Ли G выбе-
/ 1 0\ / 0 1\
рем базис ех = 1 , е2— , а в G* — сопряженным
базис /i, f2, где /,(e,) ==б,;. В этом базисе зададим координаты хи
х2. Простые вычисления показывают, что
Ad
(Г
поэтому орбиты устроены так, как показано на рис. 40. В частно-
частности, представления Ad и Ad* этой группы неэквивалентны.
■•«•»»>(
. Рис. 39
Рис. 40
Если на алгебре Ли существует симметричное невырожденное
скалярное произведение (,) такое, что (AdgX,'AdgY) = (X, У),
то присоединенное и коприсоединенное представления эквивалент-
эквивалентны, т. е. они имеют, в частности, одинаковые орбиты. Все так на-
называемые полупростые алгебры Ли удовлетворяют этому усло-
условию. Билинейная форма Spurad.tady (или Re Sp'ur ad^ ady) на-
называется формой Киллшга на алгебре Ли. Обозначим ее просто
через {X, Y). Полупростые алгебры характеризуются тем, что эта
форма невырождена.
Напомним вкратце структурную теорию комплексных полу-
иростых алгебр Ли. Максимальная абелева подалгебра TczG та-
такая, что ad/i для всех элементов h^T является полупростым ли-
линейным преобразованием G (т. е. приводится к диагональному
ниду), называется подалгеЬрой.Картана. Если XeG — произволь-
произвольный элемент, то через Т(Х) обозначим подпространство коммути-
коммутирующих с X элементов в G. Элемент X называется регулярным,
Рис. 41
если dimT(X) минимальна. Если X — регулярный элемент, то
Т(Х)—подалгебра Картапа.
Регулярные элементы образуют в G открытое всюду плотное
подмножество. Если алгебра Ли полупроста, то любая ее подал-
подалгебра Картана коммутативна.
Пусть дана" нолупростая алгебра Ли над полем комплексных
чисел. Фиксируем некоторую подалгебру Картана Т. Линейная
форма, a(h) на Т называется корнем, если существует такой эле-
элемент Ea<=G, ЕаФ0, что \h,
Ea] = tt{h)Ea для любого hdT.
Пусть Ga — собственное подпро-
подпространство, отвечающее элементу*
а. Тогда G=r®Za^oGa, где знак
Ф обозначает прямую сумму ли-
линейных подпространств. В полу-
полупростой алгебре Ли все подпро-
подпространства Ga одномерны при
афО (над полем комплексных
чисел).
Известно, что [Ga, Gf]czGa+Si,
т. е. [Еа, Еь]==ЫацЕп+р. Если
а + р=т^0, то E.j, и £е ортогональ-
ортогональны относительно формы Киллинга.
Векторы Па и Е-а, напротив, ие-
ортогональиы (рис. 41). Ограни-
Ограничение формы Киллинга иа картановскую подалгебру невырожде-
невырождено. Если r=dimcT (число г называется рангом алгебры Ли), то
существует г линейно независимых корней алгебры Ли (относи-
(относительно Т). Полное число всех корней, вообще говоря, больше г.
Поэтому множество всех корней не является линейно независи-
независимым. Если а, р, а4 |3 — корни, не равные пулю, то [Ga, Gf,\=Ga+i.
Единственные корни, пропорциональные корню аФО, это 0, ±а.
Корни можно представить векторами Н'а^Т. Так как форма Кил-
Киллинга невырождена на Т, то для каждого аеГ* (где Т* — про-
пространство, дуальное к Т) существует единственный вектор Н'а^Т
такой, что u(h)={h, Ha') для всех йеГ, Тогда если а^О, то
[£«, Х]={Еа, Х)На' для X<=G_a и (а, а>^0. Через ТоаТ обозна-
обозначим подпространство в Т, порожденное всеми векторами //«' с ра-
рациональными коэффициентами. Ясно, что Го является «веществен-
«вещественной частью» плоскости Т. Оказывается, что dirriQ 7=dimc T =
1
= — dimR7\ Здесь Q — поле рациональных чисел (не путайте с
прежним обозначением алгебры кватернионов!).
Далее, ограничение на То формы Киллинга положительно опре-
определено и принимает рациональные значения; a(li')eQ при любоу
й'еГс В частности, а(п')—вещественное число, если h'^Tu
В дальнейшем через А мы обозначим множество ненулевых кор-
корней алгебры Ли. Пусть Н\,...,НТ — какой-нибудь фиксированный
базис в То. Если К, ц — две линейные формы па 70, то говорят, чт(
114
\;>\i, если k(tti)=i\(tli) при t=i, z,...,n и A.(nn+l)](+)
Напомним, что если к, ц^корни, то Х(п'), ц (ft') — вещественные
числа для любого Л'еГ0. Таким образом, на множестве А возни-
возникнет естественное линейное упорядочение.
Корень аеД называется положительным, если а>0, т. е.
u(#i)=0 при t=l, 2,...,п и а(Яп+1)>0. Положительность корня
и означает тем самым, что первая ненулевая его координата по-
положительна. Линейная упорядоченность вводится неоднозначно.
В дальнейшем будем предполагать, что базис Н\,...,НГ (где г=
ранг алгебры) фиксирован. Обозначим множество положительных
корней через Л1. Тогда A = A+UA~, где A+(]h~ = 0, причем суще-
существует взаимно однозначное соответствие между Л+ и Д~, уста-
устанавливаемое инволюцией а-*—а. Ясно, что если аеД+, то —аЕ
е=Д-.
Положительный корень а называется простым, если его. нельзя
представить в виде суммы двух положительных корней. Если г=
= ранг G = dimc Т, то существует ровно г простых корней ai,..,
..., а,-, образующих базис в Т над С и базис в То над Q. Кроме
того, каждый корень |3geA можно представить в виде p = 2m,a;,
где т, — целые числа одного знака. Если т,^0, то PgeA+; если
tn^O, то р^А~. Система простых корней а\,...,аг обычно обо-
обозначается через П. Система А однозначно восстанавливается по
системе П.
Положим V+=Sa>oGa, V-=2a<oGa, тогда G = T®V+®V~.
Для дальнейшего в алгебре Ли фиксируем базис специального
вида. Произвольный базис Ни...,Н,- в Т (над С) порождает ба-
базис На в То (над Q) и в Т (над Q). Этот базис дополним векто-
векторами E^Ga, a^O, аеД. Векторы Еа можно выбрать так, что
(Еа, E-a)=i. Тогда операция коммутирования в алгебре G за-
задается так:
[ft, Ea]=a{h) Ea, hesT (a(ft) = Q, если ft GE To),
afi£«-P> a + ^ 0—корень,
'Qf ■ а + р^0--не корень,
(<ft, H'a)=*(h), he^T.
Векторы Еа можно выбрать так, что JVaB = JV_a-,_B. Постоянные
Л^ац можно считать вещественными (после соответствующей нор-
нормировки векторов Еа).
Рассмотрим коприсоединенное представление Ad* группы Ли,
т. е. Ad*: ®-±GL(G*), где G* — пространство, дуальное к алгеб-
алгебре Ли. Если .f^G*, то множество 0([)={Adg* f, geE®} назы-
называется орбитой, проходящей через точку f.
Как мы уже отмечали, на орбитах коприсоединенного пред-
представления любой группы Ли имеется естественная симплектиче-
ская структура (форма Кириллова), инвариантная относительно
коприсоединенного представления. Остановимся па этом по-
подробнее.
115
^ \l ) pd 1Ш1фШ.иСДШ1СППи1 U ф
касательное пространство к ней имеет вид TfO(f) ={adx*/,
geG}c=G*.
Определение 2. Пусть |, r)er;0(f). Тогда, как было дока-
доказано выше, можно считать, что | = ad*-;i/, ti = ad*n, f. Положим
по определению o>(s, r\)=f{[h, *li])-
Проверим корректность этого определения формы Кириллова.
Вообще говоря, gi, r)i определены неоднозначно. Пусть /eG*. То-
Тогда аннулятором ковектора f называется подпространство Апп/=
= {IeG : adx* f=0}. Подпространство Ann/ является, как легко
видеть, подалгеброй. Очевидно, что s=ad*5l/=ad*E! f тогда и
только тогда, когда gi — |2^Апп f. Поэтому для проверки кор-
корректности определения симплектической структуры надо показать,
что f\h + h, 4\ + 4o]=f[h, Л|]. где |0, r)o^Annf, а это вытекает
из линейности f и определения аннулятора.
Утверждается далее, что со.— невырожденная внешняя 2-форма
на орбитах. Это означает, что либо a) det(o>,-;) ¥=0, либо б) если
A'(ь, ч) — 0 для любого l^TfO(f), то ц — 0. Проверим второе
утверждение. Пусть о>(£, тг|) = f [si, r\]] ~0 для любого |ь где | =
==ad*5l f, Ti = ad*tllf. Тогда (ad*n,f)gi = O для любого |ieG, по-
поэтому ad*,,, /:=0 и, следовательно,.Ti = ad*^,/=0.
В частности, размерность каждой орбиты коприсоединенного
представления четна. Ясно также, что симплектическая форма ин-
инвариантна относительно коприсоединенного действия группы на
орбите. Оказывается далее, что dw = 0' (т. е. форма замкнута),
см. [5]. Как мы уже знаем, теперь мы можем определить на каж-
каждой орбите скобку Пуассона.
3.2. Модельный пример: SL(n, С) и sl(n, С). Все основные эф-
эффекты, связанные с системой корней полупростых алгебр Ли, в
полном объеме проявляются на примере важной полупростой ал-
алгебры Ли sl(n, С). Поэтому для удобства читателя мы проиллю-
проиллюстрируем на ее примере основные свойства системы корней. После
этого заинтересованный читатель уже без особого труда сможет
уверенно оперировать с корневыми системами и в других полу-
полупростых алгебрах Ли. Кроме того, уверенное владение техникой
корней сегодня необходимо во многих вопросах гамильтоновой
механики и геометрии.
Если алгебра Ли является матричной (каковой является sl(n,
С)), то операция коммутирования в ней задается так: \Х, Y] —
= XY—YX, где XY и YX — обычные произведения матриц из ал-
алгебры Ли. Для алгебры sl(n, С) форма Киллинга имеет простой
вид (X, Y) = Spur XY. Напомним, что алгебра sl(n, С) состоит из
комплексных квадратных матриц X размером (пХп) таких, что
SpurX = 0. В качестве картановской подалгебры Т можно взять
семейство диагональных матриц
/а, 0.
V 0 аП1
116
*де oi+ ... +ап=0. Элемент h регулярец тогда и только тогда,
<огда все собственные числа матрицы I1 Различны, т. е. а^Фа-, при
1
Через Tij обозначим элементарную матрицу, в которой отли-
'ен от нуля лишь один элемент на м^ст^ (г, /), равный единице.
Здесь i — номер строки, /— номер столбца. Картановская подал-
подалгебра уже описана нами выше. Векторы Еа, являющиеся соб-
•твенными для всех преобразований ad;,, имеют вид Tiit если /</,
л —Tih если г>/ (рис. 42). В самом Дбле> вычисляя ad^r,;, полу-
У J
-\-~<л)
\ о
о \
\
- ч
Рис. 43
l-, Тц]; т. е. а{1г)~щ — Qj. Таким образом, корни
оры si(ti, С) нумеруются парой индексов г, /. Мы будем пи-
ienepb a=a,j; aij(h)=cii — af (р'Ю. 43). Итак, алгебра s/(n,
к;) представляется в виде ГФЕСГ,-,-. Та^им образом, в качестве
корневого разложения алгебры можно ^зять ее стандартное раз*
-пожение в прямую сумму одномерных подпространств ' СГ^- и
:кости Т.
.^етим, что картановскую подалгебру J можно при желании
рассматривать как собственное подпр<^ранство преобразований
adr, отвечающее собственному значеда^ равному нулю. Крат-
-jCTb нулевого собственного значений Равна рангу алгебры, т. е.
размерности картановскои подалгебрь1 (рис. 44).
Так как Ea = Tij, то, коммутируя матрицы Еа = Тц и Е$ — ТРA,
мы получаем соотношение [Г,,-, Tpq) =*NE Л^ 0
если все индексы г, /, р, q различны и \ц q
формы Киллинга мы указали выше. Поэтому если а+$Ф0, то
{Еа, £B) = Spur TijTpq=O. Таким образам, Еа и Eg, ортогональны '
лри а+|3#Ю. Если же а+р = 0, то векторы Еа=Тц и Е_а =—Тп
неортогональны, так как (fa, f^^Spur Тц(—Т^)——1. Нако-
Наконец, равенство [Ga, GB]=Ga+B, где, Например, a=alb- i<j, p =
= аРч, p<q, может иметь место в то^ Ч только в том случае, ко-
когда среди четырех индексов г, /, р, q есть два совпадающих: либо
/ = р, либо i=q. Это эквивалентно условию, что сумм_а корней
a+р также является корнем. В саМо^ деле, ац{1г) +apq{h) =
= {a+$)h = at — aj + ap — aQ равняется at — aq, если j = p, и рав-
равняется ар — CLj, если i=q. Этот механизм показан на рис. 45, где
так
Tjq]=T
iq
как Л^аВ = 0,
Явный вид
117
корень a,j (/*)== а* — а,- при i</ изображен стрелкой,
щей, что. аг вычитается а,-.
В случае sl(n, С) корень На', где a=aj.,-( i<j, изобоажае
матрицей, показанной на рис. 46. Если a=a,,-, i>j, то па см
рис. 47. Итак, Н'а=а.1.= Ти — Ти. Отсюда следует, что лине-
оболочка матриц Та — Тц совпадает с подалгеброй Т.
Рис. 44
Рис. 46
Рис. 47
3.3. Вещественные, компактные и нормальные подалгеин.
сих пор мы рассматривали в основном комплексные полупоо'.
алгебры Ли. Однако большую роль играют также различные
вещественные подалгебры. Одна из них особенно замечате;.-.
так как соответствующая ей группа Ли является компактно*
группой.
Определение 3. Пусть G — комплексная полупростая ал-
алгебра Ли. Вещественная подалгебра Go алгебры Ли G (рассмат
риваемая как алгебра над полем R) называется вещественно'
формой комплексной алгебры Ли G, если каноническое отображе
ние комплексного расширения Goc = Go®rC алгебры Go в алгес-
ру G является изоморфизмом. В этом случае мы имеем равенствс-
dimRG(j=dimc G.
Это означает, что, комплексифицируя вещественную алгебра
Go, т. е. рассматривая линейные комбинации ее элементов с
118
илексными коэффициентами, мы получаем всю объемлющую ал-
алгебру G.
Пусть Go— какая-либо вещественная форма комплексной по-
полупростой алгебры Ли G. Тогда всякий элемент, из алгебры G од-
однозначно представляется в виде X + iY, где X, Y^G^ Это разло-
разложение алгебры G порождает естественную инволюцию а, отобра-
отображающую алгебру G в себя. А именно o{X + iY)=X — iY. Эта ин-
инволюция зависит от подалгебры Go и обладает следующими оче-
очевидными свойствами: ст2=1, оХ = Х, если IeG0; a(A + B) =оА + оВ,
<у(Ы)=коА,л[А, В] = [оА, оВ).
Лемма 1. Пусть на алгебре Ли G задана инволюция а, об-
обладающая перечисленными выше свойствами. Тогда эта инволю-
инволюция определяет некоторую подалгебру Go в алгебре G, являющую-
являющуюся вещественной формой.
Доказательство. Обозначим через Go множество непо-
неподвижных точек инволюции о на G. Из свойств а следует, что Go —
вещественная подалгебра в G. Любой элемент А из алгебры G
представляется в виде X+iY, где X, Y^G0. В самом деле, А —
= (A + oA)/2+i(A — oA)jBi), где Х= (A + oA)/2<eeG0, Y=(A —
— oA)/Bi), так как оХ = о{А + оА)/2 = Х, oY=Y. Лемма доказана.
Рассмотрим на алгебре G форму Киллиига < ,). Ее можно
ограничить на вещественную подалгебру Go. Обозначим это огра-
ограничение формы через (, H'. На подалгебре Go определена своя
форма Киллинга ( , )о- Возникает вопрос: совпадают ли эти две
формы (с точностью до скалярного ненулевого множителя)? Во-
Вообще говоря, ограничение формы Киллинга с объемлющей алгеб-
алгебры на произвольную ее подалгебру не совпадает1 с формой Кил-
Киллинга этой подалгебры. Однако в случае вещественных форм си-
ситуация более благоприятная.
Лемма 2. Если Go — вещественная форма полупростой ал-
алгебры Ли, то две указанные выше формы совпадают (с точностью
до ненулевого скалярного множителя).
Определение 4. Вещественная алгебра Ли называется
компактной, если ее форма Киллинга отрицательно определена,
т. е. если соответствующая квадратичная форма удовлетворяет не-
неравенству (X, Х)<0, если ХфО.
Определение 5". Вещественная форма Go комплексной ал-
алгебры Ли G называется компактной вещественной формой алгеб-
алгебры G, если Go — компактная вещественная алгебра.
Название «компактная алгебра» обусловлено тем, что группа
Ли, имеющая компактную алгебру Ли, сама оказывается компакт-
компактным многообразием.
Лемма 3. Для того чтобы вещественная форма Go алгебры
Ли G была компактной, необходимо и достаточно, чтобы эрмито-
эрмитова форма (А, сгЛ) на алгебре G была отрицательно определена.
Доказательство. Пусть Go — компактная алгебра Ли и
A = X+iYe=G, тогда <Л, oA) = (X+iYt X — iY) = (X, X) + {Y, У><
<0. Обратно, если форма (А, оА) отрицательно определена, то
при /4eG0, АфО имеем оА = А и (А, Д)<0. Лемма доказана.
119
и дальнейшем компактную форму мы будем обозначать
рез Gc.
Задача классификации всех вещественных форм алгебры
сводится к классификации всех неэквивалентных инволюций
полупростых алгебрах. Компактная форма определяется спе
альиой инволюцией, которую мы сейчас опишем.
Сначала рассмотрим наш модельный пример sl(n, С). Р
смотрим на G инволюцию оА=А, т. е. операцию комплексного
пряжения. Множество неподвижных точек этой инволюции сов.
дает, очевидно, с подалгеброй вещественных матриц, являющей
алгеброй Ли sl(n, R). Ясно, что форма Киллинга на алгеС
Т=Тоф[Т0'
Рис. 48
Рис. 49
sl(n, R) является вещественной формой вида Spur Х2=1,х2ц. Она,
очевидно, не является отрицательно определенной (она индефи-
индефинитна!). Поэтому $l(n, R) —вещественная, но не компактная фор-
форма комплексной алгебры Ли sl(n, С).
Компактная форма Gc строится так. Рассмотрим инволюцию
T.G-+G, тА——Ат, где Т — транспонирование. Неподвижными
точками этой инволюции являются косоэрмитовы матрицы со сле-
следом ноль. Легко видеть, что это пространство является алгеброй
Ли компактной группы SU(n). И в самом деле, вычисляя на этой
вещественной форме Go форму Киллинга, мы сразу получаем, что
она отрицательно определена.
Оказывается, рассмотрев случай алгебры sl(n, С), мы факти-
фактически смоделировали ситуацию, общую для всех комплексных по-
полупростых алгебр Ли.
Теорема 1. Каждая полупростая комплексная алгебра Ли
обладает компактной вещественной формой.
120
Доказательство, мы просто предъявим в явном виде вло-
жеипе компактной подалгебры в'алгебру Ли. Рассмотрим базис
Иенли в алгебре G (см. его определение выше). Рассмотрим инво-
инволюцию а, задаваемую на базисе Вейля так: оЕа = Е-а, если аф$,
ah = —h для любого вектора /igT0, где ГосГ — «вещественная
часть» подалгебры Картана Т. При этом будем считать, что
а (XX) —ХоХ. Итак, отображение а действует так, как показано
на рис. 48, т. е.
O-.V+-+V-, a:V--vV+, а:Т0-+-Т0, <J:iT0~+iT0.
Из свойств базиса Вейля сразу следует, что а—автоморфизм ал-
алгебры. Найдем теперь вещественную форму, отвечающую этой
инволюции.
Из явного вида инволюции следует, что в качестве веществен-
вещественного базиса в подалгебре неподвижных точек инволюции а можно
взять векторы Еа+Е-а\ i(Ea—Е.-а); iHa. Утверждается, что это
и есть компактная подалгебра в алгебре>С В самом деле, так как
{Е„, Еа) = 0 и (Еа, £-а)= — 1, то достаточно вычислить сле-
следующие скалярные произведения:
(Еа+Е-а, Еа+ Е-а) = — 2, (i (Еа— Е-а), i (Еа~Е-а)) =
{Еа + Е-а, i {Еа — Е-а)) = 0, (ili'a, Ша)== —а(Н'а) <0,
учитывая при этом, что а(#а)>0 и что'вектор На является
двойственным к линейной форме а. Следовательно, форма Кил-
линга отрицательно определена на всей подалгебре неподвижных
точек. Теорема доказана.
Рассмотрим теперь более подробно вложение компактной фор-
формы в алгебру. В G можно выбрать, очевидно, следующий вещест-
вещественный базис: Еа -т.Е-а, i{Еа—~£-<*). Еа—-Е-а, i(Ea +£-«), На, Ша.'
Это означает, что наряду с корневым разложением алгебры G =
= T®V+®V~ (над С) имеется еще одно естественное разложение"
(уже над R): G = T0®iT0®W+®W-, где W+=-.{Ea +E-a, i(Ea-~
-Е-а)}, W-^iEa-E-a, i {Ea + Е-а)},Ть ={На), гТи-{Ша}.В фи-
фигурных скобках (не путайте со скобкой Пуассона!) указаны век-
векторы, образующие базис в соответствующей плоскости (рис. 49).
Ясно, что а= + 1 на плоскости W+@iT0 и а= — 1 на плоскости
W~@T0. Следовательно, плоскость W+@iTa является подалгеброй
(в отличие от плоскости W~(BT0). Эта подалгебра неподвижных
точек совпадает с компактной подалгеброй Gc в алгебре G, т. е.
\V4-@iTo=Gc. Итак, компактная алгебра Ли Gc в комплексной
л.небре G натянута на следующие векторы:
{£« + £_«, i {Еа—Е-а), Ша).
121
Рассмотрим присоединенное действие алгебры Ли Gc на себе,
т. е. изучим действие преобразований вида аф, : Gt.-+Gc, где /ig
&Го. Так как элемент h лежит в картановско'й подалгебре, то
преобразование adft переводит в себя плоскость W+, ортогональ-
ортогональную к плоскости it о- Мы пользуемся тем, что операторы ad/, ко-
сосимметричны относительно формы Киллинга, а потому сохра-
сохраняют ортогональное дополнение, переводя его в себя.
Пусть h — iq, где q^.T0. Ясно, что
adh {Еа + Е-а) =- i adp (Еа + Е-а) = га (q) (£„—£_„),
где а(^)—вещественное число. Следовательно, adk(Ea +Е-а) =
= a(q)i(Ea— Е-а.). Аналогично ad/,/(£«— £_«) = —a(q)(Ea +
+ £_«).
Итак, оператор адн переводит в себя двумерную вещественную
плоскость, натянутую на векторы Ea + E-a, i(Ea — E-a), и па этой
плоскости задается следующей кососимметрической матрицей вто-
, / 0 a(q)\ , . тл
рого порядка: ad,= - . гДе h=iq. Итак, мы видим
\ — a(q) 0 /
отличие действия оператора adh на компактной алгебре от анало-
аналогичного действия на комплексной алгебре.
Если в комплексном случае этот оператор приводился к диаго-
диагональному виду в базисе, составленном из корневых векторов, то в
вещественном компактном случае этот оператор пе имеет вещест-
вещественных собственных векторов в ортогональном дополнении к кар-
тановской подалгебре iT0. Он приводится к блочно-диагоналыюму
виду, т. е. записывается в виде матрицы, по диагонали которой
стоят блоки размером Bx2). Каждый из них соответствует одно-
одному корню и записывается указанной выше матрицей.
В нашем модельном примере компактная алгебра Gc=su(n),
где GcczG — sl(n, С), разлагается в прямую сумму подпространств
su(n)=W+®iT0 где »Т0 =
где
Р/ вещественны,
О
Re №+ = {£«+£_»} = .
— 1
122
вумерное инвариантное подпространство, натянутое на пару век-
■1в Еа + Е а, г(£а — Е-а), имеет в данном случае вид
а + ib
+ ib
I, где а, Ь вещественны.
шается, компактная форма единственна в G с точностью
омопфизма алгебры G.
мы изучили корневое разложение алгебры sl(n, С). По-
-""Db мы можем легко выписать в явном виде канониче-
чие компактной формы Gc в алгебру sl(n, С).
чторы Еа совпадают с элементарными матрицами
а>0, и_с матрицами —TPq, p>q, если а<0. Сле-
= Jp,— Tqp, i(Ea — E-^—lTpq + iTqp И, НЭ-
Tq<i), если a{h)=ap — aq, p<q (рис. 50).
Рис. 51
подпространство iTQ совпадает с подпростран-
диагональных чисто мнимых матриц со следом ноль.
_._остранство {Еа + Е-а} совпадает с подпространством всех
-цественных кососимметрических матриц. Подпространство
(£а — Е-а)} совпадаете подпространством всех симметрических
.исто мнимых матриц с нулями по диагонали.
Подалгебра Gc=W+@iT0 совпадает с подпространством всех
косоэрмитовых матриц со следом ноль, т. е. с алгеброй Ли группы
SU(n). Итак, нами фактически доказано следующее утверждение.
Лемма 4. Стандартное вложение подалгебры su(n) в алгеб-
алгебру Ли sl(n, С) совпадает с каноническим вложением компактной
формы Gc в G.
123
Наряду с канонической компактной формой каждая полупро-
полупростая комплексная алгебра Ли обладает канонической некомпакт-
некомпактной формой, называемой иногда нормальной некомпактной
формой.
Рассмотрим снова базис Вейля в алгебре G и построим инво-
инволюцию T.G-+G, где tEa=Ea, т#а' = Яа', т. е. отображение т
тождественно на вещественной части плоскостей V+ и V~, а так-
также на вещественной части Го картановскои подалгебры Т. Но эта
инволюция отнюдь не является тождественной на всей алгебре,
так как ■z(kX)=kzX. Следовательно, t(iT0)=—iT0, t(iEa.) =—iEa.
Множество неподвижных точек инволюции т совпадает с плос-
плоскостью fo®Re V+®Re V~, т. е. с линейной оболочкой (над R) век-
векторов Еа, Е-а, На.'. Ясно, что это подалгебра.
Определение 6. Вещественная подалгебра {Еа, £_а, #«'}
называется нормальной некомпактной формой алгебры Ли G.
В нашем модельном примере эта подалгебра совпадает с под-
подалгеброй вещественных матриц со следом ноль, т. е. с sl(ii, R).
Инволюция т совпадает здесь с инволюцией тЛ=Л, где черта
означает комплексное сопряжение.
Как и компактная форма, некомпактная нормальная форма
определена однозначно с точностью до автоморфизма объемлю-
объемлющей комплексной алгебры.
Взаимное расположение ком-
компактной и некомпактной форм
в алгебре G см. на рис. 51,
а более подробную схему на
рис. 52. Это разложение по-
показано над полем R, поэтому
отдельно изображены как ве-
вещественные, так и мнимые
плоскости. ,
Компактная вещественная
форма Ос допускает еще одну
инвариантную характеристи-
характеристику. Эта подалгебра является
максимальной компактной под-
подалгеброй в комплексной ал-
алгебре Ли.
Укажем еще одну часто
появляющуюся в конкретных
задачах гамильтоновой гео-
геометрии и механики компакт-
компактную подалгебру в комплекс-
комплексной полупростой алгебре.
Рассмотрим две описанные
выше инволюции: а (опреде-
(определяющую компактную форму)
и % (определяющую пеком-
Рис. 52 пактную нормальную форму).
124
Рассмотрим множество Gn точек, неподвижных относительно
обеих инволюций. Так как а=1 на W+®rT0, а т=1 на
То®{Еа}Ф{Е-а}, то Сп натянуто на векторы Еа + Е-а, так как они
и только они остаются на месте при действии обеих инволюций
одновременно. Следовательно, Сп является компактной подалгеб-
подалгеброй. Она совпадает с пересечением в алгебре двух ее вещест-
вещественных форм: компактной и некомпактной нормальной.
Отметим, что подалгебра Gn отнюдь не является вещественной
формой алгебры, так как ее комплексификация не совпадает с G.
Подалгебра Gn иногда называется нормальной компактной подал-
подалгеброй (но не формой! Не путайте!).
В нашем модельном примере алгебры sl(n, С) получаем Gn=
= Gcf1 (нормальная некомпактная форма) =so(n) —su(n)f}sl(nr
R), так как косоэрмитовы вещественные матрицы являются косо-
симметрическими.
Изоэнергетический инвариант интегрируемых систем. В за-
заключение настоящего параграфа сделаем анонс. В следующей
главе будет предъявлен, в частности, обнаруженный автором го-
пологический инвариант интегрируемых систем v на четырехмер-
четырехмерных симплектических многообразиях М*. Инвариант представляет
из себя граф К, двумерную поверхность Р2 и вложение т: К-*~Р2.
Наряду с К можно рассматривать сопряженный граф К* = Г.
В случае нерезонансных систем v все эти объекты не зависят от
выбора второго интеграла. Вкратце опишем построение инвари-
инварианта.
Пусть /:Q-»-R—боттовский интеграл на компактной неособой
'"связкой трехмерной изоэиергетической поверхности Q, т. че. инте-
интеграл, все критические точки которого организованы в невырож-
невырожденные критические подмногообразия. Пусть fa — связная компо-
компонента поверхности уровня /"' (а) интеграла / иа Q. Совокупность
всех связных компонент уровня а обозначим через {fa}- Пусть а —
регулярные,-а с—критические значения интеграла f. Множество
критических точек интеграла {, лежащих на множестве (на кри-
критическом 'слое) /с обозначим через Nc. Для простого интеграла
множество Nc связно, для сложного — несвязно.
Пусть U(fc)—связная компонента трехмерного многообразия
/"'[с + е, с — е], где е—мало, содержащая связное множество fc.
Тогда t/ (fc)—3-многообразие, край которого состоит из торов.
Можно считать, что Q имеет вид склейки 2t/(/c), где сумма бе-
берется по всем критическим значениям с и по всем компонентам
{fc}. Обозначим U(fc) через Qc. Тогда Q=SQC.
Оказывается, каждое 3-многообразие Qc является расслоением
Зейферта со слоем 51 иад базой.Рс2, являющейся некоторым дву-
двумерным многообразием с краем. При этом, особая поверхность f,.,
вложенная в Qc, является подрасслоением этого расслоения.
•В частности, поверхность /с является расслоением Зейферта со
слоем S1 над .некоторым одномерным графом Кс, вложенным в по-
поверхность Рс2. При этом база Рс2 и граф Кс однозначно определя-
определяются заданием гамильтоновой системы v и интеграла f.
125
Пусть рс—проекция описанного расслоения Зейферта. Тогда
имеем рс'- Q<-+Pc2 и pc'-fc-*~Kc- Край поверхности Рс2 состоит из
окружностей. Их прообразы при проекции рс являются торами
■Лиувдлля в Qc. По этим торам происходит склейка 3-мпогообра-
зин Qr и Qr' внутри Q. Эти склейки граничных торов, очевидно,
индуцируют склейки соответствующих граничных окружностей по-
поверхностей Рс и РС'- В результате получаем некоторую двумер-
двумерную замкнутую поверхность Р = ИРС-
На поверхности Р естественно возникает некоторый граф К.
Для его построения возьмем объединение всех графов Кс (каж-
(каждый из них вложен в Рс) и добавим к этим компонентам окружно-
окружности К,-, являющиеся результатом склейки граничных окружностей
поверхностей вида Ре и Рс> пр.и конструировании поверхности Р.
Итак, положим К = {КС}+{КГ}-
В результате получили пару: замкнутую 2-поверхность Р (ори-
(ориентируемую или неориентируемую), а на ней — граф К.
Имеет место важная теорема. Пусть v — гамильтонова не-
нерезонансная система (т. е. система общего положения) на Q, а
f — боттовский интеграл. Сконструируем пару I(H, Q, /) = (Р2, К),
исходя из v и из /. Тогда пара (Р, К) не зависит от выбора вто-
второго интеграла f. А именно, если' f и /' — любые боттовские инте-
интегралы системы v, то существует гомеоморфизм ф: Р->-Р' такой,
что следующая диаграмма коммутативна:
К —-> Р
Следовательно, пару (Р, К) можно обозначить через /(#, Q).
Этот объект является топологическим инвариантом самого инте-
интегрируемого случая (гамильтониана) и позволяет классифициро-
классифицировать интегрируемые гамильтонианы по их топологическому типу
и по сложности. Пару /(#, Q) мы назовем изоэнергетическим то-
топологическим инвариантом ^интегрируемого гамильтониана'(инте-
гамильтониана'(интегрируемой системы). Фиксировав Н и меняя постоянную энергии
h (т. е. мёйяя Q), мы, получаем дискретное множество I (H) =
= {I(H, Q)}. Назовем его полным топологическим инвариантом
интегрируемой системы.
Детали см. в Приложении 7.
ГЛАВА 4
ЭЛЕМЕНТЫ СИМПЛЕКТИЧЕСКОИ ТОПОЛОГИИ.
КАЧЕСТВЕННАЯ ТОПОЛОГИЧЕСКАЯ ТЕОРИЯ
ИНТЕГРИРУЕМЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
НА СИМПЛЕКТИЧЕСКИХ МНОГООБРАЗИЯХ
§ 1. Классификация трехмерных поверхностей постоянной
энергии интегрируемых уравнений. Оценка количества
устойчивых периодических решений на поверхности
постоянной энергии.
Препятствия к гладкой интегрируемости уравнений на
симплектических многообразиях
■ 1.1. Случай четырехмерных симплектических многообразий.
,, Хорошо известно (см., например, [65—70]), что системы «общего
Положения» обычно иеинтегрируемы. Поскольку для приложений
фсобук? важность представляет случай, когда система интегри-
интегрируется (например, по Лиувиллю), то становится понятно, насколь-
насколько сложен поиск таких редких интегрируемых систем в необозри-
необозримом океане систем, из которых «большинство» неинтегрируемо.
]|Начиная с этой главы мы переходим к рассмотрению самого фе-
феномена интегрируемости и к поиску эффективных условий инте-
интегрируемости, дополняющих уже известные.
•|, Естественно начать со следующего вопроса: как связан факт
^интегрируемости гамильтоновой системы с топологией фазового
■\*(или конфигурационного) многообразия?
|_ Традиционно считается, что полная интегрируемость по Лиу-
Лиувиллю гамильтоновой системы дает более или менее полное каче-
качественное описание поведения интегральных траекторий системы.
Безусловно, в принципе это так. Однако при этом часто игнори-
игнорируется то обстоятельство, что для такого описания требуется эф-
эффективно найти переменные действие — угол (относительно кото-
которых траектории системы превращаются в прямолинейные обмотки
торов) в окрестности торов Лиувилля. Вложения торов Лиувилля
в объемлющее фазовое многообразие могут быть весьма сложны-
сложными (и примеры этого мы вскоре увидим). Ясно, что сложность
вложения торов растет по мере усложнения интегралов системы.
Так как обычно интегралы являются полиномами (с растущими
степенями) или рациональными функциями, то конкретное иссле-
исследование торов и переменных действие — угол часто затруднено,
поскольку связано с решением нетривиальных алгебраических и
иналитических проблем. На этом пути фундаментальные резуль-
результаты .получены С. П. Новиковым и его школой.
Ь А. Т, Фоменко . . 129
Поэтому уместно поставить следующий вопрос. Как распола-
располагаются торы Лиувилля в фазовом пространстве? Как они примы-
примыкают друг к другу? Как они заполняют открытые области? Кар
они перестраиваются'в окрестности критических поверхностей ин
тегралов? Другими словами, как построить качественную теории
топологического расположения и взаимодействия торов Лиувилля
(и тем самым расположения интегральных траекторий системы)
например, на поверхности постоянной энергии системы?
В настоящей главе мы дадим ответы на некоторые из этих во
просов. Для простоты изложения мы. начнем с четырехмерной
случая, хотя почти все формулируемые здесь результаты доказы
ваются нами и в многомерном случае. Об этом подробнее будс
рассказано в § 2.
В последние годы получено много новых результатов в направ
лении интегрирования гамильтоновых систем на симплектически:
многообразиях. См., например, [103—106] (С. П. Новиков); [10G
ПО] (М. . А. Ольшанецкий, А. М. Переломов); [123, 124
(А. Г. Рейман, М. А. Семенов-Тян-Шанский, И. И. Френкель)
[16—18] (О. И. Богоявленский); [22—27] (А. В. Браилов); [21
(А. В. Болсинов); [29] (А. П. Веселое); [50—52] (Б. А. Дубрс
вин, В. Б. Матвеев, С. П. Новиков); [55] (В. Е. 3axapoi
Л. Д. Фаддеев); [84] (С. В. Манаков); [93—100] {А. С. Мищен
ко, А. Т. Фоменко); [134—144] (В. В. Трофимов); [146—149
(В. В. Трофимов, А. Т. Фоменко); [152—157] (А. Т. Фоменко)
[266] (М. В. Карасев, В. П. Маслов); [5] (В. И. Арнольд)
[168—169] (Адлер, ван Мёрбеке); [101] (Мозер); [201—203
(Гийемин, Стернберг); [206] (Хольм, Купершмидт); [225-] (Mai
ри); [226] (Мамфорд); [227] (Марсден, Вейнстейн); [228] (Mai
Кин); [245—246] (Ратью) и др. (см. список литературы в кони
книги).
Таким образом, накоплен богатый экспериментальный матер!
ал. В связи с этим особый интерес представляет задача обнар]
жения устойчивых замкнутых интегральных траекторий интегр1
руемых систем. Такие траектории отвечают периодическим движ!
ниям системы.
В настоящей главе автор доказывает, что в некоторых случая
можно гарантировать существование по меньшей мере двух усто,
чивых периодических решений на трехмерных поверхностях пост*
янной энергии (изоэнергетических поверхностях) у интегрируемс
системы, исходя всего лишь из данных об одномерных гомология
этих поверхностей (теорема 1) или из данных о фундаментально
группе.
Этот результат следует из общей классификационной теор
Мы 3 автора о полной топологической классификации и о канон
ческом представлении поверхностей постоянной энергии интегр
руемых систем (на четырехмерных симплектических многообр
зиях М4) в виде объединения (склейки) трехмерных многообр
зий трех простейших типов. В частности, это дает простую кла
130 .
сификацию всех неособых поверхностей постоянной энергии инте-
интегрируемых систем.
При этом мы предполагаем, что система обладает вторым
гладким интегралом, который мы назовем «боттовским». Это ин-
интеграл, критические точки которого могут быть вырождены, но
обязательно организованы в невырожденные гладкие критические
подмногообразия.
В связи с этим нам потребовалось развить новую специфиче-
специфическую «теорию типа Морса» интегрируемых гамильтоновых, систем,
отличающуюся от обычной теории Морса и от теории Ботта
функции с вырожденными особенностями [180].
В частности, мы развиваем также некоторые важные идеи, вы-
высказанные Д. В. Аносовым [1], С. П. Новиковым [103, 105],
В. В. Козловым [65], С. Смейлом [126].
Мы ставим затем следующий вопрос: обладают ли неособые
поверхности постоянной энергии интегрируемых систем специфи-
специфическими свойствами, выделяющими их среди всех гладких трех-
трехмерных многообразий?
Естественно ожидать, что в боттовском, аналитическом и ал-
алгебраическом случаях далеко не всякое многообразие может вы-
выступать в такой роли. Другими словами, вероятно, далеко не вся-
всякое многообразие реализуется в виде поверхности постоянной
энергии интегрируемой системы.
В следствии 4 эта гипотеза доказана нами в боттовском слу-
случае. Отсюда, в частности, мы получаем некоторые новые тополо-
топологические препятствия к интегрируемости гамильтоновых систем в
классе гладких боттовских функций (следствие 2). Исследуя гео-
геодезические потоки на двумерной сфере (и доказывая неинтегри-
.руемость потоков общего положения в указанном классе интегра-
интегралов), мы опираемся'на работу Д. В. Аносова [1], а также на ре-
результаты Клингенберга и Такенса [63].
Как отмечалось выше, сегодня известно много способов дока-
доказательства аналитической неинтегрируемости систем общего по-
положения. См., например, работы [62—68] (В.4 В. Козлов), [70]
(В.-В. Козлов, Д. А. Онищенко), [20] (С. В. Болотин), [56, 57]
(С. Л. Зиглин) и др. Некоторые из этих способов обобщают ме-
методы А. Пуанкаре [121, 122]. Наши результаты дополняют эти ис-
исследования, поскольку позволяют эффективно давать ответ на во-
вопрос о существовании или о несуществовании (в некоторых слу-
случаях) боттовских интегралов. Этот класс интегралов отличается
от класса аналитических интегралов.
Подчеркнем, что, по нашему мнению, следует уделить особое
■внимание изучению эффекта интегрируемости на- одной, отдельно
взятой, фиксированной поверхности постоянной энергии. На это
обстоятельство неоднократно указывали С. П. Новиков- и
В. И. Арнольд. Это связано с тем, что часто встречаются ситуации
в механике и физике, когда гамильтонова система интегрируема
лишь на одной поверхности постоянной энергии и неинтегрируема
на остальных поверхностях. Аналитические же системы обычно
*)• ■ ■ 131
либо интегрируемы сразу на всех поверхностях уровня гамильто-
гамильтониана, либо ни на одной. Поэтому нам представляется полезным
рассматривать гладкие системы и гладкие интегралы, допускаю-
допускающие одновременное присутствие как «интегрируемых», так и «не-
интегрируемых» поверхностей постоянной энергии.
В связи с этим возникает следующая общая задача. Пусть за-
задана гамильтонова система с гамильтонианом Я. Требуется выяс-
выяснить: существует ли среди поверхностей постоянной энергии этой
системы хотя бы одна поверхность, на которой система интегри-
интегрируема?
Возникает естественная гипотеза, что у многих гамильтоновых
систем (в целом неинтегрируемых) такая «одинокая» поверхность
существует. Ясно; что гладкий (или аналитический) интеграл f,
интегрирующий систему t> = sgrad# лишь на одной поверхности
уровня гамильтониана, удовлетворяет более слабому уравнению,
чем обычное уравнение инволютивности {Я, f}=0. А именное он
должен коммутировать с гамильтонианом Я лишь на самой по-
поверхности уровня, а вне ее он уже не обязан коммутировать с Я.
В простейшем виде это условие можно записать равенством {Я,
f}=K(H), где функция К(Н) такова, что Л@)=0 н —- =0
/ ап я=о
(см. [65]). Здесь мы считаем, что интересующая нас изолирован-
изолированная поверхность уровня гамильтониана задается уравнением Н=
=0. Таким образом, общее уравнение {Я, f}=X(H) заслуживает
самого тщательного изучения. Рассмотрим на поверхности уровня
гамильтониана два векторных поля: 8§гас1Я и sgradf. Для того
чтобы они коммутировали на поверхности уровня, достаточно,
чтобы градиент функции {Я, /} обращался в ноль на поверхности
Я=0 [65]. В самом деле, мы знаем, что [sgrad#, sgradf] =
= sgrad{//, /}. Итак, функция К{Н) должна быть квадратичной
по Я в окрестности значения Я=0. В частности, можно было бы
сначала изучать общие свойства уравнения {Я, /}=еЯг, где е —
постоянная, отличная от нуля.
Перечисленные выше задачи являются частными случаями об-
общей задачи некоммутативного интегрирования, фактически восхо-
восходящей еще к Э. Картану [61]. Разные современные версии этой
задачи проанализированы В. В. Трофимовым и А. Т. Фоменко в
обзоре [145].
Из теоремы Лиувилля следует, что все неособые двумерные
компактные поверхности уровня второго интеграла / (на многооб-
многообразии по'стоянной энергии), т. е. совместные поверхности уровня
обоих интегралов Я и f, являются объединениями торов. Оказы-
Оказывается, можно полностью описать структуру особых поверхностей
постоянной энергии. Они оказываются гомеоморфными двумерным
клеточным комплексам, получающимся специальной (легко описы-
описываемой) склейкой двух двумерных торов. Это описание позволяет
' в частности, полностью описать поведение интегральных траекто-
траекторий системы на особых поверхностях уровня интегралов.
132
В § 2 настоящей главы мы строим новую многомерную топо-
топологическую теорию интегрируемых систем. В качестве одного из
сг приложений мы даем полную классификацию перестроек обще-
i-ii положения торов Лиувилля в окрестности бифуркационных
диаграмм отображения момента интегрируемых систем. Оказы-
нается, канонические перестройки торов могут быть описаны явно:
и эффективно. Это позволяет описать события, происходящие с
торами Лиувилля и с интегральными траекториями системы на
критических уровнях энергии (т. е. в тот момент, когда тор Лиу-
Лиувилля «натыкается» на критическое значение интеграла энергии).
Перейдем к точной формулировке наших результатов. Пусть
М4 — четырехмерное гладкое симплектическое многообразие, на
котором задана гамильтонова система t> = sgrad#, где Н — глад-
гладкий гамильтониан. Положения равновесия хо системы v — это кри-
критические точки функции Н. Так как Н—интеграл системы v, то
поле v можно ограничить на инвариантную трехмерную поверх-
поверхность Q постоянной энергии, т. е. Q={x^M : Н{х)= const}. Яв-
Являясь симплектическим многообразием, М4 ориентируемо, а пото-
потому многообразие Q также ориентируемо.
Рассмотрим некритические поверхности уровня Q, т. е. такие,
на которых gradH=£0. Для полной интегрируемости по Лиувиллю
системы v на многообразии М достаточно найти еще один (вто-
(второй) интеграл f, независимый с Н (почти всюду) и находящийся
с ним в инволюции на поверхности уровня. Пусть такой интеграл
существует. Ограничим его па поверхность Q и получим гладкую
функцию. Как уже отмечалось, мы будем рассматривать интегри-
интегрируемость системы лишь на какой-то одной поверхности постоян-
постоянной энергии.
Определение 1. Будем называть гладкий интеграл / бот-
товским па поверхности Q, если критические точки функции f на
Q образуют невырожденные критические гладкие многообразия.
Общие свойства таких гладких функций (не интегралов) изу-
изучены в известных работах Р. Ботта (см., например, [180]). На
этом основании такие функции уместно назвать боттовскими.
У нас не возникнет путаницы с обычными функциями Морса, так
как последние в нашем анализе будут встречаться редко (такие
случаи мы оговорим). Напомним, что критическое подмногообра-
подмногообразие для функции f называется невырожденным, если гессиан d2fs
функции / невырожден на плоскостях, нормальных к подмногооб-.
разию. В нашем случае невырожденные критические подмногооб-
подмногообразия для функции / на Q могут быть нульмерными, одномерными
и двумерными. Мы будем интересоваться существованием именно
боттовских интегралов у гамильтоновой системы. Дело в том, что
из накопленного опыта исследования конкретных систем (см., на-
например, [117, 118] (Т. И. Погосян), [120] (Т. И. Погосян,
М. П. Харламов), [163] (М. П. Харламов), [131] (Я. В. Татари-
пов)) можно извлечь, что подавляющее большинство уже обнару-
обнаруженных интегралов являются боттовскими в указанном нами,
смысле. Недавно А. Ошемков доказал боттовость хорошо извест-'
13а
ных интегралов для движения четырехмернога твердого тела (слу-
(случай типа Эйлера). Поэтому введенный нами класс боттовских ин-
интегралов представляется естественным.
Определение 2. Пусть у — замкнутая интегральная тра-
траектория системы v на поверхности Q (т. е. периодическое реше-
решение). Будем говорить, что траектория у является устойчивой, ес-
если некоторая ее трубчатая ок-
окрестность целиком расслоена
(без щелей) на концентриче-
концентрические двумерные торы, инвари-
инвариантные относительно системы
v. Это означает, что все инте-
интегральные траектории, близкие
к у, «укладываются» на инва-
инвариантные двумерные торы, об-
общей осью которых является
траектория у (рис. 53).
Устойчивость траекторий
означает, что нормальный дву-
двумерный диск (малого радиуса)
целиком, без щелей, расслоен
на концентрические окружно-
Рис. 53
Рис. 54
сти. Поскольку мы главным образом рассматриваем интегри
руемые системы, то данное определение устойчивости совпа
дает с традиционным понятием сильной устойчивости. Дело i
том, что неособые поверхности уровня второго интеграла тако{
системы являются двумерными торами Лиувилля. Следователь
но, устойчивые траектории — это те, на которых второй (допол
нительный) интеграл достигает локального минимума или мак
симума.
Система может быть интегрируемой, но не иметь при этом ш
одной замкнутой устойчивой траектории (хотя замкнутых траекто
рий может быть очень много). Простой пример: геодезический по
ток двумерного плоского тора, т. е. тора Т2 с локально евклидово!
134
метрикой gij = 6ij. Легко видеть, что этот геодезический поток
имеет дополнительный линейный интеграл, однако все замкнутые
траектории системы являются неустойчивыми (I).
Оказывается, существует простая качественная связь между
следующими тремя объектами:
а) Дополнительный боттовский интеграл f на поверхности по-
постоянной энергии Q (т. е. система вполне интегрируема).
б) Устойчивые периодические решения системы на. этой по-
поверхности. /
в) Группа одномерных целочисленных гомологии #i(Q, Z)
(или фундаментальная группа ni(Q)) этой поверхности.
Итак, мы рассматриваем одну поверхность Q постоянной энер-
энергии, на которой задан второй интеграл. Если он определен не толь-
только на поверхности Q={#=0}, но и в некоторой ее окрестности,
то f удовлетворяет уравнению {#, f}=K(H) (см. выше).
Рассмотрим критические невырожденные подмногообразия Т
интеграла f на Q. Каждое из них обладает сепаратрисной диа-
диаграммой. Напомним, что сепаратрисная диаграмма — это объеди-
объединение интегрльных траекторий поля grad/, входящих вТи исхо-
исходящих из Т. В соответствии с этим будем говорить о входящей
сепаратрисной диаграмме Р-(Т) и исходящей сепаратрисной диа-
диаграмме Р+{Т). В малой окрестности подмногообразия Т обе диа-
диаграммы (входящая и исходящая) являются двумерными гладки-
гладкими многообразиями с общим краем Т. Они могут быть как ориен-
ориентируемыми, так и неориентируемыми.
Определение 3. Будем говорить, что боттовский интеграл
/ на поверхности Q является ориентируемым, если все его крити-
критические подмногообразия ориентируемы. Если хотя бы одно крити-
критическое подмногообразие неориентируемо, то будем говорить, что
интеграл неориентируем.
Изоэнергетическую поверхность, на которой существует боттов-
боттовский интеграл, будем иногда называть для краткости «интегриру-
«интегрируемой поверхностью».
Оказывается, без существенного ограничения общности можно
изучать лишь ориентируемые интегралы f на Q. Дело в том, что,
рассматривая изоэнергетические поверхности Q с точностью до
двулистного накрытия (над ними), можно всегда считать, что ин-
интеграл f ориентируем (А. Т. Фоменко).
Утверждение 1. Пусть Q3 — неособая компактная поверх-
поверхность постоянной энергии в М4 и f — боттовский неориентируемый
интеграл на Q. Тогда все его неориентируемые критические под-
подмногообразия гомеоморфны бутылке Клейна (рйс. 54), причем ин-
теграл f достигает на них либо минимума, либо максимума (ло-
(локального). Пусть U(Q) — достаточно малая трубчатая окрест-'
ность поверхности Q,e M. Тогда существует двулистное накрытие
n:(O(Q), Я, ~f)-+(U(Q), H, f) (со слоем Z2), где С(й) - сим-
плектическое многообразие с гамильтоновой системой и=
—8grad# (где гамильтониан Я имеет вид. Я=я*Н), интегрируе-
интегрируемая на Q—n~l(Q) при помощи боттовского ориентируемого (I)
135
интеграла f = n*f. При этом все критические бутылки Клейна
■«разворачиваются» в критические торы Т2 в Q (максимумы или
минимумы интеграла J). Многообразие 0 (Q) является трубчатой
окрестностью Q.
Отсюда следует, что если f — неориентируемый интеграл на
Q, то автоматически n\(Q)¥=0 и в группе Л\ (Q) содержится под-
подгруппа индекса два. Если, например, Q гомеоморфно сфере S3
'(частый пример в механике), то любой боттовский интеграл f на
£3 всегда ориентируем.
В дальнейшем через m—m(Q) будем обозначать число устой-
устойчивых периодических решений системы v на Q. Пусть далее г=
= f(Q) — число критических подмногообразий интеграла f на Q,
томеоморфных бутылке Клейна. Если интеграл ориентируем, то
г=0.
Теорема 1 (А. Т. Фоменко). Пусть М* — гладкое симплекти-
ческое четырехмерное многообразие (компактное или некомпакт-
пое) и f=sgrad Н — гамильтоново векторное поле на М4, где
Я — гладкий гамильтониан. Предположим, что система интегри-
интегрируема по Лиувиллю на какой-то неособой компактной трехмерной
поверхности уровня Q гамильтониана Н, причем второй гладкий
-интеграл f коммутирует с Н на Q и является боттовским на Q.
Тогда число m—m(Q) устойчивых периодических решений си-
системы v на поверхности Q следующим образом оценивается снизу
через топологические инварианты поверхности Q:
1) В случае, когда интеграл f ориентируем на Q:
а) т>2, если группа гомологии #i(Q, Z) конечна;
б) т>2, если фундаментальная группа ni(Q)=Z. '(
2) В случае, когда интеграл f неориентируем на Q:
а) т+г>2, если группа гомологии HX(Q, Z) конечна;
б) т>2, если HX(Q, Z)=0 (при этом группа n{(Q) может
быть бесконечной);
в) т>1, если группа #i(Q, Z) — конечная циклическая;
г) т>1, если ni(Q)=Z или если n\(Q) — конечная группа;
д) т>2, если группа H{(Q, Z) — конечная циклическая и
поверхность Q не принадлежит к небольшой серии мно-
многообразий Qo= (S1x£J)+s/l3+rK'3, которые легко описы-
описываются в явном виде (см. описание ниже).
В обоих случаях интеграл f достигает локального минимума
или максимума на каждом из этих устойчивых периодических ре-
решений системы v (или на бутылках Клейна). Если группа гомо-
гомологии Я, (Q, Z) бесконечна, т. е. ранг #i>1, то система v может
-вообще не иметь на поверхности Q устойчивых периодических ре-
решений.
Полученный критерий достаточно эффективен, так как провер-
проверка боттовости интеграла и вычисление ранга группы одномерных
гомологии обычно не составляет труда. У многих интегрируемы?
систем поверхности постоянной энергии часто диффеоморфны ли
бо сфере S3, либо проективному пространству RP3, либо S'xS2
Например, для уравнений движения тяжелого твердого, тела в зо
136
ие больших скоростей после некоторой факторизации (см. гл. 3^
можно считать, что поверхности Q гомеоморфны R.P3. Кроме того,
если гамильтониан Я имеет изолированный минимум или макси-
максимум (т. е. изолированное положение равновесия системы) на М*г
то все достаточно близкие поверхности уровня Q={#=const} яв-
являются трехмерными сферами S3. Через Lp,q обозначим так назы-
называемые линзовые пространства (факторы сферы S3 по действию
циклической группы). Выделим случаи, представляющие интерес
для гамйльтоновой механики, в виде отдельного утверждения
(А. Т. Фоменко).
Предложение 1. Пусть гамильтонова система i>=sgradtf
интегрируема при помощи боттовского интеграла f на какой-то от-
отдельной поверхности Q постоянной энергии, гомеоморфной одному
из трёхмерных многообразий S3, RP3, S'xS2, Lp,q. Тогда
1) В случае, когда интеграл f ориентируем, всегда т>2, т. е„
система v обязательно имеет по меньшей мере два устойчивых
периодических решения на каждой из этих поверхностей.
2) В случае, когда интеграл f неориентируем, т>2 для S3 и
т>1 для многообразий RP3, S^S2, Lp,q. В частности, на сфере
S3 интегрируемая система всегда имеет по меньшей мере два ус-
устойчивых периодических решения для любого боттовского ин-
интеграла.
Итак, два устойчивых периодических решения у интегрируемой
системы существуют не только на трехмерных малых сферах, близ-
близких к изолированному положению равновесия (минимуму или
максимуму энергии Н), но и на всех расширяющихся поверхно-
поверхностях уровня функции Н до тех пор, пока они остаются гомеоморф-
ными сфере 53.
Критерий теоремы 1 является точным в следующем смысле:
Известны случаи, когда интегрируемая система v имеет на поверх-
поверхности Q=RP3 или на Q—S3 ровно два (и не больше\) устойчивых,
периодических решения [65].
Из результатов Аносова, Клингенберга и Такенса следует, что*
в множестве всех геодезических потоков на гладких римановых
многообразиях существует открытое всюду плотное подмножест-
подмножество потоков без замкнутых устойчивых интегральных траекторий
(см. Аносов [1], Клингенберг [63]). Это означает, что свойство гео-
геодезического потока не иметь устойчивых траекторий является
свойством общего положения. Напомним еще раз, что здесь,
имеется в виду «сильная устойчивость» (см. определение 2).
Следствие 1 (А. Т. Фоменко). Пусть двумерная гладкая по-
поверхность гомеоморфна сфере и снабжена гладкой римановой
метрикой общего положения, т. е. на поверхности нет ни одной
устойчивой замкнутой геодезической. Тогда соответствующий этой
метрике гладкий геодезический поток неинтегрируем (на каждой
неособой поверхности постоянной энергии) в классе гладких бот-
товских интегралов.
Назовем рангом R фундаментальной группы n\(Q) наимень-
наименьшее возможное число образующих (в копредставлении этой груп- ■
137-
пи). Итак, если ранг ni(Q) = l, то система v, интегрируемая на
Q при помощи- боттовского интеграла f, обязательно имеет на Q
хотя бы одно устойчивое периодическое решение. Например, в не-
некоторых интегрируемых случаях задачи движения четырехмерного
твердого тела по инерции с закрепленной точкой (см.[151]) неко-
некоторые трехмерные неособые поверхности постоянной энергии диф-
«реоморфны SlXS2 (замечание А. В. Браилова; до конца ситуации
проанализирована А. Ошемковым). Это означает, что n^S'xS2)^
=Z и jR=1. Аналогично, как хорошо известно, в интегрируемом
случае Ковалевской (для трехмерного тяжелого тела) некоторые
поверхности постоянной энергии (после подходящей факторизации,
см. выше) также гомеоморфны S'xS2.
Предложение 2. Пусть гамильтонова система v интегри-
интегрируема на какой-то одной неособой компактной трехмерной по-
поверхности Q постоянной энергии с помощью боттовского интегра-
интеграла f. Тогда, если система v не имеет на Q устойчивых периодиче-
периодических решений, то
1) группа H](Q, Z) не является конечной циклической,
2) ранг iii(Q)>2, причем хотя бы одна из образующих в груп-
группе ni(Q) имеет бесконечный порядок.
Рассмотрим геодезический поток плоского двумерного тора,
т. е. снабженного локально евклидовой метрикой. Этот поток ин-
интегрируем в классе боттовских интегралов и, очевидно, не имеет
замкнутых устойчивых траекторий. В силу предложения 2 мы
должны иметь ранг ni(Q)>2. В самом деле, неособые поверхно-
поверхности Q диффеоморфны здесь трехмерному тору Г3, у которого
л, Gз, z)=zezez.
Следствие 2. Пусть f=sgrad# — гладкая гамильтонова
•система на М4 и Q — некоторая неособая компактная трехмерная
поверхность постоянной энергии, пусть выполнены следующие два
условия:
1) система v имеет на Q не более одного устойчивого перио-
периодического решения;
2) группа Нг (Q, Z) — конечная циклическая или ранг ni (Q) <:
<1.
Тогда система неинтегрируема в классе гладких боттовских ин-
интегралов на данной поверхности Q.
В качестве приложения этого утверждения укажем на следст-
следствие 1 о неинтегрируемости гладких геодезических потоков общего
положения на двумерной сфере. В случае геодезического потока
плоского тора Т2 имеем Q=P, Я, (Г3, Z)=Z3, #=3 (т. е. условия
следствия 2 не выполнены). Хотя поток не имеет на Q замкнутых
устойчивых траекторий, тем не менее он интегрируем в классе бот-
боттовских интегралов.
В работе [97] была доказана теорема о некоммутативной ин-
интегрируемости гамильтоновых систем с симметриями, обобщаю-
обобщающая классическую теорему на тот случай, когда гамильтониан Я
включается в некоторую конечномерную алгебру Ли функций G,
удовлетворяющую условию dim G+ранг G = dimM Хотя здесь
138 - ' '
функции из алгебры Ли G уже не обязаны быть интегралами по-
поля sgrad#, тем не менее оказывается, что такие системы также
обладают инвариантными торами размерности, равной рангу G,
па которых траектории системы задают условно периодическое
движение [97].
Следствие 3. Пусть гамильтонова система u=sgrad# «к-
тегрируема на М2" в некоммутативном смысле и G — алгебра Ли
функций на М2п (относительно скобки Пуассона) с функциональ*
но независимыми (вообще говоря, некоммутирующими) образую*
щими f\, ..., fk, где /ч=#, &=dim G и dimG+ранг G—dimM.
Пусть ранг G = 2. Предположим, что среди функций fi есть хотя
бы одна функция fa такая, что ее ограничение на какую-то одни
совместную трехмерную компактную поверхность уровня Q осталь-
остальных функций fj, где ]фа, является боттовской функцией. Тогда
для системы v на Q выполнены все утверждения из теоремы 1.
Напомним, что ранг группы гомологии (в отличие от ранга
фундаментальной группы) — это число независимых образующих
бесконечного порядка. Выше мы сформулировали вопрос: любое
ли трехмерное замкнутое многообразие может быть реализована
как поверхность уровня гамильтониана некоторой интегрируемой
системы? Ответ на него дает
Следствие 4. Далеко не каждое трехмерное гладкое ком-
компактное замкнутое ориентируемое многообразие может выступать
в роли поверхности постоянной энергии гамильтоновой системы*
интегрируемой при помощи боттовского гладкого интеграла.
Таким образом, препятствием к интегрируемости гамильтоно*
вой системы может быть топология поверхности постоянной энер*
гии. Ниже мы подробнее расшифруем слова «далеко не каждое
многообразие». Мы предъявим в явном виде топологическое пре*
пятствие, мешающее «подавляющему большинству» трехмерных
многообразий реализовываться в виде поверхностей постоянной
энергии интегрируемых систем. Можно построить конкретные при-
примеры достаточно простых многообразий, которые не могут являть-
являться такими поверхностями.
Перечисленные выше результаты в действительности являют-
являются следствиями общей теоремы о топологической классификации?
поверхностей постоянной энергии интегрируемых систем. Прежде
чем сформулировать ее, опишем пять типов простейших трехмер-
трехмерных многообразий, оказывающихся теми «элементарными кирпи-
кирпичами», из которых, оказывается, склеена произвольная поверхность
постоянной энергии интегрируемой системы.
Тип 1. Прямое произведение SlxD2 назовем полноторием*.
Ето край — один тор Т2 (рис. 55).
Тип 2. Прямое произведение T2xDl назовем цилиндром. Его
край — два тора Р (рис. 55).
Тип 3. Прямое произведение N2xSl назовем ориентированным
седлом (или более образно «штанами»), где N2 — двумерная сфе-
сфера с тремя выброшенными дисками (или диск с двумя дырками).
13Ф
Многообразие N2 гомотопически эквивалентно восьмерке, т. е. бу-
букету двух окружностей. Край N2xSl — три тора Т2 (рис. 55).
Тип 4. Реализуем многообразие N2 как диск с двумя дырка-
дырками, которые фиксируем и занумеруем цифрами 1 и 2. Рассмотрим
нетривиальное расслоение /!3->-S1 с базой окружность S1, со сло-
слоем N2. Ясно, что над окружностью существует лишь два неэкви-
неэквивалентных расслоения со слоем N2. Это — прямое произведение
(см. выше тип 3) и расслоение А3 (рис. 56). Оно харак-
тпип!
Рис. 55
Рис. 56
теризуется тем, что после переноса слоя N2 вдоль базы S1 он воз-
возвращается на прежнее место с переменой местами дырок \ и 2.
Так как N2 гомотопически эквивалентно восьмерке, составленной
из двух окружностей 1 и 2, то типы 3 и 4 можно представить еще
и так. В типе 3 (с гомотопической точки зрения) мы имеем пря-
прямое произведение восьмерки на окружность, а в типе 4 восьмерка
движется по окружности так, что после полного оборота две ок-
окружности 1 и 2 меняются местами (восьмерка переворачивается)
■(рис. 56). Получаем бутылку Клейна, погруженную в R3-(рис. 57).
Малая окрестность окружности-базы S1 гомеоморфна в этом
случае двум листам Мебиуса, пересекающимся трансверсально по
общей оси. Краем многообразия А3 являются два тора. Ясно, что
А3 можно для наглядности реализовать в R3 и тогда оно имеет
следующий вид. Рассмотрим полноторие, ограниченное стандарт-
стандартно вложенным тором, внутри которого высверлим тонкое полно-
полноторие, два раза наматывающееся на образующую большого пол-
нотория (рис. 57). Многообразие А3 мы назовем неориентируемым
седлом. Ясно, что Л3 является пространством ориентированного
140
косого произведения N2xSl. Впрочем, с топологической точки зре-
зрения многообразие Л3 не является новым. Оно получается склей-
склейкой полнотория и штанов по некоторому диффеоморфизму тора.
Условно это можно записать так: Л3 = /+///= (S1XD2) + (N2xSl).
Доказательство будет дано ниже.
Тип 5. Через К2 обозначим бутылку Клейна,'а через /С3 —
пространство ориентированного косого произведения К2 на отре-
зок.'т. е. K?=K2XD1 (рис. 58). Границей А'3 является тор Т2. С то-
лологической точки зрения многообразие /С3 также не является
Рис. 57
Рис. 58
принципиально новым, так как (см. доказательство ниже) оно
представляется в виде склейки следующего вида: /C3=/+/V=
() ()
Таким образом, из указанных пяти типов многообразий лишь 1
•и 3 являются топологически независимыми. Типы 2, 4, 5 разлага-
разлагаются в комбинации многообразий типов 1, 3. Однако при изуче-
изучений траекторий системы v (динамики системы) многообразия Л3
и К3 представляют большой самостоятельный интерес, так как
соответствуют различным движениям механической системы.
Теорема 2 (теорема топологической классификации трехмер-
трехмерных поверхностей постоянной энергии интегрируемых систем;
А. Т. Фоменко). Пусть М4 — гладкое симплектическое многообра-
многообразие (компактное или.некомпактное) и u = sgradН — гамильтоно-
ва система, интегрируемая по ^Лиувиллю на какой-то одной неосо-
неособой компактной трехмерной поверхности постоянной энергии Q
при помощи боттовского интеграла f. Пусть m — число периоди-
141
ческих решений системы v на поверхности Q, на которых интеграл
f достигает строгого локального минимума или максимума (тогда
они устойчивы). Пусть далее р — число двумерных критических
торов интеграла f (минимумов или максимумов интеграла); q —
число критических окружностей интеграла f (неустойчивых траек-
торий системы) с ориентируемой сепаратрисной диаграммой; s —
число критических окружностей интеграла^ (неустойчивых траек-
траекторий системы) с неориентиру<емой сепаратрисной диаграммой;
г — число критических бутылок Клейна (минимумы или максиму-
максимумы интеграла). Это — полный список всех возможных критиче-
критических подмногообразий интеграла f на Q. Тогда многообразие Q
представляется в виде склейки (по некоторым диффеоморфизмам
граничных торов) следующих «.элементарных кирпичей-»:
Q=mI+pII+qIII+sIV+rV=
=m(S1xD2)+p(T2xDl)+q(N2xSl)+sA*+rK3.
Если интеграл f — ориентируемый, то последнего слагаемого нет*
т. ё. г=0. Указанное разложение поверхности Q назовем гамиль-
тоновым.
Таким образом, в полученном нами каноническом гамильто-
новом представлении многообразия Q все неотрицательные целые
числа m, p, q, s, r имеют четкую интерпретацию: они сообщают
нам, сколько критических подмногообразий каждого типа имеет
данный интеграл f на данном многообразии Q, Если же мы бу-
будем игнорировать эту интерпретацию чисел m, p, q, s, r и поста-
поставим вопрос о наиболее простом топологическом представлении
изоэнергетической поверхности Q, то на этот вопрос отвечает сле-
следующая теорема.
Теорема 3 (А. Т. Фоменко). Пусть Q — компактная неосо-
неособая поверхность постоянной энергии гамильтоновой системы v—
=sgrad# на Q, интегрируемой при помощи боттовского интегра-
интеграла f. Тогда Q допускает топологическое представление Q — m4+
+ p'II + q411 = m'(&xD2)+p'(FxD>)+q'(N*xSi), где m', p',q'~—
некоторые неотрицательные целые числа. Эти числа связаны с чис-
числами т, р, q, s, г из теоремы 2 гак: m'=m+,s+2r, p'=p, q'—
= q + s + r. Более того, Q = m"l+q"III, где m"=m' + p', q" = q'+p'.
Таким образом, для изоэнергетической поверхности Q3 возни-
возникают два разложения: Q=mI+pH+qIH+sIV+rV и Q = m'I+p'II+
+q'III. Первое из них — гамильтоново разложение, второе—топо-
второе—топологическое разложение. Ясно, что гамильтоново разложение — бо-
более «подробное», оно «помнит» структуру критических подмного-
подмногообразий боттовского интеграла. Топологическое разложение — бо-
более грубое (хотя и более простое). Его элементарные блоки уже
частично «забыли» исходную гамильтонову картину. В дальней-
дальнейшем мы будем пользоваться каждым из этих разложений в зави-
зависимости от интересующей нас задачи.
Теперь мы можем дать полную классификацию всех перестроек
торов Лиувилля, возникающих при изменении значения интегра-
142
via f. Меняя Я и f местами, можно было бы говорить о бифурка-
бифуркации торов Лиувилля, когда они проходят через критический уро-
уровень энергии при фиксированном втором интеграле f.
Рассмотрим следующие 5 типов перестроек тока Р, отвечаю-
отвечающих указанным выше многообразиям I, II, III, IV, V. Реализуем
тор Р как одну из компонент
края соответствующего много-
многообразия. Тогда тор Р, увле-
увлекаемый изменением интеграла
/, преобразуется в объедине-
объединение торов Лиувилля, являю-
являющихся остальными компонен-
компонентами края. Эти перестройки
имеют вид рис. 59:
1) Тор Р стягивается на
осевую окружность полното-
рия и «исчезает» затем с по-
поверхности уровня интеграла f.
Обозначим эту перестройку
так: Р—*-S'—>-0.
2) Два тора Р движутся
навстречу друг другу по ци-
цилиндру, сливаются в один тор
и «исчезают». Обозначение:
3) Тор Р распадается на
два тора, проходя через центр
штанов (ориентированного
седла), которые затем «оста-
«остаются» на поверхности уров-
уровня интеграла f. Обозначение:
7'22Р
Рис. 59
4) Тор Р два раза наматы-
наматывается на тор Р (следуя при
этом топологии неориентиро-
неориентированного седла Л3) и остается
затем на поверхности уров-
уровня интеграла f. Обозначение:
5) Тор Р превращается в
бутылку Клейна (два раза на-
накрывая ее) и затем «исчезает»
с поверхности уровня интеграла f. Обозначение:
Пять перестроек, получающихся из указанных выше заменой
стрелок на обратные, мы не будем считать новыми.
Теорема 4 (теорема_классификации бифуркаций двумерных
торов Лиувилля; А. Т. Фоменко). Пусть f — боттовсшй интеграл
на неособой поверхности постоянной энергии Q3. Тогда любая пе-
перестройка общего положения тора Лиувилля, возникающая при
143
его ■ проходе через -критическую поверхность уровня интеграла ft
является композицией перечисленных выше элементарных пере-
перестроек 1—5. Более того, из этих пяти перестроек независимы (с
топологической точки зрения) лишь первые три. Перестройки 4 .
и 5 распадаются в композиции перестроек вида 1 и 3.
Общая теорема классификации бифуркаций многомерных то-
торов Лиувилля будет сформулирована нами ниже.
В качестве важного следствия этих результатов мы получаем
возможность представить каждую изоэнергетическую поверхность
Q с интегралом f на ней в виде одномерного графа T(Q, f), все
типы вершин которого E типов), оказывается, допускают точное и
полное описание. Для построения графа достаточно изобразить
каждый тор Лиувилля точкой. Меняя значение функции f, мы за-
заставляем эти торы (т. е. «точки») перемещаться, в результате че-
чего они заметают ребра одномерного графа. Подробное описание
см. ниже.
Рассматривая все неособые поверхности Q, на которых интег-
интеграл f — боттовский, мы получаем конечный набор графов {Г (Q/)}.
Оказывается, в случае общего положения этот набор графов за-
зависит только от самого интегрируемого гамильтониана Я и не за-
зависит от конкретного вида второго интеграла f. При замене f на
другой интеграл f графы T(Q, f) заменяются на гомеоморфные им
графы F(Q, f). Поэтому набор графов F(Q) является инвари-
инвариантом самого «интегрируемого случая», т. е. интегрируемого га-
гамильтониана. Подробнее о построении нового топологического ин-
инварианта интегрируемых уравнений см. в приложении 7.
Рассмотрим теперь четыре класса трехмерных компактных ори-
ориентируемых замкнутых многообразий.
1) Класс (Я) состоит из поверхностей Q3 постоянной энергии
{изоэнергетических поверхностей) интегрируемых гамильтоновых
систем (при помощи боттовского интеграла).
2) Класс (Q) состоит из всех многообразий, разлагающихся в
сумму «элементарных кирпичей» типов 1, 2, 3, т. е. в сумму
m'(SixD»)+p'(T*xDl)+q'(N*xSi). Как доказано автором (тео-
(теорема 2), класс (Я) содержится в классе (Q).
3) Исходя из внутренних задач трехмерной топологии, Вальд-
хаузен в [255] ввел класс (W) трехмерных многообразий. W, на-
названных им Graphenmannigfaltigkeiten. Определяются они так.
Требуется, чтобы в W существовал набор непересекающихся дву-
двумерных торов, выбросив которые мы получаем многообразие,
каждая компонента связности которого расслаивается со слоем
окружность над двумерным многообразием (возможно с краем).
4) Недавно, развивая идеи автора, описанные в настоящей гла-
главе, С. В. Матвеев рассмотрел класс (S) трехмерных -многообра-
-многообразий, на которых существует гладкая функция g, все критические
точки которой организованы в невырожденные окружности, а все
неособые поверхности уровня функции g являются объединениями
двумерных торов.;
144
Оказывается, для классов (Я) и \Q) имеет место обратное
включение, т. е. в итоге классы (Я) и (Q) совпадают.
Утверждение 2 (А. В. Браилов, А. Т. Фоменко). Имеет
место равенство (H)=i(Q), т. е. любое многообразие, полученное
склейкой полноторий, цилиндров и штанов, может быть реали-
реализовано в виде компактной поверхности Q3 постоянной энергии не-
некоторой интегрируемой (при помощи боттовского интеграла) га-
мильтоновой системы на подходящем симплектическом многообра-
многообразии М4 {быть может, некомпактном).
Далее, А. Т. Фоменко и X. Цишанг доказали равенство (W) —
= (Q), а С. В. Матвеев — равенство E) = (Q). Собирая вместе
все эти результаты, получаем следующую теорему.
Утверждение 3. Все четыре класса трехмерных многооб-
многообразий, описанных выше, совпадают, т. е. (Я) = (Q) = (W) = (S).
Оказывается далее, что число критических подмногообразий ин-
интеграла f на Q можно оценить снизу универсальной постоянной,
зависящей только от первой группы гомологии Hi(Q, Z). Пусть
р-ранг H\(Q, Z) (т. е. одномерное число Бетти), е — число эле-
элементарных множителей в конечной части Tor#i группы #i(Q, Z).
Если Тог Я] разложена в упорядоченную сумму подгрупп, где по-
порядок каждой подгруппы делит порядок предыдущей, то е — чис-
число таких слагаемых.
Утверждение 4 (А. Т. Фоменко, X. Цишанг). Пусть Qe
е (Я), т. е. Q3 — поверхность постоянной энергии интегрируемой
системы (при помощи боттовского интеграла f). Пусть m — чис-
число устойчивых периодических решений системы, s — число неус-
неустойчивых периодических решений с неориентируемой сепаратрис-
ной диаграммой, г — число критических бутылок Клейна. Тогда
всегда выполнены неравенства m/=m+s+2r»E—2p+l, <7'>т'—2
при m+r+s+q>0. Если m=r=s=^=0, то е-2р«:0> причем равен-
равенство г — 2$ действительно достигается для некоторых (Q,f). Кроме
того, q>m+r—2 (где числа q', q определены выше). Если инте-
интеграл f ориентируем и все сепаратрисные диаграммы его критиче-
критических подмногообразий также ориентируемы, то s = r=0, г. е. в
этом случае мы получаем следующую оценку снизу на число m
устойчивых периодических решений системы: пг^-е—2р+1, а также
q^m — 2 (если m+q>0).
Следствие 5 (А. Т. Фоменко). Пусть интеграл f «полностью
ориентируем», т. е. он ориентируем и ориентируемы все сепарат-
сепаратрисные диаграммы его критических подмногообразий на Q. Тогда
многообразие Q допускает следующее представление. Пусть m —
число устойчивых периодических решений системы на Q, на кого-
рых f достигает локального минимума или максимума. Рассмот-
Рассмотрим двумерное замкнутое связное компактное ориентируемое мно-
многообразие Mg2 рода g, где g^-Х (т. е. сферу с g ручками) и рас-
рассмотрим прямое произведение Mg2xSK Выделим в Mg2 произволь-
произвольный конечный набор непересекающихся и самонепересекающихся
гладких окружностей аи, среди которых есть ровно m стягиваемых
145
окружностей (остальные негомотопны нулю в Mg2). В прямом
произведении Л1Я2Х«51 окружности щ определяют двумерные торы
r;2=a/xS1. Разрежем Mg2xSl no всем этим торам 7\-2, после чего
обратно отождествим эти же торы (два берега разреза) при по-
помощи,, вообще говоря, нетождественных диффеоморфизмов. В ре-
результате получается новое трехмерное многообразие. Оказывает-
Оказывается, связная поверхность постоянной энергии Q является многооб-
многообразием именно такого типа и все получающиеся таким образом
многообразия являются изоэнергетическими поверхностями неко-
некоторых интегрируемых систем.
Выше мы рассматривали случай, когда совместная поверх-
поверхность уровня обоих интегралов Я и f компактна. Однако не со-
составляет труда сформулировать и доказать аналогичные утверж-
утверждения и для некомпактного случая.
1.2. Краткая сводка необходимых сведений из классической
теории Морса гладких функций. Если на гладком многообразии
-Q задана гладкая-функВД4*-?— а невырожденными критическими
точками, т. е. функция Морса, Jp, как хорошо известно, знание
этих точек и их индексов позволяет многое сказать о топологии
многообразия Q. Как мы покажем в настоящей главе, аналог этой
теории существует и в том случае, когда на симплектическом мно-
многообразии задан набор независимых функций в инволюции, коли-
количество которых равно половине размерности многообразия.
Напомним, что точка Xo^Q называется критической для функ-
функции J, если grad/(ATo)=O. Критическая точка называется невы-
невырожденной, если матрица второго дифференциала d2f, т. е. матри-
матрица ( —|, невырожденна в точке ха. Индексом критической
\ dXidxj )
й
точки х0 называется максимальная размерность линейного под-
подпространства в касательной плоскости TXoQ, на котором били-
билинейная симметричная форма d2f отрицательно определена. Други-
Другими словами, форму d2f всегда можно привести в критической точ-
точке х0 к диагональному виду, и тогда индекс критической точки
«будет числом отрицательных квадратов в диагональной записи
этой формы.
Функция f называется функцией Морса, если все ее критиче-
критические точки невырожденны. Хорошо известно (см., например, кни-
ту Дж. Милнора [91]), что на любом гладком компактном много-
многообразии всегда существуют функции Морса. Причем они всюду
плотны в пространстве всех гладких функций на многообразии.
Каждая функция Морса имеет на компактном многообразии Q
лишь конечное число критических точек, в частности, все они изо-
изолированы. В множестве всех функций Морса существует всюду
плотное подмножество, состоящее из таких функций, что каждо-
каждому критическому значению такой функции отвечает одна и только
одна критическая точка на многообразии. Другими словами, «а
каждом критическом уровне такой функции находится в точности
одна критическая точка (рис. 60).
J46
Важным этапом в построении обычной теории Морса является
шестная лемма Морса. Она утверждает, что в некоторой откры-
открытой окрестности невырожденной критической точки Хо функции
\^орса f всегда существуют такие локальные регулярные коорди-
КП1.1 г/ь ..., уп, что в этих коорди-
штах функция f запишется в виде
(У)=-Ух2- ■ ■--У2>.+У\+1+У2п, где
» — индекс критической точки.
■ Пусть f — функция Морса на Q.
Введем обозначения.: fa = f~l(a) — по-
зерхность уровня функции f, отвечаю-
отвечающая значению a; Qa= (x^Q :f (л;)<а),
". е. Qa состоит из всех точек х, в ко-
горых значения f не превосходят а. Яс-
Ю, ЧТО 6Qa = fa.
Пусть отрезок [а, Ь] (где а<Ь на ве-
дественной оси) не содержит критиче-
■ких значений функции f, т. е. в множе-
множестве f~[[a, b], лежащем в многообразии Q, нет критических точек
эункции f. Тогда многообразия fa и fb диффеоморфны и, кроме4
-ого, многообразия Qa и Qb также диффеоморфны. При этом Qa
чляется деформационным ретрак^ом Q& (рис. 61).
Рис. 60
Рис. 61
Рис. 62
Пусть в слое f~l[a, b]=Qb\Qa имеется ровно одна критическая
точка индекса К. Тогда многообразие Qb гомотопически эквива-
эквивалентно конечному клеточному комплексу, получающемуся из мно-
многообразия Qa приклейкой к краю fa=dQa одной клетки о*1 размер-
размерности К (рис. 62). Ручкой Я*" размерности п и индекса i назы-
называется прямое произведение двух дисков D^xD"-*. Край ручки
имеет вид дЯ^^-'хD"-K)\J(D*xSn->~1). Пусть Sx-lczfa - глад-
гладко вложенная сфера такая, что -ее достаточно, малая трубчатая;
147"
окрестность NtSt~1 радиуса е>0 представляется в виде прямого
произведения S^-'x^""*, где Z)"-* — нормальный диск размерно-
размерности п—К радиуса е. Тогда можно построить новое гладкое много-
многообразие Qa с краем, рассмотрев склейку многообразия Qa с руч-
ручкой //*" по диффеоморфизму g:Sx~lxDn-t--^N^S'-1=S^1xDn-\
Имеет место важное утверждение (М. Морс). Оказывается,
многообразие Qb получается из многообразия Qa именно такой
операцией, т. е. Q& является результатом приклейки к краю мно-
многообразия Qa ручки- #хп индекса К. Другими словами Qa~Qb-
Как мы покажем ниже, важный аналог этих утверждений име-
имеет место, если заменить функцию f на отображение момента сим-
плектического многообразия, порожденное полным набором ком-
коммутирующих интегралов. В частности, можно рассмотреть один ин-
интеграл на трехмерной поверхности постоянной энергии интегрируе-
интегрируемой системы.
Перейдем к доказательству теорем п. 1.1.
1.3. Топологические перестройки торов Лиувилля интегрируе-
интегрируемой системы при изменении значения второго интеграла. Пусть
в дальнейшем выполнены все предположения теоремы 2.
Лемма 1. Гладкий боттовский интеграл f не может иметь на
меособой компактной поверхности постоянной энергии Q изолиро-
изолированных критических точек.
Доказательство сразу следует из того, что на Q3 нет кри-
критических точек функции Н. Поэтому из каждой критической точ-
та хо функции / на Q вырастает невырожденная интегральная тра-
траектория поля v, целиком состоящая из критических точек функ-
функции f.-
Лемма 2. Критические точки гладкого боттовского интеграла
на компактной неособой поверхности Q заполняют либо изолиро-
изолированные гладкие критические окружности, либо гладкие двумер-
двумерные торы, либо бутылки Клейна.
Доказательство. Если невырожденная интегральная тра-
траектория поля v, выходящая из критической точки х0 интеграла f,
замкнута, то она является окружностью. Если траектория незамк-
незамкнута, то ее замыкание Р является двумерным связным подмно-
подмножеством, состоящим из критических точек интеграла. Поэтому Р
.лежит на какой-то двумерной критической совместной поверхно-
поверхности уровня L интегралов Н и f. Вообще говоря, особая поверхность
уровня интеграла не обязана быть многообразием. Так как интег-
интеграл f — боттовский, то его критические точки организованы в не-
невырожденные подмногообразия. Следовательно, Р лежит в дву-
двумерном критическом подмногообразии Р' для функции f. Утверж-
Утверждается, что пересечение L с достаточно малой открытой окрестно-
окрестностью Р' в Q совпадает с Р'. Так как по нормали к Р' функция
f невырожденна, то она либо строго возрастает, либо строго убы-
убывает по обе стороны вдоль нормали к Р'. Следовательно, близкая
неособая поверхность уровня Р двулистно накрывает Р'. В силу
интегрируемости системы неособые компактные поверхности уров-
уровня Р (на Q) являются торами Лиувилля, а потому Р' гомеоморф-
.148
ло либо тору, либо бутылке Клейна. Дело в том, что на многооб-
многообразии. Р' есть ненулевое векторное поле sgrad#. Такое поле мо-
может быть лишь на торе Г2 и на К2. На проективной плоскости
RP2 такого поля нет. Лемма доказана.
В лемме 2 мы имели дело с критической поверхностью уровня
L, вообще говоря, не гомеоморфной объединению торов, так как
она может иметь особенности (но вдали от Р'). Неособые поверх-
поверхности уровня интеграла f на Q компактны по теореме Лиувилля
являются объединениями торов.
Пусть S1 — критическая окружность интеграла f на Q. Припи-
Припишем ей индекс 0, 1 или 2 в зависимости от того, какой индекс
имеет ограничение -f на нормальный двумерный диск к окружно-
окружности. Ясно, что индекс S1 не зависит от выбора точки на S1. Окруж- .
ности индекса ноль — это локальные минимумы интеграла f, ин-
индекса два — максимумы, а индекса 1 — седловые окружности.
Лемма 3. Критические окружности интеграла f на Q могут
иметь индексы 0, 1, 2, а критические торы и бутылки Клейна —
талько индексы 0 и 1.
Доказательство следует из,леммы 2.
Изучим теперь перестройку поверхностей уровня Ва—(х^
^Q:f(x)=a)=f-l(a) функции f при увеличении а. Полбжим Са=
= (jceQ;/(x)<a). Ясно, что Ва=дСа. Если а — некритическое зна-
значение, то Ва — это объединениелщюв^Диувилля.
Определение 4. гКруглой ручкой_у{азовеи прямое произве-
произведение окружности на двУмерныиТгискТна границе которого выде-
выделены две связные непересекающиеся дуги А и h (рис. 63). Круг-
Круглая ручка (полноторие) —,-это утолщенный цилиндр с подошвами
(основаниями) liXS1 и kxSK
Опеределим операцию приклейки круглой ручки к трехмерно-
му многЬобраТшкГСг<Гс~ краём?аГ~11усть на Ва лежат две непересе-
кающиеся и самонепересекающиеся окружности Yi и у2. Рассмот-
Рассмотрим их малые трубчатые окрестности Ni и N2. В силу ориентируе-
ориентируемости Ва эти окрестности гомеоморфны SlXDl, где D1 — отрезок.
Приклеим круглую ручку к Ва, отождествив с помощью гомео-
гомеоморфизма кольцо hxS1 с кольцом Ni и кольцо kxS1 с Л^г- Полу-
Получим новое трехмерное многообразие. Окружности Yi и Y2 назовем
осями подошв круглой ручки (рис. 64). Сепаратрисную диаграм-
диаграмму критической окружности S1 мы обозначим через sdS1.
Лемма 4. Пусть а — критическое значение интеграла f на
Q. Предположим, что на критической поверхности уровня Ва ле-
лежит роено одна критическая седловая окружность S1. Пусть е>
>0 настолько мало, что на отрезке [а—е, а+е] нет других критиче-
критических значений функции f, кроме а.
1) Пусть sdS1 ориентируема. Тогда Са+е получается из Са~..
приклейкой к краю Ва-е многообразия Са-е круглой ручки. При
этом Са+е гомотопически эквивалентно Са-„ к которому своими
обеими краями приклеен цилиндр SXXDK
2) Пусть sdS1 неориентируема. Тогда Са+г гомотопически эк-
эквивалентно Са-г, к которому приклеен лист Мебиуса.
149
Доказательство. Начнем со случая 1. Рассмотрим седло-
вую критическую окружность S1 индекса 1. В каждой ее точке х
рассмотрим нормальный диск D2(x) малого радиуса е. Рассмот-
Рассмотрим поле grad/ на Q, вводя на многообразии Q какую-нибудь ри-
манову метрику. Из каждой точки xeS1 выпустим сепаратрисы
поля grad f. Их объединение — это сепаратрисная диаграмма сед-
ловой окружности. В силу невырожденности функции f на диске
D2(x) сепаратрисная диаграмма каждой точки x^S1 является ги-
Рис. 63
Рис. 64
перболической (седло). Меняя точку х вдоль S1, мы гладко де-
деформируем сепаратрисы в нормальном диске D2(x). Рассмотрим
«входящую» часть Р-=Р-2 сепаратрисной диаграммы, содержа-
содержащуюся в слое a—z<.f*g.a (рис. 65). Так как е мало, то Р- являет-
является гладким двумерным подмногообразием, содержащим S1 и име-
имеющим край, гомеоморфный либо окружности, либо несвязному
объединению двух окружностей. Одна из них — критическая ок-
окружность S1. В первом случае многообразие Р_ гомеоморфно ли-
листу Мебиуса, во втором случае — цилиндру S^xD1.
Так как сепаратрисная диаграмма критической окружности S1
предположена нами пока ориентируемой, то первый случай (лист
Мебиуса) здесь невозможен. Следовательно, трубчатая окрест-
окрестность поверхности Р- гомеоморфна круглой ручке. Она приклеена
к Со-е именно так, как это требуется определением операции при-
приклейки круглой ручки (см. выше). Оси обеих подошв круглой
ручки приклеены к двум гладким окружностям yi и ^2, которые
150
f'l
f>/0
прочерчиваются на Ba~t точками А и В (рис. 65) при скольжении
точки х по S1. Лемма доказана в случае, когда sdS1 ориентируема.
Если же sdS1 неориентируема, то из предыдущего рассмотре-
рассмотрения, ясно, что вместо толстого цилиндра (полнотория) приклеи-
приклеивается «толстый лист Мебиуса,». Лемма доказана полностью.
Отметим, что круглая ручка
может приклеиваться к Ва-е лишь
двумя способами: к одному тору
или. к двум разным торам. «Тол-
«Толстый лист Мебиуса» может при-
приклеиваться лишь к одному тору,
так как его граница связна (в отли-
отличие от границы цилиндра).
1.4. Сепаратрисные диаграммы
высекают нетривиальные циклы на
неособых торах Лиувилля.
Лемма 5. Пусть на критиче-
критическом уровне Ва расположена роено
одна критическая седловая окруж-
окружность SK
1) Пусть sdS1 ориентируема.
Рассмотрим круглую ручку, соот-
соответствующую критической окружно-
окружности S1 и приклеенную своими
двумя подошвами к Ва-г. Тогда
каждая из подошв лежит на каком-
то торе Лиувилля. Кроме того, ось
каждой из подошв ручки является
гладкой самонепересекающейся ок-
окружностью, реализующей ненулевой
элемент фундаментальной группы
тора. Если обе подошвы приклеены к одному и тому же тору, то
оси у\ и 72 обеих подошв круглой ручки не пересекаются на торе,
реализуют одну и ту же образующую фундаментальной группы
гора и изотопны друг другу на этом торе.
2) Пусть sdS1 неориентируема. Тогда входящая сепаратрисная
диаграмма Р-, гомеоморфная листу Мебиуса, приклеена своей
граничной окружностью к одному тору Лиувилля, на котором эта
гладкая самонепересекающаяся окружность реализует одну из не-
ненулевых образующих фундаментальной, группы тора.
Трубчатую окрестность сепаратрисной диаграммы Р_ в неори-
ентируемом случае мы называем утолщенным (или толстым) ли-
листом Мебиуса.
Лемма 6. 1) Пусть sdS1 ориентируема. Если круглая ручка
приклеивается к двум разным торам, то эти торы перестраивают-
перестраиваются в один тор после прохода через критическую седловую окруж-
окружность S\ соответствующую ручке. Если же ручка приклеивается
к одному тору, то он распадается в объединение двух торов пос-
после прохода через критическую окружность S1.
Рис. 65
151
'be
Рис. 66A)
Рис. 66C)
Рис. 66B)
Рис. 66D)
Т.,
Рнс. 66E)
2) Пусть sd S1 неориентируема. Тогда тор Лиувилля, к кото-
которому приклеен лист Мебиуса (в виде диаграммы PJ), преобразу-
преобразуется снова в один тор Лиувилля после прохода через критическую
седловую окружность Sx.
Доказательства лемм 5 и 6. Пусть sdS1 ориентируе-
ориентируема. Рассмотрим первый случай, когда ручка приклеивается к раз-
разным торам Г1 и Т2. Пусть yi и уг — однократные оси подошв руч-
ручки, a S1 — критическая седловая окружность на уровне Ва. Рас-
Рассмотрим два тора Т\,, и T2,t, лежащие на Ва-С и являющиеся дву-
двумя компонентами связности Ва-, (не считая остальных его ком-
компонент, которые сейчас нас не интересуют). Пусть 71е и у2е— Две
окружности, высекаемые на Т\,, и Т2л входящей сепаратрисной
диаграммой Р- (рис. 66 A—5)). Можно считать, что 7\=7\> и
Yi=Y'8'. гДе i=1.2 и ео — достаточно малое фиксированное число.
С уменьшением е окружноети yf и ^2е, конечно, сближаются и
при s=0 сливаются в одну окружность S\ являющуюся критиче-
критической седловой окружностью.
Так как f — боттовский интеграл, то сближение однократных
окружностей Yie и Y2e происходит гиперболическим образом. Торы
7"i,e и T2,t при изменении s не пересекаются и сближаются лишь
в окрестности своих окружностей Yie и Y2e- Поэтому можно счи-
считать, что на каждом из неподвижных торов Т\ и Т2 выделены две
достаточно малые трубчатые окрестности U\ и £/j окружностей
Yi и Y2 соответственно, внутри которых (окрестностей) -шевелятся
окружности Yie и Y2e, не выходящие за пределы U\ и U2, причем
Yie изотопны Yi. t—1. 2. Ясно, что все торы Г,-,, (при переменном
е) канонически отождествляются при помощи диффеоморфизма
вдоль интегральных траекторий поля gradf с неподвижным то-
тором Т,=Т,-,Р0, i=l,2.
Рассмотрим точку М на окружности Yie и выпустим из нее ин-
интегральную траекторию т поля v. Возможны два случая: а) она
замкнута, б) она незамкнута. В ^случае а) окружность т, целиком
лежащая на торе 7\,в," близка^ к замкнутой траектории S1,
«ели е достаточно мало. В таком случае окружность т замкнута
на неособом торе 7\,е. Так как система v интегрируема, то к тору
Т\л применимы утверждения теоремы Лиувилля. • Следовательно,
на каждом из торов 7\е и Т2,г существуют регулярные криволи-
криволинейные координаты, относительно которых ограничение поля v
иа торе определяет условно периодическое движение. Поскольку
у поля v на Т\,е обнаружилась замкнутая интегральная траекто-
траектория т, то все остальные траектории этого поля на Ti,e также замк-
замкнуты. В таком случае однократная траектория т, сделав полный
оборот по тору 7,р,.*реализовала нетривиальный элемент фунда-
фундаментальной группы n\(Ti]C), поскольку она порождена прямоли-
прямолинейной обмоткой тора. Но траектория т сколь угодно близка -к
Yie, так как обе они близки к седловой окружности S1. Следова-
Следовательно, Yie реализует ненулевой элемент группы ni(fi,e), а пото-
потому yi реализует ненулевой элемент группы ni(Ti). Аналогично
в случае а) кривая Y2 реализует ненулевой элемент ni(T2).
.153
Рассмотрим случай б), когда траектория т незамкнута на
7\,е. Так как т при уменьшении е можно считать проходящей сколь
угодно близко от интегральной траектории S1 (седловой окружно-
окружности) на каждом наперед заданном (но фиксированном) интерва-
интервале времени, то, уменьшая е, можно добиться, что через некоторое
время траектория т. снова (и впервые!) вернется в малую окрест-
окрестность точки М. Пусть Л^ет — точка возврата, расположенная
около точки М в Q. При этом траектория т не покинула окрестно-
окрестности Ui окружности YiE на торе ТЬе, Следовательно, траектория т
совершила по тору TUz один полный оборот и снова вернулась в
малую окрестность начальной точки М на торе.
Очевидно, что здесь мы воспользовались ориентируемостью се-
паратрисной диаграммы. Соединяя точки М и Mi малым геодези-
геодезическим отрезком на торе 7\,Е, получаем из траектории т новую
замкнутую траекторию т', целиком лежащую в окрестности Ui.
Из теоремы Лиувилля следует, что т/ реализует ненулевой эле-
элемент группы ni(Tl]t), так как она получена малым замыканием-
почти периодической траектории, совершившей один полный обо-
оборот по тору и вернувшейся в точку, близкую к начальной (пер-
(первое возвращение). Так как однократная траектория т' сколь угод-
угодно близка к однократной траектории yie, to Yie и, следовательно,
Yi реализуют ненулевые элементы в группах niG\,e) и ni(T{) со-
соответственно. Мы существенно использовали то, что траектория тг
вернувшись в точку Ми совершила по 7\,8 один полный оборот.
Итак, если ручка приклеивается к двум разным торам, то лем-
лемма 5 доказана в ориентируемом случае. Пусть теперь ручка при-
приклеивается к одному тору (случай 2). Можно считать, что теперь
торы 7*1,,, и Гг.е (из предыдущего рассуждения) совпали. Обозна-
Обозначим этот тор через Т-„ Мы получаем на торе Т-, две окружности
Yi~e и Y2~e, которые при уменьшении е слегка деформируются
внутри своих первоначально выбранных (конечных) окрестностей
Ui и U2 и не покидают их. Окрестности (кольца) U] и t/2 можно,
очевидно, выбрать на* торе Т-г непересекающимися, так как слия-
слияние окружностей уге и Y2~e при уменьшении е происходит морсов-
ским образом (рис. 65). Снова рассмотрим случаи а) и б).
В случае а) (замкнутая интегральная траектория т.) доказав
тельство повторяется дословно. В случае б) требуется дополни-
дополнительное рассуждение. ■
Пусть траектория т незамкнута. Уменьшая е, можно добиться
того, что она через некоторое время (впервые) вернется в неко-
некоторую точку Mi, лежащую в малой окрестности точки М. Здесь
нуждается в доказательстве тот факт, что точка Мх расположена
близко к точке М с точки зрения (топологии) тора Т-е. Близость
точек М и Mi в многообразии Q .еще не гарантирует, что они
близки в топологии тора Т-е. Из леммы 4 следует, что тор Т-г
пересекается с трубчатой окрестностью окружности S1 по двум-
окрестностям Ui и U2. Можно считать, (при малом s), что Ui(]
П^2=0 (вследствие боттовости интеграла /). Но тогда за один
оборот траектория т не сможет выйти из Hi и попасть в £/2, так
154
как во время первого оборота траектория т движется близко от
окружности угв, оставаясь в ее трубчатой окрестности Ux. Факти-
Фактически мы снова опираемся на ориентируемость сепаратрйсной диа-
диаграммы, вследствие чего после одного полного оборота точки В
на yi (рис. 65) вернется в свое прежнее положение, а не в точку
А. Другими словами, использован тот факт, что пересечение Р-
с Ва-г состоит ровно из двух непересекающихся окружностей у\
и Y2- Итак, в случае 2 обе окружности yi~e и уг~е реализуют не-
нетривиальные циклы на одном и том же торе Т~г. Эти окружности
не пересекаются, так как сепаратрисы критических точек не пе-
пересекаются вне критических течек. Из элементарных свойств дву-
двумерного тора следует, что эти окружности изотопны и реализуют
один и тот же цикл на торе Т~е.
Пусть теперь sdS1 неориентируема, т, е. сепаратрисная диа-
диаграмма Р- гомеоморфна листу Мебиуса. Здесь после первого обо-
оборота вдоль окружности S1 точка А перейдет в точку В (рис. 65),
т. е. точка Мл не будет близка к точке М в топологии тора Т-е.
Другими словами, траектория т совершит лишь половину полного
оборота по тору Т-г. Сделав еще один оборот вдоль S1, траекто-
траектория т завершит свое движение по тору Т-Е, вернувшись в некото-
некоторую точку М2, близкую к точке М в топологии тора Т_е. Дальней-
Дальнейшее рассуждение, очевидно, повторяет рассуждение ориентируемо-
ориентируемого случая. Лемма 5 доказана.
Перейдем к доказательству леммы 6. Начнем с ориентируемого
случая. Пусть круглая ручка, отвечающая седловой окружности,
приклеивается к разным торам Т\ и Т% по кольцам, осями кото-
которых являются нестягиваемые (в силу леммы 5) окружности Yi
и Y2 соответственно.
Разрезая торы по этим окружностям, мы получаем два кольца
(из каждого тора). Приклеивая круглую ручку и рассматривая
границу получившегося трехмерного многообразия, мы получаем
один тор в качестве верхней компоненты границы. Обращая рас-
рассуждение, получаем перестройку двух торов Лиувилля в один.
В неориентируемом случае обе компоненты Р+ и Р- сепаратрйс-
сепаратрйсной диаграммы sdS1 критической окружности S1 гомеоморфны
листу Мебиуса (по отдельности). Следовательно, их границы
связны и гомеоморфны окружности. Отсюда следует, что один тор
Т-е перестраивается в точности в один тор Т+е. Лемма 6 доказана.
При доказательстве лемм 5 и 6 существенно использовался
тот факт, что седловая окружность является интегральной траек-
траекторией поля v. Если ограничиться рассмотрением лишь гладкой
боттовской функции f, неособые поверхности уровня которой яв-
являются двумерными торами (т. е. если отбросить условие, что
f — интеграл гамильтонова поля), то число вариантов перестроек
набора торов Лиувилля в набор торов сразу увеличится.
Приведем соответствующую таблицу, например, для ориенти-
ориентируемого случая. Возможны следующие четыре случая расположе-
расположения двух гладких самонепересекающихся и непересекающихся ок-
окружностей yi и Y2 на торе (рис. 67 A—4)).
155
1) Окружности yi и Y2 нестягиваемы. Тогда они реализуют один
и тот же нетривиальный цикл на торе и изотопны друг другу.
2) Окружность yi нестягиваема, а окружность у2 стягиваема.
3) Окружности yi и Y2 стягиваемы и расположены вне друг
друга.
4) Окружности yi и уг стягиваемы и уг расположена внутри yi-
В результате приклейки круглой ручки один тор превращается
соответственно в следующие поверхности (в случаях 1—4):
Рис. 67A)
Рис. 67B)
Рис. 67C)
Рис. 67D)
1) два тора, 2) один тор, 3) крендель (т. е. сфера с двумя
ручками) и сфера, 4) два тора.
Итак, по сравнению с утверждением леммы 6 добавились бы
еще два новых превращения тора: тор превращается в тор (нетри-
(нетривиальное преобразование) и тор превращается в крендель и сфе-
сферу. Случаи 2, 3, 4 запрещены леммами 5 и 6, если sdS1 ориенти-
ориентирована. Итак, опираясь на условия теоремы 3, мы отбрасываем
«75 процентов» всех возможных перестроек тора и оставляем лишь
случай 1, т. е. те «25 процентов», которые разрешены теоремой
Лиувилля.
1.5. Изоэнергетические поверхности задаются одномерными
графами, вершины которых разбиваются на пять канонических
типов. Рассмотрим интеграл f на Q. Возможны следующие два
случая: А) функция f имеет хотя бы одну критическую седловую
окружность на поверхности Q, Б) функция / не имеет критиче-
критических седловых окружностей.
Начнем со случая А и предположим, что sdS1 ориентируема.
Пусть S1 — седловая окружность на Q. Рассмотрим две близкие
некритические поверхности уровня Ba+t и Ba-t- Согласно лемме 6
окружность S1 порождает либо распад тера Лиувилля на два то-
156
pa, либо слияние двух торов в одни тор. Рассматривая вместо t
функцию —f, Можно считать, что мы изучаем распад одного тора
на два тора.
Выделим в слое (а—е</<а+е) связную компоненту V(Sl)
(трехмерное многообразие с краем), содержащую S1 и имеющую
в качестве границы: один тор Т~с в составе «нижней» поверхности
Рис 68
Рис. 69
Ba-t и два тора 7i,e и Гг.е в составе «верхней» поверхности Ва+С
(рис. 68). Тор Т-е распадается на два тора 7\,е и Гг,г при про-
прохождении через критическое значение а. Сепаратрисная диаграм-
диаграмма Р- выходит из критической окружности S1 и, спускаясь вниз,
встречает тор Г-, по двум окружностям yi и уг (см. выше). Из
лемм 5 и 6 следует, что yi и Y^ являются границами кольца, ле-
лежащего на торе Г_е.
Обозначим оба кольца, в объединение которых окружности yi
и Y2 разбивают тор Т-с, через /Ci и /Сг- Построим новую поверх-
151
ность Pi, добавив к сепаратрисной диаграмме Р_ кольцо К\ и вто-
вторую поверхность Р2, добавив Р_ кольцо /Сг (рис. 68). Ясно, что
обе поверхности Pi я Рг гомеоморфны тору (рис. 69).
Лемма 7. Пусть sdS1 ориентируема. Тогда торы Pi и Р2 изо-
изотопны в многообразии U (S1) торам 7\,е и Г2,е соответственно. Ок-
Окружности yi> Y2. S1 леоюат на каждом из торов Р\, Рг и реализуют
на них нетривиальные образующие циклы, (они не пересекаются
и негомотопны нулю).
Доказательство. Изотопию тора 7\> на тор Pi можно
построить при помощи рассуждений, использующихся в обычной
теории Морса при деформации поверхности уровня вдоль интег-
интегральных траекторий векторного поля до тех' пор, пока поверх-
поверхность не окажется в малой окрестности сепаратрисной диаграм-
диаграммы, после чего стягивание производится «по нормалям» к сепа-
сепаратрисной диаграмме. Остальные утверждения следуют из лемм 5
и 6. Лемма доказана.
Выше мы постоянно предполагали, что на критическом уровне
Ва находится ровно одна критическая седловая окружность. Рас-
Рассмотрим теперь общий случай, когда на Ва находится, вообще
говоря, несколько таких окружностей (их всегда конечное число).
'Лемма 8. Всегда можно считать (при изучении перестроек
торов Лиувилля), что на каждом критическом уровне Ва находит-
находится роено одна критическая седловая окружность. Другими слова-
словами, можно всегда считать, что круглые ручки или толстые листы
Мебиуса приклеиваются последовательно, а не одновременно.
Доказательство. Аналог этой леммы в обычной теории
Морса хорошо известен, однако в нашем случае его доказатель-
доказательство более деликатно, так как здесь мы имеем дело с интегралом
f (а не просто с гладкой функцией). Поэтому нужно существенно
использовать условия теоремы 3. Произвольное гладкое возмуще-
возмущение интеграла дает, вообще говоря, уже не интеграл. Рассмотрим
близкую неособую поверхность Ва-е — объединение нескольких
торов. Предположим, что с каким-то одним из этих торов Г_е
встречается несколько сепаратрисных диаграмм седловых окруж-
окружностей. В силу боттовости интеграла / каждая сепаратрисная диа-
диаграмма пересекает тор Г_е по гладкой самонепересекающейся
окружности, причем окружности, отвечающие разным диаграм-
диаграммам, не пересекаются. К каждой из окружностей по отдельности
применимы все предыдущие рассуждения. Следовательно, каждая
из них является осью узкого кольца, по которому приклеивается
подошва одной круглой ручки- или подошва толстого листа Ме-
Мебиуса. Из рис. 70A) (изображающего для простоты лишь ориен-
ориентированный случай) видно, что все круглые ручки и толстые ли-
листы Мебиуса можно считать приклеивающимися независимо друг
от друга к тору Т_е. Пусть, .например, .на ;гор Г_е «вышли» сепа-
ратрисные диаграммы нескольких седловых окружностей 1—4 (на
рис. 70A) они изображены точками). Сначала можно выполнить
перестройку по окружности 1. В результате тор 7\^ распадется
на два тора, изображенных пунктиром. Очевидно, что пересечения
158 '
этих пунктирных торов с прежними сепаратрисными диаграммами
окружностей 2, 3, 4 имеет тот же топологический тип, что и преж-
прежде (нестягиваемые образующие на торе). Пунктирные торы мож-
можно считать близкими к тору Т-„ объединенному с сепаратрисной
диаграммой Р- окружности 1. Поэтому прежние диаграммы высе-
высекают на них изотропные образующие (на рис. 70A) они показаны
белыми кружками).
. Теперь можно выполнить следующую перестройку по окружно-
окружности 2 и т. д. Итак, можно считать, что каждый раз мы приклеи-
приклеиваем лишь одну круглую ручку или один толстый лиет Мебиуса,
Рис. 70A)
Рис. 70B)
т. е. проходим только одну критическую седловую окружность.
Важно, что в нашем случае круглые ручки и толстые листы Ме-
Мебиуса приклеиваются не друг к другу (что запутало бы картину),
а к одному и тому же неособому тору (причем а разных его мес-
местах) или к его малому сдвигу по интегральным траекториям поля
grad/ (рис. 70B)). Благодаря'этому обстоятельству мы можем
теперь коммутировать приклейку круглых ручек и листов Мебиу-
Мебиуса, порожденных критическими седловыми окружностями, отвеча-
отвечающими одному и тому же критическому значению интеграла. Кро-
Кроме того, непересекающиеся и самонепересекающиеся окружности
на торе (в любом числе), реализующие ненулевые элементы фун-
фундаментальной группы, реализуют один и тот же элемент, а потому
попарно изотопны.
Теперь мы можем соответствующим образом деформировать
функцию /, чтобы на каждом " ее критическом уровне осталась
ровно одна седловая окружность. Гладкая деформация поверхно-
поверхностей уровня функции /, позволяющая задать и гладкую деформа-
деформацию самой функции, показана на рис. 71. Здесь изображено сече-
сечение трехмерного многообразия Са в окрестности его особой по-
159
верхности уровня Ва. При деформации функции f она, конечно,
перестает быть интегралом поля v в целом, но остается интегра-
интегралом в малой окрестности каждой отдельной сепаратрисной диаг-
диаграммы. Лемма доказана.
Можно также считать, что все локальные минимумы функции f
расположены на одном уровне f @), а все локальные максимумы
интеграла — на одном уровне f~l(l). Этого можно добиться изме-
изменением функции f лишь в малой окрестности минимальных и мак-
__
ft
1
I
л
*
4
У
щп
A
tt;;
% >
2
*
I
с
Рис. 71
Рис. 72
-симальных подмногообразий. Новых критических точек при этом
не возникает.
Многообразие Q удобно задавать в виде некоторого графа Г =
= F(Q, f). Пусть O^f^l на поверхности Q. Все минимумы ,и мак-
максимумы интеграла можно считать абсолютными (см. выше). Так
как f — боттовская функция на Q, то картина распада и уничто-
уничтожения неособых торов Лиувилля вблизи критических седловых
окружностей —- строго определенная. См. леммы 5 и 6.
Изобразим неособые двумерные торы Лиувилля обычными точ-
точками (на каждый тор отведем по одной точке). Меняя значение
-функции f, мы заставляем эти точки перемещаться, так как каж-
каждый неособый слой функции (интеграла) изображается теперь на-
набором точек (по числу торов Лиувилля). В результате получится
160
некоторый одномерный граф, начинающийся на плоскости (f=0)
И заканчивающийся на плоскости (f—\). При этом введем следу-
следующие обозначения.
1) Большой черной точкой (черным кружком) с исходящим
(соответственно входящим) ребром графа мы обозначим мини-
минимальную соответственно максимальную окружность -для интег-
интеграла.
2) Белым кружком с двумя исходящими (соответственно вхо-
входящими) ребрами графа мы обозначим минимальный (соответ-
(соответственно максимальный) двумерный тор для интеграла.
3) Трилистником («треножником»), т. е. точкой с тремя ребра-
. ми графа, встречающимися в атой точке, мы обозначим связную
трубчатую окрестность критической седловой окружности с ориен-
ориентированной сепаратрисной диаграммой sdS'.
4) Звездочкой (с входящими и исходящими ребрами) обозна-
обозначим трубчатую окрестность критической седловой окружности с
неориентированной сепаратрисной диаграммой sdSK
5) Кружком с точкой внутри и с исходящим (соответственно
входящим) ребром графа мы обозначим минимальную (соответ-
(соответственно максимальную) критическую бутылку Клейна.
Каждый трилистник (треножник) описывает либо распад одно-
одного тора на два тора, либо, наоборот, слияние двух торов в один.
Это зависит от того, как ориентирован треножник: либо двумя
ребрами вверх, либо одним ребром вверх.
Получающийся граф показан на рис. 72. Ясно, что- его можно
реализовать в R3. Очевидно, существует непрерывное отображение
h поверхности Q на граф T(Q,f). Меняя интеграл f (но сохраняя
поверхность Q), мы будем, вообще говоря, менять граф. Поэтому
в обозначении графа учтено как многообразие Q, так и слегка
возмущенный интеграл /.
Однако, если заменять интеграл f на боттовский интеграл, не
меняя гамильтониана Я, мы в случае общего положения не изме-
изменим граф Г(<2, }). Точнее, мы заменим граф на граф, ему гомео-
морфньщ. Другим* словами, замена второго интеграла приводит
к гомеоморфизму нашего графа. В основе доказательства лежит
тот факт, что тор Лиувилля почти всегда (в случае несоизмери-
несоизмеримых частот, т. е. в нерезонансном случае) является замыканием
любой интегральной траектории, лежащей на нем. Следовательно,
тор Лиувилля полностью определяется только гамильтонианом Я
(в интегрируемом случае). Таким образом, мы, оказывается, по-
получаем возможность сопоставлять каждому «интегрируемому га-
гамильтониану» его характеристический набор графов T(Q). Это
позволяет наглядно различать между собой различные случаи ин-
интегрируемости. Каждый случай .интегрируемости, например, в тео-
теории движения тяжелого твердого тела получает свое наглядное
изображение, отличающее его от других случаев.
На рис. 73а мы занумеровали все эти типы вершин графа Г
цифрами 1, 2, 3, 4, 5 не случайно. Дело в том, что имеется взаим-
взаимно однозначное соответствие между этими пятью видами вершин
(J Л. Т. Фоменко 161
"ШЛУА'ЦТ
m=0
О i
/77=/
m--0
z О/
- fl>'0
/U>/2
/77=/ m*o
Q/oo 20 2Q/« 207oo
V V
2
►2. 2 %
B)
1 9 1
C)
D)
m=Z
E) F)-
(г)
т-0
т-0
/и ьЗ
(О
т-0
т = 1
© 2О°° 2®'~ 1*
\у л/
2X2,
у\ А
(DIoi 2(Э7„ 2<Ь1 2Э
J3>,0
m=0
Y-IY-I Y-1
m>2
Рис. 73
графа г и пятью простейшими типами трехмерных многообразий,
перечисленных нами в теореме 2. Оказывается, достаточно малая
«окрестность»-вершины графа типа I (где i=l,2,3,4,5) гомео-
морфна (с точки зрения поверхности Q) элементарному много-
многообразию типа i в теореме 2.
Рассмотрим связное критическое подмногообразие L и близкие
к нему неособые поверхности уровня Ва+г и Ва-е. Пусть U(L) —
связная компонента слоя между 5а+Е и Ва~г, содержащая L.
Лемма 9. 1) Пусть 51 — критическая седловая окружность
и ее сепаратрисная диаграмма Р_ ориентируема. Тогда трехмерное
многообразие £/(S!) с краем TUt,\jT2,t\jT-t гомеоморфно прямому
произведению N2XS\ где N2 — двумерная сфера с тремя дырка-
дырками {диск с двумя дырками).
2) Пусть теперь сепаратрисная диаграмма Р- неориентируема..
Тогда U (S1) гомеоморфно многообразию А3, т. е. нетривиальному
расслоению Л3->5' со слоем N2; U(Sl) =N2XSl (косое произве-
произведение).
3) Пусть L = Sl — максимальная (или минимальная) окруж-
окружность для интеграла. Тогда f/(S1)=5'xD2 (полноторие).
4) Пусть L = T2 — максимальный или минимальный тор. Тогда
T2) = T2xDl (цилиндр).
5) ПустьЬ = К2 — максимальная (или минимальная) бутылка
Клейна. Тогда U(K2)=K3 = K2XDl- (косое произведение).
Двумерное многообразие N2 можно рассматривать как элемен-
элементарный кобордизм («штаны»),
содержащий ровно одну кри-
критическую точку индекса 1
(рис. 74).
Доказательство. Нач-
Начнем с ориентируемого
случая. Из лемм 5, 6, ■ 7
следует, что многообразие
U(Sl) содержит два тора
P^P-UKiK P2 = P[}K2, изотоп-
изотопные торам 7*1,е и Г2,8 соответ-
соответственно. Фиксируем эти изото-
Рис. 74
Рис. 75
164
пин. Поднимающаяся вверх (вдоль поля gradf) часть сепарат-
сепаратриснои диаграммы окружности 5! высекает на торе Г1|8 образую-
образующую 7ie> а ца торе Г2,8 — образующую у2е (Рис- 69, 75). При
изотопии тора Т\,Е вниз на тор Р\ окружность yf переходит в S1.
Аналогично пр.и изотопии тора 7,е на тор Рг окружность 72"-
переходит в S1. Любая образующая на двумерном торе всегда
может быть дополнена (неоднозначно) другой окружностью, явля-
являющейся второй образующей на торе и пересекающейся с первым
циклом ровно в одной точке. Выберем такую вторую образующую
на торе Т\,е (рис. 69,75). Опуская ее вниз при изотопии тора Т\л
на Р\, получаем на торе Р\ некоторую его образующую у, изоб-
изображенную пунктиром на рис. 69, 75 и являющуюся дополнитель-
дополнительной к окружности (образующей) 51. Окружность 7 распадается
на две дуги: y = yUy' в кольце К\. Ясно, что циклы усе ,и \2~г изо-
изотопны на торе Г_е и разбивают его в объединение колец К\ и К%.
Дополним дугу у дугой у" в К2, чтобы окружность,yUY" была бы
образующей на торе Рг, дополнительной к S\ а окружность т~Е =
= y'Uy" была бы образующей иа торе 7"_е, дополнительной к уге
(или к у2~г, что эквивалентно), см. рис. 69, 75, 76. Это можно сде-
сделать, так как б достаточно мало и часть сепаратриснои диаграм-
диаграммы Р- диффеоморфна цилиндру. Очевидно, что цикл yUy" являет-
Рис. 76
165
ся образующей на торе Р2, дополнительной к 51. Пр.и изотопии
тора Р2 на Ту,* его образующая 51 перейдет в у2в на^тор Т2,„ а
цикл yUy" перейдет в кривую Т2Е, являющуюся на торе Т2>е обра-
образующей дополнительной к образующей у2е.
Итак, мы построили систему координат в многообразии {/(S1).
В качестве N2 возьмем поверхность, заметаемую двумя окружно-
окружностями yUy' и 7Uy" пРи изотопии торов Р, на торы Г,,«, где i=l,2.
Ясно, что Т1Е = ЛГ2ПГ!е и Т2Е=Л[2П7'2 „ где т;е — образующая на торе
Ти, i=l, 2. Далее, yV2nr_e = <rE = YW. где T-e = Ki[jK2. Очевидно,
что окружности, изотопные S'-при указанных изотопиях Р,- на
торы Г,-,е, i=l, 2, задают слои прямого произведения A/^XS'3
= {7E'). В ориентированном случае.лемма доказана.
Теперь рассмотрим нео.риентируемый случай. Гранич-
Граничная окружность сепаратрисной диаграммы Р_ (листа Мебиуса)
приклеена к тору Г_г по какой-то его образующей y~e- Дополним
эту образующую на торе Г_е второй образующей, которую обозна-
обозначим через т~Е. Вторая образующая т"Е определяется неоднозначно,
но для нас это не имеет значения.
Так как окружность т~е лежит на неособом торе Лиувилля,
то в каждой ее точке определено нормальное векторное поле
gradf. Это поле увлекает за собой окружность тгЕ. Очевидно, мож-
можно корректно определить непрерывную деформацию окружности
тгЕ, индуцированную деформацией поверхности уровня. При этом
возможны два варианта:
1) Окружность тгЕ сначала превращается в восьмерку (две ее
точки склеиваются на особой поверхности уровня Ва), после чего
восьмерка разрывается и превращается в пару непересекающихся
окружностей.
2) Обратный процесс, когда окружность т~Е и ее дубликат, по-
получившийся после однократного обхода вдоль критической окруж-
окружности 51, сначала сливаются в одной точке, образуя восьмерку,
после чего восьмерка перестраивается и превращается в одну ок-
окружность.
Очевидно, что при обоих вариантах перестройки деформирую-
деформирующаяся окружность т"Е (или удвоенная окружность т~е) заметает
двумерный диск с двумя дырками. Более того, после одного пово-
поворота вдоль окружности 51 этот диск возвращается на прежнее
место, но две его дырки меняются местами. Мы получаем много-
многообразие Л3, расслоенное над базой 51 со слоем Л^2.
Пусть 51 — критическая окружность индекса 2 или 0. Рас-
Рассмотрим ее трубчатую окрестность U{Sl). Из боттовости функции
f следует, что U(S]) расслаивается на торы, сжимающиеся на
окружность 51 и являющиеся поверхностями уровня функции f.
Так как они лиувиллевы, то .интегральные траектории системы v
лежат на них. Тогда окружность S1, очевидно, устойчива.
Лемма 10. Имеют место следующие гомеоморфизмы:
1) Л3 = Л'2х51=E1Х/J) + (ЛГ2х51), т. е. А3 получается в ре-
результате склейки полнотория со штанами;
166 ,
2) K* = () () + (
получается склейкой двух полноторий со штанами.
Доказательство. 1) Рассмотрим на рис. 57 точку 0 —
центр восьмерки. Выбрасывая трубчатую окрестность окружности
р (т. е. выбрасывая полноторие), получаем многообразие R, по-
показанное на рис. 77. На рис.78
показано расслоение многообра-
многообразия R со слоем окружность над
двумерным многообразием с кра-
краем. Эта база гомеоморфна диску с
двумя дырками, т. е. ./V2. На рис. 78
показана соответствующая проце-
дура получения N2. Разрезая пер-
воначальное кольцо пополам и
склеивая два отрезка в соответ-
соответствии со стрелками, получаем N2.
Склейки определяются характе-
характером расслоения R на окружности.
Рис. 77
Рис. 78
2) Рассмотрим меридиан h на бутылке Клейна К2, показанный
на рис. 79. Этот меридиан можно считать базой нетривиального
s>
расслоения K2-*h со слоем окружность. Поэтому многообразие К3
расслаивается над окружностью h со слоем кольцо, т. е. SlXD{.
Итак, имеем р: /С3-»-/». При этом граничный тор Т2 (где Т2 = дК3)
расслаивается при проекции р со слоем, состоящим из пары ок-
окружностей (граница кольца). Это расслоение условно изображе-
изображено на рис. 79. Ясно, что бутылка Клейна К2 может быть вложена
в пространство расслоения К3 как «нулевое сечение» (рис. 79).
Следовательно, в К3 можно выделить окружность Я,
лежащую на «нулевом сечении» и проектирующуюся (гомеоморф-
но) на базу h при проекции р. Выбросим окружность h из К3.
167
В результате получаем новое расслоение р: /С3\Я—*-/г со слоем N2
(так как, выбрасывая из кольца точку, получаем N2). Ясно также,
что полученное расслоение нетривиально, т. е. /С3\й = Л3. Итак,
/С3 = Л3+E!Х/J)=2E1 + /J) + (ЛГ2х51), .что и требовалось до-
доказать.
1.6. Любая поверхность постоянной энергии интегрируемо*
системы представляется в виде склейки простейших трехме'рны.
многообразий трех типов. Пусть Q3—«интегрируемая» повег--
К2-
Рис. 79
ность постоянной энергии. Выделим в Q все критические
гообразия интеграла /. Имеем:
1) т>0 максимальных и минимальных окружностей S1;
2) р>0 максимальных и минимальных торов Г2;
3) 9>0 седловых окружностей 5+1, для которых сепаратрисная
диаграмма ориентируема;
4) s>0 окружностей SL, для которых сепаратрисная диаграм
.ма неориентируема;
5) г>0 максимальных и минимальных бутылок Клейна.
Тогда Q допускает гамильтоново представление Q = mU(S1) —
'+pU(T2)+rU-{K2)+qU{S+l)+sU(SJ), где через U(L) обозначен;
.связная регулярная трубчатая окрестность критической поверхно-
поверхности уровня, содержащей критическое подмногообразие L (см. вь-
168
шс). В лемме 9 все эти многообразия полностью описаны:
U(S1)=S1XD2, U(T2)=T2XD\ U{S+l)=N2xS\ U(SJ)=A\
U(К2) =К3. Отсюда, очевидно, следует утверждение теоремы 2.
Доказательство теоремы 3 получается из теоремы 2 и из лем-
леммы 10.
1.7. Двулистные накрытия над изознергетическими интегрируе-
интегрируемыми поверхностями всегда обладают ориентированным интСгра-
лом. Пусть К\2,...,Кг2 — конечное число бутылок Клейна, явля-
являющихся минимумами или максимумами интеграла f. Поверхности
уровня интеграла, близкие к /С,-2, гомеоморфны тору Т2, причем
этот тор двулистно накрывает бутылку Клейна К . Вырежем из
Q3 все многообразия Ki3, окружающие Ki2. Напомним, что /G3—
это трубчатая окрестность бутылки Клейна Ki2. Возьмем два эк-
экземпляра- Q+ и Q-, гомеаморфные Q\\]ri=iKi3. Ясно, что край
d(Q+\JQ-) состоит из 2г торов T2i+, T2i-, получающихся удвоением
торов дК?, \<i<r. Рассмотрим 2г экземпляров Л,-, В,- цилиндров
T2Y.Dl, причем сопоставим каждой паре торов 7;+) T2t- два ци-
цилиндра: Ai = T2i+XD1 и Bi — T2i-XDK Отождествим у каждого из
цилиндров его основание T2i+ (соответственно Г2,-) с тором Г2,-+
(соответственно Г2,_) в Q+ (соответственно Q-). Два оставшихся
основания цилиндров отождествим так, чтобы было корректно оп-
определено двул,истное накрытие Ai\JBt-+Ki3 (рис. 80). В результате
Рис. 80
169
получается новое многообразие Q=Q+\JQ-[](\]ri=iAi{]Bi). Очевид-
Очевидно, мы построили двулистное накрытие я: <3->-Q, причем Q+ и Q-
проектируются на Q\\Jri=iKi3 тождественно. Так как трубчатая
окрестность U(Q) поверхности Q в М4 гомеоморфна прямому
произведению QXD\ то можно построить двулистное накрытие
O(QU(Q)
Так как проекцию я: Q—>Q можно считать гладкой, то задан-
заданные на Q симплектическую структуру со, гамильтоново поле
sgrad H и интеграл f можно перенести обратно на Q. При этом
все эти объекты сохраняют свои характеристические свойства.
Утверждение доказано.
1.8. Нижние оценки на число устойчивых периодических реше-
решений системы. В силу теоремы 2 для Q3 имеет место гамильтоново
разложение
Q = mI + pII + qIII+sA3+rK3.
Копредставление конечно порожденной группы G с образующими
п\,...,ап и соотношениями W\,... ,Wm будем записывать так:
G— (а\,..., ап\ W\ = 1,..., Wm= 1^- Легко вычислить фундаменталь-
фундаментальные группы этих пяти элементарных кирпичей:
1) ni(S1XD*)=Z;
2) n1(PxZI)=ZeZ;
3) n\(N2XS1) =F2{a, b)@Z{c), где F2 — свободная группа;
далее tfi^xS^-ZezeZ;.
4) ni{A*)=m{A2)=F2(a, b)/(ab2 = b2a), далее tf,^3)=Z®Z;
5) ni{K3)=ai{K2) = {a, b\aba-*b = l), далее Я,(/С3) =Z©Z2.
Рассмотрим Q, интеграл f и соответствующий им граф Г =
= Г(<2, /). Выделим следующие 4 случая: 1) ^ = 0 (т. е. нет шта-
штанов), 2) q=\, 3) q = 2, 4) q>2. Опишем все возможные связные
графы T(Q, /) в случаях 1—3.
Лемма 11. Пусть q = 0. Тогда все возможные связные графы
Г(<2, f) показаны на рис. 736. Для т<1 графы T(Q, f) приведены
на рис. 736A—3). Число экземпляров А3, т. е. число s звездочек
на ребрах графа, моЖет быть произвольно.
Доказательство сводится к простому перебору всех воз-
возможных случаев. На рис. 73 рядом с каждым из узлов (вершин)
на графе Г мы поставили два числа: количество свободных обра-
. зующих (со значком оо) и число всех образующих в группе Hi
соответствующего элементарного многообразия. Например, рядом
с полноторием (черная вершина на графе) стоят числа 1» и 1.
Пусть р — одномерное число Бетти, ц — число всех образующих
в группе гомологии H{(Q, Z).
Лемм а-12. Пусть q=l. Все связные возможные графы Г по-
показаны на рис. 73в. Графы Г, для которых т<1, приведены на
рис. 73вA—4). Число s (т. е. число звездочек) может быть произ-
произвольно.
Лемма 13. Пусть q — 2. Все связные возможные графы Г, для
которых т<1, приведены на рис. 73г. Число звездочек любое.
170 ' .
Теперь перейдем к доказательству тех утверждений теоремы 1,
в которых участвует группа гомологии H\(Q, Z).
Лемма 14. 1) Пусть граф T(Q, f) связен и q = 0. Для графа
Г рис. 736A) группа Hi всегда бесконечна, т. е. C>1. Для графа
Г рис. 736B) группа HY имеет не менее одной (возможно, конеч-
конечной) образующей, т. е. цзП и р>0. В частности, Hi может быть
циклической конечной группой, если Qo= (SlXD2) +sA3+K3. Для
графа Г рис. 736C) группа Hi имеет не менее двух независимых
(возможно конечных) образующих, т. е. ц>2, р:>0.
2) Пусть граф Г связен и q—l. Для . графов Г рис. 73вA,2)'
группа Hi всегда бесконечна, т. е. р>1. Для графов Г рис.
73вC,4) р>0, ц>2 (для рис. 73вC)) и р>0, ц>3 (для рис.
73вD)). В частности, в случаях рис. /ЗвC,4) группа Нх всегда
отлична от нуля и не может быть конечной циклической.
3) Пусть граф Г связен и q = 2, пг^.1. Если граф Г содержит
сотя бы один цикл (см. рис. 73гA)), то группа Hi всегда беско-
гечна, т. е. р>1. Для графа рис. 73гB) Р>0, \к~>А, для графа
оис. 73гC) р^О, \£^. В двух последних случаях группа Hi всег-
всегда отлична от нуля и не может бьпь конечной циклической.
4) Пусть граф Г связен и q>2. Если граф Г содержит хотя бы
один цикл,"то группа Hi бесконечна. Если нет ни одного цикла,
то граф Г является деревом. В этом случае всегда \i^\ + q>3,
поэтому группа HY всегда отлична от нуля и не может быть конеч-
конечной циклической группой.
Доказательство. Пусть комплекс X получен склейкой двух
■своих подкомплексов У и Т, пересекающихся по связному подком-
подкомплексу R. Пусть Ру (соответственно \iY) и Рг (соответственно
[хт) — числа Бетти (соответственно количество, всех образующих),
причем здесь имеется в виду наименьшее число образующих) для
групп гомологии Hi(Y, Z) и Hi(T, Z). Пусть цл — минимальное
число образующих в группе Hi(R, Z). Тогда из теоремы ван Кам-
пена следует, что рх>6к+Ру—Рн и \1Х>Цг+Цт—\ir. Далее, если
граф T(Q, f) содержит хотя бы один замкнутый цикл, то из той
же теоремы ван Кампена (примененной для случая несвязного
пересечения R) следует, что группа Hi(X, Z) содержит по крайней
мере одну бесконечную образующую. Комбинируя эти два прос-
простых наблюдения, следует перебрать все случаи, перечисленные на
рис. 73:
1) В случае рис. 736A) граф Г содержит цикл, т. е. Hi — oo.
В случае рис. 736B) p(Q) >p(SIX£>2) +P(/C3) +s$(A*) — (s +
+ l)P(r2) = l + l + 2s — 2(s+l)=0, т. е. р>0. Аналогично n(Q)^
>jxE'XD2) + \i(K3) +sv(A*) — (s+ 1)VG) = 1 +2 + 2s—2(s+ 1) = 1.
Легко построить пример (подбирая нужные диффеоморфизмы
двумерных граничных торов), когда Hi = Za. Следовательно, здесь
группа Hi может быть конечной циклической, но в рассматривае-
рассматриваемом случае мы имеем т=1. Это событие происходит, .если Qo=
= (SlXD2) +sA3+K3= (s + 4) (S1XD2) + (s + 2) (WxS1).
Если же нам заранее известно, что многообразие Q недиффео-
морфно Qo, то этот особый случай (когда Н\ — конечная цикли-
171
,ческая) вычеркивается. Все остальные случаи рассматриваются
аналогично. Приведем только окончательные ответы. Для рис.
736C)
. Р (Q) > 2Р (К3) + sp (Л3)- (s + 1) р G2) =
= 2+2s— 2(s+l) = 0, т. е. p(Q)>0; n(Q)>
>2ц(А:з) + 5и(Л3)-E+ 1)hG") = 4 + 2s—2(s + 1) =
= 2, т. е. ц(<Э)>2.
2) При q—l графы рис. 73вA,2) имеют циклы, поэтому Н\ =
= оо. Для рис. 73вC)
р (Q) > 2р (К3) + р (S1 х D2) + р (Л^2 х S1) + sp (Л3)—
-(s+3)p(r2) = 2 + l+3 + 2s— 2(s+3) = 0; p(Q)>0;
H(Q)>2pi(K3)+n(S1xD2)+n(^2xS') + sn^3)-
= 4+l+3 + 2s—2(s + 3) = 2;
Для рис. 73в D) P(Q)>3p(/C3) + PC^xS^ + sp^3) — (s +
3)p(T2)>0; M(Q)>3n(/C3) + n(^2xS1)+snn3)-(s+3)n(n>3.
3) При <7 = 2 и m<l графы р.ис. 73гA) имеют цикл, поэтому
\ = оо. Далее, для рис. 73гB)
Для рис. 73гC)
51KЛ3 (
[() ( )j()^
4) Пусть q>2, m^l. Если Г содержит цикл, то #i = oo. Пусть
Т — дерево. Тогда возможны лишь два случая:
Q=
В первом случае
Во втором случае n(Q) >2 + <7>4. Лемма 14 доказана.
Доказательство гомологической части теоремы 1 завершаете^
следующим образом. Если интеграл ориентируем, то г = 0, следо-
следовательно, при условии конечности группы Hi на рис. 736, в, г, ос-
остаются лишь графы, расположенные справа от вертикальной пунк-
пунктирной линии, т. е. при т>2. Если интеграл неориентируем, то
томологические утверждения теоремы следуют из леммы 14. Нера-
172
ненство m + r>2 (при условии конечности группы Hi), очевидно,
.эквивалентно неравенству пС^2 (в ориентируемом случае), если
засчитывать каждое Къ за полноторие (см. лемму 14).
Осталось доказать утверждения теоремы 1, связанные с груп-
группой n\(Q). Пусть n\(Q)~Z в случае ориентируемого интеграла.
Из леммы 14 (рис. 73) следует, что для графов вида рис.
736B,3), 73вC,4), 73гB,3), 73дB,3) группа Hi(Q, Z) имеет не
менее двух независимых образующих, следовательно, п\{Q)ФZ.
Таким образом, эти графы нас сейчас не интересуют. Осталось
-проверить, что если граф T(Q,f) содержит хотя бы один цикл, то
тогда в группе iti(Q) есть по крайней мере две независимые обра-
образующие.
Рассмотрим случай рис. 736A), т. е. склейку двух цилиндров.
Нужно изучить случаи рис. 736A), 73вA, 2), 73гA), 73дA). В слу-
случае рис. 73г( 1) два седла могут быть склеены по двум (из трех)
своих граничных торов, см. рис. 73г A) слева. Подсчет дает, что
здесь ц>3, а потому zti{Q)=£Z. Если два седла склеены в виде
дерева (рис. 73гA) справа), то нужно заклеить четыре граничных
тора. Возможны два варианта: приклейка двух цилиндров (тогда
j3>2 и л\фТ) либо приклейка одного цилиндра и двух полното-
рий (но в таком случае т = 2).
Аналогичные рассуждения показывают, что в случае рис.
73дA), т. >е. при <7>2, тем более п\фХ. Осталось разобрать слу-
случаи рис. 73вA) слева и рис. 736A). Ясно, что достаточно изучить
«случай рис. 736A), так как в случае рис. 73вA) слева вклейка
полиотория в штаны может дать в худшем случае коммутативную
группу с двумя образующими, а это как раз случай нижнего, ци-
цилиндра рис. 736A).
Итак, рассмотрим случай Q = 2(T2XDl) + sAz (см. рис. 736A)).
Граф. Г содержит один нетривиальный цикл. Соответствующую
•ему образующую в группе iti(Q) мы обозначим через t. Предста1
■вим Q в следующем виде.
Разрезав на графе Г одно ребро, получим цилиндр T2XDl, в
который вклеено несколько неориентированных седел. Предполо-
Предположим сначала, что этих седел нет, т. е. что s = 0. Пусть G = hi(T2) =
= Z©Z и i\, i-2 — два вложения тора Т2 в верхний и нижний края
цилиндра T2XDl соответственно. Получаем гомоморфизмы t"i*:G->
-+m(T2xDl)=Z®Z и i2.: G->ni(T2xDl). Ясно, что ii* и i2* —
изоморфизмы групп. Обозначим через C?i и Ог образы группы G
лри этих гомоморфизмах. Тогда группа Jti(Q) получается из сво-
свободного произведения Z(t)*G введением соотношений tiXi(h)t~l =
-= t2*(/г), где h^G. Сокращенно совокупность этих соотношений
запишем так: tG\t~l = G2-
В нашем случае Gi«sG2~Z©Z=G, так как i\ и г2 — гомеомор-
гомеоморфизмы торов. Можно было бы с самого начала считать, что Gi = G,
т. е. что отображение h тождественно, a h — некоторый гомео-
гомеоморфизм. Тогда i2* можно задать унимодулярной матрицей \
и соотношения примут вид /а^' = аарс, /p^~1 = abpd, где аир —
173
образующие группы Gi = G = Z©Z. Отсюда видно, что ранг
nt(Q)>2, причем по крайней мере одна образующая t имеет бес-
бесконечный порядок.
Пусть теперь в цилиндр Рх/51 вклеено ровно одно неориенти-
неориентированное седло. Поступая по предыдущей схеме, оценим снизу
ранг Jti(Q). Найдем ni(Q), где <5 получено из Q разрезом вдоль
одного тора Лиувилля, т. е. на графе Г разрезается одно ребро.
Ясно, что Q гомеоморфно Л3, а Л3 гомотопически эквивалентно-
двумерному комплексу Л2, который можно получить следующим
образом. Возьмем окружность и ортогональную ей достаточно ма-
малую восьмерку. Затем будем перемещать восьмерку вдоль окруж-
окружности ортогональным образом, одновременно вращая восьмерку
так, чтобы после одного полного оборота она вернулась в прежнее
положение, но чтобы при этом две ее окружности а :и у поменя-
поменялись местами. Из рис. 57 следует
к, (Q) = F2 (а, у) * Z (PVtfap-1 = Y,
= Z (о) * Z (р)/(р2сф-2 = a) = F2 (а, Р)/(Р»а = «р»).
Здесь F2 — свободная группа с двумя образующими. Вычислим
группу iti(Q). Пусть i\ и ii — снова два вложения тора Т2 на
верхний и нижний края многообразия Q=A3. Считаем, что вложе-
вложение h тождественно. Здесь iu и i2*, отображающие группу Z©Z
в Я1(Л3), устроены следующим образом. Будем считать, что обра-
образующие группы niG'2)=Z0Z при гомоморфизме ti* переходят в
элементы аир2 группы ni (Л3). Чтобы понять, что произойдет с
элементами а и р2, после того как мы обойдем их вдоль образую-
образующей t, обратимся к ,рис. 57. Из него видно, что при этом нужно-
сравнить образующие на двух торах Лиувилля, расположенных по
разные стороны от особого слоя, гомеоморфного изученному нами
выше двумерному комплексу Л2. Имеем tatl=ix$a$-1, /p2^=|j3.
В самом деле, образующие аир можно считать образующими;
на внутреннем тонком торе в Л3, обходящем два раза ось р боль-
большого полнотория. При этом a — меридиан тонкого внутреннего
то.ра. Используя структуру Q, выводим внутренний тор из Л3 в Q
и переводим его на внешний тор Л3. При этом, элемент tat'1 (т. е.
образ а при этой операции) охватит восьмерку снаружи. Ясно, что
восьмерка'имеет вид a(pap~!). Мы проверили первое, утвержде-
утверждение.
Аналогично длинная параллель внутреннего тонкого тора поки-
покидает Л3 и возвращается на Л3 «снаружи» (.рис. 57). При этом она
превращается в элемент t$2t~l ,и разматывается, однократно пок-
покрывая р, что и требовалось проверить. Итак,
zti(Q)=Fs(a, Р, О/Самара?-1, /р2^ = р).
Отсюда следует, что ранг iti(Q)>2, причем по крайней мере одна
образующая, а .именно t, имеет бесконечный порядок.
Ясно, что увеличение числа неориентированных, седел в составе
Q не может уменьшить ранг ниже двух. Итак, в ориентируемом
случае теорема 1 доказана.
174
Пусть теперь интеграл неориентируем. Докажем, что т>1, ес-
если ni(Q)=Z. Рассмотрим двулистное накрытие л : Q->Q, построен-
построенное в утверждении 1. Так как щ(й) — подгруппа индекса два в
группе iti(Q), то jti(<5)=Z. Но теперь на й мы имеем ориенти-
ориентированный интеграл и по предыдущему рассуждению для f=n*f
получаем т>2. При проектировании вниз на Q две устойчивые
периодические траектории могут слиться в одну, следовательно,
Л1>1. Теорема 1 доказана.
Легко видеть, что в случае графа рис. 736A) путем выбора
подходящей склейки цилиндра можно добиться, чтобы Hi (Q, Z) =
= Z, хотя группа Jti(Q) остается при этом по крайней мере с дву-
двумя образующими. В самом деле, выше мы выписали соотношения
в фундаментальной группе jti(Q). Переходя к гомологиям, полу-
получаем соотношения а = аа + сC, p = ba+dp, т. е. а(а—1) + рс=О,
b (d—1)=0. Рассмотрим матрицу этой системы:
г- а—
'-{ ь d
-.)■
Если ее определитель отличен от нуля, то #i(Q, Z)=Z, по-
поскольку в этом случае система имеет лишь нулевое решение, т. е.
«=р=о.
В качестве примера возьмем унимодулярную матрицу (а \\ =
= [ ^ }V, в этом случае /=( J ^ У] и det/=l=^O. Следова-
Следовательно, многообразие Q, полученное из цилиндра T2xDl склейкой
двух его граничных торов диффеоморфизмом с матрицей ( , : ),
имеет группу Hi(Q, Z)=Z, т. е. ранг Т/i = 1. Этот пример основан
лишь на топологических соображениях. Однако всегда можно реа-
реализовать такое многообразие Q в виде поверхности постоянной
энергии некоторой интегрируемой системы.
Важно, что многообразия Л3 и К3 действительно возникают в
конкретных механических интегрируемых системах. Например, в
работе М. П. Харламова П^З] предъявлены топологические пере-
перестройки в динамике трехмерного тяжелого твердого тела, эквива-
эквивалентные А3.
Далее, геодезический поток плоской метрики-на бутылке Клей-
Клейна К2 обладает, как легко вычислить, изоэнергетической поверхно-
поверхностью Q3 = 2/C3, на которой определен боттоюский интеграл. При
двулистном накрытии обе бутылки Клейна К2 (минимум и макси-
максимум интеграла) разворачиваются в двумерные торы, в результате
чего получается многообразие <33 = 2G12XDI) с ориентированным
интегралом.
Пусть выполнены все условия следствия 5. Пусть система име-
имеет на Q ровно, т периодических траекторий, являющихся локаль-
локальными минимумами или максимумами интеграла f. В силу теоре-
теоремы 3 поверхность Q склеена из цилиндров, ориентируемых седел,
175
неориентируемых седел и ровно из т полноторий. Так как теперь
f предполагается полностью ориентированным интегралом, то в
составе Q нет неориентированных седел. Число цилиндров равно
числу максимальных и минимальных критических торов интегра-
интеграла. В каждом из этих элементарных кирпичей мы ввели выше
систему координат прямого произведения, которую мы зафикси-
зафиксируем. Попробуем ввести единую систему координат прямого про-
произведения на всем многообразии Q. Ясно, что, вообще говоря,
этого сделать нельзя. Дело в том, что если два «кирпича» склеены
по тору, то каждый из них индуцирует на торе свою пару обра-
образующих, ^задающих на нем систему координат. Любая пара обра-
образующих на торе совмещается при помощи некоторого его диффео-
диффеоморфизма. Разрезая Q по этому тору и применяя указанный диф-
диффеоморфизм, мы, очевидно, совмещаем две системы координат
прямого произведения (согласовываем их на общей части). По-
Последовательно продолжая этот процесс, мы распространяем эту
единую систему координат на все остальные «кирпичи».
Процесс завершится т тот момент, когда перестраиваемая
нами поверхность Q превратится в прямое произведение M2sXSl.
Ясно, что при этом интеграл f изменится и превратится в некото-
некоторую гладкую функцию на прямом произведении, постоянную на
■сомножителе S1. Следствие 5 доказано.
1.9. Топологические препятствия к гладкой интегрируемости.
Далеко не каждое трехмерное многообразие может реализовы-
заться как изоэнергетическая поверхность интегрируемой системы.
Докажем следствие 4. Привлечем результаты Вальдхаузена,-изло-
Вальдхаузена,-изложенные в [255]. На эту работу мое внимание обратил X. Цишанг.
В [255] изучается специальный класс трехмерных многообразий
W, названных Вальдхаузеном «многообразиями, подобными гра-
графам». Они определяются следующим образом. В многообразии W
должно существовать семейство Т непересекающихся торов Т2,
выбросив которое мы получаем многообразие, каждая связная
компонента которого расслаивается со слоем окружность над дву-
двумерным многообразием (возможно, с краем).
Легко видеть, что многообразия W содержат все поверхности
Q постоянной энергии гамильтоновых систем, интегрируемых при
помощи боттовского гладкого интеграла. Это вытекает из теоре-
теоремы 3. В самом деле, в силу этой теоремы классификации изоэнер-
гетических поверхностей многообразия первых трех типов, а имен-
именно: 1) полнотория, 2) цилиндры, 3) ориентированные седла (шта-
(штаны),'очевидно, расслаиваются со слоем окружность над двумерным
многообразием с краем.
Рассмотрим многообразие четвертого типа, т. е. Л3. Его, ко-
конечно, нельзя представить в виде расслоения Л3 — -*-М2, где
М2 — двумерная поверхность с краем. Однако Л3 можно разре-
аать на два куска Л] и Л2, каждый из которых допускает нужное
нам представление. На рис. 78 показано такое разбиение. Выре-
Вырезаем маленький диск с центром в точке О на N2. Этот диск опре-
определяет в Л3 тонкое полноторие, один раз обходящее вдоль оси Л3,
176
Выбрасывая это полноторие из Л3, получаем многообразие Р, рас-
расслаивающееся со слоем окружность над диском с тремя дырками.
На рис. 78 показан один такой слой, два раза обходящий вдоль
оси Л3' и в двух точках протыкающий диск с тремя дырками.
Итак, AS = P + (SlXD2), где каждое ,из этих многообразий явля-
является «многообразием-графом» (в смысле Вальдхаузена).
Аналогично проверяется, что и К3 принадлежит множеству
«многообразий-графов».
Итак, изоэнергетические поверхности интегрируемых систем
имеют вид склейки элементарных кирпичей, каждый из которых
распадается в объединение косых произведений двумерных много-
многообразий с краем на окружность, т. е. является многообразием
типа W.
В действительности можно показать, что' класс многообразий
вида W в точности совпадает с классом поверхностей постоянной
энергии интегрируемых систем.
Далее, в [255] отмечено, что класс многообразий вида W не
совпадает с классом всех трехмерных многообразий. Таким обра-
образом, следствие 4 доказано.
В [255] указаны примеры трехмерных многообразий (с краем),
не принадлежащих классу W (а потому и нашему классу поверх-
поверхностей Q). Возьмем сферу S3 и высверлим в ней полноторие U(K),
ось которого задается каким-либо узлом (или зацеплением) К.
■ Если получившееся многообразие S3\U(K) имеет тип W, то узел
(зацепление) К должен, оказывается, быть определенным обра-
образом связанным с торич-ескими узлами. Точное определение мы
здесь опустим, см. [255]. Поскольку такие узлы ^близкие к тори-
ческим) составляют «малый процент» в множестве всех узлов, то
мы видим, что многообразия типа W (и потому поверхности по-
постоянной энергии интегрируемых систем) «очень редки-», их отно-
относительно мало в множестве всех трехмерных многообразий.
X. Цишанг отметил, что этот пример можно модернизировать,
и в результате получить замкнутое многообразие, не принадлежа-
принадлежащее классу Q. Достаточно заклеить границу указанного выше
многообразия полноторием так, чтобы получить гомологическую
(но не стандартную) сферу. Таким образом, явно указываются
многообразия, не являющиеся поверхностями постоянной энергии
интегрируемых систем.
Если допустить у интеграла f на Q минимальные и максималь-
максимальные окружности в числе, превышающем единицу, то утверждение
о бесконечности группы #i(Q, Z) становится неверным. Приведем
пример: линзовые пространства, получающиеся склейкой двух
иолноторий по граничному тору. На них можно задать функцию
ровно с двумя критическими окружностями: минимумом и макси-
максимумом.
1.10. «Достаточно большие» трехмерные изоэнергетические по-
нерхности полностью определяются своими фундаментальными
группами. Здесь мы приведем обнаруженную X. Цишангом и
Л. Т. Фоменко универсальную оценку снизу на число полноторий
177
зп' в топологическом разложении изоэнергетической поверхности
<23 в сумму элементарных кирпичей.
Оказывается, что m'=»m + s + 2r^(e — 2$+l) q'^m'— 2, q^
^m + r — 2, где числа m, q, s, r и m', q' задают число соответ-
соответствующих элементарных кирпичей в гамильтоновом и топологиче-
топологическом разложениях изоэнергетической поверхности.
В дальнейшем мы будем рассматривать лишь топологическое
(разложение Q, т. е. разложение в сумму тп' полноторий, р' ци-
цилиндров и q' штанов.
Объединим некоторые штаны, полнотория и цилиндры в мак-
максимальные блоки Si, являющиеся многообразиями Зейферта
[239]. При этом некоторые полнотория могут оставаться, а ямен-
во те, некоторые из меридианов которых являются слоями сосед-
соседних штанов. Такие полнотория назовем тривиализирующими. Сна-
Сначала, склеивая разные блоки Si цилиндрами, получаем «дерево».
Остальные цилиндры определяют . «ручки». Пусть Si имеет m(i)
особых слоев с инвариантами (ац, Ьи),..., (а,-т(о> bim(i))- Здесь
можно предполагать, что ац>\, 0<.Ьц<.щ/ и НОД (а,-,-, Ьц) = \,
т. е. числа взаимно простые, а НОД — наибольший общий дели-
делитель). Пусть k(i) — число тривиализирующих полноторий. Пусть
n(i) — число компонент края dSi, соответствующих ручкам или
цилиндрам в дереве. Пусть g(i) — род базисной поверхности про-
пространства Зейферта S,-. Напомним, что S,- ориентируемо; это
©лияет на соотношение Bа), указанное ниже.
Утверждение 5 ([239]). Фундаментальная группа jti(S,-)
имеет следующее копредставление, задаваемое следующей табли-
таблицей.
A) Образующие:
(а) hi (соответствует слою),
(б) {гц\ l^j<m(i)}\]{Xij] \<.j^k(i)} (соответствует компонен-
компонентам dSi),
(в) {stj\ l</<m(i)} (соответствует особым слоям S,-),
(г+){^,;, м,-/| l^j<g(i)} (соответствует ручкам базы, если она
ориентирована),
"(г") {vi,-\ 1</<^@) (если база — неориентированная поверх-
поверхность).
B) Определяющие соотношения группы:
(а) [ri,,h{]==\, [xij,hi] = \, [sij,hi] = \, [^ЛЛ£] = 1, [uil,hi\ = \,
vijhivT.1hi= 1, где / пробегает все подходящие числа (см. выше);
(б) s,e/;-A?f/ = l, 1</<т@;
n(i) k(i) m(i) g(i)
(в) /!-'Пг<|Пх(/П s<7 K=l, где K = Y\[tij, «,,], если база
;=i /=i /=i /=1
g(O
ориентирована, и К= П v\n если ^аза неориентирована. Если n{i) +
+ k(i)yO, то можно предполагать, что et = Q.
Приклеивание цилиндров индуцирует соответствие Ф между
178
нсеми граничными компонентами, не заклеенными тривиализиру-
ющими полноториями. Здесь Ф(£, j)¥=(i, j) и Ф2 = 1с1. Получаем
изоморфизмы
Ь/ ■ (П/, ^) -*• (гфA-,/), АФ1(£,/)\. где Фг (i, /) —первый • член пары
ФA, /). При этом ^Ф(г./> = Ч7/1- Пусть
Здесь определитель имеет вид a(i, j)8(i, /)—P(i, /)v(i. /) — ±
Теперь приклеивания определяют новые образующие:
C) {ш,|< 1 <()}
и соотношения:
D) (а) и^1г£;
(В)-Шф(;>/) = Ш-.1 ДЛЯ 1<1<р; 1</<ПA).
Ясно, что для каждой пары (i, /), ФA,/) потребуется только од%а
пара соотношений D а, б). Для склеивания требуется новая обра-
образующая только в том случае, когда склеивание порождает ручку.
Если (г, /) отвечает цилиндру, включенному в дерево, то имеем:
(Г) Wi}=\.
Наконец, приклеивание тривиализирующих полноторий добавит
■соотношения:
(о) до;/= 1, если k(i)>\.
Теорема 5 (А. Т. Фоменко, X. Цишанг). Фундаментальная
группа трехмерного многообразия Q (т. е. изоэнергетической по-
поверхности интегрируемой системы) имеет непредставление с обра'
зующими Aа—г), C) и определяющими соотношениями Bа—в),
Dа-г), E).
Тем самым мы в явном виде описали фундаментальные груп-
группы класса поверхностей постоянной энергии интегрируемых сис-
систем.
Теорема 6 (А. Т. Фоменко, X. Цишанг). Если все блоки Si
«достаточно сложны» (в точном смысле, указанном в [239, 255])
(например, если k(i) +m(i) +n(i) +g(i) >3) и если нет тривиали-
тривиализирующих полноторий, то фундаментальная группа Jti(Q) опреде-
определяет изоэнергетическую поверхность Q однозначно с точностью до-
гомеоморфизма, и числа, определяющие копредставление группы,
являются (почти-) инвариантами этой группы.
Из теоремы 6 следует, что все «достаточно большие» неприво-
неприводимые многообразия Q3 (изоэнергетические поверхности) класси-
классифицируются своими фундаментальными группами. Тем самым мы
указали дискретный набор инвариантов, задающих «большие»
изоэнергетические поверхности достаточно сложных интегрируе-
интегрируемых гамильтоновых систем.
Остается вопрос: сколько имеется «маленьких» изоэнергетиче-
ских поверхностей Q3? Задача (пока нерешенная) заключается в.
•их полной классификации. ,
179
Ниже автором будет дано "полное описание интегральных мно-
многообразий Хп+\ обобщающих трехмерные изоэнергетические по-
поверхности и описывающие бифуркации торов Лиувилля общего
положения в окрестности критических точек отображения момента
интегрируемой гамильтонавой системы. Другими словами, Xn+i —
прообраз регулярной кривой (при отображении момента), транс-
версально пересекающей бифуркационную диаграмму. Они имеют
вид
()p()q()
где Тг — r-мерный тор. Задача: описать фундаментальную груп-
группу таких интегральных многообразий. Здесь можно ож,идать ре-
результатов, близких к теоремам, приведенным выше. Возможно,
здесь окажется полезной теория многомерных многообразий Зей-
ферта, развитая В. Нейманом, Ф. Раймондом, Б. Циммерманом,
X. Цишангом и др.
§ 2. Классификация перестроек торов Лиувилля на
многомерных симплектических многообразиях в окрестности
бифуркационной диаграммы отображения моме'нта
: 2.1. Бифуркационная диаграмма отображения момента интег-
интегрируемой систе'мы. Перестройки общего положения. В настоящем
лараграфе мы даем классификацию перестроек общего положения
торов Лиувилля, возникающих в тот момент, когда тор «пересе-
«пересекает» критический уровень интеграла энергии. Оказывается, такие
перестройки распадаются в композиции некоторых канонических
■перестроек четырех типов и эти последние явно описывают и
•имеют простую геометрическую природу. При этом мы, в частно-
частности, развиваем некоторые идеи, высказанные С. Смейлом в его
известной работе «Топология и механика» [126].
Пусть u = sgrad# — гладкая система на гладком симплекти-
ческом многообразии М2п. Пусть система интегрируема, т. е. су-
существуют п независимых (почти всюду) гладких интегралов
fi,...,fn, находящихся в инволюции. Будем считать, что fi = H.
Пусть /;: AJ2"->R" — соответствующее этим интегралам отображе-
отображение момента, т. е. F(x) = (f\(x),... ,fn(x)). Напомним, что точка
лгеМ называется регулярной для отображения F, если ранг
dF(x)=n, т. е. отображение dF(x) : TxM-+Rn = TF{x)Rn является
эпиморфизмом. В противном случае точка х называется критиче-
критической, а ее образ F(x) — критическим значением.
Пусть N<=M — множество всех критических точек отображе-
отображения момента. Ясно, что оно замкнуто. Пусть X=F(N) — множе-
множество всех критических значений. Оно называется бифуркационной
диаграммой (бифуркационным множеством). Так как отображение
F гладко, то dimS^/z—1. Если точка xeR" не является критиче-
критическим значением, т. е. xeRn\2, то ее полнь;й прообраз Ва =
■=/7~1 (а) с=М (т. е. неособый слой) не содержит критических точек
отображения F. В силу теоремы Лиувилля каждая его компактная
компонента связности диффеоморфна тору Лиувилля Тп. Предпо-
180
южим пока для простоты, что весь слой Ва компактен (рис. 81).
Ij полученных нами ниже результатов будут легко следовать со-
ггветствующие утверждения и для некомпактных слоев, т. о. для
■«.цилиндров». Если d<^2, то совместная поверхность уровня (т. е.
•лой) Ва является особой (критической) и dim Ba^.n.
При деформации точки а в R" ее прообраз, т. е. слой Ва%
<ак-то деформируется. До тех пор пока точка а, двигаясь по R",
ie встречается с бифуркационной диаграммой S, слой Ва преоб-
Рис. 81
Рис. 82
разуется посредством диффеоморфизмов, т. е. не претерпевает ка-
качественных топологических перестроек. В частности, любые два
слоя Ва и Вь, где точки а и Ь могут быть соединены гладкой
кривой y^^XS (т. е. не содержащей ни одного критического
значения отображения момента), диффеоморфны, состоят из одно-
одного и того же числа торов Лиувилля.
Если Же непрерывная кривая у встречает в какой-то точке с
бифуркационную диаграмму S, то слои Ва и Вь могут быть раз-
различны. Если точка а при своем движении протыкает 2, то слой
Ва подвергается, вообще говоря, качественному топологическому
преобразованию, перестройке (рис. 82).
181
Сформулируем общую задачу: описать топологические пере
стройки торов Лиувилля, возникающие в тот момент, когда точке
а пересекает бифуркационную диаграмму 2.
Изучение указанных перестроек позволяет описать механиз\
перестройки движения интегрируемой системы в зависимости о:
фиксированных значений интегралов. Напомним, что интегральные
траектории интегрируемой системы определяют (при выборе под
ходящих координат действие—угол) прямолинейные обмотки то
ров Лиувилля (условно периодическое движение). Преобразование
этих движений при переходе от одного совместного уровня интег-
интегралов к другому и задается перестройками торов Лиувилля пр>
изменении точки aeR".
Как мы покажем ниже, перестройки общего положения можне
классифицировать, и они имеют достаточно простой вид. Ясно
что выделяются следующие ч два случая: 1) dimS<n—1, 2)
dim2 = «—1. В случае 1 диаграмма 2 не разделяет -R", т. е. лю-
любые две точки a, beR" соединяются гладкой кривой y^^X^
Следовательно, компактные неособые слои диффеоморфны межд>
собой, в частности, состоят из одного ,и того же числа торов Лиу-
Лиувилля. Сущестюен-но более сложным является случай 2. Здесь
диаграмма 2, вообще говоря, разбивает R" на несколько откры-
открытых непересекающихся областей. В каждой из них топология не-
неособого слоя (например, количество торов Лиувилля), вообще го-
говоря, своя. Она может меняться от области к области.
Итак, пусть dim2 = n—1. Рассмотрим точку с на 2 и изучим
перестройки торов Лиувилля, когда гладкая кривая у (след дви-
движения точки .а) протыкает'диаграмму 2 в точке с. При этом дос-
достаточно рассматривать лишь малую окрестность U=U(c) точки
с в R".
Мы изучим случай «общего положения», т. е. когда путь \
трансверсально протыкает 2 с ненулевой, скоростью в точке с, ле-
лежащей на (п—1)-мерном гладком страте (листе) диаграммы 2.
Другими словами, будем предполагать, что £/|~|2 является гладким
(п—1)-мерным подмногообразием в R". В случае общего положе-
положения можно считать, что множество N^F'^U) критических точек
является объединением конечного числа гладких 'подмногообразий
в М, стратифицированных рангом dF. Это означает, что N можно
представить в виде объединения непересекающихся подмногооб-
подмногообразий N;, на каждом из которых ранг dF в точности равен i (не-
(некоторые из этих подмногообразий могут быть пустыми).
Понятие общего положения можно уточнить еще и так. По-
Поскольку мы -предположили, что в окрестности точки с множество
2 является (п—1)-мерным подмногообразием, то можно считать,
что в окрестности какой-то одной связной компоненты Вс° особо-
особого слоя Вс последние п—1 интегралов f2,...,fn независимы, а
первый интеграл /i = # (энергия) становится зависимым с ними
на подмножестве критических точек T=N[\BC°. В самом деле, ог-
ограничим отображение F на подмножество Nf\F'l(U), являющееся
согласно требованию общего положения объединением конечного
182
числа гладких подмногообразий. Так как ограничение F на каж-
каждый, в том числе и на максимальный, страт N'[]F~l(U) является
ишдким отображением гладкого подмногообразия, то dF(x):
: TxN'-+-Tfu)% является эпиморфизмом и ранг dF(x)>-n—1, по-
поскольку" dim£/(~|2 = rt—1. В то же время так как x^N — крити-
критическая точка, то ранг dF(x)^n—1. Следовательно, ранг dF(x) =
— п—1. Поэтому можно считать (в случае необходимости заменяя
базис в множестве интегралов), что }г,•■.,}» независимы на Вс°.
Следовательно, интеграл fi становится зависимым с ними на мно-
множестве T=N(]BC°.
Теперь мы рассмотрим несколько типов (п+1)-мерных много-
многообразий, краями которых являются торы.
1) Рассмотрим стандартное вложение в Rra+1 «сполнотория»
В2хТп'1 с «осью», являющейся тором Т"~1. Его граница — тор
Тп. Назовем D2xTn~l диссипативным полноторием. По поводу этой
терминологии, восходящей к механике, см. ниже.
2) Прямое лроизведение TnX~Dl назовем цилиндром. Его
край — два тора Г".
3) Пусть N2 — диск с двумя дырками. Прямое произведение
N2XTn~l назовем торическим ориентированным седлом. Его
край -<- три тора Тп.
4) Над тором Тп~1 рассмотрим все неэквивалентные друг другу
■расслоения со слоем отрезок Dl=[—1, +1]. Они классифициру-
классифицируются элементами а группы гомологии Н\(Тп~х, Z2) =Z2©...©Z2
{п—1 раз). Обозначим пространство расслоения, отвечающего
элементу а, через Уап. Ясно, что Yan является «-мерным гладким
многообразием, край которого состоит из двух торов 7я, если
а = 0, и из одного тора, если афО. Поскольку нас интересуют ин-
' тегрируемые системы, то мы будем- рассматривать далее только
такие расслоения, краями которых являются торы. Выделим в
расслоении нулевое сечение и обозначим его через Г™. Оно го-
меоморфно базе, т. е. тору. Имеем расслоение У£ — -»■ Т"~\
Рассмотрим теперь новое расслоение (ассоциированное с пер-
вым) вида Aan+1-~>-Tn'] с базой тор Г"-.1 и со слоем N2. Оно опре-
определяется следующим образом. Диск с двумя дырками гомотопи-
чески эквивалентен восьмерке. На Л^2 рассмотрим отрезок D1 —
= [—1, +1], проходящий через центр диска и соединяющий (пос-
(после его продолжения) центры двух выброшенных дисков (дырок).
С каждым расслоением Уа— -^-Т можно, заменив слой D1 на
слой N2, ассоциировать расслоение Л£+1 — -э-Т (причем та-
такое, что его границей являются торы). Частным его случаем явля-
является прямое 'произведение N2XTn~l, т. е. многообразие типа 3.
Оно получается в том случае, если а = 0. Если же а=^Ю, то соот-
соответствующее расслоение Аап+1 нетривиально. Напомним, что при
афО краем «-мерного многообразия Yan является один тор Тп~1.
Назовем (п+1)-мерные многообразия Aan+l неориентированными
торическими седлами, если а=?^0. Краем многообразия Аап+1 явля-
являются два тора, если афО.
183
Легко видеть, что все многообразия Аап+1 при афО диффео-
морфны друг другу, поэтому будем записывать их так: Лап+1 =
— N2xTn~l (косое произведение). Это следует из того, что любая
несамопересекающаяся траектория на торе может быть взята в
качестве одной из образующей на нем. Таким образом, как и в
четырехмерном случае, получаем лишь два топологически различ-
различных многообразия типа 4, а именно: N2xTn~\ N2xTn~K-
Многообразия типа 4 допускают наглядное описание. При п = 2
мы получаем многообразие Л3, уже встретившееся нам в § 1.
В многомерном случае нужно реализовать аналогичную конструк-
конструкцию.
5) Пусть р: Тп->Кп — двулистное накрытие над неориентируе-
мым многообразием Кп. Все такие накрытия р можно классифи-
классифицировать (см. Приложение 4 в конце книги). Для каждого Р = 0,1
обозначим через Gp группу преобразований тора Tn—Rn(Zn, по-
порожденную инволюцией (А. В. Брзилов, А. Т. Фоменко)
(—«1. «2 + —. «з. • • • . ап), Р = 0,
(а2, av а3+ -J-, а4, ... ,ап), р = 1,
где u=(ab...,fln)eRn/Zn. Здесь предполагается, что п>2 при
Р = 0 и rt>3 при р=1. Группа Gp действует на торе Тп без непод-
неподвижных точек, следовательно, фактор-множество K&n = Tn/G$ явля-
является гладким многообразием. Преобразование R$ меняет ориента-
ориентацию, поэтому К»п — неориентируемое многообразие. Многообра-
Многообразия Коп и К\п не гомеоморфны. В Приложении 4 доказано, что
любое неориентируемое связное многообразие минимума или мак-
максимума .интеграла f гомеоморфно либо Коп, либо К\п- Пусть Кп =
Через K»n+l обозначим цилиндр отображения р : Tn-*Kpn.
Ясно, что dim К»п+1==п+ 1 и дК»п+1 = Тп, р = 0,1.
Оказывается, что многообразия Л„п+1 и Крп+1 представляются
в виде склейки многообразий первых трех типов, т. е. с топологи-
топологической точки зрения независимыми «элементарным,и кирпичам-и*
являются лишь многообразия T"XDl, N2XT"~\ D2xTn~x.
Доказательство этого утверждения проводится аналогично
четырехмерному случаю и мы его здесь опустим. *■
Теперь опишем 5 типов перестроек тора Тп.
1) Тор задается как граница диссипативного полнотория
D2XTn~l и затем стягивается на его ось, т. е. на тор Тп'К Назовем
эту операцию предельным вырождением. Условно обозначим эту
перестройку так: Тп-*-Тп~1-*-0 (рис. 83).
2) Два тора Т\п и Т2п, являющиеся границей цилиндра TnxDxb
движутся по нему навстречу друг другу и в середине цилиндра
сливаются в один тар Тп. Условное обозначение: 2Тп-у-Тп-у0-
(рис. 84).
184
3) Top Tn, являющийся нижним краем ориентированного тори-
ческого седла N2XTn~\ поднимается вверх и в соответствии с то-
топологией многообразия №хГга~' (см. выше и § 1) распадается на
<)ва тора Tin и Т2п. Обозначение: Тп-+2Тп (рис. 85).
4) Тор Тп, являющийся одним из краев многообразия Aan+l,
<v)e афО (например, реализованный как граница внутреннего тон-
Рис. 83
Рис. 84
Рис. 85
"кого полнотория, см. рис. 57), поднимается по Аап+1 «вверх» и в
его середине перестраивается, превращаясь в один тор — в верх-
верхний' край многообразия Аа. Обозначение: Тп-*Тп. Все такие пере-
перестройки параметризуются ненулевыми элементами aeZ2ra~1 =
■=Н1(Т»-\ Z2) (рис. 86).
; 5) Реализуем тор Т" как край многообразия К&п+1. Деформи-
Деформируя тор внутрь Яр"+|, вдоль проекции р, мы, наконец, двулистно
накрываем тором Тп многообразие К$п. После этого тор «исче-
'зает». Условное обозначение: Гга->Яц"->0.
185
Сформулируем теперь окончательное определение перестройки
общего положения тора Лиувилля. Фиксируем значения последних
п—1 интегралов fi,...,fn и рассмотрим получившуюся (я+1)-
мерную поверхность уровня Xn+l. Ограничивая на нее первый ин-
интеграл (энергию) fi = H, мы получаем гладкую функцию f на мно-
многообразии Х"+1, которую будем называть интегральной поверх-
поверхностью. . - ' '
Рис. 86
Определение 1. Будем говорить, что перестройка торов
Лиувилля, образующих неособый слой Ва, является перестройкой
общего положения, если в окрестности перестраивающегося тора
Тп поверхность Хп+1 является компактным и неособым подмного-
подмногообразием, а ограничение энергии f\ = H на Хга+1 является (в этой
окрестности) боттовской-функцией (в смысле § 1).
2.2. Классификация бифуркаций торов Лиувилля.
Теорема 1 (теорема классификации перестроек торов Лну-
вилля, А. Т. Фоменко).
1) Если dimlKrt—1, то все неособые слои Ва диффеоморфны
между собой.
2) Пусть dimS = «—1 и невырожденный тор Лиувилля Тп дви-
движется вдоль совместной неособой поверхности Хп+1 уровня послед^
них интегралов /г, • • ■, fn, увлекаемый изменением значения интег-
интеграла энергии fi = H. Это эквивалентно тому, что точка a = F(Tn)&
R" движется по гладкому отрезку у по направлению к бифурка*
186
ционной диаграмме 2. Пусть в некоторый момент времени тор
Г" подвергся топологической перестройке, т. е. вышел на критиче-
i кий уровень энергии. Это происходит 'в том и только- в том слу-
случае,, когда тор Тп встречает на своем пути критические точки N
отображения момента F :M2n->Rn (т. е. путь у в точке с трансвер-
(■ильно и с ненулевой скоростью протыкает (п—I)-мерный лист
диаграммы 2). Предположим, что эта перестройка является пе-
перестройкой общего положения. Тогда все возможные типы пере-
перестроек тора Лиувилля исчерпываются композициями указанных
выше {и обратных к ним) канонических перестроек типов 1, 2, 3,
4, 5. В действительности с топологической точки зрения независи-
независимыми из них являются лишь первые три, а перестройки 4 и 5 яв-
являются их композициями.
Перестройки первых трех типов 1, 2, 3 назовем топологически-
топологическими, а все перестройки типов 1, 2, 3, 4, 5 — гамильтоновыми.
При этом в случае 1 (перестройка Г"-»-7'п~1-»-0) с ростом энер-
энергии Н тор Тп сначала превращается в вырожденный тор Г",
после чего вообще исчезает1 с поверхности постоянной энергии
//—const (предельное вырождение). В этом случае тор Тп «не
пробивает» критический уровень энергий, «тормозится» и исче-
исчезает.
В случае 2 (перестройка 2Г"->Г"->0) с ростом энергии Н два
тора Т\п и Т2п сначала сливаются в один тор Тп, после чего-исче-
зают с поверхности уровня #='Const. Здесь тор Тп также «не
Ьробивает» критический уровень энергии. Впрочем, можно считать,
гго здесь тор Тп «отражается» от критического уровня энергии.
В случае 3 (перестройка Тп-*-2Тп) с ростом энергии Н тор Тп
кпробивает» критический уровень энергии w на поверхности Н =
J=>const распадается на два тора: 7\" и Тгп.
' В случае 4 (перестройка Тп-уТп) с ростом энергии Я тор Тп
также «пробивает» критический уровень энергии ,и превращается
снова в тор Тп (нетривиальное преобразование двухкратной 'на-
'намотки, см. выше).
В случае 5 (перестройка 7""->/Ср"->0) тор Тп двулистно накры-
накрывает неориентируемое многообразие К»п, после чего исчезает с по-
поверхности # = const.
Меняя направление движения тора Лиувилля, мы получаем-5
обратных процессов:
1) рождение тора Тп из тора Т"-'1,
2) тривиальное рождение двух торов Т\п и Т2п из одного тора
Т\
3) нетривиальное слияние двух торов Т\п и Т2п в один тор Г",
4) нетривиальное превращение тора Тп в тор Тп,
5) рождение тора Тп из многообразия К»п, т. е. K»n->~Tn.
Некоторые из указанных выше канонических, перестроек уже
обнаруживались в конкретных примерах важных механических
систем (см., например, работы М. П. Харламова ,и Т. И. Погосяна
[163, 119]). В частности, таковы перестройки торов в случае Ко-
Ковалевской и в случае Горячева—Чаплыгина [163]. Можно пока-
187
зать, что перестройки двумерных торов, найденные в [163] и
обозначенные там следующим образом: 0->-S1->7'2, P->#->2F
2P—>Q->2r2, Г2->Р->Г3, являются частными случаями перестрое!,
описанных нами в теореме 1. Первая из них порождена диссипатиь
ным полноторием и является перестройкой типа 1 (в нашей клас-
классификации). Вторая из них порождена ориентированным седлом i.
есть перестройка типа 3. Третья из них порождена двумя ориеь-
тированными седлами, т. е. распадается в композицию 2Г2-*-Г2—
->2Г2 двух перестроек типа 3. Четвертая из них, порожденная не-
неориентированным седлом Аъ, и есть перестройка типа 4.
Как и в четырехмерном случае, можно было бы различат!,
ориентируемые 11 неориентируемые гамильтонианы Н. Гамильто
ниан назовем ориентируемым, если все его критические подмного
образия (на Хга+1) ориентируемы, т. е. нет ни одного критической
многообразия К&п. В противном случае гамильтониан называется
неориентиру емым.
Предложение 1. Если (U(Xn+l); sgradH; /2, ■■■,fn) — ut-
тегрируемая гамильтонова система с боттовским неориентируемыл
гамильтонианом Н на поверхности Хп+\ то ее всегда можно дву
листно накрыть гамильтоновой системой (O(Xn+l); sgrad/7,
h,■■■,{п) с ориентируемым гамильтонианом Я на накрытии Xn+l.
Здесь О (Xn+l) — двулистное накрытие окрестности U(Xn+l) мно-
многообразия Хп+\
Доказательство аналогично доказательству утвержде-
ния-1 § 1.
Пусть v — интегрируемая система на М2п. Фиксируем значе-
значения всех последних лнтегралов /2 fn и предположим, что полу-
получающаяся при этом (я-Ь1)-мерная поверхность Xn+l компактна и
неособа, т. е. интегралы f2,...,fn независимы на Xn+l. Поверхность
Хп+1 является инвариантным подмногообразием системы v. Меняя
значение энергии Н, мы перемещаем тор Лиувилля Тп вдоль по-
поверхности Xn+l. Иногда при этом возникают предельные вырожде-
вырождения, т.'е. тор Тп стягивается на тор Г" (см. перестройки типа1).
В. В. Козлов обратил внимание автора на то, что предельные вы-
вырождения реально возникают в конкретных механических систе-
системах с диссипацией. При я=1 перестройки Г'-vO и Т1-*-2Т1' можно
увидеть в задаче о движении тяжелой точки в «двухгорбой» яме.
За счет малой диссипации энергии движение точки в фазовом про-
пространстве происходит по одномерным торам (т. е. по окружнос-
окружностям), которые слегка эволюционируют и, встречая, наконец, кри-
критический уровень энергии, подвергаются перестройкам.
Если в интегрируемую систему вводится малое трение, то в
первом приближении можно считать, что рассеяние энергии моде-
моделируется уменьшением значения интеграла f\ = H и вызывает, сле-
следовательно, медленную эволюцию (дрейф) торов Лиувилля вдоль
поверхности уровня Xn+l. Рассмотрим описанный выше пример■
движения шарика в яме под действием силы тяжести (рис. 87).-
Это движение (в отсутствие силы трения) может быть полностью^
описано. Если ввести малое трение, то можно считать, что на
188
каждом достаточно малом отрезке времени движение по-прежне-
по-прежнему интегрируемо. Однако с ростом времени трение начинает ска-
скачиваться все больше и больше. В результате шарик будет подни-
подниматься на все меньшую и меньшую высоту. Наконец, в некоторый
момент времени опускающийся уровень коснется седла и движение
качественно перестроится: шарик окажется либо в левой, либо в
правой яме. Это и есть момент пере-
перестройки тора Лиувилля в момент пе-
пересечения критического уровня энер-
энергии. Ясно, что характер такой пере-
перестройки полностью определяется топо-
топологией поверхности уровня Хп+К .
Ответ на вопрос, как устроены инте-
интегральные поверхности Хп+1, дает сле-
следующая ' ■ ' '
Теорема 2 (А-. Т. Фоменко).
Пусть М2п—-гладкое симплёктическое многообразие и система
u = sgrad# интегрируема с помощью гладких независимых ком-
коммутирующих интегралов H—fi, fa,...,jn. Пусть Xn+l — любая
фиксированная, компактная неособая совместная поверхность
уровня последних п—1 интегралов f2>. .-., fn. Пусть ограничение
Н на Xn+l является боттовской функцией. Тогда поверхность
Хп+г имеет вид m{D2xTn-1)+p{TnxD>) + q(N2XTn-1)+sAan+1 +
+ гЯрп+1, т. е. получается в результате склейки граничных торов
(при помощи некоторых диффеоморфизмов) следующих «элемен-
«элементарных кирпичей»: m диссипативных полноторий, р цилиндров, q
торических ориентированных седел, s торических неориентирован-
неориентированных седел и г многообразий К»п+>- Число m в точности равно
числу предельных вырождений системы v на поверхности Хп+1, на
которых энергия Н достигает локального минимума или макси-
максимума.
2.3. Торические ручки. Сепаратрисная диаграмма всегда прик-
приклеивается к неособому тору Лиувилля по нетривиальному циклу.
Перейдем к доказательству теорем 1 и 2. Нам придется построить
для этого новую многомерную теорию «типа Морса» интегрируе-
интегрируемых гамильтоновых систем. При этом мы будем следовать схеме
§ 1. Мы не будем повторять уже изложенные в § 1 рассуждения
и лишь дополним их теми новыми моментами, которые нуждаются
в особом доказательстве в связи с многомерностью системы.
Введем следующие обозначения. Пусть ceS и ма-
малая окрестность £/(с)(]2 точки с на 2 является гладким
(п—1)-мерным подмногообразием. Пусть 7 — гладкий
путь, трансверсально протыкающий 2 в точке с и соединяющий
два некритических значения а и Ь, расположённых по разные сто-
стороны от гиперповерхности 2. Рассмотрим связную компоненту
Вс° особого слоя Bc = F-1(c). Пусть T=Bc°r\N, a Xon+i — связная
компонента слоя F~lU(c), заключенная между двумя близкими
неособыми слоями Ва и Вь. Так как ,а и Ь — некритические значе-
значения, то Ва и Въ являются объединениями торов Лиувилля.
18»
пусть 0аи = Лоя+1ПВа и #йи=Xon+*[)Bb, т. е. dX0"+i = Ba0(\Bb°.
Обозначим через f ограничение первого интеграла fi на интег-
интегральную поверхность Хоп+1 = ХО (рис. 88).
Лемма 1. Точка хеХ0 является критической для функции
f тогда и только тогда, когда в -ней первый интеграл fi зависил
(на М) с последними п—1 интегралами fi,...,fn.
Доказательство. Так как Хо — совместная поверхность
уровня последних интегралов, то их градиенты образуют базис f
плоскости, нормальной к Хо в М. Зависимость функции fi с функ-
В,
Рис. 88
циями f2,...,fn эквивалентна тому, что в этой точке
grad/i является линейной комбинацией градиентов gradf,, ^
^п. Ясно, что gradf на Хо получается ортогональным проектирг-
ванием gradf] на Хо. Лемма доказана.
Лемма 2. Множество Т критических точек функции f на А,
является несвязным объединением некоторого числа п-мерных тс-
ров Тп, (п— I)-мерных торов Тп~\ п-мерных неориентируемы:
многообразий К.9п.
Доказательство. Если Т=ВС°, то Т является совместной
(особой) поверхностью уровня всех л интегралов fi,...,fn- Близ-
Близкие к ней поверхности уровня R являются неособыми, компактны-
компактными торами Лиувилля. Ясно, что R — граница трубчатой окрест-
окрестности У"+1 подмногообразия Т в Хо. Если d\mT=k, то R^T0 рас-
расслаивается над Т со слоем Sn~h. Это может быть только в том
случае, когда n — k—О или 1, т. е. когда dim Т=п, либо л—1,
Если Гоп — связная компонента Т, то Топ = Тп, или ' Топ = К»п.
Если Вс°фТ, то рассуждение усложняется. Ясно, что в этом слу-
случае dim7<dimBc°=n, т. е. dimr<n—1. Из условий, наложен-
наложенных на интегралы системы, следует, что на Т интегралы f2>..., fn
независимы (они независимы на всем Вс°). Следовательно, на
190
Ге" имеется п—1 независимых коммутирующих векторных по-
полей sgrad fi 2<t^re. Как известно, отсюда сразу следует, что
f0"- \ = Тп~1. Лемма доказана.
Если критический тор имеет размерность п, то он является
либо множеством локального минимума, либо локального макси-
максимума энергии Я. В этом случае два близких неособых тора Лиу-
вилля либо сливаются в один тор Тп, либо тор Тп распадается на
два тора Тп. Пусть P-n = P-n{Tn~x) и Р+П = Р+П(Г"-1)—соответ-
Р+П(Г"-1)—соответственно входящая и исходящая сепаратрисные диаграммы крити-
критического подмногообразия Р1.
Определение 2. Назовем торйческой ручкой индекса X и
степени вырождения k прямое произведение ThxDKxDn+1-h~xr
подошвой ручки — следующую часть ее границы: (Г^Х^-■) X.
XDn+i~h-1, осью подошвы — пространство TkxSK~l.
Определим операцию приклейки торйческой ручки к краю Vn
(п+ 1) -мерного многообразия Wn+1. Пусть край содержит вложен-
вложенное подмногообразие JhXSx~l. Предположим, что его трубчатая
окрестность гомеоморфна прямому произведению (PxS^") X
Х£)п+1-ь-я; Можно выбросить эту трубчатую окрестность, край
которой гомеоморфен ThXSk~lXSn~h~\ С другой стороны, край
подошвы торйческой ручки также гомеоморфен произведению
ThxSk~lXSn~h~K. Отождествляя этот край с краем выброшенной
окрестности, получаем новое (п+1)-мерное многообразие. Его-
край будем называть торйческой перестройкой края' Vn. Для даль-
дальнейшего можно считать, что гладкий путь y—y(t)czRn модели:
руется отрезком иа вещественной оси R1, на которой лежат три
точки: а<с<Ь, где с — критическое значение, а и Ь близки к с.
Положим Ca=F~1(t^a), Cb — F-l(t^b); тогда CaczCb. Другими:
словами, можно считать, что / ^o^+'-vR1 и Ca=(f^a), Cb=(
Лемма 3. Предположим, что на особом слое Вс° лежит ров-
ровно один критический (седловой) тор' Тп~1.
1) Пусть P_n(J"-') ориентируема. Тогда Сь получается из С„
приклейкой к краю Ва торйческой ручки индекса 1 и степени вы-
вырождения п—1. При этом Сь гомотопически эквивалентно Са, к
которому приклеено многообразие Tn~lxDl no двум непересекаю-
непересекающимся ТОраМ Than-1 U Т2,ап~1.
2) Пусть P_n(rn-') неориентируема. Тогда множество Сь го-
гомотопически эквивалентно Са, к краю Ва° которого по тору
Та71 приклеено п-мерное многообрЬзие Ya, имеющее край Тп~1 и
являющееся расслоением Yan-*-Tn~l, отвечающим ненулевому эле-
менту aeZ2"-' = Я, (Г", Z2).
Доказательство проводится по схеме доказательства
леммы 4 из § 1 с уточнениями, вызванными многомерностью си-
системы. Эти технические подробности мы здесь опустим.
.Лемма 4. Пусть тор Га", вложенный в какой-то неособый
тор Лиувилля Тап<=Ва°, является либо одной из подошв торйче-
торйческой ручки (индекса 1 и степени вырождения п — 1), либо краем
191
жнигиииризия га" {в случае, когда Р-(Тп~1) неориентируема). То-
Тогда этот тор Га" всегда реализует одну иэ образующих в группе
гомологии Нп-Л(Тап, Z)=Zn-'. Если обе подошвы торической руч-
ручки приклеены к одному и тому же тору Лиувилля Тап, то соответ-
соответствующие оси этих подошв, т. е. торы Т\,ап~1 и T%an~i, не пересе-
пересекаются, реализуют одну и ту же образующую группы гомологии
Нп-\{Тпп, Z) и, следовательно, изотопны внутри тора Тап.
Доказательство. Рассмотрим критический седловой тор
Тп~\ Из леммы 2 следует, что он является орбитой действия абе-
левой подгруппы R"-1, вложенной в группу R", порожденную по-
полями sgrad/,-, 1<л^л. При этом базис в подгруппе Rn-1 обра-
образуют поля sgrad/г, 2^t^n. Фиксируем эту подгруппу. Так как
действие Rn (и Rn~') определено на всем М2п, то мы всегда мо-
можем рассмотреть орбиты группы Rn~', близкие к орбите Тп~\
Рассмотрим достаточно близкий к слою Вс° неособый тор Лиувил-
Лиувилля Т„п, ни котором сепаратрисная диаграмма Р_п высекает неко-
некоторый тор Тап~1. Этот тор, конечно, не является орбитой действия
группы R"~' на торе Гп". Однако, как мы сейчас покажем, тор
Го" можно аппроксимировать некоторой орбитой действия груп-
группы R"-1. Для этого рассмотрим элемент аеЯ^^Г"-1, Z2). Из
леммы 3 мы знаем, что тор Тап~1 является одной из компонент
края многообразия Yan, приклеенного к тору Га". Если а=^=0, то
аУ„» = Го»-1; если а=0, то дУа» дТ^О<) ТТ\
Задание элемента а определяет некоторое число k образующих
в критическом торе^?п~1,. обходя вокруг которых нормальный от-
■резок сепар^трисной диаграммы Р- меняет свою ориентацию. Вы-
Выделим эти образующие. В ориентируемом случае k — О, так как
а=0. Поскольку тор Гп~' является орбитой действия группы
Rn~', то, заменяя образующие в группе.R"~' (если это необходи-
необходимо), всегда можно считать, что в неориентируемом случае (fe^l)
среди полей sgrad f,-, 2^t^n, есть ровно k полей: sgrad /2,...
.:.,sgradfk+\ таких, что однократный обход вдоль орбит,точки
хеГ", порожденных соответствующими им одномерными под-
подгруппами R21,.... R'/i+i, меняет ориентацию нормального отрезка
сепаратрисной диаграммы. Рассмотрим сначала ориентируемый
случай, когда k — Q. Тогда в подгруппе Rn~' можно выделить
{п—1)-мерный параллелепипед П — фундаментальную область
действия группы Rn-1 на торе Тп~1._ При естественном отображе-
отображении группы Rn~' на тор Гп~' 'этот параллелепипед П накрывает
весь тор, т. е. тор Тп~{ получается отождествлением противопо-
противоположных граней этого параллелепипеда. Так как параллелепи-
параллелепипед П состоит- из преобразований на М, то можно рассмотреть
орбиту этого параллелепипеда при его действии па некоторую
точку /геГ[/"'cTj", Конечно, эта орбита уже не будет-замкну-
будет-замкнутым (п— 1)-мерным тором в Тап. .
Однако так как точка /ге^/ близка к точке х<=Тп~1, то
■можно считать, что орбита П(/г) является «почти-тором», т. е.
каждая из образующих параллелепипеда П переходит в отрезок,
192
концы которого близки на торе Тап (т. е. получается «почти-
окружность»). Выберем на торе Тап координаты (pi,...,cpn в соот-
соответствии с теоремой Лиувилля. Мы используем здесь то обстоя-
обстоятельство, что точки параллелепипеда П представлены симплекти-
ческими преобразованиями.
Тогда в этих координатах «почти-тор» П (h) является линей-
линейным, вполне геодезическим подмногообразием, быть может с не-
непустым краем. Изображая тор Тап (в этих координатах) в виде
стандартного куба, противоположные грани которого отождествле-
отождествлены, мы получаем в нем плоскость П'. Ее пересечения с противопо-
противоположными гранями являются (п — 2)-мерными подпространствами,
которые оказываются близкими после отождествления граней.
Ясно, что плоскость П' можно слегка повернуть так, что она пре-
превратится (после факторизации куба на тор) в некоторый (п—1)-
мерный линейный, вполне геодезический тор Т*п~' в торе Тап.
-Ясно, что тор Г»п~' близок к «почти-тору» H(h) и в то же время
близок к тору Ti,an~l. Отсюда следует, что эти торы изотопны.
Итак, мы доказали существование малой изотопии тора
Т\,ап~{ в торе Тап, переводящей его в линейный тор. Но в таком
случае тор Тиап~1 реализует образующую в группе #n_iGV\ Z),
что и требовалось доказать. Итак, в ориентируемом случае лемма
доказана. Отметим, что при малом шевелении плоскости П мы
получили новую плоскость П*, образующие которой уже могут
включать в себя образующую sgradfi, которая была исключена
на исходной плоскости П. Ясно, что Г*п-'=П*(/г).
, Рассмотрим теперь неорйентируемый случай. Здесь рассужде-
рассуждения более деликатны. Дело в том, что здесь нельзя обойтись са-
самим параллелепипедом П. В самом деле, из определения неори-
:нтируемой сепаратрисной диаграммы следует, что орбиты (ПП
f\R2l)h,..., (nf\Rlh+i)h образующих^ R2',..., R'h+i (соответствую-
(соответствующих полям sgradfi, 2^i^k+l) не являются «почти замкнуты-
замкнутыми» траекториями на торе Тап. Обозначим соответствующие ребра
параллелепипеда П через Ш, т. е. П,- = ПЛКЛ 2<1£<1&+1. При
действии Пг- на точку h она успевает пробежать лишь половину
полного оборота на торе Тап. Для того чтобы она сделала почти
полный оборот, следует еще раз подействовать на нее ребром па-
параллелепипеда Пг-. Другими словами, чтобы заставить точку h
сделать почти полный оборот на торе Тап, к пей следует приме-
применить преобразования из 2II2-, т. е. удвоить соответствующую сто-
сторону параллелепипеда П. Итак, мы подходим к следующей схеме.
Нужно удвоить все стороны параллелепипеда П2,... ,П&+ь
В результате получится новый (вытянутый) параллелепипед П,
растянутый в k направлениях в два раза. Теперь подействуем
этим растянутым параллелепипедом П на точку h. В результате
мы получим некоторую орбиту U(h). Ясно, что теперь эта орбита
изображается (в переменных действие — угол на торе Лиувилля)
линейной плоскостью, которая «почти замкнута» после фактори-
факторизации куба на тор. Дальнейшие рассуждения повторяют рассуж-
рассуждения ориентируемого случая. Лемма доказана.
7 Л. Т. Фоменко 193
Все остальные построения проводятся по аналогии со схемой
§ 1 и мы их здесь опустим. Теоремы 1 и 2 доказаны.
Возникает естественный вопрос: как устроены топологические
перестройки торов Лиувилля, когда путь у протыкает бифуркаци-
бифуркационную диаграмму 2 в ее особых точках, не лежащих на внутрен-
внутренности ее (п—1)-мерных листов? Другими словами, как устроены
перестройки особых типов (не общего положеиия)?
Далее, аналогичная теория типа Морса имеет место и для га-
мильтоновых систем, допускающих некоммутативное интегрирова-
интегрирование. При этом сохраняются все утверждения, доказанные в на-
настоящей главе, но только п-мерные торы Лиувилля заменяются
всюду на r-мериые торы, где г<п. .
§ 3. Свойства разложения изоэнергетических поверхностей
интегрируемых систем в сумму простейших многообразий
3.1. Фундаментальное разложение Q = mI + pII + <7lII + sIV+/-V
и структура особых слоев. Выше мы доказали, что кажда.я неосо-
неособая трехмерная поверхность Q3 постоянной энергии интегрируе-
интегрируемой системы представляется в виде ml + pII + glll + sIV+rV, где
т, р, q, s, г—неотрицательные целые числа, а через I, И, III, IV;
V обозначены элементарные многообразия пяти простейших ти-
типов, описанных в § 1,2. Таким образом, с каждым таким многооб-
многообразием естественно связываются пять целых чисел. Если указан-
указанное-разложение порождено боттовским интегралом f, т. е. яв-
является гамильтоиовым, то число т равно количеству устойчивых
периодических решений исследуемой гамильтоновой системы.
Если же забыть о существовании второго интеграла, то указан-
указанное разложение можно упростить и рассматривать его самостоя-
самостоятельно с точки зрения теории трехмерных многообразий. В таком
случае числа т', р', q' определяются по заданному многообразию
Q, вообще говоря, неоднозначно. Например, на рис. 73е показаны
два графа F(Q), задающие многообразия Q, допускающие разное
представление в виде склейки простейших многообразий.
Предложение 1. Каждое из элементарных многообразий
I, II, III, IV, V действительно встречается в разложениях вида Q =
=mI + pII + GlII + sIV + rV для поверхностей постоянной энергии
конкретных механических гамильтоновых интегрируемых систем.
Следующий вопрос касается свойств чисел m, p, q, s, r, a
именно: любое ли трехмерное многообразие вида ml + pll + <7lll +
+ sIV+rV (где m, p, q, s, r — произвольная пятерка чисел и
склейки граничных торов — также произвольны) можно реализо-
реализовать в виде поверхности постоянной энергии некоторой интегри-
интегрируемой системы? Ответ положительный. См. выше теорему
А. В. Браилова и А. Т. Фоменко (утверждение 2 в § 1). Аналогич-
Аналогичный вопрос возникает, конечно, и в многомерном случае и /также
решается положительно.
Мы видели далее, что любая перестройка торОв Лиувилля об-
общего положения распадается в композицию пяти канонических пе-
перестроек типов I, II, III. IV, V.
194
Предложение 2. Каждая из указанных канонических пе-
перестроек в четырехмерном случае действительно реализуется в
конкретных механических интегрируемых системах.
Вероятно, это утверждение справедливо и в многомерном слу-
случае. Возможно, все канонические перестройки реализуются в слу-
случаях интегрируемых систем уравнений движения многомерного
твердого тела [151].
Полученные выше результаты позволяют наглядно описать
структуру особых слоев, т. е. особых поверхностей уровня второго
интеграла f (в четырехмерном случае) и особых слоев отображе-
1
\_ Jj > >• УУ\
J
Рис. 89
Рис. 90
ния момента F (в многомерном случае). Для определенности оста-
остановимся на более простом четырехмерном случае.
Как было показано выше, каждый особый слой,, содержащий
седловую критическую окружность, получается так. Нужно взять
два неособых тора Лиувилля, задать на каждом из них по циклу
(т. е. нарисовать нестягиваемые окружности), после чего склеить
оба тора по этим циклам. Другими словами, два тора должны
коснуться друг друга таким образом, чтобы две нарисованные иа
них окружности совпали. На рис. 89, 90 показаны простейшие
случаи касания двух торов, которые можно изобразить в R3. Ана-
Аналогичная картина получается и в многомерном случае (см. § 2).
Здесь только нужно заменить окружность S1 на тор Тп~К Два
195
тора Лиувилля Тхп и Т2п должны коснуться друг друга так, что-
чтобы два «нарисованных» на них (п—1)-мерных тора совпали, сли-
слились в один тор Тп~1. В результате получится особый слой отоб-
отображения момента F : Af2n—>-Rn.
Возникает следующий вопрос: как устроены интегральные тра-
траектории системы на особых слоях (особых поверхностях уровня)?
Согласно лемме 2 см. § 2 седловое критическое множество интег-
интеграла f на поверхности Хп+1 состоит из (п—1)-мерных торов в
компактном случае. Можно доказать, что на особых поверхностях
уровня интегральные траектории системы либо лежат на этих
критических торах, либо асимптотически наматываются на эти
торы (рис. 91). Таким образом, мы получаем полное описание по-
п-2
Рис. 91
Рис. 92
ведения траекторий системы на особых поверхностях уровня ин-
интегралов.
Теорема 1 (А. Т. Фоменко). Пусть u = sgradtf — гамиль-
тонова система на МА, интегрируемая по Лиувиллю на какой-то
одной поверхности постояннай энергии Q3 при помощи боттовско-
го интеграла /. Тогда каждая критическая поверхность уровня
второго интеграла, являющаяся гладким подмногообразием, обя-
обязательно диффеоморфна либо тору Г2, либо окружности S1, либо
бутылке Клейна. Далее, каждая особая седловая поверхность
уровня f"](c) интеграла f, не являющаяся многообразием (это бу-
будет в том случае, когда критические точки заполняют седловую
окружность), получается склейкой двух двумерных торов Т{2 и
2V по нетривиальным циклам (окружностям) yi и у^, располо-
расположенным соответственно в торах Т^ и Г22. При этом, интегральные
траектории системы на таком особом слое асимптотически нама-
наматываются (в случае общего положения) на этот нетривиальный
цикл или совпадают с ним.
Справедлив и аналог этой теоремы в многомерном случае.
Выше в § 2 мы описали перестройки торов Лиувилля, возни-
возникающие в тот момент, когда точка а, двигаясь вдоль гладкого от-
отрезка у в R", пересекает (с ненулевой скоростью) бифуркацион-
196
иую диаграмму 2 в ее неособой точке на страте размерности п —
— 1. Что произойдет, когда путь у проткнет 2 в какой-то ее осо-
особой точке, т. е. пройдет через страт меньшей размерности?
Предположим, для простоты, что диаграмма 2 является объ-
объединением непустых стратов 2°, 2', 22, . ..,ЕП~', каждый из кото-
которых выделяется «своим» интегралом. Тогда операцию «протыка-
«протыкания» диаграммы 2 в какой-то ее особой точке можно (в частных
случаях) разложить в композицию последовательных более про-
простых операций, показанных на рис. 92. Сначала путь у трансвер-
сально встречает (п—1)-мерный страт 2й", затем движется по
этому страту до тех пор, пока трансверсально пе встречает сле-
следующий (п — 2)-мерный страт, затем движется по страту 2П~2 до
встречи со стратом 2"~3 и т. д. Каждый раз можно считать, что
возникающие перестройки торов Лиувилля классифицируются ти-
типами I, II, III, IV, V (с понижением размерности).. Это можно
сделать, если на страте 2* зависимы в точности п — i+\,интегра-
i+\,интегралов. Зависимые интегралы можно устранить и свести задачу к
меньшей размерности. В общем случае задача, конечно, сущест-'
венно сложнее. , -
3.2. Гомологические свойства изоэнергетических повёрхнрстей.
Мы уже знаем, что трехмерное многообразие Q, являющееся по-
поверхностью постоянной энергии и обладающее ориентированным
интегралом f, склеивается из четырех типов многообразий: 1) пол-
полноторий, 2) цилиндров, 3) ориентированных седел (штаны), 4) не-
неориентированных седел. Таким образом, многообразие Q точно
описано, если нам известно, сколько экземпляров элементарных
многообразий .каждого типа в нем содержится и, что особенно
важно, посредством каких склеиваний границ оно получено, дру-
другими словами, какие диффеоморфизмы граничных торов мы ис-
используем. Склеивая элементарные многообразия, мы должны по-
получить связное замкнутое (т. е. без края) многообразие. Как было
доказано автором выше, класс таких (изоэнергетических) много-
многообразий не совпадает со всем классом трехмерных многообразий.
Более того, изоэнергетические поверхности образуют «тощее» под-
подмножество в множестве всех трехмерных многообразий. Дальней-
Дальнейшее изучение класса изоэнергетических поверхностей по предложе- •
нию автора было предпринято Г. Мамедовым, некоторые из ре-
результатов которого мы здесь изложим.
Практический интерес (для оценки снизу числа устойчивых пе-
периодических решений интегрируемой системы) представляет ответ
на следующий вопрос: сколько полноторий участвует в склейке
изознергетической поверхности? Отметим сначала два особых
случая.
Случай 1. Многообразие Q3 склеивается из двух полноторий.
Для такой склейки достаточно задать диффеоморфизм между дву-
двумя торами, каждый из которых является границей соответствую-
соответствующего полнотория. Два многообразия Q, полученные таким обра-
образом, не отличаются топологически, если соответствующие диффео-
диффеоморфизмы, участвующие в их построении, гомотопны в множестве
197
непрерывных отображений тора в тор. Напомним, что классы го-
гомотопных непрерывных отображений тора в тор, в каждом.из ко-
которых содержится диффеоморфизм, находятся во взаимно одно-
однозначном соответствии с матрицами
A =
где a{ e Z и det Л = ±
цилиндр
тор
В этом случае можно получить: а) трехмерную сферу, б) мно-
многообразие SlXS2, в) линзовые пространства. Обратим внимание,
что в случаях а) и в) ранг группы Н\ (Q, Z) равен нулю.
Случай 2. Многообразие Q получается склейкой двух или
нескольких цилиндров. В этом случае можно получить многообра-
многообразие Q, у которого Я,(<3, Z)=Z (см. пример выше в § 1).
Отметим следующее наблюде-
наблюдение. Если в построении многооб-
многообразия Q участвуют еще какие-
либо элементарные многообразия,
кроме цилиндров, то многообра-
многообразие Q можно склеить вообще без
цилиндров. Действительно, мно-
многообразие Q получается из Q\
\(цилиндр) добавлением цилин-
цилиндра посредством приклеивания
границы цилиндра (являющейся
объединением двух торов) к
двум торам из множества Q\
\ (цилиндр). Очевидно, что ци-
цилиндр T2XDl можно продефор-
мировать в тор (стянуть на тор).
Это означает, что, вместо - того
чтобы «соединять» два тора из
множества Q\(цилиндр) с помощью цилиндра, можно просто
склеить эти два тора диффеоморфизмом (рис. 93).
Если же Q склеено из одних цилиндров, то, конечно, описан-
описанный процесс редукции осуществить до конца не удастся.
Нижеследующие утверждения, полученные Г. Мамедовым, ос-
основаны на чисто топологических соображениях.
Теорема 2. Если трехмерное связное многообразие Q склее-
склеено из q штук ориентированных седел, m штук полноторий и любо-
любого числа s неориентированных седел и если известно, что ранг
Hi(Q, Z)^.k, то выполнено неравенство tn^q + 2 — 2k.
Теорема верна и при q=0.
Следствие 1. Если ранг HX{Q, Z) равен нулю, то в состав
Q входит ровно q + 2 полнотория.
Следствие-2. Если ранг Hi (Q, Z) равен нулю, то tri^-2.
Это следствие мы, впрочем, уже знаем (см.§ 1).
Напомним, что для каждой изоэнергетической поверхности
можно построить граф T(Q) этого многообразия. Каждое ориен-
ориентированное седло (штаиы) будем изображать в виде «треножни-
Рис. 93
198
ка» (трилистника) (рис. 94), а полноторие— в виде черного круж-
кружка с одним ребром, исходящим из него. Места склеек на графе
мы изображать не будем. Примеры графов см. на рис. 95 A). Нас
интересуют только связные многообразия, а значит, и связные
графы. Итак, число черных кружков (вершин графа) равно т,
число треножников равно q. Концы «ног» тре-
треножника — это двумерные торы. В графах, Ч у
изображающих многообразия Q, не может \S ^
быть свободных концов, так как мы рассмат- | Т
риваем замкнутые многообразия. Графы, ' I
склеенные из треножников (с пока еще не „.
заклеенными концами) , могут содержать в
себе замкнутые подграфы, или замкнутые
ломаные, а могут и не 'содержать ни одной замкнутой ломаной.
Последние графы мы будем называть "ветвящимися (деревом).
Лемма {.'Число концов связного графа, склеенного из q тре-
треножников, не превосходит q+2, причем число концов равно q+2
в том и только в том случае, когда граф ветвящийся.
Эта лемма легко доказывается индукцией по q.
Итак, если m — число черных кружков, которыми (т. е. полно-
ториями) заклеены концы графа, то tn^q+2. Теперь предполо-
предположим, что задан неветвящнйся граф. Это означает, что в нем со-
содержится некоторая замкнутая ломаная (цикл). Разрежем граф
по любому месту склейки, лежащему на этой ломаной. Если граф
Рис. 95A) Рис. 95B)
не стал после этого ветвящимся, то в нем есть еще одна замкну-
замкнутая ломаная. Продолжаем разрезы; в результате превратим граф
в ветвящийся. Каждое такое разрезание обладает следующими
свойствами: 1) оставляет граф связным, 2) не меняет число тре-
треножников, 3) увеличивает число свободных концов графа на две
единицы. Если было выполнено k разрезаний, то q+2—m + 2k,
где m — число концов первоначального графа, q — число тренож-
треножников (т. е. штанов). Число концов окончательного графа равно
q+2.
Доказательство теоремы 2. Рассмотрим сначала для
простоты полностью ориентированный случай, т. е. когда в соста-
составе Q.HeT неориентированных седел. Докажем, что ранг H\(Q,
Z)^, где k — число разрезов, необходимых для того, чтобы пре-
199
j ииидныи граф в ветвящийся. Рассмотрим любой разрез.
Небольшая его окрестность является цилиндром T2XDl. Можно
считать, что изоэнергетическая поверхность Q получена объедине-
объединением двух своих подмногообразий: 1) k цилиндров, 2) связного
многообразия, являющегося дополнением к внутренности первого
подмногообразия.
Если пространство Q является объединением двух своих под-
подпространств Y] и Уг, причем Yi(]Y2=Y — их пересечение, то при
незначительных ограничениях имеет место следующая точная по-
последовательность Майера—Вьеториса:
... -► Hw (Q) -* Ht (Y) Ь-+ Ht (К\) 0 Hi (Yt)-+ Нс (Q) -*...,
где /»(*) = G'i.(*). —/2.W), a j1: Y-*-Yv ja: Y-+Ya~вложения.
Если обозначить объединение к цилиндров через Yu а допол-
дополнение к их внутренности в Q — через У2, то Yl(]Y2=Y представ-
представляет собой несвязное объединение 2k торов. Рассмотрим конец
последовательности Майера—Вьеториса
В нашем случае эта последовательность имеет вид
* Z -у 0.
Из точности последовательности легко следует, что ранг #i(Q,
)k а так как по условию /гарант Hi(Q, Z), то получаем ti^s
q + 2— m)/2, т. е. m^sq + 2 — 2k.
^ что переход к общему случаю, т. е. после вклейки неори-
неориентированных седел, не влияет на результат. Дело в том, что по-
прежнему 1) у каждого многообразия есть граф, 2) число разре-
разрезов, необходимых, чтобы граф стал ветвящимся, равно k=(q +
+ 2 — /п)/2, 3) в месте каждого разреза можно вырезать цилиндр
(граница которого — два тора Г2). Отсюда следует, что ранг
#,(B, Z)>£, т. е. 2k^2M=q + 2 — m, где.£ = ранг #i(Q, Z). От-
Отсюда получаем, что trC^q+2 — 2k. Теорема доказана.
Следствие 2 очевидно. Учитывая, что m^.q + 2, получаем след-
следствие 1. , '
Доказательство было фактически проведено для q~^\. Но если
в' построении многообразия не используются седла, то возможны
лишь следующие два случая.
1) Два полнотория соединяются с помощью некоторого числа
цилиндров. Фактически (см. выше) этот случай сводится к склей-
склейке двух полноторий.
2) Многообразие склеено из одних цилиндров. При этом можно
считать, что число цилиндров равно двум.
В случае 1 условие теоремы 2 выполняется тривиально. В слу-
случае 2 это условие легко доказывается; а именно докажем, что у
200
многообразия, склеенного из двух цилиндров, ранг #i(Q,
Действительно, Q является объединением двух цилиндров Yx и
У2, причем Y=Yif)^2 — это два тора. Из последовательности Май-
ера—Вьеториса получаем
Отсюда видно, что ранг HX(Q, Z)^l. Итак, утверждение теоре-
теоремы 2 верно и «ри <7—0.
В § 1 доказано, что из двух цилиндров можно склеить много-
многообразие Q, для которого #i(Q, Z)=Z.
Как уже отмечалось, из обнаруженных нами пяти типов эле-
элементарных многообразий невозможно склеить произвольное трех-
трехмерное многообразие. Тем более любопытен следующий резуль-
результат Г. Мамедова.
Теорема 3. Из ориентированных седел '(штанов) и полното-
рий можно склеить трехмерное ориентированное многообразие с
любыми возможными (для ориентированных многообразий) груп-
группами целочисленных гомологии.
Этот результат можно вывести, используя свойства многообра-
многообразий Зейферта, но можно дать ему и элементарное доказательство,
которое мы здесь приведем. ^
Прежде прокомментируем условие теоремы. В силу теоремы 3
с точки зрения гомологии класс изоэнергетических поверхностей
«совпадает» с классом всех трехмерных многообразий. Другими
словами, опираясь лишь на группы гомологии, невозможно выде-
выделить изоэнергетические поверхности среди всех трехмерных мно-
многообразий.
Заметим, что группы гомологии компактных многообразий все-
всегда конечно порождены и абелевы. Хорошо известно, что любое
трехмерное ориентированное многообразие W склеивается из двух
шаров с g ручками. Для таких многообразий H?.(W, Z)—свобод-
Z)—свободная абелева группа и ранг #s(W, Z)=paHr H^(W, Z). Для ори-
ориентированных связных замкнутых трехмерных многообразий
Hz(W, Z)=Z. Из сказанного ясно; что для доказательства теоре-
теоремы достаточно склеить из ориентированных седел и полноторий
трехмерное многообразие с любой абелевой конечно порожденной
группой Нх.
Ясно, что ориентированное седло — это полноторие, из которо-
которого параллельно вырезаны два полнотория (рис. 95B)). Вклеивая
вместо одного из них повое ориентированное седло, мы получаем
полноторие с тремя вырезанными полноториями (рис. 95C)),
Итак, из q— 2 полноторий можно склеить полноторие, из которо-
которого параллельно вырезаны q—1 полноторий, т. е. можно склеить
(S2\qD*)XSK
Докажем, что можно так вклеить q— 1 полноторий вместо вы-
вырезанных полноторий и одно полноторие—снаружи, что в резуль-
результате получится любая абелева конечно порожденная группа в ка-
201
честве H^Q, Z). Рассмотрим последовательность Манера—Вьето-
риса:
О -> Я3 (Q) -»■ Я2 (К) ->- Я2 GJ ф Я2 G2) -»- Я2 (Q) ->•
-*• Ях (К) -^//j (Kj) ф Ях (К2) _► Нх (Q) -> Z" -> Z"+1 -> Z -+. 0.
Здесь Y\—это q полноторий, Уг — это полноторие с вырезанными
q—1 полноториями, т. е. (S2\qD2) XSl, a Y—Yif\Y2 — это q дву-
двумерных торов. Поскольку Hz(Q, Z)=Z и Я;(У), Нг(Ук) для i =
i-й тор
Рис. 95C)
= 1, 2 и &=1, 2 — свободные группы, то легко видеть, что из по-
последовательности Майера—Вьеториса выделяется следующий
фрагмент:
О -*• Яа (Q) - Н, (Y) -U Я, (Кх) ф Ях (К2) - Я, (Q) - О,
где
Итак, f: Z2i-+Z2i. По-разному вклеивая полнотория, мы будем
получать различные гомоморфизмы f. Очевидно, Z2«/Imf=#i (Q)
и Я2(С)=Кег/. Чтобы исследовать гомоморфизм f, нам нужно
представить его в матричной форме. Для этого нужно задать ба-
-e помоторие
Рис. 95E)
Рис. 95F)
202
зисы (образующие циклы) в группах HX(Y), HX(YX), Hi(Y2). На
рис. 95 D)—95 F) показаны соответствующие образующие.
1) Для тора см. рис. 95D); 2) для полнотория см. рис. 95E);
3) для полнотория с вырезанными полноториями см. рис. 95F).
Если для г-го полнотория матрица склейки имеет вид (д' Y'l, то
\ Р» о* /
я,- переходит в atCi+pid и Ь{ переходит в yiCi + bid, \^i^.q—1.
Особый случай — полноторие,
которое приклеивается снаружи к
нолноторию с вырезанными полно-
полноториями (см. рис. 96). Здесь, aq пе-
переходит в aq{cx + c2-\-. •• + cq-\) + P4(i
И bq-*-yq(C\ + C2+ . . . +Cq-\)bqd. Оче-
видно, вложение Y-+Yx следующим
образом действует на образующие:
щ~*-\-еи bi~+-O-ei, l^ii^q. Упоря-
Упорядочим базисы HX{Y) и HX(YX)@ ' Рис д6
(BHX(Y2) следующим образом: для
Hx(Y) — (ax, ..., aq, bx, ..., bq), для
Hi(Yx)(BHx(Y2)-(e1, ...,'eq, cx, ..., cq-u d). Отсюда следует, что
матрица гомоморфизма / в этих базисах имеет вид
1
0
о ' •'•
1
а\ о £
0 '■ • :
а„-х ■ а9
о ft
0
\ о Y?
о '•. ;
Ye-i Y?
Строго говоря, в нижней части матрицы всюду перед числами
нужно поставить знак минус. Однако, очевидно, от минуса можно
избавиться, если считать, что матрицьГсклейки имеют вид
— а,- — у,-
-р£ -6,
Числа <ц, p,, Yj, Sj зависят от того, как мы склеиваем торы. Пусть
(а„
Тогда матрица / имеет вид
203
1
0
о. "•
Pi...
0
•0
a<7-i
P«-i
1
1
1
0
Yi
0
Si •
0
0
Ye i
■ • 8,_,
1
Обозначим группу, в которую отображает f, через N. Имеел
f : Z2«->Z2« = N. Мы уже задали базис в N. Пронумеруем его одь
паковыми буквами (е\,... ,eq,... ,e2Q). Если менять базис в груп-
группе .V, то матрица гомоморфизма будет также изменяться. Прег
положим,'что склейка уже произведена. Заметим, что если для
какого-то i имеет место равенство уг=О, то из условия целочи;
(а< у,\
ленности и унимодулярностн матрицы следует бг-^±1
Теперь предположим, что для некоторого t, например для г= 1
Ь. Сделаем следующую замену базиса в группе JV:
в-, в,, ... , в„ в„,
— ^9-Н I
Vi
•
В новом базисе ei,...,e2q матрица гомоморфизма / имеет виг
1
■
а,
и
'Р
0
0
•
п
• р,-1
1
1
i
0
Yi
0
0
0
•
и
Yrr-i
Г
где / = —«A/Yi+Pi- Мы видим, что матрица изменилась сле-
следующим образом: 1) число 8{ стало равным пулю, 2) число Pi
заменилось числом t.
Сделаем аналогичную аамену для всех, i таких, что угфО. Для
удобства обозначений будем считать, что уг=^О для 1^л<!/г и -у* —
= 0 для k+l^i^q—l. После произведенной замены базиса в
группе N матрица гомоморфизма f примет'вид ' .':
1
■ • . °
0
1
0
0 aft±i :
' •. i
h • • • h pft+i • • • P<7—l 0
0
Yx
0
Y*
0
о ••
0
+ 1 +1 1
Обозначим новый базис по-прежнему через ех e2q и произве-
произведем последнюю замену:
ek+\ =ek+i ±
eq-\ = e?_i ±
В новом базисе гомоморфизм f имеет матрицу
1
■ . о
о • .
'l
0
0
Yi
о'-.
Yfe
±1...±1 1
205
Теперь очевидно, что JV/Im / = ZVl ф ... ф ZVft ф Z'~*+1, где Z?( = О,
если Yi=l. Беря q достаточно большим и матрицы склейки беря
с нужными нам числами уь мы можем в качестве N/lmf полу-
получить произвольную конечно порожденную группу, что и доказы-
доказывает теорему. ^.
В4 частности, отсюда видно, что одномерной группой гомологии
связного компактного ориентированного замкнутого многообразия
(размерности три) может быть любая конечно порожденная абе-
лева группа.
Известно, что трехмерные многообразия могут иметь одинако-
одинаковые группы гомологии, но не быть диффеоморфными.
Можно доказать следующие утверждения.
а) Из -трех полноторий и одного ориентированного седла мож-
можно склеить гомологическую, ло не гомотопическую сферу.
б) Из «-мерных ориентированных седел, неориентированных
седел, цилиндров и полноторий (при я>3) нельзя склеить много-
многообразие с H\(Q, Z)=0.
ГЛАВА 5
СИМПЛЕКТИЧЕСКИЕ ДЕЙСТВИЯ КОММУТАТИВНЫХ
И НЕКОММУТАТИВНЫХ ГРУПП ЛИ
НА СИМПЛЕКТИЧЕСКИХ МНОГООБРАЗИЯХ.
ГАМИЛЬТОНОВЫ УРАВНЕНИЯ С СИММЕТРИЯМИ
§ 1. Полные инволютивные наборы функций и максимальные
линейные коммутативные подалгебры в алгебре функций на
симплектическом многообразии
Напомним, что действие группы Ли диффеоморфизмов гладко-
гладкого симплектического многообразия называется симплектическим,
если все эти диффеоморфизмы сохраняют на многообразии сим-
плектическую структуру.
Определение 1. Пусть на гладком симплектическом мно-
многообразии (М2п, со) задан набор F из п функционально независи-
независимых гладких функций f\,...,fn, находящихся в инволюции, т. е.
{{и fj}=0. Тогда будем говорить, что функции f\,...,fn образуют
полный инволютивный (коммутативный) набор.
Особый интерес представляет тот случай, когда одна из этих
функций является гамильтонианом какой-либо интересующей нас
гамильтоновой системы и. В этом случае все функции fi,...,fn яв-
являются интегралами системы и. В силу теоремы Лиувидля каж-
каждый такой интеграл «засчитывается за два интеграла», в резуль-
результате чего удается достаточно полно описать поведение интеграль-
интегральных траекторий системы. С .другой стороны, если на многообразии
обнаружен полный инволютивный набор функций, то все они яв-
являются интегралами каждого гамильтонова потока вида sgradf,
где f<=F.
Рассмотрим гладкие векторные поля а(/;) = sgradf,-. Каждое
из -них касается поверхности уровня, поэтому мы получаем набор
п касательных векторных полей на торе Лиувилля .Тп (см. выше
теорему Лиувилля). Мы утверждаем, что эти поля попарно ком-
коммутируют и линейно независимы в каждой точке. В самом деле,
симплектическая структура со определяет каноническое отождест-
отождествление е касательного и кокасательного пространств, в результа-
результате которого ковектор gradf, переходит в вектор sgrad/,. Посколь-
Поскольку е — изоморфизм Тх и Тх*, то линейная независимость ковекто-
ров grad/г эквивалентна линейной независимости векторов-
sgradf;. Далее, a{ft-, fj}= [afu afj]—O, так как функции /,-, f5 на-
находятся в инволюции. Следовательно, поля sgradf* попарно ком-
коммутируют, что и требовалось доказать.
20»
Таким образом, поля sgradfi образуют базис в каждой плос-
плоскости, касательной к тору Тп. Отсюда, в частности, следует, что
ограничение формы со на касательные плоскости ТхТп равно нулю,
т. е. каждый тор Лиувилля является лагранжевым подмногообра-
подмногообразием в объемлющем симплектическом многообразии.
Рассмотрим абелеву группу Rn, образующие которой обозна-
обозначим через е\,...,еп. Каждая образующая е\ порождает одномер-
одномерную подгруппу R,-1, которую мы представим в виде однопарамет-
рической группы ®И диффеоморфизмов, порожденной векторным
полем Ui = sgradfj на торе Тп. Тем самым мы представили все об-
образующие et, ...,en группы Rn с помощью диффеоморфизмов, со-
сохраняющих симплектическую структуру.
Теперь мы можем определить гладкое действие всей группы R™
на всем многообразии. Для этого фиксируем на многообразии точ-
точку х и сопоставим элементу r=t\e\+ .■.. +tnen гладкое преобра-
преобразование а(г):М-*-М, являющееся следующей композицией:
'a(r)x = ®tl6 ■ ■ • °®1п(х)- Поскольку векторные поля v{ коммутируют
на многообразии, то наше определение гладкого действия комму-
коммутативной группы R™ на всем многообразии (при изменении точки
х) корректно.
Поскольку векторные поля Vi линейно независимы в каждой
точке на поверхности (на торе) Тп, то группа Rn действует ло-
локально тр~анзитивно на торе, следовательно, отображение а: R™-*-
—>-Гп является отображением «Сна!». Такое действие группы R'
называется пуассоновским. Отличие от симплектического действие
в том, что каждая однопараметрическая группа порождена гг-
мильтоновым полем, гамильтониан которого является однозначно1
функцией, определенной на всем многообразии. Из определения '
следует также, что тор Т7' является орбитой действия группы R'
Эта орбита <Свырастает^> из точки хо^Тп. Таким образом, на то
ре Тп задано п линейно независимых коммутирующих векторны:
полей. Отсюда следует, что Г" является фактором группы Rn m
некоторой решетке. Рассмотрим в R" стационарную подгруппу Г
точки х0, т. е. множество всех элементов r = Rn, таких, что ohi
оставляют точку х0 на месте: г(хо)=хо. Из предыдущего следует
что Г — дискретная подгруппа. Можно доказать, что существую"
л линейно независимых векторов ei,...,eneRn таких, что Г с(-
впадает с множеством всех их целочисленных линейных комбина-
комбинаций, т. е. r = Z(e,,...,en)Z».
Таким образом, мы можем определить на симплектичесжп
многообразии М2п гладкое симплектическое (пуассоново) дейс~
вне коммутативной группы R". Компактными связными неособь-
ми орбитами этого действия являются торы Лиувилля Тп. Следо-
Следовательно, с каждым полным инволютивным набором функцш
естественно связано гладкое действие «-мерной коммутативно!
"группы на многообразии, сохраняющее симплектическую структу-
структуру (и даже пуассоново).
Итак, каждая вполне интегрируемая гамильтонова системе
обладает определенным типом симметрии, а именно: с ней связа
Но симплектическое (даже пуассоново) действие коммутативной
«-мерной группы на М2п. При этом связные, компактные, неосо-
неособые поверхности уровня интегралов совпадают с орбитами дейст-
действия этой группы.
Возникает естественный вопрос: на каждом ли гладком много-
многообразии существует хотя бы один полный инволютивный набор
функций?
Оказывается, если требовать от искомых функций только глад-
гладкость, то ответ положителен (замечание А. В. Браилова).
Предложение 1. На каждом симплектическом гладком
многообразии всегда существует полный инволютивный набор
гладких функций, функционально независимых почти всюду на
многообразии.
Доказательство. Согласно теореме Дарбу в некоторой
шаровой окрестности любой точки х на М2п существуют снмплек-
тические координаты р,-, G,-. Рассмотрим этот шар с центром в
точке х и зададим на нем функции fi=Pi2+qi2. Ясно, что {fit f;} =
=0, т. е. эти функции находятся в инволюции. Рассмотрим теперь
п
функцию /=V fi = 2 р? + <7?, которую можно рассматривать как
«квадрат расстояния» от переменной точки до центра шара. По-
Построим теперь на шаре гладкую функцию h(p, q)=g(f), завися-
зависящую только от радиуса (расстояния до центра шара), равную
единице в центре шара, равную тождественно нулю на границе
шара и монотонно убывающую с ростом f от нуля до границы
шара (рис. 97). Эту функцию можно продолжить нулем на все
многообразие. Ясно, что {h, /,-}«= 0, следовательно, {hfu hfj}=0.
Ряс. 97 Рис. 98
Мы утверждаем, что функции- hfu... ,hfn независимы внутри
диска (шара). В самом деле, если допустить функциональную за-
зависимость, то существует функция F такая, что F(hfu... ,hJn)s=Or
т. е. /=1(gBfi)/1,...,gBfi)fr.)=0. Ясно, что функции /i,...,/» не-
независимы, поэтому можно заменить их формальными переменны-
переменными tit...,tn. Если мы докажем, что функция F(gB,ti)ti,..*
...,g(Z,ti)tn) не равна тождественно нулю, тем самым мы дока-
докажем независимость функций ftfi,..., hfn.
211
Допустим противное: пусть указанная функция тождественно
обращается в ноль, т. е. функции gCLti)t\,... ,g{J>t{)tn функцио-
функционально зависимы. Якобиан / этой системы функций, очевидно,
имеет вид ,
где /=2/{. Если /=0, то g±t —^-=0, т. е. g(t) —линейная функ-
. dt
ция, что противоречит построению. Итак, нам удалось построить
на открытом шаре набор из п независимых функций, находящихся
в инволюции и (что важно!) обращающихся в ноль вне шара.
Следовательно, покрывая почти все многообразие М2а (за ис-
исключением замкнутого множества меры ноль) открытыми непере-
непересекающимися шарами и строя на каждом из них указанный набор
функций, мы можем определить п функций, заданных уже на
всем многообразии, находящихся в инволюции и независимых на
открытом всюду плотном множестве (рис. 98). Предложение до-
доказано. *
Из приведенного доказательства видно, что построенный нами
гладкий полный инволютивный набор функций принципиально не
может быть набором аналитических функций (если многообразие
аналитическое), поскольку каждая из функций этого набора тож-
тождественно равна нулю на связном замкнутом множестве, являю-
являющемся дополнением-к объединению счетного числа открытых не-
лересекающихся шаров. Таким образом, следует еще выяснить
возможность существования: а) аналитических полных инволю-
тивных наборов, б) боттовских полных инволютивных наборов.
В гл. 2 мы познакомились с теоремой Лиувилля, позволяющей
описывать поведение интегральных тректорий систем, обладаю-
обладающих полным набором интегралов в инволюции. В этой главе мы
лознакомимся с современными новыми методами интегрирования,
частным случаем которых является классический метод интегри-
интегрирования с помощью теоремы Лиувилля.
Через С°°(М) обозначим линейное (бесконечномерное) про-
пространство всех гладких функций на симплектическом многообра-
многообразии М2п. Как мы уже знаем из гл. 2,' это пространство естествен-
естественно превращается в бесконечномерную алгебру Ли относительно
скобки Пуассона {f, g}, где f, g&.C°°(M). С точки зрения гамиль-
тоновой механики значительный интерес представляют различные
подалгебры (как конечномерные, так и бесконечномерные) в ал-
тебре Ли С°°(Л4). При таком подходе теорема Лиувилля приобре
Тает следующее освещение. Гамильтониан Н системы .u=sgrad h
можно представить как вектор (т. е. функцию) в алгебре СХ(М)
Если система v вполне интегрируема по Лиувиллю, то Н вклю
"чается в коммутативную подалгебру функций G(H), с размер-
212-
иостью, в точности равной п (половине размерности многообра-
многообразия); при этом в G(#) можно выбрать аддитивный базис /i,...
...;/„, все функции которого функционально независимы (почти
всюду) на М. Можно считать, что f\ — H (рис. 99).
Конечно, такая коммутативная подалгебра G(#) может не су-
существовать. Тогда система u = sgrad# неинтегрируема по Лиу-
виллю. Как мы уже отмечали, «большинство» систем неинтегри-
руемы в указанном смысле. Поэтому обнаружить достаточно боль-
большую коммутативную оболочку функции Н — это редкое событие.
Если geG(#)—любая другая функция из коммутативной
подалгебры G(H), то система sgradg также интегрируема на М с
тем же набором первых интегралов, чт«г и система sgrad H. По-
Рис. 99
Рис. 100
этому обнаружение на М2п коммутативной подалгебры функций
GczC°°(M) размерности п, обладающей аддитивным базисом из
л функционально независимых функций, сразу дает нам целое се-
семейство интегрируемых систем.
Определение 2. Будем говорить, что на симплектическом
многообразии М2п задана максимальная линейная коммутативная
подалгебра функций Go (в алгебре Ли С°° (М) относительно скоб-
скобки Пуассона), если dimG0=n и в Go можно выбрать аддитивный
базис, состоящий из п функционально независимых на М2" (почти
всюду) функций /i,...,/n. Иногда будем называть такую алгебру
функций полным инволютивным (коммутативным) набором
функций.
В дальнейшем термин «почти всюду» будем опускать как
очевидно подразумевающийся. Если ,g — произвольный элемент
(функция) из Go, то g=cifi+ ... +cnfn, где с\,... ,сп — некоторые
постоянные (вещественные) числа. Следовательно, любой элемент
.geGo представляется в виде линейной комбинации с постоянными
коэффициентами независимых функций f\,...,fn- Поэтому в опре-
определении 2 мы ввели термин «линейная алгебра». Термин «макси-
«максимальная» в этом определении также имеет смысл, проясняемый
следующей простой леммой.
Лемма 1. Если Т — коммутативная линейная подалгебра (не
обязательно максимальная) в алгебре функций ^(М), причем
addutueubiu базис в подалгебре образуют функции fi,...,fr, неза-
независимые на М2п, то всегда г^п. ■
213
В самом деле, линейная оболочка L линейно независимых век-
векторов sgrad/ь...,sgradfr имеет размерность г и является изо-
изотропной плоскостью в касательном пространстве к М2п (в точке
общего положения). Так как размерность изотропных плоскостей
не превышает п (см. гл. 1), то лемма доказана.
Итак, максимальная линейная коммутативная подалгебра G№
действительно имеет максимально возможную размерность среди
всех коммутативных подалгебр, аддитивный базис в которых со-
состоит из независимых функций. Если же отказаться от последнего
условия, то в С°°(М) существует много других коммутативных
подалгебр, размерность которых больше п. Однако в них нельзя
выбрать аддитивный независимый (в функциональном смысле)
базис. В классе таких коммутативных подалгебр есть подалгебры
бесконечной размерности. Для их построения достаточно, напри-
например, рассмотреть линейную оболочку следующей бесконечной по-
последовательности независимых (в аддитивном смысле, но зависи-
зависимых функционально) функций: f, f2, f3,..., f\...
Таким образом,^в дальнейшем ие возникнет путаницы в терми-
терминологии и, говоря о максимальной коммутативной подалгебре, мы
автоматически будем всегда подразумевать, что речь идет о под-
подалгебре, обладающей аддитивным функционально независимым ба-
базисом.
В этом смысле теория бесконечномерных алгебр Ли сущест-
существенно сложнее теории конечномерных алгебр Ли, так как здесь
понятие подалгебры Картана нуждается в специальном обсуж-
обсуждении.
Итак, важная задача симплектической и гамильтоновой гео-
геометрии формулируется следующим образом. . -
Дано симплектическое многообразие М2п с 2-формой со. Суще-
Существует ли на нем хотя бы одна максимальная линейная коммута-
тивная подалгебра Go в алгебре Ли функций С°°(Л4) (относитель-
(относительно скобки Пуассона)? При этом наибольший интерес представ-
представляют аналитические, боттовские и алгебраические наборы функ-
функций. Если такие подалгебры существуют, то требуется узнать —
сколько их? Сколькими параметрами они задаются? Каковы алго-
алгоритмы их эффективного построения? Как связаны эти подалгебры
(и их «количество») с метрическими и топологическими свойст-
свойствами исходного многообразия? Существуют ли топологические
препятствия, мешающие существованию на данном многообразии
М2п таких подалгебр?
Если эта задача решена (в каком-то разумном смысле), то
следующим шагом является такой.
Какие конкретные интересные (с механической, физической то-
точек зрения) гамильтонианы попали в.такие максимальные комму-
коммутативные подалгебры? Все такие гамильтонианы порождают инте-
интегрируемые гамильтоновы системы.
Пусть симплектическое многообразие М2п фиксировано. Априо-
Априори неясно, существует ли на нем хотя бы одна максимальная ли-
линейная коммутативная подалгебра функций, т. е. существует ли
214
ua M2n хотя бы одна интегрируемая система? В гладком случае
(см. выше) формальный ответ положителен. Пример такой систем
мы мы построили выше. В то же время ясно, что построенный
нами набор функций патологичен и не представляет абсолютно
никакого интереса с точки зрения содержательных приложений.
Поэтому следует сузить класс функций, среди которых нужно ис-
искать максимальные коммутативные подалгебры. Естественно рас-
рассмотреть следующие классы:
1) Боттовские наборы функций на гладких многообразиях.
2) Вещественно-аналитические функции на многообразиях это-
этого же класса.
3) Алгебраические функции на алгебраических многообразиях.
4) Имеет смысл изучить комплексно-аналитический случай.
Пока неясно, на любом ли из симплектических многообразий
перечисленных четырех категорий существует максимальная ли-
линейная коммутативная подалгебра функций соответствующей ка-
категории.
Оказывается, гамильтонова система может быть проинтегри-
проинтегрирована не только в том случае, когда ее гамильтониан включает-
включается в максимальную линейную коммутативную подалгебру функ-
функций, но и в том случае, когда он включается в некоммутативную
алгебру Ли G функций на М, обладающую тем свойством, что
dim G+ранг G=dimAf2n. Этому и посвящеи следующий параграф.
§ 2. Гамильтонова система уравнений интегрируема, если ее
гамильтониан включается в достаточно большую алгебру Ли
функций
Огромная роль коммутативных максимальных линейных под-
подалгебр хорошо известна. Поэтому задача их обнаружения весьма
актуальна. Однако, как показали исследования последних лет, ва
многих важных случаях полные инволютивные наборы функций
«маскируются» в пространстве всех гладких функций настолько
удачно, что следует затратить большие усилия, чтобы их обна-
обнаружить. Это ставит перед нами задачу эффективного распознава-
распознавания (обнаружения) максимальных линейных коммутативных под-
подалгебр.
А. С. Мищенко и А. Т. Фоменко обнаружили, что в некоторых
случаях существование максимальной линейной коммутативной
подалгебры функций (т. е. интегралов) можно вывести из факта
существования некоммутативной алгебры функций, не являющих-
являющихся, вообще говоря, интегралами данной, системы. Это естественно
иногда упрощает поиск вполне интегрируемых сис.тем, что и под-,
твердилось на практике. К изложению этого нового метода неком-
некоммутативного интегрирования мы сейчас перейдем.
Пусть G — конечномерная алгебра Ли, G* — ее сопряженное
пространство, geG* — некоторый ковектор. Рассмотрим в алгеб-
алгебре Ли G линейное подпространство #s=Anng, состоящее из всех
векторов X таких, что adx*£=0. Подпространство Н% называется
215
аннулятором ковектора £. Будем говорить, что | является ковек-
тором общего положения, если размерность его аннулятора наи-
наименьшая. Индексом ind G алгебры Ли G назовем размерность ан-
аннулятора ковектора общего положения. Если G — полупростая
алгебра Ли, то ее индекс совпадает с ее рангом, т. е. с размер-
размерностью подалгебры Картаиа (максимальной коммутативной под-
подалгебры в G).
Сформулируем теорему, доказанную А. С. Мищенко и А. Т. Фо-
Фоменко (см. [97], [100], [151]) и обобщающую классическую теоре-
теорему Лиувилля. Сначала сделаем несколько вводных замечаний.
Определение 1. Пусть G — конечномерная подалгебра в
алгебре Ли функций С°° (М) (относительно скобки Пуассона). Под-
Подалгебру G назовем максимальной линейной на симплектическом
многообразии М2", если dim G+ind G=dimM2" и если в G можно»
выбрать аддитивный базис, состоящий из функционально незави-
независимых (почти всюду) функций на многообразии М.
Ясно, что если G — максимальная линейная коммутативная •
подалгебра, то она является максимальной линейной подалгеброй.
Обратное, вообще говоря, неверно, и в первую очередь в силу
того обстоятельства, что максимальная линейная подалгебра МО'
жет быть некоммутативной. Такие примеры мы скоро увидим (их
будет много).
Пусть G — некоторая подалгебра (не обязательно максималь-
максимальная), в которой можно выбрать аддитивный базис нз функцио-
функционально независимых функций fu ..., fk. Тогда dim G=k. Рассмот-
Рассмотрим отображение момента F : M2n-+G*, где F(x) = (f\(x),...,
..., fft(x))=geG*. Здесь G* является ^-мерным линейным про-
пространством. Каждая его точка £ определяет некоторую совместную
поверхность М% уровня функций-/ь ..., fk, т. е. Мг=р-1(%), Мъс
аМ2п.
Фиксируем неособую поверхность уровня Мь задав какой-
то ковектор £eG*. Тогда | определяет также подалгебру #5 =
=Апп |, т. е. свой апнулятор. Итак, с каждым ковектором одно-
однозначно связаны два важных объекта:
а) поверхность уровня M%~F-X (£), <
б) аннулятор Ann %.
При этом если g=2|i£(, где ковекторы еи ■ • •, ей двойственны
к векторам базиса /ь ..., fk, то поверхность Мъ задается в М си-
системой уравнений Ы*)=1ь ■•■, fk{x)=\k- Аннулятор Ann£ лежит
в исходной алгебре функций G.
При изменении ковектора \ его аннулятор тоже как-то меняет-
меняется в алгебре Ли G. Это же изменение можно моделировать изме-
изменением совместной поверхности уровня М% базисных функций-
fi, • • ■, fit- ■
Поверхность уровня М% назовем неособой, если все функции
/i, ..., fk независимы в каждой ее точке. Тогда dimМ5=2п—k.
Теорема 1. Пусть G — максимальная линейная конечномер-
конечномерная алгебра функций на Мы, пусть geG* — ковектор общего по-
положения и М% — соответствующая совместная неособая поверх-
216
пость уровня независимых функций f\, ..., fk, образующих адди-
аддитивный базис в G. Если поверхность М% компактна и связна, то
она биффеоморфна r-мерному тору Т, где r=ind G (г. е. г=
~2n—k). При этом на торе ТГ и на всех близких к нему
поверхностях уровня, также диффеоморфных тору Тг, можно вве-
ввести такие регулярные координаты фЬ ..., qv, что в этих коорди-
координатах все векторные поля sgradft, где /геАпп|, задают условно,
периодическое движение по тору Тг (т. е. являются полями с по-
постоянными компонентами).
В этой теореме мы не имели в виду какую-либо конкретную
гамильтонову систему, а описали свойства целого класса полей
вида sgrad/г, порожденных аннулятором ковектора общего поло-
положения.
Частным случаем нашей теоремы 1 является, конечно, клас-
классическая теорема Лиувцлля. В самом деле, если максимальная ли-
линейная подалгебра функций G является коммутативной, то ее ин-
индекс r=indG равен ее размерности k и, следовательно, условие
максимальности превращается в условие k+,k=uim М=2п, т. е.
k=n. В таком случае все торы Тг из нашей теоремы 1 оказывают-
оказываются обычными n-мерными торами Лиувилля.
Теперь посмотрим на теорему 1 с точки зрения возможности
интегрирования конкретных систем вида w = sgrad#. Фиксировав
гамильтониан Н, мы тем самым задаем некоторый элемент алгеб-
алгебры Ли С°°(М). Рассмотрим в ней всевозможные максимальные ли-
линейные подалгебры G (если они существуют) и попытаемся найти
хотя бы одну такую, чтобы гамильтониан Н попал в G.
Определение 2. Скажем, что гамильтониан Н допускает
правильное вложение в максимальную линейную алгебру функций
G, если H&G, и, кроме того, существует ковектор |еб* общего
положения такой, что #eAnn|crG (рис. 100).
Если гамильтониан Н допускает правильное вложение в не-
некоторую максимальную линейную подалгебру G, то определена
некоторая (по крайней мере одна) совместная неособая поверх-
поверхность уровня F-1 (|) =М|СгМ) отвечающая ковектору общего поло-
положения i (относительно отображения момента).
Теорема 2. Пусть w = sgrad# — гамильтонова система на
М2п, где гамильтониан Н допускает правильное вложение в неко-
некоторую максимальную линейную подалгебру функций G на М. Тог-
Тогда" существует по крайней мере один такой ковектор geG* об-
общего положения, что ЯеАпп g и соответствующая ему совмест-
совместная неособая поверхность уровня Mt инвариантна относительно
поля v. Если поверхность М6 компактна и связна, то она диффео-
морфна тору ТГ, где r = dimM—dim G, и на Тг существуют регу-
регулярные координаты фь ..., <рг, относительно которых поле v оп-
определяет условно периодическое движение на торе Тг {т. е. интег-
интегральные траектории поля v задают прямолинейную обмотку то-
тора Г).
Определение 3. Назовем гамильтоиовы системы, допуска-
допускающие интегрирование в смысле теоремы 2, вполне интегрируемы-
217
ми в некоммутативном смысле (или некоммутативно интегрируе-
интегрируемыми) .
Теорема 2 является очевидным следствием нашей теоремы 1
Подчеркнем важное обстоятельство: далеко не все функции g w
максимальной линейной подалгебры G являются настоящими ин
тегралами поля v—sgradH. Интегралами (в обычном смысле
являются лишь функции h из аннулятора AnngcrG ковектора п
Если алгебра G некоммутативна, то {g, H}=£0 при g^Ann|.
Как применять теоремы 1 и 2 на практике? Сначала нужш
найти наибольшее число независимых функций, коммутирующие
с Н. Затем нужно попытаться включить это семейство функций /■
в некоторую большую (вообще говоря, некоммутативную) алгег-
ру Ли функций G так, чтобы А можно было представить в вид!-
аннулятора ковектора общего положения. Если при этом алгебо*.
G окажется максимальной линейной, это позволит проинтегриро-
проинтегрировать систему в тех же терминах, что и в классической теорем;-
Лиувилля (т. е. торы, условно периодическое движение и т. п.)
Оказывается, такие ситуации часто встречаются в конкретны;'
задачах симплектической и гамильтоновой геометрии. Доказателг-
ство теорем 1 и 2 см. в наших работах [97], [100], [151]. В нем мы
используем, в частности, известную редукцию Марсдена и Ваиь
стейна [227], результаты Дюфло, Вернь [187], Бернат, Конзь
Вернь [178].
Замечания к теоремам 1 и 2:
1) В некоммутативных алгебрах Ли G выполняется неравен
ство &=dim G>ind G=r. Например, это имеет место в полупро
стом случае, когда г«у/г,.т. е. существенно меньше k. Так как
r+k=2n, то г-мерные инвариантные торы Тг, по которым движутся
интегральные траектории системы, являются «маломерными», т. е.
их размерность меньше (иногда существенно меньше), чем поло-
половина размерности симплектического многообразия М2п. Это озна-
означает, что гамильтоноаа система, допускающая некоммутативное
интегрирование в нашем смысле, вырождена, т. е. ее интеграль-
интегральные траектории ложатся в действительности не на «-мерные торы
Лиувилля, а на торы меньшей размерности.
2) В силу замечания 1 гамильтоновы системы, допускающие
некоммутативное интегрирование, естественно называть системами
с вырождением. Поэтому, с одной стороны, они устроены сложнее,
чем системы, интегрируемые в обычном коммутативном смысле.
С другой стороны, запас максимальных линейных подалгебр су-
существенно больше запаса максимальных линейных коммутатив-
коммутативных подалгебр. В симплектической геометрии часто встречаются
гамильтоновы системы, гамильтониан которых правильно вклю-
включается в максимальную линейную алгебру функций (и, как мы
теперь знаем, допускающие некоммутативное интегрирование).
Поэтому наш метод позволяет теперь интегрировать значительный
запас конкретных систем, обычное коммутативное интегрирование
которых представляет затруднения.
218
Как показал опыт последних лет, обнаружить некоммутативную
максимальную линейную алгебру функций часто бывает сущест-
существенно проще, чем обнаружить максимальную линейную коммута-
коммутативную алгебру интегралов.
3) Интересен случай, когда гамильтониан Н правильно вклю-
включается в максимальную линейную алгебру функций G и попадает
при этом в ее центр. В этом случае все функции из алгебры G
коммутируют с гамильтонианом, т. е. являются обычными интег-
интегралами системы. При этом сами интегралы не обязаны коммути-
коммутировать между собой (друг с другом), т. е. в целом алгебра G мо-
может быть некоммутативной. Такую алгебру G естественно назвать
некоммутативной алгеброй интегралов данной гамильтоновой си-
системы. В силу теорем 1 и 2 траектории такой системы задают ус-
условно периодическое движение на торах Тг, где r=ind G.
Доказательства перечисленных ниже фактов см. в наших ра-
работах [97], [100], [151].
Пусть гамильтониан системы u=sgrad# правильно включает-
включается в некоторую конечномерную линейную алгебру G функций на
М2п. Через <3 обозначим соответствующую ей односвязную груп-
. пу Ли, действующую на М симплектическими преобразованиями
1; (пуассоново действие). Пусть fu ..., fk — аддитивный базис в G
/<из независимых функций и F:M-*-G* — отображение момента,
;;т. е. F{x) = (h(x), ..., f,(x)). Через М^-Щ), где £e=G*, обо-
• значим совместную поверхность уровня функций f\, ..., fk, за-
< даваемую, следовательно, системой уравнений f» (лс) =£,-, l<t<
• ■- <:«, i=(£i, ..., %п)- Операция в алгебре Ли G задается скобкой
)i Пуассона f, g-*-[f, g}. Если |eG* и g^G, то значение ковектора
f:- (линейного функционала) % на элементе g обозначим через
"■ <5, g)=l(g)- Тогда (I, {g, /}} = <adg*€, f). Удобно ввести следую-
следующее соглашение: ковектор adg*-g обозначить через {!;, g). Следует
отдавать себе отчет в том, что это не обычная скобка Пуассона,
поскольку здесь geG*, geG, {£, g}eG*. В этих обозначениях
<l {g, /}> = <{£, g), f). Ясно, что «t = Ann|=.(geG:{g, g}=0).
Пусть элемент / алгебры G лежит в аннуляторе Н% и х^Мх,
где Мг — неособая поверхность уровня. Тогда sgrad f (х)<=ТхМг.
Это означает, что косые градиенты функций из аннулятора ко-
ковектора | касаются поверхности уровня М%.
Далее, оказывается, имеет место равенство (см. рис. 101)
• TxMlr\(sgradf,fe=G)=Hx='(sgradh,h(=Hl).
Рассмотрим теперь группу $Q% с алгеброй Ли #Е, т. е. ijgc:®.
Можно доказать, что поверхность уровня М% инвариантна относи-
относительно действия группы §Е на многообразии М. Далее, рассмот-
рассмотрим форму ш, и пусть ш — ее ограничение на поверхность уров-
уровня _М%. Действие подгруппы фЕ на многообразии М% порождает
в каждой точке xeMs плоскость НхсТхМь образованную векто-
векторами вида sgrad f, где |еЯЕ (рис. 101). .
Можно убедиться в том, что ядро формы ш совпадает с плос-
плоскостью Нх.
219
Соберем вместе сформулированные выше факты. Основными
объектами здесь являются:
а) поверхность уровня Мг, где dim Ml=2n—k;
б) орбита @ {х) точки х при действии группы @, здесь*
@()/
();
в) орбита $2г(х) точки х при действии подгруппы ФЕ=ехр#6.
Ясно, что Тх @(x) = (sgradf, f<=G), Тх§ (х)=Нх. Отсюда сле-
следует, что® (*)ПМ|=ф5(*) (Рис- 102)- Отметим, что размерность
орбиты ф {(х) равна размерности ф5 и равна г.
Рассмотрим пуассоново действие группы & на многообразии
М и предположим, что в малой окрестности поверхности уровня
Рис. 101
Рис. 102
М% это действие имеет один тип стационарных подгрупп, т. е. что
все орбиты группы ®, близкие к орбите & (х), ей диффеоморфны.
Рассмотрим проекцию р:М-*-М/ & многообразия М на простран-
пространство орбит M/®—N. Это пространство может не быть гладким
многообразием и иметь особенности. Однако в силу сделанных
выше замечаний в малой окрестности точки /j(@(je))eJV про-
пространство N является гладким многообразием размерности 2«—k.
В действительности, если группа @, например, компактна, то
объединение множества орбит общего положения (максимальной
размерности), диффеоморфных друг другу, является „открытым
всюду плотным подмножеством в многообразии М. Поэтому N
является многообразием всюду, за исключением множества точек
меры ноль.
Многообразие N не обязано быть симплектическим. Например,
оно может иметь нечетную размерность.
Проекция р, будучи ограничена на поверхность уровня М5,
проектирует ее на пространство Qi==Mtl ф{. Поэтому N расслоено
на поверхности вида QE (рис. 103).
Оказывается (доказательство мы здесь опускаем), что много-
многообразия Q% являются симплектическими многообразиями с невы-
невырожденной замкнутой формой р, являющейся проекцией формы го
на поверхность уровня Мъ при отображении prAfj-vQ^. При этом
p*p=w.
Вернемся к изучению гамильтоновых систем на М. Нусть v—
=sgrad# — система с алгеброй интегралов G, т. е. {Я, G}=0.
220
Так как гамильтониан Я коммутирует со всеми элементами из ал-
алгебры G, то функция Я инвариантна относительно действия груп-
группы ©.В самом деле, (sgrad /)Я={/, H}=0, /gG. В частности,,
подгруппа Six, действуя на М, также переводит функцию Я в се-
себя. Итак, определена естественная проекция поля sgrad Я на
пространство N. При этом поле sgrad Я касается поверхности
уровня М% и также проектируется в некоторое поле £(Я)~на фак-
фактор-пространстве QE, так как поле sgrad// инвариантно относи-
относительно подгруппы ф5.
Рис. 103
Рис. 104
Итак, мы видим, что пространство N расслоено на симплек-
тические многообразия Q%, и на N определено векторное поле
Е{Н), касающееся всех поверхностей QE (рис. 104). Итак, мы со-
сопоставили тройке объектов (М, sgrad Я, со) новую тройку анало-
аналогичных объектов (Qi, E(H), р).
Можно доказать, что в.екторное поле Е(Н) гамильтоново от-
относительно симплектической формы р на многообразии QE для
функции Гамильтона Я, равной проекции функции Я|м^ на много-
многообразие Qs, т. е. E{H)=sgradp(p*H).
Построенное выше соответствие (М, sgrad Я, (i))->(QE, Е(Н), р)
называется редукцией исходной гамильтоновой системы sgrad Я.
При этом мы получаем новую гамильтонову систему на многооб~
разии Qi меньшей размерности In—k—т. При этом dimQE<
<.&SmMx=<ln—k. Может оказаться, что редуцированная система
на Q% оказывается проще, чем исходная система на М.
Предположим, что редуцированную систему удалось тем или
иным способом проинтегрировать. Тогда, оказывается, это позво-
позволяет увеличить число интегралов у исходной системы sgradЯ на
М, «подняв» эти новые интегралы с пространства N на много-
многообразие М. *■
Можно проверить справедливость следующего утверждения.
221
Пусть G — конечномерная алгебра интегралов поля sgrad Я
на М, удовлетворяющая перечисленным условиям. Пусть Е(Н) —
редуцированная система на пространстве N—\JQi, являющаяся
гамильтоновой на каждом подмногообразии Qs. Пусть G' — ли-
линейное пространство функций на N таких, что их ограничения на
подмногообразия Qs образуют конечномерную алгебру интегралов
потока Е(Н). Тогда пространство .функций G&G", где G" = p*G',
т. е. G"=(gp, g^G', р-.M-^N), является алгеброй Ли интегралов
системы sgrad Я, причем {G, G"}=0.
Пусть v — одна из гамильтоновых систем,-указанных выше,
т. е. либо v = sgrad Я, {Я, G}=0, либо y=sgradft, где fie Ann |.
Рассмотрим описанную выше редукцию. Поскольку теперь выпол-
выполнено дополнительное условие dim G+ind G=dimM, т. е. k+r=2n,
то размерность поверхности уровня Ms равна г.. Размерность орби-
орбиты 5}5(лг), содержащейся в Мь также равна г (рис. 103). Отсюда
следует, что Мг=$%(х), т. е. в предположениях теоремы 2 поверх-
поверхность уровня является орбитой точки х при действии группы Jpj.
В частности, dim Qi—Zn—k—r—O. Поэтому в данном случае струк-
структура редуцированной системы осо-
особенно проста. Так как QE является
точкой (!), то поток Е(Н) — нуле-,
вой (рис. 105). Здесь пространство
N имеет размерность г. Так как МЕ —
поверхность уровня интегралов G
для потока v, то этот поток касается
М%, т. е. М% — r-мерное подмногообра-
_ зие, инвариантное относительно всех
ис' полей вида sgrad ft, /ieAnn|, и отно-
относительно полей sgrad Я, где {Я, G} = 0.
Осталось доказать, что поверхность уровня является г-мер-
иьгм тором в том случае, когда поверхность МЕ компактна и
связна.
Пусть £eG* — ковектор общего положения. Тогда оказывает-
оказывается, что его аннулятор Ann \ коммутативен. В частности, подгруп-
подгруппа ijE коммутативна.
Итак, поверхность уровня М% — орбита группы §{, и так как
dimME=dim5}s, то М% является фактор-группой группы фЕ по дис-
дискретной решетке Г. Так как группа §s коммутативна, то Мг в
случае компактности и связности оказывается r-мерным тором.
Подробное доказательство теорем 1, 2 и перечисленных выше ут-
утверждений см. в [97] и в книге автора [151].
§ 3. Общие свойства инвариантных подмногообразий
гамильтоновых систем дифференциальных уравнений
3.1. Редукция системы на одной изолированной поверхности
уровня. Рассмотрим наши результаты § 2 с более общей точки
зрения. Выделим в чистом виде наиболее общие элементы описан-
описанных конструкций. Напомним, что гладкая функция / на многооб-
222
разии М называется интегралом векторного поля v, если она по-
постоянна вдоль всех интегральных траекторий поля. Другими сло-
слонами, производная функции / по направлению поля v равна пулю»
т. е. у(/)=0. В этом случае интегральные траектории поля лежат
на поверхностях уровня Mc=(f=c) функции f.
Гладкая функция / называется частным интегралом поля уг
если одна (!) из ее поверхностей уровня инвариантна относитель-
относительно поля v (в частности, относительно потока, порожденного по-
полем). Остальные поверхности уровня функции могут быть неин-
неинвариантными. Если инвариантный уровень имеет вид M0=(f = 0),
то указанное условие инвариантности запишется так: у (/) | </=о> = 0.
В случае общего положения поверхность Мо является инва-
инвариантным подмногообразием коразмерности 1. Более общо под-
подмногообразие L коразмерности k в М, задаваемое уравнениями
L=(fi=O, ..., /fc=0), называется инвариантным (относительно по-
поля и), v(fi)\L=Q. В частности, если задано несколько функцио-
; нально независимых первых интегралов fi, ..., fk системы v, то-
.< каждое подмногообразие вида MCl,Cl ck = {f1 = c1, ... ,fk = ск)
\ будет инвариантным.
I Предложение 1. Пусть v=sgradH — гамильтоновб поле
'' на симплектическом многообразии М2п и f — гладкая функция,
коммутирующая {в смысле обычной скобки Пуассона) с гамиль-
, тонианом Н этого поля, т. е. {Н, /}=0 на М. Тогда функция f яв-
является интегралом поля v. Далее, подмногообразие L2n~k—
= (fi=0, ..., /ft=0) является инвариантным относительно поля v
при условии, что {#, f;}i.=0.
Замечание. Можно сказать, что функции /г- должны комму-
коммутировать с гамильтонианом Н только на поверхности L (а вне
ее, вообще говоря, коммутировать не обязаны).
Доказательство. Вычисляя производную функции f вдоль,
поля v, получаем v(f)=a,(v, sgradf)={H, /}=0 либо на всем мно-
многообразии М, либо только на поверхности L, что и требовалось
доказать,
В теореме Лиувилля утверждается, что каждое связное ком-
компактное подмногообразие Ln в М2п (для интегрируемой системы)
является тором. Н. Н. Нехорошее и В. В. Козлов отметили, что-
можно выделить случай, когда одно изолированное инвариантное
подмногообразие L= (/,=.. .=/„+*=0) в М2п является тором. Для
этого нужно потребовать, чтобы на подмногообразии L выполня-
выполнялись соотношения {/,-, /г}=0, t=l, 2, ..., п—k, /=1, ..., n+k
(т. е. векторные поля sgrad/,-, l<t<«—k, касаются поверхности'
L), а также чтобы rf{f,, fj}=0 при i, /=l, 2,...,«— ky причем эти
тождества должны выполняться в каждой точке подмногообразия
L (но не вне него, вообще говоря). Это означает, что ограничения
(сужения) полей sgrad fi на поверхность L коммутируют на L
(но не вне L).
Сейчас мы опишем, следуя Я. В. Татаринову, простую и полез-
полезную конструкцию, позволяющую превращать гамильтонову систе-
22а
му, обладающую, вообще говоря, некоммутативной группой сим-
симметрии (см. выше § 1), или, более общо, инвариантным подмного-
подмногообразием, в гамильтонову систему на симплектическом многооб-
многообразии меньшей размерности.
Эта процедура может быть названа редукцией гамильтоновой
системы на одной поверхности и фактически может быть извле-
извлечена из работ Э. Картана. Ее современный вариант, изложенный,
правда, в других терминах, содержится в работе Л. Лоско [224].
Пусть на симплектическом многообразии (М2п, ш) задана га-
мильтонова система y=sgrad# и пусть L=(/i=.. . = /fe=0) — инва-
инвариантное подмногообразие этой системы, т. е. {/,-, #}|l=(X
Предложение 2. Пусть Gi — множество всех гладких функ-
функций F таких, что подмногообразие L является инвариантным для
соответствующей гамильтоновой системы sgrad F. Тогда GL яв-
является алгеброй Ли относительно скобки Пуассона.
Доказательство. Тот факт, что Gl — векторное простран-
пространство, очевиден. Пусть F\, F2^.GL- Тогда в силу тождества Якоби
Ui, {Л, F2}}+{FU {F2, m+{F2, {fi, /r.}}=0. Если /U=0, то f =
k
Safa- В частности, {fi, /7,} = 2ф«1'7«, {fi, F2}=STa2'7a. Под-
ставляя эти выражения в тождество-Якоби, получаем
<fi, {F» m = ~{{fi, Ft), FJ + {{f(, FJ. F2} =
- -{2;<P^«, Fi) + {2 <7«,- F,} = - 2 Ф« {/«, FJ -f
. + S q>» {fa, F2}-2 fe {Ф«, FJ + 2 fa {cpb\ F2).
Это выражение обращается в ноль на поверхности L, что и тре-
требовалось доказать.
Пусть У — векторное поле на многообразии Р и К — некоторая
внешняя 2-форма на Р. Через «Y(A.) обозначим 1-форму, получаю-
получающуюся подстановкой в форму К одного аргумента — поля У. Если
'А = 2 \; dxt A dxh то iY (I) = у (V Kt,dXt (К)) dx, = J] B(Л(/К') Лсл
Предложение 3.- Рассмотрим сужение oil канонической
еимплектической структуры о) на подмногообразие L, и в каждом
■его касательном пространстве T2LcTzM' выделим плоскость
nz(L)=K,erzbSL=(Y<=TzL:iY(i)L=O). В плоскости ТгМ это есть пе-
пересечение TZL с его косоортогональным дополнением. Предполо-
Предположим, что dim Яг=соп51. Тогда:
1) Распределение плоскостей П2 вполне интегрируемо по тео-
теореме Фробениуса. Обозначим через zx ~ z2 отношение эквивалент-
эквивалентности, в силу которого Z\ и z2 принадлежат одному и тому же ин-
интегральному подмногообразию этого распределения (максимально
продолженному и, вообще говоря, погруженному). Предположим,
что корректно определено фактор-многообразие N—L/~, и обо-
обозначим через n:L-*-N соответствующую проекцию.
224
2) Положим а>(Я\, X2)=o)l(X\, Х2)=(л(Хи Х2), где Xi=a*Xi,
X,-e7V-. Тогда ш — корректно определенная каноническая струк-
структура на N.
Ясно, что это предложение аналогично доказанным выше ут-
утверждениям для случая семейства инвариантных подмногооб-
подмногообразий.
Доказательство. Отметим, во-первых, что a>L является так
называемой пред канонической структурой на L (т. е. снято усло-
условие невырожденности, но зато постоянен ранг и по-прежнему со-
сохраняется замкнутость формы: й!(со^) = (с!со)/:=0). В работе Лос-
ко [224] использовалось то обстоятельство, что для предканониче-
ских структур теорема Дарбу сохраняет силу. Мы пойдем другим
путем. Заметим, что если векторное поле У (на L) таково, что
У(г)еПг, то 2')'(o)£.)=iy(d(uL)+d(iya)i.)=O, где S — производная
Ли. Распределение П2 является так называемым характеристиче-
характеристическим для о г,, т. е. n2=Ker,@L = Ker соьПКег dcoL. Онсмштегрируемо
по теореме Фробениуса. А'именно если Y\{z), У2B)еПг, то
'[у.-уи mt = №yi> 'VJ o>l = iffy, (*y,wL)—iY2 {S£v^d '■"-■ 0,
гак как iY2«£. = 0, 36yfiiL~0. Что касается корректности определения
(о, то оно следует из следующих замечаний (везде УеГГ,).
Во-первых, (.>(*,+У, Х2)=ю(Хи Х2) + со(У, Х2)=ы(Хи Х2), т. е.
значение w не зависит от выбора Хи Х2 в дашюй точке zeL. Во-
вторых, если Xi(z), У(z)—векторные поля, то [У, Х,]=0; отсюда
«.следует, что Y(u>l{Xi, X2)) = (S'yMl) (X\, Х2) =0 согласно опреде-
определению S7, т. е. любое смещение Х\, Х2 вдоль слоев не меняет их
кососкалярного произведения.
Форма о невырожденна (что очевидно) и замкнута, так как
<о = я*(о, поэтому й!ш/.=я*с!а)=0.
П р е д л о ж е п и е 4. Пусть выполнены предположения пред-
предложения 3 и, кроме того, подмногообразие L инвариантно для по-
поля sgradf. Тогда
1) Функция F постоянна на интегральных многообразиях рас-
распределения Ш, так что корректно определена функция F'.N-y-Ц
такая, что F\L=F°z..
2) В структуре со выполнено тождество sgradf=sgrad/r.
Доказательство. Поскольку sgradFeT^L, то для всякого
У<ееП2 имеем Y(F)=®{Y, sgradF)=O. Далее «(F, sgradF) =
= ?(F) =Y(F) =а)(У, sgrad F) =co(F, sgradf), что и требовалось
доказать.
3.2. Некоммутативное интегрирование в тех случаях, когда на-
набор интегралов не образует алгебры. Описанный выше наш ме-
метод некоммутативного интегрирования был затем развит по не-
нескольким направлениям. В этом пункте мы кратко изложим ре-
результаты А. В. Стрельцова, являющиеся модификацией теорем.
Э. Картана.
g Л Т. Фоменко 225
Не следует думать, что наложенное выше на функции fi, ...
..., fs требование, чтобы они были аддитивными образующими
G, существенно. Это требование можно сильно ослабить. В част-
частности, можно .избавиться от требования замкнутости G относи-
относительно скобки Пуассона. Пусть fu ..., fn+k, 0<k-^n—\, — функ-
функции класса С°° на М. Введем в R"+* декартовы координаты |i, ...
..., ln+k и определим отображение момента (p:M2n-+Rn+k, т. е.
4>(x) = (}i(x), ••-, fn+k(x)). Пусть |oeR"+* — регулярная точка
этого отображения и подмногообразие^ Р=ф~' (g0) в М компактна
и связно.
Н. Н. Нехорошее в [107] доказал, что если скобки Пуассона
каждой из n—k функций fi,--.,fn-h со всеми остальными функ-
функциями равны пулю па Mt то в окрестности многообразия Р, яв-
являющегося тором, можно ввести обобщенные переменные дейст-
действие — угол /, ф(тос12я), р, q, в Которых симплсктическая фор-
п—к к *
ма примет вид со= d
Укажем более слабые условия на функции /ь ... ,fn+k, при ко-
которых введение таких переменных возможно. А именно потре-
потребуем, чтобы скобки Пуассона {fit fj} функционально зависели от
li,..-,fn+h, т. е. {/,-, }i} = ~fi](fu...,fn+h) и ранг матрицы ('fij(D)
был бы равен 2k на некотором открытом множестве. Эту теорему
можно применить к случаю, когда функции fi,...,fn+h образуют
базис конечномерной алгебры Ли G. Для каждого ковектора |
определен его аннулятор Н%. Ковекторы, для которых размерность
апнулятора минимальна (т. е. равна рангу G), являются ковекто-
рами общего положения. Если G удовлетворяет условию нашей
некоммутативной теоремы Лиувилля, т. е. dimG + ранг G =
= dimAf = 2n, goSG* — регулярная точка отображения ф и под-
подмногообразие Р связно и компактно, то в окрестности подмного-
подмногообразия Р, являющегося тором, можно ввести обобщенные пере-
переменные действие — угол. _,
Более точно: пусть А — алгебра Ли функций, порожденная (в
функциональном смысле) функциями fi,.-. ,fn+k, аддитивно по-
порождающими линейное пространство GczA. Пусть £0^R"+* — ре-
регулярная точка для отображения момента ф. Тогда существует ок-
окрестность U(£о) такая, что ф:ф ' (£/(£о))-^(£о) — локально три-
тривиальное расслоение, диффеоморфное прямому произведению
^(ЫХф":(Ь)- Поскольку каждый элемент /еЛ — функция, фун-
функционально зависящая от образующих f\,... ,fn+k, то функции /
сопоставляется функция f на £У(£0) такая, что f (x) =/(/i (x), ...
..., fn+k(x)). Положим ftj={fi, //}. Тогда возникают функции /",;,
l<t, j^n+k.
Предложение 5. Пусть |0 — регулярная точки для ц>, а
Р — компактная связная компонента ф~'(|о); в некоторой окрест-
окрестности точки go ранг {Uj(%))=2k. Тогда
226
1) Существуют п—k функций g\,...,gn-h из А, дифференциа-
дифференциалы которых линейно независимы на Р и {ga, />}(х)=0, 1
<n~k, 1<р<«+йпргг хеР.
2) Векторные поля sgradga, \<.a<n—k, в каждой точке
■образуют базис касательного пространства ТХР и попарно комму-
коммутируют между собой на Р.
3) Многообразие Р диффеоморфно (n—k)-мерному тору.
■ Теорема 1 (А. В. Стрельцов). В предположениях предложе-
предложения 5 существуют: окрестность многообразия Р и гладкие функции
£i, ..., gn-k вида ga{x)=ga{f\(x), ..., fn+k(x)) с независимыми
дифференциалами, определенные на этой окрестности, такие, что
з ней {ga, g>)=0, l<a<n—k, l<p<n+fe. В частности, сущест-
существует окрестность тора Р, в которой можно ввести координаты I,
n—k k
<р (mod 2л), р, q такие, что w =d\V 1^%-т £ Pfdqf\. При этом
координаты I, p, q являются функциями от f\, ..., fn+k.
Следствие 1. Пусть (М2п, ш, Н) — гамильтонова система,
fu • • ■, fn+k — ее интегралы, удовлетворяющие указанным выше
предположениям предложения 5, и Н^А. Тогда траектории систе-
системы, лежат на (n—k)-мерных торах, причем в окрестности Р мож-
можно ввести координаты так, что движение по торам будет условно
гериодическим с частотами, гладко зависящими от /ь ..., fn+k-
Функции g\,...,gn-h можно считать принадлежащими G.
Итак, G функционально порождает бесконечномерную алгебру Ли
А. В каждой точке отличными от нуля являются только конечное
число линейно независимых полей sgradf, f&A. Остальные по-
попадают в ядро представления /->-sgrad /, меняющееся от точки к
точке. Вдоль Р£ = Р s качестве линейно независимых полей можно
выбрать sgradfi, ..., sgradfn+*, изображающие «эффективную
■часть» G, нетривиально действующую в выбранной точке (в дру-
другой точке эта «эффективная часть» изменится). В предположении
ранг (fij(x))<^.2k среди функций пространства G можно найти
ровно n—k коммутирующих (также изображающих «эффектив-
«эффективную часть» аннулятора ковектора общего положения), для кото-
которых sgradg,-, l<i<n—k, порождают касательное пространство к
Pi. Функции gi,..., gn-k коммутируют между собой, вообще гово-
говоря, только на торе Р%. При изменении g они изменяются. Так как
[n+k) + (n—k)=2n и n+k=dimG, n—k=dim(gi, ..., gn-k), то это
условие является аналогом условия dimG+ранг G=dimM. Это
и означает, что прежнее «конечномерное условие» заменяется в
бесконечномерном случае условием ранг (fa(x))—2k.
3.3. Некоторые дальнейшие обобщения метода некоммутатив-
некоммутативного интегрирования. Предложенный нами в [97, 100] метод не-
некоммутативного интегрирования был затем развит А. В. Браило-
вым и расширен им на случай большего запаса подалгебр в ал-
алгебре Ли функций С°°(Л1). В настоящем пункте мы вкратце изло-
изложим эти результаты.
Напомним определение индекса конечномерной алгебры Ли G.
«• 227
Пусть G*- — дуальное пространство. Тогда \
indG-- inf A\тНь A)
gee
где //E=(geG:adg* g=0). В этом пункте мы рассмотрим (воз
■ можно бесконечномерные) алгебры Ли функций на многообразии
М со скобкой Пуассона {,}, определим дифференциальный индекс
таких алгебр Ли и дадим условие интегрируемости в квадратурах
динамических систем на М, гамильтоповых относительно {,}, в тер-
терминах алгебры Ли (первых) интегралов.
Пусть М — симплектическое многообразие. Удобно также рас-
рассмотреть случай, когда AT=G*, т. е. когда такое многообразие не
является симплектическим в обычном смысле. Скобка Пуассона
на пространстве G* задается следующей формулой. Пусть /, g —
гладкие функции па G*. Тогда положим
Пусть ^"crC°c(Af) — некоторая, возможно бесконечномерная,,
подалгебра в алгебре Ли С""(М). Дифференциальной размер-
размерностью алгебры в точке .teM назовем максимум числа линейно
независимых дифференциалов среди df^Tx*M, где f^&". Диффе-
Дифференциальной размерностью алгебры £Г назовем максимум диффе-
дифференциальных размерностей 3~ в точке х по всем хеМ. Те точки
х, в которых этот максимум достигается, назовем неособыми.
Дифференциальная размерность будет обозначаться нами че-
через ddirn^". Далее, для любой точки х определим &"х — (/^
е^": {f, g}{x)=0 для всех g<^@~). Нетрудно видеть, что ЗГХ яв-
является подалгеброй в ^". Пусть х^М — псособая точка.
Определим конечномерную алгебру Ли Kx@'=(df<=Tx*M:f<=.
^£ГХ), операция коммутирования в которой задается формулой
[df, dg]=d{f, g}; I geESTx. - B)
Докажем корректность этого определения. Действительно;
пусть с//=0. Всегда можно выбрать локальную систему координат
У\, ..., у,п на М в окрестности точки х так, что любая функция
&~ выражается через у\, ..., yk, /2=ddimSr<m. Поэтому
i-\ ~ i=k-\\
Вторая сумма равна нулю, так как / не зависит от yt при i>-k+\.
Первая сумма, равна нулю, так как g<^£Tx. Таким образом, ком-
коммутатор [|, г|] элементов |, т] не зависит от произвола в выборе
f, g таких, что %=df, r\ = dg. Тождество Якоби
Ms, b\, SD-Кл, Е, 1Л+Е, [I, ц}]=0.
для |, т], t,^Kx@~ проверяется следующим образом.
Пусть g = <#, Ц- dg, l = dh, где /, g, h<=3x. Тогда / = [d/,
dA]l + [dff, [d/t, d/]]~[dA, [df, dg]]-[d/, d{gf, A}] -l-[dg, d{h, f}]
d{f,g}]^d {f, {g, h}} -[- d {g, {h, f.}} -i d {A, {/, g}} = 0
228 -
вследствие тождества Якоби для классической скобки Пуассона.
Итак, Ккд~ — конечномерная алгебра Ли для каждой неособой
точки хеМ. Алгебра Ли Kx.ST является дифференциальным ^на-
^налогом алгебры Ли Нх. Дифференциальный индекс алгебры Ли 9~
функций на многообразии М со скобкой Пуассона определяется
согласно формуле
— inf dim/C^S?. • C)
Если, например, M=G*, x=\, Sr=Gc:C00(G*), то дифференци-
дифференциальный индекс C) совпадает с обычным индексом A) и K*G =
= НХ. Если MczG*— орбита коприсоеди'нснного представления, а
G рассматривается как алгебра функций на М, то ddim G=dimAf,
dindG = 0. Если для любой гладкой функции f на М производная
(sgrad//)f вдоль векторного поля sgrad# выражается через
скобку Пуассона (sgrad H)f={H, /}, то поле sgrad# называется
гамильтоновым. Предположим, что гамильтонова система обладает
рядом известных интегралов f\, ..., /*.. Вычисляя попарные скобки
Пуассона, мы получаем, как отмечалось ранее, некоторые, возмож-
возможно новые, интегралы системы. Добавив новые интегралы к исход-
пому набору /i, ..., fk, можно получить расширенный набор ин-
интегралов /i, ..., fm, m>k. Затем процедура вычисления скобок
Пуассона повторяется с расширенным набором интегралов и т. д.
В результате некоторого конечного числа расширении исходно-
исходного набора интегралов получается набор интегралов f\, ..., fm та-
такой, что для любых /, /=1, 2, ..., m скобка Пуассона {f,-, fj)
функционально зависит от функций f\, ..., fm. Это свойство набо-
набора F=(f\, ..., fm) можно записать следующим образом:
{ft, f,}C7:?(F) для любых ft, fj€=F. D)
Здесь и далее @~(F) — множество гладких функций на М, фун-
функционально зависимых от fi<=F. Произвольный набор F гладких
функций на М назовем замкнутым (относительно скобки Пуас-
Пуассона), если для него выполнено условие D). Таким образом, по-
поиск новых интегралов гамильтоновой системы уравнений неизбеж-
неизбежно приводит нас к замкнутым наборам интегралов.
Пусть F — замкнутый набор функций. Для набора F можно
определить алгебру Ли KXF, размерность и индекс, подобно тому
как это было сделано выше для алгебр Ли функций. Так как на-
набор F не является алгеброй Ли, ни даже векторным пространст-
пространством, то при определении индекса и размерности F можно опустить
прилагательное «дифференциальный», подразумевая его. Итак, по
определению, положим
dim F = ddim & (F), indF =
Пусть F=(fu ..., fm) — замкнутый набор, состоящий из неза-
независимых функций, m=dim/\ Пусть £</={/<, fi), где i,/=l, .... m,—
попарные скобки Пуассона. Нетрудно видеть, что алгебра Ли КХР
допускает следующее эффективное описание:
229
Рассмотрим задачу о построении базиса алгебры Ли KxF, гладко
зависящего от точки хеМ. Разрешая систему уравнений
£ &&/(*) = 0, /=1, ... , т, E)
относительно |(-, находим рациональные функции |i'(g"n, .... gmm),
i=l, ..., m; /=1, ..., k; fe=indF, такие, что дифференциалы
т
V = £ & (£"• • • • • £™»)d/< e ^*M образуют базис алгебры Ли KXF
для Каждой иеособой точки x^U. Здесь и далее UcuM — область,
в которой не обращаются в ноль знаменатели рациональных функ-
функций !,-'". С дифференциалами |' связаны векторные поля
т
У' =
1=1
Отметим, что в общем случае векторные поля У не гамильто-
новы, так как дифференциалы Ъ> не являются точными. Совмест-
Совместная поверхность уровня Л1г= (х<=Л1 :fi(x)=fi{z), i=\, ..., т) на-
называется неособой, если каждая точка хеМг является неособой
точкой для алгебры @~(F).
Следующая теорема тесно связана с нашими обобщениями
классической теоремы Лиувилля о вполне интегрируемых систе-
системах. Детальное изложение см. в {151].
Теорема 2 (А. В. Браилов [23]). Пусть М — симплектиче-
ское многообразие и F=(H=fu f2, ..., fm) — замкнутый относи-
относительно скобки Пуассона набор независимых известных функций.
Тогда
а) Гамильтоново уравнение i=sgrad Я. с начальными данны-
данными x@)=z интегрируется в квадратурах, если Мг — неособая изо-
изотропная поверхность, dH^KzF и ШН — одномерный идеал в раз-
разрешимой алгебре Ли KZF.
б) Определенные в области U векторные поля У1, ..., Yk по-
попарно коммутируют и KzF — коммутативная алгебра Ли для точ-
точки z общего положения в М.
в) Если F= (H = fu f2, ...,fm) — набор интегралов гамиль-
тоновой системы i = sgrad# и для точки z общего положения в
М имеем MzczU, где Мг — неособая изотропная поверхность, то
уравнение x=sgrad# с начальными данными общего положения
интегрируется в квадратурах.
230
Будем говорить, что гамильтонова система i=sgrad# полно-
полностью интегрируется, если для нее выполнены условия теоремы
2, в). .
Замечание 1. В окрестности компактной поверхности уров-
уровня Mz полностью интегрируемой системы всегда существуют обоб-
обобщенные (в смысле [107]) переменные действие — угол. Это легко
следует из теоремы Нехорошева [107].
Замечание 2. Для проверки изотропности поверхности уров-
уровня можно использовать формулу Э. Картана (см. [61], с. 137):'
dim GV17V-) =т-ранг (gi, (z)), F)
где Тгх — косоортогональное дополнение относительно симплекти-
ческой формы.
Как мы покажем ниже, факт полной интегрируемости гамиль-
топовой системы позволяет не только проинтегрировать ее в квад-
квадратурах (пример интегрирования интересной механической систе-
системы при помощи интегралов, не образующих алгебры Ли, но по-
попарные скобки Пуассона которых выражаются через эти же инте-
интегралы, см. в работе В.-Л. Голо [198]), но и организовать изотроп-
изотропные торы Mz в лагранжевы торы (торы Лиувилля) размерности
V2dimM.
Доказательство теоремы 2. а) Линейную оболочку га-
мильтоновых векторных полей sgrad/,, где i = l, ..., m, на поверх-
поверхности уровня Мг обозначим через Х(Мг). Линейное подпростран-
подпространство в Х(Мг), состоящее из векторных полей, касающихся Мг,
обозначим через K{MZ). Пространство К(Мг) является алгеброй
Ли относительно операции коммутирования векторных полей. Хо-
Хорошо известно, что коммутатор [sgradf, sg'radfr] любых гамиль-
тоновых полей, совпадает с гамильтоновым полем sgrad {/, К). От-
Отсюда следует, что отображение p:KzF-*-K(Mz), определенное co-
corn m
гласно формуле р(£) = £ Ht- sgrad/t-, где | = £ 1сй[с <= KZF, явля-
£=1 1=1
ется изоморфизмом алгебр Ли. Пусть D\,...,Dh — линейные об-
образующие алгебры Ли К(Мг). Будем считать, что sgrad#=.Di.
Векторные поля Du ..., Dk образуют разрешимую алгебру Ли и
[Д, Dx]=CiD\ для каждого i=l, ..., k. Здесь с, — подходящие по-
постоянные, не зависящие от точки x^Mz. Векторные поля Du .}.
..., Dk линейно независимы и покрывают поверхность уровня Мг
вследствие ее изотропности.
Из вышесказанного следует, что дифференциальное уравнение
—- =DX (^eMJ интегрируется в квадратурах в силу известной
теоремы Софуса Ли.
б) Для каждой поверхности Мг, лежащей в области U, век-
векторные поля У1, ..., У* образуют базис алгебры Ли K{MZ).
Вследствие изоморфное™ алгебр Ли KzF и К(Мг) для доказа-
доказательства утверждения б) достаточно проверить, что векторные по-
поля Y* попарно коммутируют. Действительно,
231
^ -l+y^mfi, £?} sgrad/,—
ii - ij
£?{//. Ш sgrad/;. G)
, и'
Далее
гни, m^YjHfi, м^?=.о,
s
где ds^=djdfs. Аналогично £/{//, Й} — 0- Рассмотрим сумму
• (8)
Все входящие в эту сумму функции |?. £/ и gi;- являются функци-
функциями от /ь ,.., fm. Дифференцируя (8) по fs, находим
/ = 0, (9)
откуда
f5? [sgrad/ь sgrad/,] = J^tli ( £(W sgrad /s) = 0
Итак, мы. доказали, что все три суммы в правой части равенства
G) равны пулю. Следовательно, [У", У?]=0.
в) Из утверждения б) следует, что KzF — коммутативная ал-
алгебра Ли, поэтому утверждение в)'^следует из доказанного выше
утверждения а). Теорема 2 доказана.
3.4. Канонический вид скобки Пуассона в окрестности особой
точки. Случай вырожденных скобок Пуассона. Пусть М — глад-
гладкое многообразие, снабженное скобкой • Пуассона,' причем эта
1 скобка теперь может быть вырожденной. Как доказал А. В. Браи-
лов, некоторый аналог теоремы Дарбу верен и для вырожденных
скобок. Вкратце опишем эти результаты. Пусть Q: Т*М->ТМ — со-
соответствующий скобке Пуассона гамильтопов оператор, т. е.
{f, g} = {df, Qdg). Здесь Т*М и ТМ обозначают кокасательное и
касательное расслоения к М. Следуя схеме предыдущего пункта,
можем рассмотреть' алгебру Ли KXF, где в качестве набора функ-
функций F возьмем локальные координаты на многообразии М. Ясно,
что этот набор функций является функционально замкнутым в
смысле п. 3.3.
Рассмотрим гамильтонов оператор Qx в точке х^М. Тогда
QX:TX*-^TX. Фиксируя локальные координаты на многообразии,
мы тем самым получаем некоторую матрицу Qx, задающую дейст-
действие оператора пх:Т/-+-Тх. Ясно, что эта матрица является матри-
-цей. Пуассона для локальных координат, рассматриваемых как
функции на многообразии. Как и в п. 3.3, рассмотрим ядро мат-
232
1>нцы Пуассона {F, /■"}=({/;, //}) = (gij) на линейной оболочке диф-
дифференциалов функций, являющихся локальными координатами.
Так как в данном случае эта линейная оболочка совпадает со всем
касательным пространством, то алгебра Ли KxF, введенная в
п. 3.3, совпадает со всем ядром матрицы Пуассона па кокасатель-
ном пространстве ТХ*М.
Таким образом, в каждой точке многообразия мы корректно
определили некоторую алгебру Ли Ker Qx=KxF, определяемую ли-
линейной аппроксимацией скобки Пуассона. Так как алгебра KXF',
соответствующая набору функций F', функционально выражаю-
выражающихся через функции исходного набора F, совпадает с алгеброй
KxF (см. п. 3.3), то алгебра KerQ* корректно определена в том
смысле, что не зависит от выбора локальных координат. Ясно, что
другой выбор локальных координат даст нам набор F', завися-
зависящий от F. Поскольку алгебра KxF совпадает с KerQx, то она опре-
определяется только точкой х и симплектической .структурой. Обозна-
Обозначим ее через КХМ.
Пусть xi — локальные координаты в окрестности точки х.
Матрица функций сц(х) = {х,, xj){x) является матрицей Пуассона,
соответствующей координатным функциям, и в то же время эта
матрица является матрицей оператора пх. Иногда мы будем на-
настать матрицу Q* координатным представлением данной скобки
Луассона.
Предложение 6 (А. В. Бранлов). В некоторой окрестно-
■ ти U(х0) точки лоёМ всегда можно выбрать такие локальные
соординаты, что локальное представление скобки Пуассона в каж-
юй точке x^U(xo) будет иметь вид
A(x)
.0
0
— 1
0
1
0
0
0
0
— 1
1
0)
«^ А (х) — матрица функций, равных нулю в точке х0, т. е. в
лентре окрестности.
Другими словами, каждая скобка Пуассона, в том числе и вы-
южденная, в целой координатной окрестности может быть ло-
локально приведена к каноническому виду, указанному выше. В слу-
случае невырожденной скобки матрица А (х) отсутствует и мы полу-
получаем классическое утверждение теоремы Дарбу. Этот результат
тесно связан с теоремой Э. Картаиа, о которой будет рассказано
ниже.
Доказательство предложения 6. Схема рассуждений
в значительной мере аналогична доказательству теоремы Дарбу.
233
Предположим, что мы уже построили функции xit у\, ..., хк, ук
такие, что{х,-, х;} = {г/г, г//} = 0, {xit г/;} = 6(/. Пусть N - многооб-
многообразие уровня, т. е. Л/= (Xi=yi=0). Координатам Х\, ..., уь. соот-
соответствует локальная коммутативная группа Ли <32к, действующая
в окрестности E(N) многообразия N. Пусть n:E(N)-+N — рас-
расслоение окрестности на орбиты действия группы @2*. Пусть f, g —
две функции на многообразии N. Тогда {fn, gn}=hn для некоторой
функции h на N. Действительно, {xt, (fn, gn}} = {{x(, fn}, gn} -f
+ {/я, {хи gn}} = 0, так как fn ,и gn — постоянны на слоях проек-
проекции я. Аналогично получаем {gi, {fn, gn}} = 0. Отсюда следует, что
скобка {/л, #л} также постоянна на слоях проекции я, следова-
следовательно, {fn, gn} — hn. Определим на многообразии N скобку {,}~
следующим равенством: {/, g}~ = h. Из Определения операции лег-
легко следует, что {,}~ — скобка Пуассона на многообразии N. Если
ditn/GyV = dimAf, то искомое утверждение доказано.
Если dim/;CxiV<dimAr, то найдутся две функции f, g на N та-
такие, что {/, g}~{x)¥=0. Это означает, что векторное поле Qdf не
равно нулю в точке х. Пусть Lo — многообразие, трансверсальное
к векторному полю 'QJ/ в окрестности точки х, а © f' — поток, со-
соответствующий векторному полю Qdf. Определим t(y) так, чтобы
<8f~'(y)eL0. Очевидно, {t, f}=(dt, Qdf}=\. Пусть, кроме того,
xk+\ = t, yk+i = f. Функции Xk+i, Ук+i можно добавить к набору функ-
функций. х\, уи...,Хк, Ук- После этого применим описанную выше про-
процедуру к набору функций х\, ..., уь+i и т. д. В результате полу-
получим набор функций х\, ..., ys таких, что для многообразия Ns и
скобки {,}~ на этом многообразии будет выполнено равенство
dim Ns = dim KXNS. Предложение доказано.
Следствие 2. Множество точек л;оеМ таких, что матрица,
А(х) тождественно равна нулю в окрестности точки хо, открыто
(т. е. матрица А(х) отсутствует).
Таким образом, множество «регулярных точек хо» открыто в
М. Если скобка {,.} такова, что {f, g} — аналитическая функция
для аналитических функций f и g, то такая скобка будет назы-
называться аналитической.
Следствие 3. Пусть {,} — аналитическая скобка на М.
Тогда для точки х0 общего положения матрица А (х) тождествен-
тождественно равна нулю (т. е. отсутствует) в некоторой окрестности точки
ха и, следовательно, алгебра Кх М является коммутативной алгеб-
алгеброй Ли. .
Следствие 4. Распределение плоскостей Qx(Tx*M)czTxM
интегрируемо.
Таким образом, локальная классификация скобок Пуассона (в
том числе и вырожденных) сводится к классификации скобок,
имеющих максимальное вырождение в точке, т. е. когда
dim Ker Qx=d\mM. Оказывается далее, что по крайней мере для
некоторых алгебр Ли G скобка Пуассона однозначно восстанав-
восстанавливается по ее линейной части, если KXM—G. Примером такой ал-
алгебры Ли является алгебра Ли soC) группы SOC).
234
Предложение 7 (А. В. Браилов). Пусть в трехмерном про-
пространстве R3 задана скобка Пуассона {,} такая, что ее линеариза-
линеаризация в начале координат О имеет вид /CoR3 = soC). Тогда в неко-
некоторой открытой окрестности нуля в R3 можно выбрать такие функ-
функции /, g, h, что /@) =g@) = /i@) =0 и для всех точек х из окрест-
окрестности точки х0 выполняются следующие коммутационные соотно-
соотношения: {f, g} = h, {g, h} = f, {h, f}=g.
Следствие 5. Пусть xeAf — такая точка, что алгебра Ли
КхМ, изоморфна soC). Тогда для достаточно малой проколотой
окрестности U точки х (т. е. в U = D\x, где D — диск с центром
в х) алгебра Ли КУМ изоморфна R, т. е. является одномерной
алгеброй Ли для всех точек уе£/.
Доказательство предложения 7. Не ограничивая
общности, можно считать, что {хи x2} = x3+o(|xj), {х2, х3} =
= Х! + о(|х|), {х3> Х|}=х2+о(|х|). Пусть Пх — образ оператора
/0 х3 — х2\
Qx. Оператор Q* задается матрицей j — х3 0 хх ), отку-
V Ч -Ч 0 /
да следует, что в проколотой окрестности нуля Пж является дву-
двумерной площадкой с нормалью пх = х+о(\х\). Так как распреде-
распределение Пх интегрируемо, то интегральными многообразиями слу-
служат концентрические сферы S2. Пусть Sx2 — интегральная сфера,
проходящая через точку х, а со — форма Кириллова.
Рассмотрим Dx2 = {y^Sx2: х3(г/)^х3}, Sxl = dDx2. Определим
искомую функцию h по фор-муле h — I со. Окружности Sxl
является интегральной кривой векторного поля Qdh. Пусть Г(х)=
— Т — время обхода этой окружности. Мы хотим^ показать, что
Г=2я—const. Пусть L = {xeR3: х= (хь 0, х3), х;^0} — полуок-
полуокружность. Определим функцию ф(х) (многозначную, с периодом
Т) как время, необходимое для того, чтобы попасть из полуокруж-
полуокружности L в точку х. Очевидно, что {ф, ^}=1, поэтому <a = d(f/\dh л
d(f = i _a_ (to). Отсюда получаем
dh
Т= Гс*Ф= Г d(i а (со)) = — Г со = — BяА) = 2я.
.3 J ~; dh J dh '
Здесь через tV обозначена операция подстановки векторного поля
У в качестве аргумента в 2-форму; осуществление этой операции
дает 1-форму. Пусть г(х)=. \ со. Так как г — постоянная
4п J
функция на интегральных многообразиях, то она находится в ин-
инволюции со всеми остальными функциями. Поэтому, не меняя по
существу коммутационные свойства функции h, мы можем заме-
. • 235
нить Л на функцию h—г. Очевидно, что теперь выполняется нера-
венство — г (х) ^h (х) :g> (х). Определим функции f = Vr2—h2 coscp,
g = Vr2—ft2 sin ф. Функции f, g, h являются искомыми. В этом
можно убедиться непосредственной проверкой коммутационных
соотношений, которую мы здесь опустим. Предложение доказано.
§ 4. Системы уравнений, вполне интегрируемые в
некоммутативном смысле, часто вполне интегрируемы по
Лиувиллю в обычном смысле
4.1. Формулировка общей гипотезы эквивалентности и ее спра-
справедливость для компактных многообразий. Оказывается, сущест-
существует интересная связь между процедурами коммутативного и
некоммутативного интегрирования на симплектических многооб-
многообразиях. Например, как мы покажем ниже, если система вполне
интегрируема в некоммутативном смысле, то во многих случаях
она вполне интегрируема и в коммутативном смысле. Обнаружив
этот факт, мы в [97, 100] сформулировали следующую естествен-
естественную гипотезу.
Гипотеза 1 (гипотеза эквивалентности). Пусть гамилыоно-
ва система u = sgradf на симплектическом многообразии вполне
интегрируема в некоммутативном смысле, т. е. коммутативная
алгебра ее интегралов Н (где [еЯ) включается в некоторую объ-
объемлющую, вообще говоря, некоммутативную алгебру функций G
такую, что dim G + ранг G = dim М (см. нашу теорему 1 в § 3).
Тогда эта же система вполне интегрируема и в обычном коммута-
коммутативном смысле (по Лиувиллю), т. е. существует другая коммута-
коммутативная алгебра Go независимых интегралов такая, что 2dimG0 =
= dimAf и feG0. При этом интегралы алгебры Go принадлежат
к тому же функциональному классу, что и функции, составляющие
алгебру G (если, например, функции из G аналитические, то и
функции из Go также аналитические). При этом функции алгебры
Go функционально выражаются через функции алгебры G.
Эта гипотеза, оказывается, тесно связана с другой нашей гипо-
гипотезой о существовании на орбитах общего положения коприсоеди-
ненного представления групп Ли полных инволютивиых наборов
функций (см. [100]).
Гипотеза 2 (гипотеза о слоении орбит на торы Лиувилля).
Пусть G — произвольная конечномерная алгебра Ли. Тогда суще-,
ствует конечномерное пространство F функций, в котором можно
выбрать базис из функционально независимых функций, опреде-
определенных на дуальном пространстве G*. При этом любая пара функ-
функций f, g^F находится в инволюции на орбитах коприсоединенного
представления Ad* группы © =expG на G* (относительно стан-
стандартной симплектической структуры на орбитах) и dimf =
=—(ранг G + dim G). Тогда ограничения этих функций на орбиты
общего положения образуют линейное пространство размерности
236
— (dim G—ранг G) (т. e. размерности, равной половине размер-
размерности орбиты общего положения), в котором можно выбрать ли-
линейный базиб из функционально независимых на орбите функций.
Другими словами, ограничения этих функций на орбиты общего
положения образуют полный инволютивный набор. При этом, если
орбиты общего положения являются аналитическими, алгебраичес-
алгебраическими и т. п. подмногообразиями, то и функции из F также явля-
являются соответственно аналитическими, алгебраическими и т. п.
Между гипотезами 1 и 2 имеется тесная связь. А именно нами
доказана следующая теорема (см. [100]).
Теорема 1. Пусть М2п — симплектическое многообразие и
пусть на М2п задан полный некоммутативный набор функций, т. с.
образующих алгебру Ли G с условием dim G + ранг G = 2n. Если
для алгебры G выполнена гипотеза 2 (см. выше), то на М найдет-
найдется полный инволютивный набор функций Go, т. е. dim Go = я, при-
причем коммутативная алгебра Ли Go состоит из функций, функцио-
функционально выражающихся через функции исходной некоммутативной
алгебры G. Другими словами, при условии выполнения гипотезы 2
из некоммутативной интегрируемости гамильтоновой системы вида
sgradn, где heaHi, следует ее коммутативная интегрируемости
(по Лиувиллю):
Таким образом, доказательство гипотезы .2 позволяет не только
предъявить значительный запас вполне интегрируемых систем на
орбитах коприсоединенного представления в конечномерных ал-
алгебрах Ли, но и редуцировать некоммутативную интегрируемость
гамильтоновых систем к классической, коммутативной интегрируе-
интегрируемости. В настоящее время гипотеза 2 доказана нами для всех
полупростых и редуктивных алгебр Ли (см. [96—100, 231]), для
многих бесконечных серий разрешимых алгебр Ли (В. В. Трофи-
Трофимов [135, 136, 139], А. В. Болсинов |21]), нилыютептных алгебр
Ли (М. Вернь [363], А. А. Архангельский [7], Ле Нгок Тьеуен
[81]) и для некоторых других (см. обзор в работе В. В. Трофимо-
Трофимова, А. Т. Фоменко [145]). Рассмотрим отдельно случай компакт-
компактных замкнутых симплектических многообразий. Оказывается,
в этом случае некоммутативная полная интегрируемость всегда
сводится к коммутативной полной интегрируемости.
Теорема 2 [100]. Пусть М2п — компактное симплектичес-
симплектическое многообразие и u = sgradf/ — гамильтонова система, вполне
интегрируемая в некоммутативном смысле на М (или в окрестнос-
окрестности какой-то одной фиксированной поверхности уровня функций,
порождающих максимальную линейную алгебру G (см. выше).
Тогда зта же система вполне интегрируема по Лиувиллю и в
обычном смысле, Причем коммутирующие интегралы новой алгеб-
алгебры Ли Go (т. е. максимальной линейной коммутативной подалгеб-
подалгебры на М) функционально (и явными формулами) выражаются
через прежние функции алгебры Ли G.
Эта наша теорема сразу открывает новые возможности для
поиска интегрируемых (по Лиувиллю) систем. Мы обнаружили.
237
что такие системы могут «маскироваться» под видом систем,
допускающих некоммутативное интегрирование. Тем самым мы
существенно расширили запас признаков, позволяющих распозна-
распознавать и конкретно указывать интегрируемые системы на симплек-
тических многообразиях. Как мы уже отмечали, во многих кон-1
кретных случаях проще обнаружить максимальную линейную не-
некоммутативную алгебру Ли G функций, чем сразу найти макси-
максимальный коммутативный набор интегралов Go. Особенно часто
(как мы покажем ниже) вполне интегрируемые по Лиувиллю сис-
системы маскируются «в одежды» некоммутативно интегрируемых
систем в случае геодезических потоков левоинвариантных метрик
на тех или иных группах Ли и симметрических пространствах.
Доказательство теоремы 2 будет дано ниже. Полезно представ-
представлять себе ее геометрический смысл. Если исходная гамильтонова
система обладает некоммутативной группой симметрии, т. е. до-
допускает максимальную линейную некоммутативную алгебру G, то
в силу нашей теоремы 1 (см. § 2) траектории системы определяют
условно периодическое движение на r-мерных торах Тг (где
r = dimAf—dimG). Как уже отмечалось, эти торы «маломерны»,
т. е. r<.n = — dim M. Если же система v, кроме того, допускает
максимальную коммутативную алгебру интегралов Go, то эти же
интегральные траектории уклады-
укладываются и на торы Лиувилля раз-
размерности п. Следовательно, в этом
случае маломерные торы Тг можно
естественно организовать в «боль-
«большие» торы Лиувилля Тп.
Так как торы Тп расслоены на
маломерные инвариантные roppi Тг,
траектории системы v не задают
всюду плотной (иррациональной)
обмотки торов Тп (рис. 106). В этом
смысле система v вырождена.
Именно этим обстоятельством
объясняется тот' «эксперименталь-
«экспериментальный» факт, что для многих систем
такого рода легче сначала найти
некоммутативную максимальную
линейную алгебру функций (пра-
(правильно содержащую гамильтониан
системы), а затем, опираясь на нашу общую теорему 2 настоя-
настоящего параграфа (в компактном случае), найти уже «настоящую»
максимальную коммутативную алгебру интегралов.
Впрочем, эта схема действует пока лишь на компактных симп-
лектических многообразиях. Дело в том, что в случае некомпакт-
некомпактных многообразий аналог теоремы 2 пока еще не доказан в пол-
полном объеме. Поэтому априори не исключено, что могут существо-
существовать гамильтоновы системы, вполне интегрируемые в некоммута-
г<п
Рис. 106
238
тивном смысле, но неинтегрируемые в классическом коммутатив-
коммутативном смысле. Это открытая проблема, имеющая далекие "и инте-
интересные выходы в разные области геометрии и механики.
Резюме. Таким образом; мы ввели в рассмотрение новый ши-
широкий класс некоммутативно интегрируемых гамильтоновых сис-
систем. Пока неясно, совпадает ли он с классом классических вполне
интегрируемых по Лиувиллю систем. Кроме того, пересечение
класса некоммутативно интегрируемых систем с классом систем,
интегрируемых по Лиувиллю, состоит из интересных «систем с вы-
вырождениями».. Интегральные траектории таких систем на торах
Лиувилля никогда не определяют иррациональную обмотку этих
торов. Траектории укладываются на маломерные торы, регулярно
расслаивающие большие торы Лиувилля. Таким образом, установ-
установление факта некоммутативной интегрируемости системы дает нам
■существенно больше информации о поведении ее интегральных
траекторий по сравнению с тем, что сообщает нам обычная ин-
интегрируемость по Лиувиллю.
Дополнительная информация о поведении траекторий системы
получается из рассмотрения расслоения торов Лиувилля на мало-
маломерные торы (таких неэквивалентных расслоений может быть
много). Данные об этом расслоении можно извлекать из формул,
выражающих связь между коммутирующими и некоммутирующи-
ми интегралами системы. Здесь возникает много интересных пока
еще не решенных задач. Например, представляет интерес уста-но-
вить геометрический смысл аналитических формул, превращаю-
превращающих некоммутативную алгебру интегралов в коммутативную. Как
мы покажем- ниже, эти формулы определяются отображением
мом«нта и коммутативной алгеброй интегралов, которая часто
существует на некоммутативной максимальной линейной алгебре
функций. Меняя эти алгебры, мы будем менять расслоения торов
Лиувилля на меньшие (маломерные) торы.
4.2. Некоммутативная интегрируемость и ее связь с канони-
каноническими подмногообразиями и .изотропными торами. Между раз-
различными вариантами некоммутативного интегрирования, изложен-
изложенными выше, имеются разнообразные связи. Мы не будем здесь
давать полную таблицу их взаимоотношений, а ограничимся лишь
указанием на наиболее интересные из них. В частности, мы вос-
воспользуемся работой Я- В. Татаринова [132], который по просьбе
автора специально исследовал этот вопрос.
Пусть М2п — симплектическое многообразие со структурой со.
Как и выше, мы считаем, что {f, g} = <o(sgrad/, sgradg).
Теорема 3. Пусть /СсМ — гладкое подмногообразие, кото-
которое задано как совместная неособая поверхность уровня некото-
некоторых функций G\, ..., Gm, т. е. K = {Gl = .. . = Gm = 0}. Пусть
Ни..., Hi — набор функций, определенных в некоторой открытой
.окрестности подмногообразия К. Тогда имеют место следующие
.утверждения:
1) Векторные поля sgrad Hi касаются поверхности К тогда и
239
только тогда, когда {G,, Hj}\K = O, т. е. когда ограничения указан-
указанных скобок Пуассона на поверхность К равны нулю.
2) Касательные к поверхности К векторные поля sgrad Я, ком-
коммутируют на этой поверхности тогда и только тогда, когда
d{H,,Hj}\K = O.
3) Множества SK всех функций Н таких, что их косые градиен-
градиенты sgrad Н касаются поверхности .К, является подалгеброй в про-
пространстве всех гладких функций на многообразии М.
Доказательство. Утверждения 1), 2) легко следуют из
определения скобки Пуассона. Докажем 3). Факт принадлежности
функций Ни Н2 пространству SK в точности эквивалентен условию
{Gi, Ha} = I>j<piJGi. Отсюда и из тождества Якоби вытекает
{Gc, {Hlt HJ} = {{Glt HJ, H2}-{{Giy H2}, H1} =
ад =
Таким образом, скобка {Н\, Яг} функций Н\ и Hi удовлетворя-
удовлетворяет критерию принадлежности функции к пространству SK; следо-
следовательно, SK является подалгеброй Ли, что и требовалось дока-
доказать.
Лемма 1. Подмногообразие N в М, задаваемое как поверх-
поверхность уровня, т. е. N={Fl = .. . = F2k = 0}, является каноническим в
индуцированной на N структуре тогда и только тогда, когда ранг
матрицы Пуассона равен 2к, т. е. ранг {F, F}\fi = 2k, где F =
= (F\, ..., F2k)-
Считая подмногообразие N каноническим, введем в рассмотре-
рассмотрение 2-форму Тд, = — 2ya$dFa/\dFp, где матрица Ф коэффициен-
коэффициентов формы является обратной к матрице Пуассона, т. е. Ф =
= (фар) ={Ff F)- Оказывается, существует тесная связь между
исходной симплектической структурой со на М и формой таг на N.
Теорема 4. Пусть N — каноническое подмногообразие
в симплектическом многообразии (М, со). Пусть геЛ1 и Х^ТгМ —
произвольный касательный вектор. Представим его в виде Л' =
= XN + XF в соответствии с разложением пространства ТгМ в пря-
прямую сумму подпространств TzM = TzN(&Ilz(F). где через UZ(F)
обозначена линейная оболочка векторов sgradFu ..., sgrad/^k-
Здесь F=(FU ..., F2k) — функции, задающие подмногообразие
N, т. е. N={F\ = ... = F2k = Q}. Обозначим через НЫ = Н\Ы ограни-
ограничение (сужение) произвольной функции Н на подмногообразие
NcM. Тогда выполняются равенства
240
XN = Х- 2ФаРХ (Fa) sgrad Fp - X- XF,
©(Xf, X?) = <D(Xlf X2)-%(XXJ X2).
При этом косой градиент сужения функции на N равен проекции
на /V косого градиента самой функции, т. е. sgradЯл' = (sgradI1)N,
Наконец, скобка Пуассона на подмногообразии имеет вид
■{Н?, H?) = {Hlt //,}"-!„(sgrad/^ sgrad//,) =
= [{Я,, Я2}-2ФаР{Fa, Hx) {/> H2}f.
Последнее выражение в теореме 4 (т. е. скобка на подмного-
подмногообразии /V — так сказать поправка к исходной скобке Пуассона
на М) рассматривалось Дираком. Указанную скобку будем
называть скобкой Дирака, а форму xn — формой Дирака.
Можно проверить, что скобка Дирака, форма Дирака и все ос-
остальные соотношения, указанные в теореме 4, корректно опреде-
определены в том смысле, что не зависят от выбора функций Fa, за-
задающих N.
Теорема 5. Пусть L — неособая компактная связная компо-
компонента совместной поверхности уровня независимых n + k функций
в М2", т. е. L = {/71 = Ci, ..., Fn+k = cn+k]. Предположим, что во всех
точках поверхности L выполняются следующие соотношения:
а) {Fa, Fp} = 0 при а = 1, . .. , п—k\ р = 1, .. . , п + k;
б) d{Fa,Fd=:0 при а,р = 1, ...,n~k.
Другими словами, матрица Пуассона {F, F) для набора F функ-
функций Ри ..., Fn+k на поверхности L является следующей матрицей
порядка n + k:
„_Л{ /0_j_04
Тогда L является изотропным подмногообразием в М2п, т. е.
to17- l = 0, и, кроме того, оно диффеоморфно (п—к)-мерному
тору.
Отметим, что в теореме 5 речь идет об одной фиксированной
поверхности уровня L. В частности, скобки {Fa, Fp}, равные нулю
на L, могут быть отличны от нуля вне L. Эта теорема может быть
применена и в той ситуации, которая рассматривалась в нашей
теореме о некоммутативном интегрировании (см. [97], [100]),
см. теорему 1 из § 2. Напомним, что мы рассматривали случай,
когда задана некоммутативная алгебра G функций, аддитивный
базис в которой образован функционально независимыми функ-
функциями на М. В обозначениях теоремы 5 эта ситуация описыва-
описывается так. На М2п рассматривается набор функций Fi, ..., Fn+k
таких, что {Fl,Fj} = I,q=\CijFin где с% = const.
241
Далее, подмногообразие L задается как поверхность уровня
L = {Fi = pu ..., Fn+k = Pn+k}- В условиях теоремы 1 § 2 все функции
F\, ..., Fn+k предполагаются независимыми на неособой поверх-
поверхности L, поэтому ее размерность равна dim M—(n + k) =-2п—п—
—k = n—k. Покажем, что система функций Fu ..., Fn+k, удовлет-
удовлетворяющая условиям теоремы о некоммутативной интегрируемости
(теорема 1 § 2), удовлетворяет и условиям теоремы 5. В самом
деле, пусть функции Fx, ...,Fr образуют аддитивный базис й ан-
нуляторе ковектора | общего- положения, определяющего выбран-
выбранную нами поверхность уровня Ln~k. Напомним, что ковектор g
лежит в пространстве G*, дуальном к алгебре Ли G, являющейся
линейной оболочкой функций F\, ..., Fn+k. Так как общий элемент
-алгебры Ли G записывается в,виде V^/7;, то значение ковек-
ковектора | на общем элементе имеет вид (на поверхности L)
n+k n+k n+k
1 Zl ^
i=l
так как l(Fi)=Pi, i=l, ..., n+k, и значения pt определяют по-
поверхность уровня L: Мы . утверждаем, что линейная оболочка
•функций Fu ..., Fr является аннулятором ковектора \ общего по-
положения в том и только в том случае, когда {Fa, Fq}\l = 0 для
l^a^r, l^p^n + ^. В самом деле, согласно определению копри-
соединенного представления ad* мы имеем
(adp |, Fp) = (|, (F , Fp}) = /l Vca/r\=VlCa(i, F ) =
q=\ q=\
n+k
capPq = \fa> rp)\L.
Итак, (ай*ф Fp)^{Fa, FP}\L. Поэтому {adpj, /гР>=0 для всех
•c=l, ..., г и р=1, ..., n + k тогда и только тогда, когда
{Fa, /rP}U = 0. Но так как функции Fp при р=1, ..., n + k образуют
линейный базис в алгебре Ли G, то последнее равенство возможно
ъ том и только в том случае, когда ad^ | = 0, что и требовалось
доказать.
Таким образом, матрица скобок Пуассона функций F, на по-
поверхности L приобретает вид
г{( О I О
n + k—r{\ 0 | *
Согласно условию теоремы о некоммутативной интегрируемос-
интегрируемости r+dimG = 2n, т. е. r+n + k — 2n, или r=n—k. Но в таком случае
542
мы получаем, что существуют n-\-k независимых функций, совме-
совместной поверхностью уровня которых является поверхность Ln+!ir
причем выполнено условие а) теоремы 5, так как мы только что
подсчитали явный вид матрицы Пуассона на поверхности L. Ус-
Условие б) теоремы 5 также выполнено, так как аннулятор ковек-
ковектора общего положения коммутативен. Последний факт доказан
в [187] и был использован нами для целей некоммутативного
интегрирования в работах [97], [100]. Таким образом, {Fa, F^^O
при а, р=1, ..., п—k, что и требуется для выполнения условия б)
теоремы 5. В данном случае это условие выполнено «с избытком»,
так как равны нулю не только дифференциалы скобок, по и сами,
скобки. Итак, в сделанных выше предположениях, связная и
компактная совместная поверхность уровня диффеоморфна
(и—k) -мерному тору.
Отметим в заключение, что теорема 5 применима к отдельной
поверхности L, которая оказывается тором при сформулирован-
сформулированных предположениях. Однако полученное нами условие {Fa, FA}\l =
= 0 при а=1, ..., п—k, p=l, ..., n + k отнюдь не означает, что
аннулятор ковектора общего положения является центром алгебры
G=(FU ..., Fn+k). Дело в том, что вне поверхности L скобки
{fa, Fp} уже не обязаны быть равными нулю.
Замечание. Поскольку общее число функций F, в наборе F
равно n + k, то всегда выполнено неравенство ранг {F, F}^2k. Из
утверждения а) теоремы 5 вытекает, что ранг {F, F}^.2k, следова-
следовательно, ранг {F, F} — 2k. Более того, можно считать, что ранг
{Fn-k+u • ••> Fn+n\ Fn-k+u • ••> Fn+k\ = 2k. Поэтому для поверхности
уровня N={Fn-k+\ = cn-k+u ..., Fn+ft = Сл+fe}, dimJV = 2(n—k), вы-
выполнены все условия леммы 1. По крайней, мере это имеет место
в некоторой открытой окрестности поверхности LczN. Формула
Дирака для скобки Пуассона, суженной (ограниченной) на под-
подмногообразие, показывает, что {FaN, F(,N} = 0 при а, р=1, 2, ...
..., п—k в точках поверхности L. Это означает, что L является
изотропным подмногообразием максимальной размерности (т. е.
лаграижевым) в подмногообразии N. Наконец, условие б) теоремы
5 после сужения функций на поверхность Af сохраняет свою силу.
Следовательно, векторные поля sgradfa'*' касаются поверхности
L и коммутируют. Таким образом, из обычной теоремы Лиувилля
следует, что L является тором.
Рассмотрим интересный вопрос о свойствах алгебр функций на
симплектическом многообразии. Локальные результаты, которые
мы сейчас изложим в- принятой сегодня терминологии, были фак-\
тически получены Э. Картаном или легко следуют из его исследо-
исследований. На этот факт нам указал Я. В. Татаринов.
Определение 1. Будем говорить, что семейство В гладких
функций на многообразии М или в какой-то открытой области в М
имеет класс I и порождено набором функций G — (Gh ..., Gi)t
если функция F принадлежит семейству В Тогда и только тогда,
когда dT/\dG\/\ .., /\dGis=0, а функции Gu...,Gi независимы
в каждой точке.
24а
Таким образом, множество заданного класса / (т. е. семейство
В) содержит все функции, функционально выражающиеся через
функции Gi, ..., Gi. Для дальнейшего особенно важно, что семей-
семейство функций В является бесконечномерным линейным простран-
пространством, состоящим из всех (!) функций, функционально выражаю-
выражающихся через базисные 'функции Qu ■ • ■, G/. Такие семейства функ-
функций естественно назвать функционально полными. Вообще говоря,
это пространство не обязано быть алгеброй Ли относительно скоб-
скобки Пуассона.
Ясно, что корректно определены подмногообразия В4 ={ге М:
для любой функции ГеВ выполнено равенство Г(г)=ГB0)}. По-
Поскольку функции G\,...,Gi являются функциональными образу-
образующими семейства В, то поверхность Вг° полностью определяется
функциями G\, ..., G/. В каждой точке z^M можно рассмотреть
плоскость nz(G), являющуюся линейной оболочкой косых гради-
градиентов sgrad Gi, ..'., sgrad Gi. Ясно, что для каждой функции
ГеВ ее косой градиент sgrad Г лежит в плоскости n^(G).
Определение 2. Будем говорить, что множество функций
В класса / имеет симплектический ранг 2а, если ранг {G, G}=2q.
Рассмотрим такие семейства функций В заданного класса / и
постоянного симплектического ранга 2ц, которые являются ал-
алгебрами Ли относительно скобки Пуассона. Локально семейство
функций В имеет вид {Г = -ф(Gi, ..., G/)}. Здесь под термином
«локальность» мы понимаем некоторую открытую окрестность сов-
совместной поверхности уровня функций Gi, .... G/.
Теорема 6. Для функционально полного множества функций
В класса I и постоянного симплектического ранга 2q следующие
условия локально (т. е. в окрестности одной компактной связной
совместной поверхности уровня функций из В) эквивалентны:
а) Семейство функций В является алгеброй Ли относительно
скобки Пуассона. Эта алгебра Ли бесконечномерна.
б) Скобки Пуассона {Ga, G,,} функционально выражаются че-
через функции Gi, ..., G;, т. е. {Ga, Gp} = i|3ap(Gb ..., Gt).
в) Распределение плоскостей Oz(G) интегрируемо.
г) Рассмотрим отображение g : M'2n-*-Rl, y = g(z) =± (Gi(z), ...
..., Gi{z)). Другими словами, мы отображаем М2п в пространство
значений функций G\, ..., Gi. Тогда при отображений g коррект-
корректно определено и интегрируемо распределение плоскостей &у =
gy y g{)
д) Существуют функции Fu ..., F2q, F24+i, ..., Fi<=B такие, что
{Fa, Fq+a} = —{F4+a, Fa} = — 1, a=l, ..., q, а остальные скобки Пу-
Пуассона равны нулю. Другими словами, матрица Пуассона функций
./■'= {Fu ..., Fi) имеет вид
Доказательство теоремы мы опустим. Прокомментируем лишь
некоторые из связей между пунктами а)—д). Утверждение об эк-
эквивалентности а) и б) очевидно. Эквивалентность условий а) и
д) принадлежит Э. Картану. То, что из д) следует в) и что из д)
следует г), очевидно. Утверждение в) вытекает из а) как следст-
следствие одного наблюдения В. В. Козлоза [65], см. § 2. Цепочка
б)->г)->д) практически доказана А. В. Стрельцовым.
Опишем теперь все неизоморфные алгебры функций класса I.
Теорема Э. Картана дает классификацию таких алгебр, поскольку
указывает канонические образующие в каждой алгебре класса /
и постоянного симплектического ранга 2q на многообразии М2п.
Так как матрица Пуассона функций, являющихся функциональ-
функциональными образующими в алгебре JB, может быть приведена к канони-
каноническому виду
l-2q{ \0
то каждая алгебра Ли указанного типа однозначно задается парой
целых чисел qv.ni, где 1q — симплектическин ранг семейства В,
а пг = 1—2q, т. е. m — размерность центра. Ясно, что разные пары
(q, m) и (q', m') определяют неизоморфные алгебры Ли В и В'.
Сколько неизоморфных алгебр Ли В данного симплектического
ранга 2q и данного класса I существует на симплектическом мно-
многообразии М2п в окрестности одной компактной связной поверх-
поверхности уровня (т. е. «локально»)?
Все такие алгебры легко описать наглядно, изобразив их целы-
целыми точками на двумерной плоскости. Для удобства выберем в ка-
качестве координат ,на плоскости параметры q и пг, где q'^0, m^O.
Образующие в алгебре Ли В запишем, используя теорему Э. Кар-
Картана, в виде
В — \Х\, . . . , Xq\ У\, . . . , t/ijj Z\, . . . , Zm}-
♦
Матрица Пуассона функций Х{ и г// имеет вид ( А, а
функции zk соответствуют центру.
Ясно далее, что q + m^in в том и только в том случае, когда
1^2п, q~^l—п. Таким образом, множество всех алгебр указан-
указанного типа изображается целыми точками, расположенными в тре-
треугольнике, показанном на рис. 107, 108. На рис. 107 изображен
случай нечетного л = 7, а на рис. 108 — случай четного п = 8. По-
Показаны прямые, задаваемые уравнением l = 2q + m. Точки, лежа-
лежащие на стороне треугольника q + m = n, отвечают алгебрам Ли В,
удевлетворяющим условиям теоремы о некоммутативной интегри-
интегрируемости [97], [100]. В этом случае q = l—n. Подробнее об этом
см. ниже. Ясно, что при фиксированных / и п число различных
алгебр класса I равно [(min(/, 2л—/))/2] + 1.
245
Вернемся теперь к нашей гипотезе 1 об эквивалентности неком-
некоммутативного и коммутативного интегрирования, сформулированной
выше (см. [97], [100]). Справедливость гипотезы 1 локально из-
извлекается из теоремы 6, т. е. фактически из результатов Э. Карта-
на [61]. • . ■ ,-
Теорема 7. Пусть на симплектическом многообразии задана
гамильтонова система, вполне интегрируемая в некоммутативном
смысле. Тогда локально, в некоторой окрестности неособой совме-
совместной поверхности уровня эта система вполне интегрируема и в
классическом коммутативном смысле (по Лиувиллю). При этом.
1
ч
«nT
1=0
т'
NN
\\
NN
\\
NN
NN
7 2
\\
\\
\\
\\
\\
\\
3 <
\\
\\
\\
\\
\\
\\
п =
Л
7
\\
5 7 8 9,10,11.
V.
п
#-?' '
ч
п=8
_ т \
\
I
f/77
N)
\\
\N
\\
\s
\N
-
V-,
\\
\\
Л1
NN
w
\\
N^
NN
\\
N>,
\N
■\-i
w
N\
N:
n
Рис. 107
1= 0 1 2 3 4 5 6 1 8 9 7011 П,ЩЦ 7t
a=f f 23 3 3 44 54433 2 2-Г t
Рис. 108
новые интегралы, находящиеся в инволюции, функционально вы-
выражаются в окрестности поверхности уровня через исходные функ-
функции, образующие некоммутативную алгебру Ли.
■ В самом деле, пусть на многообразии М задано семейство
функций, линейная оболочка которых образует алгебру Ли с усло-
условием ранг G + dim G = dim М. Пусть Gi, .... G; — независимые
функции, образующие аддитивный базис в алгебре Ли G, т. е.
dimG = /. Рассмотрим бесконечномерную алгебру Ли В всех (!)
функций, которые функционально выражаются через функции
Gi, ..., G/. Локально можно считать, что симплектический ранг
этого семейства постоянен и равен 2а. Оказывается, число 2ц
в этом случае не может быть произвольным и равно 2A—и).
Напомним, что функции Gb ..., Gi, удовлетворяющие условиям
нашей теоремы о некоммутативной интегрируемости, удовлетво-
удовлетворяют и условиям теоремы 5 на отдельной поверхности уровня (на
торе L). Рассмотрим матрицу Пуассона набора функций Gu ...
.... G;. Из замечания, к теореме 5 следует, что ее ранг равен 2k.
246
'Приводя в соответствие обозначения теорем 5 и 6, получаем
ранг {G, G} = 2k = 2q, т. е. k = q, r = n—k, l = n + k, /+r=2n=--
= dimM, q = l—п. Таким образом, бесконечномерная алгебра В,
окутывающая исходную конечномерную алгебру Ли G, имеет сим-
плектический ранг, равный 2q = 2(l~— n). Следует при этом отме-
отметить, что матрица Пуассона из теоремы 6 отличается от матрицы
Пуассона из теоремы 5 лишь перестановкой нулевого блока. При-
Приведение обеих матриц в соответствие осуществляется подходящей
перенумерацией функций из набора В. Согласно утверждению д)
теоремы 6 искомый набор функций F\, ..., Fi содержит подмно-
подмножество функций, находящихся в инволюции. Это подмножество
задает в матрице Пуассона две нулевые матрицы порядка q-k
в левом верхнем углу и в правом нижнем углу. Это означает, что
независимые функции F\, ..., Fq, Fi-->4+\, ..., Fi образуют инво-
лютивный набор. Число этих функций равно q + l—2q = l—q — l—
— A—п)=п, Таким образом, мы предъявили полный инволютив-■
ный набор функций по крайней мере локально, в окрестности ком-
компактной неособой поверхности уровня.
Итак, локально из некоммутативной интегрируемости всегда
следует коммутативная интегрируемость, что и доказывает нашу
гипотезу 1 {гипотезу эквивалентности) в окрестности одной по-
поверхности уровня.
Определение 3. Будем называть семейство функций В
класса / невырожденным, если для некоторого (и тогда для любо-
любого) семейства порождающих его функций F ранг матрицы Пуас-
Пуассона {F, F} максимален. Тогда l = 2q, где I — число функций в на-
наборе F. Это означает, в частности, что введенные выше подмного-
подмногообразия Вг° являются каноническими.
Предложение 1. Следующие условия локально эквива-
эквивалентны:
а) Невырожденное семейство функций В является алгеброй
Ли относительно'скобки Пуассона.
б) Форма Дирака iN= —Ecp^d/^ /\dF$~ замкнута, причем от
выбора порождающих функций F это условие не зависит.
в) Существует такое распределение Р невырожденных плоско-
плоскостей Рг на многообразии М, что замкнута форма wp'(^i, X2) =
= co(Xip, X2P) и векторы sgrad/, где f<=B, косоортогональны рас-
распределению Pz. Здесь через Хр обозначена корректно определен-
определенная проекция произвольного вектора X на плоскость распределе-
распределения Р.
Определение 4. Будем далее называть семейство функций
В класса n + k радикальным, если для некоторого (и тогда для
любого) набора порождающих его функций F ранг матрицы Пуас-
Пуассона {F, F} минимален (и равен 2k).
Предложение 2. Пусть LczM2'1 — неособая связная ком-
компактная совместная поверхность уровня порождающих функций
F=(Fi, •••. Fn+k), т. е. L = {Fl = cx, ..,, Fn+Ii = cn+k). Будем считать,
247
что индексы а, К принимают значения а=1, ..., п—k и Х = п—k-\-
+ 1, ..., п. Тогда следующие условия эквивалентны:
а) Семейство функций В является алгеброй Ли относительно
скобки Пуассона в некоторой открытой окрестности компактной
поверхности L.
б) В некоторой окрестности поверхности L существуют такие
канонические координаты ра, cpa(mod 2л), хи ук, что Fi = Fi(x, у, р).
Здесь фь ..., <fn-k — угловые координаты на торе Ln~kczM, пере-
переменные pi, ..., р„_/г сопряжены им, а переменные xn-k+i, ■ ■ ■, %п
и Уп-k+u ..., уп являются дополнительными к поверхности N в
М2п. Общее число координат х, р, <р, у равно 2(п—k) +2k = 2п~
=dimM. Таким образом, в окрестности компактной неособой по-
поверхности возникает расслоение на близкие изотропные торы.
Эта ситуация отличается от утверждения теоремы 5, где гово-
говорится только об одном торе на каноническом, подмногообразии
[132], [133].
4.3. Свойства отображения момента системы, интегрируемой
в некоммутативном смысле. Пусть G — конечномерная алгебра
Ли и G* — дуальное пространство, расслоенное на орбиты О* ко-
присоедйненного представления Ad* группы @, отвечающей ал-
алгебре Ли G, т. е. @ =expG. Тогда на каждой орбите О* опреде-
определена форма Кириллова и соответствующая ей скобка Пуассона.
Однако для наших целей сейчас будет б^рлее удобна другая опера-
операция — {,}', которую мы назовем вырожденной скобкой Пуассона
на G*. Дело в том, что отдельные скобки Пуассона, заданные на
орбитах О*, можно склеить в некоторую единую скобку {,}'. Для
этого поступим так. Пусть /, g-eC°°(G*). Положим по определению
Так как G* расслаивается на орбиты О*, то это определение кор-
корректно. Эту скобку можно явно вычислить в терминах структур-
структурного тензора с'/р, задающего алгебру Ли G. Оказывается,
где е\, ..., ek — базис алгебры Ли G, а е1, ..., ek — сопряженный
базис в G*. Соответствующие этим базисам координаты обозна-*
чены соответственно через х\ ..., xk и х\, ..., х*; ср,;- — структур-
структурный тензор алгебры G в базисе е-„ т. е. [е,-, е}] =2рс*)г,-ер. Эта скоб-
скобка удовлетворяет тождеству Якоби, хотя является вырожденной..
Чтобы не усложнять обозначения, построенную выше скобку
Пуассона обозначим снова через {,}. Это тем более естественно,
что, ограничивая ее на каждую отдельную орбиту, мы получаем
прежнюю невырожденную скобку Пуассона.
Таким, образом, теперь мы можем говорить о функциях, нахо:
аящихся в инволюции на всей коалгебре G*, а не только на ор-
5итах. Выделим важный для дальнейшего класс алгебр Ли.
>48
ипределение о. оудем говорить, что алгеира ли и яили-
.ется интегрируемой, если на G* существует линейное подпростран-
подпространство VczC°°(G*), в котором можно выделить аддитивный базис
функционально независимых функций gu ..., gq, где q — dimV,
таких, что они находятся в инволюции на G* относительно скобки
Пуассона, причем q = dimV = — (indG-Ь dim G) =— (r+k).
Тогда отсюда следует, что ограничения функций gu ..., g4 на
орбиты общего положения в G* задают на них максимальную Ли-
Лилейную коммутативную алгебру Ли функций.
Напомним, что означает последнее условие. Ограничения
функций gu ..., gq-алгебры V на орбиту дает набор функций
Ни ..., hs, где s = — dimO'=— (dimG*— r) = — (/e— r), r = indG.
Теорема 8 (А. С. Мищенко, А. Т. Фоменко [97], [100]).
Пусть М2п — симплёктическое многообразие (компактное или не-
некомпактное) и пусть на М2п задана максимальная линейная под-
подалгебра Ли гладких функций G (т. е. dim G + ind G = dimM). Если
■алгебра Ли G интегрируема (см. определение 5), то на М2п всегда
найдется максимальная линейная коммутативная алгебра функ-
функций (функционально зависимая от функций подалгебры G), т. е.
такая, что dimG0 = — dimAP1.
Теорема, следовательно, утверждает, что система, вполне ин-
интегрируемая в некоммутативном смысле на М, при помощи интег-
интегрируемой алгебры Ли функций автоматически оказывается интег-
интегрируемой и в классическом коммутативном смысле.
Мы изучим некоторые важные свойства отображения момента,
представляющие интерес и вне зависимости от теоремы 8.
Пусть па М2" задана максимальная линейная алгебра Ли глад-
гладких функций G. Рассмотрим отвечающее ей гладкое отображение
момента Г : M->G*, т. е. F(x) ~.(fx(x), ..., Ы*))> гДе /ь -. ■ •. h ~
аддитивный'независимый базис в G. Другимисловами, /;(х)=|е
^G*, где £,(f)=f(x) для /eG. Так как компактные связные сов-
совместные поверхности уровня Мг = /г~1(|) всех функций из алгебры
G днффеоморфны (согласно теореме 1 § 2) r-мерным торам Тг, где
r = indG, то неособыми слоями общего положения отображения
момента F являются именно эти торы Тг. Для удобства ссылок
приведем здесь использующиеся в дальнейшем обозначения.
1) Алгебра G: & = dimG; flt ... , fk—функционально независимые
аддитивные образующие (функции) алгебры G; r — indG; s = —dim 0*,
где О*—орбита общего положения в G*; s = — (k— г), 2п = k + г,
т. е. dim М = dimG + indG.
2) Алгебра V: q = dlmV; gv ... , gq—функционально независимые
аддитивные образующие в коммутативной алгебре V; ind У = dim V = q,
q = -]r(k-rr)~ — (dim G +indG); <7 = s+ r = — dim 0* + indG. Ясно,
249
что q<C k (в случае некоммутативной алгебры G), так как <7 = — (k +.r),
& r<k.
3) Алгебра Go: n = dimG0, indG0 = dimG0 = —-dimM2".
На рис. 109 наглядно изображены все участвующие в рассмот-
рассмотрении поверхности и размерности. Отображение F целиком накры-
накрывает всю открытую окрестность точки geG*. Пусть прообраз
F~l{l) содержит компактную связ-
связную компоненту. Тогда она гомео-
морфна тору Тг (рис. 109). Из точ-
точки х вырастает орбита @ (х) груп-
группы @ (симплектически действую-
действующей на M)t локально гомеоморф-
ная окрестности единицы группы®.
Часть этой орбиты составляет тор
Тг. По нормали к тору остается
2и—k независимых направлений.
Соответствующее ему «нормаль-
«нормальное» подмногообразие (в орбите
®(х)) при отображении момента
(локально) гомеоморфно отобража-
отображается на орбиту O*czG*. Число не-
независимых направлений по норма-
нормали к орбите О* общего положения
в G* равно г, т. е. ind О. При ото-
отображении F тор Тг переходит в то- -
чку |, а нормальная к нему пло-
площадка размерности 2л—г перехо-
переходит (в силу условия 2и—r=k) в от-
открытую окрестность точки | в G*
(размерности k). Если а(|) — не-
некоторая функция па G*, то, перено-
перенося ее на многообразие М при по-
помощи отображения момента, по-
получаем гладкую функцию aF на М. Эта функция, очевидно, пос-
постоянна на каждом торе ТгсМ2п. Если две функции аир незави-
независимы (в точке общего положения) на G*, то их прообразы; т. е.
функции aF и р/\ также независимы на М. Важное значение при-
приобретает следующее свойство отображения момента.
Лемма 2. Отображение момента F : M->-G* является @ -ин-
-инвариантным, где группа @ =expG действует на G*- коприсоеди-
ненным образом, а на многообразии М действует как группа симп-
лектических преобразований, порожденных алгеброй Ли G вектор-
векторных полей sgrad/, /eG, , .
Доказательство следует непосредственно из определения
действия группы @ .
Лемма 3. Если функции а и р па G* находились в инволюции
относительно канонической скобки Пуассона, т. е. {а, р}о»=0 {см.
Рис. 109
250
тределение скобки выше), то их прообразы находятся в инволю-
ши относительно исходной скобки Пуассона, порожденной на М
2-формой ш, т. е. {aF, pF}M = O.
Доказательство. Это вытекает из ©-инвариантности
отображения момента и из определения скобки Пуассона. Остано-
эимся на этом факте подробнее. В действительности для любых
вункций а и' р на G* справедливо - тождество {aF, $F}m =
— ({а. Pb» )F. Пусть f\, ,.., fk — линейный базис в алгебре Ли G.
Рассмотрим функции a(fu ..., fk) и b(fu ...,/*) от исходных
вункций /,, ..., fk. Тогда скобка Пуассона функций а и b будет
.{меть вид
{a, b}M = 2JL^-{ft;f,}M..
В то же время на функции а и Ъ можно взглянуть и с другой
точки зрения. Каждая функция а от k переменных /ь ..., fk опре-
определяет функцию а* на дуальном пространстве G* по формуле
a'(g)=fl«g, h), ... , (I, Ъ))= :
Далее, скобка Пуассона функций а*(|) и 6*(|) на G* имеет
к,
/*))•{<£, Д). F, //)Ь«=2-|-«6, /г) (I, h)) X
х~«|. /i). •••• <6. МХЕ. Vu
Теперь мы можем перейти кдоказательству теоремы 8.
Естественное отображение а->о*, очевидна, переводит скобку Пу-
Пуассона снова в скобку Пуассона и, следовательно, определяет изо-
изоморфизм двух бесконечномерных алгебр JJu. Рассмотрим обратное
отображение р : a*->a. Оно сопоставляет функции а*(|) на G*
функцию a(fu ..., fk), т. е. функцию a(fu ..., fk) (x) на М. Оче-
Очевидно, p(a*)=a*i\ Таким образом, мы доказали, что отображение
момента F индуцирует встречное отображение C°°(G*)->CIX4(M),
переводящее скобку {, }с* в скобку {, }м. Очевидно, что отсюда
следует утверждение леммы 3. Завершим теперь доказательство
теоремы 8. "Согласно предположению теоремы в алгебре Ли
C^Ig*) выделена коммутативная подалгебра V, удовлетворяющая
требованиям определения 5. Выделим в ней аддитивный базис
£ь • • •, gq {gi — функции на G*) и рассмотрим их прообразы:
функции g\F, ..., gqF на М. Согласно леммам 2 и 3 все они неза-
независимы на М (в точках общего положения) и находятся в инво-
инволюции. Полное их число равно q= (fe-fr)/2 = 2n/2 = n. Следова-
Следовательно, мы можем взять эти функции в качестве аддитивных об-
образующих коммутативной алгебры Go, которая, очевидно, является1
251
максимальной линейной коммутативной алгеброй Ли функций на
М. Теорема 8 доказана.
4.4. Теорема существования и явная конструкция максимальных
линейных коммутативных алгебр функций на орбитах в полупрос-
полупростых и редуктивных алгебрах Ли. Согласно теореме 8 предыдущего
пункта для доказательства коммутативной интегрируемости сис-
систем, допускающих некоммутативное интегрирование, нужно на-
набрать как можно больший запас интегрируемых алгебр Ли G, т. е.
обладающих набором функций V на G*, удовлетворяющих услови-
условиям определения 5 (см. п. 4.3).
Начнем с важного случая полупростых алгебр Ли G.
Здесь G канонически отождествляется с дуальным пространством
G* при помощи невырожденного © -инвариантного скалярного
произведения Киллинга. Через /G обозначим кольцо (алгебру)
инвариантов алгебры G. Напомним, что функция f (X) на G назы-
называется инвариантом алгебры G, если f(X) — f(AdgX) для любого
ge О. В случае матричных алгебр Ли это условие эквивалентно
условию f(X)=f(gXg~l). В полупростом случае все алгебры ин-
инвариантов найдены в явном виде, их свойства хорошо изучены
в литературе, см., например, [28]. Нас будут интересовать лишь
полиномиальные инварианты полупростых алгебр, поэтому в даль-
дальнейшем будем считать, что IG обозначает кольцо инвариантных
полиномов на G. Образующие в кольце /G явно вычислены и хоро-
хорошо известны [28].
В [96], [98] мы доказали следующий результат (подробные
изложения см. затем в [99], [100], [151]).
.Теорема 9. Пусть G — одна из следующих алгебр Ли:
а) полупростая комплексная алгебра Ли,
б) компактная вещественная форма Gc полупростой комплекс-
комплексной алгебры Ли, ■
в) нормальная компактная подалгебра G,, в компактной ал-
алгебре Ли.
Тогда каждая из этих алгебр Ли интегрируема. Редуктивные
алгебры Ли также интегрируемы. Максимальные линейные ком-
коммутативные алгебры функций строятся при этом явно и оказыва-
оказываются полиномиальными алгебрами.
Это означает, что на каждой такой алгебре Ли G — G*,всегда
существует набор gb ..., gq независимых функций, находящихся
в инволюции на G*, причем q=-- (dim G + ind G)/2. В нашем случае
indG = panrG, т. е. ind G равен размерности картановской'подал-
картановской'подалгебры в G. В частности, ограничения функций gu ■•-, gq на орбиту
общего положения в G определяют максимальную линейную ком-
коммутативную алгебру функций на орбите.
В теореме 9 функции gu ■■■, gq указываются в действительнос-
действительности явно, поэтому алгоритм выписывания функций gi абсолютно
эффективен, а именно имеет место следующее утверждение.
Теорема 10. Пусть G — одна из алгебр Ли, перечисленных
в теореме 9. Пусть IG — кольцо инвариантных полиномов на ал-
252 -
гебре G. Рассмотрим в G элемент а общего положения и пусть
f(X) — произвольный инвариантный полином на G. Тогда семей-
семейство всех функций вида f(X+Xa), где X — произвольное числог
дает набор V, превращающий алгебру в интегрируемую алгебру.
В частности, ограничения всех функций, вида f(X+Xa) на орбиты
общего положения в G дают нам максимальные линейные ком-
коммутативные алгебры функций на орбитах.
Утверждение нашей теоремы 10 можно переформулировать еще
более наглядно. Пусть Р\(Х), ..., Pg(X) — инвариантные одно-
однородные полиномы, являющиеся образующими в кольце 1G. Рас-
Рассмотрим сдвиг аргумента Х->Х+Ха, т. е. вычислим функции
Pt(X-\-Xa). Разлагая получившиеся полиномы по степеням пара-
параметра X, получаем Pi(X + Xa) =2,Q;/(-X, a)XL Здесь полиномы
Qu(X, а) зависят от X и от а, причем а можно рассматривать как
параметр. Фиксируя элемент а (общего положения), получаем
набор функций Qij(X, а) на орбитах алгебры G. Оказывается, они
образуют коммутативную алгебру Ли размерности A/2) dim О,
где О — орбита общего положения. При этом следует подчерк-
подчеркнуть, что набор полиномов Qa(X, а) является, вообще говоря,
избыточным. После ограничения на орбиты О некоторые из ука-
указанных полиномов становятся зависимыми. Тем не менее, как до-
доказано нами, из них можно выбрать ровно A/2) dim О независи-
независимых полиномов, коммутирующих относительно канонической
скобки Пуассона. Идея сдвига аргумента появилась в работе
С. В. Манакова [84].
. А. В. Браилов в [23] развил теорему 10, а именно он доказал,
что максимальная линейная коммутативная алгебра функций
найдется не только на орбитах общего положения в G (см. тео-
теорему 10), но и на сингулярных орбитах, т. е. на орбитах меньшей
размерности. Сформулируем этот результат более точно. Пусть
G — полупростая алгебра Ли. Элемент X^G называется полу-
полупростым, если эндоморфизм ad* полупростой. Орбита О в G на-
называется полупростой, если каждый ее элемент является полупрос-
полупростым (т. е. она порождена полупростым элементом). Полупростые
орбиты могут быть как 'орбитами общего положения, так и сингу-
сингулярными. Если алгебра Ли компактна, то все се орбиты являются
полупростыми (в этом случае каждая орбита обязательно пересе-
пересекается с подалгеброй Картана).
Тео.рема 11 (А. В. Браилов). Пусть О — произвольная по-
полупростая орбита (общего положения или сингулярная) в полу-
полупростой алгебре Ли G. Пусть а — регулярный полупростой эле-
элемент из G (т. е. элемент общего положения). Пусть Р\(Х), ...
..., Pg(X) — независимые инвариантные полиномы, образующие
алгебры инвариантов 1G. Тогда из ограничений всех функций вида
Pi(X+Xa) (где ХфО) на любую полупростую орбиту (в том числе
и на сингулярную) всегда можно выбрать независимые функции^
находящиеся в инволюции и в количестве, равном A/2) dim О,
т. е. эти ограничения порождают максимальную линейную комму-
коммутативную алгебру функций на орбите.
253/
4.5. Доказательство гипотезы эквивалентности для случая ком-
компактных многообразий. Теперь мы можем доказать нашу тео-
теорему 2.
Утверждение 1 [170]. Пусть М — компактное симплекти-
ческое многообразие, на котором задана конечномерная алгебра.
Ли функций G (относительно скобки Пуассона), эффективно дей-
действующая на М (т. е. каждый ненулевой элемент geG представ-
представлен ненулевым векторным полем sgradg на М). Тогда алгебра G
редуктивна, т. е. G = KQZ, где /( — полу простая, a Z — коммута-
коммутативная алгебры.
В предположениях теоремы 2. на многообразии М задана ко-
конечномерная максимальная линейная алгебра Ли G. Так как мно-
многообразие М компактно, то в силу утверждения 1 эта алгебра ре-
редуктивна. В силу нашей теоремы 9 эта алгебра интегрируема.
В силу теоремы 8 на М существует максимальная линейная ком-
коммутативная алгебра Go функций, функционально зависящих от
функций алгебры G. Теорема 2 доказана.
4.6. Отображение момента систем, интегрируемых в некомму-
некоммутативном смысле при помощи избыточного набора интегралов.
Здесь мы изложим обнаруженное А. В. Браиловым обобщение
теорем предыдущих пунктов на Случай, когда алгебра функций G,
заданная на М, является избыточной в том смысле, что размер-
размерность подпространства, заметаемого в точке хеА( векторами
sgrad g, где g^G, меньше размерности алгебры G.
Предположим, что функции f\,...,fh являются интегралами та-'
мильтоновой системы sgrad H, где хеМ, обеспечивающими ее
полную некоммутативную интегрируемость (см. выше). Из опре-
определения полной интегрируемости следует, что свойство функций
fi,...,fh обеспечивать полную интегрируемость является внутрен-
внутренним свойством набора f\,...,fk, т. е. не зависит от того, интегра-
интегралами какой именно гамильтоновой системы вида sgrad Я они яв-
являются. Это внутреннее свойство набора функций ii,...,fh До-
Допускает следующее переопределение.
Предложение 3. Пусть G — конечномерная или бесконеч-
бесконечномерная подалгебра в алгебре Ли С°°(М); fu... ,fh^G — функ-
функции такие, что всякая функция feG. зависит от fu...,fh. Тогда
эквивалентны следующие два условия:'
а) Всякая неособая поверхность Mz*=(xeM:fi(x)=fi(z)) яв-
является изотропным подмногообразием в М.
б) dimM=ddimG + dindG.
Доказательство. Предположим, что выполнено усло-
условие б). Пусть z — неособая точка. Выберем из набора f\,...,fk
функции в количестве m = ddimG, дифференциалы которых неза-
независимы. Для простоты считаем, что функции f\K...,fm независи-
независимы. Применяя к fi,...,fm формулу Э. Картана, находим
dim Tz П Tt = ddim G— ранг ({/,, f,) (z)).
-Следовательно, с одной стороны, ddim G — ранг ({/,,
254 -~
< Tz = dim M — ddimG; с другой стороны, ddim U —
— ранг ({/,-, fj}(z))^dind СТак как dimM— ddim G = dind G, то в
действительности оба эти неравенства являются равенствами.
В частности, dim Тг(]Тг±=dim Tz. Следовательно, из б) следует а).
Предположим, что выполнено условие а). Из определения
dind G следует, что найдется такая неособая точка zeAf, что
ddimG — ранг ({ft, fj)(z)) =dind G. Из формулы Э. Картана для
точки г следует, что TZ[)TZX = TZ —dim M— ddim G = dindG. Сле-
Следовательно, dim M = ddim G + dind G, что и требовалось дока-
доказать.
Пусть f\,...,fm — гладкие функции на М, образующие замкну-
замкнутый относительно скобки Пуассона набор, причем
где числа скц не зависят от точки х. Линейная оболочка G функ-
функций ft в пространстве С°°(М) является конечномерной алгеброй
Ли относительно скобки Пуассона. Предположим, что G — редук-
тивная алгебра Ли и (,) — фиксированная билинейная симмет-
симметричная невырожденная форма на G, инвариантная относительно
всех внутренних автоморфизмов. Дуальное пространство G* отож-
отождествляется с G при помощи формы (,).
Напомним определение отображения момента с учетом отож-
отождествления G и G*. Отображение момента F: M-*-G сопоставляет
точке хеМ элемент F(x)^G такой, что (F(x), fi) — U(x) для каж-
каждого i=l,...,т. Элемент | называется полупростым, если опера-
оператор adj днагонализируем или становится таким после комплекси-
фикации.
Теорема 12. Пусть GaC°°(M)—редуктивная подалгебра в
алгебре Ли гладких функций на симплектическом многообразии
М. Пусть F-.M-+G — соответствующее отображение момента.
Пусть 1\,...,1Т — набор однородных образующих алгебры инвари-
инвариантов алгебры Ли G, а — элемент из G. Функциональный коэффи-
коэффициент при ti в полиноме Рг(К, I) =/*(!+А,а) обозначается через
^г.а(Е), i^G. Предположим, что dimM = ddim G + dind G и что
для элемента х общего положения в М элемент F (х) является по-
полупростым в алгебре G. Тогда все функции IU,a°F попарно ком-
коммутируют и для элемента а общего положения в G из них можно
выбрать независимые функции в количестве A/2) dim G. В частно-
частности, если гамильтонова система sgrad H, где хеМ, полностью ин-
интегрируется в некоммутативном смысле с набором интегралов
m
f\,---,fm таким, что G = © R/j, то функции Iji,a{l) образуют пол-
ный коммутативный набор интегралов этой гамильтоновой систе-
системы, т. е. их линейные комбинации порождают максимальную ли-
линейную коммутативную подалгебру в С°°(М).
255
Наша теорема 2 (см. [97]) утверждает, что система sgrad#
на М, обладающая набором независимых интегралов f\,...,fm та-
таких, что О = фЯ/,-— редуктивная алгебра Ли и
МО, ■ B)
вполне интегрируема по Лиувиллю. Теорема Браилова 12 яв-
является развитием этой теоремы, так как в теореме 12 полная ин-
интегрируемость утверждается без предположения независимости ин-
интегралов.
Из предложения 3 следует, что определение полной некомму-
некоммутативной интегрируемости, данное выше, можно сформулировать
в форме, близкой к формуле B), а именно гамильтонова система
на многообразии М с алгеброй Ли интегралов G полностью инте-
интегрируется в некоммутативном смысле, если
dimAf=ddimG + dindG C)
Лемма 4. Пусть G — комплексная или вещественная редук-
редуктивная' алгебра Ли, a<=G — полупростой элемент, Ga— централи-
централизатор элемента a, ZGa — его центр; Iu...,Ir — образующие алгеб-
алгебры инвариантов алгебры Ли G. Тогда дифференциалы dl\{a),...
...,dlr(a) порождают ZGa.
Доказательство. Достаточно доказать лемму для полу-
полупростой алгебры Ли G. Рассмотрим сначала случай поля ком-
комплексных чисел. Пусть К — подалгебра Картана. Как известно,
■отображение ограничения /: IG-ySK, где /G—алгебра инвариан-
инвариантов, SK—алгебра полиномиальных функций на К, является моно-
мономорфизмом и j(IG)=SKw. Здесь SKW—множество полиномов
на К, инвариантных относительно группы Вейля W. Пусть бе
<=ZGa, Wa — стабилизатор а в W, Wb— стабилизатор Ь. Тогда
WaczWb. Пусть (а\,... ,а„)—орбита элемента а относительно
группы W,'a g — полином на' К такой, что dg(a)—'b и dg(ai)=Q
при й[фа. Определим функцию
\-w\
1>
где \W\ —число элементов в группе Вейля. Для g имеем dg(a) —
— b и g<=SKw. Следовательно, /=/"'(#)—инвариант алгебры G
такой, что dl(a)~b. Так как 1\,...,1Т—образующие алгебры ин-
инвариантов, то /=/>(/ь"... ,/г) для подходящего полинома Р. Сле-
Следовательно,
В случае поля С лемма доказана. Вещественный случай легко
следует из комплексного.
256
Доказательство теоремы 12. Пусть G— алгебра Ли
группы Ли®, х — элемент общего положения в М, О—орбита
(ко)присоединенного действия & на G, проходящая через F(x).
Пусть k — число независимых функций среди /i,...,/m. Л =
= ddimG. Существует малый диск Ds размерности s = k —
— dimO = dindG, трапсверсально пересекающий орбиту О в точ-
точке F(x) так, что 7>(Х)Оф TF(X)DS— TFix)F{M). Вследствие леммы
2 среди инвариантов I\,...,Ir найдется s инвариантов, ограниче-
ограничения которых на Ds независимы. Вследствие теоремы 11 из функ-
функций IU,a можно выбрать A/2) dim О функций так, что при ограни-
ограничении этих функций на орбиту они остаются независимыми. Сле-
Следовательно, па М имеется s + A/2) dim О независимых функций
вида Ih,a°F. Так как dim M = ddim G + dind G и ddim G = dind G +
+ dim О, то s + A/2) dim О = dind G + — dim О = BdindG +
+ dim 0I2= (dind G + ddim G)/2= A/2) dim M.
Так как функции I~U,a°F, очевидно, являются интегралами, то га-
мильтонова система sgrad Н вполне интегрируема по Лиувиллю.
Теорема доказана.
4.7. Достаточные условия компактности алгебры Ли интегра-
интегралов гамильтоновой системы. Алгебра Ли G называется компакт-
компактной, если существует положительно определенное скалярное про-
произведение (,) на G, инвариантное относительно всех внутренних
автоморфизмов. Пусть редуктивпая алгебра Ли G является алгеб-
алгеброй Ли функций относительно скобки Пуассона на симплектиче-
ском многообразии (М, со). Условие полупростоты образа отобра-
отображения момента F:M-+G из теоремы 12 автоматически выполне-
выполнено для компактных алгебр Ли. В связи с этим представляют ин-
интерес достаточные условия компактности алгебры Ли G интегра-
интегралов системы sgrad Я. Как следует, из [170], таким достаточным
условием является компактность многообразия М. Дело в .том,
что в этом случае для любых функций f, geG определено инва-
инвариантное скалярное произведение (/, я) = 1м/£юп. Ниже мы при-
приводим более слабое условие, обеспечивающее компактность ал-
алгебры Ли интегралов и, используя теорему 12, получим следующее
утверждение.
Теорема 13 (А. В. Браилов). Пусть гамильтонова система
sgrad Н на М полностью интегрируема в некоммутативном смыс-
смысле с набором интегралов fi,...,fm, образующих алгебру Ли G==
= ®mi=iRf,-. Если всякая изоэнергетическая поверхность Mh —
= (xgM : Н (х) =п) компактна, то гамильтонова система sgrad Я
вполне интегрируема по Лиувиллю с полным набором коммути-
коммутирующих интегралов, полиномиально зависящих от f\,...,fm.
Теорема 13 является развитием нашей первоначальной теоремы
(см. [100]), утверждающей полную интегрируемость гамильтоно-
гамильтоновой системы sgrad Н при условии компактности М и полной ее
интегрируемости с набором независимых интегралов f\,...,fm, об-
образующих алгебру Ли G такую, что dim M = dim G + ind G.
У Л. Т. Фоменко . 257
Доказательство теоремы 13. Пусть G — алгебра Ли
интегралов системы sgrad/У, каждая изоэнергетическая поверх-
поверхность которой компактна. Тогда оказывается, что G— компактная
алгебра Ли. Хотя доказательство этого утверждения легко следует
из результатов п. 4.5, тем не менее мы приведем рассуждение, по-
полезное для дальнейшего.
Пусть g— произвольный элемент G, sgradg—соответствую-
sgradg—соответствующее поле. Поле sgradg касается Mh для любого h. Так как Mh
компактно, то все интегральные траектории поля sgradg продол-
продолжаются неограниченно. Поэтому определено действие связной од-
носвязноп группы Ли @, алгеброй Ли которой является G, на М
такое, что элемент exp(tg) группы @ переводит всякую точку
Y@) многообразия М, лежащую на интегральной траектории у:
: R-кМ поля sgradg, в точку y(t).
Отображение момента F-.M-^G* переводит указанное действие
группы @наМв коприсоединенное действие па G*. Следователь-
Следовательно, образ F(Mh) поверхности Мн инвариантен относительно Ad*.
Пусть geG — нильпотентпый элемент, ^o^F(Mh). Рассмотрим
отображение g : R->G*, определенное формулой Ad*exP(fg)(|o) =
= s@- Из инвариантности F(Mh) следует, что %(t)=F(Mh). И»
нильпотентности g следует, что | — полиномиальное отображение-
Компактность Мн дает компактность F(Mh). Так как отображение
s: R-^F(Mh) полиномиально, а множество F(Mh) компактно, то
|(/)=|0Для всякого t. Поэтому'adg*(go) = 0 для каждого J-oe.
e.F(Mh) и для любого нильпотентного geG.
Следовательно, для нильпотентного g и любых feG, xeM
имеем F(x)[g, h]={g, f}(x)=O. Значит, каждый нильпотентный
элемент g алгебры Ли G содержится в ее центре, который мы
обозначим через Z. Отсюда легко получить компактность алгебры
Ли G. Действительно, пусть R — разрешимый радикал алгебры G^
Тогда множество \R, R] состоит из иильпотентных элементов ал-
алгебры Ли G и весь радикал состоит из ннлыютентных элементов.
Поэтому [R, R]dZ = R. Следовательно, G — редуктивная алгебра
Ли. Пусть S=[G, G] —полупростой идеал в G. Так как S(]Z=Or
то в S нет непулевых иильпотентных элементов. Значит, G — ком-
компактная алгебра Ли. Теорема 13 доказана.
§ 5. Динамические системы и симплектические структуры,
порождаемые секционными операторами
5.1. Общая схема построения секционных операторов. Автором
настоящей книги в [152—156] была предложена конструкция по-
построения операторов, названных секционными и позволяющих по-
получать достаточно богатые серии как вполне интегрируемых га-
мильтоповых систем на орбитах представлений групп Ли, так и
примеры разнообразных симплектических структур, обладающих
интересными свойствами.. Частными случаями таких гамильтопо-
вых систем оказываются, например, уравнения движения много-
многомерного твердого тела с закрепленной точкой в отсутствие силы
258
тяжести, уравнения движения многомерного твердого тела по
инерции в идеальной жидкости и т. п., см. [152—156, 146, 148,
149). Как было обнаружено затем В. В. Трофимовым, существует
тесная связь между тензором римановой кривизны симметриче-
симметрических пространств и секционными операторами, индуцированными
коприсоединенным представлением стационарных групп симметри-
симметрических пространств. Напомним конструкцию секционных опера-
операторов.
Пусть Н — алгебра Ли, 5з = ехр/У — соответствующая группа
•Ли, р : #->End V — представление Н на линейном пространстве
V и О(Х) —орбита действия & на V. Пусть XeV. Если задать
линейный оп'ератор Q:V-*-H (который назовем секционным), то
на орбитах возникает векторное поле X—p(QX)X. Предъявим
специальный класс секционных операторов, образующих многопа-
многопараметрическое семейство, основными параметрами которого явля-
являются два элемента: аеУ и Ье/С=КегФа, где Фа: H-+V, Фап=
= (рА)а.
Пусть а — элемент общего положения в Н. Предположим, что
в алгебре К есть полупростые элементы. Пусть Ье/С — произ-
произвольный полупростой элемент. Рассмотрим П = Кег(рЬ)сг V; пусть
Н=К+ К', где К' — произвольное алгебраическое дополнение к
К. Имеем V=n + Im(pfr) (в силу полупростоты Ъ), ПП1трЬ = 0;
плоскость Фа/С = Ф,(/7сг V определена однозначно (при заданном
а). Положим Я = ]1Г)Ф«К', R' = <baK'[\\n\pb. В силу выбора b
оператор рЬ изоморфно отображает Ini(>/> па себя. Пусть (pb)—
обратный оператор и /?= {pb)~^R'. Тогда lmpb = R + Z, где Z —
произвольное алгебраическое дополнение. Пусть Т—алгебраиче-
Т—алгебраическое дополнение к о в П.
Окончательно получаем разложение V в прямую сумму четы-
четырех подпространств V=T+B + R + Z. Если на V задано скалярное
произведение, то Z и Т однозначно определяются как ортогональ-
ортогональные дополнения. Положим В = Фа~1В, Фа~^'=В, получаем раз-
разложение алгебры Н в прямую сумму четырех подпространств Н=
= K+B + R + Z, где 2—алгебраическое дополнение к B+R в К'
{см. рис. 110). Определим секционный оператор Q : T+B + R + Z-*-
KB положив
/о
■ «-I f *л
1 0 Фа pb
\ D>,
где D : Г->/С и Ь': Z-+Z — произвольные линейные операторы,
Ф7 :В~*-В, Ф^pb^.R-*-R. Такие операторы назовем канониче-
каноническими секционными. Таким образом, операторы Q = Q(a, b, D, D')
образуют многопараметрическое семейство. В дальнейшем будем
рассматривать динамические системы вида X = p(QX)X.
5.2. Секционные операторы на симметрических пространствах.
Пусть Н—алгебра Ли, представленная операторами на простран-
9* 259
стве V, Пусть заданы два секционных оператора Q и С, отобра-
отображающие V в Н. Рассмотрим в пространстве V точку X общего по-
положения и пусть ф —ехр/У — группа Лн, отвечающая алгебре Ли
Н. Так как алгебра Н действует на V посредством представления
р, то и группа Ли § представлена линейными операторами на
том же пространстве V. Рассмотрим это линейное представление
eQ:S).-*-AuiV. Будем обозначать операторы e°q, где q^. ф, снова
через q. Действие группы ф на V расслаивает V на орбиты. Рас-
л1
/
/
II
1
1
1 hb.
■ X
1 \
R
/
К
к
j\
i\
в \
lrnpbj
■ Rjh
fas'
N.
:\
R'
■ к
\ ro
\^
''л
Рис. ПО
смотрим орбиту О(Х), проходящую через точку X. Согласно ее
определению каждая точка Y'^O(X) представима в виде q(X)r
где q^lQ. Поскольку основные приложения секционных операто-
операторов будут здесь интересовать нас лишь в случае полупростых ал-
алгебр Ли и полупрямых сумм полупростых алгебр Ли с абелевыми
подалгебрами, то в качестве § возьмем полупростую алгебру.
Рассмотрим следующий частный случай.
Пусть М= @/ф — компактное однородное пространство. Тогда
алгебра Ли G группы движений @ разлагается в прямую сумму
двух подпространств: G = ff+V, где Н=Те$> — стационарная под-
подалгебра (касательная плоскость к стационарной подгруппе), а
V — касательное пространство к многообразию М. Ясно, что под-
подалгебра // присоединенным образом действует на пространстве Vr
т. е. можем положить p=ad.
Особый интерес представляет случай, когда стационарная под-
подгруппа § совпадает с множеством неподвижных точек некоторого
инволютивного автоморфизма о, определенного на всей группе ©
т. е. а: @-»-@, а2=1. В таком случае пространство М ==■&/§ на-
называется симметрическим.
Теорема 1. (А. Т. Фоменко). Пусть М= @?/ф — компактное
симметрическое пространство, где <3 и § — полупростые компакт-
компактные группы Ли. Пусть аеУ—точка общего положения. Тогда
разложение пространства V = T + B + R + Z, определяющее канони-
канонический секционный оператор С: V-+H (см. определение выше),
имеет следующий вид: Т — максимальное коммутативное подпро-
подпространство в пространстве V, аеГ, R=^R', Z=0, фаН+Т =
= V=T + B + R, (t)aH=B + R, # = Impb. Плоскости Т, В, R по-
попарно ортогональны. Если Q, С: V-+H — два канонических секци-
260
'онных оператора, то наряду с динамической системой X=p(QX)X
на орбитах 0{X)czV возникает внешняя 2-форма F(X; |, ri) =
ж(СХ, [£, 1]]); где £, ц^ТхО(Х). Через (,) здесь обозначено не-
невырожденное скалярное произведение Киллинга на полупростой
алгебре Ли Н.
Иногда векторное поле X и форму F будем обозначать через
Хя и Fc соответственно, указывая явно порождающие их секци-
секционные операторы. В предположениях теоремы 1 секционный опе-
оператор С задает линейное отображение пространства V в Я, услов-
условно изображенное на рис. 111. В частности, матрица оператора С
задается так:
D
О
О
Фа'
Доказательство теоремы 1. Пусть aeV — произволь-
произвольный элемент общего положения. Из теории симметрических про-
пространств следует, что в плоскости V всегда существует макси-
максимальное коммутативное подпрост-
подпространство Т, содержащее а. Фиксиру-
Фиксируем такое подпространство и пусть
Т' — ортогональное дополнение к
Т относительно формы Киллинга.
Напомним, что на алгебре G = H +
+ V задана форма Киллинга, огра-
ограничение которой на V также зада-
задает невырожденное положительно
определенное скалярное произведе-
произведение на V.
Следуя общей схеме построения
секционного оператора, мы долж-
должны теперь рассмотреть в подалгеб-
подалгебре Н аннулятор К=К{а\ элемента
а, т. е. совокупность всех таких /ге
еЯ, что [k, a] =0. Это означает ра-
равенство К=КегФа. Из тождества
Якоби следует, что аннулятор яв-
является подалгеброй в Н (не обяза-
обязательно коммутативной). Можно считать, что К(а) является ан-
нулятором любого элемента t общего положения из Т, т. е. К{а) =
— K(t), где a, t — элементы общего положения в Т. Теперь мы
должны рассмотреть в К произвольный элемент Ъ общего положе-
положения. Отметим, что при этом элемент Ь не обязан быть элементом
общего положения с точки зрения всей алгебры Я. Согласно нашей
общей схеме мы должны рассмотреть подпространство П = Кегр6
в V. Ясно, что оно совпадает с аннулятором К, т. е. Ker pb='
= (oeK:[t), 6]=0). Ясно, что подпространство П не зависит от
Рис. 111
261
выбора элемента b общего положения в К. Очевидно, ГсП.
Пусть В — ортогональное дополнение к плоскости Г в П.
Лемма 1. Плоскость В совпадает с ФаЯПП, где Фа :#->-]/,
3>a(h) = (ph)a = [h, о]. Кроме того, ФаН±Т.
Доказательство. Согласно определению Фа пересечение
3>аН с П состоит из всех элементов вида [h, a], коммутирующих
z а, где h^H. Докажем, что плоскости Ф,;Я и Т ортогональны.
Рассмотрим скалярное произведение (Ф<А t), где АеЯ, t^T.
Тогда <Фа/г, t) = ([h, a], t) = (h, [а, t]) = 0, так .как t^T, т. е.
[a, t] = 0. Кроме того, мы использовали свойство операции ad:
(acbsT, Z)=—{Y, ad^Z). Другими словами, операторы adjr косо-
симметричны относительно формы Киллинга. Таким образом, Т_]_
ХФаН и Т_]_(фа#ПП), следовательно, В = ФаН(]11. Лемма дока-
доказана-.
В частности, использованное нами обозначение В для плоско-
плоскости, ортогональной-к Т в II, полностью согласуется с обозначения:
ми п. .1, где дана общая схема построения секционного операто-
оператора. Так как мы рассматриваем случай симметрического простран-
пространства М== ®/ф, то разложение алгебры G = H+V обладает важ-
важными свойствами. В частности, легко видеть, что [Н, H]czH,
[Н, V]czV, [V, V] czH. Пусть Т — ортогональное дополнение к Т
в V, а К' — ортогональное дополнение к К в Н.
Лемма 2. Для элемента а^Т общего положения отображе-
отображение Фа-H^-V, где Фап— [h, а], устанавливает линейный изомор-
изоморфизм между плоскостями К' и Т. При этом К=КегФа, Т'=
= ФаК'.
Доказательство. Отметим, что плоскости Н и V ортого-
ортогональны в О. Так как Д=КегФа, то фаН=Фа{К + К')=ФаК'.
В силу леммы 1 плоскость ФаЛ7 ортогональна Т в V, следователь-
следовательно, ФаК'сТ'. При этом отображение Фа является мономорфизмом
на плоскости К', так как КегФаГ\К' = КГ\К' = 0. Исследуем дейст-
действие стационарной подгруппы § на плоскости V. Ясно, что из каж-
каждой точки te7 вырастает орбита этого действия. Рассмотрим ор-
орбиты общего положения O(t), вырастающие из точек t общего по-
положения, лежащих в Т. Имеем dim V=dimO(t) +dim Т. Ясно,
что dim О (t) — dim Т. В то же время касательная плоскость к ор-
орбите O(t) в точке t естественно отождествляется с фактор-про-
фактор-пространством Н/К.етФа=Н/К. = К'. Отсюда следует, что dimK' =
— dim O(t) =dim T. Но так как отображение Фа мономорфно
вкладывает К.' в V, то фаК' = Т', что и требовалось доказать.
» * Лемма 3. В пространстве V выполнены следующие соотно-
соотношения:
а) l/=Impb + KerрЬ, причем ImpbflKerpb = O,
б) /? = 1трЬсг1тФа = ФаД''=/? + 5, в частности, в обозначе-
обозначениях п. 5.1 R=R' и R + B = T'.
Доказательство. Оператор рЬ, будучи ограничен на плос-
плоскость V, кососимметричеп относительно формы Киллинга, поэтому
может быть записан кососимметрической матрицей. При подходя-
подходящем выборе базиса она принимает канонический блочно-диаго-
262
пильный вид и соответствующее разложение пространства V в
сумму плоскостей, на одной из которых оператор pb тривиален, а
на другой сводится к поворотам в двумерных плоскостях, совпа-
совпадает с разложением в сумму образа и ядра оператора pb.
Далее, образ pb ортогонален ядру pb, а так как КегрЬ = П и
ТсП, то Im pb J- П и Im pb Л.Т. Поэтому impbcT'= ФиК', т. е.
Im рЬаФаК' = ФаН: Поскольку R'= ФаК' П Im рб, то R' = lmpb.
Отсюда фаК' = Im pb + Кег pb П ФаК' = Im pb + В.
Итак, фаК'=1?' + В. Так как i?'=Impb, то # = #', т. е. ФаК'~
— R + B. Лемма доказана.
Таким образом, канонический секционный оператбр С: V-*-H
приобретает в нашем случае вид С: T+B + R^-K+B + R, где ое
6= Г, К=К(а)=Апп(а), Ь^К, П = £ + Т=КегрЬ, R = lmpb,
HB R 5 1 ^ Ф1ад Фа-1^/.-Значит,
Первые утверждения теоремы 1 доказаны. Осталось опреде-
определить внешнюю 2-форму F. Пусть С — секционный оператор. Рас-
Рассмотрим произвольную точку X^V и пусть |, т} — произвольные
векторы из V, приложенные и точке X. Тогда [|, т]]е# и СХ^Нг
следовательно, определено скалярное произведение (СХ, [|, ti]),
которое мы и примем за значение формы Fc в точке X на паре
векторов g, ц. Корректность определения основана на свойстве
симметрического пространства: \V, V]czH. Теорема доказана.
Ясно, что формате определена на всем пространстве V, но мо-
может быть ограничена па орбиты О(Х) действия группы Ь на V.
"Отметим полезное для дальнейшего свойство формы F.
Лемма 4. Пусть f — гладкая функция на пространстве V.
Обозначим через sgradc/eV векторное поле на V такое, что для
произвольного векторного поля Y<=V выполнено равенство
Fc(sgradcf, Y)=Y(f). Здесь Y(f) — производная функции f вдоль
поля Y. Тогда grad/=[CX, sgradc/]. Поле sgradcf определено,
вообще говоря, неоднозначно.
Доказательство. Из равенства Y(f)=(Y, grad/) следует
(Y, gradf> = (CJ," [sgradc/, Y]) = ([CX, sgradcf], Y). Отсюда
(Y, gradf— [CX, sgradcf] ) = 0. В силу произвольности поля Y
получаем gradf— [СХ, sgradcf] =0, что и требовалось доказать.
Рассмотрим некоторые примеры построенных нами 2-фо'рм
Fc. Существуют такие важные симметрические пространства, что
форма F (при подходящем выборе канонического секционного
оператора) определяет на орбитах (или почти всюду на орбитах)
симплектическую структуру. Возьмем, например, в качестве сим-
симметрического пространства полупростую группу Ли §=М. Тогда
М= ©/§,' где @ = § х & и инволюция а:@->-@ задается фор-
формулой о(х, у) = (у, х). Соответствующее разложение в алгебре
Ли Н + Н имеет вид V=(X, —X), ХеЯ, Н=(Х, X). Здесь одной
263
буквой обозначена Я и ее реализация в G = H-\-H. Далее aV=*
=—V, aH=H.
Лемма 5. Имеют место равенства В = В = 0, H—K+R и V=
= T-rR — картановское разложение алгебры Н.
Доказательство. Здесь 7={(/, —/), tt=Tr}, где Тг—кар-
тановская подалгебра в Я. Ясно, что K={(t, t)}, feT'', поэтому Т
и К изоморфны Тг. Поскольку V и Я соответствуют одной и той
же группе, то присоединенное действие а&н на V имеет вид
ad(kik)(X, —X) = ([h, X], —[hti X])<=V, т. е. совпадает с дейст-
действием ad/jX Следовательно, для нахождения В достаточно найти
централизатор Тг в Я. Отсюда (ввиду полупростоты) получаем,
что В=0 и централизатор совпадает с Тг. Вследствие полупросто-
полупростоты ортогональное дополнение R к Т (и Я к К) натянуто на корне-
корневые подпространства алгебры Я, что и означает, что разложения
V—T+R и Н — К+К. изоморфны картановскому разложению. От-
Отметим, что хотя М и диффеоморфно £>, но вложено в @ = © X ф
не как подгруппа. Можно считать, что плоскости Н={(Х, X)} и
V={(X, —X)} отождествлены с помощью естественной операции
а: (X, Х)-+(Х, —X). В частности, орбиты OczV совпадают с ор-
орбитами стандартного присоединенного действия.
Предложение 1. Форма FC(X, \, г\), где С=С(а,а, О, Е),
совпадает с формой Кириллова на алгебре Н (линейно изоморф-
изоморфной V); в частности, невырождена и замкнута (и инвариантна) на
орбитах О присоединенного действия $Q на V.
Доказательство. Так как V=T+R, то X=nX+Y, где
лХ<=Т, Yz=R и CX=DnX+ada-ladbY=nX+Y=X^H. Следова-
Следовательно, FC = (X, [|, ti]). В полупростом случае эта форма факти-
фактически совпадает с формой Кириллова, отличаясь от нее на линей-
линейное преобразование в одной точке. Формы (X, [|, л]} и (X, [|',
г\'] > инвариантны на У относительно. Ad, поэтому достаточно
сравнить их только в одной точке X общего положения на V; |=
= ad*£', T1 = adXT1/; <*, [adxt,' adxi\']), (X' [l\ л'1 > отличаются
на невырожденное линейное преобразование ad*, переводящее ка-
карательное пространство ТХО в себя.
Таким образом, общая конструкция секционных операторов
позволяет с единой точки зрения охватить широкий класс важных
примеров структур, использующихся в гамильтоновой геометрии.
5.3. Тензор римановой кривизны и порождаемые им симплек-
тические структуры. В качестве следующего примера рассмотрим
симметрические пространства максимального ранга. Оказывается,
здесь форма F, построенная по секционному оператору, тесно^ свя-
связана с тензором римановой кривизны симметрического простран-
пространства.
Напомним основные свойства пространства yVf=@/Sj макси-
максимального ранга. Рангом симметрического пространства (компакт-
(компактного) М называется размерность максимального коммутативного
подпространства Т в плоскости V, где G = H+V. Рангом компакт-
компактной группы @ называется размерность максимальной коммута-
коммутативной подалгебры в G. Такая подалгебра называется картанов-
264
ской. Пространство М. называется пространством максимального
ранга, если ранг М равен рангу группы @.
Л е м м а -6. В случае пространства максимального ранга раз-
разложение пространств V и Н, соответствующее каноническому сек-
секционному оператору; имеет вид С: Т+В-+Е, т. е.
Z = Z = 0, R = R = 0, К = 0, а^Т, Ь = 0, С=@, Фа-').
Доказательство. Так как ранг М максимален, подпро-
подпространство TczV является одновременно и картановской подалгеб-
подалгеброй в G. Следовательно, аннулятор плоскости Т в G равен Т и,
значит, его пересечение с HczG нулевое, т. е. К = 0 и Ь = 0. Так
как pb = O, то n = Ker-.pb = G, Impb = 0, т. e. R = R = O и ФаН = В +
+ R = B. Поэтому V — T+ФаН и группа 5} действует на плоскости
V таким образом, что все орбиты общего положения в V диффео-
морфиы группе -t>. Итак, из всех компонент оператора остается
только отображение Фа~', что и доказывает лемму.
В качестве примера симметрического пространства максималь-
максимального ранга рассмотрим подмногообразие SU'(n)/SO(n) в уже хо-
хорошо знакомом нам лагранжевом . вещественном грггссмановом
многообразии U(n)/O(n). Здесь группа SO(n) вложена в SU(n)
как подгруппа вещественных матриц. Можно проверить, что ранг
этого пространства максимален п равен п—1.
Предложение 2. Если симметрическое пространство М =
— ®/ip имеет максимальный ранг, то внешняя 2-форма Fc на про-
пространстве V (и, в частности, на орбитах группы ф в V, гомео-
морфных §), определяемая каноническим секционным оператором
С—С(а, 0, 0, 0) = @, Фа~'), порождается тензором римановой
кривизны симметрического пространства. А именно имеет место
равенство FC(X; |, т})=4(а, R(X, с,)ц), где R — тензор римановой
кривизны, а аеГ — фиксированный вектор.
Таким образом, мы получаем многопараметрическое семейство
замкнутых внешних 2-форм на орбитах действия группы S)', пред-
представленной как стационарная группа на плоскости V. Как мы уже
знаем, в случае пространств максимального ранга орбиты общего
положения в V диффеоморфны самой группе &. Следовательно,
указанные выше замкнутые 2-формы определены на группе &. На-
Напомним, что мы рассматриваем компактные симметрические про-
пространства с компактной стационарной группой Ф. Отсюда сле-
следует, что все замкнутые 2-формы Fc, построенные согласно пред-
предложению 2, вырождены на ij. Дело в том, что все они являются
точными формами. Это следует из того, что для всех полупростых
компактных групп Ли § имеет место утверждение: Я2(§, R)=0,
т. е. любая замкнутая 2-форма точна. В то же время точная 2-фор-
2-форма на замкнутом компактном ориентируемом многообразии обя-
обязательно вырождена. В частности, "компактное замкнутое сим-
плектическое ориентируемое многообразие М обязательно имеет
нетривиальную группу когомологий Й2(М, R). Поэтому па § сим-
плектическая структура вообще не может существовать (в клас-
классическом смысле).
265
Однако, как мы видели выше, изучение вырожденных скобок
Пуассона (отвечающих замкнутым, но, вообще говоря, вырожден-
вырожденным 2-формам) представляет большой интерес с точки зрения
разнообразных приложений. Такова, например, форма Кириллова,
рассматриваемая не на орбитах, а на всей объемлющей алгебре
Ли. Кроме того, каждая вырожденная скобка Пуассона опреде-
определяет слоение многообразия на гладкие подмногообразия, обла-
обладающие симплектическими структурами, т. е. слоение на сим-
плектические подмногообразия. В таких случаях говорят, что на
многообразии задана слоеная симплектическая структура. Напом-
Напомним здесь следующий известный классический результат.
Лемма 7. Пусть на многообразии М задана (вырожденная)
скобка Пуассона {f, g}. Пусть А : Т*М^-ТМ — соответствующий ей
гамильтонов оператор, т. е. (Axd(p, Л|)) = {ф, \^}(х), где лг&М.
Тогда
а) Распределение х-*-Ах(Тх*М) интегрируемо в многообра-
многообразии М.
б) На интегральных подмногообразиях этого распределения
оператор А индуцирует настоящую симплектическую структуру,
т. е. невырожденную замкнутую 2-фдрму.
Остановимся подробнее на соответствии между вырожденными
2-формами и вырожденными скобками Пуассона. Пусть на глад-
гладком многообразии М задана вырожденная замкнутая 2-форма со.
Она определяет отображение расслоений Q : ТМ-+Т*М по форму-
формуле Q(s) (у) =co(s, у), где s, у — сечения касательного расслоения
ТМ. Пусть F = {feC°°(M) : cf/elm Q}. Очевидно, что F — линейное
подпространство всех гладких функций на М. Каждой функции
/е/7 мы можем- сопоставить, следуя обычному правилу, косой гра-
градиент sgrad/, обладающий свойством со (sgrad f, v)=v(f). Этот
вектор определен с точностью до элементов ядра формы со.
Для функций из подпространства F определим скобку Пуассо-
Пуассона {/. gf^w (sgrad/, sgrad g). Это определение корректно, так как
соответствующие добавки к косым градиентам sgrad f и sgrad g
из ядра формы со не влияют на результат. Таким образом, про-
пространство функций F превращается в алгебру Ли. На все про-
пространство гладких функций скобка {,} продолжается тривиаль-
тривиальным образом, а именно если df^£ImQ, то положим по определе-
определению {/, g} = 0 для любой гладкой функции на М. Таким образом,
пространство гладких функций С°°(М) превращается в алгебру
Ли. Если, например, форма « тождественно равна пулю, то эта
алгебра Ли оказывается абелевой.
Таким образом, согласно предложению 2 тензор рпмановой
кривизны симметрического пространства @/ф максимального
ранга всегда определяет на группе $ слоеную симплектическую
структуру. Аналогичная ситуация возникает и в других геометри-
геометрических вопросах. Так, например, в связи с конструкцией приве-
приведенного фазового пространства симплектические структуры на ко-
касательных расслоениях, ассоциированные с тензором римановой
кривизны главных расслоений, рассматривались Куммером. Не-
266
давно В. В. Трофимов обнаружил, что описанное в предложении 2
соответствие между секционными операторами, слоеными сим-
илектическими структурами и тензором римаиовой кривизны од-
однородных пространств носит весьма общий характер, см. работу
B. В. Трофимова [140].
Объемы гиперболических многообразий. В 1986—1987 гг.
C. В. Матвеев и А. Т. Фоменко вычислили объемы нескольких се-
серий 3-многообразий, долускающих гиперболическую структуру,
т. е. полную риманову метрику постоянной отрицательной кри-
кривизны (равной —1). Эти исследования были стимулированы из-
известными работами С. П. Новикова. Гиперболические объемы
входят в общие неравенства Морса—Новикова, а именно в обоб-
обобщенные числа Бетти.
Развернутая теория гиперболических многообразий построена
в работах Тёрстона, где, в частности, предложен способ эффектив-
эффективного построения большой серии .гиперболических многообразий.
Отдельные примеры гиперболических многообразий были постро-
построены еще Вебером и Зейфертом в 1933 г., однако до недавнего вре-
времени не было известно достаточно больших серий з-амкнутых ги-
гиперболических многообразий. Построение замкнутых многообра-
многообразий гораздо сложнее конструирования некомпактных многообра-
многообразий (см., в частности, работы И. С. Гуцула, Б. Н. Апанасова,
Э. Б. Винберга, Адамса).
Метод Тёрстона основан на идее построения гиперболических
структур склейкой так называемых идеальных симплексов и за-
заключается, по существу, в подборе параметров идеальных сим-
симплексов и вычислении их объемов. Обе задачи решаются нами с
помощью ЭВМ. Принципиально важен вопрос о правильном вы-
выборе объектов машинного счета. Выбор Адамса гиперболических
узлов и зацеплений с восемью и менее самопересечениями естест-
естествен с точки зрения теории узлов, но в достаточной мере случаен
с точки зрения гипербол,инеской геометрии. Поэтому вычисленные
им объемы некомпактных многообразий (всего около 40) мало
говорят о структуре всего ряда объемов. С. В. Матвеев и автор
подошли к решению задачи принципиально с другой точки зре-
зрения. Наш подход основан на соединении топологической теории
автора для изоэнергетических поверхностей интегрируемых га-
мильтоновых систем с теорией С. В. Матвеева сложности 3-много-
3-многообразий. Обозначим класс изоэнергетических 3-многообразий
(для интегрируемых систем) через (Я). Как доказали С. В. Мат-
Матвеев и А. Т. Фоменко, все 3-многообразия малой сложности лежат
в классе (Я), причем первые многообразия не из класса (Я) яв-
являются гиперболическими. Далее было выяснено, что среди не-
неприводимых атррических многообразий сложности не более чем 3
с краем тор .имеется ровно два гиперболических многообразия
Q\d и О_2д сложности 2 и девять гиперболических многообразий
Qid, 3^t^ll, сложности 3. Каждое из них порождает серик^ зам-
замкнутых гиперболических многообразий (Qid)P,q, где р и q — целые
взаимно простые числа. Затем -с помощью геометрического мето-
267
да были вычислены объемы около 100 многообразий каждой се-
серии, т. е. всего около тысячи объемов. Минимальный объем среди
многообразий (Qid)p,q имеет замечательное многообразие Qi =
= (QiaM,-2, следующий объем — многообразие Q2=(Q2a)s.i. Мно-
Многообразие Q2, как выяснилось, было известно Тёрстону, который
выдвинул его в качестве кандидата в гиперболическое многообра-
многообразие минимального объема. Так как объем многообразия Q\
( = 0.94) меньше объема многообразия Q2 ( = 0.98), то это предпо-
предположение неверно. Итак:
1). Все замкнутые ориентируемые 3-многообразия сложности
не больше 8 лежат в классе,(Я).
2) Все компактные неприводимые атор,ические ориентируемые
многообразия сложности не более 3 с торическими краями лежат
в классе (Я), кроме ровно двух многообразий Q\d и Q2d сложно-
сложности 2 и девяти многообразий Qf сложности 3. Эти 11 многообра-
многообразий допускают гиперболическую структуру и поэтому заведомо не
лежат в классе (Я).
3) Результатом вычислительного эксперимента (на ЭВМ) яв-
является таблица, состоящая примерно из 1000 объемов гиперболи-
гиперболических многообразий вида (Qid)P,q, вычисленных до 5-го знака.
- 4) Следствие: многообразие Q\ .имеет наименьший объем
.среди многообразий (Qid)p,q- Гипотеза 1: многообразие Q\
имеет наименьший объем среди всех 'замкнутых гиперболических
многообразий. Гипотеза 2: обнаруженное нами распределение
объемов многообразий (Qid)p,q изображает начальный отрезок
ряда объемов всех гиперболических замкнутых многообразий. Эта
информация очень важна, так как, согласно Тёрстону, гиперболи-
гиперболический объем является топологическим инвариантом многообразий
постоянной отрицательной кривизны. Следовательно, эти объемы
изображаются какими-то замечательными числами, изучение ко-
которых представляет п самостоятельный интерес. Гипотеза 3:
внутри каждой серии многообразий Мр,п (где М — многообразие с
торическим краем) объем растет вслед за ростом сложности. Да-
Далее мы приводим некоторые обоснования этих гипотез.
5) Найдено много замкнутых негомеоморфпых гиперболических
многообразий одинакового объема. Подробная статья, посвящен-
посвященная этому вопросу, будет опубликована в «Успехах математиче-
математических наук», 1988 г.
ГЛАВА 6
ГЕОДЕЗИЧЕСКИЕ ПОТОКИ НА ДВУМЕРНЫХ
РИ1У1АНОВЫХ МНОГООБРАЗИЯХ
-§ 1. Топологические препятствия к аналитической полной
интегрируемости
1.1. Неинтегрируемость уравнений движения натуральных ме-
механических систем с двумя степенями свободы на поверхностях
большого рода. Рассмотрим натуральную механическую систему с
двумя степенями свободы. Это означает, что ее конфигурационное
пространства двумерно. Будем предполагать, что оно является
двумерным компактным ориентируемым вещественно-аналитиче-
вещественно-аналитическим многообразием М2. Из элементарной топологии известно, что
такое многообразие диффеоморфно сфере S2, к которой приклеено
некоторое количество g ручек (рис. 112). Число g обычно назы-
называется родом поверхности. Известно также, что род — единствен-
единственный топологический инвариант замкнутых ориентируемых связных
поверхностей, т. е. две поверхности указанного типа диффеоморф-
ны в том и только в том случае, когда их род совпадает.
Рассмотрим кокасателыюе расслоение Т*М2 к многообразию
М2. Хорошо известно, что кокасателыгое расслоение Т*Мп произ-
произвольного гладкого многообразия Мп можно естественным образом
превратить в симплектическое многообразие. Для этого достаточ-
достаточно предъявить симплектическую структуру на Т*Мп, т. е. замкну-
замкнутую невырожденную 2-форму. Рассмотрим проекцию р:Т*М—>М,
где р(х, |) =х, х^М, |еГж*М. Многообразие Т*М является рас-
расслоенным пространством, базой которого будем считать М, а
•слоями р (х) — кокасательные пространства ТХ*М.
Определим на Т*М 1-форму а. Пусть а^Ту(Т*М)—вектор,
касательный к многообразию Т*М в точке у=(х, £). Так как р
отображает Т*М в М, то его дифференциал dp отображает
ТУ(Т*М) в TP{V)M, где р(у)=х и у=(х, 1). Положим а(а)=A,
■dp(а)), где через (,) обозначено значение ковектора | на векто-
векторе dp(а). В других обозначениях значение ковектора на векторе
можно записать как l(dp(a)). В качестве 2-формы мы возьмем
■м---da, где d — внешнее дифференцирование.
Лемма 1. Определенная выше замкнутая дифференциальная
2-форма со невырождена, а потому задает симплектическую струк-
структуру на 2п-мерном многообразии Т*М.
Доказательство. Введем на Мп локальные регулярные
координаты' х\,... ,хп- Тогда ковектор g, являющийся 1-формой
на ТХМ, задается сопряженными координатами |ь...,^„. Из
271
эпределенпя формы со следует, что w = d%i/\dxi + ... + d%nf\dxn.
Это означает невырожденность формы м.
Итак, фазовое пространство механической системы имеет есте-
естественную симплектическую структуру. В нашем примере системы
: двумя степенями свободы кокасательное расслоение Т*М2 имеет
структуру четырехмерного симплектического, многообразия. Дви-
Движение системы описывается гамильтоновыми уравнениями
igradF, где F — вещественно-аналитическая функция на Т*М. Га-
Рис. 112
Рис. 113
иильтониан будем брать в виде F = K(x, %) + U(x), где К(х, |)
при всех х^М является квадратичной формой по переменным
1^ТХ*М, а функция U(х) зависит только от х. Функции К и U
будем считать вещественно-аналитическими. Обычно квадратич-
квадратичная форма К отождествляется с кинетической энергией системы, а
функция U—с потенциальной энергией системы (п называется
потенциалом). Тогда гамильтоновы уравнения системы (отиоси-
гелыю введенной выше симплектической структуры) запишутся
. I dF •. OF _
каноническим образом: s = , х = ——. be решения изобра-
дх dl
каются интегральными траекториями на многообразии Т*М. Воз-
Возникает вопрос: в каких случаях эта система интегрируема?
"Если конфигурационное пространство достаточно простое, то
гакие системы часто интегрируются. Таково, например, движение-
материальной точки по инерции по двумерной сфере или по дву-
двумерному тору, заданным в стандартных метриках. Здесь поверх-
поверхность имеет малый род: ноль (для сферы) и единица (для тора).
Если же риманова метрика на сфере и на торе не стандартная, то
:оответствующая система может не допускать интегрирования.
Тем не менее можно дать описание всех метрик на сфере и на
горе, для которых полное интегрирование возможно (в принци-
принципе), см. ниже.
272
В описанном случае препятствие к интегрируемости лежит в
свойствах метрик, т. е. носит метрический характер. Оказывается,
если конфигурационное пространство достаточно сложное (напри-
(например, если число-ручек больше единицы), то появляются чисто то-
топологические препятствия, запрещающие аналитическим гамиль-
тоновым системам иметь достаточное число аналитических ком-
коммутирующих интегралов.
Теорема 1 (В. В. Козлов [280]). Пусть вещественно-анали-
вещественно-аналитическое конфигурационное пространство М2 имеет род, больший
единицы, т. е. оно гомеоморфно сфере с g ручками, где g>l. Тог-
'т 9F • dF ,
да гамильтоновы канонические уравнения 1 = —, х=-£г, где
F(x, g) •—вещественно-аналитический гамильтониан на Т*М2, не-,
имеют первого интеграла, вещественно-аналитического на Т*М2 и
функционально независимого от интеграла энергии F(x, |).
В случае аналитических функций их независимость имеет ме-
место, если они независимы лишь в одной точке.
Если ослабить предположения теоремы 1 и ограничиться рас-
рассмотрением лишь гладких многообразий М2 и гладких гамильто-
гамильтонианов, то ее утверждение не имеет места, см. [65, 280].
Теорема 1 вытекает из более общего утверждения В. В. Козло-
Козлова о пеиптегрируемостн уравнений движения при фиксированных
достаточно больших значениях полной энергии (см. теорему 2
ниже). Рассмотрим четырехмерное многообразие Т*М2 и систему
sgrad-F, где F = K+U. Поверхности уровня Qh=((x, |)e7"*Af:
:F(x, g) =h = const) задаются уравнением K+U = h и являются"
трехмерными аналитическими подмногообразиями в 7"*Л12, если
постоянная энергии h достаточно велика. А именно достаточно
предположить, что /г>тах U, где максимум потенциальной энер-
энергии U берется по всему многообразию М. Тогда K — h — £/>0 иа
поверхности уровня F = h. Так как К является положительно опре-
определенной квадратичной формой, то в каждой точке х&М уравне-
уравнение К(х, |) =h+ U(x)>0 определяет окружность в касательной-
плоскости (рис. 113). Здесь мы использовали предположение, что
h достаточно велико. Итак, при достаточно больших К поверх-
поверхность уровня гамильтониана оказывается трехмерным аналитиче-
аналитическим Многообразием Q, расслаивающимся над М2 со слоем окруж-
окружность. Так как поле sgradF касается поверхности Qh= (F = h), то
иа Qh3 мы получаем аналитическую систему уравнений.
Теорема 2 ([65]). Если род аналитической поверхности М2
(конфигурационного пространства исходной системы) больше
единицы, то при всех /i>max£/ аналитический поток sgrad Z7jq на
многообразии Q/,3 не имеет дополнительного непостоянного веще-
вещественно-аналитического интеграла.
1.2. Неинтегрируемость геодезических потоков на римановых
поверхностях большого рода с выпуклым краем. Пусть М — связ-
связное компактное двумерное аналитическое риманово многообразие
с краем дМ, гомеоморфным окружности (т. е. край связен). Из
элементарной топологии известно, что каждое такое многообразие
27а
получается следующим образом. Нужно выбросить из сферы с g
ручками некоторое число достаточно малых непересекающихся
дисков (рис. 114). Такое многообразие гомеоморфно плоской об-
области (граница которой связна) с g ручками. Рассмотрим эйле-
эйлерову характеристику %(М) такой поверхности. Она равна 1 — ранг
Я](М, Z). Предположим, что поверхность связна. Такая поверх-
поверхность гомотопически эквивалентна так называемому «букету» не-
нескольких окружностей, т. е. получается'из набора окружностей их
склейкой в одной точке (рис. 115). Число k таких окружностей
как раз и равно рангу одномерной группы гомологии Н\(М, Z).
Эта группа свободна и изоморфна Z0...0Z (k раз). Например,
Рис 114
Рис. 115
:выбрасывая из тора диск, получим тор с дыркой, гомотопически
•эквивалентный букету двух окружностей. Здесь k = 2, %(M) = l —
— 2 = — 1 (рис. 115).
Рассмотрим на М геодезические, определяемые римаповой мет-
метрикой. Край дМ (вообще говоря, несвязный) называется локально
геодезически выпуклом, если любые две достаточно близкие точ-
„ки х и у, лежащие на крае, соединяются единственной минималь-
минимальной геодезической, .целиком лежащей внутри многообразия М
(рис. 116).
Пусть Т*М — кокасательное расслоение и Н—квадратичная
■форма, задающая метрику. В каждой точке х^М она задает фор-
форму Н(х, |) =l1gij(x)%ic,j. Геодезический поток имеет функцию Я
своим первым интегралом. Трехмерные поверхности уровня Qh3
интеграла Н расслаиваются над поверхностью М со слоем окруж-
окружность, если /г>0. Фиксируем значение h=\ и рассмотрим! много-
многообразие Qi3.
274 -
Теорема 3 (С. В. Болотин). Пусть М — связное риманова
компактное двумерное вещественно-аналитическое многообразие с
локально геодезически выпуклым краем и такое, что х(М)<0 То-
toa геодезический поток римановой метрики на трехмерном 'мно-
'многообразии постоянной энергии h=\ не имеет аналитического пер-
первого интеграла (независимого с интегралом энергии и находя-
находящимся с ним в инволюции на Т*М).
0"
A
'о
и-
В
с
о1
А1
и
Рис. 117
1.3. Неинтегрируемость задачи п гравитирующих центров при
я>2. Пусть zu...,zn — различные точки комплексной плоскости
•С. Функция Гамильтона задачи п притягивающих центров имеет
вид ..
где U = C\(zu ... ,zn) — конфигурационное пространство, а V —
потенциал гравитационного притяжения точки z<=U точками zu...
п
...,zn, т. е. V(z)=—J |i,/|z—z,|; |i/>0. Так как V<0, та
при /г>0 уровень (H = h) интеграла энергии И является аналити-
аналитической гиперповерхностью в фазовом пространстве Qi3.
Теорема 4 (С. В. Болотин [20]). Пусть п>2. Тогда при
/г>0 задача п гравитирующих центров не имеет аналитических
первых интегралов на уровне интеграла энергии (H = h).
Таким образам, задача п гравитирующих центров интегрируе-
интегрируема но Лиувиллю в области (Я^О) только в случаях Кеплера и
Эйлера. Вопрос об интегрируемости задачи п гравитирующих цен-
центров в области (Я<0) остается пока открытым. Классические ме-
методы теории возмущений (А. Пуанкаре), по-видимому, неприме-
неприменимы для доказательства неинтегрируемости этой задачи.
1.4. Неинтегрируемость некоторых гироскопических систем. На-
Назовем механическую систему с конфигурационным пространством
М и кинетической энергией Т гироскопической, если кроме потен-
27S
идеальных сил, задаваемых потенциальной энергией V, па нее дей-
действуют гироскопические силы, задаваемые дифференциальной
2-формой Г на М. В локальных координатах Г — кососимметриче-
кососимметрическая матрица гироскопических сил'. Обычно предполагается, что
форм*а Г замкнута, т. е. cfF = O. Тогда гироскопическая система яв-
является гамнльтоновой системой с функцией Гамильтона H=T-*-V
на фазовом пространстве Т*М и гамильтоновой структурой Q-b
+ л*Т, где Q — стандартная гамильтонова (симплектическая)
структура наТ*М, а я : Т*М-*-М — проекция.
Для применения методов вариационного исчисления в целом
важно знать, когда гироскопическая система является лагранже-
вой, т: е. описывается уравнениями Лагранжа с функцией Лагран-
жа L на ТМ. Для этого необходимо и достаточно, чтобы форма
гироскопических сил была точна, т. е. T = dA, где Л — дифферен-
дифференциальная 1-форма на М.
Тогда симплектическая структура на Т*М имеет вид Q + jx*F =
= d(pdq + n*A), где pdq — каноническая 1-форма на Т*М. Преоб-
Преобразование f :T*M^>~T*M, p-yp + A(q)eT,,*M переводит Q + jt*F в
стандартную гамильтонову структуру на Т*М, т. е. /*Q = Q + n*F.
Для соответствующей функции Гамильтона HA=f*H на Т*М
имеет место выражение
pe=Tq*M,
а для полученной преобразованием Лагранжа функции Лагранжа
L на ТМ — выражение LA(q, q) =T(q, q) — V(q) — A(q) q,
Пусть рассматриваемая гироскопическая система имеет две
степени свободы. Тогда условие dY = 0 удовлетворяется автомати-
автоматически и по теореме де Рама гироскопическая система лагранжева,
если М некомпактно или если М компактно и ПлгГ = 0. Если же
М компактно и Jf^F^O, то гироскопическая система не является
лагранжевой.
Пример 1. Для гироскопической системы, возникающей на
•сфере Пуассона М после исключения интеграла площадей в ди-
динамике твердого тела (см. [65]), имеем Y = odS, где а — значение
постоянной площадей, a dS — элемент площади на сфере М. По-
Поэтому $)мГ==4яа, так что при афО гироскопическая, система не
является лаграпжевой.
Формулируемые ниже результаты принадлежат С. В. Боло-
типу.
Без ограничения общности можно считать, что конфигурацион-
конфигурационное'пространство М является аналитическим многообразием. Имея
в виду приложения к небесной механике, предположим, что потен-
потенциальная энергия V имеет особенности в точках конечного множе-
множества Ес:/И. Тогда фазовым пространством гироскопической снете-
мы является Т*(M\Z). Пусть H = T+V — интеграл энергии на
7*(M\S). Болотин показал, что для лагранжгвых гироскопиче-
гироскопических систем с двумя степенями свободы наличие п~>2%{М) осо-
особенностей ньютоновского типа потенциальной энергии препят-
276
п'вует существованию аналитических первых интегралов на Т* (М\
.2), независимых с интегралом энергии И.
В случае п = 2%(М) наличие нетривиальных гироскопических
сил (например, если H-m1V=0) препятствует существованию пер-
пых интегралов класса С1 на Т*(М\2), полиномиальных по им-
импульсу и независимых с Н. Здесь %(М)—эйлерова характеристи-
характеристика М.
Пример 2. Ограниченная задача многих тел. Пусть п точек
ги...;2п закреплены в плоскости М, вращающейся вокруг точки
О с постоянной угловой скоростью о), а точка zeAf движется под
действием гравитационного притяжения точками Zi,...,zn. Потен-
п
циальная энергия V (г) = —( V \ij|г—г,-1 + со21z\2/2), ц/ > 0 име-
имеет особенности на множестве 2 = {zi,... ,zn}czM. Матрица гиро-
гироскопических сил имеет вид 2 1 1, а форма—вид Г =
\о) 0 /
= 2(odS, где dS — элемент площади на М. Эта гироскопическая-
система интегрируема при я=1 и всех <о (задача Кеплера), а так-
также при п = 2 и » = 0 (задача Эйлера). При п — 2 и «=^=0 (ограни-
(ограниченная задача трех тел) А. Пуанкаре доказал несуществование
аналитических первых интегралов, аналитических по параметрам
\ц и независимых с интегралом Якоби II, а К. Л. Зигель доказал
несуществование алгебраических первых интегралов, независимых
с Н. Оказывается, что при п>2 для всех ы не существует анали-
аналитических первых интегралов задачи многих тел, независимых с
интегралом Якоби. Поскольку х(М) = 1> эти свойства ограничен-
ограниченной задачи многих тел согласуются с приведенным выше общим
•утверждением.
§ 2. Топологические препятствия в аналитической
интегрируемости геодезических потоков на многомерных
неодносвязных многообразиях
Мы уже видели, что в двумерном случае пеодпосвязпость мно-
многообразия может влиять на интегрируемость системы, а именно:
если фундаментальная группа «достаточно большая», то аналити-
аналитических интегралов не существует (см. выше). В этом параграфе
мы изложим обобщение теорем 1 и 2 § 1. Это обобщение недавно
пблучепо И. А. Таймановым и справедливо для римаповых анали-
аналитических многообразий произвольной размерности, обладающих
«достаточно большой» фундаментальной группой.-
Пусть М" — замкнутое многообразие. Рассмотрим геодезиче-
геодезический поток на М, который па кокасательном расслоении Т*М
(снабженном естественной симплектической структурой) является
гамильтоповым с гамильтонианом Я (х, p)^(\j2)I1g[jpjpl; где х е
gM, р( —координаты в слое кокасателыюго. расслоения ТХ*М,
gij — риманова метрика на М.
' 277
По теореме Лиувилля для достаточно хорошего описания гео-
геодезического потока следует найти набор из п функционально неза-
независимых инволютивных первых интегралов потока. Один интеграл
мы уже имеем — это гамильтониан Н. Поэтому всегда можно ре-
редуцировать геодезический поток на уровень постоянной энергии
Н=\, который мы обозначим через L. На многообразии L задано
отображение момента frL-^R", F(q) = (Ii(q),...,In-\(q)), где
/i,...,/n_i, In — H — полный набор функционально независимых
первых интегралов в инволюции. Определим понятие геометриче-
геометрически простого набора первых интегралов.
Определение 1. Полный'набор инволютивных первых ин-
интегралов геодезического потоке Л In-\, In^H называется гео-
геометрически простым, если:
1) в поверхности L содержится замкнутое множество Г такое,,
что L\T открыто и всюду плотно, имеет конечное число компо-
компонент линейной связности L\r = U'a=i^a и па £\Г отображение
момента F имеет максимальный ранг;
2) отображение F: Ua-+F(Ua) является расслоением на га-
мильтоновы n-мерные торы над областями F(Ua), гомеоморфны-
ми (п — 1)-мерным дискам F(Ua) »Dn~';
3) для любой точки q^L существует окрестность W(q) такая,,
что №(д)П(£\Г) имеет конечное число компонент линейной связ-
связности.
Оказывается, геометрически простые полные инволютивные на-
наборы интегралов могут существовать лишь на многообразиях с
«достаточно небольшой» фундаментальной группой (или группой
одномерных гомологии). Более точно, имеет место следующее
утверждение.
Теорема 1 (И. А. Тайманов). Если фундаментальная груп-
группа п\ (М) замкнутого риманова многообразия Мп не является по-
почти коммутативной, т. е. не содержит коммутативной подгруппы
конечного индекса, то геодезический поток на М не допускает гео-
геометрически простого набора первых интегралов.
Т е о р е м а 2 (И. А. Тайманов). Если 6\mH\ (M, Q) >dimAf, та
геодезический поток на Мп не допускает геометрически простого-
полного набора первых интегралов.
Если конфигурационное пространство двумерно, то отсюда
следует (в аналитическом случае) теорема 1 § 1. Отметим, что-
теоремы 1 и 2 настоящего параграфа применимы лишь к геодези-
геодезическим, потокам на кокасательных расслоениях к римановым мно-
многообразиям. Было бы интересно получить аналогичные утвержде-
утверждения для произвольного симплектического многообразия. Это поз-
позволило бы выяснить, какие универсальные топологические препят-
препятствия мешают существованию полного набора инволютивных ин-
интегралов в многомерном случае (например, боттовских интегра-
интегралов). В этом направлении следует развить наши результаты гл. 4.
Рассмотрим аналитический случай. Пусть Мп — аналитиче-
аналитическое многообразие с аналитической метрикой. В этом случае с по-
помощью результатов А. М. Габриэлова [111, 36], продолжающих
278
работы С. Лоясевича [223], доказывается тот факт, что полный
набор инволютивных аналитических интегралов геометрически
прост. Это следует из полуаналитичности множества критических
шчек отображения момента F: L-vR" и вытекающей отсюда
конструктивности (в смысле работы [111]) множества критиче-
критических значений, дополнение к которому в Rn~~' имеет конечное чи-
число компонент линейной связности. Дополнив множество критиче-
критических значений d добавочным конструктивным множеством С2, со-
состоящим из «перегородок», можно добиться того, чтобы множест-
множество Rn~1\(CiLJC2) распадалось на конечное число дисков. Тогда
Y = F~X (C1LJC2) и условие 3 следует из замкнутости семейства кон-
конструктивных множеств относительно взятия полного прообраза
при собственном аналитическом отображении.
Таким образом, из этих замечаний и из теорем 1 и 2 вытекают
следующие утверждения
Теорема 3 (И. А. Тайманов). Если фундаментальная груп-
группа п\(М) аналитического замкнутого риманова многообразия Мп
не является почти коммутативной, то геодезический поток не об-
обладает полным инволютивным набором аналитических функцио-
■ нально независимых первых интегралов, т. е. не интегрируем по
Лиувиллю в классе аналитических интегралов.
Теорема 4 (И. А. Тайманов). Если &\тН\(М, Q)>dimM,
то геодезический поток на замкнутом аналитическом многообра-
многообразии не обладает полным инволютивным набором аналитических
функционально независимых первых интегралов.
Замечание 1. С топологической точки зрения почти комму-
коммутативность фундаментальной группы ni {M) эквивалентна сущест-
существованию конечнолистного накрытия р : М->-М, где группа п\(М)
уже коммутативна.
Замечание 2. Известно, что если замкнутое многообразие
М допускает метрику строго отрицательной кривизны, то группа
п\ {М) некоммутативна и максимальная коммутативная подгруп-
подгруппа в ni(Af) является бесконечной циклической [243]. Ясно, что
такие фундаментальные группы щ{М) не являются почти комму-
коммутативными и к таким многообразиям указанные теоремы неприме-
неприменимы.
§ 3. Интегрируемость и неинтегрируемость геодезических
потоков на двумерных поверхностях, на сфере и торе
3.1. Голоморфная 1-форма полиномиального по импульсам ин-
интеграла геодезического потока и случай рода g>\. Напомним не-
некоторые определения. Рассмотрим симплектическое многообразие
Т*Мп. Пусть на М заданы локальные координаты qx qn. Тогда
координаты на Т*М записываются в виде 9i.---.9n, р\,...,рп-
(Тёо&езическим потоком*) риманова многообразия М с метрикой
us^ = 2gjjdqjdq) называется лагранжева система в касательном
расслоении ТМ с функцией Лагранжа L = 2g',j^^-. Отождествляя
ТМ и Т*М при помощи римановой метрики, можно считать, что
279
геодезический поток действует в Т*М. Соответствующая система
оказывается гамильтоновой, причем гамильтониан Н является
преобразованием Лежандра функции Лагранжа L, т. е. Я = 2а^Х
XpiPj, где матрица А—(ац), задающая гамильтониан Н, связана
с матрицей G—{gij), задающей L, соотношением A = G~xj\.
Полиномиальным по скоростям интегралам в ТМ соответ-
соответствуют полиномиальные по импульсам интегралы соответствую-
соответствующей системы в Т*М. Перечислим новые результаты, которые были
получены В. Н. Колокольцовым. При этом следует отметить, что
теоремы 1 и 3 (см. ниже) фактически являются переформулиров-
переформулировкой в современной терминологии результатов, полученных
Дж. Д. Биркгофом в [281]. Биркгоф рассматривал не только аб-
абсолютные, по и условные интегралы (на одной поверхности
уровня).
Теорема 1. Предположим, что в области f/ciR2 задана та-
такая риманова метрика ds2 = k(x, у) (dx2 + dy2) класса гладкости
С1, что определяемый ею локальный геодезический поток, т. е. га-
милътонова система в T*U с гамильтонианом Н = Х~Х (рх2 + ру2)/2у
имеет однородный по импульсам интеграл
т=0
Тогда функция R(z) = (b0—b2+...)+i(bl — Ь3+...) является
голоморфной функцией комплексного переменного z = x+iy. Кро-
Кроме того, если в некоторых других изотермических координатах (и,'
v), связанных с (х, у) голоморфным преобразованием w(z), где
w = u+iv, интеграл Fn выражается формулой
т=0
Ч
то голоморфные функции R(z) и
п.
- S(w) = (c0—c2\-...)+i{c1—c3+...)=yj
т=0
связаны формулой
Отсюда вытекает, что в окрестности всякой точки, не принад-
принадлежащей множеству нулей функции R(z), инвариантно определе-
определена голоморфная 1-форма w =dzj-\fR (г), которую естественно на-
назвать голоморфной формой, ассоциированной с данным полиноми-
полиномиальным интегралом.
Из теоремы 1 сразу получаем следствие.
Теорема 2 ([72]). Геодезический поток класса гладкости
С1 на компактном двумерном ориентируемом многообразии М ро-
280
не может обладать дополнительным аналитическим по
импульсам первым 'интегралом (непрерывно дифференцируемым в
Т*М), независимым с интегралом энергии.
Поскольку аналитический по импульсам интеграл можно раз-
разложить в сходящийся ряд по однородным полипомам, которые,
очевидно, инвариантно определены в Т*М и также являются инте-
интегралами заданного геодезического потока, то теорема 2 эквива-
эквивалентна следующему утверждению: всякий однородный полиноми-
полиномиальный по импульсам интеграл этого потока имеет вид F = cHm,
где c<=R, meZ.
Пусть Fn — однородный степени п полиномиальный интеграл.
Тогда функция R{z), определяемая в силу теоремы 1 интегралом
Fп в произвольных изотермических координатах, тождественно
'равна нулю.
Далее, обращение функции R(z) тождественно в ноль эквива-
эквивалентно тому факту, что интеграл Fn разлагается в произведение
гамильтониана Н и однородного интеграла Fn-2 степени п — 2.
Функция F на Т*М является первым интегралом системы с га-
гамильтонианом Н тогда и только тогда, когда {//, F} = 0. Если мно-
многообразие М двумерно, то квадратичные по импульсам интегралы
имеют вид F = I,bij(qu q2)PiPj, где B=(bi}) —симметрическая мат-
матрица порядка два. Воспользовавшись координатным представле-
представлением скобки Пуассона
2
,„ д.ч _Y1 dF дН дН 3F
' '~U dPi d4i dPi dqi
и приравняв нулю коэффициенты этого полинома, получим систе-
систему уравнений на коэффициенты матриц А и В. Запишем эти урав-
уравнения в изотермических координатах х, у, в которых метрика при-
принимает вид К(х, y)(dx2 + dy2). Такие координаты, как хорошо из-
известно, всегда существуют (локально) для любой метрики класса
гладкости С2 на двумерном многообразии. В них функция Н имеет
вид Н= (pi2 + p22)/4A,. Если ввести новую функцию v = —lnDX), то
система уравнений примет вид
y, '
b22Vy,
bl2vx + b22vy,
Отсюда следует, что R(z) = (bn — Ь22) + 2/t»i2 — голоморфная
функция от переменной z=x+iy. Если Ri==bn — bi2, 2R2 = 2bl2 —
соответственно вещественная и мнимая части функции R(z), то
матрица интеграла имеет вид В— J * 2 I, где b — b22.
\ R2 b }
281
Получаем следующее основное уравнение на функцию X:
ду* дх2 ) 1 дхду дх дх
^^ -^=0, ' B)
+ 3 + 20,
ду ду 5у2
которое является линейным уравнением второго порядка, гипербо-
гиперболическим во всех точках за исключением нулей функции R.
Предложение 1. Пусть A, :Z)->-R—положительная функция
класса С2, заданная в области Z)c=R2. Риманова метрика Х(х, у)Х
X{dx2 + dy2) определяет в T*D геодезический поток, который
имеет дополнительный квадратичный по импульсам интеграл F
тогда и только тогда, когда функция X удовлетворяет уравнению
B), где R = R\ + 2iR2 — голоморфная в D функция, не являющаяся
тождественным нулем, причем в этом случае коэффициенты мат-
матрицы (bjj) интеграла F выражаются через X и R по формулам
b\2 = R2, b\\ = b22 + Ru где Ь22 — Ь выражается через функцию X в
явном виде.
Посмотрим теперь, как преобразуются функции R и X при про-
произвольной голоморфной замене координат. Пусть w(z)—u(x, у) +
+ iv(x, у) —голоморфная замена координат, X\(w)=X\{u, v) —
функция, задающая метрику Х\{и, v)(du2 + dv2) в изотермических
координатах и, v, a S(w)—связанная с интегралом Г голоморф-
голоморфная функция, соответствующая координатам и, v. Тогда справед-
справедливы формулы
Xl(w)-\w'(z)\^ = X(z), . C)
S (ш) (ш'(*))-*= Я (z). D)
Теорема 3 ([281], [72]). Геодезический поток в Т*М, где
М — двумерное риманово многообразие, имеет дополнительный
квадратичный по импульсам интеграл тогда и только тогда, когда
■ в любых изотермических координатах х, у функция X, задающая
метрику, удовлетворяет уравнению B), где R = R\ + 2iR2 — голо-
голоморфная функция от переменной z=x+iy, не равная тождествен-
тождественно нулю и преобразующаяся при переходе к другим изотермиче-
изотермическим координатам в соответствии с формулой D).
Рассмотрим решения основного уравнения B) при произволь-
произвольной голоморфной функции R(z)^kO. Тогда Х\\и, v)=f(u) + h(v),
где / и h — произвольные функции класса С2. Из формулы C) по-
получаем .
^/ ч _ МИ*. У)) + М»(*. У))
1 ' |Л(г)|
Метрики вида (f(x)+h(y))(dx2 + dy2) называются лиувилле-
выми. В последних рассуждениях содержится, в частности, клас-
классический результат (Биркгоф), согласно которому любая римано-
282
ни метрика, геодезический поток которой имеет дополнительный
квадратичный по импульсам интеграл, в некоторых . подходящих
Координатах имеет лиувиллев тип. Следовательно, в этом случае
уравнения геодезических интегрируются методом разделения пе-
переменных.
3.2. Случай сферы и тора. Задание метрики класса С2 на ком-
компактном двумерном ориентируемом многообразии превращает его
о риманову поверхность. Картами на ней служат локальные кар-
карты изотермических для этой метрики координат. Риманова метри-
метрика на сфере S2 порождает риманову поверхность, которая гомео-
морфна S2 и, следовательно, конформно эквивалентна сфере со
стандартной комплексно-аналитической структурой. Следователь-
Следовательно, для любой римановой метрики на сфере существуют изотерми-
изотермические координаты, заданные на всей сфере без одной точки. Та-
Такие координаты естественно назвать глобальными изотермически-
изотермическими координатами. Ясно также, что все системы глобально изотер-
изотермических координат связаны между собой дробно-линейными пре-
преобразованиями. Оказывается, для тех метрик на сфере, которые
допускают дополнительный интеграл, квадратичный по импуль-
импульсам, описание можно получить в «явном виде».
Теорема 4 (В. Н. Колокольцов [72]). Метрика на двумер-
двумерной сфере класса С2, геодезический поток которой имеет дополни-
дополнительный квадратичный по импульсам интеграл, независимый с ин-
интегралом энергии, в некоторых изотермических координатах 2 =
= x+iy, заданных на сфере без одной точки (на сфере с выколо-
выколотой точкой), обязательно имеет вид Х(х, у) (dx2 + dy2), где функ-
функция X имеет один из видов, перечисленных ниже:
1) X — f(x2jry2), где f—положительная функция класса С2 такая,
что f (t) = — (а + О(I)) при t-^-oo; такие геодезические потоки име-
имеют линейный по импульсам интеграл;
1 г>\ 1 f(u(x> У)) + h (v (x> У)) ■ л
2) X = ——^—i-U—i—i—i—-LL—, где g2, g3 —■ такие вещественные
постоянные, что g^ —. 27g2 > 0, при этом и, v соответственно ве-
вещественная и мнимая части преобразования w (г) = Р (г), где Р (w) —
это ^-функция Вейерштрасса с инвариантами g2, g3 и парой перио-
периодов вида со1 и £сог с вещественными а>х и ©2, a f и h — функции клас-
класса С2 такие, что
а) /(«)==(«—&со1/2J(а + 0A)) при и-^-Ьш^ и аналогично h(v) =
= (v—k(o2/2J (a + О A)) при 1>->-&й2/2 для любого фиксированного це-
целого k, a > 0;
б) их значения на отрезках [(OJ2, ©J, [со2/2, <в2] определяются
через их значения на отрезках [0, ©1/2], [0, со2/2] по формулам
/(и1/2 + т)=/((о1/2-т), те [0, aJ2],
/г(аJ/2 + т)=/г(аJ/2—т), г е= [0, со2/2];
в) функции f и h периодические с периодом ол и со2 соответ-
соответственно; ясно, что при таких функциях i и h значение f(u(z)) +
283
■+h(v(z)) не зависит от выбора значения многозначной функции
P-'(z).
Обратно, положительная функция %: R2->-R, имеющая один из
двух указанных выше видов, задает риманову метрику на сфере
S2, геодезический поток которой имеет дополнительный квадратич-
квадратичный по импульсам интеграл, независимый с интегралом энергии.
Формулы для коэффициентов матрицы этого интеграла даны в
предложении 1.
Метрики из теоремы 4, отвечающие различным парам функций
/, h, неэквивалентны относительно действия группы диффеомор-
диффеоморфизмов сферы. Кроме того, группа движений каждой метрики рас-
рассматриваемого класса в том случае, когда функции f и h не совпа-
совпадают, состоит из четырех преобразований, задаваемых в координа-
координатах и, v формулой (и, и)->-(±а, ±v), а в случае совпадения функ-
функций { и h эта группа имеет еще один образующий элемент, зада-
задаваемый (как преобразование) формулой (u, v)->(v, и) (см.
рис. 117).
Классическими примерами геодезических потоков с квадратич-
квадратичными дополнительными интегралами являются геодезические по-
потоки на стандартных эллипсоидах (вообще, на квадриках в R3) и
геодезический поток фактор-метрики на сфере Пуассона, возни-
возникающий в классических задачах аналитической динамики.
Теперь рассмотрим геодезический поток на торе с дополни-
дополнительным, квадратичным по импульсам интегралом. Соответствую-
Соответствующая риманова поверхность имеет род один'и конформно эквива-
эквивалентна фактор-пространству С/Г группы С по подгруппе сдвигов
Г, порожденной двумя элементами gx : z-*-z+tou g2: 2-кг+со2, где
Im (©i/coa) Ф 0. Риманова метрика, заданная на С/Г, может быть
очевидным образом поднята на накрывающую поверхность, т. е.
на С. В результате получаем метрику на С, инвариантную отно-
относительно сдвигов g\ и #2. геодезический поток которой, очевидно,
имеет дополнительный квадратичный интеграл, также инвариант-
инвариантный. Так как при сдвигах координаты импульсов и скоростей пре-
преобразуются тождественно, то функция К, задающая метрику на С,
и голоморфная функция R, связанная с интегралом, инвариантны
относительно сдвигов g\ и g2- Следовательно, поворотом можно
добиться того, чтобы /?= 1.
Эти координаты лиувиллевы, и в них функция имеет вид к =
= f(x)+h(y). Выше было показано, что такая функция класса С2
инвариантна относительно g\ и g2 лишь в том случае, когда среди
ее параллелограммов периодов есть прямоугольник и функции f
и h периодичны. Обратно, всякая положительная функция Л,=
— f (x) +h(y) с периодическими f и h задает метрику на некотором
торе. При этом первый интеграл геодезического потока этой мет-
метрики имеет вид
' Иу) 9 fix) 9
/(х)+/!(</)' f(x)+h(y)yr
284
Таким образом, описан класс римановых метрик на сфере и
на торе, допускающих дополнительный интеграл, квадратичный
по импульсам.
Полезно сделать следующее замечание. Описанные выше не-
необходимые и достаточные условия пока еще недостаточно эффек-
эффективны в следующем смысле. Пока нет ответа на следующий во-
вопрос: как узнать, допускает ли заданная метрика иа сфере или на
торе дополнительный интеграл? Согласно теореме 4 это будет так
в том и только в том случае, когда в некоторых изотермических
координатах (на сфере с выколотой точкой) исследуемая метрика
приводится к одному из двух видов, указанных в теореме. Однако
для окончательного ответа на вопрос следует найти эти подходя-
подходящие изотермические координаты или же, напротив, доказать, что
таких нет. В последнем сдучае надо доказать, что ни в каких изо-
изотермических координатах исследуемая метрика не допускает ка-
канонического представления, указанного в теореме.
Другими словами, нужен эффективный критерий проверки сле-
следующего факта: допускает ли данная метрика нужный вид в не-
некоторых изотермических координатах? Возможно, это ее свойство
может, быть «уловлено» какими-то инвариантами и связано с воз-
возможностью изометрического вложения метрики в трехмерное ев-
евклидово пространство.
3.3. Свойства геодезических интегрируемых потоков на сфере.
Говорят, что риманоно многообразие М называется SCi-многооб-
разием, если все геодезические на М являются простыми (т. е. са-
самонепересекающимися) замкнутыми кривыми длины /. При этом
мы рассматриваем, конечно, лишь однократные геодезические.
Среди двумерных ориентируемых замкнутых многообразий
только сфера допускает геодезические потоки, у которых все гео-
геодезические замкнуты. Классическими примерами многообразий с
такими метриками являются поверхности вращения Цолля и их
модификации, предложенные Бляшке и Томсоном. Эти модифици*
рованные поверхности составлены из кусков поверхностей вра-
вращения.
Впервые вопрос о построении нетривиальных поверхностей с
замкнутыми геодезическими обсуждался, по-видимому, Дарбу
ЦЯЦ-г~&уд£м говорить, что риманово многообразие удовлетворяет
SC-свойству^уеслп существует такое число £>0, что любая геоде-
"зи^гест^ан нам является простой замкнутой кривой длины / (или ее
кратностями).
Дарбу установил условие, которому должно удовлетворять
уравнение плоской кривой для того, чтобы получаемая вращением
этой кривой поверхность обладала свойством SC. Он предложил
также красивый геометрический критерий, характеризующий та-
такие кривые. Однако у Дарбу не доказано существование глобаль-
глобальной, определенной на сфере S2 метрики, удовлетворяющей SC-
свойству.
Следующий шаг был сделан в конце прошлого века Таннери,
который построил так называемую «грушу», на которой все гео-
285
дезические замкнуты и имеют наименьший период /, за исключе-
исключением экватора, наименьший период которого равен IJ2. Эта груша
является алгебраической поверхностью, но не является гладким
многообразием, потому что в одной точке имеет особенность.
Вопрос о построении нетривиальной гладкой SC-метрики на
S2 был решен в 1902 г. Цоллем [262], который в явном виде скон-
сконструировал вещественно-аналитическую SC-поверхность враще-
вращения, го,меоморфную S2. Несложное обобщение конструкции Цолля
приводит к построению зависящего от функционального параметра
семейства гладких SC-метрик на S2, инвариантных относительно
вращений вокруг некоторой оси [14]. В своей книге [15] Бляшке
предложил изящную модификацию конструкции Цолля, позволяю-
позволяющую строить гомеоморфные сфере SC-мпогообразия, не являю-
щиеся поверхностями вращения. Поверхности Бляшке склеивают-
склеиваются из кусков различных SC-поверхностей вращения с помощью
пленок, изометричных частям стандартной сферы.
В 1913 году в статье [194] Функ попытался построить однопа-
раметрическое семейство SC-метрик вида ф@й./ на S2, где g(/ —
стандартная метрика, в виде суммы ряда с начальными условия-
условиями ф @) = 1 и — h для произвольной нечетной функции
At
h на S2, т. е. такой функции, что ha =—h для антиподального
отображения а -сферы S2. Ему, однако, не удалось доказать сходи-
сходимость построенных рядов.
Существование деформаций этого вида для каждой нечетной
начальной производной недавно доказал Гийемин в работе [200],
используя мощные средства современного глобального анализа.
Из результата Гийемина вытекает, в частности, что в достаточно
малой окрестности стандартной метрики на сфере S2 существует
весьма богатое семейство гладких метрик, удовлетворяющих
5С-свойству, но не допускающих никаких изометрий, кро-
кроме тождественного отображения. Отметим здесь, что это, по суще-
существу, лишь теорема существования, так как явных формул для этих
метрик в [200] не приведено. Глубокое доказательство Гийемина
основано на применении теоремы о неявных функциях для функ-
функциональных многообразий типа Фреше.
Современное состояние проблемы описания многообразий
с замкнутыми геодезическими наиболее полно представлено в кни-
книге А. Бессе [14].
Опуская здесь обсуждение проблемы для многообразий раз-
размерности, большей двух, где имеется много красивых результатов,
но, как отмечал Бессе, многие основные вопросы остаются пока
открытыми, укажем лишь на единственное общее условие, необхо-
необходимое для того, чтобы риманово многообразие удовлетворяло
SC-условию. А именно, как показал Вейнстейн [257], полный объ-
объем римаиова d-мерного SC-многообразия с периодом 2я равен
целому кратному объема стандартной d-мерной сферы.
Даже в размерности два проблема классификации и описания
SC-многообразий еще далека от полного разрешения. Из общей
286
теоремы Ботта и Самельсона о топологии 5Ст-многообразий (т. е^
таких многообразий, у которых все геодезические, исходящие и?
некоторой точки т, замкнуты) вытекает, что среди двумерных
многообразий лишь на сфере и на проективном пространстве RP2
существуют метрики, удовлетворяющие SC-свойству.. В 1961 г.
Л. Грин доказал гипотезу Бляшке [199]. Согласно этой гипотезе
ьсякая SC-метрика на RP2 изометрична стандартной. Поэтому
среди двумерных многообразий лишь на сфере существуют не-
нетривиальные SC-структуры. Про них известны два общих резуль-
7ата Вейнстейна. Первый заключается в том, что геодезические
потоки, порожденные двумя метриками на сфере, обладающими.
SC-свойством, сопряжены посредством симплектического диффео-
диффеоморфизма. Из второго результата следует, что объем любого
SC-многообразия с периодом 2я (гомеоморфного сфере) равен
объему стандартной сферы.
Как мы видели выше, существует достаточно богатое семейство
метрик на двумерной сфере (зависящее от функционального па-
параметра), геодезический поток которых имеет дополнительный
интеграл, квадратичный по импульсам. Как недавно показал
В. Н. Колокольцов (см. [73]), в этом семействе можно явными
формулами выделить класс SC-метрик, т. е. таких метрик, для
которых все геодезические замкнуты.
Можно качественно описать поведение таких геодезических.
На сфере существуют две пары «точек округления» таких, что
все геодезические, выходящие из одной такой точки, собираются
в противоположной ей точке. Касательные векторы к этим геоде-
геодезическим образуют в расслоении векторов единичной длины, ка-
касающихся сферы (это трехмерное расслоение PS2 является частью
касательного расслоения TS2 к сфере), двумерную пленку, есте-
естественным образом разбивающую расслоение PS2 (гомеоморфное
трехмерному проективному пространству) на два полнотория.
Эта картина аналогична структуре геодезического потока на эл-
эллипсоиде. —j
Новые инварианты интегрируемых сйстем\ В заключение вер-
вернемся к инварианту интегрируемых систем, обнаруженному авто-
автором [290].
В Приложении 7 доказывается, что несовпадение значений
I(H\, Qi) и I(H2, Qz) изоэнёргетического инварианта для двух ин-
интегрируемых гамильтоновых систем означает, что системы тополо-
топологически неэквивалентны (т. е. не существует диффеоморфизма
изоэнергетической поверхности, переводящего торы Лиувилляс
1-ii системы в торы Лиувилля 2-й системы). Однако пока из со-
совпадения. 1{Н\, Qi) ,и 1{Н2, Q2), вообще говоря, не следует, что си-
системы эквивалентны. Оказывается, можно снабдить изоэпергети-
ческий инвариант /(//, Q) числовыми метками, после чего этот
меченый инвариант /(//, Q)* приобретает следующее важное
свойство: если его значения для двух систем совпадают, то систе-
системы эквивалентны, и если его значения для двух систем различны,
то системы не эквивалентны. «Изготовление числовых меток» для
28Г
инварианта I(H, Q) выполнено А. Т. Фоменко и X. Цишангом.
Тем самым, получается классификация всех интегрируемых, га-
мильтоновых систем (с точностью до их топологической эквива-
эквивалентности) и наглядное описание всего множества интегрируемых
систем. ■ . .
Вкратце опишем схему построения меченого инварианта. По-
Поверхность Р2 склеена из кусков Рс. Стянем на окружности все ци-
цилиндры, входящие в состав Р. В соответствии с этим стянем з
3-многообразии Q каждое многообразие Qc, являющееся произве-
произведением T2XD\ на критический тор. Эту операцию назовем редук-
редукцией. При стягивании цилиндра Рс (на Р), его образ, т. е. окруж-
окружность, обозначим через Кг, добавив ее к прежним окружностям
вида Кг. Рассмотрим над каждой окружностью вида Кг гранич-
граничный в (Qc) тор Лиувилля Тг2 = рс~1{Кг), где pc'Qc-^Pc. — проек-
проекция. Выберем базисы на каждом из таких торов. Допускаемая
при этом степень произвола це влияет на дальнейшую конструк-
конструкцию. Так как Q склеено из кусков Qc, то соответствующие торы
Ту2 и ТГ'2 склеены в Q при помощи некоторого диффеоморфизма
1. Учитывая выбранные базисы циклов па торах, получаем цело-
целочисленные унимодулярные матрицы, отвечающие этим склейкам.
Обозначим матрицу через (л )• где а& — Py= 1 - Числа аир
можно считать взаимно простыми, <х>Р^О. Выделим среди окруж-
окружностей Кг те из них, для которых пара чисел (а, Р) имеет вид
,(±1, 0). Изобразим их на Р тонкими линиями, а остальные
окружности типа Кг — толстыми линиями. На каждой толстой
окружности поставим рациональное число а/р (или a/p(mod 1)),
Разрежем поверхность Р толстыми окружностями па набор обла-
областей, которые обозначим через Rb. Все прежние тонкие окружно-
окружности Кг лежат строго внутри областей Rb. Над каждой областью
Rb получаем расслоение Qb со слоем S1. Можно ввести некоторый
целочисленный инвариант вь, характеризующий топологию этого
расслоения. Грубо говоря, это — препятствие к продолжению сече-
иия, заданного на граничных торах, внутрь многообразия Qb. Да-
Далее рассмотрим числа ц.ь = еь — 2а/р.
Определение.-Объект /(//, Q)*={I(H, Q), {а/р}, Ы) на-
назовем меченым изоэнергетическим инвариантом интегрируемой си-
системы v на изоэнергетической поверхности Q. Мы скажем, что
значения этого инварианта для двух систем совпадают, если есть
■ гомеоморфизм, переводящий поверхность в поверхность, граф в
граф и числовые метки в числовые метки. Как доказали Фоменко
и Цишанг, меченый инвариант различает неэквивалентные си-
системы.
ГЛАВА 7
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КОНКРЕТНЫХ
ГАМИЛЬТОНОВЫХ СИСТЕМ УРАВНЕНИИ
В ГЕОМЕТРИИ И МЕХАНИКЕ.
МЕТОДЫ И ПРИЛОЖЕНИЯ
§ 1. Алгебры Ли и механика. Вложения динамических систем
в алгебры Ли на канонические симплектические многообразия
В главе 3 мы уже встретились с важным обстоятельством:
некоторые уравнения, описывающие движение механических сис-
систем, могут интерпретироваться как гамильтоновы системы (век-
(векторные поля) на подходящих алгебрах Ли. Здесь мы подробнее
познакомимся с этим эффектом, позволяющим, оказывается, ин-
интегрировать многие интересные и важные механические системы
и их многомерные аналоги. Поскольку сегодня разработано много
методов интегрирования, то мы не в состоянии здесь дать даже
краткого изложения всех этих направлений. Поэтому мы отсылаем
читателя к списку литературы в конце книги. Здесь же мы скон-
сконцентрируем внимание лишь на некоторых принципиальных меха-
механизмах, управляющих интегрируемостью или неинтегрируемостью
систем.
Многие классические уравнения механики записываются как
системы дифференциальных уравнений на евклидовом пространст-
пространстве. Как мы видели, например, в гл. 3, уравнения движения трех-
трехмерного твердого тела, закрепленного в центре масс, записыва-
записываются в R3(jf, у, г) так:
к + к у' у ъ + ъ *• + *. у
Как было отмечено, эта система тесно связана с трехмерной ал-
алгеброй Ли soC) группы вращений SOC). Дело в том, что прост-
пространство R3 можно естественно отождествить с пространством
soC) кососимметрических вещественных матриц Х=(хц). Для
этого достаточно положить Х\2 — х, Х\г—у, хчг — ** т. е. сопоставить
вектору с координатами (х, у, z) матрицу
/ 0 х у\
= [-х О г).
\-y-zO)
Далее, рассмотрим в алгебре Ли soC) (ко) присоединенное пред-
представление (действие) группы SOC). Легко видеть, что орбитами
10* . 291
этого действия являются стандартные двумерные сферы с центром
в начале координат.
Отождествляя R3 с soC), мы интерпретируем уравнения Эйле-
Эйлера (см. выше) в виде некоторого векторного поля v на алгебре
Ли soC). Подвергнем его теперь простому преобразованию, инду-
индуцируемому следующей заменой координат в R3:
у-
~Ь
(преобразование подобия). Поле v повернется и превратится в но-
новое поле v.
Утверждение 1. Поле v, изображающее уравнения Эйлера
движения твердого тела, закрепленного в центре масс, касается
орбит присоединенного представления в алгебре Ли soC) и яв-
является гамильтоновым на этих орбитах (гомеоморфных сферам
Доказательство сводится к прямому вычислению и мы его здесь
опустим* Таким образом, вложив уравнения движения твердого
тела в подходящую алгебру Ли, мы обнаружили, что они превра-
превратились в гамильтонову систему на орбитах действия группы
SOC). Этот факт является отражением общего механизма, поз-
позволяющего интегрировать многие механические системы, анало-
аналогичные только что описанной.
Сейчас мы сформулируем общую идею алгебраизации механи-
механических систем, позволяющую интегрировать некоторые многомер-
многомерные уравнения типа Эйлера.
Определение 1. Мы будем говорить, что динамическая си-
система v на многообразии М допускает вложение в алгебру Ли
(или допускает алгебраизацию), еслм многообразие М можно
отождествить с некоторым подмногообразием NaG* в сопряжен-
сопряженном пространстве G* некоторой алгебры Ли G (дл,я некоторой,
группы Ли @) так, что выполняются следующие условия:
1) Подмногообразие N является объединением орбит О*(|)
коприсоединенного представления группы Ли @ на G*.
2) Векторное поле и касается орбит О*(|).
3) Векторное поле v на N оказывается гамильтоновым на ор-
орбитах О*(£) относительно канонической симплектической структу-
структуры со и имеет вид u = sgrad#, где Н — гладкая функция. Если
исходное многообразие было симплектическим, та естественно по-
потребовать, чтобы симплектическая структура на нем 'индуцирова-
'индуцировалась канонической симплектической структурой, заданной на G*~
Другими словами, система v допускает алгебраизацию, если
она обладает скрытыми групповыми симметриями, выявляющими-
выявляющимися при ее вложении в подходящую алгебру Ли.
Что дает алгебраизация какой-либо конкретной механической
системы? Это позволяет применить к ее изучению развитый аппа-
аппарат современной теории групп и алгебр Ли. Как показали иссле-
исследования последних лет," это позволяет достаточно эффективно
292
предъявлять (в явном виде!) полиномиальные и рациональные
интегралы многих интересных динамических систем.
Это в первую очередь относится к разнообразным многомер-
многомерным аналогам уравнений движения твердого тела, а именно: в от-
отсутствие силы тяжести, в присутствии силы тяжести, в идеальной
несжимаемой жидкости по инерции, в намагниченной "жидкости
и т. п.
Выше* мы видели, что в современной теории интегрирования
одно из центральных мест занимают максимальные линейные
коммутативные (и, как мытеперь знаем, некоммутативные) под-
подалгебры Ли У функций на орбитах O*czG* (ко)присоединенных
представлений. В настоящее время они обнаружены в достаточно
большом количестве. В следующем пункте мы дадим список ос-
основных примеров.
Здесь же мы поставим вопрос: что дает с точки зрения прило-
приложений обнаружение таких максимальных линейных алгебр функ-
функций?
Ответ очень прост. Дело в том, что любая гладкая функция f.
из максимальной линейной коммутативной алгебры - функций V
порождает вполне интегрируемую (по Лиувиллю) гамильтонову
систему sgrad f. Варьируя функцию / внутри алгебры V, мы ме-
меняем соответствующую систему.
Запас таких систем определяется, следовательно, размерностью
коммутативной алгебры Ли интегралов V. Оказывается, таким
путем часто получаются интересные механические системы и их
аналоги. Другими словами, оказывается, что уже построенные,
коммутативные алгебры V часто содержат в себе интересные ме-
механические гамильтонианы. Нужно лишь уметь находить их среди
функций алгебры V.
Имеются обстоятельства, иногда облегчающие такой поиск.
Дело в том, что гамильтонианы, возникающие в механике и фи-
физике, обычно являются квадратичными (билинейными) функция»
ми. Поэтому в первую очередь следует изучить линейное подпро-
подпространство квадратичных функций, попавших в коммутативную
алгебру Ли V. Это исследование обычно несложно, и ниже мы его
продемонстрируем на примерах.
§ 2. Левоиивариантные гамильтоновы системы на группах Ли
' и уравнения Эйлера на алгебрах Ли
2.1. Симплектическая структура и левоинвариантные гамильто-
гамильтонианы. К настоящему времени разработано много методов пост-
построения вполне интегрируемых гамильтоновых - систем, связанных
с группами и алгебрами Ли. Ввиду недостатка места мы ограни-
ограничимся здесь лишь изложением метода, разработанного для полу-
полупростых алгебр Ли в [96—100] (Мищенко, Фоменко). Изложение
других интересных результатов и методов, относящихся к другим
конечномерным и бесконечномерным алгебрам Ли, см., например,
293
в [104—106] (Новиков), [168] (Адлер! ван Мёрбеке), [182] (Ка-
лоджеро), [217] (Констант), [211] (Каждан, Костант, Стернберг),
[228] (Маккин), [84] (Манаков), [226] (Мамфорд), [238] (Оль-
шанецкий, Переломов), [114] (Переломов), [248] (Рейман, Семе-
нов-Тян-Шанский), [136—139] (Трофимов), [16—17] (Богоявлен-
(Богоявленский), [22] (Браилов), [81] (Ле Нгок Тьеуен), [12] (Беляев),
[21] (Болсинов), [51] (Дубровин), [55] (Захаров, Фаддеев), [85]
(Манин), [89] (Мещеряков), [112—113] (Певцова), [127] (Сте-
пин), [247] (Ратью, ван Мёрбеке) и др.
Пусть ® — группа Ли, Т®— пространство касательного рас-
расслоения, Т*® — пространство кокасательного расслоения. Группа
@ действует на многообразиях ®, Т®, Т*& двумя способами:
е помощью левых и правых сдвигов. Левые сдвиги мы будем обо-
обозначать через Lg, правые сдвиги — через Rg. Естественные проек-
проекции расслоений обозначим через я : Т® -*■ & , я* : Т* ®-*-@ . Мно-
Многообразие Т*& снабжается естественной симплектической струк-
структурой, т. е. замкнутой невырожденной формой со, равной d£i, где
Q является 1-формой на многообразии Т*& , задаваемой следую-
следующим образом. Пусть X — касательный вектор в точке /еГ*@,
Y — dn{X) •— касательный вектор к многообразию ® в точке
g=n(t). Положим Q(X)—t(Y). Если хи .... Хы, где.N = dim @ , —
локальная система координат на группе ® в окрестности точки
g = n(t); X), ..., in — координаты кокасательного вектора t;
1ь ■ ■ • i Sat, t)i, ..., щ — координаты касательного вектора X к мно-
многообразию Т* ® в точке t, то вектор Y имеет координаты т^, ...
..., г|лг и Q(X) =STaria. Следовательно, в локальных координатах
Ti,...,xjv, Xi,...,xN форма со имеет вид Q=2xad*a, а значит,
о) = 2^ТаЛ^л;а, т. е. форма со является невырожденной формой. Та-
Таким образом, каждая функция Гамильтона H(t), заданная на
пространстве Т* ®, порождает гамильтоново векторное поле
sgradtf, т. е. co(sgrad#@, X)=(dH, X), Xf=Tt(T*@ ).
Мы ограничимся рассмотрением левоинвариантных функций
Гамильтона, т. е. таких функций H(t), что H{Lgt) =H(t), t^T*@,
ge ©•
Лемма 1. Если функция Гамильтона H(t), t^T* ®, лево-
инвариантна, то векторное поле sgrad H тоже левоинвариантно.
Доказательство. Требуется доказать, что sgrad#(Lg<) =
=dZ.£sgradH(t), - или, что то же самое, тождество
to (dLg sgrad H(t), X) = со (sgrad #(L^), X) верно для любого ка-
касательного вектора A"e7\(T* ®). Проверим, что форма со левоин-
вариантна, т. е.
<o(dLg(X),' dLg(Y))=u(X, У); X, УеТ((Г*@).
Поскольку Lg:T*@ ~*T* ® является диффеоморфизмом, то иско-
искомое равенство эквивалентно равенству Zjr*co=co.
Учитывая равенство co = dQ, достаточно доказать левоинвари-
антность 1-формы Q, т. ё. Le*Q = Q, или U(dLg(X))=Q(X). Так
как О(Х)=/(У), то Lg(t)(dn(dLg(X)))=t(djt(X)). Поскольку
dn°dLg=Lgodn, то Lg(t)(Le(dn(X)))=t(dn(X)). Последнее ра-
равенство уже очевидно. Лемма доказана.
294
Таким образом, если функция Гамильтона левоинвариантна, то
соответствующее ей гамильтоново векторное поле sgfad H тоже
левоинвариантно и, значит, проекция 1:Т*& -+Те*, задаваемая
с помощью левых сдвигов формулой l(t) = Ln»w_. (/), согласована
с векторным полем sgrad Я. Следовательно, иа кокасательном
пространстве Те* существует векторное поле Е(Н), согласованное
с полем sgrad//. Соответствующие полю Е(Н) уравнения назы-
называются уравнениями Эйлера данной гамильтоновой системы.
Пусть |еГе*, х^Те. Обозначим через {|, х) ковектор из Те*, зада-
задаваемый равенством (|, *}(«/) =<t, [х, у)), у(=Те, т. е. {£, Ar} = ad**£.
Пусть / — гладкая функция на Те*\ тогда форма df естественно
принимает значения в дуальном пространстве Те, т. е. df(%) =
= <l, df).
Лемма 2. Пусть Н — левоинвариантная функция на Т* ®.
Тогда E(H)t = {t, dH(t)}, teT/, где dH(t)e=Te —значение dH
в точке t.
Доказательство. Представим пространства расслоений
Т®, Т*® в виде декартовых произведений: у:ТеХ ®->■ Т@,
1р : Те*Х & ->Г* & , положив ф(А', g) =Lgx, ф(/, g) =Lgt. Нетрудно
проверить, что спаривание Г^хГ^-vR в декартовом произведе-
произведении имеет вид ((х, g), (t, g)) = (x, t). При этом оператор левого
сдвига Lh действует по формуле
Далее, касательное расслоение Т{Те*Х& ) канонически изоморф-
изоморфно прямому произведению Т(Те*)ХТ® , которое в свою очередь
изоморфно Те*ХТе*ХТеХ ® . Таким образом, касательное прост-
пространство T(t,g)(Te*x ®) в точке (t, g) изоморфно Те*ХТе. Вычис-
Вычислим значение формы Q на векторе X(=T(t,g)(Te*X @), -^=A. х).
Поскольку проекция я* : Т*0 -»■ 0 в декартовом произведении пе-
переходит в композицию n' = n*^:Te*X @->® , причем n*(t, g)=g,
то ее дифференциал dn''(£, х)=х. Следовательно, согласно опре-
определению Q{X)={t, х). Вычислим значение формы ш на паре век-
векторов Хи X2t=T{t,g){Te*X ®), Xi=(lu xi), X2=(h, X2). Восполь.
зуемся формулой для вычисления форм на векторных полях
du(X ?)X(a(?))?(Q(X))Q[x ?])
(, )(())(()){[, ])
Для этого включим векторы Хь Х2 в два векторных поля J?i, X2.
Положим в произвольной точке (/, g)(=Te*X & значения вектор-
векторных полей Хи Х2 равными Xi—(£,u X\), Хъ—^Хъ х2). Каждое из
векторных полей Яи Х2 разлагается в сумму: Хг= (|ь 0) + @, х^) —
^ + Х
причем первые слагаемые коммутируют между собой и со вторы-
вторыми слагаемыми. Что касается вторых слагаемых Х12, Х22, то они
являются левоинвариантными полями на группе @ и их комму-
коммутатор снова является левоинвариантным полем @, [xi, x2)). Та-
295
ким образом, значение формы ш на векторах Х\, Х2 принимает
следующий вид:
. со(Х1( X2) = X1(Q(X2))-X2(Q(X1))-Q([X1, Х2]) =
= X1{{i, x2))-%((t, Xl))-(t, [xv x2}) =
■ ={li, Ч) — (£2. Xi)—-{t, [хг, х2]).
» Пусть теперь H(t, g) — левоинвариантная функция Гамильто-
Гамильтона на Т*(8 =Те*Х @, т. е. Н(t, g)=~H(t). Вычислим значение
векторного поля sgradЯ в точке (t, g); sgradH—(vu vz)(=Te*X
%,Te. Рассмотрим произвольный вектор X=(g, x)^Te*XTe. Тогда
f, g)rX)=(vu x)-(l,v2)-{t, [v,,x))=
= ((dH(t),0), &,x)) = -{l,dH(t)).
В силу произвольности I и х получаем
ux) = (t, [i>2l *]> = {/, v2}(x).
Таким образом, sgrad H(t, g) — ({t, dH(t)}, dH(t)) и, следователь-
следовательно, E(H)t = {t, dH(t)}. Лемма 2 доказана.
Предложение 1 ([98]). Пусть f(t, g) =ft(ad*g-i (/)), te7e*,
g^ @. Тогда функция f является первым интегралом движения.
Доказательство. Применим sgradH(t, g) к произвольной
функции /. Пусть (t{s), g{s)) — интегральная кривая, тогда
h (ad;@,f (s)) | s=o + -js h
V dh(t)} =
ds
■ =(({t, dH(t)}-{t, dH(t)}), dft(f))=O. .
Таким образом, уравнения Эйлера
i = {t,dH(t)}, tf=Te*, (E)
задают динамическую систему на дуальном к алгебре Ли Те* про-
пространстве. В силу предложения 1 мы получаем следующее утверж-
утверждение.
296
Предложение 2. Пусть f — функция на Те*, постоянная на
орбитах коприсоединеиного представления. Тогда f является пер-
пым интегралом системы (Е). . .
В самом деле, тогда продолжение f{t, g)=f(Ad*g^(t))=f(t)
является интегралом системы sgrad H. Поскольку f не зависит от
g, то (sgrad H)] = E(H)f = 0.
Предложение 2 показывает, что векторное поле (Е) касается
орбит коприсоединенного представления. Обозначим через O*(t)
орбиту коприсоединенного представления: O*(t) ={Ads*t, ge ©}.
Орбита O*(t) диффеоморфна однородному пространству @/5? (/),
где £ (/) — стационарная подгруппа, S} (t) ={g : Adg*t = t}. Тогда
касательное пространство. TtO* (i) состоит из векторов вида
&6.x*t — {t, х}, х^Те. Пусть / — произвольная гладкая функция на
Те*. Функция f постоянна на орбитах тогда и только тогда, когда
({t, x}, df(t)) = O для любого вектора х, т. е. когда (t, [x, df(t)]) = O,
или {t, [df(t), x]) = ({t, df(t)}, х)=£). Таким образом, мы доказали
следующее утверждение.
Лемма 3. Функция f постоянна на орбитах коприсоединен-
коприсоединенного представления тогда и только тогда, когда выполнено тож- ■
дество {t, df(t)} = 0.
На орбитах O*(t) имеется каноническая симплектическая
структура, свойства которой мы уже неоднократно обсуждали. На-
Напомним, что она задается так. Если X = {t, x), Y = {t, у) — два ка-
касательных вектора к орбите, то со(Х, У) —(t, [x, у] >.
Лемма 4. Уравнения Эйлера (Е) образуют гамильтоноео
векторное поле на каждой орбите O*(t), снабженной стандартной
симплектической структурой, с функцией Гамильтона, равной ог-
раничению функции H(t) на орбиту.
Доказательство. Требуется доказать, что имеет место тож-
тождество со ({t, dH(t)}, X) = (do* (t)H(t), X) для любого касательного, к
орбите, вектора X = {t,x). Действительно,. a({tydH (t)}, {t, x}) =
= {t, [dH(t),x]); <dG.«, H(t), X) = (dH(t), X) = -({t,x}, dH(i)) =
= -{t, [x, dH(f)]) = (t, [dH(t), x}).
Сравнивая правые части равенств, приходим к искомому равен-
равенству. Лемма доказана.
2.2. Квадратичные гамильтонианы, порожденные методом сдви-
сдвига аргумента. Опишем важный класс функций на орбите 6*(t),
находящихся попарно в инволюции относительно симплектической
структуры на орбите. Каждая из таких функций автоматически
будет интегралом для гамильтонова поля, порожденного любой
другой функцией из этого же класса.
Напомним, что функция f является первым интегралом для
гамильтонова поля Е{Н), построенного по функции Гамильтона
Н на орбите O*(t), в том и только в том случае, когда скобка Пу-
Пуассона {/, Я} тождественно равна нулю. Пусть f,g — две гладкие
функции, тогда {f, g} = со (sgrad f, sgrad g). Ясно, что £(/) =
-sgrad/={f, d/(/)}. Следовательно, {/, g}(t)=(t, [df(t), dg(t)]l
В частности, функция / является интегралом уравнений Эйлера
297
для функции Гамильтона Я, если выполнено тождество
[d/dO
<, [/(),(O])O
Предложение 3 [98]. Пусть f, g — две функции на Те*,
постоянные на орбитах коприсоединенного представления, sg
(=Те* — фиксированный ковектор, X, \i — фиксированные числа.
Функции ]K(t)—f(t+Xa) и gix(t)=g(t+iia) находятся в инволюции
на каждой орбите относительно канонической симплектической
структуры.
Доказательство. Следует доказать тождество S = (t,
ldh(t), d£(f)])=O. Пусть ХФц, t = a
А/(—ц), а = ц/(ц — X). Тогда
@,
Поскольку в силу леммы 3 функции /, g постоянны на орбитах, то
оба слагаемых в последнем равенстве обращаются в ноль, что и
доказывает утверждение. .
Перечисленные выше максимальные линейные коммутативные
алгебры полиномов (и рациональных функций) на орбитах алгебр
Ли представляют интерес не только с точки зрения взаимосвязи
коммутативного и некоммутативного интегрирования гамильтоно-
вых систем. Оказывается, эти алгебры V полиномов часто содер-
содержат важные квадратичные гамильтонианы аналогов классических
механических систем. Это означает, что все такие системы вполне
интегрируемы по Лиувиллю. Более того, алгебры V обычно содер-
содержат целое линейное подпространство квадратичных гамильтони-
гамильтонианов, что открывает возможности их варьирования и поиска но-
новых интегрируемых систем.
Чтобы не загромождать изложение, мы остановимся здесь лишь
на одной серии таких примеров, связанных с различными вариан-
вариантами, уравнений движения твердого тела (в многомерном случае).
Чтобы продемонстрировать наш общий метод сдвига аргумента,
мы осветим более или менее подробно способ изучения макси-
максимальной линейной коммутативной алгебры полиномов, построен-
построенной нами для случая комплексной полупростой алгебры Ли.
Пусть V — максимальная линейная коммутативная алгебра
полиномов на орбитах полупростой алгебры Ли G, предъявленная
в п. 4.5 § 4 гл. 5. Сейчас мы опишем содержащееся в V подпро-
подпространство квадратичных гамильтонианов.
Теорема 1 [99, 100]. Пусть G — конечномерная алгебра Ли
и Р — множество функций, функционально порожденное функци-
функциями вида f(l + ka), где f(|) — инвариант алгебры G (метод сдви-
сдвига аргумента), т. е. функция, постоянная на орбитах O*czG* ко-
коприсоединенного представления Ad*; a^G* — фиксированный
298
ковектор; К — вещественное число, КфО. Квадратичный многочлен
//(|) принадлежит множеству функций Р тогда и только тогда,
когда существует такой элемент (вектор) 6eG, что выполняются
тождества {a, d#(|)} = {£, b} и {а, Ь} = 0, где {,} — операция в ал-
алгебре Ли G {коммутатор или скобка Пуассона) и {£, fc} = adu*£.
Замечание. Здесь йН{1) (т. е. дифференциал функции Я)
изображается вектором (элементом) алгебры Ли G, так как Я —
функция на дуальном пространстве G* и G** = G.
Из теоремы 1 получается важное следствие.
Теорема 2 [99, 100]. Пусть G —полупростая комплексная
алгебра Ли, a^G — вектор в общем положении, V — множество
функций на алгебре G, функционально порожденных функциями
вида f(X+Xa), где f(X) —. функции, постоянные на орбитах 0<zzG
присоединенного представления группы &. Квадратичная функция
Я(Х) принадлежит семейству V тогда и только тогда, когда най-
найдется такой вектор beG (не обязательно общего положения), что
выполнены тождества [grad Я(А')-, а] = [Х, Ъ\\ [а, Ь] —0. Соответ-
Соответствующее такой функции Я гамильтоново векторное поле X —
= sgrad#(X) будет вполне интегрируемо по Лиувиллю на всех
орбитах общего положения в алгебре Ли G.
Здесь gradH(X) можно считать элементом алгебры Ли G,
отождествляемой с G* посредством формы Киллинга.
Доказательство теоремы 1. Функция Гамильтона
Я(|) должна функционально зависеть от функций вида f(£ + A,a),
где К — некоторые числа, а — ковектор, a<=G*, a f — функции,
постоянные на орбитах коприсоединенного представления. Таким
образом, H{l)=F(fi(l + Kia), ..., fN{l+hNa)). Мы предполагаем,
что все функции f!( ..., fN и F являются гладкими. Без ограниче-
ограничения общности можно считать, что функции fk, l^k^N, являются
однородными полиномами некоторых степеней р*.. В самом деле,
условие постоянства функции f на орбитах означает выполнение
тождества {£, d/(|)} —0, %(=G*. Следовательно, эти же тождест-
тождества выполняются и для формального ряда Тейлора, а значит, и
для отдельных его членов, которые уже являются однородными
полиномами.
Таким образом, члены ряда Тейлора можно взять за новые об-
образующие в новом преддтавлении для гамильтониана Я. Рассмот-
Рассмотрим разложение функции /&(|+Яа) по степеням К, а именно:
fk°{Z)+fkl{£,)&+..■+f &{%)№. Многочлен fkf является однород-
однородным многочленом степени pk—/, в.частности f%k =const. Таким об-
образом, в новом представлении для Я можно без ограничения общ-
общности считать, что
11—Г\п • •••» In ' /i > •••> In >■>
flk~l l^k^Nмногочлены первой ^степени fk~2
где flk~l, l^.k^N,—многочлены первой ^степени, fkk~2—много-
fkk~2—многочлены второй степени по \. Тогда
H—F lfPr~l fpN~l\\p (fPi-2 fPN—2\
299
где F = F(ul, .... uN)—квадратичная, а/1, = /7а(ы1, .... uN)~линей-
uN)~линейная функции. Имеем
Отсюда получаем
О = {{I + to), dfl (?) + df{
или
{а,
F.
Так как df^~O, то из первых трех тождеств остаются только два:
1 #' 2
{a, dfpkb~l}^0, {%, dfpkir-l) + {a,
Вычислим {a, dfl*~1}. Получаем
N
{a,
где 6= — y]~-dfPkk~l^G- Так как {а, ^*-'} = 0, то {a, 6}=0.
Обратно, если существует вектор 6eG, удовлетворяющий этим
условиям, и ковектор a^G* находится в общем положении, то
функция #(|) функционально зависит от функций fk'(E). В самом
деле, поскольку 6eKer(a) = (X<=G : {а, Х} = 0) и ковектор а нахо-
находится в общем положении, то найдется такой полином f, постоян-
постоянный на орбитах, что df(a)—b. Положим
При 1 — 0 получаем df(a) = dfi>-l=b. Таким образом, {I, Ь} =
— {a, dH(l)}, а это означает, что функция Н = Н + f~2 удовлетво-
удовлетворяет соотношению {a, dli (£)} = {£, b).
300
При 6 = 0 имеем {a, dH(Q} — 0. Это значит, что dH является ли-
| «ейиым самосопряженным оператором dH : G* -> Ker (a) cr G. Фикси-
: русм базис Ьх, ..., 6seKer(a) и функции-^, ..., /s—постоянные
на орбитах, у которых dfk(a)=bk, lsSZ&sgls. Будем считать, что
fk(a) = O, l^.k^.s. Положим, как и ранее,
Здесь f"kk = 0, т. е. fk (а) = 0. Рассмотрим функцию
(Б) /?"' (Б) + ГГХ (Б) </-1 (Б)) =
Легко видеть, что для любого самосопряженного оператора
кр: G*->Ker(a)cG найдутся такие числа р,,-/ = ц/«, что ф(§) =
=SW|r bj))Mj. В самом деле, пусть VcG* — подпространство, ан-
аннулирующее Ker(a), т. е. V = {£: ||кег(а) = 0). Тогда <pv = O, посколь-
поскольку если gie'G*. h&V, то (%и ср(|2)> = <|2, q>(|i)> = 0. Следовательно,
разлагая значение ф(|) по базису Ь\, .... ^еКег(а), получаем
<р(|) =ЕЬ,-ф,-(|), где ф/F) — линейные функции, равные нулю на
V. Полный набор таких функций порожден функциями вида
<|, Ь/>, т. е. ф,-(|) =2ц;,-<!, bj). Условие ц1; = ц/; следует из самосоп-
самосопряженности оператора ф. Таким образом, применяя вышеизложен-
вышеизложенные рассуждения к оператору d/7(|), получаем, что Я(|) =
= zl'viifii~i (i)/^'" (Б) с точностью до постоянной. Теорема дока-
доказана.
2.3. Свойства общих уравнений Эйлера. Уравнение Эйлера для
квадратичной функции Гамильтона имеет вид
/ = {', <р@). (КЕ)
где ф : G*^-G — самосопряженный оператор. Рассмотрим подпро-
подпространство VczG*. Пусть GvdG — подпространство векторов
таких, что {У, x}aV.
Лемма 5. Подпространство Gv является подалгеброй.
Доказательство. Пусть х, уенGv. Тогда
= (/. [х, \У, z]])-{t, \y, [x, z]]) = ({t, x},[y, z))-{{t, у}, [х, г]) =
= {{{t, х), у), z) — ({{t, у), х), z).
Следовательно, {t, [х, «/]}=={{/, х), y}—{{t, у), х). Если feV, то
\t, x}eEV, {t, y}^V и, значит, {{t, x), {/}eV, {{t, у}, x}ceV. Таким
образом, {t, [x, y]}eEV, т. е. {V, [х, y]}cV, [x, y]s=Gv. Лемма
.доказана.
301
Обозначим через (G/Gv)*czG* подпространство- элементов
G*, аннулирующих Gv, таких, что (/, Gv) = 0.
Лемма 6. Пусть VaG*,. Gv, (GjGv)* имеют смысл, указан-
указанный выше. Рассмотрим Ov*(t)czV — орбиту коприсоединенного
действия группы ® v, ассоциированной с подалгеброй Gv. Форма
Кириллова невырождена на орбитах Ov*(t), teV, тогда и только-
тогда, когда (G/Gv)*f]{V, Gy} = 0. .
Доказательство. Касательное пространство в точке t
к орбите Ov*(t) состоит, из ковекторов вида ! = {?, х}, x^Gv. Зна-
Значение симплектической формы со на паре векторов |={^, х}, rj =
= {t, у} равно И, [х, у] > = &>(£, ti). Пусть %={t, х)ФО. Если бы
(I, Gv) = 0, то |e(G/Gv)* и, значит, £ = 0. Поэтому существует
вектор yeGv такой, что (%, у}фО. Тогда, положив т) = {^, у}, полу-
получаем и(|, t0=<*. [*> У]> = <^> *}> У) = И, у)Ф0. Обратно, пусть су-
существует вектор %ф0, l(=(G/Gv)*(]{V, Gv}. Тогда %^{V, Gv}, т. е.
£,={t, x}, t^V, xgCv и (|, Gv) = 0. Поэтому для любого вектора
y^Gv имеет место равенство <£, у) = 0. Следовательно, при ц =
~{t, у) имеем ш(£, r\) =({t, x}, у) = (%, у) = 0.
Предложение 4 [98]. Пусть VcG* — линейное подпрост-
подпространство, (G/Gv)*n{V, Gv} = 0, <f:G*^*G — самосопряженный опе-
оператор, ф(V)czGv. Тогда
а) Уравнения Эйлера (КЕ) оставляют подпространство V ин-
инвариантным.
б) Орбиты Ov* коприсоединенного представления подгруппы
@ у, ассоциированной с подалгеброй Gv, являются инвариантными
подмногообразиями уравнений (КЕ).
в) Система уравнений (КЕ) является гамильт'оновой системой
на орбитах Ov* относительно симплектической структуры, задава-
задаваемой канонической, симплектической структурой, с функцией Га-
Гамильтона Н\ *. • .
г) Пусть SF — множество функций, порожденных методом
сдвига аргумента, т. е. функционально порожденных функциями
вида f(t+Xa), где f — функции, постоянные на орбитах коприсо-
коприсоединенного представления группы @. Пусть g, h^@~ таковы, что-
dg(t), dh(t)^Gv при teV. Тогда функции g, h находятся в ин-
инволюции на орбите Ov*(i) относительно стандартной симплекти-
симплектической структуры.
Доказательство. Пункт а) очевиден. Пусть /еУ. Тогда
{t, cp(i)} — касательный вектор к орбите, так что пункт б) дока-
доказан. Докажем пункт в). Пусть d(H(t)l» ) — /el/*. Если я: G->
°V{t)
~>V* — естественная проекция, то n,dH(t)=l. Пусть Е(Н) —
такой вектор касательного пространства TOv*(t) к орбите, что
Пусть r\ = {t, у}, y^Gv. Будем искать Е(Н) в виде {t, x}, v
Имеем (о(£(Я), ц) =<*, [х, у]), /(г,) =(dH(t), {t, y}) = -({t, y)y
dH{t)) (t, [dH(t), у]). Поскольку dH(t) =<p(t)<=Gv, то
3D2
{/, x—dH(t)}<={V, Gv) и, значит, если бы {t, x—dH(t)}--£0, то в
силу равенства (G/Gv)*f\{V, Gv} — 0 для некоторого y^Gv имели
<5ы равенство ({t, х—dH(t)}, у> = 0. Таким образом, {t, dH(t)} =
■={i, л;}, или E(H)={t, dH(t)}, т. е. гамильтоново векторное поле
£ (Я),'ассоциированное с функцией Гамильтона #|0*, совпадает
с (КЕ).
Пусть g, h^&~ и dg(t), dh(t)^Gv. Пусть £|, |г — двойственные
ковекторы к d(g\Q*), d(h\0*). Как и для Е(Н), имеем gi =
= {', dg(t)}, h = {t, Vdh(t)}; V {g, h} = (t^[dg{t), dh(t)]). Правая
часть последнего равенства совпадает с значением симплектичес-
кой структуры на орбите коприсоединенного представления. При-
Применяя теорему 1, получаем {g, Л}=т=0. Предложение 4 доказано.
Напомним, что комплексные полупростые алгебры Ли харак-
характеризуются наличием невырожденной комплекснозначной симмет-
симметрической формы Киллинга (, >•, для которой выполнено соотноше-
соотношение (х, [у, z]) = (y, [z, x]). Невырожденность этой формы означает,
что соответствующий ей гомоморфизм спаривания В: G-+-G*
является изоморфизмом. Таким образом, уравнение Эйлера i —
={t, dH(t)}, t^G*, можно переписать в переменных алгебры G,
положив * = В~'@-
Пусть Н(В(х))^Н(х), тогда dtl (x) = B dH (t). Положим
<grad#(A:), y)=(dH{x), у). Тогда х = В~' (i) =B~l {/, dH{t)), т.е.
{х, y) = (B~1{t, dH{t)}, y) = ({t, dH(t)}, y) = {t. [dH(t), y]) =
= (Bx, [gradH(x), y]) = (x, [grad/?W, {/]) = (?, [x, gradH(x)]). •
Следовательно, х— [x, gradR(x)]. Эта формула имеет классичес-
классический вид уравнения Эйлера для полупростой группы. Если }(t) —
■функция, постоянная на орбитах коприсоединенного представле-
представления, то очевидно,.что функция h(x) =f(Bx) тоже является посто-
постоянной на тех же орбитах. При этом формула {t, df(t)}-=0 прини-
принимает вид [х, gradh(x)] =0, а формула для скобки Пуассона двух
функций hi, h2 — вид {х, [grad /г, (*), grad/i2(A;)]>.
§ 3. Секционные операторы в случае полупростых алгебр Ли
и соответствующие им левоинвариантные твердотельные
метрики
3.1. Секционное разложение полупростой алгебры Ли совпада-
совпадает с картановским разложением. Рассмотрим полупростую комп-
комплексную алгебру Ли G, отвечающую полупростой группе @. Тогда
группу & можно представить в виде симметрического простран-
пространства @ х @/@, где стационарная подгруппа © вложена в группу
•® х @ как множество точек вида (g, g), ge@ . Приводя эти
обозначения в соответствие с обозначениями § 5 гл. 5, возьмем
в качестве V плоскость {(X, —X)}, где X пробегает G, а в качестве
подалгебры Н — плоскость {(X, X)}, где X^G. Отметим, что обо-
обозначение G в настоящем пункте и в § 5 гл. 5 снабжены разным
«смыслом (не путайте!). Рассматривая присоединенное представле-
303
ние р = аа, получаем v = l~-H, li'=K-\-R. Здесь, как легко прове-
проверить, Т является картановской подалгеброй в G, a R — ортого-
ортогональным дополнением. Следовательно, R натянуто на корневые
подпространства. Таким образом, здесь разложение V=T+R сов-
совпадает с классическим картановским разложением V=G = TQ)
Далее, a^TczV, 6<=/<Cc//~G. Совершенно ясно, что Т явля-
является картановской подалгеброй в алгебре И, изоморфной G. Удоб-
Удобно отождествить // и V с помощью естественного изоморфизма
(X, Х)^*(Х, —X). При этом Г«/\, R^R. Значит, элементы а и Ь
можно рассматривать как элементы общего положения в одной,
картановской подалгебре алгебры Ли G.
Лемма 1. Динамическая система Х= (pQX)X на комплексной
полипростой алгебре Ли G, построенная по секционному оператору
Q(a, Ъ, D) : T+R^-T+R, совпадает с уравнениями движения мно-
многомерного твердого тела в отсутствие силы тяжести (с закреплен-
закрепленным центром масс) с полу простой группой симметрии. Пусть X —
=X'+t, где t<=T, X'^R = T\ Тогда Q(a, b, D)X = aua-ladbX' +
+ D(t), где D : T-+T — линейный оператор.
Доказательство легко вытекает из конструкции секцион-
секционного оператора и из сопоставления с результатами § 5 гл. 5.
Таким образом, частным случаем общей динамической системы,
построенной по секционным операторам, являются важные урав-
уравнения движения твердого тела, ранее рассматривавшиеся во мно-
многих работах, например, в [5, 84, 96—100] и т. д.
Пусть / — гладкая функция на алгебре G. С каждой такой
функцией можно естественно связать, как мы знаем, гамильтонову
систему на кокасательном расслоении Т* & к группе & = expGv-
продолжив функцию f до левоинвариантной функции F, заданной
на всем пространстве Т* &. Пространство Г*@ является симплек-
тическим многообразием, а потому, взяв F в качестве гамильто-
гамильтониана, мы получаем на Т* © гамильтонову систему. Эта система
также левоинвариантна и распадается на две системы, одна из ко-
'■торых задается на кокасательном пространстве в единице группы,
и называется системой уравнений Эйлера (см. выше). В данном
случае эти уравнения допускают здесь простое описание.
Пусть grad/ обозначает векторное поле на G, двойственное
относительно формы-Киллинга к дифференциалу df, т. е. удов-
удовлетворяющее условию (grad/, g) = |(f). Тогда уравнения Эйлера
записываются в коммутаторном виде: Х= [X, grad/(Я)]. Особый
интерес представляет случай потока геодезических левоинвари-
антных метрик на группе. Впервые внимание на этот факт обра-
обратил В. И. Арнольд в [5]. В этом случае функция / является не-
невырожденной квадратичной формой на алгебре Ли G, a grad/(X)
задается самосопряженным оператором в G. Это означает, что
вектор grad/(X) представим в виде <рХ, где ср: G^-G — самосоп-
самосопряженный оператор.
Приведем теперь уравнения, описывающие движение многомер-
многомерного твердого тела с закрепленной точкой. Рассмотрим сначала
304
чистый случай, пусть u — so(n) — алгеора ли ортогональной
M, / — диагональная вещественная матрица
где ХгФХ,- при 1ф\. Рассмотрим на so(n) линейный оператор"
tyX — IX+XI. Тогда уравнения грХ=*[Х, $Х] называются уравнени-
уравнениями движения п-мерного твердого тела с неподвижной точкой (»
отсутствие силы тяжести). Запишем эти уравнения в явном виде,
используя стандартные координаты в алгебре Ли so(n). Предста-
ним алгебру so(n) как алгебру кососимметрических вещественных
матриц Х=(хц). Тогда
грХ = ((лг + л;)л:(/). Ясно, что
А.; — Af
X
При п = 3 мы получаем
• А^ - — /*1 * Ад А]
* ~ XX Х~
*12 Т л XV.\X32> Х13Т ГТ Х12Х23' *23 ^ Т ^21^1.
■ Ajj -1 • Л! Aj -(- Aj A3 -f- A2
Отождествляя soC) с R3, мы получаем классические уравне-
уравнения движения трехмерного твердого тела. На этом основании
уравнения tyX= [X, \рХ] для произвольного п называются уравне-
уравнениями движения (многомерного) твердого тела. Перепишем их
в более удобной форме. Будем считать, что матрица / выбрана
так, что fo + Xj^O при всех i, /. Тогда оператор г|з обратим на
so(n) и обратный оператор г[;~1 = ф имеет вид (фХ)(/= Хц-
А; -г- А/
Произведем в so(n) замену координат Y.—^X. Тогда уравнение
движения твердого тела преобразуется к форме У= [г^>—1 У, У].
Умножая это уравнение на —1 и переобозначая У через X, полу-
получаем уравнение Эйлера [X, цХ] =Х, где ср: so(n)^-so(n) — ли-
линейный самосопряженный оператор.
Изучим теперь более подробно гамильтоповы системы, отвеча-
отвечающие указанному многопараметрйческому семейству общих сек-
секционных операторов, введенных нами выше. Для сокращения
записи обозначим оператор Q(a, b, D) просто через ср.
В этом параграфе мы построим многопараметрические семей-
семейства операторов ср: G^-G не только для комплексных полупростых
алгебр Ли, но и для их вещественных компактных форм. В даль-
дальнейшем эти операторы используются для предъявления вполне
интегрируемых уравнений Эйлера на алгебрах Ли.
3.2. Различные виды секционных, операторов (твердотельных
метрик). Комплексная серия. Нормальная нильпотентная серия.
Нормальная разрешимая серия. Пусть G — полупростая комп-
305-
лексная алгебра Ли, G = V+®T®V~ — корневое разложение для
некоторой картановской подалгебры. Пусть а, ЬеГ, аФЪ — два
произвольных регулярных элемента. Рассмотрим оператор ada:
:G^-G. Ясно, что ada|r^0, ada : V+r-*-V+, ada: V--*-V~, т. е. ada
«охраняет корневое разложение G над С. Действительно, ada£a =
— а(а)Еа для любого аеА. В дальнейшем будем считать, что а
и b выбраны в общем положении, т. е. a (a), а(Ь)ф§. Тогда опе-
операторы ada и ad& обратимы на V+®V~ : aAa~lEa=EJa(a).
Линейный оператор ф имеет вид <pX=q>(X'+t)=(pabX'+Dt =
— ada~ladbX' + Dt, где Х=Х' + 1 — однозначное разложение X по
V— V+(BV- и Т, a D : Т^-Т — произвольный линейный оператор,
симметричный на Г по отношению к форме Киллинга. Оператор ф
параметризован a, b, D. Ясно, что ф£и— а Еа. В базисе Вейля
£а, Е~а, На' оператор ф задается матрицей
«(а)
Лх 0
о \
0
0
кг 0
о К
о
0
D
где 4ab-:V+@V--+V+@V-, Xa=a{b)/a(a), q = dim V+= dim V~ =
= (число корней а>0).
Предложение 1. Оператор ф симметричен по отношению
к форме Киллинга при любых значениях параметров а, Ь, D, удов-
удовлетворяющих указанным ограничениям.
Доказательство. Обозначим базис Вейля в V+©V~ через
(£>■)• Достаточно проверить, что (ф£,-, е/) = (е,-, ще,) для любых i, j.
В силу симметрии скалярного произведения можно считать, что
1ф\. Плоскость Т ортогональна плоскости V+(BV~. Отметим, что
ялоскости V~ и V- неортогональны. Так как оператор ф перево-
переводит в себя плоскости V = V+®V~ и Г, а оператор D симметричен
на плоскости Т, то достаточно проверить симметрию оператора
<рй* на плоскости V. Поскольку Еа (при сст^О) — собственные век-
векторы оператора ф, то
«(а)
= 0
при
*> р(а)
, так как (Еа, £р)=0. Если
= О, то
«F)
а (а) Р(а)
Предложение доказано.
306
В случае общего положения оператор ф на плоскости V имеет
// различных собственных чисел %и ..., Xq (где <7=dimc V+) крат-
кратности два. Собственные векторы Еа и Е-а, отвечающие числу
и(Ь)/а(а), неортогональны, но подпространство Ga®G-a ортого-
ортогонально подпространству G(j©G-p, если аф±$. Оператор ф: V-+-V
сохраняет и это разложение. В частности, отображение ф: V+-»-V+
является изоморфизмом пространства V+ на себя. С другой сто-
стороны, плоскость V+ — это нильпотентная подалгебра размерности
q. Например, в нашем модельном примере (см. выше) V+ — это
подалгебра верхнетреугольных матриц с нулями по главной диа-
диагонали. Так как подпространство V+ порождено векторами Eai.
«>0, то оператор ф|у+симметричен относительно формы Киллин-
га. Собственные числа этого оператора (в случае общего положе-
положения) различны: Xi,...,Xg. Эту серию операторов ф|у+ мы назовем
нормальной нильпотентной серией. По построению каждой комп-
комплексной серии операторов (т. е. соответствующих «твердотельных
метрик») отвечает одна нормальная нильпотентная серия операто-
операторов (и отвечающих им метрик).
Не каждая нильпотентная алгебра Ли«может быть реализована
как подалгебра V+ (или V~) в какой-либо полупростой комплекс-
комплексной алгебре Ли.
Оператор ф переводит также в себя подалгебру V+®T, причем
оператор, ф задает изоморфизм пространства V+®T на себя. В мо-
модельном примере Vм ©Г — это подалгебра верхнетреугольных
матриц. Как и в предыдущем случае, получаем, что все собствен-
собственные числа оператора ф|у+фг различны (в общем положении) и
что он симметричен. Эту серию операторов (и отвечающих им мет-
метрик) мы назовем нормальной разрешимой серией. По построению
каждой комплексной серии операторов отвечает одна нормальная
разрешимая серия операторов (метрик). Не каждая разрешимая
алгебра Ли может быть реализована как подалгебра У+ФГ (или
V~(BT) в какой-либо полупростой комплексной алгебре Ли. В ба-
базисе Вейля операторы ф1у+ и Ф1у+фг изображаются матрицами
'К о
о
К
0
а(а)
Отметим, что комплексная серия операторов (метрик) существует
на любой комплексной полупростой алгебре Ли.
3.3. Компактная серия операторов (твердотельных метрик).
В этом пункте строится аналогичное семейство секционных опера-
операторов ф на произвольной простой компактной вещественной алгеб-
алгебре Ли. Воспользуемся теоремой Картана о связи между вещест-
ЗОГ
венными формами и инволюциями в комплексной полупростой ал-
алгебре Ли.
Ниже приведен полный список всех простых алгебр Ли G над
тюлем С и их компактных вещественных форм Gc-
К
вп
сп
Dn
Е*
Е,
Es
F,
G,
п
>1
>2
>3
>4
G
sl(n+ly С)
soBn+ 1, С)
sp(n, С)
so{2n, С)
е,(С)
е,(С)
е8(С)
/*(С)
ft (С)
su{n+ 1)
soBn+"l)
so{2n)
e7
e8
/*
ft"
dim
n{n + 2)
nBn+ 1)
nBn+ 1)
nBn —1)
78
133
248
52
14
В качестве вещественного базиса в Gc (над полем R) можно
взять векторы Ша'; £а + £-а; ЦЕа—£_а). Векторы Ша' порождают
картановскую подалгебру Тс в 6'с,' т. е. Tc = iT0. Соответствующее
разложение алгебры G условно показано на рис. 118. Над пунк-
пунктирной линией показаны плоскости, на которых о=1, внизу —
плоскости, на которых о = — 1. Подалгебра Г = Г0Ф(То является
картановской подалгеброй в G; П'о — максимальная коммутатив-
коммутативная подалгебра в GC=W+(BTC, где подпространство W+ порожде-
порождено векторами £a + £_tt и i(Ea—Е^.). Подпространство Gn (над по-
полем R), порожденное векторами Еа + Е-а, является подалгеброй,
что устанавливается непосредственной проверкой. Напомним, что
числа iVa(i (в базисе Вейля, см. выше) вещественны и N-a-(,=
— Na(,. Форма Киллинга отрицательно определена на Gc.
В модельном примере G = sl(n, С), оХ=—Хт. Корни а и век-
векторы Еа были указаны ранее. Имеем
308
1 n- =
(ъ о \
о • . •
p, = 0, <p<eR, Tc = \
Подалгебра GnczGc изоморфна алгебре so(n, R) (веществен-
(вещественных кососимметрических матриц), Gc = su(n) (косоэрмитовы комп-
комплексные матрицы). Подалгебра Go — нормальная вещественная
форма, изоморфная sl(n, R), Gof|
flGc=Gn, т. е. sl(n, R)ns«(n) =
— so(n). Отметим, что Go определя-
определяется инволюцией т: G-+G, хХ=Х и
Gn — множество неподвижных то-
точек одновременно для двух инволю-
инволюций т и ст. Кроме того, ранг G =
= ранг Gn-
Перейдем к построению ком-
компактной серии операторов (мет-
(метрик). Пусть a, b^iT0=Tc — два
элемента общего положения. Так
как adaEa=[a, Ea]=i[a', Ea], где
где число а(аг) вещественно. Сле-
Следовательно, ada (Еа+Е-ъ) =
= a.(a')i(Ea-^-E-a), adai(Ea—£-«) =
-—а(аг)(Еа+Е-а).
Итак, оператор ada: U7+->-W+
поворачивает вектор Еа + Е-а в
вектор, пропорциональный вектору
i(Ea—Е-а), и наоборот. Аналогич-
Аналогично действует и оператор adb, при-
причем в силу выбора аегТ0 оператор ada обратим на плоскости W+.
Тогда оператор ф = аda~1аdь : W+-*-W+ имеет все векторы Еа+Е-а,
ЦЕа—Е^а) своими собственными векторами с собственными чис-
числами а(Ь)/а(а) =а(Ь')/а(а'), где a = ia', b = ib', Ь'еГ0.
■ В точности аналогичные события происходят и на подпрост-
подпространству W~. Линейный оператор ф : Gc-+-Gc определим так: фХ=--
=<p(X'+t) ~(fabX'+D,t = ada~xadbX'+DI, где X = X' + t — однознач-
однозначное разложение вектора X в алгебре Gc —\^+фгГ0, X'eW'+,
t^iT0, D — произвольный линейный оператор на iTQ, симметрич-
симметричный относительно формы Киллинга. В базисе £■„ + £■_„, i(Ea—Е-а),
iHa' оператор ф задается матрицей
Рис. 1*18
309
где числа Ka = a(b)/a(a) вещественны и q=dimW+. Ясно, что опе-
операторы ф компактной серии аналогичны по своему действию опе-
операторам комплексной серии.
Предложение 2." Оператор ф : GC->GC симметричен при
любых значениях параметров а, Ь, D, удовлетворяющих указан-
указанным выШе ограничениям.
Доказательство. Проверка этого факта аналогична дока-
доказательству предложения 1. Единственное, что следует Доказать
отдельно, это — ортогональность выбранного нами базиса в плос-
плоскости W+. При этом отметим, что плоскость iT0 ортогональна плос-
плоскости W+. Далее, (£a+£-d, i(Ea—E~a))=Q.. Ортогональность ос-
остальных векторов следует из свойств, перечисленных в § 2. Дока-
Доказательство закончено. ■ ■
Оператор ф: W+-+-W+ имеет (в случае общего положения) cf
различных собственных, чисел К\, ..., Xq кратности 2. Но, в отли-
отличие от операторов (метрик) комплексной серии, здесь все собст-
собственные векторы ортогональны. Компактная серия операторов су-
существует на любой компактной полупростой алгебре Ли Gc.
3.4. Нормальная серия операторов (твердотельных метрик).
В этом, пункте мы построим аналогичное семейство операторов
(метрик) на некоторых простых компактных вещественных алгеб-
алгебрах Ли, отвечающих классическим нормальным компактным под-
подалгебрам. В предыдущем пункте мы предъявили в каждой ком-
компактной вещественной форме Gc подалгебру Gn, натянутую на
векторы Еа+Е-а, аеА. Так как все эти векторы являются собст-
собственными для операторов ф компактной серии, то, ограничивая эти
операторы на G«, получаем нормальную серию операторов. Эти
операторы совпадают с операторами ц>аь: Gn-^-Gn; qp^=ada~IadbX,
XGn; a, b(=LT0; а(а), а(Ь)Ф0. В базисе Еа + Е-а операторы
задаются матрицами
Отметим, что здесь элементы a, b не принадлежат подалгебре
Gn (!), т. е. операторы нормальной серии требуют для своего оп-
определения использования -элементов некоторой большей алгебры.
Это обстоятельство существенно отличает нормальную серию опе-
310
риторов (метрик) от комплексной и компактной серий, для кото-
которых элементы а и b принадлежали самой изучаемой алгебре Ли.
Не любую компактную простую (или полупростую) алгебру Ли
можно представить в виде подалгебры Gn в некоторой компактной
вещественной форме Gc. Ниже приводится полный список таких
алгебр Ли. Как было показано, алгебра Gn совпадает с неподвиж-
неподвижными точками автоморфизма т, хХ=Х, после его ограничения на
алгебру Gc. Пусть PczGc — подпространство, ортогональное к
плоскости Gn в Gc, иа котором т= — 1. Тогда очевидны следующие
коммутационные соотношения: [Gn, Gn]czGn, [P, P]czGn,
[Gn,P]czP.
Это означает, что пара алгебр (Gc, Gn) образует так называе-
называемую симметрическую пару, т. е. фактор-пространство ©с/@п
является компактным симметрическим пространством. Здесь, как
обычно, через @с, Э„ обозначены группы Ли, имеющие своими
алгебрами Ли Gc и Gn соответственно. Тогда плоскость Р естест-
естественно отождествляется с касательной плоскостью к многообразию
©с/®„, которое канонически вкладывается в группу Ли ©с как
вполне геодезическое подмногообразие (так называемая картанов-
ская модель симметрического пространства). Подробности см., на-
например, в [151].
Таким образом, изучение инволюций на группе @с означает
изучение компактных симметрических пространств с группой дви-
движений &с. Эта задача была решена Э. Картаном. Приведем этот
список, сохраняя стандартные обозначения. Отметим, что хотя на
одной и той же алгебре Gc может существовать несколько инво-
инволюций, однако инволюция, соответствующая нормальной форме,
определена однозначно. Ниже указаны также и соответствующие
•симметрические односвязные пространства ®с/®п-
Тип Л/. Здесь G = sl(n, С), G0 = sl(n, R), Gc--=su(n), Gn =
=so(n), aX=X, /г>1. Алгебра Gn реализована в алгебре Gc как
подалгебра вещественных кососимметрических матриц. Соответ-
Соответствующее симметрическое пространство имеет вид SU (n)fSO(n).
Далее, ранг su(n)—n—1 = рангР, где через ранг Р обозначена
размерность максимальной коммутативной подалгебры, содержа-
содержащейся в плоскости Р (вложенной в объемлющую алгебру).
Тип BDI. Здесь G = so(p + q, С), G0 = so(p, q), so(p, q) —
алгебра Ли группы SOQ(p, q) — компоненты единицы группы
SO(p, q). Группа О(р, q) — это группа матриц из SL(p + q, R),
оставляющих инвариантной квадратичную форму —Х\2—...—хр2 +
+х2р+1 + .. . + x2p+q. Алгебра Ли so(p, q) реализована в sl(p + q, R)
в виде матриц! J. 2 , где все матрицы л,- вещественны,
\ 3/
матрицы Х\, Хг — кососимметрические, порядков р и q соответ-
соответственно, матрица Х2 произвольна. Далее, Gc = so(p + q), G'' —
= so(p)®so(q), р>1, , <7>1, p + q¥=4, p^q, oX=IpqXIpq, где
, / — En 0\ г. ,-
Ipq—\ р , Ег — единичная матрица порядка г. Соответ-
311
ствующее симметрическое пространство SO(p + q)/SO(p)XSO(q)
является грассмановым многообразием. Нормальным формам со-
соответствуют значения p = q и p = q+\, при которых Gn = so(p)(B
®so(p) и Gre=so(<?)®so(<7+1).
Тип CI. Здесь G = sp(n, С), G0 = sp(n,, R), п^\, где через
/ X X \
sp(n, R) обозначена алгебра вида г \), где X,- — вещест-
\Х3 —Х\)
венные матрицы порядка /г, матрицы Х2 и Хз симметричны. Алгеб-
Алгебра sp(n, R) является алгеброй Ли группы Sp(n, R).
Далее, Gc=sp(n), Gn—u(n); вложение Gn->GC задается фор-
формулой А -Ь iB~*- ( . ], где Л + Шем(п), Л и 5 веществен-
\ —В А)
f г\ С \
ны, aX = JnXJn~\ где У„ = ( "I. Соответствующее симмет-
V п /
рическое пространство имеет вид Sp(n)/U (п).
Приведенным списком исчерпываются все нормальные формы
Gn, для которых Gc—r классическая простая алгебра Ли (т. е. типа
Ап, В„, Сп, Dn). Кроме этих форм существуют нормальные формы,
порожденные особыми алгебрами Ли, т. е. когда Gn является осо-
особой алгеброй Ли. Этот список -мы опустим ввиду громоздкости опи-
описания соответствующих алгебр Ли и их взаимных вложений.
§ 4. Явное построение интегралов уравнений Эйлера,
отвечающих комплексной, компактной и нормальной сериям
операторов (левоиивариантных твердотельных метрик)
4.1. Интегралы комплексной серии. Рассмотрим комплексную'
полупростую алгебру Ли G, фиксируем в ней картановскую под-
подалгебру и выберем в этой подалгебре два элемента
а и b общего положения. Тогда возникает симметричный опе-
оператор ф".G-vG, зависящий от параметров а, Ь, D и задающий
комплексную серию (см. § 3). Рассмотрим соответствующую этой
серии систему уравнений Эйлера (Е). Тогда к этим дифференци-
дифференциальным уравнениям полностью применимы все утверждения, дока-
доказанные нами выше в § 2 гл. 7. Сформулируем здесь эти утверж-
утверждения применительно к комплексной серии уравнений Эйлера. В
дальнейшем изложении мы будем следовать нашим работам [98],;
[99].
Лемма 1. Любая гладкая функция f{X), где XeG, заданная
на алгебре Ли G и инвариантная относительно присоединенного
действия группы Ли @ на% полу простой алгебре Ли G (т. е. по-
постоянная на орбитах этого действия), является интегралом урав-
уравнений Эйлера Х=[Х, <рХ], где ср: G-vG — произвольный самосопря-
самосопряженный относительно формы Киллинга оператор.
Доказательство следует из предложения 2 § 2 гл. 7.
Замечание. В комплексном случае не каждый элемент 1е
eG принадлежит орбите O(t) при некотором t^T, если Т — фик-
фиксированная подалгебра Картана.
312
Рассмотрим множество всед комплексных векторов grad/(X),
где /e/G. Через, IG мы обозначаем кольцо инвариантных полино-
полиномов на алгебре G. Пусть Т (X) — подпространство в G, состоящее
нэ всех элементов, коммутирующих с X. Если XeRegG (т. е. яв-
является регулярным элементом), то Т(Х) является некоторой кар-
тановской подалгеброй. Напомним, что в полупростой алгебре G
(над полем С) любые две картановские подалгебры сопряжены.
В частности, если XeRcg G, то Т(Х) =
~-goT(a, b)go~l для некоторого
ОН)
Рис, 119
Т(а, Ь) — это картановская подалгебра,,
содержащая элементы а, Ъ.
Ясно, что Т (X) содержится в подпро-
подпространстве, порожденном векторами
gradf(X), fe=/G. Если XeReg G, то
T(X) = (gradf(X), /e/G). Действитель-
Действительно, форма Киллинга невырождена на
алгебре G, и плоскость Т(Х) ортогональ-
ортогональна к .плоскости ТХО(Х) (рис. 119). Ор-
Ортогональность векторов grad/(X) к
плоскости ТхО (X) следует из определе-
определения 1G и соотношения (gradf, i) = |(f).
Лемма 2. Гладкая функция J по-
постоянна на орбитах алгебры G тогда и
только тогда, когда для любого XeG
выполнено тождество [X, grad f(X)] —0.
Здесь через gradf(X) обозначается
значение векторного поля grad f в точ-
точке X. Доказательство сразу следует из
леммы 4 § 2 гл. 7.
Предложение 1. Пусть fe/G, т. е. функция постоянна на
орбитах полупростой алгебры G. Тогда комплексные функции
К(Х) =f (Х+Ка) являются (при любом К) интегралами уравнения
Эйлера Х=[Х, срХ], где ср — оператор (метрика) комплексной се-
серии. Интегралом является и функция F(X)=<X, фХ>.
Доказательство вытекает из предложения 3 и теоремы 3
§ 2 гл. 7.
, Таким образом, интегралы f порождают целую серию новых
интегралов hx. Отметим, что функции (полиномы) К(Х, а) зави-
зависят только от элемента а и не зависят от элемента Ь, в то время
как операторы ф зависят и от а, и от Ь. Рассмотрим наш стан-
стандартный модельный пример: G=sl(n, С). Ясно, что стандартные
симметрические полиномы от собственных чисел матрицы X яв-
являются интегралами, постоянными на орбитах алгебры sl(n, С).
Следуя работе [8,4] (С. В. Манаков), преобразуем уравнение Х--=.
= [Х, фХ], записав его виде (Х+Ка)' =[Х+%а, фХ+А,Ь]. Действи-
Действительно,
[X + Ка, фХ + Щ = [X, фХ] + К ([X, Ь] +
Х»[а, Ь] = [Х,<рХ].
313
Здесь мы использовали то, что [а, Ь]—0 и [X, Ь]+[а, ц>Х]—0 в силу
определения оператора ср. Таким образом, уравнение формально
не изменилось, однако мы получили новую серию интегралов.
Это — симметрические полиномы от собственных чисел матрицыа
Х+Ка. Эти интегралы можно изобразить следующими двумя спо
собами.
1) Можно рассмотреть разложение полинома det(X+Xa— \iE) —
=2РаДац.е по степеням переменных Яиц,. Тогда все полиномы
Рар[Х, а), очевидно, являются интегралами уравнения Эйлера. •
2) Можно рассмотреть функции Sk=Spur(X+Xa)k, 1<&«:я,
и их разложения по степеням переменной X. Тогда Sk—
= SaQ*a(X, a)Ka. Связь полиномов Ньютона с симметрическими
полиномами сг, и определяет связь полиномов Q*a и Рар.
4.2. Интегралы компактной серии. Пусть Gc — компактная ве-
вещественная форма алгебры G. Пусть XeGc; a, be.Tc; Х+Ха^
еСс, если X вещественно. Алгебра Gc рассматривается над по-
полем R. Рассмотрим присоединенное действие группы ®с на ал-
алгебре Gc, расслаивающее алгебру Gc на орбиты. В отличие от
комплексного случая объединение орбит, «вырастающих» из Тс—
= Тс(а, Ъ), совпадает со всей алгеброй Go. Подалгебру Тс мы счи-
считаем фиксированной. Пусть <p:Gc->-Gc — оператор компактной
серии.
Лемма 3. Любая гладкая функция /, инвариантная относи-
относительно присоединенного действия группы ®с (т. е. постоянная на
орбитах), является интегралом движения, т. е. интегралом урав-
уравнения Эйлера Х=[Х, фХ], где <p:Gc->-Gc — произвольный самосо-
самосопряженный оператор (в том числе и оператор компактной серии).
Доказательство аналогично доказательству леммы 1.
Пусть IGC — кольцо инвариантных полиномов на алгебре Gc.
Предъявим в явном виде мультипликативные образующие кольца
IGc. Пусть N=N(TC) — нормализатор подалгебры Тс в Gc. Тогда
N/Tc=(b(Gc) — конечная группа, называемая группой Вейля ал-
алгебры Gc. Группа <b(Gc) изоморфна группе автоморфизмов под-
подалгебры Тс, индуцированных внутренними автоморфизмами труп-'
пы ©с Следовательно, группа Вейля тесно связана с орбитами
алгебры Gc. Более точно: пусть t^Tc, тогда орбита O(t) ортого-
ортогональна подалгебре Тс. Эта орбита возвращается снова на Тс, про-
протыкая Тс ортогонально в конечном числе точек. Эти точки, очевид-
очевидно, и являются образами элемента t при действии группы Вейля
(рис. 120).
Дольцо IGc отождествляется с кольцом полиномов на Тс, инва-
инвариантных относительно группы Вейля. Это кольцо допускает про-
простое описание: если группа ®с связна, то кольцо IGC является
свободной алгеброй с г образующими, где г=ранг Gc, в качестве
которых можно выбрать однородные алгебраически независимые
полиномы Pkl, Pk,, ...,Pkr, где degPft. = fei. Для простых . алгебр
Ли числа ki имеют следующий вид:
, для Ап: 2, 3, 4, ..., п, п+\;
для Вп: 2, 4, 6, ..., 2/г;
31? ;
для С п. 2, 4, 6, ..., 2л;
для Dn: 2, 4, 6,...,2/г—2, п;
для G2: 2,-6;
для F4: 2, 6, 8, 12;
для Е6: 2, 5, 6, 8, 9, 12;
для Ег. 2, 6,8, 10, 12, 14, 18;
для £8: 2, 8, 12, 14, 18, 20, 24, 30.
Полиномы PkC можно указать явно. Рассмотрим линейное пред-
представление минимальной размерности для алгебры Gc матрицами
размером (тхт). Пусть Л,, ..., Ат - веса представления, т. е.
линейные функционалы на Тс, отвечающие собственным векторам
XJ
Рис. 120
Рис. 121
операторов из Тс в пространстве представления. Отме-
Отметим, что координаты Ль ..., Ат на Тс могут быть линейно
зависимы (избыточный базис). Тогда полиномы Рк( имеют вид:
для А„:-
«+1
/»; для Вп: £ Л,*'; для Cn:J] Л^; для Dn
=i /=i /=i /=i
Л-= 2, 4, 6, ...,2«~2; и Р^Л^Л,-... -Л„.
m
Если Gc — особая алгебра Ли, то Р*. =V Л?'. Ясно, что
все кольца /Gc являются подкольцами кольца симметричных по-
полиномов S(Ab ,.., Ajv). Все указанные функции имеют вид
SpurX i==J] Л^, з'к исключением серии Dn, где добавляют еще
/=i
один полином 1/det X. Все функции кольца Юс можно считать
вещественными. Так как Gcc=G, то в точке X<=GC определены два
вектора: gradf(X) и gradcf(X), которые, вообще говоря, различ-
ны. В предыдущем пункте мы изучали векторы grad f. Векторы
315
graac f являются (в отличие от векторов gradf) вещественными
векторами с точки зрения инволюции cr:G-vG, oGc=Gc.
Рассмотрим множество всех вещественных векторов gradcf(X),
где f&IGc. Пусть ТС(Х) — подалгебра Картана, содержащая Хе
eGc, Tc(X)czGc. Отметим,, что если XeReg Gc, то XeReg G.
Плоскость Тс(Х) имеет вид g0Tc(a, b)go~\ где X—gotgfT1, t<=
еГс(о, b), причем ТС(Х) ортогонально ТХО(Х). Ясно, что Oc(X)cz
сО(Х), X^GC. Плоскость ТС(Х) порождается векторами
gradc f(X), где f^!Gc.
Лемма 4. Гладкая функция f постоянна на орбитах алгебры
Gc (можно считать, что /e/Gc) тогда и только тогда, когда вы-
выполнено тождество [X, grade/(Х)]=0 для любого IeGc.
Так как ТХОС(Х) = ([Х, |], |eGc), то для доказательства доста-
достаточно провести рассуждения из леммы 2.
Предложение 2. Пусть fs.IGc, т. е. функция постоянна на
орбитах алгебры Gc. Тогда функции hx(X)=f(X+Xa) являются
(при любом X) интегралами уравнения Х=[Х, грХ], где ф — опера-
оператор компактной серии, X+%ae.Gc. Интегралом является и квадра-
квадратичная функция (метрика) F(X)=<X, фХ>.
Доказательство. Требуется проверить, что (graded(Х)„
Х}с=0, где X^Gc и форма <,>С является ограничением формы
<,> на Gc. Форма <,> отрицательно определена на Gc и невырож-
невырождена. Далее, по определению (gradcM-X), l)c = lK(X)=dK(i)\x.
Как и в комплексном случае, вектор gradceGc . определен одно-
однозначно. Поскольку a, bs.Tc, X+ka^Gc, то равенство
<gradcK(X), ^>=0 проверяется, как при доказательстве предло-
предложения 1. Предложение 2 доказано.
Отметим, что так как T = Te®iTc, T=To@iTo, то веса Aj можно
продолжить на всю алгебру Т, а потому любую функцию f^.IGc
можно однозначно продолжить до комплекснозначной функции на
G, инвариантной относительно Ad. Таким образом, кольцо JGC
можно рассматривать как ограничение кольца IG на подалгеб-
подалгебру Gc.
Если g — гладкая функция на G и gradg — комплексный век-
вектор, то для функции q(X), XeGc, где q=g\cc, имеем grades
^GC) и этот вектор получается ортогональным проектированием
вектора gradg на Gc. Так как crG,;=Gc и а ортогонально относи-
относительно формы Киллинга, то из очевидных геометрических сообра-
соображений следует, что gradcg' = — (gradg + a^(grad g)) (рис. 121). Ко-
Конечно, это соотношение можно получить и формальной выкладкой»
которую мы здесь опустим.
Лемма 5. Пусть функции g, q совпадают с указанными вы-
выше. Тогда grado</(X) = (gradg(X) +grad(ga) (X))/2.
Доказательство. Достаточно доказать, что a(gradg(X)) =
=grad (ga)X, если XeGc, т. е. если аХ = Х. Достаточно доказать;
более общую формулу: a(gradg(X))=grad(ga) (стХ) для любого
XeG. Здесь через go обозначена композиция £(X)=g(a(X)). Ec-
316
ли g неинвариантен относительно а (т. е. ёаФё), то
tfrad(ga) (aX)¥=gradg(X) при XeGc, так как дифференциальная
операция grad чувствует поведение функции в окрестности точки.
Итак,
(cr(gradg), £) = (gradg, о£) = (o£)g = 2 ^
где o=(a,-ft) — матрица, записанная в координатах х\, ..., xNr
A/=dim G. Введем новую переменную Y=oX, г/а=2рорал:в, X—
=<s~lY. Тогда
^,Strife — = * Si^.-ftCTta 5 — ^ 5( I" )io
' дхк дуа дуа
Так как а — инволюция, то
<a(gradg(X))( t>=<grad(ga)y, |>,
т. е. CT(grad^(X))=grad(^a) (аХ), что и требовалось доказать.
Замечание. При исследовании интегралов алгебры Gc мы
обойдемся без леммы 5. Однако аналог этой леммы необходим
при исследовании интегралов нормальной серии, для которых Х+
+ka££Gn, если X<=Gn, a<=Tc{a, b)<=Gc.
4.3. Интегралы нормальной серии. Рассмотрим стандартное •
вложение Gn в Gc. Операторы y:G~>G порождаются векторами
а,Ь^Тс. В частности, a, bepGn, а потому X+ka<^Gn, если XeGn.
Это существенно отличает нормальную серию от комплексной и
компактной серий. Напомним, что операторы компактной серии ср
переводили Gn в себя, откуда следует, что ц>аь является ограниче-
ограничением ф на Gn.
Предложение 3. Пусть f^.IGCj т. е. функция f постоянна
на орбитах алгебры Gc. Рассмотрим функции Я\(Х), где \eR,
JeGn, являющиеся ограничениями функций f(X+Ka) на Gn. Тог-
Тогда функции qt. являются (при любом К) интегралами уравнения
Х=[Х, файХ], где ц>аь — оператор нормальной серии. Интегралом
является также и функция (метрика) F (Х)=<Х, фХ>.
Доказательство следует из того, что фаь — это ограни-
ограничение ф на инвариантное подпространство Gn-
4.4. Инволютивность построенных интегралов. Рассмотрим сна-
сначала комплексную серию операторов ф.
Предложение 4. Пусть fug — произвольные гладкие
комплекснозначные функции на полупростой комплексной алгебре
Ли G, постоянные на ее орбитах. Рассмотрим функции К(Х, а) —
=f(X+Xa), dtl{X, а)=£(Х+ца), где а<=Т(а, Ь). Здесь Т(а, Ъ) -
фиксированная картановская подалгебра, а числа % и ц — произ-
произвольны. Тогда интегралы hx и d^ находятся в инволюции. Кроме
того, {f, /tx}=0 для любой функции вида К, где f^IG.
Доказательство сразу следует из теоремы 1 § 2 гл. 7.
Аналогично проверяется инволютивиость интегралов компакт-
компактной серии. Пусть Gc — вещественная компактная форма ком-
31Т
плексной простой алгебры, G, сос — симплектическая форма на ор-
орбитах Gc. Ясно, что Юс совпадает с ограничением формы ю (в G)
на подалгебру Gc.
Лемма 6. Для любой гладкой функции f на Gc выполнено
тождество sgradf (X)=[gradf (X), X].
Лемма 7. Для любых двух гладких функций f и g на Gc вы-
выполнено тождество {f(X), g(X)) = <X, [gradf(X), gradg(X)]>.
Лемма 8. Пусть fu f2^IGc. Тогда [grad/,(X), gradf2(X)]=0
для любого ХеСс
Предложение 5. Пусть f, g^IGn. Положим К(Х, а) —
= /(Х+Яа), dB(X, a)=g(X+\ia), где а<=Тс(а, b); \ ц — про-
произвольные вещественные числа. Тогда интегралы hk и йЛ комму-
коммутируют. Кроме того, {f, hK}=0 для любой функции f^IGc.
Докажем инволютивность интегралов нормальной серии. Отме-
Отметим, что симплектическая форма соп на орбитах Gn совпадает с
«граничением сос на подалгебру Gn. В самом деле, если XeGn,
то On(X)czOc(X), так как @п — подгруппа в ©с. На Gn рассмот-
рассмотрим операцию gradn и операцию sgrad,,.
Лемма 9. Для любой гладкой функции f на Gn выполнено
тождество sgradnf(X)=[gradnf(X), X].
Лемма 10. Для любых двух гладких функций f и g на Gn
выполнено тождество {f(X)t g(X)} = (X, [gradnf(X), gradng(X)]}.
Лемма 11. Пусть fu f2<=IGn. Тогда [gradn fi (X), gradnf2(X)]=
=0 для любого IeGn.
Предложени-е 6. Пусть f, ge=IGn, hx(X, a)=f(X+ka),
-dtt(X, a)=g(X+\ia), aeT(a, b) (s частности, a, b^Gn); I, \i^
eR. Положим
•Функции fug можно считать вещественными, поэтому не следует
путать знак «черта» с комплексным сопряжением. Пусть ф=фаь —
оператор нормальной серии. Тогда интегралы Я* и $„ находятся
в инволюции. Кроме того, {F, йх}п=0, где F(jt)=<X, фХ>, X<=Gn.
Доказательство. Поскольку элемент Х+Ка не принадле-
принадлежит Gn, если XmGn, то, в отличие от комплексной и компактной
серий, следует провести дополнительные рассуждения. Отметим,
что 'Fn—Fc\on. В силу леммы 10 достаточно доказать, что
<Х, [gradnЯх.(Х, a), gradn5w(X, а)]>=0. Выразим gradnSx через
gradc ft*. Как и в лемме 5, устанавливается, что gradn 7п=
= (gradcft».+gradc^x)/2, где XeGn, Hx=hKox, t — инволюция, опре-
определяющая Gn, т. е. xGn=Gn. Доказательство этой формулы для
gradn Я». аналогично доказательству леммы 5. Так как
тgradcf(X+Xa)=gTadcfx(X-la), где Xf=Ga, тХ=Х, ае=Те(а, Ь),
то ха—~а, тТс——Тс. Напомним, что хХ=Х (комплексное сопря-
сопряжение) на Gc и Tc = iT0, где То — вещественная часть в Т. Окон-
Окончательно
gradn fh{X, a) = (gradcf(X + Xa)+gradcf(X — Я,а))/2, :
318
■ др /—/т. Так как т — автоморфизм, то функция f также постоян-
постоянна на орбитах Gc, т. е. отображение f-*f переводит Юс в себя.
II гак, достаточно доказать, что {X, [grade/ (X+Ka) +gradcf(^—
ка); gradeg[X + \ia) + gradcg(X—ца)]> = 0. Это соотношение
||азбивается в сумму
(X, [gradc/(X + Яд), gradcg(X + ул)]) + (X, [grad,/(X + Яд),
grad,i(X-fia)]) + (X, [gradJ(X-^a), gradc g(X + ул)]} +
+ (X, [gra"dc f(X~ Яд), grad, g (Х-ца)]>. |
Так как f, g, f, g&Gc, то, как и при доказательстве предложе-
предложения 4, проверяется, что каждое из этих четырех слагаемых рав-
равно нулю, что и доказывает инволютивность й* и <2ц. Остается
проверить равенство (X,'[gradnF_(X), gradnhk.(X, a)]} = 0. Так как
фХ=фаЬЛ при X^Gn, то gradnF=gradcF. Осталось проверить,
что (X, [ц>Х, gradef(X+ka)]) + {X, [<?X, gradc~f(X~Xa)}) = 0. Так
как f, l^.Gc, то равенство нулю каждого из этих двух слагаемых
проверяется так же, как и при доказательстве предложения 4.
§ 5. Случаи полной интегрируемости уравнений Эйлера на
полупростых алгебрах Ли
5.1. Комплексная серия твердотельных метрик. Пусть G —
комплексная простая алгебра Ли, X — регулярный элемент, т. е.
точка общего положения. Напомним, что <а, Х}¥*0 для любого
корня а из подалгебры Картана Т(Х), содержащей X. Пусть
■f\,...,fr^IG — полный набрр функционально независимых поли-
полиномов на G, постоянных на орбитах алгебры. Так как 1G являет-
является комплексным расширением кольца Юс, то /ь ..., fr можно счи-
считать комплексными полиномами от комплексных координат на ал-
алгебре G. На протяжении настоящего пункта элемент X будем
считать фиксированным. В точке X возникает набор комплексных
векторов grad/u.h, где h%th{X, a)=fk(X+Ka), l^fe^r, a^G — про-
произвольный элемент. Переменные X и а входят в hKk равноправно
в следующем смысле:
Ам(Х,а) = Я'*+|Ал_1>/к(а,Х), где feghKk = qk+ 1,
В дальнейшем в качестве а выберем регулярный элемент, на кото-
который натянем Т(а, Ь). Пусть V(X, a)—комплексное подпростран-
подпространство в G, порожденное всеми векторами grad h^k.
Наша цель: оценить снизу размерность dime V(X, а). Элемент
а выберем в соответствии с дальнейшими потребностями. По-
Поскольку hy>k — полиномы по X, то рассмотрим разложения
+l
hx,k— V Pfi't гДе ^+l=degfj:. Будем считать, что полиномы
fh упорядочены по возрастанию степеней: qk<qii+i- Пусть N+1 =
319
=qr+\=iegfr — наибольшая степень среди образующих fk- Счи-
Считаем, что Pkqk+2 = Pkqk+b=- -.=PkN^x=0, если k<r, поэтому все по-
полиномы hx,k рассматриваем как полипомы степени N+1, у кото-
которых некоторые коэффициенты при больших степенях К равны ну-
нулю. Полиномы Pkqk+l{a) не зависят от X. Имеем
"к
£=0
где ик'=ик'(Х, a)=gra&Pk'(X, а) — полиномы степени i no X я а.
Ясно, что- Up (а) не зависит от X, так как Рр линеен по X. Как
■показано ниже, все векторы Up (а) порождают картановскую под-
подалгебру Т(а), не зависящую от выбора X.Ясно,что V(X,а) порож-
порождено всеми векторами £/*.'. Дело в том, что h%.,k — интегралы век-
векторного поля X при любом X, а потому интегралами являются в
действительности все функции Р/Л градиенты которых совпадают
•с векторами IV, порождающими V(X, а).
Лемма 1. Для каждого ky \<k^cr, выполняются следующие
основные рекуррентные соотношения на векторы IV:
Доказательство. В силу леммы 2 из §4 0=
= [X, grad/>t(X)] для любого X. Применяя это тождество к функ
циям hi,k, Получаем [Х+Ка, gradhX:k{X, а)]=0, т. е.
£] = 0,
[=0
откуда и следует утверждение леммы, так как тождество должт
быть верно при любом К.
Эта «каскадная» система уравнений '(«каскад») играет фунда
ментальную роль в дальнейших исследованиях. •
Так как Т(Х) — подалгебра Картана, то можно построить ког-
невое разложение алгебры G по отношению к Т(Х) и выбрать ое-
зис Вейля. Пусть 2 = 2(Х)={а} — система корней на Т(Х) и 2 =
=2+U2_ — разложение этой системы на положительные и отрица
тельные корни относительно некоторого базиса в Т(Х), Г1уст1
n=(ai cir) — система простых корней и Ха — собственные
320
некторы корней а. Положим V+(X) = (подпространство, порожден-
порожденное векторами Ха, аеЕ+); V~(X) = (подпространство, порожден-
порожденное векторами Хр, ре2_). ■ ...
Считаем, что векторы Ха, ае2, дополненные базисом Вейля в
Т (X), дают базис Вейля в G. Подпространство T(X)®V+(X) яв-
является разрешимой подалгеброй в G. Плоскость V+(X) является
ппльпотентной подалгеброй в G. Для каждого k<r указанная це-
цепочка тождеств (см. лемму 1, каскадную систему уравнений)
обрывается раньше, чем на М-и шаге, а именно: [Ukq^, c]=0.
Лемма 2. Если a<=T(X)®V+(X), то graAhkk{X, a)T{
<BV+(X),T.e.
Доказательство. Так как G = T(x) ф V+(X) ф V~(X), то
вектор gmdh\,k можно разложить по базису Вейля:
grad«M = a+ JiieXa, u<=T(X).
аб2(Х)
Докажем, что \ха = 0; если a e 2_. Допустим противное и пусть
а,б2-—наименьший корень, для которого \\аф0. Так как qe
! (X), то a = f+ £ vaXa, тогда X+Ха = (X +Щ +
a. Отсюда
X
где W и Z — оставшиеся слагаемые при разложении по базису
Вейля. Далее,
Z L = [\ia.Xa.; X + Щ + [W, X + М + {ца.Хао. 2] + [Г, Z].
Последние три слагаемых содержатся в подпространстве S®T(X),
где 5 порождено векторами Ха, а>а0. Напомним, что
[Ха, Хр] =AfapXa+p. Так как в силу леммы 2 из § 4 L=0, т»
[(ХаДао. Х + Ь] = 0, т. е. 0=(оо, X + Яи) Ha,Xao; отсюда <а0, Х+
+Я,и>=0. Однако в силу выбора X имеем <ao, Х}¥=0 и, следова-
следовательно, (а0) Х+Я,и)=^0 при достаточно малых X. Полученное проти-
противоречие доказывает лемму.
В дальнейшем будем считать, что a^T(X)®V+(X). Рассмот-
Рассмотрим простые корни си, ..., аг, тогда каждый положительный ко-
г
рень а можно представить в виде V #№, где т,->0, причем чис-
£=1
ла Шг — целые. Так как ab...,ar — базис, то это разложение оп-
определено однозначно. Порядком (или высотой) корня аеЕ+ на-
зывается целое число k — k (a) = V m£. Через Vk+(X) обозначим
11 А. Т. Фомеикв ,321
подпространство в V+(X), порожденное векторами Ха, для кото-
которых k (а) — k. Тогда очевидно, что V+ (X) = V\+® ... ф Vs+, причем
Vi+ порождено Ха„ ... , Хаг, т. е. простыми корнями си, ..., аг.
Уточним теперь выбор элемента a^T(X)®V+(X). Пусть V+
и o = J] v,Xa., где все v^O. Тогда [V+k> a]czV+k+u [T(X), а]а
czVi+.
Лемма 3. Пусть X, а выбраны, как показано выше. Тогда
Vi+=[T(X), а] и ada:T(X)-*-Vi+ - изоморфизм.
Доказательство. Так как dim Г(Х)=сНт V\+=paHr G, то
достаточно убедиться, что ada — мономорфизм на Т(Х). Допустим
противное. Пусть существует УеГ(Х) такой, что [У, а]=0. Отсю-
г г
да получаем [Y, a] = Y \( [Y, Xa.] = ][] vc(Y, at) Xar Следова-
тельно, <У, а,->=0 для всех простых корней а, (так как все );
это означает, что У = 0. Здесь (У, ai) = aj(y) и форма (,} невы-
рожденна. <
Лемма 4. Пусть G — полупростая алгебра Ли; X, а — век-
векторы, указанные выше. Тогда [V+k, a]=V+k+u т. е. ada: V+*-*-
-*-V+k+i —эпиморфизм (рис. 122).
Это утверждение легко извлекается из известной работы Ко-
станта [265]. Полное доказательство приведено также в нашей
первоначальной работе [98]. См. также рис. 123. Так как доказа-
доказательство леммы 4 технически громоздко, то мы его здесь опускаем.
Лемма 5. Имеют место соотношения: 1) Uk°^T(X), 2) tVe
e=7(X)ewe...eVi+ для любого l<k<cr.
Доказательству Соотношение 1) следует из леммы 1 и
того, что X — регулярный элемент, т. е. G(X, 0)=T{Xy. Соотно-
Соотношение 2) докажем по индукции. Так как при /=0 соотношение уже
доказано выше, то можно считать, что ^'-'еГ^)® 1Л+Ф.. .©
®V+i-u Отсюда [tV'-1, й]еГ (X)®Vl+®.. .0V^ в силу выбора
a<=Vi+. Из леммы 1 имеем [Uk\ X]=[Uk'-1, a]e7(XHK,+0.. .0
®Vi+. В силу леммы 2 и*к = р{к + О\, где pi,!e7(X), D;he=V+(X).
Поэтому [Uih, X]=[D'k, XleErfX)©^©...©^, но так как Dlk<=
eV+(X), то [D'k, X]eУ!+©...©У,+. Поскольку оператор adx:G->-
r>-G сохраняет корневое разложение алгебры G и поскольку X
выбран в общем положении, то ad* обратим на V+(X) и, следо-
следовательно, D'/eeW"©...©^, т. е. Uik£ET(X)®Vl+®...®Vi+. Лем-
Лемма доказана.
Лемма 6. Векторы U'k, j<£i, порождают все подпространство
X)®V+®(BV+
)l
Доказательство. При / = 0 векторы Uh° лежат в Т(Х)
(см. лемму 5). Напомним, что при >,=0 имеем ho,k=fk, т. е. U°k=
=grad/zMU=0=grad/ft. Так как IG — свободная алгебра от г об-
образующих fi, ..., fr, то все векторы U°k линейно независимы и
порождают Т(Х). Дальше движемся по индукции. Рассмотрим
произвольный вектор |'еК+,-+ь Положим %=[%', Х]еУ+,+1. В силу
322 , ■ :
леммы 4 существует элемент r\^Vi+ такой, что | —fa, с]. По пред-
предположению индукции r\=I1!<i,kr[ikUlk. Следовательно, .
£=h, a] = 2t],ft[l«ft, а] =Ъыкг\}ь[ик1+\ X] = [£', X].
Так как X выбран в общем положении, то яйх обратим на плос-
плоскости V+(X), поэтому l'-'Li<i,kr\ikUk!+l=p^,T (Х)в т. е. |' разла-
разлагается в линейную комбинацию векторов И'к,_ где j<i+l, что и
требовалось доказать.
Лемма 7. Пусть а — регулярный элемент (в общем положе-
положении). Тогда dim V{X, a)»dim7(X)eV+(X) = (dim G+ранг G)/2,
£.
Рис. 122
Рис. 123
где V (X) — комплексное подпространство, порожденное всеми век-
векторами gradhKk(X, а) для всех точек XeG из всюду плотного от:
крытого подмножества в алгебре Ли G.
Доказательство. Пусть X'eReg G, (a, Х')Ф0 при всех a
и элемент a'=EviXaj-, где все v^O (см. выбор элемента а' перед
леммой 3), принадлежит Vi+(X'). Тогда из леммы 6 следует, что
векторы gra.dhx,k(X', а') порождают подпространство Т(Х')(В
4BV+(X')=V\X', а'), которое является разрешимой подалгеброй,
содержащей элементы X и а'. Поэтому dim V(X', а') = dimT(X') +
+dimVl (X')=paHrG+— (dim G-ранг G)=—(dim G+ранг G).
Таким образом, для указанных элементов X' и а' искомое не«
равенство достигается на точном равенстве. При малом шевелении
а' получаем, что dim{grad/zl)ft(X/, а'}± может только увеличиться.
Так как множество Reg G открыто и всюду плотно в G, то сколь
угодно близко к а' найдется элемент a"eReg G и, следовательно,
11'
323
dim{grad/zl,ft(X', a")}>(dim G+ранг G)/2. Так как это неравенст-
неравенство означает отличие от нуйя некоторой комплекснозначной функ-
функции на G (это некоторый мииор) как функции от переменного
вектора X' (при фиксированном а"), то неравенство справедливо
в некотором открытом, всюду плотном в G подмножестве {X}. Бо^
лее того, это множество связно, так как множество особых точе!
(в которых неравенстно заменяется на обратное) выделяется гк
крайней мере одним комплексным уравнением, т. е. имеет вещесТ'
венную коразмерность не меньше двух. Для перекода к оконча-
окончательному утверждению для aeReg G достаточно заметить, что
элементы X и а входят симметрично во все предыдущие утверж-
утверждения, так как f (X+la) =X9/(X/A,+a). Здесь /e/G — полином сте-
степени q.
Замечание.-НПодпространство V(X', a')=-T{X')®V+(X') яв-
является разрешимой подалгеброй в алгебре G, только если а'е
^V^(X'). Как только точка а" выходит за пределы Т(Х')@
(&V+(Xr), подпространство V(X', а"), порожденное градиентами
функций hx(X', а"), не совпадает с Т(Х')<$V+(X') и начинает, во-
вообще говоря, удаляться от него.
Теорема 1. Пусть G — комплексная полупростая (или ре-
дуктивная) алгебра Ли, Х=[Х, ц>Х] — уравнение Эйлера с опера-
оператором ф комплексной серии. Тогда эта система вполне интегрируе-
интегрируема по Лиувиллю на орбитах алгебры G, находящихся в общем
положении. Более точно: пусть f — любая гладкая инвариантная
функция на G. Тогда все функции hk(X, a)=f(X+ka) являются
интегралами векторного поля X при любых комплексных числах
X. Любые два интеграла /г* и dw построенные по функциям
f, g^IG, находятся в инволюции на любой орбите (регулярной
или сингулярной). Гамильтониан /7=(Х, фХ> векторного поля X
также находится в инволюции со всеми интегралами вида hk. Из
множества указанных интегралов можно выбрать функционально
независимые на орбитах общего положения интегралы в количе-
количестве, равном половине размерности орбиты. Интеграл F функцио-
функционально выражается через интегралы вида hk.
Эта теорема была сформулирована и доказана нами в [96, 98].
Доказательство. Пусть сначала G — простая алгебра.
Полная интегрируемость системы X на орбитах общего положе-
положения следует из леммы 7. В силу этой леммы все интегралы можно
взять в виде hk. Осталось доказать утверждение, относящееся к
интегралу F. Ясно, что gradF(X)=(pX. Так как в силу леммы 8
градиенты интегралов hk{X, а) порождают V(X, а), где
dim V(X, a)^(dim G + ранг G)/2, то достаточно проверить, что
, а), где Xe=V(X, а). В силу леммы 1 [tfy, а} = 0,
*, X)+[Ul4~\ a] = 0 для всех k, где qk=degfk. Напомним, что
+2=...=I/^=s0. Итак, 1/**еГ(а), причем векторы У**
порождают всю картановскую подалгебру Т(а). Действитель-
Действительно, векторы U°h порождают всю подалгебру Т(Х), и так как
324 _.,
tih,k(X, а) = Я,'/*+1/гя->,*(а, X), то в силу этой симметрии векторы
UtH порождают Г (а).
Отметим, что Г(а) вложено в V(X, а) «наискосок», пересе-
киясь, вообще говоря, со всеми плоскостями Va+(X). Об этом мож-
можно говорить, только если aeV+(X). Обозначим через b произволь-
произвольный вектор общего положения в Т(а), ЪФа. Тогда в силу замена-
иия существуют такие числа pi, ..., рг, что Ь — У\ Р*^1*- Рассмот
„-1
рим векторы Uik ' и их линейную комбинацию ft = 2
В силу соотношений \U9kk, Xj+lU^1, «1 = 0, суммируя по k, полу-
получаем [Ь, X] + [h, a] =0, где h<=V(X, a).
Пусть Х=Х+а, где as Г (a, b), XeV+(a). Тогда [b, X]+[h, a]=
=0, т. е. h=aia~l айьХ=<раьХ- Пусть, далее, D:T(a, b)-*-T(a, b) —
произвольный симметричный оператор. Тогда <рХ=фа&.Х>+/)а=
=h+Da^V(X, а), так как Г (о, b)aV(X, a), h<=V{X, а), что и
требовалось доказать..
^Случай полупростой алгебры, очевидно, сводится к рассмотре-
рассмотрению простых алгебр ввиду распадения системы корней полупро-
полупростой алгебры в ортогональную сумму систем корней простых под-
подалгебр. Теорема доказана.
Ясно, что теорема 1 верна и для редуктивных алгебр Ли.
5.2. Компактная серия твердотельных метрик. Пусть Gc — ве-
вещественная компактная форма простой комплексной алгебры Ли;
a: G-+G — соответствующая инволюция; XeGc — элемент общего
положения; О(Х) — орбита элемента X в Gc- Наша цель: изучить
подпространство, порожденное векторами gradchK(X, а), где
f<=IGc.
Теорема 2([96], [98]). Пусть Gc — вещественная компактная
форма полупростой комплексной алгебры Ли G и [X, q>X]=X -*
уравнение Эйлера с оператором компактной серии. Тогда эта сис-
система дифференциальных уравнений вполне интегрируема по Лиу-
виллю на орбитах общего положения. Более точно: пусть f^.IGc —
любая гладкая инвариантная функция. Тогда все функции вида
ht.(X, a)=f(X+Xa) являются интегралами векторного поля для
любого вещественного X. Любые два интеграла hx и da, построен-
построенные по функциям f, g^IGc, находятся в инволюции на любой ор-
орбите (регулярной или сингулярной). Гамильтониан F—(X, <pX>
векторного поля 1 также находится в инволюции со всеми инте-
интегралами вида hx. Из множества указанных интегралов (оно, во-
вообще говоря, избыточно) можно выбрать функционально незави*
симые в количестве, равном половине размерности орбиты общего
положения. Интеграл F '(порождающий твердотельную метрику)
функционально выражается через интегралы вида hx.
Доказательство. Интегралы.компактной серии предъявле-
предъявлены нами выше. Их инволютивность доказана нами в предложении
5 § 4. Все интегралы компактной серии можно получить как огра-
325
ничения комплексных интегралов алгебры G. Рассмотрим функци
fh на G, являющиеся комплексными продолжениями функций у
на -Gc, где glt .,., gr — образующие кольца IGC. Найде!
dim VC(X, а), где пространство VC(X, а) порождено векторам!
grad^^.ft(X, a); q\,k{X, a) =(X + Xa), a&Gc. Пусть простра«
•ство V{X, а) порождено grad^,ft; h\,k{X, a)=/fe(X +Ал). В сил
леммы 5 § 4 пространство VC(X, а) является ортогональной про*
•екцией пространства V(X, а) на Gc, так как gradc qitk^4
(dhuh)l2 ' I
Докажем, что векторы gradc^fe образуют вещественный баз»
в VC{X, а), размерность которого равна dim V(X, а). Пусть вектф
ры gradhx.,k образуют базис V(X, а) над С. Покажем, что посЛ
их проектирования на Gc все векторы остаются линейнс
независимыми над полем R. В самом деле, пусть нашлис!
вещественные числа о),& такие, что 2co,ftgradc<7At.,ft =0. Тогд
2(i>lkgradh),.,k +u>lkograuhxi,k = 0 и в силу вещественности co,fe имее|
grad (Z«itkhx.,k) + (tgrad Е(о,й/гх(,/=О, т. е. к~Ъо1к grad Ая..,*а
е (ортогональному дополнению в G к Gc, на котором о=—1).Эп
означает, что вектор grad f=h, где ^=2<о^/й(ЯЧ-Л,-а), ортогопале:-
к Gc. Так как кФО (по предположению не все со^ равны нулю^
то 1Фconst на картановской подалгебре в С и в то же времг
/^const на Gc, в частности, f^const на картановской подал-
подалгебре в Gc- Но так как IG — комплексное расширение кольца /ос
то f==const на G, т. е. все со«=О. Отсюда следует, чтг
dimRVc{X, a)>(dimR Gc+ранг Gc)/2= (dime G + paHrG)/2.
Таким образом, плоскость VC(X, а) накрывает по крайней мер
половину касательной плоскости, к орбите О(Х) в Gc, откуда i
следует полная интегрируемость системы Я на Gc. Утвержденш
теоремы 2, относящиеся к гамильтониану F на Gc, следуют из сп
ответствующих утверждений о комплексном гамильтониане F нг
G. Теорема 2 доказана.
5.3. Нормальная серия твердотельных метрик. Пусть GndGc —
нормальная подалгебра. Предварительно опишем Gn как пода/
гебру неподвижных точек некоторой инволюции. Пусть o:G-*~G-
инволюция, отвечающая компактной форме. Тогда а£а=£'-'
<j(iEa)=—iE-a, a(iT0)=iT0, где tT0=7c — картановская подалгег-
ра в Gc, аТ0=—Т0, где T=To®iTo— картановская подалгебра в (
Подалгебра Gc совпадает с неподвижными точками о и имеет ве
щественный базис Еа+Е-а, i(Ea—E-a), iT0- Вторая инволюция
определяется так: %Еа — Еа, r(iEa) =—iEa, x(iT0)=—lT0.
Как показано выше, инволюция т определяет нормальную Bt
щественную подалгебру Go, причем Gn=Gof]Gc, т. е. Gn совпадае
с множеством точек, неподвижных относительно инволюций т и г
Рассмотрим отображение v=ta. Так как т и а коммутируют, т
v2=l и v£a=£-a, v(t£'!x)=i£_a, v(iT0)=—tT0. В частности, эт
означает, что v является комплексным автоморфизмом G. Напоь
ним, что т и о — антикомплексные инволюции. Поэтому неподвия-
326
Mi.it" точки для v образуют комплексное подпространство Uxa( — Uax)
и (!. Вещественная подалгебра Gn натянута на векторы £«+£-<*>
Лемма 8. Комплексное подпространство GT0 является комп-
псксификацией вещественного подпространства Gn=R{£a+£-a} «
A„ - (С{Еа + Е-а})х, т. е. Gn совпадает с неподвижными точками т
mi G™. Аналогично Gn— (C{Ea+Е-а})а, Кроме того, алгебра G рас-
распадается в прямую сумму ортогональных подпространств G=
- T®G™@B~, где 5~ = C{t(£„ — £_„)}.
Дока з ат ел ьство. Тот факт, что Gxa юС{Еа + £_„}, очеви-
очевиден. Докажем обратное включение. Разложим G в прямую сумму
ортогональных подпространств: G =
а,
где Ра=
*=С{Еа+Е-а}. Это разложение G инвариантно относительно v.
Пусть XeG и \Х=Х. Представим X в виде h + Г &, Тогда в
6
силу инвариантности разложения vh=h, vga=ga, откуда /г=0,
ga=p(£a+£-a), где реС, т. е. ХеС{Яв+£_а}, что и требовалось
доказать.
Итак, G™=C{£a+£-a}=CGn. Соотношения Gn = (О" = (СТУ
очевидны. Так как dim y+(a)=dim GT0, то пространство T@Gxa@
®В~, очевидно, совпадает с G. В плоскости, ортогональной к Т,
вместо базиса Еа, £_„ введен базис £a + £_a, i(£«—£a~). Таким об-
образом, Г-L (G™@B~). Ортогональность G™ и В~ устанавливается
простым вычислением. Напом-
П'ИМ, что Еа и Еа~ неортого-
нальны. Кроме того, Gza®T —
не подалгебра. Лемма дока-
доказана.
Все эти подпространства
показаны на рис. 124. Подал-
Подалгебра Gc изображена в виде
двумерного плоского диска;
Gc = Gn@A-®Tc(a) = А+®
®А~(ВТс(а), где а —элемент
общего положения. Остальные
плоскости, частично изобра-
изображенные пунктиром, не при-
принадлежат Gc.
Дальнейшее исследование
интегралов нормальной серии
проводится по схеме, изложен-
изложенной выше для полупростой
комплексной и компактной Рис. I24
серий. Ввиду недостатка, ме-
места мы не будем здесь оста-
останавливаться на подробностях, отсылая заинтересованного читателя
к нашим первоначальным работам [96, 98]. Здесь мы приведем
лишь окончательную формулировку.-
Теорема 3. Пусть Gn — нормальная компактная подалгебра
е полупростой комплексной алгебре Ли G и Х—[Х, фХ] — уравне-
уравнение Эйлера с оператором нормальной серии. Тогда эта система
вполне интегрируема по Лиувиллю на орбитах алгебры Gn, нахо-
находящихся в общем положении. Более точно: пусть fe/Gc — любая
•гладкая инвариантная функция. Тогда все функции hk(X, a) =
=f(X+ka)\Gn являются интегралами потока X для вещественногс
.1. Любые два таких интегрйла находятся в инволюции на любой
юрбите (регулярной или сингулярной). Гамильтониан F={X, q>X]
потока X также находится в инволюции со всеми этими интеграла-
интегралами. Из множества указанных интегралов можно выбрать функцио-
функционально независимые на орбитах общего положения в количестве,
равном половине размерности орбиты. Интеграл F функционально
выражается через интегралы вида /г*. В частности, мы получаем
полную интегрируемость уравнений движения классического пг-
мерного твердого тела.
5.4. Интегрируемость уравнений Эйлера на сингулярных орби-
орбитах. Выше мы доказали интегрируемость уравнения Эйлера для
Метрик, обобщающих метрики твердого тела на всех орбитах об-
общего положения,вчпроизвольной полупростой алгебре Ли. Однако
в действительности это утверждение можно еще расширить. Ока-
Оказывается, полный инволютивный набор полиномов существует и
«а любой полупростой орбите в алгебрах Ли. В частности, эта
■орбита не обязана быть орбитой общего положения (т. е. может
<быть сингулярной); кроме того, полный набор- существует на лю-
любой сингулярной орбите в компактной алгебре Ли. Впервые этот
■важный результат был анонсирован Дао Чонг Тхи в [45], однако
доказательство этой теоремы в [45] содержало пробелы. Эти про-
пробелы были окончательно устранены А. В. Браиловым. В настоя-
настоящем пункте мы приведем полное доказательство этой теоремы.
Пусть G — полупростая алгебра Ли группы Ли @. Орбита О
представления Ad группы Ли & в алгебре G называется полупро-
полупростой, если она состоит из полупростых элементов алгебры Ли. Как
и выше," мы будем обозначать ассоциативную коммутативную ал-
алгебру полиномов на G, инвариантных относительно присоединен-
присоединенного представления, через IG. Пусть fi, ..., fr — набор однород-
однородных инвариантов, порождающих алгебру IG, и а — произвольный
элемент в G. Коэффициенты при К' в полиноме #;(>., X)=fi(X+Xa)
обозначим через Hh,a- Как мы уже знаем, эти функции являются
интегралами уравнений Эйлера.
Теорема 4. Для любой полупростой орбиты О в алгебре Ли
С и для элемента 'а общего положения в G из функций Hh,a всег-
всегда можно выбрать независимые функции в количестве, равнол
половине размерности орбиты, так, что после ограничения эти>
функций на орбиту они останутся функционально независимыми
При этом орбита не обязана быть орбитой общего положение
(может быть сингулярной). Эти функции образуют на орбже пол
ный инволютивный набор.
328 •
Сначала мы рассмотрим случай комплексных пол у про-
простых алгебр Ли. Пусть G — такая алгебра. Фиксируем1 полу-
простой элемент X. Фиксируем также подалгебру Картана Т та-
такую, что Х^Т и базис Вейля Еа алгебры G по модулю Т. Здесь
неД, А — система корней. Для каждого базиса В системы корней
А элемент V Еа обозначим через е+. Множество положитель-
пых корней обозначим, как и раньше, через Д+, множество отрица-
отрицательных керней — через Д~. Определим также множества корней
A)
Я^Я'ПА*. B)
Лемма 9. Найдется базис В такой, что
C)
Доказательство. Пусть z— такое комплексное число, что
для всякого корня ае/?' вещественная часть Rea(zX) не равна 0.
Выберем базис В так, чтобы для каждого корня аёВ веществен-
вещественная часть Ree,(zX)^0. Тогда в случае pe7?'+, aeB имеем
RepBX)>0, ReaBX)>0 и Re(a+P) (zX)>0. Следовательно, если
a + peA, то а + Э&/?'+. Лем,ма доказана.
Для каждого корня аеД определяется пространство
Ga={XeEG;[h, X]=a(h)X}, /г<=7\ D)
Элемент Ha^[Ga, G-a] определяется равенством а(Яа)=2.
1 Лемма 10 [23]. Пусть G — комплексная полупростая алгебра
flu, г — ее ранг, Т — подалгебра Картана, А — система корней,
В — базис системы Д, h — элемент из Т такой, что a{h)=2 для
любого аеВ. Положим
саНа = п. Пусть b = у. с« '£_а, 5 = Се+ + С/г + СЬ.
а) Тогда \h, е+] —2е+, [п, Ь] =—2b, \e+, b] =h, причем dim Ge+ =
=dim Gb=r, где G<={g^G : [t, g]=0}.
б) Рассмотрим G как S-модуль, соответствующий присоединен*
ному представлению. Пусть G=Ai® ... ФЛ„ — некоторое разложе-
ние этого модуля в прямую сумму простых S-модулей размерно-
размерностей vi + 1, ..., Vn+1, где vi<s ... <vn. Тогда n=r.
в) Пусть fu ..., fr — однородные алгебраически независимые
образующие (полиномы) алгебры инвариантов IG, степеней
1,..., mr+ 1, где mi^...^mr. Тогда Vi = 2m.i для любого i —
г) Дифференциалы функций fu ..., fr линейно независимы &
любой точке множества е+А. Gb.
Для элемента h из леммы 10 все собственные значения эндо-
эндоморфизма adh — четные целые числа. Для всякого целого числа.
329-.
п собственное подпространство эндоморфизма adh с собственные
Значением 2/г обозначим через Gn. Пространство G" назовем п-и
диагональю алгебры Ли G. Пусть а — корень и а = V трр, где
Рев
тэ — подходящие целые числа. Высотой корня а называется (см
выше) число |а| = V тр. Из определения диагоналей алгебрь
рев шя-
Ли G следует, что G°=T и Gtl= ф Ga при пФО. Пусть Д, ..
|о|=п
..., /г — набор однородных образующих алгебры IG степеней
/П[+1, ..., trir+l. Для произвольного элемента a^G дифферен-
дифференциалы dHii,a(X) удовлетворяют «каскаду», состоящему из следую
щих равенств (см. [98] или предыдущие пункты):
[X, dHl
[X, йН\,а(Х)] + [п, dHla{X)]=0,
E.
JX, dH?'a (X)l + [a, dtfft ~\Х)\ = О,
[a,
Для каждого целого числа /?>0 линейную оболочку дифферен
циалов dH!i,a{X), для которых /</?, обозначим через Vp(X, a)
Линейная оболочка всех дифференциалов dWi,a{X) обозначаете
через V(X, а). Выше мы доказали следующие утверждения (см
также [98]).
Лемма 11. Пусть fi, ..., fr — однородные образующие алгеб
ры IG. Тогда для любого базиса В системы корней А и для любо
го /?>0 имеем VP(X, е+) с: G0 + ... -\-Gp, где G' (i=0, ..., р) -
i-я диагональ алгебры G.
Лемма 12. Пусть fi, ..., fr — однородные алгебраически не
зависимые образующие алгебры IG степеней m.i+1, ..., тг+1
Для каждого целого /?>0 определим пространства
■ Gp=G°+...+G", GeP+ = Gp()Ge+.
Для любого />>0 имеет место включение Gep+cz VP(X, e_|_).
Доказательство. Заметим, что dHpe {X)=dft (e+). Линей
ную оболочку тех dH™le (X), -для которых nii<p, обозначим че
рез Wp. Вследствие п. а)_и г) леммы 10 dimGe+ = r и дифферен
циалы dfi(e+) порождают пространство Ge+. Поэтому дифферен
циалы df{(e+) — dHpe+(X) линейно независимы. Следовательно
dim Wp/Wp-i=m(p), где m(p) — количество чисел т(-, равных р
ззо . '
Пусть пространства Ль ..., Аг и элемент h такие, как в лемме 10;
Определим пространства Ai=Al[\G"t,... , A? — Ar{\Gp. Так как
(if — собственное подпространство эндоморфизма айн, то
Заметим, что АР [}Ge+ фО только в том случае, если nii = p; тогда
dim А? П Ge+ = 1. Поэтому dim Gp C\Ge+ — m (р). Следовательно, dim Wp=
— dimGp+. Из леммы 11 имеем WpczG",?, откуда Wp = Gep. Оконча-
Окончательно, G"p czVp(X, e+). Лемма доказана.
.Лемма 13. Пусть G — комплексная полупростая алгебра Ли;
X^.G — полупростой элемент; Т — подалгебра Картана, содержа-
щая X; В — базис системы, корней Д такой, что выполнено вклю-
включение C); fi,...,fr — набор однородных образующих алгебры
инвариантов IG; для всякого элемента a<=G пусть VP(X, а) -~
линейная оболочка дифференциалов сШи,а{Х), для которых j<pT
V(X, a) — линейная оболочка всех дифференциалов йНи,а{^)'>
Т'=[Х, G]; T(}Gp=Tp, где Gp - диагональ алгебры Лив; Г+=
= V Тр\ {Еа} — базис Вейля алгебры Ли G по модулю Т. Тог*
да для элемента а = е+ = V Еа выполнены включения T+cz
aV(X, e+) и TpczVp(X, e+) для каждого р>0.
Доказательство. Докажем по индукции, что TpczVp{X,e+).
Если р больше всех степеней инвариантов f\, ..., fr, то T[\Gp=Q и
начальное предположение индукции выполнено. Пусть а — корень,
высоты р и a(J)=?fc0. Поскольку базис В выбран так, что выполне-
выполнено включение C), то [е+, Ea]^Tp+i. Пусть U^TP+1 — такой эле»
мент, что
[X, U]+[e+, £«]=0. №
По предположению индукции Tp+iczVp+\{X, e+). Следовательно»
для подходящих комплексных чисел ch
т р+1
Используя формулы E) для а=е+, из равенства G) получаем
г Р+1
Р+1
[X,U]+[e+, £ j cidH'-el(X)] -0. : (8>
il /1
Вычитая H3J6) равенство (8), находим
г Р+1
33L
Следовательно,
г p+J
Так как Еа е Тр и dH'ite+ (X) е Gp для всех i — 1 ги| =
... ,р + 1 (вследствие леммы 11), то
г Р+1
Из леммы 12 имеем Gp+с:Ур (X, е+), поэтому £aeVp(X, e+). Так
как а — произвольный корень такой, что |а| = р и а(ЛГ)=й=О, то Грс:
*crVp(X, e+). По индукции получаем, что для любого целого р>0
1;меет место включение TpczVp(X, e+). Следовательно, Т+а
dVp(X, e+). Лемма доказана.
Доказательство теоремы 4 (А. В. Браилов). Фиксиру-
Фиксируем произвольный элемент Х^О. Так как по предположению О —
полупростая орбита, то X—полупростой элемент в G. Пусть Gc—
комплексификация вещественной алгебры Ли G; Т — подалгебра
Картана в Gc , содержащая X; Д— система корней. Фиксируем
базис В системы корней Д так, чтобы было выполнено включение
C). Выберем базис Вейля {£«} алгебры Ли Gc по модулю Т.
Применяя лемму 13 к алгебре Ли Gc, находим, что для элемента
л=е+=Ба<={*£а из функций Я';,а можно выбрать независимые функ-
функции в количестве dimcT'+ = — dirriRO так, что после ограниче-
ограничения этих функций на орбиту они остаются независимыми. Так
как полиномы H!t,a алгебраически зависят от параметра а, то это
же верно не только для элемента а=е+, но и для элементов а из
открытого по Зарисскому подмножества Z в Gc . Для элемента а
общего положения в Gc имеем a<=.Z. Теорема 4 доказана.
§ 6. Список обнаруженных максимальных линейных
коммутативных алгебр функций на орбитах коприсоединенных
представлений групп Ли
Здесь мы перечислим далеко не все, а лишь некоторые приме-
примеры указанных алгебр, представляющие интерес с точки зрения
многомерных аналогов уравнений движения различных механиче-
механических систем.
Теорема 1 [96, 98, 100]. Пусть G — одна из следующих ко-
конечномерных алгебр Ли: а) комплексная полупростая алгебра Ли
Gs, б) компактная вещественная форма Gc комплексной полу-
полупростой алгебры Ли Gs, в) нормальная компактная подалгебра
Gn в компактной алгебре Ли Gc. Тогда на каждой орбите общего
положения О в алгебре G (канонически отождествляемой с G*)
всегда имеется максимальная линейная коммутативная алгебра
332
полиномов (относительно канонической скобки Пуассона в G*).
Эти полиномы в явном виде вычислены как функции канонических
координат в алгебре Ли G.
Важно отметить, что образующие коммутативных алгебр в
теореме 1 указываются явно. Они имеют чрезвычайно простой вид.
Предложение 1 [96, 98, 100]. Пусть 10 — кольцо инвариант-
инвариантных полиномов на алгебре G, где G — либо комплексная полу-
полупростая алгебра Ли, либо ее компактная вещественная форма, ли-
либо нормальная компактная подалгебра. Пусть а — элемент общего
положения в G. Применяя метод сдвига аргумента к инвариантам
f(X) алгебры G, мы получаем новые полиномы вида f(X+Xa), где
X, a^G, кФО. Ограничивая эти функции-на орбиты общего поло-
положения, получаем максимальную коммутативную линейную алгеб-
алгебру полиномов на орбите. Далее, пусть Gn-^-Gc — каноническое
вложение нормальной компактной подалгебры в компактную ве-
вещественную форму. Ограничивая на орбиты общего положения в
Сп полиномы вида f(X+laf), f<^IGc, a'<=Gc, определенные на ал-
алгебре Gc, мы также получаем максимальную линейную коммута-
коммутативную алгебру полиномов на орбите в Gn (отличную, вообще го-
говоря, от предыдущей).
Прокомментируем эти наши теоремы. Случаи а), б), в) одно-
однотипны с точки зрения построения явных формул для образующих
коммутативных алгебр функций. Случай нормальной компактной
подалгебры богаче. Он отличается тем, что здесь мы можем так-
также рассматривать вложение Gn-+Gc и элемент а' выбирать как
элемент общего положения с точки зрения большей объемлющей
алгебры Gc (а не подалгебры Gn).
В полупростом случае эти результаты остаются справедливы-
справедливыми и для сингулярных орбит (заполняющих множество меры нуль
в алгебре Ли).
Теорема 2 (Дао Чонг Тхи, А. В. Браилов). Пусть О — про-
произвольная полупростая орбита (либо общего положения, либо
сингулярная) в полупростой алгебре Ли G (комплексной или ве-
вещественной). Тогда на ней всегда имеется максимальная линейная
Еоммутативная алгебра полиномов. Как и в предложении 1, их
вная конструкция выглядит так. Нужно рассмотреть все полино-
ы вида f(X+Xa), где f(X)—инвариантные полиномы на G, и
fa — произвольный фиксированный регулярный полупростой эле-
элемент в G. Так как f(X) —полиномы, то, разлагая f(X-\-la) no сте-
степеням параметра % получаем 2Pj(X, a) k'. Тогда набор полиномов
Pi и образует максимальную линейную коммутативную алгебру
функций на орбите.
В полупростой компактной алгебре Ли каждая орбита (обще-
то положения или сингулярная) обязательно встречается с кар-
тановской .подалгеброй, а потому каждая орбита полупростая.
В комплексной полупростой (а также в вещественной) алгебре Ли
имеются уже как полупростые, так и неполупростые орбиты. По-
Последние не встречаются с подалгеброй Картана и заполняют мно-
ззз
жество меры ноль в алгебре. Относительно этих орбит ситуация
пока неясца.
Во всех перечисленных случаях максимальный набор незави-
независимых функций в инволюции на орбитах получался путем ограни-
ограничения на орбиту сдвигов инвариантов алгебры Ли. Этот механизм
достаточно общий, хотя, как мы покажем ниже, он не всегда дает
достаточный набор функций в инволюции. Идея сдвигов инвари-
инвариантов впервые появилась в работе С. В. Манакова [84] для случая
алгебры Ли so(n). Доказательство инволютивности и максималь-
максимальности получившегося набора функций было дано в работах
А. С. Мищенко и А. Т. Фоменко. [96, 98],распространивших затем
этот метод уже на произвольные полупростые и редуктивные ал-
алгебры Ли (см. теорему 1 настоящего параграфа или [96, 98—100,
151, 192, 191]). Затем В. В. Трофимов разработал метод сдвига
полуинвариантов и «метод цепочек», развивая некоторые идеи
М. Вернь (см. [134—139, 258]). Некоторые другие максимальные
линейные коммутативные алгебры функций па полупростых ал-
алгебрах Ли были затем построены О. И. Богоявленским в [17].
Следующим классом алгебр Ли, в некотором смысле достаточ-
достаточно близким к классу полупростых алгебр, являются расширения
полупростых алгебр Ли по линейным представлениям минималь-
минимальной размерности. Напомним некоторые классические определения.
Пусть р — линейное представление некоторой алгебры Ли К
линейными операторами на линейном пространстве V представле-
представления р, т. е. р: /C-vEnd V. Тогда можно построить новую алгебру
Ли, обозначаемую G=K®PV и образованную парами (X, v), где
Х^К, dgV и правило коммутирования элементов задается сле-
следующей формулой. Линейное пространство новой алгебры Ли G
можно считать прямой суммой линейных подпространств К и V,.
т. е. G=/CeV, q=X+v, q<==G. Тогда
foi, ?2]=[*i+wi, X2+v2]=[Xu X2]+(pXi)v2-(PX2)vl.
Это означает, что подпространство V в G является абелевой,
подалгеброй, а подалгебра К действует на V посредством представ-
представления р. Среди описанных расширений содержится важный класс,.'
отвечающий точным представлениям минимальной размерности
полупростых алгебр Ли, т. е. стандартным представлениям р, при
которых алгебры Ли изображаются, матрицами наименьшей воз-
возможной размерности.
Одной из таких наиболее популярных алгебр Ли является ал-
алгебра Ли e(rt)=so(rt)®pRn, являющаяся алгеброй группы £(«) —
собственных движений евклидова пространства Rn, В матричном
виде эта алгебра имеет вид
К
so (га) :
о ( о
334
где Fi, ..., &я) — вектор из R". Ясно, чтв
„ . . . SO(n)
Е(п) = \ v
1 а»
О I 1
где а=(аи ..., an)
Если g^.E{n), то #(л:)=Лл:+а, где xeR", A^.SO(n), a — вектор
сдвига. Естественно, что алгебра Ли е(п) некомпактна и не явля-
является полупростой.
Теорема 3 (В. В. Трофимов, А. Т. Фоменко [148, 149, 193]).
На каждой орбите О* общего положения в пространстве е(п)*,
дуальном к алгебре Ли е(п) группы движений пространства R",
всегда имеется максимальная линейная коммутативная алгебра
полиномов. Она образована всеми полиномами вида f(X+ka), где
f(X) — инвариант алгебры е(п) и а<=е* (п) — ковектор общего
положения. Все инварианты f(X) вычислены в явных формулах.
В случае сингулярных орбит ситуация пока неясна. Обнару-
Обнаруженная нами коммутативная алгебра полиномов является в неко-
некотором точном смысле аналогом «интегралов компактной серии»,
построенной нами в теореме 1 для компактных вещественных
форм полупростых алгебр Ли. Оказалось далее, что на некомпакт-
некомпактной алгебре Ли е(п) есть и другие коммутативные алгебры поли*
номов, аналогичные «нормальной серии» (см. теорему 1). Эта тео-
теорема доказана А. В. Браиловым. Изложим ее доказательство.
Наборы функций этой серии являются интегралами уравнений
вида
x=ad*dH(X)(x), хее(л)*, A)
которые тем самым вполне интегрируемы по Лиувиллю. Отметим,
что при га=3 и при положительно определенной квадратичной
функции Н это уравнение совпадает с известной системой Кирх-
Кирхгофа динамики твердого тела в идеальной жидкости. В нашем
случае, однако, квадратичная функция Н невырождена, но знако-
определена. Определим стандартный базис алгебры Ли е(п),
состоящий из элементов хц и $/*, хц — инфинитезймальное враще-
.ние в (£, /) -плоскости, y~k — инфинитезймальное движение вдоль
k-й координаты. Линейные координатные функции на е(п)*, соот-
соответствующие элементам хц и ун, обозначим через хц и yk. Далее
нам потребуются матрицы X и А размером (л+1)Х(я+1). Пусть
Л], ..., ап — произвольные числа. Определим матрицы
Л+]
335
л =
1=1
i --" 0; X_i = Лу(К,->п:н; X = X14-X
Теорема 4 (А. В. Браилов). Пусть п\>...>ап-и ;
&i, •••, bn — произвольные числа. Тогда уравнение Эйлера A) с
квадратичной функцией
1=1
nfcn — aibj 2 ц J>n_ 2
<*" - "
вполне интегрируемо по Лиувиллю на орбитах О* коприсоединен-
-ного действия группы E(ji) общего положения в е(п)*. Полным
набором коммутирующих интегралов являются коэффициенты hks
(k=2, ..., n+1; s=0, ..., k) при Х2ц~2 в многочлене
hk(K, ц-») = Д*(Х1 + М1 + ц-1(Х_1 + М_,)),
•где Д* — сумма всех симметричных миноров k-го порядка.
-' Рассмотрим алгебру Ли G, допускающую представление в
виде G=/C©PV, где К — подалгебра, V — коммутативный идеал.
Пусть p=acU: V-*~V — присоединенное представление алгебры К
в пространстве V: Фактически G является полупрямым расшире-
расширением /СФрУ алгебры Ли G по представлению p = ad. Такие алгеб-
алгебры Ли называются аффинными алгебрами Ли.
Отметим важный частный случай, когда пространство V явля-
является линейным пространством алгебры К, на котором К действует
присоединенным образом. При этом мы считаем, что второй (пра-
(правый) экземпляр К, на котором действует первый экземпляр К,
рассматривается как абелев идеал. В. В. Трофимов обнаружил
алгоритм, позволяющий «размножать» алгебры Ли, обладающие
полным инволютивным набором. Другими словами, этот алгоритм
-позволяет строить по одной такой алгебре целую серию новых,
неизоморфных алгебр Ли, также обладающих полным инволютиВ-
ным набором. Алгоритм Трофимова был затем усовершенствован
и расширен А. В. Браиловым. Сформулируем полученные резуль-
результаты.
Теорема 5 (В. В. Трофимов, А. В. Браилов). Пусть G=
=/СФр/С — расширение компактной алгебры Ли К по присоединен-
присоединенному представлению К на абеле'вом идеале К, т. е. p=ad. Тогда
на каждой орбите общего положения в G* всегда имеется макси-
максимальная линейная коммутативная алгебра полиномов. Ее образу-
336
ющие явно выписываются через 'полиномиальные образующие
кольца инвариантных полиномов Щ на алгебре К.
Дальнейшие конструкции Трофимова и Браилова см. в [143,
144, 22, 25, 27]. В этих работах построен большой запас полных
инволютивпых наборов на широком классе алгебр Ли. Грубо гово-
говоря, оказывается, что если на алгебре К имеется полный инволю-
тивный набор функций, то на алгебре К®А, полученной тензор'
ным домножением алгебры К на алгебру Фробениусаг А, также
существует полный инволютивный набор функций. Ввиду недостат-
недостатка места мы не можем здесь более подробно коснуться этого ин-
интересного вопроса. Алгоритм Трофимова был использован такж$
в работах Ле Нгок Тьеуена [81, 82] для построения новых полных,
инволютивных наборов функций.
Если р — некоторое представление алгебры Ли, то через Лйр и
5*р обозначим соответственно fe-ю внешнюю и k-ю симметриче-»
скую степени представления р.
Теорема 6 (Т. А. Певцова [112, 113]). Пусть G=/C©PV - по-
полупрямая сумма простой алгебры Ли К и абелевого идеала V=K"
по представлению ц: /C-vEnd R*. Тогда если алгебра Ли К и пред-
представление \i имеют один из следующих видов: :
'-■ a) K=glBn), [х=Л2р;
б) K=sl{2n), [i=52p;
в) K=spffn), ц=р+т,
где р — представление минимальной размерности, ах — одномер-
одномерное тривиальное представление, то на орбитах общего положения
в G* всегда имеется максимальная линейная коммутативная ал-
алгебра рациональных функций. Рациональность понимается относи-
относительно канонических координат в алгебре Ли G.
Пусть G — комплексная простая алгебра Ли, Т — ее картанов-
ская подалгебра, G = r©Ea^0Ga— разложение Картана, Еа—век-
Еа—векторы, описанные выше. Корневое разложение алгебры G можно-
теперь записать в виде G=T@V+(BV~, где V+=Sa>oGa) V-=Sa<»Ga.
В случае sl(n, С) подпространство V+, очевидно, отождествляет-
отождествляется с подпространством всех верхпетреугольных матриц с нулями
по главной диагонали. Подпространство V" отождествляется с
подпространством всех нижнетреугольных матриц с нулями на
главной диагонали. Это разложение см. на рис. 125. Отметим^ что«
скалярное произведение векторов базиса устроено следующим
образом: (Еа, £_«»>=— 1, {Еа, Еа}=0.
Ясно, что подпространства V+ и V~ — нильпотентные подалгеб*
ры в алгебре ли G. Подпространства ГФУ+ и T(BV~ являются
разрешимыми подалгебрами в алгебре Ли G (см. рис. 126).
Рассмотрим подалгебру T(BV+. Базисом в ней (над полем
комплексных чисел) служат векторы £, в G, и Н'а в Т, а>0.
Вещественная подалгебра BG = (фаЯЯа) ф (J] R£a). очевид-
а>е
но, вложена в T(BV+. Подалгебра BG называется веществеянош
337
формой борелевской подалгебры (в полупростой комплексной ал~
яебре Ли). Она является разрешимой алгеброй Ли.
Теорема 7 (В. В. Трофимов [134—137]). Пусть G — простая
.алгебра Ли одного из следующих типов: so(n), su(n), sp(n), G2-
Тогда на каждой орбите общего положения в вещественной форм'
борелевской (разрешимой) подалгебры BG (алгебры G) всегда
имеется максимальная линейная коммутативная алгебра полино
мое. Эта полиномы записываются явными формулами.
Частным случаем борелевских подалгебр является алгебра Ли
Тп вещественных верхнетреугольных матриц порядка п. Для этой
алгебры максимальная линейная коммутативная алгебра пояино-
Рис, 126
мов была ранее обнаружена А. А. Архангельским в [7]. При этом
выяснилось, что (как и в общем случае борелевских подалгебр)
•сдвиги инвариантов не дают полного набора независимых комму-
коммутирующих полиномов. Поэтому В. В. Трофимову пришлось разра-
'ботать новую, более глубокую технику, основанную на рассмотре-
рассмотрении цепочек подалгебр, см. [134—137].
Теорема 8 (Ле Нгок Тьеуен [81]). Пусть G — произвольная
подалгебра в разрешимой алгебре Ли Тп верхнетреугольных мат-
матриц, имеющая вид G =
R£a, где £,-,- — эле-
a>0
j
ментарная матрица порядка п (на пересечении i-й строки и j-го
столбца стоит единица, остальные элементы нулевые), L — произ-
произвольное подпространство п-мерного пространства диагональных
матриц. Тогда на дуальном пространстве G* всегда имеется мак-
максимальная линейная коммутативная алгебра полиномов.
Ле Лгок Тьеуен усилил результаты А. А. Архангельского ич
В. В. Трофимова. А именно он доказал следующий результат.
.338
Теорема 9. Пусть BG — борелевская подалгебра в полупро-
полупростой, комплексной алгебре Ли О. Тогда на BG всегда имеется мак'
симальная коммутативная линейная алгебра полиномов.
Построенные в теореме 9 вполне инволютивные наборы поли-
полиномов отличаются от полных инволютивных наборов, построенных
ранее В. В. Трофимовым.
В симплектической топологии большую роль играют характе-
характеристические классы Маслова <и классы Маслова—Арнольда ла-
гранжевых подмногообразий в R2n и в Т*Мп. Недавно В. В. Тро-
Трофимов обобщил конструкцию этих классов на случай лроизволь-
ных лагранжевых подмногообразий в произвольных симплектиче-
ских многообразиях. Эти новые- классы Маслова—Трофимова
определяются при помощи групп голономий связностей.
Таблица
Алгебры Ли
Полные инволютнвные
наборы функций.
Орбиты общего положе-
положения
Полные инволютивные
наборы функций.
Полупростые сингуляр-
сингулярные орбиты
Остальные
сингулярные
орбиты
1. Произвольная по-
полупростая комплекс-
комплексная. Затем — вещест-
вещественная полупростая
Мищенко, Фомеико,
см. теорему 1 и [96],
[981, [100]. «Общая се-
серия». Полиномы
Дао Чонг Тхи (дока-
(доказательство с лакунами).
Браилов, см. теоре-
теорему 2. «Сингулярная
серия». Полиномы
2. Компактная ве-
вещественная форма Gf
полупростой алгебры
Ли
Мищенко, Фоменко,
см. теорему 1 и [96],
[98], [100]. «Компакт-
«Компактная серия». Полиномы
Дао Чонг Тхи (дока-
(доказательство с лакуна-
лакунами). Окончательно:
Браилов, теорема 2.
Компактная серия. По-
Полиномы
Таких
бит нет
ор-
ор3. Нормальная ком-!
пактная подалгебра Gn
в компактной вещест-
вещественной форме Gc
Мищенко, Фоменко,
см. теорему 1 и [96],
[98], [100J. «Нормаль-
«Нормальная серия». Полиномы
Браилов, см. теоре
му 2. «Нормальная се-
серия». Полиномы
Таких ор*-
бит иет
4. £(n)=so(n)®pR",
где р — представление
минимальной размер-
размерности
1) Трофимов, Фо-
Фоменко, см. теорему 3 и
[148], 1149]. Эта алгеб-
алгебра интегралов V —
аналог алгебры инте-
интегралов «компактной се-
серии» для so(n). Поли-
Полиномы. 2) Браилов, см.
теорему 4. Другая ал
гебра интегралов V —
аналог «нормальной се-
серии» для .ад (л). Поли-
Полиномы
33»
Продолжение табл.
Алгебры Ли
Орбиты общего положения
5. su (л) фр С", где р — представле-
йие минимальной размерности
а) Браилов (полиномы);
б) Болсинов (полиномы)
6. и (п) фр С", где р — представле-
представление минимальной размерности
Браилов (полиномы)
7. K®PV, где p=adK:V-*-K, V —
.идеал, К —компактная алгебра Ли
Трофимов (в некоторых частных случа-
случаях); Браилов (в общем случае). Полино-
Полиномы. См. теорему 5
8. gl Bл) фц R*. где ц = Л»р, р -
шредставление минимальной размернос-
размерности, Л8р — вторая внешняя степень
/представления р
Певцова [112], [113], см. теорему 6.
Рациональные функции
9. si Bл) фц Rw, где ц = S*p, p -
представление минимальной размернос-
размерности, Sap — вторая симметрическая, сте-
степень представления р
Певцова [112], [113], см. теорему 6.
Рациональные функции
10. sp Bл) фц R^, где ц = р+т,
.$> — представление минимальной раз-
размерности, т — одномерное тривиальное
представление
Певцова [112], [113],
Рациональные функции
см. теорему 6. ■•
И • К фр V, где К — произвольная
простая алгебра Ли, ар — произволь-
яое неприводимое линейное представ-
-ление, )у—абелев идеал, причем V —
■пространство представления р
Болсинов. Этот результат обобщает мно-
многие из перечисленных выше результатов.'
Полиномы. Таким образом, абелево рас-
расширение простых алгебр Ли по любому
точному неприводимому представлению
обладает полным коммутативным набором
полиномов
12. Иолупростые алгебры Ли. Но-
<вые наборы функций (см. справа) от-
отличаются от известных ранее (см. вы-
лпе п. 1—3)
Богоявленский. Построенные недавно в
[16], [17] полные коммутативные наборы
функций основаны на новой идее исполь-
использования фильтраций в алгебрах Ли. По-
Полиномы
13. Вещественные формы BG боре-
левских подалгебр всех простых алгебр
Ли: Bso(n), Bsu(n), Вчр(п), BG2, BF^,
BEt, BE-,, BEt; BG — борелевская под-
.алгебра в произвольной пол у простой
-алгебре G
.340
Трофимов, см. теорему 6, [134] —[137].
Для частного случая верхиетреугольных.
матриц — ранее А. А. Архангельский [7].
Для BEt — С. Сяров. Полиномы. Для BG
в произвольной полупростой алгебре G —
В. В. Трофимов
Продолжение табл.
Алгебры Ли
Орбиты общего положения
14. 0S S
KI ■ а>0
разрешимая алгебра, где L — подал-
подалгебра алгебры диагональных матриц,
?а>о R Ей — алгебра верхнетреуголь-
верхнетреугольных нилыютентных матриц
Ле Нгок Тьеуен, см. теорему 9. Поли-
Полиномы
15. Серии алгебр Ли h(G), полу-
получающиеся «размножением» алгебр Ли
G, уже обладающих иа орбитах макси-
максимальными линейными коммутативными
алгебрами полиномов (рациональных
функций). Тогда (при правильном вы-
выборе операции «размножения» ft) ал-
алгебры ft (G) также обладают полными
коммутативными наборами полиномов
(рациональных функций)
Трофимов [139], [142]. Далее алгоритм
Трофимова был существенно развит Браи-
ловым. Операция «размножения» сводится
к тензорному умножению [исходной алгеб-
алгебры Ли на алгебру Фробениуса. Затем эти
идеи были дополнены теоремой Ле Нгок
Тьеуеиа. Полиномы.
Итак, h (G) = G ® А, где А — алгебра
Фробеииуса
16. Полу простые алгебры Ли. Но-
Новые наборы функций, отличающиеся от
известных ранее ,
Богоявленский [283]. Построение этих
наборов основано иа новой идее использо-
использования фильтраций в алгебрах Ли. Поли-
Полиномы
17. Рассматривается одна особая ор-
орбита в (so (я) X 5)*, где S — симметри-
ческие матрицы
Ратью [245]. Особые случаи см. выше
в п. 7
18. Алгебры Ли малых размернос-
размерностей. Их классификация известна
Трофимов [143]. Полиномы, рациональ-
рациональные Функции
19. K(BpV, где К — полу простая
алгебра • Ли, р: К -*■ End V -*- линейное
представление, причем стационарная
лодалгебра регулярного элемента oeV
•относительно представления р триви-
тривиальна (т. е. размерность орбиты равна
размерности алгебры). В случае комп-
комплексной полупростои алгебры К и не-
лриводимого представления р достаточ-
достаточным условием является неравенство
dim К < dim V
Браилов, Певцова [112], [113]. Все функ-
функции этих полных инволютивиых наборов
являются линейными (это — элементы про-
пространства представления V)
20. GQadG, где G — полупростая
алгебра Ли (комплексная или вещест-
вещественная). Эта алгебра является частным
случаем алгебр Ли типа 6®Д (см.
выше п. 15). Для этого нужно взять
А = R[x]/(x2) (или в комплексном слу-
случае Л = С[х]/(х2))
Болсинов [21]. Построенные им пол-
полные инволютявные наборы функций от-
отличаются от построенных ранее Трофимо-
Трофимовым В. В. и Браиловым А. В. (см. выше
п. 15). Недавно Болсинов обнаружил кри-
критерий полноты набора интегралов, полу-
получаемых методом сдвига аргумента на ко-
конечномерных алгебрах Ли. Многие из пе-
перечисленных выше результатов получаются
как частные случаи этого универсального
критерия. Краткое изложение этого резуль-
результата см. в Приложении 6 этой книги
341.
Продолжение табл.
Алгебры Ли
Орбиты общего положения
Г 21. G=so (я) фр R", где р — пред-
представление минимальной размерности
Переломов [114], Рейман [124]. Полино-
Полиномы, которые являются интегралами «ге-
мерного случая Клебша»
22. G = so (я) фр R", где р — пред-
представление минимальной размерности
Переломов [276], Рейман [124]. Полино-
Полиномы, которые являются аналогами интегра-
интеграла Ковалевской в и-мерном случае
23. G=so(tt)®Rn, где р—пред-
р—представление минимальной размерности
Беляев [12]. Полиномы, которые яв-
являются интегралами аналога случая Лаг-
ранжа в я-мерном случае
24. Алгебры Ли so D) и so C)(£PR3
См. изложение соответствующих резуль«
татов в Приложении 2
25. G — нильпотентная вещественная
алгебра Ли
Вернь [263]. Полный инволютнвный на-
набор полиномов
26. G— вполне разрешимая вещест-
вещественная алгебраическая алгебра Лн
Гинзбург A980 г.). Полный инволютив-
ный набор состоит нз полиномов, причем
этот набор инвариантен относительно дей-
действия групп (копрнсоединенного). Отдель-
Отдельные полиномы, конечно, неинварнантны
27. G—разрешимая вещественная
алгебраическая алгебра Ли, причем для
G существует флаг из алгебраических
подалгебр G = Gn=3 Gn.i =>...=> d =>
dCo=O, где dimGi = i
Бодсинов A985). Полный инволютивный
набор состоит нз полиномов. Возможно,
этот набор и набор из п. 25 отличаются
друг от друга
28. Алгебры вида К® (У, где Я —
произвольная простая алгебра Ли, р —
произвольное неприводимое линейное
представление, V — абелев идеал, при-
причем, V — это пространство представле-
представления р. Полный набор интегралов
Болсинов. Этот результат обобщает мно»
гие из перечисленных ранее теорем. Итак,
абелево расширение простых алгебр Ли
по любому точному неприводимому пред-
представлению всегда обладает полным комму-
коммутативным набором интегралов (полиномов)
на орбитах общего положения
29, Новые полные наборы интегра-
интегралов на конечномерных алгебрах Ли
(см. приложение 6)
Болсинов. Этот новый метод построения
интегралов обобщает многие изложенные
выше результаты
30. Одна особая орбита в простран-
пространстве, дуальном к алгебре Ли В (su (я))
(борелевской подалгебре). На этой ор-
орбите реализуется цепочка Тода
342
Рейман, Семенов-Тян-Шанский, Френ-
Френкель [123]. Полиномы
ПРИЛОЖЕНИЕ 1
ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ТВЕРДОТЕЛЬНЫХ
' ИНВАРИАНТНЫХ
МЕТРИК НА ОДНОРОДНЫХ ПРОСТРАНСТВАХ
Качественный анализ поведения экстремалей инвариантных
гамильтоновых систем на однородных пространствах был недав-
недавно выполнен М. В. Мещеряковым. Такая гамильтонова система
определяется как пара [Т*М, Н), где М= ®/§ — однородное
пространство конечномерной группы Ли ® и Н — функция на ко-
касательном расслоении Т*М, инвариантная относительно индуци-
индуцированного гамильтонова действия группы @ на Т*М. Перечисляе-
Перечисляемые ниже результаты получены М. В. Мещеряковым в работах
[87—90].
Теорема 1. Каждая экстремаль любой &-инвариантной га-
мильтоновой системы на кокасательном расслоении Т*М однород'
ного пространства М— @/ф является либо вложенной окружно-
окружностью, либо инъективным погружением интервала вещественной
оси.
Теорема 1 имеет приложения к случаю левоинвариантных га-
гамильтоновых систем на группах Ли.
Следствие 1. Экстремали левоинвариантных гамильтоновых
потоков на Т*@ с фиксированным значением момента F, где
F: Т*® ->-G* — отображение момента, не пересекаются и одно-
однократно покрывают группу Ли ®.
Можно указать серии однородных пространств, на которых
все геодезические инвариантной метрики замкнуты или все не-
незамкнуты.
Предложение 1. Пусть ®— связная группа Ли с левоин-
вариантной римановой метрикой, все геодезические которой замк-
замкнуты. Тогда ® изометрична или группе Ли SOC), или группе
SUB) с биинвариантной метрикой.
С другой стороны, справедлив следующий результат.
Теорема 2. Траектории любого левоинвариантного гамильто-
гамильтонова векторного поля на кокасательном расслоении связной одно-
связной разрешимой группы Ли, в которой некоторая степень каж-
каждого элемента лежит в образе экспоненциального отображения
(алгебры в группу), проектируются на группу Ли в незамкнутые
кривые без самопересечения.
Описанный подход позволяет изучить свойство «жесткости»
отображения момента по отношению к пульверизациям левоинва-
левоинвариантных аффинных связностей на полупростых группах Ли, при
этом М. В. Мещеряков развивает работы Лакомба [221], Костанта
[216]. В случае группы 50C) результаты М. В. Мещерякова при-.
343
водят к известной в классической динамике интерпретации дви-
движения твердого тела по Пуансо.
Рассмотрим теперь левоинвариантные квадратичные функции
Гамильтона на Т*@ , связанные с методом сдвига аргумента. Точ-
Точнее, рассмотрим уже хорошо знакомый нам класс функций /и(Х) =
=f(X+Xa), где XeR, Си/ принадлежит кольцу инвариантов IG
алгебры Ли. Квадратичные формы F на G*, функционально зави-
зависящие от функций вида hK, имеют согласно работе Мищенко и Фо-
Фоменко [98] вид (X, q>abD{X))=F(X). Здесь (, ) — форма Киллинга
алгебры G, а операторы «многомерного твердого тела» были оп«
ределены выше.
Напомним, что скобка Пуассона на симплектическом много
образии Т* © индуцирует в кольце гладких функций на простран-
пространстве G* скобку Пуассона (X, [gradH(X),gradF(X)] > = {#, F)(X),
GzszG*. Зададим в этом кольце функций еще одну скобку Пуас-
Пуассона, а именно положим (a, [grad^(Z),grad/r(X)] ) = {#, F}a, т. е'.
«заморозим» один аргумент. В обоих случаях градиент берется от-
относительно невырожденной формы Киллинга.
Теорема 3. Пусть ф : G-*-G—самосопряженный относитель-
относительно формы Киллинга линейный оператор на полупростой алгебре
Ли G. Уравнение Эйлера Х=[Х, ц>Х] гамильтоново одновременно
относительно обеих скобок Пуассона (здесь элемент а — ковектор
общего положения) {,} и {,}а тогда и только тогда, когда ф = фа&о
для некоторых элемента Ь^Т и оператора D : Т-+-Т.
Этот результат Мещерякова дополняет полученное нами выше
характеристическое описание операторов типа «твердого тела».
Оказывается гамильтоновость уравнений Эйлера с операторами
Ф: G-+G одновременно в двух скобках Пуассона (т. е. бигамиль*
тоновость) является характеристическим свойством именно твер-
твердотельных метрик фаыэ, порожденных методом сдвига аргумента.
Теорема 3 мотивирует изучение пар скобок Пуассона, возникаю-
возникающих из двух различных структур алгебр Ли на одном и том же
векторном пространстве. Две такие структуры мы назовем согла-
согласованными, тесли сумма коммутаторов снова является коммутато-
коммутатором. Естественный класс" согласованных скобок Пуассона опреде-
определяют двойственные по Картану эффективные симметрические ал-
алгебры Ли. Пусть тройка (G, К, о) —эффективная симметрическая
алгебра Ли и G = K@P — ее разложение относительно инволютив-
ного автоморфизма а. Предположим, что представление ad: К-*-
->-End P неприводимо.
Предложение 2. Уравнения Эйлера, определенные самосо-
самосопряженным оператвром С: G-+G таким, что С=СХ@С2, Ci:K-^K,
C'i: P-+P, будут гамильтоновы одновременно относительно скобок
Пуассона двойственных по Картану алгебр Ли тогда и только то-
тогда, когда оператор Сг — скалярный.
Теорема 4. Функции /u(£, s)=f(k+Xs), K^R, f^lG, являют-
являются первыми интегралами в инволюции уравнений Эйлера с гамиль-
гамильтонианом Н(Х)={Х, СХ). Здесь X=k+s — разложение вектора
XG отвечающее разложению G — K©P.
344
Оказывается далее, что уравнения Эйлера с функцией Гамиль-
Гамильтона Н на неприводимых эффективных симметрических алгебрах
Ли обладают следующим свойством.
Предложение 3. Если (k(t), s(t)) — решение уравнений
Эйлера, то (k(t), [&@> s@1) ~ также решение этих уравнений.
Соглггсованные скобки Пуассона на алгебрах Ли рассматрива-
рассматривались в работе А. Г. Реймана [124], где такие скобки возникали
из бесконечномерных градуированных алгебр Ли и применялись
к изучению обобщений цепочки Тода.
ПРИЛОЖЕНИЕМ
УРАВНЕНИЯ ЭЙЛЕРА НА АЛГЕБРЕ ЛИ so D).
Рассмотрим частный случай теоремы 6 § 6 гл. 7, а именно
уравнения Эйлера движение многомерного твердого тела на ал-
алгебрах Ли soC) и so D). Случай алгебры so{3) фактически разоб-
разобран нами выше, когда мы продемонстрировали, что проинтегриро-
проинтегрированные нами уравнения совпали с классическими уравнениями
движения трехмерного твердого тела при п—Ъ. Случай алгебры
so D) заслуживает более детального разбора.
Рассмотрим потоки нормальной серии для Gn = soD)c:Gc =
= smD)cG=s/D, С). Алгебра soD) реализуется в виде кососим-
метрических матриц и натянута на векторы Е^ — Еа + Е-о, стан-
стандартного вида. Запишем XesoD) в виде Х — аЕх2 + $Е{г-{-
+^14 + б£гз+р£'24+е£з4, где все коэффициенты вещественны. Ор-
Орбитами общего положения здесь являются четырехмерные много-
многообразия S2X52. Пусть a, b<=TcasuD), тогда
— a-, aL — а3
Ьг — bi v .
а3 —
Для каждой пары а, b получаем поток X на S2 X S2. Интегралами
будут функции Spur (X + КаI', 1 < k < 4, где
X,aL a
— а ка2 й
-г- р — б Яа,
— Y —р —е
Вычисления дают четыре интеграла: hi~SpX2, /t2 = Sp-^4, hz =
= SpX2a, /t4 = 2SpX2a2+Sp(A'aJ. Интегралы /ti и h2 постоянны
на орбитах (это инварианты алгебры) и имеют вид
345
h2 = h\ + 4 (рбур—абуе + арре)—2 (аге2 + р2р2 + tf
_ „—. ..v.iU..w.r. ,v-i ЛШ1ЛСШ1 квадратом интеграла q степени
два (после вычитания из h2 функции /и2), где q = as—Рр + -у6.
Таким образом, два квадратичных интеграла hi и q являются
образующими кольца инвариантов l(soD)), т. е. любой полином,
постоянный на орбитах, разлагается no hi и q, Легко проверяется,
что. hi n q независимы. Уравнения /ii = p, q — l, где р и t — посто-
постоянные числа, определяют орбиты общего положения. Эти интегра-
интегралы, в частности q, рассматривались ранее в [222] (Ланглуа).
Интегралы h% и /i4 уже непостоянны на орбитах. Они имеют
следующий вид:
h3 = а2 (аг + а,) + Р2 (ах + а,) + у2 К4- а4) +б2 (а2+а3) +р2 (а
.+ е2(а3 + а4); ht = а2 (а2 + аха% + с&) + Р2 (а? + аха3 + а§) +
+ у2 (а\ + оа + а\) + б2 (а\ + аА + а\) + р2 (а! + а^ + а\) +
Легко проверить, что интегралы hu q, h3, hA функционально
независимы, а интегралы h3 и ft4 находятся в инволюции на орби-
орбитах. Итак, уравнения Эйлера Х= [X, ц>Х] на алгебре Ли soD)
полностью интегрируются для твердотельных операторов ф = фа1>о,
описанных нами выше. Интеграл /t4 можно также взять в виде
/ц = а3а4а2+а2а4 р2+а2а3у2+а 1 а4б2+а 1 а3р2 + а 1 а2 е2.
Как мы видели в гл. 4, задание интеграла f на изоэнергетичес-
кой трехмерной поверхности Q3 позволяет однозначно построить
граф P(Q, /), наглядно изображающий как качественное строение
многообразия Q, так и поведение интеграла / на Q (т. е. какие
у него критические многообразия, как они расположены и т. п.).
Граф строится так. Рассмотрим интеграл / как отображение мно-
многообразия Q на вещественную прямую R1. Взяв неособое значение
aeR1, мы получаем в качестве прообразов /~' этого значения a
набор неособых торов Лиувилля. Изображая их точками и меняя
а, мы заставляем эти точки перемещаться. В результате они за-
заметают ребра одномерного графа. Как было доказано в гл. 4»
можно дать полную классификацию всех типов взаимодействия
этих ребер, всех вершин графа. Следовательно, мы можем описать
пару Q, / при помощи канонического (довольно простого по струк-
структуре) графа. Проиллюстрируем общую качественную теорию пере-
перестроек изоэнергетических поверхностей, развитую автором в гл. 4,"
на важном примере интегрируемого случая движения четырехмер-
четырехмерного твердого тела, т. е. на примере алгебры soD). Эта работа
была выполнена А. А. Ошемковым.
Алгебра so D) реализуется как алгебра кососимметрических
матриц Х=(хц). Интегралы hi = ~Li<jXij2 и h2=xl2X34—xnx2i+хих2г.
выделяют орбиты присоединенного представления группы SO (А).
Орбиты общего положения гомеоморфны
52xS2 = {/i1-p?) /t2 = p2}, |2/>2|<р2.
346
Уравнения движения твердого тела, отвечающие нормальной се-
серии, соответствуют гамильтониану
;— а,-
Интегралы этой системы
и Л* =
находятся в инволюции на орбитах и независимы. Вершины графа
T(Q, f) согласно общей теории гл. 4 разбиваются на 5 типов,
соответствующих пяти перест-
перестройкам торов Лиувйлля. Вы-
Выяснилось, что в случае урав-
уравнений движения твердого тела
(случай so D)) на изоэнерге-
тических поверхностях реали-
реализуются лишь две из этих ряти'
перестроек. Они показаны .на
рис. 127а и рис. 1276. Иногда,
оказывается, происходит пере-
перестройка двух торов Лиувилля
в два тора Лиувилля на одном
критическом уровне. Критиче-
Критическая поверхность уровня инте-
интеграла f • гомеоморфиа здесь
PXSX, где Р — сечение сферы
S2 (стандартно вложенной в
R3) парой плоскостей, прохо-
проходящих через ее центр. Эту
. перестройку мы изобразили на
1
1
Рис. 127
Рис. 128
рис. 127в; она является композицией двух перестроек типа 1276.
Предложение 1 (А. А. Ошемков). Пусть дана гамильтонова
система твердого тела нормальной серии на алгебре Ли so D)
с гамильтонианом h^. Тогда неособые орбиты 52XS2 в soD) рас-
расслоены на изоэнергетические поверхности Q = {h3=const}, облада-
обладающие тем свойством, что Для этих поверхностей Q3, кроме, воз-
возможно, конечного числа, функция / = /u|s*xs* является боттовским
интегралом. В зависимости от численных значений параметров
Р\ и pi, определяющих орбиту общего положения S2XS2 — {hi—P\2,
Ь-2=Р2}, бифуркационные диаграммы для отображения момента
F—h3Xhi:S2XS2-^R2 могут быть лишь трех типов. Их явный вид
показан на рис. 128.
Цифрами на рис. 128 указано количество торов Лиувилля, из
которых состоит прообраз F~l(y) для точек у из данной области.
Перестройки вдоль стрелок на
рис. 128 имеют вид А, В, С,
показанный па рис. 129.
Предложение 2 (А. А.
Ошемков). Пусть дана гамиль-
тонова система твердого тела
нормальной серии на алгебре
Ли so D) с гамильтонианом Н
общего вида, указанного вы-
выше. В качестве второго инте-
интеграла f, функционально неза-
независимого с Н почти всюду,
выберем из или h^. Тогда не-
неособые орбиты (т. е. общего
положения) S2XS2 в so D)
расслоены на изоэнергетиче-
И
'л/ уу
Рис. 129
Рнс. 130
ские поверхности Q3={#=const}, обладающие тем свойством, что
интеграл f является боттовским для всех этих поверхностей Q, кро-
кроме, быть может, конечного их числа. Полный набор всех девяти
связных графов Г (Q,/), описывающих все неособые поверхности Q,
представлен на рис. 130. Все эти графы действительно реализуются
для некоторого общего гамильтониана Н (при подходящем выборе
определяющих его параметров и поверхности уровня).
Отметим, что произвольный гамильтониан Н нормальной серии
представляется в виде #^^Ч-^/и+^з^з, где коэффициенты
ki, 1ц, kz не зависят от хц. Поэтому бифуркационные диаграммы
для системы с произвольным гамильтонианом Н нормальной серии
получаются из бифуркационных диаграмм для системы с гамиль-
348
гонианом h% (см. рис. 12b) применением некоторого
ного линейного преобразования.
Сформулируем программу дальнейших исследований в этом
направлении. Поскольку теперь, как выяснилось, мы можем на-
наглядно изображать топологию поверхности Q и поведение на ней
интеграла / при помощи одномерного графа F(Q, /) (с пятью ти-
типами вершин), то следует составить, возможно более полный спи-
список всех известных на сегодня интегрируемых случаев систем на
четырехмерных многообразиях М4. Затем, следуя схеме гл. 4
(и описанной выше), можно построить графы F(Q, f). Это даст
качественно важную и наглядную информацию о топологии обна-
обнаруженных интегрируемых случаев.
Замечательным обстоятельством оказалось то, что для метрик
определенного вида на soD) соответствующие уравнения Эйлера'
имеют естественную механическую интерпретацию. В первую оче-
очередь это относится к метрикам вида (X, уХ), где ф = фаьо
(С. В. Манаков, А. С. Мищенко, А. Т. Фоменко). Затем О. И. Бо-
Богоявленский, А. П. Веселов, Л. Е. Веселова отметили в [16, 30,
31], что уравнения Эйлера описывают движение по инерции твер-
твердого тела с эллипсоидальной плоскостью, заполненной идеальной
несжимаемой жидкостью, совершающей однородное вихревое дви-
движение (см. также |102] (Н. Н. Моисеев, В. В. Румянцев)). Пос-
Последняя система является классической и рассматривалась многи-*
ми авторами, в том числе А. Пуанкаре и В. А. Стекловым.
Другая интерпретация этих уравнений была предложена в [32]
(А. П. Веселов), где однородная динамика магнитных моментов
для двухрешеточного магнетика описывается уравнениями Эйлера
на soD).
Следует отметить, что первый после важной работы В. И. Ар-
Арнольда [5] пример подобной интерпретации уравнений Эйлера на
алгебре Ли был обнаружен С. П. Новиковым для алгебры Ли
группы движений трехмерного пространства,см. [105],где указано,
что соответствующие уравнения есть уравнения Кирхгофа—Том-
сона, описывающие свободную динамику твердого тела в жидкос-
жидкости. Эти уравнения были исследованы на интегрируемость
В. В. Козловым и Д. А. Онищеико [70].' Работы А. П. Веселова
(в частности, C0]) посвящены условиям существования допол-
дополнительного интеграла для уравнений Эйлера на so D) и соответ-
соответствующих механических систем. Изложение этих результатов (см.
[30, 31]) посвящена первая часть данного приложения.
Во второй части приложения рассмотрены некоторые известные
интегрируемые случаи уравнений Эйлера на soD). Среди них от-
отметим уравнения движения «четырехмерного твердого тела», отве-
отвечающие метрике фаЬО специального вида. В работе [93] были най-
найдены квадратичные интегралы для уравнений движения «-мерного
твердого тела, инволютивность которых была доказана в [46].
В случае п=4 найденных интегралов оказалось достаточно для
полной интегрируемости этих уравнений. С. В, Манаков в [84]
нашел представление Лакса для более широкога семейства метрик
34S
на SU(n), диагональных в стандартном представлении, включаю-
включающего в себя классические уравнения движения n-мерного твердо-
твердого тела. Доказательство независимости достаточного числа полу-
получающихся интегралов и соответствующее обобщение результатов
работы (84] на случай произвольных полупростых алгебр Ли
были получены в [98, 99].
Другое интегрируемое, семейство метрик на SO D), интегралы
которого также квадратичны, было обнаружено довольно давно
в работе В. А. Стеклова [251]. Эти случаи интегрируемости с но-
новой точки зрения многократно переоткрывались в последние годы
в рамках более общих конструкций [209, 30, 16, 174]. Представ-
Представление Лакса со спектральным параметром для них было найдено
А. П. Веселовым [32], явные формулы в 6-функциях для решений
этих систем, как и для систем в [84], недавно получены А. И. Ба-
бенко.
Примеры интегрируемости с дополнительным интегралом чет-
четвертой степени при выполнении некоторого соотношения между
значениями других интегралов найдены О. И. Богоявленским
[18]. В недавней работе М. Адлера и П. ван Мёрбеке [173] при-
приведено семейство метрик на SO D), для которых утверждается
наличие интеграла четвертой степени без каких-либо ограничений
на значения других интегралов.
1. Условия интегрируемости общих уравнений Эйлера на
soD). Алгебра Ли so D) не является простой и изоморфна прямой
сумме so(.3)©soC). Именно в таком виде она и появляется при
описании указанных выше механических систем. Грубо говоря,
один экземпляр soC) отвечает твердому телу, а другой — «квази-
«квазитвердому» движению жидкости [16, 31]. Пусть Mit /,-, где i==l,
2, 3, — естественный базис в алгебре soC)©soC) или координа-
координаты на сопряженном к ней пространстве. Рассмотрим квадратичную
форму от переменных Mit U, отвечающую левоинвариантной мет-
метрике общего вида:
Н = (АМ, М)+2(ВМ, 1) + (С1, I), A)
где (, > — евклидово скалярное произведение в R3, матрицы А и
С симметричны, В произвольна. На пространстве, сопряженном
к алгебре Ли, естественно действует группа Ли. В данном случае
это действие имеет вид
M-4-RiM, l-*R2l; Ru /?2eSOC). B)
Лемма 1. Заменой B) форма A) может быть приведена
к виду, в котором матрица А диагональна, а В — верхнетреуголь-
верхнетреугольная, т. е. Aij—AiSij, а Вц = 0 при i>j.
Если собственные значения матрицы Л различны, то с точ-
точностью до знака элементы верхнетреугольной матрицы В опреде-
определяются однозначно.
350
Уравнения Эйлера, отвечающие метрике A), имеют вид
j
li=[/, вм+ci], -
где [, ] — векторное произведение в R3. Это — гамильтоновы
уравнения с гамильтонианом Н для скобки Пуассона
{Ми Af,}=*iftAfft, {k, tj}=Biiklh, {Ми /,} = 0. • D)
Кроме интеграла энергии 1\ = Н уравнения C) всегда обладают
интегралами I2=M2, h — l2, порождающими аннулятор скобки
Пуассона и фиксирующими орбиту коприсоединенного представ-
представления: М2 = т02, ./2 = /02. На этой орбите мы имеем гамильтонову
систему с двумя степенями свободы, для интегрируемости кото-
которой необходим дополнительный интеграл, независимый с Н.
Рассмотрим вопрос о существовании такого интеграла для всех
достаточно малых т0 и 10. Более точно: когда у системы C) в ок-
окрестности точки Л1 = / = 0 имеется аналитический интеграл h —
— F(M, I), независимый с J\, h, /3? Необходимые условия были
получены А. П. Веселовым.
Отметим, что формы, отличающиеся заменой B), отвечают
эквивалентным уравнениям. Ограничимся случаем, когда собствен-
собственные значения матрицы А различны, т. е. A = diag(Au A2, As),
Ai>A2>A3. Случай совпадающих собственных значений см. в
[31]. Нам потребуется также условие невырожденности матрицы
В. Рассмотрим наряду с C) систему, получающуюся из нее в пре-
пределе при малых /, т. е. заменим / на г1 и устремим г к нулю [70]
(этот прием был использован В. В. Козловым, Д. А. Онищенко).
Получим
М=[М,АМ], 1=[1,ВМ]. E)
Система E) всегда имеет три интеграла: 1\=НО — {АМУ М)B, /2 =
=М2, /з = /2, однако, в отличие от исходной системы C), она уже
не гамильтонова. Но вопрос о дополнительном интеграле имеет
смысл и для нее.
Лемма 2. Если система C) в окрестности М = 1 = 0 обладает
дополнительным аналитическим интегралом h = F{M, l), то систе-
система E) имеет полиномиальный интеграл /4 = G(AI, /), независимый
с указанными выше интегралами.
Займемся теперь системой E). Первые три уравнения
М=[М, AM] F)
— это обцчные уравнения Эйлера свободного движения твердого
тела, интегрируемые в эллиптических функциях. Вторая тройка
уравнений
1=[1,ВМ) G)
— это линейные уравнения с коэффициентами, зависимость от
351
времени которых определяется системой F). Эта зависимость яв-
является периодической, а если рассматривать и комплексные зна-
значения времени, то даже двоякопериодической. Для линейных сис-
систем с периодическими коэффициентами важным является понятие
оператора монодромии. Например, роль этого оператора в изуче-
изучении уравнений Янга—Миллса была продемонстрирована в [56,
5?].
Пусть x=A(t)x, jc^R", — линейная система, такая, что
A(t+T) =A(t) — матрица, периодически зависящая от времени;
X(t, to) — ее фундаментальное решение: X(t0, to)=E. Оператор
(матрица) монодромии • f(to) определяется равенством
X(t+T, t0) =T(to)X(t, to). Операторы T(t0) при разных t0 сопря-
сопряжены между собой:
C = X(tut0). , Ю
В нашем случае оператор монодромии
принадлежит группе 50C), т. е. является
поворотом вокруг некоторой оси на угол ф.
Можно показать (при невырожденной матри-
матрице В), что ф не постоянен, а зависит от ре-
решения уравнения F).
-Лемма 3. Если система E) имеет до-
дополнительный интеграл, то система G) имеет
решение 1=п(М), полиномиально зависящее
от М. Вектор п(М) является собственным век-
вектором оператора монодромии Т(М).
Когда существует такое решение у системы G)? Воспользуем-
Воспользуемся явными формулами для решений уравнений Эйлера F) (см.,
например, [79]):
+ --
•
в
+ + +
•
А
- + +
•
С
— +
•
В
Рис. 131
Ml=c1cnkt,
(8)
Здесь фигурируют стандартные эллиптические функции Якоби,
отвечающие эллиптической кривой с параметром &2= — —
Аг — A-i
.—iz; L auk — постоянные, также выражающиеся через ин
М*АХ — 2Н0.
тегралы Яо и М2, см. [79]. Отсюда следует, что Mt — двоякопе-
риодические функции комплексного времени t, имеющие в дтрямо
угольнике периодов полюса первого порядка в точках А, В, С, L
с вычетами af = ±УhilYЬ.^^, где S.\—A2—А3, А2=Л3—Аи
Аз=^1—А.2 для подходящего выбора знаков (рис. 131). Координа-
Координаты вектора п(М), будучи полиномиальными функциями М, также
представляют собой эллиптические функции с теми же полюсами.
Запишем их разложение в окрестности одного из полюсов:
(акф0, k >0). В силу системы G)
-2*-+ —+
352
и (<xi, а2, аз), откуда [а&, Ba]+kctk = 0. Последнее равенство
янляется линейной системой, ненулевое решение которой сущест-
иует лишь при обращении в ноль соответствующего определителя.
Простое вычисление приводит нас к равенству 0 = k(k2 + |£<х|2),
или, так как ft>0,
Ва\2 = 0. - (9)
Рассматривая аналогичные равенства в оставшихся трех полю-
полюсах, можно показать, что все внедиагональные элементы матрицы
В — нулевые. Остается лишь одно требование:
=BUt или
= 0. bmN. A0)
Приведенные выкладки напоминают рассуждения С. В. Кова-
Ковалевской, которая обнаружила свой случай интегрируемости дви-
движения тяжелого волчка. Подобный подход' для уравнений Эйлера
на 50D) был предложен в работе М. Адлера и П. ван Мёрбеке
[173]. Они рассматривали следующую постановку задачи: когда
уравнения Эйлера на SO D) имеют дополнительный алгебраичес-
алгебраический интеграл, такой, что общая поверхность уровня всех интегра-
интегралов при продолжении в комплексную область является абелевым
многообразием? Предполагается, что динамика на нем линеари-
линеаризуется, исходные координаты являются абелевыми функциями и,
следовательно, зависят от комплексного времени мероморфно.
., При выполнении этих свойств система называется алгебраически
. вполне интегрируемой.. - ■
Основной результат работы [173] такой. Среди уравнений
; Эйлера, отвечающих диагональным в стандартном представлении
>'-so(i) метрикам, при некоторых предположениях невырожденнос-
невырожденности алгебраически интегрируемы только метрики, порожденные
операторами фаьо (см. их описание выше).
Этот результат был обобщен Хайне [204] на случай so'(n)
для произвольного п. Подведем итоги.
Теорема 1 (А. П. Веселое [30]). Уравнения Эйлера на ал-
алгебре Ли soD) с гамильтонианом общего вида A), отвечающим
невырожденной матрице В и симметрической матрице А с различ-
различными собственными числам, могут иметь дополнительный анали-
аналитический в окрестности М = 1 = 0 интеграл только в том случае,
когда заменой B) матрицы А и В могут быть одновременно диа-
гонализированы. При этом соответствующие диагональные эле-
элементы Bu = bi должны удовлетворять соотношению A0) для не-
некоторого натурального k. Если при всем этом собственные числа
матрицы С также различны, то в результате той же замены она
тоже приводится к диагональному виду, а ее собственные числа
Ci удовлетворяют аналогичному соотношению
0, m<=N,
6i = c2—с3, б2 = с3—си бз = с,—с2. A1)
12 А. Т. Фоменко 353
Следовательно, среди общих метрик, зависящих по модулю за-
замен B) от 15 параметров, при соответствующих предположениях
невырожденности лишь 7-параметрические семейства A0) и A1)
могут отвечать интегрируемым случаям уравнений Эйлера. Изве-
Известные сегодня случаи интегрируемости (см. ниже) образуют 6-па-
раметрическне семейства. По всей видимости, найденные условия
не являются достаточными для интегрируемости, хотя и довольно
сильно ограничивают класс соответствующих метрик.
Следствие 1 [31, 32]. Уравнения свободной динамика
твердого тела с эллипсоидальной полостью, заполненной идеаль-
идеальной жидкостью, совершающей однородное вихревое движение, в
общем случае не имеют дополнительного аналитического интег-
интеграла.
Следствие 2 [31, 32]. Уравнение Ландау—Лифшица для
двухподрешеточного магнетика (см. [32]) в общем случае явля-
является неинтегрируемым.
2. Интегрируемые случаи уравнений Эйлера на SO D). Рас
смотрим вопрос о дополнительном квадратичном интеграле. Этот
случай интересен тем, что при этом вся коммутативная алгебрг
интегралов состоит из многочленов одной степени, и задача сос-
состоит в описании всех таких четырехмерных алгебр. Ограничимс*
невырожденным случаем,, когда собственные числа матриц А и С
для некоторого представителя алгебры различны. Для 'простоть
будем считать, что матрицы А, В, С, отвечающие элементам ал
гебры, могут быть одновременно диагонализированы (см. преды
дущий раздел).
Коммутативная алгебра порождается формами М2, I2, а такж>
некоторыми H = Ho+Hi + H2 и I — I0+Ii + h, где Hk и lk — член!
степени k по /. Будем считать, что Н — невырожденный предстг
витель, т. е. собственные числа форм Но и Я2 различны. Запись
вая условие {#, /} = 0 в компонентах, получаем (см. [115]
А. М. Переломов) {Яо, /о} = 0, откуда /о = Я#о+цМ2. Перейде
к другому интегралу / = /—КН--\iM2, J^Ji + .f2, /() = 0. Точно та
же {Я2, /2} = 0 и /2 = а#2 + р/2. Здесь возникают две возможност)
а = 0 и а=£0.
1-й случай. Пусть а = 0. Вычитая р/2, приходим к интегра/
вида J' = Ji.
2-й случай. Пусть cr^O. Здесь удобнее рассмотреть
—L/—Li* =
Иными словами, невырожденная коммутативная алгебра ква
ратичных интегралов порождается формами М2, /2 и либо 1) фс
мами вида Н = {АМ, М) + 2(ВМ, l)-\-(Cl, I), J = (DM, l), ли
2) формами вида Н = {АМ, М) + 2{ВМ, I), J = 2(DM, D+{Cl, I). P<
смотрим эти случаи отдельно:
354 '
1) Условие {#, /}=0 эквивалентно системе уравнений
A2 3) •
1 Dx (С2— С5) = ВаД3— В3£>г A2 3) (перестановки)
Из нее следует, что А — С + КЕ и выполнено условие A0) (совпада-
(совпадающее с A1)) при fe=l. Случай А = С отвечает формам, диагональ-
диагональным в стандартном матричном представлении SOD), а условие
A0) выделяет среди них уже хорошо знакомые нам метрики типа
При ХФО получаем тривиальное расширение семейства метрик
типа фаьо до шестипараметрического семейства уже недиагональ-
недиагональных метрик. Представление Лакса для них было найдено еще
в [84], явные формулы для решений в 6-функциях многообразий
Прима получены недавно А. И. Бабенко (см. также работы
М. В, Мещерякова [87] и Хайне [205]).
2) Во втором случае условие {Я, /}=0 приводит к системе
j D1H,-4,)=fl,D,-flA A23) '
\ — B1(Ca—C3) = BiD3—B3D2 A2 3) (перестановки)
Эта система в предположении В{Ф0 имеет следующее решение:
А, = — :-^3- + а, Д=—, С,= ^- + с. A23)
if £> о
Соответствующие'формы имеют вид
3
2Я = £ (ybjm-j + 2blMItl) + aM\
2J =
Общий интеграл алгебры имеет вид H + J и зависит от шести
параметров bu b2, Ь3, а, с, К. Отметим, что система имеет и три-
тривиальное решение В = /) = 0, А и С — любые, отвечающие случаю
распадения: Н — {АМ, М), J = (Cl, l), который также зависит от
шести параметров. Как уже указывалось, 2-й случай интегрируе-
интегрируемости был впервые получен В. А. Стекловым [251] и затем пере-
переоткрывался в различных видах (см. выше). В указанной здесь
форме алгебра представлена в [32]; в [16] и [174] она задается
в виде соотношении на коэффициенты квадратичных форм, ее по-
порождающих.
Укажем связь этих случев с известными интегрируемыми слу-
случаями уравнений Кирхгофа—Томсона движения твердого тела
в жидкости, описываемых уравнениями Эйлера на алгебре Ли
группы движений £C) трехмерного пространства R3. Как указал
С. П. Новиков в [105], при стягивании алгебры soD) на алгебру
еC) семейство метрик вида уаьо (первый случай) переходит в
12* . 355
случай Клебша. Затем аналогичное наблюдение для второго слу-
ча_я интегрируемости сделано в [33]. Этот случай переходит в из
вестное семейство Стеклова—Ляпунова—Колосова. Недавж
А. И. Бабенко и П. И. Голодом [10] независимо было обнаруже
но, что эти системы не только переходят друг в друга при стяги
вании алгебры Ли,, но просто эквивалентны, т. е. после замень
переменных совпадают.
Обсудим вопрос об интегрируемых случаях с интегралом сте
пени больше двух. О. И. Богоявленский [18] нашел следующи]
случай частной интегрируемости, т. е. при определенных ограни
з
чениях на начальные данные. Пусть 2Ц~ S\ а* (Mf+ /?) + 2fJjMj/i
i—\
причем р, = а—За,-, а==а1 + а2таз. Тогда на одиопараметрическо!
множестве орбит, задаваемом условием Л12 = /2, имеется дополни
тельный интеграл
J = [(а,-о,) (M.-l.r + (аа-а,) (М2-/2J +
+ («,-04) (М3-/3J]2- 4 (а,-а,) (а,-а,) • (М,- l,f (M,-/2J.
Для указанных параметров аир выполняются соотношения A0,
и A1) для k = m = 3. Случай общей интегрируемости с интегралов
четвертой степени анонсирован в недавней работе М. Адлера \
П. ван Мёрбеке [174].
В ряде астрономических задач необходимо исследовать враше
ние твердого тела Т вокруг центра масс в поле гравитационной
притяжения других тел. "Особенно важен случай, когда расстояние
до притягивающего объекта V много больше размеров твердой
тела Т. В специальном случае осесимметричного гравитационного
поля интегрируемость вращения твердого тела была доказан;.
Ф. Бруном A893). Полное решение задачи дано О. И. Богоявлеь
ским в [282], где доказан следующий результат.
Теорема 2. Вращение произвольного твердого тела Т, име-
имеющего малые размеры, вокруг неподвижного центра масс О в пом
гравитационного притяжения любого объекта V описывается неко-
некоторой универсальной вполне интегрируемой по Лиувиллю динами
ческой системой. Интегрируемость динамики твердого тела осуии-
ствляется в тэта-функциях Римана. •
Доказательство теоремы 2 основано на представлени:
уравнений движения в виде одного матричного уравнения изоспе*
тральной деформации, зависящего от произвольного параметра L
L=[L,Q], L = BE*+ME+u, Q = W—1E.
Динамические переменные, входящие в трехмерные матрицы М
и, проинтегрированы в тэта-функциях римановых поверхносте£
R(E, tw)=det(L(£)— aM)=0.
Эквивалентная формулировка теоремы 2 утверждает итгтегрт
руемость вращения произвольного твердого тела в ньютоновско
356
гравитационном поле с любым однородным квадратичным потен-
потенциалом.
В конкретных астрономических задачах движущиеся объекты
не имеют неподвижных точек и их поступательное и вращательное
движение взаимосвязаны. Следующая теорема,, доказанная в
[283}, является усилением теоремы (О. И. Богоявленский).
Теорема 3. Поступательно-вращательное движение произ-
произвольного твердого тела Т в ньютоновском поле с произвольным
(неоднородным) квадратичным потенциалом определяется гамиль-
тоновой системой, интегрируемой по Лиувиллю. Динамика центра
масс О интегрируется в элементарных функциях; вращение твер-
твердого тела вокруг центра масс интегрируется в тэта-функциях Ри-
мана.
Эта теорема применима для исследования поступательно-вра-:
щательного движения произвольного твердого тела в окрестности
точек экстремума ньютоновского потенциала, где квадратичное
приближение является достаточно точным.
ПРИЛОЖЕНИЕ 3
ВЫПУКЛОСТЬ ОТОБРАЖЕНИЯ МОМЕНТА ПРИ
ПУАССОНОВОМ ДЕЙСТВИИ ТОРА
Здесь мы вкратце обсудим результаты Атьи, Гийемина, Штерн-
Штернберга о выпуклости образа отображения момента некоторых ин-
интегрируемых систем [177, 202, 203].
Рассмотрим компактное связное симплектическое многообразие
(М2п, ш) и пуассоново действие тора Tk на нем. Возникает отобра-
отображение момента [i : Af-v/* = Rft; R;' = G*, G — TeTk.
Теорема 1. Образ \i — выпуклый многогранник, вершины
которого содержатся в множестве [л^ХГ*).
Теорема 2. Пусть М дополнительно обладает кэлеровой
структурой, инвариантной относительно действия тора. Пусть Т с—•
соответствующий комплексный тор, Y — некоторая его орбита,
Y — ее замыкание. Пусть /\, i= 1, ..., г, — компоненты множеств
ва неподвижных точек тора в У, С; = |л(/\). Тогда
A) n(F)=conv(c,, ..., с г);
B) для каждой открытой грани a<=conv(cb ..., сг) ее прообраз
^-'(о) состоит из одной Тс-орбиты;
C) |л : F/7'*«!conv(c1 cr); в частности, над внутренностью
Conv(c , сг) отображение \ц является расслоением со слоем Tk.
В общем случае пуассонова действия компактной группы @
отождествим G* с G; обозначим через / алгебру Ли максималь-
максимального тора Та @ , а через /+ — камеру Вейля. В этом случае
[x:M-*-G* = G является ©-эквивариантным отображением (при-
(причем каждая орбита О в G пересекает-1+ в единственной точке).
Теорема 3. Множество ц.(М)(](+ является выпуклым много-
многогранником.
357
Анализируя указанные выше работы, С. Л. Табачников полу-
получил следующее утверждение.
Теорема 4. Пусть на компактном симплектическом много-
многообразии М2п задана вполне интегрируемая система f ь ..., fn, отве-
отвечающая пуассонову действию тора Тп на многообразии. Тогда
числа Бетти многообразия М с нечетными номерами равны нулю,
а равенство df\ = .. .=dfn = O выполнено ровно в k изолированных
точках, где k = dim H*(M).
ПРИЛОЖЕНИЕ 4
ЛЮБАЯ КОМПОЗИЦИЯ ЭЛЕМЕНТАРНЫХ БИФУРКАЦИИ
(ТРЕХ ТИПОВ) ТОРОВ ЛИУВИЛЛЯ РЕАЛИЗУЕТСЯ ДЛЯ
НЕКОТОРОЙ ИНТЕГРИРУЕМОЙ СИСТЕМЫ НА
ПОДХОДЯЩЕМ СИМПЛЕКТИЧЕСКОМ МНОГООБРАЗИИ.
КЛАССИФИКАЦИЯ НЕОРИЕНТИРУЕМЫХ
КРИТИЧЕСКИХ ПОДМНОГООБРАЗИЙ БОТТОВСКИХ
ИНТЕГРАЛОВ
Выше мы обнаружили 3 перестройки торов Лиувилля, в ком-
композиции которых распадается любая перестройка общего поло-
положения (см. гл. 4). Возникает вопрос: любая ли композиция таких
элементарных перестроек реализуется в некотором симплектиче-
симплектическом многообразии с интегрируемой системой? Ответ — положи-
положительный.
Теорема 1 (А. В. Браилов, А. Т. Фоменко). Пусть ХпН —
гладкое компактное замкнутое ориентируемое многообразие, по-
получающееся склейкой произвольного чи'сла элементарных много'
образий типов I, II, III (т. е. диссипативных полноторий, цилинд-
цилиндров и штанов) по любым диффеоморфизмам их граничных торов
Т". Тогда всегда существует гладкое компактное симплектическое
многообразие М2п с краем, диффеоморфным несвязному объедине-
объединению некоторого числа многообразий вида Sn-'xrn и полный ин-
волютивный набор гладких функций /i,...Jn на М2п такой, что
Х"+>={х<=М2п : f2(x) = ... =fn{x) =0}.
По-видимому, есть топологические препятствия к реализации
многообразия Xn+l в компактном замкнутом симплектическом
многообразии М2п. Из теоремы 1 следует доказательство утверж-
утверждения 2 § 1-гл. 4 о реализуемости любого трехмерного многообра-
многообразия из класса (Q) в виде изоэнергетической поверхности-некото-
поверхности-некоторой интегрируемой гамильтоновой системы на подходящем симп-
симплектическом многообразии М4. Другими словами, из теоремы 1
следует, что (Q) = (#).
Доказательство теоремы 1. Искомое многообразие М2п
конструируется из симплектических многообразий, соответствую-
соответствующих тем «элементарным кирпичам», из которых склеено многооб-
358
разие Хп+У. Поэтому на первом шаге доказательства мы построим
примеры интегрируемых систем, в которых реализуются перестрой-
перестройки типов I, II, III.
Пусть ш„ — симплектическая структура на торе Тгп = {(ц>1,...
п
... , Ф2„): modd2n}, ш„= V с?ф21—i Л йф2;-На торе Т2 можно, оче-
видно, построить гладкие функции ф[б], где s=l, 2, 3, и подмного-
подмногообразия MsCzT2 так, что Nt — точка невырожденного максимума
для /ш, a N2 — невырожденная седловая точка для /[2] и N3—■
невырожденная критическая окружность для /[3]. Можно, напри-
например, взять /П5 = /[2]=соз(ф1 + 2ф2))Л^1 = {@,0)})^2 = {(л,0)}, pj =
= созф1, yv3- {@,ф2)тоA2л}. Если cs = fls]{Ns) — критичес-
критические значения, то Ci = с3= 1, Ci =— 1.
Пример s, где s—l, 2, 3. Многообразие М'2п = Т2п, ш„ — симп-
симплектическая структура на нем. Для г = 2, ..., п имеем
Ыфь ..., ф2п)=5тф21-+1-Для t=l имеем Л(фь • ■ • .фг«) =/[1;](фь фг).
Тогда гамильтонова система y = sgrad/i вполне интегрируема на
М2п с полным инволютивным набором интегралов /,-, a N — NSX
ХТ2п~2 — невырожденное критическое подмногообразие функции
/ilxn+l, где Хг>+1 = {/2 = ... =fn = 0}. Критическое значение:
h(N)=cs.
Пусть многообразие X" = (J"L'1 х-, склеено из «кирпичей» X; и
s(/) — тип %i- Если многообразие X; типа II склеивается с раз-
различными многообразиями Xfl и Х/2 по диффеоморфизмам dx и
d2, то из разбиения Xn+l можно удалить А'/, склеив X/, и- Х/2
по диффеоморфизму d2d\~]. Описанный процесс назовем" сокраще-
сокращением разложения многообразия Xn+l на элементарные кирпичи.
Обратный процесс, при котором в разложении Хп+1 добавляется
новый кирпич типа II, назовем вставкой. Оба процесса не меняют
многообразия Хп+1 с точностью до диффеоморфизма. Далее оче-
очевидно, что путем подходящей последовательности сокращений и
вставок из исходного разложения многообразия Хп+1 можно полу-
получить такое разложение, для которого будут выполнены следующие
условия:
1) для любого кирпича X/ типа II номера склеенных с X, кир-
кирпичей либо оба больше /, либо оба меньше /;
2) для любого кирпича X/ типа III номера всех трех склеенных
с X/ кирпичей не могут все быть одновременно больше или мень-
меньше /. *
Итак, пусть Xn+l = \jjl=1 X,-— разложение, удовлетворяющее
этим двум условиям. Для каждого /=1, .... m копии объектов
/,-, N, М2п из примера s = s(j) обозначим соответственно через /,-/,
N/, Mj2n. Путем подходящей линейной замены fij-*-f'\j = cijfui + bj
можно добиться того, чтобы отображение момента Fj(x) =
= (fu(x), ■•■■, fnj{x)) удовлетворяло следующим условиям:
1) для каждого /—1, ..., m при движении точки «/eRn вдоль
первой координатной оси от 0 до пг+ 1 точка у пересекает бифур-
359
кационное множество 2; отображения Fj только один раз — в точ-
ке^=(/, 0,.:.,0);
2) если S"(/) = 1 и кирпич Xjl склеен с кирпичом X, , то при ука-
указанном движении в точке г/ = £/ происходит рождение тора /r/"~1(f/)
в случае /i>/ и уничтожение — в случае /i</;
3) если s(/)=II и кирпич X, склеен с X/, и X , то . в точке
y = li происходит рождение двух торов /7/~1(г/) в случае ju /2>/
и уничтожение двух торов в случае /ь /2</;
4) если s(j) =111 и кирпич X/ склеен с X/,, Х/„ Х/„ то при
/Y</</2, /з в точке (/ = £/ происходит перестройка одного тора
в два тора, а при /i, /2</</з — перестройка двух торов в один.
Для любых г > 0, а <Ь. определим цилиндр Cr (a, b) = ly е Rn :
:2»=2^2 <г2, а < ух < 6}. Нетрудно видеть, что 2/ П Ст @, т + I) =
= П/ П Ci/2 @, т + 1), где П/ = (у EER" :«/! = /}—гиперплоскость.
Многообразие М2п получается'из многообразий
М; = M/Vy1 (С,/а @, /-1/2)) U С/2 (/ + 1/3, т + 1)
приклеиванием соединяющих их трубок. Возможность приклеива-
приклеивания трубок вытекает из следующей леммы.
Лемма. Пусть заданы числа •ai<bi<ci<a2<b2<c2, г>0.
Предположим, что^для каждого /=1, 2 имеется симплектическое
многообразие Mj2n и на нем — полный инволютивный набор глад-
гладких функций fa, где i=l,...,n такой, что отображение момента
Fj является расслоением со слоем тор Тп яад цилиндром Cr(ai,c,).
Тогда для достаточно малого г~>0 существует симплектическое
многообразие Z, содержащее в качестве открытых подмногообра-
подмногообразий прообразы Vi = F\'l(Ct(ait &i)), V2=/V(C'«(/;2, c2)) и полный
■инволютивный набор гладких функций ft на V такой, что соответ-
соответствующее отображение момента F является расслоением со слоем
Тп над Ce(ai, с2) и F\vf =^i\vj для /=1, 2.
Доказательство. Пусть bi<idi<ici и a2<d2<c2, D,=
= (dj, 0, ...,0), /=1, 2. Выберем в окрестности б/ тора 7,-я =
■=Fj~l(Dj) переменные 1ц, <р,-у типа действие—угол. Уменьшая при
необходимости О,-, мы будем считать, что переменные 1ц задают
расслоение /,-: Оу—+В& над малым шаром Be = {yeR" : \y\ <б}.
Таким образом, переменные /,-,■, ф,;- задают диффеоморфизм
IBT
Положим Р= (/2Хф2)(^1Хф1). Очевидно, что Р : Oi->O2 —
симплектический диффеоморфизм. Так как переменные /,•/ выра-
выражаются через fi,- и независимы, то существует диффеоморфизм
Jj:Bu-+0i = Fj@j) такой, что Fj = ]jli. Пусть, наконец, Р = /2/г'.
В итоге имеем следующую коммутативную диаграмму:
360
at
Ее построение неоднозначно, поскольку введение переменных типа
действие—угол зависит от выбора базиса циклов на торе, в окре-
окрестности которого эти переменные вводятся. Обсудим характер
этой неоднозначности. Пусть (Л,-) и (A/) = Л(А;) — два различных
базиса в группе HX{F2^{D2), l)=ln. Тогда A/ = 2"*=iA;*A* для
подходящей матрицы A<=GL(n, Z). Так как переменные /; типа
действие определяются путем интегрирования фиксированной
1-формы по циклам hi, то замена Л,—*-А/ приводит к линейной за-
замене /,->/,•'?= 2nft=iA,-*/ft. Замена угловых переменных производит-
п
ся при помощи обратной матрицы Ф< -»■ Ф< — J] (Л )»*Ф*-
Заменяя при необходимости Ai на Ai'= —Ль мы можем считать,
что якобиан диффеоморфизма Р больше нуля.
Пусть Cs(ax, e) — такой цилиндр, что правый его торец нахо-
находится внутри Оь а точка Dx — внутри Сг{а, е) (рис. 131A)).
•о,
Or ^,
—1 hr-Hlllln
mill
(Ж ж
1
-*•
сг
Рис. 131A)
Соединим цилиндр Ct(b2, c2) трубкой Т с образом цилиндра
Ct(.a\, е) при диффеоморфизме Р таким образом, чтобы трубка Т
была бы гладким продолжением обоих цилиндров и имела откры-
открытые непустые пересечения с ними. Пусть
Ах = СЕ
Т U С£ (&„ с,), Z, = F,-' (А,), / = 1,2.
361
Диффеоморфизм Р_ симплектический, следовательно, склеивая Z\
и Z2 при помощи Р, мы получим симплектическое многообразие
Z = Z,UpZ2. Для А=А\\}рА2, учитывая положительность якобиана
диффеоморфизма Р, имеем, что существует диффеоморфизм
L: А->Се(а\, с2), тождественный на С,(а\, Ь\) и С„(Ь2, с2). Отоб-
Отображение F(x) =L(Fj(x)), x^Zj, является искомым расслоением.
Вернемся к доказательству теоремы. Для каждого /=1,...,т
ограничение отображения момента F/ на М{ будем обозначать
через Fj'. Для любых a<Lb. Пусть [а, Ь]{ — отрезок первой коор-
координатной оси в R" от а до Ь. Нетрудно видеть, что прообраз
{F'i)~l{[0, m + l^^iF',)-1 ([/—1/3, / + 1/3],) диффеоморфен кир-
кирпичу Xj. Далее эти многообразия отождествляются. При этом
каждый тор TKlt ограничивающий Xit является, очевидно, авяз-'
ной компонентой множества
(^/Г'а-1/з, о, .... о)и(^/)~1(/ + 1/з, о 0).
Для кирпичей Xj,, Xj,, /\< j2, склеенных no торам T^czdXj,, Tk2cz
сг дХ/2, положим а=(Х/„ 7\, X,,, 7\)- Для любой такой четверки а,
используя предыдущую лемму, можно .построить симплектическое
многообразие Za, имеющее непустые (размерности 2п) пересече-
пересечения Vks и Vk2 с Mj\ и М1г соответственно, а также отображение
момента Fa : Za-^R", продолжающее отображения Fjl\Vk и f/J^.
Более подробно: пусть Vkt—связная компонента прообраза (Т*1/,) X
X (Се 0\ + 1/5, }х + 1/3)), содержащая тор T^ciFfS ih +1/3, 0, ...
... , 0); Vkt—связная компонента прообраза FJ[l (Се(/2—1/3, /2—1/5)),
содержащая fop Tklcz F~l (j2—1/3, 0, ... ,0). Здесь черта сверху
обозначает топологическое замыкание в R". Из леммы вытекает,
что существуют симплектическое многообразие Za и отображение
момента Fa :Za->CE(/i + 1/5, /2—1/5) такие, что для каждого ^=1,2
пересечение M]t ("]Za совпадает с ^*г ^а\\ - Flt\vk, и ото-
отображение Fa является расслоением со слоем Тп.
Пусть Fa" : M'j \jZa\jM'. -^R" — отображение, совпадающее
с F',-, на Мп, с Fa на Za и с Fj, на М/2. Тогда прообраз
(Fa")~l([0, m+l]i) диффеоморфен склейке Xj^Xj, кирпичей
X/, и Xj, по диффеоморфизму граничных торов 0 : Г*, -+Тк2- Воз-
Возможно, однако, что диффеоморфизм в неизотопен диффеоморфиз-
диффеоморфизму 0а, при помощи которого торы Г л, и Т кг отождествляются в
многообразии Хп1¥\ В этом случае при построении многообразия
Za необходимо изменить выбор базисных циклов hi в Н\(Ткг, Z),
hi-*-hi' = 2"=i Auht, A^SL(n, Z) так, чтобы диффеоморфизм в' =
= Л"'0 стал изотопен €>а.
Таким образом, мы можем считать, что каждое многообразие
(^а")~'([0> /п+ 1] 1) диффеоморфно объединению Xj, и Х/2 в Х"+1.
Следовательно, для многообразия М'= (\jjMj')\j([jaZa) и отображе-
отображения F, совпадающего по определению с F'. на M's и с F, на Za,
имеем /^'([0, m+ l]i) ~Xn+1. К сожалению, многообразие ЛГ яв-
362
ляется многообразием с кусочно гладким краем и поэтому не
удовлетворяет требованиям теоремы. Однако можно гладким об-
образом обрезать углы многообразия М' и получить многообразие
MczM', сколь угодно мало отличающееся от М' и уже с гладким
краем" дМ. Вырезаемое множество W необходимо взять в виде
W=M'\M = F~X(-Y), YczF(M'). Тогда край дМ тривиально рас-
расслаивается над F(dM) со слоем Тп. Образ F((dM)a) каждой ком-
компоненты связности (дМ)а края дМ является связной суммой двух
(п—1)-мерных сфер и, следовательно, диффеоморфен S". Сле-
Следовательно, край дМ диффеоморфен несвязной сумме г копий
многообразия Sn~1XTn, где г — число пар склеиваемых торов в
данном разложении многообразия Xn+l. Теорема доказана.
Выше мы обнаружили неорцентируемые многообразия /Св" —
минимумы или максимумы боттсвского интеграла f на поверхности
Х"+>. Дадим полную классификацию таких многообразий.
Для каждого р обозначим через Gp (при Р = 0, 1) группу пре-
преобразований тора rn = Rn/Zn, порожденную инволюцией
(—а1Уа2+ -j, а3, ... ,ап), р = 0,
(а^а^,а3-\- —, а4, ... ,ап), р = 1,
где a=(ai,...,a«)eR"/Z", Здесь предполагается, что «>2 при
Р = 0 и «>3 при р=1. Группа Go действует на торе Тп без непод-
неподвижных точек, следовательно, фактор-множество K»n=Tn/Gfi явля-
является гладким многообразием. Преобразование #о меняет ориента-
ориентацию, поэтому многообразие К$" — неориентируемо. Многообразия
Ко" и Kin негомеоморфны, так как имеют разные группы гомоло-
гомологии, а именно Hi (Ко", Z)=Z'l-1®Z2, а W, (Kin, Z)=Z"-1. -
Из определения К»" сразу следует, что Коп = Ко2ХТп~2, Ki" =
= KizXTn'z. При этом Ко2 — обычная бутылка Клейна, а Ki3 —
ее естественное обобщение.
Теорема 2 (А. В. Браилов, А. Т. Фоменко). Пусть f ь ... ,fn —•
полный инволютивный набор гладких функций на симплектиче-
ском многообразии М2п и F: M2n-+Rn — соответствующее отобра-
отображение момента. Пусть X"+l = {fi(x)=%i, t=l,,.. ,п— 1} — интег-
интегральное подмногообразие отображения момента. Предположим,
что ограничение fn\ n+\ является боттовской функцией и Хо =
= {fi(x)=>li, t=l, 2, ...,«}•— неориентируемое многообразие ми-
минимума функции fn\ n+i. Тогда Хо диффеоморфно либо Ко"
Л.
(при га>2), либо К\п (при п>3).
Доказательство. На многообразии Хо глобально опреде-
определены векторные поля V, = sgradf,- (при t=l,...,«—1) и локально
определено векторное поле Vn = sgradYfn—In- Эти поля комму-
коммутируют друг с другом и в каждой точке xeio линейно независи-
независимы. Пусть W — трубчатая окрестность Хо в Xn+l вида W — {fi(x) =
= ii, i=l,...,n—1; fn(*X£n+.e}. Пусть я : dW-+X0 — соответ-
363
ствующее двулистное накрытие. Нетрудно видеть, что на 3W име-
имеется глобально определенное векторное поле Vn' такое, что
n*Vn'=Vn. Векторные поля V», i=\,.,.,n—1, также поднимаются
в dW, n*Vi'=,Vi. Все векторные поля V/, i=\,...,n, по-прежнему
коммутируют и независимы в каждой точке x^dW. Преобразова-
Преобразование dW, состоящее в сдвиге вдоль интегральной кривой поля V/
за время t, обозначим gi'. Для а— (щ,... ,Qn)eR" композицию
8а\°---°8аг? обзначим ga.
Итак, группа R" действует на dW по формуле x-+ga(x). Из не-
неориентируемости Хо вытекает, что многообразие dW связно. Сле-
Следовательно, для любой точки Хо^Хо ее ^"-орбита совпадает с
6W. Пусть L = LX, — стационарная подгруппа точки хо в R".
Тогда отображение a-+ga(Xo), aeR"/L, является диффеоморфиз-
диффеоморфизмом R"/L на dW. Для любой точки x^dW компоненты щ вектора
aeR" такого, что ga(xxj)=x, назовем {неоднозначными) коорди-
координатами точки х. Пусть а — инволюция dW, переставляющая лис-
листы. Тогда o*Vn' = — V,/. Следовательно, о(8й{х)) — ^'{а)(а(х)),
где (—аи а2 ап)=щ(а).
Фиксируем точку Xo^dW и соответствующие ей (многознач-
(многозначные) координаты ,ai. В этих координатах преобразование а зада-
задается формулой o(a) = (q]—au q2 + a2,...,qn+an), где qi — коорди-
координаты точки а(хо). Заменяя при необходимости точку хо на точку
с координатами {qi/2, 0, ...,0), мы будем считать, что qi = 0.
Пусть Tq{a)—a + q — преобразование сдвига на (вектор q по мо-
модулю L. Ясно, что &=OoTq и' ooTq=Tqao. Так как ао = оТ-ч — кор-
корректно определенное преобразование многообразия dW и ао(хо) =
= х0, то cto(L)=L. Поскольку T2q = Oo2T2q = ст2 ==id|aw, то 2q^L.
Определим решетки L± = {/eL : ао(/) = ±0. Ь'—Ь+-\-Ь~. Тогда
либо L=:L', либо ЬФ\Ь'. Рассмотрим сначала первый случай. Вы-
Выберем базис (/,).^i в L~ и базис (U)i=2 п в L+. Тогда (/{) =
= (/j)i=i,2,...,п — базис в L' — L. Следовательно, в базисе (/,■) ли-
линейный оператор ао задается матрицей diag(—1, 1.....1)- Выше
мы видели, что ^i —0> 2q^L. Следовательно, 2q^L+ и можно счи-
считать, что базис (/,-) выбран таким образом, что h = 2q. В коорди-
координатах, связанных с базисом (/,-), имеем а{а\,.,. ,ап) = (—ai,
«2+1/2, а3)...,.an), следовательно, Хо диффеоморфно Ко".
Пусть Ь'ФЬ. Для.любого aeRn/L определим а±= (а±ао{а))/2.
Пусть li^L\L'. Предположим, что lr^L~. Так как h+=l\—/г,
то в этом случае и l\+^L+. Следовательно, /i = /i+ + /reL'; полу-
получили противоречие. Поэтому 1гФь~, тогда как, очевидно, 2/г(=2>.
Покажем, что h порождает L по модулю U. Действительно, пусть
l^L\L'. Тогда 2/~eL- и l'^L~. Следовательно, /г—l~^Lr и
{/,—/)+sL+. Поэтому /]—/eL', что и требовалось доказать. Пусть
/* — образующий элемент в L~. Тогда для li^L\L' и подходяще-
подходящего целого числа m имеем 2/г = т/*. Число т нечетно, так как
h-<qEL-. Заменим h на U' — U—nl*, где т = 2«+1. Тогда 2/г=
= ml*—2nl* = l*. Таким образом, /iSL\L' можно выбрать так,
что 2/г — образующий элемент в L~.
364
Пусть (/i)i=2,...,n — базис в L+. Докажем, что '(/<) =
= (U)i=i,2 п — базис в L. Пусть /<=L — произвольный элемент.
Необходимо найти целые числа Ш{, 1=1,...,п, такие, что I —
— ^iiriili. Так как U порождает L по модулю U, то можно считать,
что l = L'. Но тогда / = /++/-, где PeiA А так как l~ = 2mlr, то
отсюда следует, что /=2imj/i для подходящих чисел т*. В базисе
</,•) линейный оператор о0 задается матрицей
S21
1
о
1
Так как
<det(Si/) = —1, то su =—1. Путем элементарных преобразований
базиса (It) i=2 п в L+ можно добиться того, чтобы выполнялась
цепочка равенств s3i = S4i = ... = sni==0. В итоге получаем, что (То
-задается матрицей
г — 1
со.
0
1
0
1
1
•
0
0
0
*
• 1
Заменим теперь в базисе (/;),«=1,2 л первый вектор U на // =
— l] + kl2. Так как
О
р
1 О
— k О
1
Р—2k
-то в новом базисе его задается той же матрицей, но с заменой р
~на Р' = Р—2k. Поэтому можно считать, что C = 0 или 1. Первый
-случай соответствует L — L' и был разобран ранее. Осталось рас-
рассмотреть случай jj=l. Вектор q^L+[\(L/2\L) координат точки
а{х0) определен по модулю L. Поэтому можно считать, что q —
п
il(, где <7г = 0, 1/2. Если qi— 1/2, то заменим точку отсчета х0
на точку с координатами A/2, 0, ...,0). Так как <To(/i) = —/1 + /2,
то сдвиг q в новых координатах даст тождество цЛ /2=0 (modL).
Следовательно, можно считать, что <72 = О. Далее, совершая
элементарные преобразования над векторами /,-, i = 3,...,«, можно
добиться того, чтобы <7— (/3/2)mod L. Наконец, заменяя /2 на
h'——U + к, получаем, что а задается в координатах, связанных
>с базисом .(/,■)> формулой а(аь ... ,а„) = (.а2, аь.а3+1/2, а4, ...,'ап).
365
Следовательно, многообразие Хо диффеоморфно Kin. Теорема до-
доказана.
В заключение докажем, что трубчатая окрестность W миниму-
минимума Хо в Хп+Х разрезается на «элементарные кирпичи» описанных
выше типов I и III. Так как Хп+1 ориентируемо, а Хо — К(,п, то W
диффеоморфно фактор-М'ногообразию Wp"+i многообразия ТпХ{—1,
+ 1] по инволюции Rfiw, определяемой формулой
R%(t, a) = (—t, Др(а)), fe=[—1, 1], a^T".
Так как <'=--^хГ, Wi+l = WlxTn~\ то, по существу, доста-
достаточно рассмотреть Wo и W\. Оба этих многообразия можно получить
склеиванием штанов с полноториями.
ПРИЛОЖЕНИЕ 5
. НЕКОТОРЫЕ ДРУГИЕ МЕТОДЫ ПОСТРОЕНИЯ
ИНТЕГРАЛОВ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ НА
АЛГЕБРАХ ЛИ
Сегодня известно несколько методов построения инволютивных
наборов функций на пространствах G*, дуальных к алгебре Ли
G, т. е. методов построения коммутативных подалгебр в алгебре
Ли С°° (G*) гладких функций на G* относительно скобки Пуас-
Пуассона
Здесь ckij — структурный тензор алгебры Ли G. Здесь мы рас-
смотрим два общих метода, предложенных В. В. Трофимовым со-
соответственно в [134, 136].
1. Индуктивное построение интегрируемых динамических сис-
систем на орбитах коприсоединенного представления (цепочки под-
подалгебр). Эта конструкция впервые была описана в контексте гео-
геометрического квантования построения поляризаций — в работе
М. Вернь [258], а в контексте интегрируемых систем — в работе
В. В. Трофимова [134] (метод цепочек).
Конструкция. Пусть в алгебре Ли G имеется фильтрация
подалгебрами G=dGi=>G2=>...:=>G<,. Тогда, возникает цепочка отоб-
отображений G*-+Gi*-*~G2*-*-...-+Gq*. Каждое такое отображение
я,: Gi*-^G*i+i является отображением ограничения на подалгебру,
т.е. m{f)=f\ol+l.
Поэтому функции, заданные в пространстве G,*, можно подни-
поднимать на пространство G*, т. е. если f^C°°(Gi*), то /еС°°(б*),
J = fniX2...ni-u где я,-: Gj*-^G*I+i — построенное выше отображе-
отображение.
Определение. Пусть Fc=C°°(G*), где G — алгебра Ли,
Ad*: ®-+GL(G*) — коприсоединенное представление группы
366
Ли @, отвечающей алгебре Ли G. Тогда функция F называется
инвариантом, если F (Adg* х) = F (х) для всех xgG* и всех ge®.
Функция F называется полуинвариантом, если F(Adg*x) =
' —X(8)^ix)', %{g)<^R, Для всех ge© и для всех xeG*.
Теорема (В. В. Трофимов [134]). Пусть задана цепочка под-
подалгебр Vz3S. Тогда, если функции f, g на пространстве S* нахо-
находится в инволюции на всех орбитах коприсоединенного представ-
представления Ads», где S" — группа Ли, отвечающая алгебре Ли S, то
функции J, g находятся в инволюции на всех орбитах коприсоеди-
коприсоединенного представления Ady», где V" .— группа Ли, отвечающая
алгебре Ли V, и f=fn, g = gn, где л: V*-*~S* — отображение огра-
ограничения.
Пусть f — в частности, инвариант коприсоединенного пред-
представления Ady» группы Ли V" и § — подъем функции ge
eC°°(S*); тбгда {f, g}=0 на всех орбитах коприсоединенного
представления Ady. Если цепочка V^dS такова, что VidVidS,
я f — полуинвариант коприсоединенного представления Ady<;
где V — производная -подалгебра для V, и g — подъем функции
g^C°°(G*), то {f, g} = 0 на всех орбитах коприсоединенного пред-
представления Adv.
Методика, изложенная в этой теореме, является обобщением
конструкции М. Вернь [258]. В работе [258] для построения гло-
глобальных симплектических координат на орбитах максимальной
размерности коприсоединенного представления нильпотентных ал-
алгебр Ли использовались цепочки идеалов G\CzG2a...ciG такие,
что dim GJGi-i = 1 и инварианты представления Ad* идеалов G,-,
где 1= 1,..., dim G, поднимались с помощью естественной проек-
проекции G*-^Gi* на G*, что и давало требуемые координаты.
Отметим отдельно частные случаи, часто использующиеся при
построении инволютивных семейств функций.
Простейший вариант конструкции, изложенный в теореме Тро-
чримова, получается в случае пары ОгэЯ, где Н — максимальная
абелева подалгебра в G, см. [134]. В качестве инвариантов абс-
левой подалгебры можно взять любой ее элемент, рассматривая
его как функцию на дуальном пространстве. Если GzzG'zdH, то к
инвариантам подалгебры Н можно добавить полуинвариантные
.алгебры Ли G.
Иллюстрация. Рассмотрим простой пример применения
изложенной выше конструкции. Пусть и(п) — алгебра Ли группы
Ли унитарных матриц. В этой алгебре Ли имеется стандартная
^фильтрация и(п)^>и(п—1)=)... Если к ней применить метод цепо-
цепочек подалгебр, то получим инволютивное семейство функций на
пространстве «(«)*. Кроме того, построенное семейство функций
•обладает дополнительным важным свойством: оно является пол-
полным инволютивным семейством функций.
Пусть so(n) — алгебра Ли кососимметрических матриц. В ней
также имеется стандартная фильтрация so(«)z5so(«—1)=)... При-
367
менение к этой цепочке подалгебр изложенной методики дает пол-
полное инволютивное семейство функций на пространстве so(n)*.
Вообще говоря, выбирая цепочку подалгебр «как попало», полно-
полноту набора поднятых функций гарантировать нельзя.
2. Представления группы Ли и инволютивные семейства функ-
функций. Эта конструкция впервые была описана в работе В. В. Тро-
Трофимова [136].
Конструкция. Пусть G — алгебра Ли, &— односвязная
группа Ли, отвечающая алгебре Ли G, G* — пространство, дуаль-
дуальное к G, #(G*) — пространство аналитических функций на G*,
(Ad*f) {x) =/(Adg_i x). Обозначим через W конечномерное под-
подпространство в H(G*), инвариантное относительно Ad*©. Фикси-
Фиксируем в пространстве W базис f\,...,fs. Тогда каждая функция
feW определяет набор ковекторов c*'(f)^G* по следующему
правилу. Если /ef, то для любого элемента ge ® в силу инва-
инвариантности подпространства W имеем f(Ada*x)^W. Если в W
фиксировать базис fi,...,fs, то каждая функция f^W определяет |
функции Cfl{g) по правилу f(Adff*je) =2tv'(g)fi(x), поэтому на (?.?-!
возникает, набор линейных функционалов с1' (/): с' (/) (В =— X
* * at *=о
X с\ (ехр^З-) =dclf (|), т. е. c*'(f) — дифференциал отображения с/' в
единице группы. Итак, построены ковекторы cJ(f)^G*.
Через ковекторы c*'(f) легко выразить косые градиенты а
sgradf функций feW. "
Предложение. При сделанных выше предположениях
имеет место равенство (sgradf) (x) =c*1(f)/i(x) +.. . + c*s(/)fs(x). i.
Определение. Конечномерное подпространство W в прост-
пространстве функций Н(G*) с выделенным набором функций h\,...
. ..,ApeG назовем S-представлением группы Ли @, если выпол-
выполнены следующие условия:
а) пространство W инвариантно относительно коприсоединен-
ного представления Ad«* группы Ли @,
б) на G* выполнено равенство (cj'(hj), dli,,(x))==Q.
Замечание. Условие <с,*(Ау), dhp(x))^0, очевидно, не за-
зависит от выбора базиса f\ fs в пространстве W. В следующей
теореме раскрывается смысл S-представления -в терминах функ-
функций в инволюции.
Теорема (В. В. Трофимов [136]). Пусть (hu...,hs; W) —
5-представление группы Ли ©. Тогда
а) все функции hu...,hs находятся в инволюции на всех орби-
орбитах коприсоединенного представления Ad*@ группы Ли ©;
б) сдвиги функций hi находятся в инволюции на всех орбитах
коприсоединенного представления Ad*@ группы Ли @, т. е.
, п,{х+ца)} = 0; l<i, /<s; К,
Пример. Пусть hi,...,hs — полуинварианты коприсоединен-
коприсоединенного представления группы Ли &, №=©s,=iR/i<; тогда (Ль... ,fts;
W) всегда является S-представлением, что оказывается достаточ-
368
но глубоким результатом теории представлений групп Ли. Полез-
Полезно иметь алгоритм, позволяющий строить S-представления из уже
известных S-представлений. Такой алгоритм (тензорное расшире-
расширение алгебр) предложен в [144], но мы не будем здесь на нем
останавливаться.
Пусть h\,...,hs — инварианты коприсоединенного представле-
представления группы Ли ©. Тогда представление (h\,...,hs; ®s;=iR/i;),
очевидно, является S-представлением группы Ли @ и мы полу-
получаем нашу теорему о сдвиге инвариантов коприсоединенного пред-
представления (см. [96, 98]).
Операция сдвига аргумента, описанная выше, может быть
скомбинирована с операцией подъема функций.
Предложение. Пусть К — подалгебра в алгебре Ли G;
VczH(G*) — подпространство, инвариантное относительно Ad*@
и dim 1/<оо. Функция /eV, как описано выше, при выборе базиса
пространства V определяет некоторые ковекторы c.'eG*. Если
продолжение g^H(G*) функции g^H(K*) постоянно вдоль этих
ковекторов, то оно находится в инволюции с функцией f на всех
орбитах коприсоединенного представления группы Ли ®, т. е.
if, g)^0.
Как показал Трофимов в [134, 136], процесса, описанного в
этом предложении, достаточно для явного построения полного ин-
олютивного семейства функций на произвольной борелевской
■ одалгебре в полупростой алгебре Ли.
3. Инволютивные наборы функций на полупрямых суммах.
Пусть K=G(BPV — полупрямая сумма простой комплексной ал-
алгебры Ли G и линейного пространства V. относительно непроводи-
мого представления р : G-^-End V. Пространство, двойственное к
алгебре Ли /C=G©PV, отождествим с G*@V*, полагая G* = VX,
V* = G-L. Рассмотрим сдвиги инвариантов алгебры К на элемент
aeG*cr/(*. Оказывается, этот набор можно пополнить функция-
функциями на V*, а.,именно справедлива следующая
Теорема (А. В. Браилов). Набор функций{Д(л:)} \i
[)V~ где f\,...,fa — инварианты алгебры Ли К, являются инво-
лютивным набором функций на пространстве К*.
Рассмотрим вопрос полноты построенного семейства инволю-
тивных функций. Обозначим через St(t>) стационарную подалгеб-
подалгебру элемента иеУ относительно представления, р* : G-^-End-V*,
сопряженного к р. Тогда имеет места следующая
Теорема (А. В. Браилов). Линейные функции Uf=V на про-
пространстве V* вместе со сдвигами инвариантов алгебры Ли К на
ковектор из G* дают полный инволютивный набор функций на
пространстве К* тогда и только тогда, когда сдвиги инвариантов
алгебры Ли St(u) дают полный инволютивный набор функций на
пространстве St(o)*, где v — элемент общего положения.
В качестве частного случая получаем
Предложение. Если St-(w)=O, то элементы из V образуют
полный инволютивный набор функций.
369>
Известно, что St(w)=O (ю случае неприводимого р) тогда и
только тогда, когда dimG<dim1/ (Е. М. Андреев, Э. Б. Винберг,
А. Г. Элашвили [277]). При этом в большинстве случаев стацио- i
парные подалгебры являются полупростыми. Следовательно, для
лих выполнены условия полноты сдвигов и описанная выше кон-
струкция дает полный набор функций в инволюции. Если G —
простая комплексная алгебра Ли, ар — неприводимое представ-
представление, то имеется лишь'несколько исключений:
1) sl(n, С)фрС" со стационарной подалгеброй sl(n—1,
CjeC1
2) so A0, С) фрС16 со стационарной подалгеброй so G, С) фаС8;'
3) sp(n, С)ФрС2" со стационарной подалгеброй sp(n—1, С)фа
^2(л-о+ь где Я2(П-1)+1 — алгебра Гейзенберга размерности
'2 (га—1) + 1; а = (г+т, где ц — стандартное B«—2)-мерное пред-
представление sp(n—1, С), а т —* одномерное тривиальное представ-
представление;
4) s/B/2+1, С)фрЛ2С2п+1 со стационарной подалгеброй sp(n,
с) еас2".
Более тщательный анализ всех этих случаев позволяет дока-
доказать следующий важный результат.
Теорема (А. В. Болсинов). Пусть K=G(&PV — полупрямая
сумма простой комплексной алгебры Ли G и линейного простран- ■
£Тва V относительно представления р : G-*-End V. Тогда на двой-
двойственном пространстве К* всегда существует полный инволютив-
ный набор полиномов.
4. Индекс алгебры Ли GA = G®A. Пусть Л— коммутативная,
ассоциативная, конечномерная алгебра с единицей. . Рассмотрим
тензорное произведение G®A, являющееся расширением алгебры
Ли G, с коммутатором [|®а, ч\®Ь] = [|, Л]®^- i, "H^G, a, b<=A.
Легко видеть, что эта операция превращает пространство G®A в
алгебру Ли, которая далее обозначается Ga. Для любой алгебры
Ли G Ж- Диксмье дал общее определение ind G. Важность индек-
индекса в теории интегрируемых систем на алгебрах Ли проиллюстри-
проиллюстрирована в настоящей книге на многих примерах и объясняется тем,
что индекс алгебры Ли совпадает с коразмерностью орбиты (ко-
присоединенного действия группы) общего положения в простран-
пространстве G*. Для проверки полноты наборов коммутирующих функций
на G* необходимо знать индекс алгебры Ли G.
Теорема (А. В. Браилов). Для любой алгебры Ли G и для
любой коммутативной ассоциативной с единицей фробениусовой
алгебры А размерности N имеет место равенство ind G^ = A^-ind G.
Ввиду важности рассматриваемого вопроса сделаем краткий
экскурс в историю. Легко убедиться, что эту теорему достаточно
доказать лишь для неприводимых алгебр Л, т. е. для таких ал-
алгебр, которые нельзя представить в виде А—А\®А2 или А —
= Л1®Л2, где Л, и Л2 — алгебры меньших размерностей. Поэтому
будем считать, что алгебра Л неприводима. Первая важная ра-
работа в этом направлении — это работа С. Такиффа [252]. В ней
для полупростой алгебры Ли G и для алгебры Л=/г[е]/(е2) пол-
.370
ностью описано кольцо инвариантов, ь частности, для
А получается равенство mAGA = 2-mAG. В случае Л = й(е)/(е2)
алгебра Ли GA является полупрямым расширением G по присое-
присоединенному представлению. Следовательно, используя формулу
М. Рамса [244] для индекса полупрямого расширения, получаем
равенство ind GA = 2 т'А G уже для любой алгебры Ли G.
Дальнейшие результаты В. В. Трофимова, а затем А. В. Браи-
лова позволили доказать теорему для алгебр Ли G, обладающих
достаточным количеством функционально независимых полино-
полиномиальных инвариантов f\,...,f, (r = indG), в случае когда А =
= fe(e)/(e") — алгебра усеченных полиномов [139] и когда А —
алгебра с двойственностью Пуанкаре [22]. При наличии инвари-
инвариантов f\,...,fr и для алгебр Фробениуса А теорема .доказана
Ле Нгок Тьеуеном [82]. В качестве гипотезы теорема в общем
случае была сформулирована А. Г. Элашвили [274].
приложение: б
КРИТЕРИЙ ПОЛНОТЫ НАБОРА ИНТЕГРАЛОВ,
ПОЛУЧАЕМЫХ МЕТОДОМ СДВИГА АРГУМЕНТА
Здесь мы вкратце изложим результаты А. В. Б.олсинова. В ча-
частности, он доказал, замечательный результат окончательного ха-
характера, подводящий итог большому циклу работ разных мате-
математиков, изучавших метод сдвига аргумента.
Пусть © — односвязная группа Ли, G — .ее алгебра Ли;
/],...,/* — полный набор локальных инвариантов представления
Ad* © в некоторой окрестности регулярной точки xeG*. Рассмот-
Рассмотрев сдвиги этих инвариантов на ковектор общего положения
a^.G*, мы получим функции, коммутирующие между собой отно-
относительно скобки Ли (см. [96], [98]). При этом следует отметить,
что такая конструкция является локальной, т. е. не позволяет,,
вообще говоря, получать глобально определенные на G* функции
в инволюции, если инварианты глобально не определены. Однако
этот недостаток легко устранить, заменив семейство сдвигов экви-
эквивалентным набором полиномов. Эквивалентность в данном случае
означает, что пространства, порожденные дифференциалами функ-
функций из этих семейств в точках yeG*, совпадают почти для всех
у из общей области определения. Очень простой способ такой за-
-мены предложен А. В. Браиловым. Для этого достаточно рас-
рассмотреть разложения в ряд локальных инвариантов в точке
a<=G*:
=PP (x) + Ptl (x)
где Pih — однородный по х многочлен степени к. Легко проверя-
проверяется, что набор, составленный из полиномов РД эквивалентен в
указанном смысле семейству сдвигов на ковектор a^G*: Поэтому
в дальнейшем мы можем под семейством сдвигов понимать набор
371
jfVh не накладывая при этом никаких ограничений на алгебру
'Ли G.
Теорема (А. В. Болсинов). Пусть G — произвольная конеч-
конечномерная комплексная алгебра Ли, S = {y^G*; codimC(y)>
>ind G}— множество сингулярных точек из G*. Сдвиги инвариан-
инвариантов на ковектор общего положения образуют полный инволютив-
ный набор на G* тогда и только тогда, когда codim5^2.
Следствие 1. Пусть G — произвольная конечномерная
вещественная алгебра Ли, Gc — ее комплексификация. Сдвиги
инвариантов алгебры G на ковектор общего положения образуют
на G* полный инволютивный набор тогда и только тогда, когда
codimSc ^-2, где Sc — множество сингулярных элементов (точек)
s (GC)*.
Следствие 2. Пусть G — произвольная конечномерная ком-
комплексная (вещественная) алгебра Ли, S — множество сингуляр-
сингулярных точек из G*, x^S. Пусть ind Annx=incl G, codimS>2
(codimSc^2). Тогда сдвиги инвариантов на некоторый ковектор
общего положения образуют полный инволютионый набор на син-
сингулярной орбите О(х).
Доказательство теоремы (краткая схема). Фиксируем
произвольный элемент общего положения a^G*. Рассмотрим ре-
регулярный элемент x^J3*. Пусть fu-..,fk — полный набор локаль-
локальных инвариантов в точке х. Полнота означает, что дифференциалы
df\,... ,dfb в точке х порождают подпространство Ann*, где
Annx = {eeG : adE*х = 0}. Известно, что дифференциалы сдвигов
fih-(x) =fi(x+Xa) в точке х порождают подпространство
MczG, которое представимо в виде суммы M = U0+U1 + U2 + ...,
где подпространства Uo, U\,... удовлетворяют следующей цепочке
рекуррентных соотношений (см. [96], [98]):
A)
{Uk,
По этой цепочке подпространство MczG восстанавливается
однозначно, поэтому при доказательстве можно забыть о природе
пространства М и использовать только соотношения A).
Семейство сдвигов инвариантов образует полный инволютив-
инволютивный набор тогда и только тогда, когда почти для всех xeG* со-
соответствующее подпространство М имеет размерность, равную
(dim G + ind G)/2. Однако такое определение полноты не очень
удобно в данный момент, и мы заменим его другим. Рассмотрим
для этого подпространство ^ = {|eG : *([£, п,])=0, ц^М}, где
М — косоортогональное дополнение к пространству М в точке
х. Ясно, что Май.
372 . "
Лемма 1. Равенство dimAf = (dim G + ind (i)j2 имеет место
тогда и только тогда, когда М = М.
Итак, семейство сдвигов полно тогда и только тогда, когда для
почти всех регулярных элементов xgG* соответствующее под-
.пространство MczG совпадает со своим косоортогональньш допол-
дополнением М. Оказывается, подпространство MczG допускает доста-
достаточно простое описание.
Лемма 2. Подпространство М является максимальным среди
всех подпространств LczG, удовлетворяющих условию {L, a)cz
c{L, x}.
Из этого утверждения легко следует, в частности, что М содер-
содержит аннуляторы всех элементов вида а+Хх, teC. С другой сто-
стороны, из -рекуррентных соотношений A) легко устанавливается,
что подпространство М удовлетворяет условию {М, х} = {М, а +
-\-Хх}. Отсюда следует, что если элемент -а + Хх при некотором
teC нерегулярен, то Axm(a+Xx)gzM и поэтому МФМ. Оказыва-
Оказывается, справедливо « обратное утверждение, но его доказательство
менее тривиально. Итак, имеет место следующее утверждение.
Лемма 3. Равенство М = М имеет место тогда и только тогда,
когда все элементы вида а+Хх, ХеС, регулярны.
С геометрической точки зрения, регулярность элементов вида
а+Хх означает, что комплексная аффинная прямая а + Хх не пе-
пересекает множество сингулярных точек S. Ясно, что это возможно
для почти всех xeG* тогда и только тогда, когда codim5^2.
Теорема доказана.
Оказалось, что идея доказательства критерия полноты семей-
- ства сдвигов инвариантов может быть перенесена на более общую
ситуацию, а именно на случай инволютивного семейства функций,
построенного по произпольной паре согласованных скобок Пуассо-
Пуассона. Пусть {,}о и {,}i — две согласованные скобки Пуассона, задан-
заданные на области UczRn. Согласованность означает, что любая ли-
линейная комбинация этих скобок вновь является скобкой Пуассона
(см. [39], [225]). Обозначим через S двумерное линейное семей-
семейство скобок, порожденное скобками \,}о и {,}ь и отождествим его
с соответствующим подпространством в пространстве всех косо-
симметрических тензорных полей типа B,0). Положим R— max
tangC(x). В окрестности точки xo^U рассмотрим семейство
функций Fs, состоящее из центральных функций тех скобок Пуас-
Пуассона из' S, которые в этой точке имеют ранг R. Легко проверяет-
проверяется, что семейство Fs является инволютивным относительно всех
скобок {,}eS.
Отметим, что семейство Fs определено локально, поскольку в
общем случае локально определены центральные функции. Пусть
Ох — симплектический слой, проходящий через точку x^U и от-
отвечающий скобке {,}. Скажем, что инволютивное семейство F пол-
полно в точке х относительно скобки {,}, если подпространство в
Тх*Ох, порожденное дифференциалами функций |ef, ограничен-
ограниченных на Ох, имеет размерность dim ОХ12. Обозначим через S c
373
комплексификацию пространства S, т. е. множество линейных ком
бинаций xAo+iiAi с комплексными коэффициентами, где Ао i
А\ — тензорные поля, отвечающие скобкам {,}0 и {,}ь
Теорема (А. В. Бр аилов). Пусть размерность симплекти-
ческого.слоя ОХа, отвечающего скобке {,}&S равна R (т. е. мак-
сималь'на). Инволютивное семейство Fs полно в точке х0 относи
тельно скобки {,}eS тогда и только тогда, когда все нетривиаль
ные тензорные поля A^SC имеют в точке х0 ранг R.
Болоиновым А. В. затем было доказано более общее утверж
дение, позволяющее, в частности, проверять полноту семейств*
Fs на сингулярных симплектических слоях. Обозначим через N.
подпространство в T*XJU), порожденное дифференциалами функ
ций fe=Fs. Пусть М = {£ е= Т*х, (U)\В(£, М) = О, Ве= S}— косо
ортогональное дополнение к М в TXo(U). Оказывается, косоорто-
тональное дополнение М не зависит от выбора нетривиальной:
тензорного поля B^S. Пусть rang A (x0) =R почти для всех A^S
Тогда с точностью до пропорциональности имеется лишь конечное
число нетривиальных тензорных полей С\,..., Cjve5c таких, чте
rangC,-(xo)</?. Положим /С,= {?еКег &(х0) |В(|, КегС/(дс0))=С
для всех ZJ&S}. Легко проверяется, что dimKi>n—R.
Теорема (А. В. Болсинов). Мс = Мс + V Кег С,- (ха) (сумме
непрямая) тогда и только тогда, когда dim Кг = п—R, i=\,...,N,
В противном случае имеет место строгое включение .
N
Мс+
Отметим простую связь между полнотой семейства Fs и под-
подпространствами М in M: семейство Fs полно в точке xo^U относи-
относительно скобки {,}е5 тогда и только тогда, когда М = М +
+ KerC(*o), где С(хо) — 2-форма на TXa(U), отвечающая
скобке {,},
Нетрудно видеть, что семейство сдвигов инвариантов строите?;
по паре согласованных скобок, одна из которых — стандартная
скобка Пуассона — Ли, другая — скобка {,}а, задаваемая форму-
формулой {f, g}a=(a, [d.f, dg]).
Имеется еще одна интересная серия согласованных скобо}»
Пуассона на алгебрах Ли, на которую обратили внимание
И. Л. Кантор « Д. Персии, занимаясь классификацией лиевых
пучков. Опишем частный случай этой конструкции. Пусть L —
пространство кососимметрических матриц размерности пХп. Нг
L можно задать семейство лиевых структур (лиев пучок), рас-
рассматривая коммутаторы [,]А : [X, Y]A — XAY—YAX, где X, Y^L
А пробегает пространство симметрических матриц пХп. Линейная
комбинация двух коммутаторов снова задает структуру алгебрь:
Ли на L, поскольку Л[,]л + н.[,]в=[,]и+рв. На пространстве L*
374
тем самым, задано линейное семейство скобок Пуассона—Ли
{,}а. Рассматривая произвольное двумерное подпространство в
этом семействе скобок, можно построить инволютивное семейство
функций на L*. Пусть A = diag(l,..., 1), В — произвольная сим-
симметричная матрица, 5 (А, В) — семейство скобок вида {,}\а+цв- От-
Отметим, что скобка {,}л является стандартной скобкой Пуассона —
Ли, отвечающей алгебре Ли so(n). Наблюдение, сделанное
А. В. Болсиновым, состоит в том, что семейство Fsh.b) (см. обоз-
обозначения выше), построенное по паре {,}а и {,}в, совпадает с семей-
семейством интегралов уравнений нормальной серии на so(n), описы-
описывающих движение «-мерного твердого тела. Другой интересный
пример получается, если i4 = diag(l,..., 1,0), В — произвольна.
Скобка {,}а отвечает в этом случае алгебре Ли Е(п—1) группы
движений (л—1)-мерного евклидова пространства. Инволютивное
семейство Fs(a,b) состоит в этом случае из первых интегралов
уравнений движения (п—1)-;мерного твердого тела ib идеальной
жидкости, обобщающих второй случай Клебша (см. работу
А. М. Переломова [114]). Квадратичные гамильтонианы, задаю-
задающие эти уравнения, содержатся в семействе Fs(a,b) и имеют вид
h(X) =Tr(XCkA + ix,B)-1J. Общий метод проверки полноты семейств
функций в инволюции, построенных по паре согласованных ско-
скобок, позволяет строго доказать полную интегрируемость этих урав-
уравнений.
ПРИЛОЖЕНИЕ 7
НОВЫЙ ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ
ГАМИЛЬТОНОВЫХ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИИ, ИНТЕГРИРУЕМЫХ ПО ЛИУВИЛЛЮ.
ИНВАРИАНТНЫЙ ПОРТРЕТ ИНТЕГРИРУЕМЫХ
ГАМИЛЬТОНИАНОВ
Автором обнаружен топологический инвариант, характеризую-
характеризующий гамильтоновы системы дифференциальных уравнений, инте-
интегрируемые по Лиувиллю. Настоящее приложение посвящено топо-
топологической характеризации гамильтонианов, интегрируемых по
Лиувиллю. При этом, в частности, развиваются важные идеи сим-
плектической топологии, заложенные в работах С. П. Новикова,
В. И. Арнольда, И. М. Гельфанда, Л. Д. Фаддеева, С. Смейла,
Ю. Мозера, В. В. Козлова. Для простоты мы рассмотрим лишь
случай уравнений на четырехмерных симплектических многообра-
многообразиях, хотя некоторые результаты переносятся и на многомерный
случай. Построение нового инварианта опирается на развитую ав-
автором в [159] — [161] (и в гл. 4) теорию «типа Морса» для инте-
интегрируемых систем. Более точно, здесь имеется в виду теория пере-
перестроек поверхностей уровня для боттовских интегралов, опреде-
определенных на изоэнергетических поверхностях интегрируемых систем.
Развивая эти результаты, мы предъявляем новый топологический
375
инвариант интегрируемых систем: граф Г, двумерную поверхность
Р2 и вложение h: Г->-Р2; причем в нерезонансном случае все эти
геометрические объекты не зависят от выбора дополнительного
интеграла и описывают, следовательно, сам интегрируемый случай
(гамильтониан). Оказывается, этот инвариант можно эффективно
вычислять. В качестве примеров мы вычисляем его для1 некоторых
классических случаев интегрируемости уравнений движения тяже-
тяжелого твердого тела (случаи Ковалевской, Горячева—Чаплыгина,
гиростата).
Классическая бифуркационная диаграмма 2, при помощи ко-
которой обычно описывают топологию интегрируемых случаев, при
всех несомненных достоинствах обладает существенным недо-
недостатком — она зависит от выбора второго интеграла, т. е. не
является топологическим инвариантом системы. Обнаруженный
нами новый объект {Г, В, И), во-первых, является топологическим
инвариантом, а во-вторых, по нему восстапавлипается бифурка-
бифуркационная диаграмма (если фиксировать -какой-либо вид второго
интеграла).
Пусть МА — гладкое симплектическое многообразие и у =
= sgrad# — гамильтонова система с гладким гамильтонианом Я,
вполне интегрируемая по Лиувиллю на какой-то неособой ком-
компактной изоэнергетической поверхности Q3, т. е. задаваемой урав-
уравнением # = const. Пусть /: Q->-R — второй независимый интеграл
на Q3, коммутирующий с Я. Здесь sgrad — операция взятия косо-
симметрического градиента. Известно, что связные неособые по-
поверхности уровня функции f на Q являются двумерными торами
Лиувилля. Предположим, что интеграл / является боттовским па
Q, т. е. его критические точки организованы в невырожденные
критические подмногообразия в Q. Боттовость некоторых извест-
известных интегралов доказал А. А. Ошемков в [289].
Определение 1. Назовем гамильтониан Я нерезонансным
на данной -изоэнергетической поверхности Q3, если в Q всюду
плотны торы Лиувилля, на которых интегральные траектории си-
системы v образуют плотную иррациональную обмотку.
Опыт изучения конкретных известных физических систем пока-
показывает, <цто на четырехмерных многообразиях в большинстве слу-
случаев гамильтонианы являются нерезонансными на почти всех по-
поверхностях Q. В многомерном случае, т. е. на М2п, где п>2, из-
известны примеры, когда гамильтониан Я «по существу» является
резонансным на почти всех поверхностях Q. Это происходит, в
частности, когда система является интегрируемой в некоммутатив-
некоммутативном смысле. Анализ основных случаев некоммутативной интегри-
интегрируемости см. выше, а также в обзоре В. В. Трофимова и А. Т. Фо-
Фоменко [145]. Напомним, что в этих случаях система интегрируется
при помощи интегралов, образующих некоммутативную алгебру
Ли. Тогда система «вырожденна» (резонансна) в том смысле, что
ее траектории всюду плотно заполняют" «маломерные торы». Они
организуются-* «большие» настоящие торы Лиувилля (в компакт*
ном случае). Следовательно, исходная система иррациональна
376
лишь на малых торах, но не является таковой на «больших то-
торах». В четырехмерном же случае нерезонансность—«типичная»
ситуация.
Теорема 1 (А. Т. Фоменко). Пусть v — гамильтонова систе-
система с нерезонансным гамильтонианом Н, интегрируемая при помо-
помощи некоторого боттовского интеграла f на компактной неособой
трехмерной изоэнергетической поверхности Q. Тогда можно одно-
однозначно построить некоторый граф Y(Q, }) со следующим свой-
свойством: по графу T(Q, f) однозначно (с точностью до гомеомор-
гомеоморфизма) восстанавливается вся топологическая картина эволюции
и перестроек (бифуркаций) торов Лиувилля внутри поверхности
Q при изменении значения интеграла f.
Пусть / : Q->R — боттовский интеграл, aeR и /a = /~'(a)—
связная компонента поверхности уровня интеграла (особая или
неособая). Если а = а — регулярное (некритическое) значение для
/, то fa — это объединение конечного числа торов Лиувилля. Кри-
Критические значения для / обозначим через с, связную компоненту
критической поверхности уровня интеграла — через /с, а множест-
множество критических точек интеграла / на fc—через Nc. Как доказано
автором в гл. 4 (см. также [159] — [161]), связные компоненты
множеств Nc могут быть только следующих типов:
тип I — минимаксная окружность S1 (локальный минимум или
максимум для /), тогда A/r = /(. = S1;
тип II — минимаксный тор Г2, тогда Nc = f,:—T2;
тип III — седловая критическая окружность 51 с ориентируе-
ориентируемой сепаратрисной диаграммой, тогда Nc = S^fc;
тип IV — седловая критическая окружность S1 с неориенти-
руемой сепаратрисной диаграммой, тогда N,. — Slz/=fc\
тип V—минимаксная бутылка Клейна К2, тогда Nc=fc = К2.
Через LJ(fr), где с —критическое значение интеграла, обозна-
обозначим регулярную связную замкнутую трубчатую окрестность ком-
компоненты /с в многообразии Q3. Можно считать, что U(fc)—связ-
U(fc)—связное трехмерное многообразие, край которого состоит из несвязно-
несвязного объединения торов. В качестве U(fc) можно взять связную
компоненту многообразия f~l[c — е, с+е]. Можно считать, что
Q = ~LU(fc), т. е. Q получается из всех многообразий V(fc) склей-
кой их границ по некоторым диффеоморфизмам граничных торов.
Теорема 2 (А. Т. Фоменко). Пусть Q — компактная неосо-
неособая изоэнергетическая поверхность системы у с гамильтонианом
Н (не обязательно нерезонансным), интегрируемая ,при помощи
некоторого боттовского интеграла f. Тогда многообразия U(fc),
входящие в разложение Q = St/(/c), допускают следующие пред-
с
ставления (в зависимости от типа множества Nc):
тип I: Uifc) =Pc2XS\ где P2 = D2 (диск);
тип II: U(fc)=Pc2xS\ где Pc2 = SlxDl (цилиндр);
тип III: U(fc) —PC2XS\ где Рс2 — некоторая двумерная поверх-
поверхность с краем;
тип IV: U(fc)=Pc2xSl, где Рс2 — некоторая, двумерная поверх-
377
ность с краем, a P^xS1 — пространство расслоения Зейферта с
базой Рс2 и слоем~3{ (описание см. ниже);
тип V: U(fc)=Pc2xS\ где Рс2 = ц (лист Мебиуса), a (aX-S1 обо*
значает косое произведение (с краем — тор Т2).
Следстви-е 1. С каждой изоэнергетической поверхностью Q
(в условиях теоремы 2) можно однозначно (с точностью до го-
гомеоморфизма) связать некоторую замкнутую двумерную поверх-
поверхность P2(Q, /)=2РС2, получающуюся склейкой поверхностей Рс2,
с
индуцируемой склейкой Q = I,U(fc).
с
Теорема 3 (основная; А. Т. Фоменко). Пусть v — гамильто-
нова система, интегрируемая на Q при помощи боттовского инте-
интеграла. Тогда существует однозначное (с точностью до гомеомор-
гомеоморфизма) каноническое вложение h(Q, f) графа T(Q, /) в поверх-
поверхность P2(Q, f). Если гамильтониан Н — нерезонансный на Q, та
тройка (Г, Р, h) не зависит от выбора второго интеграла /.
А именно, если f и f—любые боттовские интегралы системы v,
то соответствующие графы T(Q, f) и V(Q, f), как и поверхности
P(Q, f) и P{Q, f), гомеоморфны, а следующая диаграмма комму-
коммутативна:
h : Г ->Р
h':T'-+P''
Следствие 2. В нерезонансном случае тройка (Г, Р, h) яв-
является топологическим инвариантом самого интегрируемого слу-
случая (гамильтониана) и позволяет классифицировать интегрируе-
интегрируемые гамильтонианы по их топологическому типу и сложности.
Эту тройку мы назовем топологическим портретом интегрируе-
интегрируемого гамильтониана. Разбиение поверхности P(Q) на области
(определяемое графом F(Q)) также является топологическим ин-
инвариантом. Поверхность P(Q) не обязана вкладываться в Q. Те-
Теперь определим многообразие Pc2xS{. Расслоенным полноторием
типа (а, Ь) называется полноторие, полученное склейкой двух ос-
оснований полного цилиндра D2xDl при помощи отображения (г,
0)->(ехрBш6/а), 1), где геС, |гК1, а, 6eZ, а и b взаимно
простые. Слоем является
{(z, t), (-expBnib/a)z, t), (expDmb/a)z, t),..., (ехрBя£(а —
•-l)&/a)z, t),
Тогда на полнотории D2xS\ определяется расслоение со слоем
S1 над D2, локально тривиальное для всех ненулевых точек диска
D2. Слой — окружность {@, t), O^t^l} является особым, если
а>\.
Теперь рассмотрим многообразие Рс2 с отмеченными на нем
точками х\,...,хт и окружим их малыми дисками D,2,... ,Dm2.
Затем возьмем прямое произведение Pc2XSl и выбросим из него
378
m полиоторий Dt2xSl, l^i^m. Вклеим вместо них расслоенные
полнотория типа B, 1). Полученное многообразие обозначим че-
через Pc2xSl. Оно является расслоением Зейферта, а Рс2 — его база.
Дадим явное построение инвариантов. Предположим сначала
для простоты, что на каждом критическом уровне /с расположено
ровно одно критическое связное многообразие Nc. В этом случае
построение графа Y(Q, f) было фактически описано в гл. 4 (а так-
также в [159]—[161]). Построим те-
теперь граф Г в общем случае. Те-
Теперь на одном критическом уров-
уровне может лежать несколько кри-
критических многообразий. В отли-
отличие от обычных функций Морса,
критические многообразия бот-
товского интеграла, лежащие на
одном уровне, вообще говоря,
нельзя «развести» на разные уров- '
ни путем малого возмущения
интеграла (оставаясь в классе ин-
интегралов). Возмущение f инте-
интеграла f может не быть интегра-
интегралом. Пусть fa — поверхность
уровня интеграла, т. е. fn = f~x{a).
Если а — регулярное значение, то
,fa — объединение конечного чис-
:Jia торов. Изобразим их точками
в R3 на уровне а, где ось R на-
направлена вверх. Меняя а в обла-
области регулярных значений, мы за-
заставляем эти точки заметать не-
некоторые дуги — часть ребер бу-
будущего графа Г. Пусть Nc — мио-
• жество критических точек f на fc.
Выделим два случая: a) Nc = fc,
, б) NcCifc, причем Nc=£fc. В рабо-
: тах автора [159]—[161] (см. так-
также гл. 4) найдены все возможно-
возможности для Nc. Рассмотрим случай
а). Здесь возможны лишь 3 ти-
типа критических множеств.
Тип «минимаксная окружность». Здесь Nc = fc гомеоморфно
окружности, на которой / достигает локального минимума или
максимума. Ее трубчатая окрестность SlxD2 гомеоморфна пол-
ноторию (в Q3). При а^-с неособые торы стягиваются на ось пол-
полнотория и при а = с вырождаются в S1. Условно изобразим эту си-
ситуацию черной жирной точкой (вершина графа), в которую вхо-
входит* (или из которой выходит) одно ребро графа (рис. 132).
Тип «тор». Здесь Nc = fc и гомеоморфно тору Р, на котором
/ достигает локального минимума или максимума. Его трубчатая
Рис. 132
379
окрестность гомеоморфна цилиндру T2xDl. Граница цилиндра -
два тора. При а-^с они движутся навстречу друг другу и при а-
— с сливаются в один тор. Изобразим эту ситуацию белым круа
ком (вершина графа), в которую входят (или выходят) два per
pa графа (рис.. 132).
Тип «бутылка Клейна». Здесь Nc=fc и гомеоморфно бутылк
Клейна К2, на которой / достигает локального минимума или Mai.
симума. Ее трубчатая - окрестность K2XDl гомеоморфна косом
произведению К2 на отрезок. Граница K2XD]— один тор. Когд
а^-с, он стремится к К2 я двулистно накрывает ее при а = с. Изои-
разим эту ситуацию белым кружком с точкой внутри (вершин
графа),, в который входит (или выходит) одно ребро граф
(рис. 132).
Рассмотрим случай б). Здесь Ncczfc, причем dimЛ^с= I, r
dim/c=2. Тогда (см. гл. 4 и [160], [161]) Nr есть несвязное объ
единение непересекающихся окружностей. Каждая из них — се£
ловая для /. Компоненту fr. также назовем седловой. Условно е'
можно изобразить плоским горизонтальным квадратом, лежаида
на уровне с bR3 (рис. 133). Снизу в него втыкаются некоторые
/ТП гпгл
г г ♦ \ • \ ' 1
* • ' I 111) •
I I I I III, I
Рис. 133
ребра графа (при а->с и а<с), вверх уходят другие ребра графе
(когда а>с). В результате мы определили некоторый граф А, О'
стоящий из регулярных дуг (ребер), некоторые из которых вть
каются в квадраты, а некоторые заканчиваются вершинами тре;
описанных типов.
Фиксируем седловое значение с и построим граф Тс, показы
вающий, как именно соединяются ребра графа А, взаимодейс*
вующие с /с- Рассмотрим на Q векторное поле w — gradf. Его трь-
ектории, входящие в критические точки интеграла или исходящие
из них, называются сепаратрисами. Их объединение — это cenapt
380
трисная диаграмма критического подмногообразия. Из каждой
седловой критической окружности 51 на уровне /с выпустим ее се-
паратрисную диаграмму. Если она ориентируема, то она полу-
получается склейкой двух плоских колец (цилиндров) по осевой
окружности (см. гл. 4). Если она неориентируема, то она полу-
получается склейкой двух листов Мебиуса по их осевой окружности.
Рассмотрим некритические зна-
значения с—е и с + е, близкие к
с. Поверхности fc-8 и fc+t со-
состоят из торов (рис. 134). Се-
паратрисные диаграммы кри-
критических окружностей, лежа-
лежащих в fc, пересекают эти торы
трансверсально по некоторым
окружностям и разбивают то-
торы в объединение областей,
которые, мы назовем регуляр-
регулярными. Выберем на - уровне
fc-t в каждой из них по точ-
точке и выпустим из этих точек
интегральные траектории поля
до. Они пройдут мимо крити-
критических окружностей па уровне
fc и попадут и некоторые дру-
другие регулярные области то-
торов, составляющих ff+«. Оче-
Очевидно, что тем самым мы по-
получаем гомеоморфизм между
открытыми регулярными обла-
областями из /6_.« и открытыми ре-
регулярными областями из fc+l.
Рассмотрим сначала ориен-
ориентируемый случай, т. е. когда
все сепаратрисные диаграммы
ориентируемы (т. е. нет лис-
листов Мебиуса). Так как каж-
каждый неособый тор — это точ- рис 134
ка на графе А, то можно сое-
соединить точки на уровне /с--8
и на уровне fc+E.дугами (отрезками), изображающими пучки инте-
интегральных траекторий поля до. Получаем некоторый граф Тс. Его
ребра показывают нам движение открытых регулярных областей
торов. Торы разваливаются на куски, которые затем поднимаются
(спускаются) и перегруппировываются в новые торы. Каждый
верхний тор составлен из кусков нижних торов (и наоборот).
Теперь рассмотрим неориентируемый случай, т. е. когда на fc
есть хотя бы одна критическая окружность с неориентируемой
диаграммой. На каждом торе, подходящем к fc, отметим звездоч-
звездочками регулярные области, инцидентные с неориентируемыми сепа-
.381
ратрисными диаграммами (т. е. с листами Мебиуса). Следова-
Следовательно, мы можем пометить звездочками и соответствующие реб-
ребра конструируемого графа. Итак, строим граф по схеме ориенти-
ориентируемого случая, после чего отмечаем звездочками те его ребра,
которые изображают движение регулярных областей со звездоч-
звездочками. Полученный граф обозначим через Тс (рис. 134A)). Ясно,
т
Рис. 134A)
Рис. 134B)
что концы ребер графа Тс отождествляются с концами некоторых
ребер графа А. Окончательно определим граф Г как объединение
(склейку) Т = А+Х?ТС, где {с} — критические седловые значе-
с
ния интеграла.
Предложение 1. Пусть f и f — два любых боттовских.ин-
боттовских.интеграла. Тогда при гомеоморфизме q(Q, f, f) :T.(Q, /)->Г(<5, f)
(см. теорему 3) седловые подграфы Тс для интеграла f гомеоморф-
но переходят в седловые подграфы Тс' для интеграла /'. Звездоч-
Звездочки графа Г переходят в звездочки графа Г". Вершины типов «ми-^
. нимаксная окружность». и «бутылка Клейна» графа Г переходят
s вершины того же типа (соответственно) на графе Г". Вершины
типа «тор» графа Г могут отобразиться в обычные внутренние точ-
точки ребер графа V. Наоборот, обычные внутренние точки ребер
графа Г могут отобразиться в вершины типа «тор» на графе V.
С аналитической тонки зрения изменение типа вершины соот^
ветствует (локально) операции /->/2 или, напротив, операции f-*-
Определение 2. Тройку F(Q), P(Q), h(Q) назовем топо-
топологическим инвариантным портретом /(Я, Q) интегрируемого га-
гамильтониана Н на данной изоэнергетической поверхности Q. Пол-
Полным топологическим инвариантным портретом 1{Н) назовем на-
набор всех троек {F(Q), P(Q), h(Q)} по всем Q. Гомеоморфные
тройки считаем, конечно, эквивалентными. Полный портрет /(Я)
382
зависит уже только от гамильтониана Я. Итак, если две интегри-
интегрируемые системы имеют негомеоморфные топологические портреты,,
то системы не эквивалентны, между ними нельзя установить, на-
например, траекториый изоморфизм. В то же время существуют за-
заведомо не эквивалентные интегрируемые системы с одинаковыми
токологическими портретами /(Я).
Теперь построим поверхность P(Q, f). Мы определим ее как
объединение (склейку) вида Р(А)+2Р(ТС), где Р(А) и Р{ТС) —
с
двумерные поверхности с краем. Определим Р(А) — (S'Xlnt A)" +
+ E-D2+2|A+ES1X.D1. Здесь IntА — объединение всех открытых
ребер графа А. Следовательно, 51 X Int Л — это объединение от-
открытых цилиндров. Многообразие (S1 X Int Л) * получается из него- .
добавлением граничных окружностей. Пусть ребро графа А за-
заканчивается черной вершиной. Тогда заклеим диском D2 соответ-
соответствующую ей граничную окружность на крае многообразия (S'X
Xlnt Л)'. Приклейку таких дисков мы и обозначаем ID2'. Пусть
два ребра графа А встретились в белой вершине. Она определяет
две граничные окружности на (S'XlnM)', которые мы заклеим
(соединим) цилиндром SlXDl. Эту операцию мы обозначаем
I>SlXDl. Пусть ребро графа А заканчивается белой вершиной с
точкой внутри. Заклеим соответствующую ей граничную окруж-
окружность на (S'X Int Л) листом Мебиуса ц. Эта операция обозна-
обозначается 2|х. Итак, £D2, SS'X/I, 2ц соответствуют минимаксным
окружностями, торам и бутылкам Клейна. Теперь построим
Р(ТС) =РС. Рассмотрим сначала ориентируемый случай, когда все
критические седловые окружности па fr имеют ориентированные
сепаратрисные диаграммы. Как показано автором в [160], [161]
(см. также гл. 4), fe гомеоморфпо прямому произведению KcXSlf
где Кс—некоторый граф, получающийся из нескольких окружно-
окружностей путем отождествления па них некоторых пар точек. Локально
из каждой вершины графа Кс выходит ровно 4 ребра. В общем,
случае имеем следующее утверждение.
Предложение 2. Комплекс /с получается склейкой несколь-
нескольких двумерных торов по окружностям, реализующим ненулевые
циклы у на торах. Если на одном торе расположено несколько та-
таких окружностей, то они не пересекаются. Окружности, по кото-
которым касаются торы, входящие, в состав fc, являются критическими
для f. Они гомологичны и разрезают fc в объединение нескольких
плоских колец.
Итак, на fc однозначно определен цикл у. Выберем на каждом
торе в fc некоторую окружность-образующую а, дополнительную к
V (пересекающуюся с v ровно в одной точке). Назовем ее овалом.
Можно считать, что овалы касаются друг друга в точках, лежа-
лежащих на критических окружностях интеграла. В ориентируемом
случае объединение овалов дает граф Кс- Он не обязан быть плос-
плоским. Пусть х — точка касания двух овалов, т. е. критическая для
/. Тогда отрезки интегральных траекторий поля w и линии уровня
функции f определяют (на двумерном диске с центром в точке х,
лежащем в Q и ортогональном критической окружности, на кото-
385
рой лежит точка х) около точки х «координатный крест», на каж
дом конце которого стоит стрелка, указывающая направление ь
{рис. 134B)). Построим такие нормальные двумерные кресты i
каждой вершине графа Кс- Разные кресты соединены отрезками
являющимися частями овалов.. Соединим теперь концы кресто:
узкими лептами, идущими вдоль дуг овалов. Эти ленты состоя1
из отрезков интегральных траекторий поля w, ортогонально пере
секающих овалы (вне критических точек). Дуги овалов идут т
оси этих лент. В результате получаем гладкую двумерную поверх'
ность с краем (рис. 134B)). Знаком «—» отметим граничнь^
•окружности, соответствующие торам, подошедшим к fc сииз}
Знаком « + » отметим граничные окружности, соответствующие то
рам, подходящим к /с сверху. На рис. 134B) в качестве примера
показано три положительных (верхних) тора и два отрицатель-
отрицательных (нижних). Число отрицательных (положительных) торов раь
но числу ребер графа Г, снизу (сверху) подходящих к /г. Получен-
Полученную поверхность обозначим Р(Т,)=РС. Ее граничные окружностг
разбиты на два класса: нижние (отрицательные) и верхние (по
ложительные). Граф Кс однозначно (с точностью до гомеоморфиз-
гомеоморфизма поверхности) вложен в Рс2.
Построим теперь Рс2 в неориентируемом случае. Схема рассуж-
рассуждений в основном сохраняется. Пусть сначала, для простоты, hi
fc лежит ровно 1 критическая окружность с неориентируемой диа-
диаграммой. Тогда fc имеет вид, показанный на рис. 134C) (частньн
случай). Следовательно, каждый овал а, лежащий на таком /,,
должен быть удвоен. Любая другая критическая окружность •.
ориентируемой диаграммой, лежащая на этом fc, встречает дв:
экземпляра цикла а в двух точках. Это заставляет нас удваиватг
циклы а и на тех торах, которые касаются друг друга вдол1
окружностей с ориентируемыми, диаграммами, но входят в соста!
"связного fc,, содержащего окружность с неориентируемой диаграм-
диаграммой. Количество окружностей с неориентируемыми диаграммам!
на связном /с не влияет на процесс удноепил, т. е. удвоить цикль
нужно лишь один раз. Дальнейшие построения повторяют ориеь
тируемый случай. В результате получаем поверхность Рс. Отличи^
лишь в том, что теперь каждая граничная окружность поверхно
сти Рс (т. е. соответствующая одному тору) встречается ровно t
двух экземплярах (удвоена).
Теперь построим поверхность Р(ТС). Из построения Рс виднс
что на ней корректно определено гладкое действие группы Z2 (ин-
(инволюция а). При этом о(х)—х в том и только в.том случае, когд;.
точка х принадлежит критической окружности с неориентируемо!
сепаратрисной диаграммой. Обозначим такие точки через х\,..
...,хт, а соответствующие им окружности через Si,...,Sm. Рас
смотрим факторпространство PC = PC/Z2. Ясно, что РС = Р(ТС) яь
ляется двумерным многообразием с краем. Теперь каждая еп
граничная окружность отвечает ровно одному тору Лиувилл*
(верхнему или нижнему). Легко видеть, что точки Xi,...,xm явля-
являются внутренними точками на поверхности Рс. Отметим их зве?
384
дочками. В частном случае, когда /с имеет вид, показанный на
рис. 134C) (т. е. т=1), поверхность Рс является двумерным ци-
цилиндром с одной звездочкой (рис. 134D)). Теперь мы можем по-
построить всю поверхность P(Q, f).
Ясно, что существует взаимно однозначное соответствие меж-
между граничными окружностями поверхности Р(А) и граничными
окружностями объединения поверхностей Рс- Это соответствие за*
дается ребрами графа А. Отождествив соответствующие окружно-
Рис. 134C)
Рис. 134D) '
сти при помощи некоторых гомеоморфизмов, однозначно получаем
замкнутую двумерную поверхность P(Q, f) (ориентируемую или
неориентируемую). Очевидно, что замена склеивающих гомеомор-
гомеоморфизмов другими индуцирует лишь гомеоморфизм поверхности на
себя. На P(Q, f) однозначно (с точностью до гомеоморфизма по-
поверхности) расположен некоторый, вообще говоря, несвязный
граф, который мы обозначим через K(Q, /). Рассмотрим окружно-
окружности, рассекающие пополам цилиндры, входящие в состав поверх-
поверхности S'XlnM. Можно считать, что каждая из них имеет вид
SlXp, где р— середина соответствующего ребра графа А. Телерь
определим граф $ как несвязное объединение всех графов Кс и
окружностей вида SlXp. Граф К имеет лишь вершины кратно-
кратности 4.
13 А. Т. Фоменко
385
Построение поверхности P(Q, f) полностью завершено.
Предложение 3. Если f и /' — любые боттовские интегра-
интегралы на Q, то P(Q, f) гомеоморфно P(Q, f) (в нерезонансном-слу-
нерезонансном-случае).
Обозначим через К* граф, сопряженный графу К в поверхно-
поверхности P(Q, /). Его вершины — это центры областей, на которые граф
К разбивает Р, а ребра — это дуги, соединяющие вершины через
середины ребер графа К.
Предложение 4. Граф T(Q, f) совпадает с графом K*(Q,
f). Следовательно, граф T(Q, f) допускает вложение h(Q, f) :
:T(Q, f)-+P(Q, /), однозначно (с точностью до гомеоморфизма
поверхности) определяемое исходной интегрируемой нерезонанс-
нерезонансной системой. Граф К разбивает поверхность Р на области, гомео-
морфные либо диску, либо плоскому кольцу, либо листу Мебиуса,
Следовательно, с каждой интегрируемой гамильтоновой нерезо-
нерезонансной системой естественно связано некоторое целое число, ко-
которое мы назовем «родом системы». Это род поверхности P{Q)~
Так как, согласно теореме 3, граф Г, поверхность Р и вложение k
не зависят от выбора /, то все эти объекты можно определить*,
опираясь лишь на геометрические свойства слоения Q3 на торы
Лиувилля, т. е. в итоге лишь на свойства гамильтониана. Мы не
будем здесь этого делать, поскольку читатель может самостоятель-
самостоятельно, опираясь на результаты гл. 4, восстановить необходимые рас-
рассуждения.
Приведем примеры вычисления топологических портретов не-
некоторых классических интегрируемых механических систем. Клас-
Классические уравнения движения тяжелого твердого тела имеют вид
^co + coX^co=vXqradII, v=vX<o,
где axb — векторное произведение, П — потенциал. Интегралы си-
системы имеют в данном примере следующий вид:
F = v2 + ,
G = Aj/tujVi + A,oJv2 + ^aftKv8 = g,
H = -L (A&l + Л*ш» + Л3©2) + П (v) = A.
а) Случай Ковалевской характеризуется тем, что Ai=A2=
= 2Л3, П = —vi. Тогда, как хорошо известно, возникает еще одш
дополнительный независимый интеграл f= (coi2 — W22+viJ-i-
+ B<oi(o2+v2J. Рассмотрим четырехмерное симплектическое мно
гообразие M4 = {f (со, v) = l; G{ay, v)=g}. Оно диффеоморфно кока
сательному расслоению к сфере T*S2. На Af4 задан гамильтониа1
Я и дополнительный интеграл /. Следовательно, можно применит]
изложенную выше конструкцию и вычислить топологический пор
трет интегрируемого случая Ковалевской. Это исследование бьш
проведено автором совместно с А. А. Ошемковым. Берем отобра
жение момента m = Hxf: Af4~>R2, отвечающее двум интегралам /
386
я f. При различных значениях g получаются различные бифурка-
бифуркационные диаграммы ScrR2, вычисленные М. П. Харламовым
(рис. 135). В интересующем нас примере трехмерные связные ком-
компоненты неособых изоэнергетических поверхностей задаются урав-
уравнениями Q3={F=1, G=g, H = h). Оказалось, что полный список
всех графов T(Q), встречающихся в случае Ковалевской, состоит
яз 6 графов (риа 136).
б) Случай Горячева—Чаплыгина. Он характеризуется тем, что
-|-=Л2 = 4Лз, П = —vi. Известно, что при G = 0 существует допол-
':'•". ■'Л/>
.•"■А1
к.-
ж
^■/•■•■••.*v:
/ 2 * '*■'.'*
г *9 w .■;.;•
Рис. 135
нительный интеграл /=2(u3((ui2+(u22) + 2(uiV3. Вычисления показы-
показывают, что здесь полный список графов T(Q) состоит всего из
двух графов. Бифуркационная диаграмма показана на рис. 137, а
топологический портрет (графы) см. на рис. 138.
в) Можно обобщить решение Горячева—Чаплыгина на случай
гиростата. В уравнениях движения и в интегралах G и Н нужно
заменить Л со на Аа + %. Тогда известно, что дополнительный инте-
интеграл имеет вид f=2(co3 — I) (coi2+<o22) + 2coiV3. При Я = 0 мы полу-
получаем обычный случай Горячева—Чаплыгина. При К¥=0 оказы-
оказывается, что полный список графов F(Q), встречающихся в этом
интегрируемом случае, имеет вид рис. 139. Здесь мы снова имеем
6 типов графов.
Вывод. Полные топологические портреты трех перечисленных
интегрируемых классических случаев не гомеоморфны. Графы 5 и
6 случая Ковалевской не гомеоморфны никакому графу случая Го-
Горячева—Чаплыгина (гиростат). Графы 5 и 6 случая гиростата не
аз»
387
гомеоморфны никакому графу случая Ковалевской. Итак, тополо-
топологические портреты наглядно различают между собой разные инте
грируемые случаи.
А. А. Ошемков построил графы T(Q) для интегрируемого ел"
.чая уравнений движения 4-мерного твердого тела. Полный тополо-
топологический портрет этого случая отличается от всех трех перечне
Рис. 137
Рис. 138
Рис. 139
ленных выше случаев. В частности, среди поверхностей P(Q) по
являются торы.
Предъявим вложения графов Г(<2) в поверхности P(Q). Д^
тальный анализ аналитических выражений для интегралов позв1
ляет в явном виде построить все эти вложения. В качестве иллн.
страции приведем сначала результат для случая Ковалевско
(рис. 140). Видно, что здесь во всех случаях поверхность P{Q) гг
меоморфна сфере. На рис. 141 графы Г(<2) и K(Q) случая KoBi
левской изображены на плоскости, получающейся выкалывание
из сферы одной точки. Возникают системы овалов, дальнейше
388
Рис. 140
изучение которых можно вести методами теории классификации
алгебраических кривых. На рис. 140 и 141 графы Г изображены
сплошными дугами, а графы К—пунктирными дугами. Наглядно
видно, что Г = /С*.
' Построенные автором поверхности склеены из базисных по-
поверхностей расслоений Зейферта. Это открывает интересные связи
с теорией трехмерных многообразий. Этот материал мы изложим:
389
Рис. 141
в отдельной работе. Все перечисленные результаты относятся
каждой отдельно взятой неособой изоэнергетической поверхног
на которой система интегрируема. Вне этой поверхности cacTt
может быть неинтегрируемой.
Укажем связь графа T(Q) с бифуркационным мнoжecтвo^
отображения момента т интегрируемой системы. Здесь т:№
-*-R2(//, f), где tn[x) = (H[x), f\x)). Фиксируя некоторое значе.
390
h для Н, мы получаем, что изоэнергетическая поверхность Q —
= (#=Л) является полным прообразом (связной компонентой)
прямой с уравнением H=h на плоскости R2(#, f). Ограничение т
с М* на Q3 совпадает с отображением f, изученным выше. Пересе-
Пересечения прямой H—h с множеством 2 (являющимся образом при
отображении т множества критических точек отображения т) со-,
ответствуют критическим уровням fc интеграла /. Легко видеть,
что замена интеграла / на другой интеграл /' меняет, вообще го-
, воря, множество 2. Следовательно, 2 не является топологическим
инвариантом интегрируемой системы. Построенный нами выше ин-
инвариант— тройка (Г, Р, К) — не восстанавливается полностью по-
геометрии множества 2, поскольку требует более тонкого анализа
критических множеств интеграла и соответствующих динамиче-
динамических формул.
Имеют место и многомерные аналоги перечисленных выше ре-
результатов, мы изложим их в отдельной работе.
Вкратце изложим схему доказательства перечисленных теорем.
Начнем с доказательства предложения 1. Пусть / и f — два бот-
говских интеграла на Q. В силу нерезонансности гамильтониана
Н каждый неособый тор с иррациональной обмоткой одновремен-
одновременно является компонентой поверхности уровня для каждого из ин-
гегралов, поскольку интегралы постоянны на траекториях системы
v и, следовательно, постоянны на замыкании каждой траектории. ■
Каждый неособый тор с рациональной обмоткой аппроксими-
аппроксимируется сколь угодно близко неособыми торами с иррациональны-
иррациональными обмотками. Следовательно, он тоже является компонентой по-
поверхности уровня для каждого из интегралов.
Рассмотрим поля oi = grad/ и w' — gradf. Они определяют
одно и то же одномерное слоение поверхности Q на интегральные
траектории, ортогональные (в какой-либо метрике) всем неособым,
поверхностям уровня, т. е. торам. Скорость движения по траекто-
траекториям (определяемым полями w и w') может быть различной и
может обращаться в ноль сразу Яа всем торе для одного из полей
(в то время как другое поле ненулевое). Так как особые компо-
компоненты уровня аппроксимируются неособыми торами (при их дви-
движении вдоль w и w'), то особые компоненты связности поверхно-
поверхности уровня для /, отличные от тора, совпадают с аналогичными
компонентами для /'. Если же поверхность уровня была критиче-
критическим тором для /, то она может стать некритической для f (и на-1
оборот). Однако каждая особая компонента для f является особой
компонентой и для /' (н наоборот). Торы образуют одномерное се-
семейство в окрестности каждого неособого тора. Локально, рас-
рассматривая операции f-»-/2=/' или f-*-~\/f=f', мы можем превратить
некритический тор в критический и наоборот. Все другие функ-
функциональные операции, локально сохраняющие боттовость, сво-
сводятся к этим двум, так как гладкая морсовская функция на одно-
одномерном многообразии может иметь лишь квадратичные особенно-
особенности. С геометрической точки зрения операция f-*»f2 отвечает пере-
перегибанию ребра графа и появлению на нем локального минимума
Э91
"или максимума. Операция f-**~yf отвечает распрямлению ребра
графа и уничтожению локального миннмакса.
Построим гомеоморфизм графа Г на граф Г'. Чтобы опреде-
определить его на подграфе А, достаточно рассмотреть каждый неосо-
неособый тор для интег£ала f как тор для интеграла f (особый или не-
неособый). Это отображение продолжается и на подграфы вида Тс
так как одномерные слоения поверхности Q, порожденные w i
■w', совпадают всюду, кроме, быть может, некоторых критически)
«ли некритических торов (где скорость движения вдоль w ил!
w' обращается в ноль). Как следствие, отметим, что полные по
верхности уровня интегралов f и f (содержащие одну и ту ж<
компоненту связности) могут состоять из разного числа связны:
компонент. При этом значения" f и f могут быть различны на од
ной и той же* компоненте связности. Предложение 1 доказано.
Предложение 2 доказано автором в [160], [161] (см. гл. 4)
Для доказательства предложения 3 рассмотрим подробнее про
цесс построения поверхности Р. Ограничимся пока ориентируемы!
случаем. Комплекс Д. получается склейкой нескольких экземпля
ров торов T\,...,Tn по циклам, гомологичным циклу у на fc (си
выше). Пусть S\,...,SP — критические окружности на fc. Выбёре!
на каждой из них по точке: q\,...,qp. Рассмотрим какоё-нибуд
ш плоских колец г, на которые fc разрезается окружностями S
Тогда на каждой из его граничных окружностей лежит ровно п
одной точке вида qa. Пусть это точки qa и q$. Соединим их гла,л
кой дугой та|), целиком лежащей внутри кольца. Эта дуга стрс
ится, конечно, неоднозначно, но на окончательный результат эт
не влияет. Самонепересекающуюся дугу тар можно было бы cbs
зать с интегралом f. Для этого нужно рассмотреть поле sgrad
на кольце г. Это поле, может обращаться в ноль только на граш
де кольца. Можно было бы выпустить из точки qa короткий отр<
аок, идущий внутрь кольца, затем юз его конца выпустить инк
Тральную траекторию поля sgrad f н двигаться по ней, пока i
Приблизимся достаточно близко к противоположной границе кол:
Ца, на которой расположена точка q». Затем свернем с интеграл:
ной траектории и проведем короткий отрезок в точку q^.
Повторим процесс построения гладкой дуги в следующем кол
це, начиная с точки q^ и т. д., пока не исчерпаем все кольца, вх'
дящие в состав fc. В результате получим систему окружносте
овалов. Каждая из них составлена из дуг вида тар. Рассмотрим i
всех внутренних точках дуги тар нормальные отрезки вдоль инт
тральных траекторий поля grad/. Концы полученной ленты опр
деляются координатными крестами точек qa и q$. Заменяя ду
таР дугой т'ар, лежащей в г и соединяющей qa и q$, получаем п
верхность, гомеоморфную предыдущей. Замена f на f приводит
гомеоморфизму Р и может существенно повлиять на вид влож
ния Рс b_Q. Предложение 4 следует из конструкции, изложенн<
выше. Граф Кс состоит из дуг вида таР. Каждая из них определя
свое кольцо вида г на fc.
392
Доказательство теоремы 2 следует из [160], [161], а также иу
явной конструкции Рс, описанной выше. Остановимся подробнее
на случае PcXSl. Пусть U(fc) ={x<=Q : с — e<f(*Xc+e} — регу-
регулярная окрестность fc, причем fc содержит критические окружно-
окружности Si,...,Sm с неориентируемыми диаграммами. Пусть lf(Si) —
малая трубчатая окрестность St- (полноторие) в U(fc). Тогда
^(fc)\(t/(Si)U---Ut/(Sm)) гомеоморфно прямому произведению
(Pc\(*iU ... (]хт)) XSK Тогда (см. рис. 134D)) каждое полното-
полноторие U(S{) является расслоенным полноторием типа B,1).
Важный комментарий. Как мы отмечали, классическая
бифуркационная диаграмма 2 (Я, f) не является топологическим
инвариантом интегрируемой системы. С этой точки зрения обна-
обнаруженный нами топологический портрет /(Я) является более есте-
естественным объектом — он зависит только от нерезонансного га-
гамильтониана Я и не зависит от выбора второго интеграла f. Би-
Бифуркационная диаграмма 2 в елучае общего положения изобра-
изображается кривой (графом) -с особенностями, лежащей в плоскости.
Наш инвариант /(Я, Q) также изображается некоторым одно-
одномерным графом, но вложенным в некоторую замкнутую двумер-
двумерную поверхность. Отсюда видно, что инвариантность топологиче-
топологического портрета /(Я) достигается ла счет более глубокого проник-
проникновения в геометрию интегрируемой системы. Инвариантный топо-
югический портрет /(Я) «знает» о системе больше, чем неинва-
шантная бифуркационная диаграмма 2 (Я, /). При этом плос-
сость заменяется на двумерную замкнутую поверхность Р, а кри-
зая 2 — на более «тонко организованный» граф Г.
ПРИЛОЖЕНИЕ 8
ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ^
ИНТЕГРИРУЕМЫХ ПРИ ПОМОЩИ НЕБОТТОВСКИХ
ИНТЕГРАЛОВ .. . _
В гл. 4 и в Приложении 7 мы рассматривали случай, когда га-
мильтонова система имеет дополнительный боттовский (морсов-
ский) интеграл. Как показали конкретные исследования реальных
систем, этот случай действительно типичен. Однако встречаются1
ситуации, когда второй дополнительный интеграл не является бот-
товским. Естественно поставить вопрос: сохраняются ли получен-
полученные выше результаты в этом случае? Конечно, на интеграл па-
прежнему нужно наложить какие-либо разумные ограничения,,
поскольку гладкие функции могут иметь чрезвычайно сложные'
I особенности. Изучение реальных систем показало, что от интегра-
j ла достаточно требовать, чтобы он был «ручным». Термин заим-
I ствован из топологии, где им обозначаются объекты, локально»
\ устроенные «достаточно хорошо», в отличие от патологических,,
«диких» пространств. Ниже будет дано точное определение. Ока-
Оказалось, что многие из обнаруженных нами результатов остаются
39»
справедливыми и в" том случае, когда гладкий интеграл является
всего лишь ручным (а не боттовским).
Рассмотрим четырехмерное симплектическое гладкое многооб-
многообразие, и пусть a = sgrad# — гамильтонова система с гладким га-
гамильтонианом Я, интегрируемая по Лиувиллю при помощи неко-
некоторого гладкого интеграла f на какой-то неособой компактной
изоэнергетической поверхности Q3= (H = const). Ограничивая ин
теграл f с многообразия М4 (или с окрестности подмногообрази?
Q3) на подмногообразие Q3, получаем гладкое отображение f
: Q+R.
Onр.еделение. Гладкий интеграл f назовем ручным, есл!
для любого критического значения a^R множество /~'(а) яв
ляется ручным, т. е. существует гомеоморфизм всего многообра
зия Q на себя, сдвигающий его (это множество) в полиэдр.
Обозначим через (Я*) класс трехмерных компактных замкну
тых многообразий, являющихся изоэнергетическими поверхностя
ми гамильтоновых систем, интегрируемых при помощи некоторой
ручного интеграла (дополнительного к Я, гладкого, независимой
и находящегося с Я в инволюции).
Так как каждый боттовский интеграл, очевидно, является руч
иым, то имеет место тривиальное включение (H*)zd(H). Другим;
словами, расширив класс рассматриваемых интегралов, мы рас
ширили и класс трехмерных многообразий, являющихся изоэнер
гетическими поверхностями. С точки зрения трехмерной топологи
и ее приложений к гамильтоновой механике очень интересен вс
прос: совпадают или нет классы (Я*) и (Я)? Другими словам*
насколько существенно предположение боттовости во многих тес
ремах теории типа Морса, разработанной в гл. 4 (см. такж
[159] —[161]).
Теорема 1 (С. В. Матвеев, А. Т. Фомеико). Классы (Я*)
(Н) совпадают.
Этот результат (который мы докажем ниже) имеет много ра;
личных интерпретаций. Укажем здесь лишь на одну из них. Ка
мы знаем из гл. 4, топология многообразия Q из класса \Н) пс
казывает нам, как перестраиваются 2-торы Лиувилля при изм<
нении значения интеграла. Мы знаем уже, что все возможные п<
рестройки в боттовском случае являются композициями трех о<
новных перестроек типов I, II, III. Расширив класс интегралов
введя в рассмотрение ручные интегралы, мы тем самым априор
расширили и запас возможных перестроек торов Лиувилля. Сфо!
мулированная выше теорема фактически утверждает, что тако1
расширения не произошло. Другими словами, хотя перестроив
торов Лиувилля в неботтовском ручном случае, конечно; силы
усложняются, тем не менее все они по-прежнему являются комт
зициями все тех же трех основных перестроек типов I, II, III, ю
торые были обнаружены автором в гл. 4. При этом следует имет
в виду, что, раскладывая эти «ручные перестройки» в композици
перестроек типов I, II, III, мы должны, вообще говоря, замени'
исходный интеграл на другой, уже боттовский. Сформулированнг
-394 '
теорема утверждает, что такая замена всегда возможна, т. е. «ря-
«рядом» е ручным интегралом всегда находится боттовский интеграл-
(на том же самом многообразии Q), осуществляющий разложение
ручных перестроек торов Лиувилля в композицию элементарных
перестроек типов I, П, III.
Перейдем к доказательству теоремы. Сначала изучим многооб-
многообразия сложности ноль. Определим классы (TS) и (TSH) компакт-
компактных ориентируемых 3-многообразий. Многообразие Мь принадле-
принадлежит классу (TS) тогда и только тогда, когда каждая компонента
его края гомеоморфна тору или сфере. Пусть М обозначает много- .
образие, получающееся из многообразия М заклеиванием шарами
всех сфер на его крае. Многообразие М3 принадлежит классу
(TSH) тогда и только тогда, когда многообразие М можно полу-
получить склеиванием краев нескольких экземпляров полного тора
SlXD2 и многообразия NaxS\ где N2 обозначает диск с двумя
дырками (см. гл. 4). Здесь следует отметить, что цилиндр можно
представить как результат склейки штанов с полноторием, воэто»
му в действительности в качестве элементарных кирпичей доста-
достаточно взять лишь два многообразия: штаны и полнаторие.
Кан доказано в [284], имеют место следующие утверждения:
1) связная сумма Aft#Af2 принадлежит классу (TSH) в том к
только в том случае, когда М\ и М2 принадлежат (TSH); 2) еслк
Mi и М2 принадлежат (TSH) и М получается из Mi и М2 склеива-
склеиванием нескольких торов на их краях, то М принадлежит (TSH);
3) если М принадлежит {TSH) и М) получается из М приклеива-
приклеиванием невырожденной круглой ручки, то Mi принадлежит (TSH).
При этом круглая ручка называется невырожденной, если низ
одно из колец ее основания не содержится в диске, лежащем т
дМ. Пересечение класса {TSH) с классом замкнутых 3-многооб»
разий совпадает с классом (Я), определенным А. Т. Фоменко в.
[159] —[161].
Нам понадобится понятие почти специального спайна 3-много*
образия. Напомним, что полиэдр Р коллапсируется на свой под*
полиэдр Q (обозначение:. Р \ Q), если в некоторой триангуляции
(К, L) пары (Р, Q) от комплекса К можно перейти к комплексу
L с помощью последовательности элементарных симплициальных
стягиваний, где каждое элементарное симплициальное стягивание
состоит в отбрасывании главного симплекса вместе с его свобод-
свободной гранью. Напомним также, что полиэдр РсМ является спай-
спайном многообразия М, если М (или М с удаленным шаром, если
дМ = 0) коллапсируется на Р.
Определение. Полиэдр Р называется почти специальным,.
если 1) Р не коллапсируется на собственный подполиэдр; 2) каж-
каждая точка полиэдра Р имеет окрестность, гомеоморфную конусу
над некоторым подграфом графа Г, где Г — окружность с тремя
радиусами.
Точки с окрестностью типа Con Г называются вершинами по-
полиэдра Р. Из определения следует, что любой неколлапсируемый
подполиэдр почти специального полиэдра почти специален.
395-
• Определение. Сложностью с(М) компактного 3-многообра-
зия М называется число вершин его минимального (в смысле чйс-
сла вершин) почти специального спайна (С. В. Матвеев).
Теория специальных спайнов и сложности 3-многообразий да-
далеко продвинута в цикле работ С. В. Матвеева. Оказалось, что
она тесно связана с рассматриваемыми нами здесь вопросами га-
мильтоновой геометрии.
Теорема 2. Если М принадлежит (TS) и его сложность с\М)
равна нулю, то М принадлежит (TSH).
Для доказательства нам понадобится следующая лемма.
Лемма 1. Пусть Aft получается из М приклеиванием ручки
индекса 1 или невырожденной круглой ручки. Тогда из того, чтс
Mi принадлежит (TS) и не принадлежит (TSH), следует, что М
принадлежит (TS) и не принадлежит (TSH).
Доказательство. Рассмотрим случай ручки индекса 1
Так как приклеивание ручки индекса 1 ие может уменьшить ро;
поверхности, то из того, что M\&(TS), следует, что M^(TS). Бу-
Будем рассуждать от противного. Допустим, что Me.(TSH),
а) Ручка приклеивается к компонентам Fi, F2 двух различны?
компонент М', М" многообразия М. Одна из них (пусть Fx) обя
зана быть сферой. Тогда М1 = М'#М", где разбиение в связнук
сумму осуществляется продавленной внутрь многообразия сферо!
Fi. Так как М' M"^(TSH) и класс (TSH) замкнут относителен
связной суммы, то Mi^(TSH). Это противоречит условию.
б) Ручка приклеивается к различным компонентам F\, F2 кра$
связного многообразия М. Одна из них (пусть Ft) по-прежнему
обязана быть сферой. Тогда M1=M#S2x51, где неразбивающе1
сферой в S2XS' служит продавленная внутрь сфера F\. Так ка!
S2XSl<=(TSH) и №<=(TSH), то Mi<=(TSH), что противоречит ус
ловию.
в) Ручка приклеивается к одной компоненте F края связноп
многообразия М. Тогда F — сфера и Mi = M^DixS1. Как и рань
ше, это противоречит условию.
Случай невырожденной круглой ручки очевиден (как отмеча
лось, класс (TSH) замкнут относительно операции приклеивани;
невырожденной круглой ручки).
С л е д с тв ие. Пусть М\ получается из М приклеиванием вы
рожденной круглой ручки по кольцам Аи А2, где А\ содержится
диске DczdM, а М2 — приклеиванием ручки индекса 2 по кольц
А2. Тогда из того, что М\ принадлежит (TS), но не принадлежи
(TSH), следует, что М2 принадлежит (TS) и не принадлежи
\TSH).
Доказательство. Легко видеть, что М\ получается из М
приклеиванием ручки индекса 1. Секущим диском этой ручки сл>
жит продавленный относительно края внутрь многообразия дис
D. Остается применить'лемму 1. • ■ •
Пусть Р — почти специальный полиэдр. Назовем ^-компоненте
ми полиэдра Р связные компоненты множества точек, линки кс
396
торых не содержат окружности с диаметром. Каждая 2-компонен-
та является 2-многообразием без края. Назовем дугой в Р связ-
связную компоненту множества точек, имеющих в Р гомеоморфную
интервалу окрестность. Сопоставим каждому почти специальному
полиэдру Р тройку чисел (Л(Р), В(Р), С(Р)), где 4(Р)—число
2-компонент полиэдра Р, В(Р)—сумма их эйлеровых'характери-
эйлеровых'характеристик, взятая с обратным знаком, С(Р)—число дуг в Р. Скажем,
что Р,<Р2, если A(Pi)<A(P2), или Л(Р1)==Л(Р2) и B(PX)<L
<В(Ра), или Л(Р1)=Л(Р2), В(Р,)=В(Яа) и С(Р1)<С(Р2).
Доказательство теоремы 2. Будем доказывать от про-
противного. Пусть имеется контрпример. Среди всех почти специаль-
специальных спайнов без вершин всех контрпримеров выберем минималь^
ный в смысле введенного порядка. Обозначим его через Pi, а от-
отвечающее ему 3-многообразие — через М\.„ Отождествим Mi с ре-
регулярной окрестностью Р-,.
Пусть C(Pi)>0. Выберем дугу в Р, и разрежем М, по нор-
нормальному к ней диску с краем в дМь Получим многообразие М с
меньшим (в смысле порядка) почти специальным спайном Р, ко-
который получается разрезанием спайна Pt по точке и коллапсиро-
ванием (дуга исчезнет, так что С(Р)<С(Р[)). По лемме 1 много-
многообразие М также является контрпримером, а это противоречит
минимальности. Итак, C(Pi)=0.
Пусть на одной из 2-компонент спайна Pi найдется нетриви-
нетривиальная сохраняющая ориентацию кривая с. Обозначим через с',
с" ее сдвиги на край дМ\. Возможны следующие два случая.
1) Кривые с' и с" нетривиальны в dMt. Разрежем Мх по нор-
нормальному к Pt кольцу со средней линией с. Спайн Р получивше-
получившегося многообразия М получается из спайна Pt разрезанием по
кривой с и коллапсированием. Поэтому А(Р)<А{Р\). С другой
стороны, многообразие Мх получается из многообразия М при-
приклеиванием невырожденной круглой ручки. По лемме 1 многооб-
многообразие М также является контрпримером, что противоречит мини-
минимальности.
2) Пусть хотя бы одна из кривых с', с" тривиальна в дМ\. Раз-
Разрежем Mi по кольцу со средней линией с. Одно из колец, возник-
возникших после разрезания на крае получившегося многообразия М,
вырождено (содержится в диске, лежащем в дМ)'. Заклеив другое
кольцо ручкой индекса 2, получим многообразие Мг. Спайн Рг
многообразия М2 получается из спайна Pt разрезанием по кривой
с, заклеиванием диском одного из краев разреза и коллапсирова-
коллапсированием. Поэтому B(P2)<B(Pi). По следствию леммы 1 многообра-
многообразие М2 также является контрпримером, что противоречит мини-
минимальности.
Итак, в Р] нет дуг и 2-компонент, содержащих нетривиальные
сохраняющие ориентацию кривые. Тогда либо Ргне имеет особых
точек и тогда он гомеоморфен сфере или проективной плоскости,
либо Pi имеет одну особую окружность и все его 2-компоненты —
клетки. В первом случае Й\ — сфера S3 или проективное про-
пространство RP3, во втором — линза L3,i или сфера. Все эти много-
397
образия лежат в классе (TSH), что противоречит условию. Это»
завершает доказательство теоремы 2.
Замечание. Теорема 2 справедлива для многообразий
сложности 1. Для многообразий сложности 2 имеем контпример— ■
дополнение к узлу восьмерки (С. В. ]Цатвеев).
Рассмотрим теперь многообразия с ручной функцией. Пусть
М — компактное ориентируемое 3-многообразие.
Определение. Дифференцируемая функция f:M-*-R назы-
называется ручной, если
1) множество критических точек функции /состоит из конеч-
конечного числа компонент, каждая из которых является гладкой
окружностью, тором или бутылкой Клейна в IntAf;
2) каждая не содержащая критических точек компонента лю-
любой поверхности уровня функции / является тором;
3) для любого критического значения а множество /-1(а) яв*
ляется ручным, т. е. существует гомеоморфизм всего многообра-
многообразия М на себя, сдвигающий его в полиэдр.
Теорема 3. Если на многообразии М существует ручная
функция, то многообразие принадлежит классу (TSH).
Для доказательства теоремы 3 нам понадобится несколько
лемм.
Лемм.а 2. Пусть F— замкнутая Ловерхность и i:Fx[0, 1)-*»
-»-Int(Px [0, 1))—собственное вложение. Тогда многообразие
N = C\(T2X [О, 1) — i(F2X [0, 1)) гомеоморфно РХ/.
Доказательство. Из теоремы об инвариантности области
следует, что образ вложения i содержит конец (окрестность бес-
бесконечности) многообразия Г2Х [0, 1). Так как фундаментальные
группы тора Г2Х{0} и поверхности i(Fx{0}) совпадают с фунда-
фундаментальной группой конца, то они изоморфны, а тогда F — тор.
Присоединяя к многообразию Г2Х [0, 1) тор Г2Х{1} и тор Fx{\}*.
получим две компактификации поверхностью многообразия Г2Х
X [0, 1). По известной теореме единственности они гомеоморфны,.
т. е. многообразие Г2Х [О, 1)U^X{1} гомеоморфно Г2Х/. Многооб-
Многообразие N получается из него вычитанием воротника края Fx{l}»
поэтому оно гомеоморфно многообразию Т2ХА
Лемма 3. Пусть f — ручная функция на М, имеющая одно
критическое значение. Тогда М имеет спайн Р, все особенности
которого содержатся в нескольких окружностях, торах и бутыл-
бутылках Клейна, лежащих в Р.
Доказательство. Докажем, что критическая поверхность,
уровня Р является спайном многообразия М (после ее сдвига в=
долиэдр). Это получается применением леммы 2 к каждой компо-
компоненте многообразия N(P) — Р, лежащей в соответствующей п>-
меоморфной Т2Х [0, 1) компоненте многообразия М — Р, где
N(P) —регулярная окрестность полиэдра Р.
Лемма 4. Пусть M^(TS) имеет такой спайн Р, что все его-
особенности содержатся в нескольких окружностях, торах, бутыл-
бутылках Клейна, лежащих в Р. Тогда М можно разрезать по несколь-
398
ким торам и получить такое многообразие Afie(TS), что c(Aft) = .
= 0.
Доказательство. Так как М\ Р, то М\ P\jN, где N —
регулярная окрестность упомянутых окружностей, торов, бутылок
Клейна. Разрежем ее (и вместе с ними многообразие М) по то-
торам, параллельным компонентам ее края. Получившееся многооб-
многообразие Mi коллапсируется на почти специальный полиэдр Pi без
вершин, который состоит из полиэдра (Р — N)\JdN и нескольких
окружностей, торов, бутылок Клейна (спайнов отрезанных ча-
частей). Поэтому с (МО =0.
Доказательство теоремы 3. Разрежем М по неосо-
неособым поверхностям уровня на части, в каждой из которых функция
/ принимает только одно критическое значение. Последовательное
применение лемм 3, 4 и теоремы 2 к каждой из этих частей пока-
показывает, что все они лежат в классе (TSH). Отсюда следует, что и
многообразие М также лежит в классе (TSH), что и требовалось
доказать.
Теорема 1 является очевидным следствием теоремы 3.
НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
1) Rn — евклидово пространство, (,) — евклидово скалярное
произведение в Rn, gradf — обычный градиент функции на
римановом многообразии М относительно римановой метри-
метрики gu.
2) (,) — кососимметрическое скалярное произведение в R2n,
со — симплектическая структура на симплектическом многооб-
многообразии М2п, sgradf—кососимметрический градиент функции f
на М2п.
3) С°°(М) —пространство гладких функций на М.
4) @, ^ — группы Ли, G, Н — соответствующие алгебры Ли,
[,] —коммутатор в алгебре'Ли (или векторное произведение
в R3); G*, Н* — пространства, сопряженные (дуальные) к
G, Н.
5) А = (аи) — квадратная матрица.
6) Т—картановская подалгебра в алгебре Ли G; а — корни по-
^лупростой алгебры Ли; На' — вектор в Г, соответствующий
'корню а; Д — система ненулевых корней а в алгебре Ли G,
П — система простых корней.
7) Adg, Adg* — присоединенное и коприсоединенное представле-
н"ия группы Ли, ad*, ad** — присоединенное и коприсоединен-
коприсоединенное представления алгебры Ли G.
8) Gc — компактная вещественная форма полупростой алгебры
Ли G. ■ .
9) Gn — вещественная нормальная подалгебра в простой алгеб-
алгебре Ли, причем Gnc:Gc.
10) IG — кольцо (алгебра) инвариантных полиномов на алгебре
Ли G.
11) ТХМ, ТХ*М — касательное и кокасательное пространства к
гладкому многообразию М в точке х.
ДОПОЛНЕНИЕ. О РИСУНКАХ
К каждой из семи глав книги предпослан графический лист.
Вкратце прокомментируем их содержание. Графический лист не
обязательно непосредственно связан с содержанием данной главы,,
так как может отражать общую идею, присутствующую в книге и
распределенную по нескольким главам. Перед гл. 3 изображены
различные виды тяжелых волчков Лагранжа, т. е. осесимметрич-
ных тел вращения, закрепленных в точке, лежащей на оси. Если
же центр смещен с оси вращения, то тяжелый волчок под влия-
влиянием сил инерции может разорваться при больщих оборотах, что
400 '
показано перед гл. 5. Перед гл. 2 помещен графический лист,
изображающий покрытие плоскости (более общо, многообразия)
непересекающимися дисками, объединение которых дает всю плос-
плоскость за исключением замкнутого множества нулевой меры. Это
покрытие используется при построении на гладком симплектиче-
ском многообразии простейшего полного набора гладких функций
в инволюции.
Перед главами 1, 6, 7 помещены рисунки, наглядно изобра-
изображающие три типичные перестройки двумерных торов Лиувилля
на критических уровнях интеграла энергии. Перед гл. 1 показан
распад одного тора на два, когда внешняя граница полноториж
«садится» на внутренних тонких полнотория, «обжимает» их и,,
перестраиваясь, распадается на два тора. Перед гл. 6 показан
аналогичный процесс перестройки тора в тор, когда внешняя гра-
граница полнотория «садится» на внутреннее тонкое полноторие, два
раза обходящее вдоль оси большого полнотория, затем перестраи-
перестраивается и превращается в один тор (два раза закрученный). Перед
гл. 7 показана перестройка тора в бутылку Клейна. Изображено
погружение бутылки Клейна в трехмерное пространство. Затем
рассматривается граница нормальной трубчатой окрестности этога
погружения. Эта граница является погруженным тором. Затем тор
«садится» на бутылку Клейна, двулистно накрывая ее. Для этого
достаточно отобразить два конца отрезка, нормального к бутылке
Клейна, на его центр (лежащий на бутылке Клейна). Перед гл. 4
показаны графы Г (Q, /), подробно описанные в гл. 4 и наглядно»
изображающие изоэнергетические поверхности интегрируемых си-
систем.
ЛИТЕРАТУРА
I. Аносов Д. В. Замкнутые геодезические//Качественные методы исследо
вання нелинейных дифференциальных уравнений и нелинейных колеба-
колебаний. — Киев: Ин-т математики АН УССР, 1981. С. 5—24.
5. Аносов Д. В. О типичных свойствах замкнутых геодезических//Изв
АН СССР. Сер. матем., мех. 1982. Т. 46, № 4. С. 675—7Q9.
3. А и о с о в Д. В. Геодезические потоки на замкнутых "многообразиях отри-
отрицательной кривизны // Труды МИАН им. В. А. Стеклова. Т. 90. М.: Наука,
1967. С. 3—209.
4. А р и о л ь д В. И. Гамильтоновость уравнений Эйлера динамики твердого
тела в идеальной жидкости // УМН. 1969. Т. 24, вып. 3. С. 225—226.
5. Арнольд В. И. Математические методы классической механики. — М.:
Наука, 1974.
Ч>. Арнольд В. И., Варченко А. Н., Гуссйн-Заде С. М. Особен-
Особенности днфференцнруемых отображений. Т. 1, — М.: Наука, 1982.
7. Архангельский А. А. Вполне интегрируемые гамильтоновы системы
на группе треугольных матриц // Матем. сб. 1979. Т, 108, № 1. С. 134—
142.
8. Архангельский Ю. А. Аналитическая динамика твердого тела. — М.:
Наука, 1977.
9. Бальдассарри М. Алгебраические многообразия. — М.: ИЛ, 1961.
10. Барьяхтар В. Г., Белоколос Е. Д., Голод П. И.//Препринт
ИТФ АН УССР, ИТФ-84-128Р, 1984.
II. Белавнн А. А., Дринфельд В. Г. О решениях классического уравне-
уравнения Янга—Бакстера для простых алгебр Ли//Функц. анализ н его прилож.
1982. Т. 16, вып. 3. С. 1—29.
'12. Беляев А. О. О движении многомерного тела с закрепленной точкой в
поле силы тяжести//Матем. сб. 1981. Т. 114, № 3. С. 465—470.
'13. Берез ни Ф. А., Переломов А. М, Теоретико-групповая интерпрета-
интерпретация уравиеннй Кортевега-де Фриза//Функц. анализ и его прилож. 1980.
Т. 14, вып. 2. С. 50—51.
- 14. Бес се А. Л. Многообразия с замкнутыми геодезическими. — М.: Мир,
1981.
05. Бляшке В. Введение в дифференциальную геометрию. — М.: Гостех-
нздат, 1957.
16. Богоявленский О. И. Новые алгебраические конструкции уравнений
Эйлера//ДАН СССР. 1983. Т. 268, № 2. С. 277—280.
17. Богоявленский О. И. Интегрируемые уравнения Эйлера, связанные с
фильтрациями алгебр Ли //Матем. сб. 1983. Т. 121, № 2. С. 233—241.
18. Богоявленский О. И. Динамика твердого тела с п эллипсоидальными
полостями, заполненными магнитной жидкостью // ДАН СССР. 1983. Т. 272,
№ 6. С. 1364—1367.
19. Б ого я в л е иски й О. И., Ивах Г. Ф. Топологический анализ интегри-
интегрируемых случаев В. А. Стеклова//УМН. 1985. Т. 40, вып. 4. С. 145—146.
20. Болотин С. В. Неинтегрируемость задачи п центров прн я>2//Вестн.
Моск. ун-та. Сер. матем., мех. 1984. № 3. С. 65—68.
'■21. Б о лея но в А. В. Вполне интегрируемые системы на ' сжатиях алгебр
Ли //Труды семинара по векторному и тензорному анализу. Вып. XXII.
М.: Изд-во Моск. уи-та. 1985. С. 8—16.
22. Б р а и л о в А. В. Ииволютивные наборы иа алгебрах Лн и расширение
кольца скаляров//Вести. Моск. ун-та. Сер. матем., мех. 1983. № 1. С. 47—
51.
23. Б р а и л о в А. В. Некоторые случаи полной интегрируемости уравнений
Эйлера и приложения//ДАН СССР. 1983. Т. 268, № 5. С. 1043—1046.
-402
24. Б р а и л о в А. В. Полная интегрируемость некоторых геодезических пото-
потоков и интегрируемые системы с уиекоммутнрующнми интегралами // ДАН'
СССР. 1983. Т. 271, № 2. С. 273—276.
25. Б р а и л о в А. В. Серия вполне интегрируемых гамильтоновых систем на
полупрямом произведении so(n) XR" // Геометрия и топология в глобальных
нелинейных задачах. — Воронеж: Изд-во Воронежского ун-та. 1984.
С. 145—148.
26. Б р а и л о в А. В. Полная интегрируемость с некоммутирующнми интегра-
интегралами некоторых уравнений Эйлера // Применение топологии в современном'
анализе. — Воронеж: Изд-во Воронежского ун-та. 1985. С. 22—41.
27. Б р а и л о в А. В. Некоторые конструкции полных семейств функций, ка«
хедящихся в инволюции//Труды семинара по векторному н тензорному
анализу. Вып. XXII. М.: Изд-во Моск. ун-та. С. 17—24.
28. Б у р б а н и Н. Группы и алгебры Лн. — М.: Мир, 1978.
29. Веселое А. П. Конечнозонные потенциалы и интегрируемые системы иа
сфере с квадратичным потенциалом//Функц. анализ и его прилож. 198.0.
Т. 14, вып. 1. С. 48—50.
30. В е с е л о в А. П. Об условиях интегрируемости уравнений Эйлера и».
so D) //ДАН СССР. 1983. Т. 270, № 6. С. 1298—1300.
31. Веселое а Л. Е. О динамике тела с эллипсоидальной полостью, напол-
наполненной жидкостью//Вестн. Моск. ун-та. Сер. матем., мех. 1985. MS.
С. 64—67.
32. В е с е л о в А. П. Кнондальиые решения уравнения Ландау—Лифшица Для
двухподрешеточного магнетика//ДАН СССР. 1984. Т. 276, № 3. С. 590—•
593.
33. Веселое А. П. Уравнение Ландау—Лифшица н интегрируемые системы-
классической механики // ДАН СССР. 1983. Т. 270, № 5. С. 1094—1097.
34. В и п о г р а д о в А. М., Купершмндт Б. А. Структура гамильтоновой
механики//УМН. 1977. Т. 32, вып. 4. С. 175—236.
35. В и ш и к С. М., Должанскнй Ф. В. Аналоги уравнений Эйлера—Пуас-
Эйлера—Пуассона и магнитной гидродинамики, связанные с группами Лн//ДАН СССР,
1978. Т. 238, № 5. С. 1032-1035.
36. Габриэлов А. М. О проекциях полуаналнтнческих множеств//Функц.
•анализ и его прилож. 1968. Т. 2, вып. 4. С. 18—30.
37. Гайдуков Е. В. Асимптотические геодезические на римановом много-
многообразии, негонеоморфном сфере//ДАН СССР. 1966. Т. 169, № 5. С. 999—
1001.
38. Г е л ь ф а н д И. М., Д и к н й Л. А. Дробные степени операторов и гамиль-
тоновы системы//Функц. анализ и его прилож. 1976. Т. 10, вып. 4. С. 13—•
29.
39. Гельфанд И. М., Дорфман И. Я. Гамильтоновы операторы и свя-
связанные с ннмн алгебраические структуры // Функц. анализ и его прилож.
1979. Т. 13, вып. 4. С. 13—30.
40. Гельфаид И. М., Чередник И. В. Абстрактный гамнльтонов форма-
формализм для классических пучков Янга—Бакстера//УМН. 1983. Т. 38, вып. 3.
С. 3—21.
41. Гинзбург В. А. Эквиварнантные когомологни и кэлеровы многообра-
многообразия // Функц. анализ н его прилож. — В печати.
42. Г о д б и й о н К. Дифференциальная геометрия н аналитическая механи-
механика. — М.: МИР. 1973.
43. Г о р р Г. В., К у Д р я ш о в а Л. В., .С т е п а и о в а Л. А. Классические за-
задачи дниамики твердого тела. — Киев: Наукова думка. 1978.
44. Гото М., Гроссханс Ф. Полупростые алгебры Ли. — М.: Мнр. 1981.
4ё. Дао Чонг Тхи. Интегрируемость уравнений Эйлера на однородных
снмплектнческих многообразиях//Матем. сб. 1978. Т. 106, №2. С. 154—
161.
46. Д н к и й Л. А. Замечание о гамильтоиовых системах, связанных с труппой
вращений//Функц. анализ и его прилож. 1972. Т. 6, вып. 4. С. 83—84.
47. Диксмье Ж. Универсальные обертывающие алгебры. — М.: Мир, 1978.
48. Дирак Л. М. Обобщенная гамильтонова динамика//Вариационные прин-
принципы механики. — М.: Физматгиз, 1959.
49. Дринфельд В. Г., Соколов В. В. Уравнения типа Кортевега-де Фри
■за и простые алгебры Лн//ДАН СССР. 1981. Т. 258, № 1. С. 11—16.
50. Ду-бровин Б. А. Тэта:функцйя и нелинейные уравнения//УМН. 1981
Т. 36, вып. 2. С. 11—80.
-51. Дубровин Б. А. Вполне интегрируемые гамильтоновы системы, связан
ные с матричными операторами, н абелевы многообразия // Функц. анали
и его прилож. 1977. Т. 11, вып. 4. С. 28—41.
52. Д у б р о в и н Б. А., М а т в е е в В. Б., Новиков С.1 П. Нелинейны
уравнения типа Кортевега-де Фриза, конечнозонные линейные оператор1
и абелевы многообразия//УМН. 1976. Т. 31, вып. 1. С. 55—136.
/53. Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современна
геометрия. — М.: Наука, 1979. Ч. 1 н 2; 1984. Ч. 3.
4. 3 а х а р о в В. Е., М а н а к о в С. В., Новиков С. П., Питаев
скнй Л. П. Теория солйтонов. Метод обратной задачи /Под общей ре;
Новикова С. П. — М.: Наука, 1980.
.55. Захаров В. Е., Фаддеев Л. Д. Уравнение Кортевега-де Фриза -
вполне интегрируемая гамильтонова система // Функц. анализ н его npt
лож. 1971. Т. 5, вып. 4. С. 18—27.
6. Зиглнн С. Л. Ветвление решений и несуществование первых нитеграло
в гамнльтоновой механике. I//Функц. анализ н его прнлож. 1982. Т. К
вып. 3. С. 30—41.
57. Зиглнн С. Л. Ветвление решений н несуществование первых ннтеграло
в гамильтоновой механике. II//Функц. анализ и его прилож. 1983. Т. 1"
_ вып. 1. С. 8—23.
158. Ибрагимов Н. X. Группы преобразований в математической фнзнке. -
М.: Наука, 1983.
59. Илюшечкин Н. В. О многообразии вполне интегрируемых левоинвг
риантных метрик на полупростой группе Лн // Вести. Моск. ун-та. Се]
матем., мех. 1979. № 3. С. 35—37.
450. Идельсон Н. И. Этюды по нсторнн небесной механики. — М.+ Наук;
_ 1975.
ДбуКартан Э. Интегральные ннварнанты. — М. — Л.: Гостехнздат, 194(
-8Z Кириллов А. А. Элементы теории представлений. —.М.: Наука, 197!
63. КлингеибергВ. Лекции о замкнутых геодезических. — М.: Ми]
1982.
Б4. К о б о я с и Ш., Номидзу К. Основы дифференциальной геометри:
Т. 1. — М.: Наука, 1981.
,65. Козлов В. В. Интегрируемость и неинтегрнруемость в гамнльтоново
, , '-г механике//УМН. 1983. Т. 38, вып. 1. С. 3—67.
6. Козлов В. В. Методы качественного анализа в динамике твердог
V— Тела. — М.: Изд-во Моск. ун-та, 1980.
Б7. Козлов В. В. Две интегрируемые задачи классической динамики
Вестн. Моск. ун-та. Сер. матем., мех. 1981. № 4. С. 80—83.
68. Козлов В. В. Несуществование дополнительного аналитического интегр;
ла в задаче о движении несимметричного тяжелого твердого тела вокрз
неподвижной точки//Вестн. Моск. ун-та. Сер. матем., мех. 1975. №
С. 105—110.
69. Козлов В. В., Колесников Н. Н. Об интегрируемости гамильтоиовы
систем//Вестн. Моск. ун-та. Сер. матем., мех. 1979. № 6. С. 88—91.
70. Козлов В. В., Онищенко Д. А. Неинтегрируемость уравнений Кир:
гофа//ДАН СССР. 1982. Т. 266, № 6.' С. 1298—1300.
71. Колесников Н. Н. Натуральные системы с разрешимой группой си»
метрий//Вестн. Моск. ун-та. Сер. матем., мех. 1978. Л» 5. С. 99—103.
' 72. Колокольцов В. Н. Геодезические потоки на двумерных многообр;
зиях с дополнительным полиномиальным по скоростям первым ннтегр
лом//Изв. АН СССР. Сер. матем. 1982. Т. 46, № 5. С. 994—1010.
73. Колокольцов В. Н. Новые примеры многообразий с замкнутыми rei
дезическими. — Вестн. М°ск. ун-та. Сер. матем., мех. 1984. № 4. С. 80-
82.
74. Красильщик И. С. Гамильтоновы когомологии канонических алгебр
ДАН СССР. 1980. Т. 251, № 6. С. 1306—1309.
404
75. К р и ч е в е р И. М. Алгебраические кривые и нелинейные разностные урав-
.,- нения //УМН. 1978. Т. 33, вып. 4. С. 215—216.
76. Кричевер И. М. Методы алгебраической геометрии в теории нолиней-
иых уравнений//УМН. 1977. Т. 32, вып. 6. С. 183—208.
77. К у л и ш П. П., Рейман А. Г-. Иерархия симплектическнх форм для
уравнений Шредингера и Дирака иа прямой//Записки научи, семмн,
ЛОМИ. 1978. Т. 77. С. 134—147.
78. Лаке П. Д. Интегралы нелинейных уравнений эволюции и уединенные
волны//Математика. 1069. Т. 13, № 5. С. 128—150.
79. Ландау Л. Д., Лифшиц Е. М. Механика. — М.: Наука, 1968.
80. Л е б е д е в Д. Р., М а н и н Ю. И. Гамильтонов оператор Гельфанда—Ди-
Гельфанда—Дикого н коприсоединенного представления группы Вольтерра ■// Функц. ана-
анализ и его прилож. 1979. Т. 13, вып. 4. С. 40—46.
81. Ле Нгок Тьеуен. Коммутативные наборы функций иа орбитах общего
положения конечномерных алгебр Ли//УМН. 1983. Т. 38, вып. 1. С. 179—
180.
82. Ле Нгок Тьеуен. Полные инволютивные наборы функций на расши-
расширениях алгебр Ли, связанных с алгебрами Фробеннуса//Труды семийара
по векторному н тензорному анализу. Вып. XXII. — М.: Изд-во Моск.
ун-та. 1985. С. 69—106.
■83. Лоос О. Симметрические пространства. — М.: Наука. 1985.
84. М а н а к о в С. В. Замечание об интегрировании уравнений Эйлера дина-
динамики гс-мерного твердого тела//Функц. анализ и его прнлож. 1976. Т. 10,
вып. 4. С. 93—94.
■85. М а н и н Ю. И. Алгебраические аспекты нелинейных дифференциальных
уравнений // Современные проблемы математики. — М.: Изд-во ВИНИТИ,
1978. С. 5—152. — Итоги" науки. Вып. 11.
■86. Маннн Ю. И. Матричные солнтоны н расслоения над кривыми с осо-
особенностями // Функц. анализ и его прнлож. 1978. Т. 12, вып. 4. С. 53—
63.
■87. М ещер я ко в М. В. Интегрирование уравнений геодезических левоинва-
рнантных метрик на полупростых группах Лн с помощью специальных
функций//Матем. сб. 1982. Т. 117, № 4. С. 481—493.
88. Мещер яко в М. В. О характеристическом свойстве тензора инерции
многомерного твердого тела//УМН. 1983. Т. 38, вып. 5. С. 201—202.
89. Мещер я ко в М. В. Решение уравнений Эйлера на особых орбитах
простых групп Лн // Геометрия н топология в глобальных нелинейных за-
задачах. -— Воронеж: изд-во Воронежского ун-та. 1984. С. 158—162.
90. Мещеряков М. В. Замечание о динамических системах на полупростых
алгебрах Лн//Вестн. Моск. ун-та. Сер. матем., мех. 1980. № 6. С. 17—
19.
91. Ми л нор Дж. Теория Морса. — М.: Мир, 1971.
92. Мищенко А. С, Фоменко А. Т. Курс дифференциальной геометрии
н топологии. — М.: Изд-во Моск. ун-та, 1980.
93. Мищенко А. С. Интегралы геодезических потоков иа группах Лн//
Функц. анализ н его прилож. 1970. Т. 4, вып. 3. С. 73—77.
94. М и щ е н к о А. С. Интегрирование геодезических потоков на симметри-
симметрических пространствах//Матем. заметки. 1982. Т. 31, № 2. С. 257—262.
, 95. Мищенко А. С. Интегрирование геодезических потоков на симметриче-
симметрических пространствах//Труды семинара по векторному "и тензорному анализу.
Вып. XXI. — М.: Изд-во Моск. ун-та. С. 13—22.
'96. Мищенко А. С, Фоменко А. Т. Об интегрировании уравнений
Эйлера на полупростых алгебрах Ли//ДАН СССР. 1976. Т. 231, № 3.
С. 536—538.
97. Мищенко А. С, Фоменко А. Т. Обобщенный метод Лнувилля интег-
интегрирования гамильтоновых систем//Функц. анализ и его прнлож. 1978.
Т. IE, вып. 2. С. 46—56.
58. Мищенко А. С, Фоменко А. Т. Уравнения Эйлера на конечномер-
конечномерных группах Ли//Изв. АН СССР. Сер. матем. 1978. Т. 42, № 2. С. 396—
415.
405
99. М и щ е н к о А. С, Ф о м е и к о А. Т. Интегрируемость уравнений Эйлер»
на полупростых алгебрах Ли//Труды семинара по векторному н тензорно-
тензорному анализу. Вып. XIX. — М.: Изд-во Моск. ун-та. 1979. С. 3—94.
100. Мищенко А. С, Фоменко А. Т. Интегрирование гамильтоновых
систем с некоммутативными сннметрнямн // Труды семннара по векторному
и тензорному анализу. Вып. XX. — М.: Изд-во Моск. уи-та. 1981. С. 5—
54.
101. Моз ер М. Некоторые аспекты интегрируемых гамильтоновых систем//
УМН. 1981. Т. 36, вып. 6. С. 109—151.
102. Моисеев Н. Н., Румянцев В. В. Динамика тела с полостями, содер»
жащими жидкость. — М.: Наука, 1965.
103. Новиков С. П. Периодическая задача Кортевега—де Фриза. 1//ФункЦ,
анализ н его прилож. 1974. Т. 8, вып. 3. С. 54—66.
104. Новиков С. П. Гамнльтонов формализм и многозначный аналог теории
Морса//УМН. 1982. Т. 37, № 5. С. 3—49.
105. Новиков С. П., Шмельцер И. Периодические решения уравнения
Кирхгофа свободного движения твердого тела в идеальной жидкости м
расширенная теория Люстерника—Шннрельмана—Морса - (ЛМШ). I//
Функц. аиалнз и его прилож. 1981. Т. 15, вып. 3. С. 54—66.
106. Новиков С. П. Вариационные методы и периодические решения урав-
уравнений типа Кирхгофа. II//Функц. анализ и его прилож. 1982. Т. 15, вып. 4.
С. 3—49.
107. Нехорошее Н. Н. Переменные действия — угол и их обобщении//
Труды ММО. 1972. Т. 26. С. 181—198.
108. Ни ко л ей ко Н. В. О полной интегрируемости нелинейного уравнения
Шредингера // Функц. анализ и его прилож. 1976. Т. 10, вып. 3. С. 55—69.
109. Ольшанецкнй М. А., Переломов А. М, Геодезнчесние потоки на
симметрических пространствах нулевой кривизны и явные решения обоб-
обобщенной модели Калоджеро для классического случая // Функц. анализ к
его прилож. 1976. Т. 10, вып. 3. С. 86—87.
ПО. О л ьш а нецки й М. А., Переломов А. М. Явные решения некоторых
вполне интегрируемых гамнльтоновых систем // Функц. анализ и его при-
прилож. 1977. Т. 11, вып. 1. С. 75—76.
111. Паламодов В. П. Об устойчивости равновесия в потенциальном но*
ле// Функц. анализ и его прилож. 1977. Т. 11, вып. 4. С. 42—55.
112. Певцова Т. А. Один способ построения коммутативной алгебры интег-
интегралов на алгебрах Ли // Всесоюзн. конференция по соврем, проблемам
геометрии: Тезисы докладов. — Мниск, 1979. С. 149.
ИЗ. Певцова Т. А. Симплектнческая структура орбит копрнсоедннениого
представления алгебр Ли типа £фрС//УМН. 1982. Т. 37, вып. 2. С. 225—
226.
114. П ер е л о мо в А. М. Несколько замечаний об интегрировании уравнений
движения твердого тела в идеальной жидкости // Функц. анализ и его-
прнлож. 1981. Т. 15, вып. 2. С. 83—85.
115. Переломов А. М. Интегрируемые системы классической механики и
алгебры Ли/Препринт ИТЭФ-147. 1983.
116. Пид к у йко С. И., С те пи н А. М. О решении одного дифференциально-
функционального уравнения//Функц. анализ и его прилож. 1976. Т. 10я.
вып. 2. С. 84—85.
117. Погосян Т. И.' Критические интегральные поверхности в задаче Клеб-
ша//МТТ. Киев. № 16. "С. 19—24.
118. Погосян Т. И. Построение бифуркационных множеств в одной задаче
динамики твердого тела//Механика твердого тела, 1980. Вып. 12. С. 9—
16.
119. Погосян Т. И., Харламов М. П. Бифуркационное множество и ин-
интегральные многообразия задачи о движении твердого тела в линейном
поле сил//ПММ. 1979. Т. 43, № 3. С. 419—428.
120. Погосяи Т. И., Харламов М. П. Области возможности движения в
некоторых механических системах // ПММ. 1981. Т. 45, №4. С. 605—610.
121. Пуанкаре А. Новые методы небесной механики//Избр. труды. Т. L
. М.: Наука, 1971; Т. 2, 1972.
406
122. Пуанкаре А. О проблеме трех тел и об уравнениях динамики//Иабр.
труды. Т. 2. — М.: Наука, 1972.
123. Рейман А. Г., Семеиов-Тян-Шанский М. А., Френкель И И,
Градуированные алгебры Лн и вполне интегрируемые дниамическне систе-
система //ДАН СССР. 1979. Т. 247, № 4. С. 802—805.
.124. Рейман А. Г. Интегрируемые гамнльтоновы системы, связанные с rpt-
дунрованнымн алгебрами Лн//Записки научных семинаров ЛОМИ. 1980.
Т. 95. С. 3—54.
125. Рыбников А. К. История математики. — М.: Изд-во Моск. уи-та. 1974.
126. Смей л С. Топология н механика//УМН. 1972. Т. 27, № 2. С. 77—133.
127. Степи н А. М. Интегрируемые гамнльтоновы системы. I. Методы интег-
интегрирования гамнльтоновых систем. II. Серии интегрируемых систем // Ка-
Качественные методы исследования иелннейных дифференциальных уравне-
уравнений и нелинейных колебаний. — Киев: Ин-т математики АН УССР, 1981,
328. Стернберг С. Лекции по дифференциальной геометрии. — М.: Мир,
1970.
129. Стройк Д. Я- Краткий очерк нсторнн математики. — М.: Наука, 1984.
130. Сян У. Ч. Когомологическая теория топологических групп преобразова-
преобразований.—М.: Мнр, 1979.
131. Татарннов Я. В. Портреты классических интегралов задачи о враще-
вращении твердого тела вокруг неподвижной точки // Вести. Моск. ун-та. Сер.
матем., мех. 1974. № 6. С. 99—105,
132. Татар ино в Я. В. Лекции по классической динамике. — М.: Изд-во .
Моск. ун-та, 1984.
133. Татаринов Я. В. Геометрический формализм классовой динамики; ка-
канонические первообразные // Вести. Моск. ун-та- Сер. матем., мех. 1983.
№ 4. С. 85—95.
134. Трофимов В. В. Уравнения Эйлера на борелевскнх подалгебрах полу-
полупростых алгебр Ли//Изв. АН СССР. Сер. матем. 1979. Т. 43, № 3. С. 714—
- 732.
135. Трофимов В. В. Уравнения Эйлера на конечномерных разрешимых
группах Лн//Изв. АН СССР. Сер. матем. 1980. Т. 44, № 5. С. 1191—
1199.
136. Трофимов В. В. Конечномерные представления алгебр Лн и вполне,
интегрируемые системы//Матем. сб. 1980. Т. 111, № 4. С. 610—621.
137. Трофимов В. В. О полной интегрируемости уравнений Эйлера на боре-
левских подалгебрах простых алгебр Ли//VII Всесоюзная конференция по
современным проблемам геометрии: Тезисы докладов. — Минск, 1979.
С. 201.
138. Трофимов В. В. Теоретико-групповая интерпретация уравнений магнит-
магнитной гидродинамики идеально проводящей жидкости // Нелинейные колеба-
колебания и теория управления. — Ижевск, 1981. Вып. 3. С. 118—124.
139. Трофимов В. В. Вполне интегрируемые геодезические потоки лево-
инвариантных метрик на группах Ли, связанные с коммутативными градуи-
градуированными алгебрами с двойственностью Пуанкаре//ДАН СССР. 1982.
Т. 263, № 4. С. 812—816.
140. Трофимов В. В. Снмплектические структуры иа группах автоморфиз-
автоморфизмов симметрических пространств // Вести. Моск. ун-та. Сер. матем., мех
1984. № 6. С. 31—33.
141. Трофимов В. В. О вполне интегрируемых геодезических потоках на
группе движений евклидова пространства // Некоторые вопросы математики
н механики. — М.: Изд-во Моск. ун-та. 1983. С. 8—9.
142. Трофимов В. В. Коммутативные градуированные алгебры с двойствен-
двойственностью Пуанкаре и гамильтоновы системы//Топологические и геометриче-
геометрические методы в математической физике. — Воронеж: Изд-во Воронежского
ун-та, 1983. С. 128—132.
143. Трофимов В. В. Расширения алгебр Ли и гамильтоновы системы//
Изв. АН СССР. Сер. матем. 1983. Т. 47, № 6. С, 1303—1321.
144. Трофимов В. В. Методика построения S-представленнй//Вести. Моск.
ун-та. Сер. матем., мех. 1984. № 1. С. 3—9,
407
145. Трофимов В. В., Фоменко А. Т. Интегрируемость по Лиувиллю га-
мильтоновых систем на алгебрах Лн//УМН. 1984. Т. 39, вып. 2. С. 3—56.
146. Трофимов В. В., Фоменко А. Т. Методика построения гамильтоновых
потоков на симметрических пространствах и интегрируемость некоторых
гидродинамических систем//ДАН СССР. 1980. Т. 254, № 6. С. 1349—1353.
147. Трофимов В. В., Фоменко А. Т. О реализации механических систем
на орбитах разрешимых алгебр Ли // Изв. АН СССР. Сер. механики твер-
твердого тела. 1981. № 3. С. 163.
148. Трофимов В. В., Фоменко А. Т. Динамические системы на орбитах
линейных представлеинй групп Ли н полная интегрируемость некоторых
гидродинамических систем//Функц. анализ и его прнлож. 1983. Т. 17,
вып. 1. С. 31—39.
149. Трофимов В. В., Фоменко А. Т. Групповые неинвариантные симплек-
тические структуры и гамильтоиовы потоки на симметрических простран-
ствах // Труды семинара по векторному и тензорному анализу. Вып. XXI. —
М.: Изд-во Моск. ун-та. 1983. С. 23—83.
150. Тюлина И. А. Жозеф Луи Лагранж. — М.: Наука, 1977.
151. Фоменко А. Т. Дифференциальная геометрия и топология. Дополни-
Дополнительные главы. — М.: Изд-во Моей, ун-та. 1983.
152. Фоменко А. Т. О симплектическнх структурах н интегрируемых систе-
системах на симметрических пространствах//Матем. сб. 1981. Т, 115, № 2.
С. 263—280.
153. Фоменко А. Т. Групповые симплектические структуры на однородных
пространствах//ДАН СССР. 1980. Т. 253, № 5. С. 1062—1067.
154. Фоменко А. Т. Алгебраическая структура некоторых классов вполне ин-
интегрируемых гамильтоновых систем иа алгебрах Ли // Геометрическая тео-
теория функций н топология. — Киев: Ин-т математики АН УССР, 1981.
С. 85—126.
155. Фомеико А. Т. Полная интегрируемость некоторых классических га-
гамильтоновых систем // Моногениые функции и отображения. — Киев: Ии-т
математики АН УССР, 1982. С. 3—19.
156. Фоменко А. Т. Алгебраические свойства некоторых интегрируемых га-
гамильтоновых систем // Тезисы Ленинградской международной топологиче-
топологической конференции. — Ленинград: ЛОМИ, 1982, С. 46.
157. Фоменко А. Т. Алгебраическая структура некоторых интегрируемых га-
гамильтоновых систем // Топологические и геометрические методы в матема-
математической физике. — Воронеж: Изд-во Воронежского ун-та, 1983. С. 84—
ПО.
158. Фоменко А. Т. Симметрические пространства н интегрирование некото-
некоторых гамильтоиовых систем//О. Лоос. Симметрические пространства. — M.J
Наука, 1985.— Приложение. С. 183—201.
159. Фоменко А. Т. Топология трехмерных многообразий и интегрируемые
механические гамильтоновы системы |/ V Тнраспольский симпозиум по
общей топологии и ее приложениям. — Кишинев, 1985. С. 235—237.
160. Фоменко А. Т. Топология поверхностей постоянной энергии интегрируе-
интегрируемых гамильтоновых систем и препятствия к интегрируемости // Изв. АН
СССР. 1986. № 6. С. 1276—1307.
161. Фомеико А. Т. Теория Морса интегрируемых гамильтоновых систем//
//ДАН СССР. 1986. Т. 287, № 5. С. 1071—1075.
162. Фомеико А. Т., Цншанг X. О топологии трехмерных многообразий,
возникающих в гамильтоновой механике//ДАН СССР. —. В печати.
163. Харламов М. П. Топологический анализ классических интегрируемых
систем в динамике твердого тела//ДАН СССР. 1983. Т. 273, № 6. С. 1322—
1325.
164. Харламов М. П. К исследованию областей возможности движения в
механических снстемах//ДАН СССР. 1982. Т. 267, № 3. С. 571—573.
165. Хелгасон С. Дифференциальная геометрия и симметрические простран»
ства. — М.: Мир, 1964.
(^166. Якоби К. Лекции по динамике. — М.—Л., 1933.
167. Я но К., Бохнер G. Кривизна и числа Бетти. — М.: ИЛ, 1957.
408 " -
168 Adler M., Moerbeke P. van. Completely Inteerahl» Systems, Euclidian
Lie Algebras and Curves//Advances in Math. 10Ж). V. аи, N 3, P. 207—
317.
169. Adler M., Moerbeke P. van. Linearization ol Ilimttlonian Systettti,
Jakoby varieties and Representation Theory//Adv. in Math, I9H0. V. 38, N .'»
P. 318—379.
170. Avez A., Li ch n e г о w I с h Л., Diaz-Miranda Л. Ниг I'ulfjebre des
automorphiser infeniteslmnux d'mw varlete symplectique//,), ut Differential
Geometry. 1974. V. 9, N 1. P. 1-40.
171. Adler M., Moser J. On n claaa polynomials connected with tin1 Korleweg
de Vries equation"//Comm. Math. Phys, I07H. P. 1—30.
172. Airault H., McKean H. P.. Mo ser J. Rational and elliptic solution oi
the Korteweg—de Vries equation and relnlmt many body problem//Comm.
Pure Appl. Math. 1977. V. 30, N I. P. 0B I4H
173. Adler M., Moerbeke P. van. Tht> «Igt'bitili1 Ililegrability of geodesic flow
on SOD)//Invcnt. Math. 1982. V. 07. P. 807-39».
174. Adler M., Moerbeke P. van. Proc, Net, Aead, ol Sri. USA//1984. V. 81.
P. 4613—4616.
175. Atiyah M. F. Convexity and commuting hnmlltonlatis//Bull. London Math.
Soc. 1982. N 14. P. 1—15.
176. Atiyah M. F., Bott R. The moment шли and «qulvarlniil cohomology//
//Topology. 1984. V. 23, N 1. P. 1—28.
177. Atiyah M. F. Angular momentum, convex polyhedra and algebraic goonict-
ry//Proc. Edinburgh Math. Soc. Ser. 2. 1983. V. 26. P. 121—133.
178. Bernat P., Conze N., Vergne M. Representations des groupes de Lie
resolubles. A paraftre dans collection «Monographios de la Socl6te Matema-
tique de France». — Paris//Dunod, 1972.
179. В о go у a v 1 e n sk у О. I. Integrable Euler equations on SOD) and their
physical applications//Comm. in Math. Phys. 1984. V. 93. P. 417—436.
180. Bott R. Non-degenerate critical manifolds//Ann. of Math. Ser. 2. 1954.
V. 60, N 2. P. 248—261.
181. В u r ch n a 11 J. L., Chaurtdy T. W. Commutative ordinary differential
operators//Proc. London Math. Soc. Ser. 2. 1923. V. 21, N 6. P. 420—440;
Proc. Royal Soc. London (A). 1928. V. 118. P. 557—593; Proc. Royal Soc.
London (a). V. 134. P. 471—485.
182. Calogero F. Solution of the one-dimensional n-body problems with qu-
quadratics and/or inversely quadratic pair potenzials//J. Math. Phys. 1971.
V. 12. P. 419—436. , - '
183. Conley C, Zehnder E. Morse-type index theory for flows and periodic
solutions for Hamiltonian equations//Comm. Pure Appl. Math. 1984. V. 37,
N 2. P. 207—255.
.184. Darboux G. Lecons sur la theorie generale des surfaces et les applica-
applications geometriques du surfaces et les applications geometriques du calcul
infinitesimal. V. 3. — Paris: Gauthier—Villar, 1891.
185.'Dickson L. E. Differential equations from the Group Standpoint//Annals
of Math. 1924. V. 25, N 4. P. 287—378.
186. Dixmier J., Duflo M., Vergne M. Sur la representation coadjointe
d'une algebre de Lie//Composito Math. 1974. V. 29, N 3. P. 309—323.
187. Duflo M., Vergne M. Une propriete de la representation coadjointe d'une
algebre de Lie//C. R. Acad. Sc- Paris. 1969. V. 268. P. 583—585.
188. Duistermaat J., Heckman G. On the variation in the cohomology of
the symple'ctic form of the reduced phase space//Invent. Math. 1982. V. 69,
N 2. P. 259-268.
189. Ebin D. Integrability of perfect fluid motion//Comm. Pure and Appl. Math.
1983. V. 36, N 1. P. 37—54.
190. Flaschka H. Toda lazzice II//Progr. Theor. Phys. 1974. V. 51. P. 703—
716.
191.Fomenko A. T. The integrability of some hamiltonian systems//Ann. of
global Analysis and Geometry. 1983. V. 1, N 2. P. 1 — 10.
409
192. Fomenko A. T. Algebraic Structure of Certain Integrable Hamiltonianj
Systems//Global Analysis—Studies and Appl. I. 1984. P. 103—127. — (Lec-
(Lecture Notes in Math. V. 1108).
193. Fomenko A. T. Algebraic properties of some integrable hamiltonian sys-
tems//Topology, Proceedings, Leningrad 1982. 1984. P. 246—257. — (Lec-
(Lecture Notes in Math. V. 1060).
194. Funk P. Uber Flachen mit lauter geschlossenen geodatischen Linien//Math.
Ann. 1913. Bd 74. S. 278—300.
195. Galgani L., Giorgilli A., Strelcyn J.-M. Chaotic motions and tran-
transition to stochaslicity in the classical problems of the heavy rigid body with:
a fixed point//Preprint, 1980.
196. Gardner С S. Korteweg—de Vries equation and generalization. IV. The
Korteweg—de Vries equation as a hamiltonian system//J. Math. Phys. 1971.
V. 12, N 8. P. 1548—1551.
197. Gardner C.S, Green J. M., Kruskall M. D., Miura R. M. Korte-
Korteweg—de Vries Equation and Generalization. VI. Methods for Exact Solu-
tion//Comm. Pure Appl. Math. 1974. V. 27, N 1. P. 97—133.
198. Golo V. L. Nonlinear regimes in spin dynamics of superfluid 3He//Letter in.
Math. Phys. 1981. V. 5. 155—159.
199. Green L. W. Auf Wiedersehenflachen//Ann. Math. 1963. Bd 78, H. 2.
S. 289—299.
200. Guil I em in V. The Radon transform on Zoll surfaces//Preprint. 1976;.
Advances in Math. 1976. V. 22, N 1. P. 85—119.
201. Guillemin V., Sternberg S. Symplectic technique in physics. —
L.—N. Y.—Cambridge: Camtiridge Univ. Press, 1984.
202. Guillemin V., Sternberg S. Convexity properties of the moment map-
mapping. I//Invent. Math. 1982. V. 67, N 3. P. 491—513.
203. Guillemin V., Sternberg S. Convexity properties of the moment map-
mapi II//It Mth 1984 V 77 N 3 P 533546
ll V., Sg . y pprt
ping. II//Invent. Math. 1984. V. 77, N 3. P. 533—546.
4. Hai L Th lbi lt itbilit f
pg // ,
204. Haine L. The algebraic complete integrability of geodesic flow on SO(n)..
Comm. Math. Phys. 1984. V. 94. P. 271—287.
205. Haine L. Geodesic flow on SOD) and abelian surfaces. Math. Ann. 1983.
Bd 263, H. 4. S. 435—472.
206. Holm D. D., Kupershmidt B. A. Poisson brackets and Clebsch rep-
representations for magnetohydrodynamics, multifluid plasmas, and elasticity-
Physica D. Nonlinear phenomena. 1983. V. 6 D, N 3. P. 347—363.
207. Iacob A., Sternberg S. Coadjoint structures, solutions and integrabi-
integrability//Lecture Notes in Phys. V. 120. — Springer-Verlag, 1980.
208. К а с V. Infinite-Dimensional Lie Algebras. — Boston—Basel—Stuttgart:
Birkhauser, 1983. — (Progress in Math. V. 44).
209. Kalnins E. G., Mtller W., Winternitz P. The group 0D), separa-
separation of variables and the hydrogen atom. SIAM Journal- of Appl. Math. 1976..
V. 30, N 4. P. 630—634.
210. Kama 1 in S. A., Perelomoy A. M. Construction of Canonical Coordi-
Coordinates on Polarized Coadjoint Orbits of Lie Groups//Comm. Math. Phys. '1985.
V. 97. P. 553—568.
211. Kazhdan D., Kostant В., Sternberg S. Hamiltonian group Actions
and Dynamical systems of Calogero Type//Comm. on Pure and Appl. Math.
1978. V. 31, N 4. P. 481—507.
212. Kir wan F. Convexity properties of the moment mapping. III//Invent. Math.
1984. y. 77, N 3. P. 547—552.
213. Klein F. Vorlesungen uber die Entwicklung der Mathematik im 19 Jahr-
hundert. II. — Berlin, 1927.
214. Knorrer H. Geodesies on the ellipsoid//Invent. Math. 1980. V. 59, N 2.
P. 119—143.
215. Koblitz A. H. A convergence of lives Sofia Kovalevskaia: scientist, wri-
writer, revolutionary. — Boston—Basel—Stuttgart: Birkhauser, 1984.
216. Kostant B. On differential geometry and homogeneous spaces. I//Proc.
Nat. Acad. Sci. USA. 1956. V. 42, N 5. P. 258—261; Troc. Nat. Acad. Sc«;
USA. 1956. V. 42, N 6. P. 354—357.
410
217. Kostant B. The solution to a generalized Toda lattice and representation
theory//Advances in Math. 1979. V.,34, N 3. P. 195—338.
218. Kostant B. On convexity, the Weyl group and the Iwasawa decomposite
on//Ann. Sci. Ec. Norm. Sup. Ser. 4. 1973. V. 6. P. 413—455.
219. Kupershmidt B. A., Ratiu T. Canonical maps between semidirect pro-
products with applications to elasticity and superfluids//Comm. Math. Phys.
1983. V. 90. P. 235—250.
220. Kupershmidt B. A., Wilson G. Modifying Lax Equations and the
Second Hamiltonian Structure//Invent. Math. 1981. V. 62, N 3. P. 403—436.
221. La comb a E. Mechanical systems with symmetry on homogeneous spaces//
//Trans. Amer. Math. Soc. 1973. V. 185. P. 477—491.
222. L a n g 1 о i s M. Contribution a l'etude, du mouvement du coups rigide a N
dimensions auto d'un point fixe//These presentee a la faculte des sciences
de 1'universite de Besamjon.— Besanc.on, 1971.
223. Lojasiewicz S. Triangulation of semi-analytic sets//Annali della Scuo-
la Normale Superiore di Pisa. 1964. Serie III. V. XVIII, N 4. P. 449—474.
224. Lose о L. Integrabilite en mecanique celeste//J. Mecanicue. 1974. V. 13,
N 2. P. 197—223.
225. M a g r i F. A simple model of the integrable Hamiltonian equation//J. Math.
Phys. 1978. V. 19. P. 1.156—1162.
226. M u m f о г d D. An algebro-geometric construction of commuting operators
and of solution to the Toda lattice equation and related non linear equati- -
ons//Proc. Intern. Syrhp. on Algebraic Geometry. — Kyoto, 1977. P. 115—
153.
227. Marsden J., Weinstein A. Reduction of symplectic manifolds with
symmetry//Reports on Math. Phys. 1974. V. 5, N 1. P. 121—130.
228. McKeen H. Integrable systems and algebraic curves//Global Analysis.—
Berlin—Heidelberg—New York: Springer, 1979. P. 83—200. — (Lecture No-
Notes in Math. V. 755).
229. McKcan H.t Trubowitz E. Hill's operator and hyperelliptic function
theory in the presence of in finitely many brunch points//Comm. Pure Appl.
Math. 1976. V. 29. P. 143—226.
230. M i 1 п о г J. Curvature of left invariant metrics on Lie groups//Adv. in
Math. 1976. V. 21, N 3. P. 293—329.
231.Mishcenko A. S., Fomenko A. T. Symplectic Lie group action//Al-
action//Algebraic Topology Aarhus, 1978, Proceedings. Springer-Verlag, 1979. P. 504—
539. (Lecture Notes in Math. V. 763).
232. Moerbeke P. van. The spectrum of Jacoby matrices//Invent. Math. 1976.
V. 37. P. 45—81.
233. Moerbeke P. van., Mumford D. The spectrum o.f difference operators
and algebraic curves//Acta Math. 1979. V. 143, N 1, 2. P. 93—154.
234. Moody B. A new class of Lie algebras//J. Algebra. 1968. V. 10. P. 211—
230.
235. M о s e r J. Three 'integrable Hamiltonian systems connected with lsospectral
deformations//Advances in Math. 1975. V. 16, N 2. P. 197—220.
236. M о s e r J. Geometry of quadrics and spectral theory//The Chern symposium,
1979. Springer Verlag, 1980. P. 147—188.
237. 01 sh a net sky M. A., Per el ото v A. M. Explicit solutions of the clas-
classical generalized Toda models//Invent. Math. 1979. V. 56. N 3. P. 261—
269.
238. О 1 s h a n e t s"k у M. A., Perelomov A. M. Completely integrable Ha-
miltonian systems connected with semisimple Lie algebras//Invent. Math.
1976. V. 37. N 2. P. 93-108.
239. О r 1 i к P., V о g t E., Z i e s с h a n g H. Zur Topologie. gefaserter dreidimen-
sionaler Mannigfaltigkeiten//Topology. 1967. Bd 6. N 1. S. 49—65.
•240. Paters J., Sharp R. Т., Winternitz P., Zassenhaus H. Invari-
Invariant of real low dimension Lie algebras//J. Math. Phys. 1976. V. 17. N 6.
P. 986—994.
241. Pe r e lo m о v A. M. The simple relation between certain dynamical sys-
systems/Math. Phys. 1978. V. 63. P. 9—11.
Ill
242. Ре r el ото v-A. M.-Lax representation for the systems of S. Kovalevsky
type//Comm. Math. Phys. 1981. V. 81. P. 239—241.
243. Preissmann A. Quelques propertietes global des espaces de Rieman//
//Comment. Math. Helv. 1943. V. 15, N 2. P. 175—216.
244. RaisM. Indeces of semi-direct product. £XPG//C. R. Acad. Sc. Paris. 1978.
V. 287. N 4. Ser. A. P. 195—197.
245. R a t i u T. The C. Neumann problem as a completely integrable system on
an adjoint orbit//Trans. of the Amer. Math. Soc. 1981. V. 264. N 2. P. 321—
329.
246. R a t i u T. Euler-Poisson equations on Lie algebras and the N-dimensional
heavy rigid body//Amer. J. of Math. 1982. V. 104. N 2. P. 409—448.
247. Ratiu Т., Moerbeke P. van. The Lagrange rigid body motion//Annales
de l'lnstitut Fourier. 1982. V. 32. N 1. P. 211—234.
248. Reyman A. G., Semenov-Tian-Shansky M. A. Reduction of Ha-
miltonian systems, affine Lie algebras and Lax equations I//Invent. Math.
1979. V. 54. N 1. P. 81—100.
249. Reyman A. G., Semenov-Tian-Shansky M. A. Reduction of Ha-
miltonian systems, affine Lie algebras and Lax equations. II//Invent. Math.
1981. V. 63. N 3. P. 423—432.
250. Sourian J. M. Structure des systems dynamiques. — Paris, 1970.
251. Steklof f W. Ann. Fac. Sci. Univ. de Toulouse//1909. V. 1, ser. 3. P. 145—
256.
252. Takiff S. J. Rings of Invariant polynomials for a class of Lie algebras//
//Trans, of the Amer. Math. Soc. 1971. V. 160. P. 249—262.
253. Tischler D. Closed 2-forms and an embedding theorem for symplectic ma-
nifolds//J. Diff. Geom. 1977. V. 12. P. 229—235.
254. T i m m A. Integrable geodesic flows on homogeneous spaces//Ergod. Theory
and Dynam. Syst. 1981. V. 1. N 4. P. 495—517.
255. Waldhausen F. Eine Klasse Von 3-dimensional Mannigfaltigkeiten. I//
//Invent. Math. 1967. V. 3. N 4. P. 308-333.
256. Weinstein A. Symplectic geometry //Bull. Aner. Math. Soc. 1981. V. 5.
N 1. P. 1—13.
257. Weinstein A. On the volume of manifolds all of whose geodesies are
closed//! Diff. Geom. 1974. V. 9. P. 513—517.
258. V e r g п е М. La structure de Poisson sur l'algebre symmetrique d'une al-
gebre de Lie nilpotente//Bull. Soc. Math. Fance. 1972. V. 100. N 3. P. 301—
335.
259. Wilson G. Commuting flows and conservation laws fod Lax equations//
//Math. Proc. Cambridge Philos. Soc. 1979. V. 86. N 1. P. 131—143.
260. Wolf J. A. Representations associated to minimal coadjoint orbits//Lecture
Notes in Math. 1978. V. 676.
261. Yau S. T. On the Ricci curvature of a compact Kahler manifold and the
complex Monge-Атрёге equations. I//Comm. Pure. Appl. Math. 1978. V. 31.
N 3. P. 339-411.
262. Z о 11 О. Uber Flachen mit Scharen geschlossener geodatischen Linien//
//Math. Ann. 1903. Bd 57. S. 108—133.
ДОПОЛНИТЕЛЬНЫЙ СПИСОК ЛИТЕРАТУРЫ
263. V e r g n e M. La structure de Poisson" sur l'algebre symeirique d'une al-
gebre de Lie nilpotente//Bull. Soc. Math. France. 1972. V. 100. N 3. P. 301—
335.
264. В и н б е р г Э. Б., О н и щ и к А. Л. Семинар по алгебраическим группам и
группам Ли. 1967/1968. — М.: Изд-во Моск. ун-та. 1969.
265. Kostant В. The principal three-dimensional subgroup and the Betti num-
numbers of a complex simple Lie groups//Amer. J. Math. 1959. V. 81. N 4.
P. 973-1032.
266. Кар а сев М. В., Ma слов В. П. Асимптотическое и геометрическое кван-
товаиие//УМН. 1984. Т. 39, вып. 6. С. 115—173.
267. М а с л о в В. П. Теория возмущений и асимптотические методы. — М.:
Изд-bd Моск. ун-та, 1965. "
412
288. Mac лов В. П. Операторные методы. — М.: Наука, 1973.
269. Фаддеев Л. Д. Квантовые вполне интегрируемые модели теории поля//
//Проблемы квантовой теории поля. — Дубиа, 1979. Р-12462. С. 249—
299.
270. Gromov M. L. A topological technique for construction of solutions of
differential equations and inequalities//Actes Congres Intern. Math. (Nice,.
1970). N 2. — Paris: Gauthier—Villard. P. 221—225.
271. Moser J. On the volume elements on a manifolds//Trans< Amer." Math.
Soc. 1965. V. 120. N 2. P. 286—294.
272. Милнор Дж., С та шеф Дж. Характеристические классы. — М.: Мир,. /
1979.
273. Фукс Б. А., Ш а б а т Б. В. Функции комплексного переменного. — М.:
Гостехиздат, 1949.
274. Элашвили А. Г. Фробениусовы алгебры Ли. П//Труды Тбилисского ма-
математического ин-та. Т. 77. — Тбилиси: Изд-во Мецииереба, 1985. С. 127—
137.
275. Ле Хоиг Ван, Фоменко А. Т. Лагранжевы многообразия и индекс
Маслова в теории минимальных поверхностей//ДАН СССР. 1987. — В пе-
печати.
276. Переломов А. М. Представление Лакса для систем типа С. Ковален-
ской//Функц. анализ и его прилож. 1982. Т. 16, вып. 2. С. 80—81.
277. Андреев Е. М., Винберг Э. Б., Элашвили А. Г. Орбиты наиболь-
наибольшей размерности полупростых регулярных линейных групп Ли//Функц.
анализ и его прнлож. 1967. Т. 1, вып. 4. С. 3 7.
278. Элашвили А. Г. Канонический вил и стационарные подалгебры точек
общего полбжеиия для простых линейных групп Ли//Фупкц. лнали.1 и его-
прнлож. 1972. Т. 6. № 1. С. 51—62.
279. Э л а Ш в и л и А. Г. Стационарные иодплгебры Точек общего положение
для неприводимых линейных групп Ли//Фупкц. аинли» и его прилож. 1972.
Т. 6, цып. 2. С. 65—78.
280. Ко я л oil В. В. Топологические препятствия к интегрируемости натуряль-
ных механических систем//ДАН СССР. 1Н7Й. Т. 24». № 0. С. 1290—
1302.
281. Биркгоф Дж. Д. Динамические системы. М. Л.: ОГИЗ, 1941,
282. Богоявленский О. И. Интегрируемые урапиении Эйлеиа на алгебрах
Ли, иозникающие в задачах математической фи.1ики//И.щ. АИ СССР. Сер.
матем. 1984. Т. 48. № 5. С. 883—938.
283. Богоя в л е н с к и й О. И. Некоторые интегрируемые случаи уравнений
Эйлера//ДАН СССР. 1986. Т. 287. № б. С. 1105- 1108.
284. Матвеев С. В., Фоменко А. Т., 111 а р к о П. Н, Круглые функции'.
Морса и изоэнергетические поверхности интегрируемых гймнльтоновых си-
стем/Преприит. — Киев: Ин-т математики ЛИ УССР, 1988,
285. Браилов А. В. Построение вполне интегрируемых гепдмических потоков
на компактных симметрических простри11Стнйх//И:1П. АН СССР. Сер. ма-
матем. 1986. Т. 50. № 4. С. 661—674.
286. Болей нов А. В. Новые примеры пполмс интегрируемых систем на ал-
алгебрах Ли//Геометрия, дифференципльные урапнення и механика. — М.!
Изд-во Моск. ун-та, 1980. С. 54—58.
287. Б о л с и и о в А. В. Инволютивные семейства функций на некоторых ал-
алгебрах Ли//Современные вопросы мехнннки и технологии машиностроения.
П. — М.: ВИНИТИ, 1936. С. 57.
288. Болсииов А. В. Полная интегрируемость урянпений Эйлера на орбитах
Ad* групп £/(п)хФС" и SU(n) Х*С"//Вестн. Моск. ун-та. Сер. матем.,
мех. 1986. № 4. С. 79—81.
289. Ошемков А. А. Боттовскне. интегралы некоторых интегрируемых га-
мильтоновых систем // Геометрии, дифференциальные уравнения и механи-
механика. — М.: Изд-во Моск. ун-тн, 1986. С. 115-117.
290. Fomenko А. Т. New lopologlcal Invariant of integrable Hamiltonians//'
//Baku International Topologlcul Conference. Abstracts, Part 2,, 1987..
P. 316.