Author: Абрамович Г.Н.
Tags: экономическая геология месторождения полезных ископаемых механика газовая динамика
ISBN: 5-02-014015-5
Year: 1991
Text
Г. Н. АБРАМОВИЧ
ПРИКЛАДНАЯ
ГАЗОВАЯ
ДИНАМИКА
ЧАСТЬ 1
ИЗДАНИЕ ПЯТОЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1991
ББК 22.25
А16
УДК 553@75.8)
Рекомендовано Государственным комитетом СССР
по народному образованию
д хр использования в учебном процессе
студентами высших технических учебных заведений
Л б р i
руководство:
рамович Г. II. Прикладная газовая динамика. В 2 ч. Ч. 1: Учеб
ство: Для втузов.— 3-е изд., перераб и доп.—М.: Наука. Гл. ред.
^,т, ,. IOOI (И\(Л „ Т СТЗЛТ tt ПО (Л А /, П 1 ч ^
РУКОВОДСТВО: /1,. Г; 1 ЫуЗОВ. O-U 1ЫД., JlfpUfJclU 11
физ-маг. лиг, 1991.— E00 с—ISBN 5-02-014015-5.
Изложены основы газовой динамики в применении к теории реактшшых
двшагелеп и других газовых машин и аппаратов.
В части 1 рассмотрена теория одномерных 1азовых течений, на которой
базируются методы расчета реактивных двигателей, лопаточных машин,
эжекторов, аэродинамических труб и испытательных стендов. Изложены
теория пограничного слоя и теория струй, лежащие в основе определения
сопротивления трения, полей скорости и температуры в соплах, диффузо-
диффузорах, камерах сгорания, эжекторах и т. и.
В части 2 рассмотрены гпнерзвуковые течения, элементы магнитной
гидродинамики, течения разреженных газов, а также теории крыла и реше-
решеток крыловых профилей. В пятое издание D-е изд—1976 г.) включены
материалы по численным методам св-ерхзвуковой газовой динамики, повью
сведения о струях и спутпом потоке.
Для студентов авиационных вузов, инженеров и специалистов в обла-
области газовой динамшат.
Табл. 11. Ил. 299 Библиогр. 69 назв.
Рецепзепт доктор физико-математических наук А. Н. Крайко
„,,„,_„
А
ISBN 5-02-014015-5 (ч. 1)
ISBN 5-02-014961-6
©«Наука» Фияматлит, 197G;
с изменениями, 1991
ОГЛАВЛЕНИЕ
Предисловие к пятому изданию 8
Предисловие к четвертому изданию 8
Предисловие к третьему изданию 9
Глава I. Уравнения газовой динамики для единичной струйки 11
§ 1. Уравнение неразрывности 11
§ 2. Уравнение энергии 13
§ 3. Предельная скорость движения газа. Число Маха .... 22
§ 4. Механическая форма уравнения энергии (уравнение Бер-
нулли) 27
§ 5. Уравнение количества движения 37
§ 6. Уравнение моментов количества движения 45
§ 7. Энтропия 48
§ 8. Расчет реактивной силы (тяги) 51
Глава II. Элементы гидродинамики i 58
§ 1. Движение жидкой частицы 58
§ 2. Уравнение неразрывности 61
§ 3. О силах, действующих в жидкости 62
§ 4. Связь между напряжениями и деформациями .... 65
§ 5. Уравнения Навье — Стокса 68
§ 6. Уравнение энергии 69
§ 7. Гидродинамическое подобие 75
§ 8. Слоистые течения 86
§ 9. Уравнения движения идеальной жидкости 90
§ 10. Плоские установившиеся движения идеальных жидкости и
газа 95
§ 11. Циркуляция скорости 99
§ 12. Примеры плоских потенциальных установившихся течений
несжимаемой жидкости 108
§ 13. Интегральная форма уравнений газовой динамики . . . 111
Глава III. Скачки уплотнения 114
§ 1. Прямые скачки уплотнения 114
§ 2. Косые скачки уплотнения 126
§ 3. О применении пневматического насадка в сверхзвуковом
потоке 140
Глава IV. Ускорение газового потока 143
§ 1. Сверхзвуковое сопло 143
§ 2. Нерасчетные режимы истечения из сопла Лаваля . . . 150
§ 3. Сверхзвуковое течение газа с непрерывным увеличением ско-
скорости (течение Прандтля — Майера) 155
§ 4. Обтекание плоской стенки 167
§ 5. Обтекание выпуклой криволинейной стенки 169
§ 6. Истечение из единичного плоского сопла с косым срезом в
пространство с пониженным давлением 171
§ 7. Характеристики уравнений установившегося течения
идеального газа ............. 173
1*
4 ОГЛАВЛЕНИЕ
§ 8. Плоские изэнтропические и изоэнергетические течения 176
§ 9. Взаимодействие однородных сверхзвуковых потоков . . . 178
Глава V. Одномерные течения газа 181
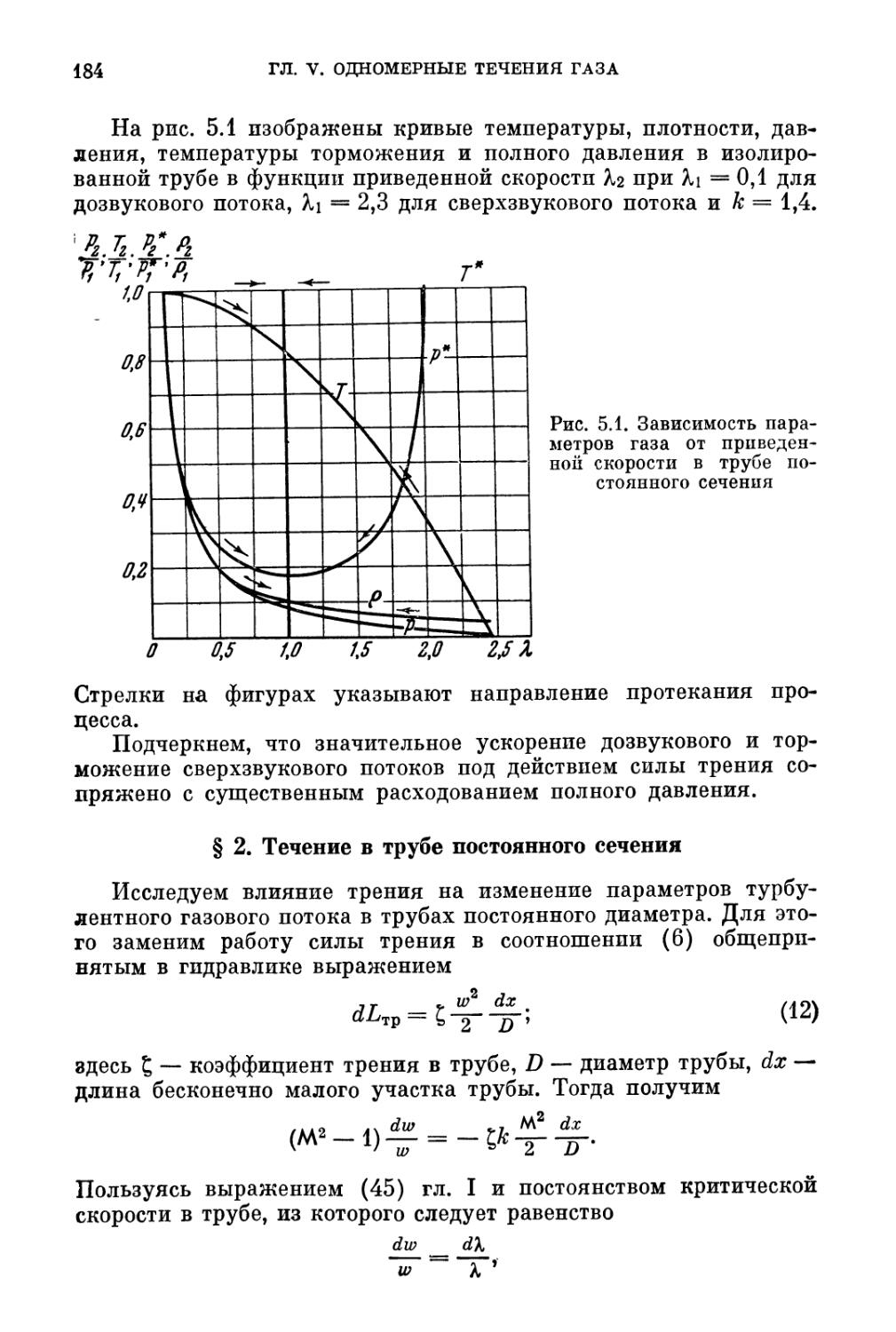
§ 1. Адиабатическое течение газа с трением. Кризис течения 181
§ 2. Течение в трубе постоянного сечения 184
§ 3. Движение подогреваемого газа по трубе постоянного сечения 192
§ 4. Общие условия перехода от дозвукового течения к сверх-
сверхзвуковому и обратно 201
§ 5. О распространении детонации и горения в газах .... 218
§ 6. Расчет газовых течений с помощью газодинамических
функций 233
§ 7. Течение газа с трением в цилиндрической трубе при задан-
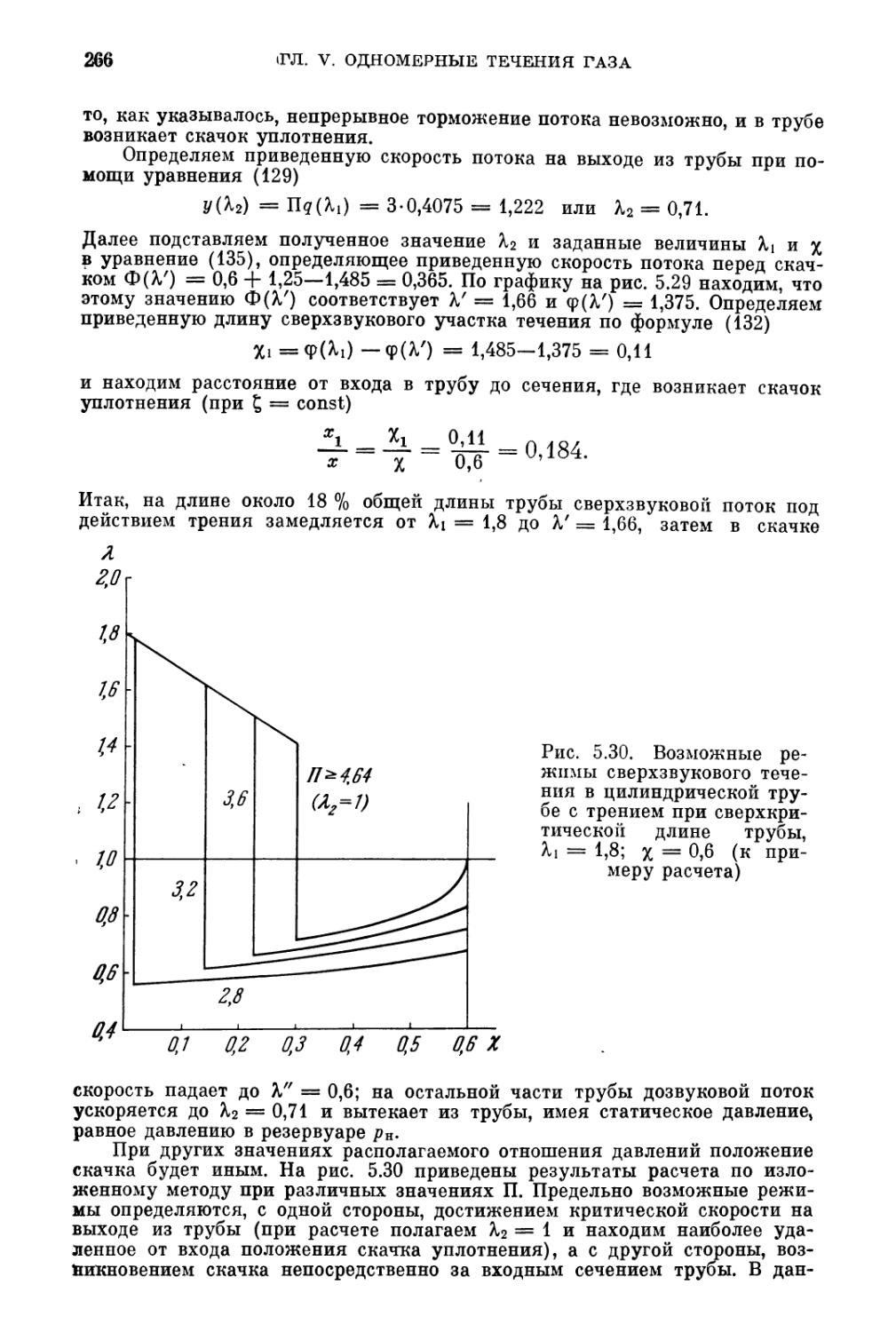
заданном отношении давлений на входе и выходе 259
§ 8. Осреднение параметров неравномерного потока .... 267
Глава VI. Теория пограничного слоя 276
§ 1. Основные понятия пограничного слоя 276
§ 2. Ламинарный пограничный слой 283
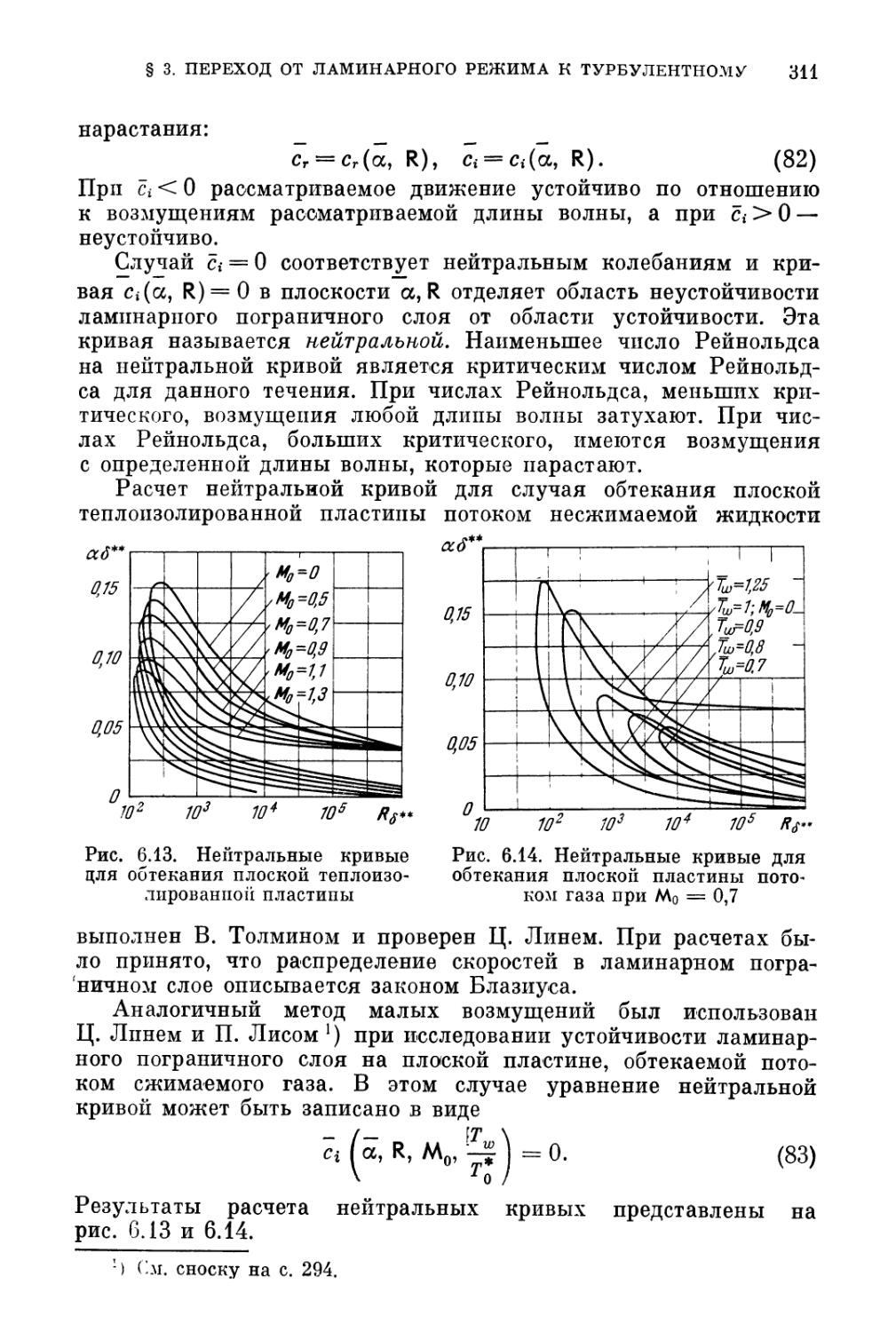
§ 3. Переход от ламинарного к турбулентному режиму течения
в пограничном слое 308
§ 4. Турбулентный пограничный слой 314
§ 5. Отрыв пограничного слоя 329
§ 6. Взаимодействие пограничного слоя со скачками уплотнения 338
§ 7. Течение жидкости в трубах 348
Глава VII. Турбулентные струи 361
§ 1. Общие свойства струй 361
§ 2. Изменение параметров по длине струи 377
§ 3. Начальный и переходный участки струи 389
§ 4. Основной участок струи в спутном потоке 393
§ 5. Влияние неизобаричности струи на закономерности ее рас-
распространения 397
§ 6. Одномерная теория начального («газодинамического») участ-
участка нерасчетной сверхзвуковой струи 408
Глава VIII. Течения газа в соплах и диффузорах ..... 429
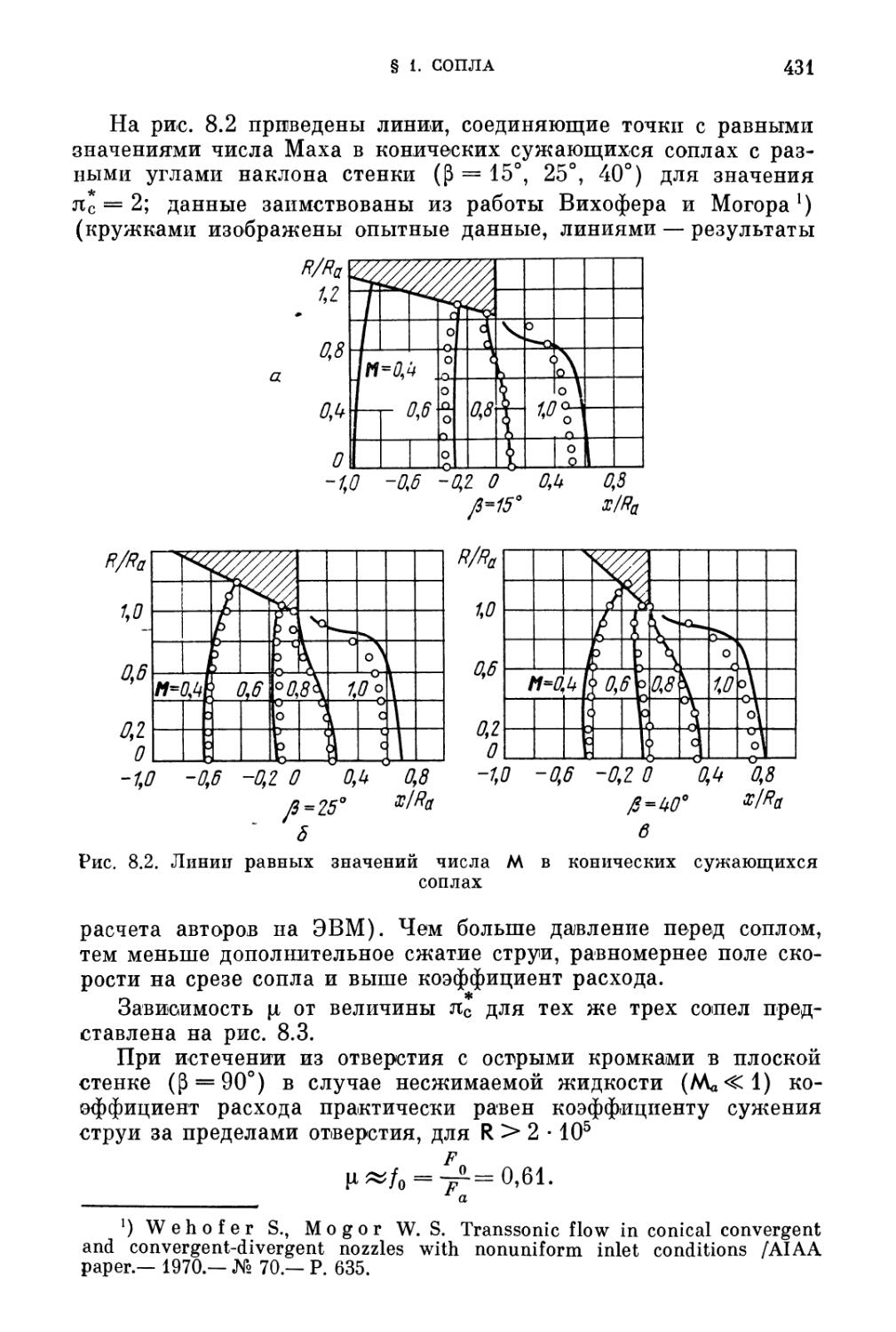
§ 1. Сопла 429
§ 2. Формы сопел 443
§ 3. Дозвуковые диффузоры 452
§ 4. Сверхзвуковые диффузоры 464
Глава IX. Газовые эжекторы . 492
§ 1. Назначение и схемы эжекторов 492
§ 2. Рабочий процесс эжектора 496
§ 3. Расчет газового эжектора 505
§ 4. Критические режимы работы эжектора. Запирание эжектора 518
§ 5. Характеристики эжектора 525
§ 6. О режиме течения на выходе из смесительной камеры 528
§ 7. Особенности работы эжектора со сверхзвуковым соплом 535
§ 8. Приближенные формулы расчета эжектора 543
§ 9. Примеры расчета эжектора 548
§ 10. Теория эжекторного увеличителя реактивной силы . . . 553
Приложения I—V 566
Список литературы 590
Именной указатель 593
Предметный указатель t « • * . » * « 594
ОГЛАВЛЕНИЕ ЧАСТИ 2
Глава X. Элементы газовой динамики единичного профиля и ре-
решетки профилей 5
§ 1. Основные геометрические параметры крылового профиля и
решетки профилей 5
§ 2. Теорема Жуковского о силовом воздействии потенциаль*
ного потока 8
§ 3. Влияние вязкости на силовое воздействие потока ... 13
§ 4. Аэродинамические коэффициенты 17
§ 5. Профиль в плоском потоке несжимаемой жидкости ... 19
§ 6. Дозвуковое обтекание профиля 30
§ 7. Сверхзвуковое обтекание профиля 41
§ 8. Околозвуковое обтекание профиля 54
§ 9. Обтекание решетки профилей дозвуковым потоком газа 64
§ 10. Обтекание решетки профилей потоком газа со сверхзвуко-
сверхзвуковой осевой составляющей скорости 73
§ 11. Обтекание решетки сверхзвуковых профилей потоком газа
с дозвуковой осевой составляющей скорости 83
§ 12. Некоторые сведения о пространственном обтекании единич-
единичного крыла и решетки крыльев 98
Глава XI. Гиперзвуковые течения газа 106
§ 1. Изменение параметров газа в изоэнтропическом гиперзвуко-
гиперзвуковом потоке 106
§ 2. Гиперзвуковое течение около выпуклого тупого угла 108
§ 3. Плоская ударная волна в гиперзвуковом течении . . . . 110
§ 4. Гиперзвуковое обтекание плоской пластины при малом угле
атаки 115
§ 5. О гиперзвуковом обтекании тонких заостренных спереди тел
§ 6. Закон сопротивления Ньютона 116
§ 7. Влияние малого затупления переднего конца тонкого тела 118
на его обтекание при гиперзвуковых скоростях . . . . 124
§ 8. О влиянии вязкости в гиперзвуковых течениях .... 128
Глава XII. Течения разреженных газов 132
§ 1. Различные типы течений разреженных газов 132
§ 2. Скачки скорости и температуры у стенки при течении газа
со скольжением 135
§ 3. Течение газа со скольжением в трубе 140
§ 4. Внешнее сопротивление тел в потоке разреженного газа при
наличии скольжения 145
§ 5. Свободно-молекулярные течения газа и элементы кинетиче-
кинетической теории газов 147
§ 6. Давление и напряжение трения при свободно-молекулярном
обтекании твердого тела 153
§ 7. Расчет аэродинамических сил при свободно-молекулярном
обтекании твердых тел 163
6
ОГЛАВЛЕНИЕ
§ 8. Свободно-молекулярное течение газа в длинной трубе 169
§ 9. Молекулярное истечение газа через отверстие в стенке и
через короткую трубу 175
Глава XIII. Элементы магнитной газовой динамики . . . . 177
§ 1. Введение 177
§ 2. Элементы электростатики и электродинамики .... 178
§ 3. Электромагнитные поля 192
§ 4. Уравнения магнитной газодинамики 197
§ 5. Критерии подобия в магнитной гидродинамике .... 204
§ 6. Течение вязкой электропроводной жидкости по плоскому
каналу в поперечном магнитном поле 207
§ 7. Магнитогидродинамические насосы, ускорители, дроссели и
генераторы 215
§ 8. Вход потока электропроводной жидкости в магнитное поле
и выход из него v. 217
§ 9. Уравнения магнитной газовой динамики, для единичной
струйки 223
§ 10. Магнитогазодинамические ударные волны и слабые возму-
возмущения 229
§ 11. Условие обращения воздействия при течении газа в элект-
электромагнитном поле 238
§ 12. Простейшие решения уравнений одномерного течения газа
в скрещенных полях 242
§ 13. Магнитогидродинамические турбулентные течения . . . 249
Глава XIV. Численное решение задач газовой динамики . . . 266
§ 1. Введение 266
§ 2. Основные понятия теории разностных схем 268
§ 3. Метод характеристик 273
§ 4. Метод сквозного счета для двумерных сверхзвуковых тече-
течений идеального газа 276
§ 5. Задача о взаимодействии двух сверхзвуковых потоков 281
§ 6. Примеры расчета двумерных сверхзвуковых течений . . . 286
Список литературы 294
Именной указатель 297
Предметный указатель . 298
ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
В пятое издание книги внесены некоторые изменения, отно-
относящиеся к главам I, II, VI, VIII и X, посвященным гидравлике,
основным уравнениям гидрогазодинамики, теории пограничного
слоя, соплам и диффузорам, крылу и решеткам лопаток; заново
написана мною глава VII (кроме § 6) о турбулентных струях,
добавлена глава XIV о численных методах расчета газовых те-
течений, составленная В. В. Дугановым (§ 2, 4, 5, 6) и В. Д. За-
Захаровым (§ 1, 3), и дополнена В. В. Дугановым глава IV (§ 7—
9) некоторыми сведениями по теории сверхзвуковых течений.
В связи ic появлением учебников по теории лопаточных ма-
машин, включающих сведения о расчете решеток крыловых про-
профилей, соответствующая глава предлагаемой книги (гл. X) со-
сокращена. Главы I—III, V, IX, XI—XIII перенесены из четвер-
четвертого издания. Поправки к главе VI внес автор этой главы
Н. М. Белянин. Главы VIII, X, взятые из предыдущего издания,
исправлены мною.
Пятое издание книги состоит из двух частей (часть 1 —
главы I—IX, часть 2 — главы X—XIV), отвечающих двум се-
семестрам при чтении курса прикладной газовой динамики.
Большую помощь в подготовке к печати пятого издания ока-
оказал В. Д. Захаров. Полезные замечания при чтении рукописи
сделал рецензент книги А. Н. Крайко. Всем упомянутым товари-
товарищам автор выражает свою признательность.
Г. Н. Абрамович
ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
В четвертое издание книги внесены небольшие исправления
и добавления, относящиеся главным образом к главам, посвя-
посвященным теории пограничного слоя, течениям газа в соплах и
диффузорах, теории газовых эжекторов, газодинамике крыла и
решетки крыльев и магнитной гидрогазодинамике.
В этом издании используется система единиц СИ вместо
применявшейся в предыдущих изданиях технической системы
единиц.
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ 9
Поправки к главам VI, IX, X вносили авторы этих глав
Н. М. Белянин, А. Я. Черкез и С. И. Гинзбург. При подготовке
к печати рукописи четвертого издания автору оказали большую
практическую помощь В. Д. Захаров и Д. С. Ковнер. Всем ука-
указанным товарищам по работе автор выражает свою призна-
признательность.
Г. Н. Абрамович
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
В книге излагаются основы газовой динамики в применении
к теории реактивных двигателей и других машин и аппаратов.
Третье издание книги существенно переработано и допол-
дополнено.
Современные методы расчета реактивных двигателей, лопа-
лопаточных машин, эжекторов, аэродинамических труб и испытатель-
испытательных стендов основываются по преимуществу на одномерных
представлениях гидрогазодинамики, поэтому одномерным тече-
течениям в книге отведено значительное место.
Вместе с тем многие вопросы, например определение сопро-
сопротивления трения и полей скорости и температуры, построение
картины течения в камере сгорания, эжекторе и сверхзвуковом
диффузоре, выяснение силового и теплового воздействия выхлоп-
выхлопной струи реактивного двигателя на органы управления и дру-
другие части летательного аппарата, а также на стенки испытатель-
испытательного стенда и т. п., не могут быть разрешены без привлечения
дифференциальных уравнений гидрогазодинамики или уравне-
уравнений пограничного слоя. В связи с этим в книге значительное
внимание уделено основам гидродинамики, теории пограничного
слоя и теории струй.
За 15 лет, прошедших со времени выхода в свет предыду-
предыдущего издания, приобрели большое значение летательные аппа-
аппараты с реактивными двигателями новых типов, обеспечиваю-
обеспечивающими полет с большой сверхзвуковой (гиперзвуковой) ско-
скоростью, выход в космическое пространство и возвращение в
плотные слои атмосферы. Это привело к быстрому развитию
разделов газовой динамики, в которых изучаются течения раз-
разреженного газа, гиперзвуковые течения и движения жидкости и
газа в электромагнитных полях; в настоящем третьем издании
книги изложены основы также и этих разделов современной га-
газодинамики.
Ряд важных вопросов (теория сверхзвуковых сопел, диффу-
диффузоров, эжекторов и решеток крыльев, использование газодина-
газодинамических функций и др.) в новом издании излагается более об-
обстоятельно, чем прежде. Появление специальных учебников и
jO ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
монографий по теории лопаточных машин и теории реактивных
двигателей позволило исключить из книги эти разделы.
Книга составлена как учебник для моторных факультетов
авиационных институтов по программе, утвержденной Мини-
Министерством высшего и среднего специального образования СССР,
и может рассматриваться как учебное пособие также для маши-
машиностроительных и энергетических институтов.
Автор стремился достигнуть возможно большей наглядности
и доступности изложения и в освещении каждого вопроса искал
наиболее простых средств. Поэтому некоторые задачи рассмот-
рассмотрены дважды: сначала в упрощенной постановке, а затем более
глубоко в специальных разделах книги. Для того чтобы сделать
книгу доступной инженерам и студентам, не изучавшим кинети-
кинетическую теорию газов и электродинамику, даны краткие сведения
из этих разделов физики.
Несколько разделов этой книги написали: Н. М. Белянин
(гл. VI), А. Я. Черкез (§ 6-8 гл. V, § 6 гл. VII и гл. IX),
С. И. Гинзбург (гл. X).
Автор выражает глубокую благодарность С. О. Апельбауму,
А. И. Бунимовичу, А. Б. Ватажину, А. С. Гиневскому, А. Л. Го-
Гонору, И. П. Смирновой и А. А. Степчкову за ценные замечания,
сделанные ими при просмотре отдельных глав книги.
Г. Н. Абрамович
Глава I
УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ
ДЛЯ ЕДИНИЧНОЙ СТРУЙКИ
§ 1. Уравнения неразрывности
Основные уравнения газовой динамики мы введем для эле-
элементарной (единичной) струйки газа, поперечные размеры кото-
которой настолько малы, что в каждом ее сечении можно считать
постоянными все основные параметры потока: скорость, давление,
температуру и плотность газа. Именно в таком виде уравнения
газовой динамики применяются обычно в теории реактивных
двигателей. В тех случаях, когда в пределах поперечного сече-
сечения рабочей струи параметры потока меняются (например, не-
неодинаковы значения скорости или темпе-
температуры), вводится представление о сред-
средних по сечению значениях этих величин,
и тогда при помощи соответствующих,
в большинстве случаев незначительных,
поправок удается использовать все урав-
уравнения, полученные для элементарной
струйки. Метод элементарной струйки
лежит в основе гидравлики, поэтому га-
вовую динамику элементарной (единич-
(единичной) струйки иногда называют «газовой
гидравликой».
Чтобы получить уравнение неразрыв-
неразрывности, рассмотрим стационарное (устано-
(установившееся) движение элементарной струй-
струйки газа (рис. 1.1). При стационарном
движении в любой точке пространства сохраняются неизменны-
неизменными по времени скорость движения и состояние газа или жидко-
жидкости (плотность, давление, температура). Траектории частиц при
таком движении называются линиями тока1). Боковая поверх-
поверхность струйки, носящая название поверхности тока, является для
жидкости (газа) непроницаемой (векторы скорости течения ка-
сательны к ней); образующие поверхности тока являются ли-
линиями тока.
Рассмотрим некоторый участок струйки между двумя нор-
нормальными к поверхности тока сечениями 1 и 2\ заметим, что
Рис. 1.1. Элементарная
струйка
*) При неустановившемся движении линии тока определяются иначе
и не совпадают с траекториями частиц.
12 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
в соответствии с указанным на рис. 1.1 направлением движения
в объеме 1—2 приток газа осуществляется только через попереч-
поперечное сечение 1, а расход газа — только через сечение 2.
За бесконечно малый промежуток времени dx выделенная
часть струйки переместится в новое положение V—2'. Переме-
Перемещение состоит в том, что за время dx заштрихованный объем
1'—2Г вместит газ, вытесненный из области 1—Т', а известное
количество газа за то же время вытечет из этого объема и за-
заполнит область 2—2'. Приток газа в объем 1'—2 составляет
h [кг], A)
где pi — плотность газа в поперечном сечении 2, F\ — площадь
поперечного сечения 1. Расстояние dl\ между сечениями 1 и Г
равно произведению скорости движения на элементарный проме-
промежуток времени:
dl\ = w\ dx,
где w\ — скорость в сечении 2, откуда
dG\ = p\W\Fi dx.-
Расход газа из объема Г—2 равен, очевидно,
dx.
При установившемся режиме и отсутствии разрывов сплош-
сплошности в движущейся среде приток газа должен равняться рас-
расходу:
dGi = dG2 = dG.
Отсюда после соответствующей подстановки получаем уравне-
уравнение неразрывности — закон сохранения массы — для единичной
струйки газа при установившемся течении
piiviFi = p2w2F2. B)
В случае несжимаемой жидкости, т. е. при р = const, урав-
уравнение B) принимает более простую форму:
wiFi = w2F2i C)
которая применима к газовым течениям в тех случаях, когда
изменениями плотности газа можно пренебречь.
На основании уравнения неразрывности C) по расположе-
расположению линий тока в несжимаемой среде можно судить о скорости
движения. В местах сгущения линий тока скорость растет; если
линии тока раздвигаются, то скорость ладает. При движении
газа не всегда можно непосредственно по расположению линий
тока определить изменение скорости, так как изменения плот-
плотности газа могут быть значительными.
В газе, как нетрудно видеть из уравнения неразрывно-
неразрывности B), картина линий тока однозначно определяет изменение
плотности тока
§ 2. УРАВНЕНИЕ ЭНЕРГИИ 13
G
представляющей собой произведение плотности газа на скорость,
т. е. массовый расход газа через единицу площади поперечного
сечения.
В местах сгущения линий тока плотность тока увеличивается,
а в местах расхождения линий тока — убывает.
Уравнение постоянства расхода газа G = pwF = const можно
представить также в дифференциальной форме
dG = pwdF + wF dp + pF dw.
Поделив почленно это соотношение на pwF, получим
G ~ w ~Г~ p l F ' KV
Уравнение неразрывности, так же как и уравнение энергии,
выводимое в § 2 для единичной струйки, широко применяется
при расчете газопроводов, гидравлических и энергетических ка-
каналов и трубопроводов, реактивных двигателей и различных ап-
аппаратов, в которых происходит движение газа или жидкости.
В этих случаях под единичной струйкой понимается не часть
общего течения, ограниченная поверхностью тока малого сече-
сечения, а весь поток жидкости или газа, и используется следующая
гидравлическая модель.
В каждом поперечном сечении скорость течения относитель-
относительно стенок и параметры, описывающие свойства среды (давление,
температура, плотность и др.), считаются постоянными и равны-
равными соответствующим средним значениям, для определения кото-
которых существуют специальные методы (см. гл. V, § 8).
Изменения средних величин скорости и параметров среды от
сечения к сечению в такой (модели подчиняются одномерным
уравнениям «условной» единичной струйки, анализу свойств ко-
которой посвящена гл. I.
§ 2. Уравнение энергии
Следуя первому началу термодинамики (закону сохранения
энергии), составим баланс энергии в неподвижной системе коор-
координат (рис. 1.1), т. е. рассмотрим преобразование энергии в од-
одной и той же массе газа, заполнявшей вначале объем 1—2,
а через бесконечно малый промежуток времени dx переместив-
переместившейся в лоложение 1'—2'.
Приращение любого вида энергии равно разности количеств
этого вида энергии в положениях V—2' и 1—2. Ввиду того,
что заштрихованный объем Г—2 является общим для этих
14 гл. i. уравнения газовой динамики для струйки
двух положений, энергия массы газа, заполняющей объем Г—2У
при вычитании сокращается1), и приращение энергии измеря-
измеряется разностью количеств энергии в бесконечно малых объемах
2—2' и 1—1'. Отсюда следует, что приращение кинетической
энергии равно
w% — w^
dEK = 2 о х dG;
здесь dG — массовый расход газа через поперечное сечение
струйки за время dx. Приращение потенциальной энергии (энер-
(энергии положения)
dE ( — zx)dG,
где z2 и %\ — высоты расположения (нивелирные уровни) сече-
сечений 2 и i, g— ускорение силы тяжести. Приращение внутрен-
внутренней (тепловой) энергии
dET=(U2 — Ux)dG9
где U = cv T — тепловая энергия единицы массы газа (произ-
(произведение теплоемкости при постояшшм объеме на абсолютную
температуру). Если теплоемкость газа в сечениях 1 и 2 одина-
одинакова, то прирост внутренней энергии равен
dEr = cv(T2 — Tx)dG.
На основания выделенной части струйки газа действуют на-
направленные внутрь и по нормали к ним внешние силы давле-
давления р. При перемещении газа внешние силы давления произво-
производят работу. Например, перенос газа из сечения 1 в сечение V
происходит как бы под действием поршня площадью F\ с дав-
давлением р\. Работа поршня за время dx равна
PiF-^w^dx = —dG.
Точно так же можно представить себе, что давление р2 на сече-
сечение 2 осуществляется поршнем площадью F2. За время dx газ
переместит поршень в положение 2, производя отрицательную
работу
р
— p2F2w2dx = dG.
Силы давления, действующие на боковую поверхность струй-
струйки (поверхность тока), никакой работы не производят, так как
они нормальны к траекториям движения частиц газа. Таким об-
образом, энергия, внесенная силами давления, равна разности
!) Движение газа предполагается, как и в предыдущем параграфе, уста-
установившимся.
§ 2. УРАВНЕНИЕ ЭНЕРГИИ 15
между работами поршня 1 и поршня 2:
К газовой струйке на участке 1—2 может быть за время dx
подведено тепло в количестве dW. Далее газовая струйка за
время dx может произвести техническую работу dl, например,
приводя во вращение колесо турбины, установленное между се-
сечениями 1 и 2. Наконец, следует учесть энергию, расходуемую
газом за время dx на преодоление сил трения dZTp.
Согласно первому началу термодинамики- подведенные к газу
тепловая энергия и работа сил давления расходуются на со-
совершение технической работы, работы сил трения, а также на
повышение запасов потенциальной, внутренней и кинетической
энергии:
= dl + rfZTp + g(z2 - Zl) dG + (U2 - Ux) dG + 2 2 * JG,
Разделив все члены полученного выражения на dG, приходим
к уравнению энергии для единицы массы A кг) газа
v р wl — w2
Q + — — — = L + L^ + g(z2 — z1) + U2 — U1+ 2 2 г. E)
Здесь введены обозначения: Q = dW/dG — тепло, подводимое к
1 кг газа на участке 1—2, L = dl/dG — техническая работа, со-
совершаемая 1 кг газа на том же участке, LTp = dlrv/dG — работа
сил трения, приходящаяся на 1 кг газа.
Приток тепла в общем случае осуществляется двумя спосо-
способами: извне ((?наР) за счет теплообмена через боковую поверх-
поверхность струйки, изнутри ((?вн) за счет преобразования в тепло
работы трения. Таким образом,
Q = <?нар + #вн. F)
Вторая часть теплового потока, очевидно, в точности равна
энергии, расходуемой газом на совершение работы трения:
(?вн = ^Тр. G)
Из термодинамики известно уравнение состояния совершен-
совершенного газа
pv = RTy (8)
где R — газовая постоянная, а удельный объем газа и есть
16 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
величина, обратная плотности: v = 1/р. Отсюда
7 = RT- (9)
Кроме того, известно соотношение, связывающее теплоемкость
при постоянном объеме (,cv) и теплоемкость при постоянном дав-
давлении (ср):
cP = cv + R. A0)
Введем в рассмотрение теплосодержание (или энтальпию)
газа, т. е. произведение теплоемкости при постоянном давлении
на абсолютную температуру
i = cPT. (И)
Тогда соотношение A0) примет несколько иной вид
i = U + RT, A2)
или, на основании (9),
j. A3)
, Используя выражения F), G) и A3), можно придать урав-
уравнению энергии следующую форму:
W2 — W2
<?наР — L = g (z2 — гг) -j ^2—L + h — h' A4)
Уравнение энергии A4) иногда называют также уравнением
теплосодержания. Существенно то обстоятельство, что уравнение
теплосодержания не содержит работы трения. В самом деле, по-
поскольку энергия, расходуемая на преодоление трения или любого
другого вида сопротивления, преобразуется полностью в тепло,
а последнее остается в газовой струе, наличие сил трения не
может нарушить общий баланс энергии, а лишь приводит к пре-
преобразованию одного вида энергии в другой.
Обычно в технике приходится 'иметь дело с частными фор-
формами уравнения теплосодержания. Так, в большинстве случаев
изменение потенциальной анергии пренебрежимо мало в срав-
сравнении с другими частями уравнения энергии, и членом g(z2 — z\)
пренебрегают. Тогда уравнение теплосодержания имеет следую-
следующий вид:
Qh*»-L= W\Wl +i2-h. A5)
При отсутствии технической работы и теплообмена с окру-
окружающей средой, т. е. в случае энергетически изолированного
процесса в газе, имеем
§ 2. УРАВНЕНИЕ ЭНЕРГИИ ч 17
В частности, уравнение A6) определяет движение газа по трубе,
если нет теплопередачи через стенки. Согласно сказанному это
уравнение справедливо вне зависимости от того, учитываются
или нет силы трения. Иначе говоря, изменение теплосодержания
(температуры) в энергетически изолированном процессе связа-
связано только с изменением скорости. Если скорость газа не ме-
меняется, то остается постоянной и температура.
Отсутствие влияния сил трения можно объяснить следующим
образом. Под действием трения давление вдоль трубы падает,
т. е. газ расширяется, и, следовательно, температура должна
была бы уменьшаться. Однако работа сил трения преобразуется
в тепло; и так как работа сил трения в точности равна теплу,
подведенному за счет этой работы, то подогрев компенсирует
охлаждение.
Вдоль трубы постоянного сечения под влиянием сил трения
температура газа в дозвуковом течении даже убывает. Происхо-
Происходит это потому, что падение давления сопровождается уменьше-
уменьшением плотности газа, а плотность тока остается неизменной:
] = G/F = pw = const. Поэтому скорость газа возрастает, и тем-
температура в соответствии с уравнением A6) понижается. При
малой скорости движения температура изменяется только за
счет теплообмена или в тех местах, где газ проходит через тур-
турбину (расходует энергию, LT > 0) или через компрессор (полу-
(получает энергию, LK<0).
Если изменением скорости и теплообменом можно прене-
пренебречь, то уравнение теплосодержания принимает следующую
форму:
i2-U = -L. A7)
Иначе говоря, изменение теплосодержания газа при этом
равно механической работе. В колесе турбины температура газа
уменьшается:
i2 = U-Lr (LT>0), A8)
в колесе компрессора температура возрастает
h = ii — LK (LR<0).
Напомним, что здесь имеется в виду работа L, отнесенная к 1 кг
газа. Таким образом, следуя уравнению теплосодержания, мы
получаем простые соотношения для расчета температурных пе-
перепадов на турбине и компрессоре при малых изменениях кине-
кинетической энергии:
Vi J A9)
ср ср
Здесь ср — среднее значение теплоемкости при постоянном дав-
давлении на данном интервале температур.
2 г. Н. Абрамович, ч. i
1Й ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
Если скорость изменяется существенно, то расчет лишь не-
немного усложнится. Именно:
2 2
i2-h+^^-=-L. B0)
Наконец, при изотермическом процессе (J2 = U = const) ме-
механическая работа расходуется целиком на изменение кинетиче-
кинетической энергии
<^L = -L. B1)
Режим, близкий к изотермическому, можно получить в много-
многоступенчатом компрессоре с промежуточным (между каждой па-
парой ступеней) охлаждением газа.
Когда технической работы нет, уравнение теплосодержания
дает
(?нар = h — h -\
в таком виде оно применяется к теплообменным процессам.
Возвратимся теперь к энергетически изолированным течениям
газа, когда выполняются условия
(?нар = 0, L = 0 B3)
и уравнение теплосодержания приобретает форму A6). При
этом его можно записать следующим образом:
i2 + -J- = ix + -J- = i+ J = const. B4)
Отсюда нетрудно видеть, что если газовую струю затормозить
полностью, то теплосодержание газа достигает максимально воз-
возможного значения:
i* = i + ?. B5)
Получающееся при этом .значение теплосодержания i* мы будем
называть полным теплосодержанием, а соответствующую абсо-
абсолютную температуру
Г* = — B6)
ср
— температурой торможения.
С помощью B5) из уравнения теплосодержания A5) можно
исключить скорости; получаем уравнение
/1 Т 4* 4* /07\
ЧГнар — Ь = 12 — &!• \?1)
§ 2. УРАВНЕНИЕ ЭНЕРГИИ
19
Итак, температура газа получается равной температуре тор-
торможения в том случае, когда скорость течения уменьшается до
нуля при отсутствии энергетического обмена с окружающей сре-
средой. Пользуясь средним значением теплоемкости, можно вычис-
вычислить температуру торможения по следующей формуле:
B8)
Для воздуха (ср ~ 1005) имеем приближенно
Т* « Т +
2010*
B9)
Например, в воздушном потоке нормальной температуры (Г«
« 300 К) при скорости движения w = 100; 350; 1000 м/с полу-
получается соответственно температура торможения: Г* ~ 305, 360,
800 К.
Следует подчеркнуть, что, согласно уравнению энергии B4) г
в энергетически изолированном потоке идеального газа сущест-
существует однозначная зависимость между температурой газа Т (теп-
(теплосодержанием i) и скоростью течения w. Повышение скорости
в таком потоке всегда сопро-
сопровождается снижением темпера-
температуры независимо от изменения
других параметров газа. Если
в двух сечениях энергетически
изолированного потока одина-
одинакова скорость течения, то в
них будет одинаковой и темпе-
температура газа, какие бы процессы
ни происходили в потоке меж-
между рассматриваемыми сечения- Рис. 1.2. Диффузор воздушно-реак-
ми. При уменьшении скорости тивного двигателя
течения до нуля газ приобрета-
приобретает одинаковую температуру Г* независимо от особенностей про-
процесса торможения и возникающих при этом необратимых
потерь.
В конце входного диффузора (рис. 1.2) воздушнореактивного
двигателя обычно вне зависимости от скорости полета устанав-
устанавливается сравнительно малая скорость потока. По этой причине
температура воздуха в диффузоре двигателя получается близкой
к температуре торможения. Пусть скорость воздуха в конце диф-
диффузора W2 = 100 м/с. Тогда температура здесь при различной
скорости полета получается из условия
2010
2010
2*
20 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
В нашем случае (w2 = 100 м/с, Т{ = 300 К)
Г2«295 +
2010'
C0)
Результаты подсчета температуры T<i по формуле C0) сведены
в следующую таблицу:
wu м/с
Г*, К
т2, к
100
305
300
350
360
355
1000
800
795
Как видим, разогрев воздуха только за счет торможения при
большой скорости потока (полета) получается весьма значи-
значительным.
Уравнение теплосодержания объясняет следующий весьма
интересный факт. При течении газа возле твердой поверхности
без теплообмена температура последней близка к температуре
торможения в газе. Дело в том, что в связи с вязкостью газа
возле твердой стенки всегда образуется тонкий пограничный
-слой, в котором скорость газа относительно стенки меняется от
величины, равной скорости обтекающего потока, до нуля (на
стенке). Но раз частицы газа непосредственно возле стенки за-
затормаживаются, то при отсутствии теплообмена температура на
стенке должна быть равна температуре торможения. Так, на-
например, в рабочей части аэродинамической трубы сверхзвуковых
скоростей (рис. 1.3), где скорость газа очень велика, его тем-
температура Гр.ч должна быть значительно ниже, чем в предкамере,
из которой покоящийся газ (Го) поступает в трубу. Например,
при скорости в рабочей части wv ч = 600 м/с и температуре тор-
торможения в предкамере То = То = 300 К получается темпера-
температура в потоке
Т* _ Р ч
1 1о1<Г~
р.ч
Несмотря на это, как показывают опыты, температура стенки на
всем протяжении аэродинамической трубы, включая рабочую
часть, остается постоянной и приблизительно равной темпера-
температуре торможения: Тст = Г* = const.
Температура термометра, помещенного в рабочую часть,
также приблизительно равна температуре торможения. Это объ-
объясняется образованием у стенок трубы и термометра погранич-
пограничного слоя, в котором обтекающий газовый поток полностью за-
затормаживается. Таким образом, неподвижный термометр не мо-
§ 2. УРАВНЕНИЕ ЭНЕРГИИ
21
жет измерить температуру в потоке газа. По тем же причинам
поверхность тел, движущихся с большой скоростью в воздухе,
бывает сильно разогрета. Например, поверхность снаряда, вы-
вылетающего из орудия со скоростью w = 1500 м/с, за счет обра-
образования воздушного пограничного слоя, в котором относитель-
относительная скорость полностью гасится, должна была бы иметь тем-
температуру (Г*), превышающую на Г* — Т = и;2/2010 = 1125 °С
Рис. 1.3. Схема аэродинамической трубы сверхзвуковых скоростей
температуру окружающего воздуха. В действительности темпе-
температура снаряда меньше полученной здесь за счет теплоизлучения
в пространство. При очень большой скорости полета делается
невозможным обледенение поверхности самолета. Например, при
скорости и; = 900 км/ч B50 м/с) температура торможения на
величину Д77 = 2502/2010 == 31 °С выше, чем в окружающей ат-
атмосфере. Температура поверхности самолета близка к темпера-
температуре торможения, поэтому в данном примере даже при морозе
в 20—25 °С обледенения не получится.
Истинная температура обтекаемой газом поверхности обычно
отличается от температуры торможения. Для определения тем-
температуры поверхности пользуются следующей формулой:
2
^пов = Т + Ф"оТ"« C1)
или, для воздуха,
2010'
C2)
Здесь ф — поправочный коэффициент, который определяется
большей частью опытным, а иногда теоретическим путем. При
<р = 1 выражения C1) и C2) превращаются в известные уже
формулы для температуры торможения. Для дозвукового ско-
скоростного самолета приближенное значение поправочного коэф-
коэффициента равно 0,8. Для сверхзвуковой высотной ракеты попра-
поправочный коэффициент может уменьшиться до значения ср ~ 0,5.
Остановимся еще на одном примере из практики. При обте-
обтекании выпуклой поверхности в некоторой области вне погранич-
пограничного слоя скорость выше, чем в набегающем потоке, и, следова-
22 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
тельно, температура в таких местах ниже, чем в набегающем
потоке. Этим объясняется одно явление, иногда наблюдаемое
летчиками при пикировании даже на дозвуковых самолетах. Оно
состоит в том, что в момент пикирования с большой скоростью
часть верхней поверхности крыла скрывается от глаз летчика
под пеленой молочного цвета. Как только летчик выходит из
пикирования, т. е. скорость резко снижается, пелена исчезает.
По-видимому, при этом в слоях воздуха, имеющих повышенную
скорость и пониженную температуру, происходит конденсация
влаги, которая прекращается при выходе на меньшую скорость,
т. е. при более высокой температуре.
§ 3. Предельная скорость движения газа.
Число Маха
Рассматривая истечение газа при отсутствии энергетического
обмена, нетрудно убедиться в том, что скорость истечения ни
при каких условиях не может быть выше некоторой максималь-
максимальной величины. В самом деле, из соотношения
2
следует, что максимальная скорость достигается в том случае,
когда теплосодержание в потоке равно нулю, т. е. когда полное
теплосодержание газа целиком преобразуется в кинетическую
энергию
Отсюда получим формулу для максимального значения скорости
в газе
ttW=V2F. C3)
Соответствующая приближенная формула для воздуха, выве-
выведенная в предположении постоянства теплоемкости (ср«1005),
имеет следующий вид:
HW « 44,8У Г*7
Если температура торможения воздуха (температура в сосуде,
из которого воздух вытекает) близка к нормальной (Г* «
«300 К), то максимальная возможная скорость истечения
г^тах = 776 м/с.
Увеличение максимального значения скорости может быть
достигнуто только путем повышения температуры торможения
(полного теплосодержания).
Для того чтобы перевести газ из состояния покоя в движе-
движение со скоростью w, необходимо израсходовать часть его теплосо-
§ 3. ПРЕДЕЛЬНАЯ СКОРОСТЬ ДВИЖЕНИЯ ГАЗА. ЧИСЛО МАХА 23
держания, равную
— - i* z
2 -I — г.
Разделив обе части этого равенства на полное теплосодержание,
получим
г* — i w2
г* ~~ 2t* #
При постоянной теплоемкости это соотношение примет следую-
следующий вид:
Т* — т_ w2
Т* ~ 2срТ* "
Если теперь умножить и разделить правую часть на газовую
постоянную R, учесть 'соотношение R = cv — cv и обозначить от-
отношение теплоемкостей через к = cp/cv, то получится
Т* — Т w2 k—i
Т* ~ kRT* 2 *
Но, как известно из физики, скорость звука в газе равна1)
. C4)
Поэтому степень использования теплосодержания газа для полу-
получения заданного значения скорости потока определяется отно-
отношением скорости потока к скорости звука в неподвижном газе;
Т* — Т _ w2 к — 1
Г* - а*2 2 *
Отсюда выводится новое выражение для максимальной скорости
истечения (Г = 0):
^max = a*
Для воздуха (к = 1,4) получаем
"W = 2,24а*,
т. е. максимальная скорость истечения воздуха не может превос-
превосходить скорость звука в неподвижном воздухе более чем в
2,24 раза; при к = 1,2 максимальная скорость газа выше:
&Wt = 3,16а*.
1) Эта формула будет выведена в § 1 гл. III.
24 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
Можно тепловой перепад разделить не на полное теплосодер-
теплосодержание, а на теплосодержание в потоке; тогда получим
Т ~~ kRT 2 "
В этом случае скорость потока оказывается отнесенной к скоро-
скорости звука в потоке, а не в неподвижном газе:
Т*-Т w2 к-1
Отношение скорости потока к скорости звука в потоке при-
принято называть числом Маха и обозначать буквой М:
М = А C7)
Число Маха характеризует степень преобразования теплосодер-
теплосодержания в кинетическую энергию потока
Т - —2~т '
Число Маха является основным критерием подобия (см. § 7
гл. II) для газовых течений большой скорости.
Если М < 1, то течение газа называется дозвуковым, если
М > 1, то — сверхзвуковым.
Из последнего выражения можно получить расчетную фор-
формулу для отношения температуры торможения к температуре
в потоке как функцию числа Маха:
•у- = 1 + ^- М2. C8)
Нетрудно видеть, что максимальное значение числа М (при
Т = 0) равно бесконечности. Этот факт объясняется тем, что
при достижении максимальной скорости вместе с абсолютной
температурой обращается в нуль и скорость звука.
Поскольку скорость потока может быть как выше, так и
ниже скорости звука, существует и такой режим, когда скорость
потока равна скорости 'звука, т. е. М = 1. Этот режим называ-
называется критическим] ему соответствует значение температуры в
потоке
^. C9)
В воздухе (к = 1,4) критическая температура на 20 % ниже
температуры торможения. Само значение скорости звука для
критического режима отличается от такового для заторможен-
заторможенного газа, но также является вполне определенным:
D0)
§ 3. ПРЕДЕЛЬНАЯ СКОРОСТЬ ДВИЖЕНИЯ ГАЗА. ЧИСЛО МАХА 25
откуда
Для воздуха R = 287,3, поэтому имеем
акр = 1
акр
Можно характеризовать степень преобразования теплосодер-
теплосодержания в кинетическую энергию еще одним способом, поделив
тепловой перепад на теплосодержание при критическом режиме:
Т* — т i* — i w2 к — 1
Отсюда с помощью равенства D0) получаем новую формулу для
отношения температур в энергетически изолированном газовом
течении:
Здесь принято обозначение
Величину Я, измеряющую отношение скорости потока к крити-
критической скорости, будем называть приведенной скоростью. На кри-
критическом режиме (w = wKp = акр) Лкр = Мкр = 1. Максимальной
скорости потока при Т = 0 соответствует определенное макси-
максимальное значение приведенной скорости
^max —
Для воздуха (к = 1,4) имеем Лтах = 2,45. Для случая к = 1,2
соответственно А,тах = 3,31.
Приведенная скорость, как и число М, может считаться кри-
критерием подобия для газовых течений, характеризующим степень
преобразования теплосодержания в кинетическую энергию.
Данному значению числа М соответствует совершенно опре-
определенное значение приведенной скорости. Найдем формулу пе-
перехода от числа М к приведенной скорости:
2 2 2 *2
2 9 *2 2 '
a alp a a
откуда на основании C9), D0) и D2) получаем
•Я2
М2 = "У , ш D5)
i-Tqrr^
26
ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
ИЛИ
D6)
В газовой динамике и теории реактивных двигателей приме-
применяются оба безразмерных числа — X и М. В одних случаях более
простые соотношения получаются при использовании приведен-
приведенной скорости, а в других — числа Маха. На рис. 1.4 представ-
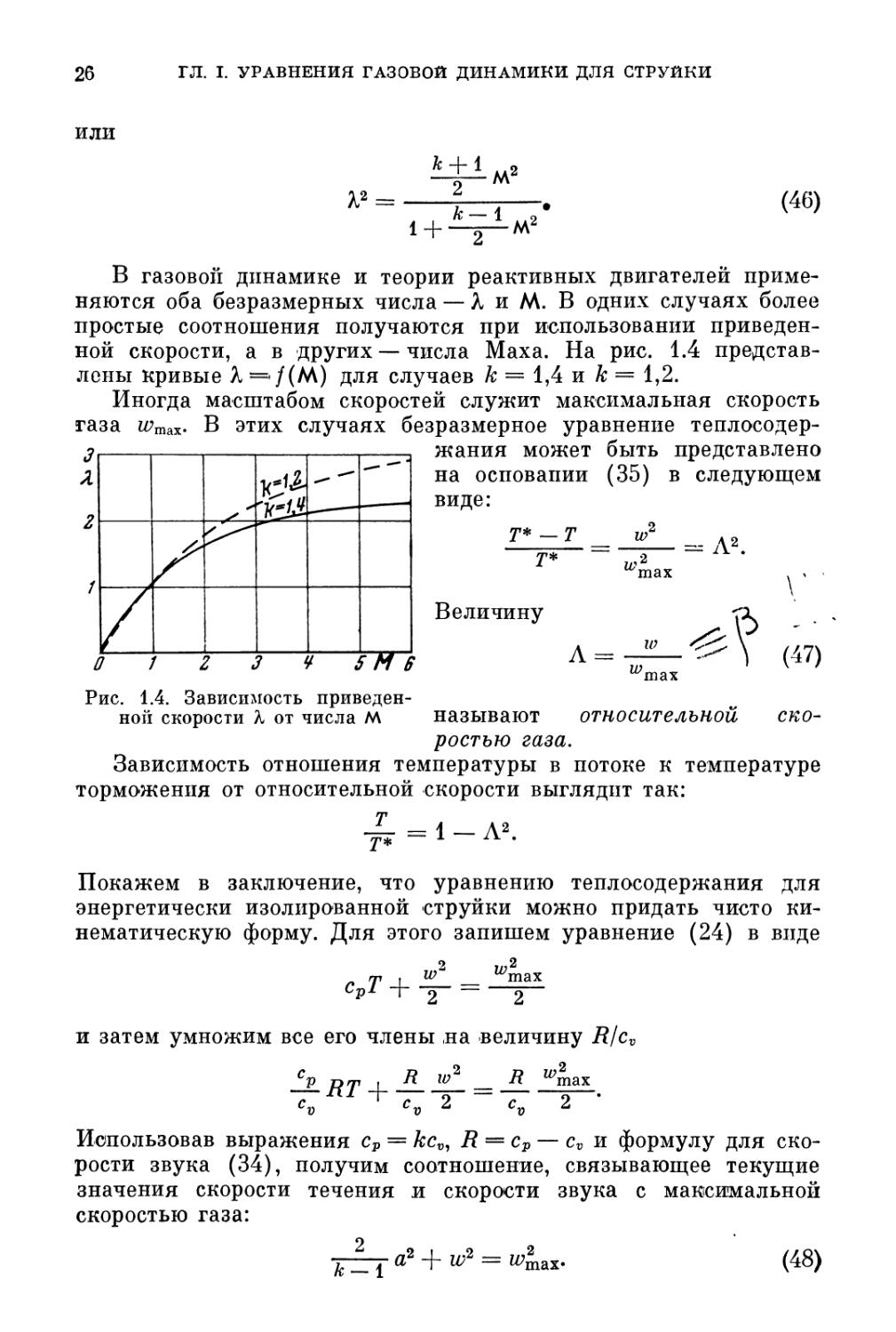
представлены кривые X ='/(М) для случаев к = 1,4 и к = 1,2.
Иногда масштабом скоростей служит максимальная скорость
газа wmax. В этих случаях безразмерное уравнение теплосодер-
теплосодержания может быть представлено
на основании C5) в следующем
виде:
я
2
1
/
Т* — т
-Л2.
Величину
5 М В
Л =
D7)
Рис. 1.4. Зависимость приведен-
приведенной скорости К от числа м называют относительной ско-
скоростью газа.
Зависимость отношения температуры в потоке к температуре
торможения от относительной скорости выглядит так:
т
__?_ _ А Д2
j* — L 1Y •
Покажем в заключение, что уравнению теплосодержания для
энергетически изолированной струйки можно придать чисто ки-
кинематическую форму. Для этого запишем уравнение B4) в виде
и затем умножим все его члены на величину R/cv
И. w H ^max
Использовав выражения ср = kcv, R = cv — cv и формулу для ско-
скорости звука C4), получим соотношение, связывающее текущие
значения скорости течения и скорости звука с максимальной
скоростью газа:
D8)
§ 4. УРАВНЕНИЕ БЕРНУЛЛИ 27
§ 4. Механическая форма уравнения энергии
(уравнение Бернулли)
Выше мы подробно рассмотрели уравнение теплосодержания.
Оно связывало температуру газа со скоростью движения с уче-
учетом энергетических воздействий (подвода тепла, технической
работы и изменением потенциальной энергии). Такие факторы,
как давление и плотность газа, в уравнение теплосодержания
не входили.
Можно получить иную (механическую) форму уравнения
энергии, куда, наоборот, не входит температура газа, а скорость
движения связана с давлением и плотностью. В дифференци-
дифференциальной форме уравнение энергии E) может быть записано
в виде
dQ -d(pv) — dL — dLTV = dU + d^- + gdz. D9)
Согласно первому закону термодинамики тепло, подводимое к га-
газу, может расходоваться только на повышение внутренней энер-
энергии и работу расширения (деформации), т. е.
dQ = dU + pdu. E0)
Вычитая из уравнения D9) равенство E0), получим
2
— dL — dLTV = d ~2—h g dz + d (pv) — p dv. E1)
Подставляя в E1) выражение удельного объема (v = ljp), по-
получаем
^dL = d^- + gdz + ^- + dLTp. E2)
Это есть механическая форма уравнения энергии, или, что то
же, уравнение живых сил для единичной струйки.
После интегрирования будем иметь
2
7
^+L^. E3)
Выведенное уравнение носит название обобщенного уравне-
уравнения Бернулли. Оно выражает скорость движения в функции
давления и плотности газа с учетом производимой газом техни-
технической работы (L), изменения потенциальной энергии g(z2 — z\)
и работы сил трения (?тр). В газовой динамике часто пользу-
пользуются упрощенной формой уравнения Бернулли, соответствую-
соответствующей режиму, когда отсутствует техническая работа (L = 0), нет
гидравлических потерь (LTp = 0) и запас потенциальной энергии
не изменяется (z2 = zi). Для этого режима уравнение Бернулли
28 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
запишется в следующей форме:
Уравнение Бернулли иногда используется в несколько ином
виде. Для этого интеграл разбивается на две части:
2 2 1
2 0 2 2 1
Г dp _ Г dp С dp С dp С dp ^a
110 0 0
Тогда из E4) следует
= — + JT = -r + )-f = const- (o6)
0
В этом случае вычисление интегралов ведется каждый раз от
абсолютного вакуума до давления, соответствующего заданной
скорости потока. Постоянную этого уравнения можно получить,
исходя из того, что при расширении газа до абсолютного вакуума
достигается максимальная скорость пото>ка.
Поэтому уравнению Бернулли можно придать следующий
вид:
о
В тех случаях, когда плотность газа на участке 1—2 элемен-
элементарной струйки остается практически постоянной, интеграл в
уравнении Бернулли равен
2
C_dp _
J Р "
1
и уравнение Бернулли выглядит особенно просто:
2 2
2 ^1 _|_ __2 1^ — г\
р + 2 ~U'
ИЛИ
Р2 , "I _ Pi , ^21 /r:ov
В такой форме оно применяется в гидравлике идеальной несжи-
несжимаемой жидкости. Иногда уравнение Бернулли для идеальной
несжимаемой жидкости записывается так:
л + р4-А + р4. E9)
§ 4. УРАВНЕНИЕ БЕРНУЛЛИ 2?
В этом случае оно составлено для 1 м3 жидкости. Кинетическую
энергию 1 м3 жидкости (pw2/2) называют скоростным напором.
Если нельзя пренебречь технической работой, гидравличе-
гидравлическими потерями и изменением потенциальной энергии, то обоб-
обобщенное уравнение Бернулли для 1 кг несжимаемой жидкости
имеет такой вид:
_L=^lzjl + g(,2_Zl)+^A + JLTp. F0)
Посредством этого равенства можно вычислить, например, ра-
работу, которую отдает жидкость колесу турбины (L>0), стоя-
стоящему между сечениями 1 и 2, если все прочие члены этого урав-
уравнения известны.
Для того чтобы пользоваться уравнением Бернулли для сжи-
сжимаемого газа, нужно заранее знать термодинамический процесс
изменения состояния газа, так как без этого неизвестна зависи-
зависимость плотности газа от давления и нельзя взять интеграл
2
—, выражающий работу проталкивания. Вычислим этот ин-
1
теграл для основных термодинамических ^процессов.
При изохорическом процессе (постоянный удельный объем,
т. е. постоянная плотность), типичном для гидравлики капель-
капельных жидкостей, как уже указывалось,
'2
I
1
В изобарическом процессе (постоянное давление)
2
J-f=O. @2)
Если осуществляется изотермический процесс (постоянная
температура), то, согласно уравнению состояния газа (8), р/р —
= RT = const, т. е. давление прямо пропорционально плотности
газа p = pi/?//?i, откуда
2
Г dp _ рх Г dp _ рг , р2
F3)
Предположим теперь, что состояние газа изменяется по идеаль-
идеальной адиабате
-4- = const;
9k
30
ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
тогда
п, следовательно,
2
Г dp РГ С
dp
ft-i
F4)
Наконец, в политропическом процессе с постоянным показа-
показателем политропы (п = const)p/pn = const получим
J P - n-lPl [-p-j
n—i
n
F5)
Следует отметить, что подводимое к газу тепло непосред-
непосредственно не отражено в уравнении Бернулли. Однако оно учиты-
учитывается при вычислении интеграла, так как влияет на вид функ-
функции р = /(/?), т. е. на характер процесса, по которому изменяется
состояние газа.
Наибольшее значение в газовой динамике имеет идеальный
адиабатический процесс, который предполагает отсутствие тепло-
теплового воздействия и работы сил трения. По этой причине при
идеальной адиабате энтропия1) газа остается неизменной, т. е.
такой процесс является идеальным термодинамическим — изо-
энтропическим — процессом. Напомним, что далеко не всякий
адиабатический процесс является идеальным. Например, при
выводе уравнения теплосодержания мы показали, что наличие
трения не нарушает адиабатичности процесса, но процесс с тре-
трением уже не может быть идеальным, так как он протекает с
увеличением энтропии. Иначе говоря, адиабатичность процесса
требует только отсутствия теплообмена с внешней средой, а не
постоянства энтропии. Таким образом, адиабатичность совме-
совмещается с постоянством энтропии только в идеальном процессе.
Если изменением потенциальной энергии можно пренебречь
(z\ ~ Z2) и нет технической работы (L = 0), а процесс является
идеально адиабатическим, то уравнение Бернуллп на основании
E4) и F4) имеет следующий ©ид:
1 K2 1
Cm.
к
ниже,
к
—
§
7.
Pi
ft-i
(pAk
w\ — i
F6)
§ 4. УРАВНЕНИЕ БЕРНУЛЛИ 31
Рассмотрим случай идеального торможения газовой струи,
т. е. определим давление р2 = /?*, которое получится, если ско-
скорость течения изоэнтропическим путем уменьшится от w\ = w
(при этом pi=p, pi = р) до i#2 = 0. Уравнение Бернулли в этом
случае дает
откуда
Используя выражение C4), связывающее скорость звука с пара-
параметрами состояния газа,
получим формулу для вычисления давления в идеально затор-
заторможенной газовой струе, в функции давления (р) и числа М
перед торможением:
k
(^1Г1- F8)
Величина р* носит название полного давления. Как и темпера-
температура торможения, полное давление является удобной характе-
характеристикой газового потока, так как оно связывает сразу два фак-
фактора: скорость и давление в потоке; последнее обычно называют
статическим давлением. Итак, отношение полного давления к
статическому есть функция числа М.
Формулу F8) можно получить непосредственно из выраже-
выражения D0) для температуры торможения
пользуясь соотношениями для идеальной адиабаты
k
п* / т* \h—i
т-W ' <69>
Отсюда же получается формула для вычисления плотности
32 ГЛ I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
в идеально заторможенной газовой струе
1
о* / *
С помощью функции D2), связывающей температуру торможе-
торможения с приведенной скоростью, находим из соотношения F9) за-
зависимость полного давления от приведенной скорости
k
1- G2)
Для плотности идеально заторможенного газа соответственно
получим
1
ft —1
Нужно отметить, что истинное давление, которое получается
при торможении струи газа, может существенно отличаться от
полного давления, определенного по формуле F8). Объясняется
это тем, что в действительности торможение струи часто проте-
протекает не по идеальной адиабате, а с более или менее существен-
существенными гидравлическими потерями. Например, в диффузоре при
дозвуковом течении газа уменьшение скорости обычно сопровож-
сопровождается вихреобразованиями, вносящими значительные сопротив-
сопротивления в газовый поток. При торможении сверхзвукового потока
почти всегда образуются ударные волны, дающие специфическое
«волновое» сопротивление. Итак, действительное давление в за-
заторможенной струе газа обычно ниже полного давления набе-
набегающей струи.
Вообще, если на участке струи 1—2 наблюдаются потери, то
это обязательно приводит к тому, что полное давление в сече-
сечении 2 будет ниже полного давления в сечении 1:
* *
Если ввести безразмерную величину, носящую название коэф-
коэффициента сохранения полного давления
<т = 4. G4)
Pi
то чем больше потери, тем ниже значение коэффициента сохра-
сохранения полного давления и меньше полное давление в конце рас-
рассматриваемого участка струи:
pt = ар\. G5)
§ 4. УРАВНЕНИЕ БЕРНУЛЛИ
33
Можно оценивать потери и по разности полных давлений:
G6)
На применении уравнения Бернулли основан пневматический
способ определения скорости потока, который состоит в том, что
в поток вводится насадок (рис. 1.5), состоящий из двух трубок.
Открытое отверстие одной из этих трубок A) размещается в но-
носовой части насадка (перпендикулярно к потоку), а отверстия
второй трубки B) расположены в боковой поверхности насадка
(вдоль потока); при дозвуковой скорости замедление струи газа
от встречи с насадком проходит без каких-либо потерь, так как
трение и вихреобразование возникают уже на боковой поверх-
поверхности насадка, т. е. после того, как струя минует область своего
полного торможения, размещающуюся
перед самым носиком насадка. По этой
причине в первой трубке создается
давление, почти в точности равное пол-
полному давлению набегающего потока;
во второй трубке, если ее входное от-
отверстие достаточно удалено от носика,
устанавливается давление, близкое к
статическому давлению потока. Трубки
1 ж 2 сообщаются с манометром, изме-
измеряющим давление. Отношение измерен-
измеренных давлений
Рг _ р*
дает возможность по формуле F8) или Рис {5 Схема пневматиче,
Gz) вычислить значения числа Маха ского насадка
или приведенной скорости потока.
Расчеты по этим формулам достаточно точны только для до-
дозвукового потока. Объясняется это тем, что при торможении
сверхзвукового потока перед насадком возникает ударная волна,
пересекая которую газовые струи претерпевают значительные
гидравлические потери. Поэтому давление в трубке 1 пневмати-
пневматического насадка при сверхзвуковом течении существенно отли-
отличается от полного давления набегающего потока, что делает фор-
формулы F8) и G2) в этом случае неприменимыми.
Нужно заметить, что пользоваться пневматическим насадком
можно и для измерения сверхзвуковой скорости, но при этом
следует применять специальные расчетные формулы, учитываю-
учитывающие волновое сопротивление. Такие формулы мы выведем в
дальнейшем.
Итак, предельное значение скорости, выше которого нельзя
применять формулы F8) и G2) при торможении газового по-
потока, равно скорости звука (М = X = 1).
Г. Н. Абрамович, ч. 1
34 ГЛ. I. УРАВНЕНИЕ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
Для ускоряющегося газового потока этими формулами можно
пользоваться и при сверхзвуковых скоростях, так как увеличе-
увеличение скорости происходит обычно без заметных потерь (изоэн-
тропически) не только в области М < 1, но и в области М > 1,
т. е. полное давление в ускоряющейся газовой струе почти не
меняется. В частности, по формулам F8) или G2) вычисляется
скорость истечения газа. При этом в сосуде, где газ покоитсяг
давление равно полному давлению вытекающей струи р*, а в вы-
выхлопном отверстии сопла — статическому да*влению р. Из фор-
формулы F8) получим
G7)
а из формулы G2)
» = Т±1 {}-(¦$) !• G8)
Отсюда определим скорость истечения w:
где
k-i
1т (^), G9)
ИЛИ
где
"'кр — «*
i —
Как нетрудно видеть, расчет скорости истечения более удобно
вести по приведенным скоростям, чем по числам М. Истинные
значения скорости истечения немного ниже определяемых по
формулам G7) — (80), так как некоторых потерь трения избе-
избежать нельзя, но погрешность этих формул обычно не больше
1-5%.
Кривые зависимости X = f(p*/p) Для случаев к = 1,4 и к =
= 1,2 представлены на рис. 1.6.
Исследуем с помощью уравнения Бернулли техническую ра-
работу компрессора и турбины. В компрессоре полное давление
газа увеличивается: р*> р\, а в газовой турбине падает: р2<
</?х. Отношение давлений pjp\ в компрессоре соответственно
больше единицы, а в турбине — меньше единицы. Для большей
наглядности предположим, что работа трения и изменение по-
потенциальной энергии отсутствуют и изменение давления в ма~
§ 4. УРАВНЕНИЕ БЕРНУЛЛИ
35
шине идет по изоэнтролическому закону. В этом случае уравне-
уравнение Бернулли напишется так:
— L
w\-w\
ft-1
JL2.I _1
(81)
Компрессор или турбина, работающие в таких условиях, носят
название идеального компрессора или идеальной турбины.
Рис. 1.6. Зависимость приведен-
приведенной скорости истечения от отно-
отношения полного давления к ста- *»\
тическому давлению в выходном ' '
сечении сопла
0,5
ZS 50 75 100 J*t2S
Р
Используя равенство F1), введем в выражение (81) полные
давления перед и за машиной, исключив из него скорости:
f
I
—
— ¦-
к ¦
А —1
Р2
к
fe-l
-1 --3-
ft-1
( — ) k
Pi
— 1
/ \
[ 2
__\ Р± /
ft-i
ft
|
откуда
но в идеальном адиабатическом процессе имеет место равенство
3*
36 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
с помощью которого после несложных преобразований полу-
получается
_*
Рл
к —I
4i -i
(82)
Итак, в идеальном случае техническая работа может быть
определена по изменению полных давлений без учета конкрет-
конкретных значений скорости газа до и после машины. Работа, пере-
передаваемая газовой турбине, является положительной {р2 *)
а подводимая компрессором,— отрицательной
Отклонение от идеального изоэнтропического процесса в ма-
машине учитывается обычно с помощью дополнительного множи-
множителя, представляющего собой коэффициент полезного действия
машины. В случае компрессора получим
LK = Л- (83)
В случае турбины
ZT = r,:L. (84)
Отношение значений полного давления за и перед машиной
я* = ^| (85)
1
будем называть в дальнейшем степенью повышения давления
(для компрессора) или степенью понижения давления (для тур-
турбины). Уравнение идеальной технической работы можно запи-
записать также в следующем виде:
Г *zi 1
|[Дж/кг]. (86)
Наиболее существенной особенностью технической работы
является то, что ее величина, как видно из выражения (86) г
прямо пропорциональна начальной температуре газа. Это свой-
свойство технической работы лежит в основе рабочего процесса лю-
любой тепловой газовой машины. Например, в двигателе внутрен-
внутреннего сгорания всегда рабочее тело вначале сжимается, затем
подогревается и расширяется. В соответствии с изложенным ра-
работа, затраченная при сжатии холодного газа, меньше работы,
которую он произведет после подогрева при расширении до пер-
первоначального давления. Из разности этих работ, собственно го-
говоря, и получается полезная работа, совершаемая двигателем
внутреннего сгорания.
Г *Lzi ]
§ 5. УРАВНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
37
§ 5. Уравнение количества движения
Согласно второму закону Ньютона элементарное изменение
количества движения равно элементарному импульсу силы:
d(mw) = Pdx. (87)
Здесь Р — сумма проекций на какую-либо ось всех сил, прило-
приложенных к телу массы т, w — проекция скорости на ту же ось,
dx — время действия силы Р. В таком виде закон Ньютона ис-
используется в механике твердого тела.
Применительно к потокам жидкостей и газов более удобна
несколько иная (гидродинамическая) форма уравнения для ко-
количества движения, которую получил впервые Эйлер. Выведем
уравнение количества движения
в гидродинамической форме. Для
этого выделим элементарную
струйку (рис. 1.7) и проведем два
нормальных к ее оси сечения 1
и 2. Разобьем всю массу жидко-
жидкости, заключенную в объеме 1—2,
на большое число частей так,
чтобы в пределах каждой из них,
имеющей массу т, скорость дви-
движения w можно было считать по-
постоянной, и установим связь меж-
между проекциями сил и количества
движения на ось х. Согласно
уравнению (87) сумма проекций импульсов всех сил, прило-
приложенных к массе жидкости 1—2, равняется изменению проекции
суммарного количества движения:
(88)
Рис. 1.7. Элементарная струйка
Рассмотрим изменение суммарного количества движения
d^mwx за время dx, в течение которого выделенная масса
жидкости переместится из положения 1—2 в положение 1'—2\
Предположим, как это мы делали в предыдущих параграфах,
что жидкость находится в установившемся движении, тогда ко-
количество движения массы Г—2, входящее как в начальное, так
и в конечное значение суммарного количества движения, остает-
остается неизменным и при вычитании сокращается. Иначе говоря,
прирост суммарного количества движения должен быть равен раз-
разности количества движения, взятого соответственно для масс
2—2' и 1—1', которые в установившемся движении одинаковы:
= (wx2 — wxl) dG.
Здесь dG — масса жидкости элемента 1—Г (или 2—2'), wX2,
wx\ — проекции на ось х скорости потока в сечениях 2 и 1. Эле-
38 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
ментарная масса dG равна произведению секундного массового
расхода жидкости на промежуток времени dx\
dG = G dr.
Отсюда
d^/riWx =(и?х2 — Wxi) G dx.
Величина Gw носит название секундного количества движения.
Подставляя полученное выражение в исходное равенство
(88), приходим к уравнению количества движения в гидродина-
гидродинамической форме (первому уравнению Эйлера), согласно кото-
которому сумма проекций всех сил, приложенных к струе жидкости
на любом ее участке, равна приращению проекции секундного
количества движения на этом участке, или, что то же, произве-
произведению секундной массы на приращение проекции скорости:
Px=G{wx2-wxl). (89)
Аналогичные уравнения можно составить и для двух других осей.
Применим уравнение количества движения к прямолинейной
струйке постоянного сечения F. Проведем торцовые части кон-
контрольной поверхности нормально к направлению потока, причем
пусть образующая боковой поверхности струйки параллельна
оси х. Скорость потока w направлена в сторону положительной
оси х. Составим уравнение количества движения в направлении
потока. На контрольную поверхность действуют силы давления,
нормальные к ней. Поэтому проекции на ось х сил давления,
приложенных к боковой поверхности, равны нулю. Изменение
давления на участке между торцовыми сечениями струйки про-
пропорционально силе, действующей на выбранный элемент жидко-
жидкости. Эта сила, па!раллельная оси х, равна (р\—P2)F. К боковой
поверхности приложена сила трения, направленная параллельно
потоку, против него: —Ртр. Кроме того, между торцовыми сече-
сечениями струйки может находиться какая-либо машина, получаю-
получающая от газа техническую работу. Пусть проекция на направле-
направление движения силы, с которой действует машина на газ, равна
—Р1). Итак, сумма проекций всех сил на ось х равна
По уравнению количества движения эта сила должна быть
равна изменению количества движения:
wl). (90)
Если расстояние между сечениями 1 ж 2 бесконечно мало, то
уравнение количества движения нужно записать в дифференци-
]) Проекция силы, приложенной газовым потоком к машине, считается
положительной.
§ 5. УРАВНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ 39
альной форме:
Gdw + Fdp = —dPTp — dP.
Умножив все члены этого уравнения на скорость движения и
разделив на массовый расход газа, получим уравнение работы
всех сил для цилиндрической струйки, отнесенное к 1 кг газа,
dp wdPTV
Здесь использовано уравнение расхода в цилиндрической струйке
pw = -г: = const.
Нетрудно видеть, что стоящие в правой части члены представ-
представляют собой работу сил трения
—
и техническую работу
Таким образом, уравнение количества движения для цилиндри-
цилиндрической струйки газа легко преобразуется в уравнение Бернулли
^+dLTp. (91)
J3 дальнейшем уравнение количества движения для цилиндри-
цилиндрической струи газа мы будем применять в следующей форме:
dp + pw dw = - ijfi- - ^г-. (92)
При отсутствии трения и силового воздействия газа на какую-
либо машину дифференциальное уравнение количества движения
приобретает особенно простой вид:
dp = —pwdw. - (93)
Уравнение (93) выражает важное свойство газового потока.
При отсутствии внешних сил и сил трения увеличение скорости
потока может быть вызвано только уменьшением статического
давления, и наоборот, торможение потока в этом случае всегда
связано с увеличением давления в нем независимо от характера
других процессов, происходящих в потоке, и изменения осталь-
остальных параметров газа. В интегральной форме уравнение количе-
количества движения для цилиндрической струйки запишется так:
Р2 — Р1+ PH> К Щ) F
40
ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
или при условии Ртр = 0 и Р = 0:
p + pw2 = const.
(94)
или
Итак, в цилиндрической струйке давление может измениться
даже в том случае, когда нет трения и технической работы. Для
этого достаточно, чтобы изменялась скорость течения, что может
быть достигнуто при подводе или отводе тепла. Например, при
подогреве газа, в связи с уменьшением его плотности, скорость
растет (piM?i =ргм>2), а давление падает.
Важная особенность уравнения количества движения состоит
в том, что с его помощью расчет действующих сил производится
только по состоянию потока, на контрольной поверхности без
проникновения в сущность процессов, происходящих внутри
этой контрольной поверхности. Поэтому уравнение количества
движения позволяет во многих случаях достаточно точно рас-
рассчитать гидродинамический процесс, не вникая в его детали.
Следует отметить, что эффективность использования уравне-
уравнения количества движения зависит в основном от того, насколько
удачно выбрана в потоке контрольная поверхность.
Рассмотрим несколько примеров применения уравнений коли-
количества движения и энергии.
Пример 1. Определим гидравлические потери в потоке несжимаемой
жидкости при внезапном расширении канала (рис. 1.8). Опыт показывает,
что в этом случае струя, выходящая из узкой части канала, не заполняет
вначале всего поперечного се-
сечения широкого канала, а рас-
растекается постепенно. В углах
между поверхностью струи и стен-
стенками образуются замкнутые то-
токи жидкости, причем давление на
торцевой стенке 1 по опытам
оказывается почти равным стати-
статическому давлению на выходе из
узкой части канала (р\). При
внезапном расширении канала на-
наблюдается значительное гидрав-
гидравлическое сопротивление, т. е. про-
Рис. 1.8. Схема течения при внезапном
расширении канала
исходит уменьшение полного дав-
давления в потоке. Если поместить
сечение 2 в таком месте, где
поток уже полностью выравнялся, т. е. статическое давление pi и скорость
потока w2 по сечению постоянны, то потери будут равны разности полных
давлении
Полное давление р* в случае движения несжимаемой жидкости опре-
определяется совершенно аналогично тому, как это делалось для идеального
адиабатического процесса в § 4, т. е. как давление в полностью затормо-
заторможенной струе без потерь и в отсутствие технической работы; при z = const,
§ 5. УРАВНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ 41
согласно уравнению Бернулли для несжимаемой жидкости F0), имеем
Таким образом, для несжимаемой жидкости
Ар* =
Скорости wi ш и?г можно связать уравнением неразрывности
= w2F2;
изменение статического давления (pi—р2) заранее неизвестно, т. е. полу-
получается одно уравнение с двумя неизвестными. Дополнительно можно ис-
использовать уравнение количества движения. Учитывая, что участок расте-
растекания струи 1—2 имеет не слишком большую длину, силой трения обычно
пренебрегают. Тогда уравнение количества движения можно применить в
простейшей форме (94):
Р\ — рг =' pw2(w2 — w{).
Здесь используется постоянство давления в сечении 1, что не является
самоочевидным, но, как указано выше, подтверждается опытами. В отличие
от уравнения Бернулли, уравнение количества движения дает возможность
сразу определить разность значений статического давления, получающихся
в потоке при внезапном расширении канала. Если этот результат подста-
подставить в уравнение Бернулли, то найдутся и потери полного давления при
внезапном расширении канала:
Следует обратить внимание на то, что применение уравнения количе-
количества движения принесло в данном случае успех благодаря удачному вы-
выбору контрольной поверхности 1—2, на которой оказались известными
основные действующие силы.
Пример 2. Произведем расчет простейшего эжектора, состоящего из
сопла А и цилиндрической смесительной трубы В, расположенных в про-
пространстве, заполненном неподвижной жидкостью (рис. 1.9). Из сопла по-
подается струя, которая подсасывает жидкость из окружающего пространства.
Пусть на выходе из смесительной трубы скорость и плотность смеси
примерно постоянны. Построим
контрольную поверхность из сечений г -¦
1 и 2, проходящих нормально к по- | В \
току по срезу сопла и срезу смеси- д \ i l
тельной трубы, и боковых поверхно- / ;
стей, направленных параллельно по- — -f* 1
току. На всей контрольной поверхно- j |
сти господствует одно и то же дав- ! ' 'i
ление покоящейся жидкости, т. е. ; j
главный вектор сил давления равен ) ^
нулю.
Если пренебречь силой трения Рис- 19- Простейший эжектор
на стенках смесительной трубы, то
окажется, что сумма проекций на ось трубы всех сил в пределах контроль-
контрольной поверхности 1—2 равна нулю, а следовательно, не должно быть измене-
изменения количества движения.
Изменение количества движения у активной струи на участке 1—2
Gi(u>2 — ^i)-
42
ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
То же у жидкости, подсосанной из окружающего пространства, где она
находилась в покое (w = 0):
(G2 — Gi)(w2 — 0);
суммарное изменение количества движения
— G\Wi = 0.
Здесь G\, G2 — секундные массовые расходы жидкости соответственно в соп-
сопле и на выходе из смесительной трубы, w\ и w2— значения скорости исте-
истечения из сопла и смесительной трубы.
Отсюда получаем, что расходы жидкости в сопле и на выходе из сме-
смесительной трубы обратно пропорциональны величинам соответствующих
скоростей
С другой стороны, очевидно, что
Gn
где р — плотность, F — площадь сечения. Сравнивая последние два выра-
выражения, приходим к следующей расчетной формуле:
Если плотность жидкости в активной струе и в окружающем пространстве
одинакова, то отношение массовых расходов жидкости равно отношению
диаметров смесительной трубы и сопла:
Пример 3. Вычислим силу, действующую на стенки диффузора
(рис. 1.10) при отсутствии гидравлических потерь в потоке несжимаемой
жидкости. Пусть давление и ско-
скорость в сечении 1 перед диффузором
постоянны и равны ри wu а в сече-
сечении 2 после диффузора также по-
постоянны и равны р2, и?2. Уравнение
Бернулли, если нет потерь, дает
pi + ~2~ = '
Рис. 1.10. К расчету силы давления
в диффузоре
Из уравения
чаем
неразрывности полу-
полуw2F2 = Gfp.
Проведем контрольную поверхность из поперечных сечений 1 и 2 и боко-
боковых поверхностей, расположенных параллельно потоку и охватывающих
диффузор. Вследствие наклона стенок диффузора сумма проекций на про-
продольную ось сил давления, приложенных от стенок к жидкости, не равна
нулю (Рлф0).
Сумма проекций всех сил на продольную ось, которая получается путем
сложения силы Рд с силами давления на торцевые сечения, равна измене--
§ 5, УРАВНЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
43
нию количества движения
— p2Fz= G{w2—wx).
Производя замену величин wx и р2 с помощью уравнений неразрывности и
Бернулли, приходим к следующему выражению для проекции на направ-
направление потока силы, действующей на поток от стенок диффузора:
Gwn
Пусть внешнее давление — рн, тогда проекция на продольную ось силы
внешнего давления на дуффузор
В итоге получаем следующее значение проекции на продольную ось
результирующей силы, которая действует на стенки диффузора:
Gw2
F2-
В частном случае, когда внешнее давление одинаково с давлением в узком
сечении диффузора, эта сила равна
Последнее выражение применяется иногда при вычислении силы, действую-
действующей на входной диффузор воздушно-реактивного двигателя.
Пример 4. Установим взаимосвязь между скоростью полета и ско-
скоростью истечения из прямоточного воздушно-реактивного двигателя, схема
которого изображена на рис. 1.11. Во входном участке двигателя происхо-
происходит преобразование скоростного напора набегающего потока в давление,
Рис. 1.11. Схема прямоточного воздушно-реактивного двигателя: е — вход-
входное сечение, к — начальное сечение камеры сгорания, w — конечное сечение
камеры сгорания, а — выходное сечение сопла
т. е. динамическое сжатие воздуха. В камере сгорания подводится тепло,
и образующаяся смесь сжатого воздуха с продуктами сгорания нагревается.
В выходном сопле нагретые газы расширяются: здесь давление преобра-
преобразуется в скоростной напор.
Основы теории прямоточного воздушно-реактивного двигателя даны
впервые Б. С. Стечкиным в 1929 г.1).
1) Стечкин Б. С. Теория воздушного
Техника Воздушного Флота.— 1929.— № 2.
реактивного двигателя /J
44 гл. i. уравнения газовой динамики для струйки
Наиболее совершенный цикл работы прямоточного воздушно-реактив-
воздушно-реактивного двигателя был бы получен в том случае, если бы сжатие воздуха на
участке н — к (рис. 1.11) осуществлялось по идеальной адиабате и скорость
потока была бы доведена до нуля, подвод тепла в камере сгорания к — ю
происходил бы при постоянном давлении, после чего выхлопная смесь
расширялась бы в сопле w — а до атмосферного давления также по идеаль-
идеальной адиабате. Прямоточный воздушно-реактивный двигатель, работающий
по указанному совершенному циклу, называют идеальным.
Полное давление в камере сгорания может быть найдено из уравнения
Бернулли, которое интегрируется в этом случае с помощью идеальной
адиабаты:
Г *=i 1
к Р„ / Р*
Скорость истечения найдется из аналогичного выражения при ра = t
h P I / n* \ ft I M>
к-
Отсюда мы получаем основное соотношение
w2 w2
Рн ~2~ = ра~*-
Итак, в идеальном прямоточном воздушно-реактивном двигателе скоростной
напор потока в выхлопном отверстии равен скоростному напору полета.
Используя это же равенство, получим для идеального двигателя
\Pft== Рн1 Р& == Рн) еш>е °ДИН важный результат:
т. е. приведенные скорости в выходном отверстии идеального двигателя
и в набегающем невозмущенном потоке равны. Отсюда вытекает также и
равенство чисел Маха полета и истечения
Ма = Мн.
Эти соотношения справедливы для идеального двигателя как при до-
дозвуковой, так и при сверхзвуковой скорости полета.
В реальном двигателе в связи с потерями давления во входном и вы-
выходном участках и в камере сгорания скоростной напор па выхлопе ниже
скоростного напора полета:
^а 2 ^н 2
По этой же причине число Маха и приведенная скорость в выходном отвер-
отверстии имеют меньшие значения, чем в набегающем потоке:
Ма < Мн, Аа "^ Ан-
Таким образом, увеличение скорости истечения по сравнению со скоростью
полета получается не в результате увеличения скоростного напора в двига-
двигателе, а за счет уменьшения плотности газа при подогреве.
Полученные соотношения приводят к простой расчетной формуле для
скорости истечения в идеальном двигателе
§ 6. УРАВНЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ
45
где аКр to, якр ь — критическая скорость газа соответственно после и до по-
подогрева. Из этой формулы следует, что отношение скорости истечения к
скорости полета для идеального двигателя пропорционально корню квад-
квадратному из отношения температур торможения, взятых в конце и начале
камеры сгорания:
Следует подчеркнуть при этом, что температура торможения в начале
камеры сгорания может быть подсчитана по формуле D2) как функция
температуры в атмосфере и приведенной скорости полета:
"* К
а температура торможения в конце камеры сгорания определяется расхо-
расходом горючего в двигателе и расходом воздуха.
§ 6. Уравнение моментов количества движения
Как известно из теоретической механики, изменение суммар-
суммарного момента количества движения относительно какой-либо оси,
например оси г/, равно сумме моментов импульсов всех сил,
приложенных к телу, z
относительно той же
оси (рис. 1.12):
= My dx. (95)
Здесь mwz, mwx — про-
проекции количества дви-
движения некоторой эле-
элементарной массы m на
оси z и х; х, z — соот-
соответствующие координа-
координаты, m(wxz — wzx) — мо-
момент количества движения элементарной массы тп относительно
оси у.
Если движение жидкости является установившимся, то изме-
изменение суммарного момента количества движения жидкости, пере-
перемещающейся за время dx из объема 1—2 в объем 1'—2', равно
разности моментов количества движения в элементарных объемах
2-2' и 1-Г
d^m(wxz — wzx) = G [(wx2z2 — wz2x2) — (юх1гг — wzlxx)] dx, (96)
где G — секундный расход жидкости. Объясняется это тем, что
тмомент количества движения заштрихованной массы Г—2 при
вычитании сокращается, так как движение жидкости предпола-
тается установившимся.
Рис. 1.12. К выводу уравнения моментов ко-
количества движения
46 гл. i. уравнения газовой динамики для струйки
Подставляя (96) в левую часть равенства (95), получим
второе уравнение Эйлера, т. е. уравнение моментов количества
движения в гидродинамической форме
My = G[(wX2Z2— wz2x2) — (wxizi — wz\xi)\. (97)
Аналогичные уравнения могут быть составлены для осей z
и х. Согласно второму уравнению Эйлера сумма моментов отно-
относительно любой оси всех сил, приложенных к жидкому объему,
равна разности моментов относительно той же оси секундных
количеств движения выходящей и входящей жидкости.
Уравнение моментов количества движения приобретает более
простую форму, если ввести полярные координаты1); в этом
случае скорости раскладываются на радиальные и окружные
составляющие, причем моменты радиальных составляющих ко-
количества движения равны нулю. Уравнение (97) при этом имеет
вид
М = G(wU2r2— Wuiri), (98)
где М — ,сумма моментов всех сил, приложенных к какому-либо
жидкому объему относительно начала координат, wu — окруж-
окружная составляющая скорости.
Если сумма моментов всех сил равна нулю (ilf = 0), полу-
получим известный закон площадей
wur = const. (99)
Остановимся на одном примере приложения уравнения момен-
моментов количества движения.
Пример. Выясним влияние температуры газа перед компрессором на
степень увеличения давления в нем. По уравнению моментов количества
движения (98) можно найти момент сил, возникающих на колесе компрес-
компрессора. Для этого нужно знать окружные составляющие скорости газа за
(и?2и) и перед (шщ) колесом, а также расстояния от оси выходящей (г2)
и входящей (г\) массы газа. Секундная работа на валу колеса, как извест-
известно, равна произведению момента сил на угловую скорость (со), откуда по-
получаем для 1 кг газа
—L = (х)Aйи2Г2 — Wuir\).
Таким образом, работа 1 кг газа на колесе определяется кинематикой
потока и угловой скоростью колеса, но не зависит от температуры и давле-
давления газа (жидкости) перед колесом. Выше было показано, что работа коле-
колеса пропорциональна разности полных теплосодержаний за и перед колесом:
Поэтому при постоянных значениях числа оборотов и объемного расхода
газа, определяющих кинематику потока, перепад теплосодержаний на ко-
колесе не изменяется:
г* — г* = const.
!) При этом движение предполагается плоскопараллельпым, т. е. траек-
траектории частиц суть плоские кривые.
6. УРАВНЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ
47
Следовательно, при постоянной теплоемкости (ср = const) перепад
температур торможения на колесе также не изменяется:
ДГ* = Г* - 7* = const.
Отсюда, пользуясь уравнением работы компрессора в форме (86), заме-
замечаем, что степень повышения давления зависит от температуры газа перед
колесом:
= const.
Пусть, например, степень повышения давления в компрессоре на старте
\ТН = ТН = 288 К) равна як0; при увеличении скорости полета, влеку-
влекущем за собой увеличение температуры торможения перед колесом Г*,
степень повышения давления в компрессоре при постоянных объемном
расходе и числе оборотов может быть вычислена из условия постоянства
работы:
fe-1
к
Если в первом приближении пренебречь зависимостью коэффициента по-
полезного действия компрессора от температуры на входе, то'получится
<*-! = •
откуда с учетом равенства
к + 1 Л«
имеем
fe-1
Итак, в конечном счете из уравнения моментов количества движения выте-
вытекает, что степень повышения давления в компрессоре турбореактивного
двигателя падает с увеличением скорости полета. Результаты расчета по
этой формуле при стартовой степени повышения давления я*0 = 4 и
к = 1,4 представлены в следующей таблице:
Мн
0
4
0,5
3,8
1
3,2
1,5
2,75
2
2,3
2,5
2
3
1,75
48 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
Проведенный расчет величины як условен, так как основан на пред-
предположении о независимости величины работы от температуры даже при
значительном ее изменении.
Основное назначение турбокомпрессорного устройства в турбореактив-
турбореактивном двигателе состоит в том, чтобы создать в выходном сопле (за турбиной)
большее полное давление, чем в диффузоре (перед компрессором):
на основании этого должно выполняться неравенство
дкятак.с> *•
Здесь ак.с — коэффициент сохранения полного давления в камере сгорания
(при подводе тепла).
Ввиду того что с ростом скорости полета величина лк уменьшается,
а величины ят и ок с остаются практически неизменными, при некотором
значении скорости полета двигатель перестает удовлетворять последнему
неравенству.
В разобранном выше случае (л*0 = 4) при л* = 0,5 и ак с =0,95 это
неравенство не выполняется уже при значениях
и выше.
Прирост полного давления в турбокомпрессорном устройстве в целом
(рс > рд) зависит также от выбранной температуры перед турбиной,
с увеличением которой уменьшается потребный перепад давления в
турбине.
При некотором значении скорости полета турбокомпрессорное устрой-
устройство в целом перестает повышать давление в двигателе, т. е. становится
нецелесообразным. На этих скоростях полета работа воздушно-реактивного
двигателя обеспечивается сжатием воздуха только за счет скорости
наддува.
При дозвуковой, околозвуковой и не очень большой сверхзвуковой ско-
скорости полета, когда сжатие газа в компрессоре существенно преобладает
над расширением в турбине, турбореактивный двигатель сохраняет все
свои преимущества перед прямоточным реактивным двигателем.
§ 7. Энтропия
Согласно второму закону термодинамики при реальных не-
необратимых процессах, протекающих в конечной изолированной
системе, энтропия возрастает, а при обратимых — остается не-
неизменной.
Математически прирост энтропии dS определяется так:
здесь dQ — полное количество тепла, подводимое как извне, так
и изнутри (например, за счет работы сил трения), Т—абсолют-
Т—абсолютная температура.
По первому закону термодинамики E0)
dQ = dU+pdv.
§ 7. ЭНТРОПИЯ 49>
В случае идеального газа имеем
dU = cv dT;
отсюда с помощью уравнения состояния (pv = RT) получаем
откуда после замены
и интегрирования находим
S
-*.-{¦?-«.'¦??.
2
1 l L
или на основании уравнения состояния
S2-S1 = cvln-^. A00)
Изменение энтропии в идеальном адиабатическом процессе,
который является обратимым, равно нулю, так как в этом случае1
p2v\ = pxv\ — puk = const.
Всякий реальный процесс для изолированной конечной системы
протекает в таком направлении, что энтропия возрастает:
S2 — S{> 0.
Для того чтобы убедиться в этом на примере идеального газа,
перейдем в равенстве A00) от параметров потока к параметрам
торможения, используя очевидное соотношение
pvh = p*v*k.
Выразив удельный объем через давление и температуру
17* =
RT*
получим
^ -± . A01)
^1 \ 1 2 /
В изолированной системе теплообмен с внешней средой отсут-
отсутствует (й(?наР = 0) и температура торможения не изменяется:
4 Г. Н. Абрамович, ч 1
.50 гл. i. уравнения газовой динамики для струйки
Для такой системы, согласно A01), изменение энтропии
2 #
^ = Rlnf±. A02)
Так как полное давление в газовом потоке вследствие потерь
падает:
* *
P2<Pl
и соответственно тепло трения имеет всегда положительный
внак:
dQBB > 0,
то энтропия в изолированной системе при необратимом процессе
всегда увеличивается.
Вводя коэффициент сохранения полного давления, учиты-
учитывающий гидравлические потери, о = р2/рг, получим для энерго-
энергоизолированного газового потока (без теплообмена и механиче-
механической работы) прямую связь между гидравлическими потерями и
(приростом энтропии:
S2 — Si = —R]nc. A03)
В теплоизолированном газовом потоке (dQH3iP = 0) без по-
потерь (dQBH = 0) энтропия останется неизменной и при совер-
совершении механической работы, несмотря на то, что полное тепло-
теплосодержание газа при этом изменяется:
— L = г* — h Ф0.
Это значит, что в идеальном компрессоре и в идеальной тур-
турбине
В реальных машинах энтропия рабочего тела всегда изменяется.
Пусть отличие реального процесса от идеального учитывается
некоторым множителем т
Тогда, согласно A01), изменение энтропии
S2 — Si = -cv(k - l)ln m. A04)
Как в компрессоре, так и в турбине при теплоизолированном
§ 8. РАСЧЕТ РЕАКТИВНОЙ СИЛЫ (ТЯГИ)
51
процессе (<2(?нар = 0) гидравлические потери выражаются в под-
подводе тепла к газу (dQBB>0), т. е. в обоих случаях т<11).
Поэтому в реальных турбомашинах энтропия возрастает
(S2-Sx>0).
§ 8. Расчет реактивной силы (тяги)
Полет реактивного аппарата осуществляется под действием
реактивной силы, или, как ее часто называют, тяги, которую
сообщает ему струя выходящих газов. Для нахождения вели-
величины реактивной силы Р нет необходимости рассматривать де-
детально распределение давления по внутренним и наружным
стенкам реактивного аппарата. Реактивную силу можно опреде-
определить в конечном виде с помощью уравнения количества дви-
движения.
Совершая полет, тело производит возмущение в окружаю-
окружающей среде. Всегда можно выделить некоторую, достаточно боль-
большую, например цилиндрическую, область, границы которой вы-
выходят за пределы возмущенной части потока (рис. 1.13). На
4-
„j J/
Рис. 1.13. Контур для определения реактивной силы
боковых границах этой области давление и скорость потока
(считаем двигатель неподвижным, а воздух — движущимся со
скоростью полета) равны их значениям на бесконечности перед
двигателем.
Пусть ось х совпадает с направлением полета и является
осью симметрии двигателя; спроектируем на ось х сдлы, дей-
действующие на двигатель и на поверхность выделенного контура.
Так как силы давления в жидкости нормальны к поверхности,
то проекции на ось х сил, действующих на боковые поверхности
контура, обращаются в нуль. Поэтому уравнение Эйлера (см..
!) И в компрессоре, и в турбине при заданных перепаде температур и
начальном давлении конечное давление тем ниже, чем больше гидравли-
гидравлические потери.
4*
?2 ГЛ. I. УРАВНЕНИЕ- ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
(90)) запишется так:
оо оо оо ^Г
J pHdF — J pxdF + P = j (^ - и;,,) dGB + }' wxdGv.
0 0 0 0
Здесь площади, на которые распространяются интегралы, и об-
область интегрирования первого члена правой части бесконечны.
Сила Р берется со знаком плюс потому, что при выводе формулы
(90) предполагалось, что эта сила приложена телом к потоку,
а равная ей по велиичне реактивная сила действует на тело,
т. е. имеет обратный знак R = — Р\ 0в — секундная масса воз-
воздуха, втекающая в контур через сечение F; Gv — дополнительная
секундная масса горючего, которая подается в двигатель.
Если взять левую торцовую поверхность далеко перед дви-
двигателем, то давление на ней постоянно и равно атмосферному
(/>н), а скорость потока равна скорости полета (и)я). Кроме того,
можно допустить, что в поперечном направлении уже на неко-
некотором конечном расстоянии от поверхности двигателя поток яв-
является невозмущенным и площадь F, на которую распространя-
распространяются интегралы левой части, считать конечной; точно так же
конечной будет и область интегрирования в первом члене пра-
правой части. Тогда следует написать:
F gb Gr
pHF — J p±dF + P = J (wx — wn) dGB + j WydGT.
0 0 0
В большом числе случаев возмущение, вызываемое летящим те-
телом, настолько незначительно, что в плоскости среза сопла а
(вне струи выхлопных газов) давление обтекающего потока мало
отличается от давления на бесконечности (/?н). Тогда силы дав-
давления на передней и задней торцовых поверхностях контура
уравновешиваются везде, кроме участка, соответствующего по-
поперечному сечению выхлопной струи {Fa). Скорости потока во
всех элементарных струйках, кроме проходящих через двига-
двигатель, одинаковы (здесь мы пренебрегаем влиянием трения, вих-
вихревых и волновых потерь на наружной поверхности двигателя).
Следовательно, изменение количества движения получается
только в струе, протекающей сквозь двигатель. Тогда уравнение
Эйлера принимает следующий вид:
(Рш ~ Pa)Fa + P = G3{wa- wa)+ GTwai
откуда получается основная формула для модуля реактивной силы
P = GB(wa-wB)+GTwa + (pa-pB)Fa. A05)
В этих выражениях wa — средняя скорость истечения.
Следует подчеркнуть, что полученное соотношение справед-
справедливо только в том случае, если скорость и давление в плоско-
§ 8. РАСЧЕТ РЕАКТИВНОЙ СИЛЫ (ТЯГИ) 53
сти а (за исключением участка рабочей струи) равны в точно-
точности их значениям на бесконечности перед двигателем. Кроме
того, мы здесь пренебрегаем внешним лобовым сопротивлением
двигателя, которое всегда может быть учтено отдельно.
На расчетном режиме работы реактивного двигателя давле-
давление в выхлопной струе равно давлению окружающего воздуха
(/?а = /?н); в этом случае тяга равна изменению количества дви-
движения газа, прошедшего через двигатель:
P = GB(wa-wn)+Grwa. A06)
В воздушно-реактивных двигателях второй член правой части
мал, и им часто пренебрегают1), т. е. принимают для воздушно-
реактивных двигателей в расчетном случае2)
P = GB(wa-wn). A07)
Тяга жидкостного реактивного двигателя, в котором не ис-
используется атмосферный воздух, определяется для расчетного
режима по формуле
р =i(Gr + Go) wa A08)
или на нерасчетном режиме
-pB)Fa. A09)
Здесь Go — секундный массовый расход окислителя.
Рассмотрим теперь влияние на реактивную силу непостоян-
непостоянства давлений в плоскости выходного среза двигателя. Построим
эпюру давления и скорости на срезе сопла (рис. 1.14). Для про-
простоты остановимся на случае дозвукового истечения. Можно,
например, представить себе такое обтекание двигателя, при ко-
котором давление вблизи выходного среза понижено, за счет чего
местная скорость во внешнем потоке увеличивается. Давление
внутри дозвуковой выхлопной струи является примерно таким
же, как и на ее границе.
Для подсчета реактивной силы воспользуемся основным
свойством неравномерных (по величинам полного давления) по-
потоков, заключающимся в том, что неравномерность в распреде-
распределении скорости исчезает очень медленно, а давление выравни-
выравнивается быстро.
Так, например, неравномерность в поле давления, возникаю-
возникающая при повороте потока, выравнивается на расстоянии 1,5—
2 диаметров прямой трубы за местом поворота, скорость же вы-
выравнивается на расстоянии 20—30 диаметров. Этим свойством
можно воспользоваться при подсчете тяги. Из опытов известно,
1) Весовая доля горючего в воздухе, проходящем через двигатель, не
превышает одного — пяти процентов: &г « @,01 -f- 0,05) GB.
2) Следует особо подчеркнуть, что величина шн есть скорость полета,
а отнюдь не скорость во входном отверстии двигателя.
54
ГЛ. I. УРАВНЕНИЕ ГАЗОВОЙ: ДИНАМИКИ ДЛЯ СТРУЙКИ
что если плоскость Ъ отстоит от среза сопла на расстоянии аЬ,
большем одного диаметра 'среза (рис. 1.14), то поле давлении
уже равномерно. Таким образом, несколько отойдя от среза
сопла, мы попадаем в плоскость постоянного давления (рь = Рн)У
Рн
WH WH I
Рис. 1.14. Распределение давления и скорости потока перед и за двигателем
в связи с чем можно определить реактивную тягу по формуле1
Остается только найти величину скорости wb, которую имеет
рабочая струя в плоскости Ъ (рис. 1.14). Для этого при дозву-
дозвуковом истечении можно воспользоваться уравнением Бернулли
без учета гидравлических и тепловых потерь, ибо, как ука-
указывалось, участок струи, заключенный между плоскостями &
и Ь, мал.
Рассмотрим в качестве примера случай не слишком большой дозвуко-
дозвуковой скорости (М < 1). Тогда по уравнению Бернулли
При такой скорости разность давлений (р& — рн) бывает невелика, вслед-
вследствие чего мы приняли плотность газа неизменной.
Итак,
Ра - Рн
откуда
wh = w,
/Ра fH+1'
CL
О
В большинстве случаев при дозвуковой скорости на срезе сопла уста-
устанавливается давление, очень близкое к атмосферному, и тогда полагают
§ 8. РАСЧЕТ РЕАКТИВНОЙ СИЛЫ (ТЯГИ)
55
¦Wb = wa. При сверхзвуковом истечении между плоскостями а и Ъ могут
образоваться скачки уплотнения. В этом случае расчет поправки несколько
усложняется, но также вполне доступен.
Интересна одна особенность прямоточного воздушно-реактивного дви-
двигателя: если сохранять неизменной температуру в камере сгорания, то ве-
величина реактивной тяги (см. § 5, пример 4)
p = <
вначале возрастает с увеличением скорости полета, а затем, пройдя через
максимум, начинает убывать и при некотором значении скорости падает
до нуля. Объясняется это тем, что увеличение скорости полета вызывает
рост температуры торможения в начале камеры (^к)» но ПРИ этом Для
сохранения неизменной температуры торможения в конце камеры прихо-
приходится уменьшать подвод тепла. В том случае, когда температура торможе-
торможения в набегающем потоке становится равной предельно допустимой тем-
температуре в двигателе (Г* = Г^), подвод тепла приходится прекратить.
При этом величина тяги падает до нуля. Из формулы D2) получается сле-
следующее условие исчезновения тяги как для дозвукового, так и для сверх-
сверхзвукового идеального двигателя:
т т
JiLijL *l «
откуда приведенная скорость полета, при которой идеальный двигатель
перестает развивать тягу, равна
Повышение давления в прямоточном воздушно-реактивном двигателе
достигается за счет динамического сжатия воздуха перед входом в двига-
двигатель и в его диффузоре. Такой двигатель, как мы видели, эффективен
только при очень большой скорости полета и вовсе не способен развивать
Рис. 1.15. Схема турбореактивного двигателя: D — диффузор, К — компрес-
компрессор, Т — газовая турбина, А — камера сгорания, В — выходное сопло
тягу на месте. Для получения в воздушно-реактивном двигателе достаточ-
достаточной тяги на старте и при умеренной скорости полета приходится приме-
применять механическое сжатие воздуха. Воздушно-реактивный двигатель с ме-
механическим сжатием нашел широкое применение в современной авиации.
Наиболее распространенным типом воздушно-реактивного двигателя с ме-
механическим сжатием является турбореактивный двигатель (рис. 1.15).
В этом двигателе1) воздух засасывается компрессором. После сжатия в
!) Подробное изложение теории турбореактивного двигателя см. в кни-
книге: Теория воздушно-реактивных двигателей/Под ред. С. М. Шляхтенко.—
М.: Машиностроение, 1987.
56 ГЛ. I. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ СТРУЙКИ
компрессоре воздух поступает в камеру сгорания, откуда смесь разогретого*
воздуха и продуктов горения направляется на лопатки турбины. Обычно в
турбине используется только часть энергии газов (для получения механи-
механической работы, потребной на вращение компрессора). Остальная (свобод-
(свободная) часть энергии газов преобразуется в кинетическую энергию вытекаю-
вытекающей струи.
В случае, если весь избыток давления, имеющийся в камере сгорания,
используется на колесе турбины, двигатель перестает развивать реактив-
реактивную силу, но при этом мощность турбины превосходит мощность, потреб-
потребляемую компрессором; избыток мощности можно использовать, например,
для вращения авиационного винта или динамомашины.
Работа, затрачиваемая на сжатие 1 кг газа в компрессоре, как показано
в § 4, равна
Здесь рк, /?д — полные давления соответственно за и перед компрессором,
т)* — коэффициент полезного действия компрессора, Г* — температура тор-
торможения перед компрессором.
Если пренебречь отводом тепла в диффузоре, то можно считать, что
у* = 7*. Условимся, как прежде, под степенью повышения давления в
компрессоре понимать отношение значений полного давления газа за и пе-
перед компрессором
• р*
Под степенью уменьшения давления в турбине будем по-прежнему
понимать отношение значений полного давления за и перед турбиной:
* Р*с
Величина ?* = л*-л* характеризует избыток давления в сопле.
Работа, производимая 1 кг газа в турбине, равна
д-1
Ы) ~k -i
здесь Т*— температура торможения за турбиной, т]т— коэффициент по-
полезного действия турбины.
В турбореактивном двигателе работа турбины используется практиче-
практически целиком на привод компрессора: LT « LK. Если пренебречь небольшими
изменениями газовой постоянной и показателя адиабаты, то будем иметь
fe-i
•-* откуда < k -I ^c
§ 8. РАСЧЕТ РЕАКТИВНОЙ СИЛЫ (ТЯГИ) 57
Обычно температура заторможенного газа в выходном сопле значитель-
значительно выше температуры заторможенного газа в диффузоре (Г* > Г*). Тог-
Тогда из равенства работ компрессора и турбины вытекает, что степень уве-
увеличения давления воздуха в компрессоре выше степени уменьшения дав-
давления в турбине (я* >1/я*), т. е. при г]*т1*« 1 имеется избыточное
давление в реактивном сопле двигателя. Это необходимо для того, чтобы
скорость истечения из сопла wa и соответственно реактивная тяга были
достаточно велики (как на старте, так и в полете). Турбореактивный дви-
двигатель развивает обычно значительную стартовую тягу.
Существенной особенностью этого типа двигателя является также его
малая чувствительность к изменению плотности воздуха. Плотность воз-
воздуха, поступающего в двигатель, заметно повышается с увеличением ско-
скорости полета, благодаря чему растет массовый расход воздуха в компрес-
компрессоре. Мощность, потребляемая компрессором, изменяется пропорцонально
массовому расходу; однако последний возрастает одновременно и в турби-
турбине. Следовательно, мощность турбины увеличивается пропорционально мощ-
мощности компрессора, т. е. баланс мощности сохраняется.
Суммарная работа газа в двигателе складывается из работ расширения
ъ турбине и в сопле !):
Таким образом, как уже отмечалось, после использования некоторой доли
энергии в турбинном колесе остальная ее часть (свободная) может быть
использована в выходном сопле.
Доля работы компрессора (^к/2^) обычно значительно больше по-
половины, следовательно, на образование свободной мощности в турбореак-
турбореактивном двигателе тратится относительно малая часть располагаемой
энергии.
Тяга турбореактивного двигателя определяется скоростью истечения
из сопла
где
Если давление за турбиной выше, чем перед компрессором, то приведенная
скорость истечения при одинаковых условиях полета у турбореактивного
двигателя выше, чем у прямоточного воздушно-реактивного двигателя. Но
в последнем возможны более высокие температуры. Поэтому прямоточный
воздушно-реактивный двигатель может развивать большие удельные тяги
даже при меньших давлениях в реактивном сопле. Однако для увеличения
тяги в турбореактивном двигателе можно поместить за турбиной вторую
камеру сгорания (так называемую форсажную камеру), в которой газ мо-
может дополнительно нагреваться до такой же температуры, как и в прямо-
прямоточном воздушно-реактивном двигателе. В этом случае тяга турбореактив-
турбореактивного двигателя существенно возрастает.
Если пренебречь потерями давления во второй камере сгорания, то
приведенная скорость истечения (Яа) сохранит то же значение, что и без
форсажной камеры, а скорость истечения (wa) возрастет пропорционально
корню квадратному из температуры.
1) Как показано выше, в турбореактивном двигателе всегда выпол-
выполняется равенство LT = LK.
Глава II
ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
§ 1. Движение жидкой частицы
Рассмотрим движение бесконечно малой жидкой частицы,,
имеющей первоначальную форму параллелепипеда (рис. 2.1).
В отличие от твердого тела жидкая частица при своем движении
может сильно деформироваться.
Грани бесконечно малой частицы жидкости, имеющей в на-
начале движения форму прямого параллелепипеда с ребрами dx,
dy, dz, с течением времени могут скашиваться и растягиваться
(рис. 2.2 и 2.3).
Пусть составляющие скорости движения частицы в точке а
(рис. 2.1) суть и, v, w; тогда составляющие скорости в точке Ъ
равны
¦ ди , , dv 7_
dx
в точке d
ди
и -J ах, v —
dw
W -f- (
и в точке е
dv
x
Рис. 2.1. Элементарный параллелепи-
параллелепипед в потоке жидкости
ди
dv
1 dz
Скашивание ребра ab частицы за бесконечно малое время dtf
которое вызывается разностью компонент скорости в точках а
и Ъ (рис. 2.2), характеризуется смещением точки &, равным
Относительное смещение или угловая деформация
W _ ди 7.
пЪ ду
§ 1. ДВИЖЕНИЕ ЖИДКОЙ ЧАСТИЦЫ
59
Скашивание ребра ad приводит к угловой деформации
dd' _ dv d
ad dx
Ввиду того что угловые деформации за время dt незначительны,
угол наклона грани можно считать равным тангенсу этого угла.
а
ъ'_^~—~~~~~~
/ - —
i_ —*—
с/
'dr
d
ь
a
с
d
С"
rt"
X
X
Рис. 2.2. Угловая деформация граней Рис. 2.3. Линейная деформация
граней
Полное скашивание первоначально прямого угла в точке а
в этом случае равно
du . dv l ,,
а скорость соответствующей угловой деформации
ди ди
Aа)
Индекс z указывает на то, что рассматривается деформация
частицы в плоскости ху, перпендикулярной к оси z; в остальных
двух плоскостях скорости скашивания координатных углов рав-
равны, очевидно,
dv , dw
dw , ди
Используя те же угловые смещения граней частицы, можно
определить угловые скорости ее вращения. Поскольку направле-
направления вращения ребер аЪ и ad противоположны, средняя угловая
скорость вращения частицы в целом около оси z составляет
dv
ди
Для остальных двух осей вращения имеем соответственно
ди d
60 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
Вектор угловой скорости вращения со, составляющие кото-
которого суть со*, (оу и coz, носит название завихренности, или вихря
скорости, его величина определяется, очевидно, следующим
равенством:
0) = у со* + со* + cof. Bв>
Остановимся теперь на линейных деформациях частицы. Ско-
Скорости движения точек and (рис. 2.3) в направлении оси х от-
отличаются на величину
ди т \ ди 7 /qv
В связи с этим частица удлиняется за время dt на величину
dd" = —r— dx dt.
дх
Относительное удлинение частицы
dd" ди ,.
—— = -т- at,
ad дх '
а скорость относительного удлинения частицы в направлении
оси х равна
ди
По аналогии, скорости относительного удлинения по другим осям
dv dw
Удлинение сторон параллелепипеда, изображающего жидкую
частицу (рис. 2.1), в общем случае ведет к изменению ее объема*
умножая разность скоростей поступательного движения противо-
противоположных граней параллелепипеда, определенную по формуле
C), на площадь каждой из этих граней, получим скорость изме-
изменения его объема за счет линейной деформации в направлении
оси абсцисс; составляя подобные выражения для скоростей из-
изменений объема по остальным двум координатным осям и сум-
суммируя все три величины, найдем полную скорость изменения
объема жидкой частицы:
dV ди -. -. j dv , л 7 . dw , 7 7
-jf = -fa dx dV dz + -щ; dy dzdx + — dz dx dy =
= Ы + ?y + ez) dx dy dz.
После деления этого выражения на первоначальный объем
жидкой частицы V = dx dy dz, приходим к важной в газовой
динамике величине скорости относительного изменения объема
§ 2, УРАВНЕНИЕ НЕРАЗРЫВНОСТИ 61
жидкой частицы:
6 ^ Т Ил = 8х + гу + 8z# ( '
На основании D) имеем окончательно
ды . dv . dw
^ + +
§ 2. Уравнение неразрывности
<6>
Выражение, стоящее в правой части равенства F), называ-
называется дивергенцией (или расхождением) вектора скорости и обо-
обозначается так:
7 ди , ди , dw /Г7Ч
где W — скорость.
В сплошной несжимаемой среде объем частицы не изменяет-
изменяется, следовательно, равенство
представляет собой уравнение неразрывности жидкости.
Условие постоянства массы жидкой частицы может быть за-
записано в следующем виде:
G = pF = const. (9)
Здесь под плотностью жидкости р понимается предел отношения
массы частицы к ее объему
^G dG
причем предполагается, что, стремясь к нулю, объем AF стяги-
стягивается к некоторой внутренней точке.
Продифференцировав по времени обе части равенства (9) и
поделив результат на величину G, получим
Отсюда на основании E) приходим к уравнению неразрывно-
неразрывности для сжимаемой сплошной среды
Заменяя полную производную плотности жидкости по времени
частными производными и используя G), получаем
ди . ди . dw\ до . до , др , до
162 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
В соответствии с правилом дифференцирования произведений
это уравнение неразрывности для сжимаемой среды (газа) при-
приводится к виду
Сумма последних трех членов представляет собой дивергенцию
плотности тока pW, поэтому уравнение неразрывности для газа
можно записать также в форме
-^ + div(pW) = 0. A26)
При выводе дифференциального уравнения неразрывности рас-
рассматривалось движение отдельной жидкой частицы; такой метод
исследования ввел в гидродинамику Лагранж. В другом методе
исследования, развитом впервые Эйлером, рассматривается не
поведение отдельных частиц, а изменение по времени парамет-
параметров жидкости в фиксированных точках пространства; метод
Эйлера во многих случаях удобнее метода Лагранжа — ив гид-
гидродинамике, и в газовой динамике им пользуются чаще.
§ 3. О силах, действующих в жидкости
Выделим некоторый объем жидкости и рассмотрим его изоли-
изолированно от окружающей жидкой среды.
Силы, действующие на заданный объем жидкости, могут быть
двоякого рода: объемные и поверхностные. Объемные силы при-
приложены ко всем материальным частицам, составляющим объем.
К объемным силам относятся: сила тяжести, силы магнитные и
электрические. Поверхностные силы распределены по поверхно-
поверхности выделенного объема. Они возникают в результате воздейст-
воздействия окружающей среды на данный объем.
Поверхностные силы, в зависимости от того как они направ-
направлены по отношению к данному элементу поверхности, подразде-
подразделяются на нормальные и тангенциальные.
Для того чтобы характеризовать изменение от точки к точке
объемной силы АР или поверхностной силы AF, вводят понятие
о напряжении, подразумевая под ним предел отношения силы
к объему AF (или соответственно к поверхности AS), который
достигается при стягивании объема (или поверхности) к неко-
некоторой внутренней точке.
Итак, напряжение объемной силы в данной точке среды есть
о ,. АР dV
поверхностное напряжение
- ,. AF d?
Д5-*0 AS dS
§ 3. О СИЛАХ, ДЕЙСТВУЮЩИХ В ЖИДКОСТИ
Силы нормальные действуют как в покоящейся, так и в движу-
движущейся жидкости; силы касательные возникают только при дви-
движении жидкости, да и то лишь в том случае, когда жидкие ча-
частицы деформируются.
Для большинства жидкостей, как показывает опыт, справед-
справедлива гипотеза Ньютона, согласно которой напряжения пропор-
пропорциональны скоростям деформаций. Коэффициент пропорцио-
пропорциональности, зависящий от рода жидкости и ее состояния, носит
z i
Рис. 2.4. Схема сил, действующих на две грани элементарного параллеле-
параллелепипеда
название коэффициента динамической вязкости или попросту
вязкости.
Составим уравнения движения вязкой сжимаемой жидкости
для элементарного параллелепипеда со сторонами dx, dy, dz
(рис. 2.4).
Обозначим компоненты объемного напряжения R буквами
X, У, Z, нормальные напряжения, приложенные к граням па-
параллелепипеда и параллельные соответствующим координатным
осям,— ох, ау, oz, касательные напряжения, лежащие в плоско-
плоскости каждой грани,— буквой т с двумя индексами (первый ука-
указывает ось, перпендикулярную данной грани, а второй — ось,
параллельную направлению напряжения, например т^, xxzi %yz).
Заметим, без доказательства, что из условия равновесия парал-
параллелепипеда следует равенство моментов сил относительно произ-
произвольной оси и равенство касательных напряжений с одинаковы-
одинаковыми, но расположенными в обратном порядке индексами:
%ху=== Тдо, T&z == Tz#, Tyz =: Tzy. ^loaj
По закону Ньютона произведение массы параллелепипеда на
его ускорение равно равнодействующей всех сил, приложенных
к параллелепипеду.
Составим соответствующее уравнение для проекций ускоре-
ускорения и равнодействующей силы на ось х. Нормальные напряже-
^54 гл. ii. элементы гидродинамики
ния, приложенные к торцовым граням, дают составляющую
^илы:
(<*х + —jr- dx) — ox\dydz — —z— dx dy dz.
Составляющие силы от тангенциальных напряжений, действую-
действующих на боковые и верхние грани:
— twx \dz dx = --?-
ух + "~^Г d^j ~~ Tv*
\Uzx + —^- dzj — xzx\ dy dx = —jj?- dx dy dz.
Если компоненты вектора скорости по осям х, у, 2 обозна-
обозначить через u, v, w и учесть, что масса частицы dG = p dx dy dz,
то уравнение движения вдоль оси х для единицы объема жидко-
жидкости примет вид
Полную производную скорости в уравнении A36) можно вы-
выразить через частные производные:
^^ dt [ dx [ dy x dz v '
Тогда уравнение движения вдоль оси х можно представить
в виде
Таким же образом можно вывести уравнения движения в на-
направлении осей у и z:
dv . 5i; . du . du v . ( дтху , ^a?/ .
P + P^hPhP^ ^+ —t^" + ""^ H
dy ' r ^z ' \ ^ж ' dy ' dz
Среднее арифметическое трех нормальных напряжений (среднее
нормальное напряжение)
<г= у (а^ + °у + az) A5а)
не изменяется при преобразовании координат и для невязкой
жидкости равно давлению, взятому с обратным знаком.
Для дальнейшего удобно выделить из нормальных напряже-
напряжений так называемые дополнительные напряжения, определяемые
§ 4. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ 65
из условий
<*х = Gx — °"»
о'у = Оу — а, A56)
o'z = gz — а.
Используя эти соотношения, систему дифференциальных
уравнений движения можно представить в виде
дх 1 у дх
+ ¦
ду l dz
до[, дху..
дх
ndw __ 7 да ( ^хг . ^yz_ , d°'z \
РЧГ~^^ ~dz~ + \1Г ~г ~~д1Г ~r dz у
Разумеется, в каждом из этих уравнений можно в соответст-
соответствии с A3в) в левой части полную производную составляющей
скорости заменить частными ее производными, а касательные
напряжения с одинаковыми, но переставленными индексами со-
согласно A3а) считать равными.
§ 4. Связь между напряжениями и деформациями
Связь между напряжениями и скоростями деформации, как
уже указывалось, устанавливается законом трения Ньютона.
Касательные напряжения вызывают деформации сдвига (уг-
(угловые деформации), определение которых было дано в § 1 этой
главы. Так как согласно гипотезе Ньютона в жидкости напряже-
напряжения пропорциональны скоростям деформаций, то в соответствии
с A) имеем
1ху =
где, как уже указывалось, коэффициент пропорциональности jj,
есть коэффициент динамической вязкости, зависящий от рода
жидкости и ее состояния (температуры, давления).
Касательные напряжения в двух других координатных пло-
плоскостях суть соответственно
(dv . dw \ ,л-7^\
7 + -^-J = №, A76)
dw . du
Сложнее обстоит дело с нормальными напряжениями.
5 Г. Н Абрамович, ч 1
66 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
Распространяя гипотезу Ньютона о пропорциональности на-
напряжений скоростям деформаций на нормальные напряжения и
деформации растяжения (сжатия), следует иметь в виду, что
растяжение жидкой частицы сопровождается ее поперечным
сжатием, т. е. объемной деформацией; иначе говоря, деформация
в направлении любой оси вызывается напряжениями, как парал-
параллельными этой оси, так и перпендикулярными к ней.
Подробный анализ полей напряжений и деформаций, выпол-
выполненный двумя разными методами в гидродинамике и в кинети-
кинетической теории газов1), позволил установить связь между нор-
нормальными и касательными напряжениями, из которой следует,
что добавочное нормальное напряжение равно
o'x = ox-o = 2ii(sx-je)j, A8)
где гХ1 е — относительные линейная и объемная деформации,
определяемые соответственно из D) и F).
Кроме того, в гидродинамике вязкой сжимаемой жидкости
принимается второе обобщение гипотезы Ньютона, согласно ко-
которому среднее нормальное напряжение равно сумме двух чле-
членов: первый член есть давление, взятое с отрицательным зна-
знаком, которое не зависит от скорости объемной деформации,
а второй член пропорционален последней:
о = — р + це; A9)
здесь ц — коэффициент, который можно назвать второй вяз-
вязкостью. Знак минус при давлении учитывает, что оно всегда на-
направлено внутрь выделенного объема жидкости; значение а при-
принято считать положительным, если оно направлено наружу.
Итак, согласно A8) и A9), нормальные напряжения выра-
выражаются следующим образом:
i о у ( 2
ох= — р + 2\кгх + IЛ о"
оу=—р + 2ixey + (л — з" v) e> B°)
/ 2 \
Ог = — Р + 2[A8Z + Л — "о" И' Iе-
\ ° J
В несжимаемой жидкости е = 0, откуда а = —р,
В кинетической теории газов доказывается, что для одно-
одноатомного совершенного газа отношение ц/уь должно иметь поря-
!) Паттерсон Г. Н. Молекулярное течение газов.— М.: Физматгиз,
1960; Л о й ц я н с к и й Л. Г. Механика жидкости и газа.— М.: Наука,
4987.
§ 4. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ 67
док квадрата отношения объема, занятого молекулами, к объему
газа, т. е. является весьма малой величиной, что дает право
пренебречь второй вязкостью.
Мы будем счдтать это справедливым для всех газов, хотя
строгого обоснования такого предположения для многоатомных
газов не существует. Для весьма плотного газа (при очень вы-
высоком давлении), двухфазного (газо-жидкостного) течения и в
других особых случаях допущение т] « 0 заведомо несправедли-
несправедливо. Следует заметить, что часто второй вязкостью называют ве-
величину % = ц — -о- fi, которая никогда не может быть принята
равной нулю, но выпадает из уравнения движения при div W =
= 0, так как является множителем при последней.
В дальнейшем мы положим ц = 0, т. е. будем рассматривать
газ без второй вязкости, тогда нормальные напряжения опреде-
определяются следующими выражениями:
ох= — р + 2
2
°У = — Р + 2|Л8у — "g- М^> B2)
2
CTz = — Р + 2|182 q- [А?.
Из A8) следует, что добавочные нормальные напряжения воз-
возникают только в вязких жидкостях, когда \х Ф 0.
Подставляя в A8) значения гх и е из D) и F), получим
' _ 2 _^_ _ ^ (ди_ 1—4- —) ^2Я ^
и соответственно для осей у и z
' п dv 2 I du , dv , dw
dw 2 I du , dv , dwx ' ^
Для несжимаемой жидкости
^ B4)
1 п dw o
В несжимаемой жидкости добавочные нормальные напряже-
напряжения связаны со скоростями линейной деформации точно такими
же соотношениями, как касательные напряжения со скоростями
угловых деформаций.
В этом нетрудно убедиться, сравнивая равенства B4) и A7).
68 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
§ 5. Уравнения Навье — Стокса
Пользуясь формулами F), A7), A9) и B3), можно в диф-
дифференциальных уравнениях A4), с учетом ц = 0, т. е. о = —р,
заменить напряжения скоростями деформаций. При этом мы
получим так называемые дифференциальные уравнения движе-
движения вязкой жидкости Навье — Стокса.
Например, для движения параллельно оси х
ди . ди ди . ди
Р —^г + ри —^ г Р^ ~^ г Pw -^— =
r dt ' v дх ' v ду ' r dz
dp , д \~ ди 2 I ди
\1 Г / ди
После несложных преобразований в случае неизменного зна-
значения вязкости во всей области течения (\х = const) имеем
ди , ди . ди ди
Р + Р" + РУ + Р"' =
2 ^ (ди до . дш
B5)
Используя обозначения для оператора Лапласа
и дивергенции скорости
т \\7 ди . ди . dw
div W = ——\- ——\- -j-,
дх 1 ду l dz
запишем уравнение B5) в более компактной форме:
ди . ^w , 5м , 5м
и по аналогии для движения в направлении осей у и z
dv , 5у . ду 5у
р-аг + рц^ + Рг;-%+р";^г =
= y--| + ^ + 4^^(divW). B66)
dw . dw , дш , дм;
P + P" + Pi; + P";
liu^(divW). B6в)
§ 6. УРАВНЕНИЕ ЭНЕРГИИ 69
Уравнения B6) называются уравнениями Навъе — Стокса.
В векторной форме уравнения Навье — Стокса сводятся к одно-
одному уравнению
р _^ = R _ grad р + jxAW + 1 [г grad (div W), B7)
где R — напряжение объемной силы.
В вязкой жидкости имеет место прилипание частиц жидкости
к стенкам, ограничивающим течение, поэтому при интегрирова-
интегрировании дифференциальных уравнений Навье — Стокса нужно ис-
использовать в качестве граничного условия равенство нулю ско-
скорости течения у стенки (Ww = 0).
В случае несжимаемой жидкости (р = const) последние чле-
члены в уравнениях Навье — Стокса B6) и B7) отсутствуют
(divW = 0), вследствие чего эти уравнения принимают более
простой вид:
du v dp . А
<28>
p ™L = R - grad p + цДW. B9)
Решение уравнений Навье — Стокса даже для несжимаемой
жидкости представляет собой очень сложную задачу.
До сих пор удалось получить точные решения этих уравне-
уравнений лишь в некоторых простейших случаях, например для тече-
течения вязкой жидкости по прямой трубе — задача Пуазейля; для
течения между двумя параллельными плоскими стенками, из ко-
которых одна неподвижна, а другая движется,— задача Куэтта;
для течения вблизи критической точки — задача Хименца —
Хоуарта и др.
Задачи гидродинамики вязкой жидкости решаются обычно
приближенно путем отбрасывания в уравнениях Навье — Стокса
членов, которые в тех или иных конкретных условиях могут
быть малы по сравнению с другими членами.
§ 6. Уравнение энергии
Составим дифференциальное уравнение сохранения энергии
для движущейся частицы сжимаемой среды. Согласно первому
закону термодинамики подведенное к телу тепло идет на повы-
повышение его внутренней энергии и на совершение работы дефор-
деформации
dQ = cvdT + p dv. C0)
70 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
Здесь dQ = dQB + dQTV — суммарное количество тепла, подведен-
подведенное к 1 кг вещества за счет теплообмена частицы с окружающей
средой (dQa) и работы сил трения (d(?Tp), p du — работа сжа-
сжатия (деформации), dU = cvdT — внутренняя энергия газа.
Для частицы с объемом V = dx dy dz и массой G = pV усло-
условие сохранения энергии запишется в следующем виде:
dq = dqB + dqTV = Gcv dT + p dV. C1)
Здесь dqB — тепло, полученное частицей извне, dgTp — тепло тре-
трения, выделяющееся на ее гранях.
Тогда секундный поток тепла, приходящийся на единицу
объема частицы, равен
Если подвод тепла из окружающей среды осуществляется
только путем теплопроводности, то через единицу поверхности,
согласно гипотезе Фурье, проходит в единицу времени поток
тепла
4-igL = -*<?.. C3)
F dt дп v '
Здесь % — коэффициент теплопроводности, зависящий от свойств
?кидкости (температуры, давления), dTjdn — градиент темпера-
температуры по нормали к поверхности, dqF/dt — секундный поток теп-
тепла, F — площадь поверхности частицы.
Возвращаясь к элементарному параллелепипеду (рис. 2.4),
запишем секундный расход тепла через грань площадью dy dz
в направлении оси х
Секундный приток тепла через противоположную грань со-
составляет
Таким образом, увеличение запаса тепла в объеме dx dy dz
вследствие притока тепла через указанную пару граней в тече-
течение промежутка времени dt составляет
±(x?L)dxdydzdt.
Аналогично, приток тепла в направлении осей у и z состав-
составляет соответственно
д U д?
ду \ ду
-т— А -т- \dz dx а у dt.
§ 6. УРАВНЕНИЕ ЭНЕРГИИ 71
Общее количество тепла, подведенное к частице путем тепло-
теплообмена с внешней средой за время dt, равно
Найдем теперь количество тепла, поступающее в объем dx dy dz
вследствие работы сил трения.
Силы вязкости, приложенные к противоположным граням па-
параллелепипеда, имеют противоположные направления. Секунд-
Секундная работа равна произведению силы на проекцию скорости на
направление силы. Например, дополнительные нормальные на-
напряжения ох, действующие на гранях площадью dy dz, соверша-
совершают за одну секунду работу (при учете только членов первого
порядка малости)
I — о'хи+ \°'x + j§dx) (и
dxdydz.
Таким же способом определяется работа, которую производят
касательные напряжения хху и тХ2, приложенные к тем же гра-
граням, в направлении двух других составляющих скорости (ишю):
dJ^l dxdydz, dJ^pdxdydz.
Работа нормальных и тангенциальных напряжений, действу-
действующих на остальных двух парах граней, рассчитывается анало-
аналогичным образом. В итоге получается следующее выражение для
суммарной секундной работы сил трения, действующих на по-
поверхности параллелепипеда:
c (GxU + т*Уи + TxzW ) + "%" (хухП
+ -^ (ъхи + tzyV + a^)J dx dy dz. C5)
Однако не вся работа вязких сил превращается в тепло.
Часть этой работы, соответствующая равнодействующей вязких
сил, которая вызывает ускорение частицы, расходуется на при-
приращение механической энергии частицы.
Компоненты равнодействующей вязких сил в направлении
осей х, г/, z были определены в § 4 при выводе уравнений дви-
движения; работа, совершаемая этими компонентами равнодейству-
72 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
ющей сил в единицу времени, очевидно, равна
~Tt [ и\~Ш ~Т~ ду ~т~ dz ) "+" V \ дх "f" ду "^ дг
дх..
Вычтя из полной работы C5) работу перемещения частицы
C6), получим искомую часть секундной работы вязких сил,
трансформирующуюся в тепло:
+х) + [ху*дУ- + ау-дТ+Ху*-ду-
ди . 'dw\] , , , ^?тр /о7\
gr + azlFjjcfa^dz = -5iB. C7)
Если теперь в уравнении C2) величину суммарного секунд-
секундного притока тепла dq = dqB + dgTp заменить с помощью C4) и
C7), то получим уравнение энергии
dT , p dV \ д I* дТ\ . д (* дТ\ . д Л дТ
ди>\ , ( ди , ' dv , dw
"to + т^ И + Тжг^ 1
/ ди . ди
<г-ЪЧ)[ Cg)
После замены в C7) вязких напряжений их значениями со-
согласно A7) и B4) получим тепло трения, выделяющееся за од-
одну секунду в элементарном параллелепипеде:
dqTXi ~тг C9)
где множитель
vf. 1 Г/ ' ди . ди , dw \ . ( ди . ' dv . dw
ди , dv , 'dw\\ 0\(duY , /^\2 . (dw
5" V j_ (ди j_йц; Y
"^"У + 1"Л + "to/ ""
2 /Зм . dv . dw \2 //Л,
носит название диссипативной функции.
§ 6. УРАВНЕНИЕ ЭНЕРГИИ 73
Используя определение функции Ф C9) и D0), получаем
уравнение сохранения энергии в виде
D1а)
Преобразуем второй член левой части этого уравнения с по-
помощью условия сохранения массы (На):
Г d(-L.Y]
У dt p dt Idt V dt J-
Тогда уравнение энергии можно представить также в сле-
следующем виде]):
d \г Т 4- р 1 dp м д U дТ ) -и
дТ\ , д L дТ
Для идеального газа, подчиняющегося уравнению состояния
р/р = ДГ, уравнение энергии упрощается, так как
Отсюда
di
p
Если коэффициент теплопроводности не изменяется во всей
области течения, то имеем уравнение энергии в следующей
форме:
^=^4t=d-dJ + ЫТ + уД>. D2)
В несжимаемой жидкости второй член левой части уравне-
уравнения энергии D1а) равен нулю и, кроме того, ср = cv = с, поэто-
поэтому уравнение энергии получается в следующем виде:
^ D3)
Диссипативная функция Ф в этом случае также принимает
более простую форму, так как последний член правой части
D0) равен нулю.
j.
1) Здесь U = ^ cvdT = CVT, где Cv — среднее значение теплоем-
теплоемкости.
74 гл. п. элементы гидродинамики
Для стационарного двумерного (плоскопараллельного) тече-
течения уравнение энергии D2) примет следующий вид:
дТ , дТ\ I др . др \ . . (д2Т . д2Т
««*V , (9v\2] . (ди . dv\2 2
В некоторых случаях в газовой динамике удобнее пользо-
пользоваться другой формой уравнения энергии, которую можно полу-
получить с помощью уравнений Навье — Стокса.
Умножим первое из уравнений Навье — Стокса A6) на со-
составляющую скорости щ второе — на у, третье — на w и сложим
почленно все три уравнения. Тогда будем иметь
W2
W) [dp
P~~di U^ dt ) "i" u \ dx ~r~ dy "*" dz
Здесь для простоты отброшена работа объемных сил как не иг-
играющих роли в газовой динамике и среднее нормальное напря-
напряжение заменено давлением (а = —р).
Складывая уравнение D5), отражающее изменение кинети-
кинетической энергии, с уравнением D2), учитывающим изменение эн-
энтальпии, и используя выражение D0), получаем после некото-
некоторых преобразований
+ ijf (%yxU + Gyv + %yzW} + 4i (XzxU + XzyV + GzW")-
Как известно из § 2 гл. I, сумма энтальпии и кинетической
энергии называется полной энтальпией (полным теплосодержа-
теплосодержанием)
W2
i + ^=i*. D7)
Подставляя D7) в левую часть уравнения D6) и заменяя с по-
помощью (8), A7) и B4) напряжения скоростями деформаций,
получаем после преобразований уравнение энергии в таком виде:
+ -J- [I (W • V) div W + -|- ц (div WJ + 2^fi, D8)
§ 7. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ 75
где
о — (^lIL ^1± —\ л_(E1L — — — —\ л. [H]L — _ dv dw \
W ~~ \~ду дх дх ду ) "¦ \ dz дх дх dz ) + \ dz ду ду dz )щ
В газовой динамике имеет большое значение (см. следующий
параграф) безразмерная величина
?-»¦
носящая название числа Прандтля. Введем это число в правую
часть уравнения D8). Для этого прибавим и вычтем член
используем D7) и учтем, что при сР = const
ср
Итак, имеем
^ . D9)
Значение числа Прандтля зависит от физических свойств среды.
Для газов число Прандтля близко к единице (например для воз-
воздуха Рг = 0,72). При Рг = 1 третий член правой части равен ну-
нулю и уравнение энергии упрощается:
E0)
§ 7. Гидродинамическое подобие
Ввиду невозможности получить точное решение уравнений
Навье — Стокса и уравнения энергии для подавляющего боль-
большинства задач гидродинамики и газовой динамики прибегают
либо к приближенным решениям, либо к экспериментам на мо-
моделях. В последнем случае возникает вопрос об условиях подо-
подобия для обтекания натурного объекта и его модели.
Первым условием такого подобия является геометрическое
подобие, которое выполняется, если размеры всех сходственных
элементов модели и натуры отличаются в одно и то же число
раз и, кроме того, если сходственные элементы расположены
под одинаковыми углами к вектору скорости набегающего
потока.
76
ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
Пусть любой характерный размер модели гм отличается от
соответствующего характерного размера натуры гн в kt раз. Тог-
Тогда величина
ГМ 7 /ГЛ\
— = kt (М)
'и
есть линейный масштаб моделирования (рис. 2.5). Кинематиче-
Кинематическое подобие течений около модели и натуры выполняется, если
Рис. 2.5. Иллюстрация геометрического подобия
в сходственных точках, координаты которых пропорциональны:
E2)
-2L = — = — = —— = к\,
х„ у„ zrr гул
"н ^н Лн 'н
компоненты векторов скорости удовлетворяют условию
U
н
"н
"н
и
оон
E3)
где Uoo м, Uoo н — скорости невозмущенного набегающего потока
соответственно у модели и у натуры на большом расстоянии
(«на бесконечности») от тела. Величина ки называется кинема-
кинематическим масштабом моделирования.
Из условия E2) вытекает, что сходственные точки двух те-
течений можно определить следующим образом:
JL
н
н
E4)
т. е. как точки с одинаковыми относительными значениями
координат.
Точно так же из условия E3) получаем, что в сходственных
точках двух кинематически подобных течений, вне зависимости
от кинематического масштаба моделирования, безразмерные зна-
значения соответственных составляющих скорости одинаковы:
Условие динамического подобия двух течений, очевидно, выпол-
выполняется в том елучае, когда значения соответственных сил, при-
приложенных к модели и натуре, отличаются в одно и то же
§ 7, ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ 77
число раз:
duM dvM. dwM
~dwn
1 dt
kR, E6)
Л1хм Л1ум -"zm 7
XH J/H ZH
Первое из приведенных равенств содержит проекции сил
инерции, стоящие в левой части уравнений Навье — Стокса, вто-
второе — сил объемных, третье — сил гидродинамического давления
и четвертое — сил трения, сгруппированных в правой части
уравнений Навье — Стокса.
Коэффициент kR характеризует динамический масштаб моде-
моделирования. Из равенств E6) видно, что вне зависимости от мас-
масштаба kR динамическое подобие имеет место в случае, если без-
безразмерные значения соответствующих сил, приложенных к мо-
модели и натурному объекту, одинаковы:
V V V V
Ам Ан хш хк „ _ _
Рм —
RXM
_ duM
Рн —
duH
H~df
duM duR ' duM duB
dt dt dt dt
T) T)
И Т. Д.,
И Т. Д.
Гидродинамически подобными являются течения, в которых
выполняются одновременно условия геометрического, кинемати-
кинематического и динамического подобия.
Если записать уравнения Навье — Стокса в безразмерном ви-
виде, то для двух гидродинамически подобных течений эти урав-
уравнения окажутся совершенно идентичными.
Приведем к безразмерному виду уравнение Навье — Стокса
B5), для чего сначала все величины, входящие в уравнения,
выразим в долях соответствующих величин для невозмущенно-
невозмущенного течения вдали от тела (и,*, р^, ?«>) и также характерных
78 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
значений времени (to) и размера (I):
(
ОО СЮ | ОО
и и и
Ф— д— д—-
и ~оо , и ~оо ,
II Ф > и 11 '
"">т
Р 'Р. Р д±. + р„!« Р
К Р W
д— д— 5 —
" U 11
д~т д~г
. E7)
а затем разделим на величину и{
инерции для единицы массы:
и и и
д д д <
_Z "оо U Uoo , V "оо W_
пропорциональную силе
_ _?/ loo Poo loo 11 Poo
.^^ *(+)'.
JL i Э
u v w
д д д —
и и и
+¦
•т ei
Z
¦ E8)
Здесь принято, что массовая сила X представляет собой силу
земного тяготения, т. е. Х/р = g.
Безразмерное уравнение Навье — Стокса E8) содержит сле-
следующие безразмерные комплексы:
gl
'о"»'
,2 >
р=х
P<x,'"oo#
Очевидно, что для геометрически и кинематически подобных те-
течений безразмерные уравнения движения E8) будут одинако-
одинаковыми в том случае, если каждый из этих комплексов имеет одно
и то же значение для натурного объекта и модели и если
в сходственных точках этих потоков относительные значения
плотности и значения вязкости одинаковы (р/р«> = idem,
§ 7. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ 79
[Л = idem)
л __^ н ___ с 1«
"сом "сон E9)
Безразмерные комплексы E9) являются, таким образом,
критериями динамического подобия для геометрически и кине-
кинематически подобных систем. Этим критериям подобия присвоены
следующие обозначения и названия:
— = Sh — число Струхаля,
ut
•^r- = Fr — число Фруда,
—г = Ей — число Эйлера,
— = R — число Рейнольдса.
F0)
В выражениях F0) индексы опущены, так как в них следу-
следует подставлять некоторые характерные значения параметров,
которые не обязательно соответствуют их значениям на «беско-
«бесконечности».
Вспомним, что каждый из критериев динамического подобия
был образован делением соответствующей силы на величину,
пропорциональную силе инерции; поэтому число Фруда опреде-
определяет по существу отношение веса (объемной силы) к силе инер-
инерции, число Рейнольдса — отношение силы вязкости к силе инер-
инерции, число Струхаля — отношение дополнительной (локальной)
силы, вызванной неустановившимся характером движения, к си-
силе инерции, число Эйлера — отношение силы гидродинамическо-
гидродинамического давления к силе инерции.
В несжимаемой жидкости критерий Эйлера не является оп-
определяющим, так как в качестве характерного давления р мож-
можно взять динамическое давление р^2/2, и тогда Ей — есть по-
постоянное число.
В сжимаемой среде критерий Ей можно представить с по-
помощью известного выражения для скорости звука а2 = кр/р
в виде
это значит, что в случае газовых течений появляются два допол-
дополнительных критерия подобия:
80 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
ЧИСЛО
и число Маха
значения которых при подобии течений около модели и натуры
должны быть соответственно одинаковыми
К = &н, Мм = Мн.
Выполнить' условия полного динамического подобия при мо-
моделировании в общем случае весьма затруднительно. Если мо-
модель испытывается в той же среде (вода, воздух и т. д.), в кото-
которой работает натуральный объект, и при одинаковом ее состоя-
состоянии (р = idem, [x = idem, a = idem), то для обеспечения одина-
одинаковых значений каждого из критериев динамического подобия
необходимо из условия Fr = idem при переходе к модели изме-
изменить скорость прямо пропорционально__корню квадратному из
линейного размера (и~У1 или ku = yki), из условия R = idem
следует скорость изменить обратно пропорционально линейному
размеру (и ~ 1/1 или ки = 1/кг), а из условия M = idem скорость
на модели должна быть такой же, как и для натуры. Нетрудно
видеть, что одновременное выполнение этих условий невозмож-
невозможно. Впрочем, в большинстве случаев добиваться полного динами-
динамического подобия и не нужно. Обычно в каждой конкретной гид-
гидродинамической задаче часть членов уравнения Навье — Стокса
либо равны нулю, либо представляют собой пренебрежимо ма-
малые величины. Например, для самолета число Фруда не имеет
значения, так как сила тяжести на частицы воздуха, обтекаю-
обтекающего самолет, не действует (воздух в воздухе невесом, Х = 0);
если к тому же моделируется самолет малой скорости (М < 1),
то сжимаемость воздуха не проявляется, т. е. нет необходимости
в выполнении условия М = idem; наконец, в случае установив-
установившегося движения самолета (t = °°, Sh = 0) отпадает и условие
Sh = idem.
В рассматриваемом примере достаточно удовлетворить усло-
условиям геометрического и кинематического подобий и единственно-
единственному условию динамического подобия: R = — =idem. В таком
случае число R является определяющим критерием подобия.
В частности, при испытании модели такого самолета в аэродина-
аэродинамической трубе (при р = idem, \i = idem) необходимо вести ра-
работу при скорости потока во столько раз большей скорости поле-
полета, во сколько раз натура больше модели (им1м = ин1в, ки = l/kt).
При этом будет реализовано так называемое приближенное по-
§ 7. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ 81
добив (по определяющему критерию подобия). Естественно, что
масштаб модели не должен быть очень мал, так как потребуется
слишком большая скорость потока в аэродинамической трубе,
что может привести к таким значениям числа Маха в модельном
эксперименте (Мм~1), при которых начнет сказываться сжи-
сжимаемость газа, т. е. нарушаться одно из принятых условий
(М < 1). Из-за этого хорошая дозвуковая аэродинамическая труба
должна иметь относительно большие размеры. Известен способ
обойти эту трудность: построить аэродинамическую трубу с вы-
высоким давлением воздуха, в которой малый размер модели I при
R=(—= idem) частично или полностью компенсируется по-
повышенной плотностью воздуха.
Выполнения условия R = idem можно также добиться путем
перехода к среде с другими физическими свойствами: в некото-
некоторых случаях модель испытывают не в воздухе, а во фреоне, ис-
используя малую вязкость последнего.
Вторым примером реализации приближенного подобия может
служить экспериментальное исследование сверхзвукового лета-
летательного аппарата с большим сопротивлением давления. В этом
примере сопротивление трения (вязкость) играет второстепен-
второстепенную роль, т. е. не обязательно выдерживать условие R = idem.
По тем же причинам, что и в предыдущем примере, не нужно
выполнять условия Fr = idem, Sh = idem, и остается основным
определяющим критерием (условием приближенного подобия):
М = idem (при к = idem). Это во многих случаях позволяет осу-
осуществлять моделирование в сверхзвуковой аэродинамической
трубе относительно малых размеров.
Остановимся еще на одном примере корабля не очень обтекае-
обтекаемой формы, который при своем движении порождает большие
волны на поверхности воды. В этом случае сопротивление тре-
трения играет второстепенную роль по сравнению с волновым со-
сопротивлением (затратой энергии на преодоление силы тяжести
воды), и для обеспечения приближенного динамического подо-
подобия становится определяющим критерием число Фруда Fr —
= —f = idem. При испытании модели корабля в гидроканале
скорость ее движения следует принять меньше, чем у натуры,,
в корень квадратный раз из отношения линейных размеров.
В ряде случаев нельзя добиться приближенного динамиче-
динамического подобия, выдерживая постоянство одного критерия подо-
подобия. Например, при моделировании хорошо обтекаемого сверх-
сверхзвукового летательного аппарата необходимо выдержать посто-
постоянство по крайней мере двух определяющих критериев подобия
(M = idem, R = idem), так как сопротивления давления и тре-
трения у такого аппарата соизмеримы. Для этого приходится
6 Г. Н. Абрамович, ч. i
82
ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
создавать сверхзвуковую аэродинамическую труоу сравнительна
больших размеров, а иногда и с переменным давлением воздуха
в ней. Для приближенного моделирования судна обтекаемой
формы требуется выполнить условия: Fr = idem, R = idem. Мож-
Можно привести большое число примеров, в которых условия при-
приближенного динамического моделирования не сводятся к посто-
постоянству одного какого-либо критерия подобия.
Перейдем теперь к рассмотрению уравнения энергии. Для
приведения уравнения энергии D2) к безразмерному виду отне-
отнесем, как и раньше, все значения скоростей к скорости невозму-
невозмущенного набегающего потока ^го, все линейные величины —
к характерному линейному размеру объекта Z, все давления —
к давлению в набегающем потоке /?«>, все температуры — к раз-
разности температур набегающего потока (вдали от тела) и стенки
тела АГо = ^оо — Tw. Для простоты исследуем уравнение энер-
энергии для установившегося режима течения (нетрудно показать,
что учет нестационарных членов в уравнении энергии приводит
к числу Струхаля, т. е. к критерию, полученному ранее из урав-
уравнений Навье — Стокса).
Тогда из D2) и D0) имеем
•т
AT
uZ ~ у "^
АГ
U Роо
р
U Роо
uZTT
W Р
и
д~Г
I
ДГ„
+
, AT -
A+f >(+Г i^L
2
и
оо
д
д
V
у
2
1
Г
д
д
w у
z
Т
2—
1"
д д
я v я х
а 2- *-^
9±
~г
д
д
w
X
"Г
2
2
3
•-г
0±
в^-
l-f- 5-
и далее, после деления всех членов на общий множитель левой
§ 7. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ
83
части:
AT
AT
AT
у Poo
J
+ ¦
Д7\.
4
f и 1
2
2
-г
2
д — д
I
F1)
Здесь АТ = Т—rw — избыточная местная температура (по срав-
сравнению с температурой стенки), причем dT = d(AT). Левая часть
уравнения энергии отражает конвективный перенос тепла, по-
поэтому деление всех членов на размерный множитель левой части
означает, что все виды тепловых потоков выражены в долях от
конвективного.
Тепловое подобие двух процессов осуществляется в том слу-
случае, когда оба они описываются одним и тем же безразмерным
уравнением энергии. Это условие выполняется при соблюдении:
1) гидродинамического подобия;
2) подобия полей температуры, т. е. равенства безразмерных
значений избыточной температуры в сходственных точках двух
течений АГ/АГ«> = idem при x/l = idem, y/l = idem, z/l = idem;
3) равенства в обоих течениях значений каждого из следую-
следующих безразмерных комплексов уравнения F1):
Poo Woo % М'^оо
Pwco P0 "роо РрО
Эти комплексы целесообразно несколько преобразовать. Так,
первый из них представляет собой произведение известного уже
б*
84 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
критерия Эйлера на так называемый температурный критерий
kR Tx ul
0 =
kRTj
Так как R = ср — с„, k = cp/cv, kRT^ = a|L, то
в (Ь1) ML
F2)
о
Следовательно, температурный критерий, учитывающий отноше-
отношение работы сжатия, осуществляемой динамическим давлением,
к конвективному тепловому потоку, пропорционален квадрату
числа Маха и отношению полной температуры набегающего по-
потока к избыточной его температуре. Величина
2
и т1* Т ЛТ*
есть прирост температуры при адиабатическом торможении пото-
потока, поэтому имеем также
^
F3)
Таким образом, температурный критерий равен удвоенному от-
отношению прироста температуры при торможении потока к избы-
избыточной температуре газа; отсюда ясно, что этот критерий имеет
значение лишь при больших скоростях потока.
Множитель при втором члене правой части уравнения F1),
выражающий отношение тепла, переносимого теплопроводностью,
к конвективному тепловому потоку, преобразуем так:
ЯМ- 11
Один из его безразмерных сомножителей есть обратная вели-
величина известного нам числа Рейнольдса, второй безразмерный со-
сомножитель, обратно пропорциональный величине числа Прандтля
зависит лишь, как указывалось, от физических свойств среды.
Величина 8 = —, которая называется коэффициентом темпера-
температуропроводности, имеет размерность коэффициента кинематиче-
кинематической вязкости v.
Произведение чисел Прандтля п Рейнольдса называют чис-
числом или критерием Пекле
Ре = i± = PrR. F5)
§ 7. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ 85
Этот критерий широко используется при моделировании процес-
процессов теплообмена. Множитель при третьем члене правой части
уравнения F1), представляющий собой отношение рассеивае-
рассеиваемого тепла к конвективному тепловому потоку, не приводит
к новым критериям, так как равен отношению температурного
критерия к числу Рейнольдса:
^оо *2~ i* e F6)
cpATQpl cpATQ plUoo R •
К сказанному следует добавить, что для среды переменной
плотности в уравнениях Навье — Стокса массовые силы суть
объемные силы Архимеда, так как по закону Архимеда «части-
«частица, окруженная жидкостью отличной плотности, теряет в своем
весе столько, сколько весит вытесненный ею объем жидкости».
Таким образом, сила Архимеда, приложенная к частице, имею-
имеющей объем F, равна
Проекции силы Архимеда, отнесенной к единице объема, ко-
которые должны быть подставлены в уравнения Навье — Стокса,
можно представить в виде
X = gx(p — poo), Г = &,(р — poo), Z = g2(p — pTO),
где gx, gy, gz — проекции ускорения силы тяжести на координат-
координатные оси.
Отношение силы Архимеда к инерционной силе, которое
должно стоять в этом случае в правой части уравнения Навье —
Стокса для оси г/, запишется в виде
Относительное изменение объема, а следовательно и плотно-
плотности, пропорционально изменению температуры:
AV _ Р - Роо = р т _
V р
где [} — коэффициент объемного расширения.
В идеальном газе при постоянном давлении р/р» — Тоо/Т,
т. е. к8 = 1/Гоо, поэтому
Безразмерный множитель
А^Л 1
Аг = ^— F7)
86 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
называют числом Архимеда; оно имеет значение для гидродина-
гидродинамического подобия в том случае, когда перепады температур
в газовом потоке велики, а скорости малы.
Как видим, критерий Архимеда получается от деления отно-
относительного перепада температур на число Фруда.
В общем случае (jJ Ф 1/Гоо)
Безразмерную величину
выражающую отношение силы Архимеда к силе вязкости, назы-
называют числом Грасгофа.
Итак, для выполнения условий гидродинамического и тепло-
теплового подобия нужно, чтобы в модели значения критериев по-
подобия:
и I
числа Рейнольдса: R = -^—,
числа Прандтля: Рг =—= —?,
Е Л
Е
—* G0)
числа Грасгофа: Gr ==
V
;/2
температурного критерия: 0 =
были такими же, как и в натурном объекте.
Для газов должно соблюдаться также равенство значений
числа Маха
М = —
и отношения теплоемкостей
СР
§ 8. Слоистые течения
К одному из простых частных случаев точного решения урав-
уравнений Навье — Стокса мы приходим в случае так называемых
слоистых течений, когда сохраняется лишь одна составляющая
скорости, а остальные две всюду равны нулю:
и = и(х, у, z, t), v = 0, w = 0.
§ 8. СЛОИСТЫЕ ТЕЧЕНИЯ
87
Если массовые силы пренебрежимо малы, то в этом случае урав-
уравнения движения имеют вид
ди , ди 1 др (д2и д2и д2и\ 1 д (ди
а уравнение неразрывности — вид
dp д{ри) = q
Если, кроме того, ограничиться случаем установившегося
течения несжимаемой жидкости (du/dt = O, р = const), то из
уравнения неразрывности вытекает неизменность скорости в на-
направлении течения ди/дх = О, а из последних двух уравнений
движения — постоянство давления в поперечных направлениях:
= 0, dp/dz = O. Тогда
dp
из первого уравнения дви-
движения получим
?д\_ д2и
Кду2 д:
У///////////////////////////////////////////////////////////,
Рис. 2.6. Плоскопараллельное течение
в канале
Пусть слоистое течение вяз-
вязкой несжимаемой жидкости
является плоскопараллель-
плоскопараллельным, причем скорости тече-
течения в направлении оси z не изменяются: du/dz = 0. Тогда в пер-
первом уравнении движения сохранятся только тангенциальные вяз-
вязкие напряжения, действующие в плоскости х, у: огх=0, xzx = 0 и
du ,ПЛк
tyx = [i^7. G1)
Соотношение G1) выражает закон вязкого трения
в простейшем виде; дифференцируя G1), получим
Ньютона
дх..
d2u
Тогда первое из уравнений движения примет вид
dp d2u
17 ~~ И» TJ
dx
dy
,2*
G2а)
Рассмотрим плоскопараллельное слоистое течение вязкой не-
несжимаемой жидкости в канале, образуемом двумя бесконечными
параллельными пластинами.
Если расстояние между пластинами равно 26 и начало коор-
координат лежит на оси канала (рис. 2.6), то в качестве граничного
88 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
условия задачи можно принять условие прилипания жидкости
к стенке
и = 0 при у = ±Ь. G26)
Интегрируя дифференциальное уравнение G2а), имеем
dp , „ du /ПСк ч
•?у + с1 = рщг- <72в)
Из условия симметрии следует, что в средней плоскости (у = 0)
du/dy = 0, и, значит, С\ = 0.
Интегрируя теперь уравнение G2в), получим
откуда на основании G26) имеем
q = 1 dp ^2
и, следовательно,
и = ~т~%№~-&2)- G2г)
Скорость течения на оси канала (при у = 0)
uo = -4rd<nrb2- <72д>
Поделив почленно равенство G2г) на G2д), получим
~k = i~l?* G3a)
Из G3а) следует, что безразмерный профиль скорости при сло-
слоистом движении жидкости в плоском канале не зависит ни от
величины вязкости, ни от величины продольного градиента дав-
давления и представляет собой квадратичную параболу.
Пользуясь условием постоянства расхода жидкости, можно,
исходя из G3а), определить так называемую среднюю скорость
течения в канале
ь
| udy
Иср = V" = 1
Вычислим градиент давления вдоль канала. Для этого опре-
определим из G3а) вторую производную скорости в поперечном на-
направлении
§ 8. СЛОИСТЫЕ ТЕЧЕНИЯ 80
и подставим ее значение в G2а)
dp 2Уир
dx fe2 •
Итак, потери давления при слоистом течении жидкости в пло-
плоском канале пропорциональны скорости и обратно пропорцио-
пропорциональны квадрату высоты канала. Изменение давления на участ-
участке конечной длины х ==¦ I равно
G4)
или в безразмерном виде
Ар
= _
Р~
Здесь h = 26 — полная высота канала. Заменяя с помощью
G36) максимальную скорость на среднюю, получаем известную
формулу Дарси
Ap = -X-Lpl^>1 G5)
в которой коэффициент потерь на трение
* = ТГ
выражается через число Рейнольдса, определяемое по средней
скорости и высоте канала
Знак минус в формуле G5) указывает на то, что давление вдоль
канала убывает.
Вычислив с помощью G3а) значение поперечного градиента
скорости у стенки (у = Ь), найдем из G1) напряжение трения
у стенки
2\iu 6иы„Л
*» = - "IT2 = - Л22. G8)
или в безразмерном виде
= Тц7 == _. 12^1 = _ il /79)
р^ср р%г л
2
Величина С/ называется коэффициентом поверхностного трения.
Значения xw и с} можно определить и непосредственно из G5),
90 гл. ii. элементы гидродинамики
если учесть, что сила разности давлений, действующая на стол-
столбик жидкости высотой h и длиной Z, должна уравновешиваться
силой трения, приложенной к стенкам *):
tw2l = Aph.
Отсюда
о
тю = 4-Д/>4-==--ГР^?' (80)
т. е.
Дифференциальное уравнение G2а) описывает также слои-
слоистое течение между двумя параллельными стенками, из которых
одна движется в своей плоскости со скоростью С/, а другая не-
неподвижна (течение Куэтта).
§ 9. Уравнения движения идеальной жидкости
Анализ уравнений движения Навье — Стокса, проделанный
Прандтлем еще в 1904 г., показал, что в случае жидкости малой
вязкости (вода, воздух и т. п.) при достаточно больших значе-
значениях числа Рейнольдса влияние вязкости сказывается лишь
в тонком слое, прилегающем к поверхности обтекаемого тела,—
пограничном слое 2). Вне этого слоя роль вязкостных сил ока-
оказывается настолько малой, что соответствующими членами
в уравнениях Навье — Стокса B6) или B7) можно пренебречь.
В таком случае получим уравнения движения идеальной
сжимаемой жидкости (идеального газа)
ди . ди . ди . ди v dp
dv лг dp
или,
или,
о dv
dw
в векторной
наконец,
<:
4- и ди
dw
форме,
t
Э\Л7
+ f
+ f
J\\7
Щ
It
•v)
dv
dw
= R
W =
(82a)
^gradp. (826)
1) Профиль скорости в поперечном сечении стабилен и плотность
жидкости неизменна, а следовательно, суммарное количество движения
вдоль ще/ли постоянно.
2) Подробнее о пограничном слое см. гл. VI.
§ 9. УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ «ЖИДКОСТИ 91
Так как во многих случаях при этих условиях теплопередача
существенно проявляется тоже лишь в пограничном слое, то в
остальной части газового потока согласно уравнению энергии E0)
и, в частности, при установившемся движении
i* = const. (84)
Но в отсутствие трения и теплообмена в газе осуществляется
идеальный адиабатический процесс, в связи с чем вместо урав-
уравнения энергии можно использовать уравнение идеальной
адиабаты
-4- = const. (85)
Уравнение энергии может быть также записано в виде
* ^ (856)
w2
w
где е = U + ~2 полная (внутренняя + кинетическая) энергия
единицы массы движущегося газа. Правая часть уравнения
(856) представляет собой работу сил давления.
В случае, если жидкость является идеальной и несжимаемой
(р = const), задача интегрирования уравнений движения (81)
сильно упрощается. На это указал впервые еще Эйлер, чье имя
носят уравнения движения (81). Аналитические методы реше-
решения уравнений движения идеальной жидкости получили боль-
большое развитие, и в настоящее время изучено множество случаев
обтекания тел (крылья, решетки крыльев, тела осесимметричной
формы, всевозможные каналы и т. п.). Из совокупности работ
этого направления образовалось важное направление современ-
современной механики — классическая гидродинамика.
В сочетании с теорией пограничного слоя гидродинамика
идеальной жидкости стала мощным средством решения задач
аэродинамики самолета, гидродинамики корабля, механики дви-
движения жидкости по трубам и многих других.
Например, в случае обтекания тела плавной формы при
больших значениях числа Рейнольдса пограничный слой на-
настолько тонок, что распределение давлений по поверхности тела
определяется в первом приближении из уравнений движения
идеальной жидкости. Далее, как будет показано в гл. VI, по из-
известному распределению давлений можно рассчитать погранич-
пограничный слой и найти напряжения трения у поверхности. При необ-
необходимости можно во втором приближении рассчитать влияние
пограничного слоя на внешнее обтекание тела (за пределами
слоя) и затем определить более точно напряжения трения. Но
92 гл. ii. элементы гидродинамики
часто к расчету второго приближения не прибегают, так как
первое приближение дает удовлетворительные результаты.
Особенно простой вид имеет решение уравнений движения
(81) в случае безвихревого движения идеальной жидкости, ког-
когда завихренность равна нулю (см. выражения B)), т. е.
+-Mi-?)-<>• <¦*»
1 / dv ди\ А
@2 = —- — — = 0.
2 2 \дх ду I
Из условий (86) следует, что существует некоторая функция ф,
частные производные которой по координатам #, г/, z равны со-
соответствующим компонентам скорости, т. е.
дф d(p дф
dx ' ду dz
Действительно, подставляя эти значения в (86), получаем
тождества
dm dv д2(р д2(р А
_— ' J_ Г)ИТ Я
ду dz dzdy ду dz ~ д*
Функцию ф принято называть потенциалом скорости, а безвих-
безвихревое движение — потенциальным.
Заменим в левой части первого из уравнений (81) полную
производную скорости суммой ее частных производных и приба-
прибавим к ней равную нулю сумму
dv dw dv dw
dx dx dx dx
Тогда это уравнение приводится к виду
ди . 1 dW2 o/ N v I dp /Q7 ч
~dt + Т-^Г - 2 (™* - W^ = X p-S" (87a)
где W = 1/u2 + v2 + w2 — полная скорость течения жидкости.
Аналогичным путем можно преобразовать уравнения движе-
движения по остальным двум координатным осям:
dv . 1 dW2 o/ \ v * дР
о (О /О)
dw , 1 dW2 o/ N rr 1 dp v
Система уравнений (87) называется уравнениями Ламба —
Громеко. Если существуют потенциал скорости ф, потенциал
§ 9. УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ 93
объемных сил О:
дф дф дф
а также некоторая функция Р(х, у, z, t), удовлетворяющая ус-
условиям
dP__J_dp_ дР__±_др_ дР _ 1 др
дх ~~ р дх ' "ду" ~~ р ду ' dz ~~ p dz '
то уравнения (87) записываются так:
дх [ dt ) + 2 дх ~~ дх дх'
д
L @!L\ и L ^1 д® дР
dz \ dt ) ' 2 dz dz dz*
Здесь использовано условие независимости смешанной производ-
производной от порядка дифференцирования
ди д fdcp \ д (dm \
— = — —— = — I -т— и т. д.
dt dt \dx ] дх \ dt J
Согласно (88) производные от комбинации
по х, у и z равны нулю. Значит указанная комбинация являет-
является функцией только оставшейся переменной — времени t. Это
приводит нас к так называемому интегралу Лагранжа:
где C(t)— произвольная функция времени.
Так как по определению
Р-$Ц; (906)
то интеграл Лагранжа можно представить в следующем виде:
Г + ?+! = » + С@- (90-)
В случае установившегося движения (dy/dt = 0, C(t) = const)
имеем
94 гл. п. элементы гидродинамики
Если жидкость баротропна, т. е. плотность является однозначной
функцией давления, то интеграл (906) всегда может быть
вычислен; при установившемся движении несжимаемой жидко-
жидкости (р = const) интеграл Лагранжа выглядит так:
-J- + \ = Ь + const.
Важной особенностью интеграла Лагранжа является то, что он
справедлив во всем пространстве, заполненном жидкостью.
Если потенциала скорости не существует, т. е. движение яв-
является вихревым, то уравнения движения идеальной жидкости
(81) также можно проинтегрировать, но только вдоль линии
тока и при условии установившегося движения.
При установившемся движении элементарное перемещение
частицы вдоль линии тока ds = W dt или в проекциях на коор-
координатные оси х, у, z
dx = u dt, dy = v dt, dz = w dt.
Умножим теперь каждое из уравнений (81) на соответствующую
проекцию элементарного перемещения вдоль линии тока и сло-
сложим эти три уравнения:
и du + v dv -j- w dw =
= Xdx + Ydy + Zdz - f—d/-dx + —^dy + — Ц- dz).
Левая часть данного уравнения есть полный дифференциал от
(W2/2). Если существует потенциал силовой функции (dd =
= X dx + Y dy + Z dz) и жидкость баротропна l-?-=dPL то это
уравнение можно записать в виде
р?) = ЙО — dP.
После интегрирования приходим к известному интегралу
Бернулли
w2
Р + ^- = ft + const,
или
J
— + -5 Ф = const.
Если силовое поле обусловлено только земным притяжением
и ось z направлена вертикально вверх, то проекции силы, дейст-
действующей на единицу массы, равны
§ 10. ПЛОСКИЕ УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ 95
В таком случае интеграл Бернулли принимает уже известную
из гл. I форму
— + -х- + 8Z — const, (91)
или для несжимаемой жидкости
— + -Т5~ + gz = const. (91a)
Напомним еще раз, что в отличие от интеграла Лагранжа интег-
интеграл Бернулли справедлив только вдоль линии тока, т. е. значе-
значение константы в правой части (91) для разных линий тока
неодинаково. Лишь в случае установившегося потенциального
течения интеграл Бернулли переходит в интеграл Лагранжа и
делается пригодным для любой точки пространства.
§ 10. Плоские установившиеся движения
идеальных жидкости и газа
Плоские (двумерные) установившиеся движения идеальной
сжимаемой жидкости описываются следующей системой диффе-
дифференциальных уравнений:
уравнениями движения
ди ди др
dv , dv dp
pu -z f- pi; -r— = — -г—
r дх ' r ду ду
(здесь объемные силы опущены), уравнением неразрывности
д (ри) д (ру) n K. Q4
—т -z—- = (J, , (УО)
дх ' ду х 7
уравнением идеального адиабатического процесса (вместо урав-
уравнения энергии)
_| = const. (94)
В несжимаемой жидкости (р = const) уравнение (94) отпа-
отпадает, а уравнение неразрывности упрощается:
ди , dv ^
Если существует потенциал скорости ф, то
d(p d(p /ГкГ ч
fe = "' w = v- (95а)
Подставляя (95а) в (95), получаем для потенциала скорости
96 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
уравнение Лапласа
<9561
к решению которого и сводится задача построения плоскопарал-
плоскопараллельного потенциального потока идеальной несжимаемой жидко-
жидкости. При этом используется граничное условие непроницаемости
для жидкости твердой границы обтекаемого тела Wnw = О, т. е.
равенство нулю около стенки нормальной к ней составляющей
вектора скорости.
При движении вдоль линии тока частица жидкости за время
dt проходит путь dS = W dt или в проекциях на координатные
оси dx = u dt, dy = u dt. Исключая отсюда время, получаем урав-
уравнение линии тока
dx dy
ИЛИ
udy—vdx = 0. (96)
Как известно из математики, если выполняется равенство
ди ди
Ту = ~"дх~'
то левая часть уравнения (96) представляет собой полный диф-
дифференциал некоторой функции г|)(#, у). Для потенциальных те-
течений несжимаемой жидкости это условие, как следует из урав-
уравнения неразрывности (95), всегда выполняется.
Таким образом, дифференциальное уравнение линии тока
можно записать следующим образом:
dty = udy — v dx = О,
или (96а)
t|)(#, z/) = const.
Функция 1|), значение которой вдоль линии тока сохраняется по-
постоянным, называется функцией тока.
Составляющие скорости можно, согласно (96а), выразить как
частные производные от функции тока
Если подставить (97) в уравнение неразрывности (95), то оно
обратится в тождество
дх ду ду дх
Физический смысл функции тока очень прост. Проведем в пото-
потоке две близкие линии тока через произвольные точки 1 и 2
§ 10, ПЛОСКИЕ УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
97
(рис. 2.7). Нетрудно видеть, что объемный расход жидкости в
плоском течении между соседними линиями тока равен
dV = udy — v dx = di|).
Таким образом,
2
V = j (и dy — и dx) = \|) (#2, у2) — г|) (а^, г/х),
1
т. е. секундный объемный расход жидкости, протекающей между
линиями тока 1 и 2, равен разности значений функции тока на
этих линиях.
Ввиду непроницаемости линий тока для жидкости значение
функции тока на каждой линии тока постоянно.
Сравнивая (97) и (95а), мы видим, что семейства линий то-
тока (г|) = const) и линий равного значения потенциала скорости
(ф = const) образуют ортогональную сетку кривых.
Если известны два каких-либо плоскопараллельных устано-
установившихся течения идеальной несжимаемой жидкости, т. е. для
каждого из этих течений известны
величина и направление скорости в
каждой точке плоскости, то можно
построить новое результирующее те-
течение, которое возникнет в резуль-
результате наложения этих двух известных
У
х
Рис. 2.7. К определению рас-
расхода жидкости между сосед-
соседними линиями тока
Результирующий поток
Рис. 2.8. Графическое сложение
потоков
течений. Для этого в каждой точке плоскости нужно построить
векторы скорости каждого из двух известных течений. Сумма
этих векторов представляет собой вектор скорости нового резуль-
результирующего течения.
Дадим простой способ графического определения линий тока
результирующего потока по линиям тока накладываемых пото-
потоков. Для этого нанесем на чертеж линии тока двух каких-либо
плоских потоков (рис. 2.8). Пересечение этих линий тока образует
сетку. Линии тока надо вычертить так, чтобы стороны клеток
7 г. Н. Абрамович, ч. 1
98 гл. ii. элементы гидродинамики
этой сетки изображали в определенном масштабе векторы скоро-
скорости накладываемых потоков в данной точке 1). Тогда для полу-
получения линий тока результирующего потока достаточно соеди-
соединить между собой последовательные точки пересечения линий
тока накладываемых потоков, т. е. провести диагональ в каждой
клетке сетки. Эти диагонали изображают в том же масштабе
векторы скорости результирующего потока в соответствующих
точках (рис. 2.8).
В случае сжимаемой жидкости (газа) уравнения (92) —(94)
удобно преобразовать, вводя в них скорость звука а = У dp/dp.
Для этого уравнение неразрывности (93) представим в виде
и выразим градиенты плотности через градиенты давления и
скорость звука:
dp __ dp др _ 1 др др _ dp_ др_ _J_ др_
Тх ~~!рдх'~'^дх~' ду ~~Tp!ty~~~?!hj'
Выражая в (99) градиенты давления с помощью (92) через ско-
скорости, получим
до р { ди . ди\ др р / dv . ди\ /ПП ч
дх а2 ^ дх 1 ду у ду а2\ дх дУ)
Подставляя (99а) и (95а) в уравнение неразрывности (98) г
имеем
{а2 _ И2} Лр _ 2uv -^ + (а2 - i;2) ** = 0. A00)
V ' дх2 дхдУ ду2
Мы вывели основное дифференциальное уравнение гааовой ди-
динамики для плоского потенциального установившегося течения.
В частном случае малых скоростей движения газа {и < а,
v < а) уравнение A00) переходит в уравнение Лапласа (956),
определяющее движение несжимаемой жидкости.
Для построения поля скоростей в сверхзвуковом потоке обыч-
обычно решают уравнение A00) методом характеристик.
При исследовании обтекания тонких тел на малых углах ата-
атаки как в дозвуковом, так и сверхзвуковом потоке уравнение A00)
решают методом малых возмущений (метод линеаризации).
1) Легко показать, что для выполнения этого условия достаточно про-
провести линии тока так, чтобы расход между любыми двумя соседними
линиями тока для обоих потоков был одинаковым.
§ 11. ЦИРКУЛЯЦИЯ СКОРОСТИ
99
§ 11. Циркуляция скорости
В установившемся плоском движении скорость частицы w яв-
является функцией двух координат
w w^x, у).
Эта векторная функция определяет поле скоростей.
При исследовании различных случаев газовых течений, в част-
частности обтекания крыльев и иных тел, полезно ввести некоторую
величину, связанную с полем скоростей рассматриваемого тече-
течения и называемую циркуляцией скорости.
Под циркуляцией скорости Г по замкнутому контуру L пони-
понимают интеграл
М) dl. A01)
Здесь w — величина скорости, (w, I)—угол между скоростью и
направлением контура в данной точке, dl — элемент длины дуги
контура. Знак у показывает, что интеграл берется по замкнуто-
замкнутому контуру.
Таким образом, циркуляция скорости представляет собой пре-
предел суммы произведений тангенциальной к контуру проекции
Рис. 2.9. К суммированию цир-
циркуляции
Рис. 2.10. К суммированию
циркуляции
скорости на соответствующий элемент длины контура. Положи-
Положительным направлением обхода на контуре будем считать направ-
направление обхода против часовой стрелки1).
Из самого определения циркуляции следует, что циркуляция
по любому контуру L может быть выражена в виде суммы цир-
циркуляции по отдельным клеткам произвольной сетки, покрываю-
покрывающей площадь, ограниченную контуром L (рис. 2.9). В самом
х) Иногда удобнее считать положительным противоположное направ-
направление.
ЮО ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
деле, рассмотрим некоторый замкнутый контур ADCBA. Пусть
произвольная дуга АС разбивает область, ограниченную этим
контуром, на две клетки: АСВА и ABC А (рис. 2.10). Выразим
циркуляцию для каждой клетки. Для первой клетки
ф w cos (
(АСВА)
При этом интеграл по контуру АСВА может быть разбит на два
интеграла: интеграл по дуге СВА и по дуге АС. Для второй
клетки
9 w cos (w, I) dl.
(ADCA)
Интеграл по этому контуру составляется из интегралов по дуге
ABC и по дуге С А. Сумма циркуляции по контурам АСВА и
ABC А равна сумме четырех интегралов, причем интеграл по ду-
дуге А С, входящий в первую циркуляцию, и интеграл по дуге С А,
входящий во вторую циркуляцию, взаимно уничтожаются, ибо
они представляют интеграл по одной и той же дуге, проходимой
в противоположных направлениях (подынтегральная функция в
обоих интегралах одна и та же). Поэтому сумма циркуляции па
контурам АСВА и АВСА равна сумме интегралов по дугам СВА
и ABC, т. е. интегралу по контуру АВСВА. Итак,
. • TaDCA == ГADCBA»
Таким образом, сумма циркуляции по контурам двух смежных
клеток равна циркуляции по всему контуру L. Если каждую ш
клеток АВСА и АСВА разбить еще на две клетки, то для каж-
каждой из них можно полностью повторить приведенное выше рас-
суждение. Продолжая процесс разбиения дальше и повторяя
каждый раз такие же рассуждения, мы приходим к высказан-
высказанному выше положению о суммировании циркуляции (см. рис. 2.9).
Выразим теперь подынтегральное выражение в формуле A01)
с помощью полярных координат (г, ср). Для этого рассмотрим
рис. 2.11. Пусть М(г, <р)—точка произвольного контура L, dl =
=• MN — элемент дуги этого контура, w — скорость в точке М с
проекциями wr и wu. Обозначим угол (w, I) = ?- NMP = аг
?- РМК = р, Z. NMK = у. Из рисунка видно, что
а = Tf - р.
Поэтому
cos (w, I) = cos a = cos (y ~~ P) — cos if cos p + sin f sin p.
Но из малого криволинейного прямоугольного треугольника
MNK получаем
МК dr . NK dw
§ 11. ЦИРКУЛЯЦИЯ СКОРОСТИ
101
Далее, очевидно, что
cos В = —, sin В = —.
Подставляя эти значения в выражение для cos(w, Z), найдем
v ' ' dl w ' dl w
Тогда подынтегральное выражение в формуле A01) принимает
вид
х\ w dr -f- w r d(p
w cos (w, l)dl = w dl j^ = wr dr + wu
Таким образом, в полярных координатах получаем следую-
следующую формулу для циркуляции скорости:
Г = ф wr dr + wur dcp.
A02)
Элементарное перемещение частицы жидкости или газа в общем
случае, как указывалось, состоит из трех частей: поступательно-
поступательного перемещения, вращения и деформации частицы. Движения,
Рис. 2.11. К определению связи меж- Рис. 2.12. К определению завихрен-
ду вихрем и циркуляцией ности в полярных координатах
в которых вращение частиц отсутствует, называются безвихре-
безвихревыми, движения с вращением — вихревыми.
При движении жидкой частицы MKNR (рис. 2.12) с враще-
вращением форма ее в общем случае изменяется. Пусть через малый
промежуток времени dx грани MR и МК займут положение MR'
и МК'. Перемещение частицы в целом, определяемое поступа-
поступательной скоростью, в данном вопросе не имеет значения. Опре-
Определим угловые скорости вращения точек R и К относительно точ-
точки М. Если составляющие скорости в точке М обозначить через
102
ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
wr и wu, то составляющие скорости в точке К равны
dwr dwu
Wr -\ -z— Дг И Wu -\ Дг,
а составляющие относительной скорости точки К (относительно
dwr dwu
точки М) ~^: &г и ~д^^г- Очевидно, вращение точки К отно-
относительно точки М создает только вторая из этих составляющих,
так как первая перпендикулярна к направлению вращения (на-
(направлена по МК). Таким образом, окружная скорость вращения
точки К относительно М, за счет которой проделывается путь
ди?.. .
А..&..Л.Л. • Yf \Л.Л-9 J^M.
тельная
вращения
центра М
(Ох =
" дг
угловая
точки
равна
dw
«Дг
дг
Аг =
7 V4. V/X J_L WJJ,
скорость
К ОКОЛО
dwu
\<р
Рис. 2.13. К определению приращений
скорости в полярных координатах
Составляющие скорости в
точке R равны (рис. 2.13)
dw dw
Wr + -d^AV И ^ + -^-A(P-
Вращение точки R относи-
относительно М происходит по на-
направлению, перпендикуляр-
перпендикулярному к хорде MR. В силу
малости угла Аф можно счи-
считать хорду MR перпендику-
перпендикулярной к радиусу СМ, а длину хорды MR — равной длине ду-
дуги MR. Тогда направление вращения точки R относительно М
параллельно радиусу СМ. Найдем проекции обеих составляющих
скорости точки R по направлению вращения. Из рис. 2.13 видно,
что эти проекции соответственно равны
/ dw \ / dw \
— ( wr + -j- AcplcosAcp и I wu + -^— Аф ) sin Аф.
Знак минус у первой проекции принят потому, что эта проекция
создает вращение по часовой стрелке, а положительным считает-
считается вращение против часовой стрелки. Считая приближенно
cos Аф « 1 и sin Аф « Аф и отбрасывая член второго порядка
малости, имеющий множителем (АфJ, получим следующие зна-
значения рассматриваемых проекций:
/ dwr . \
~ [Wr + 1ф"Аф/
и
§11. ЦИРКУЛЯЦИЯ СКОРОСТИ ЮЗ
Чтобы получить окружную скорость вращения точки R относи-
относительно Л/, из полученных выражений нужно, очевидно, вычесть
проекции составляющих скорости в самой точке М на то же на-
направление СМ. Но проекция wr на СМ равна самой величине wr,
а проекция wu на СМ равна нулю. Таким образом, окружная
скорость точки R относительно М, которая обусловливает пере-
перемещение RR' (рис. 2.12), выражается так:
dwr \
г ~\~ ~Ъ— Дф — М?г 1 •
Тогда относительная угловая скорость вращения точки R около
центра М равна
_^Аф-^А(Р_^ jdwr
так как
MR « гАф.
За среднюю угловую скорость частицы относительно точки М
принимают среднюю арифметическую угловых скоростей крайних
точек R и К:
wcp — 2 " 2 Ur т г г дер
Это выражение удобно преобразовать к виду
Формула A03) определяет величину завихренности или вихря
скорости (см. § 1) в полярных координатах.
В гидродинамике доказывается, что движения идеальной жид-
жидкости, бывшие безвихревыми в некоторый момент времени, всегда
остаются безвихревыми. Если же движение было в некоторый мо-
момент вихревым, оно всегда будет вихревым. Возникновение вих-
вихрей должно быть вызвано специальными причинами, например
вязкостью газа или жидкости.
Условием отсутствия вихрей является
сОср = О, A04)
или в полярных координатах
в-Щ-р = 0. A05)
дг с?ф v '
Чтобы выяснить связь между понятиями вихря и циркуляции
скорости, преобразуем подынтегральное выражение в формуле
A02). Рассмотрим элементарную площадку MKNR, ограничен-
ограниченную координатными линиями МК, MR и RN, KN (рис. 2.14).
104
ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
Составим подынтегральное выражение для циркуляции по
контуру MKNR. Очевидно, получим
/ dw \ [ dw \
dT = wrdr + \wu -f — dr) (r + dr)dcp — (wr + — dy I dr —wur dtp.
Здесь wr — тангенциальная проекция скорости на отрезке
МК = dr, wu+ -^dr — тангенциальная проекция скорости на ду-
дуге KN = (г + dr) йф, wr + -^ г?ф — тангенциальная проекция
скорости на отрезке NR = dr и м;и — тангенциальная проекция
скорости на дуге RM = г <&р.
У последних двух членов принят знак минус потому, что по-
положительное направление скорости на отрезке NR и на дуге RM
Рис. 2.14. К определению цирку-
циркуляции в полярных координатах
Рис. 2.15. К суммированию цирку-
циркуляции и завихренности
противоположно направлению обхода по контуру MKNR. Произ-
Производя выкладки и отбрасывая член третьего порядка малости
dw
—?^ (drJ <2ф, получим
Сравнивая это выражение с выражением A03) для вихря ско-
скорости со и замечая, что произведение г Ар dr представляет собой
элементарную площадь dF, охватываемую контуром MKNR, за-
запишем последнее выражение в такой форме:
dT = 2о) dF.
Если теперь разбить площадь, охватываемую произволь-
произвольным контуром L, на элементарные площадки, образованные сет-
сеткой координатных линий (рис. 2.15), и использовать правило
суммирования циркуляции, то получим
§11. ЦИРКУЛЯЦИЯ СКОРОСТИ 105
или, если перейти от сумм к интегралам:
= 2 f
A06)
(F)
Полученный результат и выражает искомую связь между вих-
вихрем скорости и циркуляцией1). Если величина вихря одинакова
во всех точках: ш = ©о = const, то
1 = 2ш0 f dF =
(F)
т. е. в этом случае циркуляция по некоторому контуру равна
удвоенному произведению величины вихря на площадь, охваты-
охватываемую контуром.
Предположим далее, что движение является установившимся
и безвихревым (со = 0). В этом случае циркуляция по любому
неподвижному контуру равна нулю2). Последнее заключение, од-
однако, верно лишь в том случае, если внутри неподвижного кон-
контура находятся только частицы жидкости, совершающие безвих-
безвихревое движение. Циркуляция по неподвижному замкнутому кон-
контуру отлична от нуля, если контур охватывает область, внутри
которой находится, например, одиночный вихрь3) или обтекае-
обтекаемое тело.
Таким образом, мы видим, что возникновение циркуляции
всегда связано с образованием вихрей в потоке жидкости или
газа.
Рассмотрим теперь некоторые простейшие примеры движе-
движения жидкости, которые позволяют выяснить физический смысл
понятий вихря и циркуляции.
Пример 1. Вращение жидкости как твердого тела. Пусть жидкость
вращается как твердое тело вокруг начала координат с постоянной угловой
скоростью е. Тогда величина скорости в каждой точке w = ег, где г — рас-
расстояние точки от начала координат. Найдем радиальную и окружную со-
составляющие скорости. Ясно, что в данном случае
wr = 0, wu = w = ег.
1) Формула A06) выражает для плоского движения теорему Стокса
(см., например, Фабрикант Н. Я. Аэродинамика.—М.: Наука, 1964).
2) В гидродинамике доказывается для весьма широкого класса прак-
практически важных движений, что и в случае неустановившегося движения
циркуляция по замкнутому контуру постоянна, однако в этом случае рас-
рассматривается так называемый жидкий контур, т. е. контур, состоящий из
одних и тех же частиц. Последнее утверждение называется теоремой
Томпсона. Из этой теоремы следует, что если некоторая масса жидкости
в начальный момент времени имела безвихревое движение или покоилась,
то и впредь в этой части жидкости не возникает вихрей, о чем уже упоми-
упоминалось выше (см. также учебник Н. Я. Фабриканта, цитированный выше,
в первой сноске).
3) Об одиночном вихре см. ниже — пример 2.
106 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
Составим выражение для вихря скорости. По формуле A03)
2г[ дг ду\ 2гдгУ '
Величина вихря скорости во всех точках одинакова и равна постоянной
угловой скорости вращения частиц жидкости. Этот результат был заранее
очевиден, ибо он непосредственно следует из самого определения вихря.
Найдем теперь циркуляцию по контуру, окружающему начало коорди-
координат. В качестве такого контура возьмем окружность радиуса г. Из форму-
формулы A02) получим
Г = ф wr dr + wur dcp = I err dq> = 2лег2.
L 0
Циркуляция пропорциональна квадрату радиуса. Разделив ее на пло-
площадь круга F, найдем
или
Г = 2coF.
Это равенство иллюстрирует теорему Стокса A06); в данном случае цир-
циркуляция по окружности равна удвоенному произведению постоянной вели-
величины вихрж со на площадь круга.
Пример 2. Безвихревое циркуляционное движение. В качестве вто-
второго примера рассмотрим такое плоское движение жидкости, когда части-
цы жидкости движутся по концентрическим окружностям вокруг начала
координат со скоростями, обратно пропорциональными расстояниям частиц
от начала координат, так что скорость в каждой точке w = с/г, где с — по-
постоянная. Здесь радиальная и окружная составляющие скорости равны
wr = 0, wu = w = с/г. Найдем величину вихря:
со = л. __. (rw ) — — .
2r [ dr v u/ дф J 2r dr
Таким образом, величина вихря во всех точках, кроме начала координат,
равна нулю. В начале координат (г = 0) скорость равна бесконечности, т. е.
начало координат математически является особой точкой. Физически такое
движение возможно лишь вне некоторого ядра конечного радиуса г0. Ядро
может состоять из твердого тела или из жидкости той же или другой плот-
плотности. Вне ядра течение является безвихревым. На поверхности ядра ско-
скорость имеет некоторую конечную величину w0 = с/г0.
Найдем значение циркуляции по окружности с центром в начале коор-
координат:
J г
' — const.
В данном случае циркуляция по любой окружности есть величина постоян-
постоянная. Так как w = с/г, то можно записать
Г = 2пс = 2ягш = const = 2яг0ш0,
§11. ЦИРКУЛЯЦИЯ СКОРОСТИ
107
где r0 —радиус ядра, a w0 — скорость на его поверхности1). Таким образом,
скорость в любой точке
W r 2яг' '
Рассмотренное движение жидкости носит название безвихревого циркуля-
циркуляционного движения, а соответствующее ему поле скоростей называется
полем скоростей плоского изолированного вихря. Если считать жидкость
несжимаемой, то давление
2 r2w2
р = const — 2Е- = const — р ° °
2 2г2
убывает с уменьшением расстояния от начала координат, т. е. от центра
вихря.
При го-^0 ядро переходит в точку. Эту точку называют точечным изо-
лированным вихрем. Поэтому безвихревое циркуляционное движение мож-
можно связать с точечным вихрем; последний индуцирует в каждой точке
плоскости скорость, перпендикулярную к отрезку, соединяющему эту точку
с вихрем, и равную по величине Г/2яг, где г — длина указанного отрезка,
т. е. индуцирует безвихревое движение с циркуляцией Г.
Отметим теперь одно важное явление, относящееся к обтека-
обтеканию тел потоком идеальной жидкости. Если контур обтекаемого
тела имеет участок, представляющий собой дугу с малым радиу-
радиусом закругления (рис. 2.16, а), то часть потока вблизи этой дуги
походит на циркуляцион-
циркуляционное движение: скорость
увеличивается по мере
приближения к контуру
дуги и при достаточно ма-
малых радиусах закругле-
закругления может стать очень
большой. При некотором
(достаточно малом) ради-
радиусе закругления скорость , _
должна быть столь вели- —* — ¦ — -*¦
ка, что давление (вычис- в
ляемое по уравнению Бер- рис. 2.16. Схема обтекания закругленных
нулли для несжимаемой и острых кромок
жидкости) должно стать
отрицательным, что невозможно. Когда радиус закругления равен
нулю, т. е. когда жидкость обтекает острую кромку (угловую точку
контура рис. 2.16, б), скорость обращается в бесконечность точ-
точно так же, как в центре точечного вихря, индуцирующего цир-
циркуляционное движение. Но бесконечно большая скорость требу-
требует нереального бесконечного отрицательного давления. Поэтому
бесконечно большая скорость невозможна, следовательно, невоз-
невозможно безотрывное обтекание острых кромок, и происходит срыв
!) Как нетрудно показать, циркуляция по любому замкнутому конту-
контуру, не охватывающему ядро, равна нулю, т. е. ядро играет роль вихря.
108
ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
струй1). Единственно возможным случаем безотрывного обтека-
обтекания тела с острой кромкой (крылового профиля) потоком идеаль-
идеальной несжимаемой жидкости является случай, изображенный на
рис. 2.16, в; здесь острая кромка лежит на линии раздела пото-
потоков, обтекающих верхнюю и нижнюю стороны профиля, и струи
жидкости плавно сходят с контура тела.
В реальной жидкости, обладающей вязкостью, при срыве
струй из завихренных частиц пограничного слоя образуется
вихрь, который как бы «округляет» острую кромку, и струи
жидкости обтекают уже не острую кромку, а этот вихрь.
§ 12. Примеры плоских потенциальных
установившихся течений несжимаемой жидкости
Определим потенциальную функцию <p(#, у) и функцию тока г|)(#, у)
для некоторых простейших случаев безвихревого течения несжимаемой
жидкости.
Пример 1. Плоскопараллельный поток. Выберем систему координат
так, чтобы ось х была направлена по скорости потока W\\ тогда (рис. 2.17)
Подставляя значения этих составляющих скорости в (95а) и (97), получим
после интегрирования следующие выражения для потенциальной функции
и функции тока:
<p = Wi*, A07)
Ф = Wiy. A08)
Пример 2. Источник и сток. В случае источника жидкость движется
по прямым, исходящим во все стороны из начала координат как из центра.
у
> X
Рис. 2.17. Плоскопараллельный
поток
Рис. 2.18. Источник на пло-
плоскости
Мощность источника характеризуется секундным расходом жидкости Q,
зная который легко определить зависимость радиальной и окружной со-
составляющих скорости потока от расстояния г до центра источника
1) В дальнейшем будет показано, что в сверхзвуковом потоке газа
возможно безотрывное обтекание острой кромки; при этом скорость нигде
не обращается в бесконечность.
§ 12. ПРИМЕРЫ ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ТЕЧЕНИЙ ДО9
(рис. 2.18):
Соответственно
л Q
u = w7. cos 6 = о
v=wr sin 0 = «г -«
7 2Я д;2
Производя интегрирование согласно (96а), находим уравнение линий тока
которые представляют собой семейство лучей, исходящих из начала коор-
координат.
В полярной системе координат выражение для произвольной потен-
потенциальной функции (95а) записывается так:
дг
(HI)
тде wr определяется формулой A09). В соответствии с этим получаем
после интегрирования следующее выражение для потенциала:
Ф = ^1пг. A12)
Линии равного потенциала представляют собой семейство концентрических
окружностей, центры которых совпадают с центром источника.
В приведенных выше выражениях расход Q можно рассматривать как
-алгебраическую величину. Положительные значения Q соответствуют
источнику, отрицательные — стоку. В последнем случае жидкость движется
к центру по тем же линиям тока, что и в случае источника.
Пример 3. Точечный вихрь. В предыдущем параграфе было пока-
показано, что в случае точечного вихря
о
В соответствии с этими значениями проекций скорости, индуцируемой вих-
вихрем интенсивности Г, получаем следующие выражения искомых функций:
Г Г
в ^ l
Выше уже указывался (см. § 10) графический способ построения неко-
некоторого результирующего течения, образующегося в результате наложения
двух известных плоскопараллельных установившихся течений идеальной
несжимаемой жидкости. Эту же операцию можно провести и аналитиче-
аналитическим путем, используя известное свойство линейных функций (к которым
принадлежат и потенциальная функция (956), и функция тока), что сумма
любого числа частных решений также является решением.
Таким образом, если имеются два течения с потенциалами (pi и ф2 и с
«функциями тока rfi и фг, то соответствующие функции результирующего
течения будут равных их суммам:
ф =
110
ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
В качестве примера рассмотрим поток, который получается от нало-
наложения источника и стока равных расходов.
Поместим начало координат посредине расстояния между центром
источника и центром стока и за ось х примем прямую, соединяющую эти
центры. Пусть абсцисса источника —8, абсцисса стока +е. При таком рас-
расположении системы координат потенциал скоростей и функция тока для
источника и стока определяются, согласно A10) и A12), следующими фор-
формулами:
8'
Для результирующего потока
ф = 2- [in V
- In /(z-
— arctg
ib = -i- arc tg —-—
Y 2я L x + 8
Рассмотрим предельный случай, когда расстояние между центрами источ-
источника и стока, равное 2е, стремится к нулевому значению и одновременно
расход каждого из них Q стремится к бесконечности,
но так, что произведение 2eQ остается все время по-
постоянной величиной
2е<? = М = const.
Поток, который получается в пределе, называется ди-
диполем, постоянная Л/, его характеризующая,— момен-
моментом диполя, а ось х (в данном случае) — осью диполя.
Вычислим потенциал скоростей и функцию тока ди-
диполя.
По определению имеем
г = — lim
1 2я е-*о
In
- In V(x-
2е
arctg
-arctg
2я
e-»o
28
Рис. 2.19. Линии
тока плоского ди-
диполя
Заметим, что знаменатель каждого из выражений, ко-
которые стоят здесь под знаком предела, можно рассмат-
рассматривать как приращение независимого neip-еменного,
а числитель — как соответствующее приращение функ-
функции. В соответствии с этим по определению производной мы можем написать:
т дип оГГ я^
м д
[ = ^^:(arctgji-
(ИЗ)
§ 13. ИНТЕГРАЛЬНАЯ ФОРМА УРАВНЕНИЙ Ш
После дифференцирования) получаем
М х М cos 6 _ М у М sin 8
«Рдип = 2я J + у2 — 2л г ' ^дип = — 2я = —
Анализ выражения A14) показывает, что линии тока суть окружности, про-
проходящие через начало координат и имеющие центры на оси у. Жидкость
но указанным окружностям вытекает из начала координат и вновь в него
втекает. Очевидно, что в этом случае расход жидкости через произвольный
-замкнутый контур, окружающий диполь, равен нулю (рис. 2.19).
Согласно A14) линии равного потенциала также являются окружно-
окружностями, проходящими через начало координат, но с центрами, расположен-
расположенными на оси х.
§ 13. Интегральная форма уравнений газовой динамики
Математическое исследование течений с резким изменением
параметров (например, в ударных волнах) с помощью дифферен-
дифференциальных уравнений (A2) и B6), E0)—для вязкого газа или
(81), (83)—для идеального) оказывается затруднительным в
связи с необходимостью выделения особых поверхностей (разры-
(разрывов) и расчета изменения параметров на них по специальным
соотношениям. Эти трудности можно избежать, применяя инте-
интегральные уравнения, не содержащие производных от функций,
характеризующих состояние среды. Для этого получим уравне-
уравнения, выражающие законы сохранения массы, количества движе-
движения и энергии в интегральной форме.
Выделим в пространстве, заполненном потоком, фиксирован-
фиксированный (не зависящий от времени) объем F, ограниченный поверх-
Рис. 2.20. К выводу интегральных уравнений законов сохранения: а) рас-
рассматриваемый объем V с поверхностью S, б) скорость, поверхностная сила
и внешняя нормаль к элементу поверхности dS
ностью S (рис. 2.20, а). В рассматриваемом объеме в каждый
момент времени заключена масса газа J pdV. Количество газа,
v
покидающего объем V за единицу времени, составляет величину
\ p(Wn) <25 *) (рис. 2.20, б), где п — единичный вектор внещней
!) (Wn) — скалярное произведение векторов W и п.
112 ГЛ. II. ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ
нормали к элементу поверхности dS. Так как скорость изменения
массы в объеме V равна скорости потока массы через его грани-
границу S, то получаем закон сохранения массы, или уравнение не-
неразрывности, в виде
^JpdF+ fp(Wn)dS = 0. A15)
V S
Получим уравнение количества движения. Газ в объеме V об-
обладает количеством движения \ pW dV. Изменение этой величи-
v
ны происходит за счет вытекания газа через границу S, причем
за единицу времени теряется величина J p(Wn) W dS. Кроме того.
s
на газ, заключенный в объеме F, действует сила со стороны
остальной части газа. В общем случае эта поверхностная сила
действует под углом к внешней нормали. Касательная составля-
составляющая напряжения рх связана € вязкостью. Для идеального газа
напряжение поверхностной силы сведется к нормальной состав-
составляющей, которую можно представить в виде рп = —/ш, где р —
давление. Так как скорость изменения количества движения в
объеме V равна действующей силе плюс скорость потока им-
импульса через границу S, получим закон сохранения количества
движения
= - \pndS. A16)
S
Полная энергия газа (внутренняя плюс кинетическая) в
объеме V равна jpf?7 +-yjdF, где U = к_ ^ Ее изменение
V
V-
связано с переносом энергии через поверхность uS, причем за еди-
ницу времени уносится ] р (U + -у) (Wn) dS, а также с работой
s
сил давления р, которая за единицу времени равна \ р (Wn) dS»
s
Скорость изменения энергии в объеме V равна мощности дей-
действующих сил плюс скорость потока энергии через границу S*
В результате получаем уравнение сохранения энергии в фиксиро-
фиксированном объеме V
^ Jp (с/ + ^) dF + Jp («7 + ?) (Wn) J^ = _ [^(Wn) Й5. A17)
V S S
Эти уравнения представляют собой наиболее общую форму запи-
записи уравнений газовой динамики. Они допускают существование
разрывных решений. Уравнения газовой динамики в диффереи-
§ 13. ИНТЕГРАЛЬНАЯ ФОРМА УРАВНЕНИЙ US
циальной форме могут быть получены из интегральных урав-
уравнений.
Для получения единственного решения задачи, кроме системы
уравнений, необходимо задать дополнительные начальные и гра-
граничные (или краевые) условия. При этом важно, чтобы задача
была корректно поставлена. Это означает, что решение задачи
существует, оно единственно и непрерывно зависит от исходных
данных (малому изменению исходных данных соответствует ма-
малое изменение решения). Требование корректности важно при
численном решении задачи, так как всякое численное решение
является приближенным и необходимо, чтобы метод решения был
устойчив к малым погрешностям в исходных и промежуточных,
данных.
Абрамович, ч. 1
Глава HI
СКАЧКИ УПЛОТНЕНИЯ
§ 1. Прямые скачки уплотнения
В случае полета тела со сверхзвуковой скоростью (wu>aa)
перед ним возникает ударная волна (скачок уплотнения), вы-
вызывающая значительное сопротивление.
Если рассматриваемое тело представляет собой летательный
аппарат, снабженный воздушно-реактивным двигателем, то в
сверхзвуковой струе воздуха, которая тормозится при втекании
в двигатель, также происходит скачок уплотнения. Принципиаль-
Принципиально можно представить себе и плавный переход сверхзвукового
потока в дозвуковой, осуществляемый посредством специального
обратного сопла, установленного на входе в двигатель. При этом
не было бы потерь полного давления. Однако торможение сверх-
сверхзвукового потока таким способом осуществить в полной мере не
удается, в силу чего приходится мириться с существованием
ударных волн и наличием соответствующего волнового сопро-
сопротивления.
Многочисленные опыты показывают, что всякое повышение
давления, возникшее в каком-либо месте газовой среды, распро-
распространяется в ней с большой скоростью во все стороны в виде
волн давления. Слабые волны давления движутся со скоростью
звука; их изучением занимается акустика. Сильные волны дав-
давления, как видно из опытов, распространяются со скоростями,
значительно большими, чем скорость звука. Основная особен-
особенность сильной волны давления заключается в том, что фронт
волны очень узок, в связи с чем состояние газа (давление, плот-
плотность, температура) изменяется скачком1).
Можно дать следующее качественное объяснение этому фак-
факту. Пусть в некоторой области (рис. 3.1) произошло изменение
давления, и вначале волна получила плавную форму 1АВ2. На
отдельных бесконечно узких участках волны давление возраста-
возрастает незначительно, поэтому распространение такой волны проис-
происходит со скоростью звука. В области высоких сжатий (А)
наблюдаются, естественно, более высокие температуры, чем в об-
области малых сжатий (В), в силу чего «вершина» волны давления
1) Приближенная теория гласит, что толщина области, в которой уме-
умещается сильная волна давления, должна быть порядка длины свободного
.пробега молекул.
§ 1. ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ
115
движется быстрее, чем ее «подножие». В сторону меньших дав-
давлений (вправо) волна распространяется как волна сжатия, в сто-
сторону высоких давлений (влево)—как волна разрежения. Таким
образом, если даже вначале волна сжатия является пологой, то
со временем она делается все круче и круче; процесс этот оста-
остановится и волна приобретет устойчивую форму только в тот мо-
момент, когда фронт волны станет совсем плоским A' — 2'). Итак*
х
Рис. 3.1. Схема образования волн сжатия и разрежения
волны сжатия распространяются как скачки давления (разрывы),,
в связи с чем их называют ударными волнами.
По тем же причинам, т. е. вследствие того, что в точке А
волна разрежения движется быстрее, чем в точке В, фронт вол-
волны разрежения со временем растягивается. Иначе говоря, возник-
возникновение волны разрежения не должно приводить к образованию
скачков разрежения.
Ниже будет показано, что в адиабатических (без подвода
тепла) скачках сжатия происходит увеличение энтропии газа,
а в адиабатических скачках разрежения, если бы они существо-
существовали, энтропия должна была бы уменьшаться. Этим доказы-
доказывается законность существования адиабатических скачков дав-
давления и одновременно невозможность возникновения адиабати-
адиабатических скачков разрежения (как известно из термодинамики,
в конечной замкнутой системе энтропия убывать не может).
В полном соответствии с этим находится тот известный факт,
что наблюдаемые иногда в действительности скачки разрежения
(скачок конденсации, фронт пламени) получаются только при
подводе тепла в область скачка, т. е. в таких условиях, когда и
при скачке разрежения энтропия газа растет. Нужно заметить,
что возникновение скачков разрежения при подводе тепла к газу
отнюдь не противоречит процессу, изображенному на рис. 3.1.
В самом деле, если в области пониженных давлений В за счет
подвода тепла получается температура выше, чем в областж
116
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
высоких давлений А, то скорость звука у подножия волны выше,
чем у вершины; в связи с этим со временем должна усилиться
крутизна фронта волны разрежения, что приведет к образованию
теплового скачка разрежения.
Остановимся теперь на теории ударных волн. Представим
себе, например, что под влиянием резкого смещения поршня
{рис. 3.2) в трубе возникла и распространяется слева направо
Рис. 3.2. Схема распространения ударной волны
сильная волна сжатия,
времени фронт волны
чит, что в области 1 —
ления от величины pR
чины р\ (давление за
с чем в области 1 — Н
сти газа на величину
Пусть за бесконечно малый промежуток
переместился на расстояние dx. Это зна-
Н за время dx произошло повышение дав-
(давление невозмущенного газа) до вели-
фронтом волны сжатия), в соответствии
должно наблюдаться повышение плотно-
Ар = pi — рн.
Однако это может произойти только в том случае, если не-
некоторое количество газа, равное
перетечет из объема 1 — 2 в объем Н — 1 (здесь F — площадь
поперечного сечения). Итак, при распространении сильной волны
сжатия газ позади фронта волны должен находиться в движе-
движении, следуя в том же направлении, что и волна. Из уравнения
неразрывности можно определить скорость газового потока (wn):
dG = p\Fwnd%,
откуда
A)
Но производная пути по времени есть не что иное, как скорость
движения волны:
dx
^в = т-- B)
dx * '
Отсюда получаем равенство, связывающее скорость распро-
распространения волны со скоростью газа, движущегося за фронтом
§ 1. ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ 117
волны в том же направлении
Применяя к области Н — 1 уравнение количества движения,
можно получить другое соотношение между теми же величи-
величинами. В самом деле, за время dx масса газа, заполнявшая
объем # — 2, AGH = Рн^ dx перейдет из состояния покоя в дви-
движение со скоростью wn. Соответствующее изменение количества
движения должно быть равно импульсу силы, вызванной раз-
разностью давлений, действующих в сечениях 1 и Н:
(Pi - Pn)F dx = paF(wa - 0)dx,
откуда скорость волны равна
D)
Подставив выражение для скорости газа C) в уравнение D),
получим скорость распространения волны сжатия как функцию
прироста давления и прироста плотности
В случае слабой волны, когда повышение давления (и плотно-
плотности) получается незначительным: pi « рн, р\ » рн, имеем
Слабая волна является не чем иным, как акустической волной,
поэтому выражение F) представляет собой определение скоро-
скорости звука.
Из сравнения равенств E) и F) видно, что скорость распро-
распространения сильной волны сжатия всегда выше скорости звука.
Обычно распространение звука сопровождается столь незначи-
незначительным изменением состояния газа, что энтропию можно счи-
считать практически постоянной, т. е. полагать, что при этом имеет
место идеальный адиабатический процесс p/ph = const. Но в этом
случае
или на основании уравнения состояния для идеального газа
dp
Отсюда получается уже применявшаяся выше формула [C4)
118 гл. ш. скачки уплотнения
гл. I] для скорости звука в идеальном газе
а = УЦ =
Подставляя выражение E) в равенство C), найдем формулу
для скорости газового потока за фронтом волны сжатия
Нетрудно видеть, что с ослаблением волны сжатия скорость
движения газа падает. В случае слабой звуковой волны газ за
ее фронтом неподвижен, так как согласно равенству G) при
Рх^Рп и pi « рн получается wn « 0. В действительности, как
известно, звуковая волна состоит из правильно чередующихся
областей сжатия и разрежения, причем газ за ее фронтом на-
находится в очень слабом колебательном движении; средняя по-
поступательная скорость газовых частиц равна нулю.
Заметим теперь, что вследствие истечения газа из области
1 — 2 (рис. 3.2), расположенной позади фронта сильной волны
сжатия, давление в этой области со временем убывает. По ука-
указанной причине ударная волна, возникшая в неподвижном газе
под влиянием единичного сжатия (например, взрыва или сме-
смещения поршня), всегда более или менее быстро затухает.
И только в том случае, когда источник возмущения не прекра-
прекращает своего действия, можно получить незатухающую ударную
волну. Обнаруженное выше свойство ударных волн распростра-
распространяться со скоростью, большей, чем скорость звука, приводит
к тому, что незатухающие ударные волны образуются перед те-
телом только в тех случаях, когда движение происходит со сверх-
сверхзвуковой скоростью. Например, при движении в газе с постоян-
постоянной сверхзвуковой скоростью твердого тела перед последним
образуется ударная волна постоянной интенсивности, которая
движется с той же скоростью, что и тело.
Исследуем более детально изменение состояния газа, полу-
получающееся при прохождении в нем стационарной ударной волны.
Обратимся сначала к простейшей схеме, когда фронт волны со-
составляет прямой угол с направлением распространения. Такая
волна называется прямой ударной волной.
Ради удобств расчета выгодно обратить движение, т. е. оста-
остановить фронт волны, направив поток навстречу волне со ско-
скоростью, равной скорости распространения волны (рис. 3.3):
тогда относительная скорость газа за фронтом волны
w\ = wn — wB. (8)
Остановив ударную волну встречным потоком газа, мы получи-
§ i. ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ 119
ли некоторую неподвижную поверхность, пересекая которую
все элементарные струйки газа одновременно претерпевают
скачкообразные изменения скорости движения, плотности, дав-
давления и температуры. По этой причине ударную волну называ-
называют также скачком уплотнения. Скачки уплотнения удобно на-
наблюдать в сверхзвуковых аэроди-
аэродинамических трубах при обтекании
воздухом неподвижных твер-
твердых тел.
Примем площадь поперечного
сечения струи равной единице рис 3.3. Схема прямого скачка
(F = 1 м2) и, пользуясь извест- уплотнения
ными уравнениями газовой дина-
динамики, найдем связь между значениями скорости газа до и после
скачка уплотнения (рис. 3.3). Уравнение неразрывности дает
Пренебрегая силой трения ввиду малой толщины скачка уплот-
уплотнения из уравнения количества движения получим
Р\ -рн = рнн;н(м>н- wi).
Сопоставляя эти уравнения, найдем
Pi — Рн = Рн^н ~ Pi^i = ЩМк (Pi — Рн), (9)
откуда
Если извне тепло не подводится, то полное теплосодержание
газа остается постоянным. Теплоотдачей можно пренебречь, так
как боковые поверхности струи в области скачка ничтожно малы.
Поэтому из уравнения теплосодержания следует
**=срГ* = СрТн + -| = срТг + ^ = const;
здесь Т* — температура торможения. Из этого уравнения имеем
Согласно уравнению состояния газа
Pi -Рн
следовательно,
*
Т* = —
120 гл. ш. скачки уплотнения
Здесь рп ри— полное давление соответственно за и перед скачком
уплотнения, р*, рн — плотность газа, соответствующая полному
торможению, в тех же сечениях. Следовательно,
Из термодинамики известно соотношение
о „ А-1
поэтому
л-рь(-§-тг«4 <">
По аналогии получаем
_ftfe_L_
2&
/рн А: — 1 2
Pi = Pi -у - ^г- ^i
\^н
Вычтя равенство A1) из равенства A2), имеем
р* h | .
Pi — Pn =(Pi — Рн)-* +
23Г
откуда на основании (9) выводится
н 2k РН* A3>
р1 - рн
Используя выражение [D1) гл. I] для критической скорости
2 _ 2к RT* 2к
"ко — Т. i
найдем
Наконец, сопоставляя равенства A0) и A4), приходим к сле-
следующему простому соотношению между величинами скорости
газа до и после прямого скачка:
WkWi = 4р. A5)
Это кинематическое соотношение можно привести к безразмер-
безразмерному виду, вводя приведенные скорости (X = м>/акр):
§ 1. ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ 121
ИЛИ
ХЛх = 1, A6)
•откуда видно, что в прямом скачке уплотнения всегда сверхзву-
сверхзвуковая скорость газа переходит в дозвуковую, так как если wB >
> Окр, то w\ < Окр. Одновременно можно заметить, что чем боль-
больше значение приведенной скорости перед скачком, тем меньше
ее значение после скачка, т. е. чем выше начальная скорость wR,
тем сильнее получается скачок уплотнения. С уменьшением на-
начальной скорости скачок ослабевает и исчезает совсем при
wB « w\ « a.
Установим теперь связь между давлением и плотностью газа
в скачке уплотнения. Для этого сложим равенства A1) и A2):
Pi + Рк = (Pi + Рн)^| -
Рн
Из уравнения неразрывности следует
Рн"? + PiWj = WaW± (рх + рн).
Подставляя этот результат в предыдущее выражение, имеем
откуда на основании A0) и A3) получаем основное динамиче-
динамическое соотношение
согласно которому отношение прироста давления к приросту
плотности в скачке уплотнения пропорционально отношению
среднего давления к средней плотности. Отсюда, между прочим,
следует уже известный нам результат, что при бесконечно малом
скачке уплотнения (р\ » рн, pi » рн) получается
Это подтверждает сделанное выше предположение, что звуковой
волне отвечает идеальный адиабатический процесс.
Рассмотрим более детально термодинамический процесс из-
изменения состояния газа в скачке уплотнения. Для этого пред-
представим динамическое соотношение A7) в несколько ином виде:
Pl+Рн
Pl-Рн
Разделим числитель и знаменатель в левой части этого равен-
122 ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
ства на величину рн, а в правой на р\:
?1 Рн
Отсюда после несложных преобразований получается зависи-
зависимость отношения pi/рн от отношения pjpa в скачке уплотнения,,
носящая название ударной адиабаты:
Рн
9г Л-1
Рн . . Л+1 Р]
Существенной особенностью ударной адиабаты является тог
что при неограниченном возрастании давления в скачке уплотне-
уплотнения (р\ -* оо) увеличение плотности имеет определенный пределг
который как это видно из уравнения A8), равен
Рн
Например, для воздуха (к = 1,4) увеличение плотности в скачка
уплотнения не может быть более шестикратного:
h
Рн
При скачке уплотнения в газе с меньшим значением показате-
показателя к может наблюдаться более сильное, но также ограниченное-
возрастание плотности; например, при к = 1,2
= 11.
Следует подчеркнуть, что в отличие от ударной адиабаты в слу-
случае идеального адиабатического процесса, в котором имеет место»
зависимость
увеличение плотности с ростом давления является неограничен-
неограниченным (pi -* оо при р\ -* °°).
Сравнение адиабат ударной и идеальной произведено на
рис. 3.4.
Изменение давления и плотности газа в прямом скачке уплот-
уплотнения можно представить в функции числа М перед скачком. Иа
уравнения количества движения с учетод формулы для скорости
§ 1. ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ
звука [C4) гл. I] и уравнения неразрывности найдем
123
Если с помощью ударной адиабаты заменить отношение pH/pi
его выражением через отношение pi/pa, то после некоторых пре-
преобразований получим
Г~ ~ ?_!_ \ ^н 5ПГТ# (^)
В частности, для воздуха (к = 1,4)
Можно выразить отношение давлений в прямом скачке уплот-
уплотнения и в функции приведенной скорости перед скачком Ян; для
-этого следует в равенстве
B0) произвести замену
переменных по формуле
D5) из гл. I:
Ъ
2 к-1
B1)
f
ч§а>0~
10
рис з.4. Сравнение ударной и идеальной
адиабат
При уменьшении скоро-
скорости набегающего потока
до критического значения
(Мн = 1) скачок уплотне-
уплотнения вырождается (/?1=/?н).
В дозвуковом потоке, как
уже указывалось выше,
скачки уплотнения невоз-
невозможны. В прямом скачке
уплотнения повышение
давления зависит только от значения числа М в набегающем
потоке, причем с возрастанием М давление увеличивается неог-
неограниченно (р\-+о° при Мн->оо). Подставив результат B0)
в уравнение A8), нетрудно вывести зависимость плотности за
прямым скачком уплотнения непосредственно от числа М или
с помощью D5) гл. I от приведенной скорости Кв в набегающем
потоке:
&+1
'^= к7\ ~*i B2)
Рн
1 + -
fc-i
124
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
Из равенства B2) еще раз заключаем, что даже при бесконечна
большом значении числа М плотность газа увеличивается в скач-
ке не более чем в
Определим потери полного давления в прямом скачке уплот-
уплотнения.
Полное давление в струе после скачка, очевидно, равно
Pi
h '
B3)
iLzl
к+1
1 ~~ 7 | л с*
Полное давление перед скачком равно
поэтому коэффициент сохранения полного давления, учитываю-
учитывающий волновое сопротивление (потери в прямом скачке), можно
представить, если использовать выражение B1), следующим об-
образом:
1 —
k—1 J_
_
k-l
B4)
большой скорости полета
При скорости полета, равной или меньшей скорости звука
(Ян ^ 1), волновое сопротивление исчезает
оп = 1;
формула B4) справедлива только при Я„ > 1. При бесконечна
> k+l\ n
I = "jriri) п0ЛУчается ап = 0, од-
однако при этом потери не поглотят всего первоначального запаса
полного давления, так как другой множитель (рн) стремится к
бесконечности. Кривая зависимости 0П = /(Я) для воздуха
(к = 1,4) приведена на рис. 3.5.
Из равенств G3) гл. I и B2) можно получить формулу для
определения плотности заторможенного газа после прямого
скачка уплотнения
B5)
*-*
§ i. ПРЯМЫЕ СКАЧКИ УПЛОТНЕНИЯ
125
В заключение заметим, что выведенное выше равенство A0)
и уравнение неразрывности дают возможность представить ско-
скорость потока перед скачком как следующую функцию возраста-
возрастания давления и плотности:
Но это есть уже известное выражение E) для скорости распро-
распространения прямой ударной волны в неподвижном воздухе. Такой
результат является вполне естественным, так как для того, чтобы
Рис. 3.5. Зависимость коэффициента
сохранения полного давления за
прямым скачком уплотнения от при-
приведенной скорости
0,5
\
\
\
остановить ударную волну, следует направить газовый поток на-
навстречу волне и сообщить ему скорость, равную скорости волны.
Подставляя выражение B2) в соотношение A5), получаем
новую формулу для относительной скорости газа за фронтом
скачка
w, = а
кр
Отсюда с помощью A9) обнаруживается, что относительная при-
приведенная скорость газа за скачком не может быть меньше неко-
некоторого определенного значения:
I «-.„a 1-1/1^|. B8)
Если перейти от неподвижного скачка уплотнения к скачку,
распространяющемуся в неподвижном газе со скоростью wB =
= — и>н, то с помощью полученных равенств можно определить
абсолютную скорость, которую приобретает газ в следе за скач-
скачком:
B7)
126
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
или на основании B2)
и в безразмерном виде
J_
B8)
B9)
Согласно закону A6) за ударной волной скорость газа отно-
относительно фронта волны получается всегда меньше звуковой
(A,i<l); на основании этого становится ясным, почему всякое
изменение давления, происходящее позади волны и распростра-
распространяющееся со скоростью звука, может догнать фронт волны.
Именно по этой причине описанное выше (рис. 3.2) падение дав-
давления в следе за ударной волной, возникшей в неподвижном га-
газе, приводит к ослаблению перепада давления на фронте волны
и вызывает ее затухание.
§ 2. Косые скачки уплотнения
Характерной особенностью прямого скачка уплотнения, как
можно было заметить, является то, что, пересекая его фронт,
газовый поток не меняет своего направления, причем фронт пря-
прямого скачка располагается нормально к направлению потока. По-
Помимо прямых скачков уплотнения, встречаются и так называемые
косые скачки уплотнения. Фронт косого скачка располагается
Рис. 3.6. Схема косого скачка
уплотнения
Рис. 3.7. Образование косого
скачка уплотнения при обтека-
обтекании клина
наклонно к направлению потока (рис. 3.6). Косой скачок полу-
получается в том случае, когда, пересекая фронт скачка, газовый по-
поток должен изменить свое направление. Например, при сверх-
сверхзвуковом обтекании газом клиновидного тела, которое отклоняет
поток от начального направления на угол со, перед телом образу-
образуются косые скачки уплотнения, сходящиеся на его носике
(рис. 3.7). Косой скачок уплотнения образуется и при обтекании
§ 2. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ
127
конуса (рис. 3.8). Поверхностью разрыва в этом случае будет ко-
конус с вершиной в носике обтекаемого тела. Таким образом, если
до встречи струи с фронтом косого скачка скорость wH составля-
составляла с ним угол а (рис. 3.6), то после пересечения фронта струя
отклоняется на угол со, а
угол между скоростью и
фронтом скачка становится
равным
|3=а-со. C0)
Разложим вектор скоро-
скорости на две составляющие,
из которых одна нормальна
(wn), а другая параллельна
(wt) фронту скачка (рис. 3.9).
Нетрудно показать, что при
пересечении струей фрон-
фронта косого скачка модуль
нормальной составляющей
скорости уменьшается:
win<wnni C1)
а модуль тангенциальной составляющей остается неизменным;
wt = const. C2)
Обратимся для этого к рис. 3.10, на котором нанесен прямоуголь-
прямоугольный контур НИН, охватывающий часть фронта косого скачка.
Боковые участки контура (Н — 1) проведены перпендикулярно к
Рис. 3.8. Теневая фотография косого
скачка уплотнения при сверхзвуковом
обтекании конуса
Щи
*е
Рис. 3.9. Кинематика пото-
потока при косом скачке уплот-
уплотнения
Рис
ма ]
у/
у
. 3.10.
косого
Расчетная схе
скачка уплот
нения
фронту, а торцовые (Я-Я и 1 - 2) — параллельно ему. Соста-
Составим баланс количества движения для этого контура сначала в
проекции на направление фронта. Ввиду того что силы давления
на обеих боковых поверхностях (Н — 1) одинаковы, соответствую-
соответствующая проекция количества движения остается неизменной, от-
откуда и вытекает условие C2), указывающее на постоянство тан-
тангенциальной составляющей скорости. Если теперь составить урав-
уравнение количества движения в направлении Н — 2, перпендику-
128 гл. ш. скачки уплотнения
лярном к фронту, то ввиду того, что на поверхностях Н — Н и
1 — 1 действуют существенно разные давления, получится
Р\ - Р* = РнЫ>нп(н>нп - Win).
Давление в скачке уплотнения возрастает (pi>pH), откуда сле-
следует условие C1), согласно которому нормальная составляющая
.скорости в скачке уменьшается.
Приведенные соображения показывают, что косой скачок уп-
уплотнения сводится к прямому скачку, который сносится вместе
с потоком газа вбок со скоростью wt. В отличие от прямого скач-
скачка в косом скачке претерпевает разрыв (скачкообразное умень-
уменьшение) не полная скорость газового потока, а только ее состав-
составляющая, нормальная к фронту скачка. В самом деле, согласно
уравнению неразрывности,
Уравнение теплосодержания в адиабатическом случае (нет теп-
теплообмена) дает
Далее мы имеем
откуда
w\ = w2ln
Введем в рассмотрение температуру частичного торможения, по-
понимая под этим следующую величину:
7/9 7/9 7/7
т. е. температуру, которая получится не при полном торможении
потока, а лишь при погашении нормальных к фронту скачка со-
составляющих скорости. Как показывает это равенство, темпера-
температура частичного торможения имеет одно и то же значение перед
и за фронтом скачка, что вытекает из условия wt = const. Если
присоединить к этим уравнениям еще и уравнение состояния
Рг _ Ря
то окажется, как и следовало ожидать, что косой скачок уплот-
уплотнения описывается в точности теми же соотношениями, что и
прямой скачок уплотнения (см. стр. 119), с той лишь разницей,
что в первом случае вместо полной скорости фигурируют нор-
§ 2. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ 129
малыше к фронту скачка ее составляющие, а вместо температуры
полного торможения Г* — температура частичного тормо-
торможения Г*.
По этой причине, не повторяя всех выкладок, которые были
подробно приведены в теории прямого скачка, можем написать
сразу ряд готовых выражений. Например, вместо равенства A0)
имеем
-^l5- = вд». C3)
Соответственно вместо равенства A4) получим
2 /о/ч
р^р7т+т = а«Рл- C4)
Здесь акр п — условная критическая скорость, которая соответ-
соответствует температуре частичного торможения Тп. Основное кине-
кинематическое соотношение для косого скачка принимает следую-
следующую форму:
WinWnn = Якрп- C5)
Равенство C4) дает возможность связать полную критическую
скорость с условной критической скоростью:
RT* = а«ря + i^jwl C6)
Пользуясь этим выражением, можно получить вторую часто
встречающуюся форму основного кинематического соотношения
для косого скачка уплотнения:
+
8 частном случае, когда косой скачок переходит в прямой
(а = 90°, wt = 0, wan = wH, win = wi), из соотношений C5) и
C7) получаем уже известное соотношение A5). Переходя к при-
приведенным скоростям %\п = w\JaKVn, Квп = мнп/акрп, получим в слу-
случае косого скачка безразмерное кинематическое соотношение
hlnXan = 1, C8)
которое соответствует равенству A6) для прямого скачка. Есте-
Естественно, что динамическое соотношение A7) пригодно для ко-
косого скачка уплотнения без каких-либо изменений, и ударная
адиабата применима к косому скачку уплотнения точно в таком
же виде A8), как и к прямому скачку.
Изменения статического и полного давлений в косом скачке
находятся соответственно из зависимостей B1) и B4), если
9 rt H. Абрамович, ч. 1
130
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
вставить в эти формулы вместо Ха величину Ян„:
Рн
°я = -5" =
Хтл~
нп к + 1
fe — 1 9 '*
к — 1
т+т
л
к — 1 1
Л + 1 а2
1 Лм
1_
C9)
D0)
причем приведенная скорость Хнп подсчитана здесь по нормаль-
нормальной составляющей скорости и условной критической скорости:
"крп
Можно, разумеется, получить и такие формулы, которые связы-
связывают изменение давления в косом скачке непосредственно с аб-
абсолютной скоростью набегающего потока.
Согласно уравнению импульсов прирост статического дав-
давления в косом скачке равен
Р\ -/>н =
нп- win).
Подставляя уравнение C7) в это уравнение импульсов и пере-
переходя к приведенным скоростям X, получим
Pi ~ Рк = РнЯкр ( А? sin2 а — 1 + |qry ^н cos2 aj.
Однако из D2) и D1) гл. I следует
Рн Л+1
Отсюда отношение значений статического давления за и перед
косым скачком уплотнения равно
^ п х _ Л - 1
^н
D1)
к + 1 лн
Выражение D1) при увеличении угла косого скачка до зна-
значения а = 90° переходит в известное выражение B1), получен-
полученное выше для прямого скачка. Вычислим значение pi/pa для
§ 2 КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ 131
воздуха (к = 1,4):
Р] _ ^h(! — 0,972 cos2 a)-0,167
Отношение значений полного давления за и перед косым скач-
скачком является функцией приведенных скоростей и может быть
определено следующим образом:
где
а отношение значений статического давления р\/рш берется по
формуле D1).
Таким образом, для определения ск в косом скачке уплотне-
уплотнения нужно знать приведенную скорость Х\. Из треугольников
скоростей за и перед косым скачком (рис. 3.9) следует
w\ = win + и??, wHn = wH sin a, wt = wK cos a. D3)
Используя эти соотношения, a также C7), выведем расчетную
формулу для приведенной скорости за косым скачком уплот-
уплотнения:
л 2 1 ln_ I t
hi hi
Подставляя значения win и wt в выражения для A,i, получим
I 1 л 2 2 1
I? = >i cos2 a + i -j- ^—L. D4)
Яд A — cos* a)
Увеличение угла скачка до прямого (a = 90°) приводит к из-
известному соотношению A6) для прямого скачка.
Увеличение давления в косом скачке уплотнения можно так-
также представить в функции числа М набегающего потока и уг-
угла а, который образует скорость wH с фронтом скачка. Подста-
Подставим в уравнение импульсов
9*
132 гл. ш. скачки уплотнения
значение wan из D3) и разделим обе части последнего на рп.
Тогда, используя уравнение неразрывности и формулу для скоро-
скорости звука [C4) гл. I], получим
Выразив с помощью уравнения ударной адиабаты A8) отноше-
отношение плотностей pH/pi через отношение давлений и подставив его
в последнее уравнение, приходим к искомой зависимости:
При одной и той же скорости набегающего потока косой
скачок, как это следует из D5), всегда бывает слабее прямого.
Интенсивность косого скачка уплотнения изменяется с изме-
изменением угла наклона его фронта к направлению набегающего
потока. В предельном случае, когда косой скачок переходит в
прямой (а = 90°), увеличение давления получается максималь-
максимальным. При этом равенство D5) переходит в равенство B0), из-
известное из теории прямого скачка уплотнения.
В другом предельном случае, когда угол наклона скачка к
направлению потока перед ним определяется условием
=-^-, D6)
косой скачок вырождается в бесконечно слабую волну (pi ~ рн)^
Разъясним этот факт несколько подробнее. Пусть в некоторой
точке О сверхзвукового газового потока возникло бесконечна
шн
1с 2 с" ' Зс
Рис. 3.11. Образование волны слабых возмущений
малое возмущение (рис. 3.11) давления. Слабая волна сжатия
(или разрежения) побежит из центра возмущения во все сторо-
стороны со скоростью звука а. Через единицу времени (т = 1 с) фронт
волны будет представлять собой сферу радиуса г = а. Однако вся
масса газа, в которой возникла волна, сносится по потоку со
§ 2. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ 133
сверхзвуковой скоростью wa > а. По этой причине слабые волны
давления никогда не выйдут за пределы конуса, поверхность ко-
которого является огибающей для сферических волн. Образующая
такого конуса носит название волны Маха или характеристики.
Угол cto между образующей и осью называется углом Маха или
углом распространения слабых возмущений. Этот угол, как видно
из рис. 3.11, определяется равенством
sina0 = -!.=_.
Итак, фронт очень слабого косого скачка уплотнения располага-
располагается по отношению к набегающему потоку под углом ао, который
определяется равенством D6). Сильные Еозмущения, как было по-
показано выше, распространяются со сверхзвуковой скоростью,
в связи с чем фронт сильного скачка образует с набегающим по-
потоком больший угол, чем характеристика: а > ао.
Диапазон изменения угла а для косого скачка уплотнения
определяется, таким образом, следующими пределами:
90° > а > а0.
Подставив выражение D5) в уравнение ударной адиабаты A8),
получим равенство, связывающее отношение pi/pH в случае ко-
косого скачка уплотнения с числом М набегающего потока и углом
наклона скачка:
D7)
Это равенство при М « 1/sin а дает pi ~ рн, а в случае а = 90°
переходит в сооответствующее равенство B2) для прямого скачка
уплотнения.
Зная отношение плотностей газа за и перед косым скачком,
можно вычислить угол со, на который отклоняется поток в скачке
(рис. 3.6). Из уравнения неразрывности имеем
В то же время из треугольников скоростей (рис. 3.9) следует
тЛп tg P //Q4
= . . Dо)
Отсюда получаем
~tga D9)
134 гл. ш. скачки уплотнения
или на основании равенств D7) и C8)
А+1
Л| sin2 a
- <50>
Но если известен угол [J между скоростью за скачком и фронтом
последнего, то угол отклонения потока определяется соотноше-
соотношением C0).
Мы указали способ определения угла, на который отклоняет-
отклоняется поток в скачке, когда положение фронта известно. Если,
наоборот, задано определенное отклонение сверхзвукового пото-
потока, то в тех случаях, когда в результате отклонения величина
скорости должна уменьшиться (например, при сверхзвуковом об-
обтекании клипа, изображенного на рис. 3.7, а), возникает косой
скачок уплотнения; при этом по формулам C0) и E0) может
быть вычислен угол а, под которым расположится фронт скачка
по отношению к потоку.
На рис. 3.12 представлены кривые а = /(со), соответствующие
различным значениям числа М набегающего потока, построен-
построенные для воздуха (к = 1,4). Как видим, каждому значению чис-
числа М отвечает некоторое предельное отклонение потока
(со = (Ощах). Так, при М = 2 поток может быть отклонен не более
чем на угол ©шах = 23°, при М = 3 — на сотах = 34°, при М =
= 4—на (Отах = 39°. Даже при бесконечно большой скорости
(М = оо) поток можно отклонить максимум на угол о)тах = 46°.
Наличие такого ограничения в отклонении потока после скачков
уплотнения является вполне естественным фактом, ибо как при
бесконечно слабом скачке, т. е. когда угол а равен углу распро-
распространения слабых возмущений, а образующая конуса возмуще-
возмущения является характеристикой, так и при наиболее сильном —
прямом скачке угол отклонения потока'становится равным нулю,
следовательно, кривые со = /(а) имеют максимумы.
На кривых рис. 3.12 видно также, что одному и тому же от-
отклонению потока отвечают два положения фронта скачка. Косой
скачок с большим углом наклона (верхнее значение на кривой
а (со)) называют сильным скачком, косой скачок с меньшим уг-
углом наклона — слабым скачком. Опыты показывают, что из двух
возможных положений плоского косого скачка более устойчивым
является то, при котором угол между направлением потока и
фронтом скачка меньше. Таким образом, на рис. 3.12 более важ-
важны нижние ветви кривых, лежащие под точками максимумов.
Нижнее пересечение каждой из кривых а = /(со) с осью ординат
соответствует перерождению скачка в слабую волну, а получаю-
получающийся при этом угол ао представляет собой угол слабых воз-
возмущений.
§ 2. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ
135
При сверхзвуковом обтекании клина, у которого угол при
вершине больше, чем допускается по рис. 3.12, образование пло-
плоского косого скачка уплотнения невозможно. Опыт показывает,
что в этом случае образуется скачок уплотнения с криволиней-
криволинейным фронтом (рис. 3.13), причем поверхность скачка разме-
размещается впереди, не соприкасаясь с носиком клина. В централь-
центральной своей части скачок получается прямым, но при удалении от
33'
13" 23° ЗЗ9 ?3' S3'со
Рис. 3.12. Зависимость направления косого скачка от угла отклонения
потока
оси симметрии переходит в косой скачок, который на больших
расстояниях вырождается в слабую волну. Такая же форма
скачка уплотнения наблюдается при сверхзвуковом обтекании
тела, имеющего закругленную носовую часть (рис. 3.14). В кри-
криволинейной ударной волне реализуются полностью обе ветви кри-
136
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
вой а (со), начиная от прямой ударной волны (на оси симметрии)
и кончая волной Маха (на периферии). Каждый элементарный
участок криволинейной ударной волны отвечает касательной к
этому участку плоской волне.
Иногда необходимо вычислить скорость потока после косого
скачка уплотнения. Проще всего это сделать, пользуясь треуголь-
Рис. 3.13. Скачок уплотнения
при сверхзвуковом обтекании
клина со слишком большим
углом при вершине (о)кл >
> о)тах)
Рис. 3.14. Теневая фотография скачка
уплотнения при сверхзвуковом обтека-
обтекании тела вращения
никами скоростей (рис. 3.9), из которых следует
Отсюда получаем
или в безразмерных обозначениях
H cos Р *
E1)
E2)
Используя формулу D5) гл. I, можно найти соответствующее
значение числа Маха за косым скачком:
Mj-
т+т К1
На рис. 3.15 приведены кривые зависимости числа Mi за скач-
скачком уплотнения от положения фронта Mi = /(a) для трех зна-
значений числа М в набегающем потоке (М = 2, 3, 4). Как видим,
во всех трех случаях при углах наклона фронта a < 60° скорость
потока после косого скачка уплотнения оказывается сверхзвуко-
§ 2. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ
137
вой. Крайняя левая точка каждой кривой отвечает режиму пере-
перехода косого скачка уплотнения в слабую волну, крайняя правая
точка — в прямой скачок уплотнения, скорость за которым мень-
меньше скорости звука.
В соответствии с результатами, представленными на рис. 3.15,
находится тот факт, что позади центральной части криволинейной
ударной волны (рис. 3.13) течение газа является дозвуковым,
\
№
\
\
О
20° М9 60° 80°а
Рис. 3.15. Зависимость числа Mi
за скачком уплотнения от угла
наклона скачка
Рис. 3.16. Схема сверхзвукового об-
обтекания конуса
а за пределами этой зоны — сверхзвуковым. В точке, разделяю-
разделяющей эти две зоны на линии ударной волны, угол ее наклона а
соответствует максимальному углу поворота потока со.
Случай, когда образуется прямой скачок, является наиболее
простым, так как при этом сразу получается дозвуковое течение.
После косого скачка поток замедляется, но, как мы видели, мо-
может оставаться сверхзвуковым. В таком случае последующее
торможение должно сопровождаться вторым скачком, который
может быть как прямым, так и косым. В последнем случае мо-
может понадобиться еще один скачок. Итак, полное торможение
сверхзвукового потока требует либо одного прямого скачка, либо
системы из нескольких косых скачков, обычно завершаемой сла-
слабым прямым скачком. Можно представить себе такую систему
скачков, в которой потери меньше, нежели в одном прямом
скачке 1).
Остановимся теперь на сверхзвуковом обтекании конуса. При
симметричном сверхзвуковом обтекании конуса (рис. 3.16) перед
]) Петров Г. И., Ухов Е. П. Расчет восстановления давления при
переходе от сверхзвукового потока к дозвуковому при различных системах
плоских скачков уплотнения.— М., 1947.
138
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
последпим устанавливается коническая ударная волна
(рис. 3.7, б), причем вершины конуса и ударной волны (поверх-
(поверхности скачка) практически совпадают. Ввиду того что толщина
скачка всегда очень мала, приведенные выше формулы для рас-
расчета плоскопараллельного косого скачка применимы и к осесим-
метричному скачку. В частности, если известны угол между фрон-
фронтом и направлением потока а и скорость перед скачком
(рис. 3.16), то по формулам E0) и C0) можно отыскать направ-
направление потока со™, по формуле E1)— скорость и по формуле D5) —
статическое давление непосредственно за скачком. Однако, в от-
отличие от плоского в осесимметричном потоке направление струй
70е
а
ВО9
so9
3D9
20е
/
• У
/
4''
У
1
1
/
/ л
У
1
/
Рис. 3.17. Сравнение углов
косого скачка на конусе и
на клине
10° 20е 30е W 50° со 60°
газа непосредственно за скачком (сокл) не параллельно поверхно-
поверхности тела (сокл ^ сокон). В связи с этим угол отклонения струй за
скачком постепенно изменяется, приближаясь асимптотически к
полууглу при вершине конуса. Непосредственно за скачком угол
отклонения имеет наименьшее значение соКл < сокон и, как упоми-
упоминалось, получается таким же, как для плоского потока, т. е. мо-
может быть определен с помощью рис. 3.12.
Зависимость угла а между фронтом скачка и направлением
потока от полуугла при вершине конуса ((оКОн) для случая Ян ==
= 2(МН = 3,16) приведена на рис. 3.17 (сплошная). Здесь же
нанесена кривая а = /(сокл), дающая углы отклонения потока не-
непосредственно за скачком (штриховая), т. е. отвечающая плос-
плоскому потоку (обтеканию клина). Как видим, при одинаковых уг-
углах конуса и клина на конусе скачок получается слабее (более
наклонным).
Выше было указано, что изменения направления потока, ско-
скорости и состояния газа в самом скачке не зависят от формы
§ 2. КОСЫЕ СКАЧКИ УПЛОТНЕНИЯ
139
поверхности скачка; при заданной скорости потока (Ян) и угле
скачка а эти изменения получаются одинаковыми в плоскопа-
плоскопараллельном и осесимметричном течениях. Различие этих двух
случаев состоит только в том, что при одинаковых углах раство-
раствора конуса и клина получаются разные углы наклона скачка. Ина-
Иначе говоря, при сравнении осесиммметричного и плоского косых
50°
?0°
30°
20е
10°
0
у
*/
у
у
1
J
' /
Si
г
у
/у
у
ш
/
у
f/
wfl
у
у
/
у
у
/
л
тл
У
Z
У
к
J
л
20й
уё
/
А
г/
/
у
/
Y\
у
у
А
г
V
30°
у
А
о
1
и
у
509а)
Рис. 3.18. Зависимость полуугла при вершине копуса от угла поворота
потока в скачке для различных скоростей потока
скачков целесообразно выражать все факторы в функции угла
скачка, а не угла при вершине обтекаемого тела. В этом случае
результаты расчета осесимметричного и плоского скачков полу-
получатся одинаковыми.
Течение газа за скачком в осесимметричном случае отличает-
отличается от плоского: скорость потока, статическое давление и плот-
плотность газа с удалением от скачка немного изменяются, а углы
поворота потока в скачке (угол клина) и на бесконечности (угол
конуса) существенно различны. На рис. 3.18 приведены кривые
«кон = /(о)кл) для различных значений чисел Маха. На рис. 3.19
изображены кривые значений числа Mi за скачком (штриховая)
и Мг на поверхности конуса (сплошная) в функции угла поворо-
поворота в скачке при различных значениях скорости. Как видим,
уменьшение скорости между областью, лежащей непосредствен-
непосредственно за Ькачком (соответствует плоскому течению), и поверхностью
конуса получается незначительным; так как числа М за скачком
и на поверхности конуса близки, то близки и соответственные
140
ГЛ. III. СКАЧКИ УПЛОТНЕНИЯ
числа %. Для практических расчетов скорость за коническим скач-
скачком можно принимать равной средней арифметической величине
1 I Л
E3)
или даже скорости за плоским скачком
Xi « А,1„„. E4)
При этом для осесимметричиого течения оказываются пригодными
S
?
1
<в
т
к*
i
ч
Ч
и
н
N
ч
чЛ
ч^
*ч»
ч^
V
^ч,
•*>
ч
ч
"Ч^
ч
ч
ч
•ч^
ч»
*ч
СЧ
ч
«ч^
X»
ч
ч.
"ч^
ч^
ч
ч
Чч
Ч
Ч;
ч
Г\
ч
ч
S
i i
\ \
Л
го'
30°
икл
Рис. 3.19. Значения чисел М за скачком (штриховая линия) и на поверхно-
поверхности конуса в зависимости от угла поворота в скачке
формулы, полученные выше для плоскопараллельного течения,
с той лишь разницей, что одним и тем же углам скачка соответ-
соответствуют разные углы при вершине тела (рис. 3.17).
§ 3. О применении пневматического насадка
в сверхзвуковом потоке
Для измерения скорости сверхзвукового газового течения
можно пользоваться обычным пневматическим насадком
(рис. 3.20). Нужно только учесть, что при сверхзвуковом обте-
обтекании насадка перед ним возникает ударная волна. Если ось сим-
симметрии насадка параллельна направлению потока, то центральная
§ 3. ПРИМЕНЕНИЕ НАСАДОК В СВЕРХЗВУКОВОМ ПОТОКЕ
141
газовая струйка, претерпевающая полное торможение, сначала
проходит через прямую часть ударной волны, где ее скорость
становится дозвуковой, затем при подходе к отверстию 1 скорость
плавно уменьшается до нуля.
Давление в трубке 1 (р\) может быть вычислено следующим
способом. Из выражения F8) гл. I имеем
h
vfc-1
Pi \
где р\ и Mi — статическое давление и число Маха непосредствен-
непосредственно за ударной волной. Используя формулы D5), D6) гл. I и
формулу A6) данной главы,
переходим к числу М в набега-
набегающем
M2
1
h
ИЛИ
потоке:
2
k + l\
к — 19
1 к+1Х1
2 1
& — 1 1
+ 1 ^н
2 '"г
1
к~1 (
2
н
2 J ^
2 н
2
i2
А 2 >1 \
-^0. Пневматический: насадок
в сверхзвуковом потоке
Отсюда на основании равенства B0) получаем общеизвестную
формулу Релея, выражающую отношение давления р! в трубке 1
к статическому давлению в набегающем потоке (рв) как функ-
функцию числа М в набегающем потоке:
ii -(*±±\к-Ч 2 >fe-i
2k
1
E5)
Для воздуха (к = 1,4) эта формула приводится к следующему
виду:
E6)
142 гл. ш. скачки уплотнения
Если боковые отверстия 2 находятся на расстоянии, равном не
менее 4—6 диаметрам насадка от переднего его края, то, как
показывает опыт, давление в трубке 2 равно статическому дав-
давлению набегающего потока (рн). Таким образом, величины Р\
и рв измеряются непосредственно на манометрах, присоединен-
присоединенных соответственно к трубкам 1 ж 2 насадка.
Для вычисления скорости потока по формулам E5) или E6)
нужно еще знать скорость звука, или, что то же, температуру
набегающего потока:
В некоторых случаях удобнее пользоваться формулой, выражаю-
выражающей отношение давлений в трубках насадка в функции приве-
приведенной скорости набегающего потока (Хв). Эту формулу можно
получить из выражений B1) и B3) данной главы:
=ГГ. E7)
1 —¦ ~~
Для воздуха (к = 1,4)
л* л
E8)
Вычисление скорости набегающего потока по формуле E7) мож-
можно выполнить, если известно значение критической скорости:
wB = Лнакр,
где
причем
т
1 н
& + 1 Лн
Заметим, что, например, в аэродинамической трубе всегда из-
известна именно температура торможения, т. е. температура всасы-
всасываемого в трубу воздуха.
Глава IV
УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
§ 1. Сверхзвуковое сопло
В сверхзвуковом сопле, называемом соплом Лаваля, газовый
поток преобразуется таким образом, что скорость истечения ста-
становится больше скорости звука:
М > 1,
wa
a.
Рис. 4.1. Сопло Лаваля
Рассмотрим случай одномерного течения газа по сверхзвуко-
сверхзвуковому соплу. Уравнение неразрывности дает
G = pwF = const.
Газ движется по соплу с ускорением, поэтому при малой скоро-
скорости, когда плотность газа можно считать неизменной, необходимо
уменьшать сечения. Этим обусловлено сужение начальной части
сопла. При дальнейшем рас-
расширении газа увеличение
скорости сопровождается за-
заметным уменьшением давле-
давления и, следовательно, плот-
плотности газа, что частично
компенсирует рост скорости,
и поэтому сужать сечение
канала нужно уже не гак
быстро. Наконец, процесс
проходит через такую стадию, когда плотность расширяющегося
газа уменьшается обратно пропорционально скорости. Как из-
известно, в этом сечении канала скорость потока равна скорости
звука. Дальнейшее увеличение скорости сопровождается еще бо-
более быстрым падением плотности, вследствие чего, как это следу-
следует из уравнения неразрывности, сечение сопла должно увели-
увеличиваться.
Таким образом, сверхзвуковое сопло, предназначаемое для
получения сверхзвукового потока, должно состоять из сужаю-
сужающейся (дозвуковой) и расширяющейся (сверхзвуковой) частей
(рис. 4.1). В самом узком сечении сверхзвукового сопла (крити-
(критическом сечении) скорость потока равна звуковой.
Рассмотрим совместно уравнения неразрывности и Бернулли
(без учета трения) в дифференциальной форме:
d(pwF) = О, dp + pw dw = 0.
144 гл. iv. ускорение газового потока
Разделим второе уравнение на pw2 и умножим и разделим пер-
первый его член на dp. Тогда получим
1 dp dp , dw л-ч
w2 dp p w
Из первого уравнения имеем, согласно D) гл. I, при dG = О
dp dF dw
р ~~ F w
Подставляя этот результат во второе уравнение и учитывая, что
согласно равенству C4) гл. I производная давления по плотно-
плотности в идеальном адиабатическом процессе равна квадрату ско-
скорости звука в газе, получим
w2 Л dw_ dF
w
Анализируя это равенство, можно заметить, что при расширении
(ускорении) газа, когда dw/w > 0, сечение сопла должно изме-
изменяться так, как указывалось выше, а именно:
если w <Са, то -тг- < 0 (сужение),
если w = а, то —=- = 0 (кризис),
если w > а, то -тг- > 0 (расширение).
Таким образом, наблюдаются три режима: дозвуковой w < акр,
критический w = акр, сверхзвуковой w > а„р.
Следует отметить, что около критического сечения поток
очень чувствдтелен к изменению поперечного сечения канала.
Так, например, для изменения числа М на 10 % (от М = 0,9 до
М = 1) достаточно изменить площадь сечения на 1 %, а для пе-
перехода от М = 0,95 к М = 1 — на 0,25%. По этой причине
нельзя поддержать критический режим на достаточно протяжен-
протяженном участке прямой трубы (пограничный слой, образующийся
за счет торможения газа у стенок, как бы сужает сечение струи).
Плотность, как уже отмечалось, с ростом скорости умень-
уменьшается. В критическом сечении сопла dF/F = 0, это значит, что
площадь поперечного сечения проходит через экстремум (мини-
(минимум). Из соотношения A) следует, что именно в узком сечении
сопла Лаваля получается скорость потока, равная местной ско-
скорости звука.
Рассмотрим зависимость скорости от площади поперечного
сечения сопла. Для этого, пользуясь уравнением неразрывности,
свяжем произвольное сечение сверхзвукового сопла с его мини-
минимальным сечением:
1 = Ркр^кр^кР;
§ 1. СВЕРХЗВУКОВОЕ СОПЛО 145
отсюда
Однако w = аМ и Мкр = 1, поэтому
F РКракр
Но, как известно,
* 1/2
акр _ / Укр )
а -\ Т J
и при идеальном процессе
Р
кр
следовательно,
F /rKP\2U-D
/Гкр\2(й-1) !
На основании равенств C8) и C9) гл. I имеем
Т 1 +
1 кр '
Отсюда следует
й+1
Для воздуха к = 1,4, поэтому имеем
F A + 0,2М2K
FKX) = 1,73М
B)
C)
Из этих формул видно, что безразмерное значение площади се-
сечения сопла является функцией только числа М. Следует под-
подчеркнуть, что все приведенные выражения справедливы при от-
отсутствии тепловых и гидравлических потерь, т. е. при изменении
состояния газа по идеальной адиабате.
Если задается конфигурация сверхзвукового сопла, то можно
указать, какое число М получается в любом сечении. Каждому
Ю г. Н. Абрамович, ч. 1
146
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
-значению числа М соответствует определенная величина отно-
отношения F/FKp. Кривая F/FKV = /(М), построенная по формуле C),
приведена на рис. 4.2. При этом, как видно из кривой, уравне-
уравнение C), и значит уравнение B), имеет два решения; одному и
тому же F/FKp отвечают два значения числа М: одно при дозву-
дозвуковой скорости и другое при сверхзвуковой скорости. Для вход-
входной части сопла, предшествующей критическому сечению, годны
все дозвуковые решения, а для
выходной части — все сверхзву-
сверхзвуковые. Однозначное решение по-
получается только в критическом се-
сечении (F/FKP = 1).
Давление и плотность газа при
идеальном процессе зависят од-
однозначно от числа М и определя-
определяются формулами F8) и G1) гл. I.
Отсюда следует, что, выбрав про-
произвольное сечение, мы получим в
этом сечении определенное значе-
значение числа М, которому соответ-
соответствуют определенные значения
температуры, давления и плотно-
плотно)
F 1
f
з
z
0
1
i
A
/
1 1 I
3 М ?
Рис. 4.2. Зависимость безразмер-
безразмерной площади сопла Лаваля от
числа М (к = 1,4)
сти газа (с точностью до влияпия пограничного слоя).
Величина скорости в данном сечении сверхзвукового сопла
зависит только от температуры торможения Т*. Изменение пол-
полного давления р* на скорость не влияет, так как пропорциональ-
пропорционально ему изменяется и местное давление /?, а их отношение остает-
остается неизменным, также остается неизменным и отношение тем-
температур
Для получения на срезе сверхзвукового сопла определенного
значения числа М необходимо соответствующим образом подо-
подобрать площадь сечения и, кроме того, надо иметь достаточный
запас давления в камере перед соплом. Другими словами, для
достижения требуемого числа М на срезе сопла давление в ка-
камере должно в известное число раз превосходить давление окру-
окружающей среды.
Предположим, что давление в камере р* возросло, тогда на
срезе сопла давление также увеличивается и газ истекает с
избыточным давлением. Где-то за срезом сопла давление урав-
уравняется с атмосферным, избыток давления израсходуется в струе
на увеличение скорости, а так как для сверхзвукового потока
увеличение скорости требует увеличения поперечного сечения
струи, то струя как бы образует в пространстве расширяющееся
сверхзвуковое сопло. Если же давление в камере по какой-либо
§ 1. СВЕРХЗВУКОВОЕ СОПЛО 147
причине понизится, то на срезе произойдет понижение давления,
причем давление в некоторых случаях может получиться ниже
атмосферного; скорость истечения при этом не изменится, так
как она являетоя функцией только отношения площадей выход-
выходного и критического сечений оопла. Изменение давления в ат-
атмосфере не сказывается на истечении из сопла, так как волна
давления, распространяющаяся со скоростью звука, сносится
сверхзвуковым газовым потоком. По выходе газовой струи из
сопла давление в ней в конце концов должно сравняться с ат-
атмосферным, т. е. повыситься за счет торможения сверхзвукового
потока; этот процесс сопровождается возникновением ударных
волн и будет ниже разобран более подробно.
Таким образом, давление на срезе данного сверхзвукового
сопла не связано с давлением атмосферы, а зависит только от
давления в камере и формы сопла.
Лишь в случае так называемого расчетного режима давление
на срезе сопла равно атмосферному давлению: ра = /V На не-
нерасчетных режимах, когда давление на срезе больше или мень-
меньше атмосферного, должно происходить изменение давления в
струе вне сопла (см. с. 159 и 160).
Уже отмечалось, что процесс преобразования давления в ско-
скорость в сверхзвуковом и в дозвуковом потоках протекает без су-
существенных потерь, т. е. примерно при постоянной энтропии и,
следовательно, очень близок к идеальной адиабате. Имен-
Именно поэтому приведенные выше формулы расчета идеального
сверхзвукового сопла дают хорошие результаты для реальных
сопел«.
Во многих случаях расчетные формулы упрощаются, если па-
параметры состояния газа определяются в функции не от числа М,
а от приведенной скорости. Удобство оперирования приведенной
скоростью связано с тем, что ее знаменатель (критическая ско-
скорость) зависит только от температуры торможения, которая по-
постоянна для любого участка потока с изолированным процес-
процессом. Законы изменения температуры, давления и плотно-
плотности газа в функции К выражаются формулами D2), G2)
и G3) гл. I.
Выведем выражение, связывающее площадь сечения сверх-
сверхзвукового сопла с приведенной скоростью. Обратимся к уравне-
уравнению неразрывности
F PkdSd
^кр Рш
Подставляя сюда
" = я«кР, 9-f
л т ) '
10*
148 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
получим
F
" ^кр
1
X
1-
2
к-1
к + 1
я2
1
k-1
D)
Выведем в заключение формулу для расчета секундного рас-
расхода газа в сверхзвуковом сопле. Удобно находить расход газа
по критическому сечению сопла:
G = ркрЯкр^кр, E)
так как из выражений D2), G2), G3) гл. I легче всего опреде-
определить состояние газа в критическом сечении (X = 1):
1
Г* к+1 _р* /
I
_
^нр 2 ' Ар I 2 J
-L 1 1 F)
р* _ / Ar + I \fe-l a* _ (_T*i_Y _ ( к + 1 \2
J ' «кр ~UkPJ "" I 2 J
В частности, для воздуха (к = 1,4) имеет место
Т* = 1,2Гкр, р* = 1,58ркр, /?* = 1,89/?кр, а* = 1,1акр. G)
Заменяя с помощью соотношений F) критические значения
плотности и скорости звука в выражении E) значениями, соот-
соответствующими состоянию торможения, т. е. состоянию в камере
перед соплом, получим
&+1
или, используя уравнение состояния и формулу C4) гл. I:
fe+i 1
Итак, расход газа через сверхзвуковое сопло зависит только от
состояния газа в камере перед соплом. Для воздуха (к = 1,4,
R = 287,3) имеем следующую упрощенную формулу расхода:
G = 0,0404-~^ [кг/с]. (8а)
По формулам (8) определяют размер критического сечения
сверхзвукового сопла для заданного расхода и известного со-
состояния газа перед соплом.
В тех случаях, когда скорость истечения меньше критиче-
критической, в качестве сопла применяют простой сходящийся наса-
§ i. СВЕРХЗВУКОВОЕ СОПЛО 149
док — конфузор. Состояние газа и скорость течения в различных
сечениях конфузора можно определять по тем же формулам,
что и в случае сверхзвукового сопла. Однако поток в коыфузоре
имеет ряд особенностей, которые нельзя не учитывать.
Наиболее важно, что при дозвуковом режиме истечения дав-
давление в струе на срезе сопла ра практически равно давлению
в окружающей среде рн, так как при этом режиме любое измене-
изменение давления в атмосфере в виде волны давления проникает
внутрь сопла, вызывая изменение давления перед соплом и со-
соответствующее изменение скорости истечения; перестройка по-
потока продолжается до тех пор, пока давление в струе на срезе
сопла не сравняется с атмосферным. Поэтому в отличие от сверх-
сверхзвукового сопла в простом конфузоре скорость истечения опреде-
определяется не его формой, а только давлением в камере перед кон-
фузором. Таким образом, если известно давление в камере /?*, то
при заданном давлении в плоскости выходного среза рв приведен-
приведенная скорость истечения находится непосредственно по форму-
формуле G8) гл. I:
>2 * + 1 , (Рв\ k
Величина скорости истечения равна wa = А,аакр, где критическая
скорость зависит согласно D1) гл. I только от температуры в ка-
камере перед соплом (температуры торможения):
= «* V
k+1
Расход газа в конфузоре найдем по уравнению неразрывно-
неразрывности, применив его к выходному сечению:
G = paWaFa.
Если использовать известные уже зависимости
1 1
2
то получится
или
«о»
Формулу A0) можно использовать и для определения расхода
газа в сверхзвуковом сопле на расчетном режиме истечения,
150
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
когда давление в выходном сечении сопла Fa равно давлению
в окружающей среде ра = рп. Необходимо, однако, иметь в виду,
что при Fa = const и р* = const из формулы A0) следует, что
с понижением давления ра = Рн, т. е. с ростом скорости истече-
истечения Яа в области значений Яа> 1, расход газа через сопло умень-
уменьшается: G -> 0. Это объясняется тем, что одновременно с увели-
увеличением Ха должно расти отношение площади Fa к площади кри-
критического сечения FKp, величина которой не зависит от ра = ра;
Рис. 4.3. Зависимость расхода
газа от отношения давлений
в камере и окружающей среде
иначе говоря, при увеличении р* для поддержания условия
ра = Ря при Fa = const следует уменьшать площадь критического
сечения сопла, что и вызовет уменьшение расхода газа через
сопло.
На рис. 4.3 представлен график функции
1 1
ft-i
G
кр
которая описывает изменение отношения расхода газа через вы-
выходное сечение расчетного сопла к расходу газа через критиче-
критическое сечение той же площади в зависимости от перепада давле-
давлений /?*//?н. Как видим, при_/?*//?н ~^ °° расход газа в выходном
сечении стремится к нулю: Ga -* 0.
§ 2. Нерасчетные режимы истечения из сопла Лаваля
Рассмотрим сверхзвуковое нерасчетное истечение из сопла
Лаваля, когда ра > рн. На значительном удалении от сопла дав-
давления в струе и в атмосфере должны уравняться. В связи с этим
давление в струе по мере удаления от выходного отверстия сопла
постепенно уменьшается, скорость газа возрастает и поперечное
сечение сверхзвуковой струи увеличивается (рис. 4.4). Опыт
показывает, что при этом происходит перерасширение струи,
т. е. в некотором наиболее широком сечении струи устанавли-
устанавливается давление ниже атмосферного ра\ < рн. После этого струя
начинает сужаться, так как давление должно приблизиться к
§ 2. НЕРАСЧЕТНОЕ ИСТЕЧЕНИЕ ИЗ СОПЛА ЛАВАЛЯ
151
атмосферному, а скорость соответственно уменьшиться. Тормо-
Торможение сверхзвукового потока приводит, естественно, к возникно-
возникновению скачков уплотнения. В результате этого в некоторой части
сечения струи скорость становится дозвуковой, а давление выше
атмосферного. Затем давление вновь уменьшается, сближаясь с
атмосферным. При достаточно большом
избытке давления скорость вновь дости-
достигает критического, а затем и сверхзвуко-
сверхзвукового значения, т. е. появляется второй
сверхзвуковой участок, на котором струя
расширяется. В результате второго пере-
перерасширения и последующего увеличения
давления возникает вторая группа скач-
скачков уплотнения. Естественно, что вслед-
вследствие потерь в первой группе скачков
второе перерасширение струи и вторая
группа скачков уплотнения получаются
слабее первой. Таким образом, постепен-
постепенно струя рассеивает свою энергию (под-
(подробнее об этом см. § 6 гл. VII). При небольшом избытке давле-
давления на срезе сопла также получаются колебания скорости и
давления вдоль оси струи, но без скачков уплотнения.
Сверхзвуковое истечение из сопла в том случае, когда на
срезе давление меньше окружающего, осуществляется посред-
посредством сложной системы скачков. Рассмотрим, например, плоско-
плоскопараллельную струю газа1), вытекающую в среду большего
Рис. 4.4. Схема сверх-
сверхзвукового истечения с
избытком давления: 1 —
сопло, 2 — граница
струи, 3 — скачки уп-
уплотнения
Рис. 4.5. Схема истечения из плоскопараллельного сопла Лаваля на режиме
перерасширения
давления (рис. 4.5). От краев сопла отходят косые скачки уплот-
уплотнения, встречающиеся на оси струи в точке О. Элементарные
струйки газа, пересекая фронт косого скачка (а — О), перехо-
переходят в область атмосферного давления ра > Ра. Отклонение струек
от первоначального направления, происходящее при скачке,
должно было бы привести к их столкновению на оси симметрии.
В действительности происходит второй поворот струек, возвра-
*) Речь идет о сопле, поперечное сечение которого имеет форму вытя-
вытянутого прямоугольника. Сверхзвуковое истечение из осесимметричного соп-
сопла сложнее, и мы его здесь рассматривать не будем (см. гл. VII).
152
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
щающий их к первоначальному направлению, но это приводит
к возникновению второй группы скачков (Ob). Естественно, что
если в областях аОЪ господствует атмосферное давление, то пра-
правее линий О — Ъ (рис. 4.5) получится давление выше атмосфер-
атмосферного. Поэтому за второй группой скачков устанавливается такой
же режим, как при истечении с избытком давления (Ра>Рн)'
Чем меньше давление ра на срезе сопла, тем больше получится
угол между фронтом косого скачка и направлением потока; при
этом увеличивается угол, на который должен повернуться поток
во второй группе скачков Ob. Одновременно уменьшается ско-
скорость потока за первой груп-
группой скачков (в области аОЬ),
поэтому в конце концов на-
наступает такой режим, при
котором нужный угол пово-
поворота (со) потока в скачках
Ob не может быть осуществ-
осуществлен, т. е. со > (отах. С этого
момента в центральной ча-
Рис. 4.6. Мостообразный скачок при не- стп струи образуется удар-
расчетном истечении из сопла Лаваля над вшша? а вся смма скач_
ков принимает мостообраз-
ную форму (рис. 4.6). С увеличением противодавления участок
ударной волны с — с увеличивается. При большом противо-
противодавлении сверхзвуковое истечение оказывается невозможным,
и скачки давления перемещаются внутрь сопла, т. е. осу-
осуществляются в меньшем сечении, на меньшей скорости для
данного сверхзвукового течения. В таком случае выходная часть
сопла за фронтом скачка работает как обыкновенный дозвуковой
диффузор. Если внутри сопла возникает отрыв потока от стенок,
сопровождающийся обычно сложной системой скачков (§ 6,
гл. VI), то истечение в атмосферу происходит со сверхзвуковой
скоростью, меньшей, чем на расчетном режиме.
С падением давления в камере скачок все ближе подходит
к критическому сечению, одновременно становясь более слабым.
Приблизившись вплотную к критическому сечению, скачок ис-
исчезнет, сверхзвуковое сопло при этом превратится в трубку
Вентури (рис. 4.7).
Местоположение плоскости скачка определяется отношением
давления в камере (перед соплом) к давлению в той среде, куда
истекает газ. Следует отметить, что режимы, при которых скачки
получаются внутри сверхзвукового сопла, встречаются в двига-
двигателях редко. Обычно газ расширяется до выходного сечения со-
сопла и вытекает со сверхзвуковой скоростью.
Более детальное рассмотрение сверхзвуковой струи, вытекаю-
вытекающей из сопла на нерасчетном режиме, дается в гл. VII, а вопрос
об истечении с образованием скачков внутри сопла— в гл. VIII.
§ 2. НЕРАСЧЕТНОЕ ИСТЕЧЕНИЕ ИЗ СОПЛА ЛАВАЛЯ
153
Остановимся на работе двигателя в нерасчетных условиях
истечения газа из сопла.
При работе двигателя на расчетном режиме давление в пло-
плоскости выходного среза сопла как в рабочей струе, так и во
внешнем потоке равно атмосферному. Однако такое условие вы-
выполняется лишь при одном значении отношения давлений pjp*.
0,528
Рис. 4.7. Кривые давлений
при скачке уплотнения
внутри сопла Лаваля
С изменением скорости полета давление на срезе сопла в воз-
воздушно-реактивном двигателе изменяется. По этой причине неиз-
неизменное выходное сечение становится не соответствующим расчет-
расчетному режиму. Можно выделить две области нерасчетных усло-
условий: первая — при недостаточной, вторая — при слишком боль-
большой площади выходного отверстия сопла.
В первом случае на срезе сопла Лаваля поддерживается по-
постоянное давление, величина которого выше атмосферного, ибо
выходное сечение меньше расчетного, вследствие чего газ в сопле
расширяется не полностью. Величина давления на срезе равна
и
: —1 .
Ра-Р [l —
Чем меньше безразмерная площадь выходного отверстия (/а),
тем ниже приведенная скорость (Ха) и, следовательно, тем выше
давление на срезе (ра). Выходя из сопла, струя продолжает
расширяться в атмосфере, а скорость потока растет. На рис. 4.8
показаны границы области в струе, внутри которых среднее
давление остается избыточным.
Если достроить сопло до расчетных размеров, то из-за того,
что внутри дополнительной части сопла господствует повышен-
повышенное давление, получится прирост тяги АР. Следовательно, при
недостаточной площади выходного отверстия тяга двигателя
меньше, нежели на расчетном режиме.
154
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
Другая область работы сопла Лаваля отвечает тому случаю,
когда площадь выходного отверстия превосходит расчетную, т. е.
когда величина полного давления недостаточна для того, чтобы
получить на выходе атмосферное давление. На этом режиме
сопло Лаваля заполнено сверхзвуковым потоком до самого среза,
а давление на срезе получается ниже атмосферного, т. е. сопло
работает с перерасширением. При выходе струи в атмосферу в
Рис. 4.8. Истечение из сопла с избыт- Рис. 4.9. Истечение из сопла с пе-
пеком давления - рерасширением
ней устанавливается сложная система скачков уплотнения, кото-
которая поддерживает разрежение на срезе сопла.
Работа на режиме перерасширения возможна лишь до дав-
давлений ра^Рат\п. В ином случае, как указывалось, скачок уплот-
уплотнения переместится внутрь сопла Лаваля, давление на срезе
сравняется с атмосферным и скорость истечения станет дозвуко-
дозвуковой. Этот режим работы, как уже упоминалось, в двигателях
почти никогда не встречается и практического значения не имеет.
Иначе говоря, при слишком широком сопле скорость на вы-
выходе обычно такая же, как и на расчетном режиме, а давление
здесь согласно приведенной формуле ниже атмосферного; при
этом в выходной части сопла Лаваля получается участок пере-
перерасширения, на котором к стенкам приложена сила АР, направ-
направленная по потоку (рис. 4.9). Итак, на режиме перерасширения
реактивная тяга ниже расчетной. Для увеличения тяги выгодно
отбросить участок перерасширения, укоротив сопло до расчет-
расчетных размеров.
Таким образом, во всех случаях отклонения от расчетного
режима истечения при р* = const реактивная сила меньше, не-
нежели на расчетном режиме. Как следует из формулы A05) гл. I,
реактивная тяга
На режиме перерасширения третий член в правой части этого
равенства отрицателен (/?а</?н), а первые два члена больше,
чем на расчетном режиме (из-за увеличения wa); на режиме
избытка давления (ра> р*) третий член положителен, а первые
два члена вследствие уменьшения wa меньше, чем на расчетном
режиме.
§ 3. ТЕЧЕНИЕ ПРАНДТЛЯ — МАЙЕРА 155
Вычисления показывают, что некоторый отход от расчетных
условий не влечет за собой значительного уменьшения реактив-
реактивной тяги. Получается это потому, что изменение третьего члена
в формуле тяги компенсируется в значительной мере изменением
первых двух членов. По этой причине в тех случаях, когда вы-
выходное сечение сопла больше, чем сечение камеры сгорания,
в целях снижения лобового сопротивления можно без особого
ущерба для тяги укоротить сопло, приняв Fa = FT, т. е. работая
на нерасчетном режиме. Можно доказать теоретически, на чем
мы здесь не останавливаемся, что в ПВРД величина P/Fa дости-
достигает максимума при условии, что скорость истечения в точности
равна скорости полета (wa=wH), а давление на выходном срезе
значительно выше расчетного (/?а>/?н). На таком режиме тяга
образуется только вследствие избытка давления на срезе сопла:
Выше установлено, что при постоянных значениях полного
давления и температуры торможения в двигателе наибольшая
тяга получается на расчетном режиме истечения.
Естественно, что в случае нерегулируемого выхлопного сопла,
т. е. сопла с постоянными сечениями, тяга возрастает при уве-
увеличении полного давления, так как при этом давление на срезе
сопла растет, а приведенная скорость истечения не изменяется.
§ 3. Сверхзвуковое течение газа
с непрерывным увеличением скорости
(течение Прандтля — Майера)
Рассмотрим сначала простейший вид сверхзвукового течения
газа — поступательный равномерный поток. При таком течении
все частицы газа движутся по параллельным траекториям с по-
постоянной по величине скоростью. Траектории частиц являются
одновременно линиями тока, непроницаемыми для газа.
Если поток не встречает никаких препятствий в виде твер-
твердых тел или границ (стенок), то газ не испытывает никаких воз-
возмущений. Простейшей границей, могущей изменить характер
равномерного поступательного течения газа, является прямоли-
прямолинейная твердая стенка. Рассмотрим сначала случай, когда такая
стенка расположена параллельно направлению течения, т. е.
совпадает с одной из линий тока. Если движущийся газ зани-
занимает всю бесконечную область над стенкой и сама стенка тоже
бесконечна по длине, то ясно, что в этом случае стенка не ока-
окажет никакого влияния на течение газа1). Отметим, что это по-
положение справедливо и в общем случае для кривых линий тока:
Влияние вязкости газа здесь не учитывается.
156 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
если стенка совпадает с линией тока, то она не оказывает воз-
воздействия на движущийся газ.
Если бы в некоторой точке А стенки (рис. 4.10) имелось ка-
какое-либо малое препятствие, то оно вызвало бы слабое возмуще-
возмущение равномерного потока. Такое возмущение распространилось
бы в равномерном сверхзвуковом потоке по прямой линии — ха-
характеристике, составляющей с направлением скорости угол аог
определяемый из условия
Этот угол, как нам уже известно, называется углом распростра-
распространения слабых возмущений.
Теперь мы можем дать картину обтекания внешнего тупого
угла. Пусть в некоторой точке С стенка поворачивает, образуя
с первоначальным направлением угол бо (рис. 4.11). При сверх-
сверхзвуковом обтекании внешнего ту-
тупого угла АСВ газ расширяется,
ибо область, занятая газом, уве-
увеличивается; при расширении газ
* В
Рис. 4.10. Параллельный равно- Рис. 4.11. Поворот сверхзвукового
мерный поток над плоской стен- потока газа при обтекании угла
кой АСВ
ускоряется. Вдоль участка стенки АС скорость газа постоянна.
Угловая точка С при обтекании ее газом является препятствием,
которое служит источником возникновения слабых возмущений
в газовом потоке. Эти возмущения, как было показано, распро-
распространяются в равномерном потоке по прямой линии — характе-
характеристике СК, которая отделяет невозмущенный газовый поток от
возмущенного. Вдоль участка стенки СВ скорость газа снова
принимает постоянное значение, большее, чем в исходном потоке
вдоль АС. Это значит, что возмущение, возникшее вследствие
обтекания угловой точки С, закончится на другой характеристи-
характеристике CL', которая также прямолинейна. Таким образом, поворот
потока к новому направлению осуществляется внутри угла KCL'
между двумя прямолинейными характеристиками. Для большей
наглядности разобьем участок непрерывного расширения газа
внутри угла KCU на большое число участков с незначительны-
незначительными, но прерывными изменениями параметров.
§ 3. ТЕЧЕНИЕ ПРАНДТЛЯ — МАЙЕРА 157
Первый малый скачок скорости и давления произойдет на
плоскости, следом которой является прямая СК; так как давле-
давление при этом падает, то согласно теории скачков нормальная к
плоскости СК составляющая скорости увеличивается; ввиду не-
неизменности тангенциальной составляющей скорости поток немно-
немного изменяет свое направление, отклоняясь от плоскости скачка
разрежения в сторону, противоположную той, в которую он от-
отклонился бы в скачке сжатия. Итак, за плоскостью СК слабого
скачка разрежения поток получил несколько большую скорость,,
немного отклонился в соответствующем направлении, а давление,
плотность и температура газа слегка уменьшились. Возмущение,,
распространяющееся из области более низких давлений, теперь
уже должно быть ограничено новой характеристикой СК', кото-
которая вследствие отклонения потока и увеличения числа М распо-
располагается правее прежней характеристики СК, Левее характери-
характеристики СК' никакие возмущения не проникают, поэтому вдоль
линии СК', так же как перед этим вдоль линии СК, параметры
газа и скорость движения неизменны.
Если скорость потока, которая несколько увеличилась в пер-
первом скачке, спроектировать на направления, нормальное и тан-
тангенциальное ко второй характеристике СК', то окажется, что
нормальная составляющая скорости здесь меньше {wu<^wu), а ра-
радиальная— больше (ir'r>wr), чем на линии СК.
Второй слабый скачок разрежения, который мы совместим
с плоскостью СК', вызывает новое отклонение потока в сторону
СВ и дальнейшее расширение газа, сопровождающееся увеличе-
увеличением скорости.
Поворот потока, очевидно, завершится, если струйка, /при-
/прилегающая к стенке, станет параллельной направлению СВ
(рис. 4.11). Следовательно, у самой стенки вектор скорости па-
параллелен СВ.
Но в силу того, что все характеристики, исходящие из точ-
точки С, прямолинейны, т. е. скорость (и остальные параметры газа)
вдоль них не изменяется, то и вдоль последней характеристи-
характеристики CL' вектор скорости сохраняет постоянное (по величине и
направлению) значение wkl). Таким образом, за последней ха-
характеристикой CL' поток снова становится поступательным. Но
за точкой С поток не испытывает более никаких возмущений. Сле-
Следовательно, после поворота около угла поток будет над стен-
стенкой СВ таким же, каким был поток над стенкой АС, т. е. равно-
равномерным и параллельным потоком с постоянной скоростью wK > wn.
Последняя характеристика CL', на которой завершается поворот
газового потока около точки С, располагается под углом ah к
1) Точка С является особой точкой, так как в этой точке сходятся лучи,
на каждом из которых значения скорости и давления постоянны. Эти:
постоянные значения скорости и давления различны для разных лучеГи
158 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
стонке СВ, соответствующим равенству
sinaft = J-,
тогда как первая характеристика располагается под углом а„
к стенке АС в соответствии с равенством
здесь Мн, Mfe—значения чисел М до и после поворота потока.
Как известно, конечные адиабатические скачки разрежения
невозможны. Однако если разбить угол RCL' на бесконечно боль-
большое число бесконечно малых углов, то мы перейдем от рассмот-
рассмотренной выше условной схемы с малыми скачками разрежения
к непрерывному расширению газа; вместо конечного числа сла-
слабых скачков получается бесконечное число характеристик — пучок
характеристик.
Таким образом, поворот потока около тупого угла и связанное
с этим расширение газа (уменьшение давления) можно рассмат-
рассматривать как последовательность слабых возмущений источником
которых служит вершина угла; эти возмущения распространя-
распространяются в потоке по прямолинейным характеристикам, исходящим
из вершины.
Приведенные рассуждения показывают, что при повороте
сверхзвукового газового потока около внешнего тупого угла зна-
значения скорости, давления и плотности остаются постоянными
вдоль лучей, исходящих из угловой точки и являющихся харак-
характеристиками. Поэтому при аналитическом исследовании обтека-
обтекания тупого угла удобно воспользоваться полярными координа-
координатами, поместив начало координат в этой угловой точке. Коор-
Координатными линиями тогда служат лучи, исходящие из угловой
точки, и концентрические окружности с центром в этой угловой
точке. Координатами точки на плоскости являются радиус-век-
радиус-вектор г этой точки и угол ф, составляемый радиусом-вектором с
лучом, имеющим фиксированное направление, которое мы опре-
определим позже. Все параметры газа будем рассматривать как функ-
функции от г и ф: w = w(r, ф), р=р(г, ф), р = р(г, ф). В силу того,
что параметры газа вдоль лучей в нашей задаче сохраняются
постоянными, частные производные от w, p и р по г равны нулю
(при перемещении вдоль луча не происходит изменения пара-
параметров газа). Таким образом,
Составляющие скорости по радиусу-вектору и по направле-
направлению, перпендикулярному к нему, обозначим соответственно че-
через wr и wu. Тогда величина скорости w =]/ w\ + w\. В силу
§ 3. ТЕЧЕНИЕ ПРАНДТЛЯ — МАЙЕРА
159
того, что dw/dr = О, имеем также
dw^ dw^
dr
dr
A2)
Основное свойство характеристики, как уже известно, состоит
в том, что нормальная к ней составляющая скорости равна ско-
скорости звука а, но характеристика совпадает с радиусом-вектором,,
поэтому в выбранной нами полярной
системе координат нормальная со-
составляющая скорости может быть
найдена из условия
wu = a. A3)
Рис. 4.12. К выводу усло-
условия отсутствия завихрен-
завихренности
Течение газа около внешнего тупо-
тупого угла является плавным и уско-
ускоренным, поэтому его можно считать
безвихревым. Но тогда циркуляция
по любому замкнутому контуру рав-
равна нулю. Составим выражение для
циркуляции по контуру MRNK, огра-
ограниченному отрезками двух радиусов-
векторов, проведенных из вершины угла, и двух дуг, обходя этог
контур по часовой стрелке (рис. 4.12):
Cdw \ I dw
wu + -^ArJ(r + Аг) Аф - [u>r+-0j
— wurAq> == 0»
учитывая постоянство скорости по радиусу-вектору, являющему-
являющемуся характеристикой, имеем
dw.
L-Wu= 0.
A4)
Это и есть условие отсутствия завихренности в сверхзвуковом
газовом потоке, обтекающем внешний тупой угол. Его можно
было бы получить также непосредственно из выражения A03)
гл. П. Каждую струйку рассматриваемого течения можно счи-
считать энергетически изолированной, причем уравнение энергии це-
целесообразно использовать в кинематической форме D8) из гл. I:
-Lj-a' + i^-auax. A5)
В плавно ускоряющемся газовом потоке, который мы рассмат-
рассматриваем в данном случае, потери полного давления обычно незна-
незначительны, поэтому термодинамический процесс обтекания угла
мы будем считать изоэнтропическим, т. е. подчиняющимся урав-
уравнению идеальной адиабаты:
p/pfc = const. A6)
160 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
Четыре уравнения A3) — A6) составляют систему, к решению
которой сводится задача об обтекании внешнего тупого угла
сверхзвуковым потоком газа.
Из уравнений A3) и A5) следует
• +
к-1
или
2 I к — 1 2 к — 1
w + w
Используя теперь уравнение A4), приходим к следующему диф-
дифференциальному1) уравнению:
/ awr у
\ 5ф J
Разделяя в этом уравнении переменные wr и ф получим
V2 —W2
max r
ИЛИ
d '
Производя интегрирование, получаем
Ti arcsinT;— = Ф + ci»
Л"~ L шшах
где ci — постоянная интегрирования. Разрешая это выражение
относительно искомой величины wr, найдем
Тогда из уравнения A4) сразу следует
Определим теперь постоянную интегрирования с\. Рассмотрим
случай, когда скорость невозмущенного потока (до поворота)
1) Так как параметры газа вдоль линий ф = const при обтекании внеш-
внешнего угла не изменяются, то они являются функциями лишь одного пере-
переменного—полярного угла ф. Поэтому в уравнении A8) и далее частные
производные по ф заменены полными.
§ 3. ТЕЧЕНИЕ ПРАНДТЛЯ — МАЙЕРА 161
равна скорости звука (Мн = 1). Это значит, что начальная ха-
характеристика КС (рис. 4.11) перпендикулярна к стенке АС, так
как
т. е. полярные углы ф нужно отсчитывать от перпендикуляра
к направлению скорости невозмущенного потока. Тогда при
Ф = 0 имеем wr = О, wu = w, и выражение для wr превращается
в уравнение для определения ci:
Отсюда ясно, что с\ — 0. Таким образом, получаем следующие
выражения для составляющих скорости wr и wu:
= ^шах Sin [ у ^j ф],
м>.
Wu = Wmax V ,. , . COS
Пользуясь выражениями C5) и D1) гл. I, можно перейти от
максимальной скорости газа к критической
a
и выражения для wr и wu записать в следующем виде:
= «kPcos 1/-Ь-гФ. B0)
При ф = 0 получим wr == 0, wu = w = акр, т. е. скорость невозму-
невозмущенного потока равна критической скорости звука.
Найдем теперь величину полной скорости на каждом из лу~
чей: w = у wf -f w>l. Из уравнений A9) и B0) получим
Отсюда определяется приведенная скорость
11 Г. Н. Абрамович, ч. 1
162 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
Все остальные параметры газа выражаются через приведенную
скорость по формулам, полученным в гл. I:
B2)
B3)
B4>
= 1/ k+lx* .
М = I/ ftl. .- B5)
Таким образом, определив по формуле B1) величину К2 для со-
соответствующих значений ф, мы сможем по формулам B2) —B5)
полностью рассчитать состояние газа на каждом из лучей, про-
проходящих через вершину угла. При ф = 0 получается Л = 1, при
Ф>0 имеем А>1. По мере увеличения полярного угла скорость
газа возрастает, а давление, плотность и температура умень-
уменьшаются.
Как видно из выражения B1), при некотором значении по-
полярного угла приведенная скорость может достигнуть максималь-
максимального значения
когда давление, температура и плотность газа равны нулю. Оче-
Очевидно, что дальнейшее возрастание скорости невозможно, а сле-
следовательно, прекратится и поворот потока. Иначе говоря, суще-
существует предельное значение полярного угла, определяемое из
условия
Отсюда следует
УШ- B6)
Заметим, что полученное решение пригодно для всех значе-
значений скорости сверхзвукового невозмущенного потока, а не только
в случае Кв = 1. Если скорость невозмущенного потока больше
скорости звука, то отсчет по формуле B1) следует начинать не
от нулевого полярного угла (ф = 0), а от того значения угла
{фн)э которое соответствует заданной скорости невозмущенного
§ 3. ТЕЧЕНИЕ ПРАНДТЛЯ — МАЙЕРА
163
потока (Ян). Из формулы B1) следует
arcsin
B7)
Пригодность полученного решения для любого значения скорости
основывается на том, что в данной задаче вдоль любой характе-
характеристики скорость и остальные параметры газа не изменяются,
т. е. на любой характеристике поток является равномерным и
параллельным. И поэтому для поворота потока, происходящего
правее данной характеристики, не может иметь значения пре-
предыстории потока, т. е. достигнуто ли данное значение Ян в ре-
результате ускорения газа при предварительном повороте от К = 1
и ф = 0 до А, = Ян и ф = фн или поворот начинается сразу при
значении приведенной скорости К = Ян. Итак, в случае Кя > 1
при ф ^ фн поток остается невозмущенным, т. е. все параметры
газа сохраняют свое значение. При ф > фн параметры газа вы-
вычисляются по полученным выше формулам B2) — B5). Надо
О
Рис. 4.13. Схема отсчета углов
wa при акр
Рис. 4.14. К определению линии то-
тока при обтекании внешнего тупого
угла
только помнить, что при скорости невозмущенного потока, боль-
большей скорости звука, углы ф нужно отсчитывать не от перпен-
перпендикуляра к направлению невозмущенного потока, а от прямой,
составляющей угол фн + ан с направлением невозмущенного по-
потока, где ан = arcsin^- (рис. 4.13) является углом распростра-
распространения слабых возмущений, т. е. углом между характеристикой
и направлением заданного невозмущенного потока.
Чтобы получить наглядную картину обтекания внешнего ту-
тупого угла, найдем форму линий тока. Для этого составим диф-
дифференциальное уравнение линий тока в полярных координатах.
Вспомним, что направление касательной к линии тока в каждой
ее точке совпадает с направлением вектора скорости в этой точ-
точке. Возьмем два бесконечно близких радиуса-вектора, составля-
составляющих друг с другом угол йф, и проведем в точке А первого ра-
радиуса отрезок линии тока АС, вектор скорости w = АЕ, направ-
11*
164 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
ленный по касательной к линии тока в точке А и дугу окруж-
окружности АВ радиуса г (рис. 4.14). Рассмотрим бесконечно малый
прямоугольный криволинейный треугольник ABC, Тангенс угла А
этого треугольника равен отношению
ВС = dr
АВ ~
Но угол между кривыми АВ и АС равен углу между их каса-
касательными AF и АЕ, т. е. tg(^-EAF) = dr/rdq. Вектор скорости w
разложим на составляющие wr и wu. Из треугольника ADE вид-
видно, что tg(^-DEA) = WrJWu. Но из построения ясно, что ^-DEA =
~ ^- EAF. Таким образом,
4- = — • B8)
Уравнение B8) представляет собой дифференциальное уравне-
уравнение линий тока в полярных координатах.
В случае обтекания угла wr и wu определяются формулами
A9) и B0), поэтому дифференциальное уравнение B8) примет
вид
Его можно переписать также в таком виде:
Интегрируя это дифференциальное уравнение, найдем
где через lnro обозначена произвольная постоянная интегриро-
интегрирования. После потенцирования получим
Уравнение B9) есть уравнение линий тока в полярных коорди-
координатах. Здесь го — длина радиуса-вектора линии тока при ф = 0,
т. е. в невозмущенном потоке. Из уравнения B9) видно, что все
линии тока представляют собой подобные кривые с центром по-
подобия в вершине угла. Расстояние по нормали между двумя
соседними линиями тока увеличивается в направлении течения.
§ 3. ТЕЧЕНИЕ ПРАНДТЛЯ — МАЙЕРА
165
Найдем теперь угол б, между касательной к линии тока и
направлением невозмущенного потока, движущегося со скоростью
звука, т. е. угол, на который поворачивается поток, дойдя до
соответствующего луча, составляющего угол ср с перпендикуля-
перпендикуляром к направлению скорости невозмущенного потока (приЯн = 1).
Для этого рассмотрим рис. 4.15. Здесь w — вектор скорости в
Рис. 4.15. Связь между
углами а, ф и б при обтека-
обтекании тупого угла
точке 5, направленный по касательной к линии тока. Угол а —
местный угол распространения слабых возмущений. Этот угол
равен, как известно, углу между направлением скорости w и ха-
характеристикой BE в данной точке. Угол б — искомый угол пово-
поворота потока. Из рисунка ясно, что ^- ABD = б, а угол ABC = a.
Тогда из треугольников ABC и ABD имеем
= n — ср — а и Z А = ^- — 8.
Таким образом,
п — ф — а = -2~- б,
или
Угол распространения слабых возмущений
а = arcsin -п-
C0)
C1)
Поэтому для вычисления угла поворота потока б, соответствую-
соответствующего заданному значению угла ф, нужно проделать следующие
операции:
1) определить по формуле B1) приведенную скорость X для
заданного значения ф,
2) по формуле B5) определить число М,
3) по формуле C1) определить угол а и, наконец,
166
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
4) вычислить угол б по формуле C0) для заданного значе-
значения ф. Таким образом, мы получим угол поворота потока б в
функции от полярного угла ф.
До сих пор независимым переменным являлся полярный
угол ф и все параметры газа вычислялись в функции от этого
угла. В действительности же обычно бывают известны величина
обтекаемого тупого угла, т. е. величина угла поворота потока бо
и значение скорости набегающего потока. По этим данным нуж-
нужно определить все параметры газа (скорость, давление, темпера-
ТУРУ и т. д.) после поворота потока около заданного тупого угла.
Поэтому для практических расчетов удобно составить таблицу,
где за основной параметр принят угол поворота потока б, а все
остальные параметры газа вычислены в функции этого угла. Та-
Такая таблица, рассчитанная по формулам B1) — B5), C0) и C1),
приводится в приложении I на с. 566—568. Пользоваться этой
Рис. 4.16. Линия тока сверхзвукового потока, обтекающего внешний тупой
угол
таблицей нужно следующим образом: по заданной скорости невоз-
невозмущенного потока wn определяется приведенная скорость Ян. Да-
Далее отыскивается фиктивный угол поворота потока бн, соответ-
соответствующий значению А,н (угол, на который должен повернуться
поток, текущий со скоростью звука, чтобы достичь заданной ско-
скорости wH). Затем находится угол 6к = бн + бо, где бо—заданный
угол поворота потока (рис. 4.16). Для значения бк из таблицы
1 Рк Рк Тк АА
выписываются величины Ак, —, —, -~г- и Мк, которые опре-
опрело ро о
деляют соответственно приведенную скорость, давление, плот-
плотность, температуру и число М после поворота потока около за-
заданного тупого угла. Кривые ф(б), М(б), а(б) и ~г = /(б) изо-
изображены на рис. 4.17.
§ 4. ОБТЕКАНИЕ ПЛОСКОЙ СТЕНКИ
167
При желании можно найти форму линии тока по формуле
B9), задавшись величиной го и рядом значений ф от ф = фн до
ср = фк (рис. 4.16).
Для определения угла поворота потока 6о в зависимости от
начальной и конечной скорости можно пользоваться предло-
предложенной А. Я. Черкезом простой формулой, хорошо аппроксими-
аппроксимирующей точные соотношения и табличные данные при /с = 1,4:
.« —А»). C2)
Здесь %в и Я„ — соответственно приведенные скорости потока до
9
a
\4
4
n
и
г
0
п
-150'-
fff'-
\
a
ou
1
I-
\
/
/
у
й^<
¦*•
***
*»
—*
5S9
¦аи
tea
>
У
—-
1 !
1
Ч-т-ч
0
-0,5
¦з,з
-0,2
и09 10° 20" 30° W 50° ВО" 70° 80° 30е 100° 110° 120° 130°д
Рис. 4.17. Вспомогательные кривые к расчету сверхзвукового обтекания
внешнего тупого угла
и после поворота. При X < 2,3 (-^г> 0,0005j погрешность опре-
определения угла бо по этой формуле обычно не превосходит Г.
Изложенная теория обтекания внешнего тупого угла сверх-
сверхзвуковым потоком газа применяется для решения большого чис-
числа конкретных задач газовой динамики; некоторые из них мы
рассмотрим ниже.
§ 4. Обтекание плоской стенки
Пусть сверхзвуковой поток газа течет с заданной скоростью
над плоской неподвижной стенкой. В точке С (рис. 4.18) стенка
обрывается, а давление в пространстве за точкой С меньше, чем
давление в невозмущенном потоке вдоль стенки. Тогда точно
так же, как в случае обтекания внешнего тупого угла, точка С
168 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
явится источником возмущений. Поток, обтекая точку С, повер-
повернется на некоторый угол б. Скорость его увеличится, а давление
в потоке упадет до величины давления, существующего в про-
пространстве за точкой С. Картина течения при этом совершенно
аналогична обтеканию внешнего тупого угла. Различие заключа-
заключается лишь в том, что в случае обтекания тупого угла задан угол
поворота потока б и требуется найти все параметры газа после
Рис. 4.18. Схема сверхзву-
сверхзвукового обтекания стенки
поворота, а в рассматриваемом нами случае обтекания полубес-
полубесконечной плоской стенки задано давление в потоке после пово-
поворота и требуется найти угол поворота потока и все остальные
параметры газа. Угол б определяет границу, отделяющую повер-
повернутый поток газа от неподвижного газа под стенкой (штриховая
линия на рис. 4.18).
Для расчета обтекания плоской полубесконечной стенки мож-
можно воспользоваться таблицей приложения I на с. 566—568.
По заданной величине давления находят угол поворота потока
и все остальные параметры газа.
Легко вычислить максимальный угол бшах, на который может
повернуться газовый поток, сходящий с плоской стенки. Этот
угол представляет собой угол поворота потока, начальная ско-
скорость которого равна скорости звука, при истечении в вакуум.
Положим в формуле B2) р = 0. Тогда
Подставляя А=Ятах в формулу B7), найдем
Фтах- 2 У k-lm
Так как при Я = Хтах из B5) имеем М = °°, то а = arcsin— = 0.
Тогда из формулы C0) получаем
§ 5. ОБТЕКАНИЕ ВЫПУКЛОЙ КРИВОЛИНЕЙНОЙ СТЕНКИ
169
"/7/7
125°
100е
75е
50'
При ?=^1,4 ЗНачеНИЯ фтах И бтах будут фтах = 220°27', бтах^
= 130°27/. Отсюда следует, что поток, стекающий с плоской
стенки в вакуум, не заполняет всего свободного пространства
под стенкой. Луч ф = фтах
отделяет этот поток от пу-
пустоты под стенкой. Ясно, что
это положение справедливо
не только для случая А,н = 1,
но также прп А,н > 1. Угол
поворота такого потока при
истечении в вакуум равен
бтах ~ бн, ГДе бн — фиКТИВНЫЙ
угол поворота потока, соот-
соответствующий заданному зна-
значению Ян. Этот предельный
угол, на который может по-
повернуться сверхзвуковой по-
поток заданной скорости, обо-
вначим бпр. Таким образом,
бпр = бгаах — бн.
Зависимость бпр от числа М
невозмущенного потока (при
к = 1,4) представлена на
графике рис. 4.19. При
М = 1 имеем бн = О и бпр =
= бтах- ПрИ М = °°
бн = бтах И бпр = 0.
Если сверхзвуковой по-
поток должен обтекать тупой
угол, для которого б > бпр, то после поворота около вершины угла
лоток отрывается и следует не по стенке, а по лучу, соответствую-
соответствующему б = бпр; между лучом и стенкой образуется область ваку-
вакуума. Это явление можно назвать срывом сверхзвукового потока.
§ 5. Обтекание выпуклой криволинейной стенки
Чтобы составить себе представление о картине, возникающей
при обтекании выпуклой криволинейной стенки, рассмотрим вна-
вначале одну из линий тока, полученных при обтекании тупого
угла и примем ее за проекцию твердой стенки (рис. 4.20). Над
этой стенкой параметры потока известны, ибо они останутся
такими же, какими они были над соответствующей (теперь
отвердевшей) линией тока при обтекании угла.
Через каждую точку обтекаемой кривой линии проходит пря-
прямолинейная характеристика, вдоль которой все параметры газа
остаются неизменными. Состояние газа на каждой характери-
V
\
\
\
\
i
1
1
1
f
\
\
\
А
\
\
\
L
о
\
rax
7/7
i
i
1
ч
_,
!
i
!
i
:
!
1
i
!
i ; !
!
i !
I
i j
! i
i
t
I
1
s
1
25"
123Ц56783М11М
Рис. 4.19. Предельные углы поворо-
поворота потока в скачке уплотнения и
при обтекании внешнего тупого угла
170
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
стике определяется по углу поворота потока б, соответствующе-
соответствующему этой характеристике и равному углу, между касательной к
стенке в начальной точке характеристики и направлением
невозмущенного потока. При расчете параметров газа нужно
воспользоваться выведенными ранее формулами или таблицей
приложения I к книге на с. 566—568.
Заметим, что такая же точно качественная картина имеет
место при обтекании выпуклой криволинейной стенки любой
Рис. 4.20. Схема сверхзву-
сверхзвукового обтекания выпуклой
кривой
формы. Необходимо только, чтобы выпуклость стенки была на-
направлена всегда в сторону газа. Чтобы показать это, заменим
произвольную кривую стенку вписанной ломаной линией, со-
состоящей из последовательности прямолинейных отрезков
(рис. 4.21, а). Обтекание такой ломаной сводится к обтеканию
последовательности внешних тупых углов и, следовательно, мо-
может быть полностью рассчитано. Картина обтекания показана
Рис. 4.21. Переход от обтекания ломаной стенки к обтеканию выпуклой
кривой
на рис. 4.21, б. Если теперь безгранично увеличивать число вер-
вершин ломаной, вписанной в данную кривую, то в пределе мы по-
получим обтекание кривой, причем ясно, что через каждую точку
кривой проходит прямолинейная характеристика, вдоль которой
параметры газа не меняются (рис. 4.21, в).
Чтобы рассчитать обтекание произвольной кривой выпуклой
стенки, нужно знать лишь угол поворота, т. е. направление ка-
касательной для каждой точки стенки. Если, .например, форма
стенки задана уравнением в виде у = у(х) (ось х направлена
ио вектору скорости невозмущенного потока), то, дифференцируя
§ 6. ИСТЕЧЕНИЕ ИЗ СОПЛА С КОСЫМ СРЕЗОМ 171
это уравнение, мы найдем угол касательной с осью х для каж-
каждого значения абсциссы х, равный углу поворота потока б.
Таким образом,
6
Зная б, легко определить все параметры газа, действуя точно
так же, как в случае обтекания тупого угла. В частности, можно
найти распределение скоростей и давлений вдоль стенки. При
обтекании кривой выпуклой стенки, так же как и при обтекании
угла, газ разгоняется. Скорость газа непрерывно увеличивается,
а давление падает.
Если окажется, что в какой-либо точке стенки
б>бпр,
то произойдет срыв потока.
Нахождение формы линий тока при обтекании выпуклой
стенки произвольного вида является более трудной задачей, и мы
ее здесь рассматривать не будем.
§ 6. Истечение из единичного плоского сопла
с косым срезом
в пространство с пониженным давлением
Рассмотрим истечение сверхзвукового потока газа из плоского
сопла. Пусть сопло обеспечивает равномерную скорость на его
срезе, а давление в свободном пространстве, в которое вытекает
газ, меньше, чем давление в плоскости среза сопла. Изложенная
выше теория обтекания плоской стенки позволяет определить
направление границ струи непосредственно после среза сопла.
Поведение газа вблизи кромок сопла А ж В (рис. 4.22, а) точ-
точно такое же, как при обтекании одной плоской стенки. Около
каждой из кромок поток повернется на такой угол б, чтобы дав-
давление в потоке стало равным заданному давлению в свободном
пространстве. Следовательно, струя в целом при истечении рас-
расширяется. Угол поворота потока б около каждой из кромок мож-
можно найти по заданным величинам скорости и давления на срезе
сопла и давлению в свободном пространстве так же, как при обте-
обтекании одной плоской стенки. Этот угол б определяет направление
границ струи за срезом сопла. Вдоль всей свободной границы
струи существует постоянное значение скорости, которое соответ-
соответствует внешнему давлению и легко может быть вычислено по
приведенным выше формулам и таблице.
Пучки прямолинейных характеристик, исходящих из точек А
и В, пересекаются, как показано на рисунке. После пересечения
характеристик скорость потока изменяется, и, как это следует из
§ 2 гл. III, характеристики перестают быть прямолинейными.
Если плоскость среза сопла не перпендикулярна к оси пото-
потока, то такое сопло называют соплом с косым срезом. Наличие
172
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
косого среза нарушает симметрию потока. Изучение истечения из
каналов с косым срезом имеет важное практическое значение,
так как такое истечение имеет место при работе паровых и газо-
газовых турбин, где обычно сопловые аппараты представляют собой
каналы с косым срезом.
Рассмотрим сверхзвуковое истечение газа из плоского сопла
с косым срезом в пространство, в котором давление меньше, чем
давление в потоке внутри
сопла. Косой срез образует-
образуется при смещении кромки В
сопла относительно кромки
А назад, против потока. При
небольшом смещении кром-
кромки S, т. е. при небольшом
наклоне плоскости среза АВ
(рис. 4.22, б), получится,
очевидно, несимметричная
свободная струя. При этом
область пересечения пучков
характеристик, исходящих из
кромок А и В, перемещает-
перемещается к точке А,
Следовательно, прямоли-
прямолинейные характеристики, ис-
исходящие из кромки А, начи-
начинают искривляться раньше,
чем в случае прямого среза.
За плоскостью среза АВ
струя расширяется. Углы
поворота потока около каж-
каждой из кромок А и В, оче-
очевидно, такие же, как и в
случае прямого среза.
Предельным положением
кромки В для течения тако-
такого вида является то ее поло-
положение, при котором «пер-
«первая» характеристика, прове-
проведенная из кромки 5, прохо-
проходит точно через кромку А.
Такой случай изображен на рис. 4.22, #. Картина течения вблизи
кромки В по-прежнему аналогична обтеканию одной плоской
стенки. Поэтому направление границы струи за кромкой В со-
сохраняется прежним и его легко можно определить. Характери-
Характеристики, исходящие из кромки А, начнут искривляться сразу за
точкой А. Это усложняет определение второй границы струи за
точкой А.
Рис. 4.22. Различные схемы истече-
истечения из сопла с косым срезом
§ 7. ХАРАКТЕРИСТИКИ УРАВНЕНИЙ 173
Если за кромкой А сделать направляющий козырек, выпол-
выполненный по линии тока, соответствующей повороту потока около
кромки В (рис. 4.22, г), то течение можно рассчитать полностью.
Обтекание кромки В при заданном внешнем давлении аналогично
обтеканию внешнего тупого угла. Поэтому форму линии тока
можно определить по формуле B9).
Таким образом, мы получаем профиль направляющего ко-
козырька АС. Давление на луче ВС равно заданному внешнему
давлению, вследствие чего за лучом ВС струя опять становится
параллельной и равномерной. Скорость в этой струе больше, чем
скорость внутри сопла в сечении BD. Струя отклоняется от оси
сопла на угол б, определяемый отношением внешнего давления
к давлению внутри сопла в сечении BD.
Смещая кромку В еще дальше назад, мы получим случай
истечения из косого среза, изображенный на рис. 4.22, д. Здесь
«первая» характеристика, исходящая из кромки В, приходит на
противоположную стенку внутри сопла в некоторой точке ле-
левее А. Если, как и в предыдущем случае, сделать направляю-
направляющий козырек, поместив начало его в точку встречи первой ха-
характеристики со стенкой Л, то мы сведем рассматриваемый
случай к предыдущему.
Практически применимыми случаями истечения из косого
среза являются случаи в, г и д. В случаях вид пользуются
приближенным расчетом, определяя скорость истечения и угол
поворота струи в целом так же, как в случае г, т. е. пренебре-
пренебрегают небольшим изменением параметров потока, связанным с
нарушением принятой при расчете картины течения вблизи
кромки А.
Подчеркнем еще раз, что во всех практически применимых
случаях истечения из плоского канала с косым срезом в прост-
пространство с пониженным давлением поток в косом срезе испыты-
испытывает расширение, а струя получает добавочное отклонение; при
этом скорость истечения увеличивается по сравнению со ско-
скоростью, которую может обеспечить то же самое сопло с прямым
срезом.
§ 7. Характеристики уравнений установившегося течения
идеального газа
Установившиеся плоские течения идеального газа описывают-
описываются системой уравнений (92) — (94) гл. П. Уравнение неразрыв-
неразрывности (93) может быть приведено к виду (98), и после подста-
подстановки соотношений (99) получаем уравнение
ра2 ** ра2 dy+~te + ду ~ и'
174 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
В общем случае двумерного течения газа уравнение нераз-
неразрывности может быть представлено в виде
* ? ^ ? + 4 = 0, C4)
pa2 дх ' pa2 ду ' дх ду ' z/^ '
где v = 0 для плоского течения и v = 1 для осесимметричного
течения.
Учитывая, что для двумерных установившихся течений вдоль
линии тока i* = const, или
а,
+" а, -"• <35»
уравнения движения (92) гл. II при использовании термодина-
термодинамического равенства
TdS = di dp C6)
р
можно привести к виду
W2 r W2
дх ду [ р \ дх ду J
Здесь W2 = и2 + v2. Преобразуем уравпепия неразрывности и
движения, выбирая в качестве неизвестных модуль скорости W
и угол 0 наклона вектора скорости к оси х:
и = W cos 0, i> = H^sin0. C8)
Подставляя эти выражения в уравнение C4) и используя урав-
уравнение C7), преобразуем уравнение неразрывности к виду
где ? = tg9. Подставим теперь C8) в уравнения движения (92) f
гл. II;
W cos 9 д (W;os 6) + W sin 9 д (W/os-9) = - ± » D0)
дх 1 ду р2 дх ' ч '
ТУ cos 9 d(W^Q) g(**.e) 1
Умножая первое уравнение на sin 0, второе — на cos 0 и вычи-
вычитая одно из другого, получим
-)-C-?+ ¦?-<>. D1)
Составим линейную комбинацию уравнений C9) и D1). Для
этого умножим уравнение C9) на неопределенный множитель т
§ 7. ХАРАКТЕРИСТИКИ УРАВНЕНИЙ 175
и сложим его с уравнением D1). Тогда получается уравнение
j ду J -Г
дх
Распоряжаясь величиной т/г, определим в каждой точке пло-
плоскости х, у такое направление с угловым коэффициентом с ==
= dy/dx, чтобы выражения в квадратных скобках равенства D2)
представляли производные по этому направлению от 0 и р:
??_—_?§. . лам. — j^ 4- ^ё.
dx ~ дх ^ ду dx ~ дх + С ду '
* dp___dp^.^dy__^P_ др_
dx ^х ' ^у dx дх ду
Таким образом, из уравнения D2) имеем
_g ду1
dp _ dp g(M2 —1) + трИ72 dp * *
Сравнивая D3) и D4), получаем
трТУ2? + 1 = gp2 + mpPF2 =
mpW2 — S р2 — т?рИ^2 '
Здесь Р2 = М2—1. Из D5) получается следующее соотношение
для тга:
Линии, получающиеся из D5) после подстановки D6)
с =
называются характеристиками первого и второго семейства —
с4-характеристиками и с~-характеристиками соответственно. «
Подставляя полученные значения га в уравнение D2), полу-
получим соотношения, выполняющиеся вдоль с+ и ^-характеристик
соответственно:
Ум2 — 1 • t, dx ,Q 1^м2 — i ^ dx
у/Li r rl r\ п.* * /71-1 W-г» J_ л» _5
* D9)
Эти соотношения называются условиями совместности.
176 ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
Линия тока (96) гл. II является еще одной характеристикой
(^-характеристикой или характеристикой нулевого семейства)
двумерного установившегося течения идеального газа.
Уравнения характеристик D7) и D8) можно записать и в
таком виде:
-|==-ffl = tg(e±a), E0)
где sin a = 1/М или a = arcsin A/M).
Характеристики первого и второго семейства наклонены к
вектору скорости (к линии тока) под углом Маха ос. Следова-
Следовательно, проекция скорости на нормаль к характеристике всегда
равна скорости звука.
Таким образом, система уравнений C9) и D1) при М>1,
т. е. при сверхзвуковых скоростях, имеет два семейства (с+ и
с~) действительных характеристик и относится к гиперболиче-
гиперболическому типу. При М = 1 имеем Р = 0, что соответствует двум
совпадающим семействам характеристик, и система имеет пара-
параболический тип. При М<1, т. е. при дозвуковых скоростях,
система не имеет действительных характеристик и является
эллиптической.
Тип системы уравнений определяет особенности постановки
задачи, методы и свойства решения. В случае эллиптической
задачи на решение в некоторой точке области оказывают влия-
влияние краевые условия, заданные на всей границе области. При
решении гиперболической задачи возмущения сносятся только
вниз по потоку.
§ 8. Плоские изэнтропические и изоэнергетические
течения
Условия совместности D9) могут быть проинтегрированы,
если v == 0, а энтропия и энтальпия торможения являются по-
постоянными в рассматриваемой области течения. В этом случае
условия совместности можно записать в виде
E1)
и коэффициент при dp зависит только от давления.
После интегрирования, обозначая постоянные /+ и /-, полу-
получаем для характеристик первого и второго семейства соответ-
соответственно
1 dp==J+' dy = ^S(Q + a)dxt E2)
i dp = /_) d = tg (е _ ^ dx^
§ 8. ИЗЭНТРОПИЧЕСКИЕ И -ИЗОЭНЕРГЕТИЧЕСКИЕ ТЕЧЕНИЯ 177
Таким образом, вдоль характеристик dJ+ = 0 и dJ- = 0, т. е. зна-
значения /+(/>, 0) и /-(/?, 0) сохраняются неизменными. Эти вели-
величины аналогичны инвариантам Римана в одномерных неустано-
неустановившихся течениях. Если один из инвариантов J-(p, 0) сохра-
сохраняет постоянное значение во всей области течения
J-(p, 0) = const, E4)
то вдоль каждой характеристики первого.семейства, где к тому
же /+(/?, 0) = const, все параметры, а следовательно, и угловой
коэффициент tg@ + a) сохраняются постоянными и эти харак-
характеристики являются прямыми линиями. Такие течения называют
простыми волнами, а в установившемся течении — волнами
Прандтля — Майера.
Условие совместности E1) можно записать и в другом виде.
Учитывая, что в рассматриваемом течении выполняется соотно-
соотношение
dp = -9W dW, E5)
и подставляя его в E1), получим
dQ =p ctg a -т- = 0. E6)
Здесь
ctg a = //Л2 -1=1/ *-1 2# <57>
V 1—FT!'1
Интегрируя E6), получаем
9 zp Г ctg a -у- =¦• /± (К 0). E8)
Подставляя сюда выражение E7) для ctg a, можно получить
E9)
Рассмотрим пример обтекания выпуклой криволинейной стен-
стенки сверхзвуковым однородным потоком, имеющим скорость A,i
(рис. 4.23). Аналогичный пример приведен в § 5. До точки О
газ движется вдоль прямолинейной стенки, а затем огибает уча-
участок криволинейной стенки и после поворота на некоторый угол
вновь движется вдоль прямолинейной стенки. В этом течении
/-(Я, 0) = const. E9а)
12 г. Н. Абрамович, ч. 1
178
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
Значение этой константы может быть найдено из условия К = Х\
при 0 = 0 подстановкой в E9).
Так как угол 6 в каждой точке стенки известен, то из урав-
уравнения E9) можно найти К, а из E7) — угол наклона характе-
характеристики. Так как dQ и dK имеют разные знаки, то при движении
вдоль стенки угол 0 уменьшается,
а скорость К возрастает.
Таким образом, течение
Прандтля — Майера есть течение
разрежения, в котором прямые
характеристики образуют расхо-
расходящийся пучок. Параметры пото-
потока вдоль этих характеристик по-
постоянные и равны их значениям
в точке их пересечения со стен-
стенкой. За прямолинейной характеристикой, замыкающей течение
Прандтля — Майера, течение вновь становится однородным.
Если уменьшить протяженность участка вдоль стенки с течением
Прандтля — Майера до нуля, а угол разворота потока сохранить,
то получим центрированное течение Прандтля — Майера, кото-
которое подробно исследовано в § 3.
Рис. 4.23. Простая волна Прандт-
Прандтля — Майера
§ 9. Взаимодействие однородных сверхзвуковых потоков
Взаимодействие однородных сверхзвуковых потоков удобно ис-
исследовать, используя зависимости давления от угла поворота по-
потока. Это связано с тем, что на тангенциальном разрыве, разде-
разделяющем две области течения после взаимодействия, значения дав-
давления и направления потоков непрерывны. Для косого скачка
уплотнения эта зависимость имеет вид 1)
tgO =
2fe .., fc-1
к + 1 mi ~ к + 1
k-i p
F0)
Здесь 0 — угол поворота потока, Mi, p\ — число Маха и давление
в набегающем потоке, р — давление за косым скачком уплот-
уплотнения.
В течении Прандтля — Майера для определения скорости в
зависимости от угла поворота потока используется уравнение
E9) с /-(^, 0) из E9а). Давление определяется по изоэнтропи-
1) Курант Г., Фридрихе К. Сверхзвуковое течение и ударные
волны.— М.: ИЛ, 1950.
§ 9. ВЗАИМОДЕЙСТВИЕ СВЕРХЗВУКОВЫХ ПОТОКОВ
179
ческому соотношению
ft
F1)
Графически эти зависимости для фиксированного значения Mi
представлены на рис 4.24. Значения р/ри расположенные выше
p/pi = 1, представляют так называемую ударную поляру для ко-
косого скачка уплотнения. Как
известно, при данном значении
угла поворота 6 существует два
решения для plpu соответству-
соответствующие слабому и сильному скач-
скачкам уплотнения. При решении
газодинамических задач обыч-
обычно выбирается меньшее значе-
значение р/ри отвечающее слабому
скачку. Значения р/ри располо-
расположенные ниже р/р\ = 1, получе-
получены для течения Прандтля —
Майера. Правая половина гра-
графика соответствует положитель-
положительным значениям угла 6 относи-
9
Рис. 4.24. Зависимость давления от
тельно оси абсцисс, а левая по- угла ПОВорота потока в косом скач-
ловина графика — отрицатель- ке уплотнения и течении Прандтля —
ным значениям угла поворота Майера
потока 6 для скачка уплотне-
уплотнения и течения Прандтля — Майера, как это показано на рисунке.
При решении задачи о взаимодействии двух однородных сверх-
сверхзвуковых потоков для каждого из потоков записываются соотно-
соотношения F0) или E9) и F1) и ищутся удовлетворяющие им
значения отношения давлений р/р\ и угла поворота 0. При этом
Рис. 4.25. Схемы взаимодействия двух сверхзвуковых потоков: а) две удар-
ударные волны, б) ударная волна и течение Прандтля — Майера
давление выражается в долях от давления в одном из потоков.
Если, например, имеет место картина взаимодействия с двумя
косыми скачками уплотнения, как на рисунке 4.25, а, то графиче-
графически решение представляет пересечение двух ударных поляр, со-
12*
180
ГЛ. IV. УСКОРЕНИЕ ГАЗОВОГО ПОТОКА
ответствующих потоку с числом Маха Mi и с числом Маха Мг,
причем за решение принимается точка пересечения в области
слабых скачков уплотнения (рис. 4.26). Если же имеет место
картина взаимодействия, изображенная на рис. 4.25, б с волной
в
Рис. 4.26. Взаимодействие
двух потоков с образованием
скачков уплотнения
Рис. 4.27. Взаимодействие двух
потоков с образованием скачка
уплотнения и волны разрежения
разрежения Прандтля — Майера для потока с числом Маха Mi и
со скачком уплотнения для потока с числом Маха Мг, то графиче-
графически решение представляется точкой пересечения ударной поляры
для потока с числом Маха Мг с кривой для течения разреже-
разрежения с числом Маха Mi (рис. 4.27). Аналогично можно провести
анализ других случаев взаимодействия.
Глава V
ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
§ 1. Адиабатическое течение газа с трением.
Кризис течения
Рассмотрим установившееся течение газа в трубе постоянного
сечения при наличии трения, но без теплообмена с внешней
средой.
Уравнение неразрывности в этом случае (G = const, F = const)
имеет следующий вид:
pw = const,
или в дифференциальной форме
dp __ dw m
Дифференциальное уравнение состояния
dp=R(pdT + Tdp). B)
Из уравнений A) и B) получаем
lE- = RdT-RT — . C)
Используя уравнение Бернулли в дифференциальной форме
и известное выражение для скорости звука
а2 = kRT,
преобразуем выражение C) к новому виду
RdT + {ujt-J^i^. + dLTp = 0. D)
Ввиду того что рассматриваемый процесс является энергети-
энергетически изолированным, температура торможения вдоль трубы не
изменяется: Г* = const. Это эквивалентно условию
ср w
или, принимая во внимание известные равенства Л == сР — cv,
182 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Ср — КСх))
к
E)
Подставляя E) в D), приходим к соотношению, связывающему
изменение скорости вдоль трубы постоянного сечения с работой
сил трения:
Существенно, что трение является односторонним воздейст-
воздействием: работа сил трения всегда положительна (dZ/TP>0). Поэтому
согласно соотношению F) под влиянием трения дозвуковой по-
поток (М < 1) ускоряется (dw > 0), а сверхзвуковой (М > 1)— за-
замедляется (dw<0). Непрерывный переход через скорость звука
при воздействии только трением невозможен.
Выведем формулы, определяющие изменение параметров газа
вдоль изолированной трубы при наличии трения.
Ввиду того что процесс в газе энергетически изолирован, тем-
температура торможения не меняется:
п*
Tl = T\ = const. G)
Термодинамическая температура, если воспользоваться уравне-
уравнениями D2) гл. I и G), определяется из соотношения
k-l 2
А_Ц*±^. <8)
Вследствие постоянства температуры торможения критическая
скорость вдоль трубы также не изменяется; отсюда отношение
приведенных скоростей равно отношению скоростей и на основа-
основании уравнения неразрывности — обратному отношению плот-
плотностей
Подставив равенства (8) и (9) в уравнение состояния, получим
зависимость давления от приведенной скорости:
к-\
Р2 __ К 1- к+1 *2
Р1 \ л К г ;2
1— Л: -4- 1 А1
Ввиду постоянства температуры торможения полное давление про-
§ 1. АДИАБАТИЧЕСКОЕ ТЕЧЕНИЕ ГАЗА С ТРЕНИЕМ 183
порционально плотности заторможенного газа1)
h
Отсюда на основании A0) получаем
р!
Дадим A,i какое-либо постоянное значение и будем рассмат-
рассматривать %2 как переменную величину, а параметры Т2, р2, р2, р2, Рг —
как функции переменного Яг. Выше было установлено на осно-
основании соотношения F), что трение ускоряет дозвуковой и замед-
замедляет сверхзвуковой поток. Тогда нужно считать Яг возрастающим
при дозвуковом и убывающим при сверхзвуковом потоке. Поэто-
Поэтому согласно зависимостям (8), (9) и A0) термодинамическая
температура, плотность и статическое давление вдоль изолирован-
изолированной трубы под влиянием трения падают в дозвуковом и растут
в сверхзвуковом течении. Из равенства A1) следует, что в кри-
критическом сечении при Яг = 1 полное давление /?г имеет минималь-
минимальное значение2), но тогда из выражения A02) гл. I вытекает,
что в критическом сечении энтропия достигает максимального зна-
значения. Полное давление и плотность заторможенного газа в соот-
соответствии с равенством A1) как в дозвуковом, так и в сверхзвуко-
сверхзвуковом потоке вдоль трубы убывают, и только один параметр — тем-
температура торможения — не меняется.
То обстоятельство, что энтропия достигает максимума в кри-
критическом сечении, как раз и обусловливает существование кри-
кризиса течения в изолированной трубе, делающего невозможным
плавный переход через скорость звука под влиянием трения; при
таком переходе энтропия должна была бы уменьшаться, а это
противоречит второму началу термодинамики.
*) Это вытекает из уравнения состояния и формулы G2) гл. I.
2) В этом можно убедиться, дифференцируя равенство A1) по Я2. Под-
Подставляя в выражение производной вместо Яз единицу, получим
(?\ -о
Вторая производная положительна при Яг = 1.
184
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
На рис. 5.1 изображены кривые температуры, плотности, дав-
давления^ температуры торможения и полного давления в изолиро-
изолированной трубе в функции приведенной скорости К2 при К\ =0,1 для
дозвукового потока, К\ = 2,3 для сверхзвукового потока и/с = 1,4.
Рис. 5.1. Зависимость пара-
параметров газа от приведен-
приведенной скорости в трубе по-
постоянного сечения
ZJSЯ
Стрелки на фигурах указывают направление протекания про-
процесса.
Подчеркнем, что значительное ускорение дозвукового и тор-
торможение сверхзвукового потоков под действием силы трения со-
сопряжено с существенным расходованием полного давления.
§ 2. Течение в трубе постоянного сечения
Исследуем влияние трения на изменение параметров турбу-
турбулентного газового потока в трубах постоянного диаметра. Для это-
этого заменим работу силы трения в соотношении F) общепри-
общепринятым в гидравлике выражением
аЬтр=?-2--^-, A2)
здесь ? — коэффициент трения в трубе, D — диаметр трубы, dx —
длина бесконечно малого участка трубы. Тогда получим
2
4г
D
Пользуясь выражением D5) гл. I и постоянством критической
скорости в трубе, из которого следует равенство
dw dX
§ 2. ТЕЧЕНИЕ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ
185
перейдем в соотношении F) от числа М к приведенной ско-
скорости X:
(^-1)^ = ттт^- <13>
Допустим в первом приближении, что коэффициент трения в
трубе как в дозвуковых, так и в сверхзвуковых потоках не зави-
зависит от числа М, а следовательно, и от приведенной скорости X.
В шероховатых трубах величина ? для несжимаемой жидкости
не зависит также от числа Рейнольдса R и определяется по фор-
формуле 1)
1 i?> A4)
где е = 2h/D = h/r — относительная шероховатость трубы (h —
высота выступов шероховатости).
Рассмотрим далее трение в так называемых технически глад-
гладких трубах. Технически гладкая труба характеризуется тем, что
1,0
по
о, и
0,7
\
§
t
V
V
]
\
jn
i
Л\
\
га
о » =$0
• •» =126
• » =152
® » =507
л*
41
&&
«Г*
У5Яс5ЙЕ
И"
sja
3,8
5,0
ft*
ft*
Рис. 5.2. Зависимость козффициента трения ? от R в трубах с различной
шероховатостью по опытам Никурадзе
выступы шероховатости в ней покрываются ламинарным подсло-
подслоем2). Толщина подслоя уменьшается с ростом числа R; поэтому
одна и та же труба при малых R является гладкой, а при боль-
больших R шероховатой (рис. 5.2).
1) См. Проблемы турбулентности.—М.: ОНТИ, 1936.—С. 29.
2) Подробнее о ламинарном подслое см. гл. VI.
186 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
В технически гладких трубах для турбулентного потока не-
несжимаемой жидкости коэффициент трения зависит от числа R и
может быть определен по формуле
С = 0,0032+ Ag-, A5)
Поскольку в трубе постоянного сечения согласно уравнению
неразрывности pw = const, то число R по длине трубы изменяется
незначительно (только за счет изменения вязкости).
Итак, приближенно полагаем коэффициент трения в трубе по-
постоянной величиной
? « const.
В этом случае уравнение A3) легко интегрируется:
здесь к\ — значение приведенной скорости в начале трубы при
z = 0, А,2 — значение приведенной скорости в произвольном сече-
сечении трубы на расстоянии х — Х2 от начала. С помощью выраже-
выражения A6) можно определить значение приведенной скорости в про-
произвольном сечении трубы, если известны приведенная скорость в
начале трубы Хь диаметр трубы D, коэффициент трения ? и по-
показатель идеальной адиабаты к.
Введем функцию ср (к) = —%• + 2 In X и назовем безразмерную
А
величину, находящуюся в правой части уравнения A6)
к + 1 & D ~ Х'
приведенной длиной трубы. Тогда уравнение A6) можно пред-
представить в виде
= Х. A7)
Таким образом, изменение скорости потока между двумя се-
сечениями трубы таково, что разность функций ср(Я) в них равна
приведенной длине данного участка трубы. Пользуясь графи-
графиком функции ф(^) (рис. 5.3), можно определить изменение при-
приведенной скорости потока по длине трубы в зависимости от зна-
значений X и |. Функция ф(Х) имеет при Я = 1 минимум, равный
ф(Я)=1. Поэтому при заданном значении К\ величина разности
в левой части уравнения A7), а следовательно, и приведенная
длина трубы % не могут быть больше некоторой критической ве-
величины, определяемой из условия ta = 1:
-l. A8)
§ 2. ТЕЧЕНИЕ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ
187
Действительно, приравняем нулю производную приведенной дли-
длины % по %2 при %\ = const:
Отсюда находим
Так как при %2 — 1
)- —- —-О
А.2 == 1.
то условие Яг = 1 определяет максимум величины приведенной
длины трубы для заданного значения приведенной скорости на
входе в трубу Яь Поскольку уравнение A7) справедливо не толь-
только для всей трубы, но и для любого ее
участка, то из него следует, что скорость,
равная скорости звука, может быть достиг-
достигнута только в выходном сечении трубы.
Действительно, если представить, что при-
приведенная скорость Я равна единице в ка-
каком-либо промежуточном сечении цилинд-
цилиндрической трубы, то из уравнения A7),
записанного для последующего участка
трубы, получится
16
14
12
Ю
'0,4 0,8 12 1,6 2,0 2,4А
Рис. 5.3. График функ-
функции ф (X) = -о" + 2 In I
К
Так как по определению
(рис. 5.3), то этот случай нереален.
Выше было показано, что при течении
в цилиндрической трубе с трением дозву-
дозвуковой поток ускоряется, а сверхзвуковой
тормозится, причем предельно возможным
состоянием в обоих случаях при не-
непрерывном изменении параметров является критический ре-
режим, т. е. достижение потоком скорости звука в выходном се-
сечении трубы. Уравнение A7) позволяет установить количествен-
количественную связь между изменением скорости и приведенной длиной тру-
трубы %. Если на входе в трубу поток дозвуковой и приведенная ско-
скорость его равна Я1 и если приведенная длина трубы меньше кри-
критического значения, определяемого формулой A8), то на выходе
из трубы поток будет также дозвуковым, причем из уравнения
A7) следует, что Яг > %\. Если поток на входе дозвуковой и при-
приведенная длина трубы равна критической (максимальной) для
данного Я1 величине, то на выходе из трубы скорость потока рав-
равна скорости звука и Яг = 1.
188
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Если, наконец, приведенная длина трубы больше максималь-
максимальной, определяемой из формулы A8), то уравнение A7) не имеет
решения для Яг (ф(А,г)< 1). Это означает, что принятое началь-
начальное значение приведенной скорости Xi не может быть реализова-
реализовано. В начале трубы с заданной приведенной длиной % скорость
потока не может превышать величины, получаемой из формулы
= X+i, A9)
так как при этом скорость на выходе из трубы равна критической,
и через трубу протекает максимально возможный секундный рас-
расход газа.
Чпр
0,8
0,6
ПН
ОЛ
п
1
\
ч
50
100
-
— ^
150
I
X
D
Рис. 5.4. Зависимость предельного значения приведенной скорости в начале
трубы от ее длины
На рис. 5.4 представлена зависимость предельного значения
приведенной скорости на входе в трубу Xinp от безразмерной дли-
длины трубы x/D для дозвукового потока при ? = 0,015 и к = 1,4.
При этих значениях ? и к
Следует отметить, что полученному изменению приведенной ско-
скорости (формула A6)) как при Х\ < 1, так и при Х\ > 1 соответ-
соответствует вполне определенное изменение полного и статического
давления газа (см. формулы A0) и A1) § 1). Выше мы везде
полагали, что такое изменение давления может быть всегда осу-
осуществлено: это являлось условием сохранения постоянного значе-
значения Х\ при изменении приведенной длины трубы вплоть до по-
получения Л2 = 1. Если почему-либо указанное изменение давления
невозможно, например при заданной величине перепада давле-
давлений на входе и выходе, то рассматриваемое течение с заданной
начальной приведенной скоростью может оказаться нереальным.
Подробнее этот вопрос рассмотрен ниже, в § 7.
§ 2. ТЕЧЕНИЕ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ 189
При сверхзвуковом течении, для которого формула A6) так-
также пригодна, возможны следующие режимы. Если при заданной
начальной скорости К\ приведенная длина меньше максимальной
1(%<%кр)> то в конце трубы получается сверхзвуковое течение
(Хг > 1). Если приведенная длина равна максимальной (% = %кр),
то скорость в конце трубы равна критической (%2 = 1). Если же*
приведенная длина, вычисленная по формуле A7), получается
больше максимальной, определенной по формуле A8) при задан-
заданном значении приведенной скорости в начале трубы Ль то плав-
плавное торможение сверхзвукового потока на протяжении всей тру-
трубы невозможно; в некотором сечении трубы произойдет скачок
уплотнения, за которым установится ускоренное дозвуковое те-
течение.
Определение положения этого скачка уплотнения можно про-
произвести следующим образом. Пусть задана сверхзвуковая ско-
скорость в начале трубы Х\, длина трубы х, диаметр трубы D, коэф-
коэффициент трения ? и показатель идеальной адиабаты к. Вычисля-
Вычисляем по формуле A7) приведенную длину трубы %. По формуле
A8) определяем максимальную приведенную длину /кр и убеж-
убеждаемся в том, что истинная приведенная длина больше макси-
максимальной (% > %кр)« В этом случае, как было указано, в некотором
сечении, отстоящем на расстоянии хСК от начала трубы, возни-
возникает скачок уплотнения. Для простоты допустим, что скачок уп-
уплотнения прямой, тогда приведенные скорости до скачка (А/)
и после скачка (X") связаны соотношением A6) гл. III
AV =1.
Приведенную скорость перед скачком (к') можно найти из фор-
формулы A6):
^2 ^/2 Ш ^2 к + 1^ D
Приведенная скорость за скачком, где устанавливается ускорен-
ускоренное дозвуковое течение (%" < 1), связана с длиной дозвукового
участка трубы, в конце которого имеет место кризис {%2 — 1)»
формулой A8):
^,2 1 Ш ^,2 — ? + 1
откуда
Л'2-1-1пГ2 = Х-Хск. B1)
Решая совместно два уравнения B0) и B1) с двумя неизвест-
неизвестными (%ск, V), приходим к уравнению с одним неизвестным, по
которому вычисляется скорость перед скачком:
я"+^""Р~1п^я=х' B2>
190
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
после чего по формуле B1) определяется местоположение скачка.
Формулы B0)— B2) для определения местоположения скачка
уплотнения неудобны, так как по ним приходится вести расчеты
методом последовательных приближений. Можно рекомендо-
рекомендовать вспомогательные графики
(рис. 5.5), существенно упро-
упрощающие расчеты. Кривая 1 от-
отвечает вспомогательной зависи-
зависимости
ф Ш = —-f In №, B3)
изображенной на рис. 5.3. Кри-
Кривая 2 изображает функцию B1)
2,0
Д5
У
г*
у
/
/
у
\
;
у
тл
к
/
и
с
у/
У
7
t
)^
1
1
/
f
1
1
-<
у
/
у
X
-1
**0)^ I I I I I iWI I I I I I L I Кривая 3 соответствует функции
A8)
1 , __ j J_
^кр л 2 л 2
А1 А1
Поясним способ пользова-
пользования этими кривыми на конкрет-
конкретном примере. Пусть дана труба
с приведенной длиной % = 0,6.
По кривой 3 видно, что в этой
трубе установится критический
режим (А,2=1) при значении
приведенной скорости на входе
А.1 = 1,95. Проверим сначала характер течения в трубе в случае
К\ > 1,95, например для Xi = 2,2. По формуле A6) можно вы-
вычислить скорость в конце трубы
2,0
2,5 X
Рис. 5.5. Вспомогательные кривые
для расчета сверхзвукового потока
в трубе постоянного сечения
или в соответствии с обозначением B3)
Ф2 = Ф1 - Х- B4)
На кривой 1 при Х\ = 2,2 находим точку cpi = 1,78, откуда
ф2 = 1,78 - 0,60 = 1,18,
чему на кривой 1 отвечает значение приведенной скорости в кон-
конце трубы Лг = 1,4. Итак, в трубе, имеющей приведенную длину
X = 0,6, при начальном значении приведенной скорости К\ = 2,2
происходит плавное торможение сверхзвукового потока до значе-
значения приведенной скорости %2 = 1,4.
§ 2. ТЕЧЕНИЕ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ
191
Пусть теперь труба имеет приведенную длину больше макси-
максимальной (х>Хкр)? т- е- в данном примере к\ < 1,95. Положим
^ = 1Д Тогда, согласно кривой 5,
ХкР = 0,48, т. е. ХкР < Х-
В этом случае в трубе возникает скачок уплотнения, в результа-
результате чего на участке трубы длиной % — %ск установится дозвуковое
течение, причем, как видно из сравнения кривых 2 и 3, критиче-
критическая длина трубы существенно увеличивается. Для отыскания
местоположения скачка уплотнения преобразуем формулу B0)
2,2
Л
2,0
1,8
1,2
ч
ч
ч
Ч
Ч
ч
0
ч
^Ч
ч.
ч^
Ч> '
24
ч
\
N
ч,
ч
0,1
— —
——
ч
ч
NN
ч
ч
ч
ч
ч
ч.
ч
ч
ч.
0,
ч
N
3
——'
ч
ч^^
0,?
ч
ч
Чч
L
^^!ч!
ЧчJ
ч>
is
0,8
0,8
Рис. 5.6. Кривые распределения значений приведенной скорости по трубе»
с приведенной длиной % = 0,6 при различных начальных скоростях
с помощью обозначений B3). Тогда расстояние от начала тру-
трубы до сечения, в котором происходит скачок уплотнения, равна
Хек = Ф1 - ф'. B5)
Но, с другой стороны,
X = (X "~ Хек) ~» Хск5
заменяя последнее слагаемое в правой части этой формулы по
кB5), получаем
Ф1-Х = ф'-(Х-Хск). B6)
192 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Теперь, пользуясь кривыми рис. 5.5, определим местоположение
скачка уплотнения в трубе при Х\ = 1,8. По кривой 1 находим
<Pi = 1,148,
откуда
ф1-х = 1,48-0,60 = 0,88.
Остается найти значение Я', при котором расстояние между кри-
кривыми 1 и 2 равно согласно B6)
ф'- (Х- Хек) =0,88.
Получается по рис. 5.5
Г = 1,4, ф' = 1,18,
чему соответствует по формуле B4) приведенное расстояние от
начала трубы до скачка уплотнения:
Хек = ф1 - ф' = 0,3.
Описанным способом по кривым рис. 5.5 вычислены и нане-
нанесены на рис. 5.6 кривые изменения приведенной скорости
^= /(х) в трубе с приведенной длиной % = 0,6, получающиеся при
различных значениях приведенной скорости К\ в начале трубы
(при % = 0). Как видим, скачок уплотнения располагается тем
ближе к началу трубы, чем меньше начальная сверхзвуковая ско-
скорость газа. Значения дозвуковой скорости после скачка уплотне-
уплотнения лежат во всех случаях на универсальной кривой, соответст-
соответствующей формуле
При Х\ = 1,6 скачок помещается в начале трубы (Ki =A/), т. е.
участок сверхзвукового течения вовсе ликвидируется. Течение га-
газа в трубе при заданном перепаде давлений рассмотрено в § 7.
§ 3. Движение подогреваемого газа
по трубе постоянного сечения1)
Процесс подвода тепла вносит особый вид сопротивления: при
подогреве движущегося газа полное давление падает.
Т>удем рассматривать движение газа в трубе, изображенной
на рис. 5.7. Обозначим Ях и Яг приведенные скорости в соответ-
соответственных сечениях. Пусть скорость в трубе мала:
Прибегнем к следующей идеализированной схеме. Газ посту-
поступает в трубу х — г из канала с большим поперечным сечением /
(рис. 5.7). На участке / — х реализуется течение без потерь
*) См. Абрамович Г. Н. О тепловом кризисе в газовом течении
ДАН СССР,- 1946.- Т. 54, № 7.
§ 3. ДВИЖЕНИЕ ПОДОГРЕВАЕМОГО ГАЗА ПО ТРУБЕ
J93
и теплообмена. Подвод тепла осуществляется только в цилиндри-
цилиндрической трубе х — г. После этого газ без потерь и теплообмена вы-
вытекает в широкий канал //. Несмотря на то, что в каналах I ж II
скорость мала, а гидравлическими потерями можно пренебречь,
значения полного давления в
сечениях I ж II неодинаковы;
как мы покажем сейчас, вслед-
вследствие подогрева полное давление
во втором канале меньше.
Согласно уравнению Бер-
нулли
Px=JPi—Рх~» Рт=Р2 —Рг"~2~'
Отсюда изменение полного давления
К определению теплового
сопротивления
Из уравнения неразрывности~р*м>* — РгХ#? „еледует, что если вслед-
вследствие подогрева плотность газа уменьшается, то скорость его рас-
растет и, следовательно, статическое давление падает.
И^ можно определить падение статиче-
статиче(б
^рМ? р
ского давления при подогреве на участке х — г (пренебрегая
трением): J
или
Подставив эту разность в уравнение B7), имеем
B8)
Отсюда видно, что при подогреве медленно движущегося газа
величина потерь мала. При значительной же скорости ими пре-
пренебрегать уже нельзя.
Обнаруженное «тепловое» сопротивление нетрудно объяснить
с точки зрения термодинамики. В рассмотренном примере имеет
место расширение газа в конфузоре, затем подогрев его при
пониженном давлении и, наконец, сжатие в диффузоре. Но такой
цикл противоположен обычному циклу тепловой машины, в кото-
котором подвод тепла идет при повышенном давлении. По_этой причи-
причине рассматриваемый процесс связан с поглощением, а не выделе-
выделением энергииГ
Можно предложить и другой способ термодинамического ис-
истолкования «теплового сопротивления». Как известно, повышение
13 г. Н. Абрамович, ч. i
194 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
энтропии в газе зависит как от количества подведенного тепла,
так и от температурного уровня:
При одном и том же количестве тепла прирост энтропии, а сле-
следовательно, и потери тем больше, чем ниже средняя температу-
температура процесса, т. е. чем выше скорость потока.
Оценим влияние подвода тепла на расход газа в трубе. Пусть исте-
истечение газа происходит через трубу постоянного сечения (рис. 5.8),
в которой температура газа увели-
"Ч^ ^" чивается от значения Тх до Тт. Ог-
_^ раничиваясь случаем малых скоро-
. *• стей (Яг<1), при котором абсо-
; | ~** лютная величина давления меня-
х^/ кется незначительно, получим
и? р Тх Т*
Рис. 5.8. К учету влияния подо- -—- = —- »-=- &—+»
грева на расход газа в трубе "'г Рх * г Тт
Из уравнения импульсов, пренебрегая сопротивлением трения,
имеем
и по определению
Рх — Рх = -у
Тогда
¦ / \ , / * п \ 1 п 2 I 9 L A I B,Q\
Здесь рх = р* есть полное давление в сосуде, из которого газ выте-
вытекает, а рт = рв. — статическое давление в выходном сечении
трубы.
Расход газа при заданном перепаде давлений Н == р* — ря
равен
где F — поперечное сечение трубы. Так как из B9) следует, что
IV* =
§ 3. ДВИЖЕНИЕ ПОДОГРЕВАЕМОГО ГАЗА ПО ТРУБЕ 195
то отношение расходов газа при отсутствии и наличии подогрева
в трубе
Как видим, подвод тепла при заданном перепаде давлений ведет
к уменьшению расхода газа при одновременном увеличении ско-
скорости истечения.
Исследуем теперь падение давления на участке х — г трубы
при большой дозвуковой скорости движения газа.
При значительных скоростях течения плотность газа при по-
подогреве уменьшается не только из-за повышения температуры,
но и вследствие понижения статического давления. В связи с
этим скорость газа увеличивается вдоль трубы быстрее, чем тем-
температура. Скорость звука, которая пропорциональна корню квад-
квадратному из абсолютной температуры, увеличивается вдоль трубы
значительно медленнее, чем скорость потока. По этой причине
число М = w/a по длине трубы растет.
Поток, имеющий любую начальную скорость, можно за счет
соответствующего подогрева довести до критической скорости
(Мг = 1). При большом начальном значении числа М понадобит-
понадобится незначительный подогрев. Чем ниже скорость, тем более силь-
сильный критический подогрев необходим. Но никаким подогревом
нельзя перевести поток в цилиндрической трубе в сверхзвуковую
область. Это явление носит название теплового кризиса1).
Естественно, что после того, как в конце трубы достигнут кри-
кризис, скорость потока в начале трубы не может быть увеличена
никакими способами. Если по достижении кризиса продолжать
подогрев газа, то величина критической скорости в конце трубы
растет, а скорость в начале трубы падает. Иначе говоря, заданно-
заданному количеству тепла соответствует совершенно определенное пре-
предельное значение числа М в начале трубы.
Теплосодержание заторможенного газа складывается из тепло-
теплосодержания в потоке и кинетической энергии:
.* . , wl .* . , wl
*х = *х + ~2"> гг = h Т" ~2" •
Вследствие подвода тепла теплосодержание в конце трубы боль-
больше, чем в начале, на количество подведенного тепла
Отсюда получаем
Q = ср (Т* - Tt) = ср (Тт - Тх) + -f (и* - ">!)• C1)
*) Более подробное обоснование явления теплового кризиса дается в
следующем параграфе.
13*
196 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Уравнение C1) вместе с уравнениями неразрывности, коли-
количества движения и состояния образуют систему, достаточную для
определения четырех неизвестных параметров газа — рг, рг, Гг,
wr — в конце трубы.
Из уравнения количества движения имеем
Рт
(*-')-
Вставляя в это уравнение значения рх и рт из уравнения со-
состояния
/
Рг
и учитывая, что по формуле C4) гл. I крт/рг = а?, получим
?.?*_1 = /cM*(l--M. C2)
"г х г \ ^х /
Отношение температур Гх и Гг можно представить в виде
w2 T* и,2
сР К 2срТ*
Вводя критическую скорость акр г, получим
1 Лг
Вставляя в C2) это выражение для TJTr и заменяя М? по фор-
формуле D5) гл. I, приходим к квадратному уравнению
pw 1+л? Рх г* 1+я.а v '
решая которое, находим')
Р
'х~ 2Я? L К A + «)"^J
Л ол 2 I - -1- ¦/ ~ /j i лЗ\2 /л* I" N '
]) Один из корней уравнения, отвечающий дозвуковой скорости тече-
течения, получается при знаке «минус», второй корень (при знаке «плюс»)
дает решение для сверхзвуковой скорости течения.
§ 3. ДВИЖЕНИЕ ПОДОГРЕВАЕМОГО ГАЗА ПО ТРУБЕ
197
или
Уравнение C5) используется в тех случаях, когда известно
состояние газа в начале трубы. Если же скорость газа в конце
трубы доводится до критической, то удобнее применять уравне-
уравнение C4).
При отсутствии подогрева (Г* = Т*) имеем рг ^рх.
Если в конце трубы имеет место тепловой кризис (Яг = 1)т
то уравнение C4) примет следующий вид:
C6)
При этом
Предельное значение скорости в начале трубы в этом случае
равно
=/
1-?|
C7)
Разделив обе части равенства C7) на акр.х, можно перейти к при-
приведенной скорости:
^ |np :
Так как
то
np
C8)
Данные об изменении максимальной дозвуковой скорости на вхо-
входе в трубу при варьировании подогрева приведены в нижеследую-
нижеследующей таблице:
Ыпр
1
1
2
0,41
4
0,27
6
0,22
8
0,17
198 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Уменьшение скорости в начале трубы (при Ях < 1) с усиле-
усилением подогрева в условиях теплового кризиса объясняется сокра-
сокращением расхода газа. В самом деле, при тепловом кризисе ско-
скорость газа увеличивается пропорционально корню квадратному
из температуры:
а плотность газа падает быстрее, чем величина 1/Тт (ввиду умень-
уменьшения давления):
Рг
Рг~ у-,
¦* г
G = pTwrF ~ yj^.
поэтому расход газа
Так как плотность в начале трубы не зависит от подогрева, то
падение расхода газа приводит к уменьшению скорости в начале
трубы. Малые значения приведенной скорости на входе в камеру
сгорания, получающиеся при сильном подогреве, приводят к боль-
большим габаритам двигателя. С увеличением скорости полета растут
начальная температура Т\ и предельное значение скорости на
входе в камеру сгорания.
Согласно уравнению импульсов перепад давления в трубе
равен
I L
На основании формул C4) и D5) гл. I имеем
к— = а? =
Рг
поэтому
|Хг ' "' C9)
Предельное изменение давления получается при достижении теп-
теплового кризиса (Лг = 1). В этом случае на основании C6)
Е
D0)
пр Г /Р
Здесь знак минус отвечает Ях > 1, знак плюс отвечает Лх < 1. Осу-
§ 3. ДВИЖЕНИЕ ПОДОГРЕВАЕМОГО ГАЗА ПО ТРУБЕ
199
ществляя при Ях < 1 1) очень сильный подогрев I —у -> 0 , можно
довести падение давления до следующей величины:
Рт
пр
или при & ¦« 1,4
2,4,
пр
Напомним, что падение давления, необходимое для получения
критической скорости в сопле, составляет
т. е. при к = 1,4
V
?
Определим теперь падение полного давления в цилиндриче-
цилиндрической трубе. В начале и в конце трубы имеем соответственно
Р* =
- 1
Разделив первое уравнение на второе, получим
к + 1
Отсюда коэффициент сохранения полного давления в трубе
равен
D1)
к+1лт)
Наибольшее падение полного давления получается при тепловом
кризисе. Подставляя выражения C8) и D0) в равенство D1),
') О случае Xz > 1 будет сказано ниже.
200
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
получим для этого режима течения
D2)
i±*l/ !--?
Здесь верхние знаки соответствуют режиму А* > 1. Зависимость
изменения полного давления при тепловом кризисе в трубе от
отношения температур торможения, вычисленная для Я* < 1 по
«формуле D2), представлена в нижеследующей таблице (ft = 1,4):
т*/т*
1
1
1,5
0,89
2
0,86
4
0,82
6
0,81
8
0,80
оо
0,79
Как видим, при Ях < 1 потери полного давления при реальном
подогреве {Т*/Тх&4—8) получаются такого же порядка, как
и при бесконечно сильном подогреве.
Итак, при Ях<1 и ft = 1,4 полное давление в конце подо*
ерева составляет не меньше 80 % от полного давления в начале
подогрева.
Для большей наглядности результатов несколько преобразуем
выражение D2). Для этого из C8) получим связь между крити-
критическим подогревом газа (А,г = 1) и соответствующим значением
начальной скорости до подогрева:
\ х/кр
D2а)
Отсюда следует, что при максимально возможной скорости газа
до подогрева (Я| = ,__ Л критический подогрев не превосходит
значения
кр.тах
(*-!)(*+!)*
что при к = 1,4 дает
v х/кр.тах
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС
201
Подставляя D2а) в D2) и отбирая знаки по физическому
смыслу задачи, имеем
lV-i (, к - 1. ,\*-i
к + lV-
Отсюда следует: при А,х = 0, т. е. -? = оо, акр =
D26)
1; при
^ =1, т. е. -рг = 1, акр = 1, и при А| = |i|, т. е. ^ = -г^>
огКр = 0.
/ т*\
Кривые Окр(Аа) и I—^\ =f(K), полученные с помощью
А/кр
формул D2а) и D26), нанесены на рис. 5.9.
б
7 -
Рис. 5.9. Зависимость степени
подогрева и коэффициента со-
сохранения полного давления от 0,5-
приведенной скорости потока
при кризисе (Хг = 1)
Выше было показано, что при малых скоростях течения газа
по трубе с подводом тепла в случае постоянного перепада давле-
давлений усиление подогрева ведет к снижению расхода газа.
В § 6 будет показано, что при постоянном перепаде давлений
подогрев вызывает уменьшение расхода газа и при больших ско-
скоростях течения.
§ 4. Общие условия перехода от дозвукового течения
к сверхзвуковому и обратно
В предыдущих параграфах было показано, что при подводе
тепла или совершении работы трения в движущемся по цилиндри-
цилиндрической трубе с дозвуковой скоростью газе происходит увеличение
числа М; то же явление наблюдается в дозвуковом потоке при
течении без теплообмена и трения в суживающейся трубе.
Ниже будет доказано, что изменение числа М в газовом пото-
потоке происходит не только под влиянием трения, теплового и гео-
геометрического воздействий, но также при изменении расхода гаэа
202 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
в канале и при совершении механической работы. Указанные воз-
воздействия вызывают изменение числа М как в дозвуковом, так и в
сверхзвуковом потоке газа.
Рассмотрим в общем виде влияние этих воздействий на ско-
скорость движения газа. Для простоты будем считать газ идеальным.
Расход газа равен G = pwF.
Отсюда после дифференцирования и почленного деления на G
имеем
dG dF dp , dw
~G = — + T + ~
Дифференцируя уравнение состояния для идеального газа (р
= pRT), получаем
d
или
jf=R(dT + Tf). D4)
Сопоставление выражений D3) и D4) дает
¦f =RdT+RT(*. -%¦-%). D5)
С другой стороны, из уравнения Бернулли в дифференциальной
форме (формула (91) гл. I) имеем
w dw- dL - dLTp, D6)
где L — техническая работа, LTp — работа трения. Сопоставляя
D5) и D6), а также освобождаясь от членов, содержащих плот-
плотность и давление, получим
D) + ^ + ^p = 0. D7)
Здесь используется выражение для скорости звука (а2 = kRT).
От члена, содержащего температуру (RdT), можно избавиться
с помощью дифференциального уравнения энергии
dQK3LP=di + d (^-) + dL = ^A- R dT +w dw+ dL, D8)
где ()нар — тепло, подводимое к газу извне, di = cvdT =
= Л^-—rd?7— прирост теплосодержания. Подставляя D8) в D7)
и производя элементарные преобразования, приходим к соотно-
.шению, связывающему изменение скорости газового потока
с внешними воздействиями (геометрическим, расходным, механи-
механическим, тепловым и трением):
dw dF &G 1 йТ к—^ЛП к ЙТ //Q\
^4 ^^?. D?)
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС 203
Это соотношение было установлено Л. А. Вулисом *) и полу-
получило название условия обращения воздействия. Особенность это-
этого соотношения состоит в том, что знак его левой части изменяет-
изменяется при переходе значения скорости через критическое. Поэтому
характер влияния отдельных физических воздействий на газовое
течение противоположен при дозвуковом и сверхзвуковом режи-
режимах. Воздействия, вызывающие ускорение в дозвуковом потоке
(сужение канала, подвод дополнительной массы газа, совершение
газом работы, трение и подвод тепла: dF < 0, dG > 0, dL > 0,
йфнар > 0), приводят к замедлению сверхзвукового потока; воз-
воздействия обратного знака (расширение канала, отсос газа, сооб-
сообщение газу механической энергии и отвод тепла: dF > 0, dG < 0,
dL < 0, d^nap < 0) приводят к замедлению дозвукового и уско-
ускорению сверхзвукового потоков. Отсюда следует важный вывод, что
под влиянием одностороннего воздействия величину скорости га-
газового потока можно довести только до критической, но нельзя
перевести через нее. Например, путем подвода тепла можно уско-
ускорять дозвуковой поток, но только до тех пор, пока не получится
М = 1. Для того, чтобы перевести дозвуковой поток в сверхзвуко-
сверхзвуковой, нужно переменить знак воздействия, т. е. в зоне М = 1 на-
начать отводить тепло. Таково обоснование описанного в предыду-
предыдущем параграфе явления теплового кризиса в камере сгорания.
Подогрев газа в сверхзвуковом течении вызывает торможение по-
потока, но переход к дозвуковому течению и дальнейшее торможе-
торможение станут возможными только в том случае, если, начиная
с М = 1, мы переключимся на охлаждение газа.
Разумеется, что ускорение газового потока в сопле при любой
комбинации воздействий требует достаточного перепада давлений
между сечениями, расположенными перед и за соплом.
Рассмотрим раздельно каждое из четырех воздействий.
При этом получим в дополнение к известному соплу Лаваля
(геометрическое воздействие) еще три указанных Л. А. Вулисом
способа перехода через скорость звука, т. е. расходное, механиче-
механическое и тепловое сопла.
Геометрическое сопло, т. е. известное сопло Лаваля, представ-
представляет собой канал, в котором только за счет придания ему соответ-
соответствующей формы можно осуществить переход от дозвуковой ско-
скорости к сверхзвуковой. В этом частном случае чисто геометриче*
ского воздействия на поток (dF Ф0) отсутствуют прочие воздей-
воздействия, т. е. не меняется расход газа (dG = 0), нет обмена теплоШ
и работой с внешней средой (dQB< = O, d.L = Q) ш нет трения
(dL (T)
l) By лис Л. А. О переходе через скорость звука в гзюовом течении.—
ДАН СССР.— 1946.— Т. 54, № 8; By лис Д. А. Термодинамика газовых
дотохов.—:М.:_анерголздат,.1950;„ . .-. jr.с . s , Г .: -:i
204 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Но тогда соотношение D9) переходит в полученное ранее ра-
равенство A) гл. IV:
Не останавливаясь вторично на исследовании течения в con
ле Лаваля, напомним только, что ускорение потока в дозвуково!
части сопла Лаваля (М<1) получается путем сужения канал г
(dF < 0), но, начиная с критического сечения (М = 1), для полл
чения сверхзвукового потока и дальнейшего его ускорения при
ходится изменять знак воздействия, т. е. расширять канал
)
Течение идеального газа в геометрическом сопле (рис. 4.1)
при отсутствии трения является изоэнтропическим. В критиче
ском сечении (М = 1) сопла воздействие проходит через минимум
(dF 0)
)
Расходное сопло дает возможность получить переход через ско
рость звука за счет изменения расхода газа в трубе постоянного
сечения (dF = 0) при отсутствии обмена с внешней средой рабо
ты (dL = 0) и тепла (dQB2iV = 0) и без трения (dLTp = 0). В этом
случае соотношение D9) принимает следующую форму:
Ускорение движения (dw > 0) достигается здесь за счет под-
подвода дополнительной массы газа в дозвуковой части канала и от-
отсоса газа в сверхзвуковой его части. В критическом сечении
(М = 1) расход газа и, следовательно, плотность тока проходят
через максимум.
Расходное сопло в принципе аналогично геометрическому. Ес-
Если разбить поток в расходном сопле на отдельные струйки по-
постоянного расхода, то каждая из них представляет собой геомет-
геометрическое сопло с наиболее узким сечением в области кризиса
(М = 1); однако сужение элементарных струек в нем осуществля-
осуществляется не путем сужения общего канала, а за счет подвода и отвода
дополнительных количеств газа (рис. 5.10).
Естественно, что изменение состояния идеального газа в рас-
расходном сопле (без трения) идет по изоэнтропическому закону.
Механическое сопло дает еще один принципиально возможный
иуть перехода через скорость звука: за счет технической работы
при отсутствии других воздействий (dF = 0, dG = 0, dQEup = 0,
Ц0)
р)
В этом случае основное соотношение D9) выглядит так:
<M«-iLr---yrfb
из чего следует, что если газовый ноток совершает работу
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС
205
(dL > 0), например, на колесе турбины, то в дозвуковом режиме
(М < 1) он ускоряется (dw > 0), а в сверхзвуковом (М > 1) за-
замедляется (dw<0). При подводе работы к газу (dL<0), т. е.
на лопатках компрессора, в дозвуковом течении наблюдается за-
замедление, а в сверхзвуковом — ускорение.
Непрерывный переход через скорость звука в механическом сои
ле получается при изменении знака воздействия в критическом
ПП1АААА
V II I
Рис Г) 10. Схема течения в расход-
расходном сопле
Рис. 5.11. Схема механическою
сопла
сечении. В принципе, пропуская дозвуковой поток газа через тур-
бину, можно разогнать его до критической скорости; после этогб
нужно пустить его через компрессор, и тогда получится ускоряю-
ускоряющийся сверхзвуковой поток (рис. 5.11).
Таким образом, сверхзвуковое механическое сопло должно
состоять из последовательно включенных турбины (в области
М< 1) и компрессора (в области М> 1), между которыми рас-
располагается критическое сечение (М = 1).
Особенностью механического сопла является то, что парамет-
параметры торможения проходят в его критическом сечении через мини-
минимум. В самом деле, уравнение теплосодержания для механическо-
механического сопла можно записать следующим образом:
Здесь iH, ?* — значения полного теплосодержания газа соответ-
соответственно в начальном и произвольном сечениях сопла, L — техни-
техническая работа, совершенная газом между начальным и произ-
произвольным сечениями сопла. Поэтому в дозвуковой части механиче-
механического сопла, где газ совершает работу LT (на турбине), т. е. L > 0,
полное теплосодержание (и температура торможения) убывает
*•<?.
В сверхзвуковой области, где к газу подводится компрессором
механическая энергия LK(L<0I происходит увеличение полного
теплосодержания по сравнению с его значением в критическом
сечении:
**>ЙР или Г*>ГкР.
В том, что полное давление и плотность заторможенного газа
проходят вместе с температурой торможения в критическом
206 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
сечении механического сопла через минимумы, можно убедиться
и иным способом. Для двух произвольных сечений идеального ме-
механического сопла, представляющего собой, по определению, ка-
канал постоянного сечения, имеем
АЛ iv п р п
* X X 2 2 2
Ввиду отсутствия трения и теплоотдачи параметры газа в таком
сопле изменяются как при идеальном адиабатическом процессе:
fi. = (рЛ * = (?i
Р2 \ Р2 ) \Т2
Учитывая, что отношение значений скорости звука
получим следующие простые зависимости между значением чис-
числа М и параметрами газа в идеальном механическом сопле:
(so>
Итак, монотонное возрастание значения числа М в механиче-
механическом сопле сопровождается монотонным падением температуры,
давления и плотности.
Кривые изменения параметров потока и торможения в сверх-
сверхзвуковом механическом сопле при Mi =0,1 представлены на
рис. 5.12 и 5.13.
Из E0) следует, что максимальная скорость истечения из ме-
механического сопла ничем не ограничена, так как из
при М2 -»- «> имеем 1^2-^°°. Этот результат не должен вызывать
удивления, так как в сверхзвуковом участке механического сопла
к газу подводится энергия (dL < 0).
Тепловое сопло, пока еще не осуществленное, дает принципи-
принципиальную возможность перехода газового потока через скорость зву-
звука за счет еще одного — чисто теплового — воздействия при отсут-т
ствии других воздействий, т. е. в цилиндрической трубе (dF = 0),
при постоянном расходе газа (dG = 0), без совершения механиче-
механической работы (dL• = 0) и без трения (dLTp = 0). Основное соотно-
D9), применительно к теиловому соилу имеет следующий
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС
207
вид:
/ХА2 4\ dw —
Ускорение газа (dw > 0) в дозвуковом потоке (М < 1) здесь свя-
связано с подводом тепла (dQB&v> > 0), а в сверхзвуковом — с его от-
отводом (й(?наР < 0)- Подвод тепла при сверхзвуковом и отвод тепла
рг.ТгЛ
0,8
0,6
0,4
0,2
к
\
1
\
V
\
\
N
V
ч
ч
Ч
ч
ч
2
ч*.
г
мм
зм2
Рис. 5.12. Зависимость параметров газа от числа М2 в механическом сопле
при Mi в 0,1; к = 1,4
Тг. рг*Л*
0.8
0,6-
0,4
0,2
1
1
и
1\
1
U
\
¦MB
^^
¦о
-—
**
f*
/\
У
гг4
/
/
м2 з
Рис. 5.13. Зависимость параметров торможения от числа М2 в механиче-
механическом сопле при Mi = 0,1; к = 1,4
при дозвуковом режиме вызывают замедление потока (dw<0).
Таким образом, для того чтобы преобразовать дозвуковой поток в
сверхзвуковой посредством теплового сопла, в дозвуковом участке
последнего нужно повышать теплосодержание газа, ав сверхзву-
сверхзвуковом—понижать его, т. е*. в.. критическом сечрццд: теплового
208 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
сопла, где количество подведенного к газу тепла проходит через
максимум (й^наркр = 0), следует изменить знак воздействия.
Температура торможения в критическом сечении теплового соп-
сопла (в противоположность случаю механического сопла) достига-
достигает максимального значения; это вытекает из уравнения теплосо-
теплосодержания, которое применительно к тепловому соплу имеет сле-
следующий вид:
^н = 1 чгнар*
Из предыдущего параграфа, содержащего теорию теплового
сопротивления, следует, что^при подводе теплая газовому потоку
полное давление в нем падает, а при отводе тепла — растёт. Фор-
Формулы теплового сопротивления были выведены применительно
к случаю движения газа без трения по трубе постоянного сечения,
т. е. именно к случаю теплового сопла.
Из этой теории следует, что полное давление в критическом
сечении теплового сопла, как и в механическом сопле, проходит
через минимум. Плотность заторможенного газа, прямо пропор-
пропорциональная полному давлению и обратно пропорциональная тем-
температуре торможения, достигает в критическом сечении мини-
минимального значения.
В рассмотренных выше идеальных соплах: геометрическом,
расходном и механическом, изменение состояния газа было изо-
энтропическим, т. е. описывалось уравнением идеальной адиабаты
plpk = const.
В тепловом сопле в связи с подводом и отводом тепла энтропия
изменяется.
Исследуем термодинамический процесс, который имеет место
в тепловом сопле1). Дифференциальная форма уравнения коли-
количества движения применительно к цилиндрической трубе при от-
отсутствии трения имеет следующий вид:
dp =• —ipu; dw.
Уравнение неразрывности в этом случае (dF — 0, dG = 0) дает
dp dw в
р w '
отсюда
dp
d9 - Л <51>
1) См. В у л и с Л. А. О переходе через скорость звука в газовом тече-
течении.- ДАН СССР.- 1946.- Т. 54, № 8.
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС 209
Для политропического процесса при постоянном показателе по-
политропы р/рп = const, после дифференцирования 1) имеем
%. = п JL = п ¦?, E2)
dp р к ' v '
так как скорость звука в газе а2 = кр/р. Приравнивая правые час-
части выражений E1) и E2), замечаем, что показатель политропы
в тепловом сопле является существенно переменной величиной
п = Ж2. E3)
Формула E3) показывает наличие двух характерных сечений
в тепловом сопле. _
В сечении, где М = 1/УА, местное значение показателя поли-
политропы равно единице: п = 1, т. е. элементарный термодинамиче-
термодинамический процесс в этом сечении — изотермический (dT = 0), и, следо-
следовательно, температура газа здесь проходит через максимум.
В критическом сечении теплового сопла, т. е. при М = 1, по-
показатель политропы на основании формулы E3) равен показате-
показателю идеальной адиабаты: п = ft, т. е. здесь имеет место элементар-
элементарный изоэнтропический процесс, при котором, как уже указыва-
указывалось выше, количество подведенного к газу тепла и температура
торможения проходят через максимум {dQBap = 0, dT* = 0).
От изотермического до критического сечений теплового сопла
наблюдается интересное явление: понижение температуры газа
(dT<0) при подводе тепла (d(?HaP>0). На этом участке сопла
прирост кинетической энергии газа больше прироста полного теп-
теплосодержания.
Для отыскания зависимости давления газа от числа М в теп-
тепловом сопле без трения используем уравнение количества движе-
движения в следующей форме:
Pi + рМ = Р2 + Р2^; E4)
отсюда
р1A
или
р 1+*м;
( }
Иначе говоря, давление газа в тепловом сопле с ростом числа М
монотонно падает, несмотря на увеличение полного давления
в сверхзвуковой части.
1) При плавном протекании термодинамического процесса на любом
участке малого изменения параметров состояния можно допустить, что
локальное значение показателя п постоянно, хотя в целом процесс проте-
протекает с изменением показателя политропы,
14 г. н. Абрамович, ч. i
210 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Зависимость плотности газа и скорости течения в тепловом соп-
сопле от числа М можно найти следующим способом:
М2 w2 a2 w2 T
2 2 1 __ _2 22
М1 ~ »\ *\ Т2 w*
но из уравнений состояния и неразрывности имеем
Т2 Р2 Pi' Pi W2*
поэтому . I
М2 Pi Pi
Используя зависимость E5), получаем
E6)
откуда видно, что плотность газа вдоль теплового сопла монотон-
монотонно падает с ростом числа М.
Температура газа в тепловом сопле как функция числа М мо-
может быть получена делением равенства E5) на равенство E6):
т,
Как нетрудно убедиться из выражения E7), кривая температу-
температуры имеет максимум в точке *.)
В любых двух сечениях теплового сопла с одинаковой темпе-
температурой (T2 = Ti) значения числа М, как это явствует из вы-
выражения E7), связаны следующей зависимостью:
м2м, = 4-.
Выведем формулы для параметров торможения в тепловом
сопле. Эти формулы приобретают более простой вид, если в них
]) Для этого в равенстве E7) будем рассматривать Mi и Т\ как по-
стоянные величины. Приравнивая нулю производную ^м~» находим
i 1
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС 211
число М заменить приведенной скоростью Я, для чего можно
воспользоваться известным соотношением D5) гл. I.
Температуру торможения найдем, пользуясь формулой D2)]
гл. I, из равенства
1 "" к + 1 Л2
подставив сюда E7), предварительно заменив М на К по форму-
формуле D5) гл. I, получаем
Т* I2 ( \ Л- ^2\2
р-? 7ТГ* • E8)
Полное давление в тепловом сопле может быть получено с
помощью формулы G2) гл. I из выражения
отсюда, используя равенство E5), приходим к следующей зави-
зависимости:
Плотность заторможенного газа в тепловом сопле можно оп-
определить путем деления выражения E9) на выражение E8):
Кривые изменения параметров потока в тепловом -сопле в за-
зависимости от числа Мг при Mi = 0,1 даны на рис. 5.14 и 5.15.
Определим количество тепла (Q), которое нужно подвести
в тепловом сопле, чтобы изменить скорость газа от какого-либо
одного значения (к\) до другого (Яг). При постоянной теплоем-
теплоемкости имеем:
или в безразмерном виде - ),
e-JL.U-i. ' '
' * ~ с 'Т* ' Т*
14*
212
ГЛ. V, ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
подставляя сюда отношение температур торможения из равен-
равенства E8), находим
Максимальное количество тепла, отвечающее критическому пс»
догреву (до %2 = 1), равно
ftnax
= уж) •
Оно резко уменьшается с ростом начальной скорости газа (Х\)\
о чем свидетельствует график рис. 5.16. Предельно возможная
2,0
18
16
1,2
ио
0,8
0,6
0,4
о,г
\
\
7
}
/
1
/
/
/
/
/
р
3 М,
Рис. 5.14. Зависимость статиче-
статического и полного давлений от чис-
числа М2 в тепловом сопле при
М! = 0,1; к = 1,4
'1 h
22
20
18
16
12
10
8
6
?
2
Рис. 5.15. Зависимость темпера-
температур потока и торможения от чис-
числа М2 в тепловом сопле при
Mi = 0,1; к = 1,4
Г
/ ,1
1 \
к
/.
1 •
Г"
1
$
i
|
\
\
\
Ч
\
ч
ч
к
ч
7м
скорость истечения из теплового сопла (при Мг = °°) согласно
равенству E6) зависит от начального значения числа1 fA\:
"max
l
В частности, если вести отсчет от критического сечения, т. е.
положить1)
¦
1) Следует учитывать, что в связи с подводом тепла значение критиче-
критической скорости по длине сопла меняется.
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС
213
то получится
Помимо четырех описанных «чистых» схем сверхзвуковых ее*
пел, принципиально возможны комбинированные схемы. Нак
более реальным комбинированным соплом является так назы
ваемое полутепловое сопло, в котором дозвуковой участок являете?
тепловым, а сверхзвуковой -
геометрическим (рис. 5.17 .
В таком сопле газ ускоряет
ся от некоторого начального
дозвукового значения скоро
сти до критического в цтт
линдрической трубе 1—2 за
счет подвода тепла, а пере-
переход к сверхзвуковой скоро-
скорости и дальнейшее ускорение
потока осуществляются бег
теплообмена в расширяю-
расширяющейся трубе 2—3. Расчет до-
дозвукового участка полутеп -
лового сопла ведется по
г-г* 1
Ч
го
15
10
5
A
\
\
\
!
V
\
ч
ч
О 0,2 Ot? Of OJS 1,0 Xf
Рис. 5.16. Зависимость критического по-
подогрева в трубе постоянного сечения от
начального значения приведенной ско-
скорости
Рис. 5.17. Схема полутепло-
полутеплового сопла
формулам теплового сопла, а сверхзвукового участка — по фор-
формулам геометрического сопла.
Сравним полутепловое сопло с геометрическим при одинако-
одинаковом конечном значении полного теплосодержания \}ъ), имея
в виду, что в полутепловом сопле подогрев газа совершается в ци-
цилиндрической трубе 2—2, а в геометрическом сопле то же ко-
количество тепла подводится к газу до его входа в сопло. Значения
скорости истечения из обоих сопел одинаковы, так как в кри-
яических сечениях величина температуры торможения одна и
214 гл. v. одном йрные течения газа
та же. Полное давление на выходе из полутеплового сопла ниже
в связи с наличием теплового сопротивления в его дозвуковом
участке, поэтому ниже и статическое давление на выходе из
полутеплового сопла.
Рассмотрим пример полутеплового сопла с начальной ско-
скоростью газа, соответствующей значению приведенной скорости
Кг = 0,2. При этом безразмерная величина подогрева газа в до-
дозвуковом участке сопла согласно выражению F1) должна быть
равна
Потери полного давления в полутепловом сопле (^2 = 1) можно
вычислить по формуле E9):
1 Ar + 1 Л1 I*-1
* + l J
' ПТ \ x J ПТ
При ^i = 0,2 и fe = 1,4 имеем j
j^L j =anT=o,82.
Полное давление в геометрическом сопле сохраняет постоянное
значение:
Поэтому статическое давление на выходе из полутеплового соп-
сопла при одной и той же скорости истечения в опт раз отличается
от статического давления на выходе из геометрического сопла:
далее
где Лз — приведенная скорость истечения из сопла, Р\ — полное
давление в начальном сечении сопла. При равных перепадах
давления ^„
скорость истечения из полутеплового сопла меньше,, чем из хео?
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС 215
метрического сопла (Хзпт < ^зг); это вытекает из равенства
f k ~~ * ? 2 ^
связывающего отношение статического давления к полному с
приведенной скоростью. Например, при опт = 0,82 и Язг = 2
приведенная скорость истечения из полутеплового сопла Язпт я
в 1,97, т. е. на 1,5 % меньше приведенной скорости истечения
из геометрического сопла.
Рассматривая различные типы сопел, предназначаемых для
перехода через скорость звука, мы во всех случаях имели в ви-
виду переход от дозвуковой к сверхзвуковой скорости. Полученные
формулы принципиально пригодны и для обратного случая, т. е.
плавного преобразования сверхзвукового потока в дозвуковой,
однако при торможении сверхзвукового потока могут возник-
возникнуть^ скачки уплотнения, которые усложняют явление.
Остановимся теперь кратко на совместном проявлении двух
или нескольких воздействий. В качестве первого примера разбе-
разберем случай геометрического сопла с трением. Основное соотно-
соотношение D9) имеет в этом случае вид
/кАо м dw dF к jj
(M2-l)— = — -—riLTp.
Наиболее интересной особенностью этого сопла является то, что
критическая скорость получается в его расходящейся части, так
как при М = 1
dF к ,, ^п
а в узком сечении {dF = 0 при dw > 0) имеет место дозвуковая
скорость и М < 1.
Выясним теперь главные особенности геометрического сопла
с теплообменом. Из основного соотношения D9) в этом случае
имеем
Местоположение критического сечения (М=1) определяется
равенством
dF __ fe-1 дп
-у — -^2~- "ЧГнар-
При подводе тепла {dQUSiV> 0), например при догорании газов
• в сопле, критическая скорость достигается в расходящейся части
сопла (dF>0I при отводе тепла (d@Hap<0), т. е. теплоотда-
теплоотдаче через стенки сопла, критическая скорость достигается в схо-
сходящейся части сопла (dF<df;* В первом'бл^аё в уйкбк сече-
216 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
пии сопла (dF = 0) имеет место дозвуковая, а во втором слу-
случае — сверхзвуковая скорость.
Таким же путем можно исследовать совместное влияние в га-
газовом течении любых других воздействий. При этом важно
подчеркнуть, что в соответствии с уравнением D9) переход от
М < 1 к М > 1 требует в любом случае изменения знака сум-
суммарного воздействия.
В заключение отметим одно обстоятельство, приводящее иног-
иногда к недоразумениям при качественном анализе закономерно-
закономерностей некоторых течений. В связи с этим вновь вернемся к урав-
уравнению D9).
Выше при анализе уравнения количества движения (92) гл. I
мы отмечали, что независимо от процессов, происходящих в по-
потоке, изменение скорости течения всегда вызывается действием
силы трения, внешних сил, а также разности сил давления на
выделенный элемент газового потока. Различные виды внеш-
внешнего воздействия по разному влияют на статическое давление
в потоке. Смысл совместного решения уравнений D3) — D7),
в результате которого было получено соотношение D9), сво-
сводился к тому, чтобы величину градиента давлений в потоке вы-
выразить через внешние воздействия; величина dp при этом исклю-
исключалась из уравнения импульсов или уравнения Бернулли D6).
При анализе уравнения D9) выявлено, что: а) изменение
скорости газа вызывается и такими факторами, которые не свя-
связаны с непосредственным силовым воздействием на поток (на-
(например, подвод тепла), б) суммарный эффект в ряде случаев
оказывается обратным тому, который можно ожидать, исходя
из анализа действия внешних сил. Действительно, например,
сила трения, всегда действующая против направления движения,
в дозвуковом потоке приводит не к торможению, а к ускорению
потока. Последнее означает, что при течении с трением проис-
происходит такое снижение статического давления, что действующая
по потоку сила давления превышает силу трения.
Точно так же при подводе механической энергии к дозвуко-
дозвуковому газовому потоку давление его повышается настолько, что
сила давления, действующая навстречу потоку, превышает выз-
вызвавшую ее внешнюю силу. В результате поток, к которому при-
приложена внешняя сила в направлении движения, при М < 1 не
ускоряется, а тормозится.
Таким образом, выше, при анализе внешних воздействий на
газовый поток, везде предполагалось, что в потоке возникают
соответствующие градиенты давления, которые в конечном итоге
и определяют изменение скорости течения. Так, например, для
ускорения дозвукового газового потока в тепловом сопле (т. е,
при F = const) давление на входе в сопло должно превышать
давление на выходе на величину, определяющуюся начальным и
конечным числами М (см. формулу E5)).
§ 4. УСЛОВИЯ ПЕРЕХОДА ТЕЧЕНИЯ ЧЕРЕЗ КРИЗИС 217
Такой же смысл имеют полученные выше соотношения ме-
между статическими давлениями газа при течении с трением E0),
при течении с подводом механической энергии и т. п. Во многих
случаях, однако, заранее известно, что в рассматриваемом по-
потоке нет продольного градиента давления. Изменение скорости
газа в этом случае (dp = 0) полностью определяется уравнением
количества движения в виде
pw dw = — -у (dP + dPTp),
где dPrp — сила трения, a dP — внешняя сила. Отсюда следует,
что в изобарическом потоке как при дозвуковых, так и при
сверхзвуковых скоростях трение приводит к уменьшению ско-
скорости; внешние силы, действующие по потоку, или подводимая
внешняя механическая энергия (dP < 0) всегда ускоряют газо-
газовый поток; подвод тепла при dp = 0 вообще не изменяет ско-
скорости направленного движения газа, так как при этом нет внеш-
внешних сил.
Примером изобарического течения может быть, в частности,
сверхзвуковое течение у твердой стевки. Пограничный слой
вблизи такой стенки образуется в результате непрерывного тор-*
можения потока силами внешнего воздействия (трения). В итоге
величина скорости течения в нем уменьшается при р = const от
сверхзвукового до небольшого дозвукового значения.
Точно так же изобарическая сверхзвуковая струя, смеши-
смешиваясь с неподвижным атмосферным воздухом, разгоняет его ча-
частицы до сверхзвуковой скорости путем одностороннего механи-
механического воздействия — подвода количества движения при соуда-
соударении частиц газа и воздуха.
При дальнейшем течении в любой струйке тока внутри изо-
изобарической сверхзвуковой струи происходит непрерывное тормо-
торможение — с переходом через скорость звука — до малых скоростей,
также за счет одностороннего внешнего воздействия — передачи
количества движения во внешнюю среду.
Эти примеры не противоречат установленным выше законо-
закономерностям и уравнению обращения воздействий D9). Дело в том,
что при наличии какого-либо внешнего воздействия условие изо-
баричности (р = const) может быть выполнено только при впол-
вполне определенном изменении площади сечения F.
Так, например, при дозвуковом течении в цилиндрической
трубе с трением скорость газа увеличивается, а статическое дав-
давление падает. Чтобы давление в потоке было постоянным, ка-
канал надо сделать расширяющимся, т. е. к воздействию трения
добавить геометрическое воздействие dF>0. Так как независи-
независимо от формы канала при течении с трением полное давление сни-
снижается, то в таком изобарическом потоке скорость газа умень-
уменьшается.
218 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
§ 5. О распространении детонации и горения в газах *)
Творцом теории распространения детонации в газах является
известный русский физик В. А. Михельсоя, посвятивший в 1889 г.
этому вопросу работу «О нормальной скорости воспламенения
гремучих газовых смесей»2).
Выдающиеся теоретические и экспериментальные исследо-
исследования в области горения и детонации принадлежат Н. Н. Семе-
Семенову, Я. Б. Зельдовичу, Д. А. Франк-Каменецкому, К. И. Щел-
кину и другим советским ученым3).
Распространение пламени в горючей газовой смеси вне за-
зависимости от механизма воспламенения (теплопроводностью при
медленном горении или ударной волной при детонации) подчи-
подчиняется основным законам газовой динамики и, следовательно,
может быть описано уравнениями сохранения массы, количества
движения и энергии.
Фронт пламени представляет собой тонкий слой газа прак-
практически постоянного сечения, по обе стороны которого значения
скорости движения (относительно фронта волны), температуры,,
давления и других параметров различны. В соответствии с этим
фронт пламени можно трактовать как поверхность сильного раз-
разрыва (теплового скачка).
В современном представлении детонационная волна, распро-
распространяющаяся в горючей газовой среде, является двухслойной.
Первый слой представляет собой адиабатическую ударную вол-
волну, при прохождении через которую газ сильно разогревается.
В химически активном газе разогрев этот, если он достаточна
интенсивен, может вызвать воспламенение. В связи с тем что
толщина ударной волны ничтожно мала (порядка длины свобод-
свободного пробега молекулы), в пределах ее процесс горения, по-ви-
по-видимому, развиться не в состоянии. Поэтому область, в которой
протекает горение, образует второй, более протяженный, но пра-
практически также весьма тонкий слой, примыкающий непосредст-
непосредственно к ударной волне (рис. 5.18).
Разогрев газа при прохождении его через ударную волну в де-
детонационном горении заменяет собой в сущности подогрев его»
теплопроводностью в нормальном горении.
Рассмотрим явление детонации в условиях одноразмерной
задачи. В этом случае для плоской ударной волны по известному
соотношению A5) гл. III произведение скоростей газа относи-
1) В этом параграфе дается расширенное изложение работы: Абра-
Абрамович Г. Н., By лис Л. А. К механике распространения детонации-
и горения.— ДАН СССР.— 1947.— Т. 55, вып. 2.
2) М и х е л ь с о н В. А. Полное собрание сочинений. Т. 1.— М.: ГТТИ,
1930.
3) См., например, Зельдович Я. Б. Теория горения и детонации
газов.— Изд-во АН СССР, 1944.
§ 5. О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ
219
тельно фронта волны (взятых соответственно перед и за фрон-
фронтом) равно квадрату критической скорости
wifv% = акр.
Величина w\ является скоростью распространения ударной вол-
волны (в нашем случае волны детонации в неподвижном газе). Для
исследования процесса удобнее считать, что газ притекает со
•скоростью w\ к области детонации, а фронт волны неподвижен.
Эта обращенная схема явления при-
принята нами в последующем изло-
изложении.
Ударная волна (скачок уплотне-
уплотнения), как известно, распространяет-
распространяется €0 сверхкритической скоростью
(wi>aKp), поэтому скорость газа за
' -фронтом волны всегда ниже крити-
критической (и?2<акр). Иначе говоря,
яроц°сс горения при детонации, как
is при медленном горении, протекает
в дозвуковой части газового потока. w
В конце второго слоя детонаци-
детонационной волны вследствие подвода теп-
тепла при горении скорость газа выше,
чем вначале, а давление соответ-
соответственно ниже. Таким образом, пер- / z S х
вый слой детонационной волны Рис. 5.18. Схема детонацион-
лредставляет собой скачок сжатия, ной волны: А — свежая смесь,
а второй слой, где происходит горе- fK~ о^°д^лотненияРа//— зона
тше,— скачок разрежения. Пример- скачок упл??рения'
ный характер распределения давле-
давления и скорости газа в детонационной волне показан на рис. 5.18.
Перейдем к расчету окачка уплотнения.
При расчете изменения состояния газа в первом слое пло-
плотской детонационной волны мы можем воспользоваться сотноше-
ниями для прямого скачка уплотнения.
Для рассматриваемого случая существенно, что в первом
юлое детонационной волны (адиабатическом скачке уплотнения)
температура торможения остается неизменной: Т1 = Т2. Следо-
Следовательно, критическая скорость в первом слое не изменяется:
*Я1кр = #2кр, тогда Как в продуктах сгорания значение ее увели-
увеличивается, Т3 > 7\ и, соответственно, азкр > #1кР. Это обстоятель-
обстоятельство необходимо учесть в дальнейшем при вычислении приве-
приведенных скоростей:
"ЗКр
Из уравнения неразрывности pii#i=p2itf2 и выражения A6)
220 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
гл. III найдем для изменения плотности и скорости соотношения
Закон изменения давления в прямом скачке уплотнения может
быть получен из уравнения импульсов в виде известного равен-
равенства B1) гл. III
—
к + 1
F3)
Из F2) и F3) следует, что изменение температуры газа в скач-
скачке уплотнения
т
-г = —
1 1
к + 1
Например, при скорости распространения ударной волны w\ =
= 2000 м/с, начальной температуре газа Т\ = 400 К, R =
=• 300 Дж/(кг -К) и & = 1,4 имеем Г? « 2340 К, ах кр « 900 м/с,
%х « 2,2, Я2 « 0,45, чему соответствует Т2 « 2260 К.
Нет сомнений, что в данном случае ударная волна может
вызвать воспламенение горючей газовой смеси.
Займемся теперь расчетом зоны горения.
Естественно, что все формулы, выведенные в §§ 3 и 4 для
случая подогрева газа в цилиндрической трубе, пригодны и для
расчета второго (теплового) слоя детонационной волны, так
как при выводе указанных формул длина трубы не имела зна-
значения (трением и теплоотдачей через боковую поверхность мы
пренебрегали).
Для расчета состояния газа во втором (дозвуковом) слое де-
детонационной волны — в области горения —- проще всего прибег-
прибегнуть к соотношению E8) между температурой торможения и
приведенной скоростью
откуда после решения биквадратного уравнения получим сле-
следующее выражение:
31 F6)
§ 5. О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ 221
ИЛИ
Здесь отброшены корни, дающие сверхзвуковые решения, так
как рассматривается зона горения, где относительные скорости
ниже скорости звука (Яг<1); кроме того, принято Т\ = Т\.
Приведенная скорость Х% — непосредственно за скачком уплот-
уплотнения — обычно значительно меньше единицы; если при этом и
относительный прирост температуры торможения в области горе-
горения невелик (Т7*/^* «О» то формулу F7) можно существенно
упростить:
1 ^2
(так как при сделанных предположениях Х\<^.1). Таким обра-
образом,
Г +4?. F8)
где А Г* = Q/cp, если (? — количество теплоты, выделяющейся
при сгорании единицы массы смеси. Из формулы F8) видно,
что при слабом разогреве (АГ*/Г*«0) приведенная скорость
для продуктов сгорания близка к приведенной скорости за скач-
скачком уплотнения.
С усилением скачка уплотнения, т. е. с увеличением скоро-
скорости распространения ударной волны, температура торможения
исходной смеси Т* = Г* резко возрастает согласно известному
равенству D2) гл. I:
при этом резко увеличивается и температура в потоке перед об*
ластью горения Гг. В пределе при Mi = «> иХ1=|/^-^ имеем
Т\ = Т\ = оо и Т2 == °°. С увеличением температуры Гг в связи
с возрастающей ролью термической диссоциации1) несколько
уменьшается абсолютная разность температур торможения:
ДГ* = Г* ~ Т\.
1) Термической диссоциацией называется наблюдающееся при высоких
температурах, а также при низких давлениях явление частичного разло-
разложения продуктов горения; реакция идет в обратном направлении и сопро-
сопровождается поглощением теплоты.
222 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Следовательно, с усилением ударной волны уменьшается как от-
относительный разогрев газа AT*/TV так и приведенная скорость
продуктов сгорания Яз.
Наиболее отчетливо это видно, если в формулу F8) вместо
деременной температуры торможения ввести постоянную тем-
температуру холодного газа:
<70>
Горение, протекающее за фронтом очень сильной ударной
волны, начинается на столь высоком тепловом уровне, что мо-
может вызвать лишь относительно небольшой прирост темпера-
температуры торможения. Поэтому в пределе
п \ ^ 1 _ *
\™3/ПР ^^ 2 — л »
т. е. детонационная волна сближается с обычным скачком уп-
уплотнения.
Изучим стационарный режим детонации.
Изложенные соображения позволяют представить себе про-
процесс образования стационарной волны детонации в следующем
виде.
Обычно детонационная волна возникает как результат
местного взрыва в горючей смеси. В области взрыва развиваются
весьма высокие давления и от нее устремляется очень сильная
ударная волна. При прохождении через холодную горючую смесь
эта волна, как указывалось выше, вызывает значительный разо-
разогрев газа и может довести его до воспламенения. Именно в этом
случае за фронтом ударной волны следует область горения, об-
образующая в совокупности с ударной волной волну детонацион-
детонационную. Так как вблизи центра взрыва скорость распространения
волны и интенсивность ее очень велики, то относительные ско-
скорости газа в начале области горения и в конце ее близки между
собой и существенно ниже критической скорости:
Яг ^ Яз ^ 1.
Однако с удалением от центра взрыва волна детонации ослаб-
ослабляется м скорость распространения ее Я1 падает. В связи с этим
происходит снижение температуры торможения в начале области
горения {Т*2) и рост приведенной скорости газа (Яг). При этом
увеличиваются относительный разогрев газа {АТ^/Т^ и ско-
скорость движения F8) продуктов сгорания (Яз). Очевидно, что,
когда детонационная волна ослабится настолько, что Яз подни-
§ 5. О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ 223
мется до критического значения (Хзкр = 1), дальнейшее снижение
скорости детонации окажется невозможным *).
Следовательно, процесс детонации, начавшийся со взрыва,
непрерывно ослабевает до тех пор, пока скорость распространен
ния не снизится до минимального значения, отвечающего на-
наступлению теплового кризиса в зоне горения. С этого момента
распространение детонационной волны приобретает устойчивый
стационарный характер.
Как было указано в § 4, дальнейшее ускорение и переход
в сверхзвуковую область возможны единственно при перемене
знака воздействия — в данном случае при переходе от выделе-
выделения тепла в зоне горения к отводу его, начиная от критического
сечения (тепловое сопло). Таким образом, наступление тепло-
теплового кризиса в зоне горения приводит к установлению стацио-
стационарных значений Яь Яг и Яз.
Мы можем определить приведенную скорость распростране-
распространения установившейся детонационной волны, подставив в уравне-
уравнение F0) значение Аз = 1. При этом
! f т\ Г Т*
G1)
или после освобождения от радикалов
?I
Заменяя Т3 = Тг -f- А Г*, получим также
AT*
G3)
Последние два выражения, так же как и уравнение F5),
сохраняют одинаковый вид при подстановке в них приведенных
скоростей Ai и Яг. Тем самым изменение температуры торможе-
торможения связывается здесь или со скоростью распространения дето-
детонации (Xi), или с максимальной скоростью распространения
зоны горения (Лг). Существенно, что максимальное значение %2
сохраняется вне зависимости от механизма зажигания, т. е. от-
относится как к детонационному, так и к нормальному распро-
распространению пламени.
Перейдем к вычислению скорости распространения волны.
Обозначим для краткости тепловую характеристику горючей
*) В отличие от этого простая ударная волна, образовавшаяся в резуль-
результате взрыва и распространяющаяся в инертной среде, по мере удаления
от центра взрыва полностью вырождается в волну акустическую.
224 гл- V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
смеси ft 1)
1 11
Из формул F9), G2) имеем
откуда квадрат приведенной скорости распространения волны
равен
G4)
В уравнении G4) оба знака перед корнем отвечают реаль-
реальным значениям приведенной скорости. Положительный знак со-
соответствует детонационному горению (Xi>l), т. е. скорости
распространения ударной волны. Отрицательный знак отвечает
распространению медленного горения. Следует заметить, что
формула G4) также и при отрицательном знаке пригодна для
детонации. В этом случае она связывает приведенную скорость
непосредственно за фронтом скачка уплотнения Хг (вместо К\)
с величиной
ft' = ДГ*/Г2 (вместо ft = AT7*/!7!).
В практически интересных случаях, когда ft > 1, вместо выра-
выражения G4) можно с ошибкой менее 2 % принять лриближенно:
а) для скорости распространения стационарной волны детона-
детонации
,2 2 + 4ft .
к — V
G5)
б) для предельной скорости распространения волны горения
^ = 2Т4Г G6)
Пользуясь известной связью между приведенной скоростью
и числом М, можно получить также аналогичные зависимости
числа М для волн детонации и горения от тепловой характери-
характеристики газовой смеси.
На рис. 5.19а и 5.196 изображены графики зависимостей
Я,1 = /(О) и Mi = F(ft)
1) По смыслу ата величина равна отношению количества выделившего-
выделившегося тепла к начальной энтальпии газа ft = QI(cvT\). Например, для холод-
холодной (Т\ & 300 К) смеси бензина с воздухом (при а « 1) ft « 6,5.
§ 5, О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ
225
для газовой смеси (при fc = l,4). Верхние ветви обеих кривых
(в сверхзвуковой области движения Х\ > 1, Mi > 1) отвечают
установившейся минимальной скорости распространения детона-
детонации, нижние ветви (в дозвуковой области %\ < 1, Mi < 1)— мак-
максимальной скорости горения, т. е. предельно возможной скоро-
скорости нормального распространения пламени.
Рис. 5.19а. Зависимость экст-
экстремальной величины приве-
приведенной скорости распростране-
распространения волны горения от тепло-
тепловой характеристики смеси:
1 — область нестационарной
детонации; 2 — стационарный
режим детонации, 3 — макси-
максимальная скорость горения,
4 — область нормального го-
горения
Мы приходим, таким образом, к единому представлению
о скорости распространения горения. При этом в сверхзвуковой
области (выше кривой) лежат значения, соответствующие не-
неустановившемуся режиму детонации, тогда как в дозвуковой
(ниже кривой)—бесчисленное множество значений, отвечающих
Рис. 5.196. Зависимость экст-
экстремальной величины числа Mi
для распространения волны
горения от тепловой характе-
характеристики смеси: 1 — область
нестационарной детонации,
2 — стационарный режим де-
детонации, 3 — максимальная
скорость горения, 4 — область
нормального горения
10
5
А
/
(/
*•'
У
//
/,
/\
/
А
у
7
7
7
/
/
У/
7
/\
/,
А
/
7
V
V
V/
'V
о
Л
/,
/,
/
/J
/,
7
V
V
//
/
V
/,
/,
/,
/
7
/,
/,
7
7
7
7
//
//
/
г/
7
7
/,
/,
/,
/
/
7
/ /
/,
/,
/
7
7
7
7
//
/,
7
7
/А
/,
/,
/,
/
7
7
у,
/,
/
7
7
7
//
7
//
/,
-И
7
7
Л
//
'Л
/,
Г
7,
7
7
Т/
/,
/,
7
7
7
7
//
/'
/,
/,
to
20
30
стационарному нормальному распространению горения при ма-
малых скоростях движения газа. Наконец, режимы, отвечающие
заштрихованной области (рис. 5.19а и 5.196), не могут быть
15 г. Н. Абрамович, ч. 1
226 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
реализованы в связи с явлением теплового кризиса (т. е. невоз-
невозможностью перейти через скорость звука при подводе тепла).
Именно этим, по-видимому, следует объяснить тот факт, что
переход от медленного горения к детонации, как показывают
опыты в трубах, всегда осуществляется скачкообразно.
Следует отметить одну интересную особенность полученных
кривых. Как видно из графиков, достаточно самого незначитель-
незначительного теплового воздействия, чтобы предельная скорость горения
стала существенно ниже, а скорость детонации существенно вы-
выше звуковой.
Дадим расчет давлений при детонации и горении.
Расчет предельного скачка разрежения во фронте пламени,
достигаемого при тепловом кризисе, можно произвести посред-
посредством уравнения импульсов. В случае Яз = Мз = 1 имеем 1)
но на этом режиме
3
откуда на основании зависимости G1) получается
1 - ? G7>
3
Таким образом, предельное падение давления в газовом по-
потоке в области горения равно
-А = 1 + Лу i__;f G8)
или на основании выражения G2)
Т) ' л' I л 2 ' л 2 i /< * ^ '
') Чтобы получить это выражение, напишем уравнение импульсов (94)
гл. I для нашего случая:
Р2 — РЗ
ИЛИ
во
§ 5. О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ 227
При этом значение приведенной скорости как в детонационном,
так и в предельном случае нормального горения берется из соот-
соотношения G4).
Если воспользоваться равенством G5), то найдется следую-
следующая приближенная формула падения давления во второй обла-
области волны детонации (для О* > 1):
i+
Р3 1^
Соответственно равенство G6) приведет к приближенному
выражению перепада давлений для предельной скорости нор-
нормального горения:
? #& (8D
Изменение давления при прохождении через всю область де-
детонации, состоящую из адиабатического скачка уплотнения и
зоны горения, получится при делении равенства F3) на G9):
Весьма простые зависимости получаются для изменения плот-
плотности газа. При предельной скорости нормального горения на
основании уравнения неразрывности и выражений G7) и G2)
получаем
^ = W-± = _L_ = 2Х* (83)
Р W ^l + i Xj + l'
При стационарном режиме детонационного горения, исполь-
используя равенства A6) гл. III и F2), имеем
(84)
pi р2 Pi я; + 1
Остановимся более подробно на некоторых общих свойствах
одноразмерных неадиабатических волн и дадим, в частности,
расчетные формулы для определения абсолютной скорости рас-
распространения волны. Из уравнений импульсов и неразрывности
следует, что в любом случае ударной волны (в пренебрежении
силами трения) справедливо следующее соотношение:
^р = wLwz. (85)
С другой стороны, уравнение теплосодержания с учетом урав-
уравнения состояния идеального газа дает для скачка давления при
15*
228 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
любом подводе (или отводе) тепла1)
Г5г = в»р + р4р" Dф-<4ф)- (86)
Из уравнений (85), (86) и неразрывности нетрудно вывести со-
соотношение между скоростями для произвольного скачка давле-
давлений:
ЩЩ (wi — ws) = Яз2кр^1 — a21KV>w3. (87)
В частном случае, когда подвод тепла отсутствует и #iKp =
= ^зкр» мы снова получаем соотношение A6) гл. III для адиаба-
адиабатического скачка уплотнения.
В интересующем нас случае установившейся детонации (или
распространения горения с предельной скоростью), когда насту-
наступает тепловой кризис, т. е. Яз = 1 и 1#з = язкр, уравнение (87)
принимает вид
(w± — азкрJ = Язкр — а?Кр, (88)
причем для детонации
для медленного горения
Как и в приведенных ранее безразмерных уравнениях, мы имеем
здесь два решения:
w, =
у ^зкр ^1кр»
отвечающих минимальной скорости распространения детонации
(при знаке +) и максимальной скорости медленного горения
(при знаке —).
Полученные общие соотношения применимы к любым не-
неадиабатическим скачкам давления вне зависимости от меха-
*) Напишем уравнение теплосодержания B5) гл. I для газа до и после
ударной волны
о о
с (т* _Т \ — Wl с (т^ — ТЛ— W*
или, заменяя из уравнения состояния Т = p/(Rp),
Вычитая из второго уравнения первое, с учетом равенств
2ср— 2к ' акр""Л +
и закона импульсов, получим (86).
§ 5, О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ 229
низма выделения тепла. Мы видели, что в рассмотренных выше
двух случаях распространения фронта пламени непосредственно
тепловой скачок (т. е. зона горения) представлял как при дето-
детонации, так и при нормальном горении скачок разрежения в до-
дозвуковом течении. Нетрудно указать и случай теплового скачка
сжатия в сверхзвуковом потоке. Мы имеем в виду хорошо из-
известные скачки конденсации, сопровождающейся переходом от
большей сверхзвуковой скорости к меньшей, но все еще сверх-
сверхзвуковой скорости. И в этом случае приведенные выше уравне-
уравнения и выводы остаются справедливыми.
В заключение исследуем движение газов за фронтом волны.
Выше были получены основные соотношения, характеризую-
характеризующие газовый поток, проходящдй через область скачка детона-
детонации или пламени с неподвижным фронтом, т. е. в обращенной
схеме. Рассмотрим теперь, какой вид приобретут все соотноше-
соотношения, если перейти к нормальной схеме, когда газ неподвижен,
а в нем распространяется волна детонации или горения со ско-
скоростью w\. В этом случае за фронтом ударной волны следуют
еще не воспламенившиеся частицы газа со скоростью
а позади области горения движутся продукты горения со ско-
скоростью
Wr = W\ — Wz,
где под wx и wr мы понимаем абсолютные скорости. Нетрудно
видеть, что в случае детонации
W^l > ^3 > ^2»
т. е. фронт пламени и продукты горения движутся в том же на-
направлении, что и фронт ударной волны, но только скорость ча-
частиц во фронте пламени выше, чем в продуктах горения:
wx > wr.
В случае нормального горения, когда
величина wv получается отрицательной, т. е. направления дви-
движения продуктов горения и фронта пламени противоположны.
Как было установлено, при стационарном режиме детонации
и при предельной скорости нормального горения имеет место ра-
равенство
и?з = азкр, или Хз = 1,
вследствие чего в этих режимах скорость движения продуктов
горения равна
230 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
где согласно полученной выше зависимости (89)
= а3кр ± У а\^ — а
Пкр*
Отсюда приходим к следующему выражению для скорости рас-
распространения продуктов горения в случаях стационарной дето-
детонации и предельного режима нормального горения:
шг = ±|/а2зкр-а21кр. (90)
Знак плюс отвечает детонации, знак минус — нормальному го-
горению.
Найдем теперь значения приведенных скоростей. Для фронта
ударной волны получим Х\ = wila\KV. Для частиц, следующих
непосредственно за фронтом ударной волны,
(91)
а1кр
так как а\кр = а2Кр. Наконец, для продуктов горения согласно
(90) имеем
Отсюда с помощью G2) находим
(92)
Положительные значения К получаются при детонации (К\ > 1),
отрицательные — при нормальном горении (A,i<l). В случае
Л,1 = 1 имеем К = 0, т. е. при движении волны со скоростью
звука газ остается неподвижным, что вполне соответствует фи-
физической природе явления 1).
Наибольшее значение скорости продуктов нормального горе-
горения Яг = — 1 получается, естественно, в неподвижной смеси
бесконечно большой калорийности [Ф = <», т. е. К\ = 0, см. G6)].
Максимум скорости продуктов детонации достигается также
при бесконечно большой калорийности. по G5) О1 = оо, %\ =
]с j jl
^fcZTl Г но в этом случае, как нетрудно видеть из (92), он равен
лг = -г.
1) Выше [см. G4)] было показано, что %\ = 1 получается только при
нулевой калорийности смеси, когда детонация и горение вырождаются в
обычные звуковые волны.
§ 5. О РАСПРОСТРАНЕНИИ ДЕТОНАЦИИ И ГОРЕНИЯ 231
Итак, абсолютная скорость движения сгоревших частиц всеь-
да меньше скорости звука. Этот результат справедлив как при
нормальном горении, так и при детонации.
Между тем, как нетрудно видеть из (91), скорость несгорев-
ших частиц (в начале зоны горения) в случае детонации может
быть больше звуковой; получается это на режиме
Ях = кг — ^- > 1, т. е. при Х\ — %г — 1 > 0.
Решая это неравенство, получаем
1,62 и Мх>2.
Максимальное значение этой скорости, очевидно, получается на
режиме Mi = оо и Ai = ^—т, оно равно
л 1/Л-Г1 1 / # — 1
лх max — r
Если к = 1,4, то Xxmax = 2,04 и Mxmax = 3,4.
Интересный результат получится, если связать абсолютные
скорости газа в начале и в конце зоны детонационного горения:
wr К азкр *
Отсюда, используя зависимости (91), (92) и G2), находим сле-
следующее простое соотношение:
wx = 2wr, (93);
т. е. при детонации скорость частиц перед фронтом пламени
всегда вдвое выше скорости сгоревших частиц.
Давления как за фронтом ударной волны (/?г), так и в конце
зоны горения (/?з), очевидно, не изменяются от того, что мы об-
обратили движение, т. е. могут быть определены по формулам F3)
и G9). Можно, однако, посредством (92) придать формуле G9)]
следующий особенно простой вид:
РЛ. = 1 ± kXT. (94)
Здесь минус берется при нормальном горении, знак плюс — при
детонации. В предельных случаях нормального горения (КГ =
= — 1) и детонации (К = 1/к) получаем соответственно для мак-
максимальной скорости нормального горения
232 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
и для минимальной скорости детонации
у = 2. (96)
При встрече продуктов горения с плохообтекаемым телом
произойдет повышение давления до величины р5, которая для
обоих этих режимов найдется из одного и того же выражения,
соответствующего изоэнтропийному процессу сжатия:
Более значительное повышение давления произойдет при
остановке частиц еще не загоревшегося газа, движущихся со
скоростью wx. На режимах Хх < 1 действует та же изоэнтропи-
ческая зависимость:
/QQ4
(98)
Для сверхзвуковых режимов (Хх>1), когда торможение начи-
начинается с прямого скачка уплотнения, переводящего поток к до-
дозвуковой скорости Я,х = 1 Ах и давлению, определяемому форму-
формулой F3),
(99)
имеем при полном торможении
или окончательно
В предельном случае ^i = jrirp т. е. Ях = 2,04 (при А: = 1,4),
получим предельное повышение давления при торможении
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 233
или по сравнению с давлением в продуктах горения
^«30.
При встрече газов, следующих непосредственно за фронтом
детонационной волны, с остроносым препятствием может воз-
возникнуть вместо прямого косой скачок уплотнения. В последнем
случае повышение давления при торможении газов оказывается
меньшим.
§ 6. Расчет газовых течений
с помощью газодинамических функций
Выше были установлены количественные соотношения ме-
между давлением, плотностью, температурой и приведенной ско-
скоростью газового потока, а также параметрами торможения для
некоторых течений газа. Эти уравнения содержат параметры
газа, в частности приведенную скорость Я, в высоких и дробных
степенях, поэтому преобразование их, получение явных зависи-
зависимостей между параметрами в общем виде и решение численных
задач часто представляют значительные трудности. Вместе с тем,
рассматривая различные уравнения газового потока, выведен-
выведенные, например, в § 4 гл. I и § 4 гл. V, можно заметить, что ве-
величина приведенной скорости к входит в них в виде нескольких
часто встречающихся комбинаций или выражений, которые по-
получили название газодинамических функций. Этим функциям
присвоены сокращенные обозначения, и значения их в зависи-
зависимости от величины X и показателя адиабаты к вычислены и
сведены в таблицы.
Расчет газовых потоков при помощи таблиц газодинамиче-
газодинамических функций получил широкое распространение и является
в настоящее время общепринятым. Помимо сокращения вычис-
вычислительной работы, преимуществом расчета с использованием
газодинамических функций является значительное упрощение
преобразований при совместном решении основных уравнений,
что позволяет получать в общем виде решения весьма сложных
задач. При таком расчете более четко выявляются основные ка-
качественные закономерности течения и связи между параметрами
газового потока. Как можно будет видеть ниже, использование
газодинамических функций позволяет вести расчет одномерных
газовых течений с учетом сжимаемости практически так же про-
просто, как ведется расчет течений несжимаемой жидкости.
Рассмотрим основные из применяющихся в настоящее время
газодинамических функций и на ряде примеров проиллюстри-
проиллюстрируем использование их для решения различных задач.
Первая, простейшая группа газодинамических функций вве-
введена для упрощения записи соотношений между параметрами
234
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
в потоке, параметрами торможения и приведенной скоростью
газа. В § 3 гл. I путем преобразования уравнения теплосодержа-
теплосодержания была получена формула D2)
т*
к +1Л '
связывающая температуру торможения Т* с температурой в по-
потоке Т ж приведенной скоростью %. Обозначим
l — ~jX2 = r(X). A01)
В § 4 гл. I были получены выражения G2) и G3) для отно-
отношения давления и плотности в потоке к полному давлению и
Рис. 5.20. Графики газодинамических функций т(А,), г (к), л (К) при
к *¦ 1,4
плотности изоэнтропически заторможенного газа. Введем для них
обозначения
h__
"\ (Ю2)
A03)
Связь между газодинамическими функциями т(Х), я (к) и г (К)
вытекает из очевидного соотношения между величинами р, р и Т:
л (Я)
A04)
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 235
Следует заметить, что уравнения A01), A02), A03) связывают
параметры газа в одном и том же сечении потока и справед-
справедливы независимо от характера течения и происходящих в газе
процессов: переход от параметров в потоке к параметрам за-
заторможенного газа по определению происходит по идеальной
адиабате. Характер изменения газодинамических функций т(Л),
я (X) и г(Х) в зависимости от X показан на рис. 5.20: с увеличе-
нием л от нуля до максимального значения Атах = у j—t
функции х(Х), п(Х) и г(Х) монотонно уменьшаются от единицы
до нуля. Это вполне соответствует и их физическому смыслу:
при весьма малых скоростях (X -*¦ 0) параметры в потоке прак-
практически не отличаются от параметров полностью заторможен-
заторможенного газа; с увеличением скорости до предельного значения
(М ->¦ оо, Х-*- Хтгх) температура, давление и плотность газа при
конечном значении параметров торможения стремятся к нулю.
Располагая графиками или таблицами, в которых для каж-
каждого значения X приведены значения функций л(Х), е(Х), т(Х),
можно быстро определять параметры торможения по параме-
параметрам в потоке и наоборот. Такие таблицы для значений к = 1,40
и 1,33 приведены на с. 569—586. Имеются (с. 587, 588) вспомо-
вспомогательные графики, которыми можно пользоваться вместо таб-
таблиц, если не требуется высокая точность вычислений.
Пример 1. В сечении 1 дозвуковой части идеального сопла Л аваля
известны: давление в потоке />i = 16-105 Н/м2, температура торможения
Г* = 400 К, приведенная скорость Х\ = 0,6. Требуется определить приве-
приведенную скорость Яг и давление газа в сечении 2, где температура Т2 рав-
равна 273 К.
Поскольку температура торможения и полное давление газа в рассмат-
рассматриваемом идеальном сопле не меняются, то Г2 = Тг и Р2== Р±- Исполь-
Используя первое равенство и соотношение A01), записываем
Т Т
Подставив сюда заданные значения Гг и Г1? находим т(Яг) =0,6825 и по
таблицам определяем (при к = 1,40) Я2 = 1,38. Таким образом, искомое
сечение находится в сверхзвуковой части сопла. Далее используем условие
постоянства полного давления в сопле. Выражая полное давление через
давление в потоке и функцию л(Х) согласно A02), получаем
или р* =
Для Xi = 0,6 и %2 = 1,38 в таблицах находим значения функций я (Я) и
определяем
р2 =16.105.^
Найдем теперь, какова при тех же исходных данных будет темпера-
температура газа в сечении сопла 5, где давление газа равно атмосферному'
236 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
рх= 1,01-105 Н/м2. Записываем
я(Х3)=;1=А или я(*3) = Рз^
Отсюда находим
а затем из таблиц определяем величину Хз = 1,855. Этому значению при-
приведенной скорости в таблице соответствует т(^3) =0,4265. Далее легко на-
находим температуру газа в сечении 3
Г3 = Г*т(Я3) = 400-0,4265 =170,6 К.
Таким же образом решаются и другие задачи, связанные с нахождением
зависимости между параметрами газа в различных сечениях потока.
Рассмотрим далее две газодинамические функции, которые
используются в уравнениях неразрывности потока. Подставим
в выражение секундного расхода газа G = pwF через сечение пло-
площади F соотношения, выражающие плотность газа р и скорость
потока w через параметры торможения р* и Г* и приведенную
скорость Я:
- о* U -
Тогда получим
1 Г
Умножив обе части этого выражения на акр = у
после сокращения имеем
; A06)
Это уравнение связывает расход газа в данном сечении с пол-
полным давлением, критической скоростью звука й некоторой функ-
функцией приведенной скорости
где е (Я)—введенная выше газодинамическая функция A03).
Новая Газодинамическая функция q(X) определяется как вели*
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ
237
чина, пропорциональная произведению Кг (X):
1 1
q (Я) =
X (l - j
A07)
Коэффициент пропорциональности выбран так, чтобы при; % = 1
иметь д(А,)=1. Вследствие этого газодинамическая функция
12 IS 2,0 Л Д^
Рис. 5.21. Графики газодинамических функций <?(Я), у(У) при /с = 1,4
5 (А,) приобретает физический смысл безразмерной плотности
тока:
где (р^)кр — максимальное значение плотности тока (при за-
заданных параметрах торможения), соответствующее течению со
скоростью звука. Действительно,
1
Р* Р
кр"'кр
[
График функции д(Я) приведен на рис. 5.21. При увеличении
приведенной скорости К от нуля до единицы величина q(X)
растет от нуля до своего максимального значения #(А,)= 1, а да-
далее вновь снижается до нуля при значении к = Ятах. Таким об-
образом, плотность тока максимальна при #(А,)=1 и снижается
как с уменьшением, так и с увеличением скорости по сравнению
с критическим значением. Одно и то же значение функции (Х)
238
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
соответствует двум возможным значениям приведенной скоро-
скорости, одно из которых больше, а другое меньше единицы.
Подставляя в выражение A06) функцию #(А,), имеем
A08)
Заменяя в A08) величину а„р ее значением, получаем следую-
следующую формулу для вычисления расхода газа (см. также § 1
гл. IV):
A09)
где
В нижеследующей таблице приведены значения L для раз-
различных значений А::
к
L
1,67
0,725
1,4
0,685
1,35
0,676
1,33
0,673
1,30
0,667
1,25
0,658
1,10
0,628
Для воздуха (к = 1,4, R = 287,3 Дж/(кг-К)) численный коэф-
коэффициент в уравнении A09) т = 0,0404 [м • с • К05]. Для вых-
выхлопных газов в турбореактивных двигателях (к = 1,33, R =
= 288,3 Дж/(кг-К)) т = 0,0396. Для пороховых газов в сред-
среднем можно считать т = 0,035.
При течении со скоростью звука д(Я)= 1 и уравнение A09)
сводится ^полученному^ ш._ ГУ-ДЩ^жвнию (8) для._вычисле-
ния расхода газазёрёз „сопло Лаваля по параметрам газа в кри-
критическом сечении сопла,
При решении ряда задач требуется связать расход газа не
с полным, а со статическим давлением в потоке. Такую связь
легко получить из выражений A08) или A09), если заменить
в их правых частях величину полного давления согласно вы-
выражению
р
Тогда получаем соотношения
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 239
(Ill)
у т"
где функция
1
,.т _*(*)/* + *
k-i 2
является второй газодинамической функцией, с помощью кото-
которой можно вычислять расход газа (см. рис. 5.21). Значения ее,
так же как и значения функции q(X) для различных значений к
приведены в таблицах (Приложение II) и на графиках (Прило-
(Приложение III). С увеличением X функция у (X) монотонно возрастает,
причем при X -*¦ Хтах у(^)~^°°- Как формула A09), так и фор-
формула A11) выражают расход газа через параметры его состоя-
состояния в рассматриваемом сечении потока, и потому справедливы
независимо от характера процессов, происходящих в потоке газа.
Формулами A09) и A11) удобно пользоваться при составлении
уравнений неразрывности для газового потока, причем для каж-
каждого сечения может быть выбрана та из формул, которая лучше
соответствует заданным или искомым величинам.
Выражения A09)» A11) и составленные при их помощи урав-
уравнения неразрывности непосредственно приводят к ряду зависи-
зависимостей, выведенных ранее более сложным путем, а также по-
позволяют достаточно просто решать разнообразные задачи. При-
Приведем несколько примеров расчета.
Пример 2. Определить зависимость между площадью какого-либо
сечения идеального сопла Лаваля и приведенной скоростью потока в этом
сечении, т. е. найти закон изменения площади в сопле Лаваля. Так как для
любого сечения идеального сопла расход, полное давление и температура
торможения одинаковы, то из A09) следует Fq(X) = const. Так как для
F 1
критического сечения q(X)KV = 1, то Fq(X) = FKP или т;—= т, т. е. пло-
щадь сечения сопла изменяется обратно пропорционально значению функ-
функции q(X). В соответствии с графиком функции q(X) это означает, что с
увеличением скорости площадь уменьшается при дозвуковых скоростях и
увеличивается при сверхзвуковых скоростях, имея минимум при X = 1.
Пример 3. На участке цилиндрической трубы между двумя сече-
сечениями 1 и 2 в результате гидравлических потерь (трение, местные сопро-
сопротивления) снижается полное давление движущегося газа. Потери полного
давления между сечениями 1 ж 2 оцениваются величиной коэффициента со-
сохранения полного давления о = р2/р1<1. Определить характер измене-
изменения скорости и статического давления газа в трубе при отсутствии тепло-
теплообмена с внешней средой. Запишем, воспользовавшись формулой A09), усло-
условие равенства расходов газа в сечениях 1 и 2:
240 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Поскольку в данном случае Fx = F2 и Г* = Г*, то
Отсюда по заданным значениям Xi и о можно с помощью таблиц газо-
газодинамических функций определить Х2. Полученный результат справедлив
как для дозвуковых, так и для сверхзвуковых скоростей потока. Так как
а < 1, то q(l2) > q(hi).
Из этого неравенства следует (см. график функции д(А,) на рис. 5.21),
что при наличии гидравлических сопротивлений (при G = const, F = const,
Т* = const) скорость дозвукового потока по длине трубы возрастает, а ско-
скорость сверхзвукового потока уменьшается.
Чюбы определить изменение статического давления, можно сравнить
между собой величины рг = р*п (Я2) и р2 = р*п (Я2). Однако более на-
наглядно искомый результат может быть получен из условия равенства рас-
расходов газа, если воспользоваться при этом выражением A11):
V|g(*l) PlFf»^t) Р, У (К)
или
Так как функция у (А,) возрастающая, то отсюда заключаем, что при нали-
наличии сопротивления, в соответствии с найденным выше изменением приве-
приведенной скорости, статическое давление будет уменьшаться, если скорость
потока дозвуковая, и увеличиваться, если скорость сверхзвуковая.
Пример 4. Определить приведенную скорость Я2 и статическое дав-
давление воздуха р2 на выходе из диффузора, если известно, что на входе в
диффузор полное давление р* = 3-Ю5 Н/ма, приведенная скорость Х\ =
= 0,85, отношение площадей выходного и входного сечений F2/Fi = 2,5 и
коэффициент сохранения полного давления o^/^/^i =0,94. Для решения
задачи записываем уравнение неразрывности, пользуясь формулой A09):
Пренебрегая теплообменом через стенки диффузора, имеем Г* = Г* и,
1 ^i
следовательно, ?(y = "a"F?(^i)' ^° та^лицам для Xi = 0,85 находим
q(l{) = 0,9729. Тогда q(l2) = 0,425 • 0,9729 = 0,413, чему соответствует
ta = 0,27 и л(Я2) = 0,9581. Из соотношения A02) имеем р2 = р*л (К2) =
= ор*±л (Х2) или
р2 = 0,94 . 3 • 105 • 0,9581 = 2,7 • 10Ч1/м2.
Пример 5. При испытании компрессора в выходном его сечении,
площадь которого F = 0,1 м2, измерены статическое давление р = 4,2 X
X Ю5 Н/м2 и температура торможения воздуха Т* = 480 К. Определить пол-
полное давление воздуха, если его расход G = 50 кг/с.
Из выражения расхода A11) определяем функцию у (X) по известному
значению статического давления воздуха:
G УТ* 50 Т/480
У W = 1^Г
0,0404-4,2.105.0,1
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 241
По таблицам газодинамических функций находим, что этому значению у(Х)
соответствуют величины X = 0,399 и л(Х) = 0,9101. Отсюда полное давле-
давление воздуха р* = р/п(Х) = 4,2 • 105/0,9101 = 4,61 • 105 Н/м2.
Если не пользоваться газодинамическими функциями, то подобные вы-
вычисления, которые часто делают при обработке экспериментальных данных,
приходится проводить более сложным методом, путем последовательных
приближений.
Рассмотрим газодинамические функции, которые используются
в уравнении количества движения газа. Сумму секундного коли-
количества движения и силы давления газа в рассматриваемом по-
поперечном сечении потока принято называть полным импульсом
потока /:
( ±). (ИЗ)
Если в A13) подставить соотношения
w = Яакр;
Р ЯТ РТ* М ^ ~~ 1 J ] к -\- 1 2 / л к — { «2
то получим
Gw + pF = СЧ JuzKp + 2fe "PH ~FT1^2) г A14)
После раскрытия скобок и упрощений приводим выражение A14)
к виду
Gw -\- pF = "Г, GaKpZ (X), A15)
где
z(X) = X + ±. A16)
График газодинамической функции z(X) приведен на рис. 5.22.
Минимальное значение функции z(X) = 2 соответствует крити-
критической скорости течения (Х = 1). Как в дозвуковых, так и
в сверхзвуковых потоках z(X)>2; значениям z(X)<2 не соот-
соответствуют какие-либо реальные режимы течения. Легко видеть,
что при замене величины X обратной ей величиной X' = 1/Х зна-
значение функции z(X) не изменяется. Таким образом, одному зна-
значению z(X) могут соответствовать два взаимно обратных значе-
значения приведенной скорости X — одно из них определяет дозвуко-
дозвуковое, а другое — сверхзвуковое течение газа. Отметим также, что
функция z(X), в отличие от всех остальных газодинамических
функций, не зависит от величины показателя адиабаты к.
Выражение A15) для импульса потока значительно упро-
упрощает запись и преобразования уравнения количества движения
газа. Оно оказывается чрезвычайно полезным при решении пш-
16 Г. Н. Абрамович, ч. 1
242
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
рокого круга задач газовой динамики, как, например, в расчете
течений с ударными волнами, подводом тепла и охлаждением,
течений с трением, с ударом при внезапном расширении канала,
при расчете процесса смешения потоков, при определении сил,
о
о ом о,д iz i,6
Рис. 5.22. Графики газодинамических функций
Z,0 A W
к), /(Я), г(Х) при к = 1,4
действующих на стенки канала, при вычислении реактивной тя-
тяги и др.
Следующие два примера позволяют наглядно показать, на-
насколько упрощается решение задач при использовании соотно-
соотношения A15). В первом из них рассмотрена ранее решенная за-
задача (гл. III, § 1) о прямом скачке уплотнения, во втором— за-
задача о течении подогреваемого газа в цилиндрической трубе
(гл. V, §3).
Пример 6. Определить соотношения между параметрами газа до и
после прямого скачка уплотнения.
Связь между параметрами газа в скачке уплотнения мы выше уста-
устанавливали исходя из того, что при переходе через прямой скачок сохра-
сохраняются неизменными полная энергия, расход и импульс потока. Запишем
те же уравнения с использованием газодинамических функций.
Уравнение количества движения или импульса потока
PlFi = G2w2 + pqF2
с учетом выражения A15) принимает вид
Из уравнений сохранения расхода и полной энергии имеем
Gi = Gr T\ = T\, или акр1=акр2.
Учитывая это и сокращая соответствующие величины расхода и скорости
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 243
ввука в уравнении импульсов, получаем
Это уравнение имеет два решения: либо Я2 = Яь что соответствует безудар-
безударному течению с неизменными параметрами газа, либо
что соответствует прямому скачку. Такое же выражение — основное кине-
кинематическое соотношение теории ударных волн — было получено выше,
см. формулу A6) гл. III.
По известному значению приведенной скорости с помощью уравнения
неразрывности легко определяем изменение полного и статического давле-
давлений в скачке уплотнения. Так как F2 = F\ и T2 = TV то, используя фор-
формулы A09) и A11), можно уравнение неразрывности для потока газа до
и после скачка представить в виде
Отсюда, учитывая, что Х2 = 1Дь получаем р\/р\ = Я (^i) (i)
= 2/(^i)/#(lAi). Эти соотношения эквивалентны уравнениям B4) и B1)
гл. III, но получены значительно более простым путем.
Пример 7. Газ, движущийся в цилиндрической трубе, подогревается
от 400 К на входе в трубу до 800 К на выходе из нее. Приведенная скорость
потока на входе в трубу hi = 0,4. Требуется определить, пренебрегая тре-
трением, приведенную скорость потока после подогрева, а также изменение
полного и статического давлений в потоке.
Основное соотношение, определяющее закономерности течения газа в
цилиндрической трубе с подводом тепла, получим из уравнения количества
движения. В данном случае оно имеет вид
так как подвод тепла не связан с силовым воздействием на поток и силы
давления в начальном и конечном сечении являются единственными сила-
силами, вызывающими изменение количества движения газа. Заменяя выраже-
выражения для импульсов потока газа согласно соотношению A15) и считая, что
теплоемкость газа и показатель адиабаты при подогреве не изменяются,
получаем
а„„л СкЛ = avintkzCkX или z (X)=z(X,
Так как при Ki = 0,4 z(X,i) = 2,9, то
»<Ч>-'.» 1/31 = 2,05.
С помощью таблиц функции z(%) или непосредственным вычислением из
квадратного уравнения Я2 + 1Д2 = 2,05 определяем два возможных значе-
значения приведенной скорости на выходе: Х'2 = 0,8, Х2 = 1/х'2 = 1,25. Реаль-
Реальным будет только первое решение, поскольку подогревом невозможно пере-
перевести дозвуковой поток в сверхзвуковой (см. § 4).
Зная приведенную скорость потока Я2 = 0,8, легко определить измене-
изменение полного и статического давлений в процессе подогрева. Для этого, как
и в предыдущем примере, можно воспользоваться уравнением неразрывно-
16*
244 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
сти, из которого для данного случая (G = const, F = const) следует
^2_g(Mi A*'„0,5897 1/800 = о,875,
Р2_У(К)
р1 у{К) У Т* I»4!26 * 400 ' "
Таким образом, как полное, так и статическое давление в результате подо-
подогрева газа уменьшается. Полученное значение рг/pi = 0,648 и есть то соот-
соотношение статических давлений газа в начальном и конечном сечениях рас-
рассматриваемого участка трубы, которое необходимо создать, чтобы поддер-
поддержать при данном подогреве заданную величину приведенной скорости на
входе X = 0,4.
Уравнение сохранения количества движения позволяет установить не-
некоторые общие закономерности течения в цилиндрической трубе с подогре-
подогревом или охлаждением. Так, например, легко видеть, что с увеличением
отношения ^*/^1 значения функции z(K2) (при z(X\) = const) всегда
уменьшаются. В соответствии с характером функции z(X) (рис. 5.22) это
означает, что с ростом подогрева в дозвуковом потоке приведенная скорость
увеличивается, а в сверхзвуковом — уменьшается. В обоих случаях ско-
скорость потока будет приближаться к критическому значению %ч = 1, при
котором функция z(А,) принимает минимально возможное значение я(А,г) =
= 2. Этим обусловлено значение предельно возможного подогрева для за-
заданной начальной скорости (^/^l/max (^i)/^* Для принятых в данном
примере значений параметров предельная величина подогрева соответствует
7*2— 840 К. Из уравнения расхода можно определить отношение давлений
Р2/Ри необходимое для реализации такого режима при сохранении К\ = const.
При увеличении подогрева сверх найденного значения получим 2(^2) < 2,
что указывает на физическую невозможность такого подогрева при задан-
заданной скорости течения на входе.
Заменив в соотношении A15) произведение GukV его значе-
значением согласно A08) или A10), получим выражение для им-
импульса газового потока в первом случае через полное давление,
а во втором случае через статическое давление:
'1p*Fq(k)z(l)
Gw + PF = (щ-^1 pFy (ty z (К).
Введем обозначения для двух новых функций приведенной ско-
скорости Я, входящих в правые части этих выражений:
1 1
/ (*¦) = (Т1 (*>(*> ^2 + DI1
. fc-1 ,2
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 245
Подставляя эти обозначения, получаем окончательно
A19)
A20)
Функция г(Х) введена как величина, обратная произведению
y(X)z(X) с тем, чтобы облегчить пользование таблицами (произ-
(произведение у (X)z (X) быстро возрастает с увеличением X, стремясь
к бесконечности при X -+• Хтах; величина же г(Х) изменяется в
пределах от единицы до нуля). Графики функций f(X) и г(X)
приведены на рис. 5.22.
Уравнения A19) и A20) показывают ряд свойств импульса
газового потока. Обратим внимание на то, что в правой части
этих уравнений отсутствуют величины расхода газа и температу-
температуры или критической скорости. Из этого следует, что если при
заданной площади сечения F и приведенной скорости X полное
или статическое давление в потоке постоянно, то импульс сохра-
сохраняет постоянное значение независимо от температуры и расхо-
расхода газа.
Физический смысл этого состоит в том, что при изменении
температуры (или температуры торможения) газа при X = const
скорость течения изменяется прямо пропорционально, а рас-
расход — обратно пропорционально корню квадратному из темпера-
температуры, так что произведение Gw остается постоянным. Отметим,
что функция f(X) в области дозвуковых и небольших сверхзву-
сверхзвуковых скоростей изменяется очень мало (приблизительно на
10% в интервале X = 0,55 -г-1,35). Отсюда согласно A19) сле-
следует, что импульс газового потока при постоянных полном дав-
давлении и площади сечения слабо зависит от величины X в широ-
широком диапазоне ее изменения и определяется в основном величи-
величиной произведения p*F.
Выражения A19) и A20) для импульса газа очень удобны
при решении задач, связанных с определением сил, действующих
со стороны газа на стенки канала, что необходимо, в частности,
при вычислении реактивной тяги различных двигательных ус-
установок.
Для реактивной тяги ракетного двигателя выше (§ 8 гл. I)
было получено выражение
Эта же формула определяет тягу воздушно-реактивного двигате-
двигателя любого типа при работе на месте, когда начальное количество
движения воздуха, поступающего в двигатель, равно нулю. Пре-
Преобразуем эту формулу при помощи полученных выше соотноше-
соотношений, для чего в ее правой части заменим выражение импульса
газа в выходном сечении сопла согласно формулам A19) и
246 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
A20). В первом случае получаем
*-p*Fa ИЛИ P = PnFa[Jtcf(K)—l), A21)
где пс = pl/pn — так называемое располагаемое отношение
давлений в сопле. Точно так же можно получить второе выражение
где N = pJPh — так называемая степень нерасчетиости сопла,
т. е. отношение статического давления газа на срезе сопла к ат-
атмосферному давлению.
Формула A21) весьма удобна для вычисления реактивной
тяги и широко применяется в расчете двигателей. Приведенная
скорость Ха определяется типом реактивного сопла и располагае-
располагаемым отношением давлений. Если сопло выполнено нерасширяю-
нерасширяющимся и отношение давлений превышает критическое значение,
то Ха=1\ для сверхзвукового сопла Ka = KvaC4 при всех значе-
значениях яс, больших расчетного значения, и в значительной части
диапазона jtc < лс Расч- Отсюда следует, что в широком диапазоне
режимов современных двигателей К = const, и формулой A21)
определяется линейная зависимость реактивной тяги от распо-
располагаемого отношения давлений пс, так как /(Ха)= const. Напом-
Напомним, что и при Ка Ф const функция f(k) весьма мало изменяется
в значительной области до- и сверхзвуковых скоростей.
Формула A22) удобна для вычисления тяги на режимах,
когда статическое давление на срезе сопла равно атмосферному
и N = 1. Такие условия существуют, в частности, при дозвуковой
скорости истечения газа из сопла, а также при работе сверхзву-
сверхзвуковых сопел на расчетном режиме.
Отметим, что для вычисления реактивной тяги согласно A21)
и A22) не требуется знать расход газа и его температуру. Из-
Изменение температуры, как видно из A21) и A22), при ра =
= const, p* = const и Fa = const вообще не влияет на величину
тяги, что связано с взаимно обратной зависимостью скорости ис-
истечения и расхода газа от температуры.
Выражения A21) и A22) могут быть применены также для
вычисления тяги воздушно-реактивных двигателей в полете; при:
этом з правой части необходимо вычесть так называемый вход-
входной импульс потока воздуха GBwH, где GB — расход воздуха,,
ам?н- скорость полета (см. § 8 гл. I).
Рассмотрим примеры использования приведенных выражений
реактивной тяги.
Пример 8. Определить, как зависит величина реактивной тяги от*
приведенной скорости газа на выходе из сопла при лс = const.
Из формулы A21) непосредственно следует, что если Fa = const и яс =
= const, то зависимость тяги от приведенной скорости Яа определяется:
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ
247
изменением функции f(X). При этих условиях, однако, с изменением X
изменяется и расход газа.
Больший практический интерес представляет другой случай изменения
приведенной скорости Яа, когда секундный расход и начальные параметры
газа сохраняются постоянными. Это условие может быть реализовано, если
при постоянной площади критического сечения сверхзвукового сопла FK9
изменять площадь выходного сечения Fa. Характер зависимости тяги от
величины Ха в этом случае позволит опре-
определить рациональную степень расширения р- ?
сопла для двигателя с заданными пара-
параметрами и расходом газа. Уравнения A22)
и A21) не вполне удобны для такого рас-
расчета, так как содержат две переменные ве-
величины Ха и Fa. Поэтому преобразуем
уравнение A21), заменив в нем величи-
величину Fa с помощью выражения расхода A09)
1,4
F —
а
С,8
Учитывая соотношение между функциями
/(A) q(X) и z(X), получаем
р =
а* кр
¦5Р
¦4
-3
¦2
-1 *
ItL. /
FKp ч/
—^
/ \
/ ^
Ha расчетном режиме истечения газа, т. е.
при расширении до атмосферного давле-
давления, приведенная скорость определяется
из соотношения
1,2 1,4 1,6 7,8 2,0 2,2 Яа
Рис. 5.23. Изменение тяги дви-
двигателя в зависимости от при-
приведенной скорости на выходе
из сопла при постоянных на-
начальных параметрах и расхо-
расходе газа (к примеру 8)
По этому значению %а отыскивается расчетная степень расширения сопла
FJFKv = l/q(%a) и величина реактивной тяги на расчетном режиме. В дан-
данном расчете потери полного давления между сечениями FKP и Fa не учи-
учитываются.
Пусть к = 1,33 и яс = 25; тогда на расчетном режиме работы сопла
M^a) = i=°>04> К = 1&' Я(К) = °>279> 2{К) = 2Л77.
Площадь выходного сечения такого сопла равна FKV/q(Xa) = 3,58FKP,
а тяга Р = 1,417 P^FK^. Значения Р при других значениях ка, т. е. дру-
других значениях Fa, определяются с помощью таблиц. Результаты таких рас-
расчетов приведены на рис. 5.23. Там же показаны значения FJFKV для каж-
каждого значения %а. Из графика видно, что наибольшее значение тяги полу-
получается при полном расширении газа в сопле, т. е. при расчетном режиме
истечения. Однако характер функциональной зависимости тяги от приведен-
приведенной скорости таков, что даже при заметном снижении Ха и FJFKV по срав-
сравнению с их значениями на расчетном режиме тяга уменьшается незначи-
незначительно. Это позволяет в некоторых случаях применять сопла с неполным
расширением газа, а при небольших сверхкритических отношениях давле-
давлений Р*а/Рн использовать даже простые нерасширяющиеся сопла, в которых
ha = 1,0. Если учесть, что в сопле с неполным расширением будут меньши-
меньшими потери трения, то снижение тяги по сравнению с расчетным режимом
будет еще меньшим.
248
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Наряду с этим, как видно из рис. 5.23, при Яа > Храсч тяга резко умень-
уменьшается, т. е. сопло с перерасширением газа применять нецелесообразно,
если даже не учитывать повышенных потерь трения в нем и возможности
образования скачков уплотнения при уменьшении величины лс.
При истечении газа в пустоту (рн = 0) величина тяги изменяется про-
пропорционально значению функции z(X), т. е. монотонно увеличивается с ро-
ростом Ка > 1. Действительно, в этом случае расчетным режимом является
^a
= о, xn =;
кр
ПК)
= оо.
Поскольку площадь выходного сечения сопла нельзя сделать бесконечно
большой, то такой расчетный режим не может быть реализован. При любом
конечном значении FJFKV тяга двигателя, работающего в пустоте, будет
меньше теоретически возможного значения. Однако из графиков функций
z (Я) и q(X) видно, что при значительном уменьшении FJFKV снижение тяги
получается не очень большим. Так, если вместо FJFKV = оо принять (при
к = 1,33) FaIFKV = 10, q(Xa) = 0,1, К = 2,208, то тяга по отношению к мак-
максимальному теоретическому значению (при Ка = Яшах = 2,657) составит
MM 2,661
~ 3,033
= 0,88;
при Fu/FkV = 20, т. е. при q(K) = 0,05 и К = 2,313, P/Pmax = 2,745/3,033 =
= 0,905.
В следующем примере рассматривается задача о течении сжимаемого
газа при внезапном расширении канала, встречающаяся в ряде практиче-
практических вопросов. Выше (§ 5 гл. I) мы
решили эту задачу для потока с ма-
малыми скоростями, когда можно бы-
было пренебречь изменением плотно-
плотности газа.
Пример 9. Для измерения
расхода воздуха в трубопроводе на
прямом его участке установлено
мерное сопло с площадью проходно-
проходного сечения F2, равной 0,45 площади
трубопровода Fi=F3 (рис. 5.24).
Требуется определить потери пол-
полного давления, возникающие в пото-
потоке за соплом вследствие внезапного
расширения канала, а также приве-
приведенную скорость Я3 после выравни-
1
^
1
и
щ
3
2\
3
Рис. 5.24. Схема сопла для измере-
измерения расхода газа в трубопроводе
(к примеру 9)
вания поля скоростей, если по ре-
результатам измерения давлений Ри Ар
известна приведенная скорость потока в сопле К2 = 0,52. Определить также
снижение статического давления в трубопроводе, вызванное установкой
сопла.
Запишем уравнение количества движения для участка потока между
сечениями 2 и 5, пренебрегая трением о стенки и учитывая, что при дозву-
дозвуковых скоростях воздуха в сопле статическое давление постоянно во всем
сечении 2:
G(w2—wz) = psFs — p2F3,
или
Gw3 + p3Fz — Gw2 — p2F2 = p2(F3 — F2).
Заменим теперь выражения импульсов согласно A15), а статическое
давление р2 выразим с помощью уравнения (НО). Уравнение количества
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 249
движения принимает вид
к + 1 [ к + 1 X^i r
Ga*
А ++ [ + X r
G i (h) (К)] l j Ga**
После сокращения получаем
Из этого уравнения по величинам Яг и F3/F2 определяется приведенная ско-
скорость Кз после расширения трубы. Отметим, что результат не зависит от
значений давления и температуры газа и мало меняется в зависимости от
показателя адиабаты к. Подставив в последнее уравнение заданные величи-
величины К2 = 0,52, z(l2) = 2,44, у(К2) = 0,859, F2/F3 = 0,45, получаем z(A,3) =
= 2,44 4-1,577 q g^g 1,22 = 4,68; отсюда по таблицам находим Яз = 0,225,
ъ) = 0,3475, у(Х3) =0,358.
Потери полного давления воздуха между сечениями 2 и 3 определяем
из уравнения неразрывности
С помощью таблиц
G —
отсюда
^3
Ут\
находим
F2 q(k2)
F3 Я (К)
V
0,45
" 0,
•0,7309
3475
= 0,948.
Чтобы определить изменение статического давления, необходимо предвари-
предварительно найти величину приведенной скорости потока в трубе перед соплом.
Запишем уравнение равенства расхода воздуха в сечениях 1 и 2, причем,
учитывая, что длина участка 1—2 невелика, очертания сопла плавные и
поток течет с ускорением, считаем полное давление воздуха в сечениях
1 и 2 одинаковым. В этом случае уравнение неразрывности принимает вид
Flq{'kl)==F2q(%2). Отсюда находим q(h) = 0,45 • 0,7309 == 0,329, Xi = 0,213,
г/(Tti) ===== 0,338. Легко видеть, что аналогично может быть получен резуль-
результат в случае, если между сечениями 1 и 2 существуют потери полного дав-
давления, оцениваемые коэффициентом о~х = р1/рх » величина которого извест-
известна. При этом получим
Изменение статического давления на всем участке между сечениями 1 и 3
можно определить из уравнения неразрывности
Ут\
Так как Г* = Т* и Fx = F3, имеем р3/р{ = у(Х0/у(Я,3) = 0,338/0,358 =
= 0,944.
250
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Такой результат можно получить также из соотношения
= а -
Так как Хз > Х\, т. е. я(Яз) < Jt(Xi), то отсюда видно, что вследствие увели-
увеличения скорости потока в трубе снижение статического давления здесь, как
и в других местных сопротивлениях при X < 1 и F^ = Fu получается не-
несколько большим, чем снижение полного давления. В данном случае ввиду
малости приведенных скоростей в трубе Х\ и Яз это различие невелико.
В следующем примере мы вновь вернемся к рассмотрению течения
подогреваемого газа в цилиндрическом канале. В отличие от анализа, про-
проведенного в § 3 гл. V и в примере 7 данного раздела, будет рассмотрен
случай, когда задан перепад давлений в потоке. Это определяет ряд особен-
особенностей течения, которые не могли быть выявлены выше, когда предполага-
предполагалось, что перепад давлений всегда достаточен для поддержания заданных
приведенных скоростей в начале и в конце трубы.
Пример 10. Форсажная камера турбореактивного двигателя пред-
представляет собой установленную за турбиной цилиндрическую трубу с соп-
соплом регулируемого сечения на выходе. В камере происходит горение допол-
дополнительно впрыскиваемого топлива, вследствие чего повышается температу-
температура газа. Пусть параметры потока газа на входе в камеру р* = 1,94» 105 Н/м2,
Г* =880 К, Ях = 0,4. Эти величины должны сохраняться постоянными
независимо от величины подогрева газа, иначе будет изменен режим рабо-
работы турбины и компрессора.
Определим максимально возможное увеличение температуры газа и
величину потерь полного давления в камере на этом режиме.
Заданными начальными параметрами потока определен расход газа.
Как можно видеть из выражения расхода A09), чем больше температура
Рис. 5.25. Схема форсажной камеры турбореактивного двигателя: а) исход-
исходное положение сопла, Ъ) раскрытое сопло (к примеру 10)
торможения на выходе из камеры, тем большей — при прочих равных усло-
условиях — должна быть площадь сечения сопла. Поэтому максимально воз-
возможный подогрев газа соответствует полному раскрытию сопла.
Допустим, что сопло выполнено таким образом, что при полном рас-
раскрытии площадь его выходного сечения равна площади камеры, т. е.
F3 = F2 = F\ (положение Ъ на рис. 5.25). Отношение полного давления на
входе в камеру к атмосферному давлению у Земли равно П = Р±/рн =
= 1,94-105/1,01-105 = 1,92. Это несколько превышает критическое
1,33): —f- =1,85.
значение (при А: = 1,33): I—^—) =1,85. Поэтому если бы полное
давление потока при подогреве газа сохранялось постоянным, то в выход-
§ 6. газодинамические функции 251
ном сечении скорость течения была равна скорости звука и Х3 = 1. Однако,
как мы видели выше (см. пример 7), при подводе тепла к потоку полное
давление его снижается, поэтому в данном случае может оказаться, что
р*/рн< 1,85 и скорость истечения будет дозвуковой.
Чтобы выяснить это, записываем уравнение количества движения по-
потока, выражая импульс в сечении 1 через известное полное давление Рг
по формуле A19), а в сечении 3 — через статическое давление рз A20),
причем пока полагаем, что давление рг равно атмосферному давлению рНу
т. е. режим истечения дозвуковой. Трением о стенки и изменением пока-
показателя адиабаты пренебрегаем:
Отсюда (при к = 1,33) находим
РК 1,01-105
Г W = ^ЖУ = 1.94-101-1.0822 °'483'
и далее по таблицам Я3 = 0,91, т. е. л(А,3) = 0,6048, /(Я3) = 1,2525,
*(Х3) =2,01.
Режим истечения газа действительно будет дозвуковым, сколь бы велик
ни был подогрев в камере: заданное полное давление газа, снижающееся
в процессе подвода тепла, недостаточно для создания звуковой скорости
истечения в атмосферу. Если бы полное давление р* было большим, на-
например р* = 2,4-105 Н/м2, то из последней формулы следовало бы
г(%з) = 0,390; это значение меньше критического, так как гA) =0,429.
Следовательно, при таком давлении режим истечения был бы критическим
и К3 = 1,0.
Найденное значение приведенной скорости потока на выходе из сопла
(Яз < 1 или Х3 = 1) позволяет найти все параметры течения. Для опреде-
определения температуры газа удобно воспользоваться, например, уравнением
импульсов A15), из которого следует
Это и есть предельное значение температуры торможения на выходе из
сопла. Если увеличить подогрев газа сверх этого значения, то снизится
скорость потока на входе в камеру.
Для того чтобы определить полное давление газа в выходном сечении,
в данном случае можно воспользоваться соотношением р* = Рн/п (к3) =
= 1,0М0б/0,6048 =1,68-10б Н/м2, которое справедливо при Я3 < 1, т. е.
при р3 = рп. Зпая р3, вычисляем коэффициент сохранения полного давления
а = рЦр1 = l,68-106/l,94-105 = 0,865.
Для определения изменений полного и статического давлений в процес-
процессе подогрева можно получить простые соотношения, если записать равен-
равенство импульсов газа в начальном и конечном сечениях в виде
Отсюда получаем
P3
252 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Эти соотношения справедливы при любом режиме течения газа. В част-
частности, для условий данного примера определяем а = 1,0822/1,2525 = 0,865.
Полученные для а и ръ1р\ выражения удобны для анализа характера
изменения давления, определения предельных потерь полного давления и
для получения некоторых других результатов, найденных более сложным
путем в § 3 гл. V.
Так, например, из уравнения для определения а следует, что подогрев
газа приводит к снижению полного давления как в дозвуковом, так и в
сверхзвуковом потоках. Действительно, поскольку при подогреве величина
приведенной скорости всегда приближается к единице (растет при X < 1 и
уменьшается при X > 1), то, согласно рис. 5.22, значение функции f(X) в
процессе подогрева всегда увеличивается f(X$) > /(^0 и о < 1. Так как
в области дозвуковых скоростей пределы изменения величины f(X) неве-
невелики B5 %), то коэффициент сохранения полного давления о при X < 1
не может быть ниже некоторой предельной величины
amin— /A) — 1,2591 — u»/yD l«—l.odj.
В сверхзвуковом потоке, согласно рис. 5.22, возможны любые значения
коэффициента сохранения полного давления @ < a < 1).
С другой стороны, по изменению величины функции г(X) можно уста-
установить характер изменения статического давления в потоке подогреваемого
газа. При дозвуковой скорости, когда приведенная скорость при подогреве
газа возрастает, имеем (см. рис. 5.22) г(А,3) < г(Х\) или рз<Р\, T- е. стати-
статическое давление в потоке уменьшается. Предельное изменение статического
давления, очевидно, равно
_
г @) - к + 1 '
В сверхзвуковом потоке, когда Х$ <С Х\, имеем г(Хз) > г(Х\) или рз > р\.
Таким образом, при подогреве сверхзвукового потока, несмотря на сни-
снижение полного давления, статическое давление возрастает вследствие
уменьшения приведенной скорости потока.
Что будет, если при сохранении заданного отношения давлений Р*/рн
повысить температуру газа сверх полученного выше значения Т* =1835 К,
т. е. увеличить подогрев?
Отвлекаясь от рассмотрения действующего перепада давлений, на осно-
основании формулы, выведенной в примере 7, можно было бы прийти к выводу,
что поскольку Л,1 <С 1 и Х$ < 1, то с увеличением подогрева приведенная
скорость Хг будет возрастать, приближаясь к X = 1. Однако зто неправиль-
неправильно, так как при использовании этой формулы всегда следует иметь в виду,
что полученные из нее результаты справедливы только при условии доста-
достаточности действующих на поток перепадов давления', чем больше подогрев,
тем большим должно быть отношение давлений Р*/рн> На это неоднократ-
неоднократно указывалось выше при решении задач.
Действительно, в данном случае при рг = const с ростом подогрева
увеличиваются потери полного давления газа и снижается полное давление
газа в выходном сечении трубы, вследствие чего уменьшается приведенная
скорость Я3, зависящая только от отношения полного и статического давле-
давлений в потоке
Таким образом, если Рг/рв — const, то с увеличением подогрева, когда
величина а снижается, величина приведенной скорости па выходе из ка-
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 253
меры (трубы) не возрастает, а уменьшается. Одновременно уменьшается
приведенная скорость потока на входе в трубу.
Чтобы определить действительные значения приведенных скоростей на
входе и выходе при заданных значениях подогрева ^з/^i и перепада
давлений между входным и выходным сечением, необходимо найти совмест-
совместные решения уравнения (см. пример 7)
с одним из следующих уравнений, выражающих постоянство заданного пе-
перепада давлений, например
If = W f
если задано отношение полных давлений;
=const или ~pf = W V 11 =const-
1
7f = const)
если задано отношение статических давлений;
. = const или —JL = _
если задано отношение полного давления на входе к статическому давле-
давлению на выходе из трубы (располагаемое отношение давлений). Последний
случай встречается наиболее часто. Совместное решение уравнений удобнее
всего проводить графическим способом с помощью таблиц газодинамиче-
газодинамических функций.
Общим в рассмотренных выше примерах течения газа явля-
являлось то, что скорость потока была направлена по оси канала.
В ряде задач прикладной газовой динамики приходится рас-
рассчитывать такие течения, в которых абсолютная скорость газа
составляет некоторый угол с осью потока. Помимо осевой скоро-
скорости wa, определяющей расход газа и количество движения вдоль
оси потока, здесь имеются составляющие скорости в плоскости,
перпендикулярной к оси,— радиальная wT или окружная wx
скорость частиц газа. Примером может служить течение закру-
закрученного газа в кольцевом канале, встречающееся в различных
вихревых аппаратах (окружная составляющая), или расширение
сверхзвуковой струи газа, вытекающей в атмосферу с большим
избыточным давлением (радиальная составляющая).
Если параметры газа в поперечном сечении потока можно
полагать постоянными, то для расчета таких течений могут быть
использованы методы и формулы, изложенные в данном пара-
параграфе.
На первый взгляд может показаться, что для этого достаточ-
достаточно во всех выведенных соотношениях принимать во внимание
254 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
лишь осевую составляющую скорости. Это, однако, не так, по-
поскольку при заданных параметрах торможения значения темпе-
температуры, статического давления, плотности газа будут зависеть
также от величины окружной (радиальной) составляющей ско-
скорости; изменения последней будут влиять на значение расхода
и импульса потока. Дело в том, что, согласно уравнению энергии
и полученным из него соотношениям A01) —A03), связь между
параметрами в потоке и параметрами торможения определяется
изменением абсолютной скорости (или приведенной скорости,
вычисленной по абсолютной скорости и полной температуре тор-
торможения), независимо от угла, составляемого скоростью с осью.
Покажем, как обобщить полученные выше соотношения на
случай движения с тангенциальной (радиальной) составляющей
скорости. Рассмотрим одномерный поток газа с параметрами
торможения р* и Т* и абсолютной скоростью w, составляющей
угол а с осью течения. Секундный расход газа через поперечное
сечение площади F, перпендикулярное оси, равен . * :;
G = pFwa = pFw cos a, (•<^ •"'" ^
где wa — осевая составляющая скорости газа. Таким же путем,
как при выводе формулы A09), отсюда можно получить
1
7й* ( Т+Т ) р y±} cos а,
где
•RT*
к+1
Последнее соотношение можно переписать в виде
G = mp*F^la\ A23)
где
K a)=g(A,)cosa A24)
— газодинамическая функция #(А,), обобщенная на случай дви-
движения газа с составляющей скорости в плоскости, перпендику-
перпендикулярной оси. Точно так же можно получить формулу, аналогич-
аналогичную A11),
FUa\ A25)
где
у(Х, a)=i/(X)cosa. A26)
Таким образом, если угол а задан, то для вычисления расхода
газа и составления уравнений неразрывности используются те
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ
255
же формулы, что и при а = О, так как обобщенные функции
q(k, а) и у (Я, а) определяются по углу а и по значениям q(k)
и у (к) для приведенной скорости в абсолютном движении газа.
Импульс потока газа в направлении оси равен
/ = Gwa + pF = Gw cos a + pF.
Преобразуя это выражение подобно тому, как это было сделано
при выводе формулы A15), имеем
/ = G I w cos a +
pw cos a
или после упрощений
где
^,a),
A27)
Выражение A27) аналогично выражению, полученному при
а = 0, но содержит вместо z (X) обобщенную функцию z(k, cc),
график которой приведен на рис. 5.26. При а = 0 функция
z(k, а) сводится к z(X) = K+lJX; минимальное значение ее
z (к) = 2 соответствует к = 1. 2(Л .
При а?=0 минимальные значе-
значения функции z (к, а) меньше
двух, причем с увеличением
угла а минимумы кривых сме-
смещаются в область сверхзвуко-
сверхзвуковых скоростей.
Для проведения численных
расчетов можно составить таб-
таблицы функции z(k, а) или бо-
более подробную, чем на рис. 5.26,
сетку кривых при различных
значениях а (см. график в при-
приложении). ''"О 0,4 0,8 12 1,6 2,0 24 Я
Формулы A23) и A27) по- Рис. 5.26. График функции z(K, а)
зволяют установить характер
изменения плотности тока, площади сечения, удельного импульса
и других величпн, характеризующих газовый поток, в зависимо-
зависимости от приведенной скорости к и угла а между вектором скоро-
скорости и осью. На этом, однако, мы здесь останавливаться не будем.
При использовании обобщенных функций q(k, а), у (к, а)г
г(Я, а) и их комбинаций все полученные в данном разделе урав-
256
ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
нения можно применять для расчета течений с окружной или
радиальной составляющей скорости.
Пример И. Закрученный поток газа движется в кольцевом канале
между двумя цилиндрическими поверхностями (рис. 5.27). Приведенная
скорость потока на входе в канал Ki = 0,85, направление абсолютной скоро-
скорости задано углом oti = 30° к оси канала. При течении в канале температура
Рис. 5.27. Закрученный газо-
газовый поток в кольцевом канале
(к примеру И)
торможения газа понижается от 900 до 700 К. Пренебрегая трением, а так-
также изменением параметров по радиусу канала, определить параметры газа
на выходе из канала. Показатель адиабаты к = 1,40.
Как и выше, при рассмотрении потока в цилиндрическом канале с под-
подводом тепла, основное уравнение получаем из условия постоянства импуль-
импульса газа в поперечных сечениях канала. В данном случае это условие имеет
вид
Г
или z (л2, а2) = 1/
н
Подставляя заданные значения температур торможения и z(Xu oti)= 2,055
(см. рис. 5.26), получаем
z(K2, cc2)=2,33.
Данному значению функции могут соответствовать, вообще говоря, раз-
различные комбинации значений %2 и «2, поэтому для определения этих вели-
величии используем условие постоянства момента количества движения
(см. § 6 гл. I). Поскольку средний радиус канала не изменяется и отсут-
отсутствуют моменты внешних сил, то в потоке независимо от происходящих
процессов должна быть постоянной окружная составляющая скорости. По-
Поэтому
wX2 = wxi или А^Якрг sin ai = ^i^kpi sin obi.
Отсюда определяем
sin a2
Совместное решение двух полученных уравнений удобнее всего проводить
графически. Задаваясь рядом значений угла а2, находим соответствующие
им значения приведенной скорости Х2 = 0,482/sin a2; подставляя эти зна-
значения а2 и %2 в z(X, а), строим график этой функции. Точке кривой, где
2(Х, а) = 2,33, соответствуют значения параметров в выходном сечении
канала, в данном случае находим Х2 = 0,72, а2 = 42°. При расчетах можно
также воспользоваться вспомогательным графиком или таблицами функции
z(X, a).
Условие сохранения расхода газа в сечениях 1 и 2 при использовании
выражения A23) позволяет определить отношение полных давлений газа —
§ 6. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ 257
коэффициент сохранения полного давления
р\ _ gftjcosc^ л[ Т\ _ 0,9729.0,865 ,/00 _. 1 10
р" Q(K)cosa2 V Т*х 0,9061-0,743 У 900
(охлаждение потока сопровождается увеличением полного давления).
Изменение статического давления легко определить из соотношения
^^л(/д 0,7289
Р1 ~ р* п(кг) ~ MU* 0,6382 ~ г>*™
или из условия равенства расходов, записанных в форме A25).
В заключение перечислим введенные газодинамические функ-
функции и соотношения между ними.
1. Простейшие функции, которые выражают связь между па-
параметрами газа в потоке и параметрами торможения:
k
^1^ «(^)
при этом
2. Функции, позволяющие выразить расход газа через полное
давление
или через статическое давление
С помощью этих функций получаем два выражения для расхо-
расхода газа
3. Функция
Г-тп P*Fq Щ - m РРУ (Я)
VJT — III >_:—: — Ui . —•
ут* ут*
с помощью которой импульс газового потока можно представить
в виде произведения температуры торможения (критической ско-
скорости звука) на расход газа
17 Г. Н. Абрамович, ч. 1
258 ГЛ V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
4. Функции /(Я), г (А,), при помощи которых импульс газово-
газового потока выражается через полное или статическое давление:
Соответственно получаем два выражения для импульса газового
потока:
Константа, входящая в выражения для функций #(А), г/ (Л,),
/(Я), г(Я)
" 8A)
равна 1,577 для к = 1,4 и 1,588 для к = 1,33.
5. Функции д(Я, а), г/(А, а) и 2(А,, а), позволяющие распро-
распространить рассмотренные выше методы и расчетные формулы на
случай течения газа с окружной или радиальной составляющей
скорости.
6. При решении некоторых задач используются также произ-
производные от различных газодинамических функций. Путем диффе-
дифференцирования и несложных преобразований можно получить их
выражения через исходные функции.
Например,
dn Ш
dlM _„т1 *__ I 2 i^.nu и Т#д#
В чем смысл упрощений, получаемых при записи основных
уравнений с помощью газодинамических функций?
Как можно видеть из приведенных выше примеров, основное
преимущество полученных здесь выражений заключается в том,
что они содержат такие параметры потока, характер изменения
которых может быть легко установлен из условий задачи, на-
например постоянство температуры торможения Г* в адиабатиче-
адиабатических течениях и рост Г* при подводе тепла, сохранение полного
давления р* в изоэнтроппческом течении и падение р* при на-
наличии потерь и т. д. Выбором соответствующего выражения для
расхода или импульса можно свести к минимуму число неиз-
неизвестных параметров в основных уравнениях. При этом часто
удается найти неизвестные величины непосредственно из исход-
исходных уравнений, минуя громоздкие преобразования.
§ 7. ТЕЧЕНИЕ ГАЗА ПРИ ЗАДАННОМ ОТНОШЕНИИ ДАВЛЕНИЙ 259
Отметим некоторые общие правила, полезные при решении
уравнений в общем виде и вычислениях с помощью таблиц газо-
газодинамических функций.
Во всех случаях, когда получено общее или численное выра-
выражение величины приведенной скорости X или какой-либо одной
из его функций, можно считать, что известны все газодинамиче-
газодинамические функции и X (из таблиц или графиков). Это является ос-
основным условием упрощения выкладок, так как исключает не-
необходимость получения в явном виде зависимостей между X и
его функциями. При численных расчетах следует учитывать, что
функции т(Я), я (Я), г(Х) в области малых скоростей и функции
q(X), z(X), f(X) при околозвуковых скоростях очень мало изме-
изменяются с изменением величины X. Поэтому в указанных обла-
областях незначительная погрешность в значении функций может
привести к большой ошибке при вычислении приведенной ско-
скорости X. Таких вычислений следует избегать и по возможности
использовать в этих случаях другие уравнения, включающие, на-
например, функции у (к), г (К). Если это по каким-либо причинам
невозможно, то надо вести все предварительные подсчеты с вы-
высокой степенью точности. Понятно, что в этих областях не реко-
рекомендуется определять X по указанным функциям с помощью
графиков. В особенности это относится к функции z(X), которая
в широких пределах изменения X (от 0,65 до 1,55) изменяется
всего на 10 %. Поэтому для нахождения X по значению функ-
функции z(X) в области околозвуковых скоростей можно вычислять
возможные значения X непосредственно из уравнения
откуда
(Я) ± Vz2 (X) - 4
Для того чтобы избежать погрешности, связанной с вычитанием
близких величин, сверхзвуковое решение находится по первому,
а дозвуковое решение — по второму из этих выражений.
Из примеров, рассмотренных в данном разделе, можно видеть
эффективность метода расчета с использованием газодинамиче-
газодинамических функций при решении достаточно сложных задач, имею-
имеющих практическое значение.
§ 7. Течение газа с трением в цилиндрической трубе
при заданном отношении давлений на входе и выходе
Используя соотношения, выведенные в предыдущем парагра-
параграфе, дополнительно выясним некоторые закономерности одномер-
одномерного течения газа в цилиндрической трубе с трением. В §§ 1 и
2 было установлено, что трение приводит к увеличению скорости
17*
260 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
дозвукового потока и уменьшению скорости сверхзвукового по-
потока, причем в обоих случаях предельный режим соответствует
критической скорости в выходном сечении трубы.
Полученные в § 2 результаты справедливы, однако, только в
том случае, когда приведенная скорость на входе в трубу Х\ под-
поддерживается постоянной, что требует создания вполне опреде-
определенного перепада давлений в потоке для каждого режима и
каждого значения приведенной длины трубы. В действительно-
действительности чаще всего бывает наоборот: заданной величиной является
перепад давлений между входным и выходным сечениями трубы,
а величины скорости, расхода и других параметров течения оп-
определяются действующим перепадом давлений и сопротивлением
на рассматриваемом участке трубы. Для потока во входном се-
сечении трубы наиболее характерной величиной, которая обычно
известна или может быть легко определена, является полное
давление рг; для характеристики потока на выходе из трубы
важно знать статическое давление во внешней среде или резер-
резервуаре, куда вытекает газ из трубы ра. Если скорость потока
в выходном сечении меньше скорости звука, то статическое дав-
давление потока, как известно, равно внешнему давлению, то есть
Р2 = Рн. Если А,2 = 1, то в выходном сечении трубы /?2 ^ ра. На-
Наконец, при %2 > 1 возможны также режимы, когда /?2 < рн.
Назовем величину П = Рх/Рн располагаемым отношением дав-
давлений. Параметры потока в цилиндрической трубе в основном
определяются располагаемым отношением давлений П: процесс
по существу является как бы истечением газа из сосуда с дав-
давлением Рх в среду с давлением ра через канал с заданным со-
сопротивлением. Поэтому при рассмотрении закономерностей тече-
течения с трением необходимо учитывать величину располагаемого
отношения давлений в потоке; без этого полученные результаты
могут оказаться нереальными.
Пусть, например, при дозвуковой скорости на входе в трубу
располагаемое отношение давлений П меньше критического от-
отношения давлений
1 _ / А + 1 ^*=Г.
для воздуха Пкр = 1,893. Вследствие трения полное давление
потока по длине трубы уменьшается, поэтому в выходном сече-
сечении тру бы р%/рк<Ср*/рн< 1,893. Это значит, что поток вытекает
из трубы под действием докритического отношения давлений,
следовательно, скорость такого потока всегда будет дозвуковой.
Сколько бы не увеличивать приведенную длину трубы, получить
величину А,2 = 1 не удастся: действующий в потоке перепад дав-
давлений недостаточен для создания звуковой скорости истечения
на выходе из трубы.
§ 7. ТЕЧЕНИЕ ГАЗА ПРИ ЗАДАННОМ ОТНОШЕНИИ ДАВЛЕНИЙ 261
Таким образом, полученный ранее вывод о том, что при уве-
увеличении приведенной длины трубы до максимального (критиче-
(критического) значения скорость потока на выходе из трубы достигает
скорости звука, справедлив только в том случае, если обеспечи-
обеспечивается достаточное (зависящее от величин Х\ и %) отношение
давлений П.
Покажем, как проводится расчет параметров потока при те-
течении в трубе с трением, если Х\ < 1 и задано располагаемое от-
отношение давлений.
Запишем уравнение неразрывности для потока в трубе, при-
причем расход во входном сечении выразим с помощью формулы
A09) через полное давление, а расход в выходном сечении —
через статическое давление с помощью формулы A11)
Так как для адиабатического течения в цилиндрической трубе
Т* = Т7* и F2 = F\, то отсюда следует
Если %2 < 1, то, как указывалось, р2 = рш или
. A29)
Уравнение A29), связывающее между собой значения при-
приведенных скоростей во входном и выходном сечениях трубы при
заданном значении П и К\ < 1, справедливо вне зависимости от
характера течения и длины трубы. С другой стороны, изменение
параметров газа в трубе определяется коэффициентом трения и
длиной трубы. Ранее в § 2 была получена формула, описываю-
описывающая изменение параметров потока вследствие трения:
<Р(М-Ф(М = Ь A30)
2к х
где X ~ д. I i ?~л"—приведенная длина трубы. Уравнение A30)
устанавливает зависимость между приведенными скоростями Х\
и Ад при заданном значении %. Уравнения A29) и A30) можно
рассматривать как систему двух уравнений с двумя неизвестны-
неизвестными, совместное решение определяет значения Х\ и %2 в функции
заданных величин П и %• Этими значениями приведенных ско-
скоростей определяется реальный режим течения газа через трубу
с заданным сопротивлением (приведенной длиной) под действи-
действием располагаемого перепада давлений П.
Рассмотрим некоторые из следующих отсюда свойств течения
при дозвуковой скорости потока на входе в трубу. В первую
очередь сравним одномерное дозвуковое течение газа в трубе при
262 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
наличии трения с идеальным течением при одинаковом распо-
располагаемом отношении давлений П. Изменение параметров газа по
длине трубы связано с трением, поэтому в идеальном течении,
когда pt = pi, параметры газа постоянны во всех сечениях тру-
трубы. Приведенная скорость в выходном сечении %2 == hi < 1, ко-
которая в идеальном случае определяется располагаемым отноше-
отношением давлений л;(А,2)= 1/П, больше, чем при течении с трением,
когдар*<Pi» и я(Яг)= 1/(оП). Чем больше приведенная длина
трубы, тем большими будут потери полного давления и тем
меньше будет скорость потока на выходе из трубы по сравнению
со скоростью в идеальном случае течения. Таким образом, сле-
следует иметь в виду, что, хотя при течении в трубе с трением ско-
скорость потока по длине трубы возрастает, наибольшая ее величи-
величина — скорость на выходе — всегда остается меньшей, чем при
том же отношении давлений П в случае течения без трения (на-
(например, при очень короткой трубе, когда %~0). Чем больше
приведенная длина трубы, тем меньше (при данном П) скорость
потока как на выходе, так и на входе.
Интересно отметить, что если П = const, то при Яг < 1 изме-
изменение приведенной длины трубы % всегда приводит к изменению
скорости на входе в трубу, независимо от того больше или мень-
меньше величина % ее критического значения для данного К\ < 1.
Сохранение Х\ = const при изменении приведенной длины трубы
и Яг < 1 требует соответственно изменения величины располагае-
располагаемого отношения давлений: чем длиннее труба, тем большее зна-
значение П необходимо для поддержания заданного режима на вхо-
входе, т. е. сохранения расхода газа.
С другой стороны, если при заданной длине трубы (% =
= const) увеличивать отношение давлений П, то будут возра-
возрастать скорости как на входе, так и на выходе, пока величина Яг
не достигнет критического значения Яг = 1. Дальнейшее увели-
увеличение П не изменяет ни Х\, ни Яг, однако в выходном сечении
трубы установится избыточное по сравнению с окружающей сре-
средой (резервуаром) давление. Для этого режима уравнение A29)
несправедливо, так как при выводе его предполагалось р2 = рв\
связь между параметрами потока определяется только уравне-
уравнением A30). Из условия неразрывности можно лишь найти ми-
минимальное потребное значение П, при котором установится ре-
режим с Яг = 1 и заданным значением Яь так как, согласно урав-
уравнению A29),
п _ У (О _ (b±±\h=i 1 _ Пкр
Так как qCk\)< 1, то из последнего соотношения видно, что при
течении в трубе с трением критическая скорость на выходе уста-
устанавливается при отношении давлений П > Пкр, где Пкр — отно-
§ 7. ТЕЧЕНИЕ ГАЗА ПРИ ЗАДАННОМ ОТНОШЕНИИ ДАВЛЕНИЙ 263
0,8
0,6
0,4
0,2
*
$?/
/
/
/
(
1
.'/
/
/
/
1
1
1
1
in
ы
* м»
'Ъ
7/
щ
V
Q4 0,6 0,8 Л,
шение давлений, необходимое для получения А = 1 при течении
без трения. Режим Аг = 1 для данного значения Х\ наступает
при увеличении приведенной длины х до значения
х —ЭЬф —ф(Я0— 1; A31)
при этом должно соблюдаться условие П > Птт.
На рис. 5.28 приведены результаты расчетов дозвукового те-
течения в трубе с трением. График иллюстрирует изложенные
выше основные закономерности л2
течения и, в частности, показы-
показывает, что
а) при Ai = const с ростом при-
приведенной длины х величина Аг ра-
растет, причем всегда Ai<A2^1;
б) при постоянном располага-
располагаемом отношении давлений П с
ростом х величина Ai всегда па-
падает; уменьшается также и Аг,
если Аг< 1;
в) для каждого значения при-
приведенной длины х существует
вполне определенное значение от-
отношения давлений Pi/pn = П, ко-
которому соответствует заданная
скорость потока на выходе и со-
соответственно на входе в трубу;
г) предельное значение Ai, соответствующее Аг = 1, для каж-
каждого значения % устанавливается при определенном, увеличиваю-
увеличивающемся с ростом х значении отношения давлений и не растет
при дальнейшем возрастании П.
Рассмотрим теперь особенности течения с трением при сверх-
сверхзвуковой скорости на входе в трубу. Из формулы A30) следует,
что если приведенная длина трубы меньше критического значе-
значения, определяемого для данного значения Ai > 1 формулой
A31), то по длине трубы скорость потока будет уменьшаться,
оставаясь сверхзвуковой. На выходе из трубы при непрерывном
торможении потока будет получено Аг > 1. При некотором зна-
значении приведенной длины трубы, называемом критическим, из
уравнения A30) следует ср(А2)=1, т. е. Аг = 1. Этой длине со-
соответствует предельно возможный режим течения с непрерыв-
непрерывным изменением скорости от заданного значения Ai > 1 до
А2 = 1. Если % > %кр> то непрерывное торможение потока в трубе
невозможно. В этом случае уравнение A30), описывающее тече-
течение с непрерывным изменением скорости, не имеет решений для
Аг, так как из него следует <р(Аг)< 1. В действительности при
этом в начальном участке трубы сверхзвуковой поток тормозится
0,2
Рис. 5.28. Зависимость
параметрами дозвукового
между
потока
в начальном и конечном сече-
сечениях цилиндрического канала
при наличии трения
264 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
до некоторого значения X' > 1, затем в трубе возникает скачок
уплотнения, за которым устанавливается дозвуковое течение
с увеличением скорости по длине трубы от значения X" (за
скачком) до А,2 < 1, как указывалось выше.
Местоположение скачка и относительную длину сверхзвуко-
сверхзвукового и дозвукового участков течения в зависимости от заданных
параметров можно определить следующим образом. Обозначим
приведенную длину трубы от начала ее до скачка уплотнения
(сверхзвуковой участок течения)
_ 2к ^ *!
%х ~~ к + 1 * D '
Запишем уравнение A30) для участков с непрерывным измене-
изменением скорости, т. е. раздельно для сверхзвукового и дозвукового
участков:
-Xi, A32)
!Х-Хь A33)
Произведем почленное сложение уравнений A32) и A33), пред-
предполагая при этом, что скачок уплотнения является прямым,
и поэтому справедливо соотношение X" = 1/А/. В результате
получаем
Ф (^i) — Ф (К) + Ф [jrj — Ф (^') = Х-
Обозначим
ф(А,) = ф [^) — Ф(^)==^2 — -JJ — 4 In А,. A34)
Тогда последнее уравнение можно записать в виде
Ф(Х') = % — ф (A/i) Ч~ ф (Л12). A35)
На рис. 5.29 приведен вспомогательный график для определения
функции Ф(^) по величине X. Соотношение A35) устанавливает
связь между параметрами потока, движущегося с трением в
трубе с приведенной длиной %, при условии, что в трубе возни-
возникает прямой скачок уплотнения.
В формулу A35), помимо известных величин % и Х\, входит
также неизвестное пока значение приведенной скорости на вы-
выходе из трубы Х2. Так как за скачком течение дозвуковое, то
для определения Яг воспользуемся уравнением неразрывности
которое справедливо как при Х\ < 1, так и при К\ > 1. Если из
этого уравнения следует г/(Хг)^ г/A), то А.2 = 1, если г/(А,г)<
<#A), то Яг < 1. Подставляя найденное таким образом значе-
значение Яг ^ 1 в уравнение A35), определяем Ф(А/). Далее по гра-
§ 7. ТЕЧЕНИЕ ГАЗА ПРИ ЗАДАННОМ ОТНОШЕНИИ ДАВЛЕНИЙ
265
фику (рис. 5.29) находим значения Я' и ф(А/), и, воспользовав-
воспользовавшись уравнением A32), вычисляем величину %\ — приведенную
длину трубы, необходимую для безударного торможения сверх-
сверхзвукового потока от К\ до Я'. Величина %i и определяет располо-
расположение скачка по длине трубы, так как при g = const имеем
xi/x = Xi/X-
При критическом режиме течения на выходе из трубы, когда
%2 = 1, результат вычисления, как легко видеть, не зависит от
П: скачок возникает в определенном сечении трубы независимо
Фп),<р(Л)
18
Рис. 5.29. Графики функций
Ф(Я) и Ф(Я) для расчета
сверхзвукового течения в ци-
цилиндрическом канале при на-
наличии трения,
ф (Я) = ?5+2 In Я,
Я2
1,4
1,2
1,0
0,8
0,6
0,4
0,2
/
1
Ф(Л)/
/
/
А
/
1
j
7
и1,0 1,2
1,6 1,8 2,0 2,2 2,41
от располагаемого отношения давлений. Расчет по формулам
A29), A32), A35) показывает, что при Яг < 1 скачок уплотне-
уплотнения с уменьшением П будет перемещаться от своего предельного
положения, соответствующего Яг = 1, к входному сечению трубы.
Минимальное значение располагаемого отношения давлений, при
котором возможно течение с заданной начальной приведенной
скоростью Я1 > 1, определяется тем, что скачок уплотнения, про-
продвигаясь вверх по потоку, подходит непосредственно к входно-
входному сечению.
Приведем пример расчета течения со скачком уплотнения внутри тру-
трубы. Пусть заданы приведенная скорость на входе в трубу Я = 1,8 и общая
приведенная длина трубы % = 0,6 (при обычных значениях коэффициента
трения это соответствует примерно 30 калибрам трубы). Располагаемое
отношение полного давления потока на входе в трубу к статическому дав-
давлению в резервуаре, куда вытекает газ из трубы, П = 3,0.
Определяем критическое значение приведенной длины трубы для задан-
заданного значения Яь
Х*Ф = <p(A,i) — 1 = 0,485
(величину ф(ЯО находим по вспомогательному графику рис. 5.29). Так как
заданная приведенная длина трубы % = 0,6 больше критического значения,
(ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
то, как указывалось, непрерывное торможение потока невозможно, и в трубе
возникает скачок уплотнения.
Определяем приведенную скорость потока на выходе из трубы при по-
помощи уравнения A29)
У(Х2) =
= 3-0,4075 = 1,222 или Я2 = 0,71.
Далее подставляем полученное значение Яг и заданные величины Х\ и %
в уравнение A35), определяющее приведенную скорость потока перед скач-
скачком Ф(Я') = 0,6 + 1,25—1,485 = 0,365. По графику на рис. 5.29 находим, что
этому значению Ф(А/) соответствует V = 1,66 и ф(А/) = 1,375. Определяем
приведенную длину сверхзвукового участка течения по формуле A32)
-Ф(Я') = 1,485-1,375 = 0,11
и находим расстояние от входа в трубу до сечения, где возникает скачок
уплотнения (при ? = const)
Итак, на длине около 18 % общей длины трубы сверхзвуковой поток под
действием трения замедляется от Jli = 1,8 до X' = 1,66, затем в скачке
Л
2,0
1,8
1,6¦
1,4
1,2
Ю
0,8
0,6
0,4
h
3,2
I —
i
3,6
-
~~2~J
¦
—
"Л
yd
Рис. 5.30. Возможные ре-
режимы сверхзвукового тече-
течения в цилиндрической тру-
трубе с трением при сверхкри-
сверхкритической длине трубы,
Аи = 1,8; % = 0,6 (к при-
примеру расчета)
0,1 0,2 0,3 0,4 0,5 0,6 X
скорость падает до %!' = 0,6; на остальной части трубы дозвуковой поток
ускоряется до %2 = 0,71 и вытекает из трубы, имея статическое давление»
равное давлению в резервуаре рн.
При других значениях располагаемого отношения давлений положение
скачка будет иным. На рис. 5.30 приведены результаты расчета по изло-
изложенному методу при различных значениях П. Предельно возможные режи-
режимы определяются, с одной стороны, достижением критической скорости на
выходе из трубы (при расчете полагаем Я2 = 1 и находим наиболее уда-
удаленное от входа положения скачка уплотнения), а с другой стороны, воз-
йикновением скачка непосредственно за входным сечением трубы. В дан-
§ 8. ОСРЕДНЕНИЕ ПАРАМЕТРОВ НЕРАВНОМЕРНОГО ПОТОКА 267
ном случае (Xi = 1,8, % = 0,6) критический режим течения на выходе по-
получается при П = y(l)/q(hi) = 1,893/0,4075 = 4,64.
По формулам A35) и A32) с помощью графика на рис. 5.29 находим:
ф(А/) = 0,6 + 1-1,485 = 0,115, V = 1,41, <р(Я') = 1,185. Далее имеем:
Xi = 1,485—1,185 = 0,3 и, следовательно, xjx = 0,3/0,6 = 0,5.
Минимальному значению П, при котором возможно сверхзвуковое тече-
A х
-г—1—0,6 = 2,07 — 0,6= 1,47
или Х2 = 0,66. Поэтому имеем
П = 7(Х7) = = 0^075 =2'74'
Для определения полного и статического давления по величине приведен-
приведенных скоростей на входе и на выходе достаточно записать условия равен-
равенства расходов газа во входном и выходном сечениях, воспользовавшись вы-
выражениями A09) или A11).
Выше указывалось, что если приведенная длина трубы меньше крити-
критической для данного значения Xi, то закономерности течения с трением до-
допускают существование потока с непрерывным изменением (снижением)
сверхзвуковой скорости на всей длине. Можно показать, однако, что наряду
с полностью сверхзвуковым течением здесь также возможно течение со
скачком уплотнения внутри трубы и с дозвуковой скоростью на выходе.
Такой режим течения в случае % <С %кр может существовать только в опре-
определенном интервале значений р*//?н = П, который находят из условия, что
в выходном сечении трубы статическое давление дозвукового потока долж-
должно равняться давлению внешней среды.
§ 8. Осреднение параметров неравномерного потока
На практике часто приходится рассчитывать газовые потоки
с переменными по сечению параметрами. В ряде случаев эти
потоки можно рассматривать как одномерные с некоторыми
средними значениями параметров в каждом сечении. При этом
возникает задача об осреднении параметров газа в поперечном
сечении неравномерного потока.
Иногда принимают в качестве средних значений параметров
средние по площади скорости, давления, температуры и т. д.
Можно показать, однако, что такое простейшее осреднение яв-
является, вообще говоря, неправильным и может привести к оши-
ошибочным результатам: отношение средних значений полного и
статического давлений не будет соответствовать среднему значе-
значению приведенной скорости, расход газа, вычисленный по сред-
средним параметрам, будет больше или меньше действительного
и т. п. Если исходная неравномерность потока невелика, то ко-
количественно эти погрешности незначительны; при большой не-
неравномерности параметров ошибка может быть существенной.
Поэтому к решению поставленной задачи в общем случае под-
подходят иным путем.
Заданный неравномерный поток характеризуется рядом сум-
суммарных (интегральных) величин, как-то: расходом газа, энергии
268 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
ей, импульсом, теплосодержанием, энтропией и т. д. Заменяя
этот поток одномерным — осредненным,— следует стремиться к
тому, чтобы сохранить неизменными суммарные характеристики
(свойства) потока. Поскольку состояние одномерного газового
потока определяется тремя независимыми параметрами^ (напри-
(например, полным давлением р*, температурой торможения Г* и при-
приведенной скоростью Я), то при осреднении одновременно можно
сохранить постоянным только три суммарные физические харак-
характеристики исходного течения.
Наиболее распространенным является метод нахождения
средних значений параметров />*, Г* и к при сохранении в ис-
исходном и осредненном потоках одинаковыми расхода газа G,
полной энергии Е и импульса I. Условия G = const, E = const и
/ = const дают необходимые для решения задачи три уравнения
с тремя неизвестными. Пусть в поперечном сечении исходного
неравномерного потока известны (заданы или измерены) поля
температуры, полного и статического давлений. Тогда можно
считать в каждой точке сечения известными полное давление /?*,
температуру торможения Г* и приведенную скорость X. По ве-
величине X для каждой точки сечения могут быть найдены газоди-
газодинамические функции д(Л), z(X) и др. Для потока в целом рас-
расход, импульс и энергия определяются путем интегрирования со-
соответствующих элементарных выражений по всему сечению. Так,
например, расход газа равен
J J^ A36)
(F) (F) V
Если поле параметров задано в виде графика или таблицы, рас-
расход газа можно вычислить графическим или численным интег-
интегрированием.
Аналогичным образом определяются суммарные значения
энергии Е и импульса /.
Переходим к решению задачи об осреднении параметров /?*,
Г*, X. Приравняем величины полной энергии газа, вычисленные
в одном случае по истинным, а в другом — по средним значени-
значениям параметров газа:
Gcpl*= f cpT*dG = E. A37)
<G)
Теплоемкость газа ср считаем постоянной по всему сечению.
Подставим в это уравнение выражение для элементарного расхо-
расхода газа и записанное выше выражение для суммарного расхода
газа в потоке. Отсюда получаем первую искомую величину —
§ 8 ОСРЕДНЕНИЕ ПАРАМЕТРОВ НЕРАВНОМЕРНОГО ПОТОКА 269
среднюю температуру торможения газа:
p*q(l
f
F) V
A38)
J
(F)
Из формулы A38) видно, что Г* является среднемассовым зна-
значением температуры торможения. Воспользуемся полученной
средней величиной температуры торможения для вычисления
среднего значения критической скорости звука
Среднее значение приведенной скорости потока X найдем из
условия равенства действительного импульса потока и импульса,
вычисленного по средним значениям параметров. Для упроще-
упрощения расчета выразим полный импульс посредством формулы
A15) через функцию z(X), а элементарный импульс представим
по формуле A19) через полное давление и функцию ()
В результате получим
KV>z(X) = \ p*f{X)dF,
откуда
2к ~~КР
(F)
В соответствии с заданным режимом течения газа из двух зна-
значений приведенной скорости Я, определяемых функцией z{X),
выбираем реальное значение А, > 1 или X < 1. Причина неодно-
неоднозначности решения задачи в данном случае вполне очевидна: за-
заданное условие сохранения расхода, импульса и полной энергии
не нарушится, если в осредненном потоке возникнет скачок уп-
уплотнения; приведенная скорость при этом приобретает новое,
обратное по величине значение, так что функция z(X) будет
постоянной величиной (см. § 6, пример 6).
Определив температуру торможения и приведенную скорость
в осредненном потоке, найдем среднюю величину полного давле-
давления р* из выражения для расхода газа:
р* v l . A40)
)
Интересное соотношение можно получить, если использовать для
270 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
определения среднего полного давления уравнение импульсов:
p*Ff(X)= f !
Cf)
Отсюда имеем
с*
)dF
J
р* =
Ff(X)
Величина f(X) представляет собой значение функции f(X) для
найденной выше средней по сечению величины приведенной ско-
скорости X. На основании известной из интегрального исчисления
теоремы о среднем последнее соотношение можно представить
в виде
П p*dF
Р /(I) F *
Здесь f (X)—значение функции f(X) в некоторой точке области
интегрирования, т. е. в некоторой точке сечения F. Как уже ука-
указывалось, функция f(X) изменяется очень мало в широких пре-
пределах изменения X (при дозвуковых и небольших сверхзвуковых
скоростях). Поэтому два средних значения функции f(X) в дан-
данном сечении потока f(X) и f(X) будут близки по величине. От-
Отсюда следует
Г p*dF
р*^<П——. A41)
Полученное соотношение означает, что полное давление р* мало
отличается от среднего по площади полного давления. Расчеты
показывают, что если приведенная скорость X по сечению изме-
изменяется в пределах 0,4—1,0 или 1—1,4, то погрешность вычисле-
вычисления р* по формуле A41) обычно не превышает 2—3 %.
По найденным значениям Г*, X и р* однозначно определяют-
определяются все остальные параметры осредненного потока: скорость w,
плотность р и т. д. Отметим, что средние значения параметров,
удовлетворяющие поставленным в задаче условиям, получаются
вполне определенными независимо от способа и порядка реше-
решения основных уравнений, хотя при этом могут быть получены
различные по внешнему виду выражения.
Остановимся на физическом смысле полученных осредненных
параметров потока. Легко видеть, что значения параметров Г*,
р* и X и др. равны соответствующим значениям параметров та-
такого газового потока, который может образоваться при выравни-
§ 8. ОСРЕДНЕНИЕ ПАРАМЕТРОВ НЕРАВНОМЕРНОГО ПОТОКА 271
вании (например, за счет турбулентного перемешивания) исход-
исходного неоднородного потока в теплоизолированной трубе постоян-
постоянного сечения без трения о стенки; при этом расход, импульс и
полная энергия газа также сохранят постоянные значения. Дру-
Другими словами, найденный эквивалентный (осредненный) поток
может быть действительно получен при течении исходного газа
без внешних воздействий. Если вычислить и сопоставить энтро-
энтропию газа в неравномерном и осредненном потоке, то окажется,
что осредненным параметрам соответствует большее значение
энтропии. Это объясняется тем, что при перемешивании частиц
газа с разными скоростями возникают потери на удар, умень-
уменьшается суммарная кинетическая энергия и возрастает тепловая.
В связи с этим изложенный способ осреднения в некоторых
случаях может оказаться неприемлемым. Так, например, если
по найденным таким способом средним значениям параметров
потока в выходном сечении компрессора вычислить его к. п. д.,
то будет получена величина, меньшая действительной, так как
к реальным потерям (возрастанию энтропии) в процессе сжатия
газа будут добавлены фиктивные потери, появляющиеся в ре-
результате указанной выше замены действительных параметров
потока средними значениями. Поэтому в тех случаях, когда по
смыслу задачи требуется оценить работоспособность исходного
потока газа, целесообразно проводить осреднение так, чтобы со-
сохранить постоянной суммарную величину энтропии газа1).
Для определения трех параметров осредненного потока, по-
помимо условия сохранения энтропии, используем также уравне-
уравнения постоянства расхода и полной энергии.
Средние значения параметров вычисляем следующим путем.
Из уравнения A36) находим суммарный расход газа. Далее,
как и выше, из уравнения энергии A38) определяем температу-
температуру торможения 71*. Условие постоянства энтропии (см. § 8 гл. I)
в осредненном и действительном потоках записываем в виде
k k
J
ln-^H= dG.
p*
(G)
В это уравнение входит только один неизвестный параметр —
среднее полное давление р*. Для определения р* подставляем
вместо dG его значение, полученное выше, а затем преобразуем
уравнение к виду
!) Седов Л. И., Черный Г. Г. Об осреднении неравномерных пото-
потоков газа в каналах / Теоретическая гидромеханика (Сб. статей), № 12,
вып. 4.— М.: Оборонгиз, 1954.
272 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
Часто температуру торможения Т можно считать одинаковой
во всех точках сечения, т. е. полагать Т* = Т*. В этом случае
уравнение A42) принимает вид
= -L J In p*dG. A43)
(G)
Следовательно, среднее полное давление находится осреднением
логарифма полного давления в исходном потоке по расходу.
Интегралы правой части уравнений A42), A43) вычисляют-
вычисляются обычно путем графического или численного интегрирования.
Если величина скорости в исходном потоке переменна по сече-
сечению, то вычисленные по формулам A42), A43) значения р*
всегда будут больше значений р*, определенных для тех же ус-
условий по формуле A40) (при / «= const)*
Приведенную скорость потока находим из выражения для
расхода газа
Щ A44)
В связи с указанным увеличением полного давления р* это зна-
значение q(X) оказывается меньшим, чем ранее найденное. Это зна-
значит, что средняя скорость в дозвуковом потоке будет меньшей,
а в сверхзвуковом — большей соответствующих величин, полу-
полученных при первом способе осреднения. В обоих случаях это
означает, что импульс осредненного по энтропии потока, пропор-
пропорциональный значению функции z(X), будет большим, чем сум-
суммарный импульс исходного неравномерного потока.
Возможны и другие способы осреднения параметров неравно-
неравномерного потока. Однако очевидно, что при любом способе осред-
осреднения параметров неравномерного потока сохраняется только
часть его суммарных характеристик и неизбежно утрачиваются
некоторые свойства потока. Мы видели, что в первом случае при
осреднении изменялась энтропия, во втором — импульс потока.
Можно указать и на другие условности, связанные с процессом
осреднения параметров. Так, пусть в исходном потоке статиче-
статическое давление р одинаково по всему сечению. После замены дей-
действительных параметров средними вычисленное по р* и % стати-
статическое давление р окажется иным, чем в исходном потоке. Тоже
возможно и в отношении величины приведенной скорости, пол-
полного давления и др., если они постоянны по сечению исходного
потока. Отсюда следует, что в каждом реальном случае необхо-
необходимо выбирать такой способ осреднения, который наиболее пол-
полно отражал бы особенности поставленной задачи. Так, например,
при вычислении потерь или к. п. д. рационально пользоваться
осреднением параметров потока, при котором выполняется уело-
§ 8. ОСРЕДНЕНИЕ ПАРАМЕТРОВ НЕРАВНОМЕРНОГО ПОТОКА 27$
вие сохранения энтропии. При осреднении параметров потока^
вытекающего из реактивного сопла, такой способ будет непри-
неприемлемым, так как в этом случае наиболее существенным явля-
является сохранение действительной величины импульса потока, ко-
которая характеризует реактивную тягу.
Отметим далее одну особенность нахождения средних пара-
параметров газа в сверхзвуковом потоке.
Пусть во всех точках поперечного сечения сверхзвукового по-
потока температура торможения Т* постоянна. Определим средние
значения параметров в таком потоке, пользуясь вторым из рас-
рассмотренных выше способов осреднения, при котором в осреднеде-
ном потоке сохраняются действительные значения полной энер-
энергии, энтропии и расхода газа. Из уравнения энергии получаем
очевидный результат Т* = Г*. Из уравнения A43) найдем вели-
величину р*. Третий параметр — среднюю приведенную скорость
X — находим из выражения для расхода
J VT* ;
(F) V
отсюда при Т* = T* имеем
F. A45)
Полный импульс исходного неравномерного потока равен, со-
согласно A19),
J P*f(X)dF.
(F)
Для того чтобы осредненный поток при найденном выше зна-
значении полного давления р* имел такой же импульс, приведен-
приведенная скорость в нем X должна удовлетворять соотношению
A46)
В общем случае величина Я будет отличаться от X. Действи-
Действительно, условие сохранения импульса дает четвертое уравнение
для определения трех неизвестных величин; такая система урав-
уравнений будет несовместной. Однако в данном случае осреднения
имеются некоторые особенности. Заменим в выражении A46)
величину функции f(X) по A17) и, воспользовавшись теоремой
о среднем, вынесем за знак интеграла некоторое среднее значе-
значение функции z(X). В результате получим
p*Fz (X) q(X) = z (X) J p*q (X) dF,
(F)
18 Г. Н. Абрамович, ч. 1
274 ГЛ. V. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ГАЗА
ИЛИ
$) = iM.JL.jp*q(X)dF.
Сравнивая это выражение с уравнением A45), отмечаем, что
они отличаются только множителем в правой части, поэтому
l^ A47)
В области сверхзвуковых скоростей функция z(X) (рис. 5.22)
изменяется весьма мало: при возрастании скорости от звуковой
до предельной (от X = 1 до Х = Хтах) z (X) возрастает всего на
~40 % (к = 1,40), при этом отношение давлений р/р* падает от
0,528 до нуля. Если рассматривать реально встречающуюся сте-
степень неравномерности потоков, то z (X) в пределах сечения обыч-
обычно изменяется не более чем на 15—20 %. Поэтому два средних
значения функции в этом интервале z(X) и z(X) будут мало от-
отличаться одно от другого.
Расчеты, проведенные для сверхзвуковых потоков при раз-
различных законах изменения приведенной скорости по сечению,
показывают, что даже при весьма большой неравномерности по-
потока — например, при изменении полного давления р* в 5—
10 раз при р = const — множитель правой части уравнения A47)
отличается от единицы всего на 0,5—1,5 %. Поэтому можно
считать, что q(X)^q(XI т. е. результаты определения средней
приведенной скорости из уравнения расхода и уравнения им-
импульсов практически совпадают. Точность этого приближенного
соотношения тем выше, чем больше значения X в потоке, однако
и при умеренных сверхзвуковых скоростях (X > 1,2 -f- 1,3) раз-
различие между значениями X и X составляет доли процента1).
Таким образом, при осреднении указанным способом пара-
параметров потока с большими сверхзвуковыми скоростями и посто-
постоянной по сечению температурой торможения одновременно с вы-
высокой степенью точности удовлетворяются четыре интегральных
соотношения, выражающих равенство полной энергии, расхода,
импульса и энтропии в исходном и осредненном потоках. Усло-
Условие Г* = const является в данном случае весьма существенным,
так как иначе величина q(X), полученная из уравнения расхода,
будет зависеть от закона распределения температуры торможе-
торможения и может сколь угодно отличаться от величины д(Х), найден-
найденной из уравнения импульсов, в которое величина Г* не входит.
Физический смысл полученного результата заключается в том,
1) См. Черкез А. Я. О некоторых особенностях осреднения пара-
параметров в сверхзвуковом газовом потоке / Изв. АН СССР. ОТН.— 1962,—№4.
§ 8. ОСРЕДНЕНИЕ ПАРАМЕТРОВ НЕРАВНОМЕРНОГО ПОТОКА 275
что при больших сверхзвуковых скоростях и Г* = const сущест-
существенные изменения давлений, плотностей и других параметров
потока незначительно изменяют величину скорости. Еще меньше
изменяется пропорциональная значению функции z (X) величина
импульса газа при заданном его расходе: увеличение количества
движения в значительной степени компенсируется снижением
статического давления, так что
Gw + pF = ^±^ Ga^z (к) « const- G.
Указанное свойство сверхзвуковых потоков означает возмож-
возможность одномерного рассмотрения и применения изложенных
в данной главе методов для расчета потоков с весьма большой
неравномерностью.
Так, например, в гл. VII показана высокая точность такого
расчета применительно к потоку, в поперечном сечении которого
статическое давление изменяется в 10—20 раз (начальный уча-
участок сверхзвуковой струи).
Глава VI
ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
§ 1. Основные понятия пограничного слоя
Широко разработанная теория движения идеальной жидко-
сти обычно дает вполне удовлетворительную картину действи-
действительных течений, за исключением областей, расположенных в
непосредственной близости от поверхности обтекаемого тела.
В этих областях существенное значение приобретают силы внут-
внутреннего трения, или силы вязкости, которые являются опреде-
определяющими в возникновении сопротивления тел при движении
в жидкости. Пренебрежение этими силами приводит к тому, что
сопротивление тела, равномерно движущегося в неограниченном
пространстве, оказывается равным нулю, что противоречит дан-
данным опытов.
Величина силы трения, действующей на единицу площади,
т. е. напряжение трения, обозначается обычно через т. Напря-
Напряжение трения в пограничном слое, согласно гипотезе Ньютона,
пропорционально градиенту скорости в направлении нормали
к поверхности тела (§ 4 гл. II), т. е.
ди ...
т = ^; (!)
коэффициент пропорциональности \х характеризует вязкие свой-
свойства жидкости и носит название коэффициента динамической
вязкости.
Теоретическое истолкование закона Ньютона A) можно по-
получить для газов на основании кинетической теории. Согласно
предположению, лежащему в основе кинетической теории, мо-
молекулы газа находятся в беспрерывном, но беспорядочном дви-
движении, так что газ в целом остается неподвижным. Кинетиче-
Кинетическая энергия этого беспорядочного движения молекул представ-
представляет тепловую энергию газа. Предположим теперь, что наряду
с беспорядочным движением молекул имеется упорядоченное пе-
перемещение конечных, очень больших по сравнению с отдельны-
отдельными молекулами масс газа параллельно некоторой плоскости Fq,
причем скорость этого движения и пропорциональна расстоянию
у от рассматриваемой плоскости (рис. 6.1). На произвольном
расстоянии г/i проведем плоскость F\, параллельную Fo, и рас-
рассмотрим перенос количества движения за счет беспорядочного
движения молекул через эту плоскость. Молекулы, которые
§ 1. ОСНОВНЫЕ ПОНЯТИЯ ПОГРАНИЧНОГО СЛОЯ
277
проходят через плоскость снизу вверх, обладают меньшим коли-
количеством движения в направлении скорости и, чем молекулы,
проходящие сверху вниз, вследствие этого скорость слоя газа,
лежащего выше плоскости Fi, будет уменьшаться, а скорость
слоя газа, лежащего ниже плоскости F\,— увеличиваться. Для
получения количественной характеристики этого взаимодействия
проведем следующие упрощенные вычис-
вычисления. Пусть в единице объема в среднем
находится N молекул, которые имеют
среднюю скорость беспорядочного движе-
движения с. В направлении, перпендикулярном Fj
плоскости F\, движется iV/З молекул, при-
причем из них 7V/6 движется сверху вниз
и столько же снизу вверх. За время dt г°ъ
через площадку dF на плоскости Fi в „ п . _.
^ ^ " J ^ Рис. 6.1. К истолкова-
каждом направлении пройдет -«- Nc dF dt нию закона Ньютона на
0 основании кинетической
молекул. Введем еще понятие длины теории
свободного пробега. Под длиной свободно-
свободного пробега I подразумевается такое среднее расстояние, которое
молекулы проходят между столкновениями друг с другом. Моле-
Молекула, которая находилась на расстоянии / вниз от плоскости F\,
обладала количеством движения
Сди ,
(т — масса молекулы, щ — скорость упорядоченного движения
в плоскости F\). Так как на длине свободного пробега количест-
количество движения сохраняется, то молекулы, движущиеся снизу
вверх, переносят количество движения, равное
-^-IJdF dt.
-±-Ncm
Соответственно сверху вниз переносится количество движения
II I ____ 7 I /7 г> fit
ду I
Этот перенос количества движения обусловливает появление в
плоскости F\ касательного напряжения т. Так как изменение
количества движения равно импульсу действующей силы
xdFdt = ±-
jjj-l) dFdt -±-
то для касательного напряжения получим выражение
1 т ди
B)
278
ГЛ. VI ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
которое представляет собой не что иное, как закон Ньютона,
причем \i = -j- pel.
Более точные расчеты, сделанные Энскогом и Чепменом,
учитывающие влияние скорости и на распределение скоростей
молекул, приводят к несколько иному числовому множителю
\i = 0,499pd.
В соответствии с кинетической теорией коэффициент динами-
динамической вязкости газов не должен зависеть от давления — он дол-
должен изменяться пропорционально квадратному корню из
абсолютной температуры (так как р~р/Т, с ~ У Г, 1~Т/р).
Таблица 6.1
Газ
Воздух
Азот
Кислород
Гелий
Водород
Аммиак
Водяной пар
Углекислый газ
Метан
Фреон-12
с, к
122
107
126
90
85
270
1100
238
160
60
и -10* Нс
1,72
1,66
1,92
1,86
0,84
0,98
0,81
1,37
1,03
1,17
Диапазон тем-
температур, К
180-1400
170-1300
180-1500
240-900
220—900
300—520
373—1000
260—1800
170—560
250-370
Погрешность
0,5
0,5
0,5
2
2
2
1
1
0,5
1
Первый вывод приблизительно оправдывается на опыте в до-
довольно широких пределах. Что же касается увеличения значе-
значений |х с возрастанием температуры, то оно происходит быстрее,
чем это следует из кинетической теории. Более точный подсчет
с учетом молекулярных сил притяжения и отталкивания приво-
приводит к формуле Сатерленда, которая удовлетворительно согласу-
согласуется с опытными данными,
\i __ I T \з/2 273 + С
1 О<7О 1 Ф I П '
1273/ Т+С
C)
где Т выражено в К.
В табл. 6.1 для различных газов приведены значения С и (Яо,
а также диапазон изменения температур, в котором погрешность
формулы Сатерленда не превышает значений, указанных в по-
последнем столбце таблицы.
При практических расчетах, однако, удобнее пользоваться
степенной зависимостью \х от температуры
-(JL
~ 1^273
т y
273/
D)
§ 1. ОСНОВНЫЕ ПОНЯТИЯ ПОГРАНИЧНОГО СЛОЯ
279
Результаты расчета коэффициент^ вязкости воздуха по фор-
формулам C) и D) (при со = 0,75) в диапазоне температур от 100
до 1000 К приведены на рис. 6.2. Сплошная кривая соответству-
соответствует формуле Сатерленда, а штриховая — степенной формуле. На
этом же рисунке точками показаны экспериментальные зна-
значения JLI.
Коэффициент динамической вязкости для капельных жидко-
жидкостей очень слабо зависит от давления и довольно быстро убыва-
убывает при увеличении температуры. Так как в капельной жидкости
A
3
2
1
^+
^^
200
400
800
т, к
Рис. 6.2. Зависимость коэффициента динамической вязкости воздуха от
температуры
длина свободного пробега молекулы соизмерима с размером мо-
молекулы, то кинетическая теория в этом случае непригодна. Боль-
Большое значение в этих условиях приобретают силы сцепления мо-
молекул. Ввиду сложности взаимодействия отдельных молекул
в капельной жидкости в настоящее время нет полной теории
жидкости и, следовательно, нет теории вязкости.
Рассмотрим ламинарное слоистое движение вязкой жидкости
около неподвижной твердой стенки. На самой стенке скорость
жидкости равна нулю, а вблизи стенки жидкость подтормажива-
подтормаживается под действием сил вязкости. Эта область течения вязкой
жидкости, расположенная около обтекаемого тела, называется
пограничным слоем. Вне пограничного слоя влияние вязкости
обычно проявляется слабо и картина течения близка к той, ко-
которую дает теория идеальной жидкости. Поэтому для теоретиче-
теоретического исследования течения вязких жидкостей все поле течения
можно разбить на две области: на область пограничного слоя
вблизи стенки, где следует учитывать силы трения, и на область
течения вне пограничного слоя, в которой можно пренебречь си-
силами трения и поэтому применять закономерности теории иде-
идеальной жидкости. Следовательно, пограничный слой представля-
представляет собой такую область течения вязкой жидкости, в которой
величины сил трения и инерции имеют одинаковый порядок.
На основании этого можно оценить толщину пограничного слоя.
280
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Для простоты рассмотрим течение жидкости вдоль плоской
пластины. Ось х направим вдоль пластины, ось у — перпендику-
перпендикулярно к ней. Для движения, происходящего в основном в на-
направлении оси х, сила инерции, отне-
~dy сенная к элементарному объему
dx dy dz, равна р -?• dx dy dz, где и —
скорость движения жидкости в направ-
направлении оси х. Для установившегося
движения
du ди dx ди
It
дх dt~~U'dx
сила инерции равна
Рис. 6.3. Силы трения, при-
приложенные к элементарно- следовательно,
му объему pudJLdxdydz.
Равнодействующая сил трения, параллельных направлению
движения, как легко видеть из рис. 6.3, равна
(т + -^ dy) dxdz—xdxdz =-^ dx dy dz.
Приравнивая силу инерции силе трения, получим соотношение
ди дт
или, используя закон Ньютона A),
ди
E)
Для пластины длиной I величина ди/дх пропорциональна ио/1>
где щ — скорость внешнего течения. Следовательно, сила инер-
инерции имеет величину порядка pul/l. Градиент скорости в направ-
направлении, перпендикулярном к стенке, т. е. величина ди/ду, имеет
порядок wo/б, где б — толщина пограничного слоя. Поэтому сила
трения пропорциональна [Шо/б2. Подставляя эти значения сил
в соотношение E), получим для толщины пограничного слоя
выражение
,/"и/ 6 1 1
Л/ -*—, ИЛИ -г- ~ = —т=
у р"о l i/pV VRi
F)
1^
Безразмерная величина puol/\i = Ri представляет собой число
Рейнольдса, подсчитанное по длине пластины.
Аналогичным образом можно оценить напряжения трения на
стенке т^= \i(du/dy)w. Используя полученные выше оценки
dy
-, 8
—, находим выражение для напряжения
§ 1. ОСНОВНЫЕ ПОНЯТИЯ ПОГРАНИЧНОГО СЛОЯ 281
трения и
Разделив напряжение трения xw на ргг0, получим связь между
tw
безразмерной величиной —- и числом Рейнольдса
Р"о
xw 1 /7\
Р"о /Rz
Соотношения F) и G) показывают, что число Рейнольдса явля-
является основной характеристикой ламинарного пограничного слоя.
Как толщина пограничного слоя, т. е. размеры области, где су-
существенное влияние оказывают силы трения, так и сама величи-
величина этих сил трения определяются в основном значением числа
Рейнольдса. Аналогичный результат можно получить также из
теории размерностей.
Для газов коэффициенты динамической вязкости малы
(рис. 6.2), поэтому числа Рейнольдса будут довольно большими
даже при относительно низких значениях скорости течения. Как
следует из соотношения F), толщина пограничного слоя вслед-
вследствие этого мала по отношению к длине пластины, т. е. все влия-
влияние вязкости сосредоточено в тонком слое вблизи обтекаемой по-
поверхности. Этот вывод находится в хорошем согласии с резуль-
результатами опытов по исследованию течений маловязких жидкостей.
Поясним эти качественные соображения численным примером. Оценим
порядок толщины пограничного слоя на конце пластины длиной I = 1 м,
обтекаемой воздухом при температуре Т = 300 К со скоростью щ = 15 м/с.
Плотность воздуха при этой температуре и атмосферном давлении равна
р = 1,18 кг/м3, а коэффициент динамической вязкости |Л = 1,82-10~5 Н-с/м2
(рис. 6.2). Этим параметрам соответствует число Рейнольдса Ri = piiol/\i »
» 105. Согласно формуле F) относительная толщина пограничного слоя
имеет порядок 6/1 ~ 10~3.
Число Рейнольдса является определяющим параметром не
только для количественных характеристик пограничного слоя,
но и для самого характера течения. При небольших числах
Рейнольдса движение частиц газа имеет упорядоченный слои-
слоистый характер, такое течение называется ламинарным. При
больших числах Рейнольдса движение частиц газа становится
беспорядочным, возникают неравномерные пульсации скорости
.в продольном и поперечном направлениях, такое течение назы-
называется турбулентным. Переход ламинарного течения в турбу-
турбулентное происходит при определенном значении числа Рейнольд-
Рейнольдса, называемом критическим. Критическое число Рейнольдса не
постоянно и в очень сильной степени зависит от величины на-
начальных возмущений, т. е. от интенсивности турбулентности па-
бегающего потока.
282
ГЛ VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Экспериментальные исследования перехода ламинарного по-
пограничного слоя в турбулентный на плоской пластине показали,
что критическое значение числа Рейнольдса
puQx
кр
= ю5 ч- юв.
(Здесь х — расстояние от передней кромки пластины.) Наиболее
характерным признаком такого перехода на пластине является
резкое увеличение толщины пограничного слоя и напряжения
трения на стенке. Одной из особенностей пограничного слоя на
пластинке является то, что вблизи передней кромки он всегда
ламинарен и только на некотором расстоянии хкр начинается пе-
переход в турбулентный режим течения. Ввиду сложности движе-
движения в переходной области и небольшой ее протяженности обычно
пренебрегают конечными размерами этой области, т. е. считают,
что переход ламинарного пограничного слоя в турбулентный
происходит при х = #Кр скачком.
Р1сследования течений в круглой трубе с острыми кромками
входного сечения показали, что
RKn =
кр
2300.
(8)
U — dn
(Здесь 1?Ср — средняя скорость, d — диаметр трубы.) Это значе-
значение является нижней границей критического числа Рейнольдса.
При меньших значениях R турбулентное течение не может су-
существовать даже при сильных начальных возмущениях. Если
обеспечить вход жидкости в трубу с малыми начальными возму-
возмущениями, то критическое число Рейнольдса может превышать
значение 100000.
Жидкость, заторможенная в пограничном слое, в некоторых
случаях не прилегает по всей обтекаемой поверхности тела в ви-
виде тонкого слоя. Таким особым
случаем является движение
вязкой жидкости вдоль стенки
против нарастающего давле-
давления во внешнем потоке (тече-
(течение в диффузоре). Как показы-
показывают результаты многочислен-
/Ш) =о ш ных опытов и теоретические
ду w оценки (§ 2), давление остается
постоянным поперек погранич-
пограничного слоя, следовательно, про-
продольный градиент давления,
который имеется во внешнем потоке, оказывает влияние на весь
пограничный слой. Если положительный градиент давления до-
достаточно велик, то слои жидкости, прилегающие непосредственно
Рис. 6.4. Схема образования отрыва
пограничного слоя
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 283
к поверхности тела и обладающие незначительным количеством
движения, могут остановиться и даже начать двигаться в обрат-
обратном направлении. Это явление, носящее название отрыва погра-
пограничного слоя, схематически изображено на рис. 6.4.
§ 2. Ламинарный пограничный слой
Существует два способа расчета параметров жидкости в по-
пограничном слое. Первый способ заключается в чпсленном реше-
решении системы дифференциальных уравнений пограничного слоя,
впервые полученных Прандтлем, и основывается на использова-
использовании вычислительных машин. В настоящее время разработаны
различные математические методы, позволяющие создавать ра-
рациональные алгоритмы для решения уравнений параболического
типа, к которому относится уравнение пограничного слоя. Такой
подход широко используется для определения характеристик ла-
ламинарного пограничного слоя. Развиваются приближенные мо-
модели турбулентности, применение которых делает возможным
проведение расчета конечно-разностными численными методами
и для турбулентного потока. Второй способ состоит в нахожде-
нахождении методов приближенного расчета, которые позволяли бы по-
получить необходимую информацию более простым путем. Такие
методы можно получить, если отказаться от нахождения реше-
решений, удовлетворяющих дифференциальным уравнениям для каж-
каждой частицы, и вместо этого ограничиться отысканием решений,
удовлетворяющих некоторым основным уравнениям для всего по-
пограничного слоя и некоторым наиболее важным граничным усло-
условиям на стенке и на внешней границе пограничного слоя. Основ-
Основными уравнениями, которые обычно используются в этих мето-
методах, являются уравнения количества движения и энергии для
всего пограничного слоя. При этом, однако, необходимо задавать
профили скорости и температуры. От того, насколько удачно вы-
выбрана форма этих профилей, в значительной степени зависит
точность получаемых результатов. Поэтому получили распростра-
распространение методы расчета параметров пограничного слоя, в которых
для нахождения формы профилей скорости и температуры ис-
используются дифференциальные уравнения Прандтля или их
частные решения. Далее расчет производится с помощью ин-
интегрального уравнения количества движения.
Выведем дифференциальные уравнения для ламинарного по-
пограничного слоя при установившемся плоскопараллельном тече-
течении вязкого сжимаемого газа, используя отмеченный ранее факт,
что для маловязких жидкостей (при больших 'числах Рейнольд-
са) влияние вязкости и теплопроводности сосредоточено в тон-
тонком слое вблизи обтекаемой поверхности, т. е.
284 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
где I — характерная длина обтекаемой поверхности, б — толщи-
толщина динамического пограничного слоя, бт — толщина теплового
пограничного слоя.
Преобразуем уравнения Навье — Стокса, уравнение энергии
и уравнение неразрывности (§ 5 и 6 гл. II), вводя безразмерные
величины следующим образом:
м"' ""' х=~' у^~' ~' er = -f,
р== p= Г=Т Р = ^ Х = 1Г с = Г~
причем ось х направлена вдоль обтекаемой поверхности, ось у —
перпендикулярно к ней; и, v—проекции скорости на оси х и у;
Т, Р? Р — температура, плотность и давление; \i, X — коэффициен-
коэффициенты вязкости и теплопроводности, ср — удельная теплоемкость
при постоянном давлении.
Величины с индексом 0 представляют собой параметры пото-
потока в некоторой точке вне пограничного слоя (например, в не-
невозмущенном потоке). Тогда
- -ди . — ди Ро др .
р U— + QV — = — -=г- +
дх ду pnw* дх
Г- / 4 d~ii 2 dv \ I , 5 I-
" dv , — to = Pp dp
д \ - (ди . dv\]\ //|nv
ду
дх
Безразмерные величины
^о _ 1 ^о _Ь-
dj^l = 0> A2)
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 285
не зависят от числа Рейнольдса, тогда как остальные обратно
пропорциональны числу Рейнольдса Ro:
JL =
Ro' PoVpo' RoPr'
Здесь к — отношение теплоемкостей; Мо — число М невозмущен-
невозмущенного потока; Рг — число Прандтля, подсчитанное по параметрам
вне пограничного слоя.
Приступим_теперь к_ оценке отдельных членов уравнений. Ве-
Величины и, р, р, f, jlx, К, ср имеют порядок единицы. При изме-
изменении х от 0 до 1 значения п, р, Т могут изменяться на вели-
величину порядка единицы, поэтому производные дп/дх, др/дх, дТ/дх
также имеют порядок единицы. Из уравнения неразрывности сле-
следует, что, поскольку величина дп/дх имеет порядок единицы,
такой же порядок имеет и величина dv/dy. Так как при у = О
v = О, то v будет порядка б. Такой же порядок б имеет вели-
величина^ ди/дх. При у = 0 и = 0, а при у = б и = 1, потому
ди/ду - 1/6. Тогда
— / 4 ди 2 ди \ I . & I — ди
д I — ди \ 1 ди л —ди л
ду \ ду j 6 дх ду
Так как в пограничном слое члены, зависящие от вязкости,
имеют одинаковый порядок с инерционными членами, то из пер-
первого уравнения движения следует, что
-i-r-1, или б~-т=. A3)
Эта оценка толщины пограничного слоя подтверждает более
грубый подсчет, сделанный в § 1. Сохраняя в первом уравнении
движения лишь члены, имеющие порядок единицы, получим
dTj i —ди 1 др 1 д /— ди \ ....
^ ^ А:М^ ^ % ду \г ду )
Во втором уравнении движения члены, зависящие от вязкости,
и инерционные члены имеют порядок б, следовательно, др/ду ~
~ б. Полное изменение давления на протяжении толщины по-
пограничного слоя по нормали к стенке может быть вычислено
путем интегрирования этого соотношения и имеет порядок б2,
т. е. очень мало. Поэтому можно считать, что давление
286 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
в поперечном сечении пограничного слоя остается практически
постоянным и равным давлению во внешнем потоке. Таким об-
образом, второе уравнение движения может быть записано в виде
у- = 0. A5)
Произведем аналогичную оценку для отдельных членов урав-
уравнения энергии. Так как число Прандтля для газов близко к еди-
единице, то множитель 1/PrRo, стоящий перед членами, зависящи-
зависящими от теплопроводности, будет малым при больших числах
Рейнольдса. Следовательно, члены зависящие от теплопровод-
теплопроводности, будут иметь одинаковый порядок с членами, зависящими
от конвекции тепла, только в том случае, если градиент темпе-
температуры дТ/ду велик, т. е. вблизи обтекаемой поверхности имеет-
имеется тонкий слой жидкости, в котором происходит резкое измене-
изменение температуры в направлении, перпендикулярном _ стенке.
Пусть толщина этого теплового пограничного слоя будет бг, тогда
df \ 1
Для того чтобы перенос тепла вследствие теплопроводности
был одного порядка с переносом тепла вследствие конвекции,
толщина теплового пограничного слоя должна удовлетворять
соотношению
PrR06|
¦* 1
или бг ~ —г- « A6)
/RPr
Учитывая оценку для б A3), получим соотношение
A7)
6Г
которое показывает, что при Рг ~ 1, т. е. для газов, толщина ди-
динамического пограничного слоя будет одного порядка с толщи-
толщиной теплового пограничного слоя. Так как
-др , - др -о д (тгдт\
дх ду дх \ дх )
ди У А2 9 dv ди \ (ди У
О Zl
дх ду \ду ) б2
то, оставляя в уравнении энергии члены порядка единицы,
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 287
получим
pu-L (cpT) + pv4=-(cplt) =
к— 1 — др , 1 д I г-
Возвращаясь в уравнениях A4), A5), A8) к размерным
переменным и присоединяя уравнение неразрывности A2), по-
получим дифференциальные уравнения ламинарного пограничного
слоя для установившегося плоскопараллельного течения сжи-
сжимаемого совершенного газа:
ж-0- <20>
<22>
Чтобы замкнуть данную систему, к уравнениям A9) — B2)
нужно присоединить уравнение состояния
P = pRT, B3)
а также определить зависимости коэффициентов вязкости и теп-
теплопроводности от температуры.
Необходимо еще сформулировать граничные условия. Для
непроницаемой стенки скорость должна удовлетворять условию
и = и = 0 при у = 0.
Для проницаемой стенки при подаче газа по нормали к по-
поверхности со скоростью vw граничные условия записываются в
виде и = 0, и =• vw при у = 0. Температура может удовлетворять
условию отсутствия теплоотдачи на стенке (обтекание теплоизо-
теплоизолированной поверхности)—в этом случае дТ/ду = О при z/ = 0;
в другом случае температура стенки Tw может быть задана.
Возможны и другие граничные условия, например может быть
задан тепловой поток на стенке.
При у = °° задаются значения и = ио, Т = То, где щ и То —
скорость и температура внешнего потока.
Так как толщина пограничного слоя мала, то уже на не-
небольшом расстоянии от обтекаемой поверхности параметры по-
потока практически совпадают с параметрами при у = °°. Поэтому
граничные условия можно задавать не при у = °о? а при у = б,
где б — толщина пограничного слоя, т. е. такое расстояние от
стенки, на котором, например, скорость отличается от скорости
при у = о© меньше чем на 1 %.
288
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Уравнение энергии B1) при сР=>const удобнее преобразо-
преобразовать, вводя вместо температуры Т температуру торможения
Т* =Т + и2/Bср). Для этого умножим уравнение движения A9)
на и и сложим с уравнением B1):
дт* . дт* д L дт \ . д Г д fu2\] /о/х
рг ^ i pr ^ ^ ^ <fy / ' дг/ [r dz/ V 2 / ] v '
Прибавляя и вычитая в правой части этого соотношения член
и деля обе части равенства на ср, получим
дТ* дТ* 1 д г ц 5 /а2
р"^г + ру^г = V??-№(Рг~ 1}^Ы
tkw.srk B5)
где ?т — число Прандтля, которое характеризует отношение теп-
яа, выделяющегося за счет трения, к теплу, передаваемому за
счет теплопроводности. Число Прандтля для газов обычно незна-
незначительно отличается от единицы. В табл. 6.2 приведены значе-
значения коэффициента вязкости, коэффициента теплопроводности,
Т а б лица 6.2
Газ
Воздух
Азот
Кислород
Гелий
Водород
Аммиак
Водяной пар
Углекислый газ
Метан
Фреон-12
г, к
300
300
300
300
300
300
373
300
300
293
и ю* н;с
м2
1,846
1,782
2,072
1,977
0,894
1,06
1,210
1,499
1,114
1,22
X W вт
м-град
2,62
2,57
2,67
15,2
18,3
2,44
2,52
1,66
3,42
0,98
ср. ю 3
Дж
кг-град
1,007
1,041
0,920
5,193
14,31
2,158
2,038
0,851
2,24
0,600
Рг
0,71
0,72
0,71
0,68
0,70
0,93
0,98
0,77
0,73
0,75
удельной теплоемкости и числа Прандтля для различных газов
при определенной температуре. С ростом температуры коэффи-
коэффициент теплопроводности увеличивается обычно несколько быст-
быстрее, чем коэффициент вязкости, но так как при этом немного
возрастает также удельная теплоемкость, то число Рг изменяется
слабо. Поэтому очень часто при построении метода расчета па-
параметров пограничного слоя предполагают, что число Прандтля
постоянно или даже равно единице. При Рг = 1 уравнение энер-
энергии B5) упрощается, так как первый член в правой части
равен 0.
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 289
Систему уравнений A9), B2), B5) целесообразно преобра-
преобразовать к виду, который является более удобным для исследова-
исследования частных случаев течения, допускающих получение автомо-
автомодельных решений. Преобразованные уравнения также широко
используются при применении численных методов расчета по-
пограничного слоя.
Как следует из соотношения B0), давление поперек погра-
пограничного слоя остается постоянным. Поэтому продольные гра-
градиенты давления в пограничном слое и во внешнем потоке сов-
совпадают. Дифференцируя по х интеграл Бернулли (§ 4 гл. I),
который связывает значения давления и скорости при течении
идеального газа, получим
dp du0
Здесь и дальше индексом 0 обозначены параметры внешнего
потока.
С помощью полученного соотношения можно исключить дав-
давление из уравнения движения A9):
^и 4- ^и ^U° J_ ^ ( ^U \ (9(\\
Уравнение неразрывности B2) проинтегрируем от 0 до у,
учитывая граничное условие для непроницаемой стенки v = О
при у = 0:
у
1у = —тт- \pu dy. B7)
о о
Введем новые независимые переменные Лиза — Дородницына
х у
I (ж) = j Po^o"o dx, т) (х, у) = ^= j p dy. B8)
При этом производные произвольной величины Q в различ-
различных системах координат связаны соотношениями
dQ ^ п .. 7, dQ д. дг* dQ W рио д$
В качестве зависимых переменных введем безразмерные ве-
величины
19 Г Н. Абрамович, ч 1
290 гл. vi. теория пограничного слоя
Преобразуем к новым переменным соотношение B7)
дх дц
и дифференциальные операторы в уравнениях B5) и B6)
dQ . дП РРпН'о^О Го* / df dQ df дО\ rdQ~\
Oil — f- OV —b- = e\ ^U " ~ I / ~^
* ox dy 2g L \дЦ ^ъ &ъ дЦ I дц J
д ( дО\ РРл^о^о д ( лтд0) лт р|Л
—— Li —— I = —^гт 7V — \ч -/V = •
оу у ду) 2д дц \ дц J p j-i
Используя полученные формулы перехода к новым перемен-
переменным, преобразуем уравнения движения B6) и энергии B5):
dg df dg
дЪ д\ дч\Г р
Величина р определяется распределением скорости внешне-
внешнего потока
Ло — относительная скорость внешнего потока (§ 3 гл. I), а па-
параметр N характеризует зависимость коэффициента вязкости
от температуры.
Так как г) = 0 при у = 0, ц -* °° при у -> оо? то граничные
условия имеют вид
f = ^ = °' 8= gw или 2L = 0 при т] = 0,
^• = 1, g = l при т|->оо.
Для решения системы уравнений в частных производных
C1), C2) в общем случае необходимо знать начальные про-
профили скорости и температуры.
После того, как решение уравнений C1), C2) найдено, мо-
могут быть определены напряжение трения на стенке
C3)
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 291
тепловой поток к стенке
_. (дТ\ _ су9у№ч
расстояние от обтекаемой поверхности
Индексом w обозначены параметры на поверхности обтекаемо-
обтекаемого тела.
Для некоторых практически важных случаев течение в по-
пограничном слое является автомодельным, т. е. не зависит от
переменной |.
Рассмотрим продольное обтекание плоской непроницаемой
пластины потоком несжимаемой жидкости с постоянным зна-
значением коэффициента вязкости при отсутствии теплообмена.
В этом случае duo/dz = O, Р = 0, iV = l, Л? = 0, а уравнения
движения C1) и энергии C2) становятся независимыми, при-
причем уравнение энергии C2) имеет тривиальное решение g = l,
т. е. температура сохраняется постоянной в пограничном слое.
Так как граничные условия и коэффициенты в левой части урав-
уравнения C1) не зависят от |, то существует автомодельное ре-
решение /(г)O зависящее лишь от переменной rj,
которое может быть найдено из обыкновенного дифференциаль-
дифференциального уравнения
Г + //"=о C6)
при граничных условиях
Этот случай впервые был рассмотрен Блазиусом, причем
решение уравнения C6) было получено путем применения раз-
разложения функции f(r[) в степенной ряд, асимптотического раз-
разложения для больших т] и последующей стыковки обоих разло-
разложений в некоторой определенным образом выбранной точке т|.
В настоящее время решение уравнения C6) легко может быть
получено численными методами с высокой точностью. Значения
функции м/мо = /'(т|) приведены в табл. 6.3.
Соотношение C3) для определения трения на стенке в рас-
рассматриваемом случае принимает вид
Ро^о
19*
292
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Как следует из результатов численных расчетов (табл. 6.3),
/" @) = 0,4696, и формула для определения коэффициента тре-
трения принимает вид
2tw 0,664 р и х
Сопротивление пластины шириной Ъ и длиной Z, которая
обтекается потоком с одной стороны, равно
i
W = bl%wdx.
о
Подставляя значение rw из соотношения C7) и интегрируя,
получим
0,664^p0ug R
Следовательно, коэффициент сопротивления пластины будет
равен
- ._ ™ „и* C8)
Толщина пограничного слоя не может быть определена точ-
точно, так как продольная составляющая скорости асимптотически
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
V СП)
0,0000
0,0469
0,0939
0,1408
0,1876
0,2342
0,2806
0,3266
0,8
0,9
1,0
1,2
1,4
1,6
1,8
2,0
0,3720
0,4167
0,4606
0,5453
0,6244
0,6927
0,7610
0,8167
*
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
/' (п)
0,8633
0,9011
0,9306
0,9529
0,9691
0,9804
0,9880
0,9929
Таб.
3,8
4,0
4,2
4,4
4,6
4,8
5,0
5,2
лица 6.3
/'(л)
0,9959
0,9978
0,9988
0,9994
0,9997
0,9999
0,9999
1,0000
переходит в скорость внешнего потока (функция f'(y\) асимпто-
асимптотически приближается к единице). Если условно за толщину по-
пограничного слоя принять расстояние от стенки, на котором и =
= 0,99^0, то из табл. 6.3 следует, что это расстояние соответ-
соответствует ц ~ 3,5, и следовательно,
Р0"о
4=
§ 2 ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 293
В тех случаях, когда при обтекании пластины скорость ста-
становится соизмеримой со скоростью звука или существенное зна-
значение приобретает теплообмен, необходимо учитывать сжимае-
сжимаемость. Предположим, что зависимость коэффициента вязкости
от температуры описывается степенной формулой D), а Рг = 1.
Температура и величина N могут быть выражены через иско-
искомые величины и параметры внешнего потока (штрихом обозна-
обозначено дифференцирование по у\)
Граничные условия имеют вид
Г@) = 0, /'(->)=•!, C9)
или g'@) = 0, *(оо)=1. D0)
Если температура стенки постоянна (gw = const) или тепло-
теплообмен отсутствует (g'@)=0), то система уравнений C1) и
C2) имеет автомодельное решение. При этом уравнения в част-
частных производных C1) и C2) становятся обыкновенными диф-
дифференциальными уравнениями
(#/")' + //"=(), (Ngy + fg' = 0. D1)
Из сравнения этих уравнений следует, что искомые функции
g и /' связаны линейной зависимостью g = а + bf\ причем не-
неизвестные коэффициенты а и Ъ могут быть определены из гра-
граничных условий. В зависимости от вида граничных условий для
температуры можно выделить два частных случая.
Если обтекаемая пластина теплоизолирована, то g'@) = 0
и fe='O, g(oo) = a = 1. Следовательно, в этом случае температу-
температура торможения остается постоянной в поперечном сечении по-
пограничного слоя, а температура поверхности равна температуре
торможения внешнего потока
k^i) D2)
Для определения профиля скорости и напряжения трения
на стенке необходимо решать одно обыкновенное дифференци-
дифференциальное уравнение третьего порядка D1)
+ к-=± м; A - г2)]*'1 /"}' + /г = о D3)
с граничными условиями C9).
Если функция }(ц) при заданных значениях Мо и со найде-
найдена, то можно определить профили скорости и температуры в
294
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
параметрическом виде
D5)
так как при обтекании плоской пластины | = po|io^o.r.
Соотношение C3) для определения трения в рассматриваем
1/ 2р ц ЖГ(^)' Тогда
мом случае принимает вид xw = pw\iwU0
для коэффициента трения cf в данной точке имеем
П)г0
D6)
Выражая отношение температур TJTq с помощью соотноше-
соотношения D2), окончательно получим
'~V'@). D7)
Величина /" @) зависит от числа Мо и показателя со в сте-
степенной зависимости коэффициента вязкости от температуры.
Расчеты профилей скорости и температуры, а также напряже-
напряжения трения на стенке для сжимаемого газа при со = 0,76 были
0,8
0,6
0,4
of/2
Г /
1/у
///
г
/
У
6/
/
Рпс. 6.5. Распределение скоро-
скорости в ламинарном погранич-
пограничном слое на теплоизолирован-
теплоизолированной пластине при Рг = 1,
со = 0,76, к = 1,4
О 4 8 72 16 20 24 28 32
проведены Карманом и Цзяном1). Результаты этих расчетов
приведены на рис. 6.5, 6.6 и 6.7.
Если задана постоянная температура пластины, то а —
^^(О) —?«» g{°°) = gw+b=*l. Поэтому распределение темпера-
температуры торможения в пограничном слое описывается формулой
1) Современное состояние аэродинамики больших скоростей/Под ред.
Л. Хоуарта.— М.: ИЛ, 1955.
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
295
Тогда
— — M _L
0
— 1 лА 2
М
-Mq — ^ )f + jT- — ¦
— 1 лл2,,2
ло / "о
и вместо уравнения D1) получим новое уравнение
D8)
1 +
- ^) /' + ^ -
+ //" = 0. D9)
Граничные условия C9) при этом остаются справедливыми.
Расчет профилей скорости и температуры по уравнению D9)
для различных чисел Мо при со = 0,76 и TJT0 = 0,25 также был
Рис. 6.6. Распределение тем-
температуры в ламинарном по-
пограничном слое на теплоизо-
теплоизолированной пластине при
Рг = 1, со = 0,76, к = 1,4
20
16
12
Мо=
Hi
— —
—^.
¦^^.
s-—
s
ч
ч
\
|
I
i
\
К
О 4 8 12 16 20 24 28 32 36 у
проведен Карманом и Цзяном. Результаты расчета показаны на
рис. 6.8, 6.9.
Коэффициент трения может быть подсчитан по формуле
D6), причем величина /" @) будет в этом случае зависеть от
0,65
0,55
О,<5\ ! : i I I I I L
О 2 < 6 8
Рис. 6.7. Коэффициент трения для ламинарного пограничного слоя на теп-
теплоизолированной пластине при Рг = 1, со = 0,76, к = 1,4
числа Мо, отношения температур TJTo и показателя степени о>.
Для определения удельного теплового потока qw используем
соотношение C4). Так как g'{0) = {! — gw)f" @), то при Рг = 1
!*Ns44
1
i
1
1
!
qw
E0)
Вводя безразмерный коэффициент теплоотдачи (число Станто-
на St) и выражая напряжение трения tw через коэффициент
296
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
трения cf D6) получаем
St = -
E1)
Таким образом, если коэффициент трения cf найден, то легко
определяется число Стантона.
При линейной зависимости коэффициента вязкости от темпе-
температуры (о) = 1) уравнения D3) и D9) совпадают с уравне-
уравнением C6) для несжимаемой жидкости. В этом случае функция
и/и0
0,6
0,4
0,2
0
1/
1/
1/'
V
А
/
/
i
Рис. 6.8. Распределение скорости
в ламинарном пограничном слое
на пластине при наличии тепло-
теплоотдачи и TJT0 == 0,25, Рг = 1,
со = 0,76, к = 1,4
6 8 10 12
}(ц) и, следовательно, величина /" @) не зависят от числа Мо
и температурных условий на обтекаемой пластине. Тогда фор-
формула для определения коэффициента трения D6) превращает-
превращается в соотношение C7), полученное для несжимаемой жидкости,
т/т0
¦5
4
3
Mq^Wj/
/
\
Рис. 6.9. Распределение темпера-
температуры в ламинарном пограничном
слое на пластине при наличии
теплоотдачи и Tw/T0 = 0,25,
Рг = 1, со = 0,76, к = 1,4
4 6 8 10 12 14J./EUL
а формула для коэффициента теплоотдачи E1) принимает вид
St = 0,332/V R*.
Влияние сжимаемости газа проявляется лишь в том, что
профили скорости, температуры и плотности зависят от числа Мо
и интенсивности теплообмена, как следует из формул D4) и
D5) или D8).
Для выяснения влияния числа Рг на параметры погранич-
пограничного слоя рассмотрим обтекание пластины потоком сжимаемого
газа при со = 1. Число Прандтля будем считать постоянным, но
§ 2 ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 297
отличным от единицы. Уравнение движения C6) при этом не
изменяется, а уравнение энергии C2) принимает вид
Интегрируя это линейное уравнение с учетом граничных усло-
условий C9), D0) и преобразуя интегрированием по частям с ис-
использованием уравнения C6), получим
где
*j ft) =
= ] [/" (л)//* @)]Рг *ь о2 (т|) = 2Pr J [Г (л)]Рг J [Г (л)]2"Рг
0 0
Так как *i@) = I, *i@)=0, то
Согласно численным расчетам в широком диапазоне изме-
изменения числа Рг справедливы приближенные формулы
oo)= 0,4696 Рг1/3,
Тогда выражение C4) для теплового потока к стенке преобра-
преобразуется следующим образом:
qw = Q,bZ2cv9ouuTl \\-gw- Л«A -
При обтекании теплоизолированной поверхности (qw = 0) из
этого соотношения следует, что безразмерная равновесная тем-
температура стенки равна
Полученное выражение может быть представлено в размер-
размерном виде
(^) E2)
где г = УРг — коэффициент восстановления температуры. Следо-
Следовательно, равновесная температура при обтекании пластины от-
отличается от температуры торможения внешнего потока, если
число Прандтля не равно единице. Например, равновесная тем-
тература пластины при Мо = 5, Т = 100 К для воздуха (к =
= 1,4, Рг = 0,7) будет равна 518 К, т. е. на 13 % ниже, чем
температура торможения (Г* = 600К).
Таким образом, в этом случае тепловой поток пропорциона-
пропорционален разности равновесной температуры и температуры стенки.
гл. vi. теория пограничного слоя
Вводя безразмерный коэффициент теплоотдачи, получим
Sf = coat?" -Т\ = °'332 Pr/3R^/2-
SP00 \* ПО 1w)
Коэффициент трения не зависит от величины Рг и может
быть найден по формуле C7). Число Стантона и коэффициент
трения связаны соотношением
Sf = -^С/Рг-2/3. E3)
Пограничный слой на плоской пластине является автомо-
автомодельным и в том случае, когда число Прандтля и показатель
степени со отличны от единицы. Однако уравнения движения и
энергии оказываются взаимосвязанными и совместное решение
возможно лишь численными методами. Результаты расчетов Брай-
нерда и Эммонса, Крокко, Копа и Хартри 1) показывают, что и
в общем случае равновесная температура определяется соотно-
соотношением E2). Коэффициент трения на пластине хорошо опи-
описывается приближенной формулой Янга
cf VK = 0,664 I 0,45 + 0,55 ^ + 0,09 (к - 1) Mj /Pr I ш E4)
а коэффициент теплоотдачи может быть вычислен по формуле
E3) после определения величины cf.
В качестве второго примера реальных течений, для которых
пограничный слой является автомодельным, рассмотрим течение
вблизи критической точки для несжимаемой жидкости при
о) = 1. Так как скорость внешнего течения в этом случае ли-
линейно изменяется вдоль обтекаемой поверхности щ = сх, то
р = 1, щ<^.срТ0. Тогда уравнения C1) и C2) принимают вид
В этом случае численные расчеты позволяют найти значение
функции /(т]), причем /г/ @) =• 1,233. Используя соотношение
C3), можно определить значение коэффициента трения вблизи
критической точки
cf = 1,233/lC.
Решение уравнения энергии записывается в следующем виде:
*=*
где
') См. сноску на с. 294.
§ 2„ ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 299
Тогда
' /
причем результаты численных расчетов аппроксимируются при-
приближенной формулой
В этом случае коэффициент теплоотдачи может быть найден по
формуле
Sf = 0,57Pr-°>6R-°'5.
Выражения для коэффициентов трения и теплоотдачи имеют
особенность, так как щ -> О при х -> 0. Поэтому удобнее в ка-
качестве характерной скорости использовать скорость невозму-
невозмущенного потока. При обтекании круглого цилиндра диаметром
d вблизи критической точки справедливо соотношение
Щ = Aueox/d,
с помощью которого можно представить формулы для коэффи-
коэффициентов трения и теплоотдачи в следующем виде:
2т„ 9,86 ж ,t Qw 1,14
где Roo =' рWood/|x — число Рейнольдса, подсчитанное по скорости
невозмущенного потока и диаметру цилиндра. Отличительной
особенностью рассмотренного течения является то, что коэффи-
коэффициент трения линейно растет по мере удаления от критической
точки, а коэффициент теплоотдачи сохраняется постоянным
вблизи критической точки.
Описанные результаты относятся к наиболее простым слу-
случаям течения в ламинарном пограничном слое. При более слож-
сложной форме обтекаемой поверхности и произвольном распределе-
распределении параметров внешнего потока необходимо решать систему
уравнений в частных производных C1), C2) численными ме-
методами. Наряду с разработкой численных методов были сдела-
сделаны попытки создать приближенные методы расчета, основанные
на решении интегральных соотношений, составленных для все-
всего пограничного слоя. Составим интегральное соотношение им-
импульсов при установившемся течении в пограничном слое сжи-
сжимаемой жидкости. Применяя уравнение количества движения
к элементу пограничного слоя длины dx и единичной ширины,
получим (§ 5 гл. I)
где ДB/т0 есть изменение проекции на ось х количества
движения жидкости, протекающей за единицу времени через
300
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
поверхность, ограничивающую рассматриваемый объем
(рис. 6.10), а Рх — проекция на ось х равнодействующей всех
сил, приложенных к выделенному объему. Подсчитаем сначала
изменение количества движения. Через элемент площади dy в
сеченни 1 протекает в единицу времени масса жидкости pu di/,
переносящая количество движения pu2dy. Поэтому количество
движения, переносимое жидкостью,
^^ втекающей через сечение 1, равно
{IimuI=)pu*dy.
О
Количество движения жидкости, вы-
вытекающей через сечение 2:
б / б \
Рис. 6.10. Силы, приложенные
к элементу пограничного слоя
о ^ о J
Масса жидкости, втекающей через границу пограничного слоя
на участке 1—2, равна разности расходов через сечения 2 и 1,
т. е.
/6 N
Так как скорость на границе пограничного слоя равна ско-
скорости внешнего потока мо» то количество движения, вносимое
этой массой жидкости в рассматриваемый объем, будет
Следовательно, изменение проекции на ось х количества дви-
движения равно
иг) 2 — B mu)i — B tf&w)i-2 =
( d\ /f \
= I —- \ pu2 dy — uQ -j— \ pu dy I dx.
V о о
/
Теперь найдем равнодействующую всех сил, приложенных
к рассматриваемому объему. При этом массовыми силами мож-
можно пренебречь. Силы трения в сечениях 1 и 2 не дают состав-
составляющей на ось х. Сила трения на границе пограничного слоя
равна нулю, так как ди/ду=^О при у = б. Сила трения, дей-
действующая со стороны стенки на рассматриваемый объем, равна
Рххс = — Twdx.
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 301
Проекции сил давления на ось х равны: в сечении 1 Рх\ =
= /?о6, в сечении 2 РУ2 = — \ро8 + ^ da], на границе погра-
ничного слоя ^xi—2 = Pq ~jZ~ dx- ьумма проекции сил давления
Тогда проекция равнодействующей всех сил, приложенных к
выделенному объему, будет
Подставляя найденные значения А B таи) и Рх в уравнение ко-
количества движения, получим интегральное соотношение импуль-
импульсов в пограничном слое
б
^ б^Г +т^- E5)
В этом уравнении ^0 и ро являются известными функциями
х и определяются при расчете внешнего потока.
Из уравнения движения следует
dx ro ° dx
Записав также очевидное равенство
б б
0 0 0
подставим эти выражения в соотношение E5). В результате
имеем
6 б
-^ J Р^ (Щ — и) dy + ~ J (Ро^о — Р^) аУ = т"» E6)
о о
Это уравнение можно получить и непосредственно из диф-
дифференциальных уравнений пограничного слоя. Для этого необ-
необходимо сложить почленно уравнение движения A9) с уравне-
уравнением неразрывности B2), умноженным на (u — uo), а затем
прибавить и вычесть ри дщ/дх в правой части полученного со-
соотношения
i [P" (и ~ ио)] + 9и в-^ + -щ [pv (и - щ)] = ро^о ^ + ±(р ^-)
302 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
я проинтегрировать в пределах пограничного слоя от 0 до б
с учетом граничных условий.
Введем теперь понятия о толщине вытеснения б* и толщине
потери импульса б**, которые определяются соответственно сле-
следующими выражениями:
б
J(P0*0-P*)«*y б
/ОйК E7)
6
ри («0 -u)dy 6
=(i_JL)^_^. E8)
Эти величины имеют определенный физический смысл. Тол-
Толщина вытеснения есть расстояние, на которое отодвигаются от
тела линии тока внешнего течения вследствие уменьшения ско-
скорости и изменения плотности в пограничном слое. Толщина по-
потери импульса есть толщина слоя газа с постоянными парамет-
параметрами и импульсом, равным разности импульсов потока газа с
неравномерной плотностью тока, но постоянной скоростью ио
и потока с переменными значениями скорости и плотности.
Используя введенные величины б* и б**, интегральное со-
соотношение количества движения E6) можно представить в виде
или
dx
где #=*6*/6**. Если задать законы распределения скорости и
температуры, то напряжение трения будет выражаться через
толщину потери импульса б**. Тогда соотношение E9), кото-
которое является обыкновенным дифференциальным уравнением,
может быть использовано для нахождения распределения вели-
величины б** вдоль обтекаемой поверхности.
Рассмотрим сначала пограничный слой несжимаемой жидко-
жидкости при заданном произвольном распределении скорости во
внешнем потоке. Профили скорости в пограничном слое будем
описывать многочленом четвертой степени (следуя Польгаузену)
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 303
причем для определения коэффициентов Ак используем гранич-
граничные условия
' ду2 ~~ Iя dx
— _?ii _ л ^ — 0 — Я
Второе условие при г/ = 0 вытекает из уравнения движения
B6) и граничных условий на непроницаемой поверхности.
Вводя безразмерный параметр
\i dx [lu dx'
получим (у =
•?- = B» - 2? + ?) + A Q _ 3^ + 3? - ?). F0)
Используя F0), находим напряжение трения на стенке,
толщину вытеснения б* и толщину потери импульса б**
= т°Л
2 +^"е"
6 10 120' 6 ~ 315 945 9072*
Если теперь подставить полученные выражения в интеграль-
интегральное соотношение количества движения E9), то получим обыкно-
обыкновенное нелинейное дифференциальное уравнение первого по-
порядка для определения толщины пограничного слоя Ь{х) или
параметра А(х), однозначно связанного с б. После того как
распределение толщины пограничного слоя и параметра Л
вдоль обтекаемого контура найдено, можно вычислить напря-
напряжение трения по формуле F1) и профиль скорости по форму-
формуле F0) в произвольном сечении пограничного слоя.
На рис. 6.11 показаны распределения скорости в погранич-
пограничном слое при различных значениях параметра Л. Профиль ско-
скорости при Л=-0 соответствует обтеканию плоской пластины.
Профиль скорости в точке отрыва определяется условием xw = 0,
в этом случае Л = —12. При Л<—12 имеется область возврат-
возвратного течения, а при Л>12 внутри пограничного слоя возника-
возникает область течения, где и/щ> 1. Поэтому описанный прибли-
приближенный метод расчета параметров пограничного слоя имеет
смысл лишь при —12<Л<12. Из анализа уравнения количест-
количества движения E9) вблизи критической точки, которая является
особой точкой (uq — 0), следует, что в этом случае Л = 7,052.
304
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
При обтекании плоской пластины интегральное уравнение
количества движения E9) принимает особенно простой вид
dx
F2)
причем, как следует из соотношения F1) при Л = 0, напряже,
ние трения обратно пропорционально толщине потери импульса,
т OD L_0
37
Выполняя интегрирование, получим распределение толщины
потери импульса б** вдоль пластины, а затем коэффициента
трения с1 и толщины вытеснения б*:
_?!!_ 0,685 _б^ _ 1,75 R _ Р V
с* ~~ х ~~ VK1 x ~~ VK1 х ~~ fl
Эти значения близки к значениям, найденным при численном
интегрировании уравнений пограничного слоя.
1,0
0,8
0,1
о
-о,г\ 1 1 1 1 1 1 1 1 L—\
О 0,2 0,4 0,6 0,8 у/<У
Рис. 6.11. Распределение скорости в пограничном слое при наличии гра-
градиента давления во внешнем потоке
Для сжимаемого газа, как показано выше, уравнения погра-
пограничного слоя в переменных Лиза — Дородницына имеют такой
же вид, как для пограничного слоя несжимаемой жидкости.
Поэтому следует ожидать, что зависимость скорости от перемен-
переменной т] в пограничном слое сжимаемого газа будет близка к за-
зависимости скорости от физической переменной у для несжимае-
несжимаемой жидкости. При обтекании плоской пластины (Л = 0) по-
положим
12 ^
1/Хл
к
к
УА
//
//
/
/
¦»
= 0
-6
-12
w
U
uo
[F3)
§ 2. ЛАМИНАРНЫЙ ЙОГРАНИЧНЫЙ СЛОЙ 305
где г] — переменная Дородницына, а А — значение этой пере-
переменной при у = б:
й idy- F4>
Используя F3) и F4), находим напряжение трения на стенке
ди\ ( да \ 9W o 9W u0
и толщину потери импульса
6
причем коэффициент В имеет ту же величину, что и для пе-
сжимаемой жидкости. Полученные выражения позволяют уста-
установить связь между xw и б**
tw = 2B^u0. (Г,5)
Подставляя выражение для tw из F5) в интегральное со-
соотношение количества движения, которое при обтекании пласти-
пластины имеет такой же вид F2), как в несжимаемой жидкости,
и интегрируя, получим распределение толщины потери импуль-
импульса и коэффициента трения
Используя степенной закон для зависимости вязкости от
температуры D), окончательно получим
б** 0,685 (Tw\^T
C = ^
Для определения профиля скорости в физических координа-
координатах необходимо установить связь между переменными у и z=*
=»т|/А, преобразовав первое соотношение F4) к виду
dz. F7)
Если ограничиться случаем Рг = 1, то зависимость темпера-
температуры торможения от скорости будет линейной и согласна
20 Г. Н. Абрамович, ч. 1
30U ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
соотношению D8)
Подставляя это выражение в формулу F7) и интегрируя с ис-
использованием профиля скорости F3), найдем зависимость у от z
Так как у = б при z =¦ 1, то
F8)
Тогда соотношение
и соотношение F3) дают в параметрической форме распреде-
распределение скорости в пограничном слое сжимаемого газа на плоской
пластине.
Так как А = б**/5, а б** связано с числом Рейнольдса фор-
формулой F6), то выражение F8) для толщины пограничного
слоя примет вид
б 5,84 /Г«Л-Г / 7 , 3 Г 37*-1м2
Преобразуя формулу для толщины вытеснения
и подставляя значения А и б из соотношений F8) и G0), по-
получим
@-1
б* 1,75 (Tw\— [Tw > 74^-l
^0
§ 2. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
307
При отсутствии теплоотдачи Tw = Г011 4— 2 ^о)' как сле~
дует из уравнения энергии D2). Тогда
„ 6** 0,685 , ,
со—1
— * М2\ 2
~2— °у '
о—1
2
@—1
Л0
G1)
G2)
G3)
Результаты расчета коэффициента трения на теплоизолиро-
теплоизолированной пластине для сжимаемого газа по формуле G1) при
со'^ 0,76, к = 1,4 показаны на рис. 6.7 штриховой линией.
Сплошная линия соответствует точным значениям. На рис. 6.12
16
12
8
4 -
О
-==
-*
— —'
-—
«8
8
Рис. 6.12. Зависимость толщины пограничного слоя, толщины вытеснения
и толщины потери импульса на плоской теплоизолированной пластине от
числа Мо (Рг = 1, со = 0,76, к = 1,4)
приведены значения толщины пограничного слоя, толщины вы-
вытеснения и толщины потери импульса на плоской теплоизоли-
теплоизолированной пластине для различных чисел Мо при со =•0,76,
/с=>1,4. Величины 8Н, 8Ю бн представляют собой характерные
толщины в несжимаемой жидкости, вычисленные при том же
числе Рейнольдса, что и для сжимаемого газа. Значение числа
Мо существенно влияет на характерные толщины погранично-
пограничного слоя, так при Мо = 10 толщина пограничного слоя увеличи-
увеличивается в 6 раз, а толщина вытеснения — в 20 раз по сравнению
с их значениями в несжимаемой жидкости.
Для сжимаемого газа при линейной зависимости коэффици-
коэффициента вязкости от температуры (co^l) приближенные значения
напряжения трения и толщины потери импульса не будут за-
зависеть от числа Мо в полном соответствии с результатами чис-
численных расчетов, основанных на использовании дифференци-
20*
308 гл. vi. теория пограничного слоя
альных уравнений пограничного слоя и описанных раньше.
Влияние сжимаемости будет проявляться лишь в профилях ско-
скорости и температуры и, соответственно, в значениях толщины
вытеснения и условной толщины пограничного слоя.
§ 3. Переход от ламинарного к турбулентному режиму течения
в пограничном слое
Ламинарное течение, как показывает опыт, устойчиво только
при некоторых условиях, определяемых значением критического
числа Рейнольдса. При числах Рейнольдса, больших критиче-
критического, ламинарное течение становится неустойчивым и переходит
в турбулентное. Этот переход связан с возникновением в потоке
незатухающих возмущений. Если образующиеся вследствие ка-
каких-либо внешних причин возмущения скорости и давления сте-
стечением времени затухают, то основное течение считается устой-
устойчивым, если же с течением времени они нарастают, то это сви-
свидетельствует о неустойчивости основного течения и возможном
переходе ламинарного режима в турбулентный. Исходя из такого
предположения о природе перехода, можно попытаться опреде-
определить значение критического числа Рейнольдса с помощью теории
устойчивости.
Рассмотрим плоскопараллельное течение несжимаемой жид-
жидкости, причем будем для простоты считать, что составляющая
скорости U зависит только от координаты г/, а составляющая
скорости V всюду равна нулю. Давление жидкости Р в основном
движении есть функция координат х и у. Течение в пограничном
слое можно приближенно считать именно таким течением, так
как изменение продольной составляющей U в направлении ко-
координаты х значительно слабее, чем в направлении координаты
у, а поперечная составляющая V мала по сравнению с вели-
величиной U.
Наложим на это основное течение двумерное возмущающее
движение, скорости и давление в котором зависят от времени t:
и'{х, г/, t), v'{x, у, t), p'{x, у, t).
Тогда давление и скорости результирующего движения будут
равны
р=Р + р\ u = U+u', v = v'.' G4)
Основное ламинарное течение должно удовлетворять уравнениям
Навье — Стокса. Будем предполагать, что результирующее дви-
движение также удовлетворяет уравнениям Навье — Стокса, а нало-
наложенные возмущения настолько малы, что можно пренебрегать
квадратами возмущающих скоростей. В зависимости от того, за-
затухает или нарастает с течением времени возмущающее движе-
движение, основное течение будет либо устойчивым, либо неустойчи-
§ 3. ПЕРЕХОД ОТ ЛАМИНАРНОГО РЕЖИМА К ТУРБУЛЕНТНОМУ 309
вым. Подставляя значения G4) в уравнения Навье — Стокса и
отбрасывая квадраты малых величин, получим
aw ,n*iLdU 1 дР i дР' _ (d2u 2 \\
Учитывая, что основное движение подчиняется уравнениям
Навье — Стокса, которые для рассматриваемого случая принима-
принимают вид
1 дР d2U 1 дР
v
G6)
получим для возмущающего движения следующую систему
уравнений:
ди' , ттди' , ,dU , 1 dp' ж /dV . ^2^'
дг)Г . ndv'
Дифференцируя первое уравнение системы G7) по у, а вто-
второе уравнение — по х и исключая из полученных таким образом
соотношений величину д2р'/дхду, т. е. давление, получим урав-
уравнение, связывающее составляющие скорости возмущающего дви-
движения и' и v'. Это уравнение движения вместе с уравнением
неразрывности служит для определения и и и'. Граничные ус-
условия для течения в пограничном слое заключаются в том, что
скорости возмущающего движения и и v' должны быть равны
нулю на стенке и на большом расстоянии от стенки, т. е.
tt' = i/ = 0 при г/ = 0; u' = v' = 0 при z/ = °°. G8)
Предположим, что на ламинарное течение налагается возму-
возмущение, состоящее из отдельных колебаний, каждое из которых
представляет собой волну, распространяющуюся в направле-
направлении х. Введем функцию тока для отдельного колебания в виде
следующего комплексного выражения:
Ф(*, У, О = ф(?)е'а(х-е'\ G9)
где ф = фг + г'фг- есть комплексная амплитуда, а — действительная
величина, связанная с длиной волны возмущения соотношением
3io гл. vi. теория пограничного слоя
X = 2я/сс; с = сг + iCi — комплексная величина, сг — есть скорость
распространения волн в направлении х, а с* — коэффициент на-
нарастания, от знака которого зависит, нарастают колебания или
затухают. Если Сг < 0, то колебания затухают и ламинарное те-
течение устойчиво, если же с{ > 0, то колебания нарастают и лами-
ламинарное течение неустойчиво.
Физический смысл, конечно, имеет только действительная
часть функции тока, т. е. величина
Re (if) = еач [фг cos а (х — crt) — (pi sin a (x — [crt)].
Составляя производные от функции тока, найдем для составля-
составляющих скоростей возмущающего движения значения
(80)
v' = — -g? = _ fctcp (у) **<*-<*>.
Уравнение неразрывности при этом будет удовлетворяться,
а уравнение движения, которое получается после исключения
давления, принимает вид
(С/ _ с) (ф" _ а2ф) _ с/"ф = _ SL (ф1у — 2а2ф" + а4ф).
Перейдем в этом уравнении к безразмерным величинам, для чего
разделим все скорости на скорость вне пограничного слоя но,
а все длины—на толщину потери импульса б**:
— U — с — O!fe!fc — ш
и ——, с = —, а = ао**, Ф =
% и
—, а = ао, Ф = —hrz.
Тогда получим
(Л -~с) (ф" - а2ф) - С/"ф = — J- (ф1у - 2а2ф" + а4ф), (81)
где R = C/6**/v есть число Рейнбльдса для основного ламинарно-
ламинарного течения, а дифференцирование ведется по переменной (#/6**).
Уравнение (81) называется дифференциальным уравнением
возмущающего движения. Исследование устойчивости решения
этого уравнения представляет собой задачу о собственных зна-
значениях дифференциального уравнения (81) при граничных усло-
условиях G8). Предположим, что основное течение задано, то есть
известно распределение скоростей в ламинарном пограничном
слое U(у). Тогда уравнение (81) будет содержать четыре па-
параметра: R, а, Сг, Си Для каждой выбранной пары R и а можно
найти собственную функцию ф и комплексное собственное зна-
значение с — Сг + ici, причем здесь сг — безразмерная скорость рас-
распространения возмущений, а с, — безразмерный коэффициент
§ 3. ПЕРЕХОД ОТ ЛАМИНАРНОГО РЕЖИМА К ТУРБУЛЕНТНОМУ
311
нарастания: __ __ __
сг = Сг{а, R), ci = d(a1 R). (82)
При Ci < 0 рассматриваемое движение устойчиво по отношению
к возмущениям рассматриваемой длины волны, а при с» > 0 —
неустойчиво.
Случай di = 0 соответствует нейтральным колебаниям и кри-
кривая с* (a, R)= 0 в плоскости a, R отделяет область неустойчивости
ламинарного пограничного слоя от области устойчивости. Эта
кривая называется нейтральной. Наименьшее число Рейнольдса
на нейтральной кривой является критическим числом Рейнольд-
Рейнольдса для данного течения. При числах Рейнольдса, меньших кри-
критического, возмущения любой длины волны затухают. При чис-
числах Рейнольдса, больших критического, имеются возмущения
с определенной длины волны, которые нарастают.
Расчет нейтральной кривой для случая обтекания плоской
теплоизолированной пластины потоком несжимаемой жидкости
а1Г ***
0,15
010
0,05
f
I
I
/a
//
/ /
•us
' Mq-
=0,7
101
10*
10s
10
10
Рис. 6.13. Нейтральные кривые
цля обтекания плоской теплоизо-
теплоизолированной пластины
Рис. 6.14. Нейтральные кривые для
обтекания плоской пластины пото-
потоком газа при Мо = 0,7
выполнен В. Толмином и проверен Ц. Линем. При расчетах бы-
было принято, что распределение скоростей в ламинарном погра-
пограничном слое описывается законом Блазиуса.
Аналогичный метод малых возмущений был использован
Ц. Линем и П. Лисом1) при исследовании устойчивости ламинар-
ламинарного пограничного слоя на плоской пластине, обтекаемой пото-
потоком сжимаемого газа. В этом случае уравнение нейтральной
кривой может быть записано в виде
= 0. (83)
Результаты расчета нейтральных кривых представлены на
рис. 6.13 и 6.14.
!) См. сноску на с. 294.
312 ГЛ VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Эти расчеты показали, что критическое число Рейнольдса
уменьшается при увеличении числа Мо внешнего потока при от-
отсутствии теплоотдачи от пластины. Охлаждение пластины при-
приводит к увеличению критического числа Рейнольдса при посто-
постоянном значении числа Мо, т. е. оказывает стабилизирующее
влияние на пограничный слой.
Таким образом, с помощью метода малых возмущений можно
получить значение критического числа Рейнольдса. Начиная
с того места на пластине, где число Рейнольдса достигает своего
критического значения, начинают нарастать возмущения с опре-
определенной длиной волны. Далее вниз по потоку становятся не-
неустойчивыми возмущения и с другими длинами волн. Наконец,
на некотором расстоянии от начала потери устойчивости лами-
ламинарное течение переходит в турбулентное. Критическое число
Рейнольдса, определенное экспериментальным путем из наблю-
наблюдения перехода ламинарного режима течения в турбулентный,
соответствует тому месту пластины, где турбулентность потока
приводит к перестройке всего течения. Поэтому найденные из
экспериментов критические числа Рейнольдса обычно превыша-
превышают по величине их теоретические значения.
Таким образом, метод малых возмущений позволяет опреде-
определить лишь нижнюю границу значений критических чисел Рей-
Рейнольдса, то есть дает те значения чисел Рейнольдса, меньших
RKp, при которых ламинарное течение всегда устойчиво. Кроме
того, с помощью этого метода можно выяснить влияние на
устойчивость ламинарного пограничного слоя таких параметров,
как Мо и TjTl.
Второй важной задачей, связанной с переходом ламинарного
пограничного слоя в турбулентный, является вычисление основ-
основных параметров течения в переходной области. В настоящее
время нет строгой теории переходной области в силу сложности
происходящих процессов, поэтому при проведении количествен-
количественных оценок в переходной области приходится использовать раз-
различные эмпирические и полуэмпирические методы.
Рассмотрим один полуэмпирический подход к определению
параметров в переходной области. Область перехода заменим
одной точкой, а в качестве условия сращивания решений для
ламинарного и турбулентного режимов течения используем не-
непрерывность изменения толщины потери импульса. Это условие
является наиболее оправданным с физической точки зрения, так
как изменение толщины потери импульса характеризует воздей-
воздействие вязких сил и тесно связано с величиной сопротивления.
В качестве примера рассмотрим обтекание плоской теплоизоли-
теплоизолированной пластины потоком несжимаемой жидкости. Интегрируя
уравнение импульсов F2) от 0 до Z, получим соотношение меж-
между коэффициентом сопротивления пластины длиной I и значени-
§ 3. ПЕРЕХОД ОТ ЛАМИНАРНОГО РЕЖИМА К ТУРБУЛЕНТНОМУ 313
ем толщины потери импульса в конце пластины
Cw = 26**/Z. (84)
Это соотношение справедливо для любого режима течения, в том
числе и для течения при наличии области перехода от ламинар-
ламинарного к турбулентному пограничному слою. Таким образом, для
определения коэффициента сопротивления Cw достаточно опре-
определить толщину потери импульса в конце пластины. Как пока-
показано выше, при ламинарном течении величина б** определяется
формулой
6** 0,664
X
Е'сли через хкр обозначить расстояние от кромки пластины до
начала области перехода, а через RKp — соответствующее число
Рейнольдса, то толщина потери импульса в начале области пере-
перехода будет равна
* 0,664*к
При турбулентном режиме течения в пограничном слое, как
будет показано дальше (§ 4), напряжение трения может быть
выражено через толщину потери импульса. Для этого заменим
число Re в уравнении A31) через величину Re** = РоМоб**/(Ао:
-^- = 0,0226 f^)°>25R6"*0*25 = 0,0126R^0*25.
о
Подставляя полученное выражение для напряжения трения
в уравнение импульсов F2) и интегрируя в области турбулент-
турбулентного течения (от хкр до Z), получим
б;;1>1в+ 0,0158 (Zi.«r-o.25_ xweRjrp0'")]e'8f (86)
**
где R = pouol/\io — число Рейнольдса, подсчитанное по длине пла-
пластины. Используя соотношения (85), (86), преобразуем формулу
(84) следующим образом:
0,625\0,8
j . (87)
Эта формула справедлива при R > RKp и позволяет определить
коэффициент сопротивления пластины в переходной и турбу-
турбулентной областях течения.
Значения CWi рассчитанные по формуле (87) при RKP = 5 • 105,
приведены на рис. 6.15 (кривая 2). На этом же рисунке пока-
показаны значения Cw для ламинарного режима течения в погранич-
пограничном слое (кривая 2), для турбулентного (кривая 3) и экспери-
314
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
\
ч
ч
•к
\
3
105 2 4 68106 2 4 6вЮ7 2 4 68R
Рис. 6.15. Коэффициент сопро-
сопротивления плоской пластины в
переходной области
ментальные данные, полученные для переходной области Ге-
берсом 1).
При этом следует иметь в виду, что величина RKp зависит от
начальной турбулентности основного потока и может быть опре-
определена в настоящее время только экспериментально.
Отметим, что величина критического числа Рейнольдса суще-
существенно зависит от многих параметров течения. Так, в области
ускоренного внешнего потока величина RKp увеличивается, а в
п 1п3 области замедленного потока —
уменьшается. Теоретическое опре-
определение нижнего критического
числа Рейнольдса, характеризую-
характеризующего сечение пограничного слоя,
в котором теряется устойчивость
движения, может быть выполне-
выполнено, например, с помощью приме-
применения устойчивости к однопара-
метрическим профилям скорости
F0).
На величину критического чис-
числа Рейнольдса влияет также ин-
интенсивность турбулентности 8
внешнего потока, определяемая отношением среднего квадратич-
квадратичного значения пульсаций скорости к средней скорости. Согласно
имеющимся экспериментальным данным, при малых значениях 8
(е<0,1%) RKp не зависит от интенсивности турбулентности
внешнего потока, и основной причиной возникновения перехода
является потеря устойчивости. При б > 0,1 % возрастание интен-
интенсивности турбулентности внешнего потока приводит к значитель-
значительному сокращению ламинарного участка течения (например, при
8 = 1% протяженность ламинарного участка на плоской пла-
пластине почти в 4 раза меньше, чем при 8 = 0,1%). Еще более
сложным образом на переход влияют масштаб турбулентности
и шероховатость обтекаемой поверхности.
§ 4. Турбулентный пограничный слой
Уравнения движения, энергии и неразрывности для турбу-
турбулентного пограничного слоя могут быть получены путем осред-
осреднения по времени исходных уравнений пограничного слоя A9) —
B2). Для простоты рассмотрим сначала несжимаемую жидкость.
Разложим турбулентное течение на осредненное движение и на
пульсационное движение. Обозначив осредненное по времени
значение составляющей скорости и через гг, а пульеационную
скорость — через и' и т. д., получим следующие выражения для
!) Современное состояние гидродинамики вязкой жидкости/Под ред.
С. Гольдштейна. Т. 2.— М.: ИЛ, 1948.— 408 с.
§ 4. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 315
составляющих скорости, для давления и для температуры:
и = п+и\ v = v + v', p=p+p\ Т = Т + Г. (88)
Под средним значением здесь и далее мы имеем в виду средние
значения по времени в фиксированной точке пространства, на-
например:
J udt. (89)
u = _*. j udt.
4
Для осреднения необходимо брать такой большой промежу-
промежуток времени t, чтобы осредненное значение не зависело от вре-
времени. Тогда осредненные по времени значения пульсационных
величин будут равны нулю:
Из определения (89) вытекают следующие правила осреднения:
а)
Действительно,
to+t
1 С
.+,=41 <»+=
'о
б)
Действительно,
и +
и.Л
V — U + V.
*0 + *
'о
5-в.
- I udt —
'о
to+t
4J"
'о
и,
(90)
й = й + v. (91)
(91)
так как, по определению, и не зависит от времени.
в) Uv^uv. (92)
Действительно,
uv = — \ uvdt = и — 1 udt = wi\
') 1-Е- <93>
Действительно,
ди
~дх~
i С ди ,^ д I 1 Г ,. \ ^гг
^ J d.r ^ \ i J / дх
так как пределы интегрирования не зависят от х.
316 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Теперь перейдем к выводу уравнений турбулентного погра-
пограничного слоя. Для случая несжимаемой жидкости с постоян-
постоянными физическими свойствами уравнения A9), B0), B4), B2)
принимают вид
¦1-0, (95)
дТ* , дТ* . д2Т . д2
(97)
дТ* , дТ* . д2Т . д2 ( и2 \ /пе.
-^ +cppv — = X— + [l— ^-j, (96)
Умножим обе части уравнения неразрывности (97) на ри и сло-
сложим его почленно с уравнением движения (94):
^_ер Л (98)
дх г дуЪ ч 7
г дх ' г ду дх у
Умножая обе части уравнения неразрывности на сррТ* и скла-
складывая его почленно с уравнением энергии, имеем
Подставим в уравнения (95), (97), (98), (99) вместо и, v, pr
Т их значения из (88) и произведем осреднение по времени. Ис-
Используя правило осреднения (93), из (95) получим
f = 0. A00)
Используя правила осреднения (90) и (93), уравнение нераз-
неразрывности (97) преобразуем к виду
Перейдем к осреднению преобразованного уравнения движе-
движения (98). На основании правил осреднения (90) — (93) получим
дх дх v~ ' """" ~ " } ~ дх ~ дх '
д 7=—=~; ; '~~'
д\_ dV _ Л* dp _ dp
ду2 + ду2 ~ ду2' ~д^~~Ы;
§ 4 ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 317
поэтому уравнение движения (98) после осреднения принимает
вид
д(п2) д(пЪ) д'р д~2 дИ^' дЧ
P + P =^-Р~ТГ-р~^ + Р
Вычитая почленно из этого соотношения уравнение нераз-
неразрывности A01), умноженное на рй, и (пренебрегая производной
по х от пульсационных составляющих по сравнению с производ-
производной по г/, как это делается при выводе уравнений пограничного
слоя, окончательно получим дифференциальное уравнение дви-
движения для турбулентного пограничного слоя
— ди , - ди др . д ( ди —,
A02)
Аналогичные преобразования проделаем с уравнением энер-
энергии (99). Так как
д(иТ*) __ д (иТ*) , дИ7!*' д(ьТ*) _ ~(FvT*) dVW1 д?Т_ == d2f
дх ~~ дх ^ дх ' ду ~ ду + ду ' д^ ду2%
то уравнение энергии (99) после _почленного вычитания соотно-
соотношения A01), умноженного на сррГ*, принимает вид
-д~Т* . -дГ* д L дТ -77р,\ , д - ( дп
и +cpv [X cPv Tj+u^
о — i ou —;>i /лг\о\
-^- U [и, -г 0U V , A03)
причем
Сравнивая уравнения для турбулентного пограничного слоя
A00) — (ЮЗ) с уравнениями для ламинарного пограничного слоя
(94) —(97), можно отметить следующее. Уравнение неразрывно-
неразрывности и второе уравнение движения имеют одинаковый вид. Пер-
Первое уравнение дзижения и уравнение энергии для осредненных
параметров турбулентного пограничного слоя отличаются от со-
соответствующих уравнений для ламинарного пограничного слоя
наличием дополнительных касательных напряжений и дополни-
дополнительных тепловых потоков.
Простое истолкование этих дополнительных членов было дано
Праыдтлем. Для изложения идеи Прандтля рассмотрим плоско-
плоскопараллельное течение, скорость которого по направлению совпа-
совпадает с осью х, а величина скорости зависит лишь от координа-
координаты у. Следовательно, й = м(у), г;=0, причем пусть дп/ду>0.
Механизм турбулентного течения можно представить следую-
следующим упрощенным образом. В процессе турбулентного течения
318 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
возникают жидкие объемы, каждый из которых на некотором
расстоянии движется в любом направлении как целое с опреде-
определенной скоростью. Предположим, что такой жидкий объем, воз-
возникший в слое с координатой у\ — V и обладающий скоростью
п(у\ — Z'), перемещается на расстояние V как целое в направле-
направлении оси у. Когда этот жидкий объем попадает в слой с коорди-
координатой i/i, то скорость в этом слое изменится на величину
W = u(y1-l')-u(jfl) =
которая представляет собой пульсационную составляющую. При
этом v' > 0. Аналогично жидкий объем, попадающий в слой у\
из слоя у\ +1', имеет большую скорость, чем окружающая его
среда. Следовательно, пульсациоыная составляющая и будет
равна
при этом г/ < 0.
Путь перемешивания V в известной степени аналогичен пути
свободного пробега молекул в кинетической теории газов с той
лишь разницей, что там происходят микроскопические движения
молекул, а здесь — макроскопические движения турбулентных
объемов. В общем случае длина пути перемешивания зависит от
времени и может принимать положительные или отрицательные
значения. Поэтому пульсационная составляющая также зависит
от времени _
u'-Z'-g. A04)
Возникновение пульсаций скорости в поперечном направле-
направлении можно представить следующим образом. В слое с координа-
координатой у\ за счет каких-либо причин происходит увеличение скоро-
скорости, т. е. появляется положительная пульсационная составляю-
составляющая и'>0. Жидкий объем, имеющий эту скорость п(у\)+и',
сталкивается с находящимся впереди объемом, имеющим ско-
скорость п(у\), и поэтому возникает поперечное движение, направ-
направленное в обе стороны от слоя у\. Если в слое с координатой у\
происходит уменьшение скорости (гг'<0), то жидкий объем,
имеющий эту скорость, отстает от объема, имеющего скорость
п(у\), и возникает поперечное движение, направленное с обеих
сторон к слою z/i. На основании этих рассуждений можно сде-
сделать вывод, что величина поперечной пульсационной скорости v'
имеет такой же порядок, как и величина продольной пульса-
пульсационной скорости и . Как показано выше, объем жидкости, при-
приходящий в слой г/i с положительным значением г/, вызывает
обычно отрицательную пульсационную скорость и. Объем жид-
жидкости, приходящий в слой г/i с отрицательным значением i/, вы-
§ 4. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 319
зывает обычно положительную пульсационную скорость и', т. е.
v' = -ku\ A05)
где к — коэффициент пропорциональности, имеющий порядок
единицы.
Тогда произведение uv' будет обычно отрицательным, и по-
поэтому осредненное по времени значение uv' будет отличным от
нуля и отрицательным
Ввиду некоторой неопределенности пути перемешивания мож-
можно включить коэффициент к в эту величину. Тогда получим
UV = — I2 (j^J, где Z2 = кТ2. A06)
Следует отметить, что все проведенные выше рассуждения
относились к случаю положительного значения производной
du/dy. Аналогичные рассуждения для du/dy < 0 показывают, что
в этом случае произведение u'v' обычно положительно. Тогда
A07)
Формулы A06) и A07) можно, следовательно, представить
одной формулой
u'v' = -
du
du
, -,-. A08)
dy Л" v /
Совершенно так же можно вывести формулу для осреднен-
ного значения произведения v'T', если предположить, что меха-
механизм переноса тепла подобен механизму переноса количества
движения. В этом случае Т' = I'dT/dy, и поэтому
du
dJ
A09)
Выражения A08) и A09) получены для частного случая те-
течения, когда п = п(у), однако они могут применяться и в общем
случае распределения скоростей в пограничном слое.
Используя соотношения A08) и A09), уравнение движения
A02) и уравнение энергии A03) преобразуем к виду
•"¦B+'-f —Й + ^^ + М^]. <)
?+*»>? -§ + ^.[(V+Mf ] + (и + М(-|)'. («О
320 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
где |iT = pi21 -^- J есть коэффициент турбулентной вязкости,
Ят = cpl2 ( — ] — коэффициент турбулентной теплопроводности.
Здесь и далее черта над осредненными параметрами опускается.
Гипотеза Прандтля о пути перемешивания оказалась весьма
плодотворной, так как открыла реальные возможности для рас-
расчета турбулентных течений. Хотя длина пути перемешивания и
не является физической постоянной для каждой жидкости в от-
отличие от молекулярных коэффициентов вязкости и теплопровод-
теплопроводности, однако, она, как показывают опытные данные, не зависит
от параметров потока. Длина пути перемешивания в основном
является функцией координаты у. Так как при течении вдоль
гладкой стенки в непосредственной близости от ее поверхности
пульсации скорости равны нулю, то I = 0 при у = 0. Принимая
простейшую гипотезу, что вблизи стенки длина пути перемеши-
перемешивания пропорциональна расстоянию от стенки
l = ky, A12)
можно получить, следуя Прандтлю, профиль скорости в турбу-
турбулентном пограничном слое при течении несжимаемой жидкости
вдоль плоской пластины (др/дх = 0). В этом случае из уравне-
уравнения A10) следует, что при у = 0, когда и = v = 0,
Дифференцируя по у уравнение A10) и учитывая уравнение
неразрывности A01), получим д2т/ду2 = 0 при г/ = 0, т. е. вблизи
стенки напряжение трения остается постоянным:
т = т„. " (ИЗ)
Пренебрегая коэффициентом молекулярной вязкости \х по срав-
сравнению с коэффициентом турбулентной вязкости jit и подставляя
вместо jnT его выражение через длину пути перемешивания, по-
получим соотношение
которое при замене величины I выражением A12) принимает
вид
т =
Проинтегрировав это уравнение, с учетом равенства (ИЗ) по-
получим
u = -tV -flny+C. A14)
§ 4. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
321
Это соотношение можно записать в следующем безразмерном
виде:
Vif
T~ Ш h Ci, Mini
где ^ = /т^/р, v -= ц/р.
Величина А:, согласно результатам измерений, является уни-
универсальной постоянной турбулентного течения и равна 0,4 Вто-
Вторая постоянная С\ зависит от свойств обтекаемой поверхности.
Универсальный закон распределения скоростей A15), выведен-
выведенный для течения вдоль плоской стенки, оказывается справедли-
справедливым и при течении жидкости в круглой трубе. На рис. 6.16 про-
проведено сравнение результатов расчета по формуле D15) при
30
25
20
15
10
Рис. 6.16. Распределение скорости в гладкой трубе. Кривая 1 соответствует
универсальному логарифмическому закону
С\ = 5,5 с опытными данными для труб, полученными Нику-
радзе при различных числах Рейнольдса1).
Следует отметить, что универсальный закон распределения
скорости выведен в предположении, что в основной части тур-
турбулентного пограничного слоя коэффициент молекулярной вйз-
кости мал по сравнению с турбулентным коэффициентом вяз-
вязкости. Такое допущение оправдано лишь при очень больших
числах Рейнольдса, поэтому универсальный закон распределе-
распределения скорости следует рассматривать как асимптотический закон
для очень больших чисел Рейнольдса. Опыты, проведенные при
!) Шлихтинг Г. Теория пограничного слоя.—М.: Наука, 1974.
21 Г. П. Абрамович, ч 1
о
10—
°R=4,0-W3
• 2J-10*
• 1,1-10s
ф 4JJ'10s
e tf.fff»
в 2,0-10е
• 3,2- 10е
322 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
обтекании плоской пластины потоком несжимаемой жидкости,
показывают, что при умеренных числах Рейнольдса распределе-
распределение скорости хорошо описывается степенным законом
причем величина п слабо зависит от числа Рейнольдса. При
rx = ifN—Ю8 можно принимать п = 7.
Уравнения движения, энергии и неразрывности для турбу-
турбулентного пограничного слоя сжимаемого газа могут быть также
получены путем осреднения по времени исходных уравнений по-
пограничного слоя A9) — B2). Для осредненных параметров эти
уравнения принимают вид (при постоянной теплоемкости)
ди . ди др . д Г, , ч ди ~
PU-to +*»-%=—? +¦[<» +1*)
дТ . дТ
dp . д (\л . л ч дТ
и + Р + ^
дх ^~ ду '
Здесь ^iT и К — коэффициенты турбулентной вязкости и Турбу-
Турбулентной теплопроводности, которые характеризуют nepenqc ко-
количества движения и тепла за счет поперечных пульсаций ско-
скорости. j *
Граничные условия этой системы уравнений имеют такрй же
вид, как и для ламинарного пограничного слоя:
и = v;= О, T = TW при у = О,
u = uo, Т = Го при у = б.
Для решения уравнений A17) — A19), кроме уравнения со-
состояния и зависимостей коэффициентов |я и X от температуры,
необходимо знать значения коэффициентов турбулентного пере-
переноса jit и Хт. Ввиду отсутствия в настоящее время законченной
теории турбулентности определение этих коэффициентов носкт
полуэмпирический характер и основывается на ряде гипотез.
Поэтому при расчете турбулентного пограничного слоя обыч-
обычно используют приближенный метод, основанный на решении
интегрального уравнения количества движения E9). При- этом
необходимо задавать распределение скоростей и температур в по-
пограничном слое.
Рассмотрим случай обтекания плоской пластины при числэ
Прандтля, равном единице. Сначала преобразуем уравнение
энергии. Умножая A17) на и, складывая с A18) и вводя
§ 4. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ 323
температуру торможения
золучим
Величина Ргт = (сРцт) /Ят есть число Прандтля для турбулент-
турбулентных параметров. Согласно имеющимся в настоящее время дан-
рым число Ргт близко к единице. Поэтому в дальнейшем будем
принимать Ргт = 1. При Рг = Ргт =• 1 соотношение A21) упро-
упрощается и принимает вид
.»?+<»?-?[*•+•->?]• <122>
Так как при продольном обтекании плоской пластины -^ —
= 0, то из уравнения A17) получим
ди . да д
Р + Py
Вследствие подобия уравнений A22) и A23) решение урав-
уравнения энергии A22) может быть представлено в виде
Т* = аи + 6,
где неизвестные коэффициенты а и 6 определяются из гранич-
граничных условий A20):
и = 0, Т*= Tw = b; и = и0; Т* = Т*0 = аи0 + Tw,
a = (T*0-Tw)/u0.
Следовательно,
T* = (Tl-Tv)^- + Ttt. A24)
Прежде чем переходить к нахождению профиля скорости, пе-
ибходимо отметить следующее обстоятельство. Вблизи обтекае-
обтекаемого тела число Рейнольдса, определенное по местным парамет-
параметрам жидкости, может быть сколь угодно малым. Поэтому в этой
•бласти должно существовать ламинарное течение, где трение
л теплообмен определяются молекулярным переносом, т. е. \х >
~> цт, X > хт. Эта часть пограничного слоя называется ламинар-
иым подслоем. В остальной, основной части пограничного слоя
лределяющую роль играет перенос посредством турбулентных
21*
324
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
пульсаций, т. е. [i < \iT, X < Лт. Будем считать, что число Рей-
нольдса на границе ламинарного подслоя не зависит от числа
Маха Мо и интенсивности теплообмена
Р-Щ^ = а2; A25)
согласно опытным данным коэффициент а равен 12,5.
Распределение скорости в ламинарном подслое можно счи-
считать линейным:
и
У
7
A26)
Закон распределения скорости в основной части турбулент-
турбулентного пограничного слоя может быть получен на основании ана-
анализа экспериментальных данных.
Фс
0,8
0.6
о о
*Hi49 Тш=0,93
А 5,0 0,71 •
v 5,1 0,53 Ў
¦ 5,6 0,90 *
о 9,1 0,55 ¦
2,0 1
2,4 1
2,4 1,57
2,8 1,35
0,1
0,2
0.4
0,6 0,8 у/8
Рис. 6.17. Профиль скорости в турбулентном пограничном слое сжимаемого
газа на плоской пластине
Результаты экспериментального исследования профиля ско-
скорости в основной части турбулентного пограничного слоя сжи-
сжимаемого газа на пластине представлены на рис. 6.17. Оказы-
Оказывается, что число Маха Мо и температурный фактор Tw = Tw/T0
мало влияют на форму распределения скоростей. Поэтому сте-
степенной закон A16) будем считать справедливым и для сжи-
сжимаемого газа.
Найдем выражение для напряжения трепия на стенке, ис-
используя A26):
ди
A27)
Так как на границе ламинарного подслоя значения скорости,
вычисленные по формулам A26) и A16), должны совпадать,
то ил/во = Fл/6I/п. Принимая для зависимости коэффициента
§ 4 ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
вязкости от температуры степенной закон D), получим
325
Здесь Re = роиоб/jxo — число Рейнольдса, подсчитанное по толщи-
толщине пограничного слоя, а величина ujuo должна быть определена
из условия A25).
Разрешая соотношение A25) относительно 6Л, получим
-2L
~ R6
С другой стороны, бл/б =|(ил/ио)п, поэтому
Используя связь между температурой торможения и ско-
скоростью A24), найдем следующее алгебраическое уравнение для
определения относительной скорости на границе ламинарного
подслоя:
_ а
к —
X
. A29)
Это уравнение надо решить методом последовательных прибли-
приближений, то есть задавать произвольно величину uJuq, подстав-
подставлять это значение в правую часть соотношения A29), находить
новое значение uJuq и т. д. Так как величина ujuo обычно
равна 0,3—0,7, то в качестве первого приближения возьмем
ujuo = 0,5. Тогда во втором приближении получим
п+1
1+0)
Величина, стоящая в квадратных^ скобках, слабо меняется
при изменении числа Мо. Так, при 7^ = 0,5 она изменяется от
0,750 до 0,672 при изменении числа Маха от 0 до 10. Ограничи-
Ограничиваясь первыми двумя приближениями, окончательно получим
* / .1+(о / -. д+о)
( )[1+^у A30)
326
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Тогда выражение для напряжения трения A28) при п = 7, ©«
= 0,75 принимает вид
*w = 0,0226
л „2 pO,25
»0,75
L,31 iw>
»31
. A31)
Прежде чем переходить к интегрированию уравнения коли-
количества движения E9), которое в случае пластины выглядит так:
dd**
dx
A32)
необходимо еще найти связь между б** и б. Используя про-
профиль скорости A16) и профиль температуры A24), получим
б*»
_
1
_ . б* Г
_l _ _Wj
zn+1dz
Результаты расчета величин 6*/б и б**/б для п
ведены на рис. 6.18, 6.19.
7, к = 1,4 при-
при0,8
0.8
ОА
0,2
r 1 '
, -
.——
—¦—
,——
—-—
1 —
Рис. 6.18. Относительная
толщина вытеснения для
турбулентного погранично-
пограничного слоя
О 12 3 4 5 6 7 8 9 Mo
Для несжимаемой жидкости (при Мо = О, TW — 1)
6** п б* 1
Интегрируя соотношение A32) с начальным условием 6 = 0 при
х = 0, получим распределение толщины пограничного слоя вдоль
пластины
0,0575 /б**^-°>8 A+-2~Мо] _06/ 2 у,05
R0.2 \ б
/т»0,6
1,05 -1 w
§ 4. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
327
Подставляя найденное значение б из A33) в A31), получим вы-
выражение для коэффициента трения
/Л**\о,2 1+—2~"мо
0,0922
После того как толщина пограничного слоя найдена, толщи-
толщина вытеснения и толщина потери импульса находятся по извест-
известным отношениям 6*/6 и 6**/б.
6J6
0,08
0,06
0,04
0,02
TW=O,L
X
*—
¦¦*¦—
-—
*- —
' w,
¦
2 3 4 5 6 7 в
9 Мо
Рис. 6.19. Относительная толщина потери импульса для турбулентного по-
пограничного слоя
Коэффициент сопротивления пластины длиной I и шириной Ъ
равен
После подстановки значения xw из соотношения A34) и инте-
интегрирования получим
0,116
1,05
Результаты расчета_ коэффициента сопротивления по форму-
формуле A35) для случая Tw=i (отсутствия теплоотдачи) представ-
представлены на рис. 6.20.
6** Для7 не'°жимаемой жидкости при Мо = 0, Тw == 1
Г = 2*» и поэтому
X
0,37
: R2'2'
Cjk
0,058
= 0,073
R0.2 *
328
ГЛ VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Для определения теплового потока воспользуемся интегралом
A24) уравнения энергии
Это выражение совпадает с формулой D8) для ламинарного
Cw
0,008
0,006
0,004
0,002
0,001
0Ш8
0,0006
0,0004
Ц0002
0,0001 -=—
W5 2 4 6 010е 2 4 6 8107 2 4 6 8R
Рис. 6.20. Коэффициент сопротивления пластины при Tw = 1
пограничного слоя. Поэтому для безразмерного теплового потока
имеем (при Prw = 1)
-^=
¦^—
—^
' -^
6
6
10
-*•
У
^«,
"*¦
f2
у
У/
/
/
1
—^
^*
^*
¦*»
¦»»
—*
—*^
¦^•^
*.
^=а
— и^.
¦*¦
««.
¦¦»
^
st =
2 -
A36)
Соотношение A36) является следствием предположения о на-
наличии аналогии между процессами переноса количества движе-
движения и тепла при Рг = Ргт = 1 {аналогия Рейнольдса).
Изложенный метод расчета турбулентного пограничного слоя
сжимаемого газа подтверждается результатами эксперименталь-
экспериментальных исследований. На рис. 6.21 приведены расчетные значения
0,6
0,5
— > -
—
J/ г п т
Пд—и,и nj = J
—
-
О
—
—¦ ¦
Рис. 6.21. Относительная скорость
на границе .ламинарного подслоя
0,4 0,5 0,6 0,7 0,8 0,9 Тш
относительной скорости на границе ламинарного подслоя (по
формуле A30)) и опытные значения Лобба, Винклера и Пер-
Перча1). Сравнение экспериментальных и вычисленных коэффици-
') Лапин Ю. В. Турбулентный пограничный слой в сверхзвуковых
потоках газа.— М.: Наука, 1970.
§ 5. ОТРЫВ ПОГРАНИЧНОГО СЛОЯ
329
ентов трения для плоской пластины показано на рис. 6.22.
Сплошная кривая представляет собой расчетное отношение С/А?/н,
вычисленное при одинаковых числах Рейнольдса, отнесенных к
0,8
0,6
0,4
0,2
N
1
i
D (
Рис. 6.22. Коэффициент трения для турбулентного пограничного слоя сжи-
сжимаемого газа
толщине потери импульса. Черными точками обозначены экспе-
экспериментальные значения этого отношения. Штриховая кривая со-
соответствует отношению С//с/н, подсчитанному при одинаковых Rx.
Опытные значения для этого случая показаны светлыми точками.
§ 5. Отрыв пограничного слоя
При наличии градиента давления во внешнем потоке течение
в пограничном слое становится более сложным, чем при обтадса-
нии плоской пластины. Так как давление остается постоянным
поперек пограничного слоя, то влияние градиента давления во
внешнем потоке распространяется на весь пограничный слой.
Это влияние в основном сводится к изменению профиля скоро-
скорости в пограничном слое.
Причину такого изменения профиля скорости можно понять,
если рассмотреть следующую упрощенную схему течения. Пусть
в некотором сечении пограничного слоя имеется профиль ско-
скорости и(у), причем на границе пограничного слоя иF)~щ. На
некотором малом расстоянии Ах от этого сечения давление во
внешнем потоке, а следовательно, и во всем пограничном слое
изменится на Ар. Пренебрегая силами трения и считая, что те-
течение происходит параллельно стенке, для каждой струйки жид-
жидкости можно написать уравнение Бернулли
риАи = — А/?, или — = ~.
и ри
Следовательно, в сечении, расположенном на расстоянии Ах от
330 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
начального сечения, скорость щ будет равна
Соответственно во внешнем потоке
и<>1 = ио | ! — '
Тогда окончательно имеем
Если течение происходит против нарастающего давления, то
Ар > 0, и при и < но множитель в скобках будет меньше еди-
единицы. Следовательно, профиль скорости в этом случае стано-
становится менее наполненным. Если давление вдоль потока умень-
уменьшается, то Ар<0, и при и<щ множитель в скобках будет
больше единицы. В этом случае профиль скорости становился
\
\
V
J
1
1
/
/
/ •
/
——
о
0,4 0,6 0,8 у/6 30 30 60 90' 120 /SO
Рис. 6.23. Профили скорости при
наличии градиента давления (по
опытам Никурадзе)
Рис. 6.24. Распределение давления
на круглом цилиндре
более наполненным. Результаты экспериментального исследова-
исследования пограничного слоя при наличии градиента давления во
внешнем потоке качественно подтверждают полученные выводы.
На рис. 6.23 приведены профили скорости в турбулентном по-
пограничном слое несжимаемой жидкости при наличии как поло-
положительного, так и отрицательного градиента давления. Опыты
проводились в суживающихся плоских каналах (течение с отри-
отрицательным градиентом давления: а < 0) и в расширяющихся
§ 5. ОТРЫВ ПОГРАНИЧНОГО СЛОЯ 331
каналах (течение с положительным градиентом давления: а>0).
Половина угла раствора а характеризует величину градиента
давления.
При достаточно большом положительном градиенте давления
во внешнем потоке слои жидкости вблизи стенки могут остано-
остановиться и даже начать двигаться в обратном направлении, т. е.
происходит отрыв пограничного слоя (рис. 6.4). Сечение погра-
пограничного слоя, начиная с которого возникает обратное движение
жидкости, носит название точки отрыва пограничного слоя.
В этой точке выполняется соотношение
(ди/ду)„ = О, то есть tw = 0. A37)
Отрыв пограничного слоя обычно связан с образованием вих-
вихрей, которые проникают во внешний поток и существенно иска-
искажают картину течения, полученную по теории идеальной жидко-
жидкости, даже вдали от тела. Для пояснения приведем некоторые
сведения об обтекании круглого цилиндра несжимаемой жид-
жидкостью. На рис. 6.24 показаны две кривые распределения давле-
давления вдоль окружности цилиндра; штриховая кривая построена
по теории идеальной жидкости, сплошная кривая получена экс-
экспериментально Флаксбартом при числе Рейнольдса
т. е. при турбулентном пограничном слое. Индексом °° здесь
обозначены параметры в невоамущенном потоке. На передней
стороне цилиндра измеренное распределение давления более или
менее совпадает с теоретическим распределением для идеальной
жидкости. На задней стороне цилиндра измеренные значения
давления существенно отличаются от теоретических. Это объяс-
объясняется тем, что при ф = 125° происходит отрыв пограничного
слоя. Вследствие отличия распределения давления от теоретиче-
теоретического возникает сопротивление давления. Аналогичная картина
наблюдается и при обтекании крыловых профилей. Таким обра-
образом, отрыв пограничного слоя оказывает существенное влияние
на картину обтекания различных тел, а следовательно, и на та-
такие основные характеристики, как сопротивление и подъемная
сила. В связи с этим становится очевидной необходимость уметь
рассчитывать положение точки отрыва пограничного слоя. В наи-
наиболее общем виде условия отрыва пограничного слоя были полу-
получены Г. М. Бам-Зеликовичем на основании теории размерности.
Течение в произвольном сечении пограничного слоя будет
определено, если задать:
а) профиль скорости в некотором начальном сечевии погра-
пограничного слоя;
б) распределение давления на границе пограничного слоя;
в) значение скорости щ и плотности ро внешнего потока
в какой-либо^ одной точке;
332 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
г) характерный линейный размер, соответствующий рассмат-
рассматриваемому сечению (например, расстояние х этого сечения от
начального).
Распределение давления на границе пограничного слоя мо-
может быть задано значением самого давления ро и всех его про-
наводных \р0, Ро и т- Д•) в рассматриваемом сечении.
Основное предположение, на котором основываются все даль-
дальнейшие выводы, заключается в следующем: на течение в некото-
некотором сечении пограничного слоя существенное влияние оказывает
внешний поток только в близкой окрестности этого сечения.
Это предположение подтверждается следующими эксперимен-
экспериментальными фактами. Во-первых, профиль скорости в пограничном
слое на стенках прямолинейных участков цилиндрических труб
такой же, как и профиль скорости на плоской пластине, незави-
независимо от того, какое течение — ускоренное или замедленное —
предшествовало течению около прямолинейного участка трубы.
Во-вторых, профиль скорости над точкой отрыва в турбулентном
пограничном слое несжимаемой жидкости не зависит от пара-
параметров течения во внешнем потоке до точки отрыва. Универсаль-
Универсальность отрывного профиля при различном характере течения до
сечения отрыва также говорит о том, что можно пренебречь
влиянием внешнего потока вне небольшой окрестности рассмат-
рассматриваемого сечения. Наконец, опыты по исследованию взаимодей-
взаимодействия скачка уплотнения с пограничным слоем непосредственно
показывают, что заметные изменения в пограничном слое проис-
происходят лишь на расстоянии, равном всего нескольким толщинам
пограничного слоя. Следовательно, даже очень сильное измене-
изменение давления во внешнем потоке, вызванное скачком уплотне-
уплотнения, влияет на характер течения в пограничном слое впереди
скачка уплотнения лишь в малой окрестности.
Итак, эксперименты показывают, что на течение в некотором
сечении пограничпого слоя влияют лишь параметры внешнего
потока вблизи этого сечения. Отсюда следует, что влиянием про-
профиля скорости в начальном сечении можно пренебречь. Вслед-
Вследствие этого за характерный линейный размер целесообразно
брать не расстояние х от начального сечения, а какую-либо ли-
линейную характеристику z пограничного слоя в рассматриваемом
сечении (например, толщину вытеснения б* или толщину потери
импульса б**). Из основпого предположения оледует также, что
если во внешнем потоке все производные давления ро по х в дан-
данной точке конечны, то в разложении давления ро по х можно
ограничиться первой производной ро.
При сделанных предположениях получаем следующую си-
систему параметров, определяющих течение в произвольном сече-
сечении ламинарного или турбулентного пограничного слоя:
щ —- скорость, ро — плотность, ро — давление внешнего потока
в рассматриваемом сечении, /?0— первая производная давления
§ 5. ОТРЫВ ПОГРАНИЧНОГО СЛОЯ 333
по х, z — характерный размер пограничного слоя, |яо — коэффи-
коэффициент динамической вязкости, Ко — коэффициент теплопроводно-
теплопроводности, к — отношение теплоемкостей.
По основной теореме теории размерностей любой безразмер-
безразмерный комплекс является функцией только безразмерных комби-
комбинаций определяющих параметров.
Тогда, например, для безразмерного напряжения трения на
стенке имеем
Ромо
где Mo — число Маха внешнего потока.
Функция Ф[ должна, очевидно, зависеть еще от чисел Рг и
к, но эти аргументы опущены, так как для данного газа их
можно считать постоянными.
В точке отрыва пограничного слоя xw = 0. Разрешая уравне-
уравнение A38) относительно (Poz)/(poWo) и разлагая в ряд по степе-
степеням \M)/(pqUqz), получаем
Совершим теперь в равенстве A39) тот предельный переход,
который делается при выводе уравнений пограничного слоя, т. е.
предположим, что вязкость стремится к нулю (jio-^O).
В ламинарном пограничном слое при стремлении коэффици-
коэффициента вязкости к нулю (число Рейнольдса R -* °°) характерный
размер пограничного слоя также стремится к нулю (z/l ~ 1/Vif->¦
-*•(), где / — характерный размер обтекаемого тела). Следова-
Следовательно, (p'oz)/(poul) стремится к нулю, как 1/IR.
Кроме того, имеем
Отсюда получаем, что ^~ стремится к нулю (при \ю-+0)
так же, как 1/YR. Вследствие этого в формуле A39) члены, про-
—2- I (^г>0), стремятся к нулю, как (l/VR)n.
Так как фо(Мо) не стрем>ится к нулю (при цо-^О), то для ла-
ламинарного пограничного слоя величина фо(Мо) должна тождест-
тождественно равняться нулю. Умножая обе части равенства A39) на
PoHoz/jzo и переходя к пределу при R -»- <»? получим, что в точке
отрыва ламинарного пограничного слоя справедливо соотношение
. A40)
334 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
В случае турбулентного пограничного слоя характерный раз-
размер пограничного слоя при \хо -> 0 не стремится к нулю, так как
толщина пограничного слоя определяется турбулентным пере-
перемешиванием. Следовательно, не стремится к нулю и величина
—-2—. В этом случае Фо(Мо)^0, все же остальные члены
Ро"о
в равенстве A39) стремятся к нулю при цю -* 0. Поэтому для
турбулентного пограничного слоя в точке отрыва должно выпол-
выполняться соотношение
2
Vo
A41)
Функции фо(Мо) и cpi(Mo) могут быть определены теоретически
и экспериментально. Их значения, конечно, зависят от того, ка-
какой из параметров принимается за характерный размер погра-
пограничного слоя z. Для турбулентного пограничного слоя в несжи-
несжимаемой жидкости (Мо = О) величина фо(О) равна примерно
0,015, если за характерный размер z принять толщину вытесне-
вытеснения б*. Бели за характерный размер принять толщину потери
импульса б**, то фо(О)== 0,005.
Для ламинарного пограничного слоя в несжимаемой жидко-
жидкости (Мо = 0) величина ф1'@) зависит от предыстории течения,
Согласно расчетам, проведенным с использованием профилей ско-
скорости в виде полиномов (по методу Польгаузена), величина
ф1@) равна 1,92, если за характерный размер принята толщина
вытеснения б*, и 0,157, если за характерный размер принята
толщина потери импульса б**. Если использовать автомодельные
решения уравнений пограничного слоя при постоянном значении
параметра р, то величина ф1 @) будет соответственно равна 1,11
и 0,068.
Для турбулентного пограничного слоя при Мо Ф 0 величина
Фо(Мо) может быть определена следующим образом. Будем
искать распределение напряжения трения поперек пограничного
слоя в точке отрыва в виде многочлена от у/б
причем для нахождения коэффициентов а<>, а\, съ, а$ используем
следующие условия:
у = 0, %w = 0 (в точке отрыва),
у==®' VWjw^ix (слеДУет из уравнения движения A17))
у = б, т == 0 (на границе пограничного слоя).
Еще одно необходимое условие может быть получено дифферен-
S 5. ОТРЫВ ПОГРАНИЧНОГО СЛОЯ 335
джрованием по у уравнения движения A17):
'сРи , до ди , ди ди . д2и . ди ди др ди д2т
Отсюда при г/ = 0 имеем (и = и = 01 ди/ду = 0) д2х/ду2 = 0. Тог-
Тогда, для коэффициентов полинома A42) получаем
ао = а2 = О, аг = - а3 = ——.
и соотношение A42) принимает вид
Напряжение трения в турбулентном пограничном слое можно
представить в виде суммы
Т = Тм + Тт,
где тм = [idu/dy — напряжение трения, обусловленное молекуляр-
молекулярным переносом, а тт — касательное напряжение, вызванное тур-
турбулентными пульсациями.
Согласно гипотезе Прандтля
тт = р,
причем I — длина пути смешения. Поэтому соотношение A43)
можно переписать в виде
Вдали от точки отрыва напряжения вязкого трения прене-
пренебрежимо мало по сравнению с напряжением турбулентного тре-
трения ,для всех расстояний от стенки, превышающих некоторую
определенную величину, которая называется толщиной ламинар-
ламинарного подслоя. Внутри этого подслоя напряжение вязкого трения
достигает больших значений, так как производная ди/ду здесь
велика. Однако в точке отрыва (ди/ду)w = 0 (при i/ = 0) и на-
напряжение вязкого трения будет малым даже у стенки. Поэтому
вязким трением можно пренебречь во всем сечении. Тогда из
A44) получим
Это уравнение может служить для определения профиля скоро-
скорости в точке отрыва.
Так как начиная с точки отрыва поток ведет себя приблизи-
приблизительно как свободная турбулентная струя, то можно предполо-
336 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
жить, что путь смешения в сечении отрыва постоянен и равен по
величине пути смешения для свободных турбулентных струй.
Как известно, из теории струй (§ 1 гл. VII) отношение пути
смешения к ширине струи, которой в нашем случае эквивалент-
эквивалентна толщина пограничного слоя 6, есть постоянная величина, т. е.
1 = 1/8 = const. Вводя безразмерные величины р = р/ро, и = и/щ;
У = у/&1 из соотношения A45) получим
В случае отсутствия теплообмена и Рг = 1 температура торможе-
торможения постоянна, и поэтому
Интегрируя уравнение A46) по пограничному слою от у=*0 до
у, получим
или
= -
A47)
При у = 1 и = 1, поэтому из соотношения A47) следует
где
Подставляя A48) в A47), получим окончательно для распреде-
распределения скоростей в точке отрыва
2 1 J
A49)
§ 5. ОТРЫВ ПОГРАНИЧНОГО СЛОЯ
337
Из A41) и A48) следует, что если за характерный размер при-
принять толщину вытеснения 6*, то
о
V
Для несжимаемой жидкости (Мо = 0) имеем
Исключая из этих двух соотношений неизвестную величину 1Т
окончательно получим
Фо(Мо)= ^±
A50)
Отношение 6*/б определяется выражением E7), так как про-
профили скорости и температуры в пограничном слое известны.
Изменение фо(Мо) в зависимости от числа Мо, рассчитанное
по формуле A50), показано на рис. 6.25 сплошной кривой. Там
6*i
0,0/ -
•
JL
«^
•
ш
¦^
U
^^
f
О
•
С,
=^
¦*>»
^^
V
Ml
Рис. 6.25. Зависимость параметра отрыва турбулентного пограничного слоя
от числа Маха Мо
же нанесены результаты опытов. Светлые точки соответствуют
безотрывному течению, темные точки относятся к течению с от-
отрывом пограничного слоя.
Таким образом, отрыв пограничного -слоя возникает в том
случае, когда параметр
достигает некоторого критического значения, которое зависит от
числа Мо и определяется формулой A50). Поэтому для обеспе-
обеспечения безотрывного течения при торможении потока газа
(dpo/dx>O) необходимо осуществлять торможение таким обра-
22 г. Н. Абрамович, ч. 1
338 гл. vi. теория, пограничного слоя
зом, чтобы параметр | нигде не достигал своего критического
значения.
Для определения распределения параметра | вдоль обтекае-
обтекаемой поверхности, кроме параметров внешнего потока, необходи-
необходимо знать характерный размер пограничного слоя (например тол-
толщину вытеснения). Расчет пограничного слоя при наличии гра-
градиента давления во внешнем потоке является довольно сложной
задачей, так как в этом случае профили скорости (и температу-
температуры) будут зависеть от градиента давления и изменяться от се-
сечения к сечению.
Для ламинарного пограничного слоя как несжимаемой жид-
жидкости, так и сжимаемого газа при переменном давлении во
внешнем потоке существуют различные методы расчета. Наибо-
Наиболее точные методы основываются на численном интегрировании
дифференциальных уравнений и требуют применения вычисли-
вычислительных машин. Для турбулентного пограничного слоя несжи-
несжимаемой жидкости разработаны приближенные, полуэмпириче-
полуэмпирические методы расчета. В случае небольшого градиента давления
во внешнем потоке расчет турбулентного пограничного слоя сжи-
сжимаемой жидкости может быть произведен при условии, что
влияние градиента давления учитывается лишь в интегральном
соотношении количества движения E9). При этом считается, что
профили скорости и температуры, а также зависимость напря-
напряжения трения от характерной толщины пограничного слоя имеют
такой же вид, как и в случае обтекания плоской пластины.
§ 6. Взаимодействие пограничного слоя
со скачками уплотнения
Нарастание пограничного слоя на обтекаемой поверхности
всегда оказывает влияние на внешний поток. При отсутствии
скачков уплотнения это влияние сводится к следующему. Утол-
Утолщение пограничного слоя в направлении течения связано с уве-
увеличением толщины вытеснения б*, что приводит к отклонению
линий тока внешнего потока. Поэтому течение во внешнем по-
потоке будет таким же, как при обтекании фиктивного контура,
смещенного по отношению к действительному на толщину вытес-
вытеснения. Следовательно, при расчете течения нужно применять
метод последовательных приближений: сначала рассчитывается
обтекание тела потоком идеальной жидкости, затем по найден-
найденному распределению давления вдоль поверхности тела находятся
параметры пограничного слоя (в том числе толщина вытесне-
вытеснения), далее рассчитывается обтекание фиктивного тела, контур
которого смещен на величину б* и т. д. Однако обычно толщина
вытеснения мала по сравнению с размерами тела и поэтому
можно ограничиться первым приближением.
§ 6. ВЗАИМОДЕЙСТВИЕ ПОГРАНИЧНОГО СЛОЯ СО СКАЧКОМ 339
При наличии скачков уплотнения пограничный слой обычно
оказывает более сильное влияние на внешний поток, в некото-
некоторых случаях существенно изменяя картину всего течения. Дела
в том, что в скачке уплотнения изменения скорости и темпера-
температуры по направлению нормали к фронту скачка, которое обычно
мало отличается от направления потока, велики по сравнению
с изменениями этих величин вдоль скачка. В пограничном слое
изменения скорости и температуры в направлении потока обычно
незначительны, в то время как изменения этих величин поперек
пограничного слоя велики. Следовательно, в области взаимодей-
взаимодействия скачка уплотнения с пограничным слоем скорость и тем-
температура существенно изменяются как вдоль, так и поперек по-
потока. Поэтому основные допущения теории пограничного слоя
в этом случае перестают быть справедливыми и теоретическое
исследование области взаимодействия скачков уплотнения с по-
пограничным слоем представляет чрезвычайно сложную задачу.
Экспериментальные исследования этой области течения тоже яв-
являются не простым делом, однако полученные данные позволяют
представить физическую картину взаимодействия и определить
некоторые количественные закономерности.
Наличие даже слабого скачка уплотнения приводит к рез-
резкому увеличению давления во внешнем потоке. Рост давления
передается навстречу потоку по дозвуковой части пограничного
слоя. Линии тока отклоняются от стенки, порождая в сверхзву-
сверхзвуковой части пограничного слоя семейство волн сжатия, которые
распространяются во внешний поток и оказывают влияние на
форму и интенсивность скачка уплотнения вблизи области взаи-
взаимодействия. Продольный градиент давления в пограничном слое
оказывается значительно меньше, чем во внешнем потоке. Если
скачок слабый, то движение в пограничном слое происходит под
воздействием небольшого положительного градиента давления
и отрыв потока не происходит. С увеличением интенсивности
скачка уплотнения во внешнем потоке возрастает градиент дав-
давления вблизи стенки и возникает отрыв пограничного слоя. При
этом увеличивается отклонение линий тока в сверхзвуковой ча-
части течения, благодаря чему поддерживается необходимое рас-
распределение давления, соответствующее данной интенсивности
скачка уплотнения. В зависимости от условий во внешнем по-
потоке (интенсивности скачка уплотнения, местного числа М, уско-
ускоренного или замедленного характера течения) и формы обтекае-
обтекаемого тела возможны два случая. В первом случае поток после
отрыва присоединяется снова к стенке. Сразу за скачком уплот-
уплотнения возникают волны разрежения, как при обтекании внеш-
внешнего тупого угла. В месте присоединения поток направлен под
некоторым углом к стенке, поэтому здесь возникает новый ска-
скачок уплотнения, который может вызвать иногда новый отрыв
пограничного слоя. Таким образом, могут появиться несколько
22*
340
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
последовательных скачков уплотнения, что наблюдается при об-
обтекании крыловых профилей с образованием местных сверхзву-
сверхзвуковых зон и при течении в каналах с замыкающим скачком уп-
уплотнения. Во втором случае возникает развившийся отрыв, ос-
основные закономерности которого определяются условиями сме-
смешения и в очень сильной степени зависят от характера течения
за точкой отрыва. Развившийся отрыв наблюдается, например,
при обтекании кругового цилиндра, сферы, крылового профиля
под углом атакн, при течении перед уступом.
Таким образом, при малой интенсивности окачка уплотнения
картина течения во внешнем потоке мало отличается от карти-
картины, предсказанной теорией идеальной жидкости. Это отличие
заключается в небольшом искривлении скачков уплотнения в об-
области взаимодействия. Развитие пограничного слоя в этой обла-
области происходит под воздействием плавного повышения давления
и описывается обычными уравнениями пограничного слоя. Одна-
Однако в большинстве случаев на практике приходится иметь дело
со скачками уплотнения, интенсивность которых такова, что воз-
возникает отрыв пограничного слоя. Хотя качественная картина
Рис. 6.26. Схема течения и характерное
распределение давления при взаимодей-
взаимодействии скачка уплотнения с ламинарным
пограничным слоем: 1 — начало повыше-
повышения давления, 2 — точка отрыва, 3 — на-
начало области постоянного давления,
4 — место падения скачка уплотнения,
5 — точка присоединения
взаимодействия скачка уплотнения с ламинарным и турбулент-
турбулентным пограничными слоями принципиально одинакова, количе-
количественные характеристики взаимодействия различны из-за суще-
существенного отличия в профилях скорости при ламинарном и тур-
турбулентном течениях.
Типичная схема взаимодействия падающего скачка уплотне-
уплотнения с ламинарным пограничным слоем на плоской поверхности
и соответствующее распределение давления на стенке показаны
на рис. 6.26. В невозмущенном потоке давление ро постоянно.
При приближении к точке отрыва давление начинает повышать-
повышаться и продолжает расти за точкой отрыва, достигая некоторого
постоянного значения р\ в отрывной зоне. Затем давление повы-
повышается до значения /?2, соответствующего давлению за падающим
§ 6. ВЗАИМОДЕЙСТВИЕ ПОГРАНИЧНОГО СЛОЯ СО СКАЧКОМ
341
и отраженным скачками. В этой области повышения давления
располагается точка присоединения. Таким образам, при отрыве
пограничного слоя, вызванном взаимодействием со скачком уп-
уплотнения, существуют два важных параметра, связанных с дав-
давлением. Первый параметр представляет собой отношение давле-
давления в точке отрыва /?отр к давлению в невозмущенном потоке р0,
второй — отношение давления в зоне отрыва р\ к давлению ро.
Второй параметр носит название критического отношения давле-
давлений и характеризует перепад давлений в косом скачке, возника-
возникающем перед точкой отрыва.
- Замечательная особенность явления взаимодействия заклю-
заключается в том, что параметры потока вблизи точки отрыва не
зависят от причины, вызвавшей отрыв, а зависят лишь от чисел
Маха и Рейнольдса в невозмущеином потоке. Бели числа Мо и
R совпадают, то распределение давления вблизи точки отрыва
оказывается одинаковым при взаимодействии пограничного слоя
с падающим извне скачком уплотнения, со <скачком уплотнения,
образующимся при обтекании вогнутой криволинейной стенки,
Рис. 6.27. Распределение давления в зоне отрыва при различных условиях
взаимодействия при Мо = 2, Rx = 2-105: 1 — падающий скачок уплотнения,
2 — обтекание тупого угла, 3 — обтекание вогнутой стенки, 4 — течение
перед уступом, х0 — расстояние от передней кромки до начала взаимодей-
взаимодействия
внутреннего тупого или прямого угла, со скачком уплотнения
в сопле на режимах истечения с большим перерасширением
(рис. 6.27). При этом относительное давление в точке отрыва
PotJpo и критическое отношение давления pi/po также являются
универсальными функциями чисел Маха и Рейнольдса. Согласно
приближенным теориям Г. Гэдда и Р. Хаккинеяа1) относитель-
1) Чжен П. К. Отрывные течения.—М.: Мир, 1972.
342
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
ное давление в точке отрыва при Мо > 1,2 может быть найдено
по формуле
^? = 1 + 0,57
A51)
Критическое отношение давления определяется по аналогич-
аналогичной формуле, отличающейся лишь значением численного коэф-
коэффициента,
-?¦ = 1+0,94-
A52)
Значения pmjpo и pjpo для»Мо = 2, рассчитанные по форму-
формулам A51) и A52) (сплошные кривые) и полученные экспери-
экспериментально различными авторами при исследовании обтекания
Po
1
¦»—i
О
1 4
-
Pi
Po
Ротр
Po
о
8
R-10~5
Рис. 6.28. Зависимость характерных отношений давлений от числа Рей-
нольдса для Мо = 2 при взаимодействии скачка уплотнения с ламинарным
пограничным слоем
внутреннего тупого угла и при исследовании отражения косого
скачка от плоской стенки, приведены на'рве. 6.28. Сравнение
расчетных и экспериментальных значений р0т$/ро и pi/ро при
Рис. 6.29. Зависимость характерных
отношений давлений от числа Мо
для Rx = 106 при взаимодействии
скачка уплотнения с ламинарным
пограничным слоем
различных Мо показано на ри?с. 6.29. Оплошная кривая соответ-
соответствует расчету по формулам A51) и A52) при R^^IO6, экспе-
экспериментальные данные приведены к тому же значению R* с ис-
§ 6. ВЗАИМОДЕЙСТВИЕ ПОГРАНИЧНОГО СЛОЯ СО СКАЧКОМ
343
пользованием установленной зависимости от числа Рейнольдса.
Учитывая сложность измерений и приближенный характер тео-
теории, следует считать совпадение расчетных и экспериментальных
результатов удовлетворительным.
Как следует из формул A51) и A52), относительное давле-
давление в точке отрыва и критическое отношение давлений увеличи-
увеличиваются при уменьшении числа R* или увеличении числа Мо. Фи-
Физически это означает, что чем меньше число R*, тем больше силы
шязкости, препятствующие отрыву. Увеличение числа Мо ведет
к увеличению количества движения массы газа в пограничном
слое, что затрудняет отрыв.
Отношение давлений в косом скачке, возникающем из-за
утолщения пограничного слоя вблизи точки отрыва, практически
совпадает с критическим отношением давлений. Па извест-
известному числу Мо и перепаду давлений на косом скачке мож-
можно определить угол наклона скачка относительно набегающе-
набегающего потока.
Для полного построения картины течения необходимо еще
уметь определять расстояние &, на которое отходит косой ска-
скачок уплотнения навстречу потоку. Согласно имеющимся в на-
сюящее время экспериментальным данным это расстояние про-
пропорционально толщине вытеснения невозмущенного погранично-
пограничного слоя и увеличивается при увеличении интенсивности скачка
уплотнения во внешнем потоке. Значения величины 6, найден-
найденные Г. И. Петровым и его сотрудниками при исследовании обте-
обтекания внутреннего тупого угла потоком с числом Мо = 2,0,
в зависимости от интенсивности основного скачка приведены на
Рис. 6.30. Величина отхода косого
скачка в зависимости от интенсив-
ности основного скачка при лами-
ламинарном пограничном слое
PilPo
рис. 6.30. Светлые кружки соответствуют Rx = 3,5 • 105, а тем-
темные — R* = 5,3 • 105.
Большое количество экспериментальных исследований посвя-
посвящено изучению взаимодействия скачка уплотнения с турбулент-
турбулентным пограничным слоем. Теоретическое рассмотрение этого во-
вопроса затруднительно вследствие сложности явления, в то же
время на практике этот случай встречается очень часто. Схема
взаимодействия скачка уплотнения с турбулентным пограничным
344
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
слоем при обтекании внутреннего тупого угла и соответствующее
распределение давления на стенке показаны на рис. 6.31. Давле-
Давление непрерывно увеличивается от значения ро в невшмущенном
потоке до значения /?2, которое обычно совпадает с давлением за
скачком уплотнения во внешнем потоке. Характерной особен-
особенностью распределения давления является наличие точки переги-
перегиба, причем значение давления в этой точке р\ оказывается таким
же, как за первым косым скачком уплотнения. Отношение
Р\/ро — критическое отношение давлений — является одним из
Рис. 6.31. Схема течения и ха-
характерное распределение давле-
давления при взаимодействии скачка
уплотнения с турбулентным по-
пограничным слоем: 1 — начало по-
повышения давления, 2 — точка
отрыва, 3 — точка перегиба в
распределении давления, 4 —
точка присоединения
I 3
основных параметров при взаимодействии скачка уплотнения с
турбулентным пограничным слоем. Относительное давление в
точке отрыва p0jp0 несколько меньше, чем критическое отноше-
отношение давлений. Различие в величинах этих двух параметров ме-
менее значительно при взаимодействии скачка уплотнения с турбу-
турбулентным пограничным слоем, чем при взаимодействии с лами-
ламинарным пограничным слоем.
Если перед скачком пограничный слой турбулентный, то рас-
распределение давления в области взаимодействия практически не
зависит от числа Рейнольдса (рис. 6.32). Это объясняется сла-
слабым влиянием числа Рейнолвдса на основные хараотеристки
турбулентного течения (толщину пограничного слоя, профиль
скорости, напряжение трения на стенке).
Аналогичная картина взаимодействия имеет место при нали-
наличии во внешнем потоке косого окачка уплотнения, при возник-
возникновении скачка уплотнения в местной сверхзвуковой зоне на
крыловом профиле, при нерасчетном истечении из сопла.
Такое же распределение давлепия вплоть до точжи отрыва
наблюдается при обтекании уступа сверхзвуковым потоком. Од-
§ 6. ВЗАИМОДЕЙСТВИЕ ПОГРАНИЧНОГО СЛОЯ СО СКАЧКОМ
345
нако в этом случае обычно не возникает точки перегиба в рас-
распределении давления, а происходит дальнейший монотонный
рост давления за точкой отрыва до некоторого максимального
значения, соответствующего давлению в отрывной зоне (рис. 6.33).
Это связано с особенностью течения при наличии фиксированной
точки присоединения на кромке уступа. На распределение дав-
давления за точкой отрыва сильно влияет высота уступа, если она
-соизмерима с толщиной пограничного слоя. Протяженность зоны
отрыва при турбулентном пограничном слое значительно меньше,
м
л
f
1
г
п 1,Ы06
0 Щ-106
1,0
Рис. 6.32. Влияние числа Рейнольд-
са на распределение давления в
области взаимодействия при обтека-
обтекании тупого угла сверхзвуковым по-
потоком, Мо = 2,7; хо — расстояние от
передней кромки до точки излома
контура
Pa
1,8
1,0
о /
а г
• а отрыв
f
Г
0,6
х/ц
Рис. 6.33. Распределение давле-
давления при обтекании уступа сверх-
сверхзвуковым потоком, Мо = 2,3: 1 —
ламинарный пограничный слой,
Rx = 2-105; 2 — турбулентный по-
пограничный слой, Rjc=1,5.106;
хо — расстояние от передней
кромки до уступа
чем при ламинарном. Это вызывает более сильное отклонение
линий тока внешнего потока и более значительное повышение
давления (рис. 6.33).
Опытные данные показывают, что отношение давлений в ото-
отошедшем косом скачке р\/ро (критическое отношение давлений)
не зависит от способа осуществления и интенсивности основного
скачка уплотнения и от числа Рейнольдса, а определяется зна-
значением числа Мо внешнего невозмущенного потока. На рис. 6.34
приведены значения отношения давлений в отошедшем косом
346
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
скачке, полученные И. П. Некрасовым при исследовании взаи-
взаимодействия падающего извне скачка уплотнения с пограничным
слоем на пластине при различных числах Рейнольдса. Экспери-
Экспериментальные значения критического отношения давления при
различных случаях взаимодействия в зависимости от числа Мо
приведены на рис. 6.35. На этом же рисунке сплошной линией
1,8
о
и
и О
м °!
с
Рис. 6.34. Зависимость кри-
критического отношения дав-
давлений от числа Рейнольд-
Рейнольдса при турбулентном по-
пограничном слое при Мо =
= 1,95
10°
10°
10' Яг
4 5
1 1
//
/о/
О
лоо
/
6 1
/о >^«*
/•
о 1
Д2
^ 3
Рис. 6.35. Зависимость критического отношения давления от числа Мо прп
турбулентном пограничном слое: 1 — нерасчетное истечение из сопла, 2 —
обтекание тупого угла, 3 — падающий извне скачок уплотнения, 4 — отно-
отношение давлений в прямом скачке, 5 — отношение давлений в косом скачке
при а = 60°, 6 — отношение давлений в косом скачке при а = 30°
обозначены значения этого отношения, вычисленные по формуле
^- = 1+0,2
а штриховой —по формуле Г. Гедда1) при к = 1,4
A53)
l) Gadd G. E. Interaction between wholly laminar or wholly turbulent
boundary layers and shock waves strong enough to cause separation /f
J. Aeron. Sci.— 1953.—V. 20, № 11.— P. 729—739.
§ 6. ВЗАИМОДЕЙСТВИЕ ПОГРАНИЧНОГО СЛОЯ СО СКАЧКОМ 347
Экспериментальные значения относительного давления в точ-
точке отрыва Ротр/^о в зависимости от числа Мо приведены на
рис. 6.36. Сплошная кривая рассчитана по формуле
^23» -1 + 0,15
U/4 "
Величина отхода косого скачка от точки пересечения падаю-
падающего скачка со стенкой зависит от интенсивности падающего
Ротр
Ро
ДД§^^
О А
D ° ^
А
п
д-/
11 5 Мо
Рис. 6.36. Зависимость относительного давления в точке отрыва от числа
Мо при турбулентном пограничном слое: 1 — обтекание тупого угла; 2 —
падающий извне скачок уплотнения, 3 — обтекание уступа
скачка, от числа Мо и от местных параметров пограничного слоя.
На рис. 6.37 приведены результаты опытного определения этого
линейного размера. Величина б* представляет собой толщину
вытеснения пограничного слоя при отсутствии скачка уплотне-
уплотнения во внешнем потоке.
Следует иметь в виду, что наличие скачков уплотнения во
внешнем потоке оказывает влияние на распределение скорости
и давления в пограничном слое. При небольшой интенсивности
падающего скачка это влияние сводится к некоторому утолще-
утолщению пограничного слоя; профиль скорости при этом изменяется
мало. При большой интенсивности падающего скачка уплотнения
возникает отрыв пограничного слоя и образуется вихревая зона.
Вниз по потоку от точки отрыва начинается перемешивание отор-
оторвавшихся струек и нарастание нового пограничного слоя на стен-
стенке. Благодаря передаче давления по дозвуковой части погранич-
пограничного слоя вверх по потоку давление перестает быть постоянным
поперек пограничного слоя, т. е. др/ду Ф 0. Поэтому в>се методы
расчета, разработанные в предположении постоянства стати-
статического давления в поперечном сечении пограничного слоя, мо-
могут быть использованы лишь в достаточном удалении от места
взаимодействия. Сравнение приведенных выше данных показы-
348
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
вает, что отрыв ламинарного пограничного слоя возникает при
небольшой интенсивности скачка уплотнения, в то время как
при турбулентном режиме течения величина критического пере-
перепада значительно больше. Это объясняется тем, что профиль
скорости при турбулентлном режиме течения значительно более
наполненный, чем при ламинарном, т. е. соответствует большему
количеству движения. Поэтому для от-
отрыва турбулентного пограничного слоя
необходим более интенсивный скачок
уплотнения, чем для отрыва ламинар-
ламинарного. По этой же причине повышение
давления вблизи стенки, вызванное
скачком уплотнения одинаковой интен-
интенсивности, передается навстречу потоку
в турбулентном пограничном слое на
меньшее расстояние, чем в лами-
ламинарном. Вследствие этого величина
отхода первого косого скачка уплот-
уплотнения при турбулентном режиме те-
течения меньше, чем при ламинарном
(рис. 6.30, 6.37).
Величина критического перепада
для турбулентного пограничного слоя
при Мо<1,2 больше отношения дав-
давления в прямом скачке уплотнения
(рис. 6.35) и отрыв не может возник-
возникнуть. На рис. 6.35 приведены также
значения отношения давления в косых
скачках уплотнения с углами наклона
а =* 60° и 30° относительно скорости набегающего потока, подсчи-
подсчитанные по формуле D5) гл. III. Эти значения при Мо<1,4
(а = 60°) и Мо<3 (а = 30°) оказываются меньше критического
отношения давления, и отрыв турбулентного пограничного слоя
не возникает.
Рис. 6.37. Величина отхода
косого скачка в зависимо-
зависимости от интенсивности на-
дающего скачка при турбу-
лентном пограничном слое
§ 7. Течение жидкости в трубах
Течение жидкости в каналах различного сечения очень часто
встречается на практике. При этом обычно скорость движения в
канале значительно меньше скорости звука, и поэтому жидкость
считается несжимаемой. Рассмотрим установившееся ламинарное
осесимметричное течение в круглой цилиндрической трубе диа-
диаметра d. Пусть жидкость втекает в трубу с равномерной ско-
скоростью. На стенках образуется пограничный слой, толщина кото-
которого увеличивается вдоль трубы. Так как плотность и расход
через каждое сечение остаются постоянными, то сохраняется и
средняя скорость. Поэтому уменьшение скорости вблизи стенки.
§ 7. ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ 349>
вызванное наличием трения, привадит к увеличению скорости
вне пограничного слоя (в ядре потока). Эта область течения на-
называется начальным участком. На некотором расстоянии от вхо-
входа толщина пограничного слоя становится равной радиусу тру-
трубы, т. е. происходит смыкание пограничных слоев. Эта область
течения называется основным участком и характеризуется неиз-
неизменным профилем скорости. Длина начального участка прибли-
приближенно может быть определена по формуле
ZH = 0,03dR, A54)
которая была получена теоретически Шиллером1). Так, при R =
= 1000 и R = 5000 величина ZH составляет соответственно 30 и.
150 диаметров трубы. В дальнейшем мы будем ра<ссматр»ать
только течение в основном участке. Направим ось х вдоль оси
трубы, а координату у будем отсчитывать от оси трубы. Считая,
что течение во всех сечениях одинаково (составляющая скорости
в осевом направлении не зависит от х), из уравнения неразрыв-
неразрывности в цилиндрических координатах получим
= 0, или yv = const,
где v — составляющая скорости в радиальном направлении. Так
как v = 0 при у — г (где г — радиус трубы), то, следовательно,
v = 0 во всем потоке. Тогда уравнение Навье — Стокса в цилинд-
цилиндрических координатах принимает вид
;.-?=<>, да
причем граничным условием является и = 0 при у = г. Интегри-
Интегрируя уравнение A55), получим распределение скоростей в сече-
сечении трубы
и = --^-%^-у^- A56>
Максимальная скорость достигается на оси трубы при у = О
A57)
Градиент давления dp/dx связан с расходом жидкости через тру-
трубу. Действительно,
г
Г* 4 / , \
A58>
1) Шиллер Л. Движение жидкостей в трубах.—М.: ОНТИ.— 1936.—
232 с.
350
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
откуда средняя скорость течения будет
^СР 8\i \ dx !'
A59)
В технических расчетах принято вводить коэффициент сопротив-
сопротивления ?:
где d — диаметр трубы. Подставляя в соотношение A60) значе-
значение dp/dx из равенства A59), получим
ри
ср'
Если ввести число Рейнольдса R = pucvd/\i, то закон сопротив-
сопротивления в круглой трубе при ламинарном течении будет иметь вид
t-s-
A02)
Этот закон хорошо подтверждается результатами эксперимен-
экспериментальных исследований (рис. 6.38). Оплошная кривая рассчитана
_ • р_т_^_1 по формуле A62), а точ-
* ' ^ I ' ' ' ' 1 ки соответствуют опыт-
опытным данным, полученным
Гагеном.
Ламинарный режим те-
течения имеет место только
при числах Рейнольдса,
меньших своего критиче-
критического значения. Согласно
опытам в трубах критиче-
критическое число Рейнольдса
приближенно равно RKp =
= 2300. Однако необходи-
необходимо иметь в виду, что ве-
величина RKp в значитель-
значительной мере зависит от усло-
условий течения и в первую
очередь от начальной тур-
турбулентности втекающего потока. В специальных экспериментах,
где турбулентность внешнего потока была незначительной, уда-
удалось > сохранить ламинарный режим течения до значительно
'больйшх, чем критическое^ значений чисел Рейнольдса.
В общем случае при R > RKp возникает турбулентный режим
течения в пограничном слое, причем так же, как и при ламинар-
ламинарном режиме, течение в трубе можно подразделить на входной
\
\
\
\
\
\
0,2
0,08
Ц06
OtO4
002 ,
' 100 200 400 BOO 800 WOO 2000 n
Рис. 6.38. Коэффициент сопротивления
для гладких круглых труб при лами-
ламинарном течении
§ 7. ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ 351
начальный и основной участки. Длина начального участка со-
составляет по измерениям Кирстена от 50 до 100 диаметров трубы,
а по опытам Никурадзе — от 25 до 40 диаметров *).
Рассмотрим течение в основном участке цилиндрической круг-
круглой трубы. Выделим в жидкости цилиндр, имеющий длину I и
радиус у. В основном участке трубы распределения скоростей
в различных сечениях одинаковы, поэтому силы инерции отсут-
отсутствуют и цилиндр будет находиться в равновесии под действием
касательных напряжений, приложенных к его боковой поверх-
поверхности, и разности давлений pi — P2, действующих на его основа-
основания, т. е.
bl Aбз>
Согласно этой формуле касательное напряжение пропорцио-
пропорционально расстоянию от оси трубы и достигает наибольшего зна-
значения на стенке.
!±2 A64)
Коэффициент сопротивления ?, определяемый соотношением
A60), будет в этом случае при замене градиента давления его-
значением из формулы A64) равен
\ . A65)
В отличие от ламинарного течения, для которого связь меж-
между коэффициентом сопротивления (или перепадом давления)
и расходом жидкости определяется теоретически из решения
уравнений Навье — Стокса, при турбулентном режиме такая
связь может быть найдена только в том случае, если профиль
скорости известен из эксперимента. Как уже указывалось в § 4,
профиль скорости в пограничном слое на плоской пластине при
Rx=106—108 (R6 =2- 104—106) хорошо описывается степенной
формулой с показателем 1/7, которая в выбранной системе коор-
координат имеет вид
_г/\1/7
Тогда выражение для коэффициента сопротивления ? мЬжет
быть сразу получено из соотношения A31) при f„ = 1, Мо = О
См. сноску на о. 349.
352 ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
я замене Re через R — pucvd/\i (считая 6 = г), а щ через иС1>:
г
2л \ иу dy 1
о о,
-^I/7fd(x) = 0,817^,
"° - |i ~ 2 «ср "'
Тогда, согласно A65), имеем
Г 8 Ttp о т»/"о\2 о 0,0226 о0,25 / ио У'75 _ 0,306
fe ри|р ~ ри* \ «Ср J ~" R0-28 V иср / R0'25 '
A66)
Эта формула близка к формуле Блазиуса
у 0,316
Ь ^0,25 '
полученной на основании обработки обширного эксперименталь-
экспериментального материала при R = 4 • 103—105.
При больших числах Рейнольдса опытные значения коэффи-
коэффициента ^ оказываются выше рассчитанных по формуле Блазиуса
или по формуле A66).
Для устранения этого расхождения следует при вычислении
коэффициента сопротивления использовать логарифмический
профиль скорости, который является асимптотическим при R -*¦
-*• °°, так как при выводе этого профиля пренебрегается моле-
молекулярной вязкостью по сравнению с турбулентной (§4). Для
выбранной системы координат логарифмический закон распреде-
распределения скорости A15) имеет вид
-?- = 2,5 In -2*. (г — у) + 5,5 A67)
и хорошо подтверждается опытными данными Никурадзе для
больших чисел Рейнольдса (рис. 6.16). На оси трубы г/ = 0, по-
поэтому из равенства A67) имеем
-^ = 2,51п-^ + 5,5. A68)
Зная профиль скорости A67), легко найти среднюю по сечению
трубы скорость течения
-^ = 2,5 In -^L + l J5. A69)
§ 7. ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ
353
Выразим величину ? через v* и иср, подставляя в равенство
A65) значение rw = pv% (согласно определению A15)):
? = 8—— , или —— = ,-.
\ucv) llcp 21/2
Кроме того, преобразуем величину v%r/v:
A70)
Тогда соотношение A69) можно записать в виде
ИЛИ
A71)
Эта формула качественно хорошо описывает характер изме-
изменения коэффициента сопротивления для гладких труб при боль-
больших числах Рейнольдса. Лучшее количественное совпадение
С
4
10~2
8
6
4
/<?¦¦
оо
ей
о*
V
н
ОС
2 4 6 8104 2 4 6 6W5 2 4 66106 2 4 6 8R
Рис. 6.39. Коэффициент сопротивления для гладких круглых труб при
турбулентном течении
получается, однако, если несколько изменить теоретически
числовые множители и принять
-0,8. A72)
На рис. 6.39 приведено сравнение значений величины ?, рас-
рассчитанных по формуле Блазиуса (сплошная кривая) и по фор-
формуле A72) (штриховая кривая), с экспериментальными значе-
значениями коэффициента сопротивления труб, полученными различ-
различными авторами. Как видим, для определения коэффициента
23 Г. Н. Абрамович, ч. 1
354
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
\
ч
\
ц
V
3
2
Л А
CD D
О о
4
сопротивления гладких круглых труб при R = 4 103—105 можно
использовать формулу A66), а при R> 105 — формулу A72).
Исследования течения жидкости в трубах с некруглым попе-
поперечным сечением показали, что законы сопротивления как для
ламинарного, так и для турбулентного режимов имеют такой же
С
8
В
4
7О'7
8
6
4
10* 2 4 B8103 2 4 ВвЮ4 2 4 68R
Рис. 6.40. Коэффициент сопротивления для труб с некруглым поперечным
сечением
вид, как и для круглых труб, если вместо диаметра ввести гид-
гидравлический диаметр, равный отношению учетверенной площади
сечения к периметру. На рис. 6.40 приведены эксперименталь-
экспериментальные значения ?, полученные Шиллером и Никурадзе1), и значе-
значения ?, рассчитанные по формулам A62) (кривая 1) и A72)
(кривая 2). Здесь в качестве характерного размера использова-
использовалась величина гидравлического диаметра.
Наконец, рассмотрим движение совершенного газа с постоян-
постоянной теплоемкостью в канале постоянного сечения при наличии
трения и теплообмена. Температуру стенок будем считать посто-
постоянной. Уравнения неразрывности, количества движения и энер-
энергии для средних параметров имеют вид
PUF = ?r, F — (ри2-\-р) = —Utw, cpF-j—(риТ*) = —Uqw, A73)
где F — площадь поперечного сечения канала, U — его периметр,
G — массовый расход газа, qw — поток тепла через 1 м2 поверх-
поверхности стенки.
Вводя безразмерные коэффициенты трения с} и теплоотдачи
St в последние два уравнения и учитывая, что ри = const, как
следует из уравнения неразрывности A73), получим
Л Л 2
dT*
dx
См. сноску на о. 349.
= -USi(T*-Tw),
A74)
A75)
§ 7. ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ 355
причем величины cf и St зависят от режима течения (ламинар-
(ламинарного или турбулентного) и от следующих безразмерных пара-
параметров:
{^) A76)
A77)
где X — приведенная скорость, представляющая собой отноше-
отношение скорости течения к критической скорости.
При небольших скоростях течения (А,< 1) величина X не яв-
является определяющим параметром. В этом случае коэффициент
теплоотдачи будет изменяться лишь за счет изменения темпера-
температуры газа вдоль канала. Тогда уравнение энергии A75) инте-
интегрируется и определяется распределение температуры торможе-
торможения вдоль канала. Распределение скорости находится из урав-
уравнения количества движения A74). Именно такой подход обычно
используется при рассмотрении движения несжимаемой жидко-
жидкости в канале постоянного сечения. При изучении движения сжи-
сжимаемого газа раздельное интегрирование уравнений энергии и
количества движения невозможно, так как коэффициент тепло-
теплоотдачи в этом случае зависит от скорости газа. Вводя газодина-
газодинамические функции и безразмерную температуру торможения
e = T*/Tw1 получим
G = т pmFfq3], m = const, A78)
\ Т*
-g = -^Sf@-l). A80)
Разделив соотношение A79) почленно на соотношение A80),
исключим переменную х
fc+1 d\YQz(X)] с/ХТ/е
Zk dQ 2StF—1)"
Выполняя дифференцирование в левой части, получим диф-
дифференциальное уравнение первого порядка, связывающее безраз-
безразмерную температуру торможения 0 и приведенную скорость К:
Для простоты дальнейших выкладок предположим, что вы-
выполняется аналогия Рейнольдса как при ламинарном, так и при
турбулентном режиме течения, т. е. cf = 2St. Тогда уравнение
23*
356
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
A81) примет вид
29
A82)
Интегральные кривые этого уравнения показаны на рис. 6.41
для к = 1,4. Для определения направления процесса при тече-
течении газа в канале используем уравнение энергии A80). Если
в канал поступает газ, температура торможения которого ниже
температуры стенки @<1), то газ будет нагреваться (dQ/dx>0)
и 8 -+¦ 1. Если в канал посту-
поступает газ, температура тормо-
торможения которого выше темпе-
температуры стенки F>1), то
газ будет охлаждаться
(dQ/dx < 0) и 6 -> 1. Следо-
Следовательно, течению газа в ка-
канале соответствует движение
вдоль интегральных кривых
к 9 = 1. В области 8 < 1 оба
воздействия (подвод тепла и
трения) влияют в одном
направлении: при дозвуко-
дозвуковом течении (А,<1) проис-
происходит ускорение потока, а
при сверхзвуковом — тормо-
торможение. В области 0 > 1 со-
совместное влияние отвода тепла и трения более сложно, так как
трение оказывает ускоряющее действие, а отвод тепла — тор-
тормозящее.
Рассмотрим сначала дозвуковое течение (А,<1). При боль-
больших разностях температур газа и стенкп (при больших 8) и ма-
малых скоростях (малых К) влияние теплообмена оказывается бо-
более существенным и происходит торможение потока (dX/dQ>0).
При больших X и малых 8 преобладает влияние трения и поток
ускоряется (dX/dQ<0). Вдоль линии перехода от торможения
к ускорению dX/dQ = O. Тогда из уравнения A82) получим урав-
уравнение этой линии в следующем виде:
Рис. 6.41. Интегральные кривые диф-
дифференциального уравнения, описываю-
описывающего течение сжимаемого газа в кана-
канале постоянного сечения с трением и
теплообменом при к = 1,4. Штриховая
линия — dk/dQ = 0
е-1
Эта кривая показана на рис. 6.41 штриховой линией. При сверх-
сверхзвуковом течении нагретого газа (8>1, А,>1) преобладающее
влияние оказывает трение и происходит торможение потока.
После того как зависимость К от 8 найдена, можно опреде-
определить остальные параметры потока. Из уравнения неразрывности
§ 7. ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ 357
A78) следует
р* " I/ 0н
н У
индексом «н» обозначены параметры в начале канала.
Используя основные соотношения между параметрами тор-
торможения и статическими параметрами, получим
6 ^н к + 1 Г 9
тп
Так как w = аЯ, то
Наконец, интегрируя соотношение A80), найдем связь между
х и 9
х
_ F_ Г ^В
~ U ) St (9 - 1)'
так как зависимость X от 0 уже известна и, следовательно, из-
известна зависимость St от 9.
Большинство используемых в технике труб являются шеро-
шероховатыми. Шероховатость стенки обычно характеризуется сред-
средней высотой бугорков /г, которая называется абсолютной шеро-
шероховатостью. Используя абсолютную шероховатость в качестве
характерного линейного размера для течения вблизи стенки,
представим универсальный логарифмический закон распределе-
распределения скоростей A14) в безразмерном виде
-^- = 2,5 In -| + В. A83)
Это соотношение хорошо описывает результаты многочисленных
экспериментальных исследований турбулентного течения в ше-
шероховатых трубах. В этом случае величина В является функцией
безразмерной величины hv%/v, которая может рассматриваться
как число Рейнольдса, составленное из абсолютной шероховато-
шероховатости и динамической скорости (рис. 6.42). Так как по опреде-
определению v* = Пш/р, то, используя условие постоянства числа
Рейнольдса на границе ламинарного подслоя A25) и линейный
358
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
характер распределения скорости в ламинарном подслое A26),
получим
Ни* __ h_
V б
Таким образом, величина hvjv пропорциональна отношению аб-
абсолютной шероховатости к толщине ламинарного подслоя. Если
/&< 0,256л» —-<3,
то все элементы. шероховатости расположены внутри ламинар-
ламинарного подслоя, их обтекание происходит без вихреобразований и
В
0,8
1,6
Рис. 6.42. Зависимость величин В от параметра vjilv: 1 — режим без про-
проявления шероховатости, 2 — режим с полным проявлением шероховатости
шероховатость не оказывает влияние на характеристики турбу-
турбулентного течения. При этом, как следует из рис. 6.42,
В = 5,5 + 2,5 In &-,
и соотношение A83) принимает вид
JL =2,5111^ + 5,5,
т. е. совпадает с универсальным логарифмическим распределе-
распределением скоростей при течении в гладких трубах. Такой случай те-
течения получил название режима без проявления шероховатости.
Как и для гладких труб, коэффициент сопротивления зависит
лишь от числа Рейнольдса, причем эта зависимость описывается
формулой A72). Если
°Л
то элементы шероховатости выступают из ламинарного подслоя
и вызывают дополнительное сопротивление. Профиль скорости
§ 7. ТЕЧЕНИЕ ЖИДКОСТИ В ТРУБАХ 359
A83) можно использовать для получения закона сопротивления
таким же способом, как это было сделано для гладких труб.
Определив из уравнения A83) среднюю по сечению трубы ско-
скорость течения, получим (г — радиус трубы)
^ = 2,5 In ? + В (*f) -3,75. -A84)
Выразим отношение ucv/v* через коэффициент сопротивления
в соответствии с уравнением A70) и преобразуем величину
v%r/v следующим образом:
v 41/2 b
где R = ucv>d/v — число Рейнольдса, подсчитанное по средней
скорости и диаметру трубы. Тогда соотношение A84) может
быть записано в следующем виде:
21/2
.j_2,51n^-3,75. A85)
Таким образом, коэффициент сопротивления при переходном
режиме течения зависит как от числа Рейнольдса, так и от
относительной шероховатости h/r, причем эта зависимость зада-
задается в неявном виде. Значения функции В определяются на
основании данных рис. 6.42.
Если
то элементы шероховатости значительно выступают из ламинар-
ламинарного подслоя и сопротивление в основном вызывается обтека-
обтеканием элементов шероховатости турбулентным потоком. Этот слу-
случай течения называется режимом с полным проявлением шеро-
шероховатости и характеризуется постоянным значением величины
5 = 8,5. Формула для коэффициента сопротивления A85) при
этом принимает простой вид
С = l/B lg-? + 1,68)*. A86)
Коэффициент сопротивления не зависит от числа Рейнольдса,
а определяется только относительной шероховатостью.
Результаты экспериментального исследования коэффициента
сопротивления в шероховатых трубах при различных значениях
относительной шероховатости приведены на рис. 6.43. Эти дан-
данные свидетельствуют о том, что относительная шероховатость
не влияет на критическое число Рейнольдса, характеризующее
начало перехода ламинарного режима течения к турбулентному.
360
ГЛ. VI. ТЕОРИЯ ПОГРАНИЧНОГО СЛОЯ
Зависимость коэффициента сопротивления от числа Рейнольдса
в области перехода оказывается одинаковой при различных зна-
значениях h/r. Для режима течения с полным проявлением шерохо-
шероховатости величина ? может быть определена по формуле A86).
k 6 810Ъ 1
6 810Ц 1 U 6 8105 I Ц 6 8W6 R
Рис. 6.43. Коэффициент сопротивления для шероховатых труб: 1 — по фор-
формуле A62) для ламинарного течения, 2 — по формуле A72) для турбу-
турбулентного течения без проявления шероховатости, сплошные горизонталь-
горизонтальные прямые —по формуле A86) для турбулентного течения с полным про-
проявлением шереховатости
Приведенные результаты получены при условии, что элемен-
элементы шероховатости имеют примерно одинаковый размер и распо-
располагаются плотно друг к другу. Соотношения, полученные для
такой идеализированной шероховатости, могут применяться для
практических расчетов течения в технических трубах при усло-
условии, что установлена эквивалентная шероховатость данной по-
поверхности. Эквивалентная шероховатость для многих типов
реальной шероховатости найдена экспериментальным путем.
В заключение отметим, что вопросам теории пограничного
слоя посвящена многочисленная специальная литература1).
!) Лойцянский Л. Г. Ламинарный пограничный слой.— М.: Физ-
матгиз, 1962; Шлихтинг Г. Теория пограничного слоя.—М.: Наука,
1974; Хейз У. Д., Пробстин Р. Ф. Теория гиперзвуковых течений.—
М.: ИЛ, 1962; Дорренс У. X. Гиперзвуковые течения вязкого газа.—
М.: Мир, 1966; Лапин Ю. В. Турбулентный пограничный слой в сверх-
сверхзвуковых потоках газа.— М.: Наука, 1970; Ч ж е н П. К. Отрывные тече-
течения.— М.: Мир, 1972.
Глава VII
ТУРБУЛЕНТНЫЕ СТРУИ
§ 1. Общие свойства струй
Во многих случаях движения жидкости и газа в потоке воз-
возникают так называемые поверхности тангенциального разрыва;
течения жидкости по обе стороны такой поверхности называются
струйными. В зависимости от относительного направления дви-
движения струй они могут быть спутными или встречными. Харак-
Характерной особенностью струйных течений является то, что танген-
тангенциальный разрыв на поверхности раздела терпят такие, напри-
например, величины, как скорость течения, температура, концентра-
концентрация примеси, тогда как распределение статического давления
оказывается непрерывным.
На поверхности тангенциального разрыва в связи с ее не-
неустойчивостью возникают вихри, беспорядочно движущиеся
вдоль и поперек потока; вследствие этого между соседними
струями происходит обмен конечными массами (молями) веще-
вещества, т. е. поперечный перенос количества движения, тепла и
примесей. В результате на границе двух струй формируется об-
область конечной толщины с непрерывным распределением скоро-
скорости, температуры и концентрации примеси; эта область называ-
называется струйным турбулентным пограничным слоем. При очень
малых значениях числа Рейнольдса струйный пограничный слой
может быть ламинарным, но на этом сравнительно редком слу-
случае течения мы не останавливаемся.
Наиболее простой случай струйного пограничного слоя имеет
место при истечении жидкости с равномерным начальным полем
скорости (ио) в среду, движущуюся с постоянной скоростью (мн),
так как при этом в начальном сечении струи толщина погранич-
пограничного слоя равна нулю. Утолщение струйного пограничного слоя,
состоящего из увлеченных частиц окружающей среды и затор-
заторможенных частиц самой струи, приводит, с одной стороны, к уве-
увеличению поперечного сечения, а с другой стороны, к постепен-
постепенному «съеданию» ядра струи — области, лежащей между внутрен-
внутренними границами пограничного слоя. Принципиальная схема та-
такого струйного течения изображена на рис. 7.1. Часть струи,
в которой имеется ядро течения, называют начальным участком.
Как показывают многочисленные опыты, одним из основных
свойств такой струи является постоянство статического давления
362
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
во всей области течения1), вследствие чего скорость в ядре струи
остается постоянной. Размывание струи за пределами начального
участка выражается не только в ее утолщении, но также и в из-
изменении скорости вдоль ее оси.
На некотором расстоянии от конца начального участка струй-
струйное течение приобретает такой же вид, как течение жидкости
из источника бесконечно малой толщины (в осесимметричном
случае источником служит точка, в плоскопараллельном случае —
прямая линия, перпендикулярная к плоскости течения струи);
Начальный Переходный Основной
участок , j/час то к _, _ участок
Рис. 7.1. Схема течения в струе
соответствующий участок струи называют основным. Между ос-
основным и начальным участками струи располагается так назы-
называемый переходный участок.
Часто пользуются упрощенной схемой струи и полагают дли-
длину переходного участка равной нулю; в этом случае сечение,
в котором сопрягаются основной и начальный участки, называют
переходным сечением струи. Если 'в расчетах переходный уча-
участок не учитывают, то переходное сечение считают совпадаю-
совпадающим с началом основного участка.
Наиболее изученным видом турбулентного струйного течения
является струя, распространяющаяся в покоящейся среде; такая
струя называется затопленной.
В описанной схеме струи предполагается, что пограничный
слой имеет конечную толщину; в некоторых теориях затоплен-
затопленной струи предлагается, что пограничный слой имеет беско-
бесконечную толщину с асимптотическими профилями скорости, тем-
1) В некоторых случаях (при взаимодействии струи с каким-либо пре-
препятствием) условие постоянства давления может нарушиться, но на этих
особых случаях мы остановимся отдельно.
§ 1. ОБЩИЕ СВОЙСТВА СТРУЙ
363
пературы и других величин. Оба эти представления о погранич-
пограничном слое удается практически примирить между собой, так как
асимптотический пограничный слой можно всегда приближенно
заменить слоем конечной толщины1).
Характерной особенностью турбулентной струи, как показы-
показывают теория и многочисленные опыты, является малость попе-
поперечных составляющих скорости в любом сечении струи по срав-
сравнению с продольной скоростью. Следовательно, если ось х совме-
совместить с осью симметрии струи, то составляющие скорости по
перпендикулярной к ней
оси у окажутся настолько
малыми, что в инженер-
инженерных приложениях теории
струи ими можно прене-
пренебречь.
Опыты показывают,
что профили избыточных
значений скорости, темпе-
температуры и концентрации
примеси как в затоплен-
затопленной турбулентной струе,
так и в струе, распростра- , . . .. _ .
няющейся в спутном по- О 0,5 1,0 1,5 2,0 1—
токе, имеют одинаковую °м
универсальную форму На Рис- 7*2- ПР°ФИЛЬ безразмерной избыточ-
птгл 79 ттгчт,«л«л^г , нои скорости в основном участке осесим-
рис. 7.2 приведен унгавер- метричной воздушной струи, распростра-
сальныи профиль скоро- няющейся в спутном потоке воздуха
сти, полученный в опытах
Форсталя и Шапиро2) в основном участке осесимметричной
струи воздуха, втекающей в воздушный поток того же направ-
направления и той же температуры, причем безразмерные избыточные
значения скорости Аи/Аит построены в зависимости от безраз-
безразмерных ординат '
0J5
0,5
025
\
\
\
\
Q
\
\
\
По опытам
° Форсталя и
Шапиро
Ч\р
о с
Аи
A)
Здесь и — скорость на расстоянии у от оси струи, ит — скорость
на оси струи, ия — скорость спутного потока, уо,5и — расстояние
от оси струи до места, в котором избыточная скорость вдвое
меньше своего максимального значения: и — uH = 0,5(wm — uR).
1) В этом случае «границами» асимптотического слоя считают поверх-
поверхности, на которых значения скорости (или, например, температуры) отли-
отличаются от краевых на некоторую наперед заданную малую величину, на-
например на 1 %.
2) Используемые в данной главе литературные источники содержатся
в списке литературы, помещенной в монографии «Теория турбулентных
струй» под ред. Г. Н. Абрамовича, указанной в списке литературы к на-
настоящей книге. . ^ .
364
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Эти опыты проводились при разных отношениях скорости
спутного потока к скорости истечения: т = ив/и0 = 0,2; 0,25; 0,46.
На рис. 7.2 изображен также профиль скорости в затопленной
струе (штриховая линия), взятый из опытов Трюпеля; универ-
универсальные профили скорости при наличии спутного потока и в его
отсутствие оказались практически одинаковыми.
Согласно опытам Вайнштейна, Остерле и Форсталя, а также
Фертмана профили безразмерных избыточных скоростей в пло-
плоских спутных и затопленных струях описываются той же уни-
универсальной зависимостью, что и в осесимметричных струях.
У
Ли
Ли0
п я
и,о
ПС
Цо
А
п °
л
о т=0 \„
• т=023 опытам
a m-D43v' L
а т=Ь}64) U P'
По опытам An
сома и др.
чстша
ьберт-
-1,0 -0,6 -0,6 ,4 -0,2 О 0,2 Ц4 0,6 0,8
Рис. 7.3. Профиль безразмерной избыточной скорости в пограничном слое
двух плоских спутных струй воздуха (начальный участок)
Исследованные в работах Б. А. Жесткова, В. В. Глазкова и
М. Д. Гусевой поля скорости в зоне смешения двух плоскопа-
плоскопараллельных турбулентных струй одного направления при раз-
различных соотношениях скоростей (т = 0; 0,23; 0,43; 0,64) пред-
представлены на рис. 7.3 в следующих безразмерных координатах:
Аи
Аи
B)
Здесь Аи = и — иш — избыточная скорость в струе; Аио = щ — ив —
начальная разность скоростей в струях; Ауо,ъи = У — Уо,ьи — по-
поперечное расстояние от места измерения до точки, в которой
Аи « 0,5Аи0; Ауь = Уо,9и — Уо,и — расстояние между точками,
в которых избыточные значения скорости равны соответственно
Ди1 = 0,9Ди0 и Att2 = ОДА^о.
На тот же рисунок нанесена кривая скорости в пограничном
слое начального участка затопленной плоской струи, полученная
в опытах Альбертсона и др. И в этом случае профиль скорости
является универсальным, но несколько отличается от такового
для основного участка.
Измерения, проведенные автором совместно с Ф. М. Вафиным
в начальной области течения за кормой плохообтекаемого тела,
§ 1. ОБЩИЕ СВОЙСТВА СТРУЙ
365
установленного на оси канала постоянного сечения (в плоском
и осесимметричном случаях), показали, что несмотря на суще-
существование зоны обратных токов, профили безразмерной скорости
B), при построении которых принималось во внимание, что ско-
скорость обратного тока (ия < 0) изменяется с удалением от кормы
тела, оказались такими же, как в пограничное слое обычной
струи.
Подобные же результаты получаются и в камере сгорания га-
газотурбинного двигателя. В начале камеры обычно создается
Рис. 7.4. Профили скорости в камере сгорания турбореактивного двигателя
(при холодной продувке) по опытным данным А. И. Михайлова
большая область обратных токов, примыкающая к оси симмет-
симметрии. Типичные профили скорости в различных сечениях такой
камеры, полученные при «холодной продувке» ('без горения)
в работе А. И. Михайлова, нанесены на рис. 7.4. Эти же про-
профили, но в безразмерных координатах типа B) совпадают с при-
приведенными на рис. 7.3.
Опыты Л. А. Вулиса, Ю. В. Иванова и других исследовате-
исследователей показывают, что профили безразмерных избыточных значе-
значений скорости в струе, охватываемой встречным потоком, также
универсальны и близки к таковым для затопленной струи.
Для описания универсальных профилей скорости могут быть
подобраны приближенные аналитические зависимости.
В дальнейшем для описания профилей скорости -в основном
участке струи любой формы будем пользоваться функцией /(г//Ь),
которую теоретически получил впервые Шлихтинг:
C)
Здесь т| = у/Ь — расстояние от точки со скоростью и до оси струи,
выраженное в долях от полутолщины (или радиуса) данного
сечения струи Ь.
366
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Относительное расстояние до точки, в которой избыточная
и — м„
скорость вдвое меньше, чем на оси струи
определяется из C):
Ло,5и = %^ = 0,441.
-^- = 0,5 ), легко
D)
Профили скорости, рассчитанные по формуле C), хорошо согла-
согласуются с экспериментальными профилями скорости.
В начальном участке струи (ит = щ) иногда используется
универсальная кривая скорости
ил — и
E)
где безразмерная ордината х\в отсчитывается от наружной гра-
границы струи (рис. 7.5):
у-у2
~ у7Г,
Кривая E) вследствие изменения начала отсчета отличается от
C) К
() д
кривой C). Координаты точек
Покоящийся
воздух
Рис. 7.5. Схема пограничного слоя за-
затопленной струи
, Уо,9и, Уод«, которыми поль-
пользуются для сравнения теоре-
теоретической кривой с опытными
данными, находят из E)
с помощью определения F)*
Лучшее, чем E), согла-
согласование с опытными данны-
данными для слоя смешения на-
начального участка струи дает
профиль скорости, получен-
полученный Толмином из теории
турбулентности Прандтля.
При решении задачи Тол-
мина используются диффе-
дифференциальные уравнения
двухмерного пограничного
слоя (97) и A02) или (НО)
из гл. VI, которые при постоянных плотности и давлении с уче-
учетом формулы для турбулентного трения A07) гл, VI
Fа)
р
можно представить в следующем виде:
и — 4- v — - 272 —
ди
Ну ~" '
§ 1. ОБЩИЕ СВОЙСТВА СТРУЙ 367
В уравнении движения предполагается, что турбулентный путь
смешения I в поперечном сечении слоя не изменяется, т. е. за-
зависит лишь от продольной координаты х, что объясняется отсут-
отсутствием ограничивающей турбулентную струю твердой стенки, га-
гасящей поперечные движения частиц жидкости.
Приведем уравнение движения к безразмерному виду, исполь-
используя следующие величины (для затопленной струи):
uQ VT/' ^ ах 1 дх х ' ду ах ' х х *'
о /*
где а = у 2с\ — эмпирическая постоянная; Ъ — толщина слоя
смешения, причем из уравнения неразрывности получим выра-
выражение для поперечной составляющей скорости
v = - J g- dy = аи0 J Г (Ф) ЙФ
Подставляя все эти величины в уравнение движения, приво-
приводим его к виду
F"(F'" + F) = 0,
причем внутри слоя смешения F" (у)?=0. Граничные условия
на линиях сопряжения слоя смешения с ядром постоянной ско-
скорости
JL = ^'(ф1) = 1; v = 0, т. е. F(yJ = Фх; (-^j = 0, т. е.
и с наружной неподвижной средой
^- = F' (ф2) - 0, (-g] = 0, т. е. F" (Фа) = О,
дают возможность решить дифференциальное уравнение Толми-
на, определить профиль скорости в слое смешения:
JL = р' (ф)=0,0176^ф + 0,6623еф/2 cos (ф J^|)
("/4) F6)
и найти границы слоя смешения:
Ф1 = 0,98; ф2 == -2,04.
В табл. 7.1 приведены значения функций F(cp),F'(у)^" (ф).
На рис. 7.6 профили скорости Толмина и Шлихтинга E) в пло-
плоском слое смешения сопоставляются с экспериментальными
данными.
Наряду с примененной Толмином первой теорией свободной
турбулентности Прандтля, основанной на постоянстве пути сме-
368
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
шения, получила применение вторая («новая») теория Прандтля,
предполагающая постоянство турбулентной кинематической вяз-
вязкости в поперечном сечении струи. Для этой величины Прандтль
предложил зависимость
-р = vT = к (ит — ии) Ь; Ъ = сх,
Fв)
где ит — скорость на оси струи, Ъ — ширина струи, к — коэффи-
коэффициент пропорциональности, зависящий от турбулентной струк-
структуры потока. Подставляя эту зависимость в уравнение движения,
Таблица 7.1
Основные функции для расчета пограничного слоя струи
ф
0,98
0,93
0,88
0,83
0,78
0,73
0,68
0,63
0,58
0,53
0,48
0,43
0,38
0,33
0,28
0,23
0,18
^ 0,13
0,08
0,03
-0,02
-0,07
—0,12
-0,17
F
0,981
0,930
0,880
0,831
0,781
0,732
0,684
0,636
0,589
0,543
0,498
0,453
0,410
0,368
0,326
0,286
0,247
0,209
0,172
0,137
0,103
0,070
0,038
0,008
F'
1
0,999
0,995
0,990
0,982
0,972
0,961
0,947
0,932
0,916
0,898
0,871
0,859
0,838
0,816
0,793
0,769
0,745
0,720
0,695
0,670
0,644
0,618
0,592
F"
0
0,048
0,093
0,136
0,176
0,214
0,249
0,282
0,313
0,341
0,367
0,391
0,413
0,432
0,449
0,465
0,478
0,489
0,499
0,507
0,513
0,517
0,520
0,521
ф
—0,22
—0,27
—0,32
-0,37
—0,42
-0,47
—0,52
—0,62
—0,72
—0,82
—0,92
—1,02
-1,12
—1,22
—1,32
—1,42
—1,52
—1,62
—1,72
—1,82
—1,92
—2,02
—2,04
F
-0,021
—0,048
—0,075
—0,100
-0,124
—0,146
-0,167
-0,206
—0,241
—0,270
-0,296
—0,317
—0,335
—0,350
—0,361
—0,370
—0,377
-0,381
-0,384
—0,387
-0,388
—0,389
-0,389
F'
0,566
0,540
0,514
0,489
0,463
0,438
0,413
0,365
0,319
0,275
0,234
0,196
0,161
0,128
0,101
0,077
0,056
0,039
0,026
0,017
0,011
0,009
0
F"
0,520
0,519
0,516
0,511
0,506
0,499
0,491
0,472
0,450
0,424
0,396
0,365
0,333
0,300
0,263
0,226
0,189
0,151
0,113
0,074
0,036
0
0
Гертлер получил автомодельное решение задачи о слое смеше-
смешения для начального участка струи, справедливое как для затоп-
затопленной .струи, так и при наличии спутного потока:
-1—3. = 0,5A + erf!
Уд
I/ ~"~~ If
Здесь ? = a x 0>5u; erf g — табличная функция; у — ордината, от-
отсчитываемая от оси абсцисс, которая начинается на кромке сонла
§ 1. ОБЩИЕ СВОЙСТВА СТРУЙ
369
и направлена параллельно скоростям щ и иа; о = 13,5 — эмпи-
эмпирическая постоянная. Положение слоя смешения в пространства
при ия = 0 и отсутствии поперечной скорости (v = 0) на линии
и = ио определяется линией —~^- = — 0,528.
Асимптотический профиль скорости Гертлера близок к про-
профилю конечной ширины Толмина. Если считать шириной про-
профиля Гертлера зону, лежащую между ординатами go.oiu и ?о,99и*
бу/х
Рис. 7.6. Сравнение теоретических профилей скорости на краю плоском
струи с опытными данными Рейхардта
на которых безразмерная скорость имеет соответственно значе-
значения и _цн = 0,01 и 0,99, то ширина слоя смешения по Гертле-
ру составит
для тех же условий по профилю Толмина получается
Ь = 2,75ах;
сопоставляя последние два выражения, получаем формулу, свя-
связывающую экспериментальные константы Гертлера и Толмина:
оа = 1,194 при а = 0,09; а = 13,5. Профиль скорости Гертлера
приведен на рис. 7.6. Описанные результаты получены при
умеренных скоростях струй (Мо<1) и мало отличающихся зна-
значениях плотности вещества струи р0 и окружающей среды рНг
т. е. при п = рн/ро = 1. Опыты, однако, показывают, что универ-
универсальность профилей скорости не нарушается и при значитель-
значительном изменении отношения плотностей @,25 < п < 4). Если п от-
отличается от единицы не более чем в 4 раза, то профили темпе-
температуры в струях при ср = const также универсальны1), причем
1) При переменной теплоемкости универсальны профили теплосодер-
теплосодержания.
24 г. Н. Абрамович, ч. 1
S70
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
для начального участка можно воспользоваться линейной зави-
зависимостью, которую получим из теплового дифференциального
уравнения A11) гл. VI, решая ©го совместно с уравнением дви-
движения при использовании теории Прандтля — Толмина для зна-
значения турбулентного числа Прандтля 0,5:
1 1 н
Т — Т
1 о ^
= Y1H ИЛИ
Т Т
1 0 "~iH
A_f = l_TiHI G)
1,0
0,9
где г]н определяется в соответствии с F), а индексы при значе-
значениях температуры те же, что и в E) при значениях скорости.
Зависимость G) сопо-
сопоставлена с опытными
данными на рис. 7.7.
В поперечных сече-
сечениях основного участка
справедлива следующая
зависимость избыточ-
избыточной температуры от из-
избыточной скорости, ко-
которая также выводит-
выводится из совместного ре-
решения уравнений A02)
и A18) гл. VI при ги-
1
!
i
\
огп=0 n=1t12 По опытам &
• п?=О п=7,43 \ По опыта
д т=0,2 п=0,32) Яковлеве/а
Линия 0р = 1-7]н
\
1
ч
\
\
втора,
м
si
OJ
0,6
0,5
0,4
0,3
0,2
0,1
О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 7]н
Рис. 7.7. Профиль температуры в погранич-
пограничном слое струи
() . V при ги
потезе Прандтля A07)
для турбулентного тре-
трения, а также переноса
тепла:
(8)
Здесь, как и в A0), знак приблизительного равенства предпола-
предполагает постоянство теплоемкости (ср = const), PrT — «турбулентное»
число Прандтля, пропорциональное отношению тепла, выделяю-
выделяющегося вследствие турбулентного трения, к теплу, отводимому
путем турбулентного перемешивания.
Опыты, проведенные при значениях п = 0,03 -5- 300, показыва-
показывают, что для осесимметричных струй можно принять Ргт = 0,7 -5-
-т- 0,8, а для плоских струй Ргт = 0,5.
Сопоставление профиля температуры (8) в основном участке
с опытными данными демонстрируется на рис. 7.8.
Согласно опытным данным Б. А. Жесткова, М. М. Максимова
и др. зависимости G) и (8) справедливы д для струй с большей
начальной скоростью истечения (Мо>1). Однако в этом случае
§ 1. ОБЩИЕ СВОЙСТВА СТРУЙ
371
вместо статических температур в эти зависимости следует под-
подставлять температуры заторможенного потока.
Распределение примеси в поперечных сечениях турбулентной
струи подчиняется той же закономерности, что и распределение-
температуры:
71 —
Здесь с —массовая концентрация примеси, представляющая со-
собой отношение массы примеси к массе всей смеси в том же
объеме.
Справедливость равенства (9) подтверждена многочисленны-
многочисленными опытными данными.
Заметим, что профиль скорости ддя__оснрвнрго участка затоп-
затопленной струи, а также зависимости (8) и (9)" можно получить
из уравнений Прандтля —
Толмина, как и для на-
начального участка. Мы не
приводим формулу Тол-
Толмина, так как формула
C) Шлихтинга имеет бо-
1,0
0,8
0,6
0,4
0,2
—А.
*^
"^
^Д
Д /7 = 1, ТЛ=О ПО ОПЫГ
Рвпхардта,
— Кривая -4^-=/-/
нам
Щ5
,АТт *о*
L^ при ?=0,44
Т*>^д
I
лее простой вид, но дает
практически те же резуль-
результаты. Следует отметить,
что формула Шлихтинга
выводится также из тео-
теории Прандтля (при нали- Рис. 7.8. Профиль избыточной температу-
О
0,4 0,8 1,2 7,6 2,0 К-
ры в основном участке плоской струи
(Рг = 0,5)
чии спутного потока, име-
имеющего скорость, близкую
к скорости струи).
Рассмотрим вопрос о расширении границ турбулентной струи.
Предположим, что скорость нарастания толщины пограничного
слоя пропорциональна средней квадратичной величине пульса-
ционной составляющей поперечной скорости:
которая в свою очередь пропорциональна поперечному градиен-
градиенту продольной (главной) скорости потока:
y
Здесь I — путь турбулентного смешения.
Ввиду подобия профилей скорости в различных сечениях по-
пограничного слоя поперечный градиент продольной скорости про-
пропорционален разности скоростей на границах
du
dy
24*
372 гл. vii. турбулентные струи
Вследствие этого имеем
<*>'> ~ j (ui — и2).
Из подобия профилей следует также, что отношение характерных
линейных размеров есть величина постоянная:
-т- = const, *
поэтому пульсационная составляющая поперечной скорости про-
пропорциональна разности скоростей на границах слоя:
<i/> ~ щ — U2.
Так как, по предположению,
, /ч db db dx db
<и> и
то закон нарастания толщины пограничного слоя по длине струи
можно представить в следующем виде:
dx
(Ю)
Величина ev= (и'У/и, называемая степенью турбулентности по-
потока, всегда положительна, так как вычисляется по средним
квадратичным значениям поперечной пульсационной скорости и
некоторой характерной величине осредненной продольной скоро-
скорости потока М, в связи с чем во всех случаях db/dx>0. Оста-
Остается выяснить, какое значение поступательной скорости следует
подставить в знаменатель выражения A0).
Характерное значение средней скорости можно определить
различными способами. Осреднение, однако, следует вести по
толщине (а не площади поперечного сечения) струи; это выте-
вытекает из того экспериментального факта, что законы нарастания
толщины плоской и осесимметричной струй приблизительно оди-
одинаковы.
Пусть
1
udy
~ ~o,5[K| + KH. (И)
В таком случае получим следующий закон увеличения толщины
пограничного слоя:
db К-ц21
Выражение A2) приводит к интересным выводам. В погранич-
пограничном слое, возникающем на границе двух беспредельных струй
§ i. ОБЩИЕ СВОЙСТВА СТРУЙ 373
(^i = const, W2 = const), толщина пропорциональна удалению от
начала смешения:
-— = const, Ь = const *х,
ах
где
const = с
ы+кг
Значение коэффициента с должно быть определено экспери-
экспериментально, например, по результатам исследования струи, рас-
распространяющейся в неподвижной среде (затопленная струя: иг =
= 0), когда имеет место равенство
Ъъ — сх. A3)
Опыты показывают, что на величину коэффициента с для
слоя смешения влияют число Маха и отношение плотностей
смешивающихся сред в начальном сечении струи (Mo, ft = P2/pi).
Часто это влияние оценивают произведением соответствующих
функций:
с = <усрм(М0).фп(и), A4)
где со — значение коэффициента в несжимаемой жидкости (при
фм = фп = 1). в начальном участке со = 0,27 как для плоской,
так и для осесимметричной задач.
В общем случае (иг^О) толщину пограничного слоя найдем
на основании A2), A3) и A4)
В частном случае спутного движения двух беспредельных
струй скорости на границах слоя имеют одинаковые знаки, вслед-
вследствие чего угол утолщения пограничного слоя уменьшается с
ростом скорости спутного потока U2*.
причем знак минус берется при
При распространении струи во встречном потоке скорости на
границах слоя имеют разные знаки, т. е. алгебраическая разность
скоростей равна сумме их абсолютных значений, поэтому
К
Иначе говоря, при встречном движении струй (иг < 0) угол утол-
утолщения пограничного слоя не зависит от соотношения скоростей
374
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
на границах, т. е. получается во всех случаях примерно таким
же, как и при распространении струи в неподвижной среде.
На рис. 7.9 изображена теоретическая кривая, соответствую-
соответствующая формуле A5) для интервалов значений и2/и\ = т от —1
до 0 и от 0 до 1:
— — fh. <• О — — 1"" m dbs ^>О
dx dx dx 1 —j— тп dx "***"^
Ввиду сложности определения из опытов истинного значения Ь
здесь в качестве толщины пограничного слоя было принято рас-
расстояние Ауь между точками со значениями избыточной скорости
(
. По о/
Э по
штам
• •
и. D. лпиолооиписи
По опытам
к Б.А.Жестковаидр.
» По опытам ПН. Абра
мовича и Ф.М.Вафина
_ Теория
> Ъ
п я
и,0
ПС
U,D
- 0,4
П о
\
\
1
о
ч
X
\
-1,0 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8
Рис. 7.9. Зависимость толщины пограничного слоя струи несжимаемой
жидкости от скорости внешнего потока
, и Am2 = 0,1Awo. При универсальном профиле ско-
скорости величина Ауь составляет во всех случаях одну и ту же
долю от толщины пограничного слоя:
Ауь Ь
где Ь3 — толщина пограничного слоя затопленной струи, ДуЬз —
величина Ауь для затопленной струи.
Для сравнения на рис. 7.9 приведены экспериментальные точ-
точки, которые при одном и том же значении опытной постоянной
(с = с3) располагаются близко к теоретической кривой в области
значений — 0,4 < m ^ 0,4, но отходят от нее при 7?г > 0,5. Этот
результат, обнаруживаемый также и на теневых фотографиях
струи, можно объяснить следующим образом. При выводе фор-
формулы A0) мы предполагали, что турбулентность в пограничном
§ 1. ОБЩИЕ СВОЙСТВА СТРУЙ 375
слое порождается только разностью скоростей на его границах,
а вне этих границ вовсе отсутствует, т. е. <i/>->0 при т-+1.
В действительности же и в «невозмущенном» потоке имеется
некоторая начальная турбулентность, поэтому в тех случаях,
когда скорости и\ и U2 близки между собой, т. е. интенсивность
турбулентности, порождаемой в струе, меньше исходной интен-
интенсивности турбулентности невозмущенного потока, влияние пер-
первой прекращается и перемешивание определяется турбулент-
турбулентностью невозмущенного потока, которая не зависит от величи-
величины т. Естественно, что в этой области угол утолщения погра-
пограничного слоя почти не связан с соотношением скоростей на
границах слоя.
Однако существует еще более важная причина, нарушающая
зависимость A0) толщины слоя смешения струи от параметра т.
Она состоит в том, что начальные профили скорости и плотно-
плотности в струе и спутном потоке чаще всего бывают неравномер-
неравномерными из-за наличия пристенных пограничных слоев, которые
оказывают сильное влияние на структуру струи. Подробно этот
вопрос будет рассмотрен ниже.
Результаты, полученные для зоны смешения двух беспре-
беспредельных струй, справедливы также и для начального участка
струи конечной толщины, распространяющейся в спутном или
встречном потоке, поскольку в начальном участке на обеих гра-
границах зоны смешения скорости остаются неизменными.
Очертания основного участка струи конечной толщины при
встречном движении окружающей жидкости ввиду того, что
скорость встречного движения согласно A7) не влияет на угол
утолщения зоны смешения, остаются примерно такими же, как
и в затопленной струе.
Более сложной задачей является определение очертаний ос-
основного участка струи в спутном потоке жидкости. В этом слу-
случае формула A2) приобретает следующий вид:
где ит — скорость на оси основного участка струи, ив — скорость
спутного потока (знак минус берется при ия > ит). В связи с
тем, что величина ит на оси струи изменяется, так как ит =
= ит(х), граница струи в спутном потоке должна быть криво-
криволинейной. Для ее определения необходимо знать вид зависимо-
зависимости ит(х), которую можно получить из условия сохранения ко-
количества движения; решение этой задачи приводится ниже.
В формулах A2) —A8) использовано выражение A1) для
средней скорости, справедливое в случае несжимаемой жидкости.
При величинах w = pH/po, существенно отличающихся от едини-
единицы, необходимо учитывать влияние сжимаемости.
376
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Основываясь на экспериментальных данных, можно принять
для срм в слое смешения начального участка струи (рис. 7.10):
Фм = 1 * при Мо<1,2,
срм = 1-0,4/М0-1,2 при 1,2<М0<3,6,
Фм = 0,4 при 3,6<М0<4,8
A9)
и для фп:
711/3). B0)
На рис. 7.10 расчетная зависимость от числа Маха относи-
относительной толщины изобарической зоны смешения сопоставляется
с экспериментальными данными. По длине основного участка
vj
>-
4
i ¦
0,5
0 1 2 Z И
Рис. 7.10. Зависимость толщины изобарической зоны смешения от М
струи параметры струи быстро приближаются к их значениям
в окружающей среде, поэтому здесь можно в первом приближе-
приближении положить
фм = Фп= If
т. е. считать форму границы основного участка такой же, как
в струе однородной несжимаемой жидкости.
Формулы A4), A9) и B0) справедливы при равномерном
распределении параметров потока в начальном сечении струи.
Поправки на неравномерность начальных профилей, особенно
значительные при наличии спутного потока, приводятся в § 4.
Отношение плотностей в изобарической струе с помощью
уравнения состояния заменяется отношением температур
Рн
¦* н
Т9
B1)
Основываясь на многочисленных опытах, принимаем значе-
значения коэффициента с в A4) для начального участка со = 0,27 и
для основного участка с = 0,22.
§ 2. ИЗМЕНЕНИЕ ПАРАМЕТРОВ ПО ДЛИНЕ СТРУИ 377
§ 2. Изменение параметров по длине струи
Для отыскания закономерностей изменения скорости, темпе-
температуры и концентрации примеси по длине турбулентной струи
газа или жидкости, а также для определения границ струи мож-
можно воспользоваться условиями сохранения количества движения,
теплосодержания и массы примеси, а также законом нараста-
нарастания толщины струи A8), который напишем в следующем виде
(для т< 1):
dx 2т 1
C
н а — m — н
где m = , Aum = , причем йот— значение скорости
U0m uom ~~ ин
на оси начального сечения струи. Как указывалось, в случае не-
пзотермической струи в спутном потоке можно для основного
участка в первом приближении пользоваться тем же законом
нарастания толщины струи, или, как его иногда называют, урав-
уравнением распространения, что и для изотермической струи. Это
уравнение справедливо как для плоской, так и для осесиммет-
ричной струи; в последнем случае нужно только заменить полу-
полутолщину Ъ радиусом струи г.
Для установления из уравнения B2) вида функции Ь(х)
нужно знать закон изменения скорости по оси струи кит(х),
который может быть найден с помощью уравнения сохранения
количества движения. Для изобарической струи это уравнение
имеет следующий вид:
g Go
Д/ = J (и — ин) dG = J (и0 — мн) dG0. B3)
о о
Здесь G—секундная масса газа (или жидкости), протекающая
через произвольное поперечное сечение струи, Go — то же в на-
начальном сечении струи, dG = ри dF — секундная масса элемен-
элементарной струйки в произвольном сечении. Из уравнения B3) по-
получаем
1
Аи и dF _ A/
о
1
F0 \Ди0т/ J Рот'
Рр *2о ^о »н Г
Рот и*т ^о U0mJ
Рот и*т ^о U0mJ POmwOm F0
Используя принятые вьппе обозначения тп = ——, . от = 4 ,
применение которых удобно при равномерном поле скорости
378 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
внешнего потока и неравномерном начальном поле скорости в
струе (здесь йот — скорость на оси струи в начальном сечении,
= йот — ии), а также величины
1 1
р Д« dF_ . _ Г р / Аи \2 dF_
приходим к следующему уравнению, выражающему закон сохра-
сохранения количества движения в струе:
FAUm \А2 A - т) Апт + А.т] = ^^^. B7)
Правая часть этого выражения отличается от единицы только
при неравномерных профилях скорости и плотности в начальном
сечении струи (ftiu^l, ^u^l, пФ1). Умножив и разделив
интегралы А\ и А2 на плотность окружающей среды рн, имеем
Рот-' Рн Д"т F ° 2 PomJ Рн\Дцт/ F
О О
B8)
где введено обозначение для отношения плотностей вне струи
и на ее оси ft = pH/pom. Интегралы А\о и А2о при тг = 1 во всей
области течения, а при п Ф 1 вдали от сопла являются констан-
константами, которые определяются по профилю скорости C).
С учетом этих обозначений при F = F/F0 из B7) следует
— — — Паи тП1„
FnAum [А20 A - т) Аит + тА10] = 2\_т1и . B9)
Составим теперь уравнение сохранения избыточного тепло-
теплосодержания при неравномерных полях скорости и температуры
в начальном сечении струи:
g Go
AQ = J (t _ fH) dG - J (*0 - у dG0, C0)
§ 2. ИЗМЕНЕНИЕ ПАРАМЕТРОВ ПО ДЛИНЕ СТРУИ 379
или, в безразмерном виде,
A f
f_4i» 1
J p0TO A»m Д«т * + m AiomJ pom
о о
Вводя обозначения
1
р л*
*^ * 0ТЛ QTfl QTTl Q
—— Al ^— С
д • 771 • гтт PH /Q/\
m = "SI ' l = Cp ' Cp = "c ' ^ '
приводим уравнение сохранения избыточного теплосодержания
к следующему виду:
FnAim[B2o{l — m)Aum+ тВю] = пТ. C5)
Если смешиваются газовые струи с равномерными полями ско-
скорости, плотности и температуры в начальном сечении, то пт = 1.
При тг = 1 и сР = 1, а также вдали от сопла при п?=1 и сР^1
интегралы В10 и В20 суть константы, определяемые по профи-
профилям-скорости C)ч и температуры (8).
Поделив левую и правую части уравнения B9) на соответ-
соответствующие части уравнения C5), можно установить связь между
безразмерными избыточными значениями теплосодержания и ско-
скорости на оси основного участка струи:
C6)
где
nT(i-m) AumA2Q(l-m)+A10m
„^ _ mriiu ATimB2Q A - m) + Blom
В случае затопленной струи (Дwm = um, m = 0) с равномер-
равномерными начальными полями скорости и температуры (щи = щи =
380 . ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
== 71т === 1)
Дг ^4
/сТз = —— = -^- = const, C8)
wm 20
где
ит = — • C9)
В случае смешения струй одинаковой скорости (т = 1) с рав-
равномерными начальными полями
Подынтегральные выражения в Аю, А2о, Вю, #го содержат один
и тот же множитель р/рн, поэтому величина кТ очень слабо за-
зависит от отношения плотностей в струе и окружающей среде.
При смешении струй разных газов (или жидкостей) распре-
распределение плотности зависит также от поля концентраций каждого
из газов (или жидкостей), составляющих смесь. Поле безраз-
безразмерной избыточной концентрации любого из газов в поперечном
сечении струи подчиняется зависимости (9). Распределение из-
избыточной концентрации примеси по оси струи устанавливают с
помощью уравнения сохранения избыточного количества приме-
примеси в струе
AGnp = } (с - сп) dG = J (с0 - св) dG0, D1)
о о
которое после приведения к безразмерному виду можно предста-
представить так:
1
F I " m) AC™ AU™ [ Р Ас Аи dF
Дсл Аил .1 ол«^ Ас^ Аим F
\j7Yl 0•»• * О"» "• "•
"__ Г Рр ц0 Асо dFo
Введем обозначения
о
1
J Pom Лст Лмт ^ 20' V '
§ 2. ИЗМЕНЕНИЕ ПАРАМЕТРОВ ПО ДЛИНЕ СТРУИ 381
' "от иот
О
Тогда уравнение сохранения избыточного содержания примеси
запишется так:
Fn&cm [E2o(l - т) Апт + тЕ10] = пс. D7)
Поделив левую и правую части уравнения B9) на соответствую-
соответствующие части уравнения D7), устанавливаем связь между концен-
концентрацией примеси и скоростью на оси струи:
Acm = /ccAMw, D8)
где
- т) + Е10т
10
В случае затопленной струи (т = 0) с равномерными началь-
начальными полями скорости и концентрации примеси (п\и = Щи = пс =
1
В случае смешения струй одинаковой скорости (/тг = 1) с равно-
равномерными начальными полями имеем
ксс = --^ = const. E1>
ю
Решая совместно уравнения B2), B9), C5) и D7), можна
найти зависимости изменения толщины струи, а также скорости,,
температуры и концентрации примеси вдоль оси основного участ-
участка струи. Для вычисления коэффициентов начальной неравно-
неравномерности ttiw, Щи, nT, nc нужно знать поля скорости, плотности,
температуры и других параметров жидкости (или газа) в на-
начальном сечении струи. Используя поля скорости C), темпера-
температуры (8) и концентрации примеси (9) в поперечных сечениях
основного участка, можно вычислить определенные интегралы
А ю, ^20, #ю, #20, ^ю и ?20, которые являются коэффициентами
уравнений B9), C5) и D7). При струйном смешении сред оди-
одинаковой плотности (р = const) получаются следующие величины
этих интегралов:
для плоской струи (PrT = ScT = 0,5)
0,45, Л20 = 0,316, #ю = #ю = 0,6, Яго = #20 = 0,368, E2>
382 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
для осесимметричной струи (PrT = ScT = 0,75)
Al0 = 0,258, Л20 = 0,134, В10 = Е10 = 0,328, #2о = #20 = 0,155. E3)
В соответствии с этим связь между избыточной скоростью и зна-
значениями избыточных теплосодержания и массовой концентрации
примеси _
Aim = Аст = кТАит E4)
определяется следующим значением коэффициентов, практиче-
практически одинаковым для плоской и осесимметричной струй:
&т = &с = 0,86. E5)
Значения кТ относятся к случаю затопленной струи (т = 0) при
р = const, но с ошибкой менее 10 % могут использоваться при
ль Ф 0 и р = var.
При равномерных полях скорости, температуры и концентра-
концентрации примеси в начальном сечении струи семейство кривых, опи-
описывающих изменение относительной избыточной скорости Апт
(а также температуры АТт ^ Aim и концентрации Аст) по без-
безразмерной длине струи1) х=х/Ьо, имеет параметром величину
т = ujuo при п = рн/ро = const или величину п при т = const.
С уменьшением т и ростом п «затухание» струи ускоряется.
Для полного расчета турбулентной струи необходимо прежде
всего найти изменение скорости вдоль ее оси, что достигается
путем совместного решения уравнений B2) и B9). В простей-
простейшем случае равномерного поля скорости в начальном сечении
струи (ri2u = п\и = 1) и постоянной плотности (р = const, лг = 1)
в B9) следует подставить значения интегралов Ai=Aw и^ =
= А20; для затопленной струи (т = 0) получается из B9) при
п = var:
Fnum = -j- E6)
или при п = 1:
772 TJ + 1 __ П2и
т — -A" i
«где
/ = 0 — для плоской, / = 1 — для осесимметричной струи. Соглас-
Согласно B2) в основном участке затопленной струи (х>хп)
l) bo — полуширина начального сечения плоской струи (или начальный
^радиус осесимметричной струи).
§ 2 ИЗМЕНЕНИЕ ПАРАМЕТРОВ ПО ДЛИНЕ СТРУИ
383
В переходном сечении (Aw
= хп) из E6) получаем
Tj+l
П2и
пА,
20
E7>
Величины xn = xjbo определяются в § 3.
Опыты показывают, что при р = const границы основного
участка затопленной струи пересекаются на оси выходного сече-
сечения сопла F = 0 при # = 0), откуда
53 = сх, 5ПЗ = схп.
E8)
Подставляя полученные зависимости в E6), устанавливаем пря-
прямую связь между безразмерной скоростью на оси основного»
лип
Рис. 7.11. Зависимость Амт от хп/х
для плоской струи. Обозначения см.
на рис. 7.16.
Рис. 7.12. Зависимость Амт от
ха/х для осесимметричной струи
участка затопленной струи при р = const и отношением расстоя-
расстояния от сопла до переходного сечения к расстоянию до данного
сечения:
E9>
Представим результаты совместного решения уравнений B2) и
B9) при р = const и т = var также в виде зависимости Awm =
Результаты соответствующих расчетов изображены на-
рис. 7.11 для плоской струи (/ = 0) и на рис. 7.12 для осесим-
метричной (/==1). Как видим, полученные зависимости являют-
являются прямыми линиями при т < 1 и мало отличаются от прямых
при т>1. Опыты показывают, что при неравномерных полях
384
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
скорости на срезе сопла и всегда имеющихся других начальных
возмущениях влияние величины т на линейную зависимость
Лит от (xjxK+l также несущественно и можно во всех случаях
пользоваться формулой
т
Иначе говоря, влияние спутного потока, начальной неравномер-
неравномерности полей скорости, плотности и концентрации сводится толь-
только к соответствующему из-
изменению местоположения пе-
переходного сечения:
На рис. 7.13 зависимость
F0) для дозвуковых изотер-
изотермических осесимметричных
струй разных газов, вытека-
вытекающих в поток воздуха, пред-
представлена в логарифмических
координатах сплошной ли-
линией. Здесь же нанесены экс-
экспериментальные точки, взя-
взятые из монографии Г. Н. Аб-
Абрамовича и др. [2].
Табл. 7.2 дает значения
XnJbo=Xnu (при Дйт=1)
для разных опытов с профилированными соплами, т. е. при рав-
равномерных полях скорости и концентрации в начальном сечении
отруи. При наличии спутного потока (пг Ф 0) и равномерных на-
начальных полях скорости (п\и = П2и = 1) из B9) следует выраже-
выражение для безразмерной ширины переходного сечения (AMwn = l):
Z+1 = {п [А20 A - т) + А1от)у\ F0а)
Для крайних режимов пг = 0 и пг = 1 получается соответственно
Р+1 — (rt A \~x tf+1~(r?A )~1-
отсюда отношение ширин переходного сечения для этих режи-
мов
Рис. 7.13. Затухание избыточной скоро-
скорости вдоль оси газовой струи в потоке
воздуха
1
3 + 1
Отношение интегралов слабо зависит от распределения плотно-
плотности в сечении струи, т. е. в последнюю формулу можно подста-
лзить их значения при р = const из E2) и E3). Тогда для пло-
§ 2. ИЗМЕНЕНИЕ ПАРАМЕТРОВ ПО ДЛИНЕ СТРУИ
385
ской и осесимметричной струй отношение этих величин оказы-
оказывается одинаковым:
Ьпз = 1,4ЬПС.
При равномерных полях скорости, температуры и концентра-
концентрации примеси в начальном сечении струи семейство кривых, опи-
описывающих изменение относительной избыточной скорости Дцт
1 Т а б лица 7.2
га
0
0,2
0,48
1
3
0
0,16
0,42
0,32
0
0,28
п
0,27
0,31
0,31
0,33
0,29
1,34
1,75
1,79
1,98
7,25
6,3
25
30
32
13
11
12
18
4,2
4,5
7
25
28
35
52
11,5
—
2,7
5
25
4«г>
7
7
10,5
14
2,5
—
Обозначения на рис.
7.13 и 7.16
1
2
3
4
5
6
7
8
9
10
11
(а также теплосодержания Aim и концентрации Аст) по безраз-
безразмерной длине струи х = х/Ьо, имеет параметром величину п при
т = var или величину т при n = var. С уменьшением т и ро-
ростом п затухание струи ускоряется.
Начальная неравномерность потока существенно искажает
влияние параметра т на характер зависимости Апт(х). При
значительной начальной неравномерности (например, при исте-
истечении из длинной цилиндрической трубы в неравномерный по-
поток) влияние т как на Дйт, так и на ха перестает ощущаться.
Об этом можно судить по экспериментальным данным для до-
дозвуковой струи (рис. 7.14) и для сверхзвуковой струи при Мо = 3
(рис. 7.15). Степень подогрева струй Э в этих опытах1) была
примерно одинаковой (соответственно Э = Т0/Тп = 1,85 и Э* = 2).
Расчеты и эксперименты показывают, что переходные коэф-
коэффициенты кт и &с, определяемые равенствами C7) и D9), почти
не изменяются по длине струи и не зависят от параметра сжи-
сжимаемости п.
1) Для сверхзвуковых струй под 9* понимается отношение температур
торможения в начальном сечении струи и в окружающей среде.
25 Г. Н. Абрамович, ч. 1
386
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Таким образом, если установлена зависимость кпт(х), то от
нее легко перейти с помощью C6), C7), D8) и D9) к зави-
зависимостям Мт(х) и Аст(х); для этого нужно знать, однако,
Лпп
0,75
0,5
0,25
О
+A
хо
л
+ хО
Д
Л
О
+ 777 =0
х 777 = 0,114
Д 777 П 911
° /77 =
0,305
о
120
х
Рис. 7.14. Избыточная осевая скорость в неизометрической (9 = 1,85) осе-
симметричной струе газа, распространяющейся в спутном потоке (т = var);
опытные данные О. В. Яковлевского и В. К. Печенкина
коэффициенты неравномерности в начальном сечении струи п\иу
П2ч, ПТ И Пс.
В переходном сечении для скорости (Аггтп = 1) концентра-
концентрация и теплосодержание меньше, чем в начальном сечении струи,
Ла0
0,6
0,4
0,2
О 20 40 50 80 100 120 140 150 180 я
Рис. 7.15. Избыточная осевая скорость в сверхзвуковой осесимметричной
струе газа (Мо = 3), распространяющейся в спутном потоке (га = var);
опытные данные Б. А. Жесткова и др.
так как кс<1 и Лг<1. Следовательно, переходные сечения для
последних двух параметров (Acmn = 1, Aimn = l) расположены
ближе к началу струи {хпс<хпи, хпТ<хпи). Если для каждого
-а—с
?
д •
С
<
о 777=0
a m-0,081
+ m=0,204
• 777
1
§ 2. ИЗМЕНЕНИЕ ПАРАМЕТРОВ ПО ДЛИНЕ СТРУИ
387
параметра ввести свою абсциссу переходного сечения, то форму-
формулу E5) можно использовать для расчета изменения любого па-
параметра по оси струи:
r
Экспериментальное подтверждение этого факта иллюстрирует
рис. 7.16, на котором представлена зависимость концентрации на
оси газовой струи круглого сечения в спутном потоке воздуха
(сн = 0, Acw = ст) от величины х/хае. Экспериментальные точки
для газов разной плотрости и
при разных относительных зна-
значениях скорости спутного по-
потока заимствованы из моногра- 0^6
фии Г. Н. Абрамовича и др.
[2]. Опыты велись со струями 04
фреона (я = 0,25 4-0,35), ге-
гелия (тг = 7,25) и подогретого
воздуха. Условные обозначения
и соответствующие значения
абсцисс переходного сечения
для каждого сочетания па-
параметров т, п приведены в О,/
табл. 7.2. / 2 4 6 8'
+ 8
\|
N
• 2
хЗ
04
+6
+ 7
\
—
3 вдолГоси базовой1 струи
в потоке воздуха
На рис. 7.16 сплошной ли-
линией нанесена расчетная кри-
кривая F0) с использованием со-
соответствующих значений хпс,
хпт (табл. 7.2). Согласование расчетных данных с эксперимен-
экспериментальными получилось вполне удовлетворительным.
Следует отметить, что для перехода от поля теплосодержа-
теплосодержания (энтальпии) к полю температуры требуется знание зависи-
зависимости теплоемкости газа от молекулярного веса и температуры.
Простейшее решение задачи о турбулентной струе получа-
получается в случае затопленной струи, для чего используются усло-
условия сохранения импульса E6) и уравнение распространения
струи A3) при с = 0,22:
= п2и, Ъ =
F2)
откуда скорость на оси
3 + 1
где х = х/Ьо.
Согласно E2) и E3) в плоской струе (/ = 0) 42о = 0,316 и
в осесимметричной струе (/==1) Л20 = 0,134. Таким образом,
25*
388 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
при / = О
г
а при / = 1
/ \1/2 12,4
Длину хаи находим из условия пт = 1, откуда при /
)
Коэффициент неравномерности потока в начальном сечении струи
щи зависит от профилей скорости и плотности. Например, в слу-
случае р = const и пограничном слое, заполняющем по «закону 1/7»
(см. гл. VI) все сечение, в осесимметричном сопле получается
Щи = 0,68, а в плоском — щи = 0,7775. Если пристенный погра-
пограничный слой составляет 30 % от полутолщины (радиуса) сопла,
то получается соответственно в осесимметричном случае щи =
= 0,77, а в плоском — щи = 0,864. Однако обеспечить достаточ-
достаточную равномерность потока в прямоугольном сопле труднее, чем
в круглом, поэтому влияние начальной неравномерности в пер-
первом случае больше. Практически согласуется с опытными дан-
данными для хороших сопел следующая универсальная формула
падения скорости вдоль основного участка струи:
5+1
F3)
Для концентрации примеси и теплосодержания имеем согласно
E5)
Аст = АГт = 0,86Амт. F4)
Из этих соотношений можно получить расстояние от начала
струи до переходного сечения (хпи при Дмт = 1, хпс при Аст =
= АГт=1):
xnu = i2An i+\ inc = 5nu0,86i+1. F5)
Из F3) и F5) следуют уже известные зависимости F0) и
F1). Более детальное изложение теории струи в потоке можно
найти в монографии Г. Н. Абрамовича и др., ссылки на которую
приведены выше, где показано, что при большой начальной не-
неравномерности струи (толстых пограничных слоях на срезе соп-
сопла) при изменении относительной скорости спутного потока в
интервале 0,5 < т < 2 влияние величины т на законы измене-
изменения основных параметров по длине струи (Ь(х), кит(х), Мт(х)
и т. п.) невелико, причем минимальная интенсивность изменения
§ 3. НАЧАЛЬНЫЙ И ПЕРЕХОДНЫЙ УЧАСТКИ СТРУИ
389
осевых параметров в основном участке струи имеет место при
таком режиме течения (таком соотношении скоростей и плот-
плотностей спутного потока), когда величина избыточного импуль-
импульса А/ обращается в нуль (см. выражение B3)). Это условие
может выполняться лишь при т < 1. Чем тоньше начальные
пограничные слои, тем ближе к единице значение параметра
т = т%, соответствующего Д/ = 0, т. е. при неограниченном
уменьшении толщины пограничных слоев минимальный уровень
смешения реализуется при т = 1. С ростом толщины погранич-
пограничных слоев и уменьшением относительной плотности струи
(ро/рн = 1/п) величина т% все больше отличается от единицы,
и при малой плотности центрального потока для выполнения
условия А/ = 0 необходимо, чтобы он имел значительно большую
скорость, чем наружный поток {т% <С 1).
§ 3. Начальный и переходный участки струи
В предыдущем параграфе показано, что для расчета основ-
основного участка турбулентной струи нужно определить расстояние
от сопла до переходного сечения, которое зависит от особенно-
особенностей течения в начальном и переходном участках струи. Была
получена зависимость, характеризующая нарастание толщины
44
Рис. 7.17. Схема струйного слоя смешения
слоя смешения db/dx, охватывающего ядро невозмущенного по-
потока в начальном участке. Однако для определения длины на-
начального участка струи необходимо найти также положение слоя
смешения в пространстве, которое определяется углом наклона
обращенной к ядру границы слоя У\{х) или величиной у\1Ъ при
известной зависимости Ь(х). Такую задачу позволяет решить
условие сохранения избыточного количества движения для сре-
среды, поступающей в слой смешения из невозмущенного потока.
В случае равномерных профилей на срезе сопла имеем
(рис. 7.17):
F6)
7
у±роио (и0 — ик) = J ри (и — мя) dy.
390
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Через штриховую линию а — 1 притока массы в контур нет,
так как скорость щ параллельна этой линии; через внешнюю
границу 0—2 струйки втекают со скоростью внешнего потока,
поэтому их избыточное количество движения в проекции на на-
направление струи равно нулю.
Из F6) с учетом E), F), G), B1), B4) и B8) следует
при М < 1
-2L---5—(НКв),
0 = „ = g>_.
F7)
Интегралы в F6) берутся, но представляют собой громоздкие
функции от п = 8; приближенно
In 8 Я 0,45 B — та) , 0,316A— та)
- 1
+ 0,375 (б0'75 - 1) 1 + 0,28 (G0'75 - 1)
F8)
Ввиду прямолинейности границы зоны смешения в начальном
участке струи величина yjb является постоянной и зависит толь-
только от 0. В конце начального участка (х = хн) внутренние гра-
границы зоны смешения
хн ! j j 1 1 j 1 1 смыкаются (У\ = Ь0),
поэтому относитель-
относительную длину начального
участка (хп == xjbo)
можно получить с по-
помощью F7) из условия
подобия треугольников,
образованных лучами
0—1 и 0—2 и сечения-
сечения50
25
ч
— Теория
о По опытам О.В.Яко
сто и ВЛПечен/а
т=О
те-
теша
в
Рис. 7.18. Зависимость длины начального уча-
стка неизотермической струи газа от пара-
метрав
ми, параллельными ли-
нии j ?.
F9)
Согласно B0) относительная толщина зоны смешения в началь-
начальном участке затопленной струи при Мо< 1,2
График зависимрсти длины начального участка струи от 6
при 771 = 0, рассчитанный по формулам F7), F9) и G0), нане-
нанесен на рис. 7.18.
В случае затопленной струи несжимаемой жидкости (п = 8 =
= 1) из A3), F8) и F9) получаем следующую длину началь-
начального участка:
0,27-0,416
9.
§ 3. НАЧАЛЬНЫЙ И ПЕРЕХОДНЫЙ УЧАСТКИ СТРУИ
391
Пользуясь формулами A3), A4), B0) и F8), F9), можно
установить влияние сжимаемости газа на длину начального
участка затопленной струи.
Абсцисса переходного участка может быть найдена из при-
принятого в теории струи допущения, что граница переходного
участка является линейным продолжением границы начального
участка:
— ^г = —Т~^' GОа)
хн хи
если подставить сюда из F7), F) и A8)
1 —та
1 + та
G06)
и начальную полутолщину основного участка Ьп, которая опре-
определяется из F0а) при х = хп, т. е. Дйт=1. На рис. 7.19 пред-
Рис. 7.19. Влияние степени
предварительного подогре-
подогрева 0 на абсциссу переход-
переходного сечения для осесим-
метричной A) и плоской
B) струй
20
10
_ 2
=====
==
О
ставлены результаты расчетов величины #п(9) для плоской и
осесимметричной затопленных струй.
Рассмотрим влияние спутного потока на длину начального и
переходного участков струи. При равномерных профилях скоро-
скорости в струе и в спутном потоке на срезе сопла и постоянной
плотности согласно F7) и F8):
S- = ?± = 0,416 + 0,134m.
bH b
После подстановки этого результата и выражения A8) при
ит = и = const в F5) получаем
*н 1 + та
с (I-™) @,416+ 0,134^) '
G0в)
Эта зависимость, изображенная на рис. 7.20, имеет две ветви,
уходящие в бесконечность при m = 1. В действительности даже
небольшая начальная неравномерность потока при значении /п,
близком к единице, ведет к существенному уменьшению длины
начального участка. На рис. 7.20 нанесены экспериментальные
точки С. Ю. Крашенинникова, которые показывают длину на-
начального участка при одинаковых пограничных слоях на наруж-
92
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
ной и внутренней сторонах сопла в начале струи (с толщинами
потери импульса бн = So = 0,02&0). Соответствующее сильное
влияние начальной неравномерности потока при т Ф 0 сказыва-
сказывается и на абсциссе переходного сечения. При равномерных по-
полях из G0а, б) и F0а) имеем
ос,
10
10
О
A - yjb) A - т) ск '
откуда
'-¦5-
G0г)
0,5 f,0
uz/ut _1Е=
В плоской струе (у = 0) при
р = const:
@,684-0,134/71) @,416+0,134m)
Рис. 7.20. Относительная длина на-
начального участка струи по расчету
и опытам [2]
@,584—0,134m) @,316+0,134m)«
т. е. при т = 0 и т = 1:
хп « 1,5хн. G0д)
Если использовать формулы для bn и у\/Ь из теории осесим-
метричной струи, то соотношение G0д) окажется также спра-
справедливым. Для учета сжимаемости газа при М < 1 следует в
G0г) подставить зависимости G0а) и F7) при w = 8 = var.
Вопрос о сверхзвуковых струях рассматривается ниже. Рассмот-
Рассмотрим изменения по длине скорости и ширины струи в спутном
потоке применительно к большим расстояниям от начала струи,
где Дмт<1. При этом можно пренебречь первым слагаемым в
квадратной скобке уравнения импульсов B9), откуда
5i+1-(Аиш)-1. G0е)
Из уравнения распространения струи B2) имеем
Aum~-g. G0ж)
Следовательно,
4- = const.
dx
После интегрирования получаем для больших удалений от на-
начала струи г
F~xj+2 Аи ~х i+2.
Для осесимметричной и плоской струй соответственно
хт,
G0з)
§ 4. ОСНОВНОЙ УЧАСТОК СТРУИ В СПУТНОМ ПОТОКЕ 393
§ 4. Основной участок струи в спутном потоке
Задачи о струе в спутном потоке, следе за обтекаемым телом
п т. п. сложнее, чем задача о затопленной струе; они требуют
использования некоторых дополнительных физических сообра-
соображений.
Дело в том, что решенная выше задача о слое смешения на
основе гипотез турбулентного трения Прандтля Fа) и Fв)
предполагают существование локальной связи между турбулент-
турбулентными и осредненными характеристиками потока. Опыт показы-
показывает, что такая связь реализуется в том случае, когда коэффи-
коэффициент турбулентной вязкости (или диффузии) в направлении
течения растет или остается постоянным. В тех случаях, когда
теоретическая локальная связь указывает на уменьшение коэф-
коэффициентов переноса, в действительности этого не наблюдается,
фактические значения коэффициентов переноса на очень протя-
жевных участках течения сохраняются почти неизменными.
Но при этом становятся неприменимыми зависимости Fв) и
G0ж), опирающиеся на локальные связи турбулентных характе-
характеристик с осредненными. В таком случае непригодны и зависи-
зависимости G0з).
Однако и в этом случае зависимости F0) и F1) удается
обосновать. Их можно получить теоретическим путем, если учесть
нарушение локальных автомодельных связей между коэффици-
коэффициентами турбулентной вязкости, а также диффузии, и осреднен-
осредненными параметрами потока. Дело в том, что при наличии спут-
ного потока (^н^О) согласно автомодельной теории коэффици-
коэффициенты вязкости и диффузии по длине струи должны уменьшаться,
а в действительности, как показывают опыты, значения этих
коэффициентов на очень протяженном участке струи (до х«
«B00—400) bo) не изменяются. Данный факт объясняется тем,
что возмущения сносятся по потоку, т. е. влиянием его
предыстории.
Описанный выше метод расчета струи, основанный на при-
применении формулы A8) для db/dx = f(m), опирается на локаль-
локальную связь степени турбулентности с избыточной скоростью на
оси струи (<г/> ~ ит—ин). Коэффициент турбулентной вязко-
вязкости (или диффузии) в свою очередь пропорционален произ-
произведению избыточной скорости на ширину струи: vT ~ v'l ~
~(ит — ин)Ь. Поэтому в тех задачах, где принято допущение о
постоянстве величины vT, зависимость A8) не должна при-
применяться.
Исключение составляют два частных примера (затопленная
осесимметричная струя и дальний плоский след за телом), в ко-
которых из условия сохранения импульса получается vT = const,
не противореча зависимости A8).
394 ra- VII. ТУРБУЛЕНТНЫЕ СТРУИ
В работе В. Е. Козлова, А. Н. Секундова и И. П. Смирновой !)
показано, что абсцисса переходного сечения в общем случае мо-
может быть выражена следующей приближенной зависимостью для
теесимметричной струи:
л о / к ! + ^м /7/|ч
хии = 12,4——тт=-- \1ч
ктуп
Здесь поправка &м учитывает влияние скоростной сжимаемости
(числа Маха) и тепловой сжимаемости (отношения температур
торможения в струе и внешнем потоке Э* = ТЦТ%) на интен-
интенсивность смешения:
т)]1-5| G2)
а поправка кт — влияние начальной неравномерности, зависящее
от близости режима течения к режиму нулевого избыточного
импульса, и параметров тип:
ь _ т*—т 2A — кг») т
т* -г т т^уп
где т# —параметр спутности на режиме нулевого избыточного
импульса. Из сказанного следует, что при тп < т% и т>т%
длина начального участка и абсцисса переходного сечения мень-
меньше, чем при ш = т%.
Условие равенства потери импульса в пограничных слоях
избыточному импульсу струи с равномерными профилями скоро-
скорости и плотности uom, pom, значения которых взяты на оси струи,
имеет следующий вид:
Рот (Щт — UK) ЩтГ20 = 2г\ [р<>тИотб J* + Рн^1 (бн* + бд) ] • G4)
Здесь б0 , бн и бд — толщина потери импульса соответственно
во внутреннем и наружном пограничных слоях, а также в следе
за задней кромкой сопла толщиной бд. Это квадратное уравне-
уравнение относительно т% приводится к следующему виду:
i-m+ = 26** + 2nml (б** + б„). G5)
Здесь
бд = |l, G6)
о
Вводя обозначение б = бн + бд, пренебрегая обычно отно-
относительно малой величиной 60 и полагая плотность в наружном
!) Козлов В. Б., Секундов А. Н., Смирнова И. П. Осесим-
метричная турбулентная сжимаемая струя в дозвуковом спутном потоке //
Сборник «Проблемы турбулентных течений»/Под ред. В. В. Струминского.—
М.: Наука, 1987.
§ 4. ОСНОВНОЙ УЧАСТОК СТРУИ В СПУТНОМ ПОТОКЕ 395
пограничном слое постоянной, получим
*-™* = 2б**/г. G7)
Если кольцевой пограничный слой развернуть на плоскости и
использовать толщины потери импульса для плоской задачи:
то при профиле скорости «1/7» и б** < 1 справедлива следую-
следующая приближенная зависимость:
Расчеты показывают, что для типичных схем расположения
газотурбинного двигателя в мотогондоле или фюзеляже получа-
получается б** == 0,02 или 0,06; при п — 2,5 имеем соответственно
т% = 0,9 или 0,8. При отсутствии информации о величине б**
можно ее оценить следующим грубопряближенным соотноше-
соотношением:
8** - °'04 тф + °-02 (г,-Т^г^ + °'2бд- (80)
Здесь первый член учитывает в соответствии с данными гл. VI
трение на поверхности мотогондолы; второй член, учитывающий
сопротивление ее сужающейся хвостовой части, получен обобще-
обобщением данных работы Д. Бергмана; третий член, аппроксимирую-
аппроксимирующий простейшей зависимостью сопротивление донного уступа,
основан на экспериментальных данных монографии Чжена1);
гм обозначает максимальный радиус мотогондолы, I — длину су-
сужающейся части, L — длину фюзеляжа, ReL = -^ число
Рейнольдса. В случае дозвуковой затопленной осесимметричной
струи (т = 0, йгм = О, кт=\) из G1) —G6) получается
гпз - 12,4гс-1/2. (81)
При п = 1 имеем
*пз='12,4. (82)
Близкий к этому результат следует непосредственно из зависи-
зависимостей G06, д), полученных в § 3 при со = О,27 и л = 1. В са-
самом деле, для этого случая (п = 1) в осесимметричной струе
*) См. сноску на cs 394.
396 гл- VII. ТУРБУЛЕНТНЫЕ СТРУИ
получаем ^/6 = 0,416 и — Ц- = 1 — Ц- = 0,584, 6 = 0,27а:; хп
= 9Ь0 и &н = 2,4Ь0. Из E7) при А20 = 0,134 и / = 1: Ьп = 2,74Ь0,
откуда хп = 1,24#н = И,2Ьо. В плоской струе (А2о = 0,316, /=0)
согласно E7): &п = ЗДббо; остальные величины не отличаются
от вычисленных в предыдущей задаче, поэтому xjxu = 1,54,
хп = 13,76о. В действительности, как следует из опытов, абсцис-
абсциссы переходного сечения в плоской и осесимметричной струях
практически одинаковы: хпи = 12,4. Это расхождение теории с
экспериментом устраняется, если учесть повышенную степень
неравномерности потока в прямоугольном сопле и использовать
в расчетах для начального участка вместо профиля скорости
Шлихтинга более близкий к экспериментальным данным теоре-
теоретический профиль Толмина, который выведен в § 2.
При равномерном распределении скоростей в начальном се-
сечении струи (б** = 0): т% = 1, откуда на основании G1) и G3)
Km —
-m I 1 — m\
В этих идеализированных условиях зависимость хп(т) имеет
две ветви (при т<1 и иг>1), уходящие в бесконечность при
т = 1. В реальных условиях даже при незначительной началь-
начальной неравномерности потока ха, так же как и хя, является всегда
конечной величиной, о чем свидетельствуют данные, приведен-
приведенные на рис. 7.20. Абсциссу переходного сечения хп иногда удоб-
удобнее определять не по кривой изменения осевой скорости Апт(х),
а по кривой концентрации Аст(х) или температуры Ain((x).
Соответствующий пересчет можно выполнить с помощью выра-
выражений E4), F0) и F1), из которых следует зависимость
(84)
Согласно E5) получаем для осесимметричной струи (/ = 1) при
хии = 12,4:
хпс = 0,86?nu = 10,7. • (85)
На рис. 7.21 расчетная зависимость хпи(Мо) для затопленной
осесимметричной струи при трех значениях 6* = 1, 2, 6 сопостав-
сопоставляется с экспериментальными данными. Следует отметить, что
формулы G1) и (83) согласуются с экспериментальными дан-
данными и результатами теоретических расчетов в диапазоне пара-
параметров 0 < Мо < 3; К 0* < 7,5 при наличии спутного потока
для Мн < 1. В случае затопленной струи лучше соответствует
§ 5. ВЛИЯНИЕ НЕИЗОБАРИЧНОСТИ СТРУИ 397
эксперименту эмпирическая формула1)
хв = ZL = 12 + 2,5М* - 11,2 [1 - (б*)'25] A + Nil)-1,
О
по которой выполнен расчет кривых на рис. 7.21.
При расчете местного значения температуры торможения по
местному значению энтальпии или концентрации (для струй вы-
высокой температуры) следует учитывать зависимость теплоемкости
40
го
——
—-—ч
6
е*=т*/тн
• /,5-2,3
*2,8
о 1ь4-4
0 6,5
А /
*2
f4
о
0
>
I
|
I
Рис. 7.21. Абсцисса переходного сечения изобарической затопленной осе-
симметричной струи
газа от температуры. Соответствующую поправку можно полу-
получать по приближенной формуле
§ 5. Влияние неизобаричности струи на закономерности
ее распространения
Расчеты и опыты показывают, что распределение параметров
по длине струи и ее поперечные размеры зависят от разности
давлений в струе и внешнем потоке на срезе сопла. При малых
дозвуковых скоростях эта разность давлений относительно мала,
зависит от формы выходного устройства, из которого вытекает
струя, и, как показано в § 8 гл. I, определяется по уравнению
!) Козлов В. Е., Секундов А. Н., Смирнова И. П. Модели
турбулентности для описания течения в струе сжимаемого газа / Изв.
АН СССР. МЖГ.— 1986.— № 6.
398 гл- VII. ТУРБУЛЕНТНЫЕ СТРУИ
Бернулли для идеальной несжимаемой жидкости:
r/2
(86)
Здесь ие — скорость в струе, которая получается при выравнива-
выравнивании давления в струе с давлением во внешнем потоке. Гидрав-
Гидравлическое сопротивление не учитывается в связи с тем, что при
Мо < 1 и Мн < 1 постоянное давление в поперечном сечении по-
потока устанавливается на очень близком расстоянии от начала
струи (х< bo).
Изменение скорости влечет за собой изменение поперечного
сечения. При ро = ре:
Ъ V+1 и
*) -* <87)
После того как найдены скорость и размер (радиус ге или полу-
полутолщина be) в изобарическом сечении струи, ее можно рассчи-
рассчитать как струю постоянного давления с этими начальными дан-
данными (ие, Ье).
В случае околозвуковой или небольшой сверхзвуковой ско-
скорости истечения и отношения давлений она срезе сопла (N =
==>Ро/Рн), мало отличающегося от единицы (Мо<2; 0,7 < N < 2),
следует также пользоваться уравнением Бернулли (без учета
потерь, но принимая во внимание сжимаемость газа). Тогда ис-
искомая приведенная скорость и размер изобарического сечения
Хе, Fe определяются по таблицам газодинамических функций
Fe g(^0) ло\
~кт+т 7fo w
Если форма среза сопла отличается от круга или прямоуголь-
прямоугольника, то можно обойтись без знания площади выходного сечейия
сопла и скорости истечения, заменив это сечение равновеликим
кругом. Для этого достаточно знать, статическое давление снару-
снаружи, полное давление в начале струи, расход газа G и восполь-
воспользоваться вместо второй формулы (88) известными зависимостями
A09) или A11) да гл. V:
Y л о Y i о
которые предполагают сохранение постоянства полного давления
и температуры торможения на участке выравнивания статиче-
статического давления.
Метод расчета, основанный на формулах (86)—((89) в указан-
указанном диапазоне параметров М и iV, ведет к нарушению постоян-
постоянства избыточного импульса не более чем яа 2—4 %.
§ 5. ВЛИЯНИЕ НЕИЗОБАРИЧНОСТИ СТРУИ 399
Кривая изменения любого параметра вдоль оси струи, рас-
рассчитанная по формулам E9) или F1), имеет излом в переход-
переходном сечений и дает постоянное (значение параметра, равное еди-
единице, при х ^ хп.
В действительности, начиная с конца начального участка, ве-
величины Аиш, Acm, Aim плавно изменяются, и строго говоря, лишь
с некоторого расстояния х > хп справедливы указанные простые
формулы. Существуют различные способы описания соответст-
соответствующего переходного участка струи1).
В работе В. Е. Козлова и др.2) предложена следующая не-
непрерывная зависимость, подобранная на основании опытных
данных и численных расчетов, учитывающих неавтомодельность
струн:
Аит = г|) (а*) у *1^ , (90)
причем
Здесь х° = х/хпи, /см определяется из G2). При &M<Cl и х°>2
формула (90) дает результаты, близкие к гиперболе E9), так
как ф-М/я0, г|)@,5я°)->- 2/х°. При я°<0,5 ^«1. Зависимость
(90) справедлива только для осесимметричной струи при опре-
определении величины хпи по формуле G1).
.*
Переход к зависимостям Aim и Аст осуществляется по фор-
формуле (90) путем замены хпи величиной
Япт = *пс = 0,86я„„. (92)
Формула (90), описывающая зависимость Апт(х°) плавной кри-
кривой, при х = хпи, т. е. при #°=1, дает АггтA) = 0,9 (вместо
Апт = 1 по формуле E9)).
Радиус границы основного участка струи г при универсаль-
универсальных профилях параметров в поперечных сечениях пропорциона-
пропорционален расстоянию го,5 от оси до точки с половинным значением
безразмерного параметра (Аи = 0,5Аит; Аг* = 0,5A^).
Для профилей C) и (8) при Sc = 0,75 получается соответ-
соответственно
rOMu = 0,441г, гОMг = 0,515г. (93)
Величина го,5 измеряется в эксперименте более надежно, чем г,
поэтому для описания границы струи и для сравнения теории с
!) Гиневский А. С. Теория турбулентных струй и следов.—М.:
Машиностроение, 1969.
2) См. сноску на с. 394.
400 ГЛ., VII. ТУРБУЛЕНТНЫЕ СТРУИ
экспериментом удобно пользоваться «зависимостью ro,s(#) с по-
последующим ее пересчетом на г(х) по формуле (93). Основываясь
на условии сохранения избыточного импульса и применяя (91),
В. Е. Козлов и др.1) вывели следующие зависимости для поло-
половинных радиусов, определенных по полной энталыши и 'ско-
'скорости:
2 *i
(94)
Здесь
/cmoc = 1 + 2myb~1 (x°) + wz ~ д . (95)
Значение кт находят из G3). При некруглом выходном сечении
сопла в эти формулы подставляется ге вместо г0. Для сравнения
с экспериментальными данными эмпирической кривой G5) за-
затруднительно фиксировать величину хп (см. рис. 7.21). Увязка
значений хп с экспериментом выполнена в соответствии с ра-
равенством
Как следует из рис. 7.21, влияние степени подогрева струи на
величину ха при околозвуковых и сверхзвуковых скоростях мож-
можно не учитывать.
Что касается границ затопленной сверхзвуковой струи, то они,
вообще говоря, являются криволинейными. На практике, однако,
этой криволинейностью можно пренебречь и аппроксимировать
границы струи на некотором удалении от переходного сечения
прямыми линиями, наклоненными к оси струи под тем же уг-
углом, что и в несжимаемой жидкости. Точка пересечения этих
прямых с осью хо (полюс струи) изменяет свое положение от-
относительно среза сопла в зависимости от значения N. Влияние
числа Мо на полюсное расстояние показано на рис. 7.22. Вели-
Величина хо = хо/Ь0 характеризует дальнобойность струи; результаты,
представленные на рис. 7.22, указывают на значительное увели-
увеличение дальнобойности с ростом параметра Мо.
При работе реактивных двигателей, различных струйных ап-
аппаратов, например эжекторов, и в некоторых других практически
важных случаях истечение сверхзвуковой струи из сопла проис-
происходит в условиях нерасчетного режима, когда давление в потоке
на выходе из сопла существенно отличается от давления в среде,
1) См. сноску на с, 394,
§ 5. ВЛИЯНИЕ НЕИЗОБАРИЧНОСТИ СТРУИ
401
в которую вытекает струя. При этом возможны как недорасши-
рение газа в сопле (ра>рн, iV>l), так и перерасширение его
(Ра<Рп, iV<l). Вследствие этого на участке струи, прилегаю-
прилегающем к соплу, возникает система волн расширения и сжатия,
а также скачков уплотнения, _
благодаря которым и осуществ- х°
ляется постепенное выравнива-
ние давления в струе с давле-
давлением, господствующим в окру-
окружающей среде. W
На некотором расстоянии от
сопла давление в струе стано-
становится равным давлению в
окружающей среде, и струя
уже ничем не отличается от
обычной расчетной струи, ко-
которую мы рассматривали выше, дг
Условия нерасчетного исте-
истечения сверхзвуковой струи Рис. 7.22. Влияние скорости истече-
принято характеризовать сте- ния м° и степени предварительного
прнью ирппгиетипг'гп ттт^оттпггог, подогрева 9 на положение полюса
пенью нерасчетности, представ- осесимметричной струи по опытным
ляющеи собой отношение деи- данным Б. А. Жесткова, М. М. Мак-
ствительного давления тормо- симова и др.
жения в ресивере к расчетно-
расчетному1), которое может быть приближенно заменено отношением
давления на выходе из сопла к давлению в окружающей среде:
о-—=
//
у/
У
Остановимся на некоторых экспериментальных данных, отно-
относящихся к сверхзвуковым струям при нерасчетном истечении из
сопел. На рис. 7.23 внизу сплошной линией изображено из-
изменение полного давления Px/pq, отнесенного к давлению в ре-
ресивере, вдоль оси затопленной сверхзвуковой (Мо=1,5) нерас-
нерасчетной (N = 5) струи, а штриховой — максимальное полное дав-
давление в струе; в верхней части рис. 7,23 показаны результаты
экспериментального изучения картины течения в сверхзвуковой
струе при нерасчетном режиме истечения, профили полного дав-
давления <в поперечных сечениях струи и области дозвуковых (за-
(заштрихованы) и сверхзвуковых скоростей. Как видим, в началь-
начальном участке струи максимальное значение давления имеет место
не на оси струи. Опыты показывают, что на некотором расстоя-
расстоянии от того сечения, где струя становится изобарической («изо-
*) Расчетным называют давление, соответствующее расчетному числу
Маха истечения, значение которого определяется заданным отношением
площадей критического и выходного сечений сопла.
26 г. Н. Абрамович, ч, 1
402
ГЛ., VII. ТУРБУЛЕНТНЫЕ СТРУИ
барическое сечение»), максимальная скорость наблюдается на
оси струи (начиная с места слияния сплошной и штриховой ли-
линий в нижней части рис. 7.23).
О 4 8 12 16 20 24 28 32 36 х
Масштабр?/рх
О 0,5 1,6
28 32 36 Я
Рис. 7.23. Картина течения и распределение полного давления в сверхзву-
сверхзвуковой нерасчетной струе газа (Ма = 1,5 N = 5) по опытам Б. А. Жесткова,
М. М. Максимова и др.
Используя условие сохранения импульса между плоскостью
среза сопла (индекс а) и «изобарическим сечением» (индекс с),
имеем1)
Gaua + (pa - pB)Fa = Gcuc, (96)
где Ga и Gc — массовые расходы воздуха в струе в сечениях а
и с; иа, ис — средние значения скорости б этих сечениях; Fa —
площадь сопла в сечении а.
1) Применявшееся в § 5 для расчета изобарического сечения в идеаль-
идеальной жидкости условие р* = const в данном случае непригодно в связи
с потерями в скачках уплотнения и за счет турбулентного трения.
§ 5. ВЛИЯНИЕ НЕИЗОБАРИЧНОСТИ СТРУИ
403
Переходя к безразмерным величинам
Paul
2к
кр
' PaFa
k+i
A
k+i
из (96) получаем (при постоянном вначении критической ско-
скорости)
с "ёГ I1
I1 + К ~ "FI1 -
F
(97)
Площадь изобарического сечения струи Fc рассчитывают с по-
помощью уравнений расхода и состояния '):
Gc 9au
'aua
(98)
fc + 1
Перемешивание приводит к увеличению массы струи и рез-
резкому возрастанию неравномерности профиля скорости, который
в изобарическом сечении "носит типично струйный характер.
Вследствие подсасывания струей лш
вещества из окружающей среды ла
значение Хс всегда должно быть if2
несколько ниже, чем в случае
Ga = Gc. При этом с ростом пара-
параметра N отмеченный эффект про-
проявляется слабее.
Неравномерность профиля ско-
скорости в изобарическом сечении
струи выражается в значительном
возрастании осевой скорости (А,ст)
по сравнению со средним ее зна-
значением: ХстЖс.
Скачки уплотнения в неизоба-
неизобарической части струи создают зо-
зону пониженной скорости.
Действие отмеченных выше
1,0
0,8
0,6
0.4
0.2
X
А
——
Л
0 123456789 ЮМ
факторов всегда происходит одно- рис. 7.24. Влияние степени не-
невременно и, как мы видели, ока- расчетное™ N на величину при-
призывает противоположное влияние веденной осевой скорости в изо-
на величину 1ст. На рис. 7.24 "'"* ~~ ~"
приведена кривая, рассчитанная
с помощью (97) в предположении
об отсутствии смешения (Ga = Gc) для Ла = 1,37 и к =• 1,4. Опыт-
ные данные, взятые из экспериментов Б. А. Жесткова и др. (при
1) Более детальный анализ изменения параметров газа по длине на-
»го лтягтт^ нерасчетной сверхзвуковой струи в одномерной постанов-
д еой скорости в изо
барическом сечении по опытам
Б. А. Жесткова, М. М. Максимо-
Максимова и др. (Ма = 1,5)
26*
404 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Яа=1,37), показывают, что при больших степенях нерасчетности
(N > 3) получаются завышенные расчетные значения скорости в
изобарическом сечении. При N~10 воздействие всех факторов
на величину Хст взаимно уравновешивается и скорость на оси
струи в изобарическом сечении становится очень близкой к ка.
Вычисление скорости на оси потока, после того как затоплен-
затопленная струя становится изобарической, может быть произведено на
основании уравнения импульсов (с учетом неравенства давления
в сопле и в окружающей среде) -и уравнения распространения
струи B2). В случае осесимметричной струи имеем
г
/ = J pu22nr dr = paulnrl -f- (Pa — Рн) пг2а. (99)
о
Параметры газового потока на выходе из сопла (обозначенные в
уравнении (99) индексом «а») могут быть определены по извест-
известным параметрам газа в ресивере и геометрическим размерам
сопла, так как при любом значении iV>l в сопле срабатывается
тот же относительный перепад давлений, как и при расчетном
режиме истечения.
Приведем уравнение (99) к безразмерному виду делением
обеих его частей на величину пгарК ,, ,. После некоторых пре-
преобразований ПОЛуЧИМ При П2и = 1
2 = N + l^L j^jiN- 1), A00)
где г——, a = , , . , r—радиус струи. Интеграл Ач из B4) вы-
ражается следующей приближенной зависимостью, учитывающей
неизобаричность струи:
А2 = пА20 = 0,1347V A - all) (l + 0,45аЯ;&).
Сравнивая A00) с выражением B7), видим, что уравнение им-
импульсов для нерасчетной струи отличается от соответствующего
выражения в случае расчетного истечения множителем
который зависит только от условий в начальном сечении струи и
не изменяется по координате х. Это обстоятельство позволяет
использовать полученное выше решение E6) для сверхзвуковой
струи газа при расчетном режиме истечения.
Из формулы A00) следует, что нерасчетная струя при iV>l
обладает значительно большей дальнобойностью, чем соответ-
соответствующая (при том же значении а%1) изобарическая сверхзву-
§ 5. ВЛИЯНИЕ НЕИЗОБАРИЧНОСТИ СТРУИ
405
ковая струя; при этом дальнобойность струи, определяемая, на-
например, как расстояние от сопла, на котором осевая скорость
составляет половину начальной, возрастает примерно пропорци-
пропорционально УР или при больших значениях величины aXl пропор-
пропорционально VN. Из выражения A01) следует, кроме того, что
когда скорость истечения незначительно отличается от звуковой
(параметр akl мал), то даже небольшая нераочетность струи
может приводить к заметному увеличению ее дальнобойности.
Например при а%1 = 0,2 хп
(Ма=1,11) и TV = 1,2 вели-
величина Р составляет 1,36, т. е.
дальнобойность нерасчетной
струи оказывается на 17 %
больше расчетной.
Для отыскания значения
абсциссы переходного сече-
сечения хп, которое необходимо
для расчета струи, нужно
знать характеристики турбу-
турбулентного расширения струи
в начальном ее участке. Вви-
Ввиду сложности теории началь-
начального участка нерасчетной
струи обычно используют
для вычисления либо зависи-
зависимости, полученные для со-
соответствующей расчетной
струи, либо эксперименталь-
экспериментальные данные. Зависимость
xn(N, а%1), определенная в
предположении о справедли-
справедливости в случае нерасчетного истечения соотношений для началь-
начального участка расчетной струи, изображена на рис. 7.25.
Сравнение значений осевой скорости, вычисленных по фор-
формуле A00), с результатами измерений скорости в сверхзвуковых
нерасчетных струях газа представлено на рис. 7.26 и 7.27. Экс-
Экспериментальные данные, приведенные <на рис. 7.26, получены
для сопла, рассчитанного на число Маха Ма = 1,5 (Яа= 1,37), при
следующих значениях параметра нерасчетности iV = 0,8; 1; 2; 5;
10. Опытные значения скорости на рис. 7.27 соответствуют исте-
истечению из сопла, рассчитанного на число Маха Ма = 3, дри N = 1
и N = 2. Из рассмотрения этих рисунков следует, что теоретиче-
теоретические результаты в первом приближении удовлетворительно со-
согласуются с опытными данными, хотя в отдельных случаях на-
наблюдается заметное количественное расхождение между ними.
Отмеченное несоответствие может являться следствием иопользо-
25
О
0,25 0,5 0,75 а.
Рис. 7.25. Зависимость абсциссы
переходного сечения сверхзвуко-
сверхзвуковых нерасчетных струй от пара-
параметров а\г и N
406
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
вания в начальном участке нерасчетной струи зависимостей для
струи при расчетном истечении.
Аналогичные выводы следуют и из анализа рис. 7.28 и 7.29Г
на которых представлены опытные данные о расположении ли-
линий половинной скорости в сверхзвуковых струях при различных
значениях расчетного числа Маха Ма и параметра нерасчетности
ZO 40 60 ВО 100 720 140 160 180 «Z
Рис. 7.26. Сравнение расчетных и экспериментальных значений осевой ско-
скорости в сверхзвуковой осесимметричной струе газа (Ма = 1,5) на расчет-
расчетном (N = 1) и нерасчетных (N = var) режимах истечения по опытам
Б. А. Жесткова, М. М. Максимова и др.
N, а также результаты соответствующих расчетов по формулам
A00) — A01). Линии половинной скорости (и соответствующие
им границы) в сверхзвуковых нерасчетных струях, вообще гово-
гово"о
0,8
0,6
О,*
0,2
\о
\ °
\
1
N
Ы=1
° 9 У По опытам
По формуле A15)
—^,
20
60
100
fao ш
Рис. 7.27. Сравнение расчетных экспериментальных значений осевой скоро-
скорости в сверхзвуковой осесимметричной струе газа (Ма = 3) на расчетном
(N = 1) и нерасчетном (N = 2) режимах истечения по опытам Б. А. Жест-
Жесткова, М. М. Максимова и др.
ря, криволинейны, особенно вблизи переходного сечения, но кри-
кривизна границ мала, и поэтому они могут быть в первом прибли-
приближении заменены прямыми линиями. Угол наклона этих линий
§ 5. ВЛИЯНИЕ НЕИЗОБАРИЧНОСТИ СТРУИ
407
не зависит от параметров Ма и N (тангенс этого угла равен,
как и в струе несжимаемой жидкости, 0,22), а положение точек
пересечения их с осью х относительно среза сопла (полюсное
15
10
у •
N=0,8^
у.
о А/=
У
•
0,8
д /V=/
• N=5
Расчет
50
100
150
х
Рис. 7.28. Сравнение расчетных и экспериментальных значений половинно-
половинного радиуса гс в сверхзвуковых (Ма = 1,5) струях газа при расчетном и
нерасчетных режимах по опытам Б. А,. Жесткова и М. М. Максимова и др.
Jc
15
/
// °
о
о N=1
• N=2
— Расчет
I
50
100
150
х
Рис. 7.29. Сравнение расчетных и экспериментальных значений половинно-
половинного радиуса гс в сверхзвуковых (Ма = 3) струях газа при расчетном и
нерасчетном режимах по опытам Б. А. Жесткова, М. М. Максимова и др.
расстояние х$) изменяется в зависимости от значений Ма и N.
Экспериментальная зависимость величины х0 от N для двух зна-
значений числа Ма приведена на рис. 7.30. Как видим, полюс струи
408
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
с увеличением как параметра нерасчетности N, так и значения
АДд смещается вниз по потоку.
Метод расчета сверхзвуковой струи при N?=1, изложенный в
настоящем параграфе, следует рассматривать как грубо прибли-
приближенный. В нем не учитываются конкретные условия развития
струи в «газодинамиче-
«газодинамическом» участке, примыкаю-
примыкающем к соплу, на котором
давление (при N Ф i) су-
существенно отличается от
атмосферного. Наиболее
слабым местом этого мето-
метода является способ опре-
определения абсциссы пере-
переходного сечения, а также
то, что он пригоден лишь
для той части изобариче-
изобарического течения, в которой
скорость на оси струи яв-
ляется максимальной; в
" между
участ-
участСО,
40
20
[Ма-3,0
\
/о
о
Рис. 7.30. Влияние степени нерасчетности
на положение полюса сверхзвуковой струи действительности
газа по опытам Б. А. Жесткова, М. М. Мак- газодинамическим
симова и др. / , ч
ком (где р^Рп) и этой
частью изобарического те-
течения расположена изобарическая зона с пониженной скоростью
на оси. Приближенная теория газодинамического участка струи
излагается ниже.
Мы рассмотрели при нерасчетном режиме истечения лишь
затопленную сверхзвуковую струю. Влияние спутного потока на
этом режиме как при Мн > 1, так и при Мн < 1 удается уче-сть
лишь с помощью численных методов расчета, изложенных в мо-
монографии Г. Н. Абрамовича и др. [2] и других источниках, ука-
указанных в ней. Некоторые соображения по этому поводу приво-
приводятся в конце следующего параграфа.
§ 6. Одномерная теория начального («газодинамического»)
участка нерасчетной сверхзвуковой струи
Характерной особенностью 'нерасчетной сверхзвуковой струи
является существенная неравномерность потока: параметры газа
значительно изменяются как по длине струи, так и по радиусу
поперечных сечений. Для расчета такого потока обычно приме-
применяется метод характеристик, позволяющий по исходным значе-
значениям параметров на срезе сопла найти параметры газа во всей
сверхзвуковой части потока, примыкающей к соплу. В ряде слу-
случаев, однако, необходимо знать только некоторые суммарные ха-
характеристики потока, например полный импульс, суммарные по-
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ 409
тери давления, площадь сечения, и не требуется определения
внутренней структуры струи. Для решения таких задач вместо
громоздкого и трудоемкого метода характеристик было бы жела-
желательно применить более простые расчетные методы.
Ниже излагается один из таких методов, базирующийся на
осреднении параметров струи в поперечном сечении и прибли-
приближенном рассмотрении ее как одномерного газового потока1).
Выясним прежде всего, насколько допустимо пользоваться
осреднением параметров в потоке столь большой неравномерно-
неравномерности, как нерасчетная сверхзвуковая струя, где, например, ста-
статическое давление может уменьшаться от периферии к оси в
10—20 раз, соответственно с этим изменяется и скорость те-
течения.
При расчете струи используются уравнения энергии, нераз-
неразрывности и количества движения. Поэтому необходимо, чтобы
значения полной энергии, расхода и импульса газа в попереч-
поперечном сечении, вычисленные по средним значениям параметров,
были равны их действительным значениям в исходном неравно-
неравномерном потоке. Кроме того, для расчета важно правильно оце-
оценить энтропию потока: это дает возможность использовать усло-
условие сохранения полного давления на участках, где отсутствуют
потери, а также определять действительную величину суммар-
суммарных потерь по изменению среднего полного давления.
Как известно (гл. V), при осреднении неравномерного потока
в общем случае могут быть сохранены неизменными только три
его суммарные характеристики. Однако для сверхзвукового пото-
потока с постоянной по сечению температурой торможения, каким
является начальный участок нерасчетной струи идеального газа
при отсутствии смешения, можно найти такие средние значения
параметров в поперечном сечении, при переходе к которым од-
одновременно с высокой степенью точности сохраняются значения
расхода, полной энергии, импульса и энтропии при неизменной
площади сечения. Эти средние значения параметров газа в по-
поперечных сечениях начального участка струи и будем вводить в
уравнения неразрывности, энергии, импульсов. Совместные ре-
решения этих уравнений поэтому будут также относиться к сред-
средним значениям параметров, а определяемая отсюда площадь се-
сечения будет равна действительной площади соответствующих се-
сечений струи. Почти все основные свойства потока при таком
одномерном рассмотрении не изменяются и оцениваются правиль-
правильно. Утрачивается лишь одно существенное свойство течения,
а именно равенство статического давления на границах струи и
во внешней среде; поэтому приходится условно полагать, что в
каждом поперечном сечении потока существует некоторое по-
J) Черкез А. Я. Об одномерной теории нерасчетной сверхзвуковой
струи газа / Изв. АН СССР. ОТН.- 1962.- № 5.
410
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
стоянное среднее статическое давление /?, в общем случае от-
отличное от давления внешней среды ря.
Остановимся на случае сверхзвуковой струи, вытекающей из
недорасширенного сопла, т. е. имеющей па срезе сопла избыточ-
избыточное давление ра>р* (рис. 7.31). Схематическая картина такого
течения описана в § 2 гл. IV; более детальное рассмотрение вы-
выявляет следующие особенности недорасширенной сверхзвуковой
\т
Рис. 7.31. Схема струи, вытекающей из сопла с избыточным статическим
давлением: 1 — висячий скачок, 2 — линия тока, d — d — диск Маха,
d _ п _ отраженный скачок, agmnc — граница струи
струи. Около кромки сопла а возникает пучок характеристик
(волн разрежения), обеспечивающий расширение газа в струе
от давления на срезе сопла ра до давления окружающего газа
рш. Ускорение потока сопровождается отклонением линий тока от
первоначального направления, в связи с чем поперечное сечение
струи возрастает. Угол б, который .составляет граница струи с
направлением потока на срезе сопла, можно определить по таб-
таблице плоского течения Прандтля — Майера (приложение I). До
точки пересечения первой характеристики aOg с границей струи
последняя остается прямолинейной.
Правее точки g граница струи искривляется (вследствие
уменьшения давления ев пучке характеристик). Заметим, что лю-
любая характеристика, выходящая из данной точки на кромке
сопла, является отрезком прямой только до пересечения с пер-
первой характеристикой, выходящей из диаметрально /противополож-
/противоположной точки. Участки характеристик, лежащие правее (ниже по
потоку) этого пересечения, должны быть криволинейными, так
как они проходят в области ускоряющегося течения газа. Отра-
Отраженные от поверхности струи характеристики образуют сходя-
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ 411
щийся пучок, который постепенно формирует сверхзвуковое те-
течение сжатия, вызывающее сужение и торможение струи, сопро-
сопровождаемое появлением криволинейной ударной волны 1 — d
(огибающей волн сжатия).
Как показывают расчеты и эксперименты, в наибольшем по-
поперечном сечении струи т среднее давление ниже давления
окружающей среды (рт<Рк), хотя на поверхности струи agmn
давление равно окружающему.
Около оси струи на участке торможения криволинейный ска-
скачок переходит в прямой скачок уплотнения, получивший назва-
название диска Маха, за которым скорость течения становится дозву-
дозвуковой. Периферийные линии тока образуют сверхзвуковое тече-
течение, которое, как следует из теоретических расчетов х) и экспери-
экспериментов 2), дважды пересекает криволинейный скачок 1 — 1 — d
и отраженный скачок d — п. Одна из линий тока B—2) этой
зоны течения изображена на рис. 7.31. Поверхность 1—1 (часть
криволинейного скачка) представляет собой так называемый ви-
висячий скачок уплотнения, постепенно ослабляющийся с прибли-
приближением к кромке сопла и полностью вырождающийся, немного
не доходя до последней.
Причиной возникновения висячего скачка в осесимметричной
струе является сверхзвуковое радиальное растекание газа, при
котором происходит перерасширение (р<Рн), завершаемое удар-
ударной волной, выводящей линии тока в зону давления, близкого
к окружающему. Ослабление висячего скачка с приближением к
началу струи объясняется тем, что при этом уменьшается ради-
радиальное смещение линий тока, а следовательно, ослабляется и пе-
перерасширение.
За отраженным скачком d — n, который возникает в месте
пересечения криволинейного скачка 1 — d с диском Маха, так
же как и за центральным прямым скачком, давление обычно
выше окружающего, из-за чего газовый поток вновь ускоряется:
в центральной части струи осуществляется переход к сверхзву-
сверхзвуковой скорости, в периферийной части, где линии тока пересекли
два косых скачка, сохраняется сверхзвуковая скорость, которая
за отраженным скачком d — п .возрастает.
1) Ашратов Э. А. Расчет осесимметричной струи, вытекающей из
сопла при давлении в струе, большем давления в окружающей среде /
Изв. АН СССР. МЖГ.—1966.—№ 1; А верен ко в а Г. И., Ашра-
Ашратов Э. А. и др. Сверхзвуковые струи идеального газа. Ч. I. Труды
ВЦ МГУ, 1970; Иванов М. Я., Край ко А. Н., Михайлов Н. В.
Метод сквозного счета для двумерных и пространственных сверхзвуковых
течений. Ч. 17 / Журнал вычисл. мат. и мат. физ.—1972.—Т. 12, № 2.—
С. 441-463.
2) Бондарев Е. Н., Лисичко И. Д. О влиянии вязкости на те-
течение недорасгаиренной струи, распространяющейся в спутном сверхзвуко-
сверхзвуковом потоке / Изв. АН СССР. МЖГ.— 1973.— № 2.
412 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
В итоге за так называемой первой «бочкой» недорасширенной
сверхззуковой струи формируется вторая, а затем третья и т. д.
«бочки». Потери полного давления в системе скачков уплотнения
первой «бочки» приводят к тому, что вторая «бочка» всегда сла-
слабее первой (меньше избыток давления в начале, меньше пере-
перерасширение в средней ее части и меньше площадь максимального
сечения). При большой степени нерасчетности струи (iV>5)
потери в первой «бочке» настолько велики, что давление во вто-
второй «бочке» практически равно окружающему и, следовательно,
струя за первой «бочкой» становится изобарической, т. е. после-
последующие «бочки» можно не принимать во внимание.
Наряду с более строгими теориями, позволяющими построить
всю картину течения в недорасширенной сверхзвуковой струе,
получила практическое применение простая теория, основанная
на одномерном представлении.
Несмотря на значительную неравномерность полей скорости и
давления в поперечных сечениях нерасчетной сверхзвуковой
струи, одномерная теория дает правильное приближенное пред-
представление об истинных размерах и форме начальной части такой
струи. Одномерная теория нерасчетной сверхзвуковой струи при-
приводится ниже. Газ полагаем совершенным, параметры газа на
срезе сопла считаем постоянными по сечению, векторы скорости
газа на срезе сопла — параллельными оси сопла. Смешением га-
газа в начальном участке с газом окружающей неподвижной среды
пренебрегаем.
Запишем основные уравнения, связывающие параметры газа
в свободной струе с параметрами в выходном сечении сопла.
В первую очередь в качестве характерного сечения начального
участка струи выберем максимальное сечение первой «бочки»
(рис. 7.31).
Уравнение равенства расходов записываем в виде
G=Ga, A02)
или, использовав известное выражение расхода через параметры
торможения р* и Г* и приведенную скорость X,
М Aоз)
л/т* - у
где индекс а относится к параметрам в выходном сечении сопла.
Величины р* и X представляют собой средние значения полного
давления и приведенной скорости в рассматриваемом сечении
свободной струи.
Согласно уравнению сохранения энергии
GcpT* = GacpaT*a A04)
при G = Ga и Ср = Сра температура торможения в струе остается
§ 6. ОДНОМЕРНАЯ' ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ 413
постоянной. Поэтому уравнение неразрывности A03) принимает
вид
Здесь / = FjFa, а о = р*1ра — коэффициент сохранения полного
давления, оценивающий суммарные потери полного давления на
участке между начальным и рассматриваемым сечениями струи.
Для того чтобы из уравнения A05) получить зависимость между
относительной площадью сечения / и приведенной скоростью
% в этом сечении, необходимо оценить величину коэффициента
сохранения полного давления о. Для передней части «бочки»
недорасширенной струи потерями полного давления можно пре-
пренебречь, так как в плоской струе между начальным и максималь-
максимальным сечением висячие скачки отсутствуют, а в осеоимметричной
недорасширенной струе интенсивность висячего скачка вблизи
сопла невелика. Будем считать, что и в осесимметричной струе
для первой «бочки» о = 1.
Уравнение количества движения для рассматриваемого уча-
участка ;струи запишем в виде
Gu — Gaua = PaFa- pF + pn{F - Fe), A06)
где последний член правой части представляет собой осевую со-
составляющую силы внешнего давления рв на боковую поверхность
струи. Заменим выражения импульса газа в обоих рассматривае-
рассматриваемых сечениях согласно формуле A15) гл. V, учитывая при этом,
что G = Ga и акр = aKp a. В результате получаем
^1 - z (*«)] = Л^в (/ - 1). (Ю7)
Выразим в A07) произведение GaKp согласно формулам A08)
и A10) гл. V:
через параметры газа в выходном сечении сопла. В результате
имеем
A08)
\ ?> J XiQi V'vu./
ИЛИ
где По = Ро/рц — располагаемое отношение давлений в струе,
N = pjpn — степень нерасчетносш струи, q(k) ж у (К) — извест-
известные газодинамические функции.
414
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Отметим, что согласно уравнению A06) или уравнениям
A08) и A09) импульс газа в струе не остается постоянным,
а возрастает по мере увеличения площади струи за счет дей-
действия оилы внешнего давления.
Таким образом, мы получили два уравнения A05) и A08),
содержащих две неизвестные величины: относительную площадь
сечения / и среднее значение приведенной скорости в этом се-
сечении X. Совместное решение уравнений, а также качественное
Л
2,2
2,0
1,8
16
14
1,2
го
- а1
/
f
>
———
— —
2 3 4
7 8 9 Wf
Рис. 7.32. Диаграмма состояния недорасширенной (iV>l) сверхзвуковой
струи: 2 —уравнение неразрывности A05), 2 — уравнение количества дви-
движения A08), 3 — уравнение неразрывности (ИЗ), а —выходное сечение
сопла, т — максимальное сечение первой «бочки», d — выходное сечение
идеального расчетного сопла, с — изобарическое сечение
исследование закономерностей течения наиболее удобно прово-
проводить графически. Получающийся график называют диаграммой
состояния нерасчетной струи. На рис. 7.32 для начальных пара-
параметров струи М<,= 1,5 (Ка= 1,365) niV = 6,8 (По = 25) построена
зависимость А,(/) по уравнению расхода A05) при о =* 1
(кривая 1) ж та же зависимость по уравнению количества дви-
движения A08) (кривая 2). Пересечение полученных кривых 1
и 2 дает две пары значений переменных / и К, удовлетворяющих
обоим уравнениям. Первая точка пересечения / = 1 и X = Ха со-
соответствует исходным параметрам газа на срезе сопла и интере-
интереса не представляет. Вторая точка пересечения; как показано
ниже, дает значения fm и Кт в максимальном сечении первой
«бочки». Обе точки пересечения соответствуют сверхзвуковой
скорости потока. По значениям функций q(X) и z (X), опреде-
определенных из уравнений A05) и A08), можно найти и вторые,
дозвуковые значения приведенной скорости Я. Однако совмест-
совместных решений в дозвуковой области эти уравнения не имеют.
Рассмотрим подробнее смысл полученного решения. На пер-
первый взгляд представляется странным, что условие постоянства
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ 415
расхода и уравнение количества движения одновременно удов-
удовлетворяются только в двух сечениях начального участка струи,
тогда как эти условия должны выполняться для любого сечения
потока. Однако следует учесть, что в уравнениях A05) и A08)
/при выражении расхода и количества движения газа через па-
параметры торможения и приведенную скорость предполагалось,
что скорость, соответствующая расширению от полного давления
р* до статического давления р в этом сечении, направлена по
оси струи, так что расход газа и количество движения его в осе-
осевом направлении определяются абсолютной скоростью газа.
Уравнения расхода и количества движения A05) и A08) спра-
справедливы только для таких сечений потока, в которых скорость
газа можно полагать осевой. Таким сечением, помимо выходно-
выходного* сечения сопла, в рассматриваемой части струи является мак-
максимальное сечение первой «бочки». Поэтому из совместного ре-
решения получаем / = /w и Я = Хт. Во всех остальных промежу-
промежуточных сечениях расширяющейся части первой «бочки» имеются
радиальные составляющие скорости, вследствие чего уравнения
одномерного потока A05) и A08), как видно из рис. 7.32, здесь
одновременно не выполняются.
Это означает, что не существует потока с осевым направле-
направлением скорости, который при заданных начальных параметрах на
срезе сопла и р* = const (о = 1) мог бы иметь площадь попереч-
поперечного сечения, равную площади какого-либо промежуточного се-
сечения первой «бочки».
Для определения параметров газа в этих промежуточных се-
сечениях выражения расхода и импульса следует записать с уче-
учетом радиальной составляющей скорости. Пользуясь, как и выше,
средними значениями параметров газа в каждом сечении, допу-
допустим, что среднее значение радиальной скорости таково, что век-
вектор средней абсолютной скорости составляет некоторый угол а
с осью потока.
Выше в § 6 гл. V были получены выражения для расхода
A23) и A25) и для импульса газа A27) в одномерном потоке,
имеющем составляющую скорости в плоскости, перпендикулярной
к оси.
При помощи этих выражений для расхода и импульса можно
составить уравнения неразрывности и количества движения для
любых сечений начального участка струи. Уравнения эти имеют
вид
) = -^?(U (HO)
К a)
Для каждого выбранного сечения струи с относительной пло-
площадью f = F/Fa при заданных начальных параметрах потока и
416
ГЛ. УН. ТУРБУЛЕНТНЫЕ СТРУИ
величине а (в частности, для первой «бочки» при а = 1) полу-
полученные уравнения содержат две неизвестные величины Я и а.
Совместное решение уравнений проводится графически с исполь-
использованием таблиц газодинамических функций и графика функции
z(k, а) (см. § 6 гл. V), где
К — приведенная абсолютная
скорость.
На рис. 7.33 приведены
результаты такого расчета.
Как можно видеть, во всех
(промежуточных сечениях оп-
определяется некоторое дей-
действительное значение угла
а, как бы компенсирующее
несовместность • уравнений
одномерного параллельного
потока A05) и A08) для
промежуточных сечений бо-
бочек. Естественно, что в се-
cos# чениях /==1 и / = /т, для
которых уравнения A05) и
A08) одновременно удовлет-
удовлетворяются, имеем а = 0, и
приведенная радиальная ско-
скорость Кг равна нулю.
Отметим, что абсолютная
скорость или приведенная
скорость в промежуточных
сечениях (см. штриховую
кривую на графике рис. 7.33),
а следовательно, и статиче-
статическое давление Р = /?*я(Х),
полученные при расчете с
учетом радиальных состав-
составляющих скорости, очень
близки к соответствующим
значениям, получаемым из
обычного уравнения расхода
-0,80
0,80
0,40
О
/
1
^
—-
\
\
12 16 20 24 f
Рис. 7.33. Параметры газа в промежу-
промежуточных сечениях первой «бочки» нера-
нерасчетной струи: 1 — уравнение количе-
количества движения A08), 2 — уравнение
неразрывности A05), 3 — уравнение
неразрывности (ИЗ), штриховая ли-
линия — приведенная абсолютная ско-
скорость газа с учетом радиальной состав-
составляющей скорости (Ма = 1,0; По = 46,5;
N = 24,6)
A05) . (сплошная кривая)
без поправки на угол а.
Если попытаться опреде-
определить значение угла а, прини-
принимая площадь сечений больше Fm или меньше Faj то окажется, что
coscc>l, а радиальная составляющая скорости — мнимая вели-
величина. Это указывает на физическую невозможность такого тече-
течения и, следовательно, на то, что в начальном участке недорасши-
ренной струи площадь поперечного сечения не может стать
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ
417
меньшей площади выходного сечения сопла Fa или большей пло-
площади Fm, найденной из совместного решения уравнений A05)
и A08); величина fm поэтому, действительно, является макси-
максимальной относительной площадью первой «бочки» струи.
Для определения параметров струи в сечениях, следующих
за максимальным сечением первой «бочки», можно воспользо-
воспользоваться уравнениями, которые были выведены выше для первой
«бочки», с тем отличием, что величину а — коэффициент сохра-
сохранения полного давления — в уравнениях A05) или A10) уже
нельзя полагать равной
единице. Потери полно-
полного давления в скачках
уплотнения при тормо-
торможении газа после пере-
перерасширения приводят к
тому, что в конце су-
сужающейся части первой
«бочки» и во всех по-
последующих сечениях
Р* <Ра и а < 1. На
рис. 7.34 приведено се-
семейство кривых X =
= /\(/), полученное из
уравнения неразрывно-
неразрывности при а<1. Пересе-
Пересечение этих кривых с
2,0
i О
1,6
1,4
1?
а,
А
7
<
2
' О
3
6 Г
Рис. 7.34. Диаграмма состояния нерасчетной
сверхзвуковой струи с учетом потерь полно-
кривой 2, рассчитанной го давления: 1 — уравнение неразрывности
по уравнению количе- A06), 2 — уравнение количества движения
ства движения A08), A08), 5 —уравнение неразрывности (ИЗ)
дает возможные пара-
параметры газа в максимальных и минимальных сечениях последую-
последующих «бочек» начального участка струи. Из диаграммы состояния
очевидно, что в каждой последующей «бочке» максимальные зна-
значения площади и приведенной скорости меньше, а минимальные
значения больше, чем в предыдущей; снижение полного давле-
давления приводит к уменьшению диапазона изменения параметров
газа в «бочках». При некотором значении а = amin получается
^min —Fmgix; это показывает, что в потоке, если не учитывать
смешения с внешней средой, устанавливаются постоянные значе-
значения параметров, соответствующие точке с диаграммы состояния.
Это и есть предельное состояние газа, достигаемое в начальном
участке нерасчетной струи, если не учитывать смешения с внеш-
внешней средой.
Можно показать, что статическое давление в этом сечении,
называемом изобарическим, равно внешнему давлению, вслед-
вследствие чего и прекращается дальнейшее изменение параметров
потока. Для определения параметров газа в изобарическом
27 Г. Н. Абрамович, ч. i
418
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
сечении запишем условие постоянства расхода, выразив расход
газа через статическое давление (рс—'Рв):
VI
или
VK s
/с
A12)
(ИЗ)
Совместное решение этого уравнения с уравнением количества
движения в виде A08) позволяет найти величины Кс и /с =
Отметим, что во всех случаях из расчета получается Яс>1,
т. е. при G = const струя в конце начального участка всегда оста-
остается сверхзвуковой; переход через скорость звука становится
возможным только в ре-
результате смешения с
внешней средой, кото-
которое здесь не учитыва-
учитывается.
По величине Хс лег-
легко определить
давление
и вычислить величину
суммарных потерь пол-
полного давления газа в
начальном участке
0J
0,6
0,5
0,4
0,3
0,2
0,1
К -
'"С
18-
л
<е\
Л
In
/
tk-гр
1,0
>
7,0
/
\
У
^=
*¦
полное
М (К) = Р
1
A14)
0
5 W 15 20 25 30 35 40п
Таким образом, величи-
величина суммарных потерь
полного давления во
всех «бочках» началь-
начального участка может
быть определена без
детального рассмотре-
рассмотрения процессов, происхо-
происходящих в струе. Расчеты
показывают, что эти потери весьма велики и определяются глав-
главным образом степенью нерасчетности N (рис. 7.35).
На диаграмме состояния (рис. 7.34, 7.32) кривая 5, построен-
построенная по уравнению A13),указывает возможные состояния газово-
газового потока (с заданными начальными параметрами), при которых
среднее статическое давление равно /?н; выше этой кривой р <
Рис. 7.35. Приведенная скорость газа в изо-
изобарическом сечении и суммарные потери пол-
полного давления в начальном участке нерасчет-
нерасчетной сверхзвуковой струи
§ 6, ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ 419
< ри1 ниже — р> р*. Легко видеть, что точка пересечения кри-
кривой 3 с кривой 1 \Р* = Ра) указывает параметры газа при
идеальном расширении от ра до рв в сопле Лаваля; точка с дает
параметры свободной струи в изобарическом сечении. Диаграмма
состояния непосредственно показывает качественные соотношения
между параметрами газа в точках с, т, d и а. В частности, от-
отметим, что площадь максимального и изобарического сечений
свободной струи при N > 1 получается всегда большей, чем пло-
площадь выходного сечения расчетного сопла Лаваля. Чем меньше
участок свободного расширения газа, тем ближе между собой
параметры газа в состояниях с, й, т и а.
Влияние степени нерасчетности сопла можно связать с изме-
изменением внешнего силового воздействия на струю. В самом деле,
при увеличении степени расширения сопла (уменьшении N)
часть свободного течения заменяется дополнительной частью соп-
сопла. Вместо внешнего давления ра на границах струи теперь дей-
действует переменное давление р>рв, так как N>1. Увеличение
силы, действующей на струю в направлении движения,
F
Рос- f (p-p*)dF A15)
Fa
равно силе избыточного давления на стенки дополнительной ча-
части сопла. Величина Рх войдет дополнительным слагаемым в пра-
правую часть уравнения количества движения A06), записанного
для участка потока от исходной выходной площади сопла до про-
произвольного сечения струи, вследствие этого импульс газа в се-
сечении с площадью F увеличивается. Уравнение A08) для этого
случая имеет вид
где
К =
Уравнение неразрывности не зависит от величины силы Рх.
С помощью диаграммы состояния (рис. 7.36) легко установить
качественное влияние силового воздействия на струю. Параметры
газа в максимальном и изобарическом сечениях определяются
точками пересечения неизменных кривых 1 и 3 с кривой 2\ по-
построенной по уравнению A16). При Рх>0 кривая 2' всегда ле-
лежит выше исходной кривой 2. Поэтому площади максимального
и изобарического сечений получаются меньшими, чем в свобод-
свободной струе; приведенная скорость Хт в максимальном сечении
уменьшается, а приведенная скорость Яс в изобарическом сече-
27*
420
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
Я
2,2
нии возрастает. Таким образом, увеличение силы, действующей
на поток в направлении движения (или увеличение реакции на
\стенках сопла), приводит к уменьшению перерасширения газа
в «бочках» и к уменьшению суммарных потерь полного давления
газа в начальном участке струи.
Полученный при помощи диа-
диаграммы состояния результат не
является очевидным. Действи-
2t0 tV j^^ ~^~ тельно, несмотря на то, что до-
дополнительная сила Рх направ-
направлена по потоку, импульс газа
в максимальном сечении струи
Im = Gum + PrnFm = COnSt ' Z (Xm) ,
как показывает совместное ре-
решение уравнений импульсов и
неразрывности, не увеличива-
увеличивается, а уменьшается, что свя-
связано с уменьшением площади
этого сечения.
Указанный метод анализа
силового воздействия на струю
оказывается полезным и при
рассмотрении более сложных
случаев течения газа. Зада-
Задаваясь различными начальными
параметрами струи, по указан-
1,4
1.2
>
ь
К'
G
'с
\
3
|
А
0
8 Wf
Рис. 7.36. Изменение параметров га-
за в максимальном (т) и изобари-
стТв з(а1и^ГтиХоГвеГЧ°инь^и:
лы, действующей на границах струи:
i A05)
, дущ рц ру
—уравнение неразрывности A05), ным выше соотношениям мож-
~ъ по/ ,ллп^ но определить зависимость па-
при Р = 0 2 —уравнение A16), *
при Р > 0, 3 — уравнение неразрыв- раметров газа в характерных
ности A13). Ма== 1,5, iV==6,8. сечениях струи от степени
нерасчетности и числа Ма
на срезе сопла (рис. 7.37, 7.38).
Из проведенных расчетов следует, что во всех случаях при
N > 1 средняя величина статического давления в максимальном
сечении струи
Рт == Ро№ \Л"т)
значительно ниже внешнего давления ря. Результаты расчета,
полученные в широком диапазоне начальных параметров струи,
близко соответствуют приближенной зависимости (для iV>2,5;
к = 1,4)
— = 4- + 0,07.
рн JM
A17)
Из рис. 7.39, 7.40 можно видеть, что результаты расчета пло-
площади (диаметра) максимального и изобарического сечений струи
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ
421
Рис. 7.37. Параметры газа в
максимальном сечении струи
в зависимости от степени не- 16
расчетности N = pjpn
8 70 72 74N
Рис. 7.38. Отношение площа-
площадей максимального и изобари-
изобарического (штриховые линии)
сечений нерасчетной сверх-
сверхзвуковой струи к площади
критического сечения сопла
Лаваля, к = 1,4
16
14
72
10
Л/
у
А
/
у
у
/ \
°acven
- Jim
/
шля
••*
2^&
10 14 18 22 26 30 34 38
*
422
ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
по изложенному методу хорошо соответствуют эксперименталь-
экспериментальным данным различных авторов. Отметим, что при заданных на-
начальных параметрах струи соответствие рассчитанной и измерен-
измеренной площади сечения одновременно означает, что совпадают так-
также средние значения скорости в этом сечении (см. уравнение
A08)) и величипа полного давления — коэффициент о (см.
уравнение A05)).
Из рассмотрения диаграммы состояния можно получить ка-
качественные результаты для ряда предельных условий истечения.
0,04 0,08 0,12 0,16 0,20 0,24 0,23 0,32 0,38 0,40 0t44jf
Рис. 7.39. Диаметр максимального сечения недорасширенной сверхзвуковой
струи по экспериментальным и расчетным данным: 1 — опыты Л. П. Волко-
Волковой, 2 — опыты Цзян Чжесиня, 3 — опыты Г. А. Акимова, 4 — опыты Е. Ла-
Лава, о — опыты Т. Адамсона, 6 — расчет по методу характеристик. Кривые —
расчет по одномерной теории, к = 1,4
В частности, при истечении газа в пустоту через сопло конечных
размеров (рн = 0, По = 00, д(^а)^О) в уравнении количества дви-
движения A08) исчезает второе слагаемое правой части, вследствие
чего оно принимает вид
Z(k) = z(Xa), ИЛИ Я=Ха.
Кривая 2 на диаграмме состояния (см. рис. 7.32) при этом
превращается в прямую, параллельную оси абсцисс, и точка
пересечения ее с неизменной кривой 2, выражающей уравнение
неразрывности, уходит в бесконечность(/ш-> оо, Ят-> J/^-—jj»
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ
423
Это означает, что струя, вытекающая в пустоту, не образует «бо-
«бочек», а беспредельно увеличивается в сечении, сохраняя везде
радиальную составляющую скорости.
Если профилировка сопла не обеспечивает получения парал-
параллельного равномерного потока газа в выходном сечении, как при-
принималось выше, то в уравнениях A05) и A08) следует учесть
О
*
i
А /
v 2
* 3
0,04 0,08 0,12 0,16 0,20 0,24 0,28 0,32 jf
Рис. 7.40. Диаметр изобарического сечения струи по экспериментальным и
расчетным данным. Кривые — расчет по одномерной теории; 1 — опыты
Г. А. Акимова, 2 — опыты Е. Лава, 3 — опыты Т. Адамсона
наличие радиальной составляющей скорости в сечении а. Для
этого, как делалось при выводе уравнений A10) и A11), сле-
следует заменить функции q(ka) и z(Xa) обобщенными функциями
#(А<а, аа) и z(Xai аа), где аа— среднее значение угла между век-
вектором абсолютной скорости газа на выходе из сопла и осью
сопла. Для конического сопла легко получить следующее выра-
выражение для среднего значения угла аа:
которое при р < 30° с достаточной степенью точности аппрокси-
аппроксимируется формулой
Здесь р — угол между образующей конуса и осью.
Решение системы уравнений после подстановки в правую
часть A05) и A08) величин q(Ka, aa) и z(A,«, aa) проводится,
как и для случая аа = 0. Расчеты показывают, что с увеличением
угла конусности сопла увеличивается площадь максимального се-
сечения струи, увеличивается перерасширение газа в струе и ра-
растут суммарные потери полного давления при данных значениях
По И Яа.
424 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
При решении ряда задач необходимо знать конфигурацию
начальпой части струи и расстояние между соплом и максималь-
максимальным сечением первой «бочки». Одномерное рассмотрение газовых
потоков обычно не позволяет получить такого рода данные.
Здесь, однако, можно указать способ, позволяющий приближен-
приближенно определить контур расширяющейся начальной части струи на
основании результатов, полученных из одномерного расчета.
При определении параметров газа в промежуточных сечениях
первой «бочки» для каждого сечения площадью F < Fm с по-
помощью уравнений A10) и A11) может быть найдено, как ука-
указывалось выше, некоторое значение угла а, характеризующего
величину радиальных составляющих скорости газа в этом сече-
сечении. Угол а составляют между собой вектор абсолютной сред-
немассовой скорости газа и ось струи. В действительном нерав-
неравномерном потоке углы отклонения векторов скорости от оси раз-
различны в разных точках сечения и увеличиваются от оси к пе-
периферии, поэтому найденное выше значение угла а будет не-
некоторым средним. Однако, учитывая, что основная часть расхода
газа проходит через периферийную зону "сечения как из-^за боль-
большей площади ее, так и из-за малой плотности тока в централь-
центральной перерасширенной части струи, можно полагать, что это сред-
среднее значение угла будет близко к значению угла расширения у
границы струи агр. Условно полагая агр ~ а, получаем возмож-
возможность приближенного построения границ струи.
Начальный угол отклонения границы струи у среза сопла,
где из-за наличия ядра иевозмущенного потока указанные сооб-
соображения неприемлемы, определяется аналогично углу поворота
сверхзвукового потока, обтекающего тупой угол (см. § 4, гл. IV),
по формуле
ао = Р + 6. A19)
Здесь р — угол между касательной к образующей сопла в выход-
выходном сечении и осью, а б — угол поворота потока от первоначаль-
первоначального направления, который находится из таблицы (см. приложе-
приложение I) по заданным значениям числа М на срезе сопла и отно-
отношения давлений ра/рц или pjpn. Вместо таблиц для нахождения
6 при к = 1,40 может быть рекомендована приближенная форму-
формула (для X < 2,3)
6 = 7,6(^3-А»), A20)
где Яо = А,(По) — приведенная скорость на границе струи (т. е.
при полном расширении газа до внешнего давления).
По величине начального угла ао и значениям угла а, найден-
найденным из уравнений A10) и A11) для нескольких E—6) значе-
значений относительной площади сечения / < /т, можно построить
приближенные очертания расширяющейся части первой «боч-
«бочки». Для этого к прямой, проведенной через кромку сопла под
§ 6. ОДНОМЕРНАЯ, ТЕОРИЯ НЕРАСЧЕТНОЙ СТРУИ
425
углом ао, в точках, соответствующих радиусам выбранных про-
промежуточных сечений гь гг, г3 и т. д., последовательно достраива-
достраиваются отрезки под углами ось «2, аз и т. д. до пересечения с
прямой г = гт; полученная ломаная линия скругляется.
Несмотря на условность изложенного построения, получен-
полученный таким образом контур близко соответствует видимой на фо-
фотографии форме струи, а также результату расчета по методу
характеристик, если степень нерасчетыости струи не превышает
J
з
2
1
Л
А
^—"
•6
о-
2
1
Рис. 7.41. Контур расширяющейся части первой бочки сверхзвуковой струи.
Кривые — по теневой фотографии струи, точки — расчет по шести сече-
сечениям: 1 — М = 2,5, N = 6,43, р = 5, 2 — М = 1,0, N = 24,6
значений iV=100—150 (рис. 7.41). Расстояние от среза сопла
до максимального поперечного сечения начального участка струи
при N > 1 удовлетворительно аппроксимируется следующей фор-
формулой:
f? = 0,7М„ VkN.
A21)
Длину первой бочки 1п и расстояние от среза сопла до диска
Маха ld можно приближенно определить из соотношений
Все приведенные выше результаты получены в предположе-
предположении о том, что в начальном участке струи отсутствует смешение
с внешней средой. Это имеет смысл постольку, поскольку позво-
позволяет выявить закономерности, присущие самой струе, и опреде-
определить потери, возникающие в процессе стабилизации параметров
нерасчетной струи. При большой степени нерасчетности, когда
начальный участок ограничен одной-двумя «бочками», указанное
допущение не вызывает значительной погрешности. При большой
длине участка увеличение массы струи может быть заметным,
что изменит параметры потока в изобарическом сечении. Дей-
Действительные средние значения параметров можно получить из
426 ГЛ. VII. ТУРБУЛЕНТНЫЕ СТРУИ
расчета, аналогичного изложенному выше, если при выводе ос-
основных уравнений учесть различие расхода газа в начальном и
конечном сечениях. Величина G или G/Ga должна при этом быть
вадана или определена из рассмотрения турбулентного смешения
струи с внешней средой.
Изложенная методика расчета по средним значениям пара-
параметров в основных сечениях нерасчетной струи может быть рас-
распространена также и на случай истечения с перерасширением
(W<1).
В заключение напомним, что приведенная одномерная теория
не позволяет получить данных о внутренней структуре струи и
распределении параметров по ее сечению; для этой цели необхо-
необходимо применение более сложных методов, например метода ха-
характеристик. В то же время некоторые полученные выше резуль-
результаты, например значения параметров в изобарическом сечении,
не могут быть найдены методом характеристик без дополнитель-
дополнительных предположений.
Заканчивая рассмотрение одномерного метода расчета, заме-
заметим, что этот метод может быть применен при расчете парамет-
параметров газа в промежуточных сечениях струи, при построении гра-
границы струи, при истечении газа из конического сопла и при
истечении в вакуум или среду с повышенным уровнем стати-
статического давления (N < 1).
В случае больших нерасчетностей (iV> 100) характерные ли-
линейные масштабы и конфигурации границы струи и контура ви-
висячего скачка уплотнения недорасширенной осесимметричной
сверхзвуковой струи могут быть определены при помощи соотно-
соотношений, предложенных в работе Н. Н. Шелухина *). Для расстоя-
расстояния от среза сопла до максимального сечения струи хт и для
максимального радиуса струи в этой работе получены следую-
следующие выражения:
xjra = 0,95f, rjra =
где
p —угол полураствора солла. Границы струи r = r/(gra) и кон-
контура висячего скачка уплотнения rb = rb/(gra) аппроксимируются
!) Шелухин Н. Н. Параметры подобия формы недорасширенной
струи при истечении в затопленное пространство // Ученые записки
ЦАГИ.- 1979.—Т. 10, № 2.—С. 130-136.
§ 6. ОДНОМЕРНАЯ ТЕОРИЯ НЕРАСЧЕТНОЙ, СТРУИ
427
следующими выражениями:
г =¦ 0,0312х4 + 0,238*3 - 1,468г2 + 2,008х + 0,107,
гь = —0,674я4 + 2,108я3 - 3,Ш2 + 2,465* + 0,058.
(Здесь х = x/(fra).) На рис. 7.42 и 7.43 представлены эти зави-
зависимости. Заштрихованная область характеризует разброс точек,
полученных в результате точных расчетов системы уравнений
Эйлера, при этом параметры недорасширенных струй менялись
Рис. 7.42. Форма границы струи
Рис. 7.43. Форма висячего скачка
уплотнения
в диапазонах Ма=1^5, к = 1,3 -f-1,4, TV = 50-МО6, ^ = 0-М5°.
Мы рассмотрели особенности газодинамического участка нерас-
нерасчетной сверхзвуковой струи без учета влияния вязкости, с ко-
которым связан неизбежный процесс образования граничного слоя
смешения. Выше получены закономерности для нарастания тол-
толщины слоя смешения по длине начального участка изобариче-
изобарической струи. При N > 1 давление в струе уменьшается, линии
тока сверхзвукового течения раздвигаются, что ведет к дополни-
дополнительному увеличению толщины струи. А. Н. Секундов и
И. П. Смирнова, пользуясь методом интегральных соотношений
и полагая слой смешения наложенным на границу одномерной
струи, получили следующую приближенную зависимость для тол-
толщины слоя смешения l
db
dx
12vT
(u± - uH)
hdr
г dx*
A22)
Здесь Ъ — толщина слоя смешения, х — продольная криволиней-
криволинейная координата, отсчитываемая вдоль границы струи, определен-
определенной по изложенной одномерной теории без учета вязкости, vT =
vT
= b(u __ и v — безразмерный коэффициент турбулентной кине-
V 1 Н/
матической вязкости, щ — переменная по длине скорость в одно-
одномерной струе, ия — скорость внешнего потока, г — текущий ра-
радиус границы одномерной струи. Первый член правой части
428 гл- VII. ТУРБУЛЕНТНЫЕ СТРУИ
в A22) учитывает влияние вязкости, а второй — расширение слоя
за счет уменьшения плотности газа.
Наложение слоя смешения на «границу» одномерной струи
производится так, чтобы текущее расстояние его внутреннего и
наружного краев от этой «границы» соответствовали приведенно-
приведенному в § 4 решению для изобарического слоя:
? = /A11,11), * = ?, m = X A23)
Сочетание формул A22) и A23) позволяет получить прибли-
приближенно неравномерный профиль скорости за первой «бочкой» не-
нерасчетной струи; при больших значениях N в этом месте струя
становится изобарической, т. е. может быть рассчитана по дан-
данным § 4. Расчет по формулам A22) — A23) для режима истече-
истечения воздушной струи из плавного сопла (аа = 0°) в поток воз-
воздуха при Ма = 1, Мн = 4, N = 82, к = 1,4 дает толщину слоя сме-
смешения в долях от его длины b/х = 0,058, f = 14, g = 13,4. При-
Принимая f = g = 13,7, получаем длину зоны смешения хш = 26га,
радиус диска Маха rd = 10,2га, относительно малую толщину слоя
смешения Ъ = l,52ra = 0,15rd.
Следует отметить, что длина начального участка неизобариче-
окой струи в спутном потоке большой скорости (/71 = 0,65-^0,8)
в диапазоне значений числа Маха Ма = 2 -т- 3,4 хорошо аппрок-
аппроксимируется формулой (при N = 0,5 -г- 3)
хн = *-* = 50№>6.
га
Глава VIII
ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
§ 1. Сопла
Потери полного давления в правильно спрофилированном
сопле сводятся главным образом к потерям на трение. В идеаль-
идеальном случае при отсутствии потерь скорость истечения из сопла
связана с отношением статического давления в выходном сече-
сечении ра к полному давлению в сопле рс известным равенством
k
—*— I1 —к I ^ даид1
При наличии потерь истинная скорость истечения меньше
идеальной:
'ка ^ фДа ид, A)
где фс — коэффициент скорости сопла; его значение равно обыч-
обычно фс = 0,97—0,99. Вводя коэффициент сохранения полного дав-
давления, учитывающий потери полного давления в сопле ас =
= Ра/Рс» ПОЛУЧИМ
k
отсюда устанавливается зависимость коэффициента сохранения
полного давления от коэффициента скорости:
о Л =
*=i,» ^
B)
Например, при Ха ид = 1 и фс = 0,98 получаем ас = 0,975.
Зависимость 0с = /(фс) при различных значениях числа Мид
в выходном сечении представлена на рис. 8.1; кривые рассчи-
рассчитаны по формуле B) с использованием выражения D6) из гл. I.
Рис. 8.1 показывает, что при скоростях истечения, значительно
превосходящих скорость звука (М>1,5), даже умеренным
430
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
потерям скорости (фс>0,97) соответствуют большие потери
полного давления.
Для вычисления расхода газа в сопле с учетом потерь в фор-
формулы (8) и A0) гл. IV добавляют множитель (я<1, носящий
название коэффициента
расхода; тогда, например,
при сверхзвуковом исте-
истечении
fe+1
где пг =
множитель, зависящий от
свойства газа; р*, Т* —
значения полного давле-
давления и температуры тормо-
торможения перед соплом.
Коэффициент расхода
можно представить как
произведение двух коэф-
коэффициентов: ji = <JKp/, из ко-
которых первый учитывает
потери полного давления
в сужающейся части соп-
сопла (до критического сече-
сечения) : акр = рКр/р*, а вто-
второй — неравномерность
поля плотности тока (pw)
в узком сечении. Потери
я дозвуковой части сопла всегда относительно невелики (акр =
= 0,98-0,998).
В случае простого сужающегося сопла с круто сходящимися
стенками струя газа продолжает сужаться за пределами сопла,
т. е. фактическое узкое сечение струи меньше узкого сечения
сопла. Теоретические и экспериментальные исследования пока-
показывают, что при этом на срезе сопла скорость потока меньше
скорости звука и распределена по сечению неравномерно. Если
при истечении газа в неподвижную среду отношение полного
давления перед соплом р* к давлению вне сопла рп превышает
критическое (яс= Р*//?н^2), то в узком сечении струи (за пре-
пределами сопла) скорость близка к скорости звука. Иначе говоря,
при истечении из сужающегося сопла коэффициент / отражает
дополнительное сужение струи за пределами среза сопла \f=FK9/
)
Рис. 8.1. Зависимость коэффициента со-
сохранения полного давления от коэффи-
коэффициента скорости
§ 1. СОПЛА
431
На рис. 8.2 приведены линии, соединяющие точки с равными
значениями числа Маха в конических сужающихся соплах с раз-
разными углами наклона стенки (E == 15°, 25°, 40°) для значения
пс = 2; данные заимствованы из работы Вихофера и Могора1)
(кружками изображены опытные данные, линиями — результаты
1Л
R/Ra
0,6
0,1
0
1
t
\
\ о,б\°оЛ
11°
1
<
1
К
11
0А
-%0 -0,6 -0,1 О 0,U
/345°
Фа
W
0,6
0,2
О
0,3
xlRa
M=O,L,
А
Л
k 0,6
\
?
\
А
О
о\ I
-1,0 -0,6 -0,1 О 0,U 0,8 ~1у0 -0,6 -0,2 0 0,Ц 0,8
s в
Рис. 8.2. Линии равных значений числа М в конических сужающихся
соплах
расчета авторов на ЭВМ). Чем больше да/вление перед соплом,
тем меньше дополнительное сжатие струи, равномернее поле ско-
скорости на срезе сопла и выше коэффициент расхода.
Зависимость |х от величины яс для тех же трех солел пред-
представлена на рис. 8.3.
При истечении из отверстия с острыми кромками в плоской
стенке ([} = 90°) в случае несжимаемой жидкости (M^^l) ко-
коэффициент расхода практически равен коэффициенту сужения
струи за пределами отверстия, для R > 2 • 105
) Wehofer S., Mogor W. S. Transsonic flow in conical convergent
and convergent-divergent nozzles with nonuniform inlet conditions /AIAA
paper.— 1970.— № 70.— P. 635.
432
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
При истечении газа коэффициент расхода \х зависит от отно-
отношения полного давления в струе р* к статическому давлению в
/
р
среде, окружающей струю (П = р*/ря). Если это отношение дав-
лений является критическим
то скорость
0,85
в
1л
R.JLR.q .0 О
I
а-/5-25°
о -fi-UO9
расчет
О
6,0 . 8,0
газа в узком сечении струи постоянна и равна скорости звука
„ . ^_^__^ (ко = 1), причем (Хо ~ /о = 0,75.
" b a k . A I I ПрИ П>ПКР1 получается />
>/о и \х> \хо, т. е. расход газа
G через отверстие, как и в ко-
коническом сопле, больше, чем в
режиме Пкр1. Росту значений jx
и G при увеличении П в режи-
режиме П > ПКР1 способствует нали-
наличие дозвуковой скорости в от-
отверстии (см. рис. 8.2), когда
волны давления проникают на-
навстречу потоку сквозь отвер-
отверстие. При некотором значении
П = Пкр2 скорость газа в сече-
сечении отверстия становится рав-
равной или больше скорости звука.
На таком режиме, называемом
иногда вторым критическим,
величины |х и G достигают
максимума, а давление в от-
отверстии оказывается выше, чем
за пределами струи; в связи
с зтим струя становится сверхзвуковой недорасширенной (см.
§ 6 гл. 7). По опытам М. Е. Дейча и др.1) при к = 1,4
[Хкр2 = 0,86, Пкр2 = 0,1.
Структура потока газа в узкой части сверхзвукового сопла
Лаваля зависит от формы сопла и в первую очередь от двух фак-
факторов: угла конусности сужающейся части и относительной кри-
кривизны стенок в области узкого сечения.
Известны теоретические и экспериментальные исследования,
которые позволяют достаточно надежно определять параметры
потока в соплах различной формы для идеального невязкого га-
газа, а также с учетом сопротивления трения, теплоотдачи и ре-
реальных свойств газа (диссоциация, химические реакции, конден-
конденсация и др.). В частности, можно рассчитать поле плотности то-
тока в узком сечении сопла, что позволяет вычислить коэффици-
Рис. 8.3. Зависимость коэффициента
расхода от отношения полного дав-
давления перед коническим сужающим-
сужающимся соплом к статическому давлению
на срезе
*) Дейч М. Е., Зарянкин А. Е. Гидрогазодинамика.--М.: Энерго-
атомиздат, 1984.
§ 1. СОПЛА
433
ент расхода, который для сопла Лаваля хорошей формы может
достигать очень высокого значения (ц, = 0,998).
Для расчета реактивной силы, кроме расхода газа, нужно
знать давление на срезе и скорость истечения, которые зависят
от потерь как в дозвуковой, так и в сверхзвуковой части сопла.
Выше предполагалось, что потери распределяются равномерно
по сечению сопла, однако истинная картина течения газа внутри
сопла не отвечает этому простейшему предположению. При боль-
большой кривизне стенок в области горловины сопла возможен ме-
местный отрыв пограничного слоя от стенок, кроме того, в начале
расширяющейся части ссшла некоторые линии тока сверхзвуко-
сверхзвукового течения сужаются, что приводит к образованию местных
косых скачков уплотнения.
На рис. 8.4 представлена кривая зависимости коэффициента
расхода от отношения радиуса закругления стенки г в узкой
0,96
0,92'
0,88
г
О.
* S
^45° о
-75-90° •
i
1
0,8
/
Рис. 8.4. Коэффициенты расхода в сверхзвуковых конических соплах со
скругленной стенкой в окрестности критического сечения при разных углах
конусности дозвуковой части (Р = 30°, 45°, 75 -г- 90°) и постоянном угле
конусности сверхзвуковой части (а = 15°)
части сопла Лаваля к радиусу поперечного сечения его горло-
горловины /?Кр для сопел с различными углами наклона стенки су-
сужающейся части ((} = 30°, 45°, 75-^90°) и постоянным углом на-
наклона стенки расширяющейся части A5°). Сопла представляют
собой конусы, сопряженные в области горловины дугой крута
(см. схему на рис. 8.7). Кривые проведены по опытным данным
Бекка и Куффеля1), точками различной формы нанесены опыт-
]) Back L. H., Cuff el P. F. Flow coefficient for supersonic nozzles
with comparatively small radius of curvature throat II J. of Spacecraft and
Rocketes.—1971.— V. 8, № 2.—P. 196—198.
28 Г. Н. Абрамович, ч. 1
434
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
ные данные Бекка, Маосира и Гира, а также Дюрхама и Норто-
Нортона и Шелтоиа 1).
Все значения \х взяты в автомодельной области (для чисел
Рейнольдса, подсчитанных по параметрам потока перед соплом
и диаметру горлошшы сопла, порядка RD = 106-^ 107), когда они
перестают зависеть от числа Рейнольдса.
Характерно, что при r/i?Kp ^ 0,3 кривые [х(г/Дкр) сливаются,
а при r/RKp = 2 выходят на почти горизонтальный участок с
очень высоким значением \i > 0,98; при столь большом радиусе
скругления стенки горловины вихревые и ударные потери прак-
практически отсутствуют и остается только сопротивление трения.
Дальнейшее увеличение радиуса скругления нецелесообразно,
так как удлиняет околозвуковую часть сопла и приводит к уве-
увеличению сопротивления трения. На рис. 8.5 показана зависимость
0,80
0,60
1 1 1
1 1 1
\
! ! 1 1
сг- аргон
о-аргон
д- гелии
d — азот
расчет
111и i it
tin
10ъ
Рис. 8.5. Зависимость от числа Рейнольдса коэффициента расхода кониче-
конического сверхзвукового сопла со скругленной стенкой в окрестности критиче-
критического сечения (Р = 30°, а = 15°, г/Дкр = 4)
коэффициента расхода конического сопла Лаваля с большим
скруглением горловины от числа Рейнольдса RD, полученная в
опытах с различными газами; число Рейнольдса варьировалось
изменением давления перед соплом.
В тех случаях, когда поле полного давления во входном сече-
сечении сопла равномерно, а очертания сопла настолько плавны, что
в нем нет вихревых областей и скачков уплотнения, сопротивле-
сопротивление сопла сводится к сопротивлению трения в пограничном слое.
Ввиду того что длина сопла обычно не больше нескольких диа-
диаметров сопла, толщина пограничного слоя составляет малую
l) Back L. H., Massier P. F., Gier H. L. Comparison of messured
and predicted flows through conical suppersonic nozzles with emphasis on the
transonic regions / AIAA J.— 1965.— V. 3, № 9.— P. 1606—1614
§ 1. СОПЛА
435
Рис. 8.6. Схема изменения тол-
толщины вытеснения б* по длине
сопла
долю радиуса сопла, т. е. большая часть поперечнего сечения
сопла заполнена ядром потока, состоящим из струй постоянного
полного давления, в которых параметры газа изменяются по за-
законам идеальной адиабаты. В таком случае полные давления в
ядре потока в выходном и входном сечениях сопла одинаковы,
но из-за существования пограничного слоя точное значение ско-
скорости истечения не может быть определено непосредственно по
формулам B) и C) или D) гл. IV.
Однако можно воспользоваться эти-
этими формулами, если внести поправ-
поправку в величину площади поперечного
сечения сопла, применяя понятие о
толщине вытеснения пограничного
слоя (см. § 2 гл. VI).
Как известно, смещение стенкп
от ее истинного положения в сторо-
сторону от оси сопла на расстояние, рав-
равное толщине вытеснения (рис. 8.6),
ведет к тому, что распределение
статического давления и скорости по отклоненной стенке при
обтекании ее вязкой жидкостью получается таким же, как по
истинной стенке, обтекаемой идеальной жидкостью. Иначе гово-
говоря, соответствующим увеличением поперечных сечений сопла
можно компенсировать влияние пограничного слоя на распреде-
распределение скорости и давления по оси сопла. Наоборот, если заме-
заменить заданное сопло фиктивным, контур которого в каждом се-
сечении смещен к оси сопла на расстояние, равное толщине вы-
вытеснения б*, то распределение скорости по длине фиктивного
сопла можно определять по изоэытропическим формулам B),
C) или D) гл. IV, причем оно получается таким же, как в за-
заданном сопле.
В плоскопараллельном сопле площадь фиктивного сечения F$
найдется из условия
^Ф _ , _ 26* 3
F Ъ * ^ '
где Ъ — ширина поперечного сечения заданного сопла.
В осесимметричном сопле
Г \ It J IX ч '
здесь R — радиус заданного сопла.
Тогда скорость истечения из заданного сопла определяется по
формуле
1 1
Тр
E)
фкр
j КI1 ~ ЗГ+1К) =
В этой формуле F4o — площадь выходного сечения фиктивного
сопла, .Рфкр — площадь критического сечения фиктивного сопла.
28*
436 ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
В ядре постоянного полного давления, заполняющем боль-
большую часть поперечного сечения заданного сопла, скорость газа
определяется уравнением E). По этому значению скорости,
пользуясь известной формулой G2) гл. I, отвечающей идеаль-
идеальному адиабатическому процессу в газовом потоке, можно найти
статическое давление в соответствующем поперечном сечении за-
заданного сопла:
k
здесь р* — полное давление на оси сопла, значение которого во
всех сечениях одинаково.
Учет влияния пограничного слоя путем замены истинного
контура сопла фиктивным контуром приводит к сужению сопла,
поэтому в дозвуковом течении пограничный слой вызывает уве-
увеличение, а в сверхзвуковом — уменьшение скорости (по сравне-
сравнению со случаем течения невязкого газа в сопле истинного кон-
контура).
Итак, несмотря на сохранение полного давления в ядре те-
течения, скорость в ядре в дозвуковом сопле получается больше,
чем в идеальном случае: Яа>ЯаиД, а в сверхзвуковом сопле —
меньше, чем в идеальном случае: Ха < Ха ид. В соответствии с этим
статическое давление в любом сечении истинного сопла при до-
дозвуковом потоке понижается, а при сверхзвуковом потоке повы-
повышается по сравнению с давлением в таком же сечении идеаль-
идеального сопла.
Ввиду малости поправок, учитывающих влияние погранич-
пограничного слоя на скорость и давление, их величину можно получить
путем разложения формулы E) в ряд. Опуская в E) индексы,
имеем
Mi — '
Если изменение площади поперечного сечения на малую ве-
величину AF вызывает изменение скорости также на малую вели-
величину ДЯ, то при к = const
[
1-
§ i. сопла 437
После разложения в биномиальный ряд и отбрасывания вслед-
вследствие малости всех членов с множителями порядка ДА,3 и выше
получим
AF АХ Х2-1 , АХ2 C - X2) т
F ~ X к—
Во всех случаях, кроме А, « 1, эту формулу можно упростить,
отбросив также член с множителем ДАЛ Тогда имеем
AF _ ДА, X2 — 1 /я.
В случае Я = 1, т. е. в окрестности постоянного критического се-
сечения сверхзвукового сопла формула G) приобретает особенно
простой вид:
^ = А^2. (9)
Отсюда следует, что незначительное изменение площади сечения
сопла вблизи критического сечения вызывает заметное измене-
изменение скорости. Например, изменение площади сопла около крити-
критического сечения на 1% (AF/F = 0,01) дает изменение скорости
на 10% (ДА, = 0,1).
Формула (8) устанавливает связь между малыми отклоне-
отклонениями площади сечения и соответствующими малыми измене-
изменениями скорости газового потока. При учете влияния погранич-
пограничного слоя на скорость потока можно вместо изменения площади
сечения ввести толщину вытеснения; для осесимметричного соп-
сопла согласно D) имеем
*?~ 2^
р ~ R
Отсюда связь между толщиной вытеснения и изменением ско-
скорости приобретает следующий вид (при А, Ф 1):
Например, изменение приведенной скорости на 3 % при к = 1,4
и Я = 1,5 (М = 1,73) достигается за счет толщины вытеснения
б*, составляющей ~3 % от радиуса сопла.
Малые изменения давления, вызываемые малыми изменения-
изменениями скорости, можно также вычислить по формуле, полученной
путем разложения равенства G2) гл. I в биномиальный ряд
и отбрасывания всех членов с множителями порядка ДА,2
и выше.
438
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
В самом деле
п ( h \ \Ь—1
Р — М К~~ г >2
р* \ к + 1 } '
отсюда
Р + Ар
ft—1
'Ar + 1(
Л—1
и далее
Ap_
P '
1 —¦
2fe
АЛ Л + 1
h
h-i
'k+1
A1)
Для рассмотренного выше примера (АЯ/Я = 0,03, Л = 1,5)
из A1) получим Ар/р «0,12. В случае К = 1 для зависимости
прироста давления от прироста скорости получаем следующую
простую формулу:
*? = _ МЯ, A2)
т. е. изменение давления пропорционально изменению скорости.
Ввиду наличия пограничного слоя средняя скорость газа в по-
поперечном сечении меньше скорости в ядре течения: Яср<Ла. Для
вычисления средней по массе газа скорости
G
можно использовать понятие толщины потери импульса в погра-
пограничном слое б** (см. гл. VI). Эта величина показывает, на ка-
какое расстояние б** нужно сместить контур сопла (в сторону к его
оси) для того, чтобы равномерный поток в фиктивном сопле при
той же скорости, что и в ядре течения истинного сопла, имел та-
такое же секундное количество движения, как и в истинном сопле„
Тогда
Отсюда коэффициент скорости, учитывающий влияние погранич-
пограничного слоя, равен
\ п г?
A3)
§ i. СОПЛА
439
Отметим, что величина фс в формуле A3) выражает отношение
средней по массе газа скорости к скорости в ядре течения, а ие
к скорости в идеальном сопле. Переход к величине
ер =
может быть осуществлен следующим путем:
^аид
где, согласно A0),
Г*
I2 — 1
Ааид L
2Я,
а ид
к + 1
Опыты Кинана и Неймана1) дают возможность оценить отно-
отношение фиктивного диаметра выхода из сопла Иф к истинному
диаметру выхода (Da) при различных значениях чисел R и М.
Результаты этих опытов сведены в таблицу.
Номер сопла
1
2
3
4
5
0,562"
0,186"
0,175"
0,107"
0,186"
Da
0,945"
0,498"
0,438"
0,498"
0,498"
2,06
3,14
3,87
2,84
К
3,9-105
3,9-105
3,8-105
1,2-103
0,27-105
ма ид
2,58
3,56
—
4,80
3,58
Da
0,79
0,82
0,67
0,71
Диаметры критических Z>Kp и выходных Da сечений даны в
этой таблице в дюймах, числа Ra рассчитаны по выходному диа-
диаметру сопла. Как видим, истинные значения числа Ма в выход-
выходном сечении ниже расчетных (Ма<МаиД) и фиктивный диаметр
выходного отверстия меньше истинного на 18-нЗЗ%, т. е. без-
безразмерная толщина вытеснения
б* = 0,18 -5- 0,33,
причем меньшие значения толщины вытеснения соответствуют
более высоким значениям числа Ra.
Наличие больших градиентов давления крайне осложняет
расчет пограничного слоя в соплах, особенно при сверхзвуковых
скоростях. Приближенная методика расчета турбулентного по-
1) Кеепап I. N аи man Е. / J. of Applied Mechanics.—1946.—
V. 13, № 2.— June.
440
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
750"
граничного слоя в сопле Лаваля, разработанная Бартцем1), осно-
основана на следующих предположениях: профили скорости и избы-
избыточной температуры во всех сечениях сопла подчиняются «зако-
«закону 1/7», местные значения коэффициента трения на стенке и
толщины пограничного слоя связаны такой же зависимостью, как
в случае пластины, число Нуссельта является функцией числа
Рейнольдса, поток вне пограничного слоя рассчитывается как
одномерный (без учета
влияния пограничного
слоя). Результаты такого
расчета для сопла, изобра-
изображенного на рис. 8.7, при-
приведены на рис. 8.8, где по
оси ординат отложены
толщины динамического
пограничного слоя б (в
дюймах), а по оси абс-
абсцисс — расстояние от на-
начала сопла до текущего
сечения, выраженное в до-
долях от приведенной дли-
Рис. 8.7. Сопло Лаваля (из работы
Бартца)
ны сопла хп (в данном примере яп = 8,02"). Расчет производится
для двух случаев, когда в начале сопла толщина пограничного
слоя бо = 0,188" и когда бо = 0. Важнейший результат этого рас-
расчета, подтверждаемый опытными данными, заключается в том,
что толщина пограничного слоя в критическом сечении очень
мала (бкр =0,028"; бкр = 0,0035) и практически не зависит от
толщины пограничного слоя в начальном сечении сопла. Это
0/0
015
Ц05
Горло
О 0,1 0,2 0,3 0,4 0,5 0,8 0,7 0,8 0,9 1,0
Рис. 8.8. Изменение толщи-
толщины пограничного слоя б по
длине конического сопла
Лаваля (см. рис. 8.7): 1 —
толщина слоя в начальном
сечении б0 = 0,188", 2 —
то же при 6 = 0, 3 — тол-
толщина слоя в горле бКр = О
значит, что толщину пограничного слоя в выходпом сечении сопла
Лаваля можно приближенно определить в предположении, что в
критическом сечении она равна нулю Fкр~0). Этот случая
показан на рис. 8.8 штриховой кривой.
l) Bartz D. R. An approximate solution of compressible turbulent boun-
boundary layer development / ASME Paper.—1954.— N54—A—153; Trans.
ASME.— 1955.— V. 77, № 2.— P. 1235—1245.
§ 1. СОПЛА
441
Полное давление (с учетом пограничного слоя) в выходном
сечении конического сверхзвукового сопла можно оценить при-
приближенно по следующей формуле1):
Up)
_2_tg_a
fee,
1 +
к— 1
k+1
M2-i
A4)
здесь р* — среднее по сечению полное давление на выходе, ркр —
то же в критическом сечении сопла, М — расчетное значение чис-
числа Маха, а — полуугол раствора сопла, cf — коэффициент трения.
Кривые, рассчитанные по
формуле A4) при к = 1, 4,
изображены на рис. 8.9.
Для расчета коэффи-
коэффициента трения в сопле
можно пользоваться при-
приближенной зависи-
зависимостью2), которая нахо-
находится в хорошем соответ-
ствии с данными гл. VI:
с} = 0,003 х
1—0,578
0.9
0,8
|
1
ZtffX
->—t?Cf
^200
100
\
\
25
1.0
2,0
3,0
М
Рис. 8.9. Изменение полного давления по
длине сопла, представленное в зависимо-
зависимости от местного значения числа Маха
A5)
Помимо сопротивления
трения, имеют значение
потери, связанные с не-
неравномерностью потока в зоне критического сечения и отклоне-
отклонением потока от осевого направления на выходе из сопла.
Полный коэффициент скорости сопла фс можно представить
в виде произведения трех коэффициентов, учитывающих потери
на трение (ф/), потери от неравномерности потока и наличия
местных скачков уплотнения в горле сопла (фР) и потери вслед-
вследствие отклонения потока в выходном сечении от осевого направ-
направления (фа):
фс=ф/фрфа. A6)
Величина ф/ рассчитывается с помощью методов теории по-
пограничного слоя сжимаемого газа (см. гл. VI).
1) Evvard J. Difiusers and nozzels / High speed aerodynamics and
jet propulsion.— 1957.— V. 7.— P. 638—654. Русский перевод: М.: ИЛ, 1959.
2) Ahlberg J., Hamilton S., Migdal D., Nil son E. Trunca-
Truncated perfect nozzles in optimum nozzles design / ARS J.—1961.—№ 5.—
P. 614—620.
442 ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
Величина фр в конических соплах зависит главным образом
от относительного радиуса кривизны стенки сопла в области
горла; соответствующие опытные данные Рао1) хорошо аппрок-
аппроксимируются степенной формулой
(^J6; A7)
здесь к — показатель адиабаты (в опытах к = 1,23 и 1,4), <ЙКР —
радиус критического сечения сопла (горла), г — радиус кривизны
стенки сопла в области горла. В опытах Рао отношение R^/r
изменялось от 0 до 1.
Коэффициент фа для равномерного конического потока на сре-
срезе сопла определяется по среднему значению проекции скорости
на ось сопла
1 + cos а
Фа = § '
Здесь а — полуугол раствора сопла.
Уменьшая а, т. е. удлиняя сопло (при неизменной величине
FJFKV), можно уменьшить значение фа; при этом растет поверх-
поверхность трения, т. е. увеличивается значение ф^; оптимальное ко-
коническое сопло, в котором суммарный коэффициент скорости фс
достигает максимума, получается при а = 8—12°.
Если имеются потери, то максимальная тяга достигается не
при расчетной форме сопла, а при некотором недорасширении
газа, так как небольшое сокращение выходного импульса в этом
случае с избытком компенсируется выигрышем за счет умень-
уменьшения потерь.
В хорошем соответствии с опытными данными находится сле-
следующая аналитическая зависимость оптимальной степени расши-
расширения сопла от коэффициента скорости2):
где Fa, FHp — площади выходного и критического сечений, ра —
давление на срезе сопла, р* — полное давление на входе в сопло,
фс — коэффициент скорости сопла, фкр — коэффициент скорости
с учетом потерь только в сужающейся части сопла. При фс =
= фкр = 1 формула A9) тождественна с формулой D) гл. IV,
1) Rao G. V. Evaluation of conical nozzle thrust coefficient II ARS J.—
1959.- № 8.— P. 606-607.
2) Durham F. P. Thrust characteristics of underexpanded nozzles //
Jet. Prop.—1955.—№ 12.—P. 696—700. Формула A9) пригодна, если нет
ограничений на длину сопла.
§ 2. ФОРМЫ СОПЕЛ
443
полученной для идеального сопла, в чем можно убедиться, под-
подставив в A9) зависимость F).
На режимах истечения из сопла с большим перерасширением,
когда на срезе сопла устанавливается мостообразный скачок
(рис. 8.10), отношение давлений на срезе pjpa может оказаться
выше критического для пограничного слоя сопла при его взаимо-
взаимодействии с косым скачком уплотнения ab. В этом случае возни-
возникает отрыв пограничного слоя
от стенки и система скачков
смещается внутрь сопла в се-
сечение а\ где скорость меньше
(Xs<ha) и давление перед
скачками выше (р8 > Ра), чем
в сечении а; при надлежащем
уменьшении отношения давле-
давлений в КОСОМ скачке Рис. 8.10. Истечение из сопла Лава-
ля при сильнОхМ перерасширении,
^ ^н abc — мостообразный скачок на сре-
^ р зе, а' — скачок внутри сопла, вызы-
а вающий отрыв потока
система стабилизируется и про-
происходит истечение с отрывом от стенки со сверхзвуковой ско-
скоростью, меньшей, чем на расчетном режиме. За местом отрыва
давление на стенке внутри сопла увеличивается, приближаясь
у среза сопла к атмосферному, в связи с чем тяга получается
выше, чем на режиме полного перерасширения, когда в выход-
выходном участке сопла господствует разрежение (см. § 2 гл. IV).
Расчет отрыва потока в соплах представляет собой трудную
задачу. Экспериментальное изучение этого явления позволило
получить следующую обобщенную зависимость1):
г расч
/расч
B0)
Здесь ротр — полное давление, при котором происходит отрыв,
Ррасч— полное давление на расчетном режиме. Только при сме-
смещении системы скачков к зоне с числом Маха М < 1,3 (см. § 8
гл. VI) отрыв пограничного слоя прекращается и система вырож-
вырождается в скачок, близкий к прямому, за которым устанавливает-
устанавливается дозвуковое диффузорное течение вплоть до среза сопла.
§ 2. Формы сопел
На рис. 8.7 показано сопло Лаваля, составленное из двух ко-
конусов, соединенных горловиной, которая описана дугой окруж-
окружности. Такие сопла применяются при не очень больших сверх-
l) Ash wood P. F., Higgins D. G. The influence of design pres-
pressure ratio and divergence angle on the thrust of convergent-divergent propel-
propelling nozzles / ARC СР.— 1957.— № 325.
444
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
звуковых скоростях истечения (М>3). Рекомендуется боковые
углы сужающейся части сопла брать в пределах 15—30°, рас-
расширяющейся части — в пределах 5—8°; радиус кривизны стенки
горловины должен быть не меньше диаметра критического сече-
сечения. При этих условиях такое конусное сопло дает (по экспери-
экспериментальным данным) уменьшение импульса в сравнении с соп-
соплами специального профиля не более чем на 1—2 %.
Для получения равномерного параллельного потока (приме-
(применительно к сверхзвуковым аэродинамическим трубам и реактив-
реактивным аппаратам с очень большой скоростью истечения) поль-
пользуются соплами со специально профилированными стенками, для
/г k
Рис. 8.11. Схема построения контура сопла
построения которых применяются методы характеристик или
функциональных рядов *).
Приведем простой геометрический метод расчета сопла2),
дающий контуры, очень близкие к оптимальным. Горловина та-
такого сопла описывается двумя окружностями; дозвуковая
часть — радиусом 1,5 Дф и сверхзвуковая часть — радиусом
0,4i?Kp, где i?KP — радиус критического сечения (рис. 8.11).
К отрезку дуги радиуса 0,4i?Kp под заданным углом 0^ к оси
сопла проводится касательная NQ до пересечения с отрезком
Qa, проходящим через срез сопла и наклоненным к оси под за-
заданным углом 0а (в случае аэродинамической трубы 0в = О).
Отрезки NQ и Qa разбиваются на равное число участков, при-
причем точки деления линии Qa соединяются с одноименными точ-
!) Кацкова О. Н., Наумова И. Н., Шмыглевский Ю. Д.,
Ш у л и ш и н а Н. П. /I Опыт расчета плоских и осесимметричных сверх-
сверхзвуковых течении газа методом характеристик.—М.: ВЦ АН СССР, 1961.
2) R а о G., Approximation of optimum thrust nozzle contour / ARS J.—
I960.—№ 6.—P. 561.
§ 2„ ФОРМЫ СОПЕЛ
445
ками деления линии NQ; огибающая полученной сетки прямых
образует искомый контур сопла.
На рис. 8.12 приведены графики для определения углов на-
наклона QN (сплошные линии) и 0а (штриховые линии) по задан-
заданным значениям относительной длины сопла L/i?Kp и относительно-
относительного радиуса выходного R
сечения RJRKp. О каче- т!
стве описанного геомет-
геометрического способа по-
построения сопел можно
судить по такому при-
примеру: максимальное ли-
линейное отклонение кон-
контура от оптимального,
рассчитанного по точ-
точной методике, для соп-
сопла Ra = 5i?KP, L = 12Якр
составляет 0,03i?Kp.
Контур предельно
короткого сопла опреде-
определяется путем смеще-
смещения точки N (рис. 8.11)
в критическое сечение
10 11 12 13 14 15 1S 17 18 19 20 j-
Рис. 8.12. Зависимость углов QN (сплошные
линии) и 0а (штриховые линии) от относи-
относительных значений длины и радиуса на срезе
сопла
(«угловое сопло»); угол 8* выбирается так, чтобы увеличение
числа Маха в течении Прандтля — Майера (около точки N)
происходило до значения числа Маха на срезе сопла.
Большой практический интерес представляет сопло с цен-
центральным телом, принципиальная схема которого дана на рис. 8.13.
В таком сопле газ течет по
кольцевому каналу (между
центральным телом и обе-
обечайкой) ; критическое сече-
сечение может регулироваться
либо продольным перемеще-
перемещением центрального тела, ли-
либо поворотом створок на обе-
обечайке. На рис. 8.14 пред-
представлены два типа сопла с Рис- 8-13. Схема сопла с центральным
центральным телом: а) с ча- телом: 1~ центральное тело, 2 — обе-
стичным внутренним и б) с ча"Ка' 3 ~ Щ^К"Ъ^Г* *~
чисто внешним расширением
газа. В первом случае от критического сечения до сечения А
сверхзвуковая струя расширяется в канале, а начиная от точки
А, внешняя граница расширяющейся струи является свободной.
Если угловая точка О сверхзвуковой части сопла помещается в
критическом сечении, то отходящие от нее в виде пучка харак-
характеристики (первое семейство) отражаются от обечайки, а отра-
446
ГЛ ЛГ1П. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
женные характеристики (второе семейство) падают на стенки
центрального тела.
Поток поворачивается к оси симметрии, пересекая характе-
характеристики первого семейства, а затем возвращается к первона-
первоначальному направлению, пересекая характеристики второго се-
семейства.
Профиль центрального тела подбирается таким образом, что-
чтобы в точке падения любой характеристики направление потока
за ней совпадало с на-
КР А • гг правлением стенки. За
крайней характеристикой
АВ газ течет равномерно
и прямолинейно.
В сопле с чисто внеш-
внешним расширением (рис.
8.14,6) критическое сече-
сечение и угловая точка тече-
течения расположены на срезе
обечайки.
Расширение газа при
этом является односторон-
односторонним, а критическое сече-
сечение наклонено к оси на
угол б, равный углу пово-
поворота газового потока око-
около точки А при разгоне
от критической скорости
(М=1) до расчетного
значения числа Маха (М^) для данного отношения давлений.
Полная длина выступающей за обечайку (хвостовой) части цент-
центрального тела определяется точкой пересечения последней ха-
характеристики АВ с осью. Опыты показывают, однако, что хво-
хвостовая часть центрального тела может быть без заметного сни-
снижения тяги укорочена на 30 -f- 50 % •
В критическом сечении сопла, выполненного по второй схеме
{рис. 8.14, б), обечайка должна быть параллельна стенке цен-
центрального тела; это приводит к дополнительному лобовому со-
сопротивлению в связи с потерями на внешнее обтекание сходя-
сходящейся части обечайки.
При не очень больших расчетных значениях числа Маха
(Ма ^ 2) центральное тело можно делать коническим.
Сопла с центральным телом получаются значительно короче
обычных сопел Лаваля и в отличие от последних дают очень не-
небольшие снижения относительного импульса при давлениях зна-
значительно ниже расчетного (из-за отсутствия стенок в сверхзвук
ковой части не происходит перерасширения газа).
Рис. 8.14. Схемы сопел с центральным
телом: а) с угловой точкой при смешан-
смешанном расширении, б) с чисто внешним
расширением
§ 2„ ФОРМЫ СОПЕЛ
447
На рис. 8.15 приведены опытные данные Пирсона1) об изме-
изменении относительной величины выходного импульса / при откло-
отклонении от расчетного режима \Ра/Рн = 8) для сопла Лаваля и
сопла с центральным телом (штриховая линия).
Расчетную степень расширения сопла с центральным телом
можно определять по отношению площади сечения а — а
I
го
0,9
0,8
7,0 2,0 4,0 6,0 8,010 20
2
д—д--.
7
1
fern
*—
40 60 80тф^-
Рис. 8.15. Сравнение характеристик сопла Лаваля A) и сопла с централь-
центральным телом B)
(рис. 8.14) цилиндрической поверхности, имеющей диаметр вы-
выходного сечения обечайки, к площади критического сечения.
В случае плоского сопла контуром центрального тела явля-
является линия тока течения Прандтля — Майера (около выпуклого
угла) при плоской звуковой линии (рис. 8.14, б).
В случае осесимметричного сопла контур центрального тела
отыскивается по методу характеристик. Однако при укороченной
хвостовой части контур осесимметричного центрального тела бли-
близок к линии тока плоского течения.
Известна схема сопла с центральной вставкой (рис. 8.16),
у которого критическое сечение также кольцевое, но расширение
сверхзвукового потока происходит в нем с поворотом около на-
наружной стенки, а не центрального тела. За центральной встав-
вставкой А образуется полость со свободной границей, размеры кото-
которой зависят от числа Маха на выходе из сопла (с увеличением
числа М полость сокращается).
Большое практическое значение, особенно для ТРД, имеет
эжекторное сопло (рис. 8.17), в котором продукты сгорания из
двигателя вытекают через простое сужающееся сопло, помещеп-
l) Krase W. H. Performance analisysis of plug nozzles for turbojet and
rocket exhaustes / Paper ASME.— 1958.— A248, № 58.
448
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
иое внутрь соосной с ним наружной обечайки, имеющей спе-
специальный профиль (рис. 8.17, а) или форму цилиндрического
кольца (рис. 8.17, б). На срезе внутреннего сопла (сечение 1—1)
устанавливается критическая скорость, и если давление здесь
выше окружающего, то центральная струя внутри эжектора рас-
расширяется, стесняя проходные сечения эжектпруемого ею по-
потока воздуха, который попадает в кольцевой канал из промежу-
промежуточной ступени компрессора или из атмосферы.
2, Л
в
Рис. 8.16. Режимы течения с
центральной вставкой: а)
у земли; б) на средних высо-
т.ах; в) на больших высотах
Рис. 8.17. Схемы эжекторных со-
сопел: а) с профилированной обе-
обечайкой, б) с цилиндрической обе-
обечайкой
Скорость эжектируемого потока обычно меньше звуковой,
поэтому он в выходном участке эжектора ускоряется. В некото-
некотором сечении 2—2 (рис. 8.18) граница двух потоков становится
параллельной оси сопла; это сечение расположено тем дальше
от среза внутреннего сопла, чем больше избыток давления в нем.
Поперечный размер внутренней струи увеличивается, а эжекти-
руемой — уменьшается с ростом избытка давления во внутрен-
внутреннем сопле. Конфигурации двух потоков при разных значениях
избытка давления показаны на рис. 8.18. Режим работы эжек-
эжектора, при котором вторичный поток разгоняется (в сечении 2—2)
до звуковой скорости, называется критическим (рис. 8.18, в);
если центральная струя расширяется настолько, что заполняет
все выходное сечение эжектора (рис. 8.18, г), то наступает ре-
режим запирания, когда расход эжектируемого газа равен нулю.
§ 2. ФОРМЫ СОПЕЛ
449
Для регулирования эжекторного сопла можно устаповить по-
поворотные створки как на внутреннем сопле, так и на внешней
обечайке (рис. 8.19).
1\\2 1\ 2\
Рис. 8.18. Схемы течения в эжекторном сопле на нерасчетных режимах:
а) давление на срезе внутреннего сопла равно атмосферному, б) небольшой
избыток давления на срезе внутреннего сопла, в) критический режим эжек-
эжектора, г) режим запирания эжектора
Тяга эжекторного сопла больше, чем у простого сужающегося
сопла, так как давление со стороны эжектируемого газа на стен-
стенку внутреннего сопла выше атмосферного. Сечение обечайки
0,4
0,2
/
j
1
0,04 0,03
0J5 ^
Рис. 8.19. Эжекторное сопло с
регулируемыми сечепиями
горловины и среза
Рис. 8.20. Характеристика эжектор-
эжекторного сопла
эжекторного сопла должно быть таким, чтобы на расчетном ре-
режиме расход эжектируемого газа уменьшался до минимально не-
необходимого для целей охлаждения стенки.
29 г. Н. Абрамович, ч 1
450
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
Снижение избытка давления в эжекторном сопле ведет
к уменьшению скорости внутренней струи в сечении 2—2, чем
предотвращается возможность перерасширения газа и соответ-
соответствующей потери тяги (по сравнению с соплом Лаваля).
Типичная характеристика эжекторного сопла ТРД, т. е. зави-
зависимость между коэффициентом эжекции /сэж = Ga7K/GBa и отноше-
отношением полного давления п#
внутренней струи к атмос-
атмосферному, изображена на
рис. 8.20. Для того чтобы 7,0
эжекторное сопло работало
в наивыгоднейших услови-
условиях, необходимо регулиро-
регулировать расход вторичного 6,0
воздуха (увеличивая при
малых скоростях полета
коэффициент эжекции до
значений порядка /сэж =• 5,0
= 0,1 и снижая его при
больших скоростях до ми-
минимума порядка /сэж =
4,0
НА
0,9
0,8
OJ
0,6
0,5
0,4.
\
\
3,0
2,0
го.
/
J
Л
^-=1,73
у
CL
/
а
п
/
а
о
с
/
/
4,6%
9,2%
18,6%
QfffJO/
oo,U7o
О 0,5 1,0 1,5 2,0 Мо
Рис. 8.21. Отношение полного
давления вторичного воздуха
к полному давлению во вход-
входном канале двигателя для
оптимальных условий в
торном сопле
2,0 3,0 4,0 5,0 6,0
• Эксперимент
7,0 40 9,0
Теория
Рис. 8.22. Характеристики эжекторного
сопла (при Fa = 1,73 и / = 0,6)
= 0,01—0,02). Отношения полного давления эжектируемого воз-
воздуха в сопле к полному давлению во входном канале двигателя
\Рэж/рд)ч которые можно рекомендовать для получения оптималь-
оптимальных режимов работы эжекторного сопла при разных скоростях
полета (или Мо), приведены на рис. 8.21.
§ 2. ФОРМЫ СОПЕЛ
451
Оптимальная относительная длина эжекторного сопла, обес-
обеспечивающая наименьшие потери тяги на расчетном режиме1),
7 =-
4-1,2,
где I — расстояние от среза внутреннего сопла до среза обечай-
обечайки, Jf?T — радиус критического (выходного) сечения внутренне-
внутреннего сопла.
Тяга эжекторного сопла равна суммарному импульсу двух
струй на срезе обечайки. Параметры струй при цилиндрической
обечайке определяются из условий со-
сохранения расхода и импульса (без уче-
учета трения) между сечениями 1 ж 2
срезов внутреннего сопла и обечайки
(см. § 6 гл. VII и § 10 гл. 1Х)в пред-
предположении об отсутствии смешения
струй. Эта задача имеет два решения,
из которых выбирают то, при котором
внутренняя струя в сечении 2 являет-
является сверхзвуковой, а эжектируемая —
0,4
Рис. 8.23. К определению
оптимальных значений ко-
коэффициента эжекции
Рис. 8.24. Эжекторное сопло с регули-
регулируемыми створками внутреннего сопла
и обечайки: 1 — створка центрального
сопла, 2 — створка обечайки
дозвуковой или звуковой. О том, в какой мере данные такого
расчета соответствуют экспериментальным, можно судить по
рис. 8.22, где по оси ординат отложено отношение полных давле-
давлений двух потоков, а по оси абсцисс — отношение полного давле-
давления внутренней струи к атмосферному. Приведенные данные от-
относятся к случаю, когда отношение площадей на срезе обечайки
Fa и внутреннего сопла FKp составляет 1,73. Переменным парамет-
параметром для кривых служит произведение &эж ]/ (Г*/Г*), где Т\ и
Та — температуры торможения наружной и внутренней струй.
Горизонтальные участки кривых отвечают критическим режи-
режимам сопла.
l) Person H., H oil i day J., Smith S. A theory of the cylindrical
ejector supersonic propelling nozzle / RAS.— 1958.— V. 62, № 573, 574.
29*
452
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
Потери в эжекторном сопле достигают минимума, когда от-
отношение скоростей двух струй на срезе внутреннего сопла равно
отношению их полных энтальпий 1).
Примерный характер зависимостей тяги ТРД от коэффици-
коэффициента эжекции при разных значениях числа Мн полета показан
на рис. 8.23. Штриховая линия соединяет режимы максимумов
тяги. Ввиду пологости кривых Р(кэт) можно выбирать значения
коэффициентов эжекции значительно ниже оптимальных, что
позволяет уменьшить расход вторичного воздуха.
На рис. 8.24 изображена схема эжекторного сопла с регули-
регулируемыми створками центрального сопла, обеспечивающими плав-
плавный переход сужающегося канала к соплу Лаваля, и соответ-
соответствующим регулированием створок профилированной обечайки.
а 5
Рис. 8.25. Ирисовое сопло. Режимы форсажный (а) и крейсерский (б)
Такое сопло позволяет осуществить широкий диапазон регулиро-
регулирования расхода газа при относительно малых потерях тяги.
Нашли применение сопла, названные «ирисовыми» (рис. 8.25).
Регулируемые створки ирисового сопла перемещаются в продоль-
продольных направляющих, расположенных в конце форсажной камеры
двигателя. В крайнем выдвинутом положении (рис. 8.25, а)
створки создают сужающийся канал плавной формы. В убран-
убранном положении рис. 8.25, б они образуют сопло Лаваля с отно-
относительно небольшим расширением на выходе (FJFKV ~ 1,3—1,4).
При дозвуковых режимах полета потери тяги в ирисовом сопле
вдвое меньше, чем в эжекторном, а на максимальной сверхзву-
сверхзвуковой скорости полета (при включенной форсажной камере)
вдвое больше (из-за недостаточного расширения сверхзвуковой
части сопла).
§ 3. Дозвуковые диффузоры
Рассмотрим диффузор двигателя, установленного на движу-
движущемся самолете. Пусть скорость самолета wa, а скорость звука,
отвечающая температуре атмосферы, аК. Введем обозначения:
FB — площадь поперечного сечения струи на бесконечности пе-
J) Knox R., The optimized ejector nozzle thrust augmenter // J. ASS.—
1962.— № 4.— P. 470—471.
§ 3. ДОЗВУКОВЫЕ ДИФФУЗОРЫ
453
ред двигателем, рн — плотность воздуха вдалеке перед двигателем,
Рв — давление в атмосфере. Значения площади, скорости, давле-
давления во входном отверстии диффузора обозначим Fe, wei pe- Значе-
Значения тех же величин в конце диффузора РД1 и;д, рд.
Работа диффузора зависит от отношения скорости полета
к скорости во входном его отверстии. Рассмотрим сначала режим
шн < ан, т- ©• полет с дозвуковой скоростью. Расход воздуха че-
через двигатель и, следовательно, через диффузор GB кг/с.
Можно представить себе такой случай, когда струя входит
в диффузор без изменения своей конфигурации. Площадь по-
поперечного сечения струи на бесконечности перед двигателем Fn
при этом равна площади входного от-
отверстия диффузора Fe:
Вообще же форма струи на входе в
двигатель определяется отношением
FJFe. В приведенном выше случае
Fn = Fe, следовательно, преобразования
скорости и давления перед диффузо-
диффузором нет (рис. 8.26, б):
We = WB И /?в = рп.
Если расход воздуха через диффу-
диффузор будет увеличиваться, то струя из-
изменит свою форму, как показано на
рис. 8.26, в. Изменение формы струи
сопровождается преобразованием ско-
скорости и давления:
We > М>н, Ре < Ря.
При уменьшении расхода воздуха
струя как бы образует диффузор еще в
атмосфере (перед двигателем) в связи
с уменьшением скорости и повышением
давления (рис. 8.26, а).
При постоянном расходе воздуха
форма струи перед двигателем зависит
от величины входного отверстия диффузора. Изменяя размеры
диффузора, мы можем получить любой из трех приведенных ре-
режимов работы. Для рабочего процесса двигателя выгоден
такой случай, когда поток подтормаживается еще перед диф-
диффузором, так как торможение струи перед диффузором идет
без каких-либо потерь, и собственное сопротивление диффузора
уменьшается вследствие понижения скорости на входе. Необхо-
Необходимо, однако, заметить, что, кроме внутренних потерь, следует
Рис. 8.26. Возможные кон-
конфигурации струи перед
диффузором
454
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
учитывать также внешнее лобовое сопротивление двигателя, уве-
увеличивающееся с укорочением диффузора. Объясняется это тем,
что при растекании потока перед носком двигателя струи под-
подходят к его поверхности под большими углами атаки и может
образоваться срыв на внешней поверхности носка (рис. 8.27).
Для удовлетворения этим противоречивым требованиям необхо-
необходимо отыскать оптимальные усло-
условия работы входного участка дви-
двигателя.
Опыты показывают, что для
дозвукового воздушно-реактивного
двигателя оптимум лежит вблизи
режима
we « 0,5м?н.
Если бы в диффузоре потери
отсутствовали, газ в любоом его
сечении имел бы одно и то же
полное давление, равное (при до-
дозвуковых скоростях полета) пол-
полному давлению в набегающей
струе воздуха. Наличие потерь на-
нарушает это равенство, и полное давление в конце диффузора всег-
всегда ниже, чем в начале:
* . *
Р <Ре-
Статическое давление вдоль диффузора, наоборот, увеличивается
за счет уменьшения скорости.
Величину гидравлических потерь в диффузоре удобно выра-
выразить в долях скоростного напора в широком его сечении:
Рис. 8.27. Срыв струи при боль-
большом входном отверстии диффу-
диффузора
Ре — Рц =
2 '
B1)
где ?д — коэффициент гидравлического сопротивления диффузо-
ра. Обычно потери в диффузоре относительно невелики: —*¦< 1.
Ре
Поэтому плотность заторможенного газа в диффузоре можно
считать практически постоянной: Рд«р*. Приведем формулу
B1) к безразмерному виду:
к—
Рн
здесь
¦2
и
§ 3. ДОЗВУКОВЫЕ ДИФФУЗОРЫ 455
После соответствующих преобразований имеем
а - р« _ 1 к г ю»
Заметим, что wja^v = Лд представляет собой приведенную ско-
скорость в конце диффузора. В результате получим следующее вы-
выражение для коэффициента сохранения полного давления в диф-
диффузоре:
^д = 1-^1^д. B2)
Сопротивление диффузора слагается из потерь на трение и
на вихреобразования. Вихревые потери вызываются отрывом по-
пограничного слоя от стенок диффузора, причины которого объяс-
объяснены в гл. VI; они зависят от угла раствора диффузора и играют
главную роль. При малых углах раствора диффузора гидравли-
гидравлические потери невелики, но по мере увеличения утла они воз-
возрастают. С ростом угла раствора зона вихрей перемещается от
конца диффузора к его началу и при больших углах вся стенка
покрыта вихревой областью.
Многочисленные эксперименты приводят к заключению, что
вихревые потери в диффузоре можно оценивать как смягченное
сопротивление удара (в сравнении с внезапным расширением
канала)
Ар* = г|)А^уд, B3а)
где потери удара
Здесь г|) — коэффициент полноты удара (г|)<1). Опыты пока-
показали *), что коэффициент полноты удара <ф является функцией
одного только угла раствора диффузора а.
Соответствующая зависимость для прямолинейного диффу-
диффузора с круглым поперечным сечением дана на рис. 8.28. Боль-
Большим углам раствора (а>40°) соответствует <ф ^ 1, т. е. смяг-
смягчения удара нет. При угле а = О имеем я|> = 0, т. е. удара нет.
Максимальное значение коэффициента полноты удара (г|э = 1,2)
достигается при угле а = 60°. В этом случае потери даже боль-
больше, чем при внезапном раскрытии канала, когда г|> = 1. Объ-
Объясняется это тем, что вихревая зона в прямом угле устойчива,
в то время как при наклонной стенке (а « 60°) вихревая зона
периодически уносится потоком. Таким образом, дополнительные
!) Абрамович Г. Н. Аэродинамика местных сопротивлений / Тру-
Труды ЦАГИ.— 1935.— Вып. 211.
456
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
потери при таких углах обусловливаются затратами энергии на
возобновление вихревой зоны.
Обычно применяют диффузоры с углами а = 6—8°. Таким
значениям углов раствора соответствуют значения i|) = 0,ll—
ОД5. В этой области не наблюдается видимого отрыва струй от
стенки диффузора.
Ф
1,2
0,8
0,6
0,4
о zo°
/
»
/
/
/
/
/
/
п
/
/
J
/
—¦-
—
во° во" юов шв № Warn"
Рис. 8.28. Зависимость коэффициента полноты удара от угла раствора диф-
диффузора круглого сечения
Если пренебречь изменением плотности воздуха в пределах
диффузора, то имеем
подставляя это равенство в B3а), получим
= чЬ -=5-1
B36)
В качестве примера вычислим коэффициент потерь для диф-
диффузора с соотношением поперечных сечений FJFe = 3 при угле
раствора а = 8°. Можно принять для этого случая (с учетом
трения) ф = 0,2. Тогда ?д = 0,2 • 4 = 0,8, од = 1 — 0,44А,?. Приве-
Приведенная скорость в конце диффузора дозвукового воздушно-реак-
воздушно-реактивного двигателя обычно бывает порядка Яд = 0,2 — 0,4. Тогда
Од = 0,98 -*- 0,94.
На расчете сопротивления трения мы не останавливаемся, так
как он достаточно подробно освещается в гл* VI.
Сопротивление безотрывного диффузора можно заметно сни-
снизить, если его стенке придать колоколообразную форму
(рис. 8.29) вместо прямолинейной. Теоретические и эксперимент
§ 3. ДОЗВУКОВЫЕ ДИФФУЗОРЫ
457
тальные исследования показали, что наиболее эффективен диф-
диффузор с «предотрывным» состоянием пограничного слоя во всех
поперечных сечениях. Идея предотрывного диффузора высказы-
высказывалась Л. Г. Лойцянским еще в тридцатых годах. Теоретическое
выражение для контура плоского предотрывного диффузора по-
получил впервые Г. М. Бам-Зеликович, детальное теоретическое и
Рис. 8.29. Колоколообразный
«предотрывный» диффузор.
6 — толщина пограничного
слоя
экспериментальное исследование предотрывных диффузоров раз-
различной формы (плоских, осесимметричных, кольцевых, радиаль-
радиальных) выполнено А. С. Гиневским и Л. А. Бычковой1). Форма
стенки предотрывного диффузора подбирается исходя из того,
чтобы в каждой ее точке состояние пограничного слоя было
близким к отрывному, при котором напряжение трения на стенке
равно нулю. В случае турбулентного пограничного слоя (см.
§ 6 гл. VI) несжимаемой жидкости это означает, что параметр
&\2 __ б dp
~~ ри26 dx
должен быть нем!ного меньше значения, отвечающего отрыву
(ф <фотр). Из работы Л. А. Бычковой следует, что для плоского
диффузора можно принять к = 0,225, а для осесимметричного
диффузора /с = 0,325. Расчет скорости потока и давления подли-
подлине диффузора ведется из условий сохранения массы и импульса
при постоянном давлении в каждом поперечном сечении. Профиль
скорости в пограничном слое при предотрывном режиме (т«, = 0)
получается в форме и/и6 = (у/бH'5, где б — толщина погранич-
пограничного слоя, иь — скорость на его границе; толщина вытеснения
для данного профиля скорости б* = 0,333 б; толщина потери им-
импульса б** = 0,167 б, т. е. формпараметр Н = б*/б** = 2.
Расчет пограничного слоя ведется по уравнению E9) гл. VI
при т„ = 0.
1) Гиневский А. С, Бычкова Л. А. Аэродинамические характе-
характеристики плоских и осесимметричных диффузоров с предотрывным состоя-
состоянием турбулентного пограничного слоя / Тепло- и массоперенос. Т. 1.—
М.: Энергия, 1968; Бычкова Л. А. Экспериментальное исследование диф-
фузорных каналов с предотрывным турбулентным течением / Ученые
записки ЦАГИ.—1970.— Т. 1, № 5; Бычкова Л. А. Аэродинамические
характеристики плоских и радиальных диффузоров с предотрывным тур-
турбулентным пограничным слоем / Промышленная аэродинамика, вып. 30.—
М.: Машиностроение, 1973.
458 ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
В начальном участке диффузора, где имеется невозмущенное
ядро течения, очерченное штриховой линией на рис. 8.29, погра-
пограничный слой не заполняет всего сечения канала (А = 26/й- < 1).
На этом участке и получается колоколообразная форма стенки
предотрывного диффузора.
Для расчета начального участка вводится безразмерное рас-
расстояние от начального сечения диффузора ? == к2 -г-; скорость в
о
ядре в долях от начальной получается
где А* = 260/fe0, а ширина поперечного сечения
В основном участке предотрывного диффузора осуществляет-
осуществляется течение со стабилизированным профилем скорости, так как
здесь пограничный слой заполняет все поперечное сечение кана-
канала. Угол раскрытия канала в основном участке остается постоян-
постоянным и равным а = 2 arctg 0,5 к2 или а « 6° при к = 0,225.
Для расчета куполообразного начального участка осесимме-
тричного предотрывного диффузора в цитированной работе также
получены соответствующие аналитические зависимости. Угол рас-
раскрытия основного участка предотрывного осесимметричного диф-
диффузора получается равным а = 4° при к = 0,325.
Предотрывные диффузоры имеют значительно меньшую дли-
длину, чем безотрывные диффузоры с прямолинейной формой (на
всей длине), и при этом потери в первых получаются замет-
заметно ниже.
Остановимся теперь на диффузорах с заведомо отрывным те-
течением жидкости.
Опыты показывают, что в диффузорах с вогнутыми криволи-
криволинейными боковыми стенками при больших углах раскрытия ги-
гидравлические потери могут быть существенно меньше1), чем в
диффузорах с прямолинейными стенками.
Результаты экспериментального определения потерь (вклю-
(включая трение) в плоских диффузорах одной и той же длины прц
постоянном среднем угле раскрытия а = 38° 40', но с разными
очертаниями боковых стенок, приводятся ниже. На рис. 8.30
представлены контуры испытывавшихся диффузоров. Первый
контур — прямая, второй — дуга окружности, третий — соответ-
*) Идельчик И. Е. Аэродинамика потока и потери напора в диффу-
диффузорах / Сборник статей по промышленной аэродинамике/Под ред.
К. А. Ушакова.— М.: БНТИ ЦАГИ, 1947.
§ 3. ДОЗВУКОВЫЕ ДИФФУЗОРЫ
459
ствует постоянному градиенту давления по длине диффузора
dp/dx = const, четвертый — постоянному градиенту скорости
dw/dx = const, пятый — построен по формуле
d \
dx[
Ц
Ц—?2
dx 1_
const > О,
где р — безразмерное давление, определяемое из соотношения
Наименьшее значение коэффициента сопротивления ?д = 0,24
получено для диффузоров 3 и 4 с постоянным градиентом давле-
давления и постоянным градиентом скорости. Для диффузора 5 ?д =
= 0,26, для диффузора 2 со стенками, выполненными по дуге
5.
0
Рис. 8.30. Контуры испытывавшихся диффузоров
окружности, получен коэффициент сопротивления ?д = 0,27, а для
диффузора 1 с прямыми стенками ?д = 0,32.
Таким образом, в диффузорах с постоянными градиентами
давления или скорости достигнуто снижение потерь примерно
на 25 % по сравнению с прямым диффузором.
На рис. 8.31 представлены графики зависимости коэффициен-
коэффициента потерь от длины (т. е. от угла а) для диффузоров типа 1 к 3.
У достаточно длинных (близких к оптимальным) диффузоров
этих типов разница в потерях становится малой.
Мы рассматривали сопротивление диффузора в таких усло-
условиях, когда можно пренебрегать влиянием сжимаемости возду-
воздуха, которая, как показывают опыты, начинает сказываться на
величине коэффициента потерь лишь в том случае, если скорость
во входном отверстии диффузора -близка к скорости звука
(Л>07)
460
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
На рис. 8.32 даны графики экспериментальных зависимостей
отношения полных давлений в конце и начале диффузора од =
~Рл/Ре от числа Мв во входном отверстии диффузора1) (при
центральных углах раскрытия а = 4, 6, 8, 10°, диаметре вход-
входного сечения 100 мм и диаметре выходного сечения 222 мм). Рез-
Резкое падение значений сд, наступающее при значениях числа
Рис. 8.31. Зависимость коэффициента потерь от длины диффузора
М, около 0,9, объясняется тем, что на этих режимах в началь-
начальной части диффузора развивается зона сверхзвуковых скоро-
скоростей, замыкающаяся скачком уплотнения, который вносит боль-
большое волновое сопротивление.
Для оценки влияния числа R на сопротивление диффузора
К. С. Сциллард испытывал также геометрически подобные диф-
диффузоры меньшего размера (с диаметром входного отверстия
18 мм). Результаты испытаний диффузоров увеличенного и ма-
малого размеров оказались близкими, что свидетельствует о сла-
слабом влиянии числа R на потери в диффузоре.
Зависимость од = /(Мв) не дает наглядного представления
о влиянии сжимаемости на сопротивление, так как величина ад
изменяется со скоростью даже при постоянном значении коэф-
коэффициента потерь.
^Сциллард К. С. Исследование диффузоров при больших скоро-
скоростях / Технические заметки ЦАГИ.— 1938.— № 160.
§ 3. ДОЗВУКОВЫЕ ДИФФУЗОРЫ
461
Удобной характеристикой потерь при течении сжимаемого
газа в диффузоре является коэффициент
л
B4)
Здесь числитель представляет собой адиабатическую работу, ко-
которую надо затратить, чтобы поднять в идеальном компрессоре
0,375
0,350
43Z5
0,300
0,875
0,850
от
0,800
к „
О 0,1 0,2 0,3 W Ц5 0,6 0,7 0,8 0,3
6й
0,375
U3SO
0.3ZS
0,300
0,675
0.8S0
№5
0,800
О Ц1 02 0J0,? 0,5 0,6 07 ЦвЦЗ 10
бд
0J375
0,950
0,325
0,300
0.875
0,850
0025
0,800
S
N.
3'
\
О 0.1 0,2 Q3 04-OSЦ6 0.7 Q5 п310
0,975
0,350
0,325
0,300
0,875
ЩО
0,825
0,800
/0*
О 0,1 0,2 0,3 ОЛ0,50,50,7'Q8 Цд4,0
Рис. 8.32. Зависимость коэффициента сохранения полного давления в диф-
диффузоре от числа Мв перед диффузором при углах раскрытия а = 4, 6, 8
и 10° (по опытам К. С. Сцилларда)
полное давление в конце диффузора до величины полного дав-
давления в начале диффузора, а знаменатель выражает кинетиче-
кинетическую энергию струи газа во входном отверстии диффузора.
Зависимости ?сж = /(Мв) для четырех диффузоров К. С. Сцил-
Сцилларда, пересчитанные по кривым рис. 8.32, изображены на
рис. 8.33. Как видим, влияние сжимаемости газа на значение
коэффициента потерь начинает сказываться лишь при околозву-
околозвуковых скоростях (Мв>0,7). Некоторое падение кривых ^сш^
462
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
= /(Ме) в области Ме < 0,3, где заведомо немыслимо влияние
сжимаемости, можно объяснить только влиянием числа R, кото-
которое возрастает с увеличением числа Ме.
Описанные опыты Сцилларда проводились на диффузорах с
постоянным отношением площадей выходного и входного сече-
сечений (п = Fa/Fe = 5), причем перед входом в диффузор устанав-
устанавливалось плавное сопло, соединявшееся с входным отверстием
о,з
0,2
0,1
СС=6'
сх
\
— —
1—
- —
шва
1 -.
!=&
и-
— —
——
- I
¦
S
=====
намм
.
——I
-——
/
0,1 OJ, 0,3 O,b Of
US 0,7 0,8 0,$ 1,0
ме
Рис. 8.33, Зависимость коэффициента сопротивления диффузора от числа М#
на входе при углах раскрытия a = 4, 6, § и 10 (по опытам К. С, Сцилларда)
диффузора патрубком постоянного сечения и относительной дли-
длины II de = 1,5. I
Более детальное экспериментальное исследованде диффузоров
с углами раскрытия a = 4, 6, 8, 10 и 14° при отношениях площа-
площадей п = 2, 4, 6, 10, 16 и длинах входного участка l/de = 0, 2, 5Г
Рис. 8.34. Зависимость коэффициен-
коэффициента сопротивления диффузора от| сте-
степени расширения его канала (а — 6;
h = 2d; Me = 0,665) по опытам
Гинзбурга и Идельчика *
10, 20 проведено Я. Л. Гинзбургом и И. Е. Цдеяьчиком1). На
рис. 8.34 изображена зависимость ?(гс), рассчитанная по этим
экспериментальным данным для диффузора а = 6°, l/de = 2 при
%e = 0J (Me = 0,665), и нанесена соответствующая эксперимен-
экспериментальная точка Сцилларда (п = 5).
Рассмотрим теперь работу диффузора ВРД, имеющего обыч-
обычную («дозвуковую») форму, при сверхзвуковой скорости потока
на входе. Перед входом в такой диффузор образуется скачок
1) Гинзбург Я. Л., Идельчик И. Е. Экспериментальное опреде-
определение коэффициентов восстановления давления в конических диффузорах
при больших дозвуковых скоростях и различных условиях на входе //
Ученые записки ЦАГИ.— 1973.— Т. 4, № 3.
§ 3. ДОЗВУКОВЫЕ ДИФФУЗОРЫ 463
уплотнения с криволинейным фронтом (рис. 8.35). В централь-
центральной части, т. е. в той, которую пересекает рабочая струя возду-
воздуха, поступающая внутрь двигателя, скачок должен быть прямым.
Последнее вытекает из того, что рабочая струя сохраняет после
скачка свое первоначальное направление. Таким образом, ско-
скорость в рабочей струе после скачка дозвуковая.
В зависимости от величины входного отверстия диффузора
(Fe) имеет место то или иное соотношение между значениями
скорости после скачка (w\) и на
входе в диффузор (we). Принци-
Принципиально возможны два случая:
а) w\ > wei т. е. поток между
фронтом сказка и входом в диф-
диффузор тормозится;
б) W\ — we, т. е. скорость после
скачка и скорость на входе в диф-
диффузор одинаковы.
Возможен чи такой случай, ког-
когда рабочая струя входит в диффу-
диффузор со сверхзвуковой скоростью,
тогда скачок уплотнения полу- рис g.33. Теневая фотография
чится не перед диффузором, сверхзвукового потока перед про-
а внутри неяо. Режим wi<we, стьш диффузором
т. е. ускорение потока между фрон-
той скачка и, входом в диффузор, на практике не реализуется.
Итак, в двигателе с простым диффузором торможение вхо-
входящей cipyi* ?фи сверхзвуковой начальной скорости начинается
с прямого езЦчка уплотнения. Потери в скачке и параметры по-
потока за еш^ком определяются по формулам, приведенным
в i^. Ш.
Шшдаьку, поток в простом диффузоре является дозвуковым
да>*е щш сверхзвуковой скорости полета (A,i < 1, Яе>1), гид-
ращи^еские потери в канале такого диффузора можно рассчи-
рассчитывать по формулам B2) и B3) настоящей главы.
Если для случая дозвуковой скорости полета потери полного
давления при торможении рабочей струи определялись только
внутренним сопротивлением диффузора <тд, то для случая сверх-
сверхзвуковой скорости эти потери включают также волновое сопро-
сопротивление Оп, т. е. определяются произведением коэффициентов
сохранения полного давления в прямом скачке и в диффузоре
(cnaH).
В воздушных трактах реактивного двигателя встречаются ме-
места, в которых изменяется направление потока,— колена, отво-
отводы. Потери при повороте связаны с отрывом потока от стенки и
последующим выравниванием поля скорости. В колене на стыке
двух участков разного направления имеются острые кромки, от
которых происходит отрыв потока. В отводе направление потока
464
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
й*
г
I/
//
1
изменяется плавно, но у внутренней стенки газовый поток сна-
сначала ускоряется, а при переходе к новому прямому направле-
направлению — замедляется; на этом втором участке возникает диффузор-
ного характера отрыв погранично-
пограничного слоя.
Сопротивление колен и отво-
отводов, а также других местных со-
сопротивлений, главным образом в
условиях несжимаемой жидкости,
изучается в курсах гидравлики.
Подробный справочник по
гидравлическим сопротивлениям
опубликован И. Е. Идельчиком 1).
Мы остановимся лишь на влия-
влиянии сжимаемости газа на сопро-
сопротивление при повороте потока. На
рис. 8.36 нанесены эксперимен-
экспериментальные данные Н. Н. Круминой2)
для зависимости отношения коэф-
коэффициентов сопротивления от при-
приведенной скорости перед поворо-
поворотом в колене C) и отводе A, 2).
В несжимаемой жидкости |зо =
= 1,05; Ъо = 0,3 при ro/d = 0,75
скорости на сопротивление при и ?20 = 0,2 при ro/d = 1; |ю = 0,1
при ro/d = 2,5. Влияние сжимае-
сжимаемости газа на потери в очень
плавном отводе не проявляется, а в колене становится наи-
наиболее значительным, особенно при Хвх > 0,4. Опыты ве-
велись при R = —>2»105,т. е. в области, где влияние вязкости
несущественно.
§ 4. Сверхзвуковые диффузоры
Применяя диффузоры специальной формы, можно осуще-
осуществлять ступенчатое торможение сверхзвукового потока посред-
посредством различных систем косых скачков уплотнения. Так как за
обычным плоским косым скачком скорость остается сверхзвуко-
сверхзвуковой, то для полного торможения потока нужно за последним ко-
косым скачком поместить прямой скачок или особый участок
криволинейной ударной волны, элементами которой являются
«сильные» косые скачки, переводящие поток в дозвуковой.
1) Идельчик И. Е. Справочник по гидравлическим сопротивле-
сопротивлениям.— 2-е изд.— М.: Машиностроение, 1975.
2) Ульянов И. Е., К р у м и н а Н. Н., В а к а р Н. В. Проектирова-
Проектирование воздуховодов самолетных силовых установок.— М.: Машиностроение,.
1979.
0,8
О 0,2 0,4 Абх
Рис. 8.36. Влияние приведенной
[ на сопротивле!
повороте потока
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ 465
На рис. 3.12 сильные косые скачки отвечают верхним ветвям
кривых а = /(сэ), лежащим выше максимумов, причем фронт
сильного косого скачка располагается по отношению к набегаю-
набегающему потоку под углом не менее 60°. Только при этом условии
(а>60°) можно получить за фронтом косого скачка дозвуковую
скорость потока (Mi < 1).
Различные комбинации скачков исследованы в работе
Г. И. Петрова и Е. П. Ухова1). Рассмотрим вопрос о сверхзву-
сверхзвуковом диффузоре, используя результаты этой работы. Обратимся
сначала к наиболее простой схеме сверхзвукового диффузора,
в которой торможение потока осуществляется посредством двух
скачков: косого и прямого. В косом скачке происходит умень-
уменьшение сверхзвуковой скорости, а в прямом скачке — пониженная
сверхзвуковая скорость переводится в дозвуковую.
Обозначим приведенную скорость невозмущенного потока че-
через Ян, приведенную скорость за косым скачком через Х\ и при-
приведенную скорость за прямым скачком через Яп = 1/Ль Как было
установлено выше, косой скачок уплотнения представляет собой
прямой скачок в отношении нормальных к его фронту состав-
составляющих скорости. Поэтому расчет первого косого скачка системы
можно произвести по формулам для прямого скачка. Формулы
C8), D0) и D3) гл. III дают возможность рассчитать изменение
полного давления в косом скачке уплотнения.
Теперь, пользуясь выражениями B1) и B4) гл. III, нетрудно
определить изменение статического и полного давлений в пря-
прямом скачке, расположенном за косым скачком. Для этого нужно
только учесть, что приведенная скорость перед прямым скачком
есть Ль тогда
B5)
Общее изменение полного давления в сверхзвуковом диффузор^
содержащем косой и прямой скачки, определяется произведени-
произведением коэффициентов сохранения полного давления:
оКап = ^-. B6)
При изменении угла а между фронтом косого скачка и направ-
направлением невозмущенного потока отношения значений полного и
статического давлений за и перед системой скачков изменяются.
Л1 Л + 1
&— 1 2 '
1 Л + 1 *i
p* 2
1-
1-
Ar— 1 9
k-\- 1 ^1
A —1 1
А: + 1Я2 I
!) Петров Г. И., Ух о в Е. П. Расчет восстановления давления при
переходе от сверхзвукового потока к дозвуковому при различных системах
плоских скачков уплотнения.— М., 1947.
30 г. Н. Абрамович, ч. 1
466
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
На рис. 8.37 изображены графики зависимости отношения
полных давлений за и перед системой скачков от угла косого
скачка при различных значениях скорости невозмущенного
потока (т. е. при различных значениях Мн или Ян), вычисленные
для диффузора с двумя скачками: косым и следующим за ним
прямым. Каждому значению числа Мн (рис. 8.37) отвечает не-
некоторый угол косого скачка (аопт), при котором восстановление
полного давления в диффузоре
достигает максимума; чем мень-
меньше скорость потока, тем ближе
оптимальный угол к прямому.
Штриховой линией А соеди-
соединены точки (а =ао), в кото-
которых косой скачок вырождается
в слабую волну; в этом случае
система состоит из одного пря-
прямого скачка. Штриховой ли-
линией В соединены точки, пра-
правее которых скорость за косым
скачком дозвуковая. Иначе го-
70е а 90° воря, ветвь каждой кривой, ле-
лежащая правее линии В, отвеча-
отвечает сильному косому скачку, по-
позади которого нет прямого скач-
скачка. При а = 90° сильный косой
скачок переходит в прямой
скачок. В силу изложенного на каждой из кривых коэффициенты
сохранения полного давления окоп при а = 90° и при а = ао
(угол слабых возмущений) получаются одинаковыми.
На рис. 8.37 видно, что превосходство системы — косой скачок
с последующим прямым скачком перед одним скачком, становит-
становится существенным только при М > 1,5. В случае Мн = 2 опти-
оптимальное восстановление полного давления в системе двух скачков
составляет <7к0п = 0,91 (при аОпт = 50°), тогда как один скачок
дает 0,72, т. е. на 27 % меньше. При Мн = 3 получается соответ-
соответственно для системы из двух скачков акоп = 0,58 (а0Пт = 43о) и
для одного прямого скачка ап = 0,33 (а = 90°), т. е. два скачка
дают выигрыш в полном давлении около 70 %. При дальнейшем
увеличении скорости набегающего потока преимущество двух
скачков становится еще более значительным.
Мы рассмотрели подробно систему из двух скачков. Приме-
Применяя сложные системы, состоящие из трех, четырех и большего
числа скачков, можно получить лучшие результаты, чем в двух-
скачковой системе. Расчет любой системы плоских скачков уп-
уплотнения производится с помощью формул C8)—-E2) гл. III и
формул B5), B6). Можно отыскать оптимальные режимы для
сложной системы скачков путем последовательного расчета.
Рис. 8.37. Зависимость отношения
полных давлений за и перед си-
системой из двух скачков (косой +
прямой) от угла косого скачка
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
467
Укажем сначала, как рассчитывается система из трех скачков
(два косых и завершающий прямой). При этом сначала опреде-
определяются приведенная скорость (или число М) и давление за пер-
первым косым скачком при различных углах наклона его фронтаг
и на основе уже имеющихся данных для каждого значения при-
приведенной скорости за первым скачком подбирается оптимальная
система из остальных двух скачков (косой с последующим пря-
прямым). В результате получаются кривые 0д = /(а), аналогичные
приведенным на рис. 8.37; по
ним устанавливаются оптималь-
оптимальные соотношения для системы
из трех скачков. Далее можно
найти оптимальные соотноше-
соотношения для системы из четырех
скачков (три косых с последую-
последующим прямым). Для этого нужно
вести расчет при различных по-
положениях первого косого скач-
скачка, подбирая к каждому его
положению (по значению ско-
скорости за первым скачком) опти-
оптимальную систему из трех скач-
скачков. Таким же последователь-
последователь0,8
0,6
\
\
л
ч
ч
—
Рис. 8.38. Зависимость оптимального
коэффициента сохранения полного
давления в различных системах
скачков уплотнения от числа М в.
набегающем потоке
ным расчетом можно опреде-
определить оптимальные режимы для
любого заданного числа скачков.
На рис. 8.38 приведены кривые оптимальных значений 0Д —
отношений полного давления за системой скачков к полному
давлению перед ней в зависимости от числа Мн перед диффузо-
диффузором для случаев: у
1) прямой скачок,
2) косой скачок с последующим прямым скачком;
3) два косых скачка с последующим прямым скачком,
4) три косых скачка с последующим прямым скачком.
Оптимальные режимы получены описанным способом и со-
соответствуют максимальному восстановлению полного давления.
Из рис. 8.38 видно, что сложные системы скачков могут дать
большой эффект лишь при очень высокой скорости. Так, при
М < 1,5 хорошие результаты дает один прямой скачок, и более
сложные системы в этой области скоростей не требуются. При
М ^ 1,5 целесообразно применять двухскачковую систему (ко-
(косой с последующим прямым). Преимущества четырехскачковой
системы (три косых с последующим прямым) становятся суще-
существенными только при М ^ 2,5.
Выше рассматривались различные системы скачков уплотне-
уплотнения вне зависимости от конфигурации диффузора, которая необ-
необходима для того, чтобы осуществить нужную систему. Получен-
30*
468
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
ные результаты применимы непосредственно к плоским диффу-
диффузорам и с незначительными изменениями к диффузорам осесим-
метричным.
Принципиальная схема плоского диффузора с двумя скачка-
скачками уплотнения изображена на рис. 8.39. Для того чтобы полу-
получить первый косой скачок с нужным углом наклона а, следует
устроить клинообразный выступ, отклоняющий поток на угол со,
который для заданного значения Мн подбирается по рис. 3.12.
Наличие клина не нарушает внешнего обтекания диффузора, ес-
если расстояние ОС выбрано из условия встречи фронта скачка О А
с кромкой входного отверстия. Площадь входного отверстия диф-
диффузора должна быть рассчитана так, чтобы скорость потока в
нем равнялась скорости за прямым скачком. В этом случае пря-
прямой скачок помещается в плоскости С А и не влияет на внешнее
обтекание диффузора.
На рис. 8.40 изображена принципиальная схема диффузора с
тремя скачками уплотнения. В этом случае поверхность клина
должна иметь излом. Угол отклонения невозмущенного потока
coi и угол вторичного отклонения 0J подбираются по-прежнему
Рис. 8.39. Схема плоского диффузора Рис. 8.40. Схема плоского диффузо-
с двумя скачками: О А — первый ко- ра с тремя скачками: О А — первый
сой скачок, С А — прямой скачок, косой скачок, DA — второй косой
АВ — косой скачок внешнего обте- скачок, С А—прямой скачок, АВ —
кания косой скачок внешнего обтекания
по кривым рис. 3.12 в соответствии с заданными углами наклона
первого (ai) и второго (с&г) косых скачков и с учетом скоростей
перед первым (Мн) и перед вторым (Mi) скачками. Площадь
входного отверстия СА подбирается по скорости за прямым скач-
скачком (Мп). Расстояния OD и DC вычисляются из условия пересе-
пересечения скачков СА и DA на кромке входного отверстия. При дан-
данных условиях через систему из трех скачков проходит только
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
469
1,0
*д
0,3
0,8
0,7
воздух, поступающий внутрь диффузора; внешнее же обтекание
не возмущается этой системой скачков.
Принципиальная схема осесимметричного сверхзвукового
диффузора ничем не отличается от схемы плоского диффузора.
Состояния газа за сложными системами осесимметричных
и плоских скачков (при равных
углах наклона скачков с одинако-
одинаковыми порядковыми номерами)
должны быть близки между собой.
В этом можно убедиться на
рис. 8.41, на котором представле-
представлены отношения значений полных
давлений за и перед системами из
двух скачков (косой с последую-
последующим прямым) при оптимальных
углах наклона косого скачка в за-
зависимости от числа Мн набегаю-
набегающего потока. Одна из кривых
рис. 8.41 сооответствует осесим-
метричному, другая (штрихо-
(штриховая)— плоскому течению. При
расчете замыкающего прямого
скачка в осесимметричном случае
скорость перед ним (^i) определя-
определялась по формуле E2) гл. III.
В сложном осесимметричном диф-
диффузоре все скачки, кроме первого,
можно рассчитать как для плоско-
плоского потока ввиду того, что они раз-
размещаются в относительно узких
кольцевых каналах.
Аналитические исследования,
проведенные Г. И. Петровым и
Е. П. Уховым *), а также К. Осва-
0,3
0,2
OJ
к
\
\
H/ruiA
\
\
'С
ч.
5 6М77
Рис. 8.41. Коэффициент сохране-
сохранения полного давления за систе-
системой из двух скачков (косой +
прямой) при оптимальных уг-
углах косого скачка в зависимости
от скорости потока для осесим-
осесимметричного и плоского (штрихо-
(штриховая линия) течений
тичем2), показали, что макси-
максимальное отношение полных давлений (минимум потерь) в си-
системе из нескольких плоских косых скачков уплотнения и замы-
замыкающего прямого скачка, равное
(Од)тах = Ol<J2G3 . . . Оп, B7)
получается в том случае, когда косые скачки имеют равные
1) См. сноску на с. 465.
2) Oswatisch К. Der Druckruckgewinn bei Geshossen mit Rueck-
stossantrieb bei hohen Ueberschallgeschwindigkeiten II Forschungen und
Entwicklungen des Heerswaffenamtes.— Gottingen, 1944.— Bericht №2 1005
January. - » t
1960.
Герман Р. Сверхзвуковые входные диффузоры.—М.: Физматгиз,
470 ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
потери, т. е. одинаковую интенсивность:
С\ = 02 = 03 = • • • == Ок. B8)
При этом условии из B7) имеем
<С-Ч. B9>
Здесь т — общее число скачков, (т — 1)— число косых скачков,
ак — отношение полных давлений за и перед единичным косым
скачком, оп — то же для прямого скачка.
Из формулы D0) гл. III следует, что при: равных потерях
полного давления (ак = idem) приведенные нормальные состав-
составляющие скорости перед скачком должны быть одинаковыми
(ЯНп = Ли = ... = idem, т. е. МНЛ = Min = ... = idem или
Мн sin ан = Mi sin ai = ... = idem); вследствие этого отношение
статических давлений, плотностей и других параметров во всех
( Рл Р* ., Pi Р2
косых скачках одни и те же I — = ¦—¦=...= idem, — = — =
Т Т \
= ... = idem, ^ = jr- = ... = idem, -!- = _JL = ... = idem J
HI /
и приросты энтропии в них равны {s\ — sn = 52 — S\ = ... = idem).
Аналитическое исследование показывает, что все параметры замы-
замыкающего прямого скачка в оптимальной системе лишь немного
отличаются от параметров единичного косого скачка этой систе-
системы. Так, в диапазоне значений числа Маха набегающего невозму-
щающего потока 1,5 ^ Мн ^ 5 относительная величина числа
Маха перед прямым скачком практически постоянна и равна
Mm-i = 0,94Мн sin ab C0)
Зная величину Мт-ь можно вычислить приведенную скорость
перед прямым скачком, отношение полных и статических давле-
давлений, а также всех прочих параметров за и перед скачком.
Для приближенных предварительных расчетов можно опреде-
определить число Маха перед прямым скачом по нормальной состав-
составляющей скорости перед единичным косым скачком (Mm-i «
«MHsinai). Тогда оптимальное отношение полных давлений в
системе скачков равно
<7д)тах = Ок • (о1)
Это выражение дает тем лучшее приближение к точному вы-
выражению B9), чем больше число скачков m в системе. При ис-
использовании многоскачковой системы интенсивность каждого
скачка относительно невелика, а это означает, что скорость до-
дозвукового течения за замыкающим прямым скачком близка к ско-
скорости звука (Мп « 1). Но при этом достаточно небольшого су-
сужения струи, обычно происходящего перед входным отверстием
диффузора, для того чтобы в этом отверстии установилась кри-
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ 471
тическая скорость (Мвх = 1). Опыты показывают, что данное
условие реализуется на практике на основных режимах работы
многоскачкового диффузора в системе двигателя.
В таком случае расход воздуха через диффузор определяется
по формуле (8а) гл. IV:
GB да 0,04 Й?. кг/с. C2)
У г*
Здесь /?д = сГдРн— полное давление во входном сечении диффу-
диффузора (за системой скачков); Т^= Тп— температура торможения
во входном сечении диффузора, равная температуре торможения
в набегающем невозмущенном потоке; FbX = FKV> — площадь вход-
входного сечения диффузора.
Скорость течения в каналах двигателя (в частности, перед
компрессором и перед камерой сгорания) обычно должна быть
значительно ниже скорости звука, вследствие чего внутренний
канал сверхзвукового диффузора, куда воздух попадает из вход-
входного отверстия, делается расширяющимся. Но если во входном
отверстии скорость равна критической, то такой канал может
работать и как расширяющаяся часть сопла Лаваля с образова-
образованием сверхзвукового течения, завершаемого дополнительным
скачком уплотнения.
Форму внутреннего канала и условия работы диффузора ста-
стараются выбрать такими, чтобы потери в дополнительном скачке,
по крайней мере на основном (расчетном) режиме, были как
можно меньше, а это достигается предельно возможным сокра-
сокращением дополнительной сверхзвуковой зоны течения.
При плавной форме и малых углах раскрытия начальной ча-
части (горловины) внутреннего канала диффузора удается избе-
избежать отрыва пограничного слоя в скачке (при Мн<3,5), замы-
замыкающем дополнительную сверхзвуковую зону, и свести потери
полного давления во внутреннем канале до 3—5 % (Овн —
= 0,97-0,95).
Описанные выше сверхзвуковые диффузоры, в которых основ-
основная система скачков уплотнения расположена перед входным от-
отверстием (перед обечайкой), относят к категории диффузоров
с внешним сжатием (несмотря на наличие дополнительного сжа-
сжатия во внутреннем канале). Если в таком диффузоре все скачки
пересекаются на кромке А обечайки (рис. 8.40), то, как уже от-
отмечалось, система скачков не нарушает внешнего обтекания
обечайки. Однако внутренняя стенка обечайки должна быть
ориентирована по направлению потока в замыкающем прямом
скачке, которое тем сильнее отклонено от направления набегаю-
набегающего невозмущенного потока, чем больше косых скачков имеется
на центральном теле диффузора.
В свою очередь наружная стенка обечайки составляет с вну-
внутренней угол Дсо = 3—5°, поэтому угол встречи наружной
472
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
стороны обечайки с набегающим невозмущенным потоком равен
m-i f
сон = 2 coft + Асе = сон + Aw, C3)
где cda — отклонение потока в единичном косом скачке, сон =
= 2 ®ь. — суммарное отклонение потока в системе косых скачков»
В многоскачковом диффузоре с внешним сжатием угол сон
велик и скачок АВ на наружной стороне обечайки (рис. 8.40)
оказывается интенсивным. Возможны и такпе случаи, когда
угол Он7 больше предельного со
угла поворота потока в пло-
плоском косом скачке уплотне-
уплотнения. При этом вместо плос-
кого скачка АВ образуется °°
70°
/
у
** г
¦—
L_ m-*
т=2
3
4
Рис. 8.42. Система скачков при
угле наклона обечайки, превы-
превышающем предельное значение
(для косого скачка)
Рис. 8.43. Зависимость суммарного угла
поворота потока в оптимальной систе-
системе скачков от числа Маха при разном
количестве т скачков: ©max — предель-
предельный угол поворота в косом скачке,
Фтах — ПОВОРОТ ПОТОКа при ИЗОЭНТрОПИ-
ческом сжатии около центрального
тела
отошедшая криволинейная ударная волна, которая объеди-
объединяется в одно целое с замыкающим прямым скачком си-
системы (рис. 8.42) и приводит к большому внешнему сопротивле-
сопротивлению обечайки.
Входной канал диффузора (между обечайкой и центральным
телом) обычно сначала немного сужается, а затем расширяется,
т. е. имеет узкое сечение, перед которым (за системой скачков)
дозвуковой поток разгоняется до критической скорости.^ Далее
формируется участок сверхзвукового течения, завершаемый удар-
ударной волной (волнистые линии на рис. 8.42, 8.44—8.46), за кото-
которым следует область дозвукового диффузорного течения.
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ 473
На рис. 8.43 штриховой линией изображена зависимость пре-
предельного угла поворота потока в присоединенном плоском скачке
ют числа Маха сота*(Мн) при к = 1,4. Здесь же нанесены кривые
значений суммарного угла поворота потока о>н в оптимальной си-
системе плоских скачков (для диффузора с внешним сжатием),
состоящей из различного числа скачков (т = 2, 3, 4). Как видно
из рис. 8.43, суммарный угол поворота потока в оптимальной
системе из трех скачков приблизительно равен предельному углу
поворота невозмущенного потока у обечайки, а в случае четырех
окачков — больше предельного. Иначе говоря, при т > 3 (для
Рис. 8.44. Изоэнтропическое внеш-
внешнее сжатие в сверхзвуковом диф-
фузоре: 1 — центральное тело,
2 — обечайка, DA'GB — отошед-
отошедшая ударная волна, OA'D — об-
область изоэнтропического внеш-
внешнего сжатия, GH и АС — линии
звуковых скоростей
к = 1,4) в оптимальном диффузоре с внешним сжатием неиз-
неизбежно образование отошедшей ударной волны на наружной сто-
стороне обечайки.
Как показывает рис. 8.38, увеличение числа скачков ведет
к уменьшению суммарных потерь полного давления в системе.
При увеличении числа скачков до бесконечности потери в си-
системе должны упасть до нуля (<тд ->• 1), т. е. осуществляется пе-
переход к изоэнтропическому торможению. Форма центрального
тела плоского «нзоэнтропического» сверхзвукового диффузора с
внешним сжатием изображена на рис. 8.44.
Полный угол поворота потока около такого центрального тела
рассчитывается по формулам и таблицам течения Прандтля —
Майера (см. § 3 гл. IV), так как изоэнтропическое сжатие пред-
представляет собой обращенное изоэнтропическое расширение.
Иначе говоря, угол поворота потока у плоского изоэнтропиче-
изоэнтропического центрального тела при торможении от значения числа Мн
до М = 1 равен углу поворота в течении Прандтля — Майера с рас-
расширением от М = 1 до М = Мн(сон = бн). Кривая со(Мн) для к =
= 1,4 приведена на рис. 8.43 (тга = <*>). Если бы пучок характе-
характеристик изоэнтропического течения сжатия сходился на кромке
обечайки диффузора, то струя, входящая в диффузор, не возму-
возмущала бы внешнего обтекания обечайки.
В действительности полное изоэнтропическое торможение по-
потока газа осуществить не удается, так как на поверхности цен*
трального тела происходит увеличение давления, которое вызы-
474
ГЛ VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
вает деформацию профиля скорости в пограничном слое, при-
приводящую к отрыву последнего. В точке отрыва пограничного слоя
возникает сильное возмущение сверхзвукового потока, вследствие
чего образуется скачок уплотнения (рис. 8.44), переходящий в
ударную волну внешнего обтекания обечайки.
Все же выбор соответствующей формы центрального телаг
особенно при осуществлении отсоса пограничного слоя, дает воз-
возможность частично использовать изоэнтропическое торможение
потока в диффузоре внешнего сжатия и получить восстановле-
восстановление давления несколько более высокое, чем в трех-, четырех-
скачковом диффузоре.
Если точка пересечения скачков (или волн Маха в изоэнтро-
пическом диффузоре) не совпадает с кромкой обечайки, то от
этой точки в сторону внешнего потока отходит скачок уплотне-
уплотнения, интенсивность которого определяется двумя условиями:
1) совпадением направления внешнего потока и внутренней
струи;
2) равенством давления по обе стороны поверхности, отде-
отделяющей внешний поток от внутренней струи.
Кривая значений угла поворота потока 'вшах, определяемого
данными условиями, приведена на рис. 8.43 (для изоэнтропиче-
ского сжатия).
Если угол поворота струек в скачке оказывается больше
максимального возможного при данной скорости набегающего
потока, то скачок преобразуется в криволинейную ударную
волну, которая проникает во внутреннее течение и дотягивается
Рис. 8.45. Сверхзвуковой диффузор Рис. 8.46. Сверхзвуковой диффу-
с частичным внешним сжатием зор с внутренним сжатием
до стенки центрального тела (рис. 8.44). За криволинейной вол-
волной сверхзвуковое течение разрушается вблизи как внешней, так
и внутренней стороны обечайки.
Для уменьшения внешнего сопротивления применяют диффу-
диффузоры с неполным (частичным) внешним сжатием (рис. 8.45).
В таком диффузоре обечайка составляет с направлением невоз-
невозмущенного потока меньший угол, чем последняя грань централь-
центрального тела. Поэтому поток встречает внутреннюю поверхность
обечайки под некоторым углом и вынужден отклониться с об-
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ 475
разованием косого скачка АС, идущего от кромки обечайки
к той части центрального тела, которая расположена во внутрен-
внутреннем канале диффузора; замыкающий прямой скачок EF поме-
помещается около узкого сечения внутреннего канала. Обечайка
диффузора с частичным внешним сжатием может иметь малое
внешнее сопротивление. Если обечайка направлена параллельно
скорости невозмущенного потока, то ее внешнее волновое сопро-
сопротивление равно нулю.
Сверхзвуковой диффузор с полным внутренним сжатием мо-
может быть осуществлен без центрального тела (рис. 8.46). В та-
таком диффузоре косой скачок отходит от кромки обечайки А и
пересекается в точке О на оси диффузора со скачком, идущим
от противоположной кромки. Поток газа в скачке АО отклоня-
отклоняется от первоначального направления и становится параллель-
параллельным стенке АС. В точке О линии тока вынуждены возвратиться
к первоначальному направлению, в связи с чем возникает от-
отраженный скачок OD. В точке D поток вновь отклоняется от
осевого направления и становится параллельным стенке диффу-
диффузора; это вызывает новый скачок, который отражается от оси
диффузора, образуя следующий скачок и т. д. Так как в скачках
уплотнения поток тормозится, то предельный угол поворота в
каждом последующем скачке меньше, чем в предыдущем. Опи-
Описанный процесс продолжается до тех пор, пока требуемый угол
отклонения потока не оказывается больше предельного (со >
> «шах); с наступлением этого режима вместо очередного пло-
плоского скачка образуется криволинейная ударная волна EF, за
которой поток становится дозвуковым. Дальнейшее течение
в сужающем канале идет с увеличением скорости, причем в уз-
узком сечении скорость должна быть ниже или равна критической;
в последнем случае за узким сечением может возникнуть до-
дополнительная сверхзвуковая зона, завершаемая скачком уплот-
уплотнения GH.
При очень малом угле наклона боковой стенки диффузора
с полным внутренним сжатием (со < 1°) возможно частичное
нзоэнтропическое торможение; оно осуществимо до места отрыва
пограничного слоя, вызывающего скачок уплотнения.
Сверхзвуковой диффузор с полным внутренним сжатием ис-
используется в аэродинамических трубах. Вследствие частичного
изоэнтропического сжатия в диффузоре малого угла удается
вдвое уменьшить потери по сравнению с таковыми в прямом
скачке (подсчитанными по числу Маха перед диффузором).
Пограничный слой влияет на работу диффузора не только
в случае изоэнтропического сжатия. В диффузорах других схем
влияние пограничного слоя также весьма ощутимо; оно не ска-
сказывается только на первом скачке, который устанавливается при
встрече невозмущенного потока с передней кромкой централь-
центрального тела или обечайки. .
476
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
Все последующие скачки возникают или отражаются в местах
взаимодействия пограничного слоя со скачком (при перепаде
давлений на скачке выше «критического», см. § 6 гл. VI). В ре-
результате этого взаимодействия потери давления увеличиваютсяг
а скачки уплотнения деформируются и смещаются. Если послед-
последнее обстоятельство не учтено при выборе формы центрального те-
тела диффузора с внешним сжатием, то не будет обеспечено пересе-
пересечение всех скачков на кромке обечайки (рис. 8.47), из-за чего на-
нарушится и внешнее обтекание диффузора. Следует принять во
Пограничный
слой
Рис. 8.47. Искажение системы скачкоз
при взаимодействии их с пограничным
слоем. Штриховая линия — скачки в
идеальном газе, сплошные линии —
скачки в вязком газе
Рис. 8.48. Форма струи, входя-
входящей в диффузор, при скорости
полета ниже расчетной
внимание также влияние вязкости при выборе поперечных разме-
размеров канала диффузора (путем увеличения проходных сечений в
соответствии с нарастанием по длине канала толщины вытесне-
вытеснения пограничного слоя, как это было показано на примере соп-
сопла в § 1 настоящей главы).
В частности, площадь узкого сечения диффузора (горла)
с учетом влияния пограничного слоя приходится увеличить на
5—15 % по сравнению с определенной без поправки на его влия-
влияние. Чтобы обеспечить безотрывное течение газа в расширяющей-
расширяющейся дозвуковой части канала, следующей за горлом диффузора,
ее сопряжение с концом сверхзвуковой части осуществляют с по-
помощью специального переходного канала, имеющего весьма плав-
плавные очертания с участком постоянного сечения (в зоне горла).
Иногда для улучшения характеристик диффузора применяют слив
или отсос пограничного слоя через специальные отверстия или
щели в стенках диффузора.
До сих пор мы рассматривали сверхзвуковые диффузоры, ра-
работающие на основном, расчетном значении скорости набегающе-
набегающего потока. При отклонении от расчетного режима форма системы
скачков изменяется, в связи с чем некоторые из заданных усло-
условий нарушаются. В частности, в нерегулируемом диффузоре
с внешним сжатием при уменьшении числа Маха набегающего
потока скачки уплотнения становятся более крутыми (рис. 8.48);
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
477
из-за этого крайняя линия тока внутренней струи (попадающей в
диффузор) проходит через точки аЬА, отклоняясь в каждом скач-
скачке системы. Но тогда сечение струи F0H, захватываемой диффу-
диффузором, оказывается меньше, чем на расчетном режиме, для кото-
которого оно равно полному сечению Fqa (от кромки А обечайки до
оси диффузора, см., например, рис. 8.45).
Отношение
называется коэффициентом расхода. Потери во внутренней струег
как видно из рис. 8.48 1), не должны зависеть от того, пересека-
пересекаются ли скачки на кромке А обечайки или нет; внешнее же соп-
сопротивление диффузора под действием сместившихся скачков воз-
возрастает, так как часть потока, обтекающего диффузор, вынужде-
вынуждена пересечь эти скачки до встречи с обечайкой.
Характер зависимости коэффициента сохранения полного дав-
ления Од и коэффициента расхода <р от числа Маха в трехскачко-
вом диффузоре постоянной формы (с внешним сжатием) показаа
на рис. 8.49 (расчетное ^
значение Мн = 3). Здесь д
же нанесены кривые
(Топт (Мн) И фопт(Мн) ДЛЯ
оптимального диффузора
(штриховые линии), гео-
геометрическая форма кото-
которого с изменением величи-
величины Мн должна изменяться
(идеально регулируемый
диффузор). На всех режи-
режимах, кроме расчетного, не-
нерегулируемый диффузор
имеет значения ад ниже
оптимальных; величины
ф < 1 получаются только
в области значений Мн ни-
ниже расчетного.
Расчет кривых на рис.
8.49 произведен следую-
следующим образом. По данным
рис. 8.38 берется значе-
значение ((Тд)тах = 0,73 для оптимальной системы из трех скачков при
Мн = 3 и умножается на коэффициент сохранения полного давле-
давления внутренней части диффузора (принимаем авн = 0,95); произ-
произведение этих коэффициентов характеризует полные потери внутри
1) Скачки на рис. 8.48 построены без учета влияния пограничного слоя.
О
Рис. 8.49. Зависимость от скорости полета
кооффициентов сохранения полного дав-
давления и расхода для трехскачкозого
сверхзвукового диффузора с внешним
сжатием, имеющего оптимальные характе-
характеристики при Мп = 3
478 гл- VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
диффузора на расчетном режиме (ад = 0,7), для которого коэф-
коэффициент расхода равен единице. Приближенное значение ск для
«единичного косого скачка оптимальной трехскачковой системы, со-
3 ,
гласно C1), ак = уад = 0,89. Этому значению аи отвечает на
основании B5) нормальная составляющая приведенной скорости
(при к — 1,4) Янп = 1,43 и число Маха, подсчитанное по нормаль-
нормальной составляющей скорости набегающего потока:
4=1,6.
1 "" к + 1 Анп
Отсюда угол наклона первого скачка ai = arcsin( 1,6/3)= 32°. По
кривым на рис. 3.12 гл. III отыскиваем угол первого клина цент-
центрального тела (при Мн = 3 и ai = 32°), coi = 15° и по рис. 3.19
тл. III — число Маха за первым скачком Mi = 2,3.
Значение числа Маха для нормальной составляющей скорости
перед вторым скачком в оптимальной системе должно быть таким
же, как и перед первым скачком МНп = Min = Mi sin 0&2 = 1,6. От-
Отсюда угол наклона второго скачка к направлению потока за пер-
первым скачком
1,6 ,/о
a2 = arcsin ^ = 44 ,
чему соответствует угол отклонения потока на втором уступе
клина 0J =* 18°. Полный угол поворота потока в рассматривае-
рассматриваемой оптимальной системе скачков (coi + 02)= 33°, а число Маха
за вторым скачком Мг = 1,6. Уточненное значение числа Маха
перед -замыкающим прямым скачком согласно C0) равно
Мт_! = 0?94Мнп = 1,5.
Теперь можно уточнить расчет системы скачков, для чего сле-
следует определить значение ап в прямом скачке при М = 1,5, значе-
значение о/ в каждом из двух одинаковых косых скачков
адтах
приведенную скорость и число Маха для нормальной составляю-
составляющей скорости в косых скачках Янп и МНп> углы наклона косых
скачков а± и а2 и углы уступов на центральном теле диффузора
<он, сог После этого можно уточнить значения числа Маха Mm-i
перед замыкающим прямым скачком. Ввиду того что уточненные
величины мало отличаются от полученных в первом приближе-
приближении, мы их не приводим.
Для облегчения расчетов можно воспользоваться рис. 8.50,
ла котором приведены кривые Мн sin ai = /(Мн), отвечающие дан-
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
ным оптимального диффузора с системами из двух, трех и четы-
четырех скачков. На рис. 8.51, а, б, в изображены графики углов от-
отклонения потока в косых скачках со(Мн) для тех же трех систем^
на рис. 8.52, а, б — значения чисел Маха за косыми скачками^
а на рис. 8.53, а, б, в — зна-
значения углов наклона скач-
скачков в этих системах.
Описанная методика от-
относится к расчету плоского
сверхзвукового диффузора с
внешним сжатием и опти-
оптимальной системой скачков
уплотнения на расчетном ре-
режиме, при котором все скач-
скачки пересекаются на кромке
обечайки.
При скорости полета ни-
ниже расчетной и неизменной
форме диффузора, как уже
говорилось, углы наклона
скачков уплотнения станут
больше. Например, если
Мн = 2,5, то для описанного
диффузора, получим угол на-
наклона первого скачка cti =
= 36° (при coi = 15°), число
3
2
1
-+
i
!
f
1
I
/
/
/
A
/
/
=/
у
~m=2
= 3
--4
4
Рис. 8.50. Нормальная составляющая
Мн sin o&i в зависимости от Мн для оп-
оптимальной системы т скачков
Маха для нормальной составляющей скорости перед первым скач-
скачком Мнп = Мн sin ai == 1,48 и соответствующее значение приведен-
приведенной скорости Янп == 1,35. Коэффициент сохранения полного дав-
давления в первом скачке составляет при этом ок{ = 0,936, число Ма-
Маха за первым скачком Mi = 1,9, угол наклона к потоку второга
скачка оы = arcsinA,48/1,9) = 53° (при со2 == 18°), коэффициент
сохранения полного давления во втором скачке аК2 = 0,929, числа
Маха перед замыкающим прямым скачком Mw_i = 1,2, коэффи-
коэффициент сохранения полного давления в прямом скачке ап = 0,993 и
суммарное значение этого коэффициента
fbh = 0,825.
Если угол поворота потока во втором косом скачке оказывается
больше максимального возможного (со2 > сотах) при полученном:
значении Мь то вместо трехскачковой системы реализуется двух-
скачковая (ак2«1); приближенное значение коэффициента со-
сохранения полного давления при этом равно
Од = oKianoBH,
причем оп вычисляется по значению числа Маха за первым
скачком.
480
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
Коэффициент расхода ф = FJFoA при скорости, равной или
больше расчетной, близок к единице. При пониженных значениях
Мп зависимость ф(Мн) для диффузора с внешним сжатием
О)
251
20°
75'
10°
5е
О
1
I
I
/
i
1
у
A
f
i
i
i
1
\ j
!
2 3
а
5МН
(О
2h°
Z0°
15°
10°
5°
A°
i
к
и
V
/
У
/
/
i ^
CO;
i -^i
!
ia
20°
15°
10°
5"
0°
J
/
A
f
/A
4
y^
^-^
»/,
^ —
I
/ 2 3 4 5МН 1 2 3 4 5МН
Рис. 8.51. Зависимость углов отклонения потока в скачках оптимальной
системы от Мн: а) при т = 2, б) при т = 3, в) при т = 4
определяется из условия равенства расходов во входном (кри-
(критическом) сечении и перед системой скачков
-Здесь (адрКр) — плотность воздуха в критическом сечении, вы-
вычисленная с учетом потерь полного давления в системе скачков
^без учета потерь во внутренней части диффузора: огд = о^авн).
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
481
Отсюда, используя выражение A09) гл. V, имеем
_ адРкракр
C4)
На расчетном режиме сечение струи, захватываемой в диффу-
м\ I | | I I I I I I М
А 1 1 | ' I 11 11 4
У
1
!
1
У1
/
/ 1
fy у
т
/
/
/
/
j
/
/
/
/
/
/
/
У
/
/
у*
М,
У
у
М3=Нп-
>**
1
2 3 4
а
5 Мн 1
3 4 5 Мн
б
Рис. 8.52. Зависимость числа Маха за косыми скачками оптимальной си-
системы от Мн: а) при m = 3, б) при m = 4
зор, равно полному сечению последнего в плоскости входа
(Fa = FA), поэтому
У
C5)
где Янр — расчетная приведенная скорость набегающего потока.
Разделив почленно C4) на C5), получаем выражение для коэф-
коэффициента расхода диффузора
C6)
Для любого диффузора имеем
И ф =
"нр
При Лн = AHI
при Ян = 1,
при Ян->0.
ад = 1» q &н) ->¦ 0 и ср ->> сю
Для 1 < Ян < Янр по заданному значению Ха находим с по-
помощью таблицы газодинамических функций величину q(ka) и
31 Г. Н. Абрамович, ч. 1
482
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
90°
80°
70°
60°-
50°-
40°
30°
20°\
90е
80е
701
&01
50°
40
30°
1
1
1
1
1
\
\
\
1
\
\
\
>
\
ч
ч
"h
5МН
\
1
и
|\
•и
\\
\
\
\
\
\
ч
\
ч
\
Ч
ч
1
L
90°
80°
70°
60°
50°
40°
30°
?,0°
\
\\
\\
\\
\\ \
\\ \
W
\ ^
\'
\
\
\
\
V
\
N
ч,
ч
s
0L2
¦—¦
•—
2 63
5МН
5МН
Рис. 8.53. Углы наклона скачков: а) при т = 2, б) при т = 3, в) при
т = 4
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
483
в
рассчитываем коэффициент сохранения полного давления в си-
системе скачков ад, получающейся на центральном теле диффузо-
диффузора заданной формы. Например, для оптимального диффузора с
внешним сжатием при расчетном режиме Янр = 1,97 (Мнр = 3)
выше было получено о>д = 0,73; для того же диффузора при
Мн = 2,5 (Ха = 1,825, g (Ян) =0,38) было найдено ад = 0,825, че-
чему соответствует, согласно C6), ф = 0,76. Рассчитанные по та-
такому методу кривые ф(Мн) и ад(Мн) приведены на рис. 8.49.
Ступеньки на кривой
Од(Мн) соответствуют пе-
переходам от трехскачковой
системы к двухскачковой
и от последней к одному
прямому скачку.
Штрихами, как указы-
указывалось ранее, нанесены
кривые, отвечающие иде-
идеально регулируемому
трехскачковому диффузо- Рис- 8-54- Течение на входе в диффузор
ру, у которого формы при скорости полета выше расчетной
центрального тела и обе-
обечайки, а также проходное сечение горла изменяются по такому
закону, что для каждого значения скорости устанавливается опти-
оптимальная система из трех скачков, пересекающихся на кромке
обечайки.
При значениях скорости выше расчетной (Мн > Мнр) можно
полагать ф = 1 и од<огдопт- Первое из этих условий связано
с тем, что скачки на данном режиме не фокусируются на кромке
обечайки, а заходят внутрь диффузора (рис. 8.54), вследствие
чего во входное отверстие диффузора попадает струя невозмущен-
невозмущенного потока, сечение которой равно сечению диффузора.
Второе условие (суд<Ссгдопт) предопределяется тем, что при
Мн > Мнр плотность газа в критическом сечении выше, чем на рас-
расчетном режиме (несмотря на рост потерь, полное давление за си-
системой скачков при увеличении скорости возрастает). Из-за этого
горло (D) нерегулируемого диффузора при Мн > Мнр оказывает-
оказывается перерасширенным и скорость в нем получается выше крити-
критической. Но тогда за горлом происходит дальнейшее ускорение
сверхзвукового потока, что приводит к повышенной интенсивно-
интенсивности прямого скачка EF, замыкающего сверхзвуковую зону (вели-
(величина оп уменьшается вследствие роста значения числа Маха
Mm_i перед прямым скачком).
При работе входного диффузора на скорости ниже расчетной,
когда в диффузор захватывается струя неполного сечения
(ф < 1), возникает (как уже указывалось при обсуждении схемы
обтекания, изображенной на рис. 8.48) сила дополнительного
31*
484
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
внешнего сопротивления, равная проекции на направление потока
силы избыточного давления, действующего на поверхность аЬА:
Хдоп =(р\ — РвI\ sin o)i +(p2 — рв) h sin 02. C7)
Здесь Zi, h — длины отрезков ab, bA; coi, сог — углы наклона этих
отрезков, которые параллельны соответствующим участкам цент-
центрального тела; /?i, P2 — давления за первым и вторым косыми
скачками. Разделив силу Хдоп на скоростной напор набегаьрщего
потока и площадь лобового сечения обечайки FA, получим коэф-
коэффициент дополнительного сопротивле-
сопротивления «жидкого контура» аЪА:
C8)
фузора55с °криволинейн?й
волной перед ним
Наибольшее значение коэффициента
схж имеет место в случае образования
перед диффузором криволинейной удар-
ударной волны (рис. 8.55), когда на границе внутренней струи аА дав-
давление приблизительно такое же, как за прямым скачком
уплотнения:
1~Т
(Рп - ft) (Fa - Fa) =
Здесь рп — давление за прямым скачком при скорости, соответ-
соответствующей числу Маха Мн; Fa — площадь сечения струи в точке
a, FA — площадь сечения диффузора в плоскости входного от-
отверстия.
Подставляя в C9) выражение D5) из гл. III для давления
за прямым скачком, получим
A - Ф).
D0)
При Мн < 1 дополнительное сопротивление исчезает в связи с от-
отсутствием ударных волн.
На рис. 8.56, а, б изображены результаты расчета зависимостей
<р(Мн) и С:сж(Мн) для сверхзвуковых диффузоров с одноступенча-
одноступенчатым и двухступенчатым центральным телом, имеющим различ-
различные суммарные углы поворота потока сон = coi + ©2. Как видим,
при одном и том же значении суммарного угла поворота потока
кривые ф(Мн) и с*ж(Мн) для двухступенчатого и одноступенча-
одноступенчатого клиньев мало отличаются.
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
485
Для предварительной оценки работы диффузора на расчетном
режиме (при проектировании двигателя и летательного аппара-
аппарата) в США рекомендуется так называемая «стандартная» кривая
зависимости коэффициента сохранения полного давления от чис-
числа Маха полета, изображенная на рис. 8.57 !); эта кривая полу-
Одноступенчатый клин Ж
1,8 2,0 2,2 2,4 2,8 2,8 3,0Мн 1,8 2,0 2,2 2,4 2,8 2,8 3,0Мн
а 5
Рис. 8.56. Сравнение величин ф и схт для одно- и двухступенчатого клина
чена в результате обобщения обширных экспериментальных ис-
исследований.
На работу диффузора оказывает влияние угол атаки ^ (угол
между осью диффузора и направлением набегающего потока),
Рис. 8.57. «Стандартная» кривая
(США) зависимости коэффициен-
коэффициента сохранения полного давления
в сверхзвуковом диффузоре от
числа Маха полета
1,0
0,6
0,2
О
I I I I
с увеличением которого уменьшаются коэффициенты сохранения
полного давления о и расхода ф и возрастает дополнительное ло-
лобовое сопротивление схж. Характер зависимостей о('у), ф('у) и
Схж{ч) Для различных типов воздухозаборников неодинаков.
J) Gregory Т. J., Petersen R. H., Wyss J. A. Performance tra-
doffs and research problems for hypersonic aerodynamics II J. Aircraft.—
1965.- № 4.- P. 266-271.
486 ГЛ VIII ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
До сих пор мы приводили данные о работе плоских сверх-
сверхзвуковых диффузоров. Основные зависимости для осесимметрич-
ных, а также боковых 1) и других типов диффузоров имеют тот
же характер, но их расчет представляет большие трудности.
При рассмотрении диффузоров предполагалось, что в горле
диффузора скорость равна критической, а за горлом имеется не-
небольшая сверхзвуковая зона, завершаемая дополнительным скач-
скачком уплотнения. В таком случае система скачков и расход возду-
воздуха на входе в диффузор не зависят от режима работы двигателя.
Однако при глубоком дросселировании двигателя (значитель-
(значительном изменении числа оборотов или проходного сечения сопла
и т. п.) указанный режим работы диффузора — воздухозаборника
нарушается. Так, при уменьшении объемного расхода через дви-
двигатель противодавление за диффузором увеличивается, в связи
с чем дополнительная сверхзвуковая зона сокращается и потери
в дополнительном скачке падают (ад растет). При некотором дрос-
дроссельном режиме дополнительная сверхзвуковая зона в диффузо-
диффузоре исчезает. Дальнейшее сокращение расхода приводит к тому,
что в горле диффузора устанавливается дозвуковая скорость, пос-
после чего дросселирование начинает воздействовать на интенсив-
интенсивность замыкающего скачка входной системы: из-за уменьшения
расхода уменьшается скорость за скачком, что заставляет его сме-
смещаться в область больших значений скорости перед ним, но при
этом система скачков не будет фокусироваться на кромке
обечайки.
Начиная с данного режима, наблюдается рост потерь полного
давления и внешнего сопротивления и снижение коэффициента
расхода в диффузоре. Увеличение интенсивности замыкающего
скачка уплотнения может привести к тому, что перепад давлений
на нем станет выше критического для пограничного слоя и воз-
возникнет отрыв последнего, причем вихреобразования вызовут ко-
колебания расхода воздуха и местоположения системы скачков.
В момент наибольшего сокращения расхода система скачков
превращается в криволинейную ударную волну, выбитую вперед
за пределы центрального тела. Это приводит к устранению отрыва
пограничного слоя и увеличению расхода воздуха, вследствие че-
чего система скачков восстанавливается, а замыкающий ее скачок
подходит к тому месту, где вновь происходит отрыв пограничного
слоя и т. д. На этом режиме наблюдается сильная тряска («пом-
паж») двигателя — низкочастотные пульсации давления, связан-
связанные с колебанием расхода воздуха. Ввиду возможного разруше-
разрушения двигателя работать на режиме помпажа нельзя.
1) Боковыми называются диффузоры, пристроенные к фюзеляжу или
поверхности крыла летательного аппарата, т. е. имеющие общую стенку
с какой-либо частью последнего.
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
487
При увеличении объемного расхода воздуха в двигателе (вы-
(выше расчетного) дополнительная сверхзвуковая зона (за горлом
диффузора) расширяется и дополнительный скачок смещается
в область больших скоростей, из-за чего потери полного давления
в нем растут, а плотность воздуха перед двигателем падает (это
и обеспечивает рост объемного расхода при постоянном массовом
расходе через диффузор).
При некотором увеличении объемного расхода дополнитель-
дополнительный скачок становится столь интенсивным, что вызывает отрыв
пограничного слоя(во внутреннем
канале за горлом диффузора). Для
этого режима характерны высо-
высокочастотные пульсации давления,
Линия критических
режимов
М„=1,4 '
60 80 100 123 140 160 у- 100%
60 80
120 WO 160 -jr 100%
p
0,2
\
Д
1
..—
i
\
-1,7
\?0
'2,2
0,6
0,8
1.0<p
Рис. 8.58. Характеристики нерегули- Рис. &59. Дроссельная характери-
руемого входного сверхзвукового стика нерегулируемого сверхзвуко-
диффузора вого диффузора
сопровождаемые высоким неприятным звуком — «зудом». Помпаж
и «зуд» ограничивают дроссельные режимы двигателя, снабжен-
снабженного диффузором.
Источником сильных пульсаций может быть также поверх-
поверхность тангенциального разрыва скорости (от точки пересечения
скачков), если она заходит внутрь диффузора. Типичные кри-
кривые зависимости величин од и схт от относительного объемного
расхода воздуха V/Vv (отношение действительного расхода V к
расчетному Vv) при разных значениях числа Маха Мн приведены
на рис. 8.58. Применяют также дроссельные характеристики диф-
диффузоров в виде зависимостей од(ф) и сяж(ф) при Мн = const
Хрис. 8.59).
488
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
р.ч.
Для расширения рабочего диапазона дроссельных режимов
и улучшения характеристик диффузора на нерасчетных скоро-
скоростях полета прибегают к различным методам регулирования диф-
диффузоров (изменение проходного сечения горла и взаимного поло-
положения центрального тела и обечайки, выпуск воздуха через отвер-
отверстия в стенке диффузора, слив или отсос пограничного слоя на
центральном теле или на обечайке и др.)? описанным в специ-
специальной литературе1). Регулировоание расхода воздуха через гор-
горло сверхзвукового диффузора необходимо также для вывода по-
последнего на рабочий режим («запуска»). Дело в том, что расчет-
расчетная скорость потока устанавливается не внезапно, а путем пере-
перехода от положения покоя к движению с постепенно нарастающей
скоростью. Рассмотрим этот
процесс на примере работы
диффузора аэродинамической
трубы (рис. 8.60). Разгон по-
потока воздуха в аэродинамиче-
аэродинамической трубе происходит следую-
следующим образом. Вначале — при
пуске трубы — скорость в ее
канале всюду ниже звуковой
и имеет наибольшее значение в
самом узком месте — горле соп-
сопла (г. с). Постепенно увеличи-
увеличивая расход воздуха, приходят
к режиму, на котором скорость
в горле сопла становится кри-
критической, а во всех остальных
сечениях остается дозвуковой.
Дальнейшее увеличение
объемного расхода на выходе
из трубы (в эксгаустере) не
сопровождается ростом массо-
массового расхода в горле сопла, од-
однако приводит к появлению
сверхзвуковой зоны за горлом
сопла, завершаемой скачком
уплотнения (рис. 8.60, а); в
последнем полное давление и
плотность заторможенного газа
г. с.
г. д.
Рис. 8.60. Различные режимы тече-
течения газа в аэродинамической трубе:
а) скачок помещается в сопле Ла-
валя (недостаточное разрежение пе-
перед эксгаустером), б) течение в ра-
рабочей части трубы сверхзвуковое
(режим после «запуска»); в) рабо-
рабочий режим (при суженном горле
диффузора)
уменьшаются, вызывая относи-
относительный рост объемного расхода в диффузоре трубы, горло кото-
которого (г. д.) поэтому должно иметь площадь большую, чем горло
сопла: FT.n > Fv c.
1) См. книги Р. Германа и Ю. Н. Нечаева, указанные в списке лите-
литературы.
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ 489
При некотором режиме работы эксгаустера плотность затор-
заторможенного воздуха за счет потерь в скачке может уменьшиться
настолько, что скорость в горле диффузора станет критической.
При одинаковых значениях температуры торможения (Г* = const)
одинаковая критическая скорость устанавливается как в горле
сопла, так и диффузора (акр = idem). Тогда из уравнения нераз-
неразрывности имеем
Рг д-* г д Рг о* г.о
Плотность газа в критическом сечении при Т* = const про-
пропорциональна полному давлению
которое изменяется за счет потерь в скачке. Таким образом, пло-
площади двух горловин при критических режимах в них связаны со-
соотношением
/ = JLi = PLc=J_. D2)
^ ^ °
Для того чтобы в рабочей части (р. ч.) аэродинамической трубы
получилась нужная сверхзвуковая скорость (Мн), скачок уплот-
уплотнения следует поместить в конце рабочей части. За скачком
(в сужающемся канале диффузора) дозвуковой поток ускоряется
и только в горле диффузора скорость вновь становится крити-
критической. За горлом диффузора образуется дополнительная сверх-
сверхзвуковая зона, завершаемая скачком, интенсивность которого
тем больше, чем сильнее разрежение, создаваемое эксгаустером
трубы.
Итак, величина а(М), от которой согласно D2) зависит от-
относительный размер «критического» горла диффузора, в свою оче-
очередь определяется интенсивностью скачка, соответствующего чис-
числу Маха в рабочей части. Если считать, что возникает прямой ска-
скачок, то, согласно формуле B4) гл. III,
1 - к 4- 1 Ан
к — 1 1
'-*+! А2
н_
где Ян — приведенная скорость в рабочей части трубы. Переходя
к газодинамическим функциям из гл. V, находим
'ТО
490
ГЛ. VIII. ТЕЧЕНИЯ ГАЗА В СОПЛАХ И ДИФФУЗОРАХ
Из D2) и D3) следует, что для выхода аэродинамической трубы
на заданное значение сверхзвуковой скорости относительное сече-
сечение горла диффузора должно быть не меньше следующей ве-
величины:
г.с
D4)
Если сделать относительное сечение горла диффузора немного
больше, чем по формуле D4), то можно «вытянуть» скачок уп-
уплотнения из рабочей части в расширяющуюся часть диффузора
(рис. 8.60, в), тогда в суженной части диффузора установится за-
замедляющееся (за рабочей частью) сверхзвуковое течение газа,
причем в горле диффузора приведенная скорость Ягд > 1; соглас-
согласно формуле D) гл. IV имеем
/ =
или
к+1
После того как скачок перешел в расширенную часть диффу-
диффузора, можно, плавно сужая (регулируя) горло диффузора, посте-
постепенно уменьшить скорость в
нем до критического значе-
значения, а затем, ослабляя раз-
разрежение эксгаустера, подвес-
подвести скачок уплотнения в рас-
расширяющейся части диффу-
диффузора почти к его горлу
(штриховые линии на рис.
8.60, в). На таком рабочем
режиме горло диффузора
должно быть лишь немного
больше горла сопла (за счет
толщины вытеснения погра-
пограничного слоя, т. е. только в
связи с потерями трения), а
F
10
0,8
0,6
0,2
О
1
\
\
Fr.A
Fr.c
'
1,0 15 2,0 2,5 3,0 3,5 4,0Мн
Рис. 8.61. Относительные площади гор-
горловин диффузора (при «запуске») и
сопла аэродинамической трубы
потери полного давления в
диффузоре (в скачке) стано-
становятся значительно меньше,
чем на режиме запуска.
Отношение площади сечения горла диффузора на режиме за-
запуска к площади сечения струи новозмущенного потока Fa (рабо-
§ 4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ 491
чей части трубы), согласно D2), D4) и D5),
Величины относительной площади горла диффузора FTJJ)(bAa), не-
необходимой для запуска последнего, и относительной площади
горла сопла Fr.c(MB) = FrJFB при & = 1,4 приведены на рис. 8.61.
Интересно отметить, что число Маха в горле диффузора Мг д, нуж-
нужное для «проскока» сквозь него прямого скачка уплотнения (до
сужения горла диффузора), составляет около 0,875 от значения
числа Маха в набегающем потоке Мн (для Мн = 1,5—5 при
к = 1,4). Описанные особенности запуска диффузора аэродина-
аэродинамической трубы относятся и к запуску входного диффузора дви-
двигателя. Для того чтобы, переходя от малых скоростей полета
к расчетной скорости, осуществить расчетную систему скачков,
следует при малых скоростях горло диффузора расширить (или
лишнюю часть воздуха перепустить перед горлом наружу), а по
выходе на расчетную скорость сузить горло (до расчетного разме-
размера) или прекратить перепуск воздуха (прикрыть отверстие для
перепуска). Без этого запуск сверхзвукового диффузора на рас-
расчетный режим невозможен.
Глава IX
ГАЗОВЫЕ ЭЖЕКТОРЫ
§ 1. Назначение и схемы эжекторов
Газовым эжектором называется аппарат, в котором полное дав-
давление газового потока увеличивается под действием струи друго-
другого, более высоконапорного потока. Передача энергии от одного
потока к другому происходит путем их турбулентного смешения.
Эжектор прост по конструкции, может работать в широком диапа-
диапазоне изменения параметров газов, позволяет легко регулировать
рабочий процесс и переходить с одного режима работы на другой.
Поэтому эжекторы широко применяются в различных областях
техники. В зависимости от назначения эжекторы выполняются
различным образом.
Так, в показанной на рис. 9.1 схеме аэродинамической трубы
эжектор выполняет роль насоса, позволяющего подать большое
количество газа сравнительно невысокого давления за счет энер-
энергии небольшого количества газа высокого давления. В баллоне 1
содержится воздух более высокого давления, чем необходимо для
работы трубы. Однако количество сжатого воздуха невелико, и
ч v Q
Рис. 9.1. Схема аэродинамической трубы с эжектором: 1 — баллон со сжа-
сжатым воздухом, 2 — эжектор, 3 — рабочая часть трубы
для обеспечения достаточно продолжительной работы трубы сжа-
сжатый воздух выпускают в эжектор 2, где к нему примешивается
атмосферный воздух, который засасывается эжектором через ра-
рабочую часть трубы 3. Чем больше давление сжатого воздуха, тем
большее количество атмосферного воздуха можно привести в дви-
движение с заданной скоростью.
Часто эжектор используется для поддержания непрерывного
тока воздуха в канале или помещении п выполняет, таким обра-
§ 1. НАЗНАЧЕНИЕ И СХЕМЫ ЭЖЕКТОРОВ
493
зом, роль вентилятора. Примером может служить изображенная
на рис. 9.2 схема стенда для испытания реактивных двигателей.
Струя выхлопных газов, вытекающая из реактивного сопла, под-
подсасывает в эжектор 3 воздух из шахты 2, обеспечивая тем самым
вентиляцию помещения и охлаждение двигателя 2. При этом
Рис. 9.2. Схема стенда для испытания турбореактивных двигателей:
1 — входная шахта, 2 — двигатель на балансирном станке, 3 — эжектор,
4 — выхлопная шахта
горячие газы смешиваются с атмосферным воздухом, что сни-
снижает температуру газа в выхлопной шахте 4 и улучшает усло-
условия работы выхлопных устройств (шумоглушителей и др.)«
Во многих случаях эжектор используют в качестве эксгаустера
для создания пониженного давления в некотором объеме. Таково,
например, назначение эжектора в конденсационных системах па-
паросиловых установок. Для увеличения мощности паровой машины
Рис. 9.3. Схема эжектора паровой конденсационной установки: 1 — пар вы-
высокого давления, 2 — пар из конденсатора
или турбины требуется поддерживать возможно меньшее давление
в конденсаторе, куда выпускается отработанный пар. Эжектор
(рис. 9.3) создает необходимое разрежение вследствие того, что
находящиеся в конденсаторе частицы пара и воздуха подхваты-
подхватываются и уносятся высоконапорной струей пара или воды. В ва-
вакуумной технике эжекторы аналогичной схемы, работающие на
494
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
парах ртути, используются для создания глубокого разрежения
порядка миллионных долей атмосферы.
Примером удачного использования свойств эжекторов являет-
является применение их в газосборных сетях. Источники (скважины)
природного газа, расположенные в одном районе, могут давать
газ различного давления. Если просто подключить их в общую
магистраль, то давление в магистрали необходимо уменьшить не-
несколько ниже давления самого низконапорного источника. Расход
газа из низконапорных скважин будет в этом случае невелик из-за
малого перепада давлений, а энергия давления газа из высокона-
высоконапорных скважин будет бесполезно тратиться при расширении
(дросселировании) его до давления в общей магистрали. Для эф-
эффективного использования всех источников низконапорные сква-
скважины целесообразно подключить в магистраль при помощи эжек-
эжектора, в котором давление низконапорного газа повышается за счет
энергии некоторой части газа высоконапорных скважин. Эжектор
в этом случае является компрессором. Таким путем удается од-
одновременно повысить давление' газа в" магистрали, увеличить про-
производительность низконапорных скважин и подключать в сеть
такие источники газа, которые из-за низкого напора невыгодно
использовать при простом объединении в общую сеть.
Ниже будет рассмотрена еще одна возможная область исполь-
использования свойств эжектора, а именно увеличение реактивной тяги
путем подмешивания внешнего воздуха к струе газа, вытекающе-
вытекающего из сопла реактивного двигателя.
Независимо от назначения эжектора в нем всегда имеются
следующие конструктивные элементы: сопло высоконапорного
(эжектирующего) газа 2, соп-
сопло низконапорного (эжекти-
руемого) газа 2, смеситель-
смесительная камера 3 и, обычно, диф-
диффузор 4 (рпс. 9.4).
Назначение сопел — с ми-
минимальными потерями под-
подвести газы к входу в смеси-
смесительную камеру. Расположен
ние сопел может быть таким,
как на рис. 9.4 (эжектирую-
щий поток внутри, а эжек-
тируемый—по периферии ка-
камеры), и обратным (рис. 9.1),
когда эжектирующий газ подается в камеру по внешнему коль-
кольцевому соплу. Для сокращения длины камеры смешения один
или оба потока могут быть разделены на несколько струй, что
требует соответствующего увеличения количества сопел.
Взаимное расположение, число и форма сопел не оказывают,
однако, существенного влияния на конечные параметры смеси га-
Рис. 9.4. Принципиальная схема эжек-
эжектора: 1 — сопло эжектирующего газа,
2 — сопло эжектируемого газа, 3 — ка-
камера смешения, 4 — диффузор
§ i. НАЗНАЧЕНИЕ И СХЕМЫ ЭЖЕКТОРОВ 495
зов. Важным является лишь соотношение между величинами
поперечных сечений потоков эжектируемого и эжектирующего
газов на входе в камеру, т. е. отношение суммарных площадей
сопел.
Если перепад давления в сопле эжектирующего газа значи-
значительно превышает критическую величину, то в ряде случаев ока-
оказывается выгодным применение сверхзвукового сопла. При этом
могут быть улучшены параметры эжектора на расчетном режиме.
Однако и при больших сверхкритических отношениях давлений
можно использовать эжектор с нерасширяющимся соплом, в ко-
котором скорость истечения эжектирующего газа не превышает ско-
скорости звука. Такой эжектор принято называть звуковым. Это наи-
наиболее распространенный тип эжектора, эффективно работающий
в широком диапазоне изменения параметров газов.
Камера смешения может быть цилиндрической или иметь пе-
переменную по длине площадь сечения. Форма камеры оказывает
заметное влияние на смешение газов. Поэтому, хотя ниже будут
рассматриваться в основном эжекторы с цилиндрической смеси-
смесительной камерой, мы расскажем также о принципе расчета эжек-
эжекторов с камерой переменного сечения.
Длина камеры выбирается такой, чтобы в ней практически ус-
успел закончиться процесс смешения потоков, однако по возможно-
возможности короткой, с тем чтобы не увеличивать гидравлических потерь
и сократить общие габариты эжектора.
В эжекторе, показанном на рис. 9.4, выходное сечение сопел
совпадает с входным сечением цилиндрической смесительной ка-
камеры. Существующие методы расчета эжектора составлены имен-
именно для такой схемы, поэтому она и будет рассматриваться в даль-
дальнейшем. Однако на практике сопла часто располагают на некото-
некотором расстоянии от входного сечения камеры. Так, например, соп-
сопло двигателя на стенде (рис. 9.2) нельзя поместить во входное
сечение цилиндрической камеры эжектора, так как существую-
существующее в этом сечении разрежение изменит распределение давления
на внешней поверхности сопла, что внесет погрешность в величи-
величину измеряемой реактивной тяги.
Диффузор устанавливается на выходе из смесительной камеры
в тех случаях, когда желательно повысить статическое давление
смеси газов на выходе из эжектора или когда при заданном дав-
давлении на выходе желательно получить низкое статическое дав-
давление в камере смешения и во входном сечении эжектора.
Следует отметить, что эжектор может работать и без диффузо-
диффузора. В этом случае конечное сечение смесительной камеры одновре-
одновременно является выходным сечением эжектора. Иногда вместо диф-
диффузора на выходе из смесительной камеры устанавливается су-
сужающееся сопло или сопло Лаваля. Это бывает целесообразным
тогда, когда конечной задачей является ускорение потока газа
после смешения. Так, например, в различных схемах двухконтур-
496
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
ных реактивных двигателей газовые потоки, выходящие из кон-
контуров, смешиваются в общей камере, а затем вытекают в атмос-
атмосферу через общее реактивное сопло дозвукового или сверхзвуково-
сверхзвукового типа.
§ 2. Рабочий процесс эжектора
Рабочий процесс эжектора сводится к следующему. Высокона-
Высоконапорный (эжектирующий) газ, имеющий полное давление Рц вы-
вытекает из сопла в смесительную камеру. При стационарном режи-
режиме работы эжектора во входном сечении смесительной камеры ус-
устанавливается статическое давление р2, которое всегда ниже пол-
полного давления низконапорного (эжектируемого) газа р2-
Под действием разности давлений низконапорный газ устрем-
устремляется в камеру. Относительный расход этого газа, называемый
коэффициентом эжекции п = G2/Gu зависит от площадей сопел, от
плотности газов и их начальных давлений, от режима работы эжек-
дора. Несмотря на то, что скорость эжектируемого газа во вход-
входном сечении w2 обычно меньше скорости эжектирующего газа w\9
надлежащим выбором площадей сопел F\ и F2 можно получить
сколь угодно большое значение коэффициента эжекции п.
В камеру смешения эжектирующий и эжектируемый газы вхо-
входят в виде двух раздельных потоков: в общем случае они могут
Рис. 9.5. Схема течения и изменение поля скоростей по длине камеры сме-
смешения при дозвуковой скорости потоков
различаться по химическому составу, скорости,, температуре и дав-
давлению. Смешение потоков означает, в конечном счете, выравни-
выравнивание параметров газов по всему сечению камеры.
Весь процесс смешения можно условно разделить на два эта-
этапа — начальный и основной. Соответственно выделяются два
участка смесительной камеры (рис. 9.5). Течение в начальном
участке камеры смешения с известным приближением можно
уподобить турбулентной струе, движущейся в спутном потоке.
Ввиду наличия поперечных пульсационных компонент скорости,
свойственных турбулентному движению, потоки внедряются друг
§ 2. РАБОЧИЙ ПРОЦЕСС ЭЖЕКТОРА 4^7
в друга, образуя постепенно уширяющуюся зону смешения — по-
пограничный слой струи. В пределах пограничного слоя происходит
плавное изменение параметров газовой смеси от значений их в
эжектирующем газе до значений в эжектируемом газе. Вне погра-
пограничного слоя в начальном участке камеры смешения имеются
невозмущенные потоки эжектируемого и эжектирующего газов.
В начальном участке камеры частицы эжектируемого газа
непрерывно захватываются высоконапорной струей и увлекаются
ею в зону смешения. Благодаря этому и поддерживается разре-
разрежение на входе в смесительную камеру, которое обеспечивает вте-
втекание низконапорного газа в эжектор. В зависимости от относи-
относительных размеров эжектора с удалением от сопла последователь-
последовательно исчезают обе зоны невозмущенного течения газов; так, на
рис. 9.5 первым ликвидируется ядро эжектирующей струи.
На некотором расстоянии от сопла, в сечении Г — Г, называе-
называемом граничным сечением, пограничный слой струи заполняет все
сечение смесительной камеры. В этом сечении уже нет областей
невозмущенных течений, однако параметры газа существенно раз-
различны по радиусу камеры. Поэтому и после граничного сечения
в основном участке смесительной камеры продолжается выравни-
выравнивание параметров потока по сечению. В конечном сечении камеры,
отстоящем в среднем на расстоянии 8—12 диаметров камеры от
начального сечения, получается достаточно однородная смесь га-
газов, полное давление которой р3 тем больше превышает полное
давление эжектируемого газа р2» чем меньше коэффициент эжек-
ции п. Рациональное проектирование эжектора сводится к выбо-
бору таких его геометрических размеров, чтобы при заданных на-
начальных параметрах и соотношении расходов газов получить наи-
наивысшее значение полного давления смеси, либо при заданных на-
начальных и конечном давлениях получить наибольший коэффици-
коэффициент эжекции.
Описанная выше схема процесса смешения газов в эжекторе
при дозвуковых скоростях принципиально ничем не отличается
от процесса смешения несжимаемых жидкостей в жидкостном
эжекторе. Как будет показано ниже, даже при больших докрити-
ческих отношениях давлений не только качественные закономер-
закономерности, но и многие количественные зависимости между параметра-
параметрами газового эжектора практически не отличаются от соответству-
соответствующих данных жидкостного эжектора.
Качественно новая картина течения наблюдается при сверх-
сверхкритических отношениях давлений в сопле. При дозвуковом исте-
истечении давление газа на выходе из сопла равно давлению в окру-
окружающей среде, другими словами, статические давления газов на
входе в камеру смешения р\ и р2 одинаковы. При звуковом или
сверхзвуковом истечении эжектирующего газа давление на срезе
сопла может существенно отличаться от давления эжектируемого
газа.
32 г. Н. Абрамович, ч. i
498
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
p*,F2.l2<1
Рис. 9.6. Схема течения в начальном участке
камеры смешения при сверхкритическом от-
отношении давлений в сопле
Если сопло эжектирующего газа выполнено нерасширяющим-
нерасширяющимся, то при сверхкритическом отношении давлений статическое дав-
давление на срезе сопла превышает давление в окружающей среде —
эжектируемом газе. Поэтому после выхода из сопла А струя эжек-
эжектирующего газа В (рис. 9.6), движущаяся со скоростью звука
(к{ = 1), продолжает
расширяться, скорость
ее становится сверхзву-
сверхзвуковой, а площадь сече-
сечения — большей, чем
площадь выходного се-
сечения сопла.
Точно так же ведет
себя сверхзвуковая
эжектирующая струя,
вытекающая из сопла
Лаваля, если в эжекто-
эжекторе применено сверхзву-
сверхзвуковое сопло с неполным
расширением. В этом
случае скорость газа на
срезе сопла соответству-
соответствует Х\ =Я]Р > 1,^где Xip — расчетная величина скорости для дан-
данного сопла Лаваля, определяющаяся отношением площадей вы-
выходного и критического сечений.
Таким образом, при отношениях давлений, больших расчетно-
расчетного для данного сопла, эжектирующий газ в начальном участке
смесительной камеры представляет собой расширяющуюся сверх-
сверхзвуковую струю. Поток эжектируемого газа на этом участке дви-
движется между границей струи и стенками камеры. Так как ско-
скорость эжектируемого потока в начальном участке дозвуковая, то
при течении по суживающемуся «каналу» поток ускоряется и
статическое давление в нем падает.
При дозвуковом истечении эжектирующей струи наибольшее
разрежение и максимальные скорости потоков достигались во
входном сечении камеры. В данном случае минимальное значение
статического давления и максимальная скорость эжектируемого
потока достигаются в сечении 1', находящемся на некотором рас-
расстоянии от сопла, там, где площадь расширяющейся сверхзвуко-
сверхзвуковой струи становится наибольшей. Это сечение принято называть
сечением запирания.
Особенностью сверхзвуковой струи является то, что смеше-
смешение ее с окружающим потоком на этом участке проходит значи-
значительно менее интенсивно, чем смешение дозвуковых потоков. Это
связано с тем, что сверхзвуковая струя обладает повышенной ус-
устойчивостью по сравнению с дозвуковой струей, и размывание
границ такой струи происходит слабее. Физические основы этого
§ 2. РАБОЧИЙ ПРОЦЕСС ЭЖЕКТОРА
499
явления легко уяснить на следующем примере (рис. 9.7). Если
граница дозвукового потока в силу какой-либо причины (напри-
(например воздействия частиц газа спутного потока) искривлена, то в
этом месте из-за уменьшения площади сечения уменьшается ста-
статическое давление и возникает сила внешнего давления, увеличи-
увеличивающая начальную деформацию границы: при взаимодействии
рЛ
Я7>7
Рис. 9.7. Схема силового воздействия газа на тело, искривляющее границу
дозвукового (а) и сверхзвукового (б) потоков
с окружающей средой дозвуковая струя «втягивает» частицы
внешнего потока и граница ее быстро размывается. В сверхзву-
сверхзвуковом (относительно внешней границы) потоке аналогичное ис-
искривление границы и уменьшение сечения приводит к росту дав-
давления; возникающая сила направлена не внутрь, а наружу пото-
потока и стремится восстановить исходное положение границы струи,
выталкивая частицы внешней среды.
Интересно отметить, что это различие в свойствах дозвуковой
и сверхзвуковой струй можно наблюдать буквально на ощупь.
Рис. 9.8. Шлирен-фотография потока в камере смешения плоского эжектора
при дозвуковом режиме истечения газа из сопла: а = FUF2 « 1, По =
Дозвуковая струя втягивает внутрь поднесенный к границе лег-
легкий предмет, сверхзвуковая струя на расстоянии нескольких ка-
калибров от сопла имеет «жесткую» границу; при попытке ввести
в струю извне какой-либо предмет ощущается заметное сопротив-
сопротивление резко выраженной границы струи.
На рис. 9.8 и 9.9 приведены фотографии течения в начальном
участке смесительной камеры при дозвуковом и сверхзвуковом ис-
32*
500
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
течении эжектирующей струи. Фотографии получены на плоской
модели эжектора, режим изменялся путем увеличения полного
давления эжектирующего газа перед соплом рх при постоянном
давлении эжектируемого газа и постоянном давлении на выходе
из камеры.
На фотографиях видно различие между двумя рассмотренны-
рассмотренными режимами течения в начальном участке камеры.
При анализе процессов и расчете параметров эжектора на
сверхкритических отношениях давлений в сопле будем полагать,
Рпс. 9.9. Шлирен-фотография потока в камере смешения плоского эжектора
при сверхкритическом отношении давлений в сопле По = 3,4
что до сечения запирания V (рис. 9.6) эжектирующий и эжекти-
руемый потоки текут раздельно, не смешиваясь, а интенсивное
смешение происходит за этим сечением. Это весьма близко к дей-
действительной картине явления.
Сечение запирания является характерным сечением началь-
начального участка смешения, а параметры потоков в нем, как будет
показано ниже, существенно влияют на рабочий процесс и пара-
параметры эжектора.
С удалением от сопла граница между потоками размывается,
сверхзвуковое ядро эжектирующей струи уменьшается, происхо-
происходит постепенное выравнивание параметров газа по сечению
камеры.
Характер смешения газов в основном участке смесительной
камеры до режима запирания практически такой же, как и при
докритических отношениях давлений в сопле, скорость смеси га-
газов ws в широком диапазоне начальных параметров газов остает-
остается меньше скорости звука. Однако при увеличении отношения на-
начальных давлений газов сверх некоторого определенного для каж-
каждого эжектора значения поток смеси в основном участке камеры
становится сверхзвуковым и может остаться сверхзвуковым до
конца смесительной камеры. Условия перехода от дозвукового
к сверхзвуковому режиму течения смеси газов, как будет показа-
§ 2. РАБОЧИЙ ПРОЦЕСС ЭЖЕКТОРА 501
но ниже, тесно связаны с режимом течения газов в сечении запи-
запирания. Таковы особенности протекания процесса смешения газов
при сверхкритических отношениях давлений газов в эжектирую-
шем сопле. Заметим, что под отношением давлений в сопле мы
подразумеваем отношение полного давления эжектирующего га-
газа p*i к статическому давлению эжектируемого потока во вход-
входном сечении смесительной камеры р2, которое зависит от полного
давления ft и приведенной скорости Яг.
Чем больше Яг, тем больше (при постоянном отношении пол-
полных давлений газов) отношение давлений в сопле:
р1 ?! по
Здесь я (Я) < 1 — известная газодинамическая функция, см. § 6
гл. V.
Таким образом, сверхкритический режим истечения эжектиру-
эжектирующего газа из сопла может существовать и тогда, когда отноше-
отношение начальных полных давлений газов р\/р\ = По ниже критиче-
критического значения.
Независимо от особенностей течения газов при смешении про-
происходит выравнивание скорости газов по сечению камеры путем
обмена импульсами между частицами, движущимися с большей
и меньшей скоростью. Этот процесс сопровождается потерями.
Помимо обычных гидравлических потерь на трение о стенки со-
сопел и камеры смешения, для рабочего процесса эжектора харак-
характерны потери, связанные с самим существом процесса смешения.
Определим изменение кинетической энергии, происходящее
при смешении двух газовых потоков, секундный массовый расход
и начальная скорость которых равны соответственно 6?i, G2, w\
и W2. Если предположить, что смешение потоков происходит при
постоянном давлении (это возможно при специальной профили-
профилировке камеры), то количество движения смеси должно быть рав-
равно сумме начальных количеств движения потоков:
(Gi + G2) w3 = Giwi + G2w2, A)
откуда
G
Кинетическая энергия смеси газов равна
Легко убедиться, что эта величина меньше суммы кинетических
энергий потоков до смешения, равной
502
ГЛ. ГХ. ГАЗОВЫЕ ЭЖЕКТОРЫ
на величину
АЕ = Ех
?2-?3 =
Величина АЕ представляет собой потери кинетической энер-
энергии, связанные с процессом смешения потоков. Эти потери ана-
аналогичны потерям энергии при ударе неупругих тел. Независимо
от температуры, плотности и других параметров потоков потери,
как показывает формула B), тем больше, чем больше разность
скоростей смешивающихся потоков. Отсюда можно сделать вывод,
что при заданной скорости эжектпрующего газа и заданном отно-
относительном расходе эжектируемого газа GWd (коэффициенте
эжекции) для получе-
получения наименьших по-
потерь, т. е. наибольшей
величины полного дав-
давления смеси газов, же-
желательно увеличивать
W2 так, чтобы возможно
более приблизить ско-
скорость эжектируемого
газа к скорости эжекти-
рующего газа при вхо-
входе в камеру смешения.
Как увидим ниже, это
действительно приво-
приводит к наивыгоднейшему
протеканию процесса
смешения.
При смешении газов в цилиндрической смесительной камере
эжектора статическое давление газов не остается постоянным.
Для того чтобы определить характер изменения статического
давления в цилиндрической смесительной камере, сравним пара-
параметры потока в двух произвольных сечениях камеры 1 и 2, на-
находящихся на различном расстоянии от начала камеры
(рис. 9.10). Очевидно, что в сечении 2, находящемся на большем
расстоянии от входного сечения камеры, поле скорости более рав-
равномерно, чем в сечении 1. Если принять, что для обоих сечений
р = const (для основного участка камеры, где статическое давле-
давление изменяется незначительно, это приближенно соответствует
действительности), то из условия равенства секундных расходов
газа I*
р
0,5
0,6
Г
\
\
I
/Г
^—-
Z
S
Рис. 9.10. Изменение статического давления
по длине камеры смешения при дозвуковом
течении газов
pj wdF = p J wdF = pwF
A) B)
следует, что в сечениях 1 и 2 сохраняет постоянное значение сред-
§ 2. РАБОЧИЙ ПРОЦЕСС ЭЖЕКТОРА 503
няя по площади величина скорости потока
lfr. C)
(F)
Рассмотрим далее величину
Легко убедиться, что при w = const, т. е. в случае равномерного
поля скорости в сечении F, величина т равна единице. Во всех
других случаях числитель в D) больше знаменателя и т > 1 (не-
(неравенство Коши— Шварца).
Значение величины т может служить характеристикой степе-
степени неравномерности поля скорости в данном сечении: чем более
неравномерно поле w, тем больше т. Будем называть величину
т коэффициентом поля.
Возвращаясь к рис. 9.10, теперь нетрудно заключить, что ко-
коэффициент поля т в сечении 1 больше, чем в сечении 2. Количе-
Количества движения в сечениях 1 ж 2 определяются интегралами
Jj^Y-T j
A) \A) J К B)
Так как t\ > тг, то отсюда следует
f w2dF> f w2dF. E)
A) B)
Итак, количество движения в потоке при выравнивании поля ско-
скорости в процессе смешения уменьшается, несмотря на то, что
суммарный расход и средняя по площади скорость w остаются
постоянными.
Запишем теперь уравнение импульсов для потока между сече-
сечениями 1 и 2:
р f w2dF — p f w2dF
)
A) B)
На основании неравенства E) левая часть данного уравнения
всегда положительна. Отсюда следует, что р2 > р\, т. е. выравни-
выравнивание поля скорости в цилиндрической смесительной камере соп-
сопровождается возрастанием статического давления] во входном се-
сечении камеры существует пониженное давление по сравнению
с давлением на выходе из камеры. Это свойство процесса непо-
непосредственно используется в простейших эжекторах, состоящих из
сопла и одной цилиндрической камеры смешения, как, например,
504 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
показано на рис. 9.10. Благодаря наличию разрежения на входе
в камеру, этот эжектор подсасывает из атмосферы воздух, а затем
смесь выбрасывается вновь в атмосферу. На рис. 9.10 также пока-
показано изменение статического давления по длине камеры эжектора.
Полученный качественный вывод справедлив в тех случаях,
когда изменение плотности газа в рассматриваемом участке про-
процесса смешения незначительно, вследствие чего можно прибли-
приближенно считать р = const. Однако в некоторых случаях цри сме-
смешении газов существенно различной температуры, когда имеется
большая неравномерность плотности по сечению, а также при
сверхзвуковых скоростях в основном участке смешения, когда
плотность заметно изменяется по длине камеры, возможны режи-
режимы работы эжектора, при которых статическое давление газа
в процессе смешения не возрастает, а снижается.
Если смесительная камера не целиндрическая, как предпола-
предполагалось выше, а имеет переменную по длине площадь сечения, то
можно получить произвольное изменение статического давления
по длине.
' Основным геометрическим параметром эжектора с цилиндри-
цилиндрической смесительной камерой является отношение площадей вы-
выходных сечений сопел для эжектирующего и эжектпруемого газов
а ~ Т~ ~~ F —F f
2 3 1
где Рз — площадь сечения цилиндрической смесительной камеры.
Эжектор_с большим значением а, т. е. с относительно малой
площадью камеры, является высоконапорным, но не может рабо-
работать с большими коэффициентами эжекции; эжектор с малым
а позволяет подсосать большое количество газа, но мало повы-
повышает его напор.
Вторым характерным геометрическим параметром эжектора
является степень расширения диффузора / = FJFs — отношение
площади сечения на выходе из диффузора к площади на входе
в него. Если эжектор работает при заданном статическом давле-
давлении на выходе из диффузора, например при выхлопе в атмосферу
или в резервуар с постоянным давлением газа, то степень расши-
расширения диффузора / существенно влияет на все параметры эжекто-
эжектора. С увеличением / в этом случае снижается статическое дав-
давление в камере смешения, растет скорость эжектирования и ко-
коэффициент эжекции при не очень значительном изменении пол-
полного давления смеси. Разумеется, это справедливо лишь до того
момента, когда в каком-либо сечении эжектора будет достигнута
скорость звука.
Третий геометрический параметр эжектора — относительная
длина камеры смешения h/dz — в обычные методы расчета эжек-
эжектора не входит, хотя и существенно влияет на параметры эжек-
§ 3 РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 505
тора, определяя полноту выравнивания параметров смесп по се-
сечению. Ниже будем полагать, что длина камеры достаточно ве-
велика (h/dz > 8 -г- 10) и коэффициент поля т в ее выходном се-
сечении близок к единице.
§ 3. Расчет газового эжектора
Сопла и диффузор эжектора ничем не отличаются от обыч-
обычных сопел и диффузоров, расчет которых изложен в гл. VIII. При
определении параметров эжектора существенны лишь коэффици-
коэффициенты сохранения полного давления газа в этих устройствах, по-
позволяющие по начальным давлениям смешивающихся газов найти
полные давления на срезе сопел рх и р2 и по полному давле-
давлению смеси р3 — полное давление на выходе из диффузора /?4. Эти
коэффициенты выбираются по экспериментальным данным в за-
зависимости от формы сопел и диффузора и величины скорости
потока.
Основная задача при расчете эжектора заключается в опреде-
определении параметров смеси газов на выходе из смесительной камеры
но параметрам газов до смешения. Замечательным является тот
факт, что для определения параметров потока на выходе из ка-
камеры рассмотрение самого процесса смешения не обязательно.
Нет необходимости также предварительно вычислять потери, воз-
возникающие в процессе смешения, и анализировать механизм про-
процесса передачи энергии.
Течение газа в любом участке смесительной камеры описы-
описывается тремя уравнениями сохранения: энергии, массы и коли-
количества движения. Если поток газа в выходном сеченпи камеры
считать одномерным, т. е. полагать процесс выравнивания пара-
параметров смеси по сечению полностью закончившимся, то указан-
указанных трех уравнений достаточно для определения трех парамет-
параметров потока в выходном сечении по заданным начальным парамет-
параметрам газов на входе в камеру. Три параметра, как известно, пол-
полностью характеризуют состояние потока газа и позволяют найти
любые другие его параметры. В частности, если это требуется,
по величине полного давления смеси р\ можно определить поте-
потери в процессе смешения потоков. Таким образом, при составлении
основных уравнений мы не вводим никаких условий о необрати-
необратимости процессов, однако после решения уравнений приходим к ре-
результату, который свидетельствует о том, что в рассматриваемом
процессе есть потерп полного давления, тЛ е. рост энтропии. Ана-
Аналогичное положение возникало при решении задачи о парамет-
параметрах газа за скачком уплотнения, которые, кстати сказать, опре-
определялись по начальным параметрам потока теми же тремя
уравнениями.
506 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
Такой подход к решению задачи приводит к правильному ко-
конечному результату независимо от того, какие процессы происхо-
происходят между рассматриваемыми начальным и конечным сечениями
камеры, насколько интенсивно идет процесс смешения, возника-
возникают ли скачки уплотнения, имеется ли отрыв потока, вихри, встреч-
встречные токи и т. д. Принятое допущение об одномерности потока в
конечном сечении является весьма существенным, так как очевид-
очевидно, что никаких сведений о характере поля скорости в конце сме-
смешения такой расчет дать не может; они должны быть заданы до-
дополнительно, если т Ф 1.
^Запишем основные уравнения, связывающие параметры пото-
потока во входном и выходном сечениях цилиндрической смесительной
камеры. Параметры эжектщщщцего газа во входном сечении бу-
будем отмечать индексом 1, параметры эжектируемого газа — ин-
индексом 2, параметры смеси в выходном сечении — индексом 3. Бу-
Будем считать заданными все параметры потоков во входном сече-
сечении камеры и построим решение таким образом, чтобы из уравне-
уравнений сохранения массы, энергии и импульса потока определить
температуру торможения, приведенную скорость и полное давле-
давление смеси газов в выходном сечении камеры.
Закон сохранения массы записываем в виде
G3 = G1 + G2 или !»=и+1> F)
где п = G2/G1 — коэффициент эжекции.
На основании закона сохранения энергии имеем
где Q — общее количество тепла, подводимое за 1 с к газу в сме-
смесительной камере путем теплопередачи через стенки камеры или
выделяющееся вследствие химических реакций в потоке.
Переходя к параметрам торможения, получаем
G,cvzT\ = GlCplTl + G2cp2T*2 + <?, G)
т. е. суммарное теплосодержание смеси, отвечающее состоянию
полного торможения, отличается от суммы полных теплосодержа-
теплосодержаний газов перед смешением лишь на количество тепла, подведен-
подведенного в процессе смешения. Если пренебречь различием в тепло-
емкостях смешивающихся газов и смеси, то, разделив обе части
уравнения G) на G1cplT1 и подставив в него соотношение F),
получим
(n + l)-i—1+B-L
cprlGl
§ 3. РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 507
Введем обозначения
4 = е, -4—*.
Тогда из последнего уравнения получаем
К 1 + п9 + О
Т{
(8)
где 'О — отношение подведенного секундного количества тепла к
теплосодержанию секундного расхода эжектирующего газа. Если
при смешении газов не происходит горения или какой-либо иной
реакции, сопровождающейся выделением или поглощением тепла,
а теплопередачей через стенки смесительной камеры пренебречь,
то величина относительного теплоподвода Ф = 0. При расчете
обычных эжекторов принимаем # = 0и получаем
Уравнения (8) или (9) позволяют по заданным величинам непо-
непосредственно определить первый искомый параметр смеси газов —
температуру торможения (или критическую скорость звука)
в выходном сечении смесительной камеры.
Составим уравнение количества движения. Внешние силы,
действующие на боковую поверхность потока со стороны стенок
цилиндрической камеры смешения, не дают составляющих, парал-
параллельных оси камеры (если не учитывать трения о стенки каме-
камеры). Поэтому изменение секундного количества движения пото-
потоков в цилиндрической камере смешения равно разности сил дав-
давления в граничных сечениях камеры. В общем случае, когда во
входном сечении камеры статические давления эжектирующего
и эжектируемого газов различны (но постоянны по сечению каж-
каждого потока), уравнение количества движения записывается в виде
G3.W3 — G\Wi — G2W2 = p\F\ + P2F2 — PbFz,
или
G$W3 + p3Fz = Giwi + piFi + G2w2 + P2F2. A0)
Преобразуем это уравнение при помощи газодинамических
функций. Заменим в A0) выражения импульсов согласно фор-
формуле A15) гл. V:
к -4- 1
Пренебрегая пока различием в величинах —т— для газов
и смеси, из A0) получим
2z(X2). A1)
508 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
Это уравнение имеет такой же вид, как уравнение A), записан-
записанное без учета сжимаемости газа и изменения давления в потоке,
причем величина
aKVz (к) = ъ
играет ту же роль, что и величина скорости w в уравнении A).
Так как величина акрз уже определена, то решение уравнения
A1) по существу не отличается от решения уравнения A).
Разделим обе части уравнения A1) на
Заменяя в этом уравнении отношения расходов и критических
скоростей введенными выше безразмерными величинами
а также используя уравнения F) и (8), получим окончательно
" • A2)
Это уравнение называют основным уравнением эжещии. По на-
начальным параметрам газов и коэффициенту эжекции из него мож-
можно определить газодинамическую функцию z (k3) = Х3 + -г— и при-
Лз
веденную скорость смеси Яз.
Для нахождения полного давления смеси р3 воспользуемся
уравнением F).
Заменив в F) величины расхода газа G$ и G\ при помощи со-
соотношения A09) гл. V, получим
Pi
Здесь предполагается, что значение коэффициента т в A09)
гл. V, зависящее от к и R, одинаково для обоих газов и смеси. За-
Заменим в этом уравнении отношение температур Т*х/Т$ согласно
(8) и учтем, что при цилиндрической камере смешения F$ = F\ +
F i
+ F2 или jr- = 1 H . Тогда получаем окончательно
а
§ 3. РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 509
Так как Яз известно из уравнения A2), то, определив из таб-
таблиц значение функции #(Хз), по уравнению A3) можно найти
полное давление газа на выходе из камеры смешения />3.
В уравнениях (8), A2) и A3), помимо параметров эжектп-
рующего и эжектируемого газов перед смешением, фигурирует
безразмерная величина п — коэффициент эжекции. Эта величина
может быть выражена через параметры потоков во входном сече-
сечении камеры и не является, таким образом, независимой. Подстав-
Подставляя в выражение для коэффициента эжекции величины расходов
смешивающихся газов, записанные при помощи соотношения
A09) гл. V, получаем
_ G9 P*2F2q
*F (\ \ 1/
1 1 V 1/ V
ИЛИ
п= 1 д(К) A4)
Соотношение A4) связывает коэффициент эжекции п с геомет-
геометрическим параметром эжектора а и параметрами газов на входе
в камеру. Полученные уравнения (8), A2) и A3) вместе с со-
соотношением A4) достаточны для определения состояния потока
в выходном сечении по заданным начальным параметрам потоков
и коэффициенту эжекции (или геометрическому параметру а).
Рассмотрим теперь некоторые возможные уточнения изложен-
изложенного метода расчета эжектора.
а). Учет сил трения о стенки камеры. Напомним, что в этом
простейшем расчете цилиндрической смесительной камеры учи-
учитываются лишь основные потери, свойственные процессу смеше-
смешения — потери на удар при обмене количеством движения между
частицами, движущимися с разной скоростью, а также потери
в скачках уплотнения, если они имеют место. В ряде задач, од-
однако, существенную роль играют потери на трение о стенки ка-
камеры. Чтобы учесть влияние трения, необходимо изменить вид
уравнения импульсов A0).
Действительно, при наличии трения количество движения по-
потока в смесительной камере изменяется не только под действием
сил давления в граничных сечениях камеры, но и под действием
суммарной силы трения Ртр о стенки смесительной камеры:
р . г 1в Wl р
ТР ~~ fe d 2 3"
3
После несложных преобразований представим эту формулу в виде
510 гл. ix. газовые эжекторы
Прибавляя в A0) силу трения Р1ф к действующим на поток
силам давления, после преобразований получаем следующее ос-
основное уравнение для расчета эжектора с учетом трения:
[*(К) + у Х^з] /(п + 1)A + лв + 0) = z(Я,,) + п /вz(Х2). A5)
Здесь величина % — , , 1 ? -т- называется приведенной длиной
смесительной камеры. Коэффициент трения ? выбирается в за-
зависимости от числа Рейнольдса и числа М потока, как указано
в § 2 гл. V. При расчете звуковых эжекторов обычно хорошее
соответствие с экспериментальными данными получается при
? = 0,015 - 0,025.
Что касается остальных уравнений, использованных в расчете
смесительной камеры, то при наличии трения вид их не изме-
изменяется — равенство суммарного расхода и полной энергии газов
во входном и выходном сечениях камеры сохраняется независи-
независимо от величины силы трения.
Для учета трения о стенки камеры смешения можно также
воспользоваться результатами, полученными в § 2 гл. V. Опреде-
Определив величину приведенной скорости смеси при отсутствии трения
по формуле A2) (назовем ее ^1), находим изменение этой вели-
величины, связанное с трением, по формуле A7) гл. V
где
Отсюда с помощью графика функции ф(А,) (рис. 5.3) получа-
получаем Яз — приведенную скорость смеси на выходе из камеры с при-
приведенной длиной %. Далее по формуле A3) находим полное дав-
давление смеси с учетом трения.
б) Расчет камеры при смешении разнородных газов. При вы-
выводе уравнений для расчета камеры смешения было принято, что
для обоих смешивающихся газов и для смеси значения удельных
теплоемкостей ср и газовых постоянных R одинаковы; отсюда сле-
следовало и равенство показателей адиабаты /с. Это упрощает вид
уравнений и их решение без заметной погрешности в результатах
численных расчетов. Если в эжекторе смешиваются газы с суще-
существенно различными значениями физических констант, то можно
провести расчет с учетом этого различия. Для этого по заданным
значениям cPi R и к для смешивающихся газов и коэффициенту
эжекции п необходимо вычислить значения этих величин для сме-
§ 3. РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 511
си в выходном сечении камеры. Обозначив
получаем
1 + ПС т. т 1 -\- ПС ту у> 1 + TlR
Далее, из исходных уравнений сохранения массы, энергии и ко-
количества движения надо вывести уравнения, подобные (8), A2),
A3) и A4), не пренебрегая разницей в сР, R и к и не сокращая
численных коэффициентов, зависящих от к. Значения газодинами-
газодинамических функций q(k) также надо определять из таблиц, вычис-
вычисленных для соответствующих значений к.
Путем несложных преобразований можно привести уравнения
энергии, количества движения и расхода для общего случая сме-
смешения различных газов к виду
Т1 1 + пев + Ф
В3 Y(n + 1) A + пев +*) z (Я8) = Byz (К) + В2п Y'cQ z (X2j, A7)
^з Ал V(n+1) (l + nri + Ъ) Я (К,)
Р А l V(h)
где величины
определяются для газов и смеси по известным значениям показа-
показателя адиабаты. Вместо соотношения A4) получим
Л1 Поа/св ?(Ai)
Расчет по формулам A6)—A9) дает возможность определить
влияние величин к и ср смешивающихся газов на параметры сме-
смеси в выходном сечении цилиндрической камеры.
в) Расчет камеры смешения переменной площади. В отличие
от течения в цилиндрической камере при смешении в камере пе-
переменного сечения на поток действует дополнительная сила —
осевая составляющая силы реакции стенок. Это существенно ус-
усложняет расчет, так как сила реакции, входящая в уравнение
512 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
количества движения:
Р= f pdF,
не может быть просто выражена через параметры газов в началь-
начальном и конечном сечениях камеры. В общем случае для определе-
определения этой силы необходимо знать закон изменения статического
давления по длине смесительной камеры, что требует специаль-
специального рассмотрения протекания процесса смешения. Только в не-
некоторых частных случаях здесь возможно достаточно простое ре-
решение.
Так, камера смешения может быть спроектирована таким об-
образом, что статическое давление в ней сохраняется постоянным
(изобарический процесс смешения). Осевая составляющая всех
сил давления, действующих на газовый поток между входным и
выходным сечениями такой камеры, равна нулю. Поэтому коли-
количество движения потока в камере, если не учитывать действия
силы трения, остается неизменным. Уравнение количества дви-
движения
G2W2
в этом случае приводится к виду
Это уравнение используется в расчете вместо уравнения A2).
Полное давление смеси газов р3 может быть найдено из условия
изобаричности процесса
t = р*2л(к2).
Из уравнения неразрывности F) для F$?= F{ + F2 легко по-
получить выражение, аналогичное формуле A3):
Отсюда определяется величина площади выходного сечения ка-
камеры, обеспечивающая равенство статического давления потока
на входе и выходе.
В других случаях (р Ф const) расчет камеры переменного
сечения может быть проведен приближенно, если принять упро-
упрощающие предположения о законе изменения давления в камере.
Так, иногда полагают, что давление изменяется по линейному
закону в зависимости от площади сечения камеры, так что сред-
среднее значение давления р равно полусумме значении р2 и р$ в
начальном и конечном сечениях.
§ 3. РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 513
В этом случае сила реакции стенок равна
й может быть учтена при составлении уравнения количества
движения, которое после соответствующих преобразований при-
принимает вид
Расче?ы и эксперименты показывают, что при смешении по-
потоков в сужающейся камере (частным случаем которой является
изобарическая камера) полное давление смеси может быть более
высоким, чем на выходе из цилиндрической камеры при тех же
начальных параметрах газов.
Основной причиной несколько большей эффективности су-
сужающихся камер при дозвуковых скоростях является уменьше-
уменьшение разности скоростей потоков и снижение ударных потерь при
смешении, так как процесс смешения происходит в ускоряющем-
ускоряющемся потоке. При этом, однако, следует учитывать, что увеличение
выходной скорости wz может привести к возрастанию потерь
в диффузоре.
При сверхзвуковой скорости потока сужение камеры смеше-
смешения приводит к уменьшению скорости течения и к снижению по-
потерь полного давления в прямом скачке, если он возникает
вблизи выходного сечения камеры (см. § 7), или в системе скач-
скачков, переводящих поток в дозвуковой. В результате как при до-
дозвуковых, так и при сверхзвуковых скоростях отмечается возра-
возрастание полного давления смеси, в ряде случаев составляющее до
15—20 %. В связи с этим эжекторы с камерой смешения пере-
переменной площади, чаще всего с конической сужающейся камерой,
находят применение в технике.
Рассмотрим теперь основные особенности расчета диффузора
эжекторного- устройства. Температура торможения потока при
течении в диффузоре не изменяется, поэтому Т± = Т3 и акр4 =
= акрз. Вследствие возникающих в диффузоре потерь полное дав-
давление в выходном сечении диффузора меньше, чем во входном
сечении:
Р* = ^дРз > B0)
где ад — коэффициент сохранения полного давления.
Коэффициент Од зависит от конфигурации диффузора и при-
приведенной скорости потока на входе в нею Яз. Зависимость ад
33 г. Н. Абрамович, ч. i
514 ГЛ. IX. ГАЗОЁЫЕ ЭЖЕ^ТбРЫ
от К для конических диффузоров с несколькими углами угйире-
ния приведена на рис. 8.32.
Следует иметь в виду, что при работе диффузора в эжекторе
со сравнительно короткой камерой смешения поле скорости на
входе в диффузор обладает заметной неравномерностью, и это
несколько снижает вначение коэффициента полного давления
по сравнению с данными, полученными в условиях равномерного
поля скоростей.
Для определения приведенной скорости X* на выходе из
диффузора воспользуемся уравнением неразрывности потока
в диффузоре
VTl
Учитывая условие Т± = Т3 и соотношение B0), приводим это
уравнение к виду
q (\ \ __ * а (% ) B1)
где / = FjFz — геометрическая степень расширения диффузора.
При помощи таблиц газодинамических функций по значению
qCkt) находим Ха и значения функций п(Х) и е(Я), а затем оп-
определяем все параметры потока в выходном сечении диффузора
Часто бывает заданным статическое давление на выходе из диф-
диффузора Ра (например, при выходе газа из эжектора с дозвуковой
скоростью в атмосферу или в резервуар с постоянным давлени-
давлением). В этом случае удобно выразить расход газа в выходном се-
сечении диффузора через статическое давление ра и газодинамиче-
газодинамическую функцию у(Х) (см. гл. V). При этом вместо уравнения
неразрывности B1) получим
1 Рз -" * B2)
Пользуясь таблицами газодинамических функций, по значению
у (к*) можно найти ^4 и п(Ха) и, далее, полное давление в вы-
выходном сечении
*-4:>- B3)
В зависимости от заданных величин и условий работы эжек-
эжектора приведенными соотношениями пользуются различным обра-
образом. Если поток на выходе из смесительной камеры дозвуковой
§ 3. РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 515
и параметры его Кг и р3 определены, а также известен коэффи-
коэффициент ад, то из соотношения B0) определяем р4» из соотношения
B3) п(Ха) и А,4, а из уравнения неразрывности B1) или B2) —
необходимую степень расширения диффузора /, обеспечивающую
при заданных начальных параметрах газа торможение потока до
заданного статического давления /?4. Если сделать диффузор с
другой степенью расширения, то при заданном давлении на вы-
выходе р\ изменятся параметры Яз и /?з в выходном сечении смеси-
смесительной камеры и соответственно на входе в нее, т. е. эжектор
будет работать на другом режиме.
Если скорость потока на выходе из смесительной камеры
больше скорости звука (Яз>1), то при заданном статическом
давлении Ра определяем из соотношения B2) значения */(А,4) и
Ха, из соотношения B3)—значениер4» а из B0)—значение ко-
коэффициента сохранения полного давления ад. Физически это
означает следующее. При сверхзвуковой скорости потока на вы-
выходе из смесительной камеры эжектор может работать на данном
режиме при любой степени расширения диффузора /. Соответст-
Соответственно изменению степени расширения диффузора изменяется
скорость потока в выходном сечении и перемещается скачок (или
система скачков) уплотнения, возникающий в диффузоре из-за
перерасширения потока. Скачки уплотнения перестраиваются та-
таким образом, что суммарное изменение давления на участке
перерасширения, в скачках и при торможении дозвукового пото-
потока после скачка обеспечивает получение в выходном сечении
статического давления ра\ при этом суммарные потери полного
давления оцениваются значением коэффициента ад, найденным,
как указывалось, из соотношений B2), B3) и B0). Если давле-
давление ра достаточно низко, то поток на выходе из диффузора, пред-
представляющего в этом случае расширяющуюся часть сопла Лаваля,
может быть сверхзвуковым.
Таким образом, если считать известными полные давления,
температуры торможения и приведенные скорости газовых по-
потоков во входном сечении цилиндрической камеры смешения,
а также соотношение расходов п = G2IG1 или площадей а =
= F\/F2, то, пользуясь уравнениями, выведенными в этом пара-
параграфе, можно определить конечные параметры смеси газов на
выходе из эжектора.
Рассмотрим, какими условиями связаны между собой величи-
величины, которые должны быть заданы для расчета. Температуры тор-
торможения эжектирующего и эжектируемого газов обычно известны;
полные давления известны или легко определяются по парамет-
параметрам газов перед соплами эжектора и коэффициентам сохранения
полного давления в соплах. Что касается значений приведен-
приведенной скорости газов Х\ и Хг, то они до расчета камеры смеше-
смешения и диффузора, вообще говоря, неизвестны и могут быть раз-
33*
516
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
личными на различных режимах работы одного и того же эжек-
эжектора. Поэтому в большинстве случаев для расчета эжектора при-
приходится задаваться рядом значений Xi и Яг и находить зависи-
зависимость конечных параметров эжектора и его размеров от скоро-
скоростей газов во входном сечении камеры. По этой зависимости и
выбирают оптимальный режим или режим, соответствующий ус-
условиям данной конкретной задачи. Такими условиями могут
быть, например, полу-
получение данного статиче-
статического давления смеси
няг выходе, получение
заданного коэффици-
коэффициента эжекции при наи-
наивысшем полном давле-
давлении смеси или мини-
минимальном диаметре ка-
камеры смешения, полу-
получение максимальной
реактивной тяги и т. п.
Так, на рис. 9.11 при-
приведена полученная та-
таким способом сетка
кривых pt/pl=f(^n)
для заданного отноше-
отношения полных давлений
газов Рг/ръ = 5.
Из графика видно,
что полное давление
смеси газов увеличива-
увеличивается с уменьшением
коэффициента эжек-
эжекции п — при этом уве-
увеличивается энергия
эжектирующего газа, приходящаяся на единицу расхода эжек-
тируемого газа. Кроме того, при данном значении п полное дав-
давление возрастает с увеличением начальной скорости эжектируе-
мого газа, что объясняется согласно B) уменьшением потерь
при смешении потоков.
Следует иметь в виду, что при различных значениях %2 для
получения данного коэффициента эжекции необходимо выбирать
согласно формуде A4) различные значения геометрического па-
параметра а. Поэтому точки кривых п = const на рис. 9.11 соответ-
соответствуют различным эжекторам: чем больше Яг, тем меньше отно-
относительная площадь камеры смешения (больше величина а).
Выбирая значения приведенной скорости Я1 и Яг для расчета
эжектора, необходимо учитывать, что эти величины не являются
независимыми. На любом режиме работы эжектора при задан-
и0 0,1 0,2 0,3
Рис. 9.И. Зависимость степени повышения
полного давления Р^/р* в эжекторе от при-
приведенной скорости эжектируемого газа на
входе в камеру смешения; По = 5, ^i == 1,0,
0 = 1, ft = 1,4. ab — линия предельных зна-
значений А,2
§ 3. РАСЧЕТ ГАЗОВОГО ЭЖЕКТОРА 517
ных полных давлениях газов величины Х\ и Яг связаны дополни-
дополнительными условиями, ограничивающими область возможных ско-
скоростей потоков. Эти условия различны в зависимости от того,
являются потоки дозвуковыми или сверхзвуковыми.
E оба потока во входном сечении камеры смешения дозву-
. е. Xi < 1 и Яг < 1, то можно считать, что статическое
давление постоянно по всей площади входного сечения камеры.
Это условие связывает между собой значения %\ и Яг, так как
при р\ = р2 имеем
р\п (Я2) = р\п (Я2), или я (Я2) = Поя (Я2). B4)
Таким образом, при дозвуковой скорости потоков произвольно
можно задать приведенную скорость только одного из них, ско-
скорость другого при этом определяется отношением полных давле-
давлений газов.
Для каждого значения По = pt/p* можно выбрать такое зна-
значение коэффициента скорости Яг, при котором, как следует из
уравнения B4),
Это значение Яг ограничивает область докритического истечения
эжектирующего газа из сопла: при всех больших значениях Яг
истечение газа будет происходить под сверхкритическим перепа-
перепадом давлений Pi/p2- Если в сопле эжектирующего газа отноше-
отношение давлений превышает критическое значение, то скорость исте-
истечения газа из сужающегося сопла достигает скорости звука
(Xi = l), и струя покидает сопло со статическим давлением,
более высоким, чем давление окружающего сопло потока эжек-
тируемого газа. При этом равенство давлений р\ и /?г и вытекаю-
вытекающее из него соотношение B4) между возможными значениями
Х\ и Яг не соблюдаются. То же будет и в случае применения
в эжекторе сопла Лаваля с неполным расширением; при этом с
некоторого значения По на срезе установится постоянная ско-
скорость (Х\ =XPi), не зависящая от статического давления в эжек-
тируемом потоке. При постоянном значении К\ = 1 (нерасширяю-
(нерасширяющееся сопло) или Я1=Яр1>1 приведенная скорость эжектиру-
емого газа Яг может иметь различные значения. Однако произ-
произвольно выбирая значение Яг для подстановки в расчетные
уравнения, нельзя заранее быть уверенным, что такой режим
работы эжектора реально осуществим. Имеется предельное зна-
значение Ягшах, ограничивающее область возможных режимов; реаль-
реальны лишь режимы, соответствующие Яг ^ Ягшах. Ниже в § 4 этот
вопрос рассмотрен подробнее.
•34 г. Н. Абрамович, ч. i
518 гл. гх. газовые эжекторы
§ 4. Критические режимы работы эжектора.
Запирание эжектора
Эксперименты показывают, что для каждого эжектора при за-
заданных начальных параметрах торможения газов имеется неко-
некоторое максимальное значение коэффициента эжекции п и соот-
соответствующие ему максимально возможные значения расхода и
скорости эжектируемого газа. Никаким снижением давления на
выходе из эжектора не удается превысить эти предельные значе-
значения. Явление это напоминает работу сопла Лаваля на режимахг
когда в минимальном сечении его достигнута скорость звука;
скорости газа во всех сечениях дозвуковой части при этом при-
принимают предельно возможные значения и не зависят от давле-
давления на выходе из сопла.
Режим работы эжектора, при котором коэффициент эжекциж
не зависит от давления на выходе из диффузора, называется
критическим. Особенности работы эжектора на критическом ре-
режиме связаны с характером течения в начальном участке смеси-
смесительной камеры — между входным сечением и сечением запира-
запирания 1' (рис. 9.6). Как уже указывалось, дозвуковой поток эжек-
эжектируемого газа движется здесь по каналу с уменьшающимся
сечением, ограниченному стенками камеры и границей сверхзву-
сверхзвуковой эжектирующей струи. Скорость эжектируемого потока в
минимальном сечении — оно совпадает с сечением запирания —
не может превысить скорости звука; этим и определяются пре-
предельные значения скорости во входном сечении и максимального»
расхода эжектируемого газа. Для того чтобы определить эти макси-
максимально возможные значения, необходимо найти соотношения
между параметрами потоков во входном сечении и в сечении за-
запирания.
Из приведенного выше описания физической картины тече-
течения следует, что на рассматриваемых режимах оба потока между
указанными сечениями движутся с ускорением, практически не*
смешиваясь между собой.
Поток эжектируемого газа на этом участке можно считать
одномерным, т. е. параметры его полагать постоянными по сече-
сечению. Что касается течения эжектирующего газа — сверхзвуко-
сверхзвуковой недорасширенной струи, то, как указывалось в гл. VII, § 6,.
этот поток характеризуется существенной неодномерностью, па-
параметры газа в нем сильно меняются от оси к периферии.
Детальный расчет такого течения проводится с помощью спе-
специальных методов, которые в данной книге не рассматриваются.
Для расчета эжектора, однако, внутренняя структура потока
несущественна, важны только некоторые его интегральные ха-
характеристики, и потому можно воспользоваться более простыми:
методами, основанными на осреднении параметров неодномернога
газового потока (см. гл. V, § 8). Так же, как при рассмотрении
§ 4. КРИТИЧЕСКИЕ РЕЖИМЫ РАБОТЫ ЭЖЕКТОРА 519
свободной недорасширенной сверхзвуковой струи (см. гл. VII,
§ 6), будем характеризовать эжектирующий поток в сечении
запирания некоторыми средними, постоянными по всему сечению
значениями скорости, давления, температуры; полное давление,
температура торможения и расход, как и для потока эжектиру-
емого газа, сохраняются такими же, как на входе в камеру
смешения *).
При этом условии из уравнений неразрывности каждого из
потоков между входным сечением камеры и сечением запирания
(рис. 9.6) легко получить соотношения
. B5)
Поскольку суммарная площадь потоков в обоих сечениях
одинакова, т. е.
или
F F' F f'
ТГ + 1 = -1Г-г + -г> B6)
Г2 1 Г2 2
то, заменив отношения площадей отношениями соответствующих
величин q(X) согласно уравнениям B5), можно получить
а я (К) , q(K)
{\) (К)
или
(;){[l^]} B7)
Для критического режима работы эжектора, когда А,2 = 1, от-
отсюда следует
ffi] B8)
Из последнего уравнения видно, что при а = const и увели-
увеличении приведенной скорости ^i(^i>l), когда д{^[) уменьшает-
уменьшается, величина ?(Лг), а следовательно, и скорость эжектируемого
потока на входе в камеру смешения уменьшаются. Если величи-
величина Ях увеличится настолько, что значение функции q {^г) станет
равным
я М = -^pi я (К) = т;
1) Васильев Ю. Н. Теория сверхзвукового эжектора с цилиндриче-
цилиндрической камерой смешения / Лопаточные машины и струйные аппараты,
вып. 2.— М.: Машиностроение, 1967.
34*
520
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
то из уравнения B7) получим <7(Х2)=О, т. е. Ад = 0. При этом
втекание эжектируемого газа в камеру прекращается, эжектиро-
вание не происходит. Физически это означает, что при таком
значении Ях расширяющаяся эжектирующая струя в максималь-
максимальном сечении заполняет всю площадь камеры смешения и для
прохода эжектируемого газа не остается места. Это явление на-
называется запиранием эжектора. На рис. 9.12 и 9.13 показаны
Рис. 9.12. Шлирен-фотография потока в камере смешения на критическом
режиме работы эжектора; Па = 3,6
Рис. 9.13. Шлирен-фотография потока в эжекторе на режиме, близком к
запиранию; До = 5,5, а » 1
теневые фотографии течения в камере смешения на критическом
режиме и режиме, близком к запиранию.
Если в уравнении B7) величина а неизвестна (например,
при проектировании эжектора по заданным значениям По, битг),
§ 4. КРИТИЧЕСКИЕ РЕЖИМЫ РАБОТЫ ЭЖЕКТОРА 521
то ее следует предварительно выразить из уравнения A4). Урав-
Уравнение B7) в этом случае принимает вид
ИЛИ
C0)
Для критического режима работы эжектора аналогично
получается
_ л
В уравнения B7) или C0), полученные из условия нераз-
неразрывности потока в цилиндрической камере смешения, помимо ис-
искомой величины Яг, входят приведенные скорости потока Хг, Хг и
Х2. Величина Х\ представляет собой приведенную скорость эжек-
тирующего газа на срезе сопла; для рассматриваемых здесь ре-
режимов она известна: Х\ = 1 в случае истечения из нерасширяю-
нерасширяющегося сопла или Х\ = Хр\ > 1 для сверхзвукового сопла.
Величиной Х2 ^ 1 в расчете надо задаваться, она определяет
режим работы эжектора и ограничивает область реальных значе-
значений Х2 и п максимальными значениями, соответствующими Х2 = 1;
собственно для нахождения этих максимальных значений и про-
проводится расчет начального участка течения.
Приведенная скорость Хг в уравнениях B7) или C0) неиз-
неизвестна, и для того чтобы исключить ее, надо составить еще одно
уравнение, связывающее между собой параметры потоков во
входном сечении камеры и сечении запирания.
Взаимодействие потока со стенками цилиндрической камеры
смешения (без учета трения) не дает сил, направленных вдоль
оси течения. Поэтому изменение количества движения газа про-
происходит только под действием разности сил давления на грани-
границах выделенного участка потока.
Уравнение количества движения, записанное для обоих пото-
потоков между входным сечением цилиндрической смесительной ка-
камеры и сечением запирания
G, (Wl - w[) + G2 (w2 - w2) = pxF'x + p2F2 -PlF1 - p2F2, C2)
позволяет исключить неизвестную по величине силу давления
522 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
на границе эжектирующего и эжектируемого потоков, которая
вошла бы в уравнения импульсов для каждого потока в отдель-
отдельности. Группируя члены, относящиеся к одному сечению, и при-
применяя соотношение A15) гл. V
приводим уравнение количества движения к виду
G^kpi U (Ю — z (К)] = ?2Якр2 [z (А,2) — z
или
Для критического режима работы эжектора, когда ^2 — l| уравне-
уравнение C3) принимает вид ~— ¦
Вместе с уравнением C0) уравнение C3) позволяет для за-
заданного значения к2 и пУд определить Хг и Х2; для__критического
режима из уравнений C1) и C4) можно определить максималь-^
ные значения ^i и Х^. Решение в обоих случаях проводится мето-
методом последовательных приближений или графически.
На режиме запирания, когда расширяющаяся сверхзвуковая
(^) 0
струя заполняет все сечение смесительной камеры, д(^2) = 0, по-
поэтому из уравнения B8) следует
Я(К) = -^Г1Я(К), C5)
или, для звукового эжектора,
По найденному отсюда значению Хг можно определить отноше-
отношение давления По, при котором запирается эжектор с данным
геометрическим параметром а.
Непосредственное применение уравнения C4) для расчета
эжектора на режиме запирания (п = 0, Аг = 0, 2(^2)=°°) за-
затруднительно, так как оно обращается в неопределенность. Пре-
Преобразуем уравнение C4), подставив в него
Л2
§ 4. КРИТИЧЕСКИЕ РЕЖИМЫ РАБОТЫ ЭЖЕКТОРА
Предельным переходом %2 -*• 0 приводим уравнение к виду
1
П - (t±l)k L
ио~{ 2 ) адП
523
C6)
или, для звукового эжектора (К\ = 1),
1
Подставив в последнее уравнение значение A,1? найденное из C5),
определяем предельное значение отношения полных давлений
газов, сверх которого эжектор р#
становится неработоспособным. ^o=-pf
На рис. 9.14 приведены предель- 28
еые значения По, вычисленные
по формулам C5) и C6).
Рассмотрение критических ре-
режимов работы эжектора, помимо
теоретического интереса, имеет
важное практическое значение.
Расчеты показывают, что крити-
критические режимы работы являются
не только предельными, но и в
большинстве случаев наивыгод-
наивыгоднейшими режимами эжектора. Ра-
Работая на критическом режиме,
8
4
О 0,2 0,4 0,6 0,8 1,0 Цсс
эжектор при данном значении ко- Рис g 14 зависимость отноше-
эффициента эжекции обеспечи- ния полных давлений газов, при
вает наибольшее полное давление котором происходит запирание
смеси газов, а при заданном пол- эжектора, от отношения площа-
ном давлении имеет наибольший деи ' 1 ~~
коэффициент эжекции. Это связа-
связано с тем, что при критическом режиме разность скоростей
газов на входе в камеру смешения w\ — wi становится мини-
минимально возможной; наименьшей величины достигают и потери
при смешении (см. B)). Одновременно эжектор, рассчитанный
для работы на критическом режиме, будет при заданном значе-
значении п иметь наименьшие относительные размеры смесительной
камеры, т. е. наибольшее значение а.
На рис. 9.15 приведен график для определения параметров
звукового эжектора на критическом режиме. График этот рас-
рассчитан по уравнениям A2), A3) и A4) путем подстановки
в них для заданных значений nl/Q и По, величины Х\ = 1 и пре-
предельного (критического) значения fa согласно C1) и C4). При
определении р$ в уравнение A3) подставлялось дозвуковое зна-
524
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
чение Яз, найденное из уравнения A2). По рис. 9.15 можно гра-
графически определить наивыгоднейшие параметры звукового эжек-
эжектора и решать другие задачи расчета эжекторов.
График рис. 9.15 применим только для 0,6 < 9 < 1,7; при
большем различии в температурах газов пользование графиком
приводит к заметной погрешности в величине pl/p2- Что касает-
касается величин a, nl/Q, По, то соотношения между ними на критиче-
критическом режиме можно определять по рис. 9.15 при любом значе-
значении б1). Семейство линий а = const показывает, что при посто-
постоянном отношении начальных полных давлений По и Кг < 1 сте-
степень повышения давления Р3/Р2 тем больше, чем больше вели-
величина а. Другими словами, для увеличения напорности эжектора
8 10 12 14 16
Рис. 9.15. График для определения параметров звукового эжектора на кри-
критическом режиме; %\ = 1, Л'2= 1, к = 1,4
следует выполнять эжектор с возможно меньшей относительной
площадью камеры.
Верхняя кривая на рис. 9.15 соответствует режиму запирания
(?г = 0). Эта предельная кривая показывает, какие максималь-
максимальные значения степени повышения давления Р3/Р2 можно полу-
получить в эжекторе с заданным геометрическим параметром а или
заданным отношением полных давлений газов По. Отметим, что
этот предельный режим для каждого заданного отношения дав-
давлений По соответствует своему значению а, т. е. режим запира-
запирания в камере заданных относительных размеров наступает при
вполне определенном отношении полных давлений газов.
') При этом, однако, следует учитывать ограничения, накладываемые
условием запирания в выходном сечении камеры, см. ниже § 6 и рис. 9.19.
§ 5. ХАРАКТЕРИСТИКИ ЭЖЕКТОРА
График на рис. 9.15 показывает также, что в звуковом эжек-
эжекторе существует предельная степень повышения полного давле-
давления Рз/Р2^3,55, которая достигается при отношении началь-
начальных полных давлений По ~ 12 и не возрастает более даже при
беспредельном увеличении полного давления эжектирующего га-
газа. Физический смысл этого состоит в следующем. При повыше-
повышении начального отношения полных давлений газов По увеличи-
увеличивается степень сжатия низконапорного газа, однако одновремен-
одновременно увеличивается и площадь максимального сечения эжектирую-
щей струи в сечении запирания. Вследствие этого даже при
весьма малом расходе эжектируемого газа (п ->• 0) необходимо
увеличивать относительную площадь камеры смешения. Перерас-
Перерасширение газа повышает потери в струе и потери при смешении
и, начиная со значений По = 10—11, сводит на нет увеличение
степени сжатия, получающееся вследствие возрастания энергии
эжектирующего газа.
Следует иметь в виду, что при определении параметров эжек-
эжектора на режимах, близких к запиранию, и при очень малых
значениях коэффициента эжекции (п = 0,01 — 0,05) возможны
погрешности, связанные с условностью допущения об отсутствии
смешения потоков в начальном участке камеры (до сечения за-
запирания). Незначительное количество эжектируемого газа, под-
подмешиваемое к струе на этом участке, при малых значениях п
становится соизмеримым с расходом эжектируемого газа череа
кольцевую площадь F2 в сечении запирания.
В частности, при F2 = 0, когда из расчета следует, что п = 0,
в начальном участке эжектирующей струи будет подсасываться:
некоторое, хотя и весьма малое, количество газа. Действительно,
в некоторых экспериментах при малых значениях а (т. е. при
большой длине начального участка) наблюдалось отклонение
предельных значений По, соответствующих режиму запирания,
от расчетных значений; в соответствии с этим увеличиваются по
сравнению с данными рис. 9.15 предельно возможные значения:
степени сжатия Рз/Р2- Однако уже при п > 0,05 — 0,1 этот эф-
эффект становится слабым, и расчетные данные хорошо согласуют-
согласуются с результатами экспериментов.
§ 5. Характеристики эжектора
Один и тот же эжектор может работать на различных режи-
режимах и при различных соотношениях между начальными пара-
параметрами газов. Характеристикой эжектора называется зависи-
зависимость между параметрами эжектора и условиями его работы.
Экспериментально или в результате расчета можно получить
разнообразные характеристики эжектора, однако наибольший
интерес представляют обобщенные характеристики, позволяющие
-526
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
4-
-одним графиком охватить всю область возможных режимов рабо-
работы эжектора.
Из расчета эжектора следует, что его параметры определя-
определяются несколькими безразмерными величинами, например коэф-
коэффициентом эжекции тг, отношением начальных полных давлений
газов По, степенью сжатия эжектируемого газа /?*/р2. Характери-
Характеристику эжектора поэтому
рационально строить в ви-
виде зависимости между
ос = 0,5 этими безразмерными па-
параметрами.
На рис. 9.16 приведе-
на типовая сетка характе-
ристик, построенная для
эжектора с нерасширяю-
щимся соплом эжектирую-
щего газа и цилиндриче-
2.2
18
скои смесительной каме-
камерой с геометрическим па-
параметром а = 0,5. Эта ха-
характеристика показывает
О
0,1 0,2 0,3 0,4 0,5 0$ 0,7л зависимость степени сжа-
сжатия эжектируемого газа
Рис. 9.16. Расчетная характеристика эжек- * / * ~ v
тора: ab — критические режимы работы, Рь/Ръ от коэффициента
а — запирание эжектора, 0 = 1
4
18
1,6
1,4
ос=0,725
звукового
'О 0,1 0,2 0,3 0,4
эжекции при нескольких
значениях По= v\lv\- На
рис. 9.17 показана сетка
таких же характеристик,
полученных эксперимен-
экспериментально для
эжектора при
отчески получить харак-
Рассмотрим, как прак-
теристику {Р*/р*) = Кп)
при По = const. Будем
ш снижать статическое дав-
0,5 0,6 0,7п ление на выходе из диф-
диффузора, поддерживая по-
Рис. 9.17. Экспериментальная характери- СТОянными полные давле-
стика эжектора: АВ — докритические ре- * * тт
жимы, ВС — критические режимы ния газов Pi и р2. иря
этом будет уменьшаться
статическое давление на входе в смесительную камеру, что при-
приведет к увеличению скорости и расхода эжектируемого газа G2
при незначительном увеличении расхода эжектирующего газа Gi,
(если Яг < A,i < 1, и без изменения Gu если Х\ ^ 1. В результате
увеличивается коэффициент эжекции п. Как бы мало ни было
§ 5. ХАРАКТЕРИСТИКА ЭЖЕКТОРА 527
отношение полных давлений газов По, при некотором значении
статического давления /?4 в сопле эжектирующего газа будет до-
достигнута скорость звука. Дальнейшее снижение давления на вы-
выходе из диффузора приводит к сверхкритическому режиму.
Коэффициент эжекции при этом продолжает расти вслед-
вследствие возрастания скорости эжектируемого газа на входе в сме-
смесительную камеру.
Когда скорость эжектируемого потока в сечении запирания
достигнет скорости звука, наступает критический режим работы
эжектора: коэффициент эжекции принимает предельно возмож-
возможное (для данного отношения полных давлений) значение и не
изменяется при дальнейшем снижении давления на выходе из
эжектора.
Степень повышения полного давления \pjp2 вдоль кривых
По = const с увеличением коэффициента эжекции несколько
уменьшается вследствие увеличения расхода эжектируемого газа
и увеличения потерь в диффузоре, связанного с ростом скорости
потока на входе в диффузор. Чем больше отношение полных
давлений По, тем выше проходит характеристика (p*/pV) = f(n)i
т. е. тем большую напорность имеет эжектор. Однако предель-
предельные (критические) значения коэффициента эжекции с ростом По
уменьшаются, протяженность характеристики становится мень-
меньшей. Это связано с тем, что с увеличением перепада давлений
растет площадь сверхзвуковой эжектирующей струи в сечении
запирания и уменьшается критическое сечение эжектируемого
потока.
Кривая, соединяющая предельные точки кривых По = const,
является линией критических режимов. Реальными являются
лишь режимы, соответствующие области характеристики между
этой линией и осями координат. С увеличением отношения дав-
давлений По критическая линия приближается к оси ординат и при
некотором значении По max пересекается с ней. Эта точка, в кото-
которой коэффициент эжекции равен нулю, а степень повышения
давления достигает максимально возможного для данного эжек-
эжектора значения, соответствует режиму запирания эжектора. Изме-
Изменение режима работы реального эжектора может происходить
более сложным образом, с одновременным изменением как пол-
полных давлений газов на входе, так и давления на выходе, и опре-
определяется выбранным способом регулирования режима. Смещение
кочки, соответствующей рабочему режиму, на поле характери-
характеристик эжектора в каждом случае может быть определено расчетом
по методу, изложенному в § 3.
На рис. 9.18 приведена расчетная характеристика другого
типа, связывающая коэффициент эжекции с полным давлением
эжектирующего газа рх при постоянных значениях полного дав-
давления эжектируемого газа и статического давления на выходе из
528
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
эжектора. При расчете принято ръ = р2\ такая характеристика
представляет интерес при оценке параметров эжектора, работаю-
работающего по схеме рис. 9.2 или рис. 9.10, т. е. когда воздух засасы-
засасывается из атмосферы и после смешения с эжектирующим газом
вновь подается в атмосферу. При малых значениях По значение
коэффициента эжекции п
совпадает с соответствую-
соответствующим значением п для эжек-
эжектора несжимаемой жидкости
и может быть оценено (см.
§ 8) по формуле
л
1,6
0,8
0г4
Л/в:
О 0,1 0,2 0,3 0,4 0,5
Рис. 9.18. Характеристика эжектора:
АВ — критические режимы, С — коэф-
коэффициент эжекции при По -> 1
С увеличением отноше-
отношения давлений значение п
для эжектора с данным зна-
значением геометрического па-
параметра a, = F\/F2 уменьша-
уменьшается. Причиной является то, что расход эжектирующего газа
с ростом pi увеличивается пропорционально P*q(K)i тогда как
возрастание расхода эжектируемого газа происходит менее ин-
интенсивно и связано лишь с понижением давления на входе в ка-
камеру и ростом д(А,2). При докритических режимах работы эжек-
эжектора уменьшение коэффициента эжекции невелико. По мере уве-
увеличения отношения давлений По, когда камера смешения все бо-
более заполняется расширяющейся сверхзвуковой струей, расход
эжектируемого газа начинает уменьшаться, коэффициент эжек-
эжекции резко снижается; в точке В характеристики 6?2 = 0, п = 0.
§ 6. О режиме течения на выходе из смесительной камеры
Согласно изложенному в § 3 методу расчета приведенная
скорость потока в выходном сечении цилиндрической смеситель-
смесительной камеры определяется, как указывалось, из уравнения коли-
количества движения
Z (До) =
C7)
При этом обычно возникает затруднение, связанное с неодно-
неоднозначностью решения относительно величины Лз, так как каждо-
каждому значению ?(Яз)>2 соответствуют два возможных зна-
§ 6. О РЕЖИМЕ НА ВЫХОДЕ ИЗ СМЕСИТЕЛЬНОЙ КАМЕРЫ 529
чения
Первое значение соответствует сверхзвуковому, а второе — дозву-
жовому режиму течения, причем Я3 ^ 1Аз» Такая же зависи-
зависимость была получена в § 1 гл. III для величин Я до и после
прямого скачка уплотнения. Параметры смеси газов, вычислен-
вычисленные по сверхзвуковому и дозвуковому значениям Яз, будут раз-
различными. Из аналогии со скачком уплотнения следует, что пол-
полное давление при Яз > 1 будет большим, а статическое давле-
лие — меньшим, чем для Яз<1. Диффузор, установленный на
выходе из камеры, будет работать в различных условиях при
Хг > 1 и Я3 < 1.
Рассмотрим соображения, позволяющие установить, какой из
двух возможных режимов течения на выходе из цилиндрической
смесительной камеры будет реальным. Очевидно, что если при
Ti = Т\ оба потока на входе в камеру дозвуковые, то выравнива-
выравнивание скоростей при смешении также приведет только к дозвуко-
дозвуковой скорости на выходе из камеры, т. е. Яз < 1. Сверхзвуковое
решение уравнения C7) в этом случае соответствует физически
невозможному скачку разрежения.
При сверхкритическом отношении давлений в сопле (Х\^ i)
эжектирующий газ в начальном участке камеры движется со
сверхзвуковой скоростью. Чтобы на выходе из камеры получить
Яз > 1, необходимо дозвуковой поток эжектируемого газа
(Яг<1) в процессе смешения также перевести в сверхзвуковой.
Необходимые для этого условия можно качественно установить
на основании рассмотренных в § 4 гл. V закономерностей пере-
перехода через скорость звука под влиянием внешних воздействий
на газовый поток.
Введем условную поверхность раздела, ограничивающую ядро
постоянного расхода эжектирующей струи. В кольцевом канале
вне этой поверхности, очевидно, G = С?2 = const. Взаимодействие
потоков можно в этом случае свести к переносу количества дви-
движения через поверхность раздела, а течение эжектируемого газа
в первом приближении рассматривать как движение одномерного
газового потока, на который оказывают влияние внешние воз-
воздействия: геометрическое — вследствие изменения площади сече-
сечения и механическое — связанное с переносом количества движе-
движения из эжектирующего потока.
Между сечением запирания и выходным сечением камеры
площадь сечения выделенной трубки тока эжектируемого газа
увеличивается — это следует из закономерностей течения нерас-
нерасчетной сверхзвуковой струи, согласно которым максимальное се-
530 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
чение первой «бочки» является наибольшим сечением струи, воз-
возможным при G = const (§ 6 гл. VII).
Уравнение D9) гл. V, определяющее изменение скорости по-
потока под влиянием внешних воздействий, в данном случае мож-
можно записать в виде
Согласно этому уравнению, увеличение площади сечения (dF >
> 0) и подвод механической энергии (dLl<0) качественно оди-
одинаковым образом влияют на скорость течения: оба эти вида
внешнего воздействия вызывают торможение (dw < 0) дозвуко-
дозвукового потока и ускорение сверхзвукового потока.
Если скорость эжектируемого газа в минимальном сечении
дозвуковая (докритические режимы эжектора, ^2<1)>т<> при
дальнейшем течении скорость потока в камере будет уменьшать-
уменьшаться, оставаясь дозвуковой.
Таким образом, при докритических режимах работы эжекто-
эжектора, несмотря на наличие сверхзвуковой скорости в эжектирую-
щей струе, эжектируемый газ в результате смешения не может
приобрести сверхзвуковой скорости. Скорость смеси в камере бу-
будет дозвуковой, т. е. Яз < 1.
Если скорость эжектируемого газа в сечении запирания рав-
равна скорости звука (критические режимы работы эжектора), то»
увеличение площади сечения приводит к тому, что поток эжек-
эжектируемого газа становится сверхзвуковым, и скорость его про-
продолжает увеличиваться. В результате переноса механической
энергии из сверхзвукового эжектирующего потока в сверхзвуко-
сверхзвуковой эжектируемый первый поток тормозится, второй ускоряется,
скорости потоков сравниваются по величине и могут остаться
сверхзвуковыми в выходном сечении камеры, если не возникнет
скачок уплотнения. Таким образом, сверхзвуковой режим тече-
течения смеси становится возможным только при критическом режи-
режиме работы эжектора.
Приведенный выше анализ усложняется, если температуры
торможения газов различны, т. е. 9 Ф 1. В этом случае к рас-
рассмотренным двум видам воздействия на эжектируемый поток до-
добавляется существенное тепловое воздействие; здесь могут быть
получены качественно новые результаты.
С приближением к критическому режиму увеличение скоро-
скорости течения на выходе из камеры не происходит непрерывно;
при достижении Х2 = 1 скорость смеси изменяется скачкообразно
от дозвуковой (Аз) до сверхзвуковой AДз), минуя некоторую
область околозвуковых режимов, подобно тому как изменяется
скорость потока на выходе из сопла Лаваля при постепенном
увеличении перепада давлений. Это можно видеть на фотогра-
фотографиях потока в начальной части смесительной камеры (рис. 9.9 и
§ 6. О РЕЖИМЕ НА ВЫХОДЕ ИЗ СМЕСИТЕЛЬНОЙ КАМЕРЫ 53 $
9.12). На рис. 9.9 режим работы эжектора докритический. Ядра
сверхзвуковых скоростей в эжектирующем потоке уменьшается,
на выходе из эжектора скорость дозвуковая. При незначительном:
увеличении давления перед соплом режим работы становится
критическим, причем картина течения резко изменяется
(рис. 9.12): характеристики, пересекающие поток, свидетельству-
свидетельствуют о наличии сверхзвуковых скоростей, соответствующих Л « 1,6.
Поток смеси при этом эксперименте оставался сверхзвуковым и
на выходе из камеры.
К выводам, полученным выше из качественного рассмотрения;
упрощенной схемы течения в камере, можно прийти и иным пу-
путем, анализируя обычную характеристику эжектора v\lVi — f(n)*
представленную на рис. 9.17. Как указывалось, изменение рабо-
рабочего режима эжектора при снятии такой характеристики дости-
достигается изменением статического давления на выходе из эжекто-
эжектора при постоянных условиях на входе. Пологая ветвь характери-
характеристики (АВ) соответствует докритическим режимам. Уменьшение
противодавления здесь приводит к увеличению коэффициента
эжекции, т. е. к росту скорости эжектируемого газа и разреже-
разрежения на входе в эжектор. Отсюда можно заключить, что в смеси-
смесительной камере нет таких сечений, где оба потока (или поток:
смеси в целом) сверхзвуковые, так как в этом случае передача
возмущений вверх по течению невозможна.
Следовательно, на режимах, соответствующих пологой ветви
характеристики, реализуется дозвуковое течение в выходном се-
сечении камеры и Яз < 1.
Точка В характеристики соответствует такому режиму, когда
в сечении запирания эжектируемый поток становится звуковым:
\%2 = !)• После этого, действительно, дальнейшее снижение про-
противодавления не изменяет расхода газов через эжектор. Постоян-
Постоянные предельные значения, не зависящие от противодавления,,
принимают коэффициент эжекции п и параметры смеси газов —
приведенная скорость Хз и полное давление Р3- ^ случае дозву-
дозвукового течения (А,з<1) при этом был бы постоянным коэффи-
коэффициент сохранения полного давления в диффузоре ад—/(Яз)г
а следовательно, и полное давление газа на выходе из диффузо-
диффузора Р*=:(УдРз- Другими словами, все режимы работы эжектора,,
соответствующие противодавлению, меньшему критического зна-
значения, при Яз < 1 выражались бы одной точкой характеристики
Л(/?4 = const, n = const). Однако экспериментальные данные по-
показывают, что характеристика эжектора не обрывается в точке-
В; снижение противодавления на критическом режиме всегда
приводит к падению полного давления смеси при постоянном
значении коэффициента эжекции (ветвь ВС). Легко убедиться,,
что это возможно только при сверхзвуковой скорости потока на
входе в диффузор. Действительно, при Хг > 1 диффузор работает
332 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
как расширяющаяся часть сопла Лаваля на нерасчетном режиме
(§ 2 гл. IV). С уменьшением противодавления скачок уплотне-
уплотнения приближается к выходному сечению диффузора, приведен-
приведенная скорость перед скачком и потери полного давления в скачке
возрастают, что приводит к снижению величины ад и уменьше-
уменьшению Г & при Х3 = const, p3=constH n — connt. Таким образом, на-
наличие вертикального участка ВС на характеристике эжектора
свидетельствует о том, что при критических режимах работы
эжектора реальным является сверхзвуковое течение на выходе
из смесительной камеры.
При достаточно низком противодавлении на критическом ре-
режиме поток смеси может остаться сверхзвуковым и на выходе из
диффузора. Это может представлять интерес в тех случаях, ког-
когда используется скоростной напор потока смеси или возникаю-
возникающая при истечении реактивная сила; полное давление смеси при
этом будет значительно выше, чем при Х^< 1. Однако в обыч-
обычных схемах работы эжектора требуется получить возможно боль-
большее статическое давление газа на выходе из эжектора. Для это-
этого сверхзвуковой поток, полученный на выходе из камеры сме-
смешения при критических режимах работы эжектора, необходимо
перевести в дозвуковой. Принципиально здесь возможно приме-
применение сверхзвукового диффузора, где торможение будет происхо-
происходить без скачков или в системе скачков с небольшими потерями.
Обычно, однако, в эжекторах применяются конические диффузо-
диффузоры дозвукового типа, в которых сверхзвуковой поток тормозится
€ образованием скачка уплотнения. Если считать скачок уплот-
уплотнения прямым, то легко видеть, что минимальные потери полно-
полного давления в нем будут тогда, когда скачок располагается непо-
непосредственно перед входным сечением диффузора, т. е. возникает
в сверхзвуковом потоке с приведенной скоростью Яз.
За скачком приведенная скорость потока в этом случае будет
равна 1Дз < 1, что соответствует дозвуковому решению уравне-
уравнения C7) Я3. Точно так же значения полного и статического дав-
давлений за скачком — на входе в диффузор — в этом случае полу-
получаются такими, как при дозвуковом режиме течения смеси для
заданных начальных параметров газа.
Таким образом, при проектировании эжектора, который при
работе на критическом режиме должен давать дозвуковой поток
смеси, приведенную скорость Яз следует находить из дозвукового
решения уравнения C7), т. е. так же, как и на докритических
режимах. Это соответствует оптимальному режиму торможения
полученного сверхзвукового потока. В выходном сечении диффу-
диффузора на этом режиме получается максимально достижимое при
п = птах значение полного и статического давления смеси. При
любом увеличении давления на выходе (например, при дроссели-
дросселировании выходной магистрали) эжектор должен перейти на до-
§ 6. О РЕЖИМЕ НА ВЫХОДЕ ИЗ СМЕСИТЕЛЬНОЙ КАМЕРЫ 533
критический режим с понижением Яг и п. Однако анализ про-
процесса с учетом трения о стенки камеры смешения показывает,
что изменение режима от оптимального к докритическому проис-
происходит не сразу, а постепенно, и требует некоторого конечного
приращения величины /?4. При достаточно длинной камере сме-
смешения возможна область режимов эжектора с критическими ус-
условиями течения в начальном участке, т. е.
Л2 = 1, А2 = ^2П)ах> п = ^тах?
и дозвуковым потоком на выходе из камеры. При этом скачок
уплотнения образуется в некотором промежуточном сечении ос-
основного участка камеры и с ростом противодавления постепенно
перемещается к сечению запирания. В камере возникает течение,
аналогичное движению одномерного сверхзвукового потока в
трубе с трением, когда располагаемый перегаад давлений недо-
недостаточен для поддержания на выходе Х> 1 (см. § 7 гл. V).
Выше были рассмотрены условия, при которых реализуется
дозвуковой или сверхзвуковой режим течения на выходе из сме-
смесительной камеры. С помощью уравнения количества движения
можно определить условия, когда на выходе из камеры будет по-
получен звуковой режим течения (Л-з = 1). Для случая равных
температур торможения смешивающихся газов F = 1) и без
учета трения уравнение C7) преобразуется к виду
Отсюда легко получить выражения
z(X3) = z(?g + —J-- Az и z(X3) = z(X2) - -^j Az,
где &z = z(X2)—z(K\).
Независимо от знака величины Az из двух последних соотно-
соотношений видно, что численное значение функции z(Xs) будет ле-
лежать между величинами z(X\)> 2 и z(X2)^2. Исключая как не
представляющий интереса случай Х\ = Яг = 1 (w\ = w<i = w?),
устанавливаем, что для любых начальных условий при 6 = 1 из
уравнения C7) определяется значение г(Яз)>2, которое соот-
соответствует двум действительным значениям Хз, отличающимся от
единицы. Таким образом, при равных температурах торможения
газов звуковой режим течения смеси на выходе из камеры не-
невозможен. Если температуры торможения смешивающихся газов
различны F^1), то из уравнения количества движения, наря-
наряду с действительными решениями з(Хз)>2, при определенных
сочетаниях начадьных параметров газов могут быть найдены ре-
решения 2(?1з)<2, соответствующие физически невозможным ре-
режимам течения и указывающие на то, что принятые значения
скорости и расхода эжектируемого газа не могут быть реализова-
534
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
ны. Область реальных режимов ограничивается звуковой ско-
скоростью течения на выходе из камеры. Из уравнения C7) легко
определить, при какой скорости эжектируемого газа наступает
этот режим. Положив z(Xz)= 2, находим
Z (Я2) = Z
В области дозвуковых скоростей минимальному значению
;(Яг) соответствует максимально возможное значение приведен-
приведенной скорости эжектируемого газа Яг. Это значение Яг может ока-
оказаться меньшим предельного значения Ягпр, которое мы выше
находили из условий достижения скорости звука в сечении запи-
запирания (^2— 0« Таким образом, здесь реально возможные режимы
работы эжектора ограничены кризисом течения смеси в выход-
выходном сечении камеры смешения (Яз = 1). Это возможно только
/ при значительном раз-
; Т личии начальных тем-
температур торможения
газов как при Э > 1,
так и при 0 < 1, при-
причем свидетельством вы-
выхода в область нового
ограничения режима
является получение из
уравнения C7) вели-
величины я(Яз)< 2.
На рис. 9.19 приве-
приведены результаты рас-
расчета предельных режи-
режимов звуковых эжекто-
эжекторов с различными на-
начальными параметрами.
12
10
8
6
4
О 0,5 1 1,5 2 2,5 3 3,5
Рис. 9.19. Предельные режимы работы эжек-
эжектора, соответствующие звуковой скорости
смеси в выходном сечении камеры; к = 1,4
Ниже каждой из кри-
кривых, показанных на графике, находится область, в которой пре-
предельный режим определяется сечением запирания, и звуковое
течение на выходе из камеры не реализуется. При большем раз-
различии в температурах торможения скорость эжектирования ли-
лимитируется звуковым режимом в выходном сечении камеры.
Чем больше отношение давлений газов Р1/Р2 = По, тем большим
должно быть различие температур, при котором возможен кри-
кризис течения на выходе из камеры. Отметим, что кризис течения
на выходе из цилиндрической смесительной камеры возможен в
ряде случаев и при равных температурах торможения газов, ес-
если в процессе смешения к газу подводится тепло или если в ка-
камере имеются значительные потери, связанные с трением
о стенки.
§ 7, ОСОБЕННОСТИ РАБОТЫ СВЕРХЗВУКОВОГО ЭЖЕКТОРА 535
§ 7. Особенности работы эжектора со сверхзвуковым соплом
При выводе основных уравнений для расчета смесительной
камеры, а также при рассмотрении условий существования ре-
Жима не вводилось каких-либо ограничений величины приведен-
приведенной скорости эжектирующего газа в выходном сечении сопла Ль
Поэтому изложенный выше метод расчета смесительной камеры
по конечным сечениям в равной степени применим к эжекторам
как с нерасширяющимся, так и со сверхзвуковым соплом эжек-
тирующего газа. Однако протекание процессов в начальном уча-
участке камеры в случае применения сверхзвукового сопла имеет
некоторые особенности.
При сверхкритических отношениях давлений эжектирующий
Газ покидает нерасширяющееся сопло со звуковой скоростью,
причем статическое давление в нем превышает давление в окру-
окружающем его эжектируемом газе; дальнейшее расширение и раз-
разгон газа до сверхзвуковых скоростей происходит в начальном
участке свободной струи. Если применить расчетное сверхзвуко-
вое__српло^ то расширение "газа пр^ои^ОЙдат„-пллшас1ЬШ внутри
сопла* на срезе"соплаг давление газа.^д сравняется с давлением
эжектируемого потока^г; рассмотренного выше начального уча-
участка не будет.
Различие между этими процессами состоит в том, что тече-
течение газов в начальном участке свободной струи происходит без
воздействия внешних сил, т. е. при сохранении суммарного им-
импульса потоков, в то время как при ускорении в сверхзвуковом
сопле вследствии силового взаимодействия с его стенками сум-
суммарный импульс потока может измениться. В первом случае
сверхзвуковой поток в сечении запирания существенно перерас-
перерасширен: в центральной части потока статическое давление значи-
значительно ниже, а скорость соответственно выше, чем на границе
струи.
Во втором случае при надлежащей профилировке сопла мож-
можно на выходе из него получить сверхзвуковой поток с постоян-
постоянными по всей площади параметрамиТГ~статическим давлением,
равным давлению в окружающем его эжектируемом потоке.
Осредняя в звуковом эжекторе параметры эжектирующего
потока в сечении запирания так, чтобы сохранить значения рас-
расхода, импульса и энергии, получаем, как указывалось выше, не-
некоторый эквивалентный одномерный поток, статическое давление
в котором Рх меньше, а приведенная скорость Ях больше, чем
при расширении газа от начального полного давления р± до ста-
статического давления р2 в идеальном сверхзвуковом сопле. Ско-
Скорость же эжектируемого потока в сечении запирания при данном
значении /?2 будет в обоих случаях одинаковой и, в частности,
на критическом режиме равной скорости звука.
536 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
Таким образом, разность средних скоростей эжектирующеГо й
эжектируемого газов перед смешением в случае нерасширяю-
нерасширяющегося сопла будет большей, чем для расчетного сверхзвукового
сопла, где отсутствует перерасширение газа в сечении запира-
запирания. Большими будут и потери на удар при смешении потоков.
Другим следствием перерасширения потока и увеличения сред-
средней величины Ях для эжектора с нерасширяющимся соплом
является увеличение площади эжектирующей струи в сечении
запирания Fx по сравнению с площадью выходного сечения рас*
четного сверхзвукового сопла. Поскольку при заданном расходе
эжектируемого газа площадь критического сечения Fu одинако-
одинакова в обоих случаях, то суммарная площадь потоков в сечении
запирания F± + F2 для эжектора с нерасширяющимся соплом
будет большей, чем для эжектора с расчетным сверхзвуковым
соплом. Иными словами, применение сверхзвукового сопла по-
позволяет при заданных начальных параметрах и расходах газов
получить эжектор с меньшей площадью камеры смешения.
Очевидно, что различие в площади камеры будет тем больше,
чем больше отношение давлений По, т. е. чем больше увеличение
площади потока в сечении запирания, и чем меньше коэффици-
коэффициент эжекции. С уменьшением относительной площади камеры,
как уже указывалось, можно при тех же начальных параметрах
газов и Хз < 1 получить эжектор с большей напорностью. По-
Поэтому в случае больших отношений давлений (По > 5—7) и при
малых значениях коэффициента эжекции (п < 0,4—0,5) может
быть целесообразным применение в эжекторе сверхзвукового
сопла для эжектирующего газа.
Результаты расчетов эжектора для различных сочетаний на-
начальных параметров и расходов газов показывают следующее:
если эжектор работает на критическом (т. е. наивыгоднейшем)
режиме и скорость смеси превышает скорость звука (Яз>1),
то полное давление смеси на выходе из камеры pz практически
одинаково для эжекторов с нерасширяющимся и сверхзвуковым
соплом даже при весьма больших значениях отношения давле-
давлений (По = 20—100) и при любых коэффициентах эжекции; про-
процесс смешения происходит в ускоряющемся потоке, потери на
удар невелики и различие между ними в различных эжекторах
несущественно. Однако поскольку потребная площадь камеры
смешения при сверхзвуковом сопле получается меньшей, то
меньше и величина Яз сверхзвукового потока, так как при
G = const, Т* = const и pi = const
const
Если в выходном сечении камеры возникает скачок уплотнения
(как указывалось, это соответствует наивыгоднейшему критиче-
§ 7. ОСОБЕННОСТИ РАБОТЫ СВЕРХЗВУКОВОГО ЭЖЕКТОРА 537
скому режиму работы эжектора с дозвуковым потоком на выхо-
выходе из диффузора), то потери полного давления в нем будут
меньшими в случае сверхзвукового сопла, при котором меньше
скорость сверхзвукового потока перед скачком. Таким образом,
прл^абот^эжектора на критическом режиме с дозвуковым пото-
ком_смесиТ1римёненйе сверхзвукового сопла позвбляет получить
большее значение полного давления р3- Это преимущество сохра-
сохраняется также и при работе на докритических режимах(Я2< l),
следовательно, во всех случаях, когда в выходном сечении каме-
камеры поток дозвуковой.
Возникает допрос, на какое отношение давлений должно быть
рассчитано сверхзвуковое сопло, чтобы полное давление смеси
газов было наивысшим? Это можно установить исходя из того,
что при оптимальном сопле площадь эжектирующей струи в се-
сечении запирания будет наименьшей для заданного расхода и на-
начальных параметров газов. Из теоретических и эксперименталь-
экспериментальных исследований нерасчетных сверхзвуковых струй известно,
что максимальная площадь первой «бочки» струи будет тем
меньше, чем меньше избыточное статическое давление на срезе
сопла, т. е. чем меньше степень нерасчетности. Поскольку мак-
максимальная площадь первой «бочки» свободной струи всегда боль-
больше площади выходного сечения идеального сопла Лаваля, то ес-
естественным был бы вывод о том, что площадь струи в сечении
запирания будет наименьшей, если степень расширения сверх-
сверхзвукового сопла эжектирующего газа будет соответствовать рас-
располагаемому отношению давлений
P*ij = JK
Расчеты, однако, показывают, что наивыгоднейшие параметры
эжектора получаются при степени расширения сопла, заметно
меньшей-расчетного значения. На рис. 9.20, 9.21 приведены рас-
расчетные кривые Ю. Н. Васильева, показывающие изменение пол-
полного давления смеси газов (Яз< 1) в зависимости от выбранной
величины приведенной скорости эжектирующего газа в выходном
сечении сопла A,i при постоянных значениях коэффициента
эжекции и отношения полных давлений газов. Кривые п = const
соответствуют, таким образом, эжекторам с одинаковыми началь-
начальными параметрами и расходами газов, но с различной степенью
расширения сверхзвукового сопла эжектирующего газа. Значение
Х\ = Яр1 соответствует расчетному сверхзвуковому соплу (для
По = Ю, A,pi = 1,85; для По = 50, XPi = 2,09).
Из графиков на рис. 9.20 и 9.21 видно, что степень расшире-
расширения сверхзвукового сопла существенно влияет на эффективность
эжектора, в особенности при малых значениях коэффициента
эжекции. Максимальное значение полного давления газов полу-
35 г. Н. Абрамович, ч. 1
538
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
чается при A,i=Xo<APi, т. е. соответствует соплу с неполным
расширением. Из изложенных выше соображений следует, что
при этом значении %\ площадь эжектирующего потока в сечении
запирания будет минимальной, т. е. меньшей, чем площадь вы-
выходного сечения расчетного сопла Лаваля. Физический смысл
этого результата, на первый взгляд противоречащего известным
свойствам нерасчетной сверхзвуковой струи, можно выяснить
при помощи данных, полученных в § 6 гл. VII 1). При рассмот-
рассмотрении закономерностей начального участка недорасширенной
сверхзвуковой струи было
доказано следующее положе- ?±
ние: площадь максимального ^
#
12
10
в
6
4
V 1,2 1,4 1,6 1,8 Л, W 12 1,4 1,6 18 2,0 Л7
Рис. 9.20. Параметры эжекторов Рис. 9.21. Параметры эжекторов со
со сверхзвуковым соплом в зави- сверхзвуковым соплом в зависимости
симости от приведенной скорости от приведенной скорости в выходном
в выходном сечении сопла; По = сечении сопла; По = 50, к = 1,4
== 10, к = 1,4
сечения первой «бочки» струи, перерасширение газа в этом се-
сечении и суммарные потери полного давления в системах скачков
в начальном участке струи уменьшаются, если увеличить силу,
действующую на струю со стороны ее границ в направлении
движения газа. Это означает, что для уменьшения максимальной
площади струи и снижения потерь целесообразно увеличивать
степень расширения сопла лишь до таких значений, при кото-
которых сила реакции, действующая на стенки сопла в направлении,
обратном движению газа, будет увеличиваться.
Статическое давление в эжектируемом потоке переменно и
обычно уменьшается по длине камеры, поэтому эффективность
1) Черкез А. Я. О некоторых свойствах сверхзвукового течения в
начальном участке газового, эжектора // Изв. АН СССР. ОТН.—1962.—№ 6.
§ 7. ОСОБЕННОСТИ РАБОТЫ СВЕРХЗВУКОВОГО ЭЖЕКТОРА
539
каждого дополнительного участка сверхзвуковой части сопла
AF (в отношении влияния на максимальную площадь струи я
потери полного давления) может быть оценена по величине и
знаку силы реакции на стенках этого участка
лр= Д1 <*-ft>dF'
где pi и р2 — давление внутри и снаружи сопла соответственно.
Пусть сопло выполнено с расчетной степенью расширения, т. е.
в выходном его сечении
статические давления
эжектирующего иэжек-
тируемого газов равны. р*J*
Чтобы установить, яв-
является ли такое сопло
(рис. 9.22) оптималь-
оптимальным в указанном вы-
выше смысле, определим,
как меняется статиче-
статическое давление в каж-
каждом из потоков на не-
небольшом участке с — с
вблизи выходного сече-
сечения сопла.
Из уравнения неразрывности потока при G = const, p* = const
и Г* = const следует
Fq(k)= const,
причем статическое давление в любом сечении равно
Рис. 9.22. Схема эжектора с расчетным
сверхзвуковым соплом
Логарифмированием и дифференцированием этих соотношений
получаем
dF _ __ dq (X) dp_ __ dn (X)
F q {X) ' p л (X)
Записав последние соотношения в виде
или
L
6F
и .8р = 6я(А,),
6я Щ
&q Ш'
C8)
будем считать их приближенно справедливыми и для малых ко-
конечных приращений параметров, связанных с переходом от сече-
сечения с к сечению с' и соответствующим изменением площади
сопла F\ на величину AFX = F[ — Fx и площади F2 на величину
AF AF
35*
540
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
Записав выражения вида C8) для каждого из потоков на
участке с — с' и обозначив логарифмическую производную
бл (к) бл (к) 6А.
2к
бд(к)
можно получить
8q(k)
= Ъ (I),
Hh)
C9)
Поскольку абсолютные значения р\ и Р2 в сечении с одинаковый
= — а,
v 1 2 1
то из выражения C9) можно получить соотношение между при-
приращениями статических давлений в потоках на участке с — с
в виде
Арх Ь (Я2) #
На рис. 9.23 приведен график функции Ъ (к) для к = 1,4. В об-
области дозвуковых скоростей 6(Я)<0, при А>1 6(Х)>0, при
ьт
з
/
/7
-2
-3
_| I I I
Рис. 9.23. График функции Ь{К)
б(Я)/6(Я), /с = 1,4
Рис. 9.24. Изменение статического
давления внутри A) и вне B) рас-
расчетного сверхзвукового сопла эжек-
эжектора на критическом режиме:
По= Ю
Я -> 1 |&(ЛI-*«>. Последнее означает, что в околозвуковом
эжектируемом потоке абсолютная величина Ъ (Я) будет значи-
значительно больше, чем в сверхзвуковом эжектирующем потоке, и
при любом конечном значении а для критического режима ра-
работы эжектора (Аг = 1) получается Д/?2 > А/?ь Другими словами,
давление с внешней стороны сопла будет при уменьшении Fi
§ 7. ОСОБЕННОСТИ РАБОТЫ СВЕРХЗВУКОВОГО ЭЖЕКТОРА 541
возрастать значительно быстрее, чем давление газа внутри соп-
сопла; поскольку в сечении с р\=р2, то вблизи среза расчетного
сопла всегда будет участок, на котором давление /?2 будет боль-
больше, чем р\.
Расчеты показывают (рис. 9.24), что действительно на конеч-
конечном участке расчетного сверхзвукового сопла при всех значениях
По, п и а давление во внешнем потоке выше, чем во внутреннем.
Сила реакции АР, действующая на стенки этой части сопла, на-
направлена в сторону движения струи, т. е. АР < 0. Как было ус-
установлено выше, действие этой силы приводит к увеличению
площади максимального сечения струи. Если отбросить конце-
концевую часть сопла от сечения, где /?i=/?2, то суммарная сила из-
избыточного давления, действующая на поток со стороны стенок
сверхзвуковой части сопла1), возрастет и площадь максимально-
максимального сечения струи уменьшится. При этом появляется возможность
уменьшить суммарную площадь канала, если заданы параметры
и расход внешнего потока и, следовательно, площадь его крити-
критического сечения FKP2.
Если сохранить постоянной площадь канала, то увеличится
расход внешнего газа — режим работы отдалится от режима
запирания.
Одновременно из-за уменьшения перерасширения газа сни-
снизятся суммарные внутренние потери в скачках уплотнения на
начальном участке струи и повы- jj
сится полный напор полученной
смеси газов.
Заметим, что при По < 5 и
малых значениях коэффициента 6
эжекции участок местного „пере-
„перерасширения велик, и суммарная 4
сила реакции на сверхзвуковой
части расчетного сопла Лаваля 2 ?±у^rj_
оказывается направленной по по- V '* 7>° ^ 4° ^ f7
току. Переходя в этом случае к рис g 25 Предельное отношение
нерасширяющемуся соплу, т. е. полных давлений газов (режим
отбросив всю сверхзвуковую часть запирания) для эжекторов со
сопла Лаваля, можно получить звуковым A) и расчетным сверх-
сверхуказанный выше полезный эф- звуковым B) соплом
фект. Действительно, расчеты и
опыты показывают, что при малых значениях По звуковой эжек-
эжектор обеспечивает большее полное давление газа и запирается
при больших значениях По и а (рис. 9.25), чем эжектор с рас-
]) Эта сила, равная Р — f (р1 — р2) dF, пропорциональна площади,
заключенной между кривыми р\ и р/2 на рис. 9.24. В «петле» перерасшире-
перерасширения между точками пересечения кривых сила отрицательна.
542
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
четным сверхзвуковым соплом. При По > 5 имеем всегда Р > О,
поэтому эжектор с расчетным сверхзвуковым соплом эффектив-
эффективнее звукового эжектора, хотя и уступает в эффективности эжек-
эжектору с оптимальной степенью расширения сопла.
На рис. 9.26 приведены зависимости F0/Fv = /(дУ0), где FP —
расчетная, Fo — оптимальная площадь выходного сечения сопла.
Эти зависимости аппроксимируются формулой
i-0,7
0,3л
D0)
0,1 0,2 0,3 0,4 0,5 0,8
Рис. 9.26. Соотношение между площадью вы-
выходного сечения оптимального и расчетного
сверхзвукового сопла
справедливой для По = 5—300 при nl/Q = 0—0,6. Если сравнить
результаты расчета по формуле D0) с данными, приведенными
выше (рис. 9.20, 9.21),
Fo • • - ¦ - то можно отметить хо-
рошее соответствие по-
полученных оптимальных
значений степени рас-
расширения сопла.
Таким образом, фи-
физический смысл сущест-
существования оптимальной
степени расширения
сопла, которая меньше
расчетного значения,
заключается в том, что
вследствие различного
градиента давлений в
эжектирующем и эжек-
тируемом потоках вблизи выходного сечения расчетного сопла
всегда имеется участок перерасширения, которое отрицательно
сказывается на параметрах системы.
Принципиальным преимуществом эжектора со сверхзвуковым
соплом перед эжектором с нерасширяющимся соплом является
возможность получения больших степеней повышения давления
эже^стируемого газа. На рис. 9.15 было показано, что максималь-
максимальная степень увеличения давления Р3/Р2 = 3,55 в эжекторе с не-
нерасширяющимся соплом получается при По = 11—13. В эжекто-
эжекторе со сверхзвуковым (расчетным или оптимальным) соплом при
возрастании По потребная площадь сечения камеры смешения
растет медленнее и полное давление р3 непрерывно увеличивает-
увеличивается с увеличением По (рис. 9.27). Теоретически и эксперимен-
экспериментально показана возможность получения в таком эжекторе сте-
степени повышения давления эжектируемого газарз/р* = 10 —20 и
более, разумеется, при^ очень малых значениях коэффициента
эжекции. С увеличением коэффициента эжекции до 0,5—0,6 пре-
§ 8. ПРИБЛИЖЕННЫЕ ФОРМУЛЫ РАСЧЕТА ЭЖЕКТОРА
543
имущества эжектора со сверхзвуковым соплом уменьшаются,
даже при достаточно больших значениях По.
Следует учитывать, что при уменьшении отношения давлений
по сравнению с расчетным значением сопло начинает работать
с перерасширением газа, характеристики эжектора со сверхзву-
сверхзвуковым соплом значительно ухудшаются и, начиная с некоторого
0,2
О
8 12
Рис. 9.27. График для определения параметров эжектора с оптимальным
сверхзвуковым соплом на критическом режиме (к = 1,4)
значения По, становятся по всем показателям хуже характери-
характеристик эжектора с нерасширяющимся соплом. На рис. 9.20, 9.21
это видно по резкому падению значений функции р*/Р2 — f ftp)
при Х\ > Хо и особенно при Xi >KP\. Поэтому если эжектор дол-
должен работать в широком диапазоне режимов, то, несмотря на
некоторое ухудшение данных на расчетном режиме, целесообраз-
целесообразно значительно уменьшить по сравнению с оптимальной степень
расширения в сверхзвуковом сопле или применять нерасширяю-
нерасширяющееся сопло.
§ 8. Приближенные формулы расчета эжектора
Изложенный метод расчета эжектора позволяет разрешать
любые задачи, связанные с определением размеров, параметров
и характеристик эжектора.
Недостатком этого метода является отсутствие явных анали-
аналитических зависимостей искомых величин от заданных и необхо-
необходимость при вычислениях применять метод последовательных
приближений. Поэтому влияние того или иного фактора на па-
параметры эжектора обнаруживается лишь после детальных расче-
расчетов. Существуют, однако, некоторые приближенные соотношения,
544 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
позволяющие более просто и наглядно оценивать связь между
различными параметрами эжектора и их взаимное влияние.
Рассмотрим некоторые из таких соотношений. В уравнения
для расчета эжектора A2) и A3) при О = О входит выражение
Можно показать, что погрешность приближенного равенства
Г(л+1)(лв+1)»пГв + 1 D1)
в широком диапазоне изменения величин п и 0 не превосходит
3—5%. Поэтому заменим радикалы У (п + 1) (пд + 1) в форму-
формулах A2) и A3) их приближенным значением D1). Рассматри-
Рассматривая теперь систему основных уравнений эжектора, отметим, что
коэффициент эжекции п и отношение температур торможения _0
в уравнения входят только совместно, в виде комплекса ?гУ0.
Если величины п и 0 изменять таким образом, чтобы выполня-
выполнялось равенство 7гУ0 = const, то эти уравнения будут удовлетво-
удовлетворяться при одних и тех же значениях всех параметров потока
как на входе, так и на выходе из эжектора.
Представим теперь, что для заданного эжектора (для фикси-
фиксированных значений геометрических параметров аи/) при сохра-
сохранении полных давлений газов р±, р2 и давления на выходе р\
изменится отношение температур торможения 0. Согласно основ-
основным уравнениям при этом произойдет изменение коэффициента
эжекции
где щ и 0о — значения величин на исходном режиме. Равенство
D2) является первым приближенным соотношением, позволяю-
позволяющим оценить параметры эжектора при изменении 0; оно хорошо
подтверждается экспериментом.
Рассмотрим, например, что происходит с эжектором при по-
повышении температуры торможения эжектирующего газа Тг при
Т\ = const Если F\ = const и р* = const, то расход газа через
сопло G\ изменяется обратно пропорционально корню квадратно-
квадратному из Т\, так что G1yT* = const. Из приближенной формулы
D2) в данном случае следует
С / Т1* G
п /в = -± А/ -г = const, или « = const.
Gx
Сравнивая это выражение с предыдущим, получаем G<i = const.
Таким образом, увеличение коэффициента эжекции при повыше-
§ 8. ПРИБЛИЖЕННЫЕ ФОРМУЛЫ РАСЧЕТА ЭЖЕКТОРА
545
нии температуры торможения эжектирующего газа связано лишь
со снижением расхода этого газа G\\ расход G<± эжектируемого
газа при изменении Т\ не изменяется. Так как р*2, F2 и Г* по-
постоянны по условию, то последнее возможно только в том слу-
случае, если статическое давление р2 во входном сечении смеситель-
смесительной камеры не зависит от температуры торможения Т*. Таким
образом, из приближенной зависимости D2) следует практиче-
практически важный вывод: при изменении температуры одного из газов
расход и скорость другого, а также статическое давление на
входе в камеру смешения остаются неизменными. На рус. 9.28
. Ар мм вод, ст.
Рис. 9.28. Зависимость разрежения на входе в камеру смешения от отпо-
шения полных давлений газов; р* = р3, Ар = р* — р2
приведены экспериментальные данные, подтверждающие эту
приближенную зависимость.
Из общих уравнений процесса смешения потоков можно по-
получить еще одну важную приближенную зависимость. Заменим
в уравнении A0) полные импульсы потоков согласно A19) гл. V:
D3)
Тогда уравнение A0) примет вид
К) = plFj {К) + p\FJ (X,).
Учитывая, что при дозвуковой скорости на выходе из камеры
обычно Я2<Я3<Яь т. е. /(ta)< f(h)< f(k\), а также принимая
во внимание пологость функции f(K) в области дозвуковых ско-
скоростей, можно без заметной погрешности отбросить множители
/(А,) при всех членах уравнения D3) и записать следующее
приближенное выражение:
Используя здесь условие
F\ + F-2, получим после деления
546 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
правой и левой части на F2 приближенную формулу для опреде-
определения полного давления в потоке после смешения
Формула D4) показывает, что в процессе смешения газовых по-
потоков происходит осреднение полного давления по сечению, т. е.
полное давление потока на выходе из цилиндрической смеситель-
смесительной камеры равно среднему по площади значению полного дав-
давления во входном сечении камеры.
Расчеты по формуле D4) показывают также, что точность ее
вполне удовлетворительна, если величины A,i, Я2 и Хз лежат в об-
области значений 0,15—1,1 и отношение температур торможения
0,3 < 0 < 3, причем погрешность незначительно увеличивается
с ростом отношения давлений p*/pt- Если обратиться к рис. 9.15,
на котором приведены результаты расчетов звуковых эжекторов
с различными геометрическими параметрами, то можно заметить,
что сетка прямых а = const устанавливает связь между полными
давлениями рх, р2 и/?з> соответствующую формуле D4), которую
можно представить в виде линейной зависимости
Р*з = а п , 1
р* а + 1 а + 1'
Значения P*/pt по формуле D4) всего на 2—4 % меньше значе-
значении, приведенных на рис. 9.15.
Согласно приближенной формуле D4) полное давление смеси
при заданных начальных давлениях газов и постоянных разме-
размерах эжектора не зависит от относительного расхода эжектируе-
мого газа. Это практически совпадает с данными точной характе-
характеристики эжектора (рис. 9.16), которая показывает, что полное
давление смеси весьма мало изменяется с увеличением коэффи-
коэффициента эжекции п, несмотря на то, что количество энергии
эжектирующего газа, приходящееся на единицу расхода эжекти-
руемого газа, при этом уменьшается во много раз.
Сохранение полного давления смеси является следствием то-
того, что одновременно с ростом коэффициента эжекции увеличи-
увеличивается скорость эжектируемого газа и уменьшаются ударные по-
потери при смешении потоков.
Формула D4) удобна тем, что позволяет по заданным вели-
величинам Pi* P% и а непосредственно определять полное давление
смеси р3, которое почти всегда является конечным искомым па-
параметром. Это значительно уменьшает объем вычислительной
работы по сравнению с точным методом расчета, согласно кото-
которому полное давление смеси определяется лишь после нахожде-
нахождения . всех—приведенных скоростей и коэффициента эжекции;
§ 8. ПРИБЛИЖЕННЫЕ ФОРМУЛЫ РАСЧЕТА ЭЖЕКТОРА 547
Следует, однако, иметь в виду, что при таком упрощенном рас-
расчете нельзя выяснить, будет ли реальным рассматриваемый ре-
режим работы эжектора; это устанавливается изложенными в § 4
условиями существования.
Из формулы D4) вытекает следующее практически важное
правило, справедливое не только для звуковых, но и для сверх-
сверхзвуковых эжекторов: для получения большего значения полного
давления смеси на выходе из эжектора следует, сколько возмож-
возможно, уменьшать относительную площадь камеры смешения, т. е.
увеличивать а. При сверхкритическом отношении давлений в
сопле эжектирующего газа наименьшая возможная площадь се-
сечения смесительной камеры соответствует разгону эжектируемо-
го потока в сечении запирания до скорости звука, т. е. критиче-
критическому режиму работы эжектора. Таким образом, согласно изло-
изложенному правилу критический режим работы эжектора оказыва-
оказывается наивыгоднейшим, что соответствует данным расчетов и экс-
экспериментов. Следует, однако, учитывать, что чем меньше пло-
площадь смесительной камеры, тем больше при данных расходах га-
газов скорость на входе в диффузор, т. е. больше потери в диф-
диффузоре.
Приближенные формулы D2) и D4) позволяют установить
простую зависимость между температурой газа и полным давле-
давлением потока после смешения. Здесь надо различать два случая
вычисления полного давления смеси:
а) при изменении температуры одного или обоих газов и ус-
условии а = const,
б) при изменении температуры газов и условии п = const.
В обоих случаях предполагается р± = const и р2= const. Со-
Согласно приближенной формуле D4) в первом случае полное дав-
давление смеси р3 при изменении 9 не изменяется и не зависит от
начальных температур торможения газов. Однако при этом, со-
согласно D2), изменится коэффициент эжекции, так как чем боль-
больше 9, тем меньше величина п. Чтобы сохранить прежнее значе-
значение коэффициента эжекции, необходимо увеличить относитель-
относительную площадь сопла, расход через которое уменьшился. Соответ-
Соответственно при п = const среднее по площади входного сечения
полное давление и равное ему полное давление смеси р3 прибли-
приблизятся к полному давлению более нагретого газа. Поэтому, на-
например, повышая температуру эжектирующего газа и изменяя
отношение площадей FJF2 таким образом, чтобы сохранить по-
постоянным коэффициент эжекции, можно получить большее зна-
значение полного давления смеси газов.
Приближенные соотношения D2) и D4) весьма полезны при
качественном анализе параметров эжектора. Если же допустима
погрешность в 3—5 %, то этими соотношениями можно пользо-
пользоваться и для предварительного количественного расчета.
548 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
§ 9. Примеры расчета эжектора
Пример 1. Для испытательного стенда, показанного на рпс. 9.2,
требуется подобрать эжектор, обеспечивающий поток воздуха для венти-
вентиляции помещения и охлаждения испытуемого двигателя. Расход воздуха
нужно выбрать так, чтобы температура газов в выхлопной шахте была не
выше 600 К. Параметры газа на выходе из реактивного сопла двигателя
р* = 2- 105Н/м2, Г* = 900 К. Параметры воздуха в боксе: р*= 1,03-105 Н/м2,
Т2 = 300 К. Статическое давление в выхлопной шахте 1,05 • 105 Н/м2.
Расчет начнем с определения потребного коэффициента эжекции. Пре-
Пренебрегая различием в теплоемкостях газа и воздуха, из формулы G) по-
получаем
или
900 — 600 _
Таким образом, требуемое по условию задачи снижение температуры газов
может быть достигнуто путем подмешивания воздуха в количестве равном
расходу газа через двигатель.
Определяем безразмерные параметры
П104 е|0333
Так как предполагается, что отношение давлений в сопле двигателя выше
критического значения, а сопло выполнено нерасширяющимся, то Ki = 1.
Как указывалось, для расчета эжектора необходимо задать К2 и воспользо-
воспользоваться последовательно уравнениями (8), A2) и A3). Легко убедиться,
что решение поставленной задачи неоднозначно. Заданным условиям удов-
удовлетворяет ряд эжекторов, отличающихся геометрическими параметра-
параметрами а и /.
Найдем критическое значение Я2 — предельно возможное значение ^2,
при котором в сечении запирания скорость эжектируемого воздуха достиг-
достигнет скорости звука, т. е. Х2 = 1. Для этого подставляем в уравнения C1)
и C4) значения п ув = 0,577, По = 1,94, A,i = 1 и, задавшись рядом зна-
значений Я^ > 1, определяем из каждого уравнения соответствующее значе-
значение Я2<1. Пересечение двух полученных кривых \ = f {^^) Дает сов-
совместное решение уравнений — предельные значения приведенных скоростей
на критическом режиме
А,'= 1,351 и %= 0,674.
Однако, подставив такую величину ^ и ^ = 1 в уравнение количества
движения A2), находим г(Я3) = 1,982, т. е. z(A,3) < 2, что нереально и ука-
указывает на физическую невозможность режима: при заданных значениях
п, По и 9 расход эжектируемого газа ограничен кризисом течения в выход-
выходном сечении камеры смешения (см. § 6 и рис. 9.19). Поэтому принимаем
%г = 1, т. е. z(%3) = 2, и из уравнения A2) находим
21/^666 — 2
(Я) зЗ = ' *
§ 9. ПРИМЕРЫ РАСЧЕТА ЭЖЕКТОРА 549
Этому соответствует максимально возможное значение К2 = 0,643, что не-
несколько меньше, чем было определено из рассмотрения потоков в сечении
запирания.
Теперь можно задаться несколькими значениями К2 ^ 0,643 и провести
расчет по изложенному выше методу. Выберем, например, К2 = 0,6. Из фор-
формулы A4) находим, что для заданного коэффициента эжеТЙщи^=~1 гео-
геометрический параметр а должен быть равным
1 0,8109 _n79q
W 1,941/0,333 1 ' '
Подставляя значения z(K\) = 2,0 и z(%2) = 2,267 в уравнение A2) и пола-
полагая Ф = 0, определяем
2 + 2,2671/0,333
Так как Х2 <С к2кр = 0,674, то реальным будет только дозвуковой режим
течения на выходе из камеры. Чтобы повысить точность вычисления Л3
по функции z(X3), рекомендуется дозвуковое решение квадратного урав-
уравнения
1
2i026
представить в виде
X3 = 2 = лг 2 = °'854;
отсюда следует
q(k3) =0,974, я(Х3) =0,635.
При пользовании таблицами значений функции z(X) следует иметь в виду,
что в некоторых таблицах через z(X) обозначают функцию
1
Теперь по формуле A3) можно вычислить полное давление газа после
смешения:
*- .У(» + 1)(и8 + 1) 9 (К) 21/2-^66 105 ,/п-4
^з = Pi ГГШ 7^7) = 2,38 0^74 = 1'405> 1
Статическое давление смеси в выходном сечении камеры
рз = р*я (Я3) = 1,405-0,635.105 = 0,895-10* Н/м2
на выбранном режиме ниже заданного давления в выхлопной шахте
/?4 = 1,05-105 Н/м2. Поэтому на выходе из камеры необходимо установить
диффузор. Легко убедиться, что необходимое увеличение площади потока
в диффузоре FJFs = / и соответственно потери полного давления будут не-
небольшими. Примем ад = 0,98. Тогда по формулам B0) — B3) получаем
Pi = адр* = 1,377-105 Н/м2, я (Я,4) = Ц = 0,764; Я4 - 0,667,
?(Х4) = 0,868, /=y^J—=-0^3-Q-gg- = 1,14.
550
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
Таким образом, один из возможных вариантов эжектора, обеспечивающий
заданные значения коэффициента эжекции и статического давления потока
на выходе, определяется геометрическими параметрами
F р
а = -тг- = 0,723; /=/=1,14.
Точно так же, задаваясь другими значениями Яг, определяем ряд возмож-
возможных сочетаний аи/. Результаты расчета приведены на рис. 9.29. Поскольку
требуемое изменение площади диф-
диффузора во всех случаях невелико, це-
целесообразно выполнить эжектор без
диффузора, т. е. в виде одной ци-
цилиндрической трубы. Для этого, со-
согласно рис. 9.29, достаточно выбрать
а = 0,575, / = 1 что соответствует
Я2= 0,445.
Заметим, что для всех вариантов
эжекторов, удовлетворяющих усло-
условиям задачи, получается примерно
одинаковое значение отношения пло-
площади выходного сечения F4 к площа-
площади сопла F\. В данном случае, как
ос
0,8
0,7
0,6
0,5
0,4
0,4 0,45 0,5 0,55
06 065 можно видеть из рис. 9.29,
**г F т гу 4- 1
• 2,72.
Рис. 9.29. Геометрические парамет- F ' а
ры эжекторов а и / в зависимости
от выбранного в расчете значения 12 Эту приближенную закономер-
закономерность полезно иметь в виду при под-
подборе размеров эжектора, работающего по схеме рис. 9.2 в выходных систе-
системах различных установок.
Пример 2. Эжектирующий газ имеет полное давление р* =
= 12- 105Н/м2,* полное давление эжектируемого газа р*2= 10°Н/м2; темпера-
температуры торможения газов равны. Требуется определить геометрические пара-
параметры эжектора, обеспечивающего на выходе из диффузора дозвуковой поток
смеси газов с ^возможно большим полным давлением при работе с коэффи-
коэффициентом эжекцшГТг == 0,2. Диффузор эжектора — обычного дозвукового типа.
Будем рассчитывать эжектор для работы на наивыгоднейшем крити-
критическом режиме. Ввиду того, что отношение полных давлений газов По = 12
достаточно высокое, а коэффициент эжекции небольшой, здесь целесообраз-
целесообразно подобрать оптимальное сверхзвуковое сопло для эжектирующего газа.
Для полного расширения эжектирующего газа сопло должно быть спроек-
спроектировано на отношение давлений (к = 1,4).
_ По _
12
р
лA) 0,5283
= 22,75,
так как выходное сечение его совпадает с сечением запирания, где
тируемый газ движется с критической скоростью. Определяем приведенную
скорость К\ на выходе из такого сопла
я (Aj) =—t = 0,044, Я1р = :
= 0,3211
§ 9. ПРИМЕРЫ РАСЧЕТА ЭЖЕКТОРА 551
и площадь его выходного сечения
(потерями полного давления в сопле пренебрегаем).
Для получения наибольшей величины полного давления смеси сопло
должно быть выполнено с неполным расширением газа, так что площадь
выходного сечения его меньше площади расчетного сопла; в данном случае,
согласно формуле D0),
у- = 0,7 + 0,ЗгсУ~ё = 0,76, F =2,S7F
г р
Приведенную скорость эжектирующего газа на выходе из оптимального
сверхзвукового сопла находим из уравнения неразрывности
*Ы = т; = т=0422 Ч=1787
Далее с помощью уравнений C0) и C3) определим значение приведенной
скорости К2 на критическом режиме (^2 = l)«
Совместное решение этих уравнений находим подбором. Задаемся ря-
рядом значений Xv причем в первом приближении ориентируемся на полу-
полученное выше для расчетного сопла значение Xip = 1,88 и учитываем, что
для оптимального сопла %1 < Х1р.
Поскольку параметры газа на срезе оптимального сопла мало отличают-
отличаются от параметров в сечении запирания, то в правых частях выражений C0)
и C3) образуются малые разности. Поэтому вычисления по этим формулам
необходимо вести с высокой степенью точности.
В данном случае, задавшись значениями ^=1,88; 1,84; 1,82, указан-
указанным выше способом определяем
Xi = l,85, Я2 = 0,636, g (А,2) = 0,842, *(Я,2) = 2,205.
Находим требуемую величину геометрического параметра эжектора а по
ФОРМУЛ6A4) 1М42
а—12-0,2 0,422 —°>83>
что дает для отношения площади сечения камеры к площади выходного
сечения сопла
^^
2203
и к площади критического сечения сопла
Л 2,203 2,203
^Кр1~9(М~°.422~ '
Подставляя Х\, Я2 и п в уравнение количества движения A2), находим
2,346 -f 0,2-2,205
z(h)= . 1,2 =2>322'
Несмотря на то, что в данном случае (Я^ = l) поток в смесительной камере
будбт сверхзвуковым, ищем дозвуковое решение уравнения.,Как указыва-
552 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
лось, это решение соответствует наивыгоднейшему режиму торможения
потока смеси в скачке, расположенном непосредственно в выходном сече-
сечении камеры (на выходе в диффузор):
2
^3== 2,322 + /5,40 -4 =0'571' q(Кз) = °'783*
Определим полное давление потока смеси на входе в диффузор из A3)
По рис. 8.32 находим для данного значения Я3 значение коэффициента
сохранения полного давления в диффузоре стд = 0,96. Полное давление
потока на выходе из диффузора составляет
р* = 3,52-0,96.105 = 3,38-105 Н/м2,
а максимально возможное статическое давление в резервуаре, куда выбра-
выбрасывается смесь из эжектора при Я4 « 0,2,
р4 = р*л (А,4) = 3,3-105 Н/м2.
Для этого степень расширения диффузора необходимо выбрать равной
g(A3) 0,783
f— ад^(Х4)~ 0,96-0,310 — 2'63-
Если такой же расчет произвести для эжектора с нерасширяющимся соп-
соплом, т. е. принять A,i = 1, то необходимая площадь сечения смесительной
камеры будет больше площади критического сечения сопла не в 5,23, а в
7,45 раза, и полное давление на выходе из диффузора будет на 35 % меньше
значения, полученного выше. Как видим, в данном случае применение
сверхзвукового сопла дает заметньп1ПшигрБ1Ш"^-тгоз^^ Выбор
рациональной степени расширения в сопле также дает~ некоторый эффект.
Если вместо выбранного выше оптимального сопла с неполным расшире-
расширением применить расчетное сверхзвуковое сопло (Х\ = 1,88), то, как пока-
показывает расчет, пришлось бы площадь камеры смешения увеличить на 55 %
(F3/FKp = 5,52), в результате чего полное давление смеси снизилось
бы на 4 %.
Отметим, что все эти результаты получены при условии, что диффузор
эжектора — дозвуковой и перед диффузором возникает прямой скачок уп-
уплотнения, который переводит полученную при смешении потоков сверхзву-
сверхзвуковую скорость в дозвуковую. Приведенная скорость потока смеси перед
скачком может быть определена из соотношения
лз—
__L \ 175
з— Я, ~ 0,571 — 1'ii>-
При такой скорости потери полного давления в прямом скачке весьма ве-
велики (согласно рис. 3.5 коэффициент сохранения полного давления оп « 0,6)
и составляют большую часть общих потерь в эжекторе. Действительно, пол-
полное давление сверхзвукового потока смеси значительно выше полученного
для Лз < 1 значения и равно
а
Поэтому в данном случае применение сверхзвукового диффузора с торможе-
торможением потока в системе скачков может дать заметный эффект.
§ 10. ТЕОРИЯ ЭЖШТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ 553
§ 10. Теория эжекторного увеличителя реактивной силы
Рассмотрим величину реактивной силы, возникающей при
истечении газа из эжектора, схема которого приведена на
рис. 9.30. Эжектирующим газом является выхлопная струя ре-
реактивного двигателя. Эжектируемый газ (воздух) поступает в
смесительную камеру
непосредственно из ат-
атмосферы, поток смеси
выбрасывается также в
атмосферу.
Предположим пока,
что сопло и диффузор ^* V 2 1 3 4
эжектора спроектиро-
спроектированы так, что статиче- Рис. 9.30. Схема эжектора, установленного на
ские давления газа в сопле ракетного двигателя
выходном сечении соп-
сопла и потока смеси на выходе из диффузора равны давлению
внешней среды рн. В этом случае суммарная реактивная сила,
действующая на все элементы эжектора, неподвижного относи-
относительно внешней среды,
где G\ и С?2 — секундные расходы эжектирующего газа и возду-
воздуха, a W4 — скорость истечения смеси из диффузора эжектора.
Реактивная сила (тяга) двигателя при тех же начальных
параметрах газа, но без подмешивания внешнего воздуха, равна
где w\ — скорость истечения газа из сопла.
Поскольку процесс смешения в эжекторе сопровождается по-
потерями на удар, то кинетическая энергия смеси газов
(Gx -f G2) wl/2 будет меньше начальной кинетической энергии
струи Gj^i/2, так что
Величину г] можно считать условным коэффициентом полез-
полезного действия эжектора, оценивающим совершенство процесса
смешения. Из последнего соотношения легко получить
36 г. Н. Абрамович, ч.
554 гл- 1Х- ГАЗОВЫЕ ЭЖЕКТОРЫ
ИЛИ
JL = /(л + 1)т], D5)
о
где п = G2/G\ — коэффициент эжекции.
Если при данном значении г| присоединить к струе газа до-
достаточное количество внешнего воздуха так, что п + 1 > 1/rj, то
Р/Ро > 1. Другими словами, путем распределения первоначаль-
первоначальной энергии эжектирующего потока на большую массу газа
можно увеличить реактивную тягу без затраты дополнительной
энергии. Приведенное рассуждение носит качественный харак-
характер. Количественные зависимости можно определить, рассчитав
эжектор по изложенным выше методам. Расчеты, а также экс-
эксперименты показывают, что с помощью эжектора можно реа-
реализовать такие значения коэффициента эжекции п и к. п. д. ц?
что выигрыш в тяге достигает в определенных условиях значи-
значительной величины.
Увеличение тяги при подсасывании внешнего воздуха к эжек-
тпрующей струе объясняется тем, что на элементах эжектора
возникают дополнительные силы, равнодействующая которых,
направленная по оси потока, суммируется с реактивной тягой
сопла. Основной из этих сил, определяющей выигрыш в тяге,
является неуравновешенная сила внешнего давления, действую-
действующая на входной раструб (заборник) эжектора. Ее появление
обусловлено понижением давления на стенках раструба при
втекании в него эжектируемого воздуха.
Для выяснения принципиальных свойств эжектора как эле-
элемента реактивной системы пренебрежем сжимаемостью газа, ко-
которая в данном случае оказывает не очень существенное влия-
влияние на конечные параметры системы.
Составим систему основных уравнений для эжектора, который
перемещается вместе с соплом (двигателем) относительно внеш-
внешней среды со скоростью wH. Предположим пока, что плотности
смешивающихся жидкостей (газов) одинаковы, камера смеше-
смешения — цилиндрическая, а гидравлические потери во всех эле-
элементах эжектора отсутствуют (учитываются лишь потери на
смешение). Уравнение энергии для втекающего в эжектор по-
потока внешней среды
i!" + fl = i!L + —.
Уравнение неразрывности для потоков в смесительной камере
Уравнение количества движения для потоков в смесительной
камере (при р\ = р2)
G\W\ + G2W2 —(Gi + G$) wz ==(/?з—p2) (F\ + F2). D8)
§ 10. ТЕОРИЯ ЭЖЕКТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ 555
Уравнения неразрывности и энергии для потока в диффузоре
D9)
Здесь и ниже предполагается, что в конце смесительной камеры
скорость потока постоянна по сечению.
Решение этой системы строим таким образом, чтобы по из-
известном параметрам газа (жидкости) в сопле и геометрическим
параметрам эжектора определить относительный расход эжек-
тируемой внешней среды (коэффициент эжекции) и скорость
истечения смеси из эжектора, необходимые для вычисления ре-
реактивной силы. Для этого при помощи первого и последнего
уравнений системы исключаем величину (р$ — р2) из уравнения
количества движения. Подставив в полученное выражение без-
безразмерные величины
а также полученные из уравнений неразрывности соотношения
!!^=ап, f» =-?Ц.(л + 1), !!l= * " (л + 1), E1)
приходим к квадратному уравнению относительно величины п
a(l + a2-f)n2 + 2cc(l + f)n- а/2 - 2/2 + а- ^ /2(а+ 1Jсо2 = 0.
Положительный корень этого уравнения
гт^? 52)
показывает, какое относительное количество газа подсасывает
эжектор с геометрическими параметрами аи/, движущийся от-
относительно внешней среды со скоростью wn = (uw\, при условии
полного использования скоростного напора pw^/2.
Заметим, что величина со2 здесь характеризует превышение
полного давления эжектируемого газа над статическим давле-
давлением на выходе из эжектора:
Скорость истечения смеси из эжектора wa можно определить,
подставив найденное значение п в уравнение неразрывности
(см. E1)).
Из уравнения энергии определим необходимую для дальней-
дальнейшего величину разрежения во входном сечении смесительной
36*
556 ГЛ. IX, ГАЗОВЫЕ ЭЖЕКТОРЫ
камеры
ИЛИ
о
L?(a*n*-tf). E3)
Реактивная тяга системы вычисляется по формуле
или
Р = Gm [j-^riin + IJ - nv] E4)
(полагаем, что направления векторов w^ и wa совпадают).
При составлении выражения E4) предполагалось, что из
внешней среды поступает в систему только эжектируемый газ,
а эжектирующий газ (жидкость) первоначально движется вме-
вместе с системой со скоростью wB (схема работы ракетного дви-
двигателя) . *
Если эжектирующий газ поступает из внешней среды (как,
например, в воздушно-реактивных двигателях), то следует до-
дополнительно вычесть «входной импульс» G\Wn. Тогда для реак-
реактивной тяги получим выражение
Р = GlWl Ц- ^ (» + IJ - (п + 1) со ]. E5)
Для того чтобы правильно записать выражение для исход-
исходной тяги сопла (двигателя) без эжектора, по отношению к ко-
которой будем оценивать эффективность системы, следует учесть,
что при работе сопла в эжекторе скорость истечения эжектиру-
ющего газа (жидкости) при заданных начальных параметрах
увеличивается вследствие разрежения, образующегося при входе
в камеру. Если эжектор отсутствует, то скорость истечения w±
получится меньшей, так что
или, с учетом соотношения E3),
Отсюда получаем выражение для исходной тяги без эжектора
р'о = G[w[ = pFxw'* = G1w1 A — а2п2 + со2). E6)
Для определения эффективности процесса с точки зрения
увеличения тяги целесообразно сравнить полученную реактив-
§ 10. ТЕОРИЯ ЭЖЕКТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ
557
ную тягу с исходной при равных расходах газа через сопло. При
этом получим для ракетного двигателя
<57)
для воздушно-реактивного двигателя
К ""н)
X
—(лг + 1) со].
E8)
Величину б назовем коэффициентом увеличения тяги. В даль-
дальнейшем будем пользоваться только формулой E8), имея в виду,
что для малых относительных скоростей движения со = wjwi
обе последние формулы дают близкие результаты. Заметим, что
1.6
Рис. 9.31. Зависимость параметров
реактивной системы с эжектором от
геометрического параметра эжекто-
ра a; / = 1
1.0
Щ
0,8
0;6
0,2
0,4 0,8 1,2 1,6 2,0 а
поскольку п:=п(а1 /, со), то для заданной относительной ско-
скорости движения системы со выигрыш в тяге определяется только
геометрическими параметрами аи/.
При работе эжектора на месте (со = 0), когда формулы E2)
и E8) принимают вид
п
/ A + 1/оь) /2а + а2 (/2 - l) -1 - /2
а2/2
S =
1J
E9)
F0)
коэффициент эжекции п, отношение скоростей wjw\ и коэффи-
коэффициент увеличения тяги б являются монотонными функциями
геометрических параметров аи/ (рис. 9.31, 9.32).
58
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
При этом оказывается, что для эжекторов с любыми значе-
значениями геометрических параметров аи/ коэффициент увеличе-
увеличения тяги б больше единицы, и выигрыш в тяге может достигать
значительной величины. Таким образом, в неподвижном эжек-
эжекторе подмешивание дополнительной массы к струе, вытекающей
из сопла, происходит достаточно эффективно, вследствие чего
^ при полном смешении пото-
потоков всегда образуется выиг-
выигрыш в реактивной тяге. На-
Напомним, что этот результат
получен без учета потерь на
трение.
Уменьшение а, т. е. уве-
увеличение относительной пло-
площади камеры смешения, при-
приводит к увеличению коэффи-
коэффициента эжекции п и умень-
уменьшению относительной скоро-
1f5 2,0 ~25 1.0 f стп потока на выходе из
II
3,0
2,0
W
ш4
-0,4
0,2/"
1 1 !
-14
- 1,0
Рис. 9.32. Зависимость параметров
реактивной системы с эжектором от
степени расширения диффузора /;
а = 0,3
2,5 3,0Г
эжектора wjw\. Выигрыш в
тяге (коэффициент б) при
этом возрастает (рис. 9.31).
Если беспредельно увеличи-
увеличивать относительную площадь
камеры (а-^0), то коэффициент эжекции п, согласно уравне-
уравнению E9), неограниченно возрастает, а скорость потока после
смешения стремится к нулю. Коэффициент увеличения тяги,
который в основном определяется произведением (п+ l)wjw\7
при а ->¦ 0 возрастает до максимального значения. Подставив E9)
в уравнение jF0), получим
/l-aV(l+cc2/2J
Найдем предел этой величины при а ->¦ 0. С помощью урав-
уравнения E9) легко установить, что при а -*- 0 an -> 0 (что впол-
вполне очевидно по существу, так как согласно E1) an = W2/wi).
Учитывая это, из последнего выражения определяем
lim б = 2/.
а-»о
Это значит, что коэффициент увеличения тяги неподвижного
эжектора даже при отсутствии потерь на трение не может йре-
высить некоторого конечного значения, зависящего от степени
уширения диффузора /. Так, например, эжектор без диффузора
(/ = 1) даже при беспредельном увеличении его размеров и от-
отсутствии трения не может увеличить тягу более чем в 2 раза.
§ 10. ТЕОРИЯ ЭЖЕКТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ 559
Влияние скорости движения (полета) на параметры реактив-
реактивного двигателя с эжектором сводится к следующему. Разреже-
Разрежение во входном сечении смесительной камеры E3) с увеличе-
увеличением скорости движения уменьшается, однако благодаря уве-
увеличению скоростного напора эжектируемого газа расход его С?2
возрастает. Скорость эжектируемого потока на входе в камеру
растет, разность скоростей потоков уменьшается — это снижает
потери при смешении потоков.
«Выходной импульс» системы (G\ + ?2)^4 растет вследствие
увеличения как расхода 6% так и скорости w*. Одновременно
увеличивается «входной импульс» эжектируемого потока G^w*,
а в схеме ВРД также и эжектирующего потока (G\wa). В ре-
результате этого с возрастанием относительной скорости движения
со выигрыш в тяге уменьшается, несмотря на увеличение коэф-
коэффициента эжекции и снижение потерь при смешении. Можно
показать, что падение выигрыша в тяге с ростом скорости дви-
движения является свойством не только эжектора, но и любого,
даже идеального аппарата, в котором к основной струе прибав-
прибавляется дополнительная масса без подвода дополнительной энер-
энергии. Уже при сравнительно небольших относительных скоростях
движения (полета) со коэффициент увеличения тяги для идеаль-
идеального смесителя, а следовательно, и для любой эжекторной си-
системы приближается к единице. Поэтому анализ влияния со на
коэффициент увеличения тяги можно ограничить рассмотрением
области малых скоростей движения.
При выводе соотношений E2) — F0) предполагалось, что
плотности смешивающихся газов одинаковы. Точно так же мож-
можно выразить коэффициент эжекции, скорость истечения смеси
и выигрыш в тяге для случая смешения газов различных плот-
плотностей (pi/p2 = р ^ 1).
При этом получаются следующие выражения для коэффици-
коэффициента эжекции и выигрыша в реактивной тяге:
а2 (/2 - 1) р + Вг + A + а2/2) ^-^
F1)
где
а
и
t' .;.+'., [тя^+'Н-(б2)
— а п р + -=- со4 — со
560 ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
Расчеты показывают, что формула F1) приближенно соот-
соответствует зависимости
f P
где по — значение коэффициента эжекции при р = 1.
Различие в плотностях газов, существенно изменяющее ко-
коэффициент эжекции, мало сказывается на выигрыше в тяге, так
как одновременно с ростом коэффициента эжекции уменьшается
скорость истечения газа, и наоборот. Наибольший для данного
эжектора выигрыш получается при равной плотности смешива-
смешивающихся газов, т. е. при р = 1.
Для подмешивания внешнего воздуха к струе газа можно
применить многоступенчатый аппарат, состоящий из нескольких
эжекторов, причем поток смеси, вытекающий из предыдущей сту-
ступени, является эжектирующим потоком последующей ступени.
Хотя принципиально в такой конструкции смешение в каждой
ступени происходит при меньшей разности скоростей, чем в од-
одноступенчатом эжекторе, и потери на удар будут меньшими,
количественный эффект — выигрыш в реактивной тяге — оказы-
оказывается примерно таким же, как в одноступенчатом эжекторе с
равной площадью выходного сечения.
Все рассмотренные выше результаты получены в предполо-
предположении, что потери трения в элементах эжектора пренебрежимо
малы, и эффективность эжектора зависит только от ударных
потерь, возникающих в процессе смешения. В действительности,
помимо потерь при смешении, в элементах эжектора имеются
дополнительные, вторичные потери, не связанные с самим су-
существом процесса подмешивания дополнительной массы. Это в
первую очередь гидравлические потери в соплах (потери пол-
полного давления газов до входа в камеру), потери на трение в
смесительной камере и потери при торможении потока в диф-
диффузоре.
Для того чтобы определить параметры эжекторной реактив-
реактивной системы с учетом этих потерь, необходимо ввести соответ-
соответствующие коэффициенты потерь в уравнения энергии и силу
трения в уравнение количества движения.
Решение основной системы уравнений позволяет определить
коэффициент эжекции, скорость истечения потока из эжектора
и коэффициент увеличения тяги в зависимости от геометриче-
геометрических параметров эжектора и потерь в его элементах.
Расчеты показывают, что гидравлические потери в элементах
эжектора уменьшают разрежение на входе в камеру и приводят
к снижению коэффициента эжекции и скорости истечения сме-
смеси w*. В результате значительно уменьшается выигрыш в реак-
реактивной тяге. Тем не менее при реальных значениях коэффици-
коэффициентов потерь возможный выигрыш в тяге на месте (со = 0) со-
§ 10. ТЕОРИЯ ЭЖИКТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ 561
ставляет заметную величину. Так, например, эжектор с геомет-
геометрическими параметрами а = 0,05—0,1 и /= 1,5—2 позволяет уве-
увеличить тягу на месте на 25—35 % без затраты дополнительной
энергии.
Влияние вторичных потерь на реактивную тягу в полете бо-
более существенно, чем при работе на месте. Дело в том, что
с увеличением скорости движения аппарата увеличиваются рас-
расход и скорость эжектируемого газа и соответственно возрастают
потери на трение, примерно пропорциональные количеству дви-
движения Gzivz. Поскольку ударные потери в процессе смешения
при этом уменьшаются, то вторичные потери, связанные с тре-
трением, становятся преобладающими и в основном определяют
совершенство процесса. Если без учета этих потерь выигрыш
в тяге лишь снижается с ростом со, то при реальных значениях
коэффициентов потерь уже при со = 0,2—0,3 выигрыш в тяге
исчезает, а для больших значений скорости движения вместо
прироста получится снижение тяги.
Этот результат, качественно справедливый для эжекторной
системы с любыми начальными параметрами смешивающихся
газов, указывает на то, что такого рода системы могут быть
полезны только в тех случаях, когда скорость перемещения ап-
аппарата мала по сравнению со скоростью истечения газа из сопла.
Эти условия соответствуют, например, старту и начальному
периоду движения ракеты, а также различным режимам полета
аппаратов, использующих реактивную тягу для создания подъ-
подъемной силы при небольшой вертикальной скорости (вертикаль-
(вертикальный взлет самолета, режим «висения» и т. п.).
Приведенный в § 3 метод расчета газового эжектора позво-
позволяет определить параметры эжектора — увеличителя тяги с уче-
учетом сжимаемости при больших отношениях давлений смешиваю-
смешивающихся газов, больших скоростях и температурах в эжектирую-
щей струе и тем самым уточнить полученные выше результаты.
Расчет проводится для эжектора с заданными геометрическими
размерами, т. е. параметрами а и /. Полное давление и темпе-
температура эжектирующего газа рг и Тг для данного режима ра-
работы двигателя известны. Полное давление и температура тор-
торможения эжектируемого воздуха р\ и Т2 определяются по па-
параметрам атмосферы ра и Тв и скорости полета с учетом потерь
полного давления в воздухозаборнике. Далее, последовательно
задаваясь различными значениями Лг, определяем параметры
смеси газа и воздуха на выходе из диффузора. Реальным будет
такой режим (такие значения коэффициента эжекции п и ско-
скорости истечения w*), при котором давление дозвукового потока
в выходном сечении диффузора получается равным атмосфер-
атмосферному давлению рн.
Реактивная тяга системы Р, а также исходная тяга двига-
двигателя Pq определяются по параметрам газа в выходном сечении
562 ГЛ. IX ГАЗОВЫЕ ЭЖЕКТОРЫ
эжектора и сопла1). Коэффициент увеличения тяги для воз-
воздушно-реактивного двигателя вычисляется по формуле
где wH — составляющая скорости полета в направлении истече-
истечения газа из эжектора. Для ракетного двигателя эта формула
имеет вид
6. р pIV^V^^h
Результаты расчета для различных соотношений начальных
параметров газов и размеров эжектора позволяют, в первую оче-
очередь, сделать вывод о слабом влиянии сжимаемости газа па эф-
эффективность эжекторного увеличителя тяги. Изменение отноше-
отношения полных давлений газов от весьма малых значений, при ко-
которых сжимаемостью газа можно пренебречь, до значений
Pi/Pu = 3 — 3,5, когда режим истечения эжектирующей струи
сверхкритический, практически не влияет на выигрыш в тяге
при фиксированных значениях а и /.
Как показывают расчеты, изменение отношения температур
газов в пределах 0,25 < 6 < 4 оказывает незначительное влия-
влияние на коэффициент увеличения тяги эжектора с данными гео-
геометрическими параметрами, хотя при этом сильно изменяется
коэффициент эжекции. Максимального значения коэффициент б
достигает при 9 = 1, так же как в случае несжимаемой жид-
жидкости при равных плотностях pi и р^.
Наконец, расчет скоростных характеристик эжекторного уве-
увеличителя тяги с учетом сжимаемости также дает результаты,
мало отличающиеся от приведенных выше данных, полученных
без учета сжимаемости.
На рис. 9.33—9.37 приведены некоторые результаты испы-
испытания моделей эжекторных реактивных систем на установке с
непосредственным измерением реактивной тяги. Из этих графи-
графиков видно, что эжектор действительно позволяет заметно уве-
увеличить реактивную тягу при работе на месте. В соответствии с
данными теоретического анализа выигрыш в тяге оказывается
главным образом функцией геометрических параметров эжекто-
эжектора а ж /, причем если с уменьшением а (увеличением относи-
относительного диаметра камеры) выигрыш в тяге монотонно возра-
возрастает, то по величине / имеются оптимальные значения, зави-
зависящие от потерь в диффузоре.
!) При докритическом режиме истечения газа из сопла необходимо
учитывать изменение режима работы двигателя и расхода газа Gu обу-
обусловленное разрежением на входе в камеру смешения.
§ 10. ТЕОРИЯ ЭЖЕКТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ
563
Отметим, что как по экспериментальным данным, так и по
результатам расчетов выигрыш в тяге резко снижается при
дросселировании эжектируемого потока, т. е. при уменьшении
/•=/
О 0,1 0,2 0,3 0,4 0,5ос
Рис. 9.33. Коэффициент эжек-
ции модельных эжекторных
реактивных систем при работе
на месте; Э = 1, По = 1,6—2,4
6
?
13
V
10
0,1 0,2 0,3 0,4 а
Рис. 9.34. Выигрыш в тяге
при работе на месте (по экспе-
экспериментальным данным); 9 =
= 1, По = 1,6—2,4
его полного давления по сравнению с давлением внешней среды.
При значительном дросселировании тяга системы оказывается
меньше тяги сопла без эжектора, т. е. 6 < 1. Изменение полного
давления эжектирующего газа
д
13
1,2
1.1
' 0,4 0,5 0,6 0,7
сс=0,042
о о
О
0 и о
п
1 1
п
а
о
а
i
о
° О
=0,086
о п
=0,10
I
в пределах, реальных для ВРД,
практически не изменяет ко-
д
120
a Tf=330 /Г
о Т*=750-850 /<
1,00
0,3 0,4 0,5
0,6
Рис. 9.35. Выигрыш в тяге для эжек- Рис. 9.36. Выигрыш в тяге при раз-
торов без диффузора по эксперимен- личной температуре эжектирующего
тальным данным при изменении газа; а = 0,11, /= 1
полного давления газа перед соплом
эффициент увеличения тяги эжектора без диффузора, что ука-
указывает на слабое влияние сжимаемости газа (рис. 9.35). Из-
Изменение температуры эжектирующего газа почти в 3 раза
(рис. 9.36) вызывает очень небольшое снижение выигрыша в
тяге. Испытания эжекторов в условиях, соответствующих ус-
564
ГЛ. IX. ГАЗОВЫЕ ЭЖЕКТОРЫ
ловиям полета, показывают, что выигрыш в тяге быстро умень-
уменьшается с увеличением относительной скорости полета, причем
изменение начальных параметров газа не оказывает заметного
влияния на характер снижения выигрыша в тяге.
При проектировании эжектора важно правильно выбрать
длину камеры смешения, обеспечивающую достаточно полное
выравнивание поля скорости в поперечном сечении потока. Рас-
Расчет показывает, что при неполном смешении, когда коэффици-
коэффициент поля на выходе из камеры т>1 (см. § 2), эффективность
эжектора ухудшается: при заданном давлении на выходе р± сни-
снижается разрежение на входе в камеру, падает коэффициент
эжекции и выигрыш в тяге. Если не учитывать трения о стенки,
то максимальный эффект соответствует т -* 1, т. е. неограничен-
неограниченному увеличению длины камеры. В действительности, однако,
существует конечное оптимальное значение длины камеры, так
как при малой неравномерности поля скорости полезный эф-
эффект, получаемый за счет дальнейшего выравнивания, не ком-
компенсирует возрастающих гидравлических потерь. Эксперимен-
Экспериментально это определяется по наличию максимума статического
давления смеси на некотором конечном расстоянии от входа в
б
1,20
V5
1,10
1,05
100t
камеру. Анализ основных урав-
уравнений процесса смешения по-
показывает, что эта длина каме-
камеры соответствует оптимально-
оптимальному (минимальному) значению
суммы т + l/2^h/ds, где ? —
коэффициент трения.
Чтобы теоретически опреде-
определить оптимальную длину каме-
камеры смешения, надо знать за-
закон изменения коэффициента
поля т = /(/з/^з). Такой метод
расчета, разработанный на ос-
основании обнаруженного нами
экспериментального подобия
профилей скорости в раз-
различных сечениях камеры,
изложен во втором издании
этой книги (М.: Гостехиздат,,
1953).
Можно показать, что для эжекторного увеличителя тяги по-
потребная длина камеры смешения меньше определяемой по мак-
максимуму разрежения на входе или по максимуму коэффициента
эжекции п. Дело в том, что при данном расходе смеси коли-
количество движения ее пропорционально коэффициенту поля т > 1
(см. § 2); это смещает оптимум тяги в сторону больших зна-
значений т, т. е. меньших h/dz. Эксперименты действительно по-
в
Рис. 9.37. Влияние относительной
длины камеры смешения на вы-
выигрыш в тяге на месте (а = 0,11,
/=1). 1 — эжектор с одним цент-
центральным соплом, 2 — эжектор с
8-секционным соплом
§ 10. ТЕОРИЯ ЭЖЕКТОРНОГО УВЕЛИЧИТЕЛЯ ТЯГИ 565
называют, что наибольшее приращение тяги получается при
длине камеры смешения 6—7 калибров, в то время как обычно
для эжекторов оптимальная длина камеры равна 8—12 ее ка-
калибрам.
Потребную длину камеры можно существенно сократить, ес-
если раздробить эжектирующую струю на несколько струй; для
этого применяют многосопловую конструкцию или специальное
секционное сопло (рис. 9.37). С помощью такого эжектора прин-
принципиально можно получить выигрыш в реактивной силе, не-
несколько больший указанных выше значений, поскольку в резуль-
результате уменьшения длины камеры смешения снижаются потери
на трение о ее стенки, сильно влияющие на эффективность
эжекторной реактивной системы.
Многосопловые эжекторы различной конструкции с укоро-
укороченной камерой смешения установлены на ряде современных
самолетов вертикального взлета и посадки с целью увеличения
реактивной тяги подъемных или подъемно-маршевых двигателей.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ I
Таблица для расчета сверхзвуковых течений газа с непрерывным увеличением
скорости (к = 1,4)
6°
0°00'
0°10'
0°20'
0°30'
0°40'
0°50'
1°00'
1°30'
2°00'
2°30'
3°00'
3°30'
4°00'
4°30'
5°
6°
7°
8°
9°
10°
11°
12°
13°
14°
15°
16°
17°
18°
19°
0°00'
13°08'
16°05'
18°24'
20°25'
22°06'
23°32'
27°08'
30°00'
32°33'
34°54'
37°00'
38°52'
40°39'
42°18'
45С24'
48°18'
51°00'
53°28'
55°50'
58°06'
60°20'
62°24'
64°25'
66°24'
68°24'
70°18'
72°06'
73°57'
м
1,000
1,026
1,039
1,051
1,062
1,073
1,083
1,109
1,133
1,155
1,178
1,199
1,219
1,238
1,257
1,294
1,331
1,367
1,401
1,435
1,469
1,504
1,536
1,569
1,603
1,639
1,673
1,705
1,741
1,000
1,022
1,032
1,042
1,051
1,060
1,067
1,088
1,107
1,125
1,142
1,157
1,172
1,186
1,200
1,227
1,253
1,277
1,300
1,323
1,345
1,367
1,388
1,408
1,428
1,448
1,467
1,486
1,505
Р/Ро
0,528
0,512
0,504
0,497
0,490
0,484
0,479
0,463
0,450
0,464
0,424
0,413
0,402
0,392
0,383
0,364
0,346
0,330
0,314
0,299
0,285
0,271
0,258
0,246
0,234
0,222
0,211
0,201
0,190
Р/Ро
0,634
0,620
0,613
0,607
0,601
0,596
0,591
0,577
0,565
0,553
0,542
0,532
0,522
0,513
0,504
0,497
0,468
0,452
0,437
0,422
0,408
0,393
0,380
0,367
0,354
0,341
0,329
0,318
0,306
т/т0
0,833
0,826
0,822
0,819
0,816
0,813
0,810
0,803
0,796
0,789
0,783
0,777
0,771
0,766
0,760
0,749
0,738
0,728
0,718
0,708
0,698
0,688
0,679
0,670
0,660
0,650
0,641
0,632
0,622
90°00'
77°02'
74°15'
72°06'
70°15'
68°44'
67°28'
64°24Г
62W
59°57'
58°06г
56°30'
55°08'
53°51'
52°42'
50°36'
48°42'
47°00'
45°32'
44°10'
42°54'
41°40'
40°36'
39°35'
38°36;
37°36'
36°42'
35°54'
35°03'
г/го
1
1,027
1,041
1,049
1,065
1,077
1,087
1,108
1,147
1,176
1,205
1,234
1,262
1,290
1,312
1,372
1,437
1,498
1,559
1,626
1,690
1,772
1,845
1,923
2,005
2,094
2,183
2,291
2,394
ПРИЛОЖЕНИЕ I
567
Продолжение
6°
20°
21°
22°
23°
24°
25°
26°
27°
28°
29°
30°
31°
32°
33°
34°
35°
36°
37°
38°
39°
40°
41°
42°
43°
44°
45°
46°
47°
48°
49°
50°
51°
52°
53°
54°
55°
56°
57°
58°
59°
60°
61°
62°
63°
64°
75°42
77°27
7912
80°52
82°30
84°10
85°48
87°24
89°00
90°30
92°00
93°36
95°05
96°33
98°03
99°33
101°00
102°30
103°57
105°24
106°48
108°12'
109°36'
111°00'
112°21'
113°48'
115°12'
116°36'
117°54'
119°15'
120°36'
12Г57'
123°18'
124°38'
126W
127°18'
128°36'
129°55'
131°15/
132°36'
133°54'
13540'
136°30'
137°48'
139°03'
м
1,775
1,809
1,846
1,880
1,914
1,951
1,988
2,028
2,063
2,096
2,130
2,173
2,209
2,245
2,285
2,327
2,366
2,411
2,454
2,498
2,539
2,581
2,624
2,670
2,717
2,765
2,816
2,869
2,910
2,959
3,010
3,064
3,119
3,174
3,236
3,289
3,344
3,404
3,470
3,542
3,606
3,666
3,742
3,814
3,876
1,523
1,542
1,559
1,576
1,594
1,610
1,628
1,644
1,660
1,675
1,691
1,706
1,722
1,737
1,752
1,767
1,782
1,796
1,810
1,824
1,838
1,852
1,865
1,878
1,891
1,905
1,918
1,930
1,943
1,955
1,967
1,978
1,990
2,002
2,014
2,025
2,036
2,047
2,058
2,069
2,080
2,090
2,100
2,111
2,121
Р/Ро
0,181
0,171
0,162
0,154
0,146
0,138
0,130
0,123
0,116
0,1100
0,1040
0,0980
0.0920
0,0867
0,0814
0,0764
0,0717
0,0672
0,0630
0,0590
0,0552
0,0514
0,0481
0,0450
0,0419
0,0388
0,0360
0,0334
0,0310
0,0288
0,0267
0,0249
0,0229
0,0211
0,0194
0,0178
0,0164
0,0151
0,0138
0,0126
0,0115
0,0105
0,954-10-2
0,869-Ю
0,784-10-2
Р/Ро
0,295
0,284
0,273
0,263
0,253
0,243
0,233
0,224
0,215
0,207
0,198
0,190
0,182
0,174
0,167
0,159
0,152
0,145
0,139
0,132
0,126
0,120
0,114
0,109
0,104
0,098
0,093
0,088
0,084
0,079
0,075
0,071
0,067
0,063
0,060
0,056
0,053
0,050
0,047
0,044
0,041
0,039
0,036
0,034
0,031
т/т0
0,613
0,604
0,595
0,586
0,576
0,568
0,558
0,550
0,541
0,532
0,523
0,515
0,506
0,497
0,488
0,480
0,417
0,462
0,454
0,446
0,437
0,428
0,420
0,412
0,404
0,395
0,387
0,379
0,371
0,363
0,355
0,348
0,340
0,332
0,324
0,316
0,309
0,302
0,294
0,286
0,279
0,272
0,265
0,258
0,250
а0
34°18
33°33
32°48
32°08
31°30
30°50
30°12
29°33
29°00
28°30
28°00
27°24'
26°55'
26°27'
25°57'
25°27'
25°00
24°30'
24°0.7
23°36'
23°12'
22°48'
22°24'
22°00'
21°36'
21°12'
20°48'
20°24'
20°06'
19°45'
19°24'
19°03'
18°42'
18°22'
18°00'
17°42'
17°24'
17°05'
16°45'
16°24'
16°06'
15°50'
15°30'
15°12'
14°57'
г/г0
2,500
2,612
2,735
2,858
2,993
3,163
3,319
3,476
3,647
3,820
4,046
4,256
4,436
4,710
4,955
5,236
5,521
5,741
6,166
6,472
6,919
7,362
7,758
8,260
8,710
9,184
9,954
10,57
11,20
11,97
12,94
13,62
14,72
15,78
16,90
18,62
19,49
20,89
22,49
24,38
26,30
28,32
30,55
33,89
36,40
568
ПРИЛОЖЕНИЯ
Продолжение
6°
65°
66°
67°
68°
69°
70°
71°
72°
73°
74°
75°
76°
77°
78°
79°
80°
81°
82°
83°
84°
85°
86°
87°
88°
89°
90°
91°
92°
93°
94°
95°
96°
97°
98°
99°
100°
101°
102°
103°
104°
105°
130°27'
Ф°
140°2В'
141°36'
142°54'
144°12'
145°27'
146°42'
147°57'
149°12'
150°30'
151°42'
153°00'
154°15'
155°30'
156°45'
158W
159°15'
160°30'
161°42'
162°57'
164°12/
165°27'
166°42'
167°54'
169°06'
170°21'
171°36'
172°48'
174W
175°15'
176°27'
177°40'
178°54'
179°06'
18Г2Г
182°34'
183°48'
185W
186°12'
187°24'
188°36'
189°48'
[220°27'
М
^3,949
4,021
4,124
4,193
4,268
4,348
4,429
4,515
4,621
4,695
4,810
4,912
5,015
5,126
5,241
5,362
5,488
5,593
5,731
5,875
6,028
6,188
6,321
6,464
6,649
6,845
7,013
7,184
7,413
7,610
7,837
8,091
8,326
8,636
8,928
9,259
9,569
9,891
10,245
10,626
11,037
оо
2,130
2,140
2,150
2,159
2,168
2,177
2,186
2,195
2,204
2,212
2,220
2,228
2,237
2,244
2,252
2,260
2,267
2,274
2,282
2,289
2,296
2,302
2,309
2,315
2,321
2,328
2,334
2,340
2,345
2,350
2,356
2,361
2,366
2,371
2,376
2,380
2,385
2,389
2,393
2,397
2,401
2,449
Р/Ро
0J12.10-2
0,645-Ю-2
0,584.10-2
0.525-10-2
0,474-10-2
0,426-10-2
0,380-10-2
0,339-10-2
0,301-10-2
0,270-10-2
0,241-10-2
0,214-10-2
0,186-10-2
0,165-10-2
0,145-10-2
0,126.10-2
0,112.10-2
0,971-Ю-3
0,836-Ю-3
0,722-Ю-3
0,631-Ю-з
0,545-Ю-з
0,460-Ю-з
0,398-Ю-з
0,340-Ю-з
0,285-Ю-з
0,236-Ю-з
0,197-Ю-з
0,168-Ю-з
0,139-Ю-з
0,114-Ю-з
0,954- Ю
0,778.10-*
0,628-10-*
0,502-10-4
0,403-Ю-4
0,321-Ю-4
0,257-10-4
0,202-10-*
0,156-10-4
0,118-10-4
0
Р/Ро
0,029
0,027
0,025
0,0235
0,0219
0,0203
0,0187
0,0172
0,0158
0,0146
0,0135
0,0124
0,0112
0,0103
0,940-10-2
0,851-10-2
0,780-10-2
0,705-10-2
0,633-10-2
0,570-10-2
0,518-10-2
0,466-10-2
0,413-10-2
0,373-10-2
0,333-10-2
0,294-10-2
0,257-10-2
0,226-10-2
0,202-10-2
0,176-10-2
0,153-10-2
0,134-10-2
0,116-10-2
0,996-Ю-з
0,849-Ю-з
0,726-Ю-з
0,617-Ю-з
0,526-Ю-з
0,444-Ю-з
0,368-Ю-з
0,302-Ю-з
0
т/т0
0,244
0,237
0,230
0,223
0,217
0,210
0,204
0,197
0,190
0,184
0,179
0,173
0,166
0,160
0,155
0,149
0,144
0,138
0,132
0,127
0,122
0,117
0,111
0,107
0,102
0,097
0,092
0,087
0,083
0,079
0,075
0,071
0,067
0,063
0,059
0,055
0,052
0,049
0,046
0,042
0,039
0
ос0
14°40'
14°24'
14°02'
13°48'
13°33'
13°18'
13°03'
12°48'
12°30'
12°18'
12°00'
11°45'
11°30'
11°15'
11°00'
10°45'
10°30'
10о18'
10°03'
9°48'
9°33'
9°18'
9°06'
8°54'
8°39'
8°24'
8°12'
8°00'
7°45'
7°33'
7°20'
7°06'
6°54'
6°39'
6°26'
6°12'
6°00'
5°48'
5°36'
5°24'
5°12'
0°00'
г/г0
39,63
43,15
47,85
51,62
56,00
62,50
68,50
75,00
82,75
91,20
101,4
111,7
123,5
143,3
154,8
177,0
196,8
219,8
247,0
279.3
316,2
361,0
409,0
466,0
537,0
631,0
724,5
841,2
977,0
1135
1334
1478
1622
2240
2680
3092
3890
4730
6080
7440
9360
оо
ПРИЛОЖЕНИЕ II
Таблица газодинамических функций
0,00
0,01
0,02
0,03
0,04
0,05
о;Об
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0>23
0>24
т
1,0000
1,0000
0,9999
0,9998
0,9997
0,9996
0,9994
0,9992
0,9989
0.9986
0,9983
0,9980
0,9976
0,9972
0,9967
0,9963
0,9957
0,9952
0,9946
0,9940
0,9933
0,9927
0,9919
0,9912
0,9904
зх
1,0000
0,9999
0,9998
0,9995
0,9990
0,9986
0,9979
0,9971
0,9963
0,9953
0,9942
0,9929
0,9916
0,9901
0,9886
0,9870
0,9851
0,9832
0,9812
0,9791
0,9768
0,9745
0,9720
0,9695
0,9668
8
1,0000
0,9999
0,9998
0,9996
0,9993
0,9990
0,9985
0,9979
0,9974
0,9967
0,9959
0,9949
0,9940
0,9929
0,9918
0,9907
0,9893
0,9880
0,9866
0,9850
0,9834
0,9817
0,9799
0,9781
0,9762
q
0,0000
0,0158
0,0315
0,0473
0,0631
0,0788
0,0945
0,1102
0,1259
0,1415
0,1571
0,1726
0,1882
0,2036
0,2190
0,2344
0,2497
0,2649
0,2801
0,2952
0,3102
0,3252
0,3401
0,3549
0,3696
У
0,0000
0,0158
0,0316
0,0473
0,0631
0,0789
0,0947
0,1105
0,1263
0,1422
0,1580
0,1739
0,1897
0,2056
0,2216
0,2375
0,2535
0,2695
0,2855
0,3015
0,3176
0,3337
0,3499
0,3660
0,3823
/
1,0000
1,0000
1,0002
1,0006
1,0009
1,0015
1,0021
1,0028
1,0038
1,0047
1,0058
1,0070
1,0083
1,0100
1,0113
1,0129
1,0147
1,0165
1,0185
1,0206
1,0227
1,0250
1,0274
1,0298
1,0315
г
1,0000
0,9999
0,9996
0,9989
0,9981
0,9971
0,9958
0,9943
0,9925
0,9906
0,9885
0,9860
0,9834
0,9806
0,9776
0,9744
0,9709
0,9673
0,9634
0,9594
0,9551
0,9507
0,9461 '
0,9414
0,9373
м
0,0000
0,0091
0,0183
0,0274
0,0365
0,0457
0,0548
0,0639
0,0731
0,0822
0,0914
0,1005
0,1097
0,1190
0,1280
0,1372
0,1460
0,1560
0,1650
0,1740
0,1830
0,1920
0,2020
0,2109
0,2202
*=1,4
X
0,25
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33 ?
0,34
0,35
0,36 ;#
0,37 #
0,38 *
0,39 f
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
т
0,9896
0,9887
0,9879
0,9869
0,9860
0,9850
0,9840
0,9829
0,9819
0,9807
0,9796
0,9784
0,9772
0,9759
0,9747
0,9733
0,9720
0,9706
0,9692
0,9677
0,9663
0,9647
0,9632
0,9616
0,9600
0,9640
0,9611
0,9581
0,9550
0,9518
0,9485
0,9451
0,9415
0,9379
0,9342
0,9303
0,9265
0,9224
0,9183
0,9141
0,9097
0,9053
0,9008
0,8962
0,8915
0,8868
0,8819
0,8770
0,8719
0,8668
8
0,9742
0,9721
0,9699
0,9677
0,9653
0,9630
0,9605
0,9579
0,9552
0,9525
0,9497
0,9469
0,9439
0,9409
0,9378
0,9346
0,9314
0,9281
0,9247
0,9212
0,9178
0,9142
0,9105
0,9067
0,9029
4
0,3842
0,3987
0,4131
0,4274
0,4416
0,4557
0,4697
0,4835
0,4972
0,5109
0,5243
0,5377
0,5509
0,5640
0,5769
0,5897
0,6024
0,6149
0,6272
0,6394
0,6515
0,6633
0,6750
0,6865
0,6979
у
0,3985
0,4148
0,4311
0,4475
0,4640
0,4804
0,4970
0,5135
0,5302
0,5469
0,5636
0,5804
0,5973
0,6142
0,6312
0,6482
0,6654
0,6826
0,6998
0,7172
0,7346
0,7521
0,7697
0,7874
0,8052
1,0350
1,0378
1,0406
1,0435
1,0465
1,0496
1,0528
1,0559
1,0593
1,0626
1,0661
1,0696
1,0732
1,0768
1,0805
1,0842
1,0880
1,0918
1,0957
1,0996
1,1036
1,1076
1,1116
1,1156
1,1197
r
0,9314
0,9261
0,9207
0,9152
0,9095
0,9037
0,8977
0,8917
0,8854
0,8791
0,8727
0,8662
0,8595
0,8528
0,8460
0,8391
0,8321
0,8251
0,8179
0,8108
0,8035 |
0,7963
0,7889
0,7816
0,7741
продолжение
M
0,2290
0 2387
0,2480
0,2573
| 0,2670
0,2760
0,2850
0,2947
0,3040
0,3134
0,3228
0,3322
0,3417
0,3511
0,3606
0,3701
0,3796
0,3892
0,3987
0,4083
0,4179
0,4275
0,4372
0,4468
0,4565
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
0,82
0,83
0,84
0,9583
0,9567
0,9549
0,9532
0,9514
0,9496
0,9477
0,9459
0,9439
0,9420
0,9400
0,9380
0,9359
0,9339
0,9317
0,9296
0,9274
0,9252
0,9229
0,9207
0,9183
0,9160
0,9136
0,9112
0,9087
0,9063
0,9037
0,9012
0,8986
0,8960
0,8933
0,8907
0,8879
0,8852
0,8724
0,8616
0,8563
0,8509
0,8455
0,8400
0,8344
0,8287
0,8230
0,8172
0,8112
0,8053
0,7992
0,7932
0,7870
0,7808
0,7745
0,7681
0,7617
0,7553
0,7488
0,7422
0,7356
0,7289
0,7221
0,7154
0,7086
0,7017
0,6948
0,6878
0,6809
0,6738
0,6668
0,6597
0,6526
0,6454
0,8991
0,8951
0,8911
0,8871
0,8829
0,8787
0,8744
0,8701
0,8657
0,8612
0,8567
0,8521
0,8475
0,8428
0,8380
0,8332
0,8283
0,8233
0,8183
0,8133
0,8082
0,8030
0,7978
0,7925
0,7872
0,7819
0,7764
0,7710
0,7655
0,7599
0,7543
0,7486
0,7429
0,7372
0,7314
0,7091
0,7201
0,7309
0,7416
0,7520
0,7623
0,7724
0,7823
0,7920
0,8015
0,8109
0,8198
0,8288
0,8375
0,8459
0,8543
0,8623
0,8701
0,8778
0,8852
0,8924
0,8993
0,9061
0,9126
0,9189
0,9250
0,9308
0,9364
0,9418
0,9469
0,9518
0,9565
0,9610
0,9652
0,9691
0,8230
0,8409
0,8590
0,8771
0,8953
0,9136
0,9321
0,9506
0,9692
0,9880
1,0069
1,0258
1,0449
1,0641
1,0842
1,1030
1,1226
1,1423
1,1622
1,1822
1,2024
1,2227
1,2431
1,2637
1,2845
1,3054
1,3265
1,3478
1,3692
1,3908
1,4126
1,4346
1,4567
1,4790
1,5016
1,1239
1,1279
1,1320
1,1362
1,1403
1,1445
1,1486
1,1528
1,1569
1,1610
1,1651
1,1691
1,1733
1,1772
1,1812
1,1852
1,1891
1,1929
1,1967
1,2005
1,2042
1,2078
1,2114
1,2148
1,2183
1,2216
1,2249
1,2280
1,2311
1,2341
1,2370
1,2398
1,2425
1,2451
1,2475
0,7666
0,7592
0,7517
0,7442
0,7366
0,7290
0,7215
0,7139
0,7064
0,6987
0,6912
0,6836
0,6760
0,6685
0,6610
0,6535
0,6460
0,6386
0,6311
0,6237
0,6163
0,6090
0,6017
0,5944
0,5872
0,5800
0,5729
0,5658
0,5587
0,5517
0,5447
0,5378
0,5309
0,5241
0,5174
0,4663
0,4760
0,4858
0,4956
0,5054
0,5152
0,5251
0,5350
0,5450
0,5549
0,5649
0,5750
0,5850
0,5951
0,6053
0,6154
0,6256
0,6359
0,6461
0,6565
0,6668
0,6772
0,6876
0,6981
0,708? .
0,7192
0,7298
0,7404
0,7511
0,7619
0,7727
0,7835
0,7944
0,8053
0,8163
к =1,4
Продолжение S3
to
Л,
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
х
0,8796
0,8767
0,8739
0,8709
0,8680
0,8650
0,8620
0,8589
0,8559
0,8527
0,8496
0,8464
0,8432
0,8399
0,8367
0,8333
0,8300
0,8266
0,8232
0,8197
0,8163
0,8127
0,8092
0,8056
0,8020
0,7983
0,7947
0,7909
0,7872
0,7834
я
0,6382
0,6310
0,6238
0,6165
0,6092
0,6019
0,5946
0,5873
0,5800
0,5726
0,5653
0,5579
0,5505
0,5431
0,5357
0,5283
0,5209
0,5135
0,5061
0,4987
0,4913
0,4840
0,4766
0,4693
0,4619
0,4546
0,4473
0,4400
0,4328
0,4255
8
0,7256
0,7197
0,7138
0,7079
0,7019
0,6959
0,6898
0,6838
0,6776
0,6715
0,6653
0,6591
0,6528
0,6466
0,6403
0,6340
0,6276
0,6212
0,6148
0,6084
0,6019
0,5955
0,5890
0,5826
0,5760
0,5694
0,5629
0,5564
0,5498
0,5432
q
0,9729
0,9764
0,9796
0,9826
0,9854
0,9879
0,9902
0,9923
0,9941
0,9957
0,9970
0,9981
0,9989
0,9993
0,9999
1,0000
0,9999
0,9995
0,9989
0,9980
0,9969
0,9957
0,9941
0,9924
0,9903
0,9880
0,9856
0,9829
0,9800
0,9768
У
1,5243
1,5473
1,5704
1,5938
1,6174
1,6412
1,6652
1,6895
1,7140
1,7388
1,7638
1,7891
1,8146
1,8404
1,8665
1,8929
1,9195
1,9464
1,9737
2,0013
2,0291
2,0573
2,0858
2,1147
2,1439
2,1734
2,2034
2,2337
2,2643
2,2954
/
1,2498
1,2520
1,2541
1,2560
1,2579
1,2595
1,2611
1,2625
1,2637
1,2648
1,2658
1,2666
1,2671
1,2676
1,2678
1,2679
1,2678
1,2675
1,2671
1,2664
1,2655
1,2646
1,2633
1,2620
1,2602
1,2584
1,2564
1,2543
1,2519
1,2491
г
0,5107
0,5040
0,4974
0,4908
0,4843
0,4779
0,4715
0,4652
0,4589
0,4527
0,4466
0,4405
0,4344
0,4285
0,4225
0,4167
0,4109
0,4051
0,3994
0,3938
0,3882
0,3827
0,3773
0,3719
0,3665
0,3613
0,3560
0,3508
0,3457
0,3407
м
0,8274
'• 0,8384
* 0,8496 \
0,8608 }
0,8721 "
0,8833
0,8947
0,9062
0,9177
0,9292
0,9409
0,9526
0,9644
0,9761
0,9880
1,0000
1,0120
1,0241
1,0363
1,0486
1,0609
1,0733
1,0858
1,0985
1,1111
1,1239
1,1367
1,1496
1,1627
1,1758
1,15
1,16
1,17
1,18
1,19
1,20
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,30
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
0,7796
0,7757
0,7719
0,7679
0,7640
0,7600
0,7560
0,7519
0,7478
0,7437
0,7396
0,7354
0,7312
0,7269
0,7227
0,7183
0,7140
0,7096
0,7052
0,7007
0,6962
0,6917
0,6872
0,6826
0,6780
0,6733
0,6687
0,6639
0,6592
0,6544
0,6496
0,6447
0,6398
0,6349
0,6300
0,4184
0,4111
0,4040
0,3969
0,3898
0,3827
0,3757
0,3687
0,3617
0,3548
0,3479
0,3411
0,3343
0,3275
0,3208
0,3142
0,3075
0,3010
0,2945
0,2880
0,2816
0,2753
0,2690
0,2628
0,2566
0,2505
0,2445
0,2385
0,2326
0,2267
0,2209
0,2152
0,2095
0,2040
0,1985
0,5366
0,5300
0,5234
0,5168
0,5102
0,5035
0,4969
0,4903
0,4837
0,4770
0,4704
0,4638
0,4572
0,4505
0,4439
0,4374
0,4307
0,4241
0,4176
0,4110
0,4045
0,3980
0,3914
0,3850
0,3785
0,3720
0,3656
0,3592
0,3528
0,3464
0,3401
0,3338
0,3275
0,3212
0,3150
0,9735
0,9698
0,9659
0,9620
0,9577
0,9531
0,9484
0,9435
0,9384
0,9331
0,9275
0,9217
0,9159
0,9096
0,9033
0,8969
0,8901
0,8831
0,8761
0,8688
0,8614
0,8538
0,8459
0,8380
0,8299
0,8216
0,8131
0,8046
0,7958
0,7869
0,7778
0,7687
0,7593
0,7499
0,7404
2,3269
2,3588
2,3911
2,4238
2,4570
2,4906
2,5247
2,5593
2,5944
2,6300
2,6660
2,7026
2,7398
2,7775
2,8158
2,8547
2,8941
2,9343
2,9750
3,0164
3,0586
3,1013
3,1448
3,1889
3,2340
3,2798
3,3263
3,3737
3,4219
3,4710
3,5211
3,5720
3,6240
3,6768
3,7308
1,2463
1,2432
1,2398
1,2364
1,2326
1,2286
1,2244
1,2200
1,2154
1,2105
1,2054
1,2000
1,1946
1,1887
1,1826
1,1765
1,1699
1,1632
1,1562
1,1490
1,1417
1,1341
1,1261
1,1180
1,1098
1,1012
1,0924
1,0835
1,0742
1,0648
1,0551
1,0453
1,0351
1,0249
1,0144
0,3357
0,3307
0,3258
0,3210
0,3162
0,3115
0,3068
0,3022
0,2976
0,2931
0,2886
0,2842
0,2798
0,2755
0,2713
0,2670
0,2629
0,2574
0,2547
0,2507
0,2467
0,2427
0,2389
0,2350
0,2312
0,2275
0,2238
0,2201
0,2165
0,2129
0,2094
0,2059
0,2024
0,1990
0,1956
1,1890
1,2023
1,2157
1,2292
1,2428
1,2566
1,2708
1,2843
1,2974
1,3126
1,3268
1,3413
1,3558
1,3705
1,3853
1,4002
1,4153
1,4305
1,4458
1,4613
1,4769
1,4927
1,5087
1,5248
1,5410
1,5575
1,5741
1,5909
1,6078
1,6250
1,6423
1,6598
1,6776
1,6955
1,7137
fc-1,4
Продолжение
1,50
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
1,60
1,61
1,62
1,63
1,64
1,65
1,66
1,67
1,68]
1,69]
1,70
1,71
1,72
1,73
1,74
1,751
1,76]
1,77
1,78
1,79
т
0,6250
0,6200
0,6149
0,6099
0,6047
0,5996
0,5944
0,5892
0,5839
0,5786
0,5733
0,5680
0,5626
0,5572
0,5517
0,5463
0,5407
0,5352
0,5296
0,5240
0,5183
0,5126
0,5069
0,5012
0,4954
0,4896
0,4837
0,4779
0,4719
0,4660
я
0,1930
0,1876
0,1824
0,1771
0,1720
0,1669
0,1619
0,1570
0,1522
0,1474
0,1427
0,1381
0,1336
0,1291
0,1248
0,1205
0,1163
0,1121
0,1081
0,1041
0,1003
0,0965
0,0928
0,0891
0,0856
0,0821
0,0787
0,0754
0,0722
0,0691
8
0,3088
0,3027
0,2965
0,2904
0,2844
0,2784
0,2724
0,2665
0,2606
0,2547
0,2489
0,2431
0,2374
0,2317
0,2261
0,2205
0,2150
0,2095
0,2041
0,1988
0,1934
0,1881
0,1830
0,1778
0,1727
0,1647
0,1628
0,1578
0,1530
0,1482
0,7307
0,7209
0,7110
0,7009
0,6909
0,6807
0,6703
0,6599
0,6494
0,6389
0,6282
0,6175
0,6067
0,5958
0,5850
0,5740
0,5630
0,5520
0,5409
0,5298
0,5187
0,5075
0,4965
0,4852
0,4741
0,4630
0,4520
0,4407
0,4296
0,4185
у
3,7858
3,8418
3,8990
3,9574
4,0172
4,0778
4,1398
4,2034
4,2680
4,3345
4,4020
4,4713
4,5422
4,6144
4,6887
4,7647
4,8424
4,9221
5,0037
5,0877
5,1735
5,3167
5,3520
5,4449
5,5403
5,6383
5,7390
5,8427
5,9495
6,0593
/
1,0037
0,9927
0,9816
0,9703
0,9590
0,9472
0,9353
0,9233
0,9111
0,8988
0,8861
0,8734
0,8604
0,8474
0,8343
0,8210
0,8075
0,7939
0,7802
0,7664
0,7524
0,7383
0,7243
0,7100
0,6957
0,6813
0,6669
0,6523
0,6378
0,6232
г
С,1923
0,1890
0,1858
0,1825
0,1794
0,1762
0,1731
0,1700
0,1670
0,1640
0,1611
0,1581
0,1552
0,1524
0,1495
0,1467
0,1440
0,1413
0,1386
0,1359
0,1333
0,1306
0,1281
0,1255
0,1230
0,1205
0,1181
0,1156
0,1132
0,1108
м
1,7321
1.7506
1,7694
1,7885
1,8078
1,8273
1,8471
1,8672
1,8875
1,9081
1,9290
1,9501
1,9716
1,9934
2,0155
2,0380
2,0607
2,0839
2,1073
2,1313
2,1555
2,1802
2,2053
2,23081
2,2567
2,2831
2,3100
2,3374
2,3653
2,3937
1,80
1,81
1,82
1,83
1,84
1,85
1,86
1,87-
1,88
1,89
1,90
1,91
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
2,00
2,01
2,02
2,03
2,04
2,05
2,06
2,07
2,08
2,09
2,10
2,11
2,12
2,13
2,14
0,4600
0,4540
0,4479
0,4418
0,4357
0,4296
0,4234
0,4172
0,4109
0,4047
0,3983
0,3920
,0,3856
0,3792
0,3727
0,3662
0,3597
0,3532
0,3466
0,3400
0,3333
0,3267
0,3199
0,3132
0,3064
0,2996
0,2927
0,2859
0,2789
0,2720
0,2650
0,2580
0,2509
0,2439
0,2367
0,0660
0,0630
0,0602
0,0573
0,0546
0,0520
0,0494
0,0469
0,0445
0,0422
0,0399
0,0377
0,0356
0,0336
0,0316
0,0297
0,0279
0,0262
0,0245
0,0229
0,0214
0,0199
0,0185
0,0172
0,0159
0,0147
0,0136
0,0125
0,0115
0,0105
0,0096
0,0087
0,0079
0,0072
0,0065
0,1435
0,1389
0,1343
0,1298
0,1253
0,1210
0,1167
0,1124
0,1083
0,1042
0,1002
0,0962
0,0923
0,0885
0,0848
0,0812
0,0776
0,0741
0,0707
0,0674
0,0642
0,0610
0,0579
0,0549
0,0520
0,0491
0,0464
0,0437
0,0411
0,0386
0,0361
0,0338
0,0315
0,0294
0,0273
0,4075
0,3965
0,3855
0,3746
0,3638
0,3530
0,3423
0,3316
0,3211
0,3105
0,3002
0,2898
0,2797
0,2695
0,2596
0,2497
0,2400
0,2304
0,2209
0,2116
0,2024
[0,1934
0,1845]
0,1758
[0,1672
0,1588
0,1507
0,1427
0,1348
0,1272
0,1198
0,1125
0,1055
0,0986
0,0921
6,1723
6,2893
6,4091
6,5335
6,6607
6,7934
6,9298
7,0707
7,2162
7,3673
7,5243
7,6858
7,8540
8,0289
8,2098
8,3985
8,5943
8,7984
9,0112
9,2329
9,464
9,706
9,961
10,224
10,502
10,794
11,102
11,422
11,762
12,121
12,500
12,901
13,326
13,778
14,259
0,6085
0,5938
0,5791
0,5644
0,5497
0,5349
0,5202
0,5055
0,4909
0,4762
0,4617
0,4472
0,4327
0,4183
0,4041
0,3899
0,3758
0,3618
0,3480
0,3343
0,3203
0,3074
0,2942
0,2811
0,2683
0,2556
0,2431
0,2309
0,2189 If
0,2070
0,1956
0,1843
0,1733
0,1626
0,1522
0,1085
0,1062
0,1039
0,1016
0,0994
0,0971
0,0949
0,0928
0,0906
0,0885
0,0864
0,0843
0,0823
0,0803
I 0,0782
0,0763
0,0743 i
0,0724
0,0704
0,0685
0,0668
0,0648
0,0630
0,0612
0,0594
0,0576
0,0558
0,0541
0,0524
0,0507
0,0490
0,0473
0,0457
0,0440
0,0424
2,4227
2,4523
2,4824
2,5132
2,5449
2,5766
2,6094
2,6429
2,6772
2,7123
2,7481
2,7849
2,8225
2,8612
2,9007
2,9414
2,9831
3,0301
3,0701
3,1155
3,1622
3,2104
3,2603
3,3113
3,3642
3,4190
3,4759
3,5343
3,5951
3,6583
3,7240
3,7922
3,8633
3,9376
4,0150
й== 1,4
к
2,15
2,16
2,17
2,18
2,19
2,20
2,21
2,22
2,23
2,24
2,25
2,26
2,27
2,28
2,29
2,30
2,31
2,32
2,33
2,34
2,35
2,36
2,37
2,38
2,39
2,40
2,41
2,42
2,43
2,44
2,449
t
0,2296
0,2224
0,2152
0,2079
0,2006
0,1933
0,1860
0,1786
0,1712
0,1637
0,1563
0,1487
0,1412
0,1336
0,1260
0,1183
0,1106
0,1029
0,0952
0,0874
0,0796
0,0717
0,0638
0,0559
0,0480
0,0400
0,0320
0,0239
0,0158
0,0077
0
я
0,0058
0,0052
0,0046
0,0041
0,0036
0,0032
0,0028
0,0024
0,0021
0,0018
0,00151
0,00127
0,00106
0,00087
0,00071
0,00057
0,00045
0,00035
0,00027
0,00020
0,00014
0,988-Ю-4
0,657-10-4
0,413-10-4
0,242.lO
0,128-Ю-4
0,584-Ю-5
0,211.10-5
0,499-10-6
0,316-10-7
0
8
0,0253
0,0233
0,0215
0,0197
0,0180
0,0164
0,0149
0,0135
0,0121
0,0116
0,00966
0,00813
0,00749
0,00652
0,00564
0,00482
0,00407
0,00340
0,00280
0,00226
0,00170
0,00138
0,00103
0,00074
0,00050
0,00032
0,00018
0,884-Ю-4
0,315-10
0,410-Ю-5
0
q
0,0857
0,0795
0,0735
0,0678
0,0623
0,0570
0,0520
0,0472
0,0427
0,0408
0,0343
0,0290
0,0268
0,0234
0,0204
0,0175
0,0148
0,0124
0,0103
0,0083
0,0063
0,0051
0,0038
0,0028
0,0019
0,0012
0,0007
0,0003
0,0001
0,058-10
0
У
14,772
15,319
15,906
16,537
17,218
17,949
18,742
19,607
20,548
21,983
22,712
23,968
25,361
26,893
28,669
30,658
32,937
35,551
38,606
42,233
46,593
51,914
58,569
67,144
78,613
94,703
118,94
159,65
242,16
499,16
оо
0,1420
0,1322
0,1226
0,1134
0,1045
0,0960
0,0878
0,0799
0,0724
0,0695
0,0585
0,0496
0,0461
0,0404
0,0352
0,0302
0,0258
0,0217
0,0180
0,0146
0,0111
0,0090
0,0068
0,0049
0,0034
0,0022
0,0012
0,0006
0,0002
0,285-10
0
г
0,0408
0,0393
0,0377
0,0361
0,0346
0,0331
0,0316
0,0301
0,0287
0,0255
0,0258
0,0256
0,0229
0,0216
0,0202
0,0189
0,0175
0,0161
0,0148
0,0135
0,0122
0,0109
0,0096
0,0084
0,0071
0,0059
0,0047
0,0035
0,0025
0,0011
0
Продолжение
м
4,0961
4,1791
4,2702
4,3642
4,4633
4,5674
4,6778
4,7954
4,9201
5,0533
5,1958
5,3494
5,5147
5,6940
5,8891
6,1033
6,3399
6,6008
6,8935
7,2254
7,6053
8,0450
8,5619
9,1882
9,9624
10,957
12,306
14,287
17,631
25,367
оо
? = 1,33
л
! «и к»
i 0,02
' 0,03
U,U4
¦ Uijj
иди»
0,07
0,08
0,09
одо
0,11
! 0,12
ОДЗ
<М4
ОДо
ОДб
0,17
0Д8
ОДУ
0,11A
0,21
0,22
о,23
0,24
i
I и м и ц 1
1,0000
0,9999
0,9999
п,9998
и,9997
О49995
0,9993
0,9991
0,9989
0,998*5
0,9983
0,9980
0,9976
0,9972
о,У*Н)Ь
о,9964
0,9959
0,9954
0,9949
о,9943
0,9938
0,9932
0,9925
0,9918
л
1,0000
0,9999
0,9998
0,9995
0,9991
0,9980
0,9980
0,9972
0,9964
0,9954
0,9944
0,9932
0,9918
0,9904
0,9889
0,9872
0,9854
0,9836
0,9816
0,9796
о,9774
0,9751
0,9728
0,9702
0,9675
1,0000
0,9999
0,9999
0,9997
0,9993
0,9990
0,9985
0,9979
0,9973
0,9965
0,9958
0,9949
0,9938
0,9928
0,9917
0,9903
0,9890
0,9877
0,9862
0,9846
0,9830
0,9812
0,9795
0,9775
0,9755
ч
0,0000
0,0159
0,0318
0,0476
0,0636
0,0793
0,0952
0,1110
0,1267
0,1425
0,1582
0,1738
0,1894
0,2052
0,2205
0,2360
0,2514
0,2667
0,2820
0,2972
0,3123
0,3273
0,3423
0,3571
0,3719
У
0,0000
0,0159
0,0318
0,0477
0,0636
0,0795
0,0954
0,1113
0,1272
0,1431
0,1591
0,1750
0,1910
0,2072
0,2220
0,2390
0,2551
0,2712
0,2873
0,3034
0,3195
0,3357
0,3519
0,3681
0,3844
J
1,0000
1,0000
1,0003
1,0006
1,0009
1,0015
1,0021
1,0028
1,0037
1,0046
1,0057
1,0069
1,0081
1,0096
1,0111
1,0126
1,0143
1,0162
1,0181
1,0202
1,0223
1,0245
1,0269
1,0292
1,0317
г
1,0000
1,0000
0,9995
0,9990
0,9982
0,9972
0,9959
0,9944
0,9928
0,9908
0,9887
0,9864
0,9838
0,9810
0,9781
0,9749
0,9715
0,9679
0,9642
0,9602
0,9561
0,9518
0,9473
0,9427
0,9378
П родолжепие
м
0,0000
0,0093
0,0185
0,0278
0,0371
0,0463
0,0556
0,0649
0,0742
0,0834
0,0927
0,1020
0,1113
0,1206
0,1299
0,1392
0,1485
0,1578
0,1672
0,1765
0,1858
0,1952
0,2045
0,2139
0,2233
к =1,33
Продолжение
0,25 ;
0,26 !
0<27 ;
0,28 ,
0,29
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
т
0,9912
0,9904
0,9897
0,9889
0,9881
0,9873
0,9864
0,9855
0,9846
0,9836
0,9827
0,9817
0,9806
0,9796
0,9785
п 0,9773
1 0,9762
j 0,9750
0,9738
0,9726
0,9713
0,9700
0,9687
0,9674
0,9660
я
0,9648
0,9619
0,9590
0,9560
0,9529
0,9496
0,9463
0,9428
0,9393
0,9356
0,9319
0,9281
0,9241
0,9201
0,9159
0,9118
0,9075
0,9030
0,8985 й
0,8940
0,8893
0,8850
0,8797
0,8749
0,8699
8
0,9734
0,9712
0,9690
0,9667
0,9644
0,9619
0,9594
0,9567
0,9540
0,9512
0,9484
0,9455
0,9424
0,9393
0,9361
0,9329
0,9296
0,9262
0,9227
0,9192
0,9156
0,9123
0,9081
0,9044
0,9005
9
0,3866
0,4011
0,41§6
0,4300
0,4443
0,4584
0,4724
0,4863
0,5001
0,5137
0,5273
0,5407
0,5539
0,5670 '
0,5799
0,5928
0,6055 7
0,6179 i
0,6303
0,6425
0,6545
0,6666
0,6780
0,6896
0,7009
У
0,4007
0,4170
0,4334
0,4498
ЖР,4662
0,4827
0,4992
0,5158
0,5324
0,5491
0,5658
0,5826
0,5994
0,6162
0,6332
0,6501 1
0,6672
0,6843
0,7014
0,7187
0,7359
0,7533
0,7707
0,7882
0,8058
/
1,0343
1,0369
1,0396
1,0425
1,0455
1,0485
1,0516
1,0547
1,0579
1,0612
1,0645
1,0680
1,0714
1,0750
1,0785
1,0822
1,0859
1,0896
1,0933
1,0972
1,1010
1,1053
1,1088
1,1128
1,1167
г
0,9329
0,9277
0,9224
0,9170
0,9114
0,9057
0,8999
0,8940
0,8879
0,8817
0,8754
0,8690
0,8625
0,8560
0,8493
0,8425
0,8357
0,8288
0,8218
0,8148
0,8078
0,8006
0,7934
0,7862
0,7790
м
0,2327
0,2420
0,2515
0,2609
0,2703
0,2797
0,2892
0,2986
0,3081
0,3176
0,3271
0,3366
0,3462
0,3557
0,3653
0,3749
0,3845
0,3941
0,4037
0,4134
0,4230
0,4325
0,4424
0,4522
0,4619
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,9646
0,9632
0,9617
0,9602
0,9587
0,9572
0,9556
0,9540
0,9524
0,9507
0,9490
0,9473
0,9456
0,9438
0,9420
0,9402
0,9383
0,9364
0,9345
0,9326
0,9306
0,9286
0,9266
0,9245
0,9224
0,9203
0,9182
0,9160
0,9138
0,9116
0,8648
0,8596
0,8544
0,8491
0,8436
0,8382
0,8327
0,8271
0,8214
0,8156
0,8098
0,8040
0,7980
0,7921
0,7860
0,7798
0,7737
0,7674
0,7612
0,7548
0,7483
0,7419
0,7354
0,7289
0,7223
0,7157
0,7090
0,7023
0,6955
0,6887
0,8966
0,8925
0,8884
0,8843
0,8799
0,8757
0,8714
0,8670
0,8625
0,8579
0,8533
0,8487
0,8439
0,8393
0,8344
0,8294
0,8246
0,8195
0,8145
0,8094
0,8041
0,7989
0,7937
0,7884
0,7830
0,7777
0,7722
0,7666
0,7611
0,7555
0,7121
0,7230
0,7339
0,7445
0,7548
0,7651
0,7752
0,7850
0,7946
0,8040
0,8133
. 0,8224
0,8312
(?8399}
0,858^
0,8564
0,8645
0,8722
0,8798
0,8871
0,8941
0,9011
0,9077
0,9143
0,9204
0,9265
0,9322
0,9377
0,9430
0,9481
0,8234
0,8411
0,8589
0,8768
0,8947
0,9128
0,9309
0,9491
0,9674
0,9858
1,0043
1,0229
1,0416
1,0604
1,0792
1,0982
1,1173
1,1366
1,1559
1,1753
1,1949
1,2146
1,2343
1,2543
1,2743
1,2945
1,3148
1,3353
1,3559
1,3766
1,1207
1,1246
1,1287
1,1327
1,1365
1,1406
1,1447
1,1487
1,1526
1,1565
1,1605
1,1645
1,1684
1,1724
1,1762
1,1799
1,1838
1,1874
1,1911
1,1947
1,1981
1,2017
1,2051
1,2086
1,2118
1,2151
1,2182
1,2212
1,2241
1,2270
0,7717
0,7644
0,7570
0,7496
0,7423
0,7349
0,7275
0,7200
0,7126
0,7052
0,6978
0,6904
0,6830
0,6756
0,6683
0,6609
0,6536
0,6463
0,6390
0,6318
0,6246
0,6174
0,6102
0,6031
0,5961
0,5890
0,5820
0,5751
0,5682
0,5613
0,4717
0,4815
0,4913
0,5011
0,5110
0,5208
0,5308
0,5407
0,5506
0,5606
0,5706
0,5807
0,5907
0,6008
0,6109
0,6211
0,6313
0,6415
0,6517
0,6620
0,6723
0,6826
0,6934
0,7034
0,7139
0,7243
0,7348
0,7454
0,7561
0,7666
к = 1,33
0,80
0,81
0,82
0,83
0,84
0,85
0,8В
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
1,01
1,02
1,03
1,04
т
0,9094
0,9071
0,9048
0,9024
0,9001
0,8977
0,8953
0,8928
0,8903
0,8878
0,8853
0,8827
0,8801
0,8775
0,8749
0,8722
0,8695
0,8667
0,8640
0,8612
0,8584
0,8555
0,8527
0,8497
0,8468
п
0,6819
0,6750
0,6681
0,6612
0,6542
0,6472
0,6402
0,6332
0,6261
0,6191
0,6120
0,6048
0,5977
0,5906
0,5834
0,5763
0,5691
0,5619
0,5547
0,5476
0,5404
0,5332
0,5260
0,5188
0,5116
8
0,7499
0,7442
0,7384
0,7326
0,7268
0,7210
0,7151
0,7092
0,7032
0,6973
0,6913
0,6852
0,6791
0,6730
0,6669
0,6608
0,6545
0,6483
0,6420
0,6359
0,6296
0,6233
0,6169
0,6105
0,6042
q
0,9529
0,9575
0,9618
0,9660
0,9698
0,9735
0,9769
0,9802
0,9830
0,9859
0,9883
0,9904
0,9925
0,9943
0,9957
0,9972
0,9981
0,9989
0,9995
1,0000
1,0000
1,0000
0,9995
0,9989
0,9981
У
1,3975
1,4185
1,4397
1,4610
1,4825
1,5042
1,5260
1,5479
1,5701
1,5924
1,6149
1,6376
1,6605
1.6835
1,7068
1,7302
1,7539
1,7778
1,8018
1,8261
1,8506
1,8754
1,9003
1,9255
1,9509
/
1,2298
1,2324
1,2349
1,2374
1,2397
1,2419
1,2440
1,2461
1,2478
1,2497
1,2512
1,2525
1,2539
1,2552
1,2561
1,2572
1,2577
1,2583
1,2586
1,2591
1,2591
1,2590
1,2587
1,2583
1,2576
г
0,5545
0,5477
0,5410
0,5343
0,5277
0,5211
0,5146
0,5082
0,5018
0,4954
0,4891
0,4829
0,4767
0,4705
0,4645
0,4584
0,4525
0,4466
0,4407
0,4349
0,4292
0,4235
0,4179
0,4123
0,4068
Продолжение
м
0,7772
0,7880
0,7987 ,
0,8095 '
0,8203
0,8312
0,8421
0,8531
0,8641
0,8751
0,8862
0,8974
0,9086
0,9198
0,9311
0,9424
0,9538
0,9653
0,9768
0,9884
1,0000
1,0117
1,0234
1,0352
1,0471
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
1,20
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,30
1,31
•1,32
1,33
1,34
0,8439
0,8409
0,8379
0,8348
0,8317
0,8286
0,8255
0,8223
0,8192
0,8159
0,8127
0,8094
0,8061
0,8028
0,7994
0,7961
0,7926
0,7892
0,7857
0,7822
0,7787
0,7752
0,7716
0,7680
0,7643
0,7606
0,7570
0,7532
0,7495
0,7457
0,5045
0,4973
0,4902
0,4830
0,4759
0,4688
0,4617
0,4546
0,4475
0,4405
0,4335
0,4265
0,4196
0,4126
0,4057
0,3986
0,3920
0,3852
0,3784
0,3716
0,3649
0,3583
0,3516
0,3450
0,3385
0,3320
0,3255
0,3191
0,3128
0,3065
0,5979
0,5914
0,5850
0,5786
0,5722
0,5658
0,5593
0,5528
0,5463
0,5399
0,5334
0,5269
0,5205
0,5140
0,5075
0,5007
0,4946
0,4881
0,4816
0,4751
0,4686
0,4622
0,4557
0,4493
0,4429
0,4365
0,4300
0,4236
0,4173
0,4110
0,9972
0,9958
0,9944
U,9926
0,9907
0,9886
0,9862
0,9835
0,9806
0,9777
0,9744
0,9709
0,9674
0,9634
0,9593
0,9545
0,9506
0,9459
0,9410
0,9357
0,9305
0,9252
0,9193
0,9135
0,9075
0,9014
0,8949
0,8883
0,8816
0,8749
1,9766
2,0025
2,0280
2,0550
2,0818
2,1087
2,1360
2,1635
2,1913
2.2194
2,2478
2,2765
2,3055
2,3349
2,3646
2,3940
2,4249
2,4556
2,4867
2,5181
2,5500
2,5821
2,6147
2,6477
2,6811
2,7149
2,7492
2,7838
2,8190
2,8545
1,2570
1,2559
\ ,2548
1,2534
1,2520
1,2503
1,2484
1,2463
1,2439
1,2415
1,2388
1,2359
1,2330
1,2296
1,2261
1,2218
1,2186
1,2146
1,2102
1,2055
1,2008
1,1961
1,1907
1,1853
1,1799
1,1741
1,1680
1,1618
1,1555
1,1491
0,4014
0,3960
0,3900
0,3854
0,3801
0,3750
0,3698
0,3648
0,3598
0,3548
0,3499
0,3451
0,3403
0,3356
0,3309
0,3263
0,3217
0,3172
0,3127
0,3083
0,3039
0,2996
0,2953
0,2911
0,2869
0,2828
0,2787
0,2747
0,2707
0,2667
1,0590
1,0710
1,0830
1,0951
1,1073
1,1196
1,1319
1,1443
1,1567
1,1693
1,1819
1,1946
1,2073
1,2202
1,2331
1,2461
1,2592
1,2723
1,2856
1,2990
1,3124
1,3259
1,3396
1,3533
1,3671
1,3820
1,3950
1,4091
1,4234
1,4377
к -=1,33
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
т
0,7419
0,7380
0,7342
0,7303
0,7264
0,7224
0,7184
0,7144
0,7104
0,7063
0,7022
0,6981
0,6940
0,6898
0,6856
0,6813
0,6771
0,6728
0,6685
0,6641
0,6597
0,6553
0,6509
0,6464
0,6420
я
0,3002
0,2940
0,2878
0,2817
0,2757
0,2697
0,2637
0,2578
0,2520
0,2463
0,2406
0,2349
0,2294
0,2238
0,2184
0,2138
0,2077
0,2024
0,1973
0,1921
0,1871
0,1821
0,1772
0,1723
0,1676
е
0,4046
0,3984
0,3920
0,3857
0,3796
0,3733
0,3671
0,3609
0,3548
0,3487
0,3426
0,3365
0,3305
0,3245
0,3186
0,3126
0,3067
0,3009
0,2951
0,2893
0,2836
0,2779
0,2722
0,2666
0,2610
Q
0,8677
0,8606
0,8531
0,8455
0,8381
0,8303
0,8221
0,8140
0,8060
0,7976
0,7891
0,7805
0,7718
0,7629
0,7540
0,7449
0,7357
0,7265
0,7172
0,7077
0,6982
0,6886
0,6789
0,6691
0,6593
V
2,8905
2,9271
2,9642
3,0017
3,0398
3,0784
3,1176
3,1573
3,1977
3,2386
3,2802
3,3222
3,3649
3,4083
3,4524
3,4972
3,5426
3,5890
3,6358
3,6836
3,7321
3,7813
3,8316
3,8825
3,9345
/
1,1421
1,1351
1,1277
1,1202
1,1129
1,1051
1,0968
1,0885
1,0803
1,0717
1,0629
1,0539
1,0447
1,0353
1,0258
1,0160
1,0061
0,9961
0,9858
0,9754
0,9649
0,9541
0,9432
0,9321
0,9209
г
0,2629
0,2590
0,2552
0,2515
0,2477
0,2441
0,2404
0,2368
0,2333
0,2298
0,2263
0,2229
0,2195
0,2162
0,2129
0,2097
0,2064
0,2032
0,2001
0,1970
0,1939
0,1909
0,1879
0,1849
0,1820
Тродолжение
м
1,4521
1,4667
1,4814
1,4960
1,5110
1,5290
1,5412
1,5564
1,5719
1,5875
1,6031
1,6188
1,6349
1,6510
1,6672
1,6836
1,7002
1,7169
1,7338
1,7508
1,7680
1,7854
1,8029
1,8207
1,8386
1,60
1,61
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
1,70
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,80
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
0,6374
0,6329
0,6283
0,6237
0,6191
0,6144
0,6097
0,6050
0,6003
0,5955
0,5907
0,5859
0,5810
0,5761
0,5712
0,5663
0,5613
0,5563
0,5513
0,5462
0,5411
0,5360
0,5309
0,5257
0,5205
0,5153
0,5100
0,5047
0,4994
0,4941
0,1628
0,1582
0Д537
0,1492
0,1448
0,1404
0,1362
0,1320
0,1278
0,1238
0,1198
0,1159
0,1121
0,1083
0,1047
0,1011
0,0975
0,0941
0,0907
0,0874
0,0842
0,0810
0,0779
0,0749
0,0720
0,0691
0,0663
0,0636
0,0609
0,0583
0,2554
0,2500
0,2446
0,2392
0,2338
0,2286
0,2233
0,2181
0,2130
0,2079
0,2029
0,1979
0,1929
0,1881
0,1833
0,1785
0,1738
0,1691
0,1645
0,1620
0,1555
0,1511
0,1468
0,1425
0,1383
0,1341
0,1300
0,1260
0,1220
0,1181
0,6492
0,6394
0,6294
0,6193
0,6092
0,5991
0,5889
0,5786
0,5684
0,5561
0,5478
0,5374
0,5271
0,5168
0,5065
0,4961
0,4858
0,4755
0,4652
0,4550
0,4447
0,4345
0,4243
0,4142
0,4041
0,3927
0,3841
0,3741
0,3643
0,3545
3,9874
4,0410
4,0957
4,1514
4,2080
4,2659
4,3250
4,3849
4,4458
4,5082
4,5718
4,6362
4,7027
4,7703
4,8390
4,9090
4,9808
5,0543
5,1291
5,2057
5,2839
5,3642
5,4459
5,5297
5,6153
5,6835
5,7928
5,8850
5,9795
6,0764
0,9093
0,8981
0,8865
0,8746
0,8628
0,8508
0,8387
0,8264
0,8141
0,8016
0,7890
0,7764
0,7637
0,7509
0,7381
0,7250
0,7120
0,6990
0,6858
0,6727
0,6595
0,6462
0,6329
0,6197
0,6063
0,5930
0,5797
0,5664
0,5531
0,5398
0,1791
0,1762
0,1734
0,1706
0,1678
0,1651
0,1623
0,1597
0,1570
0,1544
0,1519
0,1493
0,1468
0,1443
0,1418
0,1394
0,1370
0,1346
0,1323
0,1299
0,1276
0,1254
0,1231
0,1209
0,1187
0,1165
0,1144
0,1122
0,1101
0,1081
1,8567
1,8750
1,8935
1,9122
1,9311
1,9503
1,9696
1,9892
2,0089
2,0290
2,0493
2,0698
2,0906
2,1112
2,1330
2,1546
2,1765
2,1987
2,2211
2,2439
2,2670
2,2905
2,3143
2,3384
2,3629
2,3877
2,4130
2,4386
2,4647
2,4911
Mo
ДХ»
1,91
1,92
1,93
1,94
1,96
1,97
1,9b
1,99
2,0i>
2,01
2,02
2,03
2,04
2,05
, 2,06
2,07
2,08
2,09
2,10
2,H
I 2,12
i '
0,4887
0,4833
0,4779
0,4724
0,4670
n,4615
0,4559
0,4504
0,4448
0,4391
0,4335
0,4278
0,4221
0,4164
• •ЛЮ6
0,4048
0,3990
0,3931
0,3873
0,3814
0,3754
0,3695
0,3635
o,3574
(»,3514
л
0,0558
0,0534
0,0510
0,0487
0,0465
0,0443
0,0422
0,0402
0,0382
0,0363
0,0344
0,0326
0,0309
0,0293
0,0277
0,0261
0,0247
0,0232
0,0219
0,0205
0,0193
0,0181
0,0169
0,0158
0,0148
0,1142
0,1105
0,1067
0,1031
0,0995
0,0960
0,0925
0,0892
0,0858
0,0826
0,0794
0,0763
0,0733
0,0703
0,0674
0,0645
0,0618
0,0591
0,0564
0,0539
0,0514
0,0489
0,0466
0,0433
0,0420
я
0,3447
0,3351
0,3256
0,3161
0,3064
0,2973
0,2881
0,2790
0,2700
0,2611
0,2523
0,2436
0,2351
0,2267
0,2183
0,2101
0,2022
0,1942
0,1864
0,1788
0,1713
0,1640
0,1569
0,1500
0,1429
у
6,1757
6,2779
6,3820
6,4899
6,5949
6,7128
6,8289
6,9487
7,0720
7,1985
7,3288
7,4635
7,6020
7,7448
7,8923
8,0444
8,2016
8,3639
8,5323
8,7059
8,8854
9,0725
9,2652
9,4829
9,6737
f
0,5266
0,5134
0,5002
0,4871
0,4740
0,4609
0,4480
0,4352
0,4224
0,4097
0,3971
0,3845
0,3723
0,3600
0,3477
0,3357
0,3240
0,3122
0,3005
0,2891
0,2778
0,2668
0,2559
0,2451
0,2345
r
0,1060
0,1040
0,1020
0,1000
0,0980
0,0961
0,0942
0,0923
0,0904
0,0885
0,0867
0,0849
0,0831
0,0813
0,0795
0,0778
0,0761
0,0744
0,0727
0,0710
0,0694
0,0678
0,0662
0,0646
0,0630
Продолжение
M
2,5180
2,5454
2,5731
2,6015
2,6302
2,6596
2,6894
2,7198
2,7507
2,7822
2,8143
2,8471
2,8806
2,9147
2,9496
2,9852
3,0215
3,0587
3,0967
3,1356
3,1754
3,2162
3,2579
3,3007
3,3446
I
2,15
2,ie
2,17
2,18
2,1У
2,20
2,21
2 22
2^23
, 2,24
, 2,25
' 2,213
2,2,
2,2b
2/2'J
i
i
J 2,30
; 2,3!
\ 2,32
2,33
• 2,34
2,35
2,36
2,37
2,38
j 2,39
0,3453
0,3392
0,3331
0,3269
0,3207
0,3145
0,3083
0,3020
0,2957
0,2894
0,2830
0,2766
0,2702
0,2638
0,2573
0,2508
0,2443
0,2377
0,2311
0,2245
0,2179
0,2112
0,2045
0,1978
о,1910
0,0138
0,0128
0,0119
0,0110
0,0102
0,0094
0,0087
0,0080
0,0074
0,0068
0,00620
0,00560
0,00512
0,00465
0,00421
0,00379
0,00341
0,00306
0,00273
0,00243
0,00215
0,00190
0,00167
0,00146
0,00127
0,0399
0,0378
0,0357
0,0338
0,0319
0,0300
0,0282
0,0266
0,0249
0,0233
0,0218
0,0204
0,0190
0,0176
0,0163
0,0151
0,0140
0,0129
0,0118
0,0108
0,0099
0,0090
0,0081
0,0074
0,0066
0,1362
0,1296
0,1232
0,1170
0,1109
0,1050
0,0993
0,0937
0,0883
0,0830
0,0780
0,0731
0,0684
0,0638
0,0595
0,0553
0,0512
0,0474
0,0437
0,0402
0,0369
0,0337
0,0307
0,0278
0,0252
9,8903
10,116
10,349
10,592
10,847
11,111
11,388
11,678
11,980
12,297
12,629
12,978
13,345
13,732
14,139
14,568
15,023
15,505
16,014
16,557
17,136
17,751
18,411
19,118
19,876
0,2242
0,2140
0,2041
0,1943
0,1847
0,1755
0,1664
0,1575
0,1488
0,1404
0,1323
0,1243
0,1167
0,1092
0,1021
0,0951
0,0885
0,0821
0,0759
0,0700
0,0644
0,0590
0,0539
0,0491
0,0445
0,0614
0,0599
0,0583
0,0568
0,0553
0,0539
0,0524
0,0509
0,0495
0,0481
0,0467
0,0453
0,0439
0,0426
0,0412
0,0399
0,0385
0,0372
0,0360
0,0347
0,0334
0,0321
0,0309
0,0297
0,0285
3,3897
3,4360
3,4836
3,5324
3,5828
3,6344
3,6877
3,7428
3,7995
3,8579
3,9185
3,9811
4,0458
4,1131
4,1828
4,2551
4,3304
4,4086
4,4903
4,5756
4,6647
4,7578
4,8557
4,9586
5,0665
fc=if33
к
2,40
2,41
2,42
2,43
2,44
2,45
2,46
2,47
2,48
2,49
2,50
2,51
2,52
2,53
2,54
2,55
2,56
2,57
2,58
2,59
2,60
2,61
2,62
2,63
2,64
2,65
2,657
X
0,1842
0,1774
0,1706
0,1637
0,1568
0,1499
0,1429
0,1359
0,1289
0,1219
0,1148
0,1077
0,1006
0,0934
0,0863
0,0791
0,0718
0,0646
0,0573
0,0499
0,0426
0,0352
0,0278
0,0204
0,0129
0,0054
0
я
0,00109
0,00095
0,00080
0,00068
0,00057
0,00048
0,00039
0,00032
0,00026
0,00021
0,000163
0,000126
0,955-10
0,710-10-4
0,514-10-*
0,362-10-4
0,240-10-4
0,160.10-*
0,986-Ю-6
0,568-10
0,299-Ю-6
0,139-Ю-6
0,536-10-в
0,153.10-е
0,243-10"?
0,728-10-»
0
0,00 о9
0,0053
0,0047
0,0041
0,0036
0,0032
0,0027
0,0024
0,0020
0,0017
0,001420
0,001169
0,000949
0,000759
0,000596
0,000457
0,000342
0,000248
0,000172
0,000114
0,702-10-4
0,394-10-4
0,193-10-4
0,750-Ю-5
0,188-Ю-6
0,135-10-в
0
Я
0,0226
0,0205
0,0181
0,0160
0,0141
0,0124
0,0108
0,0093
0,0079
0,0067
0,00503
0,00466
0,00380
0,00305
0,00240
0,00185
0,00139
0,00101
0,00070
0,00047
0,00029
0,00016
0,802-10-4
0,313-10-4
0,782-10-6
0,567-10-6
0
V
20,696
21,579
": 22,536
' 23,581
24,719
26,050
27,345
28,863
30,556
32,459
34,587
37,012
39,796
43,011
46,774
51,242
56,629
63,248
71,572
82,393
96,998
117,79
149,68
205,17
322,26
779,12
оо
/
0,0402
0,0364
0,0323
0,0287
0,0254
0,0223
0,0194
0,0168
0,0144
0,0122
0,01030
0,00853
0,00698
0,00562
0,00444
0,00343
0,00258
0,00188
0,00132
0,00088
0,00054
0,00031
0,152-10-*
0,594-10-*
0,150-10-*
0,108-10
0
Продолжение
г
0,0272
0,0261
0,0249
0,0237
0,0225
0,0214
0,0203
0,0191
0,0180
0,0169
0,01580
0,01480
0,01370
0,01273
0,01160
0,01050
0,00952
0,00850
0,00748
0,00648
0,00548
0,00450
0,00353
0,00257
0,00162
0,00067
0
м
5,1807
5,3011
5,4288
5,5645
5,7089
5,8630
6,0288
6,2067
6,3990
6,6079
6,8355
7,0851
7,3614
7,6681
8,0125
8,4028
8,8506
9,3716
9,9892
10,7387
11,6736
12,8883
14,5579
17,0777
21,5366
33,3991
оо
ПРИЛОЖЕНИЕ III
587
ffl
И
1=1 §
1
1
V
/
F
\
\
t
/
/
1
i
I/
/
•
fa
у
4
— —
/
f
— —¦
s
л
/
^/
у
**-
V
<
/
xs
\
\|
\
Ж
ч
¦—
\
\
1
/
ч
7\
i
ч
\
—^
у
->
/^
V
S
/
/
I
1
ъ
7*
Y
1
7i
(д
(т
II
/1
*
\
Л
53>
^
^
38*
588
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ V
ПРИЛОЖЕНИЕ V
Стандартная атмосфера
589
Высота Н, м
0
1000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
10 000
И 000
12 000
13 000
14 000
15 000
16 000
17 000
18 000
19 000
20 000
21000
22 000
23 000
24 000
25 000
26 000
27 000
28 000
29 000
30 000
40 000
50 000
60 000
70 000
80 000
90 000
100 000
120 000
140 000
160 000
180 000
200 000
Температура
Г, К
288,2
281,7
275,1
268,6
262,1
255,6
249,1
242,6
236,1
229,6
223,2
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
216,7
219,4
222,1
224,9
227,6
230,4
257,7
274,0
253,4
219,2
185,0
185,0
209,2
446,2
826,3
1096,8
1305,3
1536,4
Давление
р, Н/м*
101 330
89 880
79 490
70 130
61 660
54 050
47 210
41090
35 650
30 790
26 490
22 690
19 390
16 570
14 160
12 110
10 350
8 850
7 560
6 470
5 530
4 730
4 040
3 460
2 950
2 530
2 160
1 860
1 590
1 370
1200
296
84,6
44,1
5,83
1,11
1,84-10-1
3,24-10-2
3,01-10-3
1,05-Ю-3
5,45-10-*
3,21-10-4
2,09-10-4
Плотность
р, кг/м3
1,23
1,11
1,01
9,09-10-1
8,19-10-1
7,37-10-1
6,60-10-1
5,90-10-1
5,26-10-1
4,67-10-1
4,14-10-1
3,65-10-1
3,12-10-1
2,67-10-1
2,28-10-1
1,95-10-1
1,67-10-1
1,42-10-1
1,22-10-1
1,04-10-1
8,89-10-2
7,60-Ю
6,50-10-2
5,56-10-2
4,75-10-2
4,06-10-2
3,43-10-2
2,91-10-2
2,47-10-2
2,10-10-2
1,79-10-2
4,00-Ю-3
1,08-Ю-3
3,32-10-*
9,27-10-5
2,09-10-е
3,47-Ю-6
5,39-Ю-7
2,33-10-8
4,38-Ю-9
1,69-10-ю
8,24.10-ю
4,43.10-н
Вязкость
М,-105, Н-с/м2
1,79
1,76
1,73
1,69
1,66
1,63
1,60
1,56
1,53
1,49
* 1,46
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,42
1,44
1,45
1,47
1,48
1,49
1,57
1,72
1,62
1,44
1,24
1,24
1,39
СПИСОК ЛИТЕРАТУРЫ
1. Абрамович Г. Н. Теория турбулентных струй.—М.: Физматгиз,
1960.
2. Абрамович Г. Н.„ Гйршович Т. А., Крашенинников С. Ю„
Секундов А. Н., Смирнова И. П. Теория турбулентных струй.»—
2-е изд./Под ред. Г. Н. Абрамовича.— М.: Наука, 1984.
3. Абрамович Г. Н., Крашенинников С. Ю., С е к у н д о в А. Н.,
Смирнова И. П. Турбулентное смешение газовых струй.—М.: Нау-
Наука, 1974.
4. Абрамович Г. Н., Крашенинников С. Ю., Секундов А. Н.
Турбулентные течения при наличии объемных сил и неавтомодельно-
сти.— М.: Машиностроение, 1975.
5. А л ь т ш у л ь А. Д., Киселев П. Г. Гидравлика и аэродинамика.—
М.. Стройиздат, 1965.
6. Аржанников Н. С, Саддекова Г. С. Аэродинамика больших
скоростей.— М.: Высшая школа, 1965.
7. Бай Ши-и. Магнитная газодинамика и динамика плазмы.— М.: Мир,
1964.
8. Борисенко А. И. Газовая динамика двигателей.— М.: Оборонгиз.
1962.
9. Бетчелор Ж. К. Введение в динамику жидкости.— М.: Мир, 1973.
10. В а т а ж и н А. В., Любимов Г. А., Р е г и р е р С. А. Магнитогидро-
динамические течения в каналах.— М.: Наука, 1970.
И. By лис Л. А. Термодинамика газовых потоков.— М.: Госэнергоиздат,
1950.
12. В у л и с Л. А. Теория струй вязкой жидкости.— М.: Наука, 1965.
13. Газодинамика разреженных газов/Под ред. М. Девиена.— М.: ИЛ, 1963.
14. Газовая динамика: Сборник переводов.— М.: ИЛ, 1963.
15. Г а р р и с Л. Магнитогидродинамические течения в каналах.— М.: ИЛ,
1963.
16. Г е р м а н Р. Сверхзвуковые входные диффузоры.— М.: Физматгиз,
1960.
17. Г и н з б у р г И. П. Прикладная гидрогазодинамика.— М.; Л.: Изд-во
ЛГУ, 1958.
18. Г и р о Ж. Основные вопросы теории гиперзвуковых течений.— М.: Мир,
1965.
19. Дейч М. Е. Техническая газодинамика.— М.: Энергия, 1974.
20. Д е й ч М. Е., 3 а р я н к и н А. Е. Гидрогазодинамика.— М.: Энергоиз-
дат, 1984.
21. Жуковский В. С. Техническая термодинамика.— М.: Гостехиздат,
1952.
22. 3 а у э р Р. Течения сжимаемой жидкости.— М.; ИЛ, 1954.
23. 3 е л ь д о в и ч Я. Б. Теория ударных волн и введение в газодинами-
газодинамику.— М.: Изд-во АН СССР, 1946.
24. И д е л ь ч и к И. Е. Гидравлические сопротивления.— М.: Госэнергоиз-
Госэнергоиздат, 1954.
^ СПИСОК ЛИТЕРАТУРЫ 591
25. Иде л ьч и к И. Б. Справочник по гидравлическим сопротивлениям.—
М.: Машиностроение, 1975.
26. И д е л ь ч и к И. Б. Аэродинамика промышленных аппаратов,— М.: Энер-
Энергия, 1964.
27. Калихман Л. Б. Элементы магнитной газодинамики.— М.: Атомиз-
дат, 1964.
28. Коган М. Н. Динамика разреженного газа.—М.: Наука, 1967.
29. К о ч и н Н. Б., К и б е л ь И. А., Розе И. В. Теоретическая гидроме-
гидромеханика.— М.: Гостехиздат, 1963.
30. Куликовский А. Г., Любимов Г. А. Магнитная гидродинами-
гидродинамика.— М.: Физматгиз, 1962.
31. Ландау Л. Д., Лившиц Е. М. Гидродинамика.—М.: Наука, 1986.
32. Левинсон Я. И. Аэродинамика больших скоростей.— М.: Оборонгиз,
1950.
33. Л и п м а н Г. В., Р о ш к о А. Элементы газовой динамики.— М.: ИЛ,
1960.
34. Лойцянский Л. Г. Механика жидкости и газа.— М.: Наука. 1987.
35. Л о й ц я н с к и й Л. Г. Аэродинамика пограничного слоя.— М.: Гостех-
Гостехиздат, 1941.
36. Л о й ц я н с к и й Л. Г. Ламинарный пограничный слой.— М.: Физмат-
Физматгиз, 1962.
37. Магнитная гидродинамика: Труды симпозиума.— М.: Атомиздат, 1960.
38. Н е ч а е в Ю. Н., Федоров Р. М. Теория авиационных газотурбин-
газотурбинных двигателей.— М.: Машиностроение, 1978.
39. П а т т е р с о н Г. Н. Молекулярное течение газов.— М.: Физматгиз, 1960.
40. Прикладная магнитная гидродинамика: Сборник переводов.— М.: Мир,
1965.
41. П р а н д т л ь Л. Гидроаэродинамика. Т. 1, 2.— М.: ИЛ, 1949.
42. Р а х м а т у л и н X. А. и др. Газовая динамика.— М.: Высшая школа,
1965.
43. С а м а р с к и й А. А., Попов Ю. П. Разностные методы решения за-
задач газовой динамики.— М.: Наука, 1990.
44. С а м о й л о в и ч Г. С. Гидроаэромеханика.— М.: Машиностроение, 1980.
45. С е р г е л ь О. С. Прикладная гидрогазодинамика.— М.: Машинострое-
Машиностроение, 1981.
46. Современное состояние гидроаэродинамики вязкой жидкости/Под ред.
С. Гольдштейна. Т. 1, 2.— М.: ИЛ, 1948.
47. Современное состояние аэродинамики больших скоростей/Под ред.
Хоуарта.— М.: ИЛ, 1955.
48. С е д о в Л. И. Методы подобия и размерности в механике.— М.: Наука,
1987.
49. С е д о в Л. И. Плоские задачи гидродинамики и аэродинамики.— М.:
Наука, 1980.
50. Седов Л. И. Механика сплошной среды.-—М.: Наука, 1983.—1984.—
Т. 1.— 1983; Т. 2.— 1984.
51. Степанов Г. Ю. Гидромеханика решеток турбомашин.— М.: Физмат-
Физматгиз, 1962.
52. С т е п а н о в Г. Ю. Основы теории лопаточных машин комбинирован-
комбинированных и газотурбинных двигателей.— М.: Машиностроение, 1958.
53. С т е п ч к о в А. А. Задачи по гидрогазодинамике.— М.: Машинострое-
Машиностроение, 1980.
54. Теория воздушно-реактивных двигателей/Под ред. С» М. Шляхтенко.—
М.* Машиностроение, 1987.
55. Фабрикант Н. Я. Аэродинамика.— М.: Наука, 1964.
56. Ф е р р и А. Аэродинамика сверхзвуковых скоростей.— М.: Гостехиздат,
1952.
57. Франк-Каменецкий Д. А, Лекции по физике плазмы.— М.: Атом-
Атомиздат, 1968.
592 СПИСОК ЛИТЕРАТУРЫ
58. Ф р а н к л ь Ф. И., X р и с т и а н о в и ч С. А., Алексеева Р. Н. Ос-
Основы газовой динамики / Труды ЦАГИ.— 1938.— Вып. 364.
59. X е й з У. Д.. П р о б с т и н Р. Ф. Теория гиперзвуковых течений.— М.:
ИЛ, 1962.
00. Хинце И. О. Турбулентность.— М.: Физматгиз, 1963.
(П. Ч арный И. А. Основы газовой динамики.—М.: Гостоптехиздат, 1961.
02. Ч е р н ы й Г. Г. Газовая динамика.— М.: Наука, 1988.
63. Черный Г. Г. Течение газа с большой сверхзвуковой скоростью.— М.:
Физматгиз, 1959.
•Я Холщевников К. В., Е м и н О. Н., Митрохин В. Т. Теория и
расчет лопаточных машин.— М.: Машиностроение, 1986.
G5. Численные решения многомерных задач газовой динамики/Под ред.
С. К. Годунова.— М.: Наука, 1976.
Г.6. Шидловский В. П. Введение в динамику разреженного газа — М.:
Наука, 1965.
(." Ш е р к л и ф Д. Теория электромагнитного измерения pacxo.ici — М.:
Мир, 1965.
08. Шлихтинг Г. Теория пограничного слоя.—М.: Наука, 197 i
ИМЕННОЙ УКАЗАТЕЛЬ
Абрамович Г. Н. 192, 218, 387, 388, 408, Зельдович Я. Б. 218, 590
455, 590
Аверенкова Г. И. 411
Акимов Г. А. 422
Алберг Дж. (Ahlberg J.) 441
Алексеева Р. Н. 592
Альтшуль А. Д. 590
Аржанников Н. С. 590
Ашвуд П. Ф. (Ashwood P. F.) 443
Ашратов Э. А. 411
Иванов М. Я. 411
Иванов Ю. В. 365
Идельчик И. Е. 458, 462, 464. 590, 591
Бай Ши-и (Bai S. I.) 590
Бам-Зеликович Г. М. 331
Бартц Д. P. (Bartz D. R.) 440
Бекк Л. (Back L. Н.) 433, 434
Бергман Д. 395
Бетчелор Ж. К (Batchelor G. К.) 590
Блаузиус Г. (Blasius H.) 291, 352
Борисенко А. И 590
Брайнерц Дж. (Brainerd J. G.) 298
Бычкова Л. А. 457
Вакар Н. В. 464
Васильев Ю. Н. 519, 5а7
Ватажин А. В. 590
Винклер Э. М. (Winkler E. М.) 328
Вихофер С. (Wehofer S.) 431
Вулис Л. А. 590
Гаген (Hagen G.) 350
Гамильтон С. (Hamilton S.) 441
Гаррис Л. (Harris) 590
Герман P. (Hermann R.) 469, 488, 590
Гертлер Г. (Gortler H.) 368, 3G9
Гиневский А. С. 399, 457
Гинзбург И. П 590
Гинзбург Я. Л. 462
Гир Г. (Gier H. L.) 434
Гиршович Т. А. 590
Глазков В. В 364
Годунов С. К. 592
Гольдштейн С. (Goldstein S.) 314
Грегори Т. (Gregory T. J.) 485
Гусева М Д 364
Гэдд Г. (Gadd G. Е.) 341, 346
Дейч М. Е. 432, 590
Дорренс У. X. (Dorrance W. Н.) 360
Дурхам Ф. П. (Durham E. Р.) 434,
442
Жестков Б. А. 364, 370, 401—403, 406—
408
Жуковский В. С. 590
Зарянкин А. Е. 432, 590
Зауэр P. (Sawyer R. А.) 590
Калихман Л. Е. 591
Карман Т. (Karman Th. von) 294, 295
Кибель И. Д. 591
Кинан И. (Кеепап I.) 439
Кирстен Г. (Kirsten H.) 351
Киселев IL Г. 590
Кнокс P. (Knox R.) 452
Коган М. Н. 591
Козлов В. Е. 394, 397, 399, 400
Коп В. Ф. (Соре W. F.) 298
Кочин Н. Е. 591
Крайко А. Н. 411
Крашенинников С. Ю. 391, 590
Крокко Л (Сгоссо L.) 298
Крумича Н. Н. 464
Куликовский А. Г. 591
Курант Г. 178
Куффель П. Ф. (Cyffel P. F.) 433
Ландау Л. Д. 591
Лапин Ю. В. 328, 360
Левинсон Я. И. 591
Лившиц Е М. 591
Липман Г. В. 591
Лис Л. (Lees L.) 311
Лобб P. (Lobb R. К ) 328
Лойцянский Л. Г. 591
Любимов Г. А. 590, 591
Максимов М. М. 370, 401, 402, 406—408
Массир П. Ф (Massier D.) 434
Мигдал Д. (Migdal D.) 441
Митрохин В. Г. 592
Михайлов А. И. 365
Михельсон В. А. 218
Могор У. С. (Mogor W. S.) 431
Наумова И. Н. 444
Нейман Э. (Nauman E.) 439
Некрасов И. П. 346
Нечаев Ю. Н. 488, 591
Никурадзе И. 321, 330, 351, 352, 354
Нильсон Э. (Nilson E.) 441
Нортон (Norton) 434
Осватич К. (Oswatitsch К.) 469
Паттерсон Г. Н. (Patterson G. N.)
591
Персон Г. (Person H.) 451
594
ИМЕННОЙ УКАЗАТЕЛЬ
Перч Дж. (Persh J.) 328
Петерсен P. (Petersen R, Н.) 485
Петров Г. И. 137, 343, 465, 469
Печенкин В. К. 386
Попов Ю. П. 591
Прандтль Л. (Prandtl L.) 283, 317, 367.
368. 591
Пробстин Р. Ф. (Probstein R. F.) 360,
592
Рао Г. В. (Rao G. V.) 442
Рахматулин X. А. 591
Регирер С. А. 590
Рейхард A. (Reichardt A.) 369
Розе И. В. 591
Рошко А. 591
Саддекова Г. С. 590
Самарский А. А. 591
Самойлович Г. С. 591
Сатерленд Д. (Sutherland D. М.) 278
Седов Л. И. 271, 591
Секундов А. Н. 394, 397, 427, 590
Семенов Н. Н. 218
Сергель О. С. 591
Смирнова И. П. 394, 397, 427, 590
Смит С. (Smith S.) 451
Степанов Г. Ю. 591
Степчков А. А. 591
Стечкин Б. С. 43
Струминский В. В. 394
Сдиллард К. С. 460, 462
Толмин В. (Tollmien H.) 311, 366, 367
Уисс Дж. (Wyes J. A.) 485
Ульянов И. Е. 464
Ухов Е. П. 137, 465, 469
Ушаков К. А. 458
Федоров Р. М. 591
Ферри A. (Ferri A.) 591
Флаксбарт О. (Flachbart О.) 331
ФранкЧКаменецкий Д. А. 218, 591
Франкль Ф. И. 592
Хартри Д. (Hartree D. R.) 298
Хейз У. Д. (Hayes W. D.) 360, 592
Хиггинс Д. (Higgins D. G.) 443
Хинце И. О. 592
Холидей Дж. (Holliday J.) 451
Холщевников К. В. 592
Хоуарт Л. (Howart L. М.) 294
Христианович С. А. 592
Цзян X. С. (Tsien H. S.) 294, 295
Чарный И. А. 592
Черкез А. Я. 274, 409, 538
Черный Г. Г. 271, 592
Чепмен Д. P. (Chapman D. R.) 278
Чжен П. К. (Cheng P. К.) 341, 360, 395.
Шелухин Н. Н. 426
Шидловский В. П. 592
Шиллер Л. (Schiller L.) 349, 354
Шлихтинг Г. (Schlichting H.) 321, 360„
365, 369, 592
Шляхтенко С. М. 55
Шулишина Н. П. 444
Щелкин К. И. 218
Эвард Дж. (Eward J.) 441
Эммонс Г. (Emmons H. W.) 298
Фабрикант Н. Я. 105, 591
Яковлевский О. В. 386
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная шероховатость 357
Адиабата идеальная 29, 31, 159
— ударная 122, 123
Архимеда закон 85
— сила 85
— число 85, 86
Аэродинамическая труба с эжектором
492
сверхзвуковых скоростей 21
Волна сильная 117
— слабая 117
— ударная 219
прямая 118
Волны Прандтля — Майера 177
— простые 177
— ударные 115
Вязкость 63
— вторая 67
Баротропность жидкости 94
Бернулли интеграл 94, 95, 289
— уравнение 27, 29, 31, 34, 35, 39,
181, 329, 398
Блаузиуса формула 352
Газодинамические функции 569—586'
143 Гедда формула 346
1 а* Горение 218, 229
Грасгофа число 86
Вентури трубка 152
Вихрь скорости 60, 103, 106, 107
Волна акустическая 117
— бесконечно слабая 120
— давления 115
— детонационная 218. 219
стационарная 222
— звуковая 121
Давление полное 31, 244
— расчетное 401
— статическое 31, 244, 238, 244
Дрси формула 89
игатель прямоточный воздушно-реак-
воздушно-реактивный 43, 54, 55
— — — идеальный 44
— турбореактивный 55
—
Да
Дв
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
595
Движение безвихревое циркуляционное
106, 107
— вязкой жидкости слоистое ламинар-
ламинарное 279
— подогреваемого газа 192—201
— потенциальное 92
— стационарное элементарной струйки
11
Детонация 218
диаграмма состояния нерасчетной струи
Дивергенция вектора скорости 61, 68
Диполь НО
Диссипативная функция 72
Диссоциация термическая 221
Диффузор 42
— боковой 486
— дозвуковой 453—464
предотрывный 457, 458
— сверхзвуковой 464—491
нерегулируемый 487
плоский 468
с частичным внешним сжатием
474
внутренним сжатием 474
Длина свободного пробега 277
Запирание эжектора 520
"Импульс потока полный 241
"Источник 108, 109
Количество движения секундное 38
Компрессор идеальный 35, 50
Конфузор 149
"Коэффициент восстановления темпера-
температуры 297
— динамической вязкости 63, 65, 276,
278, 281
— поверхностного трения 89
— полезного действия эжектора 553
— полноты удара 455, 456
— поля 503
— потерь на трение 89
— расхода 430, 432—434
— скорости сопла 429
— сопротивления 292, 314, 350, 351, 353,
354, 359
— сохранения полного давления 32, 50,
125, 429
в диффузоре 461, 467, 477,
485
— температуропроводности 84
— теплоотдачи 295, 296, 299
— трения 292, 294, 298, 299, 327
— турбулентной вязкости 320—322, 427
теплопроводности 320, 322
— увеличения тяги 557, 559, 562
— эжекции 496, 506, 526, 527, 554, 559
•кривая нейтральная 311
Критерии динамического подобия 79
Критерий температурный 84, 86
Критический режим движения газа 24
"Критическое отношение давлений 260.
341, 346
Куэтта течение 69, 90
-Лаваля сопло 203, 432, 443, 444, 498
Лагранжа интеграл 93, 94
— метод 62
-Ламба — Громеко уравнения 92
-Ламинарный подслой 323
-Лапласа оператор 68
*^ уравр^ние 96
Лиза — Дородницына переменные 289
Линии равного потенциала 109
— тока 11
Масштаб моделирования динамический
77
кинематический 76
линейный 76
Маха волна 133
— диск 410, 411, 425
— угол 133, 176
— число 22, 24, 84, 86, 312, 478
Метод элементарной струйки 11
Навье — Стокса уравнения 68, 69, 74
в безразмерной форме 78
для пограничного слоя 284
для течения в трубах 349
Наложение двух течений 97, 98
Напряжение объемной силы в данной
точке среды 62
— поверхностное 62
Нуссельта число 440
Ньютона гипотеза 63, 276
— закой второй 37
вязкого трения 87
трения 65
, второе обобщение 66
Обтекание выпуклой криволинейной
стенки 169—171
— закругленных и острых кромок 107
— конуса 137, 138
— плоской стенки 167—169
— тела вращения 136
— тупого угла 156—166
Осреднение параметров неравномерного
потока 267—275, 322
Отрыв пограничного слоя 282, 283,
329—338
Пекле число 84
Переход через скорость звука 203—208
Плотность жидкости 61
Пневматический насадок 33
в сверхзвуковом потоке 140, 141
Поверхности тангенциального разрыва
361
Поверхность тока 11
Пограничный слой 276, 279
ламинарный 282, 283
турбулентный 282, 314
струйный 361
Подобие гидродинамическое 75, 86
— динамическое приближенное 80, 81
— кинематическое 76
— тепловое 83, 86
Поле скоростей 99, 107
Потенциал 109
— объемных сил 92, 93
— скорости 92
Прандтля гипотеза 320, 335, 370, 393
Прандтля — Майера волны 177, 178
течение 155
— теория турбулентности вторая 367,
368
первая 366, 367
— число 75, 84, 86, 286, 288, 323
турбулентное 370
Приведенная длина трубы 186, 261
Процесс адиабатический идеальный 30,
35, 121, 122
— изобарический 29
— изотермический 29
596
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Процесс изохорический 29
— изоэнтропический 30
— политропический 30, 209
Пуазейля течение 69
Располагаемое отношение давлений 246,
260
Распределение скорости в гладкой тру-
трубе 321
ламинарном подслое 324
Расход газа 198, 238
в конфузоре 149
сверхзвуковом сопле 148
Рейнольдса аналогия 328
— число 79, 80, 84, 86, 281, 299, 311
критическое 281, 282, 312
Сатерленда формула 278
Сила реактивная 51, 553
— тяги двигателя 556, 557
Силы нормальные 62, 63, 66, 67
— объемные 62
— поверхностные 62
— тангенциальные 62, 63
Скачок уплотнения 114, 119
висячий 411, 427
косой 126—137, 179
прямой 121, 124
сильный 134, 179
слабый 134, 179
Скорость газа относительная 26
— газового потока за фронтом волны
сжатия 118
— движения газа максимальная 22, 23
сгоревших частиц 231
— звука в газе 23, 79, 117, 118, 181, 202
— истечения газа 34, 35
из сопла 429, 435
— нормального горения максимальная
231
— приведенная 234, 25, 44, 157, 185, 191,
219, 221, 234
детонационной волны 224
— распространения волны 116, 117
продуктов горения 230
— частиц при детонации 231
Совместности условия 175, 176
Сопло Лаваля сверхзвуковое 143—150,
153, 154, 203
— механическое 203—206
— полутепловое 213
— расходное 203, 204
— с косым срезом 171, 172
— с центральным телом 445
— тепловое 203, 206—212
— эшекторное 447, 448, 450
Срыв сверхзвукового потока 169
Стантона число 295, 296, 298
Степень нерасчетности сопла 246, 247,
401
— повышения давления в компрессоре
36, 56, 57
— понижения давления в турбине 36,
56, 57
— турбулентности потока 372
Сток 108, 109
Струхаля число 79, 82
Струя затопленная 362
Температура в потоке 234
— торможения 18, 31, 234
, предельное значение 251
— частичного торможения 128
Тепловое сопротивление 193
Тепловой кризис 195, 203, 223
Теплосодержание (энтальпия) 1в
— полное 18, 71
Термодинамики закон второй 48, 49
первый 48, 69
Технически гладкая труба 185, 186
Течение газа адиабатическое с трением
181—184
в трубе постоянного сечения 184—
192
дозвуковое 24
ламинарное 281, 308
сверхзвуковое 24
турбулентное 281, 308, 317, 318
— жидкости в трубах 348—360
— несжимаемой жидкости при внезап-
внезапном расширении канала 40
плоскопараллельное 308
в канале 87
— Прандтля — Майера 155
— сжимаемого газа при внезапном рас-
расширении канала 248
Течения гидродинамически подобные 77
— слоистые 86—90
— струйные 361
Толщина вытеснения 302, 306, 307, 435,
437
относительная для турбулентного
пограничного слоя 326
— ламинарного подслоя 335
— пограничного слоя 280, 285, 286, 292,
306, 372, 373, 440
— потери импульса 302, 307, 313, 395
в пограничном слое 438
— слоя смешения 427
— струи 377
Томпсона теорема 105
Точка отрыва пограничного слоя 331
Турбина идеальная 35, 50
Тяга жидкостного реактивного двигате-
двигателя 53
— реактивная 154, 245
Угол отклонения потока в скачке 127,
133, 134
— распространения слабых возмущений
133, 156
Ударная поляра 179
Удельный объем газа 15, 16
Уравнение возмущающего движения 310
— живых сил 27
— идеального адиабатического процесса
95
— количества движения 37, 39, 241
в струе 378
— моментов количества движения 45
— неразрывности 11, 12, 41, 42, 61, 62,
112, 143, 230
в общем случае двумерного тече-
течения 174
для пограничного слоя 287, 316
— пограничного слоя ламинарного 287,
316
турбулентного 317
— состояния идеального газа 15—16
— теплосодержания 16—18, 20
в струе 379, 381
— эжекции основное 508
— энергии 83, 112
для пограничного слоя 288
стационарного двумерного те-
течения 74
установившегося режима 82
Уравнения газовой динамики в общей
форме 112
Условия обращения воздействия 202, 203
— совместности 175
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
597
Форсажная камера турбореактивного Шлихтинга функция 365, 371
двигателя 250
Фронт пламени 218
Фруда число 79, 81, 86
Функции газодинамические 233—245,
257—259, 569—586
Функция потенциальная 109
— тока 96, 97
диполя НО, 111
Фурье гипотеза 70
Характеристика эжектора 525
Характеристики 133, 156
Хименца течение 69
Циркуляция скорости 99—101, 106
в полярных координатах 101
Эжектор газовый 492
— звуковой 492
— простейший 40
Эйлера метод 62
— уравнение количества движения в
гидродинамической форме 38
моментов количества движения в
гидродинамической форме 46
— уравнения движения идеальной сжи-
сжимаемой жидкости 90, 91
— число 79
Элементарная струйка 11
Энтальпия (теплосодержание) 16
— полная 74
Энтропия 48, 49
Янга формула 298
Учебное издание
АБРАМОВИЧ Генрих Наумович
ПРИКЛАДНАЯ ГАЗОВАЯ ДИНАМИКА
Заведующий редакцией Л. А. Русаков
Редактор А. Г. Мордвинцев
Художественный редактор Т. Н. Кольченко
Технический редактор Л. В. Лихачева
Корректоры О. А. Бутусова, Л. С. Сомова
ИБ № 32460
Сдано в набор 01.06,90. Подписано к печати 02.07.91. Формат бОХЭО'Ае. Бумага
книжно-журнальная. Гарнитура обыкновенная. Печать высокая. Усл. печ. л. 37,5.
Усл. кр.-отт. 37,5. Уч.-изд. л. 39,82. Тираж 3500 экз. Заказ № 225. Цена 7 р. 50 к.
Издательско-производственное и книготорговое объединение «Наука».
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Четвертая типография издательства «Наука»
630077 Новосибирск 77, Станиславского, 25
i SYNOPSIS
G. N. ABRAMOVICH
«APPLIED GAS DYNAMICS»
Fifth edition, revised and supplemented, USSR, «Nauka»
The author is Professor of the Moscow Aviation Institute (MAI), Doctor
of Technical Sciences, member of the USSR National Committee on Theoreti-
Theoretical and Applied Mechanics, member of three editorial boards (MAI-, KHAI-*),
and TsAGI-**) colelctions of papers on the problems of gas dynamise, two-
phase flows, and industrial aerodynamics), State Prize laureate and Joukovski
Prize laureate, Honorary Worker of Science and Technology of the USSBf,
a recognised authority in the field of gas dynamics and the founder of the
theory of turbulent jet. Prof. G. N. Abramovich has also made a significant
contribution to the theory of jet engines.
The book covers the results of scientific research (including the author's
latest publications) treated alongside classical fundamentals of gas dynamics
and hydrodynamics.
A specific feature of the book is the wide scope of gas dynamic problems
considered in close connection with actual practical tasks of modern enginee-
engineering (aviation, space, power, machine-building, chemical technology, industrial
ventilation, environment protection from industrial exhausts etc).
The wide scope of contents and the accessibility of presentation make it
'possible to use the book as a fundamental textbook and scientific manual in
the corresponding branch of science for students, postgraduates, and scientific
workers of higher technical schools and universities. It has become a valuable
reference book in many design offices and research- and development
institutes.
Previous editions of the book were translated and published in the Germa-
Germany, Czechoslovakia, China, and Bulgaria.
A number of other books and papers by G. N. Abramovich have been pub-
published in the USA, the Germany. In particular, a large monograph «Theory of
Turbulent Jets» (republished five times in the USSR) has been printed by
the publishing house of the Massachusets Institute of Technology A963).
In the USSR, the USA, and Bulgaria this book was repeatedly reviewed and
was highly appraised. It was cited in many publications by different
authors.
A collection of the authors papers and his separate publications on tur-
turbulent flows were published in the transactions of the Karlsruhe University
A977) and by Springer Verlag.
The fifth edition of the book contains 14 chapters devoted, respectively,
to the theory of one-dimensional flows affected by heat transfer, mechanical
work, friction, and mass transfer (chapters 1 and 5); the differential equa-
equations of gas motion, integral relations and similarity theory (chapter 2); shock
waves and supersonic expansion flows (chapters 3, 4); the theory of boundary
layer (chapter 6); the theory of turbulent jets (chapter 7); the gas, flows in
nozzles, diffusers, curvilinear channels, and ejectors (chapters 8 and 9); the
theory of wing profile and airfoil cascade (chapter 10); hypersonic flows
(chapter 11); magnetic gas dynamics (chapter 13) and rarefied gas flows
(chapter 12).
*) KHAI — Kharkov Aviation Institute.
•¦) TsAGI — Central Aerohydrodynamic Institute.
The book in its fifth edition is supplemented with chapter 14 in which
the numerical methods of gas dynamics are presented (in particular, the me-
methods of characteristics and shock-capture techniques as applied to the flows
in nozzles and diffusers) and this addition of new material required a cor-
corresponding enlargement of the theoretical chapters 2 and 4.
In the fifth edition of the book some changes have been made. Chapter 7
is completely rewritten and contains new information on jets in a coflowing
stream and on supersonic jets. Chapter 6 is partly rewritten the information
is given not only on the effect of the Mach number on the boundary layer
up to M = 10 and on the interaction between the boundary layer and shock
waves, but also about the effect of longitudinal pressure gradient on the boun-
boundary layer.
Chapter 8 is supplemented with the material concerning the effect of gas
compressibility on the curvilinear channel resistance.
Chapter 10 is abridged (mainly at the expense of information of the
hydrodynamics of cascades in an incompressible fluid). This chapter con-
contains new results concerning the effect of the type of gas on the flow past
a cascade.
The practical examples of the use of the theory given in the book deal
mainly with jet technology and pawer considerations.
The chapter 1 includes 8 sections containing the basic equations derived
for an elementary stream tube (the equations of continuity, energy, Bernoulli,
momentum, and moment-of-momentum). In this chapter the examples are
given for the use of above equations in the calculation of stagnation tempe-
temperature and total pressure, compressor and turbine work, reactive force and
variation of gas parameters in jet engine channels and in elementary ejector,
-as well as resistance at sudden widening of channel etc. (About 2.5 qr.)
In chapter 2 A3 sections), the differential equations of hydrodynamics
and gas dynamics (continuity, motion and energy) are derived for an ideal
continuous medium taking into account the viscosity. The basic integral rela-
relation are presented. The conditions of hydrodynamic similarity and similarity
criteria are obtained. The theory of layered viscous flow is presented and some
examples of two-dimensional potential flows of an ideal fluid are considered.
(About 3 qr.)
Chapter 3 C sections) deals with the theory of shock waves (normal and
oblique) and its application to the problems of supersonic flow around a body
and of measurement of gas motion velocity. (About 2 err.)
Chapter 4 (9 sections) is devoted to the study of expansion flows: one-
dimensional (supersonic nozzles) and two-dimensional (flow past convex wall,
blunt corner, polyhedron, curvilinear wall, and also the flow issuing from
a scarfed nozzle). In the last three sections added to this chapter the method
of characteristics is considered in detail, as well as its application to superso-
supersonic flows with simple waves, a centered wave and in more general cases.
A graphical calculation method for the interaction of flows containing shock
waves and centered waves is also described. (About 3 qr.)
Chapter 5 (8 sections) deals with the theory of one-dimensional flows
with friction, heat transfer, mechanical work and variable gas flow rate. The
general conditions of transition from subsonic to supersonic regime and vice
versa are given. The propagation of combustion and detonation waves is also
investigated. Gas dynamic functions are derived for the simplification of cal-
calculation. The methods of averaging of nonuniform flow parameters are descri-
described. (About 5 qr.)
Chapter 6 G sections) is devoted to the theory of boundary layer (lami-
(laminar, turbulent) and the problems of its transition and separation for a wide
range of Mach numbers: M = 0 ч- 10 taking into account the effect of pres-
pressure gradient and temperature factor and also the interaction between boun-
boundary layer and shock waves. This chapter is partly remade in the fifth edition.
(About 5 qr.) . , _ A . . .
Chapter 7 F sections) which deals with the theory of turbulent jets is
completely rewritten and contains the newest information on subsonic ana
supersonic jets (including nonisobaric jets in a coflowing gas stream navmg
different temperature or being of other kind and with different initial condi-
conditions). (About 3 qr.)
In the chapter 8 D sections) the detailed study of flow in subsonic and
supers-onic nozzles and diffusers and also in subsonic curvilinear changeK
(taking into account gas compiessibility) is presented. Particular attention r>
given to the inlets and outlets of jet engines. (About 4 qr.)
Chapter 9 A0 sections) deals with the theory of working proce>s in ga<
ejector and corresponding methods of calculation for the subsonic, supersonic
and mixed regimes in tbe working chamber taking ink) account the critical
conditions. The examples of calculation are also given. (About 7 sq.)
Chapter 10 A2 sections) devoted to gas dynamics of wing profile and ail-
foil cascade is abridged in the fifth edition (mainly at the expense of the sub-
subsection dealing with incompressible fluid and of some other information of
minor importance). However, this cbaptcr is supplemented with new informa-
information concerning flows of gases with different properties streaming around the
airfoils. The corresponding regularities are considered at subsonic, supersonic
and transsonic velocities. (About 6 qr.)
Chapter 11 (8 sections) is devoted to the investigation of hypersonic gas
flows (basic regularities and problems of flow past bodies of pointed and
blunt shape). (About 1.5 qr.)
In chapter 12 (9 sections) the flow of rarefied gases with slip and in the
free-molecular regime are studied with application to the interior and exte-
exterior problems as well as in the case of flow issuing from orifices. (About 3 qr )
In chapter 13 A3 sections) the fundamentals of magnetic gas dynamics
(including the necessary information about electrostatics, electrodynamics and
electiomagnetic fields) are given. The differential and integral equations of
magnetic gas dynamics are derived and the similarity criteria aie obtained.
The methods are presented for the calculation of magnetic generators, pumps,
accelerators and throttles, channel flows in the transverse and longitudinal
magnetic fields in laminar and turbulent regimes and also in the transition
region. (About 9 qr.)
Chapter 14 E sections) devoted to modern numerical methods of super-
supersonic gas flow calculation, is added to the book in its fifth edition. It contains
the description of the principles of construction of numerical methods, conside-
consideration of the method of characteristics and a detailed presentation of the
shock-capture technique with examples of its application to Ihe construction
of flow field in supersonic nozzles and diffusers. (About 2 qr.)
In the book many openmental data are used. The book contains several
tables in the text, about 550 figures and 6 appendixes (with tables and graphs
of gas dynamic functions as a rule).
The list of lecommended books includes 08 items (references to scientific
papers widely used in the book are given in suitable places in the lert). The
total volume of the book — about 50 qr.
The book v.as approved as a textbook for higher schools