А. СТ ВСК
i

А. И. ОСТРОВСКИЙ
75 ЗАДАЧ
по
ЭЛЕМЕНТАРНОЙ
МАТЕМАТИНЕ-
ПРООТЫХ, НО...
ИЗДАТЕЛЬСТВО «ПРОСВЕЩЕНИЕ»
МОСКВА 1 θ β β

ПРЕДИСЛОВИЕ
В этой книге — 75 задач по «элементарной»-
математике.
Среди этих задач — и совсем простые, решаемые
в уме, и более сложные, требующие выполнения
вычислений и построений; и Традиционные (курьеры,
бассейны), решаемые известными приемами, и так
называемые «задачи на сообразительность», требующие
в основном отыскания подхода к решению.
Цель решения каждой отдельной задачи, конечно,
не в том, чтобы выяснить: «сколько же быков было
5на лугу?» или «когда наконец встретились туристы?»,
а в установлении особенностей данной ситуации, в
обнаружении «подводных камней», в поиске наиболее
изящного пути решения и в анализе полученного
результата. Поэтому имеется в виду, что читатель
решит каждую задачу самостоятельно и,* если захочет,
затем уже сверится с приведенными в книге
решениями.
Ко многим задачам дано несколько вариантов
решения. Какой же из них следует выбрать? Это
зависит от цели, которая ставится при решении задачи:
^получить ответ» или «разобраться, при помощи
математики- в происходящих процессах, явлениях,
состояниях». В последнем случае часто оказываются
полезными графики, хотя решение с их помощью может
оказаться и сложнее обычного аналитического
решения.
3

Если окажется, что решение, найденное читателем,
лучше приведенного в книге, он, можно надеяться,
сообщит об этом издательству.
Большинство задач составлено ςπeциaльнo для
данной книги; для тех задач, которые были
опубликованы ранее, добавлены новые решения, а иногда
несколько изменено (усложнено) условие или
поставлены дополнительные вопросы.

ЗАДАЧИ
1. ОДИНАКОВЫЕ ЦИФРЫ
Пятого мая тысяча девятьсот пятьдесят пятого го*
да я записал дату так:
О· о* DO.
В этой записи встречается только одна цифра —
«пять».
Ответьте на вопрос: сколько раз в течение
столетия запись числа, месяца и последних двух цифр года
производится при помощи только одной и той же
цифры?
Не торопитесь с ответом! Подумайте!
2. ПОЕЗД ИДЕТ ТУДА И ОБРАТНО
Поезд идет несколько дней из А в Я, а затем
возвращается нз В в А. Каков должен быть график
движения этой пары поездов, чтобы те участки пути,
которые поезд проходит в одном направлении в светлое
время суток (сбч утра до б ч вечера), он проходил
бы в обратном направлении в темное время (с 6 ч
вечера да 6 ч утра)? Скорость движения поезда
одинакова в обоих направлениях.
3. СОСНОВЫЕ И ДУБОВЫЕ ШПАЛЫ
4 1
Вес сосновой шпалы 27-^кг, а дубовой 45 γ до.
Вес 10 доставленных шпал равен 384 -ε кг. Сколько
среди втих шпал сосновых и сколько дубовых?
Эта задача опубликована в одном журнале. Об·
щий путь решения подобных задач «на смещение»
хорошо известен. Однако нельзя ли в данном случае
несколько упростить вычисления и, может быть, даже
решить задачу в уме?
β

4. РАЗНОСЧИК ТЕЛЕГРАММ
Разносчик телеграмм сказал:
— Я сегодня поднимался пять раз на десятый
этаж и десять раз на пятый этаж. Если бы я не
спускался каждый раз после вручения телеграммы вниз,
а все время поднимался бы вверх, то я поднялся бы
на ... этаж!
На какой же этаж?
б. СКОЛЬКО ЖИЛЬЦОВ В ДОМЕ?
Сколько жильцов в нашем доме, состоящем из
трех четырехэтажных корпусов, если известно, что
1) в корпусе А на 39 человек больше, чем в
корпусе В, но на 77 человек меньше, чем в корпусе С;
2) из каждых 13 детей 7 учатся;
3)к 1 мая домоуправление закупило 1400
художественных открыток; более половины было передано
другому домоуправлению; оставшиеся открытки были,
розданы жильцам нашего дома — каждому по одной;
4) взрослых на 20% больше, чем детей;
5) если в первые этажи приедет 17 новых жиль,·?
цов, из вторых этажей в третьи переедет 11 жильцов»
а из четвертых этажей уедет 15 жильцов, то во всех
четырех этажах жильцов будет поровну.
6. ПЯТИЗНАЧНЫЕ ЧИСЛА
Сколько имеется различных пятизначных чисел,
среди цифр которых имеется хотя бы одна пятерка?
7а. ЦЕЛЫЕ ЧИСЛА, У КОТОРЫХ КАЖДАЯ СЛЕДУЮЩАЯ
ЦИФРА БОЛЬШЕ ПРЕДЫДУЩЕЙ
В числе 12 578 каждая следующая цифра больше
предыдущей. Сколько всего существует таких целых
чисел? Попытайтесь сначала дать приблизительный
ответ, а потом приступите к вычислениям.
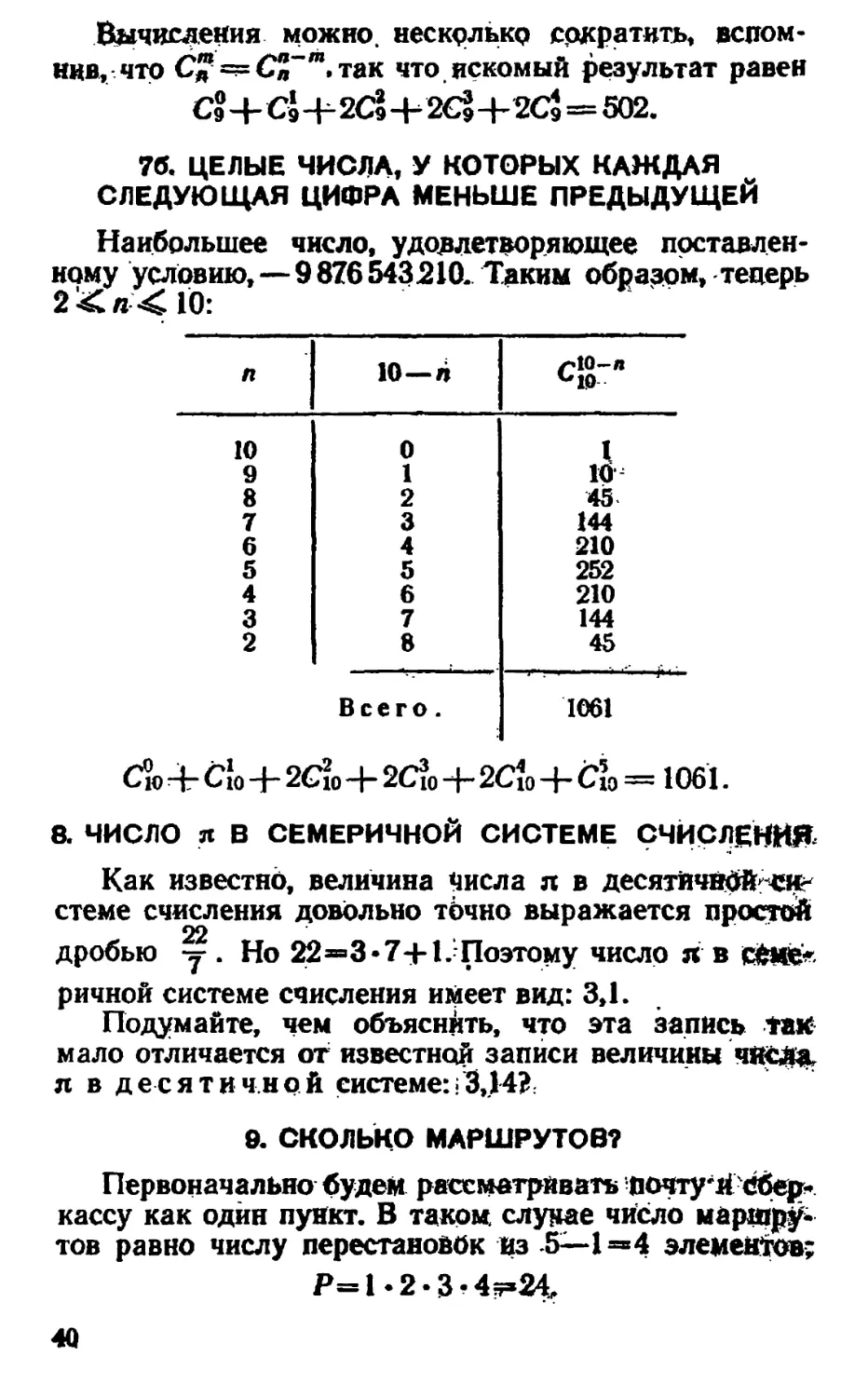
76. ЦЕЛЫЕ ЧИСЛА, У КОТОРЫХ КАЖДАЯ СЛЕДУЮЩАЯ
ЦИФРА МЕНЬШЕ ПРЕДЫДУЩЕЙ
Условие — «обратное» предыдущей задаче: иначе
говоря, теперь цифры не возрастают, а, наоборот,
убывают.
6

8. ЧИСЛО π Β СЕМЕРИЧНОЙ СИСТЕМЕ
СЧИСЛЕНИЯ
Напишите приближенное значение числа η в
семеричной системе счисления.
9. СКОЛЬКО МАРШРУТОВ?
Сегодня воскресенье, мне нужно побывать в, пяти
местах: в аптеке, химчистке, в библиотеке, сберкассе
и на почте. Для того чтобы найти самый короткий
маршрут, я решил до выхода из дома сравнить все
возможные варианты.
Сколько мне нужно сопоставить вариантов
маршрута, если почта и сберкасса расположены в одном
здании и находятся в значительном удалении от всех
остальных пунктов и от моей квартиры?
10. ТОРГОВЕЦ
Некий торговец каждый год увеличивает на одну
.огреть свое состояние, уменьшенное на 100 фунтов,
которые ежегодно затрачивает на свою семью. Через
§гри года он обнаруживает, Что его состояние
удвоилось. Спрашивается, сколько у него было денег вна-
-чале?
(Задача Ньютона из «Всеобщей арифметики» 1707 г.)
11. ТАКСИ
Четыре пассажира, которым нужно было ехать в
одном направлении, наняли такси. Когда первый
доехал до цели своей поездки, он заплатил ах рублей —·
.четверть суммы, показанной счетчиком. Через
некоторое время вышел второй; он уплатил ту же сумму,
.что и первый пассажир (at рублей), и еще одну треть
с^ммы, на которую увеличилось показание счетчика
досле выхода первого пассажира, — всего а^ рублей.
Далее вышел третий пассажир, уплативший ту же
£умму, что и виорой пассажир (т. е. аг рублей), и еще
половину суммы, на которую увеличилось показание
счетчика после выхода второго пассажира, — всего
щ рублей; наконец, вышел и четвертый пассажир; он
уплатил ту же сумму, что и третий (в3 рублей), и,
•кроме того, всю ту сумму, на которую увеличилось
f

показание счетчика после выхода третьего
пассажира, — всего л* рублей.
Требуется определить расстояние, пройденное
.такси, если за включение счетчика и за каждый
километр уплачено (строго по счетчику — условие
обязательное!) по 10 копеек.
12. ДВА СПЛАВА
Имеется два сплава серебра и золота: в одном
серебра 40%, а в другом — серебра в l·^- Раза меньше,
чем золота.
Сколько надо взять того и другого сплава, чтобы
получить 17-? кг сплава, в котором количество золота
относится к количеству серебра как 3:2?
13а. НА РЕКЕ
От пристани А вниз по течению реки отправился
катер (его· собственная скорость—12 кле/ч).
Одновременно от пристани β навстречу ему вверх по течению
реки (скорость течения — 2 м/сек) отправилась лод*
ка, собственная скорость которой равна 300 м/мин.
Встреча произошла у пункта С, отстоящего от А на
16 км, в 16 ч 45 мин.
Когда и где произошла бы встреча при скорости
течения 3 м/сек?
136. ДВА КАМНЯ
Камень отпустили свободно падать с высоты h см.
Одновременно с уровня земли навстречу ,ему бросили
с начальной скоростью v0 см/сек второй камень.
Ускорение силы тяжести — g см/сек2 Когда они
встретятся?
14. КРАЖА НА ТЕПЛОХОДЕ
В 12 «30 мин к капитану прогулочного теплохода,
шедшего вверх по. реке, влетела миссис Смит,
— Υ меня украли из каюты коробку с
драгоценностями!
1

— Подробнее?
— Горничная принесла мне кофе в 10 ч 30 мин,
после, чего она пробыла несколько минут во второй
комнате каюты, в которой находились мои
драгоценности. Затем она была в той же комнате за несколько
минут до 12 часов.
— Кто еще был в вашей каюте?
— Моя подруга миссис Браун приходила ко мне
играть на рояле, но, конечно, она вне всяких
подозрений. В 12 ч 05 мин ее игру прервал стюард, который
попросил ее выйти, пока он не исправит настольную
лампу. В 12 ч 10 мин я внезапно возвратилась в
каюту, обнаружила, что стюард рылся в моих вещах,
и начала его отчитывать. Это. продолжалось до 12 ч
25 мин, когда возвратилась моя подруга. Тут я
обнаружила пропажу и побежала к Вам.
Капитан установил, что от 12 ч 10 мин до 12 ч
20 мин горничная получала в кладовой белье. Но
никто не мог сказать, где она была от 12 ч 00 мин до
12 ч 10 мин и от 12 ч 20 мин до 12 ч 30 мин.
Так как капитан никак не мог прийти к какому-
либо определенному выводу, он в 13 ч 30 мин
повернул теплоход на обратный курс. Неожиданно в 13 ч
45 мин теплоход поровнялся с каким-то ящиком,
плывшим по воде. Миссис Смит узнала в нем свою
коробку от драгоценностей. Тогда капитан сразу
установил, что драгоценности были похищены кем?
(Из журнала «Наука и жизнь».)
16. АВТОБУС
Между пунктами А и В курсирует с постоянной
скоростью автобус, останавливающийся только л этих
пунктах (на 3 минуты). Известно следующее.
В 9 ч 08 мин автобус прошел мимо
промежуточного пункта С в направлении к В.
В II ч 28 мин автобус вышел из пункта А.
В 13 я 16 мин автобус пришел в пункт В.
В 14 ч 04 мин автобус прошел С в направлении
к Я.
Сотрудник сберкассы,, находящейся на дороге АВ,
во время обеденного перерыва сидел на крыльце
U

54 лш«; за это время мимо него автобус не прошел
ни разу.
Сотрудник почты, вышедший на улицу всего на
20 мин, видел автобус дважды.
Как расположены на АВ пункт С, сберкасса и
почта?
16. КУРЬЕРЫ
Курьеры из мест А и В двигаются, каждый
равномерно, но с разными скоростями, друг хдругу
навстречу. После встречи для-прибытия к месту
назначения одному нужно было еще 16, а другому —9
часов. Сколько времени требуется тому и другому для
прохождения всего пути между А и В?
[Задача Л. Керрола.)
17. РАЗДЕЛИТЬ ЧИСЛО 22 НА ТРИ ЧАСТИ
Разделить число 22 на три части при условии, что
если прибавить к одному из полученных чисел 0,5, от
другого отнять 1,5, а третье умножить на 2,5, то по?
лучатся одинаковые результаты.
(«Математическое просвещение», № 6, стр. 32.)
18. СЕМЬ УРАВНЕНИЙ С СЕМЬЮ НЕИЗВЕСТНЫМИ
Решите приведенную ниже систему семи линей*
ннх уравнений с семью неизвестными:
jc+ll//4-2l2-|-3U+41if4-51v + 61a»=f 77
2*+12#+22;г-г-32*-И2а4-52'0-г-62я>= 84
3^-|-13ί/-Γ-23ζ4-33/ + 43ίί+53ί; + 63α>= 91
4jc-H4i/ + 24z-[_34/-4-44w + 54'u-b64w= 98
5jc-h 15ι/ + 25ζ4-35/+45ίί+ 55<ϋ + 65да= 105
6χ+ 16</-Ь26г+36/+46и-г-56х>-Н66«» = 112
7χ -Η 1 Ту -Ь- 27ζ 4- 37/+47и + 57<υ -h 67ад = 119
Т9. ТРИ БЕГУНА
Три бегуна А> В и С участвуют в беге на 100
ярдов. Когда А финишировал, В находился в 10 ярдах
позади него, а С был в 10 ярдах позади Bt когда В
10

финишировал. На каком расстоянии находился С от
At когда А финишировал? Предполагается, что они
бежали с постоянной скоростью.
(Эта задача приведена в книге Т. Саати
«Математические методы исследования операций».)
20. ТУРИСТ
Турист, идущий из-деревни на железнодорожную
станцию, пройдя за первый час 3 кл, рассчитал, что
если он будет двигаться с той же скоростью, то
опоздает к поезду на 40 мин. Поэтому остальной путь он
проходит со скоростью 4 км/ч и прибывает на
станцию за 45 мин до отхода поезда. Каково расстояние
от деревни до станции?
Эта задача помещена в сборнике задач по
математике повышенной трудности; там же приведено ее ре-
jc 2 χ — 3 3
шение, при помощи уравнения-о-—·§-= \-\—^—1~Т'
где χ — искомое расстояние.
* Решите эту задачу арифметически.
21. ПЛОТ И МОТОЛОДКА
Из пункта А в пункт В по течению реки отплыл
плот. Через 2,4 часа вдогонку за плотом направилась
моторная лодка (ее собственная скорость — 20 км/ч).
Лодка догнала, плот и сразу же поплыла обратно в
пункт А. Через 3,6 часа моторная лодка прибыла в
пункт А, а плот в пункт В. Определить скорость
течения реки:
(Конкурсная задача.)
22. БАССЕЙН
В пустой бассейн начинают равномерно подавать
воду (ν л/сек). Как только та или иная часть воды
попадает в бассейн, начинается ее испарение; оно
происходит равномерно, ч через т секунд от данной
частицы уже ничего не остается. Требуется найти w —
количество литров воды в бассейне через t сек.
Попробуем рассуждать так. С одной стороны, за
t сек в бассейн поступит vt л воды.
11

С другой стороны, вода испаряется. Количество
испарившейся воды подсчитываем исходя из
следующих соображений. Количество испаряющейся в
каждой данный момент воды прямо пропорционально
количеству воды," находящейся в этот момент в
бассейне. Так как по условию каждую секунду в
бассейн поступает по ν л, соответственно увеличивается и
интенсивность испарения, а именно она
увеличивается каждую секунду на величину — л/сек* т. е. «при^
рост» испарения составляет ~ л/сек2.
Интересующий нас процесс оказался аналогичным
процессу равномерно переменного движения,
описываемому, как известно, так:
$ = „/ + 1^2,
где s — путь,
/ — время,
ν — начальная скорость,
а — ускорение.
Для нашего случая w—rvt — γ·^·*2) (литров).
Рассмотрим численный пример. Пусть ν —20 л{сёк
и Λΐ=10 сек.
Тогда«>=20/ — ~t* = (20t — ί2) л.
Вычислим отдельные значения
*=0 2 б (сек)
w=0 36. ν 84 (л).
Как будто бы все в порядке: количество воды в
бассейне увеличивается.
Продолжим таблицу.
t^= 8 10 И (сек)
w= 96 100 99 (л).
Количество воды в бассейне'стало уменьшаться.
Что же будет дальше? -
t== 15 20 (сек)
w— 75 О (л).
12

Через 20 сек воды в бассейне не стало вовсе! Но
эта же нелепо! Ведь в бассейн каждую секунду
поступает по 20 литров воды! Где же ошибка?
23а. ТРИ МУХИ
Во дворе стоит один шест высотой в два метра; на
его верхнем конце сидят три мухи; ровно в четыре
часа все три мухи разлетаются в разные стороны.
В котором часу все три· мухи окажутся в одной
плоскости?
(Известная задача.)
236. ЧЕТЫРЕ МУХИ
Во дворе стоит один шест высотой в два метра;
ровно в три часа с его верхнего конца вылетают в
разных направлениях четыре мухи; каждая из них
летит прямолинейно с постоянной скоростью, а именно!
первая*—50 м/мин, вторая — 60 mJmuh, третья —
70 м/мин, четвертая — 80 лЦмин. Через 9 минут все
четыре мухи оказались в одной плоскости. Когда еще
они окажутся э одной плоскости?
24. ЛЕСТНИЧНЫЙ МАРШ
На рисунке показан разрез лестничного марша.
Требуется вычислить — высоту одной ступени
(«подступенка») и ширину одной ступени («проступи»).
20. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Даны Два отрезка; известно, что один из них —«
основание, а другой — боковая сторона
равнобедренного треугольника; однако не известно, какой из этих
13

отрезков — основание, а какой— боковая сторона.
Можно ли по этим данным построить равнобедренный
треугольник?
26. В ДЕТСКОМ САДУ
Крышки столиков для детского сада имеют форму
равнобочной трапеции. Благодаря этому, поставив их
вплотную друг к другу, можно
образовать круг (точнее,
кольцо). А если каждый второй
из этих столиков повернуть йа
180°, образуется еилсйннойряд
(столики стоят в одву яинню);
в этом рлучаё "линия
соприкосновения крыше* двух
смежных столиков надбавлена то
г-^г—,,^,- ,л в одну, то в друг^^з«^ону.
\^>*\:-lh■·Ίλ-ττΐX Определите направдеш^Чво-
бодной стороны 1фсл$диего
(на рисунке крайнего правого) столика: будет .яи
она параллельна свободной стороне первого (левого!
столика?
27. ДВА КУБА
Куб, изготовленный из первого сплайа, удельный
вес которого равен 2,4, весит 41-^- г.
Сколько весит куб, изготовленный из второго
сплава, удельный вес которого равен 3,6, если известно^
что поверхность описанной, вокруг второго куба сферы
в 4 раза больше поверхности сферы, описанной во*
круг первого куба.
28а. ДОСТРОИТЬ РАВНОБОЧНУЮ ТРАПЕЦИЮ
£ f Даны три точки: А, В и С-г-верой^
ны равнобочной трапеции. Достроить
трапецию.
14

286. ТРИ ТРАПЕЦИИ
Даны три точки Dlt Dt и Da —три вершины трек
равнобочных трапеций. Известно, что ft
остальные три вершины у этих трапе- ♦' .А
циЙ-^сфщие (А, В и С). Достроить
трапеции.
29а. ТРИ ДИСКА · *
Три диска равномерно вращаются вокруг трех
параллельных осей Α, β и С (направления вращений
указаны на рисунке стрелками). До начала вращения
з дисках было просверлено отверстие О.
Дано: Л5=53 мм; ВС=34 мм; С4=40 мм;
г0=32 мм; г&=25 мм.
ωΑ=7,5 об/мин; ωΒ=10 об/мин; (йс^&ооб/мин.
Через какое время отверстия совпадут вновь?
296. ДВА ДИСКА
Два диска равномерно вращаются вокруг двух па·
раллельных осей А к В. Угловые скорости: gu=*
«=5 об/мин; ωΒ^Ι^ об/мин. До начала вращения в
дисках было просверлено сквозное отверстие О. Через
какое время отверстия совпадут вновь?
30. РАВНОСОСТАВЛЕННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
Дан четырехугольник ABCD. Требуется разбить
его на четыре части и составить из них равновеликий
laiy четырехугольник KLMN, дйа параметра которого
(например, две стороны, либо два угла, либо один
угол и одна сторона) даны.
15

81, ДВА СТОЛБА И ТЕНИ
В одной книге помещен рисунок, на котором
изображены два вертикальных столба и их тени на
горизонтальную плоскость; по этим данным требуется
найти, положение 1) источни-
| ка света (лампочки, фонаря)
В и 2) его «основания» (т. е.
V^ проекции источника света на
^' горизонтальную плоскость).
Решите эту задачу и ответьте на дополнительные
вопросы:
1) Существенно ли, что столбы вертикальны?
2) Существенно ли, что плоскость, на которую
надают тени, горизонтальна?
3) Все ли приведенные на рисунке данные
являются необходимыми?
32. КОНУС ЛЕЖИТ НА ПЛОСКОСТИ
Прямой круговой конус лежит на горизонтальной
плоскости, касаясь ее но образующей SA. Конус
перекатили без скольжения по плоскости вокруг его
вершины S на 360°, и он возвратился в исходное
положение. Каков должен быть этот конус, чтобы и
образующая SA также возвратилась в исходное
положение?
33. ДВЕ ОКРУЖНОСТИ
Две окружности произвольных размеров касаются
в точке Λί. Через Μ прове-
'-*-—^4 Дена произвольная секу»
>~~Sf/\—* щая АМВ (А и В—г точки
/ д/ ) на данных окружностях) .ι
/ /К^_У Доказать, что касательные
V / ] к окружностям, проведен-
"-*-ib^^/ ные в точках Л и В, парал-
34. ТРИ КВАДРАТА
Витя провел через вершины квадрата ABCD
четыре прямые, параллельные его диагоналям, и полу-:
чил описанный квадрат. После некоторых измерений
и вычислений он сказал:
16

— Площадь квадрата ABCD численно равна
периметру описанного вокруг него квадрата!
Сережа соединил середины сторон того же
квадрата ABCD и получил вписанный квадрат. После
некоторых измерений и вычислений он сказал:
— Площадь квадрата ABCD численно равна
периметру впйсанногов него квадрата!
Как же так? Ведь в обоих случаях квадрат ABCD
один и тот же; следовательно, и площадь одна и та
же, а описанный и вписанный квадраты — разные, и
периметр описанного квадрата в два раза больше
периметра вписанного. Не могут же две разные
величины быть одновременно равны третьей! В чем тут
может быть дело?
36. КОЛЬЦО НА ТРЕХ НИТЯХ
К крюку 5 на трех нитях подвешено кольцо
радиуса R (АВ—ВС—СА). Если все три нити одной
длины (SA—SB=SC=*L)t то плоскость кольца
горизонтальна; так, например,
подвешивают абажуры. Если же не все
нити имеют одинаковую длину
(например, SA-SB*=L=t=SC=l)\ то
плоскость кольца уже не будет
горизонтальной.
В каких пределах может
изменяться / при данных L и /??
Какой угол образует плоскость
кольца с горизонтальной
плоскостью при 1ФЬ?
Можно ли задать R и L произвольно или между
ними существует зависимость? Если да,, то какая?
86. КОРОБКА И НИТЬ
Длинная прямоугольная коробка сечением аХЬ
перевязана по середине нитью длиной 2 (а+Ь); звенья
нити перпендикулярны соответствующим ребрам
коробки. Обозначим общие точки нити и ребер через Л 0,
В0, Со и Pti зафиксируем одну из точек, скажем,
точку Ао, Возьмем вторую, более длинную нить
(длиной /); ее можно оттянуть по поверхности коробки
17

так, что звенья ломаной AqBCDAq уже не будут
перпендикулярны соответствующим ребрам коробки.
Требуется: I) определить, на какое наибольшее
расстояние от точки В0 можно удалить точку В? То
же самое для точек С и С0, а также для точек D
и D0.
2) Доказать, что получающаяся при этом
ломаная A0B'CD'A0 — плоская.
37. ПАРКЕТАЖ
На рисунке показан паркета ж: заполнение
плоскости (без пропусков и наложений) одинаковыми
плоскими фигурами. Очевидно, что каждый из
элементов любого такого паркетажа может быть
совмещен с любым другим элементом того же паркетажа
путем поступательного движения
(параллельного переноса).
В основе всякого паркетажа
лежит одна из двух схем: 1. Парал*
лелограммы (в частных случаях —
I———ΓΊ—I
I J Ι Ι Ι ι
L_J L_l I
прямоугольники, квадраты). 2. Шестиугольники с
параллельными сторонами (в частном случае —
правильные шестиугольники).
Если разрешить поворот фигур на 180°, то парке-
таж может быть образован также и произвольными
треугольниками.
Итак, из правильных фигур только трех-, четырех»
и шестиугольники образуют паркетаж.
Раздвинем эти треугольники (четырехугольники,
шестиугольники) так, чтобы между фигурами обра*
зовались полосы шириной d.
Какова должна быть ширина полос d, не занятых
фигурами, чтобы правильные треугольники
(соответственно четырехугольники, шестиугольники)
занимали бы 1/п всей площади?.
18

88. СТОЛ И СКАТЕРТЬ
Круглый стол накрыт квадратной скатертью из
тонкой ткани (центр квадрата совпадает с центром
круга).
Ла сколько углы скатерти ближе к полу, чем
середины ее сторон?
89. СИММЕТРИЧНЫЕ ТОЧКИ
1. На плоскости даны три произвольные точки А,
В и С, не лежащие на одной прямой; берем на той же
плоскости любую точку К и находим точку L,
симметричную К относительно А; затем строим точку Λί,
симметричную L относительно В, далее строим
точку Ν, симметричную Λί относительно С, и точку Я,
симметричную N относительно А. Наконец, строим
точку w, симметричную Ρ относительно В.
Требуется доказать, что точки Q и К симметричны
относительно С. (Задача была предложена на одной
из математических олимпиад.)
2. Докажите, что аналогичный предыдущему
результат будет и в том общем случае, когда при
построении каждой нечетной (т. е. первой, третьей и
пятой) симметричной точки (а именно точек L; N
и Q) мы будем
откладывать от центра
симметрии отрезок,
в φ (φ > 1) раз мены
ший расстояния
предыдущей точки до
центр» симметрии, а
при построении
каждой четной (т. е.
второй, четвертой и
шестой) симметричных
точек (а именно, Λί, Ρ и /С) откладывать от центра
симметрии отрезок, в φ раз больший расстояния
предыдущей точки до центра симметрии:
КА МС РВ LB ΝΑ Ι
= <р и — -
Яс«?»^--
ВМ
АР
<Р
AL — ΤΝ ~~ BQ
w, ^ ОС 1 , ν
В этом случае должно быть -5^ =^(см· рисунок).
19

40. СКЛАДНОЙ СТАКАНЧИК
Сколькими (и какими) параметрами определяются
форма и размеры складного стаканчика?
(Аналогично устроены складные антенны портативных
радиоприемников.)
41. МНОГОГРАННИК
Точки А, В и С находятся на трех ребрах куба,
сходящихся в его вершине О. ОА**ОВ=ОС=а
(ребро куба /.> а). Через точки А и В,
принадлежащие одной из граней куба, проведена пара плоско*
стей, перпендикулярных этой грани и параллельных
диагонали 00' куба. Аналогично проведена пара
плоскостей через точки θ и С и через точки С и А. В
результате три пары параллельных плоскостей отсекают
часть куба. Какова форма этого многогранника и
каков его о*бъем?
42. РАЗВЕРТКИ МНОГОГРАННИКОВ
На рис. а показан многоугольник, составленный из
четырех равносторонних треугольников; это — раз*-
вертка тетраэдра.
На рис. б показан многоугольник, составленный из
восьми равносторонних треугольников; это —
развертка октаэдра.
На рис. β показан многоугольник, составленный
из двадцати равносторонних треугольников; это-*-
развертка икосаэдра.
На рис. г показан многоугольник, составленный из
двенадцати равносторонних треугольников. Это
тоже развертка многогранника, правда, не столь из-
20

вестного, как тетраэдр, октаэдр или икосаэдр.
Вычертите фигуру развертки на листе бумаги, вырежьте ее
и попытайтесь склеить многогранник.
4а ГОДОВЫЕ СЛОИ
Распилив бревно (под каким-либо углом к его
оси), вы увидите рисунок годовых слоев древесины.
Что это за кривые (на языке геометрии) ?
44; ТРИ ПАРАЛЛЕЛЕПИПЕДА
1. Общий объем трех параллелепипедов равен и.
Найти объем каждого из них, если известно, что
их длины относятся как λί:λ2:λ3ί
» ширины » » μ1: μ2 : μ3,
» высоты » » Vj: ν2: ν3.
2. Та же задача, но длины относятся как а:Ь:с,
ширины » » Ь:с:а,
высоты » » с.а\Ъ.
4В. МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ
Рассмотрим выпуклый четырехугольник общего
вида (т. е. такой, что все стороны его имеют разную
длину). Пусть его стороны а, Ь, с и d — стержни, a
вершины τ—Шарниры. Такой шарнирный
четырехугольник, изменяемый при сохранении размеров сто·,
рон, может принимать различные формы. Требуется
охарактеризовать (описать) все четырехугольники,
которые может образовать данный ^^
Шарнирный «чётырехзвенник». у^\шГ]
46. УСЕЧЕННЫЙ ЦИЛИНДР / Ы|МИ I
Прямой круговой цилиндр (дна-, I шШШш
метр оснований'-— D) усечен непа-' 1>^|Шщ| I
раллельно основанию. Через, его «ШптН
ось произвольным образом прове- lUjpu^y^J
дена плоскость; оказалось, что oib —I—■
ределяемые ею образующие ци- U D }\
лнндра равны Н. и. А. Требуется нарисовать разведу
боковой поверхности усеченного цилиндра. и
вычислить ее ллощадь.
21

47. ЛИСТ БУМАГИ
Возьмите лист бумаги и сложите его пополам,
перегнув большую сторону, затем еще раз, и т. д. При
каждой такой операции длина меньшей стороны
останется неизменной, а длина другой стороны —
большей — уменьшается ровно вдвое.
Какова должна быть форма листа, для того чтобы
его половина, четверть, восьмая, шестнадцатая и т. д.
имели одну и ту же форму?
48. РУЛОН
На круглый стержень (барабан) диаметра d
плотно намотана лента; при « (п — число целое) слоях
(витках) наружный диаметр рулона — D. Известно,
что, если разрезать рулон по радиусу, проходящему
через начало и конец
ленты, лента
распадается на я кусков,
длины которых
образуют арифметическую
прогрессию. Как
нужно разрезать каждый
из η кусков на две
части, чтобы длины
получившихся 2/1
кусков образовали новую
арифметическую
прогрессию?
Для упрощения принимаем, что каждый оборот
(виток) ленты образует кольцо (т. е. полый круговой"
цилиндр), длина развертки которого определяется по
его среднему диаметру (см. рисунок).
49а. РАЗБИЕНИЕ ПРЯМОУГОЛЬНИКА
Одна сторона прямоугольника* содержит а целых
единиц, а другая — 6. Через концы единичных
отрезков проведены прямые, параллельные
соответствующим сторонам прямоугольника. Таким образом, дан-
ньпТ прямоугольник разбит на аЬ единичных квадрата.
Сколько всего образовано квадратов двумя
системами параллельных отрезков?.
22

496. РАЗБИЕНИЕ ПРЯМОУГОЛЬНОГО
ПАРАЛЛЕЛЕПИПЕДА
Аналогичный вопрос в отношении прямоугольного
параллелепипеда размерами а-Ъ>с, разбиваемого на
кубы.
49В. РАЗБИЕНИЕ «-МЕРНОГО ПАРАЛЛЕЛЕПИПЕДА
Та же задача для /ι-мерного параллелепипеда,
ребра которого имеют длины а, 6, с, .,,, ft, /, т.
бОа. В РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
ВПИСАНЫ КРУГИ
1. В равнобедренный треугольник вписан круг;
затем вписан второй круг, который касается первого
круга, а также двух боковых сторон треугольника;
далее вписан третий круг и т. д., и т. д.
Площадь каждого следующего вписанного круга
меньше площади предыдущего. Таким образом,
площади вписанных кругов — ряд убывающих чисел.
Предел, к которому стремится сумма членов этого ряда,
назовем «суммой площадей всех вписанных кругов».
Требуется найти круг, площадь которого равна
сумме площадей всех вписанных кругов.
Решить задачу вычислением и построением.
2. В равнобедренный треугольник вписан круг,
затем второй круг и т. д. Пусть основание треугольника
остается неизменным, а высота будет изменяться.
(Изменится ли при этом отношение суммы площадей всех
вписанных кругов к площади треугольника? Если да,
то в каком случае это отношение уменьшается?
Ответьте на эти вопросы, не производя никаких
вычислений и не пользуясь найденными в
предыдущей задаче соотношениями.
606. В КОНУС ВПИСАНЫ ШАРЫ
В прямой круговой конус - (высота — Я, диаметр
основания — d) вписан шар. Далее вписал шар,
касающийся всех образующих конуса и первого шара,
и т. д. Объем каждого последующего шара меньше
23

объема предыдущего. Таким образом, объемы шаг
ров — ряд убывающих чисел. Предел, к которому
стремится сумма членов этого ряда, назовем «суммой
объемов всех вписанных шаров».
Требуется найти радиус шара, объем которого
равен сумме объемов всех вписанных в конус шаров.
61а. ПОЯСА КРУГОВ ВОКРУГ ЯДРА
Возьмем круг, который назовем «ядром». Вокруг
этого «ядра» расположим пояс из кругов того же
диаметра так, чтобы каждый из этих кругов касался
ядра й двух соседних кругов пояса. Аналогично расг
положим вокруг первого пояса второй пояс из
кругов того же диаметра и т. д.
Сколько кругов во всей фигуре при наличии η
поясов?
616; ЯДРО —ТРИ КРУГА
То. же условие, что и в. предыдущей задаче, но
ядро состоит из трех одинаковых кругов, каждый из
которых касается двух других. Какова формула в
этом случае?
52. СЕМЬ ДРОБЕЙ
Расположить в возрастающем порядке
приведенные ниже дроби:
5. * 67 · 449 · 491 ' 613 -*■ 653 И 787 *
63. БРОНЗОВЫЙ ЛЕВ
«Я — бронзовый лев, две струи вытекают из моих
глаз, одна^из моего рта и еще одна из ноги. Мой npaj
вый глаз наполняет бассейн в два дня; мой левый,
глаз—в три дня; а моя нога — в четыре дня; шести
дней достаточно, чтобы наполнить его из моего рта.
Если сразу потекут все струи из. глаз, и из ноги, н
изо рта, во сколько часов наполнится бассейн?»
(Греческая задача. См/Е. С Б е ρ е з а н с к а я,
Методика арифметики, 1955 г., стр. 432.)
-Решить графически.
24

64. СВИДАНИЕ
А и В уславливались по телефону* о встрече.
— Давай, встретимся сегодня на улице т\
— Хорошо! Между переулками Ρ и Q*
— Отлично! На той стороне, где кино и ларек,
«г- В восемь ноль-ноль.
— Ну, не нужно «ноль-ноль».
-*- Ладно:- * я согласен подождать, но не более
.15 минут.
-г- И я не стану ждать более четверти часа:
сегодня большой мороз.
•г- Договорились! Между 8.00 и 8.15 я буду
маршировать от угла мимо кино и ларька и обратно;
длина квартала, мне известна: 260 метров.
— И я там буду между 8.00 и 8.15. До свидания!
— До свидания!
А и В пришли в назначенное время в назначенное
место; оба добросовестно маршировали от угла мимо
кино и ларька и обратно, но так и не встретились.
Как Зто могло случиться?
бб. ТРИ АВТОМАШИНЫ
Из пункта А через равные промежутки времени
отправляются по одной и той же дороге в пункт С
три автомашины. Через некоторое время всё они
одновременно проезжают пункт В, находящийся между
А и С. В пункт С первая машина прибывает' через
час после второй. Третья автомашина немедленно по
прибытии в С поворачивает и едет назад и в 40 км
щ С встречает первую автомашину. Определить
скорость первой автомашины, если.расстояние от Б до С
равно 120 км.
.Эта задача была предложена на вступительных
экзаменах по математике и а
механико-математическом факультете Московского университета (1963 г.).
попробуйте решить ее как арифметическую задачу.
56. ДВА ВЕЛОСИПЕДИСТА
I. Два велосипедиста выезжают из пунктов Ли В
одновременно навстречу друг другу. Каждый из них,
доехав до второго пункта, немедленно поворачивает
25

обратно и возвращается в исходный пункт. Первая
встреча произошла в 5 км от А, вторая — в 3 км от
В. Найти расстояние АВ.
(X математическая олимпиада в г. Киеве· «Успехи
математических наук», т. X, вып. 4(66).)
2. Условие задачи — то же. Но коль скоро
велосипедисты встретились дважды, предположим, что они
продолжают и дальше циркулировать между А и В,
и поставим дополнительные вопросы:
1) Когда произойдет третья, четвертая и т. д.
встречи?
2) Где будут происходить дальнейшие встречи?
3) Может ли велосипедист (1-й или 2-й),едучииз
А в В (или из £ в Л), встретить другого
велосипедиста дважды?
4) Может ли велосипедист (1-й или 2-й), едучииз
А в В (или из В в А), не встретить другого
велосипедиста ни разу?
57. ДВА ВКЛАДЧИКА
Два вкладчика положили в сберкассу одинаковые
суммы. Первый из них взял вклад по истечении т
месяцев и получил ρ рублей, а второй, взяв вклад по
истечении η месяцев, получил д рублей. Сколько
каждый из них положил в сберкассу и сколько
процентов выплачивает сберкасса?
(П. С. Моденов, Сборник задач по математике,
1954 г., зад. № 236.)
Решить графически".
58. БЫКИ НА ЛУГУ
На одном лугу площадью в fe акРа паслось
12 быков. За 4 недели они съели всю траву, которая
первоначально была на лугу, а также и ту, которая,
вырастала в течение этих 4 недель. На другом лугу
площадью 10 акров пасся 21 бык; эти быки за 9
недель съели траву, имевшуюся первоначально, а также
и ту, которая вырастала за эти дни. Сколько быков
нужно пустить на луг, площадью 24 акра, чтобы они
при тех же условиях могли прокормиться 18 недель?
(Задача Ньютона.)
26

69. ДВЕ ЛОДКИ
Из двух пунктов А и В, расположенных вдоль
течения реки, навртречу друг другу выходят
одновременно две моторные лодки, с одинаковой
собственной скоростью. Если бы первая лодка увеличила свою
скорость на χ км/ч, а вторая на столько же
уменьшила ее, то первая лодка прибыла бы в В раньше на
столько же часов, на сколько позже прибыла бы
вторая в А. Приняв скорость течения за единицу,
найти х,
60. ОТЕЦ И ТРОЕ СЫНОВЕЙ
Число лет отца на 5 больше суммы лет всех троих
его сыновей. Через десять лет отец будет вдвое
старше старшего сына, через двадцать лет он будет вдвое
старше второго сына, через тридцать лёт—вдвое
старше младшего сына. Узнать, сколько в настоящее
время лет отцу и каждому из трех его сыновей.
(Из книги П. Обера и Г. Папелье, Упражнения
по. элементарной алгебре, Учпедгиз, 1940, зад. № 52.)
61. ПОКУПАТЕЛЬ И ТРИ ПОСТАВЩИКА
Покупатель должен закупить 12 тонн продукта,
имеющегося в трех колхозах, и доставить его в город;
в его распоряжении автомашины только на 40 часов
работы. Известно следующее:
Колхоз
I
II
III
Количество
продукта
(в тоннах)
10
6 !
Цена
продукта
(в рублях
за тонну)
4
3
1
Время на
доставку
(в часах на
тонну)
1
4
3
Как следует распределить закупки между
колхозами, чтобы общий расход (денег) был бы
наименьшим?
27

62. ЧЕТЫРЕ ПУТЕШЕСТВЕННИКА
ч
Четырем лицам, отправляющимся из пункта А в
пункт Bt предстоит путь в 39,6 км. Они располагают
автомобилем, скорость которого равна 36 км/ч, но в
котором имеется только два места, кроме места
шофера; двое- из этих лиц молоды и проходят пешком
по 6 км/ч, двое других, постарше, могут
проходить только по четыре километра в час.
Уславливаются, что автомобиль доставит двух старших до
пункта Af, расположенного на пути АВУ от которого
они закончат путешествие пешком. Автомобиль;
возвратившись немедленно за двумя молодыми
путешественниками, отправившимися пешком, встретит их в
пункте Ρ и доставит их в В. Требуется определить
положение пунктов Ρ и Μ на пути АВУ зная, что все
путешественники, одновременно отправившись из Л,
одновременно же прибыли в В.
.(П. Обер и Г. Папелье, зад. № 125 на
"составление уравнений первой степени.)
еа сто петухов, кур и цыплят
Один крестьянин пошел на базар продавать кур.
Вдруг повстречался с ним император и спрашивает
крестьянина, сколько стоит его товар.
— Петух — пять! грошей, курица — три гроша, а
три цыпленка — один грош, — ответил крестьянин.
Император подумал, потом приказал:
— Принеси мне завтра сто петухов, кур и цыплят»
но столько отбери каждой птицы, чтобы все они
вместе стоили сто грошей. Если не исполнишь моего
приказания, я снесу тебе голову.
Крестьянин угрюмым возвратился домой.
■*— Не беспокойся отец, я помогу тебе, — сказал
отцу его восьмилетний сын и быстро решил задачу.
На другой день крестьянин явился к императору.
Император разгневался, что крестьянин решил за·
дачу, и приказал ему:
-т- Завтра снова принеси мне сто петухов, кур н
цыплят, но не столько каждой птицы, сколько
сегодня, и чтобы они все вместе опять стоили сто гро*
шей.
Сын снова помог отцу.
28

Когда крестьянин исполнил;» это приказание,
император еще больше рассердился и в третий раз
приказал крестьянину принести сто петухов, кур и
цыплят, но не .столько каждой птицы» как прежде, и
чтобы cum все вместе опять стоили сто грошей.
Мал>чнк и на ётот раз оказался умнее,
императора.
Определите, сколько петухов, кур и цыплят
приносил крестьянин в каждом случае.
(Старинная задача.)
64а; ТРИ ТЕЛА
Три тела движутся.по одному и тому же
направлению и начинают свое движение от одной и той
Яре точки со скоростями, равными соответственно 4,
гиб см/сек. Второе тело двинулось с места на два
Часа позже первого. Через сколько времени после
момента отправления второго тела должно двинуться
третье, чтобы одновременно со вторым догнать
первое? Решить при помощи^графика.
646, ДВА ТЕЛА
Из точки А в одном направлении одновременно
начали движение два тела: первое со скоростью
?v§TMl мин, второе — с меньшей скоростью; оба тела
Движутся равномерно ускоренно: ускорение второго —
""•'θ
%?f л/мин2. Через 1 ч 37 мин 39 сек второе тело
нагнало первое. Известно, что в тот момент, когда
скорости тел сравнялись, расстояние между ними со·
ставляло 379 м. Когда второе тело опередит первое
Йа 1137 л?
66. ПОЕЗД
Т1оезд проходит расстояние от города А до
города В за 10 ч 40 мин. Если бы скорость поезда была
на 10 км/ч меньше, то он пришел бы в В на 2 ч 8 мин
позже. Определить расстояние между городами и
скорость поезда.
(«Математика в школе», 1954, -№ 1, стр. 70.)
29

66а. ТРИ СОСУДА
В трех сосудах находится одинаковая жидкость
в неравных количествах. Если половину содержимого
(по объему) одного сосуда разлить поровну в два
другие, затем половину содержимого, оказавшегося
в другом сосуде; разлить поровну в два другие, и
после этого половину содержимого третьего сосуда
разлить поровну в два другие, то во всех сосудах
окажется жидкости поровну, а именно по 16 л.
Сколько было литров жидкости в каждом сосуде
вначале?
(К. У.^ Шахно, Пособие по математике для
поступающих в высшие учебные заведения, I960, зад.
№ 181.)
ββσ. пять разбойников
Пять разбойников отняли у прохожего кошелек,
наполненный дукатами. Самый сильный из них взял
81 дукат, каждый из четырех остальных
неодинаковую сумму.' Вследствие неравного раздела возник
спор, и пришедший в то время атаман приказал,
чтобы тот, кто взял больше всех, удвоил каждому из
остальных число его дукатов и чтобы то же самое
сделал затем захвативший второе по величине
количество дукатов, потом захвативший третье, четвертое
и пятое. В результате оказалось, что каждый из пяти
разбойников получил одно и то же число дукатов.
Узнать, сколько дукатов было в кошельке и сколько
из них каждый захватил вначале.
(Задача Желена — Г. Η. Π ο π о в, Сборник
исторических задач по элементарной математике, 1938, зад.
№ 490, стр. 62.)
67. С УДВОЕННОЙ СКОРОСТЬЮ
Некто отправился из пункта А в пункт В с
определенной скоростью; пройдя ровно половину всего
пути, он удвоил свою скорость и прибыл в В.
Во второй раз он первую половину всего времени
шел с той же начальной скоростью, а вторую
половину всего времени — с удвоенной скоростью.
Очевидно, что во второй раз он шел с удвоенной
30

скоростью дольше, чем в первый раз, и поэтому
затратил на весь путь меньше времени. Насколько
меньше?
68. КАТЕРА НА РЕКЕ
Из пункта А каждый час вверх против течения
реки отходит катер; одновременно из пункта В в н и з
по течению реки также отходит катер. Оба рейса
продолжаются целое число часов. Каждый катер,
плывущий вверх против течения реки, встречает по пути
семь катеров, вышедших из В. (не считая тех двух
катеров, которые он встретит в Л и в В). Сколько
катеров встречает каждый катер, плывущий вниз по
течению реки, если скорость катеров в стоячей воде
вдвое больше скорости течения?
69. КАТЕР И ПЛОТ
Из пункта О одновременно отплыли вниз по
течению реки катер и плот. Пройдя 1З-3 км, катер
повернул обратно и, пройдя еще 9-g км, встретился
с плотом. Требуется найти собственную скорость
катера, если известно, что скорость течения — 4 км/ч.
,(Из сборника задач по математике для подготовки
к приемным испытаниям.)
70. КОГДА НАЧИНАЮТСЯ СЕАНСЫ
Проезжая мимо кинотеатра, некто успел заметить
только^часы (но не минуты!) начала четырех сеансов:
1-й сеанс 12 ч мин.
2-й сеанс 13 ч мин.
7-й сеанс 23 ч мин.
8-й сеанс 24 ч мин.
Требуется по этим данным установить, когда
начинается каждый из восьми сеансов.
Предполагается, что
1) интервалы между началом каждых двух
последовательных сеансов (т. е. продолжительность одного
сеанса и одного перерыва) одинаковы;
2) сеансы могут начинаться в я часов и Ът
минут, где η и т — числа целые.
31

71. ДВА НОМЕРКА И ТРИ СТУДЕНТА ·
Два студента пришли в столовую пообедать; они
сдали свои пальто и шапки гардеробщику, выдавшему
им два номерка; оба номерка первый студент поло·
жил в свой карман. В конце обеда к ним подошел
третий студент-математик и завязался общий
разговор; однако второй студент должен был уйти на
лекцию, поэтому он попросил у, первого свой
номерок; так как первый студент не знал, какой из двух
номерков чей, он сказал: «Придётся тебе взять оба
номерка, получить свои вещи и возвратить мне мой
номерок». Второй согласился и взял оба номерка; но
тут математик сказал: «Тебе, может быть, не приг
дется возвращаться, если ты«.» Как вы думаете, что
посоветовал математик?
72а. ОРЕХИ
В трех мешках η орехов; какова вероятность того,
что во всех трех, мешках поровну орехов?
726. МУКА
В трех мешках я килограммов муки; какова
вероятность того, что в каждом из трех мешков по я/3
килограммов муки?
7а АВТОБУС И ТРОЛЛЕЙБУС
У остановки плакат: «Интервалы движения:
автобус — б минут; троллейбус — 8 минут».
К остановке подошли двое.
1 В этой и следующих «теоретико-вероятностных» задачах
от читателя не предполагается никаких специальных знаний,
кроме чисто интуитивного представления о «вероятности*
события, согласующегося со следующим определением:
вероятность события, имеющего η «равновероятных» исходов, равна
отношению числа «благоприятных» исходов (при которых данное
событие наступает) m к п, то есть р-» ?—*. Вероятность «досто-
вернете»события (наступающего щ>и.любом исходе) равна — =1,
вероятность «невозможного* события —нулю.
32

— Сколько в среднем приходится ждать
пассажиру?
— Если бы был только автобус, то среднее время
ожидания равнялось бы 6:2—§ мин; если бы был
только троллейбус, то среднее время ожидания—
8: 2=*4 -мйн-, но так как пассажир может поехать
либо автобусом, либо троллейбусом, то средняя' про-
доЯжительность ожидания —^— = о -^ мин.
'*' — Нет! Это неверно! Надо считать иначе.
Наименьшее общее кратное б и 8 — 24. За каждые 24
минуты будет 24 : 6= 4 рейса автобуса и 24 : 8=3 рейса
троллейбуса. Всего, следовательно, за. 24 минуты
будет 4+3=*7 рейсов. В таком случае, между каждыми
двумя рейсами, в среднем 24: 7=3 -ψ минуты, и сред-
3 5
яяя продолжительность ожидания Зу: 2 = 1уминуты.
Кто прав? (Конечно, предполагается точное
соблюдение интервалов.)
74. СИГНАЛЫ
В любые моменты времени промежутка Τ равно-
возможны поступления в приемник двух сигналов.
Приемник будет «забит», если разность *ю времени
между этими сигналами будет меньше L Определить
вероятность того, что приемник будет забит.
Эта задача приведена во многих книгах по теории
вероятностей (см., например, «Руководство для
инженеров по решению задач теории вероятностей», под
редакцией А. А. Свешникова, Судпромгиз, 1962), так
как аналогично решается широкий круг задач.
Например:
«Двое условились встретиться в определенном ме-
jCTe* между 12.00 и 12.00+Г; пришедший в усровлен-
Jioe место ждет / минут, после чего уходит. Какова
вероятность встречи, если момент прихода каждого
]равновозможен в любой момент условленного
интервала?»
«Два теплохода должны подойти к одному и тому
же причалу. Время прихода обоих теплоходов
независимо и равновозможно в течение данных суток.
аз

Время стоянки каждого теплохода у причала равно L
Определить вероятность того, что теплоход,
подошедший вторым, обнаружит, что причал занят».
Эта задача решается так. Обозначим через χ и у
моменты поступления сигналов в приемник (время
отсчитывается от начала интервала Т).
τ Областью возможных значений х, у
является квадрат со стороной Т, т. е.
площадью Т2.
Приемник будет забит, если \х—·
—y\^t, т. е. если точка (лг, у)
принадлежит заштрихованному шестиугольни-
ку (см. рисунок), ограниченному
сторонами квадрата и прямыми х—y=t и
x—y=—t. χ
Площадь шестиугольника «S= Τ2 — 2-j (Τ— (f =
«7*—(Г—*)2.
Искомая вероятность /? = -jT=l —(l —ψ\ .
Решите эту же задачу для случая трех сигналов
;(трех теплоходов и т. п.).
76. ВВЕРХ ПО ЭСНАЛАТОРУ
Вечерами я работаю в библиотеке; кончая (в
разное время), выхожу, еду в метро, затем поднимаюсь
при помощи эскалатора вверх и, наконец, еду
автобусом, который отходит каждые пять минут.
Однажды автобус отошел то что называется «перед
самым носом» и я себя ругал: «Если бы я не просто
стоял на эскалаторе во время подъема, а прошагал
бы несколько ступенек вверх, я бы вышел на 10
секунд раньше и не потерял бы пяти минут на
ожидание». Поэтому я решил впредь не стоять пассивно на
эскалаторе, а идти по нему с тем, чтобы...
Ответьте на следующие вопросы:
Если я буду каждый раз выгадывать на подъеме
по 10 секунд, то буду ли я в среднем меньше ждать
на остановке?
Буду ли я приезжать домой» раньше? Если да, то
на сколько именно?;

РЕШЕНИЯ
1. ОДИНАКОВЫЕ ЦИФРЫ
Первые девять ответов ясны сразу:
1.1.11 6.6.66
2.2.22 7.7.77
3.3· 33 о. о. 88
4.4.44 9.9.99
5.5.55
Кроме того, есть еще четыре ответа!
11. 1.11
1.11.11
11.11.11
22. 2.22
Всего, следовательно, тринадцать раз в течение
каждого столетия.
2. ПОЕЗД ИДЕТ ТУДА И QBPATHO
*,, шесть часов вечера; поезд, идущий из А в В,
пройдет следующий участок в темное время.
Следовательно, поезд, идущий из В в А, должен пройти
этот участок в светлое время. Отсюда следует, Что
поезда должны встречаться в 6 ч утра и в 6 ч
вечера.
Поэтому:
На сколько позже (раньше) 6 ч утра (6 ч вечера)
поезд выходит из А (приходит в В), на столько же
часов раньше (позже) 6 ч утра (6 ч вечера) парный
поезд должен возвращаться в А (отправляться из B)t
0. При таком расписании мимо любого пункта
между А и В поезд одного направления будет проходить
в светлое время, а поезд другого направления — в
темное время суток.
35

З..СОСНОВЫЕ И ДУБОВЫЕ ШПАЛЫ
Воспользуемся тем фактом» что вес дубовой
шпалы резко отличается от веса сосновой шпалы (он
примерно в полтора раза больше).
Если бы все шпалы были- сосновыми, обшиб вес
всех 10 шпал был бы около 270 кг.
Если бы все шпалы были дубовыми, общий вес
всех 10 шпал был бы около 450 кг.
Если бы тех и других шпал было бы поровну, то
общий вес 10 шпал был бы «средним между 270 и
450 кг>, т. е. около 360 кг, что примерно на 24 кг
меньше, чем в Действительности. По-видимому, одну
сосновую шпалу надо заменить дубовой; в таком
случае:
сосновых шпал 5 — 1—4 (штук);
дубовых шпал 5 + 1 *=»6 (штук).
Полученный в результате «прикидок» ответ
необходимо проверить точным- подсчетом.
Сосновые шпалы: 274/5*4=1084-31/б=Н11/5 (кг)
Дубовые шпалы: 45уй· 6=2704-3 .= 273 (кг)
384У5 (кг)
Верно!
Конечно, могло случиться, что наше
предположение оказалось бы не совсем точным; тогда пришлось
бы его откорректировать в соответствии с
полученным результатом.
4. РАЗНОСЧИН ТЕЛЕГРАММ
Расчет ясен без комментариев:
5.(10—1) = 45
"*~10-( 5—1) = 40
85
85+1=86
Всего, следовательно, разносчик телеграмм
поднялся бы на 86-й этаж.
Любопытно, что во Франции, где наш второй этаж
считается первым (нижний этаж называется «rez-de*

chaussee» — на уровне мостовой), расчет был бы
другим:
5,10=50
-1-кЬ 5—50
100
Иначе говоря, парижскому разносчику телеграмм
«пришлось бы» подняться на 100-й этаж (а по на·
щему, московскому, счету — на 101-й!).
б. СКОЛЬКО ЖИЛЬЦОВ В ДОМЕ?
Взрослых на 20% больше^ чем детей;
следовательно, на каждые 5 детей приходится 1,2 · 5=6 взрослых;
общее число жильцов делится на 5+6= 11.
Из каждых 13 детей 7 детей учатся;
следовательно, число детей делится на 13. Так как число детей
делится на 13, то и общее число всех жильцов,
которое в 11/5 раз больше числа детей, также делится
на 13 (числа 13 и 5 так же,· как 13 и 7, не имеют
общих множителей).
Из полученного следует, что число жильцов
кратно И-· 13=1*143.,
Если в первые этажи приедет 17 новых жильцов,
а из четвертых этажей уедет 15 жильцов» то общее
число жильцов в доме увеличится на +17—15=+2
и будет кратно 4; следовательно, действительное чи-
ело жильцов не кратно 4, но кратно 2 (приведенное
в условии число И не имеет никакого значения).
Обозначим количество жильцов в корпусе А через
А; тогда во втором корпусе А — 39 жильцов, а в
третьем А +77; всего жильцов в доме: А+{А — 39) +,
+ (А+77)=ЗЛ+38; следовательно, число жильцов не
делится на 3.
Общее число жильцов меньше, чем 1400:2 =?700.
Итак, число жильцов равно 143-2=286.
(143-3 исключается, так как число жильцов не
кратно 3;
143-4 исключается, так как число жильцов на
кратно 4;
143 · 5 исключается, так как 143 · 5=715 > 700. у
37

β. ПЯТИЗНАЧНЫЕ ЧИСЛА
Приступим к решению задачи: станем
подсчитывать количество пятизначных чисел — таких, среди
цифр которых имеется хотя бы одна пятерка.
Интересующие нас пятизначные числа содержат
либо одну пятерку, либо две, три, четыре, либо,
наконец, пять пятерок.
Подсчитаем количество чисел в каждой из этих
пяти групп. Разыскиваемые нами числа могут
начинаться либо цифрой 5, либо одной из остальных
восьми значащих цифр; в соответствии с этйм>
разбиваем каждую группу ка две подгруппы.
Обозначим:
α — любая из девяти цифр: 0, 1, 2„ J3, 4, 6, 7, 8 или 9.
β— любая из восьми цифр: 1, 2, 3, 4, б, 7, 8 или 9.
I группа — пятизначные числа, содержащие одну
пятерку.
Подгруппы:
Первая цифра 5. Первая цифра не 5.
Вид числа Количество Вид числа Количество
таких чисел таких чисел
δαααα 9·9· 9-9 —6561 βΰααδ )
βααοα
βαδαα
βοΌαα
II группа—пятизначные числа, содержащие две
пятерки.
Подгруппы:
Первая цифра 5.
Вид числа Количество,
таких чисел
4·8-9·9-9 =
==23 328
Первая цифра не 5.
Вид числа Количество
таких чисел
5ααα5 '
5αα5σ
5α5αα .
55ααα J
Ι 4·9·9·9=
= 2916
βαα55 1
pa5a5
βαδδα
β5αα5 ]
ρ5α5α Ι
β55αα |
6-89.9 =
= 3888
III группа ... Однако этот подсчет становится
скучным. Нельзя ли получить ответ на поставленный
вопрос более простым: путем?
38

Искомый ответ мы получим гораздо быстрее, если
сначала решим несколько иную задачу: «Сколько
имеется таких пятизначных чисел, которые не
содержат ни одной пятерки?» Это числа вида
βαααα. Количество этих чисел равно 8·94=52488.
Все же остальные пятизначные числа содержат хотя
бы одну пятерку, а так как общее количество всех
пятизначных чисел — 90000, то количество
пятизначных чисел, содержащих хотя бы одну пятерку, равно
90000—52488=37512.
Заметим, что таково же количество пятизначных
чисел, содержащих хотя бы одну единицу, либо одну
двойку, тройку,.,., девятку.
7а. ЦЕЛЫЕ ЧИСЛА, У КОТОРЫХ КАЖДАЯ
СЛЕДУЮЩАЯ ЦИФРА БОЛЬШЕ ПРЕДЫДУЩЕЙ
Прежде всего заметим, что наибольшее число,
удовлетворяющее поставленному условию, это число
123456789. Это единственное девятизначное число,
в котором каждая следующая цифра больше
предыдущей. Все остальные числа такого рода мы получим
из- числа 123456789 вычеркиванием из него одной или
двух,...., или, наконец, семи цифр (ясно, что два —
это наименьшее число цифр у чисел, для которых
имеет смысл говорить о выполнении интересующего
нас условия).
Итак, для определения количества л-значных чисел,
удовлетворяющих поставленному условию, следует
для каждого целого я(2<л^9) вычеркнуть 9 — η
цифр из девяти, что можно сделать С?~я способами:
η
9 —
8 —
7 —
6 —
δ—
*4 —
3— !
2 —
В
9 — η
0
1
2
3
4
5
6
7
сего. i
-с9
1
ί 9
36
84
126
126
84
36
502

Вычисления можно, нескольвд сократить,
вспомнив, что С£==С1Гт.так что яскомый результат равен
Cj+Cj+2Cl-K2Ct-H2C5=502.
76. ЦЕЛЫЕ ЧИСЛА, У КОТОРЫХ КАЖДАЯ
СЛЕДУЮЩАЯ ЦИФРА МЕНЬШЕ ПРЕДЫДУЩЕЙ
Наибольшее число, удовлетворяющее
поставленному условию,—9 876 543210. Таким образом, теперь
2£*<ί0:
λ
10
9
8
7
6
5
4
3
2
10—η
о
ι
2
3
4
5
6
7
8
Всего.
/-10-я
1
ιό
45
144
210
252
I 210
144
ι 45
1061
C?o^-Cio+2Cio+2C?o+2Cjo+C;o= 106Ϊ.
а ЧИСЛО π В СЕМЕРИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ
Как известно, величина Числа π в десятично*
системе счисления довольно точно выражается простой
дробью у . Но 22=3· 7+1. Поэтому число я в icMfc
ричной системе счисления имеет вид: 3,1.
Подумайте, чем объяснить, что эта запись так
мало отличается от известной записи величины числа,
π в десятичной системе: ·3,.14?:
θ. СКОЛЬКО МАРШРУТОВ?
Первоначально будем рассматривать почтут
сберкассу как один пункт. В таком слудае число
маршрутов равно числу перестановок из 5—1=4 элементов;
Ρ»1·2·3'4^-24,
40

А так как в каждом из этих вариантов возможны
два подварианта (раньше почта, либо раньше
сберкасса), то мне нужно сравнит!» 24· 2—48 вариантов·
ιά торговец
Вет решение Ньютона. «Чтобы решить βοπρος, за-
метьте, что в нем содержатся в скрытом виде неко-
Тэръгё предложения, которые все должны быть
выявлены н выражены.
Словесно
Алгебраически
У торговца имеется состояние
1U3 которого он в первый год
затрачивает 100 фунтов
.Остаток он увеличивает на
-здву треть
До второй год он опять
тратит 100 фунтов
Й остаток увеличивает на одну
треть
β третий год он опять тратит
100 фунтов х
И остаток также увеличивает
ца одну треть
Причем оказывается вдвое
богаче, чем был вначале
χ
jc—100
*_ι<»+Λ=ι™,
иди
4ж —400
3
4*—400
3
100, или
4* —700
4jc—700 . 4* —700
3 + 9
16* —2800
иди
9
16* —2800
или
9, т
16*—3700
9
16* — 3700 , 16* — 3700
9 ^27
64*—14 800
или w
64*—14 800
27
= 2*
Таким образом, получаем уравнение
64* —14800
—w
решая которое, мы найдем х.
— 2х,
41

Умножьте уравнение на 27, и вы получите
64л:—14800 = 54*,
вычтите из обеих частей 54*, и останется
10*—14800=0, или 10х=* 14800;
разделив на 10, вы найдете, что х=1480. Таким
образом, состояние торговца вначале, а также его
последующая прибыль и доход были равны 1480 ф>»
Вот другое решение.
Если бы торговец ничего не тратил и его состояние
увеличивалось бы каждый год на одну треть, то в
* 4
конце каждого года оно равнялось бы у того, что
было вначале. Пусть первоначально у торговца было
χ фунтов. В таком случае в конце третьего года
л /4\3 64 0 10
у него должно было оказаться I-^ J ·* = -§fχ = 2 т^χ.
По условию в конце 3-го года состояние лишь
удвоилось; разница составляет 2^*— 2лг=^-лг.
С другой стороны:
в первый год торговец
во-первых, истратил 100 ф.
во-вторых, недополучил процентов с этой
суммы "з · 100 ф.
всего потерял -§ · 100 ф.
Во второй год он потерял столько же, да еще одну
треть (недополученные проценты за потери 1-го года),
т. е. всего-^ · -g- · 100 φ.
4 4 4
Наконец, за третий год он потерял "g"" "Ϊ "5" ^0Φ»
4 /4\2
а всего- за три го^а— Ъ'^-кЫ) >V0Qjr
42

+(^ioo=4(i+i+f)-ioo=t^±^.ia.=
4 10
= 2f · 37 · 100 = ^ л; откуда
11. ТАКСИ
Задача решается в уме: всего все четыре
пассажира уплатили αι+02+03+^4 рублей; следовательно,
искомое расстояние равно (10(oi^fl2+_«3+fl4) — \]кмщ
12. ДВА СПЛАВА
Состав всех трех сплавов одинаков.
13а. НА РЕКЕ
Момент встречи совершенно не зависит от
скорости течения; поэтому и при скорости течения 3 м/сек
встреча произойдет в 16 ч 45 мин.
Место же встречи переместится на
расстояние, которое пройдет вода в реке при увеличении
Скорости течения на 3—2=1 м/сек за время движе-
16
идя катера и лодки до встречи, т. е. за 2>3600 ~
*2Ί ϊοοδ~"
«* 16:19,2-0,833 ... (часа) =50 (лш«)=3000 сек, а
именно на 3000· 1=3000 м^З км.
Итак, встреча произойдет на расстоянии 16+3=
—19 км от Л.
136. ДВА КАМНЯ
В данной задаче рассматривается система
«камень— камень», и нас интересует только их
поведение друг относительно друга (а не относительно
земли); поэтому величина ускорения силы тяжести и
даже вообще ее наличие или отсутствие нам
совершенно безразличны.
Итак, между двумя камнями расстояние h см;
один из них движется навстречу другому со скоро-
43

стью Όο 'см/сек. Встреча произрйдет через f^h'z'Pu
(сек).
Если бы нас интересовал не момент, а место
встречи камней, то было бы необходимо располагать
данными о поведении системы в целом; если вся
система движется с ускорением g см/сек\ то место
встречи можно определить по положению свободно
падающего камня через t сек. За это время он про-
летит расстояние -игт»*. е, будет находиться на вы-
соте А —%-.
Эта задача в сущности аналогична задаче на
течение, где система перемещалась равномерно.
14. КРАЖА НА ТЕПЛОХОДЕ
Авторское решение учитывает влияние течения —
изменение скорости теплохода относительно берегов
в зависимости, от того, идет ли qh по течению или
против.
Но в этой задаче течение не играет абсолютно
никакой роли. С момента, когда коробка была
выброшена в воду, теплоход удалялся от нее. С. 13 м 30 мин
до 14 ч 45 мин, т. е. 1 час 15 минут, теплоход шел на
сближение с коробкой. Следовательно, и удалялся он
от нее тоже 1 ч 15 мин. Поэтому коробка была
выброшена в 13 ч 30 мин минус 1 ч 15 мин = 12 ч
15 мин. В этот момент из трех подозреваемых-могла
выбросить коробку только миссис Браун.
16. АВТОБУС
Обозначим:
продолжительность хода на участке Л С через/д (мин)%
Тогда продолжительность· хода в одну сторону
равна tA+tB мин, продолжительность, одного, поду*
рейса t = (tA+*в+3) мин.
Автобус прошел мимо пункта· С в направлений В
в 9 ч 08 мин и в .14 ч Ы мин\ следовательно» за 14 Ч
04 мин — 9 ч 08 мин = 296 мин ой сделал целое число
44

рейсов (χ), т. е. 2х полурейсов, т. е. 2xf=296 мин,
откуда *=296:2х=148:х.
Автобус вышел из пункта А в 11 ч 28 мин; затем
он пришел в пункт В в 13 ч 16 *ш«. Следовательно,
за 13 ч 16 жин — И «28 мин = 108 жим плюс 3 *ем<
стоянки в А (или в В), т. е. за 1084-3=111 мин, он
сделал нечетное число полурейсов, т. е. (2y + \}t=*\\\\
откуда
ί =
итак, t^^^w^Y
Отсюда 3*=8у+4.
Так как χ и у целые, то χ кратно четырем.
Составим таблицу:
X
У
t
0
1
2
оо
4
1
37
8
Г 2*
»i ι
12...
4...
121
з 1
Значения х=0 и х=*8 отпадают, так как они дают
недопустимые значения у. Значение *=12 (равно, как
и последующие) отпадает, так как при *=12
продолжительность одного полурейса t —12 -g мин, а
продолжительность одного полного рейса 2
12-^ —
= 24тгИ«ш; между тем, мимо сберкассы за 54
минуты автобус не прошел ни разу; следовательно,
jf~4; #=1; /=»37 мин; ^+^=34 мин.
Автобус прошел мимо пункта С в направлении
к В в 9 ч 08 лш«, а затем вышел из пункта А в 11 Ч
28 мин. Следовательно, за 11 ч 28 мин — 9 ч
08 мин = 140 лш« автобус
прошел участок СВ> затратив на это tB мин,
стоял в β 3 мин,
сделал (2р+1) полурейсов, затратив 37 (2р+1) мин.
Итого. (*B+j2-37p-H0) мин — 140 jk««.
49

Далее. Автобус вышел из пункта А в 11 ч 28 мин
и затем в 14 ч 04 мин прошел пункт С в
направлении к В.
Следовательно, за 14 ч 04 мин — 11 ч 28 ли« =
«156 мин автобус прошел участок Л С, затратив на
это tA мин, и сделал 2q полурейсов, затратив на это
37 · 2д мин; отоюда следует, что
*А+37 · 2<7+*в+37 · 2<7-К40= 140+156=296;
37 · 2(р-К<7) =256 — 34=222;
Составим таблицу:
1 р
1 q
1 tA = 156—74?
1 'д = 100—74p
I ' °
1 3
— 66
140 ι
Ι ι
2
8
26 ,
1 2
1
82
— 48 1
3 1
0 1
156 1
— 122 j
Итак, единственно возможное решение: р=1, Ц—%
откуда /л=8 мин и /в=26 мин.
Следовательно, АС: СВ=8 :26; АС « 0,235 АВ.
Теперь относительно почты. На каком наибольшем
расстоянии от конечного пункта автобус пройдет
дважды в продолжении 20 мин? 20 — 3=17; 17:2=
=8,5; 8,5: 34=0,25.
Следовательно, почта находится где-то в одной из
двух крайних четвертей дороги АВ.
Наконец, о сберкассе. 54 — 3=51; 51:2=25,5;
25,5:34=0,75. Таким образом, о сберкассе можно
сказать то же, что и почте. Условие задачи не дает
возможности установить, находятся ли почте и йбе£к
касса в одной и той же крайней четверти дороги ASt
или в разных. Возможно даже, что сберкасса и почта
находятся в одном здании; в этом случае сотрудник
почты был на улице не в то время, когда сотрудник
сберкассы сидел. на. крыльце.
16

16. КУРЬЕРЫ
1. В книге «Рассказы о решении задач» И. Я. Деп-
мана (1957 г.) приведено следующее решение.
«Обозначим скорости курьеров через и и с, а
время от начала движения до встречи
курьеров'—через /.
Первому курьеру для прохождения всего пути
нужно f-Иб часов, второму /+9. Расстояние между
точками А и В можно выразить тремя различными
способами:
(f+l6)w, (t+9)v и f(w+t/).
Имеем равенства:
(f+16)и=t(u+v) или 16и=/а или <=-—,
о*.
(t+9)v=*(«+» или 9v=*tu или * = —.
Отсюда
1fi и л с ι*2 9 и 3
10 ν и ■ "Р"- 16 » ϋ ~Τ·
Подставив найденное значение в первое
выражение для /, имеем
. Первому курьеру для прохождения всего
расстояния необходимо 12+16=28 часов, второму—124-9=
=21 час.
2. Аналогичная задача приведена в «Сборнике
алгебраических задач повышенной трудности»
Ε. Μ. Пржевальского (Учпедгиз, 1941 г.).
«Л и В отправляются одновременно навстречу друг
другу из городов Москвы и Тулы, и каждый из них
идет все время с одинаковой скоростью. А в χ часов
проходит от Москвы до Тулы, а В в у часов от Тулы
до Москвы. В пути они встречаются за т часов
перед приходом А в Тулу и за η часов перед приходом
В в Москву. Показать, что х2 : у2=т : я».
Там же дано следующее решение.
«Пусть расстояние между Москвой и Тулой α
километров; тогда -£ и -£■ — скорости А и В. Когда они
χ у
47

встретились, то А прошел χ— m часов, а В прошел
у— η часов; следовательно, χ — т=*у— п.
К этому времени А прошел у (х — т) километров
а В прошел —(у — п) километров; поэтому
У
y(x—m)-\-j(y — n) = a,
или у(х — т)-\-х(у — п) — ху;
отсюда
(х+у) -(х — т)=хуу (1)
{х+у).(у-п)=ху, (2)
так как χ—т и у—η равны.
Из уравнения (1): х2~т(х-\-у)\ из (2): у2=п(х+
•+у); отсюда
х*: у2=т : л*.
3* Итак, подтверждено, что
отношение т: η
(отношение продолжительности движения А от
момента встречи до прибытия в свой конечный пункт
к продолжительности движения В от того же момента
встречи до прибытия в свой конечный пункт)
равно отношению- х2 : у2
(отношению квадрата времени, затраченного А на
весь путь, к квадрату времени, затраченного В на
весь путь).
Каково физическое происхождение «квадрата
времени» в данном случае? Чтобы понять это,
представим отношение двух квадратов в виде квадрата
отношения, а именно:
х2:у*=*{х:у)2.
Отношение- (х : у) имеет определенный физический
смысл — это отношение скоростей. Почему этот
фактор оказывает влияние на отношение т: η дважды?
Пусть, .для определенности, χ > у.
\) А проходит все расстояние за χ часов, afl-
за у часов, т. е. скорость А меньше скорости В в х:у
4&

раз. Поскольку оба вышли одновременно, то А
прошел до встречи расстояние, в χ: у раз меньшее,
чем Б.
2) После встречи А пройдет столько, сколько В
прошел до встречи, а В пройдет столько, сколько
прошел А; следовательно, А пройдет в χ: у раз больше,
чем В.
3)* Итак, после встречи А должен пройти в χ: у
раз больше, чем В, передвигаясь в χ: у раз
медленнее, чем В; следовательно, т: я= (х: у) · (х: у) =
=х2: у2.
Теперь значительно упростились вычисления и в
полученном ответе отчетливо видно его
происхождение.
4. Задачу Керрола можно решить и так.
Обозначим через t время, прошедшее от момента
выхода курьеров до момента их встречи. После
встречи А за т часов пройдет то расстояние, на которое В
затратил t часов, а В за η часов пройдет то
расстояние, на которое А затратил t часов; следовательно:
скорость А / я
скорость В т t '
откуда /== Утл = уг16-9^=12 («О,
ГА== 12 + 16^=28 (*), ГБ=12-Ь9 = 21 (ч).
5. Во втором варианте эту задачу интересно фор.-
мулировать в общем виде, т. е. требовать доказать,
что
т:п = (х:у)2
и / — γ7ηή.
(Если сначала доказать, что έ = γτηη, то
у* (/+/?)* (Vrnn + nf n
или, проще,
скорость А t__ Утл __ -%f*L \
скорость В л т' ~г" V т /
49

17. РАЗДЕЛИТЬ ЧИСЛО 22 НА ТРИ ЧАСТИ
Итак, сумма трех неизвестных чисел равна 22.
Если прибавить к первому из них 0,5, то сумма
также увеличится на 0,5.
Если отнять от второго из них 1,5, то сумма тоже
уменьшится на 1,5.
Если проделать обе эти операции, то сумма будет
равна не 22, а 22+0,5 — 1,5=21.
Теперь условие задачи звучит так: «Сумма трех
'чисел равна 21, первые два числа одинаковы, а третье
в 2,5 раза меньше каждого из них». Отсюда следует,
что третье число в 2-2,5=5 раз меньше суммы
первых двух чисел. Иначе говоря, если сумма первых
двух чисел — пять частей, то третье число — одна
часть всей суммы, т. е. числа 21.
Разделим число 21 на 1+5=6 равных частей:
21 : 6=3,5. Итак, третье число равно 3,5.
Первое и второе измененные числа равны
3,5-2,5=8,75.
Первое число: 8,75 —0,5=8,25;
Второе число: 8,75+1,5=10,25.
18. СЕМЬ УРАВНЕНИЙ С СЕМЬЮ НЕИЗВЕСТНЫМИ
Замечаем, что в каждом уравнении свободный
член равен коэффициенту при у, умноженному на 7.
Следовательно, система имеет решение:
x=z=t—u=v=w=0t у=7.
Это же решение будет и при любых других
значениях коэффициентов при х, г, t, ut υ и ш, за
исключением одного случая, когда эти коэффициенты
пропорциональны коэффициентам при у, в этом случае
будет не семь независимых уравнений, а лишь одно
уравнение с семью неизвестными, т. е.
неопределенное уравнение, имеющее бесчисленное множество
решений.
19. ТРИ БЕГУНА
В тот момент, когда А финишировал, т. е.
пробежал 100 ярдов, В находился в 10 ярдах позади него»
т. е. пробежал 100—10=90 ярдов; следовательно.
60

скорость В равна 0,9 скорости А; аналогично,
скорость С равна 0,9 скорости В\ следовательно,
скорость С равна 0,9 · 0,9=0,81 скорости А; в таком
случае, за то время, что А пробежал 100 ярдов, С
пробежал лишь 0,81 · 100=81 ярд, т. е. отстал от А на
100 — 81 = 19 ярдов. Таков ответ на поставленный
вопрос.
20. ТУРИСТ
Из условия следует:
1. Если турист повысит свою скорость с 3 до 4 км/ч,
то он выгадает 40-^45=85 (мин).
2. Если турист повысит свою скорость с 3 до 4 км/ч,
то он будет затрачивать на каждые 3 км не 60 мин,
а лишь-£·60=45 (мин), т. е. за каждый час хода со
скоростью 3 км\ч он будет затрачивать лишних
60 — 45=15 (мин).
Из 1. и 2. следует, что если бы турист сохранил
свою скорость (3 км/ч}, то с того момента, как он
решил повысить свою скорость до 4 км/ч, до момента
его прихода на станцию прошло бы 85 j 15=5-^ часа;
за это время (при скорости 3 км/ч) он прошел бы
5|-3=17 (км).
Всего, следовательно, от деревни до станции
3+17=20 км.
21. ПЛОТ И МОТОЛОДКА
1. Автор задачи дает следующее решение.
Пусть скорость течения реки равна χ км/ч,
расстояние от пункта А до встречи с плотом у км. Лодка
проплыла это расстояние по течению реки за <^\х %
а плот — ч. Составляем первое уравнение: -£■ —
и х
— 204-лг==^,^> Плот с места встречи с лодкой до
пункта В проплыл еще (3,6*—у) км, а лодка, возвращаясь
обратно, проплыла до пункта А еще у км. Принимая
во внимание, что эти расстояния они проплывали за
у
одно и то же время, имеем второе уравнение:-я?2—r=s
3,6*—у м-~х
Я

Таким образом, мы получаем систему двух уравне-,
ний с двумя неизвестными
(У У _ 12
Ι χ 20+* ~~ 5
{ 1*
I т*—У
I 20—χ χ
или
f 3*2+ 60*=25у
\ —9jc2-t-180;c = 5%
Разделив одно уравнение на второе, получим:
180—9х ~~ 2 ·
или 5*=20, откуда х=4.
Ответ: 4 км/ч.
2. Заметим, что можно было бы уравнивать не
промежутки времени, а расстояния.
По условию,
1) путь, пройденный плотом до встречи,
2) путь, пройденный мотолодкой до встречи и
3) путь, пройденный мотолодкой после встречи,
равны друг другу. Обозначим через ζ время,
прошедшее от момента выхода лодки до момента встречи.
Тогда:
(2,4+z)x=z(2Q+x) = (3,6 — 2,4 — 2).(20 — χ).
Откуда:
%4x+zx я 20z+z*=24—1,2*—20z+zx;
2,4*=20г=24 — 1,2* — 20z;
Z = ^JC
— 20 '
l,2x=24 — 40z=24 — 4,8*;
-6*=24; ж=4 (км/ч).
Это решение короче первого, в нем нет
квадратных уравнений.
3. Теперь попытаемся решить эту задачу, исходя
из «анализа событий» на реке.
По условию, до момента выхода лодки плот плыл
по течению .2,4 часа со скоростью χ км/ч, т. е. в мо-
Ь%

мент выхода лодки расстояние между нею и плотом
было 2,4 χ км. Лодка и плот находятся во власти
одного и того же течения; скорость плота
относительно воды — нуль, скорость лодки — 20 км/ч;
следовательно, сближение лодки и плота происходит со
скоростью 20 км/ч совершенно независимо от
скорости течения. Поэтому лодка нагонит плот через
2=2,4 х:20=0,12х (часа).
Итак, несложный анализ картины движения
быстро привел нас к зависимости, для получения
которой традиционным путем потребовалось составить
и решить систему уравнений. Далее,
мотолодка прошла по течению: (20+x)z км;
» » против течения: (20 — χ) Χ
Х(3,б — 2,4 — г) км, откуда 40z=*24— 1,2*; 4,8**=
=24 — 1,2х; 6ж=24; ж=4 {км/ч),.
4. Наконец, поищем, чисто арифметическое:
решение задачи. Плот плыл всего 3,6 часа, из них до
момента выхода лодки 2,4 ч. Следовательно, длина пути
лодки относительно воды (от А до плота) равна
2,4 : 3,6=% расстояния АВ.
Если бы течения не было, то -такова же была бы
длина пути лодки и в обратном направлении
(относительно воды). Но течение воды несло и плот, н
лодку в направлении от А к В. Так как течение
воздействовало на лодку ровно столько же времени,
сколько и на плот, считая с момента выхода лодки, и
перенесло за это время плот на расстояние тг ABt то
и лодку течение снесло также на -я- AB.
Итак, лодка прошла относительно воды
туда -$АВ.
2 1
обратно -^ АВ-\—£ АВ
всего . -$АВ
За это время, как мы выше установили, течение
прошло расстояние -^АВ; следовательно, скорость
S3

лодки в 'з:з':=:5 раз больше скорости течения.
Искомая скорость течения 20:5=4 (км/ч),
22. БАССЕЙН
Ошибка заключается в том, что составленное
нами уравнение справедливо только в определенной
области; в самом деле, если каждую секунду
испаряется — поступившей ранее частицы воды, то
через т секунд эта частица испарится целиком, и наша
формула перестанет быть справедливой.
Через т секунд после начала опыта количество
испаряющейся воды станет равным количеству
поступающей воды и объем воды в бассейне будет оста*
ваться постоянным, а именно, он будет равен (при
t=m):
Что касается равномерно замедленного движения,
то там природа процесса другая: при а < 0 и при
/=:т = ·—- точка удаляется на наибольшее
расстояние от исходного пункта и затем начинает переме-
щаться в обратном направлении; через < = 2/я=«~
она достигает исходного пункта и далее продолжает
двигаться равномерно ускоренно за исходную точку
до бесконечности*
23а. ТРИ МУХИ
Через любые три точки всегда можно провести
плоскость, поэтому три мухи будут всегда -находиться
в одной плоскости.
236. ЧЕТЫРЕ МУХИ
По условию через 9 минут все 4 мухи находились
в одной плоскости, т. е. образовали плоский
четырехугольник. Через каждую вершину этого плоского
четырехугольника проходит траектория соответствую-
64

щей мухи — луч, исходящий из верхнего конца шеста.
В таком случае верхний конец шеста можно
рассматривать как вершину четырехугольной пирамиды,
ребра которой — траектории мух, а основание —
упомянутый плоский четырехугольник. По условию все
мухи вылетели одновременно и летели равномерно; в
таком случае через α·9 минут после вылета (где
о —любое положительное число) конфигурация из
тех же пяти точек образует четырехугольную
пирамиду, подобную рассмотренной выше (коэффициент
подобия — а). Следовательно, и через α·9 минут все
четыре мухи будут находиться в одной плоскости.
Приведенные в условии цифры — лишние данные-
Плоскость, в которой в любой данный момент
находятся все четыре мухи, перемещается поступательно
(параллельно самой себе), равномерно удаляясь от
начальной точки (вершины шеста).
Если траектории трех мух лежат в плоскости,
проходящей через вершину шеста, то в этой же
плоскости лежит и четвертая траектория, и эта плоскость
остается неподвижной.
24. ЛЕСТНИЧНЫЙ МАРШ
Это — «задача на внимание»: показанное на
чертеже расстояние по вертикали охватывает
одиннадцать подступенков, а расстояние по горизонтали -ч-
десять проступей.
Ответ: 1320:11 = 120 (мм);
2310:10=231 (мм).
20. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Если меньший из двух данных отрезков не больше
половины большего отрезка, то меньший отрезок —
основание, а больший — боковая сторона; в этом
случае задача имеет одно единственное решение.
Если меньший из двух данных отрезков больше
половины большего отрезка, то любой из данных
отрезков может быть основанием равнобедренного
треугольника, а другой — его боковой стороной. Следом
вательно, в этом случае задача имеет два решения,
65

Наконец, если данные отрезки равны, to
безразлично, какой из них принять за основание, какой —
за боковую сторону: в обоих случаях мы получим
один и тот же равносторонний треугольник.
26. В ДЕТСКОМ САДУ
Ответ зависит от величины угла α между
боковыми сторонами трапеции. Для того чтобы столики
могли образовать сплошное кольцо; должно быть
360*
а__ _^ где п — чисдо целое. Если η — число чет-
п
ное, то при установке столиков в один ряд каждые
два смежные столика образуют параллелограмм.
В этом· случае свободная сторона последнего столика
параллельна свободной стороне лервого столика.
Если же η — число нечетное, свободные стороны
крайних столиков непараллельны.
27. ДВА КУБА
Для решения этой задачи «прямым» путем
следовало бы последовательно найти:
1) объем первого куба;
2) длину ребра первого куба;
3) диаметр сферы, описанной вокруг первого куба;
4) поверхность этой сферы;
5) поверхность второй сферы;
6) диаметр второй сферы;
7) длину ребра куба, вписанного во вторую сферу;
8) объем второго куба и, наконец,
9) вес второго куба.
Но можно решить эту задачу гораздо проще,
исходя из соображений подобия. В самом деле, первый
куб вместе с описанной вокруг него сферой и второй
куб вместе с описанной вокруг него сферой —
подобные фигуры.
Отношение подобия определим из заданного
отношения площадей подобных фигур (в данном случае
сфер), пользуясь тем, что отношение площадей
подобных фигур равно квадрату отношения
соответствующих линейных размеров, т. е. отношение
соответствующих линейных размеров подобных фигур
66

равно корню квадратному из отношения их. <
площадей.
По условию^ отношение поверхностей сфер равно
откуда отношение соответственных линейных
элементов равно
Следовательно, длина ребра второго куба больше
длины ребра первого куба в 2 раза.
В таком случае, объем второго куба больше
объема первого куба в 2?=*8 раз.
Но удельный вес материала второго куба больше,
удельного веса материала первого куба в 3,6:2,4 =1·^
раза. Следовательно, вес второго куба равен
4l| .8.1^ = 500 (г).
28а. ДОСТРОИТЬ РАВНОБОЧНУЮ ТРАПЕЦИЮ
Задача до того элементарна, что вы даже не стали
ее решать. Но интересно: подумали ли вы о том, что
в с е с .JL
-О .Q р*
задача имеет три решения? (Когда задача имеет два
решения? Одно решение?)
286. ТРИ ТРАПЕЦИИ
Известно, что вокруг равнобочной трапеции можно
описать окружность. Следовательно, каждая из трех
четверок точек
А В, С, Dt ι
А В, С, Οχ.
AtBtCtD>-r-
57

лежит на одной окружности;, но так как у этих трех
окружностей три точки общие (Л, β и С), то сами
окружности совпадают. Поэтому искомые точки А,
В и С лежат на окружности, проведенной через три
данные точки Dl7 D2
и D3 (рис. а). Но
где именно?
Пусть задача
решена и А, В и С —
искомые точки (рис.
б), a ABCD2 и
ABD3C— две из трех
искомых трапеций.
Тогда AD2=BC —
как боковые
стороны равнобочной
трапеции ABCDbADs^
=ВС — как
диагонали равнобочной
трапеции ABD3C.
Следовательно, AD%~
=AD3.
Отсюда вытека-
г д е ет, что для
построения точки А следует
из точки Ε — середины хорды DzD^ — восставить к ней
перпендикуляр и продолжить его через центр
окружности до пересечения с окружностью.
Аналогично находим (рис. в): с помощью хорды DiD2 точку В
и с помощью хорды DJ)3 точку С. На рис. г, д и е
даны раздельно все три решения.
Точки, получаемые при продолжении
перпендикуляра в противоположную сторону, не дают
правильного ответа. Почему?
β Oj
6
в
*i <t
η
/ \
^
ν^
В D$
29а. ТРИ ДИСКА
Все линейные размеры, а также' направления
вращений, данные в условии, излишни. Ответ зависит
только от угловых'скоростей. Совершенно очевидно,
что необходимым и достаточным условием вторичного
совпадения всех отверстий является возвращение
каждого из трех дисков в своё исходное положение.
58

Отверстие диска А будет вновь в О через
60: 7,5= 8 секунд,
Отверстие диска В будет вновь в О через
60:10 — 6 секунд,
Отверстие диска С будет вновь в О через
60: б|-=9 секунд.
Наименьшее общее кратное чисел 8, 6 и 9
равно 72.
Следовательно, каждые 72 секунды ( = 1,2 мин)
все три отверстия в дисках будут совпадать.
296. ДВА ДИСКА
60: 5=12 \ Наименьшее общее кратное чисел 12
60:12= 5 ) и 5— число 60.
Следовательно, каждую минуту система
оказывается в исходном положении и отверстия в двух
дисках будут совпадать.
Однако, в отличие от случая трех дисков, задача
о двух дисках может иметь еще и другое решение,
а именно: оба отверстия в данных двух дисках могут
совпадать также и в том случае, если они оба ока·
жутся одновременно в точке О', симметричной
точке О относительно оси АВ. Для того чтобы выяснить,
происходит ли это совпадение в данном конкретном
случае, необходимо (в отличие от задачи о трех
дисках) знать расположение отверстия О; а так как
условие не содержит необходимых данных, мы
лишены возможности выяснить, имеет ли место вторая
серия совпадений.
30. РАВНОСОСТАВЛЕННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
Как известно, четырехугольник определяется пятью
параметрами; в данном же случае даны лишь три
параметра четырехугольника KLMN: площадь и еще
два параметра. Поэтому мы располагаем, как
говорят в таких случаях, двумя степенями свободы; это
и позволяет выполнить требование: составить
четырехугольник KLMN из тех же четырех кусков, из
которых составлен четырехугольник ABCD.

Из многочисленных возможных вариантов задания-
двух параметров четырехугольника KLMN
рассмотрим один: даны сторона MN и угол /С.
Пусть Еу F, G и Я — середины отрезков — сторон
данного четырехугольника ABCD, Из точки Я, как из
центра, радиусом, равным -^-, опишем дугу. На
отрезке FG, как на хорде, построим дугу окружности,
такую, чтобы вписанный в нее угол, опирающийся
на хорду FG, был равен заданному углу
несоединим точку О — точку пересечения двух
построенных дуг — последовательно с точками Е> Ft G
и Я. Четыре отрезка ОЕ9 OF, QG и ОН. разбивают
60

веданный четырехугольник A BCD на четыре куска,
таких, что из них можно составить четырехугольник
KLMN.
В самом деле. Вообразим, что в точках £, F, О
и Η — шарниры; .пусть четырехугольник EBFO'
остается на месте, а остальные малые четырехугольники
переместятся так, как показано на рисунках 6, β и г.
В результате составится четырехугольник KLMN,
удовлетворяющий всем поставленным условиям.
Заметим еще следующее.
1. Два куска переместились поступательно (из них
один по пути перевернулся на 360°); два других
повернулись на 18СК
2. Данное выше решение не единственное. В са-
мом деле, мы провели дугу радиуса -γ с центром
в точке Н\ но в качестве центра можно было бы
принять также и любую из точек £, F или G. Мы
построили угол, равный /С, на хорде FG; но его можно
было построить также и на хорде EF. Две
построенные дуги пересекаются, вообще говоря, в двух точках.
Следовательно, в общем случае возможны 4X2X2»
«16 вариантов.
3. Мы не воспользовались «шарниром» в Н; но
Можно было бы воспользоваться им, отказавшись от
Какого-либо другого «шарнира».
31. ДВА СТОЛБА И ТЕНИ
Построения, необходимые для решения основной
задачи, даны на рисунке а.
Ответы на дополнительные вопросы.
1) Для нахождения положения самого
источника света действительное направление столбов не
имеет никакого значения; для нахождения же
положения основания источника света нужно быть
уверенным в том, что столбы вертикальны.
6!'

2) Совершенно аналогичен ответ на второй вен
прос: для нахождения положения самого
источника света направление плоскости, на которую па*
дают тени, не имеет никакого значения; для
нахождения же положения основания источника света
существенно, что тени вертикальных столбов
отброшены на горизонтальную плоскость.
3) Если — как принято в основном условии —
столбы вертикальны, а тени падают на
горизонтальную поверхность, то для решения задачи достаточно
задать на рисунке один столб с падающей от него
тенью и только направление тени второго столба;
по этим данным сначала находим «основание»
источника света, а затем и сам источник (рис. б).
Если на рисунке будут даны один столб с
падающей от него тенью и тень второго вертикального
столба, то по этим данным можно найти не только
положение источника света и его «основания», но и
высоту второго столба (рис. в).
Если же задать лишь направления двух теней, то
по этим данным легко найти положение «основания»
источника света, но и только. Положение самого
источника мы не сумеем найти даже в том случае,
если нам будут известны обе тени (но ни одного
столба).
32. КОНУС ЛЕЖИТ НА ПЛОСКОСТИ
1. Обозначим: через г—радиус основания конуса
и через а — образующую конуса.
В таком случае длина окружности, описанной в
горизонтальной плоскости точками основания конуса,
равна
L=2na.
Длина окружности основания конуса равна
/=2яг
Образующая SA возвратится после одного оборота
конуса вокруг точки S в прежнее положение только
в том случае, если
LWn, где я— число целое.
$2

Следовательно, должно быть
а=т.
Ответ: образующая конуса должна быть в целое
число раз больше радиуса основания.
Какова картина при п=1? Каков должен быть
конус, чтобы образующая А возвратилась в
первоначальное положение не после первого оборота конуса,
а только после m оборотов конуса (т -— целое число) ?
33. ДВЕ ОКРУЖНОСТИ
Приведем доказательство, не требующее никаких
вычислений.
Проведем линию центров данных окружностей,
проходящую, конечно, через точку Μ (рис. а).
Займемся сначала касательной А. Обозначим
угол АА'М, образованный этой касательной с линией
центров, через а.. Величина угла α определяется
величиной угла ΑΜΑ'=μα, так что
α=ία(μο),
где fa — некоторая функция.
Обратимся к касательной В. Обозначим угол
ВВ'М, образованный этой касательной с линией
центров, через β. Величина угла β определяется
величиной угла ВМВ'—\1ъ, так что
Ввиду полнего равноправия обоих этих случаев,
функции fа и /» — тождественны, т. е. величина угла а
определяется единственным образом величиной угла
63

μα точно таким же образом, как величина угла β
определяется однозначно величиной угла μ*,:
μ&:μα=Α>(μ*>) :/β(μο>·
Но μα = μδ. Следовательно, /α(μβ) ■· Μμ&), откуда
α=-β, что и требовалось доказать.
Совершенно аналогично можно построить
доказательство, проведя в качестве вспомогательной прямой
не линию центров, а общую касательную двух
окружностей (рис. б).
34. ТРИ КВАДРАТА
Все дело в том, что Витя и Сережа производили
измерения разными единицами.
Обозначим сторону квадрата ABCD через а; тогда
площадь квадрата равна а2.
бит*
Серело
Сторона описанного квадрата равнаι γ2а;
периметр описанного квадрата равен 4 γ2α (рис.а).
По данным Вити, а2 = 4 У%а, откуда а~4]А2; т.е.
сторона описанного квадрата равна γ2α=*γ.2χ
X 4 Υ2 — 8 Витиным единицам длины.
Сторона вписанного квадрата равна -^тра;
периметр вписанного квадрата равен 2 Υ 2а. По
данным Сережи a2 = 2"j/2a» откуда а = 2)Л2, т. е.
Ϋ~2
сторона вписанного квадрата равна -Чг-·α =
ае 1-я- · 2 Υ2 = 2 Сережиным единицам длины.
64

В Витиных единицах длины длина стороны
основного квадрата св = 4^2»
В Сережиных единицах длины длина стороны
основного квадрата ac=$V2.
Следовательно, линейная единица, которой
пользовался Витя, в 4 У~2:2 Ϋ2 — 2 раза меньше той ли-
нейаой единицы, которой пользовался Сережа.
У Вити площадь основного квадрата ABCD и
периметр описанного вокруг него квадрата
выражаются одним и тем же числом 32(4^2-41/2 = 32 и
4-8^=32).
У Сережи площадь основного квадрата A BCD и
периметр вписанного в него квадрата
выражаются одним и тем же числом 8(2 ^2·2 ]Α2=8 и 4-2=8).
36. КОЛЬЦО НА ТРЕХ НИТЯХ
Вместо кольца радиуса /? можно рассматривать
правильный треугольник со сторонами а = Y3JR:
При изменении
длины" / нити $С
положение кольца ЛВС в
пространстве будет
изменяться; при этом (рис.
а) расстояния SA, SB
vt SD будут
оставаться неизменными, а
точка О — центр кольца
и треугольника —
будет находиться на
одной вертикали с
точкой S.
Произведем
вычисления:
Площадь Δ ^С = Vp(p — а)(р — Ь){ρ—с), где
λ+ζ-Κ*
/> —:
65

Площадь &DSC=*
«>*Lsnc=—Ця> 1
Площадь &DSO=±ADSC = ±DF-SO.
"~ 2 V * б^-т-з/2—здг2'
— DF — л/\ (£a —f2)'
cosa — -щу— у ι — (б£»-{-з/2 —9tf*)tf8 '
sina =
КЗ^Чг'* — 3/?2)#
Исследуем полученное значение sin a:
1. sina = 0, если I2 — /*=(), т. е.
а = 0^ если 1 — L, что и так очевидно.
2. sina = l, если L*—Pb=Y3(2L*-\-P—3W)Ri или
Отсюда следует, что
/=|Л2-!-/?2±4#.
Этот результат может быть, конечно, получек и
непосредственно из рассмотрения рисунка б: оче-
видног что если SA=SB*=SC=L, то L^R, а если
SA=SB~L<SC, то L>¥£-R.
Возьмите кусок проволоки и нитку; изготовьте
модель; понаблюдайте за изменением положения
кольца ABC при изменении длины нити «SC
36. КОРОБКА И НИТЬ
1) Разрежем поверхность данною
параллелепипеда по ребру А н начертим развертку: пять
параллельных прямых* отстоящих друг От друга
соответственно на расстояния a, b, а и b (длина коробки —
66

параллелепипеда не имеет в данном случае никакого,
значения). Точки /& и Ло. находящиеся на одном
перпендикуляре к параллельным
прямым»—фиксированные концы нити* длиной 1>Ща+Ь). На
развертке положение нити длиной / изобразится в виде
ломаной, концы которой находятся в точках Ао и Ло»
а вершины расположены на трех параллельных пря·*
мых — трех «стальных ребрах коробкж.
Расстояяне от точки В0 До исковой точки В на
том же ребре коробки будет наибольшим из
возможных в том случае, если все три звена ломаной от
точки В до точки J& окажутся на развертке тга одной
прямой {разумеется,
'АоВ — отрезок
прямой).
Расстояние от
точки Do до искомой
точки D на том же ребре
коробки будет
наибольшим, если все три
звена ломаной от
точки D до точки Л о окажукя да развертке на одной
прямой (разумеется, AqD — отрезок прямой).
Расстояние от точки Св до искомой точны С на
том же ребре будет наибольшим, если два звена
ломаной от точки А^ до точки С окажутся ив
развертке на одной прямой, а два звена ломаной от точ«
ки С до точки X окажутся даа развертке также на
одной прямой.
Заметим, что найденные только что на развертке
точки В, С и D расположатся^ на дуге эллипса,
фокусы которого — точки Λ) « А»» а большая ось рав*
на / (эллипс — геометрическое место точек, сумма
расстояний которых от двух постоянных точек по«
стоянна).
2) Так как треугольник AqCAo—равнобедренный,
;8 A!>Bo=CoDq и ДСо=АХ»т» A&'^CD' иЯ'С =
•*bD'Ao; следовательно, на параллелепипеде будетз
ЛЖ # CD' и В'С # D'£. т. е. AqB'CD' —
параллелограмм.
67

37. ПАРКЕТЛЖ
Обозначим:
d—искомая ширина полосы,
Ь — расстояние от центра Ладанной фигуры до ее
стороны, т. е. до ближайшей полосы.
депббь ■■■■■ **У*а
Ы « W
Очевидно, что оси полос образуют сетку,
составленную из фигур (соответственно треугольников,
четырехугольников и шестиугольников), подобных
данным.
Пусть В -г расстояние от центра фигуры сетки до
ее стороны.
Тогда В = &-г--2"·
Согласно условию, должно быть:
Sb:SB=liti.
Но Sb.Ss^tfiiB2,
откуда 1 :/1 = 62:^2 = ^2:(б+-|-)2
я далее: ί#=^+Μ + γ или
d2-f 4bd+A{\ — λ)£2=0, откуда
d = 2b(Yn— 1).
Применима ли найденная формула также -для
случая паркетажа'из ромбов с углом 60°? Из любых
ромбов?
38. СТОЛ И СКАТЕРТЬ
В условии не задан ни один размер, поэтому
обозначим: через а — сторону квадрата (скатерти) и
и больше ничего не нужно.
В самом деле, вообразим, что перед нами круглый
стол, накрытый квадратной скатертью, что задача

$же решена и что диаметр стола начинает
увеличиваться. Что при этом происходит? Расстояние, на
которое свисают углы скатерти, будет уменьшаться,
но ровно на столько же будет уменьшаться и
расстояние, на которое свисают середины сторон
скатерти. В таком случае разность между этими
двумя расстояниями не изменится. Итак, искомая
разность вовсе не зависит от размеров стола.
А теперь вообразим, что крышка стола такого
размера, при котором легче решить задачу, а именно?
что диаметр крышки стола равен стороне скатерти.
В этом случае середины сторон скатерти оказываются
на окружности стола (т. е. они «свисают на нуль»),
а углы скатерти свисают на величину, равную
разности между половиной диагонали скатерти и
радиусом крышки стола, который в этом случае равен
половине стороны скатерти. Итак, искомая величина
равна половине разности между диагональю и
стороной квадрата, т. е. равна
^(Ϋ2α — α) = (^2— l)-| «0,207α.
Для решения задачи мы предположим, что
диаметр стола увеличивается. Можно было
предположить и другое: что диаметр стола остается без
изменения, но скатерть уменьшается.
А что произойдет, если при данном размере
квадратной скатерти круглый стол уменьшится до
размера точки? Тогда искомая разность будет равна
разности между половиной диагонали и половиной
стороны скатерти, т. е. мы получили тот же ответ.
Полотнище флага квадратной формы в безветренную
погоду это — «четверть скатерти на круглом столе
диаметром ноль».
Задача. То же условие, но центр квадратной
скатерти не совпадает с центром крышки круглого
стола. Чему равна разность между суммой отрезков,
образуемых четырьмя свисающими углами, и
суммой отрезков, образуемых четырьмя свисающими
серединами сторон?
Задача. То же условие, но скатерть-*
прямоугольник aXb.
69

99. СИММЕТРИЧНЫЕ ТОЧКИ
1. Для того чтобы наглядно показать, из каких
именно данных условия получаются те или иные
«первые» (непосредственные) выводы, из каких
именно «первых» выводов получаются «вторые» выводы
и т. д., а также для сокращения записей» — бывает
целесообразно изобразить на схеме все данные
условия и показать при помощи стрелок, как
последовательно получаются цепочки следствий,
приводящих нас к требуемому результату. Такой прием
весьма удобен для нашей задачи, решение которой
сразу усматривается из следующей схемы!
Дано \ka~al \ \lb^bm\ \mc=
\кммв\
1
гт
δ
i
|/№feM0| \LNU6C
ζ
7
jupecl
■-CN
1
Ε
\
ί
3
ΤΤ 4 '
"Г t —L1
I
l/W?Mfl
ш^ъ
ifiMAtBM
Д1
IKM*NQ\
I j-i-l
Λ
\nPuC8
lnr±
\
\KP'2CB
ZEZ
3_£
INQ*aPKM
\QL»MP
X
Τ
\QL\\CA\
&
£
2CAX
kc = ca
точки HuCuQ
лежат на одной прямой
[ммм|
Обозначения
АПМР*2*ВАС
Треугольники
КМРиВАС-
подобны,
отношение,
подобия-2*
^Треугольники
LNQ и РКМ
раднш: Ь*
соответствен*
нше стороны
взаимно
оараллельны
70

40. СКЛАДНОЙ СТАКАНЧИК
Напомним» что форма и размеры каждой
геометрической фигуры определяются некоторым
определенным количеством независимых параметров, из
которых хотя бы один должен быть линейным (или,
вообще, любой ненулевой степенью линейного). Так,
например, треугольник
определяется тремя
параметрами; плоский
четырехугольник— пятью
параметрами; куб — одним
параметром; треугольная
пирамида — шестью
параметрами и т. д. Какие именно
параметры будут выбраны
для данного случая,
зависит каждый раз от
конкретных обстоятельств; например, куо> можно задать либо
ребром, либо диаговалыа грана, либо диаметром
описанного шара, либо площадью одной грани, либо
полной площадью, либо объемом, либо объемом
вписанного шара, либо разностью мгежду диагональю и
ребром, либо произведением диагонали на объем,
либо частным от деления объема на произведение
диагонали куба на диагональ стороны и т. д,, и т. п.
Количество независимых параметров,
необходимых для определения данной фигуры, ке зависит
от того, какие именно параметры мы выберем в
данном случае. Количество необходимых независимых
параметров может быть определено различными
путями, в частности, это удобно сделать, если
проследить за последовательностью построения заданной
фигуры.
Складной стаканчик — комбинация из нескольких
тел вращения: диска (прямого кругового цилиндра)
и нескольких полых усеченных конусов. Полые конусы
имеют общие параметры: высоту, угол при вершине
и толщину стенки.
Для определения днища нужны два параметра
^например, диаметр и толщина).
Для определения нижнего звена4 нужны четыре
параметра (например: нижние внутренний и внешней
Диаметры, высота и внутренний объем).
71

Для определения последующих звеньев нужно
знать лишь еще один параметр (например, величину
нахлестки).
Наконец, необходимо знать число звеньев (либо
общую высоту, либо полную емкость стаканчика, либо
объем материала стаканчика и т. п.).
Всего, следовательно, требуется задать 2+4+1 +
+ 1=8 параметров.
41. МНОГОГРАННИК
Исследуемый многогранник — двенадцатигранник.
Шесть (три пары) секущих плоскостей (они все
параллельны диагонали ΟΟι куба) образуют
правильную шестиугольную
призму. Эта призма
«усечена» шестью
гранями куба. Таким
образом, шесть граней—■
параллелограммы,
пара сторон каждого из
которых параллельна
диагонали куба, а
шесть граней —
квадраты со стороной а.
Определим объем
многогранника, для
чего разобьем его на
четыре части. OBDC
(УВ'ГУС — косая
призма с квадратным основанием; ее высота равна
/ — а, ее объем: а2(/ — в). Наш многогранник
составлен из трех таких косых призм и одного куба
O'B'D'C'A'E'OxF'.
Следовательно, его объем равен
V«3o2(/ — о) +α3=3α2/— Зс3+с3=
«За2/ — 2а3=(3/ —2а)а2. '
42. РАЗВЕРТКИ МНОГОГРАННИКОВ
Изображенный на рис. г (стр. 20)
многоугольник — развертка невыпуклого многогранника;
который образуется следующим образом: установим
72

на каждую из четырех граней тетраэдра точно такой
же тетраэдр; мы получим звездчатый
многогранник; число его граней равно 4 · 3= 12; число ребер —
A Q Ч А.
4 · 3-\ ^— — 18; число вершин —А -\—*р=8.
Замечание. Представим себе, что
многоугольник-развертка вычерчен на плотной бумаге или на
картоне. Тогда, для удобства
сгибания и последующего
склеивания модели, полезно
слегка надрезать картон по
всем диагоналям развертки,
служащим ребрами
многогранника. Естественно, что
ребра выпуклого многогранника придется при
эггом надрезать с одной стороны листа картона, а у
невыпуклого (как в нашей задаче)—с разных
сторон. Это обстоятельство отмечено на рисунке
разными обозначениями диагоналей/
4а ГОДОВЫЕ СЛОИ
Форма бревна — прямой круговой конус,
усеченный параллельно основанию!; его торцы — верхнее
л нижнее основания усеченного конуса; там
отчетливо видны годовые кольца древесины (более
плотные— зимние). Таким образом, бревно можно
рассматривать как систему соосных конусов (рис. а —
число «конусов» равно числу лет дерева).
Поэтому в сечениях, перпендикулярных оси, мы
видим окружности (рис. б).
J3 поперечных сечениях,, не перпендикулярных
оси — эллипсы (рис. в).
В продольном сечении (например, на поверхности
доски)—гиперболы (рис. г).
Еслп при распиловке вдоль бревна плоскость
распила прошла через ось бревна — годовые слои обра-
1 Конечно, в действительности форма бревна более или
менее отличается от прямого кругового конуса; поэтому в
действительности рисунок годовых слоев отличается от названных
кривых.
та

зуют в сечении системы прямых, пересекающихся
в вершине ствола дерева (рис. а),
Если плоскость распила параллельна одной из
образующих конуса, годовые слои образуют
параболы Хрис. д).
44. ТРИ ПАРАЛЛЕЛЕПИПЕДА
1) ν%: ό2 : Vz^XfaVi: A^v2: λ&$/& откуда
λιΙ4Τι
_ λ ^2v,
ЯзЦаУз
«я = ч
λιμιν! + λ2μ8ν2 ~Ь ^aV8
υ
V*
2) ΐ>Ι=ζ»2='ϋ3=-3-. (Подумайте над тем, как
получить это решение непосредственно, не
используя более общего случая 1).)
45. МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ
Начертим отрезок длиной а. Его концы — две
вершины всех искомых четырехугольников.
Из концов отрезка опишем две дуги радиусами
соответственно Ь и dx Искомые третья и четвертая
74

вершины четырехугольников лежат только на этих
дугах. Но где именно?
Для дальнейших построений принимаем: b>c<d.
Кроме дуги радиуса 6, из того же центра
описываем две дуги радиусами (6+с) и (Ь — с)\ эти дуги
ограничивают возможные положения второго конца
стороны dm
Аналогично, кроме дуги радиуса d, из того же
центра опишем две дуги радиусами (d+c) и {d—с);
эти дуги ограничивают возможные положения
второго конца отрезка Ь.
По отношению к отрезку d отрезок с может
занимать два крайних положения, причем в обоих
случаях отрезки d и с лежат на одной прямой; в первом
случае сторона искомого четырехугольника является
продолжением его стороны d, а во втором —
сторона с лежит целиком на стороне d. В первом случае
четырехугольник вырождается в треугольник (рисе).
Станем изменять эту исходную фигуру.
Свободный конец отрезка d может перемещаться либо
75

внутрь треугольника (верхний ряд на рисунке), либо
наружу (нижний ряд).
Второй (свободный) конец отрезка d
перемешается:
Внутрь треугольника
рис· φ — невыпуклый
четырехугольник
рис. ж — второй конец отрезка
d занимает крайнее
левое положение;
четырехугольник выро-
дился (три вершины
"на одной прямой)
рис. и — звездчатый четырех·
угольник
рис. л — звездчатый четырех*
угольник, две стороны
которого параллельны
рис. м— звездчатый
четырехугольник
Наружу треугольника
рис. / — выпуклый
четырехугольник
рис. g— выпуклый четырех:·
угольник; между / и g
была единственная
трапеция
рис. I — второй конец отрезка
а занимает крайнее
правое положение;
четырехугольник
выродился в треугольник
рис. I — невыпуклый
четырехугольник
рис. т — невыруклый
четырехугольник
рис. я — второй конец отрезка Ъ пришел в другое
крайнее положение; четырехугольник выродился (три
вершины на одной прямой).
46. УСЕЧЕННЫЙ ЦИЛИНДР
Развертка боковой поверхности прямого
кругового цилиндра, усеченного непараллельно
основанию, показана на рис. а. Кривая — синусоида. В
самом деле (рис. б):
OB=R — BC=R — R cos α= (1 — cos a)R;
Λ=Οβ. tg β-tg β(1 — cos α)/?.
Площадь развертки боковой поверхности можно
найти двумя путями.
1 вариант. Дополним данный усеченный
цилиндр до полного цилиндра высотой //+Λ (рис. 6).
Совершенно очевидно» что дополнительная часть —
также усеченный круговой цилиндр и притом цен·
тральносимметричный заданному· Поэтому оба
усеченных цилиндра равны; следовательно, боковая
поверхность одного усеченного цилиндра равна
половине боковой поверхности всего цилиндра. Боковая,

поверхность полученного кругового цилиндра равна
5ο~π/)(//+Λ), а искомая боковая поверхность
заданного усеченного цилиндра- равна
2 вариант. Любое осевое сечение любого
кругового цилиндра (даже не прямого), усеченного
параллельно основанию, — трапеция (рис. г); следователь-
-Й0, сумма длин двух образующих цилиндра; т. е.
Обоих оснований трапеции, рав- г
на удвоенной средней линии
трапеции (2η); таким образом, «сред-(
ряя, высота» развертки равна
ц^Н+h ^ 0тсюда: s=*nDri =
***jiD—i— (эта формула
справедлива для любых цилиндров,
77
%

основание которых — фигура, симметричная
относительно центра).
Замечание. Усеченный цилиндр очень часто
встречается на практике, например, в коленах
трубопроводов, изготовленных из отдельных звеньев
.(рис. д).
47. ЛИСТ БУМАГИ
По условию, каждый следующий лист подобен
предыдущему и в два раза меньше его (по площади).
Из этого следует,
что стороны каждо-:
го следующего
листа в Ϋ2 раза
меньше соответствующих
сторон
предыдущего листа, а так как
одна из сторон у
этих двух листов
одна и та же, то
искомое отношение
равно У~2. (Именно
таково отношение длин сторон листов бумаги;
например, размер «форматки» 210X297 мм; 297:210»
48. РУЛОН
Рассмотрим прежде всего прогрессию,
получившуюся при разрезании рулона по радиусу
(«основную») ι
толщина одного слоя (ленты) δ = —~—;
торцевая поверхность рулона S = -^-(D2 —tf2);
длина ленты г= *-= "^У-У" »»~τΗ»»8
длина развертки первого слоя lx = n\d-\—^Г-)3*
(2я-1)<Н-£>„.
— 2п π»
7В

йлина развертка последнего слоя /η = πίΖ? g-— ]=
ι ι jf
резкость прогрессии ff=? £_^ » 2п(п — \\ *
ХК2л— l)D + d — (2ft— l)rf — DJ.=
ВоамОкЖИЫ два варианта прогрессии иа 2п членов.
1 вариант. Два отрезка каждого вятка
являются двумя
последовательными членами \ —' _
искомой прогрессии >-
фтс. а). Тогда сумма , !* -!_«
•двух членов ft-го вит- tIZZZZZ!^ZZr~l-
$а равна · · >
■ I ■ '
/|* "Г" ^2ft + l — Чп ~Ь *2А -Ь ι Ί ι
а сумма двух членов следующего, [(Л-И)-го» витка
равна
Чм+Чш = (Ч.+2»0+(Ч.+30 = Щ.+5?'.
Следовательно, длина (А-Ы)-го витка превышает
длину ft-ro витка на 5<7'—д'—Ад\ Но, с другой
стороны, длина каждого следующего витка превышает
длину предыдущего на д.
Итак,
/χ—2(ίι-^)==2·[ 2Н π ЪГЯ\ =
Теперь нетрудно найти длину каждого нового отрезка.
"Возникает вопрос: как расположатся в рулоне
новые разрезы? Не окажутся ли они тоже на одном
радиусе?— Нет, и вот почему. Любой радиус (после
первого) разрежет каждый виток на две части,
отношение длин которых зависит от положения
второго радиуса, но постоянно для всех витков, между
тем, как показано выше, должна быть постоянной
79

разность длин, этих двух частей (она равнаΙ ψ),
следовательно» их отношение не может быть
постоянным. Вторые разрезы расположатся по
некоторой кривой («спирального» типа).
2 вариант. Первые η членов искомой
прогрессии — соответственно длины отрезков первого, вто-
., , рого, ..., η-го витков; и
■ 't —' далее: (я-Н)-й член ис*
■ Ί комой прогрессии — оста-
Z"Z1Z.ZZZZ1Z.Z.^ ток куска ленты первого
1 *ι ■* витка; (я+2)-й; остаток
« второго витка и т. д.
IZL, (рис. б).
ζ В этом случае k-fi
член прогрессии (где
Л<л) больше (Л—1)-го члена на q*\ где q" —
разность искомой прогрессии. Аналогично, (£+л)-йчлен
прогрессии больше {k+n— 1)-го члена также на q".
В таком случае
(Ол+Юа+п) — (aft_i+aft+„_i)*=2<7";
но a* +fl#i+n — длина Λ-го витка. α*_ι+βΑ+η_ι— Длина
(k— 1)-го витка, откуда следует, что разность искомой
прогрессии в два раза меньше разности основной
прогрессии, т. е.
Обозначим первый член искомой прогрессии
через /J; поскольку /; + /;+1 =/,, т. е. /," -h l\ -+- V=
<2п — l)d + D
2/; =-|-[(2л — l)i/H-Z> — nD + nd\\
i«-£-K3«-i)rf-(«-i)^],
80

Это решение, однако, возможно не при всех
значениях й, D и п. В самом деле, условие
существования: q" · /1</ь т. е.
£^±лп<<^=^£±£я или (£>-</)л<(2«-1)Х
Xd+А или (ft— l)D<(3/i-l)rf, откуда d>£=±D.
При ρ"'Π = ίι должно быть /^ = 0, т. е.
•£L[<3«-!)<*-(«-1)01 «0,
или <3л — 1)г^ = (/г — 1)Z>. Это следует и из
формулы
Частные случаи: при л = 2
должно быть rf>-g-D
Условие существования может быть записано и так:
д< £t—3rf (л —целое число).
Два отрезка, на которые разрезан каждый виток,
отличаются друг от друга на одну и ту же
постоянную величину л^" =—γ—π. Следовательно, как и
в первом варианте, вторые разрезы расположены не
по радиусу, а по некоторой кривой.
49а. РАЗБИЕНИЕ ПРЯМОУГОЛЬНИКА
Пусть а^СЬ. Тогда наибольшая возможная
сторона квадрата — а. Следовательно, в результате
нанесения внутри заданного прямоугольника двух
систем прямых, параллельных его сторонам,
образуются квадраты со сторонами, равными 1, 2, 3,..., α
in JL л
4 и \\U
81

единицам: Сколько же образуется квадратов?
Составим таблицу.
Длина стороны
квадрата
Количество квадратов данного размера
1
2N
3
о, · Ь «в йЬ
(а— 1)'(Ь — 1) = л6 — (а+*)-И
(а—2) (ft—2) = ab—2(a-f 6)+2»
[а — (л— 1)].[6_(а-1)] =
^аб — (д^1).(Д-{-^) + (д — 1)я
2=λ*·λ—[O-f-l-f-2-Ь ...(а — 1)Иа-И)-т-
_{-[02+12+22+...(а-1)2] =
&fl^-irlfl(a+&)+2fli-63fl+1 gM
*=|·[6αί> —За2—3а&+3л+3^+2а2—3a + lJ=:
^g(a6+1)(3fr-a+l).
Формула, выведенная для случая разбиения
прямоугольника на квадраты, справедлива и для случая
разбиения параллелограмма на ромбы.
496. РАЗБИЕНИЕ ПАРАЛЛЕЛЕПИПЕДА
49в. РАЗБИЕНИЕ я-МЕРНОГО ПАРАЛЛЕЛЕПИПЕДА
Пусть а — наименьшее из чисел ак b, ct ..*4 kt I
в т. Составим таблицу. "
82

• II J ■ ■ ■
Длина
ребра
фигуры
1
2
3
с-2
а—1
а
(Л
X»
I [а
[Л
Га
-1Ь
—2)*
-<Л-
XI/·
-(а-
Х(/
-(Л-
Х[/
>
Количество фигур данного размера
<*-
(6-
-3)]
-(а-
-2)1
-(а-
-D1
-(а-
Λ·&·С.
1> - (с — 1)
2)-(с—2)
·[»--<«-
~3)].[И-
.[6Г(«-
-2) ·[/»-
. μ —(а—
-!)].[»-
..*i
• т · ^-Л
... (Л
3)]..
-(а-
2)]..

-(αϊ)!..
-(а-
1· т
-D
~2)
ί*-
3)1
♦t*-
2)1

.[ΑΙ)
■ (/-
.(/-
-<а-
-<а-
-(й-
-1).(л1-
-2). (да-
-3)1Х
-2)1Х
-D1X
ммн*«
-1)
-2)
•
MKMHrf
Обозначим произведение а~6*с..,&-/*т через s и
найдем сумму всех строк:
+[!«+*+ ... +(«_iW[£+JL + ... +£]_?
-Il.+2i+...+(a-inJi + 5£r+ ...+ш]+
-f- ... -^Ηΐ)"-1^1^ ... -Κα-ΙΓΊΧ
Х[а + 6Н- ... 4-/«Μ-(-ϊΠί»+ ... 4-(α^-1)Λ1 =
— Лс α(α~ΐ)ΓΤ ■ 1 . ■ 11· . α(α-1) ν
2*-1Τ1 . 1 . , / Ι sfr-Qw
Χ 3 ίβ*^Λβ^ #·"^ toj5 2 Α
Χ^[ά+ -+τκ]«+ - +НГХ
Χ[1"4- ·.. +(β-1Π = β[ΐ—тг(т+т +
χ(^+···+^)^···]*+<-')"Π"+-..+(*-0'']·
2я симметрична относительно 6, с, ..., k, I и я?<
Мастный случай: a=b=c= =k~l=m.
Σn=lл + 2л+...^-a',.

50а. В РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
ВПИСАНЫ КРУГИ
1. Радиус (первого) вписанного в равнобедренный
треугольник круга равен
ρ— а
Ρ
Площадь (первого) вписанного в равнобедренный
треугольник круга равна
■ ЯГ* = -т- * —-—
4 ρ
<&
Далее:
Наконец,
h: #= 1 —
: = // — 2г = Я— α·\/~·
р—а
α Υ ρ — а а
Vp~2Vp(p-a)(p-b)*
Р(р-Ь)
Равнобедренные треугольники, отсекаемые от
данного равнобедренного' треугольника касательными
к вписанному в него кругу,
параллельными основанию
треугольника, подобны данному
треугольнику.
Линейные элементы каждого
последующего треугольника
относятся к соответствующим
элементам предыдущего, как Λ: И, т. е.
соответственные (сходственные)
элементы треугольников образуют
убывающую геометрическую прогрес-
р.— а
сию со знаменателем q = -£--^— .
Следовательно, площади треуголь-
° ников (а также и вписанных в них.
кругов) образуют геометрическую прогрессию1 со
знаменателем
q0 — q -ρ

Сумма площадей всех вписанных кругов —сумма
членов бесконечной убывающей прогрессии (первый
член ее *, = $,= *...£=£ α»):
fli π (ρ — α) α2 _
4α „„Γι (Ρ — α)2
π (ρ — д) с?ρ π (ρ—α)αρ η (ρ — α) ρα
"""* 4[ρ2—ρ* + 2αρ — α2) ~ 4{2ρ — α) . Ы *
Обозначим радиус искомого круга через R0;
тогда 5г=л/Й=-£*^^-.
откуда R0=yS£^n.
2. Другой путь решения:
Площадь первой трапеции
(2/> — а) а с 2а6 с
= ρ ·>Δ = -ρΤ-«>Δ·
Доля площади трапеции, занятая кругом:
J?o_ п(р — а)а2р2 я (р — а) ар
Так как все последующие трапеции с вписанным
в каждую из них кругом подобны первой трапеции
с вписанным в нее кругом, то полученное только что
соотношение справедливо для каждой из всех
трапеций, а следовательно, и для их суммы.
Поэтому сумма площадей всех вписанных кругов
равна
п с — п(Р—<*)Р а
откуда /?о= У -f- = V —*~Ρ'Ί =
Г 86 2 V 2b *
85

3. Построение. Итак, заданный
равнобедренный треугольник разбит системой отрезков,
параллельных его основанию, на равнобочные трапеции,
в каждую из которых вписан круг; площадь каждого
из этих кругов составляет
определенную часть площади
трапеции, независимо от абсолютных
размеров трапеции.
Следовательно, искомая сумма всех
вписанных в трапецию кругов равна
площади круга, вписанного в
равнобочную трапецию,
подобную упомянутым выше, а
именно такую, площадь которой
равна площади всех трапеций, т. е.
площади заданного
равнобедренного треугольника.
Площадь первой трапеции φ
" равна площади данного
треугольника F минус площадь второго треугольника f.
Данный треугольник и второй
треугольник—подобные фигуры, поэтому их площади относятся как ква--
драты сходственных элементов:
где λ2 = £2 —Я
Обозначим через R — радиус круга, вписанного
в искомую трапецию, через г — радиус круга,
вписанного в первую трапецию. Тогда /^: <р~/с: f2; R2~
В качестве сходственного линейного элемента
возьмем половины оснований подобных треуголыш-
(f и ~-); тогда
R: а''2
КОВ
vm-wi
г.
Отсюда вытекает способ построения (рис. б). На
половине основания данного треугольника (-jj строим

полуокружность. В эту полуокружность вписываем
прямоугольный треугольник, один из катетов
которого равен "2*; второй катет— -к- (половина
основания равнобедренного треугольника, подобного
данному и равновеликому первой трапеции). Отложим
Отрезок, равный -η,, от середины основания треуголь*
ника и соединим полученную точку с центром
первого вписанного круга. Через вершину основания
данного треугольника проводим луч, параллельный
этой прямой. Получаем центр искомого круга,
откуда легко определяем и p-адиус, и сам круг. На
рисунке, кроме того,
построена и трапеция, рав- А
новеликая заданному
треугольнику.
4. Рассмотрим
частный случай, когда
данный равнобедренный
треугольник — правильный
(равносторонний).
Проведем через точки
касания каждых двух &
последовательно вписан- β
ных кругов общие
касательные, параллельные основанию треугольника
(рис. в). Тогда данный правильный треугольник
окажется разбитым на равнобочные трапеции, в ка-
ждую из которых вписан круг. Так как эти трапеции
вместе с вписанными в них кругами — подобные фи-
-гуры, то отношение площади круга к площади
описанной вокруг него трапеции одинаково для всех
фигур. Следовательно, таково же и отношение искомой
суммы площадей всех кругов к сумме площадей всех
трапеций (т. е. к площади данного треугольника).
С другой стороны, площадь каждой трапеции равна
удвоенной площади правильного треугольника,
высота которого равна /высоте трапеции, т. е. диаметру
вписанного круга. (Почему?) Площадь трапеции,
описанной вокруг искомого круга (и подобной всем
остальным трапециям), должна быть равна
площади данного треугольника; а половина площади ис-
87

комой трапеции (форма этой половины —
правильный треугольник) должна быть равна половине
площади данного правильного треугольника. В таком
случае отношение высоты искомой трапеции (она же
высота правильного треугольника, входящего в
искомую трапецию) к высоте данного правильного
треугольника равно 1 :γ2. Построения ясны из
чертежа:
На высоте AD как на диаметре строим
полуокружность AFD. Из центра Ε полуокружности
восстанавливаем к AD перпендикуляр EF (он пройдет через
точку / касания вписанного в треугольник круга).
На высоте AD отмечаем точку G на расстоянии DF
от D-DG — высота трапеции PQRS, площадь
которой равна площади данного правильного
треугольника. Следовательно, круг диаметра DG — искомый
(его площадь равна сумме площадей бесконечного
ряда вписанных в данный правильный треугольник
кругов).
Для правильного треугольника:
Sn 3π4 Зя Л —
5Δ 32/3 8>^3
2. Для ответа на поставленный вопрос достаточно
рассмотреть множество равнобочных трапеций,
описанных вокруг некоторого круга: площадь каждой
трапеции равна произведению ее высоты (т. е. диаметра
круга) л а среднюю линию; так как высоты всех
трапеций одинаковы, то отношение площадей трапеции
равно отношению их средних линий.
Наименьшая средняя линия — у трапеции,
выродившейся в квадрат. В этом случае площадь
описанной вокруг данного круга трапеции минимальная;
следовательно, отношение площади круга к площади
трапеции наибольшее, а именно, оно равно π:4«
=0,785.... По мере увеличения угла при вершине
увеличивается средняя линия трапеции, а следова-
В&

Цельно, и площадь трапеции; в таком случае
«насыщенность» трапеции кругом (т. е. треугольника
вписанными в него кругами) уменьшается (и стремится
к нулю).
606. В КОНУС ВПИСАНЫ ШАРЫ
Задача сводится к предыдущей.
61 а. ПОЯСА КРУГОВ ВОКРУГ ЯДРА
Каждый пояс состоит из кругов, центры которых
расположены на сторонах правильного
шестиугольника. Число кругов на каждой стороне следующего
шестиугольника на единицу
больше числа кругов на
стороне предыдущего
шестиугольника. Следовательно, числа
Кругов в поясах образуют
арифметическую прогрессию с
разностью d=6, αϊ=6;
следовательно,
αη=6+ {η — 1)6=6/ι.
Прибавив один круг — ядро, получим:
Nn=l+Sn+3nK
61 а. ЯДРО —ТРИ КРУГА
Ядро— 3X1 круга,
1 -е кольцо — 3X3 кругов,
2-е кольцо — 3x5 кругов.
3-е кольцо — 3χ7 кругов.
2„ = 3[l+3+5+...+
+ <2«+1)1 =
^(λ+Ι)2.
89

Какова будет формула в том случае, если ядро
составлено из четырех кругов, причем каждый круг
касается двух других, а их центры — вершины
квадрата?
62. СЕМЬ ДРОБЕЙ
Конечно, нетрудно сравнить две дроби, приведя их
к общему знаменателю, но как лучше поступить:
сравнивать их сначала попарно, затем следующие
пары и т. д., либо выбрать одну дробь и сравни·
вать ее последовательно с каждой другой дробью
и т. д., либо привести все дроби сразу к одному
общему знаменателю? Кстати, в последнем случае
общий знашйнатель будет равен 5·67·449·491Χ)
,Х613 · 653 · 787=23 265962 743672 895!
Попробуем воспользоваться графиком.
Если мы нанесем на координатное поле точку,
абсцисса и ордината· которой соответственно
знаменатель и числитель данной дроби, то величина
тангенса угла, образуемого лучом, проведенным из
начала координат через эту точку, равна величине
данной дроби. Чем больше угол (для правильной дроби
он не более 90°), тем больше тангенс угла, тем, еле*
довательно, больше и сама дробь. Таков принцип
решения задачи.
Приступим к построениям. Их проще выполнить
на миллиметровой бумаге. Какого размера лист
нужен нам? Числители (и знаменатели) данных дро·»
90

4>ей резко различны по величине: от 4 до 601 (от 5 до
787); поэтому требуется большой лист бумаги;
однако воспользуемся тем, что величина дроби не
изменится, если мы одновременно -уменьшим и
числитель, и знаменатель в 10 или в 100 раз, т. е., напри-
^53 ^5,3 * 509
мер, дробь -щ заменим дробью «gy, дробь -g^- —
509
дробью -gW Ц> τ· π· Благодаря этому все точки
разместятся на небольшом куске бумаги.
Как обычно в графических построениях, мы
наносим точку лишь приближенно, и если величины двух
дробей будут весьма близкими, график может не дать
четкого ответа; в этом случае он поможет
«рассортировать» дроби для последующего сравнения
обычным способом лишь весьма близких по величине
дробей.
Но в данном случае расположение точек
оказалось таким, что по графику читаем сразу: наимень-
^321 - * 360
шая дробь — -щ, за ней следует дробь -щ- и т. д.
63. БРОНЗОВЫЙ ЛЕВ
Строим график в системе «время — объем воды».
Отрезок ОА соответствует объему бассейна.
«Правый глаз наполняет бассейн за два дня» —
наклонная А — 2. «Левый глаз наполняег бассейн за три
дня» — наклонная О — 3.
а / г з « s в
Отметим точку В на пересечении А — 2 и О — 3.
Отрезок ВС' изображает количество воды,
поступившей в бассейн из правого глаза за промежуток
времени АС'\ аналогично, отрезок ВС" изображает
количество воды, поступившей в бассейн из левого
91

глаза за то же время. Следовательно, отрезок АС'
{=0С") изображает промежуток времени, за
который вода из обоих глаз наполняет весь бассейн, Πον
этому ОС— график работы «обоих глаз».
Аналогично строим график работы «рта» (О—6)
и «ноги» (А — 4); с помощью точки D (точки
пересечения этих двух графиков) строим АЕ — график
совместной работы «рта» и «ноги».
Суммарные графики — ОС и АЕ — пе'ресекаются
в точке F; отрезок 00 (где G — проекция точки F
на ось времени) соответствует искомой
продолжительности-наполнения бассейна при работе всех
четырех струй.
По масштабу определяем, что OG^=-^(0— 1).
4
Таким образом, бассейн заполнится за -г суток
(\9ч\2мин). °
64. СВИДАНИЕ
Как это могло быть, рассказывает график.
(Масштаб длины: 1 клеточка — 20 лс; масштаб времени:
одна клеточка — 1 минута.)
В пришел со стороны переулка Ρ за 1,5 мин до
8 часов, прошел мимо .кино и дошел до ларька; так
92

как он шел со скоростью 4 км/ч, то расстояние 200 м
200
<?н прошел за -щ^- · 60 = 3 мин. Затем он повернул
обратно и в том же темпе на том же отрезке
прошелся несколько раз.
А пришел со стороны переулка Q в 8 ч 1,5 мин —
в тот момент, когда В, дойдя до ларька, повернул
обратно; А прошел мимо ларька, затем мимо кино,
повернул обратно и т. д.
Так как А и В прохаживались маятникообразно
с одинаковой скоростью на отрезках PL и KQ
одинаковой длины (200 м), то расстояние между ними
оставалось неизменным (оно равнялось 60 м).
Вечером, в мороз, на людной улице на расстоянии 60 м
они могли и не увидеть друг друга.
Вот что может случиться, если плохо условиться!
00. ТРИ АВТОМАШИНЫ
Итак, три машины прибыли в В одновременно и
0ез остановки продолжали свое движение в С. Так
как по условию машины отправлялись из А через
Встреча
N4u№3
равные промежутки времени, то и в любой пункт
(в том числе и в пункт С) они прибудут также
через равные промежутки времени (но в обратной
последовательности). По условию, первая машина
прибыла в С через один час после второй; следователь-
дЗ

но, третья машина прибыла в С на один час
раньше второй, т. е. первая прибыла в С через 1 + 1 =
~2 часа после третьей. Вторая машина и участок АВ
нам больше не понадобятся, и теперь можно
сформулировать условие задачи так: «Из В одновременно
вышли две машины: № 1 и №3; машина №3 прибыла
в пункт С (£С=120 км) и немедленно повернула
обратно; в 40 км от С она встретила машину № 1,
которая прибыла в С через два часа после прибытия
в этот пункт машины № 3».
Машины № 1 и № 3 вышли из В одновременно.
До .встречи машина № I прошла 120 — 40=80 (км),
а машина Mb Z прошла 120+40=160 (км).
Следовательно, скорость машины № 3 в 160:80—2 раза
больше скорости машины № 1.
За 2 часа с момента прибытия машины № 3 в С
до момента прибытия в этот же пункт машины № 1
произошло следующее: машина № 3 прошла 40 км
(в направлении от С к β), а затем машина N° 1
прошла то же расстояние {в направлении от В к С).
Так как скорость машины № 3 в 2 раза больше
скорости машины № 1, то время, затраченное
машиной № 3 на участке длиной 40 км, в 2 раза
меньше времени, затраченного машиной № 1 на том же
участке, В таком случае, машина № 1 затратила на
2 4'
этот участок ^ ■ 2 2 = -^ (часа).
Итак, машина № 1 проходит 40 км за -к часа;
следовательно, ее скорость равна 40 : -*· = 30 (км/час)»
Как это все происходит, наглядно показывает
график. Расстояние АВ не дано и не может бьггь
найдено, поэтому положения точки А на графике мы
незнаем; может быть, это A'f или Л", или A"'t а может
быть, и какая-нибудь другая точка.
66. ДВА ВЕЛОСИПЕДИСТА
I. Обозначим через о скорость 1-го велосипедиста,
через w — скорость 2-го велосипедиста^ через £ —
расстояние АВ.

В таком случае:
1-й проехал (км)
2-й проехал (км)
ι до первой
встречи
5
5 —
V
до второй
встречи
1 + 3
Оба вместе (км) \ L \ 3L
Отсюда получаем два уравнения:
б.(1+£) = А О)
<L + 3).(l-f-£) = 3£. (2)
Разделив (2) на (1), получим:
£+1 = 3; Л-Ь3 = 15; 1=12 (км).
2. Воссоздать картину движения велосипедистов
ручше всего при помощи графика.
График отчетливо показывает, что после первой
(встречи велосипедисты проехали до второй встречи
Ьуть, равный удвоенному расстоянию АВ; точно так
рке и после второй встречи велосипедисты проехали
до третьей встречи путь, равный удвоенному
расстоянию Л В. Следовательно, промежуток времени между
|еторой и третьей встречами равен промежутку ме-
акду первой и второй встречами.
Однако было бы ошибкой сделать из этого вывод,
будто и впредь интервалы между каждыми двумя
последовательными встречами будут такими же. Как
видно из графика, интервалы между третьей и
четвертой встречами, а также между четвертой и пятой
95

встречами гораздо меньше первых двух интервалов;
их величину определить нетрудно: между третьей и
пятой встречами велосипедисты вновь преодолели
двойное расстояние АВ\ следовательно, промежуток
времени между третьей и пятой встречами равен
промежутку времени между первой и второй (а
также и второй и третьей встречами). Поэтому интервал
между третьей и четвертой (а также между четверг
той и лятой) встречами равен половине интервала
между первой и второй (или второй и третьей)
встречами.
Где произойдет четвертая встреча?- Из графика —
без всяких дополнительных построений или
вычислений, в силу симметрии, — видно; что четвертая
встреча произойдет в точке, равноудаленной от точек А и
В (заметьте, что на графике точка, соответствующая
четвертой встрече велосипедистов, является центром
симметрии графика).
Далее. 2-й велосипедист (тот, который едет бы·
стрее) встречает другого велосипедиста на одном
перегоне один раз и только один раз. 1-й
велосипедист (тот, который едет медленнее) встречает
другого велосипедиста либо один раз, либо (во время
своего третьего, а также восьмого полурейса) три
раза (в том числе один обгон!).
После пяти полных рейсов 1-го велосипедиста (и
семи полных рейсов 2-го) все начинается сначала.
График движения после пяти полурейсов 1-го (и
семи полурейсов 2-го) — фигура, зеркально
симметричная построенному графику.
Еще одно замечание. При решении задачи с
двумя велосипедистами мы исходили из того, что
между первой и второй встречами
каждый из велосипедистов
совершит один поворот в
противоположную сторону; между тем,
условие задачи не содержит
такого прямого указания.
Поэтому данная задача имеет и
второе решение, сущность которого ясна из графика.
Найдите расстояние АВ, в этом случае, исследуйте
решение.
96

67. ДВА ВКЛАДЧИКА
В системе координат «время — деньги», приняв
один и тот же масштаб для месяцев и для рублей,
построим две точки: В(т, р) и С(п, q) и проведем
через них прямую, которая встретит ось ординат
в точке А (рис. а).
ЫЬ
о~
т
Точка А показывает, что в момент времени 0
сумма вклада составляла ОА рублей; с этого момента
начался равномерный процесс роста вклада, что
изображается при помощи наклонной прямой; через
т месяцев размер вклада (с процентами) достиг
ρ руб., а через η месяцев — q руб.
Задача решена:
1. Ордината точки А — искомая сумма вклада.
2. Тангенс угла наклона луча АС к оси ОХ
Численно равен величине процентной суммы на вклад О А
за один месяц. Процентная сумма с того же вклада,
но не за один месяц, а за один год, т. е. за \й месяцев,
будет в 12 раз больше; процентная сумма с одного
рубля будет в О А раз меньше, чем с суммы ОА;
наконец, искомая величина процентной ставки будет в
100 раз больше, т. е. она равна 75T~tga·
Пользуясь построенным графиком, можно решить
и другие задачи, например: «Какая сумма k будет
выплачена вкладчику, внесшему υ рублей, через t
месяцев?»
Продолжим отрезок СА до встречи с осью абсцисс
в точке F (рис. б). Отрезок OF изображает тот срок,
в течение которого данный вклад удваивается (т. е.
срок, за который сумма выплаченных процентов
будет равна сумме вклада). Но коль скоро количество
процентов, выплачиваемых сберкассой, одинаково
97

для всех вкладов, точка F также постоянна для всех
вкладов. В данном случае вклад равен ν; отложим
0#=и и проведем из точки F через точку Η
полупрямую; в таком случае луч HD изобразит рост
вклада ν со временем. Отложив OG=/ и проведя GZ)|]0tf,
находим точку D. GD=k.
Если размер процентной ставки изменится, то
точка F переместится по оси абсцисс; например, если
процентная ставка увеличится в η раз, то точка F
перейдет в точку F' такую, что OF: OF'=n. В самом
деле (рис. в), по условию должно быть С'Е :СЕ—п;
из подобия треугольников СЕ А и AOF следует, что
СЕ :ЕА—АО :OF, а из подобия треугольников СЕЛ
и A OF' следует, что С'Е :ЕА=АО :OF', откуда
OF:OF'=C'E:CE=n.
Мы привели .чисто графическое решение задачи.
Если требуется найти аналитическое выражение
искомых величин, то это можно сделать, пользуясь
построенными графиками (из подобия фигур).
При небольшой величине процентной ставки
длина отрезка OF получается значительной и чертеж —
громоздким; в этом случае следует принять по оси
абсцисс меньший масштаб, чем по оси ординат.
Разумеется, выше все время речь шла о простых,
а не о сложных процентах.
68. БЫКИ НА ЛУГУ
Предварительно рассмотрим два графика; по оси
абсцисс будем откладывать время (в неделях), ведя
счет от того момента, когда быки были выпущены
на луг; по оси ординат — количество травы
(измеряемое, например, недельной порцией одного быка);
графики количества травы, съеденной быками,—
сплошные линии; графики выросшей травы —
штриховые линии.
Первый график (рис. а) показывает зависимость
количества травы, съеденной быками, от числа
недель пребывания их на лугу. Так как каждый бык
съедает каждую неделю одно и то же (пока
неизвестное нам) количество травы, то" график —луч,
проходящий через начало координат; тангенс угла
наклона луча прямо пропорционален числу быков.
98

Второй график (рис. б) показывает зависимость
количества выросшей на лугу травы от числа недель,
прошедших с момента, когда начала расти трава
(этот момент помечен на оси времени точкой Т, рас-
бремА
5
>
1*
6?
■§■*
ε t
у з
ь
з
^
|Я
Q.
7 -У
'Ъ'
' -" X —-
У-*" ~Ь^
^"-гГ
X
у
у
-"'
__ _- -"
Время
Τ ^~~-·
-iff
-5
θ+*Φ~ί
■ю
15 Недели
положенной слева от точки О). Так как каждую
неделю вырастает одно и то же количество травы
(какое именно — неизвестно), то график —луч,
проходящий через точку Т; тангенс угла наклона луча
прямо пропорционален площади луга. (Количеству
99

Травы» выросшей к тому моменту, когда быки были
выпущены на данный луг, соответствует
вертикальный отрезок, ограниченный точкой О и точкой
пересечения графика с осью ординат.)
Рассмотрим графическое решение задачи сначала
для упрощенного случая, а именно, «приведем» все
три луга к одной и той же площади, например к
площади второго луга. Тогда условие задачи запишется
так:
Луг Площадь Число Число
быков недель
I 10 36 4
II 10 21 9
III 10 χ 18
Строим график (рис. в). На оси времени
отмечаем точки Л, β и С, соответствующие 4, 9 и 18
неделям. Из точки С восставим к оси времени
перпендикуляр и на нем в произвольном масштабе будем
наносить количество быков: точка А' соответствует
36 быкам (I луг), точка β' —21 быку (II луг);
следовательно, лучи ОА' и ОВ' являются графиками
количества травы, съедаемой быками соответственно
на I и на II лугу. Однако по условию вся трава
съедается на I лугу за 4 недели, а на II лугу — за
9 недель; следовательно.^еальными являются только
участки ОА" и ОВ" этих лучей. Отрезки АА" и ВВ"
изображают (в некотором масштабе) количество
травы на лугу площадью 10 акров, съеденной двумя
группами быков за соответствующие сроки, но так
как график количества травы на лугу данной
площади в функции времени — прямая линия, то,
проведя через точки А" и В" прямую, получим график
роста травы на лугу; на этом графике отметим две
точки: Τ — определяющую момент, когда на лугу
начала расти трава (по масштабу определяем, что
70=12 недель), и С — определяющую отрезок CCft
соответствующий тому количеству быков, которое за
18 недель съест всю траву на лугу площадью 10
акров. По масштабу определяем, что СО—15 (быков).
Это и есть искомое число быков χ на III лугу для
упрощенного случая.
100

Так как площадь III луга в действительности
равна не 10 акрам, как мы приняли в упрощенном
случае, а 24 акрам, то искомое число быков равно
|р 15 = 36 (быков).
Теперь решим эту задачу, не упрощая условия.
Отметим на горизонтальной оси точки А, В и С,
соответствующие времени пребывания быков на
лугах: 4, 9 и 18 неделям (рис. г). На вертикали,
проведенной через точку С, отметим точки А' и В',
соответствующие числу быков на первом и втором
лугах — 12 и 21. Проведя лучи О А' и ОВ\ получим
графики, иллюстрирующие темпы поедания быками
травы соответственно на I и II лугах. По условию,
площади лугов I и II различны, а именно 3-я- и 10
акров. Если бы площадь I луга была бы не 3-^· акра,
а 10 акров (т. е. была бы в 3 раза больше), то
количество травы, выросшей на этом лугу к моменту,
отмеченному точкой А, изображалось бы отрезком
АА'"=ЪАА". Точки А"' и В" принадлежат графикам
лугов равной площади (по 10 акров); следовательно,
луч, проведенный через эти точки, является графиком
роста травы на лугу площадью 10 акров, а
точка Г — момент начала роста травы.
Луч Τ А"'В" пересекает ось ординат в точке F^\
отрезок OFz изображает площадь II луга (отрезок
OF ι — Ι луга).
Для построения графика роста травы на III лугу
надо найти на оси ординат такую точку F3, чтобы
отрезок OF3 изображал площадь III луга; но по
условию площадь III· луга равна 24 акрам; поэтому
FzO : F20—24 :10. Проводим луч через точки Τ и F3.
Ордината точки С на этом луче и дает ответ на
поставленный вопрос: на III луг нужно выпустить
36 быков.
С помо'щью графика мы не только получили
ответ на поставленный в задаче вопрос «Сколько
быков нужно пустить на луг площадью 24 акра, чтобы
они при тех же условиях могли прокормиться 18
недель?», но и подготовились к быстрому ответу и при
101

других цифрах. Например, для ответа на вопрос?
«Сколько недель можно прокормить β быков на лугу
площадью α акров?», достаточно провести всего два
луча, а именно: 1) из точки Τ через точку Fa на оси
ординат (ордината этой точки равна а); 2) из
точки О луч, пересекающий шкалу «количество быков»
в точке, ордината которой равна β.
Абсцисса точки пересечения этих двух лучей и
является ответом.
Аналитическое решение задачи таково:
x==:j3_. S1M2 (*а — <t) — s2bjti (<э — *г)
SjS2 t* if 2 — 11)
где: s — акры, b — быки, t — недели.
69. ДВЕ ЛОДКИ
1. Обозначим расстояние АВ через s, собственную
скорость лодки через ν, скорость течения — через а.
Тогда (при направлении течения из Л в В):
s s $ s
tz-j-л v-f-e-T*-* v — а — -* v — а *
откуда найдем:
а — ζ·
Или (при направлении течения из В в Л):
s s s s
ν-\-α — χ υ·\·α ν — α ν — а-\-х*
откуда
Следовательно, ответ таков: лодка, плывущая
против течения, должна увеличить свою
скорость, а лодка, плывущая по течению, должна
уменьшить свою скорость на х=2а.
2. В решение задачи введены величины s —
расстояние АВ и Ό — собственная скорость лодки,
которые, однако, не вошли в ответ. Почему? Если
отсутствие в ответе s более или менее понятно, то
причина исчезновения ν остается нераскрытой. И каков
физический смысл ответа?
1Θ2

Попробуем разобраться в этом. В системе
координат «время — путь» начертим график О А
движения лодки при отсутствии течения (жирная линия
на рис. с). Отложив от точки F по вертикали в
противоположные стороны отрезок а, построим графики з
ОВ — движения лодки потечению ) тонкие
ОС — движения лодки против течения ί линии.
(Величины всех взятых нами отрезков —
произвольные; из дальнейшего будет ясно, что этот произвол
нисколько не влияет на выводы.)
Увеличим скорость лодки,
плывущей по течению, на χ — получим
график ОВ'\
уменьшим скорость лодки,
плывущей против течения, на х —
получим график ОС. J
По условию задачи требуется, чтобы уменьшение
продолжительности рейса первой лодки (изображае-
штриховые
линии
мое отрезком В В') равнялось увеличению
продолжительности рейса второй лодки (изображаемое
отрезком СС')Д Но из чертежа ясно, что каковы бы ни
103

штриховые
были ν, а и х, всегда ВВ'ФСС, следовательно,
предложенное нами направление изменения скоростей не
может дать решения поставленной задачи.
Переменим направление искомой скорости к
(рис. б), т. е.
увеличим скорость лодки,
плывущей против течения, на χ—
получим график ОС"\
уменьшим скорость лодки, плы- ι линии
вущей по течению, на χ—получим I
график OB" I
Из чертежа совершенно ясно^ что ВВ" будет
равно СС" только в том случае, если точка В" совпадает
с точкой С, а точка С" — с точкой В. Тогда лодки
«поменяются графиками» и условия задачи будут
выполнены: лодка, плывущая против течения,
увеличит свою скорость на столько же, на сколько ее
уменьшит лодка, плывущая по течению (а
именно, на x=2a)t а продолжительность рейса первой
лодки уменьшится на столько, на сколько
увеличится продолжительность рейса второй лодки
(а именно, на промежуток Времени, изображаемый
отрезком ВС).
График со всей очевидностью объясняет причину
исчезновения из ответа величины собственной
скорости лодок: наши рассуждения совершенно не были
связаны с величиной vt и убеждает, что полученный
ответ -*- единственный.
А вот «чисто логическое* решение задачи. По
условию, скорость одной лодки увеличивается на
столько же, на сколько уменьшается скорость другой
лодки; физически это можно осуществить, изменив
скорость течения. Следовательно, теперь задачу
можно сформулировать так: «как должна измениться
скорость течения, чтобы время движения одной из
лодок уменьшилось ровно на столько, на сколько
увеличится время движения другой лодки?» Ответ
очевиден: если направление течения изменится на
обратное, то первая лодка будет в пути столько, сколько
была вторая, и наоборот: вторая лодка будет в пути
столько, сколько была первая; следовательно, на
сколько увеличилось время в пути одной лодки, на
столько же уменьшилось время в пути другой лодки.
104

А изменение направления течения (при сохранении
абсолютной величины скорости течения) равносильно
тому, что скорость лодки изменяется на удвоенную
величину, т. е. х=2а. Кстати, теперь совершенно
ясна причина исчезновения из ответа
как'собственной скорости лодки, так и расстояния 5.
60. ОТЕЦ И ТРОЕ СЫНОВЕЙ
1. (По книге Обера и Папелье.) Пусть и означает
возраст отца, χ— возраст старшего сына, у —
возраст второго сына и ζ — младшего.
Имеем прежде всего уравнение:
и~х+у+г+5. (1)
Через 10 лет отцу будет («+10) лет, а старшему
сыну (jc+10) лет.
Согласно условию, составляем второе уравнение
и-К10=2(*+10).
Точно так же
и+20=2(#+20) н ы-г30=2(г+30).
Из этих последних трех уравнений находим:
хшш£^-, у-£=р-. *-г^». (2)
Подставляя эти значения х, у и г в уравнение (1),
имеем:
Зи —60 -
и = —g ho,
откуда получим и = 50.
Подставив это значение и в уравнения (2),
получаем:
х=20; #=}5; г=10.
2. Через 10 лет возраст старшего сына равен
половине возраста отца. Еще через 20—16=10 лет
возраст старшего сына увеличится на 10 лет, а
половина возраста отца увеличится лишь на 10:2=
=5 лет. Следовательно, тогда число лет старшего
сына будет на 10 — 5=5 лет больше половины числа
лет отца; но в этот момент возраст среднего сына
105

станет равен половине возраста отца. Окончательно:
старший сын ыа 5 лет старше среднего. Аналогично:
средний сын на 5 лет старше младшего.
Обозначив через ζ возраст младшего сына (в
данный момент) и через и — возраст отца, получим:
г+ (2+5) + (2+5+5) +5=ы; 3z+20=w 1
(2+5+5+10) . 2=ы+10; 22+30=w J
2=10, ί/=15, х=20, и=50.
Полученные результаты наглядно иллюстрируются
следующим графиком:
Ю 20 30 40 50 60 7Q 60
61. ПОКУПАТЕЛЬ И ТРИ ПОСТАВЩИКА
Прежде всего заметим, что абсолютная величина
стоимости продукции не имеет никакого значения
для отыскания ответа: важно только то, что
наименьшая стоимость продукта в III колхозе, а
наибольшая — в I.
Решим задачу графически, путем построения
ломаной, изображающей процесс нарастания времени
работы автотранспорта по мере перевозки с его по>
мощью продукта из одного, другого, третьего
колхоза (рнс. а).
Искомая ломаная исходит из точки О (0, 0).
Процесс доставки из I колхоза изобразился бы лучом I,
106

проходящим через точку К (10, 10) —за 10ч 10тонн;
аналогично, для II колхоза луч II, проходящий через
точку L (40, 10), и для III колхоза—луч III,
проходящий через точку Μ (30, 10).
■Ρ Ν
12
Ю
I s
b/tJ
р5ч>
1
/
]/
$&
N
/
/
^
/
^
/
k^
>
/
^
^
s'
Η
:^
>
^
S
^
'
Л
s'
w
У
•
*■
*
*
яг
_
Λί
>
•
Χ
ЧГ
*7t
πι
Μ\
U-71
у
Υ
/Ι
Τ
\щ\ !
10
го
а
зо
чОчос
Искомая ломаная содержит столько звеньев,
сколько имеется поставщиков; длина проекции этой
ломаной на ось ординат должна соответствовать
общему весу продукта (12 тонн), а длина проекции
этой же ломаной на ось абсцисс не должна
превышать лимита времени
работы автотранспорта (40 н).
Так как самый дешевый
продукт в III колхозе,
сначала производим закупку
именно там; но количество
продукта в III колхозе
ограничено 6 тоннами;
поэтому первый участок
ломаной— отрезок О А.
Обращаемся в следующий (по
цене) кшхоз: проводим
через точку А луч АЩОЬ-,
но точка N оказалась вне
установленного лимита времени (суммарное время
42 ч вместо 40 ч); Поэтому проводим через
точку Ρ луч РН\\ОК; он пересечет прямую AN в
точке Q. Искомый график — OAQP; читаем ответ:
12
ю \
5
1*
-»:
к
5^
•^
а
f
-
I
f/
—
t
У
xM
А
i
λ
^
~У+Р
/У
J
f
ί
ι
/
ST. у
Ж
π
ι
ι
Ι
Ι
jj
/
t
ν
/
Ι
[Μ!
ί/
|Ί
>
S
"~
/
Ρ
Ι/,
^\
•U
,<
^
2
> Ν
4?
S
Г
д
ι
*Μ
Щ*)
го.
V2)
Μ
ϋ
*ι
2 -1 ^_α
ιο?

Решение данной задачи можно несколько
упростить, если все заданные нормы затрат на
транспортировку (1, 4 и 3 ч/т) уменьшить на единицу, т. е.
принять равными 0, 3 и 2, соответственно уменьшив
н общий лимит времени (на 12 ч). Соответствующий
график приведен на рис. б.
62. ЧЕТЫРЕ ПУТЕШЕСТВЕННИКА
1. (По книге Обера и Папелье.) Положим AM=дг,
АР—у (х>у)у причем χ и у выражены в километрах.
Старшие путешественники затратили на путь из Л в
о / χ ' 39,6—χ \
("36 ^ 4 ) часов; вРемя, затраченное на тот
же путь молодежью, составляет
ι у . 39,6—у\
ИИ 36 ) часов·
Наконец, время, затраченное автомобилем, равно
*+««-»H-cm>-i> часов.
Поскольку все эти три выражения равны между
собой, получаем:
χ . 39,6 — χ _ у . 39,6 — у _ 2х — 2f/4-39,6
Зб"г 4 ""6^36"^ 36
ИЛИ
х+9(39,6 — х) =6#+39,6 — у=2х — 2j/+39,6,
или, сперва приравнивая друг к другу первые два
выражения, а затем два последних, имеем:
8*+Ьу=8 · 39,6, 7у=2х,
откуда находим:
iL— У — в^+Зу — 8·39'6 — л о.
7 —*2"— 8,7-f5,2 ~~ 66 ~~ %°*
х=7.4,8=33,6 (км), у=2-4,8=9,6 (км).

2. Решим теперь эту задачу при помощи графика.
По условию, из А одновременно отправляются
автомобиль и молодежь; изобразим это на графике при
помощи двух лучей AM' и АР\ исходящих из одйой
точки; так как автомашина
движется быстрее пешеходов
луч AM* образует с
положительным направлением осиЛХ
больший угол, чем луч АР'
Из Μ одновременно
отправляются: автомобиль
(обратно) и старички (вперед):
графики движения —
соответственно отрезки М'Р' (ΖΛί'Ρ'Ρ=ΖΜ'ΑΚ) и Μ'В'
(угол наклона М'В' к оси АХ меньше, чем угол
наклона АР' к той же оси).
В Ρ прибывают одновременно автомобиль и
молодежь: точка Р'.
В В прибывают одновременно автомобиль и
старички:
проводим Р'В'\\АМ'-В' — точка пересечения лучей
из М' и из Р'.
Спроектируем точки Р', М' и В' на вертикальную
ось; получим точки Ρ, Μ и В.
Учитывая данные задачи, находим:
(ЛР-Ь2Л1Я):ЛЯ = 6;
таким образом, 1 -j- —^р- = 6; —др- = о; АР: МР=2:5.
2) ^^=36:4;
(МВ + 2МР):МВ = 9,
откуда 14-^ = 9; W = 8; MP.MB^A: 1.
Следовательно, АР: РМ: MB = 8: 20:5',
откуда АР — 8 ■ 2о+5 "39,6 ~ "зз ^9'6 = 9*6 (**)
РМ = ~-39,6^24 (км).
33
1 Эти отношения могли быть найдены в чисто графическим
путем.
109

При таком решении отчетливо видно, что
полученные решения не зависят от абсолютных величия
скоростей, а зависят только от отношений
скоростей автомобиля и пешеходов.
ва сто петухов, кур и цыплят
Количество петухов (П), кур (К) и цыплят (Ц)
при каждой покупке — это три целые числа,
удовлетворяющие одновременно двум уравнениям:
| П-Н К+ Ц= 100 (птиц),
Ι 5П+ЗК4-^Ц=100 (грошей).
Следовательно, задача сводится к отысканию трех
троек целочисленных корней системы двух линейных
уравнений.
Для решения этой системы воспользуемся
графиком (рис. а), изображающим нарастание стоимости
Птицы
а
всей покупки с увеличением количества купленных
птиц. Таким образом, требуется построить три
ломаные, каждая из которых должна удовлетворять
следующим условиям: \) яанало ломаной в начале
координат, конец — в точке, соответствующей 100 пти-
110

цам и 100 грошам; 2) ломаная состоит из трех
звеньев; горизонтальная проекция звена изображает
количество купленных птиц, а вертикальная — их
стоимость (соответственно: петухов, кур и цыплят);
3) абсциссы вершин ломаной — числа целые.
Из точки О(0, 0) проводим луч ОА, образующий
с положительным направлением оси ОХ угол, тангенс
которого равен 5: 1 (пять грошей за каждого
петуха) .
Из точки 0(0, 0) проводим луч ОБ, образующий
с положительным направлением оси ОХ угол,
тангенс которого равен 3: 1 (три гроша за одну курицу).
Из точки 0(0, 0) проводим луч ОС, образующий
с положительным направлением оси ОХ угол,
тангенс которого равен 1 :3 (на 1 грош три цыпленка),
Три звена искомых ломаных должны быть
параллельны этим трем лучам.
Так как количество птиц может быть только
числом целым, то мы будем иметь дело не с ломаными
линиями, а с совокупностью отдельных точек на этих
ломаных, а именно, только с теми точками на этих
ломаных, абсциссы которых числа целые. На луче ОА
несколько таких точек обозначено кружками.
Проведем через точку Со(100, 100) прямую О'С0,
параллельную лучу ОС. Она пересечет луч ОВ в
точке В0; абсцисса точки В0 — 25 — число целое.
Ломаная ОВ0Со удовлетворяет следующим условиям:
ее начальная точка — О(0, 0), конечная — Со(100,
100);
абсциссы всех вершин (0; 25 и 100) — целые
числа;
первое звено параллельно лучу OBt второе —
лучу ОС.
' Следовательно, ломаная ОВ0С0 удовлетворяет
всем условиям, кроме одного: в ней нет третьего
звена, соответствующего петухам (ломаная OBqCq
изображает покупку 25 кур и 75 цыплят: 25+75=
= 100 птиц за 25 · 3+15 · -^ = 75+25= 100
грошей). Для того чтобы включить в покупку также
и петухов, надо переместить поступательно звено
«куры» так, чтобы оно пересекло лучи ОА и O'Cq
в точках с целочисленными абсциссами.
Ш

Для облегчения построений увеличим
горизонтальный масштаб части графика (рис. б).
100
90
80
70
60-
150
30
20
Ю
О
1 -
I
2
ί
' J
А'
-£
~
4
А
t
1 i
^4
I
S'l
'
o{
^'
ЩШ
Jt
Aj£&
&$&
^βτ
HI
Ι Ί
f
_J I
«
5^
й
^
ψ
?
·-
·;
^
Λ^
i
^
^
2
>
Ρ
^
^
*'
f£
^
^
J
^
^
^
£
>
«
/l«
^
" 1
^5
,·->
£
flj
И2К
^^
jif
r —
Ή2*
Η
Λ?
t
"1
—
±
25
Как видно из графика, всем требованиям условия
задачи удовлетворяют только три ломаные:
Ломаная
Петухов
Кур
Цыплят
Всего птиц
Всего
грошей
ОЛ'В'С,
ОА"В"С0
ОАюВтС9
4
8
12
18
"
4
78
81
84
100
100
100
100
100
100
64а. ТРИ ТЕЛА
Построим графики движения трех тел. Так как
тела отправляются из исходного пункта (обозначим
в его Л) в разное время, а
затем одновременно прибывают
в пункт В, то графики
движения — три наклонные,
сходящиеся в В.
Так как по условию
скорости тел относятся как 4:5:6,
а время движения обратно про-
6ремя пбрционально скорости (дли-
112

на пути одинакова), то
AiAQ . Л2/1о . ЛэЛ>— 4-5^·^ — W 60"' 60 ~
= 15:12:10,
но ΑιΑ2=2 (часа); следовательно,
Л2^3=:Т5^15*<Л>Л2^|--2=1-|· (часа).
Заметим, что для ответа на поставленный в задаче
вопрос вовсе не нужно знать абсолютных значений
скоростей тел: достаточно знать их отношения (ответ
не изменится, если скорости тел будут равны, напри·
мер 4; 5 и б см/ч, или 4; 5 и 6 км/сек и т. д.).
646. ДВА ТЕЛА
С помощью формул равномерно переменного
движения можно составить систему из трех уравнений
с тремя неизвестными: 1) начальная скорость
второго тела, 2) ускорение первого тела и 3)
промежуток времени от начала движения до момента, когда
скорости тел сравнялись; найдя эти неизвестные,
можно приступить к дальнейшим расчетам и
определить искомый момент. Но при этом вычисления
оказываются довольно громоздкими.
Проще всего будет ответить на поставленный
вопрос, если обратить внимание на следующее.
По условию, в момент, когда скорости тел
сравнялись, расстояние между ними составляло 379 м;
требуется определить, когда второе тело опередит первое
на 1137 м. Но ведь 1137:379=3.
Значит, задаче можно придать такой вид:
«Из точки А в одном направлений одновременно
начали двигаться два тела; оба движутся равномерно
ускоренно; скорость первого больше скорости второго.
Через I ч 37 м 39 сек второе тело догнало
первое..,».
Итак, общая картина движения такова: оба тела
вышли одновременно из одной точки. Так как
скорость первого больше скорости второго, то
расстояние между ними начало увеличиваться; но, с другой
113

стороны, через некоторое время второе тело нагнало
первое; это могло быть только в том случае, если его
ускорение больше ускорения первого тела;
следовательно, до момента встречи был момент, когда их
скорости сравнялись.
Впрочем, все это проще и нагляднее изобразить
при помощи графика. Поэтому строим график в
координатах «время — скорость». Так как s=V't, то на
графике путь, пройденный телом, изобразится в виде
площади прямоугольной трапеции, а расстояние
между телами в момент Τ изобразится в виде разности
площадей двух трапеций.
Откладываем по оси скоростей два произвольных
отрезка V\ и V2{v\> ϋ2)* Через концы отрезков
проводим две наклонные (£1<£г)< Абсцисса точки
пересечения наклонных t -»- промежуток времени от
начала движения до момента, когда скорости тел
сравнялись. Разность площадей трапеций (£—379 м) —·
расстояние между телами в момент, когда скорости
сравнялись.
Далее. Для того чтобы оба тела встретились,
необходимо, чтобы площади трапеций — расстояний
сравнялись. А площади обеих прямоугольных
трапеций будут равны, если у них общие высота и средняя
линия. Отсюда следует, что 7Ό7ίβ27Ό7Ί.
По условию задачи требуется определить, когда
второе тело опередит первое на 1137 ж. Но П37«
=3 X 379=3L. Следовательно, требуется найти такую
точку 7э, чтобы разность между площадями двух
114

прямоугольных трапеций с общей стороной Т2Т3
достигла 3L. А для этого должно быть T2Ts=t
В~«.,Л». ,>„,,.„,Л τ τ о< q 1 ч 27 мин 39 сек
таком случае, Т0Тг = 3t = 3 2 =*
= 2 «ill мин 28,5 сек.
Таков ответ на поставленный вопрос.
Приведенные в условии задачи: скорость первой
точки и ускорение второй точки — лишние данные,
так как ответ совершенно не зависит от этих
величин.
65. ПОЕЗД
N Юкм/Ч
По горизонтальной оси будем откладывать
скорость, а по вертикальной — время (см. рисунок). Так
как расстояние, пройденное поездом, равно
произведению скорости на время,
то площадь
прямоугольника, стороны которого
соответственно
изображают скорость и время,
изобразит пройденное
поездом расстояние. Пусть
отрезок ОК — скорость
поезда, а отрезок — OL —
время хода (10 н40мин);
в таком случае площадь
прямоугольника OKML
изображает расстояние между городами А и В.
Если скорость поезда уменьшится на 10 км/ч (на
отрезок KN), то время хода увеличится на 2 ч 8 мин
(на отрезок LP). В этом случае расстояние АВ
изобразится площадью прямоугольника ONQP.
Так как расстояние между городами в обоих
случаях одно и то же, то площади прямоугольников
OKML и ONQP должны быть равны; так как
прямоугольник ONRL — их общая часть, то площадь
прямоугольника NKMR должна быть равна площади
прямоугольника LRQP.
Обозначив неизвестную уменьшенную скорость
поезда (отрезок ON) через х% получим:
Скоросто
115

10 ч 40 мин Χ 10 км/ч=2 ч 8 мин Χ χ км/ч,
откуда
10 ч 40 мин . , ,л 620 1Л сл . , ν
2 * 8 ли« ^ ' 128
Скорость поезда: 50+10=60 (км/ч).
г»
60
40
Расстояние между городами: 60 X 10-^=640(км).
66а. ТРИ рОСУДА
По условию, три раза повторяется одна И'та же
операция: из одного сосуда одна четверть
содержащейся в нем жидкости переливается во второй сосуд,
а другая четверть — в третий сосуд. При всех
переливаниях общее количество жидкости, находящейся
во всех трех сосудах, остается
неизменным. Представим это
неизменное количество
схематически в виде окружности (360°);
количество жидкости,
находящейся в какой-либо момент в
том или ином сосуде, будем
изображать соответствующей дугой
(рис. а). Переливанию части
воды из сосуда Я в сосуд Q (или в
сосуд R) будет соответствовать
перемещение дуги; при этом точка, где встречаются
концы дуг, соответствующих сосудам Q и /?,
останется на месте.
Пусть после переливания из сосуда Ρ одной
четверти в сосуд Q и одной четверти в сосуд R —
количество оставшейся в нем жидкости изображается
дугой АВ. Отложив А'Е' = B'D' = ·?>· А'В\ получим
точку £' (а также £У), определяющую границу между Ρ
и Q (соответственно между Ρ и R) перед
переливанием.
На рис. б внутренний круг изображает конечное
состояние системы; во всех трех сосудах по 16 л.
Предыдущее состояние системы, найденное с помощью
описанного выше приема, показано на следующем
круге. Аналогично отображены второе и первое
переливания. 'Исходное состояние системы показано на
116

внешнем круге. Последовательно вычисляем
количество жидкости в каждом из трех сосудов до
очередного переливания (цифры приведены у
соответствующих дуг).
Сначала После £ге' перелибаш»
После 1*° перегибания I После 3го перелив.
Обозначения
■■ I сосуд ЕЗЗЛсосуд ( \ Ш cocqft
δ
Ответ: в начале было: в 1-м сосуде 8 л, во 2-м —
14 л и в 3-м — 26 л.
666. ПЯТЬ РАЗБОЙНИКОВ
1. (По книге Попова.) По окончании раздела у
всех оказалось по -g· суммы; следовательно, до
последнего (пятого) удвоения у четырех было по -jq»
у 5-го i^·; перед предпоследним (четвертым)
удвоением у первых трех было по -таг, у четвертого
И 6
•kq , у пятого *2о » Перед третьим удвоением у пер-
1 21
вых двух было по -т^» у третьего -^, у четвертого
117

~, у пятого ^; перед вторым удвоением у первого
1 fi
было-gg-, у пятого -щ-, перед первым удвоением
81 41
у первого было -щ>, у второго -щ-, у третьего
-jjL·; у четвертого-щ-, у пятого -щ. Но при этом у
первого был 81 дукат, следовательно, всего было
160 дукатов.
в начале А.
После 1*°
удвоения
А,
После 2го .
удвоения Д2
После 3го л
удвоения "j
После W л
удвоения
После 5го
удвоения
В5 Cs Ds f,
Первый второй Третий Четвертый Пяты
2. (Графическое решение.) Проведем на равных
расстояниях шесть равных параллельных отрезков
A0Fq, AxFu A2F2, A3F3, A4F4 и AbFb. Нижний отрезок
AsFb делим точками Вв, С6, Ds и Еъ на пять равных
отрезков: после пятого удвоения у всех пяти
разбойников поровну. Соединим лучами точку Л3 с точками
В5, Cs, Ds и Е5. Тогда на отрезке A4F4 получим
отрезки А4В4, B4C4t C4D4 и D4E4t изображающие
количество дукатов, бывших соответственно у первого,
второго, третьего и четвертого разбойников до пятого
удвоения. Соединив лучами точку А2 с точками В4ь
С4, D4 и точку F2 с точкой Е4, получим точки Яз. Сэ,
Д, и £3, показывающие, как распределялись дукаты
перед четвертым удвоением. Дальнейшие построения
ясны из чертежа. Отрезок АХВХ получился в
результате четырехкратного деления пополам отрезка At}B6t
118

изображающего одну пятую всей суммы.
Следовательно,
АВ - AF „-AF
Λΐ°ι— 5·2·2-2·2 *"~ 80 *
Итак, у первого разбойника, после того как он
удвоил каждому число дукатов, осталась -щ всей
суммы; в таком случае у всех остальных оказалось
79 * 79
•gjg-, т. е. до удвоения у них было (-щ; значит, у пер-
79 81
вого было 1 —щ ~1ёо * а так как п0 Условию пеР*
вый взял себе 81 дукат, то всего было 160 дукатов.
Если AF=160, то i45BB=55C5=C5D5=Z)s/75=E5/?5=
=32. Для того чтобы найти, сколько было у каждого
вначале, нет необходимости возиться с дробями:
достаточно на· графике начиная с нижнего отрезка
последовательно проставить все числа.
Результат, полученный расчетом, может быть
проверен по масштабу (с точностью, допускаемой
данным построением).
67. С УДВОЕННОЙ СКОРОСТЬЮ
1. Построим графики движения в системе «вре«
мя—путь».
θ2 В,
Время
В первый раз; половина пути (AD) с начальной'
скоростью, половина, пути (DB) с удвоенной
скоростью, т. е. DiBi^^ADi,
119

Во второй раз: половина времени с начальной
скоростью, вторая половина — с удвоенной, т. е. СВ—
=2АС и АС2=С2В2.
С помощью циркуля устанавливаем, что ΒίΒ2 =
= -§ АВУ т. е. во второй раз некто был в пути на -д
меньше, чем в гтервый.
2. Оба раза первая треть пути была пройдена
с начальной скоростью за время /.
Оба раза вторая половина пути была
пройдена с удвоенной скоростью; следовательно, на нее
было затрачено -~-<г = -rt.
В первый раз на оставшуюся шестую часть пути
было затрачено -^ ·
Во второй раз на эту шестую часть было
затрачено -г.
4-
Всего было затрачено времени:
в первый раз: ί-\-^ί-\-γί = ^έ;
3 1ft.
во второй раз: t-\- -^t-\--rt=^-rt.
Следовательно, во второй раз было затрачено
времени на -к- меньше.
68. КАТЕРА НА РЕКЕ
В том случае, если течения нет, катер, идущий из
В в Ау конечно, встретит ровно столько же катеров.
идущих ему навстречу, сколько и катер» идущий из А
в В, т. е. семь. А если течение будет; то ... число
встреч не изменится, ибо нет причин для изменения
120

числа встреченных катеров. Вот и все. Но разве ничто
не изменится? Изменится вот что: так как при
наличии течения скорости катеров (относительно берегов)
будут различны (их отношение равно (2+1) : (2 —
— 1)=3: 1), то будут различны И продолжительности
каждого рейса (их отношение равно 1 :3); в
соответствии с этим, для катера, плывущего вниз по
течению, промежутки времени между каждыми двумя
встречами будут в три раза короче, чем для катера,
плывущего вверх по течению (см. график).
69. КАТЕР И ПЛОТ'
1. Обозначим через χ (км/ч) искомую
собственную скорость катера. Тогда: катер шел по течению
13 j : (χ -J- 4) (ч), против течения 9 у: (х — 4) (ч).
Плот до встречи с катером проплыл 13 тг— 9-^- =г
= 4 (км), затратив на это 4:4=1 (ч). Так как до
встречи катер и плот находились в пути одинаковое
время, то получаем уравнение:
χ + 4^ χ—4 *·
Отсюда: 13 ^(х—4)+9±(х+4)=х* —16,
или х2 —22-|jc = 0.
2
Окончательно: .к = 22 у (нм/ч).
2. Катер проплыл по течению 13-^ км, а против
течения —9-g· км, т. е. на 13.-я-—9~* = 4(км)
меньше. Следовательно, за это время плот проплыл
4 км; так как скорость течения 4 км!час, то от
момента отплытия из Ά до момента встречи прошел
1 час. Рассматривая систему катер — плот
(независимо от берегов), получаем, что катер удалялся от
плота столько же времени, сколько и шел ему
навстречу, т. е. 1: 2=0,5 часа.
121

За полчаса катер переместился (относительно бе-
регов) на 13-^ км; следовательно, его скорость была
«4
0,5 =м 26 у (км/4% собственная скорость катера
261—4 = 221 (кл/ч).
Замечание. В
условии сказано, что катер
отплыл одновременно с
плотом по течению^ однако
это обстоятельство
несущественно: если бы катер
отплыл одновременно с
плотом, но направился бы не
вниз по течению реки, а
вверх — против течения
реки, то ответ был бы тот
же (при сохранении того
условия, что катер проплыл
по течению 13-*· км, а про-
Вргмя
тив течения
*-""~ У о fCAt I ·
График показывает, как разворачивались бы
события в обоих случаях.
70. КОГДА НАЧИНАЮТСЯ СЕАНСЫ?
1. Обозначим продолжительность одного
интервала через х. Пусть 1-й сеанс начался через у часов
после 12 часов.
Тогда: начало 1-го сеанса 12-}-#,
2-го » \2 + у + х.
7-го
8-го
»
12+^+6*,
12+JH-7JC.
Отсюда и из условия следуют неравенства:
12<12-τ-ί/<13 или 0<ι/<1,
13< 12-τ-ί/-|-* < 14 или 1<0-М<2,
23<12-|-ί/+6χ<24 или ll<i/-f-6jc< 12,
24<12-Ь1/-г-7л:<25 или 12<0-т-7*< 13.
122

Отбрасывая неравенства, вытекающие из других,
получим систему:
ί О<0<1,
Ι 1<0 + *<2,
1 Π<04-6*,
Решаем систему графически.
На координатном поле проводим шесть прямых:
0 = 0,*
0=1,
л: 4-0=1,*
jc+0 = 2,
6x-\-y—l\t*
7χ-|-ί/=13.
Каждая из этих прямых — в зависимости от знака
неравенства (> или <)—определяет ту или иную
полуплоскость; на рисунке соответствующие
полуплоскости показаны штриховкой. При этом в случае
двойного знака (^) точки прямой входят в число
точек, определяемых данным неравенством
(уравнения этих прямых отмечены знаком *, а на рисунке
соответствующие прямые — толстым отрезком у
штриховки); если же знак один {<) —точки прямой не
входят в число точек, удовлетворяющих неравенству.
Искомые χ и 0 — это координаты тех точек,
которые принадлежат одновременно всем шести
полуплоскостям. Из чертежа видно, что это точки четырех-
123

угольника PQPiQu за исключением точек, лежащих
на PQ и QQt.
Дополнительному требованию (хну должны быть
кратны 5 мин) удовлетворяют только две точки:
Pi (1 ч 50 мин, 0 ч 0 мин) и
Р' (1 ч 50 мин, 0 ч 5 жмк).
Точка Q (1 «50 жи«; 10 мин) удовлетворяет
дополнительному требованию, но не удовлетворяет
требованию: у+7х<13.
Следовательно, χ — продолжительность одного
интервала — 1 ч 50 мин; начало первого сеанса 12 ч
00 мин или 12 ч 05 мин и т. д.
2. 1-й сеанс начался не раньше 12 часов, а 7-й
сеанс окончился не позже 1 часа ночи; следовательно,
эти семь сеансов заняли не более (24+1)—12=14
часов и продолжительность одного интервала (х) не
более чем 13 ч : 7=780 мин : 7» 1 ч 51 мин.
2-й сеанс начался до 14 часов, а 6-й закончился
не ранее 22 ч 55 мин; следовательно, эти пять сеансов
заняли не менее 22.55—14=8 (ч) 55 (мин} и
продолжительность одного сеанса χ не менее чем
8.55: 5=535 мин : 5= 107 мин= 1 ч 47 мин.
Итак, 1 ч 47 лш«<ж< 1 ч 51 мин.
Так как продолжительность одного интервала
всегда кратна 5 минутам, то х= 1 ч 50 лшк.
Первый сеанс окончился до 14 часов;
следовательно, он начался либо в 12 ч 00 мин, либо в 12 ч
05 мин, и т. д.
71. ДВА НОМЕРКА И ТРИ СТУДЕНТА
Третий студент предложил, чтобы второй взял у
первого не оба номерка, а только один из них. Так
как неизвестно, какой номерок первого студента,
какой второго, то номерок, взятый вторым студентом
у первого, мог оказаться либо нужным ему номерком,
либо ненужным. В первом случае ему не пришлось
бы возвращаться обратно в столовую, для того чтобы
отдать первому его. номерок. Во втором случае ему
пришлось бы возвратиться в обеденный зал за своим
номерком.
124

Итак, в половине случаев предложение третьего
студента избавляет второго студента от излишней
беготни.
72а. ОРЕХИ
Если в каждом из трех мешков будет одинаковое
количество орехов (например, по т орехов в
каждом), то общее количество орехов во всех трех
мешках будет Зт, т. е. должно быть: я=3т (где т —
число целое, положительное).
Но η — произвольное число; поэтому равновоз-
можны три случая:
я = 3т,
Л = 3/71+1,
я = Зт+2.
Поэтому только в одном случае из трех η таково,
что существует возможность того, что в каждом из
трех мешков по η: 3 орехов; в двух случаях из трех
это невозможно.
Итак, рассмотрим случай,.когда общее число
орехов во всех трех мешках n=Zm.
Эти Зт орехов могут распределиться между тремя
мешками по-разному: например в первом мешке —
ничего, во втором — один орех, а в третьем — все
остальные. Сколько же существует различных
вариантов размещения Зт орехов в трех- мешках?
Рассмотрим сначала более простой случай:
мешков всего два; пусть общее количество орехов в этом
случае равно — к. Тогда в первом мешке может быть
либо 0 орехов, либо 1 орех, либо 2 ореха, ..., либр
k орехов. Итак, в случае двух мешков существует
(k+i) вариантов размещения в них к орехов.
Возвратимся к нашей задаче, когда мешков три,
а общее число орехов —п.
Если в первом мешке ρ орехов (ρ ^ η), то
остальные (я—р) орехов могут по-разному разместиться
в двух мешках (во втором и в третьем); но задачу
о двух мешках мы только что решили; в данном
случае к—η — р\ поэтому при ρ орехах в первом мешке
остальные (п — р) орехов могут разместиться в
остальных двух мешках в {п — р) + \ вариантах.
126

Теперь можно найти общее число вариантов для
всех возможных значений величины р(/?=0, I, 2, ...
..., л), т. е. найти сумму:
/1 R
я
=(«+1)(«+1)-^=(й+1Ь^-
Ггт I П 2/* + 2-я _</*+!) (л+ 2)
Итак, общее количество всех различных случаев
размещения орехов по трем мешкам равно
(„+1).(л4-2)
2 ·
Из этих τ 2-—*--£- вариантов только один
отвечает условию задачи; следовательно, искомая ве-
2
роятность (при n—3m) равна ~. ^ . , 2>, а так как
вероятность того, что п—Ът равна -^-, то искомая
вероятность равна 3(„4-1Ы«Ч-2) '
726. МУКА
Искомая вероятность равна нулю, так как число
возможных вариантов распределения муки по
мешкам бесконечно. (А что было бы, если бы мука
в мешках была предварительно расфасована по
пакетам? Играет ли роль количество муки в пакете?)
73. АВТОБУС И ТРОЛЛЕЙБУС
Оба ответа неверны. Более того: имеющихся в
условии задачи данных недостаточно для получения
точного ответа. В самом деле. Рассмотрим более
простой случай. Пусть интервалы движения как
автобуса, так и троллейбуса — 8 мин. Если расписание
составлено так, что автобус и троллейбус отправляются
126

от данной остановки одновременно, то наличие двух
видов транспорта нисколько не сокращает
продолжительности ожидания; в данном случае средняя
продолжительность ожидания — 8 : 2=4 минуты.
Если же расписание составлено так, что
троллейбус отправляется через 8: 2=4 мин после отхода
автобуса, то средняя продолжительность ожидания
составит 4: 2=2 минуты.
Итак, при интервалах 8 и 8 мин средняя
продолжительность ожидания — от 2 до 4 мин — в
зависимости от расписания.
Приступим к решению нашей задачи
(интервалы — 6 и 8 мин).
Происходящие события будем изображать при
помощи графика. Пассажир может прийти к остановке
в любой момент. Он будет ждать 0 мин в том
случае, если он подошел как раз в момент отправления
Ш
к
Ik
ilk
Ilk
О 6 12 18
а
автобуса (или троллейбуса). Он будет ждать / мин
в том случае, если он подойдет на мгновение позже
(t мин — интервал).
На рис. а представлена картина ожидания в том
случае, когда расписание составлено так, что в
какой-то момент автобус и троллейбус отправляются от
остановки одновременно. Подсчитаем площади
заштрихованных треугольников:
^-(62-|-22 + 42+42+22-г-62) = 56.
Среднее время ожидания 56:24 = 7:3 = 2 «|· мин.
А каково будет среднее время ожидания при ином
расписании? Пусть троллейбус отправляется не одно-
127

временно с автобусом, а на χ минут позже (рис. б);
в этом, общем случае для определения среднего вр'ё*
мени ожидания необходимо вычислить площади
заштрихованных треугольников и определить, при ка^
ком лсэта площадь будет минимальной. (Заметим,
что 0-<*4^2; при *=*2 та же картина, что и при
х=0.)
1 ^^
[а
2
"VI
L-i .
б N.
. Ϊ J
Предварительно рассмотрим следующую задачу.
Дан отрезок а; на этом отрезке требуется построить
два таких равнобедренных прямоугольных
треугольника, чтобы их площадь была бы минимальной.
Докажем, что для этого искомые треугольники должны
быть равны. Итак,
построим на данном отрезке а две
пары равнобедренных
прямоугольных треугольников
(рис. в). Проведя
вспомогательные прямые,
параллельные основаниям, разобьем
треугольники на части.
Сравнивая их, убеждаемся, что
суммарная площадь двух
неравных треугольников
превосходит суммарную площадь двух равных
треугольников на фигуру, обозначенную Δ, что и требовалось
доказать.
Из этого следует, что наименьшая площадь пары
треугольников с основаниями (х+2) й (4 — х) будет
при х+2=4 — xt т. е. при х= 1.
Аналогично, для пары треугольников с
основаниями (6 — х) и (х+4) должно быть 6 — х=х+4
(т. е. х= 1).
Наконец, должно быть х=2 — χ (т. е. х=\).
'Итак, при χ = ί площадь' каждой из трех
пар.треугольников достигает наименьшей величины. Следо-
6
128

вательно, при х=1 мин сумма ожиданий будет
наименьшей; а именно, она будет равна:
^(1 4-9+25)-h-f-=-=35+18 = 53.
53 5
Среднее время ожидания: -gt = 2^ мин·
Итак, при самом неудачном расписании среднее
время ожидания равно 2 -^ мин, а при самом удач-
24
ΜΊΙ§ί·
ном —2^ мин.
Разница: -3—^"ΐϊ-
Относительная экономия времени:
3 7 3 кпу
2f* 3~~56 ~°'°·
W?
*VJ
Λ/»
74. СИГНАЛЫ
Вероятность того, что встретятся 1-й и 2-й
сигналы, определяется по предыдущему при помощи
квадрата и выделенного внутри него шестиугольника.
Аналогично
определяется вероятность встречи 2-го
и 3-го, а также 3-го и 1-го
сигналов (см. рисунок).
Теперь определим
вероятность встречи 1-го, 2-го и
3-го сигналов. Но на
рисунке мы получили три
квадрата — три ортогональные
проекции куба.
Следовательно, искомой областью ν г
точек, соответствующих
встрече всех трех сигналов, является многогранник,
три ортогональные проекции которого —
шестиугольники. Но мы уже встречались с этим
двенадцатигранником (см. задачу № 41). Его объем равен
о=*(ЗГ— 2t)P;
JU[· \ -1
129

следовательно,
Ρ — ~fz fa — \° — Δ~Τ)" \T) ·
Дополнительный вопрос: определите
вероятность встречи хотя бы двух из трех сигналов,
(Именно этот случай имеет наибольшее практическое
значение.)
75. ВВЕРХ ПО ЭСКАЛАТОРУ
Если я буду каждый раз, поднимаясь по
эскалатору, выгадывать по 10 секунд, то я буду подходить
к автобусу на 10 секунд раньше; следовательно, в
среднем я буду уезжать на 10 секунд раньше и на
10 секунд раньше приезжать домой. Так как я по-,
прежнему буду выходить к автобусу в случайные
моменты времени, то среднее время ожидания автобуса
не изменится (в обоих случаях оно равно 5: 2=а
=2,5 мин).
Другой путь решения. Интервал между двумя
последовательными отправлениями автобуса равен
5 «60=300 сек. Появляясь на остановке автобуса на
10 сек раньше, я в 10 : 300=1:30 случаев уеду
«предыдущим» автобусом. В остальных же 30—1=29
случаях из 30 я, выйдя на 10 секунд раньше, уеду тем
же автобусом, которым уехал бы, если бы и не шагал
по эскалатору^ Итак, при 30 поездках (все в
среднем) я в одном случае выгадаю 5 минут, что в
пересчете на одну поездку дает (5· 60) :30=1Ό сек (тот
же ответ).

СОДЕРЖАНИЕ
Предисловие
Л. Одинаковые цифры
2. Поезд идет туда и обратно
3. Сосновые и дубовые шпалы
4. Разносчик телеграмм
5. Сколько жильцов в доме?
6. Пятизначные числа
7а. Целые числа, у которых каждая следующая
цифра больше предыдущей
76. Целые числа, у которых каждая следующая
цифра меньше предыдущей
8, Число л в семеричной системе счисления
9· Сколько маршрутов?
10. Торговец
11. Такси
12. Два сплава
13а. На реке
336. Два камня ,
14. Кража на теплоходе
15. Автобус
.16. Курьеры
17. Разделить число 22 на три части
18. Семь уравнений с семью неизвестными
•19. Три бегуна
J20. Турист
21. Плот и мотолодка
22. Бассейн
23а· Три мухи
236. Четыре мухи
24. Лестничный марш
25. Равнобедренный треугольник
26. В детском саду
27. Два куба
28а. Достроить равнобочную трапецию
286. Три трапеции
29а. Три диска
296. Два диска
30. Равносоставленные четырехугольники
31. Два столба и тени

Задача
5
5
5
6
6
6
6
6
7
7
7
7
8
8"
8
8
9
10
10
10
10
И
11
11
13
13
13
13
14
14
14
15
15
15
15
16
Реше
ние
35
35
36
36
37
38
39
40
40
40
41
43
43
43
43
44
44
44
50
50
50
51
51
54
54
54
55
55
56
56
57
57
58
59
59
61

32. Конус лежит на плоскости 1£
ЗЗ.ч Две окружности «*
34. Три квадрата 16
35. Кольцо на трех нитях 17
36. Коробка и нить 17
37. Паркетаж 18
38· Стол и.скатерть 19
39. Симметричные точки 19
40. Складной стаканчик 20
41. Многогранник 20
42. Развертки многогранников 20
43. Годовые слои 21
44. Три параллелепипеда 21
45. Множество четырехугольников 21
46. Усеч^аный цилиндр 21".
47. Лист бумаги 22
48. Рулон 22
49а. Разбиение прямоугольника 22
496. Разбиение параллелепипеда 23
49а. Разбиение п-мерного параллелепипеда 23
50а> В равнобедренный треугольник вписаны круги 23
506- В конус вписаны шары 23
51а. Пояса кругов вокруг ядра 24
516. Ядро — три круга 24
52. Семь дробей 24
53. Бронзовый лев 24
54. Свидание 25
55. Три автомашины 25
56. Два велосипедиста 25
57. Два вкладчика 26
58. Быки яа лугу 26
59. Две лодки 27
60. Отец и трое сыновей 27
61. Покупатель и три поставщика 27
€2. Четыре' путешественника 28
63. pro петухов, кур и цыплят 28
64а. Три тела 29
646. Два тела 29
65. Поезд 29
бба. Три сосуда 30
ббб. Пять разбойников 30
67. С удвоенной скоростью 30
68. Катера на реке 31
69. Катер и плот 31
70. Когда начинаются сеансы? 31
71» Два номерка и три студента 32
72а. Орехи 32
726. Мука 32
73* Автобус и троллейбус 82
74. Сигналы 33
75. Вверх во эскалатору 34

Александр Исаакович Островский
75 ЗАДАЧ
ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ -
ПРОСТЫХ, НО . . ·
Редактор Ю. А. Гастев
Художественный редактор В. С Эрденко
Технический редактор О. Виноградова
Корректор М. Голубева
Сдано в набор 24/ΧΙ 1965 г„ Подписано к печати 7/IV 1966 г. 84 χ lOB'/ai-
Печ. л* 4,125 (6,93). Уч.-изд. л. 5,66. Тираж 150000 экз. (Тем. пл. 1966 г. Μ 155).
А12040. Заказ № 2087.
Издательство «Просвещение» Комитета по печати при Совете Министров
РСФСР. Москва, 3-й проезд Марьиной рощи, 41
Ленинградская типография № 2 нменн Евгения Соколовой
Гдавполнграфпрома Комитета по печати при Совете Министров СССР·
Измайловский проспект, £9.
Цена 15 коп·