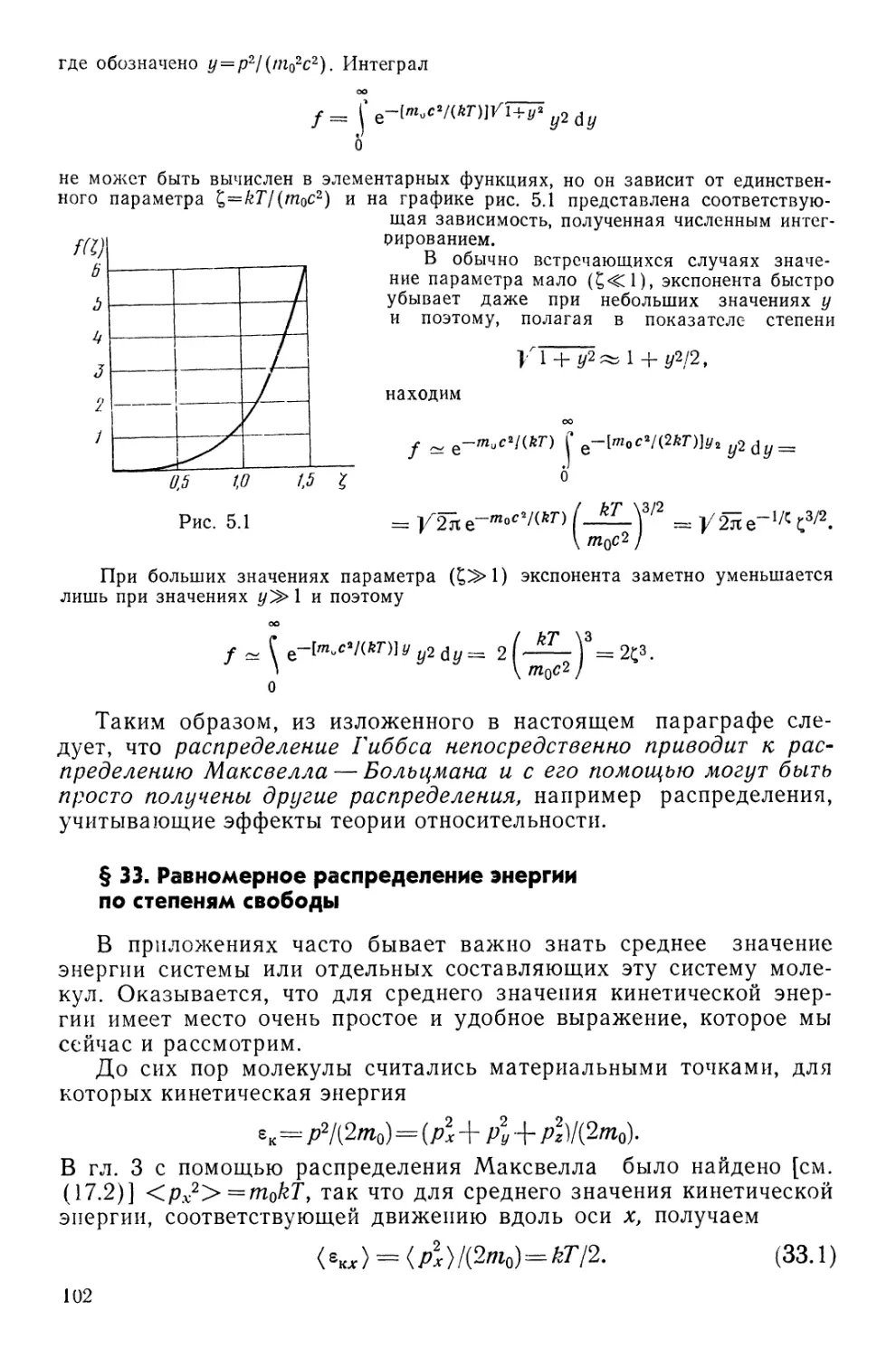
Text
А. М. Васильев
ВВЕДЕНИЕ
В СТАТИСТИЧЕСКУЮ
ФИЗИКУ
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов высших технических
учебных заведений
МОСКВА «ВЫСШАЯ ШКОЛА» 1980
ББК 22.317
В19
УДК 530.1@75)
Рецензенты:
кафедра физики твердого тела МАТИ;
проф. Б. М. Яворский
Васильев А. М.
В19 Введение в статистическую физику: Учеб. пособие. —
М.: Высш. школа, 1980. —272 с, ил.
В пер.: 80 к.
Книга является первым учебным пособием по статистической физике,
предназначенным специально для будущих инженеров. В ней излагаются
основные вопросы статистической физики и термодинамики: классическая и
квантовая статистики равновесных состояний. Большое внимание уделено
выяснению связей, существующих между различными распределениями,
и разным подходам к решению задач. Специальный раздел «Статистическая
физика неравновесных состояний» весьма полезен для многих специально-
специальностей, связанных с электроникой. Все принципиальные положения книги про^
иллюстрированы примерами.
Предназначается для студентов втузов.
г>0402 435
В 30—80 1704020000 „„, 530л
001@1)—80 ББК 22.317
© Издательство «Высшая школа», 1980
ОГЛАВЛЕНИЕ
Предисловие 6
Введение '
Част ь I
Основные сведения из теории вероятностей
Глава 1. Случайные события и вероятность И
§ 1. Понятие вероятности И
§ 2. Полная группа несовместимых событий 13
§ 3. Независимые события 16
§ 4. Условная вероятность 1*
§ 5. Биномиальное распределение вероятностей 18
§ 6. Формула Стирлинга 21
Глава 2. Случайные величины и их характеристики 23
§ 7. Случайная величина 23
§ 8. Среднее значение 27
§ 9. Распределение Пуассона 33
§ 10. Распределение Гаусса 35
§11. Вероятность как мера неожиданности 37
§ 12. Энтропия и хаотичность 38
Часть II
Классическая статистика равновесных состояний
Глава 3. Распределение Максвелла 40
§ 13. Распределение частиц в пространстве при отсутствии внешних
силовых полей 40
§ 14. Плотность вероятности для импульсов молекул 43
§ 15. Условие нормировки 47
§ 16. Связь параметра р распределения Максвелла с температурой . 47
§ 17. Плотность вероятности Максвелла для импульсов 49
-§ 18. Распределение по скоростям 53
§ 19. Распределение по модулю импульса и по энергии 54
§ 20. Функция распределения 59
§ 21. Поток частиц. Термоэлектронная эмиссия 60
§ 22. Экспериментальная проверка распределения Максвелла 66
Глава 4. Распределение Больцмана 72
§ 23. Неоднородность распределения частиц в пространстве при нали-
наличии потенциальных силовых полей 72
§ 24. Принцип детального равновесия 74
§ 25. Связь распределения Больцмана с распределением Максвелла . 74
§ 26. Барометрическая формула и экспериментальное определение по-
постоянной Больцмана 78
§ 27. Контактная разность потенциалов 80
§ 28. Метод самосогласованного поля 85
Глава 5. Распределение Гиббса 92
§ 29. Функция распределения Максвелла — Больцмана 92
§ 30. Распределение Гиббса как обобщение распределения Максвел-
Максвелла — Больцмана 93
§ 31. Пример одноатомного идеального газа 96
§ 32. Распределение Максвелла — Больцмана 100
§ 33. Равномерное распределение энергии по степеням свободы . . . 102
§ 34. Флуктуации в измерительных приборах 104
§ 35. Реальный газ 108
Глава 6. Связь статистики с термодинамикой 112
§ 36. Уравнение состояния 112
§ 37. Термодинамический смысл свободной энергии 115
§ 38. Уравнение Гиббса — Гельмгольца 116
§ 39. Энтропия и ее термодинамический смысл 117
§ 40. Статистический смысл энтропии 119
§ 41. Энтропия и второе начало термодинамики 120
§ 42. Реальный газ 123
§ 43. Теплоемкость 126
Часть III
Квантовая статистика равновесных состояний
Глава 7. Некоторые сведения из квантовой механики 130
§ 44. Квантовые свойства излучения 130
§ 45. Волновые свойства частиц 131
§ 46. Квантование излучения 133
§ 47. Принцип неразличимости 136
§ 48. Число состояний квантовой частицы в элементе объема ^-про-
^-пространства 137
§ 49. Квантование в случае частиц 139
Глава 8. Большое каноническое распределение 140
§ 50. Каноническое распределение в квантовой статистике 140
§ 51. Энтропия и третье начало термодинамики 144
§ 52. Принцип максимума энтропии 146
§ 53. Вывод большого канонического распределения Гиббса Н8
§ 54. Термодинамический смысл параметров Q*, ц, Т 150
Глава 9. Статистика Бозе — Эйнштейна 157
§ 55. Бозоны 157
§ 56. Распределение Бозе — Эйнштейна 158
§ 57. Фотоны 161^
§ 58. Законы теплового излучения 165
§ 59. Фононы 169
Глава 10. Статистика Ферми — Дирака 174
§ 60. Фермионы 174
§ 61. Распределение Ферми — Дирака 175
§ 62. Электронный газ в потенциальном ящике 177
§ 63. Невырожденный электронный газ 179
§ 64. Вырожденный электронный газ 181
§ 65. Теплоемкость газов при учете квантовых эффектов 183
4
Часть IV
Статистическая физика неравновесных состояний
Глава 11. Уравнение Больцмана 190
§ 66. Функция распределения в неравновесном случае 190
§ 67. Уравнение непрерывности 191
§ 68. Кинетическое уравнение Больцмана 192
§ 69. Взаимодействие с термостатом 194
§ 70. Уравнение Больцмана в квантовом случае 196
Глава 12. Функция распределения в диффузионном" приближении (прибли-
(приближение Лоренца) 199
§ 71. Функция распределения при малом времени релаксации .... 199
§ 72. Уравнение диффузии 201
§ 73. Функция распределения в диффузионном приближении .... 208
§ 74. Основные уравнения диффузионного приближения 211
Глава 13. Столкновения 212
§ 75. Учет взаимодействия столкновениями 212
§ 76. Член столкновений в форме Больцмана 218
§ 77. Приближение времени релаксации 223
§ 78. Эффективные сечения рассеяния 226
§ 79. Длина свободного пробега 229
§ 80. Разогрев электронного газа 231
Глава 14. Флуктуации 240
§ 81. Значение флуктуации 240
§ 82. Флуктуации числа частиц и объема 241
§ 83. Флуктуации энергии и температуры 247
§ 84. Флуктуации других термодинамических величин 249
§ 85. Шумовые токи 251
Приложения 260
1. Интеграл вероятности при малых и больших значениях аргумента 260
2. Вычисление некоторых часто встречающихся интегралов 261
3. Теорема о равномерном распределении кинетической энергии по
степеням свободы 262
4. Переход к системе отсчета, связанной с центром масс 268
Предметный указатель 270
Рекомендуемая литература 272
ПРЕДИСЛОВИЕ
Настоящая книга написана на основе лекций, которые автор читал студен-
студентам факультета электронной техники Московского энергетического института в
течение ряда лет. Несмотря на то что статистическая физика стала необходимой
дисциплиной для студентов целого ряда высших технических учебных заведений,
до настоящего времени не было выпущено учебного пособия, предназначенного
специально для этой категории читателей.
Опыт преподавания основ статистической физики в МЭИ убедил меня в том,
что существующие университетские курсы слишком сложны для студентов вту-
втузов. Они, по-видимому, сложны и для инженеров, желающих пополнить свое
образование. Более доступны учебные пособия, предназначенные для педагоги-
педагогических вузов, но даже они не совсем подходят. Дело, во-первых, в том, что в
этих курсах широко используются уравнения Гамильтона для вывода теоремы
Лиувилля, с помощью которой обосновывается распределение Гиббса. Этот путь
оказывается трудным хогя бы потому, что далеко не все втузовские программы
по теоретической механике предусматривают знакомство .с уравнениями Гамиль-
Гамильтона. Другая причина, по которой желателен специальный курс, состоит в сле-
следующем. Для многих специальностей, главным образом тех, которые связаны
с электроникой, очень существенно знакомство с основами статистической физики
неравновесных состояний (кинетики), так как при этом создается база, на кото-
которую можно опираться при изучении специальных дисциплин, где так или иначе
затрагиваются вопросы прохождения электрического тока в газах, полупроводни-
полупроводниках и металлах. Вопросы кинетики в более простых курсах почти не рассмат-
рассматриваются.
Таким образом, при написании этой книги имелся в виду читатель, подго-
подготовка которого соответствует втузовскому курсу математики и общей физики.
Хотя главной целью курса является ознакомление с основными методами
и понятиями статистической физики, но материал всюду иллюстрируется приме-
примерами, прикладное значение которых довольно очевидно и чаще всего связано с
электроникой. При изложении выдерживался давно оправдавший себя принцип:
от конкретного — к абстрактному, от простого — к сложному.
В книге не говорится об очень многих важных применениях статистической
физики, например к изучению магнитных явлений или к выяснению условий рав-
равновесия фаз и т. д. Это обусловлено прежде всего ограниченностью времени,
отводимого на изучение данного предмета. Несмотря на такие большие пробелы,
можно думать, что овладение материалом, изложенным в данном пособии, позво-
позволит читателю свободно ориентироваться в широком классе важных прикладных
задач и одновременно подготовит его к изучению более трудных книг по стати-
статистической физике.
Первая часть, посвященная основам теории вероятностей, носит вспомога-
вспомогательный характер и может быть опущена теми, кому известны сведения из этой
области в объеме практически любого курса теории вероятностей.
В книге использовался также материал, изложенный в ряде учебных посо-
пособий и монографий (см. перечень рекомендуемой литературы).
Я очень благодарен профессору В. А. Фабриканту, просмотревшему руко-
рукопись, за его благожелательную критику. Сделанные им замечания, которые были
направлены в основном на достижение большей простоты и ясности изложения,
учитывались мною при окончательной обработке рукописи.
Автор
ВВЕДЕНИЕ
В статистической физике рассмат-
рассматриваются задачи, которые, как прави-
правило, описывают явления, определяющие-
определяющиеся поведением большого числа частиц.
Для решения этих задач используются
методы теории вероятностей (статисти-
(статистики). Статистическая физика весьма
успешно применяется в самых разных
разделах физики. В молекулярной фи-
физике с ее помощью объясняют тепло-
тепловые явления, в электромагнетизме —
диэлектрические, проводящие и маг-
магнитные свойства тел, 'в оптике она по-
позволила создать теорию теплового из-
излучения, молекулярного рассеяния
света и т. д. Трудно сколько-нибудь
полно перечислить все те области, в
которых статистическая физика нашла
свое применение, тем более что в по-
последние годы круг ее приложений про*
должает расширяться.
Помимо вопросов, представляющих
большой практический интерес, в ста-
статистической физике рассматриваются
и проблемы, имеющие фундаменталь-
фундаментальное, мировоззренческое значение. Не
все они до конца решены, хотя в целом
статистическая физика выступает сей-
сейчас как наука не менее обоснованная,
чем другие разделы физики.
Статистическая физика — относи-
относительно молодая наука. Хотя ряд задач,
например объяснение свойств газов
исходя из представления о движении
молекул, рассматривались Ньютоном,
Бернулли, Ломоносовым и рядом дру-
других ученых еще в XVIII в., но, по-види-
по-видимому, более правильно отнести ее воз-
возникновение как самостоятельного
раздела физики ко второй половине
XIX в.
В 1857 г. вышла работа немецкого
физика Р. Клаузиуса «О природе двй-
Д. Бернулли A700—1782)
М. В. Ломоносов A711—1765)
Р. Клаузиус A822—1888)
Д. Максвелл A831—1879)
Л. Больцман A844—1906)
жения, которое мы называем теплом».
В ней ясно указывалось, что тепловая
энергия — это кинетическая энергия
хаотического движения молекул. Клау-
зиусу принадлежит также заслуга вве-
введения понятия длины свободного про-
пробега. Он дал правильное молекуляр-
но-кинетическое объяснение явлениям
теплопроводности и внутреннего тре-
трения. В 1859 г. появилась работа анг-
английского физика Д. К. Максвелла, в
которой он получил носящий его имя
закон распределения молекул газа по
скоростям.
Дальнейшее развитие молекулярно-
кинетической теории газов связано с
именем австрийского физика Л. Больц-
мана. Им получена формула, описыва-
описывающая распределение молекул газа во
внешнем поле (распределение Больц-
мана), и доказана теорема о равномер-
равномерном распределении кинетической энер-
энергии по степеням свободы *. Больцман
сумел выяснить вероятностный смысл
энтропии. Наконец, одним из главных
его достижений можно считать вывод
кинетического уравнения (уравнения
Больцмана), позволяющего описывать
неравновесные состояния газов. Дока-
Доказанная с похмощью кинетического урав-
уравнения теорема для функции, обозна-
обозначенной им //, позволила дать статисти-
статистическое толкование второго начала
термодинамики. Взгляды Больцмана, с
которыми боролись многие современ-
современные ему физики, получили признание
лишь после его смерти в 1906 г.
Другой подход рассматривался
американским физиком Д. В. Гиб-
бсом — современником Больцмана. В
трудах Гиббса статистическая физика
получила фундаментальное обоснова-
обоснование, пригодное для произвольных, а не
только газообразных систем. Распре-
Г. Лоренц A853—1928)
* Первые сведения о характере распреде-
распределения кинетической энергии при поступатель-
поступательном движении были получены до Больцма-
Больцмана (см : Смородинский Я А. Температура. Изд.
«Знание», № 11, М., 1977).
деление Гиббса рассматривается в на-
настоящее время как фундаментальный
принцип, который можно сравнить по
его роли в статистической физике с той
ролью, которую играют уравнения
Ньютона в классической механике или
уравнения Максвелла в электродина-
электродинамике. Книга Гиббса «Основные прин-
принципы статистической механики», вы-
вышедшая в 1902 г., сыграла в физике
такую же роль, как и «Трактат» Макс-
Максвелла, посвященный электродинамике.
Распределение Гиббса позволило
наиболее общим способом связать ста-
статистику с термодинамикой и тем самым
завершить молекулярно-кинетическое
обоснование этой феноменологической
науки, начатое Больцманом. При этом
обнаружились некоторые изъяны клас-
классической статистической физики, про-
проявившиеся, например, в невозможнос-
невозможности создания последовательной теории
теплового излучения, в вопросе о зна-
значении энтропии (третье начало термо-
термодинамики), в необъяснимости парадок-
парадокса Гиббса. Они были устранены лишь
на следующем этапе развития стати-
статистической физики, связанном с появ-
появлением квантовой механики.
Теория теплового излучения, соз-
созданная М. Планком © 1900 г., явилась
началом квантовой механики и успеш-
успешно объяснила свойства теплового излу-
излучения, наблюдаемые на опыте. Был
устранен принципиальный дефект
классической теории теплового излу-
излучения («ультрафиолетовая катастро-
катастрофа»). Индийский физик Д. М. Бозе,
рассматривая тепловое излучение как
газ фотонов, ввел в 1924 г. представ-
представление об их неразличимости, что позво-
позволило ему получить формулу Плавка
отличным от Планка способом. В даль-
дальнейшем Эйнштейн развил эту идею, и
в результате была создана квантовая
статистика, носящая название статис-
статистики Бозе — Эйнштейна.
Другая квантовая статистика поя-
появилась в 1926 г. Она была создана
Д. Гиббс A839—1903)
ГГ"
М. Планк A858—1947)
А. Эйнштейн A879—1955)
Э. Ферми A901—1954)
итальянским физиком Э. Ферми и ра-
работавшим независимо от него англий-
английским физиком П. А. М. Дираком. В
исследованиях этих ученых помимо
принципа неразличимости учитывался
также и принцип Паули, что привело
к появлению новой квантовой стати-
статистики, названной статистикой Ферми —
Дирака. Она применима к частицам с
полуцелым спином и, в частности, к
электронам.
Последующее развитие квантовой
статистики вызвало появление матема-
математического аппарата, значительно отли-
отличающегося от того, какой применяется
в классической статистике. Это, в част-
частности, связано с другим по сравнению
с классическим способом описания со-
состояний системы. Специальным, но
очень важным в прикладном отноше-
отношении классом физических систем, опи-
описываемым методом, близким к класси-
классическому, являются системы, которые
называют квазиклассическими.
Как уже упоминалось выше, стати-
статистическая теория неравновесных состо-
состояний газов была заложена Больцма-
ном, написавшим свое знаменитое ки-
кинетическое уравнение. Это уравнение
использовалось голландским физиком
Г. А. Лоренцем в его электронной тео-
теории проводимости, опубликованной в
1903 г. Им была предложена простая
приближенная форма решения, кото-
которая широко используется и в настоя-
настоящее время. Бурное развитие всех областей физим в последние де-
десятилетия XX в. сказалось, в частности, на статистической физике
неравновесных состояний, выросшей в большой и сложный раздел
науки.
Значительный вклад в статистическую физику внесли такие из-
известные советские ученые, как Н. Н. Боголюбов, Л. Д. Ландау и
целый ряд других.
Настоящая книга призвана помочь тем, кто, не имея специаль-
специального физического образования, хочет овладеть основами статисти-
статистической физики. На наш взгляд, проще всего это сделать, если сле-
следовать последовательности изложения, отражающей исторический
путь развития этой науки, кратко изложенный выше.
П. Дирак (р. 1902)
ЧАСТЬ I
ОСНОВНЫЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ГЛАВА 1
СЛУЧАЙНЫЕ СОБЫТИЯ
И ВЕРОЯТНОСТЬ
§ 1. Понятие вероятности
Все основные понятия теории вероятностей можно пояснить на
простом примере, имеющем в статистической физике и самостоя-
самостоятельный интерес. Рассмотрим молекулу Л, хаотически перемещаю-
перемещающуюся внутри сосуда, который имеет форму ящика (рис. 1.1).
Случайным событием называют явление,
которое в опыте, поставленном для его на-
наблюдения, либо имеет, либо не имеет места.
Так, например, попадание молекулы А в не-
некоторый момент времени в выделенный вну-
внутри ящика объем Дт (рис. 1.1) является
случайным событием. Если бы молекулу А
можно было сфотографировать, то на сним-
снимке она оказалась бы либо в Дт, и тогда рас-
рассматриваемое событие имело место, либо
вне Дт, и тогда событие места не имело.
Эксперимент по наблюдению случайного со-
события называют испытанием.
Обычно под вероятностью некоторого случайного события пони-
понимают отношение числа испытаний т, при которых данное событие
имело место, к полному числу М проведенных испытаний при усло-
условии, что число М достаточно велико. Если вероятность того, что
событие Л произойдет, обозначить IF (Л), то
W {A) = mlM или иначе
Рис.
Почему же -накладывается требование, чтобы число М испыта-
испытаний было достаточно велико? И (насколько велико оно должно быть?
То, что необходимо большое М9 ясно уже из соображений точности
определения значения вероятности. Допустим, что мы фотографи-
фотографировали молекулу в ящике и остановились после того, как 'получился
первый снимок, указавший на попадание молекулы внутрь Дт. Если
11
общее число фотографий оказалось при этом 127, то было бы преж-
преждевременным сделать заключение, что W(A) = 1/127. Действитель-
Действительно, сделав еще 60 фотографий, мы могли бы, например, получить,
что интересующее нас событие в дополнительных испытаниях не
имело места ни одного раза :и, следовательно, .по (новым измерениям
вероятность равна 1/187. Для получения достаточно точного резуль-
результата следует вести испытания до тех пор, пока отношения т/М не
будут отличаться друг от друга на малые величины, определяемые
той точностью, с которой желательно знать вероятность события А.
Строго говоря, поскольку -событие А (наступает случайно, нельзя
исключить из рассмотрения случай, в котором отношение т/М, по-
полученное экспериментально, не дает правильного значения вероят-
вероятности. Хотя такие случаи принципиально возможны, но они пред-
представляют собой очень маловероятные события и вероятность их
тем меньше, чем больше число испытаний.
Приведем любопытный исторический пример, иллюстрирующий это положе-
положение. Один из основоположников теории вероятностей французский ученый Лап-
Лаплас интересовался вопросом рождаемости мальчиков и девочек. Изученные им
материалы, включавшие данные по ряду европейских городов, а также в целом
по Франции, показывали, что отношение числа родившихся мальчиков т к числу
всех родившихся М близко к 0,5116. Анализ же данных по Парижу привел к
значению 0,5102. Учитывая, что число проанализированных им рождений маль-
мальчиков т было очень велико, Лаплас пришел к выводу, что обнаруженное рас-
расхождение не может быть случайным. Ему удалось выяснить, что в число рожде-
рождений по Парижу включались и подкидыши, а окрестное население по преимуще-
преимуществу подкидывало девочек. После исключения данных по подкидышам статисти-
статистика рождаемости по Парижу хорошо согласовывалась со статистикой других
городов.
Нетривиальным является и вопрос о том, как проводятся испы-
испытания. Действительно, в примере с молекулой в ящике испытания
можно поставить двумя принципиально различньши способами.
В первом способе молекулы в ящике мы фотографируем после-
последовательно в различные моменты времени. Легко видеть, что эти
моменты должны быть разделены достаточно большими промежут-
промежутками. Если серия снимков следует с очень большой скоростью, то
за время их выполнения молекула не успевает сместиться на за-
заметное расстояние и, составляя отношение т/М на основании такой
серии, мы неизбежно придем к неправильному результату. Интер-
Интервалы между фотографированиями должны быть, например, такими,
чтобы молекула успела переместиться в любую другую точку ящи-
ящика. С экспериментальной точки зрения критерий правильности вы-
выбора интервала между снимками состоит в том, что повторные се-
серии испытаний с увеличенными против первоначальных интервала-
интервалами времени приводят к тем же самым предельным значениям т/М.
Во втором способе постановки опыта изготавливается М одина-
одинаковых ящиков и в каждом из них находится молекула того же вида
Л. В определенный момент времени одновременно фотографируют-
фотографируются все молекулы и значение отношения т/М устанавливается ана-
анализом снимков различных ящиков. Совокупность одинаковых си-
систем, используемых для изучения вероятностных характеристик,
12
называется ансамблем. Таким образом, для определения вероятно-
вероятности можно было использовать ансамбль ящиков с молекулами.
Оба способа приводят к одинаковым результатам, если только
в первом выдержано условие об интервалах времени м^жду испы-
испытаниями, а во втором -все системы ансамбля действительно строго
идентичны.
Из определения вероятности следует, что ее значения заключе-
заключены между 0 и 1. Действительно, m и М — положительные числа и,
кроме того, минимально возможное значение числа m равно 0, а
максимально возможное — полиому числу испытаний М. Событие,
которое имеет место в каждом испытании и вероятность которого
поэтому равна единице, называется достоверным. Примером может
служить событие, состоящее в обнаружении молекулы Л, заведомо
помещенной в ящик, где-то внутри иего. Естественно, что на каж-
каждой фотографии всего ящика молекула А будет обнаружена, т. е.
это событие имеет место в каждом испытании и, следовательно, до-
достоверно. В противоположном случае, когда событие не имеет
места ни в одном испытании и, следовательно, вероятность его
равна нулю, оно называется невозможным. В качестве примера
можно привести событие, состоящее в том, что молекула А не будет
обнаружена в ящике: если молекула находится внутри, то такое
событие невозможно.
§ 2. Полная группа несовместимых событий
Для построения и применения теории вероятностей большое
значение имеет понятие о полной группе несовместимых со-
событий.
Два события называются несовместимыми, если реализация од-
одного исключает возможность реализации другого. Рассмотрим при-
пример. В ящике, который выбран
для наблюдения за молекулой Л,
выделены два объема: Ati и Дтг.
Если объемы не пересекаются,
как это показано на рис. 1.2, а,
то событие U состоящее в том,
что в момент t молекула А ока-
окажется в Ati, и событие 2, состоя-
состоящее в том, что в тот же момент
времени t она окажется в Дт^, не-
несовместимы. Очевидно, что в слу-
случае пересекающихся объемов
(рис. 1.2, б) эти же два события
совместимы, поскольку попадание молекулы в момент t в заштри-
заштрихованную область пересечения At означает, что она находится од-
одновременно и в том, и в другом.
Прикладная ценность понятия несовместимых событий обуслов-
обусловлена теоремой: вероятность осуществления одного из двух не-
несовместимых событий равна сумме вероятностей осуществления
13
/
/
/
?
Рис. 1.2
каждого из них. Эта теорема легко доказывается при рассмотрении
приведенного выше примера. Пусть попадание молекулы в первый
из двух непересекающихся объемов характеризуется вероятностью
где rrt\ — Ч'исло попаданий в первый объем при М испытаниях. Ана-
Аналогично, вероятность попадания во второй
Событие, состоящее в том, что молекула попала хотя бы в один из
двух объемов, осуществилось т\-гт2 раза. Теперь по общему опре-
определению можно найти, что вероятность осуществления хотя бы од-
одного из двух событий рав!на
w + w A) + w{2)
М М М К '
что и доказывает теорему. В случае совместимых событий (пе-
(пересекающихся объемов) нельзя утверждать, что число попаданий
в первый или второй объем равно mi + m2. Это число меньше, так
как имеют место случаи, когда молекула попадает в пересечение
объемов, а такие события засчитывались одновременно и в т\, и
в т2.
Полной группой несовместимых событий называется такая их
совокупность, в которой осуществление одного достоверно. Рассмот-
Рассмотренные в предыдущем примере несовместимые события (рис. 1.2, а)
не образуют полной группы, так как молекула может оказаться
вне обоих объемов Ati и Дтг, т. е. возможна ситуация, когда не реа-
реализовалось 'ни одно 1из них. Если, однако, дополнить события У и 2
событием 5, состоящим в том, что молекула будет обнаружена внут-
внутри ящика в оставшемся за вычетом Ati и Атгпространстве, то новая
группа из трех событий образует полную группу. Действительно*
поскольку объемы не пересекаются, то события несовместимы, кро-
кроме того, осуществление какого-либо из них достоверно, так как мо-
молекула находится либо в Ать либо в Дтг, либо вне их.
События называются равновозможными, если вероятность осу-
осуществления любого из них имеет одно и то же значение. Для пояс-
пояснения этого понятия предположим, что ящик разделен <на две рав-
равные части 1 и 2 (рис. 1.3), и рассмотрим группу, состоящую из
двух событий: попадания молекулы А в /и попадания ее в 2. Объ-
Объемы не пересекаются, и, следовательно, события несовместимы.
Группа полная, так как объемы 1 и 2 полностью исчерпывают объ-
объем ящика. Наконец, из полной эквивалентности обоих объемов оче-
очевидно, что вероятность попадания в / равна вероятности попадания
в 2. Таким образом, в этом примере события / и 2 образуют полную
группу несовместимых равновозможных событий. Следует подчерк-
подчеркнуть, что вывод о равновозможности событий опирается на вполне
конкретные физические представления о характере и условиях дви-
движения молекулы. Так, например, если молекула обладает магнит-
магнитным моментом и у левой стенки ящика помещен магнит, создаю-
14
щий неоднородное магнитное поле, то вероятность обнаружения
молекулы в объеме 1 окажется выше, т. е. события не будут равно-
возможными.
На рис. 1.4 показаны пять объемов равной величины, на которые
мысленно разделен ящик. Равновозможны ли события, соответст-
соответствующие попаданию молекулы в каждый из них? Ответ зависит от
тех условий, которые имеют место ори столкновении молекулы со
стенкой. Если предположить, что молекула при столкновении на
некоторое время прилипает к стенке, то естественно, что она боль-
больше времени будет проводить в объемах 1 и 5 я поэтому вероятности
/\ /
1 I
У-
/
2
— 4
/
/
/
У
1
1
1
1
У
у
\
!
\з
1
¦)-
/
у
1
1
1
1
I
-)-
/
1
1
1
1
1
/
1
1
1
1
1
1
/
ш
щ
1
Рис. 1.3
Рис. 1.4
Рис. 1.5
W(l) »и WE)> хотя и будут равны между собой, окажутся больши-
большими, чем остальные. Условия же движения в каждом из объемов 2,
2, 4 совершенно одинаковы, и поэтому вероятности WB), WC) и
WD) равны между собой. В реальной ситуации чаще всего осуще-
осуществляются условия, при которых столкновения со стенкой происхо-
происходят так, что они эквивалентны абсолютно упругому удару. При
этом вероятности всех пяти событий оказываются одинаковыми.
В дальнейшем всегда будет иметься в виду именно такой характер
столкновений, так что события, состоящие в обнаружении молекулы j
s некоторый момент времени t в равновеликих объемах, равновоз-
равновозможны.
Ценность понятия о полной группе равновозможных несовмести-
несовместимых событий состоит в том, что оно позволяет теоретически найти
значение вероятности того или иного события. Рассмотрим пример
определения вероятности того, что молекула окажется в объеме Ат,
выделенном внутри ящика.
Мысленно разобъем ящик на п одинаковых параллелепипедов
{рис. 1.5) настолько малых размеров, что объем Ат с большой точ-
точностью можно составить из некоторого их числа т. Как было пока-
показано выше, события, состоящие в том, что в момент времени t мо-
молекула А окажется в однОхМ из параллелепипедов, образуют полную
группу несовместимых равновозможных событий. Вероятность того,
что молекула А окажется в каком-то определенном параллелепипе-
параллелепипеде, одна и та же для всех параллелепипедов (условие равновозмож-
«ости) и может быть найдена из условия полноты и несовместимо-
несовместимости событий группы. Вероятность того, что молекула А находится
15
внутри сосуда, равна единице (достоверное событие). С другой сто-
стороны, по правилу сложения вероятностей несовместимых событий
эта же вероятность может быть представлена в виде суммы вероят-
вероятностей всех событий группы, т. е. l=nW. Отсюда вытекает, что
Интересующая нас вероятность W(Ax) равна сумме вероятностей
попадания в любой из параллелепипедов, составляющих Ат. По-
Поскольку их общее число т, то, снова используя теорему сложения,
найдем
/я-—= —. B.1)
п
Если умножим числитель и знаменатель на объем одного паралле-
параллелепипеда, то в числителе получится Ат, а в знаменателе — объем
всего ящика. Таким образом, вероятность того, что молекула, на-
находящаяся в сосуде объема V, в момент t окажется в элементе объ-
объема Ах, равна
B.2)
В формулу B.2) не входит число параллелепипедов /г, так что
окончательный результат не зависит от величины объемов, на ко-
которые был мысленно разбит объем сосуда. Их можно было считать
бесконечно малыми, и, следовательно, точно составить объем Дт,
так что формула B.2) абсолютно точна в отличие от приближенной
формулы B.1).
§ 3. Независимые события
В вычислениях, которые приходится проводить с вероятностями,
часто используется свойство независимости случайных собы-
событий. События называются независимыми, если осуществление одно-
одного из них не влияет на вероятность осуществления второго. Рассмот-
Рассмотрим пример. Пусть первое событие состоит в том, что в объем Дп
в момент t попадает молекула Л, а второе событие — в том, что в1
тот же момент времени в объехМ Дтг попадает другая молекула В.
Если независимо от того, попала молекула А в Дп или нет, вероят-
вероятность попадания молекулы в At2 равна одной и той же величине
Дтг/У, то события независимы. Так, например, будет, если молекулы
не взаимодействуют между собой. В этом случае даже при совпа-
совпадении объемов Дп и Дтг события независимы. Однако наличие
взаимодействия изменяет это положение. Так, при взаимном оттал-
отталкивании молекул вероятность появления молекулы В в объеме Дп
одновременно с А меньше, чем при отсутствии А. Реально все мо-
молекулы взаимодействуют между собой, но силы взаимодействия
очень быстро убывают с увеличением расстояния между ними, так
что на расстояниях порядка нескольких диаметров молекул взаимо-
взаимодействием можно полностью пренебречь. Это позволяет при малых
концентрациях (газы), когда среднее расстояние между молекула-
16
ми много больше, чем их диаметр, считать, что события, рассмотрен-
рассмотренные в приведенном выше примере, независимы. При больших кон-
концентрациях (сильно сжатые газы, жидкости) это уже не так.
Вероятность совместного осуществления независимых событий
равна произведению вероятностей каждого из них.
Для пояснения этого свойства рассмотрим разреженный газ.
Пусть при п испытаниях оказалось, что молекула А была Ш\ раз
обнаружена в объеме Ать а молекула В — т2 раз в объеме Дх2, т. е.
Из всех тех испытаний общим числом ть при которых А попала в
Дть отберем те, в которых еще и В (попала в Дтг. Поскольку веро-
вероятность, с которой случается событие 5, равна ш2/#, то число отоб-
отобранных событий должно быть равно ml(m2/n). Если отнести теперь
найденное число событий к общему числу испытаний, то вероят-
вероятность совместного осуществления событий А и В
W {AB)=
п п п
Эта формула есть математическая запись сформулированного вы-
выше 'положения.
§ 4. Условная вероятность
Возникает вопрос: каким образом можно определить вероятность
совместного осуществления двух зависимых событий? Для его ре-
решения вновь обратимся к примеру. В качестве события 1 выберем
попадание молекулы А в момент t в объем Дть а в качестве собы-
события 2— попадание этой же молекулы в тот же момент / в объем Дт2.
Эти события зависимы. Пусть, например, объемы Дтп и Дт2 не пере-
пересекаются, т. е. события 1 и 2 несовместимы, тогда если молекула
оказалась в Дл, то она, естественно, не могла в тот же момент вре-
времени находиться в Дт2. Таким образом, если вероятность события 2
есть Дт2/У, то эта же вероятность при условии, что имеет место /,
равна 0. Изменение значения вероятности события 2 из-за осущест-
осуществления события / и означает зависимость этих событий в веро-
вероятностном смысле.
В более общем случае произвольно пересекающихся объемов
Дт1 и Дт2 события 1 и 2 тоже зависимы. Чтобы убедиться в этом,
рассчитаем, как изменится вероятность события 2 при условии, что
совершилось событие 1. Осуществление события / означает,
что молекула попала в объем Д-ti и поэтому его можно рассматри-
рассматривать как «новый сосуд, содержащий молекулу. Вероятность обнару-
обнаружения молекулы в тот же момент времени в Дт2 есть вероятность
того, что она окажется в объеме Дт, являющемся общей частью
Дт1 и Дт2 (см. рис. 1.2, б). Эта вероятность равна отношению Дт к
объему «нового сосуда» Дть Таким образом, вероятность WB) со-
17
бытия 2 без условия / или, как говорят, безусловная вероятность
имеет значение
а условная вероятность W{B) есть вероятность события 2 при ус-
условии, что имело место событие Лив данном случае она равна
Ясно, что в общем случае условная и безусловная вероятности не
совпадают по величине, что и означает зависимость событий между
собой. Для независимых событий условная вероятность равна без-
безусловной.
Теперь можно сформулировать почти очевидное правило. Веро-
Вероятность W(ly 2) совместного осуществления двух событий 1 и 2
равна вероятности W(\) события 1, умноженной на условную веро-
вероятность W\ B), или вероятности WB) события 2, умноженной на
условную вероятность W2(l). Математически это записывается еле-
дующим образом:
W (I, 2) = W (l)WiB) = WB)W2(l).
Проиллюстрируем это правило на примере с двумя пересекаю-
пересекающимися объемами. Вероятность W{\, 2) попадания и в 1, и в 2
есть, по существу, вероятность попадания в пересечение этих двух
областей, т. е. в Ат, так что
2) = At;V. D.1)
Формулу D.1) можно представить либо в виде
либо
W(\, 2) = -^-=-^--^-
что полностью соответствует сделанным выше общим утверждени-
утверждениям.
§ 5. Биномиальное распределение вероятностей
Приведенные сведения позволяют решать многие задачи статис-
статистической физики. В настоящем параграфе будет рассмотрена одна
из них, имеющая большое значение как с прикладной точки зрения,
так и с точки зрения развития самой теории вероятностей.
Предположим, что в сосуде находится газ с общим числом мо-
молекул, равным N. Выделим мысленно часть объема сосуда Ат и оп-
определим, какова вероятность нахождения п молекул в Ат. Решение
этой задачи позволяет, в частности, указать вероятность того или
иного значения плотности газа, что представляет интерес для неко-
некоторых физических приложений.
18
Начнем со случая двух молекул (N--=2) и присвоим молекулам
номера 1 и 2. Для определения интересующей нас вероятности
можно рассмотреть следующую полную группу несовместимых со-
событий:
1) молекулы / и 2 находятся в Дт;
2) молекула / находится в Дт, a 2 вне этого объема;
3) молекула 2 находится в Дт, а 1 вне его;
4) обе молекулы находятся В'не Дт.
Вероятности этих событий рассчитываются следующим образом.
Вероятность пребывания молекулы У в Дт равна W = AilV, а ве-
вероятность пребывания вне этого объема —
так как сумма вероятностей обоих событий должна быть равна еди-
единице. Те же значения имеют соответствующие вероятности для мо-
молекулы 2. Обратимся теперь к первому событию, когда обе молеку-
молекулы находятся в Дт. Поскольку предполагается, что взаимодействи-
взаимодействием молекул можно пренебречь, то попадание в Дт молекул / и
2 — независимые события и поэтому вероятность первого события
W\ есть произведение вероятностей попадания в Дт молекул / и 2„
т. е.
1 V V
Аналогично можно найти:
Нас интересует вероятность того, что в Дт окажется п молекул, т. е.
в данном случае 2, 1 или 0. Легко видеть, что
так как только в случае события 1 обе молекулы находятся в Дт.
Далее,
так как во втором и третьем случае в Дт находится одна молекула.
Наконец,
Если число молекул рав'но трем и они обозначены 1, 2, 5, то
возмож'ны события, перечисленные в табл. 1. В этой же таблице
приведены значения вероятностей Wu соответствующих различным
возможным распределениям молекул, а также искомые вероятности
WC)WB)W(l) ЩО)
19
Таблица 1
Номер
события
1
2
3
4
5
6
7
8
Молекулы,
находящи-
находящиеся
в Дт
1, 2, 3
1,2
1,3
2,3
1
2
3
—
Молекулы,
находящи-
находящиеся »1
в К— Ах
—
3
2
1
2,3
1,3
1,2
1, 2, 3
Число
молекул
в Лх
3
2
1
0
Вероятности
событий Wt
U73
\F2A— W)
A— \FK
Вероятности
W(n)
W C) = 1^3
IF B) = 31*72A— U7)
Щ0) = A— WK
Переходя теперь к общему случаю yV молекул, можно пока-
показать, что
W{n)= — Wn(\-W)N-n. E.1)
V ; n\(N-n)l К J V
Действительно, вероятность того, что п определенных молекул ока-
окажется в объеме Ат, а остальные N—п молекул вне его, равна
Wn{\-V/)N-n. E.2)
Число подобных событий, отличающихся друг от друга тем, какие
именно п .молекул из общего числа Af находятся в Ат, равно числу
сочетаний ш N по я, т. е.
N\
n\(N—n)\
E.3)
Таким образом, суммирование вероятностей всех событий, в кото-
которых в Ат оказалось п молекул, т. е. умножение E.2) на E.3), при-
приводит к общей формуле E.1).
События, в которых число молекул, попавших в Ат, равно 0, 1,
2, 3, ..., несовместимы и образуют полную группу. Сумма вероят-
вероятностей этих событий должна равняться единице. Легко убедиться,
что это действительно так:
N
N
N\
Используя формулу бинома Ньютона, можно написать
N _
¦ W)]N=\X
N\
20
Связь вероятностей W(n) с формулой б'инома Ньютона послужила
основанием для того, чтобы зависимость W(n) от числа молекул п
получила «название биномиального распределения вероятностей.
В виде примера рассмотрим распределение шести молекул в
сосуде, мысленно разделенном на две равные части, т. е. при Ат =
= V/2. Рассчитав биномиальные коэффициенты, можно получить
результаты, графически представленные на рис. 1.6, где точками
обозначены соответствующие значения
вероятностей. Видно, что событие, об- УМ\
ладающее наибольшей вероятностью, '
состоит в том, что число п оказывает-
оказывается равным 3, т. е. что в половине сосу-
да окажется половина полного числа
молекул. Отсутствие молекул (/г=0)
или их полное собирание (я = 6) зна-
чительно менее вероятны и поэтому
наблюдаются гораздо реже (в 20 раз 1/RU %
Реже) • 0 1 2 J 4 5 6 7 П
Биномиальное распределение ис-
используется при решении очень многих Рис. 1.6
задач, а не только в рассмотренном
выше примере. Действительно, пусть известна вероятность W того,
что молекула обладает каким-то признаком (например, скоростью
в диапазоне от 100 до 150 м/с или тем, что она прошла без столк-
столкновений с другими молекулами путь, больший 1 мм, и т. п.). Спра-
Спрашивается, какова вероятность того, что п молекул из общего числа
N обладают этим же признаком? Если соответствующие события
для различных молекул независимы и их вероятность равна fW, то
ответ дается биномиальным распределением E.1). Чтобы убедить-
убедиться в справедливости этого вывода, достаточно учесть, что конкрет-
конкретное содержание приведенной выше задачи было использовано толь-
только при нахождении значения вероятности W=Ax/V обладания оп-
определенным признаком (попаданием в Дтв момент /). Все осталь-
остальные рассуждения не зависят от того, какой именно признак имеет-
имеется в виду.
§ 6. Формула Стирлинга
При решении статистических задач приходится иметь дело с
громадным числом молекул, поэтому использование ряда формул,
в частности биномиального распределения, оказывается неудобным
из-за того, что встречаются факториалы от очень больших чисел.
Так, например, при нормальных условиях в 1 см3 газа находится
2,69-1019 молекул. Если требуется узнать, какова вероятность того,
что 1016 из них находится в объеме Ат== 1 мм3, то для использования
формулы E.1) необходимо вычислить 1016! и 2,69-1019! Если учесть,
что при вычислении 30! или 40! уже встречаются трудности, то яс-
ясно, что желательно иметь формулу, позволяющую быстро оцени-
21
вать значения факториалов от больших чисел. Соответствующее
выражение было получено Стирлингом.
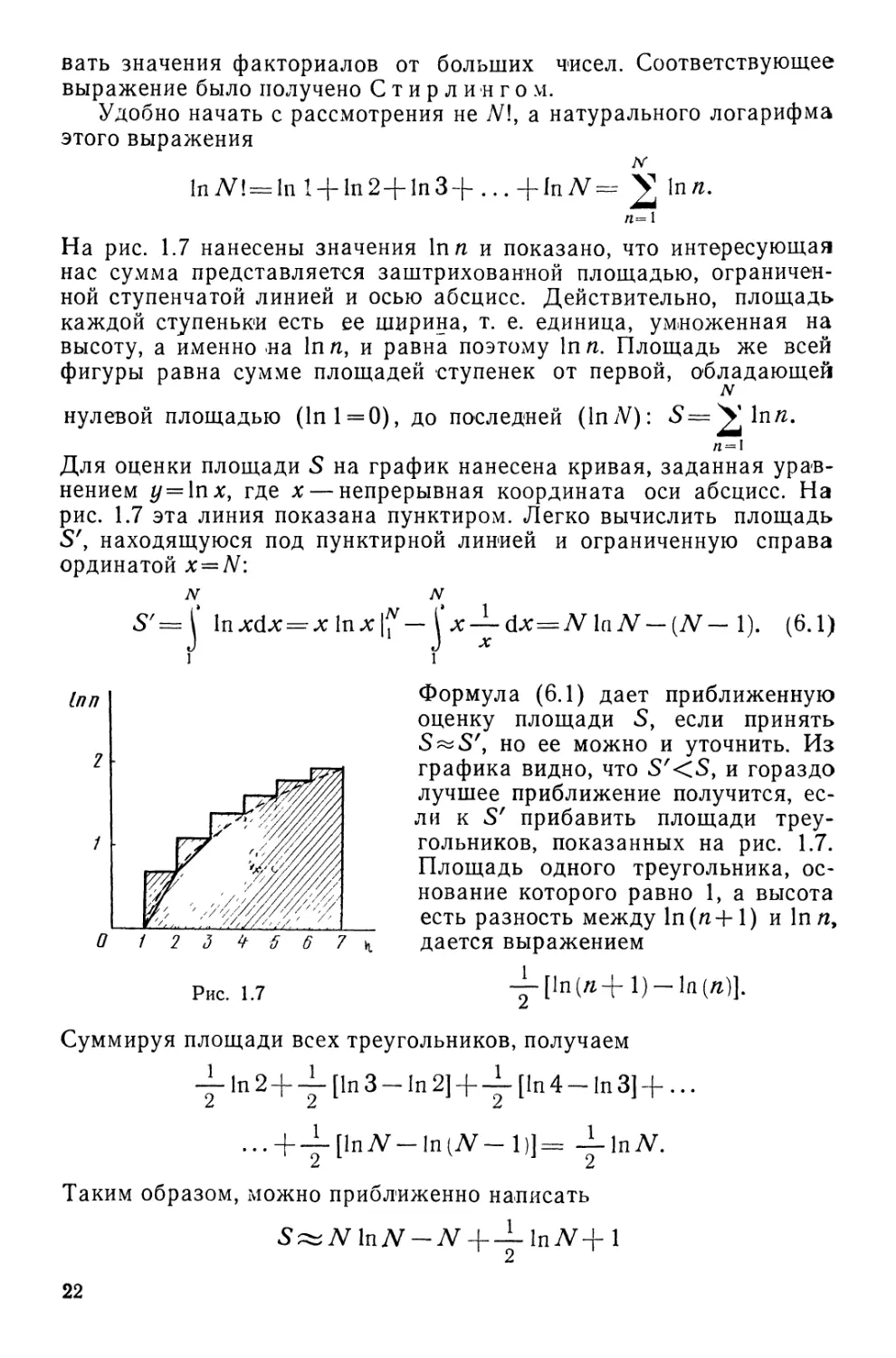
Удобно начать с рассмотрения не ЛП, а натурального логарифма
этого выражения
IV
In я.
На рис. 1.7 нанесены значения Inn и показано, что интересующая
нас сумма представляется заштрихованной площадью, ограничен-
ограниченной ступенчатой линией и осью абсцисс. Действительно, площадь
каждой ступеньки есть ее ширина, т. е. единица, умноженная на
высоту, а именно на In /г, и равна поэтому In п. Площадь же всей
фигуры равна сумме площадей ступенек от первой, обладающей
нулевой площадью (In 1=0), до последней (lruV): S=\lnn.
Для оценки площади S на график нанесена кривая, заданная урав-
уравнением у = 1пх, где х — непрерывная координата оси абсцисс. На
рис. 1.7 эта линия показана пунктиром. Легко вычислить площадь
S', находящуюся под пунктирной линией и ограниченную справа
ординатой x=N:
N N
S'=
1 2 3
-(N-l). F.1)
Формула F.1) дает приближенную
оценку площади S, если принять
S^Sf9 но ее можно и уточнить. Из
графика видно, что S'<S, и гораздо
лучшее приближение получится, ес-
если к S' прибавить площади треу-
треугольников, показанных на рис. 1.7.
Площадь одного треугольника, ос-
основание которого равно 1, а высота
есть разность между 1п(/г+1) и In/г,
дается выражением
Рис. 1.7 Y
Суммируя площади всех треугольников, получаем
--^- Г1пЛ^ — 1п(Л^— 1I= — inN.
2 2
Таким образом, можно приближенно написать
-N-\-— lniV-f 1
22
или, так как A/! =
N\nN-N+ i- 1пЛг
е 2
Приводящийся в курсах анализа строгий вывод показывает, что бо-
более точный результат имеет вид
Nl = V*iNNe-NVN, F.2)
т. е. получается небольшая разница в величине постоянного множи-
множителя (е = 2,718..., >5я = 2,506 ...).
Формула F.2) дает тем меньшую относительную погрешность,
чем больше значение N. Приведем два примера. При Л/= 4 точное
значение 4! есть 24, а по формуле Стирлинга получается
У 2к У 4 44 е ^23,7.
При N = 6 точное значение ЛП есть 720, а по формуле F.2) полу-
получается 716. В первом примере относительная погрешность равна
1,2%, а во втором — 0,55%. При больших значениях N относитель-
относительная погрешность быстро уменьшается.
ГЛАВА 2
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
И ИХ ХАРАКТЕРИСТИКИ
§ 7. Случайная величина
В приложениях теории вероятностей к вопросам статистической
физики приходится оперировать представлением о случайной
величине. Величина, которая может принимать различные числовые
значения с определенной вероятностью, называется случайной.
Фактически нам уже пришлось иметь дело с этим понятием в пре-
предыдущей главе. Действительно, число молекул в элементе объема
Ат, выделенном в сосуде объема V, представляет собой соответству-
соответствующий пример, так как это число принимает значения 0, 1,2, ..., N
и каждое из них реализуется с определенной вероятностью W(n)f
определяемой формулой E.1) биномиального распределения. Таким
образом, число молекул в элементе объема Дт есть случайная ве-
величина. Такая случайная величина носит название дискретной,
так как она принимает значения, отличающиеся друг от друга на
конечную величину (в данном примере — целочисленные значения
О, 1,2, ...,#).
Встречаются и непрерывные случайные величины, которые
принимают непрерывный ряд значений. Пожалуй, простейшим при-
примером непрерывной случайной величины может служить коорди-
координата молекулы А в сосуде V. Поместим начало координат в одном
из углов прямоугольного сосуда так, как это показано на рис. 2.1.
23
Тогда координата молекулы гА вдоль оси z может принимать лю-
любые значения в интервале от z=0 до г = а, где а — размер сосуда
в направлении оси г.
Для непрерывной случайной величины неправильно интересо-
интересоваться вероятностью данного ее значения. Правильная постановка
вопроса состоит в том, чтобы выяснить, какова вероятность того,
что случайная величина приняла значение, лежащее в интервале от
z до z + dz. Если интервал dz бесконечно мал, то бесконечно мала
и соответствующая вероятность dWy которая, следовательно, долж-
должна быть пропорциональна интервалу dz. Для искомой вероятности
можно написать следующее выражение:
tiW=w{z)&z> G.1)
где до (г)—некоторая функция, называемая плотностью вероятно-
вероятности. Ее размерность обратна размерности случайной величины z>
поскольку вероятность dW есть величина безразмерная. Таким об-
образом, плотность вероятности для некоторой случайной величины,,
значения которой обозначены z, есть такая функция w(z), которая,,
будучи умножена на dz, дает вероятность того, что значение слу-
случайной величины лежит в интервале от г до z+dz. Если интервал
dz равен нулю, то равна нулю и соответствующая вероятность, по-
поэтому не имеет смысла интересоваться вероятностью отдельного
значения непрерывной случайной величины.
Для пояснения введенного понятия обратимся к примеру, в ко-
котором непрерывной случайной величиной является координата z
молекулы А. Необходимо найти плотность вероятности для этой
случайной величины. Координата молекулы попадает в интервал
dz, если, как это видно из рис. 2.1, сама молекула оказывается
в объеме dt, ограниченном двумя плоскостями, проведенными че-
через точки z и z+dz перпендикулярно оси z. Обозначим площадь ос-
основания сосуда S, тогда объем dx = Sdz. Поскольку объем всего со-
сосуда V — aS, то для вероятности получается
d.
V aS a
Из последнего равенства видно, что плотность вероятности для ко-
координаты молекулы
w(z)= I/a.
Как и следовало ожидать, размерность плотности вероятности об-
обратна длине, поскольку сама случайная величина z имеет размер-
размерность длины.
То, что плотность вероятности оказалась постоянной величиной,
связано с конкретными особенностями данной задачи, в которой
сосуд прямоуголен и все положения молекулы А внутри сосуда
считаются равновозможными. Если бы сосуд был помещен в поле
действия каких-то внешних сил (например, учитывалось бы дейст-
действие силы тяжести) или обладал не прямоугольной, а какой-то дру-
24
гой формой, то плотность вероятности не была бы постоянной ве-
величиной.
Так, например, в коническом сосуде (рис. 2.2), пренебрегая дей-
действием силы тяжести, для вероятности dW можно найти
<™ 6%
62
где г — радиус кругового сечения конуса на высоте z от основания,
и, следовательно, nr2dz— объем слоя конуса, заключенного между
/ 1
J--
Рис. 2.1
плоскостями, проходящими перпендикулярно его оси на расстоянии
z и z-hdz от основания. Поскольку из подобия треугольников СО А
и СО'В следует —=—~^, то
Я
Г2_
Я2
„,
Если еще учесть, что объем конуса V= A/3)лЯ2Н, то
т. е. плотность вероятности
w(z) = l
Часто приходится иметь дело со случайными векторными вели-
величинами, т. е. с векторами, имеющими различную длину и направ-
направление, которые они принимают с определенной вероятностью.
Простейшим примером векторной случайной величины является
радиус-вектор молекулы Л, помещенной в сосуд объема V. Введем
декартову систему координат, по осям которой отложим компонен-
компоненты хА, Уа, za случайного вектора гА, и построим около точек х, у,
z бесконечно малый прямоугольный объем dx = dxdydz (рис. 2.3).
25
Какова вероятность того, что конец вектора г а окажется внутри
выделенного объема dx? Поскольку объем бесконечно мал, то ве-
вероятность dW должна быть ему пропорциональна, т. е.
dW=w{x,y, z)dx. G.2)
Величина w, вообще говоря, зависящая от координат х, у, г, носит
название плотности вероятности векторной случайной величины г.
Таким образом, произведение
плотности вероятности w векторной
случайной величины на элемент
объема dt дает вероятность того,
что конец вектора г окажется внут-
внутри dr, или, иначе, что одновременно
выполняются следующие условия:
х-, у- и z-компоненты г заключе-
заключены в интервалах от х до x+dx,
от у до y + dy, от z до z-\-dz соот-
соответственно.
В рассматриваемом примере
плотность вероятности w равна об-
обратной величине объема сосуда.
Действительно, еще в § 2 было ус-
Рис- 2<3 тановлено, что вероятность попада-
попадания молекулы А в элемент объема
dx, т. е. вероятность того, что конец ее радиус-вектора окажется в
этом элементе, равна
dW=dxJV.
Сопоставляя это с равенством G.2), можно заключить, что
У
G.3)
Если компоненты случайного вектора независимы, то в этом
важном частном случае плотность вероятности w(x, у, z) представ-
представляется в виде произведения трех плотностей вероятности:
, у, z) dt = wx(x)dx-wy{у)dy• wz(z)dz,
G.4)
так что вероятность попадания компоненты х в интервал dx равна
wx(x)dx и не зависит от того, какие значения принимают другие
компоненты.
Формула G.4) имеет простой вероятностный смысл и означает,
что вероятность того, что вектор г окажется в dt, равна произведе-
произведению вероятностей трех независимых событий, а именно того, что
компонента х попадет в интервал dx, компонента у — в dy, a
z — в dz. Полученная выше формула G.3) иллюстрирует этот слу-
случай. Поскольку объем сосуда, имеющего форму прямоугольного па-
параллелепипеда, равен произведению его сторон, то
26
где с, b, a — длины сторон вдоль осей х> у, z соответственно. Ис-
Используя это соотношение, можно для плотности вероятности напи-
написать
1111
w=——— . — . —,
V с b a
откуда видно, что
§ 8. Среднее значение
Знание вероятностей отдельных значений дискретной случайной
величины или плотности вероятности для непрерывной случайной
величины позволяет находить ее среднее значение, или, как говорят
иначе, математическое ожидание. Общее правило получим, рас-
рассматривая следующий конкретный пример. Пусть в сосуде V вы-
выделен объем Лт и интересующая нас случайная величина есть чис-
число молекул, находящихся в Дт в некоторый момент t. Предполо-
Предположим, что проведено большое количество опытов М, в каждом из
которых регистрировалось число молекул в Ат. Пусть пц раз заре-
зарегистрировано значение пи пг2 раз — значение п2 и т. д., тогда сред-
среднее значение числа молекул в Дт найдем по формуле
/ „ \ ш\п\ + ^2«2 + • • • ГП\П\ Л- Ш2П2 4" • . .
\ ft ) = = =
ТП\ + ГП2 + • • • М
Ш\ | /729 |
Если число испытаний достаточно велико, то отношения mJM,
tn2/M и т. д. становятся равными вероятностям соответствующих
значений я, т. е.
\\nl, (8.1)
где сумма берется по всем возможным значениям случайной вели-
величины Пг (Яг = 0, 1, ..., N, здесь Л^ — число молекул в сосуде).
Когда рассматривается непрерывная случайная величина z, то
поскольку вероятность того, что ее значение лежит в интервале de,
€сть w(z)dz, для нахождения среднего значения нужно просумми-
просуммировать выражения zw(z)dz по всем значениям г, т. е. по всем ин-
интервалам dz. Это означает, что правило для определения среднего
значения непрерывной случайной величины записывается в следую-
следующем виде:
(z) = ^zw(z)dz, (8.2)
!де интегрирование (суммирование) ведется по всем возможным
значениям случайной величины.
27
Вернемся к среднему числу частиц в объеме Ат. Пусть полное
число частиц в сосуде объема V равно N. Среднее значение опреде-
определяется формулой (8.1), в которой под w(tii) следует понимать ве-
вероятность того, что в Ат окажется п* частиц, т. е. выражение E.1).
Таким образом,
JV
ДТЗ \N-ni
' ~V
При вычислении написанной суммы следует обратить внимание на
то, что фактически суммирование ведется от /гг=1, так как слагае-
слагаемое с П{ = 0 равно нулю (необходимо учесть, что 0! = 1). В связи
с этим, сократив на щ, можно написать
N
Если обозначить щ—l = k, где k принимает значения 0, 1, ..., N—1,
то выражение для <я> можно записать в виде
N-X
Дт / Дх! \? /1 Дт! \N—I—ft
~v~\V) \ V)
jLlk\(N—\—k)\
Общий множитель N(Ar/V) выносится за знак суммы, и тогда
(
—1 — к)\ \ V
По формуле бинома Ньютона в полном соответствии с тем, что име-
имело место при аналогичных вычислениях в § 5, имеем
it
Ax\k( Ах \n-i~p г д-t ./ д-с \\N-i
*!(АГ-1-*)! I—) I1" IT) =1 — +11- —JJ =1-
Таким образом,
{n)=N-?-, (8.3)
т. е. среднее число частиц в объеме Ат равно полному числу частиц
в сосуде N, умноженному на вероятность (Дт/V) попадания час-
частицы в Ат.
Вычисление среднего значения непрерывной случайной величины
проведем на примере г-координаты молекулы, находящейся в пря-
прямоугольном сосуде. Как было показано ранее, плотность вероятно-
28
сти в этом случае равна w(z) = l/a. Среднее значение z вычисля-
вычисляется по (8.2):
~. (8-4)
т. е. мы получили результат, интуитивно ясный с самого начала.
В приложениях часто бывает важно знать среднее значение
функции от случайной величины, например квадрата (или какой-
либо другой степени) от числа частиц в объеме Ат или квадрата
координаты молекулы г2. Применяя приведенные выше рассужде-
рассуждения не к самой случайной величине niy а к некоторой ее функции
г|?(яг-), легко показать, что среднее значение следует определить
формулой
Среднее значение функции непрерывной случайной величины вычис-
вычисляется с помощью аналогичного по смыслу правила:
(z)dz. (8.6)
Интеграл берется по всем возможным значениям случайной вели-
величины z.
Таким образом, среднее значение (математическое ожидание)
функции от случайной величины вычисляется как сумма произве-
произведений этой функции на вероятность значения ее аргумента, т. е.
по формуле (8.5) для дискретной случайной величины и по форму-
формуле (8.6) для непрерывной.
Используем сформулированное правило для вычисления очень
важной характеристики, называемой дисперсией. Дисперсия —
это математическое ожидание квадрата отклонения случайной ве-
величины от своего среднего значения, т. е.
Я(*Л=<(л*-<Л/»2>. D{z)={{z-{z)f). (8.7)
Важность этой характеристики вытекает из того, что ею определя-
определяется степень разброса случайной величины, т. е. в каком-то смысле
дисперсия служит мерой случайности. Если какую-либо неслучай-
неслучайную величину рассматривать как случайную, принимающую с ве-
вероятностью единица одно и то же значение, то ясно, что отклоне-
отклонение от среднего равно для нее нулю, а следовательно, равна нулю
и дисперсия. Таким образом, дисперсия неслучайной величины
равна нулю, а у случайной она тем больше, чем шире разброс ее
значений.
Формулы (8.7) могут быть представлены в более удобном для
расчетов виде, который ниже получен только на примере непрерыв-
непрерывной случайной величины, так как в дискретном случае следует
лишь заменить интегрирование на суммирование.
29
В соответствии с определением дисперсии
)w{z)dz^ f (zJw(z)dz.
Поскольку <z>2 есть просто число, то последний интеграл равен
Г (zJ w (z)dz = (zJ tw(z)dz.
Имеет место условие нормировки плотности вероятности
случайной величины
•Оно вытекает из того, что принятые случайной величиной значения
из различных интервалов dz образуют полную группу несовмести-
несовместимых событий. Условие нормировки означает, что с вероятностью
единица случайная величина примет какое-либо из возможных
значений.
Предпоследний интеграл в выражении для дисперсии преобра-
преобразуется следующим образом:
Так как первый интеграл имеет смысл среднего значения квадрата
¦случайной величины и должен быть обозначен <г2>, то оконча-
окончательный результат с учетом условия нормировки записывается
аз виде
D{z)=(z2)-2(zJ+(zJ=(z2)-(zJ. (8.8)
Аналогичная формула имеет место и для дискретной случайной
величины:
?>(»,)=<«?>-<«,)».
На примере дисперсии легко показать, что среднее значение
^функции от случайной величины не равно значению этой функции,
когда в качестве ее аргумента берется среднее значение самой
«случайной величины. Действительно, в данном случае приходится
.вычислять среднее значение функции f(z)=z2. Ее среднее значение
есть <22> (знак усреднения относится ко всей функции), и это не
равно квадрату среднего значения <z>2. Если бы такое равенство
зшело место, то дисперсия обращалась бы в ноль. Покажем, что
это не так, на уже рассмотренном в настоящем параграфе примере.
Рассчитаем дисперсию координаты молекулы, находя-
находящейся в прямоугольном сосуде. Чтобы воспользоваться (8.8), вы-
вычисляем <z2>:
Поскольку <г>=а/2, то по (8.8) имеем
3 4 12
Для приложений очень важны следующие свойства сред-
средних значений и дисперсии.
а) Если складываются две функции f{(x, у, z) и f2(x, у, z)r
где г={#, у, г}—случайный вектор, то среднее значение сум-
суммы функций равно сумме их средних значений.
Действительно, когда г — непрерывный случайный вектор, то
= J fiw(x, у, z)dx + J f2w(x, у, z)dx =(fx) + </2>.
Аналогичным образом это свойство доказывается и для дискрет-
дискретных случайных величин.
б) Если функция от случайного вектора г умножается на по-
постоянное число а, то среднее значение произведения равно сред-
среднему значению /ь умноженному на а. Иначе это свойство фор-
формулируют так: постоянный множитель можно выносить из-под*
знака усреднения.
Доказательство проводится следующим образом:
(afx)=^a/xwdx=a J
(аналогично для дискретной случайной величины).
в) Если имеется несколько (например, три) функций /i (•*)»•
Ы#), Mz) от компонент х, у, г случайного вектора г={х, у, г}
и если случайные величины х, у, z независимы, так что
w (х, у, z) dt = wx (x) dx • wy {у) dy • wz (z) dz,
то среднее значение произведения f\(x) -f2(y) -f${z) равно про-
произведению их средних значений.
Действительно,
= J /i(x)wx(x)dx.§/2(у) wy(у)dy -L J/3{z)wz(z)dz^=
г) Дисперсия суммы нескольких независимых случайных вели
чин равна сумме их дисперсий.
Пусть х, у и z — независимые случайные величины, тогда, по оп
ределению,
3L
Возведем первую скобку в квадрат, а во второй используем свой-
свойство а):
D (jc+у + г) г= <(х2 + у2 + *2 + 2ху + 2xz + 2yz) > -
Вторую скобку возведем в квадрат, а к первой применим свойст-
свойство а):
) = ((x>) + {у2) _|_ <г.а> + {2ху) + Bxz)
-{x)*-(y)*-(z)*-2(x)(y)-2(x)(z)-2(y)(z).
По свойству б) множитель 2 выносится из-под знака среднего,
так что, например, ( 2ху)=2( ху). Более того, поскольку вели-
величины х, у, z независимы, то по свойству в)
и тогда видно, что все члены, содержащие произведения средних
значений различных случайных величин, взаимно уничтожаются.
Следовательно,
D(x + y + z)^ (jfi) - <
= D(
что и требовалось доказать.
Приведенные свойства позволяют в целом ряде случаев
упростить вычисления средних значений и дисперсии. В качестве
примера рассмотрим вновь число частиц в объеме Ат. Если сопо-
сопоставить каждой молекуле случайную величину nAi принимающую
значение 1, когда молекула находится в Ат, и 0, когда она оказы-
оказывается вне его, то число частиц в Ат можно рассматривать как
сумму этих случайных величин для всех молекул газа. По свойст-
свойству а) среднее значение числа частиц равно сумме математических
ожиданий пА. Последняя величина подсчитывается по общей фор-
формуле
V Г \ V I V
Поскольку математическое ожидание для всех молекул одинаково,
то их сумма вычисляется умножением полученного выражения на
общее число молекул N. Таким образом,
4 ' V
Столь же просто вычисляется дисперсия числа частиц в Ат. Снача-
Сначала следует найти <Да2>:
Vх \ V ) V
а затем дисперсию этой величины:
\2__ At
v \ v ) ~ v \~ v
32
^Л=<»'Д>- <*.>»=^~(^Г = -ТГ-A- -^У
Дисперсия общего числа частиц в Ат определится с помощью свой-
свойства г). Она равна
^(^) (8.9)
Прямое вычисление этой величины оказывается значительно более
громоздким.
§ 9. Распределение Пуассона
В предыдущей главе говорилось о том, что использование бино-
биномиального распределения для вычисления вероятностей при боль-
больших значениях общего числа молекул N неудобно, и была получе-
получена формула Стирлинга, облегчающая вычисление факториалов
больших чисел. Используя формулу Стирлинга, можно упростить
биномиальное распределение и свести его к другим, более удобным
для вычислений.
В настоящем параграфе рассматривается случай, когда при
большом значении числа N основной интерес представляют малые
значения числа молекул п в объеме Дт, т. е. предполагается, что
большие значения п настолько маловероятны, что ими можно пре-
пренебречь. Пусть, например, в сосуде находится N молекул, где N
порядка 1019, и выделен объем Ат, настолько малый по сравнению
с общим объемом сосуда V, что в нем может встретиться я=0, 1,
2, 3 молекулы и очень маловероятно, что число молекул превысит,
скажем, п=10. Для этого объем должен быть таким, чтобы сред-
среднее число молекул в нем, равное по (8.3) <n> = N(Ar/V), было
много меньше выбранного нами предельного числа /г=10, напри-
например <я>=3. Конечно, число 3 выбрано произвольно и с тем же
успехом могло бы быть заменено любым другим достаточно малым
по сравнению с общим числом молекул N, однако при относительно
больших <п> удобнее пользоваться другой аппроксимацией бино-
биномиального распределения, которая будет приведена в следующем
параграфе и которая заведомо непригодна при малых значениях
<п> (при <я><3).
Точное значение вероятности по формуле биномиального распределения E.1)
имеет вид
L;A_«.r
Воспользовавшись тем, что N и N—п — очень большие числа, заменим их фак-
факториалы по формуле Стирлинга:
NfrNV2h (—Y( _ Д*
Разделив и числитель, и знаменатель на Y2&NN~n NXj2 е—л/\ можно получить
;/(а^)A-ат/К)
п\ A - n/N)N~n ея A — jNI*2
2—434 33
Стоящий в знаменателе множитель
{\-nlNf
преобразуется следующим образом. Как известно из анализа, выражение
A—n/N)N при N-> оо (т. е. практически при достаточно больших N) равно е~п.
Выражение A—n/N)n, поскольку n/N — очень малая величина, близко к 1. Дей-
Действительно, если п < YD, например п = 0,3 УN, то
Таким образом,
Естественно, что при сделанных предположениях приближенно равен единице
и другой множитель из знаменателя (9.1):
A — n/NI^2 ^ 1.
Для завершения вычислений остается рассмотреть выражение, встречающееся в
числителе (9.1):
/ N(AxjV) \N
N-n \ N
(92>
Если nAx'CF, to по аналогии с предыдущим знаменатель в (9.2) равен единице.
Величина Л^Ат/У), равная среднему значению числа молекул в Дт, которое мы
обозначим <я>, по предположению много меньше iV и поэтому
Для интересующей нас вероятности оказывается, таким обра-
образом, справедливо следующее выражение:
Формула (9.3) носит название распределения Пуассона.
Она определяет вероятность того, что в Ат окажется п молекул
(при среднем значении числа молекул в Дт, равном </г>), и спра-
справедлива, если общее число молекул в сосуде много больше, чем
Поскольку распределение Пуассона есть предельный случай би-
биномиального при <я>2<сЛ/, или, иначе, при <п>/Л^=Ат/11/-^0, то
дисперсия случайной величины, подчиняющейся распределению
Пуассона, получается из (8.9) таким же предельным переходом,
т. е. оказывается равной среднему значению числа п:
?)=(»). (9.4)
34
§ 10. Распределение Гаусса
Другая полезная аппроксимация может быть использована,
когда велико не только общее число молекул N, но и число молекул
п в элементе объема Дт, а также число молекул N—я, оставшихся
вне этого объема. Такой случай очень часто реализуется на прак-
практике, так как для того, чтобы он имел место, достаточно, если сред-
среднее число молекул в элементе Ат
велико, но не слишком близко к полному их числу N, т. е. объем
Дт должен быть не слишком мал по сравнению с У, но и не слиш-
слишком близок к полному объему. Как будет видно из дальнейшего,
распределен.ие Гаусса оказывается уже достаточно точным, если
<я> и N—<п> больше 3, и его точность тем выше, чем больше
<п> и N—<n>.
Вероятность того, что в элементе объема Дт окажется п частиц,
при условии, что среднее число частиц <я> в Дт и среднее число
частиц N—<я> вне этого объема достаточно велики, дается фор-
формулой, носящей название распределения Гаусса и имею-
имеющей следующий вид:
W(n) = e-(n-(n))v(W)t (Ю.2)
Чаще всего распределение Гаусса A0.2) применяется, когда
число молекул в Дт очень велико. На практике почти никогда не
требуется знать, какова вероятность наличия в Дт ровно п молекул,
а обычно интересуются вероятностью 8W того, что число молекул
заключено в интервале значений от п до п+Ъп. Если величина 8п
достаточно мала (много меньше, чем V^5)» то вероятность
W(n)y подсчитанная по A0.2) для любого п из интервала б/г, ока-
оказывается практически одной и той же. В связи с этим вероятность
6W получается умножением вероятности W(n)y взятой для како-
какого-то (все равно какого) значения п из рассматриваемого интер-
интервала, на величину интервала бя, т. е.
] e-<«-<«»V<20) 8Л. A0.3)
Формула A0.3) показывает, что при большом числе молекул пере-
переменная п может считаться непрерывной случайной величиной и ве-
вероятность того, что ее значения заключены между п и п + Ьп, оп-
определяется формулой A0.3), т. е. соответствующая плотность веро-
вероятности равна
Если необходимо определить вероятность W того, что п заключено
в интервале от пх до п2) и интервал не предполагается малым по
2* 35
сравнению с V&* то необходимо учитывать изменение плотно-
плотности вероятности в этом интервале и использовать правило, обычное
для непрерывных случайных величин:
Точно так же при определении среднего значения функции f(n) от
числа молекул п следует воспользоваться правилом вычисления
средних значений, справедливым для непрерывных случайных ве-
величин:
= Г / (п) w (л) йп = f / (я) —-
J J )/2я?>
Пределы в последнем интеграле по смыслу переменной п не мо-
могут быть меньше 0 и больше N, однако поскольку с самого начала
предполагалось, что большие отклонения п от среднего значения
маловероятны и, как будет показано в § 13 следующей главы, при
больших <п> это действительно так, то без ущерба для точности
вычислений можно заменить эти пределы соответственно на минус
и плюс бесконечность, так что окончательно
+ 0О
Г
J
f(n) - е-(п-<п))*/BР) dftm
Y2D
Следует отметить, что распределение Гаусса часто встречается
на практике и описывает поведение очень многих непрерывных
случайных величин, т. е. оно справедливо не только для рассмот-
рассмотренного выше случая, но и в целом ряде других. На это имеются
свои причины. Дело в том, что при большом числе испытаний рас-
распределение Гаусса оказывается предельным для целого ряда рас-
распределений. Существует теорема, называемая в силу ее важности
центральной предельной теоремой теории веро-
вероятностей, которая устанавливает весьма общие условия, достз-
точные для того, чтобы предельное распределение было гауссовмм,
или, как его называют иначе, нормальным. Широкое распростра-
распространение нормального закона распределения вероятностей дало повод
для шутливого замечания, что физики считают повсеместное рас-
распространение нормального закона математической теоремой, а ма-
математики— экспериментально установленным фактом. Необходи-
Необходимо, конечно, иметь в виду, что распределение Гаусса хотя и встре-
встречается часто, но не является единственно возможным.
Если непрерывная случайная величина подчиняется нормально-
нормальному распределению, то вероятность dW того, что значения этой слу-
случайной величины z заключены в интервале от z до z+dz, определя-
определяется формулой
uW(z)= e-<*-<*»VB0> dz, A0.5)
У2О
36
где <z>—среднее значение, a D — дисперсия случайной вели-
величины г.
В заключение проведем сравнение аппроксимирующей формулы
Гаусса A0.2) с биномиальным распределением. На рис. 1.6 приве-
приведено биномиальное распределение для случая, когда N=6, а
дт/У=0,5. Результаты расчета тех же величин по A0.2) показаны
крестиками (<я>=#Дт/У=3, D = N&t/{V[1—(At/I/)]} = 1,51). Вид-
Видно, что даже в этом случае, когда <п> и N—<п> совсем не так
уже велики, получаются близкие результаты. При больших значе-
значениях <п> и N—<л> различие между расчетом по точной фор-
формуле биномиального распределения и формуле Гаусса оказывается
совсем незначительным.
§ 11. Вероятность как мера неожиданности
Вероятность какого-либо события может служить мерой его
неожиданности. Качественно это довольно очевидно. Если ве-
вероятность мала, то событие осуществляется редко и, следователь-
следовательно, относится к категории неожиданных. Наоборот, если вероят-
вероятность близка к единице, то событие случается часто и с этой точки
зрения относится к заурядным.
В теории информации за меру неожиданности события услови-
условились принимать натуральный логарифм его вероятности w, взятый
с обратным знаком: —In w.
Выбранная таким образом мера неожиданности хорошо переда-
передает многие из наших интуитивных представлений о свойствах, кото-
которыми она должна обладать. Действительно, вероятность — величи-
величина, меньшая единицы, и, следовательно, ее логарифм, взятый со
знаком минус, положителен, т. е. неожиданность — величина поло-
положительная. Если событие достоверно, то вероятность равна едини-
единице, а ее логарифм равен нулю, так что неожиданность осуществле-
осуществления достоверного события равна нулю. Наконец, если событие со-
состоит из двух независимых простых, то, поскольку его вероятность
равна произведению вероятностей, неожиданность сложного собы-
события равна сумме неожиданностей простых событий, из которых оно
состоит.
Для иллюстрации рассмотрим пример. Пусть в сосуде содер-
содержится три молекулы и в нем выделен объем, составляющий 0,1 от
-полного объема, т. е. Дт/У=0,1. Какова неожиданность того, что в
этом объеме окажутся все три молекулы? Вероятность интересую-
интересующего нас события в соответствии с биномиальным распределением
{см. также табл. 1) равна
Отсюда следует, что его неожиданность
- In WC)=3 In 10=6,9.
Этот же результат можно было получить несколько иначе. Рас-
Рассматриваемое событие состоит в осуществлении трех независимых
37
событий, а именно попадания каждой из трех молекул в Ат. Неожи-
Неожиданность попадания одной молекулы, поскольку вероятность этого
события равна Дт/У=0,1, есть
— In U7 = !n 10 = 2,3.
Неожиданность попадания трех молекул в три раза больше, т. е.
получаем тот же результат.
Поскольку отношение Ax/V мало, то попадание молекул в Дт —
маловероятное событие и поэтому гораздо менее удивительнее если
все три молекулы окажутся вне Дт. Какова неожиданность этого
события? Поскольку соответстгующая вероятность равна
то, учитывая, что Дт<с1, для неожиданности найдем
- 3 In A - At/I/) ~ 3 (Ат/1/) = 0,3.
Ее числовое значение в этом случае получилось значительно мень-
меньше, чем в предыдущем.
Если в результате измерения обнаружено, что событие осущест-
осуществилось и, например, все три молекулы оказались в Дт, то это озна-
означает, что событие стало достоверным и его неожиданность равна
кулю. Уменьшение неожиданности, явившееся следствием измере-
измерения, можно рассматривать как меру информации, которая при этом
была получена. Так как конечная неожиданность — ноль, то умень-
уменьшение неожиданности равно ее первоначальному значению, поэто-
поэтому выражение — In W(A) является также мерой количества инфор-
информации, полученной в опыте, который показывает, что событие А
осуществилось.
§ 12. Энтропия и хаотичность
Выше была введена мера неожиданности для случайного собы-
события. Пусть рассматривается некоторая полная группа несовмести-
несовместимых событий. Каждое из этих событий обладает своей неожидан-
неожиданностью, и возникает вопрос о характеристике, общей для всей си-
системы. Такая характеристика, называемая энтропией или ин-
информационной энтропией, вводится как среднее по всей системе
значение неожиданностей, т. е. неожиданность каждого 1-го собы-
события умножается на вероятность этого события W{ и все получен-
полученные результаты складываются. Таким образом, обозначив энтро-
энтропию 5, можем записать математическое выражение, определяющее
эту величину,
N
WllnWl, A2.1)
где суммирование распространено на все события, составляющие
полную группу. Энтропия характеризует степень неопределенности
или хаотичности, которая имеет место в данной ситуации. Для по-
38
яснения этого смысла энтропии обратимся к уже рассматривавше-
рассматривавшемуся ранее примеру, в котором молекула А, находящаяся в сосуде
объема V, может попасть или не попасть в выделенный объем At.
Предположим вначале, что объем Дт очень мал по сравнению
с V. Интуитивно ясно, что в этом случае неопределенность ситуа-
ситуации очень мала, так как почти наверняка молекула окажется вне
Дт. Энтропия отражает это представление. Действительно, вероят-
вероятность попадания в Дт есть W\ = &xlV, а вероятность непопадания
W2=l—W\ = l — (Дт/V). Для энтропии, следовательно, имеем
At! j Аи Л Аи \ , Л А-с \
Если Дт/V очень мало, то в первом слагаемом один сомножитель
стремится к пулю, а второй — к —оо. Поскольку, однако, возраста-
возрастание —In (Дт/V) с уменьшением Дт/V очень медленное, то при
(Дт/1/)-^0 произведение стремится к нулю*. Во втором слагаемом
первый сомножитель стремится к единице, а второй — к нулю, так
что при малом Дт/F он тоже очень мал. Таким образом, при малом
Дт/V значение энтропии мало.
Легко убедиться, что точно такое же положение имеет место,
когда объем Дт близок к V. В этом случае почти наверняка моле-
молекула А окажется в Дт. Неопределенность ситуации мала, и значе-
значение энтропии оказывается снова близким к нулю.
Когда же достигается наибольшая неопределенность? Попыта-
Попытаемся ответить на этот вопрос, выяснив, при каких условиях энтро-
энтропия достигает своего максимального значения, и рассматривая ее
как функцию вероятности Wi = Ax/V. По общему правилу нахож-
нахождения максимума функции продифференцируем S по вероятности
и приравняем производную нулю, тогда получим
= - In u?r1-l + ln(l-VF1)+ 1 = 0. A2.2)
Из этого равенства вытекает, что Wi= A—W\) или
1/2. A2.3)
Таким образом, наиболее неопределенное положение достигается
тогда, когда Дт составляет половину объема V.
Итак, мерой неопределенности или хаотичности ситуации, ха-
характеризуемой некоторой полной группой несовместимых событий
с вероятностями Wit служит функция этих вероятностей A2.1), на-
зываемая информационной энтропией.
* По правилу Лопиталя имеем
~ d In x -
lim (x In лг) == lim
0 0
—
6х
ДГ-OL —
ЧАСТЬ II
КЛАССИЧЕСКАЯ СТАТИСТИКА
РАВНОВЕСНЫХ СОСТОЯНИЙ
ГЛАВА 3
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
§ 13. Распределение частиц в пространстве
при отсутствии внешних силовых полей
Если внешние силовые поля отсутствуют, то частицы, например
молекулы идеального газа, распределяются по объему сосуда рав-
равномерно. Действительно, в § 2 были изложены соображения, по
которым можно считать, что вероятность того, что молекула нахо-
находится в объеме Дт, являющемся частью объема сосуда У, равна
Ат/У и не зависит от формы и положения этого объема. Среднее
число молекул в Ат при общем числе N определяется соотношени-
соотношением (8.3)
{n)=Nbx/V
и, таким образом, оказывается одинаковым для любых равных по
величине объемов Дт. Другими словами, среднее значение концен-
концентрации, т. е. числа молекул в единице объема (Дт=1), есть вели-
величина постоянная.
Из равенства средних значений концентрации еще не следует,
что в любой момент времени числа молекул в объеме Дт и равно-
равновеликом ему объеме Дт/ равны друг другу. Наоборот, истинное чис-
число молекул /г, как правило, отличается от <я> и различно для
этих двух несовпадающих объемов. Отклонения числа молекул от
среднего значения носят название флуктуации. Нетрудно пока-
показать, что в большинстве интересных с практической точки зрения
случаев флуктуации очень малы и с ними можно не считаться. Что-
Чтобы убедиться в этом, рассмотрим пример.
Пусть в сосуде объемом 1/= 10 см3 находится идеальный газ
с общим числом молекул iV=2,69-1020, что соответствует нормаль-
нормальным условиям (температуре 0°С и атмосферному давлению). Мыс-
Мысленно выделим часть этого объема Дт, составляющую один про-
процент от V, т. е. Дт=0,1 см3. Среднее число молекул в Дт равно
</г> = 0,0Ш=2,69-1018, а среднее число молекул вне этого объема
N—<п> ~2,66-1020. Как было показано в § 10, при таких больших
значениях чисел <п> и N—<n> число молекул п в объеме Дт
40
может рассматриваться как непрерывная случайная величина, плот-
плотность вероятности которой определяется распределением Гаусса
A0.3). Легко рассчитать вероятность любого отклонения от сред-
среднего значения. Подсчитаем, например, вероятность того, что в при-
приведенном примере число молекул в Ат будет отличаться от сред-
среднего значения больше чем на 0,01%. Другими словами, нас инте-
интересует вероятность того, что п окажется либо меньше <я>A—
—10~4), либо больше <п> A + 10~4). Соответствующая вероятность
' 1вна
— о©
оо
Если обозначить п—</i>=A/i, то
— 10~~*(п) оо
W= [ е-Ая'/(за> d(A/t) + f
4
Подынтегральная функция четна, и поэтому оба интеграла, которые
берутся в симметричных пределах, равны друг другу, так чго
W=2 f l-
ю-4<л>
Аналогичные интегралы часто встречаются в статистике, и поэтому целесооб-
целесообразно остановиться на__их вычислении подробнее. Прежде всего введем новук*
переменную х = Ап/YD и обозначим
тогда
Функция
^*1'2 A3.1)
носит название интеграла вероятности или функции ошибок, и
таблицы ее значений приводятся в справочниках по математике*. Ф(х0) опреде-
определяет вероятность того, что случайная величина х, распределенная по закону
* См., например, [12], с. 81.
41
Гаусса, по абсолютной величине окажется меньше х0. Если хо= оо, то, как ясно
из смысла интеграла вероятности,
Ф(оо)=—ТГ
V2K .
Теперь можно написать
W =
ДГо
^2 Ах - —=- \
V2K .}
Ах = 1 - Ф (х0). A3.2)
Поэтому, когда имеются таблицы функции ошибок, то легко подсчитать W. Если
хо^.\ или, наоборот, #о>1, то значение интеграла вероятности определяется
и без помощи таблиц. Как показано в приложении 1, при Хо^\
о. О3-3)
а при
интеграл вероятности оценивается формулой
1 L ^о/2
A3.4)
Применим полученные результаты для вычисления интересую-
интересующей нас вероятности. Поскольку дисперсия, как это следует из
формулы, приведенной в конце § 10, равна
ТО
При <я> =2,69-1018 это даст хо= 1,64-105, так что с очень высокой
точностью применимо соотношение A3.4). Из A3.2) с помощью
A3.4) находим
W= ^ Le~^/2 э A3.5)
/2 х°
т. е. числовое значение W имеет порядок е-1'35*1°1О= 1О-°'581°10.
Трудно представить себе, насколько мала вероятность рассмотренного собы-
события. Для иллюстрации можно сравнить ее с вероятностью того, что обезьяна, по-
посаженная за пишущую машинку, напечатала бы в нужном порядке и без оши-
ошибок полный текст «Войны и мира» (пример, предложенный Э. Борелем). В од-
одном из изданий романа три тома его содержали 2330 страниц. Если принять, что
на странице помещается 45 строк, а число знаков в строке, включая пробелы,
50, то общее число знаков в книге примерно равно 5,25-106. Поскольку предпо-
предполагается, что обезьяна нажимает все клавиши наугад, то вероятность того, что
будет нажата данная конкретная клавиша, равна 1/50 (общее число клавиш
равно 50). Считая, что все знаки печатаются независимо, легко получить для
искомой вероятности следующее значение:
\F=(l/50M-25-10e=10-8'9-107,
т. е. она в 10 ' ' раз больше, чем вероятность рассмотренного нами не*
значительного повышения концентрации молекул в объеме Ат!
42
Таким образом, при отсутствии внешних сил средняя концент-
концентрация частиц одинакова по всему сосуду и истинную концентрацию
можно считать равной ее среднему значению, так как даже очень
малое отклонение от среднего значения из-за большого числа час-
частиц обладает ничтожной вероятностью.
Для справедливости сделанного вывода очень существенно, что-
чтобы число частиц было велико. Если, например, считать, что объем
дт=Ю-3 мкм3=10~15 см3, то среднее число частиц в нем окажется
равным </г>=2,69-104, т. е. много меньше, чем в предыдущем слу-
случае. Дисперсия имеет значение D=<n>. Вероятность отклонения
концентрации от ее среднего значения на величину, большую
0,01%, определится выражением A3.1), но с другим значением па-
параметра Xq, а именно
хо= \0-*(ti)lVD=\Q-A Vln) = 1,64- Ю-2.
Поскольку значение х0 оказывается много меньше единицы, то
с помощью A3.2) и A3.3) найдем
т. е. событие практически достоверно. Однако отклонения концен-
концентрации больше чем на 10% от среднего значения будут маловеро-
маловероятны. Действительно, в этом случае
*о= / =10"
и по A3.5)
W=— — е-1б'42/2= i 9.1О-бо#
/2Л 16,4
Таким образом, в малых объемах, содержащих сравнительно не-
небольшое число частиц, относительные флуктуации могут быть за-
заметными. В некоторых явлениях они играют очень важную роль.
Б частности, флуктуациями плотности воздуха объясняется рассея-
рассеяние солнечного света атмосферой и голубой цвет неба. Последний
связан с тем, что солнечное излучение с более короткой длиной вол-
волны (синее) рассеивается более эффективно, чем красное, обладаю-
обладающее большей длиной волны.
§ 14. Плотность вероятности для импульсов
молекул
Выяснив вопрос о распределении частиц (молекул) в простран-
пространстве, мы можем поинтересоваться возможными значениями их ско-
скорости v или импульса p = mov (m0 — масса частицы). Фактически
в газе встречаются молекулы с самыми разными значениями им-
импульса, и поэтому с точки зрения теории вероятностей необходимо
43
лишь знать вероятность тех или иных его значений. Другими сло-
словами, в статистике импульс молекул, находящихся в сос\де, рас-
рассматривается как непрерывная случайная величина и для ее ха-
характеристики необходимо знать соответствующую плотность веро-
вероятности, которую мы обозначим до р.
Для дальнейшего удобно ввести представление о пространстве
импульсов. Отложим по осям прямоугольной декартовой системы
координат компоненты импульса молекулы (рис. 3.1). Если нас
интересует вероятность dW того, что
компоненты импульса какой-то оп-
определенной молекулы заключены
соответственно в интервалах
Рх-*-(Рх + *РхУ* Py-U
Рис. 3.1
то с помощью пространства импуль-
импульсов эти условия можно сформулиро-
сформулировать наглядно. Наложенные требо-
требования с геометрической точки зре-
зрения означают, что конец вектора
импульса, проведенного из начала
координат, попадает внутрь элемен-
элементарного прямоугольного объема dQ
в пространстве импульсов, изобра-
изображенного на рис. 3.1. Поскольку стороны объема равны соответст-
соответственно dpXy dpy и dpz, то
dQ = йрх dpy <5p2. A4.1)
Интересующая нас вероятность dW может быть представлена в ви-
виде dW=wv dQ, где дор—плотность вероятности импульса, которую
нужно найти.
Чтобы установить вид дор, оказывается, как это впервые показал
Максвелл, достаточно использовать следующие предположения:
а) все направления в пространстве равноправны и поэтому лю-
любое направление движения частицы, т. е. любое направление
импульса, одинаково вероятно. Это свойство иногда называют
свойством изотропности плотности вероятности дор;
б) движения по трем взаимно перпендикулярным осям неза-
независимы, т. е. значение х— компоненты импульса рх — не за-
зависит от того, каково значение его компонент ру или рг.
Второе условие менее очевидно, чем первое, и оказывается прос-
просто неверным, если учитывать движение со скоростью, близкой
к скорости света, т. е. эффекты теории от юсительности. Действи-
Действительно, поскольку по теории относителыости движение со ско-
скоростью, большей скорости света, невозмо>' но, то это означает, что
компоненты скорости вдоль различных ос й связаны между собой
неравенством
44
Так, например,если vx&cy то это возможно только при vyatvzt&0.
Таким образом, нужно быть готовым к тому, что выводы, получен-
полученные на основе принятых предположений, не будут удовлетворять
требованиям теории относительности.
Чтобы приблизиться к решению поставленной задачи, рассмот-
рассмотрим плотность вероятности для одной из компонент импульса,
например рх. Вероятность dWPx того, что компонента рх заклю-
заключена в интервале px-T-(Px+dpx), может быть записана в виде
uWpx=wPxupx9 A4.2)
где wpx— плотность вероятности для рх. Поскольку из свойст-
свойства изотропности вытекает одинаковая вероятность значений ком-
компонент рх и —рх, то плотность вероятности я^— четная функ-
функция, т. е. она зависит от квадрата рх:
«,х=?</?)- а4-3)
По тому же свойству изотропности плотности вероятности двух
других компонент выражаются аналогичным образом:
где ф — одна и та же функция. Используя независимость компонент,
легко выразить плотность вероятности Шр через плотности вероят-
вероятностей wpxf wpy, wpz. Действительно, вероятность того, что
импульс р попадет в элемент объема пространства импульсов
dQ= dpxdpydpZi равна
dW==wvdQ. (НА)
С другой стороны, это событие эквивалентно тому, что компонента
рх оказалась в интервале рх~ (рх+dpx), компонента ру — в интер-
интервале Py-r-(Py + dpy) и pz — в pz-7-(pz+dpz). Из-за независимости пе-
перечисленных событий вероятность A4.4) может быть представлена
в виде произведения:
«р<Ш=дарх dpx-wpy dprwpz d^^cp^.cp^p.cp^) dpxdpy dpz.
Если учесть A4.1), то из последнего равенства вытекает
Поскольку плотность вероятности wp не должна зависеть от на-
направления импульса (свойство изотропности), то, следовательно,
она зависит только от его величины, т. е.
где \|) — некоторая, тоже неизвестная пока, функция. Из последнего
и предыдущего равенства вытекает следующее соотношение:
121. 114.5)
45
Условие A4.5) позволяет определить вид неизвестных функций
<р и г|э, т. е. найти плотности вероятности wp и wpx. Чтобы сде-
сделать это, прологарифмируем A4.5):
In ф = 1
Продифференцируем теперь это тождество по рх:
-<—2рх — -1—2рх, A4.о)
где штрихом обозначена производная соответствующей функции
по ее сложному аргументу, т. е.
dz' dz '
После сокращения на 2рх из A4.6) получаем
Совершенно аналогично, дифференцируя по ру или р2, можно
получить еще два похожих соотношения:
Из A4.7) и A4.7') вытекает, что
9'(Pi)
Поскольку первое отношение зависит только от рх, второе —
только от ру, а третье — от pz, то написанное равенство, выполняю-
выполняющееся тождественно для всех рх, ру и pz, может иметь место только
в том случае, когда эти отношения на самом деле не зависят от
соответствующих аргументов, т. е. являются постоянными числами.
Обозначим постоянную —р и тогда получим дифференциальное
уравнение, определяющее функцию <р,
Решение этого уравнения имеет вид
где С — вторая неопределенная константа. Если известна функция
<р, то г|) определяется paseHctBOM A4.5).
Таким образом, из условия изотропности и условия независи-
независимости движения по взаимно перпендикулярным осям следует, что
46
вероятность dWpx того, что компонента импульса рх окажется за-
ключенной в интервале dpx, определяется соотношением
dWpx=C^dPx A4.8)
(аналогично для других компонент), а вероятность dW того, что
импульс окажется в объеме (Ш,— соотношением
где С и р— некоторые постоянные, которые должны быть опреде-
определены с помощью дополнительных условий.
§ 15. Условие нормировки
Одно из условий для определения постоянных Сир вытекает из
требования, чтобы интеграл от плотности вероятности по всем воз-
возможным значениям аргумента (имеющий смысл вероятности того,
что импульс молекулы имеет какое-то из возможных значений)
был равен единице. Это условие носит название условия нор-
нормировки и записывается следующим образом:
9р*дрх=1. A5.1)
Нормировочное соотношение A5.1) можно рассматривать как
уравнение, из которого постоянная С определяется через постоян-
постоянную р*.
f 92 ~\ A5.2)
Из A5.2), в частности, видно, что постоянная р должна быть
положительна, так как в противном случае интеграл в A5.2) рас-
расходится и постоянная С оказывается равной нулю. Вычисление ин-
интеграла, входящего в A5.2), приведено в приложении 2. Результат
оказывается следующим:
С=1/рм". A5.3)
Таким образом, значение нормировочной постоянной определя-
определяется через параметр р с помощью соотношения A5.3).
§ 16. Связь параметра р распределения
Максвелла с температурой
Для того чтобы завершить определение плотности вероятности
импульсов молекул, остается найти значение параметра р. Посколь-
Поскольку эта величина зависит от условий, в которых находится газ, то
ее можно найти лишь рассмотрев конкретную физическую ситуа-
47
цию. Пусть, например, имеется идеальный одноатомный газ. Его
внутренняя энергия U определяется соотношением
U=— — RT, A6.1)
2 р.
где М — масса газа, ji — его молярная масса, R — универсальная
(молярная) газовая постоянная и Т — абсолютная температура.
Обычно на опыте измеряется теплоемкость при постоянном объе-
объеме Cv, которая для одноатомного газа оказывается постоянной и
равной
Как известно из термодинамики (см. гл. 5), теплоемкость связана
с внутренней энергией соотношением
6
из которого в данном случае вытекает соотношение A6.1).
Вутренняя энергия идеального одноатомного газа — это среднее
значение кинетической энергии поступательного движения всех его
молекул, так как для такого газа взаимодействием молекул между
собой (т. е. их взаимной потенциальной энергией) можно пре-
пренебречь.
Кинетическая энергия отдельной молекулы равна
•=/*/B/Ио). A6.2)
где т0 — масса молекулы. Используя свойства средних значений,
среднее значение энергии можно представить следующим образом:
Из свойства изотропности вытекает, что средние значения квадра-
квадратов всех компонент одинаковы, так что
Величина
Поскольку С определяется соотношением A5.3), а интеграл —
формулой, выведенной в приложении 2, то для величины <рх2>
получаем
at
48
Если заданы масса М газа и его молярная масса \i, то число
молей равно Af/p, и, следовательно, общее число молекул газа
где NA — постоянная Авогадро, т. е. число молекул в одном
моле.
Среднее значение энергии газа есть сумма средних значений
энергии всех его молекул, и поэтому внутренняя энергия идеально-
идеального одноатомного газа равна
' 2 т0 2 т0 2Р fx 2 2m0P
Сравнивая последнее соотношение с A6.1), находим
Отношение универсальной газовой постоянной к постоянной Аво-
Авогадро есть постоянная Больцмана fe, и поэтому параметр
р, входящий в плотность вероятности значений импульсов A4.8)
или A4.9), носящей название плотности вероятности Максвелла,
равен
A6.3)
т. е. определяется абсолютной температурой.
§ 17. Плотность вероятности Максвелла
для импульсов
Из результатов, полученных в предыдущих параграфах, выте-
вытекает, что плотности вероятности значений импульсов (плотности
вероятности Максвелла) выражаются такими формулами:
Рассмотрим более подробно одну из компонент импульса, на-
например рх. Сопоставляя плотность вероятности этой случайной ве-
величины с A0.5), легко убедиться, что она подчиняется распределе-
распределению Гаусса, или, как принято говорить иначе, нормальному распре-
распределению. Среднее значение компоненты равно нулю, а ее диспер-
дисперсия совпадает со средним значением рх2:
D=(pl)=mokT. A7.2)
49
На рис. 3.2 изображена зависимость плотности вероятности
wpx от рх. Соответствующая кривая в силу четности wpx сим-
симметрична относительно оси ординат. Максимальное значение дости-
достигается при рх = 0 и определяется температурой газа
Рх=о= 1/ V 2,nm§kl. (i/.o>
/;.<.= Ym^kT, A7.4)
При
т. е. при среднеквадратичном значении х-компоненты импульса,
значение плотности вероятности уменьшается в "|/е=1,65 раза
по сравнению со значением в максимуме и при больших значениях
рх быстро стремится к нулю.
Если нагреть газ до более высокой температуры, то плотность
вероятности изменится. В соответствии с A7.3) максимальное зна-
значение окажется меньше, а по A7.4) сама кривая станет более ши-
широкой.
Выберем на оси абсцисс отрезок dpx, малый по сравнению
с УщкТу тогда на протяжении этого отрезка плотность вероят-
вероятности wpx почти не изменит своего значения. Вероятность того,
что значение х-компоненты импульса лежит в интервале с!/?х, оп-
определяется выражением
dw=wpxdpx
и, следовательно, изображается площадью, ограниченной осыо
абсцисс кривой распределения и ординатами, соответствующими
началу и концу интервала dpx
(двойная штриховка на рис. 3.2).
Подобная геометрическая ин-
интерпретация относится к произ-
произвольному, а не только к бесконеч-
бесконечно малому интервалу dpx. Так,
например, вероятность того, что
компонента рх больше —рь на
меньше 4-рг, изображается за-
заштрихованной на рис. 3.2 пло-
площадью. Полная площадь под кри-
кривой распределения, естественно,
равна единице, так как соответ-
соответствует вероятности достоверного события (—оо<рх< + оо).
Имея в своем распоряжении плотндсть вероятности Максвелла,
можно решать задачи двух типов.
Во-первых, можно находить средние значения различных
функций от импульса частицы. Так, например, для любой четной
степени компоненты
Рис. 3.2
</#•>=¦
1
olne
50
Соответствующий интеграл вычислен в приложении 2, и с его помо-
помощью получаем
1-3.5 ... Bлг — 1),
т. е.
2 \ A7.5)
Для любой нечетной степени рх среднее значение равно нулю, так
как эта функция одинаково часто принимает положительные и от-
отрицательные значения.
Во-вторых, можно находить вероятности тех или иных со-
событий. В виде примера найдем вероятность того, что компонент?
импульса частицы вдоль положительного направления оси х ока-
окажется больше, чем значение, соответствующее движению со ско-
скоростью 0,1 с (с — скорость света). Другими словами, нас интере-
интересует площадь под кривой распределения Максвелла от точки рх —
= 0,1ш0с и до бесконечно удаленной точки, т. е.
= Г
w=
O,\m0c
Если ввести переменную t = pxIVmokT, то
оо
0}\moc/YmokT
и при условии, что
1о=ОЛтос1УщёГ » 2, A7.6)
можно воспользоваться формулой A3.4), т. е.
1 1 -&I&
W=
6о
Легко убедиться, что почти во всех практических случаях неравен-
неравенство A7.6) выполняется. Условия для его выполнения тем менее
¦благоприятны, чем меньше масса частиц и чем выше температура,
ттри которой они находятся. Для атомарного водорода (то =
= 1,67-10—24 г) при температуре Г=3 000 К go = 6-103 и, следова-
следовательно, U7~e~207, т. е. очень малая величина.
При взрыве атомной бомбы температура продуктов реакции и,
б частности, нейтронов может достигать 10 млн. град. Поскольку
масса нейтрона тп~ 1,7- Ю~27 кг, то параметр ?0 оказывается рав-
равным 102, так что и в этом случае вероятность скоростей, близких
к скорости света, весьма мала.
В газовом разряде относительно просто создать условия, при
которых электроны плазмы обладают очень высокой температурой,
достигающей Т = 20000 К. Поскольку масса электрона те=9Х
51
Х10~29 кг, то для этого случая |о^5О и опять-таки вероятность W
очень мала.
Приведенные оценки показывают, почему тот факт, что распре-
распределение Максвелла не включает эффектов теории относительности
и теоретически допускает значения скоростей, больших скорости
света, с практической точки зрения оказывается несущественным*
В заключение отметим (в некоторых случаях это может быть
удобно), что задачу о нахождении вероятности некоторого события
формально можно рассматривать как нахождение среднего значе-
гия функции, которая в некоторой области равна единице, а во
всем остальном пространстве — нулю. Проиллюстрируем это поло-
положение примером, на котором попутно выясним связь между плот-
плотностями вероятности wpx и wp. Предположим, что нас интересует
вероятность того, что частица движется вдоль оси х в положитель-
положительном направлении, и не интересует, какое движение совершается
при этом вдоль осей у и z. Искомая вероятность совпадает с веро-
вероятностью положительного значения х-компоненты импульса, и для
ее вычисления можно найти среднее значение функции, которая
равна единице при р*>0 и нулю при рх<0:
, Л A при /?г>-0,
1 0 при рх < 0.
С помощью функции ф(Рх) для вероятности записываем
*= \
Решение этого же вопроса легко получить и исходя из плотно-
плотности вероятности wp. Выпишем интеграл от wp в пространстве им-
импульсов:
•pdQ=J d/>, J йРг J dA,^^-"
Интеграл разбивается на произведение трех интегралов:
=. С
\ Tp*n2rn°kT) dpz
\
X
Поскольку первые два интеграла по условию нормировки равны
единице, то очевидно, что получается тот же результат, что и при
52
использовании плотности вероятности wpx. Ясно, что так будет
случаться всегда, когда отыскивается среднее значение функции,,
зависящей только от компоненты рх. Если же нужно найти среднее
значение функции, зависящей от всех трех компонент рх, Ру, pz, то
необходимо пользоваться плотностью вероятности wp.
§ 18. Распределение по скоростям
В практических приложениях часто требуется найти вероятность
тех или иных значений скорости частиц или среднее значение какой-
либо величины, зависящей от скорости. Эти задачи могут быть ре-
решены с помощью плотности вероятности Максвелла для импульсов,,
если предварительно пересчитать скорости в импульсы, как, напри-
например, это было сделано в предыдущем параграфе, где фактически
определялась вероятность того, что скорость частицы больше 0,1 с.
Удобно, однако, иметь и плотность вероятности Максвелла для
скорости, чтобы не делать предварительного пересчета. Обозначим
плотность вероятности для я-компоненты скорости vx через wvx>
тогда вероятность того, что vx лежит в интервале dvx, определяет-
определяется формулой
Эту же вероятность можно выразить и через плотность вероят-
вероятности х-компоненты импульса, если только выбрать интервал dpx
так, чтобы он соответствовал dvx:
dW=wpxdpx.
Поскольку импульс и скорость связаны соотношением Px=mot;a, та
ясно, что соответствие имеет место, если dpx=modvx. Подставив в
плотность вероятности wpx значение рх, выраженное через ско-
скорость, найдем
т° e"^B>r) dv,.
Таким образом, вероятность того, что х-компонента скорости vx
лежит в интервале значений от vx до vx+dvXf определяется следу-
следующей формой распределения Максвелла:
W=wvxdvx= j/^e-^^du,. A8.1)
Аналогичные выражения имеют место и для других компонент:
A8.1)
53
В силу независимости значений компонент скорости вдоль различ-
различных осей плотность вероятности для случайного вектора скорости
получается перемножением выписанных плотностей вероятности:
wv dvx dvy dvz = (-^f e-m«/Bftr)d^ dvy dvz. A8.2)
Обратим внимание на то, что плотность вероятности wVjc не
получается подстановкой movx вместо рх в плотность вероятности
лля ^-компоненты импульса, а необходим еще и дополнительный
множитель ш0, связанный с переходом от dpx к dvx. При переходе
к новым переменным всегда нужно преобразовывать вероятность
dlF, а не отдельно взятую плотность вероятности.
§ 19. Распределение по модулю импульса
и по энергии
В некоторых случаях удобнее иметь дело с импульсом, задан-
заданным не проекциями на прямоугольные оси импульсного простран-
пространства, а модулем импульса и углами 0 и ф, характеризующими его
направление (рис. 3.3). Это соответствует переходу к сферической
системе координат, в которой вектор определяется своей длиной,
углом 9 с осью pz, совпадающей по направлению с осью z в обыч-
обычном пространстве, и углом ф между проекцией вектора р на плос-
плоскость рх0ру и осью рх. Элемент объема в сферических координатах
(рис. 3.3) имеет следующее значение:
d2 = d/?-/?d0-/?sin0dcp^/?2sin9d/?d6dcp. A9.1)
Вероятность того, что вектор импульса оканчивается в dQ, оп-
определяется произведением преобразованной к новым координатам
плотности вероятности w и преобразованного элемента объема
O9.1):
e-p4BmQkT) p2 sin 9 d/7 d8 (to. A9.2)
Предположим, что нас интересует вероятность dW того, что
модуль импульса частицы заключен в интервале от р до p + dp, и
не интересует направление этого импульса. Если через wp обозна-
обозначить плотность вероятности для модуля импульса, то по определе-
определению плотности вероятности
Поскольку, с другой стороны, эта вероятность равна вероятности
того, что импульс частицы окажется внутри шарового слоя радиуса
р и толщины dp (рис. 3.4), то dW есть сумма wpdQ по всем эле-
элементам объема dQ, составляющим шаровой слой. Так как слой бес-
бесконечно тонок, то во всех его точках импульс имеет одинаковое
значение модуля, а поэтому и плотность вероятности wv постоянна.
54
Тогда вероятность dW равна плотности вероятности wp, умножен-
умноженной на объем шарового слоя 4тср2йр, так что
Таким образом, плотность вероятности значений модуля импульса
wp определяется соотношением
-РуBтокГ)
d/7.
A9.3)
Формулу A9.3) легко получить и формально. Напишем инте-
интеграл
•л
Pz
Рис. 3.3
Рис. 3.4
в котором интегрирование ведется по шаровому слою толщины d/7.
Используя A9.2), получим
p+dp
тс 2тс
или
2тс
sin e de
BnmQkTf/2
Первый интеграл равен 2я, а второй —2. Последний в случае, когда
верхний предел бесконечно близок к нижнему, равен произведению
подынтегральной функции на dp. ]Чы снова приходим к A9.3).
От распределения A9.3) для модуля импульса можно перейти
к распределению по энергии. Частица идеального газа
обладает только кинетической энергией, которая равна е = р2/Bт0).
5S
Выражая импульс через энергию в A9.3), получаем
l e
dW=wp d/?= «r. d e=
ут
где учтено, что поскольку /?=]/2яг0е, то
Таким образом, вероятность того, что энергия частицы заключе-
заключена в интервале значений от г до e+de, определяется соотношением
2/е
¦
ds.
A9.4)
Рассмотрим подробнее плотность вероятности для модуля
импульса. Так как модуль импульса — положительная величина,
то Wp имеет смысл только для положительных значений аргумента.
График этой функции представлен на
рис. 3.5. При р = 0 получаем дор=0 и
для малых значений р, когда экспонен-
экспонента практически равна единице, плот-
плотность вероятности пропорциональна
квадрату импульса, так что начальный
участок графика представляет собой
параболу. При больших значениях им-
импульса ( р > У2щокТ) из-за экспонен-
экспоненциального множителя Wp быстро убы-
убывает. Легко найти значение импульса,
при котором достигается максимум.
Дифференцируя плотность вероятности по р и приравнивая произ-
производную нулю, получим уравнение, определяющее, как принято го-
говорить, наиболее вероятное значение импульса:
Рис. 3.5
mQkT
Отсюда наиболее вероятное значение импульса равно
pB=V2mQkT.
Для плотности вероятности в максимуме получаем
рв УшфТ '
A9.5)
A9.6)
т. е. максимальное значение плотности вероятности обратно про-
пропорционально квадратному корню из температуры. Если газ на-
назреть до более высокой температуры Т\ то плотность вероятности
изменится (рис. 3.5 — пунктирная кривая). Максимум оказывается
сдвинутым вправо и несколько более низким, кривая становится
более широкой.
С помощью плотности вероятности (Ю.З) можно находить сред-
средние значения функций от величины р^пульса. Найдем, например,,
среднее значение модуля импулься ilo общему правилу имеем
Если ввести новую леременную интегрирования x=p2/BmokT), то
( р > = -4т- VШЖ [ х е-* их.
у* J
т скольку интеграл по х равен единице *, то окончательно полу-
аем
A9.7)
или для среднего значения скорости
(v) =/8А77(шпо). A9.8)
Для среднего значения квадрата импульса следует написать
ео
( р2 J = Г р2 15?? e-
J BnmQkTf12
Если представить этот интеграл в виде
Bnm0kTK/2
/74e-
то, сравнивая его с формулой, приведенной в приложении 2, и учи-
учитывая, что подынтегральная функция четная, так что ин играл
от 0 до оо равен половине интеграла от —оо до +оо, м.>же\'. запи-
записать
<^2>= AJL4T -Г V*BmokT)W=3mot/ . A9.9)
Этот результат еще проше получить следующим образом.
Так как
¦во оо оо оо ео
f хеГх dx = — f х d(e"x) = — х ё~х I + f е~^ d*= 0 -j- ( — е""') I = 1.
0 0 0 0 0
57
то, используя соотношение A7.2), по которому <рх2> =
аналогичные ему для <ру2> и <pz2>, сразу приходим к A9.9).
Сопоставляя A9.5), A9.7), A9.9), видим, что можно говорить
¦о трех характерных средних значениях импульса и соответствующих
ям значениях скорости:
наиболее вероятном
1,41 УщкТ, va^ 1,41 VkT/mQ
среднем
и среднем квадратичном
=y 3mQkT ж 1,73Упг$Т, vk^ 1,73
Плотность вероятности для модуля импульса удобно использо-
использовать при решении одной из очень часто встречающихся задач: най-
найти вероятность того, что у частицы величина импульса превышает
Ро, или, другими словами, энергия превышает ео, где ео=
= Ро2/Bто).
Так, например, для того чтобы протекала реакция ядерного
«синтеза, при которой два ядра атомов тяжелого водорода слива-
сливаются, образуя ядро атома гелия, атомы водорода должны иметь
достаточно большую энергию. Действительно, слияние возможно
лишь после сближения на расстояние порядка размеров ядра ге-
гелия, т. е. на расстояние порядка 10~10 м. При учете так называемо-
называемого туннельного эффекта оказывается достаточным сближение до
10~9 м. Из-за кулоновских сил отталкивания такое сближение воз-
возможно лишь для ядер, обладающих достаточно большой кинети-
кинетической энергией. Поскольку потенциальная энергия двух ядер
равна
где е — заряд ядра атома водорода (положительный заряд, равный
заряду электрона), a r~10~9 м — расстояние наибольшего сбли-
сближения, то начальная кинетическая энергия, которая при сближе-
сближении переходит в потенциальную, должна быть не меньше чем
2-10~15 Дж. Если выяснить, какова вероятность того, что энерхия
частицы превышает эту величину, то можно затем оценить, на-
насколько интенсивно при данной температуре водородной плазмы
будет проходить реакция синтеза (см. задачу 1 в конце главы).
Другой пример можно взять из области физики газового раз-
разряда. Для того чтобы существовала устойчивая плазма, находя-
находящиеся в ней электроны должны обладать энергией, достаточной
для ионизации нейтральных атомов и превращения их в ионы и
новые свободные электроны. Таким путем компенсируется убыль
электронов за счет их рекомбинации. Если энергия ионизации
равна еи, то возникает вопрос о том, какова вероятность того, что
58
у электрона энергия будет больше, чем еи (см. задачу 2), или им-
импульс больше, чем Ро = У 2/гг0еи.
Вероятность соответствующего события определяется интегра-
интегралом
оо оо
W= Г wndp= [
J p i
Ро Ро
Если ввести переменную лг = /7/~|/2#го?7\ то
оо
*2йх= 2— \
Ул J
Ук } У
pQ/Y2mokT po/Y2mokT
Интегрированием по частям получим
У2тфТ
po/Y2mokT
UIEI A9.10)
где Ф — функция ошибок, определенная соотношением A3.1).
Если аргумент функции ошибок много больше единицы C или бо-
более), то, как следует из A3.4), можно оставить только первое сла-
слагаемое, т. е.
A9.11)
§ 20. Функция распределения
Знание плотности вероятности Максвелла позволяет находить
среднее число частиц, обладающих определенными значениями
импульса, скорости или энергии. Пусть, например, в сосуде вы
бран элемент объема dx и нас интересует, каково среднее число
находящихся в нем молекул с импульсами из элемента объема в
импульсном пространстве dQ. Если концентрация молекул /г, то
среднее число их в объеме dt есть nd%. Поскольку вероятность то-
того, что импульс молекулы принадлежит dQ, равна ^pdQ, то
среднее число молекул из объема dt, обладающих данным значе-
значением импульса, получается умножением их числа на соответству-
соответствующую вероятность, т. е.
dN--= ndx-WpdQ. B0.1)
59
В статистике функцией распределения принято называть такую
функцию f, которая, будучи умножена на элемент объема dx
е обычном пространстве {dx=dxdydz) и на элемент объема dQ
е пространстве импульсов (dQ=dpxdpvdpz), дает среднее число
частиц, находящихся в dx и обладающих импульсом из dQ, т. е.
dAf=/dtd2. B0.2)
Из сравнения B0.1) и B0.2) видно, что для идеального газа,
находящегося в сосуде при отсутствии внешних силовых полей,
функция распределения равна произведению концентрации на
плотность вероятности значений импульсов: f=nwv. Таким обра-»
зом, в случае максвелловского распределения
dQ = п- e~pVBm° г> dtdQ. B0.3)
Brcm0kTf/2
§ 21. Поток частиц.
Термоэлектронная эмиссия
Для решения целого ряда практических и теоретических вопро-
вопросов важно уметь рассчитывать так называемую плотность по-
потока частиц. Поясним смысл этой величины. Рассмотрим со-
сосуд, содержащий идеальный газ, в боковой стенке которого проде-
проделано малое отверстие площади ds (рис. 3.6). Через отверстие про-
Рис. 3.6
a) s)
Рис. 3.7
исходит утечка газа. Потоком частиц d/ называют число частиц,
пересекающих эту площадку, т. е. вытекающих из сосуда, в еди-
единицу времени. Под плотностью потока / понимают отношение пото-
потока к площади или поток через единичную площадку: j=dJ/ds.
Конечно, не обязательно рассматривать истечение газа из со-
сосуда. Величину потока можно относить к произвольной элементар-
элементарной площадке ds, мысленно выбранной внутри сосуда. На рис. 3.6
показана такая площадка, и вектором п°, имеющим единичную
длину, отмечено направление нормали к ней. Обычно говорят о
векторе элементарной площадки ds, подразумевая, что модуль это*
го вектора равен ds, а направление совпадает с нормалью к пло*
щадке.
60
Предположим вначале, что вместо беспорядочного хаотическо-
хаотического движения частицы идеального газа совершают упорядоченное
движение со скоростью v (импульсом p=mov). Выберем (рис.
3.7, а) элементарную площадку, перпендикулярную направлению
движения частиг, »ак, чтобы вектор ds был параллелен v, и рас-
рассчитаем поток п/. За время dt частицы проходят путь, равный
dl=vdt. Поэтому, если построить прямоугольный цилиндр, опира-
опирающийся на основание ds и имеющий высоту d/, то за dt все содер-
содержащиеся в н-м частицы пересекут основание. Если п — концентра-
концентрация частиц .-* бесконечно малом цилиндре, объем которого равен
dx=ds-dl = ds-V'<it>
то за время At через основание пройдет ndx=nvdsdt частиц. Отсю-
Отсюда по определению потока следует
H nvds, B1.1)
dJ nvds,
d t
а для плотности потока
j = ~ = nv. B1.2)
ds
Посмотрим, как изменятся формулы B1.1) и B1.2), если нор-
нормаль к площадке не совпадает с направлением движения частиц.
На рис. 3.7, б показана площадка ds, у которой нормаль составля-
составляет угол а с направлением скорости v. Проекция площадки на плос-
плоскость, перпендикулярную направлению движения, как это видно из
рис. 3.7, б, равна dsn=dscos a.
Число частиц, пересекающих ds и dsn за время dt, одно и то же,
так что, используя полученный выше результат, для потока d/ че-
через ds можно написать
dJ=nvdsn=nvcosads. B1.3)
В векторном виде последнее уравнение выглядит следующим об-
образом:
d/=/ivds, B1.4)
где учтено, что скалярное произведение векторов v и ds равно
vds=udscos а. Введем теперь понятие о векторе плотности
потока как о векторе, модуль которого равен плотности потока
частиц, а направление совпадает с направлением их движения, т. е.
J=nv. B1.5)
Тогда соотношение B1.4) записывается в виде
d/=jds. B1.6)
Формулу B1.3), непосредственно вытекающую из B1.5) и
B1.6),
d7=jds=/&vds =nvcosads
61
можно трактовать несколько иначе, чем это делалось выше. Если
обозначить через /п проекцию потока на направление нормали к
площадке ds, то, поскольку /n=/cos a=m;cos a, получаем
d/ =Jn ds = nv co»s a ds=nvn ds,
где vn — проекция скорости движения частиц на нормаль к ds..
Величина \п называется нормальной составляющей потока к пло-
площадке ds.
Перейдем теперь к случаю идеального газа, в котором имеют-
имеются частицы, движущиеся во всевозможных направлениях. Опреде-
Определение плотности потока может быть сведено к только что изложен-
изложенному, если ввести понятие об элементарной плотности потока dj.
Рассмотрим только те частицы газа, импульс которых принадле-
принадлежит элементу пространства импульсов dfi, т. е. частицы с практи-
практически одним и тем же значением импульса (скорости). Число та-
таких частиц в единице объема выражается через функцию распре-
распределения следующим образом:
Тогда плотность их потока по B1.5) определится соотношением
= {p/mQ)nwpdQ. B1.7)
Таким образом, элементарной плотностью потока dj частиц, об-
обладающих импульсом р, называется вектор, направление которого
совпадает с р, а величина равна числу частиц с импульсом из dQ,
пересекающих в единицу времени единичную площадку, перпенди-
перпендикулярную направлению их движения, т. е. вектор, определяемый
формулой B1.7).
В случае, когда распределение по импульсам оказывается макс-
велловским, для элементарной плотности потока получаем
dj = -5 - e-^2/Bmofer) dg. B1.8)
Щ {2nm0kTf/2
Поток частиц с импульсом из dQ через некоторую произволь-
произвольную площадку ds по B1.6) равен
nwn dQ nw dQ
p ds =— pnds,
p
m0 /тг0
где pn — составляющая импульса, нормальная к площадке.
Соотношение B1.8) позволяет рассчитывать плотность потока
частиц в различных конкретных случаях. Рассмотрим, например,,
электронный газ в полупроводнике. В первом приближении можно-
не учитывать взаимодействие электронов между собой и считать-
их идеальным газом, который в равновесном состоянии подчиняет-
подчиняется распределению Максвелла. Очевидно, что результирующая
плотность потока равна сумме элементарных плотностей потоков;
B1.8) для всех возможных значений импульса, т. е.
62
i =
B1.9)
где интеграл берется по всему импульсному пространству.
Выберем произвольную площадку и направим ось z декартовой
системы координат перпендикулярно этой площадке. Пусть она
обладает единичной площадью, тогда 2-компонента плотности по-
потока численно равна числу частиц, пересекающих площадку в еди-
единицу времени. Если электронный газ находится в равновесии, так
что распределение по импульсахМ максвелловское, то
- оо + оо 4- оо
Щ ,) J J
-оо —оо —оо
Bnm0kTf/2
Видно, что результат оказывается равным нулю, поскольку подын-
подынтегральная функция нечетна по рг, т. е. число частиц с данным им-
импульсом, пересекающих площадку слева направо, равно числу час-
частиц, пересекающих ее справа налево.
Другой результат получится, если интересоваться потоком элек-
электронов, пересекающих площадку слева направо, т. е. обладающих
положительным значением z-компоненты импульса. Интегрирова-
Интегрирование теперь ведется только по положительным значениям рг и по
всем (положительным и отрицательным) значениям рх и ру. Пред-
Представляя выражение для плотности потока в виде
4- оо
«о J J .'
О
BnmQkTf/2
BnmQkT)]/2
p2
p2y/BmQkT)
и учитывая, что интегралы по ру и рх согласно условию нормиров-
нормировки равны единице, можно написать
Последний интеграл просто вычисляется, если сделать замену
переменной y = pz2/BmokT). Действительно,
Щ 2 У ) 4
SkT
TtfTlQ
B1.
10)
63
Вспомним, что по A9.8) корень представляет собой среднюю ско-
скорость движения электронов, так что окончательно
jz=nvj4. B1.11)
Отметим, что формула B1.11), если не конкретизировать зна-
значение средней скорости, вытекает только из свойства изотропности
функции распределения. Действительно, можно написать
/,="</> с«в>+,
щ
где 9 — угол между направлением импульса и осью z, г знак плюс
означает, что значение функции в угловых скобках равно рг при рг
положительных и нулю при рг отрицательных. В случае изотропной
функции распределения, когда все направления одинаково вероят-
вероятны независимо от значения модуля импульса,
<СС«6>+,
т. е. среднее равно произведению среднего значения модуля им-
импульса на среднее значение функции, которая равна cos 6, когда
косинус положителен, и нулю, когда он отрицателен. Поскольку
полный телесный угол равен 4я и
2* Ti/2 %/2
Г co60sin6d8=— 2я I
\
то <cos6>+=rt/Djt) = 1/4 и, следовательно,
Если распределен,^ максвелловское, то справедлива формула
A9.8) для vc и поэтому снова получается B1.10).
Рассмотрим теперь явление термоэлектронной эмис-
эмиссии, которое состоит в том, что из нагретого до высокой темпера-
температуры металла (или в случае специальных катодов — из полупро-
полупроводника) вылетают электроны. Этот эффект качественно объяс-
объясняется так: в металле или полупроводнике всегда имеется некото-
некоторое число электронов со столь большой кинетической энергией,
что они оказываются в состоянии преодолеть силы, удерживающие
их внутри катода. Основной характеристикой катода, определя-
определяющей термоэлектронную эмиссию, является величина, носящая на-
название работы выхода. Последняя равна работе, которую нужно
совершить, чтобы вывести электрон из катода наружу. Не останав-
останавливаясь на вопросе о том, чем определяется работа выхода А, мы
можем считать ее известной из эксперимента.
Предположим, что ось z перпендикулярна плоской поверхности
катода. Для выхода электрона из плоского катода существенно
лишь движение вдоль оси z. Отсюда следует, что только те элек-
электроны покинут катод, у которых кинетическая энергия движения
64
вдоль оси z, т. е. pz2/Bm0), больше работы выхода А. Таким обра-
образом, через площадку ds на поверхности катода выйдут те электро-
электроны, которые движутся по направлению к поверхности (положитель-
(положительное направление оси z) и у которых компонента импульса pz боль-
большем, чем
рг0=У2щА. B1.12)
Поток этих электронов получим, проводя интегрирование по по-
положительным значениям импульса от р*о до оо, т. е.
J Bnm0kTI/2 то
Та же замена переменной, что и в предыдущем случае, приводит
к результату
f. ОО 2
Для плотности потока электронов с катода, т. е. для потока
с единицы поверхности, при учете B1.12) получаем
B1.13)
Выведенная ранее формула B1.11) для плотности потока элек-
электронов, не вылетающих из катода, есть частный случай формулы
B1.13) при Л = 0.
Плотность потока электронов просто связана с плотностью
электрического тока. Действительно, каждый электрон
обладает зарядом —е, и поэтому, когда через единичную площад-
площадку в единицу времени проходит / электронов, то это означает, что
ее пересекает заряд —ej, а следовательно, ток через единичную
площадку (т. е. плотность тока) определяется соотношением
Плотность тока следует считать вектором, который для электро-
электронов, обладающих отрицательным зарядом, направлен в сторону,
обратную их движению, т. е. против направления плотности потока:
i=-ej. B1.14)
Из B1.14) и B1.13) следует выражение для плотности тока
термоэлектронной эмиссии
/,= —ет>с_ 2-апкг). B1.15)
4
Последнее уравнение, показывающее зависимость тока термоэлек-
термоэлектронной эмиссии от свойств катода (п — концентрация электронов,
3—434 65
А — работа выхода) и температуры, до которой он нагрет, носит
название формулы Ричардсона [vc определяется формулой
B1.10)]. В общих чертах она хорошо описывает явление термо-
термоэлектронной эмиссии, хотя, строго говоря, не вполне точна, так как
недостаточно подробно учитывает физические свойства катодов. В
случае металлов отступления в основном связаны с тем, что в них
электроны подчиняются не максвелловскому распределению по им-
импульсам, а другому, о котором говорится в гл. 10. Впрочем, от-
отклонения, о которых только что упоминалось, носят второстепен-
второстепенный характер, так как основным является экспоненциальный
множитель, описывающий быстрое изменение тока термоэлектрон-
термоэлектронной эмиссии в функции от температуры.
При экспериментальной проверке формулы Ричардсона необ-
необходимо учитывать, что работа выхода зависит не только от свойств
материала катода, но и от состояния его поверхности. Увеличение
температуры может приводить к изменению работы выхода, и ес-
если такой эффект имеет место, то он затрудняет сравнение экспе-
экспериментальных данных с формулой B1.15).
§ 22. Экспериментальная проверка
распределения Максвелла
Экспериментальная проверка распределения Максвелла про-
проводилась в целом ряде работ. Чаще всего ссылаются на опыт, по-
поставленный Штерном A920). Экспериментальная установка, ис-
использованная в этом опыте, схематически изображена на рис. 3.8
(вид сверху). Все устройство располага-
располагается в вакуумированном объеме. В цен-
.тре помещена платиновая нить, покры-
покрытая слоем серебра. Нить нагревается то-
током до температуры, при которой сереб-
серебро начинает испаряться и которая в даль-
дальнейшем поддерживается строго постоян-
постоянной. Часть испарившихся атомов проле-
пролетает сквозь щель, имеющуюся в первом
цилиндре, окружающем нить, и устрем-
устремляется ко второму цилиндру. Если ци-
Рис. 3.8 линдры неподвижны, все атомы, прошед-
прошедшие сквозь щель, оседают на втором ох-
охлаждаемом цилиндре, образуя четкое изображение щели. Однако
в эксперименте оба цилиндра вращаются, и поэтому за то время,
в течение которого атом серебра, прошедший сквозь щель, летит
до внешнего цилиндра, последний успевает повернуться, так что
атом оседает в некоторой точке х, находящейся не прямо против
щели. Координата х зависит от времени полета, т. е. от скорости
атома серебра. Если обозначить импульс атома р, расстояние от
внутреннего цилиндра до внешнего d, массу атома т0, то время,
полета At = dmo/p. За это время внешний цилиндр повернется на
угол Аф, причем Дф = соД/, где ш — угловая скорость вращения ци-
66
линдров. Координата х связана с углом поворота Дер и радиусом
внешнего цилиндра R. Если она отсчитывается от точки, лежащей
напротив щели, то х=ЯАц>. Таким образом, атом серебра, обладаю-
обладающий импульсом р, попадет в точку с координатой х, где
x=Rk<? = Ru>M=R<udmQ/p. B2.1)
Если испаряющиеся атомы подчиняются распределению Макс-
Максвелла, то поток атомов, проходящих сквозь щель и обладающих
импульсом в интервале от р до p+dp, определяется формулой
J = С ? e-PVVmokT) dA B2.2)
Bят0кТK/2
которая вытекает из B1.8), если учесть цилиндрическую симмет-
симметрию задачи; С — некоторая постоянная, зависящая от параметров
установки (диаметра нити, размера щели, расстояния от нити до
щели и т. п.). Используя B2.1) при переходе от значений импуль-
импульса р к координате х, получим из B2.2) для скорости оседания ато-
атомов серебра в интервале dx следующее выражение:
d^ I J\ = C l ( R(»dm0 Y* e-{R<*dm0/x)>/BkTm0) 6x
dt [ ' Bnm0kTf2 \ x j x
B2.3)
Формула B2.3) определяет распределение атомов, осевших на
внешнем цилиндре, если ширина пропускающей щели Д очень ма-
мала, а именно должно быть
д2
2kTm0
Действительно, параметр б, имеющий размерность длины, харак-
характеризует форму кривой распределения, и, в частности, можно по-
показать, что максимум этой кривой располагается при х = б/4. Если
для оценки принять, что /? = 12 см, d = 8 см, число оборотов в секун-
секунду 400, а температура порядка 1000 К, то окажется, что 6^6,6 мм.
Результаты опыта в пределах точности, которую он позволял
получить, согласовывались с распределением B2.3), т. е. подтвер-
подтверждали распределение Максвелла. Опыт повторялся рядом иссле-
исследователей в различных вариантах, принципиально близких к опыту
Штерна, с использованием и других атомов, в частности висмута.
Примером другой области, в которой экспериментально уста-
устанавливается максвелловское распределение, являются зондовые
измерения в плазме газового разряда. Плазма представляет со-
собой газ, в котором некоторая часть атомов ионизована, так что на-
наряду с нейтральными атомами (или молекулами) имеется опреде-
определенное количество электронов и положительно заряженных ионов.
Б обычных условиях существования газоразрядной плазмы, когда
протекает электрический ток, она является неравновесной систе-
3* 67
мой. Однако часто условия таковы, что функции распределения
электронов и ионов в плазме, не говоря уже о функции распреде-
распределения нейтральных атомов, близки к максвелловским. Более под-
подробно вопрос об отклонении функции распределения от равновес-
равновесной рассмотрен в гл. 13.
Для изучения плазмы используют зонды — небольшие электро-
электроды, помещенные в исследуемую область. Зонды через прибор, из-
измеряющий электрический ток, и регулируемый источник постоян-
постоянного напряжения (рис. 3.9) подключе-
подключены к электроду, потенциал которого
условно принимается за ноль. Изме-
Изменяя напряжение источника, снимают
зависимость тока на зонд, регистриру-
регистрируемого токовым прибором, от напряже-
напряжения источника U, т. е. от потенциала
зонда относительно опорного электро-
электрода.
Если зонд помещен в плазму и по-
потенциал его отличается от потенциала
Рис. Зл* плазмы в этой области, то за счет пе-
перераспределения электронов и ионов
вокруг зонда образуется облако пространственного заряда, экра-
экранирующего его от остальной плазмы. Пусть, например, зонд имеет
отрицательный потенциал, тогда он отталкивает электроны и при-
притягивает положительно заряженные ионы, так что вокруг него
образуется облако положительного заряда. Вблизи зонда условия
в плазме искажаются, но плазма остается невозмущенной там, где
пространственного заряда нет. Ширина области пространственного
заряда зависит от концентрации электронов и ионов и при неболь-
небольших давлениях (менее 1 мм рт. ст.) обычно оказывается настолько
малой, что электроны проходят эту область, не испытывая столкно-
столкновений. В этих условиях ток на зонд тесно связан с потоком элек-
электронов и ионов, поступающих на внешнюю границу слоя объемного
заряда. В случае плоского зонда, т. е. электрода в форме плоской
площадки, внешняя граница слоя пространственного заряда при-
приближенно тоже плоская и имеет примерно ту же площадь s, что и
зонд.
Зондовая характеристика, т. е. зависимость силы тока на зонде
от приложенного к нему потенциала, особенно проста при отрица-
отрицательных потенциалах зонда относительно исследуемой области.
В этом случае ионы притягиваются, а электроны отталкиваются,
так что только те электроны попадают на зонд, кинетическая энер-
энергия которых достаточна для преодоления потенциального барьера:
A=-e{U-U0)9 B2 А)
где U — потенциал зонда, Uo — равновесный потенциал плазмы.
Сказанное означает, что ток электронов на зонд может быть под-
подсчитан по формуле B1.15), в которой работа выхода положена
равной значению, приведенному в B2.4):
68
Здесь п — плотность электронов в плазме, Тэ — их температура,
0с.э — средняя скорость электронов. Ионный ток не превышает тока
ионов на внешнюю границу области объемного заряда, т. е.
/u=es(nvcj4). B2.5)
Из последнего выражения видно, что при U, близких к Uq, ионный
ток меньше электронного, так как средняя скорость электронов
0с.э много больше средней скорости ионов. Отношение этих скоро-
скоростей при одинаковой температуре электронов и ионов равно кор-
корню квадратному из отношения их масс:
При атомной массе иона порядка 20—50 а.е.м. ионный ток в
50—60 раз меньше электронного.
Если полностью пренебречь ионным током, то ток на зонд
Jt/Поэ
B2.6)
При обработке зондовых характеристик принято строить за-
зависимость логарифма тока на зонд от его потенциала. Типичный
вид экспериментально снятой зависимости представлен на рис. ЗЛО.
Из B2.6) следует, что
B2.7)
U
Таким образом, логарифм тока есть линейная функция потенциала
и наклон прямой определяется температу-
температурой электронов (тангенс угла наклона ра-
равен e/kT3). По мере увеличения потенциала
зонда разность U—Uq уменьшается (напол-
(наполним, что U<Uq). Потенциальный барьер
тоже уменьшается, и электрический ток на
зонд растет. При достижении условия U=
= ?/о и дальнейшем увеличении потенциала
рост электронного юка замедляется, так
как все электроны, попадающие на внеш-
внешнюю границу области объемного заряда,
притягиваются к зонду. Рост тока продол-
продолжается лишь вследствие увеличения эффек-
эффективной площади области пространственного заряда при росте U:
f9=envC9sm/4. B2.8)
На рис. ЗЛО видно, каким образом по излому на зондовой харак-
характеристике можно найти потенциал плазмы Uq. Если считать, что
в точке излома для плоского зонда 5Эфф равна площади зонда s, то
69
Рис. ЗЛО
по B2.8) можно найти концентрацию электронов. При очень боль-
больших отрицательных потенциалах электронный ток на зонд стано-
становится меньше ионного, т. е. ток на зонд меняет знак.
Из изложенного выше ясно, что наличие линейного участка на
зависимости логарифма зондового тока от его потенциала свиде-
свидетельствует о максвелловском распределении электронов по скоро-
скоростям. Метод снятия зондовых характеристик является одним из
распространенных способов исследования плазмы газового разряда.
С помощью зондовых характеристик было показано, что в разря-
разряде могут реализовываться условия, при которых электроны рас-
распределены по закону Максвелла, но с температурой, отличной от
температуры нейтральных атомов и ионов. Такая плазма получила
название неизотермической. При обработке эксперимен-
экспериментальных ч^ндовых характеристик неизотермической плазмы тем-
температура Гэ, определенная по наклону зондовой характеристики,
оказывается выше, чем температура газа, измеренная другим спо-
способом.
Таким образом, распределение Максвелла подтверждено экспе-
экспериментально (з опытах с молекулярными пучками) и получило
широкое применение в различных прикладных вопросах (при об-
обработке зондовыл характеристик плазмы, расчете тока в некото-
некоторых полупроводниковых приборах и т. п.).
Задачи к главе 3
1. Предположим, что для поддержания непрерывной реакции термоядерного
синтеза (соединения двух ядер тяжелого водорода в ядро гелия) не менее
чем y=0,1 % от всех ядер тяжелого водорода должны обладать энергией,
превышающей <!Г0=104 эВ. Какова температура водородной плазмы, при
которой возможна самоподдерживающаяся реакция?
Решение. Если искомая температура Т удовлетворяет неравенству <§Г0> kT,
то вероятность того, что ядро дейтерия (тяжелого водорода) имеет энергию,
большую <??о, определяется формулой A9.11), т. е.
Y 2 р0 —pbBmokT) 2
100 ул
Логарифмируя, найдем
т. е.
Это уравнение можно решать последовательными приближениями, положив,
например, в нулевом приближении 3/г ЬТо=&о. В первом приближении
70
во втором
г2-—•
*| ш [—-)- In | -±r) + ~ In I -^-)j
— I
Г\ V*l "Л ШОУ '' 2
и т. д. При y=0,1%.
т i-j i-t i rvy tr •?¦* 111 П7 R* T П Q.I 07 VC
Хотя температура Го не удовлетворяет исходному неравенству, но для Гг оно
справедливо, так что искомая температура равна ~ Гг.
2. Измерения функции распределения электронов в плазме газового разряда
в водороде показали, что она максвеллов екая с температурой электронов
Т = 20 000 К. Какая доля электронов способна при этом ионизовывать
нейтральные атомы водорода, энергия ионизации которых <В% = 13,5 эВ?
Решение. По формуле, использованной в предыдущей задаче,
100 >'J V kT
Поскольку #*/6Г«8, то у»0,1%.
3. При какой температуре катода следуе-i ожидать заметного (i«l мА/см2)
тока термоэлектронной эмиссии из вольфрамового (Л =4,5 эВ) и оксидно-
оксидного (Л = 1,8 эВ) катодов? Концентрация электронов в металле п— 1022-т-
-f-1023 см~3, а в полупроводнике п— 1018-М019 см~3.
Решение. Из формулы Ричардсона, которую для оценки можно применить
как к полупроводникам, так и к металлам, после логарифмирования следует
kT
т.е. Т.
( envc \
;1пЫ
Поскольку vc = VSkTI(nme) зависит от температуры, то это уравнение решаем
последовательными приближениями:
о-
Для вольфрама Тх ^ 1700 К=1400°С. Для оксидного катода Тх ^ 1000 К=700°С.
4. Найти скорость утечки атмосферы и оценить время, за которое атмосфера
могла бы покинуть Землю. При решении задачи атмосферу Земли при-
приближенно рассматривать как однородный слой с некоторой эффективной
толщиной НЭфф. В следующей главе показано, что для Яэфф справедливо
такое выражение: ЯЭфф = /гГ/(т0^). При расчетах принять Т=300 /С>
? — 10 м/с2 (ускорение свободного падения), то=5-1О-26 кг — масса мо-
молекулы азота (кислорода).
Решение. Поскольку молекула может покинуть Землю, когда ее скорость пре-
превышает вторую космическую vo=\l км/с, то плотность потока утечки по B1.13)
равна
_ ПУ -l
j== 4 e
f 3-1019.4-102
*0 / » — • 4 ~"
: 3-10-293 м-2с-1.
71
Полный поток равен
где R — радиус Земли. Поскольку / = ——-—, где #=4я/?2#ЭффЯ— полное
at
число молекул атмосферы, то
т. е.
e
mogvc
имеет смыст времени, характеризующего продолжительность существования ат-
атмосферы. Действительно, предыдущее уравнение для концентрации можно за-
dn n -t/%
писать в виде-—'— ——• Его решение имеет следующую форму: n—Ct
at х
Подстановка числовых значений дает
X = 10319 с .
ГЛАВА 4
РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
§ 23. Неоднородность распределения частиц
в пространстве при наличии потенциальных
силовых полей
До сих пор рассматривалось поведение идеального газа, не под-
подверженного воздействию внешних силовых полей. Не все получен-
полученные результаты оказываются верными в случае, когда такие поля
присутствуют. Из опыта хорошо известно, что при действии внеш-
внешних сил равномерное распределение частиц в пространстве может
нарушаться. Это и не удивительно, так как, например, под дейст-
действием силы тяжести молекулы стремятся опуститься на дно сосуда.
Интенсивное тепловое движение препятствует осаждению, и моле-
молекулы распределяются так, что их концентрация постепенно умень-
уменьшается по мере увеличения высоты.
Задача этой главы состоит в том, чтобы выяснить закон распре-
распределения частиц в пространстве при наличии внешних силовых по-
полей. Хотя в рассматриваемом случае можно было бы ожидать на-
нарушения распределения Максвелла по импульсам, так как не вы-
выполняется условие изотропности пространства, использованное при
его выводе, однако на самом деле распределение Максвелла оста-
остается в силе.
Вопрос о характере распределения молекул в пространстве
удобно начать рассматривать с графиков зависимости потенциаль-
потенциальной энергии молекулы от ее положения. Поскольку практически
72
удобно строить такой график только при изменении одной из ко-
координат, то предполагается, что две другие сохраняют в это время
неизменное значение. Так, например, потенциальная энергия моле-
молекулы в поле силы тяготения вблизи поверхности Земли определя-
определяется уравнением
где g — ускорение свободного падения, a z — высота. Соответству-
Соответствующий график (рис. 4.1) имеет вид прямой. Аналогичный график
может быть построен и для любого друго-
другого поля сил, обладающего потенциальной
энергией.
Если идеальный газ находится в замк-
замкнутом сосуде, из которого молекулы не
могут выйти, то зависимость потенциаль-
потенциальной энергии от координаты при отсутст-
отсутствии внешних сил представляется графи-
графиком, показанным на рис. 4.2. Точки х=
= —а/2 их= +а/2 соответствуют стенкам
сосуда. Внутри сосуда, т.е. при (а/2)>
>х>(—а/2), потенциальная энергия мо-
молекул равна нулю, а вне сосуда, т. е. при \х\>а/2, — бесконечности,
что соответствует бесконечно большой работе, которую нужно со-
совершить, чтобы вынуть молекулу из сосуда через стенку. График
типа рис. 4.2 носит название потенциального ящика.
Рис. 4.1
и
Рис. 4.2
I1
1
2
А
¦
Рис. 4.3
Предположим теперь, что имеются два сосуда, разделенные
стенкой с отверстием. В пределах отверстия мы допустим суще-
существование сил, которые препятствуют поступлению молекул из со-
сосуда 1 в сосуд 2 и способствуют их обратному переходу. Если для
преодоления этих сил и перевода молекулы из первого сосуда во
второй необходимо совершить работу А, то величина потенциаль-
потенциальной энергии в 2 выше, чем в 1> на величину Аги=Л. График по-
потенциальной энергии имеет вид потенциального ящика со ступен-
ступенчатым дном (рис. 4.3; предполагается, что ось х выбрана перпен-
перпендикулярно стенке и проходит через отверстие).
73
В каждом из двух сосудов имеет место максвелловское распре-
распределение молекул по импульсам, соответствующее некоторой тем-
температуре и концентрации. Поскольку сосуды сообщаются, то через
отверстие молекулы из первого сосуда могут проникать во второй
и, наоборот, из второго в первый.
§ 24. Принцип детального равновесия
В рассмотренном в предыдущем параграфе примере равновес-
равновесное состояние характеризуется тем, что уход молекул из одного из
сообщающихся сосудов во второй компенсируется противополож-
противоположным процессом их перехода из второго в первый. Другими слова-
словами, равновесие носит динамический характер, характер постоянно-
постоянного обмена молекулами.
По примеру, предложенному Я. И. Френкелем, такой обмен можно сравнить
с положением, которое существует между двумя городами, например Москвой
и Ленинградом, вследствие постоянных переездов ленинградцев в Москву и моск-
москвичей в Ленинград. Ясно, что о равновесии населения в этих двух городах
можно говорить лишь в том случае, если среднее число переездов из Москвы в
Ленинград уравновешивается средним числом переездов из Ленинграда в Моск-
Москву. Более того, условие следует детализировать. Вряд ли можно говорить о
равновесии, если из Ленинграда выезжают только женщины, а из Москвы —
только мужчины. Даже при равных встречных потоках мужчин и женщин усло-
условия все же нельзя признать равновесными, если из Москвы выезжают только
молодые женщины, а из Ленинграда — пожилые. Следует потребовать, чтобы
возрастной контингент в обоих потоках был в среднем одинаковым.
Таким образом мы приходим к принципу детального
равновесия, который состоит в следующем. В истинном равно-
равновесии каждому потоку можно сопоставить ему противоположный,
так что равновесие имеет место не только в целом, но и детально
по каждой паре противоположных процессов.
В применении к рассматривавшимся выше сообщающимся со-
сосудам принцип детального равновесия позволяет утверждать, что
в равновесии число молекул со значечием энергии из некоторого
интервала de, уходящих из первого сосуда во второй, в среднем
равно числу молекул, поступающих обратно из второго сосуда в
первый и после перехода обладающих энергией из того же интер-
интервала de. Это положение позволяет решить вопрос о распределении
частиц в пространстве при наличии внешних сил, опираясь на рас-
распределение Максвелла.
§ 25. Связь распределения Больцмана
с распределением Максвелла
Пусть отверстие в стенке, разделяющей два сосуда, имеет пло-
площадь ds и ось х перпендикулярна стенке. Тогда по B1.8) число
молекул из интервала импульсов dQ, поступающих из первого со-
сосуда во второй в единицу времени, равно
dsdjx= ^ e-^Bif«^t) dQds, B5.1)
BkTf2
где П\ — концентрация молекул в первом сосуде, Т\ — их темпера-
температура, а рх — компонента импульса, перпендикулярная плоскости
отверстия. .Естественно, предполагается, что компонента импуль-
импульса, во-первых, направлена из сосуда 7 в 2 и, во-вторых, достаточно
велика, чтобы молекула могла преодолеть потенциальный барьер,
который имеется на ее пути. Поскольку во время прохождения от-
отверстия на молекулу действует сила, направленная в сторону от-
отрицательных х, то компонента импульса рх уменьшается, а компо-
компоненты ру и pz не меняются. Если обозначить значение х-компонен-
ты импульса после прохождения отверстия рх', то по закону со-
сохранения энергии должно быть
Рх л. . (РхJ
т. е. кинетическая энергия после перехода становится меньше, так
как увеличивается потенциальная.
По принципу детального равновесия прямой поток должен ком-
компенсироваться обратным, для которого аналогично B5.1) можно
написать
s. B5.3)
Здесь n2 и T2—.концентрация и температура молекул во втором
сосуде, а рг — их импульс, который выбирается в соответствии с
уравнением B5.2), так что после перехода молекулы из одного со-
сосуда в другой ее энергия сохраняет свое значение. Хотя направле-
направление элементарной плотности потока d/V противоположно d/x (от-
(отрицательные я), но для переходов из 2 в 1 противоположно и на-
направление нормали к площадке ds, так что поток, направленный в
первый сосуд, все равно положителен.
Из равенства потоков вытекает, что
B5.4)
При переходе значение компонент ру и рг не меняется, поэтому
все молекулы, у которых у-компонента импульса лежала в интерва-
интервале dpy, после перехода окажутся в интервале dp/, который равен
dpy. To же самое справедливо для dpz. Таким образом,
йру=йр'у> &PZ = dpi B5.5)
75
Учитывая B5.5), уравнение B5.4) можно переписать в виде
__«l__e 2mokTl д I Рх \ П2 2mokT, Л I Рх )
\ 2^0 / Bлт0кТ2K'2 \ 2ш0 )'
B5.6)
Из закона сохранения энергии B5.2) следует, что
так к?ь изменение потенциальной Эх;ергии Деп при переходе из од-
одною сосуда в другой одно и то же для молекул с любым значени-
значением импульса. Это позволяет представить условие B5.6) в виде
П2
или, поскольку ру2—ру'2} pz2=p/29 в форме
Щ.2mQkTi
Подставив в правую часть последнего равенства величину кинети-
кинетической энергии px/2lBm0) из соотношения B5.2), найдем
14
е kT2 e 2mokT2 B5 7)
Уравнение B5.7) должно быть справедливо не при одном оп-
определенном значении модуля импульса, а тождественно для лю-
любых. Но тогда ему можно удовлетворить лишь если температуры
в первом сосуде (Ti) и во втором (Т2) равны, так как только в
этом случае экспоненциальные множители с р2 сокращаются. По-
еле сокращения имеем
Л1 = л2е-^(*г), B5.8)
где T = Ti = T2 — общая для обоих сосудов температура.
Распределение B5.8), связывающее концентрации молекул в
двух сосудах, называется больцмановским. Оно справедливо
для случая любых потенциальных силовых полей, а не только для
того частного, примера, который рассматривался при его выводе.
Чтобы показать это, можно провести следующее рассуждение.
Пусть при перемещении частицы вдоль некоторого направления,
например оси х, потенциальная энергия меняется сложным обра-
76
зом (рис. 4.4). Плавный ход изменения потенциальной энергии
еи(х) можно с любой степенью точности аппроксимировать ступен-
ступенчатой линией, показанной на рис. 4.4 пунктиром, если сделать ве-
величину ступенек достаточно ма-
малой. Рассмотрим ступеньки с но-
номерами 1, 2, 3, соответствующие
положениям частицы л:ь #2, *з.
Любые две соседние ступеньки
укладываются в приведенную вы-
выше модель, и поэтому можно ут-
утверждать, что температура газа в
пределах любой из них одна и та
же, а концентрации яь #2, п$ свя-
связаны соотношениями
Рис. 4.4
где
B5.9)
B5.10)
— разности потенциальных энергий при переходе от одной сту-
ступеньки к другой. Во второе из равенств B5.9) подставим значение
/22, которое следует из первого, тогда
Но по B5.10)
Аеп21 + Аеп32 = еп (х2) - еп
так что
= еп (л:3) -
B5.11)
Таким образом, для ступенек, не находящихся в непосредст-
непосредственном соседстве и не обменивающихся частицами друг с другом,
оказывается также справедливым распределение Больцмана. Рас-
Рассматривая большее число ступенек, можно показать, что имеют
место соотношения типа B5.11) для любых двух из них; так, на-
например,
/2.c='tie п и * • а»
Если взять ступеньку, которой соответствует координата #=0,
и ступеньку с координатой х, то, обозначая концентрации на этих
ступеньках соответственно п@) и п(х), получим
п (х)=п @) е-[?пМ-6и@I/(*Г). B5.12)
Если, наконец, не связывать себя перемещениями только вдоль
оси х, а считать, что рассматриваются две произвольные точки в
пространстве с радиус-векторами r=ri и г=г2, то распределение
Больцмана можно записать в следующем общем виде:
п (г2)=л
B5.13)
77
Таким образом, из принципа детального равновесия и распре-
деления Максвелла для импульсов следует, что при наличии по-
потенциальных силовых полей для равновесия необходимо, чтобы
температура частиц всюду была одинакова, а концентрация изме-
изменялась в соответствии с соотношением B5.13), носящим название
распределения Больцмана.
§ 26. Барометрическая формула
и экспериментальное определение
постоянной Больцмана
С помощью распределения Больцмана легко получить баромет-
барометрическую формулу, описывающую изменение плотности атмосферы
с высотой. Если предположить, что атмосфера находится в равно-
равновесии и, в частности, что ее температура постоянна (на самом деле
это предположение выполняется лишь приближенно), то изменение
концентрации с высотой определяется формулой B5.13). Пусть
высота над уровнем моря обозначена через г, тогда потенциальная
энергия молекулы, обладающей массой т0, в поле тяготения Земли
равна
Обозначив концентрацию при 2=0 через щ, для концентрации на
высоте z можем написать
n{z)=n @) е-««**/<*п. B6.1)
Это соотношение является одним из возможных видов барометри-
барометрической формулы.
Поскольку при постоянной температуре давление газа пропор-
пропорционально его концентрации, то B6.1) эквивалентно следующей
форме барометрического уравнения:
B6.2)
где p(z) —давление на высоте г, р0= 1 атм — давление на уровне
моря.
Иногда формулы B6.1) и B6.2) удобно записывать несколько
иначе, выражая постоянную Больцмана через газовую постоянную
R и постоянную Авогадро jVa k = R/NAy и используя то, что m0NA=
= \i, где [л — молярная масса. Таким путем получаем:
B6.3)
B6.4)
Формулы B6.3) и B6.4) удобнее тем, что в них вместо массы мо-
молекулы входит молярная масса. Отметим, что поскольку атмосфе-
атмосфера представляет собой в основном смесь двух газов — азота N2 и
кислорода О2, то написанные выше формулы должны были бы
применяться к концентрации и парциальному давлению кислорода
и азота отдельно. Поскольку массы молекул N2 и Ог и их молярные
78
массы 0*н, = 0,028 кг/моль, ^о2-=0,032 кг/моль) близки, то часто
пренебрегают этой разницей и пользуются молярной массой воз-
воздуха (|ы = 0,029 кг/моль). В действительности по закону Больцмана
процентный состав атмосферы должен меняться с высотой в сто-
сторону обеднения ее кислородом и обогащения более легким азотом.
Уравнение B6.1) можно записать в виде
п(г) = п{0)е-г/н*ФФ, B6.5)
где #Эфф — эффективная высота:
Л =JL.= *L, B6.6)
ФФ g g
имеющая смысл такого расстояния от поверхности моря, на кото-
котором концентрация молекул, а следовательно, и давление уменьша-
уменьшаются в е раз.
При постоянной плотности атмосферы, равной ее плотности на
уровне моря, высота атмосферы оказалась бы равной #3фф. Дей-
Действительно, когда справедлива барометрическая формула, число
молекул, находящихся над единицей поверхности Земли на высоте
г в слое толщины dz, равно
d N=n (z) d г=п @) е~*/ЯзФФ dz.
Полное число молекул над единицей поверхности определится сум-
суммированием по всем слоям от примыкающего к уровню моря и до
удаленного в бесконечность, т. е.
Если бы атмосфера была однородной, то ее высота получалась бы
делением N на я@), т. е. оказалась бы равной #Эфф.
Как уже упоминалось выше, барометрическая формула лишь
приближенно описывает изменение давления с высотой, так как в
действительности атмосфера не находится в равновесном состоя-
состоянии. Все же эта формула очень важна, так как позволяет провести
ряд полезных оценок и служит основой для других более точных
соотношений, применяемых при определении высоты по давлению
атмосфеоы.
Перрен предложил использовать барометрическую формулу
для экспериментального определения числового значения постоян-
постоянной Больцмана. Поскольку постоянная Больцмана связана с мо-
молярной газовой постоянной, известной из опытов с разреженными
газами, и постоянной Авогадро, то из опыта Перрена получается
и значение постоянной Авогадро.
Идея этого замечательного опыта очень проста. Распределение
Больцмана, а следовательно, и барометрическая формула справед-
справедлива для любых частиц, находящихся в тепловом равновесии с ок-
окружающей средой. Если выбрать частицы, обладающие большой
79
по сравнению с молекулами массой, то по формуле B6.6) эффек-
эффективная высота, обратно пропорциональная массе частиц, окажется
малой. Это дает большие преимущества при проведении опыта.
Во-первых, легче измерить изменение концентрации, если измене-
изменение происходит на относительно небольших расстояниях, а не так,
как в атмосфере, где #эфф~9 км. Во-вторых, легче обеспечить рав-
равновесные условия, в частности постоянство температуры, так как
они должны иметь место в относительно небольшой области
пространства. В опыте Перрена в сосуд с жидкостью насыпался
порошок очень мелких частиц. Частицы можно рассматривать как
крупные молекулы, которые под действием силы тяжести распре-
распределяются по высоте неоднородно в соответствии с барометрической
формулой. С помощью микроскопа подсчитывается число частиц,
находящихся в поле зрения вблизи дна сосуда, а затем на некото-
некоторой высоте от дна. При этом используется то свойство микроско-
микроскопа, что в поле зрения видны лишь частицы, расположенные в уз-
узкой зоне вблизи фокальной плоскости. Отношение полученных чи-
чисел по барометрической формуле равно
где mrg — вес частицы в жидкости, т. е. вес за вычетом выталки-
выталкивающей силы Архимеда. Из написанной формулы следует
Т {n{z)\
Если известны размеры частиц (радиус г) и плотность р вещества,
из которого они состоят, а также плотность р0 жидкости, то
Зная температуру Т жидкости, по экспериментально найденному
значению отношения n@)/n(z) для выбранной высоты z опреде-
определяют k.
Из опыта Перрена для постоянной Больцмана получено значе-
значение А = 1,38 • 10~3 Дж/К, откуда для постоянной Авогадро следует
ЛгА=6,02.1023моль~1.
§ 27. Контактная разность потенциалов
В качестве другого примера использования распределения
Больцмана возьмем теорию контактной разности потенциалов.
В простейшем варианте классической (не квантовой) теории про-
проводников последние рассматриваются как своеобразные сосуды,
содержащие газ электронов. Более точно их следовало бы прини-
принимать за положительно заряженную ионную решетку, между узла-
узлами которой перемещаются электроны, взаимодействующие между
собой и с ионами решетки. В целом кристалл, состоящий из поло-
положительно заряженной решетки и электронов, нейтрален. Класси-
Классическая теория применима, например, к полупроводникам с не слиш-
слишком высокой концентрацией подвижных носителей заряда.
80
Для того чтобы вывести электрон из проводника наружу, нуж-
нужно затратить некоторую работу А, называемую работой выхода
(точнее, внешней работой выхода или электронным сродством).
Расчет работы выхода представляет собой сложную задачу, ре-
решаемую методами квантовой механики. Примем, как это уже де-
делалось при рассмотрении явления термоэлектронной эмиссии, что
для данного конкретного проводника величина А известна из
опыта.
Наличие работы выхода означает, что с энергетической точки
зрения проводник в простейшей модели представляет собой потен-
потенциальный ящик. На рис. 4.5 по оси ординат отложена энергия
1
Рис. 4.5
Рис. 4.6
электрона, а по оси абсцисс —его координата х. Если проводник
простирается от точки с координатой *=0 до точки с координатой
*=а, то потенциальная энергия электрона при этих значениях х
имеет одно значение, а для всех остальных х больше на величину
работы выхода А.
Предположим теперь, что имеются два проводника 1 и 2. Кон-
Концентрацию электронов в одном из них и его работу выхода обозна-
обозначим пх и Аи а соответствующие величины для другого — п2 и А2 Ес-
Если эти проводники находятся на столь большом расстоянии друг от
друга, что можно пренебречь обменом электронов между ними то
энергетическая диаграмма выглядит так, как показано на рис. 4.6.
Действительно, потенциальная энергия электрона, вышедшего из
проводника и находящегося вне его, имеет одно и то же значение
независимо от того, из какого проводника электрон вышел. В связи
с этим верхний край потенциального ящика, соответствующий
уровню потенциальной энергии вне проводника или уровню ваку-
вакуума, одинаков для них обоих. Глубина же потенциального ящика
зависит от работы выхода, и в случае, если Al>A2f потенциальный
ящик, соответствующий первому проводнику, оказывается глубже
следовательно, его дно располагается ниже (рис. 4.6)
Другое положение имеет место, если проводники сведены на-
настолько близко, что необходимо учитывать обмен электронами
Гакои обмен принципиально существует хотя бы из-за эффекта
термоэлектронной эмиссии, по которому из обоих проводников
81
идет электронный ток. Какова же энергетическая диаграмма в
этом случае?
Когда расстояние между проводниками много меньше, чем раз-
размеры самих образцов, можно считать, что они имеют бесконечные
размеры вдоль поверхности контакта, т. е. вдоль осей у и z, и рас-
рассматривать зависимость энергии только от координаты х, нормаль-
нормальной к поверхности контакта. Предположим для определенности,
что концентрация электронов в первом проводнике (azi) меньше,
чем во втором (Агг). Поскольку работа выхода из первого провод-
проводника выше, а концентрация элект-
электронов здесь меньше, то естествен-
естественно, что ток термоэлектронной
р. i -у/^-^-лЛ эмиссии из него меньше. Это не-
ТТ п2 I % посредственно следует из форму-
лы B1.15), примененной к плот-
плотности тока вдоль оси х в первом
и втором проводниках, если
учесть, что их температура оди-
у-,
{ I п1
0 х накова, а следовательно одина-
одинаковы и средние скорости электро-
Рис> 4-7 нов vc.- Поток электронов из вто-
второго проводника в первый превы-
превышает обратный поток, и поэтому первый проводник начинает заря-
заряжаться отрицательно, а второй — положительно. Между проводни-
проводниками возникает разность потенциалов, которая носит название кон-
контактной. Потенциальная энергия электрона в отрицательно за-
заряженном проводнике выше, чем в незаряженном, и поэтому в
процессе зарядки первый потенциальный ящик на энергетической
диаграмме поднимается вверх, а второй опускается вниз. В равно-
равновесном состоянии энергетическая диаграмма приобретает вид, по-
показанный на рис. 4.7. На этой диаграмме края потенциальных ящи-
ящиков находятся на разных уровнях. Разница в положении определя-
определяется дополнительной работой, которую нужно совершить против
появившейся разности потенциалов при перемещении электрона из
второго проводника в первый. Если обозначить электрический по-
потенциал первого проводника фЬ а второго — фг, то, поскольку заряд
электрона равен —е, дополнительная работа
ДЛ=-е(<Р1-Ч>2). B7.1)
Применяя закон распределения Больцмана к диаграмме рис.
4.7, можно выразить контактную разность потенциалов ф!—ф2 че-
через работу выхода и концентрации электронов обоих проводников.
При этом следует учесть, что частичный переход электронов из
второго проводника в первый практически не меняет концентра-
концентрацию, так как число перешедших электронов очень мало по сравне-
сравнению с общим числом электронов в каждом из проводников. Кроме
того, электрическое поле контактной разности потенциалов сосре-
сосредоточено в очень узкой области вблизи контакта. В этой области,
которая здесь не рассматривается, происходит изменение потен-
82
циала и концентрации электронов от значений, соответствующих
одному проводнику, до значений, соответствующих другому.
В глубине второго проводника концентрация, как и до приве-
приведения в контакт, равна я2, а в глубине первого — п\. Из диаграм-
диаграммы видно, что разность потенциальных энергий электрона в пер-
первом и втором проводнике равна
По закону Больцмана,
А^(«1) <^ААЛ)/AГ) B7>2)
Логарифмируя равенство B7.2) и подставляя значение АЛ из
B7.1), найдем
j /_Л1_\ А2 — ^i — g(<pi— у2)
[ ) kT
Отсюда для контактной разности потенциалов получаем
е \ п2 ) е
Таким образом, из классической теории следует, что между
двумя проводниками устанавливается контактная разность потен-
потенциалов, значение которой по закону Больцмана определяется фор-
формулой B7.3), т. е. зависит от работы выхода и концентрации элект-
электронов в обоих проводниках.
При равновесной контактной разности потенциалов ток термо-
термоэлектронной эмиссии из одного проводника в другой равен по ве-
величине обратному току. В этом легко убедиться прямыми вычис-
вычислениями, если использовать равенство B7.3). Действительно, плог-
ность тока из первого проводника во второй по B1.15) равна
B7.4)
так как хотя контактная разность потенциалов помогает переходу
электронов, но это имеет место лишь по отношению к электронам,
попавшим в контактное поле, т. е. уже вышедшим из первого про-
проводника. Плотность обратного тока определяется выражением
/21 = ЮЗЕ*. е-< А,+Ал>/<*г>, B7.5)
так как электронам необходимо преодолеть не только барьер А2>
но и дополнительный электрический барьер АЛ. Если в B7.4) под-
подставить п\ из уравнения B7.2), то получим
.
4 4 '
т. е. оказывается, что ii2=t2i> как это и должно быть.
83
Каково же значение контактной разности потенциалов? Рабо-
Работа выхода имеет значения, лежащие в пределах 0,5—4 эВ, а кон-
концентрация электронов может меняться очень сильно. Так, напри-
например, в очень чистом кремнии при комнатной температуре концент-
концентрация электронов имеет значение, близкое к 1010 см~3. С другой
стороны, используется и кремний с высокой концентрацией элект-
электронов, лежащей в диапазоне 1019—1020 см~3.
Пусть в контакт приведены два полупроводника разной хими-
химической природы, но с примерно равной концентрацией электронов,
тогда, рассчитывая контактную разность
потенциалов по формуле B7.3), легко убе-
убедиться, что основную роль играет второй
член. Поскольку работа выхода имеет зна-
значение порядка нескольких электронвольт,
то такую величину обычно имеет и разность
работ выхода. После деления на заряд элек-
электрона находим, что вклад второго слагае-
слагаемого в контактную разность потенциалов
Рис. 4.8 оказывается величиной порядка одного или
нескольких вольт. В первом слагаемом при
комнатной температуре (Г=300К) kT = 25-10~3 эВ, а следова-
следовательно, kT/e = 25 мВ. Если концентрация в контактирующих полу-
полупроводниках отличается не более чем на один-два порядка, то зна-
значение множителя ln(niln2) не превышает 2,3—4,6. Таким образом,
первое слагаемое порядка 100 мВ, т. е. на порядок меньше, чем
второе.
Совсем другое положение имеет место при контакте двух кус-
кусков полупроводника одной и той же химической природы, но об-
обладающих сильно отличающейся концентрацией электронов, на-
например двух образцов кремния с концентрацией электронов 1О10
и 1018 см~3. Работа выхода из обоих образцов одинакова, и поэто-
поэтому второе слагаемое обращается в ноль. Отношение концентрации
электронов велико A08), и поэтому логарифмический множитель
не мал:
Умножая на kT/e = 25 мВ, получим контактную разность потенциа-
потенциалов, равную 0,45 В.
С помощью формулы B7.3) просто получается закон Воль-
Вольта, утверждающий, что в замкнутой цепи, состоящей из некоторого
количества разнородных полупроводников, сумма контактных раз-
ностей потенциалов равна нулю. На рис. 4.8 изображена цепь, со-
состоящая из трех различных проводников, включенных последова-
последовательно. Для удобства дальнейших рассуждений установим направ-
направление обхода контура, например по часовой стрелке. Пусть ф12
обозначает контактную разность потенциалов на границе первого
и второго проводников, ф23 — на границе второго и третьего и cp3i —
на границе третьего и первого. По B7.3) можно написать:
84
ln(j—* ln
B7.6)
Сумму контактных разностей потенциалов в замкнутой цепи полу-
получаем сложением написанных уравнений:
е
1-(А1-А2+А2-А3+А3-А1).
е
Видно, что член, содержащий работы выхода, обращается в ноль.
Если цепь находится в равновесии, так что температура всех про-
проводников одинакова, то обращается в ноль и сумма остальных
слагаемых:
ln(J!U + in(J!L) + ta^
\ П2 J \ П3 ] \ Щ ] \ П2П3П1 I
Таким образом, сумма контактных разностей потенциалов действи-
действительно равна нулю и очевидно, что это справедливо для цепи, со-
состоящей из любого числа разнородных проводников.
§ 28. Метод самосогласованного поля
В некоторых задачах применение формулы Больцмана затруд-
затруднено тем, что потенциальная энергия, определяющая распределе-
распределение часгиц в пространстве, зависит от их положения. Типичным
примером такого случая является распределение заряженных час-
частиц (электронов и ионов) в газовом разряде. То же самое относит-
относится к распределению электронов в приконтактной области двух про-
проводников, где, как было выяснено в предыдущем параграфе, кон-
контактная разность потенциалов зависит от концентрации электро-
электронов. Подобное затруднение возникает тогда, когда, строго говоря,
пытаются выйти за рамки применимости закона распределения
Больцмана и помимо влияния внешних силовых полей, для кото-
которых распределение было выведено, учитывают поля, создаваемые
самими частицами, т. е. фактически учитывают силы взаимодей-
взаимодействия между ними. Метод учета сил взаимодействия с помощью
распределения Больцмана, который излагается в настоящем пара-
параграфе, носит название метода самосогласованного по-
поля и чаще всего применяется к заряженным частицам, поскольку
для них лучше всего выполняются условия, при которых он спра-
справедлив.
Чтобы более наглядно пояснить суть метода самосогласованно-
самосогласованного поля, целесообразно обратиться к конкретной задаче. В полу-
85
чивших распространение МОП-транзисторах один из электродов,
называемый затвором, устроен следующим образом. На полупро-
полупроводник П (рис. 4.9) наносится тонкий слой окисной пленки О, яв-
являющейся хорошим изолятором, а на нее напыляется металличе-
металлический электрод М. Потенциал затвора относительно полупроводни-
полупроводника можно менять с помощью внешнего источника, причем из-за на-
наличия окисной пленки ток через систему практически не идет.
Пусть, например, мы имеем дело с полупроводником, в котором
концентрация свободных электронов равна щ (так называемый
полупроводник /2-типа). Заряд электронов в нем скомпенсирован
положительным зарядом, связанным с
¦„.¦!?, ;,;у,„л кристаллической решеткой и распреде-
vyyyyyy* yyyyyyyyyayyyyyyy/Zl ленным равномерно. Если для упрощения
1улууа^ >>..-*> >ws,4y\ задачи не касаться сложных явлений, ко-
' п торые могут иметь место на границе по-
полупроводника с окислом и которые обус-
Рис. 4 9 ловлены структурой этой границы, то
следует считать, что концентрация элек-
электронов на границе окисел — полупроводник такая же, какая была
бы на границе металл — полупроводник при отсутствии окисной
пленки.
Предположим, что работа выхода из металла меньше, а кон-
концентрация электронов в нем выше, чем в полупроводнике, тогда
при отсутствии внешнего напряжения слой полупроводника, приле-
прилежащий к контакту, обогащается электронами и заряжается отри-
отрицательно, а соответствующий приконтактный слой металла — по-
положительно. Следует при этом иметь в виду, что изменение кон-
концентрации электронов в приконтактной области происходит путем
обмена через внешнюю цепь, а не через слой окисла.
Из-за большой концентрации электронов в металле перерас-
перераспределение заряда в нем мало сказывается на величине концент-
концентрации, поэтому в полупроводнике на границе с окисной пленкой
ее можно считать равной концентрации электронов в металле п^.
Таким образом, в полупроводнике имеется слой объемного за-
заряда и концентрация электронов в нем плавно изменяется от той,
которая устанавливается на границе, до концентрации, имеющей
место в глубине полупроводника. За счет заряда этого слоя обра-
образуется разность потенциалов, препятствующая дальнейшему пере-
перераспределению электронов. Если между затвором и полупроводни-
полупроводником приложено еще и внешнее напряжение U, то слой объемного
заряда создает такую разность потенциалов, которая достаточна
для компенсации суммы qK+U — контактной разности потенциа-
потенциалов и приложенного внешнего напряжения. Очень существенна
полярность приложенного напряжения, так как в данном примере
при плюсе на металле и минусе на полупроводнике она склады-
складывается с контактной разностью потенциалов, а при обратной поля
ности — вычитается.
Перейдем теперь к выяснению ширины области пространствен-
пространственного заряда и распределения электронов в ней. Поскольку тока
86
через систему нет, то распределение электронов равновесное, т. е.
определяется формулой Больцмана
n = nlee^kTK B8.1)
где п\ — концентрация в глубине полупроводника, причем потен-
потенциал этой области принят за ноль. Как уже отмечалось, написан-
написанная формула не дает решения задачи, поскольку потенциал оста-
остается неизвестной функцией координат. Для его определения необ-
необходимо привлечь законы электростатики (предполагается, что при-
приложенное напряжение постоянно или меняется достаточно
медленно). В электростатике выводится уравнение, связывающее
потенциал с объемной плотностью заряда р. Это уравнение, кото-
которое носит название уравнения Пуассона, имеет вид
V2<p=- —. B8.2)
где е — диэлектрическая проницаемость полупроводника, ео—элек-
ео—электрическая постоянная, а символ Y2<p обозначает
V2?=_^L +_i*L _L JtL B8.3)
Плотность заряда р связана с концентрацией электронов п и
положительным зарядом решетки соотношением
P=—en + env B8.4)
так как —еп — это отрицательный заряд электронов, приходящий-
приходящийся на единицу объема, a еп\— соответствующий положительный
заряд кристаллической решетки. Величина щ—постоянная, так
как заряд решетки распределен в ней однородно и не перераспре-
перераспределяется под действием внешнего поля.
В B8.4) можно подставить концентрацию из B8.1), тогда по-
получим
1). B8.5)
С помощью последнего выражения уравнение Пуассона представ-
представляется в форме
^ -1). B8.6)
Таким образом, если потенциал электрического поля зависит от
электрических зарядов, распределение которых определяется созда-
создаваемым ими полем, то для нахождения потенциала необходимо ре-
решить уравнение самосогласованного поля типа B8.6), а затем с
помощью найденного потенциала по закону Больцмана найти кон-
концентрацию подвижных заряженных частиц (электронов).
В уравнение B8.6) не входит внешнее поле, однако решение
существенно от него зависит. Дело в том, что для однозначного оп-
определения решения в некоторой области пространства необходимо,
чтобы были известны значения потенциала или напряженности
87
электрического поля на границе этой области, т. е. заданы так на-
зываемые граничные условия. Если в рассматриваемом при*
мере с помощью внешнего источника э. д. с. между затвором и по-
полупроводником установлена разность потенциалов U, то граничные
условия можно взять в следующем виде. В невозмущенной (т. е.
достаточно далеко отстоящей от затвора) части полупроводника
потенциал равен нулю, а в части полупроводника, примыкающей
к окисному слою, потенциал практически совпадает с суммой
Фк+f/ (предполагается, что окисный слой достаточно тонок и раз-
разностью потенциалов на нем можно пренебречь).
Уравнение самосогласованного поля нелинейно (искомая вели-
величина входит в аргумент экспоненциальной функции), и поэтому
его решение представляет известные трудности, которые преодоле-
преодолеваются, как правило, применением вычислительных машин. Суще-
Существует, однако, ряд случаев, в которых уравнение достаточно про*
сто решается приближенно. Одним из них является тот, в котором
потенциал ф мал по сравнению с величиной kT/e. При комнатной
температуре сформулированное условие выполняется, если сумма
фк+?/<25 мВ. В этом случае, пользуясь малостью аргумента, це-
целесообразно разложить экспоненциальную функцию в ряд и отста-
отставить первые два члена ряда, т. е. записать
kT
Уравнение B8.6) становится в этом приближении линейным:
~ 1 -L J!L
1 kT *
B8.7)
а поэтому может быть решено известными из математики мето-
методами.
Для выяснения некоторых характерных черт явления, описы-
описываемого уравнением B8.7), рассмотрим более детально случай,
когда задача сводится к одномерной, т. е. когда затвор и полупро-
полупроводник имеют бесконечную плоскую поверхность. Распределение
потенциала зависит лишь от одной координаты х, перпендикуляр-
перпендикулярной плоскости контакта. Уравнение B8.7) записывается в виде
B8-8)
так как производные по у и z обращаются в ноль.
Для дальнейшего удобно ввести обозначение
B8.9)
где параметр б имеет размерность длины и носит название длины
Дебая. Используя длину Дебая, уравнение B8.8) записываем
в виде
88
Общее решение имеет вид
<f=Cle-*t*+C2exl** B8.11)
где С\ и Сг — постоянные числа, значения которых определяются
с помощью граничных условий.
На достаточно большом удалении от затвора (я-^оо) полупро-
полупроводник не возмущен и потенциал равен нулю. Поскольку при
я->оо первое слагаемое в B8.11) стремится к нулю, а второе — к
бесконечности, то необходимо положить (координата контакта
0)
Таким образом, решение уравнения B8.11), удовлетворяющее
граничным условиям, имеет вид
ср=(?/+срк)е-*/'. B8.12)
Характерно, что потенциал экспоненциально убывает по мере уда-
удаления от затвора, так что на расстоянии, равном дебаевской дли-
длине, он уменьшается в е^2,7 раза. Качественно такое же распреде-
распределение встречается и в тех случаях, когда приложенный потенциал
не мал по сравнению с kT/e. Действительно, если измерять потен-
потенциал в единицах kT/е, т. е. ввести безразмерный потенциал г|) =
= еср/ (kT), то уравнение самосогласованного поля приведется к виду
--1), или V2<1>= — (e*-l), B8.13)
т. е. в качестве параметра, характеризующего распределение потен-
потенциала, снова входит дебаевская длина. Хотя закон изменения по-
потенциала теперь получается другой (не экспоненциальный), но из
физических соображений ясно, что и в этом случае тоже происхо-
происходит экранирование подвижными зарядами, причем на расстоянии
порядка длины Дебая.
В § 22 при обсуждении зондовых характеристик оговаривалось,
что толщина слоя объемного заряда около зонда должна быть ма-
мала, чтобы электроны могли проходить его без столкновений. Из
изложенного выше следует, что толщина этого слоя имеет порядок
дебаевской длины, так что ее легко оценить, если известны кон-
концентрация заряженных частиц и температура газа (см. задачу 3 к
настоящей главе).
Отметим, что выражение для электронного тока на зонд, выве-
выведенное ранее, можно получить, рассуждая иначе и используя рас-
распределение Больцмана. В соответствии с больцмановским рас-
распределением концентрация электронов непосредственно около зон-
зонда равна
Те из них, которые движутся по направлению к зонду, попадут на
него, так что плотность тока
89
Этот пример иллюстрирует ту тесную связь, которая имеется меж-
между распределениями Максвелла и Больцмана.
В заключение необходимо сделать несколько замечаний отно-
относительно применимости метода самосогласованного поля. Хотя
уравнение B8.13) может использоваться при гораздо больших по-
потенциалах, чем B8.8), но следует иметь в виду, что имеется другое
ограничение на его применимость. Используя понятие плотности
заряда в уравнении Пуассона, мы подразумеваем, что либо в объ-
объемах, в которых потенциал еще относительно мало меняется, со-
содержится много заряженных частиц, либо, если это условие нару-
нарушено, нужно брать среднее по времени значение плотности заряда.
В первом случае, оценивая объем величиной б3, должны на-
написать
я83»1.
Если т дставить сюда значение дебаевской длины из B8.9), то по-
получим, что уравнение применимо при
п «(еео?7>2K. B8.14)
Так, например, для комнатной температуры (Г=300 К) в полу-
полупроводнике с е= 10 это дает п<С Ю15 см~3.
Во втором случае, когда условие B8.14) нарушено, под фи/i
можно понимать средние по времени величины. В слабых полях
по B8.5)
Р=гя1A-е^/(«г))~-е2/11-^-, B8.15)
kT
т. е. плотность заряда линейно связана с потенциалом и, следова-
следовательно, средняя по времени концентрация определяется через
средний по времени потенциал тем же условием B8.15). Поэтому
уравнение B8.8) можно считать справедливым для средних зна-
значений потенциала. В сильных же полях, поскольку среднее значе-
значение от экспоненты при нарушении условия B8.14) не совпадает с
ее значением, вычисленным для среднего потенциала:
нельзя пользоваться соотношением B8.5), так что уравнение
B8.13) не может применяться к вычислению среднего по времени
потенциала.
Близкие уравнения и выводы можно получить и для газов. Не-
Некоторое отличие связано с тем, что в газах подвижны как отри-
отрицательные заряды (электроны), так и положительные (ионы).
Мы, однако, на этом останавливаться не будем.
Задачи к главе 4
1. На уровне Земли атмосфера состоит из 78% азота и 22% кислорода (по
объему). Каково процентное содержание этих газов на высоте, равной
эффективной толщине атмосферы, если можно считать, что атмосфера на-
находится в равновесии при температуре Г=300 К?
90
Решение. Эффективная толщина атмосферы по B6.6) при молярной массе
воздуха [хв=0,029 кг/моль равна
Концентрация на высоте #Эфф по B6.3)
лОа = лОа @) е~|хо8?яэф<|/(*7'>, nNa = /zNa @) е~
Отсюда процентное содержание кислорода
п0 100по @)
р = ЮО — = !
по> + nN> пОг @) + %з @) е-(^2-^
100пОа @) / nNf @) (fANa — [АОа) ^ЯЭфф \
/ ^ nNl@)
2(°) \ + «o2(°) + «n,
RT
где использовано, что
= 20 «/о ,
ф^г
Процентное содержание азота
/7Na= 100 —/?Оа =
2. Б опыте Перрена используются частицы с плотностью р=2,6 г-см~3 и
диаметром 2г=0,1 мкм, взвешенные в воде. Каково отношение концентра-
концентрации частиц на дне и на расстоянии 1 мм от дна при температуре Т=
= 300 К?
Решение. Эффективная масса частицы
4
т'= — яг?(р— р0) = 8• 10—5 г.
о
Отношение концентраций равно
3. В плазме концентрация электронов и ионов равна л=1012 см~3. Темпера-
Температура ионов и нейтральных молекул 300 К. Оцените порядок толщины слоя
объемного заряда около зонда.
Решение. По порядку величины толщина слоя объемного заряда равна длине
Дебая. В данном случае
Ь = У*еокТ/(еЩ = УгокТ1(еЩ « 7 мкм
(диэлектрическая проницаемость 8=1, заряд электрона — е= 1,6-10~19 Кл,
=8,85-Ю-12 Ф/м, ^ = 1,38-Ю-23 Дж/К).
91
ГЛАВА 5
РАСПРЕДЕЛЕНИЕ ГИББСА
§ 29. Функция распределения
Максвелла — Больцмана
В § 20 было выяснено, что при отсутствии внешних полей функ-
функция распределения f, которая определяет среднее число частиц
(Ш, находящихся в объеме пространства импульсов dQ и объеме
обычного пространства dt, дается выражением B0.3), которое для
удобства ссылок мы перепишем еще раз:
- e-*2/Bm0*r)d2dt. B9.1)
Bnm0kTf/2
Выясним теперь, как выглядит равновесная функция распреде-
распределения при наличии силовых полей. В этом случае рас-
распределение частиц в пространстве неоднородно и число частиц^
находящихся в элементе объема пространства dt, равно
/*(r)dt, B9.2)
где п(т) —концентрация. Распределение по импульсам по-прежне-
по-прежнему остается максвелловским, так что вероятность dw того, что им-
импульс частицы заключен в dQ, определяется по A7.1) формулой
(Щ = - е-Р*/Bто*т) dg. B9.3)
^ Bitm0kTf2
Число молекул dN, находящихся в объеме dx и обладающих им-
импульсом из dQ, может быть найдено умножением B9.2) на вероят-
вероятность соответствующего значения импульса B9.3), т. е.
dN=n (г) dt дЩ = ^ е-/>2/B/МП dt dQ. B9.4)
У B!tm0kTf2
Последнее выражение отличается от B9.1) только тем, что
теперь концентрация не является постоянным числом, а меняется
от точки к точке. Поскольку зависимость концентрации от коор-
координаты в равновесном случае определяется распределением Больц-
Больцмана B5.13), то соотношение B9.4) можно переписать в виде
n(rl)e
BnmQkTf/2
B9.5)
где n(ri) —концентрация молекул в некоторой точке гь a en(ri) —
их потенциальная энергия в этой же точке.
Другая форма соотношения получится, если множитель, не за-
зависящий от текущих координат г и импульса р, обозначить CN и
объединить экспоненциальные множители:
dN=CN е-[еп
92
Постоянный коэффициент CN равен
Для его вычисления необходимо знать концентрацию молекул
хотя бы в одной точке пространства. Существует другой способ оп-
определения этой величины, который часто более удобен.
Если известно полное число частиц N, находящихся в рассмат-
рассматриваемой системе, то, поскольку интеграл от функции распределе-
распределения по всем значениям импульса и координат должен быть равен
полному числу частиц, получаем уравнение, определяющее CN:
N== Cn | e-[?»(r)+/?2/BOToI/(fer)dt d2. B9.7)
Обычно его называют условием нормировки.
Таким образом, при наличии внешних силовых полей равновес-
равновесная функция распределения имеет вид B9.6), где константа опре-
определяется условием B9.7). Эта функция распределения объединяет
в себе закон распределения Максвелла в пространстве импульсов
и закон распределения Больцмана в обычном пространстве и по-
поэтому носит название функции распределения Максвел-
Максвелла — Больцмана.
§ 30. Распределение Гиббса как обобщение
распределения Максвелла — Больцмана
В дальнейшем нам придется все чаще и чаще говорить о части-
цах, координаты которых заключены в интервале dt, а компоненты
импульса — в интервале (Ш. Для сокращения формулировок и в
конечном счете для большей наглядности целесообразно ввести
представление о так называемом фазовом пространстве
частицы или ^-пространстве (мю-пространстве).
Под ^-пространством понимают шестимерное пространство, в
котором по трем осям откладываются координаты частицы, а по
трем остальным осям — компоненты ее импульса. Положение точ-
точки в шестимерном фазовом пространстве определяется шестью ко-
координатами. Поэтому если говорят, что молекула находится в не-
некоторой точке фазового пространства, то это означает, что заданы
пространственные координаты этой молекулы, а также компонен-
компоненты ее импульса. Элемент объема в (^-пространстве, обозначаемый
в дальнейшем dy, задается произведением дифференциалов всех,
его шесги координат, т. е.
dy = 6xuyuzupxdpyupz=dxuQ. (ЗОЛ)
Из сказанного вытекает, что когда частица находится в области
обычного пространства dt, а ее импульс попадает в область им-
импульсного пространства dQ, то это можно выразить коротко, ска-
зав, что она находится в dY-области ji-пространства.
93
Полученное в предыдущем параграфе распределение Максвел-
Максвелла — Больцмана с точки зрения введенного только что понятия дает
среднее число молекул, находящихся в элементе фазового прост-
пространства dy, и формулы B9.6), B9.7) можно переписать в виде
n=Cn j e-wr)+p-/B«.)i/(*n dYe C0.2)
Вместо того чтобы интересоваться средним числом частиц, на-
находящихся в dy, иногда задаются вопросом о том, какова вероят-
вероятность одной из них оказаться в пределах этого обгьема. Соответст-
Соответствующая вероятность dW равна
dW=dN/N=fdy/N.
Из написанного выражения видно, что эта вероятность пропор-
пропорциональна элементу фазового объема dy, т. е. величина w=f/N
имеет смысл плотности вероятности. Если подставить значение
функции распределения Максвелла — Больцмана и ввести обозна-
обозначение CW = CN/N, то
или, учитывая, что е = еп(г)+р2/Bт0) есть полная энергия моле-
молекулы,
dW=w{r, p)dy=Cwe-s/(kT>dy. C0.3)
Постоянный множитель Cw определяется условием нормировки
для плотности вероятности
J = Cw j е-/<*п dv= 1- C0.4)
Таким образом, плотность вероятности Максвелла — Больцмана
задается соотношением C0.3), где постоянная Cw находится из
условия нормировки C0.4).
Рассмотрим теперь вероятность 6W(tu Рь Гг, рг) того, что мо-
молекула / попадет в элемент объема фазового пространства dyi, a
молекула 2 — в элемент d^- Если взаимодействие между ними
пренебрежимо мало, то события независимы и тогда
r2, p2)=dW(rv Pl)dU7(r2, p2) =
dy2 =C\e-Ct+
Можно пойти дальше и определить вероятность для всех N моле-
молекул, составляющих газ. Действительно, пусть в какой-то момент
времени газ находится в таком состоянии, что первая молекула
оказалась в элементе фазового объема dyi, вторая — в элементе
dv2, третья — в dv3 и т. д. до последней N, находящейся в элементе
й- Какова вероятность такого состояния идеального газа?
94
Считая по-прежнему, что в идеальном газе движение всех мо-
молекул происходит независимо друг от друга (достаточно разрежен-
разреженный газ), нетрудно убедиться, что общая вероятность
pi; r2, p2;...; гдг
Сумма энергий всех молекул есть полная энергия газа, т. е.
$(г1, рх; г2, р2;...; *>
В дальнейшем будем писать просто &, не выписывая всех аргу-
аргументов этой функции, но всегда подразумевая, что полная энергия
является функцией координат и импульсов всех N молекул, входя-
входящих в состав рассматриваемой системы.
Удобно также обобщить понятие фазового пространства и рас-
рассматривать не ^-пространство, а полное фазовое простран-
пространство всей системы (Г — гамма-пространство). Под фазовым про-
пространством системы, состоящей из N частиц, понимается бЫ-мер-
ное пространство, по осям которого откладываются 3N координат
и 3N проекций импульсов всех составляющих систему частиц. Точ-
Точка в фазовом пространстве определяет координаты и импульсы*
всех частиц и поэтому полностью определяет состояние системы.
Элемент объема полного фазового пространства системы, обозна-
обозначаемый dr, равен
dr = dxx йуг dzx <\рхХ dpu\ dpz\
= dt1 d2x dt2
Введем еще новое обозначение для постоянного множителя
т. е., другими словами, определим величину F соотношением
Теперь общая вероятность может быть записана в следующей
форме, носящей название распределения Гиббса:
dW(rlf Pl; ...; 1>, p^)=e(F-^)/(*r)dr. C0.5)
Следует подчеркнуть, что в отличие от распределения Максвел-
Максвелла — Больцмана, говорящего о вероятности данного состояния для
одной молекулы идеального газа, распределение Гиббса определя-
определяет вероятность состояния всего газа в целом, т. е. всех его УУ
молекул.
Внешне простая формула C0.5) скрывает в себе столь богатое
и глубокое содержание, что ее по праву можно назвать централь-
центральным соотношением всей статистической физики равновесных со-
состояний. Дело в том, что хотя нами эта формула была получена
95
для идеального газа, но на самом деле, как было показано Гиб-
бсом, она справедлива для любой системы.
При построении теории каждого раздела физики обычно удобно
выбрать какие-то немногие основные положения в качестве базы,
позволяющей объяснить все относящиеся к этому разделу явле-
явления. Правильность основных положений устанавливается либо не-
непосредственной экспериментальной проверкой, либо косвенно по
соответствию всех выводов, полученных на их основе, с опытом.
Так, например, в механике роль основных положений играют за-
законы Ньютона. В электродинамике за основные принимают группу
уравнений, носящих название уравнений Максвелла. Аналогичным
образом в статистической физике равновесных состояний за основ-
основное положение может быть принято распределение Гиббса, и тогда
все свойства систем, находящихся в равновесии, получаются как
следствие справедливости этого распределения.
Распределение Гиббса, определяющее вероятность того, что
равновесная система находится в одном из состояний, принадле-
принадлежащих элементу объема фагового пространства системы dl\ дается
формулой C0.5), где & — энергия системы в состоянии из с!Г,
представленная как функция координат и импульсов всех частиц,
составляющих систему, Т — температура, F — некоторая величина,
носящая название свободной энергии и определяемая условием
нормировки C0.6):
J dW= J e(F-%m dT=eF/(kT) J e~^kT) dV= 1 C0.6)
или
F=-kTlnZ, C0.7)
где
J*/(*r)dr C0.8)
-—величина, называемая интегралом состояний.
§ 31. Пример одноатомного идеального газа
В качестве первого примера на применение распределения Гиб-
-бса рассмотрим вновь одноатомный идеальный газ. Хотя в данном
случае результат уже известен, но наша цель — показать, как рас-
распределение Гиббса применяется к конкретной задаче, и поэтому
мы не будем принимать во внимание все результаты, полученные
ранее, а используем только распределение Гиббса и сведения об
устройстве рассматриваемой системы.
Если молекулы идеального газа общим числом N находятся в
сосуде, из которого они не могут выйти, то можно считать, что они
находятся в поле внешних сил, потенциальная энергия которых об-
образует ящик бесконечной глубины. Действительно, потенциальная
энергия молекулы внутри сосуда постоянна и ее можно считать
равной нулю; кроме того, чтобы извлечь молекулу, нужно затра-
96
тить бесконечно большую работу, так что потенциальная энергия
вне сосуда практически бесконечна.
При заданной температуре Т вероятность какого-либо состоя-
состояния газа из числа описываемых точками элемента фазового объема
dF определяется распределением Гиббса C0.5). Применить эту
формулу к идеальному газу—это значит указать значение величин
ё и F для этого конкретного случая.
В идеальном газе молекулы не взаимодействуют между собой,
поэтому полная энергия & равна сумме энергий отдельных мо-
молекул:
N
C1.1)
Энергия молекулы равна сумме ее кинетической и потенциальной
энергий, т. е.
^ C1.2)
где потенциальная энергия гП{ есть такая функция координат i-u
молекулы, которая равна нулю внутри сосуда (ящика) и бесконеч-
бесконечна вне его. Таким образом,
Остается найти значение свободной энергии F, и тогда все ве-
величины, определяющие распределение Гиббса для данной конкрет-
конкретной задачи, будут известны. Поскольку свободная энергия просто
выражается через интеграл состояний Z, то все сводится к вычис-
вычислению последнего. Как в этой, так и во всех других задачах стати-
статистической физики именно здесь сосредоточены основные труд-
трудности.
По определению интеграла состояний C0.8) можно, используя
свойство идеального газа, выражаемое формулой C1.1), написать
N
2
Z=Je-*/(*r)dr=J...Je " dYi...dY*, C1.4)
N
бМ-мерный интеграл в C1.4) представляется в виде произведе-
произведения ./V шестимерных интегралов:
fe~e*/(*ndY;v, C1.5)
что и позволяет довести вычисления до конца. Действительно, все
интегралы в C1.5) одинаковы и отличаются лишь обозначением
4—434 97
переменных интегрирования, что, конечно, не сказывается на их
величине. Таким образом,
. C1.6)
Обозначим интеграл, стоящий в квадратных скобках преды-
предыдущего выражения, через z и вычислим его:
)dYi= Je Hl dtidQi.
Представляя интеграл в виде
l d2j fe dTl' C1.7)
сведем задачу к вычислению двух 3-мерных интегралов. Первый
встречался при изучении распределения Максвелла и был вычис-
вычислен, он равен Bлт0кТ)*/*. Это выражение следует из условия нор-
нормировки для распределения Максвелла, взятого в форме послед-
последнего уравнения A7.1).
Значение второго интеграла находится еще проще. Поскольку
вне сосуда eni = oo, то подынтегральное выражение вне сосуда рав-
равно нулю. Внутри 8П1 = 0, так что подынтегральное выражение рав-
равно единице. Таким образом остается интеграл по dti, взятый по
объему сосуда, т. е.
где V — объем сосуда, содержащего газ.
Таким образом,
C1.8)
и, следовательно,
Обратим внимание на то, что, как это хорошо видно из формулы
C1.9), свободная энергия F является функцией таких переменных,
как объем, занимаемый системой, и ее температура, но она же
должна рассматриваться как постоянная величина, если иметь в
виду зависимость от координат и импульсов отдельных молекул.
Таким образом, в распределении Гиббса для одноатомного
идеального газа энергия определяется формулой C1.3), а свобод-
свободная энергия — формулой C1.9). Зная распределение Гиббса, т, е.
вероятность различных состояний системы, можно вычислить сред-
среднее значение любых физических величин. В следующей главе по-
показано, что большинство из них относительно просто находится
непосредственно по свободной энергии системы F.
Чтобы лучше освоиться со смыслом распределения Гиббса, рас-
рассмотрим следующий числовой пример. Пусть имеется одноатом-
98
ный газ, например гелий, с числом молекул 1020, занимающий при
температуре 27° С объем V, равный 1 л. В этих условиях газ может
считаться идеальным. Какова вероятность состояния, в котором
все N молекул сосредоточатся в области сосуда, составляющей 0,1
всего объема, причем их скорости имеют почти одинаковое значе-
значение, а именно заключены в интервале от 300 до 301 м/с? Ответ
дается формулой C0.5). В ней
причем
a
где и = 300 м/с (или 301 м/с), сИД^= 1 м/с, то = 4,68-10~27 кг, так что
dQ = l,17.10~73 кг3.м3.с.
Энергия данного состояния
N
Свободная энергия вычисляется по формуле C1.9). В данном
случае ее удобно представить в форме
Bnm0kTf2
тогда экспоненциальный множитель в формуле Гиббса дает
е
VN
Множитель
по аналогии с множителем V может рассматриваться как эффек-
эффективный объем в пространстве импульсов, доступный молекулам
при температуре Т. Его числовое значение в данной задаче есть
4,27-102 кг3-м3.с-3.
Окончательно получаем
Множитель @,lV/l/)iv'=10-iV соответствует вероятности того, что
все молекулы сосредоточатся в объеме ОДУ. Эта вероятность очень
мала, как это уже было продемонстрировано в § 13. Второй со-
сомножитель
99
определяет вероятность того, что скорости всех молекул окажутся
в рассматриваемом диапазоне. Он тоже очень мал. Из полученных
результатов видно, что вероятность выбранного состояния ничтож-
ничтожна. Это объясняется тем, что общее число состояний системы, вклю-
включающей в себя 1020 частиц, необыкновенно велико (предполагает-
(предполагается, что фазовый объем, приходящийся на одну частицу, для всех
состояний одинаков).
§ 32. Распределение Максвелла — Больцмана
Если принять распределение Гиббса за основной постулат ста-
статистической физики равновесных состояний, то с его помощью
легко получить распределение Максвелла по импульсам и распре-
распределение Больцмана по координатам. При этом отпадает необхо-
необходимость в довольно длинных и не полностью обоснованных рас-
рассуждениях, которые привели к распределению Максвелла — Больц-
Больцмана в гл. 3 и 4.
Примем за систему одну единственную молекулу идеального
газа. Фазовое пространство «системы» в данном случае совпадает
с фазовым пространством одной частицы, так что с!Г = с1у. Для ве-
вероятности данного состояния системы из одной молекулы по фор-
формуле Гиббса получаем
dWW'-*)/(tr)dY. C2.1)
где ё> = р21Bт0) +еп(г) —энергия молекулы.
Выражение C2.1) можно записать в виде, в котором ясно вид-
видно, что оно совпадает с распределением Максвелла — Больцмана:
dW=Cw e-pf/<2«.w) е-?„(г)/(*п dt dQ>
где постоянная нормировки Cw=eF/(kT) определяется равенством
Окончательное вычисление Cw может быть выполнено, если за-
задана потенциальная энергия молекулы. Так, например, когда мо-
молекула находится в ящике и нет других внешних сил, кроме сил,
действующих со стороны стенок, то
где V — объем ящика, и
С —
Когда рассматривается столб газа с площадью основания S в
поле тяжести Земли &u = mogzt то
100
(V?n/(ftr) dt= Г их f dy f
Возможно, приведенный пример недостаточен для того, чтобы
убедить в целесообразности выбора распределения Гиббса в каче-
качестве основы для построения статистической физики равновесных
состояний, поскольку здесь были просто обращены все выкладки,
проделанные ранее и использованные для его обоснования. Однако
позднее, в частности в квантовой статистике, одна из форм распре-
распределения Гиббса будет использована для получения новых резуль-
результатов.
Предположим, что нас интересуют частицы настолько больших энергий, что
их скорость близка к скорости света с. Естественно, что для определения ста-
статистических характеристик таких частиц распределение Максвелла, которое не
учитывает эффектов теории относительности, неприменимо. Каково же распреде-
распределение частиц по импульсам при учете релятивистских эффектов? Ответ легко
получить с помощью распределения Гиббса.
Снова выбирая в качестве системы одну частицу, найдем
dw =Cwe-e/(*r)dQdi3 .
Если частица находится в потенциальном ящике, то вне его энергия частицы
бесконечна, а внутри определяется известной формулой Эйнштейна е = тс2, где
/гс = то/К 1 — t/2yc2— зависящая от скорости масса частицы, т0 — масса покоя.
В теории относительности импульс равен
р= щ v=
Выражая в последнем уравнении скорость через импульс, найдем
Если теперь подставить это в выражение для энергии, то получим последнюю кан
функцию импульса:
Таким образом,
внутри ящика и равна нулю вне его. Постоянная Cw определяется выражением
1
1 ГС -тоС*У1 + р*Цт1с*ШкТ) 1
Cw = -у U е 4лр2 dp J ,
1
V
о
о* —1
101
где обозначено y=p2l(ni02c2). Интеграл
не может быть вычислен в элементарных функциях, но он зависит от единствен-
единственного параметра ?=kT/ (т0с2) и на графике рис. 5.1 представлена соответствую-
соответствующая зависимость, полученная численным интег-
интегрированием.
В обычно встречающихся случаях значе-
значение параметра мало (?<1), экспонента быстро
убывает даже при небольших значениях у
и поэтому, полагая в показателе степени
/
/
/
7
05 1,0 1.5 1
находим
Рис. 5.1
При больших значениях параметра
лишь при значениях у^$> 1 и поэтому
~ \ е-[тиеЩКГ))у {
экспонента заметно уменьшается
Таким образом, из изложенного в настоящем параграфе сле-
следует, что распределение Гиббса непосредственно приводит к рас-
распределению Максвелла — Больцмана и с его помощью могут быть
просто получены другие распределения, например распределения,
учитывающие эффекты теории относительности.
§ 33. Равномерное распределение энергии
по степеням свободы
В приложениях часто бывает важно знать среднее значение
энергии системы или отдельных составляющих эту систему моле-
молекул. Оказывается, что для среднего значения кинетической энер-
энергии имеет место очень простое и удобное выражение, которое мы
сейчас и рассмотрим.
До сих пор молекулы считались материальными точками, для
которых кинетическая энергия
ек=р2/B/п0) = (pl + р\ + Pl)lBmo).
В гл. 3 с помощью распределения Максвелла было найдено [см.
A7.2)] <рд2>=то&7, так что для среднего значения кинетической
энергии, соответствующей движению вдоль оси х, получаем
C3.1)
102
Точно такие же равенства имеют место и для кинетической энергии
движения вдоль осей у и z:
<е,*> = <О=*772. C3.2)
Среднее значение общей кинетической энергии равно
(О = <*«> + Ы + (О =W. C3.3)
Формулы C3.1), C3.2) могут быть истолкованы таким образом,
что на каждую степень свободы частицы приходится одна и та же
средняя кинетическая энергия, равная кТ/2. У материальной точ-
точки обладающей тремя степенями свободы, среднее значение кине-
кинетической энергии равно 3/^Т. Этот результат является частным
случаем очень общего правила, по которому на каждую степень
свободы любой классической системы, находящейся в равновесии,
приходится средняя кинетическая энергия, равная kT/2.
Так, например, если рассматривать газ, состоящий из много-
многоатомных молекул, то последние должны считаться не материаль-
материальными точками, а скорее твердыми телами, обладающими хотя и
малыми, но конечными размерами. Общее число степеней свободы
твердого тела равно шести. Действительно, положение центра масс
твердого тела задается тремя координатами, что соответствует
трем степеням свободы поступательного движения, а его положе-
положение при вращении вокруг центра масс определяется тремя другими
координатами, в качестве которых обычно используются углы
Эйлера. Угловые координаты характеризуют три дополнительные
вращательные степени свободы. Таким образом, средняя кинетиче-
кинетическая энергия поступательного движения молекул газа равна
NC/2)kT и такая же энергия соответствует их вращению, так что
общая средняя кинетическая энергия равна
< ек > = 6N (kT/2) =
Полное доказательство теоремы о равнораспределении кинетиче-
кинетической энергии по степеням свободы оказывается довольно громозд-
громоздким и поэтому вынесено в приложение 3.
В общем случае результат, полученный для кинетической энер-
энергии, не имеет места для энергии потенциальной. Однако для упру-
упругой потенциальной энергии, являющейся квадратичной функцией
координат, среднее значение тоже равно kT/2 на каждую степень
свободы, соответствующую определенной координате. Так, напри-
например, в случае одномерного движения вдоль оси х упругая потен-
потенциальная энергия
где к — жесткость, и среднее значение потенциальной энергии
есть
C3.4)
103
Для трехмерного случая может быть
(U)=3kT/2.
Теорема о равномерном распределении энергии по степеням
свободы явилась очень крупным успехом классической статисти-
статистической физики, однако при сопоставлении с опытом она же пока-
показала, что классическая статистика имеет ограниченное примене-
применение. Действительно, ее применение позволило просто объяснить
различие в теплоемкостях одноатомных, двухатомных и многоатом-
многоатомных идеальных газов. Поскольку внутренняя энергия идеального
газа есть среднее значение кинетической энергии его молекул, то,
по теореме о равномерном распределении,
U=N{ij2)kT, C3.5)
где / — число степеней свободы молекулы. Одноатомному газу
следует приписать три степени свободы на атом, так как положе-
положение атома определяется тремя координатами. Положение двух-
двухатомной молекулы в пространстве можно указать, задав положе-
положение ее центра масс (три степени свободы) и два угла, определяю-
определяющие направление ее оси в пространстве (еще две степени свободы).
Таким образом, для двухатомной молекулы i равно пяти. Наконец,
многоатомная молекула, если ее рассматривать как небольшое
твердое тело, обладает шестью степенями свободы, из которых три
соответствуют поступательному движению, а три — вращательно-
вращательному. Дополнительную по отношению к двухатомной молекуле сте-
степень свободы можно рассматривать как соответствующую углу по-
поворота вокруг оси, направление которой задано двумя другими ко-
координатами.
Соотношение C3.5) в целом ряде случаев хорошо согласуется
с экспериментом, что как будто подтверждает справедливость
теории. Более внимательное рассмотрение вопроса, однако, пока-
показывает, что если бы теорема о равномерном распределении энергии
по степеням свободы была безоговорочно справедлива, то совпа-
совпадения с опытом не могло бы быть. Для того чтобы убедиться в
этом, достаточно, например, учесть, что атомы состоят из ядра и
движущихся вокруг него электронов. Если учесть степени свободы,
относящиеся к отдельным электронам, то средняя кинетическая
энергия атома должна была бы оказаться значительно больше.
§ 34. Флуктуации в измерительных приборах
С целью проиллюстрировать общность распределения Гиббса
покажем, как оно позволяет просто решить очень важный в прак-
практическом отношении вопрос о флуктуациях показаний измеритель-
измерительных приборов. Начнем наше обсуждение со случая простейшей
механической системы, изображенной на рис. 5.2. Система пред-
104
ставляет собой массу т, укрепленную на пружине с жесткостью
k, и является моделью многих измерительных приборов. Так, на-
например, гальванометр состоит из стрелки (массы) и спиральной
пружины, возвращающей стрелку в положение равновесия. В ана-
аналитических весах масса подвижной системы возвращается в по-
положение равновесия силой тяжести, момент которой оказывается
пропорциональным величине угла, характеризующего отклонение
от положения равновесия, т. е. в этом смысле момент силы тяже-
тяжести аналогичен упругой силе пружины. Можно привести и другие
примеры.
Уравнение движения пружинных весов, изображенных на рис.
5.2, имеет вид
mz'= -icz'-r\z' + F + mg C4.1)
(здесь z' — координата массы т, —кг' — упругая сила пружины,
—x\zr— сила трения, возникающая при движении массы в окру-
окружающей ее среде, F — измеряемая внешняя сила, mg — сила тяже-
тяжести, действующая на массу). Если система находится в покое, то
z' = z' = 0 и из уравнения C4.1) следует
Координата z0' соответствует равновесию массы под действием
приложенных к ней сил.
Для дальнейшего удобно ввести координату z = z'—zo\ характе-
характеризующую отклонение от положения равновесия, тогда уравнение
движения принимает вид
mz -f t\z -f- kz = 0.
C4.2)
V/////////////////. '/////,
Для рассматриваемого здесь вопроса о флуктуациях, т. е. о
беспорядочных тепловых колебаниях указателя пружинных весов
т, первостепенное значение имеет слагаемое r\z в уравнении C4.2).
Это слагаемое описывает взаимодействие указателя отклонения с
окружающей средой, которое в общих чертах состоит в том, что
молекулы среды, находящиеся в тепловом
равновесии при некоторой температуре Г,
все время бомбардируют указатель. В сред-
среднем все направления ударов равновероят-
равновероятны, поэтому среднее показание весов равно
нулю: <2> = 0. Если указатель приведен в
движение, то встречные удары начинают
превалировать и масса испытывает проти-
противодействие своему движению, описываемое
членом с силой трения — ц?. Когда весы на-
находятся в равновесии, то компенсация уда-
ударов осуществляется лишь в среднем. По-
Поскольку в какой-то момент результат бом-
бомбардировки весов молекулами среды с од- Рис. 5.2
105
т
ной стороны может оказаться больше, чем с противоположной, а в
следующий — наоборот, то внимательное наблюдение должно об-
обнаружить непрерывное беспорядочное движение указателя, так что
лишь в среднем его координата z равна 0. Величину отклонений,
т. е. величину флуктуации, принято характеризовать средним зна-
значением квадрата отклонения от положения равновесия <г2>.
С точки зрения статистики задача о весах аналогична задаче
о большой молекуле с массой т, находящейся в поле упругой силы
с потенциальной энергией /cz2/2, равной потенциальной энергии
сжатой пружины. За счет контакта со средой весы находятся в
тепловом равновесии при температуре Т. Их состояние можно оха-
охарактеризовать положением указателя (координатой z) и его им-
импульсом (тг). По Гиббсу, вероятность того, что указатель нахо-
находится в промежутке Az и обладает импульсом в интервале d(raz),
дается выражением
где ё> =mz2l2JrKz2j2 — энергия указателя, равная сумме кинетиче-
кинетической и потенциальной энергий.
Величина флуктуации определяется общим выражением
?ф
и
но в данном случае ее легче вычислить, воспользовавшись теоре-
теоремой о равномерном распределении энергии по степеням свободы.
Действительно, для потенциальной энергии выполнены условия,
оговоренные в предыдущем параграфе, и поэтому
•)= , т. е. (г2)=кТ/к. C4.3)
Числовые оценки показывают (см. за-
задачу 1 к настоящей главе), что в ре-
реально осуществимых механических си-
системах величина флуктуации очень
мала, так что они лишь в исключитель-
исключительных случаях могут влиять на точность
измерения.
Совсем другое положение имеет ме-
место в электрических измерительных
Рис. 5.3 цепях, где сплошь и рядом чувстви-
чувствительность приемно-усилительных уст-
устройств ограничена тепловыми флуктуациями. Предположим, что на
входе усилителя с большим коэффициентом усиления стоит колеба-
колебательный контур так, как это показано на рис. 5.3. На первый кас-
каскад усилителя с обкладок конденсатора колебательного контура
подается напряжение U, связанное с зарядом Q соотношением
Q = CU, C4.4)
106
где С — емкость конденсатора. Если сделать коэффициент усиле-
усиления достаточно большим и подать выходное напряжение на осцил-
осциллограф, то окажется, что на экране будут наблюдаться беспорядоч-
беспорядочные колебания, представляющие собой тепловые флуктуации 'напря-
'напряжения на конденсаторе.
Уравнение, описывающее поведение колебательного контура,
имеет вид
//?+{/= -L-^ C4.5)
и означает, что сумма напряжения на конденсаторе и падения на-
напряжения на резисторе с сопротивлением R равна действующей в
контуре э. д. с. самоиндукции катушки с индуктивностью L. Учиты-
тывая, что ток / в контуре связан с зарядом конденсатора соотно-
соотношением
¦f = /. C4.6)
хМ уравнение C4.5) переписать в виде
——Ь-^—U, (<34./)
at* dt С
где принято во внимание соотношение C4.4).
Бросается в глаза аналогия 'написанного уравнения с уравнени-
уравнением C4.2). Эта аналогия имеет глубокий смысл. Член с сопротивле-
сопротивлением R играет такую же роль, как и соответствующее слагаехмое с
коэффициентом трения в C4.2), т. е. именно им обусловлено взаи-
взаимодействие электрических колебаний в контуре с тепловым движе-
движением атомов кристаллической решетки материала, из которого
изготовлен резистор. Атомы решетки образуют термостат, и за счет
их столкновений с электронами последние приходят в состояние
беспорядочного хаотического движения. Если большее число элек-
электронов начинает двигаться в одном направлении, то 'конденсатор
заряжается в соответствии с этим направлением тока. В следую-
следующий момент времени большее число электронов движется в обрат-
обратном направлении и конденсатор перезаряжается. Таким образом,
непосредственной причиной появления электрических флуктуации
являются случайные движения электронов в резисторе, вызванные
взаимодействием с термостатом (кристаллической решеткой).
Состояние электрических колебаний в контуре задано, если из-
известны величины заряда Q (координата) и тока / (скорость). Пол-
Полная энергия контура в некотором определенном состоянии равна
сумме электрической и магнитной энергий:
S=-^- + — 9 C4.8)
2С 2 v
где электрическая энергия Q2/BC) аналогична потенциальной
kz2/2, а магнитная энергия LP/2 — кинетической mz2/2. По прин-
принципу Гиббса, вероятность того, что заряд конденсатора в конту-
107
ре имеет значение в интервале Q-±-(Q + dQ), а ток — в интервале
между I-^-1+dI, определяется распределением Гиббса
I\ C4.9)
где вместо % следует подставить C4.8), a dr = dQd/.
Теперь можно вычислить среднеквадратичное напряжение на
конденсаторе:
где среднее значение <Q2> определяется с помощью распределе-
распределения Гиббса C4.9) или еще проще с помощью теоремы о равномер-
равномерном распределении энергии по степеням свободы:
Из двух последних соотношений ©ытекает, что
((J2)=kT/C. C4.10)
Формула C4.10) дает ответ на вопрос о величине флуктуации,
но ее удобно несколько преобразовать, выразив емкость через со-
сопротивление и полосу пролускания контура. Используя методы
электротехники, можно показать, что
где Av — ширина полосы частот, на которые настроен контур, а
zR = L/(RC)—его активное сопротивление на резонансной частоте.
Таким образом, основное соотношение, связывающее среднее зна-
значение квадрата тепловых флуктуации напряжения с температурой
и параметрами цепи, имеет вид
Так, например, в приемнике с полосой пропускания Av=10 кГц,
работающем при нормальной температуре Г=300 К и обладающем
входным активным сопротивлением Zr=10 kOm, среднеквадратич-
среднеквадратичное значение напряжения шума равно
У~ЦР) = V4kTzRto ~ 1,2 мкВ.
Если входной сигнал меньше этого значения, то его невозможно
различить на фоне беспорядочных тепловых колебаний.
§ 35. Реальный газ
В качестве другого примера рассмотрим применение распреде-
распределения Гиббса к реальному газу, т. е. к газу, в котором учитывается
взаимодействие между составляющими его атомами или молеку-
молекулами. Хотя точно решить эту задачу не удается, однако даже при-
приближенный подход позволяет, как это будет видно из дальнейшего
(см. § 42), получить ряд интересных результатов.
108
Энергию системы взаимодействующих атомов можно записать
в виде
C5.1)
Пк
Рис. 5.4
где гг — потенциальная энергия i-то атома в поле внешних сил,
a Eik — потенциальная энергия взаимодействия t-ro и &-го атомов.
Сумма берется ло всем значениям i и k, не равным друг другу. Мно-
Множитель lJ2 учитывает, что в сумме по i и k энергия взаимодействия
каждых двух атомов записывается два раза. Так, (например, энер-
энергия взаимодействия третьего и пято-
пятого атомов входит один раз в форме
члена 8з5, а второй раз — в виде 853-
Свойства реальной системы зави-
зависят от энергии взаимодействия ег-А,
которая, в свою очередь, является
достаточно сложной функцией от
расстояния между атомами гщ. Ка-
Качественно характер этой функцио-
функциональной связи иллюстрируется рис.
5.4. Смысл графика может быть по-
пояснен следующим образом. На боль-
больших расстояниях друг от друга ато-
атомы практически не взаимодейст-
взаимодействуют между собой, и энергия гщ может быть принята равной нулю.
На меньших расстояниях проявляются силы взаимного притяже-
притяжения, стремящиеся сблизить атомы. Поскольку эти силы совершают
положительную работу, то это означает, что взаимная потенциаль-
потенциальная энергия атомов уменьшается, т. е. становится отрицательной.
На очень малых расстояниях, когда начинают заметным образом
перекрываться электронные оболочки атомов, проявляются силы
отталкивания, которые очень быстро увеличиваются по мере умень-
уменьшения пн. Для сближения атомов теперь нужно приложить значи-
значительные внешние силы, которые совершают положительную рабо-
работу, т. е. увеличивают энергию е*л. Для упрощения приводимых ни-
ниже вычислений удобно заменить реальную зависимость Sik(fik)
приближенной, показанной на рис. 5.4 пунктиром. Величина Ьо со-
соответствует минимально возможному расстоянию между атомами
и, следовательно, может рассматриваться как диаметр «жесткого»
атома. Параметр Ло имеет смысл работы, необходимой для того,
•чтобы отделить один атом от другого, а величина а0 может интер-
интерпретироваться как «радиус действия» сил притяжения. Выбор па-
параметров Ьо, Ло и а0 в какой-то мере произволен и ограничен лишь
требованием, чтобы реальная и аппроксимирующая зависимости
были по возможности близки друг к другу.
Для того чтабы распределение Гиббса могло считаться извест-
известным, достаточно вычислить свободную энергию F или, что по суще-
109
ству эквивалентно, интеграл состояний Z, который при учете C5.1)
имеет следующий вид:
[
Z= J e-f^/(fer) dr= Je ' l-k l dr. C5.2)
Первая сумма в показателе степени при экспоненте зависит только
от импульсов, а вторая и третья — только от координат, поэтому
C5.2) разбивается на два интеграла — по импульсам и по коорди-
координатам:
Интеграл по импульсам совпадает с вычисленным для идеаль-
идеального газа (см. § 31). Он равен
J е ' dpi... dpN
Остановимся более подробно на интеграле по координатам.
Если газ находится -в сосуде объемом F, то энергии е* так же, как
это делалось для идеального газа, можно считать равными нулю
внутри сосуда и бесконечными В'не его, так что вне сосуда экспонен-
экспонента равна нулю. Таким образом, интеграл фактически берется толь-
только по объему сосуда, и тогда все ег- следует считать равными нулю.
Интеграл .принимает вид
C5.3)
Пусть объем V настолько велик (концентрация настолько мала)^
что очень редки события, состоящие в «слипании» трех атомов и
более, тогда C5.3) приближенно можно вычислить следующим об-
образом. Зафиксируем координаты (N—1)-го атома и проведем ин-
интегрирование по координатам последнего с номером N. Когда атом
Аг находится от остальных атомов на расстоянии, большем радиуса
сил притяжения, потенциальная энергия равна нулю, так что экс-
экспонента равна единице и в результате интегрирования получается
объехМ сосуда за вычетом объема сфер притяжения всех остальных
атомов. Когда же N-й атом находится ъ сфере протяжения, то экс-
экспонента равна постоянной величине exp (Ao/kT) и интегрирование
дает объем всех областей, где е*ь = —Ло, умноженный на
exp (AolkT). Таким образом, пренебрегая пересечением сфер при-
притяжения, после интегрирования по 'координатам iV-ro атома полу-
получаем
ПО
-(N-l) —
= ^1+Л^21А_]у„_„ t35.4)
где
8 = —- яа 1'
3
i)_ J^30) C5.5)
3 о
a /jv-i — аналогичный интеграл, но для (N—1)-го атома. Оценивая
его таким же образом, найдем
Теперь уже ясно, что для C5.4) справедливо выражение
+-L]. C5.6)
Если прологарифмировать C5.6) и учесть, что малая вероятность
«слипания» трех атомов и более имеет место лишь при условии
малости отношения (N—1N/V, то
и аналогично для остальных членов, так что
m=0 m-0
Сумма в последнем равенстве представляет собой сумму N членов
арифметической прогрессии, так что
и, следовательно,
JN
Таким образом,
Z = {2nmQkTfN/2V e^-W^) C5.7)
и свободная энергия реального газа (вычисленная в предположе-
предположении, что «объем взаимодействия» N6, в котором проявляются силы
притяжения, много меньше, чем общий объем, занимаемый газом)
определяется формулой
F= -kTlnZ= - kT
или
F=-krN\jL.h]T + lnV+ ^-J"> +U>Bnm0k)H C5.8)
Последнее выражение отличается от формулы для свободной энер-
энергии идеального одноатомного газа C1.9) членом с отношением
6/V. Для газа, состоящего из многоатомных молекул, все рассуж-
рассуждения сохраняются и необходимо лишь заменить член C/2)&? на
(i/2)kT, где i— число степеней свободы молекулы.
Задачи к главе 5
1. Определить величину флуктуации указателя весов, которые обладают чув-
чувствительностью 10 мм на миллиграмм при Т=300 К.
Решение. Для среднеквадратичного отклонения по теореме о равнораспреде-
равнораспределении энергии имеем
где у — «жесткость» возвращающей системы. Поскольку у весов в равновесии
mg=yz, то
mg 10-6 кг.9,81 м-с-2
Y = —= —9- « Ю-з кг-с-2,
Z 10-2 м
т. е. в данном случае
= 2 нм.
Флуктуации имеют значение порядка десятка межатомных расстояний.
2. На входе усилителя стоит резонансный контур с емкостью С=1000 пФ.
Какова предельная теоретическая чувствительность такого усилителя?
Принять Г=300 К.
Решение. По формуле C4.10) имеем
= 2 мкВ.
ГЛАВА 6
СВЯЗЬ СТАТИСТИКИ
С ТЕРМОДИНАМИКОЙ
§ 36. Уравнение состояния
Наряду со статическим методом в физике тепловых явлений
широко используется термодинамический подход. В нем с
помощью ряда эмпирически установленных закономерностей дела-
делают выводы о тех или иных частных свойствах систем. Естественно,
что статистический и термодинамический методы тесно связаны
между собой. Цель настоящей главы показать эту связь. Мы нач-
нем с у р а в нен и я состояния системы.
Уравнением состояния называется зависимость давления Р от
объема V и температуры Т:
P=P{V, T). C6.1)
112
I V
I
I
I i
Для идеального газа уравнение состояния, носящее название урав-
уравнения Клапейрона — Менделеева, хорошо известно и
имеет вид
Р=Т^9 C6*2)
где М — масса идеального газа, \х — его молярная масса, R —
мольная газовая постоянная.
Пользуясь понятием свободной энергии, можно получить общую
форму (уравнения состояния, спра-
справедливую для любой системы, а не бп
только для идеального газа.
Предположим, что имеется со-
сосуд, содержащий рассматриваемую
систему, например жидкость или не-
неидеальный газ. Пусть координата
одной из стенок сосуда, перпендику-
перпендикулярной оси Ох, имеет значение х.
График зависимости потенциальной
энергии одной из молекул системы
от координаты х имеет вид, пока- q х хх<(/х х
занный на рис. 6.1. Действительно,
на молекулу i, находящуюся в точ- Рис. 6.1
ке Xi вблизи стенки, действует со
стороны последней отталкивающая сила, равная //. Чем ближе
молекула подходит к стенке, тем большую работу нужно совершить,
чтобы преодолеть отталкивание, и тем выше потенциальная энер-
энергия молекулы в поле отталкивающих сил. Обозначим потенциаль-
потенциальную энергию молекулы через еп. Очевидно, что еп зависит только
от взаимного расстояния стенки и молекулы, т. е.
вп=еп (* — *,). C6.3)
Из рис. 6.1 видно, что при перемещении молекулы из точки Х\ в
точку Xi + dXi, когда отталкивающая сила совершает работу
dA = /idx,9 C6.4)
потенциальная энергия уменьшается, т. е. изменяется на величину
deII = en(;c/) — еп(-?/ -\-dXi) = — dxn C6.5)
так что из сравнения C6.4) и C6.5) вытекает
j i — t
Нас будет больше интересовать сила /г-, с которой i-я молекула
действует на стенку. Поскольку, по третьему закону Ньютона, ft' =
= /г, ТО
113
или, учитывая характер зависимости потенциальной энергии от ко-
координат х и Xi по C6.3),
^E C6.6)
Jl dxi dx
Для общей силы, с которой все молекулы системы действуют
на стенку, можно написать
а для среднего значения этой силы
Последнее выражение эквивалентно следующему:
r. C5.7)
Действительно, энергия системы равна
Л' N 2
»= У *«(*-*/) + у -*- Н-^.вз+^.вн, C6.8)
где первое слагаемое представляет собой потенциальную энергию
взаимодействия со стенкой, второе — кинетическую энергию моле-
молекул, а остальные — соответственно потенциальные энергии взаимо-
взаимодействия молекул между собой ^п.вз и с полем внешних сил <§Гп.вз.
Последние три слагаемых не зависят от координаты х стенки, так
что после дифференцирования C6.8) получаем
dx dx
Давление —это сила, действующая на стенку, отнесенная к еди-
единице площади, поэтому
С^Г. C6.9)
Sdx
Произведение Sdx равно изменению объема системы dV при пере-
перемещении стенки сосуда на dx, что позволяет переписать C6. 9) в
виде
| dr. C6.10)
114
Значение интеграла C6.10) проще всего получить, исходя из
условия нормировки C0.6), которое мы выпишем еще раз:
1= ^e(/7^)/(fer)dr. C6.11)
Дифференцируя последнее соотношение по объему и учитывая, что
от объема (координаты стенки) зависят энергия <§ и свободная
энергия F, найдем
J
kT \ dV dV
После сокращения на I/(kT) можно переписать полученное усло-
условие в виде
ov
Поскольку свободная энергия не зависит от переменных интегриро-
интегрирования, то
) dV dvy Qi ~ dV '
где использовано условие нормировки C6.11). Таким образом, если
известна свободная энергия как функция объема и температуры, то
уравнение состояния вычисляется по формуле
Р=-—. C6.12)
dV y
В предыдущей главе была определена свободная энергия одно-
атом'ного идеального газа. По C1.9) она равна
F = - kTN \\nV + 3/2 In Г + 1пBя/гго&K4
Используя основное соотношение C6.12), находим уравнение со-
состояния
Если принять во внимание, что общее число молекул N выражает-
выражается через массу газа, его молярную массу и постоянную Авогадро
NA, так что N = NaM/\l, то приходим к уравнению Клапейрона —
Менделеева C6.2). Аналогичным образом можно найти уравнения
состояния для жидкости или неидеального газа, если известна их
свободная энергия.
§ 37. Термодинамический смысл
свободной энергии
Свободная энергия, формально введенная выше через статисти-
статистическую сумму, имеет определенный физический смысл. Для выясне-
выяснения его рассмотрим некоторую систему в изотермическом процессе,
т. е. при Г=const. В начальном состоянии свободная энергия име-
115
ла одно значение, соответствовавшее начальному объему, а в конеч-
конечном— другое, соответствующее конечному объему, но той же самой
температуре. При бесконечно малом изменении объема изменение
^свободной энергии равно (учтено, что Т = const и, следовательно,
4Т 0)
В силу C6.12) это можно переписать в виде
dF = -PdV.
Поскольку известно, что
где dA — работа, совершаемая системой при бесконечно малом
расширении на с!У, то оказывается, что dF = —dA. Интегрировани-
Интегрированием последнего равенства легко показать, что и для конечных изо-
изотермических расширений
Свободная энергия относится к числу функций состояния,
т. е. функций, значение которых определяется состоянием системы
(занимаемым ею объемом и температурой) и не зависит от того,
каким образом система пришла в это состояние. В связи с этим
можно сказать, что свободная энергия F — это такая функция со-
состояния, изменение которой в изотермическом процессе равно ра-
работе, совершенной системой, но взятой с обратным знаком.
§ 38. Уравнение Гиббса — Гельмгольца
При дифференцировании условия нормировки по объему полу-
получилось важное соотношение, приводящее к уравнению состояния.
Аналогичным образом дифференцирование условия нормировки по
температуре дает столь же важное уравнение, носящее название
уравнения Гиббса — Гельмгольца. После дифферен-
дифференцирования C6.11) по Т получаем
Если умножить обе части равенства на kT2 и правую часть пред-
представить в виде суммы интегралов, то
0= tT^e(F-rmkT)'dT-[Fe{F-<$)/(kT)dr+ [
) дТ J J
116
Вынося множители Т— и F, не зависящие от переменных интег-
интегрирования, за З'нак интеграла и используя значение интеграла нор-
нормировки, найдем
F+[&eu 0. C8.1)
дТ J
Интеграл в последнем выражении представляет собой среднее
значение энергии различных состояний системы. Эта величина на-
называется внутренней энергией системы и ее обозначают [/,
т. е.
Из C8.1) тогда следует
U=F-T — . C8.2)
Таким образом, внутренняя энергия есть функция состояния, рав-
равная среднему значению энергии системы, и ее значение может быть
определено через свободную энергию с помощью уравнения Гиб-
бса — Гельмгольца C8.2).
Уравнение Гиббса — Гельмгольца справедливо для любой си-
системы. Применим его в виде примера к одноатомному идеальному
газу. Подставляя в C8.2) свободную энергию, определяемую вы-
выражением C1.9), найдем
U=F-T
3 М дг
~~Т~7
dF
дТ
to со
3
"~~~2~
C8.3)
01 Z
или, иначе,
м т^ C8.3')
§ 39. Энтропия и ее термодинамический смысл
Можно дать следующее определение: энтропией S называется
функция состояния, равная
S-=- — . C9.1)
Поскольку свободная анергия есть функция состояния, то естест-
естественно, что функциями состояния являются и величины, выражаю-
выражающиеся через нее или ее производные, т. е. давление, внутренняя
энергия и энтропия. Важно, однако, выяснить термодинамический
смысл введенной таким способом новой функции состояния.
Пусть в некотором обратимом процессе состояние системы меня-
меняется. На каждом этапе обратимого процесса можно считать, что
система находится в равновесии и поэтому справедливо уравнение
117
Гиббса — Гельмгольца. При изменении состояния системы ее внут-
внутренняя энергия меняется на At/ и по уравнению Гиббса — Гельм-
Гельмгольца
Если изменение бесконечно мало, что соответствует бесконечно ма-
малому изменению объема dV и температуры d7\ то
Первое слагаемое в правой части может быть представлено в виде
где cL4 — работа, совершенная системой. Второе и третье слагае-
слагаемые взаимно уничтожаются. Наконец, последнее слагаемое по
введенному выше определению энтропии равно
[дт )
Таким образом,
dU= - dA + TdS или dS= {d(J-{-dA)/T.
По первому началу термодинамики, выражающему закон сохра-
сохранения энергии с учетом тепловых явлений, сумма изменения внут-
внутренней энергии и работы, совершенной системой, равна количеству
теплоты dQ, подведенному к системе в рассматриваемом процессе.
Итак,
dS = dQ/T. C9.2)
Следовательно, энтропия — это такая функция состояния системы,
бесконечно малое изменение которой в обратимом процессе равно
отношению бесконечно малого количества теплоты, введенного в
этом процессе, к температуре, при которой оно вводилось.
В конечном обратимом процессе изменение энтропии может быть
подсчитано по формуле
2 2
l# l'^-f C9.3)
где интеграл берется от начального состояния 1 системы до конеч-
конечного 2. Поскольку энтропия есть функция состояния, то замеча-
замечательным свойством интеграла C9.3) является его независимость
от формы контура, по которому он вычисляется.
118
В качестве примера на определение энтропии рассмотрим одно-
атомный идеальный газ. Дифференцируя свободную энергию C1.9)
по температуре, найдем
— kN =
= — R \In V + — In T + In Bя/М еK/Л,
где е — основание натуральных логарифмов Aпе=1).
§ 40. Статистический смысл энтропии
Термодинамический смысл энтропии несколько абстрактен и не
позволяет понять, почему эта функция состояния играет столь боль-
большую роль в статистической физике и термодинамике. Гораздо кон-
конкретнее тот статистический смысл, который можно вложить в эту
функцию.
Из уравнения Гиббса — Гельмгольца имеем
S=(U-F)/T.
Поскольку
то можно написать
kT J kT
Функция
есть плотность вероятности распределения Гиббса, так что энтро-
энтропия
S= — k twlnwdT=— fe(ln^). D0.1)
Формула D0.1) соответствует введенному в § 12 определению
энтропии как меры неопределенности или хаотичности. Некоторая
разница обусловлена наличием размерного множителя &, а также
тем, что в A2.1) мы «мели дело с дискретным (счетным) числом
событий и поэтому проводилось суммирование, а в D0.1)—с не-
непрерывным, так что суммирование пришлось заменить на интегри-
интегрирование.
Таким образом, статистический смысл энтропии состоит в том,
что она есть умноженная на постоянную Больцмана мера хаотич-
хаотичности состояния системы.
Впоследствии мы увидим, что соотношение D0.1) играет очень
важную роль в статистике и лежит в основе фундаментального
принципа, из которого можно последовательно вывести всю статис-
статистику равновесных состояний. Этот принцип тесно связан со вторым
119
началом термодинамики, обсуждение которого будет начато в сле-
следующем параграфе.
В одном из своих вариантов формула D0.1) запечатлена на па-
памятнике, установленном на центральном кладбище Вены крупней-
крупнейшему физику, прославившемуся своими работами в области ста-
статистической физики, — Л. Больцхману A844—1906).
§ 41. Энтропия и второе начало термодинамики
Второе начало наряду с первым является теАм основным положе-
положением, которое лежит в основе всей термодинамики и отражает глу-
глубокие закономерности явлений, наблюдаемых в системах, состоящих
из очень большого числа микроскопических частиц. Известны раз-
различные эквивалентные между собой формулировки второго начала.
Так, например, одна из формулировок гласит: невозможно, отня&
тепло от системы, полностью превратить его в работу без того, что-
чтобы в системе или окружающей ее среде не произошли другие одно-
одновременные изменения. Если >при изотермическом расширении иде-
идеального газа совершается работа за счет тепла, поступающего из;
термостата, то, когда процесс закончился, газ будет занимать боль-
больший объем, т. е. произойдут изменения по сравнению с первоначаль-
первоначальным состоянием. Можно заставить газ или какое-либо другое рабо-
рабочее тело совершить замкнутый обратимый цикл, при этом конечное
состояние будет совпадать с начальным, но тогда, по второму на-
началу, не все тепло, взятое от нагревателя, будет превращено в ра-
работу, а часть его обязательно должна быть отдана при более низ-
низкой температуре в холодильник. Отсюда следует вторая формули-
формулировка: невозможно осуществить периодически действующую
тепловую машину, полностью превращающую в работу все пере-
переданное ей тепло (вечный двигатель второго рода).
Если бы был возможен вечный двигатель второго рода, то, при-
приведя его в контакт с холодильником, мы могли бы получить неко-
некоторое количество работы. Воспользовавшись этой работой для при-
приведения в действие обратимой холодильной машины, можно было
бы, забрав еще некоторое количество тепла из холодильника, пере-
перевести его и тепловую энергию, равную полученной работе, в нагре-
нагреватель. Таким образом, оказалось бы возможным, взяв некоторое
количество тепла от менее нагретого тела (холодильник), перевес-
перевести его к более нагретому (нагреватель) так, чтобы после заверше-
завершения процесса все рабочие тела оказались в исходном состоянии.
Поскольку вечный двигатель второго рода невозможен, то невоз-
невозможен и указанный выше процесс, т. е. невозможно перевести
тепло от менее нагретого тела к более нагретому без того, чтобы
при этом не произошли другие одновременные изменения.
На первый взгляд представляется удивительным, что приведен-
приведенные выше общие формулировки эквивалентны очень простому я
точному математическому утверждению, а именно: в обратимом
процессе величина
ЩТ D1.1)
120
есть полный дифференциал. Другими словами, при переходе обра-
обратимым образом из одного состояния в бесконечно близкое другое
выражение D0.1) не зависит от того, каков был путь (процесс) пе-
перехода, а только от начального и конечного состояний.
Выше было показано, что из распределения Гиббса вытекает
соотношение
где S — функция состояния, а следовательно, dS — полный диффе-
дифференциал, т. е. было доказано второе начало термодинамики в по-
последней из приведенных формулировок. Остается лишь выяснить,
каким образом эта последняя формули-
формулировка приводит к предыдущим. Рассмот- Р
рим с этой целью какой-либо замкнутый
обратимый процесс, например представ-
представленный на Р—^-диаграмме рис. 6.2. По-
Полезная работа, полученная в этом цикле,
изображается заштрихованной на рис. 6.2.
площадью:
и равна разности между количеством те- Рнс- 6-2
плоты Qi, введенным в систему, и коли-
количеством теплоты —Q2, отданным системой в холодильник. Послед-
Последнее утверждение вытекает из первого начала термодинамики, по-
поскольку по завершению цикла система возвращается в исходное
состояние, поэтому изменение ее внутренней энергии равно нулю.
С другой стороны, если обойти цикл, то, поскольку энтропия есть
функция состояния, должно быть
-^- = 0. D1.2)
Температура Т — положительная величина, поэтому если интег-
интеграл равен нулю, то не может быть, чтобы все время было dQ>0,
т. е. чтобы тепло все время поступало в систему; должны быть
участки, на которых dQ<0, т. е. тепло отдается. Когда в цикле со-
совершена работа, то
A = Qx-Q2>0.
Условие D1.2) может при этом выполняться только в том случае,
есл<и тепло отдается при чз среднем более низкой температуре
Г2, чем средняя температура Ти при которой оно получает-
получается, так чтобы при Qi>Q2 было
Этим доказана вторая или эквивалентная ей первая формулировка.
Чтобы убедиться в справедливости третьей формулировки, пред-
предположим, что есть холодильник при температуре Г2, меньшей тем-
температуры Тх нагревателя. Пусть от холодильника взято тепло Q2 и
121
переведено в нагреватель —Q\. Если нет одновременных изменений
в системе и окружающей среде, то, следовательно, окружающая
среда не совершала работы и, по закону сохранения энергии, Q2~
= Qi, но тогда из-за неравенства температур не может выполняться
равенство
так что справедлива и третья формулировка.
Второе начало термодинамики позволяет сделать важные заклю-
заключения о к. п. д. тепловых машин. Под к. п. д. принято понимать
отношение полезной работы Л, совершенной машиной в замкнутом
цикле, к количеству теплоты Qb взятого ею от нагревателя:
А ^ Qi-Q2 1$2
1 <? "
1
Oi Qi
Максимальный к. п. д. /получается при наибольшем при данных ус-
условиях отношении Q1/Q2. Если машина обратимая, то должно вы-
выполняться условие
из которого следует, что Qi может быть тем больше, чем выше тем-
температура Т\ нагревателя, a Q2 тем меньше, чем ниже температура
Т2 холодильника. Из сказанного вытекает, что из всех циклов, об-
обладающих одной и той же максимальной температурой нагревате-
нагревателя Т°\ и минимальной температурой холодильника Г°2, наибольший
к. п. д. имеет цикл Кар но, т. е. цикл, состоящий ,из двух изотер-
изотермических (Т\ = const =T°\ и Т2 = const = Г°2) и двух адиабатических
процессов, в которых передача теплоты отсутствует.
Определим теперь к. п. д. цикла Кар«о, найисав
где опущены интегралы по адиабатам, так как в адиабатическом
процессе dQ = O. Используя условие изотермичное™, получаем
Г dQ Qi Q2
(I) i-=Jli ?± ИЛИ
J T TL T2
Q2IQ\ = T2jTl. D1.3)
Но по определению к. п. д.
так что, учитывая D1.3), найдем
г]=\-Т2/Т1 = (Т1-Т2)/Т1. D1.4)
122
Таким образом, к. п. д. цикла Карно определяется соотношением
D1.4) и не зависит от того, какое рабочее тело (газ, жидкость) ис-
используется при реализации этого цикла.
§ 42. Реальный газ
Используем полученные в настоящей главе соотношения, а так-
также выражение для свободной энергии реального газа, приведенное
в § 35, для выяснения некоторых свойств реального газа.
По C5.8) свободная энергия имеет вид
^ \ D2.1)
где i — число степеней свободы мол-екул газа.
Уравнение состояния легко получается с помощью C6.12). Дей-
Действительно,
Nlir(\ D2.2)
dV \V 2 V2 ) v }
Поскольку число молекул N = MNAf\i, где M/\i— число молей, то
D2.2) можно переписать в виде
"При очень больших объемах, когда С 1> уравнение со-
состояния реального газа переходит в уравнение состояния идеаль-
идеального газа. При меньших объемах наблюдается расхождение. По-
Поскольку вывод D2.1) с самого начала был сделан в предположении,
что ——— —<С 1» то ясно, что речь идет об относительно неболь-
небольших отличиях реального газа от идеального.
Давление реального газа при данной температуре и объеме мо-
может быть как больше, так и меньше, чем у идеального. Все зависит
от знака величины (N—1N/2, которая при учете C5.5) записывает-
записывается в виде
(ЛГ-В8 = N-l ^_{al_bs){eAoKkT)_l)_ N-\ _4*_bl
D2.3)
Отрицательная часть этой величины имеет простой физический
смысл. Действительно, поскольку Ьо — диаметр молекулы, то ее
объем равен
Число молекул в газе очень велико, поэтому можно положить
N—\ttN. Теперь видно, что отрицательный член равен учетверен-
учетверенному объему всех молекул.
123
Положительный член интерпретируется несколько сложнее.
Отметим, что при A0<^kT он упрощается, так как тогда
D2.4)
Множитель
TV 14 зз
— я (#0 — bo)
2 3
имеет смысл половины объема, в котором сказывается притяжение
молекул.
Сравним уравнение состояния D2.2) с известным из общего
курса физики уравнением Ван-дер-Ваальса, которое часто приме-
применяют для описания состояния реальных газов и их перехода в
жидкое состояние. Это уравнение имеет вид
V2
ИЛИ
№_ __а_
и.2 V2
Если мы ограничиваемся объемами V^>bM/\i, то приближенно с
точностью до членов первого порядка по отношению bM/[\V полу-
получим
P=iLj^^ *rft_AP jjl. D2.5)
Это уравнение совпадает с полученным выше теоретически урав-
уравнением D2.2), которое при учете D2.3) может быть записана
в виде
п М RT , М RT N—\ 4 ,з
II V ' (д. V2 2 3
(л V2 2 V ; 3 kT
Сравнение с D2.5) показывает, что они совпадают, если
, [л Лг—14 ,з ^а 4,з
//|О ,л
D2.Ь)
т. е. если Ъ—учетверенный объем всех молекул, содержащихся в
одном моле, и если
м. R N — 1 4 . з «.3n*
а= м~1 5 -я(а0-Ьо)Аос^
М К 2. 6
- V 4 4я («о - Ь$ Ао=Аг 4 я (а° - *о) Ло- D2.7)
Z к о 2* о
Таким образом, статистический метод приводит к уравнению
состояния, совпадающему при больших объемах с уравнением
124
Ван-дер-Ваальса, и позволяет выразить постоянные а и b этого
уравнения через параметры, характеризующие молекулы (ао, Ьот
Ло). Отметим, что в принципе вывод выражения для свободной
энергии может быть уточнен и тогда получится более точное урав-
уравнение состояния. Рассмотрение этих вопросов выходит, однако, за
рамки данной книги.
Обратимся теперь к вычислению внутренней энергии реального
газа. По уравнению Гиббса — Гельмгольца C8.2) с помощью
D2.1) получаем
2 ' V дТ L 2 J
_М-±-ПТ \ М Т9 R ° \ N~X 81
ji 2 ' н- V дТ [ 2 J*
Поскольку выражение для б (iV—1)/2 при учете соотношений
D2.6) и D2.7) в приближении, оговариваемом условием D2.4) г
может быть записано в виде
2 fx U^ j' V ;
то легко видеть, что
д Г Л^—1 Л = __а_ Г_л? /_а Л1 = _ М_ а
дГ [ 2 \~ дТ { p. \RT )] [i ЯП '
Таким образом, внутренняя энергия оказывается равной
D2.9)
\К 2 \ {А / V
Из D2.9) видно, что внутренняя энергия реального газа отличает-
ся от внутренней энергии идеального членом — — —, кото-
который учитывает потенциальную энергию взаимного притяжения мо-
молекул. Внутренняя энергия зависит от объема, занимаемого газом.
Используя уравнение C9.1), легко вычислить энтропию реаль-
реального газа. С учетом D2.8) имеем
= = Nk\ —In у +ln^ V
дТ L 2 ' \>. V ' ii VRT ~
—Nk-Nk (—) ——.
2 [ (x / VRT
Поскольку Nk=MR/\i, то
S = — x\-LinT-lnV- — -~l + const. D2.10)
Энтропия реального газа оказывается несколько меньшей, чем у
идеального, из-за наличия сил отталкивания. Это приводит к от-
12S
личию в связи между температурой и объемом в адиабатическом
процессе от той, которая имеет место для идеального газа в тех
же условиях. Более подробно этот вопрос рассматривается в зада-
задаче 3 к данной главе.
§ 43. Теплоемкость
Теплоемкостью называют величину, численно равную ко-
количеству теплоты, которое необходимо сообщить системе, чтобы на-
нагреть ее на 1 К:
/¦>
_dQ_
d T
В газах, сжимаемость которых очень велика, необходимо разли-
различать теплоемкость при постоянном объеме Су и теплоемкость при
постоянном давлении СР. В конденсированных системах (жидко-
(жидкости, твердые тела) изменение объема, как правило, настолько ма-
мало, что разницей между Су и СР можно пренебречь.
Поскольку по первому началу термодинамики
то для теплоемкости получаем
. г, dV
При постоянном объеме = 0 и, следовательно,
Cv=^r. D3.2)
Соотношение D3.2) объясняет, почему теплоемкость является ве-
величиной, представляющей большой практический интерес. Она от-
относительно просто измеряется, и поэтому ее можно использовать
для экспериментального определения внутренней энергии системы.
Если температура растет, а давление постоянно, то объем системы
увеличивается, поэтому теплоемкость при постоянном давлении
больше, чем теплоемкость при постоянном объеме:
Ср = -^-+Р-^- = СУ + Р — . D3.3)
dr ' dr ' dr к J
Очень часто имеют дело с удельной теплоемкостью,
т. е. теплоемкостью, отнесенной к массе:
cv = Су/М, ср = СР/М. D3.4)
Иногда используют молярную теплоемкость (теплоем-
(теплоемкость одного моля)
cmV = CvV.IM, cmP = CPp/M. D3.5)
126
Обратимся теперь к теплоемкости идеального газа. Если ис-
использовать соотношение C3.5) для внутренней энергии идеально-
идеального газа, то теплоемкость при постоянном объеме определится фор-
формулой
Cv^^Li-R D3.6)
[д. 2
или для молярной теплоемкости
cmV = №)R. D3.7)
Когда давление постоянно, то из D3.3) вытекает
= CV+—R. D3.8)
v-
Здесь использовано уравнение Клапейрона — Менделеева. При
учете D3.6) последнее соотношение можно записать также в форме
Cp=*L l±*R. D3.9)
p. 2
Для молярной теплоемкости при постоянном давлении из D3.8)
вытекает
cmP=caV + R. D3.10)
Это важное соотношение Майера сыграло большую роль
в истории физики при установлении закона сохранения энергии и
определении механического эквивалента теплоты.
Теплоемкости представляют собой удобные величины для про-
проверки согласия теории и опыта. Эксперимент показывает, что со-
соотношения D3.6) — D3.9) в целом ряде случаев выполняются
очень хорошо и, таким образом, как будто подтверждают справед-
справедливость теории. Однако, как уже указывалось в § 33, выводы
классической теории на самом деле противоречат эксперименту.
Если, например, учесть степени свободы, относящиеся к отдельным
электронам, то общее число степеней свободы атома i оказалось
бы значительно большим, чем допускалось до сих пор. Степени
свободы, относящиеся к электронам, тоже должны бы дать свой
вклад в теплоемкость, так что она получилась бы много больше
той, которая наблюдается на опыте.
Таким образом, часть степеней свободы по некоторым причи-
причинам, неизвестным в классической статистике, не должна учиты-
учитываться. Об этом же говорит тот факт, что при охлаждении у неко-
некоторых газов, например у водорода, еще до конденсации наблюда-
наблюдается уменьшение теплоемкости, которое можно объяснить лишь
предположив, что число степеней свободы изменяется и вместо пяти
постепенно становится равным трем. Об этом эффекте говорят как
о случае, когда вращательные степени свободы «вымерзают».
С другой стороны, лишь у относительно простых многоатомных мо-
127
лекул, таких, как молекула воды Н2 или метана СН4, число степе-
степеней свободы равно шести. В более сложных молекулах, например
этилового спирта СгНвО, теплоемкость оказывается большей, чем
та, которая соответствует идеальному газу с шестью степенями
свободы. Этот факт сам по себе не удивителен и лишь означает,
что следует принять во внимание степени свободы, учитывающие
возможность относительного движения атомов в молекуле. Попыт-
Попытка количественного учета этих степеней свободы в рамках класси-
классической статистики не может привести к согласию с опытом. В об-
общих чертах это объясняется следующим.
Движение атомов относительно друг друга при тех малых сме-
смещениях, которые обычно имеют место в молекуле, можно достаточ-
достаточно точно описать, считая, что атомы связаны квазиупругими си-
силами. Поэтому на каждую степень свободы приходится энергия
кТ/2у соответствующая кинетической энергии, и kT/2 — потенциаль-
потенциальной. Полная средняя энергия оказывается, таким образом, пропор-
пропорциональной температуре, откуда следует, что теплоемкость при
постоянном объеме постоянна. Опыт убедительно показывает, что
это не так и что теплоемкость растет с ростом температуры.
Объяснение этих парадоксов классической статистической фи-
физики было получено лишь при учете квантовых эффектов.
Задачи к главе 6
1. Исходя из выражения для свободной энергии идеального одноатомного
газа, найдите работу, которую он совершает в изотермическом процессе,
расширяясь от V\ до \\.
Решение. По термодинамическому смыслу свободной энергии,
A=F1-F2.
Используя выражение C1.9), получаем
А = — RT — [in Vi + -|- In T + In Brtm0k e)8/*l +
М* L ~ J
-f RT — [in V2 + -~ 1п т + 1п Bято? е)8/*1 =
у. I 2 J
2. Исходя из выражения для энтропии идеального одноатомного газа, най-
найдите связь между температурой и объемом в адиабатическом процессе.
Решение. В адиабатическом процессе энтропия не меняется, поэтому
ЯГ — In №).
О
= Sx - S2= — R [in Vi + -j In Tx + In BxmQk eK/*l -
— — R [in V2 + 4r ln r2 + In Bnm0k e)8/al
или
In yx -h з/2 In Ti = In V2 + з/2 in T2t
т. e.
128
3. Найдите связь между температурой и объемом в адиабатическом процессе
для реального газа.
Решение. Из условия адиабатичности S=const с помощью D2.10) находим
— 1пГ+ In V— = const
2 p. V
или после потенцирования
Поскольку по предположению M6/(jxF)<Cl, то, ограничиваясь двумя первыми
членами разложения экспоненты в ряд, можно написать
Tl'*Ve » v= const.
или окончательно
const.
-— б) =
Таким образом, в соответствии с уравнением Ван-дер-В аальса газ ведет себя
так, как будто его свободный объем меньше объема сосуда на учетверенный
объем всех входящих в его состав молекул.
6-434
ЧАСТЬ III
КВАНТОВАЯ СТАТИСТИКА
РАВНОВЕСНЫХ СОСТОЯНИЙ
ГЛАВА 7
НЕКОТОРЫЕ СВЕДЕНИЯ
ИЗ КВАНТОВОЙ МЕХАНИКИ
§ 44. Квантовые свойства излучения
К концу XIX в. было установлено, что свет имеет электромаг-
электромагнитную волновую природу, однако в начале XX в. выяснилось, что
для объяснения целого ряда явлений необходимо также привлечь
представления о квазичастицах света — фотонах. Квантовые
свойства электромагнитного излучения проявляются при его вза-
взаимодействии с веществом (при поглощении, излучении и т. д.)
и состоят в том, что передача энергии и импульса от волны к ве-
веществу осуществляется конечными порциями. Так, например, энер-
энергия све]га определенной частоты v (определенной длины волны К)
поглощается и излучается порциями — квантами, энергия которых
определяется формулой
e = 2nftv, D4.1)
где Й=1,06-10~34 Дж-с=1,06-10~27 эрг-с — постоянная Планка.
Впервые необходимость введения представления о квантах была
осознана Планком при работе над теорией излучения черного тела.
Впоследствии она была подтверждена во многих других оптических
эффектах, таких, например, как фотоэффект, излучение атомов и
молекул и т. п.
По известному соотношению Эйнштейна, уже использовавшему-
использовавшемуся в гл. 5, энергия связана с массой:
г = тс2. D4.2)
Таким образом, если сопоставить с квантом световой энергии пред-
представление о некоторой световой частице, называемой фотоном,
то, поскольку скорость распространения света равна с, импульс фо-
фотона оказывается равным
130
Подставляя в последнее соотношение энергию фотона по D4.1),
получим
p=2ahv/c=2nhlb=kh9 D4.3)
где к=2ф D4.4)
— так называемое волновое число фотона.
Отметим, что квантовые свойства излучения проявляются не
столько в том, что электромагнитные волны следует рассматри-
рассматривать как поток частиц — фотонов, сколько в учете того, что волна
обменивается с веществом конечными порциями энергии и им-
импульса в соответствии с формулами D4.1) и D4.3).
§ 45. Волновые свойства частиц
Целый ряд опытных фактов убеждает нас в том, что не только
волны, в частности свет, обладают корпускулярными свойствами,
но и, наоборот, частицы обладают свойствами волн. Пожалуй, наи-
наиболее ярким подтверждением этого положения, высказанного впер-
впервые де Бройлем в 1923 г., является дифракция электронов.
Как известно, при прохождении волн через диафрагмы (щель)
на экране, установленном вдали от щели за собирающей линзой,
наблюдается чередование максимумов и минимумов интенсивно-
интенсивности в форме полос. Все полосы, соответствующие максимуму ин-
интенсивности, кроме центральной полосы, приходятся на область
геометрической тени.
Пусть на щель нормально к ней, т. е. вдоль направления, вы-
выбранного за направление оси г, подает плоская монохроматическая
световая волна, в которой вектор напряженности электрического
поля Е описывается выражением
E=E0cos(o>/ — kz)y
где Ео — амплитуда вектора напряженности, o) = 2nv — циклическая
частота, k = 2n/X — волновое число.
Уравнение волны может быть записано и в комплексной форме:
Из теории дифракции известно, что направление ср на первый ми-
минимум дифракционной картины определяется соотношением
sincp=X/a, D5. 1)
где а — ширина щели. Это соотношение можно пояснить следую-
следующим образом. Луч 2, проходящий через середину щели (рис. 7.1),
после дифракции в направлении ф обладает разностью хода
по отношению к лучу /, проходящему через край щели. Если вы-
выполнено условие D5.1), то разность хода А приводит к сдвигу по
5* 131
фазе между лучами, равному я, и, следовательно, попадая на экран,
лучи гасят друг друга. Нетрудно убедиться, что все лучи разбива-
разбиваются на пары, гасящие друг друга, если направление ф удовлетво-
удовлетворяет условию D5.1). Действительно, лучу V (рис. 7.1) можно со-
сопоставить луч 2\ проходящий на таком же расстоянии от луча 2,
на каком луч 1' проходит от луча 1. Разность фаз между ними то-
тоже равна л. Таким образом, взаимно гасятся все лучи, а направлен
ние ф действительно соответствует минимуму интенсивности. В
нижней части рис. 7.1 представлено распределение интенсивности
света на экране в зависимости
от угла ф.
В случае дифракции на двух
щелях распределение интен-
интенсивности получается иное, оно
не совпадает с суммой интен-
сивностей, имеющих место для
каждой из щелей по отдельно-
отдельности.
В опытах Дэвисона и Джер-
мера A927) впервые было об-
^ наружено, что при отражении
от кристаллов электроны тоже
Рис- 71 испытывают дифракцию. Впо-
Впоследствии в опытах В. А. Фаб-
Фабриканта, Н. Г. Сушкина и Л. М. Бибермана дифракция наблюда-
наблюдалась при столь малой интенсивности потока электронов, что было
исключено взаимодействие между ними и каждый электрон дифра-
дифрагировал самостоятельно. Явление дифракции электронов находится
в резком противоречии с обычным представлением о них как о клас-
классических частицах. Это противоречие особенно ярко проявляется
при интерпретации дифракционного опыта на двух щелях. То, что
картина дифракции на двух щелях отлична от той, которая полу-
получается на одной, связано с прохождением волны одновременно че-
через обе щели и в интерференции этих ее двух участков между со-
собой. С точки зрения классических представлений электрон-частица
проходит либо через одну, либо через другую щель, и совершенно
непонятно, почему на него при прохождении через одну щель влия-
влияет присутствие соседней, через которую он не проходил.
Для объяснения этого и целого ряда других эффектов при-
пришлось отказаться от механики классической и перейти к кванто-
квантовой, или волновой, механике. При учете волновых свойств каждой
частице, в частности электрону, сопоставляется некоторая волна.
Если ограничиться частицами, находящимися в бесконечно глубо-
глубоком потенциальном ящике достаточно большого объема У, то каж-
каждой частице можно сопоставить волну де Бройля, имеющую
вид
W=—L. е-'С-*-*). D5.2)
132
Частота со волны и ее волновой вектор к получаются обращением
формул D4.1) и D4.3), определяющих корпускулярные свойства
волн. Таким образом, имеем:
<o = e/ft, D5.3)
k = p/ft, D5.4)
где е — энергия частицы, р — ее импульс. Физический смысл
Ч'-волны, описывающей поведение частицы, состоит в том, что ве-
величина
dU7 = |T(r, 0|2dt D5.5)
равна вероятности обнаружить частицу в объеме Ах в окрестности
точки с радиус-вектором г в момент времени t. Для частицы в
потенциальном ящике из D5.5) с помощью D5.2) следует, что
т. е. вероятности пребывания частицы в любой точке одинаковы.
Объяснение дифракционного опыта состоит в том, что при па-
падении на щель волна де Бройля свободного электрона испытывает
дифракцию и в некоторых направлениях ее интенсивность (т. е.
вероятность обнаружить электрон) оказывается максимальной, а
в некоторых — минимальной.
Таким образом, частицы обладают волновыми свойствами, для
описания которых необходимо, в частности, каждой частице, нахо-
находящейся в бесконечно глубоком потенциальном ящике большого
объема V, сопоставить волну де Бройля D5.2) с частотой и волно-
волновым вектором, определенными формулами D5.3) и D5.4).
§ 46. Квантование излучения
Электромагнитное излучение, находящееся в полости с идеаль-
идеально проводящими стенками (металлическая полость), существует в
ней в форме стоячих волн опреде-
определенных частот. Частота волны опре-
определяется из условия, что на границе
со стенкой должен быть узел элек-
электрического поля (электрическое по-
поле равно нулю), так как в противном
случае в стенке протекает большой
ток и волна быстро затухает из-за
джоулевых потерь.
Пусть, например, имеется прямо-
прямоугольная металлическая полость со
сторонами а, Ь и с, выбранными со-
ответственно за направления х, у и
z прямоугольной системы координат (рис. 7.2). Если вдоль оси х
распространяется бегущая волна с напряженностью
133
Рис* 7*2
то, отражаясь от стенки полости, она порождает обратную бегу-
бегущую волну
где а — угол, характеризующий сдвиг фазы при отражении. Интер-
Интерференция Еу и Е2 дает стоячую волну
^ e^2 cos (kxx+— \
Пусть начало координат выбрано так, что первая стенка, перпенди-
перпендикулярная оси х, расположена при #=0, а вторая — при х=а, тог-
тогда должны иметь место следующие условия:
Е\Хвя0=2Е0 е-'»' e-/a/2 cos -J-=0,
Е\х„а = 2Е0 е"« е-/а/2 cos (kxa+~- ) = 0.
Из первого находим угол а. Поскольку cos (а/2)=0, то а = я.
Второе условие приводит к равенству
cos(kxa-\——\= — si
т. е. kx=—mx, D6.1)
а
где тх — произвольное целое число, тх=1, 2, ... Таким образом,
возможны не всякие значения волнового числа kXt а только те, ко-
которые удовлетворяют условию D6.1). Используя связь волнового
числа с длиной волны, найдем, что возможны лишь длины волн,
удовлетворяющие соотношению
™>х 2 — а>
т. е. на длине стороны полости должно укладываться целое число
полуволн.
Аналогичным образом, если бегущая волна распространяется
вдоль оси у, устанавливается стоячая волна, для которой
где ту тоже принимает произвольные целые значения /пу=1, 2, ...
То же самое имеет место для волны, направленной вдоль оси z:
kz = — mz D6.3)
с
(mz=l9 2, ...). Наконец, в общем случае, когда волна распростра-
распространяется в произвольном направлении, характеризуемом волновым
вектором к с компонентами [kXy kyi kz}> устанавливается стоячая
волна, для которой компоненты волнового вектора удовлетворяют
134
всем трем условиям D6.1), D6.2) и D6.3). Поскольку длина вол-
волны связана с волновым вектором соотношением 2лД=|к|, то для
возможных длин волн получаем следующий результат:
По ряду причин удобнее иметь дело не со стоячими, а с бегу-
бегущими волнами, для которых, в частности, справедливы важные
уравнения D4.1) и D4.3). Хотя каждая стоячая волна состоит из
двух бегущих, распространяющихся навстречу друг другу, но ам-
амплитуды этих волн равны друг друг, так что их нельзя считать не-
независимыми. Таким образом, число пар бегущих волн равно числу
возможных стоячих волн. Было бы удобно считать амплитуды бе-
бегущих волн независимыми друг от друга, но тогда число незави-
независимых переменных, описывающих электромагнитные колебания в
полости, т. е. амплитуд Ео, соответствующих каждому значению
вектора к, оказывается в два раза больше, чем должно быть. Ис-
Используют следующий выход из положения. Принимают, что на
длине стороны полости укладывается целое число длин волн, а не
целое число полуволн, как это в действительности имеет место, т. е.
вместо соотношений D6.1), D6.2) и D6.3) используют следующие:
kx=Bn/a)mx, ку={2ф)ту, k2=Bn/c)m2. D6.4)
Таким образом, число возможных длин волн оказывается в два
раза меньше, но зато теперь можно амплитуды соответствующих
ИхМ бегущих волн считать независимыми, так как при этом сохра-
сохраняется правильное число независимых переменных. По существу,
в этом методе две стоячие волны с близкими Я, относящиеся к двум
значениям k [например, kx= (п/аJтх, ky=0y kz=0 и kx=
= (л/а) B/ftx+l), ky = 0y kz = 0]y заменяются двумя бегущими в про-
противоположные стороны волнами с одним и тем же значением к
[kx= Bл/а)тх, ky=0, kz=0], но с независимыми амплитудами.
Если стороны полости много больше, чем длина интересующих нас
волн, то такая замена не приведет к большой ошибке. Поскольку
в конечном счете нас будет интересовать излучение в неограничен-
неограниченном пространстве, то в окончательных результатах следует перей-
перейти к пределу при сторонах а, &, с, стремящихся к бесконечности,
и тогда переход от стоячих волн к бегущим оказывается справед-
справедливым уже не приближенно, а точно.
Из сказанного выше ясно, что электромагнитное поле, сущест-
существующее в полости, может быть представлено в виде суммы, вооб-
вообще говоря бесконечной, стоячих волн определенных частот. Если
полость достаточно велика, то поле сводится к сумме бегущих
волн. Поскольку частота электромагнитных колебаний связана с
длиной волны соотношением со = 2ясД= |к|с, то при учете D6.4)
возможны частоты бегущих волн, которые определяются формулой
- <4б-5>
135
С математической точки зрения приведенный результат является
следствием теоремы Фурье и справедлив как в классической, так и
в квантовой теории.
Обратимся теперь к тому новому, что вытекает из квантовой
механики. Поскольку энергия монохроматической бегущей волны
передается конечными порциями — квантами, то следует заклю-
заключить, что полная энергия волны состоит из некоторого целого чис-
числа таких квантов, т. е.
е = 2nhvn = Ып, D6. 6)
где п=1, 2, ... Строго говоря, D6.6) относится только к той части
энергии, которая может быть взята или передана волне, и можно
предположить, что есть еще некоторая энергия во, которая связана
с волной, но не участвует в обмене. Для простоты в дальнейшем ео
не учитывается, так что D6.6) определяет полную энергию.
Поскольку энергия отдельной монохроматической волны при-
принимает согласно D6.6) дискретные значения, а все другие значе-
значения энергии невозможны, то это означает, что по квантовой теории
амплитуда плоской волны не произвольна, а должна быть такой,
чтобы удовлетворялось уравнение D6.6). Числа тх> ту, mz, опре-
определяющие волновой вектор к, называют квантовым и числа-
числами бегущей волны. Пусть эти числа принимают некоторые кон-
конкретные значения тхау туау mza> например тха=2, туа=5,
mza=3, тогда им соответствуют частоты юа, которые вычисляются
по формуле D6.5). Энергия плоской волны с этой частотой еа мо-
может иметь значение, вычисляемое по формуле D6.6), при со = сов
и некотором значении числа м, которое обозначим na, т. е.
Следовательно, бегущая волна, которой мы приписываем индекс а,
задается тремя квантовыми числами mxa, туа, mZ0L, определяющими
ее волновой вектор, и числом па, носящим название числа запол-
заполнения, которое задает ее энергию (амплитуду). Этот же результат
можно интерпретировать, исходя из представления о корпускулах
(частицах) излучения — фотонах. С последней 'точки зрения каж-
каждая бегущая волна представляет собой совокупность фотонов. Каж-
Каждый из фотонов обладает импульсом р, который в соответствии с
формулами D5.4) и D6.4) обладает компонентами
руа= hkya=hBл/b)туа, D6. 7)
pza=HkZ(l=tb Bл/с) тгл.
§ 47. Принцип неразличимости
Представление бегущей волны в виде некоторого числа квантов
обладает одной важной особенностью, которую легко пояснить на
следующем примере.
136
Предположим, что вода наливается в стакан или вычерпывает-
вычерпывается оттуда с помощью ковшика определенной емкости. Ясно, что
полное количество воды представляет собой целое число объемов
ковшика, т. е. можно сказать, что в стакане содержится п (п —
целое) ковшиков, или «частиц», воды. Вычерпывая воду, можно
вынуть одну, две или даже все п «частиц». Однако частицы воды
в одном отношении радикально отличаются от обычных классиче-
классических частиц. Действительно, хотя в стакане содержится п частиц,
но они безличны, т. е. их нельзя перенумеровать так, чтобы при
вычерпывании можно было утверждать, что извлечена частица с
данным номером, например третья. Таким образом, говоря о фото-
нах как о частицах, необходимо иметь в виду, что они неразличи-
неразличимы между собой.
Неразличимость частиц имеет существенное значение в различ-
различных статистических приложениях. Чтобы пояснить, в чем тут дело,
рассмотрим сначала стакан с реальными частицами, например ша-
шариками. Если встряхнуть стакан, то шарики изменят свои положе-
положения, так что, хотя общее число их не изменится, но все же получи-
получилось новое состояние, поскольку одни шарики переместились в по-
положение других. При встряхивании стакана с водой нельзя гово-
говорить о новом состоянии, так как само разбиение на «частицы» во-
воды условно.
Pi
21ГЬ
§ 48. Число состояний квантовой частицы
в элементе объема ^-пространства
Представление о фотонах позволяет рассматривать их в поло-
полости как идеальный газ квантовых частиц, находящийся в замкну-
замкнутом объеме. Учтем теперь, что не вся-
всякие состояния фотона возможны. Дей-
Действительно, импульс классической час-
частицы, заключенной в бесконечно глу-
глубокую потенциальную яму, может быть
любым, а для фотона допустимы лишь
значения импульса, соответствующие
формулам D6.7). Это различие стано-
становится более наглядным при рассмот-
рассмотрении пространства импульсов. Для
классических частиц любой вектор в
этом пространстве определяет возмож-
возможные значения импульса, а для фотонов
по D6.7) допустимы лишь векторы, у
которых компоненты по осям есть це-
целые, кратные одним и тем же величинам, а именно: 2nh/a для оси
Рзс, 2nh/b для оси ру и 2лН/с для оси рг (рис. 7.3). Таким образом,
концы векторов импульса фотона образуют в импульсном про-
пространстве прямоугольную решетку. Каждому вектору решетки, т. е.
каждому ее узлу, соответствует элементарный параллелепипед с
объемом
\/
Рис. 7.3
137
D8.
Хотя объем AQ и конечен, но с точки зрения наших обычных
макроскопических представлений он очень мал. Так, например, в
кубической полости с размером а=\ см сторона AQ равна 2яН/а,
т. е. порядка 6,6• 10~27 г-см-с*1. Фотоны с такой разницей в им-
импульсе мало отличаются по длине волны, а именно:
р ) р°- 2кП а
Это соответствует относительной разности длин волн
Даже для световых волн инфракрасного диапазона (Х~ 1-МО мкм)
получается очень малая величина A0~~4—10~5). Следует отметить,
что выбранные две длины волны не являются соседними, так что
разность между соседними длинами волн оказывается еще во мно-
много раз меньшей. Таким образом, хотя в действительности импуль-
импульсы и соответствующие им длины волн фотонов дискретны, но с
макроскопической точки зрения их можно рассматривать как прак-
практически непрерывные величины.
Возникает вопрос о числе состояний, приходящихся на элемент
объема пространства импульсов dQ, который хотя и считается
бесконечно малым с точки зрения наших макроскопических пред-
представлений, но фактически много больше, чем AQ. Искомое число
состояний dG равно числу тех векторов импульса, которые закан-
заканчиваются в dQ, и приближенно вычисляется, как частное от деле-
деления dQ на AQ:
!^E2y. D8.2)
Этот результат тем точнее, чем больше dQ по сравнению с AQ. Воз-
Возможна несколько другая интерпретация соотношения D8.2). Ве-
Величина dY=dQV представляет собой элемент объема |л-простран-
ства. Выражение D8.2) можно представить в виде
dG = dY/BrtfcK, D8.3)
откуда следует, что число состояний, приходящихся на элемент
объема ^-пространства, определяется формулой D8.3).
Нетрудно показать, что приведенный результат носит весьма
общий характер. Рассмотрим, например, часть dV полного объема
сосуда и прежний объем пространства импульсов dQ. Им соответ-
соответствует фазовый объем
отличающийся от предыдущего. Сколько состояний приходится на
dy? Выделенную малую часть пространства dV следует рассматри-
138
вать как новый сосуд с меньшими размерами стенок. В нем эле-
элементарная ячейка Д?2 в соответствии с D8.1), имеет другой, боль-
больший размер, а именно
dV
Число состояний оказывается равным
ид?— dQ — dQdV dY
Bл;/гK
В новом элементе фазового объема число состояний меньше, чем
в том, который рассматривался раньше, так как объем dV меньше,
чем V. Зато в общем объеме V число малых объемов dV равно
V/dV, так что общее число состояний сохраняется прежним и при
таком расчете.
§ 49. Квантование в случае частиц
Рассмотрим частицы, находящиеся в потенциальном ящике.
В квантовой механике их поведение во многом аналогично тому,
что имеет место для излучения. Как уже говорилось в § 45, каж-
каждой свободной частице сопоставляется волна де Бройля, т. е. не-
некоторая монохроматическая волна. В бесконечно глубоком потен-
потенциальном ящике устанавливаются стоячие волны, причем на длине
стороны ящика должно укладываться целое число полуволн. Так
же как и в случае излучения, оказывается более удобным заменить
стоячие волны на бегущие и для сохранения правильного числа
независимых переменных считать, что возможны независимые вол-
волны, бегущие в противоположные стороны, но что на длине стороны
ящика укладывается целое число волн. Другими словами, для
частиц, как и для волн, имеют место соотношения D6.7), зада-
задающие возможные значения компонент импульса. Для них справед-
справедлива и формула D8.3), определяющая число состояний, приходя-
приходящихся на элемент объема [х-пространства.
Из классической механики известна связь между импульсом
и энергией частицы: е=р2/Bт0), так что возможные значения
энергии равны
е = -
Квантовая механика приводит к неожиданному с точки зрения
классических представлений выводу. Оказывается, что реальные
тождественные частицы, так же как и фотоны, подчиняются прин-
принципу неразличимости. Этот факт является отражением волновых
свойств частиц и подтверждается экспериментом.
Все имеющиеся в природе частицы разбиваются на две прин-
принципиально отличающиеся друг от друга группы. Они классифи-
классифицируются по собственному моменту количества движения, который
первоначально и, как выяснилось впоследствии, слишком упрощен-
139
но считался моментом количества движения во вращательном
движении частицы вокруг своей оси. Оказывается, что для одних
частиц проекция момента на некоторую произвольно выбранную
ось может принимать лишь полуцелые значения постоянной План-
Планка Я, а для других — только целое. Так, например, для электронов
возможны лишь два значения собственного момента количества
движения, или, как говорят иначе, спина, а именно: +Я/2 и —Я/2,
а для фотонов — значения +Я и —Я. Частицы с полуцелым зна-
значением спина носят название частиц Ферми или фермионов,
а частицы с целым спином — частиц Бозе или бозонов.
Принципиальная разница между ними состоит в следующем.
Фермионы подчиняются принципу Паули, по которому в состоянии
с определенными значениями квантовых чисел и спина может на-
находиться лишь одна частица. Так, например, в состоянии с неко-
некоторыми значениями квантовых чисел тХу туу тг, т. е. в состоянии
с данным импульсом, может находиться не более двух электронов,
причем они должны отличаться друг от друга тем, что у одного
спин равен +Я/2, а у другого —Я/2. Бозоны не подчиняются прин-
принципу Паули, и в каждом состоянии может находиться сколько
угодно частиц Бозе.
ГЛАВА 8
БОЛЬШОЕ КАНОНИЧЕСКОЕ
РАСПРЕДЕЛЕНИЕ
§ 50. Каноническое распределение
в квантовой статистике
В классической статистике распределение Гиббса, или, как его
называют, каноническое распределение, имеет вид
Оно дает вероятность того, что система находится в одном из со-
состояний, описываемых точкой в элементе объема фазового про-
пространства dr.
В квантовой механике система тоже может находиться в раз-
различных состояниях с разной энергией, но в отличие от классиче-
классической механики эти состояния дискретны, т. е., например, есть
состояние с энергией S\ и есть состояние с энергией <^2, но нет со-
состояний с энергией, промежуточной между &х и <В%
В дальнейшем будут иметься в виду только системы типа иде-
идеального газа, т. е. совокупности частиц, силовым взаимодействием
между которыми можно пренебречь. Такие системы достаточно
просты, так что можно получить окончательные результаты в про-
простой форме, а с другой стороны, модель идеального газа довольно
140
часто оказывается хорошим приближением к реальным физиче-
физическим системам.
В идеальном газе высказанное выше утверждение становится
особенно очевидным. Обозначим через 8ь 82, ... энергии состояний
отдельных частиц, а через п\у п2, ...— числа заполнения этих со-
состояний, т. е. число частиц в данном состоянии. Для энергии всей
системы можно написать
где &v — энергия системы в состоянии с номером v, в котором п\
частиц имеют энергию еь ^2 — энергию е2 и т. д. Таким образом,
состояния системы в целом могут быть перенумерованы указанием
всех чисел заполнения
а при переходе от одного состояния к другому энергия принимает
значения, отличающиеся на целое число величин еь г2 и т. д.
Распространение распределения Гиббса на квантовую механику
сводится к утверждению, что вероятность состояния v с энергией
S'y равна
E0Л)
Здесь F* — свободная энергия квантовой системы. Она определя-
определяется условием нормировки, т. е. условием, что вероятность нахож-
нахождения системы в каком-либо из всех состояний равна единице:
1. E0.2)
Поскольку из E0.2) следует, что
^е =1,
то, вводя понятие статистической суммы
__ ср 1 (Ъ,Т\
Z*=>e , E0.3)
V
можно написать
F*=-kTlnZ*. E0.4)
Таким образом, если известно, как устроена система, т. е. если
известны энергии <§v всех ее возможных состояний, то с помощью
E0.3) можно вычислить статистическую сумму, а тогда по E0.4)
находится свободная энергия этой системы.
Формулы E0.1), E0.3) аналогичны выражениям C0.5) и C0.6),
однако между ними имеется и существенная разница. Различие вы-
вызвано двумя причинами.
Во-первых, в классической механике состояния системы обра-
141
зуют непрерывную последовательность, т. е., говоря языком тео-
теории вероятностей, состояние системы есть непрерывная случайная
величина (точнее, энергия состояния есть непрерывная случайная
величина), а в квантовой механике состояния дискретны.
Во-вторых, при квантовомеханическом рассмотрении следует
учитывать принцип неразличимости, а для частиц Ферми еще и
принцип Паули.
Таким образом, свободная энергия i7*, рассчитанная квантово-
механически, не совпадает со свободной энергией F, вычисленной
классически. С одной стороны, эта разница отражает реальное от-
отличие, вызванное тем, что на самом деле точны законы квантовой
механики, а классические закономерности являются приближением
к действительности, далеко не всегда оправдывающимся для си-
систем микрочастиц. С другой стороны, бывают системы, в которых
учет принципа неразличимости и принципа Паули несуществен.
Поскольку в большинстве случаев системы, представляющие прак-
практический интерес, состоят из очень большого числа микрочастиц,
так что число возможных состояний громадно, а отличие между
близкими состояниями очень мало, то с большой степенью точно-
точности их можно считать распределенными непрерывно. Ясно, что
тогда должна существовать связь между квантовым и классиче-
классическим распределениями Гиббса, а также между свободными энер-
энергиями F* и F. Эта связь будет позднее установлена на примерах
конкретных систем частиц Бозе и Ферми, а пока отметим лишь
один общий прием, который при этом используется, а также важ-
важное следствие, которое из него вытекает.
Итак, пусть состояния системы дискретны, а учет принципа Па-
Паули и принципа неразличимости несуществен. Каждое возможное
состояние системы представляется точкой в фазовом Г-простран-
стве. В случае дискретного распределения эти точки находятся на
некотором расстоянии друг от друга. Обозначим через g"r числа
дискретных состояний, приходящихся на единицу объема Г-про-
странства, и назовем g? плотностью состояний в Г-пространстве.
На элемент объема dr при этом придется
E0.5)
состояний.
Пусть элемент dr выбран настолько малым, что вероятность
всех состояний, принадлежащих ему, практически одинакова. По-
Поскольку по распределению Гиббса вероятность зависит от энергии,
то для этого достаточно, чтобы энергии состояний, входящих в dr,
отличались на величину, много меньшую kT. Предположим так-
также, что, несмотря на малость выбранного объема dF, число при-
приходящихся на него возможных дискретных состояний достаточно
велико, тогда статистическая сумма E0.3) может быть вычисле-
вычислена следующим образом.
Разобьем все состояния, изображаемые точками в Г-простран-
стве, на группы, принадлежащие объемам dl\-, и проведем сумми-
суммирование в два этапа: сначала по состояниям внутри отдельных
142
объемов dr^./^M, а затем сложим результаты, полученные для
различных объемов, т. е. напишем
Сумма в круглых скобках вычисляется очень просто. Действи-
Действительно, по предположению, значение экспоненты для всех слага-
слагаемых этой суммы одно и то же, так что значение суммы равно
этой величине, умноженной на число членов суммы, т. е. на число
состояний в объеме dl\, или с учетом E0.5)
2 gT dr.
Таким образом,
*
Z
Вычисление второй суммы по различным элементам с!Гг есть не что
иное, как интегрирование по dr, так что
T. E0.6)
Видно, что выражение E0.6) отличается от статистического ин-
интеграла C0.8)
Z= j e-»/(*n dr
множителем g"r. Поскольку gv — постоянная величина *), то
Z*=gTZ. E0.7)
Для свободной энергии теперь получается
E0.8)
Из последней формулы видно, что свободная энергия, определен-
определенная по E0.4), не совпадает со свободной энергией, определенной
классически по C0.7). Сказывается ли эта разница при определе-
определении наблюдаемых на опыте величин?
*) По D8.3) число состояний одной из частиц системы в ее (л-пространстве
равно с!у/BлйK. Число состояний системы равно произведению числа состояний
отдельных частиц, так что
dr==
яЬK BяЬ)з
Поскольку dr=dvidY2 ••• dyN> то
143
Начнем с термодинамического смысла свободной энергии. Изме-
Изменение свободной энергии в изотермическом процессе AF*y когда вто-
второй член в правой части E0.8) постоянен, равно изменению А/7,
т. е. работе, совершаемой системой в изотермическом процессе, но
взятой с обратным знаком,
t= - АЛ. E0. 9)
Если продифференцируем E0.8) по объему, то найдем
Таким образом, уравнение состояния определяется тем же самым
уравнением.
Для внутренней энергии получаем
E0.11)
дТ
т. е. уравнение Гиббса — Гельмгольца сохраняет свой вид.
Если по аналогии с C9.1) определить энтропию соотношением
5*= —^1, E0. 12)
то легко показать, что это определение приводит к значению энтро-
энтропии, отличающемуся от того, какое следует из выражения C9.1),
на постоянную величину. Действительно,
дТ дТ
На этом различии следует остановиться несколько подробнее.
§ 51. Энтропия и третье начало термодинамики
В § 39 был выяснен статистический смысл энтропии. Получен-
Полученный там окончательный результат страдает одним существенным
недостатком, и для того, чтобы разобраться в этом вопросе, мы
вновь повторим сделанный ранее вывод, но применительно к кван-
квантовому распределению Гиббса.
Из уравнения Гиббса — Гельмгольца и определения энтропии
S* по E0.12) следует
S*=(U-F*)/T.
Но внутренняя энергия есть среднее значение энергии системы, т. е.
144
поэтому, используя условие нормировки, можно написать
-S-
т
Умножив и разделив на постоянную Больцмана, получим
MnW\, E1.
т. е. энтропия равна среднему значению логарифма вероятности со-
состояния системы. Из формулы E1.1) видно, что поскольку вероят-
вероятность есть безразмерная величина, то энтропия совпадает по раз-
размерности с постоянной Больцмана. Несколько другое положение
имеет место в случае формулы C9.1)
5= — k\
которая отличается тем, что вместо вероятности Wv входит плот-
плотность вероятности w и суммирование заменяется интегрированием.
Поскольку плотность вероятности есть величина с размерностью,
обратной элементу фазового объема, то под интегралом стоит ло-
логарифм от размерной величины, т. е. размерность энтропии оказы-
оказывается более сложной, чем в предыдущем случае. Легко видеть, что
разница между E1.1) и C9.1) получается по следующей причине.
Правильный переход от дискретного квантового случая к клас-
классическому непрерывному должен состоять в замене вероятности Wy
на вероятность wdT того, что система находится в одном из состоя-
состояний, принадлежащих dT. Тогда из E1.1) получается
5*=— Л2 wdrin(wdr) = — k
dr есть физически бесконечно малый объем фазового простран-
пространства. Если считать, что все элементы dr, на которые разбито фа-
фазовое пространство, одинаковы, то при учете условия нормировки
последнеее слагаемое примет вид
-k J
Следовательно, строгий переход от E1.1) к непрерывному распре-
распределению приводит к формуле, отличающейся от C9.1) на некото-
некоторую постоянную:
S*=—k f ^lnwdr — А1п(AГ)=— k f адlna;dr +const.
145
Постоянная зависит от величины фазового объема, который выбран
за бесконечно малый элемент интегрирования, т. е, фактически она
произвольна. Таким образом, классически энтропия определяется
всего лишь с точностью до произвольной постоянной. Это не ме-
мешает, если, как это обычно бывает, интересуются разностью зна-
значений энтропии в двух состояниях, поскольку при вычитании посто-
постоянная исключается, однако формула C9.1) не дает абсолютного
значения энтропии.
Существуют ли экспериментальные факты, говорящие о преиму-
преимуществе того или иного выражения для энтропии? Оказывается, да.
Поведение ряда термодинамических величин согласуется с предпо-
предположением о том, что при охлаждении энтропия убывает и что ее
значение при абсолютном нуле равно нулю. Таким образом, неоп-
неопределенная постоянная, о которой шла речь выше, должна быть
выбрана так, чтобы выполнялось равенство
Это условие играет важную роль в термодинамике и получило на-
название третьего начала. Легко показать, что третье начало
есть следствие определения энтропии выражением E1.1), учиты-
учитывающим квантовую дискретность состояний, если только предпо-
предположить, что основное состояние системы не вырождено, т. е. име-
имеется только одно основное состояние с наименьшим значением энер-
энергии.
Действительно, пусть ближайшее по энергии состояние облада-
обладает энергией, большей на bJS. Из распределения Гиббса E0.1) тогда
следует, что при охлаждении до температур настолько низких, что
&Г<СД<?\ вероятность всех состояний, кроме основного, будет нич-
ничтожно мала. При Г = 0 вероятность основного состояния равна еди-
единице, а всех остальных — нулю. В этом случае сумма V W\lnW\»
определяющая энтропию, обращается в ноль.
Таким образом, учет квантовых эффектов приводит к правиль-
правильному выражению для энтропии, имеющему вид E1.1), из которого,
в частности, для реальных систем вытекает равенство энтропии ну-
нулю при 7 = 0, т. е. третье начало термодинамики.
§ 52. Принцип максимума энтропии
Энтропия при ее правильном определении квантовой формулой
E1.1) с точностью до множителя k совпадает с A2.1) и, следова-
следовательно, является мерой неопределенности или хаотичности макро-
макроскопического состояния системы. Важным принципом, справедли-
справедливость которого вытекает из распределения Гиббса, а также уста-
устанавливается по совпадению всех сделанных на его основе выводов
с опытом, является принцип максимума энтропии. Энтропия опреде-
определяется формулой E1.1) ив равновесном состоянии достигает мак-
максимального значения, совместимого с теми условиями, в которых
146
находится система, т. е. равновесное состояние соответствует наи-
наиболее хаотическому или неопределенному из всех возможных. Этот
принцип можно положить в основу статистической физики равно-
равновесных состояний, так как из него, в частности, вытекает распре-
распределение Гиббса.
Посмотрим, при каком значении вероятностей отдельных состоя-
состояний Wv энтропия достигает максимального значения. Для этого
необходимо воспользоваться правилом нахождения экстремума
и учесть, что вероятности Wv связаны условием нормировки E0.2):
\=1- E2.1)
По общему методу неопределенных множителей Лагранжа соста-
составим функцию
где Х\ — неопределенный множитель Лагранжа. После дифферен-
дифференцирования f(Wv) по каждой из переменных Wy и приравнивания
производных нулю получается система уравнений, из которых v-e
имеет вид
т. е.
mrv=-A + ^-1,
откуда
где значение постоянной определяется из условия нормировки.
Таким образом, вероятности всех состояний оказываются оди-
одинаковыми. Поскольку число состояний системы бесконечно велико,
то из условия нормировки Wv-+0. Для значения энтропии при учете
равенства всех Wv получается
При Wv, стремящемся к нулю, — In Wv стремится к бесконечности,
так что значение энтропии оказывается бесконечным.
Этот результат противоречит опытным фактам и распределению
Гиббса, по которому вероятности состояний с различной энергией
не одинаковы. Он получился потому, что не было учтено одно важ-
важное обстоятельство. В реальных условиях система, находящаяся
r равновесии, не изолирована, а находится в контакте с окружаю-
окружающей средой. Обычно вводят понятие о термостате как о системе,
которая взаимодействует с рассматриваемой, но настолько велика,
что воздействие изучаемой системы не в состоянии вывести термо-
147
стат из равновесного состояния. Так как равновесие наблюдается
при контакте с термостатом, то изучаемая система непрерывно об-
обменивается с ним энергией. Поэтому хотя энергия и не постоянна,
но ее среднее значение, т. е. внутренняя энергия, имеет строго оп-
определенную величину. Следовательно, отыскивая значение вероят-
вероятностей Wv, необходимо наложить дополнительное условие следую-
следующего вида:
E2.2)
При нахождении максимума теперь составляем функцию
где %2 — Другой неопределенный множитель Лагранжа. После диф-
дифференцирования получаем уравнение вида
откуда следует
Если постоянную Хг обозначить через 1/71, а Х\ — через —[(F*/T)-h
&], то вероятность состояния v равна
т. е. совпадает с распределением Гиббса. Свободная энергия, вве-
введенная формально через множитель Х\у и температура, введенная
через множитель Яг, определяются условием нормировки E2.1)
и уравнением E2.2):
= U. E2. 3)
При выявлении связи между свободной энергией, температурой
и внутренней энергией оказывается удобнее считать заданной не
внутреннюю энергию, а температуру. Из написанных выше уравне-
уравнений F* и U могут быть вычислены как функции Т (и объема V).
§ 53. Вывод большого канонического
распределения Гиббса
Положив в основу принцип максимума энтропии, можно полу-
получить распределение более общее, чем распределение Гиббса, кото-
которое рассматривалось до сих пор. Это тот случай, когда число ча-
частиц, составляющих систему, может меняться. Так, например, если
в замкнутом сосуде находится газ с определенным числом моле-
молекул, то можно мысленно выделить небольшой объем и рассматри-
рассматривать в качестве системы газ, находящийся в этом объеме. Молеку-
Молекулы могут влетать в выделенный объем и вылетать из него, так что
148
точное значение числа молекул не определено, но в равновесии их
среднее число остается одним и тем же. Мы сразу учтем квантовую
дискретность состояний, так как из изложенного выше видно, что
такой подход оказывается более последовательным.
Обозначим через W?N вероятность vjv-го состояния системы, со-
состоящей из N частиц. Тогда максимум энтропии будет соответство-
соответствовать такому распределению, которое дает максимум выражению
при дополнительных условиях
"N
где <N> — среднее число частиц в данной системе. Составим
функцию
После дифференцирования по W?N получим уравнение
решение которого имеет вид
или если обозначить
то
Формула E3.1), дающая вероятность того, что система, находящая-
находящаяся в равновесии с термостатом, содержит N частиц и обладает энер-
энергией $»N) носит название большого канонического распределения
Гиббса.
Формально введенные величины Q*, Гиц определяются из ус-
условий
^2^*^+>т \, E3.2)
149
^N ^NU, E3.3)
2 W*sN=*?NS*-**»*™1™ =(N). E3. 4)
Вместо того чтобы определять значения \i и Г, соответствующие
данному значению внутренней энергии U и среднему числу частиц
<N>, можно считать их заданными и тогда по E3.2), E3.3)
и E3.4) найти Q*, и U и <N> как функции \х и Т (а также объема
системы V).
§ 54. Термодинамический смысл параметров Q*, \i, T
При том способе вывода большого канонического распределе-
распределения Гиббса, который был использован выше, величины Q*, [i и тем-
температура Т появились как некоторые постоянные, поэтому следую-
следующей задачей является выяснение физического смысла этих парамет-
параметров. Для этого можно с помощью E3.2), E3.3), E3.4) попытать-
попытаться получить некоторые уравнения, связывающие их между собой,
и сопоставить полученные уравнения с другими, известными из
термодинамики, т. е. в конечном счете из эксперимента. Такой путь
предполагает хорошее предварительное знакомство с термодинами-
термодинамикой, а поэтому проще, опираясь на аналогию с обычным распреде-
распределением Гиббса, признать, что Т — это температура, а п* — некото-
некоторая функция Т и [г, аналогичная свободной энергии, которую назо-
назовем ом ега~гГ6т е н ц и а л о м. Уравнения E3.2), E3.3), E3.4)
можно тогда использовать для вывода термодинамических урав-
уравнений.
Следуя этой программе, начнем с выяснения условий, при кото-
которых две равновесные системы находятся в равновесии между собой.
Пусть одна система описывается большим каноническим распре-
распределением
W', =e *N' , E4. 1)
VAT'
а вторая — распределением
(Q*"-%\ +v."N»)/(kT»)
W"* =e *N' . E4.2)
Предположим, что энергия взаимодействия этих систем между со-
собой и с термостатом много меньше, чем энергия самих систем. Если
рассматривать их как единую систему, то они подчиняются боль-
большому каноническому распределению, которое можно записать
в виде
W,N=er-^N»(kT\ E4.3)
Поскольку мы пренебрегли взаимодействием систем, то вероятность
любого состояния первой системы не зависит от того, каково со-
150
стояние второй. Кроме того, каждое состояние общей системы мож-
можно рассматривать как некоторое состояние первой и некоторое не-
независимое состояние второй, так что каждый номер vn соответст-
соответствует каким-то VJV и viv», причем
E4.4)
т. е. общее число частиц равно сумме частиц в каждой из состав-
составляющих систем, а общая энергия — сумме энергий.
Если состояния подсистем независимы, то в соответствии с ос-
основными положениями теории вероятностей вероятность состояния
сложной системы равна произведению вероятностей состояний со-
составляющих ее подсистем:
W,=W'. W\ . E4.6)
Подставляя в E4.6) значения вероятностей E4.1), E4.2) и E4.3),
можно получить
или, используя E4.4) и E4.3),
е v"' =e e
Поскольку последнее равенство должно выполняться тождест-
тождественно для всех значений #/,#», N'9 N", то это означает, что
должны выполняться следующие равенства:
Т=Т = Т\ E4.7)
|i = p' = p", E4.8)
' \ -E4.9)
Таким образом, для равновесия двух систем необходимо, чтобы
были равны их температуры Т и параметры \i (называемые хими-
химическими потенциалами). Кроме того, омега-потенциал сложной
системы оказывается равным сумме омега-потенциалов составляю-
составляющих систем.
Из изложенного выше видно, что химический потенциал играет
по отношению к числу частиц такую же роль, какую температура
играет по отношению к энергии. Так как у всех систем, нахо-
находящихся в равновесии с данным термостатом, температуры и хими-
химические потенциалы имеют одинаковое значение со значением этих
величин для термостата, то можно считать, что они являются ха-
характеристиками термостата, а не отдельных находящихся с ним в
151
равновесии систем. Именно поэтому целесообразно считать задан-
заданными ц, и 7, а другие величины, описывающие данную систему (ее
омега-потенциал, внутреннюю энергию и т. д.), определять как
функцию этих параметров.
Целый ряд важных термодинамических соотношений может
быть получен из условия нормировки. Так, например, после диффе-
дифференцирования E3.2) по химическому потенциалу \х получится
| kT \ ду.
S
или, если использовать E3.4),
?! E4.10)
Таким образом, производная от омега-потенциала по химическому
потенциалу, взятая с обратным знаком, равна среднему числу ча-
частиц в системе.
Дифференцирование условия нормировки по температуре при-
приводит к уравнению, аналогичному уравнению Гиббса — Гельмголь-
ца в системе с постоянным числом частиц. Имеем
0= J_ e V
Полученное выражение можно записать в виде
N kT2
Если умножить последнее уравнение на kT2 и использовать соот-
соотношения E3.2), E3.3) и E3.4), то
дт
т. е. U=Q*
или окончательно
U=Q* — T [х . E4. И)
152
Выражение E4.11) позволяет вычислять внутреннюю энергию по
омега-потенциалу и является обобщением уравнения Гиббса —
Гельмгольца на системы с переменным числом частиц.
Дифференцируя условие нормировки по объему У, найдем
E4.12)
Здесь учтено, что при изменении объема подсистемы, находящейся
в равновесии с термостатом, температура и химический потенциал,
которые определяются термостатом, остаются постоянными, а энер-
энергия системы из-за взаимодействия со стенками меняется. Чтобы
более конкретно представить себе рассматриваемый случай, будем
считать, что подсистема — это газ, заключенный в цилиндр с по-
подвижным поршнем. В боковой стенке цилиндра имеется отверстие,
через которое газ сообщается с другим большим сосудом, запол-
заполненным тем же газом (термостат). При перемещении поршня на dx
объем подсистемы (газа в цилиндре) изменяется на dF, где
dV=Sdx
(S — площадь поршня). Для производной энергии по объему мож-
можно написать
dV S дх
Подразумевается, что изменение энергии d%?N при смещении пор-
поршня на dx происходит при постоянном числе частиц N. Оно равно
работе силы, сжимающей систему, которая находилась в состоянии
Viv, поэтому
При этом система по третьему закону Ньютона действует на пор-
поршень с равной по величине, но противоположной по направлению
силой
р р' N_
r*N~ r>N~ дх '
Следовательно, из E4.12) вытекает
dv
N
где <F> — среднее значение силы для всех возможных состояний.
Средняя сила, деленная на площадь, есть не что иное, как давле-
давление Pt оказываемое системой на поршень, так что
Я=-^. E4.13)
dV v '
153
Таким образом, давление равно производной от омега-потенциала
по объему, взятой с обратным знаком.
Установим, наконец, связь омега-потенциала с энтропией. Из
общего выражения для энтропии при учете большого каноническо-
канонического распределения следует
Если воспользоваться условиями E3.2), E3.3) и E3.4), то
5*= L(Q*_?/4-i*(iV>). E4.14)
С помощью обобщенного уравнения Гиббса—Гельмгольца послед-
последнее уравнение можно записать в следующем виде:
^=-^, E4.15)
т. е. энтропия равна производной от омега-потенциала по темпера-
температуре, взятой с обратным знаком.
Рассмотрим, чему равно изменение энтропии в некотором обра-
обратимом процессе, в котором бесконечно мало меняются объем V,
температура Т и химический потенциал |х. Имеем из E4.14)
Это можно записать в виде
Т2 \ дТ ) Т \ дТ Г ф. Г ' 6V
Если учесть E4.10) и привести подобные члены, то
Первое слагаемое в правой части по E4.13) есть не что иное, как
работа ДЛ, совершенная системой. Поскольку по второму началу
термодинамики количество тепла, сообщенного системе, равно
то для изменения внутренней энергии находим
E4. 16)
Таким образом, в системе с переменным числом ча-
частиц изменение внутренней энергии происходит не только за
счет перехода тепла и совершения работы, но и за счет изме-
изменения среднего числа частиц. Если объем системы не меняется
(ДУ=дА = 0) и система адиабатически изолирована (AS* =
154
= AQ = O), то из E4.16) следует \x = AU/A<N>, т. е. химический
потенциал есть изменение внутренней энергии, связанное с поступ-
поступлением одной частицы в процессе, в котором AV и AS* равны нулю.
Омега-потенциал есть функция объема системы, а также темпе-
температуры и химического потенциала. В тех случаях, когда задано
среднее число частиц, а не химический потенциал, удобнее иметь
дело с другой термодинамической функцией, определяемой урав-
уравнением
F*=Q* + p(N). E4.17)
При изменении условий (объема, температуры, среднего числа ча-
частиц) функция F* испытывает изменение, равное
Поскольку d2 dr +
где учтены соотношения E4.13), E4.10) и E4.15), то
E4.18)
При неизменном среднем числе частиц и температуре изменение
введенной функции равно
т. е. работе с обратным знаком. Это дает основание по аналогии
с определением, приведенным в § 37, назвать функцию F* свобод-
свободной энергией. Из E4.18) видно, что ее удобно использовать в тех
случаях, когда за независимые переменные приняты объем, темпе-
температура и среднее число частиц. Системы с заданным числом ча-
частиц можно рассматривать как системы с заданным средним чис-
числом частиц, поэтому E4.17) является непосредственным обобщени-
обобщением свободной энергии, рассмотренной ранее.
Если температура и объем системы не меняются, а среднее чис-
число частиц увеличивается на dN, то по E4.18) свободная энергия
получает приращение
Из последнего равенства вытекает, что
E4.19)
dN
т. е. что с термодинамической точки зрения химический потенци-
потенциал — это изменение свободной энергии системы, связанное с добав-
добавлением к ней одной частицы при условии, что объем и температура
постоянны.
155
Из E4.18) видно, что при постоянных <N> и V
?L = -S; E4.20)
а при постоянных <N> и Т
— =-/>. E4.21)
Эти соотношения вполне аналогичны равенствам C6.12) и C9.1).
Задача к главе 8
1. Исходя из выражения для омега-потенциала идеального одноатомного
классического газа
где
r J m W2
найти основные термодинамические характеристики этой системы (вывод
формулы для омега-потенциала приведен в гл. 10).
Решение, а) Среднее число частиц находится по E4.10):
<N>= _ J^l= {kTft еР/(*П ус.
дц
Отсюда, в частности,
где л=<Л^>/У — концентрация частиц.
б) Уравнение состояния находится по E4.13):
р= _
oV
Если исключить jx с помощью полученного выше выражения, то
Р= nkT.
в) Внутренняя энергия подсчитывается по E4.11):
dQ* dQ* 5 fJt a
или, если использовать выражение для среднего числа частиц,
г) Для энтропии по E4.14) получается
156
Если принять во внимание связь Q* и <N>, а также выражение для [Л, то
Ч2Т \С (kTf2 )\
Последнее соотношение можно переписать в виде
S* = k {N) ["in К + -|- In Г + сЛ,
где
3 5
Ci= 1пС + — 1п& ——— ln<W>,
для чего достаточно было использовать определение концентрации n—<N>IV.
Окончательное выражение для энтропии полезно сравнить с тем, которое
было получено раньше для фиксированного числа частиц в § 39. Видно, что оба
выражения отличаются лишь на постоянную величину.
ГЛАВА 9
СТАТИСТИКА БОЗЕ — ЭЙНШТЕЙНА
§ 55. БОЗОНЫ
Как уже говорилось в гл. 7, бозонами называются частицы со
спином ноль или целым (в единицах Я). К ним относятся:
1) мезоны (/Сил), спин которых равен нулю;
2) некоторые атомы, у которых спин составляющих их электро-
электронов, протонов и нейтронов складывается таким образом, что резуль-
результирующий спин оказывается целым (примером может служить
Не2);
3) фотоны (спин 1);
4) фононы (кванты звуковых волн, спин 1).
Нас в основном будут интересовать фотоны, так как мезоны
представляют собой очень короткоживущие частицы (время жизни
10~8 с), роль которых в рассматриваемых нами процессах обычно
несущественна; атомы же обладают настолько большой массой, что
к ним чаще всего можно применять классическую статистику. Впро-
Впрочем, при очень низких температурах нужно учитывать квантовые
эффекты.
Для вещества, находящегося в твердом состоянии, где атомы
образуют кристаллическую решетку, задача сводится к изучению
колебаний решетки или, другими словами, к изучению свойств зву-
звуковых волн или звуковых квантов — фононов.
В настоящей главе совокупность бозонов рассматривается как
идеальный газ, т. е. предполагается, что между частицами нет вза-
взаимодействия.
157
§ 56. Распределение Бозе — Эйнштейна
Рассмотрим идеальный бозонный газ со статистической точки
зрения. Практически все сведения о его макроскопических свойст-
свойствах содержатся, как мы видели, в омега-потенциале Q*, и поэтому
основной задачей является вычисление этой функции. Как уже го-
говорилось в предыдущей главе, удобно считать, что рассматривае-
рассматриваемая система находится в равновесии с термостатом, температура Т
и химический потенциал \i которого заданы. Для определения Q*
нужно тогда использовать условие нормировки E3.2), которое мож-
можно записать в виде
где статистическая сумма
так что 2* = - kT In Z*. E6. 2)
Вычисления значительно облегчаются, если специальным обра-
образом выбрать систему, а именно считать системой те частицы бозон-
ного газа, которые находятся в определенном состоянии (обладают
заданными компонентами импульса). Определив омега-потенциал
выделенных частиц (подсистемы), можно затем найти омега-потен-
омега-потенциал всего газа как сумму найденных выражений для всех возмож-
возможных состояний. Применение такого способа подразумевает исполь-
использование большого канонического распределения, так как число ча-
частиц в данном состоянии не является фиксированным. Выделенная
подсистема является системой с переменным числом частиц.
Итак, рассмотрим частицы, находящиеся в некотором опреде-
определенном состоянии ?, и пусть энергия этого состояния равна &\.
Энергия подсистемы зависит от того, сколько частиц находится
в рассматриваемом состоянии, и если число их равно щ9 то
»^ = */e/. E6.3)
Одно состояние подсистемы отличается от другого лишь числом ча-
частиц П{9 так что для нумерации состояний подсистемы можно ис-
использовать это число. Статистическая сумма выделенной подсисте-
подсистемы имеет вид
^ E6.4)
где суммирование ведется от Яг = 0, когда в данном состоянии ча-
частиц нет, до Пг = оо. Число частиц Бозе в выбранной подсистеме
может быть любым, так как они не подчиняются принципу Паули.
158
Статистическая сумма легко вычисляется, поскольку видно, что
она сводится к геометрической прогрессии
Таким образом, для ?V (индекс i показывает, что это выражение
относится к f-й подсистеме, т. е. к частицам, находящимся в состоя-
состоянии i) получается
E6.5)
Омега-потенциал всей системы бозонов может быть записан в виде
E6-6>
где суммирование распространяется на все возможные состояния
бозонов, т. е. на все значения и
Следует отметить, что при вычислении статистической суммы E6.4) был
использован принцип неразличимости частиц. Действительно, считалось, что
имеется всего одно состояние, энергия" которого равна я*е*. По классическим
представлениям, когда частицы считаются различимыми, таких состояний может
быть очень много. Если общее число частиц в системе (подсистеме с термоста-
термостатом) равно N, то можно
N1
способами выбрать п% частиц из N, так чтобы наборы из п\ частиц отличались
друг от друга по крайней мере номером одной частицы. Отсюда вытекает, что
при вычислении статистической суммы в этом случае следует написать
z
1
где учтено, что значение химического потенциала классической системы jji' и ста-
статистической суммы Zi может отличаться от \х и Z**. Поскольку при использова-
использовании большого канонического распределения предполагается, что в рассматривае-
рассматриваемую подсистему может поступать любое число частиц, то N должно быть бес-
бесконечно велико и для вычисления Z\ следует перейти к пределу при N-* оо. Если
учесть, что при N^>rii
N1 N(M— 1) . ..(ЛГ— m + l) Nn'1
П[\ (N — л/)! nil nL\
то
^Г~^ Ы I XI L.. / \ Пит\Л*т ^L~^k 1 / g I
Так как Л^ бесконечно велико, то написанная сумма может иметь смысл только
если химический потенциал |j/ тоже бесконечен, так что в сумме со слагаемым
kT In N он даст конечное выражение. Целесообразно поэтому иметь дело с ко-
конечной величиной ц, равной
(х^ц' + ^ПпЛГ,
159
и ее называть химическим потенциалом системы. Тогда
Последнее выражение есть разложение в ряд Маклорена экспоненциальной функ-
функции, так что
Для омега-потенциала i-й подсистемы находим
Q,= -kTe(-^Mm, E6.7)
я для омега-потенциала всей системы
2F+11)/(ЙГ) E6.8)
Выражения E6.5) и E6.7) различны, но если в E6.5) химический потенциал
много меньше е*, так что
то показатель степени у экспоненты оказывается большим отрицательным числом:
0а-?/)/(*Г)«-1.
В этом случае сама экспонента очень мала и приближенно
lnA_e(^-»)/(W))a!_e(^-/)/(W). Eб.9)
Таким образом, омега-потенциал бозонного газа из-за принципа неразличимости
отличается от омега-потенциала классических частиц, однако при очень малых
(больших отрицательных) значениях химического потенциала эта разница стано-
становится несущественной. Для того чтобы омега-потенциал всего бозонного газа
совпадал с классическим, химический потенциал \i должен быть по крайней
мере на несколько кТ меньше, чем самый нижний уровень энергии системы, так
как тогда приближение E6.9) справедливо для всех состояний бозонов.
Когда известен омега-потенциал, легко найти самые разные ха-
характеристики системы.
Найдем, например, среднее число бозонов, находящихся в дан-
данном состоянии. По E4.10) и E6.5) имеем
<«/> = - -г1—
(*/)= с-иусаг) ' E6-10)
— 1
Формула E6.10), определяющая среднее число бозонов, находя-
находящихся в состоянии с энергией ги носит название распределения
Бозе — Эйнштейна.
Для внутренней энергии системы всех бозонов найдем по E4.11)
и E6.6)
160
Это естественный результат, если учесть, что г% — энергия бозонов,
а <пг> — их среднее число в состоянии i.
Аналогичным образом можно подсчитать и другие термодина-
термодинамические величины, характеризующие бозонный газ. Во многих
случаях эти величины выражаются через средние значения чисел
заполнения и именно этим определяется большое значение распре-
распределения Бозе — Эйнштейна.
§ 57. Фотоны
Применим теперь полученные выше общие результаты к фотон-
фотонному газу, т. е. к электромагнитному излучению.
Фотонный газ обладает важной особенностью, отличающей его
от Бозе-частиц, обладающих конечной массой покоя. Эта особен-
особенность связана с тем, что число бозонов в фотонном газе не огра-
ограничено. Так, например, нагревая стенки полости (термостата),
можно неограниченно увеличивать плотность электромагнитного
излучения внутри полости, т. е. увеличивать число содержащихся
в ней фотонов.
При выводе большого канонического распределения из принци-
принципа максимума энтропии (см. §53) использовалось условие
в котором среднее число частиц в системе <N> считалось задан-
заданным. Для фотонов это условие излишне, поскольку их среднее чис-
число определяется температурой и объемом системы. Если его не на-
накладывать (что формально можно учесть, положив множитель
Хз = — \х/Т равным нулю, т. е. фактически считая ji = 0), то придем
к выводу, что для фотонов большое каноническое распределение
применимо при значении химического потенциала, равном нулю.
По формуле E6.10) среднее число бозонов на i-м уровне равно
Для фотонов распределение Бозе — Эйнштейна имеет вид
Другой важной особенностью фотонного газа, как, впрочем, и
идеального газа любых бозонов, служит то, что хотя возможные
уровни энергии системы дискретны, но в большинстве практически
интересных случаев они расположены настолько часто, что их мож-
можно считать почти непрерывными. Остановимся на этой особенно-
особенности подробнее.
Для вычисления омега-потенциала необходимо найти сумму
6—434
Если уровни энергии г% расположены настолько близко друг к дру-
другу, что разница между соседними много меньше kT, то написанная
выше сумма может быть приближенно заменена интегралом по
энергии. Действительно, пусть de — малый интервал энергий, ко-
который, с одной стороны, много меньше кТу а с другой — много боль-
больше интервала между соседними уровнями энергии, так что в de со-
содержится много уровней энергии. Суммирование удобно провести
в два этапа. Разобьем всю шкалу энергии на интервалы величиной
de и сначала просуммируем слагаемые, относящиеся к одному ин-
интервалу. Поскольку в пределах одного интервала de энергии отли-
отличаются друг от друга на величину, много меньшую кТ, то все сла-
слагаемые имеют приблизительно одинаковое значение и их сумма
равна одному из них, умноженному на число уровней в интерва-
интервале de.
Число уровней в de, которое для малых интервалов энергии про-
пропорционально величине интервала, обозначим gede, где ge— функ-
функция, носящая название плотности состояний и имеющая
смысл числа уровней, приходящихся на единичный интервал энер-
энергии в окрестности энергии de. Например, для омега-потенциала ис-
искомая сумма будет иметь вид
Остается провести суммирование по различным интервалам de,
что, как легко видеть, сводится к интегрированию. Таким образом,
для омега-потенциала получаем
оо
Q* = kT f In A - e^-'VW) g% de. E7. 2)
Суммирование проводится от самого нижнего нулевого уровня
энергии до бесконечно большого.
Для фактического вычисления интеграла E7.2) необходимо
знать плотность состояний g8de, к вычислению которой мы теперь
и перейдем.
Почти все необходимые выкладки были проделаны ранее. Дей-
Действительно, между энергией е и величиной импульса фотона р име-
имеет место соотношение
так что в интервале энергии от е до e + de оказываются все те со-
состояния, модуль импульса которых больше р = г/'с и меньше
Другими словами, интервалу энергий de принадлежат состояния,
которые в пространстве импульсов изображаются точками, находя-
находящимися в сферическом слое толщины dp. Поскольку объем такого
162
слоя равен dQ=4jtp2d/?, то по формуле D8.2) число состояний в нем
равно
4jtp2dpV. E7.3)
ЕСли выразить импульс через энергию, то получим
dG=4*s2de
BnftcK
где dG — число состояний в интервале энергий de. По определению
введенной выше плотности состояний,
dO=g.de,
так что из E7.4) следует явное выражение для этой функции
d 4яе2 1/ds. E7. 5)
При применении E7.5) к фотонному газу нужно принять во
внимание, что имеются два вида электромагнитных волн, а следо-
следовательно, и фотонов, отличающихся друг от друга своей поляриза-
поляризацией. Для каждого вида справедлива формула E7.3), и поэтому
если нас интересует весь фотонный газ, а не одна его компонента,
обладающая данной поляризацией, то следует E7.5) умножить на
число компонент, т. е. на два.
С учетом последнего замечания для омега-потенциала фотон-
фотонного газа, химический потенциал которого равен нулю, получается
Последнее выражение часто используется в форме, когда за пере-
переменную интегрирования выбрана частота со, связанная с энергией
соотношением е=/ко. В этом представлении
Q* = 2kT \ ln(l -e-^/W)_^i deal/. E7. 6)
о
Величина
d 2*=2kTV In A - е-ь<°/<*г>У-^- du> E7. 7)
имеет смысл омега-потенциала всех фотонов, частота которых ле-
лежит в интервале dco, и поэтому функция
Bяс)з
может быть названа спектральной плотностью омега-
потенциала.
6* 163
Чтобы вычислить E7.6), удобно ввести новую переменную инте-
интегрирования
Формула для Q* принимает тогда следующий вид:
Поскольку *>
то
^ E7.8)
Таким образом, когда уровни энергии могут считаться непрерывны-
непрерывными, омега-потенциал фотонного газа определяется выражением
E7.8) или в спектральной форме уравнением E7.7).
Остановимся теперь на вопросе о том, когда справедливо при-
приближение непрерывного распределения уровней энергии. Ясно, что
это имеет место лишь в случае достаточно высоких температур, так
как основным критерием служила малость расстояния между уров-
уровнями по сравнению с kT. Условие квазинепрерывности будет вы-
выполняться, если энергия kT больше, чем энергия самого нижнего
состояния, поскольку среди состояний системы есть и такие, кото-
которые соответствуют нахождению на нижнем уровне одного, двух фо-
фотонов и т. д., причем все остальные уровни пустые. Другими слова-
словами, интервалы между соседними уровнями заведомо меньше, чем
fttoo, где coo — наименьшая частота колебаний, возможных в системе.
Пусть, например, имеется кубическая полость со стороной а =
= 1 см. Наименьшая частота определится из условия, что соответ-
соответствующая ей длина волны равна а. Хотя, строго говоря, в метал-
металлической полости возможны колебания, у которых на длине поло-
полости помещается половина длины волны, так что для наименьшей
*)
со оо
e-kx
(см. [12], с 297).
164
частоты замена стоячих волн на бегущие по правилу, изложен-
изложенному в § 46, является довольно плохим приближением, но посколь-
поскольку нас интересует выполнение условия
Ы0^кТ E7.9)
с большим запасом, то разница в множителе порядка двух не
имеет существенного значения. Таким образом, в рассматриваемом
примере наибольшая длина волны порядка а=1 см, а следователь-
следовательно, наименьшая частота
т. е. vo—3-1010 Гц. Интервалы между уровнями энергии меньше,
чем 2jt/ivo=2-10-23 Дж, и условие E7.9) выполняется уже при тем-
температурах порядка 10 К, когда &Г=1,38-10~22 Дж. Если полость ох-
охлаждена до температуры порядка 0,1 К, то переход от формулы
E6.6), учитывающей дискретную структуру уровней,' к формуле
E7.2), где они предполагаются непрерывными, неправомерен.
§ 58. Законы теплового излучения
Знание омега-потенциала позволяет рассчитать многие важные
характеристики фотонного газа, находящегося в равновесии, т. е.
равновесного теплового излучения. Одной из наиболее интересных
является внутренняя энергия U. Используя формулу E4.11) и при-
применяя ее к E7.7), найдем для внутренней энергии фотонов, часто-
частота которых лежит в интервале dco, при учете того, что |Л = О,
(da) tjt^E8.1)
Выражение E8.1) может быть истолковано следующим обра-
образом. Первый множитель представляет собой число состояний, при-
приходящихся на частотный интервал do. Второй множитель опреде-
определяет среднее число фотонов в состоянии с частотой <о, так что его
произведение на первый даст среднее число фотонов в интервале
частот от со до co + dco *
Последний множитель есть энергия одного фотона, и поэтому ум-
умножение E8.2) на ftco приводит к выражению для средней энергии
фотонного газа в рассматриваемом частотном интервале.
Если в полости, содержащей тепловое излучение, сделано не*
большое отверстие, которое практически не нарушает равновесного
состояния фотонного газа, то из отверстия выходит излучение. Мощ-
Мощность этого излучения в интервале частот dco = 1, отнесенная к еди-
единице поверхности, носит название спектральной плотности энерге-
энергетической светимости (для краткости назовем ее излучательной спо-
способностью) и в дальнейшем обозначается г^. Легко рассчитать эту
* Читатель' Здесь и далее во всех формулах вместо h следует читать Й.
165
величину, используя результаты § 21. Действительно, для плотно-
плотности потока частиц там было получено выражение B1.11)
Если под d/ понимать плотность потока фотонов, обладающих ча-
частотой в интервале do, то их концентрация я (со) do), как это выте-
вытекает из формулы E8.2), равна
Поскольку скорость всех фотонов одинакова и равна с, то
л . 8JtoJda> 1 С_
E8.4)
Каждый фотон несет с сойой энергию ftco, поэтому с помощью E8.4)
получается следующее выражение для излучательной способности,
которая по определению относится к единичному интервалу ча-
частот dco:
Если на рассматривавшееся выше отверстие извне падает излу-
излучение, то оно полностью проходит внутрь полости, не испытывая
отражения. Когда полость доста-
достаточно велика, то можно прене-
пренебречь и выходящим из полости
излучением, возникающим за счет
отражения от внутренних стенок.
Таким образом, полость с отвер-
отверстием представляет собой так на-
называемое абсолютно черное тело,
т. е. тело, полностью поглощаю-
поглощающее все падающее на него излу-
излучение. Следовательно, формула
E8.5) определяет излучательную
способность абсолютно черного
тела. Она носит название формулы Планка по имени учено-
ученого, впервые ее получившего. На рис. 9.1 показаны графики функ-
функции Планка в зависимости от частоты для нескольких температур.
При малых частотах, когда Аю/ЛГ<;1, экспоненту в знаменателе
E8.5) можно разложить в ряд и ограничиться первыми двумя чле-
членами
и>
Рис. 9.1
kT
После подстановки этого разложения в E8.5) получается
E8.6)
166
Приближенная формула E8.6) носит название формулы Р э-
лея — Джинса и показывает, что в области низких частот излу-
чательная способность черного тела пропорциональна квадрату ча-
частоты. Исторически это соотношение было получено раньше фор-
формулы Планка из чисто классических соображений и по классиче-
классической теории должно было выполняться для всех частот. Полная
энергия излучения по этой формуле равна бесконечности:
BЯСJ }
О О
поскольку последний интеграл расходится. Таким образом, клас-
классическая теория была не в состоянии объяснить лучеиспускание,
ибо приводила к абсурдному результату. Зависимость E8.6) изо-
изображена на рис. 9.1 пунктирной линией в области низких частот.
При больших частотах, когда ttid/kT^l, экспонента в знамена-
знаменателе E8.5) много больше единицы. Если последней пренебречь,
то получается так называемая формула Вина
ГшС[а) с- JO*- e-W(*r)da) E8. 7)
из которой видно, что при больших частотах излучательная способ-
способность быстро (экспоненциально) стремится к нулю. Закон Вина
представлен на графике пунктирной линией в области больших ча-
частот.
Положение максимума на кривой излучательной способности
можно определить, если продифференцировать г^ по со и прирав-
приравнять производную нулю. Имеем
dr°> _ d Г
~ l
do) lBrtcJ eAo)/<*r)
l 1
r) — 1 J
Это уравнение приводится к виду
v ; kT
или
~W~
Из последнего соотношения последовательными приближениями
легко получить:
о
1L) =3-е-з.3=2,85,
kT /
^ = 2,82.
kT
167
Таким образом, максимум излучательной способности имеет места
на частоте
которая прямо пропорциональна абсолютной температуре. Это со-
соотношение носит название закона смещения Вина и пока-
показывает, что при более высоких температурах максимум смещается
в сторону более коротких длин волн (более высоких частот).
Полную мощность, излучаемую абсолютно черным телом с еди-
единицы поверхности, называют энергетической светимостью. Ее
можно определить, вычислив интеграл
оо
Я = [ /V^O) =
BясJ(еЛо)/(*Г)— 1)
о о
Если ввести новую переменную интегрирования л: =
то*>
_J*^< *3d^
* Bл*J/гЗ )ех— 1 v '
о
где
а==6,49—-—=5,67.10-8 Вт.м-2.К-4.
BяJ^з
Соотношение E8.8) носит название закона Стефана —
Больцмана и показывает, что энергетическая светимость про-
пропорциональна четвертой степени абсолютной температуры. Постоян-
Постоянная а носит название постоянной Стефана — Больу. ма-
н а.
В заключение покажем, как применение общего аппарата позво-
позволяет вычислить давление, оказываемое тепловым излучением на
стенки полости. По формуле E4.13) с учетом E7.8) находим
dV dV \ я2ДЗсз )
дгз их
0
з их f дгз е~х
0
m = l (
(см. [12], с. 297).
168
Таким образом, тепловое излучение оказывает на стенки заключаю-
заключающей его полости давление, которое пропорционально четвертой сте-
степени температуры. Интересно отметить, что давление не зависит
от объема. Это является отражением того факта, что число фото-
фотонов в полости не фиксировано. Увеличение объема сопровождается
появлением новых фотонов, так что концентрация их, зависящая
только от температуры, сохраняется.
§ 59. Фононы
Статистика бозонов может быть использована и для описания
явлений, относящихся совсем к другой области.
При низких температурах, когда квантовые эффекты становятся
особенно существенными, большинство веществ находится в твер-
твердом состоянии и их атомы образуют кристаллические решетки. Сме-
Смещение атома в решетке вызывает смещение соседних атомов и та-
таким образом приводит к возникновению волны, распространяющей-
распространяющейся по кристаллу. Волновой характер движения атомов в кристалли-
кристаллической решетке позволяет строить статистическую теорию кристал-
кристаллов по аналогии с теорией теплового излучения в полости. Полная
теория оказывается значительно более сложной, чем для электро-
электромагнитных волн, так как решетка дискретна и в ней возможны ко-
колебания различных типов (в простейших случаях они делятся на
продольные и поперечные), наконец, свойства кристалла, а следо-
следовательно, и волн могут быть неодинаковы по различным направле-
направлениям (анизотропия). Чтобы упростить изложение, можно, как это
часто делается, приближенно заменить реальную решетку непре-
непрерывной изотропной средой с упругими параметрами, такими же,
как у решетки. Фактически это сводится к предположению, что кри-
кристаллическая решетка может быть заменена упругой средой, в ко-
которой скорость распространения звуковых волн (волн сжатия, ра-
растяжения и смещения) такая же, как и в решетке, и одинакова во-
всех направлениях. Рассматриваются всего три возможных типа
колебаний, из которых два соответствуют поперечным волнам с дву-
двумя взаимно перпендикулярными направлениями поляризации и од-
одно— продольной волне. Теория для каждого типа колебаний дает
одинаковый результат, и разница состоит лишь в том, что скорость
звука для продольных и поперечных волн различна. Имея это в ви-
виду, ограничимся лишь продольной волной, для которой скорость
распространения обозначим с\.
Если кристалл имеет ограниченные размеры, например форму
параллелепипеда со сторонами а, Ь и с, то в нем возможны коле-
колебания строго определенных частот. Частоты колебаний зависят от
размеров кристалла и условий отражения на его свободных гра-
границах. Хотя, строго говоря, набор возможных частот дискретен, но
почти во всех практически интересных случаях его можно считать
непрерывным. В этом приближении не так важно точное значение-
каждой отдельной частоты, а гораздо существеннее определить
плотность распределения этих частот, т. е. число dG различных
169
волн, частоты которых попадают в интервал dco. Другими словами,
необходимо найти плотность состояний g®, где
В полной аналогии со случаем электромагнитных волн удобно
принять, что возможны лишь такие частоты, для которых компо-
компоненты волнового вектора к, где
(ci — скорость звука, заменяющая скорость распространения элек-
электромагнитных волн с), определяются соотношениями вида D6.4)
и 2я , 2я - 2л /Р,Л i4
kx = —тх, K = -—myi kz= mz E9.1)
а о с
(mXy rrty и mz — целые числа).
Имеется, однако, и одно существенное отличие от световых волн,
которое связано с дискретной структурой кристаллической решет-
решетки. Спектр частот электромагнитных
*—.—.—.—.—. » волн не ограничен сверху, так что воз-
.^^ можны сколь угодно большие частоты
"^ ^#^--^.^-""^# или сколь угодно малые длины волн.
В кристаллах не могут существовать
^ ^ ^^ ^-^ \.-^" волны с длиной волны, меньшей неко-
некоторого значения Ящщ. Это свойство яв-
Рис 9.2 ляется следствием дискретности решет-
решетки, и его нагляднее всего можно пояс-
пояснить с помощью рис. 9.2, на котором изображены поперечные вол-
волны с уменьшающейся длиной волны для одномерной цепочки ато-
атомов (обозначенных точками). Последняя из них соответствует наи-
наименьшему возможному значению длины волны, равному удвоенной
постоянной решетки, когда соседние атомы колеблются в противо-
фазе.
Таким образом, теория тепловых колебаний решетки может
быть сведена к теории равновесных звуковых волн, аналогичной
теории равновесного электромагнитного излучения и отличающейся
тем, что возможные типы волн ограничены наименьшей длиной вол-
волны Amm или соответствующей ей максимальной частотой
сотах=2ясг/Хт1п. E9.2 )
Для внутренней согласованности теории значение сотах следует
выбирать из условия, что общее число различных волн в кристалле
равно числу степеней свободы составляющих его атомов. Если чис-
число атомов равно N, то поскольку у каждого атома три степени
свободы, то общее число степеней свободы равно 3N. Это означает,
что в простой решетке имеется N различных длин волн для каждого
из типов колебаний (продольного и двух поперечных). Таким обра-
образом, условие, определяющее сотах, может быть записано в виде
170
V = N,
BлсгK
U
т. е.
-т- -——V = N или <i)maY =
О
Поскольку в простом кубическом кристалле объем, приходящийся
на один атом, равен d3, где d — постоянная кубической решетки, то
последнюю формулу можно записать в виде
°W = / $n2Ci/d = 2nct/( 1,6 Ы), E9. 3)
ИЗ КОТОрОЙ, В ЧасТНОСТИ, ВИДНО, ЧТО Amin=l,61 d.
Используя условие ограниченности частот звуковых волн, для
омега-потенциала можем по аналогии с E7.6) написать
2*
= Г *ПпA -е-*»/<*г>) **™Z- V. E9. 4)
о
Формула E9.4) относится к волнам одного типа, например про-
продольным, и поэтому в ней опущен присутствующий в E7.6) мно-
множитель 2, который учитывает две возможные поляризации элект-
электромагнитных волн.
Следует различать два случая.
Если верхний предел интегрирования много больше kT/h,
то при интегрировании придется иметь дело и с частотами со, для
которых со^>йГ/Й, т. е.
Поскольку для этих частот
1пA — е-Ло>
— очень малая величина, то верхний предел интегрирования без
заметной ошибки можно распространить до бесконечности и тогда
теория оказывается полностью совпадающей с теорией электромаг-
электромагнитного излучения. Вместо фотонов говорят о фононах (квантах
звука), роль скорости света играет скорость звука, и для фононов
справедливы все законы, полученные для теплового излучения.
В частности, по аналогии с E7.8) для каждого типа волн (про-
(продольных и двух поперечных типов) имеем
2* = -1,07 J*3 з VT\ E9.5)
где Сф — скорость соответствующей волны. Далее обычным спосо-
способом можно найти различные термодинамические характеристики
кристаллической решетки. Так, например, используя уравнение
171
Гиббса — Гельмгольца, получаем выражение для внутренней энер-
энергии, связанной с каждой ветвью,
Здесь учтено, что для фононов р, = 0.
Теплоемкость кристалла при постоянном объеме есть сумма трех
аналогичных членов, каждый из которых обусловлен одним типом
колебаний и равен
c = 12,84 —^г- VT\
cv
v дТ |
При уменьшении температуры теплоемкость быстро (как Г3) стре-
стремится к нулю.
В другом предельном случае сотах много меньше kT/h. Все ча-
частоты, которые учитываются в интеграле, в этом случае таковы, что
Тогда, например, для внутренней энергии фононов продольных ко-
колебаний, частоты которых лежат в интервале dco, в соответствии
с E8.1) можем, раскладывая экспоненту в ряд и ограничиваясь
первыми двумя членами, получить
AtT 43tco2dco т/ ho) 4noJda> t/ —, /en e\
d(j=z V ~ V-kT. E9.6)
BясфK еЛо)/<*г>-1 BяСфK v '
Последнее равенство соответствует справедливой в классиче-
классическом случае теореме о равномерном распределении энергии по сте-
степеням свободы. Первый множитель определяет число состояний
в интервале частот dco, а второй показывает, что на каждое состоя-
состояние приходится средняя энергия kT(kT/2 на кинетическую и kT/2
на потенциальную энергию в волне). Если для электромагнитных
колебаний формула, соответствующая классическому приближению^
приводила к абсурдному результату (бесконечной общей внутрен-
внутренней энергии), то для звуковых волн этого не получается, так как
для них имеется верхняя граница возможных частот. Внутренняя
энергия в этом предельном случае описывается выражением
max 4jio>2da> 4 3 V ит /cn 74
Л;а)тах kl . E9.7)
3 Bя^K v '
Если учесть значение сотах по формуле E9.3), то формулу для
внутренней энергии продольных волн можно записать в виде
U=NkT. E9.8)
Поскольку помимо продольных колебаний в кристалле возможны
еще и два типа поперечных, то полная внутренняя энергия в рас-
рассматриваемом предельном случае равна
U=3NkT. E9.9)
172
Это находится в полном соответствии с принципом Больцмана.
Действительно, атом решетки имеет три степени свободы (движе-
(движение по осям х, у, z), причем на каждую приходится энергия kT(kT/2
на кинетическую и kf/2 на потенциальную). Общая средняя энер-
энергия одного атома равна З&Г, и, следовательно, внутренняя энергия
решетки равна E9.9).
Для теплоемкости в этом случае получается постоянное значе-
значение
Cv
v дт
Рассмотренные выше два предельных случая соответствуют низ-
низким и высоким температурам. Критерий их выполнения может быть
записан в следующем виде: при
справедливы квантовые формулы, а при
— классические (принцип равномерного распределения энергии по
степеням свободы). Параметр 0д, зависящий от универсальных
постоянных (ft, k) и параметров решетки данного конкретного кри-
кристалла (сф, d), имеет размерность температуры и носит название
температуры Дебая для этого кристалла. Таким образом,
-если температура, при которой находится кристалл, много больше
температуры Дебая, то можно пользоваться классической статис-
статистикой, а если она того же порядка или меньше, то необходимо при-
применять квантовую. Квантовые формулы значительно упрощаются,
«становясь аналогичными формулам для теплового излучения, при
температуре, много меньшей дебаевской. Следует иметь в виду, что
температуры Дебая для продольных и поперечных волн различны,
так как различны скорости распространения этих волн.
Задачи к главе 9
1. Если площадь антенны радиолокатора 5=10 м2 и его приемное устрой-
устройство регистрирует сигналы в полосе частот 1 м Гц на длине волны 0,03 м,
то какова будет мощность шумового сигнала, когда антенна направлена
на Солнце? Температура Солнца Гс = 6000 К, квадрат отношения радиуса
Солнца к радиусу орбиты Земли g=2,l7-10~5.
Решение. Излучение Солнца соответствует тепловому при температуре
€000 К. Для длины волны А,=3 см отношение h (о/?Гс равно
ho> 2л: Ьс
kT c k\Tc
173
так что для излучательной способности можно использовать формулу E8.6)t где
в данном случае ёсо=2я-106 с*1. По мере удаления от Солнца плотность энер-
энергии убывает обратно пропорционально квадрату расстояния, так что у Земли на
единицу площади поступает мощность
Полная мощность, принимаемая антенной площади S, есть
¦SSe(a,)(b>=SS ^ kTcd».
Подставляя числовые значения, найдем величину шумового сигнала: 2-10~14 Вт.
2. Оцените молярную теплоемкость меди при температуре 900 и —200° С
(скорость продольных волн в меди 4700 м/с, поперечных — 2260 м/с, плот-
плотность меди 8,9 г/см3, атомная масса 64 г/моль, постоянную решетки при-
примите равной 0,228 нм).
Решение. Для температуры Дебая находим 6Д = у бя2 Ь. c^'(kd) = 618 К
для продольных волн и Од = 297 К для поперечных. При температуре 900° С
теплоемкость может рассчитываться по формуле E9.9), так что для молярной
теплоемкости получаем 25 Дж/(К-моль). При температуре —200° С G3 К)
используем формулу
из которой для продольной ветви получаем 1,16 Дж/(К-моль), а для попереч-
поперечных— по 10 Дж/(К-моль) (объем V определяем по отношению атомной массы
к плотности).
ГЛАВА 10
СТАТИСТИКА ФЕРМИ — ДИРАКА
§ 60. Фермионы
Частицы, обладающие полуцелым спином (в единицах h), на-
называются фермионами. В отличие от бозонов они помимо принципа
неразличимости подчиняются еще и принципу Паули. Это накла-
накладывает особые ограничения на распределение фермионов по воз-
возможным состояниям, так что статистика фермионов, или, иначе, ста-
статистика Ферми — Дирака, сильно отличается от статистики Бозе —
Эйнштейна, рассмотренной в предыдущей главе.
К фермионам относятся:
1) электроны,
2) позитроны,
3) нуклоны (протоны и нейтроны),
4) некоторые ядра и атомы.
Основной интерес представляют электроны, так как позитроны
в естественных условиях встречаются редко (они быстро аннигили-
аннигилируют с электронами), а массы нуклонов, ядер и атомов настолько
174
велики, что к ним в большинстве случаев можно применять клас-
классическую статистику.
Как уже упоминалось выше, при очень низких температурах,
когда квантовые эффекты становятся особенно существенными, ве-
вещество обычно находится в твердом кристаллическом состоянии
и тогда статистические свойства удобно рассматривать, вводя пред-
представление о фононах (см. § 59). Фононы являются частицами Бозе
независимо от того, построена решетка кристалла из бозонов или
фермионов.
§ 61. Распределение Ферми —Дирака
Рассмотрим идеальный газ электронов, т. е. будем предполагать,
что взаимодействием электронов между собой можно пренебречь.
На первый взгляд такое предположение кажется необоснованным,
так как электроны обладают зарядом и электрические силы, с ко-
которыми они взаимодействуют, весьма значительны. Можно, однако,
приближенно учесть взаимодействие электронов методом самосо-
самосогласованного поля (см. § 28), т. е. принять, что они находятся во
внешнем электрическом поле, эквивалентном полю, создаваемому
самими электронами. В частном случае плазмы газового разряда
или электронов в твердом теле (металлы, полупроводники) экви-
эквивалентное поле часто равно нулю или очень мало, так как отрица-
отрицательный заряд электронов компенсируется в среднем равным ему
зарядом положительных ионов.
Система невзаимодействующих электронов может быть охарак-
охарактеризована указанием совокупности возможных состояний отдель-
отдельных электронов и их распределением по этим состояниям. Анало-
Аналогично тому, как это было сделано для идеального газа бозонов, вы-
выберем в качестве подсистемы одно-единственное состояние с номе-
номером и Если энергия этого состояния е*, то в соответствии с боль-
большим каноническим распределением (подсистема все время обмени-
обменивается электронами с остальной системой, принятой за термостат)
для омега-потенциала подсистемы получается
mkT) F1. 1)
Формально статистическая сумма, входящая в F1.1), подобна сум-
сумме E6.4), которая была написана для бозонного газа. Существен-
Существенная разница, однако, появляется вследствие учета принципа Пау-
Паули. Если для бозонов суммировние по числу частиц в данном со-
состоянии проводилось от /г = 0 до я=оо, то для фермионов п может
принимать по принципу Паули лишь два значения: /г = 0 и п=\.
Таким образом,
* _ v^
F1.2)
175
Формула F1.2) отличается от соответствующей формулы E6.5),
справедливой для бозонов, знаком перед экспонентой.
Омега-потенциал всей системы получается суммированием оме-
омега-потенциалов всех подсистем, т. е. суммированием по всем воз-
зложным состояниям:
* т F1.3)
Из соотношений F1.2) и F1.3) следует вся термодинамика иде-
идеального электронного газа. Найдем, в частности, выражение для
-среднего числа частиц в состоянии и По общему правилу E4.10)
.имеем
Формула F1.4), определяющая среднее число частиц в состоянии
с энергией ег-, носит название распределения Ферми— Ди-
Дирака.
Химический потенциал \х может быть найден из условия, что
полное среднее число частиц в системе равно сумме средних в от-
отдельных состояниях:
V V' F1.5)
Последняя формула следует и непосредственно из F1.3), если на-
написать
Для внутренней энергии по E4.11) можно получить
^kT У
. ^'^ (±=±Х\а-^ F1.6)
где использовано условие F1.5). После приведения подобных чле-
членов из F1.6) следует
F1.7)
»76
Важная формула F1.7) определяет внутреннюю энергию идеально-
идеального газа частиц Ферми и имеет смысл произведений энергий частиц
на среднее их число в каждом из возможных состояний, т. е.
§ 62. Электронный газ в потенциальном ящике
Важным в практическом отношении примером служит электрон-
электронный газ в потенциальном ящике, так как в определенном прибли-
приближении таким путем можно рассматривать металлы и полупровод-
полупроводники. Поскольку состояние электрона в потенциальном ящике за-
задается по D6.7) компонентами его импульса, а связь энергии с им-
импульсом определяется формулой
pVBmQ) = eh F2. 1)
то в принципе можно применять соотношения, полученные в пре-
предыдущем параграфе. Удобно, однако, перейти от суммирования по
дискретным состояниям к интегрированию, так как хотя состояния
дискретны, но расположены они так часто, что с практической точ-
точки зрения во многих случаях их распределение можно считать не-
непрерывным. Переход осуществляется точно так же, как это дела-
делалось в случае газа бозонов. На одно состояние в пространстве им-
импульсов приходится объем
F2.2)
где V = abc — объем в обычном пространстве. Число состояний,
энергия которых заключена в интервале от е до e + de, определится,
если разделить объем dQ, соответствующий de, на AQ. Точнее, чис-
число состояний dG равно
dG = 2 —, F2.3)
так как в каждом состоянии с данным импульсом может быть два
электрона, отличающихся друг от друга направлением своего спи-
спина.
Величина dQ — это объем импульсного пространства, заключен-
заключенный между р и p + dp, так что
Если принять во внимание F2.1), то
dQ = 4л BтоK/2
Подставляя F2.2) и F2.4) в F2.3), найдем
dQ = 4л BтоK/2 — ?1/2ds. F2. 4)
dQ y 5)
BяйK v J
7—434 177
или
где плотность состояний ge, определяющая число состояний, прихо-
приходящихся на единичный интервал энергии, по F2.5) равна
Зная плотность состояний, легко перейти от сумм к интегралам.
Пусть /(е)—функция энергии, которая практически не меняется на
интервалах de порядка kT. Суммирование по всем состояниям мож-
можно тогда выполнить в два этапа. Для этого разобьем все возмож-
возможные значения энергии на интервалы величины de и просуммируем
сначала по состояниям внутри каждого интервала de, а затем сло-
сложим полученные результаты. Внутри одного интервала по предпо-
предположению /(е) практически постоянна, поэтому результат первого
суммирования есть просто значение /(е) в этом интервале, умножен-
умноженное на число относящихся к нему состояний dG. Таким образом,
в результате суммирования по интервалу de получаем
Теперь очевидно, что суммирование по различным интервалам сво-
сводится к вычислению интеграла
Окончательно правило перехода от сумм к интегралу может быть
записано в следующем виде:
Для омега-потенциала идеального газа электронов с энергией,
заключенной в интервале от е до e+de, таким путем получается
= -kT In A + e^-*>/(^>) 4я (mo>/e/ yds, F2,7)
а для полного омега-потенциала всех электронов
оо
Q*=fd2*=-f Arin( + e^-e)/W)g-6de.
о
Введем новую переменную интегрирования | = е/(йГ), тогда
F2.8)
где lo=[i/(kT), а функция Ф(§о) равна
о
Ф(У= f ln(l + e^-E))^/2de. F2.9)
oJ
17S
Эту функцию нельзя свести к элементарным для всех значений ар-
аргумента, но можно получить простые формулы, справедливые для
больших и малых значений переменной go-
Если go—малая величина (?о<С—1), то экспонента тоже мала
и тогда
Для Ф(?о) получается
ф(?0) = е5о \ e-41/2d? = eSo -?* , F2. 10)
о
так как
В противоположном предельном случае, когда g0 — большая ве-
величина (?0>1), основной вклад в интеграл дают значения подын-
подынтегральной функции при ?<§о, так как при 1>1о
In A + е-«-*о>) те е-«-ь> <^ \.
На этом основании можно оборвать интегрирование при ? = ?о
и пренебречь единицей по сравнению с экспонентой под знаком ло-
логарифма. При этом получается
So
-^ й/2. F2. И)
§ 63. Невырожденный электронный газ
Дальнейшее исследование свойств идеального газа электронов
удобно провести отдельно для двух отмеченных выше предельных
случаев. Идеальный газ фермионов, для которого go^—1, т. е. хи-
химический потенциал \i много меньше —kT, получил название не-
невырожденного. Рассмотрим его более подробно.
Легко видеть, что невырожденный газ — это газ, подчиняющий-
подчиняющийся классической статистике. Проще всего убедиться в этом, если
проанализировать его функцию распределения. Найдем для этого
среднее число электронов, энергия которых заключена в интервале
de. По общему правилу из F2.7) получаем
0(dQ*) 1 4яBт0)/ Ч
д? — e^-^W) + 1 Bя/г)з
Если |о<С|, то |л<Се и, следовательно, с хорошим приближением
7* 179
т. е. распределение Ферми — Дирака переходит в распределение
Максвелла — Больцмана, отличающееся характерной экспоненци-
экспоненциальной зависимостью от энергии состояния. Таким образом,
F3. 1)
Bя/гK
Формула F3.1) может быть применена и к небольшой части
6.V всего объема V, тогда для среднего числа частиц, находящихся
в интервале de и объеме dV, получится
K/2 /63> 2)
Сопоставляя последнее выражение с функцией распределения
Максвелла по энергиям, для чего формулу A9.4) нужно умножить
на концентрацию электронов я, получим связь химического потен-
потенциала |i с концентрацией электронов в случае невырожденного
газа:
BяЬK
ИЛИ
{2Щ"Пт =kT\n \V2nh* (-^-Т\ . F3.4)
Конечно, этот результат можно было получить и не обращаясь
к A9.4), а просто написав, что полное среднее число частиц в dVT,
равное ndV, определяется следующим интегралом:
ndV
==dV \
Вычисление последнего снова привело бы к равенству, эквивалент-
эквивалентному F3.3) или F3.4).
Таким образом, невырожденный газ действительно подчиняется
классической статистике.
Когда же можно считать электронный газ невырожденным? Из
условия (ы<С—kT при учете F3.4) следует
т. е.
или в другой форме
180
Соотношение F3.5) является критерием невырожденности элек-
электронного газа. Оно показывает, что классическая статистика при-
применима тогда, когда концентрация частиц низка, а их температура
достаточно высока. Чем больше масса частицы, тем оправданнее
применение распределения Максвелла — Вольцмана. Примеры ис-
использования критерия F3.5) включены в качестве задач к настоя-
настоящей главе.
Поскольку в случае отсутствия вырождения газ электронов под-
подчиняется классической статистике, то ясно, что его свойства не от-
отличаются от свойств идеального одноатомного газа. В частности,
внутренняя энергия и уравнение состояния определяются соответ-
соответственно формулами C8.3) и C6.2).
§ 64. Вырожденный электронный газ
Обратимся теперь к противоположному предельному случаю,
когда 5о^>1 или, иначе, химический потенциал \i много больше kT.
Электронный гаЗ; удовлетворяющий условию \x^>kT, носит назва-
название вырожденного.
В соответствии с формулами F2.8) и F2.11) омега-потенциал
вырожденного газа имеет вид
l!L 2/я0K/2 — V>5/2- F4- !)
15 Г К
По общему правилу E4.13) для уравнения состояния получаем
5/2> F4.2)
Р
15
Для внутренней энергии, используя E4.11) и учитывая, что в F4.1)
температура не входит, найдем
L BK/2 F4. 3)
Чтобы получить явную зависимость давления и внутренней энергии
от температуры, необходимо в F4.2) и F4.3) подставить химиче-
химический потенциал, выраженный через среднее число частиц, темпера-
температуру и объем. Если <Л/Г>—среднее число электронов в системе,
то по E4.10)
таким образом,
V 5я2?3
и, следовательно,
„3/2
Г
. (б4.4)
181
Подставляя F4.4) в F4.2) и F4.3), можно найти
\ V J 15л2/и0
15я2/тг0 \ V J
i^%2
Ш
Таким образом, в случае вырожденного газа давление и объем не
зависят от температуры и давление обратно пропорционально объ-
у в степени 5/з-
По D3.2) теплоемкость при постоянном объеме равна
п dU
V дТ
Если применить эту формулу к вырожденному газу, то, поскольку
его внутренняя энергия не зависит от температуры, теплоемкость
оказывается равной нулю. Вместе с тем для невырожденного газа
электроно!В теплоемкость такая же, как и у всякого одноатомного
идеального газа, т. е. в соответствии с D3.6)
В металлах имеется большое количество свободных электронов,
и с точки зрения классической теории было загадкой, почему экс-
экспериментально найденная теплоемкость определяется только иона-
ионами решетки. Квантовая статистика просто объясняет это явление,
так как электронный газ в металлах оказывается сильно вырож-
вырожденным (см. задачу к настоящей главе), а тогда его теплоемкость
близка к нулю.
Рассмотрим теперь, каков критерий вырождения электронного
газа. Из условия
при учете выражения для химического потенциала F4.4) находим,
полагая <N>/V=n, где п — концентрация:
Если возвести обе части равенства в степень 3/г и разрешить его от-
относительно концентрации, то получится
^ F4.7)
уу\ л№ ) 5 у я
Условие F4.7) является критерием того, что электронный газ вы-
вырожден. Сравнение с соотношением F3.5) показывает, что с точ-
точностью до несущественного множителя, близкого к двум, эти нера-
неравенства обратны по отношению друг к другу.
182
В заключение остановимся на виде функции распределения Фер-
Ферми— Дирака в случае сильного вырождения. Когда \i*>kTy то все
возможные состояния электронов целесообразно разбить на две
грулпы. Для одних состояний, для которых энергия много меньше
(х, среднее число частиц в данном состоянии <П{> практически
равно единице. Действительно, если энергия состояния е* меньше \i
по крайней мере на B^-3) kT, то в формуле Ферми F1.4) экспо-
экспонента имеет очень малое значение и, следовательно, <я?>~1. На-
Наоборот, если состояние относится
к другой группе, так что энергия
8г больше jut по крайней мере на
несколько kT, то экспонента очень
велика и, следовательно, <пг>
близко к нулю. Таким образом,
функция распределения Ферми
имеет в этом случае вид, показан-
показанный на рис. 10.1. Она практически
равна единице для всех энергий,
меньших ji, и нулю для всех энер-
энергий, больших jx. Имеется относи- Рис> 10Л
тельно узкая область шириной
порядка 2&7\ в которой происходит изменение от значений, близких
к единице, до значений, близких к нулю. Для состояния с энергией
8г, равной химическому потенциалу \х, среднее число частиц <#г>
равно 72- Отсюда вытекает, что химический потенциал — это энер-
энергия такого состояния, вероятность заполнения которого равна 72*
§ 65. Теплоемкость газов при учете
квантовых эффектов
Пример электронного газа показывает, что квантовые эффекты
могут оказывать большое влияние на значение теплоемкости. Так,
при сильном вырождении теплоемкость электронов оказывается
практически равной нулю и лишь в невырожденном электронном
газе ее значение совпадает с тем, которое предсказывается класси-
классической теорией. Выше уже говорилось о том, что для объяснения
расхождений между классической теорией теплоемкости газов и
экспериментом необходимо привлечь квантовые представления.
Рассмотрим те изменения, которые при этом получаются, на, мо-
может быть, несколько искусственной, но зато очень простой модели,
позволяющей выяснить суть дела.
Предположим, что имеется жесткая двухатомная молекула, со-
совершающая плоское движение. Поскольку расстояние между ато-
атомами строго постоянно, то число степеней свободы в такой модели
равно трем. Две из них соответствуют поступательному движению
в плоскости (вдоль осей х и у) и одна — вращению молекулы от-
относительно оси, перпендикулярной плоскости (оси г). По классиче-
классической теории, внутренняя энергия в этом случае равна
183
U=±kT(N), F5.1)
я теплоемкость
Основное отличие квантовой статистики от классической состоит
в учете, с одной стороны, принципа неразличимости и принципа
Паули (для частиц Ферми), а с другой — дискретности возможных
значений энергии, которые принимает система. Обратимся к моде-
модели молекулы, совершающей плоское движение. Ее энергия пред-
представляет собой кинетическую энергию поступательного движения
вдоль осей х и у и вращательного движения относительно оси г.
Пусть т0 — масса молекулы, а /0 — ее момент инерции относи-
относительно оси, проходящей через центр масс перпендикулярно плоско-
плоскости движения. Как известно из механики, полная кинетическая
энергия может быть представлена в виде суммы кинетической
энергии поступательного движения и кинетической энергии враща-
вращательного относительно оси, проходящей через центр масс:
е = е,1ОСТ + ев?=-^- + ^, F5.2)
где через р обозначен импульс молекулы, а через Мг — проекция
момента количества движения на ось, параллельную оси z и про-
проходящую через центр масс молекулы.
Дискретность значений энергии возникает из-за того, что как
импульс, так и момент количества движения принимают дискрет-
дискретные значения. Как было выяснено в § 49, энергия поступательного
движения определяется формулой D9.1), которая в рассматривае-
рассматриваемом случае плоской модели может быть записана в виде
где а и Ь — размеры плоского «сосуда» по осям х и г/, а тх и ту —
произвольные целые числа. Рассмотрим теперь, каковы возможные
значения момента количества движения. В квантовой механике ус-
устанавливается, что для проекции момента количества движения на
некоторую ось z имеет место соотношение
Mz = mh, F5.4)
где т — произвольное целое число. Необходимость соотношения
F5.4) можно не строго, но наглядно, пояснить следующим обра-
образом. Если молекула состоит из двух одинаковых атомов, то при
вращении каждый из них описывает окружность диаметра /, где / —
расстояние между атомами. Поскольку расстояние между атомами
неизменно, то во вращательном движении они могут рассматривать-
134
ся как одна частица, обладающая суммарной массой, т. е. массой
молекулы. Момент количества движения этой частицы равен
M2 = pBpJ-, F5.5)
где рВр—количество движения во вращательном движении по ок-
окружности диаметра /. Движение по окружности следует рассмат-
рассматривать как движение в «сосуде», длина которого равна длине ок-
окружности я/. Возможные значения вращательного импульса при
таком движении в соответствии с формулами D6.7) равны
2я/г
вр л1
где т — целое число. Подставляя последнее выражение в F5.5),
найдем, что проекция момента импульса определяется формулой
F5.4), т. е. принимает дискретные значения. Ясно, что тогда дис-
дискретны и значения вращательной энергии
F5. 6)
Решение задачи об определении статистических свойств рас-
рассматриваемой модели должно начаться с определения омега-по-
омега-потенциала, для чего необходимо вычислить статистическую сумму.
Принимая за подсистему все молекулы, находящиеся в состоянии г,
характеризуемом определенным набором чисел тх, ту, т, т. е. об-
обладающие энергией
2
тхЛ гпи~\ т2, F5. 7)
В: тхЛгпи\
1 2тоа2 *2т0Ь2 У ' 2/0
для статистической суммы подсистемы можем написать
где П{ — число молекул в состоянии /. Сумма подобного вида уже
вычислялась, и результат зависит от того, каков общий спин мо-
молекулы. Если спин полуцелый, то молекула относится к частицам
Ферми и в силу принципа Паули имеется всего две возможности:
/Zi = 0 и П{= 1. Для Zi* получается
Если суммарный спин целый, то молекула есть частица Бозе и пг =
= 0, 1,..., оо. Тогда (см. § 56)
Для омега-потенциала подсистемы находим соответственно
185
для молекул — частиц Ферми и
q* = __ kT in Zt - kT In A - e(lA-?')/(*n)
для молекул — частиц Бозе.
Когда концентрация молекул достаточно низкая, так что хими-
химический потенциал отрицателен и по абсолютной величине много
больше kT, то в обоих выражениях для омега-нотенциала экспо-
экспоненциальный член под знаком логарифма оказывается малым по
сравнению с единицей и тогда приближенно оба они сводятся к од-
одному и тому же выражению
Легко видеть, что последнее совпадает с выражением E6.7), оп-
определяющим омега-потенциал системы, вычисленный без учета не-
неразличимости частиц. Оценим, при каких концентрациях справед-
справедливо сделанное выше предположение. Поскольку омега-потенциал
в этом приближении одинаков как для бозонов, так и для фермио-
нов, то можно использовать условие невырожденности газа Ферми.
Пусть масса атомов в молекуле равна массе атома водорода тн=
= 1,67-10~27 кг, тогда из "F3.5) следует, что при температурах,
больших 20 К (температура ожижения водорода при нормальном
давлении), условие невырожденности выполняется, если концент-
концентрация молекул меньше, чем я=1,7-1028 м~3. Такое высокое значе-
значение концентрации соответствует конденсированным средам (жид-
(жидкостям,, твердым телам), так что условие невырожденности в газе
можно считать выполненным. Для омега-потенциала всей системы
получается
Суммирование по i практически сводится к суммированию по тХу
где по F5.2) и F5.5)
a'~~ ' J~ ' У~ 2/0
Для дальнейшего существенно обратить внимание на большую
разницу в величине коэффициентов а, р и у. Действительно, момент
инерции молекулы равен сумме произведений масс атомов на
квадрат их расстояния от оси вращения, т. е.
Таким образом, ваи р входят произведения т0а2 и m0b2, где а и
Ь — размеры сосуда, а в у входит произведение то12, здесь /—рас-
186
стояние между атомами. Если размеры сосуда а«6~10~? м, а рас-
расстояние между атомами /— 0,7-10"0м, что соответствует расстоя-
расстоянию между атомами в молекуле водорода, то, считая массу атомов
равной массе атома водорода, для величин коэффициентов полу-
получим следующие оценки: а— р^7-10~37 Дж, y~1>4'10~21 Дж.
Предположим, что газ находится при высокой температуре и
kT много больше а, р и у. Тогда все три суммы можно приближен-
приближенно свести к однотипным интегралам, отличающимся значением па-
параметра (а, р или у). Рассмотрим одну из них, например по тх.
Учитывая, что число тх принимает значения от —оо до +оо и что
при переходе от одного слагаемого к следующему оно меняется на
Дтх=1, можно написать
'(/ftn
Используя результаты приложения 2 для определения значения
полученного интеграла, найдем
Таким образом, при достаточно высоких температурах
F5. 8)
Среднее число молекул по E4.10) оказывается равным
, F5. 9)
а внутренняя энергия в соответствии с E4.11)
дТ ф.
или, если использовать F5.9),
что находится в полном соответствии с выводом классической тео-
теории F5.1). Каковы же температуры, при которых у молекулы про-
проявляются все три ее степени свободы? Поскольку аир много мень-
меньше у, то сформулированное выше условие выполняется, если kf>y.
Учитывая численное значение y и постоянной Больцмана, найдем,
что неравенство выполняется при температурах, много больших Т'9
где
187
Выясним теперь, что происходит при температурах, много мень-
меньших Т\ Если температура такова, что ?Г<Су> но kT все е1Де много
больше а и C, то суммы с параметрами а и р не меняют своего зна-
значения, а сумма по у сводится к единице. Действительно, при y^>kT
все члены суммы, кроме того, в котором /л = 0, очень малы, так что
с хорошей точностью
V е-тю«/(*п сь* 1.
тп
Выражение для омега-потенциала оказывается следующим:
Q*= -kT&lW) ^^Lr , F5. 10)
У а?
т. е. таким, как будто у молекулы имеется всего две степени сво-
свободы, соответствующие поступательному движению. Таким обра-
образом, при Т<^Т/ вращательная степень свободы «вымерзает». Есте-
Естественно, что если с помощью F5.10) вычислить внутреннюю энер-
энергию и теплоемкость, то получатся величины, которые соответствуют
двум степеням свободы:
Cv=(N)k.
При необходимости можно проследить за изменением теплоемко-
теплоемкости от одного предельного значения до другого, для чего достаточ-
достаточно воспользоваться выражением для теплоемкости, полученным из
омега-потенциала, в котором сумма по у не заменяется интегралом.
Для переходной области достаточно учесть в сумме несколько чле-
членов (ап = О, ±1, ±2), так как влияние остальных мало. Такие вы-
вычисления, однако, целесообразно проводить для более реалистиче-
реалистической модели, чем та, которая применялась выше.
Изложенное позволяет понять причину, по которой в двухатом-
двухатомных молекулах, а также линейных, т. е. многоатомных, в которых
атомы располагаются на одной оси, следует учитывать лишь пять
степеней свободы, а не шесть, как это необходимо делать при рас-
рассмотрении нелинейных многоатомных молекул. Дело в том, что
в линейных молекулах момент инерции относительно оси, на кото-
которой лежат атомы, оказывается очень малым, так что соответствую-
соответствующий параметр у и температура V очень велики. Действительно,
при вращении молекулы вокруг этой оси момент инерции опреде-
определяется в основном электронами, масса которых на три порядка
меньше массы ядра. Что касается вклада самих ядер, то из-за ма-
малого радиуса ядра, который на четыре порядка меньше, чем ра-
радиус атома, их вклад в момент инерции относительно оси, соеди-
соединяющей ядра, оказывается на восемь порядков меньше, чем отно-
относительно осей, перпендикулярных этому направлению.
Аналогичным образом можно объяснить причину, по которой
при низких температурах не сказываются колебания атомов моле-
молекул относительно друг друга. Поскольку энергия колебательного
движения тоже принимает дискретные значения, то при энергии kTy
188
меньшей, чем минимальная энергия, необходимая для возбуждения
колебаний, вероятность возбуждения настолько мала, что колеба-
колебания не нужно учитывать при подсчете статистических сумм.
Таким образом, квантовая теория позволяет объяснить функцио-
функциональную связь теплоемкости с температурой, которая соответствует
экспериментально наблюдаемому ходу этой зависимости.
Задачи к главе 10
1. Концентрация электронов в меди равна 8,5-1028 м~3. Определить, вырож-
вырожден или невырожден электронный газ при комнатной температуре. При
какой температуре происходит переход от вырожденного к невырожден-
невырожденному при заданной концентрации?
Решение. При Г = 300 К имеем
-^L-, 1,3.1025 м-;
5уТГ
это много меньше, чем я = 8,5-1 О*8 м~3, следовательно, газ вырожден. Газ ста-
становится невырожденным при температуре, много большей, чем температура плав-
плавления и испарения меди.
2. В газовом разряде измеренная концентрация электронов /z=1018 м~3, а их
температура 2000 К. Чему равно давление электронов?
Решение. В данном случае газ невырожден, так как
что много больше значения концентрации. Отсюда вытекает, что для расчета
давления можно воспользоваться формулой C6.2)
Р== nkT ^ 3-10-2 Па.
ЧАСТЬ IV
СТАТИСТИЧЕСКАЯ ФИЗИКА
НЕРАВНОВЕСНЫХ СОСТОЯНИЙ
ГЛАВА 11
УРАВНЕНИЕ БОЛЬЦМАНА
§ 66. Функция распределения в неравновесном
случае
В гл. 5 было показано, что в классической статистике полное
описание системы, находящейся в равновесии, дается распределе-
распределением Гиббса (или большим каноническим распределением, когда
число частиц в системе переменно). На практике часто приходится
иметь дело с системами, не находящимися в равновесии, и тогда
возникает вопрос о том, какова плотность вероятности для них.
Поскольку исследование неравновесных систем представляет со-
собой очень сложную задачу, то ниже будет рассмотрен только слу-
случай идеального газа, т. е. совокупности частиц, взаимодействие ко-
которых между собой настолько слабо, что с ним можно не считать-
считаться. Движение каждой частицы идеального газа происходит неза-
независимо, и поэтому полная функция распределения системы опреде-
определяется функцией распределения одной частицы. Для того чтобы
убедиться в этом, достаточно повторить рассуждения, приведенные
в § 30. Действительно, если / (г, р) — функция распределения, то
dn/N=f(r, p)dxdQ/N=dW(r, p)
есть вероятность обнаружить частицу в объеме dy=dTdQ pi-прост-
ранства.
Вероятность того, что частица / находится в объеме dyi, а ча-
частица 2 — в dy2, вследствие независимости движения частиц дает-
дается произведением вероятностей, т. е.
u Pl; r2, p2) = dW(ru px)dW(r2y p2) =
= /(ri, Pi)dYi/(r2, P2)dY2 ~2-
Эти рассуждения можно продолжить, тогда для плотности вероят-
вероятности всей системы получим
-L/(ri, рг).../(гю pN).
190
Таким образом, основной задачей теории идеального газа явля-
является нахождение неравновесной функции распределения для одной
частицы. Поскольку имеется в виду неравновесное состояние, то эта
функция отличается от распределения Максвелла — Больцмана и
необходимо иметь некоторый общий метод, позволяющий находить
неизвестные функции распределения. Такой метод был дан Больц-
маном и состоит в решении предложенного им уравнения, носяще-
носящего название кинетического или уравнения Больцма-
н а. Прежде чем рассматривать уравнение для функции распреде-
распределения, обратимся к задаче из области гидродинамики, которая поз-
позволит лучше понять смысл кинетического уравнения.
§ 67. Уравнение непрерывности
Рассмотрим движение газа, обладающего плотностью р. Если
т0 — масса одной молекулы газа, то концентрация (число молекул
в единице объема) равна
n=Q/m().
На рис. 11.1 показана система координат и мысленно выделенный
элемент объема со сторонами dx, dy, dz. Предположим вначале, что
газ течет вдоль оси у, и рассмотрим изменение его массы в выде-
выделенном элементарном объеме. По-
Поскольку скорость изменения плот- z
ности газа в данной точке про-
пространства равна dp/dt, то измене-
изменение массы, происшедшее за про-
промежуток времени dt, можно за-
записать в виде
dM=•&
dt
F7.1)
Щ
где dx = dxdydz. Увеличение или
уменьшение массы может проис-
происходить только за счет того, что
количество газа, втекающего че- Рис. 11.1
рез левую грань с координатой у,
не равно количеству газа, вытекающему через правую с координа-
координатой y + dy. Если скорость течения равна vy, то за промежуток вре-
времени dt объем газа, совпадавший в момент t с dt, сместится на рас-
расстояние Vydt, причем он может несколько растянуться или сжаться,
если скорости у правой и левой граней не одинаковы. Из рис, 11.1
видно, что из объема выйдет количество газа, равное
Qvydtdxdz=Q(y-\-dy)vy(y-\-dy)dtdxdz. F7.2)
Вместе с тем слева в объем войдет количество газа, равное
Q{y)vy(y)dtdxdz. F7.3)
Разница между выражениями F7.2) и F7.3) состоит в том, что
значения плотности и скорости потока у левой грани у в общем
случае не равны значениям скорости и плотности у правой
За время d^ увеличение массы равно превышению втекающей мас-
массы над вытекающей, т. е. разности
g (у) vy (у) dtdxdz — Q(y-\- dy) vy {y -f d у) dtdxdz.
Поскольку у и y + dy отличаются на бесконечно малую величину
dy, то эту же разность можно представить в виде
d/dr. F7.4)
оу ~ оу
По закону сохранения массы, приравнивая F7Л) и F7.4), можно
написать '
Если поток газа имеет составляющие скорости по всем трем
осям, то рассуждения, аналогичные приведенным выше, покажут,
что уравнение непрерывности принимает вид
до_= \
д(ду2)\
dz J"
\
dt L дх
Разделив обе части уравнения F7.5) на массу одной молекулы то,
найдем, что оно может быть записано в виде закона сохранения
числа частиц
Г d(nvx) , d(nvy) д(пуж)\
[ дх ' ду dz J
dt
В обозначениях, принятых в векторном анализе, имеем
|L=-(iiv(/iv). F7.7)
Уравнение непрерывности в форме F7.6) или F7.7) показывает,
что изменение числа частиц в некотором объеме равно превышению
числа втекающих в него частиц над числом вытекающих.
§ 68. Кинетическое уравнение Больцмана
Больцман предложил находить функцию распределения из урав-
уравнения, по смыслу аналогичного уравнению непрерывности, но на-
написанного в фазовом пространстве. Вспомним, что в статистиче-
статистической физике идеального газа состояние частицы описывается за-
заданием трех ее координат (х, у, z) и трех компонент импульса (рХ)
ру, pz), т. е. шести координат фазового пространства (^х-пространст-
ва по § 30). Функция распределения должна в соответствии с ее
смыслом рассматриваться как концентрация частиц в jx-простран-
стве, поскольку выражение
d/i=/(r, p)dy
192
определяет среднее число частиц в элементе объема dy шестимерно-
шестимерного ji-пространства.
Изменение числа частиц в dy обусловлено тем, что некоторые
из них меняют свои координаты или значения импульса и выходят
из dy, а другие, наоборот, прибывают в него. Таким образом, для
функции распределения имеет место уравнение, аналогичное урав-
уравнению непрерывности, но написанное в фазовом пространстве.
Если положение частицы в фазовом пространстве задается ше-
шестимерным вектором Гф с компонентами
то скоростью движения в фазовом пространстве следует назвать
шестимерный вектор с компонентами
Vcj^U, У, Z, рх, ру, pz},
где точкой обозначена производная по времени. Поскольку по смыс-
смыслу импульса
х = Рх/т0, у = ру/т0, г = рг/щ F8. 1)
и поскольку, по второму закону Ньютона,
Px = Fx* Py = Fv Pz=Fz, F8. 1')
где FXj Fy, Fz — компоненты вектора равнодействующей всех сил,
действующих на частицу, то кинетическое уравнение Больцмана
можно записать в следующем виде:
F8-2>
или при силах, не зависящих от скорости движения частицы,
at /тг0 дх т0 ду т^ dz л дрх у дру z dpz
F8.3)
Уравнение F8.3) представляется в более сжатой форме, если
использовать понятие о градиенте функции. Градиентом функ-
функции / в обычном пространстве называется вектор, проекции кото-
которого равны
r — id-L d-L (IL\
~{дх ' оу ' дг)т
Аналогично, градиентом в импульсном пространстве называют век-
вектор
193
Легко видеть, что уравнение F8.3) эквивалентно следующему:
Цт= ~ — g™dr / - F gradp /. F8.4)
Уравнение F8.4) называется кинетическим и было предложено
Больцманом для нахождения функции распределения f.
Из уравнения F8.3) просто получается так называемая теоре-
теорема Лиувилля, точнее говоря, частный случай этой теоремы, относя-
относящийся к шестимерному ^-пространству.
Полная производная по времени от функции распределения, т. е.
производная, вычисленная с учетом изменения координат х, у, z ча-
частицы и ее импульса рх, Ру, рг в соответствии с законом движения,
равна
f • , df • , df • , df •
Если учесть уравнения F8.1) и F8.Г), то из F8.3) следует, что
полная производная равна нулю:
Предположим, что N частиц равномерно распределены по не-
некоторому объему фазового пространства Ау, тогда функция рас-
распределения отлична от нуля только в Ау и равна там
f JL
Поскольку d//d/=O, то это значение сохранится и в области Ауг, в
которую частицы из Ау перейдут за время t. Тогда из условия
N __ N
Ду Ду'
следует, что
Ду-=Ау'»
т. е. при перемещении фазового объема его величина сохраняется.
Это утверждение и составляет содержание теоремы Лиувил-
л я.
§ 69. Взаимодействие с термостатом
Практически оказывается более удобным пользоваться не точ-
точной формой кинетического уравнения F8.3), а другой — приближен-
приближенной. Для того чтобы пояснить характер используемых упрощений,
рассмотрим, например, поведение электронов в плазме газового раз-
разряда. Считая электронный газ классическим и идеальным, мы пре-
пренебрегаем взаимодействием электронов между собой, но учитыва-
учитываем воздействие внешних электрических полей, а также взаимодей-
взаимодействие с ионами и нейтральными молекулами. Когда внешних полей
нет и когда ионы и молекулы находятся в равновесном состоя-
194
нии, электроны тоже пребывают в равновесии. Более того, если
электроны каким-либо путем были выведены из равновесного со-
состояния, то за счет столкновений с ионами и молекулами они вновь
к нему возвращаются. Таким образом, ионы и молекулы следует
рассматривать как некоторый термостат, за счет взаимодействия с
которым исследуемая система (электронный газ) приходит к рав-
равновесию, характеризуемому температурой термостата.
Выделим из последнего слагаемого уравнения F8.4) ту часть,
которая описывает взаимодействие с термостатом, и напишем
F9. 1)
В F9.1) FBH — внешние силы (например, — еЕ для электронов, на-
находящихся в электрическом поле с напряженностью Е), а
(df/dt) ст — условное обозначение для результата взаимодействия
системы с термостатом (для столкновений электронов с нейтраль-
нейтральными молекулами и ионами). Вообще говоря, член (df/dt)CT имеет
различный вид в зависимости от того, какие столкновения учиты-
учитываются, однако в некотором классе случаев его можно представить
следующим образом:
(Щ = /~/о F9.2)
\ dt )ст х
где / — неравновесная функция распределения, /0 — равновесная
функция распределения, т — параметр, носящий название времени
релаксации.
Какие соображения подсказывают такое выражение?
Во-первых, столкновения не должны нарушать равновесное рас-
распределение, так как именно благодаря им оно устанавливается.
Легко видеть, что если /=/о> то (—] =0. Равенство нулю имеет
\ dt Уст
место для частиц любых импульсов, так что соотношение F9.2)
удовлетворяет принципу детального равновесия.
Во-вторых, если отступления от равновесия малы, то следует
ожидать, что скорость возвращения к равновесию должна быть
пропорциональна отклонению от равновесного состояния, т. е.
Параметр т считается известной, например из опыта, величиной.
Его смысл легко выяснить на следующем частном случае. Пусть
распределение частиц в пространстве однородно, а по импульсам
неравновесно, и внешних сил нет. Так, например, если под дейст-
действием однородного внешнего электрического поля через газ протека-
протекает электрический ток, то функция распределения неравновесна, но
однородна в пространстве, т. е. не зависит от координат. Предпо-
Предположим, что в момент времени ?=0 поле выключается и, следова-
следовательно, после этого внешние силы равны нулю. Поскольку до вклю-
включения поля функция распределения была неравновесна, то ясно,
195
что и в дальнейшем в течение некоторого времени она будет отлич-
отлична от /о- Для моментов времени после /=0 уравнение Больцмана
имеет вид
^-=- /~/о , F9.3)
поскольку член (p/mo)gradrf равен нулю, так как дифференциро-
дифференцирование по координатам дает ноль (функция распределения однород-
однородна), а слагаемое FBHgradpf обращается в ноль из-за того, что внеш-
внешние силы равны нулю. Решение уравнения F9.3) легко находится
« имеет вид
/@ = /o+[/@)-/0]e-'/*f F9.4)
где /@) —значение неравновесной функции распределения в на-
начальный момент времени. Видно, что величина
/0]е-'/*, 16Э.5)
определяющая отклонение функции распределения от равновесной,
экспоненциально уменьшается с постоянной времени т, которую по
этой причине называют временем релаксации. Итак, си-
система, отключенная от внешних воздействий, нарушающих равно-
равновесие, из-за взаимодействия с термостатом приходит в равновесие
за время, характеризующееся временем релаксации т.
Следует иметь в виду, что включение в уравнение члена вида
F9.2) было проведено не последовательно. Строго говоря, метод
Больцмана подразумевает, что должно быть детально исследовано
взаимодействие идеального газа с частицами, составляющими тер-
термостат, на основе конкретной модели строения частиц. Выражение
F9.2) может быть оправдано только если точный анализ приводит
к соотношению такого вида. Хотя в некоторых случаях это дейст-
действительно имеет место (см. гл. 13), но часто оказывается и не так.
Таким образом, приближенное уравнение Больцмана, учитываю-
учитывающее взаимодействие с термостатом членом с временем релаксации,
имеет вид
Ц-= - -В- grad, / - Fm gradp / - t=lSL . F9.6)
at niQ x
Широкое использование такой формы уравнения объясняется ее
относительной простотой, позволяющей представить решение в при-
приближенной, но не сложной и ясной по физическому содержанию
форме. В дальнейшем будет рассматриваться только этот случай.
§ 70. Уравнение Больцмана в квантовом случае
При строгом кватновомеханическом подходе метод кинетическо-
кинетического уравнения Больцмана оказывается неприменимым, так как не-
неприменимо само представление о функции распределения как о
функции координат и импульсов отдельных частиц. Причина этого
обстоятельства очень глубока и связана с так называемым прин-
196
ципом неопределенности квантовой механики, по кото-
которому частица не может одновременно иметь точное положение
(координату) и точное значение импульса. По принципу неопреде-
неопределенности если положение частицы на оси х устанавливается с точ-
точностью порядка Ал:, то ее импульс может быть известен лишь с точ-
точностью Арх, причем имеет место соотношение
kpQ\x>nh. G0. 1)
Аналогичные соотношения неопределенности справедливы и для
других осей:
Д/^Ду ^ nh, ApzLz _ nh. G0 .1)
В какой-то мере можно пояснить соотношения G0.1), используя метод
квантования, примененный в гл. 7. Предположим, что координата х фиксируется
с некоторой точностью Ах. Можно считать, что для этого частица помещается в
¦потенциальный ящик, размер которого вдоль оси х равен Да:. Состояние частицы
определяется в этом случае стоячей волной, и значение длины волны, т. е. им-
импульса, дискретно. Стоячая волна представляет собой сумму двух бегущих
навстречу волн с одинаковыми амплитудами. Это означает, что в любом из воз-
возможных состояний одинаково вероятно как положительное, так и отрицательное
значение импульса. Для среднеквадратичного разброса импульса имеем
так как
J_ _1_
<Рх>— 2 Рх+ 2 (~~~Px'--
Вычисление среднего значения квадрата импульса очень просто, а именно:
. з « L ^2 , _L , ч2 — п2
х 2 •*" 2 Л ^'
т. е. среднеквадратичное отклонение равно квадрату импульса. Поскольку по
формуле D6.1)
тпЪ.
рх = kx п = ,
VZ ..
¦ = тл Ь.
то для величины у(Ах^) у {Арх> получается
У<Ад:2> ^/<Ap2>==Ajc___
х Ах
Минимальное значение неопределенности координаты и импульса имеет место,
•когда т = \, и тогда действительно видно, что при Ах= ]/ (х? > и Арх =
АхАрх > яй .
Таким образом, в квантовой механике положение и импульс ча-
частицы не могут быть одновременно точно известны, а тогда, есте-
естественно, отпадает возможность описывать систему с помощью функ-
функции распределения, предполагающей знание как радиус-вектора,
так и импульса частицы. В связи со сказанным следует обратить
197
внимание на то, что квантовые функции распределения Ферми —
Дирака и Бозе — Эйнштейна в этом отношении отличаются от клас-
классических. Хотя они и дают среднее число частиц в данном состоя-
состоянии, но квантовомеханическое задание состояния не подразумева-
подразумевает одновременного указания импульса и координаты.
Можно все же использовать классическое представление о функ-
функции распределения и при учете квантовых эффектов, если ограни-
ограничиться так называемым квазиклассическим, т. е. почти клас-
классическим, приближением в квантовой механике. В этом приближе-
приближении состояние частицы описывается и импульсом, и координатой, но
только в той мере, в какой это допускается принципом неопределен-
неопределенности. Так, в случае одномерного движения вдоль оси х частице
приписывается импульс с точностью Арх, где Арх — некоторая вели-
величина, много меньшая, чем среднее значение модуля импульса ча-
частиц системы. По принципу неопределенности координата не мо-
может быть известна с точностью более высокой, чем
Однако если в данной задаче такая точность задания координаты
достаточна, то можно говорить и о координате х. В частности, та-
такой подход возможен, если частица находится в силовом поле, по-
потенциальная энергия которого настолько медленно меняется в за-
зависимости от координаты, что на расстоянии порядка Дл; ее следу-
следует считать практически постоянной. Вместе с тем сохраняются
такие специфические квантовые особенности, как дискретность зна-
значений импульса и энергии, необходимость учитывать принцип не-
неразличимости частиц, а также принцип Паули для частиц с полуце-
полуцелым спином.
Если привлечь понятие о плотности состояний введенное в § 48,
то в этом приближении систему можно описывать функцией рас-
распределения /(г, р). Поскольку в уравнении Больцмана функция
распределения имеет смысл среднего числа частиц в единичном
объеме фазового пространства, то следует уточнить, что понимает-
понимается под равновесной функцией распределения /0 в члене с временем
релаксации в тех случаях, когда она не может считаться клас-
классической.
Выделим элемент объема фазового пространства Ay=AtAQ, где
Ax=AxAyAz и AQ=ApxApyApz настолько велики, что удовлетворя-
удовлетворяются соотношения неопределенности G0.1), но одновременно на-
настолько малы, что в них квазиклассическая функция распределе-
распределения практически постоянна. Среднее число частиц в Ау равно
<АЛ/>
где сумма берется по всем состояниям, принадлежащим выбранно-
выбранному объему. Как было показано в § 48, число состояний в Ду выра-
выражается формулой
198
Если среднее число частиц <щ> в любом из состояний, принадле-
принадлежащих этому объему, практически одинаково, то
Таким образом, равновесная функция распределения /0 равна
Ду
ИЛИ
в случае фастиц Ферми и
в случае, когда газ состоит из бозонов. В приближении времени ре-
релаксации квазиклассическая функция распределения удовлетворя-
удовлетворяет уравнению Больцмана F9.6), однако в члене, учитывающем
столкновения, при учете квантовых эффектов следует использовать
равновесную функцию распределения Ферми — Дирака G0.2) или
Бозе — Эйнштейна G0.3) в зависимости от типа частиц, из кото-
которых состоит газ. Функции распределения G0.2) и G0.3) относят-
относятся к частицам с определенным значением проекции спина. Если в
задаче спин частиц несуществен, то их следует умножить на число
возможных значений проекций спина B для электронов и 2 для
фотонов).
ГЛАВА 12
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
В ДИФФУЗИОННОМ ПРИБЛИЖЕНИИ
(ПРИБЛИЖЕНИЕ ЛОРЕНЦА)
§ 71. Функция распределения
при малом времени релаксации
Кинетическое уравнение Больцмана при условии, что оно будет
решено, дает полную информацию о поведении идеального газа.
Поскольку уравнение даже с упрощенным членом, учитывающим
столкновения, все еще очень сложно, то получить решение для об-
общего случая в аналитическом виде практически невозможно. Есть,
однако, один частный случай, который довольно часто встречается
и в котором решение получается относительно просто. Рассмотрим
его более подробно.
Время релаксации, входящее в уравнение Больцмана, определя-
определяет время возвращения системы в равновесное состояние и харак-
199
тернзует интенсивность взаимодействия идеального газа с термо-
термостатом. Чем сильнее взаимодействие с термостатом, тем меньше
время релаксации и тем быстрее система приходит в равновесие.
Если внешние силы достаточно малы, то при малом времени релак-
релаксации они не в состоянии значительно нарушить равновесней функ-
функция распределения должна быть достаточно близкой к равновесной.
Эти физические соображения могут быть облечены в математиче-
математическую форму.
Перепишем уравнение Больцмана в следующем виде:
/ = /o-*v-t- gradr/-TFBHgradp/. G1.1)
ut m.Q
Когда время релаксации мало, слагаемые, содержащие х в качест-
качестве множителя, тоже малы и видно, что функция распределения /
близка к равновесной /0. Подставим в правую часть значение /из-
того же уравнения G1.1), тогда получится
где через 0(х2) обозначены члены второго порядка малости, т. е-
пропорциональные т2. Их можно опустить. Равновесная функция
распределения не зависит от времени, так что
г» /•
-=0.
dt
Таким образом, неравновесная функция распределения в этом при-
приближении просто выражается через равновесную:
gr/oBHg/,/o. G1.2)
щ
Однако условия, при которых справедливо решение G1.2), на-
нарушаются, если не постоянная в пространстве концентрация иде-
идеального газа отлична от равновесной. Действительно, в данной не-
небольшой области пространства равновесное распределение, соот-
соответствующее местной концентрации, устанавливается очень быстро.
В то же время установление равновесной концентрации во всей
объеме, который занимает газ, происходит диффузионным путем,
т. е. путем постепенного перемешивания. Этот процесс оказывает-
оказывается довольно медленным, и поэтому представление G1.2), где поя
/о понимается равновесная функция распределения для всего газа-
в целом, не может дать хорошее приближение. Область примени-
применимости фЬрмулы G1.2) оказывается значительно шире, если считать
ее справедливой локально, т. е. для относительно небольших обла-
областей пространства, причем равновесная функция распределения,
входящая в правую часть, не одинакова в различных областях, так
как зависит от концентрации (или, что то же самое, от химического
потенциала), меняющейся от точки к точке. Поскольку закон из-
изменения концентрации неизвестен, то формула G1.2) не может рас-
200
сматриваться как решение, во всяком случае до тех пор, пока не
-будет найдена функция n=n(rf t) или \x=\i(r, t).
Мы будем считать, что из-за эффективного взаимодействия с
термостатом температура идеального газа постоянна по всему объ-
объему и равна температуре термостата. Поскольку теперь концентра-
концентрация не предполагается постоянной, то равновесная функция рас-
распределения неявно (через концентрацию) может зависеть от вре-
времени, так что
х dfo =x dfo дп
dt дп dt
В дальнейшем при рассмотрении уравнения диффузии выяснится,
дп
что скорость изменения концентрации -— есть малая величина,
dfo
пропорциональная т, так что член t —:— второго порядка мало-
малости по т, и хотя он отличен от нуля, но все равно должен быть опу-
опущен. Иногда приходится сталкиваться с задачами, в которых внеш-
внешняя сила FBH быстро меняется во времени. Если скорость ее измене-
изменения характеризуется временами, сравнимыми с временем релакса-
релаксации т, то необходимо учитывать член т , который в этом случае
нельзя заменить на т ——. Примером такой ситуации может слу-
dt
жить воздействие инфракрасного излучения на электронный газ в
плазме и ряд других.
§ 72. Уравнение диффузии
В неравновесном случае нельзя сразу написать функцию, опре-
определяющую зависимость концентрации частиц от координат, но мож-
можно получить уравнение, носящее название уравнения диффузии,
решение которого определяет эту зависимость. При выводе уравне-
уравнения диффузии следует исходить из уравнения Больцмана
Поскольку концентрация частиц определяется соотношением
где интеграл берется по всему импульсному пространству, то попро-
попробуем проинтегрировать G2.1) по импульсам.
Меняя порядок интегрирования по импульсам и дифференциро-
дифференцирования по времени, легко показать, что
дп
dt
201
Рассмотрим теперь результат интегрирования члена, содержа-
содержащего время релаксации (т. е. описывающего столкновения). Име-
Имеем (если т не зависит от энергии частиц)
= -L($ /dQ_
Здесь учтено, что оба интеграла равны одной и той же величине,
а именно локальной концентрации частиц в области около точки г.
Следует заметить, что нулевой результат получается и при гораз-
гораздо более общих предположениях о члене, учитывающем столкно-
столкновения. Действительно, достаточно, чтобы взаимодействие носило
такой характер, что общее число частиц в данной области прост-
пространства (интеграл по всем импульсам) оставалось неизменным,
т. е. не было уничтожения или рождения частиц. Таким образом,
равенство
можно считать выполненным независимо от более частных предпо-
предположений о характере взаимодействия с термостатом.
Обратимся к вычислению интеграла.
Более подробно его можно записать следующим образом:
f
так как проекции силы Fmlx, FBHy, FBHZ по предположению не зави-
зависят от скоростей и поэтому могут быть вынесены за знак интегра-
интеграла. Вычисление каждого из трех интегралов проводится аналогич-
аналогично, и поэтому достаточно рассмотреть один из них. Имеем, напри-
например,
-[. оо -{- со + 9* -J- ею -J- оо
dp.
Поскольку число частиц с бесконечно большим значением проекции
импульса равно нулю, то
и, следовательно,
202
Оставшийся невычисленным интеграл
J-(p//no)gradr/d2
заменой порядка дифференцирования по координатам и интегриро-
интегрирования по импульсам преобразуем к следующему виду:
G2.2)
gradr/d2fr/dQf(
щ дх J т0 ду J т0
dz J m0
Каждый из приведенных выше интегралов относится к определен-
определенной области пространства, в которой концентрация почти постоян-
постоянна, так что для функции распределения можно использовать фор-
формулу G1.2). Выбрав для начала первый из них, можем написать
Щ J Щ J Щ т
^tFBHgradp/odQ. G2.3)
Щ
Рассмотрим теперь последовательно интегралы, стоящие в правой
части последнего равенства. Имеем
так как этот интеграл имеет смысл среднего значения х компонен-
компоненты скорости в равновесном состоянии, описываемом функцией рас-
распределения /о- Формально равенство нулю вытекает из нечетности
подынтегральной функции по рх-
Займемся преобразованием второго интеграла, который можно
представить в следующей форме:
gradr/od2f^^
Щ Щ J гпц дх
v
Щ ду J m20 dz
Из трех интегралов, стоящих в правой части, два последних равны
нулю, так как подынтегральная функция нечетна, например, по рх-
Остается следующий интеграл:
дх
Поскольку px2/m02=vx2 и зависимость от координаты входит через
концентрацию п, функцией которой является f0, то можно написать
203
mg дх
где
= Dx*L9 G2.5)
Величину Dx называют коэффициентом диффузии.
Рассмотрим, наконец, последний интеграл в G2.3):
J Щ
Снова в силу нечетности подынтегральной функции два последних
интеграла равны нулю. Поскольку сила не зависит от импульса,то
J Щ дрх J
m0 дрх
Назовем коэффициентом дрейфа величину
G2.6)
п j ntQ
тогда
C
J
Собирая все полученные результаты, можем для G2.3) напи-
написать
С JbL /d2= _Z)^ + ri;/-BH.v«. G2.7)
Совершенно такие же выкладки приводят к аналогичным вы*
ражениям для двух других интегралов в G2.2), а именно:
где обозначено
G2.7')
но п _ д
d ' ^—^r
G2.8)
/И0
204
Поскольку /о и т зависят только от модуля импульса, то легко ви-
видеть, что
= Dy = Dz и г\х = 1\у=
так как эти интегралы переобозначением переменных интегриро-
интегрирования переводятся один в другой. В дальнейшем коэффициент диф-
диффузии будет обозначаться ?), а коэффициент дрейфа т\'.
Таким образом, уравнение диффузии можно записать в виде
дп д Г ,^ дп | , г? '}
Ot дх I дх \
или, используя сокращенные обозначения векторного анализа,
^L FBH]. G2.10)
В тех случаях, когда рассматривают газ заряженных частиц
(электроны), на которые действует внешнее электрическое поле Е
с силой
(е — заряд частицы), вместо введенного выше коэффициента дрей-
дрейфа т]/ применяют понятие коэффициента подвижности.
Подвижность т] равна
Обычно используемая форма записи уравнения диффузии для элект-
электронов имеет следующий вид:
dv[Dgrad^ + ri/iE]. G2.11)
dt
Рассмотрим значение входящих в уравнение диффузии коэффи-
коэффициентов D и т]. Если газ невырожденный, т. е. подчиняющийся ста-
статистике Максвелла, то коэффициент диффузии
дп J
m20
A BnmQkTf2 " ^o
не зависит от концентрации. Как было выяснено выше,
поэтому, учитывая, что
(v2yx
205
можем выражение для коэффициента диффузии записать в таком
виде:
з ч '
В невырожденном электронном газе подвижность тоже не зависит
от концентрации:
epVB/«oftr) j q
т] = —— С
n J
epV() j q =
m0 Bnm0kTf/2 dPx
*l1^e-/>2/Bmo*nd2. G2 12)
v
Щ Bnm0kTK/2
После выполнения операции дифференцирования экспоненты
под знаком интеграла получается следующее выражение:
2
2
Ц = — Г -^
W J /n20
n0
Сравнение с G2.12) показывает, что
ti = —D. G2.13)
kT у
Соотношение G2.13), связывающее между собой коэффициент диф-
диффузии и подвижность частиц, подчиняющихся классической стати-
статистике, носит название уравнения Эйнштейна.
Для частиц, подчиняющихся квантовой статистике, написанные
выше уравнения несправедливы и само понятие о коэффициентах
диффузии и подвижности теряет смысл. Поясним это утверждение
на примере сильно вырожденного газа Ферми.
В случае сильного вырождения функция распределения соглас-
согласно § 64 имеет вид (см. рис. 10.1),
при е <Г т),
G2.14)
При ?>ТЬ
где уровень Ферми \х определяется уравнением F4.4)
tx = /*2/3 Eя2 Й3J/з/Bяг0). G2.15)
Таким образом, для коэффициента диффузии можно написать
дп J m\ J дп
Если использовать условие (^t) =-г— (v2x), то
3
206
где учтено, что при подынтегральной функции, зависящей от моду-
модуля импульса, dQ=4np2dp.
Целесообразно перейти к интегралу по энергиям. Поскольку
2то 2 '
то, учитывая специфический вид функции распределения G2.14),
для коэффициента диффузии получим следующее выражение:
fJL 2 4nK2/tt3o/2s1/2de. G2.16)
3 дп .) т0
о
Как показано в гл. 13, время релаксации обычно есть степенная
функция энергии электрона
х = аег, G2.17)
где а и г — некоторые постоянные. После подстановки G2.17) в
G2.16) интеграл просто вычисляется:
r!!L\ G2Л8)
D( a
дп \ Зя'^з г + 5/2 /
Поскольку уровень Ферми зависит от концентрации, то
д BуТУт0 ^+5/2 \ ф = 2У2Ут0 д..г4.3/2 ду.
дц \ Зяй^з г + 5/2 ) дп Зл:1^з k ^д '
Подставляя jx из G2.15), найдем, что коэффициент диффузии за-
зависит от концентрации по формуле
где С — постоянная, равная
2 У2 Ущ 2 Ert2ft3J/3 2у1Г52/3
Вместо того чтобы говорить о коэффициенте диффузии, зависящем
от концентрации, лучше вообще не вводить такого понятия, а про-
просто рассматривать нелинейное уравнение переноса, так же как в
задачах электротехники, когда сопротивление цепи зависит от то-
тока, лучше говорить не о сопротивлении, а о нелинейной вольт-ам-
вольт-амперной характеристике.
Аналогичным образом в случае сильного вырождения после ин-
интегрирования по частям (причем учитывается, что при рх = оо,
Рх=—оо функция распределения обращается в ноль) найдем для
подвижности
df/of
т0 дрх n J дрх \ mQ
\ е С ( х 2г дх \
/
е С - ( и дъ Рх \ А е С г ( х , 2г дх \
л J \ т0 дг гпц ) п ,) \ Щ 3/тг0 де /
207
Если использовать аппроксимацию G2.14) и перейти к интегралу
по энергии, то
iq 3 дв rriQ
о
и после подстановки G2.17) получается
п т0 \ ' 3 / BяЦK г+ 3/2
= __?_ _2_ V2 Ут0 з/2
Сравнение этого выражения с выражением для коэффициента диф-
диффузии показывает, что соотношение Эйнштейна не выполняется, а
вместо него имеет место равенство
т. е. отношение коэффициента диффузии к подвижности зависит от
концентрации (через (ы). Поскольку подвижность оказывается за-
зависящей от концентрации, то, по-видимому, лучше не вводить та-
такой характеристики для сильно вырожденного газа.
Диффузионное уравнение G2.11) при постоянной температуре
определяет концентрацию частиц в различных точках пространства,
однако для получения единственного решения необходимо допол-
дополнить это уравнение граничными и начальными условиями, т. е.
указать значения концентрации на границе той области, в которой
она определяется, а также ее значения в начальный момент вре-
времени.
§ 73. Функция распределения
в диффузионном приближении
Предположим, что путем решения уравнения диффузии удалось
найти концентрацию как функцию координат, тогда можно полу-
получить окончательное выражение для неравновесной функции распре-
распределения. Рассмотрим более подробно классический случай, когда
/о — максвелловская функция распределения:
/о = П e-pVBmokT) ^ G3.1)
По G1.2) имеем
/ = /о - * — gradr/0 - х FBH grad, /0. G3.2)
щ
Поскольку
дрх Bjtm0kTf/2 \ mokT ] тфТ *
208
то
и, следовательно,
tFBHgradp/o=-T-H^/o. G3.3)
Далее,
Поскольку из G3.1)
AlSL = lo.f G3.4)
дп п
ТО
х -JL gradr/о =^й- — (pgrad./г). G3.5)
щ п щ
Таким образом, для классической неравновесной функции распре-
распределения в диффузионном приближении справедливо следующее вы-
выражение:
^ ^/o, G3.6)
где /о — функция распределения Максвелла.
Используем формулу G3.6) для расчета плотности потока час-
частиц. В соответствии с формулой B1.9) плотность потока опреде-
определяется равенством
j= \nwD— d2.
Поскольку по определению функции распределения
то
J2. G3.7)
В равновесном случае плотность потока обращалась в ноль, так
как подынтегральное выражение оказывалось нечетной функцией
компонент импульса (/о — четная функция рх, pv, pz). В неравно-
неравновесном случае это уже не так и плотность потока отлична от нуля.
Если в G3.7) подставить выражение для функции распределе-
распределения по G3.6), то получится
Щ
8—434 209
Первый интеграл равен нулю из-за нечетности подынтегральной
функции. В оставшихся двух следует записать произведение векто-
векторов в координатной форме, отбросить члены подынтегральной функ-
функции, нечетные по компонентам импульса, и вынести за знак интег-
интеграла функции координат. Эти преобразования аналогичны тем, ко-
которые были подробно рассмотрены при выводе уравнения диффу-
диффузии. После их выполнения для потока получается
Используя определение коэффициента диффузии и подвижности,
можем написать
j=-?>gracU + riFBH/z. G3.8)
Из G3.8) видно, что поток частиц в диффузионном приближении
определяется двумя кинетическими явлениями (температура посто-
постоянна): диффузией, которой соответствует диффузный поток
3d=—
зависящий от градиента концентрации, и дрейфом с потоком
пропорциональным приложенной силе.
Сравнение уравнения диффузии с уравнением непрерывности
F7.6) показывает, что уравнение диффузии допускает следующую
физическую интерпретацию: изменение числа частиц в единице объ-
объема в единицу времени равно превышению втекающего потока над
вытекающим, причем поток имеет две составляющие — дрейфовую
и диффузионную.
Если к газу заряженных частиц приложено электрическое поле
Е, то возникает дрейфовый поток
h=r\'neE
или, если использовать определение подвижности,
Для плотности тока, связанного с движением заряженных частиц,
можно написать
G3.9)
Имеется плотность диффузионного тока
Ь== — eDgradn
и плотность дрейфового тока
iv==er\nE.
21G
Когда среда однородна и концентрация постоянна, диффузионный
ток равен нулю. Плотность тока определяется только дрейфом и
пропорциональна напряженности электрического поля:
1 = ет\пЕ.
Последняя запись представляет собой не что иное, как закон
Ома в дифференциальной форме, который обычно приводят в
форме
где а — проводимость. Видно, что проводимость определяет-
определяется через подвижность соотношением
а=епг\. G3.10)
§ 74. Основные уравнения диффузионного
приближения
Одной из главных задач при исследовании неравновесных состо-
состояний является вычисление величины возникающего в системе тока.
Для этой цели необходимо знание функции распределения. Одна-
Однако в диффузионном приближении классическая функция распреде-
распределения неравновесного состояния определяется общим соотношени-
соотношением G3.6), с помощью которого плотность тока выражается через
концентрацию заряженных частиц и напряженность электрическо-
электрического поля. При этом подразумевается, что коэффициент диффузии и
подвижность известны. Они могут быть определены эксперимен-
экспериментально или рассчитаны теоретически, причем для теоретического
расчета, как это видно из формул G2.12), G2.13), достаточно знать
локально-равновесную функцию распределения /0.
Таким образом, в диффузионном приближении для вычисле-
вычисления токов нет необходимости каждый раз обращаться к функции
распределения, а необходимо лишь знать коэффициент диффузии и
подвижность, а также концентрацию как функцию координат и вре-
времени. Последняя находится решением уравнения диффузии G2.11),
которое по этой причине является основным уравнением диффузи-
диффузионного приближения. Следует, однако, иметь в виду важную особен-
особенность этого уравнения: в него входит напряженность электрическо-
электрического поля Е. Электрическое поле определяется, с одной стороны,
внешними источниками, но с другой — зависит от распределения
заряженных частиц, дающих свой вклад в электрическое поле. Как
было выяснено в § 28, для определения Е можно использовать ме-
метод самосогласованного поля, приводящий к следующему уравне-
уравнению [см. B8.2), B8.4)]:
ее0 ее0
ИЛИ
divE=. —— (л —яЛ
?Е0
211
Здесь п — концентрация отрицательно заряженных частиц (элект-
(электронов), а п\ — положительно заряженных. Подразумевается, что
концентрация положительно заряженных частиц известна. Если это
не так, то для определения п\ следует дополнительно привлечь еще
одно уравнение диффузии, но написанное для концентрации поло-
положительных частиц.
Таким образом, решение большинства задач в диффузионном
приближении сводится к решению системы основных для этого ме-
метода уравнений, а именно уравнений диффузии в совокупности с
уравнением самосогласованного поля G4.1). Эта система в мате-
математическом отношении довольно сложна, так как оказывается не-
нелинейной (в уравнение диффузии входит член с произведением двух
неизвестных величин: напряженности электрического поля Е и кон-
концентрации частиц я).
Задачи к главе 12
1. Покажите, что в диффузионном приближении средняя энергия частицы
такая же, как и в равновесном состоянии.
Решение. Средняя энергия вычисляется по формуле
где для f следует использовать выражение G1.2). Поскольку два последних чле-
члена в G1.2)—нечетные функции рх, ру, pz, а энергия — четная, то они дадут
нулевой вклад. Таким образом,
что и требовалось показать.
2. Напишите уравнение диффузии и уравнение самосогласованного поля для
случая, когда все величины зависят только от одной координаты х (одно-
(одномерная задача).
Решение. Уравнение самосогласованного поля имеет вид
d? e
div Е= = (п— п{).
dx ее0
Для уравнения диффузии получаем
дп дЪг
—— = — div (— D grad n —- т) Е п) — и 4- ч\Ьп.
ot ох*
ГЛАВА 13
СТОЛКНОВЕНИЯ
§ 75. Учет взаимодействия столкновениями
В предыдущих главах в уравнении Больцмана для члена, кото-
который учитывает взаимодействие рассматриваемых частиц с други-
другими, находящимися в равновесии, использовалась форма с временем
212
релаксации, не имевшая строгого обоснования. Задача настоящей
главы состоит в более последовательном рассмотрении взаимодей-
взаимодействия между частицами и, в частности, в выяснении условий, при
которых можно пользоваться представлением о времени релакса-
релаксации, а также в подсчете его величины. Для определенности будем
рассматривать электроны, которые взаимодействуют с другими
частицами (нейтральными молекулами, заряженными ионами
и т. п.), представляющими термостат.
Поскольку теория неравновесных состояний рассматривается
нами для систем, представляющих собой достаточно разреженные
среды, то взаимодействие с термостатом следует трактовать как
поочередные столкновения электрона с другими частицами. В раз-
разреженной среде очень мало вероятно, что электрон столкнется сра-
сразу с несколькими другими частицами. Подавляющее большинство
столкновений носит, как говорят, парный характер, т. е. электрон
взаимодействует лишь с одной частицей, около которой он в дан-
данный момент оказался, а все остальные в это время находятся далеко
м их влиянием можно пренебречь. В конденсированных средах это
предположение нарушается.
При столкновении электрона с другой частицей у него меняются
величина и направление скорости. Описание этого процесса пред-
представляет собой задачу механики, которую мы рассмотрим в этом
параграфе более подробно. Для краткости будем называть частицу,
с которой сталкивается электрон, молекулой и обозначать все вели-
величины, относящиеся к этой частице, индексом 2 в отличие от элек-
электрона, для которого будем использовать индекс 1.
Прежде всего остановимся на некоторых общих свойствах про-
процесса столкновения. Классические уравнения движения для обеих
взаимодействующих частиц можно записать в виде
^12' G5.1)
Б этих уравнениях, представляющих собой второй закон Ньютона,
не учитываются внешние силы, которые очень малы по сравнению
с силой взаимодействия Fi2 =—F2i, возникающей при столкновении.
При взаимодействии система электрон — молекула может считать-
считаться замкнутой. Напомним, что внешние силы, играющие существен-
существенную роль в промежутках между столкновениями, учтены в уравне-
уравнении Больцмана отдельным членом.
Рассмотрение процесса столкновения заметно упрощается, если
ввести новые переменные, а именно радиус-вектор центра масс си-
системы двух частиц
G5.2)
и. радиус-вектор относительного движения
го=Г! —г2. G5.3)
Действительно, из механики известно, что центр масс замкнутой
системы движется с постоянной скоростью, так что процесс столкно-
213
вения не сказывается на этом движении. С другой стороны, если
умножить первое уравнение G5.1) на т2, а второе — на т\ и вы-
вычесть второе из первого, то получится
Разделив обе части последнего равенста на т\ + т2 и использовав
G5,3), найдем
¦V=F21. G5.4)
Если принять, что сила F2i, с которой вторая частица действует на
первую, центральная, т. е. зависит от радиус-вектора г0, соединя-
соединяющего вторую частицу с первой, то оказывается, что относительное
движение происходит так, как будто частица с некоторой эффектив-
эффективной массой
т* ~ т1т2!{т1 -f т2) G5.5)
движется относительно неподвижного центра, действующего на нее
с силой F2i. Задача сводится к задаче о рассеянии на неподвижном
центре, т. е. к более простой.
Когда известны г0 и тс, исходные радиус-векторы Г! и г2 находят-
находятся по формулам
I т2 «. _ min +/и2г2 , /Я2(Г1 —г2)
с~1 ; г0 — ¦ 1
til т т т
;г0 1 х,
till ~г т2 т\ ~г т2 т\ "г т2
G5.6)
— т2)
Щ + т2 Щ + т2 Щ -+¦ т2
¦ = г2.
Рассмотрим теперь рассеяние частицы на неподвижном центре.
На рис. 13.1 частица с эффективной массой, обладающая импуль-
импульсом р, отлетает после столкно-
столкновения под углом Э к направле-
направлению первоначального движе-
движения. Ограничимся только уп-
/ ругими столкновениями, при
v^^X^ которых полная кинетическая
Р ж jfJLSfcr=r±L энергия взаимодействующих
j>\ /\\(?а\ частиц до и после столкнове-
ния одинакова. Поскольку рас-
рассеивающий центр неподвижен»
то из закона сохранения энер-
Рис- 13-1 гии следует, что величина им-
импульса эффективной частицы
после столкновения равна его величине до столкновения. Меняет-
Меняется лишь направление движения. Угол отклонения 0 зависит от ве-
величины импульса, а также от параметра р, носящего название
прицельного расстояния и равного расстоянию между
первоначальным направлением движения и параллельной этому
214
направлению прямой, проходящей через рассеивающий центр
(рис. 13.1).
Проиллюстрируем связь угла рассеивания 8 и прицельного рас-
расстояния на простом примере взаимодействия точечной частицы
с упругим шаром радиуса а0. Из рис. 13.1 видно, что угол падения р
частицы, равный углу отражения р', связан с прицельным расстоя-
расстоянием соотношением aosinp=p. Поскольку из того же рисунка сле-
следует, что 9+ 2C=я, то
г» • / ЗХ 9 \ 8
Р = aQ sin р = aQ sin = a0 cos —,
\ 2 J 2
G5. /)
Таким образом, значение угла отклонения зависит от прицельного
расстояния р. Естественно, что для другого закона взаимодействия
эта зависимость р = р(9) окажется другой.
Если изменить прицельное расстояние на dp, то угол рассеяния
изменится на d9, причем дифференцированием легко получить
J= dp (8)
d8
de.
Так, в случае рассеяния на шаре получается
-f-ein-1-de.
G5.8)
В газе на данной молекуле может рассеиваться любой столкнув-
столкнувшийся с ней электрон. Пусть мысленно выделены только те электро-
электроны, у которых величины и направления импульса одни и те же
(точнее, импульс принадлежит бес-
бесконечно малому интервалу значе-
значений, которому соответствует объем
dQi в пространстве импульсов).
Эти электроны пролетают на раз-
разных расстояниях от молекулы, и
поэтому прицельные расстояния для
эффективных частиц могут быть лю-
любыми. Часть электронов пролетит
•практически не отклонившись от
первоначального направления, а
часть будет отклонена на опреде-
определенный угол. Для дальнейшего важ-
важно найти долю электронов, откло-
отклонившихся в определенном направ- Рис. 13.2
лении.
На рис. 13.2 принимается, что плоскость чертежа перпендику-
перпендикулярна направлению движения. Ось z проходит через центр рассея-
рассеяния в направлении движения. Все эффективные частицы, пролетев-
пролетевшие через изображенное на рисунке кольцо, обладают прицельным
расстоянием, большим р, но меньшим p + dp, и, следовательно, пос-
215
ле столкновения направление их движения окажется в интервале
углов от 6 до 9 +d0 по отношению к оси z. Ограничимся только
теми частицами, которые пересекают заштрихованную на рисунке
площадку, соответствующую углам от ф до cp + dcp. Движение элек-
электрона в процессе столкновения происходит в одной плоскости, т. е.
угол ф не меняется. Таким образом, частицы, пролетевшие через
заштрихованную на рис. 13.2 область, площадь которой равна
dso=pdpd<p, G5.9)
отклонятся в телесный угол doo, характеризующийся углами
04-(9 + d9) по отношению к оси z, параллельной направлению дви-
движения налетающей частицы, и ф-т-(ф-Мф) в плоскости ху. Величи-
Величина этого телесного угла равна
dco=sin 9d6dcp.
Площадь ds0 называется дифференциальным эффективным сечени-
сечением рассеяния в телесный угол dco.
Если в G5.9) подставить G5.7) и G5.8), то для рассеяния на
упругом шаре получится
2
d50=-aosin-yco6y--y d6dcp= --—- sin QdOdcp. G5.10)
Пусть вдоль оси z летят частицы с определенным импульсом и
поток их равен /, тогда число частиц dA/, отклоненных в телесный
угол dco за время dt, совпадает с числом тех из них, которые про-
пролетели за это время через площадку ds0, и, следовательно,
dN = juso6L G5.11)
Число частиц N, испытавших отклонение на произвольный угол,
получается интегрированием G5.11) по всем возможным углам (па
Ф от 0 до 2я, а по 9 от я при лобовом ударе до 0, когда частица
пролетает мимо):
N= J diV=j jdsodt= J6t
Величина
Jso G5.12)
называется полным эффективным сечением рассеяния. В случае
рассеяния на шаре из G5.10) и G5.12) получается
G5.13)
Этот результат имеет очевидный геометрический смысл, так как s</
совпадает с площадью рассеивающей частицы, видимой со стороны
налетающей. Как будет ясно из дальнейшего, удобнее принять за
216
полное эффективное сечение рассеяния величину, определенную
следующим образом:
Q = Г A — СОбб)A50.
G5.14)
Для простого случая рассеяния на упругом шаре сечение s0 оказы-
оказывается равным сечению So', так как
2тг 0 / 2 \
Г cos6ds0= f dcp U — — ]si
О те
sin6cos8d8 = 0.
Взаимное движение электрона и молекулы обладает важным
свойством, которое может быть пояснено с помощью рис. 13.3.
На рисунке показана траектория относительного движения. Вели-
Величина скорости (импульса)
в начале и конце движе-
движения одна и та же. Рас-
Рассмотрим траекторию, по-
показанную на рис. 13.3
пунктиром. Она соответ-
соответствует движению части-
частицы, полученному из пре-
предыдущего вращением на
180° вокруг оси, отмечен-
отмеченной штрих-пунктиром.
Ось проведена через
центр рассеяния так, что-
чтобы она лежала в плоско-
плоскости траектории и была Рис 13>з
одинаково наклонена к
начальному и конечному участкам траектории. При центральном
характере сил взаимодействия из соображений симметрии ясно, что
пунктирная траектория тоже соответствует возможному движению.
Видно также, что начальная скорость второго движения по на-
направлению и величине совпадает с конечной скоростью первого, а
конечная, наоборот, с начальной. Ясно также из тех же соображе-
соображений симметрии, что дифференциальное сечение рассеяния для пер-
первого и второго движения одинаково.
Обратимся теперь к абсолютному движению. Из G5.6) после
дифференцирования по времени вытекает
т2
mi -r i
=v2,
G5.15)
где vc — неизменная по величине и направлению скорость движения
центра масс, v0 — рассмотренная выше скорость относительного
движения, a Vi и v2 — скорости абсолютного движения. Если на-
начальное значение v0 в первом движении равно конечному значению
этой скорости во втором, то из G5.15) следует, что при одной и той
217
же скорости движения центра масс начальные скорости Vi и v2
первого равны конечным скоростям v/ и v2' во втором, поскольку
последние определяются соотношениями
=vl; vc ^L_V;=V2, G5.16)
mi 4- /П2
аналогичными G5.15).
§ 76. Член столкновений в форме Больцмана
Больцман получил выражение для члена, учитывающего взаимо-
взаимодействие между частицами, которое справедливо в приближении
парных столкновений. Вывод опирается на описание процесса
соударения, приведенное в предыдущем параграфе, при этом су-
существенно, что он дополнительно учиты-
учитывает статистический, т. е. случайный ха-
характер явления.
Выделим элемент объема dt, который
много больше среднего расстояния меж-
между частицами, но, с другой стороны, на-
настолько мал, что функции распределения
электронов и молекул в нем практически
не зависят от координат. Рассмотрим те
ис' * электроны и молекулы, импульсы кото-
которых равны соответственно pi и р2 или, бо-
более точно, принадлежат элементам импульсного объема dQi и dQ2-
Временно введем подвижную относительно лаборатории систему
координат, в которой начало помещено в центр масс какой-то про-
произвольной пары сталкивающихся электрона и молекулы. Посколь-
Поскольку скорости всех рассматриваемых электронов равны между собой,
так же как и у рассматриваемых молекул, то центры масс сталки-
сталкивающихся пар в новой системе координат неподвижны. Они, как и
сами пары, распределены в элементе пространства dx равномерно.
Выберем промежуток времени d^ достаточно малый, чтобы мож-
можно было пренебречь изменением числа частиц в dx вследствие
столкновений, но много больший самого времени столкновения, и
определим вероятность того, что эффективная частица какой-то
одной произвольной пары отклонится в телесный угол dco. Искомая-
величина есть в то же время вероятность того, что эффективная
частица, находящаяся в dr, пройдет в течение dt через площадку
ds0, соответствующую рассеянию в dco, или, другими словами, ве-
вероятность того, что эффективная частица окажется (рис. 13.4)
в цилиндрическом теле, опирающемся на площадку ds0 и обладаю-
обладающем высотой vod/. Она, таким образом, равна отношению объема
цилиндрического тела dsovodt к элементу объема dx.
Среднее число эффективных частиц dN, рассеянных в dco, мож-
можно найти, умножив полученную вероятность на число пар в dr.
Если П\ — концентрация электронов, а п2 — молекул, то число пар
218
в dt равно числу электронов ftidx, умноженному на число молекул
/22dt. Таким образом, для d/V получится
=(v0 dsQ dt/d t) nx dxn2 dt=nxn2vQ dsQ dt dt.
Поскольку рассматриваются электроны с импульсами, принад-
принадлежащими dQi, и молекулы с импульсами, принадлежащими dQ
то
так что
dN=f1f2\vl-v2\ds0dQ1d Q2dtd%, G6.1)
где учтено, что
Vo = V! — V2 = (p1//7Z1) — (p2M2)
— относительная скорость движения электрона и молекулы. Если
в G6.1) fi, f2 и относительная скорость рассматриваются как функ-
функции импульсов pi и р2 электронов и молекул в исходной лаборатор-
лабораторной системе координат, то и в дифференциальном эффективном
сечении рассеяния углы 6 и <р, а также величина относительной
скорости должны быть выражены через параметры, характеризу-
характеризующие эти импульсы. Связь между скоростями была получена
в предыдущем параграфе [см. G5.15)].
Легко найти связь между импульсом электрона pi и молекулы
р2, с одной стороны, и импульсом центра масс pc = vc(m1 + m2) и
импульсом эффективной частицы po = m*vo — с другой. Действи-
Действительно, если умножить первое уравнение системы G5.15) на т\9 а
второе — на т2, то
Pi = ЩУх = mi —^ V Ро> G6.2)
Ш\ + #*2
Рс
/tt Р
2Ро
ГП\ -f- 1712
С помощью последних соотношений выражение G6.1) мол^ет быть
представлено через переменные, описывающие движение центра
масс и эффективной частицы:
dN=fxf2v0 ds0 dQ0 d2c dt dt, G6.3)
где dQ0 и dQc — элементы объема в пространстве импульсов эф-
эффективных частиц и центров масс. Нетрудно показать (см. прило-
приложение 4), что имеет место равенство
d21d22=d2odQc. G6.4)
Оно было использовано при записи G6.3), в которой также под-
подразумевается, что /i и f2 представлены как функции рс и р0 с по-
помощью уравнений G6.2).
После столкновения импульсы электрона и молекулы изменяют-
изменяются и становятся равными р/ и р/, при этом импульс центра масс
ье меняется: рс' = рс (закон сохранения импульса), а импульс эф-
эффективной частицы меняется только по направлению, так что
219
Ро
р0' = р0. Если набор первоначальных импульсов был таким, что ин-
интервал импульсов центров масс равнялся dQc, то, поскольку каж-
каждый импульс рс не меняется, останется неизменным и интервал
dQc', так что dQc/==d!Qc-
Следующие рассуждения показывают, что и
d2; = d20. G6.5)
Действительно, хотя вектор р0 и не равен вектору рс/ (изменилось
его направление), но если вектор р0 изменить на dp0, то импульс
после столкновения изменится на такую же величину при условии,.
что прицельное расстояние ос-
осталось тем же самым. Проще
всего в этом убедиться с помо-
помощью рис. 13.5, на котором изо-
изображены импульсы до и после
столкновения. Будем менять
направление исходного им-
— пульса в определенном интер-
к вале углов. Учитывая цент-
центральную симметрию потенциа-
потенциала взаимодействия, тот же ре-
результат можно получить*
оставляя исходный вектор не-
неизменным, а поворачивая лишь
Рис. 13.5 исходную систему координат
в том же самом интервале те-
телесных углов. Ясно, что при таких поворотах с точки зрения сил,,
действующих при рассеянии, ничего не меняется, поэтому конеч-
конечное значение импульса остается неизменным. Но если считать, что
вращается не система координат, а исходный вектор импульса, то
это означает, что импульс после столкновения поворачивается точ-
точно на такие же углы, так что его изменения равны изменениям
исходного импульса. Таким образом, dpo = dpo/, а отсюда уже вы-
вытекает равенство G6.5).
Итак, оказывается, что
d2c d20 = d 2c d 2q. G6.6>
Поскольку импульсы после столкновения связаны между собой
уравнениями G6.2) такими же, как и до столкновения, то в полной
аналогии с G6.4) можно написать
Сопоставляя последнее равенство с G6.6), видим, что имеет место
условие
d2!d?2= d2i d22, G6.7)
т. е. произведение импульсных объемов электронов и молекул до
столкновения равно соответствующему произведению импульсных
объемов после столкновения.
220
Выражение G6.3) дает число электронов с импульсом рь кото-
которые вследствие столкновения с молекулами, обладавшими импуль-
импульсом р2, приобрели импульс р/, т. е. в элементе объема с!т за время
dt число электронов с импульсом pi уменьшилось на diV, а число
электронов с импульсом р/ увеличилось на ту же величину. Од-
Однако для учета полного изменения числа рассматриваемых электро-
электронов необходимо принять во внимание, что в силу отмеченного в пре-
предыдущем параграфе свойства взаимности электроны с импульсами
р/, сталкиваясь с молекулами, обладающими импульсами р2',
после столкновения приобретут соответственно импульсы pi и р2.
Эти переходы играют обратную роль по отношению к предыдущим.
Их число dN' может быть подсчитано по той же формуле G6.1),
в которой необходимо, очевидно, заменить все нештрихованные
переменные на штрихованные:
ANr = f\f2 d22 d22^o dso dtd/.
Таким образом, полное число переходов, в которых уменьшение
числа электронов с импульсом pi и молекул с импульсом р2 сопро-
сопровождается соответствующим увеличением числа электронов с им-
импульсом р/ и молекул с импульсом р2', оказывается равным
dN—diV'. Учитывая равенство G6.7), а также то, что относитель-
относительные скорости до и после столкновения равны и что при том же
прицельном расстоянии дифференциальные эффективные сечения
одинаковы, получим
UN - 6N' = (fxf2 - f{/2) d2x d22^0 ds0 dt dt. G6.8)
Для уравнения Больцмана, относящегося к электронам, пред-
представляет интерес выражение, определяющее убыль числа электро-
электронов с импульсом рь При этом безразлично, с какими именно
молекулами происходит столкновение, а также каково конечное
состояние электронов. Другими словами, равенство G6.8) следует
проинтегрировать по всем возможным значениям импульсов моле-
молекул, а также по всем конечным состояниям электронов, совместимым
с начальными. Последнее означает, что нужно проинтегрировать
это выражение по всем возможным углам рассеяния. В уравнении
Больцмана изменение числа электронов подсчитывается для еди-
единичного фазового объема исходных электронов dQidr и для еди-
единичного промежутка времени dt, так что
~ f^ ' Vl ~ V2 ' d S° 6Q>- G6-9)
Выражение G6.9) представляет собой больцмановский член, учи-
учитывающий взаимодействие в приближении парных столкновений.
Полное уравнение Больцмана должно быть записано в виде
A - J {fj2 - f\f2) | Vl - v21 d sod22,
G6.10)
221
где предполагается, что функция распределения молекул /2 из-
известна.
Если система находится в равновесии, то столкновения не меня-
меняют равновесного состояния и член столкновений оказывается рав-
равным нулю. Действительно, подставляя вместо f\ и J2 равновесные
функции распределения Максвелла — Больцмана B9.6), найдем
/1/2 —/i/2=C;vie Сдгг
__ ~^i(r)+Pj/Bm01) + e/z2(r) { pf/Bmo,)]KkT)
Разность двух экспонент в скобке равна нулю, так как полные энер*
гии до и после столкновения одинаковы. Равенство нулю подынте-
подынтегрального выражения в члене столкновений выражает собой прин-
принцип детального равновесия, по которому прямые переходы должны
в равновесии компенсироваться обратными.
При выводе G6.9) электроны рассматривались классически,
т. е. электронный газ считался невырожденным. Если концентра-
концентрация электронов высока и необходимо учесть принцип неразличи-
неразличимости и принцип Паули, то результат оказывается несколько дру-
другим. При подсчете вероятности рассеяния эффективной частицы
в телесный угол необходимо учесть, что конечные состояния, в кото-
которые совершается переход, должны быть свободны, т. е. вероятность
отклонения в телесный угол do необходимо умножить на вероят-
вероятность того, что конечное состояние свободно. Последняя равна
1—W, где W — вероятность того, что состояние занято. Поскольку
возможное число частиц Ферми в конечном состоянии равно нулю
или единице, то среднее число частиц определяется формулой
так что
1 —Н7=1 —
Из G0.2) и F1.4) имеем
Аналогичное соотношение имеет место и в неравновесном случае»
только равновесную функцию распределения следует заменить на
неравновесную:
Таким образом, в выражении G6.1) появляется дополнительный
множитель, а член столкновений принимает следующий вид:
222
dt /ст J
Vlv ir Irk AQ GF* \\\
Легко показать (см. задачу к настоящей главе), что из условия
равенства нулю подынтегрального выражения в G6.11) вытекает
равенство равновесной функции распределения электронов функ-
функции Ферми — Дирака.
§ 77. Приближение времени релаксации
Для оправдания использованной ранее формы члена, учитыва-
учитывающего столкновения, необходимо выяснить, при каких условиях
больцмановское выражение G6.9) может быть представлено в
форме
(Щ =- fi~f\ G7.1)
\ Ы /ст х v
Оказывается, следует ограничиться упругими (или почти упруги*
ми) столкновениями, в результате которых кинетическая энергия
сталкивающихся частиц до столкновения равна их кинетической
энергии после столкновения. Хотя чаще всего столкновения именно
этого типа играют доминирующую роль, но бывают существенны
и неупругие столкновения, например такие, которые сопровожда-
сопровождаются возбуждением молекул, вызывающим их последующее свече-
свечение (лазеры, газоразрядные источники света и т. п.). Важно учесть
также, что масса молекулы примерно на четыре порядка больше,
чем масса электрона. Это приводит к тому, что скорости молекул
значительно меньше скоростей электронов; в равновесном состоя-
состоянии среднеквадратичное значение скорости определяется равенст-
равенством (см. § 19)
из которого видно, что скорости молекул из-за большой их массы
на два порядка меньше, чем скорости электронов.
При рассмотрении столкновения в первом приближении мож-
ьо считать молекулы неподвижными и обладающими бесконечной
массой. В процессе столкновения молекула остается в покое, а
электрон отскакивает с той же по величине (но не по направлению)
скоростью. Лабораторная система координат в этом приближении
совпадает с системой центров масс, причем все центры масс не-
неподвижны. Поскольку скорости (импульсы) электронов оказыва-
оказываются не связанными с импульсами молекул, то интегрирование по
импульсам молекул можно выполнить независимо. Имеем
где п2 — концентрация молекул в выделенном объеме dx. Член, опи-
описывающий столкновения, упрощается:
223
) «2|Vilf(/i/OcUo. G7.2)
За знак интеграла вынесен модуль скорости относительного дви-
движения, равный в рассматриваемом приближении модулю скорости
налетающего электрона, так как интегрирование по ds0 означает
фактически интегрирование по углам рассеивания, а \\\\ от них не
зависит.
Если, как мы ожидаем, член столкновений приводится к форме
G7.1), то функция распределения в диффузионном приближении
имеет вид G3.6):
[^s] G7-з>
или
/i = /oi + A/i> G7.4)
где /oi — равновесная функция распределения, а через Aft обозна-
обозначена неравновесная часть. Неравновесную часть функции распре-
распределения можно записать в виде
A/! = Lp/01f G7.5)
где из сопоставления с формулой G7.3) видно, что L — это вектор
следующего вида:
L= %— grad, «! + -*%-. G7.6)
Он не зависит от направления импульса электрона. После подста-
подстановки G7.4) в G7.2) получается
Поскольку модуль скорости до столкновения равен модулю ско-
скорости после столкновения, а равновесная часть функции распре-
распределения зависит только от энергии, т. е. от модуля скорости, то
Таким образом,
| J tLp/oi — L pr/oi) d so= — л2|vx | /oi f(Lp-Lp')d%
G7.7)
где учтено, что /oi и fOi'» так же как и Iv^, не зависят от перемен-
переменных, по которым проводится интегрирование, и могут быть выне-
вынесены за знак интеграла.
224
Чтобы завершить вычисления, рассмотрим рис. 13.6, на котором
изображены импульсы до и после столкновения (р и р'), а также
вектор L. Сохраняя систему координат, которая была использова-
¦ча при рассмотрении сечения рассеяния, проведем ось z параллель-
параллельно вектору р. Угол между р и р' есть угол рассеяния, который обо-
обозначается 8. Для простоты примем, что вектору р' соответствует
\тол ф, равный нулю, т. е. что ось х выбрана в плоскости векторов
р и р'. Скалярные произведения
Lp и Lp', входящие в интеграл
<77.7), могут быть представлены
в виде
Lp = Lp сое ф, Lp' = Lp сев х»
где через -ф и % обозначены углы,
показанные на рис. 13.6, и учтено,
что величины импульсов р и р'
одинаковы.
Если из начала векторов про-
провести сферическую поверхность,
то точки пересечения ее с векто-
векторами образуют вершины сфери-
сферического треугольника. С помощью
формул сферической тригономет-
тригонометрии можно выразить cos х через тригонометрические функции уг-
углов 8 и г|), а также угла ф, который равен углу между плоскостями
векторов (р, р') и (р, L). По теореме косинусов,
\
\
\
Рис.
1
1
1
N
\
\
13.6
Р
\
\
cQsx=cas<j>co50-f~sin
б
Подставляя это значение в интеграл G7.7), получим три члена:
X
\ (Lp cos ^ — Lp соз ф сое Ъ — Lp sin ф sin 0 соб <р) dsQ.
Интегрирование по ds0 подразумевает фактически интегрирование
по углам 8 и ф. Поскольку в последний член входит интеграл от
со8ф по с!ф, то он равен нулю. Вынесем за знак интеграла Lpcosi|),
тогда
("?f")cr= ~^21Vl I /oi^ cosi}> JA — сое8) ds0.
Вспоминая выражение G5.14) для эффективного сечения рассеяния,
напишем
•^f )
= - п21 vi
iLp сс« ф.
Поскольку в соответствии с G7.5)
cos ф=/01Lp « д/х,
225
то
Dг) =-^lvil^/i. G7.8)
Множитель ^21Vi | s0, входящий в G7.8), имеет размерность, обрат-
обратную времени, и поэтому можно назвать временем релаксации ве-
величину
1|50). G7.9)
Если теперь выразить A/i через f{ и /Oi с помощью G7.4), то видно,
что G7.8) эквивалентно выражению для члена столкновений с вре-
временем релаксации F9.2). Итак, если рассматриваются упругие
столкновения и можно приближенно пренебречь массой электронов
по сравнению с массой молекул, то больцмановский член для
столкновений приводится к форме с временем релаксации, причем
под временем релаксации следует понимать величину, определяе-
определяемую соотношением G7.9).
Следует также отметить, что в этом приближении форма члена
столкновений с временем релаксации не меняет своего вида и тогда,
когда электронный газ оказывается вырожденным. Чтобы убедить-
убедиться в этом, достаточно выписать выражение, стоящее в фигурных
скобках под знаком интеграла в G6.11), раскрыть скобки и при-
привести подобные члены. Действительно, поскольку функция распре-
распределения f2 равна \ъ (энергия молекул не меняется при столкнове-
столкновениях с электронами), то оказывается, что
§ 78. Эффективные сечения рассеяния
Для определения времени релаксации необходимо знать эффек-
эффективное сечение рассеяния s0. Точный расчет обычно оказывается
довольно сложной задачей, однако легко получить оценку порядка
этой величины, применяя формулу G5.13) для упругого шара, если
надлежащим образом выбрать его радиус а0.
При кулоновских силах отталкивания разумно отождествить
эффективный радиус с расстоянием, на которое сближаются элек-
электрон и рассеивающий центр при лобовом ударе. Для пояснения
рассмотрим сечение рассеяния электрона на отрицательном ионе.
Эта задача представляет интерес в применении как к плазме, так и
к примесным полупроводникам. Пусть заряд иона равен — Ze.
Если кинетическая энергия электрона на большом удалении от иона
равна pi2/Bmi), то при лобовом ударе электрон сможет приблизить-
приблизиться к иону на расстояние а0, которое определится из условия, что на
этом расстоянии вся кинетическая энергия перешла в потенциаль-
226
ьую. Поскольку потенциальная энергия кулоновского взаимодейст-
взаимодействия с ионом равна Ze2/Dtteo#o)> то из условия
р\
для эффективного радиуса получается
Если выразить импульс через энергию налетающего электрона, то
после подстановки в G5.13) для сечения рассеяния на ионе на-
находим
Таким образом, сечение рассеяния зависит от энергии электрона.
В данном случае чем больше энергия, тем меньше сечение, т. е.
тем меньше рассеиваются электроны. Интересно отметить, что та-
такая грубая оценка сечения находится в довольно хорошем согла-
согласии с более строгим расчетом*. Подставляя G8.1) в формулу, оп-
определяющую время релаксации, и выражая скорость электрона
через его энергию еь придем к следующему результату:
т= * = m4V™1 ef. G8.2)
Эта формула находится в соответствии с введенным ранее предпо-
предположительно соотношением
х=аг\
[см. G2.17)], причем г=3/2.
С помощью G8.2) легко установить температурную зави-
зависимость проводимости для случая, когда доминирующую
роль играет рассеяние на заряженных центрах. Температурная
зависимость проводимости при постоянной концентрации электро-
электронов определяется температурной зависимостью подвижности или,
если иметь в виду соотношение Эйнштейна, коэффициента диффу-
диффузии D. Поскольку
г энергия невырожденного электронного газа пропорциональна
температуре, то
т т
* Случай рассеяния при кулоновском взаимодействии особый, и для полу-
получения конечного результата при «строгом» расчете приходится вводить некото-
некоторые дополнительные ограничения, приводящие к появлению логарифмического
множителя, численное значение которого обычно не превосходит нескольких
единиц.
227
т. е. в данном случае проводимость растет с повышением темпера-
температуры пропорционально Т 3/а.
При рассеянии электронов на нейтральных молекулах в плаз-
плазме или на нейтральных дефектах в кристаллической решетке твер-
твердого тела разумной аппроксимацией радиуса рассеивающего шара
служит «радиус» молекулы или дефекта. В этом случае
2
a
т. е. показатель степени 8 равен —7г- Такая зависимость времени
релаксации от энергии приводит к температурной зависимости про-
проводимости вида
Важным случаем является рассеяние электронов на тепловых
колебаниях кристаллической решетки. Когда электрон движется
вдоль правильного ряда атомов кристаллической решетки, тепло-
тепловым движением которых мы пренебрегаем, то представление о по-
последовательных столкновениях
лучше заменить картиной движе-
движения электрона в периодическом
поле потенциальных сил. Нагляд-
Наглядной моделью такого движения
может служить движение шари-
ис- 13'7 ка по идеальной гофрированной
поверхности (наподобие листа
шифера) под действием силы тяжести (рис. 13.7). Ясно, что шарик
движется с ускорением, замедляя свое движение на вершинах и
ускоряя его во впадинах, но средняя скорость такого движения
при отсутствии сил трения постоянна. Это означает, что никакого
рассеяния нет и время релаксации равно беконечности. Время
релаксации конечно только тогда, когда имеются нарушения иде-
идеальной периодичности. В реальных кристаллах такие нарушения
связаны либо с дефектами кристаллической структуры, например
наличием незанятых узлов (вакансии), атомов в междоузлиях,
присутствием атомов другого сорта (сплавы), либо с тепловым
движением, приводящим к беспорядочному отклонению атомов
решетки от положения устойчивого равновесия в узле. Рассеяние
электрона состоит в этой модели в том, что после взаимодействия
с рассеивающим центром он меняет направление и величину своей
средней скорости.
Рассмотрим роль тепловых колебаний атомов. В не строгой, но
зато наглядной трактовке можно принять, что тепловое смещение
атома из положения равновесия приводит к появлению центра рас-
рассеяния с радиусом, равным среднему смещению атома из положе-
положения равновесия. При малых отклонениях взаимодействие атома
228
с соседними почти упругое. Если обозначить коэффициент жестко-
жесткости упругой силы через р, то отклонение на расстояние г приведет
к увеличению потенциальной энергии атома на $г2/2. Поскольку
по принципу равнораспределения энергии по степеням свободы
средняя потенциальная энергия упругой силы равна 3/2kT, то для
радиуса нейтрального рассеивающего центра получается
Определив сечение рассеяния, для времени релаксации найдем
Отличие от предыдущего случая состоит в том, что сам коэффи-
коэффициент а при энергии в формуле для времени релаксации зависит
от температуры. Из-за этого проводимость пропорциональна тем-
температуре в степени —г/2, а не —7г, как при рассеянии на нейтраль-
нейтральных дефектах кристаллической решетки.
В случае вырожденного электронного газа (металлы) средняя
энергия электронов практически не зависит от температуры, поэто-
поэтому проводимость обратно пропорциональна температуре при рас-
рассеянии на тепловых колебаниях решетки и не зависит от темпера-
температуры при рассеянии на нейтральных дефектах.
§ 79. Длина свободного пробега
В модели парных столкновений электрон движется по инерции
или под действием внешних сил и время от времени сталкивается
с другими частицами, представляющими собой термостат (столкно-
(столкновение электронов друг с другом мы не рассматри-
рассматриваем, ограничиваясь случаями, в которых они не
играют существенной роли). Какова вероятность
того, что электрон испытает столкновение на
участке своего пути длиной dx?
Этот вопрос можно решить, если рассмотреть
элементарный параллелепипед, изображенный на
рис. 13.8. Грань, перпендикулярная направлению
полета электрона, имеет площадь AS, а высота па-
параллелепипеда равна dx. Пусть концентрация моле-
молекул п2, тогда в параллелепипеде имеется в среднем
n2ASdx молекул. При сечении рассеяния s0 общая Рис. 13 8
площадь для столкновения электрона, пролетающе-
пролетающего через выбранный объем в направлении оси х, с какой-либо из
молекул равна s0n2ASdx. Предполагается, что высота параллеле-
параллелепипеда dx очень мала, поэтому вероятностью того, что одна моле-
молекула «прикроет» собой другую, можно пренебречь. При этих усло-
условиях вероятность столкновения dW определяется отношением об-
общей площади молекул ко всей площади передней грани параллеле-
параллелепипеда, т. е.
AS
^Величина 1/(п250) имеет размерность длины. Если обозначить ее
Я, то
G9.1)
Рассмотрим теперь интервал длины х и определим вероятность
того, что в этом интервале электрон не испытает ни одного столкно-
столкновения. Если весь интервал х разбить на интервалы длиной dx каж-
.дый, так чтобы общее число интервалов было равно x/dx, то иско-
искомая вероятность может быть представлена как произведение веро-
вероятностей ряда независимых событий. Вероятность того, что электрон
не испытает столкновения в интервале dx, равна 1—dx/X, поэтому
вероятность отсутствия столкновений на длине х есть
x/dx
Поскольку x/dx — большая величина (в пределе бесконечно боль-
большая), то, используя известный из математики предел
получим
Наконец, найдем вероятность dW того, что электрон пройдет
без столкновений путь х и испытает столкновение в замыкающем
этот путь интервале dx. Она, очевидно, равна
d\*7' = e-*A—. G9.2)
С помощью последнего выражения можно подсчитать среднюю дли-
длину свободного пробега электрона. По общему правилу нахождения
средних напишем
Вычисление интеграла приводит к следующему результату:
<*>=ХЭ G9.3)
так что введенная выше величина X имеет смысл среднего расстоя-
расстояния от произвольной точки до точки очередного столкновения. Ес-
Если принять, что движение электрона начали рассматривать сейчас
же после столкновения, то окажется, что X есть среднее расстояние
между двумя последовательными столкновения. Это позволяет ин-
интерпретировать X как среднюю длину свободного про-
пробега.
Возвращаясь к формуле G7.9) для времени релаксации, видим,
что ее можно представить в виде
г— 1 A. /7Q А)
n2sovi vi
,230
т. е. время релаксации имеет смысл промежутка времени от како-
какого-то произвольного момента до момента ближайшего столкнове-
столкновения. Оно же может интерпретироваться как среднее время между
двумя последовательными столкновениями.
Остановимся, наконец, на вопросе о длине свободного пробега
при наличии центров рассеяния различных типов. Если имеются
молекулы различных типов A, 2, 3) с различными сечениями рас-
рассеяния 5оь 502, sO3, то вероятность столкновения электрона в слое dx~
оказывается равной
или
dx | djc _ | _ djc / 1 | X | 1_\ «
Xi X2 X3 \ Xi X2 X3 /
Поскольку выражение G9.1) можно рассматривать как определе-
определение длины свободного пробега, то
J-=J- + J- + -L. G9.5)
Xi X2 Х3
Таким образом, при наличии многих центров рассеяния обратная
величина средней длины свободного пробега равна сумме обрат-
обратных величин длин свободного пробега при рассеянии на центрах
каждого вида в отдельности. Из G9.4) вытекает, что аналогичное
правило имеет место и для времени релаксации:
—=— + — +—. G9.6)
t Xi %2 Т3
§ 80. Разогрев электронного газа
Рассмотренная в § 77 форма для члена столкновений была полу-
получена при использовании предположения, обладающего принципи-
принципиальным недостатком. Речь идет о допущении, что масса молекулы-
практически бесконечна по сравнению с массой электрона. Сделав^
его, невозможно объяснить, каким образом в стационарных усло-
условиях сохраняется постоянная средняя энергия электронов, находя-
находящихся во внешнем электрическом поле. Особенно легко в этом убе-
убедиться, если считать молекулы неподвижными. При каждом ударе-
электрон отскакивает, сохраняя величину своей скорости. Посколь-
Поскольку при наличии внешнего поля в системе идет ток, то это означает,,
что электрическое поле совершает работу, увеличивая энергию си-
системы электронов. Следует выяснить, как поддерживается стацио-
стационарное состояние. Хорошо известно, что при прохождении тока по»
проводнику в нем имеет место выделение тепла, т. е. передача
энергии термостату. Ясно, что для объяснения этого явления необ-
необходимо учесть передачу энергии от электронов к молекулам при
столкновениях, т. е. конечную величину отношения массы молекулы
к массе электрона. Поскольку при равновесии передача энергии-
от электронов молекулам компенсируется ее обратным поступле-
поступлением от молекул к электронам, то решающую роль играет неравно-
23Е
весный характер функции распределения электронов. Следует, од-
однако, учесть, что поправка к функции распределения, найденная
выше, не может дать объяснения этому эффекту. Скорее наоборот,
поскольку этой поправкой определяется ток, то она способна объ-
объяснить, каким образом электроны получают энергию или, иначе,
как они «разогреваются». Из дальнейшего будет видно, что это
действительно так. Таким образом, напрашивается вывод, что в не-
неравновесной функции распределения G7.3) функция foi, которая
считалась равновесной, в действительности таковой быть не может
и в лучшем случае близка к равновесной. Так, например, если пред-
предположить, что она максвелловская, то ей должна соответствовать
другая, более высокая температура, но возможно, что она и не яв-
является максвелловской. Изложению решения этого важного вопроса
и посвящен настоящий параграф.
Мы начнем с предположения, что искомая функция распределения имеет вид
(8ОЛ)
-и отличается от той, которая использовалась ранее, только тем, что foi не сов-
совпадает теперь с равновесной функцией распределения, но также зависит от
модуля импульса или от энергии электронов. Задача состоит в том, чтобы най-
найти эту, как принято говорить, изотропную часть функции распределения. Естест-
Естественно, что при этом нужно исходить из уравнения Больцмана G6.10). Если под-
подставить функцию распределения в предполагаемом виде (80.1) в уравнение
Больцмана, то результат можно записать следующим образом:
Ограничимся относительно простым случаем, а именно стационарной зада-
задачей в постоянном и однородном электрическом поле. Поскольку поле от времени
не зависит, то стационарное решение следует искать, положив в (80.2) члены с
производными по времени равными нулю. В других условиях, например в слу-
случае, когда электронный газ находится в переменном электрическом поле доста-
достаточно высокой частоты, эти члены необходимо учитывать. Однородность в про-
пространстве означает, что функция распределения не зависит от координат, поэто-
поэтому первые два члена в правой части уравнения (80.2) тоже равны
нулю. Уравнение принимает вид
(^) (^fi) (80.3)
0/01 \
—-—I
Если изотропная часть функции распределения равновесна, то член
равен нулю и член столкновений сводится к ——— I . В приближении вре-
\ 0* /
ст
/
мени релаксации для последнего использовалось представление F9.2)
[ dt /ст v
и полагалось [см. G3 2), где F=—еЕ], что
д/!= teEgradp /01 =те Е 4^~ (80.4)
232
(ось х выбрана в направлении электрического поля). Если сохранить эти соот-
соотношения, хотя они и не вполне точны, то окажется, что еще два члена в урав-
уравнении (80.3) взаимно уничтожаются, и тогда получается уравнение
или, если использовать (80.4) и интегральное представление для члена столкно-
столкновений,
~ V2 I ds0dQ2' (80*6>
Левая часть этого уравнения не изотропна, т. е. включает поправку и к не-
неизотропной части функции распределения Д/i. Этой поправкой мы пренебрежем?
и для получения уравнения, определяющего изотропную функцию foi, усредним*
правую и левую части по всем возможным направлениям импульса pi. Для этого-
следует умножить обе части равенства на dQi и проинтегрировать в простран-
пространстве импульсов электрона по шаровому слою, для которого величина импульса
больше ри но меньше, чем pi + dpu или, если говорить об энергии электрона, по-
слою, для которого энергия меняется от ei до ei. + dei. Интегрирование по тако-
такому слою эквивалентно усреднению по углам, характеризующим направление
импульса, и умножению на (см. § 19)
dpi = 4 уТлтУ2 "j/n d«i = g (sx) d?l. (80.7).
Правая часть (80.6) изотропна и поэтому просто умножается на g(ei)dei. Для
преобразования левой части следует от производных по р\ж перейти к производ-
производным по энергии. Так,
/=
др1х \ д*г др1х
Поскольку
р + Р)=~^Г
то далее получаем
®\х \ 04 ^1 / ^l L @Ч ор\х
Снова переходим к производной по энергии
дч
и получаем, наконец, для левой части следующее выражение:
, е2Е2 г dfoi , ftx д
Усреднение его по углам при учете того, что <Pix2>/Bml)=Ei/3, даег
e2E2 Aj
Щ L ^е1 3 двг \ дгх /J щ уч 3 дг
Следовательно, левая часть, проинтегрированная по шаровому слою в простран-
пространстве импульсов, приводит к
233J
Таким образом, уравнение для изотропной части функции распределения прини-
принимает следующий вид:
2 д ( 3/2
/72! V4 3 ^
= J (/01/2- /01 /2) I vi - v2 I ds0 dQ2? (в1) de!. (80.8)
Правая часть этого уравнения определяет число электронов, убывающих из
шарового слоя dei вследствие столкновений с молекулами, т. е. эффект передачи
энергии от электронов молекулам. Левая часть зависит от поля и показывает,
что под действием поля неизотропная часть функции распределения, которая
сама пропорциональна электрическому полю, слегка изменяется и дает при этом
добавок к изотропной части, т. е. описывает эффект разогрева электронного
газа. Дальнейшие преобразования имеют своей целью представить правую часть
этого интегрального уравнения в более простой форме. Оказывается, что, исполь-
используя условие малости передаваемой электронами при соударении с молекулами
энергии, удается привести это уравнение к относительно простому дифферен-
дифференциальному уравнению.
Чтобы сократить вычисления, целесообразно проинтегрировать обе части
(80.8) от 8i=0 до 6Ь имея, таким образом, дело не с изменением числа частиц,
энергия которых заключена в интервале deb а с изменением числа частиц, обла-
обладающих энергией, меньшей еь Левая часть, определяющая изменение, обуслов-
.ленное подогревом в электрическом поле, оказывается равной
}¦
= 4/2 Jt/n1/2 — tV2 % Ц^ е2Е2, (80.9)
3 дг\
где использовано представление g(ei)dei no (80.7). Правая часть, учитывающая
изменение вследствие столкновений, записывается следующим образом:
J J (/oi/2— /oi /2) I vi — v21 ds0 dQ2gD) d*i =
= J J /01/21 Vi — v2 I d5Od Q2 g (ч)Лч ~ [ J /01/2 I Vi — V2 I d50 dQ2? (ex) dei.
(80.10)
Пусть прямой переход состоит в том, что частицы с импульсами pi и Ра
шосле столкновения получают импульсы р/ и ргх и при этом первоначальная
энергия электрона et изменяется и становится равной 8i — 681. Если во втором
.интеграле в правой части (80.10) перейти к штрихованным переменным, т. е.
импульсам после удара, то он примет следующую форму:
/01/2K-V2 \dsQ6Q'2g(t\) <!•;,
где (ei — 681) — энергия электрона после удара, соответствующая тому значе-
значению, которое она получает при новых значениях переменных. Последнее выраже-
выражение отличается от первого члена в правой части (80.10) лишь обозначением
переменных интегрирования и значением верхнего предела. Обозначение пере-
234
менных интегрирования несущественно и не меняет значения самого интеграла.-
В связи с этим можно написать
i== \— \ = \ \/oi/2lvi — V2 | d Sq d Q2g(ei) dei.
и 0 0 ex— 8e,
(80.11>
Для продолжения выкладок необходимо подробнее рассмотреть величину
беь характеризующую изменение энергии электрона в процессе удара:
(80.12>
С помощью соотношений G5.15) и G5.16) легко получить
2/П2
так что после подстановки этих выражений в (80.12) находим
Выразив скорость центра масс и относительные скорости через абсолютные, при*-
дем к следующему удобному для дальнейшего анализа выражению:
Ъгх = ¦ (Vi — vc — Vj + vc) =
ТП\ + ГП2 Шх + /722 ^2
1
v2(vi - V!) + v^-vj). (80.13)
ГП\ + ГП2
Скорость молекулы и2 в l^/^i//W2 раз меньше, чем скорость электрона и и
поэтому первый член имеет порядок
ТП\
—v.) «
1 / /7Z1 2
V ~т~2~'
т. е. в Vm2lm\ раз больше, чем второй, имеющий порядок (mllm2)mlvl2r
Однако при оценке величины первого члена необходимо учитывать, что направ-
направление скорости v2 относительно Vi может быть любым. Хотя и имеется некоторое
влияние скорости молекулы на направление скорости электрона после удара v/,
но это влияние мало; в основном направление скорости после удара зависит от
прицельного расстояния и остается почти таким же, как и при рассеянии на
неподвижной молекуле. При произвольности направления v2 это означает, что
после усреднения первый член обращается в ноль. Среднее значение 6si опреде-
определяется, таким образом, вторым членом и может быть представлено следующим
выражением:
Vl(Vi—Vj)^ {у\-
ТП\ +/И2
о о
m\V\ Шл
A — cos6)=2—L ех A — cos0), (80.14)
ТП>2 Ttl2
235
где Ei — энергия электрона до столкновения, а 6 — угол, близкий к углу рассея-
яия, поскольку скорости vi и v/ близки к v0 и v0'.
Рассмотрим теперь квадрат ббь
2
mim v2 (V! — у\) -^- ei A — cos 6) + 4 -^§- t] A — cos 6J. (80.15)
Средний член в силу произвольности направлений v2 при усреднении дает ноль,
и его можно не учитывать. Последний член в mi/ni2 раз меньше (80.14), так как
равен квадрату этой малой величины. Первый член оказывается того же порядка
по mi/ni2, что и (80.14). Действительно,
где v2? — проекция v на направление Vi — v/. Среднее значение квадрата про-
проекции скорости молекулы в соответствии с распределением Максвелла есть
Далее,
v[2— 2v1v/l = 2v\— 2vxw\ = 2v\A — cos 0).
(Vl — vjJ = v\
Поэтому среднее значение первого члена в (80.15) равно
2
kT2v\(\ — ccs fl)= 4 —^- ^Гех A — cos6),
Л/22 ^2
т. е. того же порядка по малой пеличине tnxlrti2, что и (80.14). Таким образом,
<5е^> = 4-^ ^Г?1A — cos в) (80.16)
ffl2
и, следовательно, средние по направлениям скоростей молекул значения 6ei и
fiei2 — величины одного порядка по параметру т\1гп2. Это оказывается очень
важным для дальнейших приближенных вычислений, так как показывает необхо-
необходимость одновременного учета членов 6ei и 6ei2.
Вернемся теперь к уравнению (80.8). Из (80.13) видно, что 6ej зависит от
Vi и от угла рассеяния, так как им определяется скорость v/. В связи с этим
целесообразно сначала выполнить интегрирование по еь а затем уже по осталь-
остальным переменным:
5 I ) de',. (80.17)
Интеграл
(ei)|vi-V2U(e;)ds; (80.18)
можно вычислить приближенно, используя то обстоятельство, что интервал инте-
интегрирования 6ei мал по сравнению со средней энергией электрона 8i (в ml/m2 раз
меньше). Пренебрежем также v2 в |Vi—v$J. Функцию распределения электронов
236
fio(?i') следует разложить в ряд по отклонению энергии от ei и ограничиться
двумя членами:
, , и f \o
У10\^1/=== J 10 \^О ~Н \^1 — ^1/ л * (ои. 1У)
Действительно, следующие члены разложения после интегрирования по е^ дадут
величины порядка 6ei3 и выше, которыми можно пренебречь по сравнению с
членами, пропорциональными 6ei и 6ei2.
Итак, подставляя (80.19) в (80.18), получим
Г Г d/10 ,
\ dso/io(el)*>l?(ei) de. -f \ ds0 — (е, — q) V\g (г{) de{ =
J J dei
= d sofiQ (si) vig (?l) b&i — d s0 10 ^^ (?l) ——,
d ?i ?
где берется некоторое среднее для интервала 6ei значение величины dsov1g(ei/).
Поскольку интервал интегрирования 6ej мал по сравнению со средней энергией,
то это применение теоремы о среднем при преобразовании интеграла мало ска-
сказывается на окончательном результате. Теперь исходный интеграл (80.11) прини-
принимает следующий вид:
4" g (Sl) "Л
(80-20)
Интегрирование по dQ2 соответствует усреднению по всеАм направлениям v2 и
вычислению средних значений функции от i^, умножаемых, кроме того, на число
молекул. Таким образом,
п < s ) е
\ &?1 d 50/2 dQ2 = 2 —- /i2n \
J /и2 J
- cos
J m2 ' J
И
Г 2 т\ Г
\ Ьв, d Sq/z d?*2 == 4 kT&i \ A — cos
J Я*2 J
Здесь были использованы равенства (80.14) и (80.16), а также определение
эффективного сечения рассеяния G5.14). <so> означает сечение рассеяния сред-
среднее для интервала ббь Оно практически не отличается от s0. Этим завершается
вычисление интеграла (80.17).
Приравнивая вычисленный интеграл выражению (80.9), получаем уравнение
для функции fi0:
1 з ?l
— 4 Y2 Лт]/2 е|/2 П2 < s0 > угег — (/10 — kT
т2 \ uex /
После сокращения на общие множители и учета того, что n2<s0>vl = \/x, полу-
получается дифференциальное уравнение
237
которое просто решается методом разделения переменных. Прямой подстановкой.
легко убедиться, что искомая функция распределения имеет вид
л
/ю= Се ° (80.22)
Постоянная С, как всегда, определяется условием нормировки
где П\ — концентрация электронов.
Таким образом, при учете разогрева электронов постоянным
электрическим полем функция распределения электронов по ско-
скоростям имеет вид
f 10 — так называемая изотропная часть функции распределения^
определяемая выражением (80.22), а Д/i — поправка к ней, которая
может быть взята в форме (80.4), причем в качестве /ю подставля-
подставляется изотропная функция (80.22).
Если
Ш2 T2g2?2 _ m \2е2Е2 „
D ————— " ————— <к ft/ у I {j\J,^LiKjf
то из (80.22) получается функция распределения Максвелла
S
- f dt/<ftT)
/10=Се й =Ce-/(W)
Поскольку в этом случае средняя энергия электронов равна г/2^Тг
то из (80.23) следует, что разогрев электронного газа начинается
при электрических полях, удовлетворяющих условию
1712
или
\еЕ\ -^^Ш. (80.24)
У щ
В газах, где длина свободного пробега может быть большой, а
из-за относительно малой проводимости напряженность электриче-
электрического поля тоже велика, условие разогрева довольно легко выпол-
выполняется. В металлах проводимость очень высока и достичь напря-
напряженности электрического поля, при которой средняя энергия
электронов заметно зависит от поля, практически невозможно. В по-
полупроводниках при надлежащих условиях случай разогрева элек-
электронов возможен.
238
Если электрическое поле очень сильное, так что выполняется
неравенство, обратное по отношению к (80.23), то, пренебрегая
членом kT, можно получить
/ю=Се b ^^X*2*2 6l .
Вид функции распределения зависит от характера зависимости
длины свободного пробега от энергии. Так, например, при рассея-
рассеянии на нейтральных молекулах, когда можно считать, что длина
свободного пробега не зависит от энергии, получается так назы-
называемое распределение Дрювестейна
сильно отличающееся от максвелловского. Другой пример приведен
l задачах к настоящей главе.
На этом мы закончим изложение вопроса о неравновесных
функциях распределения, хотя рассмотренный пример далеко не
исчерпывает всех тех случаев, с которыми приходится сталкивать-
сталкиваться на практике. Поведение электронов в высокочастотном электри-
электрическом поле, влияние магнитного поля, учет неупругих ударов —
вот примеры задач, которые разрабатывались в течение ряда лет и
продолжают разрабатываться в настоящее время. Их рассмотре-
рассмотрение, однако, выходит за рамки настоящей книги.
Задачи к главе 13
1. Показать, что из принципа детального равновесия и формы члена столк-
столкновений G6.11), учитывающего принцип Паули, вытекает распределение
Ферми — Дирака.
Решение. Из принципа детального равновесия вытекает, что в равновесии
подынтегральное выражение в G6.11) должно быть равно нулю. Отсюда
/i [1 - BJthK f\] /2 = f\ [1 ~ Bяй)з /J /2
или
Здесь f2 — функция распределения Максвелла, т. е.
Если
l-BjtbK/l
где 6i — энергия электрона до столкновения, то детальное равновесие выполняет-
выполняется при условии, что
239
Находя fi из предыдущего уравнения, получим
1 1
т. е. то, что требовалось показать.
2. При какой зависимости времени релаксации от энергии неравновесная
функция распределения f]0 остается максвелловской? Какова эффективная
температура этого распределения?
Решение. Из (80.22) видно, что при x=const получается максвелловское рас-
распределение с эффективной температурой
Гэфф= Т 4- т2т?е2Е2/(Зт21 k).
ГЛАВА 14
ФЛУКТУАЦИИ
§ 81. Значение флуктуации
Рассматриваемые в статистической физике характеристики, та-
такие, например, как внутренняя энергия или давление, получаются
в результате усреднения соответствующих механических величин,
относящихся к изучаемой системе частиц. Поскольку число частиц
в системе обычно очень велико, то измеряемые на опыте значения
близки к их математическим ожиданиям (средним значениям).
Все же в некоторых случаях становятся существенными беспоря-
беспорядочные отклонения от средних значений, которые носят название
флуктуации. Величину флуктуации принято характеризовать
дисперсией, т. е. средним значением квадрата отклонения случай-
случайной величины от своего математического ожидания. Так, например,
если рассматривается энергия системы частиц, то ее флуктуация
характеризуется величиной
где U — внутренняя энергия, т. е. математическое ожидание энер-
энергии системы. Выше уже приводились примеры флуктуации. Так,
р § 13 исследовались случайные отклонения числа частиц в объеме
от их среднего значения, а в § 34 — случайные колебания указа-
указателя пружинных весов, а также напряжения на конденсаторе, вклю-
включенном в колебательный контур.
Обычно, и это отмечалось в § 13 и 34, флуктуации малы, так
что с ними можно не считаться, однако имеется очень важная для
физики и техники область, в которой они играют определяющую
роль. Речь идет о точных измерениях и технике связи. Повышение
чувствительности измерительных приборов и приемных устройств
привело к тому, что в целом ряде случаев реализуются предельные
возможности, которые определяются флуктуациями. Поясним ска-
сказанное конкретным примером.
240
Для измерения мощности излучения в видимой и инфракрасной
областях спектра иногда применяют так называемые тепловые
приемники излучения. Принцип их действия состоит в том, что под-
подлежащее измерению излучение направляется на небольшую зачер-
зачерненную площадку, на которой оно поглощается, вызывая ее нагрев.
Повышение температуры, пропорциональное величине падающей
мощности, измеряется с помощью подсоединенной к площадке чув-
чувствительной термопары или каким-либо другим способом. Предель-
Предельная чувствительность таких приемников определяется флуктуация-
ми выходного напряжения прибора, так как принимаемый сигнал,
величина которого меньше, чем величина флуктуации, не может
быть обнаружен на фоне беспорядочных всплесков выходного на-
напряжения.
Можно указать различные причины, вызывающие флуктуации
напряжения, или, как говорят иначе, шум. Прежде всего, если для
измерения перегрева используется термопара, то она обладает оп-
определенным сопротивлением и в электрической цепи термопары
с измерительным прибором возникает случайный сигнал, обуслов-
обусловленный тепловым движением электронов и флуктуацией их числа.
Этот тип шума рассмотрен в § 85. Кроме электрического шума сле-
следует учитывать, что приемная площадка, которая для повышения
чувствительности делается очень маленькой и легкой, непрерывно
обменивается энергией с окружающей ее средой. Это приводит
к случайным колебаниям температуры площадки, которые термо-
термопара превращает в случайный электрический сигнал. Флуктуации
температуры наряду с флуктуациями целого ряда других термоди-
термодинамических величин рассмотрены в § 83, 84. Наконец следует при-
принять во внимание, что на приемную площадку попадает регистри-
регистрируемое излучение вместе с фоном, обусловленным излучением нахо-
находящихся в поле видимости приемника излучающих предметов.
Фон дает излучение, мощность которого непрерывно флуктуирует,
и этим вносит свой вклад в шумовое напряжение.
Флуктуации можно условно разделить на такие, которые имеют
место в равновесных системах, и другие, которые проявляются при
отклонениях системы от равновесия. Как правило, основную роль
играют первые, поскольку отклонения от равновесия, с которыми
обычно приходится иметь дело, малы. При изучении флуктуации
в равновесных системах можно использовать распределение Гиббса,
и это позволяет дать полную теорию явления. Примером флуктуа-
флуктуации, проявляющихся в неравновесной системе, могут служить дро-
дробовые шумы, возникающие при прохождении электрического тока.
Они рассмотрены в § 85.
§ 82. Флуктуации числа частиц и объема
Применим распределение Гиббса к вычислению флуктуации
числа частиц, находящихся в определенном объеме. При этом полу-
получится общее соотношение, из которого, в частности для классиче-
классического идеального газа, следует результат, приведенный в § 13, но
9—434 241
которое зато справедливо и для других систем (таких, например,
как газ Бозе или газ Ферми).
В § 54 дифференцированием условия нормировки для большого
канонического распределения Гиббса по \i было получено условие
E4.10), определяющее среднее число частиц в системе. Это условие
может быть записано в виде
а + ЛПе *" =0. (82.1)
it
Для того чтобы получить математическое ожидание квадрата чис-
числа частиц, продифференцируем его по тому же параметру еще раз.
При этом получится
"N =0. (82.2)
Раскрывая внутренние скобки, найдем
<e-»w+*jv)/<w) = o
или
/92Q* W^ <2*-^vyv I " I ™- Г Л'р' "W
> , 1 У (MvW(«r)=
Использование условия нормировки и определения средних
позволяет приведенное соотношение переписать в виде
Поскольку
^ (82.3)
•-М2
то полученный результат сводится к
или после приведения подобных членов и умножения на kT
Так как дисперсия по определению равна <AN2> = <N2>—<Af>2,
то
(82.4)
или, если принять во внимание (82.3),
d<N> . (82.5)
Таким образом, из распределения Гиббса для величины флуктуа-
флуктуации среднего числа частиц получаются формулы (82.4) и (82.5).
Подставляя в (82.4) то или иное выражение для омега-потенциала,
можно находить дисперсию числа частиц в системе.
Для классического идеального газа по F2.8) и F2.10) имеем
т. е.
=kT d<N) = (N). (82.6)
Этот результат более прямым способом был получен в § 13.
Из (82.6) видно, что относительная величина флуктуации, т. е. от-
отношение корня квадратного из дисперсии к среднему числу частиц,
равна
Поскольку число частиц, с которыми приходится иметь дело в ре-
реальных системах, необычайно велико, то, как правило, флуктуации
оказываются незаметными и вполне достаточно знать лишь среднее
число частиц. Однако при очень точных измерениях в малых си-
системах флуктуации обнаруживают себя и ограничивают в какой-то
мере точность измерений.
9* 2U
Рассмотрим теперь Бозе-газ и определим дисперсию числа час-
частиц, находящихся в данном состоянии i. По E6.5),
Q]=kTln(l — e(|t-i/)/(*r)). (82.7)
Далее имеем
dQ* 1
<*) i. (82.8)
(распределение Бозе — Эйнштейна). Из общей формулы (82.5) для
флуктуации получается
(е — L)"
Последнее равенство удобно преобразовать следующим образом:
\ • / й _ .. \ // fc7"\ / m \ I? fcT* Ч ^
/>2^ (82.9)
где использовано выражение (82.8). Эта формула отлична от клас-
классической, но при больших отрицательных jx, когда среднее число
частиц в данном состоянии <п{> очень мало, можно пренебречь
<tti>2 по сравнению с <я*> и тогда получается классический ре-
результат.
Дисперсию полного числа частиц в системе можно получить со-
совершенно аналогичным образом, исходя из выражения E6.6) для
омега-потенциала
2* = kT ^ In A + e(lx-e<)/(ftr)). (82.10)
Поскольку вся разница между (82.7) и (82.10) состоит в том, что
в последнем случае проводится суммирование по всем состояниям
/, то естественно, что конечный результат имеет вид
^)A + <^»- (82Л1)
Таким образом, дисперсия общего числа частиц Бозе равна сумме
дисперсий числа частиц в каждом состоянии и Это указывает на
независимость числа частиц в различных состояниях.
После перехода от суммы к интегралу последнее выражение
представляется в виде
где было вновь использовано уравнение (82.9).
244
Для фотонов, полагая ц,=0, е=/ко, используя E7.5) и учитывая
две возможные поляризации, можем написать
= 2 Г
)
^ у
Если регистрируются все частоты, то нижний предел интегрирова-
интегрирования равен нулю, а верхний — бесконечности, и тогда
? e**2
J (e*-
где введена безразмерная переменная интегрирования x=h(x>/(kT).
Так как ¦>
j-^r=
е1) 3 f
то окончательно получается
Аналогичным образом можно вычислить дисперсию для частиц
Ферми. Используя выражения F1.2) и F1.3)
придем к следующим соотношениям:
Я2
3
Значение суммы > —- = —- приведено, например, в [12], с. 226.
Jmmk № и
л—1
245
Последнее равенство после перехода к интегралу представляется
в виде
Флуктуации числа частиц в заданном объеме тесно связаны
с вопросом о флуктуациях объема при заданном числе частиц.
Действительно, рассмотрим для конкретности газ в сосуде (рис.
14.1), который представляет собой систему
с заданным числом частиц. Предположим,
что произошла флуктуация, в результате
которой весь газ собрался в части сосуда
Л, так что в части В молекул не осталось.
Это же событие можно трактовать иначе.
Пусть мы рассматриваем систему, представ-
Рис- 14>1 ляющую собой газ в части сосуда А, тогда
флуктуация состоит в том, что число час-
частиц в А увеличилось на AN. Очевидно, что при не слишком малых
флуктуациях, когда часть В содержит много частиц,
kN=-^rNy (82.13)
где N — полное число частиц в сосуде, V — его объем, AV — объем
части В. Возводя предыдущее равенство в квадрат и усредняя,
найдем
(N VJ '
где отношение N/V, равное также производной [~ду—j * есть
средняя плотность частиц. Если подставить <ДЛ^2> из (82.5), то
получится
1<П/(^1)\ (82.14)
Дальнейшие преобразования имеют своей целью представить эту
формулу в более простом виде.
При постоянной температуре давление есть функция только \ху
так как омега-потенциал пропорционален объему, а давление опре-
дп*
деляется производной . В связи с этим можно написать
dV
d{N) ( d{N) \ I дР \
ф [ дР )т[дц)т'
Поскольку справедливо следующее тождество:
дР д ( dQ* \ d2Q* д I д&*\ d{N)
__ д ( dQ* \_ d2Q* _ д I
"~~ ф [ dV ) dydV ~ dV \
ду. J dV
246
то (82.14) представляется в виде
LI дР )t,
dV }t,p
Для системы с постоянным числом частиц при постоянной тем-
температуре
4 / \ dV )
и поэтому
дР
Если подставить это выражение в формулу для <AF2>, то для
флуктуации объема в системе с постоянным числом частиц при ус-
условии, что температура постоянна, получается
—\ . (82.15)
дР ),N)J K
Следует подчеркнуть, что выражение (82.15) относится к доста-
достаточно большим флуктуациям, по отношению к которым справедли-
справедливо предположение (82.13). Флуктуирующая система тоже должна
быть достаточно большой (содержать достаточно много частиц),
•чтобы к ней имело смысл применять термодинамические соотноше-
соотношения, используемые при переходе от (82.14) к (82.15).
§ 83. Флуктуации энергии и температуры
Рассмотрим флуктуации энергии в системе с фиксированным
числом частиц, находящейся в определенном объеме V. По опреде-
определению внутренней энергии и учитывая условие нормировки [см.
E3.2) и E3.3)], можно написать
(йГ)
w-tf)=0. (83.1)
Пусть число частиц в системе постоянно, т. е. N=<N>, тогда
удобно ввести свободную энергию [см. E4.17)]
Соотношение (83.1) принимает следующий вид:
0. (83.2)
247
Для того чтобы найти среднее значение квадрата отклонения
энергии от равновесного значения, т. е. <($\ —?/J>> можно про-
дифференцировать (83.2) по температуре. При этом получается
, _ и) [i?. J L. (F* -
'I дГ kT КП V
Так как по E4.20)
дТ дТ
то из уравнения Гиббса — Гельмгольца E4.11) вытекает
т1?г-р*=т i?—(o.+,»<jv»= -и
к, следовательно, (83.3) приводит к уравнению
^-^-(«.-^."^•^-(^-а (83.4)
Поскольку
то дисперсия энергии определяется следующим простым соотноше-
соотношением:
(83.5)
Так как
dtf\
где Су — теплоемкость системы при постоянном объеме, то (83.5)
можно также записать в виде
<Ав?)=*ГаСк. (83.6)
Формулы (83.5) и (83.6) и есть те основные соотношения, которые
определяют величину флуктуации энергии в системе с постоянным
числом частиц, находящейся при постоянном объеме.
Если система находится прд постоянном объеме, а число частиц
в ней постоянно, то с макроскопической точки зрения изменение
внутренней энергии связано с изменением температуры системы.
В связи с этим из (83.6) можно определить величину флуктуации
температуры. Действительно,
{ ДГСуЛТ, (83.7)
\дт )v
поэтому принимают
Сравнение последнего выражения с (83.6) показывает, что
(kT2)=kT2/Cv. (83.8)
Остановимся на смысле последнего соотношения. В теории Гиб-
бса температура выступает как постоянный параметр, характери-
характеризующий в конечном счете термостат, и поэтому говорить о флуктуа-
циях температуры вроде бы не следует. Однако при измерении
температуры в качестве термостата следует рассматривать ту часть
тела, с которой контактирует измерительный прибор. Инерцион-
Инерционность прибора, т. е. время, которое ему требуется, чтобы показания
установились, определяет в то же время объем части тела, в кото-
которой за это время успевает установиться тепловое равновесие. Под
теплоемкостью, входящей в (83.8), при условии, что теплоемкость
самого термометра пренебрежимо мала, следует понимать как раз
теплоемкость этой части. Если постоянная времени измерительного
прибора такова, что тепловое равновесие успевает устаяюбйться
во всем теле, то показания прибора характеризуют флуктуации
температуры этого тела.
§ 84. Флуктуации других термодинамических
величин
Полученные в предыдущих двух параграфах выражения для
<АУ2> и <ДГ2> позволяют рассматривать флуктуации всевоз-
всевозможных других термодинамических величин, происходящие в систе-
системах с постоянным числом частиц.
Предварительно отметим, что флуктуации объема и температу-
температуры в том смысле, в каком они были рассмотрены выше, статисти-
статистически независимы. Это следует из того, что флуктуации объема рас-
рассматривались при постоянной температуре и по существу были
обусловлены флуктуацией числа частиц, а флуктуации температуры
рассматривались при постоянном объеме и при постоянном
числе частиц, т. е. никак не были связаны с флуктуациями числа
частиц. Если составить произведение ДУД Г и усреднить его, то в
силу независимости ДУ и ДГ усреднение можно производить неза-
независимо сначала по ДУ, а затем по Д7\ Таким образом,
Поскольку как среднее значение флуктуации объема, так и среднее
значение флуктуации температуры равны нулю, то
<А1/ДГ>=0. (84.1)
Общий прием вычисления величины флуктуации рассмотрим
на примере флуктуации давления. Ограничиваясь, как и ранее, рас-
рассмотрением флуктуации в малых, но макроскопических системах,
249
по отношению к которым только и имеет смысл вводить понятие
давления, можем считать, что изменение давления при постоянном
числе частиц есть следствие изменения объема и температуры:
}т 1 \ дТ jv
Возводя это соотношение в квадрат и усредняя, найдем
или, учитывая статистическую независимость флуктуации объема
к температуры,
Выражения для величин <ДК2> и <АГ2> были получены выше,
так что после подстановки их в последнее равенство получим
dV Jv {дТ )v Cv \
(
Путем несколько громоздких преобразований, которые мы прово-
проводить не будем, можно показать, что (84.2) эквивалентно следую-
следующему равенству:
dV Js
где ( ) — производная от давления по объему при постоян-
\ dv js
ной энтропии, т. е. в адиабатическом процессе.
В качестве второго примера рассмотрим среднее значение про-
произведения флуктуации объема и давления. Поскольку
) tv+[\ tr\[\ bv+l)
dV )т \dT jv J [dVJr [dTJv
то после усреднения с учетом (84.1) найдем
или после подстановки <АУ2>
Таким образом, флуктуации давления и объема оказываются не
независимыми. Из приведенного соотношения видно, что поскольку
правая часть отрицательна, то в среднем увеличение объема сопро-
сопровождается уменьшением давления, и наоборот.
250
Аналогичным образом можно показать, что зависимы флуктуа-
флуктуации давления и температуры:
(ДРАГ) ={^
дт)уК ] Cv \dT)v
Этих примеров, по-видимому, достаточно, чтобы понять метод,
которым удобно вычислять флуктуации различных термодинами-
термодинамических величин.
§ 85. Шумовые токи
Рассмотрим теперь важный в практическом отношении вопрос
о шумовых токах, которые часто определяют предельную чувстви-
чувствительность современной измерительной радиотехнической аппарату-
аппаратуры. Ограничимся упрощенным вариантом теории, чтобы можно
было использовать простой математический аппарат.
Пусть по проводнику длиной I и площадью поперечного сечения
5 протекает электрический ток /. Говорят, что в этом случае мы
имеем дело с элементом тока //. Для исследования вопроса
о шумах элемент тока удобно представить в другой форме. По-
Поскольку сила тока связана с плотностью тока соотношением I=iSt
а плотность тока, в свою очередь, в силу формул B1.14) и B1.2)
может быть представлена в форме
1= —ej= —en(v)y (85.1)
где п — концентрация электронов, a <v> —их средняя скорость, то
Il = iSl = iV= -e(v)nV= -e(v) (N)
(V = Sl — объем проводника, <N> = nV — число электронов в нем).
Полученное выражение допускает следующую физическую ин-
интерпретацию. Электрон, обладающий зарядом —е и движущийся со
скоростью v, представляет собой элемент тока —ev. Элемент тока
И есть просто сумма элементов тока отдельных электронов. Это
положение мы примем за основу и будем считать его точным, т. е.
не только для средних значений, а и для мгновенных, так что
=2-
где vax — мгновенное значение проекции скорости электрона с но-
номером а на направление тока (ось х). Сумма берется по всем элек-
электронам, находящимся в проводнике. Из последнего соотношения
для мгновенной силы тока следует
e (85'2)
Дальнейший анализ будет опираться на это уравнение.
251
Из (85.2) вытекает, что ток — величина случайная и ее случай*
ность вызвана двумя причинами. С одной стороны, скорости элек-
электронов имеют составляющую, обусловленную тепловым хаотиче-
хаотическим движением. С другой стороны, число электронов в проводнике
тоже случайно, так что число слагаемых в сумме флуктуирует.
Рассчитаем дисперсию тока, которая по определению равна
С помощью (85.2) для дисперсии получаем
J\ (85.3)
Предполагая, что по проводнику идет ток, мы должны считать,
что скорость электрона с номером а может быть представлена
в виде
где <vax>—среднее значение скорости (отличное от нуля, посколь-
поскольку идет ток), a Avax — случайная тепловая скорость. Среднее зна-
значение тепловой скорости, естественно, равно нулю, и, кроме того,
тепловые скорости различных электронов независимы. После под-
подстановки последнего выражения в (85.2) для дисперсии тока полу-
получится
Сумма ^SiVax) равна <vax>N, где N — мгновенное значение
а
числа электронов. Положим
так что AN — отклонение числа электронов от среднего. Выраже-
Выражение для дисперсии примет следующий вид:
или после приведения подобных членов
Флуктуации числа электронов и флуктуации скорости электро
нов независимы, поэтому средние значения от произведений Av&N
252
равны нулю. Sfero позволяет после возведения в квадрат и усредне-
усреднения написать
Если еще учесть независимость скоростей различных электронов,
то усреднением по скоростям легко получить
Теперь проведем усреднение по числу электронов, тогда
(АЛ) =-?<*„>»< ДЛГ«> +%(N)(bvlx). (85.4)
Из (85.4) видно, что дисперсия тока состоит из двух составляю-
составляющих. Одна связана с флуктуациями скоростей электронов и назы-
называется тепловым или джонсоновс к и м шумом. Она не
зависит от силы тока (от скорости направленного движения) и по-
поэтому имеет место и тогда, когда по проводнику ток не идет. Вторая
составляющая носит название дробового шума или шума
Шоттки. Она связана с флуктуацией числа электронов и прояв-
проявляется только тогда, когда по проводнику идет ток. Иногда ее назы-
называют генерационно-рекомбинационным шумом, что зависит от при-
причины, вызывающей флуктуацию числа частиц.
Получим более удобные выражения для обеих составляющих
шумового тока.
Среднее квадратичное значение дробового шума, как это следует
из (85.4), равно
<Д/2,р> =-?¦<«„)»< ДЛГ»>. (85.5)
Если электроны в проводнике образуют невырожденный электрон-
электронный газ, как это, например, имеет место в электронном полупро-
полупроводнике с не слишком высокой концентрацией электронов, то в со-
соответствии с (82.6)
(LN2)=nV.
Подставляя это выражение в (85.5), сможем написать
Поскольку V/l=S есть сечение проводника, a l/<vax> = to — вре-
время пролета, т. е. время, за которое электрон проходит через провод-
проводник, то с учетом (85.1) из последнего соотношения получится
*)=e-?-~e-L. (85.6)
'о 'о
253
Физически дробовую составляющую шума можно интерпрети-
интерпретировать следующим образом. Каждый электрон, перемещаясь по про-
проводнику со средней скоростью <vax>, создает импульс тока дли-
длительностью, равной времени пролета *. Импульсы тока отдельных
электронов случайны в том отношении, что случаен момент их воз-
возникновения.
Для определения реакции цепей и приборов, подключенных
к проводнику, на дробовой шум целесообразно перейти к спек-
спектральному представлению, т. е. представить импульс тока
в виде суммы синусоидальных сигналов. Такое представление мож-
можно получить, используя разложение Фурье. Спектральное представ-
представление упрощает рассмотрение, так как прохождение синусоидаль-
синусоидального сигнала через электрическую цепь легко рассчитать, если из-
известна частотная характеристика цепи.
Из теории разложения Фурье известно, что спектральная плот-
плотность 5((о) импульса тока, форма которого определяется функцией
/(/), вычисляется по формуле (см. [12], с. 544)
В данном случае, имея в виду прямоугольную форму импульса тока,
амплитуду которого обозначим Л, и выбирая начало отсчета време-
времени посередине импульса, получим
+ *о/2
S(o))=-L Г
2л
-to/*
Вычисление этого интеграла приводит к следующему результату:
5@,)=: А 1еш°'2-е-ш°'2] _ A sin (*fo/2)
^ 2л ш 2л ° о>/0/2
Энергия спектральной составляющей с частотой со пропорцио-
пропорциональна квадрату модуля спектральной плотности на этой частоте:
8 7
4я2
График этой функции представлен на рис. 14.2. Она достигает мак-
максимального значения при нулевой частоте и постепенно убывает
с ростом абсолютного значения частоты. При о) = 2л//о функция
* В случае генерационно-рекомбинационного шума длительность отдельных
импульсов определяется не столько временем пролета, сколько так называемым
временем жизни электрона, т. е. средним временем его существования, которое
обычно много меньше, чем время пролета.
254
первый раз обращается в ноль и после этого ее значение очень ма-
мало. При со = 0
Оказывается удобным ввести понятие о полосе частот, в которой
дробовой шум отличен от нуля. Для этого заменяют реальную функ-
функцию | S (со) |2 прямоугольником
так, как это показано на рис.
14.2 пунктиром. Высота прямо-
прямоугольника равна значению квад-
квадрата модуля спектральной плот-
плотности в максимуме |S@)|2, a
ширина выбирается такой, что-
чтобы площадь прямоугольника рав-
равнялась площади под кривой
|S(<o)|2. Ширина обозначена
2Дсо, так как физический смысл Рис 14.2
имеют лишь положительные час-
частоты. Математически равенство площадей записывается следую-
следующим образом:
2Ao)|S@)|2= f
Поскольку
ТО
Если вместо циклической частоты со ввести обычную /,"то для по-
полосы частот, в которой дробовой шум отличен от нуля, получится
* Интегрирование по частям дает
+ ОО +00 +ОО
Г si
J
• d */= —
2 sin у cos у
У
-I
sin 2y
dy.
Значение последнего интеграла есть я (см., например, [12], с. 408).
255
Таким образом, для дробового шума имеет место следующее выра-
выражение:
<Д/2др)=2*/Д/лр.
Устройство, подключенное к шумящему проводнику, может
реагировать не на все частоты, содержащиеся в спектре дробового
шума. Если оно пропускает полосу частот А/, приходящуюся на
диапазон частот вблизи максимума спектральной чувствительно-
чувствительности, т. е. на частоты, много меньшие/= l/t0, при которой спектраль-
спектральная плотность обращается в ноль, то шум определяется мощностью
пропущенных спектральных составляющих. Мощность прошедшего
через устройство шума, пропорциональная квадрату силы тока, во
столько раз меньше полной мощности дробового шума, во сколько
полоса устройства А/ меньше полосы А/др. Таким образом, дробо-
дробовой шум, действующий на прибор, подключенный к проводнику, об-
обладает дисперсией
<Д/2р)=2г/Д/, (85.8)
которая пропорциональна силе тока в проводнике и полосе частот
прибора.
Прохождение случайного тока по проводнику с сопротивлением
R вызывает появление на нем случайного напряжения. Среднее
квадратичное значение этого напряжения может быть легко получе-
получено умножением (85.8) на квадрат сопротивления:
(Ш%) =/?2( Д/др) =2eIR*Lf. (85.9)
Мощность дробового шума в проводнике определяется фор-
формулой
Приведем примеры использования полученных соотношений.
Пусть по проводнику, изготовленному из кремния я-типа, идет ток
силой 10 мА. Если концентрация электронов в кремнии 1015 см~3,
что соответствует удельному сопротивлению материала около
10 Ом-см, и образец имеет длину 1 мм и поперечное сечение 1 мм2,
то его сопротивление 100 Ом. Пусть он подключен на вход усили-
усилителя, который пропускает полосу частот от 100 до 10 000 Гц. Како-
Какова величина шума, воздействующего на усилитель? По формуле
(85.9) получим
= V2-1,6- К)9- Ю-2- 10-4.9900мкВ =
= 0,45 мкВ.
Необходимо, однако, проверить, выполнены ли условия, при кото-
которых справедлива формула (85.8), а следовательно, и (85.9). Рас-
Рассчитаем поэтому полосу частот, в которой действует дробовой шум.
Для этого следует воспользоваться (85.7), определив предваритель-
предварительно время пролета. Плотность тока в кремнии равна 1 А/см2 и по-
256
этому с помощью (85.1) при учете известной концентрации элек-
электронов легко найти среднюю скорость дрейфа электронов. Имеем
1
еп
1,6-10-19.1015
= 6-103 см/с.
Следовательно, при длине образца 1 мм время пролета равно
1,6-10—5 с, т. е. полоса частот дробового шума по (85.7) равна
30 .кГц. Это перекрывает полосу частот усилителя, и, следователь-
следовательно, формула (85.9) применима.
Предположим теперь, что об- дуих
разец изготовлен из кремния с
удельным сопротивлением
1 Ом-см (концентрация электро-
электронов 1016 см~3), а его длина рав-
равна 10 мм, тогда сопротивление
образца останется прежним, но
напряжение дробового шума не
будет равно 0,45 мкВ. Действи-
Действительно, в этом случае скорость
дрейфа электронов в 10 раз мень-
меньше, чем в предыдущем случае, а время пролета в 100 раз больше,
так как в 10 раз увеличилась длина пути. Полоса частот дробово-
дробового шума укладывается в диапазон 0—30 Гц, а эти частоты усили-
усилителем не воспринимаются.
Перейдем теперь к тепловому шуму. Дисперсия тока теплового
шума по (85.4) равна
Рис. 14.3
Поскольку <v2ax>:=kT/moy а среднее число частиц <N> = nV, то
/2
щ
(85.10)
Предположим, что от столкновения до столкновения электроны
движутся одно и то же время т независимо от их скорости. Проек-
Проекция тепловой скорости отдельного электрона на оси х, как функ-
функция времени, имеет тогда вид, показанный на рис. 14.3, т. е. ток,
обусловленный данным электроном, представляет собой последова-
последовательность импульсов одинаковой длительности, но разной ампли-
амплитуды.
В рассматриваемой модели подвижность электронов оказыва-
оказывается равной
(85.11)
Действительно, в поле Е электрон движется с ускорением
а=—еЕ/то. Он увеличивает свою скорость от нулевой после
столкновения до
<vz=lqx— — еЕх/т0
257
перед следующим столкновением, после которого он снова теряет
направленную скорость движения. Средняя скорость дрейфа равна,
таким образом,
К ' 2 2 '
откуда и вытекает формула (85.11).
Если (85.10) умножить и разделить на т, то можно написать
4 ' /2тотз 2т0 /2 и /2-я
Вводя проводимость о=г\еп, найдем
2av2.
/2 тз /2/(aV) U
Поскольку сопротивление проводника равно
R=J- = JL
* cS oV9
то полученную формулу можно также записать в виде
Случайные импульсы теплового тока предполагаются имеющими
одинаковую длительность, поэтому переход к спектральному пред-
представлению осуществляется точно так же, как и в случае дрейфо-
дрейфового тока. В результате получается
где Д/т = 1/2т — полоса частот теплового шума. Поскольку т очень
мало (порядка 10~12 с при комнатных температурах), то спектр
теплового шума практически равномерен от нулевой частоты до
очень высоких частот порядка 1/т. Эти частоты соответствуют мил-
миллиметровому диапазону длин волн. Учитывая точно так же, как и
раньше, роль полосы пропускания прибора, найдем для величины
теплового шума, воздействующего на прибор с полосой пропуска-
пропускания Д/,
Для среднего значения квадрата напряжения тепловых шумов по-
получим
(LUl)=4kTRbf, (85.12)
а для мощности теплового шума
258
Последние три формулы, определяющие величину тепловых шумов
в электрической цепи, носят название формул Найквиста.
В виде примера оценим напряжение теплового шума для рас-
рассмотренного выше проводника и усилителя, считая температуру
комнатной C00 К). Так как в обоих случаях сопротивление равно
100 Ом, то по (85.13) получим
У(Ш2Т) =V4kTRLf=V4-1,38-10-23.300.100-9900=0,12 мкВ-
ПРИЛОЖЕНИЯ
1. Интеграл вероятности при малых и больших значениях аргумента
При хо^\ в интеграле
переменная х, меньшая х0, тоже меньше единицы и экспоненту можно разложить
в ряд, который быстро сходится. Тогда имеем
4 -«о
Если ограничиться первым членом ряда, то
и, как видно, из предыдущего выражения, ошибка при хо^1 меньше
т. е. 15%. Учет двух членов обеспечивает точность 2,5%.
При Хо» 1 интеграл вероятности оценивают иначе. Запишем
Ф(хо)= 1 - ]/—
Если хо велико, то интеграл мал и Ф(*о) близка к единице. Преобразуем напи-
написанное выражение следующим образом:
Если провести теперь интегрирование по частям, то
l/I \ I d(e-^)= _ l/I le^ + l/I f le-/'d,.
V Л 1 * V П *Q V Я J *2
Хо *о
Последний интеграл в правой части из-за множителя х-2 по крайней мере в Jtjj"
раз меньше, чем исходный. Поэтому если Xq велико, то
260
У я J У я
и, следовательно,
с ошибкой порядка
При *о>2 эта формула обеспечивает точность, достаточную в большинстве прак-
практических расчетов.
2. Вычисление некоторых часто^ встречающихся интегралов
Вычисление интеграла
" " = \ е
имеет смысл рассмотреть подробно, так как он и целый ряд других близких к:
нему интегралов часто встречаются в статистике. Оказывается более удобным*
вычислять не /(Р), а квадрат этого интеграла. Поскольку переменная интегриро-
интегрирования может обозначаться любым способом, то
/2(Р)= j ,-Mdx j-
Произведение интегралов может быть представлено в виде одного двойного ин-
интеграла, который берется по всей плоскости (х, у):
Дальнейшие вычисления упрощаются, если перейти к полярным координатам
на плоскости. Так как
где р — расстояние точки с координатами х, у, от начала координат, а элемент-
площади AS в полярной системе имеет вид
dS= p!d
(ф — полярный угол), то
Поскольку интегрирование ведется по всей плоскости, то р меняется от 0 до оо„
а угол ф — от 0 до 2я. Интеграл по ф дает 2я и тогда
= 2я Г е""рра рМр = я/р,
т. е.
261
По вычисленному интегралу легко находятся значения целого ряда других
интегралов, встречающихся в статистике. Так, например, если продифференци-
продифференцировать тождество
-J- OO
-i
по р, то получится
Дифференцируя последнее соотношение по р еще раз, найдем
и т. д. Этим способом легко получаются значения следующих интегралов:
f
л 1-3-5... B/1--:
3. Теорема о равномерном распределении кинетической энергии по степеням
свободы
Рассмотрим доказательство теоремы о равномерном распределении кинети-
кинетической энергии по степеням свободы. Пусть положение системы в пространстве
определяется 3N координатами. Поскольку такими координатами могут служить
не только расстояния, отсчитанные по осям де-
декартовой системы координат, но и какие-то дру-
другие величины, как, например, угол поворота при
вращении твердого тела, то будем назы-
называть их обобщенными координатами
и обозначать qi. Если минимальное число обоб-
обобщенных координат <7ь q2, ..., <7здг, необходимых
для полного определения положения системы в
пространстве, равно 3N, то говорят, что число
степеней свободы системы равно ЗЛЛ Так, поло-
положение твердого тела, закрепленного на неподвиж-
неподвижной оси, вокруг которой оно может вращаться,
определяется всего одной координатой, за кото-
которую удобно принять угол поворота <р. Если ось
вращения выбрать за ось z, то угол поворота ср может отсчитываться от неко-
некоторого направления, принятого за ось х, так, как это показано на рис. П.З.
Угол ф является обощенной координатой данной системы, которая, таким обра-
образом, обладает одной степенью свободы.
Производная от обобщенной координаты по времени носит название о б-
общенной скорости, ив приведенном примере обобщенная скорость сов-
совпадает с угловой скоростью вращения со:
Рис. П.З
Декартовы координаты любой точки системы однозначно определяются
обобщенными координатами, и поэтому ее скорость есть линейная функция
262
обобщенных скоростей. Действительно, пусть декартова координата х\ одной из-
точек системы является функцией обобщенных координат q\y Цъ, ..., qzn
•*/= fi(qi> q2, ••• » Qzn)> (П3.1>
тогда
злг
dqj
(П3.2>
dfi
где производные —~ , хотя и зависят от обобщенных координат, но не зависят
oqj
от их производных, т. е. от обобщенных скоростей. Так, например, для точек
твердого тела, вращающегося вокруг оси z,
.*/= r,-cos<p, tji= r/ sin <p» (ПЗ.З)
где Гг — расстояние точки i от оси вращения, и поэтому
*/*= -i/ == — /*/ sin<p.^,
(П3.4)
viy= ^- = r/cos<f4-
Кинетическая энергия системы
Если подставить в выражение для кинетической энергии значения компонент
скорости, выраженные через обобщенные скорости по (П3.2), то окажется, что
кинетическая энергия есть однородная функция второй степени от обобщенных
скоростей, т. е. имеет вид
2 (пз-5>
где aij — некоторые коэффициенты, которые, вообще говоря, могут зависеть от
обобщенных координат (но не от обобщенных скоростей). Для твердого тела,,
вращающегося вокруг неподвижной оси г,
где rtii — масса i-го элемента, входящая в его состав. Подставляя значения ско-
скоростей из (П.34), найдем выражение кинетической энергии через обобщенную-
скорость:
(ПЗ.б)
где
/==
— момент инерции твердого тела относительно оси вращения. Таким образом,
в данном конкретном случае имеется одна степень свободы и единственный ко-
коэффициент аи в (П.3.5) равен половине момента инерции.
263
Импульс материальной точки, входящей в состав системы, может быть пред-
предоставлен следующим образом:
/ ffliV- \ А W^ ТП fV j A<?
(П3.7)
По аналогии с (ПЗ 7), обобщенным импульсом pi называют про-
производную от кинетической энергии системы по обобщенной скорости:
Рг-
(П3.8)
Из (П3.8) видно, что обобщенный импульс есть линейная функция обобщенных
скоростей, поэтому, наоборот, обобщенная скорость может быть представлена
как линейная функция обобщенных импульсов. Так, для случая вращения твер-
твердого тела вокруг неподвижной оси обобщенный импульс есть
:/9=/@, (П3.9)
\ * /
т. е. это момент количества движения.
Если выразить обобщенные скорости через импульсы с помощью уравне-
уравнений (П3.8)
(П3.10)
щ подставить получившиеся выражения в (П3.5), то кинетическая энергия ока-
окажется однородной функцией второй степени от обобщенных импульсов, т. е.
«будет иметь вид
Для рассматриваемого примера из (П3.9)
<?> = <й = р I
m по (ПЗ.б)
-так что единственный коэффициент 6ц равен
Ьп= 1/B/).
Поскольку кинетическая энергия — однородная функция второй степени, то
но теореме Эйлера имеет место следующее тождество:
^к=уУ Pi "~• (ПЗ. 13)
Это соотношение классической механики лежит в основе вывода теоремы о рав-
равномерном распределении кинетической энергии по степеням свободы.
Кинетическая энергия, приходящаяся на t-ю степень свободы, дается сла-
слагаемым выражения (П3.13), имеющим индекс i:
<?к/ = "Г" Pi ~Т^" • (пз-14>
264
Для среднего значения кинетической энергии, приходящейся на i-ю степень сво-
свободы, следует в соответствии с распределением Гиббса написать
<(
= I —
dpi
dr.
(ГШ5>
Полная энергия системы <8 есть сумма кинетической и потенциальной, но по-
поскольку потенциальная энергия не зависит от скоростей, а следовательно, и or
импульсов, то
dpi dpi
Это позволяет переписать (П3.15) в виде
dpi
<'
где dF — элемент объема фазового пространства:
d H= d^i df/i dzi dj^2 d У2 dz2 . • • dx^ dy^ dz^j X
X dpxi dpyi dpzi dpX2 dpy2 d pZ2 ... d pxN d pyN d pzN,
Интегрирование легче выполнить, если от декартовых координат и импульсов
перейти к обобщенным. Как известно из математики, этот переход осуществляет-
осуществляется по правилу
d Г= / d qi ... d q3N d px ... d p3N, (П3.16)
где
x^yNZN PxlPylPzl
Pi
dXl
dqi
dzN
dqx
dx,
dzN
d93N
dxi
dpi
1 dzN
\ dpi '"
dXl
dP*N
dzN
dP3N
dqx
dPxi
dpi
dPzN dPzN dPzN
dPl "" dPzN
— детерминант, носящий название якобиана.
Поскольку декартовы координаты по (П3.1) зависят только от обобщенных
координат, то все производные по обобщенным импульсам, стоящие в правом1
верхнем углу и отделенные пунктиром, равны нулю. В связи с этим якобиан,
разбивается на произведение двух детерминантов:
dxx дхг
/ =
dz
N
dqi
dpi
26S
Можно показать, что это произведение равно единице. Для этого в выра-
выражении (П3.7)
Pl=
dqi
^рассмотрим кинетическую энергию как функцию декартовых переменных:
dvx
...+¦
dv
zN
dv.
uxi dqi uvzN
'Из полученного сотношения видно, что
dvxi dpi
' = Рх\
dv
zN
'zN
dqi
dv
zN
dpi
ti
Px\
dqt dp.
'zN
О другой стороны, из (П3.2) и аналогичных ему сотношений после дифферен-
дифференцирования по Ц\ следует
41 поэтому
dvxi
dqi
dpi
dx
dqi
dx
dv
zN
dqi
dPzN
d2N
dqi
dz
N
Таким образом, первый детерминант можно представить следующим образом:
dpi dp3N
"' dPxX
dpi
dPzN
dP
zN
Переставив в нем строки и столбцы, что не меняет значения детерминанта, за-
запишем якобиан в виде
dpi
dpi
dpzN
dpxi "" dpzN
dpi *" dp
3N
dpi
dPzN
дРзм
Если теперь провести умножение по правилу «строка на столбец», то
dp\ dpi dpx
dpi
dp..
'3N
dp
SN
dpi
266
т. е. фактически
так как
dpi
dpi
= 1 и
dpi
1
О
О О
1
(П3.17)
= 0
). Таким образом, показано, что яко-
p pj
биан равен единице и, следовательно, среднее значение кинетической энергии,,
приходящейся на t-ю степень свободы, определяется выражением
Выполним сначала интегрирование по ри учитывая, что возможные значения
обобщенного импульса лежат в пределах от — оо до + оо. Поскольку
if'
kT
—
2 dpi
— oo —
то после интегрирования по частям получится
f Pi
\ т
— оо
kT
kT г
2 )
Первое слагаемое обращается в ноль, так как при бесконечном значении
обобщенного импульса бесконечна и энергия системы, а тогда экспоненциальный
множитель бесконечно мал. Теперь выражение для <<^к*> можно записать
в виде
kT Р
—у
dqmdPl...
т. е.
(П3.18)
так как по условию нормировки
d,,..
= J
dr-l.
Формула (П3.18) и есть математическая запись теоремы о равномерном
распределении кинетической энергии по степеням свободы.
В заключение заметим, что аналогичное соотношение может иметь место
и для потенциальной энергии, однако для этого необходимо выполнение следую-
следующих условий.
Во-первых, потенциальная энергия должна быть квадратичной функцией
обобщенных координат q\, так что
(ПЗЛ9)
267
Во-вторых, кинетическая энергия не должна зависеть от обобщенных коор-
координат, так чтобы соотношение (П3.19) можно было переписать в виде
Теперь для среднего значения потенциальной энергии, приходящейся на t-ю сте-
степень свободы, т. е. для
учитывая, что якобиан равен единице, по общему правилу находим
1 д% {?—%)/(kT)
"i" **1 ~~д е ' * * ^т ''' ^3^
Интегрирование выполняется тем же способом, что и в предыдущем случае,
и приводит к равенству
4. Переход к системе отсчета, связанной с центром масс
По G6.2),
Pl =
(mi -f mi)
Рс-Ьро»
(П4.1)
(тх + mi)
Рс—Ро.
Поскольку
где / — якобиан преобразования от pi, p2 к рс, ро, то необходимо вычислить
якобиан. Имеем
дРсу
дР\у
дрОу
др
су
дрсу dpcz дрох дроу дрог
Соответствующие производные легко вычислить с помощью (П4.1). Отличны от
нуля
дрсх дрсу dpcZ M-i "т* т2 дрох дрОу дрог
m<z
дрсг
4- /7Z2 ' дрох дроу dpoz
268
После подстановки в (П4.2) получается
О
О
Щ
-f/7Z2
0
0
4-/7Z2
0
0
и
Щ
mi + m<i
0
п
и
/712
mi -f- /722
0
1
0
0
0
1
0
0
0
1
0—1 О О
0 0—1 О
/Wo
- 0 0—1
Если прибавить четвертую строку к первой, пятую ко второй, а шестую к треть-
третьей, то получится выписанный ниже детерминант, абсолютная величина которого,
очевидно, равна единице:
1
0
0
/712
mi ¦+• /W2
0
0
0
1
0
0
/П2
mi 4- /иг
0 -
0
0
1
0 -
0
/7*2
0
0
0
1
0
- 0
0
0
0
0
— 1
0 -
0
0
0
0
0
1
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Бозе частицы (бозоны) 140, 157
Величина случайная 23
дискретная 23
непрерывная 23
Вероятностей биномиальное распреде-
распределение 21
Вероятности плотность 24
, условие нормировки 30
Вероятность безусловная 18
— события 11, 5,1
— условная 18
Вина закон смещения 168
— формула — см. Формула Вина
Время релаксации 196, 226, 229, 231
Газ идеальный, уравнение состояния
112
— реальный 108
, свободная энергия 111
, уравнение состояния 123
— электронный 177
вырожденный 181
, критерий вырождения 182
, — невырожденности 181
невырожденный 179
Гиббса принцип — см. Принцип Гибб-
са
Градиент функции 193
Дебая температура—см. Температура
Дебая
Дисперсия 29, 240
— тока 252
, шум дробовой (Шоттки) 253,
256
, — тепловой (джонсоновский)
253, 257
— числа частиц 42, 243,
Длина Дебая 88
— свободного пробега средняя 230
Закон Вольта 84
— Ома — см. Плотность тока
— смещения Вина 168
— Стефана — Больцмана 168
Излучательная способность 165
абсолютно черного тела 166
Излучения квантованные 133
, квантовые числа 136
Интеграл вероятности 41, 260
— состояний 96
Испытание (определение) И
Карно цикл 122
270
Клапейрона — Менделеева уравнение
113
Коэффициент диффузии 204
— дрейфа 204
— подвижности 205
Майера соотношение 127
Математическое ожидание 27
Мезоны 157
Мера количества информации 38
— неожиданности 37
— неопределенности ситуации 39
Метод самосогласованного поля 85
Омега-потенциал 150
бозонов 159
электронов 178
Омега-потенциала спектральная плот-
плотность 163
Опыт Перрена 79
— Штерна —см. Распределение Макс-
Максвелла
— Дэвисона и Джермера 132
— Фабриканта, Сушкина, Бибирма-
на 132
Плазма«см. Распределение Макс-
Максвелла
Планка формула — см. Формула План-
Планка
Плотность вероятности 24
импульса 44, 54
Максвелла 49
Максвелла — Больцмана 94
, условие нормировки 30
— потока частиц 60, 62
— состояний 162, 178
— тока 65, 211
, закон Ома 21,1
Постоянная Авогадро 49, 80
— Больцмана 49, 78, 80
— нормировочная 47
— Стефана — Больцмана 168
Потенциал химический 151, 155, 176У
183
Потенциальный ящик 73, 177
Принцип детального равновесия 74
— неопределенности 197
— неразличимости 136, 139
— Паули 140, 174
Прицельное расстояние 214
Проводимость 211
—, зависимость температурная 227.
228
Пуассона уравнение — см Уравнение
Пуассона
Работа выхода 64
Разность потенциалов контактная 82
Распределение Бозе — Эйнштейна 160
для фотонов 161
— Гаусса (нормальное) 35, 36
— Гиббса 95, 96
большое каноническое 149
для фотонов 161
в квантовой статистике 140
для газа идеального одноатом-
одноатомного 97
— Дрювестейна 239
— Максвелла (по скоростям) 53
, экспериментальная проверка
(опыт Штерна) 66
, (плазма) 67
— Максвелла — Больцмана 100
— по энергии 55
— Пуассона 34
— Ферми — Дирака 176
Рэлея — Джинса формула — см. Фор-
Формула Рэлея — Джинса
Сечение рассеяния эффективное 216
дифференциальное 216
полное 216
Событие достоверное 13
— случайное 11
Событий несовместимых полная груп-
группа 11
События случайного вероятность II
— независимые 16
— несовместимые 13
— мера неожиданности 37
— равновозможные 14
Среднее значение 27, 50
, правило определения 27
Стирлинга формула — см. Формула
Стирлинга
Температура Дебая 173
Теорема Лиувилля 194
Теплоемкость 126
— газов 126, 183
— молярная 126
— удельная .126
Термодинамики начало второе 120
третье 146
Уравнение Больцмана кинетическое
194, 196, 221
— Гиббса — Гельмгольца 116
— диффузии 201
для электронов 205
— Пуассона (самосогласованного по-
поля) 87, 211
— состояния 112, 115, 153, 156
— Клапейрона — Менделеева 113
— Эйнштейна 206
Условие изотропности 44
— независимости движения 44
— нормировки 30, 47, 93, 141, 149
Фазовое пространство (^-пространст-
(^-пространство) 93
полное (гамма-пространство) 95
Ферми частицы (фермионы) 140, 174
Флуктуации 40, 104, 240
— объема 247
— температуры 248
— числа частиц 243
— энергии 248
Фонон 157, 17,1
Формула барометрическая 78
— Вина 167
— Планка 166
— Ричардсона 66
— Рэлея —Джинса 167
— Стирлинга 22
Формулы Найквиста 259
Фотон 130, 157, 161
Фотона волновое число 131
Функция распределения 60
квазиклассическая 199
Максвелла 60, 92, 209
и Больцмана 93
неравновесная 191
равновесная 93
электронов по скоростям 238
Шум дробовой — см. Дисперсия тока
, мощность 256
— тепловой 253, 257
, мощность 258
Энергетическая светимость 168
Энергия внутренняя 117, 152
свободная 116, 155
квантовой системы 141
Энтропия 117, 144, 154
—¦, принцип максимума 146
—, статистический смысл 119
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Курсы статистической физики для университетов
1. Терлецкий Я. П. Статистическая физика. 2-е изд. М., 1973.
2. Ансельм А. И. Основы статистической физики и термодинамики. М., 1973.
Пособия для пединститутов
3. Ноздрев В. Ф., Сенкевич А. А. Курс статистической физики. М, 1969.
4. Радушкевич Л. В. Курс статистической физики. М., 1966.
Монографии
5. Ландау Л. Д., Лифшиц Е. М. Статистическая физика. М., 1976.
6. Френкель Я. И. Статистическая физика. М. — Л., 1948.
7. Керзон Хуанг. Статистическая механика. М., 1966.
8. Кубо Р. Статистическая механика. М., 1967.
9. Хир К. Статистическая механика, кинетическая теория и стохастические
процессы. М., 1976.
10. Исихара А. Статистическая физика. М, 1973.
11. Чемпен С, Каулинг Т. Математическая теория неоднородных газов.
М., 1960.
Справочник
12. Бронштейн И. #., Семендяев К. А. Справочник по математике для ин-
инженеров и учащихся втузов. 10-е изд. М., 1964.
Андрей Михайлович Васильев
ВВЕДЕНИЕ В СТАТИСТИЧЕСКУЮ ФИЗИКУ
Зав. редакцией литературы по физике и математике Е. С. Гридасова. Редактор С. А. Кры-
Крылов. Младший редактор С. А. Доровских. Переплет художника В. И. Сидоренко. Художе-
Художественный редактор В. П. Спирова. Технический редактор Е. И. Герасимова. Корректор
Г. И. Кострикова
ИБ № 2150
Изд. № ФМ-642 Сдано в набор 10 04 80 Подп. в печать 09.10 80
Формат 60X90l/ie- Бум. тип. № i. Гарнитура литературная. Печать высокая.
Объем 17 уел печ л 16,32 уч.-изд л Тираж 20 000 экз. Зак. № 434. Цена 80 коп.
Издательство «Высшая школа». Москва, Пеглинная ул , д 29/14.
Московская типография № 8 Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли, Хохловский пер., 7.