ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
И ВАРИАЦИОННОЕ
ИСЧИСЛЕНИЕ
л.э.эльсгольц
КУРС
ВЫСШЕЙ МАТЕМАТИКИ
И МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
Под редакцией
А. Н. ТИХОНОВА, В. А. ИЛЬИНА,
А. Г. СВЕШНИКОВА
ВЫПУСК 3
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
И ВАРИАЦИОННОЕ
ИСЧИСЛЕНИЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19S9
л. э. эльсгольц
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
И ВАРИАЦИОННОЕ
ИСЧИСЛЕНИЕ
Издание второе, стереотипное
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебника
для студентов физических специальностей
университетов
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1869
517.2
Э 53
УДК 517.9/519.3 (075.8)
Лее Эрнестович Эльеаольц
Дифференциальные уравнения и вариационное исчисление
(Серия: «Курс высшей математики и математической физики»)
М., 1969 г., 424 стр. с илл.
Редактор Ю. А. Горьков
Техн, редактор К. Ф. Бру&но	Корректор Е. С. Статникова
Печать с матриц, 2-ой типографии им. Ев. Соколовой. Подписано к печати 26/II 1969 г.
Бумага 60х90/1в. Физ. печ. л. 26,5. Условн. Печ. л. 26,5. Уч.-изд. л. 25,04.
Допечатка тиража 40 000 экз. Цена книги 90 коп. Заказ № 104.
Издательство- «Наука»
Главная редакция физико-математической литературы
Москва, В-71, Ленинский проспект, 15
Отпечатано в 1-ой типографии изд-ва «Наука». Ленинград, В-34, 9-я линия, дом 12.
2-2-3
23—69
ОГЛАВЛЕНИЕ
От редакторов серии...................................... . .	8
Предисловие .......... ......	.............................. 8
ЧАСТЬ I
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Введение . . ......................."........................  9
Глава 1. Дифференциальные уравнения первого порядка. ... 15
§ I.	Уравнения первого порядка, разрешенные относительно про-
изводной .-............................................  15
§ 2.	Уравнения с разделяющимися переменными ............ 19
§ 3.	Уравнения, приводящиеся к уравнениям с разделяющимися
переменными ...........................................  24
§ 4.	Линейные уравнения первого порядка................  27
§ 5.	Уравнения в полных дифференциалах . . ............. 32
§ 6.	Теоремы существования и единственности решения уравне-
ния	у)................................      39
§ 7.	Приближенные методы интегрирования уравнений первого
порядка ...............................................  61
§ 8.	Простейшие типы уравнений, не разрешенных относительно
производной . .......................................... 68
§ 9.	Теорема существования и единственности для дифференциаль-
ных уравнений, не разрешенных относительно производной.
Особые решения.......................................... 75
Задачи к главе 1...................................  82
Глава 2. Дифференциальные уравнения порядка выше первого 85
§ 1.	Теорема существования и единственности для дифферен-
--циального уравнения п-го порядка...................... 85
§ 2.	Простейшие случаи понижения порядка................ 87
§ 3.	Линейные дифференциальные уравнения n-го порядка ....	93
§ 4.	Линейные однородные уравнения с . постоянными коэффи-
циентами и уравнения Эйлера ..... ..................... 107
§ 5.	Линейные неоднородные уравнения....................113
§ 6.	Линейные неоднородные уравнения с постоянными коэффи-
циентами и уравнения Эйлера.............................124
§ 7.	Интегрирование дифференциальных уравнений при помощи
рядов.................................................  137
§ 8.	Метод малого параметра и его применение в теории квази-
линейных колебаний . ...................................147
6
ОГЛАВЛЕНИЕ
§ 9.	Понятие о краевых задачах...........................159
Задачи к главе 2................................. . . 165
Глава 3. Системы дифференциальных уравнений....................168
§ 1.	Общие понятия .......................................168
§ 2.	Интегрирование системы дифференциальных уравнений путем
сведения к одному уравнению более высокого порядка ... 171
§ 3.	Нахождение интегрируемых комбинаций.................178
§ 4.	Системы линейных дифференциальных уравнений........... 181
§ 5.	Системы линейных дифференциальных уравнений с постоян-
ными коэффициентами ......................................192
§ 6.	Приближенные методы интегрирования систем дифферен-
циальных уравнений и уравнений и-го порядка ............. 199
Задачи к главе 3.................................. . 201
Глава 4. Теория устойчивости.................................  203
§ 1.	Основные понятия....................................203
§ 2.	Простейшие типы точек покоя..........................206
§ 3.	Второй метод А. М. Ляпунова  ........................215
§ 4-	Исследование на устойчивость по первому приближению . . 221
§ 5.	Признаки отрицательности действительных частей всех корней
многочлена................................................227
§ 6.	Случай малого коэффициента при производной высшего
порядка.......................•	........................230
§ 7.	Устойчивость при постоянно действующих возмущениях . . 234
Задачи к главе 4..........................................238
Глава 5. Уравнения в частных производных первого порядка . 241
§ 1.	Основные понятия....................................241
§ 2.	Линейные и квазилинейные уравнения в частных производ-
ных первого порядка ..... .............................. 243
§ 3.	Уравнения Пфаффа ...................................255
§ 4.	Нелинейные уравнения первого порядка................260
Задачи к главе 5.................	. ................278
ЧАСТЬ п
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Введение.....................................................   280
Глава 6. Метод вариаций в задачах с неподвижными границами 284
§ 1.	Вариация и ее свойства...............................284
§ 2.	Уравнение Эйлера.....................................292
х,
§ 3.	Функционалы вида J* F (х, уь у2...уп, Ур у2, .... y'^jdx 305
Хо
§ 4.	Функционалы, зависящие от производных более высокого
порядка.................................................  308
§ 5.	Функционалы, зависящие от функций нескольких независимых
переменных....................	. . . ...................312
§ 6.	Вариационные задачи в параметрической форме..........317
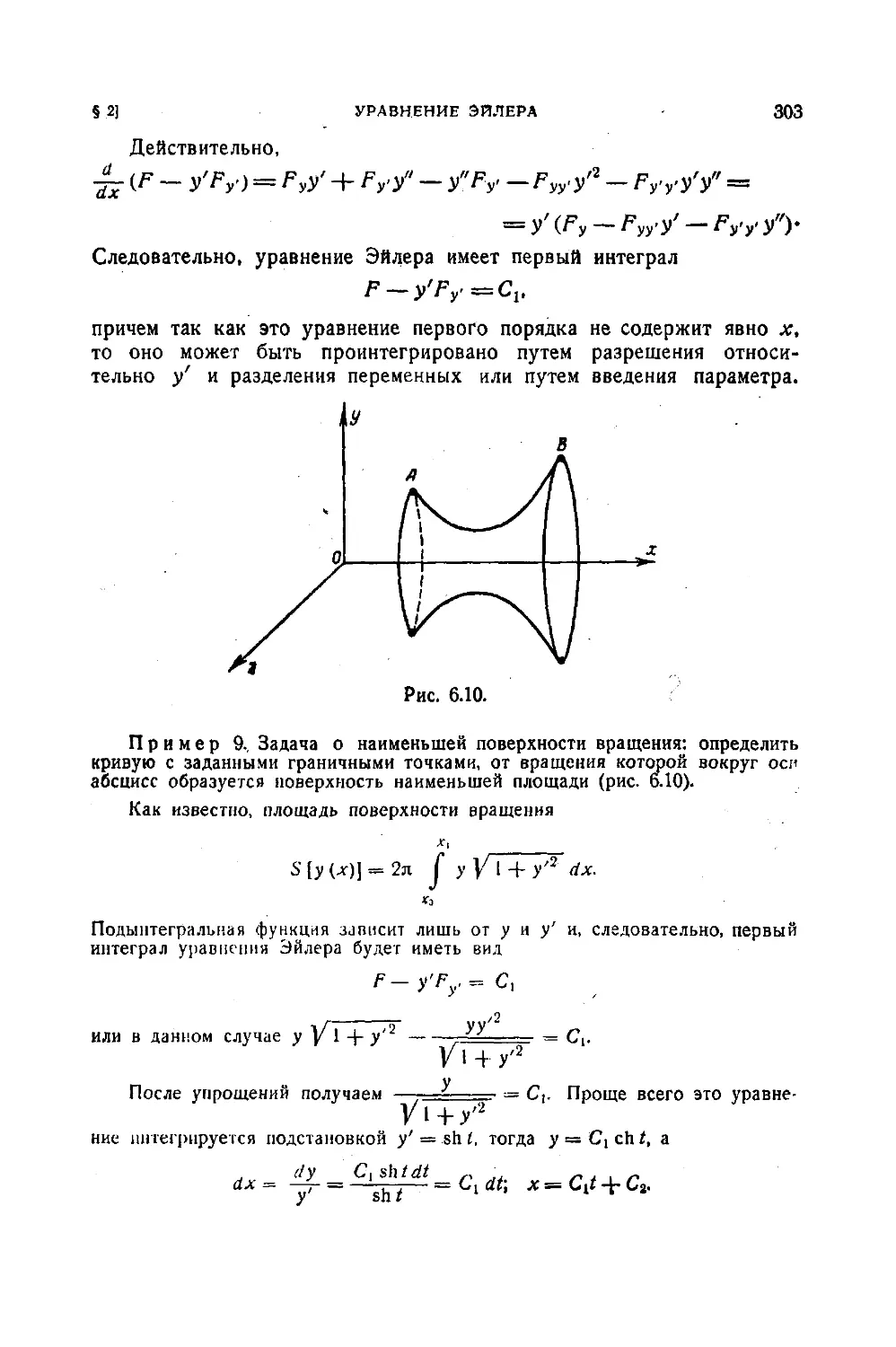
§ 7.	Некоторые приложения................................  320
Задачи к главе 6 .....................................324
ОГЛАВЛЕНИЕ
7
Глава 7. Вариационные задачи с подвижными границами и не-
которые другие задачи...............................327
§ 1.	Простейшая задача с подвижными границами......327
§ 2.	Задача с подвижными границами для функционалов вида
J F(x. у, г, у', г') dx ...... .................334
§ 3.	Экстремали с угловыми точками................ 338
§ 4.	Односторонние вариации........................346
Задачи к главе 7.............................   349
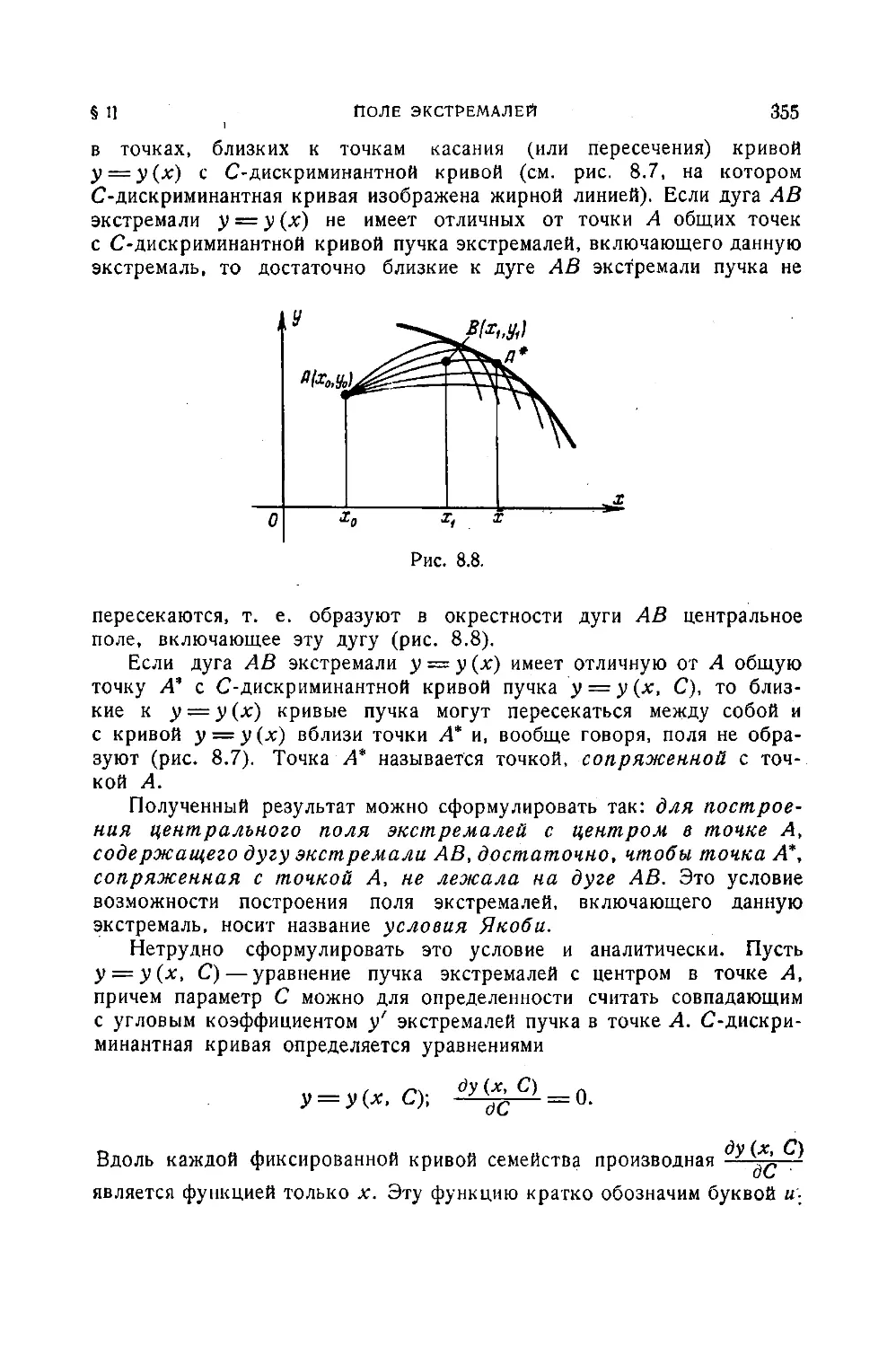
Глава 8. Достаточные условия экстремума ................351
§ 1.	Поле экстремалей..............................351
§ 2.	Функция Е(х, у, р, у')........................357
§ 3.	Преобразование уравнений Эйлера к каноническому виду . . 368
Задачи к главе 8...............  ...............	373
Глава 9. Вариационные задачи на условный экстремум.............375
§ 1.	Связи вида <р(х, у,. у2> .... уп) — 0.............. 375
§ 2.	Связи вида <р(х, уь у2, .... Уп, yj, у2.Л>) = °.....382
§ 3.	Изопериметрические задачи ..........................385
Задачи к главе 9...................................  393
Глава 10. Прямые методы в вариационных задачах.....394
§ I.	Прямые методы............................ 394
§ 2.	Конечно-разностный метод Эйлера ..........395
§ 3.	Метод Ритца.............................  397
§ 4.	Метод Канторовича.........................406
Задачи к главе 10 ..................... 412
Ответы и указания к задачам...................................  414
Рекомендуемая литература .....................................  421
Предметный указатель..........................................  422
ОТ РЕДАКТОРОВ СЕРИИ
В качестве третьего выпуска серин редакция приняла переиздание
(с некоторыми изменениями) книг Л. Э. Эльсгольца по соответству-
ющим разделам.	-
ПРЕДИСЛОВИЕ
Третий выпуск «Курса высшей математики и математической фи-
зики» для физических и физико-математических факультетов содержит
теорию дифференциальных уравнений и вариационное исчисление.
В основу книги положены лекции, которые автор в течение ряда
лет читал на физическом факультете Московского ордена Ленина
государственного университета им. М. В. Ломоносова.
Излагаемый материал хотя и близок к содержанию книг автора'
«Дифференциальные уравнения» (М., Гостехиздат, 1957) и «Вариа-
ционное исчисление» (М., Гостехиздат, 1958), однако по совету
редакторов .Курса в него внесен ряд изменений. За эти советы автор
выражает им свою искреннюю признательность.
Л. Э. Эльсголъц
ЧАСТЬ I
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВВЕДЕНИЕ -
При изучении физических явлений часто не удается непосредст-
венно найти законы, связывающие величины, характеризующие физи-
ческое явление, но в то же время легко устанавливается зависимость
между теми же величинами и их производными или дифференциалами.
При этом мы получаем уравнения, содержащие неизвестные функции
или вектор-функции под знаком производной или дифференциала.
Уравнения, в которых неизвестная функция или вектор-функция
входит под знаком производной или дифференциала, называются
дафференциальными уравнениями. Приведем несколько примеров
дифференциальных уравнений:
1)	— kx— уравнение радиоактивного распада (k — постоян-
ная распада, х— количество неразложившегося вещества в момент
,	dx
времени t, скорость распада пропорциональна количеству рас-
падающегося вещества).
I dx \
2)	т — f \t, г, ~-1 —уравнение движения точки массы т
под влиянием силы F, зависящей, от времени, положения точки, опре-
деляемого радиусом-вектором г, и ее скорости Сила равна
произведению массы на ускорение.
д2и . д2и . даи .	.	.	п
3)	“ УРавнение Пуассона, ко-
торому, например, удовлетворяет потенциал а(х, у, г) электроста-
тического поля, р(х, у, z) — плотность зарядов.
Зависимость между искомыми величинами будет найдена, если
будут указаны методы нахождения неизвестных функций, опреде-
ляемых дифференциальными уравнениями. Нахождение .неизвестных
функций, определяемых дифференциальными уравнениями, и является
основной задачей теории дифференциальных уравнений.
Если в дифференциальном уравнении неизвестные функции или
вектор-функции являются функциями одной переменной, то дифферен-
10
ВВЕДЕНИЕ
циальное уравнение называется обыкновенным (например, уравне-
ния 1) и 2)). Если же неизвестная функция, входящая в диффе-
ренциальное уравнение, является функцией двух или большего
числа независимых переменных, то дифференциальное уравнение на-
зывается уравнением в частных производных (например, урав-
нение 3)).
Порядком дифференциального уравнения называется максимальный
порядок входящей в уравнение производной (или дифференциала)
неизвестной функции.
Решением дифференциального уравнения называется функция,
которая при подстановке в дифференциальное уравнение обращает
его в тождество.
Например, уравнение радиоактивного распада
.	<в.1>
имеет решение
x — ce~kt,	(B-h)
где с — произвольная постоянная.
Очевидно, что дифференциальное уравнение (В.1) еще не пол-
ностью определяет закон распада х = х (t). Для его полного опре-
деления надо знать количество распадающегося вещества х0 в неко-
торый начальный момент tQ. Если х0 известно, то, принимая во вни-
мание условие x(t0) — x0 из (В.1!), находим закон радиоактивного
распада:
x = xoe-ktf~tl>\
Процесс нахождения решений дифференциального уравнения назы-
вается интегрированием диффе ренциального уравнения. В. рас-
смотренном примере мы легко нашли точное решение, однако в более
сложных случаях очень часто приходится применять приближенные
методы интегрирования дифференциальных уравнений. Эти прибли-
женные методы еще недавно приводили к утомительным вычислениям,
но теперь быстродействующие вычислительные машины способны
выполнять эту работу со скоростью в несколько десятков или даже
сотен тысяч операций в секунду.
Рассмотрим несколько подробнее упомянутую выше более сложную
задачу о нахождении закона движения г = г (f) материальной точки
массы т под действием заданной силы F (t, г, г). По закону Ньютона
mr = F (Л г, г).	(В.2)
Следовательно, задача сводится к интегрированию этого дифферен-
циального уравнения. Очевидно, что закон движения еще не вполне
ВВЕДЕНИЕ	И
определяется заданием массы т и силы F, надо еще знать начальное
положение точки
r(^ = r0	(B.2j)
и начальную скорость
г(/о) = го.	(В.22)
Укажем весьма естественный приближенный метод решения урав-
нения (В. 2) с начальными условиями (B.2j) и (В.22), причем идея
этого метода может служить и для доказательства существования
решения рассматриваемой задачи.
Разделим отрезок времени /0 t Т, на котором требуется опре-
делить решение уравнения (В.2), удовлетворяющее начальным уело-
т______________________________________________________t
виям (B.2j) и (В.22), на п равных частей длины А =——-:
Uo> Л1. 1^1. ^1.	Л,
где
=	(А = 1, 2.....я—1).
В пределах каждого из этих малых (при больших значениях я)
отрезков времени сила F (/, г, г) мало изменяется (вектор-функция F
предполагается непрерывной), поэтому приближенно ее можно считать
на каждом отрезке	постоянной, например, равной ее зна-
чению в левой граничной точке каждого отрезка. Точнее, на отрезке
|/0, сила F (t, г, г) считается постоянной и равной F (t0, г0, г0).
При этом допущении из уравнения (В.2) и начальных условий (B.2t)
и (В,22) легко определяется закон движения гя (/) на отрезке [/0,
(движение будет равномерно переменным) и, следовательно; в част-
ности, известны значения гя (^) и r„ (ZJ. Тем же методом прибли-
женно определяем закон движения гя (t) на отрезке [f1( t2], считая
силу F на этом участке постоянной и равной F (/v гя(^), г„ (/,)).
Продолжая этот процесс, определим приближенное решение гя (?)
поставленной задачи с начальными значениями для уравнения (В.2)
на всем отрезке [/0, Г].
Интуитивно ясно, что при я->оо приближенное решение r„(Z)
должно стремиться к точному решению.
Заметим, что векторное уравнение (В.2) второго порядка может
быть заменено эквивалентной системой двух векторных уравнений
первого порядка, если рассматривать скорость v как вторую неиз-
вестную вектор-функцию:
# = ’• £ = Г(/. г. V).	(В.З)
Каждое векторное уравнение в трехмерном пространстве может
быть заменено путем проектирования на оси координат тремя
12	ВВЕДЕНИЕ
скалярными уравнениями. Следовательно, уравнение (В.2) эквивалентно
системе трех скалярных уравнений второго порядка, а система (В.3)
эквивалентна системе шести скалярных уравнений первого порядка.
Наконец, можно одно векторное уравнение (В.2) второго порядка
в трехмерном йространстве заменить одним векторным уравнением
первого порядка в шестимерном пространстве, координатами в кото-
ром служат координаты г х, гу, гг радиуса-вектора г (t) и коорди-
наты vx, vy, vz вектора-скорости v. Такое пространство физики
называют фазовым. Радиус-вектор R (t) в этом пространстве имеет
координаты (гх, гу, rz, vx, vy, vz). В таких обозначениях система (В.З)
имеет вид:
^ = ®(f,R(/))	(В.4)
(проекциями вектора Ф в шестимерном пространстве служат соответ-
ствующие проекции правых частей системы (В.З) в трехмерном про-
странстве).
При такой интерпретации начальные условия (B.2t) и (В.22) заме-
няются условием
R(^o) = Ro-	(В.4,)
Решением уравйения (В.4) R = R(/) будет фазовая траектория,
каждой точке которой будет соответствовать некоторое мгновенное
состояние движущейся точки — ее положение г (t) и ее скорость v (t).
Если к уравнению (В.4) с начальным условием (В.4;) применить
изложенный выше приближенный метод, то на первом отрезке [Zo,
вектор-функцию Ф(/, R (£)) надо считать постоянной и равной
Ф(*о, R(A>))- Итак, ПРИ
-^ = Ф(^,
откуда, умножая на dt и интегрируя в пределах от tQ до t, получим
линейную вектор-функцию R(/):
R(O = R(Q+®tfo, R(/0))(f-f0).
В частности, при t — будем иметь
R (^) = R (£0)-|-ЛФ (£0, R(/o)).
Повторяя то же рассуждение на следующих участках, получим
Я(/2)==Р(/г)Н-ЛФ(/1, R(^)),
R = R (tk_ i) + ЛФ (^_v R (^_t)),
Применяя эти формулы n раз, дойдем до значения R(7).
ВВЕДЕНИЕ
13
В этом методе искомое решение R(0 приближенно заменяется
кусочно линейной вектор-функцией, графиком которой служит неко-
торая ломаная, называемая ломаной Эйлера.
Для уравнения (В.2) нередко в приложениях встречается и иная
постановка задачи — дополнительные условия задаются не в одной,
а в двух точках. Такая задача, в отличие от задачи с условиями (B.2t)
и (В.22), называемой задачей с начальными условиями или задачей
Коши, носит название краевой или граничной.
Пусть, например, требуется, чтобы материальная точка массы т,
движущаяся под действием силы F (/, г (О. г(0)> находившаяся
в начальный момент t == t0 в положении г = г0, попала бы в момент
t — ty в положение г^Гр т. е. надо решить уравнение (В.2) с гра-
ничными условиями г (/0) = г0, г (/]) = гг К этой граничной задаче
сводятся многие баллистические задачи, причем очевидно, что реше-
ние здесь часто может быть не единственным, так как из точки
г (70) = г0 можно попасть в точку г (Q = г, по настильной и по
навесной траекториям.
Точное или приближенное решение задач с начальными условиями
и граничных задач является основной задачей теории дифферен-
циальных уравнений, однако иногда требуется выяснить или при-
ходится ограничиваться выяснением лишь некоторых свойств решений.
Например, часто требуется установить, существуют ли периодические
или колеблющиеся решения, оценить быстроту возрастания или убы-
вания решений, выяснить, сильно ли меняется решение при малом
изменении начальных значений.
Остановимся несколько подробнее на последнем из этих вопросов
применительно к уравнению движения (В.2). В прикладных задачах
начальные значения г0 и г0 почти всегда являются результатом изме-
рения и, следовательно, неизбежно определены с некоторой погреш-
ностью. Поэтому естественно возникает вопрос / о влиянии малого
изменения начальных значений на искомое решение.
Если сколь угодно малые изменения начальных значений спо-
собны вызвать значительные изменения решения, то решение, опре-
деляемое неточными начальными значениями г0 и г0, обычно не имеет
никакого прикладного значения, так как оно даже приближенно
не описывает движение рассматриваемого тела. Следовательно, воз-
никает важный для приложений вопрос о нахождении условий, при
которых малое изменение начальных значений г0 и г0 вызывает лишь
малое изменение определяемого ими решения г (/)•
Аналогичный вопрос возникает и в задачах, в которых требуется
выяснить, с какой точностью надо задавать начальные значения г0
и г0, чтобы движущаяся точка с заданной точностью вышла на тре-
буемую траекторию или попала бы в данную область.
14	ВВЕДЕНИЕ
Столь же большое значение имеет вопрос о влиянии на решение
малых слагаемых в правой части уравнения (В.2) — малых, но
постоянно действующих сил.
В некоторых случаях эти малые силы, действующие в течение
большого промежутка времени, способны сильно исказить решение
и ими нельзя пренебречь. В других случаях изменение решения под
действием этих сил незначительно, и если оно не превосходит тре-
буемой точности вычисления, то малыми возмущающими силами
можно пренебречь.
Ниже излагаются методы интегрирования дифференциальных урав-
нений и простейшие способы исследования их решений.
ГЛАВА 1
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
§ 1. Уравнения первого порядка, разрешенные относительно
производной
Обыкновенное дифференциальное уравнение первого порядка
первой степени можно, разрешив относительно производной, пред-
ставить в виде
^- = /(х, у).
Простейший пример такого уравнения
рассматривается в курсе интегрального исчисления. В этом простей-
шем случае решение
y = ff(x)dx + c
содержит произвольную постоянную, которая может быть определена,
если известно значение у (х0) = у0. тогда
X
У = Уо+ / f(x)dx.
*0
В дальнейшем будет доказано, что при некоторых ограничениях,
налагаемых на функцию /(х, у), уравнение
й = У)
также имеет единственное решение, удовлетворяющее условию у(х0) =
= у0, а его общее решение, т. е. множество решений, содержащее
все без исключения решения, зависит от одной произвольной по-
стоянной.
16
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
[ГЛ. I
Дифференциальное уравнение = / (х, у) устанавливает зави-
симость между координатами точки и угловым коэффициентом каса-
dv .	
тельной к графику решения в той же точке. Зная х и у, можно
d,y
вычислить Следовательно, дифференциальное уравнение рассма-
Рис. 1.1.
триваемого вида определяет поле
направлений (рис. 1.1) и задача
интегрирования дифференциального
уравнения заключается в том, чтобы
найти кривые, называемые интег-
ральными кривыми, направление
касательных к которым в каждой
точке совпадает с направлением
поля.
Пример 1.
dy = у
dx х'
В каждой точке, отличной от точки (0, 0). угловой коэффициент касательной
у
к искомой интегральной кривой равен отношению — > г. е. совпадает с уг-
ловым коэффициентом прямой, направленной из начала координат в ту же
точку (х, у). На рис. 1.2 стрелками изображено поле направлений, опреде-
ляемое рассматриваемым уравнением. Очевидно, что^интегральными кривыми
в данном случае будут прямые у = ех, так как направления этих прямых
всюду совпадают с направлением поля
Пример 2.
dy	х
dx ~	у *	.
§ 1] УРАВНЕНИЯ, РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ 17
Замечаем, что угловой коэффициенз касательной к искомым интегральным
х	„	. .	„у
кривым-----и угловой коэффициент касательной — к интегральным кри-
у	х.
вым примера 1 в каждой точке удовлетворяют условию ортогональности:
——— = — 1. Следовательно, поле направлений, определяемое рассматри-
у X
ваемым дифференциальным уравнением, ортогонально полю направлений,
изображенному на рис, 1.2. Очевидно, что интегральными кривыми уравне-
dy х	9 .
ния	= —— являются окружности с центром в начале координат х2 -f-
+ у2 = сг (рис. 1.3) (точнее, полуокружности у = 1^с2—х2 и у — — \^с2—х2).
Примерз.
dx
Для построения поля направлений Найдем геометрическое место точек, в ко-
торых касательные к искомым интегральным кривым сохраняют постоянное
направление. Такие линии называются изоклинами. Уравнение изоклин по-
лучим, считая = А, где k — постоянная; J^x2 + У2 = А или х2 у2 = А2.
Следовательно, в данном случае изоклинами являются окружности с центром
в начале координат, причем угловой коэффициент касательной к искомым
Рис. 1.4.
интегральным кривым равен радиусу этих окружностей. Для построения поля
направлений дадим постоянной А некоторые определенные значения (см.
рис. 1.4 слева). Теперь можно уже приближенно провести искомые инте-
гральные кривые (см. рис. 1.4 справа).
Пример 4.
У' = 1 4- ху.
Изоклинами являются гиперболы A = xy-f-l или xy = k—1, причем при
А = 1 гипербола распадается на пару прямых х = 0 и у=0 (рис. 1.5). При
А = 0 получаем изоклину 1 -|- ху = 0; эта гипербола разбивает плоскость на
части, в каждой из которых у' сохраняет постоянный знак (рис. 1.6). Инте-
гральные кривые у — у (х), пересекая гиперболу 1 -)- ху = 0, переходят из
области возрастания функции у (х) в области ее убывание или, наоборот,
18
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
из области убывания в область возрастания, и следовательно, на ветвях
этой гиперболы расположены точки максимума и минимума интегральных
кривых.
Определим теперь знаки второй производной в различных областях
плоскости:
у* = ху'4-у или у" = х(1-f-xy)4-У =-*4" (*2 4" 1)У-
Кривая х 4- (х2 4- 1) У — 0 или
У—(ID
(рис. 1.7) разбивает плоскость на две части, в одной из которых у" < 0, и
следовательно, интегральные кривые выпуклы вверх, а в другой у* > 0, и
значит, интегральные кривые вогнуты вверх.
При переходе через кривую (1.1) интег-
ральные кривые переходят от выпуклости
к вогнутости, и следовательно, на этой
кривой расположены точки перегиба инте-
гральных кривых.
В результате проведенного исследо-
вания известны области возрастания и
Рис. 1.8.
Рис. 1.7.
убывания интегральных кривых, известно расположение точек максимума
и минимума, известны области выпуклости и вогнутости и расположение
точек перегиба, известна изоклина t»l. Этих сведений вполне достаточно
для того, чтобы сделать набросок расположения интегральных кривых
§ 21	УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ	19
(рис. 1.8). но можно было бы вычертить еще несколько изоклин, что позво-
лило бы уточнить расположение интегральных кривых.
Во многих задачах, в частности почти во всех задачах геометри-
ческого характера, переменные хну совершенно, равноправны.
Поэтому в таких задачах, если они сводятся к решению дифферен-
циального уравнения
-g- = /(x. У).	(1.2)
естественно наряду с уравнением (1.2) рассматривать также уравнение
dx —	1	(1
dy ~ fix. у)
Если оба эти уравнения имеют смысл, то они эквивалентны, так
как если функция у = у(х) является решением уравнения (1.2), то
обратная функция х = х(у) является решением уравнения (1.3), и
следовательно, уравнения (1.2) и (1.3) имеют общие интегральные
кривые.
Если же в некоторых точках одно из уравнений (1.2) или (1.3)
теряет смысл, то в таких точках естественно его заменять другим
из этих уравнений.
rfy у
Например, уравнение = у теряет смысл при х = 0. Заменив
dx х
его уравнением — ,
правая часть которого уже не
смысла при х = 0, находим в дополнение к ранее найденным
ниям у — сх (см. стр. 16) еще одну интегральную кривую
теряет
реше-
х = 0
этого уравнения.
§ 2. Уравнения с разделяющимися переменными
Дифференциальные уравнения вида
f2(.y)dy = fi(x)dx	(1.4)
называются уравнениями с разделенными переменными. Функции
(х) и /2(у) будем считать непрерывными.
Предположим, что у (х) является решением этого уравнения,
тогда при подстановке у (х) в уравнение (1.4) получим тождество,
интегрируя которое, будем иметь:
ff2(y)dy = ffl(x)dx-hc.	(1.5)
где с — произвольная постоянная.
Мы получили конечное уравнение (1.5), которому удовлетворяют
все решения уравнения (1.4), причем каждое решение уравнения (1.5)
20	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
является решением уравнения (1.4), так как если некоторая функ-
ция у(х) при подстановке обращает уравнение (1.5) в тождество,
то, дифференцируя это тождество, обнаружим, что у(х) удовлетво-
ряет и уравнению (1.4).
Конечное уравнение Ф(х, у) = 0, которое определяет реше-
ние у(х) дифференциального уравнения как неявную функцию х,
называется интегралом рассматриваемого дифференциального урав-
нения.
Если это конечное уравнение определяет все без исключения
решения данного дифференциального уравнения, то оно называется
общим интегралом рассматриваемого дифференциального уравне-
ния. Следовательно, уравнение (1.5) является общим интегралом
уравнения (1.4). Для того чтобы уравнение (1.5) определяло у как
неявную функцию X. достаточно потребовать, чтобы /2(у)4 0.
Вполне возможно, что в некоторых задачах неопределенные
интегралы J* fx (х) dx ii j" f2 (у) dy нельзя будет выразить в элемен-
тарных функциях, тем не менее мы и в этом случае будем считать
задачу интегрирования дифференциального уравнения (1.4) выполнен-
ной в том смысле, что мы свели ее к более простой и уже изу-
ченной в курсе интегрального исчисления задаче вычисления неопре-
деленных интегралов — квадратур *).
Если надо выделить частное решение, удовлетворяющее условию
у(х0) —у0, то оно, очевидно, определится из уравнения
У	х	'
J /2(У)^у= J/i(x)dx,
у->	л
которое получим из
у	х
f h (J)dy = У /1 (х) dx 4- С,
Уз
воспользовавшись начальным условием у(х0) — у0.
Пример!.
х dx 4 у dy = 0.
Переменные разделены, так как коэффициент при dx является функцией
только х. а коэффициент при dy является функцией только у. Интегрируя,
получим
У х dx 4 У у dy — c или х2 4 У2 = С1
*) Так как термин «интеграл» в теории дифференциальных уравнений
часто применяется в смысле интеграла дифференциального уравнения, то во
избежание недоразумений для интегралов функций у / (х) dx обычно при-
меняется термин «квадратура».
§ 2]	УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ	21
— семейство окружностей с центром в начале координат (сравните с при-
мером 2, стр. 16—17).
Пример 2.
Интегрируя, получаем
Интегралы J* ex'dx и f не берутся в элементарных функциях, тем не
менее исходное уравнение считается проинтегрированным, так как задача
доведена до квадратур.
Уравнения вида
Ф1 (*) Фт (У) dx — ф2 (х) ф2 (у) rfy,
в которых коэффициенты при дифференциалах распадаются на мно-
жители, зависящие только от х и только от у, называются диффе-
ренциальными уравнениями с разделяющимися переменными, так
как путем деления на ф1 (у) ф2 (х) они приводятся к уравнению
с разделенными переменными:
'	dx== Му)
Ч>2 (*) ах ф, (у) ау- '
Заметим, что деление на ф] (у) ф2 (х) может привести к потере
частных решений, обращающих в нуль произведение ф! (у) • ф2 (х),
а если функции ф2 (у) и ф2(х) могут быть разрывными, то возможно
появление лишних решений, обращающих в нуль множитель
1
Ф1 (У) ЯРа (*) ’
Пример 3.
~ = — (сравните с примером 1, стр. 16).
Разделяем переменные и интегрируем:
dy __ dx /* dy _____ Г dx
J ~у~~ J ~х"'
In I у I = 1п| X |-|-In с, с > 0.
Потенцируя, получим | у | = с | х |. Если речь идет только о гладких реше-
ниях, то уравнение | у j = с | х I, где с > 0, эквивалентно уравнению у = ± сх
или у = ctx, где Cj может принимать как положительные, так и отрица-
тельные значения, но cj 0. Если же принять во внимание, что при деле-
нии на у мы потеряли решение у = 0, то можно считать, что в решении
у = С]Х постоянная ct принимает и значение С] = 0, при котором мы полу-
чаем потерянное ранее решение у = 0.
Замечание. Если в примере 3 считать переменные х и у равноправ-
dy у	.
ными, то уравнение	, теряющее смысл при х = 0, надо дополнить
22
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
[ГЛ. I
(1х X .	1Пч
уравнением = — (см. стр. 19), 'которое, очевидно, имеет еще
“У у
х — 0, не содержащееся в найденном выше решении у = ctx.
Пример 4.
х (1 + У2) dx — У (1 + х2) dy = 0.
решение
Разделяем переменные и интегрируем:
у dy _ х dx Г у dy Г х dx (
1 + У2 ” !+х2 : J 1 + У2 “	1 + х2 + С:
In (1 + у2) = In (1 4- X2) + In с,; 1 + у2 = Cl (1 + х2).
Пример 5.
£ = 4^
Найти решение х (t), удовлетворяющее условию х(1) = 1.
Разделяем переменные и интегрируем:
х	t
I = Г 2/ dt, Vx = t2, x = t*.
J 2/x J
Пример 6. Как уже упоминалось во введении, установлено, что ско-
рость радиоактивного распада пропорциональна количеству х еще не рас-
павшегося вещества. Найти зависимость х от времени t, если в начальный
момент при t = i0 будет х = ха.
Коэффициент пропорциональности k, называемый постоянной распада,
предполагается известным. Дифференциальное уравнение процесса будет
иметь вид
/7 у
=	d-б)
(знак — указывает на уменьшение х при возрастании t, k > 0). Разделяя
переменные и интегрируя, получаем
d X
— — kdt\ In | X I — In I x01 = k (t — tQ),
откуда
x = xoe_ft(/_/o).
Определим еще период полураспада т (т. е. время, в течение которого
распадается Хо). Полагая t — /0 = т, получим х0 = хае~кх, отсюда
1 п 2
Не только радиоактивный распад, но и любая другая мономолекуЛярная
реакция на основании закона действующих масс описывается уравне-
dx ,
нием = — кх, где х — количество еще не прореагировавшего вещества.
Уравнение
4rr = kx, k>0,	'	(1.7)
§ 2]	УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ	23
отличающееся лишь знаком правой части от уравнения (1.6), описывает мно-
гие процессы «размножения», например «размножение» числа нейтронов
в цепных ядерных реакциях или размножение числа бактерий в предположе-
нии, что условия среды для них предельно благоприятны и поэтому скорость
их размножения пропорциональна наличному числу бактерий.
Решение уравнения (1.7), удовлетворяющее условию х (t0) = х0, имеет
вид x =	и, в отличие от решений уравнения (1.6), x(t) не убывает,
а возрастает по показательному закону с возрастанием t.
Пример 7.
А_Р(р_2)(р_4).
Начертить интегральные кривые, не интегрируя уравнения; р и ф— полярные
координаты.
Уравнение имеет очевидные решения р = О, р = 2 и р = 4. При 0 < р < 2
> 0; при 2 < р < 4	< 0 и при р > 4	> 0.
аф	аф	аф
Следовательно, интегральными кривыми являются окружности р = 2
и' р = 4 и спирали, наматывающиеся при возрастании ф на окружность р = 2
и разматывающиеся с возрастанием ф с окружности р = 4. Замкнутые инте-
гральные кривые, в достаточно малых окрестностях которых интегральными
кривыми являются спирали, называются предельными циклами. В данном
примере окружности р = 2 и -р = 4 являются предельными циклами.
Пример 8. Найти ортогональные траектории семейства парабол у = ах2.
Ортогональными траекториями заданного семейства кривых назы-
ваются линии, пересекающие под прямым углом линии данного семейства.
Угловые коэффициенты у[ и у'2 касательных к кривым данного семейства
и к искомым ортогональным траекториям должны в каждой точке удовле-
творять условию ортогональности у2 ---Для семейства парабол у =
У1
у	2у
= ах2 находим у' = 2ах, или так как а = то у' = —Следовательно,
х2	х
дифференциальное уравнение искомых ортогональных траекторий имеет
вид/ = -^.
Разделяя переменные, находим 2у dy -f- х dx = 0 и, интегрируя, получим
семейство эллипсов
(рис. 1.9).
Пример 9. Пусть и = ху — потенциал скоростей плоскопараллельного
течения жидкости. Найти уравнение линий тока.
Линии тока являются ортогональными траекториями семейства эквипо-
тенциальных линий ху == с. Находим угловой коэффициент касательной
у
к эквипотенциальным линиям: ху + у = 0, у =* —Следовательно, диф-
ференциальное уравнение линий тока имеет вид у’ = -у или ydy = xdx;
интегрируя, получаем л2 — у2 = с — семейство гипербол.
Пример 10. Полый однородный металлический шар, имеющий
внутренний раДиУс П» а внешний г2 находится в стационарном тепловом
24:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
(ГЛ. I
состоянии, причем температура на его внутренней поверхности равна Гц
а на наружной Г2. Найти температуру Г на расстоянии г от центра
шара, г1 < г < г2.
Из соображений симметрии следует, что Т является функцией только г.
Так как Между двумя концентрическими сферами с центрами в центре
шара (их радиусы могут изменяться от п до г2) количество тепла остается
Рис. 1.9.
неизменным, то через каждую сферу
протекает одно и то же количество
тепла Q. Следовательно, дифференци-
альное уравнение, описывающее рас-
сматриваемый процесс, имеет вид
— 4лАг2 — = Q,
dr
где k — коэффициент теплопроводности.
Разделяя переменные и интегрируя.
получим искомую зависимость Т от г:
. ,	Q dr
4nk dT = — ^2- ;
т	г
4яй j dT = -Q
Tt	ft
4лНТ’-Г1) =
Для определения Q используем условие: при г = г2. Г = Г2
4л*(Г2-Г,) ^(Тг-Т^пг,
1	1	“ П — г} 
§ 3. Уравнения, приводящиеся к уравнениям
с разделяющимися переменными
Многие дифференциальные уравнения путем замены, переменных
могут быть приведены к уравнениям с разделяющимися переменными.
К числу таких уравнений относятся, например, уравнения вида
где а и b— постоянные величины, которые заменой переменных
z = ax-}-by преобразуются в уравнения с разделяющими перемен-
ными. Действительно, переходя к новым переменным х и z, будем иметь
dz	,	dy	dz	„ .	....
: Д' -4- Ь ~т~~ , • —:— = О -f- Ь f
dp	1	dx	dx ।	\ /
s 3] УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
25
ИЛИ
. а+6/(л)
и переменные разделились. Интегрируя, получим
Г dz
х — I —. . ,, , 4- с.
J a + bf(z) '
Пример!.
Полагая г = 2х 4- у, будем иметь
dy -— — 9 dz о -
dx ~ dx ’ dx
Разделяя переменные и интегрируя, получим
=dx, 1п|г-|-2| = х4-1пс, z = — 2 + се*,
* “Г *
2х + у== — 2-^-се*. у = се*—2х—2.
П р и м е р 2.
Полагая х — у = г, получим
dy__,	dz	dz	1 ,
dx	dx'	dx	z ‘
dz 1
•^== ——, zdz = — dx z1 = — 2x + c. (x — y)2 = — 2x+ c.
К уравнениям с разделяющимися переменными приводятся и так
называемые однородные дифференциальные уравнения первого
пярядка. имеющие вид
dx ' \х)
у
Действительно, после подстановки z — или у — xz получим
dy dz ,	dz ,	. . . dz dx
— x -----h z, x -j— V z — f (z), ~rr\---= —»
dx dx 1	dx ' J ’ f(z) — г x ’
----= Inlx|4-lnc. x —
/(z) —z 1,1
Заметим, что правая часть однородного уравнения является
однородной функцией переменных х и у нулевой степени однород-
ности, поэтому уравнение вида
М (х, y}dx -\-N (x, y)dy = 0
26
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
будет однородным, если М (х, у) и N (х, у) являются однородными
функциями х и у одинаковой степени однородности, так как в этом
случае
dy___ М (х, у) _ /у \
dx N (х, у) J \ х)'
Примерз.
==Z + tgJL.
dx х 1 6 х
Полагая y — xz, = х z и подставляя в исходное уравнение по-
лучим
dz .	. . cos z dz ал
—----г г — г tg z, --------:-----= —
dx 1 г 6	sin г	х
In | sin г| = In| x|-)-lnc, sin z — ex, sin ~- = cx-
Пример 4.
(x + у) dx — (у — x) dy = 0.
Полагая у = xz, dy — x dz -j- z dx, получим
(x 4- xz) dx — (xz — x) (x dz 4* z dx) — 0,
(1 + 2z— z2)dx-j-x(l—z)dz = 0,
lln|14-2x-xM + ln|xl=	x
= -jlnc, x2(l-j-2z — z2) = c, x2 2xy — y2 = c.
Уравнения вида
dy_ _ f / Д1Х-Ь&|у + С1\
dx ~1 \a2x 4- b2y 4- c2 )	u
преобразуются в однородные уравнения путем переноса начала коор-
динат в точку пересечения (хр У1) прямых
OjX 4- Ьгу 4- = 0 и а2х 4- Ь?У + с2 = 0.
Действительно, свободный член в уравнениях этих прямых в но-
вых координатах Х = х — хр Y = y—уг будет равен нулю, коэф-
.	dy dY
фициенты при текущих координатах остаются неизменными, a
йх лл
и уравнение (1.8) преобразуется к виду
dY _ f +
dX ~~J
или
dY _ ,
dX~d
Д1 +	\
----------p- =Ф
Д2 + Ьг	j
и является уже однородным уравнением.
§ <1
ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
27
Этот метод нельзя применить лишь в случае параллельности
прямых агх t^y Cj = 0 и а2х-у Ь2ус2 — 0. Но в этом
коэффициенты при текущих координатах пропорциональны
—	= k, и уравнение (1.8) может быть записано в виде
случае
dy
dx
/ aix 4~ М 4~ ci \
\ k (аух 4- 61У) 4" С1 /
F (а,х 4- Ьгу),
и следовательно, как указано на стр. 24, замена переменных z =
= агх 4- Ь\У преобразует рассматриваемое уравнение в уравнение
с разделяющимися переменными.
Пример 5.
^У _ *-~у4-1
dx х у— 3 ’
Решая систему уравнений х — у 4-1=0, х-|-у— 3 = 0, получим х, = 1,
у, = 2. Полагая х — X 4- 1, у == Y-j-2, будем иметь
dY _ X — Y
dX ~ X+Y'
у
Замена переменных г = или Y — гХ приводит к уравнению с разделяющи-
мися переменными
. у dz _ 1—z (l-j-z)dz dX
~dX~T^7' 1—2г —г2 ~~Х~'
— 1|п|1—2г —г2| = 1п|Х| —ylnc,
(1—2г —г2)Л'2 = с, X2 — 2XY — Г2 = с,
х2 — 2ху — у2 4- 2х 4- 6У = ei-
§ 4.	Линейные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка
называется уравнение линейное относительно неизвестной функции
и ее производной. Линейное уравнение имеет вид
77 + Р(*) У = /(*),	(1.9)
где р(х) и f (х) в дальнейшем будем считать непрерывными функ-
циями х в той области, в которой требуется проинтегрировать
уравнение (1.9).
Если /(х) = 0, то уравнение (1.9) называется линейным однород-
ным. В линейном однородном уравнении переменные разделяются:
•^ + рМУ = 0. откуда ~ = ~ p{x)dx,
28	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
и, интегрируя, получаем
1п|у| =—J* р (х) dx In Ср ct > 0,	,
у^сеЧ^, с=#0,	(1.10)
При делений на у мы потеряли решение у = 0, однако оно может
быть включено в найденное семейство решений (1.10), если считать
что с может принимать и значение 0.
Для интегрирования неоднородного линейного уравнения
^-+р(х)у = /(х)	(1.9)
может быть применен так называемый метод вариации постоянной.
При применении этого метода сначала интегрируется соответствующее
(т. е. имеющее ту же левую часть) однородное уравнение
^ + />(х)у = 0,
общее решение которого, как указано выше, имеет вид
- [ р (х) dx
у = се J
«-г	.	- Г Р (х) dx
При постоянном с функция се J является решением однород-
ного уравнения. Попробуем теперь удовлетворить неоднородному
уравнению, считая с функцией х, т. е. по существу совершая замену
переменных
- f Р (X) dx
у — с (х) е J ,
где с (х) — новая неизвестная функция х.
Вычисляя производную
dy de -fp(x)dx	-fp(x)dx
dV=d^e j -c(x)p(x)e
и подставляя в исходное неоднородное уравнение (1.9), получим
de -J p(x)dx	-С p(x)dx	-f p(x}dx	•
— C(x)p(x)e +p(x)c(x)c	=/(x)
или
откуда, интегрируя, находим
С(х) = J/(x) Л rfx-l-Cp
§ 4]
ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
а следовательно,
, ч -(.p(x)dx -f р (х) dx -tpwdx’r	f p(x)dx
y = c(x)e =v1e  +e	\ fix) e dx.
(1.11)
Итак, общее решение неоднородного линейного уравнения равно
сумме общего решения соответствующего однородного уравнения
-С p(x)dx
и частного решения неоднородного уравнения
-f р (х) dx ' Г Р (х) dx
е . J f(x)eJ dx,
получающегося из (1.11) при с1==0.
Заметим, что в конкретных примерах нецелесообразно пользо-
ваться громоздкой и трудно запоминаемой формулой (1.11), значи-
тельно легче каждый раз повторять все приведенные выше вычи-
сления.
Пример 1.
dx х
Интегрируем соответствующее однородное уравнение
dy у п	dy	dx , , ,	। , , , ,
х0,	у |п । у 1 = 1П1х 1 + 1п с’ У = сх-
Считаем с функцией х, тогда у = с (х) х,	х-\- с (х) и, подставляя
(1л UX
в исходное уравнение, после упрощения получаем
de	X*
—— х = х2 или de = х dx, с (х) = -я- 4- с,.
dx	' '	2
Следовательно, общее решение
X3
y = c,x + -g-.
П р и м е р 2.
</у
— у etg х = 2х sin х.
Интегрируем соответствующее однородное уравнение
rfy . n dy cos х .	.
-f-— у etg х = 0, —— = —-------dx,
dx J b	у sin x
In | у | = In] sinx|-f-Inc. y = csinx.
Варьируем постоянную
у = с (х) sin х, у' = с' (х) sin х с (х) cos х.
30	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. t
Подставляя в исходное уравнение, получим
с' (х) sin х -|- с (х) cos х — с (х) cos х = 2л sin х,
с' (х) = 2х, с (л) = х2 -|- cit
у = х2 sin х с1 sin х.
Пример 3. В электрической цепи с самоиндукцией происходит процесс
установления переменного тока. Напряжение U является заданной функцией
времени U =U (t), сопротивление R и самоиндукция L постоянны, начальная
сила тока / (0) = /0 задана. Найти зависимость силы тока I = I (/) от времени.
Пользуясь законом Ома для цепи с самоиндукцией, получим
U-L^-=R1. .
at
Решение этого линейного уравнения, удовлетворяющее начальному условию
/(О) = /о, согласно (1.11) имеет вид
При постоянном напряжении U <=• получим
Я ,
Интересен случай синусоидального переменного напряжения U — A sin cot
При этом согласно (1.12) получим
Стоящий в правой части интеграл легко вычисляется.
Многие дифференциальные уравнения путем замены переменных
могут быть сведены к линейным. Например, уравнение Бернулли,
имеющее вид
+	=	п*1,
или
у-п-т£+р<^~п=М’	а-13)
заменой переменных y1-” = z сводится к линейному уравнению. Дей-
1	dy dz
ствительнс, дифференцируя yL~n=z, находим (1—п) у~"
и, подставляя в (1.13), получим линейное уравнение
§ 4|
ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
31
П р и м е р 4.
dy _ У . х2
dx 2х "Г 2у ’
2у
dx
4 х2, у2 = г,
я dy dz
9у__— -х___
dx dx
dy '
£
х
dz __z
dx ~~ x
и далее, как в примере 1 стр. 29.
Уравнение
+ Р (х) у Ч- q (х) у2 = / (х).
называемое уравнением Риккати, в общем виде не интегрируется
в квадратурах, но может быть заменой переменных преобразовано
в уравнение Бернулли, если известно одно частное решение У](х)
этого уравнения. Действительно, полагая y = y14-z, получим
У!4- z' + р(х)(у1Ч-г)-4-9(х)(у1 Ч-2!)2 = /(х)
или. так как у' -f- р(х) у, q (х) у] = f (х), будем иметь уравнение
Бернулли
Пример
z' 4- IP (х) + 2q (х) уiJ z 4- q (x) z2 = 0.
В этом примере нетрудно подобрать частное решение yt = —. Полагая
, 1	,	,	1	,	1	/ . I V 2
у = г + —, получим у' = г' ——j-,	д- —-_= г-|-_ — — или
Л	Л»	Л	\	Л I
z
z' =• z‘ -f- 2 — — уравнение Бернулли.
z' _ 2	_ 1	du	z'
г2 ~x7 + 1’ U~ ~z‘ dx=	z2 '
-	du 2u , du 2dx
—-  ----------1, -------------
dx x	и x
1п|и| = — 21n |x|4-lnc, “ = u = _~r^’
c'(x)	.	. . x3
—i, c(x) = _t + C1
 „ С1 X 1 С] X	1 Cl x
u ~ x2 3 ’ г ~ x2 3 ’	1 “ x2 3 ’
' y~7
1 ,	3x2
У = X ”1" C2 — Xs ’
32
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
(ГЛ. I
§ 5, Уравнения в полных дифференциалах
Может случиться, что левая часть дифференциального уравнения
М(х, y)dx-\-N(x, y)dy = 0	(1-14)
является полным дифференциалом некоторой функции и(х, у)'.
du (х, у) == М (х, y}dx 4- М (х, у) dy
и, следовательно, уравнение (1.14) принимает вид
du(x, у) = 0.
Если функция у(х) является решением уравнения (1.14), то
du(x, у(х)) = 0,
и, следовательно,
и(х, у(х)).= с,	(1.15)
где с — постоянная, и наоборот, если некоторая функция у (х) обра-
щает в тождество конечное уравнение (1.15), то, дифференцируя
полученное тождество, получим du(x, у(х)) = 0, и следовательно,
и (х, у) = с, где с произвольная постоянная, является общим инте-
гралом исходного уравнения.
Если даны начальные значения у (х0) = у0, то постоянная с опре-
деляется из (1.15) с = д(х0, у0) и
и(х, у) = «(х0, у0)	(1.150
является искомым
частным интегралом.
Если >7,— == N (х, у) ¥= 0
в точке (х0. Уд), то уравнение (1.150 определяет у как . неявную
функцию х.
Для того чтобы левая часть уравнения (1.14)
М (х, y)dx 4- Л/(х, y)dy
являлась полным дифференциалом некоторой функции а(х, у), как
известно, необходимо и достаточно, чтобы
д-М(х, у) _ dN(x, у)	.
ду	дх '	k '
Если это условие, впервые указанное Эйлером, выполнено, то
уравнение (1.14) легко интегрируется. Действительно,
du — М dx 4- N dy.
С другой стороны,
. Он ,	. Ои .
du = -^dx-\---dy.
§ 51	УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ	33
Следовательно,
ди и, , ди . т, ч
— =М(х, у);	^- = N(x, у),
откуда
и(х,у) — J М(х, y)dx + c(y).
При вычислении интеграла J* М(х, y)dx величина у рассматривается
как постоянная, поэтому с (у) является произвольной функцией у.
Для определения функции с (у) дифференцируем найденную функцию
//(х, у) по у и, так как — = Д/(х, у), получим
М(х- у)+ с'(У) = N(.K. у).
Из этого уравнения определяем с' (у) и, интегрируя, находим с (у).
Как известно из курса математического анализа, еще проще
можно определить функцию и (х, у) по ее полному дифференциалу
du — М (х, у) dx + А/(х, y)dy, взяв криволинейный интеграл от
/И (х, y)dx-\-N(x, y)dy между некоторой фиксированной точкой
(х0, Уо) и точкой с переменными координатами (х, у) по любому
пути:
(х, у)
и(х, у) = J М(х, y)dx4-W(x, y)dy.
Мз, уо
Чаще всего в качестве пути интегрирования удобно брать ломаную,
составленную из двух звеньев, параллельных осям координат (рис. 1.10);
в этом случае
(X, у)	IX, у0)	(х, у)
J* М dx -j- N dy = у Afdx-j- f N dy
(x„, у,'	(Х..У-,)	lx, y0) _
ду
ди	, , ,
— = х4у41,
дх	1/1
ди , ,, .
с' (у) = —у243,
34	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
ИЛИ
<Х, У\	у)	,л, у)
J М dx 4 N dy = J* N dy 4 J Mdx.
(Xo, Уо)	(x„ y,)	(X„ У)
Пример 1.
(х4у41)<**4(х — №4-3) dy = 0.
Левая часть уравнения является полным дифференциалом некоторой функ-
ции и (х, у), так как
<4*4У41)  d(x-ya43)
дх '
12 =-у 4 ХУ 4-* 4 с (У).
х + ? (У) = х — у2 4- 3,
V3
с (у) = — -у 4- Зу 4 clt
х2-	уЗ
« = — + *У4-*—-у43у 4-С1-
Следовательно, общий интеграл имеет вид
Зх2 4-бху 4-6х — 2у34- 18у = с2.	(1.17)
Можно применить и другой метод определения функции «(х, у):
(х, у)
и(х, у) = J (х4у4 l)dx4-(x — y243)dy.
(х„ Уо)
За начальную точку (х0, у0) выбираем, например, начало координат, в ка-
честве пути интегрирования — изображенную на рис. 1.11 ломаную. Тогда
(х, 0)	(х, у)
«(х,у) = f (x4-l)dx4- J* (х — y24-3)dy =^-4-x4xy — -уН-Зу-
(0,0)	(x, 0)
и общий интеграл имеет вид
-у 4- х 4- ху —	4 Зу == с
или как в (1. 17).
В некоторых случаях, когда левая часть уравнения
М(х, y)dx 4- (V (х, y)dy = O	(1-14)
не является полным дифференциалом, легко удается подобрать функ-
цию ц(х, у), после умножения на которую левая часть уравнения (1.14)
превращается в полный дифференциал
du — цЛ1 dx 4 |дА/ dy.
§ 51
УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ
35
Такая функция р называется интегрирующим множителем. За-
метим, что умножение на интегрирующий множитель ц(х, у) может
привести к появлению лишних частных решений, обращающих этот
множитель в
Пример
нуль.
2.
х dx -|- у dy -f- (х2	у2) х2 dx = 0.
1
------------------- —	----------- _ левая часть Пре_.
после умножения на множитель ц
Очевидно, что
вращается в полный дифференциал. Действительно, после умножения на
Н = Х2 получим
xdx-\-ydy , , .	_
----, 	„	4- х2 dx = О
v2 _J_	1
1	Xs
или, интегрируя, -~-1п(л2-|-У2) +-q-= 1° Умножая на 2 и потенцируя,
2	о
будем иметь
lx»
(x2-|-y2)c3 = C?
Конечно, далеко не всегда интегрирующий множитель подби-
рается столь легко. В общем случае для нахождения интегрирующего
множителя
не равное тождественно нулю
шение уравнения в частных
ных
надо подобрать хотя бы одно
частное ре-
производ-
РрА1 _ d\iN
ду дх
или в развернутом виде
ду ' ду дх '
dN
дх ”
которое после деления на р и переноса
некоторых членов в другую часть равенства
d 1пц	_ сИпи. ______ ON  
ду	дх	дх
приводится к
дМ
ду •
виду
(1.18)
В общем случае интегрирование этого уравнения в частных про-
изводных является задачей отнюдь не более простой, чем интегри-
рование исходного уравнения, однако в некоторых случаях подбор
частного решения уравнения (1.18) не представляет затруднений.
Кроме того, считая, что интегрирующий множитель является функ-
цией только одного аргумента (например, является функцией только
х + у или только х2-|-у2, или функцией только х, или только у
и т. д.), можно уже без труда проинтегрировать уравнение (1.18) и
36	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. !
указазъ условия, при которых интегрирующий множитель рассматри-
ваемого вида существует. Тем самым выделяются классы уравнений,
для которых интегрирующий множитель легко может быть найден.
Например, найдем условия, при которых уравнение Мdx-f-N dy—Q
имеет интегрирующий множитель, зависящий только от х, р — р (х).
При этом уравнение (1.18) упрощается й приобретает вид
d Inp	dN	дМ.
	— /у —	
dx------------dx	dy '
dM dN
ду дх
откуда, считая —-—----- непрерывной функцией х, получим
дМ dN
In р — J — dx 4" с>
дМ dN
f ду__дх
р = се-' N dx.	(1.19)
Можно считать с — 1, так как достаточно иметь лишь один интег-
рирующий множитель.
дМ dN
Если	является функцией только х, то интегрирующий
множитель, зависящий лишь от х, существует и равен (1.19), в про-
тивном случае интегрирующего множителя вида р(х) не существует.
Условие существования интегрирующего множителя, зависящего
только от х, выполнено например, для линейного уравнения
P<x)y = f(x) или [р(х)у — /(x)ldx + </y = 0.
дМ dN
Действительно, д, — р (х) и, следовательно, р = е-Г ₽	.
Совершенно аналогично могут быть найдены условия существования
интегрирующих множителей вида
р(у), р(х±у), р (х2 ± у2), р(х-у), Н^ит. д.
Пример 3. Имеет ли уравнение
х dx-j-у dyх dy — у dx = 0	(1.20)
интегрирующий множитель вида р = р (х2 -|- у2)?
Обозначим х2 + у2 = г. Уравнение (1.18) при р — р (х2 + у2) = р (г) при-
нимает вид
п,..	.. . d In p dN дМ
2 (Aly — Nx) —-=-1- = -т--,
' }	’ dz дх ду
S 5]
УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ
37
откуда	In 1 н 1 = -g- У ф (г) dz 4- in с
или	4- 1 ф(г)<Гг H = ce2J	,	(1.21)
где	dN дМ . . дх ду ч’(г)_ Му — Nx ’
Для существования интегрирующего множителя заданного вида необходимо
dN дМ
, дх ду
и в предположении непрерывности ф (z) достаточно, чтобы	— Nx—
была функцией только х2 -f- у2. В данном случае
dN дМ
дх ду
 Му —,Nx
Ч
X2 + У2 ’
следовательно, интегрирующий множитель ц = ц (х2 4- у2) существует и ра-
вен (1.21). При с = 1 получим
_1_
г
1
х24-у2 ’
Умножая уравнение (1.20) на и. = s
приведем его к виду
х dx у dy х dy — у dx _
« х2 + у2 1	х24-у2	“U
или
ld(x2+y2)
-------------1_______ =o
Х2 + У2 l + (f
. i d In (x2	y2) d arctg -y = 0.
Интегрируя, получим
In К*2 4-У2 = — arctg4- In c,
и после потенцирования будем иметь
у
________________________________- arctg —
'	ух2 -f- у2 = се х,
38	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. t
или в полярных координатах р=се ф — семейство логарифмических спира-
лей.
Пример 4. Найти форму зеркала, отражающего параллельно данному
направлению все лучи, выходящие из заданной точки.
Поместим начало координат в заданную точку и направим ось абсцисс
параллельно заданному в условиях задачи направлению. Пусть луч падает
на зеркало в точке М(х, у). Рассмотрим изображенное на рис. 1.12 сечение
зеркала плоскостью Оху, проходящее через ось абсцисс и точку М. Про-
ведем касательную MN к рассматриваемому
сечению поверхности зеркала в точке М (х, у).
Так как угол падения луча равен углу отра-
жения, то треугольник MNO равнобедрен-
ный. Следовательно,
tg <р = у
Рис. 1.12.
У
Полученное однородное уравнение легко ин-
тегрируется заменой переменных
— = z,
У
но еще проще, освободившись от иррациональности в знаменателе, переписать
его в виде
х dx 4~ у dy = х* 2 4- у2 dx.
Уравнение имеет очевидный интегрирующий множитель
1
Ц = —г  
/х24-у2
х dx 4~ y_dy_ __ d + у2 = х + с, у2 = 2сх с2
/Х2_|_у2	Г	“Г /	-Г
(семейство парабол).
Заме ч а н и е. Эта задача еще проще решается в координатах х и р,
где р — Yх2 -ф- у2, при этом уравнение сечения искомых поверхностей при-
обретает вид
dx = dp, р = х 4- с.
Можно доказать существование интегрирующего множителя, или,
что то же самое, существование ненулевого решения уравнения в
частных производных (1.18) (см. стр. 35) в некоторой области, если
функции М и N имеют непрерывные производные и по крайней мере
одна из этих функций не обращается в нуль. Следовательно, метод
интегрирующего множителя можно рассматривать дак общий метод
интегрирования уравнений вида
М(х, y)dx-]-N (х, y)dy = 0,
однако ввиду трудности нахождения интегрирующего множителя этот
метод чаще всего применяется лишь в тех случаях, когда интегри-
рующий множитель .очевиден.
$ 61	ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
39
§ 6. Теоремы существования и единственности решения
уравнения ^=/(х, j)
Класс интегрирующихся в квадратурах дифференциальных ура-
внений весьма узок, поэтому уже со времени Эйлера приближенные
методы в теории дифференциальных уравнений приобрели большое
значение.
В настоящее время в связи с быстрым развитием вычислительной
техники приближенные методы приобретают еще несравненно боль-
шее значение.
Теперь часто целесообразно применять приближенные методы даже
в тех случаях, когда уравнение интегрируется в квадратурах. Более
того, если даже решение может быть несложно выражено в элемен-
тарных функциях, то нередко ис-
пользование таблиц этих функций
оказывается более трудоемким, чем
приближенное интегрирование урав-
нения на быстродействующей маши-
не. Однако, для того чтобы приме-
нять тот или иной метод прибли-
женного интегрирования дифферен-
циального уравнения, надо прежде
всего быть уверенным в существова-
нии искомого решения, а также и в
единственности решения, так как при
отсутствии единственности остается
неясным, какое именно решение тре-
буется приближенно определить.
Чаще всего доказательство теорем
существования решения одно-
временно дает и метод точного или приближенного нахождения ре-
шения, что еще более увеличивает значение теорем существования.
Например, доказываемая ниже теорема 1.1 дает обоснование метода
Эйлера приближенного интегрирования дифференциальных уравнений,
который заключается в том, что искомая интегральная кривая диф-
d у
ференциального уравнения /(х, у), проходящая через точку
(х0, Уо)> заменяется ломаной, состоящей из прямолинейных отрезков
(рис. 1.13), каждое звено которой касается интегральной кривой
в одной из своих граничных точек. При применении этого метода
для приближенного вычисления значения искомого решения у (х)
в точке х=-Ь, отрезок ха-^х ^.Ь (если b > х0) делится на п рав-
ных частей точками х0, хР х2. .... хп_х, х„, где хп=Ь. Длина
каждой части xZ)1 — xt — h называется шагом вычисления. Прибли-
женные значения искомого решения в точках хх обозначаем yt.
40	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. I
Для вычисления у, заменяем на отрезке х0 х х} искомую
интегральную кривую отрезком ее касательной в точке (х0, у0).
Следовательно, у1 = у0Н-йуд, где у0==/(х0, у0) (см. рис. 1.13).
Аналогично вычисляем:
У2 = Уj Н- Щ где У1=/ (хг У1)<
У3=У2+АУ2’ Гле у2 = /(х2, у2);
Уп = Уп-1 + ЬУп-1> где У«-1 = /(*я-г ?„-()•
Если b < х0, то схема вычислений остается прежней, но шаг h
отрицателен.
Естественно ожидать, что при й—>0 ломаные Эйлера прибли-
жаются к графику искомой интегральной кривой, и следовательно,
с уменьшением шага й метод Эйлера дает все более и более точное
значение искомого решения в точке Ь. Доказательство этого утвер-
ждения одновременно приведет нас к следующей фундаментальной тео-
dv .,
реме о существовании и единственности решения уравнения = f(x, у)
с начальным условием у(х0) = у0 при весьма общих достаточных
условиях, наложенных на функцию f(x, у).
Теорема 1.1 {о существовании и единственности решения).
Если в уравнении
•g-=/(x. у)	О-22)
функция f(x, у) непрерывна в прямоугольнике D:
х0 — а < х < х0 +а, у0 — ь <У <Уо+А
и удовлетворяет в D условию Липшица'.
1/(*. У1) —/(*. у2)1<М|У1—У21.
где N — постоянная, то существует единственное решение
у = у(х),х0 — Их ^ха-(-Н, уравнения (1.22), удовлетворяю-
щее условию у(х0) = у0, где
Н < min (а, Лт, -тЛ.
\ М N j
7И = тах/(х, у) в D.
Условия теоремы нуждаются в некоторых пояснениях. Нельзя
утверждать, что искомое решение у = у(х) уравнения (1,22), удо-
влетворяющее условию у (х0) = у0. будет существовать при х0 — а
^х^х^а, так как интегральная кривая у = у(х) может выйти
s ei ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ	41
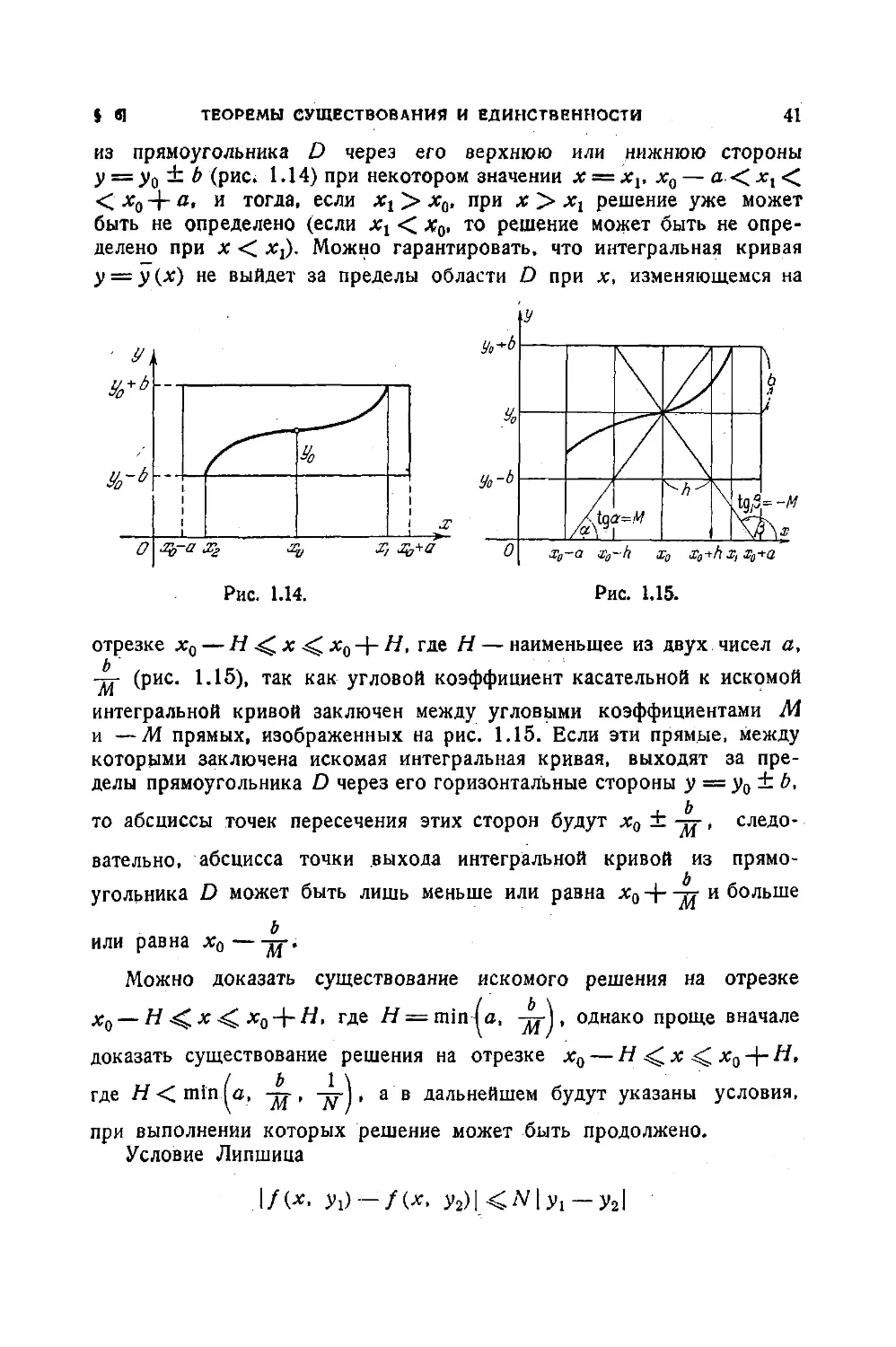
из прямоугольника D через его верхнюю или нижнюю стороны
у = у0 ± b (рис. 1.14) при некотором значении х = х0 — а <	<
< х0 4- л. и тогда, если хг > хй, при х > хг решение уже может
быть не определено (если хг < х0, то решение может быть не опре-
делено при х < Х0. Можно гарантировать, что интегральная кривая
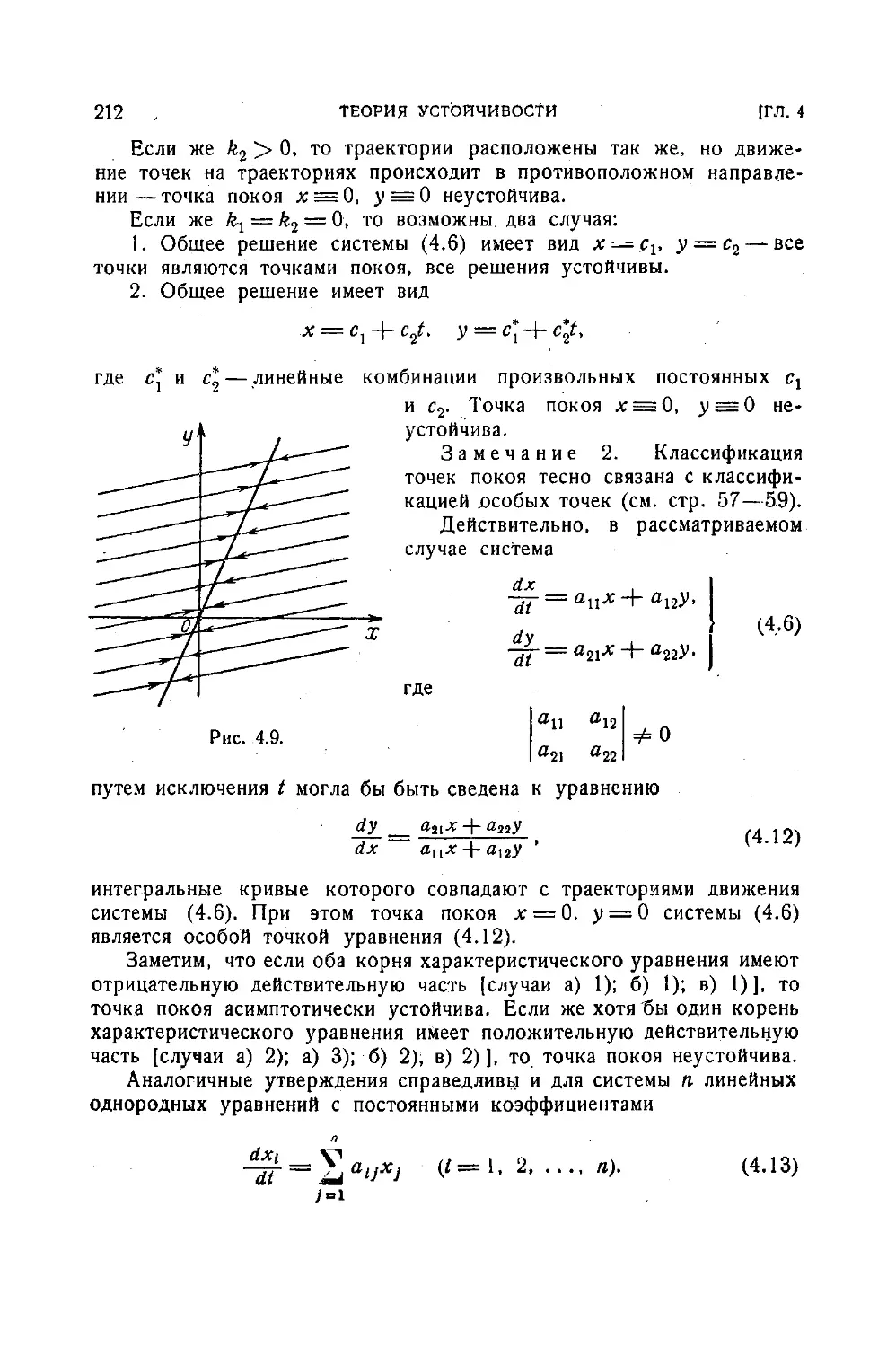
у = у(х) не выйдет за пределы области D при х, изменяющемся на
отрезке х0— Н х х0-|- Н, где Н— наименьшее из двух чисел а,
~ (рис. 1.15), так как угловой коэффициент касательной к искомой
интегральной кривой заключен между угловыми коэффициентами М
и —М прямых, изображенных на рис. 1.15. Если эти прямые, между
которыми заключена искомая интегральная кривая, выходят за пре-
делы прямоугольника D через его горизонтальные стороны у = у0 ± Ь,
то абсциссы точек пересечения этих сторон будут х0 ±	, следо-
вательно, абсцисса точки выхода интегральной кривой из прямо-
угольника D может быть лишь меньше или равна	и больше
Ъ
или равна xQ—
Можно доказать существование искомого решения на отрезке
х0 — Н ^.х	хй-\-Н, тлх /7 —min^a, однако проще вначале
доказать существование решения на отрезке х0 — И х х0-\-Н,
где Я < min (а,	, а в дальнейшем будут указаны условия,
при выполнении которых решение может быть продолжено.
Условие Липшица
1/(*. У1)~/(х. у2)| <N|yj — у21
42	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. !
может быть заменено несколько более грубым, но зато обычно легко
проверяемым условием существования ограниченной по модулю част-
ной производной /у (х, у) в области D.
Действительно, если в прямоугольнике D
(х. у)|<АЛ
то, пользуясь теоремой о конечном приращении, получим
|/(*. yj-f(x, У2)| =&)|у1 —5>2[.
где £ — промежуточное между У! и у2 значение. Следовательно,
точка (х, £) лежит в D, поэтому
|/y(*>	и У1)~/О- У2)|<А71у1 — у2|.
Нетрудно привести примеры функций / (х, у) (например,
/(х, у) = | у | в окрестности точек (х, 0)), для которых условие
тт	с*/
Липшица выполнено, но производная в некоторых точках не
существует, следовательно, условие	является более гру-
бым, чем условие Липшица.
Доказательство
ственности. Заменим
теоремы существования и
дифференциальное уравнение
еди н-
77 = /(*> У)	(1.22)
с начальным условием
у(х0) = у0	(1.23)
эквивалентным интегральным уравнением
I
X
У = Уо + J/(х, y)dx.
(1-24)
Действительно, если некоторая функция у = у(х) при подста-
новке обращает в тождество уравнение (1.22) и удовлетворяет усло-
вию (1.23), то, интегрируя тождество (1.22) и принимая во внимание
условие (1.23), получим, что у = у(х) обращает в тождество и ура-
внение (1.24). Если же некоторая функция у = у (х) при подстановке
обращает уравнение (1.24) в тождество, то она, очевидно, удовле-
творяет и условию (1.23), а дифференцируя тождество (1.24), полу-
чим, что у = у(х) обращает в тождество и уравнение (1.22).
Строим ломаную Эйлера у = у„(х), исходящую из точки (х0, у0)
с шагом — на отрезке х0 х	х0 -ф- Н, п — целое положи-
§ 6]
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
43
тельное число (совершенно аналогично доказывается существование
решения на отрезке х0 — И х х0). Ломаная Эйлера, проходящая
через точку (х0, у0), не может выйти из области D при х0 х
х0 Н (или х0 — Н х х0), так как угловые коэффициенты
каждого звена ломаной по модулю меньше М.
Дальнейшее доказательство теоремы разобьем на три этапа:
1)	Последовательность у = уп(х) равномерно сходится.
2)	Функция у (х) = lim уп(х) является решением интеграле-
п -> <х>
ного уравнения (1.24).
3)	Решение у(х) уравнения (1,24) единственно.
Доказательство 1). По определению ломаной Эйлера
У^ (*) = /(** У*) при xk<x^xk+v А==0, 1.п — 1
(в угловой точке xk взята правая производная), или
y;w = /(x, Ул(*))+ [/(**. yk) — f(x, ул(х))]	(1.25)
обозначим
f(xk, У *) — /(*• Уп (•*)) = Лл(х)-
В силу равномерной непрерывности функции f(x, у) в D получим
h«W| = |/(xft. УА) — /(х, ул(х))|<ел (1.26)
при и>/У(£л), где е„—>0 при л->оо, так как |х — хл|^йл,
a |yft —ул(х)| < (ИЛЛ и Лл=-^-->0 при л->оо.
Интегрируя (1.25) по х в пределах от х0 до х и учитывая, что
Ул (*о) = Уо> получим
Ул(*) = Уо + f	(1.27)
Xa	Ха
Здесь п может принимать любое целое положительное значение, сле-
довательно, при целом т > 0
X	X
Уя+т(*) = Уо + f fit- yn+m(t))dt+ f ^m(f)df. (1.28)
x,	xa
44	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. t
Вычитая из (1.28) почленно (1.27) и взяв модуль разности, получим
|уя+яд*) —Уя(*)1 =
X
f 1Ж y«+m(O)~/(t Уя(01^ +
Хо
Пл+Л! (0 dt - J т]„ (О dt
X
< f l/(t Уя+га(О)-/(А уя(0)М/4-
Хо
х	х
+ /|пл+л1(О|й?/ + f l^^'dt
Го	Го
при х0^. х х0-\- Н или, принимая во внимание (1.26) и условие
Липшица:
X
|Ул+т (х) — Уп (х) |< N f I у„+т (О — у„ (/) I dt 4- (en+m + e„) • Я.
Xi
Следовательно,
max |Ул+т(х) — y„(x)| <
Жо < x < xQ + n
X
max f | у
n+m (О-уя(О|^ + (ея+Л1 + ея)Я,
откуда
max | Ул+лг (x) — y„ (x) [ < (&п\т^н~ ' < c
Xo<X<X„+H	I /VZ7
для любого e > 0 при достаточно большом п >	(е).
Итак,
max |уя+я1(х) — у„(х)| < в
г„ < х < х0+ Н
при п >	(е), т. е. последовательность непрерывных функций уп (х)
равномерно сходится при х0 х х04~ И:
У„(х) г$у(х),
где у (х) — непрерывная функция.
Доказательство 2). Перейдем в уравнении (1.27) к пределу
при п—>оо: '
х х
Иш ул (х) = у0 + lim f / (х, уя (х)) dx + Jim f т]л (x) dx
n-^OO	n-^CO J	n-+<X) J
Xo	Xo
§ 6] ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ	45
ИЛИ
у(х) = уо+ lim f/(х, y„(x))dx-|- lim f^W^x. (1.29)
Л->ОО **	Г2->ОО J
X*	'	Х-) .
В силу равномерной сходимости у„(х) к у (х) и равномерной непре-
рывности функции / (х, у) в D последовательность /(х, yn(x))Zj
^f(x, у(х)).
Действительно,
|/(х, у(х)) —/(х,	(х)) I < е,
где е > 0, если |у (х) — уп (х)| < д (е), но |у (х) — уп (х) | <5 (е), если
/г > N,(д(е)) для всех х из отрезка х0 х х0-}~ И.
Итак, |/(х, у(х)) — /(х, ул(х))| <е при n>/Vj(6(e)), где Nx
не зависит от х.
В силу равномерной сходимости последовательности /(х, у„(х))
к /(х, у(х)) в (1.29) возможен переход к пределу под знаком инте-
грала. Принимая, кроме того, во внимание, что |Лл(е)| < ел, гДе
е„->0 при п—>схэ, окончательно в (1.29) получим
'	X
у(х) = уо+ f f(x, y(x))dx.
х.
Итак, у(х) удовлетворяет уравнению (1.24).
Доказательство 3). Допустим существование двух несовпа-
дающих решений ул(х) и у2(х) уравнения (24), следовательно,
шах |У1(х) — у2(х)| =£0.
Г|><х<Х(|+/Т
Вычитая почленно из тождества
X
У1(х) = Уо+/f(x, У!(х))с1х
тождество
X
у2М=Уо+У2(.х))йх,
Хй
получим
УЛх)~у2{х)^ f [/(х, yt(x))—/(х, y2(x))]rfx.
Хй
46	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
Следовательно.
max |У1О)— У2О)| =
max
Xq X Хо+ //
Уi/o. ул*))—/О- y2o))irfx
max
У I/O. У10)) — /О. у2О))И* .
X,
Пользуясь условием Липшица, будем иметь
max |yi О) — У2О)| шах
/ |У10) — у2(х)| dx
N - max |У1О) — у2(х)| max
= NH	max
Хо
|У10) — у2 О)|.
Полученное неравенство
max |У1О) —y2O)l	щах ;|У1(х) — У2О)|	(1.30)
х, <х«Сх»+Я	х0<х'О>+Н
противоречиво, если max |у1(х) — у2(х)|¥=0,таккакпоусло-
Хо<Х<Х0+//
вию теоремы	а из (1.30) следует, что (V/Y = l.
Противоречие снимается лишь при
max |У] (х)— у2(х)|=0,
х<> .< х < х,+7/
т. е. если yt(x)==y2(x) при х0 х х0 -f- Н.
Замечание I. Существование решения уравнения (1.22) можно
было бы доказать иным методом лишь в предположении непрерыв-
ности функции /(х, у) (без условия Липшица), однако одной непре-
рывности функции f (х, у) недостаточно для доказательства един-
ственности решения.
Замечание 2. Существование и единственность решения у=у(х)
доказаны лишь на отрезке х0 — Н х <1 х0 -|- Н, однако, взяв точку
(х0 + ?7, у (х04- //)) за начальную, можно, повторив рассуждение,
продолжить решение еще на отрезок длины Ну если, конечно,
в окрестности новой начальной точки выполнены условия теоремы
существования и единственности решения. Продолжая этот процесс
§ 6)	ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
47
в некоторых случаях, можно продолжить решение па всю полуось
х х0 или даже на всю ось — оо < х < оо, если продолжить реше-
ния и в сторону меньших значений х. Однако возможны и другие
случай, даже если функция f {х, у) определена для любых значе-
ний х и у.
Возможно, что интегральная кривая становится непродолжаемой
ввиду приближения к точке, в которой нарушены условия теоремы
существования и единственности решения или интегральная кривая
приближается к асимптоте, параллельной оси Оу.
Эти возможности иллюстрируются следующими примерами:
1)	= - —, у (0) = 1.
’ dx У
Разделяя переменные и интегрируя, получаем
X2 —|-у2 = С2, у=±^с2—X2, С — 1, у — У1 —X2.
Решение непродолжаемо за пределы интервала — 1 < х < 1. В граничных
точках (—1, 0) и (1, 0) правая часть уравнения — — у- разрывна. Усло-
вия теоремы существования решения нарушены (рис. 1.16).
dy
2) ^—= у2, у (1) = 1. Разделяя переменные и интегрируя, получим
1	о	1
у =----------, с = 2, у —---------5,
z х — с	J х — 2
и интегральная кривая продолжаема лишь до асимптоты х = 2 (— оо < х < 2)
(рис. 1.17).
В настоящее время теоремы существования и единственности реше-
ний не только дифференциальных уравнений, но и уравнений иных
типов очень часто доказывают методом неподвижных точек.
48	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. 1
Простейшей теоремой о неподвижных точках является принцип сжа-
тых отображений.
Принцип сжитых отображений. Если в метрическом *)
полном**) пространстве М задан оператор А, удовлетво-
ряющий условиям:
1) оператор А переводит точки пространства М в точки
того же пространства: если ycz/И, то Д[у]сЛ(;
2) оператор А сближает точки, точнее,
р(Л[у], Я [г] )<ар (у. z),
где у и z—любые точки пространства М, а< 1 и не зависит
от выбора у и г, р(у, г) — расстояние между точками у и z
в пространстве М, то существует единственная неподвиж-
ная точка у пространства М, Л[у]==у, и эта точка может
быть, найдена методом последовательных приближений, т. е.
у — lim ул, где У„ —Я[у„_1] (я=1, 2, ...), причем точка уЛ
П-^СХ)
выбирается в пространстве /И произвольно.
Доказательство. Докажем, что последовательность
Уо- Ур Уг....Ул- •  •
фундаментальна. Оценим расстояние между соседними членами этой
последовательности:
Р(Уг- У1) = Р(Л [У11- Л[у0]Хар(У1- Уб).
Р(Уз.'Уг) = Р(л 1У21- Л[Ут])<Сар(У2. У1)<а* 1 2 3р(уп у0).
р(у»+1. ул)==рИ1уп]. Аiy»-ilX	(1,31)
<«р(ул. Ул-1)<аяр(У1- Уо)>
 *) Пространство М называется метрическим, если в нем определена
функция р (у, г) пар точек этого пространства, удовлетворяющая для любых
точек у и г рассматриваемого пространства условиям:
1) Р (У< *) > 0, причем р (у, у) = 0 и из р (у, z) = 0 следует у = г;
2) Р (У. г) = Р (?, у);
3) р (у, г)< р (у, и) 4- р (и, z) (правило треугольника).
Функция р называется расстоянием в пространстве М.
♦*) Метрическое пространство М называется полным, если каждая фун-
даментальная последовательность точек пространства М сходится в этом
пространстве. Напомним, что последовательность уь у2........ул,... назы-
вается фундаментальной, если для каждого е > 0 можно подобрать число N (е)
такое, что при n~^.N(е) расстояние р (уп, ул+то) < е при любом целом т > 0.
§ 6) ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ	49
Применяя теперь п — 1 раз правило треугольника и используя
неравенства (1.31), получим
Р(УЯ. УЯ+Я1)<Р(УЯ. У»+1) + Р(Уп+р У«+2)+ •••
••• Н-р(Уя+яг-1. Л+т)<1«’ + а”+1+	+а',+'я"11р(Ур уо) =
а" — а"'101	а"
= -1_|х "Р(Ур Уо) < yzryР(Ур Уо) < е
при достаточно большом п. Следовательно, последовательность у0,
уь у2.....ул, ... фундаментальна и, в силу полноты простран-
ства М, сходится к некоторому элементу того же пространства:
lim ул = у, у с/И.
Докажем теперь, что у является неподвижной точкой. Пусть
Д[у]==у. Применяя два раза правило треугольника, получим
Р(У. У) <Р(У. УЯ) + Р(УИ. Уя+1) + Р(Ул+р У)-
Для любого е>0 можно выбрать А/(в) такое, что при п^А/(е)
1)	Р(У- Уя)<у. так как у= lim ул;
2)	Р (Уп< Ул+i) < у» так как последовательность ул фундамен-
тальна;
3)	Р(Уя+1. У)=р(Л[ул1, Д1у])<ар(Уп,У)< у, откуда р (у, у)<е,
где е можно выбрать сколь угодно малым. Следовательно,
р (у, у) = О и у = у, А [у] = у.
Остается доказать, что неподвижная точка у единственна.
Если бы существовала еще одна неподвижная точка г, то
р(Д[у], Д[г]) = р(у, г), что противоречит условию 2) теоремы.
Применим принцип сжатых отображений к доказательству тео-
ремы .существования и единственности решения у(х) (х0—
dy
x0 -J- й0) дифференциального уравнения	у), удо-
влетворяющего условию у (х0) — у0, в предположении, что в области D
хо — а<х<ЛоН-а, у0 — b <у < у0 + ^
функция / непрерывна и, следовательно, ограничена |/| Ж и удо-
влетворяет условию Липшица
I/O, у) — f(x, z)l |у — z\.
Число hQ min fa, и будет точнее выбрано ниже.
50
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
(ГЛ. 1
Рассмотрим полное метрическое пространство С, точками кото-
рого являются всевозможные непрерывные функции у (х), определен-
ные на отрезке х0— h0 х х0 h0, графики которых лежат
в области D, а расстояние определяется равенством
р(у, z) = max |у — z\,
где максимум берется при х, изменяющемся на отрезке
*о —	< x0 + h0.
Это пространство часто рассматривается в различных вопросах мате-
матического анализа и носит название пространства равномерной
сходимости, так как сходимость в смысле метрики этого простран-
ства означает равномерную сходимость.
dv
Заменим дифференциальное уравнение ^- = /(х, у) с начальным
условием у (х0) — у0 эквивалентным интегральным уравнением
Г
У = Уо + ff(x' y)dx-	О-24)-
Рассмотрим оператор
ж
А [у] = у0 + J f О- У (*)) dx>
• х,
ставящий в соответствие каждой непрерывной функции у(х), задан-
ной на отрезке х0— hQ х х0 -|- й0 и не выходящей из обла-
сти D, непрерывную функцию А [у], определенную на том же от-
резке, график которой также не выходит из области D, так как
Mh0 Ь. Оператор А [у], следовательно, удовлетво-
ряет условию 1) принципа сжатых отображений.
Уравнение (1.24) при этом запишется в виде у = А[у], и следо-
вательно, для доказательства теоремы существования и единствен-
ности остается доказать существование в пространстве С единствен-
ной неподвижной точки у (х) оператора А, так как в этом случае
у = А [у] и уравнение (1.24) удовлетворяется.
Для доказательства теоремы остается проверить, удовлетворяет ли
оператор А условию 2) принципа сжатых отображений:
X
J f(x, y)dx
х„
р(Л[у], A [z])< ар (у, г), а < 1,
где
р(А[у], А[д]) —max
X
J [/(*. У) — f(x> z)]dx
Хо
§ 6]	ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
Пользуясь неравенством ЛиЬшипа, получим
51
р(Л[у], Л [z])<;/Vшах
f |у — z\dx
X-l
N щах | у — z\ max
= Nh0 max |y — z\	VAop(y, z).
Выбирая Ло так, чтобы Nh0 <(а < 1, получим, что оператор А удо-
влетворяет условию
р (Л [у], Л [г] X ар (у, z), а < 1.
Итак, согласно принципу сжатых отображений существует един-
ственная неподвижная точка у (х) оператора Л, или, что то же самое,
единственное непрерывное решение уравнения (1.24), и оно может
быть найдено методом последовательных приближений.
Совершенно аналогично можно доказать теорему существования
и единственности решения yt(x), у2(х).........у„(х) Для системы
уравнений
dy.
— =ft(x, yv у2.........у„), y,(xo) = yzo (i — 1, 2.....п) (1.32)
ИЛИ
X
у,-= У/о-Ь J/<•*> Уг У2> •••> y'n)dx (i=l. 2........п) (1.33)
х, й
в предположении, что в области D, определяемой неравенствами
х0 — а < х < х0 + а, Ую — Ь1<У1< yi0 + t>i (/=1,2.........../г),
правые части уравнений (1.32) удовлетворяют условиям:
1) всё функции fi(x, уР у2, .... у„) (г = 1, 2, .... п) непре-
рывны, а следовательно, и ограничены, |/z|	Л4;
2) все функции ft (1=1, 2.........п) удовлетворяют условию
Липшица:
1Л(*. Ур у2. •••. Уп) — fi(x, Zp z2. ....	|yz — zt\.
i=i
Точкой пространства С будет теперь система п непрерывных
функций (ур у2......у„), т. е. n-мерная вектор-функция У(х)
с координатами у}(х), у2(х)......Уп(х)> определенная на отрезке
*0 ~ ло "С х хо + ло- гДе -С min (°-	....и будет точнее
52	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. I
выбрано ниже. Расстояние в пространстве С, определяется равен-
ством
р(К(х), Z(x)) = 2max|yz — zj,
z=i
где zx, z2, zn — координаты вектор-функции Z(x).
Нетрудно проверить, что при таком определении расстояния мно-
жество С n-мерных вектор-функций У (х) превращается в. полное
метрическое пространство. Оператор А определяется равенством
(X
Ую-F f fi(x’ Ур Уч- ••• У^Лх, .
*0
X	X
У20 + J А(х- У1’ Уч.. Уп>ах... Упо+ f fn(x- Ур У2.. yjdx j ,
г,-	Хо	/
т. е. при действии оператора 'А на точку (ур у2......у„) получаем
точку того же пространства С с координатами, равными правым
частям системы (1.33).
Точка Л[К] принадлежит пространству С, так как все ее коор-
динаты являются непрерывными функциями, не выходящими из обла-
сти D, если координаты вектор-функции У не выходили из области D.
Действительно,
X
J/((•». Ур у2> •••- Уп)<1х
Ху
и следовательно, |yz — у/0| FA-
Остается проверить выполнение условия 2) принципа сжатых
отображений:
р(Д [Г], Д[Д]) =
Л	X
==:SmaX|/ У2...............У«)~ fl(X’ ZV Z2..
/ = ]
n	x
< 2 max j f \ft (%. yP У2. .... У„) —/<(*. zv z2, .... z„) | dx | <
I = 1	xo '
n	X n
<A/]^max|J ^|yz —
1 = 1	1 = 1
n	n	X
N	max I уi — zt |	max | J dx | = Nnhffi (Y, Z).
1-Л	i = l Xo
6 61
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
53
Следовательно, если выбрать	где 0<ct< 1. или
Nnh0 а < 1, то условие 2) принципа сжатых отображений будет
удовлетворено и будет существовать единственная неподвижная
точка Y, причем ее можно найти методом последовательных прибли-
жений. Но условие Y = А (У) по определению оператора А экви-
валентно тождествам
X’
= Ь + f fdx’ Ур ••• • У^ах U = Y 2................................я),
Л*о
где yz(/=l, 2........«) — координаты вектор-функции Y, то есть Y
является единственным решением системы (1.33).
Пример 1. Найти несколько последовательных приближений ух, у2,
Уз к решению уравнения	,
g = ^ + y2; у(0) = 0, -1<х<1.
у = У (х2 4- у2) dx, Ло = min ^1,	= Р
о
Полагая у0 (х)	0, получим
f , . х3	х8\ j х3 хг
yt=sJ xldx^3' У2^] Vе +9-)rfx = 3 + 63’
о'	о
Пример 2. При каких ограничениях линейное уравнение
^+p(.x)y = f(x)
удовлетворяет условиям теоремы существования и единственности!
Для выполнения первого условия теоремы достаточно, чтобы на рассма-
триваемом отрезке изменения х, ах^х^а2, функции р(х) и /(х) были бы
непрерывны. При этом будет выполнено и второе условие теоремы суще-
ствования и единственности, так как частная производная по у от правой
dv
части уравнения -^ = — Р {х) у -|- f (х) равна — р (х) и вследствие непре-
рывности функции р (х) на отрезке ах < х <. а2 ограничена по модулю (см.
стр. 42). Итак, если р(х) и /(х) непрерывны на отрезке at<x<a2, то
через каждую точку (х0, у0), где ах < х0 < а2, а у0 задается произвольно,
проходит единственная интегральная кривая рассматриваемого линейного
уравнения.
54
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
[ГЛ. I
Теорема 1.2 (о непрерывной зависимости решения от па-
раметра и от начальны*, значений). Если правая часть
дифференциального уравнения
d^=f(x, у, р) .	(1.34)
непрерывна по ц при	и удовлетворяет условиям
теоремы существования и единственности, причем постоянная
Липшица N не зависит от ц, то решение у(х, ц) рассматри-
ваемого уравнения, удовлетворяющее условию у(х0) — у0, не-
прерывно зависит от ц.
Строим ломаные Эйлера уп— уп(х, ц), являющиеся непрерыв-
ными функциями ц, и, повторяя рассуждения на стр. 40—45, получим,
что последовательность уп(х, р) сходится равномерно не только
по х, но и по ц при х0 < х Н, р,0 ц так как N и И
не зависят от ц, если Н < min [а,	, где М | / (х, у, ц) |.
Следовательно, решение у = у(х, ц) уравнения.
У =Уо + ff(x, У, Ц)йх,	(1.35)
Ли
являющееся пределом последовательности уп (х, ц), непрерывно не
только по х, но и по J1.
Замечание. Если применить к уравнению (1.35) метод после-
довательных приближений, то последовательные приближения у —
— уП(х, ц), являющиеся непрерывными функциями х и ц, равно-
мерно сходятся к решению у (х, ц) уравнения (1.35) (так как а —
— Nh < 1 не зависит от р). Следовательно, и этим методом можно
доказать непрерывную зависимость решения от х и ц.
Очевидно, что доказательство нисколько не изменится, если
правая часть уравнения (1.34) является непрерывной функцией не-
скольких параметров в предположении, конечно, что постоянная
Липшица N от них не зависит.
Тем же методом при аналогичных условиях можно было бы
доказать непрерывную зависимость решения у(х, х0, у0) уравнения
~^ = f(x, у) от начальных значений х0 и )!0, при этом пришлось бы
лишь несколько уменьшить h0, так как в противном случае реше-
ния, определяемые начальными значениями, близкими4 к х0, у0,
могли бы выйти из области D уже при значениях х, лежащих на
интервале х0 — hQ < х < х0 Ло.
Однако еще проще заменой переменных свести вопрос о зави-
симости решения от начальных значений к уже рассмотренному выше
§ 6]	ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
55
случаю зависимости решения от параметров, содержащихся в правой
части уравнения (1.34). Действительно, полагая z — у (х, х0, у0)—у0,
t = х — х0, преобразуем уравнение = f (х, у) с начальным усло-
вием у(х0) = у0 в -^- = /(^ + *0- г + Уо)- 2(°) — °- к которому
уже можно применить теорему о непрерывной зависимости решения
от параметров х0 и у0,
если функция f непрерывна
и удовлетворяет условию
Липшица.
Аналогичные теоремы
теми же методами могут
быть доказаны для систем
уравнений.
Заметим, что непрерыв-
ная зависимость решения
у(х, х0, у0). х0<х<*
(или b х х0), от началь-
ных значений х0 и у0 означает, что для любого е>0 можно подо-
брать д(е, Ь) > 0 такое, что из неравенств
|*о — х0|<6(е, Ь) и |у0 —у0|<6(е, 6)
следует неравенство
|у(х, х0, Уо) —у(х, х0, Уо)| < е	(1.36)
при х0<х<6 (рис. 1.18).
С возрастанием b число б(е, Ь), вообще говоря, уменьшается и
при b —> оо может стремиться к нулю. Поэтому далеко не всегда
удается подобрать такое число д(е) > 0, при котором неравенство (1.36)
удовлетворялось бы для всех х > х0, т. е. не всегда решения, близ-
кие по начальным значениям,, остаются близкими при сколь угодно
больших значениях аргумента.
Решение, которое мало изменяется при произвольном, но доста-
точно малом изменении начальных значений для сколь угодно боль-
ших значений аргумента, называется устойчивым. Подробнее об
устойчивых решениях см. гл. 4.
Теорема 1.3 (об аналитической зависимости решения от
параметра, теорема Пуанкаре). Решение x(t, ц) дифферен-
циального уравнения x=f(t, х, р), удовлетворяющее условию
x(t0) = x0, аналитически зависит от параметра ц в окрест-
ности значения ц = ц0, если функция f в заданной области
изменения t и х и в некоторой окрестности точки р0 непре-
рывна по t и ' аналитически зависит от р, 'и х.
56	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. I
Аналогичное утверждение справедливо и для системы уравнений
= хр х2....................хп, ц) (/=1, 2.........п),	}
причем в этом случае предполагается, что функции t непрерывны
по первому аргументу и аналитически зависят от всех остальных
аргументов.
Подробное доказательство этой теоремы, как и других теорем,
требующих применения теории аналитических функций, мы не при-
водим, отсылая читателя к статье А. Н. Тихонова [4], где дано
наиболее простое доказательство теоремы об аналитической зави-
симости решения от параметра.
Идея доказательства А. Н. Тихонова сводится к следующему: считая,
что р может принимать и комплексные значения, доказывается существова-
Д X (4 р) дх
ние предела hm —-д-— = "ф * что и означает аналитическую зависи-
мость решения от р. Существование этого предела следует из того, что
Д„х
отношение —^—-удовлетворяет линейному дифференциальному уравнению
d Дцх fit, х it, р-|-Др), р + Др) —/(/, x(t, р), р + Др) А|Л(А И)
~dt "Др ~	Дцх (Г, р)	Др
/(Г, х it, р), р-НДр) — f{t, x(t, ц), р) Дцх I
. +	АН	’Др
решение которого единственно и при стремлении приращения Др, по любому
закону к нулю стремится к едйнствённому решению уравнения
Теорема 1.4 (о дифференцируемости решений). Если
в окрестности точки (х0, у0) функция /(х, у) имеет непре-
рывные производные до k-го порядка включительно, то реше-
ние у(х) уравнения
£=/<*• У).	(1.37)
удовлетворяющее начальному условию у(х0) = у0, в некоторой
окрестности точки (х0, у0) имеет непрерывные производные
дд (&4-1)-го порядка включительно.
Доказательство. Подставляя у(х) в уравнение (1.37), по-
лучаем тождество
-g--/(x, у(х)),	(1.370
и следовательно, решение у(х) имеет в некоторой окрестности
рассматриваемой точки непрерывную производную / (х, у (х)).
§ 6) ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ	57
Тогда, в силу существования непрерывных производных функции /,
будет существовать непрерывная вторая производная решения
d2y df . df dy df . df ,,	, ..
dx2 ~ дх + dy dx~ dx^ dy ^X' y(-X^'
Если fe> 1, то, в силу существования непрерывных производных
второго порядка функции /, можно, дифференцируя еще раз тож-
дество (1.3?!). обнаружить существование и непрерывность третьей
производной решения
_ <?7 , 9 <?7 f , ^7	, df_ (df_ df А
dxs dx2 ""г" dx dy J ' dy2 ' ' dy \dx' dy '
Повторяя это рассуждение k раз, докажем утверждение теоремы.
Рассмотрим теперь точки (х0, у0), в окрестности которых реше-
dy
ния уравнения ^ = /(х, у), удовлетворяющего условию у(х0) = у0,
не существует или решение существует, но не единственно. Такие
точки называются особыми точками.
Кривая, состоящая сплошь из особых точек, называется особой.
Если график некоторого решения сплошь состоит из особых точек,
то решение называется особым.
Для нахождения особых точек или особых кривых надо прежде
всего найти множество точек, в которых нарушены условия теоремы
о существовании и единственности решения, так как только среди
таких точек могут быть особые. Конечно, не каждая точка, в кото-
рой нарушены условия теоремы о существовании и единственности
решения, обязательно является особой, так как условия этой тео-
ремы достаточны для существования и единственности решения, но
они не являются необходимыми.
Первое условие теоремы существования и единственности реше-
ния (см. стр. 40)' нарушается в точках разрыва функции f(x, у),
причем если при приближении по любому пути к некоторой изоли-
рованной точке разрыва (х0, у0) функция / (х, у) неограниченйо
возрастает по модулю, то в тех задачах, в которых переменные х и у
dv
равноправны, как мы условились выше, уравнение = /(х, у)
должно	быть	заменено уравнением	—------,
rfy	/(х,	у)
правая	часть	уже непрерывна в	точке	(х0,	у0),
7-7——; = °-
/ (*о. у0)
Следовательно, в задачах, в которых переменные
для которого
если считать
х и у равно-
правны, первое условие теоремы существования и единственности
нарушается в тех точках, в которых и функция / (х, у) и
разрывны.
1
У)
58
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
[ГЛ. I
Особенно часто приходится рассматривать уравнения вида
dy   М (х, у)
dx	N (х, у) ’
(1.38)
где функции М (х, у) и N(x, у) непрерывны. В этом случае функ-
М (х, у) N (х, у) ,
ции N{x у)' И ~ЛГ(*~У)~ одновРеменно' разрывны лишь в тех
точках (х0, у0), в которых А1(х0, у0) = IV (х0> у0) = О и не суще-
ствует пределов
lim М (х, у)
х->х- Af(x, у)
у->у.
и
lim N (х, у)
х-»х0 М (х, у)
у->у
Рассмотрим несколько типичных особых точек уравнения (1.38).
Пример 3
dy__2y_
dx х
„	dxx
Правые части данного уравнения и уравнения	разрывны
в точке х — 0, у=0. Интегрируя уравнение, получим у = сх1 — семейство
парабол (рис. 1.19) и х = 0. В начале координат — особая точка, называемая
узлом.
Пример 4.
<У _ У
dx х
$ 6)	ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
59
_	'	dx х
Правые части данного уравнения и уравнения -j— =----разрывны
«у у
с
в точке х = 0, у = 0. Интегрируя уравнение, получаем у = — — семейство
гипербол (рис. 1.20) и прямую х = 0. В начале координат — особая точка,
называемая седлом.
Пример 5.
rfy х + у
dx х — у'
Правые части
dx х — у
данного уравнения и уравнения = ^_|_у разрывны
в точке х=0, у=0. Интегрируя рассматриваемое однородное уравнение
(сравните с примером 3 на стр. 36), получим:
у
_________. arctg —
у х2 + у2 = се х ,
или в полярных координатах р = сеф— логарифмические спирали (рис. 1.21).
Особая точка такого типа называется фокусом.
П р и м е р 6.
dy__________________________________х_
~dx ~ у'
_	dx у
Правые части данного уравнения и уравнения = — х- разрывны
в точке х = 0, у = 0. Интегрируя уравнение, получаем х2 -|- у2 — с2— се-
мейство окружностей с центром в начале координат (рис. 1.22). Особая точка
такого типа, т. е. особая точка, окрестность которой заполнена семейством
замкнутых интегральных кривых, называется центром. В этом примере не
существует решения, удовлетворяющего условию у (0) = 0.
К вопросу об особых точках и их классификаций мы с несколько
иной точки зрения еще вернемся в главе 4.
Второе условие теоремы 1.1 существования и единственности
решения — условие Липшица, или более грубое условие, требующее
существования ограниченной частной производной чаще всего
60	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ДОРЯДКА [ГЛ. Т
нарушается в точках, при приближении к которым неограни-
ченнно возрастает, т. е. в точках, в которых = 0.
Уравнение
1 ' ду
-^у-=0, вообще говоря, определяет некоторую кри-
вую, в точках которой может быть нарушена единственность. Если
в точках этой кривой единственность нарушена, то кривая будет осо-
бой, если, кроме того, эта кривая
окажется интегральной, то полу-
чим особую интегральную кривую.
Возможно, что кривая 1 ____л
df
Рис. 1.23.
Ту
имеет несколько ветвей, тогда
для каждой ветви надо решить
вопрос о том, будет ли эта ветвь
особой кривой и будет ли она ин-
тегральной кривой.
Пример 7. Имеет ли уравне-
rfy
ние = у2 -j- х2 особое решение?
Условия теоремы существования
и единственности выполнены в ок-
рестности любой точки, следователь-
но, особого решения нет.
Пример 8. Имеет ли уравне-
ние = j/(y — х)2 5 особое ре-
шение?
Правая часть непрерывна, но частная производная
<?/	2 "з
ду ~ 3 (у х}
неограниченно возрастает при приближении к прямой у = х, следовательно,
на прямой у = х может нарушиться единственность. Но функция у — х не
удовлетворяет рассматриваемому уравнению, следовательно, особого реше-
ния нет.
Пример 9. Имеет ли уравнение  = |/(у — л)2-}-! особое ре-
шение?
Как и в предыдущем примере, уравнение -~- = 0 имёет вид у = х, но
"ду
на этот раз функция у = х удовлетворяет данному уравнению. Остается
выяснить, нарушена ли единственность в точках этой прямой.'Заменой пе-
ременных г = у — х приводим исходное уравнение к уравнению с разделяю-
щимися переменными, после чего без труда находим решение: у — х =
§ 7] ПРИБЛИЖЕННЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ УРАВНЕНИИ 61
(jc_
= -—27~~- Кривые этого семейства преходят через точки графика реше-
ния у = х (рис. 1.23). Следовательно, в каждой точке прямой у — х единст-
венность нарушена и функция у = х является особым решением.
Этот пример показывает, что одной непрерывности правой части в урав-
нении
-^7 = /(•*• У)>	У(х0)=уа,
недостаточно для единственности решения основной начальной задачи, однако
можно доказать, что существование решения при этом уже обеспечивается.
§ 7. Приближенные методы интегрирования уравнений
первого порядка
В предыдущем параграфе мы уже познакомились с двумя при-
ближенными методами интегрирования дифференциальных уравнений:
методом Эйлера и методом последовательных приближений. Однако
оба эти метода имеют существенные недостатки, в силу которых ими
сравнительно редко пользуются в практике приближенных вычислений.
Достоинства приближенных методов оцениваются по. точности
даваемых ими результатов и по простоте вычислений. Недостатками
метода последовательных приближений являются сравнительно мед-
ленная сходимость приближений к решению и сложность вычислений.
Недостатком метода Эйлера является малая точность, для повышения
которой приходится брать весьма малый шаг h, что приводит к дли-
тельным вычислениям.
Впрочем, небольшое усовершенствование метода Эйлера, так
называемое уравнивание (или итерация) приводит уже к довольно
удобной вычислительной схеме. При применении метода Эйлера
с уравниванием делят отрезок х0^ х ^ Ь, на котором надо вычи-
щу г/ ч
слить решение уравнения = / (х, у), определяемое условием
у(х0) = у0, на равные части длиной h = b п*а . Обозначая
х0-\- kh = xk, у(х0Н-&Л) = уА, у'(х0-фkh) = у', вычисляют yft
если уже найдено yk, в начале по формуле Эйлера:
= или ДУ* = У*+1—О-39)
т. е. на отрезке х0 -ф- kh х х0 -ф- {k -ф- lj h заменяют интеграль-
ную кривую, проходящую через точку (хй, уА), отрезком ее каса-
тельной в той же точке (см. рис. 1.13, стр. 39). Затем уточняют
вычисленное значение ул+р для чего определяют производную
Ук^1—f (хk + v Ук+^ и снова применяют формулу Эйлера (1.39), но
вместо ук берут среднее арифметическое вычисленных значений
62
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
[ГЛ. I
Ук + Ук + У
производных в граничных точках ----%---, т. е. считают
Уа+1 = Уа + ^--+2У-'-~-	(1’40)
Вновь вычисленное значение yft+1 дает возможность вычислить новое
значение производной у*+] =/ (*й+1> УА + 1). после чего снова вы-
,	„	 Уй+Уй + 1
числяют среднее арифметическое значений производных --------•
снова применяют формулу (1.40)
и продолжают этот процесс до тех пор, пока в пределах заданной
точности не совпадут результаты двух последовательных вычисле-
ний значений ул + 1. После этого тем же методом вычисляется yft+2
и т. д.
Метод Эйлера с уравниванием дает на каждом шаге погрешность
порядка /г3 и нередко применяется в вычислительной практике.
Однако значительно чаще применяются более точные методы (методы
Штермера, Рунге, Мильна и др.), основанные на замене искомого
решения несколькими членами его тейлоровского разложения
/,2	hn
Ук^~Ук + нУ'к+^Ук + ••• +4г^!)-	<Ь41>
т. е. замене искомой интегральной кривой параболой re-го порядка,
имеющей касание л-го порядка с интегральной кривой в точке
х = хк, y = yk.
Непосредственное применение формулы Тейлора (1.41) на каждом
шаге приводит к сложным и неоднотипным вычислениям, поэтому
эта формула обычно применяется лишь для вычисления нескольких
близких к х — х0 значений, необходимых для применения более
удобных вычислительных схем, среди которых в первую очередь
следует назвать метод Штермера, в котором вычисление про-
водится по одной из следующих формул в зависимости от порядка
аппроксимирующей параболы:
Уа+i — Ук~\~ЧкЧ-у	(1-42)
1	А
У*+1 — Уй + ^* + '2	+	.	(1-43)
Уй+1 = Ул + ^* + '§’ Д‘7й-1 + ^’Д29а-2+-|-Д39'й-з'	(1-44)
Ук + 1 — Ук^~Як + f-\2^Як~1 + g-^i-3 + ^4?t-4’ (145)
§ 7] ПРИБЛИЖЕННЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ УРАВНЕНИИ 63
где
= Чг-l^a-V-l’ ДЧ_2 = Д^_1-Д?Й_2-
дз?л-з = д2<7*-2—д2?л-з- Д4<7а-4 = дз<7л-з — ДЗ(7а-4-
Формулы Штермера могут быть получены путем интегрирования
в пределах от xk до и тождества у' = /(х, у(х)), в котором
у(х) является искомым решением:
Х+1
=	/ /С*. y(x))dx,
и применения известной из курса анализа квадратурной формулы:
I
J*	+	+^д2<Р^_2 +
*k
+ 4дзФ^з+|^Д4Фа-4+ •••]• (1-46)
Напомним, что эта квадратурная формула получается путем замены
подынтегральной функции ф(х) аппроксимирующим многочленом по
интерполяционной формуле Ньютона и вычисления интегралов от
отдельных слагаемых.
Оценка остаточного члена квадратурной формулы (1.46) показы-
вает, что погрешность в формуле (1.42) при одном шаге имеет по-
рядок /г3, в формуле (1.43) А4, в формуле (1.44)/г5, в формуле (1.45) /г6.
Если же принять во внимание, что при нескольких шагах погреш-
ности могут суммироваться, то для оценки погрешности при п шагах
b — х0
надо опенки, полученные для одного шага, умножить на п = —2,
что может привести к изменению указанного выше порядка погрешности.
Замечание. Можно показать непосредственным разложением
по формуле Тейлора в окрестности точки х = хк, что правая часть
формулы Штермера (1.42) с точностью до членов, содержащих h
в степенях выше второй, совпадает с первыми тремя членами раз-
ложения уА+1 по формуле Тейлора (1.41):
/,2
’	(1.47)
правая часть следующей формулы Штермера (1.43) с точностью до
членов, содержащих h в степенях выше третьей, совпадает с
у* + кУк +	+ 4г y't
64
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО-ПОРЯДКА
(ГЛ. 1
и т. д. Длй формулы (1.42), например, получим:
или, разлагая
y'k^ — y\xk_x}
по формуле Тейлора
у'(**-1) = /(х4) — Ау"(хл)Н-уА2у'"(х^4- ...
и подставляя в (1.48), получим:
у» + лу* + 4 * (у^ - y*-i)=У* + Ау; +1 А2у" - -J- Л3у"' 4- ...,
и следовательно, три первых члена совпадают с тремя членами
разложения по формуле Тейлора (1.47).
Для начала вычисления по формулам Штермера необходимо знать
значения искомой функции не в одной, а в нескольких точках (при
применении формулы (1,42) в двух точках: х0 и х0 + Л, при
применении формулы (1.43) в. трех точках: х0, х0-}-/г и х0-]-2й,
и т. д.). Эти несколько первых значений могут быть вычисле-
ны методом Эйлера’ с уменьшенным шагом или путем использо-
вания формулы Тейлора (1.41), или кратко изложенным ниже мето-
дом Рунге.
Возьмем для определенности формулу (1.44):
Уь+1 = У» +	4 ^*-1 + ТГ Д2?л-2 + 4‘Д?<7«-з
и предположим, что, кроме заданного начального значения у0, уже
найдены уР у2 и у3. Тогда можно вычислить:
Яо = /(хо’ Уо)А. ?i = /(*i. У1)А,
?2 = /(^2- Уг)А. ?3 = /(*з> Уз) А.
а следовательно, и
д?о = <71—д?1— Яг — <7р Мг = Яз—Яг>
д2?о —	— д7о- Д2<71 = д<?2 — д?р дз?о — д2<71 — ^Яв‘
Теперь по формуле (1.44) вычисляем значение у4, зная которое
получим q4, Д^д, Д2<?2, Д39р Затем по той же формуле (1.44) вы-
числяем у5 и т. д.
§ 7] ПРИБЛИЖЕННЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ УРАВНЕНИЙ 65
Результаты вычисления заносятся в приводимую ниже, постепенно
заполняющуюся таблицу:
X	У	<7	А?	Д2<?	д39
	Уз	<7о			Д39о
*1	Уг	Vi	Л?,	Л2?,	
х2	Уз	4i	'М?		
Хз	Уз	Яз			
X,					
Хз					
X»					
Обычно требуется вычислить значение искомого решения диф-
ференциального уравнения в некоторой точке х = b с заданной
точностью. При этом сейчас же возникает вопрос, какой из формул
Штермера целесообразно пользоваться и какой шаг /г гарантирует
требуемую точность вычислений и в то же время не является
чрезмерно малым и тем самым не приводит к лишним вычислениям.
Некоторое представление о выборе формулы, по которой целесо-
образно вести вычисления, и о выборе шага дают указанные выше
порядки погрешностей при каждом шаге, при этом, конечно, надо иметь
в виду, что при нескольких шагах погрешности могут суммироваться.
При правильном выборе шага h все разности в таблице должны
меняться плавно, а последние разности в формуле (1.44) должны
'влиять лишь на запасные знаки. Резкое изменение какой-нибудь
разности указывает на то, что при выбранном шаге Л могут оказаться
неучтенными особенности изменения функции на рассматриваемом
отрезке, что может повлечь за собой значительные ошибки при вы-
числении уЛ+Р
Однако все эти соображения не являются вполне падежными,
а более точные оценки погрешности оказываются весьма громоздкими
и неудобными. Поэтому обычно применяют следующий практически до-
статочно надежный метод: выбрав, исходя из указанных выше неточных
66	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ГГЛ. t
соображений, некоторый шаг А, проводят вычисления по одной из формул
Штермера с шагом А и у и сравнивают результаты в общих точках.
Если в пределах заданной точности результаты совпадают, то счи-
тают, что шаг А обеспечивает заданную точность вычисления; если же
результаты в пределах заданной точности не совпадают, то снова
А А
уменьшают шаг вдвое и проводят вычисления с шагом у и у и
опять сравнивают результаты и т. д.
Вычисления с шагом А и целесообразно проводить парал-
лельно, чтобы как можно раньше заметить несовпадение результатов
и не производить лишней работы. Этот способ двойного счета имеет
еще то преимущество, что’ при его применении почти полностью
исключаются ошибки в вычислениях, так как они, как правило,
немедленно обнаруживаются при сравнении результатов вычислений
. А
с шагом » и у.
Для нахождения нескольких первых значений yz, необходимых
для начала вычислений по методу Штермера, кроме указанных выше
способов (метод Эйлера с уменьшенным шагом с итерациями или
без итераций или метод разложения по формуле Тейлора), можно
рекомендовать еще метод Рунге.
По методу Рунге для нахождения yft+1 надо вычислить четыре
числа:
yft). m2 = f\xk^--T,	--j-).
, h	. .	(1-49)
w3 = /(xa4--t>	+ m4 = f(xk + h, yk + mjf),
и тогда
=	+4('и1 + 2/я2 + 2/из+ »»4).	(1.50)
Обычно метод Рунге применяется лишь’ для вычисления нескольких
первых значений у1( у2...необходимых для начала вычисления по
методу Штермера, однако можно этим методом вычислять и осталь-
ные значения. Метод Рунге, так же как и метод Штермера, основан
на аппроксимации искомой интегральной кривой соприкасающейся
параболой.
Если сравнить правую часть формулы Рунге (1.50) с разложением
по формуле Тейлора
= + ••••
то окажется, что члены со степенями ниже пятой совпадают. Поэтому
при вычислении нескольких начальных значений по методу Рунге
§ 71 ПРИБЛИЖЕННЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ УРАВНЕНИЙ 67
с переходом з'атем на вычисление по методу Штермера по фор-
мулам (1.42), (1.43) или (1.44) можно вычисление вести с тем же
шагом h\ если же в дальнейшем применяется формула Штермера (1.45),
то начало вычисления по методу Рунге надо вести с уменьшенным
шагом, так как при одном и том же шаге формула (1.50) не гаран-
тирует той точности вычислений, какую гарантирует/формула (1.45).
Впрочем, нередкр даже при использовании формул Штермера (1.43)
и (1.44) начало вычислений все же ведут по формулам Рунге с умень-
шенным шагом, так как даже небольшая погрешность в вычислении
исходных для формул Штермера значений может резко уменьшить
точность дальнейших вычислений *).
Современные быстродействующие вычислительные машины дискрет-
ного действия позволяют выполнить указанные выше вычисления по
методу Штермера или Рунге с необычайной быстротой (многие десятки
и даже сотни тысяч операций в секунду), причем и процесс про-
граммирования может быть значительно упрощен применением стан-
дартных программ, разработанных для методов Штермера и Рунге.
При этом при приближенном интегрировании дифференциального
уравнения —	у), у(х0) = у0, надо составить лишь подпро-
грамму для вычисления значений у'ь — f (xk, ул) и включить ее в стан-
дартную программу.
Пример.
у' = х2 у2; у (0) = — 1.
Найти значение у (0,5) с точностью до 0,01.
Воспользовавшись разложением по формуле Тейлора
у(л) = у(0) + у'(0).+ Г^ + Ж+..,,
вычисляем значение у (х) в точках х; = 0,1 и х2 = 0,2:
у (0,1) = — 0,9088 и у (0,2) = — 0,8309
(или вместо У (0,2) вычисляем у(—0,1), что даже предпочтительнее, так
как точка х{ = — 0,1 лежит ближе к начальной точке ха = 0, чём точка
= 0,2). Дальнейшие значения вычисляем по формуле Штермера (1.43)
с шагом Л = 0,1, а результаты вычисления заносим в таблицу (без разно-
стей Д3?). После этого или параллельно проводим вычисления с шагом
-у- = 0,05. В результате получим:
у (0,5)»— 0,63.
*) Более подробно о приближенных методах интегрирования дифферен-
циальных уравнений можно прочесть в книгах А. Н. Крылова [6] и И. С. Бере-
зина и Н. П. Жидкова [7] (см. рекомендуемую литературу).
68
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
(ГЛ. !
§ 8. Простейшие типы уравнений, не разрешенных относительно
производной
Дифференциальное уравнение первого порядка, не разрешенное
относительно производной, имеет вид
F (х. у, у') = 0.	(1-51)
Если это уравнение удается разрешить относительно у', то получаем
одно или несколько уравнений
У' == /i (х, у) (/= 1, 2, ..,).
Интегрируя эти, уже разрешенные относительно производной урав-
ков решений у	с при
нения, найдем решения исходного урав-
нения (1.51).
Проинтегрируем, например, уравнение
(у')2_(А._|_у)у- + ху==0. (1.52)
Разрешая это квадратное уравнение отно-
сительно у', будем иметь: у' = х и у' — у.
Интегрируя каждое из полученных урав-
нений, находим:
у2
У-у + с	(1.53)
и
у — се*	(1-54)
(рис. 1.24). Оба семейства решений удов-
летворяют исходному уравнению.
Гладкими интегральными кривыми
уравнения (1.52) будут также кривые, со-
ставленные из дуги интегральной кривой
семейства (1.53) и дуги интегральной кри-
вой семейства (1.54), если в общей точ-
ке они имеют общую касательную. На
рис. 1.25 изображена интегральная кри-
вая уравнения (1.52), составленная из графи-
с = у, —оо<х<1, и y — cef при
с = е~1, I У х < со, а на
составленная из графиков
рис. 1.26 — интегральная кривая уравнения (1.52),
решений у = — при х-^0 и у^О при х > 0.
Итак, уравнение
F(x, у, у')==0
(1.51)
может быть проинтегрировано путем разрешения относительно у' и
интеграции полученных при этом уравнений у' = (х, у) (/ = 1,
2, ...), уже разрешенных относительно производной.
§ 81 УРАВНЕНИЯ. НЕ РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ 69
Однако далеко не всегда уравнение (1.51) легко разрешается
относительно у' и еще реже полученные после разрешения относи-
тельно у' уравнения — у) легко интегрируются, поэтому
часто приходится интегрировать уравнения вида (1.51) иными мето-
дами. Рассмотрим следующие случаи.
1.	Уравнение (1.51) имеет вид
/?(у') = 0.	(1.55)
причем существует по крайней мере один действи-
тельный корень у' = А; этого уравнения.
Так как уравнение (1.55) не содержит х и у, то kt — постоянное.
Следовательно, интегрируя уравнение у'=А/( получим у = ktx с,
или ki — -----. но kj является корнем уравнения (1.55), следова-
тельно, F = 0 является интегралом рассматриваемого урав-
нения.
Пример 1.
(у')7-(у')6 + у' + з = о.
Интеграл уравнения
(-МЧ^Ч2?^3-0-
2.	Уравнение (1.51) имеет вид
F(x, у') = 0.	(1-56)
Если это уравнение трудно разрешить относительно у', то целе-
сообразно ввести параметр t и заменить уравнение (1.56) двумя
уравнениями: х = <р(/) и у' = хр (£). Так как dy = у' dx, то в дан-
ном случае dy — т|? (/) <p' (t) dt, откуда У — f (t) ср'(t) dtс и, сле-
довательно, интегральные кривые уравнения (1.56) определяются
70	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. I
в параметрической форме следующими уравнениями:
х — <р (Z),
у = J ф (/) ф' (t) dt -I- с.
Если уравнение (1.56) легко разрешимо относительно х, х— ф(у'),
то почти всегда удобно в качестве параметра ввести у' ~ t. Тогда
х = ф(0. dy — y'dx — tq'(t)dt, у = J tq/ (t) dt ~f- с.
Пример -2.
х = (У)’-/т-1.
Положим у' = t, тогда
x = t2 — t — 1,	(1.57)
dy = у' dx = t (3t2 — I) dt,
3/4 t2 ,
У = -4----2-+C,‘	(1,58)
Уравнения (1.57) и (1.58) определяют в параметрической форме семейство
искомых интегральных кривых.
Пример 3.	_____
х/1+у'2 = У'-
Полагаем у' = tg/, —	тогда
х = sin t,	(1.59)
dy = у' dx — tgt cos t dt = sin t dt,
y = — cos <-|-Ci	(1.60)
или, исключая t из уравнений (1.59) и (1.60), получим х2-|-(у— с,)2 = 1—
семейство окружностей.
3.	Уравнение (1.51) имеет вид
F(y, /) = 0.	(1.61)
Если это уравнение трудно разрешить относительно у', то, как
и в предыдущем случае, целесообразно ввести параметр t и заме-
нить уравнение (1.61) двумя уравнениями: y — <p(t) и у'=ф(/). Так
,	, ,	, dy q>' (t) dt	Г q>' (t) dt ,
как dy — y dx, то dx =	, откуда х = J 4-с.
Следовательно, искомые интегральные кривые в параметрической
форме определяются уравнениями
Г ср' (/) dt
х==./ ш +с "
В частности, если уравнение (1.61) легко разрешимо относи-
тельно у, то обычно за параметр удобно взять у'.
§ 81 УРАВНЕНИЯ, НЕ РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ П
Действительно, если у = ф(у'), то, полагая у'=t, получим
...	, dy w'(t)dt
У—Ч>((). dx = -^- — -^-i—,
/' q>' (t) dt
X=ZJt~ + C-
П p и м e p 4.
У = (У')8 + (У')3 + у' + 5.
Полагаем у' = t\ тогда
у=/5 + /3-|_/ + 5>	(1.62)
dx = d^ = (y + 3^+i)rfz = (5/3 + 3/; dt
* = ^ + ^- + N'l + <-	(1.63)
Уравнения (1.62) и (1.63) являются параметрическими уравнениями семейства
интегральных кривых.
Примера.
--У-
1/1 +у'2
Полагаем у' = sh t, тогда
у = ch t,	(1.64)
dy sh t dt
dx = —7- = —г—.— = dt,
y' shZ
x = t + c	(1.65)
или, исключая из (1.64) и (1.65) параметр t, получаем у=>сЬ(лг — с).
Рассмотрим теперь общий случай: левая часть уравнения
F(x, у, у') = 0	(1-51)
зависит от всех трех аргументов х, у, у'. Заменим уравнение (1.51)
его параметрическим представлением:
х = <р(«, v), у = ф(а, v), у'= /(«• V)'
Пользуясь зависимостью dy = у' dx, будем иметь
ЛЬ .	, ЛЬ ,	,	. Г да ,	, да , Т
du +--+- dv = %(и, v) \-^-duA-^-dv ,
1 dv Л v [ du 1 dv j ’
dv
откуда, разрешая относительно производной , получим
dtp Лр
rfv у- ди du
^L_X(B1V)^'
dv Л ’ dv
(1.66)
В результате получено уравнение первого порядка, уже разрешен-
ное относительно производной, и тем самым задача сведена к уже
72
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
[ГЛ. I
рассмотренной в предыдущих параграфах, однако, конечно, полу-
ченное уравнение (1.66) далеко не всегда будет интегрироваться
в квадратурах.'
Если уравнение
F(x, у, у') = 0
легко разрешимо относительно у, то за параметры и и v часто
удобно брать х и у'. Действительно, если уравнение (1.51) приво-
дится к виду
у=/(х, у'),	(1.67)
то, считая х и у' = р параметрами, получим
У=/(х, р), dy — -~dx + dp
или
dy	__df	।	df	dp
dx	dx	'dp	dx ’
____i	df	dP	л
?	dx	dp	dx	( •	)
Интегрируя уравнение (1.68) (конечно, оно далеко не всегда инте-
грируется в квадратурах), получим Ф(х, р, с) = 0. Совокупность
уравнений Ф(х, р, с)=0 и у = /(х, р), где р—параметр, опре-
деляет семейство интегральных кривых.
Заметим, что уравнение (1.68) может быть получено дифферен-
цированием уравнения (1.67) по х. Действительно, дифференцируя
(1.67) по х и полагая у' — р,
падает с (1.68). Поэтому этот
df . df dp
получим р =	+	ЧТО сов-
метод часто называют интегрированием
дифференциальных уравнений с помощью дифференцирования.
Совершенно аналогично часто интегрируется уравнение
F(x, у, у') = 0,
если оно легко разрешимо относительно х:
x = f(y, у').	(1.69)
В этом случае, взяв за параметры у и у' = р
мостыо dy = у' dx, получим
^у = р[-^ру + -^]
или
1 _ I df dp
р dy ' dp dy
и пользуясь зависи-
(1.70)
Интегрируя уравнение (1.70), получим Ф(у, р, с) = 0. Это уравне-
ние совместно с х = /(у, р) определяет интегральные кривые исход-
§ 81 УРАВНЕНИЯ. НЕ РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ 73
ного уравнения. Уравнение (f.70) может быть получено из уравнения
(1.69) дифференцированием по у.
В качестве примера применения этого метода рассмотрим линей-
ное относительно х и у уравнение
у = хф(у')4-ф(у'),
называемое уравнением Лагранжа. Дифференцируя по х и полагая
у' = р, получим
P = >f(P) + xq>' (р)-^£- + ф' (р)-—-,	(1.71)
или
|р-ф(р)]-^-=хф/(р) + ф/(р).	(1.72)
dx
Это уравнение линейно относительно х и и, следовательно,
легко интегрируется, например, методом вариации постоянной.
Получив интеграл Ф(х, р, с) = 0 уравнения (1.72) и присоединяя
к нему у = хф (р)-J-ф (р), получим уравнения, определяющие иско-
мые интегральные кривые.
При переходе от уравнения (1.71) к уравнению (1.72) пришлось
делить на . Но при этом мы потеряем решения, если они суще-
ствуют, для которых р постоянно, а значит ^- = 0. Считая р по-
стоянным, замечаем, что уравнение (1.71) удовлетворяется лишь
в том случае, если р является корнем уравнения р—ф(р) = 0.
Итак, если уравнение р — ф(р) = 0 имеет действительные корни
р = ph то к найденным выше решениям уравнения Лагранжа надо
еще добавить у = хф (р) —J—ф(р), P = Pi- или, исключая р,
у — хф (pt) -]-ф (pi) — прямые линии.
Отдельно надо рассмотреть случай, когда р — ф(р) = 0, и сле-
dp
довательно, при делении на теряется решение р = с, где с —
произвольная постоянная. В этом случае ф(у') = у' и уравнение
у = хф (у') -ф- ф (у') принимает вид
у = ху' -ф-Ф (уО— уравнение Клеро.
Полагая у'= р, получим у — хр -ф-ф(р). Дифференцируя по х,
будем иметь:
ИЛИ
(х + ф'(р))-^- = 0,
откуда или-^- = 0 и, значит, р — с, или х -j- ф' (р) — 0.
74	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. I
В первом случае, исключая р, получим:
у = сх-|-1|>(с)	' '	(1.73)
— однопараметрическое семейство интегральных прямых. Во втором
случае решение определяется уравнениями
у = хр4~гр(р) и х -|~т|/(р) = 0.	(1.74)
Нетрудно проверить, что интегральная кривая, определяемая
уравнениями (1.74), является огибающей семейства интегральных пря-
мых (1.73).
Рис. 1.27.	Рис. 1.28.
Действительно,/огибающая некоторого семейства Ф(х, у, с) = 0
определяется уравнениями
Ф(х, у, с) = 0 и £ = 0,	(1.75)
которые для семейства у = сх-|-1р(О имеют вид
у = сх -Ь "ф (О. х + 1|)'(О = 0
и лишь обозначением параметра отличаются от уравнений (1.74)
(рис. 1.27)'.
Замечание. Как известно, уравнения (1.75) могут определять,
кроме огибающей, геометрические места кратных точек, а иногда
и другие кривые, однако если хотя бы одна из производных
дФ
и -т— отлична от
ду
нуля и обе ограничены в точках, удовлетворяю-
щих уравнениям (1.75), то эти уравнения определяют только огибаю-
D	'	дф	дФ .
щую. В данном случае’эти условия выполнены:	— с,	1*
Следовательно, уравнения (1.75) определяют огибающую, которая
может выродиться в точку, если семейство (1.73) является пучком
прямых.
§ 91
ОСОБЫЕ РЕШЕНИЯ
75
Примерб.
у = ху' —у'2 — уравнение Клеро.
Однопараметрическое семейство интегральных прямых имеет вид
у — сх — с2. Кроме того, интегральной кривой является огибающая этого
семейства, определяемая уравнениями у — сх — с2 и х — 2с = 0. Исключая с,
получаем у = (рис. 1.28).
Пример?.
у = 2яу'— у'3—уравнение Лагранжа.
У' = Р<
у — '2хр — /А	(1.76)
Дифференцируя, получаем
+	<1-77)
dp
и после деления на приходим к уравнению
2*+3'!-
линейное уравнение, получаем х = у р2. Следова-
ьные кривые определяются уравнениями у = 2хр — р2,
Интегрируя это .
тельно, интегральные кривые определяются уравнениями у .	.
с, . Зр2
Х=^ ~т4-~7“•
р2 1	4
п	dp
При делении на как указывалось-выше, теряются решения р — Pt,
где pi — корни уравнения р — <р (р) —V. В данном случае теряется решение
р = 0 уравнения (1-77), которому, в силу уравнения (1.76), соответствует ре-
шение исходного уравнения у — 0.
§ 9. Теорема существования и единственности
для дифференциальных уравнений, не разрешенных
относительно производной. Особые решения
В § 6 была доказана теорема существования и единственности
решения у(х) уравнения	у), удовлетворяющего условию
у(х0) — у0. Аналогичный вопрос возникает и для уравнений вида
Р(х, у, у') = 0. Очевидно, что для таких уравнений через некото-
рую точку (х0, у0), вообще говоря, проходит уже не одна, а не-
сколько интегральных кривых, так как, разрешая уравнение
F (х, у, у') = 0 относительно у', мы, как правило, получаем не одно,
а несколько действительных значений y'—f^x, у) (г = 1, 2, .. .),
и если каждое из уравнений у' — /г (х, у) в окрестности точки
(лг0, Уо) удовлетворяет условиям теоремы существования и единствен-
ности § 6, то для каждого из этих уравнений найдется единственное
76	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (ГЛ. I
решение, удовлетворяющее условию у (х0) = у0. Поэтому свойство
единственности решения уравнения F (х, у, у') = 0, удовлетворяю-
щего условию у (х0) = у0, обычно понимается в том смысле, что
через данную точку (х0, у0) по данному направлению проходит
не более одной интегральной кривой уравнения F (х, у, у') = 0.
"	/ <^У V
Например, для решений уравнения I—1=0 свойство единствен-
ности всюду выполнено, так как через каждую точку (х0, у0) проходят две
интегральные кривые, но по различным направлениям. Действительно,
dv
-£=±1, у = х-Н и у = —х + с.
Для уравнения (у')2 — (х + У) У' + ~ 0, рассмотренного на стр. 68, в точ-
ках прямой у = х свойство единственности нарушено, так как через точки
этой прямой проходят интегральные кривые уравнений у' = х и у' = у по
одному и тому же направлению (рис. 1.29).
Теорема 1.5. Существует единственное решение у —у (х),
х0—й0 <1 х <1 х0 h0, где Ао достаточно мало, уравнения
F (х, у, у') = 0,	(1.78)
у, у') удовлетворяет условиям-.
F(x, у, у') непрерывна по всем аргументам;
dF
производная существует и отлична от нуля;
удовлетворяющее условию у(х0) = у0, для которогб у' (х0^ = у'о,
где Уд— один из действительных корней уравнения F (х0, у0, у')=0,
если в замкнутой окрестности точки (х0,
F (х,
1)
2)
Уо. Уо) Функция
§ 9]
ОСОБЫЕ РЕШЕНИЯ
77
'	л	др
3) существует ограниченная по модулю производная —,
Доказательство. Согласно известной теореме о существо-
вании неявной функции можно утверждать, что условия 1) и 2)
гарантируют существование единственной непрерывной в окрест-
ности точки (х0, у0) функции у' = f (х, у), определяемой уравне-
нием (1.78) и удовлетворяющей условию у0 = f (х0, у0). Остается
проверить, будет ли функция /(х, у) удовлетворять условию Лип-
„	I d f I . .,
шица или более грубому условию |	| N в окрестности точки
(х0, Уо), так как тогда можно будет утверждать, что уравнение
у' = /(х, у)	(1.79)
удовлетворяет условиям теоремы существования и единственности
(см. § 6, стр. 40) и, следовательно, существует единственное реше-
ние уравнения (1.79), удовлетворяющее условию у(х0) = у0, а вместе
с тем существует единственная интегральная кривая уравнения (1.78),
проходящая через точку (х0, у0) и имеющая в ней угловой коэф-
фициент касательной у^.
Согласно известной теореме о неявных функциях можно утвер-
ждать, что при выполнении условий 1), 2), 3) производная су-
ществует и может быть вычислена по правилу дифференцирования
неявных функций.
Дифференцируя тождество F (х, у, у') = 0 по у и принимая во
внимание, что у' —f (х, у), получим
или
dF dF Of
ду ду' ду
др
df _	ду
ду	dF ’
W
откуда, принимая во внимание условия 2) и 3), следует, что
I I В 3аМКНуТ°й окРестности точки (*о- Уо)-
Множество точек (х, у), в которых нарушается единственность
решений уравнения
^(х, у, у') = 0,
(1.78)
называется особым множеством.
множе-
78	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ГГ.Л. 1
В точках особого множества должно быть нарушено по край-
ней мере одно из условий теоремы 1.5. В дифференциальных
ниях, встречающихся, в прикладных задачах, условия I) и 3)
6F , п
выполняются, но условие 2)	0 часто нарушается.
Если условия 1) и 3) выполнены, то в точках особого
ства должны одновременно удовлетворяться уравнения
лр
Г(х, у, у') = 0 и -^- = 0.
Исключая из этих уравнений у', получим уравнение
Ф(Х, у) = 0,
уравне-
обычно
СЕвО)
(1-81)
которому должны удовлетворять точки особого множества. Однако
не в каждой точке, удовлетворяющей уравнению (1.81), обязательно
нарушается единственность решения уравнения (1.78), так как усло-
вия теоремы 1.5 лишь достаточны для единственности решения, но
не являются необходимыми, и следовательно, нарушение какого-
нибудь условия теоремы не обязательно влечет за собой наруше-
ние единственности.	,
Итак, только среди точек кривой Ф(х, у) = 0, называемой
р-дискриминантной кривой (так как уравнения (1.80) чаще записы-
dF
ваются в виде F (х, у, р) — 0 и -^- = 0), могут быть точки осо-
бого множества.
Если какая-нибудь ветвь y = tp(x) кривой Ф(х, у)—0 принад-
лежит особому множеству и в то же время является интегральной
кривой, то она называется особой интегральной кривой, а функция
у = ф(х) называется особым решением. '
Итак, для нахождения особого решения уравнения
F(x, У- У/) = 0	,	(1'78)
надо найти р-дискриминантную кривую, определяемую уравнениями
F(x, у, р) = 0,	—0,
выяснить путем непосредственной подстановки в уравнение (1.78),
есть ли среди ветвей р-дискриминантной кривой интегральные кри-
вые, и, если такие кривые есть, то еще проверить, нарушена ли
в точках этих кривых единственность или нет. Если единствен-
ность нарушена, то такая ветвь р-дискриминантной кривой является
особой интегральной кривой.
Пример 1. Имеет ли уравнение Лагранжа у — 2ху' — (у')2 особое
решение?
Условия 1) и 3) теоремы существования и единственности выполне-
ны. р-дискриминантная кривая определяется уравнениями: у = 2хр — р2,
§9]	ОСОБЫЕ РЕШЕНИЯ	79
2х — 2р = 0, или, исключая р, у = х2. Парабола у = х2 не является интег-
ральной кривой, так как функция у ?= х2 не удовлетворяет исходному
уравнению. Особого решения нет.
Пример 2. Найти особое решение уравнения Лагранжа
4	8
*-У = |(/)2—^(/)9-	(1.82)
Условия 1) и 3) теоремы существования и единственности выполнены.
р-дискриминантная кривая определяется уравнениями
4	8,8	п
« —У = -д Р2—27 Р3. д-(Р — Р2) = 0.
Из второго уравнения находим р = 0 или р = 1; подставляя в первое урав-
нение, получим:
у — х или у — х—
Лишь вторая из этих функций является решением исходного уравнения.
проинтегрировать уравнение (1.82) и выяснить, проходят ли через точки пря-
4
мой у = х—по направлению этой прямой другие интегральные кривые.
Интегрируя уравнение Лагранжа (1.82), получим:
(у — с)2 = (х — с)3. '	(1.83)
4
Из уравнения (1.83) и рис. 1.30 видно, что прямая у = х — является
огибающей семейства полукубических парабол (у — с)2 — (х — с)3 и, следо-
4
вательно, в каждой точке прямой у = х — нарушена единственность — по
одному и тому же направлению проходят две интегральные кривые: прямая
4
у = х — и касающаяся этой прямой в рассматриваемой точке полукуби-
ческая парабола.
80
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
(ГЛ. I
Итак, особым решением является у — х—
В этом примере огибающая семейства интегральных кривых является
особым решением.
Если огибающей семейства
Ф(х, у, с) = 0	(1.84)
называть . кривую, которая в каждой своей точке касается некото-
рой кривой семейства (1.84) и каждого отрезка которой касается
бесконечное множество кривых рассматриваемого семейства, то
огибающая семейства интегральных кривых некоторого уравнения
F (х, у, у') = 0 всегда будет особой интегральной кривой.
Действительно, в точках огибающей значения х, у и у' совпа-
дают со значениями х, у и у' для интегральной кривой, касающейся
огибающей в точке (х, у), и следовательно, в каждой точке оги-
бающей значения х, у и у' удовлетворяют уравнению F (х, у, у') = 0,
т. е. огибающая является интегральной кривой (рис. 1.31). В каждой
точке огибающей нарушена единственность, так как через точки
огибающей по одному направлению проходят по крайней мере две
интегральные кривые: огибающая и касающаяся ее в рассматрива-
емой точке интегральная кривая семейства (1.84). Следовательно,
огибающая является особой интегральной кривой.
Зная семейство интегральных кривых Ф(х, у, с) = 0 некоторого
дифференциального уравнения F(x, у, у') — 0, можно определить
его особые решения путем нахождения огибающей. Как известно
из курса дифференциальной геометрии или из курса математиче-
ского анализа, огибающая входит в состав с-диСкриминантной кри-
вой, определяемой уравнениями
Ф(х, у, с) = 0 и-^- = 0,
однако, кроме огибающей, в состав с-дискриминантной кривой
могут входить и другие множества, например множество кратных
„	дФ <?Ф п
точек кривых рассматриваемого семейства, в которых ~^ =
Чтобы некоторая ветвь с-дискриминантной кривой заведомо была
огибающей, достаточно, чтобы на ней:
1)	существовали ограниченные по модулю частные производные
<?Ф , п <ЭФ , п
2)	—— Ф 0 или	-т— =# 0.
’дх	ду
Заметим, что эти условия лишь достаточны, так что кривые, на ко-
торых нарушено одно из условий 1), 2), тоже могут быть огибаю-
щими.
§ 91	ОСОБЫЕ РЕШЕНИЯ	81
Пример 3. Дано семейство интегральных кривых (у — с)г = (х—с)з
некоторого дифференциального уравнения (см. пример 2 на стр. 79). Найти
особое решение того же уравнения.
Находим с-дискриминантную кривую:
(у — с)2 = (х — с)3 и 2 (у — с) = 3 (х — с)2.
Исключая параметр с, получим
4
у = х и х - у - 27 = о.
4
Прямая у = х —2? является огибающей, так как на ней выполнены все
условия теоремы об огибающей. Функция у = х не удовлетворяет дифферен-
циальному уравнению. Прямая у = х является геометрическим местом
точек возврата (см. рис. 1.30). В точках этой прямой нарушено второе усло-
вие теоремы об огибающей.
Пример 4. Дано семейство интегральных кривых
у5— х4с = 0	(1.85)
некоторого дифференциального уравнения первого порядка. Найти особое
решение того же уравнения.
Задача сводится к нахождению огибающей рассматриваемого семейства.
Если непосредственно применить указанный выше метод нахождения огибаю-
щей, то получим противоречивое уравнение 1=0, откуда казалось бы
естественно сделать вывод, что семейство (1.85) не имеет огибающей. Однако
в данном случае производная от левой части уравнения (1.85) по у,
дФ
<Эу
_4
= =у 5, обращается в бесконечность при у = 0, и следовательно, не
□
исключена возможность того, что у = 0 будет огибающей семейства (1.85),
которую не удалось найти общим методом ввиду нарушения на прямой у = 0
условий теоремы об огибающей.
Следует преобразовать уравнение (1.85) так, чтобы для преобразованного
уравнения, эквивалентного исходному, уже выполнялись условия теоремы об
огибающей. Например, запишем уравнение (1.85) в виде у — (х—’с)6 = 0.
Теперь условия теоремы об огибающей выполнены, и, применяя общий метод,
получим:
у = (х — с)5, 5 (х — с)4 = 0,
или, исключая с, будем иметь уравнение огибающей у = 0 (рис. 1.32).
Пример 5. Дано семейство интегральных кривых
у2 — (х — с)3 = 0
(1.86)
некоторого дифференциального уравнения первого порядка. Найти особое
решение того же уравнения.
с-дискрйминантная кривая определяется уравнениями
у2 — (х — с)3 = 0 и х— с = 0,
82	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА [ГЛ. 1
или, исключая с, получим у = 0. На прямой у — 0 обращаются в нуль обе
частные производные —г— и от левой части уравнения (1.86), следова-
тельно, у = 0 является геометрическим местом кратных точек кривых семей-
ства (1.86), в данном случае точек возврата. Однако это геометрическое
Рис. 1.32.
место точек возврата в рассматриваемом примере является одновременно и
огибающей. На рис. 1.33 изображены полукубические параболы (1.86) и их
огибающая у = 0.
Задачи к главе 1
1.	tg у dx — ctg х dy = 0.	10.	x (In x — In y) dy — у dx = 0.
2.	(12хН-5у —9) dx +	11.	xy(y')2 — (^2 + №) y' +
	+ (5* + 2у — 3) dy = 0.		4-xy=o.
		12.	(yT = 9y4. X
3.	x-^- = y + V х2 + у2.		
4.	x dx +у + х3-	13.	dx	~T . x ~dt=e +t
5.	у dx — x dy = x2 у dy.	14.	x2 + (y')2=l.
6.		15.	У = ХУ' + —-
7. 8. 9.	у sin x y' cos x = I. y'=^-’’. = x 4- sin t. dt	'	16. 17. 18.	х = (у')3-У'+2. d-У _ У
			dx x 4- У3 ’ У = (У')4 —(У')3 —2.
19.	Найти ортогональные траектории семейства ху = с, т. е. найти линии,
ортогонально пересекающие кривые указанного семейства.
20.	Найти кривую, у которой подкасательная -вдвое больше абсциссы
точки касания.
21.	Найти кривую, у которой отрезок, отсекаемый касательной на оси
ординат, равен абсциссе точки касания.
22.	Найти ортогональные траектории семейства
х2 у2 — 2ах.
23.	Считая, что скорость охлаждения какого-либо тела в воздухе про-
порциональна разности между температурами тела и воздуха, решить сле-
дующую задачу: если температура воздуха равна 20° С и тело в течение
ЗАДАЧИ К ГЛАВЕ 1
83
20 Мин. охлаждается от 100 до 60° С, то в течение какого времени темпе-
ратура тела достигнет 30° С?
24.	Моторная лодка движется в спокойной воде со скоростью 10 км/час.
На полном ходу ее мотор был выключен и через t = 20 сек. скорость лодки
уменьшилась до = 6 км/час. Определить скорость лодки через 2 мин.
после остановки мотора, считая, что сопротивление воды пропорционально
скорости движения лодки.
25.	Найти форму зеркала, отражающего параллельно данному направ-
лению все лучи, выходящие из заданной точки.
26.	У,2+у2=4.
27.	Найти кривую, у которой отрезок касательной, заключенный между
осями координат^ делится в точке касания на равные части.
28.	rfy = 2У-Х-4.	29> ^У _ У + 2 = 0.
dx 2х — у + 5	dx 1 + х '
30.	Численно проинтегрировать уравнение
-g-^x+у2,	у(0)=0.
Определить у (0,5) с точностью до 0,01.
31.	Численно проинтегрировать уравнение
dy
~г~ — ХУ'
dx J
У (0) =0.
Определить у (0,6) с точностью до 0,01.
32.	у'= 1,31л — 0,2у2, у (0) = 2.
Составить таблицу пятнадцати значений у с шагом h = 0.02.
,33. у = 2лу' — у'2. 34. -^ = cos (х — у).
35.	Пользуясь методом изоклин (см. стр. 17), сделать набросок семей-
ства интегральных кривых уравнения
dy
dx
36.	(2л —|— 2у — 1) dx -f- (х у — 2)dy = 0.
37.	у'3—у'е2-г = 0.
38.	Найти ортогональные траектории парабол у2 -|- 2ах = аг.
39.	Имеет ли дифференциальное уравнение у =5лу'— (у')2 особое
решение?
40.	Приближенно проинтегрировать уравнение
^ = Х-У2. у(1)=0
у2.
методом последовательных приближений (определить и у2).
41. у = х'г
dx.
42.	Имеет ли уравнение у' = х — 5у 2 особое решение?
43.	(х — у) у dx — x2dy=0.
44.	Найти ортогональные траектории семейства у2 = cxJ.
45.	х -|- 5х = l0t-}-2 при t = 1, х = 2.
[ГЛ. I
84	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
46.	X = у + ПРИ t ~ 2' X = 4.
47.	у = ху' -f- у'2 при х = 2, у — — 1.
48.	у = ху' -j- У'2 при х = 1, у — — I.
49	.. Зх-4у-2
dx Зх — 4у — 3’
50.	х — х etg i = 4 sin t.
у'2
51.	у = x2-f-2y x-j--2y~.
52.	у' — JL 4-x3y2 = 0.
53.	у (1 4-У'2) = <z.
54.	(x2 — y) dx 4- (x2y2 4* x) dy = 0.
55.	Найти интегрирующий множитель уравнения
(Зу2 — х) dx 4- 2у (у2 — Зх) dy — 0.
имеющий вид ц = р (х 4- у2).
56.	(х — y)ydx — x2rfy = 0.
58.	ху' — у2 In х 4- У = 0.
59.	(х2 — 1) У' 4" 2ху — cos х = 0.
60.	(4у4-2x4-3)у'— 2у— х— 1 =0.
61.	(у2 — х) у' — у 4- х2 = 0.
62.	(у2 — х2) у' 4- 2ху = 0.
63.	Зху2у' 4- у3 — 2х = 0.
64.	(у')2 + (х-Ь«)У' — У = 0> где а — постоянная.
65.	(у')2 — 2ху' 4- у = 0.
66.	(у')2 4- 2уу' etgx — у2 = 0.
ГЛАВА 2
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПОРЯДКА ВЫШЕ ПЕРВОГО
§ 1.	Теорема существования и единственности
для дифференциального уравнения и-го порядка
Дифференциальные уравнения n-го порядка имеют вид
у(.«) = /(Х, у, у'..........У(л_1)),
(2.1)
или, если они не разрешены относительно старшей производной,
Д(х, у, у', ..., у<«>) = 0.
Теорема существования и единственности для уравнения п-го
порядка легко может быть получена путем сведения его к системе
уравнений, для которой на стр. 51 теорема существования и един-
ственности уже была доказана.
Действительно, если в уравнении у<я> = /(х, у, у', ..., у^-1))
неизвестными функциями считать не только у, но и у' — уР
у" — у2.....y(«-i) — уя1, то уравнение (2.1) заменяется системой
У = уР
= У2>
Ул-2 Ул-1’
y'n^ = f(x, У. У,........Ул-,)-
(2.2)
после чего уже можно применить теорему о существовании и един-
ственности решения системы уравнений (см. стр. 51), согласно кото-
рой, если правые части всех уравнений системы (2.2) непрерывны
в рассматриваемой области и удовлетворяют условию Липшица по
всем аргументам, кроме х, то существует единственное решение систе-
мы (2.2), удовлетворяющее условиям
у(Х0) = У0, У1(Х0) = У10......Ул-1(^о)	= Ул-1,О-
86	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ 2
Правые части первых п— 1 уравнений (2.2) непрерывны и удовле-
творяют не только условию Липшица, но даже более грубому усло-
вию существования ограниченных производных по у, ур у2....ул_р
Следовательно, условия теоремы существования и единственности
будут выполнены, если правая часть последнего уравнения у' =
— f(x< У< У1.....Уп-i) будет непрерывна в окрестности начальных
значений и будет удовлетворять условию Липшица по всем аргумен-
там, начиная со второго, или более грубому условию существования
ограниченных частных производных по всем аргументам, начиная со
второго.
Итак, возвращаясь к прежним переменным х и у, окончательно
получаем следующую теорему существования и единственности:
Теорема 2.1. Существует^единственное решение дифферен-
циального уравнения п-го порядка yW = f(x, у, у'........у<я-1)),
удовлетворяющее условиям
У (хо) = Уо- У' (хо) = У0’ У" (О = Уо- • У<п"У> (хо) = уГ”.
если в окрестности начальных значений (х0, у0, у', .... у^п-1))
функция f является непрерывной функцией всех своих аргу-
ментов и удовлетворяет условию Липшица по всем аргумен-
там, начиная со второго.
Последнее условие может быть заменено более грубым условием
существования в той же окрестности ограниченных частных произ-
водных первого порядка от функции f по всем аргументам, начиная
со второго.
Общим решением дифференциального уравнения га-го порядка
называется множество решений, состоящее из всех без исключения
частных решений. Если правая часть уравнения
у(«) = /(х, у, у', у"..у(я-1))	(2.1)
в некоторой области изменения аргументов удовлетворяет условиям
теоремы существования и единственности, то общее решение урав-
нения (2.1) зависит от п параметров, в качестве которых могут быть
выбраны, например, начальные значения искомой функции и ее про-
изводных у0, у', у", ..., у^"-1). В частности, общее решение урав-
нения второго порядка у" — f(x, у, у') зависит от двух параметров,
например от у0 и у'о. ^Если же фиксировать yfl и у', т. е. задать
точку (х0, у0) и направление касательной к искомой интегральной
кривой в этой точке, то при выполнении условий теоремы суще-
ствования и единственности этими условиями определяется единствен-
ная интегральная кривая.
§ 2]	ПРОСТЕЙШИЕ случаи понижения порядка	87
Например, в уравнении движения. материальной точки массы по
прямой под действием силы / (t, х, х):
тх = f(t, х, х),
задание начального положения точки х(^0) = х0 и начальной скорости
х (/0) ±= х0 определит единственное решение, единственный закон дви-
жения х = х(О. если, конечно, функция f удовлетворяет условиям
теоремы существования и единственности.
Теорема о непрерывной зависимости решения от параметров и от
начальных значений, рассмотренная на стр. 54, без изменения метода
доказательства переносится на системы дифференциальных уравнений,
а следовательно, и на уравнения n-го порядка.
§ 2. Простейшие случаи понижения порядка
В некоторых случаях порядок дифференциального уравнения может
быть понижен, что обычно облегчает его интегрирование.
Укажем несколько наиболее часто встречающихся классов урав-
нений, допускающих понижение порядка.
I. Уравнение не содержит искомой функции и ее
производных до порядка k — 1 включительно:
F(x, у(Ч у<*+1>, .... у<л>) = 0.	(2.3)
В этом случае порядок уравнения может быть снижен до п — k
заменой переменных y(ft) — р.
Действительно, после замены переменных уравнение (2.3) прини-
мает вид
F(x, р, р'.....р(л-*)) = 0.
Из этого уравнения определяется р = р(х, Ср с2, ..., cn_k), а у
находим из у!*) = р(х, ср с2.......сл-а) ^-кратным интегриро-
ванием. В частности, если уравнение второго порядка не содержит у,
то замена переменных у' = р приводит к уравнению первого порядка.
Пример!.
rf5y	1 d*y
dx5	х dxi
„ d4y	dp 1	_
Полагая = p, получаем -f----------p — 0; разделяя переменные и интегри-
dx	dx x	'
"	d* у
руя, будем иметь: 1п| р | = In | х | 4- In с, или р—сх,	откуда
у = CtXs + с2х3 + с3х2 4- с4х 4- с6.
Пример 2. Найти закон движения тела,-падающего в воздухе без
начальной скорости, считая сопротивление воздуха пропорциональным квад-
рату скорости.
88	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Уравнение движения имеет вид
где $— пройденный телом путь, т — масса тела, t — время. При i = 0
_	л d$ л
будет s=0 и —^- = 0,
Уравнение не содержит явно неизвестной функции $, следовательно,
ds „
можно понизить порядок уравнения, считая — = v. При этом уравнение дви-
жения примет вид
dw	, о
т mg — kv2.
Разделяя переменные и интегрируя, получим
V
mdv	Г dv 1	, ,, kv
mg — kv2	J mg — kv2	j/^’
откуда v =	th (fe Уg t)', умножая на di и интегрируя еще раз. найдем
закон движения:
-^-In ch (k^g t)-
2.	Уравнение не содержит независимого пере-
менного:
F(y. /, у"......у(">) = 0.
В этом случае порядок уравнения можно понизить на единицу
подстановкой у' = р, причем р рассматривается как новая неизве-
стная функция у, р = р(у), и следовательно, все производные —
dx*
надо выразить через производные от новой неизвестной функции
Р(У) по у:
d2y   dp   dp dy   dp
dx2	dx	dy dx	dy
dx3 ' dx \dy } dy dy ) dx dy2 dy I
и аналогично для производных более высокого порядка. При этом
d*y
очевидно, что производные —- выражаются через производные по-
dx*
рядка не выше k — 1 от р по у, что и приводит к понижению
порядка на единицу.
§ 21
ПРОСТЕЙШИЕ СЛУЧАИ ПОНИЖЕНИЯ ПОРЯДКА
89
В частности, если уравнение второго порядка не содержит неза-
висимого переменного, то указанная замена переменных приводит
к уравнению первого порядка.
Пример 3.
У
= 0.
разделяющимися пере-
чу
# = С1У или = cty.
In| у | — c^-t- In с2 или
v dv = — a2 sin х dx,
_ dy d2y dp
Полагая = p. = p • получим уравнение с
dp .	_	,
менными ур — р2 = 0, общее решение которого
Снова разделяя переменные и интегрируя, получим
У = с2ес'х.
Притиер 4. Проинтегрировать уравнение математического маятника
х 4- a2 sin х = 0 при начальных условиях х (0) = ха, х (0) = 0.
Понижаем порядок, полагая
•	dv
х — V, x — v ——,
dx
V2
— = a2 (cos х — cos х0),
v = ± а К2 (cos х — cos х0),
= ± а У 2 (cos х — cos х0),
dx
ay 2 > у cos х — cos х.
Интеграл, стоящий в правой части, не берется в элементарных функциях,
но легко сводится к эллиптическим функциям.
3.	Левая часть уравнения
F(x, у, у', у". .... /«))== 0	(2.4)
является производной некоторого дифференциаль-
ного выражения (я—1)-го порядка Ф(х, у, у', .... y'n~v>).
В этом случае легко находим так называемый первый интеграл,
т. е. дифференциальное уравнение (п — 1)-го порядка, содержащее
одну произвольную постоянную, эквивалентное данному уравнению
я-го порядка, и тем самым понижаем порядок уравнения на еди-
ницу. Действительно, уравнение (2.4) можно переписать в виде
У. у'....у(я“1)) = 0.	(2.40
Если у(х) является решением уравнения (2.40, т0 производная функ-
ции Ф(х, у, у'.....у<«-4) тождественно равна нулю. Следовательно,
функция Ф(х, у, у'.......у!”-1») равна постоянной, и мы получаем
первый интеграл
Ф(х, у, у', .... у<я"1)) — с.
Пример 5.
уу" + (УТ = 0.
90	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 4
Это уравнение можно записать в виде <7(уу') = 0, откуда уу' = с, или
yrfy = c,<Zx Следовательно, общим интегралом является у2 — CjX + c,
Иногда левая часть уравнения F(x, у, у', .... yW) = 0 стано-
вится производной дифференциального выражения (п — 1)-го порядка
Ф(х, у, у'.....у(л-1)) лишь после умножения на некоторый мно-
житель ц(х, у, у'....у(л-1>).
Примере.
уу" —(у')2—0.
,1	уу"—(y'V	d /v'\
Умножая на множитель ц =	получим —	’ = 0 или |yj = 0,
откуда у = Ср или уу In | у | = с,. Следовательно, In | у | = скх -f-1пс2, с2 > 0,
откуда у = е2ес,х, с2 =/= 0, как и в примере.3 этого параграфа.
Замечание. При умножении на множитель р(х, у, у'.
могут быть введены лишние решения, обращающие этот множитель
в нуль. Если множитель ц разрывен, то возможна и потеря реше-
ний. В примере 6 при умножении на ц = -у- было потеряно реше-
ние у = 0, которое, однако, можно включить в полученное решение
у = с2ес,х, если считать, ’’«то с2 может принимать значение 0.
4. Уравнение F (х, у, у', ..., у(л-) = 0 однородно от-
носительно аргументов у, у'.........у(л).
Порядок однородного относительно у, у'....у1’"’ уравнения
F(x, у, у'...yW)==0,
(2.5)
т. е. уравнения, для которого справедливо тождество
F(x. ky, ky'......Ау(я)) = kpF (х, у, у'......у<л)),
может быть понижен на единицу подстановкой y — e^zd\ где
z — новая неизвестная функция. Действительно, дифференцируя,
получаем
у" = z dx + z'\
у'" = е$ Zd\z* + $zz' + z"),
y^ = e$zdx<b(z, z’, z\ .... z<*-«>)
(убедиться в справедливости этого равенства можно методом ин-
дукции).
§ 2]	ПРОСТЕЙШИЕ СЛУЧАИ ПОНИЖЕНИЯ ПОРЯДКА	91
• Подставляя в (2.5) и замечая, что. в силу однородности, мно-
житель ep^dx можно вынести за знак функции F, получим
ep^zdxf(x, z, z'......z(n-1)) = 0
или, сокращая на ep$zdx, будем иметь,
f(x, z. z', .2(п-1,) = 0.
Пример?.
УУ" — (у')2 = бху2.
„	\ г dx	,	,	0 9.	Г (Зх’+С.) dx
Полагая у — е1 , получим г = &х, г = Зх2-(-с1, у — eJ	или
у =
Особенно часто в приложениях встречаются дифференциальные
уравнения второго порядка, допускающие понижения порядка.
1)	F (х, у") = 0.	(2.6)
В этом уравнении можно понизить порядок подстановкой у' = р
и свести его к уравнению F (х,	— 0, рассмотренному на стр. 69.
Можно разрешить уравнение (2.6) относительно второго аргу:
мента у" — f (х) и два раза проинтегрировать или ввести параметр
и заменить уравнение (2.6) его параметрическим представлением
•4^- = <Р(0> 'Не-
откуда
dy' — у" dx = ф (О'ф/ (О dt, ' у' — J" ф (О'К (О dt -ф ср
dy — y'dx, У — f [^*ф(О'Ч’л (0	(0 -ф<ф
2)	F(y'. у") = 0,	(2.7)
Полагая у' — р, преобразуем (2.7) к уравнению (1.61), стр. 70, или
представим уравнение (2.7) в параметрическом виде:
у;=ф(о. у^==11’(о.
откуда'
dy' _ <f'(t)dt	Г y'(t)dt
dx- y„ — ^{t} , x — J	-фс,
после чего у определяется квадратурой:
dy^y'dX^if^-^dt, y^=f ^^-dt + c2.
3)	F (у, y") = 0.	(2.8)
Можно понизить порядок, полагая
dy   d2y   dp dy   dp
dx	P’ dx2	dy dx	? dy '
92
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. 2
Если уравнение (2.8) легко разрешимо относительно второго
аргумента у" — / (у), то, умножая это уравнение почленно на
2y'dx — 2dy, получим d(y')'2 = 2f (y)dy, откуда
•^7= ±у 2ff(y)dy 4-Ср ±- >  —	------- d*.
у 2 f (y)rfy-f-Ci
. , „ _+ /’£У
Можно уравнение (2.8) заменить его параметрическим предста-
влением у = <()(t),	W); тогда из dy' — y"dx и dy — y'dx
получим у' dy' — у" dy. или
±d(y'y = q(f)<f'(t)dt,
(у')2 = 2 J* ф (/) ф'(/) d/-|-
у'= ± |/*2^ф(О <р' (0 dt + Ср
после чего из dy — у' dx находим dx, а затем и х:
, dy
dx =	=
У
ср' (/) dt
ф' (О dt
"Ь с2'
ф (0 ф' (0 dt 4- С)
(2.9)
Уравнение (2.9) и у = ср(£) и определяют в параметрическом виде
семейство интегральных кривых.
Пример 8.
у* = 2у3, у(0) = 1, у'(0) = 1.
Умножая обе части уравнения на 2у' dx, получим d (у')2 «= 4у3 dy, откуда
(у')2 = у’-|-с, Принимая во внимание начальные условия, находим, что
с, — 0 и у'=у2. Следовательно,
dy ,	1	.
—= dx,-------------- х + с2,
У2	у т
с2 = —1,
$ 3]
ЛИНЕЙНЫЕ дифференциальные уравнения
93
§ 3. Линейные дифференциальные уравнения и-го порядка
Линейным дифференциальным уравнением п-го порядка
называется уравнение, линейное относительно неизвестной функции
и ее производных и, следовательно, имеющее вид
«о(л;)У('’)+а1(л:)У("_1)+  • • +an-i (х)У' + ап (х)у ==<р(х). (2.10)
Если правая часть ф(х) = 0, то уравнение называется линейным
однородным, так как оно однородно относительно неизвестной
функции у и ее производных.
Если коэффициент а0(х) не равен нулю ни в одной точке некото-
рого отрезка	то, разделив на а0(х), приведем линейное
однородное уравнение при х, изменяющемся на этом отрезке, к виду
У!'!1 + Р1ИУ:"‘1)+ ••• +(Зл-1 (*)/+/>«(*) У = 0 (2.11)
или
У^=- 2 pz(x)y(«-‘).	(2.1 lj)
Z = 1
Если коэффициенты pt (х) непрерывны на отрезке а х Ь,
то в окрестности любых начальных значений
у (*о) = Уо- Уо (*0)=Уо.у(л_ (*о)=yir
где х0 — любая точка интервала а < х < Ь, удовлетворяются усло-
вия теоремы существования и единственности.
Действительно, правая часть уравнения (2.1 lj) непрерывна по
совокупности всех аргументов и существуют ограниченные по модулю
частные производные = — рп-ь(х) (Л = 0- 1..............(«—1)),
так как функции p„_k(x) непрерывны на отрезке а^х^Ь и,
следовательно, ограничены по модулю
Заметим, что линейность и однородность уравнения сохраняются
при любом преобразовании независимого переменного х = <р(/), где
<р (/) — произвольная п раз дифференцируемая функция, производная
которой <р' (/) Ф 0 на рассматриваемом отрезке изменения t.
Действительно,
dy   dy 1
dx	dt <p' (t) ’
d2y   d2y 1	dy <p* (/)
~dx?~ dt2 [<pz (X)]2	~dt~ [tp' (Z)]3 *
d^y
Производная любого порядка yy является линейной однородной
dy	d2y	d^y
функцией производных —и следовательно, при
dt	dt2	dt*
94	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. 2
подстановке в уравнение (2.11) его линейность и однородность
сохраняются.
Линейность и однородность сохраняются также при линейном
однородном преобразовании неизвестной функции у (х) — а (х) z (х).'
Действительно, по формуле дифференцирования произведения
у<*> = а(х) z^-\-ko! (х)	04- k	— а" (х)	Ч~ ... Ч-а(А)(х) г,
т. е. производная у^к} является линейной однородной функцией
г, г', г"....Следовательно, левая часть линейного однород-
ного уравнения
«О.(*) У<л) + «1 (*) у*”"1’ 4- • • • + ач (*) У = 0
после замены переменных будет линейной однородной функцией
z, г'.....z(n\
Запишем линейное однородное уравнение
У{п> + Р1 (х) у(«-1’ -4- ... Н- рп (х) у = О
кратко в виде
А[у] = 0,
где
£ [у] = у(п) 4* А (х) У<л-1) 4~ ... +р„(х)у.
Будем называть А[у] линейным дифференциальным оператором.
Линейный дифференциальный оператор обладает следующими
двумя основными свойствами:
1)	Постоянный множитель выносится за знак линейного
оператора:
L[cyl = c£[y].
Действительно,
(су)(п)+Д1(х)(су)л-14- ...
••• +PnW(cy) = c[y(',)-bp1(x)y(^11 4- ... +р„(х)у].
2)	Линейный дифференциальный оператор, примененный
к сумме двух функций yi и у2, равен сумме результатов при-
менения того же оператора к каждой функции в отдельности:
L [У 14“ Уг1 — [У 11 4- L 1Уз1 • ’
Действительно,
(У1 + Уг)’"’ + Pi (х) (yt Ч~ у2Г1 4- ... 4- /4 (х) (у, 4- У?) =
_ |у(«) Р1 (х) у(п- 1) _|_ ... _|_ рп w yj	(X) УУ - 11 Ч- . . ,
••• +P«(JC)y2].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	95
1) и 2) является
~ т	1	т
2 454^2
J = I	J	г = 1
§ 3]	ЛИНЕЙНЫЕ
Следствием свойств
L
где ct — постоянные.
Опираясь на свойства линейного оператора L, докажем ряд
теорем о решениях линейного однородного уравнения.
Теорема 2.2. Если у! является решением линейного одно-
родного уравнения L [у] = 0,' то и сур где с — произвольная
постоянная, является решением того же уравнения.
Доказательство. Дано LfyJsO. Надо доказать, что
McyJsEO.
Пользуясь свойством 1) оператора L, получим
Д[сУ1]==с4[У1]=£0.
Теорема 2.3. Сумма yt—|—у2 решений у! и у2 линейного
однородного уравнения L [у] = 0 является решением того же
у равнения.
Доказательство. Дано Z,[yJ = O и £[у2] = 0. Надо дока-
зать, что L [У1	у2] = 0.
Пользуясь свойством 2) оператора L, получим:
С 1У1 +	[У11 Н~ IЗ’г! = 0-
Следствие теорем 2.2 и 2.3. Линейная комбинация с про-
т
извольными постоянными коэффициентами У с,у, решений
<=!
Ур Уг> •••> Ут линейного однородного у равнения А[у] = 0 является
решением того же уравнения.
Теорема 2.4. Если линейное однородное уравнение Z,[y] = O
с действительными коэффициентами pt (х) имеет комплексное
решение у (х) = и(х)iv (х), то действительная часть этого
решения и(х) и его мнимая часть и(х) в отдельности являются
решениями того же одно родного у равнения.
Доказательство. Дано L [и (х) -|- lv (х)] = 0. Надо доказать,
что А[и] = 0 и L [г»] = 0.
Пользуясь свойствами 1) и 2) оператора L, получим:
L [и lv] = L [a] -j- IL [»] = 0,
откуда £[к] = 0 и £[»] = 0, так как комплексная функция действи-
тельного переменного обращается тождественно в нуль тогда и
только тогда, когда ее действительная и мнимая части тождественно
равны нулю.
Замечание. Мы применили свойства 1) и 2) оператора L
к комплексной функции и (х) -j- lv (х) действительного переменного,
96	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
что, очевидно, допустимо, так как при доказательстве свойств 1) и 2)
были использованы лишь следующие свойства производных {су)' = су',
где с — постоянная, и у2)' — у[ + у^, остающиеся справедливыми
и для комплексных функций действительного переменного.
Функции У] (х). у2(х), • • •• Уп(х) называются линейно зависимы-
ми на некотором отрезке изменения х, а х ^Ь, если существуют
постоянные величины а2, .... ая такие, что на том же отрезке
а1У1 + а2У2+ •••	=	(2-12)
причем хотя бы одно az #= 0. Если же тождество (2.12) справедливо
лишь при	... = a„ = 0, то функции ур у2, .... уп на-
зываются линейно независимыми на отрезке
Пример 1. Функции 1, х, х2, .... х" линейно независимы на любом
отрезке а < х < Ь, так как тождество
cq + <*2Х + а3х2-|- ... 4-ая+1хл = 0	(2.13)
возможно лишь, если все а,- = 0. Если бы хоть одно az #= 0, то в левой
части тождества (2.13) стоял бы многочлен степени не выше п, который
может иметь не более п различных корней и, следовательно, обращается
в нуль не более чем в п точках рассматриваемого отрезка.
Пример 2. Функции	е"1*, ..., епХ, где kx Ф kj при i =]= ],
линейно независимы на любом отрезке а < х < Ь.
Допустим, что рассматриваемые функции линейно зависимы. Тогда
а1Лх + а2Лх+ ... +а„Лг = 0,	(2.14)
где хотя бы одно az =f= 0, например для определенности ап =£ 0. Разделив
тождество (2.14) на ек,х и продифференцировав, получим:
а2(й2-*,)^2"й‘)х+ ...	(2.15)
— линейную зависимость между п — 1 показательными функциями вида ерх
с различными показателями. Деля тождество (2.15) на е<к2~к^х и дифферен-
цируя, получим линейную зависимость между п — 2 показательными функци-
ями с различными показателями. Продолжая этот процесс п— 1 раз, получим
а„(/г, — Й1)(*3 — k2) ... (kn — kn_x)e^n~kn-',X
что невозможно, так как а„, по предположению, отлично от нуля, а kj ф kj
при I =f= j-
Доказательство остается справедливым при комплексных
Пример 3. Функции
ek'\ хек'х...xn'ek-x,
екгХ, хек1Х..хП2ек2Х,
kx kx nkx
е р , хе р...х Ре р	,
где kj =# kj при i #= /, линейно независимы на любом отрезке а^х-^Ь.
Допустим, что эти функции линейно зависимы. Тогда
Р,(^)И1Л; + Р2(х)Лх+ ... +Рр(х)//30,	(2.16)
§ 3]	линейные дифференциальные уравнения	97
где Р[ (х) — многочлен степени не выше л/, причем хотя бы один полином,
например Рр(х), не равен нулю тождественно. Разделим тождество (2.16) на
ек'х и продифференцируем n, -f- 1 раз. Тогда первое слагаемое в тождестве (2,16)
исчезнет, и мы получНм линейную зависимость такого же вида, но с меньшим
числом функций:
Q2(Ar)<?(*2"A1)*+ ... + (?„(*) А’*1И = 0.	(2.17)
При этом степени многочленов Qt и P/(Z = 2, 3,...., р) совпадают, так как
при дифференцировании произведения Pi(x)epx, получим [Р/ (х) р -ф-
-|- Р’( (х)] ерх, т. е. коэффициент при старшем члене многочлена Pt (х) после
дифференцирования пройзведения Pi(x)epx приобретает лишь не равный
нулю множитель р. В частности, совпадают степени многочленов Рр (х) и
Qp (х), и следовательно, многочлен Qp (х) не равен нулю тождественно. Деля
тождество (2,17) на е(к,~ь''1Х и дифференцируя гг2 —f- 1 раз, получим линейную
зависимость с еще меньшим числом функций. Продолжая этот процесс р — 1
раз получим	>
/?р(х)
что невозможно, так как степень многочлена Rp(x) равна степени много-
члена Рр (х) и, следовательно, многочлен Rp (х) не равен нулю тождественно.
Доказательство не изменяется и при комплексных kP
Теорема 2.5. Если функции ур у2, .. у„ линейно зависимы
на отрезке а^х^.Ь; то на том же отрезке определитель
W(x) = W[yv у2.
		у2	Уп	
		у' ...	У’п	
		у; . ...	Уп	•
		уГ11 •••	У("~1)	
называемый определителем Вронского *), тождественно равен
нулю.
Доказательство. Дано, что
а1У1 Н-огУ24“	= О	(2.18)
на отрезке а х причем не все а, равны нулю. Дифферен-
цируя тождество (2.18) п — 1 раз, получим
СЧУ1	+	«2У2 + ••• + «ЯУЯ	s0’
«X	+	а2у;+ ... +<v;	^°'	(2.19)
а]у(1л-1,4-а2у<я"1'4- ... +алу(1«-1’ = 0.
*) По имени польского математика Г. Вронского (1775—1853).
58
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
ГГЛ. 2
Эта линейная однородная по отношению ко всем а; система л
уравнений имеет нетривиальное решение (т. к. не все аг равны нулю)
при любом значении х на отрезке а^х^.Ь. Следовательно, опре-
делитель системы (2.19), являющийся определителем Вронского
W (ylt у2....уп], равен нулю в каждой точке х отрезка а х < Ь.
Теорема 2.6. Если линейно независимые функции ур у2.......у„
являются решениями линейного однородного уравнения
у1Л|-|-Р1(х)у(л-‘Ч- ••• +/>Я(Х)У = О	.2.20)
с непрерывными на отрезке
то определитель Вронского
а < х коэффициентами pt (х),
Г(х) =
У1
у;
У1"-1'
У2	••• Уп
У'г	• • • У'„
z2
не может обратиться в нуль, ни в одной точке отрезка
а^.х^Ь.
Доказательство.. Допустим, что в некоторой точке х — хи
отрезка а^.х^_Ь определитель Вронского 1^(хо) = О. Выберем
постоянные а1(1=1, 2, ..., п) так, чтобы удовлетворялась система
уравнений
“i^iUo) Н-а2У2(хо) + ••• +алУя(*о) =°-
«1Х(хо) +а2У2(*о) 4-	+а»У«(хо) = °«
а	(*0) + МТ*’ (хо) + ... + а,Xя-11 (*о) = 0
и чтобы не все а, равнялись нулю. Такой выбор возможен, так как
определитель линейной однородной системы (2.21) п уравнений с п
неизвестными а; равен нулю, W (х0) = О, и следовательно, существуют
нетривиальные решения этой системы. При таком выборе линей-
ная комбинация
У = «1У1 (х) + а2у2 (х) + ... 4- а„У„ (х)
будет решением линейного однородного уравнения (2.20), удовлет-
воряющим, в силу уравнений системы (2.21), нулевым начальным
условиям
у(хо) = О, у'(хо) = О.......у<п-1>(х0) = 0.	(2.22)
Таким начальным условиям, очевидно, удовлетворяет тривиальное
решение у = 0 уравнения (2.20) и по теореме о единственности ре-
шения начальным условиям (2.22) удовлетворяет только это решение.
линейные дифференциальные уравнения
99
, на отрезке О х <1 2
§ 3]
Следовательно, (цу, (х)-|- а2у2 (х) + ... + алу„ (х)==0 и решения
Ур у2...у„, вопреки условию теоремы, линейно зависимы.
Замечание 1. Из теорем 2.5 и 2.6 следует, что линейно не-
зависимые на отрезке а^х^.Ь решения ур у2, .... уя уравнения
(2.20) линейно независимы также на любом отрезке а1^.х^.Ь1,
расположенном на отрезке а х Ь.
Замечание 2. В теореме 2.6 в отличие от теоремы 2.5 пред-
полагалось, что функции Ур у2, ..., ул являются решениями линей-
ного однородного уравнения (2.20) с не-
прерывными коэффициентами. Отказаться
от этого требования и считать функции
Ур у2, ..., ул произвольными п — 1 раз
непрерывно дифференцируемыми функция-
ми нельзя. Легко привести примеры ли-
нейно независимых функций, не являющихся,
конечно, решениями уравнения (2.20) с не-
прерывными коэффициентами, для которых
определитель Вронского не только обра-
щается в нуль в отдельных точках, но даже
тождественно равен нулю. Пусть, наприме)
определены две функции уДх) и у2(х):
у1(х) = (х — I)2
при 0 'С х 5
у1(х)=0 при 1 < х < 2,
у2(х) = 0 при
0<х< 1
и
(рис. 2.1).
Очевидно,
у2(х) = (х — I)2
при
1 < X <2
У1
у;
при
0 х 2, так как
на отрезке
0 <1 х 1 второй столбец состоит из нулей, а при 1 < х 2
из нулей состоит первый столбец. Однако функции у1 (х) и у2(х)
линейно независимы на всем отрезке 0<1х<^2, так как, рассма-
тривая тождество	а2у2 = 0, 0<^х<^2, вначале на отрезке
0^ х 1, 'приходим к выводу, что «j = 0, а затем, рассматривая это
тождество на отрезке 1^х<^2, находим, что и а2==0.
Теорема 2.7. Общим решением при а^,х^.Ь линейного
однородного уравнения
у(л>4-Р1(х)у(’1-1>-|- ... +рп(х)у = 0
(2.20)
с непрерывными на отрезке а^х^Ь коэффициентами pt{x)
п
(/=1, 2....й) является линейная комбинация
100
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
. (ГЛ. 2
п линейно независимых на том же отрезке частных реше-
ний yt (/—1, 2. .... л) с произвольными постоянными коэф-
фициентами.
Доказательство. Уравнение (2.20) при	удовле-
творяет условиям теоремы существования и единственности. Поэтому
п
решение у = У сгу; при а х b будет общим, т. е. будет со-
1=1
держать все без исключения частные решения, если окажется воз-
можным подобрать произвольные постоянные с, так, чтобы удовле-
творялись произвольно заданные начальные условия
У(хо) = Уо- У'(хоН'о......У(я-1)(а:0) = у{)«-Ч
где х0 — любая точка отрезка а х Ь.
п
Потребовав, чтобы решение у =2 С<У1 удовлетворяло поставлем-
1=1
ным начальным условиям, получим систему п линейных относительно
сz(/==l, 2, .... п) уравнений
Л
2 С1У1 (*о) = Уо>
/=1
п
Я^У'М^Уу
2 С1УГ1'(хо)=<-1)
с п неизвестными ct, с отличным от нуля определителем системы,
так как этим определителем является определитель Вронского W (х0)
для п линейно независимых решений уравнения (2.20). Следовательно,
эта система разрешима относительно с/ при любом выборе х0 на
отрезке а х b и при любых правых частях.
Следствие теоремы 2.7. Максимальное число линейно
независимых решений однородного линейного дифференциаль-
ного уравнения равно его порядку.
Замечание. Любые п линейно независимых частных решений
линейного однородного уравнения n-го порядка называются его
фундаментальной системой решений. У каждого линейного одно-
родного уравнения (2.20) существует фундаментальная система реше-
ний. Для построения фундаментальной системы решений произвольно
зададим п2 чисел
yzft)(xo) (^=1> 2.п'<	k = 0, 1....п — 1),
§ 31
ЛИНЕЙНЫЕ дифференциальные уравнения
101
подчинив их выбор лишь условию
У1 (хй) М*о)
Уп (Xq)
У»(Хо)
* о.
у<«-1)(х0) у<-»(х0) ... у<;-1>(х0)
где х0— любая точка отрезка а^х^Ь. Тогда решения уг(х),
определяемые начальными значениями ^(хо)(4«0, 1.......п—1;
I = 1, 2, .... п), образуют фундаментальную систему, так как их
определитель Вронского W (х) в точке х — х0 отличен от нуля и,
следовательно, на основании теорем 2.5 и. 2.6 решения ур у2, .... у„
линейно независимы.
Пример 4. Уравнение у" — у = 0 имеет очевидные линейно независи-
мые частные решения у, = ех и у2 = е~х (см. стр. 96, пример 2), следова-
тельно, общее решение имеет вид у = схехс2е~х.
Пример 5. Решение у = схех 4- сг ch х + с3 sh х уравнения у"' — у' = О
не является общим решением, так как решения «*, ch х, sh х линейно за-
висимы. Линейно независимыми решениями являются 1, ch х, sh х, и следо-
вательно.
у = C| -J- с2 ch х -f- с3 sh х,
где Ci, с2 и с3 — произвольные постоянные, будет общим решением рассма-
триваемого уравнения.
Зная одно нетривиальное частное решение ух линейного
однородного уравнения
у^ +рх(х)у^ + ... + />„(х)у = 0,	(2.20)
можно подстановкой у = ух j udx понизить порядок урав-
нения, сохранив его линейность и однородность.
Действительно, подстановку y = ylj' udx можно заменить двумя
подстановками: y = yxz и г' — и. Линейное однородное преобра-
зование
y = yxz	(2.23)
сохраняет линейность и однородность уравнения (см. стр. 94), сле-
довательно, уравнение (2.20) преобразуется при этом к виду
a0(x)z{ -f-ах (х) z^ ... 4~ ап (х) z == 0,	(2.24)
причем решению у = У! уравнения (2.20) в силу (2.23) со-
ответствует решение z = 1 уравнения (2.24). Подставляя z=l в
102	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. 2
уравнение (2.24), получим ап(х) = 0. Следовательно, уравнение (2.24)
имеет вид
a0(x)zw-|-a1(x)z<'I_1)-f- ... +«„-1 (*)*' = 0,
и подстановка г' — и понижает порядок на единицу:
a0(x)z/n (х) я(я '-f- ••• Н~ ая_] (х)« = 0.
Заметим, что та же подстановка у — У1J udx, где у,—реше-
ние уравнения L[у] = 0, снижает на единицу и порядок линейного
неоднородного уравнения L [у] = f (х), так как эта подстановка
не затрагивает правой части уравнения.
Зная fe линейно независимых ' на отрезке а х b решений
yv у2, Уй линейного однородного уравнения, можно понизить
его порядок до п — k на том же отрезке а^х^Ь.
Действительно, понизив подстановкой у — yft J* и dx на единицу
порядок уравнения
L[y] = O,	(2.20)
получаем опять линейное однородное уравнение
а0 (х) и{п~ b a, (х) и[п~2) + ... 4- a„_t (х) и — 0	(2.25)
порядка п — 1, причем нам известны k — 1 его линейно независимых
решений
которые получим, подставляя в у = yft J udx или и = по-
следовательно у — ур у = у2.....У — У/i-v (Заметим, что уже ис-
пользованному нами для понижения порядка решению у — ук уравнения
(2.20) соответствует тривиальное решение а = 0 уравнения (2.25).)
Решения ир и2.......ик-\ линейно независимы, так как если бы
между ними существовала линейная зависимость на отрезке а х ^Ь:
а,и1а2и2... + аЬ1иЬ|;==0
или
°-Ш'+<•’(&)'+  +«»-.(2-26>
где хотя бы одно az 0, то, умножая на dx и интегрируя тожде-
ство (2.26) в пределах от х0 до х, где	а х0 — точка
§ 35
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
103
отрезка 1а, Л»], будем иметь
„ У1(х) , „ УН*) ,	,	У*,1 (*)
1 УйС*) 2 У* (•*)''' ‘ ^ *-1 Ул(*)
_Г„ У1 <*о) I а УН*о) I	n-iWl_0
I1 Ш + °2 УА (*о) + • ’ ‘ + У4(хо) J - °’
или, умножая на уе(х) и обозначая
Г„ У1(*о) ,	у2(х0)	Уа-1 Wl_
~1а’ м^Т + а2уй^г+ •••	]““*•
получим, вопреки исходному предположению, линейную зависимость
между решениями ур у2.....ук;
«1У1+С12У2+ •••
где хотя бы одно az ф 0. Итак, использовав одно частное реше-
ние ук, мы понизили порядок уравнения на единицу, сохранив его
линейность и однородность, причем нам известно k — 1 линейно
независимых решений преобразованного уравнения. Следовательно,
тем же методом можно снизить порядок еще на одну единицу;
использовав еще одно решение и продолжая этот процесс k раз,
получим линейное уравнение п—k порядка.
Пример 6.
ху" — ху' + у = 0.	(2.27)
Уравнение имеет очевидное частное решение у1 = х. Понижая порядок
подстановкой
у — х I и dx, y'—xu-j- I udx, у" = хи'-±-2и,
приведем уравнение (2.27) к виду
х2и' (2 — х) ха = 0,
Лемма. Два уравнения вида
... + ря(х)у = 0,	(2.28)
+	... +7„(х)у = 0,	(2.29)
где функции р, (х) и qt (х) (Z — 1, 2, .... га) непрерывны на отрезке
а х </>, имеющие общую фундаментальную систему решений
Ур Уг’ • • •• Уп- совпадают, то есть р [ (х) == q£ (х) (/=1,2.га)
на отрезке а^х^Ь.
Доказательство. Вычитая из (2.28) почленно (2.29), полу-
чаем новое уравнение:
1Р1 (*) — Vi (-01 У'"" ° + lP2 W — <h (*)] У(п'2) 4- • • •
• • • 4- 1Р« (х) - qn (х)] у = 0, (2.30)
104	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
решениями которого являются функции ур у2, .... уа, удовлетво-
ряющие одновременно уравнениям (2.28) и (2.29).
Допустим, что хотя бы один из коэффициентов уравнения (2.30)
[/>, (х)— qt (х)] хотя бы в одной точке х0 отрезка а^х^.Ь отли-
чен от нуля. Тогда в силу непрерывности функций р\ (х) и qt (х)
этот коэффициент отличен от нуля в некоторой окрестности точки х0,
и следовательно, в этой окрестности функции уР у2> • • •> Уп являются
линейно независимыми решениями линейного однородного уравне-
ния (2.30) порядка не выше чем л —1, что противоречит следствию
теоремы 2.7. Значит, все коэффициенты уравнения (2.30)
Pi(x)~ qt(x)^=Q (/=1,2.............n),
т. е. />г(х) = ^(х) (/==1,2, .... п) на отрезке а х Ь.
Итак, фундаментальная система решений ур у2, .у„ вполне
определяет линейное однородное уравнение
у<^>-|-р1(х)у(«-1Ч- ... +р„(х)у = 0,	(2.28)
и следовательно, можно поставить задачу о нахождении уравне-
ния (2.28), имеющего заданную фундаментальную систему решений
Уп Уг......Ув-
Так как всякое решение у искомого уравнения (2.28) должно
быть линейно зависимо от решений уР у2...........уя, то определи-
тель Вронского W [ур у2..........................уя, у] =0. Запишем это уравнение
в развернутом виде:
У	1	Уг	•••	Уп	У
У	! Уг Уп У'
У	"1	Уг	•••	У'п	У“ =0>
у(п-1)	уИ-!)	...	у(п-1)
У	\п:	У?1	•••	У(яй' .	У'п
или, разлагая по элементам последнего столбца,
	У| у;	У2 У2	• • • Уп "'У'п		
w [уР у2	уя1у(">-	у(Л-2>	у(Л-2)	... у';-21	ytn-V>+ , .	= 0.
	уТ	уТ	••• УТ		
(2.31)
§ 3]	ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	105
Полученное уравнение (2.31) и является искомым линейным однород-
ным уравнением, имеющим заданную фундаментальную систему
решений ур у2.......Ул (так как ПРИ У = У/ (/=1. 2, .... д)
117 [ур Уг> •••> Ул> У1 = 0). Разделив обе части уравнения (2.31) на
отличный от нуля коэффициент 117[уР у2, .... уя] при старшей
производной, приведем его к виду (2.28).
Отсюда следует, в частности, что
	У1	уа	Уп
	У1	/ У2	Уп
		уГ2)-..	/Г2)
	У?1	У^	Лл)
U7[yb '		>2.	
Заметим, что определитель
У1	Уг	• ул	
У1'	У2	• Уп	
у01-2)	у^-2) ..	V(«-2) 'п	(2.32)
у(«)	у<л) ..	. у<я> •*п	-
равен производной от определителя Вронского U7[ylt Ур •••< УЯЬ
Действительно, по правилу дифференцирования определителя, про-
изводная
d	У1 У1'	У2 У2	••• Уп ... у'п
dx	у(»-2)	у(«-2)	* J п
	УГ”	у(л-1)	z п
равна сумме по I от 1 до п определителей, отличающихся от опре-
делителя Вронского тем, что в них продифференцированы элементы
/-й строки,- а остальные строки определителя Вронского оставлены
без изменения. В этой сумме только последний определитель при I = п,
совпадающий с определителем (2.32), может быть отличен от нуля.
Остальные определители равны нулю, так как их l-я и i-\~ 1-я строки
совпадают.
106
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. 2
Следовательно, рх (х) = —	. Отсюда, умножая на dx и инте-
грируя, получим
1п|Г| = -JpjUHx-Hnc, W = ce~$p'wax
ИЛИ
х
- J Pl (х) dx
W = ce х= .	(2.33)
При х — х0 получим c = W (х0), откуда
X
- J р, IX) dx
W(x)=W(x0)e *•	.	(2.34)
Формулы (2.33) или (2.34), впервые полученные М. В. Остроградским
и независимо от него Лиувиллем, называются формулами Остро-
градского— Лиувилля.
Формула Остроградского — Лиувилля (2.34) может быть исполь-
зована для интегрирования линейного однородного уравнения вто-
рого порядка
У'+ Pi (*)/ + л2 (х)у = 0,	(2.35)
если известно одно нетривиальное решение этого уравнения yv
Согласно формуле Остроградского—Лиувилля (2.34) любое реше-
ние уравнения (2.35) должно быть также решением уравнения
У1 У
У у'
или
,	:	- f Pl(х) dx
У1У —yy} = Cie J
Для интегрирования этого линейного уравнения первого порядка
проще всего воспользоваться методом интегрирующего множителя.
Умножая на и, = Д. получим
У1
d / У \ __ С1 - J Pl (X) dx
’dx\~l~/xe
откуда
- f Pl (X) dx
-------------------------------5------dx 4- Cn,
У?
или
„ - f PiWdx
= cre J
J 4] ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 107
§ 4. Линейные однородные уравнения с постоянными
коэффициентами и уравнения Эйлера
1. Линейные однородные уравнения с постоян-
ными коэффициентами. Если в линейном однородном урав-
нении
аоУ(п> О1У^П_1) -)-•••+ апУ = 0	(2.3.6)
все коэффициенты at постоянны, то его частные решения могут
быть найдены в виде у = екх, где k — постоянная. Действительно,
подставляя в уравнение (2.36) у = екх и = kpekx (р — 1,2..п),
будем иметь:
aoknekx + a\kn~xekx + ... + апекх = 0.
Сокращая на необращающийся в нуль множитель екх, получим так
называемое характеристическое уравнение
aoknalkn 1 4- ... -|- a„_tk 4- ап = 0.	(2.37)
Это уравнение ге-й степени определяет те значения k, при которых
у — екх является решением исходного линейного однородного уравне-
ния с постоянными коэффициентами (2.36), Если все корни kv k2.kn
характеристического уравнения различны, то, тем самым, найдено п
линейно независимых решений ек'х, ек'х....ек"? уравнения (2.36)
(см. стр. 96, пример 2). Следовательно,
y = cte 1 4- с2е 2 4- ... 4- спе * .
где с2 — произвольные постоянные, является общим решением исход-
ного уравнения (2.36). Этот метод интегрирования линейных уравне-
ний с постоянными коэффициентами впервые был применен Эйлером.
Пример I.
у" — Зу'4-2у = 0.
Характеристическое уравнение имеет вид А2 — ЗА -|- 2 = 0, его корни А, = 1,
А2 = 2. Следовательно, общее решение исходного уравнения имеет вид
у = Cie* -|- с2егх.
П р и м е р 2.
у'" —у'=0.
Характеристическое уравнение А3 — А = 0 имеет корни А1 =0, А2 = 1,
А3 = — 1. Общее решение рассматриваемого уравнения у = с, 4- с2ех 4* с3е~х.
Так как коэффициенты уравнения (2.36) предполагаются действи-
тельными, то комплексные корни характеристического уравнения могут
появляться лишь сопряженными.парами. Комплексные решения
и £«»-₽<)*, соответствующие царе комплексных сопряженных корней
^! = a4-p/ и A2 = a—pi,
108	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	{ГЛ. J
могут быть заменены двумя действительными решениями: действи-
тельной и мнимой частями (см. стр. 95) одного из решений
— eix (cos рх I Sjn
или
е(а-?4)Л =-e<iX (cos рх I sjn f}x).
Таким образом, паре комплексных сопряженных корней Ali2 = a ± (3Z
соответствуют два действительных решения: eIJfcospx и elXsinpx.
ПримерЗ.
у"-{-4/-|-5у = 0.
Характеристическое уравнение имеет вид k2 4- 4А -J- 5 == 0, его корни
^[.2 = — 2 ± I. Общее решение
у = е~2х (с, cos х 4- с2 sin х).
Пример 4.
у" 4- а2у = 0	--
Характеристическое уравнение й24~а2 = 0 имеет корни 2 = ± al. Общее
решение	,	«
у = С) cos ах 4- с2 sin ах.
Если среди корней характеристического уравнения имеются
кратные, то число различных решений вида екх меньше п и, следо-
вательно, недостающие линейно независимые решения надо искать
в «ном виде.
Докажем, что если характеристическое уравнение имеет корень kt
кратности ah то решениями исходного уравнения будет не только
k .X	А,-*” п lx	а,— 1 А х -
е 1 , но и хе 1 , х2е	х ' е г .
Предположим вначале, что характеристическое уравнение имеет
корень kt = 0 кратности at. Следовательно, левая часть характери-
стического уравнения (2.37) имеет в этом случае общий множитель
k°r, т. е. коэффициенты а„ '= an-i — • • • ~ ап-о- +\= и характери- ”
стическое уравнение имеет вид
<з0Ал4-«Л’"1+ ••• +а„_о// = 0.
Соответствующее линейное однородное дифференциальное урав-
нение
й0У(Л)+-й1У(Л'1,+ ••• + а„_в/у(0<) = 0,
очевидно, имеет частные решения 1, х, х2.......... х’< ', так как
уравнение не содержит производных порядка ниже чем аг. Итак,
кратному корню k,—Q кратности at соответствует а, линейно не-
зависимых (см. стр. 96, пример 1) решений
1, х, х2, .... ха<~1.
J 4] ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 109
Если характеристическое уравнение имеет корень £z=40 крат-
ности а(, то замена переменных
у = ек?г	(2.38)
сводит задачу к уже рассмотренному случаю равного нулю кратнбго
корня.
Действительно, линейное однородное преобразование неизвестной
функции (2.38), как указано на стр. 94, сохраняет линейность и
однородность уравнения. Постоянство коэффициентов при замене
переменных (2.38) тоже сохранится, так как
у^	=ek>x^P) + pz(P~ % 4-^=^ /"W -
k jg
и после подстановки в уравнение (2.36) и сокращения на е < при
Z, г'.....остаются лишь постоянные коэффициенты.
Итак, преобразованное уравнение будет линейным однородным
уравнением n-го порядка с постоянными коэффициентами
60z(n)+^2<n-I)+ ... +d„z = 0,'	(2.39)
причем корни характеристического уравнения
4- ... 4-ая = 0. s (2.37)
отличаются от корней характеристического уравнения для преобра-
зованного уравнения (2.39)
*оРя + *1Рп-1+	+*„ = 0	(2.40)
на слагаемое так как между решениями y = ekx уравнения (2.36)
и z — epx уравнения (2.39) должна быть зависимость y = ze i или
ekx = epxekix, откуда k = p~\-kt. Следовательно, корню k = kt
уравнения (2.37) соответствует корень Р(= 0 уравнения (2.40).
Как нетрудно проверить, при этом соответствии сохранится и
кратность корня, т. е. корень pt — 0 будет иметь кратность а(-
Действительно, кратный корень уравнения (2.37) можно рас-
сматривать как результат совпадения различных корней этого урав-
нения при изменении его коэффициентов, но тогда в силу зависи-
мости k — р 4- ki совпадут с р = 0 и at корней уравнения (2.40).
Корню р — 0 кратности а(- соответствуют частные решения z = l,
z — x, .... z =	'. Следовательно, в силу зависимости y = ze i •
корню kt кратности at уравнения (2.37) будут соответствовать az
частных решений
ь.х	k,x	a,-i	,,,
у = е  , у — хе 1	, у = х i е t •	(2.41)
Остается показать, что решения
ekix, xekix...хл‘~1ек1х G=l. 2, .... т),	(2.42)
110	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	ГГЛ. 2
где т — число различных корней kt характеристического уравнения,
линейно независимы, но это уже было доказано в примере 3 стр. 96.
Следовательно, обшее решение уравнения (2.36) имеет вид
У=^(с01 + сих + с2!х2+ ... +-cOt_i,zx“''>V.
где csi — произвольные постоянные.
Пример 5
у'" Зу» _|_ Зу' _ у = о.
Характеристическое уравнение k3 — 3k1 -f-ЗА — 1 =0 или (k — I)3 = 0 имеет
трехкратный корень k. 2,3 = 1. Следовательно, обшее решение имеет вил
у = (с, 4- сгх 4- с3х2) ех
Если характеристическое уравнение имеет кратный комплексный
корень р + qi кратности а, то соответствующие ему решения
e(P+4i)X^ хе{Р+Ч1]Х х2е{Р+И^Х....
можно преобразовать по формулам Эйлера
e<P4'9i)J' = e₽JC(cos^x4-^sin^x)
и, отделяя действительную и мнимую части, получить 2а действи-
тельных решений:
epxcosqx, xepxcosqx, x2epxcosqx.......хх~херх cosqx,
epxsinqx, xepx sin qx, x2epxsinqx. .... x" ~'epx sin qx.
Взяв действительные и мнимые части решений, соответствующих
сопряженному корню р— ql характеристического уравнения, мы
не получим новых линейно независимых решений. Таким образом,
паре комплексных сопряженных корней p±qi кратности а соот-
ветствуют 2а линейно независимых действительных решений (2.43)
Пркмерб.
y'v _|_2у"4у = 0.
Характеристическое уравнение А4 4- 2А2 4- 1 = 0 или (А2 4-1)2 — 0 имеет дву-
кратные корни ± i. Следовательно, общее решение имеет вид
у = (с, 4 <Чх) cos х 4 (сз 4 cix) sin х.
2. Уравнения Эйлера. Уравнения вида
аох'У"> 4- а1хл~1у<л~1> 4- ... -(-а^ху'4-а„у — 0, (2.44)
где все а{ — постоянные, называются уравнениями Эйлера. Уравне-
ние Эйлера заменой независимого переменного х = е‘ *) преобра-
*) Или х = — в‘, если х < о, в дальнейшем для определенности будем
считать х > 0.
(2.43)
§ 41 ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ |Ц
зуется в линейное однородное уравнение с постоянными коэффи-
циентами.
Действительно, как указано на стр. 93, линейность и однород-
ность уравнения при преобразовании независимого переменного
сохраняются, а коэффициенты становятся постоянными, потому что
*У _ аУ
dx dt'
<?У	1^У_ _ dy\
dx2	\ dt1	dt J ’
=	...	(2.45)
dxK	' dt dt2	dtR /
где все 0; — постоянные, и при подстановке в уравнение (2.44) мно-
жители сокращаются с множителями =
Справедливость равенства (2.45) легко может быть доказана ме-
тодом индукции. Действительно, допустив, что равенство (2.45) спра-
ведливо, и продифференцировав его еще раз по х, докажем справед-
+ 1 у
ливость равенства (2.45) и для —:
_ <?-(*+!>< (g d2y I fi d3y I 4 в V
dxkt-‘	V’ dt2 dt3 +	dtk+' /
bf+v^+...+v..,^).
где все yf — постоянные.
Итак, справедливость формулы (2.45) доказана, и следовательно,
линейно входящие в уравнение Эйлера
(2-44'’
fcsO
с постоянными коэффициентами произведения
dxk ’ dt dt?'±	dtk
линейно (с постоянными коэффициентами) выражаются через произ-
водные функции у по новой независимой переменной t. Отсюда
следует, что преобразованное уравнение будет линейным однород-
ным уравнением с постоянными коэффициентами
112
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. 2
Вместо того чтобы преобразовывать уравнение Эйлера в линей-
ное уравнение с постоянными коэффициентами, частные решения
которого имеют виду=й* , можно сразу искать решения исход-
k
нОго уравнения в виде у = х , так как
ек* — хк.
Получающееся при этом после сокращения на хк уравнение
(Ji •— 1) •• • (Jt — ti —1) -ф- ajz (k — 1) ... (k — ti 2) -|- ...
... + n„ = 0 (2.47)
для определения k должно совпадать с характеристическим урав-
нением для* преобразованного уравнения (2.46). Следовательно, кор-
ням kt уравнения (2.47) кратности az соответствуют решения i
k,t , k,t Л k.t	ль-l Jl
e ‘ , te 1 ., t e ».t » e 1
преобразованного уравнения или
xkl, xki\nx, x*zln2x, .... x*‘lna'“Ix
исходного уравнения, а комплексным сопряженным корням р ± ql
уравнения (2.47) кратности а соответствуют решения
ept cos qt, tepi cos qt.ept cos qt,
epl sin qt, tept sin qt.ta~xept sini?( ’
преобразованного уравнения или
xp cos(q In x), xp In xcos (q In x)...x₽In“-1 xcos(q Inx),
xp sin (q In x), xp In x sin(<? In x).xp ln“-1 x sin (q In x)
исходного уравнения Эйлера.
Пример?.
5
хгу" + у ху’ — у = О.
5	1
Ищем решение в виде у = хк; k(k — 1)-]-А — 1 = 0, откуда А, -
k2 = — 2. Следовательно, общее решение при х > 0 имеет вид
1
У = CjX2 с2х~2..
Примере.
х2у" — ху' у = 0.
Ищем решение в виде у = xft; k (k — 1) — k + 1 = 0, или (k — I)2 = 0,
Следовательно, общее решение при х>0 будет
У = (ci + с2 In х)х.
П р и м е р 9.
х2у" + ху' + у = Q.
$ 5]	ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ	113
Ищем решение в видеу = х.л; k(k—1) 4- k 4-1 = 0, откуда kit 2=±/.
Следовательно, общее решение при х > 0 имеет вид
у = «! cos In х + с2 sin 1пх.
Уравнения вида
а0 (ах + b)n yw + aj (ах + Ь)п~1 у(п-1)
... +й/„_1(ахН-^)у' + «пУ = 0 (2.48)
также называются уравнениями Эйлера и сводятся к уравне-
нию (2.44) заменой независимого переменного ах4-Ь = хх. Следо-
вательно, частные решения этрго уравнения можно искать в виде
у=(ах4-^)А или преобразовать уравнение (2.48) к линейному одно-
родному уравнению с постоянными коэффициентами заменой пере-
менных ах-\-Ь^=е* (или ах-\-Ь =— е*, если ах-\-Ь<.О).
§ 5. Линейные неоднородные уравнения
Линейное неоднородное уравнение имеет вид
М*)У(л) + °1	• •• 4-а„(х)у = <р(х).
Если ай(х) #= 0 на рассматриваемом интервале изменения х, то после
деления на а0(х) получим
у(л)4-Л(х)у(«-1)+ ... +/?„(*) у = /(х).	(2.49)
Это уравнение, сохраняя прежние обозначения, кратко запишем
в в иде
£[у] =/(*)•
Если при а^х~<(.Ь в уравнении (2.49) все коэффициенты pz(x)
и правая часть /(х) непрерывны, то оно имеет единственное реше-
ние, удовлетворяющее условиям
'у<*)(хо) = у<*> (А = 0, 1, .... д-1),
где у<*>— любые действительные числа, а х0 — любая точка интер-
вала а < х < Ь.
Действительно, правая часть уравнения
у(«) = —/71(х)у<л-1> —р2(^)У(л-3)— ••• — Pn{x)y-\-f(x) (2.49j)
в окрестности рассматриваемых начальных значений удовлетворяет
условиям теоремы существования и единственности:
1) правая часть непрерывна по всем аргументам;
~2) имеет ограниченные частные производные по всем у<*>
(& = 0, Г, .,., п — 1), так как эти производные равны непрерывным
по предположению на отрезке а^х^.Ь коэффициентам —Рп-^^х).
114	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Еще раз отметим, что на начальные значения у(ой не налагается
никаких ограничений.
Из двух основных свойств линейного оператора
Д|су| = с4[у],
МУ[ + Уз1 — MyJ ~Ь МУгЬ
где с — постоянная, непосредственно следует:
1) Сумма у + У1 решения у неоднородного уравнения
Му|=/(х)	>2.49)
и решения ух соответствующего однородного уравнения L[yj=O
является решением неоднородного уравнения (2.49).
Доказательство.
Му + yd = Му] H-Myd.
но £[у]=/(х), a LiyJsO, следовательно.
Му 4-У11^/(^)-
2) Если у, является решением уравнения L[y} = f!{x)
т
(1=1. 2....zw), то у = У, является решением уравнения
t=i
т
МУ1 = 2 aJi (*).
[=i
где а, — постоянные.
Доказательство.
т
2 а/У/
1 = 1
L
т	т
2 Mazyj= 2 <*МУаЬ
;=i	<=1
(2.50)
но L [у()^/( (х), следовательно,
т
2 «[У/
i- 1
L
т
= S a-ifiix).
1=1
Это свойство, называемое часто принципом суперпозиции (или
принципом наложения), очевидно, остается справедливым и при
/в->оо, если ряд 2 а;У; сходится и допускает «-кратное почлен-
/ = 1	’ .
ное дифференцирование, так как в этом случае возможен предель-
ный переход в тождествах (2.50).
3)' Если уравнение L [у] = U (x)-f- IV (х), где все коэффи-
циенты р( (х) и функции U (х) и V (х) действительны, имеет
решение у = ц (х) + tv (х), то действительная часть реше-
§ si	ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ	115
ния и(х) и мнимая часть v(x) являются соответственно реше-
ниями уравнений
L1у] = U (х), L[y\=V(x).
Доказательство.
L [и -fc- lv] г U (х) -|- IV (х)
или
L [u| + IL [-и] == U (х) + IV (х).
Следовательно, отдельно равны действительные части L\u\=U (х)
и мнимые части. L [т>] = V (х).
Теорема 2.8. Общее решение на отрезке а^х^Ь урав-
нения L[y] = f(x) с непрерывными на том же отрезке коэф-
фициентами Pi(x) и правой частью f (х) равно сумме общего
п
решения Т ciyl соответствующего однородного уравнения и
< = 1
какого-нибудь частного решения у неоднородного уравнения.
Доказательство. Надо доказать, что
Л
У = S <чУ, + у,	(2.51)
< = 1
где С; — произвольные постоянные, a yt (/=1, 2..п) — линейно
независимые решения соответствующего однородного уравнения,
является общим решением неоднородного уравнения L [у] = / (х).
Принимая во внимание 1) (стр. 114) и справедливость для рассматри-
ваемого уравнения теоремы существования и единственности, надо
доказать, что подбором постоянных cz в (2.51) можно удовлетворить
произвольно заданным начальным условиям
ycft)(^o) = y(oft’ (Л=0, 1, 2, .... га-1),	(2.52)
где а Xq^.6. Требуя, чтобы решение (2.51) удовлетворяло началь-
ным условиям (2.52), приходим к системе уравнений
п
S <чУг (*о)+У*(*о) =Уо>
' = 1
П
2/^(*о)+у'(*о) = Уо-
п
S <чУ(Г ь(*0)= У^"-1*.
116	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	ГГЛ. 8
Эта линейная по отношению к постоянным ct система п уравнений
с га неизвестными при произвольных правых частях допускает един-
ственное решение относительно сг (/ = Г, 2, .... га), так как определи-
тель системы (2.53), будучи определителем Вронского[ур у2, .... у„]
для линейно независимой системы решений соответствующего одно-
родного уравнения, отличен от нуля при любых значениях х из
отрезка а < х Ь и, в частности, при х = х0.
Следовательно, интегрирование линейного неоднородного урав-
нения сводится к нахождению одного частного решения этого урав-
нения и к интегрированию соответствующего линейного однородного
уравнения.
П р и м е р 1.
у"4-у = х.
Одно частное решение этого уравнения у — х, очевидно, общее решение
соответствующего однородного уравнения, имеет вид
у — с, cos х Ц- Са sin х (см. стр. 108, пример 4).
Следовательно, общее решение исходного неоднородного уравнения
у — сг cos х -|- с2 sin х х.
Если подбор частного решения неоднородного уравнения
труден, но общее решение соответствующего однородного
п
уравнения у = 2с/У; найдено, то можно проинтегрировать
i=i
линейное неоднородное уравнение методом вариации по-
стоянных.
При применении этого метода решение неоднородного уравнения
л	П
ищем в виде у = 2 с/(х) У/> т- е- п0 существу вместо неизвестной
/=т
функции у вводим п неизвестных функций с;(х). Так как подбором
функций сг(х) (I — 1, 2, .... га) надо удовлетворить лишь одному
уравнению
У(л)+Р1(^)У('1-1) + ...'4-Рл(-*г)у = /(х),	(2.49)
то можно потребовать, чтобы эти п функций ct(x) удовлетворяли бы
еще каким-нибудь га—1 уравнениям, которые мы выбираем так,
/г
чтобы производные функции у = 2 с/(х) У< W имели бы по воз-
‘ = 1
можности такой же вид, какой они иМейт при постоянных сГ Выбе-
рем сДх) так, чтобы вторая сумма в правой части
п	. п
' = 2 с, (х) у Ах) + 2 o' (*) У, (•*)
§ 6)	ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ	117
равнялась нулю,
2 cJWyz(x) = 0,
и, следовательно,
У' = S ct(x)y'.(x),
z=i
т, е. у' имеет такой же вид, как и при постоянных с(. Точно
так же у второй производной
п	п
у" = 2 (х) у" + 2 с\ (х) у\
1=1	Z=1
требуем обращения в нуль второй суммы и тем самым подчиняем ct (х)
второму условию:
п
2 < (*) y'i = о.
п
Продолжая вычислять производные функции у = У ct (х) yz
1=1
рядка- п — 1 включительно и требуя каждый раз обращения
п
суммы 2 c'i(x) y\k)(x):
2 с\ (х) у<?> (х) = 0	(й=0, 1, 2, .... п — 2),
z=i
получим	4
п
У , = 2 Cl (x)yz,
/=1
и
у' = 2 с, (X) у'р
f=l
. п
у" =^ci(x)y"i,
до по-
в нуль
(2.54)
(2.55)
п
у'"-1’ — 2 Ci(x) у^-1’,
1=Л
и	п
у(»), = 2 с1 (х) у<п) + 2 с' (х) У<«- ’>•
/=1	1=1
п
В последнем равенстве мы не можем потребовать, чтобы 2 с-у^"-1'—0,
так как функции с( (х) уже подчинены п — 1 условиям (2.54),
tig	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. $
а надо еще удовлетворить исходному уравнению (2.49). Подставляя
у, у'.....jAn> из (2.55) в уравнение
У('!)+Р1(-«)у('г_11+	+ P„(x)y = f(x),	(2.49)
получим недостающее уравнение для определения с( (х) (Z=l, 2, .... fl).
При этом очевидно, что в левой части уравнения (2.49) останется
п
лишь сумма 2<W так как все остальные члены имеют
/ = 1
такой же вид, как и при постоянных с;, а при постоянных cz функция
п
у = У. ctyi удовлетворяет соответствующему однородному уравнению.
/ = 1
В этом можно убедиться и непосредственным вычислением:
п	п	п	п
2	+ 2 c^ + PiWS^"'” + P2w S • ••
Z = ]	t = l	fs=l
n
... + pa(x)^iclyl = f(x)
i=l
или
n	n
2 <//’-11 + S ct Pi (x) yt/1-” + ••• + l’1Wy(]=/ (*)• (2.56)
Все у, являются частными решениями соответствующего однородного
уравнения, следовательно, у^1 + Р, (х) у^-11 + . .. + ра (х) у,зО
(i= 1, 2.....я) и уравнение (2.56) принимает вид
п
2 c'$^ = f(x).
i-1
Итак, функции с;(х) (I = 1, 2.. п)	определяются из системы п
линейных уравнений
п
2 <(^7,= о,
i»1
п
2 <(л)у;=о,
п
2 с' (х)у" = 0,
1=1
п
2 <(х)у<л2) = о,
'(2.57)
п
2 ci(x)^n-'> = f{x)
1-=1
§51	ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ	119
с отличным от нуля определителем системы, так как этот опреде-
литель
У1	Уз	••• Уп
У'з	Уз	••• у'п
у(Л-П у(Л-1)	u(n-l)
является определителем Вронского для линейно независимых реше-
ний соответствующего однородного уравнения. Определив из (2.57)
все е'(х) = <р/(х), квадратурами находим
Пример 2.
С/ (*) = / (Pi(x)dx + Ci.
у" 4- у — —J.
1	' ' COS X
Общее решение соответствующего однородного уравнения имеет вид
у = С] cos х с} sin х Варьируем ct и с2:
у = С[ (х) cos х 4- с, (х) sin х.
с1 (х) и с2 (х) определяются из системы уравнений (2.57):
С] (х) cos х 4“ с2 (•*) sin х = О,
— q(х)sin х4- Cj(•*)cosx ~ ~CJ^ x'
откуда
t	<fn x	_
ciW=-^7' c,(x) = ln|cosx|4-c1;
c'2(x)=l, c2(x) = x4-c2.
Общее решение исходного уравнения
у = с, cos х 4- «2 sin х 4- cos х In | cos x 14- x sin x.
ПримерЗ.
x 4- a2x = / (t).
Общее решение соответствующего однородного уравнения имеет вид
х «= Cj cos at 4- с2 sin at. Варьируя постоянные х = сх (t) cos at 4- с2 (t) sin al,
получим
«J (t) cos at 4- c2 (/) sin at = 0,
— acj (t) sin at 4- ac'-2 (t) cos at =f (t).
f (и) cos au du 4-
120	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. 2
откуда
с'(/) =---/(/) sinai, Cj (i) =-- j f (u) sin au du + cp
Л	a J
o
t
,	1	if	-
c2 (0 = — f (0 cos c2 (0 = — / / («) cos an du c2,
a	a j
о
i	t
cos at f ,. 4 ,	. . sin at
x(t) =------— J f (u) sin au du -|-
° 0 _ ’ _
4- c, cos at + c, sin at,
или
t,
x(t)—-^ y* f (u) [cos au sin at — sin au cos at] du -]- cj cos at 4- c2 sin at,
6
откуда окончательно получаем
t
x(t)—-^ I f(u)sina(t— U) du 4-7, cos at 4-72 sin at.
6
Заметим, что первое слагаемое правой, части является частным решением
исходного уравнения, удовлетворяющим начальным условиям х (0) = 0,
.7(0) = о.
Итак, знание п линейно независимых частных решений соответ-
ствующего однородного уравнения позволяет методом вариации
постоянных проинтегрировать неоднородное уравнение
Z.[y]=/(x).
Если же известно ' лишь k, где k < п, линейно независимых
решений ур у2.......yft соответствующего однородного уравнения,
то, как уже указывалось на стр. 102, замена переменных позволяет
понизить порядок уравнения до п—k, сохраняя его линейность.
Заметим, что если k=n.— 1, то порядок уравнения снижается
до первого, а линейное уравнение первого порядка всегда можно
проинтегрировать в квадратурах.
Аналогично могут быть использованы k решений неоднородного
уравнения ур у2, ..., yft, так как их разности являются уже реше-
ниями соответствующего однородного уравнения. Действительно,
= /(*)• ^1ур]=/(х),
следовательно,
L(?j ~ ГУ;1 — t[yp]=/M-/M=0.
§ 5]	ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ	121
Если частные решения соответствующего однородного уравнения
(51 — Ул). (У2~Ул)...................... (Ул-1~ Ул) (2.58)
линейно независимы, то порядок уравнения L(y) — f (х) может быть
понижен до п—(k — 1). Очевидно, что другие разности уу— ур
являются линейными комбинациями решений (2.58)
Уу-У/> = (У; ' Ул) — (Ур— Ул)
и, следовательно, не могут быть использованы для дальнейшего
понижения порядка.
Укажем еще метод Коши нахождения частного решения линей-
ного неоднородного уравнения
i [У W] = / (х).	(2.59)
В этом методе предполагается известным, зависящее от одного пара-
метра, решение К (х, s) соответствующего однородного уравнения
£[у(х)]=0, удовлетворяющее условиям
K(s, s) = K' (s, s)= ... = f^n~2>{s, s) — 0;	(2.60)
K(n~l}(s, s) = 1.	(2.61)
Нетрудно проверить, что в этом случае
у(х) = JК(х, s)f(s)ds
х,
(2.62)
будет частным решением уравнения (2.59), удовлетворяющим нуле-
вым начальным условиям
у(х0) = у'(х0) = .... = у(»-»(хо) = О.
Действительно, дифференцируя (2.62) и принимая во внимание
условия (2.60) и (2.61), получим
X
у' (х)	— f Кх(•*• f ds'
Xi
X
у" (X)	— J к"(х. s)f(s)ds,
х0
(2.63)
у<»-1'(х)= J/6"‘n(x, s)f(s)ds,
Хо
X
У " W = J № (X, s)f (s) ds + f (х).
Жо
122	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ.' 2
Подставляя (2.62) и (2.63) в уравнение (2.59), получаем
X
рК(х, s)l/(s)d$ + /(x) ==/(*),
г,
так как К (х, s) является решением соответствующего однородного
уравнения и L[K(x, s)]==0.
Решение К (х, s) может быть выделено из общего решения
п
у = У, с,у( (х) однородного уравнения, если выбрать произвольные
1=1
постоянные cf так. чтобы удовлетворялись условия (2.60) и (2.61).
Пример 4. Для уравнения
у" + ^у = /(л)	(2.64)
общим решением является у = с, cos ax-f- с2 sin ах, условия (2.60) и (2.61)
приводят к следующим уравнениям:
с, cos as -|- с2 sin as = 0,
— ас, sin as -j- ac2 cos as — 1.
Следовательно,
sin as cos as
и искомое решение К (х, s) имеет вид
/< (х, s) = -i- sin а (х — s).
Решение уравнения (2.64), удовлетворяющее нулевым начальным условиям,
согласно (2.62), представимо в виде
х
У (х) = у	sin а(х — s)f (s) ds.
*0
При х0 = 0 это решение совпадает с полученным выше (см. стр. 120) другим
методом решением того же уравнения.
Можно дать физическую интерпретацию функции К (х, s) и ре-
шению линейного уравнения с правой частью в форме (2.62). При
этом нам будет удобнее независимое переменное обозначить буквой t.
Во многих задачах решение у (t) уравнения
У(п’+А(0Уя-1’+ ••• +Pn(t)y=f(t) (2-65)
описывает смещение некоторой системы, а функция /(/)— силу,
действующую на эту систему, t — время.
Предположим вначале, что при t < з система находилась в со-
стоянии покоя и ее смещение вызывается силой отличной
§ 51	ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ	123
от нуля лишь в промежутке s < t < s + е, причем импульс этой
силы равен 1:
5+е
J /е(т)йт=1.
Обозначим уе(0 решение уравнения
yw-bpjoy'’-1’ + ...
Легко проверяется существование предела уе(О при е—>0, не зави-
сящего от выбора функции / (/), в предположении, что она не ме-
няет знака. Действительно,
Уе (0 = f К (t, s) fz (s) ds.
to
Применяя теорему о среднем при t > s -|- е, получим
Уе (0 = K(t, s -j- е*) J Д (т) dx = К (t, s -f- е*),
где 0 < е* < е; следовательно,
lim v (0 = K(t s)-
е->0
Поэтому функцию К (t, s) естественно назвать функцией влияния
мгновенного импульса в момент t = s.
Разбивая промежуток (Zo, /) точками s1 (I = 0, 1....п) на т
равных частей длины \s — -~ta, представим функцию f (t) в (2.65)
в виде суммы функций /t(t), где Д(() отлична от нуля лишь
на Z-м промежутке sz-1 < t < st> на котором она совпадает с функ-
цией / (t):
т
Г (0 = 2 Л (О-
(=1
В силу принципа суперпозиции (стр. 114) решение уравнения (2.65)
имеет вид
т
У V) = 2 У. (О.
где yi (t) — решения уравнений
У1л,+а(0у(п-1)4- ... +дл(0у=Л(0
124	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
с нулевыми начальными значениями. Если т достаточно велико, го
решение у,(/) можно рассматривать как функцию влияния мгновен-
ного импульса интенсивности /z(sz)As. Следовательно,
m
sz)/(sz)As.
z=i
Переходя к пределу при т—>оо, получим решение уравнения (2.65)
с нулевыми начальными условиями в виде
у = f К (t, s) f (s) ds,
it)
показывающем, что влияние непрерывно действующей силы можно
рассматривать как наложение (суперпозицию) влияний мгновенных
импульсов.	’
§ 6. Линейные неоднородные уравнения
с постоянными коэффициентами и уравнения Эйлера
При решении линейных неоднородных уравнений с постоянными
коэффициентами во многих случаях без труда удается подобрать
частные решения и тем самым свести задачу к интегрированию соот-
ветствующего однородного уравнения.
Пусть, например, правая часть является многочленом степени $,
и следовательно, уравнение имеет вид
ОоУ(л, + а1У<л-1)-+ ••• +^п-1У' + апУ =
— Aoxs-\- AiX‘-'+ ... +XS, (2.66)
где все а.] и Л( — постоянные.
Если а„ #= 0, то существует частное решение уравнения (2.66),
имеющее тоже вид многочлена степени $. Действительно, подставляя
y = BoxJ-]-B1xi-1+ ... +RS
в уравнение (2.66) и сравнивая коэффициенты при одинаковых, сте-
пенях х в левой и правой частях, получаем для определения коэф-
фициентов Bz всегда разрешимую, если «„=/=0, систему линейных
уравнений:
апВ0 = А0, Во = ^,
a^ + sa'-iB^At,
откуда определяется Bv
апв2 + (5 — 1) а„~ ,В, 4- s (s — 1) а„_2В0 = Л2,
125
НЕОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФ.
§ 6]
откуда определяется В2
оЛ + ... =Л>
откуда определяется Bs.
Итак, если а„=£0, то существует частное решение, имею-
щее вид многочлена, степень которого равна степени много-
члена, стоящего в правой части.
Предположим теперь, что ая = 0, причем для общности допу-
стим, что и ля_1==ая_2^= ... = ая_а+1 = 0, но ап_а^0. т. е. k = О
является а-кратным корнем характеристического уравнения, причем
случай а=1 не исключается. При этом уравнение (2.66) прини-
мает вид
а0У1") + а1У("_1)+ ••• + ал-аУ(0) = А)*5Н-Лх'5-1-I- ... 4-As.
(2.67)
Полагая у(а) = z, мы приходим к предыдущему случаю, и следо-
вательно, существует частное решение уравнения (2.67), для которого
^) = Вох-' + В1^-1+ ... +В„
а значит, у является многочленом степени s-(-a, причем, члены,
начиная со степени a—1 и ниже, у этого многочлена будут иметь
произвольные постоянные коэффициенты, которые могут быть,
в частности, выбраны равными нулю. Тогда частное решение примет
следующий вид:
у = х“(Вох’ + В1х^-1+ ... + BJ.
Пример 1.
у" + У = х2 + х.	(2.68)
Частное решение имеет вид
у = В0х2 Л-Btx-]-В2.
Подставляя в уравнение (2.68) и сравнивая коэффициенты при одинаковых
степенях х, получаем
Во<=1, В1 «= 1, В2 = —2, у = х2-}-х — 2.
Общее решение
у — С) cos х 4- с2 sin х 4 х2 -|- х — 2.
Пример 2.
У" + У' = х — 2.
Частное решение ищем в виде
у= х(Воа:4В1).
Подставляя в уравнение и сравнивая коэффициенты при одинаковых степе-
нях х в левой и правой частях полученного тождества, находим
— Bt = — 3, у = х (-1 х — з).
126	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Общее решение
У = Cj 4-с2<?-* +х (у х — 3).
Рассмотрим теперь линейное неоднородное уравнение вида
аоу(л) 4-	+•...+ апу = еРх (Айх* A}xs-' 4- ... 4- ДД
(2.69)
где все и At — постоянные. Как было указано выше (стр. 109),
замена переменных у = ePxz преобразует уравнение (2.69) к виду
еРх {boz^ + bxz'-n~i'i -|- ... 4- bnz} = ePx(Anxs 4- Д^-14- ... -f- ДД
или
60z(n)	. +t>nz = Aoxs + Д^5’1 + ... 4- Д,. (2.70)
где все bj—постоянные.
Частное решение уравнения (2.70), если (>л=#0, имеет вид
z = BQxs 4- B}xs~' 4- ... 4- Bs,
а значит, частное решение уравнения (2.69)
у = epx(BQxs 4- B..xs~' 4- • • • + Bs).
Условие bn 4 0 означает, что k=Q не является корнем характе-
ристического уравнения
bokn + b1kn-'+ ... +6л = 0,	(2.71)
а следовательно, k = p не является корнем характеристического
уравнения
a^k 4“ а^к 4~  • * 4“ ап ==	(2.72)
так как корни этих характеристических уравнений связаны зави-
симостью ,k — k 4- р (см. стр. 109).
Если же k = 0 является корнем характеристического уравнения
(2.71) кратности а, другими словами, k — р является корнем характе-
ристического уравнения (2.72) той же кратности а, то частные ре-
шения уравнений (2.70) и (2.69) имеют соответственно вил
z = (BQx* + BlX°-' + ... 4- Bs),
у = хаеРх (Boxs 4- В^-' 4- ... 4- ВД
Итак, если правая часть линейного дифференциального
уравнения с постоянными коэффициентами имеет вид
ерх (До^ 4- Дх^-1 4- • •  + ДД
§ 6]'	НЕОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФ.	127
то, если р не является корнем характеристического уравне-
ния, частное решение надо искать в таком же виде'.
У = еР' (Вох‘ +	4- • • • 4- В5).
Если же р является корнем характеристического уравнения
кратности а (этот случай называется особым или резонанс-
ным), то частное решение надо искать в виде
у = хаеРх (Boxs +	. -J- Bs).
Пример 3.
- у" + 9у --- eix.
Частное решение надо искать в виде
у = Ве5Х.
П р и м е р 4.
у" 4- у — e'ix (х — 2).
Частное решение надо искать в виде
-	У = eix (Вох + By).
Пример 5.
у" — у =• ех (х2 — 1).
Частное решение надо искать в виде
у = хех (Вах2 + ВуХ + S2),
так как k — 1 является простым корнем характеристического уравнения.
Пример 6.
У"' + Зу" + Зу' + у = е~х (х - 5).
Частное решение надо искать в виде
у = x2e~x(Bax-Y By).
так как k——1 является трехкратным корнем характеристического урав-
нения.
Заметим, что наши рассуждения остаются справедливыми и при
комплексном р, поэтому если правая часть линейного дифференциаль-
ного уравнения имеет вид
epx [/^ (х) cos qx Qs (x) sin qx\,	(2.73)
где один из многочленов Ps(x) или Qs(x) имеет степень $, а дру-
гой - степень не выше чем 5, то, преобразуя тригонометрические
функции по формулам Эйлера к показательному виду, получим
в правой части
e(P+4i)^fis(x) 4- е'Р~ч‘>хТг(х),	(2.74)
где Rs (х) и Ts (х) — многочлены степени s.
Для каждого слагаемого правой части можно уже применить
указанное выше правило, а именно, если p'h.ql не являются корнями
128	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	“ (ГЛ. 2
характеристического уравнения, то частное решение можно искать
в таком же виде, как и правая часть (2.74); если же p+ql являются
корнями характеристического уравнения кратности а, то частное ре-
шение приобретает еще множитель ха.
Если опять вернуться к тригонометрическим функциям, то это
правило можно сформулировать так:
а)	Если р ± ql не являются корнями характеристического
уравнения, то частное решение надо искать в виде
y — ePx\Ps{x}cosqx-\-Qs(x)sinqx],
где Р (х) и Qs(x)— многочлены степени s с неопределенными
коэффициентами.
Заметим, что если один из многочленов Ps{x) или фДх) имеет
степень ниже s или даже, в частности, тождественно равен нулю,
то все же оба многочлена Ps(x) и Qs(x) будут, вообще говоря,
иметь степень $.
б)	Если p+qi являются а-кратными корнями характери-
стического уравнения {резонансный случай}, то частное ре-
шение надо искать в виде
у = хаеР* [Ps (х) cos qx -|- Qs (х) sin qx].
Пример?.
у" + 4у' + 4у = cos 2х.
Так как числа ±21 не являются корнями характеристического уравнения,
то частное решение ищем в виде
/= A cos 2х + В sin 2х.
Примере.
' У" + 4у = cos 2х.
Так как числа ±21 являются простыми корнями характеристического урав-
нения, то частное решение ищем в виде
у = х [ A cos 2х 4- В sin 2х].
П р и м е р 9.
ylv 4-2у"4-у = sinx.
Так как числа ± i являются двукратными корнями характеристического
уравнения, то частное решение ищем в виде
у — х2 (Л cos х -|- В sin х).
Примерю.
у" + 2у' 4- 2у = е~х (х cos х + 3 sin х).
Так как числа — 1 ± I являются простыми корнями характеристического
уравнения, то частное решение ищем в виде
у = хе~х [(Л0х4- cos х 4- (Вох -|- Si)s|n
§ 61	НЕОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФ.	129
Во многих случаях при нахождении частных решений линейных
уравнений с постоянными коэффициентами с правой частью вида (2.73)
целесообразно перейти к показательным функциям.
Например, в уравнении
у" — 2у' 4* У — cos х
можно преобразовать cos х по формуле Эйлера или, еще проще, рассмотреть
уравнение
у" — 2у' + у = е‘х,	(2.75)
действительная часть решения которого должна удовлетворять исходному
уравнению (см. стр. 114—115).
Частное решение уравнения (2.75) можно искать в виде
у=ЛеЧ
Тогда
А = у , у = у (cos х -j- I sin х).
Частное решение исходного уравнения
У) = Re у = — у sin х.
Для нахождения частных решений линейных неоднородных урав-
нений с постоянными коэффициентами во многих случаях очень удо-
бен операторный метод.
Понятие об операторном методе решения линей-
ных дифференциальных уравнений с постоянными
коэффициентами. Для производных порядка k введем обозна-
чение
Пользуясь этим обозначением, запишем уравнение
йоу(я) 4-а1У<п-1> + ...+ «лу = /(х)
в виде
уaxDn ’у 4~ • • • апУ — f
(a0Dn 4- axDn-1 4- • • • + ап_ XD 4- а„) у = f (х)'.	(2.76)
Выражение
а0Ол4-а1^>” *+ ••• + ап-\В ап
называется операторным многочленом. Этот операторный много-
член кратко обозначим F(D), а уравнение (2.76) запишем в виде
F(D)y=/(x).
130	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. 2
Непосредственной проверкой легко устанавливается справедливость
следующих тождеств:
1)	F(D)ekx = ekxF(k),
2)	F (£>2) sin ах = sin axF (— а2),
3)	F (£>2)cos ах = cos axF(—а2),
4)	F (D)ekxv (x) = ekxF (D 4- k) v(x).
Действительно:
1) F(D)?x = (a0Dn + a1D'"1+	=
— ekx(aQknaxkn~'... + a„) = ekxF (k).
2) F (Z)2)sinax = (a0Z)2" 4~ a1D2n-24-... -f~	+ ajsin ax —
= [«o(— a2)n + «1 (~ a2)"'* + •••+«»-!(— °2) + an\sin ax =
= sin axF (— a2).
Тождество 3) доказывается совершенно аналогично:
F (D2) cos ax = cos axF (— a2).
4) F (D) ekxv (x) = J} an_pDp (ekx v (x)) =
p=0
= ekx ^an_p]kpv{x)-\-pkp~xDv-\-
P = 0
+	fep~2^+	+£>₽d =
21	J
= e*x 2 c«-p (D + v = e'lXF (D k) v W-
p=0
Суммой двух операторов F} (D) и F2(D) называется оператор
[Fj (£>) -j- F2 (£>)], действие которого на некоторую функцию / (х)
определяется равенством
[Fj (D) 4- F2 (D)] f (x) = Fi (D) f (x) 4- F2 (D) f (x).
Из этого определения следует, что
2оя-рОР+ ^bn_pDp= Ъ(ап_рА-Ьп,р)Вр.
р=0	р=0	р=0
так как действие левой и правой частей этого равенства на неко-
торую п раз дифференцируемую функцию /(х) приводит к одному
и тому же результату, т. е. правило сложения операторных много-
членов не отличается от правила сложения обычных (не операторных)
многочленов.
§61	НЕОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФ.	131
Произведением двух операторов Fj (£>) • F2 (О) называется опе-
ратор, действие которого на некоторую достаточное число раз диф-
ференцируемую функцию /(х) определяется равенством
F! (D) • F2 (О) / (х) = F, (D) [F2 (D) f (x)],
т. e. на функцию /(x) действует сначала правый множитель, а затем
на результат действия правого множителя на функцию /(х) действует
левый множитель.
Исходя из этого определения, нетрудно обнаружить, что правило
умножения операторных многочленов не отличается от правила умно-
жения обычных (не операторных) многочленов. Действительно,
п	гп	п гп
2 an_pD- V Ьт_^ = V £	(2.77)
/; = 0	«7 = 0	р = о 17=0
так как
п т
= 22 вп-р^_9/р+?>(х),
р=0 <7 = 0	4
что совпадает с результатом действия оператора
п т
2 2 «Я-Д1_/>Р+’
р=0 9=0
на /(х).	,
Из (2.77), в частности, следует коммутативность умножения опе-
раторов
F1(D)F2(D) = F2(D)F1(D).
Справедливость дистрибутивного закона
F (D) [F. (D) 4- F2 (£>)] = F (D) Ft (D) +'F (.£)) F2 (D)
непосредственно следует из правила дифференцирования суммы.
Следовательно, действия сложения и умножения с операторными
многочленами не отличаются от тех же действий с обычными (не
операторными) многочленами.
„ 1
Определим теперь оператор •
Результатом действия оператора -рф} на некоторую непрерыв-
ную функцию /(х) является решение уравнения
F(D)y=f(x),
(2.78)
132
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. г
Следовательно,
РФ) |.77О) f (*)] = /(*)•
(2.79)
Можно было бы считать, что рфу / (х) является решением уравне-
ния (2.78), определяемым какими-нибудь конкретными, например
нулевыми, начальными условиями, однако для наших целей удобнее
считать, что у, / (х) является одним из решений, все равно каким,
уравнения (2.78) и, следовательно, действие оператора	на не‘
которую функцию /(х) определено лишь с точностью до слагаемого,
равного решению соответствующего однородного уравнения.
„ 1
При таком понимании действия оператора будет
вым равенство
справедли-
p~lF(D)f(x)]^/(x).
так как /(х), очевидно, является решением уравнения
F(D)y = F(D)/(x).
Произведение операторов Ф (D) на определяется
Ф -FTD) f {Х> = ° (D) [m f (Х)] •
Аналогично
вее)
равенством
Ф (D) f (х) =	[Ф (D) / (х)].
Поэтому в формулах (2.79) и (2.80) скобки можно опустить. Заметим
еще, что
^pf(x) = J f ... f f(x)dxp,
1	ч 1
так как f (x) является по определению оператора реше-
нием уравнения Dpy=f(x).
Проверим следующие свойства оператора ~р~фу:
P(D) = k F(D) f
где k — постоянный множитель, так как
F k TXD) f (x) = kF (D> ~FTD) f W-
2)	7W е"Л = Й) ’ если F {k) * °’
§ 6]
НЕОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФ.
133
Действительно,
так как по формуле 1) стр. 130
р&у является решением уравнения F (D) у — е“х
F{D)
екх F(k)ekx = кх
А(А)~ F(k) ~е
3)	7>) S’n йХ = А-а2) ' еСЛИ F “2) °*
Действительно,	является решением уравнения F(D2)y =
sin ах, так как по формуле 2) стр. 130
F (D2)	j? (2. Д2) F (— a2) sin gx = sin ах,
4)	ТТ^У cos ах =	• еСЛИ F	а2) * ° ’
так как по формуле 3) стр. 130
F	д2) F (— а )cos ах = cos ах.
5)	FTD)	(Х) = gkX ~Р (/+ k) V
Действительно, екх ? v является
F (£)) у = ekxv (х), так как по формуле 4) стр.
решением уравнения
130
F(D)ekx F(D + k} v{x) — ekxF{D-\-k) P(D^ky
6)	[/i (x) + /2 (x)] = -p— f^x) -b /2 (x).
v(x) = ekxv(x);
Это равенство является следствием принципа суперпозиции (стр. 114).
7)	= Г, (£)) F2(D) (х)'
т. е.
у = Fx (D) [ F2 (D) f(x)]	(2,81)
является решением уравнения
F^(D)F2(D)y = /(x).	(2.82)
Действительно, подставляя (2.81) в (2.82), получим
^i^F))Fx (£>)	f (х)^|= F2 (D) р2^ f (-с) = /(х).
134	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Приведем несколько примеров нахождения частных решений линейных
неоднородных уравнений с постоянными коэффициентами операторным
методом:
1)	у"-|-4у = г*, или (D2 4- 4) у = еv * * * * х, откуда
1 X ех
У~ Г>24-4 е ~ 5 '
2)	y'V у — 2 cos Зх, или (D4 + 1) У = 2 cos Зх,
1 о о 2cos3x 1
У = дГТрГ 2 cos Зх = (_9)2 + 1 = 4Г cos Зх
3)	у" 4~ 9у = 5 sin х, (£>2 + 9) у = 5 sin х,
1	- ,	5 sin х 5 ,
У=	= 8 slnx
4)	у" _ 4у' _]_ 4у = х2е2х' (£> — 2)2 у = х2е2х.
5)	у'" — Зу" + Зу' - у = ех, (D — I)3 у = ех,
>,= (D —I)3
F (k) = 0, поэтому вместо второй формулы применяем формулу 5) (стр.
132—133), рассматривая ех как произведение ех-1:
1 г , к 1 1 х -*3
У — (В _ 1)3 е '1 — е рТ 1 — е 6 •
6) у”' — у = sin X,
(D3— l)y = sinx.	(2.83)
у— 2j3~—j-sinx. Так как оператор содержит нечетные степени D, то вос-
пользоваться формулой 4) нельзя. Поэтому вместо исходного уравнения рас-
смотрим уравнение (D3 — 1) у = е,х, или
(D3—1) у — cos х -j- i sin х.	(2.84)
Мнимая часть решения уравнения (2.84) будет решением исходного уравне-
ния (см. стр. 115):
v —	1 pi* — eiX _ ~е‘х _ (—1.+ 0(cosx4-Zsinx) __
У D3 — 1 г3 — 1 ~ 14-/	2	~
= — у (cos х 4- sin х) 4- 4- (cos х — sin x)
Мнимая часть решения cos-- -i* уравнения (2.83) является решением
уравнения (2.83).
7) У" + У = cos х, (D2 4- 1) у — cos х, у =	’ cos х'
' Формула 3) стр. 133 неприменима, так как F (— а2) = 0, поэтому опять
вместо заданного уравнения рассматриваем уравнение
у" + у = е1Х или у"-|-У = cos х 4-г’sin х
§ 6)	НЕОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФ.	135
и берем действительную часть его решения
(^ + 1)у = ?Л у = —1^ = (Д-0 (D[+i)	=
1 eix etx 1 . е‘хх x(cos x-f-Zsinx)
~ D — i ~2i 2Г D'l~ 2i	21	"
Взяв действительную часть найденного решения вспомогательного уравне-
xsinx
ния----, получим решение исходного уравнения
8) yIV — у = ех, (D4—1)у = е< у = -D< д- е* =
1	1	я,	1 6х 1 х 1 , хех
~ D — 1 (D4-1)(£>24-1) е ~ D — 1 4 ~ Iе ~D 1	4~*
Выясним еще, как действует оператор на многочлен
Рр(х) = Аохр + А1хр->+ ... + Ар.
Формально разделим 1 на многочлен
F(D) = ая4-оя_1О-|- ... -j-a0D", а„=£0,
расположенный по возрастающим степеням D, по правилу деления
обычных (не операторных) многочленов. Процесс деления прекратим
тогда, когда в частном получим операторный многочлен степени р:
/>0 + ^£> + ... + bpDp = Qp(D).
При этом в остатке окажется многочлен
R(D) = cp+lDp+l + cp+2Dp+2 + ... + cp+nDp+n,
содержащий оператор D в степенях не ниже p-f-l. В силу зависи-
мости между делимым, делителем, частным и остатком получим
F(D)Qp(D) + R(D)~l.	(2.85)
Это тождество справедливо для обычных (не операторных) много-
членов, но так как правила сложения и умножения операторных
многочленов не отличаются от правил сложения и умножения обыч-
ных многочленЪв, то тождество справедливо и для операторных
многочленов. Действуя правой и левой частями тождества (2.85)
на многочлен Айх? -]-	... -|- Ар, получим
(F(D)Q;,(D)-|-/?(D)](H()xp + 41xp-’+ ... + Др) =
=	+-\-ар
или, принимая во внимание, что
Я(П)(ДохР4-Л1Л;Р-Ч~ ... -ЬДР) = О,-
136
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
[ГЛ. 2
так \ак R(D) содержит D в степенях не ниже р 4- 1, будем иметь
F(/3)[<?p(D)HoxP + AlXP-'-h ... +Л,)]==
= Лохр -Ь AiXP-l-+ ... 4- Ар,
т. е. Qp (D) (АоХр 4- AiXP~lA~ . • • 4~ Ар) является решением уравнения
F (D) у = Лох'4 AlXP~' +•••+ Л,.
Итак,
'рф) <ЛхР + AixP 1 + • •  + Ар) —
= Qp (D)(АоХр 4- AiXp-> 4- ... 4- А„).
Например:
9) У"4- у = х2 —х4-2, (Р24-1)у = л-2—x4-2,y = grl-j(xa—х-1-2).
Разделив 1 на 14-D2. получим Q2 (D) — 1 — D1. Следовательно,
у = (1 — О2) (х2 — х 4- 2) = х2 — х. '
Ю) у" 4* 2у' 4~ 2у — Х2е~х, (D2 4- 2£> 4- 2) у = х2г-<
У = р2 4. 2£> 4- 2 Х^е Х=°е Х О2 4- 1	= * Л(1 — £>2)х2 = «? х(х2 —2)-
П) У" 4" У = х cos х, (D2 4- I) у = х cos х.
Перейдем к уравнению (О2 4~ 1) У = xetJC и потом возьмем действительную
часть решения
Взяв действительную часть sin х 4- cos х, получим искомое решение.
Замечание. Последний пример показывает, как надо действо-
вать оператором ~р
в виде DSfJ){D), где свободный член многочлена Ф(£>) уже не
„ 1
нулю, действуем на многочлен вначале оператором 
оператором .
Неоднородные уравнения Эйлера
аохлу<п> 4-а1хп-1у(я~1) 4- ... 4- апу = /(х)
на многочлен, если ап = 0. Представив F(D)
равен
затем
а
(2.86)
(2.87)
или
а()(ах4-/>)'’у(п'4-а1(ах4-й)л-1у('1-1) 4- ... 4- апу = /(х)
можно интегрировать путем решения соответствующих однородных
уравнений (см. стр. 110) и подбора одного частного решения неодно-
§ 7)	ИНТЕГРИРОВАНИЕ УРАВНЕНИИ ПРИ ПОМОЩИ РЯДОВ	137
родного уравнения, или применяя метод вариации постоянных. Однако
обычно проще вначале проинтегрировать однородное уравнение, а для
подбора частного решения преобразовать уравнение Эйлера (2.8,6)
заменой переменных х = + е‘ (для уравнения (2.87) ах-\-Ь — + 'е‘)
к уравнению с постоянными коэффициентами, для которых хорошо
разработаны методы нахождения частных решений.
Пример 11.
х2у" (х) — ху' (х) у (х) = х In3 х.	(2.88)
Ищем- решение соответствующего однородного уравнения в виде у = л*
й2 — 2й 4- 1 = 0;	(2.89)
йь 2 — 1, следовательно, общее решение однородного уравнения имеет вид
у = (С| 4- Сг1пх)л. Заменой переменных л = <4 преобразуем уравнение (2.88)
в уравнение с постоянными коэффициентами у (t) — 2у (/) 4~ У = № (левая
часть этого уравнения сразу может быть написана по характеристическому
уравнению (2.89)). Операторным методом легко находим частное решение
преобразованного уравнения
1	/-з t 1 е*Р х1п5аг
у~ (D — I)2 et ~ е ~ 20 ’ У~ 20 '
Следовательно, общее решение уравнения (2.88) имеет вид
У = («1 + с21 п х 4-х.
§ 7. Интегрирование дифференциальных уравнений
при помощи рядов
Задача интегрирования линейных однородных уравнений га-го
порядка
Ро(*)/п) + Р1(*)У('’_1)-|- ••• +РЯ(*)У = °-	(2.90)
сводится к подбору п или хотя бы п — 1 линейно независимых
частных решений. Однако частные решения легко подбираются лишь
в исключительных случаях. В более сложных случаях частные реше-
ОО
ния ищут в виде суммы некоторого ряда 2 <VP/ (*)• особенно часто
в виде суммы степенного или обобщенного степенного ряда.
Условия, при которых существуют решения в виде суммы сте-
пенного или обобщенного степенного ряда, обычно устанавливаются
методами теории функций комплексного переменного, знакомства
с которыми у читателя мы не предполагаем, поэтому основные теоремы
этого параграфа даны без доказательства в применении к наиболее
часто встречающимся в приложениях уравнениям второго порядка.
Теорема 2.9 (об аналитичности решения). Если
р0(х), Pi(x), р2(х) являются аналитическими функциями х
138	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
в окрестности точки х = хои ро(хо)#=О, то решения уравнения
Ро(х)У" + Pi(x)y' -I- р2(х)у = 0	(2.91)
также являются аналитическими функциями в некоторой
окрестности той же точки и,’-следовательно, решения урав-
нения (2.91) можно искать в виде
У = а0Чга1(х — х0) + а2(х — х0)2+ ... -f-ап(х — х0)" + ...
Теорема 2.10 (о разложимости решения в обобщенный
степенной ряд). Если уравнение (2.91) удовлетво ряет условиям
предыдущей теоремы, но х — х0 является нулем конечного
порядка s функции р0(х), нулем порядка s—1 ила выше
функции рх(х) (если s > 1) а нулем порядка не ниже s — 2
коэффициента р2(х) (если s > 2), то существует по крайней
мере одно нетривиальное решение уравнения (2.91) в виде
суммы обобщенного степенного ряда
у = а0(х-х0)*+а1(х-х0)*+1+ ... + ая(х-х0)*+л + ..(2.92)
где k — некоторое действительное число, которое может быть
как целым, так и дробным, как положительным, так и отри-
цательным.
Второе линейно независимое с (2.92) решение, как правило, имеет
тоже вид суммы обобщенного степенного ряда, но иногда может еще
содержать произведение обобщенного степенного ряда на 1п(х—х0).
Впрочем, в конкретных примерах можно обойтись без формули-
рованных выше двух теорем, тем более, что эти теоремы в указан-
ной формулировке все равно не устанавливают области сходимости
рассматриваемых рядов. Чаще всего в конкретных задачах подбирают
степенной или обобщенный степенной ряд, формально удовлетворяю-
щий дифференциальному уравнению, т. е. при подстановке обращающий
рассматриваемое уравнение (2.90) порядка п в тождество, если пред-
полагать сходимость ряда и возможность почленного дифференциро-
вания п раз. Получив формально решение в виде ряда, исследуют
его на сходимость и на возможность почленного дифференцирования
п раз. В той области, где ряд сходится и допускает л-кратное
почленное дифференцирование, он не только формально удовлетво-
ряет уравнению, но его сумма действительно является искомым
решением.
Пример!.
у" — ху = 0.	(2.93)
Ищем решение в виде степенного ряда
У = 2
§ 7]	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ ПОМОЩИ РЯДОВ	139
Опираясь на теорему 2.9 или формально дифференцируя этот ряд почленно
два раза и подставляя в уравнение (2.93) получим
2 апп (п — 1) х"~2 — -*2 апХ" = &
п-2	«=0
Сравнивая коэффициенты при одинаковых степенях х в левой и правой
Дл
частях тождества, получим: а2 = 0, 3-2<z3— ав — 0, откуда а3 = '2~з";
4-За, — Л1=0, откуда а4=^т; 5-4а5— а2 = 0, откуда а5 = -г^-,..
о • 4	4 • Э
п (п— I) а„ — д„_3 = 0, откуда ап =
ап-з
(п — 1) п ’
.. Следовательно,
«з/г-1	0. ^зп— 2.3.5.6 ... (дп_ 1)3„ •
Лзл+1 = 3-4-6-7 ...’зл(ЗггН-1)	(« = ^> 2,
а0 и й| остаются произвольными. Итак,
х^	х*п	*1
1 + Гз + 2 • 3 • 5 • б +	+ 2 • 3 - 5 • 6 ... (Зп — 1) Зп + •••] +
[у4	X7	X3n+l	1
+з~4 + 3.4.6 • 7 +	+ 3 • 4 • 6  7 ... Зп (Зп + 1) + •••]• (2'94)
Радиус сходимости этого степенного ряда равен бесконечности. Следова-
тельно, сумма ряда (2.94) при любых значениях х является решением рас-
сматриваемого уравнения.
П р и м е р 2.
х2у"4-лу' + (л:2 —из)у = О.	(2.95)
Это уравнение называется уравнением Бесселя порядка п, хотя впервые оно
встречается в работах Л. Эйлера и Д. Бернулли. К уравнению Бесселя сво-
дятся многие задачи математической физики, поэтому мы исследуем его не-
сколько подробнее.
По теореме 2.10 по крайней мере одно нетривиальное решение уравнения
Бесселя может быть найдено в виде суммы обобщенного степенного ряда
/ 00
У = У архк+р.
Р—0
Дифференцируя этот ряд два раза почленно и подставляя в уравнение (2.95)
получим
со
X- ^iap(k+p)(h + p—1)xk+p-i+
р=0
+ х У, ap(.k-i-p) 4-(х2 — п2) 2	=0.
рсО	р=0
140	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. 2
Сравнивая коэффициенты при одинаковых степенях х в левой и правой ча-
стях равенства, получаем
zz0 (А2 — л2} = 0,
а, [(* + I)2 - л2] - 0,
((* + 2)2 — п2] а„ + а0 •= О,
t	((й + 3)2 — п2] а3— О,
Так как коэффициент а0 при низшей степени х можно считать отличным от
нуля, то первое уравнение сводится к
k2 — п2 = 0, откуда k = ± п.
Для определенности будем пока считать k п > 0; тогда из второго уравне-
ния Л|[(п-+-1)2— н2] = 0 получим: ах = 0 и, следовательно, все а2р+1=-0,
___ __	_______Др___
а2~ (л + 2)2 — п2 =	22(л-Н)’
О>2	До
= — („ + 4)2 _ П2 “ — 22 (п + 2) 2 = 24 (л 4-1) (л + 2) 1 • 2 ’
а _____________(~1)рДо
2/,= 22р-pl(n+l)(n4-2) ... (л + р) ‘
При 4= — п совершенно аналогично получаем
а « а _______________________________(- _________________
>	2₽	22₽pt(—л-|-1)(—л4-2)... (—л-|-р) "
При А = л получаем решение
у = а0 V _________<=11РАР+П
“ 2 z’/’|(«+1)(« + 2) ... (л-hр)
Этому решению можно придать более удобный вид, если выбрать произволь-
ное постоянное йо “=	• где Г — гамма-функция Эйлера; напом-
ним, что
. ( Х>
г (р) = J* е~*хр~ xdx при р > О, Г (р + 1) == рГ (р).
о
Тогда
(-1/(^2₽+Л
р! Г (и + р + I)’
(2.96)
§ л	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ ПОМОЩИ РЯДОВ	141
Это решение обычно обозначается Jn (х) и называется функцией Бесселя
первого рода порядка п.
При k = — п, выбирая а0 =	, аналогично получаем фун-
кцию Бесселя первого рода порядка —п:
/_Я(Х)_ 2j р1Г(_п_|_р+1).	(2.97)
р=о
Ряды (2.96) и (2.97) сходятся при любых значениях х (в (2.97) х =/= 0) и
допускают двукратное почленное дифференцирование, следовательно /я(х)
J_„(х) являются решениями уравнения Бесселя (2.95).
При п, не равном целому числу, решения Jn(x) и 7_л(х), очевидно,
линейно независимы, так как их разложения в ряды начинаются с различных
степеней х и, следовательно, линейная комбинация a.\Jn (х)	(х) мо-
жет тождественно равняться нулю лишь при а, — а2 = 0.
Если же п равно целому числу, то, так как для целых отрицательных
значений р и для р = 0 функция Г (р) обращается в бесконечность, разло-
жения в ряды функций Jn(x) и J_n{x) начнутся с одинаковых степеней х
и, как нетрудно проверить, функции Jn(x) и J-„(x) будут находиться
в следующей линейной зависимости:
/_п(х)=(-1)я/„(х).
Следовательно, при целом п вместо	(х) надо искать другое решение,
которое было бы линейно независимо от /„ (х). Такое решение можно полу-
чить различными способами, например, можно, зная одно частное реше-
ние /я (х), понизить порядок уравнения (2.95) подстановкой, указанной на
стр. 101, или сразу искать решение в виде суммы обобщенного степенного
ряда и произведения обобщенного степенного ряда на 1п х. Получаемое любым
из .этих способов линейно, независимое от Jn (х) решение при вполне опре-
деленном выборе произвольного постоянного множителя называется функ-
цией Бесселя второго рода и обозначается Кя(х).
Чаще всего, однако, Y„ (х) определяют так: считая пока п не равным
целому, числу рассматривают решение Y„ (х) уравнения Бесселя, являющееся
линейной комбинацией решений Jn (х) и (х):
Jn(x) cos лл —(х) .
л< ’	sin/гл	’
затем, переходя к пределу при п, стремящемся к целому числу, получают
линейно независимое от Jn (х) частное решение уравнения Бесселя Y„ (х),
определенное уже и для целых значений /г.
Итак, общее решение уравнения Бесселя при п, не равном целому числу,
имеет вид
у= с,/л(х)-Ьсг/_„(х),
а при п, равном целому числу,
у«сЛ(х) + с2Кя(х),
где С| и с2 — произвольные постоянные.
Функции Бесселя первого и второго рода изучены весьма детально и,
в частности, составлены подробные таблицы их значений. Поэтому, если
какая-нибудь задача сведена к функциям Бесселя, то ее можно считать
142	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	(ГЛ. 2
решенной в такой же мере, в какой мы считаем решенной задачу, в которой
ответ дан, например, в тригонометрических функциях.
Часто в приложениях приходится рассматривать уравнение
х2у" + ху'+ (т2хг — пг)у = 0.	(2.98)
Это уравнение сводится к уравнению Бесселя заменой переменной xt = тх.
Действительно, при такой замене переменных
dy	e rfy rfxi	= dy	т d2y	= d2y
dx dxy dx dxx dx2 dx2	
и уравнение (2.98) переходит в уравнение Бесселя:
-ГТ + 7^-+ (x'i ~ "2) > = °-
dx] dx} '
Следовательно, общее решение уравнения (2.98) при п, не равном целому
числу, имеет вид
у = cjn (тх) + c2J -п (тх),
а при п целом
у = CiJn (тх) + с2У„ (тх).
ПримерЗ.
Х*У" + ху' + (4х2 _ j у = 0.
Общее решение уравнения имеет вид
У = ctJ3 (2x) + c2J з (2х).
"5	' 5
П р и м е р 4.
х2у" + ху’ + (Зх2 — 4) у = 0.
Общее решение
у= сЛ(хКЗ)-Ьс2Г2(лКЗ).
Пример 5. Проинтегрировать уравнение
х2у" + ху’ + ^4х2 — -1) у == 0
при условии, что решение должно быть непрерывно в точке х = 0 и у (0,3) = 2.
Общее решение имеет вид
У = Ci J i (2х) + c2J j (2х).
J	"а
Функция J j (2х) разрывна при х «= 0, так как ряд (2.97) начинается
" з
с отрицательных степеней х. Следовательно, решение у непрерывно в точке
х 0 лишь при с2 = 0:
у = С](2х).
3
§ 7)	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ ПОМОЩИ РЯДОВ	143
Удовлетворяя второму условию у (0, 3) = 2, получим
_	2
С1 “	(0,6) •
3
В таблицах Бесселевых функций находим Jj (0,6) = 0,700, следовательно,
"з
с, « 2,857 и
у « 2,857J1 (2х).
з
В приложениях часто требуется найти периодические решения
некоторого дифференциального уравнения. В этом случае обычно
целесообразно искать решение в виде суммы некоторого ряда Фурье:
Ло । V1 I л пл , , D . пл ,\
x(O = -2L+ 2j (Ллсо®—finsln—т
п=1
Заметим, что если уравнение
xW = F(t, х, х......х'"'1))	(2.99)
имеет периодическое решение х0(/) периода Т, то правая часть ура-
внения (2.99) вдоль рассматриваемой интегральной кривой является
периодической функцией периода Т по первому аргументу. Действи-
тельно, подставляя в уравнение (2.99) периодическое решение х —
— х0 (/), получаем тождество
XW(O = F(/, х0(0, x^t).......х<Г1’(0).
Заменяя в этом тождестве t на / Т, мы в силу периодичности
функции х0 (t) и ее производных не изменим левой части уравнения
и не изменим аргументов правой части, начиная со второго, следова-
тельно,
Г(Л х0(/), х0(О.....
= F(/4-T, х0(О, Xo(t), .... х^-’ЧО).
т. е. функция F вдоль интегральной кривой x — x0(t) имеет период Т
по явно входящему аргументу t.
Следовательно, если правая часть уравнения (2.99) при любом
выборе х0(/) не является периодической функцией по первому аргу-
менту, то не существует и периодических решений. Если функция F
не зависит явно от t, т. е. является постоянной по отношению к аргу-
менту t, то F можно рассматривать как периодическую по t функцию
любого периода и поэтому не исключена возможность существования
периодических решений какого угодно периода.
144	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Пусть, например, требуется найти периодические решения уравнения
х-+-а2х — f(t).	(2.100)
Для существования периодического решения необходимо предпо-
ложить, что f является периодической функцией. Без существенного
ограничения общности можно считать, что f (t)— периодическая
функция периода 2л, так как если бы функция f (f) имела период Т,
то после преобразования независимого переменного t1 — -jr-t пра-
вая часть стала бы функцией периода 2л по новому независимому
переменному
Предположим, что функция /(/), кроме того, непрерывна и раз-
ложима в ряд Фурье:
/(/)	(gfe cos kt 4- bk sin kt).	(2.101)
*=i
Периодическое решение ищем в виде
x(t)=-^- .4. V (At cos kt 4- Вк sin kt). (2.102)
л=1
Дифференцируя ряд (2.102) почленно два раза и подставляя в урав-
нение (2.100), получим
—	cos sin +
*=1
4- а?
4- cos kt 4- Bk sin kt)
k=i
==-y-4- ^(as cos kt-\-bk sin kt),
s=i
откуда, если а не равно целому числу, определяем коэффициенты -
ряда (2.102):
д __
2 “ 2 ’	а2 ’
(a2-r-£2)^ = aft, =
(2.103)'
{а1—!г2)Вк—Ьк.	=
§ 7] ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ПРИ ПОМОЩИ РЯДОВ	145
Следовательно, уравнению (2.10Q) формально удовлетворяет ряд
ао । Пк cos kt ~Ь sin kt	" /о 104\
2л2 '	а2 — k2 '	(	'
ft=i
Очевидно, что ряд (2.Г04) сходится и допускает двукратное почлен-
ное дифференцирование, так как ряд (2.101), в силу непрерывности
функции /(/), сходится равномерно, а коэффициенты ряда
оо
. (2.105)
t=i
составленного из вторых производных от членов ряда (2.104), отли-
чаются от коэффициентов ak и bk ряда (2.101) лишь не зависящим
k.2
от t, монотонно стремящимся к 1 при k -> оо множителем — а2_^2 .
Следовательно, ряд (2.105) сходится равномерно, а значит, ряд (2.104)
можно было дифференцировать почленно два раза. Итак, ряд (2.104)
не только формально, удовлетворяет уравнению (2.100), но его сумма
x(f) существует и является периодическим решением уравнения (2.100).
Если а мало отличается от целого числа гаи ап =# 0 или Ьп #= 0,
то наступает явление резонанса, заключающееся в резком возрастании
при приближении а к га хотя бы одного из коэффициентов
А —	В — Ьп
^П — аг_пг > “п ai _пг •
Если же а = га и хотя бы один из коэффициентов ап или Ьп не равен
нулю, то периодических решений не существует, так как резонирую-
щим слагаемым
ап cos nt + Z?nsin nt
в правой части уравнения (2.100), как указано на стр. 128, согласно
принципу суперпозиции соответствует в общем решении уравне-
ния (2.100) непериодическое слагаемое вида
t (Ап cos nt + Вп sin nt),
тогда как остальные слагаемые в общем решении уравнения будут
периодическими функциями. Следовательно, при а = га периодическое
решение уравнения (2.100) существует лишь в случае отсутствия
в правой части резонирующих членов ап cos nt -|- bn sin nt, т. е.
в случае
2л	2л
— f (t) cos nt dt — 0, bn — ^ I* /(Z)sin nt dt — 0.	(2.106)
.о	6
146	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
В последнем случае, т. е. при а — п, ап=Ьп — 0, периодическое
решение уравнения (2.100) существует, причем при k #= п коэффи-
циенты определяются по формулам (2.103), а коэффициенты Ап и Вп
остаются произвольными, так как A„ cos nt -|- Вп sin nt является при
произвольных Ап и Вп решением соответствующего однородного
уравнения.
Пример 6. Определить периодическое решение уравнения
. о V sin
х+2х =
i = l
Ищем решение в виде ряда
ОО
х (f) =	(Л* cos kt Bk sin kt)
4 = 1
и, определяя коэффициенты Ah и Bh по формулам (91), получаем
v sin kt
Х()=‘& k*(2 — k2)‘
4 = 1
Пример 7. Определить периодическое решение уравнения
х + 4х sin21.
Так как условия существования периодического решения (2.106) не удовле-
творяются:
2л
J* sin21 sin 2/ dt = 0,
о
но
2л
J sin2t cos 2t dt Ф 0,
о
то периодического решения не существует.
Пример 8. Определить периодическое решение уравнения
оо
Seos kt
—•
k = 2
В правой части отсутствуют резонирующие члены cos t bi sin t. Следо-
вательно, периодическое решение существует и определяется по форму-
лам (2.103):
СО
Seos kt ,	. ,	, ,
_____ + Cj cos t + c2 sin t,
k = 2
где e, и сг — произвольные постоянные.
§ 8]	МЕТОД МАЛОГО ПАРАМЕТРА	147
§ 8. Метод малого параметра и его применение в теории
квазилинейных колебаний
В предыдущем параграфе был указан метод нахождения периоди-
ческих решений линейных уравнений вида
х а?х = f (/).
Во многих практических задачах возникает вопрос о нахождении
периодического решения аналогичного уравнения, но имеющего в пра-
вой части малое нелинейное слагаемое:
х -f- а2х — f (t) -ф- \iF (t, х, х, р),	(2.107)
где p — малый параметр.
Если отбросить слагаемое pF (/, х, х, р), т. е. считать в урав-
нении (2.107) р = 0, то получим линейное уравнение
х 4- а2х = f (/),
называемое порождающим для уравнения (2.107).
Одним из наиболее эффективных методов нахождения периодиче-
ских решений уравнения нелинейных колебаний с малой нелиней-
ностью (2.107) является разработанный А. Пуанкаре и А. М. Ляпу-
новым метод разложения решения в ряд по степеням малого пара-
метра р, широко применяемый в настоящее время при решении самых
разнообразных задач.
Опираясь на теорему об аналитической зависимости решения от
параметра (см. стр. 55), легко обобщающуюся на уравнения второго
и более высокого порядков, можно утверждать, что решения x(t, р)
уравнения (2.107) будут аналитическими функциями параметра р при
достаточно малых по модулю значениях р, если функция f (t) непре-
рывна, а функция F(t, х, х, р), непрерывная по t, аналитически за-
висит от остальных аргументов: от х и х в той области, в которой
в дальнейшем будут меняться эти переменные, а от р при достаточно
малых по модулю значениях р.
Предполагая, что эти условия выполнены, ищем периодическое
решение x(t, р) в виде суммы ряда
x(t, р) = хо(0 4-рх1(0 4-р2х2(О4- ••• 4-Ц%(0+ •••
Дифференцируем этот ряд почленно два раза:
x(t, р) =x0(t) 4-pjCi(04- ••• 4-ил*я(04- ••••
X (f, Р) =*= Ха (0 4- р*1 (О 4- ... 4- p“jc„ (0 4- ....
148
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. 2
и подставляем в уравнение (2.107), в котором функция F(t, х, Д р)
предварительно разложена по степеням х — х0, х — х0 и р,
х сРх — f (/) —j— р F (f, Xq, x0,
X = Xft
H=0
x = x0
ц=0
,•	• . , / dF \
(x -x0) 4- —
\ /
(2.108)
X = Xq
H = o
Сравнивая коэффициенты при одинаковых степенях р в левой и пра-
вой частях уравнения (2.108), получим
x0 + a2x0 = f(t),
Xj + а'2хх = F (t, х0, х0, 0),
X = Хо	X = Хо	X = X
ц=0	ц=0	ц=0
Первое из этих линейных уравнений совпадает с порождающим
уравнением. Интегрируя его и подставляя найденное решение х0(7)
во второе уравнение, получим для определения хх (7) опять линейное
уравнение и т. д.	'
Для определения xn(t) ь(ы также получим линейное уравнение,
так как в правой части этого уравнения будут содержаться Лишь Ху
и Ху с индексами, меньшими п, потому что из-за наличия множи-
теля р при F члены, содержащие в правой части х„ и хп и, тем
более, xk и xk с большими индексами, будут иметь множитель р
в степени не ниже п 4-1.
В этом параграфе мы рассматриваем лишь вопрос о нахождении
периодических решений, поэтому на правую часть уравнения
х -|- а2х = /(04- \iF (t, х, х, р),
в соответствии с замечанием на стр. 143—144 естественно наложить
еще одно ограничение, а именно потребовать, чтобы правая часть была
периодической функцией по явно входящему аргументу t. Без суще-
ственного ограничения общности можно считать наименьший период
правой части, если правая часть явно зависит от t, равным 2л, при
этом, если /(/) не равно постоянной величине, периодические реше-
ния уравнения (2.107), если они существуют, при достаточно малом р
могут иметь лишь периоды, равные или кратные 2л (см. стр. 143—1'44).
§ 8]	МЕТОД МАЛОГО ПАРАМЕТРА	149
Для нахождения периодического решения уравнения (2.108) в виде
x(t. ц)=хо(О4 рх1(/) + ’... +рлхл(/)+ ...	(2.110)
надо определить периодические решения хк (f) уравнений (2.109). Дей-
ствительно, если'решение х(/, ц) имеет постоянный период 2л (или 2/пл,
т — целое число) при любом достаточно малом по модулю ц, то
хо(О 4-	(0 + ••• 4~ и"*,» (О 4“ ••• — хо(f + 2л)-|-
4-	ЦХ| (£ 4“ 2л) -р .... 4~	4~ 2л) -j- • • • (2-111)
Следовательно, коэффициенты при одинаковых, степенях ц в левой
и правой частях тождества (2.111) должны быть равны, т. е.
хп (0 == хп (t 4- 2л),
а это и означает периодичность функций xn(t) (n = 0, 1, 2, . ..).
Совпадение коэффициентов при одинаковых степенях ц в левой и
правой частях тождества (2.110) можно обнаружить, например, диф-
ференцируя тождество (2.110) п раз по ц, после чего, полагая ц = 0,
получим
хп (2л 4- t) = хп (t) (п = 0, 1, 2, ...).
Итак, нам надо найти периодические решения уравнений (2.109)^
При этом целесообразно отдельно рассмотреть следующие случаи.
1.	Нерезонансный случай: а отлично от целого
числа. Если а не равно целому числу, то первое из уравнений (2.109)
имеет единственное периодическое решение х0 = ср0(£), которое нахо-
дим методом предыдущего параграфа (см. стр. 144). Затем тем же
методом находим хх (/), х2 (0 и т. д.
Если бы этим методом мы нашли общий член ряда (2.110), уста-
новили сходимость этого ряда и законность его двукратного почлен-
ного дифференцирования, то сумма ряда (2.110) являлась бы искомым
периодическим решением периода 2л. Однако обычно нахождение
общего члена ряда (2.110) является крайне сложной задачей, в силу
чего приходится ограничиваться вычислением лишь нескольких первых
членов ряда, что было бы достаточным для приближенного нахожде-
ния периодического решения, если бы была уверенность в том, что
ряд сходится и его сумма является периодическим решением.
В связи с этим большое значение имеют теоремы А. Пуанкаре
о существовании периодических решений, позволяющие, в частности,
найти условия, при которых заведомо существует единственное перио-
дическое решение уравнения (2.107), стремящееся при р,->0 к перио-
дическому решению порождающего уравнения.
Если условия теоремы А. Пуанкаре выполнены и, следовательно,
существует единственное периодическое решение уравнения (2.107),
стремящееся при ц->0 к периодическому решению порождающего
уравнения, то сумма единственного ряда с периодическими коэффи-
.150	Уравнения Порядка выше Первого	(гл. 2
циентами (2.110), формально удовлетворяющего уравнению (2.107),
должна существовать и должна совпадать с искомым периодическим
решением. При этом отпадает необходимость нахождения общего
члена ряда (2.110) для исследования ряда на сходимость и можно,
найдя несколько первых членов ряда (2.110), утверждать, что при
малом р их сумма приближенно равна искомому периодическому
решению.
Теоремы А. Пуанкаре, опирающиеся на сведения из теории ана-
литических функций, довольно сложны, поэтому мы приводим в конце
этого параграфа лишь простейшую из этих теорем, которая, однако,
уже позволяет утверждать, что в рассматриваемом нерезонансном слу-
чае уравнение (2.107) всегда имеет единственное периодическое реше-
ние при достаточно малом р.
Пример 1. Приближенно определить периодическое решение уравнения
х -|- 2х = sin t рх2.
где ц—малый параметр (определить два члена ряда (2.110)). Ищем решение
в виде
X (t, и) = х0 (О 4- рх, (0 4- ... 4- рпхл (04- ...
Находим периодическое решение порождающего уравнения
х0 4- 2х0 = sin t, х0 (0 = sin t.
Периодическое решение уравнения
Xi 4-2xl = sin21 или X!4-2X|=----g----
имеет вид
1 . cos 2/
^ = т+-4--
Следовательно, периодическое решение
x (/, ц) « sin t 4- (1 4- cos 20 ц.
2.	Резонансный случай. Метод малого параметра может
быть применен и в резонансном случае, т. е. в случае, когда в урав-
нении (2.107) а равно целому числу п или стремится к целому
ЧИСЛУ П ПрИ р -> 0.
Если в уравнении (2.107) а мало отличается от целого числа п,
точнее, разность а2 — п2 имеет порядок малости не ниже чем р:
а2 — n2 = alii,	(2.112)
где ах ограничено при р—>0, то уравнение
х 4- а2х — f (0 + fiF (t, х, х, pi)
можно переписать в виде
х 4- п2х = /(04- («2 — о.2) х 4- pF (0 х, х, р),
§ 8]	МЕТОД МАЛОГО ПАРАМЕТРА	151
откуда в силу (2.112)
x-j~n2x = f (0+ х> х'
где функция Fx удовлетворяет тем же условиям, которым по пред-
положению удовлетворяет функция F.
Следовательно, в дальнейшем в резонансном случае можно счи-
тать а равным целому числу:
x-{-n2x = f(t)-[-iiF(t, х, х, р).
Применяя метод малого параметра, ищем периодическое решение
в виде ряда
x(t, р.) = хо(О + н*1(О+ ••• + н**л(0 +
Для определения функций xk(t) опять получаем уравнения (2.109),
в которых а2 = га2, но в данном случае порождающее уравнение
*о + л2хо = /(0	(2.113)
имеет периодическое решение лишь в случае отсутствия резонирую-
щих членов в правой части, т. е. при выполнении условий (см. стр. 145)
	2л J / (0 cos nt dt = 0, °2„	(2.106) J* / (0 sin nt dt — 0. 0
Если эти условия выполнены, то все решения уравнения (2.113)
будут периодическими периода 2л (см. стр. 146)
х0 (0 = с10 cos nt + с2о sin nt 4- Фо (*)•
Функция xx(t) определяется из уравнения
х, -f- п2хх = F (t, х0, х0, 0).	(2.114)
Это уравнение также имеет периодические решения лишь в случае
отсутствия резонирующих членов в правой части, т. е. при выпол-
нении условий
2л
J* F (t, х0, х0, 0) cos nt dt = О,
о
2я	(2.115)
J F (/, х0, х0, 0) sin nt dt = 0.
о
152
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. 2
Уравнения (2.115) содержат с10 и с20, которые, вообще говоря, и
определяются из этой системы.
Пусть с10 и с2() удовлетворяют системе (2.115); тогда все решения
уравнения (2.114) имеют период 2л:
Xj (/) = си cos nt -j- с21 sin nt —Н <Pi (0>	(2.116)
причем и с21 опять определяются из двух условий отсутствия
резонирующих членов в следующем из уравнений (2.109):	-*
.t = Xi	х = л»	х = х„
ц=0	ц=0	ц=0
И T. Д.
Следовательно, не каждому периодическому решению
Хо — С10 COS nt + с20 sin + Фо (О
порождающего уравнения, а лишь некоторым, значения с10 и с20
которых удовлетворяют уравнениям (2.115), соответствуют периоди-
ческие решения уравнения (2.107) при малых р. Конечно, и в резо-
нансном случае для того, чтобы, не находя общего члена ряда (2.110),
быть уверенным, что указанным процессом будет найдено периоди-
ческое решение, надо предварительно доказать теорему о существо-
вании периодических решений. Это замечание относится и к случаям,
изложенным в следующих пунктах 3 и 4.
3.	Резонанс л-го рода. Иногда в системах, описываемых
уравнением
х + а2х — f (t) -|- pF (t, х, х, р),	(2.107)
удовлетворяющим указанным выше условиям, наблюдаются интенсив-
х	к	1
ные колебания, когда собственная частота мало отличается от —,
п
где п — целое число. Это явление получило название резонанса
n-го рода.
 С математической точки зрения это означает, что при а, мало
1 ,
отличающемся от —, где п — целое число, большее единицы, урав-
нение (2.107) может иметь периодические решения периода 2лл, не
являющиеся в то же время периодическими решениями периода 2л.
Пусть
х^5-х == / (/) 4~ pF (Л х, х, р)	(2.117)
МЕТОД МАЛОГО ПАРАМЕТРА
153
1 ., 1
(если а мало отличается от —, точнее,	— рд,, где остается
ограниченной при р —>0, то, перенося член ^д2— х в правую
часть и включая его в р/7^, х, х, р), получим уравнение вида (2.117)).
Ищем периодическое решение уравнения (2.117) периода 2лл
в виде ряда	<
х (/, р) = х0 (t) -|- рх1 (0 -|- ... + рлх„ (0 + ...	(2.110)
Подставляя (2.110) в уравнение (2.Г17) и сравнивая коэффициенты при
одинаковых степенях р, получим уравнения (2.109), в которых
Для определения xQ(t) получаем порождающее уравнение
x0 + -^x0 = f(t),	'(2.118)
которое имеет периодическое решение периода 2лп лишь при отсут-
ствии в правой части резонирующих членов, т. е. при
2лл	2лл
j f (t) cos dt = 0 и f(t) sin ^dt — 0.
о	"	о , П
Если эти условия выполнены, то все решения уравнения (2.118)
имеют период 2лл
хо = сю cos Ч- с2о s'n 77 Ч~ Фо (0«
где с10 и с20 — произвольные постоянные.
Уравнение, определяющее xv
xi +1? Xl ~ F V' х0’ *о> И)	(2.Н 9)
будет иметь периодические решения периода 2лп лишь при отсут-
ствии в правых частях резонирующих членов, т. е. при выполнении
условий
2лл
У* F (t, х0, х0, р) cos dt = 0,
о
2ЯЯ	(2-120)
/ F(t, х0, х0, p)sin4 dt = Ot
V	fl
о
из которых, вообще говоря, определяются с10 и с20.
154	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Если условия (2.120) удовлетворяются, то все решения уравне-
ния (2.119) имеют период 2лп
•4 = си cos + с21 sin -j- Ф1 (/).
Для определения произвольных постоянных сп и с21 пользуемся
двумя условиями отсутствия резонирующих членов в- следующем
из уравнений (2.109):
х=ха	X=Xf	Х=Хц
ц=0	Ц-0	|1=0
И Т. Д.
4. Автономный случай. Предположим, что правая часть
уравнения (2..107) не зависит явно от t, и уравнение имеет вид
х 4- а2х — pF (х, х, р),	(2.121)
где функция F удовлетворяет поставленным выше условиям.
На первый взгляд может казаться, что исследование уравнения (2.121)
должно быть проще исследования уравнения (2.107), в котором
правая часть зависит от аргумента t, однако в действительности
отсутствие аргумента t в правой части уравнения приводит к услож-
нению задачи.
Если правая часть явно зависит от t, то, как уже отмечалось
выше, известны возможные периоды решений, так как периоды
решений могут быть лишь равными или кратными периоду правой
части вдоль решений по явно входящему аргументу t.
Если же правая часть не содержит t, то ее можно рассматривать
как периодическую функцию произвольного периода и, следовательно,
не исключена возможность существования решений любого периода,
причем период решений, вообще говоря, будет функцией пара-
метра р. Ввиду того, что период решения х(/, р) является, вообще
говоря, функцией р, было бы нецелесообразно искать решение
в виде ряда
x(t, p,) = x0(O + |iXi(O+ ••• -+-Нл*в(0+ •••• (2.110)
так как каждая из функций x„(t) в отдельности не обязана быть
периодической функцией и, следовательно, функции хл(/) не могли бы
быть найдены рассмотренными выше методами. Поэтому надо пре-
образовать уравнение (2.121) к новому независимому переменному
так, чтобы по новому переменному уравнение имело бы уже по-
стоянный период, а уж затем искать решение в виде ряда (2.110).
§ 8J	МЕТОД МАЛОГО ПАРАМЕТРА	155
Предварительно для упрощения преобразуем уравнение (2.121)
заменой независимого переменного tx = at к виду
А4-+ х = pFj (х, х, р).	(2.122)
dt\
Каждое решение порождающего уравнения х0 (Q = сх cos (tt — t0)
будет иметь период 2л, а периодические решения уравнения (2.122)
при р =# 0, если они существуют, будут иметь период 2л-|-а(р),
причем можно доказать, что а(р) является аналитической функцией р
при достаточно малом р.
Разложим а(р) в ряд по степеням р; тогда
2л + а(р) = 2л(1+Й1РН-А2р2+ ... +Л„рл+ ...), (2.123)
где hj—некоторые, пока неизвестные нам постоянные величины.
Преобразуем переменные так, чтобы периодическое решение x(t, р)
уравнения (2.122) имело бы период не 2л-|-а(р), а постоянный
период 2л. Это достигается заменой переменных
••• + V+ •••).	(2.124)
так как, в силу зависимости (2.123), при изменении tx от 0 до
2л-|-а(р) новое переменное t2 изменяется от 0 до 2л. При этом
уравнение (2.122) преобразуется к виду
••• Ч-й„р"+ ...)2х =
= р(1 Ч-Л1Р+ • • • Ч-йлрлЧ- • •	(1 Ч-ЛрН- ...
... -Мярл+	И)- (2.125)
Периодическое решение этого уравнения ищем в виде
x(t,, р) = х0(/2) +^1(^)4- ••• Ч-РЛ^Л(^)Ч- •••• (2-126)
где хл(/2)— периодические функции аргумента /2 периода 2л. Под-
ставляя (2.126) в уравнение (2.125) и сравнивая коэффициенты при
одинаковых степенях р в левой и правой частях равенства, получим
х0Ч~ хо~ 0. откуда x0 = ccos(t2— t0),
Ч- = — 2йхх0 +	(х0, х0, 0)
или
х1 -|- Xj = — 2hxc cos (t2 —10)
+ Fj(c cos(t2—10~), —csln(t2—10), 0) (2.127)
Для того чтобы уравнение (2.127) имело периодические решения,
необходимо и достаточно, чтобы в его правой части отсутствовали
156
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
[ГЛ. 2
резонирующие члены (см. (2.106)), т. е. чтобы
2л	
J* Рг(С COS (/2 — to)* — С Sin (t2,— ^о)» 0) sin — ^о) dt2 = 0,
о
2л
— 2Aic + ^/Pi(ccos(t2 —10),~ csin(t> — /0), 0)Х '
о
(2.128)
X cos (/2 —10) dt2 — 0.
Первое из этих уравнений дает возможность найти значения с,
а второе — hv определив которые, мы найдем те решения порождаю-
щего уравнения x0 = ccos(/2 — tQ), в окрестности которых при
малом р появляются периодические решения уравнения (2.122), и
приближенно определим период искомого решения
)	2л-|-а(р) я» 2л (1 -j-Ajp,).
Зная с и Ар можно определить хг (/2) и, если необходимо, тем же
методом вычислить х2(£2), х3(/2) и т. д.
П р и м е р 2.
х + х = рх (9 — х2).	(1.129)
Определить решения порождающего уравнения, к которым при р -> 0 при-
ближаются периодические решения уравнения (2.129).
Решения порождающего уравнения имеют вид х = с cos (t — ta). Для
определения искомых значений с воспользуемся первым из уравнений (2.128):
2л
J с (9 — с2 cos2 (t — t„)) sin2 (t — to)dt = O
0
или лс ^9 —	— 0, откуда c, = 0, c2,3 - ± 6.
При Cj = 0 получаем тривиальное решение x = 0 порождающего урав-
нения, которое остается решением уравнения (2.129) при любом и
При с2,3 = ± 6 получаем х = ± 6 cos (t — ta).
Докажем простейшую из теорем А. Пуанкаре о существовании
и единственности периодического решения, стремящегося при
р —>0 к периодическому решению порождающего уравнения, в при-
менении к уравнению вида
x—f(t, х,/х, р),	(2.130)
где функция f удовлетворяет условиям теоремы об аналитической
зависимости решения от параметра р при достаточно малых по
модулю значениях р. Кроме того, предположим, что функция f
явно зависит от t и имеет по t период 2л. Допустим также, что
порождающее уравнение х = f(t, х, х, 0) имеет единственное перио-
дическое решение х = <р0(() периода 2л.
§ 81	МЕТОД МАЛОГО ПАРАМЕТРА	157
Решение уравнения (2.130), удовлетворяющее начальным условиям
лг(/0) — <р0.(/0)-|-р0, х (t0) = фр (^о)Ч- Рр
обозначим x(t, ц,, р0, pj). Следовательно, р0 и Pi являются отклоне-
ниями начальных значений решения x(t, ц, р0, Pj) и его производ-
ной x(t, ц, р0, Pj) от начальных значений ф0(/0) и ф0(/0) периоди-
ческого решения порождающего уравнения.
Задача заключается в том, чтобы, указать условия, при которых
для каждого достаточно малого по модулю значения ц существует
единственное периодическое решение х (/, ц, р0, рх) уравнения (2.130),
стремящееся при ц,—>0 к периодическому решению ф0(/) порождаю-
щего уравнения.
Если решение х (/, ц, р0, pj является периодическим с перио-
дом 2л, то, очевидно, должны удовлетворяться следующие условия:
х (2л, и, р0, Р0— х(0, ц, р0, Рц) = О, |
х(2л, ц, р0, Pj) —х(0, ц, р0, pj) = 0. J
Обозначая левые части этих уравнений соответственно Ф0(Ц, р0, Pi)
и ФДр, Ро, Pi), запишем систему (119) в виде
Фо(Н> Ро< Pi) = 0,
Ф1(Н. Ро> ₽1) = 0.
(2.132)
Условия (2.132), называемые условиями периодичности, не только
необходимы, но и достаточны для периодичности решения x(t ц, р0, р,)
уравнения (2.130). Действительно, '
в силу периодичности правой
части уравнения (2.130) по t,
эта правая часть в. полосах
0 t С 2л, 2л < t 4л, ...
принимает в точках (t, х, х),
(t +-2л, х, х), ... одинаковые
значения. Следовательно, если в
точках t — 0 и t = 2л задать
одинаковые начальные значения х0
и хй, то ими определяются в по-
лосах 0 <11 2л и 2л t 4л
совершенно одинаковые интегральные кривые (рис. 22), точнее,
кривые, являющиеся периодическим продолжением одна другой.
По теореме о неявных функциях можно утверждать, что, если
якобиан
ЩФо. Ф.) , Л
0(Ро, Pi)
158	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
в точке ц = 0, р0 = Р] —0, то при каждом достаточно малом по
модулю значении р существует единственная пара функций р0(|1) и
pj (ц), удовлетворяющих условиям периодичности (2.132) и стремя-
щихся к нулю при р—> 0, т. е. в указанных условиях для каждого
достаточно малого р существует единственное периодическое реше-
ние уравнения (2.130), стремящееся к периодическому решению
порождающего уравнения при р—>0*). Это утверждение и составляет
содержание теоремы Пуанкаре.
Пример 3. Доказать, что в нерезонансном случае для уравнения
x-\-a2x — f(t) + рА(Г, х, х, р),	(2.107)
где f и F удовлетворяют указанным выше условиям (см. стр. 147), вы-
полнены требования теоремы о существовании и единственности периодиче-
ского решения.
Решение х (t, р, р0, р(), являющееся аналитической функцией последних
трех аргументов при достаточно малых значениях этих аргументов, ищем
в виде
х Р> 0о. 01) = хо (0 4" ли (0 0о 4" -*12 (О 01 + -к13 (t) р ... (2.133)
Подставляя (2.133) в уравнение (2.107) и сравнивая коэффициенты при оди-
наковых степенях р, 0О и Pi, получим для определения и х12 следующие
уравнения:
*и4~ а2Хц =0, Хц(0)=1, л11(б)==0,
Х12-|-а2х12 = 0, х12 (0) = 0, х12(0)=1,
(начальные значения получены из условий
х (Ль И> 0о> 01) — хо (Л) + 0о>
х <to> Н> 0о> 01) = хо (Л) + 01).
откуда
хп = cos dt, xl2 — — sin дД
Условия периодичности (2.132) имеют вид
(cos 2ап — 1)0о+ ^-sin2<znp] -f- ... =0,
— asin2ajtPo4-(cos2an—1)Pj-|- ... =(),
где невыписанные члены не влияют на величину определителя
~Z)((B°’ в*? при И = 0о = 01 = 0.
и VPo> Pi)
Определитель
= (cos 2ал — I)2 -ф sin2 2ал
и=р0= р1=о
отличен от нуля, так как а не равно целому числу.
(2.134)
D (Фо. ФО |
O(0o,Pi) |
*) Подробнее о теоремах существования периодических решений см.
И. Г. М а л к и н [3].
§ 9]
ПОНЯТИЕ О КРАЕВЫХ ЗАДАЧАХ
159
§ 9. Понятие о краевых задачах
Как уже упоминалось во введении, наряду с основной начальной
задачей часто приходится решать так называемые краевые или гра-
ничные задачи. В этих задачах
значение искомой, функции за-	—.—
дается не в одной, а в двух точ-	/
ках, ограничивающих отрезок, на	/	\
котором требуется определить ре-	/	\
шение. Например, в задаче о дви-	/	\
жении материальной точки мае-	Д———-	""	—J
сы т под действием заданной силы А	В
F (Л г, г) часто требуется найти	рис 2.3.
закон движения, если в началь-
ный момент точка находи-
лась в положении, характеризуемом радиусом-вектором г0, а в мо-
мент t = tt должна попасть в точку г = гР
Задача сводится к интегрированию дифференциального урав-
нения движения
m-7?r=F(t г, г)
с краевыми условиями г (t0) — r0; r(^1) = rv
Заметим, что эта задача имеет, вообще говоря, не единственное
решение; если речь идет о баллистической задаче и о точках земной
поверхности, то в одну и ту же точку тело может попасть по навес-
ной и по настильной траектории (рис. 2.3), более того, при очень
больших начальных скоростях можно попасть в ту же точку и после
однократного или многократного облета земного шара.
Аналогичную краевую задачу можно поставить и для луча света,
проходящую через преломляющую среду: найти направление, по
которому луч света должен выйти из точки А, чтобы он попал
в другую заданную точку В.
При этом очевидно, что задача не всегда имеет решение, а если
решения существуют, то их может быть несколько и даже беско-
нечное множество (например, если лучи, выходящие из точки А,
фокусируются в точке В).
Если удается найти общее решение дифференциального уравнения
краевой задачи, то для решения этой задачи надо определить про-
извольные постоянные, содержащиеся в общем решении, из граничных
условий. При этом, конечно, далеко не всегда существует действи-
тельное решение, а если существует, то оно не обязательно един-
ственно.
В качестве примера возникающих здесь возможностей рассмотрим
следующую краевую задачу:
160	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
Найти решение уравнения
у" + у = 0,	(2.135/
удовлетворяющее условиям: у (0) = О, у (Xj) = yv
Общее решение уравнения (2.135) имеет вил
y — ct cos х Н- с2 sin х.
Первое граничное условие удовлетворяется при с1 = 0, при этом
y = c2sinx.
. Если xt ¥= пл, где п — целое число, то из второго граничного
условия находим уг = с2sin хр с2 =	—
Следовательно, в этом
случае существует единственное решение краевой задачи
У1
у = sin х.
SinXj
Если же Xj = nn и у]=0, то все кривые пучка у — с5 sin х
являются графиками решений краевой задачи.
При X] — пл, у, ¥= 0 решений краевой задачи не существует,
так как ни одна кривая пучка y = c2sinx не проходит через точку
(хр уг), где '
х, — пл, У] #= 0.
Рассмотрим несколько подробнее краевые задачи для линейных
уравнений второго порядка
У" + Ру (*) У' + Р2 Ю У = Ф (*)•	(2.136)
у (х0) = у0, У(х1) = у1.	(2.137)
Линейной заменой переменных
z = y — (X — х0) - у0
— ЛО
краевые условия (2.137) сводятся к ..нулевым условиям z(x0) =
==гг(х1) = 0, причем линейность уравнения (2.136) не нарушается.
Умножением на е$p,wdx линейное уравнение (2.136) приводится
к виду
^(#Иу') + ?ИУ=/(4	(2.138)
где р (х) = е (Jr> Поэтому без существенного ограничения
общности можно заменить изучение краевой задачи (2.136), (2.137)
изучением краевой задачи для уравнения (2.138) с граничными
условиями
у(хо) = у(х1) = 0.
(2.139)
§9)	ПОНЯТИЕ О КРАЕВЫХ ЗАДАЧАХ	161
Вначале рассмотрим краевую задачу (2.138), (2.139), причем / (х)
является локализованной в точке х = s функцией с единичным импуль-
сом. Точнее, рассмотрим уравнение
~ (р (х) у') + q (х) у = /е (х, s)	(2.140)
с граничными условиями у (х0) = у (xt) == 0, где функция /е(х. s)
равна нулю на всем отрезке [х0> xj, за исключением е-окрестности
точки x = s, s — £ < х < s + е, причем
s+e
J /е(х, s)dx = l.
s-е
Обозначим Ge(x, s) непрерывное решение этой краевой задачи
и перейдем к пределу при е->0:
limOe(x, s) = O(x, s).	(2.141)
е-»0
Нетрудно было бы доказать существование этого предела, не
зависящего от выбора функции /е(х, s), однако в этом нет необхо-
димости, так как пока наши рассуждения носят эвристический харак-
тер, и на стр. 162 будет дано точное определение функции G(x, s).
Функция О (х, $) называется функцией влияния или функцией
Грина рассматриваемой краевой задачи. Так же как на стр. 122—124,
решение краевой задачи (2.138), (2.139) с непрерывной правой
частью в (2.138) можно рассматривать как суперпозицию решений
краевых задач, соответствующих локализованным в точке функциям
с импульсами /($,)Д$, где sz—точки деления отрезка [х0, xj на т
равных частей, As —	. Точнее, приближенное решение крае-
вой задачи (2.138), (2.139) равно интегральной сумме
tn
2 ° (* si) / (s/)
Z=1
а предел этой суммы при т -> оо:
X]
у (х) = J G (х, s) f (s) ds	(2.142)
является, решением рассматриваемой краевой задачи (2.138), (2.139).
Физический смысл функции влияния G(x, s) и решения (2.142)
станет еще яснее, если в уравнении (2.140) рассматривать у(х) как
смещение некоторой системы под влиянием непрерывно распреде-
ленной на отрезке [х0, xj силы f (х) (например, отклонение струны
от положения равновесия под влиянием распределенной нагрузки
162
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
(ГЛ. 2
с плотностью /(х)). При этом Q(x, s) описывает смещение, вызы-
ваемое единичной сосредоточенной силой, приложенной к точке x = s,
а решение (2.142) рассматривается как предел суммы решений, соот-
ветствующих сосредоточенным силам.
Функция Грина обладает следующими свойствами, вытекающими
из ее определения (2.141):
1. Q(x, s) непрерывна по х при фиксированном з при х0 <^х < хр
Хо < 3,< Xj.
2. G(x, s) является решением соответствующего однородного
уравнения
(х) /)4-д(х)у = 0
на всем отрезке [х0, xj, за исключением точки х = з (так как вне
этой точки в случае локализованной в точке х = з функции правая
часть равна нулю).
3. О(х, з) удовлетворяет граничным условиям:
О (х0. s) = О (хР з) = 0.
4. В точке х = з производная Ох (х, з) должна иметь разрыв
первого рода со скачком — • Действительно, ожидать разрыва
следует лишь в точке локализации функции—в точке х = з. Умно-
жая тождество
(Р (х) О; (х, з)) + q (х) Ge (х, з) = /е (х, з)
на dx и интегрируя в пределах от з — е до з е, получим
s+e
,	iJ+e r
р (х) Ое (х, з) 4- I q (х) Ое (х, з) dx = 1
е
и, переходя к пределу при е—>0, будем иметь
[Gz (s+ 0, з) - О' (з - О, 3)] = ‘ .
.	Р\Ъ)
Все наши рассуждения о функции Грина носили эвристический
характер. Придадим теперь им необходимую точность.
Определение. Функцией Грина G(x,s) краевой за-
дачи (2.138), (2.139) называется
указанным выше условиям 1), 2),
Непосредственней подстановкой
ряем, что
функция, удовлетворяющая
3). 4).
в уравнение (2.138) прове-
у (х) — j" О (х, з) / (з) ds
(2.142)
§ 9]	ПОНЯТИЕ О КРАЕВЫХ ЗАДАЧАХ \	163
является решением этого уравнения (краевые условия (2.139), оче-
видно, удовлетворяются в силу свойства 3)).
Действительно,
у' (х) — f Gx (х> s) f (s) ds = J G‘x{x, s) f (s) ds-\- f Gx (x, s) / (s) ds;
x0	x0	X
y"(x) = Jg^(x, s) f (s) dsGx(x, x — 0)/(x) 4-
Xo
4* J Gxx (X. s) / (s) ds — Gy(x, x 4- 0) f (x) =
X
= J* G"xx(x, s) f (s) ds [ОДх + 0, x) — Gx(x — 0, x)]/(x).
Xff
Подставляя (2.142) в уравнение (2.138), получим
J [p{x)Gxx(x, s)4- p' (x)Gx(x, s) 4- q (x) G (x, $)] dx 4-
4- p(x)[Ox(x 4-0, x) —G'(x —0, x)] f (x)== f (x)
в силу условий 2) и 4).
Рассмотрим метод построения функции Грина, из которого полу-
чим также достаточное условие ее существования.
Рассмотрим решение У](х) уравнения
^-(/’(х)у')4-?(х)у = 0,	(2.143)
определяемое начальными условиями
У(хо) = °,	У(х0) = у’ ¥=.0.
Это решение, вообще говоря, не удовлетворяет второму граничному
условию у (Xj) = 0. Случай yj (х0) == у] (Xj) = 0 является исключи-
тельным, и мы его здесь рассматривать не будем.
Очевидно, что решения С1У((х), где сг — произвольная постоян-
ная, также удовлетворяют граничному условию у (х0) = 0. Аналогично
находим нетривиальное решение у2(х) уравнения (2.143), удовлетво-
ряющее второму граничному условию У2(х1) = 0; этому же условие
удовлетворяют все решения семейства с2у2(х), где с2 — произвольная
постоянная.
164
УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
[ГЛ. 3
Функцию Грина ищем в виде
0(х, $) =
С1У1 (х)
с2у2 (х)
при
при
Xf) < X < S,
$<х < хг
причем постоянные Cj и с2 выбираем так, чтобы были выполнены
условия 1) и 4), т. е. чтобы функция G(x,s) была непрерывна по х
при фиксированном s, и в частности непрерывна в точке х = $:
с1У] ($) = с2у2 (s).	(2.144)
и чтобы Gx(x, s) в точке x—s имела скачок —
=	(2.145)
В силу предположения, что у^х^-АО, решения у^х) и у2(х)
линейно независимы, так как все линейно зависимые от yj (х) реше-
ния имеют вид с2уj (х) и, следовательно, при Cj =# 0 не обращаются
в нуль в точке х1( в которой обращается в нуль решение у2(х).
Следовательно, определитель системы (2.144) и (2.145), являющийся
определителем Вронского: W (ух (х), у2 (х)) = W (х) в точке х — s,
отличен от нуля и постоянные сх и с2, удовлетворяющие системе (2.Г44)
и (2.145), легко определяются:
откуда
_ Уз (S) У1 (X)	_ у, (S) у2 (X) -
W(s)p(s) •	с2— W(s)p(s) ’
G(x, s) —
У2 (Д) У1 (х)
!T(s)/>(s)
У1 (s) У2 (х)
' W(s)p(s)
при
при
(2.146)
Хо < X < S,
s < х < хР
Пример. Найти функцию Грина краевой задачи
у" (х) + у (х) «= / (х),	у(0) —0,	у^=0.
Решения соответствующего однородного уравнения, удовлетворяющие усло-
виям у (0) =» О и у (у) « 0, соответственно имеют вид У) =» с, sinx и
Уз «= са cos х, следовательно, сбгласно (2,146)
— cos s sin х при О < х < з,
Q (х, s)«=
— sin s cos X
я
при з < х < у
Замечание. Мы предположили (стр. 163), что не существует
нетривиального решения у (х) однородного уравнения (2.143), удо-
влетворяющего нулевым граничным условиям у(х0) = у (Х0 — 0. Это
условие гарантирует не только существование и единственность
краевой задачи (2.138), (2.139), но и единственность функции Грина.
ЗАДАЧИ К ГЛАВЕ t
165
Действительно, если допустить существование двух различных
функций Грина G] (х, s) и О2(х, $) для краевой задачи (2.138),
(2.139), то получим два различных решения этой задачи:
У1(^)= J Gi(x. s)f(s)ds
и
у2(х) = J" G2(x, s)f\s)ds,
разность которых
JlG^x, s)— G2(x. s)\ f (s) ds,
th
вопреки предположению, будет нетривиальным решением соответ-
ствующего однородного уравнения, удовлетворяющим нулевым гра-
ничным условиям.
Задачи к	главе 2
1. у" — бу' -|- 10у = 100, причем при х = 0 у = 10. у' — 5. ' 2. х + х = sin t — cos 2t.  3. у'у"' — 3(у")2=0. 4 < + ’- J-л • х 5. х*у" — 4ху' (-бу = 2. ' 6. у" + у = ch х. 7- У" + -у— (уУ =0.	• л	л dx . .	t , 2f । « *- dt> 4 dt -Нх=?-н2Ч1.	9. (1+х2)у’-Ь(у')2+1=0. d2x Ю.х3^+1=0. 11. yIV_ 16у = х2 — ^. 12. (у"’)2 + (у")2 = 1. d*x d'x dt* dt* z d^x	d2x 14-4f— 24^+*=/2-3-
15. у" + 4ху = 0; проинтегрировать с
 16. х2у" + ху- -|-
к уравнению Бесселя.
П У* 4-(у')а = 1. у(0)=0. ,/(O)-L
18.
помощью степенных рядов
у = 0; проинтегрировать путем сведения
19.
20.
/'=jKy. у (0) = 1. у'(0)-2.
у' + У — 1---г—•
’	1 sinx
d2u 2 du „
dr2 r ~dr
21.	Найти скорость, с которой тело упадет на поверхность Земли, если
считать, что оно падает с бесконечно большой высоты и движение проис-
166	УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО	[ГЛ. 2
ходит только под влиянием притяжения Земли. Радиус Земли считать рав-
ным 6400 км.
22.	Найти закон движения тела, падающего без начальной скорости,
допуская, что сопротивление воздуха пропорционально квадрату скорости
и что скорость имеет своим пределом при <->оо величину 15 м/сек.
23.	Цепь длиной 6 м соскальзывает со стола. В момент начала движе-
ния со стола свисал 1 м цепи. Во сколько времени со стола соскользнет вся
цепь. (Трением пренебрегаем.)
24.	Цепь переброшена через гладкий гвоздь. В момент начала движе-
ния с одной стороны свисает 8 м цепи, а с другой стороны 10 м цепи.
Во сколько времени вся цепь соскользнет с гвоздя? (Трением пренеб-
регаем.)
25.	Поезд движется по горизонтальному пути. Вес поезда Р, сила тяги
паровоза F, сила сопротивления при движении W = а 4- bv, сцъ а и b — по-
стоянные, a v — скорость поезда; s — пройденный путь. Определить закон
движения поезда, считая, что при t — 0 s = 0 и w = 0.
26.	Груз в р кг подвешен на пружине и оттянул ее на а см. Затем
пружина оттягивается еще на А см и отпускается без начальной скорости.
Найти закон движения пружины, пренебрегая сопротивлением среды.
27.	Два одинаковых груза подвешены к концу пружины. Найти закон
движения одного из грузов, если другой оборвется. Дано, что удлинение
пружины под влиянием одного из грузов равно а см.
28.	Материальная точка массы т отталкивается от центра О с силой,
пропорциональной расстоянию. Сопротивление среды пропорционально ско-
рости движения. Найти закон движения.
29.	Найти периодическое решение с периодом 2л уравнения
х 4-2х = /(<),
где функция =	— t3 при —л</<л и далее продолжена перио-
дически.
30.	уу" 4- (у')2 = -/22L
/14-;
31.	УУ'У" = (П3 + (У")2-
32.	х 4- 9х = t sin 3Z.
33.	у" 4- 2у' 4- у = sh х.
34.	у'" — у = ех.
35.	у" — 2у' 4- 2у = хех cos х.
36.	(х2 — 1) у" — бу = 1. Частное решение соответствующего однородного
уравнения имеет вид многочлена.
37.	Найти решение и = и (х2 4- У2) уравнения
д2и , д2и л
дх2 + ду2 ~ °’
зависящее лишь от х2 4- у2.
38.	Найти решение и = и (х2 4- у2 4- г2) уравнения
д2и ( д2и , д2и _ л
дх2"’ Ту2”*' ~dz2~ °’
являющееся функцией х2 4- У2 4* •?2-
39.	Материальная точка медленно погружается в жидкость. Найти закон
движения, считая, что при медленном погружении сопротивление жидкости
пропорционально скорости погружения.
ЗАДАЧИ К ГЛАВЕ 2
167
40.	Проинтегрировать уравнение движения тх = f (/, х. х), считая, что
правая часть является функцией только х или только х:
а)	тх — f (х);
б)	тх = / (х).
41.	yVl — 3yV-+-3ylV — у"' = х.
42.	xiv 4- 2х" -f- х = cos t.
43.	(1 + х)2 у" + (1 + х) у' + у = 2 cos In (1 + х).
44.	Определить периодическое решение уравнения
ио
/7=1
45.	Определить периодическое решение уравнения
х atx + агх = / (/),
где at и аг — постоянные, a f (t)— непрерывная периодическая функция
периода 2л, разлагающаяся в ряд Фурье, а1 Ф 0 и а2 ф 0.
46.	х -j- Зх = cos 14- рх2, р — малый параметр. Приближенно определить
периодическое решение.
47.	х3у" — ху' 4 У =* 0» проинтегрировать уравнение, если yi = х является
частным решением.
48.	Найти линейное однородное уравнение, имеющее следующую фунда-
ментальную систему решений: yj = 49.	xlv4-x = f3. 50.	х = (у")3 4- у" 4-1. 51.	х 4- 10х 4- 25х = 2' 4- 1е~ы 52.	хуу" — х (у')2 — уу' = 0. 53.	yvl — y = t?2x 54.	yVl 4- 2у IV 4- у" = х 4- ех.	=^ys = -. 55.	6y"ylV—5(у"')2 = 0. 56.	ху" = у'1п^-. 57.	у" 4- у = sin Зх cos х. 58.	у" =2у3, у(1) = 1, у'(1) = 1. 59.	УУ"-(У')2 = /.
Г Л А В A 3
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Общие понятия
Уравнение движения материальной точки массы т под действием
силы F (/, г, г)
т = г, г)
путем проектирования на оси координат может быть заменено систе-
мой трех скалярных уравнений второго порядка:
(i^X	*	*	*
т — X (t, х, у, z, х, у. г),
т = Y (t. х, у, z, х. у. z),
d2z -г	\
т-г^-— Z(t. х, у. z, х, у. z),
или системой шести уравнений первого порядка, если за неизвестные
функции считать не только координаты х, у, z движущейся точки,
dr .
но и проекции х, у, z ее скорости :
х = и,
y — v,
z = w;
mu = X(t, х, у, z, a, v.
mv = Y (t, x, у, z, и, v, w),
mw — Z (t, x, y, z, a, v, w).
При этом обычно задаются начальное положение точки х (t0) = х0,
y(t0) — y0, z(t0) — z0 и начальная скорость a(t0) = u0, v(t0) = vo.
§ 1]
ОБЩИЕ ПОНЯТИЯ
169
Эта основная задача с начальными значениями уже рассматривалась
в § 6 главы 1 (стр. 51). Там была доказана теорема существования
и единственности решения системы дифференциальных уравнений
=	хр х2.......х„).
dx2 t	,
— =/2(Л хр х2.............х„).
df ~ f п	XV •••• -'-«)
(3.1)
удовлетворяющего начальным условиям
' xl(t0) = xiti (1=1, 2.........п).	(3.2)
Напомним, что достаточными условиями существования и един-
ственности решения системы (3.1) при начальных условиях (3.2)
являются:
1)’непрерывность всех функций ft в окрестности начальных
значений;
\\ 2) выполнение условия Липшица для всех функций по всем
аргументам, начиная со второго в той же окрестности.
Условия 2) можно заменить более грубым, потребовав существо-
вания ограниченных по модулю частных производных
-иг 2.................»>
Решение системы дифференциальных уравнений х, (t), х2 (/)> . . .
x„(t) является «-мерной вектор-функцией, которую мы кратко
будем обозначать X (/). В этих обозначениях система (3.1) может
быть записана в виде
=	X).
где Р— вектор-функция с координатами (Д, /2, .... /я), а началь-
ные условия в виде X (t0) = X0, где Хо есть «-мерный вектор с коор-
динатами (х10, х20, .... хя0).
Решение системы уравнений
Xi^Xj^), х2 = х2(О, .... хя = хя(О,
или кратко X = X (t), определяет в евклидовом пространстве с коор!-
динатами t, хР х2, .... хя некоторую кривую, называемую инте-
гральной кривой. При выполнении условий 1) и 2) теоремы суще-
ствования и единственности через каждую точку этого пространств;
проходит единственная интегральная кривая и их совокупность обра-
зует «-параметрическое семейство, в качестве параметров этого семей-
ства могут быть взяты, например, начальные значения х10, х20.хя0.
170	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	[ГЛ, 3
Возможна и другая интерпретация решений
Xl = Xi(0. х2 = х2(/)....xn = xn{t),
или кратко X = X (f), особенно удобная, если правые части системы
(3.1) не зависят явно от t.
В евклидовом пространстве с прямоугольными координатами хр
х2, .... х„ решение х^х^/), х2 —х2((), .... xn — xn(t) опре-
деляет закон движения по некоторой траектории в зависимости от
изменения параметра t, который при этой интерпретации мы будем
„	dX ,
считать временем. При такой интерпретации производная будет
dx. dx2 dxn
скоростью движения точки, а	....— координатами
скорости той же точки. При этой интерпретации, весьма удобной
и естественной во многих физических и механических задачах, система
= хР х2...........хл) (/ = 1.2.........л),	(3.1)
или
обычно называется динамической, пространство с координатами
Хр х2......х„ называется фазовым, а кривая X = X (t)— фазовой
траекторией.
Динамическая система (3.1) в заданный момент времени t опреде-
ляет в пространстве хР х2......хл поле скоростей. Если вектор-
функция Р зависит явно от t, то поле скоростей меняется с тече-
нием времени и фазовые траектории могут пересекаться. Если же
вектор-функция F, или, что то же самое, все функции не зависят
явно от t, то поле скоростей стационарно, т. е. не изменяется с те-
чением времени, и движение будет установившимся.
В последнем случае, если условия теоремы существования и
единственности выполнены, через каждую точку фазового простран-
ства (Хр х2.....хл) будет проходить лишь одна траектория. Дей-
ствительно, в этом случае по каждой траектории X = X (/) совер-
шается бесконечное множество различных движений X — X -j- с),
где с — произвольная постоянная, в чем легко убедиться, совершив
замену переменных tx=t-\-c, при которой динамическая система
не изменит своего вида:
и следовательно, X = X (/J будет ее решением, или в прежних
переменных X = X (/.-|- с).
§ 2]	ИНТЕГРИРОВАНИЕ СИСТЕМЫ УРАВНЕНИЙ
171
Если бы через некоторую точку Хо фазового пространства в рас-
сматриваемом случае проходили две траектории
X = Xx(f) и X^X^tY Х1(ГО) = ^2(ГО) = Л'О,
то, взяв на каждой из них то движение, при котором точка Хо
достигается в момент времени £ = /0, т. е., рассматривая решения
X — Xx(t — /0Н-70) и X = X2{t — г04-70),
получим противоречие с теоремой существования и единственное™,
так как два различных'решения Xx(t— ^o4“A>) и	— A)~Wo)
удовлетворяют одному и тому же началь-
ному условию X (Zo) = Л’о-
Пример. Система уравнений
имеет, как нетрудно проверить непосредст-
венной подстановкой, следующее семейство
решений:
х = <4 cos (t — с2),
у = — С] stn(/ — С2).
Рассматривая t как параметр, получим на фа-
зовой плоскости х, у семейство окружностей
с центром в начале координат (рис. 3.1). Пра-
вая часть системы (3.3) не зависит от t и
удовлетворяет условиям теоремы существова-
ния и единственности, поэтому траектории не пересекаются. Фиксируя сь
получим определенную траекторию, причем различным с2 будут соответство-
вать различные движения по этой траектории. Уравнение траектории
х2 ф у2 = с2 не зависит от с2, так что все движения при фиксированном ct
совершаются по одной и той же траектории. При с1 = 0 фазовая траек-
тория состоит из одной точки, называемой в этом случае точкой покоя
системы (3.3).
§ 2. Интегрирование системы дифференциальных уравнений путем
сведения к одному уравнению более высокого порядка
Один из основных методов интегрирования системы дифферен-
циальных уравнений заключается в следующем: из уравнений си-
стемы (3.1) и из уравнений, получающихся дифференцированием урав-
нений, входящих в систему, исключают все неизвестные функции,
кроме одной, для определения которой получают\ одно дифферен-
циальное уравнение более высокого порядка. Интегрируя это урав-
нение более высокого порядка, находят одну из неизвестных функ-
ций, а остальные неизвестные функции, по возможности без интегра-
ций, определяются из исходных уравнений и уравнений, получившихся
в результате их дифференцирования.
179
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ГЛ. в',
Иллюстрируем сказанное примерами.
Пример!.
dx __ dy
dt — У’ "~dF
Дифференцируем одно из уравнений, например первое. =
dy	d2x
чая -2- с помощью второго уравнения, получим --------------
си> '	lLv
х == с,е* 4- с2е~*. Используя первое уравнение, получаем у =
Мы определили у без интеграций с помощью первого уравнения,
мы определили у из второго уравнения
dy
dt
dy
• —тг И’ исклю-
dt
х = 0. откуда
, х = с2е у = с,е‘ — с2е ‘ 4- с.
s=	•
Если бы
то ввели бы лишние решения, так как непосредственная подстановка
ную систему уравнений показывает, что системе удовлетворяют
х — с,г*4"с2е~‘, у = С{е‘— с2е~(-^-с3 не при произвольном с3,
при с3 = 0.
Пример 2.
в исход-
функции
а лишь
dx „	6
— = 3х-2у,
dy <>
(3.4,)
(3.42)
Дифференцируем второе уравнение:
d?y _с> dx	dy
dt2	dt	dt'
(3.5)
*	dx
Из уравнений (3.42) и (3.5) определяем х и
2 \ dt
dx _ 1 / d2.y
dt ~ 2 \ dt2
(3.6)
Подставляя в (3.4,), получим
^>l_2-^- + y = 0
dt2 dt
Интегрируем полученное линейное однородное уравнение с постоянными
коэффициентами у = (Ci-f-c2t) и, подставляя в (3.6), находим x(t):
х = ^-е‘(2С1 4-с2+ 2c2t).
Пример 3.
d2x d2y
dt2 ~y’ ~d^
5 2]	ИНТЕГРИРОВАНИЕ СИСТЕМЫ УРАВНЕНИЙ	173
П	&У ti‘>x
Дифференцируя первое уравнение, получим	, и, подставляя во
второе уравнение, будем иметь -рр- = х. Интегрируя это линейное одно-
родное уравнение с постоянными коэффициентами, получим
х = С!? + сге~‘ с3 cos 14- c^sln*.
и, подставляя в первое уравнение, находим
у s= с3е‘ 4- с2е~* — c3cost— c4sln/.
Опишем теперь более точно процесс исключения из системы
уравнений всех неизвестных функций, кроме одной.
Покажем вначале, что одна из неизвестных функций, например
xx(t), входящая в состав решения xx(t), x2(f)....x„(t)	системы
дифференциальных уравнений:
— хР xs, .... хп),
—pp—xp xi' •••• ’*'«)>	(ЗД)
= Xp x2..............x„).
удовлетворяет некоторому уравнению n-го порядка, при этом мы
предположим, что все функции /z имеют непрерывные частные про-
изводные до (п — 1)-го порядка включительно по всем аргументам.
Подставив в систему (3.1) некоторое решение xx{t), х2(/)........хл(0>
обратим все уравнения системы в тождества. В частности, в тожде-
ство обратится и первое уравнение системы
dx. .	.
Хр х2.......х„).
Продифференцируем это тождество по t‘.
d2xt _ <Vi , У d/i dxi
dt2 ~~ dt "г Zji dxj dt ’
z=i
или
<*2*1 __ d/l I V f	(o 7a\
dt2 ~~ dt Id dx{ 2 l'
Z=1
и, обозначив правую часть последнего тождества F2(t, xv х2........хя),
получим:
(3.7^)
dfZ —Х2.....................хп)'
(ГЛ. з
174	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Снова дифференцируем это тождество:
	п d3Xi	। 'V ^2 dxt dt3 ~ dt +1 dxt dt ' t-1
или	d3x, _ dF2 .\ldFt ,	( _a\ dt3	dt	dXf Jl'
и, обозначив правую часть последнего тождества F3(t, xv х2, .... хп),
получим:	^. = F3(t, xp x2, .... хл).	(3.7з)
Опять дифференцируем это тождество и, продолжая этот процесс
п — 2 раза, получим, наконец, тождество
——rL = F„_1(Z, хР х2.........х„).	(3.7®_1)
дифференцируя которое будем иметь: dnxx 	 dtn	еще раз Fn(r. Хр	и пользуясь Xi	хп).	тождествами		(3.1).
Итак, получены п. — 1	тождеств				
	Хр х2, .	.. Хя).	(3.7,)		
	X j. Х2» •	•ха), 	(3-72)		(3.7)
—^ = /?«-1(tXpX2.......х„)	(3.7„_,)
и еще одно тождество
^L = F„(t. хр х2.............................хя).	(3.8)
Предположим, что в рассматриваемой области изменения пере-
менных определитель
£>(/ь Fq, F3...Fn-i) , Q
D (х2, ха, х4..хп)
Тогда систему (3.7) можно разрешить относительно х2, х3.....хп,
dx	~ X
выразив их через переменные t, хр > •••• —	• Подставив
$ 2]	ИНТЕГРИРОВАНИЕ СИСТЕМЫ УРАВНЕНИИ	175
найденные из системы (3.7) переменные х2, х3, .... хп в последнее
уравнение (3.8), получим уравнение n-го порядка
Л1 = ф(;, Х1,
dtn \ dt
dn-1xl
dt"'1
(3.8!)
которому удовлетворяет функция xx(t), являвшаяся по предположе-
нию функцией *1(0 решения x^f). x2(t)........xn(t) системы (3.1).
Докажем теперь, что если взять любое решение хх (t) получен-
ного уравнения я-го порядка (3.8t) подставить его в систему (3.7) и
определить из этой . системы х2 (0. х3 (t).....хп (0, то система
функций
Xj(0. х2(0, .... х„(0	(8.9)
будет решением системы (3.1).
Подставим найденную систему функций (3.9) в систему (3.7) и тем
самым обратим все уравнения этой системы в тождества; в частности,
получим тождество
dxt ___е ,,	.
— = /l(f, Хр Х2............Хп).
Дифференцируя это тождество по t, будем иметь:
d2xx _ dfx у dfi dxt
dt2 dt ' dxt dt ’
i = \
(8.71)
(3.10)
„	dxi ,	.
В этом тождестве пока нельзя заменить функциями /г, так как
мы еще не доказали, что полученные указанным выше путем из
уравнения (3.8) и системы (3.7) функции хг, х2......х„ удовлетво-
ряют системе (3.1), более того, именно это утверждение и является
целью нашего доказательства.
Вычитая почленно из тождества (3.10) тождество (3.72), взятое
в развернутом виде (3.72), получим
У dfi idxL
Ы дхх ( dt
z=i

или, в силу (3.7Х),
У df\ (dxt
dxi \ dt
Л)^о.
176	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ	[ГЛ. 3
Совершенно аналогично, дифференцируя тождество (3.72) и вычитая
(3.7з), затем дифференцируя тождества (З.73) и вычитая (3.7<) и т. д.,
получим:
п
/=2
idxj
А дх; \ dt
i=2
Так как определитель линейной однородной системы уравнений
' 1 = 2
п
S()F2 ldxt . \ n
~dx[\~dF —
(3.11)
состоящей из (n—1)-го уравнения с п — 1 неизвестными —ftj
(1 = 2, 3, .... «), совпадает с отличным от нуля функциональном
определителем
D(/„	.... F„_,)
D(x2, х3....хп)
то система (3.11) в каждой точке рассматриваемой области имеет
только тривиальные решения,
^--Л = 0	(1 = 2, 3, .... п).
Принимая во внимание еще (3.7t), получаем, что п функций xlt
х2, .... х„ являются решением системы уравнений
^ = /((О1,х2.....х„)	(/=1, 2...п).
Замечание 1. Указанный здесь процесс исключения всех функ-
ций, кроме одной, предполагает, что
Д (/1. F2, ,.Fn^i) q
D (x2, xa,	xn)
(3-12)
$ 2]	ИНТЕГРИРОВАНИЕ СИСТЕМ^ УРАВНЕНИИ	177
Если это условие не выполнено, то можно применить тот же
процесс, но вместо функции х{ взять какую-нибудь, другую из функ-
ций х2, х3’ хп> входящих в решение системы (3.1). Если же
условие (3.12) не выполняется при любом выборе вместо какой-
нибудь функции из х2, х3, .... х„, то возможны различные исклю-
чительные случаи, которые мы иллюстрируем следующими примерами.
П р и м е р 4.
=	х3).
Система распалась на совершенно независимые между собой уравнения,
каждое из которых приходится интегрировать отдельно.
П р и м е р 5.	'
/
~ Хг' Хз)'
ut	CUfg
я Л (*' х2. Хз)-
Два последних уравнения можно указанным выше методом свести к од-
ному уравнению второго порядка, но первое уравнение, содержащее неиз-
вестную функцию X], не входящую в остальные уравнения, надо интегриро-
вать отдельно.
Замечание 2. Если применить указанный выше процесс исклю-
чения всех неизвестных функций, кроме одной, к системе
п
a=i. 2.г... п),
называемой линейной
нение п-го порядка
однородной, то, как нетрудно проверить, урав-
-^-=ф (f, Х1,
dtn \ dt
dn~'x, \
dtn~x /
(3.8Х)
тоже будет линейным однородным, причем если все коэффициенты
были постоянными, то и уравнение (3.8t) будет линейным однород-
ным уравнением с постоянными коэффициентами. Аналогичное
178	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	(ГЛ. 3
замечание справедливо и для линейной неоднородной системы
п	4
^ = 2^ (/)*/+Л (О (/=1.2..........л),
7=1
для которой уравнение (3.8!) будет линейным неоднородным уравне-
нием л-го порядка.
§ 3. Нахождение интегрируемых комбинаций
Интегрирование систем дифференциальных уравнений
^=/z(/,Xp х2........хп) (1=1.2, .... п) (3.1)
нередко осуществляется путем подбора так называемых интегрируемых
комбинаций.
Интегрируемой комбинацией называется дифференциальное
уравнение, являющееся следствием уравнений (3.1), но уже легко
интегрирующееся, например являющееся уравнением вида
</Ф(Л хр х2, .... хл) = 0
или уравнением, сводящимся заменой переменных к какому-нибудь
интегрируемому типу уравнений с одной неизвестной функцией.
Пример 1.
Складывая почленно данные уравнения, находим одну интегрируемую ком-
бинацию
<*(•* +У) ,	d (X у) .,
—	'	• = х -+- у или —Y ,1 1 = dt,
dt	' J	х у
откуда
In |х + У I =/ + ,п ci. x-^-y — cte‘.
Почленно вычитая из первого уравнения системы второе, получаем вторую
интегрируемую комбинацию
d(x — у)	.	.	d(x — y)	..
——-г,-— = — (х — у) или —-----------— — — dt,
dt	'	77 х — у
In | х — у | = — /-{-In сг, х — у = сге~*.
Итак, найдено два конечных уравнения:
х-{-у = с1г/ и х —у = с2е_/,
из которых может быть определено решение исходной системы
х=у(с,?-{-с2в_/), у — с2е~‘)
или	_	_	_	_
х = c^-j- с2е~‘, у = схе* — сге~1.
§ 3]	НАХОЖДЕНИЕ ИНТЕГРИРУЕМЫХ КОМБИНАЦИЙ	179
Одна интегрируемая комбинация дает возможность получить одно
конечное уравнение
Ф](Л Хр х2......хЛ) = Ср
связывающее неизвестные функции и независимое переменное; такое
конечное уравнение называется первым интегралом системы (3.1).
Итак, первым интегралом
Ф(Л Хр х2, .... хя) = с	(3.13)
системы уравнений (3.1) называется конечное уравнение, обращаю-
щееся в тождество при некотором значении с, если вместо х(- (/)
(z = 1, 2, ..., п) подставлено решение системы (3.1).
Часто первым интегралом называют также левую часть
Ф(Л Хр х2, ..., хя) уравнения (3.13). и тогда первый интеграл
определяется как функция, не равная тождественно постоянной, но
сохраняющая постоянное значение вдоль интегральных кривых си-
стемы (1).
Геометрически первый интеграл Ф(/, хР х2, ..., хп) = с при
фиксированном с можно интерпретировать как «-мерную поверхнбсть
в («-|- 1)-мерном пространстве с координатами t, хР х2, .... хя,
обладающую тем свойством, что каждая интегральная кривая, имею-
щая общую точку с этой поверхностью, целиком лежит на поверх-
ности. При переменном с получаем семейство непересекающихся по-
верхностей, обладающих тем же свойством, т. е. состоящих из точек
некоторого (« — 1)-параметрического семейства интегральных кривых
системы (3.1).
Если найдено k интегрируемых комбинаций, то получаем k пер-
вых интегралов:
Ф1 (t. х}, х2....хп) — с},
Ф2 (Л Хр х2, .... хя) = с2,	(3.14)
Ф*(Л Хр х2, .... хя) = сЛ.
Если все эти интегралы независимы, т. е. если хотя бы один опре-
делитель
О(ФьФг.....Ф*) а
D(xh-xJ,.....х)„)	’
где Хур Xj2.....х1к—какие-нибудь k функций из Хр х2..........хя,
то из системы (3.14) можно выразить k неизвестных функций через
остальные и, подставляя в систему (3.1), свести задачу к интегриро-
ванию системы уравнений с меньшим числом неизвестных. Если k — п
и все интегралы независимы, то все неизвестные функции определяются
из системы (3.14).
180	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	[ГЛ. Э
Примера.
Сложив почленно уравнения этой системы, получим.
dx.dy.dz п d , .	. .	_
-di+dr + ~dt^Q или -57-(* +у+ *) = <>•
откуда
Найденный первый интеграл позволяет выразить одну из неизвестных функ-
ций через остальные переменные и тем самым свести задачу к интегрирова-
нию системы двух уравнений с двумя неизвестными функциями. Однако
в данном случае легко можно найти еще один первый интеграл. Умножим
первое уравнение почленно на х, второе на у. третье на г и сложим:
или, умножив на 2, получим
4(х2+у2+г2)==0,
откуда
^ + у2 4-^ = с2.
Из двух найденных первых интегралов можно выразить две неизвестные
функции через остальные переменные и тем самым свести задачу к интегри-
рованию одного уравнения с одной неизвестной функцией.
Пример 3.
Л-^=(В-С)?г В-§- = (С-Л)гр, C~r = (A~B)pq,
. Ill	Ul	Ul
где Л, В и С — постоянные (эта система встречается в теории движения
твердого тела). Умножая первое уравнение на р, второе на q. третье на г и
складывая, получим	'
','%-+в*Тг+с'7Г-'>'	'
откуда находим первый интеграл
Ар2 + Bq2-J-Сг> = с,.
Умножая первое уравнение на Ар, второе на Bq, третье на Сг и складывая,
будем иметь
л,',4г+в,’47- + е,':гг-‘к
и, интегрируя, получим еще один первый интеграл
А2р2 4- B2q2 + С*г2 = с2.
Если исключить случай А — В — С, при котором система интегрируется не-
посредственно, то найденные первые интегралы независимы и, следовательно,
пользуясь этими первыми интегралами, можно исключить две неизвестные
$ «1 СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	181
функции, причем для определения третьей функции получим одно уравнение
с разделяющимися переменными.
Для нахождения интегрируемых комбинаций часто удобно пере-
ходить к так называемой симметрической форме записи системы урав-
нений (3.1):
dxi
Ф1 (Л Хр х2.
dx2
<р2 (4 х{,х2, .... х„)
<txn.
dt
Фл (t хг, x2,
Ф0(<, хр х2. .... х„) ' (ЗЛ5)
<р (/, хь х2, .
Л (Л xv Х2, ....	=
(/= 1, 2, ..., п).
В системе, заданной в симметрической форме,
равноправно, что иногда облегчает нахождение
бинаций.
Пример 4.
переменные входят
интегрируемых ком-
dx
Интегрируя уравнение
dy dz
х2 — у2 — z2 ~ >2ху ~ 2хг '
(3.16)
dy __ dz
2ху ~ 2xz ’
где .
первого из отношений
у
находим у = Ср Умножая числители и знаменатели
системы (3.16) на х, второго на у, третьего на z и составляя производную
пропорцию, получи^
х dx у dy z dz _ dy
х (х2 -|- у2 -|- z2)	~~ 2ху '
откуда
или
= с2.
У
Найденные независимые первые иПтегралы
у
— = с, и
z
сг
У
определяют искомые интегральные кривые.
§ 4. Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если
она линейна относительно всех неизвестных функций и их производ-
ных. Система п линейных уравнений первого порядка, записанная
182	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	(ГЛ. 3
в нормальной форме, имеет вил
=	(/=1,2.......п),	(3.17)
7=1
или в векторной форме
^ = AX + F,	(3.18)
где Д’ есть n-мерный вектор с координатами xx(f), х2(/), .... x„(/),
F есть «-мерный вектор с координатами f,(t), /2(/), •••• /„(О-
которые удобно в дальнейшем рассматривать как одностолбцовые
матрицы:
аи а12  • • Л1п
а21 «22 ... а2п
ап1 ап2 • • • апп
dX
dt
dx,
dt
dx2
~dT
dxn
dt
Согласно правилу умножения матриц строки первого множителя
должны умножаться на столбец второго, следовательно,
	1 "и'Ь<4а		2 o.xjXj-\- f\ y=i
АХ =	2 a2jX]		,2 a2jxj+A
	*11*1^3 а		2 anjxj +fn
§4] СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ 183
Равенство матриц означает равенство всех их элементов, следова
тельно, одно матричное уравнение (3.18) или
эквивалентно системе (3.17).
Если все функции а,у(£) и /,(/) в (3.17) непрерывны на отрезке
a ^.t ^.Ь, то в достаточно малой окрестности каждой точки
(Zo, х10, х20..хя0), где a^t0;^.b, выполнены условия теоремы
существования и единственности (см. стр. 169) и, следовательно, через
каждую такую точку проходит единственная интегральная кривая
системы (3.17).
Действительно, в рассматриваемом случае правые части системы (3.17)
непрерывны, и их частные производные по любому Xj ограничены,
так как эти частные производные равны непрерывным на отрезке
аП коэффициентам a^tt).
Определим линейный оператор L равенством
l\x\ = ^--ax.
тогда уравнение (3.18) еще короче можно записать в виде
£[Х]=Г.	(3.19)
Если все /;(Z) = 0 (Z=l, 2... п), или, что то же самое,
матрица F = 0, то система (3.17) называется линейной однородной.
В краткой записи линейная однородная система имеет вид
Л[АГ] = О.	(3.20)
Оператор L обладает следующими двумя свойствами:
1) L\cX]-= cL\X],
где с — произвольная постоянная.
2)	+	=£[*,] +Не-
действительно,
т—	И-
-У - А^х<+(т- - axi)+(т -•
184	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
Следствием свойств 1) и 2) является
[гл. з
L 2 с А '= 2 ctL [XJ,
где ct — произвольные постоянные.
Теорема 3.1. Если X является решением линейной однород-
ной системы £[^1 = 0, то сХ, где с — произвольная постоян-
ная, является, решением той же системы.
Доказательство. Дано L [Х] = 0, надо доказать, что
/.[cA'lssO.
Пользуясь свойством 1) оператора L, получим
L [сХ]	ct{X\ == 0.
Теорема 3.2. Сумма Х1-\-Х2 двух решений Хх и Х2 одно-
родной линейной системы уравнений является решением той же
системы.
Доказательство. Дано	и Z.|X2|sO.
Требуется доказать, что Z. [ AY+Л"2] = 0.
Пользуясь свойством 2) оператора L, получим
L [X, + Х2\ = L [4- L [Х2] = 0.
Следствие теорем 3.1 и 3.2. Линейная комбинация 2 ciXt
с произвольными постоянными коэффициентами решений
Xv Х2, .... Xv линейной однородной системы L [Х] =0 является
решением той же системы.
Теорема 3.3. Если линейная однородная система (20) с дей-
ствительными коэффициентами a^if) имеет комплексное реше-
ние X = U IV, то действительная и мнимая части
«1
«2
t/ =


в отдельности являются решениями той же системы.
Доказательство. Дано L |(7 + IV] == 0 Надо доказать, что
£[(/] = 0 и L|V] = O.
Пользуясь свойствами 1) и 2) оператора L, получаем
L [U + IV\ == L [(7Ц- IL [V]	0.
Следовательно, £[L/] = 0 и L [V] = 0.
«<1
СИСТЕМЫ ЛИНЕЙНЫХ -ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
185
Векторы Х2, .... X п, где
(О
x2i (О
хт (*)
называются линейно зависимыми на отрезке a^.t^.b, если суще-
ствуют постоянные ар а2.........ап такие, что
a!-^i а2 Х2 ... -j-anX„ = O	(3.21)
при 4^ причем по крайней мере одно а( ¥= 0. Если же тож-
дество (3.21) справедливо лишь при at = а2 = . .. = ал = 0. то
векторы Xv Х2, ...,Хп называются линейно независимыми.
Заметим, что одно векторное тождество (3.21) эквивалентно п
тождествам:
п
2а;хн(/) = 0,
п
2 atxu (О °-
/=1
(3.21J
п
2 atxnl(f)t=0.
Если векторы А'/(/=1, 2......п) линейно зависимы и значит
существует нетривиальная система az (т. е. не все az равны нулю),
удовлетворяющая системе п линейных однородных по отношению
к az уравнений (3.21!), то определитель системы (3.21х)
W =
хп х12
х21 х22
ХХп
х'2п
Хп} Хп1 • ’ • хпп
должен быть равен нулю для всех значений t отрезка a ^Ь.
Этот определитель системы называют определителем Вронского
для системы векторов Хх, Х2, ..., Xп.
Теорема 3.4. Если определитель Вронского W решений
Xv Х2. .... Хп линейной однородной^ системы уравнений (3.20)
с непрерывными на отрезке a^t^b коэффициентами a(j(t)
равен нулю хотя бы в одной точке t = t0 отрезка a^t^b,
то решения Х[: Х2...Х„ линейно зависимы на том же от-
резке, и, следовательно, на рассматриваемом отрезке W = 0.
186	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ	(ГЛ. 3
Доказательство. Так как-коэффициенты atj (О а. / = I.
2.....п) непрерывны, то система (3.20) удовлетворяет условиям
теоремы существования и единственности. Следовательно, начальное
значение X(to) = O (или, подробнее, Xj(/o)'=O, х2(/о) = О.........
хп (/0) == 0) определяет единственное решение рассматриваемой
системы и этим решением, очевидно, является тривиальное решение
системы (3.20) X(t) = 0 (или, подробнее, Х](/) = 0, х2(() = 0.....
хл(/)эО). Определитель W (ta) — 0. Следовательно, существует
нетривиальная система cv с2, .... сп, удовлетворяющая уравнению
ci^i(^o)~^~ с2-^2^о) + ••• +c„A"n(/o) = O,
так как это одно векторное уравнение эквивалентно системе п ли-
нейных однородных относительно ct уравнений с равным нулю Опре-
делителем:
п
2 Wh (to) = О,
1	= 1	'
/I
2	(^о) = °-
/ = 1
л
2«Л((У = <>-
i = 1
Соответствующее этой нетривиальной системе cv с2, ...» сп реше-
п
ние уравнения (3.20) X (t) = 2ciy’G (0 удовлетворяет нулевым на-
i=i
чальным условиям X (t0) = 0 и, следовательно, совпадает с триви-
альным решением системы (3.20):
п
2<>ВД^0,
t=i
т. е. Xt линейно зависимы.
Замечание. Эта теорема, как показывают простейшие примеры,
не распространяется на произвольные векторы Хх, Х2...Xп, не
являющиеся решениями системы (3.20) с непрерывными коэффициен-
тами.
Пример 1. Система векторов '
линейно независима, так как из
§ 4] СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 187
ИЛИ
aLt -|- a2t2 == О,
следует, что =а2 —0 (см. стр. 96, пример 1). В то же время определитель
Вронского
t t2 |
р тождественно равен нулю. Следовательно, векторы Хх и Х2
не могут быть решениями одной и той же линейной однородной системы
(3.20) с непрерывными коэффициентами ац (i) (Z, j— 1, 2).
П
Теорема 3.5. Линейная комбинация	ctX t п линейно неза-
/.= 1
висимых решений Xv Х2......Хп линейной однородной системы.
(ЗЛО) с непрерывными на отрезке a-^.t коэффициентами atj(f)
является общим решением системы (3.20) на том же отрезке.
Доказательство. Так как коэффициенты a^it) непрерывны
на отрезке	то система удовлетворяет условиям теоремы
существования и единственности и, следовательно, для доказатель-
ства теоремы достаточно обнаружить, что подбором постоянных ct
п
в решении У можно удовлетворить произвольно выбранным
i=i
начальным условиям X (t0) — XQ,
пО
где /0 — одно
из значений t на отрезке a^.t^.b, т. е. можно
удовлетворить одному векторному уравнению
2 Ci-Xi ('о) —
<=1
или эквивалентной системе п скалярных уравнений:
п
2 (ta) = х10,
1=1
п
S Cix2l ('о) = Х20*
п
2 cfMo)=
1=л

188	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ	ГГЛ, 3
Эта система разрешима относительно ct при любых х10, так как
определитель системы является определителем Вронского для ли-
нейно независимой системы решений Х{, Х7.....Хп и, следова-
тельно, не обращается в нуль ни в одной точке отрезка а t <1 Ь.
Пример 2,
dx
Нетрудно проверить, что системе (3.22) удовлетворяют решения
л, = cos t. у, =— sin/ и x2 = sin/, y2 = cos/
Эти решения линейно независимы, так как определитель Вронского
I COS / — Sin t I J
I Sin/ COS / I
отличен от нуля. Следовательно, общее решение имеет вид
х = с, cos / с2 sin /.
у = — С) sin / 4- с2 cos /,
где с, и с2 — произвольные постоянные.
Теорема 3.6. Если X является решением линейной неодно-
родной системы
L[X] = F,	(3.19)
а Хх — решением соответствующей однородной системы
£[Х] = 0, то сумма Х1Ц-Х также будет решением неодно-
родной системы £[Х] = А
Доказательство. Дано, что HX] = F и HXjssO. Надо
доказать, что L -j- X\==F.
Пользуясь свойством 2) оператора L, получим
£ 1*! + X] = £ |Х,)+ М*) = F.
Теорема 3.7. Общее решение на отрезке a^.t^b неодно-
родной системы (3.19) с непрерывными на том же отрезке
коэффициентами alf(t) и правыми частями ft(t) равно сумме»
п
общего решения 2 ci^t< соответствующей однородной системы
/=1
и частного решения X рассматриваемой неоднородной си-
стемы.
Доказательство, Так как условия теоремы существования
и единственности выполнены (см. стр. 183), то для доказательства
теоремы достаточно обнаружить, что подбором произвольных по-
СИСТЕМЫ ЛИНЕЙНЫХ дифференциальных уравнений
189
I
стоянных ct в решении X ='^iciXl-\-X можно удовлетворить
f=i .
произвольно заданным начальным условиям
X (А)) — ^0 —
*10
*20
*П0
т. е. надо доказать, что одно матричное уравнение
2C/XZ(/O)+ X(t0) = Xt
i-1
или эквивалентная система уравнений
2 С i*U (to) + *1 (to) = Х1о,
2 С/*2/ (4)) + *2 ('о) — *20-
(3.23)
2 ''(*«/(^о) Н" *л(А>) — *пС
всегда имеет решеИйе cv с2......сп, каковы бы ни были правые
части. Однако в такой ферме это утверждение очевидно, так как
определитель системы (3.23) является определителем Вронского
в точке t = ta для линейно независимых решений Х{, Х2.......X„
соответствующей однородной системы и по теореме 3.4 отличен от
нуля. Следовательно, система (3.23) имеет решение сх, с2....с„
при любых правых частях.
Теорема 3.8 (принцип суперпозиции). Решением системы
линейных уравнений
LlX\=^Fit
fm(t)
190
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ	[ГЛ. 3
т
является сумма 2 Xt решений Xt уравнений
i=i
L [А',] =/=\ (/=1,2.т).
Доказательство. Дано L [ А",] == Ft (/=1,2.т).	Надо
доказать, что
[т	т
/=1 „ J i-\
Используя свойство 2) оператора L, получим
[т ~| т	т
2 хД^цх^^р,.
i = I	J	i=1	i = 1
Замечание. Теорема 3.8 без изменения доказательства, оче-
видно, распространяется и на тот случай, когда т —> оо, если ряд
со
2 Х{ сходится и допускает почленное, дифференцирование.
z=i
Теорема 3.9. Если система линейных уравнений
где
L[X] = U + IV.
с действительными функциями ац (О, «ДО- ^ (/)(/,/=!, 2.п)
имеет решение
U =
«1
«2
v

V =
«Я
Vn
то действительная часть решения U и его мнимая часть V
соответственно являются решениями уравнений
L{X\ = U и L[X] = V.
Доказательство. Дано L [U -|- IV] = U -j- IV, надо доказать,
что L = L[V] = V.
$ 4] СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 191
Пользуясь свойствами 1) и 2) оператора L, получаем
L{0 4- IV\ == L [L7] + IL [V] == U + IV.
Следовательно. L[U\=:U и L[V]^V.
Если известно общее решение соответствующей однородной
системы L(X) — 0, но подобрать частное решение неоднородной
системы L(X) — F не удается и, следовательно, нельзя воспользо-
ваться теоремой 3.7, то можно применить метод вариации постоянных.
п
Пусть X — 2 ctXt является при произвольных постоянных ct
1=1
общим решением соответствующей однородной системы
и, следовательно, Xt(l = l, 2, .... п) — линейно независимые част-
ные решения той же однородной системы. Решение неоднородной
системы
ищем в виде
п
X = ^icl(t)Xl,
t=i
где ct (f) — новые неизвестные функции. Подстановка в неоднородное
уравнение дает
п	п	П‘
1^1	z=i
dXi л v
или, так как —^~~ = AXlt получим
п
Zc'^X^F.
t = l
Это векторное уравнение эквивалентно системе п уравнений:
п
Хи = /г (/),
1 = 1
П
х21 —(3.24)
192	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	[ГЛ. 3
Из этой системы л уравнений с п неизвестными c'(/)(Z=l,
2, .... п) с определителем системы W, совпадающим с определите-
лем Вронского для линейно независимых решений Хх, Х2..........Ха
и, следовательно, отличным от нуля, определяются все
c'(Z) = <p/(Z) (Z — 1, 2...п),
откуда, интегрируя, находим неизвестные функции С/(():
с( f	(Z = 1. 2....«).
Пример 3.
dx dy	,1
dt ~ У’ dt = Х cos t ’
Общее решение соответствующей однородной системы
имеет вид х = С! cos 14- с2 sin t, у =—с, sin t 4- c2 cos t (см. стр. 188. при-
мер 2). Варьируем постоянные
х = С] (t) cos t-j-Сц (Z) sin t,
у = — Cl (t) sin t 4- c2 (Z) cos t.
с, (Z) и c2 (Z) определяется из системы (3.24), имеющей в данном случае вид
С] (Z) cos t с'2 (Z) sin t = О,
— cj (Z) sin t + c2 (Z) cos t = -^-t ,
откуда
/... slnZ < ...	,
ci (<) “ ~ roTz ’ C2 (Z) ~ L
Следовательно,
C, (Z) = In | cos Z| cb
c2 (Z) = z 4- C2
и окончательно получаем
x = ct cos Z 4- c2 sin Z 4- cos t In | cos 114- Z sin Z,
у = — ct sin Z 4- c2 cos Z — sin Z In | cos Z | 4- Z cos t.
§ 5. Системы линейных дифференциальных уравнений
с постоянными коэффициентами
Линейной системой с постоянными коэффициентами назы-
вается линейная система уравнений
п-
+	(Z=l. 2....п),
§ 5]
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
193
или в векторной форме
в которой все коэффициенты a{j постоянны, или, что то же самое,
матрица А постоянна.
Проще всего система линейных однородных или неоднородных
уравнений с постоянными коэффициентами интегрируется путем
сведения ее к одному уравнению более высокого порядка, причем,
как отмечено на стр. 177, полученное уравнение более высокого
порядка будет линейным с постоянными коэффициентами.
Однако можно и непосредственно найти фундаментальную систему
решений линейной однородной системы с постоянными коэффи-
циентами.
Будем искать решения системы
dx,	,	,	,
— аихг -|- ai2X2 4- •   + в1ахл,
dx2	,	,	,
-sL = a21x1 + «22^2+ ••• +а2пх„.
(3.25)
~ЙГ = Wi 4 ап2х2 + • • • + алях„.
где все atj постоянны, в виде
хг = а^ем, х2 = a2eftz........хп = апеЧ
с постоянными ау (/=1, 2, .... п). Подставляя’в систему (3.25),
сокращая на а** и перенося все члены в одну часть равенства, по-
лучим
(au — k) at + a12a2 4-  • •'4' ainan — О,
fl21al 4" (a22 — a2 4 • • • 4 a2nan = 0,
(3.26)
4 an2a2 4 • • • 4 (an„ — k) a„ == 0.
Для того чтобы эта система п линейных однородных уравнений
с п неизвестными cty (/=1, 2, .... п) имела нетривиальное реше-
ние, необходимо и достаточно, чтобы определитель системы (3.26)
был равен нулю:
С2 и - /2 tZ|2 *
2Z2I Л22 -*~ k •
а1п
а2п
= 0.
(3.27)
^л2	" • • ® пп
194
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯ
[ГЛ. 3
Из этого уравнения степени п определяются значения k, при которых
система (3.26) имеет нетривиальные решения (/=1. 2.............л).
Уравнение (3.27) называется ха раитеристаческим. Если все корни
характеристического уравнения kt (I — 1, 2, .. ., п) различны, то,
подставляя их по очереди в систему (3.26), определяем соответствую-
щие им нетривиальные значения (Z, J = 1, 2, ..., л) и, следо-
вательно, находим п решений исходной системы (3.25) в виде
=	..... x<Z) = a^^'	(/=1, 2.......л),
(3.28)
где верхний индекс указывает номер решения, а нижний индекс —
номер неизвестной функции.
Пользуясь векторными обозначениями, получим тот же результат
еще короче:
dX
dt
(3.25J)
ищем решение в виде
X — Kekt, где А =
'k-kekt = AXekt,
ai
a2
или
(A —A:E)A = 0,
(3.29)
где E — единичная матрица:
E =
1.0 0 ...0
0 1 0 ... 0
0 0 0 ... 1
Для того чтобы уравнению (3.29) удовлетворяла нетривиальная
матрица А
0
0
0
§ Б]	СИСТЕМЫ линейных уравнений	195
необходимо и достаточно, чтобы матрица А — kE была бы особой,
т. е. чтобы ее определитель был равен нулю: |Л— kE\ = 0. Для
каждого корня kt этого характеристического уравнения |Л —kE\ — 0
из (3.29) определяем не равную нулю матрицу А<г) и, если все
корни kj характеристического уравнения различны, получаем п ре-
шений:
Хх = A'1'/*', Х2 = А(2’Л'........... Х„ = А1"'еЧ
где
<х</>
а<0
Л
Эти решения, как нетрудно показать, линейно независимы. Действи-
тельно, если бы существовала линейная зависимость
2 p,A(tV'z = 0,
1=1
или в развернутой форме
1=1
Z=1
(3.30)
то, в силу линейной независимости функций (/=1, 2...............к)
(см стр. 96), из (3.30) следовало бы, что
Pza(/’ = 0,
Pza^ = 0.
Р,<’ = 0.
(/=1, 2..........и).	(3.31)
Но так как при каждом I, хотя бы одно из а\1\ сйР, .. .. a(h
0 = 1, 2.......п) отлично от нуля, то из (3.31) следует, что Pz = 0
(/ = 1, 2......п).
196	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ	[ГЛ. 3
Итак, решения А*^*^ (1—1, 2, .... п) линейно независимы
и общее решение системы (3,25) имеет вид
п
/ = 1
или
х} — 5 С^е^1 (7 = 1, 2........п),
где Cj — произвольные постоянные.
Постоянные а<б (/=1, 2, .... п) определяются из системы (3.26)
при k = ki неоднозначно, так как определитель системы равен нулю
и, . следовательно, по крайней мере одно уравнение является след-
ствием остальных. Неоднозначность определения связана с тем,
что решение системы линейных однородных уравнений остается
решением той же системы при умножении на произвольный постоян-
ный множитель.
Комплексному корню характеристического уравнения (3.27)
kj = р + qi соответствует решение
A; = A(>W,	(3.32)
которое, если все коэффициенты a,j действительны, может быть
заменено' двумя действительными решениями: действительной и мни-
мой частями решения (3.32) (см. стр. 184). Комплексный сопряжен-
ный корень характеристического уравнения kJ+l — р — qi не даст
новых линейно независимых действительных решений.
Если характеристическое уравнение имеет кратный корень ks
кратности у, то, принимая во внимание, что систему уравнений (3.25)
можно свести процессом, указанным на стр. 173, к одному линей-
ному однородному уравнению с постоянными коэффициентами /г-го
или более низкого порядка (см. замечания на стр. 177), можно
утверждать, что решение системы (3.25) имеет вид
А'(/)=(А^,Н-А(Л+ ... + А!£1Л_1) екЛ (3.33)
где
а>2 — постоянные.

§ 5]	СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ	197
Следует заметить, что и в тех случаях, когда система п уравне-
ний (3.25) сводится к уравнению порядка ниже п (см. замечание 1
стр. 176), характеристическое уравнение последнего необходимо
имеет корни, совпадающие с корнями уравнения (3.27) (так как
уравнение, к которому свелась система, должно иметь решения
вида ekst, где ks—корни уравнения (3.27)). Но возможно, что
кратности этих корней, если порядок полученного уравнения ниже п,
будут ниже кратностей корней уравнения (3.27), и следовательно,
возможно, что в решении (3.33) степень первого множителя будет
ниже, чем у— 1, т. е. если мы будем искать решение в виде (3.33),
то может обнаружиться, что некоторые коэффициенты А(/\ в том
числе и при старшем члене, обращаются в нуль.
Итак, решение системы (3.25), соответствующее кратному корню
характеристического уравнения, следует искать в виде (3.33). Под-
ставив (3.33) в уравнение (3.25J и требуя, чтобы оно обратилось
в тождество, определим матрицы А^, причем некоторое из них,
в том числе и А$/—i, могут оказаться равными нулю.
Замечание. Можно точнее указать вид решения системы (3.25), со"
ответствующего кратному корню характеристического уравнения (3.27). Пре-
образовав систему (3.25) неособенным линейным преобразованием к системе,
в которой матрица || А — kE || имеет нормальную Жорданову форму, и про-
интегрировав полученную легко интегрирующуюся систему уравнений, обна-
ружим, что решение, соответствующее кратному корню ks характеристиче-
ского уравнения (3.27) краткости у, имеет вид
X (t) = (А</> + х(л + • • • +	’) г?,
где ₽ — наибольшая степень элементарного делителя матрицы || А — ££||,
соответствующего корню ks.
П р и м е р 1.
^ = х + 2у. ^=4^ + Зу.
Характеристическое уравнение
I 1 *	1 = 0 или k2 - 4Л — 5 = 0
I 4	3-А|
имеет корни £|=5, k2 = — 1. Следовательно, решение ищем в виде
х, =	у. = aVV5*,
(3.34)
х2 == а(]2^	у2 =	*.
Подставляя (3.34) в исходную систему, получим: —4</1,)-|-2а!!1? = 0, откуда
= 2a(jO; dp остается произвольным. Следовательно,
хх = уг = 2с1^5/,	= a(t4
198
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
[ГЛ. Э
Для определения Коэффициентов а'2 и а22)
_|_ 2а(22> = 0, откуда а(22) = — а^; коэффициент
Следовательно,
получаем уравнение 2а\21 4-
а(2) остается произвольным.
Общее решение
•*2 = С/ У2 = — с^~1'
с2 = а(12)-
Пример 2.
х—cteBtс2е ‘,
у = 2cteBt— с2е~*.
dx .
~dt =*-5*
-^ = 2x-v
dt y'
Характеристическое уравнение
11 — k —5
2	— 1 — k
или
А2 4-9 = 0
имеет корни й1>2 •= ± 3i, xt = а^3^, ух = a2e3it, (1 —3z) а( —5а2 = 0. Этому
уравнению удовлетворяют, например, Oj — 5, а2 = 1 — Зх. Следовательно
xt = 5e3Z/ = 5 (cos 3t + i sin 3t),
У1 = (1 _ 31) e3lt = (1 — 3Z) (cos 3t 4-1 sin 30-
Действительная и мнимая части этого решения также являются решениями
рассматриваемой системы, а их линейная комбинация с произвольными по-
стоянными коэффициентами является общим решением:
х = 5ci cos 3t -|- 5c2 sin 3t,
у = С] (cos 3t -f- 3 sin 30 4- c2 (sin 3t — 3 cos 3t).
ПримерЗ.
' dx
ST- — ’’
%-'+>>
Характеристическое уравнение
1=0 или k1 — 4k 4- 4 = 0
3 — я |
Ai,2 = 2. Следовательно, решение следует искать
х = («1 4- piO e2t, 1
У = («2 + PsO e2t. J
Подставляя (3.36) в (3.35), получим
2сц 4- Pi 4~ 2Pi< = «! 4“ P.O—<*2 — Р2Л
1 — k
1
имеет кратный корень
в виде
откуда
Oj = — Clj — Pl.
(3.35)
(3.36)
§6]	ПРИБЛИЖЕННЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ	199
а, и pt остаются произвольными. Обозначая зги произвольные постоян-
ные соответственно с, и е2, получим общее решение в виде
х = (С1 +	*2‘.
У = — (С1 + «2 + СгО е2/.
§ 6.	Приближенные методы интегрирования систем
дифференциальных уравнений и уравнений n-го порядка
Все изложенные в § 7 гл. 1 методы приближенного интегриро-
вания дифференциальных уравнений первого порядка без существен-
ных изменений переносятся на системы уравнений первого порядка,
а также на уравнения порядка выше первого, которые обычным
способом сводятся к системе уравнений первого порядка (см. стр. 85).
I.	Метод последовательных приближений. Как было
указано на стр. 51, метод последовательных приближений применим
к системам уравнений
dy,
= уР у2.............У„)	(/ = 1, 2, .... я) (3.37)
с начальными условиями у/(х0) = уго (^ — 1. 2.п), если функ-
ции ft непрерывны по всем аргументам и удовлетворяют условиям
Липшица по всем аргументам, начиная со второго.
Нулевое приближение уг0(х) (/=1, 2, .... п) может быть вы-
брано произвольно, лишь бы удовлетворялись начальные условия,
а дальнейшие приближения вычисляются по формуле
X
У/,*+1ДО=Ую+ f fi(x, ylk, у2к..... ynk)dx (7=1, 2.....я),
ж.
Так же как и для одного уравнения первого порядка, этот метод
редко применяется в практике приближенных вычислений ввиду
сравнительно медленной сходимости приближений и сложности и не-
однотипности вычислений.
2.	Метод Эйлера. Интегральная кривая системы дифферен-
циальных уравнений
dy,
Ур Уг.....У в)	а=1. 2.......я),
определяемая начальными условиями уг(х0) = уш (7=1, 2, .... я),
заменяется ломаной, касающейся в одной из граничных точек каждого
звена проходящей через ту же точку интегральной кривой (hi
рис. 3.2 изображена ломаная Эйлера и ее проекция только па
200	СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ	[ГЛ. 3
плоскость хуО- Отрезок х0 х ^.Ь, на котором надо вычислить ре-
шение, разбивается на части длиной h, и вычисление проводится
по формулам
(I — 1, 2, .... п).
Сходимость ломаных Эйлера к интегральной кривой при h —>0 до-
казывается так же, как
Рис. 3.2.
для одного уравнения первого порядка (см.
стр. 43). Для повышения точности можно
применить итерации (уравнивание).
3.	Разложение по формуле Тей-
лора. Предполагая, что правые части сис-
темы уравнений (3.37) дифференцируемы k
раз (для того чтобы обеспечить дифферен-
цируемость решений k 1 раз), заменяют
искомые решения несколькими первыми
членами их тейлоровских разложений:
у( (х) « у, (х0) + у; (х0) (х - х0) +
(1=1, 2, .... п).
Оценка погрешности может быть осуществлена путем оценки
остаточного члена в формуле Тейлора

где 0 < 0 < 1.
Этот метод дает хорошие результаты лишь в малой окрестности
точки х0.
4.	Метод Штермера. Отрезок х04х^^ разбивается на
части длиной h, и вычисление решения системы (3.37) проводится
по одной из формул:
У/, ft+i ~i>ik +	+ y^z, а-p	(3.38)
Уi. a + i — Уik	+ у k-i + '12'^i, k-2>	(3.39)
Уi, a+i = Уш т Яш +	^4i, a-i +	&2qi, n-2 + 4 а-з- (3.40)
где	(1=1, 2....n), ylk = yt(xk),
xk = x0 + kh, g^y^h.
&Я1, k-\=4ik	Яi, а-p A2<7z, k-2 — &4i, n-i k-2’
а-з ~ №qlt k-2	^24i, k-з-
§ в]
ЗАДАЧИ К ГЛАВЕ 3
201
Формулы (3.38), (3.39) и (3.40) могут быть получены совершенно
так же, как для одного уравнения первого порядка (см. стр. 63).
Порядок погрешности при применении этих формул остается
таким же, как и для одного уравнения.
Для начала вычисления по формуле Штермера необходимо знать
несколько первых значений yt (хк), которые могут быть найдены
путем разложения по формуле Тейлора или методом Эйлера с умень-
шенным шагом, причем, так же как и для одного уравнения, для
повышения точности можно применять итерации (см. стр. 61—62),
или методом Рунге.
5.	Метод Рунге. Вычисляются числа
«л = /«(*»•	У2к.......УПк)>
, {	. h . Лгаги . hm2,	. hmn<\ '
т12 ~ fl	+ у •	Умг Н---2~ ’	----~.......УлйЧ------“) ’
mi3 — fl	+ "2 > н	~ ’	У2И H ~.........Улб H-----2~) ’
>ni4 = fi(Xit-\-h, ylk+hmn, y2k + htn^............ynk + hmn3>'
зная которые, находим yit ft+1 по формуле
У i, й+i = У ik “h'g (ти %mi2 2m/3 + тм) (Z = 1, 2,..., га).
Порядок погрешности такой же, как и для одного уравнения.
Грубо ориентировочно шаг h в зависимости от требуемой точ-
ности результата выбирается с учетом порядка погрешностей в при-
меняемых формулах и уточняется путем пробных вычислений с ша-
гом п и -g- . Надежнее всего проводить вычисления с шагом га и
всех требуемых значений уДхр, и если при сравнении результатов
все они в пределах заданной точности совпадают, то шаг h считают
обеспечивающим заданную точность вычислений, в противном случае
Л h
снова уменьшают шаг и проводят вычисления с шагом у и
и т. д. При правильном выборе шага А разности &qik, Д2^(^, • • •
должны меняться плавно, а последние разности в формулах Штер-
мера должны влиять лишь на запасные знаки.
Задачи к главе 3
= ^Г = -х’ *(0) = 0, у(0) = 1.
2. -^=х2, -^ = х„ Л'<°) = 2- -М°) = 2.
х2 (0) = 2, х2 (0) = 2.
202
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
[ГЛ, 3
3.
5.
6.
7.
8.
dx . c
~dt+bx
dx
-dt^y'
dx
-dT~y'
dx , dy
dt
z dz
-,-r- = — xy.
x dx 7
dy
*У-..г,
dt
dy У2
di х
*У__х_6у^.
dz
~dt^x
9.
dt
dx
dx
г —У
dx
dx dy
dt dt
10.
11
dz
У — х
dy
dt ~ л л- / -r -> dt
Z-^ + y-O, t-^x
dx . . dy
~dt=^X' ~£-~X
1
sin t
dz
~dt
12	dx - y dy = x
’ dt x — у * dt x — у '
13.	x 4- у = cos t, у + x = sin t.
14.	x -f- 3x — у = 0, у — 8x -f- у = 0, x (0) «= 1, у (0) «= 4.
. _ d20 . , _ „	. „ „ л dO
15.	-J3T 4- sin 0 = 0 при t = 0, 0=5д,	= 0
dt2	36 dt
Определить 0 (1) с точностью до 0.001.
16.	х (t) == дх — у, у (<) = х + ау; а — постоянная.
17.	х 4-Зх +4у =0, у + 2х4-5у =0.
18.	х •= — 5х — 2у, у = х — 7у.
19.	х = у — z, у = х 4- у, z = х + z.
20.	х — у-j-z= 0, у — х — у =t, z — х — z = t.
21	dx	dy = dz
’x(y-z) y(z—x) z(x—yy
92	dx _ dy _ dz
x (у2 — г2) у (г-2 — x2) ~ z (x2 — y2) ’
23. AX, где X =P’ ||, a A = I 2	I.
Ц JCq |j	К О	j
ГЛАВА 4
ТЕОРИЯ УСТОЙЧИВОСТИ
§ 1. Основные понятия
Для возможности математического описания какого-нибудь реаль-
ного явления неизбежно приходится упрощать, идеализировать это
явление, выделяя и учитывая лишь наиболее существенные из влияю-
щих на него факторов и отбрасывая остальные, менее существен-
ные. При этом неизбежно встает вопрос о том, удачно ли выбраны
упрощающие предположения. Возможно, что неучтенные факторы
сильно влияют на изучаемое явление, значительно меняя его количе-
ственные или даже качественные характеристики. В конечном счете
этот вопрос решается практикой — соответствием полученных вы-
водов с опытными данными, но все же во многих случаях можно
указать условия, при которых некоторые упрощения заведомо не-
возможны.
Если некоторое явление описывается системой дифференциальных
уравнений
^ = Фг(/, у1( у2....у„) (/=1,2........к) (4.1)
с начальными условиями yz(£o) = y/o (/ = 1, 2... п), которые
обычно являются результатами измерений и, следовательно, неиз-
бежно получены с некоторой погрешностью, то естественно возни-
кает вопрос о влиянии малого изменения начальных значений на
искомое решение.
Если окажется, что сколь угодно малые изменения начальных
данных способны сильно изменить решение, то решение, опреде-
ляемое выбранными нами неточными начальными данными, обычно
не имеет никакого прикладного значения и даже приближенно не
может описывать, изучаемое явление.
Следовательно, возникает важный для приложений вопрос о на-
хождении условий, при которых достаточно малое изменение на-
чальных значений вызывает сколь угодно малое изменение решения.
204	ТЕОРИЯ УСТОЙЧИВОСТИ	[ГЛ. 4
Если t изменяется на конечном отрезке t0 t С Т, то ответ на
этот вопрос дает теорема о непрерывной зависимости решений от
начальных значений (см. стр. 54). Если же t может принимать
сколь угодно большие значения, то этим в.опросом занимается теория
устойчивости.
Решение cpz (t) (1 = 1,2...п) системы (4.1) называется устой-
чивым, или, точнее, устойчивым по Ляпунову, если для любого
е > 0 можно подобрать 6(e) > 0 такое, что для всякого решения у, (/)
(/=1, 2, .... п) той же системы, начальные значения которого
удовлетворяют неравенствам
|У;(*о)‘—Ф/О < 6<е) (*=1. 2.........га),
для всех справедливы неравенства
I У/(0 — Ф/(О | < Е (1=1,2......га),	(4.2)
т. е. близкие по начальным значениям решения остаются близкими
для всех t t0.
Замечание. Если система (4.1) удовлетворяет условиям тео-
ремы о непрерывной зависимости решений от начальных значений,
то в определении устойчивости вместо t^-t0 можно писать t~^-T
так как в силу этой теоремы на отрезке t0 t Т решения остаются
близкими при достаточно близких начальных значениях.
Если при сколь угодно малом 6 > 0 хотя бы для одного реше-
ния у; (О (I = 1, 2....я) неравенства (4.2) не выполняются, то
решение <pz (t) называется неустойчивым. Неустойчивые решения
лишь в редких случаях представляют интерес в практических за-
дачах.
Если решение <pz(Z) (/=1, 2......га) не только устойчиво, но,
кроме того, удовлетворяет условию
lira |yz(O — фу (01 = 0, 	(4.3)
/->00
если | yt (/0) — <pz (t0) | < 6Z > 0, то решение cpz (t) (I = 1, 2.га)
называется асимптотически устойчивым.
Заметим, что из одного условия (4.3) еще не следует устойчи-
вость решения q>z(/) (i — 1, 2..га).
Пример 1. Исследовать на устойчивость решение дифференциального
dy
уравнения = — а2у, а =/= 0, определяемое начальным условием у (Zo) = у0.
Решение
У = у0«~
асимптотически устойчиво, так как
|yoe~“i(''—у0е'а2(/_/°>| = e-a’(z“'o)|yo	<е
§ 1]	ОСНОВНЫЕ понятия	205
при Z>Z0, если I Уо ~ Уо I < ее~д!/1 и
lime-a2(Z-/o)| у0 —уо| = О.
t ->оо
Пример 2. Исследовать на устойчивость решение уравнения =
= а2у, а^О, определяемое условием у (t0) = у0.	,
Решение у — уоеа	неустойчиво, так как нельзя подобрать столь
малое 6 > 0, чтобы из неравенства |у0 — Уо I < б (е) следовало бы
—yo^'’2(,_/o)| < е
или
^('-«[Ро-Уо! <6
при всех t~^t0.	
Исследование на устойчивость некоторого решения
У/ = Уг(О а=1. 2.........п)
системы уравнений
=	У1> у2....уя) (/=1, 2.........п) (4.1)
может быть сведено к исследованию на устойчивость тривиального
решения — точки покоя, расположенной в начале координат.
Действительно, преобразуем систему уравнений (4.1) к новым
переменным, полагая
Х1 = У>1 — У/(О (/ = 1. 2......п).	(4.4)
Новыми неизвестными функциями х, являются отклонения yz— yz(Z)
прежних неизвестных функций от функций yz(Z), определяющих ис-
следуемое на устойчивость решение.
В силу (4.4) в новых переменных система (4.1) принимает вид
+	+	......*Я+М*))
(1=1, 2.......«).	(4.5)
Очевидно, что исследуемому на устойчивость решению yz = yz(Z)
(Z=l, 2........«)	системы (4.1), в силу зависимости xz=yz —yz (t),
соответствует тривиальное решение xz = 0 (I = 1, 2, ..., п) си-
стемы (4.5), причем исследование на устойчивость решения yz = yz(Z)
(i — 1, 2.....п) системы (4.1) может быть заменено исследованием
на устойчивость тривиального решения системы (4.5). Поэтому
в дальнейшем без ограничения общности можно считать, что на
устойчивость исследуется тривиальное решение' или, что одно и то же,-
расположенная в начале координат точка покоя системы уравнений
206
ТЕОРИЯ УСТОЙЧИВОСТИ
(ГЛ. 4
Сформулируем условия устойчивости в применении к точке
покоя x(s 0 (Z — 1, 2, .... л).
Точка покоя х( = 0 (/=1, 2.........п) системы (4.5) устойчива
в смысле Ляпунова, если для каждого е > 0 можно подобрать
б (е) > 0 такое, что из неравенства
|^(У|<6(е) (/=1,2....«)
следует
|х,(/)|<е (/=1,2........п) при/>Т>/0,
Или несколько иначе: точка покоя xz = 0 (/=1, 2..............п) устой-
чива в смысле Ляпунова, если для каждого е > 0 можно подобрать
б, (е) > 0 такое, что из неравенства
п
2 (*о) < (8)
1 = 1'
следует
У X? (/) < В2
< = 1
при t Т, т. е. траектория, начальная точка которой находится
в fij-окрестности начала координат при t^-T не выходит за пре-
делы е-окрестности начала координат.
§ 2.	Простейшие типы точек покоя
Ибследуем расположение траекторий в окрестности точки покоя
х — 0, у — 0 системы двух линейных однородных уравнений с по-
стоянными коэффициентами:
-^- = й]1х + а12у.
dy	(4-6>
-^-=Л21*+а22У>
где
ап а12	, п
¥= О.
а21	а22
Ищем решение в виде x = a1eA/, у = а2еА/ (см. стр. 193). Для
определения k получаем характеристическое уравнение
О,, k Hi л
. \ = О
®21	^22	*
ИЛИ
А2 — (йц а22) k -|- (<Гцй22 — fl2iai2)= О»
§ 2)	ПРОСТЕЙШИЕ ТИПЫ ТОЧЕК ПОКОЯ	207
СЦ и а2 с точностью до постоянного множителя определяются из
одного из уравнений:
(ап — k) а, +- a12a2 = 0,1
a21aj + (a22 -A)a2 = 0. |
Рассмотрим следующие случаи:
а) Корни характеристического уравнения kx и k2 действи-
тельны и различны.
Общее решение имеет вид
х = с1а1?,' + с2р1?!<, |
У — схо,2е ’ -f- с2р2е г • '
где at и pz — постоянные, определяемые из уравнений (4.7) соответ-
ственно при k — kx и при k = k2, а сх и с2 — произвольные по-
стоянные.
При этом возможны следующие случаи:
1)	Если kx < 0 и k2 < 0, то точка покоя х = 0, у = 0 асимпто-
тически устойчива, так как из-за наличия множителей ек'* и
в (4.8) все точки, находящиеся в начальный момент t = t0 в любой
d-окрестности начала координат, при достаточно большом t пере-
ходят в точки, лежащие в сколь угодно малой е-окрестности начала
координат, а при /->оо стремятся к началу координат. На рис. 4.1
изображено расположение траекторий около точки покоя рассма-
триваемого типа, называемой устойчивым узлом, причем стрелками
указано направление движения по траекториям при возрастании t.
2)	Пусть kx > 0, й2 > 0. Этот случай переходит в предыдущий
при замене / на — t. Следовательно, траектории имеют такой же
вид, как и в предыдущем случае, но только точка по траекториям
движется в противоположном направлении (рис. 4.2). Очевидно,
ТЕОРИЯ УСТОЙЧИВОСТИ
Рис. 4.3.
на-
208	ТЕОРИЯ УСТОЙЧИВОСТИ	(ГЛ. 4
что с возрастанием t точки, сколы угодно близкие и началу коор-
динат, удаляются из е-окрестности начала координат — точка покоя
неустойчива в смысле Ляпунова. Точка покоя рассматриваемого типа
называется неустойчивым узлом.
3)	Если >0, k2 < 0, то точка покоя тоже неустойчива, так
как движущаяся по траектории
х = схахек>‘, у = сха2ек,‘	(4.9)
точка при сколь угодно малых значениях ct с возрастанием t вы-
ходит из е-окрестности начала координат.
Заметим, что в рассматриваемом случае существуют движения,
приближающиеся к началу координат, а именно:
х — с$хе^1, y — c^>2eh^.
При различных значениях с2 получаем различные движения по одной
и той же прямой у==-|^-х. При возрастании t точки на этой пря-
Р1
мой движутся по направлению к началу координат (рис. 4.3). Заметим
также, что точки траек-
тории (4.9) движутся с
возрастанием , t по прямой
Оо
у = — х, удаляясь от
чала координат. Если же
Cj #= 0 и с2 =/= 0, то как при
t —>оо, так и при t-^-— ео
траектория покидает ок-
рестность точки покоя.
Точка покоя рассматриваемого типа называется седлом (рис. 4.3)
потому, что расположение траекторий в окрестности такой точки
напоминает расположение линий уровня в окрестности седлообразной
точки некоторой поверхности
z = f{x. у).
б) Корни характеристического уравнения комплексны-.
kx>2 = р + ql, q=£0.
Общее решение рассматриваемой системы можно представить
в виде (см. стр. 196)
x==ept (сх cos qt-{~c2 sin qt), |
у ж ept (с* cos qt + с* sin qt), )
где cx и c2 — произвольные постоянные, а с* и с? — некоторые ли-
нейные комбинации этих постоянных.
(4.10)
5 21
ПРОСТЕЙШИЕ ТИПЫ ТОЧЕК ПОКОЯ
209
При этом возможны следующие случаи:
1)	2 = р ± ql, р < 0. q Ф 0.
Множитель ept, р < 0, стремится к нулю с возрастанием t,
а второй — периодический множитель в уравнениях (4.10) остается
ограниченным.
Если бы р — 0. то траекториями были бы, в силу периодичности
вторых множителей в правой части уравнений (4.10), замкнутые
Рис. 4.5.
кривые, окружающие точку покоя х == 0, у—0 (рис. 4.4). Наличие
стремящегося к нулю с возрастанием t множителя epl, р < 0, пре-
вращает замкнутые кривые в спирали, асимптотически приближающиеся
при / —> эо к началу координат (рис. 4.5), причем при достаточно
большом t точки, находившиеся при t — tQ в
любой d-окрестности начала координат, по-
падают в заданную е-окрестность точки по-
коя х = 0, у = 0, а при Дальнейшем воз-
растании t  стремятся к точке покоя. Сле-
довательно, точка покоя асимптотически
устойчива — она называется устойчивым
фокусом. Фокус отличается от узла тем,
что касательная к траекториям не стре-
мится к определенному пределу при прибли-
жении точки касания к точке покоя.
2) *i,2 = Р ± Р > °, Я =# °-
Этот случай переходит в предыдущий
при замене t на — t. Следовательно, траек-
Рис. 4.6.
тории не отличаются от траекторий предыдущего случая, но движе-
ние по ним происходит при возрастании t в противоположном на-
правлении (рис. 4.6). Из-за наличия возрастающего множителя ept
точки, находившиеся в начальный момент сколь угодно близко к на-
чалу координат, с возрастанием t удаляются из е-окрестности начала
координат — точка покоя неустойчива. Она носит название неус-
тойчивого фокуса.
210	ТЕОРИЯ УСТОЙЧИВОСТИ	(ГЛ. 4
3) А1>2 = ± ql, q=h 0.
Как уже. отмечалось выше, в силу периодичности решений, траек-
ториями являются замкнутые кривые, содержащие внутри себя точку
покоя (рис. 4.4), называемую в этом случае центром. Центр является
устойчивой точкой покоя, так как для заданного е > 0 можно подо-
брать 6 > 0 такое, что замкнутые траектории, начальные точки
которых лежат в d-окрестности начала координат, не выходят за
(4.П)
пределы е-окрестности начала координат или, что то же самое, можно
подобрать столь малые сг и с2, что решения
х = Cj cos qt -|- с2 sin qt,
у — с’ cos qt -f- c* sin qt
будут удовлетворять неравенству
x1 (t) 4- у2 (О < е2.
Заметим, однако, что асимптотической устойчивости в рассматривае-
мом случае нет, так как x(t) и у(/) в (4.11) не стремятся к нулю
при t—> сю .
в) Корни кратны kx — k2.
1) kx = k2 < 0.
Общее решение имеет вид
х(0 = (<?!«! + с2р/) еЧ
у (t) = (с^ + с2₽2/) ек^,
причем не исключена возможность того, что р1 = р2 = 0, но тогда
О] и О; будут произвольными постоянными.
Из-за наличия быстро стремящегося к нулю множителя ек^ при
t -> со произведение (Cja, -f- c2(V) ек'* (1=1, 2) стремится к нулю
при t—>оо, причем при достаточно большом t все точки любой
6-окрестности начала координат попадают в заданную е-окрестность
§ 21
ПРОСТЕЙШИЕ типы точек покоя
211
начала координат и, следовательно, точка покоя асимптотически
устойчива. На рис. 4.7 изображена точка покоя рассматриваемого
вида, так же как и в случае а) 1), называемая устойчивым узлом.
Этот узел занимает промежуточное положение между узлом а) 1) и
фокусом б) 1), так как при сколь угодно малом изменении действи-
тельных коэффициентов ап, а12, а21, а22 он может превратиться как
в устойчивый фокус, так и в устойчивый узел типа а) 1), потому
что при сколь угодно малом изменении коэффициентов кратный
корень может перейти как в пару комплексных сопряженных корней,
так и в пару действительных различных корней. Если р1 = р2 = О,
то тоже получаем устойчивый узел (так называемый дикритический
узел), изображенный на рис. 4.8.
2) Если kr — k2 > 0, то замена t на — t приводит к предыду-
щему случаю. Следовательно, траектории не отличаются от траекто-
рий предыдущего случая, изображенных на рис. 4.7 и 4.8, но дви-
жение по ним происходит в противоположном направлении. В этом
случае точка покоя называется, так же как и в случае а) 2), не-
устойчивым узлом.
Тем самым исчерпаны все возможности, так как случай kt = 0
(или k2 = 0) исключен условием
аи
a2i
°12
о22
+ 0.
Замечание 1. Если
аи
а21
а12
а 22
= 0,
то характеристическое уравнение
а11	&	а12
а21	а22 —
= 0
имеет нулевой корень kx = 0. Предположим, что = 0, но k2 =# 0.
Тогда общее решение системы (4.6) имеет вид
х = CjOt, -|- с^еЫ,
У = С1а2 + с£2еЫ.
Исключая t, получим семейство параллельных прямыхр^у—с1а2)=
= р2 (х — ^а,). При с2 = 0 получаем однопараметрическое семейство
точек покоя, расположенных на прямой агу — а2х. Если k2 < 0, то
при /->оо на каждой траектории точки приближаются к лежащей
на этой траектории точке покоя х = с^, у — сха2 (рис. 4.9). Точка
покоя х = 0, у = 0 устойчива, но асимптотической устойчивости нет.
212
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
Если же /г2 > 0, то траектории расположены так же, но движе-
ние точек на траекториях происходит в противоположном направле-
нии— точка покоя №0, у = 0 неустойчива.
Если же fej = fe2 = 0, то возможны два случая:
1. Общее решение системы (4.6) имеет вид х = с1, у = с2— все
точки являются точками покоя, все решения устойчивы.
2. Общее решение имеет вид
X = Cj-i-C2t. у —с*-|-с*Л
где с* и с* — линейные комбинации произвольных постоянных Cj
и с2. Точка покоя х = 0, у = 0 не-
устойчива.
Замечание 2. Классификация
точек покоя тесно связана с классифи-
кацией .особых точек (см. стр. 57—59).
Действительно, в рассматриваемом
случае система
-^ == апх-+ а12у,
<7 у	,
-пГ=й21х-Ьа22у,
(4-6)
где
aU °12
а2) а22
путем исключения t могла бы быть сведена к уравнению
ЛУ ___ Д21-У + й2аУ	(Л 1
dx atlx4-aI2y ’	7
интегральные кривые которого совпадают с траекториями движения
системы (4.6). При этом точка покоя х = 0, у = 0 системы (4.6)
является особой точкой уравнения (4.12).
Заметим, что если оба корня характеристического уравнения имеют
отрицательную действительную часть [случаи а) 1); б) 1); в) 1)], то
точка покоя асимптотически устойчива. Если же хотя 15ы один корень
характеристического уравнения имеет положительную действительную
часть [случаи а) 2); а) 3); б) 2), в) 2)], то точка покоя неустойчива.
Аналогичные утверждения справедливы и для системы п линейных
однородных уравнений с постоянными коэффициентами
п
^Г = ^аих1	2......«>•	<4-13>
ПРОСТЕЙШИЕ ТИПЫ ТОЧЕК ПОКОЯ
213
§ 2]
Если действительные части всех корней характеристического
уравнения системы (4.13) отрицательны, то тривиальное решение
х( = 0 (Z = 1, 2, .... п) асимптотически устойчиво.
Действительно, частные решения, соответствующие некоторому
корню ks характеристического уравнения, имеют вид (стр. 193 и 196)
xt ==ctie*-s/ (I— 1, 2, ..., и),
если ks действительны,
xi = е”5' (0;cos qst 4-Nj si" Ш
если ks — ps-\-qsl, и, наконец, в случае кратных корней решения
такого же вида, но еще умноженные на некоторые многочлены
Очевидно, что все решения такого вида, если действительные части
корней отрицательны (ps < 0, или если ks действительно, то ks < 0),
стремятся к нулю при /—>оо не медленнее, чем ce~mi, где с — по-
стоянный множитель, а —т < 0 и больше наибольшей действитель-
ной части корней характеристического уравнения. Следовательно,
при достаточно большом t точки траекторий, начальные значения
которых находятся в любой 6-окрестности начала координат, попа-
дают в сколь угодно малую е-окрестность начала координат и при
>с*о неограниченно приближаются к началу координат — точка
покоя х( = 0 (Z = 1, 2, .... п) асимптотически устойчива.
Если же действительная часть хотя бы одного корня характери-
стического уравнения положительна, Re — pt > 0, то соответ-
ствующее этому корню решение вида Xj — cajekil, или в случае ком-
плексного kj его действительная (или мнимая) часть ce/’zZ(PyCos<7zZ-|-
уу sin qtt) (j = 1, 2.....п) при сколь угодно малых  по модулю
значениях с неограниченно возрастает по модулю при возрастании t, и,
следовательно, точки, расположенные в начальный момент на этих
траекториях в сколь угодно малой 6-окрестности начала координат,
покидают при возрастании t любую заданную е-окрестность начала
координат. Следовательно, если действительная часть хотя бы одного
корня характеристического уравнения положительна, то точка покоя
х, = 0 (J—1, 2........п) системы (4.13) неустойчива.
Пример 1. Какого типа точку покоя имеет система уравнений
dx
ИГ = Х~У
-g-=2x + 3y?
Характеристическое уравнение
I1”* "’bo
2	3 —
или
А2 — 4А -f- 5 = 0
214	ТЕОРИЯ УСТОЙЧИВОСТИ	[ГЛ. 4
имеет корни АЬ2 = 2 ± Z, следовательно, точка покоя х=0 у = 0 является
неустойчивым фокусом.
Пример 2. х = — а2х — 2Ьх — уравнение упругих колебаний с учетом
трения или сопротивления среды (при Ь > 0). Переходя к эквивалентной
системе уравнений, получим
х = у,
у — — а2х — 2Ьу.
Характеристическое уравнение имеет вид
о	, =0 или + %bk 4- а2=0.
— a2 — 2b — k\
откуда й|>2 = — b ± УЬ2 — а2.
Рассмотрим следующие случаи:
1)	6 = 0, т. е. сопротивления среды не учитываются. Все движения
периодические. Точка покоя в начале координат является центром.
2)	Ь2— а2 < 0, b > 0. Точка покоя является устойчивым фокусом. Коле-
бания затухают.
3)	Ь2 — а2>0, b > 0. Точка покоя является устойчивым узлом. Все
решения затухающие, неколеблющиеся. Этот случай наступает, если сопро-
тивление среды велико (Ь а).
4)	Ь < 0 (случай отрицательного трения), Ь2— л2 < 0. Точка покоя
является неустойчивым фокусом.
5)	b < 0, Ь2 — а2 > 0 (случай большого отрицательного трения). Точка
покоя является неустойчивым узлом.
Пример 3. Исследовать на устойчивость точку покоя системы урав-
нений
S- = 3x-2z,
at
dz -	.
-^=Sx-4y.
Характеристическое уравнение имеет вид
— k
3
5
2 —1
— k —2
— 4 — k
= 0
или
k2 — 9k + 8 = 0.
Определить корни кубического уравнения в общем случае довольно
трудно, однако в данном случае один корень kt = 1 легко подбирается, и
так как этот корень имеет положительную действительную часть, то можно
утверждать, что точка покоя х — 0, у — 0, z = 0 неустойчива.
§3
ВТОРОЙ МЕТОД А. М. ЛЯПУНОВА
215
§ 3. Второй метод А. М. Ляпунова
Выдающийся русский математик Александр Михайлович Ляпунов
в конце XIX века разработал весьма общий метод исследования на
устойчивость решений системы дифференциальных уравнений
= xv х2...........хп) (1=1, 2........«),	(4.14)
получивший название второго метода Ляпунова.
Теорема 4.1 (теорема Ляпунова об устойчивости). Если
существует дифференцируемая функция т»(х1( х2, .... хп), на-
зываемая функцией Ляпунова, удовлетворяющая в окрест-
ности начала координат следующим условиям’.
1) v(xi< х2....хП)^-0, причем v = 0 лишь при х£=0
(1—1, 2, .... п), т. е. функция v имеет строгий минимум
в начале координат’,
п
2)	=	....хлХ° пРи	то точка
i=i
покоя хг = 0 (I = 1, 2....п) устойчива.
Производная в условии 2) взята вдоль интегральной кривой,
т. е. она вычислена в предположении, что аргументы xt (Z = 1, 2, ...
.... п) функции v(xlt х2, .... х„) заменены решением Xj(t) (1 =
= 1, 2, п) системы дифференциальных уравнений (4.14).
л
„ „	dv dv dxt
Действительно, в этом предположении = 2j	или эа'
i=i
меняя правыми частями системы (4.14), окончательно получим .
п
dv dv .	.
dt ~ 44 dxi f ‘ У' Х1’ Х2...
z=i
Доказательство теоремы Ляпунова об устойчи-
вости. В окрестности начала координат, как и в окрестности
всякой точки строгого минимума (рис. 4.10), поверхности уровня
v(xv х2.....хя) = с функции v(xp х2, .... хп) являются зам-
кнутыми поверхностями, внутри которых находится точка мини-
мума — начало координат. Зададим е > 0. При достаточно малом
с > 0 поверхность уровня v = с целиком лежит в е-окрестности
начала координат *), но не проходит через начало координат, следо-
вательно, можно выбрать б > 0 такое, что 6-окрестность начала
*) Точнее, по крайней мере одна замкнутая компонента поверхности
уровня v = с лежит в е-окрестности начала координат.
216
ТЕОРИЯ УСТОЙЧИВОСТИ
ГГЛ. 4
координат целиком лежит внутри поверхности v = c, причем в этой
окрестности v < с. Если начальная точка с координатами xt (t0)
(Z=l, 2.......л) выбрана в б-окрестности начала координат
(рис. 4.11) и, следовательно,	х2(^0), .... хп (f0)) = q < с,
то при t > t0 точка траектории,' определяемой этими начальными
условиями, не может выйти за пределы е-окрестности начала коор-
динат и даже за пределы поверхности уровня v = c, так как, в силу
условия 2) теоремы, функция v вдоль траектории не возрастает и,
следовательно, при t t0
‘vCxj(t), x2(t).........................................................
Замечание. А. М. Ляпунов доказал теорему об устойчивости
в более общих предположениях, в частности, он считал, что функ-
ция v может зависеть и от t: v==v(t, хр х2, , хп). При этом
для справедливости теоремы об устойчивости первое условие надо
заменить следующим	'
v(t, xv х2, .... Xn)>W(Xp х2.х„)>0
в окрестности начала координат при t^-t0, где непрерывная функ-
ция w имеет строгий минимум в начале координат, v (t, 0, 0, ..., 0) =
= w(0, 0, ..., 0) = 0, а второе условие остается прежним
но только в этом случае
п
dv dv . VI dv . .	x
dt ~' dt + 1 dxt	x2......xn)-
Z = 1
§ 3]
ВТОРОЙ МЕТОД А М ЛЯПУНОВА
217
Схема доказательства остается прежней, надо только принять во вни-
мание, что, в силу условия 1), подвижная при изменяющемся t поверх-
ность уровня v(t, jfp х2.хя) —с остается при всех изменениях
t^-t0 внутри поверхности уровня w(x], х2.хя) = с (рис. 4.12).
Теорема 4.2 (теорема Ляпунова об асимптотической
устойчивости). Если существует дифференцируемая функция
ЛяЯунова v(xx, х2,  , х„), удо-
влетворяющая условиям'.
1) v(xx, х2...хП) имеет
строгий минимум в начале'
координат', г» (0, 0, .... 0) = 0;
2) производная, функции vx
вычисленная вдоль интеграль-
ных кривых системы (4.14)
dv
~dt Т
Vi dv ,
..................
Z=1
причем вне сколь угодно малой
окрестности начала коорди-
п
нат, т. е. при S х? > 0,	производная	—₽ < 0.
где 0— постоянная, то точка покоя х( = 0 (Z=l, 2........п)
системы (4.14) асимптотически устойчива.
Доказательство. Так как условия теоремы об устойчивости
выполнены, то для каждого е>0 можно подобрать д(е)>0 такое,
что траектория, начальная точка которой находится в 6-окрёстности
начала координат, при не выходит за пределы е-окрестности
начала координат. Следовательно, в частности, вдоль такой траекто-
рии при t > То выполнено условие 2), поэтому вдоль траектории
функция v монотонно убывает с возрастанием t, и вдоль траектории
существует предел функции v при t—>оо:
lim v(t, хх (i), x2(Z),
<->00
х„ (О) — а 0.
Надо доказать, что а = 0, так как если а = 0, то из условия 1)
следует, что lim xt (t) = Q (£=1,2...........n), т. e. точка покоя
/~>оо
хх = 0 (£ = 1, 2, .... n) асимптотически устойчива. Допустим, что
а > 0; тогда траектория при t > tQ находится в области v^-a,
следовательно, вне некоторой dj-окрестности начала координат, т. е.
218
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
там, где по условию 2)	—р<0 при t^TQ. Умножая неравенство
— Р на dt и .интегрируя вдоль траектории в пределах от То
до I, получим:
х2(О......xn(t)) — v(xi(T0), х2(7'0).....хДТ'оЛС
или
v (Xj (/), х2 (/), .... хп (О X
v(Х| (Т’р), х,(То)..х„(Т0))—р(t—TQ).
При достаточно большом t правая часть отрицательна, а следовательно,
и v(xA(t), x2(t), хл (/))<(), что противоречит условию 1).
Замечание. Теорема об
щается на случай функции V,
Рис. 4.13.
асимптотической устойчивости обоб-
зависящей от I, хр х2.....хл, если
первое условие, как ив предыду-
щей теореме, заменить следующим:
*! *2....хп)>
 >w(xp х2.....ХЛ)>О,
где функция w имеет строгий мини-
мум в начале координат, и, кроме
того, потребовать, чтобы функция
v(t, Хр х2...... х„) равномерно
относительно t стремилась к нулю
при У xj-*O.
Теорема 4.3 (теорема Че-
таева о неустойчивости). Если
существует дифференцируемая функция г»(хр х2, ..., хл), удо-
влетворяющая в некоторой замкнутой h-окрестности начала
координат условиям'. 1) в сколь угодно малой окрестности U
начала координат существует область (у > 0), в которой г» > 0,
причем v — 0 на лежащей в U части границы области (v > 0);
2) в области (у > 0) производная
Х1’ ...........> 0>
1 = 1
причем в области	а > 0, производная ^->Р>0, то
точка покоя х( = 0 (1= 1, 2....п) системы (4.14) неустойчива.
§ 3]	ВТОРОЙ МЕТОД а. М. ЛЯПУНОВА	219
Доказательств Начальную точку х, (f0), х2(/0).........x„(f0)
возьмем в сколь угодно малой окрестности начала координат в области
(v > 0). у(хг((д), х2(/0),	х„(/0)) = а> 0 (рис. 4.13). Так как
вдоль траектории О, то функция v вдоль траектории не убы-
вает, и следовательно, пока траектория не покинет рассматриваемую
Л-окрестность начала координат, где выполнены условия теоремы,
траектория должна находиться в области (и)>а). Допустим, что
траектория не покидает //-окрестности начала координат. Тогда в силу
условия 2) вдоль траектории при t t0 производная	> 0.
Умножая это неравенство на dt и интегрируя, получим:
к(Х1(/), х2 (/), .... хп (t)) V (X] (/0), х2(/0), .... хп (/0)) р (t-/д),
откуда следует, что при t—>са функция v вдоль траектории не-
ограниченно возрастает, что находится в противоречии с предполо-
жением о том, что траектория не выходит за пределы замкнутой
Л-окрестности начала координат, так как в этой Л-окрестности не-
прерывная функция v ограничена.
Замечание. Н. Г. Четаев доказал теорему о неустойчивости
в предположении, что v может зависеть также и от t, при этом усло-
вия теоремы несколько изменяются и, в частности, приходится требо-
вать ограниченности функции v в области (v 0) в рассматриваемой
//-окрестности начала координат.
Пример 1. Исследовать на устойчивость тривиальное решение системы:
dx	,	dy . 
ИГ = ~У~Х’	dF = x~y'
Функция v (х, у) — х2 + у2 удовлетворяет условиям теоремы А. М. Ляпу-
нова об асимптотической устойчивости:
1) v(x, у)>0, v(0, 0) = 0;
2)	— 2х (— у —- х3) + 2у (х — у3) = — 2 (х4 + у4) < 0. Вне окрестности
начала координат — ₽ <0. Следовательно, решение xsO, уиОасимп-
тотически устойчиво.
Пример 2. Исследовать на устойчивость тривиальное решение хаО,
у == 0 системы:
dx . dy
~dT = ~xy' W=yx -
Функция v (x, у) = x4 -|- У4 удовлетворяет условиям теоремы А. М. Ляпу-
нова об устойчивости:
1) v (х, у) = х4 + у4 > 0. v (0, 0) = 0;
2)	= — 4х1у4-|-4х’у4 = 0.
220
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
Следовательно, тривиальное решение хэО, у = 0 устойчиво.
Пример 3. Исследовать на устойчивость точку покой х as 0, у =i 0
системы уравнений
dx , . .
— =/ + л*.
dy
dt
х3 -|- у5.
Функция v = х4 — у4 удовлетворяет условиям теоремы Н. Г. Четаева:
1) v > 0, при | х | > | у |;
2)	= 4х3 (у3 + х5)— 4у3 (х3 +у8) = 4 (х8— у8) > 0 при | х | > | у |,
причем при о>а>0, ^>0 > 0. Следовательно, точка покоя х==0. ysO
неустойчива.
Пример 4. Исследовать на устойчивость тривиальное решение
(i = 1, 2, .... п) системы уравнений
dx^_ _ ди_(хг, х2, .... х„)	=	.....
dt	dxt	'	’	.
если дано, что функция u(xi, х2, •••< хп) имеет строгий максимум в начале
координат.
В качестве функции Ляпунова возьмем разность
aUb х2............хл)=и(0, 0.......0) —и(х,, х2, ..., х„),
которая, очевидно, обращается в нуль при х/=0(»=1, 2, .... п), имеет
строгий минимум в начале координат и, следовательно, удовлетворяет усло-
вию 1) теоремы Ляпунова об устойчивости. Производная вдоль интеграль-
ных кривых
dv _ VI ди dxi _ Vi I ди \2	_
'	dt ~ 21 dxt dt ~ .Zj \дх, /
i=i	i=i
Итак, условия теоремы Ляпунова об устойчивости выполнены, следовательно,
тривиальное решение устойчиво.
Пример 5. Исследовать на устойчивость тривиальное решение х(==0
(«=1, 2..... п) системы уравнений
п
^='^alj(t)xi, где ац (t) = — ajt (t) при i=pj и все
> = 1
п
Тривиальное решение устойчиво, так как функция v — xj удовлетво-
£= 1
ряет условиям теоремы Ляпунова об устойчивости:
1)v>0hv(0, 0............0) = 0;
п	п п	п
2) SF = 21jXz^ = 22 Ъ^х^^ ^X1<Q-
i=i	t=i j=i	t=i
§ 4]	ИССЛЕДОВАНИЕ НА УСТОЙЧИВОСТЬ	221
§ 4. Исследование на устойчивость по первому приближению
При исследовании на устойчивость точки покоя х1 = 0 (I — 1,2.п).
системы дифференциальных уравнений
=	х1( х2....х„) (Z=l, 2......п),	(4.14)
где /г — дифференцируемые в окрестности начала координат функ-
ции, часто применяется следующий метод: пользуясь дифференцируе-
мостью функций ft(t, Хр х2.....х„), представляют систему (4.14)
в окрестности начала координат х* = 0(/=1, 2, .... п) в виде
п
«= 2 “О ОТ <<	.....*»> (< = । • 2...»). (4.15)
где Rt имеют порядок выше первого относительно У, х?, и
вместо ^очки покоя х( = 0(<=1, 2, .... п) системы (4.15) исследуют
на устойчивость ту же точку покоя линейной системы
Л
^ = ^aij(t)xj (/=1, 2........п),	(4.16)
называемой системой уравнений первого приближения для
системы (4.15). Условия применимости этого метода, которым долгое
время пользовались без всякого обоснования, были детально исследо-
ваны А. М. Ляпуновым и в дальнейшем расширены трудами многих
других математиков, среди которых следует в первую очередь отме-
тить работы О. Перрона, И. Г. Малкина, К. П. Персидского,
Н. Г. Четаева.
Исследование на устойчивость системы уравнений первого при-
ближения, конечно, является задачей значительно более легкой, чем
исследование исходной, вообще говоря, нелинейной системы, однако
даже исследование линейной системы (4.16) при переменных коэффи-
циентах atj(t) является задачей весьма сложной. Если же все atj
постоянны, т. е. система стационарна в первом приближении, то
исследование на устойчивость линейной системы (4.16) не предста-
вляет принципиальных затруднений (см. стр. 212—213).
Теорема 4.4. Если система уравнений (4.15) стационарна
в первом приближении, все члены Rt в достаточно малой
окрестности начала координат при t 1() удовлетворяот
\ Г+а
неравенствам |/?/|<САН	Х?1	• г&е N и а — постоянные,
причем а>0 (т. е., если Rt не зависят от t, то их порядок
222	ТЕОРИЯ УСТОЙЧИВОСТИ	(ГЛ. 4
Г I
выше первого относительно [/ У x'j I и все корни характе-
ристического уравнения
аП	&	а12 • • •	а1л
a2i a^—k...	а2„	_Q
«Я1 ап2 ...ann — k
имеют отрицательные действительные части, то тривиаль-
ные решения x/ = 0(Z=l, 2, .... га) системы уравнений (4.15)
и системы уравнений (4.16) асимптотически устойчивы, сле-
довательно, в этом случае возможно исследование на устойчи-
вость по первому приближению.
Теорема 4.5. Если система уравнений (4.15) стационарна
в первом приближении, все функции Rl удовлетворяют усло-
виям предыдущей теоремы, и хотя бы один корень характери-
стического уравнения (4.17) имеет положительную действи-
тельную часть, то точки покоя x;=0(Z — 1, 2. .... га) системы
(4.15) и системы (4.16) неустойчивы, следовательно, и в этом
случае возможно исследование на устойчивость по первому
приближению.
Теоремы 4.4 и 4.5 в отношении ограничений, налагаемых на корни
характеристического уравнения, не охватывают лишь так называемый
критический случай: все действительные части корней характеристи-
ческого уравнения неположительны, причем действительная часть
хотя бы одного корня равна нулю.
В критическом случае на устойчивость тривиального решения
системы (4.15) начинают влиять нелинейные члены Z?z и исследование
на устойчивость по первому приближению, вообще говоря, невозможно.
Доказательство теорем 4.4 и 4.5 можно найти в книге И. Г. Мал-
кина [2].
Для того чтобы дать представление о методах доказательства таких тео-
рем, мы приведем доказательство теоремы 4.4 в предположении, что все
корни характеристического уравнения Az действительны и различны
kt < О (Z = 1, 2, ..л), Az =/= kj при i у.
В векторных обозначениях система (4.15) и система (4.16) примут соответ-
ственно вид
-g-^ДА + Я,	(4.15,)
-g- - АХ.
(4.16»)
ИССЛЕДОВАНИЕ НА УСТОЙЧИВОСТЬ
223
§ 4]
где
<гн Я|2 ... atn
л 2 к. а22 • •• а2п
&ni ^п2 • • • ^пп
R,
/?2
С помощью невырожденного линейного преобразования с постоянными коэф-
фициентами X = BY, где
В =
Ьп
&2]
612
622
«• •
• • • Ь2п
Ьп\ &П2   Ьпп
Уп
преобразуем систему (4.16,) к виду В —= ABY или ^- = В 1 ABY. Подбе-
рем матрицу В так, чтобы матрица В-1 АВ была диагональной:
В'1 АВ =
kx	0	0	...	О
О	k,	0	...	О
О	0	k3	...	О
0 0 0 ... kn
При этом система (4.16) преобразуется в
=	(f=l, 2, .... n),
а система (4.15) при том же преобразовании переходит в
= >ЧУ1 + #i (* Ун Уг...................Уп) (1=1, 2.....	п),	(4.18)
1
_______	— I V - \"	—
где I 1	УI |	, N — постоянная величина, а > 0,
w=i /
Для системы (4.18) функцией Ляпунова, удовлетворяющей условиям тео-
ремы об асимптотической устойчивости, является
2 У?.
/= 1
Действительно,
1) v(y>. У2...Уп)>®, v(0, 0, .... 0) = 0;
а	п	п	п
2} S=
<=i	i=i	i=i	»=1
224
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
при достаточно малых у/, так как все А/< 0. а удвоенная сумма 2
1 = 1
при достаточно малых yf может быть сделана по модулю меньше сум-
л
мы Mr
Т=1
Наконец, вне окрестности начала координат
Пример
системы
1. Исследовать на устойчивость точку покоя х = 0, у — Q
dx	। , , , , .
— = х — у + -* + У sin z,
dy
_ = x + y-y’.
(4.19)
Нелинейные члены удовлетворяют условиям теорем 4.4 и 4.5. Исследуем
на устойчивость точку покоя х — 0. у — 0 системы первого приближения
dx
dt
х — у.
dt
х + у.
(4.20)
Характеристическое уравнение | ।	_А|~ ® имеет корни А,.2«=1±/,
следовательно, в силу теоремы 4.5 точка покоя систем >4.19} и (4.20) не-
устойчива.
Пример 2. Исследовать на устойчивость точку покоя х = 0, у = 0
системы 1
dx л .
= 2х-(-8 sin у.
dy	(4-21)
-jj — 2 — е* — Зу — cos у
Разлагая slnj>, е* и cos у по формуле Тейлора, представляем систему,
в виде
g=2x + 8y + /?l, g = -x-3y + tf2,
где Л| и /?2 удовлетворяют условиям теорем 4.4 и 4.5.
v	12 — k 8	1-
Характеристическое уравнение ।	= 0 для системы пер-
вого приближения
^=2х + 8у. g= -x-3y	(4.22)
имеет корни с отрицательными действительными частями. Следовательно,
точка покоя х = 0, у = 0 систем (4.21) и (4.22) асимптотически устойчива.
§ 4]	ИССЛЕДОВАНИЕ НА УСТОЙЧИВОСТЬ	225
Пример системы	3. Исследовать на устойчивость точку покоя х = 0, у — 0 dx	.	3 dt	У Х’ .	(4.23) ^=3х-уз.
Характеристическое уравнение	|= 0 для системы первого
приближения имеет чисто мнимые корни — критический случай. Исследова-
ние по первому приближению невозможно. В данно.4 случае легко подби-
рается функция Ляпунова
v = Зх2 + 4уа.
1) v (х, у) > 0, v (0, 0) = 0;
2) — = 6х (— 4у — х3) 8у (Зх — у3) = — (6х4 8у4) < 0, причем . вне
некоторой окрестности начала координат < — ₽ < 0, следовательно, точка
покоя х = 0, у = 0 по теореме предыдущего параграфа асимптотически
устойчива.
Остановимся несколько подробнее на последнем примере. Система
уравнений первого приближения
% = <424>
имела в начале координат центр. Наличие нелинейных членов в си-
стеме (4.23) превратило этот центр в устойчивый фокус.
Аналогичная, но несколько более сложная геометрическая картина
наблюдается и в общем случае. Пусть система первого приближения
для системы
-^- = а11х) + ai2x2 +/?!<%!, х2),
— «21Х1 + а22Х2 + ^2 (•*!• Х2)
(4.25)
имеет точку покоя типа центра в начале координат. Предположим,
как и на стр. 221, что нелинейные члены Rl(xl, х2) и R2(xi> х2)
имеют порядок выше первого относительно ]/х^4-х2. Эти нелиней-
ные члены в достаточно малой окрестности начала координат малы
по сравнению с линейными членами, но все же они несколько иска-
жают поле направлений, определяемое линейной системой первого
приближения, поэтому выходящая из некоторой точки (х0, у0) траек-
тория после обхода начала координат немного смещается по сравне-
нию с проходящей через ту же точку траекторией линейной системы
226	ТЕОРИЯ УСТОЙЧИВОСТИ	[ГЛ. 4
и, вообще говоря, не попадает в точку (х0, у0)— траектория не за-
мыкается.
Если после такого обхода начала координат все траектории при-
ближаются к началу координат, то в начале координат возникает
устойчивый фокус; если же траектории удаляются от начала коор-
динат, возникает неустойчивый фокус.
В виде исключения возможен также случай, при котором все
траектории нелинейной системы, расположенные в окрестности начала
координат, остаются замкнутыми, однако наиболее типичным надо
считать случай, при котором лишь некоторые (может быть, и ни
Рис. 4.15.
одной) замкнутые' кривые остаются замкнутыми, а остальные превра-
щаются в спирали.
Такие замкнутые траектории, в окрестности которых все траек-
тории являются спиралями, называются предельными циклами.
Если близкие к предельному циклу траектории являются спира-
лями, приближающимися при /-»со к предельному циклу, то пре-
дельный цикл называется устойчивым (рис. 4.14); если близкие
к предельному циклу траектории являются спиралями, удаляющимися
от предельного цикла при t—»оо, то предельный цикл называется
неустойчивым', если же с одной стороны предельного никла при
t—>со спирали приближаются к предельному циклу, а с другой сто-
роны удаляются от него (рис. 4.15), то предельный цикл называется
полу устойчивым.
Итак, переход от системы первого приближения (4.16) к системе
(4.25) приводит, вообще говоря, к превращению центра в фокус,
окруженный р (случай р = 0 не исключается) предельными циклами.
На стр. 154, исследуя периодические решения автономной квази-
линейной системы
х-\- a'2x=\if (х, х, ц),	(4.26)
§ 5) ПРИЗНАКИ ОТРИЦАТЕЛЬНОСТИ ДЕЙСТВИТЕЛЬНЫХ ЧАСТЕЙ  227
мы уже встречались с аналогичным явлением. Действительно, заме-
няя (4.26) эквивалентной системой, получим
х = у,
у = _ a2x + pf(x, у, |л).
(4.27)
Соответствующая линейная система:
х = у, у = —а2х
имеет в начале координат точку покоя типа центра; добавление ма-
лых при малом ц нелинейных членов превращает центр, вообще
говоря, в фокус, окруженный несколькими предельными циклами,
радиусы которых и определялись из уравнения (2.128), стр. 156.
Различие между случаями (4.25) и (4.27) заключается лишь в том,
что члены и /?2 малы лишь в достаточно малой окрестности на-
чала координат, тогда как в случае (4.27) слагаемое ц/(х, у, ц)
может быть сделано малым при достаточно малом ц не только
в достаточно малой окрестности начала координат.
В примере 2 (стр. 156) при малом ц в окрестности окружности
радиуса 6 с центром в начале координат, являющейся траекторией
порождающего уравнения, возникает предельный цикл.
В приложениях устойчивым предельным циклам обычно соответ-
ствуют автоколебательные процессы, т. е. периодические процессы,
в которых малые возмущения практически не изменяют амплитуды
и частоты колебаний.
§ 5. Признаки отрицательности действительных частей
всех корней многочлена
В предыдущем параграфе вопрос об устойчивости тривиального
решения широкого класса систем дифференциальных уравнений был
сведен к исследованию знаков действительных частей корней харак-
теристического уравнения.
Если характеристическое уравнение имеет высокую степень, то
его решение представляет значительные трудности, поэтому большое
значение имеют методы, позволяющие, не решая уравнения, устано-
вить, будут ли все его корни иметь отрицательную вещественную
часть или нет.
Теорема 4.6 (теорема Гурвица*)). Необходимым и доста-
точным условием отрицательности действительных частей
всех корней многочлена
zn-i-a1zn-1+ ... +«„_!* +а„
*) Доказательство теоремы Гурвица можно найти в курсах высшей
алгебры, например в «Курсе высшей алгебры» А. Г. Куроша.
228
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
с действительными коэффициентами является положитель-
ность всех главных диагональных миноров матрицы Гурвица
	ах	1	0	0	...	0 а3	а2	<Zj	1	...	0 а5	а4	аз	а2	... а1	а6	й5	а4	 • • 0	0	0	0	...	ап	
По главной диагонали матрицы Гурвица стоят коэффициенты
рассматриваемого многочлена в порядке их нумерации, начиная с аг
до ап. Столбцы состоят поочередно из коэффициентов только с не-
четными или только с четными индексами, включая и коэффициент
а0 = 1, следовательно, элемент матрицы blk = a2i_k. Все недостающие
коэффициенты, т. е. коэффициенты с индексами, большими п или
меньшими 0, заменяются нулями.
Обозначим главные диагональные миноры матрицы Гурвица:
1 0 ... О
#2	• • • • «
а4 ая .....
00	0 ... ап
Заметим, что так как Дя = Ая_1ая, то последнее из условий Гур-
вица А] > 0, А2 > 0.....Ая > 0 может быть заменено требованием
°я>0*).
Применим теорему Гурвица к многочленам второй, третьей и чет-
вертой степени.
a)	z2 —|— a{z —|— а2.
Условия Гурвица сводятся к аг > 0, а2 > 0. Эти неравенства
в пространстве коэффициентов аг и а2 определяют первую четверть
(рис. 4.16). На рис. 4.16 изображена область асимптотической устой-
чивости тривиального решения некоторой системы дифференциальных
уравнений, удовлетворяющей условиям теоремы 4.1, если z2-}-alz-{-a2
является ее характеристическим многочленом.
*) Заметим, что из условий Гурвица следует, что все л/ > 0, однако
положительность всех коэффициентов недостаточна для того, чтобы действи-
тельные части всех корней были бы отрицательными.
§ 5] ПРИЗНАКИ ОТРИЦАТЕЛЬНОСТИ ДЕЙСТВИТЕЛЬНЫХ ЧАСТЕЙ 229
б)	z3 4- axz2 -\^a2z 4- йз-
Условия Гурвица сводятся к аг > 0, а}а2 — а3 > 0, а3 > 0.
Область, определяемая этим неравенством в пространстве коэффи-
циентов, изображена на рис. 4.17.
в)	Д'4 4-	+ «222 + a3Z + а4-
Условия Гурвица сводятся к
О, - Ц*з 4* б, (^4^2 — ^3^ ^4 — Д1Ц4 4* б, Й4 б.
Для рассмотренных многочленов условия Гурвица очень удобны
однако с возрастанием степени многочлена
и легко проверяемы,
условия Гурвица быстро
усложняются и часто
вместо них удобнее при-
Рис. 4.16.
менять другие признаки отрицательности действительных частей кор-
ней многочлена.
Пример. При каких значениях параметра а тривиальное решение
Л] =0, х2 = 0, х3 = 0 системы дифференциальных уравнений
^*1	dx2 __ q dx3 _	। д
~1Г~Хз' ~dF-~3x" ~аГ~а^ + 2х^ *а
асимптотически устойчиво?
Характеристическое уравнение имеет вид
— k
— 3
а
0	1
— k	0
= 0 или
кг 4- F — ak 4-6 = 0.
2	— 1 — к
По признаку Гурвица условиями асимптотической устойчивости будут at > 0,
Л| а2 — а3 > 0, а3 > 0. Эти условия в данном случае сводятся к — а — 6 > 0,
откуда а <—6.
230	ТЕОРИЯ УСТОЙЧИВОСТИ	(ГЛ. 4
§ 6. Случай малого коэффициента при производной
высшего порядка
Теорема о непрерывной зависимости решения от параметра
(см. стр. 54) утверждает, что решение дифференциального уравнения
x(t) = f(t, x(t), р) непрерывно зависит от параметра р, если в рас-
сматриваемой замкнутой области изменения t, х и р функция f не-
прерывна по совокупности аргументов и удовлетворяет условию
Липшица по х:
\f(t, х, — х, p)|<2V|x — х|,
где N не зависит от t, х и р.
В задачах физики и механики условия этой теоремы обычно вы-
полнены, однако один случай разрывной зависимости правой части
от параметра, изучению которого и посвящается этот параграф, встре-
чается в приложениях сравнительно часто.
Рассмотрим уравнение
=	х~)>	(4.28)
где р — малый параметр. Задача заключается в том, чтобы выяснить,
dx
можно ли при малых значениях |р| пренебречь членом Р~^~, т. е.
dx
приближенно заменить решение уравнения р = / (t, х) решением
так называемого вырожденного уравнения
f{t, х) = 0.	(4.29)
Мы не можем здесь воспользоваться теоремой о непрерывной зави-
симости решения от параметра, так как правая часть уравнения
dx 1
# = (4-28^
разрывна при р = 0.
Предположим пока для упрощения, что вырожденное уравнение
(4.29) имеет лишь одно решение х = (р(/), предположим также для
определенности, что р > 0. При стремлении параметра
dx „	dx 1 ,,,	.
производная решений уравнения	х) 8 каждой точке,
в которой f(t, х)=#0, будет неограниченно возрастать по абсолют-
ной величине, имея знак, совпадающий со знаком функции /(/, х).
Следовательно, касательные к интегральным кривым во всех точках,
р к нулю
в которых f(t, х) =# 0, стремятся при р->0 к направлению, парал-
лельному оси Ох, причем если f(t, х) > 0, то решение х(/, р)
уравнения (4.280 возрастает с возрастанием t, так как > 0, а если
$ в]
СЛУЧАИ МАЛОГО КОЭФФИЦИЕНТА
231
/(/. х) < 0, то решение x(t, ц) убывает с возрастанием t. так как
£<»•
Рассмотрим изображенный на рис. 4.18 случай а), при котором
знак функции /(/, х) с возрастанием х при фиксированном t ме-
няется при переходе через график решения х = ф(0 вырожденного
уравнения с -|- на — .
Стрелками показано поле направлений касательных к интеграль-
ным кривым при достаточно малом р. Поле направлений устремлено
к графику корня вырожденного уравнения. Поэтому каковы бы ни
Рис. 4.18.
Рис. 4.1ft
были начальные значения x(tQ) = xQ, интегральная кривая, опреде-
ляемая этими начальными значениями, будучи почти параллельной
оси Ох. устремляется к графику корня вырожденного уравнения и
при возрастании t уже не может покинуть окрестность этого гра-
фика. Следовательно, в этом случае при t tx > /0 при Достаточно
малом ц можно приближенно заменять решение х(/. ц) уравнения
(4.28) решением вырожденного уравнения. В рассмотренном случае
решение х=<р(0 вырожденного уравнения называется устойчивым.
Рассмотрим случай 61—знак функции f(t. х) при переходе че-
рез график решения х = <р(0 вырожденного уравнения с возраста-
нием х при фиксированном t изменяется с — на 4-. На рис. 4.19
изображено поле направлений, касательных к интегральным кривым
прн достаточно малом ц. В этом случае очевидно, что каковы бы
ни были начальные значения x(f0)=xB, удовлетворяющие лишь
условию /(<0. XqJ^O, интегральная кривая, определяемая этими зна-
чениями, при достаточно малом ц, имея почти параллельную оси Ох
касательную, удаляется от графика решения х—<р(/) вырожденного
уравнения. В этом случае решение х = *р(О уравнения (4.29) назы-
вается неустойчивым. В неустойчивом случае нельзя заменять реше-
ние х = х(0р) исходного уравнения решением вырожденного
Рис. 4.20.
232	ТЕОРИЯ УСТОЙЧИВОСТИ	[ГЛ. 4
,	. dx
уравнения, другими словами, нельзя пренебречь членом р-^- в уравне-
нии = /(/, х), как бы мало р ни было.
Возможен еще третий, так называемый полуустойчивый, случай в):
знак функции f(t, х) при переходе через график решения вырожден-
ного уравнения не изменяется. На рис. 4.20 изображено поле напра-
влений в случае полуустойчивого решения х —ф(/).
В полуустойчивом случае, как правило, тоже нельзя приближенно
заменять решение исходного уравнения x = x(t, р) решением выро-
жденного уравнения, так как,
во-первых, интегральные кри-
вые, определяемые начальными
значениями, лежащими с одной
стороны от графика решения
х = ф(/), удаляются от этого
графика, во-вторых, интеграль-
ные кривые, приближающиеся
к графику решения х = ф(/),
могут перейти через него
на неустойчивую сторону
(рис. 4.20) и после этого уда-
литься от графика решения
х = ф (/). Наконец, если даже
интегральная кривая x = x(t, р) остается в окрестности графика
решения с его устойчивой стороны, то неизбежные в практических
задачах возмущения могут перебросить график решения x = x(t, р)
на неустойчивую сторону графика решения вырожденного уравнения,
после чего интегральная кривая x = x(t, р) удалится от графика
решения х = ф (/).
Заметим, что если на графике решения вырожденного уравнения
-^- < 0, то заведомо решение х = ф(0 устойчиво; если же > 0,
то решение х = ф(/) неустойчиво, так как в первом случае в окрест-
ности кривой х = ф (/) функция f убывает с возрастанием х и, сле-
довательно, меняет знак с на —, а во втором случае возрастает
с возрастанием х и, значит, при переходе через график решения
х — ф(/) функция / меняет знак с — на .
Если вырожденное уравнение имеет несколько решений х = ф; (/),
то каждое из них должно быть исследовано на устойчивость, при-
чем в зависимости от выбора начальных значений интегральные кри-
вые исходного уравнения могут вести себя при р —>0 различно.
Например, в изображенном на рис. 4.21 случае трех решений х = фД/)
(f = 1, 2, 3) вырожденного уравнения, графики которых не пересе-
каются, решения х — х (t, р), р > 0, исходного уравнения, опреде-
§ 6]
СЛУЧАЙ МАЛОГО КОЭФФИЦИЕНТА
233
ляемые начальными треками, лежащими выше графика функции
х = ф2(/), стремятся при
вырожденного уравнения
ределяемые начальными
точками, лежащими ни-
же графика функции
х = <р2(/), стремятся при
/ > и р -> 0 кустойчи-
вому решению №ф3(7)
вырожденного уравнения
(рис. 4.21).
Пример 1.
стремится ли
X = X (t, р)
dx	л п
ц-^-=х—t, р>0, удов-
летворяющее начальным ус-
ловиям х (/0) = х0 к реше-
нию вырожденного уравне-
ния х — t = 0 при t > ta и
t>t0 и ц—>0 к устойчивому решению
решения x = x(t, ц), оп-
X = <?!((),
а
I
И*

Выясните»
решение
уравнения
ш
rdJJ—лЦНЖ Н


fftt Нин +
т h '
Решение х = х (t, ц) не
стремится к решению вы-
рожденного уравнения х = t,
неустойчиво, потому что —
Рис. 4.21.
, так
d(x-t)
как
решение вырожденного
— = 1 > 0 (рис. 4.22).
уравнения
Пример 2. Тот же вопрос для уравнения
ц = sin21 — Зе*.
Решение вырожденного уравнения jc = 2!n|slnf|—In3 устойчиво, так
<?(sin2/ — Зет)	г
как —5----—;----- =—drI<0. Следовательно, решение исходного уравнения
дх
234
ТЕОРИЯ УСТОЙЧИВОСТИ
(ГЛ. 4
х — х (t, ц) стремится к решению вырожденного уравнения для t > t0
при ц->0.
Пример 3. Тот же вопрос для решения уравнения
ц-^- = х(1!2 —х+1), р>0, x(Z0) = x0.
Из двух решений х = О и х = /2 4- 1 вырожденного уравнения
,	. л	„	дх (t2 — х +1) I
x(t2— x-f-l) = 0 первое неустойчиво, так как —=—ч----------!—£-	=
	„	с)х 1х=о
dx(t2___x-i- 1) I
= /2-|-1 > 0, а второе устойчиво, так как—-—5= —t2— 1 <0.
Ох 1х=<!+1
Если начальная точка (/0, х0) лежит в верхней полуплоскости х > 0, то
интегральная кривая исходного уравнения при ц->0 приближается к графику
решения х = t2 +1 вырожденного уравнения (рис. 4.23) и остается в его
окрестности.
Если же начальная точка лежит в нижней полуплоскости х < 0, то
lim х (t, р) = — во при t > tQ (рис. 4.23).
|1-»0
Вопрос о зависимости решения от малого коэффициента р при
старшей производной возникает и для уравнений zi-ro порядка
цх<л’ (f) = f (t, х, х, х....................х<я-п),
и для систем дифференциальных уравнений.
Уравнение n-го порядка может быть обычным способом (см. стр. 85)
сведено к системе уравнений первого порядка, и следовательно,
основная задача заключается в исследовании систем уравнений
первого порядка с одним или несколькими малыми коэффициентами
при производных. Эта задача подробно исследована А. Н. Тихо-
новым [4] и А. Б. Васильевой.
§ 7. Устойчивость при постоянно действующих возмущениях
Если исследуемая система уравнений
7Г=/|(*- *i>	......х„), Xt(f0)=xi0 (4.30)
(/ = 1, 2.....п)
подвергается малым кратковременным возмущениям, то систему (4.30)
на малом интервале изменения t, t0^t ^,t0, следует заменить
возмущенной системой
хр х2.........хя)4~/?/(/, хр х2, .... хя),
х/(/'0) = х,(Г0)	(/=1,2..........га),
где все хр х2, .... хл) малы по модулю, а затем при
возмущения прекращаются, и мы снова возвращаемся к системе (4.30),
§ 7] УСТОЙЧИВОСТЬ ПРИ ПОСТОЯННО ДЕЙСТВУЮЩИХ ВОЗМУЩЕНИЯХ 235
но уже с несколько измененными начальными значениями в точке
Го, Х1(^о) = xi <?о) + 6Д/ = 1, 2.я), где xt (t) (i = 1, 2.я) —
исследуемое решение системы (4.30), а все 6Z малы по модулю при
малых |/?;| в силу теоремы о непрерывной зависимости решения
от параметра (рис. 4.24).
Следовательно, действие кратковременных возмущений в конеч-
ном счете сводится к возмущениям начальных значений, а вопрос
об устойчивости по отношению
к таким кратковременным или,
как их часто называют, мгновен-
ным возмущениям сводится к рас-
смотренному выше вопросу об
устойчивости в смысле А. М. Ля-
пунова.
Если же возмущения дейст-
вуют постоянно, то система
(4.30) должна быть заменена сис-
темой (4.31) для всех	и
возникает совершенно новая за-
дача об устойчивости при пос-
тоянно действующих возмущениях, исследованная И. Г. Малкиным
и Г. Н. Дубошиным.
Так же как при исследовании на устойчивость в смысле А. М. Ля-
пунова, можно заменой переменных х; = у;— Ф/(0 (/= 1, 2........п)
преобразовать исследуемое решение у/==<р. (/) (Z= 1, 2, ..я)
dy.
системы = Ф(- (/, Ур у2. ..у„) (/= 1, 2, ..., я) в тривиальное
решение xz = 0 (Z = 1, 2, ..., п) преобразованной системы. Поэтому
в дальнейшем можно считать, что на устойчивость при постоянно
действующих возмущениях исследуется тривиальное решение х; = 0
(Z = 1, 2, ..., я) системы уравнений (4.30).
Тривиальное решение системы (4.30) называется устойчивым по
отношению к постоянно действующим возмущениям, если для каж-
дого е > 0 можно подобрать > 0 и б2 > 0 такие, что из нера-
Л	 п
венств У $ < 6? при и У < ^2 следует, что
z = l	i=l
п
S < е2
при

где xt(f) (Z=l, 2....я) решение системы (4.31), определяемое
начальными условиями x^t^) — xi0 (/ = 1, 2.я).
Теорема 4.7 (теорема Малкина). Если для системы урав-
нений (4.30) существует дифференцируемая функция Ляпунова
236
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
v(t, xv х2...хп), удовлетворяющая в окрестности начала
координат при следующим условиям:
1)т»(t, х2...x„)>w1(x], х2..хя)^>0, v(t, 0, 0,	0)=0,
где wl — непрерывная функция, обращающаяся в нуль лишь
в начале координат',
2) производные (s= 1, 2.....п) ограничены по модулю-,
OXS
п
S) производная =	+ fi ^.~-a>2(xv х2.......хя)<0,
t=i
где непрерывная функция w2(Xp х2, .... хя) может обращаться
в нуль лишь в начале координат, то тривиальное решение
системы (4.30) устойчиво по отношению к постоянно действую-
щим возмущениям.
Доказательство; Заметим, что в силу ограниченности произ-
водных ($ = 1, 2, .... п) функция v равномерно по отношению
п
к t при стремится к нулю при 2	-* 0- так как по тео-
п
реме о среднем значении v(t, xv х2, .... хп) =	xi где
/ dv \
— производные, вычисленные для некоторых промежуточных
между 0 и X; (Z= 1, 2.п) значений аргументов хр х2, .... х„.
Заметим также, что вне некоторой 6-окрестности начала координат
(п	\
т. е. при 2 x2i > Ф2 > 0 ) и ПРИ t>t0 в СИЛУ условий 2) и 3)
. / = ]	/
производная
п	п
£=-£+W-+S&«-<-‘<0
»=1	(=1
при достаточно малых по модулю /?( (Z = 1, 2, .... п).'
Зададим е > 0 и выберем какую-нибудь поверхность уровня
(или одну из ее компонент) те>1=/, Z > 0, целиком лежащую в е-ок-
рестности начала координат.
Подвижная при переменном t^-t0 поверхность уровня
v(t, xt, х2..хд) = /, в силу условия 1), лежит внутри поверх-
ности уровня.и в то же время, в силу равномерного по t
п.
стремления к нулю функции v при 2х/_>0- лежит вне
z=i
некоторой 62-окрестности начала координат, в которой г» < Z, и,
§ 7] УСТОЙЧИВОСТЬ ПРИ ПОСТОЯННО ДЕЙСТВУЮЩИХ ВОЗМУЩЕНИЯХ 237
следовательно, на поверхности уровня v(t, хР х2........х„) = 1 при
любом t /0 производная
п	п
/=1	f=l
п
если 2 Я/ <	> 0. где 6j достаточно мало. Траектория, опре-
< = ,
делаемая начальной точкой х((20) — х[0 (/ = 1, 2.......л), лежащей
в указанной выше б2-окрестности начала координат, не может
при t^t0 выйти за пределы е-окрестности начала координат, так
как, в силу выбора б2, f(/0, х10, х20.....хп0) </, и следовательно,
если бы при t t0 траектория выходила за пределы е-окрестности
начала координат или хотя бы за пределы поверхности уровня
а»1==/, то она должна была бы при некотором значении t = T
первый раз пересечь поверхность уровня v(t, xv х2.........хп) = 1,
причем в окрестности точки пересечения вдоль траектории функ-
ция v должна была бы возрастать, что противоречит условию
dv ,	. п
— л<0 вдоль траектории в точках поверхности уровня
V(t, Хр х2, .... х„)—1.
Сравнивая условия теоремы Малкина с условиями теоремы Ляпу-
нова об асимптотической устойчивости (см. замечание на стр. 218),
увидим, что они почти совпадают; дополнительным в теореме
Малкина является лишь требование ограниченности производных
.£^-($=1, 2.......га), так что асимптотическая устойчивость и устой-
чивость по отношению к постоянно действующим возмущениям
являются, хотя и не совпадающими, но весьма близкими свойствами.
Пример 1. Устойчиво ли по отношению к постоянно действующим
возмущениям тривиальное решение х = 0, у = 0 системы уравнений
где а и b — постоянные.
Функцией Ляпунова, удовлетворяющей всем условиям теоремы Малкина,
является v = Ъгх2 + в2у2.
Следовательно, точка покоя х = 0, у = 0 устойчива по отношению
к постоянно действующим возмущениям.
Пример 2. Устойчива ли точка покоя х.-эО (2 = 1, 2....га) системы
п
^ = '£iaiJxj + Ы{' *1- *2.....х»)	(2 = 1, 2, ..„я) (4.32)
1=1
238
ТЕОРИЯ УСТОЙЧИВОСТИ
[ГЛ. 4
по отношению к постоянно действующим возмущениям, если все ац— по-
стоянные, a Rj удовлетворяют условиям теоремы Ляпунова, стр. 221, т. е-
/ п \*/г+«
I < А'( 2j j > а > О, N — постоянная, и все корни характеристиче-
\/=1 )
скбго уравнения для системы первого приближения различны и отрицательны.
На стр. 223 после замены переменных, приводившей линейные части
уравнения (4.32) к каноническому виду, была указана функция Ляпунова
п
у|, удовлетворяющая всем условиям теоремы Малкина, следо-
вательно, точка покоя х, = О (z = l, 2.....п.) устойчива по отношению
к постоянно действующим возмущениям.
Тот же результат можно получить, предположив, что действительные
части всех корней характеристического уравнения, среди которых могут
быть и кратные, отрицательны, но только в этом случае подбор функции
Ляпунова значительно усложняется.
Задачи к главе 4
1.	Исследовать на устойчивость точку покоя х=0, у = 0 системы
d х
# = -2л-Зу + х5,
^ = х + у-у2.
2.	Исследовать на устойчивость точку покоя х = 0, у = О, z — О
системы
dx	dy t „ dz	-
_ = х_у_г, __=л + у_3г,	— = х-5у-.3г
х — 0, у = 0, z = 0 системы
dx
dt
4.
3.	При каких значениях а точка покоя
dy	dz	„	_
= ах — у, = ау — г, = az — х устойчива?
При каких значениях а система
dx . s
— =у + ах-х^,
dt	у
имеет
5.
устойчивую точку покоя х = 0, у — О?
К какому пределу стремится решение дифференциального уравнения
dx
=(х2 4-Г2 —4)(x2+l!2 —9), х(1)=1
прир->0, р > О, t > 1?
6.	К какому пределу стремится решение дифференциального уравнения
р = х — t -f- 5, х (2) = 5 при р -> О, р > 0, t > 2?
ЗАДАЧИ К ГЛАВЕ 4	239
7.	Исследовать на устойчивость точку покоя х = 0, у=0 системы
уравнений
dx , ,,
-тг = х 4- е* — cos у,
at
~~ = Зх — у — sin у.
at
8.	Устойчиво ли по отношению к постоянно действующим возмущениям
решение х — 0, у = 0 системы уравнений
9.	Устойчиво ли решение х = 0 уравнения
х 4- 5х 4* 2х 20 = 0?
10.	Устойчиво ли решение х = 0 уравнения
х 4- 5х 4- 6х 4~ х о?
11.	Какого типа точку покоя х=0, у = 0 имеет система уравнений
<Zx , о dy г
__ = х4-3у, -ЗГ = 5х-у?
12.	Определить периодическое решение уравнения х 4" 2х 4-2х = sin <
и исследовать его на устойчивость.
13.	х4-2x4-5х4-3х= cost Устойчиво ли периодическое решение
этого уравнения.
14.	Исследовать на устойчивость точку покоя xj=0, у=0 системы
х = у3 4- х\ у = х3 4- у5.
15.	Исследовать на устойчивость решения системы уравнений
х = Зу — 2х 4- е*.
у = 5х — 4у 4- 2.
16.	Исследовать на устойчивость тривиальное решение уравнения
х 4- 2х 4- Зх 4- 7 sh х = 0.
17.	Исследовать на устойчивость тривиальное решение уравнения
х 4- (а — 1) х 4- (4 — а2) х - 0,
где а — параметр.
18.	Устойчиво ли решение -tsO, у = 0 системы
х = Зу — х3, у = — 4х — Зу3
при постоянно действующих возмущениях.
240	ТЕОРИЯ УСТОЙЧИВОСТИ	[ГЛ. 4
19.	Устойчиво ли тривиальное решение системы
X (t) — AX(t),
где X (t) — вектор в трехмерном пространстве, а
А 2 0\
Д=|0 1 11.
\1 3 1/
20.	Исследовать на устойчивость решения уравнения
х + 4х -|- 5л = t.
21.	Исследовать на устойчивость решения уравнения
х -}- 9л = sin t.
22.	х'+ х = cos t. Найти периодическое, решение и исследовать его на
устойчивость.
23.	Найти область устойчивости
x-f-ax4-(l—а)л = 0.
24.	а2 л 4- 5ал = 0. Найти область устойчивости.
ГЛАВА 5
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
§ 1. Основные понятия
Как уже отмечалось во введении (стр. 10), диффе ренциальными
уравнениями в частных производных называются дифференциаль-
ные уравнения, в которых неизвестные функции являются функциями
более чем одной независимой переменной.
Очень многие физические явления описываются дифференциаль-
ными уравнениями в частных производных. Уравнение
/ ди \2 . { ди \2 । { ди \2	,	.
+ НгЧ + Н— = «(*, у, г)
\дх / 1 \ду ) 1 \дг /	4	л '
описывает распространение световых лучей в неоднородной среде
с показателем преломления п(х, у, г); уравнение
ди , d2u
dt дх2
описывает изменение температуры стержня; уравнение
' д2и , d2u
-----л*_______
at2 дх2
является уравнением колебания струны; уравнению Лапласа
д2и . д2и , д2и _______________________„
Рх2 + Ну2 + 'dz2 ~ U
удовлетворяет потенциал поля в областях, не содержащих зарядов,
и т. д.
В этой главе мы кратко рассмотрим лишь методы интегрирования
дифференциальных уравнений в частных производных первого по-
рядка, теория которых тесно связана с интегрированием некоторых
систем обыкновенных уравнений.
Уравнениям в частных производных более высокого порядка,
интегрирующимся совсем иными методами, посвящается отдельная
книга серии.
242
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА (ГЛ. б
Рассмотрим несколько простейших примеров.
Пример 1.
дг (х, у) ,
---= у + х.
дх J 1
Интегрируя по х, получаем
г(х, у) = ху + ^- + <р(у),
где <р (у) — произвольная функция у.
Пример 2.
д^г (х, у)	d J дг )
дх ду	дх ( ду J
..	dz , .	'	,
Интегрируя по х, получаем = <р (у), где ф (у) — произвольная функция у.
Интегрируя теперь по у, получим
Z= f <Р (У) dy + <р, (х),
где <р1 (х) — произвольная функция х. Или, обозначая
J Ф (У) dy = ф2 (у),
окончательно будем иметь
г(х, у) = ф! (х) + <р2(у).
где ф2 (у), в силу произвольности функции ф (у), тоже является произволь-
ной дифференцируемой функцией у.
Приведенные примеры наводят на мысль, что общее решение
дифференциального уравнения в частных производных первого
порядка зависит от одной произвольной функции, общее решение
уравнения второго порядка зависит от двух произвольных функций,
а общее решение уравнения /?-го порядка, вероятно, зависит от р
произвольных функций.
Эти предположения оказываются справедливыми, но нуждаются
в уточнении. Для их уточнения сформулируем теорему С. В. Кова-
левской о существовании и единственности решения уравнения
в частных производных.
Теорема 5.1 (теорема Ковалевской). Существует един-
ственное аналитическое в окрестности точки х10, х20, .... х„0
решение уравнения, разрешенного относительно одной из произ-
водных максимального порядка
дрг .(	дг д2г др~'г дх д2г
дх%	dxj -дх2	dxf 1 дх2 дхх дх2
д2г	др?\
дх2...... дхр J
§ 2]	ЛИНЕЙНЫЕ И КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ	243
удовлетворяющее условиям
при х = х10, г = ф0(х2, х3...Хп),	х3, .... х„), ...
др~1г	.	.
Х3.....Хп),
если функции ф0, фр ..., фр_1 являются аналитическими функ-
циями в окрестности начальной точки х20, х30, .... хп0,
a f является аналитической функцией в окрестности началь-
ных значений своих аргументов х10, х20, .... хпй, z0 =
= фо(х2о, Х3Г)...хпо)'
/ дг \	.	.	/ др г \	/ <ЭрФо \
— = ‘«’i (х20.....х«о)....... -ГТ = Т7
\^Jo	\дХп k \dxnJr.^.n
I Ю
Решение определяется заданием начальных функций ф0, фр . . .
. .., фр_р произвольно меняя которые в классе аналитических функ-
ций, мы получим совокупность аналитических решений исходного
уравнения (А), зависящую от р произвольных функций.
Доказательство этой теоремы, требующее применения теории
аналитических функций, мы опускаем.
§ 2. Линейные и квазилинейные уравнения в частных
производных первого порядка
Линейным неоднородным уравнением или квазилинейным
уравнением первого порядка в частных производных назы-
вается уравнение вида
Х^ху, х2, .... х„, z)-^--[- Л2(Хр х2, .... х„,	...
... -ф-А'^Хр х2, .... х„, z)-^ = Z(Xl, х2.....хп. z). (5.1)
Это уравнение линейно относительно производных, но может быть
нелинейным относительно неизвестной функции z.
Если правая часть тождественно равна нулю, а коэффициенты X t
не зависят от z, то уравнение (5.1) называется Линейным однородным.
Для большей наглядности геометрической интерпретации рассмо-
трим вначале квазилинейное уравнение с двумя независимыми пере-
менными:
Р(х, +	5,1 z')^r=R(-x’ У’ <5Л1)
Функции Р, Q и R будем считать непрерывными в рассматриваемой
области изменения переменных и не обращающимися в нуль одно-
временно.
244 УРАВНЕНИЯ в ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА (ГЛ. 8
Рис. 5.1.
Рассмотрим непрерывное векторное поле
F = Р(х, у, z) i 4~ Q(x, у, z)j + R (х, у, z) k.
где i, j, k — единичные векторы, направленные по осям координат.
Векторные линии этого поля (т. е. линии, касательная к которым
в каждой точке имеет направление, совпадающее с направлением
вектора F в той же точке) определяются из условия коллинеарности век-
тора t = i dx 4- j dy + k dz, направленного no
касательной к искомым линиям, и вектора поля F:
dx	dy	dz
Р (х, у. z) “ Q(x, у, z) “ R (х. у. г) '
Поверхности, составленные из векторных
линий, точнее, поверхности, целиком содержа-
щие векторные линии, имеющие хотя бы одну
общую точку с поверхностью, называются век-
торными поверхностями (рис. 5.1).
Очевидно, векторные поверхности можно
получить, рассматривая множество точек, ле-
жащих на произвольно выбранном, непрерывно
зависящем от параметра, однопараметрическом
семействе векторных линий. Векторная поверх-
ность характеризуется тем, что вектор- N, на-
нормали к поверхности, в любой точке поверхности
правленный по
ортогонален вектору поля F:
(N-F) = 0.
(5.2)
Если векторная поверхность определяется уравнением z = f (х, у),
то вектор
и условие (5.2) принимает вид
Р(х, у. 2)^-4-Q(x, у, z)^ = R(x. у, г).	(5.3)
Если векторная поверхность задается уравнением и(х, у, д) —О
„ ди ди .. ди ,	/к
и. следовательно, вектор N = -т- 1 4~ -з—j 4—т~ к, то уравнение (5.2)
(/Л
приобретает вид
Р(Х, у, z)-^-4-Q(x, у. z')-~-\-R(x, у, z)^ = o: (5.4)
Следовательно, для нахождения векторных поверхностей надо
проинтегрировать квазилинейное уравнение (5.3) или линейное одно-
§2]	ЛИНЕЙНЫЕ И КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ	245
родное уравнение (5.4) в зависимости от того, ищем ли мы уравне-
ние искомых векторных поверхностей в явном или неявном виде.
Так как векторные поверхности могут быть составлены из век-
торных линий, то интегрирование уравнения (5.3) (или (5.4)) сво-
дится к интегрированию системы обыкновенных дифференциальных
уравнений векторных линий.
Составляем систему дифференциальных уравнений векторных
линий
dx	dy _____ dz	„
Р(х. у. z) Q (х, у г) R (х, у, г)'	( • )
Пусть Ф1(х, у, z) = cx и ф2(х, у, z) — c2— два независимых
первых интеграла системы (5.5). Выделяем из двухпараметрического
семейства векторных линий фДх, у, z) = c1, ф2(х, У- z) = c2, назы-
ваемых характеристиками уравнения (5.3) (или (5.4)), произволь-
ным способом однопараметрическоё семейство, устанавливая какую-
нибудь непрерывную зависимость Ф(ср с2) = 0 между параметрами
с, и с2. Исключая из системы
Ф1(Х, у, Z) = CX, ф2(Х, у, Z) — C2, Ф(Ср с2) = 0
параметры сх и с2, получаем искомое уравнение векторных поверх-
ностей:
Ф(Ф1С*. у, z), ф2(х, у, z)) = 0,	. (5.6)
где Ф — произвольная функция. Тем самым найден интеграл квази-
линейного уравнения (5.3), зависящий от произвольной функции.
Если требуется найти не произвольную векторную поверхность
поля
F = P(X, у, 2r)i + Q(x, у, z)j ±R(x, у, г)к,
а поверхность, проходящую через заданную линию, определяемую
уравнениями Ф] (х, у, z) — 0 и Ф2 (х, у, z) — 0, то функция Ф в (5.6)
уже не будет .произвольной, а определится путем исключения пере-
менных х, у, г из системы уравнений
Ф^х, у, г) = 0,	Ф2(х, у, д) = 0,
ф,(х, у, z) = cx,	ф2(Х, У' z)~c2’
которые должны одновременно удовлетворяться в точках заданной
линии = 0 и Ф2 = О, через которую мы проводим характеристики,
определяемые уравнениями ф] (х, у, z) — cv ф2(х, у, z)—c2.
Заметим, что задача станет неопределенной, если заданная линия
Ф,(х, у, г)==0, Ф2(х, у, z) — 0 является характеристикой, так как
в этом случае эту линию можно включить в различные однопара-
метрические семейства характеристик и тем самым получить различ-
ные интегральные поверхности, проходящие через эту линию.
246 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
Итак, интеграл квазилинейного уравнения '
Р(х, у, z)~ +Q(x, у, z)~ = R(x, у, z),
зависящий от произвольной функции, может быть получен следую-
щим методом: интегрируем вспомогательную систему уравнений
dx	dy	dz
Р (X, у, z) Q (х, у, z) R (х, у, z)
и, найдя два независимых первых интеграла этой системы:
ipj(x, у, z) = c1, ф2(х, У- г)~ с2-
получаем искомый интеграл в виде Ф(ф](х, у, z), ф2(х, у, z)) = 0,
где Ф — произвольная функция.
Уравнение интегральной поверхности того же квазилинейного
уравнения, проходящей через заданную линию, определяемую урав-
нениями Ф^х, у, z) — 0 и Ф2(х, у, г) = 0, можно найти, взяв
упомянутую выше функцию Ф не произвольно, а определив функ-
цию Ф(Ср с2) путем исключения х, у, z из уравнений
Ф1(Х, у, z) = 0,	^Ф2(х, у, z) — 0,
фг(х. у, z) = cv	ф2(х, у, z) = c2,
в результате чего получим уравнение Ф(ср с2) = 0, и искомым ин-
тегралом будет Ф(ф](х, у, г), ф2(х, у, z)) = 0.
Пример 1. Определить зависящий от произвольной функции интеграл
уравнения
dz . dz _.
dx dy
Составляем вспомогательную систему уравнений
dx = dy — dz.
Ее первые интегралы имеют вид х — у = си г — х = сг. Интеграл исходного
уравнения Ф (х — у, г — х) = 0, где Ф — произвольная функция, или в раз-
решенном относительно г виде z = x-\-q(x—у), где <р — произвольная
дифференцируемая функция.
Пример 2. Найти интегральную поверхность уравнения
проходящую через кривую х = 0, г = у2.
Интегрируем систему уравнений
dx   dy   dz
— у	Т ~ "О-’
откуда z = C), x2-J-y2 = c2- Исключая х. у и г из уравнений
х2 + у2 = с2, z си х ~ 0, г = у2,
получаем с1 = с2, откуда г =± хг -|- у2.
§ 2]	ЛИНЕЙНЫЕ И КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ	247
Пример 3. Найти интегральную поверхность того же уравнения
проходящую через окружность
2=1, х2+у2 = 4.	(5.7)
Так как заданная линия (5.7) является векторной линией (характери-
стикой), то задача неопределенна. Действительно, интегральными поверх-
ностями рассматриваемого уравнения являются всевозможные поверхности
вращения z — Ф (х2 -f- у2), ось вращения которых совпадает с осью Oz.
Очевидно, существует бесконечное множество таких поверхностей вращения,
проходящих через окружность (5.7), например параболоиды вращения z ~
= х1 + у2—-3, 4г = х2 + у2, г — — х2—у2 -ф- 5, сфера х2 -f- у2 г2 = 5 и т. д.
Если уравнение кривой, через которую требуется провести интеграль-
ную поверхность уравнения (5.Т;) дано в параметрической форме:
Хй = Ха(5), у0=у0(з), 20=2-0(5),	(Б)
то обычно и решение удобно искать в параметрической форме:
X = X (t, З), у = у (t, s), z = z (t, s).
В систему (5.5), определяющую характеристики, вводим параметр t, полагая
dx _ dy _ dz _	
Р (х, у, 2) ~~ Q (х, у, z) R (х, у, г)	у
Для того чтобы характеристики проходили через заданную кривую, ищем
решение • системы (5.50, удовлетворяющее при / = 0 (или t — t0) начальным
условиям:
X = Х0 (в), у = у0 (з), Z = 20 (3).
При таких начальных условиях при фиксированном з получим характери-
стику, проходящую через фиксированную точку кривой (Б). При перемен-
ном з получим семейство характеристик
x = x(t,s), y — y(t,s), z = z(t,s),	(В)
проходящих через точки заданной кривой (Б) (при этом предполагается, что
заданная кривая (Б) не является характеристикой). Множество точек, лежа-
щих на этом семействе характеристик (В), и образует искомую интегральную
поверхность.
П р и м е р 4.
дг	дг _ .
дх	ду ~
Найти интегральную поверхность, проходящую через кривую х0 = з,
Уо = S2, 20 = s3.
Система уравнений, определяющая характеристики, имеет вид
dx = — dy= dz = dt.
Ее общее решение
X = t -|— Cj, у = — t —|- Cg, Z = t -|- Cg.
Пользуясь начальными условиями, определяем произвольные постоян-
ные и окончательно получаем
х=/-|-з, у = — t + s2, z = 1Л
248 УРАВНЕНИЯ в ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
Перейдем теперь к случаю п независимых переменных. Естест-
венно ожидать, что указанная выше для трехмерного случая схема
решения может быть распространена и на (п -|- 1)-мерный случай.
Начнем с исследования однородного линейного уравнения
х2, .... х„)	—|-Аг2(х1, х2.....xrt)-^--[-...
•••	Х2....x„)-g- = 0, (5.8)
где непрерывные функции Х^Хр х2, .... хп) не обращаются в нуль
одновременно ни в одной точке рассматриваемой области и имеют
в той же области ограниченные частные производные.
Составляем вспомогательную систему уравнений
______</xt_______________dx2_________	________dxn______ g.
Х|(хь x2....x„) ~~ X2 (Xp x2..хя) ~	•’Ш.х,.....x„)’	1	’
которая при указанных выше ограничениях удовлетворяет условиям
теоремы существования и единственности.
Находим п —. 1 независимый первый интеграл системы (5.9):
Ф1(Хр х2.......x„) = ct,
t2(*P х2.......хп) = с2.
Ч’л-Л*!- Х2....ХЯ) = С„_1.
В пространстве с координатами хр х2......хп эта система ин-
тегралов определяет (я—1)-параметрическое семейство линий, назы-
ваемых характеристиками уравнения (5.8). Докажем, что левая
часть любого первого интеграла ф(хр х2......хп) = с системы (5.91
является решением исходного линейного однородного уравнения
в частных производных (5.8).
Действительно, вдоль любой интегральной кривой системы (5.9)
функция ф = с. Следовательно, вдоль любой интегральной кривой
п
(5Л°)
t=i
Но вдоль интегральной кривой системы (5.9) дифференциалы </х(
пропорциональны функциям X следовательно, в силу однородности
относительно dxt левой части тождества
§ 2)	ЛИНЕЙНЫЕ И КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ	249
дифференциалы dxt могут быть заменены пропорциональными им
величинами Xt, при этом получим, что вдоль интегральных кривых
системы (5.9)
п
<611>
(=1
Интегральные кривые системы (5.9) проходят через каждую точку
рассматриваемой области изменения переменных хр х2..........хп и
левая часть тождества (5.11) не зависит от постоянных сР с2.сп_г
и, следовательно, не меняется при переходе от одной интегральной
кривой к другой, значит, тождество (5.11) ,справедливо не только
вдоль некоторой интегральной кривой, но и во всей рассматриваемой
области изменения переменных хр х2......хп, а это и означает,
что функция ф является решением исходного уравнения
п
( = 1
Очевидно, что Ф(фр ф2> •••• г1’я-1) = с> где Ф — произвольная
функция, является первым интегралом системы (5.9), так как вдоль
интегральной кривой системы (5.9) все функции фр ф2, ...,фл_1
обращаются в постоянные, следовательно, и Ф(фР ф2, .... фя-1)
обращается в постоянную вдоль интегральной кривой системы (5.9).
Значит, г=Ф(фР ф2......фя_1), гДе Ф — произвольная дифферен-
цируемая функция, является решением линейного однородного урав-
нения (5.8).
Докажем, что
2=Ф(ф,(Хр .... Х„). ф2(Хр .... Хп)......ФП_1(Х!.....Х„))
является общим решением уравнения (5.8).
Теорема 5.2. д=Ф(фр ф2........Фл-1)> где Ф — произвольная
функция, является общим решением уравнения
«
2 Xt (хР х2, .... хп)	(5.8)
1=}	‘
т. е. решением, содержащим все без исключения решения этого
уравнения.
Доказательство. Допустим, что г = ф(х1, х2> . ...хя)
является некоторым решением уравнения (5.8), и докажем, что суще-
ствует функция Ф такая, что ф = Ф(фр ф2.....Фл-1)>
250 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА (ГЛ. 5
Так как ф и фр ф2...........Фя—i являются решениями уравне-
ния (5.8), то
У х, -р^=о,
‘ дх,
/=1
Ух 4^ = 0,'
1 dXj
t = i
УХ;^2_ = О,-
JaJ ' дх,
i = ]
Рассматривая систему (5.12) как линейную однородную систему п
уравнений относительно X, (1= 1, 2.п) и замечая, что эта одно-
родная система в каждой точке хр х2....хп рассматриваемой
области имеет нетривиальное решёние, так как Xt (хр х2.хп),
по предположению, не обращаются в нуль одновременно, приходим
к выводу, что определитель этой системы
дф	дф	дф
		
дх,	дх2	дхп
	dip.	йф.
		
дх,	дх2	дхп
дф2	дф2	йф2
		
дх,	дх2	дхп
^Фл-1	<ЭФл-1	дфл-i
дх,	дх2	дхп
тождественно равен нулю в рассматриваемой области. Но тожде-
ственное обращение в нуль якобиана функций ф, фр ф2, .... фя_,
указывает на наличие функциональной зависимости между этими
функциями:
F(i|), фР ф2.....ф„_1) = 0.	(5.13)
В силу независимости первых интегралов фг(хр х2, .... xn) = ct
(Z=l, 2.......п — 1) системы (5.9) псу крайней мере один из мино-
ров (л — 1)-го порядка якобиана
/2(4. 4). Ф;..Фл-1)
D(xlt х2, х3, .... х„)
§ 2]	ЛИНЕЙНЫЕ И КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ	251
вида
D №. Фг.............................'Ы
D(xa,, ха2, .... ха^)
отличен от нуля. Следовательно, уравнение (5.13) можно представить
в виде
Ф = Ф(Фр Ф2......
Пример 5. Проинтегрировать уравнение
п
Система уравнений, определяющая характеристики, имеет вид
dxi _________________________ dXi _	_ dxn
Xj	~X^~'
Независимыми первыми интегралами этой системы будут:
Общее решение исходного уравнения
является произвольной однородной функцией нулевой степени однородности.
Теорема Эйлера об однородных функциях утверждает, что однородные
функции нулевой степени однородности удовлетворяют рассматриваемому
уравнению (5.14); теперь мы доказали, что только однородные функции нуле-
вой степени однородности обладают этим свойством.
Неоднородное линейное уравнение первого порядка
п
х2> .z)-^- — Z(xl, х2............х„, д), (5.15)
z=i
где все Xt и Z — непрерывно дифференцируемые функции, не обра-
щающиеся в нуль одновременно в рассматриваемой области изме-
нения переменных х2.........хп, z, интегрируется путем сведения
к линейному однородному уравнению.
Для этой цели, так же как и в случае трех переменных, доста-
точно искать решение z уравнения (5.15) в неявном виде:
и(хг, х2, .... хп, z) — d,	(5.16)
ди . „
где 77 * °-
Действительно, считая, что функция z — z (хр х2, .... х„) опре-
делена из уравнения (5.16), и дифференцируя тождество
«(-Vp Х2.....х„, z(xx, х2, .... х„)) = 0
252 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
по. xt, получим
du	du dz	g
dx,	dz dxi '
откуда
du
dz   dxj
dxj	du
~dz~
Подставляя найденное в (5.15), умножая на —и перенося
все члены в левую часть уравнения, получим однородное линейное
уравнение
II
х2.....хп- z)^ + Z(Xl, х2, ..	х„,	(5.17)
Z = 1
которому должна удовлетворять функция и, однако лишь в пред-
положении, что z является функцией хг, х2......хп, определяемой
уравнением и(хг, х2, .... хп, z') = Q.
Итак, надо найти функции а, обращающие линейное однородное
уравнение (5.17) в тождество в силу уравнения
и (хр х2......хл, z) — 0.
Найдем вначале функции и, обращающие уравнение (5.17) в тож-
дество при независимо меняющихся хР х2.........хп, z. Все такие
функции и являются решениями однородного уравнения (5.17) и
могут быть найдены уже известным нам способом: составляем си-
стему уравнений, определяющую характеристики
dx{ _	___  dx2
(Ху x2.....xn, z) X2 (xp x2, xn, z)
. .. =	-------r =	------—---------г; (5.18)
Хп{хх, x2, xn, z} Z(xi,x2.........xn, z)’ v J
находим n независимых первых интегралов этой системы:
Ф1(*1. х2.....х„, z) = c1,
ф2(Хр х2, .... хп, г) = с2,
фп(хр х2, .... хл, z) = c„;
тогда общее решение уравнения (5.17) имеет вид
а = Ф(фр ф2, .... фл),«
где Ф — произвольная функция.
§2]	ЛИНЕЙНЫЕ И КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ	253
Решение z уравнения (5.15), зависящее от произвольной функции,
определяется из уравнения
«(Хр х2......х„, г) = 0 или Ф(фР ф2, .... ф„) = 0.
Но, кроме найденных этим способом решений, могут быть ре-
шения z, которые определяются из уравнений и (хр х2....хп, г) —0,
где функция и не является решением уравнения (5.17), а обращает
это уравнение в тождество лишь в силу уравнения и(хх, х2, ...
..., хп, г) = 0. Такие решения называются специальными.
Специальных решений в некотором смысле не очень много, они
не могут образовывать даже однопараметрических семейств.
Действительно, если бы специальные решения образовали одно-
параметрическое семейство и определялись уравнением
и(хх, х2.....хп, z) = c,	(5.19)
где с—параметр, с0^.с^.с1, то уравнение (5.17) должно было бы
обращаться в тождество в силу уравнения (5.19) при любом с.
Но так-жак уравнение .(5.17) не содержит с, то оно не может обра-
щаться в тождество в силу уравнения (5.19), содержащего с, и,
следовательно, должно быть тождеством по отношению ко всем
переменным хх, х2, .... хп, z, меняющимся независимо.
Последнее утверждение допускает простую геометрическую
интерпретацию. Говоря, что уравнение (5.17) обращается в тождество
в силу уравнения и(хх, х2, •••> хп, z) — 0, мы утверждаем, что
уравнение (5.17) обращается в тождество в точках поверхности и = 0,
но может не обращаться в тождество в других точках пространства
хр х2......х„, z. Если же уравнение (5.17), не содержащее с,
обращается в тождество в силу уравнения и = с, где с — непре-
рывно меняющийся параметр, то это означает, что уравнение (5.17)
обращается в тождество на всех непересекающихся 'и заполняющих
некоторую часть D пространства хр х2.........х„, z поверхностях
и—с, cQ^c^.cx и, следовательно, уравнение (5.17) обращается
в тождество в области D при независимо изменяющихся хР х2, ...
.... xn,z.
В конкретных задачах обычно требуется найти решение уравне-
ния (5.15), удовлетворяющее еще каким-нибудь начальным условиям,
и так как специальных решений в указанном выше смысле сравни-
тельно мало, то они лишь в совершенно исключительных случаях
будут удовлетворять поставленным начальным условиям и поэтому
их лишь в редких случаях приходится принимать во внимание.
Пример 6. Проинтегрировать уравнение
Л
(»»>
i=l
где р — постоянная.
254 УРАВНЕНИЯ в ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
Система уравнений
dx} ________________ dx2 ___	__ dxn _ dz
x2 "' x„ ~ pz
имеет следующие независимые интегралы:
Следовательно, решение z исходного уравнения определяется из уравнения
.....
хп ' хп ’ хп!
откуда
Итак, решением  является произвольная однородная функция р-й степени
однородности.
Можно доказать, что уравнение (5.20) не имеет специальных интегралов
и, следовательно, теорема Эйлера об однородных -функциях обратима — урав-
нению (5.20) удовлетворяют только однородные функции степени одно-
родности р.
Понятие характеристики распространяется на системы квазилинейных
уравнений следующего специального вида:
п/	, ди ,	'	.ди п .	.
Р(х, у, и, v)	+ Q (х, у, u,v)-^- = /?, (х, у, и, v),
Р (х, у, и, v)	4- Q (х, у, и, v) ~ — Р2 (х, у, u, V).
Характеристиками такой системы называются векторные линии век-
торного поля в четырехмерном пространстве
F = Р (х, у, и, v) i -j- Q (х, у, и, v) j + Ri (х, у, и, v) к! + R2 (х, у, и, V) к2,
где i, j, kj, к2 — единичные векторы, направленные соответственно по осям
координат Ох, Оу, Ои и Ov.
Характеристики определяются системой уравнений
dx ____________ dy ___________ du
(Г)
dv
(Д)
Р (х, у, и, v) Q (х, у, и, v) (х, у, и, v) R2 (х, у, и, v)'
Система уравнений (Г) в векторной записи имеет вид
(F-N,)==0 и (F-N2) = 0,
(ди ди . _\ (dv dv
где Nj и N2—векторы с координатами	— 1, 0J и	0, — 1),
направленные по нормалям к искомым трехмерным цилиндрическим поверх-
ностям соответственно и = и (х, у) и v = v (х, у).
Следовательно, с геометрической точки зрения интегрирование си-
стемы (Г) сводится к нахождению двух трехмерных цилиндрических поверх-
ностей и = и (х, у), и v = v (х, у), нормали к которым в точках пересечения
этих поверхностей ортогональны к векторным линиям. ч
Очевидно, что это условие будет выполнено, если двухмерная поверх-
УРАВНЕНИЯ ПФАФФА
255
§ 3]
ность S, по которой, вообще говоря, пересекаются трехмерные цилиндриче-
ские поверхности и == и (х, у) и v = v (х, у), будет состоять из векторных
линий, так как эти векторные линии будут лежать одновременно на поверх-
ностях и = и (х, у) и v = v (х, у) и, следовательно, будут ортогональны
векторам N, и N2. Взяв какие-нибудь два независимых относительно и и v
первых интеграла Ф, (х, у, и, v) = 0 и Ф2 (х, у, и, v) = 0 системы (Д), дру-
гими словами, взяв две трехмерные векторные поверхности, мы, вообще
говоря, в их пересечении получим двухмерную поверхность S, состоящую
из векторных линий, так как если некоторая точка принадлежит одновре-
менно векторным поверхностям Ф] (х, у, и, v) = 0 и Ф2 (х, у, и, v) = 0, го
и векторная линия, проходящая через эту точку, лежит в каждой из этих
поверхностей.
Разрешая систему уравнений Ф[ (х, у, и, v) = 0 и Ф2 (х, у, a, v) = О
относительно и и о, получим уравнения двух трехмерных цилиндрических
поверхностей и = и (х, у) и v = v (х, у), пересекающихся по той же двух-
мерной поверхности S, состоящей из векторных линий. Следовательно, най-
денные функции м = и(х, у) и v — v(x, у) будут решениями исходной системы.
Решение системы (Г), зависящее от двух произвольных функций, можно
найти, применяя тот же метод, но взяв первые интегралы системы (Д)
в наиболее общем виде:
Ф| (ф, (х, у. u, v), ф2 (х, у, и, v), ф3 (х, у, и, v)) = 0, 1
। (М
Ф2 (Ф1 (X. у. и. V), ф2 (х, у, И, V), ф3 (х, у, «, V) ) = 0, /
где ф1.(х, у, и, v), ф2 (х, у, и, v) и ф3(х, у, и, v) — независимые первые инте-
гралы ’системы (Д), а Ф] и Ф2 — произвольные функции (см. стр. 249).
Уравнения (Е), если сложные ф)Н<ции Ф, и Ф2 независимы относи-
тельно и и v, определяют решения и (л, у) и и(х, у) системы (Г) как. неяв-
ные функции х и у, зависящие от выбора произвольных функций Ф, и Ф2.
§ 3. Уравнения Пфаффа
В § 2 мы рассматривали две задачи, естественно возникающие
при изучении непрерывного векторного поля
F = P(x, у, z)i+Q(x, у, z)j + R(x, у, z)к.
Это — задачи о нахождении векторных линий и векторных поверх-
ностей.
Почти так же часто возникает задача о нахождении семейства
поверхностей U (х, у, z) = c, ортогональных к векторным линиям.
Уравнение таких поверхностей имеет вид (F-t) = O, где t — век-
тор, лежащий в касательной плоскости к искомым поверхностям:
t == i dx + j dy + k dz,
иди в развернутом виде
Р(х, у, z)dx + Q(x, у, z)dy 4- R(x, у, z)dz = 0.	(5.21)
Уравнения вила (5.21) называются уравнениями Пфаффа.
256 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. S
Если поле F = Pi QJ 4- /?к потенциально:
а гт	в dU	MJ	r>	dU
F = gradt7,	т.	е.	Р = -^—,	Q = ~—,	Р = -т—,
ь	дх	ду ’	dz
то искомыми поверхностями являются	поверхности уровня	U(x, у, z)=c
потенциальной функции U. В этом случае нахождение искомых
поверхностей не представляет затруднений, так как
ix, у, *)
U — J Р dx 4- Q dy + R dz,
l*i, Уо. *o)
где криволинейный интеграл берется по любому пути между выбран-
ной фиксированной точкой (х0, у0, z0) и точкой с переменными
координатами (х, у, z), например, по ломаной, состоящей из прямо-
линейных отрезков, параллельных осям координат.
Если же поле F не потенциально, то в некоторых случаях можно
подобрать скалярный множитель р(х, у, z), после умножения на
который вектора F поле становится потенциальным.
Если такой множитель существует, то pF = grad U или
n dU ' dU D dU
pP = -Д--------------- , pQ = -T— , pP = —r-
dx	dy r dz
и, следовательно,		<Э(иО) _	_ d(yR)	Ф[*Р)	д(у.Р)
d(pP) __	d(pQ)				
ду	dx	’	dz ~	ду ’	дх	дг
или	дР	dQ _ 1	/л Ф	Р Ф	
	ду	дх	и	15 дх	Р ду)'	
	6Q	dR 1	/п Ф		
	дг	ду ~ I1	Г ду	Qdz)'	
	dR	дР _ 1	(р Ф	R “Н	
	дх	дг	[1	V дг	К дх)'	
Умножая первое из этих тождеств на Р, второе на Р, третье на Q
и складывая почленно все три тождества, получим необходимое
условие существования интегрирующего множителя р:
или (F-rotF) = 0, где вектор rot F —вихрь поля — определяется
равенством
„ _ (dR dQ\. . (дР dR\, . IdQ дР \.
ro1F==(^r-^r)i+(-dr--dr)j +hr~^-)k-
Если это условие, называемое условием полной интегрируемости
уравнения (5.21), не выполнено, то не существует семейства поверх-
УРАВНЕНИЯ ПФАФФА
257
§ 3]
ностей U (х, у, z) — c,
F(x, у, z).
Действительно, если
ствовало, то левая часть
ортогональных векторным линиям поля
бы такое семейство U (х,. у, z) = c суще-
уравнения (5.21) могла бы отличаться от
dU '	, OU . . dU .
-т— dx 4- -5—dy	dz
дх ду ' dz
лишь некоторым множителем jx(x, у, z), который и был бы инте-
грирующим множителем уравнения (5.21).
Итак, для существования семейства поверхностей £/(х, у, z) = c,
ортогональных векторным линиям векторного поля F, необходимо,
чтобы векторы F и rotF были бы ортогональны, т. е. (F-rotF)sO.
Замечание. Условие (F • rot F) = 0 называется также условием
интегрируемости уравнения Пфаффа Р dx 4- Q dy 4R dz — 0 одним
соотношением (J(x, у, z) — c.
Иногда требуется определить не поверхности, ортогональные
векторным линиям поля F, а линии, обладающие тем же свойством,
другими словами, надо проинтегрировать уравнение Пфаффа не одним,
а двумя соотношениями:
Ul(x, у, z) — 0 и U2(x, у, z) = 0.	(5.22)
Для нахождения таких линий можно одно из уравнений (5.22) задать
произвольно, например
(У,(х, у, д) = 0,	(5.23)
и, исключив из уравнения (5.21) с помощью уравнения (5.23) одно
из переменных, например z, получим дифференциальное уравне-
ние вида
М (х, y)rfx-|-/V(x, y)dy = 0,
интегрируя которое, найдем искомые линии на произвольно выбран-
ной поверхности их(х, у, д) = 0.
Покажем, что условие (F • rot F) = 0 является не только необхо-
димым, но и достаточным для существования семейства поверхно-
стей, ортогональных векторным линиям.
Заметим, что на искомых поверхностях U (х, у, д) = с должно
обращаться в тождество уравнение
Р dx + Q dy R dz = О
или, что то же самое, на этих поверхностях криволинейный инте-
грал
J Р dx 4 Qdy 4 R dz	(5.24)
L
258 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
должен быть равен нулю по любому пути (в том числе и по незам-
кнутым путям).
Рассмотрим всевозможные вихревые поверхности, т. е. векторные
поверхности поля rotF. Очевидно, что в силу теоремы Стокса
J* F dr — У J1 rot F • n da,
С	D
где dr — i dx-\- j dy -j- k dz, и интеграл (5.24) по любому замкнутому
пути на вихревой поверхности равен нулю (так как скалярное произ-
Рис. 5.2.
ведение единичного вектора норма-
ли к поверхности п и вектора rotF
равно нулю). Выберем теперь сре-
ди вихревых поверхностей те, на
которых все интегралы
J F dr — £ Pdx -\-Qdy Rdz
L	L
по незамкнутым путям также рав-
ны нулю. Для построения такой
поверхности, проходящей через за-
данную точку М (х0, у0, z0), про-
ведем через эту точку М какую-нибудь линию, ортогональную век-
торным линиям поля F. Такие линии определяются уравнением
Р dx Q dy + R dz = О,
(5.21)
к которому добавлено уравнение произвольной проходящей через
точку /И поверхности z = / (х, у) (чаще всего уравнение этой по-
верхности берут в виде д =/](%) или z = /2(y) или даже в виде
z — а, где а — постоянная). Подставляя z=f{x,y) в (5.21), по-
лучим обыкновенное уравнение вида
M(x, y)dx-\- N {х, y)dy = Q,
интегрируя которое и учитывая начальное условие у (х0) = у0, по-
лучи^ искомую кривую I, проходящую через точку Л1 (х0, Уо, До)
и ортогональную векторным линиям (рис. 5.2).
Если эта линия не является линией вихря, то, проводя через каж-
дую точку линии I линию вихря, получим искомую поверхность S,
ортогональную векторным линиям поля F.
Действительно, взяв любую незамкнутую кривую L на поверх-
ности S (рис. 5.2) и проведя через ее граничные точки вихревые
линии до пересечения с кривой I в точках р{ и р2, получим зам-
кнутый контур, состоящий из отрезка линии I между точками рх и р2,
кривой L и двух вихревых линий.
УРАВНЕНИЯ ПФАФФА
259
§ 3]
Криволинейный интеграл J Р dx 4~ Qdy + Rdz, взятый по этому
с
замкнутому контуру С, равен нулю, так как контур лежит на вих-
ревой поверхности, причем тот же интеграл, взятый на отрезке
дуги I, и по отрезкам вихревых линий равен нулю, так как дуга I
и вихревые линии ортогональны векторным линиям поля F (вихре-
вые линии ортогональны векторным линиям поля F в силу условия
(F • rot F) = 0). Следовательно, интеграл J Pdx 4- Qdy -\-Rdz по про-
L
извольно выбранному нами незамкнутому пути L равен нулю, т. е.
поверхность S является интегральной поверхностью уравнения (5.21),
проходящей через заданную точку М.
Этот метод доказательства достаточности условия (F • rot F) = 0
для существования семейства поверхностей, ортогональных векторным
линиям поля F, одновременно указывает путь, правда не кратчайший,
для нахождения этих поверхностей.
Прим ер I.
z dx + {х — у) dy -|- гу dz = 0.
Условие (F -rot F) = Q, где F = г! 4~ (л — у) j -|- yz к, не выполнено, сле-
довательно. рассматриваемое уравнение не интегрируется одним соотно-
шением.
Пример 2.
(6л + уг) dx + {хг — 2у) dy -|- {ху 4- 2г) dz = 0.
Так как rotF=sO, где F = (6л -|- у г) i 4- {xz—2у) j-Млу 4-2л) к. го
F = grad U, где
(X, У, г)
U = J* (6л 4- у г) dx 4- {хг — 2у) dy 4- (ху 4- 2г) dz.
(0, 0. 0)
В качестве пути интегрирования выбираем ломаную, звенья которой парал-
лельны осям координат. Интегрируя, получаем U => Зл2 — у2 4- г2 4- xyz,
и следовательно, искомым интегралом является
Зл2 — у2 4- г2 Ц- xyz = с.
Пример 3.
yz dx 4- 2xz dy ху dz = 0,
F •= yzi 4- 2лл) -j- лук, rot F = — л! 4- zk.
Условие интегрируемости (F rotF) = 0 выполнено. Находим на какой-
нибудь поверхности, например на плоскости г «= 1, кривые, ортогональные
векторным линиям:
г = 1 у dx 4- 2л dy = 0, ху2 а.
Проводим через кривые семейства г = 1, ху2 = а вихревые поверхности,
для чего интегрируем систему уравнений вихревых линий
dx dy dz
_ « _ =	' у ~ С1> кг ~ Са.
260 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
Исключая х. у и г из уравнений г — 1, луа = а, у = хг — с2, получаем
CjC2 = а. Следовательно, искомый интеграл исходного уравнения имеет
вид xy2z =* а.
Замечание. Другой, обычно применяемый метод интегрирова-
ния уравнения Пфаффа
Р(х, у, z)dx-\-Q(x, у, z)dy + R(x, у, z)dz = 0	(5.21)
заключается в том, что временно считают z (или другую переменную)
постоянной и интегрируют обыкновенное уравнение
Р(х, у, z)dx -}-Q (x, у, z)dy = 0,	(5.25)
в котором z играет роль параметра.
Получив интеграл уравнения (5.25)
U (х, у, z) = c(z),	(5.26)
в котором произвольная постоянная может быть функцией пара-
метра z, подбирают эту функцию c(z) так, чтобы удовлетворялось
уравнение (5.21). Дифференцируя (5.26), получим
dU . , dU . . Г dU ,, .1 .	„	,с п_.
-d^dx + -dTd^ + [-dr-c = °	(5-27)
Коэффициенты при дифференциалах переменных в уравнениях (5.21J
и (5.27) должны быть пропорциональными
dU	dU	dU
дх	ду	дг	С {г)
Р ~ Q ~ R
dU	„/ /	X
гл	dx dz
Из уравнения -р  =------------- можно определить с (z), так как
можно доказать, что при выполнении условия (F-rotF) = 0 это
уравнение содержит лишь z, с'(z) и U (х, у, z) = c(z).
§ 4.	Нелинейные уравнения первого порядка
Рассмотрим сначала случай, когда искомая функция зависит от
двух независимых переменных. Уравнения в частных производных
первого порядка с тремя переменными имеют вид
Г (х, у, z, р, <?) = 0,	(5.28)
где
dz	dz
& ~дх’	~ду ’
Дифференциальное уравнение (5.28) в каждой точке (х, у, z) той
области, в которой изменяются первые три аргумента, устанавливает
§ 41
нелинейные уравнения первого порядка
261
зависимость <р (/?, q) — 0 между числами р и q, определяющими на-
правление нормали N (р, q, —1) к искомым интегральным поверх-
ностям z = z(x, у) уравнения (5.28).
 Таким образом, направление нормали к искомым интегральным
поверхностям в некоторой точке (х, у, z) не определяется точно, а лишь
выделяется однопараметрическое семейство возможных направлений
нормалей — некоторый конус допустимых направлений нормалей
N(p, q, —1), где р и q
удовлетворяют уравнению	___
ф(р, ?) —° (рис. 5.3).	' х-s. МШ
Следовательно, задача
интегрирования уравнения
(5.28) сводится к нахождению
поверхностей z — z (х, у),	2а________\
нормали к которым были бы
в каждой точке направлены	.
по одному из допустимых	*~У
направлений конуса норма-
лей в этой точке.
Исходя из этой геомет- х
рической интерпретации,	рис 53
укажем метод нахождения
интеграла уравнения (5.28),
зависящего от произвольной функции, если известен его интеграл
Ф(х, у, z, а, Ь) — 0, который зависит от двух параметров а и Ь.
Интеграл Ф(х, у, z, а, Ь) — 0 уравнения (5.28), зависящий от
двух существенных произвольных постоянных а и Ь, называется пол-
ным интегралом.
Так как исходное дифференциальное уравнение (5.28) налагает
ограничения лишь на направление нормалей к искомым интегральным
поверхностям, то каждая поверхность, нормали к которой совпадают
с нормалями к интегральным поверхностям в тех же точках, будет
интегральной поверхностью. Следовательно, интегральными поверх-
ностями будут огибающие двухпараметрического или однопараметри-
ческого семейства интегральных поверхностей, так как нормаль
к огибающей совпадает с нормалью к одной из проходящих через
ту же точку интегральных поверхностей семейства.
Огибающая двухпараметрического семейства интегральных поверх-
ностей в предположении существования ограниченных частных произ-
г)Ф М> ЗФ	,
водных , -у-,	, не обращающихся в нуль одновременно,
дФ с/Ф
и существования производных и определяется уравнениями
Ф(х, у, г, а, Ь) — О,
-? = 0, ^ = 0.
да до
(5.29;
262 УРАВНЕНИЯ в ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 3
Выделяя из двухпараметрического семейства интегральных поверх-
ностей Ф(х, у, z, а, Ь) — 0 произвольным способом однопараметри-
ческое семейство, для чего считаем Ъ произвольной дифференцируемой
функцией параметра а, и находя огибающую однопараметрического
семейства Ф(х, у, z, а, Ь(а)) = 0, мы также получим интегральную
поверхность. Огибающая этого однопараметрического семейства
в предположении существования ограниченных производных функ-
ции Ф по всем аргументам и не обращения в нуль одновременно
дФ дФ дФ
производных	определяется уравнениями
Ф(х, у, z, а, Ь(а)) — 0 и -^-{Ф(х, у, z, а, Ь(а))}=0
или
Ф(х, у, z. а, Ь(а)) = 0 и +	=0.	(5.30)
Эти два уравнения определяют множество интегральных поверхностей,
зависящее от выбора произвольной функции b~b(a). Наличие
в уравнениях (5.30) произвольной функции, конечно, не дает права
утверждать, что уравнения (5.30) определяют множество всех без
исключения интегральных поверхностей исходного уравнения (5.28);
например, это множество, вообще говоря, не содержит интегральной
поверхности, определяемой уравнениями (5.29), но все же наличие
в уравнениях (5.30) произвольной функции обычно уже позволяет
выделить интегральную поверхность, удовлетворяющую заданным
начальным условиям Коши (см. стр. 242).
Итак, зная полный интеграл, уже можно построить интеграл, за-
висящий от произвольной функции.
Нахождение полного интеграла во многих случаях не вызывает
затруднений, например:
1)	Если уравнение (5.28) имеет вид F (р, <у) = 0 или p = q(q),
то, полагая q = a, где а — произвольная постоянная, получаем
р=ф(а), dz = pdx-\- qdy = q>(a)dx + ady,
откуда
z = q> (а) х ay b
— полный интеграл.
2)	Если уравнение (5.28) может быть приведено к виду ф! (х, р) =
= Ф2(у,	т0> полагая ф^х, р) = ф2(у, <?) = а, где а — произволь-
ная постоянная, и разрешая, если это возможно, относительно р
и q, получим р^хф^х, а), ^ = ф2(у, а),
dz = pdx -^qdy — ^^x, a)dx-j-ip2(y, a)dy,
z — f (x, a)dx-i~ j' ф2(у. a)dy-{-b
— полный интеграл.
§ 41	НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА	263
3)	Если уравнение (5.28) имеет вид F(z, р, q) = 0, то, полагая
z — z(u), где и — ах -j- у, получим
с, I	dz	dz\	n
F\z, a , -T-,	=0.
\	du	du /
Интегрируя это обыкновенное уравнение, получим z = Ф (а, а, Ь),
где b — произвольная постоянная, или
z = Ф(ах-|-у, а, Ь)
— полный интеграл.
4)	Если уравнение (5.28) имеет вид, напоминающий уравнение
Клеро:
г = рх + 9у + <р(/>, q),
то, как нетрудно проверить непосредственной подстановкой, полным
интегралом является
z = ах-\-Ьу + <р(а, Ь).
Пример 1. Найти полный интеграл уравнения р = З#3.
q — а, р — За3, dz = За3 dx-\- a dy,
z = За3х -|- ау Ц- 6.
Пример 2. Найти полный интеграл уравнения pq = 2лу.
р 2у	2у ,	. , 2у .
—= а,р=ах, а = —, dz = ах dx-\- — dy,
х q F ’ a	'a
ax2 . y2 .
Пример 3. Найти полный интеграл уравнения г3 = pq2.
, .	।	dz dz
z = z(u), где u=ax + y,	Я =
- I dz\3 dz	—т
z3 = al-j— I или -r- = a\Z, где a, = a J ,
\du / du
In | z | = a^u 4- In b, z= beaiU,
Пример 4. Найти полный интеграл уравнения
г= px + qy->t-p2 + q2.
Полным интегралом является
z = ах 4- by -|- а2 -|- Ь2.
В более сложных случаях применяется один из общих методов
нахождения полного интеграла уравнения
F{x, у, z, р, q) = Q.
264
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
(ГЛ. 5
Наиболее простая	идея	лежит	и основе	метода Лагранжа
и Шарпа. По этому	методу	к уравнению		
	Р (х.	у. z.	р. q)~ 0	(5.28)
подбирают' уравнение	U(x,	у, Z,	Р- q) — a	(5.31)
так, чтобы определяемые из системы уравнений (5.28) и (5.31) функ-
ции р = р(х, у, 2, а) и q=q(x, у, z, а) приводили бы к инте-
грирующемуся одним соотношением уравнению Пфаффа
dz = p(x, у, z, a)dx + q(x, у, z, a)dy (5.32)
Тогда интеграл уравнения Пфаффа Ф(х, у, z, а, (>) = 0, где b — про-
извольная постоянная, появляющаяся при интегрировании уравне-
ния (5.32), будет полным интегралом уравнения (5.28). Функция U
определяется из условия интегрируемости уравнения (5.32) одним
соотношением
(F • rot F) = 0, где F = p(x, у, z. a)i-)~q(x, у, z, a)j — k,
т. e. в развернутом виде из уравнения
<)?	др	dp дд _ дг Ч дг 'ду ' дх	:0.	(5.33)
„	дд др др дд Производные —вычисляются	дифференцированием	
тождеств		
F(x, у, z, р, q) = 0, 1 U(х, у, z, р, q) — а, J		(5.34)
в которых р и q рассматриваются как функции х, у и z, опреде-
ляемые системой (5.34).
Дифференцируя по х, получаем
<?Л , dF_ фр dP п
дх ''др дх ' дд дх ~~
dU	dU др dU eg
дх 'др Ох ' ад дх '
откуда
Р (F, U)
дд __ _ Р (р. х)
дх ~ ~ Р (F, U) '
D (р. д)
Аналогично, дифференцируя (5.34) по у и определяя
Р{Р, U)
др_______D(y. q)
ду	Р(Р Р) •
£>(Л д)
др
ду ’
получим
? 41
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
265
Дифференцируя ф.34) по z и разрешая относительно	будем
иметь
D(f, U}
_ D(z, q)
. dz ~ D(f, U) ’
D (p. q)
D (f, U)
dq __	D(p, z)
dz ~	D (f, U) '
D(p, q)
Подставляя вычисленные производные в условие интегрируемости
(5.33) и умножая на определитель
отличным от нуля, получим
idf dU df dU\ (df dU_____________________
dz dp dp dz / dz dq dq dz 1^
. Idf dU df dU\ . idf dU df dU
’ \ dy dq	dq dy / \ dx dp dp dx
4) ’ КОТОРЫЙ мы C4irraeM
df dU
или
df_dU_ . df dU
dp dx "г” dq dy
dU
dz
+	0. (5.35)
dz } op \dy 4 dz; dq '	’
Для определения функции U мы получили однородное линейное
уравнение (5.35), которое интегрируется методом, указанным в § 2
этой главы: составляется уравнение характеристик
dx dy ______ dz ___________ dp	dq •
df ~ df , df ~ ~ ~df~ df ~~~ df . df ’' ,0 }
dq ? dp dq dx + ? dz dy dz
df
ор
находится хотя бы один первый интеграл системы (5.36)
(7t(x, у, z, р, q) = a,
и если функции F и Ux независимы по отношению к р и q, т. е.
~q) Т° пеРвый интеграл Ux (х, у, z, р, q) и будет иско-
мым решением уравнения (5.35).
Следовательно, определяя р = р(х, у, г, а) и q = q(x, у, г, а)
из системы уравнений
F (x, y, z, p, q) = 0,
Ux (x, y. z, p, q) — a
266 УРАВНЕНИЯ в ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
и подставляя в
dz = p(x, у, z, a~)dx-{-q(x, у, z, a)dy,
получим интегрируемое одним соотношением уравнение Пфаффа,
решая которое, находим полный интеграл исходного уравнения
Ф(х, у, z, а, />) = 0.
Пример 5. Найти полный интеграл уравнения
угр1 — д = 0.	(5.37)
Система (5.36) имеет вид
dx _	dz	dp	dp
^.руг у 4p3yz — q ур3 гр1 УРгЯ '
Воспользовавшись исходным уравнением, упрощаем знаменатель
,	dz dp
отношения и получаем интегрируемую комбинацию
третьего
, откуда
(5.38)
Из уравнений (5.37) и (5.38) находим р=-^-, q — —% » откуда dz =
= у dx + dy. Умножая на 2г и интегрируя, находим полный интеграл
исходного уравнения г1 — Чах 4- а2у2 -f- b.
Зная полный интеграл Ф(х, у, z, а, Ь) = 0 уравнения
F(x, у, z, р, q) — 0.
можно, вообще говоря, решить основную начальную задачу (см.
стр. 242) или даже более общую задачу об определении интегральной
поверхности, проходящей через заданную кривую,
x = x(f), y = y(t), z — zif).	(5.39)
Определим функцию b-=b(a) так, чтобы огибающая однопара-
метрического семейства
Ф(х, у, z, а, b (а)) = 0,	(5.40)
определяемая уравнениями (5.40) и
^-+*P'(fl)==0,	(5.41)
проходила бы через заданную кривую (5.39),
§ 4]	НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА	267
В точках заданной кривой оба уравнения (5.40) и (5.41) по t
обращаются в тождества:
Ф(х(0, у (0, г(П, a, b{a)) — Q	(5.42)
и
дФ (х (t), у (Q, z (t), а, Ь (а)) . <ЭФ (х (t), у (t), z (t), a, b (а)) у . Q
да	'	дЬ	\	•
(5.43)
Однако определить из этих уравнений функцию b = b(a) было бы
довольно сложно. Значительно проще можно определить эту функ-
цию из системы уравнений (5.42) и
~д7 х + ~5у У + ~5Г г & °’	(5-44)
или в краткой записи
(N • t) = 0.
где t — вектор касательной к заданной кривой
x = x{t), y = y(t), z = z(t),	(5.39)
a N — вектор нормали к поверхности Ф = 0, а следовательно, и
к искомой огибающей в соответствующих точках. Условие (5.44)
геометрически очевидно, так как искомая поверхность должна про-
ходить через заданную кривую и, следовательно, касательная к этой
кривой должна лежать в касательной плоскости к искомой поверх-
ности.
Пример 6. Найти интегральную поверхность уравнения г = рх -f- qy 4-
+	, проходящую через кривую у — 0, г = х2.
Полный интеграл этого уравнения (см. случай 4 на стр. 263) имеет вид
z = ах-[ by-j-, Уравнение заданной кривой можно написать в пара-
метрической форме x = t, у = 0, z = t2.
Для определения функции b = b (а) составляем систему уравнений (5.42)
и (5.44), которые в данном случае имеют вид t2 = at -f- и It = а, откуда
а2
Ь =— а, г = а (л — у) — —. Огибающая этого семейства определяется
уравнениями
а2
ж = а(х~у)------j-
и
а „
х —у —у =0.
Исключая а, получим z = (х — у)2.
268
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА (ГЛ. 3
Если система (5.36) (стр. 265) легко интегрируется, то для реше-
ния поставленной обобщенной задачи Коши очень удобен излагаемый
ниже метод характеристик — метод Коши.
Интегральную поверхность z = z(x, у) уравнения
F (х, у, z, р, q) — 0,
проходящую через заданную кривую
х0 = х0(у), Уо = Уо(8), z0 = z0(s),
можно, как и для квазилинейного уравнения (см. стр. 247), пред-
ставлять себе состоящей из точек, лежащих на некотором однопара-
метрическом семействе кри-
Рис. 5.4.
вых
X = X {t, s), у — у (t, s),
z = z(t, s'),
где s — параметр семейства,
называемых характерис-
тиками.
Вначале мы найдем се-
мейство характеристик, за-
висящее от нескольких па-
раметров, а затем, проводя
характеристики через точки
кривой
XO = XQ(S), y0 = y0(s).
20=2()(s)
И удовлетворяя еще некоторым условиям, выделим однопараметри-
ческое семейство кривых, в которых параметром можно считать s:
х = X (t> s), у = у (t. s), z — z (t, s)
(рис. 5.4). Множество точек, лежащих на этих кривых, и образует
искомую интегральную поверхность. Такова в кратких чертах идея
метода Коши.
Пусть z — z(x, у) является интегральной поверхностью урав-
нения
f(x, у, z, р, q) = Q.	(5.45)
Тогда, дифференцируя тождество (5.45) по х и по у, получим
г.+Л+г„> + г,-Й-=о.
§ 41
да	др ,
или, так как = будем иметь
дх	ду J ,
^ + F,p + rp^ + F<^ = 0.
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
269
(5.46)
Уравнения характеристик для системы уравнений (5.46), квазилиней-
ной относительно р и q, причем z считается известной функцией
от х и у, имеют вид (см. стр. 254)
р ¥ р =dt- (5.47)
Fp Fq Рх+рРг Ру + дРг
Так как z связано с р и q уравнением
dz — pdx-\-q dy,	(5.48)
то вдоль характеристики
dz dx , dy „ .	_
~dt~-P ~dt + 4 ~dt ~ pFP чРя
или
dz ________________________________
pFp + qF. ~at'
(5.49)
что дает возможность дополнить систему (5.47) еще одним уравне-
нием (5.49).
Итак, в предположении, что z = z {x, у) является решением урав-
нения (5.45), приходим к системе
=	=-	*Р. ..	= dt. (5.50)
Fp Fq pFp-^qF, Fx+pFz F^ + qP,	>
Из уравнений (5.50) можно, не зная решения z == z (х, у) уравнения
(5.45), найти функции х = х (f), у = у (f), z — z (t), р = р (t), q — q (t),
•j. e. можно найти кривые
X = X (f), у = у (t), Z — Z (t).
называемые характеристиками, и в каждой точке характеристики
найти .числа р — p (t) и q = q(f), определяющие направление плоскости
Z — z — р(Х — х)-}-q(Y — у).	(5.51)
Характеристика вместе с отнесенной к каждой ее точке плоскостью
(5.51) называется характеристической полосой.
Покажем, что из характеристик может быть образована искомая
интегральная поверхность уравнения F (х, у, z, р, q) = Q.
Прежде всего заметим, что вдоль интегральной кривой системы
(5.50) функция F сохраняет постоянное значение
F(x, у, z, р, q) = c.
270 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 8
другими словами, функция F (х, у, z, р, q) является первым интегра-
лом системы (5.50).
Действительно, вдоль интегральной кривой системы (5.50)
— Fix v z о о) = F — 4- F — 4- F — 4- F — 4- F — —
dt r (x, y, z, p, q> rx dt 4- г y dt 4- гг dt r n dt df —
= F^+F^+F, (pFp+qF9) - Fp (F^pF,) - FQ (F^qF2) == 0,
следовательно, вдоль интегральной кривой системы (5.50)
F {х, у. z, р, q) = с. где с = F (х0, у0, z0, рп, q0).
Для того чтобы вдоль интегральных кривых системы (5.50) удовле-
творялось уравнение F (х, у, z, р, q) — 0, надо начальные значения
x0(s), y0(s), z0(s). p0(s). q0(s) выбирать так, чтобы они удовлетво-
ряли уравнению
F(x0. Уо- г0, р0, <7о) = О.
Интегрируя систему (5.50) при начальных значениях x0 = x0(s),
Уо = Уо^)- Zo = zo(s)> Po = Po(s)< 40 — q0(s), удовлетворяющих ура-
внению F (х0, у0, z0, р0, ^о) = О, получим x — x(t, s), y = y(t, s),
z = z(t, s), p — p(t, s), q — q(t, s).
При фиксированном s будем иметь одну из характеристик
х = х (/, s), у — у (/, s), z — z (t, s).
меняя s, получим некоторую поверхность. В каждой точке этой по-
верхности при p = p(t, s). q = q(t, s) уравнение F (x, у, z, p, q) — 0
удовлетворяется, но надо еще выяснить, будет ли при этом р — -^-
и
<7 =
дг
~ду'
или,
что то же самое, будет ли dz — pdx 4- Qdy, или

что эквивалентно двум условиям:
dx ,	ду	dz	п
дх ,	ду	dz
p-dr + ^-dr-ir^-
(5.52)
(5.53)
Второе из этих уравнений, очевидно, обращается в тождество, так
как при составлении системы (5.50) мы уже требовали, чтобы вдоль
характеристики dz — р dx 4* <7 dy. Впрочем, в этом легко убедиться и
непосредственно, если принять во внимание, что, в силу системы (5.50),
— = F ^- = F — — pF 4- пр
dt p’ dt 1' dt P[p^F4rq
§4)
НЕЛИНЕЙНЫЕ уравнения первого ПОРЯДКА
271
(в (5.50) вместо	-sr мы писали -~гт-, -4-, ~л~. так как
' 4	'	dt dt dt	at at at
считали s фиксированным).
Для того чтобы удовлетворялось уравнение (5.52), необходимо
наложить еще некоторые ограничения на выбор начальных значений
x0(s), Уо(5)’ ^о(5)> Ро(5)- Действительно, обозначим
дх , ду дг ,,
р-з-Д-Р-/-------(5.54)
r ds 1 7 ds ds	'
и докажем, что (7 = 0, если начальное значение (7]/=0 =0, откуда
будет следовать, что если начальные функции
*о(®)> УоО)- *o(s)> До СО- Яо («)
выбрать так, что
р0 ($) х' (s) 4- q0 (s) у0 (s) — z0 (s) = 0,
то Уs0 для всех t.
Дифференцируя (5.54) по t, получим
дЦ __ др dx	. д2х	. dq dy	.	d2y ___ d2z
dt	dt ds	'	& dt ds dt ds	’	dtds	dtds
и, принимая во внимание результат дифференцирования тождества
(5.53) по s:
dp	д2х . dq ду , d2y д2г _
ds dt ' Р dsdt ' ds dt ' dsdt dsdt ’
будем иметь
dU   dp дх . dq ду
dt	dt as ' dt ds
dp dx
ds dt
__ dq dy
ds dt
или, в силу уравнений (5.50),
т •= -	+ чг,> Д - 4г - у =
с ( дх .	ду дг\ д ,
- ч Р рГ +- ДГ - -р?) = - рг (F1 - F*U = - F’u>
так как Д = 0, и следовательно, полная частная производная
(Д) = 0. Из уравнения
(&Л5)
. 272 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА (ГЛ. В
-fa*
находим и = ийе 0	. Следовательно, если Uo — O, то £/ = 0,
что, впрочем, следует и из единственности решения U = 0 линей-
ного уравнения (5.55), удовлетворяющего условию t/|/=o = O.
Итак,' при интегрировании уравнения
F (X, у, z, р, <?) = ()	(5.45)
с начальными условиями x0 = x0(s), у0 = у0($), zQ = z0(s) по ме-
тоду Коши надо из уравнений
F(x0(s), y0(s). z0(s), p0(s), ?o(s)) = 0
и
pQ (s) xQ (s) 4- qQ (s) y0 (s) — z° (s) = Q
определить функции pQ — pQ(s) и q0 = q0(s) и затем интегрировать
систему уравнений
#=# = -р =	(5.50)
рр F<J pFp+qFq РхЛ-рРг Fy + qFz
с начальными условиями: при / = 0
x = x0(s), y = y0(s), z = z0(s), р = p0(s), q — q^s).
Три функции
x — x(t, s), y = y.(t, s), z = z(t, s')
из решения системы (5.50) и дают в параметрическом виде уравнение
искомой интегральной поверхности уравнения (5.45).
Все вышеизложенное легко обобщается на нелинейные -уравнения
в частных производных с произвольным числом независимых перемен-
ных
F(xv х2. ..., хп, z, pv р2......Ря) = 0.	(5-56)
где
л =	” = L!......">•
Требуется определить интегральную re-мерную поверхность
z = z (хр х2.....хя) уравнения (5.56), проходящую через заданную
(л — 1)-мерную поверхность:
x^ — x^Sy s2, ..., уя_1) (/=1,2........re), (5.57)
Zo = zo (Sp $2* •••• 5n-l)’
Временно предположим, что нам известны начальные значения
функций
Pio~Pio(sv s2' •••• sn-i) (/=1, 2, .... ri)’,	(5.58)
5 4]
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
273
тогда, интегрируя вспомогательную систему уравнений
с начальными условиями (5.57) и (5.58), получим
xz = x;(?, sP s2.........
Z = Z(t, Sp s2.........S„_j),
(i— 1, 2,
.... я).
(5.60)
Pi — P^t. sv s2..........5л-1)-
При фиксированных sp s2...уравнения (5.60) определяют
в пространстве с координатами xv х2, .... х„, z кривые, называе-
мые Характеристиками, каждой точке которых отнесены еще числа
pt = pt(t, $р s2, .... s„_j), определяющие направление некоторых
плоскостей
p,(Xz-xz).	(5.61)
Характеристики вместе с плоскостями (5.61) образуют так называе-
мые характеристические полосы.
При изменении параметров sp s2......s„_t получаем (п—• ^-па-
раметрическое семейство характеристик
X» = XZ(t Sj.....s„_i), z = z($, Sp .... sn_x),
проходящих через заданную (re—1)-мерную поверхность (5.57).
Покажем, что при определенном выборе функций
Pto=Pio(sv s2......s/>-i)	(/=1. 2, .... re)
точки, лежащие на характеристиках семейства (5.60), образуют иско-
мую re-мерную интегральную поверхность. Следовательно, надо будет
доказать, что при определенном выборе функций pl0(sv s2...
1) Р(хг((, Sp .... s„_j).....x„(t,	.....
s,....s„_j), px(t, s,...sn_x).....pn(t, sz......s„_i)) = 0,
2) pi—^~	(/=1, 2, .... re), или, что то же самое,
dz = 2 Pi dxi-
Нетрудно проверить, что функция F (хр х2, ..., хп, г, р{, р2, .... рп)
является первым интегралом системы уравнений (5.59). Действительно,
274 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. в
вдоль интегральных кривых системы (5.59)
dr,;
х2..............Хп’ Z> Pv Pl......Рп) =
i=l	i=1
f FxfPl + Fz 2 PiFPl - 2 FPl (FXl + PiFz) 0
Z=1	Z=1	Z=1
и, следовательно, вдоль интегральных кривых системы (5.59)
F(xv х2....................х„. z. pv р2........рп) = с.
где с — постоянная, равная F (х10, х20, .... хл0, z(j, pw, р20,.рп0).
Для того чтобы функции (5.60) удовлетворяли уравнению (5.56)
вдоль интегральных кривых системы (5.59), надо выбрать начальные
значения pl0, (sv s2, .... ая_1) так, чтобы
F(x10(Si,	s^-j), .... xM(s1, .... s„_}), z(sr..$„_!),
Pi(»i.....^-i)..... Pn<Pi....s„-i)) = 0.
n
Остается проверить, что dz — S Pidxt или
Z = 1
л—1	и /	л —1	\
dt + S dsi — X Pi I dt+X 4^ ds> •
dt	ds< J l l\ dt 1 ds> > I
j=i	i=i \	j=i J J
Это тождество эквивалентно следующим:
Л
dz \т dxi п
-dt~liPi-dt-°	<5-62)
« = 1
и
я
о=1’2......................................— » <5-бз>
/ = 1
Справедливость тождества (5.62) становится очевидной, если принять
во внимание, что, в силу системы (5.59),
п
< =	=	«=1.2........»)
1=1
dz
вместо -тт-
аг
dx.
и мы пишем частные производные, так как
ме (5.59) все st предполагались фиксированнымиj.
в систе-
§ 41
нелинейные уравнения первого порядка
275
Для доказательства тождеств (5.63), справедливых лишь при опре-
деленном выборе начальных значений pl0(sv $2, .... обозначим:
U=-^_ — V р,-^-	(J=l,2..........п—1)
7 dst 44 dsi	w	'
z=i
и, дифференцируя Uj no t, получим
__ <Fz у 32xz у dpt dxt
dt dtdSf 44 Pi didst dt dsi '	( • )
/=o	1 = 0
Принимая во внимание результат дифференцирования тожде-
ства (5.62) по Sj
d2z	у <Fxt	у dPl ах, _
dtdSj	^^‘dtdSj	44 dsi dt ’
i = 0	1=0
n
можно переписать уравнение (5.64) в виде
3(7;	уч dpt dxi	у dpi dxt
dt	44 dsi dt	^4 dt ds< '
1 = 0	1 = 0
Воспользовавшись системой (5.59), получим
3(7; уч dPi р V / о , d \ dxi
~dr=li~&sj Fpi	=
Z=1	i=l
__у (_^__dx^ | df dpi \ . dF $z	dF / dz
\ dxi dSj ' dpi dsj J'dz dSj	dz \ 3s;
= ^|-^7-
Полная частная производная -^-{F}=0, так как F^O, и сле-
довательно, функции Uj являются решениями линейных однородных
3(7;
уравнений —= —РгУр которые имеют единственное решение
(7; = 0, если U;|/=о = О. Следовательно, если начальные значения
PZo(sp s2> •••• sn-i) (^—1> 2, .... я) выбрать так, что U;|/=о = О
/	п	\	“
или
= 0 (j = 1,2
П — 1), TO
dz
dsj
n
(/=‘.2......................«-D
/•1 J
276 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 1
и, следовательно, на поверхности (5.60) dz = pt dxt, т. е. pt —
г=1
(/==1,2.......п).
Итак, для нахождения интегральной поверхности уравнения
f(xl, Х2......х„, z, pv р2......... ph) = 0, проходящей через
(л — 1)-мерную поверхность
xi0 = xi0(sv s2.....sn_j) (Z = l, 2, ..., л),
20 = г0($и s2.....S„_1),
надо определить начальные значения pl0(sv s2, .... 3„_j) из уравнений
F(X1O, X20....-*-n0> Pw Pw’ •••• Рло) “
= » »...............»-»•( <“5)
после чего, интегрируя систему (5.59) (стр. 273) с начальными усло-
виями:	•*40 —	S2' •••• 5л-1)> Д0=2Г0(51, s2	(/=1,	2	п). Рю — Pio(sv S2< • 	5л-1)
получим:	Sp s2	зл_!)	(/ = 1, 2, .... и),	(5.66) z = z(t. зр з2	зл_!),	(5.67) Л =	Sp 32	зп_,)	(/=1,2	л).
Уравнения (5.66) и (5.67) являются параметрическими уравнениями
искомой интегральной поверхности.
Замечание. Мы предполагали, что система уравнений (5.65)
разрешима относительно р10, а также, что система (5.59) удовлетво-
ряет условиям теоремы существования и единственности.
Пример 1. Найти интегральную поверхность уравнения г = pq, про-
ходящую через прямую х = 1, г = у.
Запишем уравнение прямой х = 1, г = у в параметрической форме
ха— 1, у,, = 5, z0 = з. Определяем р0 (s) и q0 (s) из уравнений (5.65): s = poqa,
1 — q0 = 0, откуда ра = s, q0 = 1. Интегрируем систему (5.59):
dx _ dy _ dz   dp _ dq _
q ~ p ~ 2pq ~ p ~ q ~
p = clet, q = c2e‘, х = с2е‘-^-с3, y = c1et-^~ci, z = c(cae2( -}-c6.
Принимая во внимание, что при / = 0
х = 1 у = s. г = s, . р = з, q = 1,
получим
р = se‘, q=- е‘, х—е1, у = se‘, z = se1*.
§ 4]
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
277
Следовательно, искомой интегральной поверхностью является
х = ef, у —set z = se21 или г = ху.
Пример 2. Проинтегрировать уравнение ~Ь ~ 2 ПРИ Усл0"
вии. что при х — 0, z = у, или в параметрической форме ха = 0, у0 — s, za = s.
Определяем рй (s) и q0 ($):
Ро + 9о = 2’ !—4'о = °-
откуда 0О= 1, р0= ± 1.
Интегрируем систему уравнений (5.59):
dx dy dz dp dq
p—c}, q — c2, x = 2c,Z + c3. у = 2c2tc4, z = 4i-f-c5;
пользуясь начальными условиями p2 = ± 1, q0 = 1, xa — 0, y0 = s, za = s,
получим p= ±1,0=1, x=±2t, y = 2t-\-s, z = 4t-\-s. Последние три
уравнения и являются параметрическими уравнениями искомой интегральной
поверхности. Исключая параметры t и $, получим z = у ± х.
В задачах механики часто приходится решать задачу Коши для
уравнения
-^-4-/У(Л х2.........х„,	р2, .... рл) = 0,	(5.68)
где р, =-г—, являющегося частным случаем уравнения (5.56) (стр. 272).
С/Х i
Метод Коши, который в- применении к уравнению (5.68) часто назы-
вается первым методом Якоби, приводит нас к системе уравнений
dt —;	dx} dH dpi dpi	dx2 	 dH ’  dpi		dxn 	dH ^Pn dpn 		_ dPi _ — dH ~ dX' dv	/
	dH dx2		dH 	V dH -4- ЪР1дР1 + i = 0	» dv dt
dx, dt	_dH dpi '	dPl _ 1 dt	dx, x	= 1, 2		n)	(5.69)
откуда
и,
или
п
dv  уч дН , dv
dt	L Pidpi di
i-=l
dv  уч dH
dt 2d dp,
t = i
- /7.
(5.70)
278 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА [ГЛ. 5
Система 2п уравнений (5.69) не содержит v и может быть проинте-
грирована независимо от уравнения (5.70), после чего из уравне-
ния (5.70) функция v находится квадратурой. В этом и заключается
некоторое своеобразие применения метода Коши к уравнению (5.68).
Кроме того, в рассматриваемом случае нет необходимости вводить
в систему (5.50) вспомогательный параметр, так как эту роль с успе-
хом может играть независимая переменная t.
Задачи к главе 5
г = у.
1 Jf_^£ = 0.
1 дх ду
2,^ + ^ = 2г.
дх 1 ду
о д?
3. X -5— = 2.
ду
, дг дг _
4.	-----у-— =0.
дх ' ду
_ дг	„
5. у^ = г при х = 2,
„ дг дг	, _	_
6-хд7-у5Г = гпри у = 1> г==3х
_ дг , дг	п ,
7. у г -ф -— = 0 при х = 0, г = у3.
J дх 1 ду г	'
8. Найти поверхности, ортогональные поверхностям семейства
9. Найти поверхности, ортогональные поверхностям семейства
10. ^Л^г-5.
3 дх 5 оу
11,|^ + |L + r2± = 0.
дх ' ду 1 дг
in	t п I о	л
12-л^+2^+32^=4“-
13.	=0.
дх2
.. дг	q дг ~	«
14.----з---- 2х з— = 0 при х ~ 1, г = у2.
дх ду	z
15.	Интегрируется ли уравнение
(у2 4- г2 — х2) dx хг dy -ф- ху dz — 0.
z ~ аху.
хуг — а.
одним соотношением?
16.	Проинтегрировать одним соотношением уравнение
(у ф- Зг2) dx 4- (х 4- у) dy 4- Ъхг dz =» 0.
17.	Найти полный интеграл уравнения
pg = х2у2..
ЗАДАЧИ К ГЛАВЕ 5	-	279
18.	Найти полный интеграл уравнения
z=^ px-Yqy-\- p*q\
19.	Найти полный интеграл уравнения
pq — 9г2.
20.	Найти полный интеграл уравнения
р — sin q.
21.	Найти поверхности, ортогональные векторным линиям векторного
поля
F = (2ху — Зуг) i + (л2 — 3xz) j — Злу к.
22.	Найти семейство поверхностей, ортогональных векторным линиям
векторного поля
F = (2х — у) i + (Зу — г) j + (х — 2у) к.
23.	Найти векторные линии, векторные поверхности и поверхности, орто-
гональные векторным линиям поля
F = xi + yj — zk.
24.	z = pq -|- 1 при у = 2, z = 2x 1.
25.	2z= pq — Зху при x = 5, z = 15y.
26.	4г = p2 -|- q2 при x = 0, z = y2.
ЧАСТЬ II
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
ВВЕДЕНИЕ
Наряду с задачами, в которых
ные и минимальные значения некот
А(х0, у0) и B(xt, у,) (см. рис. А)
на, если задано уравнение кривой
необходимо определить максималь-
орой функции z = f (х), в задачах
физики нередко возникает необхо-
димость найти максимальные или
минимальные значения величин
особого рода, называемых функ-
ционалами.
Функционалами называются
переменные величины, значения
которых определяются выбором
одной или нескольких функций.
Например, функционалом яв-
ляется длина I дуги плоской
(или пространственной) кривой,
соединяющей две заданные точки
. Величина I может быть вычисле-
у = у (х)'; тогда
/(У(х)) = J/l + (/)2d*.
Площадь S некоторой поверхности также является функционалом,
таь как она определяется выбором поверхности, т. е. выбором функ-
ции z (х, у), входящей в уравнение поверхности 2 = z(x, у). Как
известно,
5[г(х, у)] = f +
D
где D — проекция поверхности на плоскость Оху.
ВВЕДЕНИЕ
281
Моменты инерции, статические моменты, координаты центра
тяжести некоторой однородной кривой или поверхности также являют-
ся функционалами, так как их значения определяются выбором кривой
или поверхности, т. е. выбором функций, входящих в уравнение
Этой кривой или поверхности.
Во всех этих примерах мы имеем характерную для функционалов
зависимость: функции (или вектор-функции) соответствует число, в то
время как при задании функции z = f (х) числу соответствовало число.
Вариационное исчисление изучает методы, позволяющие нахо-
дить максимальные и минимальные значения функционалов. Задачи,
в которых требуется исследовать	'• ’
функционал на максимум или минимум,
называются вариационными зада-
чами
Многие законы механики и физики	\
сводятся к утверждению, что некото-	\
рый функционал в рассматриваемом	\
процессе должен достигать минимума	X.
или максимума. В такой формулировке
эти законы носят название вариацион-	В
ных принципов механики или физики.___________________________.г
К числу таких вариационных принци- О
пов или простейших следствий из них
принадлежат: принцип наименьшего	Рис
действия, закон сохранения энергии,
закон сохранения импульса, закон со-
хранения количества движения, закон сохранения момента количества
движения, различные вариационные принципы классической и реляти-
вистской теории поля, принцип Ферма в оптике, принцип Кастилиано
в теории упругости и т. д.
Вариационное исчисление начало развиваться с 1696 года и офор-.
милось в самостоятельную математическую дисциплину с собственными
методами исследования после фундаментальных работ действительного
члена Петербургской Академии наук Л. Эйлера (1707 — 1783 г.), кото-
рого с полным основанием можно считать создателем вариационного
исчисления.
Большое влияние на развитие вариационного исчисления оказали
следующие три задачи:
Задача о брахистохроне. В 1696 году Иоганн Бернулли
опубликовал письмо, в котором предлагал вниманию математиков за-
дачу о линии быстрейшего ската — брахистохроне. В этой задаче
требуется определить линию, соединяющую две заданные точки А и В,
не лежащие на одной вертикальной прямой, и обладающую тем свой-
ством, что материальная точка скатится по этой линии из точки А
в точку В в кратчайшее время (рис. Б).
282
ВВЕДЕНИЕ
Легко видеть, что линией быстрейшего ската не будет прямая,
соединяющая точки ДиВ, хотя она и является кратчайшим расстоянием
между точками А я В, так как при движении по прямой скорость
движения будет нарастать сравнительно медленно; если же мы возьмем
кривую, более круто спускающуюся около точки А вниз, то хотя
путь и удлинится, но значительная часть пути будет пройдена с
большей скоростью. Решение задачи о брахистохроне было дано
И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопита-
лем. Оказалось, что линией быстрейшего ската является циклоида
(см. стр. 304—305).
Задача о геодезических линиях. Требуется определить
линию наименьшей длины, соединяющую две заданные точки на не-
которой поверхности ср(х, у, z) = 0 (рис. В). Такие кратчайшие линии
г '	называются геодезическими.
11	\ Мы имеем типичную вариаци-
/	>А	онную задачу на так называе-
4-----Д \	мый связанный или услов-
"----—ный экстремум. Необходи-
мо найти минимум функцио-
нала
. J_____________^У
/О	х< __________
/	J /1+/2+г'2^х,
/	Ха
причем функции у (х) и z (х)
Рис. В.	должны быть подчинены ус-
ловию <р (х, у, z) = 0. Эта за-
дача была решена в 1698 году Я. Бернулли, но общий метод ре-
шения задач такого типа был дан лишь в работах Л. Эйлера и
Ж. Лагранжа.
Изопериметрическая задача. Требуется найти замкнутую
линию, заданной длины Z, ограничивающую максимальную площадь S.
Такой линией, как было известно еще в древней Греции, является
окружность. В этой задаче требуется определить экстремум функцио-
нала S при наличии своеобразного дополнительного условия—длина
кривой должна быть постоянна, т. е. функционал
/==/ /х(/)2+у(/)2^
сохраняет постоянное значение. Условия такого типа называются изо-
периметрическими. Общие методы решения задач с изопериметричес-
кими условиями были разработаны Л. Эйлером.
ВВЕДЕНИЕ
283
Ниже излагаются методы решения различных вариационных задач,
причем в основном исследуются на экстремум следующие часто встре-
чающиеся в приложениях функционалы:
J* F (х, у(х), y'(x))dx,
х,
а'(
у(х), у' (х), . .y(n>(x))dx,
Х0
Xi
f F(x, yi(x)......у«(х). y'i(x).....y'n(x))dx,
f [ F (*• У' z (х- у)> £ • 37) dx< аУ>
D
в которых функции F заданы, а функции у (х), ^(х) ... уп(г), z (х, у)
являются аргументами функционалов.
ГЛАВА 6
МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ
ГРАНИЦАМИ
§ 1. Вариация и ее свойства
Методы решения вариационных задач, т. е. задач на исследование
функционалов на максимум и минимум, весьма сходны с методами
исследования на максимум и минимум функций. Поэтому целесо-
образно напомнить кратко теорию максимума и минимума функций
и параллельно ввести аналогичные
ремы для функционалов.
1. Переменная величина z на-
зывается функцией переменной
величины х, что обозначается так:
z—f(x), если каждому значе-
нию х из некоторой области изме-
нения х соответствует значение z,
т. е. имеет место соответствие:
числу х соответствует число z.
Аналогично определяются и
функции нескольких переменных.
2. Приращением &х аргу-
мента х функции f (х) называется
разность между двумя значениями
этой переменной Дх = х — хР
Если х — независимое перемен-
понятия и доказать сходные тео-
1.	Переменная величина v на-
зывается функционалом, завися-
щим от функции у(х), что обо-
значается так: v — v [у (х)], если
каждой функции у(х) из некото-
рого класса функций у(х) со-
ответствует значение V, т. е.
имеет место соответствие: функ-
ции у(х) соответствует число
Аналогично определяются и
функционалы, зависящие от не-
скольких функций, и функцио-
налы, зависящие от функций
нескольких независимых пере-
менных.
2.	Приращением или вариа-
цией бу аргумента у(х) функцио-
нала v [у (х)] называется разность
между двумя функциями бу =
— у(х)~уг(х). При этом предпо-
ВАРИАЦИЯ И ЕЕ СВОЙСТВА
$ 1]
ное, то дифференциал х совпа-
дает с приращением dx — Дх.
3.	Функция /(х) называется
непрерывной, если малому из-
менению х соответствует малое
изменение функции /(х).
285
латается, что у (х) меняется произ-
вольно в некотором классе функ-
ций.
3. Функционал v [у (х)] назы-
вается непрерывным, если ма-
лому изменению у (х) соответствует
малое изменение функционала
г»|у(х)].
Последнее определение нуждается в уточнении и разъяснении,
так как сейчас же возникает вопрос, какие изменения функции у(х),
являющейся аргументом функционала, называются малыми или, что
то же самое, какие кривые у = у (х) и у = У] (х) считаются мало
отличающимися или близкими.
Можно считать близкими функции у(х) и у^х) в том случае,
если модуль их разности у(х)— у, (х) мал для всех значений х,
для которых задаются функции у(х) и у^х), т. е. считать близкими
кривые, близкие по ординатам.
Однако при таком определении близости кривых часто встречаю-
щиеся в приложениях функционалы вида
и[у(х)]= J Р{х, у, y')dx
из-за наличия в подынтегральной функции аргумента у' лишь
в исключительных случаях будут непрерывными. Поэтому во многих
случаях более естественно считать близкими только те кривые, кото-
рые близки по ординатам и по направлениям касательных в соответ-
ствующих точках, т. е. требовать, чтобы для близких кривых не
только модуль разности у(х) — у^х) был бы мал, но, кроме того,
был бы мал и модуль разности у' (х) — у' (х).
Иногда же оказывается необходимым считать близкими только
те функции, для которых малы модули каждой из разностей:
У (х) — У1 (х). у' (х) — У) (х),
У"(х) — у"(х).....yW(x) —yW(x).
В связи с этим приходится ввести следующие определения близости
кривых У = у (х) и у = У] (х).
Кривые у = у(х) и у — У1 (х) близки в смысле близости
нулевого порядка, если модуль разности у(х) — У1(х) мал.
286 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ G НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
Кривые у — у (х) и у=у}(х)
первого порядка, если модули
у'(х) — У, (х) малы.
Кривые
У —У(х) и
близки в смысле близости
разностей у(х)— уДх) и
У = У1(*)
близки в смысле близости k-го порядка, если модули разностей
у (х) — yt (х),
у'(х)—yj(x).
y(ft) (х) — у(*’(х)
малы.
На рис. 6.1 изображены кривые, близкие в смысле близости
нулевого порядка, но не близкие в смысле близости первого порядка.
так как ординаты у них близки, а направления касательных не близки.
На рис. 6.2 изображены кривые, близкие в смысле близости первого
порядка.
Из этих определений следует, что если кривые близки в смысле
близости А-го порядка, то они тем более близки в смысле близости
любого меньшего порядка.
Теперь мы можем уточнить понятие непрерывности функционала.
3'. Функция /(х) непрерывна
при х — х0, если для любого
положительного е можно подо-
брать д > 0 такое, что | / (х) —
—/Uo)l<e ПРИ !•»—-с01<6.
3'. Функционал v [у (х)) непре-
рывен при у==у0(х) в смысле
близости А-го порядка, если для
любого положительного е можно
подобрать 6 > 0 такое, что
Ct>lyt,x)] -»1у0(.хЯ1<е
§ I)
ВАРИАЦИЯ И ЕЕ СВОЙСТВА
287
При этом подразумевается, что
х принимает значения, в которых
функция f (х) определена.
при
IУ (х) — уо (х) | <б.
|/ (х) — у^(х)| <6,
|у;*!(х) - у'^(х) | < б.
При этом подразумевается,
что функция у(х) берется из
класса функций, на котором функ-
ционал v [у (х)] определен.
Можно было бы определить понятие расстояния р(ур у2) между
кривыми у = yj (х) и у = у2(х) (х0 х хД и тогда близкими
кривыми считать кривые, расстояние между которыми мало.
Если считать
Р(У1> У2)== тах |У1(*)— У2 WI-
< X < X,
т. е. ввести метрику пространства Со (см. стр. 50), то мы приходим
к понятию близости нулевого порядка. Если считать
*
Р(УР У2)=У max I М(1/Л (х) — У(2Р) (Х)|
р— 1 Хо х С х,
(предполагается, что yj и у2 имеют непрерывные производные до
порядка k включительно), то близость кривых понимается в смысле
близости k-ro порядка.
4. Линейной функцией на-
зывается функция I (х), удов-
летворяющая следующим усло-
виям:
I (сх) = cl (х),
где с—произвольная постоянная, и
(А +	— I (xj +I (х2).
Линейная функция одной пере-
менной имеет вид
/ (х) = kx,
где k — постоянная.
4. Линейным функционалом
называется функционал L[y(x)],
удовлетворяющий следующим ус-
ловиям:
А [су (х)1=с£[у(х)],
где с — произвольная постоянная и
L [у, (х) + у2 (х)] =
=	(х)]4-£[у2(х)].
Примером линейного функцио-
нала является
Xi
£[у(х)]== J (р(х)у-Н(х)у') dx,
*0
288 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
5. Если приращение функцио-
нала
Дг» = -ц [у (х) +'6yl — v [у (х)|
можно представить в виде
Au = Z.[y(x), бу] -Ь
ч- Р (у (х), бу) тах|бу|,
где А[у(х), бу | —линейный по
отношению к бу функционал,
max|бу | — максимальное значение
|бу| и р(у(х), бу)->0 при
max | бу ]—>0, то линейная по от-
ношению к бу часть приращения
функционала, т. е. L [у (х), бу],
называется вариацией функцио-
нала и обозначается 6г/.
это главная, линейная по отно-
5. Если приращение функции
А/ = / (х + Дх) — f (х)
может быть представлено в виде
Д/ — А (х) Дх -f- р (х, Дх) • Дх,
где А (х) не зависит от Дх,
а р(х, Дх)->0 при Дх->0, то
функция называется дифференци-
руемой, а линейная по отношению
к Дх часть приращения—А (х)Дх
называется дифференциалом
функции и обозначается df. Разде-
лив на Дх и переходя к пределу при
Дх->0, получим, что А(х) =
— /' (х), и, следовательно;
df = f' (х) Дх.
Итак, вариация функционала —
тению к бу, часть приращения функционала.
При исследовании функционалов вариация играет такую же роль,
какую играет дифференциал при исследовании функций.
Можно дать и другое, почти эквивалентное, определение диф-
ференциала функции и вариации функционала. Рассмотрим значение
функции /(х4-аДх) при фиксированном х и Дх и изменяющихся
значениях параметра а. При а — 1 получим приращенное значение
функции /(x-f-Дх), при а = 0 получим исходное значение функции
f (х). Нетрудно проверить, что производная от f(xf-a&x) по а
при а=0 равна дифференциалу функции /(х) в точке х. Действи-
тельно, по правилу дифференцирования сложной функции
+ а Дх)|а=0 ==/'(* + аДх) Дх |а=0=// (х) Дх = df (х).
Точно так же для функции нескольких переменных
z = f(xv х2.....х„)
можно получить дифференциал путем дифференцирования
/(Xj -|- а Дхр х2-|- аДх2, .... хл + аДх„)
по а, полагая затем а=0. Действительно,
п
^-/(х1-|-аДх1,х2-|-аДх2......х„ 4- аДхп) |о=0 =	Дх( = df.
/=i
И для функционалов вида v [у (х)] или более сложных, зависящих
о: нескольких неизвестных функций или от функций нескольких
§ 1]	ВАРИАЦИЯ И ЕЕ СВОЙСТВА	289
переменных, можно определить вариацию как производную от функ-
ционала v [у (х) аду] по а при а=0. Действительно, если функционал
имеет вариацию в смысле главной линейной части приращения,
то его приращение имеет вид
Дх> = г>[у (х)-|-аду] — v [у (х)] = L(у, аду)4~0 (У. аду) | а| max|ду [.
Производная от ц[у-|- а6у] по а при а = 0 равна
lim Av = lim Av = Пт L (у, a dy) + р [у (х), а ду] | а I max | ду | __
Ла >0 А« а->0 а а->0	а
= Ит	_l_ нт .Му (*)> аду] I а1 ma*l ду£ = £(у. ду),
а->0	“	а^О	«
так как в силу линейности
Л(у, аду) = а/,(у, ду),
a
1' ₽ [У (х), аду] 1 a I max I ду |	,	.. .
lim	1= 1)тр[у О),а ду] max | ду ] — 0,
а->0	а	а->0
потому что р [у (х), аду]->0 при а->0. Итак, если существует
вариация в смысле главной линейной части приращения функционала,
то существует и вариация в смысле производной по параметру при
начальном значении параметра, и оба эти определения эквивалентны.
Второе определение вариации несколько шире первого, так как
существуют примеры функционалов, из приращения которых нельзя
выделить главной линейной части, но вариация в смысле второго
определения существует.
6. Диффе ренциал функции 6. Вариация функционала
/ (х) равен	v{y(x)J равна
-^-/(х-f-a Дх)|а=0.	[у (х) Н-аду] |а=0.
Определение. Функционал v [у (х)] достигает на кривой
у = у0(х) максимума, если значения функционала ту [у (х)]
на любой близкой к у = у0(х) кривой не больше, чем fly0(x)],
то есть Дц = г/[у(х)]—‘п|Уо(х)]^О-
Если Ди С 0, причем Дц — 0 только при у (х) — у0 (х), то говорят,
что на кривой у — уДх) достигается строгий максимум. Аналогично
определяется кривая у==у0(х), на которой реализуется минимум.
В этом случае Дт»^-0 для всех кривых, близких к кривой у — у0(х).
7. Теорема. Если диффе-
ренцируемая функция /(х)
достигает максимума или
7. Теорема. Если функ-
ционал v [у (х)], имеющий ва-
риацию, достигает максимума
290 МЕТОД ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. в
минимума во внутренней точ-
ке x — xQ области определе-
ния функции, то в этой точ-
ке
df— <д.
или минимума при у = у0(х),
где у(х) — внутренняя точка
области определения функ-
ционала, то при у~у0(х),
dv = 0.
Доказательство теоремы для функционалов. При
фиксированных у0(х) и by v [у0 (х) -|- а ду] — <р (а) является функ-
цией а, которая при а — 0, по предположению, достигает максимума
или минимума, следовательно, производная
ф'(0)==.0*). или v [у0 (х) 4- a dy] I =0,
оа	1а=0
т.г е. дт — 0. Итак, на кривых, на которых достигается экстремум
функционала, его вариация равна нулю.
Понятие экстремума функционала нуждается в уточнении. Говоря
о максимуме или минимуме, точнее, об относительном максимуме
или минимуме, мы имели в виду наибольшее или наименьшее значение
функционала только по отношению к значениям функционала на близ-
ких кривых. Но, как было указано выше, близость кривых может
быть понимаема различно, поэтому в определении максимума или
минимума надо, указывать, какого порядка близость имеется в виду.
Если функционал v [у (х)] достигает на кривой у = у0(х) макси-
мума или минимума по отношению ко всем кривым, для которых
модуль разности у(х) — У0(х) мал, т. е. по отношению к кривым,
близким к у = у0(х) в смысле близости нулевого порядка, то мак-
симум или минимум называется сильным.
Если же функционал v [у (х)] достигает на кривой у=у0(х)
максимума или минимума лишь по отношению к кривым у = у(х),
близким к у — у0(х) в смысле близости первого порядка, т. е. по
отношению к кривым, близким к у = у0(х) не только по ордина-
там, но и по направлениям касательных, то максимум или минимум
называется слабым.
Очевидно, что если на кривой у = у0(х) достигается сильный
максимум (или минимум), то подавно достигается и слабый, так как
если кривая близка к у —у0(х) в смысле близости первого порядка,
то она близка и в смысле близости нулевого порядка. Однако воз-
можно, что на кривой У = у0 (х) достигается слабый максимум (ми-
нимум) и в то же время не достигается сильный максимум (минимум),
т. е. среди кривых у — у(х), близких к y = yj(x) как по ордина-
там, так и по направлению касательных, может не быть таких, для ко-
*) а может принимать в окрестности точки а = 0 как положительные,
так и отрицательные значения, так как ув (х) — внутренняя точка области
определения функционала.
$ !]	ВАРИАЦИЯ И ЕЕ СВОЙСТВА	291
торых v[y(x)] > v[y0(x)| (в случае минимума v [у (х)] < v [у0 (х)]),
а среди кривых у = у(х), близких только по ординатам, но уже не
близких по направлению касательных, могут найтись и такие, для
которых v [у (х)] > v [у0(х)| (в случае минимума v [у (х)] < v [у0 (х)]).
Различие между сильным и слабым экстремумом не будет иметь су-
щественного значения при выводе основного необходимого условия
экстремума, но оно будет весьма существенно в главе 8 при изуче-
нии достаточных условий экстремума.
Заметим еще, что если на кривой у = у0(х) достигается экстремум,
то не только® |Уо(х)Ч-абу] I = 0. но и -4- v [у (х, а)] I = 0,
аа	'а = 0	аа	1а=0
где у (х, а) — любое семейство допустимых кривых, причем при
а = 0 и при а=1 функция у(х, а) должна соответственно превра-
щаться в у0(х) и у0(х)4~6у. Действительно, v[y(x, а)] является
функцией а, так как задание а определяет кривую семейства у—у (х, а),
а значит, определяет и значение функционала v[y(x, а)].
Эта функция, по предположению, достигает экстремума при а = 0,
следовательно, производная этой функции обращается в нуль
при а = 0 *).
Итак, v (у (х, а)] I =0, однако эта производная, вообще
оа	1а=о
говоря, уже не будет совпадать с вариацией функционала, но будет,
как показано выше, обращаться в нуль одновременно с to на кри-
вых, реализующих экстремум функционала.
Все определения этого параграфа и основная теорема (стр. 289)
почти без всякого изменения переносятся на функционалы, зависящие
от нескольких неизвестных функций
Уг(х), .... у„(х)]
или зависящие от одной или нескольких функций многих перемен-
ных
х......х„)],
х2.....Х„), Z2(Xj, х2......х„)......«„'(Xj, х2, .... хл)].
Например, вариация би функционала v[z(x, у)] может быть опре-
делена или как главная линейная по отношению к бд часть прира-
щения
Av — v[z(x, у) -|- бд] — vlz(x, у)],
или как производная по параметру при начальном значении
*) Предполагается, что а может принимать любые близкие к а=0 зна-
существует.
и = и
f.'V [у (х, а)] I
С'Ц
292 МЕТОД ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
параметра
причем если при z = z(x, у) функционал о достигает экстремума,
то при z = z(x, у) вариация bv — 0, так как v[z (х, у)-\-abz]
является функцией а, которая при а = 0, по предположению, дости-
гает экстремума и, следовательно, производная от этой функции
по а при а = 0 обращается в нуль, -^-v[z(x, y)-f-a6z]|	=0
иа	1<х=о
или bv = 0.
§ 2. Уравнение Эйлера
Исследуем на экстремум функционал
v[y(x)l = J F(x, у(х), y'(xY)dx,
(6.1)
причем граничные точки допустимых кривых закреплены: у(х0) = у0
и у(х1) = у1 (рис. 6.3). Функцию Fix, у, у') будем считать трижды
дифференцируемой.
Мы уже знаем, что необходимым условием экстремума является
обращение в нуль вариации функционала. Покажем теперь, как при-
меняется эта основная теорема к
рассматриваемому функционалу,
причем мы еще раз повторим пре-
дыдущее рассуждение применитель-
но к функционалу (6.1). Предпо-
ложим, что экстремум достигается
на дважды дифференцируемой кри-
вой у — у (х) (требуя лишь суще-
ствования производных первого
порядка у допустимых кривых,
можно иным методом доказать, что
рис ез	у кривой, реализующей экстре-
мум, существует и вторая произ-
водная).
Возьмем какую-нибудь близкую к у = у (х) допустимую кривую
у = у (х) и включим кривые у — у (х) и у = у (х) в однопараметри-
ческое семейство кривых
у(х, a) = y(x)4-a(y(x) —у(х));
при а = 0 получим кривую у = у(х), при а=1 имеем у = у(х)
§ 2]
УРАВНЕНИЕ ЭЙЛЕРА
293
(рис. 6.4). Как мы уже знаем, разность у(х)— у(х) называется ва-
риацией функции у(х) и обозначается ду.
Вариация ду в вариационных задачах играет роль, аналогичную
роли приращения независимого переменного Ах в задачах на иссле-
дование экстремумов функций /(х). Вариация функции ду—у(х)—у(х)
является функцией х. Эту функцию, можно дифференцировать один
или несколько раз, причем (ду)/ = у'(х)— у'(х) = ду/, т. е. про-
изводная вариации равна вариации производной, и аналогично
(ду)" = у" (х) — у" (х) == ду", z
(dy)(fr) = у(*’ (х) — y(ft) (х) = ду<й).
Итак, рассмотрим семейство у = у(х, а), где у(х, а) = у(х)4-
-|-аду, содержащее при а = 0 кривую, на которой достигается эк-
стремум, а при а = 1 — некото-
рую близкую допустимую кри-
вую — так называемую кривую
сравнения.
Если рассматривать значения
функционала
X,
v[y(x)] = f F(x, у, y')dx
Xt>
только на кривых семейства
у = у(х, а), то функционал пре-
вращается в функцию а:
гЧуСх, а)] = <р(а),
так ка\ значение параметра а определяет кривую семейства у = у(х, а)
и тем самым определяет и значение функционала ц[у(х, а)]. Эта
функция <р (а) достигает своего экстремума при а = 0, так как при
а = 0 получаем у = у(х), и функционал, по предположению, до-
стигает экстремума по сравнению с любой близкой допустимой
кривой и, в частности, по отношению к близким кривым семейства
у = у (х, а). Необходимым условием экстремума функции <р(а)
при а = 0,
водной при
как известно, является обращение в нуль ее произ-
а = 0:
Так как
ф'(0) = 0.
<Р(а)= J F(x, у(х, а), ул(х, a))dx,
ха
294 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
ТО
-Ч
<р' (а) = f у (х. а) + Ру у' (х, а)] dx,
*0
где
Fy=-^F(x, у(х, а), у'(х, а)),
Fy = -^г Р (х, у(х, а), у'(х, а)),
или, так как
у (х, а) = [у (х) Н- аду] = бу
и
^у'(х, а) = -^[у'(х)4-аду']—д/,
получим
Х1
ф'(а)= J [Fy(x, у (х, а), у'(х, а))ду4-
*о
-\-Ру(х, у(х, а), у'(х. a))dy']dx;
<p'(0) — J |Fy(x, у(х), у'(х))ду 4- Fy (х, у(х), y'(x))dy']dx
•Vo
Как мы уже знаем, <р'(0) называется вариацией функционала и
обозначается tyv. Необходимое условие экстремума функционала v
заключается в обращении в нуль его вариации: dt» = O. Для функ-
ционала
•и[у(х')]= f F(x, у, y')dx
это условие имеет вид
•J* [Fy ду Fy-ду'] dx = 0.
Хо
Интегрируем второе слагаемое по частям и, принимая во внимание,
что ду' = (ду)', получим
х'
Ьи = IFy. ду£ 4- f (Fy - A. Fy-) ду dx.
xb
Но
U=x, = У (хо) ~ У = 0 и U=Xj = У (*1) — У (*1) — о.
§ 21
УРАВНЕНИЕ ЭЙЛЕРА
295
потому что все допустимые кривые в рассматриваемой простейшей
задаче проходят через фиксированные граничные точки, и следова-
тельно,
X,
К-)
Итак, необходимое условие экстремума приобретает вид
f (Fy--^Py’)f>ydx = O,r	(6.2)
х»
причем первый множитель Fy— Fy' на кривой у'=у(х), реали-
зующей экстремум, является заданной непрерывной функцией, а вто-
рой множитель ду, ввиду произвола в выборе кривой Сравнения
у — у (х), является произвольной функцией, удовлетворяющей лишь
некоторым весьма общим условиям, а именно: функция ду в гранич-
ных точках х = х0 и х — хг обращается в нуль, непрерывна и
дифференцируема один или несколько раз, ду или ду и ду' малы
по абсолютной величине.
Для упрощения полученного условия (6.2) воспользуемся следую-
щей леммой:
Основная лемма вариационного исчисления. Если для
каждой непрерывной функции t](x)
х,
• J Ф (х) т|(х) dx = О,
Хо
где функция Ф(х) непрерывна на отрезке [х0, xj, то
Ф(х)==0
на том же отрезке.
Замечание. Утверждение леммы и ее доказательство не из-
меняются, если на функции т| (х) наложить следующие ограничения:
•q(xo) = T](x1) = O; т](х) имеет непрерывные производные до по-
рядка р. |т](-’)(х)| < е ($ — 0, 1, ... q\ q р).	_
Доказательство. Предположив, что в точке х = х, лежа-
щей на отрезке х04х ^х;, Ф(х)^0, придем к противоречию.
Действительно, из непрерывности функции Ф(х) следует, что если
Ф(х)=/=0, то Ф(х) сохраняет знак в некоторой окрестности (x0OOt)
точки х; но тогда, выбрав функцию т](х) также сохраняющей знак
296 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ |ГЛ. 6
в этой окрестности и равной нулю вне этой окрестности (рис. 6.5),
получим
л,
Ф (х) т] (х) dx = § Ф (х) т] (х) dx4= О,
*	Z
так как произведение Ф(х)т](х) сохраняет знак на отрезке (x0^x<^xt)
и обращается в нуль вне этого отрезка. Итак, мы пришли к про-
тиворечию, следовательно, Ф(х) = 0. Функцию г)(х) можно выби-
рать, например, так: т](х) = 0 вне отрезка (Xq^x^Xj); т](х) =
— k (х — х0)2п (х — Х02" на отрезке (х0 ^х Xj), где п — целое
положительное число, k—постоянный множитель. Очевидно, что
функция т](х) удовлетворяет упомянутым выше условиям: она не-
прерывна, имеет непрерывные производные до порядка 2п — 1, об-
ращается в нуль в точках х0 и х} и может быть сделана по модулю
сколь угодно малой вместе со своими производными за счет умень-
шения модуля множителя k.
Замечание. Дословно так же можно доказать, что если функ-
ция Ф(х, у) непрерывна в области D на плоскости (х, у) и
/Ф(х, y)i)(x, y)dxdy — 0 при произвольном выборе функции
D
т](х, у), удовлетворяющей лишь некоторым общим условиям (непре-
рывность, дифференцируемость один или несколько раз, обращение
в нуль на границах области D, |т)| < е, 11)*| < е, | т)у | < Е)- то
Ф(х, у) = 0 в области D. Функцию т](х, у) при доказательстве
основной леммы можно выбрать, например, так: т](х, у) = 0 вне
круговой окрестности достаточно малого радиуса точки (х, у),
в которой Ф(х; у)#=0, а в этой окрестности точки (х, у) функция
т](х, у) = £[(х — х)2Д-(у— у)2 — е2]2я (рис. 6.6). Аналогичная лемма
справедлива и для я-кратных интегралов.
УРАВНЕНИЕ ЭЙЛЕРА
297
Применим теперь основную лемму для упрощения полученного
выше необходимого условия (6.2) экстремума простейшего функцио-
нала (6.1)
•п
f	(6.2)
ха
Все условия леммы выполнены: на кривой, реализующей экстремум,
множитель	Fy \ является непрерывной функцией, а вариа-
ция ду является произвольной функцией, на которую наложены лишь
предусмотренные в основной лемме ограничения общего характера, сле-
довательно, F,,-Ру = О
у dx у
на кривой у = у (х), реализую-
щей экстремум рассматриваемо-
го функционала, т. е. у — у (х)
является решением дифферен-
циального уравнения второго
порядка
^-^ = 0,
или в развернутом виде
Fy — Fxy —РууУ’ —
Рис. 6.6.
-FyVy" = 0.
Это уравнение называется уравнением Эйлера (оно впервые было
им опубликовано в 1744 году). Интегральные кривые уравнения Эйлера
у = у(х, С2) называются экстремалями. Только на экстремалях
может достигаться экстремум функционала,
®1У(х)) = J F(.x, у, y'}dx.
Ха
Для нахождения кривой, реализующей экстремум функционала (6.1),
интегрируем уравнение Эйлера и определяем обе произвольные по-
стоянные, входящие в общее решение этого уравнения, из условий
на границе у(х0) = у0, y(x1) = yP Только на удовлетворяющих этим
условиям экстремалях может реализоваться экстремум функционала
Однако для того чтобы установить, реализуется ли на них в дей-
ствительности экстремум, и притом максимум или минимум, надо вос-
пользоваться достаточными условиями экстремума, изложенными
в главе 8.
298 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
Напомним, что краевая задача
Fy — FV’ = 0, у (х0) = у0, у (Xj) = У1
не всегда имеет решение, а если решение существует, то оно может
быть не единственным (см. стр. 159).
Заметим, что во многих вариационных задачах существование ре-
шения очевидно из физического или геометрического смысла задачи,
и если решение уравнения Эйлера, удовлетворяющее граничным усло-
виям, единственно, то эта единственная экстремаль и будет решением
рассматриваемой вариационной задачи.
Пример 1. На каких кривых может достигать экстремума функционал
л
2
ч[у(х)] = f [(У')2 — У2] dx; у(0) = 0, у^^=1?
о
Уравнение Эйлера имеет вид у" у = 0; его общим решением является
у = Сх cos х 4- Сг sin х. Используя граничные условия, получаем: С^О,
Су — 1; следовательно, экстремум может достигаться лишь на кривой
у = sin X.
Пример 2. На каких кривых может достигать экстремума функционал
1
fly (х)] = f I(y')2+I2xy]dx, y(0) = 0, у(1)— 1?
о
Уравнение Эйлера имеет вид у" — 6х = 0, откуда у = х3 Ctx Су. Ис-
пользуя граничные условия, получаем: С} =0, С2 = 0; следовательно, экстре-
мум может достигаться лишь на кривой у = х3.
В этих двух примерах уравнение Эйлера легко интегрировалось,
но так бывает далеко не всегда, так как дифференциальные уравне-
ния второго порядка интегрируются в конечном виде лишь в исклю-
чительных случаях. Рассмотрим некоторые простейшие случаи инте-
грируемости уравнения Эйлера.
1) F не зависит от у':
F = F(x, у). .
Уравнение Эйлера имеет вид Ру(х, у) —0, так как Fy=0. Реше-
ние полученного конечного уравнения Fy(x, у) = 0 не содержит
элементов произвола и поэтому, вообще говоря, не удовлетворяет
граничным условиям у (х0) = у0 и у (Xj) = yv
Следовательно, решение рассматриваемой вариационной задачи,
вообще говоря, не существует. Лишь в исключительных случаях,
когда кривая
Fy(x, у) = 0
S 2]
УРАВНЕНИЕ ЭЙЛЕРА
299
проходит через граничные точки (х0, у0) и (Хр у^, существует кри-
вая, на которой может достигаться экстремум.
ПримерЗ.
Х1
f [у (*)]= J УгЛх-, у(х0)=уа,
У(-*1)=У1-
Уравнение Эйлера имеет вид
Fy = 0 или у = 0.
Экстремаль у = 0 проходит через граничные точки только при у0 = О И
У1 = 0 (рис. 6.7). Если yQ = 0 и у, = 0,' то, очевидно, функция у = 0 реалй-
X,
зует минимум функционала v= J* Уг dx, 1 у
Х0
так как v[y(x)]>0, причем о = 0 при
у = 0. Если же хотя бы одно из у0 и yi
не равно нулю, то минимум функционала
на непрерывных функциях не достигается,
что и понятно, так как можно выбрать
последовательность непрерывных функций ________;______А '	В
уп (х), графики которых состоят из все бо-	0	z	х
лее и более круто спускающейся из точки	°	• '
(х0, Уо) к оси абсцисс дуги кривой, за-
тем из отрезка оси абсцисс, почти совпа-	рИс. 6.7.
дающего со всем отрезком (х0, хг), и, на-
конец, возле точки хл, круто поднимаю-
щейся к точке (Х|, У1) дуги кривой (рис. 6.8). Очевидно, что на кривых
такой последовательности значения функционала сколь угодно мало от-
личаются от нуля и, следовательно, нижняя грань значений функционала
равна нулю, однако эта нижняя грань не может достигаться на непрерывной
кривой, так как для любой непрерывной кривой у = у (х), отличной от то-
X,
ждественного нуля, интеграл | у2 dx > 0. Эта нижняя грань значений
Хо
функционала достигается на разрывной функции (рис. 6.9)
У (Хо) = Уо.
у (х) = 0 при Хо < X < Хр
У(Х!) = У1-
2) Функция F линейно зависит от у':
F(x, у, у') = М(х, y)4-Af(x, у) у';
X,
® [у (х)]= f [л1(х, y) + N(x, У)
X»
30(1 МЕТОЛ ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. в
Уравнение Эйлера имеет вид
	d№ . dN , d ., .	. л —	г~У—-^—N(x, у) = 0, ay 1 dy '	dx	' х/
ИЛИ	6M. dN , _ dN   dN ,  dy * dy У	dx	dy	’
или	д/И	dN   ~dy	dx~ ~ ’
но это опять.
ренциальное уравнение. Кривая
как и в предыдущем случае, конечное, а не диффе-
удовлетворяет граничным условиям, следовательно, вариационная за-
дача, как правило, не имеет решения в классе непрерывных функций.
_ дМ dN п	.. , , .. .
Если же --------^ = 0, то выражение М ах N dy является точ-
ным дифференциалом и
v = J —	— I" (Мdx -f- Ndy)
To	*•
не зависит от пути интегрирования, значение функционала v посто-
янно на допустимых кривых. Вариационная задача теряет смысл.
П р и м е р 4.
1
» [у (*)] = J (У2 + *2у') dx\ у (0) = 0, у (1) = а.
о
,,	дМ dN п	ар.
Уравнение Эйлера имеет вид --------=0 или у — х = 0. Первое гра-
ничное условие у (0) = 0 удовлетворяется, но второе граничное условие удо-
влетворяется лишь при а — 1. Если же а 1, то экстремали, удовлетворяю-
щей граничным условиям, не существует.
УРАВНЕНИЕ ЭЙЛЕРА
301
§ 2]
Пример 5:
*1
oly(*)l= J*(y4-xy')rfx или (v[y (х)] = J (у dx-} х dy)-,
к»	r0
У(*о)=Уо. У(*1) = У|-
Уравнение Эйлера превращается в тождество 1 s 1. Подынтегральное выра-
жение является точным дифференциалом, и интеграл не зависит от пути ин-
тегрирования:
*1
v [У (*)] = J* <*(*У) = *1У1—*оУо,
по какой бы кривой мы ни интегрировали. Вариационная задача не имеет
смысла.
3)F зависит лишь от у':
F = F(y').
Уравнение Эйлера имеет вид Fy'y’y" = 0, так как Fy = Fxy. —
— Fyy- =0. Отсюда у" = 0 или Fy-y’ =0. Если у" = 0, то у—
= СуХ	—двухпараметрическое семейство прямых линий. Если же
уравнение Fy'V' (у') = 0 имеет один или несколько действительных
корней у' =k{, то у — ktx -\-С, и мы получаем однопараметрическое
семейство прямых, содержащееся в полученном выше двухпарамет-
рическом семействе у = Сгх -|- С2. Таким образом, в случае F = F (ух)
экстремалями являются всевозможные прямые линии у = CjX4~^2-
Пример 6. Длина дуги кривой
/[У (х)]= f /1 + У'2 dx
Хо
имеет экстремалями прямые линии у — CiX-\-C2.
Пример 7. Время t [у (х)), затрачиваемое на перемещение по некото-
рой кривой у •= у (х) из точки А (х0, у0) в точку В (xb yt), если скорость
= v (у ) зависит только от у , является функционалом вида
/[у(х)] = Г У1 ^,У—dx
'J ,/ v(y )
Хо
(ds ,	ds V\+y'2dx. . f -+-У'2 .
|~7r==v(y'k dt=—-------------7-^---- t= / -------------dx .
I dt	v(y') v(y')	J v(y')	/
\	x0	/
Следовательно, экстремалями этого функционала являются прямые линии.
4) F зависит лишь от х и у':
F = F(x, у').
302 МЕТОЛ ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 6
Уравнение Эйлера приобретает вид ~ Fy (х, у') = 0 и, следо-
вательно. имеет первый интеграл Fy (х, y')=sCi, причем так как
полученное уравнение первого порядка Fy (х, y') = Ct не содержит у,
то уравнение может быть проинтегрировано или путем непосредствен-
ного разрешения относительно у' и интегрирования, или путем вве-
дения подходящим образом выбранного параметра (см. стр. 69).
Пример 8. Функционал
(’ V^l -4- у^
t [у (*)] = / -——dx
ъ
(t — время, затрачиваемое на перемещение по кривой у = у(х)из одной
ds
точки в другую, если скорость движения v = х, так как если —& = х, то
ds Г V 1Ч- у/2
dt =----- и t = / —---—— dx I. Первый интеграл уравнения Эйлера
X	tf	х	/
-Vo	f Z
F , = С, имеет вид --- У 	= Ct. Это уравнение проще всего инте-
л У1 -|-у'2
грируется, если ввести параметр, полагая у' = tg t; тогда
X = —J------ У- = Д- Sin t
С' /1+у'2 с>
или х = С, sin t, где С| =	'
уу = tg t; dy = tg £ dx = tg / • C, cos tdt—Cx sin t dt;
интегрируя, получаем у = — cos t C2. Итак,
x = sin t, у — C2 =— C] cos t
или, исключая t, получаем хг + (У — С2)2 = С2 — семейство окружностей
с центрами на оси ординат.
5) F зависит лишь от у и у':
F = F(y, у').
Уравнение Эйлера имеет вид: Fy — Fyyy' — Fyyy" = G, так как
Fxy — 0. Если умножить почленно это уравнение на у’, то, как не-
трудно проверить, левая часть превращается в точную производную
hV-y'F,’)-
§ 2]
УРАВНЕНИЕ ЭЙЛЕРА
303
Действительно,
(F - y'Fy>) = Руу' 4- Fy.y" - y"Fy-Fyy.y'2 - РУ’У-у'у" =
= у' (Ру — ?уу'У' — Ру'у' у")'
Следовательно, уравнение Эйлера имеет первый интеграл
F — y'Fy==Cv
причем так как это уравнение первого порядка не содержит явно х,
то оно может быть проинтегрировано путем разрешения относи-
тельно у' и разделения переменных или путем введения параметра.
Пример 9. Задача о наименьшей поверхности вращения: определить
кривую с заданными граничными точками, от вращения которой вокруг оси
абсцисс образуется поверхность наименьшей площади (рис. 6.10).
Как известно, площадь поверхности вращения
$ [у U)J = 2л j у V 1 + у'2 dx.
Подынтегральная функция зависит лишь от у и у' и, следовательно, первый
интеграл уравнения Эйлера будет иметь вид
А-у7у=С,
или в данном случае у У 1 + у'2----- = С,.
/1 + У'2
После упрощений получаем —	  •— Ct. Проще всего это уравне-
У1+У'2
ние интегрируется подстановкой у'= shтогда у = С] ch t, а
dy CiShtdt г	г . . г
(1л = —~	д  " = Ci dtt X С it 4- Са«
у	sh/ 1	* ‘
304 МЕТОД ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. в
Итак, искомая поверхность образуется вращением линии, уравнение которой
в параметрической форме имеет вид
х " Ctt С2,
у = Cj ch t.
х___(j
Исключая параметр t, будем иметь у = С{ ch ——- семейство цепных
линий, от вращения которых образуются поверхности, называемые катенои-
дами. Постоянные Ci и С2 определяются из условия прохождения искомой
линии через заданные граничные точки (в зависимости от положения точек
А и В может существовать одно, два или ни одного решения).
Пример 10. Задача о брахистохроне (см. стр. 281): определить кривую,
соединяющую заданные точки А и В, при движении по которой материаль-
ная точка скатится из точки А в точку В в кратчайшее время (трением и
сопротивлением среды пренебрегаем).
Поместим начало координат в точку А, ось Ох направим горизонтально,
ось Оу — вертикально вниз. Скорость движения материальной точки
— Y'j.gy откуда находим время, затрачиваемое на перемещение точки
из положения А (0, 0) в положение В (хь у]):
X,
''’"-’‘“ту/
V1 + г2
Ку
dx\
у (0) = 0,	у(х1) = у1.
Так как этот функционал также принадлежит к простейшему виду и его
подынтегральная функция не содержит явно х, то уравнение Эйлера имеет
первый интеграл F — y'F?, = С, или в данном случае
/i + /2 _УЛ _
Гу Kyd + y'2)
откуда после упрощений будем иметь —	— = С или у (1 4- у/2) = Сх.
Ку(Г+у/2)
Введем параметр t, полагая у' = ctg t\ тогда получим:
у = ~4-~ctF2<~= Cl ®in2 z = -т(1 ~cos 20;
. dy 2C, sin t cos t dt „	, t
dx =-	= —!-------—--------= 2Ci sin2t dt — Ci (1 — cos 2/) dt\
У	ctg/
x = Ci (t -	4- C2 =	(2/ - sin 2/) + C3.
Следовательно, в параметрической форме уравнение искомой линии имеет
вид
х—С2 = -у-(2/ — sin 2/), у =-£1.(1 — cos 2/).
Если преобразовать параметр подстановкой 2/ = ti и принять во внимание,
§ 31	ФУНКЦИОНАЛЫ ОБЩЕГО ВИДА	305
что С2 = 0, так как при у — 0, х = 0, то. мы получим уравнение семейства
циклоид в обычной форме:
с
У = -FT- (1 — COS ti),
С,
где ~—радиус катящегося круга, который определяется из условия про-
хождения циклоиды через точку В(хх, yj. Итак, брахистохроной является
циклоида.
§ 3. Функционалы вида
f F(X, yv У2......У„, Ур у2, yn)dx
*«
Для получения необходимых условий экстремума функционала v
более общего вида
^(Уг у2.....Уя] = / Уг У2............УП’ Ур У2......Уп)ах
при заданных граничных значениях всех функций
У1(хо)~Ую’ У2 (*о) = У2о- •••• У«(^о) = Уяо>
у1(х1) = Уц, y2(X!) = y2i...УЛ(*1) = УЯ1.
будем варьировать лишь одну из функций
У/(*)	(У=1. 2......я),
оставляя все остальные функции неизменными. При этом функционал
v{yp У2> •••• УЯ1 превратится в функционал, зависящий лишь от
одной варьируемой функции, например от у,(х),
п[У1. У2. - - -• У«1 = г» 1У2]
рассмотренного в § 2 вида, и, следовательно, функция, реализующая
экстремум, должна удовлетворять уравнению Эйлера
Так как это рассуждение применимо к любой функции у(. (Z=l,
2..... п), то мы получим систему дифференциальных уравнений
второго порядка
F —	»’ =0	(i=l, 2......я),
у( dx yL	v	'
306 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
определяющих, вообще говоря, 2п-параметрическое семейство инте-
гральных кривых в пространстве  х, ур у2......... уп — семейство
экстремалей данной вариационной задачи.
Если, в частности, функционал зависит лишь от двух функций
у (х) и z (х):
и[у(х), z (х)] = J* F(x, у, z, у', z'}dx\
Xt
У(^о)==Уо-	«(x0)==z0,	у(х1) = у1,	г(Х1) = г1,
т. е. определяется выбором пространственной кривой у = у(х),
z — z(x) (рис. 6.11), то, варьируя только у(х) и фиксируя г(х),
мы изменяем нашу кривую так, что ее проекция на плоскости xOz
не изменяется, т. е. кривая все время остается на проектирующем
цилиндре z = z (х) (рис. 6.12).
Аналогично., фиксируя у (х) и варьируя z (х), мы варьируем кри-
вую так, что она все время лежит на проектирующем цилиндре
у = у (х). При этом получаем систему двух уравнений Эйлера:
Пример 1. Найти экстремали функционала
я
2
1У'2 +	+ 2уг] dx, у (0) = 0, у = 1.
О'
г(0) = 0,	----1.
f [у (X), г (х)] =
§ 3]	ФУНКЦИОНАЛЫ ОБЩЕГО ВИДА	307
Система дифференциальных уравнений Эйлера имеет вид
у" — z = 0,
г" — у = 0.	-
Исключая одну из неизвестных функций, например г, получаемую— у=0.
Рис. 6.12.
Интегрируя это линейное уравнение с постоянными коэффициентами, будем
иметь:
у =	4- С2е~х	С3 cos х С4 sin х;
г = у"', z — Схех	С2е~х — С3 cos х — Ct sin х.
Используя граничные условия, находим:
Ci = 0, С2 = 0, С3 = 0, С4 = 1;
следовательно, у = sin х, г= — sin х.
Пример 2. Найти экстремали функционала
х,
. V [у (х), z (х)] = J F (у', г') dx.
A-q
Система уравнений Эйлера имеет вид
РууУ" +	= 0; Fy,z.y" + Fz,z,z" = 0,
откуда, считая Fy,y,Fz,z,—=# 0, получим: у" = 0 и г" = 0 или
у = С|Х4" С2, г= С3х4-С4 — семейство прямых линий в пространстве.
Пример 3. Найти дифференциальные уравнения линий распростра-
нения ’света в оптически неоднородной среде, в которой скорость распро-
странения света равна v (х, у, г).
308 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
Согласно принципу Ферми свет распространяется из одной точки А (ха, у0)
в другую В(хьу|) по кривой, для которой время Т прохождения света
будет наименьшим. Если уравнение искомой кривой у = у (х) и z = г (х), то
Система уравнений Эйлера для этого функционала
У^ + У г + г'2 d______________/___________
ду	vi	dx ~
dv V1 + У|2 + *'2  d_________________________п
дг	v*	dx v /1 + у'2 + г'2
и будет системой, определяющей линии распространения света.
§ 4. Функционалы, зависящие от производных
более высокого порядка
Исследуем на экстремум функционал
Х1
У[yW] = fF(x’ yW. /(*)............y(n)(x))rfx,
где функцию F будем считать дифференцируемой п-|-2 раза по
всем аргументам и будем предполагать, что граничные условия
имеют вид
'^о) = Уо’ У'(хо) = Уо........ У(n-1)(xo):=^’^)л1,;
У(*1) = У1- У'(*1) = У1'......-	у<л-1>(лг1) = yf"-1-),
т. е. в граничных точках заданы значения не только функции, но и
ее производных до порядка п — 1 включительно. Предположим, что
экстремум достигается на кривой у = у (х), дифференцируемой 2л раз,
и пусть у = у (х) — уравнение некоторой кривой сравнения, также
дифференцируемой 2п раз.
Рассмотрим однопараметрическое семейство функций
у(х, а) = у (х)-|-а [у (х) — у(х)] или у(х, а) — у (х) + абу.
При а = 0 у(х, а) = у(х), при а=1 у(х, а) —у(х). Если рас-
сматривать значение функционала v [у (х)] только на кривых семей-
ства у = у(х, а), то функционал превратится в функцию пара-
метра а, достигающую экстремума при а —0; следовательно,
-^-v[y(x, а)11а=о = О' Эта производная в соответствии с § 1
§ 41
ФУНКЦИОНАЛЫ ОТ СТАРШИХ ПРОИЗВОДНЫХ
309
называется вариацией функционала v и обозначается б-и:
6v =
г	-Ч
f F(x. У(х, а), у'(х, а).
,,	(х, a))dx
- а= 0
= f 6У + Fy, бу' + Fy, бу"+ ... + /> dy^dx.
Х>
Интегрируем по частям второе слагаемое в правой части один раз:
X,	*1
f Ру бу' dx = [Fy- бу— f 4xFy бу dx,
«/	«л.
Xg	JCq
третье слагаемое — два раза:
Xj	XJ
f Fy6y"dx = [Fy6y']2 —	+ f -^-Fy6ydx,
Xa	X° xa
и т. д., последнее слагаемое — n раз:
/F^"dx - v-X - [-h F^>	+  • •
X,	"
•V,
••• iF^dx'
Xo
Принимая во внимание граничные условия, в силу которых при
х = х0 и при х — х} вариации бу = бу' = бу" = ... =дУя“1> = 0,
окончательно получим
 +(-!>’ST
Так как на кривой, реализующей экстремум, имеем
= /(F> -	F>- +• +<->)' 5гМ-0
То
при произвольном выборе функции бу и так как первый множитель
под знаком интеграла является непрерывной функцией х на той же
кривой у = у (х), то в силу основной леммы первый множитель
тождественно равен нулю:
310 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
Итак, функция у = у(х), реализующая экстремум функционала
ц[у(х)] = уР(х, у, у', у", .... у<л))йх,
Го
должна быть решением уравнения
+  +<-1)”^г>> = 0.
Это дифференциальное уравнение порядка 2п носит название урав-
нения Эйлера—Пуассона, а его интегральные кривые называются
экстремалями рассматриваемой вариационной задачи. Общее решение
этого уравнения содержит 2п произвольных постоянных, которые
могут быть, вообще говоря, определены из 2п граничных условий:
у (*0)=у о- у' (*о)=у'о’ ’. у{п~'} (О=1;;
У(*1) = УР у' (*1) = у;..... у^п-х\х^ = у\п-^.
Пример 1. Найти экстремаль функционала
1
. v[y(x)] = pl+y"2)^;
о
у(0) = 0,	у'(0)=1.	У(1)=1.	/(!)=!•
d2
Уравнение Эйлера — Пуассона имеет вид (2у") = 0 или yiv = 0; его
общим решением является у = С^3 С2х2 -J- С3х -|- С4. Используя гранич-
ные условия, получаем:
С1 = 0, С2 = 0,	С3=1, С\ = 0.
Итак, экстремум может достигаться лишь на прямой у = х.
Пример 2. Определить экстремаль функционала
л
2
v[y(x)] = f (,y"2 — y2 + x2)dx,
о
удовлетворяющую условиям
у(0)=1,	у'(0) = 0, у(у)=0, у' (у) = -1-
Уравнение Эйлера — Пуассона имеет вид yiv — у = 0; его общим решением
является у = C2e~x-j- С3 cos х-4- С4 sin х. Используя граничные усло-
вия, получаем Ct = 0, С2 = 0, С3 = 1, С4 = 0. Итак, экстремум может дости-
гаться лишь на кривой у = cos х.
Пример 3. Определить экстремаль функционала
I
v [У (*)] = f (у ИУ"2 +ру)
-Z
§ 4]	ФУНКЦИОНАЛЫ ОТ СТАРШИХ ПРОИЗВОДНЫХ	31 1
удовлетворяющую граничным условиям:
у(-О = 0, /(-0 = 0. У(0 = 0, /(0 = 0.
К этой вариационной задаче сводится нахождение оси изогнутой упругой
цилиндрической балки, заделанной на концах. Если балка однородна, то р
и ц постоянны и уравнение Эйлера — Пуассона имеет вид
р + -А-(МУ") = О или yiv = _£.,
dx2	'	р.
откуда
У = —24ц "I"	4" CsX2 -|- С3х + Ct.
Используя граничные условия, окончательно находим
у °= _w(x4~2/2x2+/4) или y==-w(x2~/2)2
Если функционал v имеет вид -
v [у (х), z(x)\ — j F(x, у, у'.у(я), z. z'.z(m>)dx,
то, варьируя только у(х) и считая z(x) фиксированным, мы нахо-
дим, что функции у(х) и z(x), реализующие экстремум, должны
удовлетворять уравнению Эйлера — Пуассона
//	ип
а варьируя г(х) и считая у(х) фиксированным, получим, что те же
функции должны удовлетворять уравнению
F--hF-'+ - +<-D"^r^« = 0-
Итак, функции z(x) и у(х) должны удовлетворять системе двух
уравнений
и	,	>in
••• +(-1)Я^/>=0'
F’~iF’’+ •••
Точно так же можно рассуждать и при исследовании на экстре-
мум функционала, зависящего от любого числа функций:
У2....Уя1 =
*1
= fF(x- у г Уг > у\п'\ Уг у'2.y(24 ...
..., ут, у'...у^У) dx.
J т * т	* т /
312 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
Варьируя какую-нибудь одну функцию уДх) и сохраняя остальные
неизменными, получим основное необходимое условие экстремума
в виде
.	.^1
••• +Н);7У>() = °	(* = 1- 2..т).
dx 1	dx 1 у i
§ 5.	Функционалы, зависящие от функций нескольких
независимых переменных
Исследуем на экстремум функционал
и \z (х, у)] = f f F (х, у, z, ~dx dy,
причем на границе С области D значения функции z(x, у) заданы,
т. е, задан пространственный контур С, через который должны
проходить все допустимые поверхности (рис. 6.13). Для сокращения
«	dz dz ,	„ ,
записи обозначим:	-~ = q. Функцию г будем считать
трижды дифференцируемой. Поверхность z = z (х, у), на которой
реализуется экстремум, будем предполагать дважды дифференци-
руемой.
Рассмотрим опять однопараметрическое семейство поверхностей
z — z(x, у, a) — z(x, y)-{-abz, где 6z = z(x, у) — z(x, у), вклю-
чающее при а — 0 поверхность z — z (х, у), на которой реализуется
экстремум, а при а = 1 — некоторую допустимую поверхность
z = z(x, у). На функциях семейства г(х, у, а) функционал v пре-
§ 5] ФУНКЦИОНАЛЫ ОТ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ . 313
вращается в функцию а, которая должна иметь экстремум при а — 0;
следовательно, 4-v[z(x, у, а)] I,, п = 0. Называя в соответствии
да	'	'«= °
с § 1 производную от vfz(x, у, а)] по а при а = 0 вариацией
функционала и обозначая ее би, будем иметь:
У* У" F У, z (х. у, а), р (х, у, а), q(x, у, а)) dx dy I =
' D	'а=0
= f f + Fpf>pFqbq] dx dy,
' D '
где
z(x, y, a) = z(x, y)-\-abz,
,	dz (x, y, a) ,	. ,	,
p(x, у, a) =—Z_ = P(X> у)_|_абр,
,	. dz (x, у, a) ,	, , x
q(x, y, a) =—'—z-—- = q{x, y)-Fobq.
Так как
4-{F„dz} = 4~{FP} t>z + Fpt>p,
ax 1	p	’	ox 1 P'	p
[F. bz\ = 4~ {^1 + Fa bq,
dy 1	fl	1	dy 1 *1	*	7
то
f f (Fpbp + Fqbq)dxdy =
D '
= ,/
D
D
где	—так называемая полная частная производная по х.
При ее вычислении у считается фиксированным, но зависимость z,
р и q от х учитывается:
дх 1 Р> грх^‘ pz дх i^z рр дх^ рч дх
и аналогично
ду У dl 1 ?У И 1 qz дх ЧР ду ~ dd ду
По известной формуле Грина
f f (^r^'^~}dxcly== f (Ndy — Mdx)
'a	c
314 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
получим
f f\l& \Fp6z}	dv == [ (Fpdy — Fqdx)bz = 0.
d'	c
Последний интеграл равен нулю, так как на контуре С вариация
6z = 0, потом}' что все допустимые поверхности проходят через один
и тот же пространственный контур С. Следовательно,
f f U^bp + F^bq] dxdy=- f f	-1-4-bz dx dy.
* d'	D .
и необходимое условие экстремума
/ J (Fz bz + Fp bp 4- Fq bq) dx dy = 0
D
принимает вид
f f (F* —t 1^1 - -fry- 14))6г dx d>=°-
D
Так как вариация bz произвольна (на bz наложены лишь ограниче-
ния общего характера, касающиеся непрерывности и дифференци-
руемости, обращения в нуль на контуре Сит. д.), а первый мно-
житель непрерывен, то по основной лемме (стр. 296) на поверх-
ности z — z (х, у), реализующей экстремум,
Следовательно, z (х, у) является решением уравнения
Р.—
Это дифференциальное уравнение второго порядка в частных про-
изводных, которому должна удовлетворять функция z(x, у), реали-
зующая экстремум, носит название уравнения Остроградского
по имени выдающегося русского математика М. В. Остроградского,
который в 1834 году впервые получил это уравнение, однако
для прямоугольных областей D оно встречалось уже в работах
Л. Эйлера.
— Пример!.
v [z(x, у)] = f f [(|L)2 + (-g-)2] dx dy,
D
§ 5] ФУНКЦИОНАЛЫ ОТ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 315
на границе С области D значения функции г заданы: г = /(х, у), Уравне-
ние Остроградского в данном случае имеет вид
дх2 ду2 ’
или в краткой записи
Дг = 0,
т. е. является известным уравнением Лапласа, причём надо найти непрерыв-
ное в Р решение этого уравнения, принимающее заданные значения на гра-
нице области D. Это — одна из основных задач математической физики,
называемая задачей Дирихле.
П р и м е р 2.
v [г (х, у)] = f f	+ 2г/ (х, у)] dx dy,
D ’
на границе области D функция г задана. Уравнение Остроградского в дан-
ном случае имеет вид
д2г , д2г _
дх2 + ду2 ~ f ^х’ у)’
или в краткой записи
Дг = /(х,у).
Это уравнение, называемое уравнением Пуассона, также весьма часто встре-
чается в задачах математической физики.
Пример 3. Задача о нахождении поверхности минимальной площади,
натянутой на данный контур С, сводится к исследованию на минимум функ-
ционала
- SUU. у»-///' + (»’+(»’
D
Уравнение Остроградского в данном случае имеет вид
х (' р ! 1 q	]-о
дх j К1 + р2 + <72 / ду | |/1 + р2 + ?2 I
Г. ।	<> dz дг д2г |^Г Ztein
дх2 [	\ ду / J дх ду дхду' ду2 \ дх ' ]	’
т. е. средняя кривизна в каждой точке равна нулю. Известно, что физиче-
ской реализацией минимальных поверхностей являются мыльные пленки,
натянутые на заданный контур С.
Для функционала
«кСч. х2.......*„)]==
^ff-f F(XP х2.............Хп’ Z’ Pl’ Pi’ • • •> Pn)dxldx2 • • • dxn’
D
316 МЕТОД ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. в
dz	А
где pi = -^~, из основного необходимого условия экстремума
до == 0 совершенно аналогично получим следующее уравнение Остро-
градского:

которому должна удовлетворять функция
, z = z(xv х2.........х„).
реализующая экстремум функционала V.
Например, для функционала
’=ЛЛШ+(>Г+(>)>^
D
уравнение Остроградского имеет вид
d2u . д2и . д2и _________„
дх2 ’ ду2 ' dz2
Если подынтегральная функция функционала о зависит от произ-
водных более высокого порядка, то, применяя несколько раз пре-
образования, использованные при выводе уравнения Остроградского,
в качестве необходимого условия экстремума получаем, что функция,
реализующая экстремум, должна удовлетворять уравнению, аналогич-
ному уравнению Эйлера—Пуассона (стр. 310).
Например, для функционала
v[z(x, y)]=f f f(x, у. z,	^Adxdy
J J '	dx dy dx2 dxdy dy2)	'
D
получим уравнение
IM —IM 4- £ IM + IM + ^- IM = 0.
где
__ dz _____ dz ______ d2z ' ' d2z .______ d2z
P dx ’ dy ’ Г dx2 ' S dxdy ’ dy2
Этому уравнению четвертого порядка в частных производных должна
удовлетворять функция, реализующая экстремум функционала v.
Например, для функционала
D
§ 6]	ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ	317
функция z, реализующая экстремум, должна удовлетворять так на-
зываемому бигармоническому уравнению
+ —= 0
дх'^ дх2 ду‘ ^ оу'
которое обычно кратко записывается так: AAz=0.
Для функционала
D
функция z(x, у), реализующая экстремум, должна удовлетворять
уравнению khz == f (х, у).
К бигармоническому уравнению приводят также задачи на эк-
стремум функционала
о
или функционала более общего вида
V= Г +	(/£_yn dxdy,
J J \\ дх2 1 ду2 / v [ дх2 ду2 дх ду / J J J
D
где р,— параметр.
§ 6.	Вариационные задачи в параметрической форме
Во многих вариационных задачах решение удобнее искать в параметри-
ческом виде. Например, в изопериметрическои задаче (см. стр. 282) о на-
хождении замкнутой кривой заданной длины I, ограничивающей максималь-
ную площадь S, неудобно искать решение в виде у => у (х), так как по
самому смыслу задачи функция у (х) неоднозначна (рис. 6.14), поэтому в
рассматриваемой задаче целесообразно искать решение в параметрической
форме: х — х (/), у = у (0- Следовательно, в данном случае надо искать
экстремум функционала
Т
•S [х (О, У (01 = 4" У* — У*) dt
о
т
при наличии условия Z = J" |/х2 4- у2 d/, где I — постоянная,
о
Пусть при исследовании на экстремум некоторого функционала
v [у (х)] =- J F(x, у, у') ах
Хъ
318 МЕТОД ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
оказалось более целесообразным искать решение в параметрической форме
х — х (t), у = у (0; тогда функционал преобразуется к следующему виду:
х (0 dt.
v [х (0, У (0) = I" F\x (0, у (0, 4-
t\
Заметим, что полученная после преобразования переменных подынтеграль-
ная функция
х (0, У (0. х (0
X (0 /
не содержит t явно и является по отношению к переменным хи 'у одно-
родной функцией первой степени однородности.
Таким образом, функционал v [х (0, у (0] является не произвольным
функционалом вида
J Ф (Л X (0, у(0, X (0, У(0)Л
t,
зависящим от двух
такого функционала, так как
функций х (0 и у (0, а лишь весьма частным случаем
его подынтегральная функция не содержит
явно t и однородна первой степени однород-
ности по отношению к переменным х и у.
Если бы мы перешли к какому-нибудь
другому параметрическому представлению
искомой кривой х = х (т), у у (т), то
функционал v [х, у] преобразовался бы к
Ti .	-у
/• „ /	Ух \	w г-
виду / г ( х, у, —г- I х dt. Следователь^
То
но, подынтегральная функция функциона-
ла v не меняет своего вида при изменении
параметрического представления кривой.
Таким образом, функционал v зависит от
вида кривой, а не от ее параметрического
представления.
Нетрудно убедиться в справедливости следующего утверждения: если
подынтегральная функция функционала
v[x(t), у (0] = х (0, у (0, Х(0, y(t))dt
не содержит t явно и является однородной функцией первой степени одно-
родности относительно х и у, то функционал v [х (0, у (0] зависит лишь
от вида кривой х = х (0, у = у (0, а не от ее параметрического представ-
ления. Действительно, пусть
t,
v[x(0, у (0] = Г Ф (х (0, у (0, х(0, y{t)),dt,
to
§ 6)	ВАРИАЦИОННЫЕ ЗАДАЧИ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ	319
где
Ф(х, у, kx, ky) АФ (х, у, х, у).
Перейдем к. новому параметрическому представлению, полагая
т=<р(О (ф(Т)^О), х=х(т), у = у (т).
Тогда
Л	т,
ГФ(х(<), У (О •*(/), y(t))dt = /* Ф(х(т), у (т), хт(т)ф(О. Ут(т)ф(/))-ДЬ
J 	J	<р(П‘
t	То
В силу того, что Ф является однородной функцией первой степени одно-
родности относительно х и у, будем иметь
Ф (х, у, хт<р, ут<р) = <рФ (х, у, хт, ут),
откуда
6	Т,
У*ф(х, у,хе yt)dt — j* Ф (х, у, хт, yT)dr,
h	То	'
т. е. подынтегральная функция не изменилась при изменении параметри-
ческого представления.
Длина дуги J* /х2 + у1 dt *), площадь, ограниченная некоторой кривой
4)
-j- у (ху— ух) dt, являются примерами таких функционалов.
<0
Для нахождения экстремалей функционалов рассматриваемого типа ,
г,
V [х (/), у (Z)] = J Ф (х, у, х, у) dt,
4)
где Ф — однородная функция первой степени однородности относительно х
и у, как и для функционалов с произвольной подынтегральной функ-
цией Ф(Л х, у, х, у), надо решить систему уравнений Эйлера
Фг—^Ф.=0;
at х
ф —-£ф.
у dt у
= 0.
Однако в рассматриваемом частном случае эти уравнения не являются
независимыми, так как им должны удовлетворять наряду с некоторым ре-
шением х = х (Z), у == у (Z) и любые другие пары функций, дающие другое
параметрическое представление той же кривой, что в случае независимости
уравнений Эйлера привело бы к противоречию с теоремой существования
*) Функция V^x2 -|- у2 является положительно однородной первой сте-
пени однородности, т. е. для нее условие F (kx, Ay) = kF (х, у) удовлетво-
ряется лишь при положительных k, однако этого вполне достаточно для
справедливости излагаемой в этом параграфе теории, так как при замене
переменных с =<}>(/) можно считать <p (Z)>0.
320 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 6
и единственности решения системы дифференциальных уравнений (см. стр. 75).
Это указывает на то, что для функционалов вида
v [х (0, У (01 = j Ф (х, у, х, у) dt,
ta
где Ф— однородная функция первой степени однородности относительно х
и у, одно из уравнений Эйлера является следствием другого. Для нахож-
дения экстремалей надо взять одно из уравнений Эйлера и проинтегриро-
вать его совместно с уравнением, определяющим выбор параметра. Напри-
мер, к уравнению Ф*— х = 0 можно присоединить уравнение
х2-|-у2 = 1, указывающее, что за параметр взята длина дуги кривой.
§ 7. Некоторые приложения
Основным вариационным принципом в механике является принцип
стационарного действия Остроградского — Гамильтона, утверждающий,
что среди возможных, т. е. совместимых со связями, движений си-
стемы материальных точек в действительности осуществляется дви-
жение, дающее стационарное значение (т. е. значение, соответ-
ствующее аргументу, для которого вариация функционала равна нулю)
интегралу
t,
f (Г — U) dt,
t,
где Т—кинетическая, а I) — потенциальная энергия системы.
Применим этот принцип к нескольким задачам механики.
Пример I. Дана система материальных точек с массами (Z = 1,
2, .... п) и координатами (х;, у,, х,), на которую действуют силы Т7,, обла-
дающие силовой функцией (потенциалом) — (7, зависящей только от коор-
динат:
F	F	F =
Iх dxt ’ ty dy, ’ iz dzt ’
где F x, Fy, F z — координаты вектора Ft, действующего на точку
(х;, у(-, г,). Найти дифференциальные уравнения движения системы. В дан-
ном случае кинетическая энергия
п
а потенциальная энергия системы равна U. Система уравнений Эйлера для
интеграла
ftr — U)dt
ta
5 П
имеет вид
некоторые Приложений
321
_ ди _	d7~ _ 0. _ °и _ тт_ = 0. _ dU______________L dT „ о
dxi dt d'xi ’ dyt dt dyt ’ dzt dt dzt
или
—f^-0; и^-FycO;' —Лг=-0
(/= 1, 2,..., л).
Если бы движение было подчинено еще некоторой системе независимых
связей
q>;(f, Х„ хг....х„. у1( уг....уп, г„ г2....z„) = О
(/= 1, 2, ..т, т < Зл),
то из уравнений связей можно было бы выразить т переменных через
Зл — т независимых переменных (не считая времени I) или выразить все Зл
переменных через Зл — т новых, уже независимых, координат
71> ?2> • • • . Чзп-т-
Тогда Т и U можно было бы также рассматривать как функции
?i> ?2...Язп-т и *•
Т ~ Т (71- 7зл-т' 71’ 7г>>*-> Чзп-т.’ *)>
и^и (qv q3......7зл-т> 0>
и система уравнений Эйлера имела бы вид
d4i d* dqt
Пример 2. Выведем дифференциальное уравнение свободных коле-
баний струны.
Поместим начало координат в один из концов струны. Струна в со-
стоянии покоя под влиянием натяжения расположена вдоль некоторой пря-
мой, по которой направим ось абсцисс (рис. 6.15). Отклонение от положения
равновесия и (х, t) будет функцией
абсциссы х и времени t.	ки
Потенциальная энергия U эле-
мента абсолютно гибкой струны про-
порциональна растяжению струны.
Участок струны dx в деформирован-
ном состоянии, с точностью до беско-
нечно малых более высокого поряд-	У °
К- 72	____
1 + их dx J
и, следовательно, удлинение элемента
равно {У I 4-«^2 — 1) dx. По форму-	рис. е.15.
1 /	7%	, 1 ,2
ле Тейлора у Ц-их «
Считая их малым и пренебрегая более высокими степенями их> полу»
чим, что потенциальная энергия элемента равна kiix dx, где h — множитель
322 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
пропорциональности, а потенциальная энергия всей струны равна
f *u'*dx.
о
Кинетическая энергия струны равна
о
fl
где р — плотность. Интеграл J" (Т — U) dt имеет в данном случае вид
v= У* у [у р«/'2 — j dx dt.
t, a
Уравнение движения струны будет уравнением Остроградского для функ-
ционала V. Итак, уравнение движения струны имеет вид
Если струна однородна, тори k — постоянные, и уравнение колеблющейся
струны упрощается:
д2и . д2и
Р dt2 дх2
Допустим теперь, что на струну действует еще внешняя сила f(t, х), пер-
пендикулярная к струне в ее положении равновесия и рассчитанная на еди-
ницу массы. Как легко проверить, силовая функция этой внешней силы,
действующей на элемент струны, равна р/(/, x)udx; следовательно, ин-
теграл Остроградского — Гамильтона
(J) dt имеет вид
У У* [у ри/ — 7 kux + Р/ (* x)u^dxdt,
О
а уравнение вынужденных колебаний струны
(р“3 ~ i W ~р/ (г> х)=°-
или, если струна однородна,
дги k д2и . .. .
Совершенно аналогично может быть получено уравнение колеблющейся
мембраны.
Пример 3. Выведем уравнение колебаний прямолинейного стержня.
Направим ось абсцисс по оси стержня, находящегося в положении равнове-
sn
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
323
сия. Отклонение от положения равновесия и (х, t) будет функцией х и вре-
мени t, кинетическая энергия стержня длины I
. Т — — I" puf dx.
о'
Будем считать стержень нерастяжимым. Потенциальная энергия упругого
стержня при постоянной кривизне пропорциональна квадрату кривизны.
Следовательно, дифференциал dU потенциальной энергии стержня равен
dU — ^k
д*и
дх*
а потенциальная энергия всего
говоря, переменна, будет равна
стержня, кривизна оси которого, вообще
U
д*и
дх*
dx.
Предположим,
' / ди \2
членом I
что отклонения стержня от положения равновесия малы и
в знаменателе можно пренебречь; тогда
i
Интеграл Остроградского — Гамильтона имеет вид
л '
о
Следовательно, в случае свободных колебаний упругого стержня будем иметь
следующее уравнение движения:
4(рФ>кн
Если стержень однороден, то р и k — постоянные, и уравнение колебаний
стержня преобразуется к виду
д*и , . дла _
Р dt* + k дх* “°'
Если на стержень действует внешняя сила f(t, х), то надо еще учесть
потенциал этой силы (см. предыдущий пример).
Принцип стационарного действия может быть применен при выводе
уравнений поля. Рассмотрим скалярное, векторное или тензорное
324 МЕТОД ВАРИАЦИИ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ 1ГЛ. в
поле щ> = тг>(х, у, z, f). Интеграл j (Т — U)dt в данном случае,
tfi
вообще говоря, будет равен четырехкратному интегралу по простран-
ственным координатам х, у, z и по времени t от некоторой функ-
ции L, называемой плотностью функции Лагранжа или лагран-
жианом.
,	dw dw ow dw .
Обычно лагранжиан является функцией w.	:
,	, / dw dw Ow 0w\
L==L\W' SI' S^' SI' St]'
»
и, следовательно, действие имеет вид
Г Г Г Г г I dw Ow dw dw\ , , , .. е
J J J J L(w' Sx’ Sr SI’ -or)dxdydzdt. (6.3)
D
Согласно принципу стационарного действия уравнение поля является
уравнением Остроградского для функционала (6.3):
~ SI 1 ~ Sy Ы ~SI {М ~ St 14) = °’
где
Ow	Ow	Ow	ow
dx *	dy * ^3 dz ’	di
Задачи к главе 6
1.	Найти экстремали функционала
ч [>(*)]= J	—dx.
Хо
2.	Исследовать на экстремум функционал
МУ (*)] = J (yJ + 2xyy')dx; у(х9) = у0; y(Xi) = y1.
3.	Исследовать на экстремум функционал
1
= J (ху + у2—2у2у') dx-, у(0) = 1; у(1) = 2,
о
4.	Найти экстремали функционала
v (У («)] = J у' (1 + x2y')dx.
ЗАДАЧИ К ГЛАВЕ 6
325
5.	Найти экстремали функционала
и [у (х>] = у (уА ч- -УУ' — 16/) </х.
х0
6.	Найти экстремали функционала
X,
V [у (х)] = J (ху' + y/2)dx.
Ха
7.	Найти экстремали функционала
X,
v[y(x)]~f ±±f-dx.
Хо
8.	Найти экстремали функционала
Xi
v [у (х)] « J (у' 4- у'2 — 2у sin х) dx.
ХР
9.	Найти экстремали функционала
v (У G41 = J* (1 бу2 — у"2 + х2) dx.
10.	Найти экстремали функционала
v[yWI = J (2ху + у'"2) dx.
«о
11.	Найти экстремали функционала
. v [у (х), г (х)] = J" (2уг — 2у2 4- у'! — г'2) dx.
к.
12.	Написать уравнение Остроградского для функционала
V [г (X. у)] = f f [(-« У - (Ay ] dx dy.
D
13.	Написать уравнение Остроградского для функционала
v |« (X, у. г)) = f f f [(Ay + (-g-)' + (A-)' + 2U/ (x, y, x)] dx dy dx
b
14.	Найти экстремали функционала
X.
V l> U)] = У* A- dx.
Хй
326 МЕТОД ВАРИАЦИЙ В ЗАДАЧАХ С НЕПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. в
15.	Найти экстремали функционала
v [у (х)] = (у2 + у'2 + 2уех) dx.
Xq
16.	Найти экстремали функционала
v [У (*)) = /‘(у2 — У'2 — 2у sin •*) dx.
Ха
17.	Найти экстремали функционала
v[y(x)] = J [у2 + (У')2 + -^] dx.
18.	Найти экстремали функционала
X,
V [у (*)] = J [х2 (у')2 + 2у2 + 2ху] dx.
Хо
19.	Найти экстремали функционала
v [у (х)1 = J [(У")2 — 2 (у')2 + у2 — 2у sin х] dx.
Xd
20.	Найти экстремали функционала
Xi
v ly (*)] = J* l(y"')2 + У2 — 2yx3j dx.
Хо
ГЛАВА 7
ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ
И НЕКОТОРЫЕ ДРУГИЕ ЗАДАЧИ
§ 1. Простейшая задача с подвижными границами
В главе 6 при исследовании функционала
Xi
v = j' F(x, у, y')dx
предполагалось, что граничные точки (х0, у0) и (х,, yt) заданы.
Предположим теперь, что одна или обе граничные точки могут
перемещаться. Тогда класс допустимых кривых расширяется, — кроме
кривых сравнения, имеющих общие граничные точки с исследуемой
кривой, можно уже брать и кривые со смещенными граничными
точками.
Поэтому если на какой-нибудь кривой у = у(х) достигается
экстремум в задаче с подвижными граничными точками, то экстремум
тем более достигается по отношению к более узкому классу кривых,
имеющих общие граничные точки с кривой у = у(х), и, следова-
тельно. должно быть выполнено основное, необходимое для достиже-
ния экстремума в задаче с неподвижными границами условие —
функция у(х) должна быть решением уравнения Эйлера
Fy — -4-Fy =0.
у dx *
Итак, кривые у = у(х), на которых реализуется экстремум в задаче
с подвижными границами, должны быть экстремалями.
Общее решение уравнения Эйлера содержит две произвольные
постоянные, для определения которых необходимо иметь два условия.
В задаче с неподвижными граничными точками такими условиями были
У (х0) == Уо « У (-«1) = У1-
328 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 7
В задаче с подвижными границами одно или оба эти условия отсут-
ствуют и недостающие условия для определения произвольных по-
стоянных общего решения уравнения Эйлера должны быть получены
из основного необходимого условия экстремума — равенства нулю
вариации fyv.
Так как в задаче с подвижными границами экстремум достигается
лишь на решениях у=у(х, Сх, С2) уравнения Эйлера, то в даль-
нейшем можно рассматривать значение функционала лишь на функциях
этого семейства. При этом функционал т<[у(х, Ср С2)] превращается
в функцию параметров С, и С2 и пределов интеграции х0 и, х1(
а вариация функционала совпадает с дифференциалом этой функции.
Для упрощения будем считать, что одна из граничных точек, например
(х0, у0), закреплена, а другая (xj, yt) может перемещаться и пере-
ходит в точку (xj -|- Axj, yj-j-Ayj), или, как обычно обозначают
в вариационном исчислении, (Xj-j-dXj, уг -1- ду;).
Допустимые кривые у = у(х) и у = у(х)-|-ду будем считать
близкими, если модули вариаций ду и ду' малы, "и малы модули
приращений dxj и ду, (приращения 6х} и ду] обычно называют
вариациями предельных значений хг и yj).
Экстремали, проходящие через точку (х0, у0), образуют пучок
экстремалей у = у(х, С^. Функционал и[у(х, С[)] на кривых этого
пучка превращается в функцию Сг и хР Если кривые пучка
у = у(х, Сг) в окрестности рассматриваемой экстремали не пересе-
каются, то и[у(х, Cj)] можно рассматривать как однозначную функ-
цию Xj и ур так как задание Xj и yj определяет экстремаль пучка
(рис. 7.1) и тем самым определяет значение функционала.
Вычислим вариацию функционала и [у (х, С,)] на экстремалях
пучка у = у (х, Cj) при перемещении граничной точки из положения
ХХр yj) в положение (х, -|- дх,, у\ -ф- дуj). Так как функционал v на
кривых пучка превратился в функцию Xj и yj, то его вариация
§ J) простейшая задача с подвижными границами '	329
совпадает с дифференциалом этой функции. Выделим из прираще-
ния Ат» главную линейную по отношению к 6xj и 6уг часть:
г,+бх,	х,
д-и— J F(x, уЧ-бу, у' 4- бу') dx -*• J F(x\ у, y')dx =
X)	х^
х,+бх,
= / F{x. у 4- бу, у' +6y')dx +
Xi
-4- J [F(x, у4-бу, y'+V) — F(x, у, y')]rfx. (7.1)
Первое слагаемое правой части преобразуем с помощью теоремы
о среднем значении:
Х,+бх,
J F(x. у 4-бу. y'4-6y')dx =	где 0 < 0 < I.
Xi
в силу непрерывности функции F будем иметь:
= У- УЧ=хЛеР
где et -» 0 при бХ] —> О и бу, -> 0.
Итак,
х, + бх,
J F(x, у 4-бу, у' 4- бу') dx = F (х, у. у')| бх, +-e,6xv
X,
Второе слагаемое правой части (7.1) преобразуем путем разложения
подынтегральной функции по формуле Тейлора
«I
У' + бу') — F(x, у, y')]dx =
Хо
Л)
= J [/’у (х, у, у') бу 4- РУ’ (х. у, y'}?>y'l dx 4- /?1,
х>
где /?j является бесконечно малой более высокого порядка, чем бу
или бу'. В свою очередь линейная часть
х,
J* (Fyby + FV’by')dK
330 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 7
может быть преобразована путем интеграции по частям второго сла-
гаемого подынтегральной функции к виду
ч
f (F.-^F^dx.
Хо
Значения функционала берутся лишь на экстремалях, следовательно,
Ру—Fy' s0. Так как граничная точка (х0. у0) закреплена,
то бу I = 0. Следовательно,
J (Л-бу + ^у'бу'Мх^^у.бу]^.
Заметим, что бу I* не равно бух — приращению ур так как бух —
это приращение при перемещении граничной точки в положение
(Xj-f-бхр У1~НбУ1), а бу|х=л.—это приращение ординаты в
,iO4Ke X] при переходе от экстремали, проходящей через точки
(х0, Уо) и (xi- У1) к экстремали, проходящей через точки (х0, у0)
и(х14-бх1. У] -j-бУ]) (рис. 7.2).
Из чертежа видно, что ВО = бу|л_х; FC — byf,
ЕС « у (х^бхр BD — FC — EC
или
6y|x=Xi	У (^1)6X1-
При этом приближенное равенство справедливо с точностью до бес-
конечно малых более высокого порядка.
§ 1]	ПРОСТЕЙШАЯ ЗАДАЧА С ПОДВИЖНЫМИ ГРАНИЦАМИ' 331
Итак, окончательно имеем: J* F dx F |X=X1 6xf,
Г,
•ч
J [F(x, у + бу, у'Н-бу')—F(x, у, y')]dx^
» РУ U=x, • (6У1 — У' <*1> дх1)'
где приближенные равенства также справедливы с точностью до
членов порядка выше первого относительно бл^ и бур Следовательно,
из (7.1) получим
6v = F |Л=Х1 бХ1 + Fr 1Ж=Ж1 (&У1 — У' (*1) 6*1) =
= У'Ру) |Х=Л| 6*14- Fv> |Л=Х1 буг
или
dv (х1( yj) = (F — у'Fy’) |X=X1 dXi 4- Fy’ |Х=Л1 dyx,
где v(Xj, у,) — функция, в которую превратился функционал v на
экстремалях у = у(х, Cj), a dxx = Axi — бхр dy1=Ay1=6y1 —
приращения координат граничной точки. Основное необходимое
условие экстремума 6v = 0 приобретает вид
/ (F - y'Fy.) |ж=Л| 6X1 + Ру |Х=Л1 бу, = 0. /	(7.2)
Если вариации 6xi и 6уг независимы, то отсюда следует, что
(Р-у'РУ’)\х=х=0 и Fy4,=X1 = 0.
Однако чаще приходится рассматривать случай, когда вариации бХ]
и бу! зависимы.
Пусть, например, правая граничная точка (хп ух) может пере-
мещаться по некоторой кривой
У1=ф(Х1).
Тогда 6yi»<р'(Xi) 6xj и, следовательно, условие (7.2) принимает
вид [F (<р' — у') Fy’] 6X1 = 0 или, так как 6xi изменяется произ-
вольно, то [F -(<р' — у') Fyl] х^х =0. Это условие устанавливает
зависимость между угловыми коэффициентами ф' и у' в граничной
точке. Оно называется условием трансверсальности.
Условие трансверсальности совместно с условием У1=ф(х0 по-
зволяет, вообще говоря, определить одну или несколько экстоема-
лей пучка у~у(х, Сх), на которых может достигаться экстремум
Если граничная точка (х0, у0) может перемещаться по некоторой
кривой Уо —Ф(х0), то совершенно так же обнаружим, что и в точке
(х0, Уо) Должно удовлетворяться условие трансверсальности
[F + W'-yVy'U^O.
332 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 7
Пример 1. Найти условие трансверсальности для функционалов вида
v = J" Л (х, у) V 1 + У/3 dx.
Xi
Условие трансверсальности F + Ру, (<₽' — у') =0 имеет в данном случае вид
и/г Vi	Л (Л’ •у)у' / /	п Л(х, у)(1+q>'y')	_
А (х у) у 1 + у Н .	 (<р' — у') = 0 или -;=-~ -------= 0;
V1+у	У1+у
предполагая, что А (х, у) =/= 0 в граничной точке, получим 1 + у'<р' =0 или
у' -= —, т. е. условие трансверсальности свелось в данном случае к ус-
ловию ортогональности.
х, _______________________________________________________________
Пример 2. Исследовать на экстремум функционал f J—Li_Z_ rfx,
о У
причем у (0) = 0, а у( =» X]—5 (рис. 7.3). Интегральными кривыми уравне-
ния Эйлера (пример 1, стр. 324) являются окружности (х — Cj)2 -j- у2 = С2.
Первое граничное условие дает = С2. Так как условие трансверсальности
для данного функционала сводится к условию ортогональности (см. преды-
дущий пример), то прямая yi — xt — 5 должна быть диаметром окружности
и, следовательно, центр искомой окружности находится в точке (0, 5) пере-
сечения прямой yi = X!—5 с осью абсцисс. Следовательно, (х — 5)2 4-у2=
= 25, или у = ± V 10х — х2. Итак, экстремум может достигаться лишь на
дугах окружности у = Y 10х — х2 и у = — К 10х — х2.
Если граничная точка (хр yt) может перемещаться лишь по вер-
тикальной прямой (рис. 7.4) и, следовательно, dXj = 0, то усло-
вие (7.2) переходит Ъ Fy |х = 0.
Пусть, например, в задаче о брахистохроне (см. стр. 304) левая гранич-
ная точка закреплена, а правая Может перемещаться по вертикальной
прямой.
§ 1)	ПРОСТЕЙШАЯ ЗАДАЧА С ПОДВИЖНЫМИ ГРАНИЦАМИ	333
/2
— dx являются циклоиды, урав-
нения которых, если
вид
Экстремалями функционала U=J
о
принять во внимание условие у (0) = 0,' будут иметь
х — Ci(t — sin t),
у = Ci (1 — cos t).
Для определения С,
случае имеет вид
используем условие Fv, I	= 0, которое в данном
У 'Х—Х[
У у /1+у'2
откуда у' (Xj) =0, т. е. искомая циклоида должна пересекать прямую х~ х}
под прямым углом и, следовательно, точка x—xlt y = yt должна быть
вершиной циклоиды (рис. 7.5). Так как вершине соответствует значение
t — л, то Х| = С!л, Ci = Следовательно, экстремум может реализоваться
лишь на циклдиде
x — -~(i— sinZ); у = ^-(1—cos <)•
Если граничная точка (хх, уг) в задаче об экстремуме функцио-
•и
нала v= J" F (х, у, y')dx может перемещаться по горизонтальной
Хо
прямой у = ур то ду1 = О и условие (7.2), или условие трансвер-
сальности, принимает вид

334
ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ
[ГЛ. 7
§ 2. Задача с подвижными границами
для функционалов вида J F(x, у, г, у', z')dx
Если при исследовании на экстремум функционала
v = J F(x, у, z, у', z')dx
лг,
одна из граничных точек, например B(xv ур zt), перемещается,
а другая, А (х0, у0, z0), неподвижна (или обе граничные точки под-
вижны), то очевидно, что экстремум может достигаться лишь на инте-
гральных кривых системы уравнений Эйлера
Fy-i/’r-o; F,-ir,. = o.
Действительно, если на некоторой кривой С реализуется экстремум
в задаче с подвижными границами, т. е. достигается максимальное
или минимальное значение v по сравнению со значениями v на всех
близких допустимых кривых, среди которых находятся как кривые,
имеющие общие граничные точки с кривой С, реализующей экстре-
мум, так и кривые, у которых граничные точки не совпадают с гра-
ничными точками кривой С, то тогда подавно на кривой С дости-
гается экстремум по отношению к более узкому классу близких
кривых, имеющих общие граничные точки с кривой С.
Следовательно, на кривой С должны удовлетворяться необходи-
мые условия экстремума задачи с неподвижными граничными точками,
и, в частности, кривая С должна быть интегральной кривой системы
уравнений Эйлера.
Общее решение системы уравнений Эйлера содержит четыре
произвольные постоянные. Зная координаты граничной точки
А (х0, у0, z0), которую мы считаем неподвижной, можно, вообще
говоря, исключить две произвольные постоянные.
Для определения двух других произвольных постоянных необхо-
димо иметь еще два уравнения, которые будут получены из условия
dv = 0, причем при вычислении вариации мы уже будем считать, что
функционал задается лишь на решениях системы уравнений Эйлера,
так как только на них может достигаться экстремум. При этом
функционал v превращается в функцию Ф(хр ур zj координат хр
ур точки Z?(Xp Ур zA), и вариация функционала превращается
в дифференциал этой функции *).
*) Функция Ф будет однозначной, если экстремали пучка с центром
в точке А не пересекаются, так как тогда точка В yb zt) однозначно
определяет экстремаль.
$ i]	ЗАДАЧА С ПОДВИЖНЫМИ ГРАНИЦАМИ	,	335
Вычисление вариации v может быть проведено совершенно гак
же, как на стр. 328 — 331:
«ч+йх,
Дт»= J F (х, y4-dy, z^-bz, у'4-бу', z'-\-bz'~)dx—
Же
Ж,
— J* F(x, у, z, у', z')dx —
Xi 4-OXj
= J F(x, y-\-by, z-]-bz, y'-\-by', z' -\-bz')dx-\-
Xi
4- J [F (x, y4-dy, z-}-bz, у'4-буЛ, z'-j-bz') —
Xi
— F(x, y, z, y', z')}dx.
Применим теорему о среднем значении к первому интегралу и вос-
пользуемся непрерывностью функции F, а во втором интеграле
выделим главную линейную часть с помощью формулы Тейлора.
После этих преобразований получим
bv = F |x=Jfi dx, + J [Fyby 4- Рг bz -Ь Fy’ by' -(- Fy bz'l dx.
Интегрируя по частям два последних слагаемых, стоящих под знаком
интеграла, будем иметь:
bv = F |ХвЖ16Xj 4- [fy 4~ l^' bz]x=Xt 4-
+ J	—я- '’>)б4лх-
Ха
Так как значения v вычисляются лишь на экстремалях» то
Fy —/-Fy-==0; F2-Af2,=0
у dx у	‘dx
и, следовательно,
= F | дх, 4- [Fy- ду] 4- [Рг- bz]
-V — Л |	Л— XV |	“'**1
Рассуждая так же, как и на стр. 330, получим
ду|Л=Л|—ду,—y'UJdxj и д;? | Ж=Ж1 »д2, — z'txjbxy
и, следовательно,	v
bv = [F — y'Fy — z'Fz’]x~Xi dxi 4- Fy |Ж!=Л1 dy, 4- Fy |	= 0.
336 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 7
Если вариации дх,, dy,, дат, независимы, то из условия дд = 0 по-
лучаем
[F-y'^-2^1,=x, = 0; /у[х=Л1 = 0 и ^.|л=х=0.
, Если граничная точка В(хг, у,, г,) может перемещаться по не-
которой кривой у! = <р(хг); z = ty(xl), то ду, =ф/(х,)дх1> a t>zl =
(х1)дх1 и условие дд —О или
[F — y'Fy — z'FZ'\x^Xidx, + Fy |x=Jt]dy, -I- F у |ж=х_dz, = 0
переходит в условие
[F 4- (ф' — у') Fy -И (ф' — z') By]x=Xi dx, = 0.
откуда в силу произвольности дх, получим
[^4- (ф' - /) Fy + (Ф' - z')Fy\x_X{ = о.
Это условие носит название условия трансверсальности в задаче
об исследовании на экстремум функционала
х,
v = f F(x, у, z, у', z')dx.
К-,
Условие трансверсальности совместно с уравнениями у,==ф(х,)
д, = ф(х,) дает недостающие уравнения для определения произволь-
ных постоянных в общем решении системы уравнений Эйлера.
Если граничная точка fi(x,, у,, гг) может перемещаться по не-
которой поверхности z^tp ixy у,), то дд, = ф^дх, 4 фу ду,, при-
чем вариации дх, и (>у1 произвольны. Следовательно, условие дд = 0
или, в развернутом виде,
[F — y'Fy — 2/F^)x=x 6x14-Fy |ж=ж ду, 4-^г'1ХжХ дд,= 0
преобразуется в условие
tF-y'Fy.-z'F, +фЛ,|ж=, дх, 4[Fy 4FXL=Xi6yt = 0.
Отсюда в силу независимости дх, и ду, получим
[г-уг,++
Эти два условия вместе с уравнением z, =ф(х,, у,), вообще говоря,
дают возможность определить две произвольные постоянные в общем
решении системы уравнений Эйлера.
Если подвижной является граничная точка А (х0, у0, z0), то тем же
методом в этой точке получим совершенно аналогичные условия.
$ 21
ЗАДАЧА С ПОДВИЖНЫМИ ГРАНИЦАМИ
337
Если рассмотреть функционал
® = / ?(х. Уг У2, ... Уп. Уу У2..............yn)dx.
г,'
то без изменения метода доказательства получим, что в случае под-
вижной точки В (Ху уи, у21, .... уя1) в этой точке
бх, + 2 F ,
( = Н yi
Ъуа = О.
Х = Х,
Пример 1. Найти условие трансверсальности для функционала
v = J* /1 (х, у, г) У1 4- у'2 + г'2 dx, если zt *= <p (xt, у,).
Условия трансверсальности
р- УЛ' +К~ г')Л’1х=х, = ° и PV + ^'Ч’уЬ=х, = 0
в данном случае имеют вид 1 -|- <f'xz' = 0 и у' +	= 0 при х = х, или
1	у' г’
—Г =	=------при х = Ху т. е. являются условием параллельности вектора
<Рх	Чу _~1
касательной t (1, у', г') к искомой экстремали в точ-	_______
ке (Ху уу г{) и вектора нормали -V <ру, —1) к по-	____
верхности г — <р (х, у) в той же точке. Следова- ’
тельно, условие трансверсальности становится в	Ш
данном случае условием ортогональности экстремали
к поверхности г = <р (х, у).
Пример 2. Найти экстремальное расстояние	/
между двумя поверхностями	/
z — (₽ (х, 'у) и г — ф (х, у).	/ S
Иначе говоря, найти экстремум интеграла
X,_____________ JI
Z- f /1 + у'2 + х'2 dx при условии, что коорди-
х
наты одной из граничных точек (х0. у0, га) удовлет- -------
воряют уравнению г0 — <р(х„ у0), а координаты дру-	р	„„
гой граничной точки (х1 уу гг) удовлетворяют	гис> '•а
уравнению z{ — тЦхг У<)-
Так как подынтегральная функция зависит лишь от у' и г‘, го экстре-
малями являются прямые линии (см. пример 2, стр. 307) Так как функционал
X,
f /1 + у,2 + ^72 dx является частным случаем рассмотренного в преды-
Хо
хг
дущем примере функционала J* А (х, у, г) I + у'2 + z/2 dx> то условия
х9 
338 ВАРИАЦИОННЫЕ ЗАДАЧИ 0 ПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 1
трансверсальности как в точке (х0, у0, za), так и в точке (xb ylt zt) переходят
в условия ортогональности. Следовательно, экстремум может достигаться
лишь на прямых, ортогональных как к поверхности г — <р (х, у) в точке
(х0, у0, г0), так и к поверхности ^ = i|7(x, у) в точке (хь уь (рис. 7.6).
Пример 3. Исследовать на экстремум функционал
X,
V— J* (у,24-л’/2 + 2уг) dx, причем у (0) = 0; z (0)=0, а точка (хь ур г,) может
ХЭ
перемещаться по плоскости х = xt. Система уравнений Эйлера имеет вид
г" — у = 0; у" — г — 0, откуда y,v — у = 0; у = Сх chx 4- C2sh х + C3cosx-|-
-|- С4 sin х, z — у"-, г = Ci ch х-{- С2 sh х—С3 cos х — C4sinx. Из условий
у (0) = 0 и z (0) — 0 получаем: Ci С3 = 0 и Сх — С3 = 0, откуда Ct — С3 = 0.
Условие в подвижной граничной точке
(F - у'/у - z'Fz.)x=x> Ъхх +	|Х=Х|	+ /> |ж=Л(	= 0
переходит в условия
I — 0 и Р,\	— 0,
У ix=x,	z <х=х,
так как 6х, = 0, а бу; и произвольны. В рассматриваемом примере
Fy. = 2уFz, — 2г', следовательно
У'(*1)=0 и У (*!> = 0
или
С2 ch xt + С, cos xt = 0 и С2 ch хх — С4 cos хх = 0.
Если cos л, 4= 0, то С2 = С4 = 0 и экстремум может достигаться лишь на
прямой у — 0; г — 0. Если же cos X] = 0, т. е. хх —	4- пп> где л — целое
число, то С2 — 0, С4— произвольная постоянная, у = С4 sin х, г — — С4 sin х.
Нетрудно проверить, что в последнем случае при любом С4 функционал v = 0.
§ 3. Экстремали с угловыми точками
До сих пор мы рассматривали вариационные задачи, в которых
искомая функция у = у (х) предполагалась непрерывной и имеющей
непрерывную производную. Однако во многих задачах последнее
требование является неестественным, более того, в некоторых классах
вариационных задач решение, как правило, достигается на экстре-
малях, имеющих угловые точки. К числу таких задач принадлежат,
например, задачи на отражение и преломление экстремалей, являю-
щиеся обобщением соответствующих задач на отражение и прело-
мление света.
Задача об отражении экстремалей. Найти кривую, реа-
х>
лизующую экстремум функционала v — J* F (х, у, у') dx и проходящую
х0
через заданные точки А(х0, у0) и В(х2, у2), причем кривая должна
§31
ЭКСТРЕМАЛИ С УГЛОВЫМИ ТОЧКАМИ
339
попасть в точку В лишь после отражения от заданной линии у = (х)
(рис. 7.7).
Естественно считать, что в точке
угловая точка искомой экстремали и,
производная у' (Xj — 0) и правая
производная y'^Xj + O), вообще
говоря, различны. Поэтому удоб-
нее функционал v [у (х)] предста-
вить в виде
-V.
W[y(x)]= J F(x, у, y')rfx +
+ f у, y')rfx,
х,
отражения £ (хр у^, может быть
следовательно, в этой точке левая
причем на каждом из интервалов
х0 х Xi и xt х х2 производная у' (х) предполагается непре-
рывной и, следовательно, мы можем пользоваться изложенными выше
результатами.
Основное необходимое условие экстремума — 0 принимает вид
Х|	х2
= 6 F (х, у, y^rfx-j-d J F(x, у, y')dx = 0.
X,	X,
как точка (хр у() может перемещаться по кривой у=<р(х), то
X,	Хг
вычислении вариаций 6 J* F (х, у, у') dx и 6 J F (х, у, y')dx
4 х:>	Х\
находимся в условиях задачи с подвижной граничной точкой,
Так
при
мы
движущейся по заданной кривой, и можем использовать результаты
§ 1 (стр. 327). Очевидно, что кривые АС и СВ являются экстре-
малями. Действительно, на этих участках у = у(х) является решением
уравнения Эйлера, так как если считать одну из этих кривых уже
найденной и варьировать лишь другую, то задача сводится к нахо-
X,	/	X, \
ждению экстремума функционала J* F dx ( или J* F dx I в задаче
ха \ х, /
с закрепленными граничными точками. Поэтому, вычисляя вариацию
функционала, будем уже считать, что функционал рассматривается
лишь на экстремалях, имеющих угловую точку С. Тогда
bjF(x, у, У/)^х = [/7-|-(ф'— y/)/?ylJ.=Xi_odxl
340 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 7
И
Р{х, у, y')dx = — [F + (<p' — у')
*о
(см. стр. 331), где знаки x = xt —0 и х = xf-}- 0 означают, что
берется предельное значение величины, стоящей в скобках при при-
ближении к точке X; в первом случае слева (со стороны значений х,
меньших X]) и во втором случае справа (со стороны значений х,
больших xt). Так как в точке отражения разрывна лишь производ-
ная у', то в первом случае надо взять в угловой точке левую про-
изводную, а во втором случае — правую производную.
Условие бг» = 0 принимает вид
[Г + (<р' — у')	,+ (ф' ~ У')	= 0
или, так как Ъхг изменяется произвольно, то
[F + (ф' - у') Fy’]x=Xi_0 = [F + (ф' - У')
или
F(xlt ур у'(Х1 — 0))4-(ф'(х1) —
— y'(Xj —0))/V(Xp ур у' (Xj — 0)) = Р (xv ур у'(*i + 0)) 4-
-Нф'(х,) — у'(*i-I-0)) Fy-(Хр ур у'(х, +0)).
Это условие отражения приобретает особенно простой вид для функ-
ционалов типа
«1 ______________
v = J А (х, у) _|_ у'2 dx.
«о
а именно:
А(^р У1) [У1+у- +	=
I	V1 + у Jx=x,-o
= Д(Хр У!>
/1+уМ
(<?' —уЭу']
1^1 4- у'2 Jr=x,+0
или, упрощая и . сокращая
А (Хр У!) 4 0, получим
на А(Хр yj) в предположении, что
1 + <Р'У'
/Г+Р
Х=Х,-0
1 + <Р'У'
V1 + Z
х=г, +0
Обозначив угол между касательной к кривой у = ф(х) и осью
абсцисс буквой а, а углы наклона к оси абсцисс левой и правой
§ 3]	ЭКСТРЕМАЛИ С УГЛОВЫМИ ТОЧКАМИ	341
касательных к экстремали в точке отражения С. соответственно
Р] и р2 (рис. 7.8), получим
/(*! — O) = tg pp у' (Xj 4- 0) = tg р2; <p/(x1) = tga.
Условие в точке отражения приобретает вид
1 + tga-tgP, _ l + tg«-tgPa
— sec pi	sec p2
или после упрощения и умножения на cos а:
— cos (a — pj = cos (a — p2).
Отсюда следует равенство угла падения и угла отражения.
Если точка движется в некоторой среде со скоростью v(x, у),
то время t, затрачиваемое на перемещение точки из положения А(х0> у0)
в положение В(хх, у^, равно интег-
ралу
»(х, у)
dx, который принад-
лежит к рассматриваемому виду функци-
Рис. 7.9.
оналов J А (х, у) V 1 + У'2 dx , и еле- о
fl
довательно, при любом законе измене-.
ния скорости v(x, у) в точке отражения угол падения равен углу
отражения.
Если бы точки А, В и С были расположены иначе, например так
как они расположены на рис. 7.9, то для получения того же условия
в точке отражения из-за двузначности функции у = у (х) удобнее
было бы проводить исследование в параметрической форме.
342 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 7
Преломление экстремалей. Предположим, что подынтег-
X,	'
ральная функция функционала t» — j"F(x, у, y')dx в рассматри-
ваемой области имеет линию разрыва у — <р (х), а граничные точки
А а В расположены по разные стороны линии разрыва (рис. 7.10).
Представим функционал v в виде
v = J Fi(x, у, y')dx + j'F2(x, у, y')dx,
Хо	X,
где F] (х, у, y') — F(x, у, у') с одной стороны линии разрыва,
a F2(x, у, y') = F(x, у, у') с другой стороны линии разрыва.
Рис. 7.10
Предположим, что F{ и F2 трижды дифференцируемы. В точке С
пересечения искомой кривой с линией разрыва естественно ожидать
наличия угловой точки. Дуги АС и СВ, очевидно, являются экстре-
малями (это опять следует из того, что, фиксируя одну из этих дуг
и варьируя лишь другую, мы получим задачу с закрепленными гра-
ничными точками). Поэтому можно брать в качестве кривых сравне-
ния лишь ломаные, состоящие из двух дуг экстремалей, и тогда
вариация ввиду подвижности граничной точки С(х{, у^, перемещаю-
щейся по кривой у = ф(х), принимает следующий вид (см. стр. 331):
A’i	Х2
bv = i)^Fl(x, у, y'Jdx-j-dj' F2(x, у, y')dx =
Х>	X,
= 1Л + (ф' — у') Д1у'Ь=л,_06х1 — [F2 + (ф' — у'} f2v'1a.= X]+06a:1,
и основное необходимое условие экстремума би = 0 сводится к ра-
венству
1^1 + (Ф' - У')	- У'> fyl^+o-
§ 3]
ЭКСТРЕМАЛИ С УГЛОВЫМИ ТОЧКАМИ
343
Так как в точке преломления может быть разрывна лишь у',
то это условие преломления можно записать и в следующем виде:
Л(*р ур y'(*i~ 0)) +
+ (ф'(*1) —/(*1 — 0))/>'(Хр ур yz (Xj — 0)) =
= F2(x1, Ур /(*1 + 0)) +
+ (<P/(*i) —/(*i + 0))F2y’(Xp ур у'(х, + 0)).
Это условие преломления вместе с уравнением у1=ф(х1) дает
возможность определить координаты точки С.
Если, в частности, функционал v равен
•ч	________
J* А (х, у) V\ + у '2 dx —
X,	_______ х2	_________
= j" At (х, у) V1 + у'2 dx + J А2 (х, у) V 1 + у'2 dx,
Х„	X,
то условие преломления приобретает вид
Я1(х, у)
1+фУ
/1 + у'2
= Л2(х, у)
х=х,—0
1 +<pzy'
<х=х,+0
или, сохраняя обозначения стр. 340—342, у' (xt — 0) = tgpp
yz(x,-4-0) = tgP2, <pz(x1) = tga1 после упрощений и умножения на
cos а будем иметь:
cos (a — pi) _ Яг(х„ у,)
cos (a— р2)	+(x„ у,)
sin [у — (a — Pi)
sin Г+ — (a — p2)
_ +(xi, yj
A (xb y{) ’
что является обобщением известного закона прело'мления света:
отношение синуса угла падения к синусу угла преломления равно
отношению скоростей
v^x’ лдЬ) и V2(x- у)== + (Ьо (ср‘ стр- 34°
в средах, на границе которых происходит преломление.
Не следует думать, что экстремали с угловыми точками появляются
лишь в задачах на отражение или преломление экстремалей. Экстре-
мум может достигаться на экстремалях с угловыми точками даже
Х1
в задачах на экстремум функционала v = J* Р(х, у, y'~)dx, где функ-
Хо
ция Р трижды дифференцируема, и допустимые кривые должны про-
ходить через граничные точки А и В без каких бы тО ни было
пополнительных условий.	i
344 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 7
Исследуем, например, функционал
2
v = J" у'2 (1 — у')2 dx, у (0) = 0; у(2)=1.
Так как подынтегральная функция положительна, тоя^-О, и сле-
довательно, если на какой-нибудь кривой функционал и = 0, то на
этой кривой заведомо реализуется абсолютный минимум функцио-
нала V, т. е. наименьшее значение функционала на допустимых кри-
вых. Нетрудно видеть, что на ломаной у — х при 0< х< 1 и у = 1
при 1 <х^2 (рис. 7.11) функционал
У	v = 0, так как на этой ломаной-
подынтегральная функция тождественно
If.tl У’1 /уп равна нулю. Следовательно, на этой
। ’ ломаной реализуется абсолютный ми-
tfZ	I	нимум функционала.
/	!	.Абсолютный минимум функционала:
'	у = 0, достигается также и на лома-
ных, изображенных на рис. 7.13.
рис уп	С другой стороны, легко видеть, что
на гладких кривых значения функцио-
нала строго больше нуля, хотя и могут
быть сделаны сколь угодно близкими к нулю. Действительно, подын-
тегральная функция обращается в нуль только при у = х +
или при у = С2, но линии, составленные из отрезков прямых этих
семейств, проходящие через точки А (0, 0) и В (2, 1), могут быть лишь
ломаными. Однако, сглаживая точки излома путем соответствующего
изменения функции в сколь угодно малой окрестности этих точек,
мы можем получить гладкую кривую, значение функционала на ко-
торой сколь угодно мало отличается от значений функционала на
ломаной. Таким образом, v = 0 является точной нижней гранью
значений функционала v на гладких кривых, но эта точная нижняя
грань на гладких кривых не достигается, а достигается на кусочно-
гладких кривых.
Найдем условия, которым должны удовлетворять решения с угло-
выми точками задачи об экстремуме функционала и[у(х)] =
= J* F (х. у, y')dx. Очевидно, что отдельные гладкие дуги, из кото-
Хо
рых составлена ломаная экстремаль, должны быть интегральными
кривыми уравнения Эйлера. Это следует из того, что если зафик-
сировать все звенья ломаной, кроме одного, и варьировать лишь это
одно звено, то задача сводится к простейшей задаче с закреплен-
ными границами и, следовательно, это звено должно быть дугой
экстремали.
$ 31	ЭКСТРЕМАЛИ С УГЛОВЫМИ ТОЧКАМИ	345
Считая для упрощения записи, что’ ломаная экстремаль имеет
лишь одну угловую точку *), найдем условия, которые должны удо-
влетворяться в угловой точке:
JCt
f у, y')dx = J* Р (х, у, у') dx-\- J F (х, у. у') dx,
ч	Хо	X.
где х, — абсцисса угловой точки (рис. 7.12). Считая, что кри-
вые АС и СВ являются интегральными кривыми уравнения Эйлера
и что точка С может произвольно перемещаться, получим согласно § 1.
стр. 331:
tn> — (P - //7у’)|ж=Л1_06х1
+ Ру ж.-О ~(р~ у'7» 1х=х1+0	- ру‘ к=ж1+0 6У1 = °’
откуда
(F - у'Р,.) |ж=х _0 бх, + Fy \x=Xi_Q бу, =
= (F - y'Fy) |х=х +0 бх, + Fy |X=X1+O dyj,
или, так как бх, и бу, независимы, имеем
- m) 1,=Ж1_о=- то и,1+0
1х=ж,-0 =	1х=х,+0-
Эти условия вместе с условиями непрерывности искомой экстремали
позволяют определить координаты угловой точки.
*) Если угловых точек несколько, то к каждой из них применимо то же
самое рассуждение.
346	. ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 1
Пример 1. Найти ломаные экстремали (если они существуют) функ-
а
ционала v — J* (у'2 — у2) dx. Напишем второе из условий, которые должны
о
перелома, fy, о=	+о’ или в Данном СЛУ*
чае 2у' (Xi — 0) = 2у' (xj + 0). откуда
у' (Xj — 0) = у' (%! + 0), т. е. -производ-
выполняться в точке
0
Рис. 7.13.
ная у' в точке xt непрерывна, и точ-
ки перелома нет. Следовательно, в рас-
сматриваемой задаче экстремум может
достигаться лишь на гладких кривых.
Пример 2. Найти ломаные экстрема-
х,
ли функционала v= J" у'2 (1—у')г dx. Так
Ху
как подынтегральная функция зависит
лишь от у', то экстремалями являются
прямые линии у = Сх Ц- С (см. стр. 301).
Условия в точке перелома в данном случае принимают вид
и
- У2 (1 - У'} (1 - Зу') Lx,_0 = - у'2 (1 - у') (I - Зу') |Ж=Х1+О
2у' (1 - У') (1 - 2у') 1^.0 = 2у' (1 - у') (1 - 2у') |Л=Л1+О.
Эти условия, не считая тривиальной возможности
удовлетворяются при
и
или
и
у' (х,— 0) = у' (x1-j-O),
у' (х,-0) = 0
у' (Х,4-О)=1
у' (х(-0)=1
у' (х,+0) = 0.
Следовательно, ломаные экстремали могут состоять только из отрезков пря-
мых, принадлежащих семействам у = Cj и у=х-|-С2 (рис. 7.13).
§ 4. Односторонние вариации
В некоторых вариационных задачах об экстремуме функцио-
нала v [у (х)] на класс допустимых кривых может быть наложено
ограничение, запрещающее им проходить через точки некоторой
области R, ограниченной кривой Ф(х, у) = 0 (рис. 7.14). В этих
задачах кривая С, реализующая экстремум, или проходит целиком
вне границы области R, и тогда она должна быть экстремалью, так
как в этом случае наличие запрещенной области R совершенно не
влияет на свойства функционала и его вариации в окрестности кри-
§ 4]	ОДНОСТОРОННИЕ ВАРИАЦИИ	347
вой С, и рассуждения главы 6 остаются справедливыми, или кривая С
состоит из дуг, лежащих вне границы /?, и из частей границы
области R. В этом последнем случае возникает новая ситуация:
на частях границы области R возможны лишь односторонние вариа-
ции кривой С, так как внутрь области допустимые кривые заходить
не могут. Части кривой С, лежащие вне границы области R, должны
по-прежнему быть экстремалями, так как если варьировать кри-
вую С лишь на таком, допускающем двусторонние вариации, участке,
то наличие области R на вариации у влиять не будет, и выводы
главы 6 остаются справедливыми.
Таким образом, в рассматриваемой задаче экстремум может дости-
гаться лишь на кривых, состоящих из дуг экстремалей и частей гра-
ницы области R, а следовательно, для построения искомой кривой,
реализующей экстремум, надо получить условия в точках перехода
экстремали.на границу области R, дающие возможность определить
эти точки. В случае, изображенном на рис. 7.15, необходимо полу-
чить условия в точках Л4, AZ, Р и Q. Получим, например, условие
в точке М. Совершенно аналогично можно было бы получить усло-
вия и в других точках перехода экстремали на границу области
При вычислении вариации dv функционала
v = J* F(x, у, y')dx — j' F(x, у, y')dx-|- J* F(x, у, y')dx
-Vo	.	ЛГо	r
мы можем считать, что вариация вызывается лишь смещением
точки М(х, у) на кривой Ф(х, у) = 0, т. е. можно считать, что
при всяком положении точки М на кривой Ф(.х, у) = 0 дуга AM
является уже экстремалью, а участок MNPQB не варьируется.
348 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ (ГЛ. 7
Функционал
X
©1 = J F (х, у, y')dx
Хо
имеет подвижную граничную точку, перемещающуюся по границе
области R, уравнение которой Ф(х, у) = 0, или в разрешенном
в окрестности точки М относительно у'виде: у=ф(х).
Следовательно, согласно § 1 (стр. 331)
6^1 = I/7 Ч- (ф' — У') Ру’]х=хЪ*-
Х1
Функционал v2 = J F (х, у, y')dx также имеет подвижную гра-
ничную точку (х, у), однако в окрестности этой точки кривая,
на которой может достигаться экстремум у = ф(х), не варьируется.
Следовательно, изменение функционала v2 при перемещении точки (х, у)
в положение (x-f-бх, уН~бу) сводится лишь к изменению нижнего
предела интегрирования и
Xi	Х1
Дг»2 = J* F(x, у, y')dx — J F(x, у, y')dx =
x+бх	x
х+бх	х+бх
— ~f F(x> У- y')dx = — j" F(x, <р(х), ф'(х))«Гх,
~Х	X
так как на интервале (х, х-]-бх) у = ф(х).
Применяя теорему о среднем значении и пользуясь непрерыв-
ностью функции F, получим
hv2= — F (х, ф(х), ф' (х)) |л=-бх -j- 0 • бх,
где р->0 при бх—>0.
ЗАДАЧИ К ГЛАВЕ 7
349
Следовательно, дг»2 = — Р(х, ф(х), ф'(х) )]х=-дх,
дг/—дг»1Н-дг»2 = [^(х,у,у')-|-
+ (ф'— У')^у'(х, У, У%=7дх — F (х, у, ф') | х = 7 дх =
= [F(x, у, у') —Р(х, у, ф') —(у'— ф'Иу-(х, у, у')]х=-дх,
так как у (х) ф (х).
Необходимое условие экстремума дг» = О ввиду произвольности дх
принимает вид
[F(x, у, у') —F(x, у, ф') — (у'—• ф') Fy (х, у, у')]х=- = 0.
Применяя теорему о среднем значении, получим
(у'— <p')[Fy (х. у, 9) —Fy(x, у, /)]A.=J = 0,
где q— значение, промежуточное между ф'(х) и у' (х). Снова при-
меняя теорему о среднем значении, будем иметь
(у'_ ф')(9 — y')Fyy (х, у, <7)|х=г = 0,
где q — значение, промежуточное между q и у' (х). Предположим,
что Fyy (х, у, q) 0. Это предположение является естественным
для многих вариационных задач (см. главу 8). В этом случае условие
в точке М имеет вид у' (х) = ф' (х) {q = у' только при у' (х) = ф' (х),
так как q — значение, промежуточное между у' (х) и ф' (х)).
Следовательно, в точке М экстремаль AM и граничная кри-
вая MN имеют общую касательную (левую касательную для кривой
у = у(х), правую —для кривой у = ф(х)). Итак, экстремаль
касается границы области R в точке М.
Задачи к главе 7
1.	Найти решение с одной угловой точкой в задаче о минимуме функ-
ционала
<4У (*)] = / (У' ~ И2 (У' + I)2 dx-, у (0) = 0; у (4) = 2.
о
2.	Существуют ли решения с угловыми точками в задаче об экстремуме
функционала
и 1у (X)J = J (у'2 + 2ху — у2) dx-, у (х0) = у0; у (х,) = уР
350 ВАРИАЦИОННЫЕ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ [ГЛ. 1
3.	Существуют ли решения с угловыми точками в задаче об экстремуме
функционала
ч
»[у (*)] = /(/" — 6/2) dx'< У(0) = 0; у(х1) = у1.
О
4.	Найти условие трансверсальности для функционала
*х	_______
v [у W] — J* А (х, У) earctg у + у'2 dx, А (л, у) =/= 0.
Го
5.	Пользуясь основным необходимым условием экстремума bv = 0, найти
функцию, на которой может достигаться экстремум функционала
1
V [У (•*)] = J (у"2 — 2лгу) dx; у (0) = у' (0) — 0;
о
У (1) — -[20 ! У' (О — не задано.
6.	Найти кривые, на которых может достигаться экстремум функционала
ю
v[yW]= f У'3 ^; У(0)=0; у (10) = 0,
о
при условии, что допустимые кривые не могут проходить внутри круга, огра-
ниченного окружностью
(х-5)2 + ^ = 9.
7.	Найти функцию, на которой может достигаться экстремум функционала
л
4
v [у (*)] ~ f <У2 ~ у'2) dx< у (°) = °’
о
м	Л
если другая граничная точка может скользить по прямой л==-^-.
8.	Пользуясь лишь основным необходимым условием = 0, найти кри-
вую, на которой может достигаться экстремум функционала
V [у (*)] = ] * у  dx; у(0) = 0,
о
если вторая граничная точка (xj, yj может перемещаться по окружности
(х — 9)2 + у2 = 9.
ГЛАВА 8
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
§ I. Поле экстремалей
Если на плоскости (х, у) через каждую точку некоторой области и
проходит одна и только одна кривая семейства у = у(х. С), то
говорят, что это семейство кривых в
точнее, собственное поле. Угловой
коэффициент касательной р(х, у) к
кривой семейства у = у (х, С), про-
ходящей через точку (х, у), называ-
ется наклоном поля в точке (х, у).
Например, внутри круга
х2 у2 < 1 параллельные прямые
у = х + С образуют поле (рис. 8.1),
причем наклон этого поля
р(х, у)=1. Напротив, семейство
парабол у = (х— а)2 — 1 (рис. 8.2)
внутри того же круга поля не об-
разует, так как внутри этого круга
параболы рассматриваемого семейст-
области D образует поле, или,
кУ
ва пересекаются.	рис 8 j
Если все кривые семейства
у = у(х, С) проходят через некото-
рую точку (х0, у0), т. е. образуют пучок кривых, то они заведомо
не образуют собственного поля в области D, если центр пучка при-
надлежит области D. Однако если кривые пучка покрывают всю
область D и нигде не пересекаются в этой области, кроме центра
пучка, т. е. во всех точках, отличных от центра пучка, требования,
налагаемые на поле, выполнены, то говорят, что семейство у — у(х, С)
тоже образует поле, но в отличие от собственного поля в рассматри-
ваемом случае поле называется центральным (рис. 8.3).
352
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
[ГЛ, 8
х й, а < л
Например, пучок
образует центральное
синусоид y = Csinx
поле (рис. 8.4). Тот
при О
же пучок синусоид в
Рис. 8.2.
достаточно малой окрестности отрезка оси абсцисс б х а, где
б > О, а < л. образует собственное поле (рис. 8.4). Тот же пучок
синусоид в окрестности отрезка оси
t	абсцисс 0 <1 х av at > л, поля не
' &	образует (рис. 8.4).
Если собственное или центральное
поле образовано семейством экстрема-
- X лей некоторой вариационной задачи, то
оно называется полем экстремалей.
х Понятие поля почти без изменения
—q-----------------------переносится и на случай пространства лю-
бого числа измерений. Семейство у; =
= у. (х, С’г ., Сп) (£ = 1,2.п) образует
Рис. 8.3.	поле в области D пространства х, ylt ..., уп,
если через каждую точку области D про-
ходит одна и только одна кривая семей-
ства yt = yt (х, Cj. Сп). Функциями наклона поля pt (х, ур у2....уд)
(Z = 1, 2.п) называют частные производные от функций у t (х, Ср Cv .... Сп)
по х, вычисленные в точке (х, у„ у2, ..., уя); следовательно, для получения
pt (х, yv у2...уп) надо взять у; (х, С,, С2........Qn) и заменить Су
С2, .... Сп их выражениями через координаты х, уР у2....уп. Аналогично
определяется и центральное поле.
§ I]	' ПОЛЕ ЭКСТРЕМАЛЕЙ	353
Пусть кривая у = у(х) является экстремалью вариационной задачи
об экстремуме простейшего функционала
ла
•и [у (х)] = J F(x, у, y')dx,
Xi>
причем граничные точки А(х0, у0) и B(xit у^ закреплены. Говорят,,
что экстремаль у — у (х) включена в поле экстремалей, если найдено
У
Рис. 8.4.
семейство экстремалей у — у (х, С), образующее поле, содержащее
при некотором значении С — Со экстремаль у = у(х), причем эта
экстремаль у = у(х)не лежит на границе области D, в которой
семейство у = у(х, С) образует поле (рис. 8.5). Если пучок экс-
тремалей с центром в точке Д(х0, у0) в окрестности экстремали
у = у (х), проходящей через ту же точку, образует поле, то тем
самым найдено центральное поле, включающее данную экстремаль
354
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
[ГЛ. 8
у — у (х). За параметр семейства в данном случае можно взять угло-
вой коэффициент касательной к кривым пучка в точке А (х0, у0)
(рис. 8.6).
Пример 1. Дан функционал
а
J (у'2 — У2) dx\
О
требуется включить дугу экстремали у = 0, соединяющую точки (0, 0) и (а, 0),
где 0 < а < л в центральное поле экстремалей. Общее решение уравнения
Эйлера у"-[- у = 0 (см. стр. 298, пример 1) имеет вид у = Сх cos х-|- С2 sin х.
Из условия прохождения экстремалей через точку (0, 0) получаем С-, = 0,
у = С2 sin х, причем кривые этого пучка на отрезке 0 а, а < л обра-
зуют центральное поле, включающее при С2 = 0 экстремаль у = 0. Параметр
семейства С2 равен производной у'х в точке (0, 0). Если в той же задаче
a л, то семейство у = С2 sin х поля не образует (см. стр. 352)
" Известно, что две бесконечно близкие кривые семейства
Р(х, у, С) = 0 пересекаются в точках С-дискриминантной кривой,
определяемой уравнениями
дд
F(x, у. С) = 0; -^ = 0.
Напомним, что в состав С-дискриминантной кривой, в частности,
входит огибающая семейства и геометрические места кратных точек
кривых семейства. Если F (х, у. С) —0 является уравнением пучка
кривых, то центр пучка также принадлежит С-дискриминантной кри-
вой. Поэтому если взять пучок экстремалей у — у (х. С), проходя-
щих через точку (х0, у0), и определить его С-дискриминантную кри-
вую Ф(х, у) = 0, то близкие кривые семейства у = у(х. С) будут
пересекаться вблизи кривой Ф(х, у) = 0 и, в частности, кривые
этого семейства, близкие к рассматриваемой экстремали у — у(х),
проходящей через точки Л(х0, у0) и В{хх, yt), будут пересекаться
ПОЛЕ ЭКСТРЕМАЛЕЙ
355
§ П
в точках, близких к точкам касания (или пересечения) кривой
у = у(х) с С-дискриминантной кривой (см. рис. 8.7, на котором
С-дискриминантная кривая изображена жирной линией). Если дуга АВ
экстремали у = у(х) не имеет отличных от точки А общих точек
с С-дискриминантной кривой пучка экстремалей, включающего данную
экстремаль, то достаточно близкие к дуге АВ экстремали пучка не
пересекаются, т. е. образуют в окрестности дуги АВ центральное
поле, включающее эту дугу (рис. 8.8).
Если дуга АВ экстремали у = у (х) имеет отличную от А общую
точку А* с С-дискриминантной кривой пучка у = у(х, С), то близ-
кие к у = у(х) кривые пучка могут пересекаться между собой и
с кривой у = у(х) вблизи точки А* и, вообще говоря, поля не обра-
зуют (рис. 8.7). Точка Л* называется точкой, сопряженной с точ-
кой А.
Полученный результат можно сформулировать так: для построе-
ния центрального поля экстремалей с центром в точке А,
содержащего дугу экстремали АВ, достаточно, чтобы точка А*,
сопряженная с точкой А, не лежала на дуге АВ. Это условие
возможности построения поля экстремалей, включающего данную
экстремаль, носит название условия Якоби.
Нетрудно сформулировать это условие и аналитически. Пусть
у —у(х, С) — уравнение пучка экстремалей с центром в точке А,
причем параметр С можно для определенности считать совпадающим
с угловым коэффициентом у' экстремалей пучка в точке А. С-дискри-
минантная кривая определяется уравнениями
у = у(х, С); -УУсС)=О.
Вдоль каждой фиксированной кривой семейства производная
является функцией только х. Эту функцию кратко обозначим буквой и;
356	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	ТТЛ. 8
ду (х, С)	(Ру {х, С) .
и =	где С задано; отсюда а„ =——- Функции
дС	* дС дх J
у = у(х, С) являются решениями уравнения Эйлера, поэтому
Fy(x. у(х, С), у*(х, C)) — ~Fy,(x, уU, С), у*(х. С))=0.
Дифференцируя это тождество по С и полагая	= й, получим
FyyM -у FVy u' — vy'u "Ь у'у' u') ~ 0 (
или
, (^уу —-^^уу')^ —•^(/;'у'у'и/)==0-
Здесь Fyy (x, у, у'), Fyy (x, у, у'), Fy y (x, у, у') являются извест-
ными функциями х, так как второй аргумент у равен решению урав-
нения Эйлера у = у (х, С), взятому при значении С = С$, соответ-
ствующем экстремали АВ. Это линейное однородное уравнение второго
порядка относительно и называется уравнением Якоби.
_	ду (х, С) ,
Если решение этого уравнения и = -	, обращающееся
в нуль в центре пучка при х = х0 (центр пучка всегда принадлежит
С-дискриминантной кривой), обращается в нуль еще в какой-нибудь
точке интервала х0 < х < хр то сопряженная с А точка, определяе-
мая уравнениями
у = у (х, Со) и	~~ — 0 или и — О,
лежит на дуге экстремали АВ*). Если же существует решение урав-
нения Якоби, обращающееся в нуль при х = х0 и более не обращаю-
щееся в нуль ни в одной точке отрезка х0 sj х ^Х], то точек, сопря-
женных с А, на дуге АВ нет,—условие Якоби выполнено,, и дугу
экстремали АВ можно включить в центральное поле экстремалей
с центром в точке А.
Замечание. Можно доказать, что условие Якоби необходимо
для достижения экстремума, т, е, для кривой АВ, реализующей экстре-
мум сопряженная с А точка не может лежать в интервале х0<х<х1
Пример 2. Выполнено ли условие Якоби для экстремали функционала
а
о—| (у'2 — у2) dx, проходящей через точки А (0, 0) и В (а, 0)?
*) Заметим, что все нетривиальные решения линейного однородного диф-
ференциального уравнения второго порядка, удовлетворяющие условию
и (х0) = 0, отличаются друг от друга лишь отличным от нуля постоянным
множителем и,, следовательно, обращаются в нуль одновременно.
ФУНКЦИЯ Е(х, V, р, /)
357
S 21
Уравнение Якоби имеет вид
— 2и—^-(2«') = 0 или и"-\-и — 0,
откуда
и = Ci sln(x— С2).
Так как и(0) = 0, то Са = 0; «=Ctsinx. Функция и обращается в нуль
в точках х = Лл, где k — целое число, и, следовательно, если 0 < а < л, то
на отрезке 0 < х < а функция и обращается в нуль только в точке х = О
и условие Якоби выполнено; если же а > л, то на отрезке 0 х а функ-
ция и обращается в нуль еще по крайней мере в одной точке х = л и усло-
вие Якоби не выполнено (сравните с примером 1, стр. 354).
Пример 3. Выполнено ли условие Якоби для экстремали функционала
а
v [у (*)] = J (у'2 + У2 + *2) dx,
о
проходящей через точки А (0, 0) и В
Уравнение Якоби имеет вид и" 
в форме и = Ct sh х -|- Сг ch х. Из
и = C| sh х. Кривые пучка u = Ct sh х
пересекают ось Ох лишь в точке
х = 0. Условие Якоби выполнено при
любом а.
§ 2. Функция Е(х, у, р, у')
Предположим, что в простей
шей задаче об экстремуме ф
ционала
Г|
V— J F (х, у, y’)dx\
W = уо- У(-*:1) = У1
I, 0)?
и = 0. Его общее решение возьмем
условия и (0) =» 0 находим С2 = О,
Рис. 8.9.
условие Якоби выполнено и, следовательно, экстремаль С, про-
ходящая через точки А(х0, у0) и B(xlt у^, может быть включена
в центральное поле, наклон которого равен р(х, у) (рис. 8.9)*).
Для определения знака приращения Дг» функционала v при пере-
ходе от экстремали С к некоторой близкой допустимой кривой С
преобразуем приращение Дг» = § F (х, у, у') dx — J F (х, у, у') dx
S	с
•) Можно было бы предположить, что экстремаль включена не в цен-
тральное, а в собственное поле.
358	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	(ГЛ. 8
к более удобному для исследования виду. (Символы
J* F(x, у, y')dx и J F (х, у, y')dx
С	С '
х,
представляют значения функционала v = y F(x, у, y')dx, взятые
соответственно по дугам кривых С и С).
Рассмотрим вспомогательный функционал
f (*> У> Р) + (-J7 — р\ Fp (х, у, р)] dx,
V
который на экстремали С обращается в j*F(x, у, y')dx. так как
с
на экстремалях поля Р- С другой стороны, тот же вспомога-
тельный функционал
f[F(x, у, +	— p)fp(x, у, p)]dx
с
или
J [F(x, у, p) — pFp(x, у, p)]dx~\- Fp(x. у. p)dy (8.1)
с
является интегралом от точного дифференциала. Действительно, диф-
ференциал функции v(x, у), в которую превращается функционал
•о[у(х)] на экстремалях поля, согласно § 1 главы 7-(стр. 331), имеет
вид
dw = [F(x, у, у') — y'Fyix, у. у')] dx+ у, y')dy
и лишь обозначением углового коэффициента касательной к экстре-
малям поля отличается от подынтегрального выражения в рассматри-
ваемом вспомогательном интеграле (8.1).
Итак, интеграл у [/^(х, у, Р)Н-(у' — p)Fp\dx на экстремали С
с
совпадает с интегралом £ F(x, у, y')dx, а так как функционал
с
У । у. р) + (У' ~ Р) Fp] dx является интегралом от точного
с
§21	функция er*, v. о. /)	359
дифференциала и, следовательно, не зависит от пути интегрирования, то
J F(x. у, y')dx = J(F(x, у, р) 4-(у' — p)Fp{x, у, p)[dx
с	с
не только при С —С, но и при любом выборе С.
Следовательно, приращение
А-и == J F (х, у, у') dx — J F (х, у, у') dx
Ъ	с
может быть преобразовано к следующему виду:
Ао = j*F(x, у, y')dx — J [F (х, у, р) + (у'—p)Fp(x, у, p)]dx=
с	с
= J [F(x, у, y') — F(x, у, р) — (у' — p)Fp(x, у, p)\dx.
с
Подынтегральная функция носит название функции Вейерштрасса
и обозначается Е (х, у, р, у'):
Е(х, у, р. y') = F(x, у, у') —F(x, у, р) — (у' — р) Fр (х, у, р).
В этих обозначениях
*1
Au = J*£(x, у, р, y'Jdx.
Гл
Очевидно, что достаточным условием достижения функционалом v
минимума на кривой С будет неотрицательность функции Е, так как
если Е 0, то и А® О, а достаточным условием максимума будет
Е ^0. так как в этом случае и Ав 0. При этом для слабого мини-
мума достаточно, чтобы неравенство F(x, у, р, у')^0 (или
Е 0 в случае максимума) выполнялось для значений х, у, близ-
ких к значению х, у на исследуемой экстремали С, и для зна->'
чений у', близких к />(х, у) на той же экстремали, а для сильного
минимума то же неравенство должно быть справедливо для тех же
х, у, но уже для произвольных у', так как в случае сильного экстре-
мума близкие кривые могут иметь произвольные направления каса-
тельных, а в случае слабого экстремума значения у' .на близких кри-
вых близки к значениям у' — р на экстремали С.
Следовательно, достаточными для достижения функционалом Q
экстремума на кривой С будут следующие условия.
Для слабого экстремума:
1.	Кривая С является экстремалью, удовлетворяющей граничным
условиям. 1
360	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	(ГЛ. «
2.	Экстремаль С может быть включена в поле экстремалей. Это
условие можно заменить условием Якоби.
3.	Функция £(х, у, р, у') не меняет знака во всех точках (х, у),
близких к кривой С, и для близких к р(х, у) значений у'. В случае
минимума Е 0, в случае максимума Е 0.
Для сильного экстремума:
1.	Кривая С является экстремалью, удовлетворяющей граничным
условиям.
2.	Экстремаль С может быть включена в поле экстремалей. Это
условие можно заменить условием Якоби.
3.	Функция Е(х, у, р, у') не меняет знака во всех точках (х, у),
близких к кривой С и для произвольных значений у'. В случае ми-
нимума Е 0, в случае максимума Е 0.
Замечание. Можно доказать, что условие Вейерштрасса необ-
ходимо. Точнее, если в центральном поле, включающем экстремаль С,
в точках экстремали для некоторых у'
1</	/	функция Е имеет противоположные
/ .	знаки, то сильный экстремум не до-
/ /	а 5] стирается. Если это свойство имеет ме-
/ / S ’ сто при сколь угодно близких к р зна-
///	' чениях у', то не достигается и слабый
///	экстремум.
Пример 1. Исследовать на экстре-
х чум функционал
~~О	Г з
v= I у' dx; у(0) = 0,
Рис. 8.10.	о
у (а) = b, а > X), b > 0.
Экстремалями являются прямые линии у — Ctx -ф- С2. Экстремум может
достигаться лишь на прямой у = — х. Пучок прямых у = Схх с центром
в точке (0, 0) образует центральное поле, включающее экстремаль у = у х
(рис. 8.10).
Функция
Е (х. у, р, у') = у'3 — р3 — Зр2 (у' — р) = (у' — р)2 (у' + 2р).
На экстремали у = — х наклон поля р = — > О, и если у принимает зна-
чения, близкие к р = —, то £>0 и, следовательно, все условия, достаточ-
ные для достижения слабого минимума, выполнены. Итак, на экстремали
b	_ „	„	,
у = — х достигается слабый минимум. Если же у принимает произвольные
значения, то (y'-f-2p) может иметь любой знак и, следовательно, функция Е
знака не сохраняет — условия, достаточные для достижения сильного мини-
§ 2]	ФУНКЦИЯ Е(х, у. р, д’)	361
мума, не выполнены. Если принять во внимание замечание на стр. 360, то
„	„ Ъ
можно утверждать, что сильный минимум на прямой у = — х не достигается.
Пример 2. Исследовать на экстремум функционал
а
J" (бу'2 — у'4 + уу') dx; у (0) = 0; у (а) = Ь; а > 0 и b > 0
о
в классе непрерывных функций с непрерывной первой производной.
Экстремалями являются прямые у = С\х С2. Граничным условиям удо-
влетворяет прямая у = — х, которая включается в пучок экстремалей
у = Ctx, образующих центральное поле. Функция
Е(х, у. р, у') = 6у'2 — у'4 + уу' — 6р2 + р4 — ур — (у'— р)(12р—4р3-|-у) =
== — (/ — р)г [у'2 + 2ру' — (6 — Зр2)].
Знак функции Е противоположен знаку последнего множителя
у'2+2ру'-(6-3р2).
Этот множитель обращается в нуль и может изменить знак лишь при пере-
ходе у' через значение у' =—р±]/Г6— 2р2. При 6 — 2р2<;0 или р^>КЗ
при любому' имеем [у'2-|-2ру'— (6 — Зр2)]
р<Уз, то выражение [у'2-f-2ру' —
— (6 — Зр2)] меняет знак. Если же при
этом у' достаточно мало отличается от р,
то последнее выражение сохраняет поло-
жительный знак при р > 1 и отрицатель-
ный знак при р < 1.
Следовательно, при р = — <1 или
b < а имеем слабый минимум, так как £>0
при значениях у', близких к р; при
р — — > 1 или b > а имеем слабый макси-
а	—
мум. При р = — > р^З имеем сильный мак-
симум, так как £ 0 при любых значениях
у'. Прир = — <V~3, на основании заме-
> 0, если же 6 — 2р2 > 0 или
Рис. 8.11.
чания на стр. 360, нет ни сильного минимума, ни сильного максимума
(рис. 8.11).
Даже в приведенных выше весьма простых примерах исследование
знака функции Е было сопряжено с некоторыми затруднениями, и
поэтому желательно условие сохранения знака функцией Е заменить
более легко проверяемым условием. Предположим, что функция
Е(х, у, у') трижды дифференцируема по аргументу у'. По формуле
362	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	[ГЛ. 8
Тейлора получим
у, у') =
= Е(х, у, р)+(у' — р)Рр(х. у. р) + (У Fyy (х. у, q),
где q заключено между р и у'.
Функция
Е(х, у, р, y') = F(x, у, y') — F(x, у, р) — (у' — р) F^x, у, р) ,
после замены функции F(x, у. у') ее разложением по формуле Тей-
лора примет вид	~~
Е(х, у, р, у/)= (У ~р)2 Fyy (х, у, q).
Отсюда видно, что функция Е сохраняет знак, если сохраняет знак
Fyy (х, у, q~). При исследовании на слабый экстремум функция
Fyy (х, у, q) должна сохранять знак для значений х и у в точках,
близких к точкам исследуемой экстремали, и для значений q, близких
к р. Если Fy’y’ (х, у, у') #= 0 в точках экстремали С, то в силу
непрерывности эта вторая производная сохраняет знак и в точках,
близких к кривой С, и для значений у', близких к значениям у' на
кривой С. Таким образом, при исследовании на слабый минимум
условие Е 0 может быть заменено условием Fyy > 0 на экстре-
мали С, а при исследовании на слабый максимум условие Е^О может
быть заменено условием Fyy < 0 на кривой С. Условие Fyy > О
(или Fyy < 0) носит название условия Лежандра *).
При исследовании на сильный минимум условие Е 0 может быть
заменено требованием Fyy' (х, у, q) 0 в точках (х, у), близких
к точкам кривой С при произвольных значениях q. При этом, конечно,
предполагается, что разложение по формуле Тейлора
Е(х, у, у<) =
= Е(х, у, р) + (У'~ p)Fp(x. у, р)+-(У-^Р)2- Fyy(x, у, q)
справедливо при любых у'. При исследовании на сильный максимум
получим условие Fyy (х, у, q) <10, при тех же предположениях
относительно области изменения аргументов и разложимости функции
Е(х, у, у') по формуле Тейлора.
*) Условие Fy'y' > 0 (или Fy,y, < 0) часто называют усиленным усло-
вием Лежандра, а условием Лежандра называют неравенство Ру у >0
(или Fyy < 0).
Сводка достаточных условий минимума простейшего функционала *)
v [У (-*)] = J"f(x. у. у') dx-, у (х0) = уо, у (х,) = у,
Хо
Слабый минимум	Сильный минимум	Слабый минимум	Сильный минимум	Слабый минимум	Сильный минимум	
LF, ^Гу,-0	1 р	— F , =0 У dx У	1.F	— F , =0 у dx У	'Л	1 F	— F , =0 У dx У	1 F -	— F'.—O У dx У	
2. Условие Якоби	2. Условие Якоби	2. Условие Якоби	2. Условие Якоби	2. Существует по- ле экстремалей, включающее данную экстре- маль	2. Существует по- ле экстремалей, включающее данную экстре- маль	ФУНКЦИЯ
3. Fy'y' >0	З.Еу,у,(х,у.у')>0	;3. Е (х, у, р, у')>0	3. Е (х, у, р, у')>0	3. Е (х, у. р, у')>0	3. Е(х, у.р,у')>0	Сч
на исследуемой экстремали	для точек (х, у), близких к точ- кам на исследу- емой экстрема- ли и для произ- вольных значе- ний у'. При этом предполагается, что функция F (х, у, у') три- жды дифферен- цируема по у' для любых у'	для точек (л, у), близких к точ- кам на исследу- емой экстрема- ли, и для у', близких к р(х, у)	для точек (х, у), близких к точ- кам на исследу- емой экстрема- ли, и для произ- вольных у'	для точек (х, у), близких к точ- кам на исследу- емой экстрема- ли, и :для у\ близких к р(х, у)	для точек (х, у), близких к точ- кам на исследу- емой экстрема- ли, и для про- извольных у'	(Л -а -Й
*) Для получения достаточных условий максимума в этой сводке надо взять знаки неравенства проти* воположного смысла.						363
364
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
[ГЛ. 8
Пример 3. Исследовать на экстремум функционал
v [У (-г)] = J" (у'2 — у2) dx, а > 0; у(0) = 0, у(а) = 0.
о
Уравнение Эйлера имеет вид у" + у==О, его общее решение у = cosx-{-
-|- С2 sin х. Используя граничные условия, получаем Ct = 0 и С2 = 0, если
а -4= кл, где k — целое число.
Итак, при а ф кл экстремум может достигаться лишь на прямой у = 0.
Если а < л, то пучок экстремалей у = Сг sin х с центром в точке (0, 0)
образует центральное поле. При а> л условие Якоби не выполнено (см.
стр. 352).
Так как подынтегральная функция трижды дифференцируема по у' при
любых у' и Ру, , = 2>0 при любых значениях у', то на прямой у = 0 при
а <л реализуется сильный минимум. Если учесть замечание на стр. 356,
то можно утверждать, что при а>л минимум на прямой у = 0 не дости-
гается.
Пример 4. Исследовать на экстремум функционал
*1 ________
v[yW]= Г -- Ut-— dx’ У (°) = °> У(Х1) = У1
б' Ку
(см. задачу о брахистохроне, стр. 304). Экстремалями являютсй циклоиды
х = С] (f — sin t) + С2,
у = С1 (1 — cos t).
Пучок циклоид х == С] (t — sin t), у = Ct (1 — cos f) с центром в точке (0, 0)
образует центральное поле, включающее экстремаль
х — a (t — sin t), у = а (1 — cos t),
где а определено из условия прохождения циклоиды через вторую гранич-
ную точку В (хр у]), если х, < 2ла (рис. 8.12).
Имеем
р , =-----; р , , =________________!------> 0
У Ку’/TTF УУ Уу^ + у'У’
§ 2]	ФУНКЦИЯ Е(х, у, р. д')	365
при любых у'. Следовательно, при X] < 2ла на циклоиде
х = a (t — sin t), у = а (1 — cos t)
реализуется сильный минимум.
, Пример 5. Исследовать на экстремум функционал
а
v [у (-*)] = У у'3 dx> У (0) = о, у (а) = b, а > О, Ь > 0.
о
Этот пример был решен на стр. 360, но теперь в отношении слабого экстре-
мума исследование можно упростить. ,
Экстремалями являются прямые линии. Пучок у = Сх образует централь-
ft и	b
ное поле, включающее экстремаль у~ — х. На экстремали у = — х вторая
производная — бу' = 6 — > 0. Следовательно, прямая, у = — х реали-
зует слабый минимум. При произвольных у' вторая производная Ру'у- ~ бу'
знака не сохраняет; следовательно, указанные выше достаточные условия
для достижения сильного минимума не выполнены. Однако отсюда еще
нельзя заключить, что сильный экстремум не достигается.
Пример 6. Исследовать на экстремум функционал
а
г'[у(х)] = J“-^-dx; у(0) = 1, у (а) — Ь, а > 0, 0 < b < 1.
о у
Первый интеграл уравнения Эйлера (см. случай 5 на стр. 302) имеет вид
-4~ + у'-М- = С или у'2 = 4С,у;
У' У'.	.
извлекая корень, разделяя переменные и интегрируя, получаем у = (С!Х-)-С2)2—
семейство парабол. Из условия у (0) = 1 находим С2 — !• Пучок парабол
у = (Схх + I)2 с центром в точке Д(0, 1) имеет ^-дискриминантную кривую
у = 0 (рис. 8.13). Через точку В (а, Ь) проходят две параболы этого пучкг.
366	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	[ГЛ. 8
На дуге АВ одной из них (£j) лежит точка Л*, сопряженная с точкой Л,
на другой же (£2) сопряженной точки нет, и следовательно, на дуге £2
условие Якоби выполнено и на этой дуге параболы может реализоваться
экстремум. В окрестности исследуемой экстремали Fv, , =	> 0 для про-
т У'
извольных у', однако на этом основании нельзя утверждать, что на дуге £2
у
реализуется сильный минимум, так как функция F (х, у, у') = —не может
У'
быть представлена в виде
f (х, у, у') = F (х, у, р) + (у' — р) Fp (х, у. р) 4- —-~Р)2 Руу (*. у. q)
» , 
при произвольных значениях у' ввиду наличия разрыва функции F (х, у, у')
при у' = 0. Можно лишь утверждать, что на L2 реализуется слабый минимум,
так как для значений у', близких к наклону поля на кривой L2, такое раз-
ложение функции F (х, у, у') по формуле Тейлора имеет место. Для полного
исследования этого функционала на экстремум необходимо рассмотреть
функцию Е (х, у, р, у'):
g<xу > - 4- - 4+4 <>' - я	+
У Р г
Так как множитель (2у' р) не сохраняет знака при произвольных у', то
на основании замечания на стр. 360 можно утверждать, что сильный минимум
на дуге L2 не достигается.
Изложенная теория без значительных изменений переносится и на функ-
ционалы вида	)
г1
v [Уг Уу- Уя]= J F(x> у1- Ь---. Уп> у’х> У2...уя)^;
*>
УЛЛ) = Уг-0’ У/(х1) = У/1	(/=1.2...П).
Функция Е принимает вид
£ = F(x, У1, у2..у„, X, у2....у'п) - F (х, У1, у2,..., у„, р}1 р2.рп)-
п
-2 (y'i-P^P^ Уг У2..........Уп' Рх' Р2... Рп>
где р( — функции наклона поля, на которое наложены некоторые ограни-
чения (при этих ограничениях поле называется специальным).
Условие Лежандра Fy,y, >0 заменяется следующими условиями:
F , , >0,
F , ,
>1*1
F , ,
у2Ух
F , ,
У2У2
о,
р	р	р
у'ху’х	у'ху'2”‘ у'ху'п
р	р	р
у'2у‘х	у'2у'2"‘ У2Уп
р	р	р
у'пу'х у'пУ2"‘ y'tty'n
$ 21
ФУНКЦИЯ Е(х, д. р, д')
367
Достаточные условия слабого минимума как в простейшей задаче, так
и в более сложных, можно получить иным методом, основанным на изучении
знака второй вариации.
По формуле Тейлора преобразуем приращение функционала в простей-
шей задаче к следующему виду:
х,
Д* = f У + бу' У' + by )— F (Л> у’ У И dx ~
ЛГ1 '
X!	X!
= f (ру 6У + РУ 6У")	+ 4 f [Лм W + 2руу' &У &У' + руу S^'2] dx + R,
X,	Хо
где R имеет порядок выше второго относительно бу и бу'. При исследовании
на слабый экстремум бу и бу' достаточно малы, и в этом случае знак при-
ращения До определяется знаком члена, стоящего в правой части и содер-
жащего наиболее низкие степени бу и бу'. На экстремалй первая вариация
X,
f (,руЬу + ру by')dx = 0
Хо
и, следовательно, знак приращения До, вообще говоря, совпадает со знаком
второй вариации
А1
бго = J (Fvy fy2 + 2Руу by бу' + Руу, бу'2) dx.
Хо
Условие Лежандра в соединении с условием Якоби и являются условиями,
обеспечивающими постоянство знака второй вариации, а вместе с тем и по-
стоянство знака приращения Ди в задаче о слабом экстремуме.
Действительно, рассмотрим интеграл
Г’
I К (х)бу2 + 2со(л:)бу 6y']dx,	(8.2)
Хо
где <о(х)— произвольная дифференцируемая функция. Этот интеграл равен
нулю:
г*	г'
j [со' (х)бу24-2ш(х)6у бу'] dx = f d (ш бу2) dx = [со (х) by2= О
Хо Г	Хо
(так как бу |Хо = бу Ц = 0).
Прибавляя интеграл (8.2) ко второй вариации, получим
л
62v= J [(/7уу4-со')бу24-2(/’у}„+<»)бубу'-]-Лу,у,бу'!]^.
х<>
Выбираем функцию со (х) так, чтобы подынтегральная функция, с точ-
ностью до множителя, превратилась в точный квадрат, для чего функ-
ция <о(х) должна удовлетворять уравнению
Г у'у' (Г уу 4“ ® ) (Г уу, -]- СО)2 я 0.
368	ДрСТЛТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	[ГЛ. 8
При таком выборе функции о вторая вариация принимает вид
64,= / /уу, S/ + -УУ бу dx
"	\ гу'у' /
*0
и, следовательно, знак второй вариации совпадает со знаком Ру,у,.
Однако такое преобразование возможно лишь в предположении, что
дифференциальное уравнение
Ру'у’	+ Fyy) ~ (f уу' + ®)2 = 0
имеет на отрезке (х0, xj дифференцируемое решение ш(х).
Преобразовав это уравнение к новым переменным подстановкой
где и — новая неизвестная функция, получим
{Fyy ~ Их РУУ') и ~ Их (Fy'y’u') = 0
— уравнение Якоби (см. стр. 356).
Если существует не обращающееся в нуль при х0<х<Х| решение
этого уравнения, т. е. выполнено условие’ Якоби, уо существует для тех же
значений х непрерывное и дифференцируемое решение
. .	_	_ " и'
Щ(х) = -Ауу-Лу,у, —
уравнения
Fy’y' (Fyy^~e> )	(^уу' + ®)2 = О-
Итак, условие Лежандра и условие Якоби гарантируют сохранение знака
второй вариации и, следовательно, являются достаточными условиями для
слабого минимума (Fy,y. > 0) или максимума (F , , < 0).
3. Преобразование уравнений Эйлера к каноническому виду
Систему п уравнений Эйлера (см, стр. 305)
гг'’,;-» <'=‘-2............................”>	<8-3»
можно заменить системой 2п уравнений первого порядка. Полагая
в (8.3)	F’=<}k	(А =1,2	я),	(8.4) yk
получим	dq.	dF dx-dy'		«)•	<8-5) ' R
§ 3)	ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ ЭЙЛЕРА	36#
Разрешаем систему уравнений .(8.4) относительно у'к (для возмож-
ности такого разрешения предположим, что
у1 у2 М
7ГГ>—7------°)’
D (»• >'2.Уп)
У* = ®4*' ys. qj.
(8.6)
где	'
ak(x, ys,.qs) = ak(x, у2...............уп, qv q2.........<?„),
и подставляем (8.6) в (8.5,). .При этом получим систему 2п уравне-
ний первого порядка в нормальной форме:
dyk z ч
= ys. qs),
dqk _ I dF 1
dx — j dyk
(8.7)
Здесь и в дальнейшем фигурные- скобки означают, что в скобках
вместо у'к подставлены ®к(х, ys, qs). -
С помощью функции
п
Н (х, ys, qs) = 2	— {Т7}
1=1
система (8.7) может быть записана в каноническом виде:
—__
dx dqk ’
dq.	дН
dx	ду.
(£ = 1,2..........п).	(8.8)
Заметим, что если функция F(yv У2............ Уп> Ур У2. .... у')
не зависит явно от х, то система (8.8) имеет первый интеграл Н = С.
Действительно, в этом случае
п
i = l
также не содержит х явно и, следовательно.
с/// дН dyдН dtf^
dx 2^ dy. dx + dq. dx ’
f=i 1	z=i *
370	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА	[ГЛ. 8
В силу уравнений (8.8) получим
4^ = 0, Н = С
dx
вдоль интегральных кривых системы (8.8).
Для простейшей задачи этот первый интеграл уже был получен
на стр. 303.
Пример 1. Зак'он сохранения энерг и'и. Функция
/=1
для функционала
6	п
f(r-U)dt.
Го	1=1
где сохранены обозначения примера 1 стр. 320 (Г — кинетическая энергия
системы материальных точек, U — потенциальная энергия), имеет следую-
щий вид:
п
1=1
— полная энергия системы. Применим принцип стационарного действия.
Если потенциальная энергия U не зависит явно от t, т. е. система консерва-
тивна, то уравнения Эйлера для функционала J* (Т — U) dt имеют первый
6
интеграл Н — С, Т 4- U = С.
Итак, полная энергия консервативной системы остается при движении
постоянной.
Интегрирование канонической системы (8.8) равносильно инте-
грированию дифференциального уравнения в частных производных
	=	(8.9)
где
и I	dv \	и /	dv	dv	dv \
nix, ys, — =п х, у., V,.........у„,	т— .
\	dys} \	dyt	ду2	дуп)
Уравнение (8.9) называется уравнением Гамильтона—Якоби.
Если известно однопараметрическое семейство его решений
v (х> ys> а)> т0 известен и первый интеграл = р системы (8.8),
р — произвольная постоянная. Действительно,
d j dv у d2v ! d2v дуj	d2v ( d2v dH t
~dx \ да J дхда ду.да дх дхда ду. да dq. ' (8-Ю)
7=1	’	J 1
S3]
ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ ЭЙЛЕРА
371
Дифференцируя тождество
у,.	по о.
получим
d2v ___ V дН d2v	_ ..
дх да	dqs dys да	\ • >
s=l
и, подставляя (8.11) в (8.10), получим в правой части (8.10) тожде-
ственный нуль. Итак,
dx \да )
откуда
dv —л
да Р'
Следовательно, если известен полный интеграл уравнения Гамиль-
тона — Якоби	1	'
v — v(x, Ур у2......уя, ар а2, ...,а„),
то известно и п первых интегралов системы (8.8):
= в (/=1,2.............п).	(8.12)
Если якобиан системы (8.12) отличен от нуля
то система (8.12) определяет у, как функции остальных аргументов:
У/ = У/(*. ар а2...................ал, ₽р ₽2, .... ₽„)	(8.13)
(/=1, 2......п).
Тем самым получено 2/г-параметрическое семейство экстремалей.
Можно доказать, что (8.13) является общим решением системы урав-
нений Эйлера, а функции
at.....a„, Рр .... р„)
и
((=1.2.......»)
являются общим решением системы (8.8).
Пример. Найти уравнение геодезических линий на поверхности, на
которой элемент длины кривой имеет вид
ds2 = [<₽! (х) -J- <p2 (у)] (dx2 4- dy2),
372	ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
т. е. найти экстремали функционала
[ГЛ. 8
X _____________________
5 = J (х) 4-ф2 (у)] (14-у'2) dx.
Хо
Так как	____________
н =	= уф1 (х)4-ф2 (у)- /1 — ?2.
И + у
_______у'
у 1	у,2 ’ /72 4- q2 = ф1 (х) -}- ф2(у),
то уравнение Гамильтона — Якоби имеет вид
I dv\2 I dv\2
Ы) +Ы
или
/ dv \2	, .	/ ч (dv \2	4
. Ы “'р,и)=ф2(у)_ы •
Для уравнений такого типа (уравнений с разделенными переменными)
/ dv\ . I dv\
Ф, х, -j— = Ф2 у, |
1 \ дх ) v ду )
легко находится первый интеграл. Полагая
( dv \2	. .	. . I dv\
Ы) ~ф,(х)==а и <>’*w-by)ea
или
57=/ч>1 (*)+«
И
-g- = /q>2(y)-a.
находим
v = f К<₽1 w + a dx4- J к<р2 (у) — a dy,
о dv о
следовательно, уравнение геодезических линии -— = р в данном случае
имеет вид
Г _dx -С______________.
j К<₽1(*)4-а д /ф,(у) — “
Замечание. К уравнению Гамильтона — Якоби можно прийти
и из иных соображений. Рассмотрим центральное поле экстремалей
с центром в точке А (х0, у0) для функционала
х
г» [у (х)] =• J F (х, у, у') dx.
Хо
ЗАДАЧИ К ГЛАВЕ 8
373
На экстремалях поля функционал v [у (х)] превращается в функ-
цию v(x, у), координат второй граничной точки В(х, у). Как было
указано на стр. 370,
dv	и,	. dv
-г— — — И (х, у, q),	-r-=q.
дх	\ • j"	1
Исключая q, получим
dv и ( dv \	/
-V— — — Н х, у, -д— .
dx	\ ду )
Итак, функция v(x, у) является решением уравнения Гамиль-
тона — Якоби. Совершенно аналогичные рассуждёйия справедливы
и для функционала
•ч
fF(x- Ур У2.......У,р Ур У2........y'„)dx-
Задачи к главе 8
Исследовать на экстремум функционалы:
’	2
1.	v [у (х)] = J* (ху'+ у'2) rfx; у (0) = 1; у(2)=0.
о
а
2.	v [у (х)] = у(у'2 + 2у/—16y2)rfx; а > 0; у (0) — 0; у(а) = 0.
о
2
' 3. v[y(x)]= f y'(l+x*y')dx; у(~1) = 1;
-1
- 2
4.	v[y(x)] = J y'(l + x2y')dx; у(1>3; у(2)®5.
1
2
5.	v [у (х)] = J* у' (l+x2y')dx; у (—1) = у (2) = 1.
-1
л
4
6.	V (у-(х)] = У" (4у2 — у '2 + 8у) dx; у (0) = — 1; у = 0.
о
2
7.	v(y(x)] = J(x2y'24-12y2)rfx; у(1)=1; у(2) = 8.
1
374
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА
[ГЛ. 8
8.	Чу W] = /(y'24-y24-2y^)dx; у(0) = 1; у(1) = 1^.
О
л
4
9.	v [у (х)] = у1 (у2—у'2 4-бу sin 2x)dx; у(0) = 0; у = 1.
о
Xl
/dx
yl y(0) = 0; у(х|) = у1; Xi > 0; у1 > 0.
О
Х1
И. Чу(*)] =	У(0) = 0; У(*1) = Уп *i > 0; У! > 0.
о У
2
12.	v [у (л)] = Г dx; у(1)=1; у(2) = 4.
f У
3
13.	V [у (х)] = J (12ху 4- у'2) dx; у (1) = 0; у (3) = 26.
1
2
14.	v [у (х)] = J [У2 + (У')2 — 2ху] dx; у (0) = 0; у (2) = 3.
о
ГЛАВА 9
ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ
§ 1. Связи вида t?(x, yv у2, ..., уп) — О
Вариационными задачами на условный экстремум называются
задачи, в которых требуется найти экстремум функционала v, причем
на функции, от которых зависит функционал V, наложены некоторые
связи. Например, требуется исследовать на экстремум функционал
*[У1- Уг.....Ул]==/ F(x> Уг У2........УП' y'z........У'п)ах
при наличии условий
<Р/(х. Ур у2, .... у„) = 0 (/ = 1, 2....т; т<п).
Вспомним, как решается аналогичная задача при исследовании
на экстремум функции а = /(хр х2, •••• хп)< при наличии связей
ф2(Хр х2.....хп) = 0	(7=1, 2.......т-, т<п).
Наиболее естественный путь заключается в разрешении системы
<pz(Xp х2, .... х„) = 0 (1=1, 2...../я),
уравнения которой мы будем считать независимыми, относительно
каких-нибудь т переменных, например относительно хх, х2, .... хт:
xl = xi(xm+l, хт±2......ХПУ,
х2 = х2(хт+1, хт+2, • хл);
Хщ — хт(хт + 1, хпг+2, •>., х„),
и подстановки найденных хР х2.........хт в /(хр х2, .... хл).
При этом функция /(хр х2........хл) становится функцией Ф(х,„+р
xm+a, .... хп) только л— т переменных xOT+i, хт+2............х.,
376	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ (ГЛ. 9
которые уже независимы, и следовательно, задача свелась к иссле-
дованию функции Ф на безусловный экстремум. Этим путем можно,
конечно, решать и поставленную выше вариационную задачу. Раз-
решая систему фДх, ур у2, .... уя) = 0 (Z=l, 2, ..., т) относи-
тельно ур у2, .... ут (или каких-нибудь других т функций yz)
и подставляя их выражения в v [ур у2.....уя], мы получим функ-
ционал Г[ут+р ут+2, .... У„]. зависящий только от п — т уже
независимых аргументов, и, следовательно, к функционалу W при-
менимы методы, изложенные в § 3 главы 6. Однако как для функ-
ций, так и для функционалов обычно более удобен другой метод
решения, называемый методом неопределенных множителей, сохра-
няющий полное равноправие переменных. Как известно, этот метод
при исследовании на экстремум функции z — f(xv х2, .... хя) при
наличии связей ф,(хр х2, .... хя) = 0 (Z=l, 2, .... т) заклю-'
чается в том, что составляется новая вспомогательная функция
т
=/+ 3
1=1
где — некоторые постоянные множители, и функция z* исследуется
уже на безусловный экстремум, т. е. составляется система урав-
нений ^-=° «=>•2.............»)	дополненная уравнениями
<р;=0 (/=1, 2, .... т), из которой определяются все
неизвестных xv х2, ..., х„ и Х2..........кт. Совершенно
гично может быть решена задача на условный экстремум
функционалов, а именно: если
связей
п-^-т
анало-
и для
v=fp(x, у,, у2......у„, у;, у'....y'Jdx
Ха
<fi(x, Ур у2, .... ул)==о (Z=l, 2, ..., т),
то составляют функционал
Ч / т	\
•а* — /* I F + 2 (х) Ф< I dx или v* — / F* dx,
X, V / = 1	'	А
где
т
FW+SWe
z=i
§ 1]	СВЯЗИ ВИДА Ф(лг, ,{гг)-о	377
который уже исследуется на безусловный экстремум, т. е. решают
систему уравнений Эйлера
F -4-Р /=0	(7=1, 2.......га),
у, dx у,	w
(9 i)
дополненную уравнениями связей	' ’ 7
<pz = 0	(1 = 1, 2, ..., т).
Число уравнений т-\-п, вообще говоря, достаточно для определения
т-\-п неизвестных функций ур у2, ••> Уп и	^2....^т> а гРа'
ничные условия у>(Хо) = У/о и у^(х1) = у;1 (/=1, 2........га),
которые не должны противоречить уравнениям связей, вообще говоря,
дадут возможность определить 2я произвольных постоянных в общем
решении системы уравнений Эйлера.
Очевидно, что найденные этим путем кривые, на которых дости-
гается минимум или максимум функционала v*, будут решениями и
исходной вариационной задачи. Действительно, при найденных из
системы (9.1) функциях
Хг(х) (1=1, 2, .... т) и у у (J = 1, 2, ..., п) все <pz = 0
и, следовательно, v*=v, причем если при уу = уу(х) (7=1, 2, .... га),
определенных из системы (9.1), достигается безусловный экстремум
функционала V*. т. е. экстремум по отношению ко всем близким
кривым, как удовлетворяющим уравнениям связи, так и не удовле-
творяющим им, то, в частности, экстремум достигается и по отно-
шению к более узкому классу кривых, удовлетворяющих уравне-
ниям связей.
Однако из этого рассуждения отнюдь не следует, что все решения
исходной задачи на условный экстремум будут давать безусловный
экстремум функционалу V* и, следовательно, остается невыясненным,
все ли решения могут быть найдены этим методом. Мы ограничимся
доказательством более слабого утверждения.
Теорема. Функции уР у2.......уп, реализующие экстремум
функционала
V=fF(x, У1, у2.......у„, у;, у'....y'Jdx
при наличии условий
<Р/(х, уР у2...У„) = 0	(7=1, 2......т\ т<п)
удовлетворяют при соответствующем выборе множителей
Z,(x) (7=1, 2...../га) уравнениям Эйлера, составленным для
378	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ
функционала
V* — J* I F Хг (х) <pz j dx — J F* dx.
x, \	/=1	/	x.
[ГЛ. 9
Функции K^x) и yt(x) определяются из уравнений Эйлера
F*	= °	(/=1. 2.....re)
Vj dx у j
re
q>i = 0	(Z=l, 2, .... m).
Уравнения <pf = 0 можно также считать уравнениями Эйлера для
функционала V*, если аргументами функционала считать не только
функции ур у2, .... у„, но и Х](х), Х2(х)........Хт(х). Уравнения
<pz(x, ур у2.....уп) = 0 (Z= 1, 2, .... т) предполагаются неза-
висимыми, т. е. один из якобианов порядка т отличен от нуля,
например.
В (ф|. Фг.Фт) _> л
D(yi, Уг, .... Ут) ‘	•
Доказательство. Основное условие экстремума дг» = 0 при-
нимает в данном случае вид
Хо /=1
Интегрируя по частям вторые слагаемые в каждой скобке и принимая
во внимание, что
(дууУ = ду; и (дуу)ж=Жо = О; (дуу)х=л=О,
получим
п
Хо / = 1	1
Так как функции ур у2, .... у„ подчинены т независимым связям
<Pi(x, Ур у2, .... У„) = 0	(Z=l, 2...../те),
то вариации дуу не произвольны, и пока применять основной леммы
нельзя. Вариации дуу должны удовлетворять следующим условиям,
$1]	СВЯЗИ ВИДА ф(х, »р-о	379
полученным путем варьирования уравнений связей фг = 0:
п
(^ = 1» 2...«)*).
и следовательно, только п — т йз вариаций можно считать произ-
вольными, например dym+1, 6ym+2.....бу„, а остальные опреде-
ляются из полученных уравнений.
Умножая почленно каждое из этих уравнений на Xt(x)dx и
интегрируя в пределах от х0 до хг, получим
х.
J = 0 (/ = 1> 2.......................«)•
X,	/ = 1	7
Складывая почленно все эти т уравнений, которым удовлетворяют
допустимые вариации 6у;-, с уравнением
х> п
х, / = 1	7
будем иметь
п	т
Г V dF । V1 / х <fyi d dF .	. n
/	777 + 2jM-k)~~—T7 Ъу^х = 0.
//Til" z=i дУ/ dx^'j]
или, если ввести обозначение
1=1
получим
Х1 л
Хо J =1
*) Точнее, применяя к разности
Фг(*. У1 + бУ1. .... Ул + ЪУп) — <ti(x, у„ у„)
левых частей уравнений <р/ (х, yt + byt.уп -f 6у„) = 0 и <р^ (х, ylt у„)=0
формулу Тейлора, следовало бы писать
п
где Л/ имеют порядок выше первого относительно буу(/= 1, 2,	п).
Однако, как нетрудно проверить, члены Ri не окажут существенного влия-
ния на дальнейшие рассуждения, так как при вычислении вариации функ-
ционала нас интересуют лишь члены первого порядка относительно
6y/U=l. 2.......л).
380	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ	[ГЛ. 9
И здесь пока нельзя применять основной леммы ввиду того, что
вариации буу не произвольны. Выберем т множителей Z,1(x),
Х2(х), .... Xm(x) так, чтобы они удовлетворяли т уравнениям
fy. —=0	(/=1,2.......т),
yj dx yrj	'	z
или
m
^- + 2^(x)VL-7“-F==0 (/-=1. 2, .... /п).
dyJ г=л dyJ dx ry'i
Эти уравнения образуют линейную по отношению к систему
с определителем, отличным от нуля,
£>(<Р1, фг.<Рт) , 0.
D (У1, У1..Ут)^ ’
следовательно, эта система имеет решение
^1 (х)> ^2 (х)...(”')•
При таком выборе ^(х), Х2(х)........^т(х) основное необходимое
условие экстремума
Л1 Л
принимает вид
л1 л
4	х0 j = m + l	J
Так как для функций ур у2, ул, реализующих экстремум
функционала V, это функциональное уравнение обращается в тожде-
ство уже при произвольном выборе буу (/ = /»+!, т + 2..........п),
то теперь можно применить основную лемму. Положив по очереди
равным нулю все буу, кроме одного, и применяя лемму, получим
^+2........п).
Принимая во внимание полученные выше уравнения
/V----+f<=0	(/=1,2........m),
yj dx yj	w	'
окончательно будем иметь, что функции, реализующие условный
экстремум функционала V, и множители ХДх) должны удовлетворять
СВЯЗИ ВИДА <р(лг. »;)-0
381
системе уравнений
Fy — -j—F  =0	(/=1,2........n),
yj dx yj	u	7
Фг(х, yp y2....У„) = 0 (i =1. 2, .... m).
Пример 1. Найти кратчайшее расстояние между двумя точками
Л (х0, у0, z0) и В (хь ур z^ на поверхности q> (х, у, г) = 0 (см. задачу о гео-
дезических линиях, стр. 282). Расстояние между двумя точками на поверх-
ности определяется, как известно, по формуле
Z = J /1 + у,24-^'2 dx.
X,
В данном случае надо найти минимум I при условии ср (х, у, z) — 0. Согласно
предыдущему берем, вспомогательный функционал ’
X, ____________
Z* = J [}^1 -|- у'2 4- г'2	(х) <р (х, у, z)] dx
и для него пишем уравнения Эйлера
Л (х) <ру — -4L —У-- — = 0;
У Лху^у,2+г,г
, . . d z'	п
А (х) Фг —д----------------= 0;
dX^i+y,2 + 2,2
<р(Х, у, Z) = 0.
Из этих трех уравнений определяются искомые функции
У = У(*) и z = z (х),
на которых может достигаться условный минимум функционала v, и множи-
тель Л (х).
Пример 2. Пользуясь принципом Остроградского — Гамильтона (см.
стр. 320), найти уравнения движения системы материальных точек массы
mi(i— 1, 2, п) с координатами (хр ур z() под действием сил, имеющих
силовую функцию — U, при наличии связей
<py(Z, Хр х2...х„, ур уз...у0, zp z2....zn) = 0
(J = 1. 2...m).	.
Интеграл Остроградского — Гамильтона
6
v = J (Г— U) dt
t'i
в данном случае имеет вид
v
382	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. 9
а вспомогательный функционал
Л
к
п	т
Y X mi (-*2i + И + И)—
(=1 ’ /=1
Уравнения движения будут уравнениями Эйлера для функционала V*. Они
будут иметь следующий вид:
dU . V , d(ff
т
dU- , V ,
^ = -^7 + 2Л(0
ои
-------—
dz,
(i = 1.
т	,
7=i
2, ..., ri).
§ 2. Связи вида ф(х, уь у2, ...» у„, yj, у?,	у^) = 0
В предыдущем параграфе мы рассматривали вопрос об исследо-
вании на экстремум функционала
v = fp(x, У1, у2........уп, у’р у', .... y'Jdx-,
yj(x0) — yjQ, Уу(х1) = уу1 (/=1, 2, .... п)
при наличии конечных связей
х <Рг(*. Ун У2..........Ул)==°	(*=1. 2........т).	(9.2)
Предположим теперь, что уравнения связей являются дифферен-
циальными уравнениями
<pz(x, ур у2, .... ул. yj. у', ..., у;) = 0	(7=1, 2.......т).
В механике связи такого вида называются неголономными.
а связи вида (9.2) — голономными.
В этом случае также можно доказать правило множителей, заклю-
чающееся в том, что-условный экстремум функционала v достигается
на тех же кривых, на которых реализуется безусловный экстремум
функционала
т
л.

5 2]	СВЯЗИ ВИДА <р(х. У,, vjj-o	383
где
F* = F -1- 2 К{ (х) ср(.
z=i
Однако доказательство значительно усложняется по сравнению со
случаем конечных связей.
Если же ограничиться доказательством более слабого утвержде-
ния о том, что кривые, на которых достигается условный экстремум
функционала V, при соответствующем выборе (х) являются экстре-
малями для функционала V*, то доказательство, проведенное в пре-
дыдущем параграфе, может быть с незначительными изменениями
повторено и для рассматриваемого случая.
Действительно, предположим, что один из функциональных определите-
лей порядка т отличен от нуля, например
Д(Ф1. Фа, .... фта) , 0
Это гарантирует независимость связей.
Разрешая уравнение <р/ (х, уг, у2.уп, yj, у2,	у^) =0 относительно
Ур у2....Ут, что возможно, так как
Д(Ф1. <р2,<рт) 0
D{y'v У2......Ут)
получим у'{ == фг (х, Ур у2, ..., Уп, у'т+1, у'т+2.у')	(/ = 1, 2, .... т). Если
считать ут+1. Ут+2.....Уп произвольно заданными функциями, то из этой
системы дифференциальных уравнений определяются уь у2.....ут. Таким
образом, Ут+Р Ут+2.....Уп являются произвольными дифференцируемыми
функциями с фиксированными граничными значениями и, следовательно, их
вариации в том же смысле произвольны.
Пусть ур у2........уп — произвольная, удовлетворяющая уравнениям свя-
зей <р/ = 0 (г = 1, 2.т),	допустимая система функций. Варьируем урав-
нения связей
л	п
....“>•>
; = 1	/=1
Умножаем почленно каждое из полученных уравнений на пока не опреде-
ленный множитель Л/ (х) и интегрируем в пределах от ха до х{; тогда по-
лучим
Л1	П	Х1	П л
f U) 2 ту-бу7-+ У ^-^-6yyrfx = 0;
Л у = 1 7	ХО	°yJ
*) И здесь, как и на стр. 379, следовало бы в левые части уравнений
включить слагаемые, содержащие члены порядка выше первого относительно
буу и буу (/=1, 2, ..., п), причем учесть влияние этих нелинейных членов
здесь уже значительно труднее.
384	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ [ГЛ. 9
интегрируя каждое слагаемое второго интеграла по частям и принимая во
внимание, что бу^ = (буу)' и	= (,^У/)Х~Х ~ будем иметь
-ч п
f У Гм*) —	(*) ут)] f>yjdx = Q. (9.3)
ГД dyj dx \ <ЗД
Из основного необходимого условия экстремума получим
*1 п
ж-гф'’-11 w>
X, j = 1 \	1 '
так как
Ч п	х' п
+'Ч - f Ё i'7)
Хо j = 1	Хо j = 1 ’	' '
Сложив почленно все уравнения (9.3) и уравнение (9.4) и вводя обозначение
т
F* = F 4- М (*) фр будем иметь
/=1
(9-5)
Так как вариации буу (/= 1, 2.и) не произвольны, то пока нельзя при-
менять основной леммы. Выберем т множителей (х), Л2(х).Хт (х)
так, чтобы они удовлетворяли уравнениям
/Л = 0 (/=1,2.....т).
у/ dx У]
Если написать эти уравнения в развернутом виде, то они представляют со-
бой систему линейных дифференциальных уравнений относительно
М*) и Чх~ (Z = l’ 2’	и)’
которая при сделанных предположениях имеет решение Z, (х), Л2 (х), ...
Ът(х), зависящее от т произвольных постоянных. При таком выборе
Л1 (х), Л.2 (х)...(х)	уравнение (9.5) приводится к виду
п
J Ё
Хо J = m+i '	'
где вариации буу (/ = т -f-1, «4-2, .... п) уже произвольны, и следова-
тельно, полагая все вариации byi =0, кроме какой-нибудь одной буу, и при-
меняя основную лемму, получим
S 3]	ИЗОПЕРИМЕТРИЧЕСКИЕ ЗАДАЧИ	385
Таким образом, функции ylt (х), у2 (х).уп (х), реализующие условный
экстремум функционала v, и множители 7ц (х), Л2 (х).Лт (х) должны
удовлетворять системе п-\- т уравнений:
Г* —	=0	(/ = 1, 2, .... п)
У1 dx У/
и
= 0 (Z = 1, 2, .,т),
т. е. должны удовлетюрять уравнениям Эйлера вспомогательного функцио-
нала v*, который рассматривается как функционал, зависящий от п 4- т
функций
У1> >2....Уп- .... >.т-
L
§ 3. Изопериметрические задачи
Изопериметричекими задачами в узком смысле этого слова назы-
ваются задачи об отыскании геометрической фигуры максимальной
площади при заданном периметре.
Среди таких экстремальных задач, исследовавшихся еще в древ-
ней Греции, были । вариационные задачи, например упомянутая на
стр. .282 задача о. нахождении замкнутой кривой заданной длины,
ограничивающей максимальную площадь *). Задавая кривую в пара-
метрической форме х = х (t), у— у (t), можно эту задачу формули-
ровать так: найти иаксимум функционала
<1	,	Л	X
S = У ху dt I или S = т;- У (ху — ух) dt j
z
при условии, что функционал
h ________
J* Ух1 -|- у2 dt
^0
сохраняет постоянное значение:
А _______
j V'x’2 + 'y'1dt = l.
^0
Таким образом, мы имеем здесь вариационную задачу на условный
экстремум со своеобразным условием: интеграл J" Ух1у1 dt со-
/о
храняет постоянное значение.
*) Хотя решение этой задачи было известно еще в древней Греции,
однако ее своеобразней вариационный характер был осознан лишь в конце
XVII века.
386	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ {ГЛ. 9
В настоящее время изопериметрическими задачами называется зна-
чительно более общий класс задач, а именно: все вариационные за-
дачи, в которых требуется определить экстремум функционала
®== f	У2.....У„. Ур У2. .... y'n)dx
х«
при наличии так называемых изопериметрических условий
f Ур У2............Уп’ Уу У2......У«И*=Ч
(/=1,2.......т),
где i — постоянные, т может быть больше, меньше или равно п,
а также аналогичные задачи для более сложных функционалов.
Изопериметрические задачи могут быть сведены к задачам на
условный экстремум, рассмотренным в предыдущем параграфе, путем
введения новых неизвестных функций. Обозначим
J FLdx == zt(x) (/=1,2.........tri),
ха
Х1
откуда zz(xo) = 0 и из условия J* F^x-l^ имеем zz(x1) = /i.
Хо
Дифференцируя zt по х, будем иметь
^(x) = Fz(x, уР у2......уп, у;, у'....у’)
(i = 1, 2...т).
•Г|
Тем самым интегральные, изопериметрические связи J* Fldx = ll
Хо
заменились связями дифференциальными:
^ = F/(X- Ур у2....Уп’ Уу У2. ••• Уп)
(/ = 1, 2, ..tri)
и, следовательно, задача свелась к задаче, рассмотренной в преды-
дущем параграфе.
Применяя правило множителей, можно вместо исследования на
условный экстремум функционала v= £ F dx при наличии связей
Хо
S3]
ИЗОПЕРИМЕТРИЧЕСКИЕ ЗАДАЧИ
387
Р — z'( = 0 (I — 1, 2, .... m) исследовать на безусловный экстремум
функционал
v? = f F +	(х)(Pt— Z'O dx= § F* dx,
X	Z=sl	J	Xo
где
m
Уравнения Эйлера для функционала v* имеют вид
<>=1'2.....»>
*	/7	*
FZi--^Fz'=0	(/=1.2....т),
ИЛИ
т	/	т	\
F>,+2г £ г , + 2 ’•‘Fs =0
/=Л	1	\	1	/=1	'/
(J — 1. 2.п),
= °	(/=1.2.т).
Из последних т уравнений получаем, что
вые п уравнений совпадают с уравнениями
все постоянны, а пер-
Эйлера для функционала
Таким образом, мы получаем следующее правило: для получения
основного необходимого условия в изопериметрической задаче о нахо-
X,
ждении экстремума функционала v= J F dx при наличии связей
х>
Х1
J F^x — lt (/=1, 2,..., т) надо составить вспомогательный
X,
функционал
т	\
i=l	/
где — постоянные, и написать для него уравнения Эйлера.
388
ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ
[ГЛ. 9
Произвольные постоянные Ср С2, .... С2п в общем решении
системы уравнений Эйлера и постоянные Хр Х2, ..., Хт определяются
из граничных условий
У](хо) — У}О< У)(х1) = у}1	(1=1, 2......п)
и из изопериметрических условий
У F^x — Ц (/=1,2, .... т).
-Го
Система уравнений Эйлера для функционала и** не изменяется,
если V** умножить на некоторый постоянный множитель |д0 и, следо-
вательно, представить его в виде
т
Но®** = J Pipi dx,
Х> 1=0
где введены обозначения F0 = F, Н; = Хур,0, /=1........т. Теперь
все функции Ft входят симметрично, поэтому экстремали в исходной
вариационной задаче и в задаче
на нахождение экстремума функ-
х1
ционала Fsdx при наличии изо-
Хо
периметрических условий-
X,
УF t dx — l[
Хо
(Z = 0, 1, 2, ...
..., s — 1, s + 1, .... m)
совпадают при любом выборе
s (s = 0, 1....n).
Это свойство носит название
принципа взаимности. Напри-
мер, задача о максимуме площади, ограниченной замкнутой кривой
заданной длины, и задача о минимуме длины замкнутой кривой, огра-
ничивающей заданную площадь, взаимны и имеют общие экстремали.
Пример 1. Найти кривую у = у (х) заданной длины I, для которой
площадь S изображенной на рис. 9.1 криволинейной трапеции CABD дости-
гает максимума.
Исследуем на экстремум функционал
х,
5 = у у dx, у(х0) = у0,
Хй
§ 3]	ИЗОПЕРИМЕТРИЧЕСКИЕ ЗАДАЧИ	389
у (X!) = ух, при изопериметрическом условии
Jfi ______
J ]Л+у'2 dx — I.
Составляем сначала вспомогательный функционал
s** = / G + ^/H-У'2) dx.
Хо
Так как подынтегральная функция не содержит х, то уравнение Эйлера
для 5** имеет первый интеграл F— уТу = Cj или, в данном случае,
у + х/1 + у'2----------------------
]А + /2
откуда
у-С, = -^^.
]А+у'2
Вводим параметр t, полагая у' = tg /; тогда получим
у — Ct = — X cos /;
dy . ,	. dy К sin t dt .	,
-r- = tg /, откуда dx =	— = X cos t dt;
dx b J	tg/ tg/
x = % sin 14* C2.
Итак, уравнение экстремалей в параметрической форме имеет вид:
х — Сг <= % sin t,
у — Ct——к cost,
или, исключая t, получим (х—С2)2 + (У— Ct)2 — X2 — семейство окружно-
стей. Постоянные Clt С2 и X определяются из условий
х, ________
У Оо) = Уо. y(xi) = yi и J* ]А-1-у'2 dx=Z.
. х°
Пример 2. Найти кривую АВ заданной длины I, ограничивающую
вместе с заданной кривой у = f (х) максимальную площадь, заштрихованную
на рис. 9.2.	"
Требуется определить экстремум функционала
х,
S = f (y-f(x))d#
Хц
У(*о) = Уо. УО1)=У1
при наличии условия
/ Vl + y'2dx = l.
390	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ	(ГЛ. 9
Составляем вспомогательный функционал
х-,	_______
s** = f(y-/(х) + /. /1 + у'2) dx.
- х,	.
Уравнение Эйлера для этого функционала не отличается от уравнения
Эйлера в предыдущей задаче, и следовательно, в данной задаче максимум
может достигаться лишь на дугах окружностей.
Пример 3. Найти форму абсолютно гибкого, нерастяжимого однород-
ного каната длиной I, подвешенного в точках А и В (рис. 9.3).
Так как в положении равновесия центр тяжести должен занимать наи-
более низкое положение, то задача сводится к нахождению минимума стати-
ческого момента Р относительно оси Ох, которая предполагается направлен-
 X, _______________________________________________________________
ной горизонтально. Исследуем на экстремум функционал Р = у + y's dx
Хо
X, ________
при условии 1^1 4-у'2 rfx =/. Составляем вспомогательный функционал
Хо
Х\
Р** = f (У+М /l + y'2dx,
для которого уравнение Эйлера имеет первый интеграл
F-y'Fy.=C,
или, в данном случае,
(у+X) УТ+7"2 - (у.±К]у,22 = с"
V\+y’2
откуда у 4-А. = Ci +у'2. Вводим параметр, полагая y' = sh/, откуда
У 14-У'2 = ch t и у 4- А, == Cj ch t; = sh t; dx =	= Сг dt; x = Cit 4- C2,
ил	8Л •
5 3]
ИЗОПЕРИМЕТРИЧЕСКИЕ ЗАДАЧИ
391
х__£
или, исключая t, получим y + ^ = C'i ch ——--------семейство цепных
линий.
Указанное выше правило решения изопериметрических задач рас-
пространяется и на более сложные функционалы.
Упомянем еще об одной задаче на условный экстремум — задаче
об оптимальном управлении. Рассмотрим дифференциальное уравнение
x(t), и(t))	(9.6)
с начальным условием х (t0) = х0.
Кроме неизвестной функции (или вектор-функции) х (t), это урав-
нение содержит еще так называемую управляющую функцию (или
вектор-функцию) u(t). Управляющую функцию u(t) надо выбрать
так, чтобы заданный функционал
V= JF(x(f), u(t)) dt
достигал экстремума.
Функция и (/), дающая решение поставленной задачи, называется
оптимальной функцией или оптимальным управлением.
Эту задачу можно рассматривать как задачу на условный экстре-
мум функционала v с дифференциальными связями (9.6), Однако
в практических задачах оптимальные функции часто лежат на границе
множества допустимых управляющих функций (например, если упра-
вляющей функцией является включаемая мощность моторов, то, оче-
видно, эта мощность ограничена максимальной мощностью моторов,
причем в решениях оптимальных задач нередко приходится включать
моторы хотя бы на некоторых участках на полную мощность).
Если же оптимальная функция лежит на границе множества допу-
стимых управляющих функций, то изложенная выше теория задач на
условный экстремум, предполагавшая возможность двусторонних
вариаций, неприменима.
Поэтому для решения задач оптимального регулирования обычно
применяются иные методы, разработанные Л. С. Понтрягиным (см. [8j)
и Р. Веллманом (см. [9]).
Пример. В системе дифференциальных уравнений
dx dv
-j7- = v, -^- = « if — время),	(9.7)
описывающей движение точки в плоскости с координатами х, v, определить
управляющую функцию и (t) так, чтобы точка А (х0, v0) переместилась
в точку В (0, 0) за наименьший промежуток времени, причем | и I < 1 (так
d^x
как и =	, то и можно считать силой» действующей на точку с единичной
массой).
392	ВАРИАЦИОННЫЕ ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ (ГЛ. 9
Управляющая функцйя u{t) кусочно непрерывна. Для упрощения рассу-
ждений предположим, что она имеет не более одной точки разрыва, однако
окончательный результат верен и без этого предположения.
Почти очевидно, что на оптимальных траекториях и= ±1, так как при
IdxI Idv I	,
этих значениях -тг и -тг достигают наибольших значении и, следова-
| аг |	| dt |
тельно, точка движется с наибольшей скоростью. Полагая в (9.7) и — 1,
получим
v = ^4-C1, х = -у4- Cii 4"С2,
или v2 = 2 (х — С), и аналогично при и = — 1;
/2
V — — i-f-Ci, х = —g—h£i^4"C2, с/г = —2 (х—С).
На рис. 9.4 и 9.5 изображены эти семейства парабол, причем стрелки
указывают направление движения при возрастании t. Если точка А (х0, v0)
.	лежит на проходящих через начало
v 1	' координат дугах парабол
v = — У~х или v = У—х	(9.8)
С	л
л	(рис. 9.6), то оптимальной траекто-
/	\	рией	является	дуга	одной	из этих
{ ув\.	парабол, соединяющая точку А с
Г	:	Г	1	точкой В. Если же	точка	А	не ле-
\	\	J	жит	на этих	параболах,	то	опти-
мальной траекторией будет дуга па-
j	раболы АС, проходящая через точ-
л	ку А, и дуга СВ одной из пара-
рис gg	бол (9.8) (см, рис. 9.6, на котором
указаны два возможных положения
точек А и С).
В этой задаче время Т перемещения точки из положения А в положе-
ние В является функционалом, определяемым первым из уравнений (9.7),
второе уравнение из (9.7) можно рассматривать как уравнение связи. Однако
применение к этой задаче изложенных выше классических методов решения
било бы затруднительным, так как оптимальное управление лежит на границе
области допустимых управлений | и К 1 и двусторонние вариации здесь не-
ЗАДАЧИ К ГЛАВЕ 9	' 393
возможны, кроме того, решение ищется в классе кусочно непрерывных
управлений.
Оба эти обстоятельства весьма характерны для-большинства практиче-
ских задач на оптимальное управление.
Задачи к главе 9
1
1.	Найти экстремали изопериметрической задачи v [у (х)] = £ (у/2-|-х2) dx
о
1
при условии у2 dx = 2; у.(0) = 0; у(1) = 0.
„ °
2.	Найти геодезические линии круглого цилиндра г = R.
Указание. Решение удобно искать в цилиндрических координатах
г, <р, г.	ч
3.	Найти экстремали изопериметрической задачи
X,	X,
v [у (х)] =. J* у'2 dx при условии j'ydx = a.
X.	Ху
где а — постоянная.
4.	Написать дифференциальное уравнение экстремалей изопериметриче-
ской задачи об экстремуме функционала
х-,
v [У <-*)] = J' lp U) У2 + q (х) у'\ dx
э
при условии I у (х) у'1 dx у (0) = 0; у (Xi) — 0.
V
5.	Найти экстремаль в изопериметрической задаче об экстремуме функ-
ционала 1
1
v [у (х); г (х)] = § (у'2 4- г'2 — 4хг' — 4г) dx
о
I
при условии у (у'2 — ху'—г'2) dx = 2; у (0) = 0;	г(0)=0;	у(1) = 1;
о
г(1) = 1.
ГЛАВА 10
ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ
§ 1. Прямые методы
Дифференциальные уравнения вариационных задач интегрируются
в конечном виде лишь в исключительных случаях. В связи с этим
естественно возникает потребность в иных методах решения этих
задач. Основная идея так называемых прямых методов заключается
в том, что вариационная задача рассматривается как предельная для
некоторой задачи на экстремум функции конечного числа переменных.
Эта задача на экстремум функции конечного числа переменных
решается обычными методами, а затем предельным переходом полу-
чается' решение соответствующей вариационной задачи.
Функционал v [у (х)] можно рассматривать как функцию бес-
конечного множества переменных. Это утверждение становится совер-
шенно очевидным, если предположить, что допустимые функции
могут быть разложены в степенные ряды:
У (х) = а0 + агх 4- а2х2 4- ... -}-апхП-^- ....
или в ряды Фурье:
оо
у (х) = -у- 4- (ап cos пх 4- bn sin пх),
л = 1	>
или вообще в какие-нибудь ряды вида
у(х)= 2 »яфв(х).
п = 0
где <ря (х) — заданные функции. Для задания функции у (х), пред-
ставимой в виде ряда у (х) = 2	(•*) достаточно задать значе-
п = 0
ния всех коэффициентов ап, и следовательно, значение функционала
v [у (х)] в этом случае определяется заданием бесконечной последова-
тельности чисел: ай, ах, а2..ап, .... т. е. функционал является
§ 21	КОНЕЧНО РАЗНОСТНЫЙ МЕТОД ЭЙЛЕРА	395
функцией бесконечного множества переменных:
у [у (х)] = <р («0, ах.й„, .. .).
Следовательно, различие между вариационными задачами и зада-
чами на экстремум функций конечного числа переменных состоит
в том, что в вариационном случае приходится исследовать на экстре-
мум функции бесконечного множества переменных. Поэтому основная
идея прямых методов, заключающаяся, как уже сказано выше, в том,
что вариационная задача рассматривается как предельная для задачи
на экстремум функций конечного числа переменных, является весьма
естественной.
Л. Эйлер в первый период своих исследований в области вариа-
ционного исчисления применял метод, называемый теперь конечно-
разностным прямым методом. Этот метод в дальнейшем длительное
время совсем не применялся и лишь в последние три десятилетия
был с большим успехом снова возрожден в работах советских мате-
матиков (Л. А. Люстерник, И. Г. Петровский и др.).
Другой прямой метод, известный под названием метода Ритща,
в разработку которого весьма значительный вклад внесен советскими
математиками (Н. М, Крылов, Н. Н. Боголюбов и др.), в настоящее
время находит широкое применение при решении различных вариа-
ционных задач.
Третий прямой .метод, предложенный Л. В. Канторовичем, при-
менимый к функционалам, зависящим от функций нескольких незави-
симых переменных, находит все более и более широкое применение
в тех же областях, в которых применяется метод Ритца.
В дальнейшем мы остановимся лишь на этих трех основных
прямых методах, причем доказательства многих утверждений будут
опущены. Читателя, желающего более детально ознакомиться с при-
меняющимися в настоящее время прямыми методами, мы отсылаем
к книге Л. В. Канторовича и В.. И. Крылова [10] • и к книге
С. Г. Михлина [11].
§2. Конечно-разностный метод Эйлера
Идея конечно-разностного метода заключается в том, что значе-
ния функционала v [у (х)], например
J А’(х, у, y')dx, у(х0) = а, у(х1) — Ь,
1л
рассматриваются не на произвольных, допустимых в данной вариа-
ционной задаче, кривых, а лишь на ломаных, составленных из задан-
ного числа п прямолинейных звеньев, с заданными абсциссами вершин:
х0 ф- Дх, х0-[-2Дх, .... x0-f-(zi—1)Дх, где Дх = х‘~Лс (рис. 10.1).
396	Г1РЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	(ГЛ. 19
На таких ломаных функционал v {у (х)) превращается в функцию
ф(ур у2......Ул-i) ординат ур у2, ул-1 вершин ломаной, так
как ломаная вполне определяется этими ординатами.
Выбираем ординаты уР у2, .... ул-1 так, чтобы функция
<р(Ур Уз> •••' Ул-i) достигала экстремума, т. е. определяем
Ур у2, .... y„_i из системы уравнений
*=о, -^ = 0............... А-	= 0,
ду, • ду,	dy„.t
а затем переходим к пределу при п—>оо, В пределе при некоторых
ограничениях, налагаемых на функцию F, -получим решение вариа-
ционной задачи.
Удобнее, однако, значение функционала v [у (х)] на указанных
выше ломаных вычислять приближенно, например в простейшей
задаче заменять интеграл
г,	л_ 1 *о+ (*+ 1)Дл	’	,
f р (X, у, у') dx « 2 f р(х, у, Ук+^х jdx
х-	S=0 x,+k &х
интегральной суммой
тг)Дх-
ы
В качестве примера выведем уравнение Эйлера для функционала
xi
v[y(x)] = f F(x, у, y')dx.
хь
§3)
МЕТОД РИТЦА
397
В этом случае на рассматриваемых ломаных
V [у(х)| «<р(УР у2....Уп-1) = 2/7(х'’	~9 Ах‘
1 = 0
Так как от у, зависят лишь два слагаемых этой суммы:
7-е и (I—1)-е,
то уравнения
-^-=•0 (7 = 1,
ду.
2.....п — 1) принимают вид
Fy(xi' У1' Уи\х'У'')^х+ рУ’(х1’ Ус
+ ру(х1-с уг_р -'-д^ ’) д^Дх — °
(/ = 1. 2...(п-1)).
или
S')
Fy’(xr уг 4г)-МХ'-»’
Дх
или
Ayz ) ЛЛУ' п
Хр Ур -г-М----г2-—О-
С XI	/	Длг
Переходя к пределу при п—> оо, получим уравнение Эйлера
которому должна удовлетворять искомая функция у (х), реализующая
экстремум. Аналогично может быть получено основное необходимое
условие экстремума в других вариационных задачах.
Если не совершать предельного перехода, то из системы урав-
нений -^- = 0 (7=1, 2.......п—1) можно определить искомые
ординаты ур у2, .... ул_] и тем самым получить ломаную, являю-
щуюся приближенным решением вариационной задачи.
' § 3. Метод Ритца
Идея метода Ритца заключается в том, что значения некото-
рого функционала v [у (х)] рассматриваются не на произвольных
допустимых кривых данной вариационной задачи, а лишь на все-
п
возможных линейных комбинациях =	с постоянными
/=1
398	ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	[ГЛ. 10
коэффициентами, составленных из п первых функций некоторой
выбранной последовательности функций
ИЗД. изд..........изд....
п
Функции уп=2а/^/(х) должны быть допустимыми в рассматри-
;=1
ваемой задаче, что налагает некоторые ограничения на выбор после-
довательности функций и^Дх). На таких линейных комбинациях
функционал v [у (х)] превращается в функцию ф(ар а2, ..., а„)
коэффициентов ар а2.......ая. Эти коэффициенты аР а2, .... ап
выбираются так, чтобы функция <р(ар а2,	а„) достигала экстре-
мума; следовательно, ар а2, .... а„ должны буть определены
из системы уравнений
4^ = 0 (Z = 1. 2........п).
да:	v	’
Совершая предельный переход при п—>оо, получим в случае
ОС
существования' предела функцию у = 2 ai^i (•*). являющуюся (при
i=i
некоторых ограничениях, налагаемых на функционал v [у (х)] и на
последовательность Wx (х), UZ2 (х)...Wn (х), .. .) точным реше-
нием рассматриваемой вариационной задачи. Если не совершать
предельного перехода, а ограничиться лишь п первыми членами
п
у„ = 2	(х)> т0 получим приближенное решение вариационной
i = i
задачи.
Если таким методом определяется абсолютный минимум функцио-
нала, то приближенное значение минимума функционала находится
с избытком, так как минимум функционала на любых допустимых
кривых не больше, чем минимум того же функционала на части
п
этого класса допустимых кривых — на кривых вида у,п— 2а1^Дх)-
/ = 1
При нахождении тем же методом максимального значения функцио-
нала получаем по тем же причинам приближенное значение максимума
функционала с недостатком.
Л
Для ТОГО чтобы функции уп — 2 Cl/UZ(х) были допустимыми,
1 = 1
прежде всего необходимо удовлетворить граничным условиям (конечно,
не следует забывать и о других ограничениях, которые могут быть
наложены на допустимые функции, например требованиях, касающихся
их непрерывности или гладкости). Если граничные условия линейны
и однородны, например, в простейшей задаче у (х0) — у (xj = 0 или
(7 = 0,1),
МЕТОД РИТЦА
399
§ 3]
где — постоянные, то проще всего и координатные функции
выбрать удовлетворяющими этим граничным условиям. Очевидно,
п
что при этом и уя = 2 at^t (х) при любых az будут удовлетворять
i = l
тем же граничным условиям. Пусть, например, граничные условия
имеют вид у (х0)== у (Х])= 0, тогда в качестве координатных функ-
ций можно выбрать
UZz (х) = (х — х0) (х — Xt) <pz (х),.
где cpz(x) — какие-нибудь непрерывные функции, или
Wk (х) = sin	(Л=1, 2, ...),
или какие-нибудь другие функции, удовлетворяющие.условиям
rz(xo) = rz(x1) = O.
Если условия неоднородны, например у(х0) = у0, у(х1) = у1,
где хотя бы одно из чисел у0 или У] отлично от нуля, то проще
всего искать решение вариационной задачи в виде
п
y„==Sazrz(x)4-F0(x),
z=i
где U^0(x) удовлетворяет заданным граничным условиям Ц70(х0) = у0,
Ц70(х1) = у1, а все остальные IFz(x) удовлетворяют соответствующим
однородным граничным условиям, т. е. в рассматриваемом случае
(х0) == W t (хр = 0. Очевидно, что при таком выборе при любых az
функции у„ (х) удовлетворяют заданным граничным условиям. В ка-
честве функции UZ0(x) можно выбрать, например, линейную функцию
Wo (х) = xLZ--x° <х — хо) + Уо-
Л ) AQ
Решение системы уравнений -^- = 0(Z==l, 2,
п), вообще
говоря, является весьма сложной задачей. Эта задача значительно
упрощается, если на экстремум исследуется квадратичный относи-
тельно неизвестной функции и ее производных функционал -о, так как
в этом случае уравнения — 0 (Z = 1, 2.........п) линейны относи-
тельно az.
Выбор последовательности функций U^j, 1Г2.....Wn, .... назы-
ваемых координатными функциями, сильно влияет на степень слож-
ности дальнейших вычислений, и поэтому от удачного выбора коорди-
натной системы функций в значительной мере зависит успех приме-,
нения этого метода.
400	ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	(ГЛ. Ю
Все сказанное выше в полной мере относится и к функционалам
и1г(Хр хг.....хл)], причем, конечно, в этом случае функции Wt
должны быть уже функциями переменных х1₽ х2, .... хп, а также —
к функционалам, зависящим от нескольких функций.
Метод Ритца часто применяется для точного или приближенного
решения задач математической физики. Например, если требуется
найти в некоторой области D решение уравнения Пуассона
d2z д2г
дх2 ду2 ~
при заданных значениях z на границе области D, то можно заменить
эту задачу вариационной задачей об экстремуме функционала, для
которого данное уравнение является уравнением Остроградского
(см. стр. 315). В рассматриваемом случае таким функционалом будет
J fl(^^(w)2 + 2zf(X'y)]dxdy- 
D	'
Функцию г, реализующую экстремум этого функционала, можно
находить любым из прямых методов.
Задачи математической физики обычно сводятся к исследованию
на> экстремум функционалов, квадратичных относительно неизвестной
функции и ее производных, и следовательно, как указывалось выше,
применение метода Ритца в этом случае’ упрощается.
Вопрос о сходимости приближений, получаемых по методу Ритца,
к искомому решению вариационной задачи, а также об оценке сте-
пени точности этих приближений является весьма сложным. Поэтому
ограничимся здесь лишь немногими замечаниями, отсылая читателя,
желающего подробнее ознакомиться с этим вопросом, к книгам
Михлина [11] и Канторорича и Крылова [10].
Для определенности будем иметь в виду функционал
ц[у(х)] = J F(x, у(х), y'(x))dx
и предполагать, что речь идет о его минимуме. Последовательность
координатных функций UZj(х), W2(x).....Wn(x), ... будем считать
полной в том смысле, что каждая допустимая функция может быть
с любой степенью точности аппроксимирована в смысле близости пер-
вого порядка линейной комбинацией У, (х) координатных функ-
s=i
ций, где п достаточно велико. Тогда, очевидно, что методом Ритца
Л
можно получить функции уР у2, ...» ул, ...» где у„ = У (х),
§ 3]
МЕТОД РИТЦА
401
образующие так называемую минимизирующую последовательность,
т. е. последовательность, для которой значения функционала
® 1У11. ® [у21.........г> [Ул1. • •
сходятся к минимуму или к нижней грани значений функционала'
vjy(x)]. Однако из того, что lim v [уп (х)] == min v [у (х)], отнюдь не
следует, что lim уп(х) = у (х). Минимизирующая последовательность

может и не стремиться к функции, реализующей экстремум в классе
допустимых функций.
Действительно, функционал
v [у„ (х)1 = J F (х, уп (х), у'л (х)) dx
может мало отличаться от
v [у (х)] = J F (х. у (х), у' (х)) dx,
не-только в том случае, когда на всем отрезке интегрирования у„ (х)
близка в смысле близости первого порядка к у(х), но и в том случае,
когда на достаточно малых частях отрезка (х0, xj функции у„ (х)
и у(х) или их произ-
водные резко отличаются 1У
друг от друга, оста-	-ийА________
ваясь близкими на осталь-
ной части отрезка (х0, xj
(рис. 10.2). Поэтому ми-	।
нимизирующая последо-	!	!
вательность ур у2, ...,у„	1	I
может даже не иметь пре-	i
дела в классе допустимых	j	!	х
функций, хотя функции	~q	J
У1. У2...Ул сами и бу-	°	’
дут допустимыми.	Рис
Условия СХОДИМОСТИ	'
последовательности уя,
полученной методом Ритца, к решению вариационной задачи и оцен-
ка быстроты сходимости для конкретных, часто встречающихся
функционалов были разработаны в трудах Н. М. Крылова и Н. Н. Бо-
голюбова. Так, например, для функционалов вида
® = J IP (х) у"2 + q (х) у2 + / (х) у] dx; у (0) = у (1) = 0,
402
ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ
[ГЛ. 10
где р (х) > 0; q (х)	0, часто встречающихся в приложениях, не
только доказана сходимость приближений, получаемых по методу
Ритца, к функции у(х), реализующей минимум функционала, при ко-
ординатных функциях
U7t(x)=]/r2 sin Ал х (А = 1, 2, ...),
но и даны весьма точные оценки погрешности |у(х)— уя(х)|.
Приведем одну из этих оценок максимума | у (х) — у„ (х) | на отрез-
ке (0, 1):
maxjy — у„|<
j 1/ (f2 (х) dx
1	Г z \ । шах а (х) 1 2 “	/
<< —г—г max р (х) 4-	\ 	----°-----------у
И + 1 L	) 2 Л2_|	5
2	[min р (х)] 2
X ^max|j/(x)| +-i-max<7(x)-j-ttmin p(x)j*).
Даже в этом, сравнительно простом случае, оценка погрешности
очень сложна. Поэтому для оценки точности результатов, полученных
методом Ритца или другими прямыми ме-
о	тодами, обычно пользуются следующим
теоретически, конечно, несовершенным,
но практически достаточно надежным при-
емом: вычислив уя(х) и уя+1(х), сравни-
—*" вают их между собой в нескольких точ-
z ках отрезка [х0, xj. Если в пределах
требуемой точности их значения совпа-
дают, то считают, что с требуемой точ-
Рис. 10.3.	ностью решение рассматриваемой вариа-
ционной задачи равно уя(х). Если же
значения уп (х) и уя+1 (х) хотя бы в некоторых из выбранных точек
в пределах заданной точности не совпадают, то вычисляют уя+2(х)
и сравнивают значения уя+1(х) и уя+2(х). Этот процесс продол-
жается до тех пор, пока значения y„+i(x) и ул+А+1(х) не совпа-
дут в пределах^ заданной точности.
Пример 1. При изучении колебаний заделанного клина постоянной тол-
щины (рис. 10.3) приходится исследовать на экстремум функционал
• 1
v = J* (ах’у'2— bxy2) dx\ у (1) = у' (1) «= 0,
*) См. книгу Канторовича и Крылова [10].
§ 3]	МЕТОД РИТЦА	403
где а и 6 — положительные постоянные. За координатные функции, удовлет-
воряющие граничным условиям, можно взять
(х — I)2, (х — I)2 х, (х — 1)2х2..(х — I)2 х*-1,
следовательно,
У„ =	—UV"1-
ft=l
Ограничиваясь лишь двумя первыми членами, будем иметь
Уз = (.X — I)2 (а, 4- а2х),
тогда
1
v2 = v [у2] = J* [ал3 (6а2х + 2d] — 4а2)2 — Ьх(х — I)4 (а, -|- а2х)2] dx ==
о
= а ^(а, — 2а2)2 + -у а2 (а1 ~ 2а2) + 6а2] ~ ь
а2 ( 2а , а2
30 + 105	280
Необходимые условия экстремума
случае вид
и
dv2
dat
-& = о
v0l2
принимают в
данном
( b \ I /2 ь \ л
[a-¥)a,4-^-.105) а»= °
(б а 105) а‘ + (б а 28о)“2~а
Для получения решений, отличных’ от решения сц = аг = 0, которое соответ-
ствует отсутствию колебаний клина, необходимо, чтобы определитель этой
однородной линейной системы уравнений был равен нулю:
6	2	6
а 30	5 а .105
2	6	2	6	=0
5 а	105	5 й	280
или
/ д \ / 2 b \	/2	6 \2 Л
Г ЗоДб* 280/ \5 а Юз") =а
Это уравнение называется уравнением частот. Оно определяет частоту Ъ
собственных колебаний клина, описываемых функцией
и (х, 0 = у(х) cos 6t.
Меньший из двух корней 6^ и б2 уравнения частот дает приближенное зна-
чение частоты основного тона колебаний клина.
Пример 2. В задачах, связанных с кручением цилиндра или призмы,
приходится исследовать на экстремум функционал
vk(^. у)] = f f [G&-y)2 + (^ + *f]dxdy-
D
404	ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	[ГЛ. 10
Для цилиндра с эллиптическим поперечным сечением область интегрирова
№ у2
ния D будет ограничена эллипсом	- =1. В этом случае, взяв лишь
одну координатную функцию ху, получим
Z1 = axy, v [zi] = »| =	[(а+ I)2 а24-(а — I)2 62].
Необходимое условие экстремума
(а Н* 1) а2 + (а — 1) Ь2 = 0, откуда
*1 = 0
да
принимает
в данном случае вид
Ь2 — а2	Ь2 — а2
а = а2 Ь2 ’ г' “ а2 4- Ь2 ХУ'
Пример 3. Если в условиях предыдущего примера область D будет
прямоугольником со сторонами 2а и ib, — а < х «С а; — b < у < Ь. то. взяв
за координатные функции ху. ху3, х3у. т. е. положив
z3 = atxy 4- а2ху3 4- а3х3у
получим
а ' b
V3 = V[Z3]= f Д^_уу+(^ + х)2]^у =
-а -Ь
= -| ай3(“| — 1)24-4а*5 (4- + ^)а2 + 4а5*(4г'^^Г’)аз +
4- 4 а3Ь (а! 4-1)2 4- 4 abi <°i — 1) «г 4- 4 “3Ь (а, 4- 1) а2 —
О	и	О
— 4 а66 (Ц| 4- I) а3 — 4 а3*3 (а2 + *2) “газ — 4 а’*3 <ai ~ а«-
О	D	«3
dvt „ dv« _ dv3 ..
Необходимые условия экстремума —— = 0,	= 0,	= 0 позво-
ляют вычислить ар а2,а3:
7 (а6 — Ь3) 4- 135а2 62 (а2 — Ь1)
а‘ =	7 (а6 4- Ь3) 4- 107а262 (а2 4- Ь2) ’
7а2(3а24-35д2)
“2“	21 (а«4-&в)4-321а2&2(а24-й2) ’
1Ь2 (35а2 4- З*2)
“3=	21 (а3 4- Ь3) 4- 321 а2Ь2 (а2 4- Ъ2)'
Пример 4. Найти решение уравнения
д2г . д2г
дх2 + ду2 =/(л’
внутри прямоугольника D, 0<.x<a, 0<y<S, обращающееся в нуль на
границе D. Функция / (л, у) предполагается разложимой внутри рассматри-
ваемого прямоугольника в равномерно сходящийся двойной ряд Фурье:
ОО со
7) = S Р₽« Sln Sin?
р- 1 «=1
§ 3)	' МЕТОД РИТЦА	405
Эту краевую задачу можно свести к вариационной задаче, т. е. подобрать
функционал для которого заданное уравнение было бы уравнением Остро-
градского, и затем- одним из прямых методов найти функцию, реализующую
экстремум этого функционала и тем самым найти решение исходной краевой
задачи. Как легко проверить,
d2z . d2z
дх2 ду2 у}
является уравнением Остроградского для функционала
сл[лг (лс. у)] = У J [(-57)' ++ 2z/(x. y)]dxdy
D ‘
(см. стр. 315). Граничное условие сохраняется: г=0 на границе области D.
Исследуем этот функционал на экстремум методом Ритца. В качестве си-
стемы координатных функций возьмем
, лл , лу ,	. „	.
sin/я-----slnn (т, п=* 1, 2, ...).
а Ь	'
Каждая из этих функций и их линейные комбинаций удовлетворяют гранич-
ному условию г = 0 на границе области D. Свойством полноты эти функции
также обладают Взяв
п т
V1 , лл , лу
т = 2j 2j aPV sln P — s,n 9
p= 1 <7=1	—
будем иметь
a t> r
0 0
JO 30
+ J} sin p ~ sin q
p=1 <7=1
dx dy e
-v	n m	n m
' Л2а£ V V t P2 1 Я1 \ 2 1 V V я
4 2j \ a2 b2 / аРч "I" 2 -2j «PdPp?-
p=l <7 = 1	p=l <7=1
Этот результат легко получить, если принять во внимание, что координатные
функции sin Р~~- sin q (р, q = 1, 2. ...) образуют в области D ортого-
нальную систему г. е.
Г Г , пл , лу - лл , лу ,	„
I I sin р—^~ sin9 sin pi -7-sin q, —— dx dy — 0
’ D
при любых целых положительных р, q, ръ qx, за исключением случая р =» рц
q = qt При р — ру и q <= qt получаем
Я. , лл , , лу j J ab
SHV Р — Sln^ -2- dx dy =
D
406	ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	(ГЛ. 10
Поэтому из всех членов, стоящих под знаком двойною интеграла, рав-
ного v надо учитывать лишь те, которые содержат квадраты функций
, ях , яу . ях яу	ях , яу л
sin р---s\nq-~~, sin р— cos qи cos р ——sin?—г-. Очевидно,
г а b	а * b	r а Ь
vlznm] является функцией <р(ац, <х12, ...,апт) коэффициентов ап, а12, ...
.... апт, которые определяются из основного необходимого условия экстре-
мума
1^7 = 0 ^=Е2.........л; '7=1>2........т}
Эта система уравнений в данном случае имеет вид
аР, + 7г)	+ Pw = 0 (Р = Ь 2------- ? = 1. 2....яг),
откуда
Следовательно,
, л т «
1 V V "Р?	 ЯХ , яу
гпт-=--^	1 > 7 VSln/?— Sln-7-T-
р= I 4=1 аг + J2
Переходя к пределу при пит, стремящихся к бесконечности, в данном
случае получим точное,решение:
, “ 00	д
J_ у у	w
Я2	Р2 ; q2
p=i ?=i тг + тг
. „ ЯХ .  яу
Sin Р --Sin?—Г-.
а о
§ 4. Метод Канторовича
При применении метода Ритца к функционалам v[z(xlt х2,,..,х„)],
зависящим от функций нескольких независимых переменных, выбирается ко-
ординатная система функций
W'i(xI, х2...х„), ^2(х„ х2. .... х„)....Wm(xb х2, .... хп), ...
и приближенное решение вариационной задачи ищется в виде гт =
т \
= У akWh(xb х2.......хп), где коэффициенты ак — постоянные.
k^i
Метод Канторовича также требует выбора координатной системы
функций
(х„ х2, ..., хп), х2, .... хп), .... Wm(xt, х2, .... хп), ...
и приближенное решение также ищется в виде
гт = 2 °*	• • *> х^’
А = 1
МЕТОД КАНТОРОВИЧА
407
§ 4]
однако коэффициенты (х,) не постоянные, а являются неизвестными функ-
циями одной из независимых переменных. Функционал v [г] на классе функ-
ций вида
гт = 2 “ft Wk .............хп)
й=1
превращается в функционал v [оч (xz), a2(xi), .... ат (xz)], зависящий от т
функций одной независимой переменной
Qi (Х(), а2(хг), .... am(xz).
Функции 01 (х;), a2 (х;)...ат (xz) выбираются так, чтобы функционал v
достигал экстремума.
Если после этого перейти к пределу при т -> оо, то при некоторых
условиях можно получить точное решение, если же предельного перехода
не осуществлять, то этим методом будет получено приближенное решение и
притом, вообще говоря, значительно более точное, чем при применении ме-
тода Ритца с теми же координатными функциями и с тем же числом членов т.
Большая точность этого метода вызвана тем, что класс функций гт =
т
= 2	(•*/) (xi> х2>--->х„) с переменными a*(xz) значительно шире
класса функций
^=2	Л2...Хп)
к=\
при постоянных и, следовательно, среди функций вида
т
Zfn= 2	Х2> .... */х)
£=J
можно подобрать функции, лучше аппроксимирующие решение вариационной
задачи, чем среди функций вида У, ahWh(x}, х2, ...,хя), где а* постоянны.
А=1
Пусть, например, требуется исследовать на экстремум функционал
х, <Ых)
V = ' f f F[X'y’2‘^' ^}dxdy’
Хо Ф1 (х)
распространенный на область D, ограниченную кривыми у = <Pi (х), у = <р2 (х)
( двумя прямыми х = х0 и Х = Х! (рис. 10.4). На границе области D заданы
значения функции г (х, у). Выбираем последовательность координатных
функций:
IF1 (х, у), 1Г2 (х, у).1Г„(х, у), ...
Ограничиваясь пока т первыми функциями этой последовательности, мы
будем искать решение вариационной задачи в виде суммы функций гт =»
т
= “л (х)	(х, У) или> меняя обозначения ak (х) на uj (х), получим;
/ = 1
X,л (X, у) =	(х) IF1 (х, у) + в2 (х) W2 (X, у) + ... Н- ит (X) Wm (х, у)»
408	ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	[ГЛ. 10
где Wk — выбранные нами функции, а ик — неизвестные функции, которые
мы определяем так, чтобы функционал v достигал экстремума. Имеем
Х| <h(X)
^т{х. у)] = f dx j />(х, у, гт(х, у).	^)dy.
Хо ф| (х\
Так как подынтегральная функция является известной функцией у, то инте-
грация по у может быть выполнена, и функционал v \гт (х, у)] будет функ-
ционалом вида
v [гт (х, у)] = J <р(х, и, (х).ит (х), и', ..um) dx
Хо
Функции Ul (х), u2 (х), .... ит (х) выбираются так, чтобы функционал
о [?т (х, у)] достигал экстремума. Следовательно, и/ (х) должны удовлетво-
рять системе уравнений Эйлера:
d	о
d	о
•Г2
d	л
Фи —-ТТФ - =°-
т аХ и
т
Произвольные постоянные выбираются так, чтобы zm (лг, у) удовлетворяла
ча прямых х = л0 и х = Х[ заданным граничным условиям.
Пример 1. Исследовать на экстремум функционал
а ъ
’^”1- f
§4]	МЕТОД КАНТОРОВИЧА	409
причем на границе области интегрирования z = 0. Областью интегрирования
является прямоугольник — а<х<а; —Ь<у<,Ь. Рейение/ ищем в виде
г, = (i2 — у2) и (х), при этом граничные условия на прямых у — ± b будут
удовлетворены. Функционал
-	а	•
t'l2ri]= /* [43- й6и'2 + 4- Ь3и2-^-63u]dx.
J L	о	о J
-д
Уравнение Эйлера для этого функционала
,	5	5
“	2&2 “	462
является линейным уравнением с постоянными коэффициентами, общее ре-
шение которого имеет вид
и = С’] ch j/ -у -у С? sh
Постоянные Ct и С2 определяются из граничных условий z(—а)= г(а) = 0
откуда С2 = 0, С, =----------, и окончательно получаем:
2chV 2 Т
1	/ , ch V 2 b
« = -2 1---7==—
2	\	<_ - / 5 a
A chK 7T
следовательно.
zi = j (Ъ2 — у2)
2 Ь
получить более точный ответ, то можно искать решение
г2 = (Ь2 — у2) и, (х) 4- (Ь\— у2)2 и2 (х).
Найти непрерывное решение уравнения Дг = — 1 в об-
Если необходимо
в виде
Пример 2.
ласти D, являющейся равносторонним треугольником, ограниченным прямыми
/3
у = ± -Нг— х и х = Ь (рис. 10.5) обращающееся в нуль на границе этой
О
области.
Уравнение Да = — 1 является уравнением Остроградского для функцио-
нала
Уз"
к	—5— X
о 3
f ш+ш-ч—
о УГ
х
410	ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ	[ГЛ. 10
причем на границе области интегрирования г — 0. Следуя методу Канторо-
вича, будем искать первое приближение в виде
Г / i/’T \21
и (х).
Zi
„		уз
При таком выборе гх граничные условия на прямых у = ± х удовлет-
О
воряются.
Функционал v[-2Ti] после выполнения интегрирования по у принимает вид
_ ь
V ь.1 = 2ЦЗ- Г (2х5«,2+10х4ии' 4-30x3u2 + 15x3u)dx.
о
15
Уравнением Эйлера для этого функционала будет х2и" + 5хи'— 5и = —.
Линейные уравнения такого типа в теории дифференциальных уравнений на-
зываются уравнениями Эйлера (стр. ПО).
Одно частное решение этого неоднородного уравнения очевидно: и =
____,3
-___4 ‘
и = хк и
Решение соответствующего однородного уравнения ищем в виде
окончательно получаем и = СххС^х~5~ —. Так как около
точки х = 0 решение и -должно быть
ограничено, то С2 следует выбрать рав-
ным нулю, а из условия и (Ъ) — 0 полу-
3
чаем Ci =---------------------------гт-. Итак,
4Ь
Z\ =
,2_____L
3 X ?
Замечание. Для приближенного ре-
шения краевых задач часто применяется
еще один прямой не вариационный метод —
метод Б. Г. Галеркина. Этот метод осо-
бенно удобен при решении линейных крае-
вых задач, но может быть применен и ко
многим нелинейным задачам. Для опреде-
ленности изложим метод Галеркина в применении к особенно часто встре-
чающимся в приложениях линейным уравнениям второго порядка
у" + Р (х) у’'+ q (х) y=f(x)
с однородными граничными условиями у (х0) = 0, у (Xj) — 0 (неоднородные
граничные условия у (х0) = у0, у (xj = yi заменой переменных
г = У — Уо---v° -	— х»)
Х| — Xq
(Ю.1)
легко сводятся к однородным).
МЕТОД КАНТОРОВИЧА
411
§ 4]
Уравнение (10.1) кратко запишем в виде
Д(у)=»/(х).
Выберем полную на отрезке [х0, xj систему непрерывных линейно не-
зависимых функций
t»i(4®iW.........шл(х), ....	(10.2)
удовлетворяющих граничным условиям wn (х0) = wn (xj = 0 (n=l, 2, ...).
Приближенное решение краевой задачи будем искать в виде линейной ком-
бинации первых л функций системы (10.2):
Уп = 2 a‘w‘ <•*)•
<=1
Подставляем уп в уравнение (10.1) и выбираем коэффициенты a, (I — 1,2, ..., л),
так чтобы функция
У aiWt (х)
t = i
была ортогональна на отрезке [х0, xj каждой из функций wi (х) (z = 1,2,.... п)
-/(X)
wt (х) dx — 0 (i = 1, 2, ..л). (10.3)
Естественно ожидать, что уп стремится при л -»оо к точному решению
у = 2 atwi (х),
: = 1
так как, если полученный ряд сходится и допускает двукратное почленное
дифференцирование, то функция L (у)— f (х) ортогональна на отрезке [х0, xj
каждой функции (х) системы (10.2), а так как система (10.2) полна,
то Д (у)— /(х) = 0, а это означает, что у является решением уравне-
ния (10.1). Очевидно, у удовлетворяет и граничным условиям у (х0) — у (xt) = 0
(так как все wi (х0) — wi (х^— 0).
Определить все а; из линейной по отношению к ним системы (10.3) и
совершить предельный переход при л->оо удается весьма редко, поэтому
дбычно ограничиваются лишь конечным и притом весьма небольшим
числом л (л — 2, 3, 4, 5, а иногда даже л = 1).
При этом, конечно, надо выбрать лишь л функций Wi (х), поэтому усло-
вие полноты отпадает и их надо выбирать лишь линейно независимыми и
удовлетворяющими граничным условиям
(х0) = wt (xj = 0.
Часто в качестве таких' так называемых координатных функций беру г
многочлены:
(X — Хо) (X — Xj), (X —Х0)2(Х— Х1), (X — Х0)3 (X — X,), ...
..(X — х0)п (х — Xi), . . . (10.3;
412
ПРЯМЫЕ МЕТОДЫ В ВАРИАЦИОННЫХ ЗАДАЧАХ
(ГЛ. 10
(удобно при этом начало координат перенести а точку ха, и тогда в (10.3)
х0 <= 0) или тригонометрические функции
sin ™	(Я=1, 2. ...).
*1 — *0
Этот метод применим к уравнениям любого порядка п, к системам
уравнений и к уравнениям в частных производных
Задачи к главе 10
f
1.	Найти приближенное решение уравнения Аг —— 1 внутри квад-
рата — а^х^а, —а^у-^а, обращающееся в нуль на границе этого
квадрата.
Указание. Задача сводится к исследованию на экстремум функ-
ционала	.
- /лш+ог-^-
D
Приближенное решение можно искать в виде
г0=э а (х2 — а2) (у2 — а2).
2.	Найти приближенное решение задачи об экстремуме функционала
1
' . v [у (х)] = J (х3у"2 + ЮОху2 — 20ху) dx; у (1) = у' (1) = 0,
о
Указание. Решение можно искать в виде
U) = (X — I)2 (а0 + а,х + ... 4-а„хя);
провести вычисления при п = 1.
3.	Найти приближенное ре.шение задачи о минимуме функционала
1
^[у(х)] = /(у" — у2 — ^xy)dx\ у (0) = у(1)«0,
о
и сравнить с точным решением.
У Казани е. Приближенное решение можно искать в виде
уя= х(1 — х)(ао + а,х+ ... -j-u^x");
провести вычисление при п = 0 и п = 1.
4.	Найти приближенное решение задачи об экстремуме функционала
2
«1)И|= f (ху'2 — х у2 — 2х‘‘у\ <1х; у (1) = у (2) = 0,
и сравнить с точным решением.
ЗАДАЧИ К ГЛАВЕ 10	, 413
Указание. Решение можно искать в виде
у = а(х— 1)(л — 2).
5.	Найти методом Ритца приближенное решение задачи о минимуме
функционала
2
V[y(x)]« J (yzii + у2 ч- 2ху) dx\ у (0) — у(2) = 0.
о
и сравнить с точным решением.
Указание. См. задачу 3.
6.	Найти методом Ритца приближенное решение дифференциального
уравнения у" -f- хгу — х; у (0) = у (1) == 0. Определить ys (х) и у3 (х) и срав-
нить их значения в точках х = 0,25. х = 0,5 и х = 0,75.
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
К главе 1
1. sin у cos х — с.
,	С I х3 с У*
4 у = т + т-5- ~2
8. е* — еу = с. 9. х = се' — -i- (cos t -|- sin t).
2. 6х2 4- Ъху 4- у2 — 9х — Зу — с. 3. х2 — 2су = с2.
— = с. 6. х — се~31 4* -г е2‘- 7- У = с cos х 4- sin х.
X	о
10. Однородное уравнение:
(3tW I3-'”I'I=‘-•
х - sin t,
!	t
p=2
P3 — P + 2.
3 4 P2
>=4^-2-
. X=X^P3 — ^P2 + C>
l У = P' — P3 — 2.
19. Гиперболы x2 — у2 — c. 20. Дифференциальное уравнение искомых кри-
У
вых -^- = у'. Отв. у2 — 2сх. 21. Дифференциальное уравнение искомых кри-
вых у— ху'— х. Отв. у = сх— л!п|х|. 22. х2 4-У2 — 2су = 0. Особенно
просто задача решается в полярных координатах. 23. Дифференциальное
уравнение задачи ~^-=k(T — 20). Отв. Через 1 час. 24. Дифференциаль-
х = yecy+l. 11. у = сх и у2 — х2 — с. 12. у2
14. Можно ввести параметр, полагая
15. у = сх 4- у; особое решение у2 = 4х.
у' = cos t
16.
dx	уЗ
нение линейно относительно х и х = су 4- 4г. 18.
•	dy 7 1 2
sin 2t
~~4~
17. Урав-
ное уравнение задачи = kv, где v — скорость. Отв. v а: 0,466 км/час.
25. Если поместить начало координат в заданную точку и направить ось
абсцисс параллельно данному в условиях задачи направлению, то дифферен-
циальное уравнение кривых, вращением которых образуется искомая поверх-
— х ± V X2 4- У2 I	.	.	п	,Г~
ность, имеет вид у =-------------'—2— (или dx — dp = 0, где р = у х2 4- у2) 
Отв. Осевое сечение искомой поверхности определяется уравнением
у2-2сх~1-с2, поверхность является параболоидом вращения. 26. у — 2 sin (х—с).
у
27. Дифференциальное уравнение искомых кривых у' — — — , Отв. Гипербо-
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
415
лы ху^с. 28. (х + у + 1)’ = с(х-у + 3). 29. у = -1С1±^_. 30.у(0.5) «
«0,13. 31. у (0,6) « 0,07. 32. у (0,02) « 1,984; у (0,04) « 1,970; у (0,06) « 1,955;
у (0,08)« 1,942; у (0,10)« 1,930; у (0,12)« 1,917; у (0,14)« 1,907; у (0,16) « 1,896;
у (0,18) « 1,886; у (0,20) « 1,877; у (0,22)« 1,869; у (0,24)» 1,861; у (0,26)« 1,854;
. 2р
Х р2 3 ’ и у = 0. 34. x-j-ctg = с.
у — 2рх—р2.
36. (Л'4-У 4- I)3 = сг2х+у. З7.у = с;у = гх4-с;у = —вх + с. 38. у2 = 2сх4-с2.
оа м	лп	х2~1	х2—1 , 2	1
39. Не имеет. 40. у, =---------§—; у2 = —g---------
41. у = 2х2— х. 42. Не имеет. 43. х = се у. 44. х2 -|-	*= с2. 45. х = 2/.
х'^
48. Действительного решения не
с‘^ х%
существует. 49. Зх—4у -|- 1 = сех~у- 50. х = (4Z + с) sin t. 51. у = сх 4-—
1Х^	О
и особое решение у — — х2. 52. у =	;, у = 0. 53. х — с = у (2Z—sin 2t),
у (0,28) « 1,849; у (0,30) « 1,841.33.
6	20 '
46. x = t2.
у = -^-(1—cos 2t) — семейство циклоид. Особое решение у — а. Указа-
ние: удобно ввести параметр t, полагая y' = ctgZ. 54. 3 (х2 4- у) 4" ХУ3 = сх-
X
55.	8 —	56, х=сеУ 	х24-2ху —у2—6х— 2у = с.
58.	У = । |п у и у — 0. 59. (х2—1)у — sinx = c. 69. 8у4~4х-|-5 =
= с?х-8у-4. 61. у34-х3 — Зху = с. 62. у = с(х2-|-у2). 63. у3=х4--^-.
(х I	2 с
64.	у = с (х 4- а) 4* с2 и особое решение у =--—65. х~~^ ^4"^»
3	с
у — 2xt — t2	и у	= 0, у	= -г х2.	66. у	= -т—--------.
J	2	1	4	1	1 ±	cos х
К главе 2
A	. .	... 1 A, t COS t
2. x = C] cos 14- c2 sin t -f- cos 2t-—
.	,	.	, COS2 X 1
4. у = С] COS X 4- C2 sin X 4-:----=—;---
1.	у = 5е3х sin х 4- Ю.
3. (у — с3)2 = ^х 4- с2.
5. у = CiX2 4- с2х3 4-	6. у = Ci sin х 4- с2 cos х-J- -i- ch х. 7. у =	1  4~ 1.
О	£	С]Х Cj
t2e2‘	1	х	с? 4- 1
8. x = e2t(cl +c2t) + —- + е‘ + —. 9. у =--------^.-L—lnl 14-^x14-63.
2	4	q cf
10. CjX24-1=c2 (i-|-c2)2. U.y — cle2x-[-c^~2x-{-c3cQs2x-{-cisln2x— ^+4^^
12. у = cos (x — C|)4-c2x4-c3. 13. у — c}ex+c2e~x-ircixi+cAx2+cix+c6 —
14. x = e‘ (C| 4- c2t) 4- e~‘ (ca 4- c4t) -|- 1 4" ^2-	15. у — cQ fl----+
416
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
42х6
2  3  5 • 6
(—1)* 4* л',зл
2-3-5-6 ... (ЗА — 1) 3k
4х4
3-4 т
42х’
3 • 4 • 6 • 7
••• +з
(__1)* 4*^3* + !
4 • 6 • 7 ... ЗА  (ЗА 4- 1)
16. у =
= с} J г (Зх) + c3J j (Зх). 17. у — х. 18. у = (у х 4- 1 j4. 19. у = с( cos х 4-
"5	“s’
4-с2 sin л: 4-1 4-% cos х — sin xln [ sin x |. 20. и = ~4~ c2,	21. Дифферен-
d2r A	dv k
циальное уравнение задачи — или v fa' где r — расстояние
от центра Земли до тела, v— скорость, А = —64002£. Отв. 11 :м/с&к.
d'^x	/ dx \
22. Дифференциальное уравнение движения -р- =—’
752	£
Отв. х =----Inch-^-Z. 23. Дифференциальное уравнение движения
g	!о	_
-g- = A(s4-l) или -g.= .|-(s4-i). Отв. Z=j/" jln(6+J<35).
t>g t
24. / = —^1п(94-Г8б).	25. s= - ~a t — p- (1 — г " ).
V g _	b	b2g
26; x = A cos |/ ~t. 27. x = a cos 1. 28. Дифференциальное уравне-
7 iAO
ние движения x 4- ktx — k2x = 0, As > 0.- Отв. x — c}e' 2	'4*
29. x=12V (~^\П
(n2 — 2) л3
«=1
= C| (x2 4~-*Kl 4- x24-ln [ *4-Kl 4-*21) 4- c2. 31. у — c2ec,x 4- cb у
30. y 2=>
4
— c — x'
32. x = C] cos 3? 4-c2 s|n 3/—=^-/2 cos 3<4~ -X-sin3t 33. у = e~x (c, 4- c2x —
12	Ou	\
' 1 Л 1 1 x ол x >	Кз ,	, /з \ . 1 x
— -4 X2 j 4- g- ex. 34. у = cxex A-e lc2 cos	x 4- c3 sin f~^-x j 4- -g-
«	г,'	. .vi Х0хсо8л , x2ex sin x	,
35. у — (Ci cos x + c2 sin z) -[--1--. 36. у = Cj (x—x3) -|-
+ C2r4_6x24-3(x3-x)ln|-^±j-|]-l	37. u-clln(x2 + y2) + c2.
38. и =
C|
ния mx = mg — kx. Отв. x =	1
39. Дифференциальное уравнение движе-
/	__k_ \
4O.a)Z-/o =
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
417
X	с	V
Г	dx	l‘vdv .	, Г dv
.1	/--------------------•	f~(vj’
' Т/ ,	2 f		v-	v'
V ^o + -^J f^dx
*0
•	x$ x^
гдеи = х. ’	41. у = C, + c2x + c3x2 4- ex (c4 4- c6x 4- c6x2)-g--^-.
42. x = (Ci 4- c2t) cos t 4- (c3 + c4Z) sin t — ^t2 cos t. 43. у = c, cos in<1 4- x)4-
00
.	, , ,, । .	. .. V (2—n2)sinn/—2ncosnz
4-сг sin In (1 + x)4~ln (1 4-x) sin In (1 4-x). 44. x = 2,	[(2_п2)2'_|-4^2|„4—•
/2=1
2^2 aW [n — a2y 4- a‘n	[nr — a2) 4- a[n2
где a0, an, p„—коэффициенты Фурйе функции f (t).	46. x = —* 4-
4-	(1 4“ 3 cos 2t).	47. у = cxx 4- c2xe x. 48. x2y" + xy'— у = 0.
V~2	_	___ И2	_
-5-' I v/~ 9	1/2 \	~~?~4	V~2 V 2 \
49.	x=e I Cj cos ~ t-\-c2 sin —	I c3 cos C4-ct sin Л4-<3.
50.	x = ^4-/+l.y= f-/6 + 4’<5 + 4' /4 + (c‘+t) '3 + c>*H-c2- 51- *=
= (C) 4-С20^~5< I (5-^21n2)2 + % -• 52. у = c2ec'x\ 53. у cxex+c2e~x 4-
X	___ x
4-C2 [c3 cos X 4- c4 sin xj 4- e 2 (c6 cos -^-x 4- c6 sin J~ xj 4~
'	x^ 1
+	54. №(c,* + c2) cos x+(c3x + cj slnx+c64-Qx + -£- + e\
55.	у = (CXX 4- C2)8 4- C3x4- c4. 56. у = e1+c'x(—-У\4~с2- 57. y=cx cosx -f-
\ci ci /
,	, sin 2x sin 4x _o	1	, 1
+ c2Sln.x-----_____	58, у ______	59. у = Сг^4.__,
1	К главе 3
1. x = sinZ, у = cos t. 2. xl — 2ei, хг = 2ег. 3. x= c1e(-1+4.
4-c2^-1'~’/15^ 1 4- и e1 4--g-c2/; у находим из первого уравнения: у — е‘
~^—Ьх. 4. х = схе‘->ге 2 (с2 cos 4- с3 sin t'j ; у и z опре-
деляются из уравнении: у =	, z =	5. х = схеСг1\ у = схс2еСг,
6. х = Cj cos t 4- с2 sin t 4- 3; у = — c, sir) 14- c2 cos t. 7. у = cxJ0 (x) 4- с2У0 (x);
г = x [с/0 (x) 4- c2 Гд (x)]. 8. x 4- у 4- г = Cj, x2 4- y2 4- z2 = c|. 9. x = cte' 4.'
418
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
4-с,е~2'; у = с,е/4-с3е 2г; г =	— (с2+ Сз)« ~	10. х= cj+
у =—С1< + -у-- И. х = с, cos t 4- с2 sin t — t cos t 4- sin t In | sin 11; у onpe-
d,x
деляется из уравнения у =	—1.	12. х2— у2 = с,. у — х— t — c2.
\3. х= сУ-{-с2е~‘-\-s\nt\ у —— с^е'+ с2е~‘.	14. х—е‘\ у = 4е‘-
15. 0 (1) as 0,047. 16. х =	(с, cos t -|- с2 sin t). y = ea‘(c{s\nt — c2 cos t).
17. x—	c2e~Jt, у — — c{e~f +	.	18. x = e~6t (2c, cos t 4-
4-2c2sinZ), y = e B! [(Ci — c2) cos f + (c,+c2) sin /].
= (cI<4-c3)c/ — t — 1 — c2, z = y — c}e‘.
21. x2 4- y2 4-'z2 = c2, ' xyz = c2. 22, X=
20. x-^y + z = Cj,
c,ef -j- сге~‘
4- 3c2c
19. x = cte! + c2, у ==
xyz = c2.
К главе 4
1. Точка покоя асимптотически устойчива. 2. Точка покоя неустойчива.
3. При а <---точка покоя асимптотически устойчива, при а — — у устой-
чива, при а>—неустойчива. 4. При а<;0 точка покоя асимптотически
устойчива, при а > 0 неустойчива. 5. При 1 < t < 2 x(t, ц) -> У 4 — I2; при
2 < t < 3 х (t, р) -> — У9 — t2; при t > 3 х (/, ц) ->со. 6. х (t, ц) -> со. 7. Точка
покоя неустойчива. 8. Точка покоя устойчива. 9. Точка покоя неустойчива.
10. Точка покоя устойчива. 11. Седло. 12. Периодическое решение х —
12
= -=-sin£---=- cos t асимптотически устойчиво. 13. Все решения, в том числе
О	о
и периодические, асимптотически устойчивы. 14. Точка покоя неустойчива.
Функция v = х4 — у4 удовлетворяет условиям теоремы Четарва. 15. Все реше-
ния неустойчивы. 16. Решение х = 0 неустойчиво 17. При 1 < а < 2 реше-
ние xsO асимптотически устойчиво. При а=1 и при а=2 решение х=0
устойчиво. При а>2 и при а< 1 решение хэО неустойчиво. 18. Решение
х = 0, у = 0 устойчиво при постоянно действующих возмущениях. Функция
v = 4х2 4* Зу2 удовлетворяет условиям теоремы Малкина. 19. Решение
X (/) = 0 неустойчиво. 20. Все решения устойчивы, но асимптотической устой-
чивости нет. 21. Все решения устойчивы, но асимптотической устойчивости
no п	cos t — sin t	„	„„ _,
нет. 22. Периодическое решение х —----------- неустойчиво 23. Область
устойчивости 0<;а<1, область асимптотической устойчивости 0 < а < 1.
24. Область устойчивости а >-5, область асимптотической устойчивости а > 5-
К главе 5
1. г = Ф(х4-у).
5 г==5 + Ф(^).
ys
- ( -
2. г = 02ЛФ (х — у). 3. г = ехФ (х). 4. Ф \г, уе
6. и = Ф(х — у, у—г). 7. и = х4Ф^2, pj.
х-2
г/ = 0.
8. г =
= хф, (у) 4-Ф2 (У). 9. г = (х24*У —I)2- Ю. z = ye v 11. z = Зх. 12. z =
= ^yz —	13- Ф (z2 4-х2, х2 — у2) = 0. 14. Ф(г2 — х2, х2 — у2) = 0.
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
419
уЗ
15. Не интегрируется. 16. 2ху 4-У2 4-6xz2 >= с. 17. z — ах3 -f-	4" Ь (воз-
можны и другие ответы). 18. z = ахbyа3Ь3 (возможны и другие от-
^-(а2х+у)
веты). 19. г — Ьеа (возможны и другие ответы). 20. z — х sin а 4- ay -f- b
(возможны и другие ответы). 21.x2 у— Зхуг = с. 22. Такого семейства поверх-
ностей нет, так как условие (F-rotF) = 0 не выполнено. 23. Уравнение
у
векторных линий ~^ = с> xz — с2. Уравнение векторных поверхностей
1	/ У \
г——Ф I • Уравнение поверхностей, ортогональных к векторным линиям
х2 4- у2 — г2 — с. 24. г = ху 4- 1. 25. г — Зху. 26. z — х2 4- у2.
К главе 6
1. Экстремалями являются окружности (х—С])2 + у2 — С|. 2. Интеграл
не зависит от пути интегрирования. Вариационная задача лишена смысла.
3. В классе непрерывных функций экстремум не достигается. 4. Экстремалями
С	х*
являются гиперболы у=г-^-+С2. 5. у = С, sin (4х—С2). 6. у =-----------ф-
-|—4- С2. 7. у = sh (С|% + С2). 8. у — С^ех -|- С2е~х 4- — sin х. 9. у =
= Схе2Х + Сге~2х + С3 cos 2х -f С4 sin 2х. 10. У = у + Сух3 4- С2х4 + С3х3 +
С4х2 + С5х + Св. 11. у = (С,х + С2) cos х 4- (С3х 4- С4) sin х, г = 2у>4- у", от-
д2г д2г . д2и д2и . О2и
куда г легко определяется. 12. — _ —= 0.	13.	—
= f (х. у. г). 14. у = С,х4 4- С2.	15. у — -i- хе.х 4- С,ех 4- С2е~х. 16. у=
__ — х cos х с* cos х 4- sin л. 17. у = С, ch х 4- С2 sh х 4- х sh х —
— ch х In ch х. 18. у = С,х 4-^| 4~ уI х ! 19. у = (Ci + С2х) cos хф-
4~(С'з 4- С4х) sin х — х-Sjn х 20. у — С}ех4- С2е~х + е2 [с3 cosX^- х-[-
4- С, sin xj 4- е 2 (с5 cos ~ х 4- С6 sin xj 4- х3.
К главе 7
1. у = — X npir0<x< 1; у = х — 2 при 1 <х<4иу = х при 0< х< 3»
у = — х 4- 6 при 3 < х <. 4. На той и другой ломаной функционал достигает
абсолютного минимума. 2. Не существует. 3. Ломаные, проходящие через
заданные граничные точки, составленные из прямолинейных отрезков с угло-
выми коэффициентами 3 и — У 3. 4.	= 1, т. е. экстремали дол-
жны пересекать кривую yi = <р (х,). по которой скользит граничная точка,
под углом j. 5. у =	4-	(х2 — х3).	6. у = ± х при 0 < х < -;г-;
у = ±)<9 —(х —5)2 при 4г < х < 4г; У = 4 (•* ~ Ю) при -Д < -г < 10,
420
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
т. е. кривая состоит из отрезка прямой, касающейся окружности, дуги окруж-
ности и снова отрезка касательной к окружности. 7. у s 0. 8. Дуги окруж-
ности у = ±	— х2.
К главе 8
1
1. При у =—достигается сильный минимум. 2. При у = 0 дости-
„	„л	л
гается сильный минимум, если 0 < а <	, если же а >	, то минимума нет.
4
3, Экстремум на непрерывных кривых не достигается. 4. При у = 7 —~ —
сильный минимум. 5. При у = 1—сильный минимум. 6. При y = sln2x—1
достигается сильный максимум. 7. При у — х2 достигается сильный минимум.
8. При у = -1- г2Л достигается сильный минимум. 9. При у = sin 2х дости-
О
гается сильный максимум 10. На прямой
у.
мум. .11. Непрямой у = — х достигается
xi
достигается слабый минимум. 13. При
п sh х
максимум. 14. При у =
, = *х
слабый
у = х3 — 1 достигается
-f-'х достигается сильный минимум.
достигается слабый мини-
минимум. 12. При у = х2
сильный
.К главе 9
1. у = ± 2 sin плх, где п — целое число. 2. <р = б] 4- С2г; г = R. 3. у —
— Хх2 + CiX -I- С2. где С|, Сг й X определяются из граничных условий и из
изопериметрического условия. 4. (р (х) у') + [Лг (х) — q (х)] у = 0;
у(0)=0; y(Xi) = 0. Тривиальное решение у^О не удовлетворяет изонери-
метрическрму условию, а нетривиальные решения, как известно, существуют
лишь при некоторых значениях Л, называемых собственными значениями.
Следовательно, X должно быть собственным значением. Одна произвольная
•постоянная общего решения уравнения Эйлера определяется из условия
5	7
у (0) = 0, другая — из изопериметрического условия. 5. у =— х2-|-^ х; г=х.
»	К главе 10
1. г, =	(х2 — а2) (у2 — Ь2). Если необходима большая точность, то
решение можно искать в виде г2 = (х2 — а2) (у2 — Ь2) [а0 4- а, (х2 4- у2)].
2. yi = (х—I)2 (0,124 4-0,218х). 3. Точное решение у =	—х. 4. Реше-
ние уравнения Эйлера у = 3,60727 j (х) -(-0,75195Ki (х) — х, где и К] —
2 sh х	'
функции Бесселя. 5. Точное решение у =	---х. 6 Если искать реше-
ние в виде: у2=х(х—1)(а|4*«2х), у3 = х(х—1) (а, + а2х 4~ а3х2), то
у2 = х(х— 1) (0,1708 4- 0,17436х), у3= х(х — 1) (0,1705 4-0,1760х - 0,0018х2).
В заданных точках значения у2 и у3 с точностью до 0,0001- совпадают.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
К части 1
1.	И. Г. Петровский, Лекции по теории обыкновенных дифференциаль-
ных уравнений, изд. 5-е, «Наука», 1964.
2.	И. Г Малкин, Теория устойчивости движения. Гостехиздат.; 1052
(к гл IV).	'
3.	И. Г. Малкин, Некоторые задачи теории нелинейных колебаний. Гос-
техиздат, 1956 (к § 8 гл. 2).
4.	А Н. Тихонов, О зависимости решений дифференциальных уравнений
от малого параметра, Математический сборник, т. 22 (64): 2 (1948) и т. 31
(72): 3 (1952) (к § 6 гл. 4).
5.	В. В. Степанов, Курс дифференциальных уравнений, изд. 8-е, Физмат-
гиз, 1959.
6.	А. Н. Крылов, Лекции о приближенных вычислениях, изд. 5-6, Гос-
техиздат, 1950 (к § 7 гл. 1 и § 6 гл. 3).
7.	И. С. Б е р е з и н и Н. П. Жидков, Методы вычислений, т. II, .Физ-
матгиз, 1960 (к § 7 гл. 1 и § 6 гл.,3).	*.
К части II.
1.	И. М. Гельфанд и С. В. Фомин. Вариационное исчисление, Физмат-
гиз 1961.
2,	М. А. Лаврентьев и Л- А Люстерник, Курс вариационного
исчисления, изд. 2-е, Гостехиздат, 1950.
3.	В. И. С м и р н о в, В. И. Крылов и Л. В. Канторович, Вари-
ационное исчисление, КУБУЧ, 1933.
4.	В. И. С м и р н о в. Курс высшей математики, т. 4, изд. 4-е, Физматгиз, 1958.
5.	Н. М Гюнтер, Курс вариационного исчисления, Гостехиздат, 1941.
6.	Н. И Ахиезер. Лекции по вариационному исчислению, Гостехиздат,
1955.
7.	М. А. Лаврентьев и Л. А. Люстерник, Основы вариационного
исчисления, ч. 1 и 2, Гостехиздат, 1935.
8.	Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе,
Е. Ф. Мищенко. Математическая теория оптимальных процессов, Физ-
матгиз, 1961.
9.	Р. Беллман, Динамическое программирование, ИЛ, 1960.
10.	Л. В. Канторович и В. И. К р ы лов, Приближенные методы высшего
анализа, изд. 5-е, Физматгиз, 1962.
11.	С. Г. Михлин, Прямые методы в математической физике, Гостехиздат,
1950.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Асимптотически устойчивое решение
204
Бернулли уравнение 30
Бесселя уравнение 139
— функции 141—143
Бигармоническое уравнение 317
Близость кривых 285, 286
Брахистохрона 281, 304, 332, 364
Вариации постоянной метод 28
Вариационная задача 281
----в параметрической форме
317—320
----на условный экстремум 375—
393
----, прямые методы решения 394—
413
— — с подвижными границами 327—
350
Вариационное исчисление 281
— —, основная лемма 295
Вариационный принцип 281, 320
Вариация 284, 288, 289, 309, 313
Вейерштрасса функция 359
Векторная линия 245	х
—	поверхность 244
Взаимности принцип 388
Влияния функция 123, 161 — 165 .
Вронского определитель 97, 185
Галеркина метод 410
Гамильтона — Якоби уравнение 370
Гамма-функция 140
Геодезическая линия 282, 381
Голономные связи 382
Граничная задача 13, 159
Грина функция 161 — 165
Гурвица теорема 227
Дикритический узел 211
Динамическая система 170
Дирихле задача 315
Дифференциальное уравнение 9
—	— Бернулли 30
—	— Бесселя 139
----в полных дифференциалах 32
Дифференциальное уравнение в ча-
стных производных 10
----— — — первого порядка 241—
279
----высшего порядка 85—167
—	—,интеграл 20
—	—,интегрирование 10
—	—,— с помошью рядов 137—146
—	— Клеро 73
—	— Лагранжа 73
—	— линейное высшего порядка
93—106, 113—124
—	— — неоднородное с постоянны-
ми коэффициентами 124—136
—	— — однородное с постоянными
коэффициентами 107—ПО
—	— — первого порядка 27
— — —.фундаментальная система
решений 100
----, не решенное относительно про-
изводной 68
---общее решение 15, 86
----, общий интеграл 20, 32 -
—	— обыкновенное 10
—	— однородное 25
----, операторный метод решения
129—136
—	—, особое решение 57, 78
— —, периодические решения 143—
146
----,	порядок	10
----Пфаффа	255
—	—,	решение	10, 169
----	Риккати	31
— — с разделенными переменными
19
— — с разделяющимися переменны-
ми 21
----, теорема существования и един-
ственности решения 39—61, 75—
82, 85—87
----Эйлера 110—113, 136
Изоклины 17
Изопериметрическая задача 282, 317,
385
Изопериметрические условия 282,386
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Интеграл дифференциального уравне-
ния 20
— первый 89, 179
— полный 261
Интегральная кривая 16, 169
--- особая 78
— поверхность 261, ^268
Интегрируемая комбинация 178
Интегрирующий множитель 35
Канторовича метод 406—412
Квазилинейное уравнение в частных
производных 243
Клеро уравнение 73
Ковалевской теорема 242
Коши задача 13
— метод 121, 268
Краевая задача 13, 159
Лагранжа уравнение 73
Лагранжа — Шарпи метод 264
Лагранжиан 324
Лапласа уравнение 315
Лежандра условие 362
Линейная зависимость 96, 185
— система дифференциальных урав
цений 181—192
----------с постоянными коэффи-
циентами 192—199
Линейное дифференциальное уравне
ние 27
---— в частных производных не-
однородное 243
—---------------однородное 243
—--	--высших порядков 93—106,
113—124
-------с постоянными коэффици-
ентами 107—110, 124—136
—	— —, фундаментальная	система
решений 100
Линейный дифференциальный опера-
тор 94—183
—	функционал 287
Липшица условие 40
Ляпунова второй метод 215
—	теорема 215, 217
—	функция 215
Максимум функционала 289
—	— сильный 290
---слабый 290
—	— строгий 289
Малкина теорема 235
Малого параметра метод 147—158
Метрическое пространство 48
Минимум функционала 289
423
Минимум функционала сильный 290
— — слабый 290
Наклон поля 351
Наложения принцип 114, 189
Начальная задача 13
Неголономные связи 382
Непрерывный функционал 285, 286
Неустойчивое решение 204
Неустойчивый предельный цикл 226
— узел 208, 211
— фокус 209
Общее решение дифференциального
уравнения 15, 86
Общий интеграл дифференциального
уравнения 20
Обыкновенное дифференциальное
уравнение 10
Огибающая 74
Оператор линейный дифференциаль-
ный 94, 183
Операторный метод решения диффе-
ренциальных уравнений 129—136
— многочлен 129
Определитель Вронского 97, 185
Оптимальная функция 391
Оптимальное управление 391
Особая интегральная кривая 78
— точка 57
Особое решение дифференциального
уравнения 57, 78
Остроградского уравнение 314
Остроградского — Гамильтона прин-
цип 320
Остроградского — Лиувилля форму-
ла 106
Первого приближения система урав-
нений 221
Первый интеграл 89, 179
Периодические решения дифферен-
циального уравнения 143—146
Периодичности условия 157
Плотность функции Лагранжа 324
Покоя точка 171, 205
Поле собственное 351
—	центральное 351
—	экстремалей 352
Полная интегрируемость уравнения
Пфаффа 256
Полное пространство 48
Полный интеграл 261
Полуустойчивый предельный цикл
226	/
424
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Порядок дифференциального уравне-
ния 10
Последовательных -приближений ме-
тод ,199
Предельный цикл 23, 226
-----неустойчивый 226
-----полуустойчивый 226
-----устойчивый 226
Пространство метрическое 48
— полное 48
— равномерной сходимости 50 „
— фазовое 12, 170
Прямые методы в вариационном ис-
числении 394—413
Пуассона уравнение 315
Пфаффа уравнение 255
Равномерной сходимости простран-
ство 50
Расстояние 48
Резонанс 145, 152
Риккати уравнение 31
Ритца метод 397—406
Рунге метод 64, 201
Связи голономные 382
— неголономные 382
Связный экстремум 282
Седло 59, 208
Сжатых отображений принцип 48
Сильный экстремум 290, 360
Системы дифференциальных уравне-
ний 168—202
— линейных дифференциальных урав-
нений 181—192
-----— — с постоянными коэффи-
циентами 192—199
Слабый экстремум 290, 359, 360
Собственное поле 351
Специальные решения 253
Стационарного действия принцип 320
Строгий экстремум 290
Суперпозиции принцип 114, 189
Трансверсальности условие 331, 336
Узел 58	•
— дикритический 211
— неустойчивый 208, 211
— устойчивый 207, 211
Управление оптимальное 391
Управляющая функция 391
Уравнения в частных производных 10
— —-------первого порядка 241—
279
Уравнивание 61
Условный экстремум 282, 375—393
Устойчивое решение (по Ляпунову)
204
----по отношению к постоянно
действующим возмущениям 236
Устойчивый предельный цикл 222
— узел 207, 211
—	фокус 209
Фазовая траектория 170
Фазовое пространство 12, 170
Фокус 59
—	неустойчивый 209
—	устойчивый 209
Фундаментальная система решений
100
Функционал 280, 284
—	линейный 287
—	непрерывный 285, 2S6
Характеристик метод 268
Характеристики 245, 248, 254, 268,
269, 273 
Характеристическая полоса 269, 273
Характеристическое уравнение 107,
194
Центр 59, 210
Центральное поле 351
Цикл предельный 23, 226
Четаева теорема 218
Штермера метод 62, 200
Эйлера дифференциальное уравнение
110—113, 136
—	конечно-разностный метод 395—
397
--- ломаная 13, 40
—	метод 39, 61, 199
—	уравнение (в вариационном исчис-
лении) 297, 306, 368, 377
Эйлера — Пуассона уравнение 310
Экстремаль 297, 310
Экстремум связаный 282
—	условный 282, 375—393
—	функционала 290
—	— сильный 290, 360
---слабый 290, 359, 360
Якоби первый метод 277
—	уравнение 356
—	условие 355