Author: Бутузов В.Ф. Медведев Г.Н. Крутицкая Н.Ч. Шишкин А.А.
Tags: анализ математический анализ функциональный анализ физика математическая физика издательство физматлит
ISBN: 5-9221-0284-2
Year: 2002
УДК 517
ББК 22.16
М34
Математический анализ в вопросах и задачах: Учеб. пособие/
В.Ф. Бутузов, Н. Ч. Крутицкая, Г. Н. Медведев, А. А. Шишкин; Под ред.
В.Ф. Бутузова. — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 480 с. —
ISBN 5-9221-0284-2.
Пособие охватывает все разделы курса математического анализа функ-
функций одной и нескольких переменных. По каждой теме кратко излагаются
основные теоретические сведения и предлагаются контрольные вопросы;
приводятся решения стандартных и нестандартных задач; даются задачи
и упражнения для самостоятельной работы с ответами и указаниями.
Четвертое издание — 2001 г.
Для студентов высших учебных заведений.
Рецензент: доктор физико-математических наук, профессор
А. И. Прилепко (Московский инженерно-физический институт)
© ФИЗМАТЛИТ, 2000, 2001, 2002
© В.Ф. Бутузов, Н.Ч. Крутицкая,
Г.Н. Медведев, А.А. Шишкин,
ISBN 5-9221-0284-2 2000, 2001, 2002
ПРЕДИСЛОВИЕ
Учебное пособие написано на основе многолетнего опыта чтения
лекций и ведения семинаров по математическому анализу на физи-
физическом факультете МГУ. Оно предназначено как для студентов, так и
для преподавателей, особенно молодых, начинающих вести семинары.
Пособие охватывает основные разделы дифференциального и ин-
интегрального исчисления функций одной и нескольких переменных.
Оно не является сборником задач в обычном смысле слова. Как сле-
следует из его структуры, назначение пособия — помочь активному и
неформальному усвоению студентами изучаемого предмета. Матери-
Материал каждого параграфа разбит, как правило, на четыре пункта.
В пункте "Основные понятия и теоремы" приводятся без дока-
доказательства основные теоретические сведения (определения, теоремы,
формулы), необходимые для решения задач. Формулировки определе-
определений и теорем соответствуют в большинстве случаев учебнику
В.А. Ильина и Э.Г. Позняка "Основы математического анализа". Иног-
Иногда после формулировки определения или теоремы даются поясняю-
поясняющие примеры или комментарии, чтобы облегчить студентам восприя-
восприятие новых понятий. Там, где это возможно, авторы старались указать
на физическую интерпретацию и физические приложения математи-
математических понятий. В наибольшей мере это относится к главе XV.
В пункте "Контрольные вопросы и задания" содержатся вопросы
по теории и простые задачи, решение которых не связано с больши-
большими вычислениями, но которые хорошо иллюстрируют то или иное
теоретическое положение. Назначение пункта — помочь студентам
в самостоятельной работе над теоретическим материалом, дать воз-
возможность самостоятельно проконтролировать усвоение основных по-
понятий. Предполагается, конечно, что основная работа над теорети-
теоретическим материалом с проработкой доказательств теорем ведется по
учебнику или конспектам лекций. Однако для решения задач часто
достаточно понимания сути теоремы (или формулы). Многие конт-
контрольные вопросы направлены на раскрытие этой сути. Из этого пунк-
пункта преподаватель может черпать вопросы для проверки готовности
студентов к семинару по той или иной теме.
В пункте "Примеры решения задач" разобраны типичные приме-
примеры, демонстрирующие применение на практике результатов теории.
При этом большое внимание уделяется обсуждению не только "техни-
Предисловие
ческих приемов , но и различным тонким местам , например усло-
условиям применимости той или иной теоремы или формулы. Количество
разобранных примеров варьируется в зависимости от объема и важ-
важности темы. Иногда здесь дается ответ на вопрос, поставленный в
предыдущем пункте.
Назначение последнего пункта — "Задачи и упражнения для
самостоятельной работы" — определено его названием. Авторы огра-
ограничились определенным минимумом упражнений, достаточным для
усвоения основных приемов решения задач по каждой теме. При под-
подборе упражнений были использованы различные источники, в том
числе широко известные задачники, например "Сборник задач и уп-
упражнений по математическому анализу" Б.П. Демидовича. Поэтому
многие задачи данного пособия не претендуют на оригинальность,
хотя среди них есть целый ряд новых. В конце книги даны ответы и
указания к задачам и упражнениям.
При подготовке данной книги были устранены замеченные в пре-
предыдущем издании опечатки и неточности.
Начало и конец решений задач отмечаются соответственно знака-
знаками Л и А, а вместо слова "Указание" употребляется знак *.
Авторы надеются, что пособие поможет студентам в овладении ме-
методами математического анализа при их самостоятельной работе над
предметом. Они также выражают надежду, что пособие будет полез-
полезным для преподавателей в работе со студентами, и с благодарностью
воспримут все критические замечания и пожелания, направленные
на улучшение его содержания.
Авторы
ГЛАВА I
ВЕЩЕСТВЕННЫЕ ЧИСЛА
§ 1. Сравнение вещественных чисел
Основные понятия
1. Представление вещественных чисел в виде бесконеч-
бесконечных десятичных дробей. Любое вещественное число а представи-
мо в виде бесконечной десятичной дроби:
а = =Ьао, aia2-..an...,
где из двух знаков ± берется какой-то один: плюс — для положитель-
положительных чисел, минус — для отрицательных чисел (знак плюс обычно не
пишется).
Рациональные числа представимы в виде периодических, а ирра-
иррациональные числа — в виде непериодических бесконечных десятич-
десятичных дробей. Некоторые рациональные числа представимы в виде ко-
конечной дроби или, что то же самое, в виде бесконечной дроби с нулем
в периоде. Такие числа допускают второе представление — в виде
бесконечной десятичной дроби с цифрой 9 в периоде. Например,
1/2 = 0,500...0... = 0,5@), 1/2 = 0,4999...9... = 0,4(9).
При сравнении вещественных чисел будем пользоваться для таких
рациональных чисел лишь первой формой записи (с нулем в периоде).
2. Правило сравнения вещественных чисел. Пусть а =
= ±ao, aia2-..an... и Ъ = ±&о, b\b2...bn... — произвольные вещественные
числа, представленные в виде бесконечных десятичных дробей.
Числа а и Ъ называются равными (а = Ь), если они имеют оди-
одинаковые знаки и справедливы равенства аи = bk (к = 0,1,2,...). В
противном случае считается, что а фЪ.
При сравнении неравных чисел а и Ъ рассмотрим три случая:
1) а и Ъ — неотрицательные числа. Так как а ф Ь, то существует
натуральное п (или п = 0) такое, что аи = bk (к = 0,1,...,п- 1) и
ап ф Ъп. Будем считать, что а > 6, если ап > bnj и а < 6, если ап < Ьп;
2) а — неотрицательное, Ъ — отрицательное число. Будем считать,
что а > Ь;
3) а и Ъ — отрицательные числа. Будем считать, что а > Ь, если
\а\ < |Ь|, и а < Ь, если \а\ > \Ь\.
Гл. I. Вещественные числа
3. Некоторые числовые множества. Вещественные числа
можно изображать точками на координатной прямой *). Поэтому мно-
множество всех вещественных чисел называют числовой прямой, а са-
сами числа — точками, и при рассмотрении числовых множеств часто
пользуются их геометрической интерпретацией.
Будем использовать следующие обозначения и терминологию:
N — множество всех натуральных чисел;
Z — множество всех целых чисел]
R = (—оо, +оо) — множество всех вещественных чисел {числовая
прямая);
[а,Ъ] — сегмент (отрезок), т. е. множество всех вещественных
чисел х, удовлетворяющих неравенствам а ^ х ^ Ь;
(а,Ъ) — интервал, т. е. множество всех вещественных чисел х,
удовлетворяющих неравенствам а < х < Ь;
[а,Ъ), (а,Ь] — полуинтервал (полусегмент), т. е. множество всех
вещественных чисел х, удовлетворяющих соответственно неравенст-
неравенствам а ^ х < Ь, а < х ^Ь;
[а, +оо), (а, +оо), (—оо,а], (—оо,а) — полупрямая, т. е. множество
всех вещественных чисел х, удовлетворяющих соответственно нера-
неравенствам а ^ х < +оо, а < х < +оо, —оо < х ^ а, —оо < х < а;
сегмент, интервал, полуинтервал, полупрямую и числовую пря-
прямую будем называть также промежутком;
окрестность точки с — любой интервал, содержащий точку с;
е-окрестность точки с — интервал (с — г, с + г), где г > 0.
Контрольные вопросы и задания
1. В чем состоит различие бесконечных десятичных дробей, представля-
представляющих рациональные и иррациональные числа?
2. В каком случае два числа называют равными?
3. Верны ли равенства 0,41(9) = 0,42@) = 0,42?
4. Сформулируйте правило сравнения двух неравных чисел.
Примеры решения задач
1. Доказать, что для любых вещественных чисел а и Ъ (а < Ь)
найдется рациональное число с такое, что а < с < Ъ.
Л Пусть для определенности числа а и Ъ положительны, т. е.
а = а0, aid2...ak... > О, Ъ = Ьо? ^Ьг---^... > 0.
Если какое-нибудь из них является рациональным числом, выража-
выражающимся дробью с периодом 9, то запишем его в виде дроби с перио-
периодом 0. По условию а < Ъ. Это означает, что существует неотрица-
неотрицательное целое число п такое, что а/. = bk (к = 0,1,..., п — 1) и ап < Ъп.
*) Напомним, что координатной прямой называется прямая, на которой выбра-
выбраны точка, являющаяся началом отсчета, масштабный отрезок и положительное
направление.
2. Точные грани числового множества
Поскольку цифра 9 не является периодом числа а, найдется натураль-
натуральное число г > п такое, что а^ ф 9.
Рассмотрим рациональное число с = со, C1C2...Q, где с/. = а/.
(к = 0,1, ...,г — 1), Ci = di + 1. Число с больше а, так как с/. = а/.
(к = 0,1,..., г - 1), Ci = <2i + 1 > <2i, и меньше 6, так как с^ — а^ — Ъи
(к = 0,1,..., п — 1), сп = ап < Ъп. Итак, существует рациональное число
с такое, что а < с < Ъ. А
2. Доказать, что для любых вещественных чисел а и Ъ (а < Ь)
найдется иррациональное число а такое, что а < а < Ъ.
Л При предположениях примера 1 рассмотрим число
а = с0, ciс2...Сг010010001...000...01000...01...
П 71+1
Эта дробь, очевидно, непериодическая (объясните, почему), т. е. а —
иррациональное число. Это число больше а, так как с/. = аи (к =
= 0,1, ...,г — 1), Ci = cti + 1 > cti, и меньше b, так как с/. = bk
(к = 0,1,...,п — 1), сп — ап < Ьп. Итак, существует иррациональное
число а такое, что а < а < b. A
Задачи и упражнения для самостоятельной работы
1. Докажите, что у/Е есть иррациональное число.
2. Представьте дробь 31,2 (88) в виде обыкновенной.
3. Докажите, что любую периодическую десятичную дробь, не имеющую
цифры 9 в периоде, можно получить как результат деления двух нату-
натуральных чисел.
4. Докажите, что любую периодическую десятичную дробь, имеющую в
периоде цифру 9, нельзя получить как результат деления двух нату-
натуральных чисел.
5. Докажите, что для любых двух вещественных чисел а и Ъ (а ф Ь) су-
существует бесконечно много как рациональных, так и иррациональных
чисел, заключенных между ними.
6. Докажите транзитивность знаков =, >, т. е.: а) если а = b и b = с, то
а = с; б) если а > Ъ и Ъ > с, то а > с.
7. Докажите, что для любого числа а справедливы неравенства —\а\ ^ а ^
^ И-
8. Докажите, что если х ^ у, то —х ^ —у.
§ 2. Точные грани числового множества.
Применение символов математической логики
Основные понятия и теоремы
1. Об использовании некоторых логических символов.
Пусть X — непустое множество вещественных чисел.
Определение. Множество X называется ограниченным сверху
{снизу), если существует число М (т) такое, что для любого числа
Гл. I. Вещественные числа
х из множества X выполняется неравенство х ^ М (х ^ т). Число
М (т) называется верхней {нижней) гранью множества X.
В этом определении, а также в формулировках многих других
определений и теорем используются слова "существует" и "для лю-
любого". Для краткости записи вместо этих слов будем использовать
логические символы 3 и V.
Символ 3 называется квантором существования, а символ V —
квантором всеобщности. Тот факт, что число х принадлежит (не при-
принадлежит) множеству X, будем обозначать так: х Е X (х 0 X).
С помощью указанных символов определение ограниченного свер-
сверху множества можно записать так: множество X называется ограни-
ограниченным сверху, если ЗМ Е R такое, что Vx Е X выполняется неравен-
неравенство х ^ М, или (еще более кратко)
3MeR МхеХ: х^М. A)
Использование кванторов не только сокращает запись, но и поз-
позволяет весьма простым способом строить отрицания предложений
(определений, утверждений), записанных с помощью кванторов. Про-
Проиллюстрируем этот способ на примере отрицания определения огра-
ограниченного сверху множества. Иначе говоря, сформулируем опреде-
определение неограниченного сверху множества. Неограниченность сверху
множества X означает: не существует числа М такого, что для любо-
любого х Е X выполняется неравенство х ^ М. Это значит, что для любого
числа М существует х Е X, для которого х > М. Поэтому определе-
определение неограниченного сверху множества с помощью кванторов можно
записать так: множество X называется неограниченным сверху, если
ММ Е R 3 х Е X: х > М. B)
Сравнивая A) с B), мы видим, что для построения отрицания
предложения A) нужно квантор 3 заменить на V, а квантор V на 3
и стоящее после двоеточия неравенство заменить ему противополож-
противоположным.
Это правило можно использовать и для построения отрицаний лю-
любых других утверждений, содержащих кванторы 3 и V.
2. Точные грани числовых множеств.
Определение. Число х называется точной верхней гранью огра-
ограниченного сверху множества X, если: 1°) \/х е X: х ^ ж; 2°) \/х < х
Зх G X: х > х.
Условие 1°) означает, что х — одна из верхних граней множества
X, а условие 2°), что х — наименьшая из верхних граней множества
X, т. е. никакое число ж, меньшее ж, уже не является верхней гранью.
Точная верхняя грань множества X обозначается supX.
Аналогично определяется точная нижняя грань*) ограниченного
снизу множества X; она обозначается inf X.
*)В некоторых учебниках по математическому анализу точная верхняя (ниж-
(нижняя) грань называется просто верхней (нижней) гранью.
2. Точные грани числового множества
Теорема. Ограниченное сверху (снизу) непустое множество
имеет точную верхнюю (нижнюю) грань.
Если множество X не ограничено сверху (снизу), то пишут
supX = +00 (inf X = —оо).
Множество X называется ограниченным, если оно ограничено
сверху и снизу, т. е.
ЗМ, т Уж е X: т ^ х ^ М. C)
Контрольные вопросы и задания
1. Напишите с помощью кванторов определение ограниченного снизу мно-
множества. Постройте отрицание этого определения, пользуясь правилом
построения отрицаний.
2. Дайте определение точной верхней (нижней) грани ограниченного свер-
сверху (снизу) множества.
3. Сформулируйте теорему о существовании точных граней числового
множества.
4. Докажите единственность точных граней, т. е. что ограниченное свер-
сверху (снизу) множество имеет только одну точную верхнюю (нижнюю)
грань.
5. Покажите, что точные грани могут как принадлежать, так и не при-
принадлежать множеству. Приведите примеры числовых множеств X, у
которых: a) supX ? X; б) supX 0 X; в) inf X Е X; г) inf X (jL X. Име-
Имеет ли множество X в случаях а) и б) наибольшее, а в случаях в) и г)
наименьшее число?
6. Что означает символическая запись: a) supX = +оо; б) inf X = —оо?
7. Какое множество называется ограниченным?
8. Докажите, что следующее определение ограниченного множества эк-
эквивалентно C): множество X называется ограниченным, если ЗА > О
Ух е X: \х\ ^ А.
9. Применяя правило построения отрицании к приведенному в задании 8
определению, сформулируйте определение неограниченного множества.
Примеры решения задач
1. Найти точную верхнюю грань интервала @,1).
Л Число 1 является верхней гранью интервала @,1), так как Уж Е
Е @,1): х < 1. Более того, Vх < 1 За G @,1): а > х. Действительно,
если х ^ 0, то \/a G @,1): а > х. Если х > 0, то, как показано в
примере 1 § 1, на интервале (ж, 1) найдется рациональное число а
такое, что х < а < 1, т. е. За G @,1): а > х. Таким образом, для
числа 1 выполнены оба условия определения точной верхней грани.
Следовательно, sup @,1) = 1. Заметим, что найденная точная грань
не принадлежит интервалу @,1), т. е. sup @,1) 0 @,1), в то время
как для промежутка @,1] sup @,1] = 1 G @,1]. А
2. Найти точные грани множества всех правильных рациональ-
рациональных дробей т/п (т,п е N, т < п) и показать, что это множество не
10 Гл. I. Вещественные числа
имеет наименьшего и наибольшего элементов.
Л Пусть X — множество всех правильных рациональных дробей
т/п. Так как Vm,n G N: т/п > 0, то число 0 — нижняя грань
множества X. Более того,
Уж > 0 3 a Е X: а < х. D)
Действительно, если х > 1, то правильная рациональная дробь а =
= 1/2 удовлетворяет условию D). Если 0 < х < 1, то число х можно
записать в виде бесконечной десятичной дроби:
причем Зп такое, что хп ф 0. Рациональное число
а = 0, х1х2...хп-1(хГ1 - 1I
согласно правилу сравнения вещественных чисел удовлетворяет не-
неравенствам 0 < а < х < 1, т. е. является правильной рациональной
дробью и удовлетворяет условию D).
Таким образом, для числа 0 выполнено и второе условие опреде-
определения точной нижней грани числового множества. Итак, inf X = 0.
Так как множество X содержит только правильные дроби, т. е.
т < п, то т/п < 1. Значит, число 1 — верхняя грань множества
X. Более того, Уж < 1 Зт/п Е X: т/п > х. Действительно, как было
показано в примере 1 § 1, существует рациональное число х\ такое,
что х < х\ < 1. Так как х\ < 1, то х\ — правильная дробь: х\ —
— т/п (т < п), т. е. х\ е X. Следовательно, для числа 1 выполнены
оба условия определения точной верхней грани числового множества.
Итак, supX = 1.
Однако inf X = 0 0 X, поскольку т/п = 0 лишь при т = 0, но
0 0 N. Значит, множество X не имеет наименьшего элемента. Точно
так же supX = 1 0 X, поскольку т/п = 1 лишь при т = п, что про-
противоречит требованию правильности дроби. Значит, множество X не
имеет наибольшего элемента. А
Задачи и упражнения для самостоятельной работы
9. Пусть X и Y — непустые множества вещественных чисел, причем
X ограничено сверху, а У содержится в X. Докажите, что У также
ограничено сверху и sup У ^ supX.
10. Найдите точные грани множества рациональных чисел ж, удовлетво-
удовлетворяющих неравенству х2 < 2.
11. Пусть А — множество чисел, противоположных по знаку числам из
множества В. Докажите, что: a) inf A = —sup В] б) sup A = —inf В.
§3. Арифметические операции над числами 11
§ 3. Арифметические операции
над вещественными числами
Основные понятия
1. Сложение и умножение рациональных чисел. Для рацио-
рациональных чисел известны следующие правила сложения и умножения:
777-1 ТП2 777,177,2 +777-277,1 777-1 ТП2 777-1777-2 /-* \
77-1 77-2 77-177-2 ' 77-1 77-2 77-177-2
Определим операции сложения и умножения для любых вещест-
вещественных чисел.
2. Сложение вещественных чисел. Пусть х и у — произволь-
произвольные вещественные числа, а х\ и у\ — любые рациональные числа,
удовлетворяющие неравенствам
xi ^ ж, 2/i ^ У- B)
Далее символ (х\ +у\)г будет означать, что числа х\ и у\ скла-
складываются по правилу A) сложения рациональных чисел. Рассмотрим
множество {[х\ + у\)г\ всевозможных сумм рациональных чисел х\ и
2/1, удовлетворяющих условию B). Это множество ограничено сверху
и, следовательно, имеет точную верхнюю грань.
Суммой вещественных чисел х и у называется sup{(xi +yi)r}-
3. Умножение вещественных чисел. Пусть х иу — произволь-
произвольные положительные вещественные числа, а х\ и у\ — любые рацио-
рациональные числа, удовлетворяющие неравенствам 0 < х\ ^ ж, 0 < у\ ^ у.
Далее символ {х\у\)г будет означать, что числа х\ и у\ перемножа-
перемножаются по правилу A) умножения рациональных чисел. Рассмотрим
множество {(xiyi)r} всевозможных произведений таких рациональ-
рациональных чисел. Это множество ограничено сверху и, следовательно, имеет
точную верхнюю грань.
Произведением положительных вещественных чисел х и у называ-
называется sup{(>i2/i)r}.
Произведение вещественных чисел любого знака определим сле-
следующими правилами:
^О\ х Q _ Q х _ Q.
\у\, если знаки х и у одинаковы,
\у\, если знаки х и у различны.
2°) XV = \ X
Контрольные вопросы и задания
1. Сформулируйте правила сложения и умножения двух любых вещест-
вещественных чисел. Докажите, что множества {{х\ +2/i)r} и {{xiyi)r}, фи-
фигурирующие в этих правилах, ограничены сверху.
12 Гл. I. Вещественные числа
2. Докажите, что правило сложения вещественных чисел обладает свой-
свойствами: а) х + у = у + х (переместительное свойство); б) (х + у) + z =
= х + {у + z) (сочетательное свойство).
3. Докажите, что правило умножения вещественных чисел обладает
свойствами: а) ху = ух (переместительное свойство); б) (xy)z = x(yz)
(сочетательное свойство).
Примеры решения задач
1. Доказать, что сложение двух рациональных чисел по правилу
сложения вещественных чисел дает тот же результат, что и сложение
их по правилу A) для рациональных чисел.
Л Пусть х и у — произвольные рациональные числа, (ж + у)г — их
сумма, полученная по правилу сложения рациональных чисел, (ж +
+ у) — сумма, полученная по правилу сложения вещественных чисел,
т. е. х + у = sup{(xi + 2/i)r}? гДе х\\\у\ — любые рациональные числа,
удовлетворяющие неравенствам х\ ^ ж, у\ ^ у. Нужно доказать, что
х + у = (х + у)г, или
sup{(xi + 2/i)r} = (х + у)г-
Для этого согласно определению точной верхней грани множества
нужно показать, что:
1°) V(xi + 2/i)r G {(ж! + 2/i)r}: Oi + 2/i)r ^ (ж + у)г]
2°) Уж < (х + 2/)г 3(ж1 + 2/i)r e {(xi + 2/i)r}: fai + 2/i)r > ж.
Так как х\ ^ ж и 2/i ^ 2/, то (xi + 2/1)г < (ж + у)г (для рациональных
чисел это свойство неравенств известно). Следовательно, условие 1°)
выполняется. Покажем, что выполнено условие 2°).
Пусть х — произвольное число, меньшее (ж + у)г. Между числами
х и (х + у)г найдется рациональное число а (см. пример 1 § 1): х <
< а < (х + у)г. Положим S = (х + у)г — а (вычитание производится
по правилу вычитания рациональных чисел). Тогда а = (х + y)r — S,
и так как S > 0, то существует такое натуральное п, что 2/п < S.
Рассмотрим теперь рациональные числа х\ — х — 1/п и у\ — у —
— 1/п. Так как х\ < х и у1 < у, то (х\ +2/i)r ^ {(^i +2/i)r}- При
этом (xi + 2/1)г — (ж + 2/)г ~ 2/п > (ж + 2/)г — S = а, поскольку 2/n < J.
Итак, (х\ + 2/1)г > а > ж, т. е (х\ + 2/1)г > ж. Тем самым мы пока-
показали, что выполнено условие 2°). А
2. Доказать, что \/х: х + (—х) = 0.
Л Пусть #1 и 2/1 — любые рациональные числа, удовлетворяющие
неравенствам х\ ^ ж, 2/1 ^ —ж. Нужно доказать, что supj^i + 2/i)r} —
= 0, т. е.:
1°) У(ж! + У1)г е {(ж! + У1)г}: (ж! + У1)г <: 0;
2°) Уж < 0 3(ж1 + 2/1 )г е {(ж! + 2/i)r}: (^i + 2/i)r > ж.
Так как 2/i ^ —х, то —2/1 ^ ж (это легко установить, используя
правило сравнения вещественных чисел; см. упр. 8 к § 1). Из нера-
неравенств х\ ^ ж и ж ^ -2/1 в силу транзитивности знака ^ следует, что
§4- Метод математической индукции 13
х\ ^ ~У\ и5 значит, {х\ + у\)г ^ 0. Тем самым выполнено условие 1°).
Покажем, что выполнено условие 2°). Пусть х — произвольное от-
отрицательное число. Так как —х > 0, то найдется такое натуральное
п, что 1/10п < —х, т. е. —1/10п > х. Представим число х в виде бес-
бесконечной десятичной дроби (будем для определенности считать, что
ж>0):
X = Ж
Из правила сравнения вещественных чисел следует, что
= Х0, Х\Х2...Хп ^ Ж,
УХ = -Х0, Х1Х2^Хп ~ — ^ -X.
Тем самым {х\ + y\)r G {(xi + 2/i)r}- При этом (х\ + ?/i)r = -l/10n >
> ж, т. е. мы доказали, что выполнено условие 2°). А
Задачи и упражнения для самостоятельной работы
12. Докажите, что умножение двух рациональных чисел по правилу умно-
умножения вещественных чисел дает тот же результат, что и умножение
их по правилу A) для рациональных чисел.
13. Докажите, что Уж: ж + 0 = х.
14. Докажите, что Уж, г/ существует единственное число z такое, что х =
= у + z (z называется разностью чисел х и у: z = х — у).
15. Докажите, что Уж: ж • 1 = ж.
16. Докажите, что Уж ф 0 Зж': хх = 1.
17. Докажите, что Уж и Уг/ / 0 существует единственное число г такое,
что ж = yz (z называется частным чисел х и у: z = х/у).
18. Докажите, что Уж, у, z: (x-\-y)z = xz-\-yz.
19. Докажите, что если ж > г/, то У^: ж + г > г/ + г.
20. Докажите, что если ж > у, то У^ > 0: ж^ > 2/?.
21. Докажите справедливость неравенств: а) |ж + у\ ^ |ж| + |г/|; б) |ж — г/| ^
22. Пусть X, Y — непустые ограниченные множества вещественных чи-
чисел, а Т — множество всевозможных сумм ж + г/, где х е X, у eY. До-
Докажите, что множество Т ограничено и что: a) supT = supX + sup У;
б) infT = infX + infy.
23. Пусть X, У — непустые ограниченные множества неотрицательных
вещественных чисел, а В — множество всевозможных произведений
ху, где ж G X, у Е У. Докажите, что множество Б ограничено и что:
a) sup 5 = sup X • sup У; б) inf В = inf X • inf У.
24. Вычислите три первые значащие цифры суммы: а) - + л/3; б) л/3 + у/7.
25. Найдите три первых десятичных знака произведения: а) ->/3; б) л/3 х
хл/7.
26. Пусть А и В — непустые множества вещественных чисел, у которых
каждое число из А меньше любого числа из В и для любого е > 0
существуют х ? А и у ? В такие, что у — ж < е. Докажите, что sup A =
14 Гл. I. Вещественные числа
§ 4. Метод математической индукции
Основные понятия
Чтобы доказать, что некоторое утверждение верно для любого на-
натурального числа п начиная с п0, достаточно доказать, что:
а) это утверждение верно для п = по;
б) если данное утверждение справедливо для некоторого натураль-
натурального числа к ^ по, то оно верно также и для следующего натурального
числа к + 1.
Такой метод доказательства называется методом математичес-
математической индукции.
Контрольные вопросы
1. В чем состоит метод математической индукции?
2. Методом математической индукции докажите, что Vn E N: п ^ 2п~1.
Примеры решения задач
1. Доказать, что Vn G N и \/х > -1 справедливо неравенство (не-
(неравенство Бернулли)
Л Докажем неравенство A) методом математической индукции. Если
п = 1, то неравенство A) справедливо, поскольку обращается в вер-
верное равенство. Предположим, что соотношение A) справедливо для
натурального числа к и \/х > -1:
Так как х > — 1, то 1 + х > 0. Умножим неравенство B) на положи-
положительное число 1 + х:
а\?._|_1 . л 7 7 О
—I— Т* 1 I ^> I _|_ I/* гр _|_ /у* _|_ I/* /у*
| db I ^* X | /Ъ db | db | t\j db •
Отбрасывая неотрицательное слагаемое /еж2 в правой части, получаем
неравенство
Мы доказали, что неравенство A) справедливо для натурального чис-
ла к + 1 и \/х > -1. Тем самым доказано, что соотношение A) спра-
справедливо Vn G N и\/х > —1. А
2. Доказать, что для любых п положительных чисел 2/1 ? 2/2? • • • э 2/пэ
удовлетворяющих условию
У\У2-"Уп = 1, C)
имеет место соотношение
У\ +У2 + ... + Уп^ п. D)
§4- Метод математической индукции 15
Л При п = 1 из условия C) следует, что у\ = 1. Поэтому соотношение
D) выполнено.
Пусть при п = к из условия C) следует соотношение D) и пусть
к + 1 положительных чисел 2/1 ?2/2, ~чУк,Ук+1 удовлетворяют условию
C). Докажем, что для них выполнено соотношение D). Если все эти
числа равны 1, то их сумма равна к + 1 и соотношение D) имеет
место. Если же среди указанных чисел есть хотя бы одно, отлич-
отличное от 1, то обязательно найдется еще одно число, не равное 1. При
этом если одно число больше 1, то другое меньше 1. Не умаляя общ-
общности, предположим, что ук > 1, Ук+i < 1- Произведение к чисел
У\,У2,---,Ук-1,УкУк+1 в силу условия C) равно 1. Поэтому по ин-
индуктивному предположению
У\ + 2/2 + ... + Ук-i + УкУк+i ^ к.
Отсюда получаем
У\ + 2/2 + ... + Ук+i + УкУк+i ^ к + ук + 2/fc+b
или
2/1 + 2/2 + ... + Ук+i ^ к + 1 + ук + Ук+i ~ УкУк+i - 1 =
= к + 1 + A - yk+i)(yk - 1) ^ fc + 1,
т. е. соотношение D) выполнено при п = к + 1. Таким образом, для
любых п положительных чисел, удовлетворяющих условию C), вы-
выполнено соотношение D). А
Задачи и упражнения для самостоятельной работы
Применяя метод математической индукции, докажите, что Vn E N спра-
справедливы следующие равенства:
27. 1 + 2 + 3 + ... + п = 0,5п (п + 1).
28. I2 + 22 + З2 + ... + п2 = | п(п + 1)Bп + 1).
29. I3 + 23 + З3 + ... + п3 = 0,25п2(п + IJ.
Методом математической индукции докажите справедливость следующих
неравенств:
30. 1 • I . 2п - 1
2 4 •" 2п
32. nn+1 > (n+ 1)"
33. Ж1 +Ж2 + ... + ЖК, ^ ^/Ж1Ж2...Жгг при Хк ^ 0, /г = 1,..., п (среднее геомет-
геометрическое п неотрицательных чисел не превосходит их среднего ариф-
арифметического).
34
. у а + л/а + ... + л/а ^ 0,5A + л/4а + 1) Va > 0.
ГЛАВА II
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
§ 1. Ограниченные и неограниченные
последовательности. Предел последовательности
Основные понятия и теоремы
Если каждому натуральному числу п поставлено в соответствие
некоторое число хп, то говорят, что определена числовая последова-
последовательность (или просто последовательность) х\,Х2,х%, ...,хп,... Крат-
Кратко ее обозначают символом {хп} или (хп). Число хп называется чле-
членом (элементом) последовательности, an — номером члена.
Последовательности {хп + уп}, {хп-уп}, {хпуп}, {хп/уп} назы-
называются соответственно суммой, разностью, произведением и частным
последовательностей {хп} и {уп} (для частного уп ф 0).
Определение. Последовательность {хп} называется ограничен-
ограниченной, если ЗМ > 0 такое, что Vn \хп\ ^ М.
С геометрической точки зрения это означает, что все члены после-
последовательности находятся в некоторой окрестности (М-окрестности)
точки х = 0.
Определение. Последовательность {хп} называется неограни-
неограниченной, если VM > 0 Зп: \хп\ > М.
Определение. Число а называется пределом последовательнос-
последовательности {хп}, если \/е > 0 3N G N такое, что Vn > N \хп — а\ < е. Обо-
Обозначение: lim xn = а.
п—>-оо
С геометрической точки зрения это означает, что в любой г-ок-
рестности точки а находятся все члены последовательности начиная
с некоторого номера (зависящего, вообще говоря, от г) или, что то же
самое, вне любой ^-окрестности точки а находится лишь конечное
число членов последовательности.
Последовательность, имеющая предел, называется сходящейся, а
последовательность, не имеющая предела, — расходящейся.
Теорема 1. Сходящаяся последовательность имеет только один
предел.
Теорема 2 (необходимое условие сходимости последовательнос-
последовательности). Сходящаяся последовательность ограничена.
§1. Предел последовательности 17
Контрольные вопросы и задания
1. Сформулируйте определения: а) последовательности; б) ограниченной
и неограниченной последовательности; в) предела последовательности.
Дайте геометрическую интерпретацию этих определений.
2. Эквивалентно ли определение предела последовательности такому опре-
определению: lim хп = а, если Vs > О ЗК > 0 (не обязательно натуральное)
п—)-оо
такое, что Vn > К \хп — а\ < el
3. Покажите на примере, что номер ЛГ, фигурирующий в определении пре-
предела последовательности, зависит, вообще говоря, от е.
4. Пусть последовательность {хп} и число а удовлетворяют условию: 3N
такой, что Vs > 0 и Vn > N \хп — а\ < е. Всякая ли сходящаяся к а после-
последовательность удовлетворяет этому условию? Какова геометрическая
интерпретация этого условия?
5. Пусть lim xn = а.
п—Уоо
а) Могут ли все члены последовательности быть положительными (от-
(отрицательными), если а = О?
б) Может ли последовательность иметь бесконечно много отрицатель-
отрицательных (равных нулю) членов, если: а > 0; а / 0?
в) Докажите, что lim хп+\ = a, lim жп+2 = а-
п—>og n—>og
г) Докажите, что {хп} ограничена.
6. Пусть в некоторой окрестности точки а лежит бесконечно много членов
последовательности {жп}. Следует ли из этого условия, что: a) lim xn =
п—Уоо
= а; б) никакая точка вне этой окрестности не является пределом по-
последовательности {жп}; в) {хп} ограничена?
7. Пусть в любой окрестности точки а лежит бесконечно много членов по-
последовательности {жп}. Следует ли отсюда, что: a) lim хп = а; б) {хп}
ограничена? п^°°
8. Какая последовательность называется: а) сходящейся; б) расходящейся?
9. Пусть последовательность {хп} является ограниченной (неограничен-
(неограниченной). Следует ли из этого условия, что она сходится (расходится)?
10. Пусть последовательность сходится. Является ли сходящейся последо-
последовательность, которая получается из исходной, если:
а) из нее удалить конечное число членов, а оставшиеся заново перену-
перенумеровать в порядке их следования;
б) к ней добавить конечное число членов, перенумеровав члены после-
последовательности в порядке их следования;
в) в ней изменить произвольным образом конечное число членов?
11. Докажите, что сходящаяся последовательность имеет только один пре-
предел.
12. Сформулируйте необходимое условие сходимости последовательности.
Примеры решения задач
1. Сформулировать на языке "г - 7V" определение того, что число
а не является пределом последовательности {хп\ (а ф lim xn\ и дать
геометрическую интерпретацию этого определения.
Л По определению предела последовательности а = lim жп, если
¦>оо
18 Гл. П. Предел последовательности
Vs > О 3N такое, что Vn > N: \хп — а\ < е. Пользуясь правилом по-
построения отрицаний, получаем: а ф lim хп, если Зе > 0 такое, что
п—юо
V7V Зп > N: \хп - а\ ^ г.
Более подробно это можно записать так: а ф lim жп, если Зг > О
п—>-оо
такое, что
для 7V = 1 3ni > 1: |жП1 — а\ ^ г,
для 7V = 2 Зп2 > 2: |жП2 - а\ ^ г,
для 7V = 100 Зпюо > ЮО: \х100 -а\^е,
Таким образом, а ф lim хп, если существуют е > 0 и последова-
п—>-оо
тельность номеров {пдт} GV = 1,2,3,...) таких, что пдг > ^V и \xnN —
-а\^е.
Геометрическая интерпретация этого определения: а ф lim xn,
п—>-оо
если существует некоторая г-окрестность точки а, вне которой нахо-
находится бесконечно много членов последовательности. А
2. Доказать, что последовательность хп = 2П^~1^ не ограничена.
Л В силу определения неограниченной последовательности нужно по-
показать, что VM > 0 3n G ./V, для которого |жп| > М. Зададим произ-
произвольное М > 0 и возьмем любое четное число п, удовлетворяющее
неравенству п > log2 M. Для такого п имеем
хп = 2n > 2log2M = М,
что и требовалось доказать. А
3. Пользуясь определением предела последовательности, доказать,
5 • Зп
что lim = 5.
7WOO 3П - 2
Л Зададим произвольное г > 0 и рассмотрим модуль разности между
n-м членом последовательности и числом 5:
5-Зп
Зп-2
-5
10
Зп -2'
В соответствии с определением предела последовательности мы долж-
должны указать номер N такой, что Vn > N выполняется неравенство
Для отыскания номера N решим неравенство A) относительно п. По-
Получим
Из неравенства B) следует, что в качестве N можно взять целую
часть числа log3 ( Ь 2 J:
N =
§1. Предел последовательности 19
В самом деле, если п > JV, то
т. е. справедливо неравенство B), а значит, Vn > N выполняется и не-
неравенство A). (Отметим, что при е > 10 имеем N = Iog3( Ь 2] =
= 0, и поэтому неравенство A) справедливо Vn Е N.)
Итак, для произвольного г > 0 мы указали такой номер N =
= log3 ( h 2 j , что Vn > N выполняется неравенство
5-371
-5
< г.
Зп -2
Это и означает по определению предела последовательности, что
к on
lim ±J- = 5. А
п^оо зп - 2
4. Пользуясь определением предела последовательности, доказать,
что lim —-j= = 0.
!
п—Yoo
Л Зададим произвольное г > 0. Нужно указать номер 7V такой, что
Vn > N выполняется неравенство
ti < г. C)
Мы не будем стремиться к тому, чтобы найти наименьший номер
N, начиная с которого выполняется неравенство C). Укажем номер
"с запасом", решая более простое неравенство
2/п < г. D)
Так как Vn G N п! > п(п/4) (докажите это), то Vn G TV справедливо
неравенство
1/л/п! < 2/п, E)
и поэтому неравенство C) является следствием неравенства D).
Решая относительно п неравенство D), получаем
п > 2/е. F)
Положим N = [2/е]. Если п > JV, то п ^ [2/е] + 1 > 2/е, т. е. выполня-
выполняется неравенство F), а следовательно, неравенства D) и C). Таким
образом, \/е > 0 3N (N = [2/е]) такой, что Vn > N 1/л/га! < г. Тем
самым доказано, что lim ^^ = 0. А
Рассмотренные примеры показывают, каким образом следует до-
доказывать, что lim xn = а, пользуясь определением предела последо-
п—>-оо
вательности. Надо составить выражение |жп — а| и подобрать (если
20 Гл. П. Предел последовательности
это целесообразно) последовательность {уп} такую, что, во-первых,
Vn \хп — а\ ^ уп и, во-вторых, неравенство
Уп < е G)
при произвольном г достаточно просто решается относительно п.
Пусть решение неравенства G) имеет вид
п > /(г),
где f(s) > 0. Тогда в качестве N можно взять [f(s)] (если при этом
окажется, что [f(s)] = 0, то неравенство G) справедливо Vn). Таким
образом, \/п > N = [f(e)] будет выполнено неравенство \хп — а\ < е,
а это и означает по определению предела последовательности, что
lim xn = а.
п—>-оо
5. Известно, что lim хп = 0 и хп ^ 0 Vn. Доказать, что при а > 0
п—>-оо
lim x% = 0.
га-юо
Л По условию lim хп — 0, т. е. Ms\ > 0 3Ni такое, что Vn > Ni
п—>-оо
справедливо неравенство
\хп\ < ех. (8)
Требуется доказать: \/е > 0 3N такое, что Vn > N \х^\ < г, или, что
равносильно,
\хп\<е^а. (9)
Зададим произвольное г > 0 и положим si = sl/a (e\ > 0). Для этого е\
3Ni такое, что Vn > JVi справедливо неравенство (8), т. е. \хп\ < ег/а.
Таким образом, Vn > N = JVi справедливо неравенство (9). Тем самым
доказано, что lim х® = 0. А
Задачи и упражнения для самостоятельной работы
1. Ограничены ли последовательности: а) хп = (—1)п —; б) жп = 2п;
в) жп = Inn; г) хп = sinn; д) {хп} = 1,0,2,0,3,0,4,0,5,0,6,...?
Ответы обоснуйте.
2. Пользуясь определением предела последовательности, докажите, что:
a) lim I ; = 0; 6) lim -Ш- = 2; в) lim ^^^ = 0;
Ti—У OO * v Ti—У OO * v I *J 77-—У ОО '^
r) lim logn 2 = 0; д) lim . , ^ , , = 0; e) lim @,8)" = 0;
п—)-оо гг—)-оо 77- -\- 2,71 -\- 1
3/ "
гг—^oo
ж) Ит 2 +5'6 = 5; з) lim v^sli;n = 0.
3. Известно, что lim xn = а. Докажите, что:
п—Уоо
a) lim (xn+i — xn) = 0; б) lim \хп\ = |а|; в) lim ж^ = а2.
гг—^оо гг—^оо гг—^оо
4. Пусть lim \xn\ = |а|. Следует ли отсюда, что lim xn = а?
гг—)-оо гг—)-оо
5. Докажите, что последовательность {хп} расходится, если:
а) хп = п; б) Жгг = Inn; в) хп = п^^ .
§2. Бесконечно малые 21
6. Пусть последовательность {хп} сходится и М = sup{xn}, т = inf{xn}.
Докажите, что: либо Зп такое, что хп = М; либо Зк такое, что Хк = тп\
либо Зп, А; такие, что хп = М, Хк = ш. Приведите примеры последова-
последовательности всех трех типов.
§ 2. Бесконечно малые
и бесконечно большие последовательности
Основные понятия и теоремы
Определение. Последовательность {хп} называется бесконечно
малой, если lim хп = 0.
п—юо
Определение. Последовательность {жп} называется бесконечно
большой, если VA > 0 37V такое, что Vn > N \хп > А\.
С геометрической точки зрения это означает, что в любой (сколь
угодно большой) окрестности нуля находится лишь конечное число
членов последовательности, а вне ее — бесконечно много членов.
Если последовательность {хп} бесконечно большая, то пишут
lim xn = оо. Если при этом начиная с некоторого номера все члены
п—уоо
бесконечно большой последовательности положительны (отрицатель-
(отрицательны), то пишут lim хп = +оо (—оо). Отметим, что бесконечно большая
п—>-оо
последовательность не является сходящейся и символическая запись
lim хп = +00 (—оо) означает только, что последовательность {хп}
п—>-оо
является бесконечно большой, но вовсе не означает, что она имеет
предел.
Всякая бесконечно большая последовательность является неогра-
неограниченной, поскольку вне любой окрестности нуля имеется член
последовательности (даже все члены начиная с некоторого номера).
Обратное неверно: неограниченная последовательность может и не
быть бесконечно большой.
Теорема 3. Алгебраическая сумма конечного числа бесконечно
малых последовательностей является бесконечно малой последова-
последовательностью.
Теорема 4. Произведение бесконечно малой последовательности
на ограниченную является бесконечно малой последовательностью.
Следствие. Произведение конечного числа бесконечно малых
есть бесконечно малая.
Теорема 5. Если последовательность {хп} бесконечно большая,
то, начиная с некоторого номера п, определена последовательность
{1/хп}, которая является бесконечно малой. Если последователь-
последовательность {хп} бесконечно малая и Vn xn ф 0, то последовательность
{1/хп} является бесконечно большой.
22 Гл. П. Предел последовательности
Контрольные вопросы и задания
1. Сформулируйте определения: а) бесконечно малой последовательности;
б) бесконечно большой последовательности. Дайте геометрическую ин-
интерпретацию этих определений.
2. Сформулируйте на языке "е — 7V" отрицание того, что последователь-
последовательность является: а) бесконечно малой; б) бесконечно большой. Дайте гео-
геометрическую интерпретацию этих отрицаний.
3. Дайте определение, соответствующее символической записи lim хп =
= -оо. п^°°
4. Пусть бесконечное число членов последовательности находится: а) в лю-
любой окрестности нуля; б) вне любой окрестности нуля. Следует ли из
условия а) (из условия б)), что последовательность является: бесконеч-
бесконечно малой; бесконечно большой; ограниченной; неограниченной? Следует
ли из условия а) (из условия б)), что последовательность не является:
бесконечно малой; бесконечно большой?
5. Известно, что последовательность {хп} является: а) бесконечно малой;
б) бесконечно большой. Следует ли отсюда (при условии хп ф 0 Vn), что
последовательность {1/хп} является: а) бесконечно большой; б) беско-
бесконечно малой?
6. а) Является ли бесконечно малая последовательность ограниченной?
б) Является ли бесконечно большая последовательность: неограничен-
неограниченной; сходящейся?
в) Является ли любая неограниченная последовательность бесконечно
большой?
7. Известно, что уп ф 0 Vn и: a) lim хп = lim уп = 0; б) lim xn =
п—>og n—>og n—>og
= lim уп = оо. Может ли последовательность {хп/уп} быть: бесконечно
п—^оо
большой; бесконечно малой; сходящейся; расходящейся, но не бесконеч-
бесконечно большой? Приведите примеры.
8. Докажите, что сумма двух бесконечно малых последовательностей яв-
является бесконечно малой. Верно ли аналогичное утверждение для бес-
бесконечно больших последовательностей? Ответ обоснуйте.
9. Докажите, что если lim хп = оо, то, начиная с некоторого номера п,
п—)-оо
определена последовательность {1/жп}, причем lim (l/xn) = 0.
п—Уоо
10. Пусть {хп + уп} — бесконечно малая последовательность. Следует ли
отсюда, что {хп} и {уп} — бесконечно малые последовательности? От-
Ответ обоснуйте.
11. Пусть {хпуп} — бесконечно малая последовательность. Следует ли от-
отсюда, что хотя бы одна из последовательностей {хп} и {уп} бесконечно
малая? Ответ обоснуйте.
12. Докажите, что если хп ^ уп и lim уп = +оо, то lim хп = +оо.
Примеры решения задач
1. Сформулировать на языке "г — 7V" отрицание того, что после-
последовательность является бесконечно большой. Дать геометрическую
интерпретацию этого отрицания.
Л Согласно определению бесконечно большой последовательности
§2. Бесконечно малые 23
lim xn = оо, если \/А > О 3N такое, что Vn > N \хп\ > А. Поль-
п—>-оо
зуясь правилом построения отрицаний, получаем, что последователь-
последовательность {хп} не является бесконечно большой, если ЗА > 0 такое, что
\/N Зп > N: \хп\ ^ А. С геометрической точки зрения это означает,
что найдется некоторая окрестность нуля (А-окрестность), в которой
находится бесконечно много членов последовательности. А
2. Доказать, что последовательность {а71} является: а) бесконечно
большой при \а\ > 1; б) бесконечно малой при \а\ < 1.
Л Пусть \а\ > 1. Докажем, что последовательность {а71} удовлетворяет
определению бесконечно большой, т. е. VА > О 3N такое, что Vn > N
выполняется неравенство
\а\п>А. A)
Зададим произвольное А > 0. Для отыскания номера N решим нера-
неравенство A) относительно п. Получим
п > logH A. B)
Положим N = [log|a| А]. Тогда Vn > N выполняется неравенство B),
а значит, и A). Таким образом, \/А > О 3N = [log|a| А] такое, что
Vn > N \а\п > А. Это и требовалось доказать.
б) Пусть \а\ < 1. Если а = 0, то ап = 0 Vn и, следовательно, {а71}
бесконечно малая. Пусть а ф 0. Тогда ап = (A/а)п)~1. Так как |1/а| >
> 1, то последовательность {(l/a)n} является бесконечно большой, а
последовательность (A/а)п)~1 бесконечно малой в силу теоремы 5.
Таким образом, последовательность {ап} бесконечно малая при \а\ <
< 1. А
3. Пусть хп = n(-1)n. Доказать, что последовательность {хп}:
а) неограниченная; б) не является бесконечно большой.
Л а) Докажем, что {хп} удовлетворяет определению неограниченной
последовательности. В самом деле, VM > 0 член последовательности
с номером п = 2([М] + 1) равен п и больше М. Это и означает по
определению, что {хп} — неограниченная последовательность.
б) Докажем, что последовательность {хп} не является бесконеч-
бесконечно большой. Действительно, в интервале (-2,2) находятся, очевидно,
все члены последовательности с нечетными номерами, а значит, в
этом интервале находится бесконечно много членов последователь-
последовательности {хп}. Отсюда следует, что {хп} не является бесконечно боль-
большой. А
4. Пусть {хп} — сходящаяся, а {уп} — бесконечно большая по-
последовательность. Доказать, что последовательность {хп + уп} бес-
бесконечно большая.
Л Докажем, что последовательность {хп + уп} удовлетворяет опре-
определению бесконечно большой, т. е. VA > О 3N такое, что Vn > N
\хп + Уп\ > А. Так как {хп} сходится, то она ограничена, т. е. ЗМ > О
такое, что Vn выполняется неравенство
\х„\ < М. C)
24 Гл. П. Предел последовательности
Зададим теперь произвольное А > 0. Поскольку {уп} бесконечно боль-
большая, для числа А + М 3N такое, что Vn > N имеем
\уп\>А + М. D)
Из C) и D) получаем, что Vn > TV выполняется неравенство
/"V* I ГЪ И > ГЪ И ГУ* ' ч, /J I Д /| Д /| /J
\хп ~г Уп\ iy \Уп хп *> si ~г ш ivi — -ri,
что и требовалось доказать. А
Задачи и упражнения для самостоятельной работы
7. Известно, что в некоторой окрестности нуля находится: а) конечное
число членов последовательности; б) бесконечное число членов последо-
последовательности. Следует ли отсюда, что в каждом из этих случаев после-
последовательность является: ограниченной; бесконечно малой; бесконечно
большой?
8. Известно, что последовательность {хп} сходится, а {уп} бесконечно
большая. Может ли последовательность {хпуп}'- а) сходиться; б) рас-
расходиться, но быть ограниченной; в) быть бесконечно большой; г) быть
бесконечно малой? Ответьте на эти вопросы, используя в качестве при-
примеров последовательности {п}, < п ~ >, < — >, < ^—'— >, < — >.
9. Приведите примеры последовательностей {хп} и {уп}, для которых
lim хп = 0, lim уп = оо, а произведение их {хпуп} является последова-
п—)-оо п—)-оо
тельностью: а) сходящейся; б) расходящейся, но ограниченной; в) бес-
бесконечно малой; г) бесконечно большой.
10. Докажите, что заданные последовательности бесконечно малые: а) хп =
= пк (к < 0); б) хп = (-1Г • 0,999п; в) хп = ^; г) хп = —^—.
п\ 2ns + 1
11. Докажите, что заданные последовательности бесконечно большие:
а) хп = пк (к > 0); б) хп = п(-1)п; в) хп = 2^; г) хп = Iog2(log2n)
(n ^ 2).
12. Докажите, что любая бесконечно большая последовательность являет-
является неограниченной.
13. Докажите, что последовательность {A + (—1)п)п} неограниченная, од-
однако не является бесконечно большой.
14. Докажите, что если lim хп = +оо (—оо), то последовательность {хп}
п—)-оо
достигает своей точной нижней (верхней) грани.
15. Найдите наименьший член последовательности {хп}, если: а) хп =
= п2 - 9п - 100; б) хп = п + 100/п.
§ 3. Свойства сходящихся последовательностей
Основные понятия и теоремы
Теорема 6. Пусть lim xn = a, lim yn = Ъ. Тогда:
П—У(Х> П—У(Х>
a) lim (хп + Уп) = а + Ь;
§3. Свойства сходящихся последовательностей 25
б) lim (xnyn) = ab;
п—Уоо
в) если Ъ ф О, то, начиная с некоторого номера, определена по-
последовательность {хп/уп} (т. е. 3N такое, что Vn ^ N уп ф 0) и
lim (xn/yn) = а/6.
п—юо
Если lim жп = lim ?/п = О, то lim (хп/уп) называют неопреде-
п—Уоо п—Уоо п—Уоо
ленностью типа 0/0. Аналогично определяются неопределенности
типа оо/оо, 0 • оо, оо - оо. Ясно, что для таких пределов теорема б
неприменима.
Теорема 7. Если lim хп = а и, начиная с некоторого номера,
п—Уоо
хп ^ Ъ (хп ^ Ъ), то а ^ Ъ (а ^ Ь).
Теорема 8 (теорема о трех последовательностях). Если lim xn =
п—уоо
= a, lim yn = а, и, начиная с некоторого номера, выполняются нера-
п—уоо
венства хп ^ zn ^ уп, то lim zn = а.
п—>-оо
Контрольные вопросы и задания
1. Дайте определение сходящейся последовательности.
2. Сформулируйте на языке "е — 7V" определение расходящейся последова-
последовательности и дайте геометрическую интерпретацию этого определения.
3. Сформулируйте теоремы 6-8.
4. Пусть последовательность {хп} сходится, а {уп} расходится. Докажите,
что {хп + Уп} расходится, {схп} сходится, {суп} расходится при с / 0.
Покажите на примерах, что последовательность {хпуп} может: а) схо-
сходиться; б) расходиться.
5. Пусть последовательность {хп + уп} сходится. Следует ли из этого, что
{хп} и {уп} сходятся?
6. Пусть
lim xn = а. (*)
У
п—Уоо
Докажите, что {хп} можно представить в виде
хп = а + ап, (**)
где {ап} — бесконечно малая последовательность. Докажите обратное:
из (**) следует (*).
7. Докажите теорему 6.
8. Пусть lim хп = а, причем Vn хп > Ъ. Следует ли отсюда, что: а) а > Ъ]
п—Уоо
б) а^Ы
Примеры решения задач
1. Пусть lim уп = Ъ ф 0, а последовательность {zn\ расходится.
Доказать, что {znyn} расходится.
Л Обозначим хп = znyn. Докажем расходимость последовательности
{хп} методом от противного. Предположим, что {хп} сходится. Так
как по условию lim уп = Ъ ф 0, то по теореме б последовательность
26 Гл. П. Предел последовательности
{хп/Уп} = {%п} определена, начиная с некоторого номера, и сходится.
Но это противоречит условию. Следовательно, {хп} расходится. А
2. Доказать, что последовательность {sinn} расходится.
Л Доказательство проведем методом от противного. Пусть
lim sinn = а. Тогда lim sin(n + 2) = а, откуда
п—>-оо п—>-оо
lim (sin(n + 2) - sinn) = 0. A)
n—yoo
Так как sin(n + 2) — sinn = 2sinlcos(n + 1), то, учитывая равенство
A), получаем
lim cos(n + 1) = 0. B)
n—>-oo
Из равенства cos(n + 1) = cosncos 1 — sinnsin 1 находим sinn =
= ——- (cos n cos 1 — cos(n + 1)). Отсюда в силу B) следует, что
lim sinn = 0. Таким образом, получаем lim cosn = lim sinn = 0,
n—yoo n—>-oo n—>-oo
что противоречит равенству cos2 n + sin n = 1. Следовательно,
{sinn} расходится. А
3. Найти пределы:
\ т 1Оп *\ г п2-п ч г 5-Зп
a) lim — -; б) lim — ^=; в) lim -.
Л Отметим, что каждый из этих пределов является неопределен-
неопределенностью типа оо/оо. Имеем:
а) Ит 4^= lim -^=0,
так как \ п + — \ бесконечно большая;
б) цт гг2-п = Um (п-у/п)(п + у/п) = Ит (п + ^) = +00
п^оо П — л/71 п^оо 71 — л/71 п^оо
n—yoo 6IL — I n—yoo _
11111) Vх зп,
4. Найти предел lim (y/n2 + n — n).
n—yoo
Л Отметим, что этот предел является неопределенностью типа
оо — оо. Имеем
lim (у п2 + п — п) = lim
5. Вычислить lim Vncos
П-^ОО 71 + 1
Л Последовательность {cosn} ограничена, а < ^n L бесконечно
L 77- ~г 1 J
§3. Свойства сходящихся последовательностей 27
малая, так как
п-юоп
I Ит Л А
п п-ххЛ ™/
Отсюда по теореме 4 следует, что произведение этих последователь-
последовательнее^?
га-Юо П + 1
ностей является бесконечно малой, т. е. lim vncosn = 0. А
6. Найти предел lim
га-Юо П°
Л Обозначим 5П = I4 + 24 + З4 + ... + п4. Будем искать Sn в виде
Sn = An5 + Bn4 + Cn3 + Dn2 + En + F.
Тогда
5n+1 - 5n = A[(n + IM - n5] + B[(n + IL - n4] +
+ C[(n + IK - n3] + Z3[(n + IJ - n2] + E[(n + 1) - n].
Отсюда для любого натурального п имеем
(п + IL = ЪАпА + A0А + 4Б)п3 + A0А + 6Б + ЗС)п2 +
4Б + ЗС + 2
Приравнивая коэффициенты при равных степенях п в левой и правой
частях равенства, получим
ЪА
1(L4 H
1(L4 Н
5А Н
Ь 4Б
h 4Б Н
h ЗС
ь зс
+ 2?>
= 1,
= 4,
= 6,
= 4,
Отсюда А = 1/5, Б = 1/2, С = 1/3, ?> = 0, Е = -1/30. Таким образом,
для любого п имеем Sn = - п5 + - п4 + - п3 — — n + F. Полагая п =
5 Z о о\)
= 1, получим 1 = - + - + - — — +F, откуда F = 0. Следовательно,
5 z о oU
Итак,
1 J_ J ^\ = 1 A
б 2n 3n2 30n4/ ~~ 5'
28 Гл. П. Предел последовательности
Задачи и упражнения для самостоятельной работы
16. а) Известно, что последовательность {хп} сходится, а {уп} расходится.
Может ли последовательность {хпуп} быть: сходящейся; расходящейся?
б) Известно, что последовательности {хп} и {уп} расходятся. Могут ли
последовательности {хп + уп}, {хпуп} быть: сходящимися; расходящи-
расходящимися?
Ответьте на эти вопросы, используя в качестве примеров последова-
тельности { ^±1} , {(-1)"}, { 1} , {«}, {-n}, {{-1)п+1}.
17. Даны последовательности 1-1,1—1,1 ^—^— >, < >. Выбе-
l n J I n2 J I n J'ln + lOOj
рите из этих бесконечно малых последовательностей такие, что:
a) lim (хп/уп) = 0; б) lim (хп/уп) = 1; в) lim (хп/уп) = оо;
п—)-оо п—>og n—>og
г) {хп/уп} расходится, но ограничена.
18. Дано: lim хп = Ъ ф оо, lim уп = оо. Докажите, что:
п—)-оо п—)-оо
a) lim (хп ± Уп) — оо; б) lim (xn/yn) = 0;
в) lim (уп/хп) = оо (хп ф 0); г) lim (хпуп) = оо, если Ъ / 0.
гг—^оо гг—^оо
19. Докажите, что lim (хп/уп) = оо, если lim хп = 6 ф 0, lim 2/n = 0
гг—^оо гг—^оо гг—^оо
(г/n ^ 0).
20. Известно, что lim xn = а ф оо. Найдите предел последовательности
гг—^оо
{^/гг}, если:
а) уп = 2хп - Хп + l] б) уп = Хп • Xn + 2;
в) 2/гг = (хп+1 - хп)п; г) уп = mm(xn,xn-^i).
21. Известно, что lim хп = а ф оо. Приведите пример, когда последова-
п—>оо
тельность {уп} сходится (расходится), если: а) уп = [хп\, б) уп = sgn xn.
22. Известно, что xn > 0. Докажите, что:
a) lim хп = 3, если lim (хп — хп) = 6;
б) lim хп = 1, если lim lxn + — ) =2.
гг—)-оо гг—)-оо \ Хп )
23. Исследуйте на сходимость последовательности (в зависимости от
Р + 3
24. Найдите пределы:
(n\) б) ит(л/^ТТ_01) в
2 ^V V У
а) ит б) ит(л/^ТТ01) в) lim ;
' п^оо п + 2 n^ooV V У п-юо (-2)"
гг
25. Пусть хп = У^ , Требуется вычислить lim жте.
Оценим хп сверху и снизу:
п п п
\.—^ 1 \—^ 1 \—^ 1
^—' Vn2 + п ^-^ Vn2 + к ^-^ л/п2
k=l к=1 к=1
Таким образом, имеем
, „" < ХП < 1.
§4- Замечательные пределы
29
Так как
= 1,
то по теореме о трех последовательностях lim xn = 1. С другой
71—)-ОО
стороны, произвольный член в выражении для хп равен
} (к = 1, 2,..., п). Так как lim , } = 0, то
:=0 + 0+ ... +0 = 0.
= lim
+ ... + lim
• + 1 n^oo Vn2 + 2 п^оо Vn2 + П
Итак, мы получили, что 1 = 0. Найдите ошибку в проведенных рассуж-
рассуждениях. Какой из двух результатов верен, а какой нет и почему?
26. Вычислите пределы:
a) lim (J^ + А
z /
1^ + ^ + ... + .
§ 4. Замечательные пределы
Основные понятия и формулы
Будем говорить, что бесконечно большая последовательность {хп}
имеет более высокий порядок роста, чем бесконечно большая последо-
последовательность {уп}, если {хп/уп} бесконечно большая; при этом будем
употреблять обозначение уп < хп. Этот параграф посвящен вычисле-
вычислениям некоторых пределов, с помощью которых сравниваются порядки
роста различных бесконечно больших последовательностей. Нахож-
Нахождение таких пределов основывается на применении теоремы 8 о трех
последовательностях и формулы бинома Ньютона
(а + Ь)п = ап
Ъп =
где
ск =
п(п — 1)...(п — к + 1)
k=0
m — 1
Из этой формулы получаем неравенство
(а + Ъ)
A)
30 Гл. П. Предел последовательности
справедливое для положительных а и Ъ и любого натурального
числа п.
Рассматриваемые в этом параграфе примеры и задачи приводят к
таким результатам:
log|a| п < па < ап < п! при a > 0, |а| > 1. B)
(Соотношение log|a| п ^ па справедливо при а > 0, но в упр. 27 и
упр. 28 предлагается доказать его лишь при а ^ 1.)
Контрольные вопросы и задания
1. Сформулируйте теорему о трех последовательностях.
2. Напишите первые четыре члена формулы бинома Ньютона для разло-
разложения A + а)п.
3. Даны бесконечно большие последовательности: {n!}, {log10n}, {\/n},
{4П}, {п5}. Пользуясь соотношениями B), для каждых двух последова-
последовательностей укажите, какая имеет более высокий порядок роста.
Примеры решения задач
па
1. Доказать, что lira — = 0 при а > 0, а\ > 1.
n-юо an
Л Из определения предела последовательности следует, что если
lira \ип\ = 0, то и lira un = 0. Поэтому достаточно доказать, что
п—>-оо п—>-оо
lira cjn = 0, где cjn = ——. Представим иоп в виде
Рассмотрим последовательность zn = —w и докажем, что
{\а\1/а}
lim zn = 0. Тогда из результата примера 5 из § 1 будет следовать,
п—>-оо
что lim ujn — 0. Так как а > 0, \а\ > 1, то 3/3 > 0 такое, что |a|1//a =
п—>-оо
= 1 + /3. Применив неравенство A) к биному A + /3)п, получим
(lal1^)^ = A + /3)n > n(n~1V Vn ^ 2.
Отсюда следует, что
2
Положим жп = 0 Vn и уп = —— Vn > 2. Последовательности
C2(п-1)
{жп}, {2:п}, {?/п} удовлетворяют условиям теоремы о трех последо-
последовательностях, поскольку хп ^ zn ^ уп и lira жп = 0, lira ?/n = 0.
п—>-оо п—>-оо
Следовательно, lira zn = 0, что и требовалось доказать.
§4- Замечательные пределы 31
Таким образом, можно записать
па < ап при а > О, \а\ > 1. А
2. Доказать, что lim —г = 0 при а > 1.
п—юо Tl!
Л Рассмотрим последовательность zn = ^- и докажем, что lim zn =
n! га-юо
= 0. Пусть к — натуральное число такое, что к ^ |а|, и пусть n > 2fc.
Представим zn в виде произведения п сомножителей:
И
п! ~ 1 2 2к2к + 1 п'
Поскольку к ^ |а|, дробь ^- и все дроби, следующие за ней, не больше,
чем 1/2. Поэтому получаем оценку
Так как zn > 0 и lim B|a|Jfe~1( - ) = 0, по теореме о трех после-
довательностях lim zn = 0. Отсюда следует, что lim —г = 0, т. е.
последовательность {п!} имеет более высокий порядок роста, чем по-
последовательность {а71} при \а\ > 1. Итак, an ^С п! при |а| > 1. А
3. Доказать, что lim у/п = 1.
А При п ^ 2 число >/п больше 1. Поэтому Vn ^ 2 3/3П > 0 такое, что
^=1 + /Зп. C)
Из равенства C) вытекает, что п = A + /Зп)п. Применяя к правой
части последнего равенства неравенство A), получим
Отсюда находим, что /Зп ^ J Vn ^ 2. Из неравенств 0 < /Зп
и соотношения lim л/ = 0 по теореме о трех после-
п-1 n^ooVn-1
довательностях следует lim вп = 0. Из равенства C) теперь имеем
lim V/n = 1. А
п—>-оо
Задачи и упражнения для самостоятельной работы
27. Используя определение предела последовательности и результат при-
примера 3, докажите, что lim oga n = 0 при а > 1.
71—ЮО И-
28. Докажите, что lim °^%П = 0 при a > 1, a > 1.
п—)-оо ^
32 Гл. П. Предел последовательности
29. Докажите, что заданные последовательности бесконечно малые:
a)Xn = ^-; 6)Xn = g; в)ж„=^5-1.
30. Вычислите пределы:
2п
l +A +JL + _+ M. б) lim Inn • V Х
fc=n
31. Используя результат примера 2, докажите, что lim .— = 0.
§ 5. Монотонные последовательности
Основные понятия и теоремы
Последовательность {жп} называется невозрастающей (неубываю-
(неубывающей), если Vn xn+i ^ xn (xn+i ^ жп).
Невозрастающие и неубывающие последовательности называют
монотонными последовательностями.
Последовательность {хп} называется возрастающей (убывающей),
если Vn xn+i > хп (xn+i < хп).
Возрастающие и убывающие последовательности называют также
строго монотонными.
Отметим, что монотонная последовательность всегда ограничена
хотя бы с одной стороны: невозрастающая последовательность огра-
ограничена сверху, а неубывающая — снизу своим первым членом. Если
же монотонная последовательность ограничена и с другой стороны,
то она сходится, т. е. имеет место следующая теорема.
Теорема 9. Монотонная ограниченная последовательность схо-
сходится.
Контрольные вопросы и задания
1. Сформулируйте: а) определение монотонной последовательности; б) при-
признак сходимости монотонной последовательности.
2. Является ли ограниченность последовательности необходимым и до-
достаточным условием сходимости: а) монотонной последовательности;
б) произвольной последовательности?
Пример решения задачи
Найти предел последовательности {хп}, которая определяется ре-
рекуррентным соотношением
Xn+i = xnB-xn) Vn ^ 1, A)
где х\ — произвольное число, удовлетворяющее неравенству 0 < х\ <
< 1.
§ 5. Монотонные последовательности 33
Л Докажем сначала, что последовательность {хп} ограничена, а имен-
именно, пользуясь методом математической индукции, докажем, что Vn
справедливы неравенства
О < хп < 1. B)
Для х\ неравенства B) выполняются по условию. Допустим, что не-
неравенства B) имеют место для номера п, и докажем, что тогда они
будут справедливы для номера п + 1. Запишем формулу A) в виде
хп+1 = 1 - A -хпJ.
Из неравенств B) следует, что 0 < A — хпJ < 1, поэтому 0 < жп+1 <
< 1. Тем самым неравенства B) доказаны Vn.
Докажем теперь, что последовательность {хп} возрастающая. Так
как хп < 1, то 2 — хп >1. Разделив равенство A) на хп, получим
хп+1/хп = 2-хп > 1.
Отсюда следует, что хп+\ > хп Vn. Таким образом, последователь-
последовательность {хп} монотонная и ограниченная. Следовательно, по теореме 9
существует lim жп, который обозначим а. Для отыскания а перейдем
п—>-оо
к пределу в рекуррентной формуле A). Получим
lim xn+i = lim хп • lim B — хп), или а = аB — а).
п—>-оо п—>-оо п—>-оо
Отсюда а = 0 или а = 1; так как х\ > 0 и последовательность {жп}
возрастающая, то а = 1. А
Задачи и упражнения для самостоятельной работы
п
32. Докажите сходимость последовательности {хп}, где хп =/ г-
k=i
33. Докажите сходимость и вычислите предел последовательности {хп},
если
= л/а, Х2 = д/а + л/а,..., жп = у а + у а + ... + у/а,..., где а > 0.
34. Докажите сходимость и вычислите предел последовательности
если она определяется рекуррентным соотношением:
а) Х!=а, х2=Ъ, аф Ъ, хп = xn-i+xn-2 уп ^ 3;
Z
б) х\ — произвольное положительное число,
Xn+i = \{хп + —) Vn ^ 1, а > 0;
в) х\ — произвольное отрицательное число,
Xn+i = \{хп + —) Vn ^ 1, а > 0;
2 В.Ф. Бутузов и др.
34 Гл. П. Предел последовательности
г) xi = |, xn+i = у/Зхп - 2 Vn ^ 1; д) Ж1 G 0, | , жп+1 = х\ + ж^
Vn ^ 1; е) xi = 1, хп+1 = 1 — j— Vn ^ 1; ж) х\ = О, Х2 = -,
xn+i =-A + хп + Xn-i) Vn ^ 2; з) жп > 0 Vn ^ 1; в качестве жп+1
о
берется любое число, удовлетворяющее неравенству хпF — хп+\) > 9.
35. Докажите, что неограниченная монотонная последовательность явля-
является бесконечно большой.
( 1 \п
36. Докажите существование предела lim I 1 -\— ) .
п^оо V П)
§ 6. Предельные точки
Основные понятия и теоремы
Пусть {хп} — некоторая числовая последовательность. Рассмот-
Рассмотрим произвольную возрастающую последовательность целых поло-
положительных чисел fci, &2,..., кп,... Отметим, что кп ^ п. Выберем из
{хп} члены с номерами fci, k2, ...,fcn,...:
Полученная числовая последовательность {хип} называется под-
подпоследовательностью последовательности {хп}.
Теорема 10. Если lim xn = а, то любая подпоследовательность
п—>-оо
{ж/.п} сходится к а при п —У оо.
Теорема 11 (теорема Больцано-Вейерштрасса). Из любой ограни-
ограниченной последовательности можно выделить сходящуюся подпоследо-
подпоследовательность.
Определение 1. Число а называется предельной точкой (или
частичным пределом) последовательности {жп}, если из последова-
последовательности {хп} можно выделить подпоследовательность {xkn}, схо-
сходящуюся к а.
Можно дать другое, эквивалентное определение предельной точки.
Определение 2. Число а называется предельной точкой после-
последовательности {жп}, если в любой ^-окрестности точки а содержится
бесконечно много членов последовательности {хп}.
Замечание 1. Из теоремы 10 следует, что сходящаяся последователь-
последовательность имеет только одну предельную точку, совпадающую с ее пределом.
Замечание 2. Из теоремы 11 следует, что всякая ограниченная по-
последовательность имеет по крайней мере одну предельную точку.
Наибольшая (наименьшая) предельная точка последовательности
{жп}, ограниченной сверху (снизу), называется верхним (нижним)
пределом этой последовательности и обозначается lim хп ( lim хп ).
7WOO VrWOO /
§ 6. Предельные точки 35
Очевидно, если {хп} сходится, то lim хп = Ит хп = Нт хп.
п—>-оо п^.оо п—>-оо
Если последовательность {хп} не ограничена сверху (снизу), то по-
полагают lim хп = +оо ( lim хп = —оо).
n-юо ^га-юо '
Контрольные вопросы и задания
1. Сформулируйте определения: а) последовательности; б) предельной точ-
точки (дайте два определения и докажите их эквивалентность); в) верхнего
(нижнего) предела последовательности.
2. Дайте геометрическую интерпретацию определения предельной точки.
3. Является ли предел последовательности ее предельной точкой? Ответ
обоснуйте.
4. Даны последовательности {п((—1)п + 1)}, {п}, {(—1)п + 1}. Укажите,
какая из них: а) имеет предельную точку; б) не имеет предельной точ-
точки; в) имеет две предельные точки; г) имеет только одну предельную
точку. Есть ли среди этих последовательностей сходящаяся?
5. Докажите, что сходящаяся последовательность имеет только одну пре-
предельную точку, совпадающую с ее пределом. Верно ли обратное утверж-
утверждение: если последовательность имеет единственную предельную
точку, то она сходится?
6. Дана последовательность {жп}. Известно, что любая окрестность точ-
точки а содержит бесконечно много членов последовательности и никакой
сегмент, которому не принадлежит точка а, не содержит бесконечно
много членов последовательности. Следует ли отсюда, что lim xn = а?
п—Уоо
7. Пусть lim x2n = 4. Может ли последовательность {хп} быть: а) сходя-
п—Уоо
щейся (если да, то чему может быть равен ее предел?); б) расходящейся?
8. Сформулируйте теорему Больцано-Вейерштрасса.
9. Верно ли утверждение: если последовательность не ограничена, то из
Примеры решения задач
1. Доказать расходимость последовательности хп = (—1)п.
Л Рассмотрим две подпоследовательности этой последовательности:
X2k = 1 и X2k-i — ~1 (к = 1,2,...). Очевидно, что lim х^к — 15
к—too
lim X2k-i — ~1-
к—too
Таким образом, последовательность {(—1)п} имеет две предель-
предельные точки: 1 и -1, а поэтому не может быть сходящейся, поскольку
сходящаяся последовательность имеет только одну предельную точ-
точку. А
2. Найти: а) все предельные точки последовательности {sinn°};
б) верхний и нижний пределы этой последовательности.
Л а) Каждое из чисел
О, ±sinl°, ±sin2°, ..., ±sin89°, ±1
2*
36 Гл. П. Предел последовательности
встречается в последовательности бесконечно много раз, поскольку
Vn, p Е N sinn° = sinC60°p + п°). Поэтому каждое указанное число
является предельной точкой последовательности {sinn°}. Других пре-
предельных точек последовательность не имеет, так как если число а не
совпадает ни с одним из этих 181 чисел, то существует окрестность
точки а, не содержащая ни одного члена последовательности.
б) Из указанных в п. а) 181 предельных точек наименьшей явля-
является -1, а наибольшей 1, т. е.
lim sinn° = 1, lim sinn° = — 1. A
П-ЮО П-ЮО
3. Найти: а) все предельные точки последовательности
О, 1, 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, ...;
б) верхний и нижний пределы этой последовательности.
Л а) Данная последовательность {хп} представляет собой множество
всех рациональных чисел сегмента [0,1], расположенных в указанном
порядке. Так как в любой ^-окрестности любого вещественного числа
из сегмента [0,1] содержится бесконечно много рациональных чисел
(см. упр. 5 к гл. 1), то каждая точка этого сегмента является пре-
предельной точкой данной последовательности. Если же а 0 [0,1], то эта
точка не является предельной точкой данной последовательности, по-
поскольку для нее существует окрестность, не содержащая ни одного
члена последовательности.
б) Очевидно, lim хп = 0, lim хп = 1. А
ПЮО
4. Доказать, что бесконечно большая последовательность {хп} не
имеет предельной точки.
Л Доказательство проведем методом от противного. Пусть некоторая
точка а является предельной точкой последовательности {хп}. Тогда
существует подпоследовательность {xkn} такая, что lim x^n — а. С
п—>-оо
другой стороны, {xkn} не имеет предела, поскольку является беско-
бесконечно большой. Действительно, так как {хп} — бесконечно большая,
то \/А > О 3N: Vn > N \хп\ > А. Отсюда, поскольку кп^пи кп+\ > кп,
следует, что Укп > N \xkn\ > А, т. е. {xkn} бесконечно большая. По-
Полученное противоречие доказывает, что {хп} не имеет предельной
точки. А
Задачи и упражнения для самостоятельной работы
37. Докажите, что:
а) из любой неограниченной последовательности можно выделить бес-
бесконечно большую подпоследовательность;
б) любая подпоследовательность бесконечно большой последователь-
последовательности является бесконечно большой;
в) монотонная неограниченная последовательность не имеет предель-
предельной точки;
г) у каждой ограниченной последовательности существуют верхний и
нижний пределы.
§ 7. Фундаментальные последовательности 37
38. Известно, что последовательности {хп} и {уп} имеют по одной пре-
предельной точке. Покажите на примерах, что последовательности {хп +
уп} и {хпуп} могут: не иметь предельных точек; иметь одну предель-
предельную точку; иметь две предельные точки.
39. Найдите все предельные точки последовательности {жп}, а также
lim xn, lim xn, если:
в) хп = 1 + 2(-l)n+1 + ЗС-!)"^'/2; г) хп = ^| cos Щ?;
д) хп =
и) Жп = ^l + 2-(-1)n; к) хп = cos" ^; л) хп = (-1)пп.
о
40. Исследуйте на сходимость последовательность
п п п
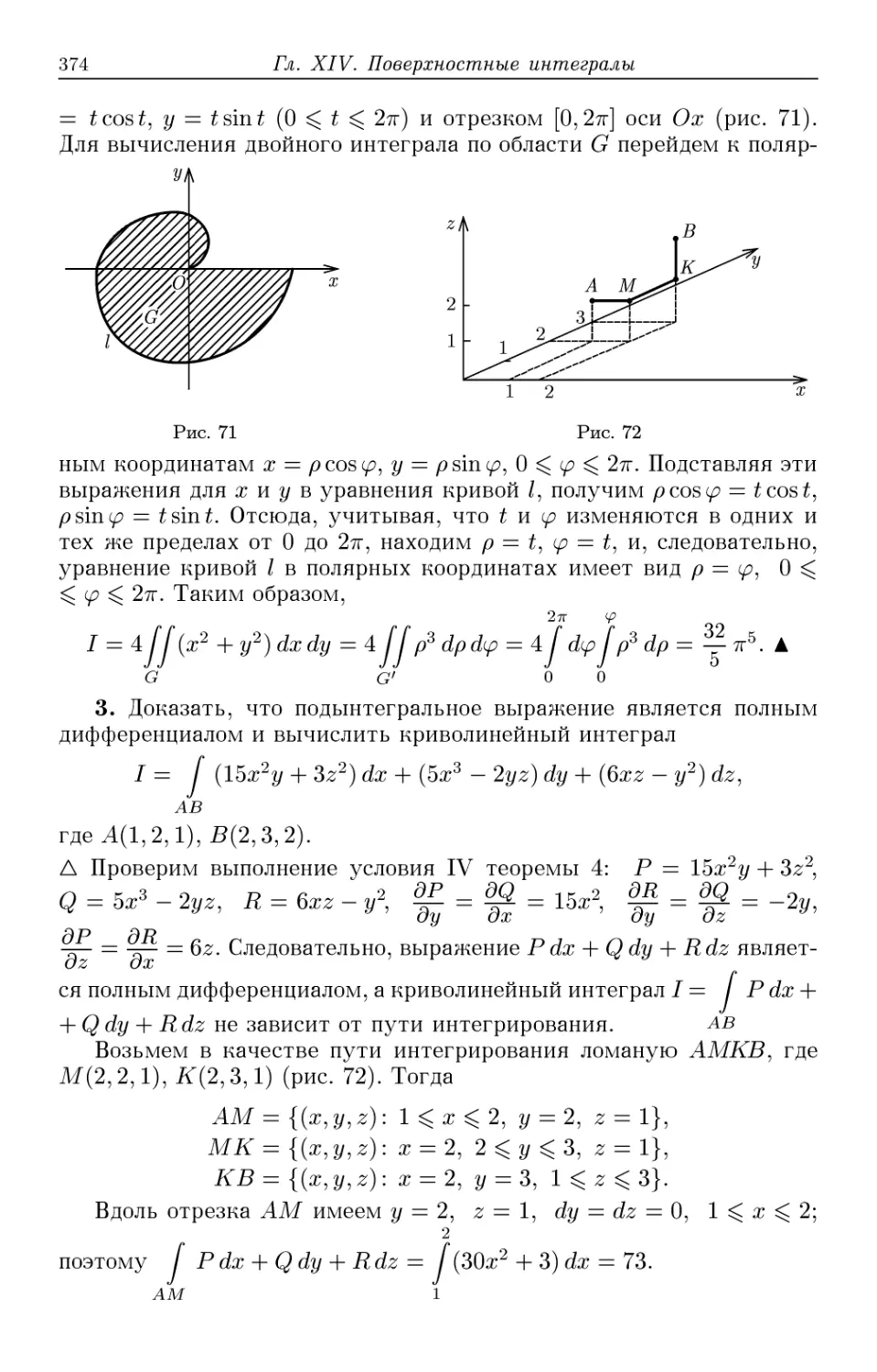
§ 7. Фундаментальные последовательности.
Критерий Коши сходимости последовательности
Основные понятия и теоремы
Определение 1. Последовательность {хп} называется фунда-
фундаментальной, если \/г > О 37V такое, что Vn > N и любого натураль-
натурального числа р выполняется неравенство \хп — хп+р\ < г.
Это определение эквивалентно следующему.
Определение 2. Последовательность {хп} называется фунда-
фундаментальной, если Vs > О 37V такое, что Vn > N и Vm > TV выполняется
неравенство |жп — жш| < г.
Геометрическая интерпретация этих определений состоит в сле-
следующем: если последовательность {хп} фундаментальная, то Vs > О
3N такое, что расстояние между любыми двумя членами последова-
последовательности с номерами, большими, чем JV, меньше г.
Теорема 12 (критерий Коши сходимости последовательности).
Для того чтобы последовательность сходилась, необходимо и доста-
достаточно, чтобы она была фундаментальной.
Контрольные вопросы и задания
1. Сформулируйте определения:
а) фундаментальной последовательности (дайте два определения и до-
докажите их эквивалентность);
б) нефундаментальной последовательности (пользуясь правилом пост-
построения отрицаний).
Дайте геометрическую интерпретацию этих определений.
2. Сформулируйте критерий Коши сходимости последовательности.
38
Гл. П. Предел последовательности
Примеры решения задач
1. Пользуясь критерием Коши, доказать сходимость последова-
тельности {жп}, где хп =
sink
к=1
Д В силу критерия Коши достаточно доказать, что последователь-
последовательность {хп} фундаментальная. Для этого оценим \хп — хп+р\. Имеем
^n %n+p
n+p
E
sin А;
А;2
п+р
Ер
к=п+1
Так как —
п+р
к2 Jfe(Jfe-l) к-I
1 + '
к=п+1
(n + lJ (n + 2J ""
< (I_ 1 ) + ( 1 _ 1 )+„.+ (_! _1) =
Vn n + l/ \n + l n + 2/ \n + » —1 n + p
Поэтому Vn, p ? N имеем
/п.
A)
Зададим теперь произвольное е > 0 и положим 7V = [1/е]. Тогда \/п> N
выполняется неравенство п ^ [1/г] + 1 > 1/г, откуда 1/п < г. Следова-
Следовательно, Vn > N и любого натурального числа р, используя неравенство
A), получаем \хп — хп+р\ < 1/п < г. Это доказывает фундаменталь-
фундаментальность последовательности {хп}. А
2. Пользуясь критерием Коши, доказать расходимость последова-
п
тельности {жп}, где хп = ^
*i
Л В силу критерия Коши достаточно доказать, что последователь-
последовательность {хп} не является фундаментальной. Для этого оценим \хп —
— х
п+р
. Имеем
X
п+р
п+р
Vn, p e N.
В частности, при р = п получаем
VJ±> J- Vn.
B)
§ 7. Фундаментальные последовательности 39
Возьмем г = 1/л/2- Тогда ViV найдутся такие п > N и натуральное
число р, что \хп — хп+р\ ^ е. В самом деле, в силу неравенства B)
достаточно взять любое п> N и р = п. Это доказывает, что последо-
последовательность {хп} не является фундаментальной. А
Задачи и упражнения для самостоятельной работы
41. Пользуясь критерием Коши, докажите сходимость последовательности
{хп}, если:
cos(fc!) . ч A
г) жп = ^afcgfc, где |g| < 1 и |afe| ^ M Vk, M > 0.
fc=0
42. Пользуясь критерием Коши, докажите, что если последовательность
п
хп = у^ ак сходится, то lim an = 0.
fc=l
43. Пользуясь критерием Коши, докажите расходимость последователь-
последовательности {жп}, если:
ГЛАВА III
ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 1. Предел функции. Теоремы о пределах.
Бесконечно большие функции
Основные понятия и теоремы
1. Предел функции в точке. Пусть ж — числовая переменная
величина, X — область ее изменения. Если каждому числу ж Е X
поставлено в соответствие некоторое число у, то говорят, что на мно-
множестве X определена функция, и пишут у = f(x). Переменная х назы-
называется независимой переменной (или аргументом функции),
множество X — областью определения функции /(ж), а число у,
соответствующее данному значению аргумента ж, — частным зна-
значением функции в точке х. Совокупность Y всех частных значений
функции называется множеством значений функции f(x).
Точка a (a Е X или а ф X) называется предельной точкой мно-
множества X, если в любой окрестности точки а имеются точки мно-
множества X, отличные от а.
В определениях этого параграфа предполагается, что а есть пре-
предельная точка множества X — области определения функции f(x).
Определение 1 (по Коши). Число Ъ называется пределом функ-
функции f(x) в точке а (при х —> а), если Vs > 0 36 > 0 такое, что Уж,
удовлетворяющего условиям х е X, 0 < \х - а\ < 6, выполняется не-
неравенство \f(x) — Ь\ < е.
Определение 2 (по Гейне). Число Ъ называется пределом функ-
функции f(x) в точке а, если для любой сходящейся к а последователь-
последовательности {хп} такой, что хп G X, хп ф а, соответствующая последова-
последовательность значений функции {/(жп)} сходится к Ъ.
Обозначение: lim f(x) = b или f(x) —у b при х —> а.
х—>а
Подчеркнем, что понятие предела функции в точке а вводится
только для предельных точек а области определения функции. Отме-
Отметим, что при этом функция может быть и не определена в точке а,
т. е., вообще говоря, а 0 X.
Сформулируем отрицания определений 1 и 2.
Отрицание определения 1. Число b не является пределом
функции f(x) в точке a (b ф lim /(ж)), если Зг > 0 такое, что \/6 > О
v х—>а '
Зх е X, для которого 0 < |ж - а\ < 6 и |/(ж) — Ь\^е.
Отрицание определения 2. Число b не является пределом
функции /(ж) в точке a (b ф lim /(ж)), если существует сходящаяся
§1. Предел функции 41
к а последовательность {хп} (хп G I, хп / а) такая, что соответст-
соответствующая последовательность {f(xn)} не сходится к Ъ.
2. Теоремы о пределах.
Теорема 1. Определения 1 и 2 предела функции эквивалентны.
Теорема 2. Пусть f(x) и д(х) определены в некоторой окрест-
окрестности точки а, кроме, быть может, самой точки а, и lim f(x) = b,
ж —>а
lim g(x) = с. Тогда:
ж —>а
lim (/(ж) + д(х)) = Ъ + с; lim (/(ж) - д(х)) = Ь - с;
ж>а ж>а
(
ж—>-а
lim f(x)g(x) = 6с; lim ^"T — ~ и/ж условии с ф 0.
ж—^а ж—^а р(ж) С
Теорема 3. Пусть функции /(ж), д(ж) и /г(ж) определены в неко-
некоторой окрестности точки а, кроме, быть может, самой точки а, и
удовлетворяют неравенствам f(x) ^ #(ж) ^ h(x). Пусть lim /(ж) =
ж—^а
= lim /i(x) = Ъ. Тогда lim д(ж) = Ъ.
х—>а х—>а
3. Односторонние пределы.
Определение 1 (по Коши). Число Ъ называется правым {левым)
пределом функции f(x) в точке а, если Vs > 0 36 > 0 такое, что \/х,
удовлетворяющего условиям xGl, а < х < а + 6 (а — 6 < х < а),
выполняется неравенство \f(x) — Ь\ < г.
Определение 2 (по Гейне). Число Ъ называется правым [левым)
пределом функции f(x) в точке а, если для любой сходящейся к а
последовательности {хп} такой, что хп е X, хп > а (хп < а), соот-
соответствующая последовательность значений функции {f(xn)} сходит-
сходится к Ъ.
Обозначения: lim f(x) = Ъ или /(а + 0) = Ъ (соответственно
ж—>а-\-0
lim f(x) = b или f(a — O) = b).
х—>а—О
Определения 1 и 2 эквивалентны.
Теорема 4. Если существуют f (а + 0) и f (а — 0), причем f (a +
+ 0) = /(а — 0) = Ъ, то существует lim f(x) = b.
х—>а
Теорема 5. Если функция f(x) определена в некоторой окрест-
окрестности точки а, за исключением, быть может, самой точки а, и су-
существует lim f(x) = b, то существуют f(a + 0) и f(a — 0), причем
/(а + О) = /(сГ-О) = Ь.
4. Предел функции при х —у оо. Пусть функция /(ж) определена
на полупрямой (с, +оо).
Определение 1 (по Коши). Число b называется пределом функ-
функции f(x) при х —у +оо (b = lim fix)), если \/г > О ЗА > 0 (а ^ с)
4 ж-^+оо '
такое, что \/х > А выполняется неравенство \f(x) - b\ < г.
Определение 2 (по Гейне). Число b называется пределом функ-
функции f(x) при х -у +оо, если для любой бесконечно большой последо-
42 Гл. III. Предел и непрерывность функции
вательности {хп} (хп > с) соответствующая последовательность зна-
значений функции {f(xn)} сходится к Ъ.
Определения 1 и 2 эквивалентны.
Аналогично определяется lim /(ж). Если lim /(ж) = lim /(ж) =
х—У — оо х—У — оо х—>-+оо
= 6, то пишут lim /(ж) = 6. Например, lim A/ж) = 0.
х—юо ж—юо
Для односторонних пределов и пределов при ж ->• оо справедлива
теорема, аналогичная теореме 2.
5. Бесконечно большие функции.
Определение 1. Функция /(ж) называется бесконечно большой в
точке а справа, если VM > 0 36 > 0 такое, что Уж, удовлетворяющего
условию х е X, а < х < а + S, выполняется неравенство
|/(ж)|>М. A)
Обозначение: lim /(ж) = оо или f(a + 0) = оо. Подчеркнем, что
х—>а+0
эта запись означает только, что /(ж) является бесконечно большой в
точке а справа, но вовсе не означает, что /(ж) имеет в точке а правый
предел; очевидно, этот предел не существует.
Если в определении 1 вместо неравенства A) выполняется не-
неравенство /(ж) > М (/(ж) < — М), то говорят, что функция /(ж)
является бесконечно большой знака плюс (минус) в точке а спра-
справа, и пишут lim /(ж) = +оо или f(a + 0) = +оо (соответственно
ж-^а+О
lim /(ж) = —оо или /(а + 0) = —оо).
х—^а+0
Аналогично определяется бесконечно большая функция в точке а
слева.
Если функция является бесконечно большой в точке а справа и
слева, то пишут lim /(ж) = оо. Например, lim A/ж) = оо.
ж-^а ж-^0
Определение 2. Функция /(ж) называется бесконечно большой
в точке а справа (слева), если для любой сходящейся к а последова-
последовательности {хп} такой, что хп G X, хп > а (хп < а), соответствующая
последовательность {/(жп)} является бесконечно большой.
Определения 1 и 2 эквивалентны.
Пусть функция /(ж) определена на полупрямой (с, +оо).
Определение 3. Функция /(ж) называется бесконечно большой
при х ->• +00, если VM > О ЗА (А^ с) такое, что Уж > А |/(ж)| > М.
Определение 4. Функция /(ж) называется бесконечно большой
при х —> +00, если для любой бесконечно большой последовательности
{хп} [хп > с) соответствующая последовательность {/(жп)} является
бесконечно большой.
Обозначение: lim /(ж) = оо.
х—>-+оо
Определения 3 и 4 эквивалентны.
Аналогично вводится понятие бесконечно большой функции при
ж ->• -оо: lim /(ж) = оо. Если функция /(ж) является бесконечно
§1. Предел функции 43
большой при х ->• +оо и при х ->• -оо, то пишут lim f(x) = оо. На-
х—>-оо
пример, lim ж = оо.
ж—>-оо
Контрольные вопросы и задания
1. Сформулируйте два определения предела функции в точке. Что означа-
означает эквивалентность этих определений?
2. Пользуясь определением предела функции по Гейне, докажите единст-
единственность предела функции в точке.
3. Докажите, что Уж о Ит ж = жо, пользуясь определением предела функ-
X—>XQ
ции: а) по Коши; б) по Гейне.
4. Дана функция /(ж) = ^. Определена ли функция /(ж) в точке ж = О?
Является ли точка ж = 0 предельной точкой области определения функ-
функции? Существует ли lim /(ж)?
5. Сформулируйте отрицание двух определений предела функции в точке.
6. Сформулируйте теоремы 2 и 3 о пределах функций.
7. Сформулируйте два определения односторонних пределов функции и
отрицания этих определений. , _ ,
8. Существуют ли /C + 0) и /C — 0), если /(ж) = ±-—^? Существует ли
lim /(ж)? 3 " х
х^-З
9. При каких условиях из существования односторонних пределов (преде-
(предела функции) следует существование предела функции (односторонних
пределов)?
10. Сформулируйте два определения предела функции при ж —»¦ +оо и от-
отрицания этих определений.
11. Докажите, что функция /(ж) = ж не имеет предела при ж —»¦ +оо.
12. Докажите, что lim ж = +оо.
х—^ + оо
13. Сформулируйте определения по Гейне и по Коши, соответствующие сле-
следующим символическим обозначениям:
a) lim /(ж) = +оо; б) /(а + 0) = -оо; в) lim /(ж) = Ь\
х—>а х—> — оо
г) lim /(ж) = оо; д) lim /(ж) = +оо.
х—> — оо
14. Докажите, что функция /(ж) = является бесконечно большой в
точке ж = 3. х - 6
Примеры решения задач
1. Доказать, что lim sin ж = 0.
Л Воспользуемся неравенством |sinx| ^ |ж| Уж. Зададим произволь-
произвольное е > 0 и положим S = е. Тогда если |ж| < 5, то | sinx| ^ |ж| < S = е.
Это и означает (согласно определению предела функции по Коши), что
lim sin ж = 0. А
2. Вычислить lim /(ж), где fix) = х ~ .
х—Yl Ж — 1
Л Так как lim (ж2 — 1) = 0 и lim (ж — 1) = 0, то этот предел является
х—vl х—vl
44 Гл. III. Предел и непрерывность функции
неопределенностью типа 0/0, и мы не можем воспользоваться теоре-
теоремой 2 о пределе частного двух функций. Воспользуемся тем, что при
рассмотрении предела функции в точке х = 1 ее аргумент не при-
принимает значения, равного 1. Поэтому lim f(x) = lim (ж + 1), так как
2 -, х—>1 х—>1
f(x) = Х Z\ = х + 1' если ХФ1-
Пусть {жп} — произвольная последовательность, сходящаяся к 1
(хп ф 1); тогда lim (хп + 1) = 2. Это означает (согласно определению
п—юо
предела функции по Гейне), что lim (ж + 1) = lim /(ж) = 2. А
~ >1 х>1
3. Вычислить предел lim
X - 1
Л Этот предел, как и в примере 2, является неопределенностью ти-
типа 0/0. Однако в отличие от примера 2 здесь нельзя непосредственно
"сократить" числитель и знаменатель дроби на х — 1. Поэтому пред-
предварительно преобразуем функцию, умножив числитель и знаменатель
на (у/3 + х + 2) — выражение, сопряженное числителю. Получим
ж- 1
х-1
Так как при рассмотрении данного предела аргумент ж не принимает
значения ж = 1, то, сокращая на ж — 1, получаем
г у/3 + х - 2 1 1
lim = lim , = -. А
ж-и ж-1 ж^1Л/3 + ж + 2 4
4. Доказать, что функция Дирихле
О, если ж — иррациональное число,
^ ' > ' если ж — рациональное число,
не имеет предела ни в одной точке.
Л Докажем, что в произвольной точке а функция D(x) не удовле-
удовлетворяет определению предела функции по Гейне. Для этого укажем
две последовательности, {жп} и {ж^}, сходящиеся к а и такие, что
lim D(xn) ф lim D(x' ). Сначала рассмотрим последовательность
п—>-оо п—>-оо
{жп} рациональных точек, сходящуюся к а. Для нее D(xn) = 1 Vn,
и поэтому lim D(xn) = 1. Теперь рассмотрим последовательность
п—>-оо
{ж^} иррациональных точек, сходящуюся к а. Для нее D(x'n) = 0 Vn,
и поэтому lim 1)(ж' ) = 0. Таким образом, lim D(xn) ф lim D(x').
Отсюда следует, что предел функции D(x) в точке а не существует. А
5. Рассмотрим множество всех иррациональных чисел интервала
(—1,1). Обозначим его 1Г. Определим на множестве 1Г функцию /(ж):
/(ж) = 1, если ж G /г. Доказать, что lim /(ж) = 1, где а — произволь-
х—>а
ная точка сегмента [—1,1] (рациональная или иррациональная).
§1. Предел функции 45
Л Пусть а е [-1,1]. Точка а является предельной точкой множества
1Г (см. упр. 5 к гл. I). Воспользуемся определением предела функ-
функции по Гейне. Пусть {хп} — произвольная последовательность точек
множества /г, сходящаяся к точке а (жп фа). По условию /(жп) = 1
\/жп Е 1Г. Поэтому lim /(жп) = 1 и, следовательно, lim /(ж) = 1. А
п—>-оо х—>а
6. Доказать, что функция sin ж не имеет предела при ж —> +оо.
Л Докажем, что эта функция не удовлетворяет определению предела
функции при ж —У +00 по Гейне. Для этого укажем такую бесконечно
большую последовательность {жп}, что последовательность {sina;n}
расходится. Положим хп = JBn + 1). Тогда lim хп = +оо, а после-
2 п-^оо
довательность {sinxn} = —1,1,-1,1,... расходится. Отсюда следует,
что функция sin ж не имеет предела при ж —У +оо. А
7. Пусть
f(x\ = { х при ж < О,
J ^ ) у sin ж при ж > О
(/(ж) не определена при ж = 0). Существует ли lim /(ж)?
х—>0
А Вычислим в точке ж = 0 односторонние пределы функции /(ж),
пользуясь теоремой 5 для функций y = sinx и у — х в точке а — 0:
/(а + 0) = lim sin ж = lim sin ж = О,
/(а — 0) = lim sin ж = lim ж = 0.
Отсюда по теореме 4 следует, что существует lim /(ж), и он равен
х—>-0
нулю. А
8. Вычислить lim /(ж), где /(ж) = 2
Л Этот предел является неопределенностью типа оо/оо, так как чис-
числитель и знаменатель — бесконечно большие функции при ж ->• оо.
Представим /(ж) в виде
ЮОж2 + 1
Так как lim A/ж2) = 0, то, используя теорему 2 (для ж —> оо), полу-
х—>-оо
чаем
lim A00 +1/ж2)
lim /(ж) = ^? =- = — = 100. А
z^oo lim A + 100/ж2) 1
ж—>-оо
Примеры 2 и 8 позволяют сформулировать общие правила вычис-
вычисления пределов вида lim R{x) и lim R{x). Здесь R{x) — рациональ-
х—>а х—Уоо
ная функция (рациональная дробь), т. е. R(x) = Pn(x)/Qm(x), где
Рп(х) и Qm(x) — многочлены соответственно степени пит.
46 Гл. III. Предел и непрерывность функции
Если lim Qm(x) = Qm(a) Ф 0, то lim R(x) = Pn(a)/Qm(a).
х—>а х—>а
Если lim Qm{x) = 0 и lim Рп{х) Ф 0, то lim R[x) = оо.
х—>а х—>а х—>а
Если lim Qm{x) = lim Pn(x) = 0, то Рп{х) = {х - а)Р*_г{х),
х—>а х—>а
Qm(x) = (х - a)Qm-i(x) и
lim R(x) = lim —™~1
Для вычисления lim R(x) надо разделить числитель и знаменатель
х—уоо
функции R(x) на хт и далее вычислять предел полученной функции,
учитывая, что lim ^ = Ьо, где Ьо — коэффициент при хш мно-
х—уоо X171
гочлена Qm(x). A
9. Пусть lim f(x) = b, lim g(x) = +00. Доказать, что
x—>a x—>a
lim (f(x) + #(ж)) = +oo.
x—>a
А Докажем, что функция f(x) + g(x) удовлетворяет определению бес-
бесконечно большой знака плюс в точке а, т. е. VM > 0 36 > 0 та-
такое, что Уж, удовлетворяющего условию 0 < \х — а\ < й, выполняется
неравенство f(x) + g(x) > М. Так как lim f(x) = b, то существует
х—>а
^1-окрестность точки а, в которой (при х/а)
I/WI < С, B)
где С — некоторое положительное число (докажите это самостоя-
самостоятельно). Зададим произвольное М > 0. Поскольку lim g(x) = +00,
х—>а
для числа М + С 36 > 0 F ^ 6i) такое, что Уж, удовлетворяющего
условию 0 < \х — а\ < ?, выполняется неравенство
д(х) >М + С. C)
Из неравенств B) и C) получаем, что при 0 < \х — а\ < 6 ^ 6i
справедливо неравенство
f{x) + q(x) 2 д(х) - \f(x)\ >M + C-C = M,
что и требовалось доказать. А
Задачи и упражнения для самостоятельной работы
1. Пользуясь определением предела функции по Коши, докажите, что
lim(xsin(l/x)) = 0.
х—>0
2. Докажите, что функция f(x) = sin(l/x) не имеет предела в точке х = 0.
3. Существует ли lim {ж}, где {х} = х — [х] — дробная часть числа ж?
§1. Предел функции 47
f(x\ = /ж2, если я
J у } у 1, если ж
4. Пусть
иррациональное число,
— рациональное число.
Докажите, что /(ж) имеет предел в точках ж = 1иж = — 1 и не имеет
предела в остальных точках.
5. Докажите, что: a) lim(l — cos ж) = 0; б) lim tgж = 0.
ж—)-0 ж—)-О
6. а) Используя неравенство sin ж <ж<tgж@<ж< тг/2) и теорему 3,
докажите, что
lim smx = 1 (первый замечательный предел).
х—>0 X
б) Используя первый замечательный предел, докажите, что
,. 1 — cos ж 1 ,. tgx
hm = -, hm -^— = 1.
ж—)-О Ж2 2 ж—)-О Ж
7. Пусть
Я(ж) =
box
Докажите, что
{оо при п > т,
ао/^о при п = т,
0 при п < т.
8. Вычислите пределы:
ч г A + жK - A + Зж + Зж2) . ж2 - 4
a) lim —г~^ -; б) lim -о—^-o~i ^;
ж-^0 Ж4 + Ж3 ж-^2 Ж3 — 2ж2 + Ж — 2
ч .. ж2 -5ж + 6 ч .. ж4 -Зж + 2
в) hm.^ o^ , 1е; г)lmi
—т ; г) hm — ;
ж2 - 8ж + 15 J x^i ж5 - 4ж + 3
-—=— (т —
Ж — 1
9. Вычислите пределы:
a) lim VT+2^-3
i->4 Vx-2
10. Вычислите пределы:
д) lim -—=— (т — натуральное число).
х—>1 Ж — 1
V Ж + 1
11. Докажите, что lim cos ж не существует.
ж—^оо
12. Существует ли lim /(ж), если:
х^а ( 1 при Ж > 0,
а) а = 1, /(ж) = #sgn (ж — 1), где sgi^=< 0 при ж = 0,
I —1 при ж < 0;
1 — cos ж _
при ж < 0,
б) а = 0, /(ж) = ^ х
жz
при ж > 0;
в) а = 0, /(ж) = <^ ж
2ж + ж2
зшж п
ж
cos ж при ж ^ 0?
48 Гл. III. Предел и непрерывность функции
13. Пусть lim f(x) = b, lim g(x) = +00. Докажите, что:
a) lim(/S-^))=^; 6) lim ^ = 00 (при b ф 0);
Jx)
x—>a
x>a J\)
в) lim Ц& = 0; г) lim f{x)g(x) = 00 (при b / 0).
14. Пусть lim f(x) = 0 (причем f(x) / 0 при х / a), lim д(ж) = 6/0.
ж—)-a ж—)-a
Докажите, что lim ^) ; = 00.
§ 2. Непрерывность функции в точке
Основные понятия и теоремы
1. Непрерывность функции в точке. Пусть функция опреде-
определена в некоторой окрестности точки а.
Определение. Функция f(x) называется непрерывной в точке
а, если lim f(x) = /(a).
х—Уа
Пусть функция f(x) определена в правой (левой) полуокрестности
точки а, т. е. на некотором полуинтервале [a, a + г) (соответствен-
(соответственно (а —г, а]). Функция f(x) называется непрерывной справа (соот-
(соответственно слева) в точке а, если /(а + 0) = /(а) (соответственно
/(а-0) = /(а)).
Теорема 6. Для того чтобы функция была непрерывна в точке а,
необходимо и достаточно, чтобы она была непрерывна в этой точке
справа и слева.
Теорема 7. Если функции f(x) и д(х) непрерывны в точке а,
то функции f(x)+g(x), f(x)-g(x), f(x)g(x), f(x)/g(x) также
непрерывны в точке а (частное — при условии д(а) ф 0).
2. Непрерывность сложной функции. Пусть функция у =
= (р(х) определена на множестве X, а Y — множество значений этой
функции. Пусть, далее, на множестве Y определена функция и = f(y).
Тогда говорят, что на множестве X определена сложная функция, и
пишут и = f(y), где у = ср(х), или и = f(cp(x)).
Теорема 8. Пусть функция у = ср(х) непрерывна в точке а, а
функция и = f(y) непрерывна в точке b = (p(a). Тогда сложная функция
и = f(if(x)) = F{x) непрерывна в точке а.
3. Непрерывность элементарных функций. Функции у =
= С = const, у = ха, у = аж, у = loga х (а > 0, а ф 1), у = sinx,
у = cos ж, у= tgx, y= ctgx, 2/ = arcsinx, ^/ = arccosx, y= arctgx,
у = arcctgx называются простейшими (или основными) элементар-
элементарными функциями.
Функция называется элементарной, если она может быть получе-
получена с помощью конечного числа арифметических операций и суперпо-
суперпозиций над простейшими элементарными функциями.
§2. Непрерывность функции 49
Совокупность всех элементарных функций называется классом
элементарных функций.
Наряду с простейшими элементарными функциями весьма широ-
широкое применение имеют так называемые гиперболические функции:
гиперболический синус shx = (ех — е~х)/2;
гиперболический косинус спж = (ех + е~х)/2;
гиперболический тангенс thx = shx/chx;
гиперболический котангенс cthx = chx/shx.
Теорема 9. Любая элементарная функция, определенная в ок-
окрестности некоторой точки, непрерывна в этой точке.
4. Второй замечательный предел.
lim A + хI/х = е « 2,718281828459045...
х^О V J
Отметим, что этот предел является неопределенностью типа 1°°.
5. Классификация точек разрыва. Пусть а — предельная точ-
точка области определения функции /(ж). Точка а называется точкой
разрыва функции /(ж), если f(x) в этой точке не является непре-
непрерывной. Пусть /(ж) определена в некоторой окрестности точки а, за
исключением, быть может, самой точки а. Тогда а называется:
1) точкой устранимого разрыва функции /(ж), если существует
lim /(ж) = Ь, но либо /(ж) не определена в точке а, либо /(а) ф Ъ (если
х—>а
положить /(а) = Ь, то функция /(ж) станет непрерывной в точке а,
т. е. разрыв будет устранен);
2) точкой разрыва I рода функции /(ж), если существуют /(а + 0)
и/(а-0),но/(а + 0)#/(а-0);
3) точкой разрыва II рода функции /(ж), если в точке а не су-
существует по крайней мере один из односторонних пределов функции
Контрольные вопросы и задания
1. Сформулируйте определения: а) непрерывности функции в точке; б) не-
непрерывности функции справа (слева) в точке.
2. Сформулируйте необходимые и достаточные условия непрерывности
функции в точке.
3. Исследуйте на непрерывность функцию /(ж) в произвольной точке а:
а) f(x) = х2;
^ч ,, ч ГО, если ж — иррациональное число, ,„ п ч
б) fix) = { -, (функция Дирихле).
' J у ' \ 1, если х — рациональное число у^и ч м н j
4. Какие функции называются элементарными?
5. Докажите, что функция у = sin ж непрерывна в любой точке а.
6. При каких значениях аргумента х функция /(ж) = агс8тAпж) является
непрерывной?
7. Какие точки называются точками разрыва функции?
8. Дайте определения точки устранимого разрыва и точек разрыва I и II
рода.
50 Гл. III. Предел и непрерывность функции
9. Найдите точки разрыва функции Дирихле. Укажите тип этих точек
разрыва.
10. Укажите тип точки разрыва функции /(ж): а) /(ж) = sgnx; б) /(ж) =
= х\/х.
11. Сформулируйте теорему о непрерывности сложной функции. Поль-
Пользуясь этой теоремой и первым замечательным пределом, вычислите
Цш In sins.
ж—)-О X
12. Какие функции называются гиперболическими? Принадлежат ли они
классу элементарных функций? При каких значениях аргумента эти
функции непрерывны?
Примеры решения задач
1. Исследовать на непрерывность функцию /(ж) и указать тип ее
точек разрыва, если:
„\f(r\_x\ 6)f()_-i/x. RW(V)_Js приж^1,
Л а) Функция /(ж) равна ж при х ф 0 и не определена при х — 0. Так
как Va lira х — а, то при а/ 0 lira /(ж) — а — /(а), и, следователь-
х—>а х—>а
но, f(x) непрерывна в любой точке а ф 0. В точке х = 0 /(ж) имеет
устранимый разрыв, поскольку существует lim /(ж) = lim ж = 0.
ж-И) ж-И)
б) Функция /(ж) = е~х'х элементарная, так как она является
суперпозицией функций у = —х~1 и / = еу. Функция f(x) опре-
определена при всех ж, кроме ж = 0; следовательно, по теореме 9 она
непрерывна в любой точке х/0. Так как /(ж) определена в окрест-
окрестности точки ж = 0, а в самой точке не определена, то ж = 0 — точ-
точка разрыва. Вычислим /@ + 0) и /@ — 0), пользуясь определением
одностороннего предела функции по Гейне. Рассмотрим произволь-
произвольную бесконечно малую последовательность {жп} такую, что хп > 0
Vn. Поскольку lim (-1/жп) = -оо, имеем lim е~1//Жп = 0. Следова-
¦>оо п—>-оо
тельно, lim e 1//ж = 0. Рассмотрим теперь произвольную бесконеч-
бесконечно малую последовательность {ж^} такую, что х'п < 0 Vn. Так как
lim (-1/ж' ) = +оо, то lim e~1^Xn = +оо. Поэтому lim е~1//ж =
7WOO ' П/ 7WOO Ж^О-0
= +оо, т. е. /(О - 0) = +оо.
Таким образом, предел /(ж) в точке ж = 0 слева не существует, и,
значит, ж = 0 является точкой разрыва II рода.
в) Докажем непрерывность /(ж) в точке аф\. Возьмем е < \а — 1|,
г > 0. Тогда ^-окрестность точки а не содержит точку ж = 1, если г <
< \а — 1|. В этой ^-окрестности /(ж) совпадает либо с функцией ср(х) =
= ж, если a < 1, либо с функцией ф(х) = 1п(ж), если а > 1. Так как
указанные простейшие элементарные функции непрерывны в точке а,
то /(ж) непрерывна в любой точке аф\. Исследуем на непрерывность
функцию /(ж) в точке а = 1. Для этого вычислим ее односторонние
§2. Непрерывность функции 51
пределы в этой точке, пользуясь непрерывностью функций ф(х) и
ip(x) в точке а = 1 и теоремой 6. Получим
/A + 0) = lim Inx = lim Inx = In 1 = 0,
ж^1+0 х>1
/A — 0) = lim x = lim x = 1.
ж-И-0 ж-И
Таким образом, /A + 0) ф /A — 0), поэтому в точке а = 1 функ-
функция /(ж) имеет разрыв I рода. А
2. Доказать, что:
а) lim 1пA+ж) =1; 6) \[m9*Lz±=\na a > 0, a ^ 1.
Л а) Представим функцию —^ -^- в виде 1пA + жI//ж = In 2/,
ж
где у = A + жI//ж. Так как НтA + жI/ж = е, а функция In 2/ непре-
х—>0
рывна в точке у = е, то lim ln(l + жI//ж = lne = 1.
х—^0
б) Рассмотрим функцию 2/ = Ц>(х) =ах — 1. Она непрерывна в точке
х = 0 и 2/@) = 0. При этом
s = log(l + y) аХ~1~ У
Вычислим lim тт г, пользуясь результатом п. а):
>olog(l + 2/)' J y
г у ,. y\na , 1 In a ,
lim j- = lim — = In a —j- r- = = In a.
Рассмотрим теперь функцию /(ж), непрерывную в точке у = 0:
{- -г г при w^O,
loga(l + 2/)
In a при у = 0.
Согласно теореме 8 сложная функция
() = |^1 при Хф0,
{ In a при х = 0
X -|
является непрерывной в точке х = 0. Поэтому lim = In a. A
х—>0 X
Задачи и упражнения для самостоятельной работы
15. Исследуйте на непрерывность функцию f(x) и укажите тип ее точек
разрыва (см. упр. 1-4):
а) f(x) = xsin(l/x); б) f(x) = sin(l/x); в) f(x) = {ж};
52 Гл. III. Предел и непрерывность функции
( 2
w/ \ _ J х •> если х — иррациональное число,
' ^ ' ~ 1 1, если ж — рациональное число;
при 0 ^ х < 1,
— х при 1 < х ^ 2;
при х\ ^ 1, ^ //г^ _ Г cos(ttx/2) при
-\|х-
1\ при
при
16. Докажите, что: a) lim Ё—zl = i; б) lim A+ж)° ~ г = а;
д) lim i^ = -I.
J x^o x2 2
§ 3. Сравнение бесконечно малых функций.
Символ "о малое" и его свойства
Основные понятия и теоремы
1. Сравнение бесконечно малых функций. Функция а(х) на-
называется бесконечно малой при х —У а (в точке а), если lim a(x) = 0.
х—Уа
Пусть а(х) и /3(х) — две бесконечно малые функции при х —> а.
Функции а(х) и /3(х) называются:
а) бесконечно малыми одного порядка при х —У а (в точке а), если
v а(х) / гл
km -)-( = с ф 0;
х^а /3(х)
б) эквивалентными бесконечно малыми при х —> а (в точке а), если
lim ^t~v = 1 (обозначение: а ~ C при х-> а).
х^а р\Х)
Если lim 2$Ц = 0, то говорят, что а(х) является бесконечно малой
хУа РуХ)
х—Уа
более высокого порядка при х ->• а (в точке а), чем /3(х), и пишут
а = о(/3) при х —У а (а равно "о малое" от C при х —У а).
Например, х2 = о(х) при х —У 0.
Аналогичные определения имеют место для случаев х —У а + 0,
х —У а — 0, х —У оо.
Следует иметь в виду, что равенства, содержащие символ "о ма-
малое", являются условными. Например, равенство х2 = о(х) при х —У О
верно, но о(х) = х2 неверно, поскольку символ о(х) обозначает не
какую-то конкретную функцию, а любую функцию, являющуюся при
х —У 0 бесконечно малой более высокого порядка, чем х. Таких функ-
функций бесконечно много, в частности, любая функция хр (где р > 1)
есть о(х) при х —У 0. Таким образом, равенство х2 = о(х) при х —У О
означает, что функция х2 принадлежит множеству бесконечно малых
§3. Сравнение бесконечно малых 53
функций более высокого порядка при х ->• 0, чем х. Поэтому "в об-
обратную сторону" это равенство (о(х) = ж2) неверно: все множество
функций о(х) не сводится к одной функции ж2.
2. Свойства символа "о малое".
Теорема 10. Пусть а\ (х) и а2 (x) — две произвольные бесконечно
малые при х ->• а функции такие, что а\{х) = о(/3) и а2{х) = о(/3).
Тогда а\(х) + а2(х) = о(/3) при х —> а.
Эту теорему кратко можно записать так:
Сформулируем наряду с указанным еще ряд свойств символа
"о малое" (всюду имеется в виду, что а —> 0 и C —У 0 при х —> а).
Г.о(р) + о(р)=о(р).
2o.o(f3)-o(f3)=o(f3).
3°. о(ф) =оЦ5) Vc^O.
4°. со(C) =о(C) Vc^O.
5°. о({Зп) = о({Зк), п^2 (п е 7V), к = 1,2,...,п-1.
6°. (о(C))п =о((Зп) VnG TV.
7°. /Зпо(/3) = o(Cn+1) Vn G TV.
8°. °ltp- = o^-1), n > 2 (n G TV).
Обозначим любую бесконечно малую при х —> а функцию сим-
символом оA). Тогда свойство 8° будет справедливо также при п = 1:
9°. of ^cfe/3fe j = о(/3), где cfe — числа.
12°. а/3 = о(а), аC = о(C).
13°. Если а ~ /3, то а-/3 = о(а) и а- E = оЦ5).
Контрольные вопросы и задания
1. Дайте определение бесконечно малой функции: а) при х —»¦ а; б) при
ж —>- оо. Приведите примеры таких функций.
2. Сформулируйте определение и приведите примеры бесконечно малой
функции а(х):
а) одного порядка с функцией /3(х) в точке а;
б) эквивалентной функции /3(х) в точке а;
в) более высокого порядка при х —»¦ а, чем /3(ж).
Что означает символическая запись а = о(/3) при ж —»¦ а?
54 Гл. III. Предел и непрерывность функции
3. Приведите примеры функций а(ж), для которых справедливы равенст-
равенства:
а) а(х) = о(ж) при ж —»¦ 0;
б) а(х) = о(д/1 — х) при ж —>- 1 — 0;
в) а(х) = оA/ж2) при ж —>- оо.
4. Докажите, что ж3 = о(ж2) при ж —»¦ 0. Верно ли равенство ж3 = о(/3) при
ж —»> 0, если:
а)/3(ж) = ж; б)/3(ж) = ж2д/[ж|; в) /3(ж) = ж3дДж|"; г) /3(ж) = ж2 sin ж?
5. Докажите, что (ж — IJ = о(х — 1) при ж —»¦ 1. Верно ли равенство (ж —
— IJ = о(/3) при ж —>- 1, если:
а) РуЛ) — yJL — л.) , U^ fjyJLJ — olil^X — 1J , d) fJyJLj -
6. Докажите, что 1/ж4 = оA/ж3) при ж —»¦ оо. Верно ли равенство 1/ж4 =
= о(/3) при ж —>- оо, если:
7. Являются ли функции sin ж и ж эквивалентными бесконечно малыми
при ж —»¦ 0? Докажите, что sin ж — ж = о(ж) при ж —»¦ 0.
8. Пользуясь свойствами символа "о малое", запишите для функции а(ж)
равенство вида a(x) = o(xk) при ж —>- 0, если:
а(х) = о(ж2) + о(ж2); а(х) = о(ж) — о(ж); а(ж) = 5о(ж);
а(ж) = оCж2); а(ж) = (о(ж)K; а(ж) = жо(ж); а(ж) = ;
а(ж) = о(—ж + 2ж +ж ); а(ж) = о(о(ж )); а(ж) = о(ж + о(ж)).
9. Пользуясь свойствами символа "о малое", запишите для функции а(х)
равенство вида а(х) = оA/хк) при ж —>- оо, если:
а(х) =о(-) -о(-); а(х) = 1000of-Y a(x) =о
х J
Примеры решения задач
1. Верно ли равенство а(х) = о{х) при х —У 0, если: а) а(х) = 2ж2;
б) а(ж) = Зж; в) а(ж) = л/Щ; г) а(ж) = г^—; д) ol(x) = 1 - cos ж?
Л а) 2ж2 = о(ж), так как Нт ^- = 0.
б) Равенство Зж = о{х) неверно, поскольку Нт — = 3^0. Функции
Зж и ж являются бесконечно малыми одного порядка при ж —> 0.
: о(ж), так как Нт ^ = оо.
§3. Сравнение бесконечно малых 55
П0СК0ЛЬКУ lim
д) 1 — cos ж = о(ж), так как lim = lim
"I • I о 111 I Jb I ? ) \ X -| r\ r\ A
= H (-^/2 ) 2 = l • ° = °- k
2. Верно ли равенство а(х) = о(ж2) при ж ->• 0, если:
а) а(х) = sin2 ж; б) а(х) = ж3; в) а(ж) = 1 — cos ж?
Л a) sin2 ж ф о(ж2), так как lim —— — ^m f sin ж J = 1. Функции
sin2 жиж2 — эквивалентные бесконечно малые в точке ж = 0.
б) ж3 = о(ж2), поскольку lim — = 0.
\ 1 / / 9\ ,. 1 — COS Ж 1 , ^
в) 1 — cos ж ^ о(х ), так как lim = -. Функции 1 —
х^о х2 2
— cos ж и ж2 — бесконечно малые одного порядка в точке ж = 0. А
3. Используя пределы:
а) Ит «М = 1; б) Щп i^?? = 1; в) lim
' х^О X ' х^О X2 2' ' х^О X
г) Нт У + % - — _ гп — натуральное число);
х^О X П V П
представить функции sin ж, cos ж, 1пA + ж), у/1 + ж в виде
т/?(ж) = ао + а1Ж^ + о(хк) при ж —>- 0,
где /с = 1 или к = 2; ао и di — некоторые числа.
Л Докажем сначала, что если а(х) и /3(х) — бесконечно малые од-
одного порядка при ж ->• а, т. е. lim ^Ц = с ^ 0, то а(х) = с/3(ж) + о(/3)
х—>а Р\Х)
при ж —>- а.
В самом деле, так как
^Н - с = 0 или hm v y ^v } = 0,
/3(ж) / х^а /3(х)
то по определению символа о(/3) имеем а(х) — с/3(х) = о(/3), или
а(х) = с/3(ж) + о(/3) при ж —>- а. A)
Из равенств а)-г), пользуясь формулой A), получаем
sinx = х + о(х) при ж ->• 0, B)
совж = 1 --ж2 + о(ж2) при ж ->• 0, C)
1пA + ж) = ж + о(ж) при ж —>¦ 0, D)
-ж + о(х) при ж -»> 0. E)
п
Формулы B)-E) называются асимптотическими формулами, а
также асимптотическими разложениями или асимптотическими
56 Гл. III. Предел и непрерывность функции
представлениями функций sinx, cosx, 1пA + ж), у/1 + х при х ->• 0.
Последнее слагаемое в правой части этих формул (о(х) или о(х2))
называется остаточным членом асимптотической формулы. А
4. Доказать свойства 2°, 3°, 6°, 9°, 10° символа "о малое".
Л Напомним, что символ о(/3), входящий в левую часть формул, озна-
означает любую бесконечно малую функцию в точке а более высокого
порядка, чем /3(х).
1. Докажем сначала свойства 2°, 3°, 6°, т. е.
о(р)-о(р)=о(C), F)
о(ф)=о({3) Vc^O, G)
(о(/3))п = о(/Зп) VnGTV. (8)
Обозначим через ai(x), a2(x), а(х) произвольные бесконечно ма-
малые функции в точке а такие, что а\{х) = о(/3), а2{х) = о(/3), а{х) =
= о(ср) при ж —> а. По определению символа "о малое" эти равенства
означают, что
Шп^М=0, (9)
lim ^ = 0, A0)
Для доказательства справедливости равенств F)-(8) нужно уста-
установить, что
а1(х) - а2(х) = о(/3), а(ж) = о(/3), (ai(rc))n = о(/Зп),
т. е.
г г а(ж) п г a- OlO)) п
L2 = hm -?-!- = 0, L3 = lim \ ; // = 0.
Учитывая (9) и A0), получим
T ,. ai(#) r аг(ж) г» г» г»
Li = lim „; / - lim ^ / =0-0 = 0,
^ Р(х) ^ Р(х)
С помощью равенства A1) находим
L2 = с lim ^L = с ¦ 0 = 0.
ж-^a Ср(Х)
Итак, справедливость формул F)-(8) доказана.
§3. Сравнение бесконечно малых 57
2. Докажем теперь свойства 9° и 10°, т. е.
A2)
--о(/3). A3)
Обозначим через ф(х), а(х) и (р(х) произвольные бесконечно малые
функции в точке а такие, что
ф(х) = of 2_^ckftk ), а(х) = о(/3), Ц)(х) = о(а) = о(о(/3)),
т. е.
lim /(ж) = 0, A4)
к=1
lim |^ = 0, A5)
lim Щ=0. A6)
х^а а(х)
Для доказательства справедливости равенств A2), A3) нужно до-
доказать, что
Учитывая A4), A5), A6), получаем
Е скРк
L± = lim /(ж) lim k=1 = 0 • а = О,
/ j ckP
Li — lim lim ^ ^ =0-0 = 0.
Таким образом, справедливость формул A2), A3) доказана. А
Задачи и упражнения для самостоятельной работы
17. Используя пределы:
a) lim -—^— = In а (а > 0, а ф 1); б) lim -—=— = 1;
в) lim ^ ^—^— = а; г) lim -^—^ = 1;
д)Пт^=1; e)limi^ = -I
х^О X х^О X2 2
выведите асимптотические формулы (при х —»¦ 0) для функций аж, еж,
A+ж)а, shx, thx, chx.
58 Гл. III. Предел и непрерывность функции
18. Докажите свойства 1°, 4°, 5°, 7°, 8°, 11°-13° символа "о малое".
19. Справедливо ли равенство о(о(х)) = о(ж1+?) при ж —»¦ 0, если: а) е > 0;
б) ? = 0; в) — 1 < е < 0? Ответ обоснуйте.
20. Верны ли равенства:
а) о(х + ж2) = о(ж2) при ж ->• 0; б) о(ж) = о(ж2) при ж ->• 0;
в) о(ж2) = о(ж) при х —>- 0; г) оA/ж) = оA/ж2) при ж —»- оо;
д) оA/ж2) = оA/ж) при ж —»> оо?
Ответ обоснуйте.
21. Пользуясь войствами символа "о малое", запишите для функции а(х)
равенство вида а(х) = оA) или а(ж) = о((ж — а)к) при ж —>- а (к нату-
натуральное), если:
а) а(х) = о(-5ж + ж2 - ж3 + о(-5ж + ж2 - ж3)) при ж ->• 0;
б) а(ж) = (ж — 1)о((ж — IJ + о(ж — 1)) при ж —»¦ 1;
в) а(х) = ^- оCж + ж2) при ж —»¦ 0.
22. Пользуясь свойствами символа "о малое", запишите для функции а(х)
равенство вида а(х) = оA) или а(ж) = оA/хк) при ж —>- оо (к натураль-
натуральное), если:
ч/ч 2 1 ^ , ^ 2/^1 / 1
б) а(х) = — - —; в)а(ж)=ж .о[ — +о[ —
х3 х2 \х3 \х3
^)-о(^)); д) а(х) = 5х-о
§ 4. Вычисление пределов функций с помощью
асимптотических формул. Вычисление пределов
показательно-степенных функций
Основные понятия и формулы
1. Асимптотические формулы. В примерах и задачах § 3 были
получены асимптотические формулы для простейших элементарных
функций при х —У 0. Запишем эти формулы в виде таблицы:
I. sin ж = х + о(х). V. A + х)а = 1 + ах + о(х).
2
Пгоч т _ 1 _ х , n(T2\ YT
III. 1пA + ж) =ж + о(ж). VII.
IV. аж = 1 + ж In а + о(х) (а > 0), VIII. chx = 1 + Цг- + о(х2).
Указанные формулы остаются справедливыми, если в них вмес-
вместо аргумента х подставить хп, где {хп} — бесконечно малая после-
последовательность, либо у(х), где lim y(x) = 0. Например, справедливо
х—>а
представление, вытекающее из формулы I:
. 1 1 , / 1 \
sin— = — +о( —),
п2 п2 \п2 /
§4- Вычисление пределов функций 59
of —J >
где ^of —J > — бесконечно малая последовательность более вы-
Г 1 1 г оA/п2) г 2 / 1 \ п
сокого порядка, чем — , т. е. lim ' = lim n o\ — = 0.
In2 ) n-Юо 1/П2 п^оо \П2 )
Функция у{х) = х — 1 является бесконечно малой при х —У 1, поэ-
поэтому из формулы III получаем равенство
1пA+ у(х))=у(х)+о(у) при х->1,
или
1пA + (х - 1)) = In ж = х - 1 + о(х - 1) при х ->• 1.
Используя это равенство и формулу II, запишем асимптотическое
представление функции cos In ж при х —У 1:
cos In ж = cos(x - 1 + о(ж - 1)) =
На основании свойств символа "о малое" получаем
\(о(Х - I)? =
Аналогично,
(х - 1 + о(х - I)J = (х - IJ + о(х - IJ.
В силу свойства 11° имеем
о((х - IJ + о(х - IJ) = о(х - IJ.
Окончательно получим
cos In ж = 1 — —h o{x — IJ при х —У 1.
2. Вычисление пределов показательно-степенных функций.
Рассмотрим вычисление предела при х —> а показательно-степенной
функции [u(x)]v(x\ где функции и(х) и v(x) определены в некоторой
окрестности точки а, причем и(х) > 0.
Возможны следующие случаи.
1. Если lim и(х) = Ъ > 0, lim и (ж) = с, то lim 'u(x)^) = bc.
х—>а х—>а х—>а
2. Если lim и(х) = 0, lim v(x) = с > 0 (или +оо), то lim uv = 0.
х—>а х—>а х—>а
3. Если lim и(х) = 0, lim v(x) = с < 0 (или — оо), то lim uv = +оо.
4. Если lim и(ж) = 0, lim v(x) = 0, то lim u(x)v^ называется не-
х—>а х—>а х—>а
определенностью типа 0°.
60 Гл. III. Предел и непрерывность функции
5. Если lim и(х) = +оо, lim v(x) = с > 0 (или +оо), то lim uv =
х—Уа х—Уа х—Уа
= +00.
6. Если lim и(х) = +оо, lim v(x) = с < 0 (или — оо), то lim uv = 0.
х—Уа х—Уа х—Уа
7. Если lim и{х) = +оо, lim v{x) = 0, то lim uv называется не-
х^-а х—Уа х—Уа
определенностью типа оо°.
8. Если lim и{х) = 1, lim v{x) = оо, то lim uv называется неопре-
х^-а х—Уа х—Уа
деленностъю типа 1°°. Примером такой неопределенности является
второй замечательный предел:
+ жI/ж =е.
Если uv представить в виде evlnu, то каждая из неопределеннос-
неопределенностей 0°, оо°, 1°° сводится к неопределенности вида 0 • оо, для функции
v\nu.
Если при этом lim vlnu = 6, то lim uv = eb.
x—Уа х—Уа
Контрольные вопросы и задания
1. Напишите асимптотические формулы для функций sin ж, tgx, cos ж,
ln(l + ж), еж, ах, A + х)а, shx, thx, chx при х —>- 0.
2. Напишите асимптотические формулы с остаточным членом вида о(ха)
при х —>- 0 или оA/жа) при ж —>- оо (а > 0) для сложных функций sin у,
tgy, cosy, ln(l + 2/), еу, ау, A + |/)а, shj/, thy, chy, если:
а) |/ = Зж и ж 4 0; б) у = -у/ж и ж —>- +0; в) у = х3 и ж —»¦ 0;
г) у = 1/х и ж —>- оо.
3. Напишите асимптотические формулы с остаточным членом вида о{1/па)
(а > 0) для последовательностей sin жп, tg жп, cos хп, 1пA + жп), еХп , аЖп ,
A+жп)а, shxn, tllжrг, сЬжп, если:
а) жп = i; б)жп = -^; в) жп = In Л + iV г) хп = е1/п - 1.
4. Дайте определение бесконечно малой последовательности {ап} более
высокого порядка, чем {1/п}, при п —»¦ оо. Дайте определение бесконеч-
бесконечно малой функции а(ж) более высокого порядка, чем 1/ж, при ж —»¦ оо.
Запишите для ап и а(ж) соответствующие символические обозначения.
5. Какой порядок малости имеют последовательность ап = поA/п2) при
п —»¦ оо и функция а(ж) = жоA/ж2) при ж —»¦ оо по сравнению соответ-
соответственно с {1/п} и /3(х) = 1/ж?
6. Пользуясь асимптотической формулой IV и определением предела
функции по Гейне, докажите, что е1^71 = 14 Ь о I — ) при п —»¦ оо.
7. Верны ли равенства:
д/l + х2 = 1 + i ж2 + о(ж2) при ж ->> 0;
- = l + i4+°f^) при ж ^ О?
Ответ обоснуйте.
§4- Вычисление пределов функций 61
8. Назовите возможные случаи вычисления пределов показательно-степен-
показательно-степенных функций. Приведите примеры трех типов неопределенностей для
таких функций.
9. Вычислите пределы:
a) lim ^4 5 б) lim ?-4 ; в) lim »
ч1/1пж
Примеры решения задач
1. Вычислить lim «т sin tg (x2/2) _
ж-^о Incos3x
Л Запишем асимптотическое разложение числителя, пользуясь асимп-
асимптотическими формулами для синуса и тангенса и свойствами символа
"о малое":
sin sin tg у = sin sin (у + <?(y)) =
= sin (у + o(x2) + o(x2)j = sin (y + o(x2)j = у + o(x2).
Здесь мы воспользовались тем, что of Цг- + of Цг- J J = о(х2) и о(ж2) +
+ о(х2) = о(ж2).
Выведем теперь асимптотическое разложение знаменателя, исполь-
используя асимптотические формулы для косинуса и логарифма:
Здесь мы воспользовались тем, что
о(CхJ) = о(х2), о( - ^ + о(х2)) = о(х2), о(х2) + о(х2) = о{х2).
Таким образом, данный предел равен
9 + о(^) 9
2 2 ж2 2 х—уо х2
Здесь мы воспользовались тем, что, по определению символа
"о малое" lim о = 0. А
62 Гл. III. Предел и непрерывность функции
2. Вычислить lim аХ ~ Q° (а > 0).
Л Положим у = ж - а, тогда данный предел запишется так:
л^+а _ „а пУ _ 1
lim = a lira .
У
Так как ay = 1 + у In a + 0B/), то
a lim = aa lim v^y = aa ( In a + lim -^ = aa In a.
2/^0 у у^О у V 2/^0 у )
Итак, lim — = aalna. A
ж —У о, X CL
3. Вычислить lim sinGrv n2 + 1).
n—>-oo
Л Используя асимптотическую формулу V при ж = 1/п2 и а = 1/2,
получим
+
2
Отсюда
+ +of)) (l)sm(+
2n \nJ J \2n
Последовательность {(—l)n} ограниченная, а < sin f^~+°(~)) f бес-
бесконечно малая, поэтому произведение этих двух последовательнос-
последовательностей является бесконечно малой последовательностью. Таким образом,
lim sinGrv n2 + 1) = 0. А
п—>-оо
4. Вычислить lim(cosx)ctg ж.
Л Данный предел является неопределенностью типа 1°°, так как
lim cosх = 1, lim ctg2x = 00. Запишем (cosx)ctg ж ввидеес*8 zincosz
и вычислим L = lim ctg 2x • In cos ж. Для этого напишем асимптоти-
ж-^0
ческое разложение для In cos ж и sin2 ж при х ->• 0:
In cos ж = In A h о(ж ) J = h о(ж ),
\ Zi / Zi
sin2 ж = (ж + о(ж)J = ж2 + о(ж2).
Используя эти равенства, находим
Т v 2 v -x2/2 + o(x2) 1
L = lim cos ж • lim f ; = --.
ж-^0 ж-^0 Ж2 + О(Х2) 2
Таким образом, искомый предел равен eL = е~1//2. А
/i\tg(l/n)
5. Вычислить lim —
Л Данный предел является неопределенностью типа 0°. Для его вы-
§4- Вычисление пределов функций
63
числения запишем
i)
в виде e
tg(Vn)in(i/n)
и вычислим пре_
дел L = lim ( tg — • In — ). Имеем
n-Юо V П nj
L= lim f-
=- lim ^
т h /1\1 n i. Inn ,. o(l/n) n
- lim Inn • о - =0- lim • lim v ' J = 0,
n-^oo L \n/ J n-^oo П n-^oo 1/n
так как lim ^ = 0 (см. § 4 гл. II) и lim ^/^ = 0.
rwoo П n^oo 1/n
Таким образом, L = 0, т. е. искомый предел равен 1. А
Задачи и упражнения для самостоятельной работы
23. Напишите асимптотические разложения следующих функций при х
0 с остаточным членом вида о(жа), где а ^ 0:
a) sin2Ev/^), sin2Ev/^ + ^) (ж > 0); б) cosDx2), cosDx2+x);
в) е2ж, е
д) 3 - ^27 - ж, 3 - ^/27 - ж + у/Б (ж>0); е) 2Ж', 2ж3+ж2;
ж) In cos 2ж, 1псо8Bж + ж2); з) совл/втж, ch л/sin ж (ж > 0);
и) 1п(еж + л/ж) (ж > 0); к) 5e*-cos^;
л) y^cos у/х (ж > 0); м) cos ж cos ж2 — 1.
24. Напишите асимптотические разложения функций при ж^2с остаточ-
остаточным членом вида о(х — 2)а, где а ^ 0:
а)8т(ж-2J; б)C-ж)/3; в) 1п(ж - 1); г) С08(тгж);
д) tg (тгж2); е) fyx - 1 - \7ж - 1; ж) хх - 4.
25. Напишите асимптотические разложения функций при ж —»¦ оо с оста-
остаточным членом вида оA/жа), где а ^ 0:
а) у/х2 + ж - ж; б) ^ж3 + ж - ж; в) {/(ж + 1)(ж + 2)(ж + 3)(ж + 4) - ж;
h)] д)С08Ш; еM1/Ж;
ж) In cos (-), lnch(-); з) е1/л/* - 1 (ж > 0).
26. Напишите асимптотические формулы для последовательностей с оста-
остаточным членом вида оA/па), где а ^ 0:
а) ^/п3 + п2 - п; б) 21/п + 71/гг - 2; в) sin (-j=\
27. Вычислите пределы:
Пт сов х-сов Зх И
Ю Ж2
x-nr/3 1-2COSX
в) lim A-х) tg 2^; г) lim
д) lim (л/1+ж + ж2 - VI-ж+ ж2); е) lim
/COS X — лУCOS Ж
64
Гл. III. Предел и непрерывность функции
ж) lir
и) lim
V
a. з) Ит (±±х\ ~~^~ при х
\2 + Ж/
(f+Ж)У82*; к) Um
, ж ^ 1, х _> +ОО;
(а > О, Ь > О);
л) lim (smx)tsx; м) lim n(ch Gr/n)~1};
x—>n/2 n—^oo
h) linr.
/
28. Вычислите пределы:
a) lim УГ
r) lim
^0
в) П
'l - ж/2
; д) lim . f*
11) — sin ж
e) lim n( \/a — 1) (a > 0); ж) lim
2 .-
/ I <-) \ ж / 3^2 _i_ ]\ ]__ж
з) lim I ) ; и) lim I — I ;
ж-юо \2ж-1/ ж^оо\2ж2-1/
к) lim sinn ( 27ГП ); л) lim cosn -^=; м) lim (tgxI
29. Вычислите пределы:
a) lim ^ —; 6) lim x ~ a (a > 0);
ж-И 1ПСО8GГ-2Ж)' ж^а Ж- a V У'
-Л, +аж-/г _ 2ax
В) Ит
д) lim
smbx
x)
; e) lim
(a > 0);
1/ In 71-1
/ / \ r / \ a i 1 n
ж) lim n sin ( In Л /cos — ); з) lim ( n л ) + sin — ;
и) lim cosGrvn2 + n); к) lim (x — In chx).
n—)-oo ж—)- + oo
30. Вычислите пределы:
a) lim ( уж3 + Зж2 — л/х2 — 2ж);
1 — cos ж cos 2ж cos Зж
6) lim xi/6[(x + lJ/d - (x - 1ГИ; в) lim
sin2 2ж
r) lim A - ж) 1оёж 2; д) lim а* ~ ж° (а > 0);
ж—>-1 ж—>а X — а
е) lim n2(^- -+-J/S) (а>0); ж) lim
П—>-ОО Ж—>-+0
\/Ж
) lim ^"ff; и) lim [cos (W-^- V)! * ;
з
к) lim
1п(ж2+еж
lVl; л) lim f
ч .. 1п(ж2 + еж)
ГЛАВА IV
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
§ 1. Производная функции. Правила дифференцирования
Основные понятия и теоремы
1. Определение производной. Пусть функция у = f(x) опреде-
определена в некоторой окрестности точки хо. Приращением этой функции
в точке хо называется функция аргумента Ах
Ау = /(ж0 + Ах) - f(x0).
Разностное отношение -^- также является функцией аргумен-
аргумента Ах.
Определение. Производной функции у = f(x) в точке хо назы-
называется lim -r-^ (если он существует).
Производная функции у = f(x) в точке хо обозначается f'(xo) или
у'(хо). Операция нахождения производной называется дифференциро-
дифференцированием.
2. Таблица производных простейших элементарных
функций.
I. [ха)' = аха~х (а — любое число).
П. (sin^y = cos ж.
III. (cos^y = -sin ж.
IV. (log. x)' = ——, в частности, (In ж)' = - (х > 0).
х та х
V. (ах)' = ах In а, в частности, (ех)' = ех.
VII. (ctgx); = %- (хфтгп, neZ).
sin х
VIII. (arcsinxy = l (-K x < 1).
X.
XL
XII. (shxO = chx.
3 В.Ф. Бутузов и др.
66
Гл. IV. Производные и дифференциалы
XIII. (cha;)' = shx.
XIV.
XV. (cthx)' = -
(x^O).
3. Физический смысл производной. Производная f'(xo) —это
скорость изменения функции у = f(x) в точке ж0 (иными словами,
скорость изменения зависимой переменной у по отношению к изме-
изменению независимой переменной х в точке жо). В частности, если х —
время, у = /(ж) — координата точки, движущейся по прямой, в мо-
момент ж, то f'(xo) — мгновенная скорость точки в момент времени xq.
4. Геометрический смысл производной. Рассмотрим график
функции у = f(x) (рис. 1). Точки М
и N имеют следующие координаты:
М(жо, /(жо)), N(xo + Аж, /(жо + Ах)).
Угол между секущей MN и осью Ох
обозначим ср(Ах).
Определение. Если существует
lim ср(Ах) = (ро^ то прямая I с
Аж-^О
угловым коэффициентом к = tg(^0,
проходящая через точку М(жо,/(жо)),
называется касательной к графику
функции у = /(ж) в точке М.
Теорема 1. Если функция y = f(x) имеет в точке ж0 производную
/'(жо), то график функции имеет в точке М(жо,/(жо)) касательную,
причем f'(xo) является угловым коэффициентом касательной, т. е.
уравнение касательной записывается в виде
у- /(ж0) = //(ж0)(ж-ж0).
Если функция у = /(ж) непрерывна в точке жо и
lim
/(ж0
Ах) - /(ж0)
-1———- = оо,
Ах
то говорят, что функция имеет в точке хо бесконечную производную.
В этом случае касательная к графику в точке Mq параллельна оси
Оу, а ее уравнение таково: х = ж0.
5. Односторонние производные. Если существует
lim
Аж-^+О
Ах
Аж-^-0
Ах
то он называется правой ( соответственно левой) производной функ-
функции у = f(x) в точке хо и обозначается /'(жо + 0) (соответственно
/;(so-0)).
Если существуют f (х® + 0) и f (х® — 0) и они равны, то существу-
существует f'(xo), и она равна f'(xo + 0). Обратно: если существует /'(жо), то
существуют f'(x0 + 0) и f'(x0 - 0), причем f'(x0 + 0) = f'(x0 - 0) =
'Ы
§1. Производная функции 67
6. Правила дифференцирования.
Теорема 2. Если и(х) и v(x) имеют производные в точке жо, тпо
сумма, разность, произведение и частное этих функций {частное при
условии v{x) ф 0) также имеют производные в точке жо, причем в
точке хо справедливы равенства
(и + v)' = и' + v1\ (и — v)' = и' — v1',
(и\ U V —
- =
\v/ v2
7. Производная обратной функции.
Теорема 3. Если функция у = f(x) строго монотонна и непрерыв-
непрерывна в некоторой окрестности точки ж0, имеет производную в точке
хо и f'(xo) ф 0, то существует обратная функция х = f~1(y)J кото-
которая определена в некоторой окрестности точки у о = /(жо) и имеет
производную в точке уо, причем
Физическая интерпретация формулы A): производная (f~1(yo))'
есть скорость изменения переменной х по отношению к изменению
переменной у, a f'(xo) — скорость изменения переменной у по отно-
отношению к изменению переменной х. Ясно, что эти величины являются
взаимно обратными.
8. Производная сложной функции.
Теорема 4. Если функция t = ip(x) имеет в точке хо производную
(р'(хо), а функция у = ф{Ь) имеет в точке to = 4>(xq) производную
ф'(го), то сложная функция у = ф(ср(х)) = /(ж) имеет производную в
точке жо, причем
/'(хо)=ф'(фо))^Ы. B)
Физическая интерпретация формулы B): производная (р'(хо) есть
скорость изменения переменной t по отношению к изменению пере-
переменной ж, а производная ф'(to) — скорость изменения переменной у
по отношению к изменению переменной t. Ясно, что скорость ср'(хо)
изменения переменной у по отношению к изменению переменной ж
равна произведению скоростей ^'(^о) и (р'(хо). (Если t "движется"
быстрее ж в к раз, а у — быстрее t в I раз, то у "движется" быстрее
ж в Ы раз.)
9. Производная функции, заданной параметрически. Пусть
функции
x = <p(t), У = Ф№ C)
определены на некотором промежутке изменения переменной ?, ко-
которую назовем параметром. Пусть функция ж = cp(t) является строго
монотонной на этом промежутке. Тогда существует обратная функ-
функция t = if~1(x), подставляя которую в уравнение у = ф(г), получим
3*
68
Гл. IV. Производные и дифференциалы
Таким образом, переменная у является сложной функцией пере-
переменной х. Задание функции у = f(x) с помощью уравнений C) назы-
называется параметрическим.
Уравнения C) можно интерпретировать как зависимость коорди-
координат точки, движущейся на плоскости (х,у), от времени t. При такой
интерпретации график функции у = f(x) представляет собой траек-
траекторию точки.
Если функции х = (p(t) и у = ip(t) имеют производные ip'(t) /Ои
ip'(t), то функция у = /(ж) также имеет производную, причем
D)
Заметим, что существование производной ip'(t) определенного зна-
знака является достаточным условием строгой монотонности функции
х = (p(t) и, следовательно, существования функции у = /(ж), задан-
заданной параметрически.
10. Производная вектор-функции. Если каждому значению
переменной t Е Т (Т — некоторое числовое множество) поставлен
в соответствие некоторый вектор г, то говорят, что на множестве Т
определена вектор-функция г = г(?).
Определение. Вектор а называется пределом вектор-функции
г = г(?) в точке ?0, если lim |r(t) - а| = 0.
ttt
M(x(t),y(t),z(t))
r'(t)
Определение. Производной вектор-функции г = г(?) в точке t
называется lim -д-(г(? + At) — r(t)) (если он существует).
Производная вектор-функции г(?) обозначается г'(?).
11. Физический смысл вектор-функции и ее производной.
Положение точки М в пространстве можно задать тремя ее коорди-
координатами или вектором г = ОМ', начало
которого совпадает с началом коорди-
координат, а конец — с точкой М (рис. 2).
Если точка М движется, то вектор г
изменяется в зависимости от време-
времени t. Таким образом, движение точки
можно описать вектор-функцией г =
= г(?), где t изменяется на некото-
некотором отрезке [а, Ь]. Множество концов
вектора г(?) (где t G [а, Ъ]) представля-
представляет собой траекторию движения точ-
точки (оно называется также годографом
вектор-функции г = г(?)). Производ-
Производная г'(?) есть вектор мгновенной скорости точки в момент времени t.
Вектор г'(?) направлен по касательной к траектории.
Если обозначить через ж(?), y(t), z(t) координаты точки М в мо-
момент времени ?, а через i, j, k — единичные векторы осей координат,
Рис.2
§1. Производная функции
69
то вектор-функцию г = г(?) можно представить в виде
а производную r'(t) — в виде
Аналогично, движение точки М на плоскости (ж, у) можно описать
вектор-функцией г = x(t) i + y(t)j.
Если x'(t) имеет определенный знак, например, x'(t) > 0, то траек-
траектория движения точки М представляет собой график функции
у = /(ж), заданной параметрически уравнениями х = ж(?), у = y(t).
Координаты вектора скорости
r'(t) равны x'(t) и y'(t), а тангенс уг-
угла между вектором r'(t) и осью Ох,
т. е. угловой коэффициент касатель-
касательной к графику функции у = /(ж),
равен y'(t)/x'{t) (рис. 3). Таким об-
образом, мы снова получили выраже-
выражение D) для производной функции,
заданной параметрически.
Вектор n(t) = {-y'(t),x'(t)} при
x'2{t) + y'2{t) Ф 0 является векто-
вектором нормали к графику функции
у = /(ж) в точке M(x(t),y(t)), т. е.
О
зу'Щ
M(x(t),y(t))
i x(t)
Рис.3
направляющим вектором прямой, проходящей через точку М перпен-
перпендикулярно касательной к графику в этой точке (эта прямая называ-
называется нормалью).
Контрольные вопросы и задания
1. Что называется приращением функции у = f(x) в точке жо?
2. От какого аргумента зависит разностное отношение Ay/Ах? Какова
область определения функции Ау/Ах?
3. Дайте определение производной функции у = f(x) в точке жо-
4. Пользуясь определением производной, выведите формулы для произ-
производных функций хп (п — натуральное число), sinx, cosx, loga ж, ах.
5. Каков физический смысл производной функции у = f(x) в точке хо? Ка-
Какое движение точки описывается уравнением у = vqx + уо (х — время,
vo и уо — постоянные)?
6. Каков геометрический смысл производной функции у = f(x) в точке
хо? Дайте определение касательной к графику функции у = f(x) в точке
(жо,/(жо)) и запишите уравнение касательной.
7. Когда говорят, что функция имеет в точке хо бесконечную производ-
производную? Приведите пример функции, график которой имеет в некоторой
точке вертикальную касательную.
8. Что такое односторонние производные функции в точке? Какова связь
между односторонними производными и производной функции в точ-
точке? Приведите пример функции, у которой существуют односторонние
производные в некоторой точке, но не существует производная в этой
точке.
70 Гл. IV. Производные и дифференциалы
9. Выведите формулы для производных суммы, разности, произведения и
частного двух функций. Используя их, выведите формулы для произ-
производных функций tgx, ctgx, shx, сЬж, thx, cthx.
10. Сформулируйте теорему о производной обратной функции. Что можно
сказать о производной обратной функции, если выполнены все условия
теоремы, кроме условия /'(жо) ф 0 (т. е. выполнено условие /'(жо) = 0)?
Приведите пример такого случая. Какова физическая интерпретация
формулы для производной обратной функции? Пользуясь этой форму-
формулой, выведите формулы для производных обратных тригонометричес-
тригонометрических функций.
11. Сформулируйте теорему о производной сложной функции. Применима
ли эта теорема к функции у = 8т2(л/ж^) в точке х = 0? Существует ли
производная этой функции в точке х = 0? Какова физическая интер-
интерпретация формулы для производной сложной функции? Используя эту
формулу, выведите формулу для производной функции ха (а — любое
число).
12. Что такое параметрическое задание функции? При каких условиях
справедлива формула D) для производной функции, заданной парамет-
параметрически?
13. Что такое вектор-функция? Дайте определения предела и производной
вектор-функции. Каков физический смысл вектор-функции и ее произ-
производной?
14. Пользуясь определением производной вектор-функции, выведите фор-
формулу г' (t) = i x' (t) + j у' (t) + kzf (t).
15. Каковы координаты единичного вектора нормали к годографу вектор-
функции г = \x(t) +iy(t) в точке M(x(t),y(t)O
Примеры решения задач
1. Пользуясь определением производной, найти производную
функции у = ж3 в точке ж = 1.
Л Находим приращение функции у = х3 в точке х = 1:
Ау = A + АхK - 1 = ЗАж + 3(АжJ + (АжK.
Отсюда получаем -^- = 3 + ЗАж + (АжJ и, следовательно, у'A) =
= lim %!L = 3. А
Аж^О Аж
2. Сравнить на промежутке 0 ^ t ^ 1 мгновенные и средние ско-
скорости двух точек, прямолинейные движения которых заданы уравне-
уравнениями si = ?2, s2 = 2?4 (t ^ 0).
Л Находим мгновенные скорости точек в момент времени t: v\{t) =
= s[(t) = 2t, v2(t) = s'2(t) = 8t3. Отсюда получаем уг@) = г;2@);
vi(l/2) = г;2A/2); v^t) > v2(t) при 0 < t < 1/2; v^t) < v2(t) при t > 1/2.
Средняя скорость первой точки на отрезке времени 0 ^ t ^ 1 равна
Vlcp = *i(l)~*i@) = L Аналогично, г;2ср = g2A)~g2(Q) = 2. Таким
образом, vicp < v2cp- A
3. Составить уравнение касательной к графику функции у = cos ж
в точке с абсциссой ж = тг/б.
§1. Производная функции 71
Л Имеем ж0 = тг/б, /(ж0) = cos(tt/6) = л/3/2, /'(жо) = - sinGr/6) =
= —1/2. Поэтому искомое уравнение касательной запишется в виде
л/3
4. Найти односторонние производные функции /(ж) = |ж — х$\д(х)
в точке ж0, где #(ж) — непрерывная в точке ж0 функция. Имеет ли
функция /(ж) производную в точке жо?
Л При Аж > 0 приращение функции в точке жо имеет вид
Ау = /(ж0 + Аж) - /(ж0) =
= |ж0 + Аж - жо| #(ж0 + Аж) - 0 = д(х0 + Аж)Аж,
откуда -г-^ = ^(жо + Аж). Так как д(х) непрерывна в точке жо, то
Л
Л
дНт Q д^ = д(хо)- Итак, /'(ж0 + 0) = #(ж0).
Аналогично, при Аж < 0 получаем Ау = -д(х0 + Аж)Аж, откуда
Ау
л ИГП п А~ = л Ит П(~#(Ж°
Аж-^-0 /лх Аж-^-0
т. е. /'Оо -0) = -р(ж0).
Если #(ж0) ф 0, то /;(^о + 0) ф ff(x0 - 0), и, значит, функция /(ж)
не имеет производной в точке жо. Если же #(жо) = 0, то /'(жо + 0) =
= f'(xo — 0) = 0, и, следовательно, функция /(ж) имеет производную
в точке жо, причем f'(xo) = 0. А
5. Вычислить производную функции:
а) у = х^х (ж > 0, хф 1); б) у = cosB^ - ж3) (-оо < ж < оо).
Л а) Пользуясь правилами дифференцирования произведения и част-
частного и таблицей производных, получаем
(ж2 sin жУ In ж — х2 sinxCinxY
= —2 =
In х
ж2 cos ж + 2xsinx) In ж — х2 sin ж • 1/х _
Ь2^ =
+ 2 sin ж) In ж — ж sin ж , ~ . 1Ч
^ (ж > 0, ж/ 1).
У (х) = —2
In
In ж
б) Функцию у = cosB^ - ж3) можно представить в виде у = cost,
где t = 2х — ж3. Пользуясь правилом дифференцирования сложной
функции, получаем
а (ii ^^ (роч/г B^ 1*] ^^
= -sinB* -ж3)Bж1п2-3ж2) (-оо < ж < оо). А
6. Найти производную у'(х) функции
_ J ж2 sin(l/x) при х/0,
О при ж = О
72 Гл. IV. Производные и дифференциалы
и исследовать, является ли у'(х) непрерывной в точке ж = 0.
Л При ж ф 0 производную у'(х) можно найти дифференцированием
функции ж2 sin(l/x) по правилу дифференцирования произведения.
Это дает
у'(х) = 2ж8тA/ж) - cos(l/ar) (ж ф 0).
Полученное выражение не определено при ж = 0. Это не означает,
однако, что у'@) не существует, поскольку выражение для у'(х) и
было получено при условии ж ф 0. Для нахождения у'@) воспользуем-
воспользуемся определением производной. Приращение Ау функции у(х) в точке
х = 0 равно (АжJ 8тA/Аж), поэтому
lim —- = lim Ажвт—- = 0,
Аж—^0 /лх Аж—^0 /лх
т. е. у'@) = 0. Итак, у'(х) существует во всех точках:
,/ ч _ Г 2жвтA/ж) — cos(l/x) при х^0,
У \х) — | q ПрИ х = 0.
Для исследования непрерывности у'(х) в точке ж = 0 рассмотрим
lim у'(х). Ясно, что lim 2жвтA/ж) = 0, a lim cos(l/x) не существует.
Поэтому и lim y'(x) не существует. Таким образом, у'(х) разрывна
в точке ж = 0, которая является точкой разрыва II рода функции
у'(х). к
7. Доказать, что уравнения ж = cost, у = sint @ ^ t ^ тг) задают
параметрически некоторую функцию у = /(ж). Найти производную
/'(ж) этой функции.
Л Функция ж = cost является строго монотонной (убывающей) на от-
отрезке 0 ^ t ^ тг и, следовательно, имеет обратную. Подставляя эту
обратную функцию в уравнение у = sint, получаем функцию вида
у = /(ж). В данном случае обратная функция находится в явном ви-
виде: t = агссовж, и поэтому для /(ж) получаем выражение /(ж) =
= 8т(агссо8ж) (—1 ^ ж ^ 1). Эту же функцию можно записать в
виде /(ж) = л/1 — х2 (—1 ^ ж ^ 1) (объясните, почему). Вычислим
производную /'(ж) двумя способами: а) используя явное выражение;
б) используя формулу для производной функции, заданной парамет-
параметрически. Имеем:
а) /'(*) = -
Так как cost = ж, sint = лД - cos2 t = л/1 - х2 при 0 ^ t
из второго выражения для /'(ж) получаем первое: /'(ж) = —
(ж ф ±1 или -1 < ж < 1). А
8. Доказать, что если вектор-функции i*i(t) и Г2(?) имеют про-
производные, то для производной скалярного произведения (i*i(t)r2(t))
§1. Производная функции 73
справедлива формула
(ri(t)r2(t))' = (ri(t)r2(t)) + (n(t)ri(t)).
Л Пусть n (t) = xi (t) i + j/i (t) j + 0i (t) k, r2 (t) = ж2 (i) i + y2 (t) j +
+ z2(*) к. Тогда (n (t) r2 (*)) = xx (t) x2 (t) + 2/i (i) y2(t) + *i (i) ?2(i). Вос-
Воспользуемся тем, что если rj(?) (г = 1, 2) имеет производную, то Xi(t),
yi(t), Zi(t) также имеют производные, причем r?(?) = x'^t) \ + y[{t)i +
+ ^(?)k (см. упр. 25). Получаем
(ri (t) r2 (*))' = x[ (t) x2 (t) + Xl (t) x'2 (t) + y[ (t) y2 (t) + t/i (t) y'2 (t) +
+ z[(t)z2(t)+z1(t)z'2(t) = {x'1(t)x2(t)+y[(t)y2(t)+z[(t)z2(t)} +
+ {Xl(t)x2(t)+y1(t)y2(t) + z1(t)z2(t)} = (г!(г)г2(г)) + (n(t)r2(t)). a
Задачи и упражнения для самостоятельной работы
1. Запишите выражение для Ау = /(жо + Аж) — /(ж) и найдите область
определения функции Ау, если:
а) /(ж) = агсвтж, жо = 1/2; б) /(ж) = агссовж, жо = 0;
в) /(ж) = In ж, жо = 2; г) /(ж) = sin ж, жо = 2тг.
2. Пользуясь определением производной, найдите производную функции:
а) у = х в точке ж = 1; б) ?/ = ж2 в точке ж = жо;
в) у = -у/ж в точке ж = 4; г) у = ж|ж| в точке ж = 0;
» = I 0 при х = 0 в точке ж = °-
3. Функция у = /(ж) имеет производную в точке а. Вычислите пределы
последовательностей:
a) lim n(f(a + 1/n) - /(а)); б) lim п(/(а) -/(а - 2/n));
в) lim п(/(а - 1/п) - /(а + 1/п));
п—)-оо
г) lim п(/(а + 1/п) + /(а + 2/п) + ... + /(а + к/п) - kf(a)).
п—^оо
4. Уравнения прямолинейного движения двух точек имеют вид: a) si = ?,
S2 = t2 (О 0); б) si = t2, s2 = ts (О 0); в) si = lnt, s2 = лД
(t ^ 1) (t — время, si и S2 — расстояния, пройденные первой и второй
точками за время t). Сравните мгновенные скорости этих двух точек,
а также их средние скорости на отрезках времени 0^t^lnl^t^2
для случаев а) и б) и на отрезках 1 ^ t ^ 4 и 1^?^25 для случая в).
5. Составьте уравнение касательной к графику функции у = /(ж) в точке
с абсциссой жо, если:
а) /(ж) = sin ж, жо = 0; б) /(ж) = ж2, жо = 1;
в) /(ж) = -§/ж, жо = 0; г) /(ж) = ап^ж, жо = 1.
6. Найдите точку пересечения касательных к графику функции у = /(ж)
в точках с абсциссами х\ и х2, если:
а) /(ж) = cos ж, Ж1=тг/6, ж2=тг/2; б) /(ж) = еж, ал = 0, ж2 = 1;
в) /(ж) = агсвтж, х\ =0, ж2 = 1/2.
7. Составьте уравнения касательных к графику функции у = -у/ж, прохо-
проходящих через точку B, 3/2).
74
Гл. IV. Производные и дифференциалы
= тг/2;
8. Найдите односторонние производные /'(жо + 0) и /'(жо — 0) и сравните
их, если:
а) /(ж) = |ж|, ж0 = 0; б) /(ж) = |ж|, ж0 = 1;
в) /(ж) = ж2 sgnж, жо = 0; г) /(ж) = vsin2 ж, жо = 0;
д) /(ж) = |ж| sin ж, жо = 0; е) /(ж) = |ж — тг/2| cos ж, ж
ж) /(ж) = |ж-1|еж, жо = 1.
Существует ли в каждом случае производная /'(жо)?
9. Найдите г/(ж), если:
а) у = ж2; 6)у = у/Е; в)у = 1/х; г) у = 2у^
р)у = log2 ж3 + log3 ж2 (вычислите ?/A)); е) у = Т + A/2)ж;
ж) |/ = sin ж — cos ж (вычислите г/@) и у/(тт/4)); з) ?/ = tgж — ctgж;
и) |/ = агсвтж + агссовж (объясните полученный результат);
к) |/ = arctg ж + ага^ж (объясните полученный результат).
10. Докажите, что если и(х) и г;(ж) имеют производные в точке ж и и(х) >
> 0, то функция [u(x)]v^ также имеет производную в точке ж, причем
[u(x)v(x)]' = ^(ж)^(ж)"(жЬ1^(ж) + u(x)v{x) \nu(x)v'(x).
11. Найдите г/'(ж), если (везде а > 0):
б) |/ = у ж + д/ж + л/ж, 2/ = sin2 (cos ж) + cos2 (sin ж);
B)i/ = sin[sin(sin*)], У=^Ь' у = 2™*+***;
а2), у = In sin ж;
±, 2/ = Jarctg?;
з) у = arctg lJij? (сравните с производной функции у = arctg ж и объ-
1 X
ясните результат);
и) у = агссо8A/ж), 2/ = arcsin(sh^), у = arctg О^ж);
к) у = 8т(агс8тж), 2/ = ctg (arcctgж);
ln^±^
-arctg-, y-^Va -ж +—arcsin-,
In ж
о) у = arctg (ж + л/1 + ж2), |/ = (sinx)cosa:, ;г/=8п^ж), 2/= th (совж);
п) 2/ = ln(shaj), y = \g(chx), у = arctg (thaj), j/= In fcth|V
12. Известно, что у(ж), ф(х) и /(ж) имеют производные. Найдите г/(ж),
если:
а) 2/ = Л/^2(ж) + ^2(ж);
б) 2/ = log^(x) ^(ж) (^(ж) > 0, ф) ф 1, ^(ж) > 0);
вJ/ = /(ж2) + /(ж-2); г) 2/ = /(/(ж)).
§1. Производная функции
75
13. Функция у = /(ж) имеет в точке ж = 0 производную, отличную от нуля.
Вычислите пределы:
; б) lim .. {(*)sin* ¦
() () у ж^о /(ж) ch ж - /@)
14. Функция у = /(ж) имеет производную в точке ж = а. Вычислите пре-
пределы:
1/ / ?, ч \ 1
б) lim Ш)
\f(a)J
a) lim (До +
(а > 0).
a) U
15. Функции /(ж) и д(ж) имеют производные в точке а. Вычислите преде-
пределы:
a»f(x)-x«f(d) {п 6 д^. б) ,im f(x)g(a)-f(a)g(x).
х—Уа Ж — CL х—Уа Ж — CL
В) Um /to In а-/(а) In s (fl Q /(fl) / Qy
' x^a g(x) -g(a) y i у \ j т j
16. Докажите (методом математической индукции), что если/i (ж), /2(ж),...
п
...,/rito имеют производные в точке ж, то сумма / j fi(x) и произве-
г = 1
дение fi(x)f2(x)...fn(x) также имеют производные в точке ж, причем
17. Докажите, что имеет место следующее правило дифференцирования
определителей n-го порядка:
/ll О)
/into
/llto ... /into
'/iito"'--V''/Lto'
/nlto ... fnn(x)
18. Можно ли применить правило дифференцирования произведения двух
функций и(х) и г;(ж) в точке жо, если:
= 0; б) и(х) = ж, г;(ж) = |ж|, жо = 1;
) )
а) гб(ж) = ж, г>(ж) = |ж| )
в) гб(ж) = sin ж, v(x) = sgnж, жо = 1;
г) гб(ж) = ж2, г>(ж) = sgпж, жо = 0;
з / \ f 8тA/ж) при ж
е) гб(ж) = [ж], г>(ж) = 8т2(тгж),
0,
Z;
ж) гб(ж) = ж — [ж], г;(ж) = sin (ттж), жо = п G ^?
Существует ли в каждом случае производная произведения гб(ж)г>(ж) в
точке жо?
19. Справедливы ли следующие утверждения?
I. Если и(х) имеет производную в точке жо, a v(x) не имеет производ-
производной в точке жо, то:
а) и(х) + v(x) не имеет производной в точке жо;
б) u(x)v(x) не имеет производной в точке жо.
П. Если и(х) и v(x) не имеют производных в точке жо, то:
а) и(х) + v(x) не имеет производной в точке жо;
б) u(x)v(x) не имеет производной в точке жо.
(Если утверждение не справедливо, то приведите соответствующий
пример.)
76 Гл. IV. Производные и дифференциалы
20. Функции /(ж) и д{х) имеют производные во всех точках ж Е R. В каких
точках не имеет производной функция:
a) |/(ж)|; б) тах(/(ж),я(ж)); в) max
21. Справедливо ли утверждение: если /(ж) < д(х), то /'(ж) < gf(x)?
22. Выведите формулы для сумм
Рп = 1 + 2х + Зж2 + ... + пжп-\ Qn = I2 + 22ж + 32ж2 + ... + п2
Rn = x + 3xs + 5ж5 + ... + Bп + 1)ж2гг+1, Sn =
k=i
23. Изобразите траекторию точки, движение которой на плоскости (ж, г/)
задается уравнениями:
а) ж = ?, y = t2, —oo < ? < oo; б) х = cos2 t, у = sin2 t, 0 ^ t < oo;
в) x = a cost, у = bsint, 0 ^ t < oo;
r) ж = acht, у = 6sh?, —oo <t< oo;
д) ж = a(? — sint), у = a(l — cost), —oo < t < oo;
е) ж = e?, 2/ = e2?, —oo < ? < oo.
В каждом из случаев укажите такой промежуток изменения параметра
?, на котором уравнения определяют функцию у = /(ж), и найдите
производную этой функции по формуле D). В случаях а), б), в), г), е)
выразите /(ж) в явном виде и сравните явное выражение для /'(ж) с
выражением, полученным по формуле D). В случаях в) и г) составьте
уравнения касательной и нормали к кривой в точке t = 0.
24. Пусть r(t) = x(t) i + y(t)j + z(t) k, а = а\ i + a2 j + as k — постоянный
вектор. Докажите утверждение: для того чтобы lim r(t) = а, необхо-
t->t0
димо и достаточно, чтобы lim x(t) = ai, lim г/(?) = a2, lim г(?) = аз.
t* ?^ ^^
25. Пользуясь результатом предыдущей задачи, докажите утверждение:
для того чтобы вектор-функция r(t) = x(t) i + y(t)j + z(t) k имела про-
производную r'(t) в точке ?, необходимо и достаточно, чтобы скалярные
функции ж(?), г/(?), ^(t) имели производные в точке t. При этом г (t) =
/() /() '()
26. Докажите, что для вектор-функций имеют место следующие правила
дифференцирования:
У = r[(t)+r'2(t),
[Г1(*)г2(*)]' = [ri(*)ra@] + [ri(t)r'2@],
где [Y\(t)Y2{t)] — векторное произведение векторов Y\(t) и
27. Движение точки в пространстве задается уравнениями:
а) ж = t, у = t, z = t2, t ^ 0;
б)ж = Ясо8^, у = Rsint, z = ht, t ^ 0, Я > 0, /г > 0 (винтовая линия);
в) ж = ?, 2/ = t2, г = f3, ? ^ 0;
г)ж = 1п?, y = t2/2, z = y/2t, t^l.
Найдите модуль и направляющие косинусы вектора скорости в мо-
момент времени: а) t = 2; б) ? = тг; в) t = 1; г) ? = 2,5.
§2. Дифференциал функции
77
§ 2. Дифференциал функции
Основные понятия и теоремы
1. Дифференцируемость функции.
Определение. Функция у = /(ж) называется дифференцируемой
в точке жо, если ее приращение Ау = /(жо + Дж) — /(жо) в этой точке
можно представить в виде
Ау = А Ах + а Ах,
A)
где А — некоторое число, а а — функция аргумента Аж, бесконечно
малая и непрерывная в точке Ах = 0 (т. е. lim а(Ах) = а@) = 0).
Теорема 5. Для того чтобы функция у = /(ж) была дифферен-
дифференцируемой в точке ж0, необходимо и достаточно, чтобы существовала
производная /'(жо).
Отметим, что при этом А = f'(xo).
Дифференциалом (или первым дифференциалом) функции у = /(ж)
в точке жо (дифференцируемой в этой точке) называется функция
аргумента Аж: dy = //(ж0)Аж.
При f'(xo) ф 0 дифференциал является главной (линейной относи-
относительно Аж) частью приращения функции в точке жо.
Дифференциалом независимой переменной ж называется прираще-
приращение этой переменной: dx — Ах. Таким образом, дифференциал функ-
функции у = /(ж) в точке жо имеет вид
dy = f'(xo)dx, B)
откуда
f(Xn) - W
[Хо)~ dx'
равна отношению диф-
дифуа
/fo+Д
т. е. производная функции у = /(ж) в точке
ференциала функции в этой
точке к дифференциалу неза-
независимой переменной.
2. Геометрический и
физический смысл диффе-
дифференциала. Геометрический
смысл дифференциала функ-
функции нетрудно уяснить из
рис. 4, на котором изображены
график функции у = /(ж)
(жирная линия) и касатель-
касательная МР к графику в точке
М(ж0, /(ж0)). Дифференциал
dy равен приращению линейной функции, графиком которой является
касательная МР.
Рис. 4
78 Гл. IV. Производные и дифференциалы
Если х — время, а у = f(x) — координата точки на прямой в
момент ж, то дифференциал dy = f'(xo)Ax равен тому изменению ко-
координаты, которое получила бы точка за время Ах, если бы скорость
точки на отрезке времени [жо,жо + Аж] была постоянной и равной
f'(xo). Изменение скорости на этом отрезке приводит к тому, что,
вообще говоря, Ау ф dy. Однако на малых промежутках времени Ах
изменение скорости незначительно и Ay « dy = f'(xo)Ax.
3. Инвариантность формы первого дифференциала. Пусть
аргумент х дифференцируемой в точке хо функции у = f(x) является
не независимой переменной, а функцией некоторой независимой пе-
переменной t: х = ip(t), причем хо = ip(to), a cp{t) дифференцируема в
точке to- Тогда дифференциал функции у = f(x) по-прежнему имеет
вид B): dy = f'(xo)dx, но только теперь dx является не произволь-
произвольным приращением аргумента х (как в случае, когда х — независи-
независимая переменная), а дифференциалом функции х = ip(t) в точке to,
т. е. dx = cpf(to)dt. Это свойство (сохранение формулы B) и в том
случае, когда х = (p(t)) называется инвариантностью формы первого
дифференциала.
4. Использование дифференциала для приближенных вы-
вычислений. Так как Ау = dy при малых Ах, т. е. /(ж0 + Ах) - f(x0) =
^ //(ж0)Аж, то
/(хо + Ах)-/(хо) + //(^о)Ах. C)
Эта формула позволяет находить приближенные значения /(жо + Ах)
при малых Ах, если известны /(жо) и /Чжо)- При этом погрешность
при замене /(ж0 + Ах) правой частью формулы C) тем меньше, чем
меньше Ах, и, более того, эта погрешность при Ах —у 0 является
бесконечно малой более высокого порядка, чем Ах.
Контрольные вопросы и задания
1. Дайте определение дифференцируемости функции в данной точке.
2. Докажите теорему о связи между дифференцируемостью функции в
точке и существованием в этой точке производной.
3. Что такое дифференциал функции в данной точке? От какого аргумента
он зависит?
4. Может ли дифференциал функции в данной точке быть постоянной ве-
величиной?
5. Для каких функций дифференциал равен приращению функции? При-
Приведите примеры.
6. Каков геометрический смысл дифференциала?
7. Каков физический смысл дифференциала?
8. Что понимается под инвариантностью формы первого дифференциала?
Докажите, что форма первого дифференциала инвариантна.
9. Как можно использовать дифференциал функции для приближенных
вычислений?
§2. Дифференциал функции 79
Примеры решения задач
1. Найти дифференциал функции у = х2 - х + 3 в точке х = 2
двумя способами: а) выделяя линейную относительно Ах часть Ау;
б) по формуле B).
А а) Ду = /B + Ах) - /B) = [B + АхJ - B + Ах) + 3] - [22 - 2 +
+ 3] = ЗАх + (АхJ. Отсюда следует, что dy = ЗАх.
б) f {х) = 2х — 1, /'B) = 3. Следовательно, по формуле B) полу-
получаем dy = 3dx = ЗАх. А
2. Найти дифференциал функции у = sin(x2): а) в точке х = х0;
б) в точке х = д/тг; в) в точке х = л/тт при dx = —2.
Л а) Согласно формуле B) dy\x=Xo = f'(xo)dx = cos(xqJxo dx.
б) Полагая в последнем равенстве х = ^/тг, получаем dy\x_/^ =
в) Имеем ф ж=у^ = 4^. А
3. Заменяя приращение функции ее дифференциалом, найти при-
приближенное значение: а) д/0,98; б) sin 31°.
Л а) Рассмотрим функцию у(х) = д/1 + х. Так как 2/@) = 1,
2/(-О,О2) = л/0^8, г/'(*) = 1A + x)-V2, ^@) = I, то по формуле C)
получаем
2/(-О,О2) « 2/@) + 2/'(О)(-О,О2) = I - 0,01 = 0,99.
Итак, дДЩ « 0,99.
б) Рассмотрим функцию у = sinx. Так как 2/C0°) = sin 30° = 1/2,
2/'C0°) = cos30° = л/3/2, 1° = 2тг/360 (радиан) « 0,0175 (радиан), то
по формуле C), получаем
Ц +f ~« 0,5151. А
Задачи и упражнения для самостоятельной работы
28. Представьте в виде A) приращение функции:
а) у = ех в точке х = 0; б) 2/ = sin ж в точке ж = тг/2;
в) у = arctgx в точке ж = 0.
Запишите выражение для функции а(Ах).
29. Найдите приращение и дифференциал функции 2/ = х3 — х2 + 1 в точке
х = 1 и вычислите их значения при:
а) Аж = 0,01; б) Ах = 0,1; в) Аж = 1; г) Аж = 3.
30. Прямолинейное движение точки задано уравнением s = 2t2 + t + 1, где
? выражается в секундах, as — в метрах. Найдите приращение и диф-
дифференциал пути s в момент времени t = 1 с и сравните их при:
a) At = 0,1 с; б) At = 0,2 с; в) At = 1 с.
80 Гл. IV. Производные и дифференциалы
31. Найдите дифференциал функции у в точке ж, если:
а) у = д/ж; б) у = —; в) у = 1п(ж + л/ж2 + 1); г) у = - In
д) у = arcsin —; е) у = - arctg —; ж) ?/ = же2ж; з) у = х sin ж + cos ж.
32. Найдите dy\x=o и с?г/|ж=1, если:
х- 1
г) 2/ = sin^; д) 2/ = cos^.
33. Постройте график функции у = 1пA + ж) и изобразите на графике dy
при: а) ж = 0, dx = 1; б) ж = 1, с/ж = 1; в) ж = 1, dx = 2.
34. Пусть у = sin ж, где ж = cost. Какие из следующих равенств справед-
справедливы:
a) dy\t=lz/2 = 0; б) dy\t=n/2 = dx\ в) dy\t=n/2 = -dt?
35. Используя формулу C) и выбирая подходящее значение жо, найдите
приближенные значения:
a) cos 151°; б) arcsin0,49; в) lg 11; г) <§/ТДГ; fl)arctgl,l; e) e0'2
36. Докажите приближенную формулу (для малых ж)
?/ап + ж и а + —^Ц- (а>0).
С помощью этой формулы найдите приближенные значения:
а) ^9; б) ^255; в) ^130.
37. Функция у = /(ж) имеет производную в точке ж = а. Вычислите предел
последовательности
lim
(/(в+±)+/(а+4) +••• + /(«+4) ""/(«))•
V V 7lZ / \ 7lZ / \ 7lZ / /
§ 3. Производные и дифференциалы высших порядков
Основные понятия и формулы
1. Определение производных высших порядков. Если про-
производная f'(x) функции у = f(x) определена в некоторой окрестности
точки жо и имеет в этой точке производную, то эта производная от
f'(x) называется второй производной (или производной второго поряд-
порядка) функции у = f(x) в точке ж0 и обозначается одним из следующих
символов: /"Оо), /B)Оо), у"(х0), уB\х0).
Третья производная определяется как производная от второй про-
производной и т. д. Если функция у = f(x) имеет (п — 1)-ю производную
в окрестности точки хо и если (п — 1)-я производная имеет производ-
производную в точке ж0, то эта производная называется п-й производной (или
производной п-го порядка) функции у = f(x) в точке хо и обозначается
Таким образом, производные высших порядков определяются ин-
индуктивно по формуле
§3. Производные и дифференциалы высших порядков 81
Функция, имеющая п-ю производную в точке ж0, называется п раз
дифференцируемой в этой точке. Функция, имеющая в точке хо про-
производные всех порядков, называется бесконечно дифференцируемой в
этой точке.
Производные высших порядков вектор-функции г = г(?) также
вводятся индуктивно:
г(п)ф = [г(п-1)ф]/в
Если r(?) = x(t) i + y(t)j + z(t) k, то
r(n) ф = ж(п) ф j + y(n) ф }+z(n) ф k
Если функция г = r(t) описывает движение точки (t — время), то
вторая производная r"(t) есть вектор ускорения в момент времени t.
2. Основные правила вычисления n-х производных.
1. (u±v)^ =u^ ±v(n\
2. Формула Лейбница:
i=0
где «(«)=«, v^=v, Cin = 1^iyv 0! = l.
3. Формулы для n-х производных некоторых функций.
1. (V*)(n) = «(« - 1)...(а - п + 1)жа~п (ж > 0, а — любое число).
2. (аж)^п) = ах(\па)п @ < а ^ 1); в частности, (ех)^ = ех.
3.
4.
4. Дифференциалы высших порядков. Пусть х — независи-
независимая переменная и функция у = f(x) дифференцируема в некоторой
окрестности точки xq. Первый дифференциал dy = f'(x)dx является
функцией двух переменных: х и dx.
Второй дифференциал d2y функции у = /(ж) в точке хо определяет-
определяется как дифференциал функции dy = f'(x)dx в точке ж0 при следующих
условиях:
1°) dy рассматривается как функция только независимой перемен-
переменной х (иными словами, при вычислении дифференциала от f'{x)dx
нужно вычислить дифференциал от f'(x), рассматривая dx как по-
постоянный множитель);
2°) приращение независимой переменной х при вычислении диф-
дифференциала от f'(x) считается равным первоначальному приращению
аргумента, т. е. тому же самому значению dx, которое входит мно-
множителем в выражение dy = f'(x) dx.
Пользуясь этим определением, получаем
d2y\x=Xo = d(dy)\x=Xo = d[f(x)]\x=Xodx =
= {[f'(x)]'\x=xodx}dx =
82 Гл. IV. Производные и дифференциалы
или (записывая {dxJ в виде dx2)
d2y\x=Xo=f"(xo)dx2.
Дифференциал произвольного n-го порядка функции у = f(x)
определяется индуктивно по формуле
dny = d{dT-xy)
при таких же двух условиях, что и дифференциал второго порядка.
При этом справедлива формула
dny\x=xo = fM(x0)dxn (dxn = (dx)n), A)
откуда
Если х является не независимой переменной, а функцией какой-то
переменной ?, то формулы A) и B) становятся неверными (неинва-
(неинвариантность формы дифференциалов высших порядков). В частности,
при п = 2 имеем
d2y = f"(x)dx2+f'(x)d2x.
Контрольные вопросы и задания
1. Дайте определение второй производной функции у = /(ж) в точке жо-
2. Может ли существовать вторая производная /"(жо), если не существует
первая производная /'(жо)?
3. Приведите пример функции, у которой существует /'(жо), но не сущест-
существует /"(ж0).
4. Дайте определение n-й производной функции ?/ = /(ж) в точке жо.
5. Известно, что n-я производная функции в точке хо существует. Что
можно сказать о существовании производных меньшего порядка в точ-
точке хо и в окрестности этой точки?
6. Дайте определение n-й производной вектор-функции. Каков физичес-
физический смысл второй производной вектор-функции, описывающей движе-
движение точки?
7. Методом математической индукции докажите правило нахождения п-й
производной суммы и разности двух функций.
8. Выведите формулу Лейбница.
9. Выведите формулы для п-х производных функций жа, аж, sin ж, cos ж,
In ж.
10. Докажите, что если /(ж) п раз дифференцируема, то
dnf(ax + b) _ пАп)(,м
— -a f (t)\t=ax+h.
11. Вычислите производные n-го порядка: (е5ж)(гг), (зтCж + 2))(гг),
§3. Производные и дифференциалы высших порядков 83
12. Дайте определение дифференциала n-го порядка функции у = f(x) в
точке жо-
13. Докажите справедливость формулы A) для дифференциала n-го поряд-
порядка в случае, когда х — независимая переменная.
14. Справедлива ли формула A), если х — функция некоторой перемен-
переменной t? Выведите в этом случае формулы для d2y и dsy. Докажите, что
формула A) сохраняется, если х — линейная функция независимой пе-
переменной ?, т. е. х = at + Ъ (а и Ъ — числа).
Примеры решения задач
1. Найти ?/10), если у = х2е3х.
Л Данная функция является произведением двух функций: х2 и е3х.
Применяя формулу Лейбница, получаем
Так как (х2)^ = 0 при п ^ 3, (е3х)^ = е3хЗк, то
Ж2езжзю + 10 . 2хе3ж39 + 45 • 2е3ж38 =
( 30). А
Рассмотренный пример показывает, что формулу Лейбница наи-
наиболее удобно применять в тех случаях, когда один из сомножителей
является многочленом невысокой степени р. В этом случае все члены
формулы Лейбница начиная с (р + 2)-го равны нулю.
2. Найти п-ю производную функции у = ——-.
2
Л Данную функцию можно представить в виде у = 1 -\— .
t \ t \ /2 \^п^ / 2 \(п} 2
Поэтому у(п> = 1 ^ + ——- = ——- . В свою очередь ——-
\х2 — 1/ \х2 — 1/ х2 — 1
можно разложить на простейшие дроби:
2 1 1
х2 — 1 х — 1 ж + 1'
Следовательно,
кх — 1,
Вычислим последовательно первую, вторую и третью производ-
производные функции
-:
X X
= (-1)(-2)(^ - I) = ("IJ • 2!(* - I),
= (-1J2!(-3)(а; - I) = (-1K ¦ Щх - I).
Гл. IV. Производные и дифференциалы
Далее по индукции нетрудно доказать, что
x-l
Аналогично,
Итак,
у(п) - (-\\пп\
У ~[ } П'
3. Функция 2/ = /(ж) задана параметрически уравнениями х =
= acos?, ^/ = asin?, 0 < ? < тг. Найти f"(x).
Л Выведем формулу для второй производной функции 2/ = /(ж), за-
заданной параметрически уравнениями х = <р(?), 2/ = ip(t), считая, что
функции (p(t) и ip(t) дважды дифференцируемы и ip'(t) ф 0.
В силу инвариантности формы первого дифференциала df'(x) =
= f"(x)dx, откуда f"(x) =
. Так как f(x) = ^Щ, то c(f'(ж) =
= ( ,; ( ) dt. Учитывая, что dx = cp'(t)dt, получаем
\(p (?) /
Положив в этой формуле ф = a sin ?, ip = a cos ?,
получим
1
. C)
(ж) = arccos(x/a),
fix) = -
- X2/a2K/2 (a2 - Ж2K/2 "
В данном примере можно найти явное выражение для /(ж): /(ж) =
= у'а2 — х2 (—а < х < а). Вычисляя f"(x), получим, разумеется, то
же самое выражение, что и по формуле C). А
4. Движение точки в пространстве задано уравнениями х = i^cost,
у = Rsint, z = /zi2/2, t ^ 0. Найти модули векторов скорости и уско-
ускорения в момент t = 1.
Л С помощью вектор-функции движение можно задать уравнением
г = R cos ? • i + R sin ? • j + — • k,
? ^ 0.
Дифференцируя, находим
r; (t) = — Д sin ? • i + R cos ? • j + /i? • k (скорость),
r"(?) = —Rcost • i — i?sin? • j + h • k (ускорение).
Отсюда получаем |r;(?)| = л/R2 + /i2?2, |г;A)| =
r"(t)| =
= л/^R2 + /u2 (абсолютная величина ускорения является постоянной). А
§3. Производные и дифференциалы высших порядков 85
5. Найти второй дифференциал функции у = cos2x, если: а) ж —
независимая переменная; б) х = ip(t), где ip(t) — дважды дифферен-
дифференцируемая функция независимой переменной t.
Л a) d2y = y"{x){dxJ = -4cos2x(dxJ;
б) d2y = y"(x)(dxJ + y'(x)d2x =
= -Acos{2if{t)){if'{t)dtJ -2sm{2ip{t))ip"{t){dtJ =
= -2[2cosB^))(pt2(t)+sinB(p^))(p"(t)}(dtJ. A
Задачи и упражнения для самостоятельной работы
38. Найдите производные указанного порядка:
а)(е-*2)C>; б) (вша*)'10'; в) (е**)<4>; г)
Д) (/(еж))B); е) (/М*)))C); ж) (^)A0); з)
; к)
C0)
39. Найдите у^п\ если:
а) 2/ = л/аж + Ь; 6) У = —:5 в) j/ = sin ж;
еж + d
г) |/ = cos2 ж; д) у = sin3 ж; е) у = cos3 ж;
ж) |/ = sin аж sin /Зж; з) г/ = cos аж cos /Зх\ и) г/ = ж sin аж;
к) |/ = ж2 cos аж; л) г/ = (аж2 + 6ж + c)efc;c;
ах + Ь N N о
н)? ж8пж о) гж
ч . ах + Ь N N о л
м) |/= In ; н)?/ = ж8пж; о) г/= ж сЬж;
ах — о
п) у = аохп + а\хп~х + ... + ап-\х + ап (а» — числа).
40. Методом математической индукции докажите равенства:
а) (essinx)(n) = 2п/2ех sin (ж + -^
б) (жп1пж)(гг) =п!
Ж74
41. Для функций из упр. 23, заданных параметрически, найдите /"(ж) и
42. Выразите производные обратной функции ж = f~1(y) до третьего по-
порядка включительно через производные функции у = /(ж).
43. Движение точки в пространстве задается уравнениями из упр. 27. Най-
Найдите модуль и направляющие косинусы вектора ускорения в указан-
указанные моменты времени.
44. Найдите дифференциалы указанного порядка, если ж — независимая
переменная:
а) ^(ж3); б) d4(>/x=T)] в)о75(ж1пж); г) dlo(x sin ж).
Гл. IV. Производные и дифференциалы
45. Найдите dny, если:
а) у = sh ж; б) у = ch (аж); в) у = ж2 In ж.
46. В каждом из следующих случаев проверьте, что функция у{х) удов-
удовлетворяет соответствующему уравнению (Ci — произвольные числа):
а) у = С\ sin кх + С2 cos &ж, г/" + к2у = 0;
б) 2/ = Cie** + С2е-кх, у" - к2у = 0;
в) у = e~ax(Ci cos /Зх + С2 sin/Зж), j/" + 2а?/' + (а2 + /32)^/ = 0;
г) у = dsinx + C2cosx + С3ех + С4е~х, уD) - у = 0.
47. Найдите /(гг)(жо), если /(ж) = (ж — жоO7^^)? где ср(х) имеет непрерыв-
непрерывную производную (п — 1)-го порядка в точке жо.
48. Докажите, что функция fix) = < е ПРИ х ' ' бесконечно диф-
^ 0 при ж = 0
ференцируема в точке ж = 0.
ГЛАВА V
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Первообразная и неопределенный интеграл
Основные понятия и формулы
1. Определение первообразной и неопределенного интег-
интеграла.
Определение. Функция F(x) называется первообразной для
функции f(x) на промежутке X, если F'(x) = f(x) \/х e X.
Теорема 1. Если F\(x) и ^(ж) — две любые первообразные для
f(x) на X, то F2(x) — Fi(x) = С — const.
Следствие. Если F(x) — одна из первообразных для f(x) на X,
то любая другая первообразная Ф(ж) для функции f(x) на X имеет
вид Ф(х) = F(x) + С, где С — некоторая постоянная.
Определение. Совокупность всех первообразных для функции
f(x) на X называется неопределенным интегралом от функции f(x)
на промежутке X и обозначается I f{x)dx.
С
В силу следствия из теоремы 1 / f(x) dx = F(x) + С, где F(x) —
одна из первообразных для /(ж), С — произвольная постоянная.
(Иногда символом f(x)dx обозначается не вся совокупность пер-
первообразных, а какая-либо одна из них.)
2. Основные свойства неопределенного интеграла.
1°. dff(x)dx = f(x)dx.
2°. fdF(x) =F(x)+C.
3°. Линейность интеграла. Если существуют первообразные функ-
функций f(x) и д(х), а а и /3 — любые вещественные числа, то существует
первообразная функции af(x) + /Зд(х), причем
f[af(x) + /Зд(х)] dx = a Г f(x) dx + C f \
д{х) dx.
Контрольные вопросы и задания
1. Дайте определение первообразной для функции /(ж) на промежутке X.
2. Приведите примеры функций, имеющих первообразные.
3. Приведите примеры двух различных первообразных для одной и той
же функции /(ж).
Гл. V. Неопределенный интеграл
4. Всякая ли функция имеет первообразную? Рассмотрите пример:
г/ \ _ Г 1 при ж > О,
/W - \ _2 при ж ^ 0.
5. Найдите первообразную для функции /(ж) = sin ж, которая в точке
х = тг/2 принимает значение, равное 10.
6. Известно, что две первообразные для функции /(ж) = ех в точке ж = 1
отличаются на 2. На сколько отличаются эти же первообразные в точке
ж = 100?
7. График какой первообразной для функции /(ж) = проходит через
точку с координатами A, 2тг)?
Примеры решения задач
1. Доказать, что функция
{1 при х > 0,
0 при х = 0,
-1 при х < 0
имеет первообразную на любом промежутке, не содержащем точку
х = 0, и не имеет первообразной на любом промежутке, содержащем
точку х = 0.
Л На любом промежутке, не содержащем точку х = 0, функция sgnx
постоянна. Например, на сегменте [1, 2] sgnx = 1 и любая первооб-
первообразная для функции sgnx на этом сегменте имеет вид F(x) = х + С,
где С — некоторая постоянная.
Рассмотрим теперь промежуток, содержащий точку х = 0, напри-
например, сегмент [—1,3]. На полусегменте [—1,0) любая первообразная
для функции sgnx имеет вид —ж + Ci, а на полусегменте @, 3] пер-
первообразная для sgnx равна х -\- С^- При любом выборе произвольных
постоянных С\ и Съ мы получаем на сегменте [—1,3] функцию, не
имеющую производной в точке х — 0. Если выбрать С\ — С2, то по-
получим непрерывную функцию у — \x\-\-C [С — С\ — С^)-, которая
также не дифференцируема в точке х — 0. Таким образом, функция
sgnx не имеет первообразной на сегменте [—1,3].
Данной пример показывает, что вопрос о существовании перво-
первообразной для функции существенно связан с тем промежутком, на
котором эта функция рассматривается. А
2. Важный физический пример первообразной дает задача восста-
восстановления закона прямолинейного движения материальной точки по
заданной скорости. Мгновенная скорость v(t) является производной
функции s(?), определяющей закон движения материальной точки.
Поэтому отыскание функции s(t) по заданной скорости v(t) сводится
к нахождению первообразной для функции v(t). Любая первообразная
для v(t) имеет вид
s(t) = fv(t)dt + C.
Постоянная С определяется из дополнительных условий. Пусть,
§2. Простейшие неопределенные интегралы
89
например, v(t) = a(t - t0) + ^о (движение с ускорением а = const),
s(t0) = s0. Тогда s(t) = а^ ~ °^ + vo(t - t0) + С. Из дополнительного
условия s(t0) = sq находим С = s0, поэтому
s(t) =
_ a(t-toJ
vo(t - to) + s0.
§ 2. Простейшие неопределенные интегралы
Таблица основных неопределенных интегралов.
П.
III.
IV.
V.
VI.
VII.
VIII.
IX.
X.
f
f
f
у
(аф-\).
у
faxdx = ^ + C @<
/ sin xdx = — cos ж + С
/ cos xdx = sin ж + С
Щ- = tgx + C (
s ж
fe
90
Гл. V. Неопределенный интеграл
Примеры решения задач
Следующие интегралы сводятся к табличным путем тождествен-
тождественного преобразования подынтегрального выражения.
1. [x-±±dx=
J у/х y/
2. |(ж4 + l)x3dx = ^|(ж4 + 1) d(x4 + 1) = \fd(x4 + IJ =
3.
x2 dx
1-х2
2-1) + 1
1-х2
= —x + - In
1+Ж
1 -Ж
c.
4. [tg2xdx= [[A+ tg2x)-l]dx= f(-L--{\dx =
= tg ж — x + G.
2
f 2/3) + 5/6] ^ _
(х + 2/3) ЙЖ "
2 , 5,
1.
8.
6. / л/1 — sin 2ж dx = / л/sin2 ж — 2 sin ж cos ж + cos2 x dx =
= / л/(^тх — cos жJ dx = \ cos ж — sin ж| б?ж =
= (sin ж + cos ж) • sgn (cos ж — sin ж) + С.
Задачи и упражнения для самостоятельной работы
Найдите следующие интегралы.
dx. 2. f(xs + l)sx2 dx. 3. [3~Х2 dx. 4. fC-x2)sdx.
г-
+ X + 2
dx.
^ri^dx- 107ctg
2xdx. 11.
Зж + 2
с/ж.
12. Г— ^-—dx. 13. fth2xdx. 14. fsh2xdx. 15. |ch Bж + 3) dx
16. fBx+3xJdx. 17. /х/1 + Ж" + х/1~ж2 W?.t. 18. fBx-3I0dx.
J J VI — ж4 </
19. /л/l + sin2xdx. 20. [ , X 21. / ^—. 22. f-
J J х/2-5ж У 2 + Зж2 У ,
23.
У sin2Bx +
тг/4)'
24
•/г
+ cos ж
25
Зж2
У 1 + sin х
dx
§3. Метод замены переменной 91
§ 3. Метод замены переменной
Основные понятия и теоремы
Теорема 2. Пусть функция х = ip(t) определена и дифференци-
дифференцируема на промежутке Г, а промежуток X — множество ее значений.
Пусть функция у = f(x) определена на X и имеет на этом промежут-
промежутке первообразную F(x).
Тогда на промежутке Т функция F(cp(t)) является первообразной
для функции f((p(t))(p'(t).
Из теоремы 2 следует, что
ff(<p(t))<p'(t)dt = F(<p(t))+C, A)
а так как F(ip(t)) + С = (F(x) + C)\x=(pW = j f{x) dx\x=(p{t), то ра-
равенство A) можно записать в виде
jf{x) dx\x=v(t) = ff{<p{t))<p'{t) dt. B)
Равенство B) называется формулой замены переменной в неопре-
неопределенном интеграле.
Если функция х = if{t) имеет обратную функцию t = (p~1(x)J то
из равенства B) следует
Jf(x) dx = Jf(v>(tW(t) dt\t=ip_1(x). C)
Эта формула является основной рабочей формулой при вычислении
интеграла / f(x) dx методом замены переменной.
Контрольные вопросы и задания
1. Запишите формулу B) замены переменной в неопределенном интеграле.
При каких условиях эта формула справедлива?
2. При каком условии из формулы B) следует формула C)?
3. Требуется найти /д/4 — х2 dx для —2 ^ х ^ 2. Допустима ли для этой
цели замена переменной:
а) ж = sin?, -тг/2 ^ t ^ тг/2; 6)x = 2sint, 0 ^ t ^ тг/2;
B)x = 2sint, -тг/2 ^ t ^ тг/2; r)x = 2cost, 0 ^ ? ^ тг/2;
д) ж = 2 cos ?, тг ^ t ^ 2тг?
Примеры решения задач
Рассмотрим некоторые приемы вычисления интегралов с помо-
помощью замены переменной.
1°. Тождественное преобразование подынтегрального выражения с
выделением дифференциала новой переменной интегрирования (прос-
(простейшая замена переменной).
Г xdx = [fa*) = ,
' J л/1-Ж2 J л/1-Ж2 J
92
Гл. V. Неопределенный интеграл
= -1/A
- х2) = -\ 2A -
С.
fx'dx = Г 1^) = Г d{
' J ж8 - 2 У (ж4J - 2 У _2[1 - (х4
л/2 п
л/2 -х4
с.
' У Жл/Ж2 + 1 У Ж2л/1 + 1/ж2
V
= -In
ж Уж2
С (ж
dx
ж In ж In In ж
к /\ у f-d(cosx) , | | , ~
5. tgxdx = / - L = _ In cos ж + С
У У cos ж ' '
а Г dx f dx
о. / -г^ = / ^—7—9 т =
У sin ж + 2со82ж У cos^ ж(tg^ж + 2)
2[l + (tgж/^/2J] 2
2°. Некоторые подстановки.
1. / = /ж2 ^1 — жб?ж. Положим t = A — жI//3, тогда ж = 1 — ?3,
б?х = — 3?2 (it. Имеем
1 = f{\- t3ft(-3t2) dt = -з|A - i3Ji3 dt =
= -з/^3 - 2t6 + t9) dt = -3(j-^t7 + ± i10) + C,
t=(l-xI/3.
2. I = (xbB-bxzJ/zdx. Положим t = 2 - bxz, тогда х =
/ cy i \ 1/3
= ^—- ) , dt = -15ж2 б?ж. Находим
V о /
75 5
j= /• sin ж cos3 x rfx = f
У 1 + cos2 ж У
75 8
1 + cos2 ж
dx
§ 3. Метод замены переменной 93
Положим t = 1 + cos2 ж, откуда dt = -2 cos x sin x dx. Значит,
I = —- (it = -- + - In |t| + С, t = 1 + cos2 ж.
Zi J T Zi Z
3°. Тригонометрические подстановки при интегрировании некото-
некоторых иррациональных функций.
1. / = / ж2 3 , . Положим х = sint, —тг/2 < t < тг/2; тогда
<ix = cos tdt. Следовательно,
г Г cos tdt j. . г ri j.
I = / -— = tgt + 6, t = arcsmx.
У cos31
2./= /—г—x' , . Положим x = atgt, —тг/2 < t < тг/2; тогда
У (ж2 +a2K/2
б?ж = a о . Поэтому
cos2 t
r fa cos3 tdt 1 • . /^ . ,ж
^ = / ~5 ^T = -^ sint + C, t = arctg -.
У a3 cos2 to? a
3* ^= / 2 ^ 3/2 • Положим ж = 1/sint, -тг/2 <t<0 и 0<t<
J (x — 1)
< 7г/2; тогда <ix = -costdt. Таким образом,
sin t
т _ f — cos t dt _ Г sin tdt _ Г d(cos t) _
~ J о / 1 \^ ~ ~J cos2t ~ У
sin1 —^ 1
Vsin
\ J У cos2t
1
l /in
= \-C, t = arcsin - .
cos t \ ж /
Задачи и упражнения для самостоятельной работы
Выделяя дифференциал новой переменной, найдите следующие интег-
интегралы.
26. [x2fyl + x3dx. 27. fsinBx + 3)dx. 28. fJL^.
29./—^^. 30. Л,, ^. 31. j J?_ ¦ 32. J-
. У^Л, 36. (-r^—v
J x J жB + In ж)
'—^-с/ж. 39. / sin5 ж cos x dx.
r sin ж + cos ж Г81пжб?ж г с?ж
40. / ч dx. 41. / 42. / .
^ Vsin ж — cos ж </ v cos 2ж ^ sin ж
г с?ж г arctg ж г 1 1
43. / . 44. / ^—dx. 45. / г-In
J shx 71 +ж2 71-ж2 1
1 + ж
dx.
94 Гл. V. Неопределенный интеграл
Используя различные подстановки, найдите следующие интегралы.
fdx
. fxs(l-5x2I0dx. 47. / fdx . 48. /cos5 xy/sfalcdx.
J J v 1 — ж2 </
46.
49. / х™ х. 50. / """ х. 51.
52. [л/а2 - х2 dx. 53. Г J ?-^ dx (*x = acos2t). 54. f—=
J J у a — x J \Ja2
55.
r x — a j ( a \ -„ Г dx „m r
3. /д/ dx *ж= . 56. / 57. /-
У V ж + a V cos 2t / У х/ж2 + a2 У л
§ 4. Метод интегрирования по частям
Основные понятия и теоремы
Теорема 3. Пусть на промежутке X функции и(х) и v(x) диф-
дифференцируемы и существует v(x)u'(x) dx (т. е. функция v(x)u'(x)
имеет первообразную на X).
Тогда u(x)v'(x)dx также существует на X и
u(x)v'(x) dx = u(x)v(x) — v(x)u'(x)
dx.
Это равенство называется формулой интегрирования по частям.
Так как и'{х) dx = du, vf(x) dx = dv, то эту формулу можно записать
в виде
udv = u(x)v(x) — vdu.
Метод интегрирования по частям удобно применять в следующих
случаях.
1. Подынтегральное выражение содержит в виде множителя функ-
функции In ж, \пср(х), arcsinx, arccosx, arctgx. Если в качестве и{х) вы-
выбрать эти функции, то подынтегральное выражение vdu нового ин-
интеграла обычно получается проще исходного.
2. Подынтегральная функция имеет вид Р(х)еах, P(x)sinax,
P(x)cosax, где Р(х) — многочлен относительно переменной х. Если
в качестве и(х) выбрать Р(х), то в новом интеграле подынтегральная
функция снова принадлежит одному из указанных типов, но степень
многочлена окажется уже на единицу меньше. Выбирая этот много-
многочлен снова в качестве и(х), понижаем степень еще на единицу и т. д.
3. Подынтегральная функция имеет вид еах s'mbx, eax cosbx,
sin(lnx), cos(lnx) и т. п. После двукратного интегрирования по частям
получается снова исходный интеграл с некоторым коэффициентом.
Полученное равенство является линейным алгебраическим уравне-
уравнением относительно искомого интеграла.
§4- Метод интегрирования по частям 95
Контрольные вопросы и задания
1. Напишите формулу интегрирования по частям неопределенного интег-
интеграла. При каких условиях эта формула справедлива?
2. Какие функции удобно интегрировать по частям?
Примеры решения задач
1. / = / arctgжdж. Положим и = arctgx, dv = dx. Тогда du =
= —^Ц-, v = х. Следовательно,
1 + х
xdx 2
J
= xarctgx
2. / = I x2e~xdx. Положим и = ж2, dv = e~xdx. Тогда (iix = 2xdx,
v = — e~x. Значит,
/ = -x2e~x + 2fxe~xdx = -x2e~x + 2^-xe~x + fe~xdx^ =
= -x2e~x - 2xe~x - 2e~x + C.
r
3. / = / sm(\nx)dx. Положим и = sin In ж, dv = <ix. Тогда du =
= - cos In xdx, v = ж. Имеем
ж
1-х sin \nx — cos In ж б?ж = ж sin In ж — (ж cos In ж + / sin In ж dx).
Мы получили линейное относительно / уравнение
/ = x(s'm In ж - cos In ж) - /,
откуда находим
I = -z (sin In ж — cos In ж) + С.
{х2 + а2)а {ol = 1,2,...). Положим и = (ж2 + д2)а, dv =
= dx. Тогда
Ка= {х* + а*У ~ jXd\{x* + a*y) =
(х2 + а2) — а2 , _
a
9 Г (х2
а + ^«У (ж2)
Г /• с?ж _ 2 у ^ж I _
откуда
^ = 1 х \2а~1К
a+1 ж2+а2)« "^ 2аа2 а
96
Гл. V. Неопределенный интеграл
Мы получили рекуррентную формулу, с помощью которой Ка+1
выражается через Ка. При а = 1 интеграл Ка есть "почти" таблич-
табличный интеграл:
Kl = [^-^ = i arctg ^ + С.
J ж + а а а
Полагая в рекуррентной формуле а = 1 и зная i^i, найдем К*}. Полагая
а = 2 и зная i^, найдем Хз и т. д.
Замечание. С помощью методов замены переменной и интегриро-
интегрирования по частям получаются следующие часто употребляемые формулы.
arcsin - + С (а > 0, |ж| < а).
' = f л/а2 - x2 + Щ- arcsin - + С (а > 0, |ж| < а).
— 2 2 I
Задачи и упражнения для самостоятельной работы
Найдите следующие интегралы.
58. An ж с/ж. 59. l^Jx\v?xdx. 60. fx^e'^dx.
61. x2sin2xdx. 62. / arcsin ж с/ж. 63. / ^—с/ж.
64. / sinжln(tgж)c/ж. 65. /ж(arctgжJ с/ж.
ж 1п(ж + Vl + ж2)
66.
- с/ж. 67.
1с/ж.
68. fcos(\nx)dx. 69. feaxsmbxdx. 70. |е2ж sin2 ж с/ж.
§ 5. Интегрирование рациональных функций
Основные понятия и теоремы
1. Разложение рациональной дроби на сумму простейших
дробей. Рассмотрим рациональную функцию (или рациональную
дробь) Pn(x)/Qm(x). Здесь Рп(х) и Qm(x) — многочлены степеней
пит относительно переменной х.
§ 5. Интегрирование рациональных функций
97
Если п ^ т, т. е. дробь неправильная, то ее можно представить в
виде
Р4Ж) _ р / \ , Rk(x) ,, ч
QmO) Сш(ж)
или, как говорят, выделить из нее целую часть Рп_т(ж).
В результате интегрирование неправильной рациональной дроби
сводится к интегрированию правильной дроби Rk(x)/Qm(x).
Теорема 4. Пусть Pn(x)/Qm(x) — правильная рациональная
дробь (п < т), а разложение Qm(x) на произведение неприводимых
вещественных множителей имеет вид
Qm{x) = {х- а)а...{х -
+rx + sN,
x2 + рх + qy.
где а,..., Ъ — вещественные корни, х2 + рх + q,..., ж2 + rx + s — квад-
квадратные трехчлены, не разложимые на вещественные множители.
Тогда
Qm(x) (х-а)
MlX
'"
х — а
х — b
X -\~ J-Jfi
E '"
где Ai, Bi, Mi, Ni, Ki, Li — вещественные числа.
Дроби, входящие в правую часть A), называются простейшими, а
само равенство A) называется разложением правильной рациональной
дроби Pn(x)/Qm(x) на сумму простейших дробей с вещественными
коэффициентами.
2. Интегрируемость простейших дробей в элементарных
функциях. Каждая из простейших дробей интегрируется в элемен-
элементарных функциях:
dx = A\n
x-a
2)
3)
(x — a)a 1 — a (x — a)a~1
Mx + N M , 2 , . ч
-Y- — dx = — \n(x + px + q)
, 2N-MP .
H arctg
f
J (
M
2A-a)
+ G;
(a > 1), где
а =у~ т*
4 В.Ф. Бутузов и др.
98 Гл. V. Неопределенный интеграл
Интеграл Ка вычисляется по рекуррентной формуле (см. § 4).
3. Практические приемы разложения правильной дроби
на сумму простейших дробей.
1°. Метод неопределенных коэффициентов. Разберем этот
метод на следующем примере. Разложение правильной дроби
-——-2 г на сумму простейших дробей согласно тео-
реме 4 имеет вид
х _ А В Сх + Р
О + 1)Bж-1)(ж2 + 1) ~ ж + 1 2ж-1 ж2 + 1
Приводя к общему знаменателю и приравнивая числители получив-
получившихся дробей, приходим к равенству
х = АBх - 1)(ж2 + 1) + В(х + 1)(ж2 + 1) +
+ Сх(х + 1)Bж - 1) + D(x + 1)Bж - 1). B)
Два многочлена тождественно равны тогда и только тогда, ког-
когда равны коэффициенты при одинаковых степенях х. Приравнивая
коэффициенты, получаем систему уравнений для определения А, В,
С и D:
-А + В- ?> = 0;
2А + В- С+ ?> = 1;
-А + В+ C + 2D = 0;
2А + В + 2С =0.
Решив эту систему, найдем коэффициенты А, В, С, D.
Такой общий подход даже в примере с четырьмя неопределенными
коэффициентами приводит к весьма громоздкой системе.
Вместе с тем, используя тождество B), можно найти искомые ко-
коэффициенты проще:
а) полагая в B) х = -, получаем - = В • - • -, откуда В = —¦;
z Zi Zi 4 X О
б) полагая в B) х = -1, получаем -1 = А • (-3) • 2, откуда А = -;
в) полагая в B) х = 0, получаем 0 = —А + В — D, откуда D =
= В~ А = То;
г) сравнивая коэффициенты при ж3, получаем 0 = 2А + В + 2G,
при
при
при
при
ж°
ж1
ж2
X3
2°. Метод вычеркивания. Отметим полезный прием вычисления
некоторых из неопределенных коэффициентов. Пусть
т. е. вещественное число а — корень кратности а многочлена Qm(x).
§ 5. Интегрирование рациональных функций 99
Кратному вещественному корню х — а соответствует в разложе-
разложении дроби Pn(x)/Qm(x) цепочка простых дробей:
Аа |Ад — 1| , А\
1 ••• \
(х — а)а (х — а)а * х — а
Для отыскания коэффициента Аа при старшей степени знамена-
знаменателя надо в знаменателе исходной дроби пч , ч вычеркнуть
(х — а)а(р(х)
(х — а)а и в оставшейся дроби положить х = а, т. е. Аа = п/ / .
(р(а)
Указанный метод особенно удобен, если все корни знаменателя
вещественные и простые. Тогда этим методом находятся все неопре-
неопределенные коэффициенты. Например,
=А+ В + С + D
¦1)(ж-2) жж-1ж + 1ж-2'
х + 2
В =
(ж -2)
х=1
+ -
х=0
С
J + 1
= 1,
3
2
и т. д.
Контрольные вопросы и задания
1. Всякая ли рациональная дробь интегрируема в элементарных функци-
функциях?
2. Почему исследуется вопрос об интегрировании только правильной дро-
дроби?
3. Что значит "выделить целую часть неправильной дроби"?
4. На какие простейшие вещественные множители можно разложить мно-
многочлен с вещественными коэффициентами?
5. Известно, что число 2 — г является корнем многочлена с вещественны-
вещественными коэффициентами. Верно ли, что число 2 + г есть корень того же
многочлена?
х + 1
6. На какие простейшие дроби разлагается дробь — ?
0 + iJo2 + ж-ы)
7. Что такое метод неопределенных коэффициентов при разложении дроби
на сумму простейших дробей?
8. Что такое метод вычеркивания при вычислении неопределенных коэф-
коэффициентов?
9. Найдите методом вычеркивания неопределенные коэффициенты в раз-
^ х
ложении дроби .
ДР (х + 2)(х - 3)
10. Найдите методом вычеркивания неопределенные коэффициенты в раз-
разложении дроби . * Положите х2 = у и затем примените
(ж2 - 2)(ж2 + 3)
метод вычеркивания.
4*
100 Гл. V. Неопределенный интеграл
Задачи и упражнения для самостоятельной работы
Найдите следующие интегралы.
_. г 2ж + 3 _о г ж3 + 1 ~п f f
71- У (ж-2)(ж + 5) ^ 72' У ,3-5,2+6, ^ 73- У l,2-
(ж-2)(
_. г ж2 + 5ж + 4 ,
74. / — dx.
У ж4 + 5ж2 + 4
ж2 -4ж + 4)(ж2 -4ж + 5)
76. /_^_. 77. [-Р-. 78. /-^. 79.
У 3 1 J 4 1 У 4 1
^. 77. [Р. 78. /. 79. / А 9 .
ж3 + 1 J ж4 - 1 У ж4 + 1 У ж4 + ж2 + 1
80. ^^
/ ^ 81. /"-^- 82. [-
J ж4 + Зж3 + 4,5ж2 + Зж + 1 У ж6 + 1 J (ж -
(ж-1I
83. /4^^- 84. / я д^ . 85.
У 6 1 У 8 З4 2
ж6 + 1 У ж8 + Зж4 + 2 У жA + ж7)
9 i -1 ^ 4 i -1
А \ dx. 87. /^-—-dx. 88. f^-—^dx.
ж4 + ж2 + 1 У ж8 + 1 У ж6 + 1
§ 6. Интегрирование иррациональных функций
Основные рационализирующие подстановки
В этом и следующем параграфах через R(x, у) обозначается ра-
рациональная функция двух аргументов х и у.
1. Интегрирование дробно-линейных иррациональностей.
Интеграл вида R[x, ?/ ах + j dx ( - ф - ) рационализируется, т. е.
сводится к интегралу от рациональной функции, подстановкой
2. Подстановки Эйлера. Вопрос об интегрировании в элемен-
элементарных функциях интегралов вида / R(x, л/ах2 + Ьх + с) dx (а ф 0)
решается с помощью подстановок Эйлера, которые рационализируют
интегралы такого вида.
Если квадратный трехчлен ах2 + Ьх + с имеет комплексные корни
(в этом случае знак а совпадает со знаком трехчлена, стоящего под
корнем, т. е. а > 0), то применяется первая подстановка Эйлера
t = у ах2 + Ьх + с + ху/а.
Если ах2 + Ьх + с = а(х — х\)(х — жг), где х\ и х<± — вещественные
корни, то для рационализации интеграла применяется вторая подста-
подстановка Эйлера
_ у/ах2 + Ьх + с
х — х\
3. Другие приемы интегрирования квадратичных ирра-
иррациональностей. Подстановки Эйлера, играя важную теоретическую
§ 6. Интегрирование иррациональных функций 101
роль, на практике приводят обычно к громоздким выкладкам, поэто-
поэтому прибегать к ним надо в крайних случаях, когда не удается более
просто вычислить интеграл другим способом. Одним из таких спосо-
способов является следующий. Если в квадратном трехчлене ах2 + Ьх + с
выделить полный квадрат, т. е. привести его к виду а\х + — ) +
( Ъ2\ V J
+ ( с - — 1 и положить
t =
(*+=)•
с-Ъ2/Dа)
то интеграл / R(x, л/ах2 + Ьх + с) dx приводится к одному из трех
видов:
Сделав в первом из этих интегралов подстановку t = sin-u, во
втором 1/t = sin и, в третьем ? = tgu, получаем интегралы вида
R(smu,cosu) du (см. § 7).
Рассмотрим еще один способ вычисления интегралов вида
R(x, л/ах2 + Ьх + с) dx (без применения подстановок Эйлера и три-
тригонометрических подстановок). Для этого преобразуем подынтеграль-
подынтегральную функцию к некоторому специальному виду.
Так как четные степени выражения л/ах2 + Ьх + с являются мно-
многочленами, то функция R(x, л/ах2 + Ьх + с) представима в виде
вт
/
R(x, у ах2 + Ьх + с) =
Ъх
где Р, Q, S и Т — многочлены. Чтобы избавиться от иррациональ-
иррациональности в знаменателе, умножим числитель и знаменатель этой дроби
на S(x) — Т(х)у^ах2 + Ьх + с. Тогда получим
, V «ж2 + for + с) =
Ъх
= д , , + Д2(ж)
Х /аж2 +6ж
С(х) С(х)л/ах2 + bx + c
где А, В и С — многочлены, R\(x) и Д2(ж) — рациональные функции.
Вычисление интеграла от Ri(x) описано в § 5.
Выделяя в рациональной дроби Д2(ж) целую часть Рп(х) и раз-
разлагая оставшуюся правильную дробь на сумму простейших дробей,
приходим к следующим трем типам интегралов:
Pn(x)dx , ч
+ Ьх + с
102 Гл. V. Неопределенный интеграл
[
Г
J
(х- C)тл/ах2 -\-bx-\-c
(Мх + N) dx
(x2 + px + q)a^ax2 -\-bx-\-c'
B)
Эти интегралы можно вычислить следующим образом.
1. Для интеграла A) справедлива формула
Pn(x)dx „ ( \ / 9 , l i , л f dx ,Л,
= = Qi(x)Vax2+ Ъх + с + \ D)
, 2 ,, = = Qn-i(x)Vax+ Ъх + с + \ Г-Г-и ,
у ах1 +Ъх + с J у ах2 +Ъх +
где Qn-i(x) — многочлен степени п — 1, а Л — некоторое число. Для
определения коэффициентов Qn-i(x) и числа Л продифференцируем
тождество D). После приведения к общему знаменателю получим ра-
равенство двух многочленов. Сравнивая коэффициенты при одинаковых
степенях, находим неизвестные коэффициенты. Входящий в правую
часть равенства D) интеграл сводится к табличному выделению пол-
полного квадрата в подкоренном выражении.
2. Интеграл B) сводится к интегралу типа A) подстановкой t =
= 1/(х-р).
3. Интеграл C) в случае, когда
а _ Ъ _ с ( ,
Т"р"? E)
т. е. когда квадратные трехчлены совпадают с точностью до множи-
множителя (ах2 + Ъх + с = а(х2 + рх + q), a > 0), можно представить в виде
суммы двух интегралов:
Mr Bx+p)dx I (N Мр\ Г dx
Mr
%^/EJ (ж2
Первый из них рационализируется подстановкой t = х2 + рх + q, a
второй — подстановкой t = (л/х2 + рх + q)' = — х +Р
2^/х2 +рх + q
Если соотношение E) не выполняется, то интеграл C) сводится
сначала к виду
Так, если j = - ф -, то вид F) достигается подстановкой х = у — ^.
Если j ф -, то для приведения интеграла C) к виду F) использу-
используется подстановка х = ^у + ^. Коэффициенты /1иг/ подбираются так,
чтобы в полученных квадратных трехчленах отсутствовали члены
первой степени относительно у.
§ 6. Интегрирование иррациональных функций
103
В интеграле F) дробь 22m~u^ является правильной, и после ее
разложения на простейшие дроби получаются интегралы типа
dy
(у2 +l)k\/ry2 + з
Г ydy Г
J (у2 + ^)k\/ry2 + s J
Первый из них рационализируется подстановкой t = л/гу2 + s, вто-
второй — подстановкой t = (л/гу2 + s/ =
Контрольные вопросы и задания
1. Какая подстановка рационализирует интеграл от дробно-линейной ир-
иррациональности?
2. Какого типа интегралы вычисляются с помощью подстановок Эйлера?
3. Какова теоретическая роль подстановок Эйлера?
4. С помощью каких тригонометрических подстановок вычисляются ин-
интегралы 1у/1 — х2 dx, \\/х2 — 3dx, Ых2 + 3dx, Ых2 — 2х + 2 dx,
2 + 2х-х2 dx?
Примеры решения задач
, откуда dx =
Ь С,
л/3
У (ж2
с/ж
(ж2 + ж + 1)л/ж2 + ж - 1
-/¦
с/ж
dx
V$
3
5
Положим t = х Т. , тогда \fbdt = 2dx и, значит,
v5
I=-
dt
-l
104
Гл. V. Неопределенный интеграл
Положим теперь - = sin и, откуда -— = cos и du. Поэтому
cos и sin и du
и ) cos и
зУ i
= --/
5У
sin и du
cosz и
5 5
d(cosu)
4 1 /3,
= - - \ / - In
где и = arcsm
л/5
л/6
8/3 - cos2 и 3 2
. Окончательно получим
Bж + 1)л/2
л/8 — \/3cosi6
Bж + 1)л/2 -
3. Вычислим интеграл примера 2 без применения тригонометри-
тригонометрических подстановок. Интеграл имеет вид C), где р = 1, q = 1, а = 1,
6 = 1, с = —1, т. е. выполнены условия а/1 = b/р ф c/q.
Полагая х = у - -, приходим к интегралу / = / — у
2 J B/2 +
(8)
типа G), который рационализируется подстановкой
Из соотношения (8) получаем t2(y2 - 5/4) = у2, откуда
2 3 = 2t2 - 3/4 , .
Записывая формулу (8) в виде ?\/?/2 - 5/4 = у и дифференци-
дифференцируя, получаем dt^/y2 — 5/4 + t(^/y2 — 5/4)'dy = <%, или, с учетом (8),
Л^- (ю)
2 — 5/4 + t • tdy = dy, откуда
Подставляя выражения (9) и A0) в интеграл /, имеем
dt 1 ,
где t =
2\/ж2 + ж + 1
/= -4= In
л/6
3/4-2
, т. е.
Bх-
Bж + 1)\/2 -
§ 6. Интегрирование иррациональных функций
105
. /= Г- -з-Й—= =.
J (х- 1Kл/ж2 + Зж + 1
(х- 1)
Положим t =
—^—-, тогда dx = -Д, dt
ж-Г Г
и / = — / . Далее воспользуемся формулой A):
J у/Ы2 + 5* + 1 V У
Ы + 1 + Л
У
Ы
Дифференцируя это тождество, получаем
^2 + Ы + 1
+ 5* + 1
+ 5* + 1
Приводя к общему знаменателю и сравнивая коэффициенты при оди-
одинаковых степенях ?, находим А = 1/10, Б = -3/20, Л = 11/40. Далее,
г, dt =4= л
d{t +1/2)
1/2J - 1/20
= 1 In
/
Окончательно имеем
где i =
1 4
10 20
11
40л/5
In
x — 1
или
1=
x2 + Зж + 1 -
11
40л/5
In
ж-1
+ С.
'+5
Задачи и упражнения для самостоятельной работы
Найдите следующие интегралы.
dx „„ г \/х + 1 — \/ж — 1
89.
91- У^
97- /-
^ ж3
100.
102.
90. fV*±±-V*Z±dx.
J у/х + 1 + у/х ~ 1
= . 92. /-
93.
X
dx
-с/ж. 95. Л
98.
ж3 с?ж
- 2ж - ж2
96.
x10dx
dx
Г б?Ж
J A-х4)у/Г
101
' J (х2 -
99
xdx
У D
х2 dx
D -
ж2)\/2
f a ^
i (ж2 +z +
(ж + 1) dx
(ж2 - 1)\/ж2 - ж - 1
103.
106 Гл. V. Неопределенный интеграл
Ю4. [ dx 105
J I
+ у/1 - 2х - х2
106. f ^-l)dx 107
§ 7. Интегрирование тригонометрических функций
Основные рационализирующие подстановки
Интеграл вида R(smx, cos ж) dx рационализируется с помощью
универсальной тригонометрической подстановки t = tg(x/2). На
практике она приводит часто к громоздким выкладкам. В ряде слу-
случаев более удобны другие подстановки:
а) t = cos ж, если R(— sin ж, cos x) = —R(sm ж, cos x);
б) t = sin ж, если i?(sin ж, — cos ж) = —R(sm ж, cos ж);
в) t = tg ж, если R(— sin ж, — cos ж) = i?(sin ж, cos ж).
Примеры решения задач
1. / = cosbxdx. Подынтегральная функция относится к слу-
случаю б). Поэтому положим t = sin ж. Тогда dt = cosxdx, cos4 ж =
= A-8т2жJ = A-?2J и
i= [(I- t2f dt = t-h3 + lt5 + c,
J о о
где t = sin ж.
2. / = s'm5xco8xdx. В данном случае проще вычислить ин-
интеграл, не прибегая к подстановкам и представив подынтегральную
функцию в виде -(зт4ж + втбж). Тогда
/ = - / (sin 4ж + sin бж) dx = - - cos 4ж - — cos бж + С
2 J 8 12
3. / = / ^Ц—:—• Здесь можно сделать универсальную под-
J a cos х + о sin ж
становку t = tgf. Тогда ж = 2arctgt, б?ж = -^^, sin ж = -г^-^,
? 1 ~\ t 1 ~\ t
cos ж = ~ 2 и интеграл / сводится к интегралу от рациональной
функции. Однако проще сначала преобразовать подынтегральную
функцию:
1 _ 1
a cos х -\-Ъ sin ж
§ 7. Интегрирование тригонометрических функций
107
где s'mtp = —j==—= , cos(p = —j= = , и положить далее t =
Va2 + b2 Vfl + b2
= tg±^?. Тогда dx = -?j^, sin(x
л/a2 + &2 J t
7
л. ~\ t
и, следовательно,
Задачи и упражнения для самостоятельной работы
Найдите следующие интегралы.
108. [sm6xdx. 109. Г sin2 x cos4 x dx. 110.
J J
111.
112
. f ,
•/ v sin3
113.
v sin3 ж cos° ж
114. / cos ж cos 2ж cos Зж с/ж. 115. / sin3 2жсов2 Зжс/ж.
116. / ^ . 117. f- dx
J 2 sin ж — cos ж + 5 7 1
2 sin ж — cos ж + 5
n2
_ + ? COS Ж
sin ж б?ж
при: a) 0 < e < 1; 6) e > 1.
118. /¦^^L. ид. f f1*^ . 120. f edx в .
J 1 + sin ж J sm° ж + cosd ж J cos0 ж + smD ж
ГЛАВА VI
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ
И ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
§ 1. Теоремы об ограниченности непрерывных функций
Основные понятия и теоремы
1. Определение ограниченной функции. Пусть функция у =
= f(x) определена на множестве X.
Определение. Функция у = f(x) называется ограниченной свер-
сверху (снизу) на множестве X, если существует число М(т) такое, что
Vx Е X выполняется неравенство /(ж) ^ M (f(x) ^ т).
Число М(т) называется верхней (нижней) гранью функции на мно-
множестве X. Функция у = f(x) называется ограниченной на множестве
X (или ограниченной с обеих сторон), если она ограничена сверху и
снизу на этом множестве.
2. Теоремы об ограниченности непрерывных функций.
Теорема 1 (о локальной ограниченности функции, непрерывной
в точке). Если функция у = /(ж) непрерывна в точке жо, тпо сущест-
существует окрестность точки ж0, в которой эта функция ограничена.
Теорема 2 (об устойчивости знака непрерывной функции). Если
функция у = f(x) непрерывна в точке хо и f(xo) ф 0, то существует
окрестность точки жо, 6 которой f(x) имеет тот же знак, что и
Теорема 3 (первая теорема Вейерштрасса). Непрерывная на сег-
сегменте функция ограничена на этом сегменте.
3. Точные грани функции.
Определение. Число М называется точной верхней гранью
функции у = f(x) на множестве X, если:
1°) \/х G X выполняется неравенство f(x) ^ М;
2°) VM; < М Зх' G X такое, что f(x') > М'.
Замечание. Условие 1°) означает, что число М является одной из
верхних граней функции у = f(x) на множестве X. Условие 2°) означает,
что М — наименьшая из верхних граней функции у = f(x) на множестве
X, т. е. никакое число М7, меньшее М, не является верхней гранью.
Точная верхняя грань функции у = f(x) на множестве X обозна-
обозначается так: sup f(x). Если функция у = f(x) не является ограниченной
х
сверху на множестве X, то пишут sup f(x) = +оо.
х
§1. Ограниченность непрерывных функций 109
Аналогично определяется точная нижняя грань функции: inf f(x).
х
Разность sup/(ж) — inf/(ж) называется колебанием функции у = /(ж)
х х
на множестве X.
Теорема 4 (вторая теорема Вейерштрасса). Непрерывная на сег-
сегменте [а, Ъ] функция /(ж) достигает на этом сегменте своих точ-
точных граней, т. е. Зж', х" Е [а, Ь] такие, что f(x') = inf /(ж), f(x") =
[а, Ъ]
= sup/O).
[а,Ч
Если функция у = f(x) достигает на множестве X своей точной
верхней (нижней) грани, то она имеет на X максимальное (минималь-
(минимальное) значение, причем max/(ж) =вир/(ж) (соответственно гшп/(ж) =
х х х
= inf/(ж)). В противном случае функция не имеет на множестве X
максимального (минимального) значения.
Контрольные вопросы и задания
1. Дайте определение ограниченной сверху (снизу) на множестве X
функции.
2. Используя правило построения отрицаний предложений с кванторами,
сформулируйте определение неограниченной сверху (снизу) на мно-
множестве X функции.
3. Докажите, что определение ограниченной функции эквивалентно сле-
следующему: функция у = /(ж) называется ограниченной на множестве
X, если существует число А > 0 такое, что ViGl выполняется нера-
неравенство |/(ж)| ^ А.
4. Сформулируйте определение неограниченной на множестве X функции
с помощью отрицания определения, приведенного в задании 3.
5. Сформулируйте теорему о локальной ограниченности непрерывной
функции.
6. Докажите, что теорема о локальной ограниченности функции остает-
остается в силе, если условие непрерывности функции в точке хо заменить
условием существования lim f(x).
X^-XQ
7. Сформулируйте теорему об устойчивости знака непрерывной функции.
8. Известно, что f(x) непрерывна в точке хо и /(ж<э) = 0. Можно ли утверж-
утверждать, что /(х):
а) имеет определенный знак в некоторой окрестности точки ж0 (кроме
самой точки жо);
б) не имеет определенного знака ни в какой окрестности точки хо?
9. Сформулируйте первую теорему Вейерштрасса.
10. Справедливо ли утверждение: непрерывная на интервале функция огра-
ограничена на этом интервале?
11. Может ли неограниченная на множестве X функция быть непрерывной
на этом множестве, если: а) X — сегмент; б) X — интервал?
12. Дайте определение точной верхней и точной нижней грани функции. В
каком случае полагают inf/(ж) = — оо?
110 Гл. VI. Непрерывные и дифференцируемые функции
13. Справедливо ли утверждение: ограниченная сверху (снизу) на мно-
множестве X функция имеет на этом множестве точную верхнюю (ниж-
(нижнюю) грань?
14. Сформулируйте вторую теорему Вейерштрасса.
15. Справедливо ли утверждение: непрерывная и ограниченная на интер-
интервале функция достигает на этом интервале своих точных граней?
16. Справедливо ли утверждение: если функция не достигает на сегменте
[а, Ь] своей точной верхней (или нижней) грани, то она разрывна на этом
сегменте?
17. Справедливо ли утверждение: разрывная на сегменте [а, Ь] функция не
достигает на этом сегменте своих точных граней?
18. Справедливы ли следующие утверждения:
а) ограниченная на сегменте [а, Ь] функция у = /(ж) имеет max/(ж) и
min/fr); [aM
[а,Ъ]
б) непрерывная на сегменте [а, Ь] функция имеет max/(ж) и тт/(ж)?
[а,Ъ] [а,Ъ]
19. Справедливы ли утверждения задания 18, если сегмент [а, Ь] заменить
интервалом (а, Ь)?
Примеры решения задач
1. Доказать, что функция у = ограничена на числовой пря-
прямой (—оо, +оо).
Л Так как х2 ^ 0, то 1 + х2 ^ 1 и, следовательно, \/х Е (—оо,+оо)
выполняются неравенства
Отсюда следует, что функция у = ограничена на (—оо, +оо). А
л. —|— X
2. Найти точные грани функции из примера 1 и установить, имеет
ли она максимальное и минимальное значения.
Л Из неравенств A) следует, что числа т = 0 и М = 1 — соответ-
соответственно нижняя и верхняя грань функции у = -. Докажем, что
эти числа и являются точными гранями данной функции. Так как
—> 0 при х —> оо, то VW > 0 Зх' такое, что — < т'. Та-
Таким образом, никакое положительное число т' не является нижней
гранью функции, а значит, число т = 0 — наибольшая из нижних
граней, т. е. inf = 0.
(-оо, + оо) 1 +Х2
При х = 0 значение функции равно 1. Следовательно, никакое чис-
число, меньшее 1, не является верхней гранью функции. Иначе говоря,
наименьшая верхняя грань функции равна 1. Итак, sup f(x) = 1.
( —оо,+оо)
Заметим теперь, что, в отличие от значения 1, которое функция
принимает при х = 0, значение 0 не принимается функцией ни при
§1. Ограниченность непрерывных функций 111
каком х (\/х > 0). Поэтому данная функция имеет на числовой
прямой (—оо,+оо) максимальное значение: max = 1, но не
( —оо, + оо) 1 + X
имеет минимального значения. А
Задачи и упражнения для самостоятельной работы
1. Докажите ограниченность функции:
а) у = на полупрямой [0,+оо);
1 + х2
2х
б) у = на числовой прямой (—оо,+оо);
1 + X2
в) у = х sin — на (—оо, +оо); г) у = arctg 2х на (—оо, +оо);
х
д) у = хе~х на @,+оо).
2. Ограничены ли следующие функции:
а) у = х2 на [-5,10]; б) у = х2 на [-5, +оо);
в) у = xcos(l/x) на (—оо,+оо);
г) Г ^/(-D при х ,4 1, на@2)
' [0 при х = 1 v ' "
д)у = 21/(*-1) на @,1)?
3. Приведите пример функции, которая на некотором множестве X:
а) ограничена сверху, но не ограничена снизу;
б) ограничена снизу, но не ограничена сверху;
в) не ограничена снизу и сверху.
4. Пусть функция f(x) определена на множестве X и пусть VxGl су-
существует окрестность, в которой f(x) ограничена. Следует ли отсюда
ограниченность f(x) на X, если:
а) X — интервал; б) X — сегмент?
5. Приведите пример функции /(ж), которая непрерывна и равна нулю в
некоторой точке хо и:
а) имеет определенный знак в некоторой окрестности точки хо (кроме
самой точки жо);
б) не сохраняет знака ни в какой окрестности точки хо.
6. Приведите пример функции, непрерывной на интервале, но не ограни-
ограниченной на нем:
а) сверху; б) снизу; в) с обеих сторон.
7. Постройте пример функции, определенной на [а, Ь], но не ограниченной
на [а, Ь\:
а) сверху; б) снизу; в) с обеих сторон.
Может ли такая функция быть непрерывной на [а, Ъ]1
8. Найдите точные грани функции:
a) f{x) = -^-з на @, +оо); б) f(x) = х2 на [-5,10];
1 -\- х
в) /(ж) = arctg 2х на (—оо, +оо); г) f(x) = sin x + cos х на [0, тг];
д) /(ж) = 2l'{x-l) на @,1).
Достигает ли f(x) своих точных граней на указанном множестве?
112 Гл. VI. Непрерывные и дифференцируемые функции
9. Приведите пример функции /(ж), у которой:
a) sup/(ж) = +оо; б) inf f(x) = — оо.
х х
10. Постройте пример непрерывной и ограниченной на интервале функции,
которая на этом интервале:
а) достигает sup, но не достигает inf;
б) достигает inf, но не достигает sup;
в) не достигает sup и inf.
11. Постройте пример ограниченной на сегменте функции, которая на этом
сегменте:
а) достигает sup, но не достигает inf;
б) достигает inf, но не достигает sup;
в) не достигает sup и inf.
Может ли такая функция быть непрерывной на сегменте?
12. Постройте пример функции, которая на некотором множестве X имеет
sup и inf, но не имеет max и min.
13. Найдите колебания функции:
а) f(x)=x2 на (-1,2);
б) /(ж) = sin(l/x) на @,е), где е — произвольное число;
в) /(ж) = xsin(l/x) на @,1);
г) f{x) = фтA/ж)| на @,1).
14. Обозначим через m[f] и M[f] соответственно точную нижнюю и точ-
точную верхнюю грани функции f(x) на множестве X. Пусть fi(x) и /2 (ж)
определены и ограничены на X. Докажите, что
m[fi + /2] ^ m[/i] + m[/2], M[h + /2] ^ М[/i] + M[/2].
Постройте примеры функций fi(x) и /2(ж), для которых в указанных соот-
соотношениях имеет место: а) знак равенства; б) знак неравенства.
§ 2. Равномерная непрерывность функции
Основные понятия и теоремы
1. Определение равномерной непрерывности функции.
Пусть множество X является промежутком или состоит из несколь-
нескольких промежутков.
Определение. Функция f(x) называется равномерно непрерыв-
непрерывной на множестве X, если \/г > 0 36 = 6(е) > 0 такое, что Vx, x' G X,
удовлетворяющих неравенству \х — х'\ < 6, выполняется неравенство
\f(x)-f(x')\<e.
Замечание. Из определения следует, что если функция равномерно
непрерывна на множестве X, то она непрерывна на этом множестве, т. е. не-
непрерывна в каждой его точке. Отличие равномерной непрерывности функ-
функции на множестве X от "обычной" непрерывности на этом множестве (т. е.
непрерывности в каждой его точке) состоит в том, что при равномерной
непрерывности Vs > 0 найдется "нужное" (такое, какое требуется по опре-
определению) 6(е) > 0, общее для всех х Е X F зависит только от е и не зависит
от ж), а при "обычной" непрерывности Vs > 0 и Ух Е X найдется "нужное" 6
§2. Равномерная непрерывность функции
113
(т. е. 5 зависит и от е, и от ж), но для каких-то е может не существовать
"нужного" 5(в) > О, общего для всех х Е X. Ясно, что в этом случае 5 изме-
изменяется в зависимости от х так (при указанных фиксированных значениях
е), что может принимать сколь угодно малые значения.
2. Геометрическая иллюстрация равномерной непрерыв-
непрерывности функции. Если f(x) рав-
равномерно непрерывна на X, то
\/е > 0 3S(e) > 0 такое, что пря-
прямоугольник со сторонами 6(г) и
г, параллельными осям Ох и Оу,
можно так переместить вдоль
графика (сохраняя параллель-
параллельность сторон осям координат),
что график не пересечет горизон-
горизонтальных сторон прямоугольника,
а будет пересекать только верти-
вертикальные стороны (рис. 5).
3. Теоремы о равномерной
непрерывности функции.
Теорема 5 (теорема Канто- Рис.5
ра). Непрерывная на сегменте функция равномерно непрерывна на
этом сегменте.
Теорема б (достаточное условие равномерной непрерывности
функции). Если функция f(x) имеет на промежутке X ограниченную
производную, то f(x) равномерно непрерывна на этом промежутке*).
О
X
Контрольные вопросы и задания
1. Дайте определение равномерной непрерывности функции.
2. Пользуясь кванторами, сформулируйте отрицание равномерной непре-
непрерывности функции.
3. Справедливы ли следующие утверждения:
а) если f(x) непрерывна на множестве X, то она равномерно непрерывна
на этом множестве;
б) если f(x) равномерно непрерывна на X, то она непрерывна на X?
4. Какова геометрическая иллюстрация равномерной непрерывности
функции?
5. Сформулируйте теорему Кантора.
6. Справедливо ли утверждение: непрерывная на интервале функция рав-
равномерно непрерывна на этом интервале?
7. Сформулируйте теорему, выражающую достаточное условие равномер-
равномерной непрерывности функции.
8. Является ли ограниченность производной необходимым условием рав-
равномерной непрерывности функции?
*) Напомним, что промежутком называется любое из следующих множеств:
сегмент, интервал, полуинтервал, полупрямая, числовая прямая.
114 Гл. VI. Непрерывные и дифференцируемые функции
Примеры решения задач
1. Исследовать на равномерную непрерывность функцию у = х2
на интервале (—1,1), где I > 0 — любое фиксированное число.
Л Докажем, что функция у = х2 равномерно непрерывна на интерва-
интервале (—1,1), причем сделаем это тремя способами: 1) пользуясь опреде-
определением равномерной непрерывности; 2) используя теорему Кантора;
3) используя достаточное условие равномерной непрерывности.
1) Составим разность у(х\) —
у(хг) - у(х2) =xj-xj = Oi + х2)(хг - х2). A)
Если xi,x2 G (—1,1), то модуль суммы \xi + х2\ ограничен числом 21.
Поэтому модуль разности \у(х±) — у(х2)\ будет сколь угодно малым
для любых х\,Х2 Е (—1,1), если только модуль разности \х\ — х2\ до-
достаточно мал. Эти качественные рассуждения показывают уже, что
функция у = х2 равномерно непрерывна на интервале (—1,1).
Проведем теперь более строгие рассуждения, пользуясь опреде-
определением равномерной непрерывности. Зададим произвольное г > 0 и
положим 6 = г/B1). Тогда \lx\,x2 Е (—1,1), удовлетворяющих нера-
неравенству \xi - х2\ < 6, выполняется неравенство
\у(хг) - у(х2)\ = |xi - х2\ • \х! + х2\ < S • 21 = е.
Это и означает по определению, что функция у — х2 равномерно не-
непрерывна на интервале (—1,1).
2) Рассмотрим функцию у — х2 на сегменте [—1,1]. Она непрерывна
на этом сегменте и, следовательно, по теореме Кантора равномерно
непрерывна на нем. Отсюда следует, что функция у — х2 равномер-
равномерно непрерывна на интервале (-1,1). В самом деле, (—/,/) С [—/,/], и
так как неравенство \у(х±) — у(х2)\ < г выполняется \/х±,х2 G [—1,1],
удовлетворяющих неравенству \х\ — х2\ < 8(е), то оно выполняется
и для любых х\,х2 G (—1,1), удовлетворяющих тому же неравенству.
3) Производная у'(х) = 2х ограничена на интервале (—1,1):
\у'(х)\ = 2\х\ ^ 21. Отсюда по теореме б следует, что функция у — х2
равномерно непрерывна на (—1,1). А
2. Исследовать на равномерную непрерывность функцию у — х2
на всей числовой прямой.
Л Из выражения A) видно, что если х\,х2 G (—оо,+оо), то при сколь
угодно малом модуле разности |^i — ж21 модуль разности
\у(х\) — у(х2)\ не будет мал при достаточно больших х\ и х2 из-за мно-
множителя (х\ -\-х2). Это качественное рассуждение наводит на мысль,
что функция у = х2 не является равномерно непрерывной на всей
прямой (—оо,+оо). Докажем это, пользуясь отрицанием определения
равномерной непрерывности. Нужно доказать, что Зг > 0 такое, что
\/5 > 0 Зх\,х2, удовлетворяющие неравенству \х\ — х2\ < 6, для ко-
которых \у(х±) -у(х2)\ ^г.
§2. Равномерная непрерывность функции 115
Возьмем г = 1 и VS > 0 положим х\ — 1/8 + 8/2, х2 = 1/8. Тогда
— х2\ = й/2 < й, но при этом
\y{xi) - у{х2)\ = ki - ж2||ж1 + ж2| = - ^ + -J = 1 + —
Это доказывает, что функция у = х2 не является равномерно непре-
непрерывной на (—оо,+оо). А
Задачи и упражнения для самостоятельной работы
15. Пользуясь определением равномерной непрерывности и его отрицани-
отрицанием, докажите, что функция у = 1/х:
а) равномерно непрерывна на полупрямой [1,+оо);
б) не является равномерно непрерывной на полупрямой @,+оо).
16. Приведите пример функции, которая непрерывна на некотором интер-
интервале, но не является на нем равномерно непрерывной.
17. Докажите равномерную непрерывность следующих функций, пользу-
пользуясь только определением равномерной непрерывности (т. е. выбирая
по заданному произвольному е нужное 8 = 8{е)):
а) /(ж) = кх + Ъ на (-оо, +оо), к / 0; б) /(ж) = ж3 на (-3, 5);
в) /(ж) = sin ж на (—оо, +оо); г) /(ж) = ех на [0, 10].
18. Исследуйте на равномерную непрерывность следующие функции (лю-
(любым способом):
а) /(ж) = 1п(ж) на @,1) и на A, 2);
б) /(ж) = sin(l/a) на @,1) и на @,01; 1);
в) /(ж) = ап^ж на (—оо, +оо);
г) /(ж) = агсвтж на (—1,1); д) f(x) = л/х на [0, +оо);
е) /(ж) = ж sin - на @,1); ж) /(ж) = е/ж на @,1);
з) /(ж) = ж sin ж на (—оо, +оо); и) /(ж) = sin2 ж на (—оо, +оо);
к) /(ж) = sin(x2) на (-оо, +оо); л) /(ж) = е~х на @, +оо).
19. Докажите, что функция /(ж) = равномерно непрерывна на ин-
х
тервалах 1\ = (—1 < ж < 0) и /2 = @ < ж < 1), но не является равномерно
непрерывной на их сумме Д + /2 = {0 < |ж| < 1}.
20. Докажите, что если функция /(ж) равномерно непрерывна на каждом
из сегментов [а, с] и [с, Ь], то она равномерно непрерывна на сегменте
[а,Ъ].
21. а) Докажите, что если функция /(ж) определена и непрерывна на по-
полупрямой [а,+оо) и существует lim /(ж), то /(ж) равномерно непре-
непрерывна на [а,+оо). ж-^+оо
б) Приведите пример функции, равномерно непрерывной на полупря-
полупрямой [а,+оо), у которой lim /(ж) не существует.
х—^ + оо
22. Приведите пример функции, которая имеет неограниченную производ-
производную на множестве X, но является равномерно непрерывной на этом
множестве.
23. Докажите, что равномерно непрерывная на интервале функция огра-
ограничена на этом интервале. Верно ли обратное утверждение?
24. Докажите, что сумма и произведение двух равномерно непрерывных
на интервале функций равномерно непрерывны на этом интервале.
116 Гл. VI. Непрерывные и дифференцируемые функции
25. Модулем непрерывности функции /(ж) на промежутке (а, Ъ) (а и Ъ мо-
могут быть соответственно равны — оо и +оо) называется следующая
функция аргумента 6 F > 0):
ш}E)= sup
(если \f(xi) — f(x%)\ является неограниченной функцией при {\х± —
— Х2\ ^ S] х\,хъ G (а,Ь)}, то пишут uJf(S) = +оо).
а) Докажите, что для равномерной непрерывности функции /(ж) на
промежутке (а, Ь) необходимо и достаточно, чтобы \imujf(S) = 0.
<5 —> О
б) Приведите пример функции /(ж), х Е (а, 6), для которой ujf(S) = +оо.
26. Пусть функция /(ж) непрерывна на множестве X, т. е. непрерывна в
каждой точке ж Е X. Тогда Vs > 0 и \/ж Е X 3? = 5(е, ж) > 0 такое, что
из неравенства |ж' — ж| < ?(е,ж) (ж7 Е X) следует неравенство [/(ж7) —
—/(ж)| < е. Докажите, что для равномерной непрерывности функции
/(ж) на множестве X необходимо и достаточно, чтобы существовала
функция 6(х,у) такая, что inf 6(е,х) > 0 (Ve > 0).
§ 3. Некоторые теоремы о дифференцируемых функциях
Основные понятия и теоремы
1. Возрастание функции в точке.
Определение. Говорят, что функция /(ж) возрастает в точке
жо, если существует такая окрестность точки ж0, в которой f(x) >
> /Оо) при х > х0, /О) < /Оо) при х < х0.
Аналогично определяется убывание функции в точке.
Теорема 7 (достаточное условие возрастания функции в точке).
Если функция /О) дифференцируема в точке хо и /'Оо) > 0 (/'Оо) <
< 0), то /(ж) возрастает (убывает) в точке xq.
2. Теоремы о возрастании и убывании функции на про-
промежутке.
Определение. Говорят, что функция /(ж) возрастает (не убы-
убывает) на промежутке X, если \/xi,x2 G X из условия х\ < х2 следует
неравенство f(x\) < f(x2) (соответственно f(x\) ^ f(x2))-
Аналогично определяется убывание (невозрастание) функции на
промежутке.
Теорема 8. Для того чтобы дифференцируемая на промежутке
X функция /(ж) не убывала (не возрастала) на этом промежутке,
необходимо и достаточно, чтобы Vx G X выполнялось неравенство
/'О)^о (/'Око).
Теорема 9 (достаточное условие строгой монотонности функ-
функции). Если /'(ж) > 0 (/'О) < 0) \/х G X, то f(x) возрастает (убывает)
на промежутке X.
§3. Теоремы о дифференцируемых функциях 117
3. Теоремы Ролля, Лагранжа и Коши.
Теорема 10 (теорема Ролля). Пусть функция f(x) удовлетворя-
удовлетворяет условиям:
1°) f{x) непрерывна на [а, 6];
2°) f(x) дифференцируема в (а, Ь);
3°) /(а) = /(&).
Тогда существует точка с Е (а, Ь) такая, что f'(c) = 0.
Физическая интерпретация теоремы Ролля. Пусть х — время,
f(x) — координата точки, движущейся по прямой, в момент време-
времени х. В начальный момент х — а точка имеет координату /(а), далее
движется определенным образом со скоростью f'{x) и в момент вре-
времени х — Ь возвращается в точку с координатой /(a) (f(b) = f(a)).
Ясно, что для возвращения в точку /(а) она должна остановиться в
некоторый момент времени (прежде чем "повернуть назад"), т. е. в
некоторый момент х = с скорость /'(с) = 0.
Геометрическая интерпретация теоремы Ролля. Существует точ-
точка с Е (а, Ь) такая, что касательная к графику функции у = f(x) в
точке (c,f{c)) параллельна оси Ох.
Теорема 11 (теорема Лагранжа). Пусть функция f(x) удовлет-
удовлетворяет условиям:
1°) f(x) непрерывна на [а,Ь];
2°) f(x) дифференцируема в (а,Ь).
Тогда существует точка с Е (а, Ь) такая, что
f(b)-f(a) = f(c)(b-a). A)
Формула A) называется формулой Лагранжа (или формулой конеч-
конечных приращений).
Физическая интерпретация теоремы Лагранжа. Пусть х — время,
f(x) — координата точки, движущейся по прямой, в момент време-
времени х. Запишем формулу Лагранжа в виде
№ - /(а) _ ,,(А
Ь-а -J^C)'
Величина в левой части равенства является, очевидно, средней ско-
скоростью движения точки по прямой за промежуток времени от а до Ъ.
Формула Лагранжа показывает, что существует такой момент време-
времени х = с, в который мгновенная скорость равна средней скорости на
временном отрезке [а, Ъ].
Геометрическая интерпретация теоремы Лагранжа. Число
f(b)-f(a)
^-^—-^—- является угловым коэффициентом прямой, проходящей че-
о — а
рез концы графика функции у = f(x) — точки (a,f(a)) и F, /(Ь)),
a f'(c) — угловым коэффициентом касательной к графику в точке
(с,/(с)). Формула Лагранжа показывает, что касательная к графи-
графику в некоторой точке (c,f(c)) параллельна прямой, проходящей через
концы графика (или совпадает с ней).
118 Гл. VI. Непрерывные и дифференцируемые функции
Теорема 12 (теорема Коши). Пусть функции f(x) и д(х) удовле-
удовлетворяют условиям:
1°) f(x) и д(х) непрерывны на [а,Ь];
2°) f(x) и д(х) дифференцируемы в (а, Ь);
3°) ф)/0 VxG (а, Ъ).
Тогда существует точка с Е (а, Ь) такая, что
№ - /(а) = /Чс) (,
g(b)-g(a) g'(c)' У }
Формула B) называется формулой Коши.
Контрольные вопросы и задания
1. Дайте определение возрастания (убывания) функции в точке.
2. Сформулируйте теорему, выражающую достаточное условие возраста-
возрастания функции в точке.
3. Справедливы ли следующие утверждения:
а) если функция возрастает в точке жо, то она имеет в этой точке по-
положительную производную;
б) если дифференцируемая в точке жо функция /(ж) возрастает в этой
точке, то /'(жо) > О?
4. Сформулируйте теорему, выражающую необходимое н достаточное
условие монотонности дифференцируемой функции на промежутке.
5. Сформулируйте теорему, выражающую достаточное условие строгой
монотонности дифференцируемой функции на промежутке.
6. Справедливо ли утверждение: если дифференцируемая на промежутке
X функция /(ж) возрастает на этом промежутке, то f (х) > 0 Уж G XI
7. Пусть функция /(ж) определена в некоторой окрестности каждой точки
множества X. Справедливы ли утверждения:
а) если /(ж) возрастает на множестве X, то она возрастает в каждой
точке жо G X;
б) если /(ж) возрастает в каждой точке жо G X, то она возрастает на
множестве XI (Рассмотрите функцию /(ж) = —1/ж.)
8. Сформулируйте теорему Ролля.
9. Останется ли справедливой теорема Ролля, если опустить условие:
а) /(а) = /(&); б) /(ж) непрерывна на [а, Ъ]1 Приведите соответствующие
примеры.
10. Сформулируйте теорему Лагранжа.
11. Сформулируйте теорему Коши.
Примеры решения задач
1. Найти промежутки монотонности функции f(x) = Зх — х3.
А Имеем f'(x) = 3 - Зх2 = 3A-ж2). Так как f'(x) > 0 при х G
G (-1,1), f'(x) < 0 при х G (-оо, -1) и х G A, оо), то функция f(x) =
= Зх - х3 возрастает на интервале (-1,1) и убывает на полупрямых
(—оо,—1) и A,+оо); можно также сказать, что /(ж) возрастает на
сегменте [—1,1] и убывает на полупрямых (—оо,—1] и [1,+оо). А
§3. Теоремы о дифференцируемых функциях 119
2. Доказать, что функция
_ { х -\- х2 sinB/x) при х/0,
\ 0 при ж = 0
возрастает в точке ж = 0, но не является возрастающей ни на каком
интервале (—?,?) (е > 0 — произвольное число).
Л Имеем
+ 2ж sinB/x) - 2 со8B/ж) при ж ф О,
1 при ж = О
(по поводу вычисления /'@) см. пример б из § 1 гл. IV).
Так как /'(О) = 1 > 0, то по теореме 7 функция /(ж) возрастает в
точке ж = 0.
Если бы /(ж) возрастала на некотором интервале (-г, г), то соглас-
согласно теореме 8 выполнялось бы условие /'(ж) ^ 0 Уж Е (—г,г). Пока-
Покажем, что это не так. Положим хп = 1/(ттп) (п — натуральное число).
Очевидно, что \/г > 0 Зп такое, что 1/(тгп) < г, т. е. хп Е (—г,г).
Подставляя ж = жп = 1/(ттп) в выражение для /'(ж) при ж /0, полу-
получим f'(xn) = -1 < 0. Это доказывает, что функция /(ж) не является
возрастающей ни на каком интервале (—?,?). A
3. Пусть функция /(ж) удовлетворяет условиям: 1) /(ж) имеет не-
непрерывную производную на [а, Ь]; 2) /(ж) имеет вторую производную
в (а, Ь); 3) /(а) = /'(а) — 0, /(Ь) = 0. Доказать, что существует точка
с е (а,Ь) такая, что f"(c) = 0.
Л Очевидно, что для функции /(ж) на сегменте [а, Ь] выполнены все
условия теоремы Ролля. Поэтому существует точка d e (а,Ь) такая,
что f'(d) = 0.
Рассмотрим функцию /'(ж) на сегменте [a, d]. Имеем: 1) /'(ж) не-
непрерывна на [а, б?]; 2) /'(ж) имеет производную (/'(ж))' = f"{x) в
(а, d); 3) f'(a) = f'(d) = 0. В силу теоремы Ролля существует точка
с е (a, d) (и, следовательно, с е (а, Ь)) такая, что (/'(ж))'|ж=с = /"(с) =
= 0. А
4. Доказать, что | cos ж - cos^/| ^ |ж - ?/| Уж, 2/.
Л По формуле Лагранжа
cos ж — cos у = sin? • (ж — у),
где ? — некоторая точка из интервала (х,у). Так как |sin?| ^ 1, то
| cos ж — cos у\ ^ |ж — у\. А
5. Пусть функции /(ж) и д(ж) определены и дифференцируемы при
ж ^ ж0, причем /(ж0) = #(жо), f'(x) > д'{х) ПРИ ж > хо- Доказать, что
/(ж) > д(х) при ж > ж0.
Л Рассмотрим функцию (р(ж) = /(ж) — д(ж) на произвольном сегменте
[жо,ж] (ж > хо). По формуле Лагранжа
(р(х) - (р(х0) = <р'(?)(х - х0), C)
120 Гл. VI. Непрерывные и дифференцируемые функции
где ? — некоторая точка из интервала (жо,ж). Так как
- д(х0) = 0, if'@ = /'(?) - я'(О > 0. х - х0 > 0,
то из равенства C) получаем (р(х) > 0, т. е. f(x) — д(х) > 0 при х > xq.
Таким образом, /(ж) > д{х) при х > xq. A
Задачи и упражнения для самостоятельной работы
27. Найдите промежутки монотонности функций:
a) /(ж) = ах2 -\-bx-\-c (а > 0); б) f(x) = ж3 + Зж2 + Зж;
2ж
в) /(ж) = -; г) fix) = ж + sin ж; д) /(ж) = ж + 2 sin ж;
1 + х2
е) /(ж) = sinGr/aO; ж) /(ж) = ж22"ж; з) /(ж) = жпе"ж (п > 0, ж ^ 0).
28. При каких значениях а функция /(ж) = ах + sin ж возрастает (убывает)
на числовой прямой?
29. Докажите, что если функция возрастает в каждой точке интервала, то
она возрастает на этом интервале. Останется ли верным это утверж-
утверждение, если интервал заменить произвольным множеством?
30. Функции /(ж) и д(х) удовлетворяют на [а, Ь] условиям теоремы Ролля
и, кроме того, /(ж) /0и д(х) ф 0 на [а, 6]. Докажите, что существуют
точки ci, C2 G (а, 6) такие, что
/Ы S(ci)' Дс2)
31. Пусть функция /(ж) удовлетворяет условиям:
1) /(ж) имеет непрерывную (п — 1)-ю производную на [жо,жп];
2) /(ж) имеет n-ю производную в (жо,жп);
3) f(xo) = f(xi) = ... = /(жп), где ж0 < Ж1 < ... < хп.
Докажите, что существует точка ? Е (жо,жп) такая, что /(гг)(?) =0.
32. Используя теорему Ролля, докажите, что если все корни многочлена
Рп(х) = аохп + сцх*1'1 + ... + ап (а0 ф 0)
с вещественными коэффициентами а& (к = 0,1, ...,п) вещественны, то
его производные Р^(ж),Р"(ж),...,Р™ (ж) также имеют лишь вещест-
вещественные корни.
33. Докажите, что все корни многочлена Лежандра
вещественны и лежат в интервале (—1,1).
34. Найдите точку с в формуле конечных приращений A) для функции
fM= f 0,5C-ж2) при 0^ж^1,
п ' \ 1/ж при 1<ж<+оо
на сегменте [0, 2].
35. Используя формулу Лагранжа, докажите справедливость неравенств:
а) | sin ж - sin у\ ^ |ж - у\ \/ж, г/;
б) |arctgж— arctg у| ^ |ж — у\ Ух,у;
в) ?Л^ < In - < ^^ при 0 < у < ж.
ж У У
§4- Правило Лопиталя 121
36. Докажите, что если производная функции во всех точках промежутка
равна нулю, то функция является постоянной на этом промежутке.
Используя это утверждение, докажите тождества:
2х
а) 2 arctg ж + arcsin = тг при ж ^ 1;
1 + х2
ч \/1 — X 1 . 7Г ., .,
б) arctg Н— arcsin ж = — при — 1 < ж < 1;
1-х2
в) arccos — 2 arctg ж = 0 при х ^ 0.
37. Докажите справедливость неравенств:
а) ех > 1 + х при ж / 0;
б) х - ^- < 1пA + х) < х при х > 0;
в) 1пA + ж) > —^— при ж > 0;
1 ~\~ х
т3
г) ж — —г < sin ж < ж при ж > 0;
о!
т3 тг
д) ж + — < tgж при 0 < ж < -;
о 2
е) Ъха — ахъ < b — а при ж > 1, 0 < а < Ъ.
Проиллюстрируйте эти неравенства геометрически.
38. Пусть функции /(ж) и д(х) определены и п раз дифференцируемы при
ж ^ жо, причем /<*>(*(,) = ?(fc)M (Л = 0,1,..., п - 1); fn\x) > д^п\х)
при ж > жо. Докажите, что /(ж) > д(ж) при ж > жо.
39. Докажите утверждения:
а) если функция имеет на интервале ограниченную производную, то и
сама функция ограничена на этом интервале;
б) если функция дифференцируема, но не ограничена на интервале, то
ее производная также не ограничена на этом интервале.
Приведите пример, показывающий, что обратное утверждение невер-
неверно.
40. Пусть функции /(ж), д(х) и h(x) непрерывны на [а, Ь] и дифференци-
руемыв(а,6),а /(ж) ^ ад
F(x)= /(a) g(a) h(a)
№ д(Ъ) h(b)
Докажите, что существует точка с Е (а, Ь) такая, что F'(с) = 0. Исполь-
Используя это утверждение, выведите формулы Лагранжа и Коши.
41. Справедлива ли формула Коши для функций /(ж) = ж2 и д{х) = ж3 на
сегменте [—1,1]? Какое условие теоремы Коши не выполнено для этих
функций?
42. Пусть функция /(ж) удовлетворяет условиям: 1) /(ж) непрерывна на
[а, Ь]; 2) /(ж) дифференцируема в (а, Ь); 3) /(ж) не является линейной
функцией. Докажите, что существует точка с Е (а, Ь) такая, что \f(b) —
-f(a)\<\f'(c)\-\b-a\.
43. Пусть функция /(ж) удовлетворяет условиям: 1) /(ж) дважды диффе-
дифференцируема на [а, Ь]; 2) /'(а) = /'F) = 0. Докажите, что существует
точка с Е (а, 6) такая, что |/(Ь) - /(а)| ^ A/4)(Ь - аJ|/"(с)|.
44. За время ? с точка прошла по прямой расстояние s м. В начальный
и конечный моменты времени скорость точки равна нулю. Докажи-
Докажите, что в некоторый момент времени абсолютная величина ускорения
точки была не меньше 4s/?2 м/с2.
122 Гл. VI. Непрерывные и дифференцируемые функции
§ 4. Правило Лопиталя
Основные понятия и теоремы
Теорема 13. Пусть выполнены условия:
1°) функции f(x) и д(х) определены и дифференцируемы в некото-
некоторой окрестности точки а {кроме, быть может, самой точки а);
2°) lim /(ж) = lim g(x) = 0;
ж —>а ж —>а
3°) д'(х) /Об указанной окрестности точки а [кроме, быть мо-
может, самой точки а);
fix)
4°) существует lim .; (
х^а д'(
lim .; (.
х^а д'(х)
Тогда существует lim ^-^-, и он равен lim ,. {.
х^а д(х) х^а д'(х)
Замечание. Если все условия теоремы 13 выполнены в правой (левой)
полуокрестности точки а, то теорема верна в отношении правого (левого)
предела функции f(x)/g(x) в точке а.
Теорема 14. Пусть выполнены условия:
1°) функции f(x) и д(х) определены и дифференцируемы на полу-
полупрямой (а, +оо);
2°) lim f(x) = lim g(x) = 0;
ж-^+оо ж-^+оо
3°) g'(x) /0 Va;G (a,+oo);
f'(x)
4°) существует lim ,, (.
ж^+оо g'yx)
Тогда существует lim ^-7—г, и он равен lim ; '.
ж-^+00 дух) ж-^+оо д ух)
Замечание. Если условие 4°) в теоремах 13 и 14 заменить условием
,. /'0*0 / ч ,. f(x)
lim .. . =00 (а — число или символ +оо), то lim . . = 00.
х^а д'ух) х^а д(х)
Теоремы 13 и 14 позволяют раскрывать неопределенности типа
0/0.
Теорема 15. Если выполнены условия 1°), 3°), 4°) теорем 13 и
14, а вместо условия 2°) выполнено условие lim f(x) = lim g(x) = оо
ж—>а х—Уа
fix)
(а — число или символ +оо), то существует lim ^-^-, и он равен
hm ^f^.
р()
Теорема 15 позволяет раскрывать неопределенности типа оо/оо.
Она справедлива также в отношении односторонних пределов.
Каждая из теорем 13-15 называется правилом Лопиталя. Неопре-
Неопределенности других типов @ • оо; оо - оо; 1°°; 0°; оо°) можно свести
к неопределенностям типа 0/0 или оо/оо и затем применять правило
Лопиталя.
§4- Правило Лопиталя 123
Контрольные вопросы и задания
1. Сформулируйте правило Лопиталя раскрытия неопределенности типа:
а) 0/0 при х —»> а; б) 0/0 при х —»> +оо;
в) оо/оо при ж —>- а; г) оо/оо при ж —»- +оо.
2. Пусть выполнены условия 1°)-3°) теоремы 13 (или теоремы 14, или
fix)
теоремы 15) и пусть не существует lim ——. Следует ли отсюда, что
х-ьа д'(х)
не существует hm ; с
х^-а дух)
ч x2sin(l/x) ч + i
Рассмотрите примеры: a) hm Н^—-\ б) hm
2х + sin ж
Примеры решения задач
_, тт „ ,. sin ах
1. Найти hm —.
ж-И) tgpx
А Данный предел является неопределенностью типа 0/0. Проверим,
выполнимость условий теоремы 13:
1°) функции s'max и tg/Зх определены и дифференцируемы в не-
некоторой окрестности точки х = 0;
2°) Hm sin ax = lim tgdx = 0;
3°) (tgCx)' = —у—- ф 0 в окрестности точки х — 0;
COS д^Ж
.оч ,. (sinax) ,. a cos аж а
4 ) hm — = hm = —
J x^o (tgf3x)f x^o f3/(cos2 f3x) 0
Следовательно, по теореме 13 hm — = —. A
x^o tg/3x /3
Иногда для раскрытия неопределенности приходится применять
правило Лопиталя последовательно несколько раз, как в следующем
примере.
2. Найти
lim *?f? A)
х^О X3 V J
А Этот предел является неопределенностью типа 0/0. Условия
1°)-3°) теоремы 13 выполнены, а предел отношения производных
,. (tgx — х)' ,. 1/cos2 х — 1 /оЧ
hm v 6 y hm -^—-— B)
х^о (х3)' х^о Зх2 v J
также является неопределенностью типа 0/0.
Для предела B) выполнены условия 1°)-3°) теоремы 13, а предел
отношения производных
,. A/cos2 ж — lV ,. 2cos~3xsinx /оЧ
hm v ' —- = hm C)
x^o (Зх2)' x^o 6x v '
снова является неопределенностью типа 0/0.
124 Гл. VI. Непрерывные и дифференцируемые функции
Для раскрытия этой неопределенности также можно воспользо-
воспользоваться правилом Лопиталя, поскольку для предела C) условия 1°)-3°)
теоремы 13 выполнены и предел отношения производных есть
,. Bcos~3xsinxV ,. 6cos~4xsin2 х + 2cos~2 х 1 //|Ч
hm 7—-, = hm = -. D)
ж^О Fж)' ж^О 6 3 V J
Итак, в силу B)-D) искомый предел A) равен 1/3. А
3. Найти Hm хх.
Л Данный предел является неопределенностью типа 0°. Представим
хх в виде ех1пх и рассмотрим Hm (ж In ж). Этот предел является не-
х>+0
определенностью типа 0 • оо. Записав ж In ж в виде -г-гт приходим к
{1/х)
неопределенности типа оо/оо. Нетрудно проверить, что для Hm ——
ж-Ц-0 1/х
выполнены все условия теоремы 15 для односторонних пределов (про-
(проверьте это самостоятельно). Применив правило Лопиталя, получим
,. In ж т 1/х v / \ л
hm —- = Hm /. = Hm (-ж) = 0.
ж-Ц-0 1/Х ж-Ц-0 —1/х2 ж-Ц-0
Отсюда следует, что Hm хх = Hm exlnx = е° = 1. А
^+0 ^+0
Задачи и упражнения для самостоятельной работы
Найдите следующие пределы.
45. lim — (а > 0). 46. lim — (а > 0, а > 1).
х—>- + оо Ха х—>- + оо пх
Л„ Л. sinax л а л- tgx — х .. chx — cos ж
47. hm . 48. hm — . 49. hm .
ж-^о sin/^ж x-i 2
50. lim fx--)ctg2x. 51. lim 1+
ж-^тг/2 \ 2/ ж-^Зтг/4 1 —
— 2 COS2 X
ро arcsinx ро ж клл- ln(sinax) . .
52. hm . 53. hm . 54. hm —) f (a > 0, /3 > 0).
ж-^о x ж-^о arccosx ж-^+о ln(sin/to)
^^ ,. cos(sinx) — cosx ^л ,. е-1/ж , ^ч
55. hm—^ '- . 56. hm (a > 0).
x^O X4 x^+0 Xa
57. lim aX ~ XU . 58. limB-x)tgGr;c/2). 59. lim (t
ж—^а Ж — a ж—>-1 ж—^тг/4
60. hm x /x. 61. hm . 62. hm —
ж-^ + оо ж-^0 \ X ) ж-^0 \ X )
63. lim fi - -^^V 64. lim (— - —^—). 65. lim fctgx- i).
ж—>-o \x ex — 1 / ж—>-i \1пж ж — 1/ ж—>-o V x/
66. lim A + жI/ж-е. 67. lim ^ ~ пХ . 68. lim 1
ж—>-0 X x^-a X — a x—>¦! —0
§ 5. Формула Тейлора 125
§ 5. Формула Тейлора
Основные понятия и теоремы
1. Многочлен Тейлора. Пусть функция /(ж) п раз дифферен-
дифференцируема в точке xq. Многочлен
к=0
называется многочленом Тейлора для функции f(x) (с центром в точ-
точке хо). Он обладает следующим свойством:
Роль многочлена Тейлора раскрывает следующая теорема.
Теорема 16. Если функция f(x) определена в некоторой окрест-
окрестности точки хо и п раз дифференцируема в точке жо, то
f(x)=Pn(x)+Rn+1(x), A)
где Rn+1(x) = о((х - хо)п).
Формула A) называется формулой Тейлора для функции f(x) с
центром в точке ж0 и остаточным членом Rn+1(x) в форме Пеано.
2. Различные формы остаточного члена.
Теорема 17. Пусть функция f(x) определена и п + 1 раз диф-
дифференцируема в некоторой окрестности точки xq. Пусть х — про-
произвольное значение аргумента из этой окрестности, р > 0 — произ-
произвольное число. Тогда существует точка ? Е (хо,х) такая, что
Rn+i(x) = f{x) - Рп{х) = (Ж~^+1 (^y)P/(w+1)@- B)
Выражение B) называется общей формой остаточного члена.
Наиболее важны следующие частные случаи общей формы оста-
остаточного члена:
а) форма Лагранжа (р = п + 1)
Rn+i(x) = ( Хо* /(п+1)(жо + 0(х - хо)) @ < 0 < 1);
б) форма Коши (р = 1)
Rn+i(x) = ——j-^ — рп+1'(хъ + в(х — хо)) @ < в < 1).
3. Основные разложения. Если хо = 0, то формулу Тейлора
принято называть формулой Маклорена. Важную роль играют еле-
126 Гл. VI. Непрерывные и дифференцируемые функции
дующие разложения по формуле Маклорена.
__ 2к — 1
П.
к=1
п
III. совж = У^(~1)^7^7ТТ + R>2n+2(x)-
к=0
IV. In A + Ж) =
к=1
п
к=1
Контрольные вопросы и задания
1. Что такое многочлен Тейлора для функции f(x) с центром в точке хо?
Каким свойством он обладает?
2. Сформулируйте теорему о формуле Тейлора с остаточным членом: а) в
форме Пеано; б) в общей форме. Как отличаются условия этих теорем?
Условия какой теоремы следуют из условий другой?
3. Выведите из общей формы остаточного члена формы Лагранжа и Коши.
Получите форму Пеано остаточного члена из формы Лагранжа.
4. Напишите формулу Маклорена для функции f(x) и остаточные члены
этой формулы в формах Пеано, Лагранжа и Коши.
5. Напишите основные разложения и остаточные члены этих разложений
в формах Пеано, Лагранжа и Коши.
Примеры решения задач
1. Разложить функцию tgж по формуле Маклорена до члена с ж3
включительно.
Л Найдем производные функции /(ж) = tgж до третьего порядка
включительно:
/'(ж) = —— = cos~2 ж;
cos2 х
/"(ж) = 2 cos~3 ж sin ж;
f'"(x) = б cos~4 ж sin2 ж + 2 cos ж.
Отсюда получаем /@) = 0, /'(О) = 1, /"@) = 0, /'"@) = 2. По формуле
Маклорена с остаточным членом в форме Пеано имеем
tgx = ж + — + о(ж3).
о
Заметим, что вычисление f^\x) дает /^4^@) = 0. Поэтому оста-
остаточный член можно записать в виде о(ж4). А
§ 5. Формула Тейлора 127
2. Разложить функцию f(x) = In cos ж по формуле Маклорена до
члена с ж4 включительно.
Л Здесь нет надобности вычислять производные f(x) до четвертого
порядка, а можно воспользоваться основными разложениями III и IV.
Пользуясь разложением III, получим
In (cos ж) = In A I—- + о(х
х2 х4
Теперь воспользуемся основным разложением IV:
-t)=t-^+o{f) =
3. Оценить абсолютную погрешность приближенной формулы
ех ~1 + х+^ + ... + ^=Рп{х) C)
при 0 ^ х ^ 1.
Л Для получения оценки абсолютной погрешности нужно оценить
остаточный член Rn+i(x) = ех — Рп{х). Остаточный член Rn+i(x)
xn+1
в форме Лагранжа для функции ех имеет вид Rn+i(x) = -( туе
(О < в < 1). Отсюда получаем
|Дп+1(*I^ (^уу при O^x^l. D)
Это и есть искомая оценка абсолютной погрешности приближенной
формулы C) при 0 ^ х ^ 1. А
4. С помощью оценки D) решить следующую задачу: сколько чле-
членов нужно взять в формуле C) при х = 1, чтобы вычислить число е
с точностью 10~6?
Л Нетрудно подсчитать, что 10! > 3 • 106. Поэтому —- < =
= 10~6. Таким образом, достаточно в формуле C) при х = 1 поло-
положить п = 9, чтобы получить число е с точностью 10~6. А
5. Используя основные разложения, найти
,. tgx + 2 sin ж — Зх
Inn — .
4
128 Гл. VI. Непрерывные и дифференцируемые функции
Л Имеем
,. tgж + 2 sin ж — Зж
lim — =
г3 / г3 \
пп _|_ |_ П(™4\ _|_ О ( Г _ |_ П(™4\ \ _ Q~>
= lim ^—; = lim -Ц
ж-^О Ж4 ж-^О Ж^
6. Найти числа а и b такие, что
lim х( ух3 + х2 + ах — ух3 — Ьх2 ) = 3.
х—>-оо
Л Используя формулу Маклорена для A + х)а при а = 1/3, получаем
х2+ах- л/х3 - bx2 ) =x2
- 2Г1 +
" L Зж
9
Чтобы предел этой функции при х —> оо был равен 3, должны быть
выполнены равенства
1 . h n За - 1 + б2
1 + 6 = 0, =3.
Отсюда находим: Ъ = —1, а = 9. А
Задачи и упражнения для самостоятельной работы
69. Разложите функцию f(x) по формуле Маклорена до члена указанного
порядка включительно:
а) /(ж) = е~х до члена с хп\ б) f(x) = e2x~x до члена с ж5;
в) /(ж) = sin sin ж до члена с ж3; г) /(ж) = cos sin ж до члена с ж4;
v x/ v sin ж 6 \ г/ \ з/—. о 13
д) /(ж) = In до члена с ж ; е) /(ж) = vsmr до члена еж;
х
ж) /(ж) = \/ап + ж до члена с ж2 (а > 0);
з) /(ж) = л/1 — ж + 2ж2 до члена с ж3.
70. Напишите разложение по формуле Тейлора с центром в точке ж = 1
функции:
а) /(ж) = ж2; б) /(ж) = л/х до члена с (ж — IK;
в) /(ж) = sinGnc/2) до члена с (ж — IL.
§ 5. Формула Тейлора
129
71. Оцените абсолютную погрешность приближенных формул:
Ж 1 X
a) sinx и ж при |ж| ^ -; б) tgx и ж Н при |ж| ^ 0,1;
6 2 3
/1 + ж й И — при О
в) у/1 + х ж 1 -\ при U ^ ж ^ 1.
72. С помощью формулы Тейлора найдите приближенные значения:
а) \/9 с точностью до 10~3; б) \У90 с точностью до 10~4;
в) sin 18° с точностью до 10~4; г) sinl° с точностью до 10~8;
д) In 1,1 с точностью до 10~3; е) е0'2 с точностью до 10~5;
ж) cos 6° с точностью до 10~5.
73. Используя основные разложения, найдите пределы:
ч ,. cos ж — е~
a) lim
г) lim ж3/2(л/ж + 1 + л/ж - 1 -
д) hm
ж—>-0
2ж2
; е) lim - - -— ;
х—>о \х smx/
ч г 1 /1 \ ч r sin sir
ж) lim — I — — ctg x ; з) lim
ж-^0 X \X J ж-^0 Х5
74. Найдите числа а и Ъ такие, что:
a) lim (л/ж2 + 2ж + л/ж2 — х + ах + 6) = 2;
б) lim
ж—)-О
sin аж — tg 6ж
= 4; в) lim
= 1.
75. Найдите /'@) и /"@), если /(ж) =
-, ж/0,
ж = 0.
76. Докажите, что:
ч ,. fix + Аж) - 2/(ж) + fix - Аж) ?п( \ ( ?п/ \ \
a) hm ^ }-—-^-—^ L = f"(x) (если/7(ж) существует);
Аж—>-0 (Аж)^
л /О + ЗАж) - 3/Q + 2Аж) + 3/Q + Аж) - /(ж) _ Ш( , (
и) nm — — — / ^ж; ^если
Аж-^0 (АжK
f'"(х) существует).
5 В.Ф. Бутузов и др.
ГЛАВА VII
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
И ПОСТРОЕНИЕ ГРАФИКОВ
§ 1. Построение графиков явных функций
Основные понятия и теоремы
1. Асимптоты графика функции. Функцию, заданную соотно-
соотношением у = /(ж), х Е D(f), принято называть явной функцией.
Определение. Прямая х = с называется вертикальной асимп-
асимптотой графика функции у = /(ж), если хотя бы один из пределов
lim f(x) или lim f(x) равен +оо или —оо.
ж->-с—О ж-^с+О
Определение. Прямая у = кх + Ь называется наклонной асимп-
асимптотой графика функции у = f(x) при х —У +оо, если эта функция
представима в виде f(x) = kx + b + а(х), где а(х) —> 0 при х —>¦ +оо.
Теорема 1. Для того чтобы прямая у = kx + b была наклонной
асимптотой графика функции у = /(ж) при х —> +оо, необходимо и
достаточно, чтобы существовали пределы
lim ZM = &5 lim [/(ж) - te] = b.
х—>-+оо Ж ж—>-+оо
Аналогично вводится понятие наклонной асимптоты графика
функции при х —> —оо.
2. Четные, нечетные, периодические функции.
Определение. Функция у = f(x) называется четной, если Vx G
€?>(/): f(x)=f(-x).
Определение. Функция у = /(ж) называется нечетной, если
VxeD(f): f(x) = -f(-x).
Определение. Функция у = /(ж) называется периодической, ес-
если существует число Т ф 0, называемое периодом функции 2/ = /(ж),
такое, что
Vx G ?>(/): f{x) = f{x + Г) = /(ж - Г).
Обычно под периодом функции понимают наименьший из положи-
положительных периодов, если такой период существует.
3. Локальный экстремум функции. Пусть функция у = f(x)
определена в некоторой окрестности точки xq.
Определение. Говорят, что функция у = f(x) имеет в точке хо
локальный максимум (минимум), если существует такая окрестность
точки хо, в которой при х ф хо выполняется неравенство f(x) < f(xo)
(соответственно f(x) > f(x0)).
§1. Графики явных функций 131
Локальный максимум и локальный минимум объединяются об-
общим названием локальный экстремум (или просто экстремум).
Теорема 2 (необходимое условие экстремума). Если функция у =
= f(x) имеет в точке хо экстремум, то производная f'{x) в точке
хо или равна нулю, или не существует.
Значения аргумента функции у = /(ж), при которых либо про-
производная функции равна нулю, либо производная не существует, но
сама функция непрерывна, принято называть точками возможного
экстремума.
Теорема 3 (первое достаточное условие экстремума). Пусть
функция у = f(x) дифференцируема в некоторой окрестности точ-
точки хо возможного экстремума (за исключением, быть может, самой
точки хо). Тогда если при переходе через точку хо (в сторону возрас-
возрастания х) производная f'(x) меняет знак с плюса на минус (с минуса
на плюс), то в точке хо функция у = f(x) имеет локальный максимум
(минимум). Если при переходе через точку х0 производная функции не
меняет знака, то в точке хо функция у = f(x) не имеет экстремума.
Теорема 4 (второе достаточное условие экстремума). Пусть в
точке хо возможного экстремума функция у = f(x) имеет вторую
производную. Тогда если f"(xo) < 0 (f"(xo) > 0), то функция у = f(x)
имеет в точке х0 локальный максимум (минимум).
4. Направление выпуклости и точки перегиба графика
функции. Пусть функция у = f(x) имеет в каждой точке интер-
интервала (а, Ь) конечную производную. Тогда в каждой точке М(ж,/(ж)),
х Е (а,Ь), график функции у = f(x) имеет касательную, не парал-
параллельную оси Оу.
Определение. Говорят, что график функции имеет на интер-
интервале (а, Ь) выпуклость, направленную вниз (вверх), если в пределах
интервала (а, Ь) график лежит не ниже (не выше) любой касательной.
Теорема 5. Если на интервале (а,Ъ) существует вторая про-
производная функции у = f(x) и если эта производная неотрицатель-
неотрицательна (неположительна) всюду на этом интервале, то график функции
у = f(x) имеет на интервале (а,Ь) выпуклость, направленную вниз
(вверх).
Определение. Точка M(c,f(c)) графика функции у = f(x) на-
называется точкой перегиба этого графика, если в этой точке график
функции имеет касательную и существует такая окрестность точки
с, в пределах которой слева и справа от точки с направления выпук-
выпуклости графика функции у = f(x) различны.
Говорят также, что в точке M(c,f(c)) график функции имеет
перегиб.
Теорема б (необходимое условие перегиба). Если график функ-
функции у = f(x) имеет перегиб в точке М(с, f(c)) и вторая производная
f"(x) непрерывна в точке с, то f"(c) = 0.
Теорема 7 (достаточное условие перегиба). Если в некоторой
5*
132 Гл. VII. Графики функций
окрестности точки с существует вторая производная функции у =
= f(x), причем f"(c) = 0; и в пределах этой окрестности слева и
справа от точки с знаки f"(x) различны, то график функции имеет
перегиб в точке М(с, /(с)).
5. Схема построения графика функции у = /(ж).
1°. Найти область определения функции и значения этой функции
в точках разрыва и граничных точках области определения.
Если в точке с функция имеет разрыв, причем /(с + 0) или /(с —
— 0) обращается в бесконечность, то х = с — вертикальная асимптота
графика функции у = f(x).
Если функция определена на полупрямой или на всей числовой
прямой, то следует установить (с помощью теоремы 1), имеет ли гра-
график функции наклонные асимптоты. Если наклонных асимптот нет,
то нужно исследовать, является функция ограниченной при х —> оо
или неограниченной (в последнем случае — является ли она беско-
бесконечно большой при х —У оо и какого знака).
2°. Установить, является ли функция четной, нечетной, периоди-
периодической.
Назначение этого пункта — сократить выкладки. Действительно,
если функция четная или нечетная, то вместо всей области определе-
определения достаточно рассмотреть лишь ту ее часть, которая принадлежит
положительной полуоси абсцисс. На этой части области определения
нужно провести полное исследование функции и построить ее гра-
график, а затем, пользуясь симметрией, достроить его на всей области
определения.
Если функция периодическая, то достаточно провести исследова-
исследование функции на любом отрезке, длина которого равна периоду функ-
функции, а затем, построив график на этом отрезке, распространить его
на всю область определения функции.
3°. Найти нули функции, т. е. решить уравнение /(ж) = 0. Эти
решения и точки разрыва функции разбивают ее область определения
на промежутки знакопостоянства функции.
4°. Найти локальные экстремумы и промежутки возрастания и
убывания функции (на графике экстремальные точки будем обозна-
обозначать символом о).
5°. Найти промежутки сохранения направления выпуклости и точ-
точки перегиба графика функции (на графике точки перегиба будем обо-
обозначать символом х или +).
Контрольные вопросы и задания
1. Дайте определение и приведите пример вертикальной асимптоты гра-
графика функции.
2. Сформулируйте определение и приведите пример наклонной асимптоты
графика функции при х —»¦ +оо (при х —»¦ —оо).
3. Сформулируйте теорему, выражающую необходимые и достаточные
условия существования наклонной асимптоты графика функции.
§1. Графики явных функций 133
4. Приведите примеры функции, у которой существуют наклонные асимп-
асимптоты графика при х —у +оо и при х —у —оо, причем эти асимптоты:
а) совпадают; б) не совпадают.
5. Дайте определение локального экстремума функции.
6. Что такое точки возможного экстремума функции?
7. Сформулируйте теорему, выражающую необходимое условие экстре-
экстремума: а) произвольной функции; б) дифференцируемой функции. Пока-
Покажите на примере, что это условие не является достаточным.
8. Сформулируйте теоремы, выражающие достаточные условия экстрему-
экстремума функции.
9. Дайте определение направления выпуклости графика функции.
10. Дайте определение точки перегиба графика функции.
11. Может ли меняться направление выпуклости графика функции при пе-
переходе через точку, не являющуюся точкой перегиба? Приведите
примеры.
12. Сформулируйте необходимое условие перегиба графика функции.
Покажите на примере, что это условие не является достаточным.
13. Сформулируйте достаточное условие перегиба графика функции.
14. Приведите схему построения графика функции у = f(x).
Примеры решения задач
2х
1. Построить график функции у = arcsin -.
Л 1°. Функция определена при тех значениях ж, для которых, как
2х
следует из определения арксинуса, выполнено неравенство
^ 1. Оно равносильно неравенству A - \х\J ^ 0. Последнее верно для
2х
любых вещественных х. Итак, D(f) = R. Функция непрерыв-
1 "т" X
на в любой точке (как частное двух непрерывных функций). Поэтому
функция arcsin также непрерывна в любой точке (как суперпо-
± ~\~ х
зиция непрерывных функций), и, следовательно, график функции не
имеет вертикальных асимптот. Для нахождения наклонной асимпто-
асимптоты при х —у оо вычислим следующие пределы:
hm ±-^L = hm - arcsin = О,
ж-^+оо X ж-^+оо X 1 + X2
2х
Hm \f(x) — kx] = Hm arcsin = arcsin 0 = 0.
ж^+оо ж^+оо 1 + X1
Отсюда следует, что прямая у = 0 является асимптотой при х —у +оо
(ее правильнее назвать горизонтальной, а не наклонной). Аналогично
можно установить, что та же прямая у = 0 является асимптотой при
х -у -оо.
2°. Очевидно, что функция непериодическая и является нечетной.
Поэтому вместо всей области определения достаточно рассмотреть
полупрямую [0,+оо).
134 Гл. VII. Графики функций
3°. Имеем у = 0 при х = О. Других нулей, а также точек разрыва
функция не имеет. На полупрямой @, +оо) функция является поло-
положительной.
4°. Найдем точки возможного экстремума на полупрямой [0, +оо).
Вычислим производную функцию при х ф 1:
, _ 1 2A+ж2)-4ж2 _ 1 + ж2 2A-ж2) _ 2sgn(l-x2)
у
A+Ж2J |1-Ж2| A+Ж2J 1+Ж2
Отсюда видно, что производная не обращается в нуль ни в одной точ-
точке. Так как у'A + 0) = -1, у'A - 0) = 1, то в точке х = 1 производная
не существует. Знак производной при переходе через точку х = 1
меняется с плюса на минус. Поэтому в точке х = 1 функция име-
имеет локальный максимум, причем у{1) = arcsin 1 = тг/2. Отметим, что
в точке х = 1 функция непрерывна, а ее производная имеет разрыв
I рода. В таком случае соответствующая точка графика (в данном
примере точка A, тг/2)) называется угловой точкой. Промежутки мо-
монотонности функции определяются знаком производной: у' > 0 при
0 ^ х < 1; у' < 0 при х > 1.
5°. Так как вторая производная
У ~ (l+ж2J ' X^ '
обращается в нуль лишь при х = 0 и при переходе через точку ж = О
2/" меняет знак, то в точке @,2/@)) = @,0) график функции имеет
перегиб. Направление выпуклости определяется знаком второй про-
производной: у" < 0 при 0 ^ х < 1; у" > 0 при ж > 1.
Исследование функции закончено. Перед тем как строить график,
удобно изобразить на схеме результаты исследования, в частности,
промежутки знакопостоянства функции, первой проиводной у' и вто-
второй производной у":
Перегиб +
У—*? ± ^х
, и + max _
у 1 ¦ 1
"-о 1 ^х
Теперь, считывая информацию со схемы, строим график функции
на промежутке [0,+оо). На отрезке [0,1]: а) функция возрастает от
значения у = 0 при ж = 0 до значения у = тг/2 при ж = 1; б) выпуклость
направлена вверх. Далее, на полупрямой [1,+оо): а) функция убыва-
убывает, оставаясь положительной; б) выпуклость направлена вниз; в) при
ж —> +оо график приближается к асимптоте — оси Ох. Отметим, что
при переходе через точку ж = 1 изменяется направление выпуклости
графика, но точка A, тг/2) не является точкой перегиба — это угловая
точка (рис. 6).
§1. Графики явных функций
135
Наконец, используя нечетность функции, достраиваем ее график
на всей области определения (рис. 7). А
\У
О
Рис. 6
Рис. 7
Замечание. Если кривая задана уравнением Ф(ж,г/) = 0 и если это
уравнение удается разрешить относительно у или относительно ж, то по-
построение кривой сводится к построению графиков явных функций.
2. Построить кривую, заданную уравнением у2 - sin4 ж = 0.
Л Это уравнение \/х Е R имеет два решения относительно у: у =
= sin2 х и у = — sin2 ж, которые являются явными функциями, опре-
определенными на всей числовой прямой. Графики этих функций симмет-
симметричны относительно оси Ох. Поэтому достаточно построить график
первой функции, а затем, воспользовавшись симметрией, построить
всю кривую. Итак, задача свелась к построению графика явной функ-
функции у = sin2 ж, которую запишем в виде
У = 2 ~ 2 cos2x-
Эту функцию исследуем по вышеизложенной схеме.
1°. Имеем D(y) = R.
2°. Функция у{х) периодическая с периодом Т = тг. Поэтому чтобы
построить график функции, достаточно рассмотреть отрезок оси Ох
длины тг, например [-тг/2,тг/2]. Так как у(х), кроме того, является
четной, то можно ограничиться сегментом [0,тг/2].
3°. Найдем нули функции на сегменте [0,тг/2]; имеем
- - - cos 2x = 0
при х = &7Г, k G Z, но из всех этих решений сегменту [0, тг/2] принадле-
принадлежит только х = 0. Функция не имеет точек разрыва. На промежутке
@,тг/2] функция положительна.
4°. Находим у' = sin2x. На сегменте [0,тг/2] производная равна
нулю при х = 0 и х = тг/2. Далее, у' > 0 при 0 < х < тг/2, у' < 0 при х < 0
и х > тг/2. По теореме 3 функция имеет локальный максимум в точке
тг/2, причем 2/(тг/2) = 1, и локальный минимум в точке х = 0, причем
2/@) = 0. Весь сегмент [0,тг/2] является промежутком возрастания
функции.
136
Гл. VII. Графики функций
5°. Имеем у" = 2cos2x. На сегменте [0,тг/2] вторая производная
обращается в нуль при х = тг/4. При переходе через эту точку у"
меняет знак. Значит, по теореме 7 график функции имеет в точке
(тг/4,2/(тг/4)) = (тг/4,1/2) перегиб. Таким образом, можно построить
следующую схему:
у ? + V2 + X
_|_
* 0 тг/2
„+. + „ -
0 тг/4 тг/2
Считывая информацию со схемы, строим график функции на сег-
сегменте [0,тг/2] (рис. 8). Используя четность функции, достраиваем ее
1
0,5
О
4 2
Рис. 8
Рис. 9
график на сегменте [-тг/2,тг/2] (рис. 9). Учитывая периодичность
функции, строим ее график на всей области определения (рис. 10).
Рис. 11
Наконец, учитывая симметричность исходной кривой относитель-
относительно оси Ох, получаем всю кривую (рис. 11). А
§2. Кривые, заданные параметрически 137
Задачи и упражнения для самостоятельной работы
Постройте графики следующих явных функций.
1. у = 1 + х2 - 0,5ж4. 2. у = (х + 1)(ж - 2J.
3. у = 0,4ж - 0,5ж3 + 0,1ж5. 4. у = A — ж2).
5. 2/ = ж4A + ж). 6. у = A Ч- жLA - ж).
7.у = х2(х - 1H + I). 8. у = хA - 22
X
9.у = 2х-1 + (х + 1)~1. 10. у =
cos 2х
11. г/ = arccos -. 12. у = arcsin(sinx).
13. у = sin(arcsinx). 14. г/ = arctg (tgx).
15. у = arctg A/ж). 16. у = (ж + 2)е1/ж.
17. 2/ = 0,5(л/ж2+ж + 1 - л/ж2 -ж + 1). 18. 2/ = \/ж2 + 1 -
19. 2/ = О + 2J/3 - О - 2J/3- 20. 2/ = О + 1J/3 + О - 1J/3-
Постройте кривые, заданные следующими уравнениями.
21. у2 = 8х2 - ж4. 22. у2 = (ж - 1H - 2H ~ 3).
23. у2 = (ж - 1H + I)- 24- 2/2 = ^2(! - ж)(! + ЖГ2-
25. ?/2 = ж4(ж + 1). 26. ж20/ - 2J + 2ху - у2 = 0.
§ 2. Исследование плоских кривых,
заданных параметрически
Схема исследования кривой
Параметрические уравнения плоской кривой имеют вид
x = x(t), y = y(t), teT. A)
Исследование и построение такой кривой можно провести по сле-
следующей схеме.
1°. Найти множество Т — общую часть областей определения
функций ж(?), y(t) (если множество Т не задано), — отметив, в част-
частности, те значения параметра ti (включая ti = ±oo), для которых хотя
бы один из односторонних пределов lim ж(?), Hm y(t) равен +оо
или —оо.
2°. Установить, обладает ли кривая симметрией, позволяющей со-
сократить выкладки.
3°. Найти нули функций ж(?), y(t) и области знакопостоянства
этих функций.
4°. Найти точки ?/,, в которых хотя бы одна из производных ж(?),
y(t) равна нулю или разрывна. Заметим, что точки ?^, отмеченные в
п. 1°, и точки ?/,, найденные в этом пункте, разбивают множество Т
на промежутки знакопостоянства производных ж(?), y(t). Поэтому на
каждом таком промежутке (tp,tp+i) функция x(t) строго монотон-
монотонна, и, следовательно, система уравнений A) на интервале (tp,tp+i)
138
Гл. VII. Графики функций
задает параметрически функцию вида у = /(ж) (см. § 1 из гл. IV).
Производные этой функции выражаются по формулам
pi _ dtu ]
Часть кривой, соответствующую изменению параметра t от tp до
tp+i, будем называть ветвью кривой. Каждая ветвь кривой является
графиком функции вида у = /(ж).
5°. Найти точки tj, в которых /" = 0.
6°. Составить таблицу следующего вида:
(tp,tp+l)
(Xp,Xp+l)
(yP,yP+i)
Знак f"
Здесь в первой строке записываются промежутки изменения па-
параметра t, граничными точками которых tp и tp+\ служат точки,
найденные в пп. 1°, 4° и 5°. Во второй и третьей строках таблицы
приводятся соответствующие промежутки изменения переменных х
и у. В последней строке таблицы указывается знак /", определяющий
направление выпуклости графика соответствующей ветви кривой.
7°. Пользуясь таблицей, построить ветви кривой, соответствую-
соответствующие промежуткам (tp,tp+i).
Замечание 1. В п. 1° схемы можно найти асимптоты кривой (если
они имеются). Для этого надо иметь в виду следующее:
а) если при t->tp (t —»> tp + 0 или t —»¦ tp — 0) x —»¦ жо, а у —>- oo, то х = xo —
вертикальная асимптота кривой;
б) если при t—ttp (t—ttp + О или t —»¦ tp — 0) х —»¦ оо, а у —>- г/о, то |/ = г/о —
горизонтальная асимптота кривой;
в) если при t —>- tp (t —>- tp + 0 или t^rtv — 0)ж—>-ооигу—>- оо, то возможна
наклонная асимптота, нахождение которой надо провести в соответствии с
теоремой 1.
Замечание 2. При изучении симметрии кривой (п. 2° схемы) следует
иметь в виду четыре случая, когда вместо всей области определения Т
достаточно рассмотреть лишь неотрицательную ее часть:
а) Vt G T: () () () () (
оси Ож);
б) Vt e T:
оси Оу);
в) Vt G T: x(t) = -x(-t), iy(t) = -y(-t)
начала координат);
г) Vt G T: x(t)=x(-t), y(t) = y(-t) (наложение).
Замечание 3. Если tp — точка, найденная в п. 4° схемы, и если на
интервале (tp_i,tp+i) x(t) сохраняет знак, то на этом интервале система
уравнений A) задает параметрически функцию вида у = /(ж), для ко-
которой точка ж^р) является точкой возможного экстремума. Является ли
ж^р) точкой экстремума функции у = /(ж), можно определить, рассмотрев
изменение у на интервалах (tp_i,tp) и (tp,tp+i).
р ру
x(t) = x(—t), y(t) = —y(—t)
x(t) = -x(-t), y(t) = y(-t)
(симметрия относительно
(симметрия относительно
(симметрия относительно
§2. Кривые, заданные параметрически 139
Замечание 4. В процессе исследования кривой можно обнаружить
одну из характерных особых точек кривой, заданной параметрически, —
точку возврата (см. пример 2 на с. 140).
Контрольные вопросы и задания
1. Как вычисляются производные функции, заданной параметрически?
2. Кривая задана параметрически: х = sin2 t, у = cos2 t. Какой промежу-
промежуток достаточно рассмотреть, чтобы при изменении параметра t на этом
промежутке точка (x(t),y(t)) оказалась в каждой точке кривой только
один раз?
3. Как найти асимптоты кривой, заданной параметрически?
4. Как исследовать и использовать симметрию кривой, заданной парамет-
параметрически?
5. Сформулируйте необходимое условие локального экстремума функции,
заданной параметрически.
6. Приведите схему исследования и построения кривой, заданной пара-
параметрически.
Примеры решения задач
1. Построить кривую, заданную параметрически:
t t(l-2t2)
Ж=Г^2' У= I-*2
Л 1°. Имеем
t е (-оо,-1) U (-1,1) U A,+оо),
х е @, +оо) U (-оо, +оо) U (-оо, 0),
у Е (—оо, —оо) U (+00, —оо) U (+00, +оо).
Отсюда следует, что х = 0 — вертикальная асимптота кривой, а при
t —У — 1 и t —У 1 возможны наклонные асимптоты. Действительно,
Нт У-= lim A-2?2) = -1, lim (y + x)= lim 2t = 2.
Аналогично находятся пределы при t —у —1:
lim - = -1, lim (у + х) = -2.
х—>-±оо X х—>-±оо
Итак, кривая имеет две асимптоты: у = —х + 2 и у = —х — 2.
2°. Так как x(t) = -x(-t), y(t) = -y(-t), то кривая обладает сим-
симметрией относительно точки 0@,0). Поэтому достаточно рассмот-
рассмотреть далее множество М = [0,1) U A, +оо).
3°. На множестве М x(t) = 0 при t = 0, y(t) = 0 при t = O,t = 1/л/2-
4°- *(*) = A^' У^ = A12J ¦ На множестве М x(i) > О,
1,51.
140
Гл. VII. Графики функций
РГО ?1 _ У _ ** ОГ + 1 ГЦ _ (Ц _
сюда //; ^ 0 при t e [0,1), /" > 0 при t e A, oo).
6°. Составим таблицу:
A+t2K
(tp,tp+l)
[Хр, Хр+1)
(yP,yP+i)
Знак /"
@;0,47)
@;0,6)
@;0,3)
+
@,47; 1)
@,6;+оо)
@,3;-оо)
+
A; 1,51)
(-оо;-0,7)
(+оо;2,3)
-
A,51;+оо)
(-0,7; 0)
B,3;+оо)
-
7°. Строим часть кривой, соответствующую множеству М
(рис. 12).
1
J
о
\У
о
Рис. 12
Рис. 13
Далее, используя симметрию кривой, построим всю кривую
(рис. 13). А
2. Построить кривую, заданную параметрически:
ж = 2?-?2, y = 3t-t3. B)
Л 1°. Имеем , ч
t e (-оо,+оо),
х G (—оо, —оо),
у G (+00, -оо).
Таким образом, при х ->• -оо (? ->• =Ьоо) возможны наклонные асимп-
п г 2/ г 3t-t3
тоты. Однако lim — = lim = оо, т. е. асимптот нет.
ж-^-оо X t^±oo 2t — tz
2°. Свойствами симметрии и периодичности кривая не обладает.
3°. Имеем х = 0 при ? = Ои? = 2;2/ = О при t = 0, t = -л/3 и t = л/3-
4°. Находим ж(?) = 2A - t) = 0 при t = 1, ?/(?) = 3A - t2) = 0 при
? = -1 и ? = 1.
" = —-
5°. Так как /" =
, то //; > 0 при t < 1, /" < 0 при t > 1.
§2. Кривые, заданные параметрически
141
6°. Составим таблицу:
(tp,tp+l)
(Xp, Xp+l)
(Ур> У p+i)
Знак /"
(-OO,
(-оо,
( + OO,
+
-1)
-з)
-2)
(-1.
(-з,
(,
+
1)
1)
2)
A.
A.
B,
+oo)
-оо)
-оо)
-
7°. Строим кривую.
Заметим, что если t рассматривать как время, а кривую, задан-
заданную системой уравнений B), — как траекторию движения точки на
плоскости (ж, у), то {х,у} есть вектор скорости движения этой точки.
При t = 1 в данном примере x(t) = y(t) = 0, т. е. скорость равна
нулю, причем при переходе через t =
= 1 x(t) и y(t) меняют знак. Это озна-
означает, что при t —> 1 — 0 точка, движу-
движущаяся по траектории, приближается
к точке W(l,2) (рис. 14), в момент
t = 1 останавливается в точке W, а
далее движется в обратном направле-
m v y(t) v y(t)
нии. Так как lim ^-г = Inn ту4,
то ветви траектории, соответствую-
соответствующие t ^ 1 и ? ^ 1, имеют при t = 1,
т. е. в точке W(l, 2), одну и ту же одностороннюю касательную. Точ-
Точка W(l,2) называется точкой возврата (такое название, очевидно,
соответствует рассмотренной выше физической интерпретации). А
Замечание 1. Для кривой, заданной уравнением вида
F(x,y) = O, C)
иногда удается получить параметрические уравнения. Обычно это делается
так. Положим у = a(t)xn, где a(t) и п — выбранные подходящим образом
функция и число. Подставляя выражение для у в уравнение C), получим
F(x,a(t)xn) = 0. Пусть х = cp(t) — решение этого уравнения. Тогда
Рис. 14
— параметрические уравнения кривой. На практике выбор функции a(t)
определяется видом функции F(x,y).
Рассмотрим кривую, заданную уравнением
х4 + у4 = 2ху. D)
Этому уравнению могут удовлетворять координаты ж, у только тех точек,
которые лежат в I и III квадрантах или на осях координат, т. е. должно быть
выполнено неравенство ху ^ 0. Для перехода к параметрическим уравне-
уравнениям кривой положим у = Хл/tgt. Подставляя это выражение в уравне-
уравнение D), получим
откуда х = 0 и х = fy4tgtcost. Первое решение х = 0 содержится во втором
при t = 0. Таким образом, параметрические уравнения кривой имеют вид
142 Гл. VII. Графики функций
Однако параметр t можно ввести и иначе, полагая, например, у = xt.
Тогда приходим к следующим параметрическим уравнениям кривой:
У =
У =
Дальнейшее исследование кривой проведите самостоятельно для обоих слу-
случаев введения параметра t.
Замечание 2. Кривую, заданную в полярных координатах, можно ис-
исследовать, используя схему, изложенную в этом параграфе. Действитель-
Действительно, пусть в полярной системе координат (<?>, р) кривая задана уравнением
р = /(<?>). Тогда, выражая декартовы координаты через полярные:
{х = pcoscp,
у = psincp,
получим параметрические уравнения кривой (ср — параметр)
х = f(cp) cos (p, y = f(cp) sin (p.
Задачи и упражнения для самостоятельной работы
Постройте кривые, заданные следующими уравнениями.
27. х = j(t + IJ, y=j(t- IJ. 28. x = ^
29. x=^, V=?^j- 3O.x = -l
31.ж=-?±^, »=-?-. 32. a;=(iz^_) j,=
, y. 32. x , у
4A -t) t + l t + 1 t-1
2 t2- t3
Переходя к параметрическим уравнениям, постройте кривые, заданные
следующими уравнениями.
34. х3 + у3 = Заху, где а > 0 (лист Декарта).
35. (х — аJ(х2 + у2) = Ъ2х2, где а > О, Ь > 0 (конхоида Никомеда).
Рассмотрите случаи: а) а > Ъ] б) а = Ъ] в) а < Ъ] установите в каждом из
них, каков характер особой точки кривой 0@,0).
36. х2/3 + у2/3 = а2/3, где а > 0 (астроида).
37. х6 + 2х3у = у3. * Положите у = x2t.
38. 4у2 = 4х2у + х5. * Положите у = x2t. 39. х4 + 2у3 = 4х2у.
40. х3 - 2х2у - у2 = 0. 41. х2у2 + у = 1. * Положите у = t/x.
42. х3 + у3 = Зх2. 43. у5 + ж4 = ж?/2.
44. ж4 - у4 + ж?/ = 0. 45. ж5 + ?/5 = ху2.
Постройте кривые, заданные в полярной системе координат следующи-
следующими уравнениями.
46. р = Ь/(р @ < ip < +оо). 47. р2 = 2а2 cos2 <p.
48. р = a cos 9? + Ъ (Ь^а>0). 49. p = asm3(p (а>0). 50. p =
ГЛАВА VIII
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Интегрируемость функции (по Риману)
и определенный интеграл
Основные понятия и теоремы
1. Интегральные суммы и определенный интеграл. Пусть
функция /(ж) определена на сегменте [а, Ь] (где а <Ъ). Произвольное
разбиение сегмента [а, Ь] точками а = жо < х\ < ... < хп = Ъ на п час-
частичных сегментов [a^-i •> xi] (i = 1, 2,..., п) будем обозначать символом
T[a,b] или просто Т. Положим Axi — Х{— Х{-\. Выберем на каждом
сегменте [xi-i^xi] произвольную точку & и составим сумму:
г=1
Число I(xi,?i) называется интегральной суммой функции /(ж), со-
соответствующей данному разбиению Т[а, Ь] и данному выбору проме-
промежуточных точек ^ на сегментах [xi-i,Xi].
Введем обозначение А = max Аж^.
Определение. Число / называется пределом интегральных сумм
I(xi,?i) при А —> О, если Vs > 0 36 > 0 такое, что для всякого разбие-
разбиения Т[а, Ь], у которого А < ?, выполняется неравенство |/(ж^, ^) — /| <
< е при любом выборе промежуточных точек & на [ж^_1,Жг].
Определение. Функция /(ж) называется интегрируемой (по Ри-
ману) на сегменте [а, 6], если существует lim /(ж^,^) = /.
При этом число / называется определенным интегралом от функ-
функции /(ж) по сегменту [а, Ь] и обозначается так:
ь
= f(x)dx.
2. Суммы Дарбу. Пусть /(ж) определена и ограничена на
[а, Ь]. Для произвольного разбиения Т[а,Ь] введем обозначения
vrii — inf /(ж), Mi — sup /(ж) и составим суммы:
я ^^ ^ т ' /\ т* ¦ S ^^
г=1 г=1
144 Гл. VIII. Определенный интеграл
Числа s и S называются нижней и верхней суммами (суммами
Дарбу), соответствующими данному разбиению Т[а,Ь].
Очевидно, что для фиксированного разбиения Т[а,Ь] и любого вы-
выбора промежуточных точек на этом разбиении s ^ I(xi,?i) ^ S.
Приведем свойства сумм Дарбу.
1°. Для любого фиксированного разбиения
8= Ш|' {I(Xi,Zi)}, S= SUp {I(Xi,ti)}-
по всем по всем
наборам наборам
точек & точек ?.
2°. Если разбиение T<i получено из разбиения Т\ добавлением
нескольких новых точек (т. е. получено измельчением Xi), то ниж-
нижняя сумма S2 разбиения Т<± не меньше нижней суммы s\ разбиения
Ть а верхняя сумма 52 разбиения Т2 не больше верхней суммы S\
разбиения Т\. si ^ S2, S2 ^ S\.
3°. Нижняя сумма произвольного разбиения не превосходит верх-
верхней суммы любого другого разбиения.
4°. Пусть {s} и {S} — множества всевозможных нижних и верх-
верхних сумм для любых разбиений [а, Ь]. Числа
7= inf {S}, I_= sup {s}
по всем по всем
разбиениям разбиениям
называются соответственно верхним и нижним интегралами Дарбу.
Нижний интеграл Дарбу не превосходит верхнего: / ^ /.
5°. Лемма Дарбу:
lim S = /, lim s = I.
3. Необходимые и достаточные условия интегрируемости.
Теорема 1. Для того чтобы ограниченная на сегменте [а, Ь]
функция f(x) была интегрируемой на этом сегменте, необходимо и
достаточно, чтобы / = /.
Теорема 2. Для того чтобы ограниченная на сегменте [а,Ь]
функция была интегрируемой на этом сегменте, необходимо и доста-
достаточно, чтобы \/е > 0 нашлось такое разбиение Т[а, Ь] (хотя бы одно),
для которого
S-S<?. A)
Напомним, что число uj{ — М{ — mi называется колебанием функ-
функции на сегменте [xi-i,Xi].
Условие A) можно записать в виде
S-S = 2^;Дж; <
§1. Интегрируемость функции (по Риману) 145
4. Некоторые классы интегрируемых функций.
Теорема 3. Непрерывная на сегменте [а,Ъ] функция f(x) интег-
интегрируема на этом сегменте.
Следствие. Всякая элементарная функция интегрируема на
любом сегменте, целиком лежащем в области определения этой функ-
функции (так как она непрерывна на этом сегменте).
Теорема 4. Пусть f(x) ограничена на сегменте [а,Ь]. ЕслиМе >
> 0 существует конечное число интервалов, покрывающих все точки
разрыва f(x) и имеющих сумму длин, меньшую е, то f(x) интегри-
интегрируема на сегменте [а,Ь].
Следствие. Кусочно непрерывная функция (т. е. имеющая на
сегменте [а, Ь] конечное число точек разрыва I рода) интегрируема на
этом сегменте.
Замечание. Если выполнены условия теоремы 4, то значение интег-
ъ
рала I f(x) dx не зависит от значений f(x) в точках разрыва. Поэтому час-
а
то ставят и решают задачу вычисления интеграла от функции, которая не
определена либо в конечном числе точек сегмента [а, Ь], либо на множестве
точек, которое можно покрыть конечным числом интервалов сколь угодно
малой длины. При этом считают, что функция f(x) доопределена в этих
точках произвольно, но остается, конечно, ограниченной на сегменте [а, Ь]
и, следовательно, интегрируемой.
Например, строго говоря, интеграл
1
-dx B)
/sin x
х
X
не существует, так как в точке х = 0 функция не определена. Однако
х
1
интеграл //(ж) с/ж, где
о
{sin ж ,
— при Хф0,
С при ж = О
(С — произвольное число), существует и не зависит от выбора С. Поэтому
1
считают, что интеграл B) также существует и равен //(ж) dx.
о
Теорема 5. Монотонная на сегменте [а,Ь] функция f(x) интег-
интегрируема на этом сегменте.
Контрольные вопросы и задания
1. Что такое разбиение сегмента [а, Ь]?
2. Что такое интегральная сумма функции /(ж) на сегменте [а, Ь]?
3. Дайте определение предела интегральных сумм при измельчении раз-
разбиений (А —»> 0) сегмента [а, Ь].
146 Гл. VIII. Определенный интеграл
4. Что такое определенный интеграл?
5. Какая функция называется интегрируемой?
6. Докажите, что неограниченная функция неинтегрируема.
7. Интегрируема ли функция /(ж) = 1/х: на сегменте [1,2]; на сегменте
[-Li]?
8. Интегрируема ли функция /(ж) = tgxctgx: на сегменте [тг/6,тг/4]; на
сегменте [—1,1]?
9. Интегрируема ли функция /(ж) = е~1/ж: на сегменте [—3,-2]; на сег-
сегменте [—1,0]; на сегменте [—1,1]?
10. Всякая ли ограниченная функция интегрируема? Обоснуйте ответ при-
примерами.
11. Что такое нижняя и верхняя суммы (суммы Дарбу)?
12. Перечислите свойства сумм Дарбу.
13. Сформулируйте необходимые и достаточные условия интегрируемости
(два варианта).
14. Назовите известные вам классы интегрируемых функций. Приведите
примеры функций из этих классов.
15. Придумайте пример монотонной на сегменте [а, Ь] функции, имеющей
бесконечно много точек разрыва. Интегрируема ли такая функция на
Примеры решения задач
1. Постоянная функция /(ж) = С интегрируема на [а, 6], так как
для любых разбиений и любого выбора точек ^ интегральные суммы
имеют одно и то же значение
пъ, &) = Е /&) д& = с Ё
i=i i=i
ъ
Отсюда \Cdx- lim /(ж^<^) = С(Ь - а).
J А-^о
а
2. Доказать, что функция Дирихле
( \ _ / 0? если х иррационально,
^ ' ~ у 1,
если х рационально,
не интегрируема на любом сегменте [а, Ь].
А В самом деле, на любом сколь угодно малом сегменте [xi-i,Xi]
найдутся как рациональная, так и иррациональная точка. Если на
всех сегментах выбрать рациональные ^, то /(ж^,^) = Ъ — а; если же
все & иррациональны, то /(ж^, &) = 0. Чередуя такие выборы при А —)>
—У 0, получаем, что предел / не существует. Значит, функция Дирихле
не интегрируема. А
3. Проверить, что для функции /(ж) = 1 + ж на сегменте [—1,4]
4
выполнено условие A) теоремы 2, и вычислить / = / A + ж) dx как
-1
§1. Интегрируемость функции (по Риману) 147
предел интегральных сумм.
Л Согласно теореме 2 для произвольного е > 0 нужно указать такое
разбиение сегмента [—1,4], при котором S — s < г.
Разобьем сегмент [—1,4] на п равных частей. На каждом сегмен-
сегменте [xi-i,Xi]= — 1 Н— -, — 1 Н непрерывная функция 1 + х
достигает точной нижней грани на левом конце сегмента, а точной
верхней — на правом. Поэтому
s = > rriiAxi = > / — Ц— • - =
i=i i=i n n
E5 (. 1 ч 5 25 \~^/. -, \
-(г- 1)- = — У (г- 1),
n n n2 *-^
n n n n
о ST^ пж л X^ *f -1 5г\5 \r^ Б . Б 25 v^ •
b = У MiAxi = у /1 — 1 H 1 • — = > — • г • — = ^t > г.
^^ ^^ V n J n *-^ n n n2 *-^
Отсюда
/ П П \
c 25 /v-> . v^/- 1Л 25 25 /
o-s = ^r > г — У u-1 =-n= — < e,
n2 \^ ^ J n2 n
если n > 25/e, т. е. при таком числе п точек разбиения сегмен-
сегмента [—1,4] выполнено неравенство A). Значит, по теореме 2 интеграл
4
/ = / A + х) dx существует.
-1
Чтобы вычислить его как предел интегральных сумм, можно рас-
рассмотреть любую последовательность интегральных сумм, у которой
А —> 0, поскольку из существования интеграла следует, что предел
любой последовательности интегральных сумм при измельчении раз-
разбиения существует и равен /.
Возьмем, например, последовательность интегральных сумм, со-
соответствующую разбиениям сегмента [—1,4] на п равных частей
(п = 1,2,...) и выбору в качестве точек ^ правых концов частич-
частичных сегментов. В этом случае для возрастающей функции f(x) =
п
= 1 + х интегральная сумма равна верхней сумме Ь = 2_^ ~ г-> от~
куда получаем i=i n
./(i+!
т //-1,\7 т \~^ 25 . т 2Бп(п +1) 25
1 = A + х) ах = lim > — г = lim ^-—- = —.
п^оо ^-^ П2 п^оо 2п2 2
4
Итак, f(l + x)dx = 25/2. A
-1
148 Гл. VIII. Определенный интеграл
4. Доказать, что функция Римана
, ч _ Г 0, если х иррационально,
Рк00) — | \jn, если х = т/п,
где тип (п ^ 1) — взаимно простые целые числа, интегрируема
на любом сегменте [а, Ь].
Л Снова воспользуемся теоремой 2. Зададим произвольное г > 0. Тог-
Тогда функция ср(х) удовлетворяет неравенствам
2{Ъ -a) ^w
только в некотором конечном числе N точек.
Это вытекает из следующих соображений. Все рациональные точ-
точки сегмента [а, Ь], т. е. точки вида т/п, можно занумеровать в таком
порядке: сначала точки вида т/1, затем т/2, затем т/3 и т. д. Соот-
Соответствующие значения функции ср(х) в этих точках равны 1/1, 1/2,
1/3, ..., т. е. уменьшаются с переходом к каждой следующей группе
точек, причем точек каждого вида имеется конечное число. Таким
образом, в число указанных N точек попадут такие, для которых
1 е 2(Ъ-а) ст
- > — -, откуда п < — -. Ясно, что таких точек конечное
п 2(Ъ — а) е
число (пусть оно равно N).
Покроем эти N точек конечной системой попарно непересекаю-
непересекающихся сегментов с общей суммой длин, меньшей г/2. Длины этих
сегментов обозначим Ах[. Получилось некоторое разбиение [а, Ь].
На сегментах с длинами Ах[ колебания uj[ функции ip(x) не больше 1,
поскольку \/х е [а, Ь] 0 ^ (р(х) ^ 1. Имеется также некоторое конечное
число остальных сегментов (обозначим их длины Ах"). Колебания и"
функции (р(х) на этих сегментах не превышают — -. Поэтому для
2(Ъ-а)
полученного разбиения справедливы оценки
S-s =
Итак, по заданному г > 0 нашлось разбиение сегмента [а, 6], для ко-
которого S — s < г; следовательно, по теореме 2 функция Римана ср(х)
интегрируема на любом сегменте [а, Ь]. А
5. Вычислить
7Г
/
J
cos2 хA + tg2x)'
о
Л Этот интеграл принадлежит к типу интегралов, рассмотренных в
замечании к теореме 4, поскольку
г/ ч 1 Г 1 при 0 ^ х < тг/2, тг/2 < х ^ тг,
cos2x(l + tg2x) | не определена при х = тг/2.
§2. Свойства определенного интеграла 149
Доопределив эту функцию в точке тг/2, например, по непрерывности,
т. е. полагая /(тг/2) = 1, мы получим /(ж) = 1 \/х Е [О,тг], и, следова-
следовательно, искомый интеграл равен тг. А
Задачи и упражнения для самостоятельной работы
1. Для данных функций на указанных сегментах найдите верхнюю S и
нижнюю s суммы Дарбу при разбиении сегментов на п равных частей:
а) /(ж) = ж3, 2 ^ ж ^ 3; б) /(ж) = 2Ж, 0 ^ ж ^ 10.
2. Вычислите определенные интегралы как пределы интегральных сумм:
2
а) I х2 dx (удобно разбить сегмент [—1,2] на равные части);
-1
2
б) / ~? (удобно выбрать ^ = ^Х{-\ • ж;);
1
3
в) / хт dx (удобно выбрать точки деления xi так, чтобы они образо-
2
вали геометрическую прогрессию).
3. Докажите, что функция /(ж) = 1/ж — [1/ж] при ж / 0 и /@) = 0 ин-
интегрируема на сегменте [0,1].
4. Докажите, что функция f(x) = sgn (вп^тг/ж)) интегрируема на сег-
сегменте [0,1].
§ 2. Свойства определенного интеграла
Основные понятия и теоремы
1. Свойства определенного интеграла.
а
1°. По определению / f(x) dx = 0.
а
Ъ а
2°. По определению / /(ж) dx = — / f(x) dx.
а ь
3°. Линейность интеграла. Если /(ж) и д{х) интегрируемы на
[а,Ь],а и /3 — любые вещественные числа, то функция af(x) + /Зд(х)
также интегрируема на [а, 6], причем
ъ ъ ъ
f(af(x) + /Зд(х)) dx = a ff(x) dx + /3 Гд(х) dx.
а а а
4°. Если f(x) интегрируема на [а, 6], то функция \f(x)\ также ин-
интегрируема на [а, 6], причем
ь ь
f(x)dx ^ J\f(x)\dx (a< b).
150 Гл. VIII. Определенный интеграл
5°. Если /(ж) и д(х) интегрируемы на [а, 6], то функция f(x)g(x)
также интегрируема на [а, Ь].
6°. Если /(ж) интегрируема на [а, 6], то она интегрируема также
на любом отрезке [c,d] С [а, Ь].
7°. Аддитивность интеграла. Если f(x) интегрируема на [а, с] и
[с, 6], то она интегрируема также на [а, 6], причем
ebb
ff(x) dx + ff(x) dx = f f(x) dx.
аса
При этом точка с может быть произвольно расположена относительно
а и Ъ.
В дальнейших свойствах 8°-10° полагаем а < Ъ. ь
8°. Если /(ж) интегрируема на [а, Ъ] и /(ж) ^ 0, то f(x)dx ^ 0.
а
9°. Если f(x) и д(х) интегрируемы на [а, Ъ] и f(x) ^ g(x) Vx G
ъ ъ
G [а, Ь], то y/(s) dx ^ Jg(x) dx.
а а
10°. Если /(ж) непрерывна на [а, 6], /(ж) ^ 0, /(ж) ^ 0 на [а, 6], то
3if > 0 такое, что / /(ж) dx ^ if.
а
2. Формулы среднего значения.
Теорема 6. Пусть /(ж) и д(х) интегрируемы на [а,Ь], д(х) ^ 0
(д(х) ^ 0) Уж G [а, Ь], М = sup/(ж), m = inf /(ж).
[а,6] [а,&]
существует число fi e [m, M] такое, что
ь ь
ff(x)g(x) dx = /ifg(x) dx. A)
a a
Следствие 1. Если в формуле A) положить д(х) = 1, то
ъ
ff(x)dx = fi(b-a), fie[m,M]. B)
а
Ъ
Число а = f(x)dx называется средним значением функции
о — a J
а
/(ж) на сегменте [а, Ь].
Следствие 2. Если выполнены условия теоремы б и функция
/(ж) непрерывна, то 3^ G [а, Ь] такое, что
x)dx. C)
§2. Свойства определенного интеграла 151
Следствие 3. Если f(x) непрерывна на [а, 6], то 3? Е [а, Ь] та-
такое, что
ъ
D)
а
и
Контрольные вопросы и задания
1. Перечислите свойства определенного интеграла.
2. Следует ли из интегрируемости суммы интегрируемость слагаемых?
Ответ обоснуйте примерами.
3. Рассмотрите аналогичные вопросы для разности, произведения и част-
частного двух функций.
4. Интегрируема ли сумма двух функций, если одно слагаемое интегри-
интегрируемо, а другое нет?
5. Рассмотрите аналогичные вопросы для разности, произведения и част-
частного двух функций.
6. Интегрируема ли сумма двух неинтегрируемых функций? Ответ обос-
обоснуйте примерами.
7. Рассмотрите аналогичные вопросы для разности, произведения и част-
частного двух неинтегрируемых функций.
8. Известно, что |/(ж)| — интегрируемая функция. Что можно сказать об
интегрируемости /(ж)? Приведите примеры.
9. Пусть /(ж) интегрируема на [а, с] и не интегрируема на [с, Ь]. Что можно
сказать о ее интегрируемости на [а, Ь]?
10
и
. Известно, что / /(ж) dx ^ 0. Следует ли отсюда, что /(ж) ^ 0 \/ж Е [а, Ъ]1
а
Приведите примеры.
ъ ъ
11. Известно, что I f(x)dx > Ig(x)dx. Следует ли отсюда, что /(ж) ^ д(х)
а а
\/ж Е [а, Ъ]1 Приведите примеры.
12. Приведите несколько вариантов формулы среднего значения. При каких
условиях они справедливы?
Примеры решения задач
1. Доказать, что сумма, произведение и частное двух неинтегри-
неинтегрируемых функций могут быть интегрируемы.
Л Пусть /(ж) = 2 + D(x), д(х) = 2 + D(x), где
j^, ч _ Г 0, если х — иррациональное число,
^ ' ~ у 1, если х — рациональное число
(т. е. D(x) — функция Дирихле).
Напомним, что функция D(x) неинтегрируема (см. пример 2 из
§ 1). Функция f(x) = 2 + D(x) также неинтегрируема. В самом деле,
152 Гл. VIII. Определенный интеграл
если допустить, что f(x) интегрируема, то разность двух интегри-
интегрируемых функций f(x) — 2 = D(x) согласно свойству 3° должна быть
интегрируемой, но это противоречит тому, что D(x) неинтегрируема.
Так как д{х) = /(ж), то д{х) неинтегрируема. Рассмотрим функцию
, / ч _ 1 _ Г 1/2, если х — иррациональное число,
^ ~ д(х) ~ \ 1/3, если х — рациональное число.
Эта функция также неинтегрируема. Доказательство аналогично до-
доказательству неинтегрируемости функции Дирихле.
Составим сумму, произведение и частное неинтегрируемых
функций:
Fi(rc) = f{x) + (-g(x)) = О, F2(x) = f{x)h{x) = 1,
F3(x)=f(x)/g(x) = l.
Функции Fi, F2, F3 как постоянные интегрируемы на любом сегменте
[а, Ь]. Таким образом, из интегрируемости суммы или произведения
не следует интегрируемость слагаемых или сомножителей. А
2. Доказать, что произведение интегрируемой функции f(x) на
неинтегрируемую функцию д(х) может быть: а) интегрируемой
функцией; б) неинтегрируемой функцией.
Л а) Рассмотрим, например, интегрируемую функцию f(x) = 0 и не-
неинтегрируемую функцию Дирихле D{x) на [а, Ь]. Так как f{x)D{x) =
= 0, то f(x)D(x) — интегрируемая функция на [а, Ь].
б) Пусть f\x) = 2, д(х) = D(x) на [а, Ь]. Тогда f(x)g(x) = 2D(x) —
неинтегрируемая на [а, Ъ] функция. А
3. Найти среднее значение функции на заданном сегменте:
a) f(x) = cosx на [0,Зтг/2]; б) f(x) = sgnx на [-1,2].
Л Находим средние значения /i, пользуясь формулой B):
Зтг/2
2 / 2
а) /i = — / cosxdx = --—. Отметим, что непрерывная функция
Зтг J Зтг
о
cosx принимает на сегменте [0,Зтг/2] значение \i = —2/(Зтг), а именно
cos? = -2/(Зтг), в точке f = arccos(-2/C7r)) G [0,Зтг/2].
2
б) \i — - I sgn х dx = -. В данном случае разрывная функция sgn x
о J о
-1
не принимает на сегменте [—1,3] значение \i — 1/3. А
Задачи и упражнения для самостоятельной работы
5. Докажите, что сумма интегрируемой и неинтегрируемой функций есть
функция неинтегрируемая.
6. Интегрируемы ли на сегменте [0,1] функции:
a)/i(x) = x; б) 91(х) = 1/х; в) h{x) + gi(x);
г) h (х)д 1 (х); я)Ых) = у&; е) /2 (х)дi (ж) ?
§3. Формула Ньютона-Лейбница 153
= {
7. Пусть
1 при - 2 ^ ж ^ О,
D{x) при О ^ ж ^ 2,
где D(x) — функция Дирихле. Интегрируема ли функция /(ж) на сег-
ментах [-2,2], [-2,-1], [-1,1], [1,2]?
ъ
8. Пусть существует l\f(x)\dx. Следует ли отсюда интегрируемость
а
функции /(ж) на сегменте [а, Ь]? Рассмотрите пример:
если ж — рациональное число,
если ж — иррациональное число.
9. Пусть /(ж) = sin ж, д(х) = 0,5 sin ж, и пусть: а) 0 ^ ж ^ тг; б) 0 ^ ж ^
^ Зтг/2. В каком из этих случаев выполнены условия свойства 9°?
10. Найдите среднее значение функции на указанных сегментах:
а) /(ж) = sin ж на [0, тг], [0, 2тг], [ipo, ipo + 2тг], [ipo, ipo + тг];
б) /(ж)= 8§пжна[-2,-1], [-2,1], [-1,3], [-2,2], [1,2].
Является ли среднее значение функции на каждом сегменте одним из
значений этой функции на этом сегменте? Объясните, почему в одних
случаях ответ положительный, а в других — отрицательный.
11. Найдите среднее значение функции на указанных сегментах:
а) f(x) = yft на [0,1], [0,10], [0,100];
б) /(ж) = 10 + 2 sin ж + 3 cos ж на [—тг, тг];
в) f{x) = sin ж sin(a; + ip) на [0, 2тг].
12. Найдите среднее значение скорости свободно падающего с высоты h
тела, начальная скорость которого равна vo.
13. Сила переменного тока меняется по закону
г = го sin
где г'о — амплитуда, t — время, Т — период, ip — начальная фаза.
Найдите среднее значение квадрата силы тока:
а) на промежутке времени [0,Т];
б) на промежутке [0,Т/2] (период функции г2(?));
в) на произвольном промежутке [0, to] и предел этого среднего при
to —»¦ оо.
§ 3. Формула Ньютона-Лейбница
Основные понятия и теоремы
1. Первообразная непрерывной и кусочно непрерывной
функции. Пусть функция f(x) интегрируема на сегменте [а, Ь].
Функция
х
F(x) = ff(t)dt (a^x О)
а
называется интегралом с переменным верхним пределом.
154 Гл. VIII. Определенный интеграл
Теорема 7. Непрерывная на сегменте [а,Ь] функция f(x) имеет
первообразную на этом сегменте. Одной из первообразных является
функция
х
= //(*) dt. A)
Замечание. Интеграл с переменным верхним пределом определен для
любой интегрируемой на [а, Ь] функции /(ж). Однако для того чтобы функ-
функция F(x) вида A) оказалась первообразной для /(ж), существенно, чтобы
функция f(x) была непрерывна.
Приведем пример, показывающий, что интегрируемая функция может
не иметь первообразной. Пусть
{1 при х > О,
О при х = 0, х Е [—1,1].
— 1 при х < 0;
Эта функция интегрируема на сегменте [—1,1], поскольку является кусочно
непрерывной, но, как уже отмечалось в гл. V, не имеет первообразной. В
самом деле, любая функция вида
р( \ _ [ —х + С\ при х < 0,
Т\х) — | х + Съ при х ^ 0,
где Ci, Сг — произвольные числа, имеет производную, равную sgnx, при
всех х ф 0. Но даже "самая хорошая" из этих функций — непрерывная
функция F(x) = \х\ + С (если С\ = Сг = С) — не имеет производной при
х = 0. Поэтому функция sgnx (и вообще всякая кусочно непрерывная функ-
функция) не имеет первообразной на любом промежутке, содержащем точку
разрыва.
Дадим теперь расширенное определение первообразной, пригодное
и для кусочно непрерывных функций.
Определение. Функция F(x) называется первообразной функ-
функции f(x) на сегменте [а, 6], если:
1°) F(x) непрерывна на [а,Ь];
2°) F'{x) = f{x) в точках непрерывности /(ж).
Замечание. Непрерывная на [а, Ь] функция f(x) является частным
случаем кусочно непрерывной ("кусок ее непрерывности" совпадает со всем
сегментом [а, Ь]). Поэтому для непрерывной функции расширенное опреде-
определение первообразной совпадает со старым, так как F (х) = f(x) Ух Е [а, Ь],
а непрерывность F(x) следует из ее дифференцируемости.
Приведем пример функции, имеющей первообразную в "новом" смысле
и не имеющей в "старом". Функция f(x) = sgnx на [—1,1] в "старом" смыс-
смысле не имела первообразной. В "новом" смысле ее первообразной является
функция F(x) = |ж|, поскольку она непрерывна на [—1,1] и F'(х) = f(x)
для х ф 0, т. е. всюду, кроме точки разрыва, х = 0.
Ценность расширенного определения первообразной ясна из сле-
следующего результата, сохраняющего для кусочно непрерывных функ-
функций теорему 7 с "новым" определением первообразной.
§3. Формула Ньютона-Лейбница 155
Теорема 8. Кусочно непрерывная на сегменте [а,Ь] функция f(x)
имеет первообразную на этом сегменте в смысле расширенного опре-
X
деления. Одной из первообразных является функция F(x) = f(t)dt.
а
2. Формула Ньютона—Лейбница.
Теорема 9. Для кусочно непрерывных функций справедлива
формула Ньютона-Лейбница
ъ
(x)dx = F(b)-F(a),
где F(x) — первообразная функции f(x) на [а,Ь] в смысле расширен-
расширенного определения.
2
/I 2
sgnxdx = |ж||_1 = 2 - 1 = 1.
-1
3. Метод замены переменной.
Теорема 10. Пусть:
1) f(x) определена и непрерывна на [а,Ь];
2) х = g{t) определена и непрерывна вместе с производной на [а,/3],
где д(а) = а, д({3) = Ь и а ^ g(t) ^ Ъ.
ъ C
Тогда ff(x)dx= f f(g(t))g'(t) dt.
a a
4. Метод интегрирования по частям.
Теорема 11. Если f(x) и д(х) имеют непрерывные производные
на [а, Ь], то
ъ ъ
Jf(x)g'(x)dx = f(x)g(x)\ba - Jf(x)g(x)dx.
Контрольные вопросы и задания
1. Что такое интеграл с переменным верхним пределом? Для каких подын-
подынтегральных функций он является первообразной?
2. Дайте расширенное определение первообразной, пригодное для кусочно
непрерывных функций.
3. При каких условиях справедлива формула Ньютона-Лейбница?
4. Известно, что функция /(ж) имеет первообразную на [а, Ь]. Интегрируе-
Интегрируема ли /(ж) на [а, Ь]? Рассмотрите пример: f(x) = Ff(x), где
F(x) = { х3/2 s^1/*) при х ф 0' х е [о, 1].
v у (^ 0 при х = 0; L J
5. Перечислите условия, при выполнении которых справедливы: а) форму-
формула замены переменной; б) формула интегрирования по частям.
156 Гл. VIII. Определенный интеграл
6. С помощью каких подстановок вычисляются интегралы, содержащие:
а) дробно-линейные иррациональности; б) квадратичные иррациональ-
иррациональности?
7. Для вычисления каких типов интегралов удобны тригонометрические
подстановки? Приведите примеры.
8. Цля вычисления каких типов интегралов удобен метод интегрирова-
интегрирования по частям? Приведите примеры.
Примеры решения задач
cos(t2) dt
1. Найти lim
ж-И) X
А Данный предел представляет собой неопределенность вида 0/0.
X
Интеграл с переменным верхним пределом / cos (t2) dt есть первооб-
Поэтому, применяя правило Лопиталя, получим
разная непрерывной функции cos ж2, т. е. ( / cos(t2)dt ] = cos(x2).
,ило Лопи
cos (t2)dt
lim
о
ж-^0 X
jujjaona/i j-\Jin. ^kjo yj"
x
,. cos (х ) 1
= lim —- = 1.
1
2
-1
\F(x)
А
1 х
Отметим, что первообразная для cos (ж2) не является элементарной
х
функцией, т. е. /cos (t2) dt не выражается через элементарные
о
функции. Это, однако, не помешало вычислению искомого предела. А
2. Найти первообразную кусочно не-
непрерывной функции
f(x)-ll ПРИ 1Ж1<1' xeR
ПХ)-\О при \х\^1; ХеН
А Одной из первообразных является ин-
Рис. 15 теграл с переменным верхним преде-
пределом, причем в качестве нижнего предела
интегрирования можно взять любое число, например х = —2. Итак,
х ( 0 при х ^ -1,
F(x) = ff(t)dt= I х + l при -l^x^l,
-2 I 2 при х ^ 1
(рис. 15). А
7Г
_ Г cos х dx
n V -1-
3. Вычислить / =
0
Л I способ. Подынтегральная функция /(ж) не определена в точке
§3. Формула Ньютона-Лейбница 157
ж = тг/2. Разобьем сегмент [0,тг] на два: [0,тг/2] и [тг/2,тг]. Полагая
на первом сегменте /(тг/2) = 1, получим интеграл от непрерывной
функции / = 1:
тг/2
— [ Л rl — I71"/2 — ^
i\ — Lax — ж|0 — —.
о
На втором сегменте положим /(тг/2) = — 1 и снова получим интеграл
от непрерывной функции / = —1:
7Г
Т /"/-14 7 I71" ТГ
/2= у (-l)dx = -rr|7r/2 = --.
тг/2
Окончательно имеем Д + /2 = 0.
II способ. Воспользуемся расширенным определением первооб-
первообразной. Функция F(x), удовлетворяющая этому определению, имеет
вид
= Г ж при 0 ^ ж <С тг/2,
\ тг — ж при тг/2 ^ ж ^ тг.
В самом деле, ^(ж) непрерывна на [0,тг] и F'(x) = /(ж) Уж Е [0,тг],
ж ^ тг/2, т. е. F'(x) = /(ж) в точках непрерывности /(ж). (Напомним,
что ж = тг/2 — точка разрыва /(ж).)
Согласно формуле Ньютона-Лейбница, справедливой для кусочно
непрерывных функций и расширенного определения первообразной,
получаем
7Г
/ = f(x)dx = ^(ж)|д = тг - х\х=7Т - х\х=0 = 0. А
о
Следующие два примера показывают, что формальное примене-
применение формулы Ньютона-Лейбница (т. е. использование этой формулы
без учета условий ее применимости) может привести к неверному
результату.
1
4. Рассмотрим интеграл /——. Взяв в качестве первообразной
J A\J X
о
подынтегральной функции /(ж) = 1/Bд/ж) функцию ^(ж) = л/х и
формально применив формулу Ньютона-Лейбница, получим
о
Однако этот результат неверен, так как функция /(ж) = 1/B^) не
1
ограничена на [0,1], и, следовательно, интеграл / —— не существует.
J A\J X
158
Гл. VIII. Определенный интеграл
5. Рассмотрим интеграл
На первый взгляд может показаться, что функция arctg A/ж) яв-
является первообразной подынтегральной функции — ( arctg - ), и тог-
ах \ х/
да по формуле Ньютона-Лейбни-
Ньютона-Лейбни-1
Ч
1
-1
_3тг
4
^Ф(я)
1 >
;
ца получаем
I = arctg -
-1
_ 7Г / 7Г\ _ 7Г
~ 4 ~ V 4У ~ 2'
Рис. 16
Однако этот результат неверен,
поскольку функция arctg A/ж)
не является первообразной для
d ( . 1\ г 1 in
— (arctg -1 на сегменте [—1,1J.
(XX \ X /
В самом деле, на рис. 16, а изображен график функции arctg A/ж).
Наглядно видно, что эта функция имеет в точке х = 0 разрыв I рода,
в то время как первообразная по самому определению должна быть
непрерывной во всех точках.
Чтобы вычислить интеграл /, заметим, что
I ~1+ 2 ПРИ Ж ^ 0'
[ не определена при ж = 0.
Доопределяя эту функцию в точке ж = 0 по непрерывности, получим
непрерывную функцию
1
Первообразной для /(ж) является
муле Ньютона-Лейбница имеем
хе[-1,1].
= —arctgж, поэтому по фор-
Отметим, что первообразную для /(ж) можно построить также с по-
помощью функции arctg A/ж), а именно:
{arctg A/ж) при -1 ^ х < 0,
—тг/2 при ж = 0,
arctg A/ж) - тг при 0 < ж ^ 1.
График Ф(ж) изображен на рис. 16, б. По формуле Ньютона-Лейбница
§3. Формула Ньютона-Лейбница 159
снова получаем
6. Применяя подходящую замену переменной, вычислить
а
I = х2 у а2 — х2 dx.
о
Л Положим х = asint, 0 ^ t ^ тг/2. Такая замена переменной
удовлетворяет всем условиям теоремы 4. Так как у/а2 — х2 = a cost,
dx = a cost (it, to
тг/2 4 тг/2 4 тг/2
/ = a4 / sin2 t cos2 t (it = ^- / sin2 2tdt = — f A - cos4t) (it =
0 0 0
_ тга
о
Следующий пример показывает, что формальное применение фор-
формулы замены переменной (без учета условий ее применимости) мо-
может привести к неверному результату.
7. Если в интеграле / = / = — сделать формально замену
-1
переменной х = 1/t и написать
г _ [ dt / 1 \ _ г dt _ тг ,9ч
-1 -1
то получается, очевидно, неверный результат.
Ошибка связана с тем, что изменению х сегменте [—1,1] соответ-
соответствует изменение t = 1/х не на сегменте [—1,1], как написано в ра-
равенстве B), а на объединении полупрямых (—оо, — 1) и A,+оо). Тем
самым указанная замена переменной не удовлетворяет требованиям
теоремы 4.
2тг
8. Вычислить / =
1 + 0,5 cos ж
о
Л Подынтегральная функция fix) = непрерывна на сег-
1 + 0,5 cos х
менте [0, 2тг] и, следовательно, имеет первообразную. Для нахождения
первообразной функции f(x) подходящей заменой переменной явля-
является t = tg (ж/2) (см. гл. V). Однако для определенного интеграла /
такая замена не удовлетворяет условиям теоремы 4, поскольку изме-
изменению х на сегменте [0, 2тг] не соответствует изменение t на некото-
некотором сегменте: t = tg (x/2) —у +оо (—оо) при х —> тг — 0 (тг + 0). Поэ-
Поэтому воспользуемся указанной заменой переменной для нахождения
160 Гл. VIII. Определенный интеграл
первообразной подынтегральной функции. Рассмотрим неопределен-
/dx
. На каждом из промежутков 0 ^ ж < тг и
1 + 0,5 cos ж
тг < ж ^ 2тг для него допустима замена переменной t = tg (ж/2).
В первом случае обратной функцией является ж = 2arctgt @ ^
^ t < +оо), во втором х = 2(тг + arctgt) (—оо < t ^ 0). В каждом
1 - ?2 , 2dt
случае cos ж = -, ах = -, и мы получаем
1 "т" Т 1 "Т" и
dx A f dt +C =
^Х) ~ J 1 + 0,5 cos ж ~ J зП
t=tg(x/2)
При любой постоянной С функция Ф(х) является первообразной для
/(ж) = Т~Г\ на промежутках [0, тг) и (тг, 2тг]. Так как она име-
1 "т" \ 1 / ^/ COS X
ет в точке х = тг разрыв I рода: Ф(тг + 0) — Ф(тг — 0) = —i, то Ф(ж)
не является первообразной для f(x) = -—р— на всем сегменте
1 + U,О COS X
[0,2тг]. Однако с помощью Ф(ж) теперь уже легко построить первооб-
первообразную для /(ж) на всем сегменте [0,2тг]. Положим
F(x) =
2тг
при 0^ж<тг,
при ж = тг,
Тем самым на [0, тг) мы взяли С = 0, в точке ж = тг доопределили Ф(ж)
(при G = 0) по непрерывности слева, а на (тг, 2тг] взяли С = 4тг/л/3-
Получилась функция F(x), производная которой во всех точках сег-
сегмента [0,2тг], в том числе и в точке ж = тг, равна функции /(ж) (для
точки ж = тг докажите этот факт самостоятельно), т. е. F(x) — пер-
первообразная для /(ж) на [0,2тг]. По формуле Ньютона-Лейбница
Замечание. Можно было бы разбить интеграл / на два интеграла:
тг 2тг
/ = I f(x)dx+ I F(x)dx, и воспользоваться тем, что первообразной для
f(x) на [0, тг] является функция
4
/1 х\
arctg I —— tg — ) при 0 ^ х < тг,
V V3 2 /
при х = тг,
§3. Формула Ньютона-Лейбница 161
а на [тг, 2тг] — функция
{^arctg(-^tg^) при тг<ж^2тг,
А* ^
-- ПРИ Ж = ТГ
(F\(x) получается из Ф(ж) при С = 0 с помощью доопределения Ф(ж) в точке
ж = тг по непрерывности слева, a F2(x) — справа). В этом случае, применяя
формулу Ньютона-Лейбница к каждому из интегралов, получаем
I = F!(x)\l + F2(x)\27r = Fi(tt) - Fi@) + F2Btt) - F2(n) =
9. Вычислить / = / | In x| dx.
l/e
А Разбивая интеграл / на сумму интегралов по сегментам [1/е, 1] и
[1,е] (чтобы "освободиться от модуля") и применяя в каждом интег-
интеграле формулу интегрирования по частям, получим
1 е 1 е
I = — In ж dx + \nx dx = — х\пх\1, + dx + ж In ж|^ — dx =
1/е 1 1/е 1
ir*r> т- /"Ж Sill Ж,
10. Вычислить / = / ^— аж.
У 1 + cos2 х
о
Л Применим формулу интегрирования по частям:
Т Г d(cosx) Г ,, , чч
I — — \ х — ^— = — ха( arctg (cosж)) =
J 1 + cos2 х J
о о
d(cosx) _
. + COS2 X
= —ж arctg (cos ж) | q + / arctg (cos x) dx = — тг f — J — 0
где h = arctg (cos ж) б?ж.
о
Чтобы найти /]_, заметим, что график функции /(ж) = arctg (cos ж)
центрально симметричен относительно точки (тт/2,/(тт/2)) = (тг/2,0).
Поэтому интегралы от этой функции по сегментам [0, тт/2] и [тг/2,тг]
равны по модулю и противоположны по знаку, а значит, в сумме
равны нулю, т. е. Д = 0. Этот же факт можно установить таким
образом: разобьем 1\ на два интеграла по сегментам [0,тг/2] и [тг/2,тг]
соответственно и во втором интеграле сделаем замену переменной
6 В.Ф. Бутузов и др.
162
Гл. VIII. Определенный интеграл
х = тг - t. Получим
тг/2 п
1\ = / arctg (cos х) dx + / arctg (cos x) dx =
7Г/2
7Г/2
= / arctg (cos x) dx + / arctg (- cos t) (—dt) =
7Г/2
7Г/2
7Г/2
arctg (cos x)dx — I arctg (cos t)dt = 0.
о
Итак, /i = 0, поэтому / = тг /4. А
Задачи и упражнения для самостоятельной работы
14. Найдите производные:
Ь Ь х2
а) — / sin(x2)dx; б) — / sin(x2)dx; в) — / sin(x2)dx;
dx J dbJ da J
a a a
~2 „2 „3
dx
dx J
о
dx
dt
dx
dx
15. Вычислите интегралы:
sh2 2
a)
^i 6) /"ll-xldx;
dx
@ < a < тг).
T _ , „ - - 2 - 2xcosa -,
shl 0 -1
16. Объясните, почему формальное применение формулы Ньютона-Лейб-
Ньютона-Лейбница приводит к неверным результатам, и вычислите, используя пер-
первообразную для кусочно непрерывной функции или разбивая на части
промежуток интегрирования, следующие интегралы:
2тг 1
, г dx
а) у СО82ж/2+ t 2ху б
о C0S X^ S Ж^ -1
17. Вычислите
, где
= { (_ x
при 1 < ж ^ 2,
двумя
способами: а) используя первообразную для /(ж), построенную на всем
сегменте [0,2]; б) разбивая сегмент [0,2] на сегменты [0,1] и [1,2].
18. Применяя формулу интегрирования по частям, вычислите следующие
интегралы:
In 2 2тг 1
а) хе~х dx; б) x2cosxdx; в) /arccosxdx.
§3. Формула Ньютона-Лейбница 163
19. Применяя подходящую замену переменной, вычислите следующие ин-
интегралы:
0,75 In 2 1
3
20. Можно ли вычислить интеграл ху/1 — ж2 с/ж с помощью замены пере-
переменной ж = sint? о
1
21. Можно ли, вычисляя интеграл / л/1 — ж2 с/ж с помощью замены пере-
0
менной ж = sint, взять в качестве новых пределов интегрирования чис-
числа: а) тг и тг/2; б) 2тг и 5тг/2; в) тг и 5тг/2? Вычислите интеграл в каждом
случае, когда указанная замена допустима.
22. Докажите, что для непрерывной на [—/,/] функции /(ж) справедливо
равенство:
i i
а) / /(ж) с/ж = 2 / /(ж) с/ж, если /(ж) — четная функция;
-I о
i
б) //(ж) с/ж = 0, если /(ж) — нечетная функция.
-I
Дайте геометрическую иллюстрацию этих фактов. Справедливы ли
эти равенства, если /(ж) — интегрируемая на [—/, /], но не обязательно
непрерывная функция?
23. Докажите, что одна из первообразных четной функции есть функция
нечетная, а всякая первообразная нечетной функции есть функция чет-
четная.
24. Вычислите интегралы:
1 е 3
а) / 2 Х ; б) /(ж In жJ с/ж; в) / arcsin \ / dx;
-11 О
2тг тг/2 тг
г) /- — -; д) / sin ж sin 2ж sin Зж с/ж; е) / (ж sin жJ с/ж.
J B + cosx)C + cos ж) J J
B
25. Пользуясь формулой Эйлера
егх = cos ж + г sin ж
(г — мнимая единица), покажите, что
2тт
= Г 0 При
[ inx . е-ггпх d (
J \ 2тт при т = п
о
& & ъ
(используйте равенство [f(x)+ig(x)]dx=f(x)dx + ig(x)dxj.
а а а
26. Покажите, что
ь
/(a-\-i0}x т G в^
a
(используйте равенство е(а+г/3)ж = eax • ег/3ж).
6*
164 Гл. VIII. Определенный интеграл
27. Пользуясь формулами Эйлера
cosx = -(егх + е~гх), sinx = — (егх - е~гх),
вычислите интегралы:
тг/2
Г
/
а) / sin х cos x dx: б) / dx:
J У sin ж
о о
7Г 7Г
в) / cosn х cos nxdx; г) / sinn x sin nxdx.
о о
§ 4. Вычисление длин плоских кривых
Основные понятия и формулы
1. Длина кривой. Рассмотрим на плоскости кривую L, заданную
параметрически:
x = ip(t), у = Ш, a^t^/3, A)
где ip(t) и ijj(t) — непрерывные на сегменте [а,/3] функции, причем
различным значениям t e [а, /3] соответствуют различные точки (ж, у)
(т. е. нет кратных точек). Такую кривую назовем простой (плоской)
незамкнутой кривой.
Если точки А(ср(а),ф(а)) и В(ср(/3),ф(/3)) совпадают, а осталь-
остальные точки не являются кратными, то кривая L называется простой
замкнутой кривой.
Пусть L — простая (замкнутая или незамкнутая) кривая, задан-
заданная уравнениями A). Рассмотрим произвольное разбиение сегмен-
сегмента [а,/3] точками а = to < t\ < ?2 < ••• < tn = C. Ему соответству-
соответствует разбиение кривой L точками А = Mq, Mi, M2, ..., Мп = В, где
Mi = М(ср(гг),ф(и)). Впишем в кривую L ломаную АМ1М2...В. Обо-
Обозначим длину ломаной через 1(М{) и положим At = max (ti — U-i).
Определение. Число I называется пределом длин ломаных 1(М{)
при At ->• 0, если Vs > 0 36 > 0 такое, что для любого разбиения
сегмента [а,/3], у которого At < 6, выполняется неравенство 0 ^
()
Определение. Если существует предел длин ломаных при
At —> 0, то кривая L называется спрямляемой, а число I — длиной
кривой L (или длиной дуги кривой L).
2. Длина кривой, заданной параметрически.
Теорема 12. Пусть простая кривая L задана параметрическими
уравнениями х = ip(t), у = ф(г), а ^ х ^ C, причем функции ip(t) и ф(г)
имеют на сегменте [а,/3] непрерывные производные. Тогда кривая L
§4- Вычисление длин плоских кривых 165
спрямляема, а ее длина вычисляется по формуле
Р
1 = Jy/Vl2(t)+V2(t)dt. B)
а
Функция
t
J^4t)+iP'2(t)dt C)
называется переменной дугой.
3. Длина кривой в декартовых координатах. Если кривая
задана уравнением у = /(ж), а ^ х ^ Ь, причем функция f(x) имеет
на сегменте [а, Ь] непрерывную производную, то длина кривой вычис-
вычисляется по формуле
ъ
^ + fl2(x)dx. D)
4. Длина кривой в полярных координатах. Если кривая за-
задана уравнением г = r((p), (fi ^ ^ ^ ^2, причем функция г(ф) имеет
на сегменте [(^1,(^2] непрерывную производную, то длина кривой вы-
вычисляется по формуле
Если кривая задана уравнением ip = ip(r), Т\ ^r ^r2, причем функ-
функция ip(r) имеет на сегменте [ri,r2] непрерывную производную, то
длина кривой вычисляется по формуле
Контрольные вопросы и задания
1. Что такое простая незамкнутая (замкнутая) кривая?
2. Дайте определение предела длин ломаных при At —»¦ 0.
3. Что такое спрямляемая кривая?
4. Что такое длина кривой?
5. По каким формулам вычисляется длина кривой: а) заданной парамет-
параметрически; б) в декартовых координатах; в) в полярных координатах?
6. Приведите примеры спрямляемых кривых.
7. Является ли прямая спрямляемой кривой?
8. Является ли окружность простой кривой?
166 Гл. VIII. Определенный интеграл
Примеры решения задач
1. Найти длину параболы у = ж2, 0 ^ х ^ 2.
Л По формуле D) получаем
2
/ = fy/l-\-4x2dx = л/17+ -1пD + л/17). А
о
2. Найти длину одной "арки" циклоиды x = a(t-sint), у —
= a(l -cost), 0 ^ t ^ 2тг.
Л По формуле B) находим
2r I
I = а / уA -costJ + sin2 tdt = 8a. A
о
Ж2 ?72
3. Найти переменную дугу эллипса — + У— = 1 (а>Ь) между
а2 о2
точкой (О, Ь) и любой точкой эллипса в первой четверти.
Л Полагая х = asint, у = 6cost, 0 ^ t ^ тг/2, по формуле C) получаем
(считая от верхнего конца малой полуоси)
t I 2 Г2 *
l(t) = a \ 1 - ^—^— sin2 t (it = a / v 1 - г2 sin2 t (it,
0 0
где г = л/a2 — b2/a — эксцентриситет эллипса.
Таким образом, переменная дуга эллипса выражается интегралом
t
l(t) = a/Vl-e2 sin2 tdt = aE(e,t),
о
который называется эллиптическим интегралом II рода.
Этот интеграл не выражается в элементарных функциях. Он ши-
широко используется в математике. Его название объясняется как раз
связью с рассмотренной задачей.
Если t = тг/2, то интеграл выражает 1/4 длины эллипса. В этом
случае эллиптический интеграл Е(е, тг/2) называют полным эллип-
эллиптическим интегралом и обозначают Е(е). А
Задачи и упражнения для самостоятельной работы
28. Найдите длины кривых, заданных уравнениями:
а) у = х3/2 @^ж^4); б)ж=*?-±1пу A ^ у ^ е);
B)y = \ncosx @ ^ж ^а <тг/2); г) ?/2 = ж3/Bа - ж) @ ^ х ^ 5а/3);
д) ж2/3 + |/2/3 = а2/3; е) х = cos4 t, у = sin4 t;
ж) х = а(? — sint), у = аA — cost) @ ^ t ^ 8тг; обратите внимание на
пределы интегрирования);
з) р = ay? @^9?^ 2тг) (спираль Архимеда);
и) р = a(l+cos<^); к) р = asin3((^/3); л) 9? = у/р @ ^ р ^ 5).
§ 5. Вычисление площадей плоских фигур
167
29. Докажите, что длина эллипса х = asint, у = 6cost равна длине сину-
синусоиды у = csm(x/b), 0 ^ ж ^ 2тг6, с = л/&2 — Ъ2. Дайте геометрическую
иллюстрацию этого результата, связав длины эллипса и синусоиды с
сечением цилиндра х2 + у2 = б2 плоскостью z = (c/b)x.
§ 5. Вычисление площадей плоских фигур
Основные понятия и формулы
1. Площадь плоской фигуры. Плоской фигурой будем называть
любое ограниченное множество точек плоскости.
Пусть в данную фигуру вписана многоугольная фигура и около
данной фигуры описана многоугольная фигура, т. е. фигура, состоя-
состоящая из конечного числа треугольников.
Множество площадей всех вписанных многоугольных фигур огра-
ограничено сверху (площадью любой описанной фигуры), а множество
площадей всех описанных многоугольных фигур ограничено снизу
(например, нулем).
Определение. Плоская фигура называется квадрируемой, если
точная верхняя грань Р_ множества площадей всех вписанных много-
многоугольных фигур равна точной нижней грани Р множества площадей
всех описанных многоугольных фигур.
Число Р = Р_ — Р называется площадью плоской фигуры (по Жор-
Дану).
Теорема 13 (достаточное условие квадрируемости). Для того
чтобы плоская фигура была квадрируемой, достаточно, чтобы ее гра-
граница была спрямляемой кривой.
2. Площадь плоской фигуры в декартовых координатах.
Пусть плоская фигура представляет собой криволинейную трапецию,
ограниченную непрерывными кривыми у = Д(ж), у = f2(x), а ^ х ^
^ Ъ (где у\{х) ^ ?/2(x))j и Двумя отрезками прямых х = а, х = Ъ
О
V=f*(x)
УI
х о
у =fi(x)
Р=Р(<Р)
/ Р=Р(<Р)
о
о
а б ~ а ~ б
Рис. 17 Рис. 18
(рис. 17, а). Отрезки прямых могут вырождаться в точку (рис. 17, б).
168 Гл. VIII. Определенный интеграл
Тогда площадь фигуры вычисляется по формуле
ъ
A)
3. Площадь плоской фигуры в случае параметрического
задания ее границы. Пусть граница плоской фигуры G — простая
замкнутая кривая, заданная параметрически уравнениями х = (p(t),
у = ?/>(?), О ^ t ^ Т, причем точка ((p(t),ip(t)) при изменении t от
О до Т пробегает границу G так, что фигура G остается слева от
движущейся точки. Тогда площадь фигуры G может быть вычислена
по любой из следующих формул:
B)
о
т
s = Jip(tW(t)dt, (з)
о
т
t. D)
4. Площадь плоской фигуры в полярных координатах.
Пусть плоская фигура представляет собой криволинейный сектор,
ограниченный непрерывной кривой р = p(ip), ipi ^ ip ^ <^2, 0 <
< (f2 — ^fi ^ 2тг, и отрезками лучей ip = ipi и (р = (р2 (рис. 18, а). От-
Отрезки лучей могут вырождаться в точку О (рис. 18, б). Тогда площадь
фигуры вычисляется по формуле
2
(<p)d<p- E)
Контрольные вопросы и задания
1. Что такое плоская фигура?
2. Что такое квадрируемая фигура?
3. Что такое площадь плоской фигуры?
4. По каким формулам вычисляется площадь фигуры: а) в декартовых
координатах; б) в случае параметрического задания границы; в) в по-
полярных координатах?
5. Приведите примеры квадрируемых фигур.
6. Является ли плоскость квадрируемой фигурой?
7. Является ли прямая квадрируемой фигурой?
§ 5. Вычисление площадей плоских фигур
169
Примеры решения задач
1. Найти площадь фигуры, ограниченной кривыми у = \х — 1|,
у = 3-\х\.
Л Данные кривые пересекаются в двух точках (рис. 19). Решив
Рис. 19
Рис. 20
уравнение 3 - \х\ = \х - 1|, найдем абсциссы этих точек: ? = —1, х = 2.
Поэтому
2
S= JC-\x\-\x-l\)dx.
-i
Разобьем интеграл на три интеграла соответственно по сегментам
[-1,0], [0,1], [1,2]. Получим
S =
-х) - (l-x)]dx
2
+ ДC - х) - (х - 1)] dx = 1 + 2 + 1 = 4. А
1
2. Найти площадь фигуры, ограниченной астроидой ж2/3 +у2/3 =
= а2/3 (рис. 20).
Л Полагая х = acos3t, 2/ = asin3t, 0 ^ t ^ 2тг, приходим к парамет-
параметрическим уравнениям астроиды (параметр ? играет роль полярного
угла точки (ж,у) на астроиде). По формуле D) получаем
2тг
S = - / (a cos3 ? • За sin2 ? cos t + За cos2 ? sin ? • a sin3 ?) eft =
27Г
= - a2 / sin2 ? cos2 ? eft = -тга2. А
2 J 8
Замечание 1. Симметричная формула D) привела здесь к более прос-
простому интегралу, чем тот, который получился бы в результате применения
формул B) или C).
170
Гл. VIII. Определенный интеграл
Замечание 2. Отметим, что интеграл по сегменту [0, тг/2]
2 ^/
-— / si
Z J
sin2 ? cos2 tdt = — тга2
о2
дает площадь той части фигуры, которая лежит в I квадранте (рис. 21), хо-
хотя в этом случае вся граница фигуры уже не описывается уравнениями х =
= acos3t, у = a sin3 ?, поскольку содержит отрезки осей координат. Поче-
Почему же получился правильный результат? Дело в том, что параметрически
отрезок [а, 0] оси Оу можно задать уравнениями х = 0, у = 2аA — ?/тг),
тг/2 ^ t ^ тг, а отрезок [0, а] оси Ох — уравнениями х = 2а(?/тг — 1), у = 0,
тг ^ t ^ Зтг/2. На этих отрезках параметр t не играет роли полярного угла.
Рис. 21 Рис. 22
Используя теперь полную параметризацию границы фигуры (параметр t
изменяется от 0 до Зтг/2) и разбивая интеграл по сегменту [0, Зтг/2] на
три интеграла, соответствующих криволинейному и двум прямолинейным
участкам границы, получаем, что интегралы по отрезкам координатных
осей обращаются в нуль, так как на каждом из них одна координата и ее
производная по параметру равны нулю.
По той же причине формула B) остается справедливой для криволи-
криволинейной трапеции, ограниченной отрезком оси Ох, двумя вертикальными
отрезками и кривой, заданной параметрически уравнениями х = <p(t),
у = if;(t), 0 ^ t ^ Т, если при изменении t от 0 до Т точка ((p(t),ifj(t))
пробегает кривую так, что трапеция остается слева от точки. В противном
случае в формуле B) перед интегралом нужно поставить знак плюс.
Замечание 3. Найти площадь фигуры, ограниченной циклоидой х =
= a(t — suit), у = a(l — cost), 0 ^ t ^ 2тг, и осью Ох.
Л По формуле B) (где в силу замечания 2 перед интегралом взят знак
плюс) имеем
2тг
*=
Замечание 4. Найти площадь фигуры, ограниченной кривой, задан-
заданной в полярных координатах уравнением р = 2a2 cos 2(p (лемниската
Бернулли).
Л Учитывая неотрицательность р, находим, что —тг/4 ^ ср ^ тг/4 и Зтг/4 ^
^ (р ^ 5тг/4 (рис. 22). По формуле E) вычисляем площадь одной из двух
равных частей фигуры и удваиваем результат:
тг/4
1 2 f 2
S = 2 • - • 2а / cos 2cpdcp = 2а . А
-тг/4
§ 6. Вычисление объемов тел 171
Задачи и упражнения для самостоятельной работы
30. Найдите площадь фигуры, граница которой задана уравнениями в
декартовых координатах:
2 2
а) ~Т + 7^" = !> х = хо, x = xi, у^О (-а < х0 < xi < а);
а2 Ь2
б) у = х , ж + 2/ = 2; в) 2/ = (х + 1) , х = sinTH/, ?/ = 0 @ ^ j/ ^ 1);
г) |/2 = х2(а2 —ж2); д) ?/ = e~x|sinx|, у = 0 (ж ^ 0) (за площадь
этой неограниченной фигуры примите предел при А —»¦ +оо площадей
криволинейных трапеций, соответствующих изменению х от 0 до А).
31. Найдите площадь фигуры, граница которой задана параметрически
(предварительно нарисуйте эскиз фигуры):
а) х = a(cost + tsint), 2/ ^ «(sint — tcost), 0 ^ t ^ 2тг, ж = а, у^О
(развертка круга);
б) х = aBcos? — cos 2?), у = aBsin? — sin2?).
32. Найдите площадь фигуры, граница которой задана уравнением в по-
полярных координатах:
а) р = a(l + cos cp) (кардиоида); 6)p = asin3(p (трилистник);
в) р = 3 + 2 cos <р; г) р2 +ср2 = 1.
33. Перейдя к полярным координатам, найдите площадь фигуры, граница
которой задана уравнением:
а) х3 + у3 = Заж?/ (лист Декарта);
б) (ж2 + у2J = 2а2ху (лемниската Бернулли).
§ 6. Вычисление объемов тел
Основные понятия и формулы
1. Объем тела (по Жордану). Телом будем называть любое
ограниченное множество точек пространства.
Пусть в данное тело вписан многогранник и около данного тела
описан многогранник, т. е. тело, состоящее из конечного числа тре-
треугольных пирамид.
Множество объемов всех вписанных многогранников ограничено
сверху (объемом любого описанного многогранника), а множество
объемов всех описанных многогранников ограничено снизу (напри-
(например, нулем).
Определение. Тело называется кубируемым, если точная верх-
верхняя грань V_ множества объемов всех вписанных многогранников
равна точной нижней грани V множества объемов всех описанных
многогранников.
Число V = У_ = V называется объемом тела (по Жордану).
2. Объем тела с известными поперечными сечениями.
Пусть каждое сечение кубируемого тела плоскостью х = const есть
квадрируемая фигура, причем ее площадь S(x) является непрерыв-
непрерывной функцией х (а ^ х ^ Ь). Тогда объем этого тела вычисляется по
172 Гл. VIII. Определенный интеграл
формуле
ъ
V = fs(x)dx. A)
а
В частном случае, когда тело получено вращением вокруг оси Ох
криволинейной трапеции, заданной непрерывной функцией у = /(ж),
а ^ х ^ 6, объем тела вращения вычисляется по формуле
ъ
V = тг Jf(x)dx. B)
Контрольные вопросы и задания
1. Что называется телом?
2. Что такое кубируемое тело?
3. Что такое объем тела?
4. По какой формуле вычисляется: а) объем тела с известными попереч-
поперечными сечениями; б) объем тела вращения?
5. Приведите примеры кубируемых тел.
6. Является ли плоскость кубируемым телом?
7. Является ли прямая кубируемым телом?
Примеры решения задач
х2 у2
1. Найти объем тела, полученного вращением эллипса — + ^— — 1
вокруг оси Ох.
Л По формуле B) имеем
a g
V = тг / -^(а2 — х2) dx = - 7гаЬ2. к
J а о
— а
2. Найти объем тела, ограниченного поверхностями х2 + у2 = а2,
Л I способ. Рассмотрим сечения этого тела плоскостями х = const.
В сечениях получаются прямоугольные треугольники с площадями
дух) — — y\x)z\x) — —у а — х у о у а — х — —— [а — х ).
По формуле A) находим
V
= — j (a2 -x2)dx= — а •
II способ. Рассекая это же тело плоскостями у = const, в сече-
сечениях получаем прямоугольники с площадями
5B/) = 2x
§ 7. Физические приложения 173
Поэтому
V = 2л/3 /у у а2 — у2 dy = а3. А
J 3
о
Задачи и упражнения для самостоятельной работы
34. Найдите объем усеченного конуса, основания которого ограничены эл-
эллипсами с полуосями А, В и а, Ъ, а высота равна h.
35. Тело представляет собой множество точек М(ж, у, z), где 0 ^ z ^ 1. При
этом 0 ^ ж ^ 1, 0^2/^1, если г — рациональное число, и —1 ^ ж ^ 0,
— 1 ^2/^0, если z — иррациональное число. Докажите, что объем этого
1
тела не существует, хотя S(z)dz = 1.
о
36. Найдите объемы тел, поверхности которых заданы уравнениями:
а2 Ь2 а ' а2 Ь2 с2
в) — + — — — = 1, z = ±с; г) ж2 + z2 = а2, у2 + z2 = а2;
az oz cz
д) ж2 +1/2 + z2 = а2, ж2 + у2 = аж (пересечение указанных сферы и
цилиндра образует два тела. Найдите объем так называемого тела Ви-
виани, вырезаемого цилиндром из сферы. Получив ответ, обратите вни-
внимание на его структуру: если из полусферы удалить тело Вивиани, то
объем оставшейся части выражается через радиус сферы без иррацио-
иррациональных коэффициентов, в частности без тг).
37. Найдите объемы тел, ограниченных поверхностями, полученными вра-
вращением следующих кривых:
а) у = 6(ж/аJ/3 @ ^ ж ^ а) вокруг оси Ож;
б) у = 2ж — ж2, у = 0 вокруг оси Ож;
в) у = 2ж — ж2, у = 0 вокруг оси Оу\
г) у = sin ж, у = 0 @ ^ ж ^ тг) вокруг оси Ож;
д) у = sin ж, 2/ = 0 @ ^ ж ^ тг) вокруг оси Оу\
е) ж = а(? — sint), ?/= аA — cost) @ ^ ? ^ 2тг) вокруг оси Ож;
ж) ж = a(t — sint), у = аA — cost) @ $J t $С 2тг) вокруг оси Оу.
§ 7. Физические приложения определенного интеграла
Основные понятия и формулы
1. Вычисление массы плоской кривой. Пусть простая кривая
L задана параметрически уравнениями х = (p(t), у = ip(t), а ^ ? ^ /3,
и пусть р(х,у) — линейная плотность массы в точке (х,у) G L. Тогда
масса кривой L вычисляется по формуле
м =
174 Гл. VIII. Определенный интеграл
Пусть простая кривая задана уравнением в декартовых коорди-
координатах у = /(ж), а ^ х ^ Ъ. Тогда масса кривой L вычисляется по
формуле
ъ
М = fp(x,/(х))л/1 + //2И dx.
а
В частности, при р = 1 числовое значение массы совпадает с длиной
кривой.
2. Вычисление моментов и координат центра тяжести
плоской кривой. Статические моменты (или моменты первого
порядка) кривой L относительно координатных осей в случае пос-
постоянной линейной плотности р = 1 (геометрические моменты) вы-
вычисляются по следующим формулам (х = (p(t), у = ip(t), а ^ ? ^ /3, —
уравнения кривой):
Мх — ip(t)^/(pf2(t) + ipf2(t) dt (момент относительно оси Ож),
а
Р
Му = / cp(t)y/(p/2(t) + i/j/2(t) dt (момент относительно оси Оу).
Если кривая задана в декартовых координатах: у = /(ж), а ^ х
^ Ь, то
ъ ъ
±у±Х — I J \**v у ' J \ ) 1 У —
а
Координаты хо и уо центра тяжести кривой L вычисляются по
формулам
хо = Му/l, уо = Мх/1,
где I — длина кривой L.
Моменты инерции (или моменты второго порядка) кривой L от-
относительно координатных осей [р = 1) вычисляются по формулам
Р
1Х = / ф2(t) vV'2(t) + гр'2(t) dt (относительно оси Ох),
а
Р
Iy = / ср2 (?) у/'ер'2 (t) + гр'2 (t) dt (относительно оси Оу),
a
или (в декартовых координатах)
ъ ъ
1,=
§ 7. Физические приложения 175
3. Вычисление моментов и координат центра тяжести
плоской фигуры. Статические моменты фигуры G, ограниченной
непрерывными кривыми у = Л(ж), у = /2(ж), а ^ х ^ b (где Д(ж) ^
^ /2(^)), и отрезками прямых ж = а, ж = 6, в случае постоянной по-
поверхностной плотности /я = 1 вычисляются по формулам
^ж = о / [^2 (ж) ~~ Л2(ж)] ^ж (относительно оси Ох), A)
ь
My = x[f2(x) — fi(x)]dx (относительно оси Оу). B)
а
Координаты ж0 и у0 центра тяжести фигуры вычисляются по
формулам
Му Мх ( v
хо = -gr, 2/о = -~-, C)
где S — площадь фигуры G.
Моменты инерции фигуры G относительно координатных осей
р = 1 вычисляются по формулам
ъ
1Х — - [/|(ж) — fl (ж)] dx (относительно оси Ож),
а
Ъ
1у = /ж2[/2(ж) - Д(ж)]б?ж (относительно оси Оу).
а
Примеры решения задач
1. Найти статические моменты и координаты центра тяжести
криволинейной трапеции, ограниченной параболой у2 = /|(ж) = 2рх и
прямыми у = Д(ж) = 0 и ж = 1.
Л По формулам A) и B) находим
1 1
»м, 1 о Г , р
2 J 2
О О
Вычислим площадь этой криволинейной трапеции:
0
Теперь по формулам C) находим координаты центра тяжести:
_ Му _ 3 _ Мж _ 3
176 Гл. VIII. Определенный интеграл
2. Применяя вторую теорему Гульдена (см. ниже упр. 44), най-
найти координаты центра тяжести плоской фигуры G, ограниченной од-
одной аркой циклоиды х = a(t - sint), у = аA - cost), 0 ^ t ^ 2тг, и
осью Ох.
Л Объем тела, полученного от вращения фигуры вокруг оси Ох,
равен
2тга 2тг
У = тг Г y2dx = тга3 ГA -costKdt = 5тг2а3.
о о
Площадь фигуры G равна
2тга 2тг
5= Г ydx= fa2(l-costJdt
о о
Пусть 2/о — ордината центра тяжести. Согласно второй теореме
Гульдена S • 2тгуо = У, откуда уо = 5а/б. Из симметрии фигуры G
относительно прямой х = тга следует, что абсцисса центра тяжести
есть хо = тгр. А
Задачи и упражнения для самостоятельной работы
38. Найдите статистический момент и момент инерции полуокружности
радиуса а относительно диаметра этой полуокружности.
39. Найдите статический момент дуги параболы у2 = 2рх @ ^ х ^ р/2)
относительно прямой ж = р/2.
40. Найдите статический момент и момент инерции однородной треуголь-
треугольной пластинки с основанием Ъ и высотой h относительно основания.
41. Найдите моменты инерции однородной эллиптической пластинки с по-
полуосями а и Ъ относительно ее главных осей.
42. Найдите момент инерции однородного круга радиуса R и массы М
относительно его диаметра.
43. Докажите первую теорему Гульдена: площадь поверхности, образован-
образованной вращением плоской кривой вокруг не пересекающей ее оси, лежа-
лежащей в плоскости кривой, равна произведению длины этой кривой на
длину окружности, описываемой центром тяжести кривой.
44. Докажите вторую теорему Гульдена: объем тела, образованного вра-
вращением плоской фигуры вокруг не пересекающей ее оси, лежащей в
плоскости фигуры, равен произведению площади этой фигуры на дли-
длину окружности, описываемой центром тяжести этой фигуры.
45. Найдите объем "баранки", полученной вращением окружности
(ж — 2J + у2 = 1 вокруг оси Оу.
46. Найдите координаты центра тяжести дуги окружности х = a cos 9?,
y = asin(p (\ip\ ^ а ^ тг).
47. Найдите координаты центра тяжести фигуры, ограниченной парабола-
параболами ах = у2, ау = х2 (а > 0).
48. Найдите координаты центра тяжести однородного полушара
х2 + у2 + z2 ^ a2, z ^ 0.
49. Найдите координаты центра тяжести фигуры, ограниченной кривой
г = аA + cos (f).
ГЛАВА IX
МЕРА И ИНТЕГРАЛ ЛЕБЕГА
§ 1. Мера множества
Основные понятия и теоремы
1. Некоторые сведения о множествах. Говорят, что между
элементами двух множеств установлено взаимно однозначное соот-
соответствие, если каждому элементу первого множества поставлен в
соответствие некоторый элемент второго множества так, что при
этом каждый элемент второго множества соответствует только од-
одному элементу первого множества.
Два множества называются эквивалентными, если между их эле-
элементами можно установить взаимно однозначное соответствие. Если
два множества эквивалентны, то говорят, что они имеют одинаковую
мощность.
Множество называется счетным, если оно эквивалентно множест-
множеству натуральных чисел (иными словами, множество называется
счетным, если его элементы можно занумеровать с помощью
натуральных чисел).
Например, множество всех рациональных чисел сегмента [0,1]
счетно, а множество всех вещественных чисел этого же сегмента не-
несчетно.
Если множество эквивалентно множеству всех вещественных чи-
чисел сегмента [0,1], то говорят, что оно имеет мощность континуума.
Объединением (суммой) множеств Е\, Е2,..., Еп называется мно-
п
жество Е — (J Ek, которое состоит из всех элементов, принадлежа-
k=l
щих хотя бы одному из множеств Е^ (к = 1,2,...,п).
Объединение множеств Е\ и Е2 будем обозначать также символом
E1UE2 или Е1 +Е2.
Пересечением множеств Е\, Е2,..., Еп называется множество
п
G — Р| Екч которое состоит из всех элементов, принадлежащих каж-
к=1
дому из множеств Е^ (к = 1, 2,..., п).
Пересечение множеств Е\ и Е2 будем обозначать также символом
Ех ПЕ2 или ЕХЕ2.
(X)
Точно так же определяются объединение |J E^ и пересечение
к=1
178 Гл. IX. Мера и интеграл Лебега
ОО
Р| Ek счетного числа множеств.
k=i
Разностью множеств Е\ и Е2 называется множество Е — Е\ \Е2,
которое состоит из всех элементов множества Е\, не содержащихся
в Е2.
Пусть Е — произвольное числовое множество. Точка х называ-
называется внутренней точкой Е, если существует окрестность точки ж,
целиком принадлежащая Е.
Множество Е называется открытым, если все его точки внут-
внутренние. Множество Е называется замкнутым, если оно содержит все
свои предельные точки.
Например, интервал (а, Ъ) — открытое множество, а сегмент
[а, Ъ] — замкнутое множество.
Объединение конечного или счетного числа открытых множеств
является открытым множеством.
Теорема 1 (о структуре открытых множеств). Любое открытое
множество является объединением конечного или счетного числа по-
попарно непересекающихся интервалов.
2. Понятие числового ряда. Пусть {ап} — числовая последо-
последовательность. Образуем формально выражение
ОО
а\ + а2 + ... + ап + ... = ^ аи
k=i
и назовем его числовым рядом (или просто рядом). п
Числа аи называются членами ряда, а число Sn = ^ аи — его п-й
частичной суммой. u=i
Рассмотрим последовательность {Sn}.
Определение. Если существует lim Sn = 5, то говорят, что
со п—>-оо
ряд V^ аи сходится, а число S называется суммой ряда.
k=i
3. Мера множества. Мерой интервала (а,/3) (где C > а) назовем
его длину C — а.
Пусть G — ограниченное открытое множество. По теореме 1 его
можно представить в виде G= U(afc?Afe)? где (ak,Pk) — попарно
непересекающиеся интервалы. к=1
Мерой \iG открытого ограниченного множества G назовем сумму
длин его интервалов: fiG = ^(/^ - аи).
k=i
Отметим, что если число интервалов (аи,Ри) счетно, то сумма
(X)
длин интервалов является числовым рядом ^(/^ - аи) с положи-
тельными членами (/3k — аи). В силу ограниченности множества G
этот ряд сходится.
§1. Мера множества 179
Пусть Е — произвольное ограниченное множество. Рассмотрим
всевозможные ограниченные открытые множества G, содержащие Е.
Множество {/iG} мер этих множеств ограничено снизу (например,
числом 0) и, следовательно, имеет inf {fiG}.
Число ~рЕ = inf {/iG} называется внешней мерой множества Е.
Определение. Множество Е называется измеримым (по Лебе-
Лебегу), если \/е > 0 существует открытое множество G, содержащее Е,
для которого Jt(G \Е) < г. При этом внешняя мера множества Е на-
называется его мерой (Лебега) и обозначается /иЕ, т. е. \iE — ~pE.
Замечание. Для открытого множества Е это определение эквивалент-
эквивалентно данному выше (в качестве G достаточно взять само Е).
Понятие меры множества обобщает понятие длины. Для достаточ-
достаточно простых множеств (интервал, сегмент) мера совпадает с длиной.
Для более сложных множеств, не имеющих длины в обычном смысле,
роль длины играет мера.
Любое замкнутое ограниченное множество измеримо.
Если Е — измеримое множество, причем Е С [а, Ь], то множество
Е — [а,Ь]\Е (дополнение множества Е до сегмента [а, Ь]) измеримо.
Объединение (если оно ограничено) и пересечение конечного или
счетного числа измеримых множеств являются измеримыми мно-
множествами. При этом мера объединения счетного (или конечного)
числа попарно непересекающихся множеств равна сумме мер этих
множеств, т. е. если
ОО
Е= U Ek,
к=1
ТО
к=1
Это свойство называется счетной аддитивностью (или а -аддитив-
-аддитивностью меры Лебега.
Контрольные вопросы и задания
1. Что такое взаимно однозначное соответствие между элементами двух
множеств?
2. Какие множества называются эквивалентными?
3. Какое множество называется счетным?
4. Является ли счетным: а) множество Q всех рациональных чисел; б) мно-
множество R всех вещественных чисел?
5. Что такое множество мощности континуума? Имеет ли множество R
всех вещественных чисел мощность континуума?
6. Что такое объединение множеств? Может ли объединение множеств
совпадать с одним из них? Может ли объединение непустых множеств
быть пустым множеством?
180 Гл. IX. Мера и интеграл Лебега
7. Что такое пересечение множеств? Может ли пересечение множеств сов-
совпадать с одним из них? Может ли пересечение непустых множеств быть
пустым множеством?
8. Что такое разность двух множеств? Может ли разность Е\ \ Еч непус-
непустых множеств совпадать: а) с Е\\ б) с ?^?
9. Что такое: а) внутренняя точка множества; б) открытое множество;
в) предельная точка множества; г) замкнутое множество?
10. Является ли множество Q всех рациональных чисел: а) открытым;
б) замкнутым?
11. Является ли множество R всех вещественных чисел: а) открытым;
б) замкнутым?
12. Докажите, что объединение конечного или счетного числа открытых
множеств является открытым множеством.
13. Докажите, что пересечение конечного числа открытых множеств явля-
является открытым множеством, а пересечение счетного числа открытых
множеств может не быть открытым множеством.
14. Докажите, что пересечение конечного или счетного числа замкнутых
множеств является замкнутым множеством.
15. Докажите, что объединение конечного числа замкнутых множеств яв-
является замкнутым множеством, а объединение счетного числа замкну-
замкнутых множеств может не быть замкнутым множеством.
16. Сформулируйте теорему о структуре открытых множеств.
17. Когда говорят, что числовой ряд сходится? Что такое сумма ряда?
оо
18. Пусть все члены ряда \. ак неотрицательны. Докажите, что в этом
к = 1
случае: а) необходимым и достаточным условием сходимости ряда яв-
является ограниченность последовательности {Sn} его частичных сумм;
б) если переставить члены ряда произвольным образом, то сумма ряда
не изменится.
19. Что такое мера: а) интервала; б) ограниченного открытого множества?
оо
Докажите сходимость ряда /iG = /(Д — ел к), где (а/., Д) — попарно
к = 1
непересекающиеся интервалы, из которых состоит открытое ограни-
ограниченное множество G.
20. Что такое внешняя мера множества? Всякое ли ограниченное мно-
множество имеет внешнюю меру?
21. Дайте определение измеримого множества и его меры.
22. Пользуясь определением измеримого множества, докажите, что сегмент
[а, Ь] измерим, причем его мера //[а, Ь] = Ъ — а (а < Ъ).
23. Пусть измеримое множество Е С [а, Ь]. Докажите, что множество
Е = [а, Ь] \ Е измеримо, причем цЕ = //[а, Ь] — цЕ.
24. Докажите, что замкнутое ограниченное множество измеримо.
25. Что такое счетная аддитивность меры? Докажите, что объединение
(если оно ограничено) счетного числа измеримых множеств является
измеримым множеством.
§1. Мера множества 181
Примеры решения задач
1. Доказать, что интервал @,1) = / и числовая прямая R — эк-
эквивалентные множества: R ~ I.
Л Чтобы доказать эквивалентность множеств /ий, нужно устано-
установить между их элементами взаимно однозначное соответствие. Такое
соответствие осуществляет функция
y= tg^rx- |), x el.
В самом деле, каждому х е I эта функция ставит в соответствие
некоторое у Е R, а так как она непрерывна и возрастает на / и,
кроме того, lim tg (тгж J = —оо, lim tg (тгж J = +оо, то
My ~ R существует единственное х G / такое, что у = tg (тгж — ^J.
Это и означает, что между элементами множеств / и R установлено
взаимно однозначное соответствие. Итак, R ~ I. А
2. Доказать, что интервал @,1) = / и сегмент [0,1] = S — экви-
эквивалентные множества: I ~ S.
Л Пусть Q — множество всех рациональных чисел сегмента S. Это
множество счетное (см. § б из гл. II). Положим Q = S\Q. Тогда
S = Q + Q. Удалим из множества Q точки 0 и 1. Получим счетное
множество Q\ рациональных чисел интервала /. Очевидно, I = Q1-\-
+ Q. Так как Q и Q\ — счетные множества, то Q ~ Q\. Отсюда сле-
следует, что Q + (J ~ Qi + Q, т. е. S - /. А
Замечание. Из утверждений примеров 1 и 2 следует, что числовая
прямая R (множество всех вещественных чисел) имеет мощность конти-
континуума.
3. Пусть открытое множество Е С [а, Ь]. Доказать, что G =
= [а,Ь]\Е — замкнутое множество.
Л Нужно доказать, что G содержит все свои предельные точки. Из
определения разности множеств следует, что \/х G [а, Ъ] либо х G Е,
либо х G G. Пусть х — предельная точка множества G, т. е. в лю-
любой окрестности точки х имеются точки множества G, отличные от
х. Очевидно, х G [а, Ь]. Докажем, что х G G. Предположим против-
противное. Тогда х е Е, и так как Е — открытое множество, то существу-
существует окрестность точки ж, целиком принадлежащая Е. Следовательно,
в этой окрестности точки х нет ни одной точки из множества G,
но это противоречит тому, что х — предельная точка G. Получен-
Полученное противоречие доказывает, что х G G, и, значит, G — замкнутое
множество. А
4. Доказать, что множество Q всех рациональных чисел произ-
произвольного сегмента [а, Ъ] измеримо, причем \iQ — 0.
Л Множество Q счетно, поэтому его точки можно занумеровать с
182 Гл. IX. Мера и интеграл Лебега
помощью натуральных чисел. Зададим произвольное г > 0 и заклю-
заключим первую точку множества Q в интервал длины г/2, вторую —
в интервал длины г/22,...,п-ю — в интервал длины г/2п и т. д.
Объединение этих интервалов является открытым множеством G, ме-
мера которого
к=1
В силу того, что е произвольно мало, отсюда следует, что ~pQ = 0.
Так как (G\Q) С G, то Jt(G \ Q) ^ JIG = \iG < г. Это означает по
определению, что Q измеримо, причем \iQ = ~pQ = 0. В таком случае
говорят, что множество Q имеет меру нуль. А
5. Пусть а — произвольное число такое, что 0 < а < 1. Построим
два множества, D и Е, с помощью счетного числа шагов следую-
следующим образом. На первом шаге удалим из сегмента [0,1] интервал Е\
длины а/2, расположенный симметрично относительно середины сег-
сегмента [0,1] (назовем такой интервал средним интервалом). На втором
шаге из оставшихся двух равных сегментов удалим средние интерва-
интервалы длины а/8 каждый. Обозначим объединение этих интервалов Е^\
длина Е2 равна а/4. На третьем шаге из оставшихся четырех равных
сегментов удалим средние интервалы длины а/32 каждый. Обозна-
Обозначим объединение этих четырех интервалов Е3; длина Е3 равна а/8.
На четвертом шаге из оставшихся восьми равных сегментов удалим
средние интервалы длины а/128 каждый и т. д. Пусть
оо
Е= U Ek, D = [0,l]\E.
к=1
Доказать, что:
а) Е — открытое, a D — замкнутое множество;
б) /иЕ = a, ijlD = 1 - а;
в) множество D не содержит целиком ни одного сегмента;
г) множество D не содержит изолированных точек;
д) \/е > 0 найдется множество D' такое, что D С D' и 0 < /iD' -
- /iD <г;
е) множество D несчетно.
Л а) Множество Е открытое, так как оно является объединением ин-
интервалов — открытых множеств; множество D замкнутое, поскольку
является дополнением открытого множества до сегмента.
б) Так как множества Еь (к = 1, 2,...) не пересекаются, то в силу
сг-аддитивности меры
k=l к=1
Множества D и Е не пересекаются, поэтому
§1. Мера множества 183
в) Предположим, что множество D содержит целиком некоторый
сегмент длины I. Заметим, что в процессе построения множества D
после n-го шага удаления средних интервалов оставшаяся часть сег-
сегмента [0,1] состоит из 2П равных непересекающихся сегментов. Дли-
Длину каждего из них обозначим dn. Очевидно, dn —У 0 при п —У оо.
При любом п множество D содержится в объединении указанных 2П
сегментов. Поэтому сегмент длины I, целиком содержащийся в D,
должен целиком содержаться в одном из указанных сегментов длины
dn, т. е. I ^ dn. Но это противоречит тому, что dn —У 0 при п —У оо.
Итак, множество D не содержит целиком ни одного сегмента.
г) Если бы множество D содержало изолированную точку, то
отсюда следовало бы, что при построении D из сегмента [0,1] уда-
удалены два смежных интервала (разделенных этой точкой). Однако лю-
любые два удаленных интервала разделены некоторым отрезком, а не
точкой.
п
д) Положим D' = [0,1] \ U Ек. Очевидно, D С D'', причем
к=1 оо
(X) ОО
D'\D= U Ek, vD>-vD= Y, №= U ? = ?•
к=п+1 к=п+1 к=п+1^ 1
Отсюда следует, что Ve > 0 Зп такое, что выполняется неравенство
О < iiD' - iiD = ? < е.
е) Счетное множество имеет меру нуль (см. пример 4). Так как
fiD = 1 — а т^ 0, то D — несчетное множество. А
Задачи и упражнения для самостоятельной работы
1. Докажите эквивалентность следующих множеств:
а) {1,2,3,4,...} и {2,4,6,8,...};
б) сегментов [0,1] и [а, Ь\\
в) интервала (а, Ъ) и числовой прямой R.
2. Докажите, что:
а) бесконечное подмножество счетного множества также счетно;
б) объединение конечного или счетного числа счетных множеств есть
счетное множество;
в) множество всех многочленов с рациональными коэффициентами
счетно;
г) множество точек разрыва монотонной функции конечно или счетно.
3. Докажите, что множество всех вещественных чисел сегмента [0,1]
несчетно.
4. Докажите, что:
а) если А — бесконечное множество, В — конечное или счетное
множество, то А + В ~ А]
б) если А — бесконечное множество, В — конечное или счетное
множество, А\В — бесконечное множество, то А \ В ~ А;
в) множество всех иррациональных чисел сегмента [0,1] имеет
мощность континуума;
г) всякое бесконечное множество содержит часть, эквивалентную
всему множеству.
184 Гл. IX. Мера и интеграл Лебега
5. Докажите, что для любых множеств А, В, С:
а) (А + В)С = АС + ВС; б) А + А = А;
в) АА = А- г) А + ВС = (А + В)(А + С);
д) А = (А \ В) + (АВ), в частности, А = (А \ В) + E), если В С А.
6. Пусть V& AkCE, Ак = Е\Ак —дополнение Ак до Е (число множеств
Ак конечно или счетно). Докажите, что (J Ак = П А&.
7. Пусть замкнутое множество Е С (а, 6). Докажите, что G = (а,Ь) \ Е —
открытое множество.
8. Докажите, что множество Q всех иррациональных чисел сегмента [а, Ь]
измеримо, и найдите его меру.
9. Пусть Е — ограниченное множество такое, что JIE = 0. Докажите, что
Е измеримо, причем /iE = 0.
10. Докажите, что всякое подмножество множества меры нуль имеет меру
нуль.
§ 2. Измеримые функции
Основные понятия и теоремы
1. Определение измеримой функции. Пусть функция f(x)
определена на измеримом множестве Е. Символом {х G E: f(x) ^ с}
будем обозначать множество всех таких значений аргумента ж, при-
принадлежащих множеству Е, для которых /(ж) ^ с (с — число).
Определение. Функция f(x) называется измеримой на мно-
множестве Е, если для любого числа с множество {х ? Е : f(x) ^ с}
измеримо.
Теорема 2. Для измеримости функции f(x) на множестве Е не-
необходимо и достаточно, чтобы для любого числа с было измеримо лю-
любое из следующих множеств: {х е Е: f(x) > с}, {х е Е: f(x) ^ с},
{хеЕ: f(x) <c].
2. Некоторые свойства измеримых функций.
1°. Если функция /(ж) измерима на множестве Е, то она измерима
на любом измеримом подмножестве множества Е.
2°. Если функция /(ж) измерима на множествах Е±, Е^,..., Еп
(X) (X)
то она измерима на их объединении (J Е\* и пересечении [\ Е\~.
3°. Если функция /(ж) определена на множестве Е меры нуль, то
она измерима на этом множестве.
4°. Если функции /(ж) и д{х) измеримы на множестве Е, то функ-
функции /(ж) + д(х), /(ж) - д(х), f(x)g(x) и f(x)/g(x) (при условии д(х) ф
Ф 0) также измеримы на множестве Е.
5°. Непрерывная на сегменте функция измерима на этом сегменте.
Говорят, что некоторое свойство справедливо почти всюду на мно-
множестве Е, если множество точек из Е, на котором оно не справедливо,
имеет меру нуль.
§2. Измеримые функции 185
Функции f(x) и д(х), определенные на измеримом множестве,
называются эквивалентными на этом множестве, если они равны поч-
почти всюду на нем.
Обозначение эквивалентности: /(ж) « /(ж) на Е.
Например, функция Дирихле
ъ, ч Г 0, если ж — иррациональное число, г ,-, /1Ч
D(x) = < -, ' xGfli, A)
v J у 1, если ж — рациональное число; L ' ¦" v J
если ж — рациональное число;
эквивалентна на [а, Ь] непрерывной функции д{х) = 0, так как мно-
множество точек х сегмента [а, 6], в которых D(x) ф д(х), является мно-
множеством Q всех рациональных чисел сегмента [а, 6], мера которого
jjiQ = 0. Заметим, что функция D(x) разрывна во всех точках [а, Ь].
Приведем еще два свойства измеримых функций.
6°. Если д{х) измерима на Е, f(x) « д{х) на Е, то /(ж) измерима
на Е.
7°. Теорема 3 (теорема Лузина, или С-свойство измеримых
функций). Для того чтобы функция f(x) была измерима на [а, 6], не-
необходимо и достаточно, чтобы Vs > 0 существовала непрерывная на
[а, Ъ] функция д{х) такая, что /i{xG [а, Ъ]: f{x) ф д(х)} ^ е.
Теорема Лузина означает, что любая измеримая на [а, Ь] функция
может быть сделана непрерывной путем изменения ее на множестве
сколь угодно малой меры, т. е. измеримые функции в этом смысле
близки к непрерывным функциям.
Контрольные вопросы и задания
1. Дайте определение измеримой функции.
2. Пользуясь определением, докажите измеримость функций:
а) /(ж) = с = const, ж G [а,Ь]; б) /(ж) = ж, ж Е [а, Ь];
' 0 при 0 ^ ж ^ 1/2,
3. Сформулируйте теорему, выражающую необходимое и достаточное
условие измеримости функции на множестве Е.
4. Сформулируйте свойства 1°-5° измеримых функций. Докажите свой-
свойства 1°-3°.
5. Когда говорят, что некоторое свойство справедливо почти всюду на
множестве Е1
6. Какие функции называются эквивалентными на множестве Е1 Докажи-
Докажите, что функция Дирихле эквивалентна на [а,Ь] непрерывной функции.
Чему равна мера множества точек разрыва функции Дирихле на [а, Ь]?
7. Сформулируйте и докажите свойство 6° измеримых функций.
8. Пользуясь свойствами 5° и 6°, докажите, что если функция /(ж) экви-
эквивалентна на [а,Ь] непрерывной функции, то /(ж) измерима на [а,Ь].
9. Сформулируйте теорему Лузина. Проиллюстрируйте ее на примере
, ,, v Г 0 при 0 ^ ж ^ 1/2,
функции /(ж) = J '
186 Гл. IX. Мера и интеграл Лебега
Примеры решения задач
1. Доказать, что функция Дирихле D(x) (см. формулу A)) изме-
измерима на [а, Ь].
Л По определению измеримой функции нужно доказать, что Vc мно-
множество {х Е [а, Ь]: /(ж) ^ с} = Ес измеримо. Рассмотрим три случая.
Если с ^ 1, то Ес = [а, Ь] — измеримое множество.
Если 0 ^ с < 1, то Ес = Q, где Q — множество всех иррациональных
чисел [а, Ь] — измеримое множество.
Если с < 0, то Ес = 0, где 0 — пустое множество. Пустое мно-
множество считается измеримым: ц0 = 0.
Итак, D(x) — измеримая функция. А
2. Доказать свойство 5°: непрерывная на [а, Ь] функция /(ж) изме-
измерима на [а, Ь].
Л Докажем, что Vc множество {х G [а, Ь]: /(ж) ^ с} = Ес измеримо.
Если Ес = 0, то Ес измеримо: \iEc — /10 = 0. Пусть Ес не пусто.
Докажем, что Ес — замкнутое множество. Отсюда будет следовать,
что Ес измеримо. Пусть хо — предельная точка множества Ес. Нуж-
Нужно доказать, что ж0 Е Ес. Ясно, что ж0 G [а, Ь]. Согласно определению
предельной точки 3{жп} —У хо, причем Vn xn G Ес. Из непрерывности
/(ж) в точке ж0 следует, что {/(жп)} ->• /(ж0), а так как хп G Ес, то
f(xn) ^ с. Значит, /(жо) ^ с, т. е. жо Е ^С5 что и требовалось дока-
доказать. А
Задачи и упражнения для самостоятельной работы
11. Докажите теорему, выражающую необходимое и достаточное условие
измеримости функции на множестве Е.
12. Пусть Л ^
^W-\l при iGD=[0,l]\E,
где Е и D — множества из примера 5 из § 1. Докажите, что:
а) /(ж) — измеримая функция на [0,1];
б) D является множеством всех точек разрыва /(ж);
в) Vs > 0 существует непрерывная на [0,1] функция д(х) такая, что
fi{xe[0,l]:f(x)^9(x)}<e.
13. Докажите, что функция (р(х) = ж, х Е D, где D — множество из упр. 12,
измерима на множестве D.
14. Пользуясь теоремой Лузина, докажите, что сумма, разность и произ-
произведение измеримых на [а, Ь] функций являются измеримыми на [а, Ь]
функциями.
§ 3. Интеграл Лебега
Основные понятия и теоремы
1. Определение интеграла Лебега от ограниченной функ-
функции. Пусть Е — произвольное измеримое множество. Разбиением
множества Е назовем любую совокупность Т = {Ek} конечного чис-
§3. Интеграл Лебега 187
ла измеримых множеств Е\, Е2,...,Еп такую, что [j Ек = Е;
Ei HEj = 0 при г ф j. k=1
Пусть на множестве Е определена ограниченная функция /(ж).
Для произвольного разбиения Т = {Ек} положим Мк = sup/(ж),
mk = inf/(ж) и составим две суммы: Ек
Ек
к=1 к=1
Числа 5т и st называются верхней и нижней суммами разбиения
Т. Очевидно, VT sT ^ ST.
Рассмотрим числовые множества {st} и {St} всевозможных ниж-
нижних и верхних сумм. Они ограничены снизу числом тцЕ, а сверху —
числом M/iE, где т = inf /(ж), М = sup /(ж), и, следовательно, имеют
точные грани. Числа / = sup {st} и / = inf {St} называются нижним
и верхним интегралами Лебега.
Определение. Ограниченная на измеримом множестве Е функ-
функция /(ж) называется интегрируемой по Лебегу на этом множестве,
если / = /.
При этом число / = / называется интегралом Лебега от функции
/(ж) по множеству Е и обозначается f (x) dfi(x).
Е
2. Связь между интегралами Римана и Лебега.
Теорема 4. Всякая функция, интегрируемая по Риману на [а,Ь],
является интегрируемой на [а, Ь] по Лебегу, причем интегралы Рима-
Римана и Лебега от такой функции равны.
Замечание. Обратное утверждение неверно (см. пример нас. 189).
3. Класс интегрируемых по Лебегу ограниченных функ-
функций.
Теорема 5. Для того чтобы ограниченная на измеримом мно-
множестве Е функция /(ж) была интегрируема по Лебегу на этом
множестве, необходимо и достаточно, чтобы /(ж) была измери-
измеримой на Е.
4. Интеграл Лебега как предел лебеговских интеграль-
интегральных сумм. Пусть /(ж) — ограниченная измеримая функция на мно-
множестве Е, т = inf/(ж), М = sup/(ж), и пусть уъ у2,...,Уп-1 — про-
Е Е
извольные числа такие, что т = у0 < у\ < у2 < ... < уп = М.
Лебеговским разбиением множества Е называется разбиение
Г = {Ек}, где Ег = {ж G Е: у0 ^ /(ж) ^ У1}, Ек = {ж G Е: ук-г <
^ J \Х) ^ ykj •) ГЪ Z5°5 •••5 lb-
Пусть ?fc — произвольная точка из Ек (к = 1,2,...,п). Число
188 Гл. IX. Мера и интеграл Лебега
k называется лебеговской интегральной суммой
k=i
(если какое-то Ек = 0, то Ек не содержит ни одной точки ?&, и со-
соответствующее слагаемое в сумме считаем равным нулю). Положим
5 = max 5k, где 5к = ук - ук-Х.
Теорема 6. Предел лебеговских интегральных сумм при 6 —> О
равен интегралу Лебега, т. е. lim I(Ekj^k) — f(x)d/i(x).
б—>о J
Е
Из этой теоремы следует, что интеграл Лебега можно определить
как предел лебеговских интегральных сумм при 5 —У 0. Такое опреде-
определение интеграла Лебега аналогично определению интеграла Римана с
той разницей, что при составлении лебеговских интегральных сумм
на частичные сегменты разбивается не область определения, а мно-
множество значений функции.
5. Свойства интеграла Лебега.
1°. fdfi(x) = fiE.
Е
2°. Линейность интеграла. Если f(x) и д(х) интегрируемы на Е, а
аи /3 — произвольные числа, то функция af(x) + /Зд(х) интегрируема
на Е, причем
J[af(x) + /Зд(х)} d/i(x) = ajf(x) d/i(x) + pfg(x
E ЕЕ
3°. Аддитивность интеграла. Если f(x) интегрируема на Е\ и Е2,
причем Ei P| E2 = 0, то f(x) интегрируема на Е\ (J Е<± и выполняется
равенство
f(x)dfi(x) = J f(x)dfi(x) + J f(x)dfi(x).
Ei E2
4°. Если f(x) и g(x) интегрируемы на Е, причем f(x) ^ g(x)
Vx e E, то
J f(x) d/i(x) ^ Jg(x)
E E
Контрольные вопросы и задания
1. Что называется разбиением измеримого множества Е?
2. Что такое верхняя и нижняя суммы данного разбиения?
3. Докажите, что если разбиение Т2 получено из разбиения Т\ = {Ek} с
помощью разбиений каких-то Ek (т. е. путем измельчения разбиения
Ti), то sTl ^st2, STl ^ St2-
4. Докажите, что втг ^ ^т2, st2 ^ Stx Для любых разбиений Т\ и Т2.
5. Что такое верхний и нижний интегралы Лебега? Докажите, что / ^ /.
§3. Интеграл Лебега 189
6. Дайте определения интегрируемой по Лебегу функции и интеграла
Лебега.
7. Какова связь между интегралами Лебега и Римана?
8. Что представляет собой класс интегрируемых по Лебегу ограниченных
функций?
9. Что такое лебеговское разбиение?
10. Что такое лебеговская интегральная сумма?
11. Можно ли определить интеграл Лебега как предел лебеговских интег-
интегральных сумм? В чем состоят общность и отличие такого определения
интеграла Лебега по сравнению с определением интеграла Римана?
12. Перечислите свойства интеграла Лебега.
Пример решения задачи
Доказать, что функция Дирихле D{x) (см. формулу A) из § 2)
интегрируема по Лебегу на [а, 6], и найти / D(x) dfi(x).
[a,b]
Д I способ. Так как D(x) ^ 0, то для любого разбиения Т имеем
st ^ 0, 5т ^ 0. Рассмотрим разбиение Г* сегмента [а, Ь] на множество
Q рациональных чисел и множество Q иррациональных чисел. Для
этого разбиения
ST* = sup D(x)fiQ + sup D(x)fiQ = 1 • 0 + 0 • (b - a) = 0.
Q Q
Таким образом, множество {St} содержит число 0. Поэтому / =
= ini{Sr} = 0.
Так как все st ^ 0, то / = sup {st} ^ 0, а поскольку / ^ /, получаем
/ = 0.
Итак, / = / = 0. Отсюда следует, что функция D(x) интегрируема
по Лебегу на [а, 6], причем / D(x) dfi(x) = 0.
[a,b]
II способ. Для любого лебеговского разбиения Г = {Ек} имеем
liEi =fi{xe[aJb}:0^D(x) <: Vl < 1} =
= fiQ = b-a, /F) = 0 VfiGBi;
цЕ2 = /nE3 = ... = /лЕп-i = /jl0 = 0;
\iEn = fi {x e [a, b]: 0 < yn-X < D(x) ^ 1} =
= »Q = 0, /(fn) = 1 V^n e En.
Поэтому I(Ek,?k) — f(^,i)/^Q + f(in)nQ — 0, T- e- любая лебеговская
интегральная сумма равна нулю. Следовательно, \im I(Ek,?k) — 05
5-И)
т.е. функция D(x) интегрируема на [а, 6], причем / D(x) dfi(x) =
= 0. А [а,Ъ]
190 Гл. IX. Мера и интеграл Лебега
Замечание. Известно, что функция D(x) неинтегрируема по Риману
на [а, Ь]. Таким образом, интегрируемая по Лебегу функция может быть
неинтегрируемой по Риману.
Задачи и упражнения для самостоятельной работы
15. Пусть f(x) — функция из упр. 12. Докажите, что f(x) интегрируема
по Лебегу, но неинтегрируема по Риману на [0,1].
16. Для функции из упр. 15 составьте лебеговские интегральные суммы и
вычислите / f(x)d/jJ(x).
[ОД]
17. Докажите, что функция (р(х) из упр. 13 интегрируема по Лебегу на
множестве D, и вычислите ср(х) d/i(x).
D
18. Докажите, что если функция f(x) = 0 почти всюду на измеримом мно-
множестве Е, то она интегрируема, причем f(x)d/i(x) = 0.
Е
19. Докажите, что если ограниченные функции f(x) и д{х) эквивалентны
на множестве Е и функция f(x) интегрируема на Е, то функция д{х)
также интегрируема на Е, причем g(x)d/i(x) = f(x)d/jJ(x).
Е Е
20. Докажите, что всякая функция, интегрируемая по Риману на [а, Ь],
является интегрируемой на [а, Ь] по Лебегу, причем интегралы Римана
и Лебега от такой функции равны.
21. Докажите достаточность в теореме 5, т. е. докажите, что ограниченная
измеримая на множестве Е функция интегрируема по Лебегу на этом
множестве.
22. Докажите, что имеет место следующий критерий интегрируемости
функций по Лебегу (аналогичный критерию интегрируемости по Ри-
Риману): для того чтобы ограниченная на измеримом множестве Е функ-
функция была интегрируема по Лебегу на этом множестве, необходимо и
достаточно, чтобы Vs > 0 существовало такое лебеговское разбиение Т
множества Е, для которого справедливо неравенство St — st < ?•
23. Докажите, что если функция f(x) ограничена и измерима на множес-
множестве Е, то предел ее лебеговских интегральных сумм при S —»¦ 0 F =
= max (ук — Ук-i)) равен интегралу Лебега от функции f(x) по мно-
жеству Е.
ГЛАВА X
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Последовательности точек
в m-мерном евклидовом пространстве
Основные понятия и теоремы
1. Понятие m-мерного евклидова пространства. Совокуп-
Совокупность т чисел называется упорядоченной, если указано, какое из этих
чисел считается первым, какое — вторым и т. д. Произвольную упо-
упорядоченную совокупность т чисел часто записывают в виде
(ж1,ж2, ...,жт), где х\ — первое число из совокупности т чисел, х2 —
второе число и т. д.
Множество всевозможных упорядоченных совокупностей т чисел
называется т-мерным координатным пространством и обозначается
Rm. Каждая упорядоченная совокупность (жь ж2,...,жт) называется
точкой этого пространства и обозначается так: M(xi,X2,...,xm). При
этом числа xi,X2, ...,хт называются координатами точки М.
Расстоянием между двумя произвольными точками Mi(xi,X2,...
...,жт) и М2B/ъ2/2? •••чУгп) координатного пространства Rm называет-
называется число p(Mi,M2), определяемое формулой
р(МиМ2) = л/(У1 -xiJ + (У2 -х2J + - + (Ут-хтJ. A)
Определение. Координатное пространство Rm с введенным по
формуле A) расстоянием между точками называется т-мерным
евклидовым пространством и обозначается Ет.
Отметим, что евклидово пространство Е1 представляет собой чи-
числовую прямую (т. е. множество всех вещественных чисел) и геомет-
геометрически изображается координатной прямой. Аналогично, евклидовы
пространства Е2 и Е3 геометрически представляют собой соответ-
соответственно плоскость и трехмерное пространство, в которых введены
прямоугольные системы координат. Формула A) обобщает известную
из аналитической геометрии формулу расстояния между точками на
случай m-мерного пространства.
2. Множества точек пространства Е™. Пусть точка А при-
принадлежит Ет, R — некоторое положительное число.
Множество точек {М: р(М, А) ^ R} (т. е. множество всех точек
евклидова пространства Ет, удовлетворяющих условию р(М,А) ^
^ R), называется т-мерным шаром радиуса R с центром в точке А.
192
Гл. X. Функции нескольких переменных
Множество точек {М : р(М,А) < R} называется открытым
т-мерным шаром радиуса R с центром в точке А.
Множество точек {М: р(М,А) = R} называется т-мерной сферой
радиуса R с центром в точке А.
Отметим, что при т = 2 (т. е. на евклидовой плоскости) эти мно-
множества представляют собой соответственно круг, открытый круг и
окружность радиуса R с центром в точке А.
Открытый шар радиуса г с центром в точке А называется
s-окрестностью точки А.
Пусть точка А имеет координаты (ai,a2, ...,am), а di,d2, ...,dm —
положительные числа. Множество точек {M(xi,X2, ...,жт): \х± — а±\^
^ б?1, |^2 — <221 ^ б?2, ..., \хт — ат\ ^ dm} называется т-мерным
параллелепипедом. При т = 2 это множество представляет собой пря-
прямоугольник.
Пусть {М} — некоторое множество точек пространства Ет.
Определение. Точка А называется внутренней точкой мно-
множества {М}, если существует ^-окрестность точки А, целиком при-
принадлежащая множеству {М}, (т. е. все точки этой ^-окрестности
принадлежат множеству {М}; рис. 23).
Определение. Точка А называется граничной точкой множест-
множества {М}, если в любой ^-окрестности точки А содержатся точки,
Рис. 23 Рис. 24
как принадлежащие множеству {М}, так и не принадлежащие ему
(рис. 24).
Отметим, что граничная точка множества может как принадле-
принадлежать этому множеству, так и не принадлежать ему.
Определение. Множество {М} называется открытым, если
все его точки внутренние.
Определение. Множество {М} называется замкнутым, если
оно содержит все свои граничные точки.
Множество всех граничных точек множества {М} называется его
границей.
Определение. Точка А называется предельной точкой множес-
множества {М}, если в любой ^-окрестности точки содержатся точки мно-
множества {М}, отличные от А.
Образно говоря, точка А называется предельной точкой множест-
множества {М}, если "к точке А можно подойти сколь угодно близко, идя по
точкам множества {М} и не наступая на саму точку А." Отметим,
§1. т-мерное евклидово пространство 193
что предельная точка множества может принадлежать, а может не
принадлежать этому множеству.
Множество {М} называется ограниченным, если все его точки со-
содержатся в некотором шаре.
Множество L = {М(х!,х2, ...,хт) : х\ = <fi(t), х2 = ^(t), ...
— ,Xm = iPm(t); a ^ t ^ /3}, где Lpi(t),..., ipm(t) — непрерывные функ-
функции на сегменте [а,/3], называется непрерывной кривой в простран-
пространстве Еш. Точки А((р1(а), ...,(рт(а)) и B((pi(/3),..., (рт(/3)) называются
концами кривой L. Говорят также, что непрерывная кривая L соеди-
соединяет точки А и В.
Множество {М(х\,х2, ...,хш) : х\ = x\ + OL\t, х2 = х® + ot2t, ...
...,жт = х^ + amt; -оо < t < 00}, где ж?, ...,ж^, аь ..., ат — числа,
называется прямой в пространстве Ет. Очевидно, эта прямая про-
проходит через точку Мо(ж^,Ж2, ...,ж^) (точка Mq соответствует t = 0).
Множество {М} называется связным, если любые две точки его
множества можно соединить непрерывной кривой, целиком принад-
принадлежащей этому множеству.
Окрестностью точки А называется любое открытое связное мно-
множество, содержащее точку А.
Открытое связное множество называют также областью, а
объединение области и ее границы — замкнутой областью.
3. Последовательности точек в пространстве Е™. Если каж-
каждому натуральному числу п поставлена в соответствие точка
Мп G Еш, то говорят, что определена последовательность точек про-
пространства Ет : Mi,M2, ...,МП,... Ее обозначают {Мп}.
Определение. Точка А называется пределом последовательнос-
последовательности точек {Мп}, если lim р(Мп,А) = 0.
п—>-оо
Обозначение: lim Мп = А или Мп ->• А при п ->• оо. Последователь-
п—>-оо
ность {Мп} называется при этом сходящейся к точке А (или просто
сходящейся). Отметим, что определение предела последовательности
{Мп} точек пространства Еш основано на понятии предела числовой
последовательности: условие lim p{Mn, А) = 0 означает, что числовая
п—>-оо
последовательность {р(Мп, А)} сходится к нулю. Согласно определе-
определению предела числовой последовательности отсюда следует, что Vs > О
3N такое, что Vn > N: р(Мп,А) < г. Геометрически это означает,
что в любой ^-окрестности точки А находятся все точки последова-
последовательности {Mn}, начиная с некоторого номера N (зависящего, вообще
говоря, от е).
Лемма 1. Если
{Мп(х{п\ 44 .-, х^))}^А(а1,а2,...,ат) при п -> оо, B)
то
{4п)}-^аь {4П)}-^а2, ..., {х^} -+ аш при п-^оо. C)
Обратно: из C) следует B).
7 В.Ф. Бутузов и др.
194 Гл. X. Функции нескольких переменных
Эта лемма показывает, что сходимость последовательности точек
{Мп(ж^п, ...,х\п )} эквивалентна покоординатной сходимости, т. е.
сходимости т последовательностей координат {х±},..., {% }.
Определение. Последовательность {Мп} называется фундамен-
фундаментальной, если Vs > О 3N такое, что Vn > N и любого натурального
числа р выполняется неравенство р(Мп,Мп+р) < г.
Теорема 1 (критерий Коши сходимости последовательности).
Для того чтобы последовательность {Мп} сходилась, необходимо и
достаточно, чтобы она была фундаментальной.
Определение. Последовательность {Мп} называется ограничен-
ограниченной, если существует число R > 0 такое, что Vn: р(Мп,О) ^ R, где
О — точка, все координаты которой равны нулю.
С геометрической точки зрения это означает, что все точки после-
последовательности {Мп} содержатся в шаре радиуса R с центром в точке
О (начале координат).
Теорема 2 (теорема Больцано-Вейерштрасса). Из любой огра-
ограниченной последовательности точек пространства Ет можно выде-
выделить сходящуюся подпоследовательность.
Контрольные вопросы и задания
1. Дайте определения: а) упорядоченной совокупности т чисел;
б) m-мерного координатного пространства; в) m-мерного евклидова
пространства.
2. Дайте определения: а) m-мерного шара; б) открытого m-мерного шара;
в) m-мерной сферы; г) m-мерного параллелепипеда; д) ^-окрестности
точки. Докажите, что во всяком m-мерном параллелепипеде содержится
некоторый m-мерный шар. Каков максимальный радиус такого шара?
3. Дайте определение внутренней точки множества. Может ли внутренняя
точка множества не принадлежать этому множеству?
4. Дайте определение граничной точки множества. Может ли точка быть
одновременно внутренней и граничной точкой какого-то множества?
Может ли точка множества быть одновременно не внутренней и не гра-
граничной точкой этого множества?
5. Дайте определение открытого множества. Являются ли открытыми сле-
следующие множества:
а) m-мерный шар; б) т-мерная сфера; в) ^-окрестность точки?
6. Дайте определение замкнутого множества. Может ли множество быть
одновременно: а) открытым и замкнутым; б) не открытым и не замк-
замкнутым? Являются ли замкнутыми следующие множества:
а) m-мерный шар; б) m-мерная сфера; в) ^-окрестность точки,
г) m-мерный параллелепипед?
7. Что представляет собой граница: а) m-мерного шара; б) открытого
m-мерного шара; в) m-мерной сферы?
8. Дайте определение предельной точки множества. Докажите, что любая
внутренняя точка множества является предельной точкой этого мно-
множества. Может ли граничная точка множества: а) быть предельной точ-
точкой этого множества; б) не быть предельной точкой этого множества?
§1. т-мерное евклидово пространство 195
9. Дайте определения: а) ограниченного множества; б) непрерывной кри-
кривой; в) прямой в пространстве Еш. Может ли непрерывная кривая
быть неограниченным множеством? Является ли прямая замкнутым
множеством?
10. Дайте определение связного множества. Являются ли связными сле-
следующие множества: а) m-мерный шар; б) т-мерная сфера; в) прямая
в пространстве Ет1
11. Дайте определение окрестности точки. Докажите, что в любой окрест-
окрестности точки А содержится некоторая ^-окрестность этой точки.
12. Какое множество точек называют: областью; замкнутой областью?
13. Сформулируйте определения: а) последовательности точек пространст-
пространства Еш; б) предела последовательности {Мп}. Дайте геометрическую
интерпретацию определения предела последовательности {Мп}.
14. Сформулируйте лемму об эквивалентности сходимости последователь-
последовательности {Мп(х{г, #2 j •••5жт )} и сходимости т числовых последователь-
ностей {х^1 }, {#2 }? •••? {хгп }• Пользуясь определением предела, дока-
докажите эту лемму.
15. Сформулируйте определения: а) фундаментальной последовательности
{Мп} точек пространства Ет; б) нефундаментальной последователь-
последовательности {Мп} (пользуясь правилом построения отрицаний). Дайте гео-
геометрическую интерпретацию этих определений.
16. Сформулируйте критерий Коши сходимости последовательности {Мп}.
17. Сформулируйте определения: а) ограниченной последовательности
{Мп}; б) неограниченной последовательности {Мп}. Дайте геометри-
геометрическую интерпретацию этих определений.
18. Дайте определение подпоследовательности последовательности {Мп} и
сформулируйте теорему Больцано-Вейерштрасса. Верно ли утвержде-
утверждение: из неограниченной последовательности {Мп} можно выделить схо-
Примеры решения задач
1. Доказать, что для любых точек M\^M^^Ms пространства Ет
справедливо неравенство треугольника
р(М1,М2)^р(М1,М3)+р(М3,М2). D)
Л Пусть точки Mi, М2, Ms имеют следующие координаты:
М1(х1,х2,...,хт), М2(у1,у2,...,ут), M3(z1,z2,...,zm). Тогда
,1/2 rjn_ -,1/2
р(МиМ2)= \^(
M=l
[га 1 1/2
^(
г=1
Для доказательства справедливости неравенства D) нам понадо-
196 Гл. X. Функции нескольких переменных
бится неравенство Буняковского для сумм*)
т г га -. 1/2 г га -. 1/2
Е Е ?
г=1 L г=1 J L г=1
Используя это неравенство, получаем
г=1 г=1
га
2
г=1 г=1 г=1
| 1/2 г т -. I/2 m
Е
i=l 4=1 J L г=1 J г=1
= [p(Mi,M3)+p(M3,M2)]2.
Отсюда следует, что р(М1,М2) ^ p(Mi,M3) +^(M3,M2). A
2. Доказать, что открытый шар п = {М: р(М, А) < R} является
открытым множеством.
Л Согласно определению открытого множества нужно доказать, что
любая точка шара П является внутренней точкой этого шара, т. е. что
для любой точки Мо Е п существует некоторая ^-окрестность этой
точки, целиком принадлежащая п. Пусть Мо — произвольная точка
шара п и пусть р(М0,А) = г. Так как Мо Е
^ G П, то г < R. Положим е = R — г и рассмот-
\ рим ^-окрестность точки Mq. Любая точка М
мо \ из этой ^-окрестности удовлетворяет условию
\ р(М, Мо) < г. Используя неравенство треуголь-
\ у^А } ника5 получаем
Ку"\( J Р(М, А) <: р(М, Мо) + р(М0, А) < е + г =
Рис. 25 Таким образом, р(М, А) < R, т. е. любая точка
М из указанной ^-окрестности точки Мо при-
принадлежит шару П, что и требовалось доказать. Отметим, что в случа-
случаях трехмерного пространства и плоскости доказанный факт является
наглядно очевидным (рис. 25). А
3. Доказать, что сфера S = {М: р(М, А) = R} является замкнутым
множеством.
Л Согласно определению замкнутого множества нужно доказать, что
*) Доказательство справедливости неравенства Буняковского для сумм приве-
приведено в учебнике В.А. Ильина и Э.Г. Позняка "Основы математического анализа",
ч. I (M., Наука, 1982), с. 349.
§1. т-мерное евклидово пространство 197
сфера содержит все свои граничные точки. Докажем сначала, что
любая точка Мо сферы является граничной, т. е. что в любой
^-окрестности точки Мо содержатся точки, как принадлежащие сфе-
сфере, так и не принадлежащие ей. Пусть точки А и Мо имеют следую-
следующие координаты: A(ai, а2,..., ат), М0(ж?,Ж2, ...,ж^). Так как Мо Е 5,
то р(М0,А) = л/И " «iJ + .- + « - ашу = R.
^ _ а
рим точку M(xi,X2, ...,жт), где а^ = х® -\— • -
Поскольку
Рассмотрим точку M(xi,X2, ...,жт), где а^ = х® -\.
R 2
, м0) =
точка М содержится в ^-окрестности точки Mq. Кроме того, точка
М не лежит на сфере 5, так как
р(М, А) = >/(rri_aiJ + ... + (rrro-aroJ = Л + | > Л.
Таким образом, в произвольной г-окрестности точки Mq сферы со-
содержатся точки, как принадлежащие сфере (например, сама точка
Мо), так и не принадлежащие ей (например, точка М). Заметим,
что в случае сферы в трехмерном пространстве этот факт нагляд-
наглядно очевиден. Итак, любая точка сферы является ее граничной точкой.
Если же точка Мо не лежит на сфере, то она не является граничной
точкой этой сферы. В самом деле, если, например, р(Мо, А) = г < R,
то, взяв г = R — г, получим, что ни одна точка М из ^-окрестности
точки Mq не лежит на сфере (р(М, А) ^ р(М, Mq) + p(Mq, А) < г + г =
= R). Это и означает, что точка Мо не является граничной точкой
сферы.
Мы доказали, что множество всех граничных точек сферы сов-
совпадает с самой сферой. Значит, сфера содержит все свои граничные
точки, т. е. является замкнутым множеством. А
4. Доказать, что если А — предельная точка множества {М}, то
существует последовательность {Мп}, сходящаяся к А, каждая точка
которой принадлежит множеству {М} и не совпадает с А.
Л Рассмотрим si-окрестность точки А, где е\ — 1. Согласно опреде-
определению предельной точки множества в si-окрестности точки А содер-
содержатся точки множества {М}, отличные от А. Возьмем одну из этих
точек и обозначим ее М\. Пусть p(Mi,A) = Si. Очевидно, Si < 1.
Положим 82 = min(Ei,l/2). В ^-окрестности точки А также со-
содержатся точки множества {М}, отличные от А. Одну из этих точек
обозначим М<2. Пусть р(М2, А) = #2. Очевидно, 82 < 1/2.
Далее, положим гз = min(E2,1/3) и аналогичным образом выберем
точку М3 G {М}. При этом р(М3,А) = S3 < 1/3.
Продолжая этот процесс неограниченно, получим последователь-
последовательность {Мп}, каждая точка которой принадлежит {М} и не совпадает
с А, причем р(Мп,А) < 1/п. Отсюда следует, что {Мп} —у А при
п —у оо. А
198 Гл. X. Функции нескольких переменных
Задачи и упражнения для самостоятельной работы
1. Докажите, что m-мерный шар {М: р(М, А) ^ R} является замкнутым
множеством.
2. Докажите, что если множество {М} точек пространства Еш ограниче-
ограничено, то оно содержится в некотором m-мерном шаре с центром в точке
О@, 0, ...,0).
3. Докажите, что ограниченность множества {M(xi, х2, •••, Хщ)} эквива-
эквивалентна ограниченности т числовых множеств {xi}, {#2},..., {хт}.
4. Докажите, что в пространстве Еш непрерывная кривая — ограничен-
ограниченное множество, а прямая — неограниченное множество.
5. Составьте уравнения прямой, проходящей через точки Mi(yi, y2,..., уш)
И M2(zi,Z2,...,Zm).
6. Докажите, что m-мерный шар {М : р(М,А) ^ R} является связным
множеством.
7. Найдите множество всех предельных точек: а) m-мерного шара;
б) открытого m-мерного шара; в) т-мерной сферы.
8. Докажите утверждение: для того чтобы множество {М} было замкну-
замкнутым, необходимо и достаточно, чтобы оно содержало все свои предель-
предельные точки.
9. Докажите, что если последовательность {Мп} граничных точек
множества {М} сходится к точке А, то А — также граничная точ-
точка множества {М}.
10. Докажите, что если все точки последовательности {Мп} принадлежат
замкнутому множеству {М} и {Мп} —»> А при п —»¦ оо, то А Е {М}.
11. Докажите, что фундаментальность последовательности Мп(х{1] х2п\ •••
...,Хт ) эквивалентна фундаментальности т числовых последователь-
§ 2. Предел функции
Основные понятия и теоремы
1. Понятие функции т переменных. Пусть {М} — множест-
множество точек пространства Ет. Если каждой точке М(х\,Х2, ...,жш) G
е {М} поставлено в соответствие некоторое число и, то говорят, что
на множестве {М} определена функция т переменных, и пишут и =
= f(M) или и = f(xi,X2,...,xm). Числовые переменные xi,X2, ...,хт
называются независимыми переменными (или аргументами) функ-
функции. Множество {М} называется областью определения функции
/(М), а число и, соответствующее данной точке М, — частным зна-
значением функции в точке М. Совокупность {и} всех частных значений
функции и = f(M) называется множеством значений этой функции.
Функции двух и трех переменных часто обозначают так:
и = f{x,y) и и = f{x,y,z).
2. Предел функции. Теоремы о пределах. Пусть функция
и = f(M) определена на множестве {М} и точка А — предельная
точка множества {М}.
2. Предел функции 199
Определение 1 (по Коши). Число Ь называется пределом функ-
функции f(M) в точке А (при М —у А), если \/е > 0 36 > 0 такое, что VM,
удовлетворяющей условиям М е {М}, 0 < р(М,А) < 6, выполняется
неравенство |/(М) — Ь\ < г.
Определение 2 (по Гейне). Число Ъ называется пределом функ-
функции f(M) в точке А, если для любой сходящейся к А последователь-
последовательности {Мп} такой, что Мп Е {М}, Мп ф А, соответствующая после-
последовательность значений функции {/(Мп}) сходится к Ъ.
Обозначение: lim f(M) = b или lim f(xi,...,xm) = b, где
ai,...,am — координаты точки А. хт^ат
Теорема З. Определения 1 и 2 предела функции эквивалентны.
Теорема 4. Пусть функции /(М) и д{М) определены на мно-
множестве {М\ и пусть lira f(M) = b, lim g(M) = с. Тогда
M^rA M^rA
lim (f(M)+g(M)) = b + c,
М^-А
lim (f(M) - g(M)) = b-c,
^A
lim f(M)g(M) = be,
^A
v f(M) b ,n
lim ^t—f = - при условии с Ф 0.
мА g(M) с ^
Функция и = /(М) называется бесконечно малой при М ->• А (в
точке А), если lim f(M) = 0. Если f(M) и g(M) — бесконечно малые
М^А f(M)
функции при М —>- А и если lim ^Ц—f = 0, то говорят, что функция
м^гА д(М)
f(M) является бесконечно малой более высокого порядка при М —>¦ А
(в точке А), чем д(М), и пишут / = о(д) при М —>¦ А.
Пусть функция IX = /(М) определена на множестве {М}, которое
содержит точки, сколь угодно удаленные от точки О@, 0,..., 0).
Определение. Число b называется пределом функции f(M) при
М ->• оо, если Vs > О ЗЛ > 0 такое, что VM, удовлетворяющей ус-
условиям М G {М}, р(М,О) > R, выполняется неравенство |/(М)—
— Ь| < €Г.
Обозначение: lim f(M) = b или lim f(xi,...,xm) = b.
жт—>-оо
3. Повторные пределы. Для функций многих переменных наря-
наряду с обычным понятием предела вводится понятие повторного преде-
предела. Оно связано с изучением предела функции при изменении только
одной независимой переменной и фиксированных значениях осталь-
остальных. Рассмотрим это понятие на примере функции двух переменных.
Пусть функция и = f(x,y) определена в прямоугольнике
Q = {(ж, у): \х - хо\ < di, \у - уо < <i2}, кроме, быть может, отрезков
прямых х = хо и у = уо. При фиксированном значении переменной
у функция f(x,y) становится функцией одной переменной х. Пусть
200 Гл. X. Функции нескольких переменных
для любого фиксированного значения у, удовлетворяющего условию
0 < \у — Уо\ < d>2, существует предел функции /(ж, у) при х —у хо (этот
предел зависит, вообще говоря, от у):
у — фикс.
Пусть, далее, предел функции ср(у) при у —у уо существует и равен Ь:
lim (/?(?/) = Ъ.
Тогда говорят, что в точке Мо(жо,2/о) существует повторный предел
функции f(x,y), и пишут
lim lim f(x,y) = b.
При этом lim f(x,y) называется внутренним пределом в повтор-
X УХо
у — фикс.
O<\y-yo\<d2
ном. Аналогично определяется другой повторный предел
lim lim f(x,y), в котором внутренним является lim f(x,y).
ж-^ж0 у->уо У^Уо
ж —фикс.
0<|ж-ж0|<Й1
Теорема 5. Пусть в точке Мо(хо,уо) существует предел функ-
функции f(x,y), равный Ъ ( lim f(x,y) = b), а также внутренние пределы
У^Уо
в двух повторных пределах этой функции. Тогда существуют повтор-
повторные пределы lim lim f(x,y) и lim lim f(x,y), причем каждый из
них равен Ь.
Отметим, что обратное утверждение неверно (см. примеры 3 и 7).
Понятие повторных пределов функции можно ввести и для того слу-
случая, когда жо (либо уо, либо xq и у$) равно +оо (или —оо, или оо).
Контрольные вопросы и задания
1. Сформулируйте два определения предела функции /(М) в точке А. Что
означает эквивалентность этих определений?
2. Для каждого из двух определений предела функции /(М) в точке А
сформулируйте отрицание определения.
3. Может ли быть так, что lim f(M) = 6, lim g(M) = с, где Ь и с —
М-*А М^-А
числа, но равенство lim (/(М) + д(М)) = Ь + с не выполняется?
М-ьА
4. Дайте определение бесконечно малой функции при М —у А. Приведите
пример бесконечно малой функции при М —у О@, 0,..., 0).
5. Сформулируйте определение бесконечно малой функции /(М) более
высокого порядка при М -у А, чем д(М). Приведите пример таких
функций.
6. Дайте определение предела функции /(М) при М —у оо. Приведите при-
пример непостоянной функции /(М), у которой lim /(M) = 1.
2. Предел функции 201
7. Дайте определение повторного предела функции /(ж, г/) в точке
Мо(жо,г/о).
8. Известно, что функция /(ж, 2/) имеет в данной точке предел и повторные
пределы. Могут ли какие-то два из них быть неравными?
9. Сформулируйте определение повторного предела:
a) lim lim /(ж, г/); б) lim lim /(ж, г/); в) lim lim /(ж, г/).
Примеры решения задач
1. Доказать, что функция /(ж, 2/) = (ж + 2/) sin - sin - является бес-
бесконечно малой в точке О@, 0). Х У
Л Согласно определению бесконечно малой функции требуется дока-
доказать, что lim /(ж, у) = 0. Отметим, что функция /(ж, у) не определена
х>0
на осях координат, но точка О@,0) является предельной точкой об-
области определения /(ж,?/), и, значит, можно рассмотреть вопрос о
пределе функции в точке О.
Воспользуемся определением предела функции по Коши. Зададим
произвольное г > 0 и положим S = г/2. Тогда если р(М(х, у), О@,0)) =
= л/х2 + у2 < 5, то |ж| < S и \у\ < S. Следовательно,
|/(ж, у) - 0| = (ж + ^/) sin - sin - ^ |ж| + \у\ < 28 = г.
х у
Это и означает, что lim f(x,y) = 0. А
х—>0
у^0
2. Вычислить предел lim A + хуJ^х +ху\
ху0
Л Представим функцию в виде [A + хуI ^хуЛ>]2у^х+у\ Так как z =
= ху -+ 0 при (^ §), то lim A + хуI^^ = lim (I + zI^ = e. Да-
лее, lim —^— = 2 (в силу теоремы 4). Поэтому искомый предел ра-
ж^0 X + у
вен е2. А
3. Существует ли предел lim
ж^0
xy ?
2
Л Пусть точка М(х,у) стремится к точке 0@,0) по прямой у = кх,
проходящей через точку О. Тогда получим
,. ху л. кх2 к
lim п у п = lim -
х2 + у2 х^о х2 + к2х2 I + к2'
(У=кх)
Таким образом, приближаясь к точке О@,0) по различным
прямым, соответствующим разным значениям к, получаем разные
202 Гл. X. Функции нескольких переменных
предельные значения. Отсюда следует, что предел данной функции в
точке 0@,0) не существует. А
4. Вычислить предел lim — -.
ж^оо х2 — 2ху + 2у2
Л Перейдем к полярным координатам х = pcostp, у = pshnp. Тогда
х + 2у _ 1 cos ср + 2 sin ср _ ()
х2 — 2ху + 2у2 р cos2 (p — 2 cos (р sin (р + 2 sin2 (р p д(<р)'
а условие М(х,у) —> оо эквивалентно условию р —> оо. При р ^ оо
первый сомножитель 1/^о стремится к нулю. Докажем ограниченность
второго сомножителя — функции $(ф)/д(ф) при 0 ^ ip ^ 2тг. Отсюда
будет следовать, что искомый предел равен нулю.
Очевидно, |/(^)| ^ 3, а для функции д(ср) нетрудно установить,
что ее минимальное значение положительно. Это можно сделать, ис-
используя известные методы исследования на экстремум функций од-
одной переменной, а можно и проще, а именно запишем д(ф) в виде
g(yj) = (cos(^ — sin(^J + sin2 if. Ясно, что g(ip) > 0 при 0 ^ (р ^ 2тг, а
так как ^((^) — непрерывная функция, то она имеет на сегменте [0, 2тг]
минимальное значение, причем т = min gUp) > 0. Итак, gUp) ^ т >
[0,2тг]
> 0. Следовательно, |/((^)/^((^)| ^ 3/ттг, т. е. функция f(cp)/g(cp) огра-
ограничена при 0 ^ ср ^ 2тг. А
5. Вычислить повторные пределы функции fix,у) = — ^ в
точке О@, 0) при условии с ф 0, d ф 0.
Л Имеем
lim lim fix,у) = lim ( lim -^ ) =
ж^Оу^о ж-^о\ y-^o cx + ay /
x — фикс. ,
^o = lim ( lim
+ dy/X
ж —фикс.
ж^0
Аналогично получаем lim lim fix,у) = -. А
у-^Ож-^о а
6. Существуют ли повторные пределы функции f(x,y) = (х + у) х
х sin - sin - в точке О@, 0)?
х у v J
Л Рассмотрим внутренний предел lim fix,у) в повторном пре-
ж-^0
у — фикс.
деле lim lim f(x,y). Представим функцию f(x,y) в виде суммы двух
у—>0 ж—^0
слагаемых: f(x,y) = ж sin- sin- +^/sin- sin-. При фиксированном
х у х у
у ф 0 первое слагаемое ж sin - sin - стремится к нулю при х ->• 0. Во
х у
2. Предел функции 203
втором слагаемом произведение у sin- является постоянным, отлич-
У
ным от нуля, если уф — (n E Z), а сомножитель sin- не имеет
ТТЛ X
предела при х ->• 0: в сколь угодно малой окрестности точки х = 0
функция sin- принимает все значения от —1 до 1. Следовательно,
второе слагаемое у sin - sin -, а значит, и вся функция /(ж, у) не име-
х у
ет предела при х —> 0 и фиксированном у, не равном 0 и —. Таким
образом, указанный внутренний предел не существует, а поэтому не
существует повторный предел lim lim f(x,y). Аналогично можно до-
у^Ох^О
казать, что не существует другой повторный предел lim lim f(x,y). A
х—>0 у—>0
Замечание. В примере 1 было доказано, что предел функции /(ж, у) =
= (ж + у) sin — sin - в точке О@, 0) существует и равен нулю. Таким обра-
х у
зом, на основании примеров 1 и 6 можно сделать вывод: из существования
предела функции в точке не следует существование повторных пределов
функции в этой точке (сравните этот вывод с утверждением теоремы 5).
7. Вычислить повторные пределы функции f(x,y) = 2 2 в точ-
точке 0@,0). +У
А Имеем
lim lim f(x. у) = lim ( lim _ _ ) = lim ( — ) =0.
ж^0у^0 ж-^0\ у-И) X2 + y2 ) ж-^0\Ж2/
ж —фикс.
xM
Аналогично получаем lim lim f(x,y) = 0. А
Замечание. В примере 3 было доказано, что предел функции /(ж, у) =
= в точке О@, 0) не существует. Таким образом, на основании при-
примеров 3 и 7 можно сделать вывод: из существования и равенства повторных
пределов функции в данной точке не следует существование предела функ-
функции в этой точке.
Задачи и упражнения для самостоятельной работы
12. Докажите, что функция /(ж, г/) является бесконечно малой в точке
О@, 0), если: а) /(ж, у) = х<2 ; б) /(ж, у) = вт(ж + у) 1п(ж2 + у2).
13. Вычислите пределы:
a) lim ^; б) lim —-—; в) lim A + ху \у у ху ^
х—>0 X х—>1 XV х—^0
У—>а У—>0 У^-3
, ах + Ьу , х2+у2 , х2+у2
г) JLim^ — ^-j; д) Jin^ ———\ е) \ш^ ——^—•
ж) Ит {х + у)е~{х2+у2)] з) Ит (х2 +
х—^оо хуо
204 Гл. X. Функции нескольких переменных
14. Докажите, что следующие пределы не существуют:
. х2+ху + у2 . \п(х + у) , sin |ж-
a) hm — —^-; б) hm — —; в) hm '
х^О X2 ХУ + у2 я->1 у х^О
х^О X2 - ХУ + у2 у
у —>0 у —>0 у—>0
2
15. Докажите, что функция /(ж, г/) = — обладает следующими свой-
свойствами: х +у
а) при стремлении точки М(х,у) к точке 0@,0) по любой прямой,
проходящей через точку О@, 0), предел функции равен нулю; б) предел
функции в точке О не существует.
16. Вычислите повторные пределы lim Иш/(ж,г/)и lim lim /(ж, г/), если:
в)
cosх - cosy
ч х/ ч cosх - cosy
в) f(x,y) = ж2 i 2—' жо = 0, 2/о = 0;
ч х/ ч sin \x\ - sin |г/|
p)f(x,y) =
ж) /(ж, 2/) =
1 ~т Ж"
з) /(ж, 2/) = sin ^+3 > жо = оо, 2/о = оо.
17. Существуют ли предел и повторные пределы функции /(ж, 2/) в точке
(жо,2/о), если:
б) /(ж, 2/) = 1с^ж(ж + 2/), жо = 1, 2/о = 0;
ч х/ ч sinх + sin?/
в) /(ж, 2/) = -, жо = 0, 2/о = О?
ж + гу
§ 3. Непрерывность функции
Основные понятия и теоремы
1. Определение непрерывности. Пусть функция т перемен-
переменных и = /(М) определена на множестве {М} и пусть А — предельная
точка множества {М}, принадлежащая этому множеству.
Определение. Функция и = f(M) называется непрерывной в
точке А, если Hm f(M) = /(-4).
M^rA
Приращением (или полным приращением) функции и = f(M) в
точке А называется функция Аи = /(М) - /(-А), М G {М}.
Пусть точка А имеет координаты (ai, ...,am), а точка М — коор-
координаты (xi,...,xm). Если ввести обозначения х\ — а\ — Axi,...,xm-
§3. Непрерывность функции 205
— ат = Ахт, то приращение функции Аи можно записать в виде
Аи = /(ai + Джь...,ат + Ахш) - /(ab ...,om).
Очевидно, условие непрерывности функции в точке А (lira f(M) =
= f (А)) эквивалентно условию lira Аи = 0 или lira Аи = 0. Это ра-
венство называется разностной формой условия непрерывности функ-
функции в точке А.
Предельные точки области определения функции и = /(М), в кото-
которых функция не является непрерывной, называются точками разрыва
этой функции.
2. Непрерывность по отдельным переменным. Зафиксируем
все аргументы функции и = /(xi, ...,жт), кроме одного из них, напри-
например, Xk, положив xi — а{ (i Ф k). Аргументу хи дадим произвольное
приращение Ахк- Функция и = /(xi, ...,жт) получит приращение
АХки = /(аь ...,ак-1,ак + Ахк, a^+i,..., am) - /(«i,..., am),
которое называется частным приращением функции в точке А, со-
соответствующим приращению Ахк аргумента хк. Отметим что, АХки
является функцией одной переменной Ахк.
Определение 1. Функция и = f(xi,...,xm) называется непре-
непрерывной в точке A(ai, ...,am) по переменной хк, если lira AXku = 0.
Можно дать другое, эквивалентное определение непрерывности по
переменной хк.
Определение 2. Функция и = f(xi,...,xm) называется непре-
непрерывной в точке A(ai, ...,am) по переменной хк, если функция /(ai,...
...,Xk,..., dm) одной переменной хк непрерывна в точке хк = ак.
В отличие от непрерывности по отдельным переменным обычную
непрерывность функции (определение п. 1) называют иногда непре-
непрерывностью по совокупности переменных.
Теорема 6. Если функция и = f(x\,...,хт) определена в некото-
некоторой окрестности точки А и непрерывна в точке А, то она непрерывна
в этой точке по каждой из переменных xi, ...,xm.
Обратное утверждение неверно (см. пример 2 на с. 208).
3. Основные теоремы о непрерывных функциях.
Теорема 7 (об арифметических операциях над непрерывными
функциями). Если функции /(М) и д{М) определены на множест-
множестве {М} и непрерывны в точке A G {М}, то функции f(M) + g(M),
f(M) - g(M), f(M)g(M) и ,Л* (частное при условии д(А) ф 0) не-
прерывны в точке А.
Пусть функции
определены на множестве {T(ti,..., tk)} С Ek. Тогда каждой точке
Т(?ь ...,?/,) е {Г} ставится в соответствие точка М(жь ...,ж/,) G Ет.
206 Гл. X. Функции нескольких переменных
Множество всех таких точек М обозначим {М}. Пусть на мно-
множестве {М} определена функция и = /(xi, ...,жт). Тогда говорят, что
на множестве {Г} определена сложная функция и = f((fi(ti, ...,?&), •••
())
Теорема 8 (о непрерывности сложной функции). Пусть функции
Xl = (?i(?i,...,?/0,...,жт = ^rn{ti,...,tk) непрерывны в точке А(а1,...
...,а/.), а функция и = f(xi,...,xm) непрерывна в точке B(bi,..., bm),
где bi = (fi(ai,...,ak) (i = l,...,m). Тогда сложная функция и =
= /(y?i(tb...,tfe),...,(pm(tb...,tfe)) непрерывна в точке А.
Функция и = f(M) называется непрерывной на множестве
если она непрерывна в каждой точке этого множества.
Функция и = /(М) называется ограниченной на множестве {}
если существуют числа с и С такие, что VM G {М} выполняются
неравенства с ^ /(М) ^ С
Теорема 9 (первая теорема Вейерштрасса). Непрерывная на
замкнутом ограниченном множестве функция ограничена на этом
множестве.
Определение. Число U называется точной верхней гранью
функции и = /(М) на множестве {М}, если:
1) VM е {М} выполняется неравенство /(М) ^ U;
2) MU1 < U ЗМ' е {М} такая, что /(М') > U'.
Обозначение: U = sup /(M).
{М}
Аналогично определяется точная нижняя грань функции
inf /(M).
{M}Jy
Теорема 10 (вторая теорема Вейерштрасса). Непрерывная на
замкнутом ограниченном множестве функция достигает на этом
множестве своих точных граней.
Пусть каждая точка М множества {М} является его предельной
точкой и пусть на множестве {М} определена функция и = /(М).
Определение. Функция и = f(M) называется равномерно
непрерывной на множестве {М}, если \/г > 0 3S = S(e) > 0 такое,
что VMi,M2 G {М}, удовлетворяющих неравенству p(Mi,M2) < S,
выполняется неравенство |/(Mi) - /(М2)| < г.
Теорема 11 (теорема Кантора). Непрерывная на замкнутом
ограниченном множестве функция равномерно непрерывна на этом
множестве.
Замечание. Обе теоремы Вейерштрасса и теорема Кантора имеют
место для функций, непрерывных на замкнутом ограниченном множестве.
В случае функций одной переменной эти теоремы были справедливы для
функций, непрерывных на сегменте. Таким образом, аналогом сегмента в
многомерном случае является замкнутое ограниченное множество.
§3. Непрерывность функции 207
Контрольные вопросы и задания
1. Дайте определение непрерывности функции в точке.
2. Что такое полное приращение функции и = /(М) в точке А? Как за-
записать условие непрерывности функции в точке А, используя ее при-
приращение в этой точке? Выразите приращение функции и = ху в точке
АA,2) через приращения Ах и Ау ее аргументов.
3. Какие точки называются точками разрыва функции и = /(М)? Приве-
Приведите примеры точек разрыва функций двух и трех переменных.
4. Что называется частным приращением функции и = /(#i,...,#m) в
данной точке A(ai,..., am)? Как получить частное приращение функции
из ее полного приращения? Напишите частные приращения функции
и = ху в точке АA, 2).
5. Сформулируйте два определения непрерывности функции и = /(#i,...
..., жт) в точке А по отдельным переменным и докажите их эквивалент-
эквивалентность.
6. Как связаны непрерывность функции в точке по совокупности аргумен-
аргументов и непрерывность в этой точке по отдельным переменным?
7. Сформулируйте теорему об арифметических действиях над непрерыв-
непрерывными функциями. Докажите эту теорему, опираясь на теорему 4.
8. Сформулируйте понятие сложной функции и теорему о непрерывности
сложной функции.
9. Дайте определение непрерывной на данном множестве функции.
Является ли функция
{ 1, х + у = 0,
непрерывной на всей плоскости?
10. Дайте определение ограниченной на данном множестве функции.
Является ли функция
{sinp + У) Т -l п
0, х = 0,
ограниченной: а) в круге {(х,у): х2 + у2 ^ 1}; б) на оси Ох?
11. Сформулируйте определение неограниченной на данном множестве
функции.
12. Сформулируйте первую теорему Вейерштрасса.
13. Справедливо ли утверждение: непрерывная в ^-окрестности точки А
функция и = /(М) ограничена в этой ^-окрестности?
14. Может ли неограниченная на множестве {М} функция быть непрерыв-
непрерывной на этом множестве, если: а) {М} — m-мерная сфера;
б) {М} = {(ж, у): х2 + у2 <: 1}; в) {М} = {(ж, у): х2 + у2 < 1}.
15. Дайте определения точной верхней и точной нижней граней функции
на данном множестве. Имеет ли функция и = — точные грани на
всей плоскости: у
16. Сформулируйте вторую теорему Вейерштрасса.
17. Справедливо ли утверждение: если функция достигает на множестве
{М} своих точных граней, то она непрерывна на этом множестве?
18. Справедливо ли утверждение: непрерывная в параллелепипеде функция
имеет в этом параллелепипеде максимальное и минимальное значения?
208 Гл. X. Функции нескольких переменных
19. Дайте определение равномерной непрерывности функции. Как связаны
между собой непрерывность и равномерная непрерывность функции на
данном множестве?
20. Пользуясь кванторами, сформулируйте отрицание равномерной непре-
непрерывности функции.
21. Сформулируйте теорему Кантора.
22. Верно ли утверждение: непрерывная в ^-окрестности точки А функция
и = /(М) равномерно непрерывна в этой ^-окрестности?
Примеры решения задач
1. Найти точки разрыва функции и = ——^-г.
х6 — у6
Л Данная функция не определена в тех точках, где знаменатель дроби
равен нулю: ж3 — у3 = 0, т. е. функция не определена на прямой у — х.
В остальных точках плоскости функция определена, поэтому каждая
точка прямой у — х является предельной точкой области определения
функции. В любой точке А прямой у — х функция не является непре-
непрерывной, так как и (А) не существует. Таким образом, любая точка
прямой у — х есть точка разрыва данной функции.
В любой точке В, не лежащей на прямой у = ж, функция и =
= ——?-г непрерывна. Это следует, например, из теоремы 7, посколь-
х6 — у6
ку функции ж, у, ж3, у3, очевидно, непрерывны в любой точке и ж3 —
-^/3/0в точке В. Итак, множество точек разрыва данной функции
есть прямая у = ж.
Отметим, что в любой точке А(а,а), лежащей на прямой у — х
и не совпадающей с точкой 0@,0) (т. е. а / 0), существует предел
Л т X — У ,. 1 1
функции: hm ——^ = hm — = —.
х^а х3 — у3 х^а х2 + ху + у2 а2
Поэтому точки А(а, а) при а ф 0 можно назвать точками устрани-
устранимого разрыва функции: если положить и(а, а) = —, то функция станет
непрерывной в точке А(а,а). В точке же О@,0) имеем Hm u(x,y) =
= Hm — = оо, т. е. О@,0) — точка неустранимого разрыва
данной функции. А
2. Доказать, что функция
{ 0, х2+у2=0,
непрерывна в точке О@,0) по каждой переменной ж и у, но не явля-
является непрерывной в этой точке по совокупности переменных.
Л Рассмотрим частное приращение функции f(x,y) в точке О@,0),
соответствующее приращению Аж аргумента ж:
Ахи = /(Аж, 0) - /@,0) = 0 - 0 = 0.
§3. Непрерывность функции 209
Очевидно, lim Axu = 0, а это и означает, что fix,у) непрерывна в
Дж-И)
точке 0@,0) по переменной х.
Этот же факт легко обосновать, пользуясь другим определени-
определением непрерывности функции по отдельным переменным. Рассмотрим
функцию f(x,y) при у = 0, т. е. /(ж,0). Поскольку /(ж,0) = 0 во всех
точках ж, функция /(ж,0) непрерывна на всей оси Ох, в частности
в точке х = 0. Согласно второму определению непрерывности функ-
функции в точке это и означает, что функция f(x,y) непрерывна в точке
О@,0) по переменной х.
Аналогично можно доказать непрерывность f(x,y) в точке О@,0)
по переменной у.
Чтобы доказать, что функция f(x,y) не является непрерывной
в точке О@,0) по совокупности переменных, используем результат
примера 3 из § 2. В этом примере было доказано, что предел функции
о о в точке О@,0) не существует. Отсюда следует, что функция
х2 + у2
f(x,y) не является непрерывной в точке О@,0). А
3. Исследовать функцию
( cos(x - у) - cos(x + у) ,
Ф,У) = { 2хУ ' У* '
I 1, ху = О,
на непрерывность по отдельным переменным и по совокупности пе-
переменных в точках О@,0) и АA,0).
Л Применяя известную формулу для разности косинусов, запишем
функцию и(х,у) в виде
{sin ж sin у . ~
у-, ху^О,
х у
1, ху = 0.
1) Так как
т / \ т sin ж ,. sin у ., /г. _ч
lim и(х, у) = lim lim = 1 = ш0, 0),
х^0 V J х^0 X у^0 у V J
у
то функция и(х,у) непрерывна в точке О@,0) и, следовательно, не-
непрерывна в этой точке по отдельным переменным.
2) Рассмотрим функцию и(х,0). Согласно определению имеем
и(х,0) = 1 для всех ж, и, следовательно, эта функция непрерывна
в точке х = 1. Это означает, что функция и{х,у) непрерывна в точке
АA,0) по переменной х.
Рассмотрим теперь функцию
иA,у)={ У
1, у = 0.
Так как lim иA, у) = lim sin I —- = sin 1^1 = иA, 0), то функция
у^0 у^0 у
210 Гл. X. Функции нескольких переменных
иA, у) не является непрерывной в точке у = 0. Это означает, что функ-
функция и(х,у) не является непрерывной по переменной у в точке АA,0).
Отсюда следует, что функция и(х,у) не является непрерывной в точ-
точке АA,0) по совокупности переменных, так как в противном случае
в силу теоремы б она была бы непрерывной в этой точке и по пере-
переменной у. А
4. Доказать, что функция и(х,у) = ——^ ограничена на мно-
X ~г У
жестве П = {(ж, у): 0 < х2 + у2 ^ 1}, и найти ее точные грани на этом
множестве.
Л Для исследования функции удобно перейти к полярным координа-
координатам х = pcoscp, у = р sin ср. Тогда
и = р2 (cos4 if + sin4 ip) = p2 (l sin2 2ipJ.
Так как VM(x,y) G П выполняются неравенства 0 < p2 ^ 1, 0 < 1 —
— - sin2 ip ^ 1, то 0 < и ^ 1, т. е. функция и(х,у) ограничена на мно-
жестве и.
При р = 1, (p = 0, т. е. в точке х = 1, у = 0, функция и(х,у)
принимает максимальное свое значение, равное 1. Таким образом,
supu(x,y) = 1.
Так как, очевидно, и —> 0 при /я —> 0, то и(х,у) принимает сколь
угодно малые положительные значения, т. е. \/е > 0 3(жо?2/о) ? ^ та~
кая, что г&(жо,2/о) ^ г* ОтсюДа и из неравенства и(х,у) > 0 следует,
что inf u(x,y) = 0.
Отметим, что функция и(х,у) не достигает на множестве п своей
точной нижней грани, т. е. ни в одной точке ее значение не равно
нулю. Следовательно, функция и(х,у) не имеет на множестве п ми-
минимального значения. А
5. Доказать, что функция и = х + 2у + 3 равномерно непрерывна
на всей плоскости.
Л Воспользуемся определением равномерной непрерывности функ-
функции. Зададим произвольное е > 0 и положим 5 = г/3. Тогда
VMi(xi,2/i), М2(х2,У2), удовлетворяющих неравенству р(М1,М2) =
= \/{х\ — х2J + B/i — у2J < S, будут выполнены неравенства \х\ —
-х2\ < S, 12/1—2/21 < ^, и, следовательно, |u(Mi) - ЦМ2)| = \xi +
+ 2^/1 — х2 — 2у21 ^ \х\ — х21 + 2\yi — у2\ < S + 25 = 35 = е. Это по опре-
определению и означает, что функция и(х,у) равномерно непрерывна на
всей плоскости. А
6. Исследовать на равномерную непрерывность функцию и =
= —z—^т на множестве п = Ux,у): 0 < х2 + у2 < 1}.
х2 + у2
Л Данная функция имеет более сложный вид, чем функция в приме-
примере 5. Поэтому исследование ее на основании определения равномерной
§3. Непрерывность функции 211
непрерывности представляет большие трудности. Проведем исследо-
исследование другим способом.
Отметим, что функция и(х,у) непрерывна на множестве П, так
как числитель х3 + у3 и знаменатель х2 + у2 являются непрерывны-
непрерывными функциями и х2 + у2 ф 0 на множестве П. Но множество П не
является замкнутым (поскольку не содержит точку 0@,0)), поэто-
поэтому теорема Кантора непосредственно здесь не применима.
Однако функцию и(х,у) можно доопределить в точке 0@,0) так,
что она будет непрерывной в этой точке. В самом деле, переходя к
полярным координатам х = р cos (р, у = р sin (р, получим и = p(cos3 ip +
+ sin3 ср), откуда следует, что и —У 0 при р —У 0, т. е. lim u(x,y) = 0.
х—>0
Таким образом, если доопределить функцию и(х,у) в точке О@,0),
положив ix@,0) = 0, то функция и(х,у) будет непрерывной в точке
О@,0) и, следовательно, непрерывной в круге П = {(х,у): х2 + у2 ^
^ 1}. Круг П — ограниченное замкнутое множество. По теореме Кан-
Кантора функция и(х,у) равномерно непрерывна в этом круге, а значит,
равномерно непрерывна и в круге П с выброшенным центром О@,0),
т. е. на множестве п. А
Замечание. Оказывается, что функция и(х,у) является равномерно
непрерывной на всей плоскости. Однако обосновать это с помощью теоремы
Кантора уже нельзя, так как плоскость — неограниченное множество, и
теорема Кантора неприменима. Равномерная непрерывность и(х,у) на всей
плоскости будет доказана в § 5 (см. пример 8 на с. 233), где будет получено
достаточное условие равномерной непрерывности функции.
Задачи и упражнения для самостоятельной работы
18. Найдите точки разрыва следующих функций:
а) и = — -; б) и = 1пD — х2 — у2)] в) и =
ж2+?/2 ж2+?/2-2;2
ч .ж v sin х sin?/
г) 16 = sin -; д) 16 = -;
2/ Ж2/
е)и= — —; ж) и = tg (ж2 + у2 + ?2).
19. Исследуйте следующие функции на непрерывность по отдельным пе-
переменным и по совокупности переменных:
в точках О@,0) и АA, 2);
/ 0,
= О,
212 Гл. X. Функции нескольких переменных
в) и= \ х + у ' ж + ^/°' в точках О@, 0) и АA, -1);
[ О, ж + у = О,
2
У
г) и= I x2+y2' X +У ^°' в точках 0@,0) и у
( sin ж + sin?/
ж+ 2/ ^ ' в точках 0@,0) и А (-,-- 1;
[ 1, ^ + ^/ = 0, V3 зу
{cos ж - cos у _ ,
i^ ' Ж ^^ ' в точках 0@,0) и AW-,-) и
О, ж-?/ = 0, V4 Aj
20. Ограничены ли следующие функции:
а) и = х2 - у2 в круге {(ж, у): ж2 + у2 ^ 25};
б) и = ж2 — у2 вне круга {(ж, у): ж2 + у2 ^ 25};
ч аж2 + by2 2 , 2 / г> / l \
в) it = —- — при ж +|/ т^ 0 (а и о — числа);
ч сов(ж + у) - сов(ж - у) .
г) и= — — при ху ф 0;
ху
, эт(ж + у) - вт(ж -у) .
д) и = — — — при ху ф 0;
ху
. In ж - In у
е) и = при х ф yl
х -у
21. Докажите ограниченность функции на указанном множестве, найдите
ее точные грани и установите, достигает ли функция своих точных
граней:
ж2 - у2
а) и = ——^тг при х -\- у ф 0;
ж2 +гу2
б) и = ——^- на множестве {(ж, у): 0 < ж2 + у2 ^ 9};
Ж ~г ?/
\ ^ У 4 | 4 _/ rv
ж4 + гу4
г) it = хуе~ху на множестве {(ж, г/): ж ^ 0, у ^ 0};
д) it = — при ж +|/ + z ф 0 (а > о).
22. Пользуясь определением равномерной непрерывности, докажите рав-
равномерную непрерывность функции на указанном множестве:
а) и = ах + by + с на всей плоскости ?72 (а / 0, b / 0);
б) it = ж2 + ?/2 в круге {(ж, у): ж2 + у2 ^ 1};
в) и = д/ж2 + |/2 + z2 во всем пространстве Е3;
г) it = ж3 — у3 в квадрате {(ж, ?/): 1 ^ ж ^ 2, 0 ^ у ^ 1}.
23. Исследуйте функцию на равномерную непрерывность на указанном
множестве:
а) и = — на множестве {(ж, у): 0 < ж2 + у2 < 25};
ж ~г у
§4- Частные производные 213
б) и = ^—^ — на множестве {(ж, ?/): 0 < х2 + у2 ^ 1};
2 2
в) и = — на множествах Q\ = {(ж, у): 1 < ж2+у2 < 2} и О2 =
= {(ж,г/): 0<ж2+т/ <1};
г) гб = — на множествах Q\ = {(ж, ?/, г): 10~2 < ж2 + ?/2 + z2 <
< 100} и ft2 = {(ж, г/, г): 0 < ж2 + у2 + ?2 < 1(Г2};
д) гб = ж sin - на множестве {(ж, у): 0 < ж < 1, 0 < г/ < 1};
2/
е) и = ху sin - на множестве {(ж, у): 0 < ж < 1, 0 < г/ < 1}.
§ 4. Частные производные
и дифференцируемость функции
Основные понятия и теоремы
1. Определение частной производной. Пусть M(xi, ...,хт) —
внутренняя точка области определения функции и = f(xi,...,xm).
Рассмотрим частное приращение этой функции в точке М(х\, ...,жш),
соответствующее приращению Axk аргумента х^\
Отношение .Хк является функцией одного аргумента Ахк (при фик-
Ахк
сированной точке M(xi,...,xm)).
Определение. Частной производной функции и = f(xi,...,xm)
Аж,п
по аргументу хк в точке М называется hm . К (если он сущест-
. Ажй^О Аж^
вует).
Эта частная производная обозначается любым из следующих сим-
символов: ——(М), -^-(М), иХк(М), fXh(M). Отметим, что при фикси-
охк ихк
рованных значениях всех аргументов, кроме хк, функция и = f(xi,...
...,хт) становится функцией одной переменной. Производная этой
функции одной переменной и есть частная производная функции и =
= f(xi, ...,xm) по аргументу хк. Поэтому вычисление частных произ-
производных производится по тем же правилам, что и вычисление произ-
производных функций одной переменной.
ди
Физический смысл частной производной: ——(М) — это скорость
охк
изменения функции в точке М в направлении оси Охк.
Замечание. Если М — граничная точка области определения функ-
функции, то для такой точки введенное определение частной производной
214 Гл. X. Функции нескольких переменных
уИ
может быть непригодным. Например, если функция и = /(ж, г/) определена
в треугольнике G (рис. 26), то для гранич-
М0(х0,у0) ной точки Мо(хо,уо) не определено частное
Мо(жо+Аа;,2/О)?C приращение Ахи, так как при любом Ах / О
точка М(жо + Дж,2/о) лежит вне области G.
Поэтому нельзя определить —(Мо), пользу-
ясь данным выше определением частной про-
производной. В таком случае, если существу-
ди
ет частная производная — во внутренних
дх
точках М области G, то по определению по-
гл ^ ди , ~ - s т ди ,, г, ,
и х лагают —(Mo) = lim —(М) (если этот
дхУ J м^м0 дхУ J v
ис# предел существует).
2. Определение дифференцируемости функции. Рассмотрим
полное приращение функции и = f(xi,...,xm) во внутренней точке
M(xi,...,xm) области определения функции
Аи = f(x! + Ажь...,жт + Ахш) -/(жь...,жт).
Оно является функцией аргументов Axi,...,Axm.
Определение. Функция и = /(xi, ...,жш) называется дифферен-
дифференцируемой в точке M(xi, ...,жш), если ее полное приращение в этой
точке можно представить в виде
Аи = AiAxi + ... + АтАхт + «iAxi + ... + атАхт, A)
где Ai — некоторые числа, с^(г = 1,...,ш) — функции аргументов
Axi,..., Ажт, бесконечно малые при Axi —>- 0, ..., Ахт —>- 0 и равные
нулю при Axi = ... = Ажт = 0.
Условие дифференцируемости A) можно записать в другой, экви-
эквивалентной форме
Аи = АгАхг + ... + АтАхт + а(р), B)
где р = y^AxiJ + ... + (АжтJ — расстояние между точками
М(жь...,жт) и M'Oi + Ажь...,жт + Ажт), а(/о) = о(р) при /о -^ 0,
а@) = 0.
Теорема 12. Е'сли функция и = f(xi,...,xm) дифференцируема в
точке М, то она непрерывна в этой точке.
Обратная теорема неверна, т. е. непрерывность является толь-
только необходимым, но не достаточным условием дифференцируемости
функции (см. замечание к примеру 1, б) на с. 219).
3. Связь между дифференцируемостью и существованием
частных производных. Напомним, что для функции одной пере-
переменной у = f(x) существование производной в точке хо является не-
необходимым и достаточным условием дифференцируемости функции
§4- Частные производные
215
в этой точке. Для функции нескольких переменных дифференциру-
емость и существование частных производных не являются эквива-
эквивалентными свойствами функции.
Теорема 13 (необходимое условие дифференцируемости). Если
функция и = /(xi, ...,жт) дифференцируема в точке М, то она имеет
в точке М частные производные по каждому аргументу xi, ...,xm.
ди
При этом ——(М) = Ak (к = 1, 2,..., т), где А\~ — числа из равен-
UXfc
ства A). Поэтому условие дифференцируемости A) можно записать
в виде
Аи = |^
атАх
C)
Обратная теорема неверна, т. е. существование частных производ-
производных не является достаточным условием дифференцируемости функ-
функции (см. пример 2 на с. 219).
Теорема 14 (достаточное условие дифференцируемости). Если
функция и = f(xi, ...,xm) имеет частные производные по каждому ар-
аргументу xi,...,xm в некоторой окрестности точки М и эти част-
частные производные непрерывны в точке М, то функция и = /(жь ...,жт)
дифференцируема в точке М.
Отметим, что непрерыв-
непрерывность частных производных яв-
является только достаточным, но
не необходимым условием диф-
дифференцируемости функции (см.
пример 3 на с. 220).
4. Геометрический смысл
дифференцируемости функ-
функции. Напомним, что для функ-
функции одной переменной у = f(x)
из дифференцируемости функ-
функции в точке хо следует сущест-
существование касательной к графику
функции в точке М(жо,/(жо)).
Рассмотрим непрерывную
функцию двух переменных и = Рис. 27
= /(ж, ?/), (х,у) е G. График
этой функции, т. е. множество точек S = {(х,у, f(x,y)), (x,y) G
G G}, представляет собой поверхность в пространстве i?3. Пусть плос-
плоскость Р проходит через точку А^о (^о ? 2/о ? f(xo,Vo)) поверхности 5;
N(x,y, f(x,y)) — произ-вольная точка на поверхности S; Ni — ос-
основание перпендикуляра, проведенного из точки N к плоскости Р
(рис. 27).
Определение. Плоскость Р, проходящая через точку Nq по-
поверхности 5, называется касательной плоскостью к поверхности S
•М(х,у)
•М0(х0,у0)
216 Гл. X. Функции нескольких переменных
в этой точке, если при N ->• No (N e S) величина p(N,N1) является
бесконечно малой более высокого порядка, чем p(N,No), т. е.
0
Nes
Теорема 15. Если функция и = f(x,y) дифференцируема в точке
Мо(хо,уо), то в точке TVq(^о?2/о? f(xo,yo)) существует касательная
плоскость к поверхности S (графику этой функции), причем уравне-
уравнение касательной плоскости имеет вид
^ ^ ~ Уо) ~{и- f(xo,yo)) = 0.
Вектор п нормали к касательной плоскости, т. е. п = < ^
—— (Mo), —If, называется вектором нормали (или нормалью) к поверх-
ду )
ности S в точке No(xo,yo, f(xo,yo)).
5. Дифференцируемость сложной функции.
Теорема 16. Пусть функции х\ = ^i(?i,..., tk), ..., хш =
— ^Prai^i-, ••••itk) дифференцируемы в точке A(ai, ...,a^), а функция и =
= f(xi,...,xm) дифференцируема в точке B(bi,...,bm), где bi =
— ^г(^1? •••? ак) (* = 15 •••5 к). Тогда сложная функция и = /((pi(?i, ...,t^),
•••?^т(*1?---^А;)) дифференцируема в точке А и ее частные производ-
производные в этой точке выражаются формулой
6. Дифференциал функции. Пусть функция и = /(жъ...,жт)
дифференцируема в точке M(xi, ...,жт), т. е. ее приращение в этой
точке можно представить в виде C):
Аи = \р-(М) Аж1 + ... + т^-(М) Ахт]
i
Выражение в квадратных скобках является линейной относительно
Axi,...,Axm частью приращения функции, а выражение в круглых
скобках — бесконечно малой функцией при Ах\ ->• 0, ...,Ажт ->• 0
более высокого порядка, чем р = ^(AxiJ + ... + (АжтJ.
Дифференциалом (или первым дифференциалом) функции
i,..., жт) в точке М называется линейная функция аргументов
du =
§4- Частные производные 217
Дифференциалом независимой переменной Х{ будем называть
приращение этой переменной: dxi = Да^. Тогда дифференциал функ-
функции и = /(xi, ...,жт) в точке М можно записать в виде
du = ——(M) dx\ + ... + ——(M) dxm. E)
Если аргументы дифференцируемой в точке МFЬ ..., Ьт) функции
и = /(ж1,...,жт) являются не независимыми переменными, а диф-
дифференцируемыми функциями каких-либо независимых переменных
причем bi = (pi(ab...,afe), ..., 6т = (рт(аи ..., а*), то дифференциал
сложной функции I/ = /((^i(ti,..., ?/.),..., ipm(ti,..., ?&)) в точке A(ai,...
...,ajfe) по-прежнему имеет вид E), но dxi,...,dxm являются не при-
приращениями переменных xi,...,xm (как в случае, когда xi,...,xm —
независимые переменные), а дифференциалами функций F) в точке
А, т. е.
dxi = -^—^-(^4) dti + ... + -^-^-(у!) <it^, i = 1,..., тп.
Это свойство называется инвариантностью формы первого диффе-
дифференциала.
Контрольные вопросы и задания
1. Дайте определение частной производной функции и = /(^i, ...,жт) по ар-
аргументу Хк во внутренней точке области определения функции.
Каков физический смысл частной производной?
2. Пользуясь определением частной производной, найдите — и —, если
2 дх ду
и = ху . у
3. Почему для граничной точки определение частной производной может
быть непригодным? Как определяются частные производные функции
в граничных точках области определения функции?
4. Дайте определение дифференцируемости функции в данной точке. Дока-
Докажите эквивалентность условий дифференцируемости A) и B). Докажи-
Докажите дифференцируемость функции и = х±Х2 в точке 0@,0), представив
ее приращение в этой точке в виде A).
5. Докажите, что дифференцируемая в данной точке функция непрерывна
в этой точке. Приведите пример, показывающий, что обратное утверж-
утверждение неверно.
6. Сформулируйте и докажите теорему о необходимом условии дифферен-
дифференцируемости.
7. Сформулируйте теорему о достаточном условии дифференцируемости.
8. Пусть дана функция
0 на осях координат,
1 в остальных точках плоскости.
218 Гл. X. Функции нескольких переменных
Она обладает следующими свойствами: —@, 0) = —@, 0) = 0; в любой
дх ду
точке М(ж, 0) (х ф 0) оси Ох — = 0, а — не существует; в любой точке
дх ду
(/II (/II
^@, у) (у ф 0) оси Оу — = 0, а — не существует; во всех остальных
ду дх
точках плоскости — = — =0 (обоснуйте эти свойства). Отсюда сле-
дх ду
ди ди ^( л
дует, что частные производные — и — непрерывны в точке 0@,0).
дх ду
Вместе с тем функция и(х,у) разрывна в точке 0@,0) (объясните, по-
почему), и, следовательно, недифференцируема в этой точке. Объясните
кажущееся противоречие этого примера с теоремой о достаточном усло-
условии дифференцируемости.
9. Каков геометрический смысл дифференцируемости функции и = /(ж, у)
в точке Мо(жо,2/о)? Дайте определение касательной плоскости к поверх-
поверхности и = /(ж, у) в точке No(xo, г/о, /(жо, г/о)) и запишите уравнение ка-
касательной плоскости в этой точке.
10. Сформулируйте теорему о дифференцируемости сложной функции и за-
запишите формулу для вычисления частных производных сложной
функции.
11. Что такое дифференциал функции и = f(xi,..., хш) в данной точке? От
каких аргументов он зависит?
12. Что понимается под инвариантностью формы первого дифференциала?
Докажите инвариантность формы первого дифференциала, пользуясь
правилом дифференцирования сложной функции.
Примеры решения задач
1. Найти частные производные функции:
а) и = ху (х > 0); б) и = дД2 +у2 + z2.
А а) При вычислении частной производной функции и = ху по
аргументу х рассматриваем функцию и как функцию только одной
переменной ж, т. е. считаем, что у имеет фиксированное значение.
При фиксированном у функция и = ху является степенной функци-
функцией аргумента х. По формуле дифференцирования степенной функции
ди 7/_i
получаем —- = уху .
ди
Аналогично, при вычислении частной производной -^— считаем,
ду
что фиксировано значение ж, и рассматриваем функцию и = ху как
показательную функцию аргумента у. Получаем — = ху\пх.
оу
б) При фиксированных значениях у и z функция и = \Jх2 + у2 + z2
является сложной функцией аргумента х. Вычисляя производную
этой функции аргумента ж, получаем
ди 1 о х
^ 2,х ^
дх 2^х2 +у2 + z2 д/ж2 + у2 + z2 '
§4- Частные производные 219
Аналогично,
ди у ди z
дУ у/х2 + у2 + z2 ' dz у/х2 + у2 + z2
Отметим, что полученные формулы теряют смысл в точке
0@,0,0). Покажем, что в этой точке частные производные функции
u(x,y,z) = д/ж2 + у2 + z2 не существуют. В самом деле, и(х,0,0) =
= л/х2 = |ж|. Эта функция аргумента ж, как известно, не имеет про-
производной в точке х = 0. Последнее и означает, что частная производ-
производная -т— в точке О не существует. Аналогично можно показать, что
дх л л
ди ди ~
частные производные — и — в точке О также не существуют. А
Замечание. Функция и = у х2-\-у2-\-z2, очевидно, непрерывна в
точке 0@,0,0), но не дифференцируема в этой точке (поскольку не име-
имеет частных производных в точке О). Это доказывает, что непрерывность
является только необходимым (теорема 12), но не достаточным условием
дифференцируемости функции.
2. Доказать, что функция
и= \ +у
О, х2+ у2=
имеет в точке О@,0) частные производные, но не дифференцируема
в этой точке.
Л Так как и(х,0) = ( п' Х - п' т- е- ^(ж'°) = ж' Т0 ^(°'°) =
I U, X — U, ох
= —и(х,0)\ _п = 1. Аналогично получаем —@,0) = 1. Итак, функ-
ах \х—о Q-y
ция и(х,у) имеет в точке О частные производные.
Докажем, что функция и(х,у) не дифференцируема в точке О.
Предположим противное. Тогда приращение функции в этой точке,
равное Аи = и(Ах,Ау) — г/@, 0) = -—^—дг"' можно представить в
виде
Аи= |^@,0) Ах +g@,0)A2/ + o(^),
где р = у/Ах2 + Ау2. Так как -—@,0) = —@,0) = 1, то из усло-
Аж3 + Ау3
вия дифференцируемости получаем -— —^- = Ах + Ау + о(р), или
Ах2 + А|/2
АхАу2 + Ах2Ау , /л 9 , л 9Л
; = «(VA^ + A?/2), т. е.
Дж-^0
220 Гл. X. Функции нескольких переменных
Покажем, что на самом деле этот предел не существует. Пусть
Ах и Ау стремятся к нулю так, что Ay = kАх (к ф 0). Тогда получим
,. АхАу2 + Ах2Ау Л. Ах3(к2 + к) к2 + к
lim - т^- = lim
(А2 А2K/2 А3(
_-^6 (Ах2 + Ау2K/2 Аж^о Ах3{1 + к2K/2 A + /с2K/2'
(Аз/=ЛАя;)
Так как величина ТТЛ. пРинимает разные значения при разных
к, то указанный предел не существует. Отсюда следует, что сделанное
предположение неверно, и, значит, функция и(х,у) не дифференциру-
дифференцируема в точке О. А
3. Доказать, что функция
х2+у2фО,
и = < х/х* + у*
х2 + у2 = О,
имеет частные производные в окрестности точки 0@,0) и дифферен-
дифференцируема в точке О, но частные производные не являются непрерыв-
непрерывными в точке О.
Л Во всех точках, кроме точки О, частные производные функции
и(х,у) можно найти, вычисляя по обычным правилам производные
функции (ж2 + у2) sin — ¦ Например,
ди
= 2ж sin —, / cos —, при х2 + у2 Ф 0.
В точке 0@,0) эта формула теряет смысл. Однако это не означает,
что -—@,0) не существует, поскольку выражение для — (х,у) было
получено при условии ж2 + у2 ф 0. Для нахождения -—@,0) восполь-
воспользуемся определением частной производной. Так как
т — 0
х — и,
vu = и(Ах, 0) — и@, 0) = Аж2 sin ——-. Отсюда lim
то l\xu = u[/\x4V) - ia(U,U) = ZXa^siiiT-r—г. итсюда lim —— =
\Ах\ Аж-^0 Аж
= lim Axsin-—=0, т. е. — @,0) = 0. Аналогично можно доказать,
|Аж
§4- Частные производные 221
ди
что —@,0) = 0. Итак, функция и(х,у) имеет частные производные
в окрестности точки О.
Докажем, что функция и(х,у) дифференцируема в точке О. Для
этого нужно доказать, что Аи = и(Ах, Ау) - и@,0) = (Аж2 +
+ Ay2) sin — — можно представить в виде
^А2 + Ау2
Аи = |^@,0) Ах + |^@,0) Ау +
т. е. справедливо равенство (учитываем, что —@,0) = —@,0) = 0
\ ОХ
(Ах2 + Ay2) sin . = о(Л/Ах2+А?/2).
д/Аж2 + Ау2
Но это равенство очевидно, поскольку
(Аж2 + Ay2) sin =
lim
= lim л/Д.т!2 + A?/2 sm —— = 0-
Аж^О v у/Дж2 + Ау2
Таким образом, функция и(х,у) дифференцируема в точке О.
Докажем, наконец, что частная производная —(х,у) не является
непрерывной в точке О. Очевидно, первое слагаемое 2xsin-
/х2 +у2
стремится к нулю при М(х,у) —> О@,0). Второе же слагаемое
( та— ) не имеет предела при Mix. у) —>¦
V ^Х2 + у2 ^Х2 +у2)
—> О@, 0). В самом деле, если точка М(ж, у) стремится к точке О@, 0)
по лучу у = кх (к ф 0, х > 0), то на этом луче указанное слагаемое
равно cos —г^=^ и, очевидно, не имеет предела при х ->• 0.
л/1 + к2 x\J\ + к2
Итак, предел —-(х,у) при М(х,у) —> О@,0) не существует. Сле-
довательно, —(х,у) не является непрерывной в точке О. Аналогично
можно показать, что —(х,у) не является непрерывной в точке О.
Рассмотренный пример показывает, что непрерывность частных
производных является только достаточным (теорема 13), но не необ-
необходимым условием дифференцируемости функции. А
4. Составить уравнение касательной плоскости к параболоиду и =
= х2 + у2 в точке NqA,2,5) и найти нормаль к параболоиду в этой
точке.
222 Гл. X. Функции нескольких переменных
ди
Л Пусть МоA,2) — точка на плоскости Оху. Так как — = 2ж,
(ill (ill (ill
¦7— = 2у, то -— (Мо) = 2, —— (Мо) = 4. Учитывая также, что u(Mq) =
ду дх ду
= 5, получаем искомое уравнение касательной плоскости
2(ж - 1) + 4(?/ - 2) - (и - 5) = 0, или 2ж + 4$/ - и - 5 = 0.
Вектор п = {2,4, —1} является нормалью к параболоиду в точке Nq. A
5. Найти частные производные функции и = f(x,xy,xyz) по аргу-
аргументам х, у и z.
Л Данная функция является сложной функцией переменных ж, у и z:
и = f(xi,X2,xs), где х\ = ж, Ж2 = ж?/, хз = ж^/2:. Обозначим частную
производную функции и = /(ж1,Ж2,жз) по аргументу ж^, через /г; (г =
= 1,2,3) (функции j[ зависят от тех же аргументов, что и функция
/, т. е. j[ — fl(x, xy, xyz)). Применяя формулу D), получим
ди
6.
М@,
А а)
/м+.
Найти
1,2); б)
Имеем
П-У + й-уг,
дифференциал
и = f(x + y2,y
~дх ~ е
ди ?,
~ду~ ~ h ' Х^
функции: а)
+ ж2) в точке
• 2ж, тг^(М)
ох
¦л-
м =
М(-1
= 0;
^,
,1)
ди
~d~z ~
W+z2
= /з
в
•Ж2/. А
точке
"г2-2г/,
^(М) = 2е5; ^ = ex'+y2+z'-2z, ^(M) = 4е5. Следовательно,
ду oz oz
du\ = f^(M) da; + |^(М) dy + |^(М) d2 = 2 ¦ e5dy + 4e5(fe.
сж ^2/ c^
б) Запишем функцию и = /(ж + у2, у + ж2) в виде и = /(?, г?), где
t = ж + у2, г? = ?/ + ж2. Вычисляя частные производные — и — по
дх ду
формуле D), получим
^ = Л(ж + ?/2, ?/ + ж2) • 1 + /,(ж + г/2, 2/ + х2) • 2ж,
-^ = ft(x + у2, у + ж2) • 2у + Д(ж + у2, у + ж2)
Следовательно,
= [Л@,2) - 2/„@,2)]йа; + [2/4@,2) + fv@,2)]dy. G)
§4- Частные производные 223
Это же выражение для du\M можно получить другим способом,
используя инвариантность формы первого дифференциала. В силу
инвариантности формы первого дифференциала имеем
du\M = Л@, 2)<Й + /w@, 2)dv, (8)
где dt и dv — дифференциалы функций t = x + y2nv = y + x2B точке
М(-1,1). Так как * (М) = 1, *(М) = 2, g(M) = -2, |(М) = 1,
то c?i|M = dx + 2dy, dv\M = —2dx + dy, и из равенства (8) получаем
du\M = /«@,2)(dx + 2dy) + /„@,2)(-2dx + dy) =
= [/(@,2) - 2/„@,2)]<*с + [2/* @,2) + /„@,2)]^,
что совпадает с равенством G). А
Задачи и упражнения для самостоятельной работы
24. Найдите частные производные следующих функций:
а) и = х2 + у3 + Зж2?/3; б) гг = ж?/? + —;
у ~
в) гг = sin(x|/ + г/г); г) гг = ^2^; д) гг = tg (ж + г/) • еж/у;
cos ?/
е) гб = arcsin — ; ж) и = arctg —; з) гб = жг/1п(жг/);
72 + 2 ж
= xyyzzx.
25. Существует ли частная производная ^ функции гб = ^/l — х2 — у2 в
точке @,1)?
26. Исследуйте, имеет ли функция и(х,у) частные производные в точке
0@, 0) и дифференцируема ли она в этой точке, если:
а) и = л/х2 + у2; 6) и =
д) и= Ух4 + у4] е) и=
} I 0, х
и) и = *§/ж • sin у; к) и = ^/у • tg x\
( (
[О, Ж2+г/2 = 0; [ 0, |ж| + Ы=0.
27. Для функций из упр. 26 исследуйте вопрос о существовании частных
производных в окрестности точки 0@, 0) и их непрерывности в точ-
точке О.
28. Докажите, что если функции f(x) и д(у) имеют производные соот-
соответственно в точках хо и г/о, то функции и(х,у) = f(x)+g(y) и
v(x,y) = /(ж) • д(у) дифференцируемы в точке (хо,уо).
29. Составьте уравнение касательной плоскости к поверхности:
а) и = ху в точке ЛГоA, 0, 0);
б) и = х + у2 в точке А@,1,1); в) и = х3 + у3 в точке БA, —1, 0);
г) и = sin(xy) в точке СA, тг/3, л/З/2); д) и = ех+у в точке ?>A, -1,1).
224 Гл. X. Функции нескольких переменных
30. Является ли плоскость и = 0 касательной в точке 0@, 0, 0):
а) к параболоиду вращения и = ж2 + у2] б) к конусу и =
в) к гиперболическому параболоиду и = xyl
31. Найдите частные производные следующих сложных функций (функ-
(функции / и д считаются дифференцируемыми):
а) и = f(x + у,х2 + ?/2); б) ^ = /(-,-); в) и = f(x-y,ху)\
\у ж/
г) и = /(яу) • ^Ы; р)и= [f(x -
е) и = f(x -у2\у - ж2, ху)\ ж) и =
32. В каждом из следующих случаев проверьте, что функция и(х,у) удов-
удовлетворяет соответствующему уравнению, если / — произвольная диф-
дифференцируемая функция:
a)u = f(x +y), у--х- = 0;
б) « = «-/D). *?+2»?=т,;
V х2) дх ду
в) и = yf(x2 - у2), у2^- + ху-^- = хщ
дх ду
г) и = — + f(xy), x2— — ху— + у2 = 0;
\ п с ( У z \ ®и ди п ди
дJ и = ж /I —, —т ), ж Ь сеу г р?— =
*)u=?»-\nx + xf(v-, z-\
Z \Х Xj
ди ди
+
ди ди
33. Вычисляя частные производные — и — и исключая производные
дх ду
функций f и g (f и g — произвольные дифференцируемые функции),
составьте уравнение, которому удовлетворяет функция и(х,у), если:
а) и = х + f(xy)\ б) и = xfU?A\ в) и = f(x -y,y-z);
n)u = Xf(X-)+y9(X-).
\yj \yj
34. Найдите решение и = и(х,у) уравнения:
а) — = cos ж + ху, удовлетворяющее условию и@,у) = у ;
^ж
б) — = ж2 + у2, удовлетворяющее условию и(х.х) = 0;
ду
ч ди ху ( 1 \ Л
в) — = е у +1/, удовлетворяющее условию и\ ж, — 1 = 1.
^ж V ж/
35. Найдите дифференциал функции:
а) 16 = х2у3 в точках М(ж, у) и МоB,1);
б)и=— в точках M(x,y,z) и ЛГA,2,3);
в) и = С08(ж?/ + ж^) в точках M(x,y,z) и ЛГA, тг/6, тг/6);
г) гб = ежу в точках М(х,у) и О@,0);
д) гб = жу в точках М(х,у) и МоB,3);
е) гб = ж1п(ж?/) в точках М(х,у) и Мо(—1, — 1).
§ 5. Частные производные высших порядков 225
36. Найдите дифференциалы следующих сложных функций в указанных
точках, если / — дифференцируемая функция; x,y,z — независимые
переменные:
a)u = f(x — y, х + у) в точках М(х,у) и МоA, — 1);
б) и = /(ху, — ) в точках М(х,у) и Мо@,1);
V у)
в) и = f(x2-у2,у2 - z2,z2 - х2) в точках M(x,y,z) и ЛГA,1,1);
г) и = /(sin х + sin у, cos x — cos 2) в точках M(x,y,z) и 0@,0,0).
37. Пусть и и v — дифференцируемые функции каких-либо независимых
переменных. Докажите, что справедливы следующие правила диффе-
дифференцирования:
1) d(cu) = с du (с — число); 2) d(u + v) = du + dv;
3) d(u — v) = du — dv; 4) d(uv) = udv + v du;
2 ^/°-
§ 5. Частные производные
и дифференциалы высших порядков
Основные понятия и теоремы
1. Частные производные высших порядков. Пусть функция
?( \ ди ,
и = j{xiJ...Jxm) имеет частную производную —— (она называется
uX<i
также частной производной первого порядка) в каждой точке некото-
некоторой окрестности точки М. Если -— имеет в точке М частную про-
иХ{
изводную по аргументу Xk, то эта производная называется частной
производной второго порядка (или второй частной производной) функ-
функции и = /(жь ...,жш) по аргументам х^ Xk в точке М и обозначается
одним из следующих символов:
d' J^ uXiXh(M), fXiXM(M).
Если к ф г, то частная производная второго порядка называет-
называется смешанной. Если к = г, то частная производная второго порядка
д2и d2f ,
обозначается ——^ или ^-^, или 1&Ж2, или /Ж2.
Частные производные третьего порядка определяются как част-
частные производные от частных производных второго порядка и т. д.
Частная производная п-го порядка (или п-я частная производная)
функции и = f(xi,...,xm) по аргументам Хгг,Хг2,...,Хг обозначает-
обозначается
ся — — и определяется формулой
дпи 3
дх
дпи _ д / дп~1и \
пдхгп-1- дхП ~ дх^п ^dxin-i- дх^'
8 В.Ф. Бутузов и др.
226 Гл. X. Функции нескольких переменных
Если не все индексы гьг2, ...,гп равны друг другу, то частная произ-
производная n-го порядка называется смешанной.
Теорема 17. Если в некоторой окрестности точки Мо(жо,2/о)
функция и = f(x,y) имеет смешанные частные производные fXy{x,y)
и fyx(x,y), причем эти смешанные частные производные непрерывны
в точке Мо, то они равны в этой точке:
1ху(хО,Уо) = 1ух(хО,Уо)- A)
Если равенство A) выполняется, то говорят, что смешанные част-
частные производные второго порядка функции и = f(x,y) не зависят от
порядка дифференцирования в точке Мо(хо,уо).
Обобщением теоремы 17 является следующая теорема.
Теорема 18. Если все смешанные частные производные п-го по-
порядка функции и = /(xi, ...,хт) существуют в некоторой окрестнос-
окрестности точки Мо и непрерывны в точке Mq, то они не зависят в точке
Mq от порядка дифференцирования.
Определение. Функция и = /(xi, ...,жт) называется дифферен-
дифференцируемой п раз в точке Мо, если все ее частные производные (п - 1)-
го порядка дифференцируемы в этой точке.
Следующая теорема дает другое, нежели в теореме 17, достаточ-
достаточное условие для выполнения равенства A).
Теорема 19. Если функция и = f(x,y) дважды дифференцируема
в точке Мо0о,2/о), rno fxy(xo,yo) = }ух(хо,Уо)-
2. Дифференциалы высших порядков. Пусть функция и(х,у)
независимых переменных х иу дифференцируема в окрестности точ-
точки Мо(хо,уо) и дважды дифференцируема в точке Mq. Первый диф-
дифференциал функции
du= ^(ж'^ж + ^(ж'^^
является функцией четырех переменных: ж, у, dx и dy, причем
— (ж,2/) и ^г(х?У) — дифференцируемые в точке Мо функции.
ох оу
Второй дифференциал d2u (или дифференциал второго порядка)
функции и(х,у) в точке Mq определяется как дифференциал в точ-
точке Мо от первого дифференциала du при следующих условиях:
1°) du рассматривается как функция только независимых пере-
переменных х и у (иными словами, при вычислении дифференциала от du
нужно рассматривать dx и dy как постоянные множители);
2°) при вычислении дифференциалов от —(х^у) и —(х^у) прира-
приращения независимых переменных х и у берутся такими же, как и в
выражении для du, т. е. равными dx и dy. На основании этого опре-
определения получается формула
Mo) dxdy+w{ 2
§ 5. Частные производные высших порядков 227
где dx2 = (dxJ, dy2 = (dyJ. Формулу B) можно записать в более
компактном виде. Для этого введем следующие понятия. Символ -т—
ох
будем называть оператором частной производной по переменной х.
При действии этого оператора на функцию и(х,у) получается новая
функция — частная производная — (х,у). Аналогично определяется
оператор — частной производной по у.
dy
Определим степени и произведения степеней операторов — и —
ох оу
следующим образом:
(—) = ——?¦ — оператор второй частной производной по ж; при
- Х Х м д"и
действии его на функцию и получается -—¦;
д д д2
____ = _—_ — оператор смешанной второй производной по у, х:
дхду дхду
д\к ( д\1 дк+1
дх^) Щ) = Ъх~кду^ ~ оператор смешаннои производной
(к + Z)-ro порядка I раз по у и к раз по х.
Символ d — — dx + — с?2/ назовем оператором дифференциала,
dx dy
При действии этого оператора на функцию и(х,у) получается диф-
дифференциал функции: du = -^-dx + -^- dy. Определим n-ю степень опе-
dx dy
ратора дифференциала как n-ю степень двучлена — dx + — dy. В
аж а?/
частности, при п = 2 получаем
б?2 = (-г- б?ж + — ф ) = ^-т б?ж + 2 б?ж ф + ^-т <i^/2.
Ч^ж dy ) dx2 dxdy dy2
При действии оператора d2 на функцию и получится, очевидно, вто-
второй дифференциал функции. Таким образом, формулу B) можно за-
записать теперь в операторном виде:
d d \2
dx dy J ^o
Дифференциал dnu произвольного п-го порядка функции и(х,у)
определяется индуктивно по формуле
dnu = d(dn-1u) C)
при таких же двух условиях, что и дифференциал второго порядка.
Для dnu справедлива операторная формула
8*
228 Гл. X. Функции нескольких переменных
Если х и у являются не независимыми переменными, а дифферен-
дифференцируемыми (нужное число раз) функциями каких-либо независимых
переменных ?ь ..., tk, то формула D) при п ^ 2 становится, вообще
говоря, неверной (неинвариантность формы дифференциалов высших
порядков). В частности, при п = 2 имеем
—rfx + —rfd, E)
dy
где dx, cfa/, cPx, d2y — дифференциалы первого и второго порядка
функции x(tu...,tk) и y(tu...,tk).
В случае функции т независимых переменных и = f(xi,...,xm)
дифференциал n-го порядка определяется индуктивно по формуле C)
при условиях, аналогичных условиям 1°) и 2°). Оператор дифферен-
дифференциала имеет вид
d = -— dxx + ... + д— dxm,
ах i axm
и справедлива операторная формула, аналогичная D):
3. Формула Тейлора.
Теорема 20. Если функция и = f(xi,...,xm) дифференцируема
п + 1 раз в некоторой г-окрестности точки Mq(xJ, ..., х™), то для лю-
любой точки M(xq + Axi, ...,х™ + Ажт) из этой г-окрестности спра-
справедливо равенство
f(x\ + Axi,..., х™ + Ажт) - /(xj,..., х™) =
+^^2^| +^ + ]_dnu + х tT+^L, G)
Mo 2! lMo n! Mo (n + 1)! l7V
г^е 7V — некоторая точка, лежащая на отрезке М0М, а дифференциа-
дифференциалы dku вычисляются по формуле F), причем dxi = Axi (г = 1, ...,т).
Формула G) называется формулой Тейлора для функции ^ =
= f(xi,...,xm) с центром разложения в точке Mq(xJ, ...,ж^).
Если положить Axi — Х{— х\ (г = 1, ...,т) и раскрыть выражения
для <^|м , то формулу G) можно записать в виде
..., хт) = /(х?,..., х°т) + ^(
М0)(а;то - x°Jn + Rn+1 = Рп(хи...,хт) + Rn+i, (8)
где Pn(xi, ...,xm) — многочлен степени п от переменных xi,...,xm, a
Rn+1 = —¦ dn+1u\N — остаточный член.
[п + 1).
§ 5. Частные производные высших порядков 229
Многочлен Pn(xi,...,xm) называется многочленом Тейлора; он об-
обладает тем свойством, что значения его и всех его частных производ-
производных до n-го порядка включительно в точке Мо соответственно равны
значениям функции и = f(xi,...,xm) и ее частных производных в
точке Mq.
При п = 0 из формулы G) получаем формулу Лагранжа конечных
приращений для функции многих переменных:
f(x\ + A*i,..., х°т + Ахт) - fix0,,..., x°J =
Введем обозначение р = р(М0,М) = \/Ах\ + ... + Лж^. Тогда оста-
остаточный член в формуле (8) можно записать в виде i2n+i = o(pn) (оста-
(остаточный член в форме Пеано).
Формула Тейлора с остаточным членом в форме Пеано справед-
справедлива при более слабых требованиях, чем в теореме 20, а именно
функция и = f(xi,...,xm) должна быть дифференцируемой п — 1
раз в ^-окрестности точки Мо и дифференцируемой п раз в самой
точке Mq.
Контрольные вопросы и задания
1. Дайте определение частной производной второго порядка функции
и = /(ж1,..., Хт) по аргументам Жг, Хк в точке М. В каком случае част-
частная производная второго порядка называется смешанной?
2. Покажите, что смешанная частная производная fXy(x,y) функции
и = /(ж, г/) представляет собой повторный предел
fxy(x,y) =
lim lim f(x + Ax,y + Ay) - f(x, y + Ay)- f(x + As, g/) + f(x, y)
Ay^O Аж-^0 Ax • A?/
3. Дайте определение частной производной n-ro порядка функции и =
= /(ж1,...,жт) по аргументам Жг15 Жг2, •••, xin. В каком случае эта част-
частная производная называется смешанной?
4. Известно, что функция и = f(x\,..., жт) имеет все частные производные
n-ro порядка в точке М. Что можно сказать о существовании частных
производных меньшего порядка этой функции в точке М и в окрест-
окрестности точки М?
5. Сформулируйте теорему о равенстве смешанных частных производ-
производных второго порядка функции и = /(ж, г/). Пользуясь этой теоремой,
обоснуйте равенство смешанных частных производных второго поряд-
порядка функции и = [sin(x-\-y)]cosху в любой точке М(ж,г/), в которой
sin(x + у) > 0 (не вычисляя самих производных).
6. Сформулируйте теорему о независимости n-х смешанных частных про-
производных функции и = /(ж1,...,жт) от порядка дифференцирования.
Опираясь на теорему о равенстве смешанных частных производных
д3и д3и
второго порядка, докажите, что = .
дх\ дх2 дхз дхз дх2 дх\
230 Гл. X. Функции нескольких переменных
7. Дайте определение n-кратной дифференцируемости функции и =
= /(ж1, ...,жт) в данной точке. Докажите, что если функция дифферен-
дифференцируема п раз в точке Мо, то эта функция и все ее частные производные
до (п — 1)-го порядка включительно дифференцируемы в точке Мо.
8. Докажите, что если функция и = f(x\,..., хш) имеет в некоторой окрест-
окрестности точки Мо все частные производные n-го порядка и эти частные
производные непрерывны в точке Мо, то функция дифференцируема п
раз в этой точке.
9. Сформулируйте вторую теорему о равенстве смешанных частных про-
производных второго порядка функции и = /(ж, г/).
10. Дайте определение дифференциала второго порядка функции и = /(ж, у)
(ж и у — независимые переменные) в данной точке Мо и, пользуясь
этим определением, выведите формулу B).
11. Напишите операторную формулу для дифференциала второго порядка
функции и = /(ж, г/) (ж и у — независимые переменные).
12. Дайте определение дифференциала n-го порядка функции и = /(ж, г/).
Методом математической индукции докажите справедливость опера-
операторной формулы D) для дифференциала n-го порядка.
13. Выведите формулу E) для дифференциала второго порядка функции
и = /(ж, у) в случае, когда жиг/ — дважды дифференцируемые функции
каких-либо независимых переменных.
14. Напишите выражение для оператора дифференциала и операторную фор-
формулу для дифференциала n-го порядка функции и = /(ж1,..., жт), где
Ж1,..., жт — независимые переменные. Докажите, что эта формула спра-
справедлива и в том случае, когда Ж1,...,жт — линейные функции незави-
независимых переменных ?i,...,?fc.
15. Сформулируйте теорему о формуле Тейлора и запишите формулу
Тейлора в двух видах (формулы G) и (8)).
16. Что такое многочлен Тейлора? Каким свойством он обладает? Докажите
это свойство.
17. Напишите формулу Лагранжа конечных приращений для функции
и = /(ж1, ...,жт). При каких условиях эта формула верна?
18. При условиях теоремы 20 (т. е. пользуясь формулой G)) выведите фор-
формулу для остаточного члена в форме Пеано. При каких более слабых
требованиях справедлива формула Тейлора с остаточным членом в фор-
форме Пеано?
Примеры решения задач
1. Найти частные производные второго порядка функции
и = ху.
Д Сначала находим частные производные первого порядка:
Затем, вычисляя частные производные от частных производных пер-
первого порядка, получаем производные второго порядка данной функ-
функции:
^ ^ = х*-1 + ухУ-1 \пх = Ху-\1 + уЫх),
= уХу \пх + ху-=ху A + 2/In ж), -д-^ = ху (\п х) . А
§ 5. Частные производные высших порядков 231
д2и д2и
Замечание. В рассмотренном примере = . Вообще, если
дх ду ду дх
функция и = /(ж, г/) является суперпозицией элементарных функций, то
ее частные производные любого порядка также являются суперпозициями
элементарных функции, а так как элементарная функция непрерывна в лю-
любой точке, в окрестности которой она определена, то частные производные
любого порядка функции и = f(x,y) не зависят от порядка дифференциро-
дифференцирования.
2. Доказать, что функция
f(x,y) = < х2 + у2
[ о, х2+у2 = 0,
имеет в точке 0@,0) смешанные частные производные второго по-
порядка, НО При ЭТОМ /Жу@, 0) ф /уж @,0).
Л Вычислим сначала частную производную первого порядка fx(x,y).
Во всех точках, кроме точки О@,0), это можно сделать, дифферен-
о о
цируя по ж функцию ху ——^г. Получаем
х2 + у2
{^$)' х2+у2^0. (9)
Чтобы найти /ж@, 0), воспользуемся тем, что /(ж, 0) = 0. Отсюда име-
имеем /ж @,0) = 0.
Для нахождения смешанной производной второго порядка /Ж2/@, 0)
нужно найти производную по у функции /ж @,2/) в точке у = 0. Из
(9) следует, что fx(O,y) = —у при у ф 0, а так как /ж@,0) = 0,
то \/у: /ж@,2/) = -у. Следовательно, fxy@,0) = — fx@,y)\y=o = -1.
х2 — у2 fx2—v2\'
Аналогично получаем fy(x,y) = х——^+ху[——^ ) при
X ~\- у \Х + у J у
х2 + у2 ф 0, /^@,0) = 0, откуда Vx: fy(x,0) = ж. Следовательно,
Таким образом, /яз/@,0) ф /^@,0). А
3. Найти о о о Q, если и = ежу.
^ж2 ду8
Л Указанная частная производная десятого порядка не зависит от
порядка дифференцирования (см. замечание после примера 1). Оче-
г)8
видно, -^-^ = х8еху . Вычисляя теперь по формуле Лейбница вторую
д8и
производную по х от тг-^5 получаем
ду8
а о и\ _ аи _ , 8yt ху | 2(г8У(гхуУ +т8(рху)" -
дхЛду8) ~ дх2ду8~[ ] +А^Де )х+х^е )хх -
= Б6х6еху + 16х7уеху + х8у2еху = еху(Б6х6 + 16х7у + ж8?/2). А
232 Гл. X. Функции нескольких переменных
4. Найти второй дифференциал функции и = ху в точке МоA,0).
Л Полагая х = 1, у = 0 в выражениях для частных производных вто-
второго порядка данной функции (см. пример 1), получим ^-^-(Mq) =
= 0, - - (Mo) = _ _ (Мо) = 1 —г (Mo) = 0. Подставляя эти зна-
ох оу оу ox oyz
чения в формулу B), находим d2u м = 2dxdy. A
5. Найти второй дифференциал функции и = f(x + у, ху) в точке
М(х,у), если х и у — независимые переменные.
Л Запишем данную функцию в виде и = /(?, г?), где t = х + у, v = ху.
Используя эти обозначения, находим
-^ = ft(x + у, ху) + fv(x + у, ху) • у,
ду у
-^ = /« + fvt'y + ftv 'У + fvv ' У2 = /« + tyftv + 2/2Лг;,
^J- = ftt +fvfX + ftv-y + fvv 'ХУ + fv =
д u _ f. , /» . . r _i_ A .r i f . r2 _ /r , Or f+ 4- Г2 f
r\ 9 — «/** ^^ JVC «^ ^^ «/cv «^ i J vv **-* — J tt ~ ^^Jtv i **-* J vv'
Подставляя эти выражения в формулу B), получаем
d2u = (ftt + 2yftv + у2fvv) dx2 + 2(ftt + (ж + 2/)/tv + xyfvv +
+ fv) dxdy + (fu + 2x/^ + x2 fvv) dy2. A
6. Разложить функцию f(x,y) = еЖ//у по формуле Тейлора (8) с
центром разложения в точке Mq@, 1) до членов второго порядка вклю-
включительно.
Л Сначала находим частные производные функции f(x,y) до второго
порядка включительно:
Ё1=ех/
дх yJ ду V у2 /
^1 = ех/у . 1_^ ^]_ = ех/у . (_ Ж \ + еХ/у 8 (^__L_
= р е
дудх \ уЧ \ у
В точке Мо@,1) имеем /(Мо) = 1, |^(М0) = 1, ^(Мо) = 0,
0(МО) = 1, ^^(Мо) = -1, 0(МО) = 0. Подставляя эти выра-
§ 5. Частные производные высших порядков 233
жения в формулу (8), получаем
ех/У = 1 + х + i х2 - х(у - 1) + R3 = 1 + 2х + i ж2 - ж?/ + Д3.
В форме Пеано Л3 = о(ж2 + (з/ - IJ). A
7. Доказать, что если функция f(x,y) дифференцируема в выпук-
выпуклой*) области G и ее частные производные fx(x,y) и fy(x,y) ограни-
ограничены в этой области, то f(x,y) равномерно непрерывна в области G.
Л Пусть \fx(x,y)\ ^ с, \fy(x,y)\ ^ с в выпуклой области G (с > 0 —
некоторое число). Зададим произвольное г > 0 и положим ? = —.
2с
Пусть Mi(xi,2/i) и М2(ж2,2/2) — любые точки области G, для кото-
которых р(М1,М2) < S. Так как область G выпуклая, то отрезок прямой,
соединяющий точки Mi и M2j целиком лежит в области G, и поэтому
к разности /(Mi) — /(М2) можно применить формулу Лагранжа:
- /(М2) = /ж(А0(*1 " х2) + /y(JV)(|/i - 2/2). (Ю)
Далее, так как р(М1,М2) = \/(хх - х2J + (у\ - у2J < 5, то \xi-
-х2\ < S, \уг -у2\ < S, и поскольку \fx(N)\ ^ 0,1/3,(^I ^ с, из ра-
равенства A0) следует, что
|/(Mi) - /(М2)| < l/.WIki - ж2| + \fy(N)\\yi - У2\ < 2cS = e.
Согласно определению это и означает, что функция /(ж, у) равномерно
непрерывна в области G. А
8. Доказать, что функция
*+yl> X +У ^U'
y
0, х2 + у2 = 0,
равномерно непрерывна на всей плоскости.
Л Докажем сначала, что данная функция имеет ограниченные част-
частные производные их и иу на всей плоскости. В самом деле,
" У3
их = X +(^Уу2"J2Жг/ при х2+у2^0и их@,0) = 1 (см. пример 2 § 4).
Переходя к полярным координатам х = pcostp, у = ps'mtp, получим
их = cos4 if + 3cos2 ipsm2 ip - 2 cos ip sin3 ip (при р ф 0) и гаж(О,О) = 1.
Отсюда непосредственно видно, что 1хж(ж, 2/) — ограниченная функция
на всей плоскости. Аналогично доказывается ограниченность иу(х,у).
Казалось бы, теперь можно воспользоваться установленным в при-
примере 7 достаточным условием равномерной непрерывности функции.
*) Область G называется выпуклой, если для любых точек М\ и М_2 этой области
отрезок прямой, соединяющий точки М\ и М2, целиком принадлежит области G.
Например, круг и прямоугольник — выпуклые области на плоскости.
234 Гл. X. Функции нескольких переменных
Однако этому мешает тот факт, что функция и(х,у) не дифферен-
дифференцируема на всей плоскости, а именно не дифференцируема в точке
0@,0) (см. пример 2 § 4). Тем не менее простые рассуждения поз-
позволяют обойти это препятствие. Если точки Mi и М2 таковы, что
точка О не лежит на отрезке M\M2l то разность и(М\) — и(М2) мож-
можно оценить с помощью формулы Лагранжа точно так же, как и в
примере 7. Если же точка О лежит на отрезке М\М2, то разность
u(Mi)-u(M2) следует заменить суммой двух разностей [u(Mi)—
— и (Ms)] + [и (Ms) — и(М2)], причем точку Мз выбрать так, чтобы
точка О не лежала на отрезках М\М^ и М^М2. Далее, каждую из
этих разностей можно оценить с помощью формулы Лагранжа. В лю-
любом случае получим \и(М\) — и(М2)\ < е, если p(Mi,M2) < S = —,
где с — верхняя грань \их\ и \иу\. Это доказывает равномерную не-
непрерывность функции и(х,у) на всей плоскости. А
Задачи и упражнения для самостоятельной работы
38. Найдите частные производные второго порядка следующих функций:
а) и = Xs + у4 + 2х3у4; б) и = xy2zs + -^-3 ; в) и = cos(xy);
г) и = sin(x + yz)\ д) и = arctg —; е) и = \Jх2 + у2 • ех+у]
т т
\ vz \ (ХХ \ Y^ , Y^ и ( и
4XJ* I /Э / ^^~ SY* & • О I /Э / ^^~ I ^^ 1 • Т Л" I /Э / ^^~ Ж /~f 1 ОТ* 1 I Ж ГЛ • 1 ОТ* • ОТ* 1 I /~f 1 f\ • 1
числа). У k=1 ''k=1
{xu пои \u\ ^C \x\
^ I имеет в точке
O@, 0) смешанные частные производные второго порядка, но иху@, 0) ф
40. Докажите, что если функция и = /(ж, г/) имеет в некоторой окрестнос-
окрестности точки Мо(жо,2/о) частные производные /ж(ж,г/), /у(ж,г/), fxy(x,y) и
смешанная частная производная fXy(x,y) непрерывна в Мо, то в этой
точке существует смешанная частная производная /уж и справедливо
равенство fyx(xo,yo) = fxy(xo,yo).
41. Найдите частные производные указанного порядка:
б) а а~ 4> если и = х cos у + у cos ж; в)
^ж4 ^?/4
дх ду dz
д1Ои дш+пи
г) д^д^' если и = 5{пхС052У' д) ЭжжЭуИ> если и =
Qrn+nu у
е) , если и = е х sin у + ех cos -;
ч ^w t 2 мо ч ^m+nw х + у
ж) -, если и = (х + у) tgx: з) , если и = -.
' дхду9 У У) ь 1 ) dxmdyni х_у
42. Найдите частные производные второго порядка следующих функций
(функции / и g считаются дважды дифференцируемыми):
§ 5. Частные производные высших порядков 235
а) и = /(ж + у, ж2 + у2); б) и = / (ху, - ); в) и = /(жгу) • g(xz)\
V у)
г) и = In/(ж, ж + |/); д) 16 = /(sinж + cos?/); e) гг = [/(ж)]5'^^.
43. Докажите, что функция
и= \ e~F~^, жгу/О,
I 0, ху = О,
имеет в точке 0@, 0) частные производные любого порядка, которые
не зависят от порядка дифференцирования, но при этом функция и
разрывна в точке О.
44. а) Докажите, что функция и = -——е ТагГ~ (а и жо — числа) удов-
ди 2®2и
~dt ~п ~дх~^'
_ ди 2
летворяет уравнению теплопроводности — = а
dt
б) Докажите: функция и = -, где г = л^(х - х0J + (у - у0J + (z - z0J,
/ гл тт л д2и д2и д2и
удовлетворяет при г Ф 0 уравнению Лапласа Аи = —- + —- + —- = 0.
дх2 ду2 dz2
45. В каждом из следующих случаев проверьте, что данная функция удов-
удовлетворяет заданному уравнению, если / и g — произвольные дважды
дифференцируемые функции:
\ ?( ±\ , / , ±\ д2и 2 д2и
а) и = f(x - at) + g(x + at), — = a —;
дхду
x^ + 2Xyf^+y^n(nl)u;
дх2 дхду ду2
ч р/ , ,, ди д2и ди д2и
д) и = f(x + g(y)), — • ——- = — • —j.
дх дхду ду дх2
46. Вычисляя частные производные первого и второго порядков и исклю-
исключая производные функции / и g (/ и g — произвольные дважды диффе-
дифференцируемые функции), составьте уравнение, которому удовлетворяет
функция и(х,у), если:
а)и = f(x) + g(y); б) и = f(x)g(y)\
в) и = f(x + y) + g(x-y)\ г) и = f(xy) + g(-J.
47. Найдите решение и = и(х,у) уравнения:
а) —- = у, удовлетворяющее условиям иуд, у) = у , —(О52/) = У]
дх2 дх
д2и
б) = —sinж, удовлетворяющее условиям и@,у) = 0, и(х,0) = х;
дхду
\ ^2>и -1 / п\ ел ®и ( с\\ , -1
в) = 1, удовлетворяющее условиям щх, 0) =0, —(ж, 0) = ж + 1,
и@,у) = у.
48. Для функций из упр. 35 найдите дифференциалы второго порядка в
указанных точках.
236 Гл. X. Функции нескольких переменных
49. Найдите дифференциалы второго порядка следующих функций в ука-
указанных точках, если / — дважды дифференцируемая функция, ж, у,
z — независимые переменные:
а) и = /(ж — у, х + у) в точках М(ж, у) и МоA,1);
б) и = /(ж + |/, z2) в точках М(ж, 2/, z) и МоA, —1, 0);
в) и = f(xy, х2 + |/2) в точках М(ж, 2/) и О@, 0);
г) и = sin /(ж) • е^у^ в точках М(ж, 2/) и О@, 0).
50. Найдите dnu, если: а) гб = /(аж + by + сг); б) гб = /(аж, by, cz); ж, ?/,
г — независимые переменные.
51. Разложите данную функцию по формуле Тейлора с центром разложе-
разложения в данной точке Мо:
а) ^=(ж-1J + (ж + 2/J, Мо@,0);
б) и = х - 2у + ж2 - Зху + %2, МоA, 2);
в) и = ж3 + у3 + ?3 - Зжг/г, МоA, 1, 1).
52. Разложите данную функцию по формуле Тейлора с центром разложе-
разложения в данной точке Мо до членов указанного порядка включительно:
а) и = д/1 — ж — у, Мо@,0), до членов второго порядка;
б) и = 1пA + ж + |/), Мо@, 0), до членов третьего порядка;
в) и = (ж + у) sin(a; — г/), Мо@, 0), до членов третьего порядка;
г) гб = ех cosy, Mo@,0), до членов четвертого порядка;
д) и = жу, МоA,1), до членов второго порядка;
е) и = жу^, МоA, 2,1), до членов второго порядка.
53. Исследуйте на равномерную непрерывность на всей плоскости следу-
следующие функции:
а) и = sin ж cos у; б) и = е~^ж +у ^; в) гб = д/ж2 +
0,
§ 6. Локальный экстремум функции
Основные понятия и теоремы
1. Определение и необходимые условия локального экст-
экстремума. Пусть функция и = /(М) = /(жь ...,жш) определена в неко-
некоторой окрестности точки Mo(xJ, ...,ж^).
Определение. Говорят, что функция и = f(M) имеет в точке
Мо локальный максимум (минимум), если существует такая окрест-
окрестность точки Мо, в которой при М т^ Мо выполняется неравенство
/(М) < /(Мо) (/(М) > /(Мо)).
Если функция имеет в точке Мо локальный максимум или ло-
локальный минимум, то говорят также, что она имеет в этой точке
локальный экстремум (или просто экстремум).
Теорема 21 (необходимое условие экстремума). Если функция
и = /(М) = f(xi,...,xm) имеет в точке М$(х\, ...,х®т) локальный
§ 6. Локальный экстремум
237
экстремум и в этой точке существует частная производная функции
по аргументу Xk, то ——(Mq) = 0.
UXfc
Следствие. Если функция и = f(M) = f(xi,...,xm) имеет в
точке Мо локальный экстремум и дифференцируема в этой точке,
то
(при любых значениях дифференциалов независимых переменных
dxu...,dxm).
Точки, в которых первый дифференциал функции равен нулю,
принято называть точками возможного экстремума этой функции.
Для отыскания точек возможного экстремума функции и = /(xi,...
...,жт) нужно решить систему уравнений fXl(xi, ...,жт) = 0, ...
...,/Жт(ж1, ...,жт) = 0 (это система т уравнений с т неизвестными
Х\ , ..., Хт) .
2. Некоторые сведения о квадратичных формах. Функция
вида
CLX2XXX2
(или, в краткой записи, Q =
аттх2т
, где ац — числа, причем
,3
dij = ctji, называется квадратичной формой от переменных xi, ...,жш.
Числа dij называются коэффициентами квадратичной формы, а
составленная из этих коэффициентов симметричная матрица
А =
аи а12
0*21 «22
— матрицей квадратичной формы.
Определители
Si = аи, S2 =
аи ai2
ац
0*11
называются угловыми минорами матрицы А.
Квадратичная форма Q(xi, ...,жт) называется положительно опре-
определенной (отрицательно определенной), если для любых значений пе-
переменных xi,...,xm, одновременно не равных нулю, она принимает
положительные (отрицательные) значения.
238 Гл. X. Функции нескольких переменных
Отметим, что Q@,0,..., 0) = 0.
Например, Q(x\,x2) = х\ + 2х\ — положительно определенная
квадратичная форма, так как Q{x\,x2) > 0 во всех точках (xi,x2),
кроме точки @,0).
Квадратичная форма называется знакоопределенной, если она
является либо положительно определенной, либо отрицательно опре-
определенной.
Квадратичная форма Q(xi, ...,хт) называется квазизнакоопреде-
ленной, если она принимает либо только неотрицательные, либо толь-
только неположительные значения, но при этом обращается в нуль не
только при х\ = ... = хш = 0.
Например, Q(x\,x2) = х\ + 2х\х2 + х\ — квазизнакоопределенная
квадратичная форма, поскольку Q{x\, х2) = (xi + х2J ^ 0 во всех точ-
точках (х\,х2), но Q(x\,х2) = 0 не только в точке @,0); так, Q(l, —1) = 0.
Квадратичная форма Q(xi, ...,жт) называется знакопеременной, ес-
если она принимает как положительные, так и отрицательные значения.
Например, Q(xi,x2) — х\— х\х2 — х\ — знакопеременная квадра-
квадратичная форма, поскольку она принимает как положительные, так и
отрицательные значения: Q(l,0) = 1 > 0, Q@,1) = —1 < 0.
Критерий Сильвестра знакоопределенности квад-
квадратичной формы.
1°. Для того чтобы квадратичная форма Q(x\, ...,хт) была поло-
положительно определенной, необходимо и достаточно, чтобы все угловые
миноры ее матрицы были положительны: 8\ > 0,S2 > 0, ...,Sm > 0.
2°. Для того чтобы квадратичная форма Q(xi, ...,жт) была отри-
отрицательно определенной, необходимо и достаточно, чтобы знаки глав-
главных миноров ее матрицы чередовались следующим образом: Si < 0,
S2 >0, 63 <0, S4 >0,...
3. Достаточные условия локального экстремума. Второй
дифференциал функции и = f(x\,..., хш), где х\,...,хш — незави-
независимые переменные, в точке Mq можно записать в виде
Это выражение показывает, что второй дифференциал функции и =
= f(xi,...,xm) в данной точке Mq является квадратичной формой
от переменных dx\,..., dxm, а частные производные второго порядка
-—-— — коэффициентами этой квадратичной формы.
uX<i vXj
Теорема 22 (достаточные условия экстремума). Пусть функция
и = f(M) = f(xi, ...,xm) дифференцируема в некоторой окрестности
точки М0(ж?, ...,ж^) и дважды дифференцируема в самой точке Мо,
причем Mq — точка возможного экстремума данной функции, т. е.
du\M =0. Тогда если второй дифференциал d2u\M является поло-
положительно определенной {отрицательно определенной) квадратичной
§ 6. Локальный экстремум 239
формой от переменных dx\,..., dxm, то функция и = f(M) имеет в
точке Mq локальный минимум (максимум). Если же сРи\м0 являет-
является знакопеременной квадратичной формой, то в точке Мо функция
и = /(М) не имеет локального экстремума.
Замечание. Если du\ = 0, a d2u
является квазизнакоопределен-
м0
ной квадратичной формой, то функция и = /(М) может иметь в точке Мо
локальный экстремум, а может и не иметь его. Например, для каждой из
функций и = х4 + у4 и и = х3у3 в точке О@, 0) выполнены условия du = О,
d2u = 0 (т. е. второй дифференциал является квазизнакоопределенной квад-
квадратичной формой). Но при этом первая функция имеет, очевидно, в точке
О локальный минимум, а вторая функция не имеет экстремума в точке О.
4. Случай функции двух переменных. Пусть функция и =
= f(x,y) дифференцируема в окрестности точки Мо(жо,2/о) и дважды
дифференцируема в самой точке Мо, причем Мо — точка возможно-
возможного экстремума данной функции, т. е. du\M = 0. Введем обозначения:
я2Л1 02и д2 и
——-(Мо), а22 = тг-2 (Мо).
дхду ду2
Тогда из теоремы 22 и критерия Сильвестра знакоопределенности
квадратичной формы следуют утверждения:
1) если D = апB22 — «12 > 0, то в точке Мо функция и = f(x,y)
имеет локальный экстремум (максимум при аи < 0 и минимум при
аи > 0);
2) если D < 0, то в точке Мо функция и = f(x,y) не имеет экст-
экстремума;
3) если D = 0, то в точке Мо функция и = f(x,y) может иметь
локальный экстремум, а может и не иметь его.
Контрольные вопросы и задания
1. Дайте определение локального экстремума функции.
2. Сформулируйте и докажите теорему о необходимом условии экстрему-
экстремума и следствие этой теоремы. Приведите пример функции и = /(ж, г/),
удовлетворяющей в некоторой точке Мо условиям —(Мо) = О,
дх
ди
— (Мо) = 0, но не имеющей в точке Мо локального экстремума.
ду
3. Какие точки называются точками возможного экстремума функции?
Приведите пример функции и = /(ж, г/), имеющей в некоторой точке
Мо локальный экстремум и такой, что —(Мо) = 0, а — в точке Мо не
дх ду
существует.
4. Какая функция называется квадратичной формой? Что такое матрица
квадратичной формы? Выпишите матрицу квадратичной формы
Q(xi, Ж2, жз) = 2жх — 4ж1^2 + 6ж1Жз — х\ — 2x2X2, + Зж2 и вычислите ее
главные миноры.
240
Гл. X. Функции нескольких переменных
5. Какая квадратичная форма называется: а) положительно определенной;
б) отрицательно определенной; в) знакоопределенной; г) квазизнако-
определенной; д) знакопеременной? Приведите примеры каждого типа
квадратичных форм.
6. Сформулируйте критерий Сильвестра знакоопределенности квадратич-
квадратичной формы. Пользуясь этим критерием, установите, является ли зна-
знакоопределенной квадратичная форма Q(xi, Х2, хз) = х\ — 1х\Х2 + 2ж| +
7. Напишите выражение для второго дифференциала функции и =
= /(xi,...,xm) в точке Мо, если xi,...,xm — независимые переменные.
Квадратичной формой от каких переменных является с/2гб|м0?
8. Сформулируйте теорему о достаточных условиях экстремума функции
и = /(ж1,..., Хга). Являются ли условия этой теоремы необходимыми
условиями экстремума?
9. Сформулируйте достаточные условия локального максимума, локаль-
локального минимума и отсутствия экстремума функции и = /(ж, г/) в точке
Мо(жо,г/о).
10. Приведите пример функции и = /(ж, г/), удовлетворяющей в некоторой
точке Мо условиям du = 0, D = 0,110,22 — а?2 = 0, причем эта функция
в точке Мо: а) имеет локальный экстремум; б) не имеет локального
экстремума.
Примеры решения задач
1. Найдите точки локального экстремума функции
и = 2х2 — ху + 2xz — у + у3 + z2.
А Для нахождения точек возможного экстремума данной функции
вычисляем ее частные производные и приравниваем их нулю:
их = 4х - у + 2z = 0, иу = -х - 1 + Зу2 = 0, uz = 2x + 2z = 0.
Решая эту систему трех уравнений, находим две точки возмож-
возможного экстремума: Mi(l/3, 2/3, -1/3) и М2(-1/4, -1/2,1/4).
Далее воспользуемся достаточными условиями экстремума. Для
этого вычислим частные производные второго порядка данной функ-
функции: ихх = 4, иху = иух = -1, uxz = г^ж = 2, г^у = 6^/, uyz = г^ = 0,
uzz = 2.
Значения этих частных производных в точке Mi являются коэф-
коэффициентами d2u
dz. Матрица этой квадратичной формы имеет вид
( 4 ^ 2\
А= -1 4 0.
V 2 0 2 У
Вычисляя главные миноры матрицы А, получаем
4-12
м квадратичной формы от переменных dx, dy,
5г = 4 > 0,
4 -1
-1 4
= 15 > 0, S3 =
-1
2
= 14 > 0.
§ 6. Локальный экстремум 241
Согласно критерию Сильвестра d2u\M является положительно опре-
определенной квадратичной формой от переменных dx, dy, dz. Следова-
Следовательно, в точке Mi функция имеет локальный минимум.
Исследуем теперь точку М2. Матрица квадратичной формы
d2u\M имеет вид
А= [ -1 3 0).
V 2 0 2/
Отсюда получаем S\ = 4 > 0, ?2 = —13 < 0, S% = —14 < 0. Следователь-
Следовательно, d2u M не является знакоопределенной квадратичной формой от
dx, dy, dz. Нетрудно видеть, что эта квадратичная форма знакопере-
знакопеременная. В самом деле, если положить dx ф0, dy — dz — 0, то получим
л2 i д2и,П/Г , , 2 А , 2 п , , п , ,п
dzu\M2 = ^~2 (М2) axz =4<ixz > 0, а если положить dx = dz = 0, dy^O,
д2и
то получим d2u\M2 = л~т(^2) ^2/2 = —3dy2 < 0. Следовательно, в точ-
ке М2 функция не имеет локального экстремума. А
2. Найти точки локального экстремума функции и = х2 — 2ху +
+ 4у3.
А Вычисляем частные производные функции и приравниваем их
нулю:
их =2х -2у = 0, иу = -2х + 12у2 = 0.
Решая эту систему уравнений, получаем две точки возможного
экстремума: Mi@,0) и М2A/б, 1/6).
Далее находим частные производные второго порядка: ихх = 2,
иху = -2, иуу = 242/. д2и д2и
В точке Mi: аи = —|(Mi) = 2, ai2 = ^—^-(Mi) = -2, а22 =
= ^-j(Mi) = 0. Следовательно, D = аца^ — ^?2 = —4 < 0, и, значит,
в точке Mi функция не имеет локального экстремума.
В точке М2: ац = 2, ai2 = —2, a22 = 4. Следовательно, D =
= 2 • 4 - (-2J = 4 > 0 и так как ац = 2 > 0, то в точке М2 функция
имеет локальный минимум. А
3. Найти точки локального экстремума функции и = Зх2у — х3 —
-у4-
А Вычисляем частные производные функции и приравниваем их
нулю:
их = —Зх2 + бху = 0, иу = Зх2 — 4у3 = 0.
Решая эту систему, находим две точки возможного экстремума:
Mi @,0) иМ2(б,3).
Вычисляем частные производные второго порядка данной функ-
функции: ихх = —6ж + 6у, иху = бж, иуу = -12у2.
В точке Mi: ац = 0, ai2 = 0, a22 = 0, и, значит, D = аца22 - а\2 =
= 0. Поэтому точка Mi @,0) требует дополнительного исследования.
242 Гл. X. Функции нескольких переменных
Значение функции и(х,у) в этой точке равно нулю: Ц0,0) = 0. Да-
Далее, при х < 0, у = 0 имеем и(х,у) = —ж3 > 0, а при х = 0, у ф 0
имеем и(х,у) = -у4 < 0. Следовательно, в любой окрестности точ-
точки Mi @,0) функция и(х,у) принимает значения, как большие 1/@,0),
так и меньшие и@, 0), и, значит, в точке Mi функция и(х, у) не имеет
локального экстремума.
В точке М.2'. аи = —18, а\2 — 36, a^i — —108, и, значит, D =
= 648 > 0. Так как ац < 0, то в точке М2 функция имеет локаль-
локальный максимум. А
Задачи и упражнения для самостоятельной работы
54. Найдите точки локального экстремума следующих функций двух пе-
переменных:
а) и = х2 — ху + у2] б) и = х2 — ху — у2;
в) и = х2 - 2ху + 2у2 + 2ж; г) и = х3 + у3 - х2 - 2ху - у2]
д) и = х3 - 2у3 -Зх + 6у); е) и = х3 - 2х2у2 + у4;
ж) и = ху + ; з) и = ех+2у(х2 - у2)]
z{x + у)
И)и = ех~у(х2 - 2ху + 2у2)- к) и = (х2 + 2у2)е-^+у'2)-
я) и = (х - 2у)е~^х +у }; м) и = ху\п(х2 + у2); н) и = - + - +у.
55. Найдите точки локального экстремума следующих функций трех
переменных:
а) и = х2 + 2у2 + z2 - 2х + 4у - 6z + 1]
б) и = 2х2 +у2 + z2 - 2ху + 4z - х]
в) и = х3 + ху + ?/2 - 2^ж + 2^2 + Зг/ - 1;
х2 у2
г) и = xyz(\ — х — у — z)\ д) и = 2 — + — — 4ж + 2z2;
2/ г
е) =(ж + ?/ + 2;ф-(ж2+*/2+г2).
56. Докажите, что функция и = (ж — у2)Bх — у2):
а) имеет в точке О@, 0) локальный минимум вдоль каждой прямой,
проходящей через эту точку;
б) не имеет локального минимума в точке О@,0).
ГЛАВА XI
НЕЯВНЫЕ ФУНКЦИИ И ИХ ПРИЛОЖЕНИЯ
§ 1. Неявные функции
Основные понятия и теоремы
1. Понятие неявной функции. Рассмотрим уравнение
F(x,y) = 0. A)
Пусть для любого х из некоторого множества X это уравнение имеет
решение относительно у. Тем самым каждому х е X ставится в со-
соответствие определенное число — решение уравнения A) (заметим,
что уравнение A) может иметь несколько решений относительно у,
но мы выбираем какое-то одно из них). Это означает, что на множес-
множестве X определена функция у = f(x). При этом правило /, ставящее
в соответствие каждому х некоторое число, не указано здесь явно,
а задано с помощью уравнения A) ("спрятано" в этом уравнении).
Такой способ задания функции у = f(x) называется неявным, а са-
сама функция у = f(x) — неявной функцией. Итак, неявная функция
у = f(x) — это решение уравнения A) относительно у, т. е. Vx Е X:
F(x,f(x))=0.
Например, уравнение х2 + у2 — 1 = 0, рассматриваемое в области
2/^0, определяет неявную функцию у = л/1 — х2. Таким образом,
здесь неявная функция найдена в явном виде. Во многих случаях
этого сделать не удается.
Аналогично уравнению A) можно рассмотреть уравнение с боль-
большим числом переменных:
F(xux2,...,xm,y) = 0, B)
и ввести понятие неявной функции у = /(xi,x2, ...,жт), определяемой
уравнением B).
2. Существование, непрерывность и дифференцируемость
неявной функции.
Теорема 1. Пусть: 1°) функция F(x, у) непрерывна в прямоуголь-
прямоугольнике Q = {(ж, у): а < х < Ь, с ^ у ^ d};
2°) \/х е (a,b) : F(x,c)F(x,d) < 0 (т. е. на нижней и верхней
сторонах прямоугольника Q функция F(x,y) имеет значения разных
знаков);
3°) \/х G (а, Ь) функция F(x,y) является строго монотонной функ-
функцией аргумента у на сегменте [с, d].
244 Гл. XI. Неявные функции и их приложения
Тогда на (а, Ъ) существует единственная неявная функция, опре-
определяемая уравнением A), и эта функция непрерывна на (а,Ь).
Следующая теорема в отличие от теоремы 1 носит локальный
характер: утверждается существование, единственность и дифферен-
цируемость неявной функции в некоторой окрестности точки.
Теорема 2. Пусть: 1°) функция F(x,y) дифференцируема в неко-
некоторой окрестности и; точки Мо(хо,уо);
2°) частная производная Fy непрерывна в точке Мо;
3°) F(xo,yo) = 0, Fy(xo,yo) фО.
Тогда существует такой прямоугольник {(х,у): \х — xq\ < d,\y —
— ?/о| ^ с, d > О, с > 0} С и, в котором уравнение A) определяет един-
единственную неявную функцию вида у = /(ж), причем /(жо) = Уо, функция
f(x) дифференцируема на интервале (ж0 - d,x0 + d), и ее производная
вычисляется по формуле
1*4
Fy(x,y)
Fx(x,f(x))
j=f(x) Fy(x,f(x))-
Замечание 1. Обратите внимание на порядок действий при вычисле-
вычислении Fx(x, f(x)) — числителя в формуле C): сначала берется частная про-
производная по х функции F(x,y), а затем вместо у подставляется /(ж) (но не
наоборот).
Замечание 2. Если функция F(x,y) дифференцируема п раз в и,
то неявная функция у = /(ж) дифференцируема п раз на интервале (ж<э —
— d,xo + d). Ее вторая производная может быть вычислена с помощью диф-
дифференцирования по х правой части равенства C):
Производные более высокого порядка вычисляются аналогично.
Замечание 3. Если условие Fy(xo,yo) / 0 не выполняется, т. е.
Fy(xo,yo) = 0, то уравнение A) может иметь не единственное решение от-
относительно у в окрестности точки Мо и может не иметь ни одного реше-
решения. Например, для уравнения F(x, у) = х2 + у2 — 1 = 0 выполнены условия
F(l,0) = 0, Fy(l,0) = 0. Очевидно, что в окрестности точки МоA,0) при
х > 1 уравнение не имеет решений (вещественных) относительно у, а при
х < 1 имеет два непрерывных решения: у = у/1 — х2 и у = —л/1 — ж2. Урав-
Уравнение F(x,y) = х2 + у2 = 0, для которого F@, 0) = Fy@,0) = 0, не имеет
решений относительно у при любом х / 0.
Вместе с тем условие Fy(xo,yo) / 0 является лишь достаточным (в со-
совокупности с остальными условиями теоремы 2), но не необходимым для
существования в некоторой окрестности точки Мо единственной неявной
функции вида у = /(ж), определяемой уравнением A). Например, для урав-
уравнения F(x,y) = ж3 — у3 = 0 это условие не выполнено в точке Мо@,0):
F@,0) = Fy @,0) = 0, но тем не менее данное уравнение определяет в
окрестности точки Мо@, 0) единственную неявную функцию вида у = /(ж):
у = х.
Теорема 3. Пусть: 1°) функция F(xi,X2, ...,жш,у) = F(M) диф-
дифференцируема в некоторой окрестности и; точки М0(ж?,Ж2, ...,ж^,2/°);
§1. Неявные функции
245
2°) частная производная Fy непрерывна в точке Мо;
3°)F(M0) = 0, Fy(Mo)?0.
Тогда существует такой параллелепипед
\у - у°\ ^ с, di > 0, с > 0} С и,
в котором уравнение B) определяет единственную неявную функцию
вида у = /(жьж2,...,жт), причем f{x\,x%, ...,ж™) = у0, функция у =
= /(^1,ж2,...,жт) дифференцируема при \xi -ж°| < di (г = 1,2, ...,ш),
и ее частные производные вычисляются по формуле
Xi, Х2, ...,
= 1,2,...,ш). E)
3. Неявные функции, определяемые системой уравнений.
Рассмотрим систему п уравнений
' F1(x1,x2, ...,хт,у1,у2, ...,Уп) = 0,
B,...,ят,2/1,2/2,...,2/п) = 0,
F)
= 0.
Решение этой системы относительно 2/ъ2/2? •••?2/п
называется совокупностью неявных функций, определяемых системой
уравнений F).
Определитель
dFx dFx dFx
dF2 dF2
дух ду2
dF2
дуп
дух ду2 '" дуп
составленный из частных производных, называется определителем
Якоби (или якобианом) функций Fi,F2, ...,Fn по переменным 2/i,2/2? ---
...,2/п и обозначается символом
Теорема 4. Пусть: 1°) функции Fb F2, ..., Fn, входящие в
систему F), дифференцируемы в некоторой окрестности и; точки
246 Гл. XI. Неявные функции и их приложения
dF
2°) частные производные ^—^ (i,j = l,2,...,n) непрерывны в точ-
точке Мо;
= 0, F2(M0)=0, ..., Fn(Mo) = 0,
yz,...,ynj Mq
существует такой параллелепипед
{(жъЖ2,...,ят,2/ъ2/2,...,2/п): \Xi ~ х®\ < di (i = 1,2,...,т),
\Уз -У®\ < Cj, (j = l,2,...,n), di > 0, Cj > 0} С и,
в котором система уравнений F) определяет единственную совокуп-
совокупность неявных функций вида G), и эти функции дифференцируемы
при \xi — х®\ < di (г = 1, 2, ...,т).
Формулы для вычисления частных производных неявных функ-
функции G) можно получить следующим образом. Предположим, что в
систему F) подставлены функции G). Тогда получатся тождества,
дифференцирование которых по переменной х\ дает систему п ли-
dfi df2 dfn
неиных уравнении относительно ——, ——, ..., -?—\
dFx df2 , , dFx dfn n
d^/2 ^ж^ a^/n dxi
"dFn ' "dh"''' "'dFn ' "dfn'L'n
уп
)( р Тр Тр \
Определителем этой системы является якобиан —^—^—^~~i—^т- В си-
D(yyy)
лу условий 2° и 3° теоремы 4 он отличен от нуля в некоторой окрест-
окрестности точки Mq. Поэтому из этой системы однозначно получаются
(например, по формулам Крамера) выражения для частных произ-
производных неявных функций G).
Контрольные вопросы и задания
1. Какая функция называется неявной? Приведите пример уравнения вида
F(x,y) = 0, определяющего неявную функцию, и пример уравнения, не
определяющего неявную функцию.
2. Сколько непрерывных неявных функций вида у = f(x) определяет урав-
уравнение х2 — у2 = 0 в окрестности точки О@, 0)?
3. Сформулируйте теорему о существовании, единственности и непрерыв-
непрерывности неявной функции, определяемой уравнением F(x,y) = 0 (теоре-
(теорему 1). Докажите существование и единственность этой функции.
4. Докажите, что уравнение х2 + у2 — 5 = 0 не определяет неявную
функцию в прямоугольнике {(ж, у) : — 1 < х < 1, 0 ^ у ^ 2}. Какое
условие теоремы 1 не выполнено в данном случае?
5. Сформулируйте локальную теорему о существовании, единственнос-
единственности и дифференцируемости неявной функции, определяемой уравнением
F(x, у) = 0 (теорему 2). Докажите, что при условиях теоремы 2 сущест-
существует такой прямоугольник, в котором выполнены условия теоремы 1.
§1. Неявные функции 247
6. Выведите формулу C) для производной неявной функции, дифферен-
дифференцируя по х тождество F(x,f(x)) = 0. Является ли такой вывод доказа-
доказательством дифференцируемости неявной функции?
7. Приведите примеры, когда невыполнение условия Fy(xo, г/о) ф 0:
а) приводит к неразрешимости уравнения F(x,y) = 0 относительно у в
окрестности точки (жо,2/о) или к неединственности решения;
б) не нарушает существования и единственности неявной функции вида
у = /(ж), определяемой уравнением F(x,y) = 0 в окрестности точки
(хо,уо).
8. Докажите, что уравнение х + у = 0 не определяет неявной функции в
достаточно малой окрестности точки A,1). Какое условие теоремы 2
не выполнено в данном случае?
9. Уравнение |ж| + у = 0 определяет в окрестности точки О@, 0) недиффе-
ренцируемую в точке х = 0 функцию у = —\х\. Какое условие теоремы 2
не выполнено в данном случае?
10. Уравнение (у — х) (у — 2х)(у + Зх) = 0 определяет в любой окрестности
точки О@, 0) три дифференцируемые функции: у = ж, у = 2ж, у = — Зх.
Какое условие теоремы 2 не выполнено в данном случае?
11. Вычислите производные /'@) и /"@) неявной функции у = /(ж), опреде-
определяемой уравнением х2 + у2 — 1 = 0 и удовлетворяющей условию /@) =
= 1, двумя способами: а) используя формулы C) и D); б) используя
явное выражение для функции /(ж).
12. Сформулируйте теорему о существовании, единственности и диффе-
дифференцируемости неявной функции, определяемой уравнением F(xi, Ж2,...
...,хт,у) = 0 (теорему 3).
13. Сформулируйте теорему о существовании, единственности и диффе-
дифференцируемости совокупности неявных функций, определяемых систе-
системой уравнений (теорему 4).
Примеры решения задач
1. Доказать, что уравнение
y + Q,5siny-x = 0 (8)
определяет единственную неявную функцию вида у = /(ж), х G
е (-оо, +оо), и найти f'(x), f"(x), f'(n), f"(n).
Л Введем обозначение F(x,y) = у + Ofis'my — х. Так как Fy =
= 1 + 0,5 cos у > 0, то при любом фиксированном значении х функ-
функция F(x,y) является возрастающей функцией аргумента у. Кроме
того, для любого фиксированного значения х при достаточно боль-
больших значениях \у\, очевидно, выполняются неравенства F(x,y) < О
при у < 0, F(x,y) > 0 при у > 0. Поскольку F(x,y) — непрерывная
функция, отсюда следует, что Уж существует единственное у такое,
что F(x,y) = 0, т. е. \/х уравнение (8) имеет единственное решение
относительно у. Это и означает, что уравнение (8) определяет един-
единственную неявную функцию вида у = /(ж), х е (-оо, +оо).
Так как F(x,y) — дифференцируемая функция и Fy(x,y) ф 0, то
и функция у = f(x) дифференцируема на всей числовой прямой. Для
248 Гл. XI. Неявные функции и их приложения
нахождения f'(x) воспользуемся формулой C):
у=Нх) 1 + 0'5 cos W
Fy(x,y)
Дифференцируя f'(x), найдем
fit, \ _ 0,5 sin/(ж) -/'(ж) _ sin/(ж)
1 У } [1 + 0,5 cos/(ж)]2 2[l + 0,5cos/(x)]3'
Чтобы найти значения f'(x) и /"(ж) в какой-либо точке ж, нужно
сначала вычислить соответствующее значение /(ж). Пусть ж = тг. Не-
Нетрудно проверить, что решением уравнения (8) при ж = тг является
у = тг, т. е. /(тг) = тг. Подставляя ж = тг, /(ж) = тг в формулы для /'(ж)
и /"(ж), получаем /'(тг) = 2, /"(тг) = 0. А
2. Найти производные /'@) и /"@) неявной функции у = /(ж),
заданной уравнением
ж2 - ху + 2?/2 + ж - у = 1 (9)
и удовлетворяющей условию /@) = 1.
Л Функция F(x,y) = ж2 — ху + 2?/2 + ж — 2/ — 1 дифференцируема в
любой окрестности точки @,1). Производная Fy = —х + 4у — 1 не-
непрерывна в точке @,1). Наконец, F@,1) = 0, Fy@,1) = 3 / 0, т. е.
выполнены все условия теоремы 2. Поэтому в некоторой окрестности
точки @,1) уравнение (9) определяет единственную дифференциру-
дифференцируемую неявную функцию вида у = /(ж), причем /@) = 1. Более того,
так как функция F(x,y) дважды дифференцируема в любой окрест-
окрестности точки @,1), то и функция у = /(ж) дважды дифференцируема
в некоторой окрестности точки ж = 0.
Производные /'(ж) и /"(ж) можно найти по формулам C) и D),
а затем, полагая ж = 0, /@) = 1, вычислить /'@) и /"@). Однако
удобнее поступить следующим образом. Предполагая, что функция
у = /(х) подставлена в уравнение (9), продифференцируем полученное
тождество по ж:
2ж - у - ху' + 42/2/' + 1 - у' = 0. A0)
Полагая в равенстве A0) ж = 0, у = 1, получаем —1 + 4^/@) + 1 —
— у'@) = 0, откуда у'@) = 0. Чтобы найти вторую производную, про-
продифференцируем тождество A0) по ж:
2-2у'- ху" + 4(у'J + 42/2/" - у" = 0. A1)
Полагая ж = 0, 2/ = 1, у' = 0, получаем 2 + 32/"@) = 0, откуда у"@) =
= -2/3. Итак, /'@) = 0, /"@) = -2/3. А
3. Найти производные первого и второго порядков неявной функ-
функции у = /(ж), заданной уравнением
у — 2жarctg — = 0. A2)
х
§1. Неявные функции
249
Л Левая часть уравнения A2) не определена при х = 0. Будем счи-
считать, что х/0. Предположим, что уравнение A2) определяет дваж-
дважды дифференцируемую неявную функцию у = /(ж). Подставляя ее в
уравнение A2) и дифференцируя полученное тождество по ж, прихо-
приходим к равенству
-^?(a;2/'-2/)=O. A3)
Уравнение A3) можно упростить, если воспользоваться исходным
уравнением A2). А именно, из уравнения A2) следует, 2arctg- =
= —. Поэтому уравнение A3) можно записать так:
2х
:{ху' -у) =0.
Из уравнения A4) находим
A4)
A5)
где у = /(ж). Для вычисления второй производной можно, как и в
примере 2, продифференцировать тождество A4) по ж и, получив ли-
линейное относительно у" уравнение, найти вторую производную. Од-
Однако в данном случае удобнее воспользоваться равенством A5), из
которого следует
„ = ху' -у
у х2 '
Подставляя в последнее равенство выражение A5) для у', окончатель-
окончательно находим у" = 0.
Задача решена в предположении, что уравнение A2) определяет
дважды дифференцируемую
функцию у = /(ж). Исследо-
Исследовать вопрос о существовании
такой функции можно, как это
было сделано в примере 2, с
помощью теоремы 2. Однако
здесь мы воспользуемся дру-
другим способом. Равенство нулю
второй производной функции
во всей области определения
означает, что уравнение A2)
может задавать только линей-
линейные функции. Если ввести пе-
переменную t = у/х, то уравнение A2) запишется в виде t = 2arctgt.
Это уравнение имеет три решения: t = -?0, t = 0, t = t0 (рис. 28). Сле-
Следовательно, уравнение A2) определяет линейные функции у = —tox,
у = 0 и у = tox при ж ф 0. А
Рис. 28
250 Гл. XI. Неявные функции и их приложения
4. Доказать, что уравнение
z3 - xyz + у2 = 16 A6)
определяет в некоторой окрестности точки A,4,2) единственную
неявную функцию вида z = f(x,y). Найти ее частные производные
dz ( ч d2z ( ч dz (Л .ч d2z (л л,
_(*,„),_(*,„), _A,4) и— A,4).
Л Функция F(x, у, z) = z3 — xyz + у2 — 16 дифференцируема в любой
окрестности точки MqA, 4, 2). Производная Fz = 3z2 — ху непрерывна
в точке Mq. Наконец, F(l,4, 2) = 0, i^(l,4, 2) = 8 7^ 0, т. е. выполнены
все условия теоремы 3. Поэтому в некоторой окрестности точки Mq
уравнение A6) определяет единственную дифференцируемую неяв-
неявную функцию вида z = f(x,y), причем /A,4) = 2. Более того, так
как функция F(x,y,z) дважды дифференцируема в любой окрестнос-
окрестности точки Мо, то и функция z = f{x,y) дважды дифференцируема в
некоторой окрестности точки A,4).
Для нахождения —(х,у) воспользуемся формулой E):
ох
dz _ Fx{x,y,z)
дх Fz(x,y,z) z=f(x<y)
A7)
Дифференцируя —— по ж, найдем
ох
2xy3f(x,y) . .
Р(ху)ху]з' У '
Теперь, подставляя в выражения A7) и A8) вместо х, у, f(x,y) coot-
ветственно значения 1, 4, 2, найдем значения -— и —— в точке A,4).
ох ох
Рассмотрим другой (эквивалентный) способ решения задачи.
Предполагая, что функция z = f(x,y) подставлена в уравнение A6),
продифференцируем полученное тождество по х:
3z2zx -yz- xyzx = 0. A9)
Решая уравнение A9) относительно zx, приходим к соотношению A7).
Если же в равенстве A9) положить х = 1, у = 4, z = 2, то получим
**A,4) = 1.
Чтобы найти zxx, продифференцируем тождество A9) по х:
6z(zxJ + 3z2zxx - 2yzx - xyzxx = 0. B0)
Отсюда следует равенство A8). Если же в равенстве B0) положить
х = 1, у = 4, z = 2, zx = 1, то получим 2:жжA,4) = —0,5. А
5. Доказать, что уравнение
Ж2 + у2 + Z2 = а2
§1. Неявные функции 251
определяет единственную неявную функцию вида z = f(x,y) в неко-
некоторой окрестности точки Мо(хо,уо, zq), где
-х2- yl ф О, B2)
и найти: а) частные производные zx и zxy; б) дифференциалы cb и
d?z этой функции.
Л Функция F(x, у, z) = х2 + у2 + z2 — а2 дифференцируема в любой
окрестности точки Mq. Производная Fz = 2z непрерывна в точке Mq,
причем Fz(xo,yo,zo) = 2z0 ф 0 в силу соотношения B2). Из того же
соотношения следует, что F(xo,2/ch ^о) = О-
Итак, выполнены все условия теоремы 3. Поэтому в некоторой
окрестности точки Mq уравнение B1) определяет единственную диф-
дифференцируемую функцию вида z = f(x,y). Более того, так как функ-
функция F(x,y,z) дважды дифференцируема в любой окрестности точки
Мо, то и функция z = f(x,y) дважды дифференцируема в некоторой
окрестности точки (жо,2/о)-
а) Предполагая, что функция z = f(x,y) подставлена в уравнение
B1), продифференцируем полученное тождество по х:
2х + 2zzx = 0. B3)
Отсюда имеем zx = —x/z, где z = f(x,y). Дифференцируя B3) по у,
получаем
2zyzx + 2zzxy = 0. B4)
Из равенства B4) можно найти смешанную производную, если из-
известна производная zy. Чтобы найти zy, продифференцируем тож-
тождество B1) по у: 2y-\-2zzy = 0. Отсюда zy = —y/z, где z = f(x,y).
Теперь из B4) находим zxy = —xy/z3, где z = f(x,y).
б) Предполагая, что функция z = f(x,y) подставлена в уравнение
B1), вычислим дифференциалы от обеих частей полученного тож-
тождества:
2х dx + 2ydy + 2z dz = 0. B5)
Отсюда имеем
dz = --dx-V-dy, B6)
где z = f(x,y). Чтобы найти второй дифференциал функции z =
= /(ж, у), вычислим дифференциалы от обеих частей тождества B5):
2{dxJ + 2{dyJ + 2{dzJ + 2zd2z = 0. B7)
Из равенства B7) получаем
W B8)
где z = f(x,y).
252 Гл. XI. Неявные функции и их приложения
Заметим, что из равенств B6) и B8) находятся все частные про-
производные первого и второго порядков функции z = f(x,y):
2 2 2 2
х у х + z ху у + z
у — у — ?_ у — у — ?_ у — 2.
^х — 1 ^у — 1 ^хх — 3 ' ^ху — з ' УУ — 3 '
где z = f(x,y). A
6. Найти производные первого и второго порядков неявных функ-
функций x(z), y(z) в точке z = 2, если эти функции заданы системой урав-
уравнений
x+y+z=2
и удовлетворяют условиям хB) = 1, уB) = —1.
Л Функции F\ (ж, у, z) = х2 + у2 — 0,5z2 и F^ (х, у, z) = х + у + z — 2
дифференцируемы в любой окрестности точки MqA,—1,2). Частные
OF! о dFx о 3F2 Л dF2 л
производные ^г— = 2х. -^— = 2у, —— = 1, ^г— = 1 непрерывны в точке
дх ду дх ду
Мо. Далее, имеют место равенства Fi(l, -1,2) = 0 и F2(l, —1,2) = 0.
Наконец, якобиан —Ц^—р- равен
D(x,y)
2 -2
1 1
= 4 и,значит, отличен от
нуля в точке Mq. Таким образом, выполнены все условия теоремы 4.
Следовательно, в некоторой окрестности точки Мо система уравне-
уравнений B1) определяет единственную пару дифференцируемых функций
x(z) и y(z). Более того, так как функции Fi(x,y,z) и F^ix^y^z) дваж-
дважды дифференцируемы в любой окрестности точки Мо, то и функции
x(z), y(z) дважды дифференцируемы в некоторой окрестности точки
2 = 2.
Предполагая, что в систему уравнений B9) подставлены функции
x(z) и y(z), продифференцируем полученное тождество по z:
Г 2хх' + 2уу' = z,
Полагая в равенствах C0) х = 1, у = —1, z = 2, получим систему
уравнений относительно х'B), у'B):
(х'B)-у'B) = 1,
\х'B)+у'B) = -1.
Отсюда находим х'B) = 0, у'B) = —1.
Теперь продифференцируем по z тождества C0):
2(х'J + 2хх" + 2(у'J + 2уу" = 1,
х" + у" = 0.
Полагая х = 1, у = —1, z = 2, х' = 0, у' = —1, получим систему урав-
уравнений относительно х"B), у"B):
(х"B)-у"B) = -0,5,
\х"B)+у"B) = 0.
§1. Неявные функции
253
Отсюда имеем х"{2) = -0,25, у"{2) = 0,25. А
7. Доказать, что неявная функция z = f(x,y), определяемая урав-
уравнением
s2+S/2 + *2 = Jtf(f), C1)
где д(и) — произвольная дифференцируемая функция, удовлетворяет
уравнению
(ж2 - у2 - z2)zx + 2xyzy = 2xz. C2)
Л Пусть жо, уо, %о — решение уравнения C1). Рассмотрим функ-
функцию F(x,y,z) = х2 + у2 + z2 — уд(-) в некоторой окрестности точки
Мо(хо,уо, zo). Пусть Fz(Mq) ф 0. Тогда в некоторой окрестности точ-
точки Мо выполнены условия теоремы 3, и, следовательно, уравнение
C1) определяет дифференцируемую неявную функцию z — f(x,y).
Подставляя эту функцию в уравнение C1), получим тождество
C3)
Вычислим дифференциалы от обеих частей тождества C3):
2xdx + 2ydy + 2zdz = <?(|) dy + 0'(|) (| dy - |J dz), C4)
где z = f(x,y). Решая равенство C4) относительно dz, получим
dz =
Следовательно,
-2x
¦¦ + ^!. . .
z=f(x,y)
Подставляя полученные выражения для частных производных в урав-
уравнение C2), приходим к тождеству C3). Таким образом, неявная функ-
функция z = /(ж,у), определяемая уравнением C1), удовлетворяет урав-
уравнению C2). А
8. Найти локальные экстремумы неявных функций вида
z = /(ж,у), заданных уравнением
F(x, у, z) = х2 + у2 + z2 - 2х + 2у - 4z - 10 = 0. C5)
Л Предполагая, что дифференцируемая неявная функция z = f(x,y)
подставлена в уравнение C5), вычислим дифференциалы от обеих
частей полученного тождества:
2ж dx + 2y dy + 2z dz - 2 dx + 2 dy - 4 dz = 0. C6)
254 Гл. XI. Неявные функции и их приложения
Отсюда (при z ф 2) находим
, х — 1 , , 2/ + 1 j
= ^—; dx + 7^—; Ф-
Используя необходимое условие экстремума dz = 0, приходим к сис-
системе уравнений для координат точек возможного экстремума:
х-1
= 0,
Y^~z ~u' {1-1 = 0,
или <
откуда х = 1, у = — 1. Подставив значения а: = 1, у = -1 в уравне-
уравнение C5), найдем соответствующие значения z\ имеем z2 — 4z — 12 =
= 0, откуда ^1 = —2 и ^2 = 6. Таким образом, получили две точки:
М1A,-1,-2)иМ2A,-1,б).
Заметим, что FZ(M\) = —8 ф 0, FZ(M2) = 8 ф 0, и, следовательно,
в окрестностях точек М\ и М2 выполнены все условия теоремы 3 для
уравнения C5). Так как функция F(x,y,z) дважды дифференцируе-
дифференцируема, то в некоторой окрестности точки М{ (i = 1,2) существует един-
единственная дважды дифференцируемая неявная функция z = fi(x,y).
При этом ДA, —1) = —2, /2A, —1) = 6. Точка A, —1) является точкой
возможного экстремума для каждой из функций fi(x,y) и f2(x,y).
Чтобы применить достаточное условие экстремума, надо найти
вторые дифференциалы этих функций. Для этого вычислим диффе-
дифференциалы от обеих частей тождества C6):
(dxJ + (dyJ +zd2z + (dzJ -2d2z = 0.
Отсюда имеем
f f 2
d2z_ (dxf + (dyf + (dzJ _
2 — z
Учитывая, что d^|(i?_i) = 0, получаем o?2/i|(i,—1) = 0,25[(dxJ + (dyJ],
бР/2|A,_1) = -0,5[(dxJ + (dyJ]. Таким образом, o?2/i|(i,—1) являет-
является положительно определенной квадратичной формой, a <i2/2|(i5_i) —
отрицательно определенной квадратичной формой. Следовательно,
функция z = fi(x,y) имеет в точке A, —1) локальный минимум, рав-
равный —2, а функция z = /2(х,у) имеет в точке A, —1) локальный мак-
максимум, равный 6. А
Замечание. Уравнение C5) приводится к виду
(я-1J + (у + 1J + (* + 1J = 16.
Это — уравнение сферы радиуса 4 с центром в точке A,-1,2). Точка
Mi(l, —I, —2) — самая нижняя, а точка МгA, —1, 6) — самая верхняя точка
этой сферы. Очевидно, неявная функция z = fi(x,y) является уравнением
нижней полусферы (в точке A, —1) эта функция имеет минимум, равный
—2), а неявная функция z = /2(^,1/) — уравнением верхней полусферы (в
точке A, —1) эта функция имеет максимум, равный 6).
§1. Неявные функции 255
Задачи и упражнения для самостоятельной работы
1. Пользуясь теоремой 1, докажите, что уравнение ж3 + у3 + ж + у = 12
определяет единственную неявную функцию вида у = /(ж) в прямо-
прямоугольнике {(ж, г/): —1 < ж < 1,5, 1 ^ ?/ ^ 3}. Найдите /A).
2. Пользуясь теоремой 2, докажите, что уравнение ж3 + у3 — -ж + 4г/ =
о
= —4,2 определяет единственную дифференцируемую неявную функ-
функцию вида у = /(ж) в некоторой окрестности точки A, —1). Вычислите
/'A) и /"(!)•
3. Пусть функция F(x,y) дважды дифференцируема в некоторой окрест-
окрестности точки Мо(жо,2/о) и пусть F(Mo) = 0, Fy(Mo) ф 0. Докажите, что
в некоторой окрестности точки Мо уравнение F(x,y) = 0 определя-
определяет единственную дважды дифференцируемую неявную функцию вида
у = /(ж), причем справедлива формула
пи / ч _ FxxFy — 2FxyFxFy + FyyF2
J Ух)~~ Бз '
rv
4. Найдите первую и вторую производные неявной функции вида у =
= /(ж), заданной уравнением:
a) In л/х2 + у2 = arctg -; б) у — scosy = ж @ < е < 1);
в) ху = ух {уф х); г) sinxy = 1 — 0,2ху.
5. Найдите первую, вторую и третью производные неявной функции вида
у = /(ж), заданной уравнением х2 + ху + у2 = 3.
6. Найдите /'@), /"@M /'"@) Для неявной функции ?/ = /(ж), удовлетво-
удовлетворяющей условию /@) = 1 и заданной уравнением:
а) ж2 + Ж?/ + у2 = 1; б) |/ sin ж + ж2 + у3 = 1.
7. Пользуясь теоремой 3, докажите, что уравнение z3 — 3xyz = 8 опре-
определяет единственную дифференцируемую неявную функцию вида z =
= /(ж, у) в некоторой окрестности точки @, —1, 2). Вычислите 2ж@, —1)
и *„((),-1).
8. Найдите частные производные первого и второго порядков неявной
функции вида z = /(ж, г/), заданной уравнением:
а) г = у/ж2 - у2 tg ^ 2; б) ?3 - Зж?/? = а3; в) ж + г/ + z = ez.
9. Найдите дифференциалы первого и второго порядков неявной функции
вида z = /(ж, г/), заданной уравнением:
а) ж + 2/ + г = e~x-y-z] б) - = In - + 1;
z у
10. Найдите все частные производные второго порядка функции z = /(ж, у)
в точке A, —2), если эта функция удовлетворяет условию /A, —2) = 1
и задана уравнением:
а) ж2 + 2у2 +3z2 +ху - z = 9; б) Зж^ + жV = 5(ж + у).
11. Докажите, что неявная функция z = /(ж, г/), определяемая уравнением
^(ж — а^, |/ — bz) = 0, где F(u,v) — произвольная дифференцируемая
функция (a, b — постоянные), является решением уравнения а • zx +
256 Гл. XI. Неявные функции и их приложения
12. Докажите, что неявная функция z = /(ж, 2/), заданная уравнением
F[x-\—, 2/Н—) =0, где F(u,v) — произвольная дифференцируемая
\ у х/
функция, удовлетворяет уравнению xzx + yzy = 2 — ж?/.
13. Система уравнений
Г ж cos г*, + ?/sin гб + In 2 = д(и),
1 — ж sin и + 2/ cos и = gf (и),
где д(гб) — произвольная дифференцируемая функция, определяет не-
неявные функции 2 = /1(ж,2/), ^ = /г(ж, 2/)- Докажите, что функция 2 =
= fi(x,y) удовлетворяет уравнению (^жJ + (%уJ = ?2-
14. Найдите производные первого и второго порядков неявных функций
жB) и 2/B), заданных системой уравнений:
а) Г ж + 2/ + 2 = 0, б) Г ж2 + |/2 - 2^ = 1,
< 2 , 2 , 2 -I
I пг —L- 7/ Ч— У —
15. Найдите производные г/@), ^'@), у"@), z"@) неявных функций г/(ж)
и г (ж), удовлетворяющих условиям |/@) = —1, 2@) = 1 и заданных
системой уравнений:
а) Г ж + 2/ + 2 = 0, б) Г ж2 - ?/2 - z2 + 2 = 0,
\ ж2 + ?/2 + z2 = 2; | ж2 + ж?/ + |/2 + 2 = 2.
16. Найдите дифференциалы cb и с/2^ в точке C, —2) неявной функции
z = /(ж, 2/), заданной уравнением z3 — xz + у = 0 и удовлетворяющей
условию /C, -2) = 2.
17. Найдите дифференциалы первого и второго порядков неявных функций
и(х,у) и г;(ж, г/), заданных системой уравнений
18. Найдите сйг, с/г>, с/2гб, d2v в точке A, 1), если неявные функции и(х,у)
и г;(ж, г/) заданы системой уравнений
и удовлетворяют условиям ггA,1) = 0, г>A,1) = тт/4.
19. Исследуйте на экстремум неявную функцию у = /(ж), заданную урав-
уравнением |/ — еsin2/ = ж2 @ < е < 1).
20. Исследуйте на экстремум неявные функции вида z = /(ж, 2/), заданные
уравнением:
a) zs - xyz + у2 = 16; б) zs - xyz + у2 + 4ж2 = 16;
в) ж2 + |/2 + z2 - xz - yz + 2ж + 2у + 2z = 2;
г) (ж2 + у2 - z2J = а2(х2 + у2 + ?2) (а > 0).
§2. Зависимость функций
257
§ 2. Зависимость функций
Основные понятия и теоремы
1. Понятие зависимости и независимости функций. Пусть
п функций
Г 2/1 = fl{x1,X2,...,Xm),
Уп =
определены и дифференцируемы в некоторой области D С Еш.
Определение. Функция yk = fk(xi,X2,...,xm) = Л(М) называ-
называется зависимой в области D от остальных функций из совокупности
A), если ее можно представить в виде
Ук = Ф(у1, ...,ук-1,Ук+1, -,Уп), B)
где Ф — дифференцируемая функция своих аргументов.
Равенство B) нужно понимать следующим образом: если в правую
часть вместо yi подставить fi(M) (i = 1,..., к - 1, к + 1,..., п), то полу-
получится /Л(М), т. е. Ф(Д(М), /2(М),..., Л_1(М), Л+1(М),..., /П(М)) =
= fk(M) для всех точек М Е D.
Определение. Функции A) называются зависимыми в облас-
области D если одна из них (безразлично, какая) зависит в области D от
остальных функций. Если же ни одна из функций A) не зависит от
остальных, то функции A) называются независимыми в области D.
Например, функции ух—х\^ у^—х\^ уз = s/l — х\— х\ зависимы
в круге D = {(xi,X2): х\ + х\ < 1}, так как для всех точек этого кру-
круга выполняется равенство у% = ^1 — у\ — У2- Примеры независимых
функций рассмотрены ниже (см. пример 1 на с. 258).
2. Достаточные условия независимости и зависимости
функций.
Теорема 5. Пусть функции уч =/i(xbx2, ...,жт), ..., уп = /п(жь
Х2,...,хга), где п ^ т, дифференцируемы в окрестности uj точки
Мо(ж?,Ж2, ...,ж^п) и пусть якобиан этих функций по каким-либо
переменным не равен нулю в точке Mq. Тогда эти функции независи-
независимы в и.
Следствие. Если функции у\ — /i(xi,?2, -,%), ..., уп — fn(xi,
D(vi V2-, •••-, V)
зависимы в uj, то все якобианы
D(Xi
г)
равны
нулю в и.
Составим матрицу из частных производных функций A):
dh \
А =
dxi
дх\
dfn
V dxi
дх2
д$2
3X2
dfn
дХ2
dxm
dfn
дХт
9 В.Ф. Бутузов и др.
258 Гл. XI. Неявные функции и их приложения
Она называется функциональной матрицей.
Сформулируем общую теорему о зависимости и независимости
функций.
Теорема 6. Пусть: 1°) функции A) дифференцируемы в окрест-
окрестности и точки Mq{x\, Ж2,...,Жгп), а частные производные —^- (г =
з
= l,2,...,n; j = l,2,...,m) непрерывны в точке Мо;
2°) функциональная матрица А имеет минор г-го порядка, не рав-
равный нулю в точке Мо;
3°) все миноры (г + 1)-го порядка матрицы А (если такие имеют-
имеются) равны нулю в и.
Тогда г функций, представленных в указанном миноре г-го порядка,
независимы в со, а каждая из остальных функций зависит в некоторой
окрестности точки Мо от этих г функций.
Контрольные вопросы и задания
1. Дайте определение функции, зависимой от других функций в некоторой
области. Зависит ли функция у\ = х2 от функции у2 = х на интервале
— 1 < х < 1? Зависит ли функция у2 от у\ на том же интервале?
2. Дайте определение зависимости и независимости функций. Приведите
пример зависимых функций. Зависимы ли функции г/i = #i, г/2 = #2 в
окрестности точки 0@,0)?
3. Сформулируйте теорему о достаточном условии независимости функ-
функций (теорему 5). Является ли это условие (отличие от нуля какого-либо
якобиана этих функций в точке Мо) необходимым условием независи-
независимости функций в окрестности точки Мо? (Рассмотрите функции у\ = х\
и г/2 = х\ в окрестности точки Мо@,0).)
4. Сформулируйте необходимое условие зависимости функций.
5. Сформулируйте общую теорему о зависимости и независимости функ-
функций (теорему 6).
Примеры решения задач
1. Доказать, что функции у\ — х\ + х2 и у2 = х\х2 независимы в
любой окрестности точки 0@,0).
Л Решим задачу двумя способами: 1) пользуясь определением за-
зависимости и независимости функций; 2) используя теорему 5 о дос-
достаточном условии независимости функций.
I способ. Предположим, что у\ и у2 зависимы в некоторой окрест-
окрестности точки О@,0). Тогда в этой окрестности либо у\ зависит от у2,
либо у2 зависит от у\. Допустим, что у\ зависит от у2, т. е. у\ = Ф(у2),
и, значит, х\ + х2 = Ф(х±х2) для всех точек (xi,x2) из указанной
окрестности.
Отсюда для точек (xi,0) этой окрестности (т. е. точек, лежащих
на оси Ох\) получаем х\ — Ф@) = const, а это противоречит тому,
что х\ изменяется вдоль оси Ох\. Следовательно, у\ не зависит от у2.
§2. Зависимость функций 259
Допустим, что у2 зависит от 2/ъ т. е. у2 — Ф{у\), и, значит, х\х2 —
— Ф[х\ + х2) для всех точек (х\,х2) из указанной окрестности. От-
Отсюда для точек (xi,-xi) (т. е. точек, лежащих на прямой х2 = —х\)
получаем —х\ = Ф@) = const, а это противоречит тому, что х\ изме-
изменяется вдоль этой прямой. Таким образом, у2 также не зависит от 2/i,
т. е. функции у\ и у2 независимы в любой окрестности точки 0@,0).
II способ. Составим якобиан функций 2/ъ у2 по переменным жь
х2:
1 1
— Х\ — Х2.
Х2 Х\ i Z
В точке 0@,0) этот якобиан, очевидно, равен нулю. Однако в лю-
любой окрестности и точки О@,0) имеется точка Mq(xi,x2), у кото-
рой х\ ф х2, и, следовательно,
0. Окрестность и точки
D(xux2)
О@,0) является также окрестностью точки Mq. Таким образом, для
окрестности и точки Mq выполнены условия теоремы 5, и, значит,
функции у\ и у2 независимы в ио. А
2. Даны функции
х2 х>0 f^2' Ж^°'
О ' х < 0- ^ = < О, -К х < О,
U' X<U' [(х + 1J, х^-1.
Доказать, что у\ зависит от у2 в некоторой окрестности любой
точки числовой прямой, но у\ не зависит от у2 на всей числовой
прямой.
Л Для любой точки х можно указать такую окрестность, в которой
зависимость у\ от у2 при х > -1 выражается формулой у\ — Ф\{у2) =
= ?/2, а при х ^ — 1 — формулой у\ — Ф2(у2) = 0. Таким образом, у\
зависит от 2/2 в некоторой окрестности любой точки х.
Вместе с тем 2/1 не зависит от у2 на всей числовой прямой Е1. В
самом деле, предположим, что это не так, т. е. 2/1 зависит от у2 на
Е1. Тогда существует такая дифференцируемая функция Ф(у2), что
сразу для всех х выполняется равенство 2/i = ФB/2), т. е. это равенство
обращается в тождество относительно х при подстановке 2/i = 2/1(^M
2/2 = у2(х): yi(x) = Ф(у2(х)). Положим в этом тождестве х = —2.
Учитывая, что yi(-2) = 0, у2(-2) = 1, получим ФA) = 0. Положим
теперь х = 1. Так как 2/i(l) — 1, 2/2A) = 1, то ФA) = 1. Равенства
ФA) = 0 и ФA) = 1 противоречат друг другу. Следовательно, функция
2/i(ж) не зависит от у2(х) на всей числовой прямой. А
3. Исследовать вопрос о зависимости функций 2/i = х\ + х2 + ж3 +
+ Ж4, 2/2 — Х\ — Х2 + Жз — #4, УЗ — (Х1 + ЖзJ + (х2 + Ж4J.
Л Составим функциональную матрицу из частных производных
9*
260 Гл. XI. Неявные функции и их приложения
ФУНКЦИЙ уЪу2,Уз-
1
1
1
-1
0 2(х2 +
хЛ
2(rri
1
1
+
хз)
1
-1
2(ж2 +
хЛ
Матрица А имеет минор второго порядка, отличный от нуля, напри-
1 Г
мер,
= -2 ф 0, а все миноры третьего порядка тождественно
равны нулю, поскольку каждый такой минор содержит два одина-
одинаковых столбца. Отсюда по теореме б следует, что функции у\ и у2
независимы в любой окрестности каждой точки М(х\,Х2,х%,Х4) и,
значит, независимы во всем пространстве Е4, а функция у3 зависит
от у\ и ?/2 в некоторой окрестности каждой точки М. Вместе с тем
это не означает, что у% зависит от у\ и y<i во всем пространстве ЕА
(см. пример 2). Однако в данном случае нетрудно проверить, что 2/1,2/2
и 2/з связаны соотношением у% = O,5B/J + 2/2)? следовательно, у% зави-
зависит от ух и у2 во всем пространстве Е4. Поэтому ух.уъ.Уъ зависимы
вЕ4. А
Задачи и упражнения для самостоятельной работы
21. Докажите, что функции и\ = ху, U2 = ж, иг = у зависимы на всей
плоскости Оху.
Хл Xе)
22. Зависимы ли функции у\ = , у2 = Ж1Ж2Ж3, уз = хз'-
хз
а) в окрестности точки @,0,1); б) в полупространстве хз > 0?
23. Пользуясь определением зависимости и независимости функции, дока-
докажите, что:
а) функции т = ху и U2 = — независимы в окрестности точки @,1);
У
б) функции и\ = и U2 = — независимы в окрестности точки
Хз Х2
A,1,1)-
24. Пользуясь теоремой 5, докажите, что функции у\ = ът.{х\Х2Хз)-, У2 =
= х\ COSX2 независимы в окрестности точки A, 0,1). Зависимы ли эти
функции в какой-нибудь окрестности точки @,0,0)?
25. Пользуясь теоремой 6, докажите, что функции и\ = sin(xyz), U2 =
= х cos 1/, из = x2 sin(xyz) — x2 sin(xyz) sin2 у зависимы в некоторой
окрестности точки A,0,1), а любые две из них независимы в любой
окрестности этой точки. Зависимы ли функции щ, г^2, г^з во всем
пространстве Е3?
26. Пользуясь теоремой 6, докажите, что функции и\ = ху + yz + zx, U2 =
= х + у + г, 1бз = ж2 + |/2 + z2 зависимы в некоторой окрестности точ-
точки A, 2, 3), а любые две из них независимы в любой окрестности этой
точки. Зависимы ли функции ui,U2,U3 во всем пространстве Е3?
27. Докажите, что п линейных функций т переменных yi = ацх\ +
+ OL12X2 + ... + OLimXrn (« = 1, 2, ..., Щ CLij ЧИСЛа):
а) зависимы при п > т во всем пространстве i?m;
б) независимы, если п = т и det Ца^-Ц / 0-
§3. Условный экстремум 261
§ 3. Условный экстремум
Основные понятия и теоремы
1. Понятие условного экстремума. Рассмотрим функцию
и = /Оьж2,...,жт) = /(М) A)
при условии, что ее аргументы являются не независимыми перемен-
переменными, а связаны между собой к соотношениями (к < т):
Fi(xuX2,...,xm) = 0 (г = 1,2,.., к). B)
Эти соотношения называются условиями связи. Пусть координаты
точки Мо(ж?,Ж2, ...,ж^п) удовлетворяют уравнениям B).
Определение. Говорят, что функция A) имеет в точке Мо ус-
условный минимум (максимум) при условиях связи B), если существует
такая окрестность точки Мо, что для любой точки M(xi,x2, ...,жт)
(М ф Мо) этой окрестности, координаты которой удовлетворяют
уравнениям B), выполняется неравенство /(М) > /(Mq) (/(M) <
< /(Мо)).
Иначе говоря, условный максимум (минимум) — это наибольшее
(наименьшее) значение функции в точке Мо по отношению не ко всем
точкам из некоторой окрестности точки Мо, а только к тем из них,
которые связаны между собой условиями связи.
Рассмотрим два метода решения задачи об условном экстремуме
функции.
2. Метод исключения части переменных. Пусть в окрест-
окрестности uj точки Мо(ж^,Ж2, ...,ж^) для уравнений связи B) выполнены
условия теоремы 4 о неявных функциях, так что в некотором паралле-
параллелепипеде Q С ио эти уравнения имеют единственное решение относи-
относительно каких-то к переменных, например, относительно xi,^2, ...,ж^:
Хг =ф{(хк+1,Хк+2,...,Хт) (i = 1,2,...,&). C)
Тогда в параллелепипеде Q условия связи B) эквивалентны соотно-
соотношениям C), в которых естественно рассматривать Xk+i,Xk+2, -,%
как независимые переменные.
Если функции C) удается найти в явном виде, то, подставляя их
в A), получим функцию т — к независимых переменных:
и =
В пределах Q значение функции F(M') в любой точке M'(xk+i,..., хт)
совпадает со значением функции /(М) в соответствующей точке
М(ж1,Ж2, ...,жт), удовлетворяющей уравнениям C), или, что то же
самое, уравнениям связи B). Поэтому вопрос об условном экстрему-
экстремуме функции A) при условиях связи B) в параллелепипеде Q сводится
к вопросу о безусловном экстремуме функции F(M').
262 Гл. XI. Неявные функции и их приложения
Если нахождение функций C) в явном виде затруднительно (или
невозможно), то можно поступить следующим образом. Предполо-
Предположим, что функции C) подставлены в A), в результате чего получается
функция F(M'), и в уравнения B), которые после этой подстановки
обращаются в тождества. Дифференциал функции F(M') в силу ин-
инвариантности формы первого дифференциала можно записать в виде
г=1
где dxk+i, dxk+2T--,dxm — дифференциалы независимых перемен-
переменных, a dxi, dx2, ...,dxk — дифференциалы неявных функций C). Диф-
Дифференцируя указанные выше тождества, получим
т—^ dxi + тг^ dx2 + ... + тг~^ dxm = О,
Из этой линейной системы выразим дифференциалы dxi, dx2,...,
неявных функций C) через дифференциалы независимых перемен-
переменных dxk+i, dxk+2, •••? dxm. Подставляя полученные выражения для
dxi, dx2,..., dxk в D), приходим к равенству
dF = ^2 Ai(xi,x2,...,xm)dxi, D')
i=k+l
где xj = <Pj(xk+i,xk+2,.->xm) (j = 1,2,..., к).
Если в точке Mq(x^+1,x^+2, ...,ж^) функция F(M') имеет экстре-
экстремум, то dF\M'Q = 0, т. е.
Q
+..,x°m)dxi = 0, F)
i=k+l
где x°j = ^К+1,х0+2,...,х^) = щ(М()) (j = 1,2,.., к). Так как dx{
(г = к + 1, /с + 2,.., ттг) — дифференциалы независимых переменных,
то из F) получаем
Ai(x°1,x02,...,x0k,x°k+1,...,x0m)=0 (г = к + 1,...,т). G)
Равенства G) являются, таким образом, необходимыми условиями
экстремума функции F(M') в точке Mq, или, что то же самое, необ-
необходимыми условиями условного экстремума функции /(М) в точке
Мо(ж^,Ж2, ...,ж^п) при условиях связи B).
Отсюда следует, что для отыскания точки М^{х\,х^, ...,ж^) воз-
возможного экстремума нужно решить систему m уравнений относи-
относительно т неизвестных xi,X2, ...,хт
( Fi(x1,x2,...,xm) = 0 (г = 1,2, ...,fe), ,яч
1 А;(ж1,ж2,...,жт) = 0 (г = fe + l,fe + 2,...,m). l ;
§3. Условный экстремум 263
Если точка Мо возможного экстремума найдена, то ее дальнейшее ис-
исследование связано с рассмотрением второго дифференциала сР/\м'-
Его можно вычислить (предполагаем, что функции A) и B) дважды
дифференцируемы), дифференцируя равенство D') для dF и исполь-
используя выражения для дифференциалов dxi, б?ж2,..., dxk неявных функ-
функций C), найденные из системы E). В итоге находим d2f\M> — квад-
квадратичную форму от переменных dxk+i, dxk+2,---, dxm. Если эта
квадратичная форма положительно (отрицательно) определена, то
функция A) имеет в точке Мо условный минимум (максимум) при
условиях связи B). Применение описанного метода, использующего
систему (8), к конкретной функции рассмотрено в примере 2 на с. 265.
3. Метод Лагранжа. Задача об условном экстремуме функции
A) при условиях связи B) эквивалентна задаче об условном экстре-
экстремуме функции Лагранжа
Ф(М) = /(М) + AiFi(M) + A2F2(M) + ... + XkFk(M)
(Xi — произвольные числа) при тех же условиях связи B), поскольку
в точках М, удовлетворяющих уравнениям связи, справедливо ра-
равенство Ф(М) = /(М).
Теорема 7 (необходимое условие Лагранжа условного экстрему-
экстремума). Пусть:
1°) функция и = /(ж1,Ж2, ...,жт) дифференцируема в точке Mq(xJ,
Ж2,...,ж^) и имеет в этой точке условный экстремум при условиях
связи B);
2°) уравнения B) удовлетворяют в некоторой окрестности точки
Мо условиям теоремы 4 о неявных функциях вида C).
Тогда существуют числа Аь А2,..., А/, такие, что все частные про-
производные первого порядка функции Лагранжа равны нулю в точке Mq.
Из теоремы 7 следует, что для отыскания точек возможного услов-
условного экстремума функции A) при условиях связи B) нужно решить
систему т + к уравнений
Fi(x1,X2,...,xm) = 0 (г = 1,2, ...,&),
— (xi,x2,...,xm,Ai,A2,...,Afe) =0 (г = 1,2,...,ш)
относительно т + к неизвестных xi,x2, ...,жт, Ai, A2,..., А/.. Если ж?,
#2,..., 4) Aj, A2,..., А^ — решение системы (9) (таких решений может
быть несколько), то M0(xi,x2, ...,ж^) является точкой возможного
условного экстремума функции A) при условиях связи B). Дальней-
Дальнейшее исследование этой точки связано, как и в методе исключения
части переменных, с рассмотрением второго дифференциала d2F\Mf
функции F(M') = F(xk+i,...,xm) = Ф((^1(ж^+1,...,жт),...,^(ж^+1,...
..., хт), xk+i,..., хт), где Ф = / + A?Fi + A^F2 + ... + X°kFk. Его можно
264 Гл. XI. Неявные функции и их приложения
вычислить по формуле
где dxk+ii dxk+2T--,dxm — дифференциалы независимых перемен-
переменных, a dxi, dx2j..., dxk — дифференциалы неявных функций C) в точ-
точке Mq. Формула A0) показывает, что для нахождения d2F\M' сначала
вычисляется второй дифференциал функции Лагранжа в точке Mq,
причем так, как если бы все аргументы Ж1,ж2,...,жт были независи-
независимыми переменными, а затем dxi, dx2,..., dxk заменяются дифферен-
дифференциалами неявных функций C) в точке M'Q. В результате получает-
получается d2F\M' — квадратичная форма от dxk+i, dxk+2, •••? dxm. Если эта
квадратичная форма положительно (отрицательно) определена, то в
точке Мо функция A) имеет условный минимум (максимум) при
условиях связи B), а если <PF\mi — знакопеременная квадратичная
форма, то в точке Mq функция A) не имеет условного экстремума.
Контрольные вопросы и задания
1. Сформулируйте определение условного экстремума функции.
2. Объясните, в чем состоит метод исключения части переменных. Све-
Сведите задачу об условном экстремуме функции и = х2 + у2 при условии
связи х + у = 2 к задаче о безусловном экстремуме.
3. Изложите схему метода исключения части переменных, не связанную
с нахождением в явном виде каких-то переменных через остальные.
4. Что такое функция Лагранжа? Напишите выражение для функции
Лагранжа в задаче об условном экстремуме из задания 2.
5. Сформулируйте теорему о необходимых условиях Лагранжа условного
экстремума. Составьте систему уравнений (9) для задачи об условном
экстремуме из задания 2 и решите ее.
6. Объясните, как исследовать далее точку возможного условного экстре-
экстремума, найденную методом Лагранжа. Проведите такое исследование
для точки, найденной в задании 5.
Примеры решения задач
1. Методом исключения части переменных найти экстремум функ-
функции
а — J/T утл V11/
при условиях связи
Л Решая систему уравнений A2) относительно у и z, находим
2/ = x2+x + l, z = x + l. A3)
§3. Условный экстремум 265
Подставляя выражения A3) в равенство A1), приходим к функции
одной переменной х: и(х) = 2х2 + 4х + 2, для которой рассмотрим за-
задачу о безусловном экстремуме. Так как и' = 4(ж + 1) = О при х = —1,
то функция и{х) имеет единственную точку возможного экстремума.
Но и"(—1) = 4 > 0, поэтому при х = — 1 функция и(х) имеет мини-
минимум. Из системы A3) находим соответствующие х = — 1 значения у
и z: у = l,z = 0. Итак, функция A1) при условиях связи A2) имеет
в точке (-1,1, 0) минимум, причем и(-1,1, 0) = 0. А
2. Методом исключения части переменных найти экстремум
функции
и = х + у — z A4)
при условиях связи
4ж3 + 4у3 + 4z3 + 12ж + 12у + 12 z = 13,
Л Воспользуемся схемой метода исключения части переменных, не
связанной с нахождением в явном виде каких-либо двух переменных
через третью из уравнений связи A5). Предполагая, что система A5)
определяет дважды дифференцируемые неявные функции у(х) и z(x),
и считая, что они подставлены в уравнения связи, будем рассматри-
рассматривать равенства A5) как систему тождеств. Вычисляя дифференциалы
от обеих частей тождеств A5), получим
(ж2 + 1) dx + {у2 + 1) dy + (z2 + l)dz = 0,
dx + dy = 0.
Отсюда находим
dy = — dx,
, -2x + 1 ,
dz = — dx.
' + 1
Подставляя эти выражения для dy и dz в выражение для дифферен-
дифференциала функции A4), которое имеет вид du — dx + dy — dz, получим
du= ^ldx = Adx. A7)
Рассмотрим теперь систему уравнений, состоящую из уравне-
уравнений A5) и уравнения А = 0 (это и есть система (8) в данном слу-
случае). Она имеет единственное решение х = 1/2, у = 1/2, z = 0, т. е.
МоA/2,1/2,0) — единственная точка возможного экстремума функ-
функции A4) при условиях связи A5). Дифференцируя выражение A7) для
du, получаем
2(z2 + l)dx-Bx-lJzdz ,
откуда, используя уравнения A6), находим d2u\M0 — 2(dxJ. Так как
2(dxJ — положительно определенная квадратичная форма (одной пе-
переменной dx), то функция A4) имеет в точке Mq минимум при усло-
условиях связи A5). А
266
Гл. XI. Неявные функции и их приложения
Замечание. Задача решена в предположении, что система A5) опре-
определяет дважды дифференцируемые функции у(х) и z(x). Теперь можно
уточнить, что это условие должно выполняться в некоторой окрестнос-
окрестности точки МоA/2,1/2,0). Покажем, что данное требование выполнено. Вос-
Воспользуемся теоремой 4. Функции F\ (ж, у, z) = 4ж3 + 4ys + 4zs + 12ж + 12у +
-\-12z — 13 и F2(x,y,z) = ж + у — 1 дифференцируемы в любой окрестное-
о тр Q тр
ти точки Мо. Частные производные = 12(?/2 + 1), = 12(z2 + 1),
dFo dFo
= 1, = 0 непрерывны в точке Мо. Функции Fi(x,y,z) и F2(x,y,z)
ду dz
равны нулю в точке Мо. Наконец,
D(FUF2)
= —12 ф 0. Поэтому в си-
м0
лу теоремы 4 система A5) в некоторой окрестности точки Мо определя-
определяет единственную пару дифференцируемых функций y(x),z(x). Более того,
так как функции F\ (ж, у, z) и F2 (ж, у, z) дважды дифференцируемы в любой
окрестности точки Мо, то и функции г/(ж), z(x) дважды дифференцируемы.
3. Методом Лагранжа найти экстремум функции A1) при услови-
условиях связи A2).
Л Составим функцию Лагранжа
Ф = x + y + z2 + AiB - ж -
и рассмотрим систему уравнений (9):
ду
Х2(у -xz-
= 0,
F1=z-x-l = 0,
{ F2 = у - xz - 1 = 0.
Она имеет единственное решение: х — —1, у = 1, z = 0, Ai = 1, А2 =
= —1, т. е. Мо(—1,1,0) — единственная точка возможного экстрему-
экстремума функции A1) при условиях связи A2). Отметим, что в окрестнос-
окрестности точки Mq система A2) определяет единственную пару неявных
функций у(х), z(x). Хотя в данном случае их легко найти в явном
виде, нам эти явные выражения не понадобятся. Предполагая, что
в систему A2) подставлено ее решение у(х), z(x), и дифференцируя
полученные тождества, приходим к равенствам
Отсюда находим
dz - dx = 0,
dy — х dz — z dx = 0.
dz = dx,
dy = (x + z) dx.
A8)
§3. Условный экстремум 267
Теперь вычисляем второй дифференциал функции Лагранжа:
d2<5> = 2(dzJ -2\2dxdz,
и, подставляя А2 = -1 и выражение A8) для dz, получаем положи-
положительно определенную квадратичную форму от одной переменной dx:
4(dxJ. Отсюда следует, что функция A1) при условиях связи A2)
имеет в точке Mq условный минимум. А
4. На эллипсоиде х2 + 2у2 + 4z2 = 8 найти точку, наиболее удален-
удаленную от точки @,0,3).
Л Расстояние р между точками (x,y,z) и @,0,3) определяется фор-
формулой р = у/х2 + у2 + (z — ЗJ. Поэтому исходная задача равносильна
задаче об условном максимуме функции
и = р2 = х2 + у2 + (z - ЗJ A9)
при условии связи
х2 + 2у2 + 4z2 = 8. B0)
Составим функцию Лагранжа
Ф = х2 + у2 + (z - ЗJ + Х(х2 + 2у2 + 4z2 - 8)
и рассмотрим систему уравнений (9):
§!- = 2х + 2Хх = 0,
ох
0' B1)
Ц = 2z - б + 8Az = 0,
[ х2 + 2у2 + Az2 = 8.
Так как эллипсоид B0) более всего вытянут вдоль оси Ох, то абсцисса
искомой точки не может быть равна нулю, т. е. х ф 0. Поэтому из
первого уравнения системы B1) следует, что А = —1. Тогда из второго
и третьего уравнений системы B1) имеем у = 0,2 = —1. Наконец, из
последнего уравнения системы B1) находим х = ±2. Итак, функция
A9) имеет две точки возможного условного максимума, Mi B,0, —1)
и M2{—2,0, — 1). Предполагая, что в уравнение B0) подставлено его
решение z = z(x, у), и дифференцируя полученное тождество, находим
х dx + 2y dy + 4:Z dz = 0,
откуда
dz = -^dx-^dy. B2)
Теперь вычисляем второй дифференциал функции Лагранжа
d4 = 2A + \){dxf + 2A + 2\){dyf + 2A + 8X)(dzf,
268 Гл. XI. Неявные функции и их приложения
и, подставляя Л = —1, координаты точки Mi или М2 и выражение
B2) для dz, получаем в каждом случае отрицательно определенную
квадратичную форму от двух переменных dx, dy: -2(dyJ - 3,5(<ixJ.
Отсюда следует, что функция A9) имеет в точках Mi и М2 условный
максимум при условиях связи B0), т. е. на эллипсоиде B0) имеются
две точки, MiB, 0, —1) и М2{—2, 0, —1), наиболее удаленные от точки
@,0,3). А
Задачи и упражнения для самостоятельной работы
28. Исследуйте на условный экстремум методом исключения части пере-
переменных функцию:
ч 9 9 X У
а) и = ж + у при условии связи —\- — = 1;
а Ъ
б) U = X + у При УСЛОВИИ СВЯЗИ — + — = —;
х2 у2 а2
в) и = ху при условии связи х2 + у2 = 1;
г) и = х2 + у2 + 2z2 при условии связи ж — у + 2 = 1;
д) и = ж3 + у2 — zs + 5 при условии связи ж + у — z = 0;
е) и = х — 2у + z при условии связи х + у2 — z2 = 1;
ж) и = xy2zs при условии связи х + 2у + 3z = 6 (х > 0, |/ > 0, 2 > 0);
з) и = х — 2у -\- 2z при условии связи х2 -\- у2 -\- z2 = 1;
2 2 2
и) 16= — + — + — при условии связи х2 + у2 + z2 = 1 (а > Ъ > с > 0);
а2 б2 с2
к) 16 = ж? + х\ + ... + ж^ при условии связи — + — + ... + — = 1
ai «-2 о,п
(ai > 0,а2 > 0,...,an > 0).
29. Исследуйте на условный экстремум методом Лагранжа:
а) функцию и = xyz при условии связи х2 -\- у2 -\- z2 = 3;
б) функцию it = xyz при условиях связи х2 + у2 + z2 = 1, х + у + z = 0.
30. При каких значениях диаметра основания d и высоты h цилиндричес-
цилиндрическая банка, объем которой равен 54тг, имеет наименьшую поверхность?
31. При каких размерах прямоугольная банка объемом 32 см3, открытая
сверху (т.е. без верхней грани), имеет наименьшую поверхность?
32. При каких размерах открытая цилиндрическая ванна с полукруглым
поперечным сечением, поверхность которой равна Зтг м2, имеет наи-
наибольшую вместимость?
33. Найдите измерения прямоугольного параллелепипеда наибольшего
х2 у2 z2
объема, вписанного в эллипсоид —- + ^— + —- = 1.
а2 о2 с2
34. Найдите наименьшее из расстояний между точкой (жо,г/о,^о) и точка-
точками плоскости Ах + By + Cz + D = 0.
35. Найдите наименьшее из расстояний между точками параболы у = ж2
и прямой ж — у — 2 = 0.
36. Найдите наибольшую площадь треугольника, у которого заданы сто-
сторона а и противолежащий угол А.
37. Известны стороны а, Ь треугольника и величина угла С между ни-
ними. Разделите этот треугольник на две равновеликие части отрезком
прямой, пересекающим заданные стороны и имеющим наименьшую
длину.
§4- Замена переменных 269
§ 4. Замена переменных
Основные понятия
1. Замена переменных в выражении, содержащем обык-
обыкновенные производные. Пусть в выражении
А = Ф(х,у,У',у",...,уЮ), A)
где у является функцией аргумента ж, требуется перейти к новым
переменным ?, и, где t — независимая переменная, а и — функция
аргумента ?, причем переменные ж, у связаны с переменными ?, и
уравнениями
g1(x,y,t,u) = 0,
2(x,y,t,u) = 0,
которые будем называть формулами замены переменных. Будем счи-
считать, что система B) определяет (в некоторой области) дифферен-
дифференцируемые достаточное число раз неявные функции х = fi(t,u), у =
= f2(t,u). Так как и есть функция аргумента ?, то х = fi(t,u(t)) =
= x(t) и у = f2(t,u(t)) = 2/(?) — сложные функции аргумента ?.
Схема решения.
1. Предполагая, что в систему B) подставлено ее решение ж(?), y{t),
получим тождества
g2(x(t),y(t),t,u(t)) =0-
Дифференцируя по t обе части этих тождеств, приходим к системе
уравнений, линейных относительно производных
dx dy . du
х = —, у = —, и = —.
dtJ y dtJ dt
2. Решаем полученную систему относительно ж, у.
3. Выражение у' в новых переменных ?, ^ находим по формуле
4. Чтобы найти выражения старших производных, пользуемся опе-
операторной формулой
— = --. D)
dx х dt
Например, чтобы найти выражение второй производной у", в левую
часть формулы D) подставляем у', а в правую — представление для
у' по формуле C). Получим
5. В исходном выражении A) переходим к переменным ?, и.
270
Гл. XI. Неявные функции и их приложения
Замечание. Если формулы замены переменных B) даны в форме,
разрешенной относительно ж, у (?, и), то изложенная схема упрощается (см.
пример 2 на с. 273).
2. Замена переменных в выражении, содержащем част-
частные производные. Ради простоты изложения ограничимся случаем
функций двух переменных. Пусть в выражении
где z является функцией аргументов х и у, надо перейти к новым пе-
переменным u, v, w, где u,v — независимые переменные, aw — функция
аргументов u,v, причем переменные x,y,z связаны с переменными
u,v,w уравнениями
gi(x, у, z, и, v,w)=0 (i = I, 2,3),
F)
которые будем называть формулами замены переменных.
Обычно формулы замены переменных F) даются в форме, раз-
разрешенной относительно либо старых переменных x,y,z, либо новых
переменных u,v,w.
Рассмотрим в отдельности оба эти случая.
1°. Пусть формулы замены переменных имеют вид
( х = fxiu.v.w),
\У = f2(u,v,w), G)
где fi(u, v, w) (г = 1, 2, 3) — функции, дифференцируемые достаточное
число раз.
Схема решения.
1. Из равенств G) получаем
(8)
у/О — U/U/ Т ^ U/1/ П^ ^Г UUUU .
аи av aw
Так как w — функция аргументов и, v, то dw = wudu + wvdv. Подстав-
Подставляя это выражение для dw в равенства (8), приходим к равенствам
Du
Du
Du
Dv
Dv
Dv
где
Du
dfi dfi Dfi dfi dfi ,. Л о oN
-±L +-J± Wu и -±l =-11 +-J± Wv (г = 1,2,3.
du dw Dv dv dw
§4- Замена переменных 271
2. Если А =
Dfi Dfi
О, то первые два уравнения систе-
Du Dv
мы (9) однозначно разрешимы относительно du и dv:
dx +
Du Du
3. Подставляя выражения A0) в последнее уравнение системы (9),
получаем
dz = - (ЕкЕк - ЕАЕА) dx + L(_?А?А + EAEA) dv
А V Du Dv Dv Du J A V Du Dv Dv Du ) y'
Сопоставляя полученное представление для dz с равенством dz =
= zx dx + zy dy, находим выражения частных производных zx и zy
в новых переменных u,v,w:
у _]_f?f1Df1_Df1Df1\ -±(_RARA + RARA\
х~ A\Du Dv Dv DuI y ~ A V Du Dv ^ Dv Du)'
4. Чтобы получить выражения вторых производных функции
z(x,y) в новых переменных, вычислим дифференциалы от первых
производных zx и zy, представленных в виде A1). Запишем первую
из формул A1) в кратком виде:
zx = F(u,v,w,wu,wv).
Отсюда d(zx) = dF или zxx dx + zxydy = Fudu + Fvdv + Fwdw +
+ FWudwu + FWvdwv. Подставив сюда выражения (iw; = wudu + wvdv,
dwu = wuudu + wuvdv, dwv = wvudu + wvvdv, а затем выражения A0)
для du,dv, и приравняв коэффициенты соответственно при dx и dy в
обеих частях полученного равенства, найдем выражения 2:жж и 2:жу в
новых переменных.
Выражение zyy получим аналогично, вычислив дифференциал про-
производной zy, представленной второй формулой A1).
Таким же образом можно найти далее выражения для производ-
производных более высокого порядка.
5. В исходном выражении E) переходим к новым переменным
2°. Пусть теперь формулы замены переменных имеют вид
Г u = fi(x,y,z),
A2)
w =
где fi(ж, у, z) (г = 1, 2, 3) — функции, дифференцируемые достаточное
число раз.
272
Гл. XI. Неявные функции и их приложения
Схема решения.
1. Из равенств A2) получаем
дх
0/2
dv = -^— dx + -^— dy + -77— dz,
дх ду dz
дх
ду
dz
Подставляя сюда выражение dz = zxdx + zydy, приходим к равенст-
равенствам
Dx
Dx
Dx
Dy
Dy
A3)
Dy ""'
T)i* Fi^r Fi у /")?/ Fin Fi у 11/
2. Так как w — функция аргументов u,v, то dw = wudu + wvdv.
Подставляя в это равенство выражения A3) для du, dv и dw, приходим
к равенству
Dfs Dfs (Dfi Dfi
Dx Dy V Dx Dy
Приравнивая в обеих частях равенства коэффициенты соответствен-
соответственно при dx и dy, получаем систему двух линейных уравнении относи-
относительно zx и zy.
3. Коэффициенты этой системы зависят от wu, wv и старых пере-
переменных x,y,z. Поэтому для zx и zy получаются выражения
= F(x, у, z, wu, wv), zy = G(x, y, z, wu, wv).
A4)
4. Чтобы получить выражения вторых производных функции
z(x,y), вычислим дифференциалы от первых производных zx и zy,
представленных в виде A4). Из первого равенства A4) имеем dzx =
= dF или zxxdx + zxydy = Fxdx + Fydy + Fzdz + FWudwu + FWvdwv.
Подставив сюда выражения dz = zxdx + zydy, dwu = wuudu + wuvdv,
dwv = wvudu + wvvdv, а затем выражения A3) для du, dv и выражения
A4) для zx, zy, и приравняв коэффициенты соответственно при dx и
dy в обеих частях полученного равенства, найдем выражения zxx и
zxy в новых переменных.
Выражение zyy получим аналогично, вычислив дифференциал про-
производной zy, представленной второй формулой A4).
Таким же образом можно найти далее выражения для производ-
производных более высокого порядка.
§4- Замена переменных 273
5. В исходном выражении E) переходим к новым переменным и,
V, W.
Примеры решения задач
1. В уравнении у у' + ху2 + х3 = 0 перейти к новым переменным
t,u, где и = u(t), если формулы замены переменных имеют вид
и2-у2-х2 = 0,
Л В соответствии со схемой, описанной в п. 1°, сначала нужно уста-
установить, что система A5) разрешима относительно х,у. Это можно
сделать, используя результаты § 1, но здесь мы не будем этим зани-
заниматься. Учитывая, что и = u(t), и предполагая, что в систему A5)
подставлено ее решение х = x(t), у = y(t), продифференцируем полу-
полученные тождества по переменной t:
Отсюда находим
ий- уу - хх — О,
хх — t + ип = 0.
t — ий . 2ип — t
х= , у= .
х у
тт 1 /о\ I У XBUU — t) т-г
По формуле C) получаем у = — = —-, ^-. Подставляя это вы-
х y(t — ий)
ражение для у' в исходное уравнение и используя формулы замены
переменных A5), приходим к уравнению в переменных ?, и
2. Решить уравнение A + х2Jу" = у, перейдя к новым перемен-
переменным ?, и, где и = u(t), если х = tgt, у = .
cost
Л Продифференцируем по t выражения для ж, у, заданные формулами
замены переменных; тогда получим
. _ 1 . _ и cos t + и sin t
cos2 t' cos2 t
Производную у' находим по формуле C): у' = % = йcost +-usin?. Ис-
Используя операторную формулу D), находим выражение второй про-
производной
у" = - — (и cos t + и sin t) = cos3 t-(u + u).
Переходя к новым переменным в исходном уравнении, получим и =
= 0. Очевидно, решением этого уравнения является линейная функ-
функция и = At + В, где А, В — произвольные постоянные. Возвращаясь
274 Гл. XI. Неявные функции и их приложения
в равенстве и = At + В к старым переменным, получаем решение ис-
исходного уравнения у = (Aarctgx + В)у/1 + ж2. А
3. Решить уравнение у"(у')~3 — х = 0, приняв 2/ за новую незави-
независимую переменную, а ж — за новую функцию.
Л Чтобы воспользоваться стандартной схемой решения задачи, вве-
введем новые переменные t и и (и = u(t)) по формулам t = у, и — х.
Продифференцируем эти равенства по t: 1 = у, п = х. Используя по-
полученные соотношения, по формулам C) и D) находим
й' х dt\u/ и3
В результате исходное уравнение примет вид й + ^ = 0. Возвраща-
Возвращаясь к прежним обозначениям, т. е. заменяя и на ж, а ? на 2/, полу-
получаем уравнение —- + х = 0, решением которого является функция
dy2
х = AsinB/ + <p), где A, ip — произвольные постоянные. Выражая
из последнего равенства у, находим решение исходного уравнения:
у = arcsin(x/A) — if или у = arcsin(??x) + С, где В и С — произволь-
произвольные постоянные, В ф 0. А
4. В выражении В — xzx + yzy — 2z перейти к новым переменным
и, v, w, где w = w(u, v), если формулы замены переменных имеют вид
х х2 + у2 ху
и = -, v = —^-, w=z'
Л Так как формулы замены переменных A6) заданы в форме, разре-
разрешенной относительно новых переменных и,у,га, т. е. имеют вид A2),
то воспользуемся схемой решения, изложенной в п. 2°. Из равенств
A6), учитывая, что dz = zxdx + zydy, получаем
1 , dx x ,
du= -dy,
У У2
dv = xdx + ydy, A7)
II ПГ 1*11
dw = - dx + - dy 1 (zx dx + zy dy).
z z z
Так как w — функция аргументов u,v, то dw = wudu + wvdv. Под-
Подставляя в это равенство выражения A7) для du, dv и dw, приходим
к равенству
wu( ody) +wv(xdx + y dy) = - dx + - dy \ (zx dx + zy dy).
V у yz J z z zA
Приравнивая в обеих частях равенства коэффициенты соответствен-
соответственно при dx и dy, получаем систему двух линейных уравнений относи-
1 У ХУ
-wu +xwv = fzx,
у z zz
§4- Замена переменных 275
Отсюда находим
zx
Zy
Z
= —
X
z
У
y2
Z
— t: W
xy2
+ z2 w
y3
2
Z
и — —
У
_ z2
xy2
Wy,
Wy.
Подставляя эти выражения для первых производных в исходное вы-
выражение, получим
В = — \xz Л— )wy.
у \ х )
Используя формулы замены переменных A6), переходим к новым пе-
переменным u,v,w в выражении В:
в = - ';:22,«va
wz(l + и2)
5. Решить уравнение zy — zx = 0, перейдя к новым независимым
переменным и = х + у, v — х — у.
Л Дифференцируя выражения для и, v, заданные формулами замены
переменных, имеем
du = dx + dy,
dv — dx — dy.
Так как в данной задаче заменяются только независимые перемен-
переменные, а переменная z (функция) не заменяется, то dz — zxdx + zydy
и, аналогично, dz = zudu + zvdv. Отсюда, используя равенства A8),
получаем
dz = zxdx + Zydy = zu(dx + dy) + zv(dx — dy).
Приравнивая в обеих частях последнего равенства коэффициенты со-
соответственно при dx и dy, находим выражения для zx и zy: zx =
= zu + Zy, Zy — zu- Zy. Следовательно, исходное уравнение примет
вид Zy = 0. Решением этого уравнения является произвольная диф-
дифференцируемая функция переменной и, т. е. z — f(u). Возвращаясь к
старым переменным, получаем, что z = f(x + у) — решение исходно-
исходного уравнения. А
6. В уравнении zxx + zxy + zx = z перейти к переменным и, v, w,
где w = w(u,v), если
Jb — LL I LJ • U — LL LJ • /0 — (JU о • I X %J )
Так как формулы замены переменных A9) заданы в форме, разре-
разрешенной относительно старых переменных х, у, z, т. е. имеют вид G),
то воспользуемся схемой решения, изложенной в п. 1°. Из равенств
A9), учитывая, что dw = wudu + wvdv, получаем
{dx = du + dv,
dy = du- dv, B0)
dz = eu~v(wudu + Wydv) + wev~u(dv — du).
276 Гл. XI. Неявные функции и их приложения
Из первых двух уравнений системы B0) находим
du = 0,5(<ix + dy),
dv = Q,5(dx-dy).
Подставляя выражения B1) для du, dv и dz = 2:жс?ж + zydy в третье
уравнение системы B0), приходим к равенству
zxdx + Zydy = 0,5ev~w[ww(dx + dy) + wv(cte - dy)] - wev~udy.
Приравнивая в обеих частях равенства коэффициенты при dx, име-
имеем zx = 0,5ev~u(wu + wv). Чтобы найти выражения вторых производ-
производных функции z[x,y) в новых переменных, вычислим дифференциал
от первой производной zx:
dzx = zxxdx + zxydy = 0,5ev~u(dv - du)(wu + wv) +
+ 0,5ev~u(wuudu + wuvdv + wvudu + wvvdv).
Подставляя сюда выражения B1) для du и di?, получаем равенство
zxxdx + 2^2/ = -0,5ev~w(w;w + wv) dy +
+ 0,2bev~u[wuu(dx + ф) + 2iyuvda: + wvv(dx - dy)].
Приравнивая в обеих частях равенства коэффициенты соответствен-
соответственно при dx и dy, находим
zxx = 0,25ev-u(wuu + 2wuv + wvv),
zxy = zyx = -0,5ev~u(wu + wv) + 0,25ev-u(wuu - wvv).
Подставив выражения первых и вторых производных в исходное урав-
уравнение, получим wuu + wuv = 2w. A
Задачи и упражнения для самостоятельной работы
38. Решите дифференциальное уравнение, вводя новую независимую пе-
переменную:
а) х2у" + ху' + у = 0, если х = е?;
б) Dж2 + 1J/" + 4жг/ + у = 0, если x=-sh2t;
в) 4A — х2)у" — 4xyf + а;22/ = 0, если х = sin 2t.
39. Преобразуйте дифференциальное уравнение, приняв у за новую неза-
независимую переменную, ах — за новую функцию:
а) у'у'" - 3(y"f - (у'Гу = 0; б) {y'fy'V ~ Wy'y"v'" + ^(v"f = (у'У¦
40. Введя новые переменные t,u, где и = u(t), преобразуйте дифференци-
дифференциальное уравнение:
а) х3у" + хуу' — у2 = 0, если х = е?, у = и-еь;
б) з/" - ж3^ + ху' - у = 0, если ж = 1/t, г/ = и ft;
ч Ж2 , . . 1ПЖ lilt
в) -—-— 2/ + У = 1, если г/ = -и + 1, — = —-;
1 — In ж ж ?
г) жщ/" -х{у'J +уу' = 0, если ? = j/, u = \n(y/x).
§4- Замена переменных 277
41. В уравнении у" + р(х)у' + q(x)y = 0 перейдите к новой функции и =
= и(х), если у = ехр^ —0,5 p(t)dt > • и.
х0
42. Преобразуйте дифференциальное уравнение, перейдя к полярным ко-
координатам x = pcos(p, у = psimp, где р = р(<р)):
а) у' = ^^; б) (ху' - уJ = 2ху{1 + у'2),
х -у
43. В системе уравнений
^ =-х + ку(х2 + у2)
перейдите к новым функциям р = p(t), ср = cp(t) по формулам ж = р cos 9?,
2/ = р sin <р.
44. Введя новые независимые переменные и, v, преобразуйте дифференци-
дифференциальное уравнение:
а) xzx + yzy = z, если и = ж, г> = |//ж;
б) г/2ж — ж^у = |/еж +у , если гб = х2 + ^Д v = у;
в) (ж + г/Jж — (ж — г/)^ = 0, если и = In у^ж2 + |/2, г; = arctg (у/х);
г) (xzxJ + ayzzy = bz2, если гб = 1пж, г; = 1п|/.
45. Решите уравнение с частными производными, введя новые независи-
независимые переменные гб, v:
а) azx + bzy = 0, если гб = ах + fo/, v = bx — ay;
б) г/2ж — ж^у = 0, если и = ж, г> = ж2 + ?/2;
в) ж^ж + г/^у = z, если гб = 4ж — 7г/, v = Sy/x.
46. Решите дифференциальное уравнение, введя новые переменные и, v, w,
где ^ = w(u, v):
а) ж^ж + (у + 1)% = 0, если ж = гб + v, у = г;/гг, ^ = гу/гг;
б) г/2;ж — xzy = B/ — x)z, если гб = ж2+^/2, v = l/x + l/y, w = \nz —
-х -у.
47. Преобразуйте дифференциальное уравнение, перейдя к новым пере-
переменным u,v,w, где w = w(u,v):
а) ж +?/ ^ж + жA + |/2)^ = — -ху, если w2 + v2 + ж2 - у2 = 0, ж =
У х
= г>?/, sin(^ — z) = щ
б) (жг/ + ^)^ж + A — y2)zy = ж + |/^, если и = yz — х, v = xz — у, w =
= ж?/-2;
в) (ж^жJ + (yzyJ = ^2^ж^у, если ж = гбе^, у = vew, z = wew.
48. Преобразуйте выражение 5 = (zxJ + (?уJ, приняв ж за функцию, а
гб = xz и г> = yz — за независимые переменные.
49. Введя новые независимые переменные, преобразуйте выражение:
а) В = (zxJ + (zyJ, если ж = рсо8^, у = psimp;
6)B = zxx+zyy, если x = pcos(p, у = psimp;
в) В = x2zxx+ 2xyzxy + y2zyy, если гб = 1пж, v = \ny;
г) В = x2zxx+ 2xyzxy+y2zyy, если x = pcos(p, у = psimp.
278 Гл. XI. Неявные функции и их приложения
50. Введя новые независимые переменные, преобразуйте уравнение:
a)zxx+Zyy=0, если и = — -, v=— -;
б) x2zxx — 2х sin уzxy + sin2 yzyy = 0, если u = xtg-, v = ж;
в) zxx + 2zxy + ?уу = 0, если и = х + z, v = у + z.
51. Решите уравнение, введя новые переменные u,v,w, где w = w(u,v):
а) ?жж — 2^жу + Zyy = 0, если и = х -\- у, xv = у, xw = 2;
б) zxx = a2Zyy, если и = у — ах, v = у + ах.
52. Преобразуйте уравнение xyRxy + yzRyz + xzRxz = 0, введя новые не-
независимые переменные гб, г>, ги по формулам ж = vw, у = гш;, z = гж.
53. Введя новые переменные и, v, w, где w = гу(гг, г;), преобразуйте уравне-
уравнение:
а) г/^у + 2zy = 2/ж, если уи = ж, v = x, w = xz — у;
б) ?жж + 2^жу + ?уу = 0, если и = х + у, v = х — у, w = ху — z;
в) zxx — 2zxy-\-A-\-y/x)zyy = 0, если и = х, v = x + y, w = х + у + z;
г) A — ж2)^жж + A — y2)zyy = xzx + г/^у, если ж = sini6, г/ = sinv,
+ X + |/ + 16=l, V — X + у — U =
= 0, ху — z = w.
54. Докажите, что вид уравнения zxxzyy = (^ЖуJ не меняется при любом
распределении ролей между переменными x,y,z.
55. Докажите, что уравнение zxx = zy не изменит своего вида при замене
( о Л
X 1 W \ X \ , v
переменных и=—, v = — -, 2= —ехр < —— >, где w = w(u,v).
У У у/У { ^У )
ГЛАВА XII
КРАТНЫЕ ИНТЕГРАЛЫ
§ 1. Двойные интегралы
Основные понятия и теоремы
1. Определение двойного интеграла. Пусть G — квадрируе-
мая (и, следовательно, ограниченная) область (открытая или замк-
замкнутая) на плоскости и пусть в области G определена ограниченная
функция и = /(М) = f(x,y). Разобьем область G на п квадрируемых
частей Gi (i = 1,2, ...,п) так, чтобы любые две части не имели общих
внутренних точек, в каждой части Gi возьмем произвольную точку
Mi(?i,rji) и составим сумму
г=1
где Asi — площадь G{. Эта сумма называется интегральной суммой
функции /(ж,у), соответствующей данному разбиению области G на
части Gi и данному выбору промежуточных точек М{.
Диаметром ограниченного множества G точек назовем точную
верхнюю грань расстояний между двумя произвольными точками
этого множества: sup p(M',M").
M'eG
M"eG
Пусть di — диаметр Gi, d = max d{.
Определение. Число / называется пределом интегральных сумм
I(Gi, Mi) при d —> 0, если \/е > 0 36 > 0 такое, что для любого разбие-
разбиения области G, у которого d < S, и для любого выбора промежуточных
точек Mi выполняется неравенство
Если существует lim I(Gi,Mi) = /, то он называется двойным интег-
ралом от функции /(ж, у) по области G и обозначается / / /(ж, у) dx dy
G
или / / f(M) ds, а функция /(ж, у) называется интегрируемой в облас-
G
ти G.
Теорема 1. Функция, непрерывная в замкнутой квадрируемой об-
области, интегрируема в этой области.
280
Гл. XII. Кратные интегралы
Теорема 2. Функция, ограниченная в квадрируемой области и не-
непрерывная всюду, кроме некоторого множества точек площади нуль*),
интегрируема в этой области.
Двойные интегралы обладают такими же свойствами, как и опре-
определенные интегралы (линейность, аддитивность, формулы среднего
значения и т. д.).
2. Вычисление двойных интегралов с помощью повторно-
повторного интегрирования. Пусть функция f(x,y) определена в области
Рис. 29 Рис. 30
G = {(х,у): a^x ^b, ух(х) ^ у ^ 2/2(я)}, где^(ж) и з/2(ж) — непре-
непрерывные функции на сегменте [а, Ъ] (рис. 29). Такую область G назовем
у-трапециевидной.
Теорема 3. Пусть:
1°) существует двойной интеграл f(x,y)dxdy;
G
2°) Vx G [а, 6] существует определенный интеграл
2/20)
0
= J
Тогда существует определенный интеграл
Ь Ь 2/2 (ж)
I(x)dx= dx / f(x,y)dy
а а у1(ж)
(он называется повторным) и справедливо равенство
Ъ 2/20)
JJ f(x,y)dxdy = Jdx J f(x,y)dy,
A)
т. е. двойной интеграл равен повторному.
Если область G является ж-трапециевидной (рис. 30), то при соот-
соответствующих условиях справедлива формула, аналогичная A):
*) Говорят, что множество точек плоскости имеет площадь нуль, если \/е > 0 су-
существует многоугольник, содержащий это множество и имеющий площадь, мень-
меньшую е (иными словами, если это множество можно заключить в многоугольник
сколь угодно малой площади).
§1. Двойные интегралы
281
JJf(x,y)dxdy =
f(x,y)dx.
B)
xi (у)
Область более сложного вида часто удается разбить на трапециевид-
трапециевидные части, к которым применима формула A) или B) (рис. 31).
3. Замена переменных в двойном интеграле. Рассмотрим
двойной интеграл f(x,y)dxdy. Замена переменных в двойном
G
интеграле состоит в переходе пе-
переменных х и у к новым перемен-
переменным и и v по формулам
х = ip(u,v),
у = ф(щу),
(u,v) е д.
C)
О
При этом каждая точка (ж, у) об-
области G соответствует некоторой
точке (и, v) области д, а каждая
точка (u,v) области д переходит в
некоторую точку (ж, у) области G
(рис. 32). Иными словами, когда
точка (и, v) "пробегает" область д, соответствующая ей точка (ж, у) =
= ((р(и,у),ф(и,у)) "пробегает" область G. Функции C) называют
Рис. 31
также отображением области д плоскости (u,v) на область G плос-
плоскости (х,у). Область G называется образом области д, а область д —
прообразом области G при отображении C).
Пусть отображение C) удовлетворяет следующим условиям.
I. Отображение C) взаимно однозначно, т. е. различным точкам
(u,v) области g соответствуют различные точки (х,у) области G.
П. Функции (p(u,v) и ip(u,v) имеют в области g непрерывные
частные производные первого порядка.
ID
и
Т/( ПР 7/1
III. Якобиан отображения ' =
во всех точках области g. \u^v)
отличен от нуля
282
Гл. XII. Кратные интегралы
Теорема 4. Пусть д и G — замкнутые квадрируемые области,
функция f(x,y) ограничена в области G и непрерывна всюду, кроме,
быть может, некоторого множества точек площади нуль, а отобра-
отображение C) удовлетворяет условиям I—III.
Тогда справедливо равенство
D(x,y)
D(u,v)
dudv.
D)
Формула D) называется формулой замены переменных в двойном
интеграле.
Замечание. Если условие I (взаимная однозначность отображения
C)) или условие III (отличие от нуля якобиана отображения) нарушается
на множестве точек площади нуль (например, в отдельных точках или на
отдельных кривых), то формула D) остается в силе.
4. Криволинейные координаты. Формулам C), которые рас-
рассматривались как отображение области g на область G, можно при-
придать другой смысл. Рассмотрим в области g отрезок прямой и = щ =
= const (рис. 33). В области G ему соответствует параметрически за-
заданная кривая
x = (p(uo,v), у = гр(ио,у), E)
где роль параметра играет переменная v. Точно так же отрезку пря-
прямой v = vq в области g соответствует в области G кривая
х = <p(u,v0), У = ф(и,у0),
F)
где роль параметра играет и. Точке (uo,vo) области g соответствует
некоторая точка Мо(хо,уо) области G(x0 = (p(uo,vo),yo = ())
Уп
О'
щ
и О х
Рис. 33
причем в силу взаимной однозначности отображения C) точке Mq
соответствует единственная точка (щ,Уо) области д, т. е. точка Mq
однозначно определяется парой чисел (uo,vo). Поэтому числа щ и г?о
можно рассматривать как координаты точки Mq (но уже не прямо-
прямоугольные, а какие-то другие), а кривые E) и F), на которых одна из
координат и или v постоянна, естественно назвать координатными
линиями v и и. Так как эти координатные линии представляют собой,
§1. Двойные интегралы
283
вообще говоря, кривые, то числа (щ,Уо) называются криволинейными
координатами точки Mq. При отображении C) сетка прямых коорди-
координатных линий в области g переходит в сетку кривых координатных
линий в области G (рис. 33). Итак, формулы C) можно рассматривать
как формулы перехода от прямоугольных координат (х,у) к новым,
криволинейным координатам (u,v) в области G.
Примером криволинейных координат являются полярные коорди-
координаты (p,ip), связанные с прямоугольными координатами (х,у)
формулами
х = р cos ip, у = psimp @^^<оо, 0 ^ ср < 2тг).
Иногда в качестве промежутка изменения ip берется промежуток
-тг < (р ^ тг. Якобиан перехода к полярным координатам имеет вид
дх дх
cos if —psimp
D(x1y)_ =
dp
ду
дер
ду
sin ip p cos cp
= p-
dp dip
5. Геометрические приложения двойных интегралов.
а) Площадь S квадрируемой области G на плоскости (ж, у) выра-
выражается формулой
S = JJdxdy. G)
G
Если G = {(ж,у): а ^ х ^ Ь, 0 ^у ^ f(x)} — криволинейная тра-
трапеция, то, сведя двойной интеграл G) к повторному, придем к из-
известному выражению площади криволинейной трапеции с помощью
определенного интеграла
ъ /О) ъ ъ
S = ffdxdy = fdx Г dy= f [y\f0(x)] dx = ff(x) dx.
G а о а а
Переходя в G) к новым переменным по формулам C), получим
выражение площади области G в криволинейных координатах
5 =
D(u,v)
dudv.
(8)
Величину ds = dx dy, представляющую собой площадь прямоуголь-
прямоугольника со сторонами dx и dy, естественно назвать элементом площади
в прямоугольных координатах х и у, а величину ds =
D(x,y)
dudv
D(u,v)
элементом площади в криволинейных координатах и и v. Модуль
' представляет собой коэффициент растяжения
якобиана
D(u,v)
площади в точке (и, v) при отображении области g плоскости (и, v)
на область G плоскости (х,у).
Если G — криволинейный сектор на плоскости (х,у), ограничен-
ограниченный лучами if = a, if = /3 и кривой р = р((р), где р и ip — полярные
284
Гл. XII. Кратные интегралы
координаты (рис. 34), то, переходя в формуле G) к полярным коорди-
У1
О
р=р(<р)
{{
T
|
Рис. 34 Рис. 35
D(x,y) u ч д
натам, учитывая, что —; ; = р, а д = \(р,т): а^(р^р,0^р^
D(p,(p)
^ у^((^)}, и сводя двойной интеграл к повторному, получаем извест-
известное выражение площади криволинейного сектора через определенный
интеграл
5 =JJdxdy = jjpdpdif = j dtp j pdp = Л у \dip = -j p2{(p)d(p.
G 9 ос о а'-0-' а
б) ОбъемУ тела Г = {(ж, ?/, z): (x,y) G G, 0^z^/(x,?/)} (рис. 35),
где G — квадрируемая замкнутая область, a f(x,y) — непрерывная
неотрицательная в области G функция, выражается формулой
(9)
V = Jjf(xJy)dxdy.
6. Физические приложения двойных интегралов. Пусть
G — материальная бесконечно тонкая пластинка (квадрируемая об-
область на плоскости Оху) с плотностью р(х,у). Тогда справедливы
следующие формулы:
а) m = p(x,y)dxdy — масса пластинки;
б) Мх = yp(x,y)dxdy, My = xp(x,y)dxdy — статические
G G
моменты пластинки относительно осей Ох и О у,
ч My Мх
в) хо = —-, уо = — координаты центра тяжести пластинки;
m m
г) Ix = у2р(х, у) dx dy, Iy = х2р(х, у) dx dy — моменты инер-
G G
ции пластинки относительно осей Ох и Оу;
д) /0 = 1Х + 1у = / / (ж2 + у2)р(х, у) dx dy — момент инерции плас-
G
тинки относительно начала координат.
§1. Двойные интегралы 285
Контрольные вопросы и задания
1. Что такое интегральная сумма? Составьте интегральную сумму функ-
функции /(ж, у) = ж2 + у2, соответствующую разбиению области G = {(ж, 2/):
а ^ ж ^ 6, с ^ ?/ ^ с/} на прямоугольники Gij = {(ж, 2/) : Жг-i ^ ж ^
^ ж;, г/j-i ^ у ^ 2/j} (а = жо < Ж1 < ... < хп = 6, с = г/о < 2/1 < •••
• •• < 2/m = d) и выбору левых верхних вершин этих прямоугольников в
качестве промежуточных точек.
2. Что называется диаметром ограниченного множества точек? Чему ра-
равен диаметр: а) квадрата со стороной 1; б) области, ограниченной
о о
эллипсом — Н—- = 1 (а> ЪI
а1 Ь2
3. Дайте определение предела интегральных сумм и двойного интеграла.
Докажите, что неограниченная в области функция не интегрируема в
этой области.
4. Сформулируйте теорему об интегрируемости непрерывных функций.
Верно ли утверждение: непрерывная в открытой квадрируемой области
функция интегрируема в этой области?
5. Сформулируйте теорему об интегрируемости некоторых разрывных
функций (теорему 2). Для каких областей (открытых, замкнутых) вер-
верна эта теорема?
6. Напишите формулы, выражающие линейность и аддитивность двойных
интегралов.
7. Сформулируйте теорему о формуле среднего значения для двойного ин-
интеграла, аналогичную теореме для определенного интеграла.
8. Сформулируйте теорему о сведении двойного интеграла к повторному
по формуле A) (теорему 3) и аналогичную теорему о сведении двойного
интеграла к повторному по формуле B).
9. Сведите двойной интеграл / / /(ж, у) dx dy к повторному двумя способа-
G
ми, если G — круг, ограниченный окружностью (ж — IJ + (у — 2J = 25.
10. Напишите формулы перехода к новым переменным в двойном интег-
интеграле и сформулируйте условия I—III, которым должно удовлетворять
отображение.
11. Используя теорему о неявных функциях, докажите, что в силу усло-
условия III некоторая окрестность произвольной точки (uo,vo) области д
взаимно однозначно отображается на некоторую окрестность точки
(жо,2/о) = (<p(v>o,vo),ip(uo,vo)) области G, т. е. локально из условия III
следует условие I. Следует ли в целом (т. е. для всей области д) из усло-
условия III условие I? (Рассмотрите пример: ж = и cos v, у = и sin v, 1 ^ и ^ 2,
0 ^ v ^ 4тг.)
12. Изобразите на плоскости (ж, у) образ прямоугольника д = {(р,ср): 0 ^
^р^1, 0 ^ (р < 2тг} при отображении х = р cos ср, у = р sin ср. Является
ли это отображение взаимно однозначным?
13. Сформулируйте теорему о замене переменных в двойном интеграле.
14. Что такое криволинейные координаты? Изобразите на плоскости (ж, у)
координатные линии полярных координат р и ср.
15. Напишите формулы для вычисления площади плоской фигуры с по-
помощью двойного интеграла. Получите из этих формул выражения пло-
площадей криволинейной трапеции и криволинейного сектора с помощью
определенного интеграла. Что такое элемент площади в прямоугольных
и криволинейных координатах? Каков геометрический смысл якобиана
отображения?
286
Гл. XII. Кратные интегралы
16. Напишите формулу для вычисления объема тела с помощью двойного
интеграла.
17. Напишите формулы для вычисления координат центра тяжести и мо-
моментов инерции материальной плоской пластины.
Примеры решения задач
1. Свести двойной интеграл f(x,y)dxdy к повторному двумя
G
способами (по формуле A) и по формуле B)), если G — область, огра-
ограниченная кривыми ж = 1, у = ж2, у = 2х (ж ^ 1).
Л I способ. Область G изображена на рис. 36, а. При каждом зна-
значении х из отрезка [0,1] перемен-
переменная у изменяется от х2 до 2ж, т. е.
область G можно представить в
виде G = {(ж,у): 0 ^ х ^ 1, х2 ^
^ у ^ 2х}. По формуле A) полу-
О
чаем
2х
dx dy =
> у)
Рис. 36
II способ. Чтобы воспользо-
воспользоваться формулой B), нужно раз-
разбить область G на две части, G\
и G2, как показано на рис. 36, б.
В области G\ переменная у изменяется от 0 до 1, а при каждом значе-
значении у переменная х изменяется от у/2 (значение х на прямой у = 2х)
до у/у (значение х на параболе у = ж2). Поэтому по формуле B) полу-
получаем _
1 у/У
JJ /(ж, у) dx dy = Jdy J /(ж, у) dx.
Gx 0 у/2
В области G2 переменная у изменяется от 1 до 2, а при каждом
значении у переменная ж изменяется от у/2 до 1. По формуле B)
имеем 2 1
тт
Итак,
G
jj /(ж, у) dx dy = jdy j /(ж, у) dx.
G2 1 y/2
= jj f(x,y)dxdy+ jj f(x,y)dxdy =
Gi G2
1 у/У 2 1
= jdy j /(ж, у) dx + уф у /(ж, ^/) б?ж. А
О у/2 1 у/2
2. Вычислить двойной интеграл (x-\-y2)dxdy по области G,
§1. Двойные интегралы
287
ограниченной кривыми у = ж и у = ж2.
Л Область G изображена на рис. 37. Сводим двойной интеграл к
повторному по формуле A):
1 х
ГГ(х + у2) dxdy = Jdxj(x + у2) dy.
G 0 Х2
Вычисляем внутренний интеграл в повторном,
пользуясь формулой Ньютона-Лейбница:
X 0 1
о Z о J- R
— х ж ж .
х2 3 3
; + y2)dy = (ж?/ + -2/3J
Теперь вычисляем повторный интеграл:
Л1 2 2 з 1
1
Рис. 37
3. Изменить порядок интегрирования в повторном интеграле
2 V2~F
I = Jdx J f(x,y)dy.
А Кривые у = л/2ж — ж2, 2/ = л/2ж и отрезок прямой ж = 2 ограни-
ограничивают область G, изображенную на рис. 38, а. Данный повторный
1 -
о
Рис. 38
интеграл равен двойному интегралу по этой области. Чтобы изменить
порядок интегрирования в повторном интеграле, нужно разбить об-
область G на три части, как показано на рис. 38, б. Кривая у = л/2ж - х2
является верхней полуокружностью окружности (х — IJ + у2 = 1.
Разрешая это уравнение относительно ж, получим два решения: х =
= 1 ± л/l — у2. В областях G\ и G^ переменная у изменяется от 0 до
1, а при каждом значении у переменная х изменяется в области G\
от у2/2 (значение х на кривой у = л/2х) до 1 - ^/1 - у2 (значение х
на окружности), а в области G2 — от 1 + ^/1 - у2 до 2. Поэтому по
288
Гл. XII. Кратные интегралы
формуле B) получаем
[Г /(ж, у) dx dy + Г Г /(ж, у) dx dy = f dy Г /(ж, у) dx +
1 1 l-^/l-y2 2 -,
+ /ф J 2f(x,y)dx = Jdy\ J f(x,y)dx+ J f(x,y)dx\.
0 1+ A_ 2 0 ^ ^2/2 1+ A_ 2
Аналогично для области G3 имеем
2 2
УУ /(ж, у) dx dy = ydy J f(x, y) dx.
G3 1 2/2/2
Таким образом, окончательно находим
1 l-y7!-?/2 2
fff(x,y)dxdy=fdy\ j f(x,y)dx+ j f(x,y)dx\
G
у f(x,y)dx.
4. В двойном интеграле / = / / (ж2 + у2) dx dy, где G — круг, огра-
G
ничейный окружностью х2 + у2 = 2ж, перейти к полярным координа-
координатам с полюсом в точке 0@,0) и вычислить полученный интеграл.
2тг
О" 1 Р
г
Рис. 39
Л Круг G изображен на рис. 39, а. Уравнения, связывающие (х,у) и
полярные координаты (р,(р) с полюсом в точке 0@,0), имеют вид
х = pcostp, у = ps'mtp, A0)
причем наглядно видно, что в качестве промежутка изменения ip
можно взять сегмент —тг/2 ^ ip ^ тг/2. Подставляя выражения A0)
в уравнение окружности, получим р2 = 2pcos(p, откуда р = 0 или
§1. Двойные интегралы 289
р = 2 cos if. Эти две кривые на плоскости (р,(р) при —тг/2 ^ <р ^ тг/2
ограничивают область g (рис. 39, б), являющуюся прообразом об-
D(x у)
ласти G при отображении A0). Якобиан ; \ отображения A0)
D(p,<p)
D(x у)
равен р. Отметим, что —; ' ' = 0 на границе р = 0 области д. одна-
ко формула D) замены переменных применима (см. замечание после
теоремы 4). Подынтегральная функция х2 + у2 в новых переменных
равна р2. По формуле D) имеем
/ = / ( р3 dp dip.
9
Полученный двойной интеграл по области д сводим к повторному:
тг/2 2 cos с/?
1= f dip I p3dp, A1)
-тг/2 О
и вычисляем повторный интеграл, применяя формулу Ньютона-
Лейбница:
тг/2
I =
-тг/2
-тг/2 -тг/2
-тг/2
/3 1 \ "/2
= - ip + sin 2ip + - sin 4(p
V z о /
Замечание 1. Расстановку пределов интегрирования в повторном ин-
интеграле A1) можно произвести, рассматривая не область д, а изменение
полярных координат в исходной области G. На рис. 39, в видно, что при
каждом значении ip из промежутка [—тг/2, тг/2] переменная р изменяется
от 0 (значение р в полюсе) до 2 cos ip (значение р на окружности, уравнение
которой в полярных координатах имеет вид р = 2 cos ip). Таким образом,
пределы интегрирования по ip — от —тг/2 до тг/2, а по р — от 0 до 2 cos ip.
Замечание 2. Обычно замена переменных в двойном интеграле про-
производится с целью упрощения области интегрирования. Если в данном при-
примере перейти к полярным координатам с полюсом не в точке 0@,0), а в
точке АA, 0) (центре круга), т. е. по формулам х — 1 = рcos ip, у = psimp, то
прообразом круга G окажется прямоугольник (наиболее простая область)
а = {(p,ip): O^p^l, 0 ^ ip ^ 2тг} (рис. 39, г). Выражение для подын-
подынтегральной функции примет вид х2 + у2 = 1 + 2pcos ip + p2. В этом случае,
используя формулу D) и сводя двойной интеграл к повторному, получим
(J
= JdipJ(p + 2р2 cos ip + ps)dp = J (д + - cos ip) dip = - тг.
0 0 0
10 В.Ф. Бутузов и др.
290
Гл. XII. Кратные интегралы
5. Вычислить двойной интеграл / = х2у2 dx dy, где G = {(ж, у):
1^х2+у2 ^4}. G
Л Область G представляет собой кольцо (рис. 40, а). Его можно раз-
разбить на трапециевидные части, к которым применима формула све-
сведения двойного интеграла к повторному, например так, как пока-
1 2
б
Рис. 40
зано на рис. 40, а. Однако удобнее сделать замену переменных —
перейти к полярным координатам: х = pcostp, у = psimp, 0 ^ (р ^ 2тг.
При этом отображении прообразом кольца является прямоугольник
д = {(^ ф); 1 ^ р^2, 0 ^(р ^ 2тг} (рис. 40, б). Применяя формулу D)
и сводя двойной интеграл к повторному, получаем
2 2тг
/ = dp I ръ sin2 ip cos2 ip dip — \ p5dp / -
63 7Г 217Г
10 10
6. Найти площадь фигуры G, ограниченной кривой
(а + б)' =
(а > О, Ь>0). A2)
Л Так как левая часть уравнения кривой неотрицательна при любых
х и у, то и правая часть должна быть неотрицательной, а значит, х иу
должны иметь одинаковые знаки. Следовательно, кривая расположе-
расположена в I и III квадрантах, причем она симметрична относительно начала
координат. В самом деле, если точка М(х,у) лежит на кривой, т. е.
х и у удовлетворяют уравнению A2), то -х и —у также удовлетво-
удовлетворяют этому уравнению, т. е. точка М'{—ж, —у), симметричная точке
М относительно начала координат, также лежит на кривой. Поэтому
и вся фигура G состоит из двух частей, симметричных друг другу
относительно начала координат. Найдем площадь Si части фигуры,
расположенной в I квадранте. Для этого удобно перейти к новым пе-
переменным — обобщенным полярным координатам. Они вводятся по
формулам
х - х0 = арр cosa ip, у - уо = bpp sma р, A3)
§1. Двойные интегралы 291
где ж0, ?/о, «, Ь, а, /3 — некоторые числа, выбираемые в каждом кон-
конкретном случае из соображений удобства. Якобиан отображения A3)
равен aba/3p2f3~1 sin" ip cosa~1 ip.
В данном случае удобно взять жо = уо = 0, а = 2, C = 1. Тогда
левая часть уравнения A2) будет равна рА и уравнение примет вид
р4 = 4abp2 cos2 ip sin2 cp,
откуда р = 0 или р = 2y/ab sin ip cos ip, причем 0 ^ ip ^ тг/2 (I ква-
квадрант). Кривые р = 0 и р = 2y/ab sin ip cos ip @ ^ cp ^ тг/2) на плос-
плоскости (/я, (р) ограничивают область д — прообраз части фигуры G,
лежащей в I квадранте. Якобиан отображения A3) в данном случае
равен 2abp sin ip cos ip. По формуле (8) получаем
тг/2 2\/a6sin cp cos cp
Si = / / 2afy? sin (^ cos ip dp dip = dip / 2а6/? sin ^ cos ipdp =
p oo
тг/2 тг/2
= 4а2 б2 / sin3 ip cos3 ipdip = 4a2 b2 / sin3 (^ A - sin2 ф) d(sin ф) =
a2b2
2
Искомая площадь фигуры G равна 2Sb т. е. -a2b2. A
7. Найти объем тела Г, ограниченного поверхностями z = 0, г =
= х2 + 2/2, у = ж2, 2/ = 1.
Л Данное тело можно представить в виде Т = {(x,y,z): (x,y) G G,
О ^ z ^ ж2 + 2/2}, где G — область на плоскости (х,у), ограниченная
кривыми у = х2 и у = 1, т. е. G = {(ж,2/) : -1 ^ ж ^ 1, ж2 ^ у ^
^ 1}. Применяя формулу (9) и сводя двойной интеграл к повторному,
получим
1 1
V = ГГ(х2+y2)dxdy = fdx Г(х2+y2)dy =
-1
-1
8. Найти моменты инерции 1Х и /у относительно осей Ох и О^/
пластины с плотностью р = 1, ограниченной кривыми ж^/ = 1, ху = 2,
у = 2х, х = 2у и расположенной в I квадранте.
Л Данная пластинка G изображена на рис. 41. По формулам для 1Х и
1У имеем
1Х = у2 dxdy, Iy = х2 dx dy.
G G
Чтобы свести каждый из этих двойных интегралов к повторному,
нужно область G разбить на три части. Удобнее перейти к поляр-
полярным координатам: ж = рcos ip, у — ps'vmp. Тогда ip изменяется от
ю*
292
Гл. XII. Кратные интегралы
= arctg- до ц>2 = arctg2 (см. рис. 41), а при каждом значении ip
из сегмента [(^1,(^2] переменная р изме-
изменяется от pi(cp) = = (значение
V sin cp cos ср \
р на кривой ху = 1, уравнение которой
в полярных координатах в I квадранте
1 \
имеет вид р = — ) до р2{ф) —
у/sin (p cos (p J
= — (значение р на кривой ху =
V sin (p cos 9?
= 2). Следовательно,
О
Рис. 41
Ix =
Ч1 ()
= dcp / /?3 sin2 (pdp =
dip
?2= arctg 2
i= arctg \
Аналогично получаем Iy = -. A
Задачи и упражнения для самостоятельной работы
1. Сведите двойной интеграл / / /(ж, ^/) с?ж dy к повторному двумя способа-
способами, если: g
а) G — треугольник с вершинами A,1), D,1), D, 4);
б) G — треугольник с вершинами B,1), E, 2), C, 7);
в) G — область, ограниченная кривыми у = Зж2, у = 6 — Зж;
г) G — круг ж2 + у2 ^ 2ж — Ау + 4;
д) 6г — треугольник со сторонами, лежащими на прямых у = 2ж, у = Зж,
х = 4;
е) 6г — трапеция с вершинами (—1, 4), E, 4), A,1), D,1);
ж) G — трапеция с вершинами (—2, 0), @, 6), @, 3), (—1, 0);
з) G — трапеция с вершинами (-2, 3), @, 6), C, -3), @, -3);
и) G — кольцо 1 ^ (ж - IJ + у2 ^ 4;
к) G — область, ограниченная кривыми ж2 — 2ж + у2 = 0 и ж2 — 2ж +
+ у2 - 1у = 2.
2. Измените порядок интегрирования в повторных интегралах:
1 Щ е2 In ж2 2 2х
a) jdy j f(x,y)dx; б) jdx j f(x,y)dy; в) jdx jf(x,y)dy;
0 i 0
1 1 —Ж
г) у с/ж J f(x,y)dy; д)
In ж
0
f(x,y)dx;
G
= 6 - Зж;
§1. Двойные интегралы 293
1/2 у/2-х 1 -л/Г^Р"
е) I dx I f(x,y)dy; ж) I dy I f(x,y)dx.
3. Вычислите двойные интегралы:
a) // (x — У) dx dy, где G — треугольник с вершинами A,1), D,1), D, 4);
G
xdxdy, где G — область, ограниченная кривыми у = Зж2, у =
G
3 — Зж;
в) / / 2\х\ dx dy, где G — трапеция с вершинами (—1, 4), E, 4), A,1), D,1).
G
4. Перейдите к полярным координатам в двойном интеграле / //(ж, у) dxdy
и сведите его к повторному двумя способами, если: g
a) G — круг х2 + у2 ^ а2; б) G — круг х2 + у2 ^ 2г/;
в) С? — кольцо а2 ^ ж2 + у2 ^ б2;
г) G — область, ограниченная кривой (ж2 + у2J = а2(ж2 — у2), ж ^ 0;
д) G — треугольник со сторонами, лежащими на прямых ж = 0, у = 0,
у = 1 — х;
е) G — область, ограниченная кривыми ж2 = ш/, у = а (а > 0).
5. В следующих интегралах перейдите к полярным координатам, а затем
сведите интеграл к повторному двумя способами:
1 х 2 л/Зу 1 Vl-ж2
a) Jdxjf(x, у) dy; б) ^ / /(ж2 + ?/2) cb; в) ^ж / /(ж,
О Ж2 О У 0 1-х
6. Перейдите к новым переменным и, v в интеграле:
3 3-у
a) dy /(ж + у,х — у) dx, если и = х + у, v = х — у;
О 2
О 2-у
3 4ж
', = X, V = —.
X
2 Зж
3 4ж
dx f(-) dy, если и = х,
7. Докажите, что замена переменных х + у = и, у = uv переводит тре-
треугольник, стороны которого лежат на прямых ж = 0, у = 0, у = 1 — ж, в
квадрат {(и, v): 0 ^ и ^ 1, 0 ^ v ^ 1}.
8. Найдите замену переменных ж = ж(гб, v), у = y(u,v), при которой об-
область G, ограниченная кривыми ху = 1, жг/ = 4, ж — 2^/ — 2 = 0, ж —
— 2^/ + 1 = 0 (ж > 0, у > 0), является образом прямоугольника, стороны
которого параллельны осям координат на плоскости (и, v).
9. Вычислите двойные интегралы, введя обобщенные полярные координа-
координаты: J
Г Г I 2 2~
а) /м/1 — ^-т — т^т dx dy, где G — область, ограниченная эллипсом
У У V or tr
G
dxdy, где G — область, ограниченная кри-
294 Гл. XII. Кратные интегралы
/х — 1 /у + 1
выми ж = 1, у = — 1, л / Ь л / = 1;
в) xdxdy и х2 dxdy, где G — область, ограниченная астроидой
10. Вычислите двойные интегралы:
а) xdxdy, где G — область, ограниченная кривой ж2 + ?/2 = 4ж —
— 2^ + 4;
б) [[ (\х\ + М)^жс^/, гДе <2 = {(ж, 2/): |ж| + \у\ ^ 1};
G
в) JJxydxdy, где G = {(ж,?/): ж4 + ?/4 ^ 1};
G
г) (x + y)dxdy, где G — область, ограниченная кривыми у2 = 2ж,
G
х + у = 4, х + у = 12.
11. Найдите площадь фигуры, ограниченной кривыми:
а)ху = а2, х + у = 2,Ьа (а > 0); б) Bж - ЗуJ + ж2 = 3;
в) ху = а2, ху = 2а2, у = ж, у = 2х (ж > 0, г/ > 0).
12. Введя полярные координаты, найдите площадь фигуры, ограниченной
кривыми:
а) (ж2 + ?/2J = -2а2(ж2 - у2), х2 + у2 = а2 (ж2 + у2 ^ а2);
б) (ж2 + у2J = 8а2ху, х2 + у2 = а2 (а > 0, ж2 + у2 ^ а2).
13. Введя обобщенные полярные координаты, найдите площадь фигуры,
ограниченной кривыми:
2 2> (ж-3J (?/ + 2J = ж «
"Ж +^'Г^ g + 4 3 2'
д) у/х - 1 + у/у + 1 = л/2, ж = 1, г/=-1.
14. Вычислите объем тела, ограниченного поверхностями:
а) г = 1пA + ж2
б) z = sin
в) г = ж?/, ж2 =у, ж2 = 2j/, j/^ = ж, J/* = 2ж, ^ = 0.
15. Найдите координаты центра тяжести однородной пластинки, ограни-
ограниченной кривыми:
а) ж + у = 4, |/ = 0,5ж ; б) + = — + -;
в) (ж2 + у2J = 2а?'ху (ж > 0, у > 0).
16. Найдите координаты центра тяжести круглой пластинки {(х,у): х2 +
+ у2 ^ а2}, если ее плотность в точке М(х,у) пропорциональна рас-
расстоянию от точки М до точки А(а,0).
17. Найдите моменты инерции 1Х и 1У относительно осей Ох и Оу одно-
однородной пластинки с плотностью р = ро, ограниченной кривыми:
а) ж = 0, у = 0, ж = a, j/ = Ь (а > 0, Ь > 0);
б) |/ = 0, у = х, у = 2 — ж;
в) (ж — аJ + (у — аJ = а2, ж = 0, у = 0, @ ^ ж ^ а);
2. Тройные интегралы 295
18. Найдите моменты инерции 1Х и 1У относительно осей Ох и Оу плас-
пластинки с плотностью р = ху, ограниченной кривыми:
а)ж = 0, у = 0, х = а, у = Ь (а > 0, &>0); б) у = 0, ?/ = ж, j/ = 2 - х.
19. Шар радиуса а погружен в жидкость постоянной плотности р, причем
центр шара находится на расстоянии h от уровня жидкости и h ^ а.
Найдите силы давления рв и рн на верхнюю и нижнюю полусферы
этого шара.
20. Докажите, что если в плоскости, где расположена пластинка G массы
т, взяты две параллельные оси ж и ж7 на расстоянии а друг от друга,
причем первая из них проходит через центр тяжести пластинки G,
то моменты инерции пластинки G относительно этих осей связаны
соотношением 1Х< = 1Х + та2.
§ 2. Тройные интегралы
Основные понятия и формулы
1. Определение тройного интеграла. Основные понятия и тео-
теоремы для тройных интегралов аналогичны соответствующим поня-
понятиям и теоремам для двойных интегралов. Пусть Г — кубируемая
область (открытая или замкнутая) в трехмерном евклидовом про-
пространстве и пусть в области Т определена ограниченная функция
u = f(M) = f(x,y,z). Разобьем область Т на п кубируемых час-
частей Т{ (i = l,2,...,n) так, чтобы любые две части не имели общих
внутренних точек, в каждой части Г^ возьмем произвольную точку
Mi(^i,T]iXi) и составим интегральную сумму
где AVi — объем Г«.
Пусть di — диаметр Tf, d = max di.
Определение. Число / называется пределом интегральных сумм
I(Ti, Mi) при d —> 0, если \/е > 0 36 > 0 такое, что для любого разбие-
разбиения области Г, у которого d < S, и для любого выбора промежуточных
точек Mi, выполняется неравенство
\I(ThMi)-I\<s.
Если существует lim I(Ti,Mi) = /, то он называется тройным ин-
тегралом от функции f(x,y,z) по области Т и обозначается
f(x,y,z)dxdydz или f(M)dV, а функция f(x,y,z) называ-
т т
ется интегрируемой в области Т.
Теорема 5. Функция, непрерывная в замкнутой кубируемой об-
области, интегрируема в этой области.
Теорема 6. Функция, ограниченная в кубируемой области и не-
непрерывная всюду, кроме некоторого множества точек объема нуль,
интегрируема в этой области.
296
Гл. XII. Кратные интегралы
Тройные интегралы обладают такими же свойствами, как опре-
определенные и двойные интегралы (линейность, аддитивность, формулы
среднего значения и т. д.).
2. Вычисление тройных интегралов с помощью повторно-
повторного интегрирования. Пусть функция f(x,y,z) определена в области
Г = {(x,y,z): (x,y) e G,
z1(xJy) ^ z ^ z2(x,y)},
где zi(x,y) и z2(x,y) —
непрерывные функции в
квадрируемой области G
(рис. 42).
Теорема 7. Пусть:
1°) существует трой-
тройной интеграл
JJJf(x,y,z)dxdydz;
т
2°) \/(х,у) G G сущест-
существует определенный интег-
интеграл
ь
Рис. 42
I(x,y) = J f(x,y,z)dz.
Тогда существует двойной интеграл zi\x^y)
I(x,y)dxdy= dxdy / f(x,y,z)dz
A)
G G Zl(x,y)
(он называется повторным) и справедливо равенство
ffff(x,y,z)dxdydz=ffdxdy Г f(x,y,z)dz,
Т G Zl(x,y)
т. е. тройной интеграл равен повторному.
Если область G является ^-трапециевидной (см. рис. 42), т. е.
G = {(ж,у) : а ^ х ^ b, yi(x) ^ у ^ у<±(%)}, то двойной интеграл
I(x,y) dxdy в свою очередь можно свести к повторному:
G Ъ У2(х) Ъ У2(х) z2(x,y)
ffl(x,y)dxdy = fdx Г I(x,y)dy = fdx Г dy Г f(x,y,z)dz.
G а У1(х) а yi(x) zi(x,y)
Таким образом, вычисление тройного интеграла сводится в этом слу-
случае к последовательному вычислению трех определенных (однократ-
(однократных) интегралов:
Ъ У2(х) z2(x,y)
Ifff(x,y,z) dxdy dz = fdx f dy f f(x,y,z)dz.
T a yi(x) Zl(x,y)
2. Тройные интегралы
297
В формуле A) повторный интеграл представляет собой двойной
интеграл, а внутренний интеграл в повторном является определен-
определенным интегралом. Возможно и иное сведение тройного интеграла к
повторному, когда повторный
интеграл представляет собой
определенный интеграл, а внут-
внутренний интеграл в повторном
является двойным интегралом.
Пусть функция f(x,y,z) оп-
определена и ограничена в облас-
области Т, которая заключена меж-
между плоскостями х — а и х — Ь,
причем каждое сечение области
Т плоскостью х = const (a ^
^ х ^ Ь) представляет собой квадрируемую фигуру G(x) (рис.43).
Теорема 8. Пусть:
1°) существует тройной интеграл f(x,y,z)dxdydz;
т
2°) \/х Е [а, Ь] существует двойной интеграл
f(x,y,z)dydz.
Рис. 43
= JJ
G(x)
Тогда существует определенный интеграл
ъ ъ
I(x)dx= dx // f(x,y,z)dydz
()
G(x)
(он называется повторным) и справедливо равенство
ъ
i У>z) dx dV dz = fdx ff Яж> 2/»z) dV dz-
3. Замена переменных в тройном интеграле. Аналогично
случаю двойного интеграла замена переменных в тройном интегра-
интеграf(x,y,z)dxdydz состоит в переходе от переменных ж, у, z к
т
ле
новым переменным и, v, w по формулам
х = ip(u,v,w), y = ip(u,v,w), z = x(u?v?w)? (u,v,w)€t. C)
При этом каждая точка (ж, у, z) области Т соответствует по формулам
C) некоторой точке (u,v,w) области г, а каждая точка (u,v,w) облас-
области т переходит в некоторую точку (x,y,z) области Т. Иными слова-
словами, функции C) осуществляют отображение области т пространства
(u,v,w) на область Т пространства (x,y,z). Пусть отображение C)
удовлетворяет таким же условиям, как и в § 1.
298
Гл. XII. Кратные интегралы
I. Отображение C) взаимно однозначно.
П. Функции if(u,v,w), гр(и,у,ъи) и x(u,v,w) имеют в области г
непрерывные частные производные первого порядка.
III. Якобиан отображения
отличен от нуля в области т.
D(u,v,w)
Теорема 9. Пусть г и Т — замкнутые кубируемые области,
функция f(x,y,z) ограничена в области Т и непрерывна всюду, кроме,
быть может, некоторого множества точек объема нуль, а отобра-
отображение C) удовлетворяет условиям I—III.
Тогда справедливо равенство (формула замены переменных в трой-
тройном интеграле)
/, z) dxdy dz =
= ffff(^(u, v, w),ip(u, v, w),x(u, v, w))
D(x,y,z)
D(u, v, w)
dudv dw.
Замечание. Формула замены переменных остается в силе, если усло-
условия I и III нарушаются на множестве точек объема нуль.
4. Криволинейные координаты. Формулы C) можно рассмат-
рассматривать как формулы перехода к новым, криволинейным координатам
(u,v,w) в области Т. Поверхности и = const, v = const и w = const
представляют собой координатные поверхности (вообще говоря, кри-
криволинейные) в пространстве (x,y,z). Кривые, на которых две кри-
криволинейные координаты имеют постоянные значения и изменяется
только одна из координат, представляют собой координатные линии.
Рассмотрим два примера наиболее употребительных криволиней-
криволинейных координат.
Цилиндрические координаты. Пусть M(x,y,z) — произвольная
точка в пространстве (x,y,z), М' — проекция точки М на плоскость
(х, у) (рис. 44). Точка М однозначно задает-
задается тройкой чисел (p,(p,z), где (р,(р) — по-
полярные координаты точки М' на плоскос-
плоскости (х,у), z — аппликата точки М. Тройка
чисел (р, if, z) называется цилиндрическими
координатами точки М. Переход от прямо-
прямоугольных координат (x,y,z) к цилиндричес-
цилиндрическим (/о,
У
задается формулами
М'(здО)
х = р cos if, у = psimp, z = z
@^р<+оо, 0^(?<2тг, -оо<2:<+оо).
Рис. 44 D)
(Иногда в качестве промежутка изменения if берется промежуток
2. Тройные интегралы
299
-тг <
тг.) Якобиан отображения D) есть
D(p,<p,z) P'
Координатная поверхность р = const представляет собой цилиндри-
цилиндрическую поверхность — отсюда и название "цилиндрические коор-
координаты".
Сферические координаты. Пусть M(x,y,z) — произвольная точка
в пространстве (x,y,z), М' — проекция точки М на плоскость (х,у)
(рис. 45). Точка М однозначно задается трой-
тройкой чисел (г, 0,(р), где г — расстояние точ-
точки М от точки О (начала координат), 0 —
угол между лучами ОМ и Oz, ip — полярный
угол точки М' на плоскости (ж, у). Тройка чи-
чисел (г, в, ср) называется сферическими коорди-
координатами точки М. Переход от прямоугольных
координат (x,y,z) к сферическим (г,в,ср) за-
задается формулами
M(x,y,z)
х — г sin в cos (р, у = г sin в sin (p, z — т cos в
М'(здО)
Рис. 45
(Иногда в качестве угла в берется угол между лучами ОМ и ОМ' со
знаком плюс, если z > 0, и со знаком минус, если z < 0. В этом случае
—тг/2 ^ 0 ^ тг/2, а в формулах E) нужно заменить sin# на cos#, a
на
Якобиан отображения E) есть
= г2 sin в (в случае второго
D(r,0,<p)
способа выбора угла в якобиан равен r2cos#). Координатная поверх-
поверхность г = const > 0 представляет собой сферу — отсюда и название
"сферические координаты".
Иногда используются так называемые обобщенные сферические
координаты. Они связаны с прямоугольными координатами (x,y,z)
формулами
х — хо = arn sina в cos^ ср, у — уо = Ьтп sina p,
z - zo = crn cosa в
@ ^ г < +оо, (К#^7г, 0^(^< 2тг),
где ж0,2/о, ^о, «, 6, с, п,а, /3 — некоторые числа, выбираемые в каждом
конкретном случае из соображений удобства.
Якобиан перехода к обобщенным сферическим координатам имеет
вид
-1 sin2^1 в cos^1 Osin
1
(р.
F)
300 Гл. XII. Кратные интегралы
5. Вычисление объемов с помощью тройных интегралов.
Объем V кубируемой области Т (кубируемого тела) в пространстве
(x,y,z) выражается формулой
V = HUxdydz. G)
т
Если Г = {(ж, з/, я): (х,у) е G, 0 ^ z ^ /(ж, 2/)}, где G — квадрируе-
мая область на плоскости (х,у), a f(x,y) — непрерывная в области G
функция (см. рис. 35), то, сводя тройной интеграл к повторному, при-
придем к формуле (9) из § 1, выражающей объем тела Т через двойной
интеграл:
f(x, у)
V = JJdxdy I dz = JJ[z\f0^y)]dxdy = JJf(x,y)dxdy.
GOG G
Если область Т заключена между плоскостями х = аих = Ьи
каждое сечение области Т плоскостью х = const представляет собой
квадрируемую фигуру G(x) с площадью S(x) (см. рис. 43), то, сводя
тройной интеграл G) к повторному по формуле B) и учитывая, что,
dydz = 5(ж), придем к известному выражению объема тела с
G(x)
помощью определенного интеграла:
ъ ъ
V = Ux И dydz = /S(x) dx. (8)
a G(x) a
Переходя в равенстве G) к новым переменным и, v, w по фор-
формулам C), получим выражение объема области Т в криволинейных
координатах:
JJJ \D(u,v,w)
dudvdw.
Величину dV = dxdydz, представляющую собой объем прямоуголь-
прямоугольного параллелепипеда с ребрами dx, dy и dz, естественно называть
элементом объема в прямоугольных координатах ж, у, z, а величину
dV =
D(x,y,z)
D(u, v, w)
du dv dw — элементом объема в криволинейных ко-
координатах и, v, w. Модуль якобиана
представляет собой
D(u, v, w)
коэффициент растяжения объема в точке (u,v,w) при отображении
области г пространства (u,v,w) на область Т пространства (x,y,z).
6. Физические приложения тройных интегралов. Пусть
Т — материальное тело (кубируемая область в пространстве Oxyz)
с плотностью p(x,y,z). Тогда справедливы следующие формулы:
2. Тройные интегралы 301
а) т = / / / р(х, у, z) dx dy dz — масса тела;
т
б) Myz = fffxp(x,y,z)dxdydz, Mzx = j j j yp(x,y,z) dxdy dz,
T T
Mxy = zp(x,y,z) dxdy dz — статические моменты тела относи-
т
тельно координатных плоскостей Oyz, Ozx, Oxy;
ч Myz MZX МХу
в) хо = ——, Уо = •> zo = — координаты центра тяжести
тела; т
г) Iyz = fffx2p(x,y,z)dxdydz, Izx = /11у2 p{x,y,z) dxdy dz,
T T
Ixy = z2p(x,y,z)dxdydz — моменты инерции тела относительно
т
координатных плоскостей Oyz, Ozx, Oxy;
Д) 1Х = hx + 1Ху, Iy = Ixy + Iyz, Iz = Iyz + Izx — моменты инер-
ции тела относительно осей координат Ox, Oy, Oz;
р) Тп — Т 4- Т 4- Т
и/ -*0 — 1yz \ 1zx \ 1ху '
т
мент инерции тела относительно начала координат;
ж) U(xo,yo,zo) = jp(x,y,z)-dxdydz — ньютоновский по-
т
тенциал поля тяготения тела Т в точке (xo,yo,zo); здесь г =
= у/(х — хоJ + (у — уоJ + (z — zoJ — расстояние между точками
M(x,y,z) и Мо(хо,уо,%о), 7 — гравитационная постоянная;
з) F = {Fx,Fy,Fz} — сила притяжения материальной точки
Мо(хо,уо, zo) массы то телом Т, где
F =JrnoJJJp{x,y,z) ^3 dxdydz,
т
Fy =
Fz =
-^- = 'ymoJJJp(x, y, z)Z ^ dx dy dz.
Контрольные вопросы и задания
1. Что такое интегральная сумма? Составьте интегральную сумму
функции f(x,y,z) = х2 + xyz, соответствующую разбиению области
Т{(ж, y,z): а ^ х ^ Ь, с ^у ^ d, e ^ z ^ g} на параллелепипеды Т^/е =
= {(ж, J/, г): Жг-i ^ ж ^ х{, yj-i ^y ^ yh zk-X ^ z ^ zk} (a = х0 <
< xi < ... < хш = Ь, с = уо < yi < ... <уп =d, e = zo < zi < ... < zi = g)
и выбору вершин (жг-i, У3 1 Zk-i) этих параллелепипедов в качестве про-
промежуточных точек.
302 Гл. XII. Кратные интегралы
2. Дайте определения предела интегральных сумм и тройного интеграла.
Докажите, что неограниченная в пространственной области функция не
интегрируема в этой области.
3. Сформулируйте теоремы об интегрируемости непрерывных и некото-
некоторых разрывных функций (теоремы 5 и 6). В какой из этих теорем су-
существенна замкнутость области, и почему?
4. Напишите формулы, выражающие линейность и аддитивность тройных
интегралов.
5. Сформулируйте теорему о формуле среднего значения для тройного ин-
интеграла.
6. Сформулируйте теорему о сведении тройного интеграла к повторному,
в котором внутренний интеграл является определенным интегралом.
7. Сформулируйте теорему о сведении тройного интеграла к повторному,
в котором внутренний интеграл является двойным.
8. Тройной интеграл f(x,y,z)dxdydz, где Т — шар, ограниченный
т
сферой (х + IJ + (у — IJ + (z + 2J = 9, сведите к повторному двумя
способами: а) так, чтобы внутренний интеграл в повторном был опре-
определенным интегралом; б) так, чтобы внутренний интеграл в повтор-
повторном был двойным интегралом.
9. Сведите тройной интеграл из предыдущего задания к последовательно-
последовательному вычислению трех определенных интегралов.
10. Напишите формулы перехода к новым переменным в тройном интег-
интеграле и сформулируйте условия I—III, которым должно удовлетворять
отображение.
11. Что представляет собой образ параллелепипеда т = {(p,ip,z): 0 ^ р ^
^ 1, 0 ^ (р < 2тг, 0 ^ z ^ 1} при отображении х = pcoscp, у = psincp,
z = z. Является ли это отображение взаимно однозначным?
12. Что представляет собой образ параллелепипеда т = {(г, в, if): 0 ^ г ^ 2,
0 ^ в ^ тг/2, 0 ^ (р ^ тг} при отображении х = г sin в cos ср, у = г sin в sin cp,
z = r cos в. Является ли это отображение взаимно однозначным?
13. Сформулируйте теорему о замене переменных в тройном интеграле.
14. Что такое криволинейные координаты? Напишите формулы перехода
от прямоугольных координат (x,y,z) к цилиндрическим координатам
(p,cp,z). Вычислите якобиан перехода. Что представляют собой коор-
координатные поверхности р = const, (p = const, z = const и координатные
ЛИНИИ /9, (р, Z?
15. Напишите формулы перехода от прямоугольных координат (x,y,z) к
сферическим координатам (г, в, if). Вычислите якобиан перехода. Что
представляют собой координатные поверхности г = const, в = const,
ср = const и координатные линии г, #, ср?
16. Напишите формулы перехода от прямоугольных координат к обобщен-
обобщенным сферическим координатам. Вычислите якобиан перехода.
17. Напишите формулу для вычисления объема тела с помощью тройного
интеграла. Получите из этой формулы выражения объема тела с по-
помощью двойного интеграла и определенного интеграла. Что такое эле-
элемент объема в прямоугольных координатах?
18. Напишите формулу для вычисления объема тела в криволинейных ко-
координатах. Что такое элемент объема в криволинейных координатах?
Каков геометрический смысл якобиана отображения?
§2. Тройные интегралы
303
19. Напишите формулы для вычисления координат центра тяжести и мо-
моментов инерции материального тела.
20. Напишите выражения для ньютоновского потенциала поля тяготения
материального тела и составляющих силы притяжения этим телом ма-
материальной точки.
Примеры решения задач
1. Дан тройной интеграл / / / f(x,y,z) dxdy dz, где Г — область,
т
ограниченная поверхностями z = 0, z — ху, у = ж, х = 1. Свести
данный интеграл к повторному двумя способами: а) так, чтобы внут-
внутренний интеграл был определенным интегралом с переменной интег-
интегрирования z\ б) так, чтобы внутренний интеграл был двойным интег-
интегралом с переменными интегрирования у и z. В каждом случае свести
тройной интеграл к последовательному вычислению трех определен-
определенных интегралов.
Л а) Область Т представляет собой "криволинейную пирамиду"
АО ВС (рис. 46, а), основанием которой является треугольник ОВС
zi
С\У=х
В
О
О
х у
X 1
а бе
Рис. 46
в плоскости (ж, у) (обозначим этот треугольник буквой G). Для каж-
каждой точки (ж, у) области G переменная z изменяется от 0 (значение z
в области G) до ху (значение z на поверхности z = ху), т. е. область
Г можно представить в виде
T = {(x,y,z): (x,y)
По формуле A) имеем
1 = ffdx dy I ^ж'у' ^ dz'
G О
Сводя двойной интеграл по области G к повторному, получим
1 х ху
1 = Jdxjdy f f(x,y,z)dz. (9)
0 0 0
ху
I
304
Гл. XII. Кратные интегралы
б) Область Т заключена между плоскостями х = 0 и х = 1. Сече-
Сечение области Т плоскостью х = const (рис. 46, б) представляет собой
треугольник G(x). Проекция этого треугольника на плоскость Oyz
изображена на рис. 46, в. По формуле B) имеем
1
1= [dx [j f(x,y,z)dydz.
О G(x)
Сводя двойной интеграл по области G(x) к повторному, получим
1 х ху
= J dxj dyj f(x,y,z)dzJ
0 0 0
что совпадает с равенством (9). А
2. Вычислить тройной интеграл
где Т — область, ограниченная по-
х верхностями
2 = 0, z = y, y = x2, у = 1.
Л Область Т изображена на рис. 47. Ее можно представить в виде
T = {(x,y,z): (x,y) GGJOO},
где G = {(ж, у): — 1 ^ х ^ 1, х2 ^ у ^ 1}. Сводя тройной интеграл к
повторному, получим
У 1 1 У
I — dx dy ху \fz dz = dx dy xy^fz dz =
G о l 2 о
-l
-1 x2
о
l
= i-y^l - \x\7) dx =
-1
-l
3. Вычислить интеграл / = / / / [(x + уJ — z] dx dy dz, если область
т
T ограничена поверхностями z = 0 и (г — IJ = х2 + ^/2.
Л Область Т представляет собой конус (рис. 48, а). Уравнение ко-
конической поверхности, ограничивающей область Т, можно записать
в виде z = 1 - л/х2 + у2, а саму область Г представить следующим
образом: Т{(х,y,z): (x,y) G G, О ^ z ^ 1 - дД2 +2/2}, гДе G — круг
2. Тройные интегралы
305
радиуса 1 с центром в начале координат. Поэтому данный тройной
интеграл можно свести к последовательному вычислению трех опре-
определенных интегралов в прямоугольных координатах:
-I;
dx
dy
— z] dz.
Однако удобнее перейти к цилиндрическим координатам (р, ip,z): x —
— pcosp, у = psimp, z — z. Тогда прообраз круга G есть прямоуголь-
прямоугольник {(p,ip): 0 ^ р ^1, 0^(^^ 2тг}, прообраз конической поверхнос-
поверхности — плоская поверхность z = 1 - р, а прообраз области Г — область
Рис. 48
г, изображенная на рис. 48, б. Якобиан перехода к цилиндрическим
координатам равен р, подынтегральная функция в цилиндрических
координатах равна р2A + sin2(p) — z. Сводя тройной интеграл по об-
области т к последовательному вычислению трех определенных интег-
интегралов, получим
/ = ГГГ[р2A + sin 2ф) - z]p dp dip dz =
2тг 1 1-p
= I dip I dp [ [p2(l + sm2ip) - z]pdz =
ooo
2тг 1
= I dip I [p3(l - p)(l + sin 2ip) -\p(l- P?] dp =
Отметим, что расстановку пределов интегрирования в цилиндри-
цилиндрических координатах можно произвести, рассматривая не область г, а
306
Гл. XII. Кратные интегралы
изменение цилиндрических координат в области Т. Наглядно видно,
что в области G переменная ip изменяется от 0 до 2тг, при каждом
значении ip переменная р изменяется от 0 до 1, а для каждой точки
(р, ср) области G переменная z изменяется в области Т от 0 (значение
z в области G) до 1 — д/ж2 + у2 = 1 — р (значение z на конической по-
поверхности). Это позволяет расставить пределы интегрирования так,
как сделано в равенстве A0). А
4. Вычислить интеграл / = /// л/х2 + у2 + z2 dxdy dz, где Т —
т
область, ограниченная поверхностью х2 + у2 + z2 = z.
Л Область Т представляет собой шар, ограниченный сферой, урав-
"s!
2тг ср
Рис. 49
нение которой удобно записать в виде х2 + у2 + (z — 1/2J = 1/4
(рис. 49, а). Данный тройной интеграл можно вычислить с помощью
повторного интегрирования в прямоугольных координатах:
1/2 y/l/4-x2 1/2+Л/1/2-х2-у2
1= I dx [ dy [
-V2 -у^/Ч-ж
1/2-у/1/2-х2-у2
У2
У2 +
Однако удобнее перейти к сферическим координатам (г,в,(р):
х — т sin в cos ср, у = г sin в sin cp, z — т cos в, A1)
причем переменная ip изменяется от 0 до 2тг, а при каждом значении
ip переменная в изменяется от 0 до тг/2. Подставляя выражения A1) в
уравнение сферы, получим г2 = г cos в, откуда г = 0 или г = cos#. Эти
две поверхности в пространстве (г,в,ср) при 0 ^ ср ^ 2тг, 0 ^ в ^ тг/2
ограничивают снизу и сверху область т (рис. 49, б), являющуюся
прообразом области Г при отображении A1). Якобиан отображения
A1) равен r2sin#, а подынтегральная функция в сферических коор-
координатах равна г. Вычисляя тройной интеграл по области т с помощью
2. Тройные интегралы
307
повторного интегрирования, получаем
2тг тг/2 cos 61
'>sm0drd0d(p= [dtp Г d0 Г r3sin0dr =
о
2тг тг/2
У dif I 4L~ - — 4 5 10'
о о
Отметим, что расстановку пределов интегрирования для переменной
г можно произвести, рассматривая не область т, а изменение г при
фиксированных значениях ip и в в области Т. Наглядно видно, что на
каждом луче ip = const, О = const переменная г изменяется в шаре Г
от 0 (значение г в начале координат) до cos# (значение г на сфере). А
5. Найти объем тела Г, ограниченного
15
Рис. 50
поверхностью S: J—Ь J - + J— = 1 и
координатными плоскостями.
Л Тело Г изображено на рис. 50. Для вы-
вычисления его объема удобно перейти к обоб-
обобщенным сферическим координатам (г,6,(р)
по формулам
х = 2r2 sin4 О cos4 cp,
у = 3r2 sin4 О sin4 <p, A2)
z = 15r2 cos4 0.
Тогда уравнение поверхности S примет про-
простой вид: г = 1. В пределах тела Т перемен-
переменная (р изменяется от 0 до тг/2, при каждом
значении ср G [0,тг/2] переменная О изменя-
изменяется также от 0 до тг/2, а на каждом луче
ip = const, О = const переменная г изменяется от 0 (значение г в нача-
начале координат) до 1 (значение г на поверхности S). Итак, прообразом
тела Т при отображении A2) является прямоугольный параллелепи-
параллелепипед в пространстве (г,6,(р):
г = {(г, в, if): 0 ^ г ^ 1, 0 ^ в ^ тг/2, 0 ^ ip ^ тг/2}.
Якобиан отображения A2) равен 2880r5 sin7 в cos3 в sin3 у? cos3 cp
(см. формулу F)).
Используя формулу (8) для объема тела в криволинейных коор-
координатах и вычисляя интеграл по области т с помощью повторного
интегрирования, получаем
тг/2 тг/2 1
V = J dip J dO /*2880г5 sin7 0 cos3 0 sin3 ip cos3 <pdr =
0 0 0
тг/2 тг/2
/ sin7 0 cos3 OdO =
/
= 480 f sin3 <p cos3
о
308
Гл. XII. Кратные интегралы
тг/2
тг/2
= 480 / sin3 if{l - sin2 ф) d(sin ф) • f sin7 0A - sin2 0) d(sin 0) =
1 1
6. Найти моменты инерции относительно координатных плоскос-
плоскостей однородного тела Т с плот-
плотностью р = 1, ограниченного по-
поверхностями х2 = 2pz, 2/2 = 2рх,
х=р/2, z = 0 (p> 0).
Л Тело Т изображено на рис. 51.
Его можно представить в виде
т =
2р ^ ^ 2' ^ ^2
Используя формулу для момента
инерции тела относительно ко-
координатной плоскости Ozx, с помощью повторного интегрирования
получаем
р р/2 х2/Bр)
1 dx dy dz = / dy / dx / у2 dz =
-P У2/AР) °
Рис. 51
P/2
f
J
J/2/Bp)
99
2p
48
108"
Аналогично находим
7»' = jjjx'dxdydz = ^, 4, = fffz'dxdydz = y^q-
7. Найти ньютоновский потенциал поля тяготения однородного
шара Г радиуса R с плотностью ^ в точке А, находящейся на рас-
расстоянии d от центра шара (d > R).
Л Введем прямоугольную систему координат так, чтобы начало ко-
координат совпало с центром шара, а точка А лежала на положительной
полуоси Oz. Тогда уравнение сферы, ограничивающей шар, примет
вид х2 + у2 + z2 = R2j а точка А имеет координаты @,0,(i). По фор-
формуле для ньютоновского потенциала имеем
ги.п * fff dxdydz
Так как тело Т — шар, то для вычисления тройного интеграла удобно
перейти к сферическим координатам: х = г sin в cos (р, у = г sin в sin (p,
2. Тройные интегралы 309
z = r cos в. Прообразом шара Г при этом отображении является пря-
прямоугольный параллелепипед г = {(г, в, ф) : 0 ^ г ^ R, 0 ^ в ^ тг,
0 ^ (р ^ 2тг}. Учитывая, что якобиан отображения равен r2sin#, a
д/ж2 + ?/2 + (z — б?J = л/^2 + сР — 2rdcos6, и сводя тройной интеграл
по области т к повторному, получим
, о, d) = 7 /77р 2
J 4JJ И Vr2 +
2тг R тг
/Г Г
dip r dr / —==
J J vr2 ¦
л/г2 + d2 - 2rdcos6
2тг R 2тг R
= jp d(p — (v r2 + d? — 2rd cos ^ ) dr = -jp dtp r2 dr =
0 0 0 0
где m — - ttR3p — масса шара.
о
Таким образом, однородный шар массы m создает в пространстве
вне шара такое же поле тяготения, что и точечная масса т, помещен-
помещенная в центр шара. А
Задачи и упражнения для самостоятельной работы
21. Сведите тройной интеграл ////(ж, г/, 2) dxdydz к последовательному
т
вычислению трех определенных интегралов шестью способами, если:
2 2 2
Ж 1/ /2
а) Т — область, ограниченная эллипсоидом — + ^— + — = 1;
а2 б2 с2
б) Т — область, ограниченная поверхностями х2 -\-у2 -\- z2 = 1, ж2 +
+ у2 + ?2 = 16, ж = 0, 2/ = 0, г = 0 (ж ^ 0, у ^ 0, г ^ 0);
в) Т — четырехугольная пирамида с вершинами (—2,0,0), @,-2,0),
B,0,0), @,2,0), @,0,4);
х2 у2 х2 у2
г) Т — область, ограниченная поверхностями — + — = 22, — + — =
a b a2 b2
= 1, г = 0 (Ь > а > 0).
22. Измените порядок интегрирования (различными способами) в интег-
интегралах:
1/а 1-ах ах+у 1 1 2ж2+3у2
a) J dx J dy J f(x,y,z)dz\ 6) Jdyjdx J f(x,y,z)dz\
0 0 0 0 0 0
в) I dz I dy I f(x,y,z)dx\ r) I dx I dy I f(x,y,z)dz.
310 Гл. XII. Кратные интегралы
23. Вычислите интегралы:
а) xzdxdydz, если Т — область, ограниченная поверхностями
т
х2 +у2 +z2 = а2, z = 0 (O0);
б) 111 (х + у + z) dx dy dz, если Т — область, ограниченная поверхнос-
т
тями х + у + z = 1, ж = 0, ?/ = 0, z = 0.
24. Перейдите к сферическим координатам в интеграле
f + y2 + z2) dx dy dz,
т
где Т — область, ограниченная поверхностями z = х2 + у2, х = у,
х = 1, |/ = 0, 2 = 0, и сведите полученный интеграл к последователь-
последовательному вычислению трех определенных интегралов шестью способами.
25. Перейдите к сферическим координатам и вычислите интегралы:
а) /// \/х<2 + у2 + z2 dx dy dz, где Т — область, ограниченная поверх-
^ 2,2,2
ностью х + у + z = ж;
з v»—ж^ у1»—ж —у
б) fx2dx f у2 dy f zdz.
26. Перейдите к цилиндрическим координатам и вычислите интегралы:
а) / / / \/х2 + |/2 2 с/ж cfa/ с/^, где Т — область, ограниченная поверхностя-
т
ми ж2 + у2 = z, z = 1;
з ~ ' ~
6)fzdzfy2dy I x2dx.
Q _ /— I 2
27. Выбрав подходящую замену переменных, вычислите интегралы:
а) (х2 -\-у2 + z2) dx dydz, где Т — область, ограниченная сферой
т
т
х2 +у2 + z2 = х + у + Z]
2 х2 2
MSz2 х2 у2 \
—2~ — — — Zj jdxdydz, где Т — область, ограниченная эллип-
-^222
соидом %- + \- + Z— = 1;
а2 б2 с2
в) / / /1/ с/ж cfa/ с/^, где Т — область, ограниченная поверхностями z = у2,
т
z = 4.y2, z = x, z = 3x, z = 3 (j/>0).
28. Вычислите объем тела, ограниченного поверхностями:
a)x + y + z = l, x + y — z = —l, —x + y + z = l, x — у + z = l, z = 0;
В) *1 + У1 = 22, ?! + ? = !, 2 = 0 (Ь > а > 0).
а о az bz
2. Тройные интегралы 311
29. Перейдите к цилиндрическим координатам и вычислите объем тела,
ограниченного поверхностями:
а) 2z = 2ж2 + —, 4ж2 + — = 1, z = 0;
1 3 9
б) у2 + z2 = а2, |/2 + ^2 = ж2, х = b (b> а> 0).
30. Перейдите к сферическим координатам и вычислите объем тела, огра-
ограниченного поверхностями:
а) ж2 + у2 + z2 = 1, ж2 + у2 + z2 = 16, z2 = ж2 + |/2, 2/ = 0, 2 = 0,
у = х (ж>0 ?/>0 ?> 0)'
31. Перейдите к обобщенным сферическим координатам и вычислите объ-
объем тела, ограниченного поверхностями:
) = Зг, ж = 0, у = 0, z = 0 (x^O, y^O, z ^ 0).
2 /
32. Найдите массу тела, ограниченного поверхностями 2z = х2 + у2, х +
+ у + г = 1, если плотность тела изменяется по закону:
а) р = ро; б) р = ро\1 + ж|; в) р = роу2\1 + х\ (р0 = const).
33. Найдите координаты центра тяжести однородного тела, ограниченного
поверхностями:
а)ж^+^2=а2, г/ = 1, г/ = 3, ^ = 0 (^ ^ 0);
б) ^ = 4-Ж2-2/2, 2 = 1, ж = 0, ?/ = 0 (ж^0, г/^0);
в) ж2 = 2р^, |/2 = 2рж, ж = р/2, 2 = 0 (р > 0);
г)^ = ж2+|/2, 2 = (ж2+?/2)/2, ^ + ^ = 1, ж + 2/ = _15 x_^ = l5
х -у = -1.
34. Найдите координаты центра тяжести тела, ограниченного поверхнос-
поверхностями 2z = ж2 + 4ж + у2 — 2у + 5, 2 = 2, если плотность тела изменяется
по закону:
а)/9 = ^; 6)/9 = /90[O + 2J + (j/-lJ]; в) p = p0z(x2 + ?/2) (ро= const).
35. Найдите моменты инерции относительно координатных плоскостей од-
однородного тела плотности ро, ограниченного поверхностями:
2 2 22ч2 х 2 2
^ ) Ь ^
B)z = A-x2-y2, 2 = 1, ж = 0, |/ = 0 (ж ^ 0, 2/^ 0).
36. Найдите моменты инерции относительно координатных плоскостей
тела:
а) плотности р = — (ро = const), ограниченного поверхнос-
х2 + у2 + ?2
2
^\ 35 2 2,22
б) плотности р = 2 , ограниченного поверхностями ж + у = а ,
128
37. Найдите моменты инерции относительно осей координат и начала ко-
координат однородного тела плотности р0, ограниченного поверхностями:
312 Гл. XII. Кратные интегралы
38. Определите момент инерции относительно начала координат тела плот-
плотности р = ро(х2 + у2 + z2), где ро = const, ограниченного поверхностью
(x2+y2+z2J=x2 + y2.
39. Пусть Т — однородный цилиндр плотности ро с высотой h и радиусом
основания R. Найдите силу притяжения этим цилиндром материаль-
материальной точки массы то, находящейся в центре основания цилиндра.
§ 3. m-кратные интегралы
Основные понятия и теоремы
1. Определение m-кратного интеграла. При m > 3 понятие
m-кратного интеграла вводится аналогично понятиям двойного и
тройного интеграла. Предварительно нужно ввести понятие объема
тела в m-мерном евклидовом пространстве Еш. Объемом тп-мерного
параллелепипеда Q = {(х\,Х2, ...,жт) : \х\ — а\\ ^ di,..., \xm — am\ ^
^ dm} назовем число V(Q) = 2di2d2...2dm (при m = 3 получается
известная формула для объема прямоугольного параллелепипеда в
трехмерном пространстве). Пусть Т — произвольное ограниченное
множество точек в пространстве Еш (для краткости будем назы-
называть его телом). Рассмотрим всевозможные многогранники QBn и
Qon, вписанные в тело Г и описанные около него и составленные из
m-мерных параллелепипедов. Объем каждого такого многогранника
положим равным сумме объемов составляющих его параллелепипе-
параллелепипедов. Числа
V= sup {V(QBn)} и V= inf {V(Qon)}
QbuCT TcQou
называются соответственно нижним и верхним объемом тела Т. Тело
Т называется кубируемым, если V_ = V, а число V = V_ = V называется
объемом тела Т.
Пусть на кубируемом множестве Т С Еш задана ограниченная
функция и = /(М) = /(ж1,ж2, ...,жт). Разобьем тело Г на кубируе-
мые части Ti (i = 1,2,...,п) так, чтобы любые две части не имели
общих внутренних точек, в каждой части возьмем произвольную точ-
точку Mf(^{,^25 •••?Cn) и составим интегральную сумму
г=1
где Al/f — объем Х^. Пусть df — диаметр Ti, d = max df. Предел
интегральных сумм при d —у 0 (его определение в точности такое же,
как и для двойных и тройных интегралов) называется тп-кратным
интегралом от функции /(xi, ...,жт) по множеству Т и обозначается
x2---dxrri. A)
§3. т-кратные интегралы 313
Как и в случае двойных и тройных интегралов, справедливы сле-
следующие утверждения:
1) функция, непрерывная в замкнутой кубируемой области Г С
С Ет, интегрируема в этой области;
2) функция, ограниченная в кубируемой области Т С Еш и не-
непрерывная всюду, кроме некоторого множества точек объема нуль,
интегрируема в этой области.
Если /(ж1,ж2, ...,жт) = 1, то интеграл A) равен объему тела Г:
= Ц J
Jdx1dx2...dxm. B)
т
2. Вычисление m-кратных интегралов с помощью повтор-
повторного интегрирования.
Теорема 10. Пусть:
1°) функция /(xi,...,xm) интегрируема в области Т = {(жь...
...,жт): (>i,...,xm_i) G G, 2/i(>i,...,xm_i) ^ жт ^ 2/2(^1,...,xm_i)},
где 2/i(xi, ...,xm_i) u 2/2(^1, ...,xm_i) — непрерывные функции в куби-
кубируемой области G С Ет;
2°) V(xi,X2, ...,xm_i) G G существует определенный интеграл
/
существует (т — 1)-кратный интеграл от функции
...,жт) по области G (повторный интеграл) и справедливо равенство
= HJ
1...dxm-1 I f(xi,...,xm)dx
В свою очередь интеграл по области G при соответствующих усло-
условиях можно также свести к повторному и т. д. В конечном итоге при
определенных условиях, которым должна удовлетворять область Т,
m-кратный интеграл сводится к последовательному вычислению т
определенных интегралов (см. пример 1 на с. 314).
3. Замена переменных в m-кратном интеграле. Замена пере-
переменных в ш-кратном интеграле A) состоит в переходе от переменных
xi,...,xm к новым переменным ui,...,um по формулам
х\ = (?i(>i,...,^m), ..., хш = (pm(>i,...,^m), (иъ...,ит) G т. C)
Функции C) осуществляют отображение области г пространства
(г*1э..., иш) на область Г пространства (xi,..., хш). На это отображе-
отображение накладываются такие же условия I—III, как и в случае двойных
и тройных интегралов.
314 Гл. XII. Кратные интегралы
Теорема 11. Пусть г и Т — замкнутые кубируемые области,
функция f(xi,...,xm) ограничена в области Т и непрерывна всюду,
кроме, быть может, некоторого множества точек объема нуль, а
отображение C) удовлетворяет условиям I—III.
Тогда справедливо равенство (формула замены переменных в
т-кратном интеграле)
JJ..J
...dxm = yy.
г
U\Ui, ..., иш
D)
При f(xi,...,xrn) = 1 из формулы D) получаем выражение для
объема тела Т в криволинейных координатах
uduo ...dum.
Контрольные вопросы и задания
1. Дайте определения кубируемого тела в m-мерном евклидовом прост-
пространстве и объема тела.
2. Дайте определения интегральных сумм и m-кратного интеграла.
3. Сформулируйте теорему о сведении m-кратного интеграла к повторно-
повторному. Сведите интеграл по параллелепипеду Q = {(х\,..., хш): \х\ — а\\ ^
^ d\,..., \хш — аш\ ^ dm} к последовательному вычислению m опреде-
определенных интегралов.
4. Сведите интеграл по m-мерному шару Т = V{(x\,..., хш) : х\ + ...
... + ж^ ^ R2} к последовательному вычислению m определенных ин-
интегралов.
5. Сформулируйте теорему о замене переменных в m-кратном интеграле.
6. Докажите, что если отображение C) линейное, т. е. (fi(u\,..., um) =
= ^ aijUj и det||aij|| ф 0, то это отображение удовлетворяет усло-
условиям I—III.
7. Напишите формулы для вычисления объема тела в пространстве Еш с
помощью m-кратного интеграла.
Примеры решения задач
1. Вычислить объем тела Т, заданного неравенствами х\ ^ 0, x<i ^
^ 0, ..., хш ^ 0, х\ + х2 + ... + хш ^ 1.
Л Согласно формуле B) V(T) = // \ dx\ dx<± ... dxm. Тело Т можно
т
представить в виде Г = {(xi,...,xm): (жь ...,xm-i) G Gm_b 0 ^ хш ^
^ 1 - х\ - х2 - ... - xm-i}, гдеОт_1 —область в пространстве Ет~1,
заданная неравенствами х\ ^ 0, ...,хш-\ ^ 0, х\ + ... + xm-i ^ 1.
§3. т-кратные интегралы
315
Сводя m-кратный интеграл по телу Г к повторному, получим
1-Ж1-...-Жт_1
V(T) = JJ]mJdx1...dxm-1 I dxm =
//A ~Xl ~ '" -zm-i)dx1...dxm-1.
Gm-1
rni
Так как область Gm_i можно представить в виде Gm_i =
...,ajm-i): (жь...,жт_2) G Gm_2, 0 ^ жт_1 ^ 1 - хх - ... -жт_2}, где
Gm-2 — область в пространстве Ет~2, которая задается аналогично
Gm_i, то (т — 1)-кратный интеграл по области Gm_i можно свести
к повторному таким же образом, как и интеграл по телу Г:
JJ...J A -xi- ... -am_i)Gtei...Gtem_i =
Gm-i
1-Ж1-...-жт_2
= JJ_Jdx1...dxm-2 J A -xi - ... -xm_i)<ixm_i =
Gm-2
Далее, аналогичным образом можно свести (т — 2)-кратный интеграл
по области Gm_2 к повторному и т. д. Через т - 1 шагов придем к
следующему определенному интегралу:
аг-1 1
Итак, V(T) = Л- ^
т!
2. Даны два материальных тела: Т\ с плотностью pi(x,y,z) и Г2
с плотностью p2{x,y,z). Найти силу F притяжения тела Т\ телом Т2.
Л Пусть M(x,y,z) — произвольная точка тела 7\, а М'(х',y',z') —
произвольная точка тела Т2. Введем (бесконечно малые) элементы
объема dV = dx dy dz и dV = dx' dy' dz' с центрами в точках М
Рис. 52
и М' (рис. 52). Масса элемента объема dV равна p1(x,y,z) dx dy dz, a
масса элемента объема dV равна р2(х',у', z') dx' dy' dz'. Силу, с кото-
которой первая из этих масс притягивается второй, можно представить в
316 Гл. XII. Кратные интегралы
виде
,._ _ pi (ж, г/, z) dx dy dz p2Jx', у', z) dx dy' dz'
d p4m,m>) e' ^
где e — единичный вектор, сонаправленный с вектором ММ'. Коор-
динаты вектора е равны
Так как р(М, М') = [(V - хJ + (у1 - уJ + (V - zJ]1/2, то состав-
составляющую силы dF по оси Ох можно записать в виде
dFx=7 ur%v\1Mxi;if!xL2
[(x' - xJ + (У - yf + 0' - zJ]3/2
Чтобы найти составляющую по оси Ох силы, с которой тело Т\ при-
притягивается телом Г2, нужно просуммировать выражения E) по всем
элементам объемов тел Т\ и Т2, или, более точно, нужно проинтегри-
проинтегрировать по телам Т\ и Т2. Таким образом, составляющая Fx искомой
силы F выражается 6-кратным интегралом:
Т\ ХТ2
Говорят, что этот интеграл берется по произведению тел Т\ и Г2.
Аналогично выражаются составляющие Fy и Fz силы F. А
Задачи и упражнения для самостоятельной работы
40. Вычислите m-кратный интеграл:
а) / / / {х\ + х\ + ... + ж2^) dxi dx2-" dxra-, где Т — m-мерный куб, за-
т
данный неравенствами 0 ^ Хк ^ 1, А; = 1, 2,..., т;
/»/» /»
б) // /y/xi + Ж2 + ... + хш dx\ dx2... dxrn, где Т — т-мерная пирамида,
т
заданная неравенствами х\ + Ж2 + ... + жт ^ 1, ж/^ ^ 0, к = 1, 2,..., т.
41. Найдите объем m-мерного параллелепипеда, ограниченного плоскос-
плоскостями пцХ\ + С^2Ж2 + ••• + UimXm = ±^г (« = 1, 2, ..., т), вСЛИ А =
= det||afci||m,m ф 0.
42. Найдите объем m-мерной пирамиды, заданной неравенствами — +
а\
+ ^ + ... + ^1^1, ж-^о (г = 1,2,...,ш), аг>0 (г = 1, 2,..., ш).
43. Найдите объем 5-мерного шара радиуса R.
ГЛАВА XIII
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. Криволинейные интегралы первого рода
Основные понятия и теоремы
1. Определение криволинейного интеграла первого рода.
Пусть кривая L на координатной плоскости Оху задана параметри-
параметрически уравнениями
x = ip(t), у = Ш, a^t^/3. A)
Напомним, что L называется простой (плоской) незамкнутой кривой,
если функции (p(t), ip(t) непрерывны на [а,/3] и различным значени-
значениям параметра t из сегмента [а, /3] соответствуют различные точки
M((p(t),ip(t)). Если точка А((р(а),ф(а)) совпадает с точкой В((р(/3),
фф)), а остальные точки не являются кратными, то L называется
простой замкнутой кривой. Простая кривая L называется спрямляе-
спрямляемой, если существует предел длин ломаных, вписанных в кривую,
при At —у 0 (этот предел называется длиной кривой L). Аналогичные
определения имеют место для пространственной кривой, заданной
параметрически уравнениями в координатном пространстве Oxyz.
Пусть L — простая, спрямляемая (замкнутая или незамкнутая)
кривая, заданная уравнениями A), и пусть на кривой L определе-
определена функция f(x,y). Разобьем сегмент [а,/3] на п частей точками
а = t0 < t\ < ... < tn = /3. При этом кривая L разобьется на п частей
точками Mo, Mi,..., Мп. Обозначим через А^ длину дуги M^_iM^,
выберем на каждой дуге Mk-iMk некоторую точку Nk(?,k,Vk) и со-
составим интегральную сумму
п
i(Mk,Nk) = ^,
к=1
Пусть Al = max
Определение. Число / называется пределом интегральных сумм
при А1 —у 0, если Vs > 0 36 > 0 такое, что для любого разбиения кривой
L, у которого А1 < 6, и для любого выбора промежуточных точек Nj*
выполняется неравенство
\I(Mk,Nk)-I\<e.
Если существует lim I(Mk,Nk) = /, то число / называется кри-
Д/-И)
волинейным интегралом первого рода от функции f(x,y) по кривой L
318 Гл. XIII. Криволинейные интегралы
и обозначается
ff(x,y)dl. B)
L
Если кривая L — незамкнутая и точки А и В — ее концы, то
криволинейный интеграл первого рода обозначается также следую-
следующим образом: / f(x,y)dl.
АВ
Из определения следует, что криволинейный интеграл первого ро-
рода не зависит от того, в каком направлении (от А к В или от В к А)
пробегается кривая L, т. е.
f(x,y)dl = J f(x,y)dl.
АВ ВА
Если f(x,y) = 1, то / dl равен длине I кривой АВ: / dl = I.
АВ АВ
Аналогично вводится криволинейный интеграл первого рода для
пространственной кривой L, заданной параметрически уравнениями
x = ip(t), у = ф[г\ z = X(t), a^t^/3. C)
2. Вычисление криволинейного интеграла первого рода с
помощью определенного интеграла. Простая кривая L, заданная
уравнениями A), называется гладкой (кусочно гладкой), если функции
ip(t) и ijj(t) имеют непрерывные (кусочно непрерывные) производные,
одновременно не обращающиеся в нуль на [а,/3] (на [а,/3], за исключе-
исключением конечного числа точек). Функция f(M) = f(x,y), определенная
на кривой L, называется непрерывной вдоль кривой L, если VMq E L
Jim /(M) = /(Mo).
меь
Если это условие выполнено в каждой точке кривой, за исключе-
исключением конечного числа точек, в которых функция имеет разрывы пер-
первого рода, то функция f(M) называется кусочно непрерывной вдоль
кривой L.
Теорема 1. Если L — кусочно гладкая кривая, заданная уравне-
уравнениями A), и функция f(x,y) кусочно непрерывна вдоль кривой L, то
существует криволинейный интеграл B) и справедливо равенство
C
j
jf(x,y)dl = ff№QMt)W<P'2(t)+*l>'2(t)dt. D)
L
Замечание. Предположим, что /(ж, г/) непрерывна вдоль кривой L.
Тогда имеют место следующие утверждения.
1°. Если кривая L задана уравнением у = у(х), а ^ х ^ 6, и у(х) имеет
непрерывную производную на [а, Ь], то существует интеграл B) и справед-
справедливо равенство
Jf(x, у) dl = Jf(x, y(x))y/l + у'Цх) dx. E)
§1. Криволинейные интегралы первого рода 319
2°. Если кривая L задана в полярных координатах уравнением г = г(<р),
<Pi ^ ? ^ ^2, и г(ср) имеет непрерывную производную на [^1,^2], то су-
существует интеграл B) и имеет место равенство
Jf(x,y)dl= Jf(r(tp) cos tp, r(ip) sin ф) л/г2((р) + r'2((p) dip. F)
3°. Для гладкой пространственной кривой, заданной параметрически
уравнениями C), справедлива формула
C
ff(x,у,z) dl = Jf{y{t)^{t),X{t))^y'2{t)+^{t)+xl2{t)dt. G)
L a
4°. Криволинейные интегралы первого рода обладают свойствами, ана-
аналогичными свойствам определенного интеграла: линейность; аддитивность;
модуль интеграла не превосходит интеграла от модуля функции. Справед-
Справедлива также формула среднего значения.
3. Физические приложения криволинейных интегралов
первого рода. Пусть L — материальная плоская кривая с линей-
линейной плотностью р(х,у). Тогда справедливы следующие формулы:
а) т = p(x,y)dl — масса кривой;
L
б) Мх = yp(x,y)dl, My = xp(x,y)dl — статические моменты
L L
кривой L относительно осей Ох и Оу;
ч My Мх
в) хо = —-, уо = — координаты центра тяжести кривой;
г) /0 = / (ж2 + у2)р(х, у) dl — момент инерции кривой относитель-
L
но начала координат (полярный момент инерции кривой);
д) 1Х = у2р(х,у) dl, Iy = x2p(x,y) dl — моменты инерции
L L
кривой относительно осей Ох и Оу;
е) F = {Fx,Fy} — сила притяжения материальной точки
Мо(хо,уо) массы то материальной кривой L, где
V _Л/ГГ1 fp(x,y)cosip _ fp(x,y) sin ip
tx — 7777,0 / 2 dli г у — 7Шо / 2 dli
L L
r = {xo — x,yo — у}, г = |r|, cp — угол между вектором г и осью Ох,
7 — гравитационная постоянная.
В случае пространственной материальной кривой справедливы
аналогичные формулы для вычисления координат центра тяжести,
статических моментов, полярного момента инерции, а также силы
притяжения материальной точки.
320 Гл. XIII. Криволинейные интегралы
Контрольные вопросы и задания
1. Какая плоская (пространственная) кривая называется: а) простой не-
незамкнутой (замкнутой); б) спрямляемой; в) гладкой; г) кусочно
гладкой?
2. Является ли кривая х = cost, у = sint, 0 ^ t ^ Зтг, простой? Является
ли кривая х = 2t — t2, у = 3t — t3, — 1 ^ t ^ 1, гладкой, кусочно гладкой?
3. Напишите параметрические уравнения плоской кривой, заданной: а) в
декартовых координатах; б) в полярных координатах.
4. Дайте определение функции: а) непрерывной вдоль кривой; б) кусочно
непрерывной вдоль кривой.
5. Сформулируйте определения: а) интегральных сумм для криволинейно-
криволинейного интеграла первого рода; б) предела этих интегральных сумм; в) кри-
криволинейного интеграла первого рода.
6. Зависит ли от направления обхода кривой: а) криволинейный интеграл
первого рода; б) какая-нибудь его интегральная сумма?
7. Составьте интегральную сумму функции /(ж, у) = х + у, соответствую-
соответствующую разбиению отрезка прямой у = х при 0 ^ х ^ 1 на п равных частей и
ЛТ fV?k \/2АЛ ^
выбору промежуточных точек Nk ( , ). Вычислите предел этих
интегральных сумм при п —»> оо.
8. Сформулируйте теорему о существовании криволинейного интеграла
первого рода и вычислении его с помощью определенного интеграла.
Напишите соответствующие формулы для: а) плоской кривой, заданной
параметрически; в декартовых координатах; в полярных координатах;
б) пространственной кривой, заданной параметрически.
9. Вычислите интеграл I (х + у) dl, где L — отрезок прямой у = х при 0 ^
L
^ х ^ 1, и сравните результат с пределом интегральных сумм задания 7.
10. Какие физические приложения криволинейного интеграла первого рода
вы знаете?
11. В случае плоской (пространственной) материальной кривой напишите
формулы для вычисления: а) координат центра тяжести; б) моментов
инерции относительно осей координат; в) силы притяжения точки Мо
массы то материальной кривой.
12. Для криволинейного интеграла первого рода сформулируйте: а) свойст-
свойства линейности и аддитивности; б) теорему об оценке модуля интеграла;
в) теорему о формуле среднего значения.
Примеры решения задач
1. Вычислить криволинейный интеграл первого рода / (ж4//3 +
+ у4/3) dl, где кривая L — астроида ж2/3 + у2/3 = a2/3. l
Л Запишем параметрические уравнения астроиды: х = acos3t, у =
= asin3t, 0 ^ t ^ 2тг. Так как х' = -3a cos2 t sint, у' = За sin2 t cost,
то х'2 + у'2 = 9a2 cos2 t sin2 t.
Отметим, что х'2 + у'2 = 0 в четырех точках t = 0, тг/2, тг, Зтг/2,
т. е. астроида является кусочно гладкой кривой.
§1. Криволинейные интегралы первого рода
321
Для вычисления криволинейного интеграла применим формулу
D). Получим
2тг
Г(х4/3 + у4/3) dl = /V/3(cos4 t + sin4 t) За | cost sint| dt =
7Г/2
= 12а7/3 [ (cos5 t sin t + sin5 t cos t) dt =
= 12а7/зГ_?2!!
L 6
sin6t
2. Вычислить криволинейный интеграл первого рода U/x2 + у2 dl,
L
где L — кривая, заданная уравнением (ж2 + у2K^2 = а2(ж2 —у2).
Л Перейдем к полярным координатам: х = rcos(p, 2/ = rsin(p.
Уравнение кривой L примет вид
г = a2 cos 2<р, <р е Ф = {(?: -тг/4 ^ у? ^ тг/4, Зтг/4 ^ у? ^ 5тг/4}.
Для вычисления интеграла применим формулу F). Так как
I'х2 + у2 — г — a2 cos (p,
то
/ \/х2 +у2 dl = / a4cos2(p у 1 + 3sin2
2л/3 У
3 sin2
sin
= 2a4 + -^ 1п(л/3 + 2). A
-тг/4
3. Найти массу m материальной кривой L, заданной уравнением
у = In ж, где 1 ^ х ^ е, если линейная плотность ее в каждой точке
пропорциональна квадрату абсциссы, т. е. р(х,у) = кх2.
Л По формуле для массы m имеем m = кх2 dl. Для вычисления
криволинейного интеграла воспользуемся равенством E). Так как
m=
J X О О
1 ^
4. Вычислить криволинейный интеграл / = (х + у) dl, где L
ньшая часть окружности
меньшая часть окружности
ограниченная точками A@,0,R) и B(R/2,R/2,R/y/2).
11 В.Ф. Бутузов и др.
322
Гл. XIII. Криволинейные интегралы
Л Запишем параметрические уравнения данной части окружности в
виде x = t,y = t,z = VR2 -2t2, 0 ^ t ^ R/2. Тогда д/ж'2 + у12 + z12 =
#л/2 . /^
, и по формуле G) находим
= А /1 + 1 +
о о
5. Найти координаты жо, уо, %о центра тяжести первого полувитка
материальной винтовой линии L, заданного уравнениями ж = a cost,
у = asint, z = 6t, 0 ^ t ^ тг, если ее линейная плотность постоянна и
равна /я.
Л Масса т равна pdl. Вычислим этот интеграл по формуле G). Так
L
как у/х'2 + у'2 + z'2 = л/a2 sin2 t + a2 cos2 t + б2 = л/a2 + б2, то m =
тг
= /я / л/^2 + b2 dt = тгру/а2 + б2. Значения жо, ^/о5 ^о находим по фор-
= — xdL уо = — lydL zo = — zdl.
mj mj mj
о
мулам
x0
Каждый из этих интегралов вычисляем с помощью равенства G):
тг тг
жо = — / a cos tya2 + b2 dt = 0, уо = — a sin tу a2 -\-b2 dt = —,
mj mj тг
6. Найти момент инерции / относительно диаметра окружности
L, заданной уравнением х2 -\-у2 = а2, если ее линейная плотность
есть р = 1.
Л Зафиксируем какой-нибудь диаметр
окружности. Имеем
М(х,у)
где d(x, у) — расстояние от точки
М(х,у) е L до диаметра. Перейдем к по-
полярным координатам: х = rcos(p, у =
= г simp, 0 ^ (р ^ 2тг. Тогда уравне-
уравнение окружности L примет вид г = а.
Рис. 53 Пусть диаметр лежит на прямой, обра-
образующей угол <?о с осью Ох, где <^о ? [0, тг) (рис. 53). При этом
d(x, у) = d(a cos cp; a sin у?) = а\ sin((p — (fo)\.
§1. Криволинейные интегралы первого рода
323
2тг 2тг
a2 sin2((p - cpo)adcp = а3 / ( - - - cosB(p - 2<?0) )d<? = тга3.
j J \ 2 2 /
Пользуясь формулой F) и учитывая, что у/г2 + г12 = а, находим
2тг 2тг
О О
7. Пусть с = {u(x,y),v(x,y)} — скорость плоского потока несжи-
несжимаемой жидкости в точке М(х,у). Найти количество Q жидкости,
вытекающей за единицу времени из области G, ограниченной глад-
гладким контуром L.
Л Разобьем кривую L на п частичных дуг. Пусть пк — единичный
вектор внешней нормали к кривой
L в точке Nk(^k,r]k) (т. е. вектор
пк направлен во вне области G),
|AQ/e| — количество жидкости, вы-
вышедшей (вошедшей) за единицу вре-
времени через дугу длины А^ из облас-
области (в область) G (рис. 54).
Так как |AQ^| есть площадь па-
параллелограмма со сторонами А^ и
|сд;|, где ск = {uk,Vk}, ик = и(?к,т),
Vk = v{?kim)i то AQk = А1к(скпк).
Если скалярное произведение (с^щ)
положительно, то жидкость вытекает из области G (AQk > 0), а ес-
если отрицательно, то втекает в G (AQk < 0). Далее, составим сум-
му *S^(cknk)Alk и перейдем к пределу при тах{А^} —у 0. Получим
к=1
Q = (en) dl, где п — единичный вектор внешней нормали в точке
L
М(х,у) е L. А
Задачи и упражнения для самостоятельной работы
1. Вычислите криволинейные интегралы первого рода:
а) l(x + y)dl, где L — граница треугольника с вершинами АA,0),
В@,1),С@,0);
б) /у2 dl, где L — арка циклоиды х = a(t — sint), у = a(t — cost),
L
0 ^ t^ 2тг;
в) /е^ x +y dl, где L — граница кругового сектора {(г, (р): 0 ^ г ^ а,
L
0 ^ (р ^ тг/4}, г и ср — полярные координаты;
г) / \Jх2 + у2 dl, где L — окружность х2 + у2 = аж;
L
р) I z dl, где L — коническая винтовая линия ж = t cos t, у = t sin t, z = t,
11*
324 Гл. XIII. Криволинейные интегралы
е) х2 dl, где L — окружность <
2. Найдите массу материальной кривой L с линейной плотностью р(ж, ?/, г),
если:
а) L : ж = e~?cos?, ?/ = e~?sin?, 2 = е~?, 0 ^ ? ^ 1пЗ; p(x,y,z) =
= Ро;
б) L: х = 3t, у = 3?2, ? = 2t3 от точки 0@,0,0) до точки АC,3,2),
p(x,y,z) = ро;
2 2
в) L — половина дуги эллипса 1 = 1, для которой у < 0, р(ж, ^/) =
= -у;
r)L:x = t, V=\t\ *=\*^ O^t^l, p(a;,y,^)
3. Найдите координаты центра тяжести:
а) однородной меньшей дуги окружности х2 + у2 = 4, соединяющей точ-
точки АB,0) и Б(-1,л/3);
б) контура однородного сферического треугольника х2 + у2 + z2 = a2,
ж ^ 0, 2/ ^ 0, z ^ 0.
4. Найдите статические моменты дуги L астроиды х2^3 + у2^3 = а2^3, х ^
^ 0, г/ ^ 0, относительно осей координат, если ее линейная плотность
р(х,у) = 1.
5. Найдите полярный момент инерции однородной кривой L плотности ро
относительно точки 0@,0), если:
а) L — контур квадрата {(ж, у): тах(|ж|, \у\) = а};
б) L — контур правильного однородного треугольника плотности ро с
вершинами в точках, заданных полярными координатами Р(а,0),
Q(a, 2тг/3), Д(а,4тг/3).
6. Найдите моменты инерции относительно осей координат одного витка
однородной винтовой линии х = cost, у = sin?, z = ?/Bтг), 0 ^ ? ^ 2тг,
если ее плотность равна ро-
7. Найдите проекции на оси координат силы, с которой материальная од-
однородная полуокружность х2 + у2 = а2, 2/ ^ 0, массы М притягивает
материальную точку О@, 0) массы т.
§ 2. Криволинейные интегралы второго рода
Основные понятия и теоремы
1. Определение криволинейного интеграла второго рода.
Пусть АВ — простая спрямляемая незамкнутая кривая, заданная па-
параметрически:
(А = А(у>(а),^(а)), В =
Пусть на кривой АВ заданы две функции, Р(х,у) и Q(x,y). Разобьем
сегмент [а,/3] на п частей точками а = to < t\ < ... < tn = C. При
этом кривая АВ разобьется на п частей точками А = M0,Mi,M2,...
§2. Криволинейные интегралы второго рода 325
...,МП = Бв направлении от А к В. Пусть (хк,ук) — координаты точ-
точки Мк, Ахк = хк -хк-х,Аук=ук -ук^,А1к — длина дуги Мк^Мк,
Al = max Alk. На каждой дуге Мк_\Мк возьмем некоторую точку
и составим две интегральные суммы:
h(Mk,Nk) = Y,P(tk,m)bxk, h(Mk,Nk) =
k=l k=l
Определение. Число Im (m = 1, 2) называется пределом интег-
интегральных сумм Im(Mkj Nk) при Al —у О, если \/г > О 3S > 0 такое, что
для любого разбиения кривой, у которого Al < 5, и для любого выбора
промежуточных точек Nk выполняется неравенство
\Im(Mk,Nk)-Im\<e.
Если существует lim Im(Mk, Nk) = /m, то он называется криволи-
нейным интегралом второго рода и обозначается следующим образом:
h = I Р{х, У) dx, h = I Q{x, y) dy.
АВ АВ
Сумма /i + /2 называется общим криволинейным интегралом вто-
второго рода и обозначается так:
P{x,y)dx + Q{x,y)dy. B)
АВ
Из определения криволинейного интеграла второго рода следует,
что при изменении направления обхода кривой АВ изменяется и знак
интеграла, т. е.
[ Р(х, y)dx = - [ Р(х, у) dx, I Q(x, у) dy = - Г Q(x, у) dy.
АВ ВА АВ ВА
Если АВ — замкнутая кривая (замкнутый контур), т. е. точка А сов-
совпадает с точкой В, то для нее можно указать два направления обхода
от А к В. Если область, лежащая внутри контура, остается слева по
отношению к движущейся по контуру точке, то такое направление
обхода кривой L назовем положительным, а противоположное ему —
отрицательным.
Интеграл B) по замкнутому контуру L в положительном направ-
направлении обозначают так: <?Р(х, у) dx + Q(x, у) dy.
L
Аналогично вводится криволинейный интеграл второго рода
J Р(х, у, z) dx + Q(x, у, z) dy + R(x, y, z) dz C)
АВ
326 Гл. XIII. Криволинейные интегралы
для пространственной кривой, заданной параметрически,
x = (p(t), y = ip(t), z = x(t), a^t^/3 D)
(A = А^{а),ф{а),Х{а)), В = В(р(/3),^(/3),Х(/3))).
2. Вычисление криволинейного интеграла второго рода с
помощью определенного интеграла.
Теорема 2. Если АВ — кусочно гладкая кривая, заданная урав-
уравнениями A), а функции Р = Р{х,у) и Q = Q(x,y) кусочно непрерывны
вдоль кривой АВ, то существует интеграл B) и справедливо равен-
равенство
Р
АВ а
Для пространственной кривой АВ, заданной уравнениями D),
справедлива аналогичная теорема, и интеграл C) вычисляется по
формуле
Pdx + Qdy + Rdz = }[P(<p(t)Mt),x(tW(t) +
АВ а
+ д(^),^(*),х(*))^(*) + й(^),^(*),х(*))х'(*)]*. (б)
Если кривая АВ задана уравнением у = у(х), а ^ х ^ Ъ, и имеет
кусочно-непрерывную производную, а функции Р(х,у) и Q(x,y) ку-
кусочно непрерывны вдоль кривой АВ, то существует интеграл B) и
имеет место равенство
ъ
J Pdx + Qdy = J[P(x, y(x)) + Q(x, y(x))y'(x)] dx. G)
АВ а
Замечание. Криволинейные интегралы второго рода обладают
свойствами линейности и аддитивности, однако теорема об оценке модуля
интеграла и формула среднего значения неверны.
3. Связь между криволинейными интегралами первого и
второго рода.
Теорема 3. Пусть АВ — кусочно гладкая кривая, заданная урав-
уравнениями A), функции Р = Р(х,у) и Q = Q(x,y) кусочно непрерывны
вдоль кривой АВ и т = {cos a, sin a} — единичный касательный век-
вектор к кривой АВ в точке М(х,у), причем направление т соответст-
соответствует направлению движения от А к В (а — угол между вектором т
в точке М(х,у) и осью Ох).
Тогда имеет место равенство
[ Р(х, у) dx + Q(x, y)dy = Г (Р cosa + Q sin a) dl = Г (ат) dl, (8)
АВ АВ АВ
где а = P(x,y)i + Q(x,y)j.
§2. Криволинейные интегралы второго рода 327
Замечание. Для пространственной кривой D) справедлива аналогич-
аналогичная теорема, а формула (8) имеет вид
/ Р(х, у, z) dx + Q(x, у, z) dy + R(x, y, z) dz =
AB
= / (P cos a-\-Q cos C-\-R cos j)dl = (ar)dl, (9)
AB AB
где a = Pi + Qj + JRk, т = cos а • i + cos /3 • j + cos 7 • k; a, /3, 7 — углы
между касательным вектором т к кривой в точке M(x,y,z) и осями Ох,
Оу, Oz.
4. Физические приложения криволинейных интегралов
второго рода.
а) Работа силы F(x,y) = P(x,y) i + Q(x,y) j при перемещении
материальной точки массы 1 из точки А в точку В вдоль кривой
АВ вычисляется по формуле
P{x,y)dx + Q{x,y)dy. A0)
AB
Таким же образом вычисляется работа силы при перемещении мате-
материальной точки вдоль пространственной кривой.
б) Пусть с = {u(x,y),v(x,y)} — скорость плоского потока
жидкости в точке М(х,у) (см. пример 7 из § 1). Тогда количество
Q жидкости, вытекающей за единицу времени из области G, равно
Q = |(cn)d/,
L
где п — единичный вектор внешней нормали к кривой L в точке
М(х,у). Если направление касательного вектора т к кривой L соот-
соответствует положительному направлению обхода кривой и а — угол
между вектором т и осью Ох, то
п = < cos (а J, sin (а ) Г = {sinQo ~ cos a},
(сп) = и sin а - v cos а,
и для величины Q, используя формулу (8), получаем выражение через
криволинейный интеграл второго рода:
{-v cos а + и sin а) dl = & — v dx + и dy.
Контрольные вопросы и задания
1. Сформулируйте определения: а) интегральных сумм для криволинейно-
криволинейного интеграла второго рода; б) предела этих интегральных сумм; в) кри-
криволинейного интеграла второго рода.
328 Гл. XIII. Криволинейные интегралы
2. Зависит ли от направления обхода кривой: а) криволинейный интеграл
второго рода; б) какая-нибудь его интегральная сумма?
3. Для криволинейного интеграла второго рода / ydx + xdy, где кри-
АВ
вая АВ задана уравнением у = 2ж, А(—1, —2), 5B,4), составьте интег-
интегральную сумму, соответствующую разбиению кривой АВ на п
равных частей и выбору промежуточных точек Щ ( ~ п, ~ ),
к = 1, 2,..., п. Вычислите предел интегральных сумм при п —»> оо.
4. Сформулируйте теорему о существовании криволинейного интеграла
второго рода и сведении его к определенному интегралу. Напишите со-
соответствующие формулы для: а) плоской кривой, заданной параметри-
параметрически; в декартовых координатах; б) пространственной кривой, задан-
заданной параметрически.
5. Какое направление обхода замкнутой кривой принимают за положи-
положительное?
6. Каков смысл обозначения <hPdx + Qdyl
L
7. Сформулируйте теорему о связи между криволинейными интегралами
первого и второго рода.
8. Криволинейный интеграл второго рода / ydx + xdy, где кривая АВ
АВ
задана уравнением у = 2ж, А(—1, — 2), БB,4), сведите к криволиней-
криволинейному интегралу первого рода и вычислите его. Сравните результат с
результатом задания 3.
9. Приведите примеры физических приложений криволинейных интегра-
интегралов второго рода.
10. Напишите формулу для вычисления работы силы при перемещении ма-
материальной точки вдоль кривой.
11. Сформулируйте свойства линейности и аддитивности криволинейных
интегралов второго рода.
Примеры решения задач
1. Вычислить криволинейный интеграл второго рода / =
= / 2ху dx + х2 dy по трем кривым, соединяющим точки А@,0)
и 5A,1), изображенным на рис. 55.
5A,1) А 1) Пусть кривая АВ задана уравнением
у — х. Тогда у1 — 1, и, пользуясь форму-
формулой G), получим
1 1
/i = / 2х • х dx + х2 dx = / Sx2 dx = x3 |Q = 1.
AF,0) GA,0)
Рис- 55 2) Для кривой АВ, заданной уравнением
у = ж2, имеем у' = 2ж, откуда
1 1
/2 = ^2ж • ж2 <ix + х2 • 2х dx = fix3 dx = ж41J = 1.
§2. Криволинейные интегралы второго рода 329
3) Интегрируя по ломаной АСВ, воспользуемся свойством адди-
аддитивности интеграла и представим его как сумму двух интегралов —
по отрезкам АС и СВ. Так как для отрезка АС у = 0,у' = О и 0 ^ ж ^ 1,
то по формуле G) получаем
1
/ 2ху dx + ж2 dy = / 2х • 0 dx + x2 • 0 dx = 0.
ас о
Для отрезка СВ имеем х = х(у) = 1, х' = 0 и 0 ^ у ^ 1; поэтому
1
Г 2xydx + x2 dy = f 2- 1 -у -Ody + I2 dy = y\l = 1.
сб о
Следовательно,
/3 = / 2ж^/ б?ж + ж2 Gfa/ + / 2ж^/ б?ж + х2 dy = 1.
АС СВ
Таким образом, Д = /2 = /3 = 1. Этот результат не случаен. Можно
доказать, что значение данного интеграла / не зависит от кривой,
соединяющей точки А и В. Вопрос о том, в каких случаях криволи-
криволинейный интеграл второго рода не зависит от кривой, соединяющей
две данные точки, будет рассмотрен в § 3. А
2. Вычислить криволинейный интеграл второго рода / = / Dж +
АВ
+ у) dx + (х + 4^/) dy, где кривая АВ задана уравнением у = ж4, АA,1),
Б(-1,1).
Л Вычислим интеграл, пользуясь формулой G). Учитывая, что у =
1
= ж4, dy = 4ж3 б?ж и ж изменяется от 1 до —1, получаем I = — Dж +
+ ж4 + (ж + 4ж4Lж3) dx = -2. А -1
3. Вычислить криволинейный интеграл второго рода <Ь{х + у) dx +
«/
+ (ж — у) dy, где L — окружность (ж — IJ + (у — IJ = 4.
Л Запишем параметрические уравнения данной окружности: ж =
= l + 2cos?, у = l + 2sin?, 0 ^ t ^ 2тг. Вычисляем интеграл, поль-
пользуясь формулой E). Так как dx = — 2 sin t dt, dy = 2 cost (it, то
2тг
x + y)dx + (ж -y)dy = /JB + 2cost + 2sint)(-2sint)(it +
0
+ Bcost- 2sintJcostdt =
2тг
= /(-4sint-8sintcost + 4cos2t)dt = 0. A
о
4. Вычислить криволинейный интеграл второго рода / = / (^/2 —
330 Гл. XIII. Криволинейные интегралы
- z2) dx + lyzdy - х2 dz, где L — кривая х = t, у = t2, z = t3, 0 ^ t ^ 1,
пробегаемая в направлении возрастания параметра t.
Л Вычислим интеграл по формуле F). Так как dx = dt, dy = 2tdt,
dz = 3t2dt, 0 ^ t ^ 1, то
/ = /(t4 - t6 + 2t5 • 2t - t2 • 3t2) dt= ^-. A
0
5. Вычислить криволинейный интеграл
/ = j(y2 - z2) dx + (z2 - x2) dy + (x2 - y2) dz
L
вдоль замкнутого контура L, являющегося границей части сферы
х2 + у2 + z2 = 1, расположенной в I октанте: х ^ 0, у ^ 0, z ^ 0, причем
направление обхода контура таково, что в плоскости Оху движение
происходит от точки АA,0,0) к точке 5@,1,0).
Л Контур L состоит из трех кривых, /]_, ^, 1з, каждая из которых
является дугой единичной окружности, лежащей соответственно в
з
координатной плоскости Оху, Oyz, Oxz. Поэтому / = У^/&, где //, =
к=1
= J(y2 - z2) dx + (z2 - х2) dy + (ж2 - у2) dz.
h
Найдем интеграл 1\ по кривой 1\. Так как кривая 1\ лежит в плос-
плоскости Оху, то z — 0, dz — 0 и /i = у2 dx — х2 dy, где 1\\ х2 -\- у2 — \,
h
х ^ 0, у ^ 0. Запишем параметрические уравнения 11: х = cost, 2/ =
= sint, 0 ^ t ^ тг/2. По формуле E) получим
тг/2 тг/2
/i = / (- sin3 t - cos3 t) dt = -2 Г sin3 t (it =
о о
= 2 / A - cos2 t) d(cost) = 2f cost - ^) Г7' = -|.
J V о / lo 3
о
Точно так же вычисляются интегралы I<i и /3. При этом Д = /2 =
= /з = —4/3. Следовательно, / = —4. А
6. Найти магнитную индукцию В = {Bx,By,Bz} магнитного по-
поля, создаваемого током /, протекающим по замкнутому проводнику
L, в точке Мо(жо,2/о,^о).
Л Рассмотрим произвольное разбиение кривой L на малые дуги
MqMi, M1M2,..., Мп-\Мп такие, что направление по дуге кривой от
точки Mfc_i(a;fc_i,2/fc_i,2]fe_i) к точке Mk(xk,yk,zk) совпадает с на-
направлением тока. На дуге Мк_\Мк выберем некоторую промежуточ-
промежуточную точку Nk(^k,T]kXk). Каждую из дуг Мк-\Мк заменим прямоли-
прямолинейным отрезком. Согласно закону Био-Савара электрический ток /,
§2. Криволинейные интегралы второго рода 331
протекающий по отрезку Мк_\Мк, создает магнитное поле, индукция
которого в точке Mq равна
АВ, = {ABkx,ABky,ABkz} = ^ [M^Ml • г,],
где гк = M0Nk = {?к -хо,т ~ УоХк - zo], Мк-±Мк = {хк - хк-Ъ
Ук -Ук-и*к - Zk-i} = {Ахк,Аук,Агк}, тк = \гк\, 7 — коэффициент
пропорциональности. Поэтому
** = Ц. ((а -
тк
АВку = ^ ((^ - xo)Azk - (Ск ~
тк
хк - (& -хо)Аук).
'к
Суммируя по к от 1 до п и переходя к пределу при А1 —> 0, получим
_ ^ Т / (z- г0) dy-(y- уд) ^
-О .г —
- Гг - гп
/(ж — жо) dz — (z — zq) dx
L
B _ Л/ T i (У - Уо) dx-(x- xp) dy
/((ЖЖо) + B/2/о) + (^го))
Ll
Если ввести векторы г = {x - xo,y - yo,z - z0} и ш = {dx, dy, dz}, то
вектор магнитной индукции В = Вх i + Ву j + Bz k можно записать в
виде -^
[ ]
Отметим, что направление обхода контура L совпадает с направлени-
направлением тока в контуре. А
7. Привести пример, показывающий, что для криволинейных
интегралов второго рода неверна, вообще говоря, формула среднего
значения
I P(x,y)dx = P(x*,y*) I dx,
АВ АВ
где АВ — гладкая кривая, Р(х,у) — непрерывная вдоль АВ функ-
функция, (ж*, у*) — некоторая точка кривой АВ.
Л Рассмотрим полуокружность {ж2 + у2 = 1, х ^ 0} с направлени-
направлением обхода от точки А@,1) к точке В@, —1). На полуокружности АВ
зададим непрерывную функцию Р(х,у) = у. Пользуясь параметри-
параметрическими уравнениями кривой АВ х = cost, у = sint, тг/2 ^ t ^ Зтг/2,
вычислим криволинейные интегралы, входящие в формулу среднего
332 Гл. XIII. Криволинейные интегралы
значения: о /о
Зтг/2
P(x,y)dx = lydx — / smt(-smt)dt =-^-^ О,
АВ АВ тг/2
Зтг/2
Г dx= Г (-smt)dt = O.
АВ тг/2
Следовательно, не существует такого промежуточного значения
Р(х*,у*) непрерывной подынтегральной функции Р(х,у) = у, для ко-
которого / Р(х,у) dx = Р(х*,у*) / б?ж. А
АВ АВ
Задачи и упражнения для самостоятельной работы
В упр. 8-18 вычислите криволинейные интегралы второго рода. Для не-
незамкнутых кривых, заданных параметрически (уравнением у = /(ж)), на-
направление обхода соответствует возрастанию параметра t (переменной ж).
8. / xdy — ydx, где 0@,0), АA,2), если: а) О А — отрезок прямой;
ОА
б) ОА — дуга параболы, осью которой является ось Оу; в) ОА —
ломаная линия, состоящая из отрезка ОВ оси Ох и отрезка В А, парал-
параллельного оси Оу.
9. xdx — ydy, где О А — кривые из пп. а), б) и в) упр. 8.
ОА
10. / (ж2 — 2ху) dx + (у2 — 2ху) dy, где L — дуга параболы: у = ж2, —1 ^
^ х <: 1.
11. Г(х2 + у2) dx + (ж2 - у2) dy, где L — кривая у = 1-\1-х\, 0 ^ ж ^ 2.
L
г х2 у2
12. ф (ж + у) dx + (ж — |/) cfa/, где L — эллипс —- + —- = 1.
/ а2 Ь2
L
13. / B — у) dx + ж cfa/, где L — арка циклоиды х = t — sin ?, г/ = 1 — cos ?,
О ^ ? ^ 2тт.
^ л Г (х -\- у) dx — (х — у) dy T о о
14. ф к У) о—Ц—^-^, где L — окружность ж2 + у2 = 1.
/ х2 + у2
15. ф , где L — граница квадрата с вершинами АA,0), 5@,1),
/ 1Ж1 + \У\
[\А + \у\
16. / у dx + zdy + ж dz, где L — виток винтовой линии ж = cos t, у = sin ?,
z = t, 0 ^ t ^ 2тг.
17. (у — z) dx -\- (z — x) dy + (ж — 2/) dz, где L — окружность ж2 + у2 +
+ z2 = a2, 2/ = x tg a, a E @, тг/2); обход окружности совершается про-
против хода часовой стрелки, если смотреть из точки Bа, — 2а, 0), а > 0.
§3. Формула Грина
333
18.
1 dx + z2 dy + ж2 dz, где L — кривая Вивиани
ж2 + у2 + z2 = а2,
х2 + у2 = ах
( 0, а ^ 0), пробегаемая против часовой стрелки, если
смотреть из точки Bа, 0,0).
19. Пусть F(M) — сила, с которой материальная точка массы т, помещен-
помещенная в начало координат 0@,0), притягивает точку массы 1, находя-
находящуюся в точке М(х,у). Найти работу силы притяжения F при пере-
перемещении материальной точки массы 1 вдоль кривой АВ, где АВ —
часть эллипса 2- + ^- = 1, при х ^ 0, у ^ О, А@,3), ВB,0).
20. Пусть с = {—ху,у2/2} — скорость плоского потока жидкости в точ-
точке М(х,у). Вычислить количество жидкости, вытекающее за единицу
времени из области G = {(ж, у): — 1 ^ х ^ 1, ж4 ^ ?/ ^ 1}.
21. Вычислить работу силы F вдоль кривой АВ, если:
а) F = {у, — ж}, А5 — окружность ж2 + ?/2 = 1, пробегаемая по ходу
часовой стрелки от точки А(—1/у/2, —1/-\/2) до точки БA/>/2,1/л/2);
б) F = {z, — ж,|/}, А5 — виток винтовой линии ж = a cost, 2/ = 6sin?,
г = ct, 0 ^ ? ^ 2тг, А(а, 0, 0), Б(а, 0, 2тгс).
22. Вычислить работу силы F вдоль замкнутого контура L в положитель-
положительном направлении, если:
a) F = {ж — у, 2ж + у}, L — треугольник с вершинами АA,1), 5C, 3),
С()
б) F = {ж + у, у — ж}, L — эллипс 5ж2 — бху + Ъу2 = 8.
§ 3. Формула Грина. Условия независимости
криволинейного интеграла второго рода
от пути интегрирования
Основные понятия и теоремы
1. Понятие простой области. На рис. 56, а изображена замк-
замкнутая область Gi, ограниченная снизу и сверху кусочно гладкими
Ук
У=Уг{х)
О а
х=х1(у)
Рис. 56
кривыми у = у\(х) и у = У2(х), а слева и справа — отрезками
прямых х — а и х — Ъ. Напомним, что такая область называется
^/-трапециевидной (отрезки прямых могут вырождаться в точку).
Аналогично определяется ж-трапециевидная область (рис. 56, б).
334
Гл. XIII. Криволинейные интегралы
Замкнутую область G назовем простой, если ее можно разбить
на конечное число как ж-трапециевидных, так и ^-трапециевидных
областей. Предполагается, что при
каждом разбиении никакие две об-
области не имеют общих внутренних
точек. Примерами простых облас-
областей являются круг, прямоугольник,
кольцо. На рис. 57, а показано раз-
разбиение кольца на ^-трапециевидные,
Рис- 57 на рис. 57, б— на ж-трапециевидные
области (стрелками указано положительное направление обхода гра-
границы кольца).
2. Формула Грина.
Теорема 5. Пусть функции Р(х,у) и Q(x,y) и их частные про-
дР дО
изводные —— и —— непрерывны в простой области G.
ду дх
Тогда справедливо равенство
A)
G
где криволинейный интеграл берется по границе L области G в поло-
положительном направлении.
Формула A) называется формулой Грина. Она связывает интеграл
по границе области с интегралом по самой области.
Замечание 1. Формула Грина справедлива не только для простой
области, но и для любой ограниченной области с кусочно гладкой границей.
Замечание 2. Полагая в формуле Грина Q = ж, Р = 0, а затем Q = О,
Р = —у и учитывая, что dxdy равен площади S области G, получим вы-
G
ражения площади фигуры через криволинейные интегралы по ее границе:
B)
S = (bxdy,
L
S = — (bydx.
L
Пусть а и C — произвольные числа такие, что а + /3 = 1. Умножая
первое из равенств B) на а, а второе на /3 и складывая, получим еще одну
формулу для площади:
S = (pax dy — Cydx (a + C = 1).
L
Наиболее употребительна эта формула при а = /3 = 1/2:
S = - р dy — у dx.
C)
§3. Формула Грина 335
3. Условия независимости криволинейного интеграла вто-
второго рода от пути интегрирования на плоскости. В § 2 был
рассмотрен пример, в котором криволинейный интеграл второго ро-
рода по трем различным кривым, соединяющим две данные точки А и
В, имел одно и то же значение. Можно доказать (см. ниже замеча-
замечание 2 к теореме 6), что этот интеграл имеет то же самое значение
для любой кусочно гладкой кривой, соединяющей точки А и В. В
таком случае говорят, что криволинейный интеграл второго рода не
зависит от пути интегрирования (т. е. не зависит от выбора кри-
кривой, соединяющей две данные точки, а зависит только от самих этих
точек).
В формулируемой ниже теореме б об условиях независимости кри-
криволинейного интеграла второго рода от пути интегрирования исполь-
используется понятие односвязной области.
Определение. Область G на плоскости называется односвязной,
если для любого замкнутого контура, лежащего в этой области, огра-
ограниченная им часть плоскости целиком принадлежит области G.
Примерами односвязных областей служат круг, прямоугольник;
пример неодносвязной области — кольцо.
Теорема 6. 1°. Пусть функции Р(х,у) и Q(x,y) непрерывны в
области G.
Тогда следующие три условия эквивалентны (т. е. из каждого из
них следуют два других).
I. Для любого замкнутого кусочно гладкого контура L, расположен-
расположенного в области G, справедливо равенство
L
П. Для любых двух точек А и В в области G криволинейный ин-
интеграл I P dx + Qdy не зависит от пути интегрирования, располо-
АВ
женного в области G.
III. Выражение Р(х,у) dx + Q(x,y) dy является полным дифферен-
дифференциалом, т. е. в области G существует функция и{М) = и{х, у) такая,
что
du = Р' dx + Q dy.
При этом для любой кусочно гладкой кривой АВ, лежащей в облас-
области G, имеет место равенство
Pdx + Qdy = u{B) - и{А). D)
АВ
2°. Пусть G — односвязная область, а функции Р и Q имеют в
области G непрерывные частные производные —— и ——.
ду ох
Тогда каждое из условий I—III эквивалентно следующему условию:
336 Гл. XIII. Криволинейные интегралы
IV. В области G выполняется равенство
дР _ 0Q
Замечание 1. Функция и(х, у) из условия III может быть найдена по
2/д формуле
и(х,у)= Г Pdx + Qdy + C,
где интеграл в правой части представляет собой
криволинейный интеграл второго рода по про-
произвольной кривой L, лежащей в области G и
* соединяющей какую-нибудь фиксированную точ-
р ку (жо,2/о) с точкой (ж,г/), а С — произвольная
постоянная. В качестве кривой L часто бывает
удобно брать ломаную, состоящую из двух отрезков, параллельных осям
координат (рис. 58). Тогда
(х,Уо) (ж,2/) х у
и(х,у) = J Pdx+ J Qdy + C = fP(x,yo)dx + JQ(x,y)dy + C. F)
(xo,yo) (x,y0) x0 У0
Замечание 2. Для рассмотренного в примере 1 из § 2 криволинейного
интеграла / = / 2xydx + х2 dy имеем Р = 2ху, Q = ж2, — = 2ж, — = 2х.
J ду дх
Таким образом, — = — и, следовательно, интеграл / не зависит от пути
ду дх
интегрирования.
Контрольные вопросы и задания
1. Какая область называется: ^/-трапециевидной; ж-трапециевидной;
простой?
2. Покажите, что область G = {(х,у): — 1 ^ х ^ 1, х2 ^ у ^ 1} является
простой. Удалив из области G круг х2 + [у — - ) < —, получим об-
V 2/ 16
ласть G\. Покажите, что область G\ также является простой. Укажите
положительное направление обхода границы области G\.
3. Напишите формулу Грина и сформулируйте условия, при которых она
верна.
4. Пусть G — ^/-трапециевидная область, L — ее граница, функция Р(ж, у)
дР
и ее частная производная — непрерывны в области G. Докажите, что
ду
дР
r r дР г
справедливо равенство / / — dxdy = — фР dx.
J J ду J
G 9У
5. Напишите формулу для вычисления площади S простой области с по-
помощью криволинейного интеграла по ее границе L. Верна ли формула
5 = /- dy - ^ dx?
/5 5
ь
§3. Формула Грина 337
6. Что означает утверждение: криволинейный интеграл / Р dx + Q dy не
зависит от пути интегрирования? ав
7. Что означает утверждение: выражение Р dx + Q dy является полным
дифференциалом в области G?
8. Пусть функции Р(х,у) и Q(x,y) непрерывны в области G. Сформули-
Сформулируйте два необходимых и достаточных условия независимости криво-
криволинейного интеграла / Р dx + Q dy от пути интегрирования.
АВ
9. Дайте определение односвязной области на плоскости. Является ли
односвязной областью: полуплоскость; круговой сектор; круг с вы-
выброшенным центром; область G\ из задания 2?
10. Пусть функции Р{х,у), Q(x,y) и их частные производные — и —
ду дх
непрерывны в односвязной области G. Сформулируйте необходимое
и достаточное условие независимости криволинейного интеграла
Р dx + Q dy от пути интегрирования, использующее указанные про-
АВ
изводные. Как связано это условие с условиями из задания 8?
11. Пусть du(x, у) = Р(х, у) dx + Q(x, у) dy в области G. Напишите формулу
для вычисления функции и(х,у).
12. Пусть Р = ху, Q = ^- , G{(x, у): х2 + у2 < 4}. Докажите, что
выражение Р dx + Q dy является полным дифференциалом некоторой
функции и(х,у) в круге G, и найдите эту функцию. Чему равен интег-
рал фР dx + Q dy для любого замкнутого кусочно гладкого контура L,
расположенного в области G? Вычислите интеграл / Pdx + Qdy, где
АA1) ВA1) л
Примеры решения задач
1. Вычислить криволинейный интеграл
/ = / (еж sin у - ру) dx + (ех cos у - р) dy,
АО
где кривая АО — верхняя полуокружность х2 + у2 = ах, А(а,0),
0@,0) (рис.59).
Л Введем обозначения: Р = ех sin у - ру,
Q = ех cosy — р. Дополним кривую ин-
интегрирования АО до замкнутого контура
L отрезком О А оси Ох. Тогда получим
- [ Pdx-\-Qdy.
О А Рис. 59
гт, dQ OP ^
Так как -^- —— = р, то по формуле Грина находим
ох ду
/г г
Р dx + Q dy = pdx dy,
L G
338
Гл. XIII. Криволинейные интегралы
где область G — верхняя половина круга радиуса а/2. Поэтому
2
jjpdxdy =p.S(G) =p- Щ-.
G
Вычислим интеграл по отрезку О А оси Ох. Учитывая, что на этом
отрезке Р = О, dy = 0, получим / Р dx + Q dy = 0. Таким образом,
2. Пусть функции и(х,у), v(x,y) и их частные производные пер-
первого и второго порядка непрерывны в замкнутой области G, ограни-
ограниченной гладкой кривой L. Доказать, что справедлива вторая формула
Грина:
и
ди
дп
V
dv
дп
dl =
Г Г
JJ
G
и
Аи
V
Av
dx dy,
ди
где —— — производная по направлению внешней нормали L, Аи =
дп
д2и , д2и „ „
= ——z + -—-;-, а интеграл в левой части есть криволинейный интеграл
дх2 ду2
первого рода.
Л Сначала докажем, что
/du „ [[( \ , dv ди , dv ди\ , ,
v — dl = (vAu+ — --- + -----)dxdy.
дп JJ \ дх дх ду ду)
G)
Пусть n = {cos(p, sin(^} — единичный вектор внешней нормали к
„ Т гтл ди ди ди .
кривой L. Так как -— = —- cos(p + —- sin о?, то
дп дх ду
Г ди ,, I ди , ди . \ ,,
фу т— dl = ф [v -^- cos х + v тг- sin cp dl.
I дп J V дх ду )
L L
Единичный касательный к L вектор т = {cos a, sin а}, направление
которого соответствует положительному направ-
направлению обхода контура, получается поворотом
вектора п на угол тг/2 против часовой стрелки
(рис. 60). Поэтому
а =
¦ж/2,
L
Рис. 60
рода через криволинейный интеграл второго рода:
ди , ди •
Учитывая эти равенства, с помощью формулы (8)
из § 2 выразим криволинейный интеграл первого
ди
§3. Формула Грина 339
Вводя обозначения Р = —v —, Q = v ^—, преобразуем последний ин-
оу ох
теграл по формуле Грина. Учитывая, что
dQ__d_( 9и\ _ д\ dv_du
дх дх\ дх) дх2 дх дх'
дР _ д ( ди\ _ д2и dv ди
ду ду\ ду) ду2 ду ду'
ду
и
dv ди dv ди
G
Таким образом, справедливость равенства G) доказана.
Поменяв в равенстве G) ролями функции г? (ж, у) и и(х, у), получим
/dv 77 tt(\ , dv ди dv ди\ , , /сЛ
u — dl = [uAv +— — + —— )dxdy. (8)
дп JJ\ дх дх ду ду)
L G
Составляя разность равенств (8) и G), приходим ко второй формуле
Грина:
(Ь [и— у — ) dl = // (и Av — v Аи) dxdy. к
L G
3. Вычислить площадь S фигуры, ограниченной астроидой
х — a cos3 ?, у — b sin3 t, 0 ^ t ^ 2тг.
Л Пользуясь формулой C), находим
2тг
Л г Л г
S = - (hxdy — у dx = - / {Sab cos4 t sin2 t + Sab sin4 t cos2 t) dt =
2 J ^ J
L 0
2тг
2тг 2тг
= - / cos2 ? sin2 tdt = - / sin2 2? (it = .
2 У 8 У 8
A
У У 8
о о
4. Доказать, что подынтегральное выражение является полным
дифференциалом, и вычислить криволинейный интеграл:
а) I xdx-ydy, где А@,1), ВC, -4);
б) J (x4+4xy3)dx + Fx2y2-5y4)dy, где А(-2, -1), ВC,0).
x2 v2
А а) Очевидно, xdx - ydy = бЬ, где -u = —— ^—. По формуле D)
находим
xdx - ydy = u{B) - u{A) = -1 - ( - I) = -3.
340 Гл. XIII. Криволинейные интегралы
б) Проверим выполнение условия IV теоремы 6: Р = ж4 + 4ж?/3,
ГЛ а 2 2 к 4 #Р 1О 2 dQ 1О 2 ™ . дР 8Q
Q = 6х у — Ъу , -г— = 12ж?/ , -г-1- = 12ж?/ . Таким образом, -^— = -^,
а?/ аж ду ох
т. е. условие IV выполнено. Следовательно, по теореме б выражение
Р dx + Q dy является полным дифференциалом, а криволинейный ин-
интеграл / = I P dx + Qdy не зависит от пути интегрирования. Возь-
АВ
мем в качестве пути интегрирования ломаную АМВ, где М(—2,0).
Тогда AM = {(ж,2/): х = -2, -1 ^ у ^ 0}, МБ = {(ж,у): у = 0, -2 ^
^ ж ^ 3}.
Вдоль отрезка AM имеем ж = —2, б?ж = 0, — 1 ^ у ^ 0; поэтому
о
/ Р dx -\- Q dy = / B4^/2 — ЪуА) dy = 7. Вдоль отрезка MB имеем у =
AM -1
= 0, dy = 0, -2 ^ ж ^ 3; поэтому
з
/" Pdx-\-Qdy= fx4dx = 55.
МБ -2
Искомый интеграл по ломаной АМВ равен сумме вычисленных ин-
интегралов, т. е. равен 62. А
5. Дважды дифференцируемая функция и(х,у) называется гармо-
гармонической в области G, если в этой области Аи = ^г-^ + ^г^- = 0. Дока-
дх2 ду2
зать, что если для функции и(х,у), имеющей непрерывные частные
производные второго порядка в односвязной области G, и для любого
гладкого замкнутого контура L, лежащего в области G, справедливо
Гди „ п ди
равенство <Ь — dl = 0, где — — производная по внешней нормали к
L
контуру L, то и(х,у) — гармоническая функция в области G.
Л Пусть n = {cos(p, simp} — единичный вектор внешней нормали к
кривой L. Так как
ди ди ди .
— = ^- COS if + — Sin (р,
дп дх ду
то
/ ди „ Г (ди t ди . \ „
ф —- ш = ф тг- cos ^ + тг- sm V>] cil.
I дп J \дх ду )
L L
Далее, пусть т = {cos a, sin a} — единичный касательный вектор к
кривой L, направление которого соответствует положительному на-
направлению обхода контура. Тогда а = ^ + ip (см. рис. 60), cos a =
= — sin(^, sin a = cos(p, и по формуле (8) из § 2 получим
/ди „ Г(ди . ди \ ,, С ди , ди ,
—- dl = ф т— sm а — -7Г- cos а ш= ф — -тг- dx + -^- dy.
дп J \дх ду ) I ду дх
§3. Формула Грина
341
Таким образом, ф — ^— dx + -^- dy = 0 для любого замкнутого
J ду дх
L
гладкого контура L, лежащего в односвязной области G, т. е. выпол-
выполнено условие I теоремы 6. По теореме б из условия I следует условие
„, д ( ди\ д (ди\ д2и д2и Л
IV, т. е. — - — = — — , откуда ^-^ + -— = 0, или Аи = 0.
<9?/V <9?// дх\дх/ дх2 ду2
Это и означает, что функция и(х,у) гармоническая в области G. А
^т-, т Г х dy — у dx T
6. Вычислить интеграл / = ф—^—^—, где L —замкнутый ку-
/ х2 + у2
L
сочно гладкий контур, окружающий начало координат, пробегаемый
в положительном направлении и ограничивающий область G.
Л Покажем, что интеграл / не зависит от выбора контура L, окружа-
ющего начало координат. Положим Р = г-^—-,
х2 + у
:. Тогда
при х2 + у2 ф 0,
dQ_ _дР_ _ у2 -х2
дх ~ ду ~ (х2 -\-у2J
т. е. условие IV теоремы б выполнено всюду в области G, за исключе-
исключением точки 0@,0). Область G с выброшенной точкой О уже не явля-
является односвязной, поэтому утверждение 2° теоремы б использовать
нельзя (нельзя утверждать, что из условия IV следует условие I).
Рассмотрим другой кусочно гладкий замкнутый контур I, окру-
окружающий начало координат. Пусть контур I лежит внутри (или вне)
области G, тогда кривые L и I ограничивают некоторую область п.
Применим к этой области формулу Грина. Если кривая I лежит
внутри G (рис. 61, а), то в формуле Грина обход контура L совер-
совершается против часовой стрелки, а контура I — по часовой стрелке.
Поэтому
)Р dx + Q dy — (ЬР dx + Q dy = //( -^- — -^— j dx dy = 0,
L I Q
откуда
(ЬР dx + Q dy = фР dx + Q dy. (9)
l i
342 Гл. XIII. Криволинейные интегралы
Если же кривая I лежит вне G (рис. 61, б), то в формуле Грина обход
контура L совершается по часовой стрелке, а контура I — против ча-
часовой стрелки. Значит,
)Pdx + Qdy- J)Pdx + Qdy = 0.
j
I L
Отсюда снова получаем равенство (9). Если контуры L и I пересека-
пересекаются в п точках (рис. 61, в), то для каждой из п полученных при этом
областей пк, не содержащих начала координат (они заштрихованы на
рис. 61, в), справедлива формула Грина. Пользуясь этой формулой,
находим
Г Pdx + Qdy+ f
(направления обхода показаны на рис. 61, в). Просуммировав эти ра-
равенства по к от 1 до п, получим, что сумма интеграла по контуру L в
положительном направлении и интеграла по контуру I в отрицатель-
отрицательном направлении равна нулю. Отсюда снова приходим к равенству
(9). Таким образом, интеграл / не зависит от выбора кривой L. Вы-
Вычислив его по единичной окружности х = cost, у = sint, 0 ^ t ^ 2тг,
получим
т
1
-/
cos2 t dt + sin2 t dt
cos2 t + sin2 t
Замечание. Рассмотренный пример показывает, что если область не
является односвязной, то из условия IV теоремы 6 может не следовать
условие I.
7. Найти функцию и(х, у), если du = [ycosxy - 2xsin(x2 - у2)] dx +
+ [х cos xy + 2у sin(x2 — у2)] dy.
Л Нетрудно убедиться, что для дифференциального выражения вы-
выполнено равенство E). Для вычисления функции и(х,у) воспользуем-
воспользуемся формулой F). Находим
{x, у) = [уо cos хуо - 2х sin(x2 - у%)] dx +
у
/ [х cos xy + 2y sin(x2 — у2)] dy =
У0
¦cos(x2 -yl)]\lQ + [sinxy + cos(x2 - у2)]\Ууо +С =
cos(x2 - 2/о) -
+ [sinж?/ + cos(x2 - у2) — sinx^/o - cos(x2 - y%)] + С =
= sinxy + cos(x2 - y2) + Ci,
где C\ — произвольная постоянная. А
§3. Формула Грина 343
Задачи и упражнения для самостоятельной работы
23. Вычислите криволинейные интегралы второго рода, применив форму-
формулу Грина:
а) Фху2 dy — ж2 dx, где L — окружность х2 + у2 = а2;
L 2 2
б) /(ж + у) dx - (ж - у) dy, где L — эллипс ^— + \- = 1;
L
в) (Ье~х +у (cos 2xydx + sin2xy dy), где L — окружность ж2 + ?/2 = Я2;
L
г) / ((р(у)ех — py)dx + ((р'(у)ех — p)dy, где АБ — кусочно гладкая
кривая, соединяющая точки А{х\,у\) и В(х2,У2), не пересекающая
отрезок А5 в его внутренних точках и ограничивающая вместе с от-
отрезком АВ область площади 5, а функция ср(у) имеет непрерывную
производную.
24. На сколько отличаются друг от друга криволинейные интегралы
h = / {х + ?/J dx — (х — уJ dy и /2 = / (ж + ?/J dx — (х — уJ dy, где
ЛтБ АпВ
АтВ — отрезок, соединяющий точки АA,1) и В{2, 6), а Ап5 — дуга
параболы, проходящей через точки А, В и начало координат?
25. С помощью криволинейных интегралов вычислите площади областей,
ограниченных следующими кривыми:
а) эллипсом х = a cost, у = bsint, 0 ^ t ^ 2тг;
б) параболой (ж + ?/J = 2ах (а > 0) и осью Ож;
в) гиперболой |/ = 1/ж, осью Ож и прямыми ж = 1 и ж = 2;
г) окружностью ж2 + у2 = 4 и параболой ж2 = 2 — у (область содержит
начало координат).
26. Вычислите интеграл / = ф (ж cos a + ycosf3) dl, где L — замкнутая
L
гладкая кривая, ограничивающая область площади S] а и C — углы
между вектором внешней нормали п к кривой L в точке М(х,у) и
осями Ох и Оу.
27. Докажите, что если функция и(х,у) имеет в замкнутой области G не-
непрерывные производные второго порядка, то справедлива формула
//[(к)E)>//
G G L
где L — гладкий контур, ограничивающий область G.
28. Докажите, что подынтегральное выражение является дифференциалом
некоторой функции, и вычислите криволинейные интегралы:
а) Г xdy + ydx, где А(-1,2), БB,3);
б) J (ж + у) dx + {x- у) dy, где А@,1), ВB, 3);
/ , где АB,1), ВA,2), АВ — кривая, не пересекающая
J х2
АВ
ось Оу;
344 Гл. XIII. Криволинейные интегралы
г) / — . где АA,0), 5F,8), АВ — кривая, не проходящая че-
J л/.Т2 -I- ?У2
/в
рез начало координат;
д) j xdx + y2dy, где
х dx -\- у dy , , 2,
у где точка М\\х\,у\) лежит на окружности х +
= а2, а точка М2(ж2,2/2) — на окружности ж2 + у2 = Ь2.
29. Выразите следующие криволинейные интегралы через определенный
интеграл:
а) / f(x + y)(dx + dy), где А@,0), B(a,b), a /(?) — непрерывная
функция;
б) У /(л/ж2 +V2)(xdx + ydy), где Mi(>i,2/i), М2(ж2,2/2), а /(*) —
непрерывная функция.
30. Выразите криволинейный интеграл / у(ж) dx + ^(г/) с/|/, где Mi(xi, г/i),
М2(ж2,2/2), а <р(ж) и ^(г/) — непрерывные функции, через сумму опре-
определенных интегралов.
31. Найдите функцию и(х,у), если:
а) cfai = (ж2 + 2ху - у2) dx + (ж2 - 2ж^/ - у2) dy;
Qn-\-m-\-l z Qn-\-m-\-l z
б) du = dx + — dy.
dxn+1 дут дхп dyrn+1
ГЛАВА XIV
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
§ 1. Площадь поверхности
Основные понятия и теоремы
1. Уравнения поверхности. В § 4 гл. X была рассмотрена по-
поверхность, являющаяся графиком непрерывной функции
z = f(x, у), (x,y)eG. A)
Задание поверхности уравнением A), а также уравнением
x = f(y,z) (V)
или уравнением
V = f(z,x) A")
называется явным.
Поверхность может быть задана уравнением
F(x,y,z)=0, B)
не разрешенным относительно ни одной из переменных (неявное за-
задание). При этом поверхность представляет собой множество всех то-
точек, координаты которых удовлетворяют уравнению B). Например,
уравнение
х2 + у2 + z2 - R2 = О C)
задает сферу радиуса R с центром в начале координат.
Наконец, поверхность может быть задана параметрически:
х = <р(и, v), у = ф(щ v), z = х(щ v), (и, v) G g, D)
где ip, ф, х — непрерывные функции в области д. Переменные и и v
называются параметрами. По формулам D) каждой точке (и, v) об-
области д ставится в соответствие некоторая точка (ж, у, z) трехмерного
пространства. Множество этих точек и образует поверхность.
Например, уравнения
х = R sin и cos v, у = R sin и sin i?, z = Rcosu,
(u,v) G g = {(u,v): 0 ^ и ^ тг, 0 ^ v ^ 2тг} ^
задают ту же самую сферу, что и уравнение C).
Уравнения D) можно записать в векторном виде
г = ip(u, v) i + ip(u, v)i + x(u, v) k, (u, v) G g, F)
346
Гл. XIV. Поверхностные интегралы
где г = xi + yj + zk — радиус-вектор точки M(x,y,z), a {i,j,k} —
ортогональный базис.
В дальнейшем, рассматривая поверхности, заданные параметри-
параметрически уравнениями D), будем считать выполненными следующие
условия.
I. Область д ограничена и замкнута; ее границей является кусочно
гладкая кривая без самопересечений.
П. Функции (р, ф и х непрерывно дифференцируемы (т. е. имеют
непрерывные частные производные первого порядка) в области д.
III. Различным внутренним точкам (и, v) области д соответствуют
различные точки (x,y,z) поверхности.
Если условие, аналогичное III, выполнено также для граничных
точек области д, то поверхность будем называть простой. Множест-
Множество точек поверхности, соответствующих граничным точкам области
д, образует в этом случае границу (или край) поверхности. На рис. 62
изображена часть конической поверхности х = ucosv, у = us'mv,
О' А(а,0)
Рис. 62
z = и, (u,v) Е д = {(u,v) : 0 < а ^ и ^ 6, 0 ^ г? ^ тт}, краем ко-
которой является замкнутый контур А'В'CD', соответствующий пря-
прямоугольнику ABCD — границе области д. Точки поверхности, не
принадлежащие краю, называются ее внутренними точками. Если
же условие типа III не выполнено для граничных точек области д,
то поверхность может не иметь края (в таком случае она называется
замкнутой). Примером такой поверхности является сфера, заданная
уравнениями E).
Замечание. Определение внутренних и граничных точек поверхнос-
поверхности можно ввести еще и так: точка М поверхности называется внутренней,
если существует окрестность точки М такая, что множество точек этой
окрестности, не принадлежащих поверхности, является несвязным; точка
поверхности, не являющаяся внутренней, называется граничной.
2. Понятие гладкой поверхности. Пусть поверхность Ф за-
задана либо явно, либо неявно, либо параметрически. Будем называть
поверхность Ф гладкой, если для любой ее внутренней точки сущест-
существует такая окрестность, которая вырезает часть поверхности Ф,
§1. Площадь поверхности
347
допускающую явное представление вида A) или (Г) или A") где / —
непрерывно дифференцируемая функция.
Из этого определения следует, что в каждой внутренней точке
гладкой поверхности существует касательная плоскость и нормаль
(см. § 4 гл. X).
Если поверхность Ф задана явно уравнением A) и функция f(x,y)
непрерывно дифференцируема в области G, то поверхность, очевидно,
является гладкой. Уравнение касательной плоскости и координаты
вектора нормали в данной точке поверхности Ф приведены в § 4 гл. X.
Пусть поверхность Ф задана неявно уравнением B) и пусть функ-
функция F(x,y,z) непрерывно дифференцируема. Точка Мо(жо,^/о5 ^о) по-
поверхности Ф называется неособой, если в этой точке F% + Fy + F^ ф 0.
В противном случае точка называется особой. Если поверхность не
содержит особых точек, то она является гладкой. Уравнение каса-
касательной плоскости к поверхности Ф в неособой внутренней точке
М)(жо,2/о,?о) имеет вид
Вектор
Fx(M0)(x - х0) + Fy(M0)(y - у0) + Fz(M0)(z - z0) = 0.
N = {Fx(Mo),Fy(Mo),Fz(Mo)}
Ф в точке M
G)
N
является вектором нормали к поверхности
Пусть поверхность Ф задана пара-
параметрически уравнениями D), или, что
то же самое, уравнением F). Точка
M0(ip(u,v), ф(и,у), x(u,v)) называется
неособой точкой поверхности Ф, если в
этой точке векторы
ги = iipu(u, v) + j фи(и, v) + k^w(w, i?),
rv = i ifv {и, v) + jфv (и, v) + k Xv (и, v)
неколлинеарны (линейно независимы).
В противном случае точка Mq называ- Рис. 63
ется особой.
Простая поверхность, не имеющая особых точек, является глад-
гладкой.
Уравнение касательной плоскости к поверхности Ф в неособой
внутренней точке M((p(u,v),ip(u,v),x(uiv)) имеет вид
А(х - х0) + В(у - у0) + C(z - z0) = 0,
где xq = ip(u,v), уо = ф(и,у), z0 = x(u,v),
А =
Фи Хи
Фv Xv
в =
Хи
Xv
с =
Фи
Фv
(8)
Вектор N = [ги -rv] = iA+jB + кС есть вектор нормали к по-
поверхности Ф в точке М. Векторы ги и rv, отложенные от точки М,
лежат в касательной плоскости (рис. 63).
348 Гл. XIV. Поверхностные интегралы
3. Понятие площади поверхности. Пусть Ф — гладкая ограни-
ограниченная поверхность. Разобьем ее с помощью кусочно гладких кривых
на конечное число п частей Ф^ (г = 1, 2,..., п) так, чтобы каждая часть
Ф^ однозначно проектировалась на касательную плоскость, проведен-
проведенную в любой точке этой части (предполагается, что такое разбиение
возможно). На каждой части Ф^ возьмем произвольную точку Mi и
проведем через нее касательную плоскость к поверхности. Обозна-
Обозначим через Si площадь проекции Ф^ на касательную плоскость (эта
проекция ограничена кусочно гладкими кривыми и потому квадри-
п
руема). Составим сумму S($i,Mi) = У^?^. Пусть di — диаметр Ф^,
d = max di. i=1
Определение. Число S называется пределом сумм 5(Ф^, Mi) при
d —> 0, если Vs > 0 36 > 0 такое, что для любого разбиения поверх-
поверхности Ф, у которого d < 6, и для любого выбора точек Mi выполняется
неравенство
\S(*i,Mi)-S\<e.
Если существует lim S{$i,Mi) = 5, то поверхность Ф называется
квадрируемой, а число S — площадью поверхности Ф.
Замечание 1. Поверхность, составленная из нескольких гладких по-
поверхностей, называется кусочно гладкой. Если каждая из этих гладких
поверхностей квадрируема, то сумма их площадей принимается за площадь
кусочно гладкой поверхности.
Замечание 2. Определение площади естественным образом распро-
распространяется на поверхности, не имеющие касательной плоскости и нормали
в конечном числе внутренних точек. Примером такой поверхности явля-
является коническая поверхность, которая не имеет касательной плоскости в
своей вершине.
4. Вычисление площади поверхности с помощью двойного
интеграла.
Теорема 1. Гладкая параметрически заданная поверхность, не
имеющая особых точек, квадрируема, и ее площадь S выражается
формулой
S = JJ^Ai+Bi + Cidudv, (9)
9
где А, В и С определяются по формуле (8).
Замечание 1. При наличии конечного числа особых точек форму-
формула (9) остается в силе.
Замечание 2. Введем функции
Е = т2и = (pl(u, v) + ф1(и, v) + х1(щ v),
G = r2v= <рЦщ v) + ф1{щ v) + xl(u, v), A0)
F = (rwr,) = (pu(fv + Фифу + XuXv-
Справедливо равенство
A2 + В2 + С2 = EG - F2, A1)
§1. Площадь поверхности 349
и поэтому формулу (9) можно записать в виде
5 = jj^EG-F2dudv. A2)
9
Замечание 3. Поверхность, определенную явно уравнением A), мож-
можно рассматривать как заданную параметрически — роль параметров игра-
играют х и у. Параметрические уравнения D) для такой поверхности можно
записать в виде
х = и, у = v, z = f(u, v), (и, v) G G.
Если область G удовлетворяет условию I п. 1, а функция /(ж, г/) непрерыв-
непрерывно дифференцируема в области G, то, используя равенство A2), получим
формулу для площади поверхности, заданной явно,
5 = JJy/1 + fl(x,y) + fl{x,y)dxdy. A3)
G
Контрольные вопросы и задания
1. Назовите способы задания поверхности. Для каждого способа приведите
пример.
2. Напишите уравнения поверхности в параметрическом и в векторном
виде. Какие требования накладываются на параметрические уравнения
поверхности?
3. Напишите параметрические уравнения сферы, конуса, круглого ци-
цилиндра.
4. Какая поверхность называется простой? Что называют границей или
краем поверхности? Является ли простой поверхностью часть эллипти-
эллиптического параболоида х = и, у = v, z = и2 + v2, (и, v) G g = {(и, v): 0 ^
^ и2 + v2 ^ а2}? Что является границей этой поверхности?
5. Приведите пример замкнутой поверхности, т. е. поверхности без края.
6. Для следующих поверхностей, заданных параметрически, определите,
в какие точки поверхности (граничные или внутренние) отображается
граница области д:
а) сфера х = i^sin^cosv, у = i^sin^smv, х = Rcosu, (u,v) G g =
= {(и, v): 0^^^7T,0^v^ 2тг};
б) конус х = г cos 9?, у = rsincp, z = г, (г, 9?) G g = {(г, ср): 0 ^ г ^
^ а, 0 ^ <? ^ 2тг};
в) цилиндр х = a cos 9?, 2/ = asin<?, z — h (a > 0), (/г, <p) G g = {(/&, <p):
-b^h^b, O^ip^ 2тг}.
Нарисуйте данные поверхности и укажите на рисунке образ границы
области д. Являются ли эти поверхности простыми?
7. Дайте определения: а) гладкой поверхности; б) касательной плоскости
к поверхности в данной точке.
8. Какая точка поверхности называется неособой (особой), если поверх-
поверхность задана: а) неявно; б) параметрически?
9. Сформулируйте достаточные условия, при которых является гладкой
поверхность, заданная: а) явно; б) неявно; в) параметрически.
10. Напишите уравнение касательной плоскости в неособой внутренней точ-
точке гладкой поверхности, заданной: а) явно; б) неявно; в) параметри-
параметрически. Каковы координаты нормали к поверхности в этой точке?
350 Гл. XIV. Поверхностные интегралы
11. Укажите особые точки сферы и конуса из задания 6. Существуют ли
касательные плоскости в этих особых точках?
12. Имеет ли особые точки цилиндр х = a cos ср, у = asincp, z = h при
-b^h^b, 0 ^ if ^ 2тг?
13. Справедливо ли утверждение: в каждой внутренней точке гладкой по-
поверхности существует касательная плоскость и нормаль?
14. Дайте определение площади поверхности. Какая поверхность называет-
называется квадрируемой?
15. Сформулируйте теорему о квадрируемости поверхности, заданной па-
параметрически, и напишите формулу для вычисления ее площади.
16. Вычислите выражение л/EG — F2 для сферы, конуса, кругового цилинд-
цилиндра из задания 6.
17. Напишите параметрические уравнения гиперболического параболоида
2 2 X2 у2 Z2 Л
z = х — у и эллипсоида — + ^- + — = 1и вычислите выражение
а2 Ь2 с2
\JEG — F2 для этих поверхностей.
18. Выведите формулу для вычисления площади поверхности, заданной яв-
явно. При каких условиях она верна?
Примеры решения задач
1. Составить уравнение касательной плоскости и вычислить на-
направляющие косинусы нормали к поверхности х = и, у = и, z —
— и3 + v2 в точке МоA,1, 2).
Л Пользуясь уравнением поверхности в векторной форме z = iu +
+ j v + к (и3 + г?2), получим
По формуле N = [rwrj находим нормаль в точке Мо:
i J k
N =
1 0 3
k.
0 12
Составляем уравнение касательной плоскости, проходящей через
точку МоA,1,2): -3(х - 1) - 2(у - 1) + (z - 2) = 0, или z - Зх -
— 2у + 3 = 0. Далее, вычислим длину вектора N и его направляющие
косинусы: |N|2 = 9 + 4 + 1 = 14, cos а = — З/д/14, cos/З = -2/л/14,
cos 7 = 1/л/14- А
2. Вычислить площадь S части гиперболического параболоида z =
= ху, вырезанной цилиндром х2 + у2 = 8.
Л Площадь S вычислим по формуле A3):
S =
G G
где G — круг х2 + у2 ^ 8. В интеграле перейдем к полярным коорди-
координатам; получим
§1. Площадь поверхности
351
2тг 2^2
S = dip p^/l + р2 dp.
о о
Вычисляя интеграл, находим S = 2бтг. А
3. Найти площадь S части поверхности z = 1 — (ж2 — 2/2K//2, отсе-
отсекаемой плоскостью г = 0.
Л Для вычисления площади S воспользуемся формулой A3). На-
Находим
9(х2
zy = -Зу(х
S = J
G
2
где G — область на плоскости Ож^/, на которую проектируется часть
поверхности, отсеченная плоскостью z = 0. Границей области G яв-
является линия пересечения поверхности с плоскостью z = 0, т. е. кри-
кривая 0 = 1 — (ж2 + 2/2K/2. Отсюда получаем ж2 + ^/2 = 1, т. е. граница
области G — окружность радиуса 1 с центром в начале координат.
Вычислим интеграл 5, перейдя к полярным координатам х =
у = y^sin^, 0 ^ ip ^ 2тг. Имеем
s =
4. Найти площадь поверхности тела, ограниченного поверхностя-
поверхностями х2 + z2 = а2, у2 -\- z2 = а2.
Л Сначала вычислим площадь 5 части поверхности Ф первого цилинд-
Рис. 64
pa, вырезанной вторым (рис. 64). Параметрические уравнения перво-
первого цилиндра имеют вид
х = acos(p, у = /i, 2 = asin(^, 0 ^ <р ^ 2тг, —оо < h < +оо.
352 Гл. XIV. Поверхностные интегралы
Для того чтобы найти уравнение линии пересечения поверхностей,
подставим параметрические выражения у и z в уравнение второго
цилиндра. Уравнение у2 + z2 = а2 в переменных (р, h примет вид
Ь2 = а2 cos2 <?, 0 ^ <? ^ 2тг.
Таким образом, для точек пересечения поверхностей при у > О
имеем h = a\ coscp\, при 2/ < 0 имеем h = —a\ coscp\. Область д изме-
изменения параметров поверхности Ф запишется следующим образом:
д = {(ip,h): 0 ^ ip ^ 2тг, —а| cos(^| ^ /i ^ a\
Пользуясь формулами A0), получаем Е = a2 sin2 у? + а2 cos(p = а2,
G = 1, F = 0, откуда \JEG — F2 = а. По формуле A2) находим
2тг a|cos(/?|
S = a dcp dh = a dcp / dh = Sa2.
9 0 —а| cos (/?|
Точно так же вычисляется площадь части второго цилиндра, выре-
вырезанной первым. В результате получаем ответ: 16а2. А
Задачи и упражнения для самостоятельной работы
1. Составьте уравнение касательной плоскости к поверхности в точке
()
а) х = a cos v sin 16, у = 6sinvsini6, z = ccosi6, М0(а/л/3, b/y/З, — с/л/З);
б) ж = г, ?/= r sin 9?, z = rcos<?, М0(-1,л/3/2,-1/2);
B)x = acos<^, |/ = a sin (p, z = h, Мо(а/л/2, а/л/2, — 1)-
2. Вычислите направляющие косинусы нормали к поверхности в точке Мо:
a)x = rcos<^, |/ = rsin(^, z = h(p, Mo(h/y/2, h/y/2, /гтг/4);
б) ж = A + cos^) cos 9?, |/ = A + cos^) sin 9?, z = sin^, МоA/л/2,
3. Пользуясь явным заданием поверхности, вычислите площадь:
а) части гиперболического параболоида az = xy, заключенной внутри
цилиндра х2 + у2 = а2;
б) части эллиптического параболоида 2az = х2 + у2, заключенной внут-
внутри цилиндра (ж2 + у2J = 2а2ху; 2 2
в) части гиперболического параболоида — — \- = 2z при г ^ 0, выре-
Т2 7.2 а о
^ 1
Т2 7.2
занной цилиндром ^ + р- = 1;
г) части поверхности ( — + f ) + — = 1, вырезанной
х = 0 2/ = 0 z = 0;
( f ) 1 й плоскостями
х = 0, 2/ = 0, z = 0;
д) части конической поверхности г = 2ху, отсекаемой плоскостями
ж + г/ = 1, ж = 0, 2/= 0;
е) части конической поверхности z = д/ж2 + у2, заключенной внутри
цилиндра ж2 + у2 = 2ж.
4. Пользуясь параметрическим заданием поверхности, вычислите
площадь:
О О О О О
а) части сферы ж + г/ + г = а , заключенной внутри цилиндра ж +
+ ?2 = fr2 если 0 < Ъ < а;
§ 2. Поверхностные интегралы первого рода 353
б) части сферы ж = Rcosvsmu, у = Rsmvsmu, z = Rcosu, ограни-
ограниченной двумя параллелями и двумя меридианами, т. е. v\ ^ v ^ г>2,
^ч* ^ч* О О О О О
в) части сферы ж + у -\- z = а , расположенной вне цилиндров х +
+ 2/2 = =Ьаж;
г) части цилиндра х2 + у2 = а2 при ж > 0, ?/ > 0, вырезанной плоскос-
плоскостями ж + ? = 0, х — z = 0;
д) части гиперболического параболоида z = (ж2 — у2)/2, заключенной
внутри цилиндра (ж2 + у2J = (ж2 — у2);
е) части геликоида ж = г cos ср, у = r sin cp, z = hep, O^r^a, 0^<^^ 2тг;
ж) поверхности тора ж = F + a cos ^) cos <^, 2/ = F + a cos ^) sin 9?,
z = asinifj при 0<a^6, 0^<^^ 2тг, 0 ^ ф ^ 2тг.
5. Вычислите площадь поверхности тела, ограниченного поверхностями:
а) ж2 +у2 = ?2/3, ж+ ?/ + ? = 2а (а > 0);
= л/ж2 +|/2 ж + 2z = а (а > 0).
§ 2. Поверхностные интегралы первого рода
Основные понятия и теоремы
1. Определение поверхностного интеграла первого рода.
Пусть на квадрируемой поверхности Ф определена функция /(М) =
= f(x,y,z). Разобьем Ф кусочно гладкими кривыми на п квадрируе-
п
мых частей: Ф = (J Ф^. На каждой части Ф^ выберем произвольную
г=1
точку Mi и составим интегральную сумму
г=1
где 5(Фг) — площадь Ф^. Пусть di — диаметр Ф^, d = max d{.
Определение. Число / называется пределом интегральных сумм
I($i, Mi) при d —> 0, если \/е > 0 36 > 0 такое, что для любого разбие-
разбиения Ф, у которого d < S, и для любого выбора точек Mi выполняется
неравенство
Предел / интегральных сумм называется поверхностным интег-
интегралом первого рода от функции /(М) по поверхности Ф и обозначается
fff(M)dS
ф
JJf(x,y,z)dS. A)
или
12 В.Ф. Бутузов и др.
354 Гл. XIV. Поверхностные интегралы
2. Вычисление поверхностного интеграла первого рода с
помощью двойного интеграла.
Теорема 2. Пусть Ф — гладкая поверхность, не имеющая осо-
особых точек, заданная параметрически уравнениями х = cp(u,v), у =
= ф(и, v), z — x(u, v), (и, v) G g, и пусть функция /(ж, у, z) непрерыв-
непрерывна на Ф. Тогда существует интеграл A) и справедливо равенство
, B)
Ф 9
функции Е, G, F переменных и, v определены формулами A0) из § 1.
Замечание 1. Если поверхность Ф является графиком непрерывно
дифференцируемой функции z = z(x,y), (ж, г/) G G, то имеет место равен-
равенство
fff(x, у, z) dS = fff(x, у, z(x, y))jl + zl+z$dx dy. C)
Ф G
Замечание 2. Формулы B) и C) остаются справедливыми для ку-
кусочно гладкой поверхности.
3. Физические приложения поверхностных интегралов
первого рода. Пусть Ф — материальная поверхность с поверхност-
поверхностной плотностью p(x,y,z) в точке M(x,y,z) G Ф.
Тогда справедливы следующие формулы:
а) М = р(х, у, z) dS — масса поверхности;
б) Мху = JJzp(x,y,z)dS, Mxz = JJyp(x,y,z)dS, Myz =
p г Ф Ф
= xp(x,y,z)dS — статические моменты поверхности относитель-
ф
но координатных плоскостей Оху, Oxz, Oyz;
в) хо = -1г^, уо = -^пг, zo = -1^L — координаты центра тяжести
1V1 1V1 1V1
поверхности;
г) 1Х = (у2 + z2)p(x,y,z) dS — момент инерции поверхности
ф
относительно оси Ох;
д) Iyz = x2p(x,y,z) dS — момент инерции поверхности относи-
ф
тельно плоскости Oyz;
е) /0 = / / (ж2 + у2 + z2)p(x, у, z) dS — момент инерции поверхнос-
ф
ти относительно начала координат;
ж) F = {Fx,Fy,Fz} — сила притяжения материальной точки
Мо(хо,уо, zo) массы то материальной поверхностью Ф, где
x,y, z) dS, Fy = imoffy^Lp(Xjy, z) dS,
§ 2. Поверхностные интегралы первого рода 355
Fz = juiq / / —-—р(х, у, z) dS,
ф
г = {х — хо,у — уо, z — zo}, г = |г|, 7 — гравитационная постоянная.
Контрольные вопросы и задания
1. Дайте определение поверхностного интеграла первого рода.
2. Сформулируйте теорему о существовании поверхностного интеграла
первого рода и сведении его к двойному интегралу для поверхности,
заданной параметрически.
3. Напишите формулу вычисления поверхностного интеграла первого рода
с помощью двойного интеграла для явно заданной поверхности.
4. Пусть Ф — материальная поверхность с поверхностной плотностью
р(М). Напишите формулы, по которым для этой поверхности вычис-
вычисляются: а) статические моменты относительно координатных плос-
плоскостей; б) координаты центра тяжести; в) моменты инерции 1ху и
Iz относительно плоскости Оху и оси Oz\ г) сила, с которой поверх-
поверхность притягивает материальную точку массы гао, помещенную в точ-
точку Mo(xo,yo,zo).
5. Пользуясь формулой C), вычислите интеграл zdS, где Ф — часть
параболоида z = х2 + у2 при 0 ^ z ^ 1. ф
6. Пользуясь формулой C), сведите поверхностный интеграл ///(ж,
ф
у, z) dS к сумме двух двойных интегралов, если Ф — сфера х2 + у2 +
Примеры решения задач
1. Вычислить поверхностный интеграл первого рода /= zdS,
ф
где Ф — часть гиперболического параболоида z = xy, вырезанная
цилиндром х2 + у2 = 4.
Л По формуле C) получаем
/ = ffzJl + zl +z%dxdy = jjxy^l + y2 +x2dxdy,
G G
где G — круг x2 + у2 ^ 4. Переходя к полярным координатам х =
= г cos(^, у = г simp и сводя двойной интеграл к повторному, находим
2тг 2
/ = / dip r3 cos if sin ip v 1 + r2 dr =
= dip cos ip sin ip • r
о о
2. Вычислить интеграл I = у dS, где Ф — часть поверхности ци-
ф
линдра х = 2у2 + 1 при у > 0, вырезанная поверхностями х = у2 + z2,
12*
356
Гл. XIV. Поверхностные интегралы
х = 2, х = 3.
Л Вычислим интеграл / с помощью двойного интеграла по области
G — проекции поверхности Ф на плоскость Oxz. Для отыскания гра-
границы области G исключим переменную у из уравнений х = 2у2 + 1 и
х = у2 + z2; получим 2z2 = х + 1.
Граница области G состоит из двух дуг этой параболы и отрезков
Рис. 65
прямых х = 2 и х = 3 (рис. 65). Уравнение поверхности запишем в
виде ^/ =
-. Отсюда следует, что
у/1 + 2/2 + 2/2 =
Пользуясь формулой
получим
Гж + 1/16 / 2 , ж 7 /15\2 1,
= [ 2^VX +8"8 "(Тб) '21П
• + Тб +
, ж 7
" ~ "
_ 98л/17-99л/3
~ 64л/2
3. Вычислить момент инерции Iz относительно оси Oz однород-
однородной сферической оболочки х2 + у2 + z2 = а2, г ^ 0 плотности ^0-
Л Имеем Iz = ро(х2 +y2)dS. Напишем параметрические уравне-
ф
ния данной полусферы: х = acosvsinu, у = a sin и sin га, z = acosix,
§ 2. Поверхностные интегралы первого рода 357
тг/2, О ^ v ^ 2тг. По формулам A0) из § 1 находим
Е = a2cos2i> cos2/u + a2sin2i> cos2/u + a2sm2u = a2
G
a2
= a2sin2i> sin2u + a2cos2i> sin2/u = a2sin2/u,
= —a2 cos v cos ix sin v sin ix + a2 sin г; cos и • cos i? sin и = 0,
откуда л/EG — F2 = a2sinix.
Выразим подынтегральную функцию в переменных и, г?; получим
2 2 2
+ з/2 = a2 sin
Вычисляем интеграл Iz по формуле B):
тг/2 2тг
Д = Ро о2 sin2 ix • a2 sin ududv = ^0«4 / sin3ix бЬ dv = -
P 0 0
4. Заряд Q равномерно распределен по сфере радиуса R. Найти
напряженность электрического поля сферы в точке А, находящейся
на расстоянии г (г ф R) от центра сферы.
Л Введем прямоугольную систему координат с началом О в цент-
центре сферы и осью Ож, направленной, как и вектор О А. Пусть Е =
= {Е1,Е2,Е3} — вектор напряженности в точке А электрического по-
поля сферы. Из соображений симметрии имеем Е2 = Е% = 0 и |Е| = Е\.
Поверхностная плотность а заряда на сфере равна —Ц-%. Вектор на-
пряженности, создаваемой в точке А элементом сферы с площадью
As, обозначим через АЕ = {A^i, AE2, А.Ез}- Заряд элемента сферы
равен a As, и по формуле напряженности поля точечного заряда полу-
получаем IAEI = а2 g, где к = , го — диэлектрическая постоянная,
р 4тт?о
р
р — расстояние от точки А(г, 0, 0) до элемента сферы, заряд которо-
которого будем считать сосредоточенным в точке M(x,y,z) этого элемента.
Пусть а — угол между вектором АЕ и осью Ох. Тогда
AEi = \AE\ cos a = ka As cos a • —.
Вычислим р и cos a:
р = \м1\ = у/(х - гJ +у2 +z2 = \JR2 + г2 - 2тх,
г — х
cos а = . .
л/Я2 + г2 - 2гх
Следовательно,
i = ко ^^ Г AS.
(Я2 + г2 - 2гжK/2
Пусть сфера разбита кусочно гладкими кривыми на п квадрируе-
мых частей (элементов). Будем предполагать, что диаметр di i-ro
358
Гл. XIV. Поверхностные интегралы
элемента достаточно мал. Для каждого элемента вычислим величину
Д-Ei, составим сумму всех п таких величин и перейдем к пределу
при d ->• 0 (d = max di). В результате получим поверхностный ин-
теграл первого рода
Е1 = ка [[ ^^ Г dS.
JJ (R2 2 2K/2
Ф
(R2
Верхняя и нижняя полусферы проектируются на координатную плос-
плоскость Оху в один и тот же круг G = {(х,у): х2 + у2 ^ R2} и для обеих
I ГУ
полусфер имеем wl + z2, + 2^ = Поэтому поверхност-
поверхностный интеграл i?i равен удвоенному двойному интегралу по кругу G:
r — х Rdxdy
Вычислим полученный интеграл с помощью повторного интегри-
интегрирования:
r VR2-x2
E1=2kaRr r~x <*- Г dy
= 2kaRir
-R
(Я2 + г2 - 2гж
О3/2 У Г \^/R2+r2 _2rxh
— R
= 2kaR7r\(R2 + г2 - 2тх)-х12 * - -\x{R2 + г2 - 2га)-1/2
v —R T L
h/2 н}=
R
-R
— R
Отсюда получаем:
если г > R, то i?
г-Я|
9 е> г\
= 2ka7rR • —т- = к • -^:
2 2
- Д| - г -
г2 г2
если г < R, то Ei = 2&сгтгЯ -0 = 0.
Таким образом, сфера, на которой равномерно распределен за-
заряд Q, создает в пространстве вне сферы такое же электрическое
поле, что и точечный заряд Q, помещенный в центр сферы. Внутри
же сферы электрическое поле равно нулю. А
§ 2. Поверхностные интегралы первого рода 359
Задачи и упражнения для самостоятельной работы
6. На сколько отличаются друг от друга поверхностные интегралы 1\ =
= Г Г (ж2 + у2 + z2) dS и 12 = Г Г (х2 + у2 + ?2) dS, где Ф: — сфе-
сфера ж2 + у2 + z2 = а2, Ф2 — поверхность октаэдра |ж| + \у\ + \z\ = a,
вписанного в эту сферу?
7. Вычислите интеграл // \Jz2 — ж2 dS, где Ф — часть конуса ж2 + у2 =
ф
= z2, вырезанная цилиндром ж2 + у2 = а2.
8. Вычислите поверхностные интегралы первого рода:
а) / / (ж + у + z) dS, где Ф — полусфера ж2 + у2 + z2 = а2, 2 ^ 0;
ф
ф
5 гДе ^ — граница тела, заданного неравенствами
в) II- ——Г2", где Ф — граница тетраэдра, заданного неравенст-
ф
вами ж + г/ + 2 ^ 1, ж^О, ^/ ^ 0, ^^0;
г) \xyz\dS, где Ф — часть поверхности г = ж2 + у2 при г ^ 1;
ф
д) zdS, где Ф — часть геликоида ж = ucosv, у = i6sinv, z = v
ф
при О^гб^ а, 0^г>^ 2тт;
е) z2 dS, где Ф — часть конической поверхности ж = г cos 9? sin a,
ф
I/ = r sin (p sin а, г = г cos а при О^г^а, 0 ^ <? ^ 2тг (а>0, а —
постоянная и 0 < а < тг/2);
ж) (ху + yz + zx)dS, где Ф — часть конической поверхности
ф
z = д/ж2 + у2, вырезанная цилиндром ж2 + у2 = 2аж.
9. Вычислите массу: а) части поверхности z = {х2 -\-у2)/2 при г ^ 1,
плотность которой в точке M(x,y,z) равна г; б) полусферы ж2 + у2 +
+ z2 = а2 при z ^ 0, плотность которой р(М) = г/а.
10. Вычислите статистические моменты относительно координатных плос-
плоскостей однородной треугольной пластинки х -\- у -\- z = а, ж^0, у ^ 0,
z ^ 0 плотности po-
poll. Вычислите момент инерции относительно оси Oz части однородной
конической поверхности ж2 + z2 = у2, у > 0 плотности ро, заключенной
внутри цилиндра ж2 + у2 = а2
12. Вычислите момент инерции однородной конической поверхности
Т2 2 2
—2" + ^ — Т2~ = 0> О^^^о, плотности ро относительно прямой — =
о о '
13. Вычислите моменты инерции относительно начала координат однород-
однородных поверхностей Ф: и Ф2 плотности 1, где Ф: — поверхность куба с
360 Гл. XIV. Поверхностные интегралы
центром в начале координат и ребром 2а; Фг — полная поверхность
цилиндра х2 + у2 ^ R , 0 ^ z ^ Н.
14. Вычислите координаты центра тяжести однородных поверхностей Ф1 и
Фг, где Ф: — часть конической поверхности z = д/ж2 + у2, вырезанная
цилиндром х2 + у2 = ах; Фг — часть поверхности z = д/а2 — ж2 — у2
при ж ^ 0, 2/^0, х + у ^ а.
15. С какой силой однородная поверхность х = г cos 92, 2/ = г sin 9?, z = r,
0 ^ <? ^ 2тг, 0 ^ 6 ^ г ^ а, плотности р0 притягивает материальную
точку массы т, помещенную в начало координат?
§ 3. Поверхностные интегралы второго рода
Основные понятия и формулы
1. Двусторонние и односторонние поверхности. Если по-
поверхность ограничивает некоторое тело, то у нее различают внеш-
внешнюю и внутреннюю стороны. Примером такой поверхности является
сфера. Если поверхность задана уравнением z = f(x,y), то у нее раз-
различают верхнюю и нижнюю стороны. Указанные поверхности имеют
две стороны. Наряду с ними существуют так называемые односто-
односторонние поверхности. Сформулируем теперь строгие определения.
Если каждой точке М области G поставлен в соответствие вектор
а(М), то говорят, что в области G задано векторное поле. Вектор-
Векторное поле а(М) = {ai(M), a2 (M), аз(М)} называется непрерывным в
области G, если его координаты — функции ai(M), 02 (М), аз(М) —
являются непрерывными в области G. Гладкая поверхность Ф в каж-
каждой внутренней точке М имеет нормаль N(M), причем существует
окрестность этой точки, вырезающая часть поверхности, на которой
поле нормалей непрерывно.
Если можно задать векторное поле нормалей, непрерывное на всей
поверхности, то такая поверхность называется двусторонней. Поверх-
Поверхность, на которой не существует непрерывного векторного поля нор-
нормалей, называется односторонней.
Двусторонняя поверхность Ф характеризуется следующим свой-
свойством: для любой точки М G Ф и для любого замкнутого контура,
проходящего по поверхности Ф и не пересекающегося с границей по-
поверхности, выбранное в точке М направление нормали, непрерывно
меняясь при движении точки по контуру, не изменит своего направ-
направления (на противоположное) при возвращении в точку М.
На односторонней поверхности существует такой контур, при об-
обходе которого направление нормали изменится на противоположное.
На каждой двусторонней поверхности можно задать два непре-
непрерывных ноля нормалей, противоположных по направлению: N(M)
и —N(M). Выбор одного из этих полей называется выбором стороны
поверхности. Таким образом, двусторонняя поверхность имеет две
стороны.
§3. Поверхностные интегралы второго рода 361
Двусторонние поверхности называются также ориентируемыми, а
выбор определенной стороны (выбор поля N(M) или —N(M)) называ-
называется ориентацией поверхности. Например, плоскость, сфера, гипербо-
гиперболоиды — двусторонние поверхности, лист Мёбиуса — односторонняя
поверхность. На рис. 66 изображен лист Мёбиуса и указан контур,
при обходе по которому направление норма-
нормали изменяется на противоположное.
Если поверхность задана уравнением z =
= /(ж,у), где функция f(x,y) непрерывно
дифференцируема, то на верхней стороне по-
поверхности непрерывное поле нормалей мож-
можно задать вектор-функцией
¦}. A)
на нижней стороне — вектор-функцией
-}• B) Рис. 66
Если гладкая двусторонняя поверхность задана параметрически, то
на одной ее стороне непрерывное поле нормалей можно задать вектор-
функцией N = {А, В, С}, а на другой — вектор-функцией
-TSI = {-A,-B,-C}.
Понятия двусторонней и односторонней поверхности можно ввес-
ввести и для кусочно гладких поверхностей. Примером кусочно гладкой
двусторонней поверхности является поверхность параллелепипеда.
2. Определение поверхностного интеграла второго рода.
Пусть Ф — гладкая или кусочно гладкая ограниченная поверх-
поверхность. Выберем одну из ее сторон, определяемую полем нормалей
N(M). Пусть а(М), /3(М), j(M) — углы, которые вектор N(M) сос-
составляет с осями координат, и пусть на поверхности Ф заданы три
функции Р(М), Q(M), R(M).
Определение. Поверхностные интегралы первого рода
) cosa(M) dS, h = ffQ(M) cos/3(M) dS,
Ф rr Ф C)
/3 = R(M) cos j(M)dS
ф
называются поверхностными интегралами второго рода соответст-
соответственно от функций Р, Q, R по выбранной стороне поверхности Ф.
Они обозначаются также следующим образом:
h = ffQ(M) dz dxi h = ffR(M) dx dV-
Такие обозначения связаны с тем, что элемент площади dy dz можно
рассматривать как площадь проекции элемента поверхности с пло-
площадью dS на координатную плоскостью Oyz, т. е. dydz — dS cos a
362 Гл. XIV. Поверхностные интегралы
(или dydz = -dScosa в зависимости от знака cos а) и, аналогично,
dz dx = dS cos C, dx dy = dS cos 7.
Из определения следует, что поверхностный интеграл второго рода
зависит от выбора стороны поверхности. Если взять другую сторону
поверхности, то вектор N(M) изменит направление на противопо-
противоположное; поэтому направляющие косинусы вектора N(M), а следова-
следовательно, и интегралы Д, /2, /з изменят знак.
Сумма
h + h + /3 = ffP(M) dy dz + Q(M) cte dx + R(M) dx dy D)
ф
называется общим поверхностным интегралом второго рода.
3. Вычисление поверхностного интеграла второго рода с
помощью двойного интеграла. Поверхностные интегралы второго
рода C) по выбранной стороне поверхности Ф являются поверхност-
поверхностными интегралами первого рода соответственно от функций
P(M)cosa(M), Q(M) cos/?(M), R(M)cosry(M). Поэтому на основа-
основании теоремы 2, считая, что функции Р(М), Q(M), R(M) непрерывны
на Ф, получаем формулы для вычисления поверхностных интегралов
второго рода.
Пусть гладкая двусторонняя поверхность Ф задана параметричес-
параметрически уравнениями
х = <р(и, v), у = ф(щ v), z = х(щ v), (и, v) G g,
и не имеет особых точек. Выберем ту сторону поверхности, на ко-
которой N(M) = {А, В, С}. Тогда, пользуясь формулой A1) из § 1,
находим
А А
cosa(M) = -
VA2 + B2 + C2
В
cos7(M) = -=
у Az
По формуле B) из § 2 получаем
Д = ГГР(М) cos a(M) dS =
А
= P((p(u,v),ril)(u,v),x(uTv))A(uTv)dudv. E)
9
Аналогично,
/2= Г Г Q(M) cos/3(M)dS= f[Q((p(u,v)^(u,v),x(u,v))B(u,v)dudv,
Ф ^ F)
§3. Поверхностные интегралы второго рода 363
/3 = /1R(M) cosт(М) d5 = f[R((p(u,v)^(u,v),x(u,v))C(u,v)dudv.
ф я G)
Если гладкая поверхность Ф задана уравнением z = f(x,y), (х,у) Е
G G, и выбрана верхняя сторона поверхности, т. е. N(M) = {-fx(x, у),
—fy(x,y), 1}, то cos 7 (-&/") = и по формуле C) из § 2
V 1 + fx+ fy
находим
/3 = JjR(M) cos7(M) dS =
ф
= f[R(x,y,f(x,y)) \ .
У V1 + fx + fy
= jjR(x,y,f(x,y))dxdy. (8)
G
Для нижней стороны поверхности имеем cosj(M) = —,
/1 —I— f^ —I— f^
откуда V i- Jx ^ jy
Is = — R(x,y, f(x,y))dxdy. (9)
G
Аналогично получаются формулы для вычисления интегралов 1\ и
/2, если поверхность Ф задана соответственно уравнением х — х(у, z\
(y,z) e G, и уравнением 2/ = y(z,x), (z,x) G G.
4. Физический смысл поверхностного интеграла второго
рода. Запишем общий поверхностный интеграл второго рода D) в
виде
П = ГГ[Р(М) cosa(M) + Q(M) cos/3(M) + R(M) cos7(M)] dS. A0)
ф
Направляющие косинусы cosa(M), cos/3(M), cosj(M) являются ко-
координатами единичного вектора нормали п(М) к поверхности Ф в
точке М. Если ввести вектор а(М) = {Р(М), Q(M), i?(M)}, то подын-
подынтегральное выражение будет представлять собой скалярное произве-
произведение векторов а(М) и п(М), а интеграл A0) можно записать в виде
L,n)dS. A1)
Интеграл A1) называется потоком вектора (векторного поля)
через выбранную сторону поверхности Ф (определяемую вектором
п(М)). В частности, если а(М) = v(M) — скорость течения жидкос-
жидкости в точке М, то П = / / (vn) dS представляет собой поток жидкости
ф
через выбранную сторону поверхности (см. также § 2 из гл. XV).
364 Гл. XIV. Поверхностные интегралы
Контрольные вопросы и задания
1. Сформулируйте понятие векторного поля.
2. Дайте определение поверхности: а) двусторонней; б) односторонней;
в) ориентируемой. Приведите примеры двусторонних поверхностей и
односторонней поверхности.
3. Каким характеристическим свойством обладает двусторонняя поверх-
поверхность; односторонняя поверхность?
4. Укажите вектор-функцию N(M), определяющую верхнюю сторону по-
поверхности z = /(ж, г/).
5. Найдите непрерывное векторное поле единичных нормалей, определяю-
определяющее внешнюю сторону сферы х = asini6cosv, у = asini6sint>,
z = a cos и, (и, v) G д = {(и, v): 0 ^ и ^ тт, 0 ^ г> ^ 2тт}.
6. Вычислите координаты единичных векторов нормалей, определяющих
нижнюю сторону части конической поверхности z = л/х2 + у2 при
0<a^z^6, а <Ь. Докажите, что это поле нормалей непрерывно.
7. Сформулируйте определение поверхностных интегралов второго рода.
Как они обозначаются?
8. Зависят ли от ориентации поверхности:
а) поверхностный интеграл первого рода и его интегральные суммы;
б) поверхностный интеграл второго рода?
9. Что такое общий поверхностный интеграл второго рода? Каков его
физический смысл?
10. Сформулируйте достаточные условия существования поверхностного
интеграла второго рода и напишите формулы сведения его к двойно-
двойному интегралу в случае, если поверхность задана:
а) параметрически; б) явно.
11. Вычислите поверхностные интегралы второго рода // dxdy, // dydz,
ф ф
/ / dzdx, где Ф — внешняя сторона сферы х2 + у2 + z2 = R2.
ф
12. Выразите поверхностный интеграл второго рода
/ / (cos a + cos C + cos j)f(x, у, z) dS
через сумму двойных интегралов, где Ф — сфера х2 + у2 + z2 = R2 и
n(M) = {cos a, cos /3, cos 7} — ее внешняя нормаль.
13. Вычислите поверхностный интеграл второго рода
/ / xdy dz + у dzdx + zdxdy,
ф
где Ф — внешняя сторона поверхности куба {(x,y,z) : 0 ^ х ^ 1,
0 ^ г/ ^ 1, 0 ^ z ^ 1}. Чему равен этот интеграл, если Ф — внутренняя
сторона поверхности куба?
Примеры решения задач
1. Вычислить поверхностный интеграл второго рода / = / / dxdy,
ф
где Ф — нижняя сторона части конуса z = л/х2 + у2 при 0 ^ z ^ 1.
§3. Поверхностные интегралы второго рода 365
Л Проекцией данной части конуса на плоскость Оху является круг
G: ж2 + у2 ^ 1. Пользуясь формулой (9), сведем поверхностный ин-
интеграл / к двойному интегралу: I = — dxdy. Так как // dxdy =
= S(G) = 7Г, ТО / = —7Г. к G G
2. Вычислить поверхностный интеграл второго рода / = у dz dx,
ф
где Ф — верхняя сторона части параболоида z = х2 + у2 при 0 ^ z ^ 2.
Л По формуле A) вычислим вектор нормали, определяющий верхнюю
сторону данной поверхности: N = {-fx(x,y), -fy(x,y), 1} = {-2ж,
—2у, 1}. Отсюда следует, что для единичного вектора п(М) =
= {cos a, cos /3, cos 7} верхней стороны справедливо равенство
Разобьем данную поверхность на две части, описываемые уравне-
уравнениями у = y/z - х2 при у ^ 0 и у = —y/z - х2 при у ^ 0. Обе части
поверхности (обозначим их соответственно <I>i и Ф2) проектируются
на область G плоскости Oxz, граница которой состоит из дуги пара-
параболы z = х2 и отрезка прямой z = 2, т. е. G = {(ж, г) : —л/2 ^ ж ^
^ л/2, ж2 ^ z ^ 2}.
Сведем поверхностные интегралы по Ф1 и Ф2 к двойным интег-
интегралам по области G подобно тому, как это было сделано при выводе
формул (8) и (9). Получим
\\ydzdx-— у(х, z)dzdx — — \\ у/z — ж2 dz dx
Ф1 G G
(здесь перед двойным интегралом стоит знак минус, так как
cos /3(М) < 0) и, аналогично,
/ / у dzdx = / у(х, z) dzdx = / / — у/z — ж2 dzdx.
Ф2 G G
Таким образом, имеем
/= ydzdx= ydzdx-\- у dz dx =—2 y/z — х2 dzdx.
Ф Ф^ Ф2 G
Двойной интеграл вычислим с помощью повторного интегрирования:
7^dz = -2 J |B-ж
-у/2
Используя замену переменной х = V2sin?, —тг/2 ^ t ^ тг/2, оконча-
окончательно получаем п ,2
/ = -- / 23/2у/2 cos4 tdt = -2тг. А
-тг/2
366 Гл. XIV. Поверхностные интегралы
3. Вычислить поток П вектора а = х2 i + у2 j + z2 k через внеш-
внешнюю сторону сферы (х — аJ + (у — ЪJ + (z — сJ = R2.
Л Согласно определению потока требуется вычислить поверхностный
интеграл второго рода
П= // (ж2 cos a + y2cosC + z2 cos 7) dS,
ф
где Ф — внешняя сторона данной сферы. Находим вектор нормали N
по формуле G) из § 1: N = {2(х — а), 2 (у — b), 2{z — с)}. Единичный
вектор нормали п = \ х ~ а, ^ ~ , z ~ с \ определяет внешнюю сторо-
l it it it j
ну сферы. Учитывая это, перепишем интеграл в виде
ф
и вычислим его по формуле B) из § 2. Для этого запишем парамет-
параметрические уравнения сферы: х = а + Rcosvsmu, у = Ъ + Rsvavsmu,
z = с + R cos и, О^г^тг, 0 ^ г> ^ 2тг. Так как \/EG — F2 = R2 sin и, то
2тг тг
П = dv R2 sin ix [(a + R cos i? sin иJ cos i? sin ix +
о о
+ (b + Rsinv sin uJ sin v sin u + (с + Д cos ixJ cos и ] du =
2тг тг 2тг
.3,
= R2 Г 2aR cos2 г; dv Г sin3 udu + R2 Г 2bR sin2 г; / sin3
о о
2тт тг
Л2 / 2cR dv / cos2 ix sin udu —
Задачи и упражнения для самостоятельной работы
16. Вычислите поверхностный интеграл второго рода:
а) xdydz + ydzdx + zdxdy, где Ф — внешняя сторона сферы х2 +
ф
+ у2 + z2 = а2;
б) f(x)dydz + g(y)dzdx + h(z)dxdy, где Ф — внешняя сторона
ф
параллелепипеда О^ж^а, 0 ^ у ^ Ь, 0 ^ z ^ с; /(ж), #(г/), /i(^) —
непрерывные функции;
в) (у — z) dy dz + (z — x) dz dx + (x — y) dx dy, где Ф — нижняя сто-
ф
рона части конической поверхности z = \/х2 + у2 при 0 ^ z ^ h;
г) /"/"Г cos_a _j_ cos^ _j_ cos_7 j^s? где ф — внешняя сторона эллипсоида
ф
ф
Т2 ?У2
а2 ^ Ь2
§4- Формула Стокса 367
17. Вычислите поток вектора а(М) через ориентированную поверхность
Ф, если:
а) а(М) = xi-\- yj -\- zk, Ф — нижняя сторона части конической по-
поверхности z = \J х2 + |/2 при 0 ^ 2 ^ h\
б) а(М) = ж i + ?/j + z к, Ф — верхняя сторона основания этого конуса,
т.е. Ф = {(x,y,z): z = h, х2 + у2 ^ /г2};
в) а(М) = yzi -\- xzj -\- хук, Ф — внешняя сторона части цилиндри-
цилиндрической поверхности ж2 + ?/2 = а2 при 0 ^ ^ ^ /г;
г) а(М) = yzi + xzj + хук, Ф — внешняя сторона границы тела
{(x,y,z): х\+у2?а2, 0 SC z SC ft};
д) а(М) = ж i + ?/j + z к, Ф — верхняя сторона части поверхности г =
= 1 - дД2 + у2 при 0 ^ z ^ 1;
е) а(М) = ж2 i + |/2 j + z2 k, Ф — верхняя сторона части сферы х2 + у2 +
+ z2 = 1 при х ^ 0, г/^0, ^ ^ 0;
ж) а(М) =|/i + ^j+xk, Ф — внешняя сторона поверхности пирами-
пирамиды, ограниченной плоскостями х + у + z = а (а > 0), ж = 0, г/ = 0,
^ = 0;
з) а(М) = ж3 i + |/3 j + z3 k, Ф — внешняя сторона сферы х2 + у2 +
-\-z2 = х.
§ 4. Формула Стокса
Основные понятия и формулы
1. Согласование ориентации поверхности с направлени-
направлением обхода ее границы. Пусть Ф — ориентированная поверхность,
ограниченная замкнутым контуром L. Введем положительное на-
направление обхода контура, согласованное с ориентацией поверхности:
если наблюдатель находится на выбранной стороне поверхности (т. е.
направление от ног к голове совпадает с направлением вектора
Рис. 67
нормали), то при обходе контура L в положительном направлении он
оставляет поверхность слева от себя (рис. 67).
Если граница поверхности состоит из нескольких замкнутых кон-
контуров, то для каждого из них положительное направление обхода
определяется таким же образом (рис. 68).
368
Гл. XIV. Поверхностные интегралы
Поверхность Ф называется xyz-проектируемой, если она однознач-
однозначно проектируется на каждую координатную плоскость прямоуголь-
прямоугольной системы координат Oxyz. Такую
поверхность можно задать с помощью
любого из следующих уравнений:
x+y+z=l
z = z(x,y),
х = x(y,z),
у = y(z,x),
(х,у)
(y,z)
(z,x)
A)
Примером такой поверхности являет-
является часть плоскости, изображенная на
рис. 69.
2. Формула Стокса.
Теорема 3. Пусть гладкая xyz-
проектируемая ориентированная по-
поверхность Ф ограничена кусочно гладким контуром L и расположена
внутри области G, в которой функции P(x,y,z), Q(x,y,z), R(x,y,z)
имеют непрерывные частные производные первого порядка.
Тогда справедлива формула
Рис. 69
\Pdx + Qdy + Rdz = JJ [^-^)dydz
L Ф
dP dR
dP
где контур L обходится в положительном направлении.
B)
Эта формула называется формулой Стокса. Она выражает криво-
криволинейный интеграл второго рода по замкнутому контуру L через по-
поверхностный интеграл второго рода по поверхности Ф, ограниченной
контуром L.
Замечание 1. Формула Стокса остается справедливой, если поверх-
поверхность Ф не является ж^-проектируемой, но ее можно разбить кусочно глад-
гладкими кривыми на конечное число ж^-проектируемых частей.
Замечание 2. Формула Стокса справедлива и в том случае, когда
поверхность Ф является плоской областью, параллельной какой-либо коор-
координатной плоскости (такая поверхность не является ж^-проектируемой).
Для такой поверхности формула Стокса переходит в формулу Грина. На-
Например, если поверхность Ф параллельна плоскости Оху, то вектор нормали
/»
п = {0, 0,1}, iRdz = 0, и из равенства B) получаем формулу Грина
Замечание 3. Если граница поверхности Ф состоит из нескольких
контуров, то формула Стокса остается в силе. При этом в левой части фор-
формулы B) нужно записать сумму интегралов по всем контурам, пробегае-
пробегаемым в положительном направлении.
§4- Формула Стокса 369
Замечание 4. Отметим, что третье слагаемое в правой части форму-
формулы Стокса представляет собой правую часть формулы Грина. Два первых
получаются из него циклической перестановкой переменных х, у, z и функ-
х Р\
ций Р, Q, R: /^Уу j{^-q •
3. Условия независимости криволинейного интеграла
второго рода от пути интегрирования в пространстве. Для
криволинейных интегралов второго рода в пространстве справедлива
теорема об условиях независимости их от пути интегрирования, ана-
аналогичная теореме б из гл. XIII. В этой теореме будет использовано
понятие поверхностно односвязной области.
Определение. Трехмерная область G называется поверхностно
односвязной, если для любого замкнутого контура L, лежащего в G,
внутри области G найдется поверхность, ограниченная контуром L.
Примерами поверхностно односвязных областей являются: шар,
область, заключенная между концентрическими сферами; примером
поверхностно неодносвязной области служит тор.
Теорема 4. 1°. Пусть функции Р{х,у, z), Q(x,y, z), R(x,y, z) не-
непрерывны в области G. Тогда следующие три условия эквивалентны
(т. е. из каждого из них следуют два другие).
I. Для любого замкнутого кусочно гладкого контура L, расположен-
расположенного в области G, справедливо равенство
j
L
П. Для любых двух точек А и В области G криволинейный ин-
интеграл / Р dx + Q dy + Rdz не зависит от пути интегрирования,
АВ
расположенного в области G.
III. Выражение Р(х, у, z) dx + Q(x, у, z) dy + R(x, у, z) dz является
полным дифференциалом, т. е. в области G существует функция
и(М) = u(x,y,z) такая, что
du = Pdx + Qdy + Rdz.
При этом для любой кусочно гладкой кривой АВ, лежащей в G, имеет
место равенство
i
Рdx + Qdy + Rdz = и(В) -и(А). C)
АВ
2°. Пусть G — поверхностно односвязная область, а функции Р,
Q, R в области G имеют непрерывные частные производные перво-
первого порядка. Тогда каждое из условий I—III эквивалентно следующему
условию.
IV. В области G выполняются равенства
дР_ _dQ_ (Ж _dQ_ дР_ _(Ж D)
ду ~ дх ' ду ~ dz' dz ~ дх' U
370 Гл. XIV. Поверхностные интегралы
Замечание. Функция и(х, у, z) из условия III может быть найдена по
формуле
u(x,y,z)= Г Pdx + Qdy + Rdz =
(ж0, УО,
х У z
= Гр(х, у0, z0) dx + [q(x, у, z0) dy + jR(x, y, z) dz + C. E)
XQ У0 Z0
Здесь (жо, 2/o, zq) — какая-нибудь фиксированная точка, С — произвольная
постоянная, и в качестве кривой интегрирования взята ломаная, отрезки
которой параллельны осям координат.
Контрольные вопросы и задания
1. Как вводится положительное направление обхода контура, согласован-
согласованное с ориентацией поверхности, ограниченной этим контуром?
2. Пусть на сфере х2 + у2 + z2 = 1 выбрана ее внешняя сторона. Контур
L: х2 + у2 + z2 = 1, х = у является границей полусферы, содержащей
точку МA,0,0). Укажите на контуре L положительное направление,
согласованное с ориентацией данной полусферы.
3. Дайте определение ж^-проектируемой поверхности.
4. Является ли ж^-проектируемой часть плоскости х + у + z = 1 при
х ^ 0, у > 0, z ^ 0? Является ли эта поверхность гладкой?
5. Является ли ж^-проектируемой сфера х2 + у2 + z2 = 1? Покажите, что
сфера допускает разбиение кусочно гладкими кривыми на конечное чис-
число гладких ж^-проектируемых частей.
6. Покажите, что часть параболоида z = х2 + у2 при 0 ^ z ^ h можно
разбить на четыре гладкие ж^-проектируемые поверхности.
7. Напишите формулу Стокса и сформулируйте условия, при которых эта
формула верна.
8. Пользуясь формулой Стокса, вычислите криволинейный интеграл вто-
второго рода фу2 dx + z2 dy + х2 dz, где L — граница тела, заданного не-
L
равенствами х + у + z ^. 1, ж^О, у ^ 0, z ^ 0, причем контур L
обходится против часовой стрелки, если смотреть из точки B,0,0).
9. Что означает утверждение: криволинейный интеграл / Р dx + Q dy +
+ Rdz не зависит от пути интегрирования? ав
10. Что означает утверждение: выражение Рdx + Q dy + Rdz является пол-
полным дифференциалом в области G?
11. Пусть функции Р(ж,г/, 2;), Q(x,y,z), R(x,y,z) непрерывны в области
G. Сформулируйте два необходимых и достаточных условия независи-
независимости криволинейного интеграла / Рdx + Qdy + Rdz от пути интег-
интегрирования. АВ
12. Дайте определение поверхностно односвязной области в пространст-
пространстве. Является ли поверхностно односвязной областью: все пространство;
часть шара, отсекаемая плоскостью; шар с выброшенным центром; тор?
13. Пусть функции Р(х, у, z), Q(x, у, z), R(x, у, z) имеют непрерывные част-
частные производные первого порядка в поверхностно односвязной области
§4- Формула Стокса 371
G. Сформулируйте необходимое и достаточное условие независимости
криволинейного интеграла / Р dx + Q dy + R dz от пути интегрирова-
АВ
ния, использующее производные первого порядка. Как связано это усло-
условие с условиями из задания 11?
14. Пусть du(x, у, z) = Р(х, у, z) dx + Q(x, у, z) dy + R(x, у, z) dz в области G.
Напишите формулу для вычисления функции u(x,y,z).
15. Пусть Р = 2ху + z, Q = х2 + z2, R = 2yz + x. Докажите, что вы-
выражение Р dx + Q dy + Rdz является полным дифференциалом некото-
некоторой функции u(x,y,z), и найдите эту функцию. Чему равен интеграл
J Pdx + Qdy + Rdz, где А(-1,1,1), БA, -1,1)?
АВ
Примеры решения задач
1. Вычислить двумя способами (по формуле F) из § 2 гл. XIII и по
формуле Стокса) криволинейный интеграл / = ф у dx + z2 dy + х2 dz,
j
L
где контур L — окружность, по которой пересекаются сфера х2 +
+ у2 + z2 =4 и плоскость z = л/3, причем направление обхода кон-
контура L выбирается против хода часовой стрелки, если смотреть из
точки @, 0, 2). В формуле Стокса в качестве ориентированной поверх-
поверхности Ф, которую ограничивает окружность L, взять:
а) верхнюю сторону части сферы z = ^/4 — х2 — у2 при у/3 ^ z ^ 2;
б) верхнюю сторону части плоскости z = л/3 при х2 + у2 ^ 1 (на-
(направление обхода контура согласовано с ориентацией поверхности).
Л Уравнения окружности L можно записать в виде х2 + у2 = 1,
z = л/3- Вычислим криволинейный интеграл /, перейдя к параметри-
параметрическим уравнениям окружности х = cost, у = sint, z = л/3, 0 ^ t ^ 2тг.
Тогда dx = — sin ? d?, dy = cost (it, dz = 0, и по формуле (б) из § 2
гл. XIII получаем 2?г
/= [(-sin2t + 3cost)dt =-тг.
о
Перейдем теперь к вычислению интеграла / вторым способом —
с помощью формулы Стокса. Поскольку Р = у, Q = z2, R = ж2, имеем
dR _ dQ_ _ _2z дР_ _ dR _ _2x dQ_ _дР_ _
ду dz ' dz dx ' дх ду '
и поверхностный интеграл второго рода в формуле Стокса равен
J = — / / 2z dy dz + 2х dz dx + dx dy.
ф
Пусть n = {cos a, cos C, cos 7} — единичный вектор нормали верх-
верхней стороны поверхности Ф.
372 Гл. XIV. Поверхностные интегралы
а) Часть сферы х2 + у2 + z2 = 4 при л/3 ^ z ^2 проектируется на
координатные плоскости Oyz, Oxz, Oxy соответственно в области
Gi = {B/,z): -V*-z2^y^V4-z2, л/3 ^ z <С 2},
G2 = {(*, ж): л/3 ^ z <С 2, -л/4-z2 ^ х <С л/4-z2},
G3 = {(x,y): x2+y2 ^1}.
Так как на область Gi проектируются две части поверхности Ф:
х = ^/4 - у2 - z2, для которой cos а ^ 0, и ж = — д/4 - у2 - z2, для
которой cos a ^ 0, то для поверхностного интеграла второго рода
Ji = — 2z dy dz получаем
ф Ji = - ( /7 2zdydz- И 2z dy dz} = 0.
Аналогично,
J2 = - |/2ж dzdx = -( № 2x dz dx - I I 2x dz dx) = 0.
Ф G2 G2
Учитывая, что cos 7 > 0, и пользуясь формулой (8) из § 3, находим
J3 = -jjdxdy = - Л dxdy = -S(G3) = -к.
Ф G3
Следовательно, J = J± + J2 + J% = —тг = /.
Отметим, что второй способ вычисления криволинейного интег-
интеграла / (с помощью формулы Стокса) является более громоздким по
сравнению с первым. Этот способ рассматривается здесь только с
целью лучшего усвоения формулы Стокса. То же самое относится к
примеру 2 и некоторым упражнениям для самостоятельной работы
этого параграфа.
б) Для верхней части плоскости z = л/3 имеем dz = 0, п =
= {0,0,1}. Поэтому
J — — \\2zdydz -\-2xdzdx -\- dxdy — — \\ dxdy — — I dx dy = —тг.
ф ф х2+у2^1
Таким образом, и в этом случае получили тот же результат. А
2. Пользуясь формулой Стокса, вычислить криволинейный ин-
интеграл / = yzdx + Sxz dy + 2ху dz, где О А — кривая, х = t cos t,
ОА
2/ = ?sin?, z = t2, 0^?^2тг, 0@,0,0), АBтг, 0,4тг2).
Л Незамкнутая кривая О А лежит на поверхности z = х2 + у2. Дейст-
Действительно, х2 + у2 = ?2(cos2 t + sin2 t) = t2, т. e. x2 + y2 = z. Дополним
кривую интегрирования ОА до замкнутого контура L дугой АО па-
параболы z = ж2, лежащей в плоскости Ozx (отметим, что эта парабола
лежит также на поверхности z = х2 + у2). Тогда
/Г
yzdx + 3xzdy + 2xy dz — I yzdx -\- 3xzdy + 2xy dz.
L АО
§4- Формула Стокса
373
Учитывая, что вдоль кривой АО у = 0, dy = 0, получим
/ yzdx + Sxz dy + 2ж?/ dz = 0.
АО
Следовательно, / = ctyzdx + 3xz cfa/ + 2xy dz.
L
Контур L лежит на параболоиде z = x2 + у2 и обходится в направ-
направлении, указанном на рис. 70. Выберем на
части параболоида, ограниченной контуром
L, непрерывное векторное поле нормалей
п(М) = {cos a, cos /3, cos 7} так, чтобы обход
контура был положительным, т. е. выберем
верхнюю сторону параболоида. По форму-
формуле A) из § 3 находим N = {—2ж, —2у, 1}.
Вычислим единичный вектор нормали п:
|N|2=4x2+4^2 + l,
-2х -2у
'4ж2 + 4у2 + 1 у4ж2 + 4|/2 + 1
1
Рис. 70
Для нахождения криволинейного интеграла
по замкнутому контуру L применим формулу Стокса. Так как
Р — yz, Q = 3xz, R = 2ху, то
dR dQ о о аР ая о
^-7 = 2жж = -ж ^-^ = у~2у = -у
дР
ду
Q
По формуле Стокса находим
/г г г
yzdx + 3xzdy + 2xydz = //
^ L
2т
(-ж)
-2j/
!+4^/2 + 1 ч ~7 ^4x2+42/2 + 1-1 ii Д/4Ж2 + 4у2 +1
Этот поверхностный интеграл первого рода вычислим по формуле C)
из § 2. В данном случае z = х2 + ^/2, 2:ж = 2ж, ^ = 2^/, ^ 1 + z2. + z
= д/l + 4ж2 + 4^/2. Поэтому
2// f+y2 + Z =dS = 4[[(x2+y2)dxdy,
JJ л/4х2 + 4^/2 + 1 У У
2 _
J + 4^/2
где G — область на плоскости Оху, ограниченная кривой I: х =
374
Гл. XIV. Поверхностные интегралы
= tcost, у = tsint @ ^ t ^ 2тг) и отрезком [0, 2тг] оси Ож (рис. 71).
Для вычисления двойного интеграла по области G перейдем к поляр-
У1К
Zj
2
1
A M^
{
Рис. 71 Рис. 72
ным координатам ж = pcostp, у = ^sin(p, 0 ^ (^ ^ 2тг. Подставляя эти
выражения для жир уравнения кривой I, получим pcostp = tcost,
yosin(p = tsint. Отсюда, учитывая, что t и (р изменяются в одних и
тех же пределах от 0 до 2тг, находим р = ?, у? = ?, и, следовательно,
уравнение кривой / в полярных координатах имеет вид р = (р, 0 ^
^ <р ^ 2тг. Таким образом,
I = 4jJ(x2+y2)dxdy =
G G' 0 0
3. Доказать, что подынтегральное выражение является полным
дифференциалом и вычислить криволинейный интеграл
I = A5х2у + 3z2) dx + Eж3 - 22/2:) б?2/ + Fxz - у2) dz,
АВ
где АA,2,1), 5B,3,2).
Л Проверим выполнение условия IV теоремы 4: Р — 1Ъх2у + 3z2,
=Ц- тг5. А
-7j— = -~— = 62:. Следовательно, выражение Р dx -\- Q dy -\- R dz являет-
является полным дифференциалом, а криволинейный интеграл / = / Р dx +
+ Q dy + Rdz не зависит от пути интегрирования. ав
Возьмем в качестве пути интегрирования ломаную АМКВ, где
МB, 2,1), КB,3,1) (рис. 72). Тогда
= {(x,y,z): l^x^2, у = 2, z = l},
= {(x,y,z): x = 2, 2О^З, * = 1},
{(x,y,z): ж = 2, 2/ = 3, 1 ^ z ^ 3}.
Вдоль отрезка AM имеем у = 2, z = 1, dy = dz = 0, 1
2
поэтому /" Pdx + Qdy + Rdz = Г(ЗОх2 + 3) dx = 73.
§4- Формула Стокса 375
Вдоль отрезка МК имеем х = 2, z — 1, <ix = dz = 0, 2 ^ у ^ 3;
з
поэтому Г Pdx + Qdy + Rdz = /D0 - 2у) dy = 35.
МК 2
Вдоль отрезка КБ имеем х = 2, у = 3, dx = cfo/ = 0, 1 ^ г ^ 3;
з
поэтому интеграл вдоль этого отрезка равен / A2 z — 9) dz = 30.
i
i
Искомый интеграл по ломаной АМКВ равен сумме вычисленных
интегралов, т. е. равен 138. А
4. Найти функцию u(x,y,z), если
du=(l-- + z-
yz
Л Нетрудно убедиться, что для дифференциального выражения du
выполнены равенства D) при yz ф 0. Для вычисления функции
и(х, у, z) воспользуемся формулой E), считая, что у0, z0, у, z отличны
от нуля. Получим
уо
Уо
уо
+(JLy-*)\v +Х-У
Хо \хо у/\уо z
+с =
Zo
У у
Следовательно, u(x,y,z) = x(l — - + У-) + Ci, где С\—произволь-
С\—произвольная постоянная и yz ф 0. А
5. Найти работу силы тяготения F = —зг (r = ix+jy + 'kz,
г = \Jх2 + у2 + ?2), действующей на единичную массу, которая пере-
перемещается ИЗ ТОЧКИ Mi(xi,yi,Zi) В ТОЧКУ М2(Х2,У2, %2).
Л Работа А силы F при перемещении материальной точки из точ-
точки М\ в точку М<2 вдоль кривой М\М<2 вычисляется (аналогично
плоскому случаю) по формуле A— I P dx + Q dy + Rdz, где F =
{P,Q,R}. MiM2
Следовательно,
/k
-{xdx + ydy + zdz).
Покажем, что подынтегральное выражение является полным диффе-
дифференциалом:
~(xdx + у dy + zdz) = -A- d(x2 + у2 + z2) =
= * d{r2) = -J^2rdr = -^ = k-
2гз 2r3 r2
376 Гл. XIV. Поверхностные интегралы
Поэтому
А = к |
М1М2
= к
у2 + z\
Задачи и упражнения для самостоятельной работы
18. Пользуясь формулой Стокса, вычислите криволинейный интеграл:
а) ydx + zdy + xdz, где L — виток винтовой линии х = cost, y =
L
= sint, z = t, 0 ^ t ^ 2тг, пробегаемый в направлении от точки A, 0, 0)
до точки A, 0, 2тг);
б) ф(у — z) dx + (z — х) dy + (ж — у) dz, где L — окружность х2 + у2 +
L
-\- z2 = а2, у = xtga, 0 < а < тг/2, обход которой совершается против
хода часовой стрелки, если смотреть из точки Bа, 0,0);
в) фу dx + zdy + xdz, где L — окружность х2 + у2 + z2 = а2, ж + ^/ +
L
+ ? = 0, пробегаемая против часовой стрелки, если смотреть из точки
(а, 0,0);
г) ф (у — z) dx + (z — х) dy + [х — у) dz, где L — эллипс х2 + у2 = а2,
L
— + j- = 1 (а > 0, /г > 0), пробегаемый против часовой стрелки, если
смотреть из точки Bа, 0,0);
Д) f (у2 + ^2) dx + (ж2 + z2) dy + (ж2 + |/2) dz, где L — кривая, по ко-
L
торой пересекаются верхняя полусфера х2 + у2 + z2 = 2Яж (^ > 0) с
цилиндром х2 -\- у2 = 2гж, где 0 < г < R. Кривая L пробегается против
хода часовой стрелки, если смотреть из точки @,0, 2R);
е) Ф (У2 — z<2) dx + (z2 — х2) dy + (ж2 — у2) dz, где L — граница сечения
L
куба О^ж^а, 0^^/^а, О^^^а плоскостью ж + у + z = За/2, пробе-
пробегаемая против хода часовой стрелки, если смотреть из точки Bа, 0, 0);
ж) f (у2 ~ z<2) dx + (z2 — ж2) dy + (ж2 — у2) dz, где L — контур, огра-
L
ничивающий часть сферы ж2 + у2 + z2 = 1 при ж ^ 0, 2/^0, z ^ 0.
Направление обхода кривой L берется против хода часовой стрелки,
если смотреть из точки B,0,0).
19. Докажите, что подынтегральное выражение является полным диффе-
дифференциалом и вычислите криволинейные интегралы:
a) J xdx + y2dy-z2'dz, где АA,1,1), БB,3,-4);
a)
АВ
б) Г yzdx + xzdy + xydz, где АA,2,3), БF,1,1);
§ 5. Формула Остроградского-Гаусса
377
•> /
мгм2
xdx + ydy
V*2-
^ где точка M1(x1,y1,z1) лежит на сфере ж2
+ у2 + z2 = а2, а точка М2(ж2, ?/2, z^) — на сфере х2 + у2 + z2 = Ъ2 и
О < а < Ъ.
20. Выразите криволинейный интеграл / f{^/x2+y2+z2){xdx-\-ydy-\-
мгм2
+ zcb) через определенный интеграл, где f(t) — непрерывная функция
и Mi = Mi(x\,yi,zi), M2 = M2(x2,y2,z2).
21. Найдите функцию u{x,y,z), если:
а) du = (ж2 — 22/z) с/ж + (у2 — 2xz) dy + (z2 — 2ху) dz;
б) du = (з/?еж + ^еу + yez) dx + (ж^еу + zex + же2) с/|/ + (xyez + |/еж +
+ хеу) dz\
в) c/w = Bxyz + |/2^ + yz2) dx + Bж^ + Л + ж^2) dy + Bxyz + ж2^/ +
+ ху2) dz.
22. Найдите работу, производимую силой тяжести, когда материаль-
материальная точка массы т перемещается из точки M\(xi,yi,zi) в точку
Мг(ж2,2/2, 22) (ось Oz направлена вертикально вверх).
23. Вычислите работу силы F вдоль замкнутого контура L, пробегаемого
против хода часовой стрелки, если смотреть из точки М:
а) F = г = {ж,|/,^}, L — окружность, по которой плоскость ж = 2у
пересекает сферу ж2 + у2 + z2 = Я2, М = BЯ, 0, 0);
б) F = {yz, zx,xy}, L — эллипс, по которому плоскость 2z — Зж = 6
пересекает цилиндр ж2 + у2 = 1, М = B, 0, 0).
§ 5. Формула Остроградского-Гаусса
Основные понятия и теоремы
Пусть функции z\ (ж, у) и z<i (ж, ^/) определены и непрерывны в огра-
ограниченной замкнутой области D и
2i(ж, ^/) ^ 22(ж, ?/). Область G = {(ж, ?/, 2):
(х,у) е Д 2i (ж, 2/) ^ 2 ^ 22 (ж, 2/)} на-
называется 2-цилиндрической (рис. 73).
Аналогично определяются ж-цилиндри-
ческая и ^/-цилиндрическая области.
Область G называется простой, если
ее можно разбить на конечное чис-
число как ж-цилиндрических, так и ^-ци-
^-цилиндрических и z-цилиндрических об-
областей.
Теорема 5. Пусть функции Р(ж,
y,z),Q(x,y,z), R(x,y,z) и их частные
производные -~—, -^, -~— непрерывны в простой замкнутой облас-
области G, ограниченной кусочно гладкой поверхностью Ф.
z=z1(x,y)
378 Гл. XIV. Поверхностные интегралы
Тогда справедлива формула
= ((Р dy dz + Q dz dx + Rdx dy, A)
G ¦ - {J
где поверхностный интеграл берется по внешней стороне поверх-
поверхности.
Формула A) называется формулой Остроградского-Гаусса.
Следствие. Если функции Р, Q, R таковы, что -=—Ь -тр + -~— =
= 1, то интеграл в левой части равенства A) равен объему области
G, т. е. HI dxdydz — V(G), и из формулы A) получается формула
G
для вычисления объема области G с помощью интеграла по ее поверх-
поверхности
V(G) = If P dydz + Qdzdx + R dx dy. B)
ф
Замечание. Формула Остроградского-Гаусса остается справедливой
для любой ограниченной области G, граница которой состоит из конечного
числа кусочно гладких поверхностей.
Контрольные вопросы и задания
1. Дайте определение: а) ^-цилиндрической области; б) ^/-цилиндри-
ческой области; в) ж-цилиндрической области.
2. Какая область называется простой?
3. Является ли простой областью: а) шар ж2 + у2 + z2 ^ а2; б) паралле-
параллелепипед О^ж^а, 0 ^ у ^ Ъ, 0 ^ z ^ с; в) тетраэдр ж + у + z ^ 1,
х ^ 0, у ^ 0, z ^ 0? Ответы обоснуйте.
4. Напишите формулу Остроградского-Гаусса и сформулируйте условия,
при которых эта формула справедлива.
5. Пусть ^-цилиндрическая область G ограничена кусочно гладкой поверх-
поверхностью Ф и пусть функция R(x,y,z) и ее частная производная ^- не-
непрерывны в области G. Сводя тройной интеграл к повторному, дока-
докажите, что 111 ^ dxdydz = И Rdxdy, где поверхностный интеграл
G Ф
берется по внешней стороне Ф.
6. Пользуясь формулой Остроградского-Гаусса, покажите, что объем об-
области G, ограниченной кусочно гладкой поверхностью Ф, можно вычис-
вычислить по формуле
V(G) = - / / ж dy dz + у dz dx + zdxdy,
ф
где интеграл берется по внешней стороне Ф.
7. С помощью формулы Остроградского-Гаусса вычислите интеграл
/ / ж2 dy dz + у2 dz dx + z2 dx dy,
ф
где Ф — внешняя сторона поверхности тетраэдра заданного неравенст-
неравенствами x + y + z^l, ж^О, у ^ 0, z ^ 0.
§ 5. Формула Остроградского-Гаусса 379
Примеры решения задач
1. Пользуясь формулой Остроградского-Гаусса, вычислить интег-
интеграл П = / / х2 dy dz + у2 dz dx + z2 dx dy (см. пример 3 из § 3), где Ф —
ф
внешняя сторона сферы (ж — аJ + (у — ЪJ + (z — сJ = R2.
Л По формуле Остроградского-Гаусса имеем
П = [[[Bх + 2у + 2z) dx dy dz,
G
где G — шар (ж — aJ + (у — ЪJ + (z — сJ ^ R2. Для вычисления ин-
интеграла перейдем к сферическим координатам
х = а + г cos ip sin 0, у = Ь + г sin ip sin в, z = с + г cos 6>,
О ^ у? ^ 2тг, 0 ^ в ^ тг.
Якобиан перехода равен г2 sin#. Уравнение границы области G имеет
вид г = R. Следовательно,
2тг тг R
П = 2 / dip I sin 6 d6 I г2 [а + Ъ + с + r(cos <p sin # + sin cp sin # +
+ cos в)] dr = - тг(а + b + с)i?3. A
о
2. Вычислить интеграл Гаусса
Ф
где Ф — поверхность, ограничивающая простую замкнутую область
G; iV(?, 77, С) — фиксированная точка вне области G; M(x,y,z) G Ф;
г = {ж - ?, ^/ - 77, г - С}, г = |г|; n = {cosa, cos/3, cos7} — внешняя
единичная нормаль к поверхности Ф в точке М; ip — угол между
векторами г и п.
Л Выразим costp через координаты векторов г и п:
- (п'г) - (^ ~ О cosa + (у - г]) cos/3 + Q - С) cos7
— —j- — .
|п||г| г
Поверхностный интеграл / запишется в виде
^)ds-
Так как точка iV(?, 77, С) лежит вне области G, то г / 0 и, следова-
тельно, функции Р = —r-^-, Q = _ , Л = —г-1 непрерывны вместе
/v»O /v»O /v»O
с их частными производными первого порядка в области G. Находим
дР _ 1 3Q-Q2 <9Q _ 1 3(у - У7J dR _ 1 3(^ - Q2
^ — ^з ^5 ' ~ду ~ ^> Тъ ' ~dz ~ гЗ ^ '
дР dQ dR _ 3 3r2 _
^ ^ ^ 3 5
380 Гл. XIV. Поверхностные интегралы
Применяя формулу Остроградского-Гаусса, получаем
//
G
3. Вычислить интеграл Гаусса /@,0,0) (см. предыдущий пример),
если Ф — сфера х2 + у2 + z2 = a2.
Л Формулу Остроградского-Гаусса применять нельзя, так как функ-
функции Р, Q, R не являются непрерывными в точке JV(O,O,O) Е G. Так
как ? = ?7 = C=U, n=s-,-,-r> и г = а, то
. а а а .
ж — ? У — V п z — С х2 -\- у2 -\- z2 1
—r-^ cos а + cos р Н т-^ cos 7 = ^ = -г
1@,0,0) = ± ff dS = ±??= 4*,
Ф
т. е. интеграл Гаусса /@,0,0) не зависит от радиуса а сферы. А
4. Пусть Ф — гладкая поверхность, ограничивающая простую
замкнутую область G, функция u(x,y,z) имеет непрерывные част-
частные производные второго порядка в области G, -^ — производная
функции и(х, у, z) по направлению внешней нормали к поверхности Ф.
Доказать, что д
JJ^-dS = JJJAudxdydz,
Ф G
д д2и , д2и , д2и
где Аи = ^-^ + ^-у + -^-з-.
аж a^/ a^
Л Пусть n = {cos a, cos C, cos 7} — единичный вектор внешней нор-
нормали к поверхности Ф. Тогда
ди ди ди о , ди
— = — cosa + ^-cos/3+ ^
an аж oy o
и поверхностный интеграл —- ds запишется в виде
JJ on
ди ди п t ди
Ф
Применяя формулу Остроградского-Гаусса, получим
++
Ф G G
5. Вычислить интеграл /= х3 dy dz + у3 dz dx + z2 dxdy, где
ф
Ф — нижняя сторона части параболоида z = х2 + 2/2, отсекаемая плос-
плоскостью 2 = 2х.
Л Дополним поверхность Ф до замкнутой частью плоскости z = 2х.
Обозначим плоскую часть через Ф1 и выберем ее верхнюю сторону.
§ 5. Формула Остроградского-Гаусса 381
Для вычисления интеграла по замкнутой кусочно гладкой поверхнос-
поверхности Ф + <I>i применим формулу Остроградского-Гаусса. Тогда для ин-
интеграла / получим
/ = ГГГ(Зх2 + Зу2 + 2z) dx dy dz - Г Г х3 dy dz + у3 dz dx + z2 dx dy,
G Фх
где G — тело, ограниченное поверхностями z = х2 + у2, z — 2х. Вы-
Вычислим тройной интеграл с помощью повторных интегралов. Область
G проектируется на плоскость Оху в область D, границей которой
является окружность 2х = х2 + у2. Находим
2х
/ТУ (Зж2 + Зу2 + 2z) dx dy dz = Г Г dx dy Г [3(х2 + у2) + 2z] dz =
G D x2+y2
= JJ[6x(x2 + y2) + 4x2 - 4(x2 + y2J] dx dy.
D
Двойной интеграл вычислим, перейдя к полярным координатам
х = rcos(p, у = г simp, 0 ^ ip ^ 2тг. В полярных координатах уравне-
уравнение окружности примет вид г = 2cos(p, и поэтому двойной интеграл
равен
тг/2 2cos(/?
dip г [бг3 cos (^ + 4r2 cos2 ср — 4r4] <ir =
— тг/2 0 тг/2
г { a O\l2 cos ^
= / (jr5cos(^ + r4cosV- ^ r6j dy? =
-тг/2
г/2 Х тг/2
/ ( Г
/ /
= 16 / (у cos6 (p + cos6 у? - | cos6 Ч>)<1ч) = Щ- Г
cos6
sin2^+sin4^ - isin3 M Г_С/2 = т
Вычислим интеграл по верхней стороне области <I>i на плоскости
z = 2ж, учитывая, что единичный вектор нормали п равен {—2/у/5, О,
1/у/Щ. Получаем
+ y3dzdx + z2dxdy= II (- -L х3 + -^
ф^ ф^
Этот интеграл вычислим с помощью двойного интеграла по облас-
области D. Находим zx = 2, zy = 0, , /l + z2 + z2 = л/5 и
7 Л
Фх D
Переходя к полярным координатам, получим
тг/2 2cos(^
dip (—2r3 cos3 <? + 4r2 cos2 cp)r dr =
-тг/2 О
382 Гл. XIV. Поверхностные интегралы
тг/2
= Г (-MCOsV + 16cos
-тг/2
Таким образом, данный интеграл / равен —-^ — ^г- = -т^- А
3 2 6
Задачи и упражнения для самостоятельной работы
24. Пользуясь формулой Остроградского-Гаусса, вычислите поверхност-
поверхностные интегралы по внешней стороне поверхности Ф (если поверхность
не замкнутая, дополните ее до замкнутой):
а) xdydz + ydzdx + zdxdy, где Ф — сфера х2 + у2 + z2 = a2;
ф
б) (у — z) dy dz + (z — x) dz dx + (ж — y) dx dy, где Ф — часть кони-
ф
х2 + у2 =
ческой поверхности ж + у = z при 0 ^ z ^ h;
в) / I yzdy dz + zx dzdx + xy dxdy, где Ф — граница тела ж2 + у2 ^ а2,
О iz sC ft;
г) 11xdydz-\-ydzdx-\-zdx dy, где Ф — часть поверхности z = 1 —
— д/ж2 + |/2 при 0 ^ 2 ^ 1;
д) / /ydydz + zdzdx + xdxdy, где Ф — поверхность пирамиды, огра-
ф
ничейной плоскостями ж + ?/ + 2 = а (а > 0), ж = 0, ?/ = 0, 2 = 0;
е) х3 dydz + у3 dzdx + z3 dxdy, где Ф — сфера ж2 + у2 + z2 = ж;
ф
ж) х2 dydz + у2 dzdx + z2 dxdy, где Ф — поверхность куба О^ж ^
ф
^а, 0 ^ у ^ а, О^^^а;
з) х3 dydz + у3 dzdx + z3 dxdy, где Ф — сфера ж2 + ?/2 + z2 = a2;
ф
и) 11 {х — у -\- z) dy dz -\- {у — z -\- x) dz dx -\- {z — х -\- у) dx dy, где Ф —
ф
поверхность \х — у + z\ + \y — z + x\ + \z — х + у\ = 1.
25. Пусть Ф — гладкая поверхность, ограничивающая область G, функции
и(х, у, z) и v(x, у, z) имеют непрерывные частные производные второго
порядка в замкнутой области G, -^ — производная по направлению
внешней нормали к поверхности Ф. Докажите справедливость формул:
ги §и ds = [[[( \(диJ + (§и\2 + (диЛ
on JJJ ll\oxj \ду) \oz j
ф ' дп дп
~ JJJ | Аи Av
dx dy dz — вторая формула Грина.
ГЛАВА XV
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
§ 1. Дифференциальные операции
в скалярных и векторных полях
Основные понятия и формулы
1. Скалярное поле. Пусть G — область в трехмерном простран-
пространстве (или на плоскости). Говорят, что в области G задано скалярное
поле, если каждой точке М е G поставлено в соответствие некоторое
число и(М).
Физические примеры скалярных полей: поле температур какого-
либо тела; поле плотности зарядов на какой-либо поверхности или в
сплошной среде; поле плотности масс какого-либо тела.
Поверхность (линия), на которой функция и(М) принимает посто-
постоянное значение, называется поверхностью (линией) уровня скалярного
поля (например, поверхность или линия постоянной температуры).
Придавая и(М) различные постоянные значения: и(М) = С, получа-
получаем семейство поверхностей (линий) уровня данного скалярного поля.
Физические скалярные поля не зависят от выбора системы коор-
координат: величина и является функцией лишь точки М и, быть может,
времени (нестационарные поля).
Если в пространстве введена прямоугольная система координат
Oxyz, то скалярное поле описывается функцией трех переменных:
и = u(x,y,z), (x,y,z) e G.
2. Векторное поле. Говорят, что в области G задано векторное
поле, если каждой точке М е G поставлен в соответствие некоторый
вектор а(М).
Физические примеры векторных полей: электрическое поле систе-
системы электрических зарядов, характеризующееся в каждой точке век-
вектором напряженности Е; магнитное поле, создаваемое электрическим
током и характеризующееся в каждой точке вектором магнитной ин-
индукции В; поле тяготения, создаваемое системой масс и характери-
характеризующееся в каждой точке вектором силы тяготения F, действующей
в этой точке на единичную массу; поле скоростей потока жидкости,
описываемое в каждой точке вектором скорости v.
Удобной геометрической характеристикой векторного поля а(М)
служат векторные линии — кривые, в каждой точке М которых век-
вектор а(М) направлен по касательной к кривой. Векторные линии поля
тяготения, электрического и магнитного полей называются силовыми
линиями, а поля скоростей — линиями тока. Так, например, силовые
384 Гл. XV. Скалярные и векторные поля
линии электрического поля двух разноименных зарядов представля-
представляют собой кривые, начинающиеся на одном заряде и заканчивающиеся
на другом. Силовые линии магнитного поля тока являются замкну-
замкнутыми кривыми.
Пусть векторная линия, проходящая через точку Мо, описывается
уравнением г = г(?), где t — параметр. Условие коллинеарности век-
вектора поля а и касательного вектора г(?) в произвольной точке этой
линии имеет вид
!=¦»-• <»
где Л — некоторое число. Условие A) можно записать также в виде
или, умножая на dt, в виде
[dra]=0. C)
Каждое из уравнений A)-C) является дифференциальным уравне-
уравнением векторных линий в векторной форме и определяет множество
векторных линий. Конкретная векторная линия, проходящая через
заданную точку Мо, определяется дополнительным условием
г(*о)=го, D)
где го — радиус-вектор точки М.
Физические векторные поля не зависят от выбора системы ко-
координат: в каждой точке М вектор а(М) полностью определяется
своим модулем |а(М)| и направлением. Если в пространстве введе-
введена прямоугольная система координат Oxyz, то векторное поле а(М)
описывается вектор-функцией трех переменных a.(x,y,z) или тремя
скалярными функциями — ее координатами:
a(x,y,z) = {P(x,y,z), Q(x,y,z), R(x,y,z)}, (x,y,z) E G.
Так как в прямоугольных координатах dr = {dx, dy, dz}, то векторное
уравнение C) для векторных линий эквивалентно системе дифферен-
дифференциальных уравнений
dx _ dy _ dz /р,ч
Т - ~Q ~ if' [b)
а дополнительное векторное условие D) эквивалентно следующим
условиям:
x(t0) = хо, у (t0) = ?/о, z(t0) = z0, F)
где жо, уо, zo — координаты точки Mq.
3. Производная по направлению. Скалярное и векторное поля
и(М) = u(x,y,z) и а(М) = {P(x,y,z), Q(x,y,z), R(x,y,z)} назы-
называются дифференцируемыми п раз, если функции u(x,y,z), P(x,y,z),
§1. Дифференциальные операции 385
Q(x,y,z), R(x,y,z) дифференцируемы п раз. В дальнейшем, не ого-
оговаривая это особо, будем считать, что рассматриваемые поля диффе-
дифференцируемы нужное нам число раз.
Пусть и{М) — скалярное поле, заданное в области G; 1 — еди-
единичный фиксированный вектор; М — фиксированная точка; М' —
любая точка из G, отличная от М и такая, что вектор ММ' коллине-
арен 1. Пусть, далее, ММ' — величина направленного отрезка ММ'
(она равна его длине |ММ'| , если векторы ММ' и 1 сонаправлены, и
равна -\ММ'\, если эти векторы противоположно направлены).
Определение. Число lim — -^—- называется производ-
м'^м ММ'
ной скалярного поля и(М) (функции и(М)) в точке М по направле-
направлению 1 и обозначается символом — (М).
к
Производная по направлению — (М) является скоростью измене-
изменения функции и(М) по направлению 1 в точке М.
Если в прямоугольной системе координат Oxyz I = {cosa, cos/3,
cos 7}, то
du du du о du /^_ч
-— = — cos а + — cos р + — cos 7. G)
dl дх ду dz v J
В частности, если вектор 1 сонаправлен с одной из координатных осей,
то производная по направлению 1 совпадает с соответствующей част-
частной производной. Например, если 1 = {1,0,0}, то
ди _ ди -, _ ди
dl дх дх'
Аналогично определяется производная по направлению векторно-
векторного поля.
п и v а(М')-а(М) .
Определение. Вектор lim — -^—- называется производ-
м'^м ММ'
ной векторного поля а(М) (вектор-функции а(М)) в точке М по на-
направлению 1 и обозначается символом —-.
Если в прямоугольной системе координат Oxyz а(М) = {Р, Q, Л},
то
да. _ (дР_ dQ_ дВЛ
di ~ I di' di' di }'
4. Градиент скалярного поля.
Определение. Градиентом скалярного поля и(х, у, z) называет-
называется вектор-функция
, du.du.du, (du du du}
giadu = — 1+ — j + -— k = <^ —, -^-, — \.
dx dy dz Idx dy dz)
Из равенства G) следует, что
^ = (gradi/.l), (8)
13 В.Ф. Бутузов и др.
386 Гл. XV. Скалярные и векторные поля
ди
откуда —(М) = | gradi&||l| cosy? = | gradi^ cosy?, так как |1| = 1.
Здесь ip — угол между векторами 1 и grad-u в точке М. Очевидно,
что — принимает наибольшее значение при ip = 0, т. е. в направле-
направлении grad-u в данной точке. Иначе говоря, вектор grad-u в данной точке
указывает направление наибольшего роста поля и (функции и) в этой
точке, а | gradi^ есть скорость роста функции и в этом направлении.
Таким образом, вектор grad-u не зависит от выбора системы коорди-
координат, а его модуль и направление в каждой точке определяются самой
функцией и(М).
5. Потенциальное поле.
Определение. Векторное поле а(М) называется потенциаль-
потенциальным в области G, если его можно представить в этой области как
градиент некоторого скалярного поля и(М):
a = grad-u. (9)
Функция и(М) называется скалярным потенциалом векторного
поля а(М). Если а = {Р, Q,i?}, то из равенства (9) следует, что
р ди ^ ди р ди
^ y K
Иногда потенциалом векторного поля а называют такую функцию и,
что а = — grad-u.
Рассмотрим, например, поле тяготения точечной массы т, поме-
помещенной в начале координат. Оно описывается вектор-функцией
F(M) = -7 — г G — гравитационная постоянная, г = х i + уj + z k,
г = |r| = у^ж2 + у2 + z2). С такой силой действует это поле на единич-
единичную массу, помещенную в точку M(x,y,z). Поле тяготения являет-
является потенциальным. Его можно представить как градиент скалярной
функции и(М) = -—, называемой ньютоновским потенциалом поля
тяготения точечной массы т. Действительно,
ди д A \ ( \\дт jm д , г^~х—^——~Л
= 7Ш — (-) =7ш -— -- = --4- ^- (Vх +У + z ) =
дх dx\rJ V г2/ дх г2 дх v v J
х
= -jm—.
г3
A ди у ди z
Аналогично, -—= —7гтг-^-, т— = — 7Ш—, откуда
ду г3 dz r3
gradix = --4-(xi + ^/j + 2:k) = -7 — г = F(M).
В качестве еще одного примера рассмотрим электрическое поле
точечного заряда е, помещенного в начале координат. Оно описыва-
описывается в точке M(x,y,z) вектором напряженности
r = |г| =
§1. Дифференциальные операции 387
Это также потенциальное поле. Его можно представить в виде
Е = — grad —. Функция и(М) = — называется потенциалом элект-
г г
рического поля точечного заряда е.
Поверхности уровня потенциала и{М) называются эквипотен-
эквипотенциальными поверхностями. В рассмотренных примерах эквипо-
эквипотенциальными поверхностями являются сферы с центром в начале
координат.
6. Дивергенция.
Определение. Дивергенцией векторного поля а = Р(х,y,z)i +
+ Q(x, y,z)j + R(x, y, z) k называется скалярная функция
,. DP 0Q , DR
diva= — + -?- + -r-.
ox oy dz
Слово "дивергенция" означает "расходимость" ("расхождение").
Дивергенция характеризует плотность источников данного вектор-
векторного поля в рассматриваемой точке.
Рассмотрим, например, электрическое поле точечного заряда е,
помещенного в начале координат:
ЕЛ/О Л/6 / • • 1 \
3 о 2 ОГ
r ~x'6r "fa г3 Зх2г г2 Зх2
п, д ( х\ fa г6 - Зх2г г2 - Зх2
Так как -— —- = ^^- = = и, аналогич-
дх\г3; г6 г6 г5
д ( у\ _ г2 - Зу2 д ( z\ _ г2 - Зх2
то
,. „ 7 3r2-3{x2+y2+z2) n
div Е = ке ^——» L = о
г5
(при г ф 0). Физически этот результат означает отсутствие источни-
источников поля в любой точке, кроме начала координат. В начале координат
divE = оо (бесконечная плотность заряда).
7. Ротор.
Определение. Ротором (или вихрем) векторного поля а =
= Р(х,у, z) i + Q(x,y, z) j + R(x,y, z) k называется вектор-функция
rota =
i
д
дх
P
J
д
ду
Q
k
д
dz
R
dR dQ\ , .(dP dR\ , , (dQ dP
ду dz J \dz dx J \дх ду
13*
388
Гл. XV. Скалярные и векторные поля
В частности, для плоского поля а = {Р(х,у), Q(x,y), 0} имеем
rota = k
, (dQ дР\
— .
дх ду J
Ротор характеризует завихренность поля а в данной точке.
Рассмотрим твердое тело, вращающееся вокруг оси Oz с постоян-
постоянной угловой скоростью uj (рис. 74). Векторное поле скоростей v(M)
точек этого тела можно представить в виде
i J k
О О
х у
Найдем ротор поля скоростей v(M):
j k
v(M) = [о; г] =
z
— —uyi + ujx].
rot v =
1
d_
дх
-uy
d_
ду
UJX
d_
dz
0
Таким образом, rotv является постоянным вектором, направлен-
направленным вдоль оси вращения Oz, а его модуль равен удвоенной угловой
скорости вращения тела: | rot v| = 2и.
Рассмотрим потенциальное поле
г = XI + 2/j + zk.
Его потенциал и = г2/2 = (ж2 + у2 +
-\-z2)/2. Вычислим ротор этого поля:
^
rot г =
i
д
дх
X
j
д
ду
У
=
к
д
dz
z
i-0+j
ОН
Ьк
•0
= 0
Рис. 74
Вообще, ротор любого потенциального поля равен нулю (см. также
§ 2). Поэтому говорят, что потенциальное поле является безвихревым.
8. Соленоидальное поле. Векторное поле а(М) называется
соленоидалъным в области G, если в этой области diva = 0. Так как
diva характеризует плотность источников поля а, то в той области,
где поле а соленоидально, нет источников этого поля.
Например, электрическое поле Е точечного заряда соленоидально
(удовлетворяет условию divE = 0) всюду вне точки, где находится
заряд (в этой точке divE = оо). Векторные линии соленоидального
поля не могут начинаться или заканчиваться внутри области солено-
идальности; они либо начинаются и заканчиваются на границе облас-
области, либо являются замкнутыми кривыми. Примером соленоидального
поля с замкнутыми векторными линиями является магнитное поле,
создаваемое током в проводнике.
§1. Дифференциальные операции 389
Если векторное поле а(М) можно представить как ротор некото-
некоторого векторного поля Ь(М), т. е. а = rotb, то вектор-функция Ь(М)
называется векторным потенциалом поля а(М).
Можно проверить (см. подробнее § 2), что divrotb = 0, т. е. поле
а = rotb является соленоидальным.
Любое векторное поле можно представить в виде суммы потенци-
потенциального и соленоидального полей (см. § 2).
9. Уравнения Максвелла. Уравнения Максвелла — фундамен-
фундаментальные уравнения классической электродинамики, описывающие
электромагнитные явления в любой среде (и в вакууме). Они связы-
связывают величины, характеризующие электромагнитное поле, т. е. на-
напряженность электрического поля Е, электрическую индукцию D,
напряженность магнитного поля Н и магнитную индукцию В с ис-
источниками поля, т. е. с распределением в пространстве электрических
зарядов и токов.
В дифференциальной форме уравнения Максвелла записываются с
помощью понятий дивергенции и ротора. В системе СИ эти уравнения
имеют следующий вид.
Это уравнение является обобщением закона Био-Савара и выража-
выражает тот факт, что магнитное поле порождается токами проводимости
(j — плотность тока) и токами смещения -^—.
dt
Это уравнение выражает закон электромагнитной индукции
Фарадея и показывает, что одним из источников электрического поля
является изменяющееся во времени магнитное поле.
III. divB = 0.
Это уравнение выражает факт отсутствия магнитных зарядов
(соленоидальность магнитного поля).
IV. div D = р.
Это уравнение выражает закон Кулона и показывает, что вторым
источником электрического поля являются электрические заряды с
плотностью р.
К уравнениям Максвелла следует присоединить так называемые
материальные уравнения поля.
V. D =гЕ.
VI. В = /Ш.
VII. j = <тЕ.
Здесь г — диэлектрическая проницаемость, \i — магнитная про-
проницаемость, а — удельная проводимость среды.
10. Оператор Гамильтона. Напомним, что символ — называ-
ох
ется оператором частной производной по х. Под произведением этого
390 Гл. XV. Скалярные и векторные поля
оператора на функцию и = (u,x,y,z) будем понимать частную про-
ди д ди . д д
изводную -т—, т. е. —-• и = -т— • Аналогично, — и операторы
дх дх дх ду dz
частных производных по у и по z.
Введем векторный оператор "набла", или оператор Гамильтона:
V
_ ._д_ ._д_ ,_д_ _ Г_д_ д_ д\
~1дх Зду dz~ \дх' ду' dz)'
С помощью этого символического (операторного) "вектора" удобно
записывать и выполнять операции векторного анализа.
В результате умножения вектора V на скалярную функцию
u(x,y,z) получается grad-u:
„ _ Л d . d , d \ _ . du . du , ди _
V дх ду dz) dx dy dz
Скалярное произведение вектора V на вектор-функцию а(ж, у, z) —
— Р\ + Qj + Rk дает diva:
(Va) = -—Р+-—Q + -—i? = diva.
dx dy dz
Векторное произведение вектора V на вектор-функцию
a.(x,y,z) = Pi + Qj + Rk дает rota:
[Va] =
i j k
д д д
= rot a.
dx dy dz
P Q R
11. Правила вычислений с оператором V.
а) Если оператор V действует на линейную комбинацию
где Fi — скалярные или векторные функции а^ — числа, то г
б) Если оператор V действует на произведение нескольких функ-
функций F, G, Н (скалярных или векторных), то результат этого дейст-
действия аналогичен результату дифференцирования произведения в том
смысле, что оператор V последовательно применяют к каждому со-
сомножителю, отмеченному знаком ^, а другие сомножители при этом
считают фиксированными. Затем результаты складывают. Итак,
V(FGH) = V(FGH) + V(FGH + V(FGH). A0)
При этом следует иметь в виду, что слагаемые в правой части
равенства A0) предварительно преобразуют по правилам векторной
алгебры так, чтобы за оператором V стоял тот множитель, который
отмечен знаком ^. После вычислений знаки I опускают.
Пользуясь этим правилом, докажем, что
div[ab] = (brota) - (arotb). A1)
§1. Дифференциальные операции 391
Учитывая, что div[ab] = (V • [ab]), по формуле A0) имеем
(V.[ab]) = (V.[ab]) + (V.[ab]). A2)
Чтобы в первом из двух смешанных произведений A2) оператор V
действовал на вектор а, воспользуемся свойством смешанного произ-
Переставляя сомножители [Va] и b в скалярном произведении и учи-
учитывая, что [Va] = rota, получаем
(V-[ab]) = (brota).
Во втором слагаемом A2) поменяем местами сомножители в вектор-
векторном произведении:
(V-[ab]) = -(V-[ba]).
После этого находим
(V • [ab]) = -(V • [ba]) = -(arotb).
Складывая полученные результаты, получаем формулу A1).
Формулу (8) для производной по направлению с помощью опера-
оператора V можно записать в виде
Эй /1Т-7 \
ж =AVu)-
С другой стороны, —- можно вычислить, "умножая" скалярное
ol
произведение векторов 1 и V на скаляр и:
| = (ivK A3)
Символ — = (IV) будем называть оператором производной по на-
направлению 1. В частном случае, когда вектор 1 сонаправлен с одной из
координатных осей, например, с Ох A = i), имеем
I=<"»=?¦
т. е. оператор производной по направлению координатной оси — это
оператор соответствующей частной производной.
Используя оператор производной по направлению, запишем с
помощью оператора Гамильтона производную векторного поля а по
направлению 1:
| = dV)a. A4)
Формула A4) эквивалентна совокупности трех формул A3) для коор-
координат вектора а.
392 Гл. XV. Скалярные и векторные поля
12. Нестационарные поля. Пусть в области G определено не-
нестационарное скалярное поле u(x,y,z,t): величина и является функ-
функцией точки M(x,y,z) e G и времени t. Физический пример такого
поля — изменяющееся со временем распределение температуры в
какой-либо среде (например, в потоке жидкости). Рассмотрим дви-
движущуюся в области G точку (частицу жидкости) M(x(t),y(t),z(t)).
Координаты точки (частицы) изменяются со временем по известно-
известному закону х = ж(?), у = y(t), z = z(t). Величина и в движущейся точке
М является сложной функцией t:
и = u(x(t),y(t),z(t),t).
Вычислим производную по t этой функции (она называется пол-
полной производной). По правилу дифференцирования сложной функции
находим
du _ ди ди dx ди dy ди dz
dt dt дх dt dy dt dz dt
т, л , г л Г dx dy dz}
Введя в точке М вектор скорости v = {vx,vy,vz\ = < —-, -^-, — >,
L, CLZ CLZ CLZ )
получаем
du ди ди ди ди
ИЛИ
du ди , , ч ди , ^п ч ди , „ч /1 гЧ
_ = _ + (vgradu) = _ + (v Vu) = - + (v V)«. A5)
Аналогично, если в области G задано нестационарное векторное
поле а(ж,2/,2,?), то Для движущейся точки M(x(t),y(t),z(t)) вектор-
векторная величина а является сложной функцией t: a.(x(t),y(t),z(t),t). Пол-
Полную производную по t для каждой координаты вектор-функции а
можно вычислить по формуле A5). Умножая результаты на базисные
векторы i,j,k и складывая, получим
В формулах A5) и A6) слагаемые — и — выражают скорости
ot ot
изменения величин и и а со временем при фиксированных коор-
координатах, т. е. характеризуют локальное изменение этих величин, и
поэтому называются локальными производными. Слагаемые (vV)u и
(vV)a образуются за счет изменения координат точки, ее движения
(конвекции). Поэтому эти слагаемые в выражениях полных производ-
производных называются конвективными производными.
Локальные производные характеризуют нестационарность
рассматриваемого физического поля в данной точке пространства.
Конвективные производные характеризуют неоднородность поля в
данный момент времени.
§1. Дифференциальные операции 393
Контрольные вопросы и задания
1. Дайте определение скалярного и векторного полей и приведите примеры
физических полей.
2. Что такое поверхности уровня? Напишите уравнение семейства поверх-
поверхностей уровня электрического поля точечного заряда, находящегося в
точке M(xo,yo,zo).
3. Что такое векторные линии? Напишите их уравнения в различных
формах.
4. Дайте определение производной по направлению для скалярного и век-
векторного полей. Как связана производная по направлению с частными
производными?
5. Найдите производную скалярного поля и = у/(х — жоJ + У2 + z2 в точке
А@, 0, 0) по направлению: а) оси Ох; б) оси Оу\ в) вектора 1 = {1,1,1}.
6. Дайте определение градиента скалярного поля. Как связана производная
по направлению 1 с градиентом скалярного поля в данной точке?
7. Для скалярного поля из задания 5 найдите gradi6 в точке А@,0,0).
Сопоставьте направление gradi*, с указанными в задании 5 направле-
направлениями и значение | gradi6(A)| с производными функции и в точке А по
этим направлениям.
8. Какое векторное поле называется потенциальным? Приведите примеры
потенциальных полей.
9. Дайте определение дивергенции векторного поля. Каков физический
смысл дивергенции?
10. Чему равна дивергенция электрического поля точечного заряда?
11. Дайте определение ротора векторного поля. Каков физический смысл
ротора?
12. Какое векторное поле называется безвихревым? Приведите примеры
безвихревых полей.
13. Какое векторное поле называется соленоидальным? Приведите примеры
соленоидальных полей.
14. Что такое скалярный потенциал; векторный потенциал?
15. Напишите систему уравнений Максвелла. Какое из уравнений Максвел-
Максвелла выражает факт отсутствия магнитных зарядов?
16. Что такое оператор Гамильтона?
17. Запишите с помощью оператора Гамильтона: а) градиент скалярного по-
поля; б) дивергенцию векторного поля; в) ротор векторного поля; г) фор-
формулы для производной скалярного и векторного полей по направлению 1.
18. Используя правила вычислений с оператором Гамильтона, докажите,
что div[ab] = (brota) — (arotb).
19. Что такое полная производная; локальная производная; конвективная
производная? Что они характеризуют и каким соотношением связаны?
Примеры решения задач
1. Найти и нарисовать линии уровня скалярного поля и = ху. Вы-
Вычислить и изобразить на чертеже градиент этой функции в точках
A,1) и A,-1).
Л Линии уровня функции и — ху задаются уравнением ху — С, где
С — произвольная постоянная, т. е. представляют собой семейство
394
Гл. XV. Скалярные и векторные поля
С
гипербол у = —, а также две прямые, х = 0 и у = 0 (рис. 75). Далее,
41,1)
grad «A,-1)
I/
grad и =
grad г^д) = i + j,
На рис. 75 видно, что в указанных точках
gradи перпендикулярен линиям уровня,
проходящим через точки. В точке A,1)
функция и — ху быстрее всего возрас-
возрастает в направлении от начала координат
по биссектрисе I квадранта, и скорость
ее возрастания в этом направлении равна
О =л/2.
Рис.75 ~dlyjJ~
В точке A, —1) функция и — ху возрастает быстрее всего в направле-
направлении к началу координат по биссектрисе IV квадранта, и скорость ее
возрастания в этом направлении также равна л/2. А
2. Найти градиент скалярного поля и = xyz в точке М(—2,3,4).
Чему равна в этой точке производная поля и в направлении вектора
а ={3,-4,12}?
Л Согласно определению градиента имеем
Далее, единичным вектором, сонаправленным с а, является вектор
1 = — = —{3, —4,12}. По формуле (8) получаем
|а| 13
3. Найти векторные линии векторного поля а(М) = grad-и, где
и = xyz.
А Для векторного поля а(М) = grad-и = yz\ + zxj + хук уравне-
уравнения E), определяющие векторные линии, имеют вид
dx dy dz 7 7 у?
— = —- = — или xdx = ydy и ydy = zdz,
yz xz ху У У У У
откуда
x _ У
Л, A7)
У ^ I Г^ (Л Q\
у = у + С2. A8)
Уравнения A7) и A8) определяют два семейства гиперболических
цилиндров с образующими, параллельными соответственно осям Oz
и Ох, а также (при С\—Сч— 0) две пары плоскостей, х = ±у иу = ±z.
§1. Дифференциальные операции 395
Любая векторная линия поля а(М) является линией пересечения
двух поверхностей, получающихся из семейств A7) и A8) при неко-
некоторых фиксированных значениях С\ и С2.
Например, при С\ — С<± — 0 линия пересечения плоскостей ж =
= у и у = z представляет собой прямую, проходящую через начало
координат. Ее уравнения имеют вид ж = у = z. В точках этой прямой
вектор поля есть а(М) = {ж2,ж2,ж2}. А
4. Найти градиент сферического скалярного поля и = ip(r), r =
= л/х2 + у2 + z2 (т. е. зависящего только от расстояния точки (ж, у, z)
до начала координат).
Л Согласно определению градиента имеем
grad^(r) = j—<p(r), -frjj<p(r), ^
Отметим, что из соотношения
а = (//(г) - = grad^(r)
следует, что векторное поле а = (р'(г) - является потенциальным, а
функция ср{г) — его потенциал. А
5. Доказать, что кулоновское поле а = — • - (С = const) потенци-
г2 г
ально, и найти его потенциал.
Л Кулоновское поле а = — • - является частным случаем потенциаль-
г2 г
ного поля (р'(г) -, рассмотренного в предыдущей задаче и имеющего
г
С
своим потенциалом функцию (р(г). Поэтому, полагая tpf(r) = —, на-
С
ходим ip(r) = h Ci, где С\ — произвольная постоянная.
г
Итак, кулоновское поле потенциально и представимо в виде
а= ^л ' ~ =
С
где ip(г) — С\ — его потенциал. Отметим, что потенциал любого
векторного потейциального поля определен неоднозначно — с точ-
точностью до постоянного слагаемого. Это слагаемое не влияет на ко-
координаты векторного поля, получающиеся дифференцированием по-
потенциала, и может быть выбрано любым удобным образом, исходя из
дополнительных соображений. А
6. Найти дивергенцию векторного поля а — ж1 + у2 j + z3kb точке
М(-2,4,5).
Л Согласно определению дивергенции векторного поля а = {Р, Q,R]
396
Гл. XV. Скалярные и векторные поля
находим
= A + 2у + 3z2)M(_2,4,5) = 1 + 8 + 75 = 84. А
7. Найти дивергенцию сферического векторного поля а = /(г) г,
г = х\ + у] + zk, г = |г|. Определить вид функции /(г), для которой
поле а является соленоидальным.
Л Данное поле в координатах имеет вид а = /(г) г = {f(r)x,f(r)y,
f(r)z}. Согласно определению дивергенции находим
diva= §-{
§;{f{r)z) =
= Г (г) у + /(г) + f (г) ? + /(г) + /'(г) у + /(г) = /'(г) г + 3/(г).
Из условия соленоидальности div а = 0 следует, что f'(r)r + 3/(r) = 0.
Далее, разделяя переменные, имеем
df _ _ 3 dr
После интегрирования получаем
In |/| = -31nr + lnC,
С
откуда /(г) = —, где С — произвольная постоянная.
Итак, дивергенция сферического векторного поля а = /(г) г равна
С
нулю только в том случае, если /(г) = —, т. е. только в случае ку-
С
лоновского поля а = — г. Это поле является соленоидальным в любой
г6
области, не содержащей начала координат. А
8. Дано векторное поле а = z2 i + х2 j + у2 к. Найти rot а в точке
()
Л Согласно определению ротора имеем
rota(M) =
i j к
д_ д_ д_
дх ду dz
9
у
9 9
z х
= i Bг/ - 0) + j Bx - 0) + к Bх - 0)м =
= 4i + 6j + 2к. А
9. Найти ротор сферического векторного поля а = /(г) г, г =
2:к, г =
г|.
||
Л Запишем данное поле в координатах: а = /(г) г = {/(г)ж, f{r)y,
f(r)z}. По определению ротора находим
rota =
J
д
i
д_ д_ д_
дх ду dz
f(r)x f(r)y f(r)z
§1. Дифференциальные операции 397
^ - ^) = 0.
Итак, ротор любого сферического векторного поля равен нулю,
т. е. сферическое векторное поле является безвихревым. А
10. Векторное поле а{М) соленоидально в области G. Доказать, что
его можно представить в виде а(М) = rotb(M), и найти векторный
потенциал Ь(М).
дР
Л Пусть а = Р(ж,?/, z) 1 + Qix^y, z) j + Rix^y, z) k и diva = ——У
ox
+ -^ + ——. Будем искать векторный потенциал поля а(М) в виде
b = b\ (ж, у, z)\ + Ь2{х,у, z)j. Из условия rotb = а получаем
i J k
д д д ^1_U_1_UI__
ду
О
откуда
дЪ2 т-у dbi ^ дЪ2 дЪ\
Интегрируя первые два уравнения A9), находим
Z Z
Ъ2 = - ГР(х,у, z) dz + <p(x,y), h = fQ(x,y,z)
Zo Zo
где zo — аппликата какой-нибудь точки (xo,yo,zo) G G, a ip(x,y) и
ф(х,у) — произвольные функции. Положим ф(х,у) = 0, а функцию
ip(x,y) выберем так, чтобы выполнялось третье равенство A9), т. е.
B0)
Покажем, что такой выбор функции (р(х,у) возможен. Действитель-
дР dQ dR ,
но, учитывая равенство ——У —— = —~к~ (оно следует из условия
diva = 0), получаем из B0)
<^Р_ - Rrx z\_]®3l(x z)dz-
дх ' J dz
zo
= R(x, y, z) - [R(x, y, z) - R(x, y, z0)] = R(x, y, z0),
Jb
откуда <p(x,y,z) = jR(x,y,zo)i
398 Гл. XV. Скалярные и векторные поля
Итак, искомый векторный потенциал Ь(М) имеет координаты
Z Z X
h = JQ(x, у, z) dz, b2 = -Jp(x> У>z) dz + JR(X> У, zo) dx, b3 = 0. A
zq zo x0
11. Пусть и{М) и v(M) — скалярные поля. Доказать справедли-
справедливость формулы grad(w) = vgr&du + ugi&dv.
Л Согласно правилу A0) вычисления оператора Гамильтона от про-
произведения функций имеем
gra,d(uv) = V(uv) + V(uv) = vVu + wVv = г; grad u + u gradг;. А
12. Пусть u(M) — скалярное поле, а(М) — векторное поле. Дока-
Доказать справедливость формулы
div(im) = [gradи • а] + и diva.. B1)
Л Используя свойства оператора Гамильтона, получаем
div(im) = (V • из) = (V • из) + (V • из) = (Via • а) + u(Va) =
= (grad и • э) + и div a. A
13. Доказать справедливость формулы
rot(im) = [gradix • а] + urota, B2)
где ЦМ) — скалярное поле, а(М) — векторное поле.
Л Имеем
rot (на) = [V • из] = [V • из] + [V • на] =
= [Vh • а] + n[Va] = [grad н • а] + и rot a. A
14. Доказать справедливость формулы
rot[ab] = a div b - b div a + (bV)a - (aV)b, B3)
где а(М) и b(M) — векторные поля.
Л Учитывая выражение ротора с помощью оператора V и правило
A0), находим
rot[ab] = [V[ab]] + [V[ab]]. B4)
Преобразуя первое двойное векторное произведение в B4) по формуле
[p[qs]] = q(ps) - s(pq), получаем
[V[ab]] = a(Vb) - b(V a) = (bV) a -b(V a) = (bV)a - b div a. B5)
Отметим, что перестановка сомножителей в скалярном произведении
(a(Vb) = (bV) а) сделана для того, чтобы оператор V действовал на
стоящий за ним вектор а.
§1. Дифференциальные операции 399
Аналогично для второго слагаемого в B4) имеем
[V[ab]] = a(V b) - b(Va) = a(V b) - (aV) b = adiv b - (aV)b. B6)
Складывая B5) и B6), получаем формулу B3). А
15. Доказать справедливость формулы
grad(ab) = [b rot a] + [a rot b] + (bV)a + (aV)b, B7)
где а(М) и b(M) — векторные поля.
Л Согласно правилу A0) имеем
grad(ab) = V(ab) + V(ab). B8)
Перепишем формулу [p[qs]] = q(ps) - s(pq) в виде s(pq) = [p[sq]] +
+ (ps)q. При этом мы переставили сомножители в произведении [qs],
изменив знак векторного произведения.
Запишем с помощью этой формулы второе слагаемое в B8):
V(ab) = [a[Vb]] + (aV) b = [arotb] + (aV)b. B9)
Аналогично для первого слагаемого в B8) имеем
V(ab) = V(ba) = [b[V a]] + (bV) a = [b rot a] + [bV]a. C0)
Складывая B9) и C0), получаем формулу B7). А
Задачи и упражнения для самостоятельной работы
1. Найдите и нарисуйте линии уровня скалярного поля и = (х — уJ. Вы-
Вычислите и начертите вектор gradi6 в точках А(—1,1) и 5A,1).
2. Найдите линии уровня скалярного поля и = е2х^х +у ^ и нарисуйте ли-
линии уровня и(х,у) = е и и(х,у) = е1^2. Вычислите и начертите вектор
gradu в точках АA,1), 5B,0), СA,-1).
3. Найдите и нарисуйте линии уровня скалярного поля и = тт(ж,г/). Вы-
Вычислите и начертите вектор gradi6 в точках АB,1) и ВA, 2).
4. Найдите векторные линии: ,
а) кулоновского поля Е = — г точечного заряда е, находящегося в
г6
начале координат;
б) векторного поля а = [с г], где с — постоянный вектор, г = х i + у j +
+ ^k;
в) векторного поля а = — а2у i + Ъ2хj (а и Ъ — числа);
г) векторного поля а = х i + у j + 2z k.
5. Вычислите производные скалярного поля и = х2 + у2 в точке МA,1)
по направлениям векторов h = {1; 1}, Ь = {0; 1}, 1з = { — 1; 1}- Найдите
gradi6 в точке М и сравните | gradi^l с найденными значениями произ-
производных по направлениям векторов li, 12, 1з-
400 Гл. XV. Скалярные и векторные поля
6. Найдите градиент скалярного поля:
а) и = x3y2z в точке МA, 2, 3);
б) и=(х-у)(у- z)(z-x) в точках MiA,2,3), М2C,1,2), М3B,3,1);
в)и=(х-1)(у- 2)(z - 3) в точке МB, 3, 4).
7. В каких точках градиент скалярного поля и = х3 + у3 + z3 — 3xyz:
а) перпендикулярен оси Oz\ б) параллелен оси Ozl
8. В каких точках градиент скалярного поля и = х2 + у2 — 2ху:
а) перпендикулярен прямой у = ж; б) равен нулю?
9. Найдите угол между градиентами скалярного поля и = — в
точках МA, 2, 2) и ЛГ(-3,1, 0).
10. В каких точках выполнено равенство
grad In -
= 1, если
г 1 г
11. Докажите, что: a) grad г = -; б) grad- = — —; в) grad sin r =
г г г6
= cosr-, где г = xi + 2/j + zk, г = |г|. Укажите скалярные потен-
„ г г г г 1 г
циалы векторных полей -, — —, - cosr, —, --.
12. Докажите справедливость формул (и, v — скалярные поля):
\ л( , \ л л *\ ли v grad w - w grad v
a) gradm + v) = gradi*, + gradv; 6) grad — = ;
v v2
в) grad f(u) = f (u) grad щ r) grad /(гг, г;) = — grad и + — grad v.
аи av
13. Найдите grad(cr) и grad(i6(cr)), где гб — скалярное поле, с — посто-
постоянный вектор, г = х i + у j + z k.
14. Для скалярного поля и = и(х,у) найдите gradi6, если функция и(х,у)
определяется неявно уравнением:
а) и3 - Зхуи = а2; б) х + у + и = еи] в) х + г/ + и = е~(х+У+и\
15. Найдите дивергенцию векторного поля а, если:
а) а = (х - у)(у -z)i + (y- z)(z - ж) j + (z - х)(х - у) к;
б) а = (у2 + z2)(x + у) i + (z2 + x2)Q/ + г) j + (х2 + 2/2)(^ + х) к;
в) а = (ж2 + у2)(у - z) i + (у2 + ?2)(? - ж) j + (?2 + ж2)(ж - у) к;
r) a = /iB/,?)i + /2(x,?)j + /3(x,2/)k;
ТТ | р\ rp I T-.J ('Jy ^) 1 I II —I— /о ( 'Т* /^ ) I 1 —I— ^ —I— I О [ ПГ II ) 1С *
е) а = ж/i (j/, ^) i + у/2 (ж, г) j + 2/3(ж, ?/) к.
16. Вычислите: a) div г; б) div-; в) div(r4 г), где г = х i + у'} + z к, г = |г|.
17. Найдите минимальное значение дивергенции векторного поля а =
= (х - а)(у -ЬJ \+ {у -Ь)(х - aJ j.
18. Докажите справедливость формулы:
а) div(a + b) = div a + div b;
б) div(i6c) = (cgradi^), где с — постоянный вектор.
19. Используя формулы B1) и A1) из § 1, преобразуйте: a) div(rc);
б) div(r2c); в) div(/(r)c); г) div(b(ra)); д) div(r(ra)); e) divr[сг];
ж) div[a[rb]]; где r = xi + |/j + ^k, г = |r|, a, b, с — постоянные
векторы.
§1. Дифференциальные операции 401
20. Твердое тело вращается вокруг оси Oz с постоянной угловой скорос-
скоростью и. Векторные поля скоростей v(M) и ускорений ио(М) определя-
определяются формулами v(M) = [о; г], и)(М) = [о;[о; г]], где и) = ш к, г = ОМ —
радиус-вектор точки М. Вычислите divv(M) и divo;(M).
21. Найдите дивергенцию гравитационного поля, создаваемого конечной
системой точечных масс mi, тг,..., тте.
22. Найдите дивергенцию электрического поля, создаваемого конечной сис-
системой точечных зарядов ei, ег, •••, ете.
23. Найдите ротор векторного поля а= — \-\—j-\— к:
х у z
а) в произвольной точке M(x,y,z); б) в точке А(—1,— 1, — 1).
24. Найдите ротор векторного поля:
а) а = yz i + ?Ж j + ху к; б) а = y2zs i + 2ж^?/2 j + 3xy2z2 к;
в) а = |/^i + ^(x + 2г/) j + г/(ж + г/) к; г) а = -^-j к;
*Х/ *Х/ *X/ *X/
25. Найдите ротор векторного поля а в точке МA,1, 2), если:
а) а = yz2 j + жк; б) а = ?/?2 i + х j; в) а = yz2 к + х i.
26. Вычислите: a) rot г г; б) rot-; в) rot —; где г = х i + у\ + 2 к, г= г|.
г г6
27. Используя формулы B2) и B4), преобразуйте: a) rot(rc)a; б) rot(rc);
в) rot /(r)c; г) rot [с • /(г) г]; где а — векторное поле, г = х i + у j + z k,
г = |г|, с — постоянный вектор.
28. Для произвольных векторных полей а, Ь, с и произвольного скалярного
поля и докажите двумя способами (с помощью оператора Гамильтона
и в прямоугольных координатах) справедливость следующих формул:
a) (aV)wb = b(aVw) + w(aV)b; б) (с • V(ab)) = (a • cVb) + (b • (cV)a);
в) (cV)[ab] = [a • (cV)b] - [b • (cV)a];
r) ([ab] • rot c) = (b • (aV)c - (a • (bV)c).
29. Пусть а и b — векторные поля. Докажите, что вектор (bV)a есть
производная векторного поля а по направлению вектора Ь, умноженная
да
на модуль вектора b: (bV)a = — |b|.
дЪ
30. Даны векторные поля а = yzi + zxj + хук и b = zx\ + ху'} + yzk.
Вычислите векторы (bV)a и (aV)b и найдите — и — (производную
db да
поля а по направлению вектора b и производную поля b по направле-
направлению вектора а).
31. Вычислите производные векторного поля а = ху\ + yzj + zxk по на-
направлениям векторов h = i, Ь = i + j, 1з = j + k, I4 = i + j + k. Вычис-
Вычислите также векторы (liV)a, (bV)a, AзУ)а, (l4V)a.
32. Покажите, что дифференциалы скалярного поля и векторного поля мо-
могут быть записаны с помощью оператора Гамильтона в виде
du = (d r • Vu) = (d rV)i6, da = (d rV)a, где d r = dx i + dy j + dz k.
33. Нестационарное поле температуры точек плоскости Оху задано фор-
формулой Т = Тое~(ж +у +t ) (t — время). Частица движется по траекто-
, ч cost . sint . , , ч ч о
рии r(t) = 1 + j (г(?) — радиус-вектор частицы). Вычислите
локальную, конвективную и полную производные по времени темпе-
температуры частицы.
402 Гл. XV. Скалярные и векторные поля
34. Нестационарное электрическое поле в пространстве задано формулой
ке
Е = — г + Aosinujt • i, r = xi + yj + zk; r = |r|, t —время.
Вычислите векторы локальной, конвективной и полной производных
по времени поля Е в точке, движущейся по винтовой линии r(t) =
= a cos t • i + b sin t • j + bt k.
35. Пусть v(x,y,z,t) — нестационарное поле скоростей потока жидкости.
Используя формулу A6) при а = v и формулу B7) при а = b = v, вы-
ведите формулу ^ ^
- = -+grad(-j +[rotv.v].
§ 2. Повторные дифференциальные операции
в скалярных и векторных полях
Основные понятия и формулы
1. Дифференциальные операции второго порядка. Пусть в
области G заданы скалярное поле и(М) и векторное поле а(М) =
= {Р, Q,R}, причем функции u,P,Q,R имеют в области G непре-
непрерывные частные производные второго порядка. Тогда grad'u(M) и
rota(M) являются дифференцируемыми векторными полями, а
diva(M) — дифференцируемым скалярным полем.
К векторным полям grad'u(M) и rota(M) можно применить опера-
операции вычисления дивергенции и ротора, а к скалярному полю
diva(M) — операцию вычисления градиента. Таким образом, по-
получаем повторные операции: divgrad-u, rotgrad-u, divrota, rot rot a,
grad div a.
Операцию div grad называют оператором Лапласа и обозначают
также символом А:
div grad и = Аи.
С помощью оператора Гамильтона оператор Лапласа записывается
в виде
Аи = div grad и = (V • (Vu)) = V2u.
Учитывая, что
_ Л д . д д \2 _ д2 д2 д2
" V1 дх + J ду + dz) ~ дх* + ду* + dz
получаем
Ди = Vu =—- + -— + -—.
аж2 оу ozl
Функция и, удовлетворяющая в некоторой области уравнению
Лапласа Аи = 0, называется гармонической в этой области. Напри-
Например, линейная функция и = ах + by + cz является гармонической в
любой области. Оператор Лапласа широко используется в уравнени-
уравнениях математической физики. Отметим, в частности, что потенциал
§2. Повторные дифференциальные операции 403
электрического поля точечного заряда или поля тяготения точечной
к /
массы, имеющий вид и—- {к — const, г = уж2 + у2 + ?2), при г ф 0
удовлетворяет уравнению Лапласа.
Как было отмечено в § 1,
rot grad и = [V • Vu] = 0
(потенциальное векторное поле grad-u является безвихревым) и
divrota= (V[V • а]) = 0
(векторное поле rota является соленоидальным).
Две остальные повторные операции rot rot а и grad diva связаны
соотношением (см. пример 3 на с. 404)
rot rot a = grad div a — Аа, A)
где Аа = A(Pi + Qj + Rk) = APi + AQj + Ark — вектор-функция,
координатами которой являются результаты применения оператора
Лапласа к функциям Р, Q, R.
2. Разложение векторного поля на сумму потенциального
и соленоидального полей. Произвольное непрерывно дифференци-
дифференцируемое векторное поле а(М) может быть представлено в виде
a(M)=ai(M)+a2(M), B)
где ai(M) — потенциальное поле, а2(М) — соленоидальное поле.
Действительно, по определению потенциальное векторное поле
ai(M) есть градиент некоторого скалярного поля и(М): ai(M) =
= grad-u(M). Поэтому для вектора а2(М) из равенства B) имеем
а2(М) = а(М) - gradu(M). C)
Чтобы векторное поле а2(М) было соленоидальным, оно должно
удовлетворять условию diva2(M) = 0, откуда, учитывая равенст-
равенство C), находим
diva2(M) = diva(M) - div grad u(M) = diva(M) - Au(M) = 0.
Таким образом, для скалярного потенциала поля ai(M) получаем
уравнение
Аи = div a, D)
где diva — известная функция данного поля а(М).
Итак, если функция и есть решение уравнения D), то, полагая
ai(M) = grad'u(M), a2(M) = а(М) — gradix(M), получаем представ-
представление поля а(М) в виде B), где ai(M) — потенциальное, а2(М) —
соленоидальное поле.
Уравнение D) — неоднородное уравнение в частных производных
второго порядка, называемое уравнением Пуассона:
л д2и д2и д2и , г л-
Аи = -?-? + -?-г + -?-г = /, / = div a.
дх2 ду2 dz2
404 Гл. XV. Скалярные и векторные поля
Отметим, что это уравнение имеет (бесконечное) множество ре-
решений, поэтому представление поля а(М) в виде B) не единственно.
Контрольные вопросы и задания
1. Перечислите повторные дифференциальные операции в скалярных и
векторных полях.
2. Результаты каких повторных дифференциальных операции тождест-
тождественно равны нулю?
3. Что такое оператор Лапласа и как он связан с оператором V?
4. Приведите примеры функций, удовлетворяющих уравнению Лапласа
Аи = 0. Как называются такие функции?
5. Объясните, как представить произвольное векторное поле в виде суммы
потенциального и соленоидального полей.
6. Вычислите graddiv г и divgradr, где г = х i + ?/j + zk, г = |г|.
Примеры решения задач
1. Доказать справедливость формулы
div(u grad v) = (grad и • grad v) + и Av, E)
где и и v — скалярные поля.
Л Используя оператор Гамильтона, получаем
div(iAgradv) = (V • (uVv)) = (Vu-Vv) + uV2v =
= (grad и • grad v) + и Av. A
2. Доказать справедливость формулы
A(uv) = v Аи + 2(grad-u • gra.dv) + uAv, F)
где и и v — скалярные поля.
Л Используя формулы Аи = (V • Via), V(uv) = vVu + uVv и
(V • v Vu) = (Vu • Vv) + v V2/u, находим
A(uv) = (V • V(uv)) = (V • 0 Vu + и Vv)) = (V • v Vu) + (V • и Vv) =
= (Vv • Via) + г; V2ix + (Via • Vv) + ia V2i; =
= г; V2ix + 2Vu Vv + ix V2v = г; Via + 2(grad и • grad г;) + и Av. A
Отметим, что формулу F) с помощью оператора Гамильтона мож-
можно записать в виде
V2(uv) = v V2u + 2(Via • Vv) + и V2v
аналогично формуле второй производной произведения двух функций
(uv)" = uv" + 2u'v' + uv".
3. Доказать, что для векторного поля а справедлива формула
rot rot a = grad div a — Аа.
§2. Повторные дифференциальные операции 405
Л Используя формулу для двойного векторного произведения [а[Ьс]] =
= Ь(ас) — (ab)c и полагая в ней а = b = V, получаем
rot rot a = [V[Va]] = V(Va) - V2a = graddiva - Aa. A
4. Вычислить A(-J, где г = д/ж2 + у2 + z2, A — оператор Лап-
Лапласа.
Л Учитывая равенство т^ - = —о т^ = —о - и аналогичные ра-
ox\rJ г2 ох г2 г
д /1\ д /1\
венства для -—- ( - 1 и -—- - , получаем
ду \г ) dz\rJ
\г/ дх2 \г/ ду2 \r/ dz2 \r/
( + ( +
дх\ г2 г) ду\ г2 г) d
rs-3r2-z
Зг3 - Зг3
= 0 при г ф 0.
Итак, функция и = - является гармонической в любой области,
г
где г ф 0. А
5. Доказать, что электрическое поле Е(М, t) при \i — г = 1 удов-
удовлетворяет телеграфному уравнению
в области, где плотность зарядов равна нулю (р = 0).
Л Рассмотрим систему уравнений Максвелла при \i — e — 1,^ = 0 (см.
п. 9 из § 1):
=j + ^, rotE = -^, divH = 0, divE = 0, j = aE. (8)
Дифференцируя первое из уравнений (8) по времени и учитывая по-
последнее уравнение, находим
Вычисляя ротор от обеих частей второго из уравнений (8),
получаем
отт
rot rot E = -rot^r-. A0)
ОТ
В силу тождества rot rot E = graddivE - АЕ и уравнения divE = 0
имеем
rotrotE = -AE. A1)
406 Гл. XV. Скалярные и векторные поля
Поэтому rot -^— = АЕ, и, следовательно, из (9) получаем уравне-
уравнение G). А
Если ток проводимости отсутствует (а = 0), то для электрического
поля Е получается волновое уравнение
<92Е
АЕ = ?-=-
dt2 '
Для стационарного электрического поля Е(М) оно переходит в урав-
уравнение Лапласа
АЕ = 0. A2)
Уравнение A2) означает, что каждая координата вектора Е является
гармонической функцией в рассматриваемой области.
6. Разложить векторное поле а = (х — у) i + (х + у) j + (z + 2) к на
сумму потенциального и соленоидального полей.
Л Как показано в п. 2, векторное поле а представимо в виде а =
= ai + а2, где ai = grad-u — потенциальное поле, а2 = а — grad-u —
соленоидальное поле, причем и — решение уравнения Пуассона
Аи = div a.
Для данного поля
Уравнение Аи = 3 в прямоугольных координатах имеет вид
д2и д2и д2и _
дх2 ду2 dz2
Частным решением этого уравнения является, например, функция
и = -(ж2 + у2 + z2). Для этой функции
grad-u = xi + yj + zk = г.
Следовательно, данное поле а представимо в виде суммы потенциаль-
потенциального поля
ai = grad u = xi + yj + z'k = r
и соленоидального поля
а2 = а - gmdu =[(x-y)-x]i+ [(x + у) - y]j + [(z + 2) - z] k =
= —y\ + xj + 2k.
Непосредственно можно проверить, что векторное поле а2 является
соленоидальным:
§3. Характеристики векторных полей 407
Задачи и упражнения для самостоятельной работы
36. Вычислите: a) div(i6gradi6); б) div(grad/(r)); в) rot(i6gradv);
г) rot[a • rotb]; где г = \/ х2 + у2 + z2, г*, и г; — скалярные поля, а и
b — векторные поля.
37. Для векторного поля а = х2у2 i + у2 z2 \ + z2x2 k вычислите rot rot а,
graddiva, Aa и проверьте справедливость формулы A).
38. Даны векторные поля ai = \е±х +je±y +ke±z, а2 = \е±у +je±z +
+ ке±ж, аз = ie±z + je±z + ke±y (возможны любые комбинации зна-
знаков). Докажите, что:
а) rot ai = 0, а поля а2 и аз удовлетворяют уравнению а + rot rot a = О,
б) diva2 = 0, diva3 = 0, а поле а\ удовлетворяет уравнению а —
— graddiva = 0.
39. Покажите, что функция и = In -, где г = л/х2 + у2, удовлетворяет при
Г д2и д2и
г ф 0 уравнению Лапласа на плоскости: Аи = —- -\ = 0.
ке дх2 ду2
40. Покажите, что электрическое поле Е = —- г точечного заряда е, на-
г3
ходящегося в начале координат, удовлетворяет при г ф 0 уравнению
Лапласа АЕ = 0.
41. Покажите, что при ц = е = 1 магнитное поле Н удовлетворяет теле-
ли Ж , <92Н
графному уравнению АН = а + ——.
dt dt2
42. Разложите следующие векторные поля на сумму потенциального и со-
леноидального полей:
а) ai = (х + у) i + (ж - y)j + (z + l) k;
б) а2 = i(x2i + |/2j + ^2k); в) а3 = х\ + yj - 2zk.
§ 3. Интегральные характеристики векторных полей
Основные понятия и формулы
1. Поток векторного поля. Рассмотрим векторное поле а(М),
определенное в пространственной области G, и некоторую кусочно
гладкую ориентированную поверхность Ф С G. Пусть п(М) — поле
единичных нормалей на выбранной стороне поверхности Ф.
Как было отмечено в § 3 из гл. XIV, поверхностный интеграл
ff(an)dS = jjandS A)
ф ф
называется потоком векторного поля а(М) через поверхность Ф в
сторону, определяемую вектором п (говорят также: поток через выб-
выбранную сторону поверхности Ф).
Если взять другую сторону поверхности (изменить ориентацию),
то вектор п изменит направление на противоположное; поэтому ска-
скалярное произведение (an), а значит, и поток (поверхностный интеграл
A)) изменит знак.
Если а = v — скорость движущейся жидкости, то / / (vn)dS пред-
ф
408 Гл. XV. Скалярные и векторные поля
ставляет собой количество (объем) жидкости, протекающей через по-
поверхность Ф в заданную сторону в единицу времени. Эта величи-
величина называется в физике (гидродинамике) потоком жидкости через
поверхность Ф. Поэтому и в случае произвольного векторного поля
а(М) интеграл A) называется потоком векторного поля через поверх-
поверхность Ф.
Рассмотрим электрическое поле Е точечного заряда е, помещен-
помещенного в точку N. Найдем поток векторного поля Е через внешнюю
сторону сферы Ф радиуса г с центром в точке N. Пусть г = NM
(М — точка на сфере Ф); тогда \NM\ = г, Е(М) = — г, п(М) = -,
(En) = —- (rr) = -r2 = -. Поэтому
(En)dS = Ц ffdS = Ц 4тгг2 = 4тг/се = -,
г2]] г2 е
ke f f 1Г1 ке
*JJ
Ф Ф
где е — диэлектрическая проницаемость среды, к = -—.
4tts
Если в системе координат Oxyz a = {P, Q, R}, a n = {cos a, cos /3,
cos7}, то выражение A) для потока векторного поля а(М) можно за-
записать в виде
Г Г (Р cosa + Q cos /3 + Rcos>y)dS =
ф = [fpdydz + Qdzdx + Rdxdy. B)
ф
Каждое слагаемое в правой части равенства B) зависит от выбора
системы координат, однако их сумма, т. е. поток / / (an)d5, очевидно,
не зависит от выбора системы координат. ф
2. Формула Остроградского-Гаусса в векторной форме.
Пусть в области G определено векторное поле а = {Р, Q,R}; Ф —
замкнутая поверхность, ограничивающая область G; n(M) = {cosa,
cos /3, cos 7} — единичный вектор внешней нормали к поверхности Ф
в точке М.
Пусть, далее, для векторного поля а (т. е. для функций P,Q,R)
и поверхности Ф выполнены условия теоремы 5 из гл. XIV. Тогда
справедлива формула Остроградского-Гаусса
III (ж + ?~ + ^)
G Х У Ф
C)
Подынтегральная функция в тройном интеграле есть diva, а по-
поверхностный интеграл представляет собой поток векторного поля а
через поверхность Ф. Поэтому формулу C) можно записать в вектор-
векторной форме:
Ш div a dV = II (an) dS. D)
G Ф
§3. Характеристики векторных полей 409
Физический смысл формулы Остроградского-Гаусса: поток вектор-
векторного поля а через замкнутую поверхность в сторону внешней норма-
нормали равен тройному интегралу по области, ограниченной этой поверх-
поверхностью, от дивергенции векторного поля а. Чтобы поток был отличен
от нуля, внутри области G должны быть источники (или стоки) поля.
Из формулы Остроградского-Гаусса следует, что тогда и div а будет
отлична от нуля. Таким образом, diva характеризует источники по-
поля. Само векторное поле как бы расходится от источников. Отсюда и
происходит название "расходимость" или "дивергенция".
3. Свойства соленоидального поля. Как известно, векторное
поле а(М), удовлетворяющее в области G условию diva = 0, назы-
называется соленоидальным в этой области. Пусть область V является
объемно односвязной. Это означает, что если кусочно гладкая замкну-
замкнутая поверхность Ф лежит в области G, то и область, ограниченная по-
поверхностью Ф, целиком принадлежит области G. Примерами объемно
односвязных областей являются шар, параллелепипед, тор. Отметим,
что тор не является поверхностно односвязной областью. Область, за-
заключенная между двумя сферами, не является объемно односвязной
(но является поверхностно односвязной; см. п. 3 § 4 из гл. XIV).
Из формулы Остроградского-Гаусса следует, что соленоидальное
поле в объемно односвязной области обладает следующим свойством:
поток соленоидалъного поля через любую замкнутую поверхность, рас-
расположенную в этой области, равен нулю. Иногда это свойство прини-
принимают за определение соленоидального поля.
Отметим, что если область не является объемно односвязной, то
поток соленоидального (в этой области) поля через замкнутую по-
поверхность, расположенную в области, может быть отличен от нуля.
Так, электрическое поле Е(М) точечного заряда, помещенного в точ-
точку JV, является соленоидальным в шаре с выброшенным центром N
(div Е(М) = 0 при М ф N). Шар с выброшенным центром не является
объемно односвязной областью, и, как мы установили в п. 1, поток
поля Е(М) через сферу с центром в точке N отличен от нуля.
Слово "соленоидальное" означает "трубчатое". Для соленоидаль-
соленоидального поля имеет место закон сохране-
сохранения интенсивности векторной трубки.
Он состоит в следующем.
Пусть а(М) — соленоидальное поле.
Рассмотрим отрезок "векторной труб-
трубки", т. е. область, ограниченную двумя
сечениями, Ф1 и Ф2, и боковой поверх-
поверхностью Фз, состоящей из векторных
линий (рис. 76). Применим к такой Рис 7б
области формулу Остроградского-Гаус-
Остроградского-Гаусса D). Так как в соленоидальном поле diva = 0, то поток векторного
поля а(М) через поверхность области равен нулю: / / (an) dS = 0
Ф1+Ф2+Ф3
410 Гл. XV. Скалярные и векторные поля
(п — единичный вектор внешней нормали). На боковой поверхности
Ф3 имеем aln, поэтому / / (ап)б?5 = 0. Значит,
ф3
И (an)dS = /7(an)dS+ /7 (an)dS = 0.
Ф1+Ф2 Ф1 Ф2
Изменим на сечении <I>i направление нормали п на противоположное
(ni — внутренняя нормаль к #i). Тогда получим
JJ (an1)dS= //(an2)d5,
ф1 ф2
где оба потока через сечения <I>i и Ф2 вычисляются в направлении
векторных линий.
Таким образом, в соленоидалъном (трубчатом) векторном по-
поле а поток через любое сечение векторной трубки имеет одно и то
же значение. Это и есть закон сохранения интенсивности векторной
трубки.
4. Инвариантное определение дивергенции. Пусть в облас-
области G, ограниченной поверхностью Ф, определено векторное поле
а(М). Запишем формулу D) для векторного поля а в области G. При-
Применяя к левой части этой формулы теорему о среднем, получим
diva(M*) ¦ V(G) = //(an) dS,
или
diva(M*) =
где V(G) — объем области G, a M* — некоторая точка области G.
Зафиксируем точку М G G и будем стягивать область G к точ-
точке М так, чтобы М оставалась внутренней точкой области G. Тогда
V(G) —> 0, а М* будет стремиться к М. В силу непрерывности diva
значение diva(M*) будет стремиться к diva(M). Таким образом, по-
получаем г г ( ч ._
// (an)dS
diva(M)= lim П*п. . E)
v J v(G)^o V[G) v J
MeG
В правую часть формулы E) входят величины, инвариантные от-
относительно выбора системы координат (поток векторного поля через
поверхность и объем области). Поэтому формула E) дает инвариант-
инвариантное определение дивергенции векторного поля. Итак, дивергенция век-
векторного поля зависит только от самого поля и не зависит от выбора
системы координат.
5. Циркуляция векторного поля. Рассмотрим векторное поле
а(М), определенное в пространственной области G, и некоторую ку-
кусочно гладкую кривую L G G, на которой указано направление обхо-
обхода (выбор направления обхода называют также ориентацией кривой).
§3. Характеристики векторных полей 411
Пусть т(М) — единичный касательный вектор к кривой L в точ-
точке М, направленный в сторону обхода кривой.
Криволинейный интеграл
f(Rr)dl= fardl F)
L L
называется циркуляцией векторного поля а вдоль кривой L в заданном
направлении.
Если взять другое направление обхода кривой (изменить ориента-
ориентацию), то вектор т изменит направление на противоположное, поэтому
скалярное произведение (ат), а значит, и циркуляция (криволиней-
(криволинейный интеграл F)) изменит знак.
Если а = F — силовое векторное поле, т. е. F — вектор силы, то
циркуляция / (Ft) dl представляет собой работу силового векторного
L
поля вдоль кривой L в заданном направлении.
Если в прямоугольной системе координат Оху а = {Р, Q,i?}, a
г = {cos a, cos C, cos 7}, то выражение F) для циркуляции векторного
поля а можно записать в виде
Г (Р cos a + Qcosf3 + R cos j)dl = Г Р dx + Q dy + Rdz. G)
L L
Каждое слагаемое в правой части G) зависит от выбора системы ко-
координат, однако их сумма, т. е. циркуляция / (ат) dl, очевидно, не
зависит от выбора системы координат. l
Если ввести вектор dr = {dx,dy,dz}, то циркуляцию можно запи-
сать в виде / (adr) (сравните с правой частью равенства G)).
L
6. Формула Стокса в векторной форме. Пусть в области G
определено векторное поле а = {Р, Q,R}; L — замкнутый контур,
лежащий в области G; Ф — произвольная поверхность, границей ко-
которой является контур L; Ф С G (говорят: поверхность Ф натянута на
контур L); n(M) = {cos a, cos C, cos 7} — единичный вектор нормали
на выбранной стороне поверхности Ф.
Пусть для векторного поля а (т. е. для функций P,Q,R) и поверх-
поверхности Ф выполнены условия теоремы 3 из гл. XIV. Тогда справедлива
формула Стокса
= //
JJ l\
dR dQ\ , (дР dR\ п , (dQ дР\ 1
я "^ cosa+ — cos/3+ Up. - — COS7
d dz) \dz dx J \dx dy J J
где ориентация контура L согласована с ориентацией поверхности Ф.
Левая часть формулы Стокса есть циркуляция векторного поля а
412 Гл. XV. Скалярные и векторные поля
вдоль контура L, а правая часть представляет собой поток через по-
dR dQ dP dR
верхность Ф векторного поля с координатами — --^, — —,
ду dz dz дх
dQ дР ^ , „
—— ——, т. е. поток rota через поверхность Ф. Поэтому формулу
дх ду
Стокса можно записать в векторной форме:
/(ат) dl = //(rot a • n)dS, (8)
или L L
/(adr) = //(rot a • n) dS.
L Ф
Физический смысл формулы Стокса: циркуляция векторного по-
поля а вдоль замкнутого контура равна потоку ротора векторного по-
поля а через поверхность, натянутую на этот контур.
Чтобы циркуляция была отлична от нуля для малого контура,
окружающего некоторую выбранную точку поверхности, поле а долж-
должно поворачиваться (иметь завихрение) вблизи этой точки. Из форму-
формулы Стокса следует, что тогда и rot а вблизи этой точки будет отличен
от нуля. Таким образом, rota(M) характеризует завихрение поля в
точке М. Отсюда и происходит название "вихрь" или "ротор".
7. Свойства потенциального поля. Как известно, векторное
поле а(М), удовлетворяющее в области G условию а = grad-u, на-
называется потенциальным в этой области (и — скалярный потенци-
потенциал поля а(М)). Если поле а(М) = {Р, Q,R} потенциально в облас-
области G, то Р = — Q = — R= — и выражение Р dx + Q dy + R dz =
дх ду dz
du , ди , du ,
= — dx + — dy + — dz является полным дифференциалом функции
их Оу 0 z
и в области G. Это означает, что выполнено условие III теоремы 4 из
гл. XIV об условиях независимости криволинейного интеграла от пу-
пути интегрирования в пространстве. Из условия III вытекают осталь-
остальные условия этой теоремы.
Таким образом, потенциальное в области G поле обладает следую-
следующими свойствами.
1°. Циркуляция потенциального поля а(М) вдоль любого замкну-
замкнутого контура L С G равна нулю:
/С
(adr) = фРdx + Q dy + Rdz = 0.
L L
Иногда это свойство принимают за определение потенциального
поля.
2°. Для любых точек А и В из области G циркуляция потенци-
потенциального поля а = gradix вдоль кривой АВ не зависит от выбора кривой
АВ С G и равна разности значений потенциала и в точках А и В:
(adr) =u(B) -и(А).
АВ
§3. Характеристики векторных полей 413
Применительно к силовому потенциальному полю это свойство
означает, что работа такого поля вдоль кривой АВ не зависит от
выбора кривой, а зависит только от начальной и конечной точек А
и В. Для поля тяготения точечной массы F = —-г этот факт был
г6
уже установлен в примере 5 из § 4 гл. XIV:
АВ
3°. Потенциальное поле а(М) является безвихревым, т. е.
rot a = rot grad и = 0.
Пусть теперь дано векторное поле а(М) = {Р, Q,R}, удовлетво-
удовлетворяющее в области G условию rota = 0. Следует ли отсюда, что поле
а(М) потенциально в области G? Ответ на этот вопрос зависит от
вида области G. Если область G является поверхностно односвязной,
то из условия rota = 0 в силу теоремы 4 из гл. XIV следует, что
существует функция u(x,y,z) такая, что
D ди ^ ди D ди
дх ду dz
Следовательно, а= т—1+^—1 + ^—k = grad-и, т. е. поле а является
дх ду dz
потенциальным в области G.
Таким образом, условие rota = 0 является необходимым и доста-
достаточным условием потенциальности поля а(М) в поверхностно одно-
связной области.
Потенциал u(x,y,z) потенциального поля а(М) = {Р, Q,R} в по-
поверхностно односвязной области можно вычислить по формуле E) из
§ 4 гл. XIV:
(ж, у, z)
u(x,y,z)= [ Pdx + Qdy + Rdz =
(xo,yo,zo)
X У Z
= JP(x, j/o, zo) dx + JQ(x, y, z0) dy + Jr(x, y, z) dz. (9)
XQ У0 ZQ
Если область G не является поверхностно односвязной, то условия
rota = 0 не достаточно для потенциальности поля а(М) в области G.
Так, например, векторное поле
х1 + у2 х2 + у2
(см. пример 13 на с. 423) удовлетворяет условию rota = 0 в шаре с
выброшенным диаметром, лежащим на оси Oz. Шар с выброшенным
диаметром не является поверхностно односвязной областью, и, как
показано в примере 13, поле а не является потенциальным в этом
шаре.
414 Гл. XV. Скалярные и векторные поля
8. Инвариантное определение ротора. Пусть в области G
определено векторное поле а(М). Зафиксируем точку М Е G и не-
некоторую плоскость, проходящую через эту точку. Пусть п — еди-
единичный вектор нормали к плоскости, L — замкнутый контур, ле-
лежащий в плоскости и ограничивающий область Ф такую, что М —
внутренняя точка области Ф. Запишем формулу (8) для векторного
поля а в области Ф. Применяя к правой части этой формулы теорему
о среднем, получим
ф (ат) dl = (rot a • п)м* • 5(Ф),
откуда
i (ат) dl
(rota.n)M* =
где 5(Ф) — площадь области Ф, М* — некоторая точка области Ф.
Будем стягивать область Ф к точке М так, чтобы М оставалась
внутренней точкой области Ф. Тогда 5(Ф) —> 0, а М* будет стре-
стремиться к М. В силу непрерывности rota значение (rota • п)м* будет
стремиться к (rota • п)м- Таким образом, получаем
(ат) dl
(rota.n)M= lim Jl_ . A0)
5(Ф)^0 5(Ф)
В правую часть формулы входят величины, инвариантные относи-
относительно выбора системы координат (циркуляция векторного поля вдоль
замкнутого контура и площадь плоской области). Поэтому данная
формула дает инвариантное определение проекции rota в точке М
на направление, определяемое заданным вектором п.
Итак, проекция ротора векторного поля на произвольное направ-
направление, а значит, и сам rota зависит только от векторного поля а и не
зависит от выбора системы координат.
Для определения вектора rota вышеуказанным способом доста-
достаточно рассмотреть в заданной точке М проекции rota на три произ-
произвольных некомпланарных направления. Такими тремя проекциями
rot а определяется однозначно.
Контрольные вопросы и задания
1. Что называется потоком векторного поля через поверхность? Напишите
выражения для потока в векторной форме и в прямоугольных коорди-
координатах.
2. Приведите примеры потоков физических векторных полей через задан-
заданные поверхности.
3. Запишите формулу Остроградского-Гаусса в прямоугольных координа-
координатах и в векторной форме.
§3. Характеристики векторных полей 415
4. Каков физический смысл формулы Остроградского-Гаусса?
5. Какая область называется объемно односвязной? Приведите примеры
объемно односвязных областей и областей, не являющихся поверхност-
поверхностно односвязными.
6. Каким свойством обладает соленоидальное векторное поле в объемно
односвязной области? Покажите, что это свойство может не иметь мес-
места, если область не является объемно односвязной.
7. Выведите закон сохранения интенсивности векторной трубки для соле-
ноидального поля.
8. Дайте инвариантное определение дивергенции векторного поля.
9. Что называется циркуляцией векторного поля вдоль кривой? Напиши-
Напишите выражение для циркуляции в векторной форме и в прямоугольных
координатах.
10. Запишите формулу Стокса в прямоугольных координатах и в векторной
форме.
11. Каков физический смысл формулы Стокса?
12. Сформулируйте свойства 1°-3° потенциального поля. Что означает свой-
свойство 2° применительно к силовому полю?
13. Сформулируйте необходимое и достаточное условие потенциальности
поля а(М) в поверхностно односвязной области и напишите формулу
вычисления потенциала поля а(М).
14. Векторное поле а(М) в области G удовлетворяет условию rot a = 0.
Следует ли отсюда, что поле а(М) потенциально в области G?
15. Циркуляция векторного поля а(М) вдоль любого замкнутого контура,
лежащего в области G, равна нулю. Является ли поле а(М) потенциаль-
потенциальным в области G?
16. Дайте инвариантное определение ротора векторного поля.
17. Каков физический смысл условия diva = 0?
18. Каков физический смысл условия rot a = 0?
19. Приведите примеры физических полей, удовлетворяющих условиям:
a) div а = 0; б) rot a = 0.
20. В области G выполнено условие diva = 0. Следует ли отсюда, что поток
векторного поля а(М) через замкнутую поверхность, лежащую в G,
равен нулю? Приведите соответствующие примеры.
21. Пусть точечный заряд находится в точке Мо. Рассмотрим электричес-
электрическое поле Е этого заряда в области G, представляющей собой окрест-
окрестность точки Мо, из которой удалена сама точка Мо. Является ли поле
Е в области G соленоидальным? Укажите какую-либо замкнутую по-
поверхность Ф С G, через которую поток поля Е равен нулю. Укажите
замкнутую поверхность Ф С G, через которую поток поля Е отличен
от нуля. Всякая ли область, в которой поле Е соленоидально, является
объемно односвязной?
22. Пусть точечная масса т находится в точке Мо. Рассмотрим поле тя-
тяготения F массы т в области G, представляющей собой окрестность
точки Мо, из которой удалена сама точка Мо. Является ли поле F
в области G потенциальным? Существует ли в области G замкнутый
контур, вдоль которого циркуляция поля F не равна нулю? Всякая ли
область, где поле F потенциально, является поверхностно односвязной?
416 Гл. XV. Скалярные и векторные поля
Примеры решения задач
1. Доказать, что поток постоянного векторного поля а через лю-
любую замкнутую кусочно гладкую поверхность равен нулю.
Л Пусть Ф — замкнутая кусочно гладкая поверхность, ограничи-
ограничивающая область G. Согласно формуле Остроградского-Гаусса имеем
[[(an) dS = HI div a dV = 0,
так как дивергенция постоянного поля а равна нулю. Следовательно,
поток постоянного векторного поля через любую замкнутую поверх-
поверхность равен нулю: / / (an) dS = 0. А
ф
2. Найти поток радиуса-вектора г = xi + yj + zk через произволь-
произвольную замкнутую кусочно гладкую поверхность Ф, ограничивающую
область G объема V.
Л Сначала найдем дивергенцию данного поля: div r = l + l + l = 3.
Далее, используя формулу Остроградского-Гаусса, имеем
/У (rn) dS = HI div г dV = 3 fffdV = ЗУ.
Ф G G
Полученный результат дает формулу для вычисления объема области
G с помощью поверхностного интеграла
Ф
или, в прямоугольных координатах,
V = - / / (х cos а + у cos C + z cos 7) dS,
ф
где п = {cos a, cos/3, cos 7} — единичный вектор внешней нормали к
поверхности Ф. Эта формула была приведена в § 5 из гл. XIV. А
3. Вычислить поток электрического поля Е точечного заряда е,
помещенного в начале координат, через произвольную замкнутую ку-
кусочно гладкую поверхность, не проходящую через начало координат.
Л Векторное поле Е точечного заряда е, находящегося в начале коор-
ке ^ ^
динат, имеет вид Е(М) = — г, где г = ОМ, |г| = \ОМ .
По определению, векторное поле Е является соленоидальным в
любой области G, где divE = 0. В п. 6 из § 1 было показано, что
/ ке \
div ( — г 1 = 0 при г ф 0. Поэтому поле Е(М) соленоидально в любой
области G, не содержащей начала координат. Однако, как было отме-
отмечено в п. 3, величина потока соленоидального векторного поля через
замкнутую поверхность Ф, расположенную в области G, существенно
§3. Характеристики векторных полей 417
связана со свойством объемной односвязности области G. Рассмотрим
два случая.
1. Пусть замкнутая кусочно гладкая поверхность Ф представляет
собой границу объемно односвязной области G, не содержащей нача-
начала координат. Тогда условие divE = 0 выполняется во всех точках
объемно односвязной области G, и в силу свойства соленоидального
поля поток вектора Е через поверхность Ф равен нулю.
2. Пусть замкнутая кусочно гладкая поверхность Ф представляет
собой границу области G, содержащей внутри себя начало координат.
Тогда поле Е не является соленоидальным в области G, так как в на-
начале координат divE = оо. Если же выбросить из области G начало
координат, то оставшаяся область не будет объемно односвязной. Для
вычисления потока Е через поверхность Ф введем сферу Ф1 достаточ-
достаточно малого радиуса с центром в начале координат, целиком располо-
расположенную внутри G, и рассмотрим область G\ между поверхностями
Ф1 и Ф. Условие divE = 0 выполнено для всех точек области G\.
Применим к этой области формулу Остроградского-Гаусса. Трой-
Тройной интеграл от дивергенции Е по области G\ равен нулю. Следова-
Следовательно, равен нулю и полный поток поля Е через поверхности Ф и Ф2:
/7(En)dS+ Г Г (En) dS = 0 A1)
Вычислим поток поля Е через сферу Ф]_:
(En) dS = -4тг/се
(см. с. 408). Знак минус означает, что внешняя к области G\ нормаль
на поверхности Ф1 направлена к центру сферы Ф1 (к началу коор-
координат) и, следовательно, противоположна вектору г. Отметим, что
поток Е через сферу Ф1 не зависит от ее радиуса, т. е. имеет одно и
то же значение для сферы любого радиуса.
Возвращаясь к соотношению A1), находим поток поля Е через
поверхность Ф:
(En) dS = - ff (En) dS = 4тг/се.
ф
Итак, поток электрического поля Е через поверхность Ф равен либо
нулю, либо 4тг&е, в зависимости от того, лежит точка, где помещен
заряд, вне или внутри области, ограниченной поверхностью Ф. А
4. Вычислить поток векторного поля а = х2 i + у2 j + z2 k через
боковую поверхность Ф1 конуса {(x,y,z): х2 + у2 ^ /i2, ^х2 + у2 ^
^ z ^ h} в сторону внешней нормали.
Л I способ. Поток // (an) dS поля а через поверхность Ф1 можно
Ф1
14 В.Ф. Бутузов и др.
jj
418 Гл. XV. Скалярные и векторные поля
вычислить по формуле B), не пользуясь формулой Остроградского-
Гаусса. Этот способ применялся ранее (см. пример 3 из § 3 гл. XIV).
Здесь мы так делать не будем.
II способ. Чтобы сделать возможным применение формулы Ост-
Остроградского-Гаусса для вычисления искомого потока, дополним за-
заданную поверхность Ф1 (боковую поверхность конуса) до замкнутой
кусочно гладкой поверхности Ф основанием конуса — кругом Ф2 :
х2 + у2 ^ /i2, z = h.
Применим теперь формулу Остроградского-Гаусса к области G,
ограниченной замкнутой поверхностью Ф:
II (an) dS + II (an) dS = 2Щ[х + у + z) dx dy dz. A2)
Ф! Ф2 G
На круге Ф2 имеем а = x2 i + y2 j + h2 k, n = k; поэтому
(an) dS = II h2dS = Д25(Ф2) = h2 • irh2 = тг/i4.
ф2 ф2
Для вычисления тройного интеграла перейдем к цилиндрическим
координатам: х = pcoscp, у = psincp, z — z. Уравнение конической
поверхности примет вид z — р. Таким образом,
2тг h h
2 (х + у + z)dxdydz = 2 dip pdp [p(cos ip + sin ip) + z]dz =
- p)(cos(p + sinip) + —— P— \pdp = ^ /i4.
о о
Из формулы A2) следует, что искомый интеграл по боковой поверх-
поверхности Ф1 конуса равен разности тройного интеграла и поверхностного
интеграла по кругу Ф2:
(an) dS = -^ тг/i4 = ~^2~.
ф2
Рассмотренный пример показывает, что применение формулы
Остроградского-Гаусса для вычисления потока векторного поля че-
через замкнутую поверхность удобно в тех случаях, когда достаточно
просто вычисляются поверхностный интеграл по поверхности, допол-
дополняющей данную поверхность до замкнутой поверхности Ф, и тройной
интеграл от дивергенции векторного поля по области, ограниченной
поверхностью Ф. А
5. Вывести формулу Грина как частный случай формулы Стокса
для поля а= {Р(ж,2/), Q(x,y)} на плоскости.
Л Рассмотрим векторное поле а = {Р(х, у), Q(x, у)} как частный слу-
случай поля а = {Р, Q,R} при R = 0. Пусть поле а = {Р, Q,0} задано в
плоской области G с границей L, лежащей в плоскости Оху. Единич-
Единичная нормаль к области G совпадает с базисным вектором к оси Oz.
§3. Характеристики векторных полей
419
Поэтому, применяя формулу Стокса (9) к полю а в области G, полу-
получим
/(adr) = Г Г (iota-k) dS. A3)
L G
Формула A3) является векторной формой формулы Грина. Вычислим
ротор поля а:
rota =
i J
д д
д
дх ду dz
Р Q О
Учитывая также запись циркуляции в прямоугольных координа-
координатах, получаем уже знакомый вид формулы Грина
= (dQ__dP\
\дх ду) '
Отметим, что по-прежнему условие rot а = 0 (т. е. в данном случае
3Q дР Л .
-^- —— = 0 обеспечивает потенциальность поля а лишь в поверх-
дх ду )
ностно односвязной области. Такую область на плоскости мы назвали
односвязной (см. § 3 из гл. XIII). А
6. Доказать, что циркуляция постоянного векторного поля а вдоль
любого замкнутого кусочно гладкого контура равна нулю.
Л Пусть L — замкнутый кусочно гладкий контур, Ф — кусочно
гладкая поверхность, натянутая на L. Согласно формуле Стокса (9)
имеем eh (adr) = / / (rota • n) dS = 0, так как ротор постоянного по-
L Ф
ля а равен нулю. Следовательно, циркуляция постоянного векторного
поля вдоль любого замкнутого контура равна нулю: i(adr) = 0. А
L
7. Найти циркуляцию плоского векторного поля а = — yi + xj
вдоль произвольного кусочно гладкого контура L, лежащего в плос-
плоскости Оху и ограничивающего область Ф площади S.
Л Сначала вычислим ротор данного поля:
i J k
д_ д_ д_
дх ду dz
0
rota =
-у
= 2 к.
Далее, используя формулу Стокса и учитывая, что для области Ф
п = к, находим
= ЦBк • к) dS = iffdS = 25.
L Ф Ф
Полученный результат дает формулу для вычисления площади
14*
420
Гл. XV. Скалярные и векторные поля
плоской фигуры с помощью криволинейного интеграла:
или, в прямоугольных координатах,
S = - фх dy — у dx.
L
Другой вывод этой формулы был получен в § 3 из гл. XIII. А
8. С помощью формулы Стокса найти циркуляцию векторного по-
поля а = — yi + xj + zk вдоль замкнутого контура L, состоящего из
отрезка винтовой линии г(?) = a cost • i + asint • j + bfk @ ^ t ^ 2тг)
и отрезка прямой, соединяющего точки
??(а, 0, 2тгЬ) и А(а, 0, 0), причем обход конту-
контура совершается так, что по отрезку прямой
движение происходит от точки В к точке А.
Д Находим
,2k
2k
В
rota =
i
д
дх
-у
j
д
ду
X
к
д
dz
Z
= 2 к.
Рис .77
Пусть поверхность Ф, натянутая на кон-
контур L, состоит из части <I>i цилиндричес-
цилиндрической поверхности х2 + у2 = а2 и круга Ф2 :
х2 + у2 ^ a2, z = 2ттЪ (рис. 77). На цилинд-
цилиндрической поверхности Ф1 имеем rota _L n,
и поэтому (rot a • n) = 0. На поверхности Ф2 имеем п = к, и поэтому
rotan = 2kk = 2.
Применяя к полю а формулу Стокса, получаем
/(adr) = /7(rota-n)dS= f + Г =0 + 2 Г Г ds = 25(Ф2) = 2тга2. А
L Ф <1>1 Ф2 Ф2
9. Найти работу силового поля F = —у\ + xj + zV. вдоль отрезка
L\ винтовой линии r(t) = a cost • i + asint • j + bfk @ ^ t ^ 2тг) от
точки А(а,0,0) до точки В(а, 0, 2тгЬ).
Л I способ. Непосредственно вычисляя криволинейный интеграл
второго рода, выражающий работу силового поля F вдоль кривой L\
в заданном направлении, находим
2тг
/г
(F dr) = / (—a sin t • i + a cos t • j + bt k) x
j
1 x (-asint • i + acost • j + bk)dt = 2тга2 + 2тг2Ь2.
II способ. Чтобы сделать возможным применение формулы
Стокса для вычисления искомого интеграла, дополним заданный от-
отрезок L\ винтовой линии до замкнутой кусочно гладкой кривой L
отрезком Ь2 прямой, соединяющим точки В(а, 0,2тг6) и A(a,0,0).
§3. Характеристики векторных полей
421
Применяя формулу Стокса к контуру L и любой кусочно гладкой
поверхности Ф, натянутой на этот контур, имеем
J (Fdr)+ I (Fdr) = Jf(TotF-n)dS. A4)
Li L2 Ф
Повторяя выкладки предыдущего примера для вектора а = F, на-
находим, что rotF = 2 k и
Г Г (mtF • п) dS = 2тга2.
= -2тг2Ъ2.
2тг6
Вычислим теперь работу силы F вдоль отрезка L2 прямой от
точки В(а,0,2тгЬ) до точки А(а,0,0). На этой прямой F = aj + zk,
dr = *kdz и 0 0
f (Fdv)=
L2 2тг6
Из формулы A4) следует, что искомый интеграл (работа силы F вдоль
кривой Li) равен разности поверхностного интеграла (потока rotF
через поверхность Ф) и криволинейного интеграла по отрезку пря-
прямой Z/2:
f (Fdr) = 2тга2 - (-2тг2Ь2) = 2тга2 + 2тг2Ъ2.
Li
Рассмотренный пример показывает, что применение формулы
Стокса для вычисления работы силового поля (а также других криво-
криволинейных интегралов второго рода) вдоль незамкнутых кривых удоб-
удобно в тех случаях, когда достаточно просто вычисляются криволиней-
криволинейный интеграл по кривой, дополняющей данную кривую до замкнутого
контура, и поток ротора данного векторного поля через поверхность,
натянутую на этот контур. А
10. Вершины D,B,A' куба ABCDA'B'C'D' находятся соответ-
соответственно в точках A,0,0), @,1,0),
@, 0,1). Применяя формулу Стокса, вы-
вычислить циркуляцию векторного по-
поля а = 2/i + zj + xk вдоль ломаной
C'CDABB'A'D' (рис. 78).
Л Обозначим данную ломаную через
L\. Чтобы сделать возможным при-
применение формулы Стокса для вычис-
вычисления искомого интеграла j (adr),
Li
дополним ломаную L\ до замкнутой
кривой L отрезком L^ прямой, соеди-
соединяющим точки D' и С. На контур L
"натянем" кусочно гладкую поверхность Ф, состоящую из трех квад-
квадратов: C'CDD', D'DAA' и А'АВВ'. Обозначим их соответственно
через Фь Ф2, Фз-
Df
/
О—7-
J
У
V(lAl
Ус
^ /
i ^
)
B'
5@,1,0)
Д1,0,0)
Рис. 78
422 Гл. XV. Скалярные и векторные поля
Применяя формулу Стокса к контуру L и поверхности Ф, имеем
J (adr) + j (adr) =
Li L2
= Г Г (rot a • n) dS + И (rot a • n) dS + /У (rot a • n) dS. A5)
Далее, находим rota = —i — j — k. Единичные векторы нормалей на
частях Ф]_, <1>2, Фз поверхности Ф с учетом направления обхода кон-
контура L имеют вид п(Ф1) = —i, п(Ф2) = j, п(Фз) = i.
Вычислим поток rota через поверхность Ф:
JJ (Tota-n(<b1))dS + ff (rota-п(Ф2)) dS + yj (rot a • п(Ф3)) dS =
Ф1 Ф2 Фз
= JfdS-JfdS-JJdS = -l.
Ф1 Ф2 Фз
Найдем теперь циркуляцию поля а вдоль отрезка Ь2 прямой от
точки D' до точки С. На этой прямой a = ^/i+j + k, dr=jdy и
1
L2 0
Из формулы A5) следует, что искомый интеграл / (adr) (цирку-
ляции поля а вдоль кривой Ь\) равен разности поверхностного интег-
интеграла (потока rota через поверхность Ф) и криволинейного интеграла
(adr) (циркуляции поля а вдоль кривой Ь2): / (adr) = — 1 — 1 =
L2 L\
= -2. А
11. Доказать, что векторное поле а = у2 i + 2x^/j + zk потенци-
потенциально, и найти его потенциал.
Л Поле а определено во всем пространстве. Пространство является
поверхностно односвязной областью; поэтому необходимое и доста-
достаточное условие потенциальности поля а имеет вид rota = 0. Находим
rota =
i J k
д_ д_ д_
дх ду dz
у2 2ху z
= 0.
Следовательно, а — потенциальное поле.
Вычислим потенциал поля а по формуле A0), взяв в качестве точ-
точки (xo,yo,zo) начало координат:
х у z 2
u(x,y,z) = / 0 • dx + / 2xydy + I zdz = xy2 + ^—. A
§3. Характеристики векторных полей 423
12. Найти работу силового поля F = у2 i + 2x?/j + zk вдоль отрез-
отрезка L линии пересечения цилиндров х2 + z2 = а2 и у2 + z2 = а2, прохо-
проходящего от точки А(-а, -а, 0) через точку G@, 0, а) до точки В(а, а, 0).
Л I способ. Как и в примере 9, можно непосредственно вычислить
криволинейный интеграл /(Fdr), выражающий работу силового по-
L
ля F вдоль данной кривой L. Здесь мы этого делать не будем.
II способ. Воспользуемся тем, что данное силовое поле F являет-
2
ся потенциальным во всем пространстве: F = grad-u, где и = ху2 + 4г
(см. пример 11). Отсюда следует, что работа силы F вдоль кривой L
равна разности значений потенциала в точках В и А:
C(Fdr) =и(В)-и(А) =а3-(-а3) = 2а3. А
L
13. Выяснить, является ли потенциальным векторное поле а =
х2 + у2 х2 + у2
Д Находим
rota =
1 J К
д_ д_ д_
дх ду dz
У Х Г)
= 0, если х +у ф 0.
х2 + у2 х2 + 2Г
Заметим, однако, что поле а не определено на оси Oz, поэтому
условие rot а выполняется во всех точках пространства, кроме точек
оси Oz. Следовательно, в любой поверхностно односвязной области,
не содержащей точек оси Oz, поле а является потенциальным. Так,
например, оно потенциально в I октанте (ж > 0, у > 0, z > 0), и его
потенциал равен и = arctg — + 2z (проверьте это).
Рассмотрим теперь область, содержащую точки оси Oz, например
шар с центром в начале координат. Удалив из этого шара точки оси
Oz (т. е. диаметр, лежащий на оси Oz), получим область G, в которой
поле а определено и rota = 0. Однако эта область не является поверх-
поверхностно односвязной, и поэтому из условия rota = 0 нельзя сделать
вывод о потенциальности поля а. Покажем, что поле а в области G не
является потенциальным.
Для этого рассмотрим окружность L = {х = Rcost, у = i^sint,
0 ^ t ^ 2тг, z = 0}, лежащую в области G, и вычислим циркуляцию
поля а вдоль окружности L, пробегаемой в направлении возрастания
параметра t от 0 до 2тг. Имеем
/
?/ Т
dX +
2 2 dX + ^Г\2 ty =
х2-\-у2 х2-\-у2
L L 2тг 2тг
— sin t)(— sin t) dt + cos t • cos tdt] = / dt = 2тг ф 0.
«у
424
Гл. XV. Скалярные и векторные поля
Итак, циркуляция поля а вдоль замкнутой кривой L не равна
нулю. Следовательно, поле а не является потенциальным в облас-
области G. А
14. Пусть векторное поле а = {P(x,y),Q(x,y)} задано в плоской
области Ь, ограниченной кусочно гладкой кривой L. Доказать, что
A6)
/У div RdS = <j>(an)dl,
D
,. дР BQ „ т
где diva = ——\- -^-, an — внешняя нормаль к кривой L.
ох оу
Л Формула A6) представляет собой "плоский" вариант формулы
Остроградского-Гаусса и может быть получена из обычной форму-
формулы Остроградского-Гаусса следующим образом. Рассмотрим вектор-
векторное поле а= {Р(х,у), Q(x,y), 0} в пространственной области G =
= {(ж, у, z)\ (x,y) e D, 0 ^ z ^ 1}. Согласно формуле Остроградского-
Гаусса имеем
HI div adV = ГГ (an) dS, A7)
G Ф
где Ф — поверхность, ограничивающая область G, a n — единич-
единичный вектор внешней нормали к поверхности Ф. Сводя тройной ин-
интеграл к повторному и учитывая, что diva не зависит от z, получим
Ш div a dV = II dx dyj div adz = If div a dS.
G DO D
Поверхность Ф состоит из оснований D(z = 0), $i(z = 1) и боковой
поверхности Ф2. На основаниях D и Ф1 имеем а 1 п, и, следователь-
но, (з.п) dS = // (an) dS = 0. На боковой (цилиндрической) по-
D Фх
верхности Ф2 введем криволинейные координаты (l,z) (рис. 79), где
Сл
I
Рис. 79
Рис. 80
I — расстояние вдоль кривой L, отсчитываемое от некоторой точки
@ ^ Z ^ Zo)- Так как на Ф2 выполняется равенство dS = dl • dz и век-
вектор нормали п совпадает с вектором нормали к кривой L, причем а
§3. Характеристики векторных полей 425
и п зависят только от I и не зависят от z, то
^0 1 ^0
(an) dS = II (an) dS = fdlf(an) dz = /"(an) d/ = /(an) dl.
Ф Ф2 0 0 0 L
Подставляя найденные выражения для тройного и поверхностного ин-
интегралов в A7), приходим к формуле A6). А
Замечание 1. Отметим, что формула A6) ("плоский" вариант фор-
формулы Остроградского-Гаусса) есть не что иное, как формула Грина, за-
записанная в специальной форме. В самом деле, запишем формулу Грина в
обычном виде:
D L
Введем теперь вектор а = {Q, — Р}. Тогда — -^— = diva, Pdx + Qdy =
ox oy
= (Р cos a + Q sin a) dl = [Q sin a + (—P) (— cos a)] dl = (an) dl, где а — угол
между касательным вектором г и осью Ox; n = <cos(a 1, sin (a —
1 > = {sin а, — cos a} — единичный вектор внешней нормали к L
(рис. 80). В силу этих равенств формула Грина принимает вид A6).
Замечание 2. Аналогично тому, как из формулы Остроградского-
Гаусса была получена формула A6), из формулы A6) (или, что то же самое,
из формулы Грина) можно получить формулу Ньютона-Лейбница ("одно-
("одномерный" вариант формулы Остроградского-Гаусса). Для этого положим
Q = Q(x), Р = О, D = {х,у: 0 ^ х ^ I, 0 ^ у ^ 1}. Тогда из формулы
Грина получим
С С dQ С
II -z—dxdy = AQdy.
J J ox J
dQ D L
Так как —— не зависит от у, а на нижней и верхней сторонах прямоуголь-
ох
ника D имеем dy = 0, то
о
^ dxjdy = Q(O)Jdy + Q(l)Jdy,
0 1 0
или
о
Это и есть формула Ньютона-Лейбница.
Таким образом, формулы Грина и Остроградского-Гаусса являются об-
обобщениями формулы Ньютона-Лейбница на случаи двумерных и трехмер-
трехмерных областей.
15. Пусть скалярные поля и и v заданы в области G, ограниченной
кусочно гладкой поверхностью Ф. Доказать, что
;-^ dS = fff(v Аи + (gradix • gradi;)) dV A8)
G
426 Гл. XV. Скалярные и векторные поля
{первая формула Грина) и
Ф G
(вторая формула Грина).
Л Применим к векторному полю а = I'grad'U в области G форму-
ди
лу Остроградского-Гаусса. Учитывая равенства ('ygrad'U • n) = v —,
diy(vgr3>du) =v diy(grdidu) + (grad-u • grad г;) (см. формулу B1) из § 1)
и div(grad'u) = Аи, получаем формулу A8).
Вторая формула Грина выводится с помощью первой: нужно в A8)
поменять и и v местами и вычесть полученное равенство из A8). А
Замечание 1. Отметим, что первую и вторую формулы Грина на
плоскости можно вывести аналогично A8) и A9), применив формулу A6)
к векторным полям v(x,y)gra,du(x,y) и u(x,y)gra,dv(x,y). Эти формулы в
координатной форме были получены в § 3 из гл. XIII.
Замечание 2. Рассмотрим широко распространенный в математи-
математической физике оператор
Ни) = div[k(M) gradw(M)] - q(M)u(M), B0)
где к(М), q(M), u(M) — скалярные функции (оператор Лапласа Аи явля-
является частным случаем Ь(и) при к(М) = 1, q(M) = 0).
Пусть векторное поле а = v(M)k(M) grad и (v(M) — скалярное поле) за-
задано в области G, ограниченной поверхностью Ф. Применяя к векторному
полю а в области G формулу Остроградского-Гаусса и учитывая равенство
div(vk grad и) = v div(k grad и) + &(grad и • grad г;)
(см. формулу B1) из § 1), получаем
} — dS= fff[vL(u) + /c(grad и • grad v) + quv] dV B1)
Ф G
(первая формула Грина для оператора L(u)).
Меняя в формуле B1) и и v местами и вычитая полученное равенство
из B1), приходим к формуле
klv и — IdS = / // (vL(u) — uL(v)) dV
JJ \ dn dn/ JJJ
Ф G
(вторая формула Грина для оператора L(u)).
В случае полей и(М) и v(M), заданных в области D с границей L на
плоскости, применяя к полям v • kgradu и u-kgradv формулу A6), для
оператора Ь(и) получаем следующие формулы:
I kv — dl = / / [vL(u) + &(grad и • grad г;) + quv] dS,
L D
jk(v—-u—\dl = jj(vL(u) ~ uL(v)) dS,
L П П D
аналогичные формулам B1) и B2).
В случае полей и(х) и v(x), заданных на отрезке 0 ^ х ^ /, для оператора
т du
kv—
dx
§3. Характеристики векторных полей 427
(одномерный вариант B0)) имеют место формулы
1 = Г \vL(u) + к — • — + quv] dx, B3)
о J L dx dx J
k(v—-u—)\l= f(vL(u)-uL(v))dx. B4)
V dx dx J |n </
о
В справедливости формул B3) и B4) можно убедиться непосредственно
интегрированием по частям.
Задачи и упражнения для самостоятельной работы
43. Применяя формулу Остроградского-Гаусса, вычислите поток вектор-
векторного поля а = (ж — у) i + (z — у) j + (z — ж) к через:
а) поверхность пирамиды, ограниченной плоскостями ж + у + z = 1,
ж = 0, ?/ = 0, z = 0 в сторону внешней нормали;
б) сферу ж2 + у2 + z2 = 1 в сторону внешней нормали.
44. Применяя формулу Остроградского-Гаусса, вычислите поток вектор-
векторного поля а = ж cos у • i — sin у • j + (z — IJ k через боковую поверхность
цилиндра, ограниченного поверхностями:
я^ т2 _i_ ?#2 — 1 г — П г — 9-
aj ж -|-г/ — 1, z — и, z — z,
б) ж2 + у2 = 1, 2 = 2, 2 = 4 в сторону внутренней нормали.
45. Вычислите поток векторного поля а = (z + 1) к через:
а) сферу ж2 + у2 + z2 = 1 в сторону внешней нормали;
б) полусферу ж2 + у2 + z2 = 1, 2 ^ 0 в сторону внешней нормали к
сфере;
в) полусферу ж2 + у2 + z2 = 1, 2 ^ 0 в сторону внутренней нормали
к сфере;
г) полусферу ж2 + у2 + z2 = 1, 2 ^ 0 в сторону внутренней нормали к
сфере;
д) полусферу ж2 +у2 + z2 = 1, 2/^0 в сторону внешней нормали к
сфере.
46. Вычислите поток векторного поля а = у\ + zj + жк через круг, полу-
получающийся при пересечении шара ж2 + у2 + z2 ^ 1 и плоскости:
а)ж + ?/ + ? = 0; б) ж+ г/ +2 = 1; в)ж —^/ + ^ = 0;
г) ж — у -\- z = 1 в сторону той нормали к плоскости, которая образует
острый угол с осью Оу.
47. Применяя формулу Остроградского-Гаусса, вычислите поток вектор-
векторного поля а = у\-\- zj + жк через каждую из частей сферы ж2 + у2 +
+ z2 = 1, получающихся при пересечении этой сферы плоскостью:
а) ж + у + z = 0; б) ж + г/+ 2 = 1; в)ж —^/ + ^ = 0;
г) ж — у -\- z = 1 в сторону внешней нормали к сфере.
48. Вычислите поток векторного поля а = у\ + zj + жк через круг, полу-
полученный при пересечении шара ж2 + у2 + z2 ^ 1 и плоскости ж + ?/ + 2 =
= а в сторону той нормали к плоскости, которая образует острый угол
с осью Ох. При каком значении а поток векторного поля а принимает
наибольшее и наименьшее значения?
428 Гл. XV. Скалярные и векторные поля
49. Даны векторные поля: ai = fi(y,z)i + /2B, ж) j + /з(ж,г/)к; а2 = ж2 i +
+ 2/j + ^k; a3 = (у — ж^/Ji + (у - yzj j+ (у - жг) к; а4 = ж2 i +
+ 2/2 J + z2 к. Выясните, какие из них являются соленоидальными. Вы-
Вычислите поток каждого из данных полей через сферу единичного ра-
радиуса с центром в начале координат в сторону внешней нормали.
50. Применяя формулу Стокса, вычислите циркуляцию векторного поля
а = О - х2) i + (ж - у2) j + (у - z2) k вдоль:
а) треугольного контура, образованного пересечением плоскости х+
+ у + 2 = 1 с координатными плоскостями и пробегаемого по часовой
стрелке, если смотреть из начала координат;
б) треугольного контура, образованного отрезками прямых, соединя-
соединяющими точки @,0,0), @,1,0) и @,0,1), и пробегаемого по часовой
стрелке, если смотреть из точки A,0,0);
в) треугольных контуров, лежащих в плоскостях Оху и Oxz, аналогич-
аналогичных контуру из п. б) и пробегаемых по часовой стрелке, если смотреть
соответственно из точек @, 0,1) и @,1, 0).
51. Применяя формулу Стокса, вычислите циркуляцию векторного поля
а = у\ + zj + ж к вдоль окружности, получающейся при пересечении
сферы х2 + у2 + z2 = 1 плоскостью: а) х + у + z = 0; б) х + у + z = 1;
в) х — у + z = 0] г) х — у + z = — 1. Контур пробегается против часовой
стрелки, если смотреть из точки @,2,0).
52. Применяя формулу Стокса, вычислите циркуляцию векторного поля
а = (у — х) i + (z — у) j + (x — z) k вдоль окружности, получающейся
при пересечении сферы х2 + у2 + z2 = 1 и плоскости х + у + z = a.
Окружность пробегается против часовой стрелки, если смотреть из
точки @, 0, 2). При каком значении а циркуляция векторного поля при-
принимает наименьшее значение?
53. Применяя формулу Стокса, вычислите циркуляцию векторного поля
а = ж cos у • i + sin у • j + (z — IJ k вдоль отрезка винтовой линии r(t) =
= cos t • i + sin t • j + — k:
7Г
а) от точки А@, 0, 0) до точки В@, 0, 2) @ ^ t ^ 2тг);
б) от точки Б@, 0, 2) до точки С@, 0, 4) Bтг ^ ? ^ 4тг).
54. Вершины D,B,A* куба ABCDA1 В'С'D' находятся соответственно в
точках A,0,0), @,1,0), @,0,1). Применяя формулу Стокса, вычисли-
вычислите циркуляцию векторного поля а = z\ + ж j + у к вдоль замкнутого
контура: а) С'СВВ'A'D'C; б) DD'A'ABCD; в) C'D'DABB'C. Ис-
Используя полученные результаты, вычислите циркуляцию векторного
поля а вдоль ломаной: г) C'CBB'A'D'- д) DD'A'ABC; e) C'D'DABB'.
55. Докажите, что векторное поле а = /(г) г, где г = х i + у j + z k, r = |r|,
является потенциальным, и найдите потенциал этого поля.
56. Даны векторные поля: ai = (у + z) i + (z + х) j + (ж + у) k; a2 = /i (ж) i +
+/2B/) j + /3B) к; а3 = ж i + у j + ^к; а4 = ^i + жj + г/к. Выясните, ка-
какие из них являются потенциальными. Вычислите циркуляцию каждо-
каждого из данных полей вдоль окружности ж2 + z2 = 1, пробегаемой против
часовой стрелки, если смотреть из точки @,1,0).
57. Найдите потенциалы потенциальных полей предыдущей задачи.
58. Докажите, что поток векторного поля а через поверхность Ф, заданную
уравнением г = r(u,v), (u,v) G д, в сторону нормали N = — • —
Idu dvJ
§3. Характеристики векторных полей 429
может быть вычислен по формуле
-//(•[?¦?])**.
Ф д
где п = — единичный вектор нормали к поверхности Ф.
Вычислите по этой формуле поток векторного поля а = cos ip • i +
+ sin Lp • j через коническую поверхность Ф, заданную векторным урав-
уравнением г(г, ф) = г cos ср • i + г sin ip • j + г cos а • к @ ^ <? ^ 2тг, 0 ^ г ^
^ 1), где г, <^ — полярные координаты, а — угол между образующей
конуса и осью Oz.
Какая из нормалей Ni = — • — и N2 = — • — образует острый
Р [дг д(р\ [д(р дг\ Р У Р
угол с осью Oz?
59. В области G = {(ж, г/) : 0 < ж2 + ?/2 ^ 1} задано векторное поле а =
= —-^—- i + —-^—- j. Докажите, что rota = 0 в G. Объясните, поче-
х2 -\- у х2 + у
му из условия rot a = 0 не следует потенциальность поля а в облас-
области G. Задав произвольную замкнутую кривую L в области G в виде
х = p(ip) cos ip, у = р(<?>) sin 9?, 0^<?^ 2тт, докажите, что циркуляция
поля а вдоль кривой L равна нулю. Найдите потенциал поля а.
60. Вычислите ротор векторного поля а и циркуляцию этого поля вдоль
окружности L, если:
а) а= Х i+ 2^ oJ + ^k, L: ж2 + ?/2 = 1, ^ = z0;
х2 +у2 х2 + ?/2
б) а = ж!+ ^ j+ ^ k, L: г/2+^2 = 1, ж = ж0;
y2+z2 y2+z2
в) а= Ж i- ^ j + ^k, L: ж2 + у2 = 1, ^ = z0;
х2 -\- у2 х2 + ?/2
г) а = ж1+ ^ j- Z к, L: ^/2 + ^2 = 1, ж = ж0.
Являются ли поля а) и в) потенциальными в шаре ж2 + у2 + z1 ^ 1 с
выброшенным диаметром, лежащим на оси Oz, а поля б) и г) потенци-
потенциальными в шаре ж2 + у2 + z2 ^ 1 с выброшенным диаметром, лежащим
на оси Ож?
61. Дано векторное поле на плоскости а = — i + — j, ж2 + у2 Ф 0.
х2 +у2 х2 + у2
Вычислите rot а и циркуляцию поля а вдоль окружности ж2 + у2 = R2.
Является ли поле а потенциальным: в области 0 < ж2 + у2 ^ 1; в области
(X - 2J + у2 4: 1?
X
62. Дано скалярное поле на плоскости и = ятггпя Вычислите
\Jx2 + у2
gradi6 и циркуляцию векторного поля а = gradi6 вдоль окружности
ж2 + у2 = В2. Является ли векторное поле а потенциальным в области
О <х2 +у2 ^ 1?
63. Дано векторное поле на плоскости а = —-^—- i + —-^—- j, ж2 + у2 ф 0.
х2-\-у2 х2-\-у2
Вычислите div а и поток поля а через окружность ж2 + у2 = 1 в сторону
внешней нормали. Объясните, почему в данном случае из соленоидаль-
ности поля а не следует, что поток поля а через любую замкнутую
кривую равен нулю.
430 Гл. XV. Скалярные и векторные поля
64. Дано векторное поле на плоскости а = о у о i -\——^—- j, х2 + у2 ф
х2-\-у2 х2-\-у2
Ф 0. Докажите, что diva = 0 и поток поля а через любую замкнутую
кривую, не проходящую через начало координат, равен нулю (кривая
может обходить начало координат).
65. Пусть в односвязной плоской области G векторное поле а(ж,г/) удов-
удовлетворяет условиям rota = 0 и diva = 0. Докажите, что поле а по-
потенциально и его потенциал является гармонической функцией в об-
области G. Объясните, почему это утверждение неприменимо к полю
а = о у о i Н——^—- j в области 0 < х2 + у2 < 1, хотя условия rot a =
х2 + у2 х2 + у2
= 0 и diva = 0 в этой области выполнены (см. упр. 61 и 64).
66. Применяя формулу Остроградского-Гаусса к векторному полю и(М) i,
где и(М) — скалярное поле в области G с границей Ф, докажите, что
Ф G
где а — угол между внешней нормалью п к поверхности Ф и осью Ох.
67. Применяя формулу Остроградского-Гаусса к векторным полям и(М) i,
и(М) j, и(М) к, где и(М) — скалярное поле в области G, ограниченной
поверхностью Ф, докажите, что
[fun dS = Г Г пи dS = fffVu dV, B5)
где п — единичный вектор внешней нормали к поверхности Ф. (Эта
формула аналогична формуле Остроградского-Гаусса, но вместо век-
векторного поля здесь фигурирует скалярное поле и(М).)
68. Используя формулу B5), докажите, что
ff
un dS
-, B6)
где V(G) — объем области G, ограниченной поверхностью Ф. (Эта
формула дает инвариантное определение градиента скалярного поля,
аналогичное инвариантным определениям дивергенции и ротора.)
69. Пусть векторное поле а = {P(M),Q(M),R(M)} задано в области G,
ограниченной поверхностью Ф, a n = {cos a, cos /3, cos 7} — единичный
вектор внешней нормали к поверхности Ф.
Примените в области G формулу Остроградского-Гаусса к векторным
полям R(M) j - Q(M) k, P(M) k - R(M) i и Q(M) i - P(M) j. Умножая
полученные равенства соответственно на i, j, k и складывая, докажите,
что
jj [na] dS = jjj rot a dV
Ф G
ИЛИ
ff[na]dS = fff\y*]dV. B7)
Ф G
Эта формула аналогична формуле Остроградского-Гаусса:
JJ (na) dS = JJJ div a dV
или
§3. Характеристики векторных полей 431
///(па) dS = ///(Va) dV. B8)
70. Используя формулу B7), докажите, что
f[[na]dS
rota(M)= lim ^ , B9)
V J v(G)^o V(G) ' V J
meg
где V(G) — объем области G, ограниченной поверхностью Ф. (Формула
B9) дает инвариантное определение ротора векторного поля, причем,
в отличие от формулы A0), она выражает сам вектор rota, а не его
проекцию на некоторое выбранное направление.)
71. В примере 4 из § 5 гл. XIV для скалярного поля и была получена фор-
формула
ir?dS=IIIAudv'
Ф G
которую с помощью оператора Гамильтона можно записать в виде
JJ(n\7)udS = JJJv2udV. C1)
Ф G
Используя формулу C0), докажите, что
Щ$Г C2)
MEG
где V(G) — объем области G, ограниченной поверхностью Ф. (Формула
C2) дает инвариантное определение оператора Лапласа.) Формулы B5),
B7), B8), C1) можно рассматривать как частные случаи следующего
операторного обобщения формулы Остроградского-Гаусса:
п) dS = JJjL{V) dV, C3)
Ф G
где L(b) — некоторое линейное однородное выражение относительно
вектора b (b — произвольный вектор, в частности вектор п или век-
вектор V ). Такими выражениями относительно вектора п в левых частях
формул B5), B7), B8), C1) являются пи, [па], (па), (nV). В правых
частях указанных формул тройные интегралы берутся от тех же выра-
выражений, в которых вектор п заменен вектором V. Поэтому формулы E),
B6), B9), C2) оказываются частными случаями операторной формулы
[Г L(n) dS
L{V)M = Hm JU ,
v(G)^o V(G)
MEG
где V(G) — объем области G, ограниченной поверхностью Ф и стяги-
стягивающейся к точке М.
72. Применяя формулу C3), докажите, что
C4)
C5)
432 Гл. XV. Скалярные и векторные поля
где а — векторное поле, заданное в области G с границей Ф; п —
единичный вектор внешней нормали к поверхности Ф; v — постоянный
вектор.
Проверьте справедливость этих формул, проделав все указанные опе-
операции в координатах. Используя формулы C4) и C5), докажите, что
/7(vn)adS
JU
/7
(vV)a(M)= lim JU , ч , Aa(M)= lim
, ч, Aa(M)= lim
() V{G) ' V J v(G)^o V{G)
M?G M?G
(эти формулы дают инвариантные определения операций (vV)a и Аа).
73. Пусть а — постоянный вектор, г = xi + yj + zk. Используя форму-
формулу C4), докажите, что //(an)rcLS' = аУ, где V — объем области,
ф
ограниченной поверхностью Ф.
74. Пусть а — постоянный вектор, г = xi + yj + zk. Используя формулу
C4) и тождество B5) из § 1, докажите, что // (ar)n dS = аУ, где V —
G
объем области, ограниченной поверхностью Ф.
§ 4. Основные дифференциальные операции
векторного анализа
в криволинейных ортогональных координатах
Основные понятия и формулы
1. Криволинейные ортогональные координаты. Пусть ж, у,
z — прямоугольные координаты точки М. Положение точки М, как
было отмечено в гл. XII, можно задать также с помощью криволиней-
криволинейных координат. Будем обозначать их gb g2, ^з, а формулы, связыва-
связывающие криволинейные координаты с прямоугольными, запишем в виде
х = x(qljq2jq3)j У = y(qi, #2, <7з), z = z(Qij Q2, Ы- (!)
При изменении q\ и фиксированных значениях q2 и q% точка с ко-
координатами x,y,z, определяемыми формулами A), описывает в про-
пространстве некоторую кривую, называемую координатной линией q\.
Аналогично определяются координатные линии д2 и дз- Криволиней-
Криволинейные координаты называются ортогональными, если в любой точке
три координатные линии, проходящие через эту точку, попарно орто-
ортогональны (т. е. попарно ортогональны касательные к координатным
линиям в этой точке).
Элемент dl\ длины дуги координатной линии q\ выражается фор-
формулой
dl\ = Hidqi,
где
Аналогично,
§4- Криволинейные координаты 433
где
Ox f ( ду \2 / Oz \2
Величины Яь Я2, Я3 называются параметрами Ламэ или масштаб-
масштабными коэффициентами криволинейных координат qi, ^2, Цз- Они ха-
характеризуют в каждой точке пространства изменение dl\ длины ко-
координатной линии в зависимости от изменения dqi соответствующей
криволинейной координаты qi.
2. Цилиндрические и сферические координаты. Примерами
криволинейных ортогональных координат являются известные нам
цилиндрические и сферические координаты.
Цилиндрические координаты q\ = p, q2 = (p, q3 = z вводятся с
помощью соотношений
х = р cos (р, у = р sin if, z = z,
p ^ 0, 0 ^ if < 2тг, -oo < z < +00.
Параметры Ламэ для цилиндрических координат имеют вид
#! = 1, Я2 = р, #з = 1.
Сферические координаты qi = г, q2 = 6, q3 = <? вводятся с
помощью соотношений
ж = г sin # cos (р, у = г sin # sin (p, z = r cos ^,
г ^ 0, 0 ^ 6> ^ тг, 0 ^ у? < 2тг. ^
Параметры Ламэ для сферических координат имеют вид
#1 = 1, Я2=г, H3=rsin0.
3. Операции grad, div, rot, А в криволинейных ортогональ-
ортогональных координатах. Пусть #ь ^2, ^з — криволинейные ортогональные
координаты точки М. Введем в точке М ортогональный базис, состо-
состоящий из трех единичных векторов ei, e2, ез, касательных к коорди-
координатным линиям в точке М и направленных в сторону возрастания
Цх-, Ц2-, Уз- Отметим, что при переходе от точки к точке направления
векторов еь е2, е3 изменяются (в отличие от векторов i, j, k), т. е.
базис {ei, в2, ез} зависит от точки М (или, что то же самое, от q\,
Пусть и{М) и а(М) — дифференцируемые скалярное и векторное
поля. Вектор а(М) разложим по базису {е1,в2,ез} в точке М: а =
= aiei + a2e2 + a3e3.
Основные дифференциальные операции векторного анализа в кри-
криволинейных ортогональных координатах имеют следующий вид:
434
Гл. XV. Скалярные и векторные поля
1 ди
1 ди
1 ди
diva =
rota =
1
Я1Я2Я3
Hi ei Я2 е2 Я3 e3
а\Н\ a^H-i CL3H3
= div grad и =
E)
^ /Я2Я3 ди\ д /Я3Я1 a^\ a /Я1Я2 ^
^"\ Я: ^"У ~dq~2\ H2 ~dq4J ~dq^\ Я3 ^з"
Контрольные вопросы и задания
1. Что такое криволинейные координаты; координатные линии? Какие
криволинейные координаты называются ортогональными?
2. Что такое параметры Ламэ? Каков их геометрический смысл?
3. Приведите примеры криволинейных ортогональных координат.
Напишите формулы, связывающие прямоугольные координаты: а) с
цилиндрическими координатами; б) со сферическими координатами.
Изобразите на рисунке координатные линии для цилиндрических и сфе-
сферических координат.
4. Вычислите параметры Ламэ для цилиндрических и сферических
координат двумя способами: а) по формулам для параметров Ламэ;
б) используя вид координатных линий и геометрический смысл пара-
параметров Ламэ.
5. Как вводится базис {е1,е2,ез}, связанный с криволинейными орто-
ортогональными координатами? В чем его отличие от базиса {i,j,k}?
Изобразите на рисунке базис {в1,е2,ез} в произвольной точке для:
а) цилиндрических координат; б) сферических координат.
6. Запишите в криволинейных ортогональных координатах:
a) grad 16; б) diva; в) rota.
7. Используя формулу Д = div grad, выведите выражение для оператора
Лапласа в криволинейных ортогональных координатах.
Примеры решения задач
1. Записать выражение градиента скалярного поля и в цилиндри-
цилиндрических координатах.
Л Полагая в формуле D) q± = p, q2 = у?, <?з = z, е1 = ер, е2 = е^,
е3 = ez и используя выражения параметров Ламэ в цилиндрических
§4- Криволинейные координаты 435
координатах, получаем
_ ди 1 ди ди
др И р dip * dz
2. Записать выражение Аи (А — оператор Лапласа) в сферичес-
сферических координатах.
Л Полагая в формуле E) q\ = r, q2 = 0, q% = ср и используя выражения
параметров Ламэ в сферических координатах, получаем
1 д ( о ди\ , 1 д ( . „ди\ , 1 #и .
3. Найти сферически симметричное решение уравнения Пуассона
Дг& = -, т. е. решение, зависящее только от г.
Л Так как искомая функция и по условию не зависит от в и (р, то
производные по этим переменным в выражении F) равны нулю, и
уравнение для функции и примет вид
}_д_Bди\ = 1
г2 дг\ дг) г
Отсюда
d du
используем обозначения обыкновенных производных, так как функ-
функция и зависит лишь от одной переменной: и = и(г). Умножая на dr,
получаем
а[г — 1 = гаг.
\ dr)
откуда, интегрируя, находим
Деля на г2 и интегрируя еще раз, имеем
Здесь Ci и G2 — произвольные постоянные. А
Задачи и упражнения для самостоятельной работы
75. Пусть ер,е^,ег — единичные базисные векторы системы цилиндри-
цилиндрических координат р, 9?, г, связанных с прямоугольными координатами
ж, 2/, г формулами B). Даны точки АA, 0, 0), В@,1, 0), С@, 0,1) (коор-
(координаты точек прямоугольные).
а) Изобразите на рисунке базис {ер,е^,ег} в точках А, В, С.
б) Найдите углы между векторами: 1°) ер(А) и ер(В); 2°) е<ДА) и
ер(Б); 3°) ер(А) и е^(Б); 4°) е,(А) и ez(B).
в) Разложите векторы: 1°) i,j,k по базису {ер,е^,ег} в точках Аи В;
2°) ер,е^,ег точках А и В по базису {i,j,k}.
436 Гл. XV. Скалярные и векторные поля
76. Пусть ег, е#, е^ — единичные базисные векторы системы сферических
координат г, #, ср, связанных с прямоугольными координатами x,y,z
формулами C). Даны точки АA, О, 0), 5@,1, 0), G@, 0,1) (координаты
точек прямоугольные).
а) Изобразите на рисунке базис {ег,е^,е^} в точках А, В, С.
б) Найдите углы между векторами: 1°) ег(А) и ее (В); 2°) е<ДА) и
ег(В); 3°) ег(А) и е^(Б); 4°) ев(А) и е*(Я).
в) Разложите векторы: 1°) i,j,k и по базису {ег,е^,е^} в точках А и
В; 2°) ег,е0,е^ в точках А и В по базису {i,j,k}.
77. Запишите выражение градиента скалярного поля и на плоскости Оху
в полярных координатах.
78. Выразите дивергенцию и ротор плоского векторного поля а(ж,г/) в по-
полярных координатах.
79. Запишите выражение градиента скалярного поля и в сферических ко-
координатах.
80. Запишите выражение дивергенции векторного поля а:
а) в цилиндрических координатах; б) в сферических координатах.
81. Выразите ротор векторного поля а:
а) в цилиндрических координатах; б) в сферических координатах.
82. Запишите выражение Аи (А — оператор Лапласа) в цилиндрических
координатах.
83. Найдите решения уравнения Лапласа Аи = 0, зависящие: а) только
от р\ б) только от if] в) только от z\ где p,ip,z — цилиндрические
координаты.
84. Найдите решения уравнения Лапласа Аи = 0, зависящие: а) только
от г; б) только от 0; в) только от ср; где г,6,ср — сферические коор-
координаты.
85. С помощью выражения оператора Лапласа в сферических координатах
вычислите A(rm).
86. Пусть {ei, ег, ез} — ортогональный базис системы криволинейных ко-
координат gi, #2, qs- Найдите divei, dive2, dive3. Запишите полученные
выражения:
а) в цилиндрических координатах, считая ei = ер, е2 = е^, е3 = ег;
б) в сферических координатах, считая ei = er, е2 = е#, ез = е^.
87. Пусть {ei, е2, е3} — ортогональный базис системы криволинейных ко-
координат gi, g2, qs- Докажите, что
1 дНг \ 1 г ,„
Выведите аналогичные формулы для rote2 и rote3. Запишите получен-
полученные выражения:
а) в цилиндрических координатах, считая ei = ер, е2 = е^, ез = ег;
б) в сферических координатах, считая ei = er, е2 = е^, ез = е^.
/ 1 дНг \ ( 1 дНг \ 1 г ,„
rot ei = е2 — I ез = — gradii
VЯзЯl dq3) \Я1Я2 dq2 ) Н^
ОТВЕТЫ И УКАЗАНИЯ
Глава I
1. * Воспользуйтесь методом доказательства от противного. 5. * Вос-
Воспользуйтесь результатами примеров 1 и 2. 15. Пусть ж — любое положи-
положительное число и пусть х\ и у\ — любые рациональные числа, удовлетво-
удовлетворяющие неравенствам
О < xi ^ ж, 0 < yi ^ 1. (*)
Тогда по определению произведения положительных чисел имеем ж • 1 =
= sup М, где М = {(xiyi)r}. Как следует из (*), V#i, у\ 0 < (x\y\)r ^ Ж1 ^ ж,
т. е. х — верхняя грань множества М. Пусть ж < х. Как показано в примере
1 из § 1, существует рациональное число ж* такое, что ж < х* < х. Возьмем
х\ = ж*, у\ = 1. Тогда (xiyi)r = ж* • 1 = ж* и, следовательно, (#ii/i)r > ж.
Итак, для числа х выполнены оба условия определения точной верхней гра-
грани множества, т. е. supM = х. Таким образом, Ух > 0 х • 1 = sup M = ж,
откуда ж • 1 = ж. Если ж = 0, то согласно правилу умножения рациональных
чисел 0-1 = 0. Если ж < 0, то согласно определению произведения вещест-
вещественных чисел ж • 1 = —|ж| • 1. Но, как только что было показано, |ж| • 1 = |ж|,
т. е. ж • 1 = —|ж| = ж. 33. * При х\Х2---хп = 0 утверждение очевидно. При
Ж1Ж2...жп ф 0 положите ук = хк == ^ — 152,...,п) и воспользуйтесь
результатом примера 2 из § 4.
Глава II
1. а) Да; б) нет; в) нет; г) да; д) нет. 4. Нет. 5. Достаточно доказать,
что последовательность {хп} неограниченная. 14. * Если lim xn = +оо, то
п—^оо
ЗА > 0 и номер 7V такие, что хп > A Vn > TV. Среди Ж1, Ж2,..., ждг существу-
существует наименьшее число. 15. а) Ж4 = хъ = —120; б) жю = 20. 20. а) а; б) а2; в) 0;
г) а. 21. а) уп = Г2 + (-1)n^| расходится; б) ?/п = Sgn((-l)nij расходит-
расходится. 23. а) Сходится, если а>0, /3>0, а^/3 или а ^ 0, C любое; б) сходится,
если 7 ^ 3/2. 24. а) 0; б) 0; в) 1/3. 26. а) 1/2; б) 1/3; в) 1. * Представь-
Представь(А; = 1,2,...,п); г) 1/4. * Представь-
виде Sn = А + ^-у + ^2 Vn;
1. 30. а) 2; б) 0. 31. Так как Уе >
= 0, то Vs > О 3N такое, что Vn > N выполняется неравенст-
)п/п\ < 1 или 1/ \/пТ < е. 33. A + л/1+4а)/2. 34. а) (а + 2Ь)/3; б) д/а;
1 = (^4)Т - ^т, 0! = 1, п
438 Ответы и указания
в) -^/а; г) 2; д) A - у/1 - 4xi)/2; е) 1/2; ж) (л/б - 1)/2; з) 3. 37. * г) До-
Докажите, что: 1°) множество U предельных точек последовательности огра-
ограничено; 2°) если inf U = с, sup U = 6, то с, 6 Е [/; 3°) с = lim хп,Ъ = lim жп.
39. а) Предельные точки: 2, —2; lim хп = 2, lim хп = —2; б) предельные
точки: 0, 1, 2; lim жп = 2, lim жп = 0; в) предельные точки: —4, 0, 2,
71->-ОО ^^^
6; lim хп = 6, lim жп = —4; г) предельные точки: —1/2, 1; lim жп = 1,
п-юо ^^оо те-э-оо
lim хп = —1/2; д) предельная точка 1; lim жп = +оо, lim хп = — оо;
п—^оо тг—^оо гг—^оо
е) предельные точки: 0, 1; lim хп = 1, lim хп = 0; ж) предельные точ-
те-Э-оо п^оо
ки: —е /=, —е Н—/=, е — 1, е, е + 1; lim жп = е + 1, lim жп = — е -j=\
V2 V2 гг-^оо гг-^оо V2
з) предельные точки: 0, 1/2, 1; lim хп = 1, lim жп = 0; и) предельные точ-
п^оо п^оо
ки: 1, 2; lim хп = 2, lim жп = 1; к) предельные точки: 0, 1; lim xn = 1,
lim хп = 0; л) нет предельных точек; lim жп = +оо, lim жп = — оо. 40. Рас-
п—^оо тг—^оо гг—^оо
ходится. * Докажите, что lim Ж2& ф Hm ^2fc+i- 41. а) Воспользуйтесь
оценкой -ру ^ , —-у = — ^ при А; ^ 2; г) воспользуйтесь оценкой
п+р
akQk\ ^ Л^ ^^ \я\к• 42. * В определении 1 фунда-
\хп+р —
ментальной последовательности положите р = 1. 43. * б) Покажите, что
для е = 1/2 и Vn |жп - ж2п| ^ 1/2.
Глава III
2. * Докажите, что f(x) не удовлетворяет определению предела функ-
функции по Гейне. 3. Нет. 4. * Для доказательства того, что не существует
lim /(х) при \а\ ф 1, воспользуйтесь отрицанием определения предела функ-
функции по Гейне 8. а) 1; б) 4/5; в) -1/2; г) 1; д) т. 9. а) 4/3; б) -2; в) 1/4.
10. а) 1; б) 510/325; в) 1; г) 1/^2. 12. а) Нет; б) 1/2; в) 1. 15. а) х = 0 —
точка устранимого разрыва; б) х = 0 — точка разрыва II рода; в) х = к
(к Е Z) — точки разрыва I рода; г) в точках х = 1 и х = — 1 функция не-
непрерывна, остальные точки — точки разрыва II рода; д) х = — 1 — точка
разрыва II рода; е) х = 0 — точка разрыва I рода; ж) х = 1 — точка разрыва
I рода; ж = 0 — точка разрыва II рода; з) х = — 1 и ж = 3 — точки разрыва
II рода; и) х = 1 — точка устранимого разрыва; к) ж = —1 — точка разры-
разрыва I рода; л) х = — 1 — точка разрыва I рода. 17. а) ах = 1 + ж In a + о(ж);
б) еж = 1 + ж + о(ж); в) A + х)а = 1 + ах + о(ж); г) вЬж = ж + о(ж); д) thж =
= ж + о(ж); е) сЬж = 1 + A/2)ж2 +о(ж2). 19. а) Нет; б) да; в) да. 20. а) Равен-
Равенство о(х + ж2) = о(ж2) при ж —>- 0 неверно. Действительно, например, функ-
функция а(ж) = ж^/ж является бесконечно малой более высокого порядка, чем
ж + ж2 при ж ->> 0 (так как lim Хл^ = о), но lim ^ф- = оо т. е. ж ?/ж / о(ж2)
Глава IV
439
при ж —»> 0; б) нет; в) да; г) нет; д) да. 23. а) 25ж + о(ж), 25ж + о(ж);
б) 1-8ж4+о(ж4), 1-A/2)ж2+о(ж2); в) 1 + 2ж + о(ж), 1 + фс + о(л/ж);
г) -ж2+о(ж2), ж + о(ж); д) A/27)ж + о(ж), (-1/27)у/х + о(у/х); е) 1 +
+ ж31п2 + о(ж3), 1 + ж21п2 + о(ж2); ж) -2ж2+о(ж2), -2ж2+о(ж2); з) 1-
- A/2)ж + о(ж), 1 + A/2)ж + о(ж); и) ^/ж" + о(л/ж"); к) 1 + (ж + A/2)|ж|) In 5 +
+ о(ж); л) 1-A/6)ж + о(ж); м) -A/2)ж2 + о(ж2). 24. а) (ж-2J+о((ж-
- 2J); б) 1 + ?B - ж) + оB - ж); в) ж - 2 + о(ж - 2); г) 1 - A/2)тг2(ж - 2J+
+ о((ж-2J); д) тг(ж2-4)+о(ж-2); е) B/35)(ж - 2) + о(х - 2); ж) 4A +
+ In ж)(ж - 2) + о(х - 2). 25. а) 1/2 + оA); б) 1/(Зж) + оA/ж); в) 5/2 + оA);
г) 1/^2+оA/^2), 1/^2+оA/^2); д) 1-1/Bж2)+оA/ж2); е) 1 +
+ (In5)/ж + оA/ж); ж) -4/ж2 + оA/ж2), 4/ж2 + оA/ж2); з) 1 Д/ж + оA/л/ж).
26. а) 1/3 + оA); б) A/n) In 14 + оA/п); в) 1Д/п + o(l/y/n). 27. а) 4;
б) 1/л/З; в) 2/тг; г) а/т-0/щ д) 1; е) -1/12; ж) 1/а; з) 1/2, л/гД 1;
и) 0; к) 0, если а < Ь; +оо, если а > Ь; е~1/&, если а = 6; л) 1; м) 1; н) у/В.
28. а) а/т + /З/n; б) -19/3; в) 1/324; г) -4/9; д) 3; е) In а; ж) е^; з) 0; и) 0;
к) 0; л) е"ж2/2; м) е. 29. а) -2; б) аа 1п(еа); в) 2а/6; г) ах In2 а; д) -2; е) е2;
ж) -тг2/4; з) в1""; и) 0; к) In2. 30. a) 2; б) 4/3; в) 7/4; г) -In2; д) аа1п(а/е);
е) In а; ж) 2; з) 45/91; и) e7^2; к) е2а; л) е; м) 1/2; н) 1/2.
Глава IV
. a)
-2 < Аж < +оо. 2. а) 1; б) 2х0; в) у'D) =
д) 1/2. 3. а) /'(а); б) 2/'(а); в) -2/'(а); г) Ifc(fc + l)f(a). 4. а) гл > v2 при
О ^ t < 1/2, гл = V2 при t = 1/2, гл < ^2 при t > 1/2; на [0,1] глср = ^2ср = 1,
на [1, 2] глср = 1 < 3 = ^2ср; б) vi = г^2 = 0 при t = 0, гл > ^2 при 0 < t < 2/3,
гл = г>2 = 4/3 при t = 2/3, vi < г>2 при t > 2/3; на [0,1] глСр = ^2ср = 1, на [1, 2]
г;1ср = 3 < 7 = ^2ср; в) vi > г^2 при 1 ^ t < 4, vi = V2 = 1/4 при t = 4, гл < V2 при
t > 4; на [1,4] глср = A/3) In4 > 1/3 = г;2сР, на [1,25] глср = A/24) In 25 <
< 1/6 = г;2сР. 5. а) у = ж; б) у = 2х - 1; в) ж = 0; г) гу = ^ж + | - 1.
6. а) (^ - V3, V3 - ) б) ( j в) ^
' 6B -
7 v -
^)( ^
= \х + I, у = |ж + 1. 8. а) /'(+0) = 1, /Ч-О) = -1; б) /'A + 0) = /'A -
- 0) = /41) = 1; в) /'(+0) = /Ч-О) = /40) = 0; г) /'(+0) = 1, /Ч-О) = -1;
Д) /Ч+О) = /Ч-О) = /40) = 0; е) /'(тг/2 + 0) = /'(тг/2 - 0) = /'(тг/2) = 0;
ж) /41 + 0) = е, /41 - 0) = -е. 9. а) 2ж; б) ^= (ж > 0); в) —^ (ж / 0);
ж) cos ж + sin ж, г/@) = 15 У {к/4) = л/2; з) l/(sin2 cos ж) (ж / тгп/2, n G ^);
и) 0 (arcsinж + arccosж = тг/2 = const); к) 0 (ап^ж+ arcctgж = тг/2 =
= const). 10. * Представьте [u(x)]v^ в виде ev(x)lnu(x) и воспользуйтесь
формулой для производной сложной функции. 11. а) , ~ ,Р9 ; , ож
(еж + a)z л/ж2 — а2
440
Ответы и указания
(ж < -а, х > а):
+ 3 ;
о ; б)
2' J
(ж > 0) — sinxsinBcosx) — cosxsinBsinx); в) cos[sin(sinx)] cos(sinx) cos ж;
xe Aпж +
+ тгп; п G Z) ; г) ех (sin ж + cos ж); 2ех
(ж > 0); д) жжAпж + 1) (ж > 0);
; еж \ee + xe (
[()]
< —a, x > a); e) - (x / 0); , o1 ; ctgx Bтгп < ж < тг + 2тгп, п G Z)\
x yxz ± a2
ж) Icos(ba;) (x > 0); x (-a < ж < a); -yi-,; з) —1 (i # 1);
•^ v CL — X X \ U -L ~T «a<
V4 ПРИ
-Зтг/4 при
sgn cos ж (х ф | +7гп, n G Z); 1 (ж / | + тгп, n G Z); к) 1 (-1 < х < 1); 1;
(» > -а); л/а2 - ж2 (-а < х < а); м) -^ccosx (Q |ж| х)
1); н) 70W {~1<х< 1);
(х + а)(х2 +b2
(sin ж)СО8 х х (cos2 ж — sin2 ж In sin ж) Bтгп < ж < тг + 2тгп, пе Z); cn I ^g ж J (ж ф
; п) cthaj (ж > 0); tha/lnlO; 1/сЬ2ж; -1/shaj
; в) 2xf(x2)-
/ | +7ГП, nG Z); - Ь2
(ж > 0). 12. а)
+ ^ / 0); б) ^
(х ф 0); г) /'(/(*))/'(*)- 13. а)
| /^/@); б) /@)//'@).
14. а) е//(а)//(а); б) е2^^(а)/^(а). 15. а) ап/'(а) - пап~^(а); б) g(a)f(a) -
-f(a)g'(a); в) [(Inа)/'(а) - A/а)/(а)]/(/(а)- 18. а) Нет, (Н'|ж=0 = 0; б) да,
' L=i=cos 1; г)нет'
L=o
=0; д)нет'
L=o
= 0; е) нет, (ш;)' _ = 0; ж) нет, (ш;)' _ =0. 19. I. а) Да; б) нет.
П. а) Нет; б) нет. 20. а) В точках ж таких, что /(ж) = 0 и /'(ж) / 0;
б) в точках ж таких, что /(ж) = д(х) и /'(ж) ф д'(х); в) в точках ж та-
таких, что /(ж) = тах/(?) и /7(ж) ф 0. 21. Нет. 22. * Для Рп(х) рассмотрите
[а,ж)
(ж + ж2 + ...+жп)/. 23. а) -оо < t < оо, /'(ж) = %t/l\t=x = 2ж, /(ж) = ж2
(-оо < ж < оо); б) 0 ^ t ^ тт/2, /'(ж) = (sin2 tO(cos2 t)' ?=ЯГГГОЧл/^ = -1
@ < ж < 1), /(ж) = 1 - ж @ ^ ж ^ 1); в) 0 ^ t^ тг, /'(ж) = 6cost
cost
VI - cos2
cos t=x/a
(-a < x < a), /(ж) = -Va2 - ж2
(—а ^ ж ^ а); касательная: ж = а, нормаль: г/ = 0; г) 0 ^ ? < оо, /7(ж) =
(ж > а), /(ж) = -\/ж2 — а2 (ж ^ а); касательная:
bcht
asht
ж = а, нормаль: г/ = 0; е) —оо < t < оо, /7(ж) =
2е2
= 2ж, /(ж) = ж2
Глава IV
441
(О < ж < оо). 27. a) |v| = л/18, cosX = cos У = l/\/l8, cos Z = 4/\/l8;
б) |v| = y/R? + /i2, cosX = 0, cosy = -Ry/WTh2, cosZ = h/y/R2 + h2;
в) |v| = л/Ti, cosX = l/\/l4, cosy = 2/\/Ti, cosZ = 3/\/l4; r) |v| = 2,9,
cos X = 2/29, cos У = 25/29, cos Z = 10\/2/29. 28. a) Ay = Ax + а(Дж) Дж,
еАж - 1 - Аж
где а(Аж) =
¦{
При
0 при Ах = 0;
Дж
0 при Дж = 0;
arctg Аж — Аж
А?/ = а(Дж)Ах, где а(Дж) =
J' в) Ау = Ах + а(Аж)Дж, где а(Аж) =
_ при ^Х г и' 29. А|/ = Аж
0 при Дж = 0.
а) Ау = 0,010201, dy = 0,01; б) Ау = 0,121, dy = 0,1; в) Ay = A, dy = 1;
г) А?/ = 48, dy = 3. 30. As = bAt + 2At2, ds = 5At; a) As = 0,52, ds =
= 0,5; 6) As = 1,08, ds = 1; в) As = 7, ds = 5. 31. a) -^ (ж > 0); 6) -4%
{x ф 0); в)
dx
dx
); д)
(-a<x<a); e)
dx
ж) A + 2x)e2xdx; з) ж cos ж с/ж. 32. а) с?г/| _ =dx,dy _ =dx;6)dy\ _ =с/ж,
d?/L=i= \dxiв) d?/L=o= dx' dy\x=i= edxir) ^L=o = \dx^ dy\x=i= 0;
д) dy\x=Q = 0, с/у|ж=1 = -\dx. 34. Равенства б) и в). 35. а) -0,8747; б) 0,5121
рад, или 29°20/; в) 1,04; г) 1,0033; д) 0,83 рад, или 47°33/; е) 1,2. 36. а) 2,08;
б) 3,9961; в) 2,0045. 37. f'(a)/2. 38. а) A2ж - 8ж3)е"ж2; б) -а10 этаж;
в) к4екх; г) 12ж/"(ж2) + 8ж3/'?2); д) ехf (ех) + е2хf"(ex); e) ipm(x)x
7
720
> 0); з) 720 7 (ж ф 1); и) 220(ж2 sin 2ж - 20ж cos 2ж - 95 sin 2ж); к) 514Eж3 -
[х 1J
-126a;)sin5a;-3-513G5a;2 -182) cos 5ж; л) - 2 ' 8! s (х ф -1); м) ^ ¦
30! хх
); н)
; о) -
; в) — 2n x cosf 2ж + n^ j; r) 2n : cosf 2ж + n^ j ; д) | sinf ж + n^ j—
3j |(a-^'bx
¦^ I; и) an~x \ax sin f ax +
n5 ) ~*~ n s^n (аж + (n ~ 1) ? ) h к) оп~\а2х2 cos [аж + n ^ j + 2паж cos ( ax +
¦Box + b)nfc + n(n-l)o]; m) (-l)n-lan(n-l)\\(nrr ^ ..„ -
442
Ответы и указания
( ax ~*~ ^ > 0 ); н) ж ch ж + n sh ж, если п нечетное, ж sh ж + n ch ж, если п чет-
ное; о) ж2 sh ж + 2пж ch ж + n(n — 1) sh ж, если п нечетное, ж2спж + 2пжх
( ) ) \ ) "() '"()
; ) ( ) , ,
х sh ж + п(п — 1) ch ж, если п четное; п) аоп\. 41. а) /"(ж) = 2; /'"(ж) =
= 0; б) /"(*) = /'"(*) = 0; в) /"(х) = -
г) f"(x) = -
f
(х2 -а2K/2
ч = cos(t/2)
f'"(T) =
2K/2' T K '
ао . ffff(T\ — ЗаЬх
a2_x2>K/2>J W- (а2_ж2M/2'
' где * =
= a(t - smt) (t ф 2т™, п € Z); e)
(х2-а2M/2' МУ J K J 4asin4(t/2)'
— обратная функция к функции ж =
с) = 2, /'"(ж) = 0. 42. {f~1{y))' = w^T>
Х) /1Q -Л l^'fOM — 9
. 4D. d^ |I \^)\ — ?•)
=
cosX = cosl" = 0, cosZ = 1; б) |г"(тг)| = 1, cosX = 1, cosY = cosZ = 0;
в) |г"A)| = 2л/Ш, cosX = 0, cosy = 1/л/Ш, cosZ = 3/л/ТО; г) |г"B,5)| =
= л/б1Т/25, cosX = -4/л/бЗТ, cos У = 25/л/б4Т, cosZ = 0. 44. а) б^ж3;
б) ~15^4 (ж>1);в)-^ (ж>0);г)A0со8ж-ж8тж)^ж10 45. а)
xdxn, если п нечетное; впжа'ж™, если п четное; б) an sh (аж) а'ж77', если п
нечетное; ап ch (аж) dxn, если п четное; в) (—1)тг~12 • (п — 3)! ^_Г2 (ж > 0,
п ^ 3). 47. 9?(жо) -п!.
Глава V
1. 2v^ + ln|aj|. 2. A/12)(ж3 + IL. 3. 2\/3 arctg (ж/\/3) - ж. 4. 27ж-
- 9ж3 + 9ж5/5 - ж7/7. 5. (-1/57)(Зж + 2)~19 6. 15Ж/ In 15. 7. 4(ж2
8. In
). 9. ж
¦2 In
1
ж- 1
10. - ctg ж - ж. 11. Зж/2 - E/4) In |ж +
+ 3/2|. 12. -^U
+ 3). 16. 4^+2^ + ^. 17. агс8тж + 1п(ж + л/1 + ж2). 18. A/22)Bж-
1п4 1п6 1п9 \ v / \//\
-ЗI1. 19. (-cos ж + sin ж) sgn (cos ж + sin ж). 20. (-2/5)\/2 - 5ж.21. -Ц х
х arctg(жv/з72). 22. A/\/3) In |ж\/3 + \/Зж2 - 2|. 23. (-1/2) ctg Bж + тт/4).
24. tg(a/2). 25. tg (ж/2 - тг/4). 26. A/4)A + ж3L/3. 27. -0, 5совBж + 3).
28. A/4) arctg (ж2/2). 29. 2 arctg л/ж. * Воспользуйтесь тем, что dx/л/х =
= 2от(л/ж). 30. 1,5A+ 2жI/3. 31. -arcsin(l/|aj|). 32. 2sgnaj 1п(-^/]ж[+
+ у^|ж-1|), ж(ж-1) > 0. 33. 2л/1пж. 34. (-1/2)е"ж2. 35. A/3) In3 ж.
36. 1п|2 + 1пж|. 37. A/30)A + 27жI0/9. 38. 0,75AпжL/3. 39. A/6) sin6 ж.
40. C/2)^/1 — sin 2ж. 41. (—1/л/2) In |л/2 совж + л/со8Bж)|. 42. In | tg (ж/2)|.
43. In I th (ж/2)|. 44. 0,5(ап^жJ. 45. \ In2 i±_?. 46. -i4J^r-(l - 5ж2)п.
47. - J-(8 + 4ж2 + Зж4)л/1 - ж2. 48. (| - % sin2 ж + ?¦ sin4
1о у о ( 11
49. -ж-2е-ж/2+21пA + еж/2). 50. ж - 21пA + УТТ~^). 51. (arctg ^x~f.
52. 0,5[жл/а2 — ж2 + а2 arcsin(#/a)]. 53. —л/а2 — ж2 + а агс8т(ж/а). 54. 0,5 х
х [ж\/а2 + ж2 — а2 1п(ж + \/а2 + ж2)]. 55. \/ж2 — а2 — 2а 1п(\/ж — а + \/ж + а),
Глава V
443
если ж > а; — л/ж2 — а2 + 2а 1п(л/—ж + а + д/—ж — а), если ж < —а. 56. In \x +
+ л/ж2 + а2|. 57. In |ж + л/ж2 - а2|. 58. жAпж - 1). 59. |ж3/2 (in2 ж - |1пж +
+ §Y 60. -0,5(ж2 + 1)е-ж2. 61. 1
2 cos2a;+|sin2a;. 62. ж arcsin ж +
-In
1 + VI - ж2
ж
. 64. In tg (ж/2) — cos ж In tgж.
+ж2)(arctgжJ - 2жarctgж
66.
х2 1п(ж
1п(еж + л/е2ж + 1)]. 68. 0,5a[sin(lna;
ж2) -ж. 67. 0,5[еж\/е2ж
+ С08Aпж)]. 69. ^
71. In |ж - 2| + In |ж + б]!* 72. ж + A/6) In |ж| - (9/2) In |ж - 2| + B8/3) In |ж -
-31-73- -^ет М|iS
I^^ ^^l 77. i
-arctg^-2). 76. I
1 оо J_ 1л (ж2 + IJ
- 1)" ' 12 1П 4 2
\/ж2 +ж + 1J. 93. -
In
. 94. Я + 1п(ж + 1 + Я) - л/2
х
х In
, где R = Vx2 + 2ж + 2. 95. - 19 + 5^ + 2x
2x-x2 -
x
x 1п(ж + л/1 + ж2). 97. -
99. arcsin
100.
х In
где z = х + л/ж2 +ж + 1. 104. In
A-ж)\/2 \/б \/б - \/2 + 2ж - ж2
101. h arcsin
. 103.
- 2 arctg *, где z = г + Vl " 2х + ж-.
105.
5A-^-^2)
5л/5
л/5 - 1 - 2z
где
444 Ответы и указания
х2 - 1
Ю6. - 4= arcsin -Зр^-. * Положите t = х + ±. 107. - -U
V2 ж2 + 1 ж /2
* Положите t = x - -. 108. E/16)ж - A/4) sin 2x + C/64) sin 4ж + A/48) x
xsin32x. 109. A/16)ж- A/64) sin4x + A/48) sin3 2x. 110. 1/C cos3 ж) -
-1/cosx. 111. (l/4)tg4x - (l/2)tg2x -ln|cosx|. 112. -2^/ctg^ + B/3) x
X\/tgsx. 113. —y= In z + ^V + arctg I , где ^ = tgx.
114. 1/4ж + 1/8 sin 2x + 1/A6) sin 4ж + 1/B4) sin 6x. 115. -3/A6) cos 2ж +
+ 3/F4) cos 4x + 1D8) cos 6x - 3/A28) cos Sx + 1/A92) cos 12ж.
119. 1 in (sinx + cosxJ
6 181ПЖСО8Ж
Глава VI
2. а) Да; б) нет; в) нет; г) нет; д) да. 4. а) Нет; б) да. 8. a) inf fix) = 0
@, + оо)
не достигается, sup f(x) = 1 = /A); б) inf /(ж) = 0 = /@), sup f(x) =
@, + оо) [-5,10] [-5,10]
= 100 = /A0); в) inf f(x) = 0, sup f(x) = тг/2 не достигаются;
[-оо, + оо] [_ОО; + ОО]
г) inf f(x) = -1 = /(тг), sup /(ж) = л/2 = /(тг/4); д) inf f(x) = 0, sup f(x) =
[0^] [О,тг] (ОД) @,1)
= 1/2 не достигаются. 13. а) 4; б) 2. 17. а) ?(е) = e/|jfe|; б) 6(е) = s/75;
в) 5(е) = s; г) ^(s) = e~10s. 18. а) Равномерно непрерывна на A, 2), но
не является равномерно непрерывной на (О, I); б) равномерно непрерывна
на @,01; 1), но не является равномерно непрерывной на @, 1); в) равно-
равномерно непрерывна; г) равномерно непрерывна; д) равномерно непрерывна;
е) равномерно непрерывна; ж) равномерно непрерывна; з) не является рав-
равномерно непрерывной; и) равномерно непрерывна; к) не является равномер-
равномерно непрерывной; л) равномерно непрерывна. 22. f(x) = arcsin ж на (—1,1).
23. Из равномерной непрерывности f(x) на (а,Ь) следует, что в точках
а и Ъ выполнено условие Коши существования предела функции. Поэто-
Поэтому функцию f(x) можно доопределить в точках а и Ъ так, что она станет
непрерывной на [а, Ь], а значит, и ограниченной на [а, Ь]. 27. а) Убывает
на (~оо^~^-)^ возрастает на I— ^-,+ooJ; б) возрастает на (—оо,+оо);
в) возрастает на (—1,1), убывает на (—оо, — 1) и на A,+оо); г) возрас-
возрастает на (—оо,+оо); д) возрастает на ( 2тгп — 4г-; 2тгп + 4г-), убывает на
( 2тгп + =?-; 2тгп + ц?-), п Е Z\ е) возрастает на ( -—3__^ —3_^ ), п е Z,
\ 3 ' 3 /' у \2га + 1,5' 2га — 0,5/'
убывает на (-оо, -2), на ( 2уг, + q 5' 2п - 0 5 ) ^ ^ ^ ^5 ^ / 0, и на B, +оо);
ж) возрастает на @, 2/In 2), убывает на (—оо,0) и на B/1п2,+оо); з) воз-
возрастает на @,п), убывает на (п, +оо). 28. Возрастает при а ^ 1, убывает
при а ^ —1. 31. * Используйте метод примера 3 из § 3. 34. с = 1/2 или
с = л/2- 37. * Используйте метод примера 5 из § 3. 39. * Воспользуй-
Воспользуйтесь теоремой 6 и результатом упр. 23. 41. Нет. 42. Рассмотрим функцию
Глава VII
445
д(х) = f(x) — f(a) ^ — (ж — а). Она непрерывна на [a, b] и диффе-
дифференцируема в (a,6), причем д(а) = д(Ъ) = 0. Так как f(x) не является ли-
линейной функцией, то д(х) ф 0 и, следовательно, д'(х) ф 0 в (а,6). Отсюда
следует, что 3ci,C2 G (a,b) такие, что g'(ci) > 0, а д'(сч) < 0 (объясните,
почему), откуда /'(ci) > /F^ ~ ^(а) - ''^ ^ /F) ~ /(а)
из точек сг имеем |/'(сг)| > /(^ I f}a)
44. * Воспользуйтесь результатом упр. 43. 45. 0. 46. 0. 47. а//3. 48. —2.
49. 1. 50. 1/2. 51. -1/3. 52. 1. 53. 0. 54. 1. 55. 1/6. 56. 0. 57. aa(lna - 1).
58. е2/7Г. 59. 1/е. 60. 1. 61. е/6. 62. е/3. 63. 1/2. 64. 1/2. 65. 0. 66. -е/2.
67. аа. 68. 1. 69. а) 1 - х + ^ - С + ... + (-1)ПС + о(хп); б)
-. Значит, в одной
,т.е. \f(b)-f(a)\<\f(ct)\.\b-a\.
\ _х _ х _ _х_ , п(тъ\. р\ т _ л _ J? I п(т^\. ж\ п
R) ~а~ Ton oqqc + °\х )•> е) х Tq QO/in ^ °1Ж ^ ж^ a
2п:
(
180 2835 ' у h > 18 3240
- Г
Г)
¦ - IJ; б) 1 + (х - 1) - 1(ж - IJ + ^(ж - IK + о((х - IK); в) 1 - ^_ х
х (х - IJ + ^(х - IL + о((ж - IL). 71. а) Меньше 1/3840; б) меньше 2 х
хЮ; в) меньше 1/16. 72. а) 2,080; б) 3,08000; в) 0,3090; г) 0,01745241;
д) 0,095; е) 1,22140; ж) 0,99452. 73. а) -1/12; б) -2; в) 1; г) -1/4; д) 1/2;
е) 0; ж) 1/3; з) 19/90. 74. а) а = -2, Ь = 3/2; б) а = Ь = -2; в) а = 1, Ь = 2
или а = -1, Ъ = -2. 75. /'(О) = 0, /"@) = -1/3.
Глава VII
На графиках функций экстремальные точки обозначены "кружками"
(о), а точки перегиба — "крестиками" (х или +).
К упр. 1 /[у К упр. 2 ^ К упр. 3
446
Ответы и указания
К упр.
-3-VU
2
7
! (
-1!
-3+VU УГ
1 2 ^УУ
/ />
К упр. 8 к
К упр. 9
К упр. 11
О 1
@,0) — угловая точка
г,|) и (-|
2У v 2
угловые точки
Глава VII
447
К упр. 14 I
_2Е|
2
К упр. 15 I
О \ / х
К упр. 17
К упр. 18 I
О
-1 О
К упр. 19 I
О 2
К упр. 20 I
-1 О
К упр. 21 у
1 х
-2
К упр. 22 i
@,0) — угловая точка
К упр. 23 ку К упр. 24 /! |^ К упр. 25 Д
-1
О
)
448
Ответы и указания
К упр. 26 , у1
К упр. 27
К упр. 28
К упр. 31 '
1
^ttTlj
! 0,5
i
-1-А. О
f '•
К упр. 32
-4
х=\
\ 16
3
Г*
К упр. 33
V2-1
•' (-4,4) — точка возврата
К упр. 34 Ау
\/2-1
Глава VII
449
(О, 0) — изолированная (о, 0) — точка возврата
точка
@, 0) — точка само-
самопересечения
К упр. 36 '
К упр. 37 I
К упр. 38 I
О
-24 О
25
¦ —а
(О, а), (-а, 0), @,-а), (а, 0)
— точки возврата
К упр. 39 I
К упр. 40 /
-1-1
! i О
[У
г
К упр. 41 *
/л
I
-0,25
О 0,25.
К упр. 42 I
15 В.Ф. Бутузов и др.
450
Ответы и указания
К упр. 45 у
+ \
/ 6
03/20^10-6^
\/10-5л/3
Ж1=22/55-1/2
Ж2=21/533/105-1/2
/р1Ж2
\ +
К упр. 46
К упр. 48
К
->*
упр.
^
i
1
50 '
Ус)
¦-'' i
.у?
X
Глава VIII
4. * Используйте то, что х = 0 — предел точек разрыва. 6. а) Да;
б) нет; в) нет; г) да, с учетом замечания в п. 4 § 1; д) да; е) нет. 7. Нет;
да; нет; да. 9. а) Да; б) нет. 10. а) 2/тг; 0; 0; B/тг) cos <^0; б) -1; -1/3;
1/2; 0; 1. 11. 2/3; A/15I03/2; A/150I003/2; б) 10; в) A/2) cos (p. 12. vcp =
= (г>о + wi)/2, где г>1 = 2g/i — конечная скорость тела. 11. го/2; го/2; г'о/2 —
-^/2)(l/to)(T/47r)[sinD7rto/T + 2^)-sin2^], г§/2. 14. а) 0; б) sinF2);
в) -sin(a2); г) 2жл/1 +ж4; д) 2жл/1 +ж4; е) Зж2/л/1 + ж6 - 2ж/л/1 + ж4;
- 2ж/л
к) 0;
л) -|ж(ж2+ t4)~s/2dx + Зж2/л/ж2+ж12. 15. а) 1; б) 1; в) тг/B sin a). 16. а) тгл/2;
б) 2/3. 17. 5/6. 18. а) 0,51п(е/2); б) 4тг; в) 1. 19. а) 1/6; б) A/л/2) 1п[(9 +
+ 4>/2)/7]; в) 2 - тг/2; г) тг2/4. 20. Нет. 21. а) Да, тг/4; б) да, тг/4; в) да, хо-
хотя в этом промежутке нарушено условие теоремы 10, тг/4. 24. а) 0,5 In 3 —
-тг/2л/3; б) E/27)е3 - 2/27; в) 4тг/3 - л/3; г) 2тгA/л/3 - 1/2л/1); д) 1/6;
) /
7гBт)\Bп)\
4
)!; б) °5
четное число; тг,
е) .3/6 - тг/4. 27. a) 2aro+an+lm!w!(m + п)!,
если п — нечетное число; в) тг/2п; г) (тг/2п) sinGrn/2). 28. а) (8/27)A0\/Т0 -
-1); б) (е2 + 1)/4; в) In tg (тг/4 + а/2); г) 4а[1 + \/31пA + \/3)/\/5]; д) 6а;
е) 1 + [1пA + \/2)]/л/2; ж) 32а; з) тга\/1 + 4тг2 + (а/2) 1пBтг + л/1 + 4тг2);
и) 8а; к) Зтга/2; л) 19/3. 30. a) (afr/2)[arcsin(xi/a) - arcsin(xo/a)] + [b/2a] x
х (xix/a2 -x\ - хол/а2 -ж2); б) 9/2; в) 1/3 + 2/тг; г) 4а3/3; д) 0,5 cth (тг/2).
31. а) (а2/3)Dтг3 + 3тг); б) бтга2. 32. а) Зтга2/2; б) тга2/4; в) 11тг; г) 2/3.
Глава IX 451
33. а) За2/2; б) a2. 34. (тгк/6)[BА + а)В + (А + 2а)Ь]. 36. а) 2а6с/3;
б) 4тга6с/3; в) 8тга6с/3; г) 16а3/3; д) 2тга3/3 - 8а3/9. 37. а) Зтга62/7;
б) 16тг/15; в) 8тг/3; г) тг2/2; д) 2тг2; е) 5тг2а3; ж) 6тг3а3. 38. 2а2; тга3/2.
39. (р2/8)[л/2 + 51пA + л/2)]. 40. bh2/6; bhs/12. 41. Мх = тга&3/4; Му =
= тга36/4. 42. 3RM/16. 45. 4тг2. 46. ж0 = (asina)/a; j/0 = 0. 47. ж0 = 9а/20;
уо = 9а/20. 48. ж0 = 0; у0 = 0; z0 = За/8. 49. <?0 = 0; г0 = 5а/6.
Глава IX
1. а) Достаточно каждому числу п из первого множества поставить в
соответствие число 2п из второго множества; б) функция у = (Ь — а)х + a
осуществляет взаимно однозначное соответствие между элементами сег-
сегментов [0,1] и [а, Ь]; в) функция ?/ = tg ^ ^,—^Ц—'- осуществляет взаимно
однозначное соответствие между элементами интервала (а, Ъ) и числовой
прямой R. 2. б) Элементы объединения счетного числа счетных множеств
{ж^}, {^/г}, {^г}, {^г}, {vi},..., {wi},... можно занумеровать по следующей
схеме:
У\ У 2 Уз У А Уъ ...
{/* S S S
Z\ Z2 Zs Z4 Z5
/ S /
U\ Vb2 Us Ua Us
if s
Vl V2 «3 Va «5
.,/. . . .
4. * а) Используйте метод примера 2 из § 1; б) воспользуйтесь равенст-
равенством А = (А \ В) + АВ (см. упр. 5) и результатом упр. 4, а); в) восполь-
воспользуйтесь результатом упр. 4,6); г) воспользуйтесь результатом упр. 4,6).
5. а) Докажем, что: 1°) любой элемент х из множества (А-\-В)С при-
принадлежит также множеству (АВ + ВС)] 2°) обратно: любой элемент х из
множества (АВ + ВС) принадлежит также множеству (А + В)С. 1°. Если
х G (А + В)С, то х ? (А +В) и х ? С. Так как х G (А + Б), то ж при-
принадлежит хотя бы одному из множеств А или В. Пусть, например, х G А.
Тогда ж G АС и, следовательно, ж G (АС + БС). 2°. Если ж G (АС + ВС),
то ж принадлежит хотя бы одному из множеств АС или ВС. Пусть, напри-
например, ж G АС Тогда ж G А и ж G С. Значит, ж G (А + В) и ж G (А + Б)С
6. Докажем, что любой элемент ж из множества U Ак принадлежит так-
также множеству Г\Ак. Если ж G UA/., то ж 0 U А/, и, следовательно, ж 0 А/.
VA;. Поэтому ж G А& VA;, а значит, ж G nib Остается доказать, что любой
элемент ж из множества П А& принадлежит также множеству UA/.. Сде-
к к
лайте это самостоятельно. 7. Если предположить, что какая-то точка ж G С
не является внутренней точкой С, то ж окажется предельной точкой Е
(объясните, почему) и, следовательно, ж G ?7. Но это невозможно, так как
С?7 = 0. Таким образом, любая точка ж G С является внутренней точкой С,
т. е. С — открытое множество. 8. * Воспользуйтесь тем, что Q + Q = [а, Ь]
и //Q = 0 (см. пример 4 из § 1); отсюда /iQ = Ь — а. 9 и 10. * Восполь-
Воспользуйтесь определением измеримого множества. 12. * а) Используйте ме-
метод примера 1 из § 2; б) воспользуйтесь результатом в) примера 5 из § 1;
15*
452 Ответы и указания
в) воспользуйтесь результатом д) примера 5 из § 1. 13. * Рассмотрите
функцию г/(ж) = ж на сегменте [0,1] и воспользуйтесь свойствами 5° и 1°
измеримых функций. 15. Интегрируемость по Лебегу следует из измери-
измеримости /(ж) (см. упр. 12, а). Чтобы доказать, что /(ж) неинтегрируема по
Риману на [0,1], достаточно доказать, что нижний и верхний интегралы
Дарбу не равны: 1_ ф I. Рассмотрите произвольное разбиение [0,1] на час-
частичные сегменты и покажите, что для него s = О, S^l — a (s и S — суммы
Дарбу). Отсюда следует, что / = О, 7^1 — а > 0. 16. / f(x)d/jJ(x) = 1 — а.
г [ОД]
17. / (р{х)Aц{х) = A — а)/2. 19. * Составьте разность /(ж) — д(х) и вос-
D
пользуйтесь для нее результатом упр. 18. 20. * Воспользуйтесь тем, что
множество всех нижних (верхних) интегральных сумм Дарбу, получаю-
получающихся при разбиениях [а, Ь] на конечное число частичных сегментов, содер-
содержится во множестве всех нижних (верхних) интегральных сумм, получа-
получающихся при разбиениях [а, Ь] на конечное число попарно непересекающих-
непересекающихся измеримых множеств. 21. * Воспользуйтесь тем, что для лебеговско-
го разбиения Т множества Е выполняется неравенство St — st ^ S • цЕ,
где 6 = max (m. — m._i), а также тем, что I — I_ ^ St — st- 22. * Для
доказательства необходимости воспользуйтесь тем, что для лебеговского
разбиения Т множества Е выполняется неравенство St — st ^ S • [iE, где
5 = max (yk — Ук-i)- Для доказательства достаточности воспользуйтесь
^^ _
неравенством I — I_ ^ St — st- 23. * Воспользуйтесь тем, что любая ле-
беговская интегральная сумма 1(Ек,?к) лебеговского разбиения Т = {Ек}
множества Е удовлетворяет неравенствам st ^ 1(Ек,?к) ^ St, а также
тем, что St — st ^ 8 • /лЕ.
Глава X
5. Xi = yi + (zi — yi)t, i = 1, 2,..., m; t G R. 7. a) m-мерный шар; б) m-
мерный шар; в) т-мерная сфера. 13. а) а; б) 2; в) е3; г) 0; д) 0; е) 0; ж) 0;
з) 1. 15. * б) Рассмотрите случай, когда точка М(х,у) стремится к точ-
точке О@,0) по параболе у = кх2. 16. а) 1 и 1; б) 1/2 и 1/3; в) -1/2 и 1/2;
г) 1 и -1; д) 1/2 и -2/3; е) 0 и 1; ж) 1/2 и 1; з) л/3/2 и 1. 17. а) Предел
не существует, lim ( lim /(ж, г/)) = 1, lim ( lim /(ж, г/)) = —1; б) предел не
ж—)-0 V у—>0 ' У^-0 v ж—)-0 У
существует, lim ( lim /(ж, г/)) = 1, lim ( lim /(ж, г/)) = оо; в) lim /(ж, г/) =
= lim (lim /(ж, г/)) = lim (Нт/(ж,^/)) = 1. 18. а) О@,0); б) все точки
х^0Ху^0 ' t/^0Vx^0 ' 2 2 2
окружности ж +|/ = 4; в) все точки конической поверхности ж + у = z ;
г) все точки прямой у = 0; д) все точки прямых ж = 0 и ?/ = 0; е) все точ-
точки прямых ж ± |/ = тгп, n G Z; ж) все точки сфер ж2 + ?/2 + z2 = тт/2 + тгА;,
А; = 0,1, 2,... 19. а) В точке О функция непрерывна по отдельным перемен-
переменным и разрывна по совокупности переменных, в точке А непрерывна как
по отдельным переменным, так и по совокупности переменных; б) в точках
О и А функция непрерывна по отдельным переменным и по совокупности
переменных; в) в точке О функция непрерывна по отдельным переменным
и разрывна по совокупности переменных, в точке А разрывна по отдель-
отдельным переменным и по совокупности переменных; г) в точке О функция
Глава X 453
непрерывна по переменной х и разрывна по переменной у и по совокуп-
совокупности переменных, в точке А непрерывна по отдельным переменным и по
совокупности переменных; д) в точке О функция непрерывна по отдель-
отдельным переменным и по совокупности переменных, в точке А разрывна по
отдельным переменным и по совокупности переменных; е) в точках О и А2
функция непрерывна по отдельным переменным и по совокупности пере-
переменных, в точке А\ разрывна по отдельным переменным и по совокупности
переменных. 20. а) Да; б) нет; в) да; г) да; д) нет; е) нет. 21. a) supu = 1
достигается, например, в точке A,0); inf и = — 1 достигается, например, в
точке @,1); б) supu = 81 достигается, например, в точке @,3); inf и = 0 не
достигается; в) supu = 0,5 достигается, например, в точке A,1); inf и = 0
достигается, например, в точке @,1); г) supi6= 1/е достигается, например,
в точке A,1); inf и = 0 достигается, например, в точке @,0); д) sup и = а
достигается, например, в точке A,0,0); inf и = Ъ достигается, например,
в точке @,0,1). 23. а) Равномерно непрерывна; б) не является равномер-
равномерно непрерывной; в) равномерно непрерывна на множестве п±, не являет-
является равномерно непрерывной на множестве ГЬ; г) равномерно непрерыв-
непрерывна на множестве Qi, не является равномерно непрерывной на множестве
ГЬ; д) не является равномерно непрерывной; е) равномерно непрерывна.
24. а) их = 2х + бху3, иу = Зу2 + 9х2у2; б) их = yz + —, иу = xz — -f-,
yz у z
uz = xy — -^2-; в) их = у • cos(xy + yz), uy = (x + z) cos(xy + yz), uz = у x
x cos(xy + yz); г) их = - jjS|, uv = _2J; д) ux = _Jf^ ^ <л + tg (x +
+ У)
In 2/In ж; м) их = жу~1^/2+1^ж + xyyzzx lnz, гбу = xyyzzx \nx + ху х
j/, 2/2/ 2/^ж. 25. Нет. 26. а) ^@,0) ищ@,0)
не существуют, функция и(х,у) не дифференцируема в точке О@,0);
б) гбж(О,О) = иу@,0) = 0 и функция и(х,у) дифференцируема в точке О;
в) их@,0) = иу@,0) = 0, но функция и(х,у) не дифференцируема в точке
О; г) их @, 0) = иу @, 0) = 0 и функция гг(ж, у) дифференцируема в точке О;
д) их @, 0) и иу @, 0) не существуют, функция и(х, у) не дифференцируема в
точке О; е) гбж(О,О) = иу@,0) = 1, но функция и(х,у) не дифференцируема
в точке О; ж) гбж(О,О) = иу@,0) = 0 и функция и(х,у) дифференцируема в
точке О; з) гг(О, 0) = иу @, 0) = 0 и функция гг(ж, г/) дифференцируема в точ-
точке О; и) гбж(О, 0) = иу@, 0) = 0 и функция и(х, у) дифференцируема в точке
О; к) их@,0) = иу@,0) = 0 и функция и(х,у) дифференцируема в точке
О; л) их @, 0) = иу @, 0) = 0 и функция и(х, у) дифференцируема в точке О;
м) их@,0) = иу@,0) = 0 и функция и(х,у) дифференцируема в точке О.
27. а) Частные производные функции и(х,у) существуют в окрестности
точки О, за исключением самой точки О; б) частные производные функ-
функции и(х,у) существуют в окрестности точки О и непрерывны в точке О;
в) частная производная их существует в окрестности точки О, за исключе-
исключением точек @, у), уфО\ частная производная иу существует в окрестности
точки О, за исключением точек (х,0), х / 0; их, иу разрывны в точке О;
454
Ответы и указания
г) частная производная их существует в окрестности точки О, за исключе-
исключением точек @,г/), у ф 0; частная производная иу существует в окрестности
точки О, за исключением точек (ж,0), х ф 0; гбж, гбу разрывны в точке О;
д) частные производные функции и(х,у) существуют в окрестности точки
О, за исключением самой точки О; е) частные производные функции и(х, у)
существуют в окрестности точки О, за исключением точек прямой у = —х
(ж ф 0), они разрывны в точке О; ж) частные производные функции и(х,у)
существуют в окрестности точки О и непрерывны в этой точке; з) частные
производные функции и(х,у) существуют в окрестности точки О и непре-
непрерывны в этой точке; и) частная производная их существует в окрестности
точки О, за исключением точек @, г/), у ф &тт, k E Z; их разрывна в точке О;
частная производная иу существует в окрестности точки О и непрерывна
в этой точке; к) частная производная их существует в окрестности точки
О и непрерывна в точке О; частная производная иу существует в окрест-
окрестности точки О, за исключением точек (ж,0), х ф ктг, к Е Z; иу разрывна в
точке О; л) частные производные функции и(х, у) существуют в окрестнос-
окрестности точки О и непрерывны в этой точке; м) частные производные функции
и(х,у) существуют в окрестности точки О и непрерывны в этой точке.
29. а) и = у; б) и = х + Чу - 1; в) и = Зх + Зу; г) и = |ж + \у - | + ^;
д) и = х + у + 1. 30. а) Да; б) нет; в) да. 31. а) их = ft + fv • 2ж, иу = ft + fv •
Чу, где t = ж + 2/, г; = х2 + 2/2; б) ^ = Н - 4Л» % = ^ft + ^Л, где t = f,
УХ у Л у
v = |; в) их = ft + j//v, uy = -ft + ж/„, где t = х - у, v = ху; г) их = ftyg,
Щ = ftxg + fgvz, uz = fgvy, где t = xy, v = yz; д) ux = f9 \gvy\nf+ jft\,
uv = f9 \gvx\nf - jft\, где t = x -y, v = xy; e) ux = ft - 2xfv +yfw,
x2 + 2/2, ^ = v^2 + ^2' w =
+ yuy = 2гб; в) их + uy + uz = 0; r)
34. а) гб = sin ж + 0,bx2y + |/2;
+ х2'
. 33. а) хих - уиу = х\ б)
+ уиу + zuz = 0; д) хих + уиу =
= х2у + \у3 - Щ-; в)и= \еху + ху -
у
35. a) du\M = 2xy3dx + 3x2y2dy, du\M = 4dx
\
, du = -6dx + 3dy
1 >
+ cfa/+
X X
+ xdy + xdz],
du\^=0; д) du
= A +lnxy)dx+ -dy,
du\
du\N = -^(^
у / \м х*
= — sinx(y + z)[(y + z)dx +
; г) du\M = exy(ydx + xdy),
= 12с/ж + 8In 2 • dy\ e) du\M =
= dx + c/j/. 36. a) dw|M = (/t + fv)dx + (/v -
y;6) du\
+ fv@,0)]dx,
= (yft + i/«
xft -
= xy, v=^; в) du\M = 2(xft - xfw)dx
\Mo = [/t@,0)
2y(fv - ft)dy
+2z(fw-fv)dz,du\ =2(/t@,0H)-/w@,0,0))da;+2(/o@H,0)-/t@,0H))di/+
Глава X
455
+ 2(/ад@,0,0) - fv(O,O,O))dz, где t = х2 - у2, v = у2 - z2, w = z2 -ж2;
I. a) uxx
2; 6) Uxx = 0, ^жу = 2yZ3 ~
г) cfaJ = (ft cos х — fv sin ж)с?ж + /* cos ydy-\-fv sin 2 cb, с?гг| = /t@, 0)dx +
/, где t = sin ж + sin у, v = cos ж — cosz. 38. a) uxx = 6x + 12ж?/4,
^3
= 3»V - ^, и„ = 2xz3 + ^, uyz = 6xyz2 ^ ^
в) гбжж = —y2cosxy, uxy = — sinx^/ — xycosxy, uyy = — x2 cosxy] r) гбжж =
2
= — sin ?, гбжу = —^ sin ?, гбжг = —г/ sin ?, гбуу = —? sin ?, гбуг = —г/2; sin t + cos ?,
^гг = — У2 SHI ?, ГДе t = X + yZ] Д) Uxx = — 16yy = . 2 _f^2\2 ? wa!J/ = / ^2 Г \\2 \
+ у2J]; ж)
+ yzlnx),
3) uxx = ?i
=yz(yz - l)xyz~2, uxy =xyz~1z(l + yzlnx), uxz =xvz~1y(l +
= xyz(z\nx) , Uyz = \nx ¦ xyz(l + yz\nx), uzz = xyz(y\nx) ;
(\ + zln I),
l)\ uxy = -z2
uxz = I (z
lcosxy, uyyx = —2x sin xy — x2у cos xy; б) л 4^ 4 = 24 x
); в) ^уж = (ж22/2^2 + Зж^ + 1)еж^; г)
^W
= —26 sin ж х
!; ej
)хтдуп - * е ътуу-t 2 у
^.42.а)^ж = /«+4ж/^
г» \ ОН
х cos 2?y; д) X ™ ^ п = 7
* у дхтдуп
хсо8Ш^;ж)^^-
^ж^?/9 V " cos^ ж,
дгп+пи _ 2(-1)ш(п + т - 1)\(пх + ту)
дхтдуп (х-у
+ 2fv, иху = fu + 2{x + y)ftv +4:xyfvv, Uyy = fu +±yftv + ty2 fw +2/v, где
t = x + y, v = x2 + у2] б) 1гжж = y2fu + 2/^ + -iffw, uxy = xyfu - -^fw +
+ ft- \fv, Uyy =x2fu - 2^ftv + ^fw + ^§Л, rj\et = xy, v=-\b) uxx =
= y2gf" + 2^/^ + ?2/<A ^yy = ж2^/^, uzz = x2fg", uxy = xygf" + xzf'g' +
+ P/'j Uxz = xyf'g' -\-xzfg" + fg', uyz =x2f'g'; г) 1гжж = -~k(ft + ЛJ +
j = ж, v = x + 2/; д) гбжж =cos2 x • f" — sin ж • /7, гбжу = — sin у cos x x
x/", %y =sin22/.r-cos2/.//; e) uxx = g • ^~2[(g - l)f'2 +//"], ^ =
= /*-У/'A+#1п/), %y = /^(^/2ln2/ + /ln/). 46. a) ^ =0; 6) uuxy =
= гбжгбу; в) ихх = гбуу; г) ж2гбжж = у2иуу — хих + уиу. 47. а) гб = 0,5ж2^/ + ху +
+ 2/2; б) гб = ycosx — у + ж; в) и = 0,5ж?/2 + жг/ + г/. 48. а) с/2гб = 2ysdx2 +
+ 12ж?/2сЬс^/ + 6ж22/с^/2, с?2^|м = 2dx2 + 24dx^ + 24^2; б) d2u\M =
= ^Щ-dx2 - ^dx dy - '^dx dz + -dy dz, d2u = 12 dx2 - 6dxdy - Adxdz +
X X X X iV
456 Ответы и указания
-\-2dydz; в) d2u\ = — cos(xy + xz)[(y + z)dx + x(dy + dz)]2 — 2sin(x|/ + xz) x
xdx(dy + dz), d2u ш = -^[^dx + dy + dz] - V3dx(dy + dz); r) ЛI =
= exy[(ydx + xdyJ + 2dxdy], d2u\Q = 2dxdy; д) Л| = жу~2[B/сЬ + ж х
xlnxdyJ + dxBxdy-ydx)], d2u\M = 2[Cdx + 2\n2dyJ + dxDdy - 3dx)];
e) Л|м = ^p -\--dxdy - -^dy2, ^и\м = ~dx2 - 2dx dy-\-dy2.
49. a) d2u\M = fu(dx-dyJ+ 2ftv(dx2 -dy2) + fvv(dx + dyJ, d2u\M =
+ dyJ, где t =
= x — y, v = x + y; 6) d2/^|M = ftt(dx + cfa/J + 4zftvdz(dx + cfa/) + 4^2/^^<i^2 +
+ 2fvdz2, d2u\Mo = fa@,0)(dx + dyJ + 2/v@, 0)^2, где t = ж + j/, v = ^2;
в) с/2гб|м=/^(|/с/ж + xdyJ + 4ftv(ydx + xdy)(xdx + 2/cfa/) + 4fvv(xdx + у х
xdyJ + 2ftdxdy + 2fv(dx2 +dy2), d2u\M^ = 2ft@,0)dxdy + 2fv@,0)(dx2 +
+ dy2), где ? = ж?/, v = ж2 +^/2; г) с?2^|м = - sin/(ж) • еПу) ff2(x)dx2 + 2 х
х cos f(x)eny)f(x)f(y)dxdy + cos/(ж) • еЯу) f" (x)dx2 + sin /(ж) • е/(г/) х
xff2(y)dy2 + sin/(ж) • efMf"(y)dy2, d2u\Q = e^[(cos/@)/"@) - sin/@)x
//2@))dx2 + 2 cos /@)//2(O)dx^ + sin /@)(/"@) + //2(O))dj/2]
x//2@))dx2 + 2 cos /@)//2(O)dx^ + sin /@)(/"@) + //2(O))dj/2]. 50. a) dnu =
= f{n)(ax + by + cz)(adx + bdy + cdz)n; 6) dnu = (adx-щ^ +bdy-J^r +
*cdz'd[czVu' 51* a) u = l~2x + Bх2+2ху+у2);б) и = 8 +(-3Ax+ 11 Ay) +
+ (Аж2 - ЗАжА^/ + 4A?/2), где Аж = ж - 1, Aj/ = j/ - 2; в) гл = 3(Аж2 + А^/2 +
^2 - АхАу - AyAz - AzAx) + (Аж3 + Ay3 + Az3 - 3AxAyAz), где
= x-l,Ay = y-l,Az = z-1.52. a) y/1 - x - у = 1 - \(x + у) - |(ж +
2+ о(ж2+ i/2); 6) ln(l +ж + 2/) = ж + |/- 0,5(ж + уJ + |(ж + |/K+ о((ж2 +
K/2); в) (z + y)sin(a-y) = ж2 - i/2 + о((ж2 + 2/2K/2); г)
= 1 + ж + 0,5(ж2 - у2) + \(х3 - Зху2) + ^(ж4 - 6жУ + у4) + о((ж2+ у2J);
д) ж^ = 1 — 2/ + жу + о((ж — IJ + (у — IJ); e) xy/z = -у + 2z + ж2 + ху -
— 2xz + о((ж — IJ + (г/ — 2J + (z — IJ). 53. а)-д) Равномерно непрерывна.
54. a) i6min = гб(О, 0) = 0; б) точек экстремума нет; в) umin = и(—2, —1) = —2;
г) ^min = Ц4/3, 4/3) = -64/27; д) ^min = ггA, -1) = -6 и ?Wx = Ц-1,1) = 6;
е) точек экстремума нет; ж) точек экстремума нет; з) ит-1П = ггB/3, —4/3) =
= -D/3)е-2; и) ^min = и@, 0) = 0; к) ^min = ц@? 0) = 0, ?Wx = гл@,1) =
= г*@, -1) = 2/е; л) ит[п = ^(-1/л/Ш, 2/л/Ш) = -у/Б/Bе), ит^ = иA/у/10,
—2/л/Ш) = у/Ь/Bе)] м) umin = гбA/л/2ё, 1/\/2е) = гг(—1Д/2е, -1/л/2е) = ^,
55. a) wmin=w(l,-l,3) = -11; б) wmin = Ц1/2,1/2, -2) = -17/4; в) wmin =
= Ц1, -2,1/2) = -9/2; г) ?wx = Ц1/4,1/4,1/4) = 1/256; д) ^min = и( '
1/4, 1/4) = -1/8; е) ит^ = Ц1/B>/3),:
),-1/Bл/3),-1/л/3) = -л
Глава XI 457
Глава XI
1. /A) = 2. 2. /(I) = -0,4, Г A) = -0,72. 4. в) у' = |±*, у" = 2jf_+ffl,
где 2/ = /(ж); б) j/' = —-^-.—, у" = scosy = уг( ч в) у' =
у2 Lin2 ^ - 2(ж - у) In ^ In ^ - ж In2 ^1
' ГДе У —
х2(\пу-1)' у х4A-\пуK
г) у1 = -У у" = 1У- где у = fix) 5 у1 = 2х + у у" = ~18 у1" =
J у ж' у ж2' у J\ г - У х + 2у' у (ж + 2?/K' у
= - 162ж Где у = f(x). 6. а) у'@) = -0,5, у"@) = -|, 2/ш@) = 0;
б) у'@) = -1/3, у"@) = -2/3, у//;@) = -7/27. 7. ^@, -1) = -0,5, *у@, -1) =
= 0 8 а) 2: = xz z = ~^z z = ~У2г z = xyz z =
X2_y2i У X2 _ y2 •> (ж2-?/2J' ЖУ (Х2~у2J' УУ
_ -x2z где ^ _ г/ ч. бч ^ _ yz z _ xz Zxx _ -2xysz
-x2y2) y = -2xsyz
(z2 — r
-, где 2 = /(ж, у). 9. a) dz = -dx - dy,
'% где z =
= f(x,y); в) dz = !!^dx + y^dy, d2z = (^ ]_ ^K {[(zy - zf + (x -
- yzJ - 2y(xy - z)(x - yz)] (dxJ + 2 [(x - yz)(y - xz) - (xy - z) (x2 + y2 -
- xyz - z2)]dxdy + [(xy - zJ+ (y - xzJ- 2x(y - xz)(xy - z)](dyJ}, где z =
¦ x
^ 2, где z = f(x,y). 10. a) zxx = -0,4, zxy =
= -0,2, zvv = -3,132; 6) zxx = Ш, Zxy = -|, Zyy = -|. 14. a) x' =
2 % 2
v" = ~x" = j^yf где x =
= -0,5, *"@) = -i/"@) = -0,75; 6) j,'@) = z'@) = -1, i/"@) = 1, z"@) =
= 0. 16. dz= U2dx-dy), d2z = -^{2{dxJ - bdxdy + 2(dyJ). 17. du =
У z4o
_ (sin v-\-x cos г;)б?ж + (ж cos г; —sin ц)ф , _ (у cos ц —sin v)dx-\-(y cos ц + sin u)dy
~ у cos и + x cos v ' ~~ у cos w + x cos v '
j2 t2 B cosv б?ж — xsmv dv)dv — Bcosw dy — у sinu du)du / \
d u= —dv = ± L -^ — L—, гдеи = и(х,у),
У COS U + X COS V \ itf/i
v = v(x, y). 18. du = 0,5(dx + dy), dv = 0,5[(l + ir/2)dy - dx], d2u = (dxJ,
d2v = 0,b(dx — dyJ. 19. /min@) = 0. 20. а) Нет точек экстремума; 6) zm8iX =
= 2@, 0) = 2 \У2; в) zmin = z(-3 - \/б, -3 - \/б) = -4 - 2\/б, ?max = ^(л/б -
- 3, л/6 - 3) = 2л/б - 4; г) ^min = 2i@, 0) = a, 2max = z2@, 0) = -а. 22. а) За-
Зависимы; б) зависимы. 24. Независимы в любой окрестности точки @,0,0).
26. Функции i6i, U2, us зависимы во всем пространстве Е3. 28. a) i6min =
= о и2 в точке ( 2 и2 •> 2й \2 ) 5 б) i6min = 2л/2а в точке (л/2а,л/2а),
а+о \а+о а + о )
458 Ответы и указания
гбтах = —2л/2а в точке (—у/2а, — л/2а); в) i6max = 0,5 в точках A/л/2,1/л/2)
и (-1/л/2,-1/л/2), ^min = -0,5 в точках (-1/л/2,1/л/2) и A/л/2, -1/л/2);
г) 'Wmin = 0,4 в точке @,4; -0,4; 0,2); д) ^min = 5 в точке @, 0, 0), ^тах = 7Щ в
точке (—4/3, 8/3, 4/3); е) нет точек экстремума; ж) гбтах = 1 в точке A,1,1);
з) ^min = -3 в точке (-1/3,2/3,-2/3), ишах = 3 в точке A/3,-2/3,2/3);
и) гбтах = с~2 в точках @, 0, —1) и @, 0,1), umin = а~2 в точках (—1, 0, 0),
A,0,0); к) umin=
—,
\г = 1 г = 1 )
29. а) ^min = -1 в точках (-1,1,1), A,-1,1), A,1,-1) и (-1,-1,-1),
«max = 1 В ТОЧКаХ A,1,1), (-1,-1,1), (-1,1,-1) И A,-1,-1); б) Um\n =
= -1/(Зл/б) в точках A/л/б, 1/л/б, -2/л/б), A/л/б, -2/л/б, 1/л/б) и (-2/л/б,
1/л/б, 1/л/б), г*тах = 1/(Зл/б) в точках (-1/л/б, -1/л/б, 2/л/б), (-1/л/б, 2/л/б,
— 1/л/б) и B/л/б, -1/л/б, -1/\/б). 30. d = h = 6. 31. Smin = 48см2 при высоте
2 см и длинах сторон основания, равных 4 см. 32. Vmin = ттм3 при радиусе
основания 1 м и длине образующей 2 м. 33. 2а/\/3, 26/л/З, 2с/\/3. 34. /9min =
= 1Лж°+,^° + С2° + -Р1. 35. 7/D^). 36. 5max = 0,25а2 ctg 4- 37. U =
= л/2а6sin тт. 38. a) г/ + г/ = 0; решение исходного уравнения есть функция
у = A sin(ln х + (р), где А, (р — произвольные постоянные; б) у + у = 0; реше-
решение исходного уравнения есть функция у = A sin ( ^ 1пBж d= \/4ж2 + 1) + 9? j,
где A, ip — произвольные постоянные; в) у + о;2|/ = 0; решение исходного
уравнения есть функция у = Asinf ^ arcsinx + (р), где А, (р — произволь-
произвольные постоянные. 39. а) х'" + у = 0; б) жD) + 1 = 0. 40. а) и + A + ^)й = 0;
б) t5u + Ct4 + 1)п + п = 0; в) t J2lnt^ + и = 0; г) tu + й = 0. 41. и" + [д(ж) -
-0,25р2(ж) - 0,5р'(^)]^ = 0. 42. а) р = р- б) р2 = p2l~{^- 43. р = kp3,
ф = —1. 44. a) uzu = z\ б) ^ = zb , v =еи; в) ^u = zv\ г) ^2 + azzv = 6^2.
V w — v2
45. a) zu = 0; решение исходного уравнения есть функция z = f(bx — ay),
где f(v) — произвольная дифференцируемая функция; б) zu = 0; решение
исходного уравнения есть функция z = /(ж2 + у2), где f(v) — произвольная
дифференцируемая функция; в) uzu = z\ решение исходного уравнения есть
функция z = /( ^ J Dж — 7г/), где /(г;) — произвольная дифференцируе-
дифференцируемая функция. 46. а) гу^ = 0; решение исходного уравнения есть z = ^ •
/ ( ^ 1, где f(u) — произвольная дифференцируемая функция; б) wv = 0,
решение исходного уравнения есть функция z = ехр {х + у + /(ж2 + ?/2)},
где f(u) — произвольная дифференцируемая функция. 47. a) v • wv = 1;
б) «,„ = 0; в) и2^ + v2w2v = W2WllW,. 48. Б = 4
49. а) 5 = zp + -j-^; б) В = zpp + -^р + —^z^^\ в) В = zuu + 2zuv
— zu — zv] г) В = р Zpp. 50. a) zuu + .z-y-y = 0; б) zvv =
Глава XII
459
+ 2zuv + zvv = 0. 51. a) wvv = 0; решение исходного уравнения есть функция
z = y • f(x + у) + х - д(х + 2/), где f(u), д(и) — произвольные дважды диффе-
дифференцируемые функции; б) zuv = 0; решение исходного уравнения есть функ-
функция z = f(y + ах) + д(у — ах), где f(v), д(и) — произвольные дважды диф-
ференцируемые функции. 52. и? (и^) + v& (y%f) + w^ (w^) =
= 2
= ( 1 — — J
dv dudw
Wvv; r) WUU
• 53. a) wuu = 0; 6) wuu = 0,5; в) wuu =
^^ = 0; д) WUU + ^иг; + ^г;г; = W.
Глава XII
4 x
3 бж-11
1. a) Jdxjf(x, у) dy, Jdyjf(x, у) dx (рис. 81); 6) Jdx J f(x, у) dy +
5 B9-5ж)/2
/ у
f(x,y)dy, Jdy J f(x,y)dx
B9-2t/)/5 1
f f(x,y)dx (рис. 82); в) f dx x
2 (t/ + ll)/6 -2
6-Зж З УуТз 12
x J f(x,y)dy, Jdy J f(x,y)dx + Jdy x
зж2 о _^тз з
2-2//3 4
x J f(x,y)dx (рис. 83); г) Jdx x
-2-\-V8-\-2x-x2
1 1ГУи~тУ~Г ^ ОЖ
f(x,y)dy, Jdy J f(x,y)dx; д) Jdx J f(x,y) dy,
460
Ответы и указания
8 У/2
hi
О у/2,
Jdy J f(x,y)dx + Jdy J f(x,y)dx (рис. 84); e) Jdx J f(x,y)dy
8 y/3
y=Q—3x
—VI-
ж=4
=2x
+ Jdxjf(x,y)dy + Jdx J f(x,y)dy, Jdy J f(x,y)dx; ж) J dx x
11 4 Зж-ll I E-2t/)/3 -2
Зж+6 О Зж+6 З У/3-1 6 О
xj f(x,y)dy+ Jdx J f(x,y)dy, Jdy J f(x,y)dx + Jdy J f(x,y)dx;
0 -1 Зж+З 0 y/3 —2 3 y/3 —2
О 1,5ж+6 З 6-Зж З 2-у/З 6
з) у^ж у f(x,y)dy + Jdx у f(x,y)dy, Jdy J f(x,y)dx + J
-2 -Зж-3 О -3 -3 -y/3-1
2-y/3
x У /О, у) dx; и) fff(x, у) dx dy = JJ /(ж, у) dx dy + JJ /(ж,
B/3)t/-4 G Gi G2
у = гМ{x)
у =у1(х)
W
Рис. 85
у =
K/
17
3 ж
Рис. 86
2 2/2 (ж) 3 2/2 (ж)
+ уу /(ж, 2/) cb <Zj/ + уу /(ж, у) dx dy = Jdx у /(ж, 2/) cfa/ + у^ж J /(ж,
С?з G4 0 2/1 (ж) 2 —У2(ж)
Глава XII
461
2 -2/1 (ж) 0 2/2 (ж)
^ ^ f(x,y)dy+ Jdx J f(x,y)dy, где yi(ж) = л/2ж -ж2, */2(ж)
О -У2(х) -1 -г/2 (ж)
2 1+ж2B/) 1 1+Ж2B/)
/ / f(x,y)dx + Jdy J f(x,y)dx
1-х2(у) -1 l+a;iB/)
= л/3 + 2ж - ж2 (рис. 85);
1+ж2B/)
()
f(x,y)dx+ j dy j f(x,y)dx, где a?i(y) = л/l - |/2, ж2(г/) =
-2 1-Ж2B/) -1 1-ж2B/)
= л/4~^25 к) fff(x,y)dxdy= JJ f(x,y)dxdy+ JJ f(x,y)dxdy +
G Gi G2
2 1+2/2 (ж) 3 1+2/2 (ж)
+ jjf(x,y)dxdy + JJf(x,y)dxdy = Jdx J f(x,y)dy + Jdx J f(x,y)x
G3 G4 0 yi(x) 2 I-2/2 (ж)
2 -2/1 (ж) О 1+2/2(ж)
xdy-\-Jdx J f(x,y)dy+ Jdx J f(x,y)dy, где yi(x) = \/2ж -ж2,
О
J J
О 1-2/2(ж)
() ()
2/2 (ж) = л/3 + 2ж - ж2 (рис. 86); J dy J f{x,y)dx+ Jdy J f{x,y)d
1 () 1 ()
-1 1-2/2(ж)
3
x
-Ж1B/)
J f(x,y)dx, где
1-ж2B/)
= л/l -1/2, ж2(г/) =
1-ж2B/)
1 х2
2. a) Jdxjf(x, y)dy (рис. 87); б) Jdyjf(x, y)dx + J dy J /(ж, j/)<te (рис. 88);
I
f(x,y)dx + Jdyx
О
О Ж3
2/
J
2/
в) Jdy J f(x,y)dx + Jdy J f(x,y)dx; r)
О t//2 2 y/2
1
— \/ж
1_-2/ О О
х / f(x,y)dx (рис. 89); д) Jdx J f(x,y)dy + Jdx J f(x,y)dy
О _A+ж)/2
О ж 1 ж
Рис. 87
Рис. 88
462
Ответы и указания
VI
1
-l/
-1
Рис
—-«^
x=^^
V >
. 89
-1
*\
Vl
Рис
V ! ж
\v=-^rx~ j
,. 90
V2-0,5 0,5 1
(рис. 90); e) ^ dy J f(x,y)dx+ j dy j f(x,y)dx+ jc
0,5^3 -s/1-2/2 ^2-0,5 Vl-2/2 -1"
л/2 —у —0,5л/3 0,5 + \/l — ж2 0
х / f(x,y)dx (рис. 91); ж) /" с?ж / f(x,y)dy+ Г dx x
0,5
-0,5^3
2tt a
x f f(x,y)dy (рис. 92). 3. а) 4,5; 6) -27/4; в) 61. 4. a) fd(pfpf(pcos(p,
VT=^ о о
а 2тг тг 2 sin <^
р simp) dp = pdp f(p cos (p, p simp) dip; б) dip j pf(p cos ip, psimp) dp =
0 0 0 0
2 7r-arcsin(p/2) 2тг &
= pdp I f (p cos ip,p simp) dip (рис. 93); в) dip pf(p cos ip, psimp)dp =
0 arcsin(p/2) 0 a
6 2tt тг/4 aVcos 2<p
= pdp f(pcos ip, psimp) dip; r) dip pf (pcos ip, psimp) dp =
-тг/4 О
Глава XII
463
а 0,5 arccos(p2/a2) тг/2 l/(sin ip+cos ip)
= [pdp f f (p cos ip,p sin ip) dip (рис. 94); p) Г dip Г рх
0 -0,5arccos(p2/a2) 0 0
1/V2 тг/2 1 а-тг/4
x f (p cos (p,p simp) dp = f pdp f f(p cos <p, p sin ф) dip-\- Г pdp\ f f(px
Рис. 93
Рис. 94
Рис. 95
x cos (р, p sin. (р>) dip + / f (p cos (p, p simp) dip , где a = arcsin —h- (рис. 95);
Зтг/4-о;
тг/4 a sin ip/ cos 9? Зтг/4 a/ sin </?
e) dip / pf (p cos (p, p sin (p) dp + / c/9? / pf(p cos (p, psimp) dp +
о о
a sin <?>/ cos (
тг/4 О
a 7Г —ai(p)
+ dip / pf (pcos (p, psimp) dp = pdp I f(pcos (p, psimp) dip ¦
Зтг/4 0 0 ai(p)
464
Ответы и указания
= arcsm ¦
f(p cos p, p sin p) dp + / f(p cos p, p sin 9?) dp , где ai (p) =
J J
I.(P) 7Г — «2(p)
, тг/4 sin (p/cos2 <p
\n ~a? a2^ = arcsin^- 5- a) [ dtp f pf(pcosp,
rr/4
p sin p) dp = pdp f(p cos p,p sin p) dp, где a = arcsin v + P .
О а
тг/4 2/sine/?
/ /
к /4
arcsinB/p)
V / (
= j f(P2)pdpjdv+ j f(P2)Pdp j
0 / /
тг/6
б) /dy /
тг/6 0
тг/2 1 /(р)
в) dp I pf (p cos p,p sin p) dp = pdp I f (p cos p, p sin p) dp;
0
тг/6
1 тг/4+а(р)
г/4-а(р)
3 4
где a(p) = arccos —h-. 6. a) ^ Мгб А/(гб, г;) <iv; 6) Ju du I f(v) dv = | j f(v)dv.
2 u-6 2 3 3
8. Положите и = xy, v = x - 2y. 9. а) 2тгаЬ/3; б) 2; в) 0 и 21тта4/29.
10. а) 18тг; б) 4/3; в) 0; г) 543^. 11. а) A5/8 - 1п4)а2; б) тг; в) 0,5а2 In 2.
12. а) а2(л/3 - тг/3); б) а2 D - л/15 + тг/2 - arccos (л/15/4)). 13. a) aV/Bc2);
б) 1/35; в) аЪ(а2 + 62)тг/2; г) Зтг; д) 2/3. 14. а) тгC1пЗ - 2); б) 2тг2; в) 3/4.
15. а) хо = —1, уо = 3,2; б) хо = 4,5, г/о = —1; в) хо = г/о = тта/8. 16. жо =
= -а/5,г/о = 0. 17. а) /ж = а63ро/3, /у = а3Ър0/3; б) /ж = ро/6, /у = 7ро/6;
в) 1Х = 1у = а4A -5тг/16)р0; г) 1Х = 1у = ^дро- 18. а) /ж = aV/8,
/у = а462/8; б) 1Х = 0,1, /у = 13/30. 19. рв = тга2р(/г - B/3)а), рн =
= 7ra2p(h + B/3)а). 20. Взяв ось ж в качестве оси абсцисс, получаем 1Х< =
= (у — аJр(х,у) dxdy = Ix — 2аМх -\- a2m. Так как по условию Мх =
G a by/l-x2/
= 0, то приходим к равенству 1Х> = 1Х + ?тга2. 21. a) I dx I dy x
f(x,y,z)dz,
-Сл/1-х2/а2-у2/Ъ2
c^/l-x2/a2-y2/b2
Jdy J dx J f(x,y,
~b -ал/1-у2/Ъ2 -Сл/1-х2/а2-у2/Ъ2
aJl-z2/c2
Сл/1-х2/а2 b^/l-x2/a2-z2/c2
z)dz, f dx f dz f f(x,y,z)dy, f dz f dx x
~C -aJl-z2/c2
-c-sjl-x2 /a2 -by/l-x2/a2-z2/c2
b cy/l-y2/b2 ay/l-y2/b2-z2/c2
by/l-x2/a2-z2/c2
x J f(x,y,z)dy, Jdy J dz
-by/l-x2/a2-z2/c
-b
J f(x,y,z)dx,
-Сл/1-у2/Ъ2 -ay/l-y2/b2-z2/c
Глава XII
465
J dy J f(x,y,z)dx; 6) Jdx J dy J f(x,y,
/1_х2_у2
z)dz-\-Jdx J dy J f(x,y,z)dz + Jdx J dy J f(x,y,z)dz,
n ) tt n 1 n n
о
0
0
0
J dx J f(x,y,z)dz-\- Jdy J dx J f(x,y,z)dz
У
о о
x J dx J f(x,y,z)dz, Jdy J dz J f(x,y,z)dx + J
Vi6-y2 Vi6-y2-22 4 Vi6-y2 Vi6-y2-2
x J dz J f(x,y,z)dx + Jdy J dz
./i_e.2 0 10 0 0
J
0
X
f(x,y,z)dx, dzx
0
dy I f(x,y,z)dx+ I dz I dy I f(x,y,z)dx+ dzx
J dy J f(x,y,z)dx, Jdx J dz J f(x,y,z)dy + Jdxx
0 0 0 0 ^!_Ж2_^2 О
dz f(x,y,z)dy+ I dx dz f(x,y,z)dy, dzx
\_X2 0 10 0 0
J dx J f(x,y,z)dy + Jdz J dx J f(x,y,z)dy+ [dzx
\/l6 —22 \/l6 — ж2— z2 2 2 —ж 4 —2ж —2t/
x J dx J f(x,y,z)dy; в) Jdx J dy J f(x,y,z)dz
J J
0 0
0 4-2ж
J J J
0 0 0
J
0
0 ж + 2
0 4-2ж + 2у О 0 4+2ж + 2у 0 ж + 2
J dy J f(x,y,z)dz + Jdx J dy J f(x,y,z)dz+jdxjdy
x-2 0 -2 -ж-2 О -2 0
4+2ж-2у
x у f(x,y,
2 2-у 4-2ж-2у
J J J
2 0 4+2ж-2у
jj J
2 2-у 4-2ж-2у 2 0 4+2ж-2у
z)dz, Jdy Jdx J f(x,y,z)dz + jdyjdx J f(x,y,
0 0 0 0 0 y-2 0
0 у+ 2 4-2x + 2y 0 0 4+2ж + 2у
z)dz + у dy J dx J f(x,y,z)dz + J dy J dx J f(x,y,z)dz,
-2 0 0 -2 -2-у О
4 2-г/2 2-y-z/2 4 0
У J J
J
О
-г/2 2-y-z/2 4 0 2/-г/2 + 2 0
J dy J f(x,y,z)dx + Jdz J dy J f(x,y,z)dx, J dy
0 y+z/22 0 г/22 у+г/22 2
x
0 0 y+z/2-2
0 г/2-2 -
466
Ответы и указания
2t/+4 2-y-z/2
x J dz J f(x,y,
0 y+z/2-2
2-x-z/2
x J f(x,y,z)dy-
x+z/2-2
2-x-z/2
z)dx
4
>/*
0 ;
2
2
+ fdy
0
0
г/2-2
4-2ж
4-2?/ г/-,г/2 + 2
0 z/2-y-2
x-z/2+2
' J f(x,y,z
-x+z/2-2
y-z/2+2
,V,z)dx,
)dy,
4
fdz
0
0
2-^/2
2; dxx
0
2ж+4
/* / *,„
-2
1
0
(l-w)/a
f(x,y,z)dy + Jdx J dz J f(x,y,z)dy. 22. а) ^с/?/ J dxx
z+z/2-l 0 0 z/2 — x — 2 О О
ax-\-y 1 2 A — 2/)/« 1 1 A — 2/)/«
J f(x,y,z)dz = Jdzjdy J f(x,y,z)dx+jdzjdy J f(x,y,z)dx =
0 0 0 (z — y)/a 0 z 0
c/^x
1 I/a 1—ax
J[Jdx j f
0 z/a 0
1 3t/2 1
J\JJ
= Jdyljdz J f(x,y,z)dx + Jdz J f(x,y,z)dx\ = Jdx\J
0 У (z-y)/a 0 0 ~
1 — ax 1 1 — ax 1 l/(
x J f(x,y,z)dy + Jdz J f(x,y,z)dy\ = Jdz\J
0 ax z-ax 0 z/a
z/a l-ax 1 1 2x2+3y2
+ J dx J f(x,y,z)dy\\ 6) Jdx Jdy J f(x,y,z)dz = Jdy\JdzJf(x,y,
0 z-ax 0 0 0 0 0 0
2+3t/2 1 3 11 2 VV3~
z)dx-\- I dz I f(x,y,z)dx\ = I dz I dy I f(x,y,z)dx + dz I dyx
l з У^Тз l 5
f(x,y,z)dx + Jdz J dy J f(x,y,z)dx + J dzx
1 1 2x2 1 2ж2+3
I dy I f(x,y,z)dx = /с/ж I dz I f(x,y,z)dy + I dzx
2 11 2 Уг/2
= I dz I dx I f(x,y,z)dy + I dz dxx
0 y^72 о oo
3 11 5 1
f(x,y,z)dy + jdzjdx J f(x,y,z)dy + Jdz J dxx
f(x,y,z)dy; в) например, Jdz Jdx J f(x,y,z)dy = Jdxx
v ~ -У2 1 У2 1 У
/^2/ / f(x,V,z)dz; r) например, /cM I dz I f(x,y,z) dx + I dz x
/(z-2
/(z-2X2)/3
1
Ж ч/ж2_2/2
0 0 У
Глава XIII 467
1 тг/4 тг/2
х Г f(x,y,z)dx . 23. а) 0; 6I/8. 24. Например, /с/у? / sin(9d(9 x
z/y 0 arcctg (I/ cos^)
l/(cos ip sin#) тг/4 тг/4 l/(cos <?> sin0)
х J f(r)r2dr = J sin в d6 J dip J f(r)r2dr +
cos6>/sin26> arctg(l/\/2) arccos(tg6>) cos6>/sin26>
тг/2 tt/4 l/(cospsin0)
+ f sm6d6 f dip f f(r)r2dr. 25. а) тг/10; б) 37тг/25. 26. а) 4тг/21;
тг/4 0 cos 0/ sin2 в
б) 81/40тг. 27. а) Зл/Зтг/5; б) 8тга6с/5; в) 9/4. 28. а) 2/3; б) 1; в) тгаЬ(а + Ь)/8.
29. а) 21тг/32; б) тг(Ъ - а)(Ъ2 + аЪ - 2а2)/3. 30. а) 21тг/Dл/2); б) тг2а3/Dл/2).
31. а) тгаЬс/60; б) 81/40; в) 6. 32. а) 4тгро; б) 128ро/15; в) 1408ро/105.
33. а) хо = О, у0 = 2, z0 = 4а/3тг; б) ж0 = уо = 16л/3/A5тг), ^0 = 2; в) ж0 =
7р/18, уо = 0, zo = 7р/176; г) х0 = уо = 0, z0 = 7/20. 34. a) x0 = -2, j/0 = 1,
?о = 4/3; б) хо = -2, 2/о = 1, г0 = 2/3; в) х0 = 32/13, у0 = 16/13, ^о =
= 33/65. 35. а) 1ху = D/15)тгроа6с3, Ixz = D/15)тгроа63с, Iyz = D/15)тгроа36с;
б) /жу = тгро/Ю, Ixz = Iyz = тгро/20; в) 1ху = 81тгро/16, Iyz = Ixz = 9тгро/16.
36. a) Ixy = D/9)тгроа6с3, Ixz = D/9)тгроа63с, /yz = D/9)тгроа36с; б) Ixy =
= 75тг, Ixz = 62тг, Iyz = 50тг. 37. а) 1Х = 1у = 0,15тгр0, /z = 0,1тгр0, /о = 0,2тгр0;
б) 1Х = 1у = тгроа5A6 - 7л/2)/60, /, = тгроа5(8 - 5л/2)/30, /0 = тгроа5B -
-л/2)/5. 38. 5тг2ро/64. 39. Fx =j fff ^^ dxdy dz = jpomo [[ dydzx
4o
40. a) f;
8тг2Д5
15 '
Глава XIII
1. а) 1 + Л/2; б) 2^; в) 2(ea - 1) + ?fea; г) 2а2; д) i[(
_2з/2]; e) W_ 2# a) 2g. 6) 5po. B) 4+^3^^. r) i
| In 3+|vI]. з. a) a.o = M, y0 = |_; б) Жо = 2/o = «o = (|fy- 4. Мж =
= My = Щ-. 5. a) 32of?0. 6) 3v^?o_ „_ Ix = Iy = б
/г = рол/4тг2 + 1. 7. Fi = 0, F2 = 7 у , где 7 — гравитационная постоян-
тга
ная. 8. а) 0; б) |; в) 2. 9. а) -|; б) -|; в) -|. 10. -И. Ц. |. 12. 0.
13. -2тг. 14. -2тг. 15. 0. 16. -тг. 17. 2тгл/2а2 sin Г| - а\. 18. -^-.
19. ^. 20. 0. 21. а) тг; б) тгаBс - 6). 22. а) 4; б) -4тг. 23. а) ^; б) -2тга6;
в) 0; г) ±pSeX2 • ^(j/2) - eXl • y?B/i) - p(y2 - yi) - 0,5р(ж2 - aji)(j/2 - yi) (вы-
468
Ответы и указания
бор знака зависит от направления обхода замкнутого контура АтВА).
24. h -72 = 2. 25. а) тгаЬ; б) ^-; в) In2; г) Зл/3 + ^. 26. I = 2S. 28. а) 8;
а+Ъ \/х1+У1
б) 4; в) -§; г) 9; д) ^; е) Ъ - а. 29. a) J f(u)du; б) | uf(u)du.
Г Г 3 3
30. / ip(x) dx+ ф(у) dy. 31. а) и = ^- + х2у - ху2 - ^- + С; б) и =
_ dn+mz _|_ ^
дхпдугп
Глава XIV
1. а) ^ + | - | - л/3 = 0; б) 2ж + л/% - z = 0; в) аж + ау - л/2а2 = 0.
2. a) cos а = ^, cos/З = — i, cos 7 = -7=; б) cos а = 0, cos/3 = 0, cos 7 = —1-
3. a)
aaB0-3,r). в)
cosщ -cosu2\] в) 8а2; г) 2а2; д) B0 - Зтг)/9; е) тгГал/а
ж) 4тг2а6. 5. а) 4тгC + 2л/3)а2; б) ^
3V3
6. h-I2 = Dтг-2л/3)а4. 7. ^f_\/2. 8. a) ^з. б) П+ + ^). в) 05C _
- л/3) + (л/3-1) In 2; г) 125^~1; д) ^(ал/ГТ^2 + 1пA + л/ГТ^2));
е) 0,57ra4sinacos2a; ж) Щ^-
11. ZL^l^o. 12. 4ттгроаCа2+ 262)л/а2+ б2. 13.40а4,
ч
^. 15. F
9. а) 2ж{1 +6х/1); б) тга2. 10. ^.
1о 2\/3
14. х0 = §, 2/о = 0, го = ^; ж0 = j/о = ^, зд = a
= {Fi,F2,F3}, где Fi = F2 = 0, F3 = тг7тро1п(| j. 16. а) 4тга3; б) абс х
У в) 0; г) if(а262 + aV + 62с2).
а 6 с
г3; ^
17. а) 0; б) тг/г3; в) 0; г) 0; д) тг; е) ^; ж) 0; з) ?. 18. -2тг * Дополните кри-
вую L отрезком так, чтобы контур стал замкнутым; б) 2л/2тга2 sin ( j — а );
в) -тга2л/3; г) -2тга(а + /г); д) 2тгЯг2; е) -|а3; ж) -4; 19. а) -53^; б) 0;
Z LZ
в)Ь-а. 20. f tf(t)dt. 21.а)^=|(ж3 + у3 + zs) -
; б)и =
= exyz + eyxz + ezxy + С; в) 16 = ж2^/^ + ж^/2^ + xyz2 + С. 22. —mg(z2 —
— z\). 23. а) 0; б) 0. 24. а) 4тга3; б) 0. * Дополните поверхность Ф до за-
замкнутой; в) 0; г) тг. * Дополните поверхность Ф до замкнутой; д) 0; е) ^;
Ж) За4; з)
; и) 1.
Глава XV 469
Глава XV
1. (х-у) = С; gradu(-l, 1) = -ni + 4j; gradu(l, 1) = 0. 2. (ж - СJ +
+ у2 = С\ х2 + у2 /0; (ж-1J+у2 = 1; (я-2J+у2=4; grad^(l,l) =
= —ej; gradi6B,0) = — (е/2) i; gradi6(l,— 1) = ej. 3. Пары лучей, сонаправ-
ленных с положительными полуосями Ох и Оу и имеющих общее начало
на прямой у = ж; gradi6B,l) = j; gradi6(l,2) = i. 4. а) Лучи, исходящие из
начала координат; б) окружности, лежащие в плоскостях, перпендикуляр-
перпендикулярных прямой, параллельной вектору с и проходящей через начало коор-
координат; центры этих окружностей лежат на указанной прямой; в) семей-
семейство эллипсов х2/а2 + у2/Ъ2 = С; г) х = С\у = С2л/Щ. 5. | grad^| = 2 л/2 =
= JJ(M), 2 = g(M), 0 = g(M). 6. a) grad^(M) = 36i + 12j + 4k;
б) grad^(Mi) = -3i + 3k, grad^(M2) = 3i — 3j, grad^(M3) = 3j-3k;
в) gradi6(M) = i+j + k. 7. а) В точках конуса z2 = xy\ б) в точках
прямой х = у = z. 8. а) Во всех точках; б) в точках прямой х = у.
9. ip = arccos(-8/9). 10. В точках сферы (ж - аJ + (у - ЪJ + (z - сJ = 1.
11. г; 1/r; sin r; In r; arctgr. 13. с; (cr) gradi*, + гбс. 14. а) 2 ц (у\ + ж j);
б) (е^ - l)-1(i+j); в) -i-j. 15. а) 0; б) 2(ж2 + у2 + z2); в) 0; г) 0; д) 3;
е) fi(y,z) + f2(x,z) + f3(x,y). 16. а) 3; б) 2/г; в) 7г4. 17. mindiva = 0 при
ж = а, 2/ = Ь. 19. а) (сг)/г; б) 2(гс); в) (/'(г)/г)(гс); г) (ab); д) 4(га);
е) 0; ж) 2(ab). 20. а) 0; б) -2и2. 21. 0 вне масс. 22. 0 вне зарядов.
23. а) -а/у) i - A/z) j - A/ж) k. 24. а) 0; б) 2xyzCz - 2) i + 2yz2(l - z) k;
в) 0; г) -(l/x2)j-B/x3)k; д) 0; e) A/x2) i + 2(y/x3) j. 25. a) —4 i — j;
б) 4j-3k; в) 4i. 26. a) 0; 6) 0; в) 0. 27. a) (re) rot a + [ca]; 6) (l/r)[rc];
в) (/'(r)/r)[pc]; r) 2/(r) с + (/'(r)/r)[cr2 - r(cr)]. 30. (bV) a = yz(x + y) i +
гж(г/ + ^) j + Ж2/(^ + x) k; (aV)b = y(z2 + ж2) i + ^(ж2 + |/2) j + x(y2 + ^2) k;
da/db = (z2x2 + ж22/2 + y2z2)-1/2[yz(x + j/) i + гж(г/ + ^) j + xy(z + ж) k];
ab/aa = (у V + ^2ж2 + жУ Г1/2^2 + ж2) i + ^(ж2 + 2/2) j + х(у2 + ^2) к].
31. da/dh =yi + zk; da/dl2 = A/>Д)[(х + у) i + z j + г к]; <9a/<9Z3 = ^
x[a;i + (j/ + ^)j + a;k]; da/dh = A/уД)[(х+ y)i +(y + z)j +(z
(liV)a = j/i + ^k; (l2V)a = (ж + ^/) i + ^j + ^k; (l3V)a = жi + (y + ^) j +
+ ж к; A4 V)a = (ж + у) i + (у + г) j + (z + ж) к. 33. <9T/<% = -2Tot ехр{-^2-
2 322
-t2}; (vV)T = 2T0t-3exp{-t-2-t2}; dT/dt = дТ/dt + (v\7)T = 2T0(-t +
+ t~3)exp{-t~2 -t2}. 34. 0Е/сЙ = iAocjeoscjt; (vV)E = (ke/r5{[asint x
хCж2 - r2) - 3bx(ycost + z)]i + [bcost(r2 - 3y2) - 3y(bz - аж8т?)^ +
+ [b(r2 - 3z2) - 3z (bycost - axsint)]k}] dE/dt = дВ/dt + (vV)E.
36. a) (grad^J + иАщ 6) /"(r) + B/r)//(r); в) [grad и grad v]; r) (rotb V) x
xa- (a V) rotb-rotb- diva. 37. rot rot a = 2B^ж - ж2) i + 2Bxy - y2) j +
+ 2B^-^2)k; grad diva = 2B^ж + у2) i + 2Bxy + z2) j + 2Byz + ж2) к;
Aa = 2(ж2 + у2) i + 2(y2 + z2) j + 2(^2 + ж2) к. 42. a) anoT = A/3)(ж i + у j +
+ г к), аСОл = Bж/3 + у) i + (ж - 4у/3) j + Bг/3 + 1) к; б) аПОт = а2, асол = 0;
в) аПот = 0, аСОл = аз. Следует иметь в виду, что ответы этой задачи
не однозначны. Например, возможно аз = аПот = аСОл, где аПот = (ж + z) i +
+ (z + ж) j + (ж + у) к, асол = (ж - у - z) i + (у - ж - z) j + Bz + у + ж) к.
43. а) 1/6; б) 4тг/3. 44. а) 0; б) 0. 45. а) 4тг/3; б) 5тг/3; в) -5тг/3; г) тг/3;
д) 2тг/3. 46. а) 0; б) 2тгЗл/3; в) 0; г) Ютгл/З/81. 47. а) 0; 0; б) -2тг/3л/3;
2тг/3л/3; в) 0; 0; г) -Ютгл/З/81; Ютгл/З/81. 48. тгаC - а2)/3л/3; а = 1; а =
470 Ответы и указания
= —1. 49. Соленоидальными являются поля ai и а3; 0; 8тг/3; 0; 0. 50. а) 3/2;
б) -1/2; в) -1/2; -1/2. 51. а) -тгл/З; б) -2л/3/3; в) тг/л/З; г) -2тг/(ЗлД).
52. -тгл/3A -а2/3); а = 0. 53. а) 2/3; б) 26/3. 54. а) 2; б) -2; в) -1;
г) 1; д) —1; е) —2. 55. и = tf(t)dt-\-C. 56. Потенциальными являют-
г0
ся поля ai и аг; 0; 0; 0; тг. 57. ai = gradi^i; u\ = ж?/ + xz + yz + G;
ж у z
а2 = gradw2; и2 = f fi(Od? + Jf2(r])dr] + J fs(OdC + С 58. Ni образует
0 0 0
острый угол с осью Oz. 59. гб = In г + С. 60. a) rot а = 0 при х2 + у2 ф
ф 0; б) rot а = 0 при у2 + z2 / 0; в) rot а = [4ж^//(ж2 + у2J] к; r) rot a =
= [4yz/(y2 + z2J] i; циркуляции всех полей вдоль указанных окружностей
равны нулю. Поле а) потенциально в указанной области, и его потенциал
есть и = In \Jх1 + у2 + ?2/2 + С. Поле б) потенциально в указанной облас-
области, и его потенциал есть и = In д/?/2 + z2 + ж2/2 + С. Поля в) и г) не яв-
являются потенциальными. 61. О при х2 + у2 / 0; 2тг; нет; да. 62. gradi6 =
= H2/|/(^2+2/2)]i + [kl/(^2+2/2)]J; 0; да. 63. 0 при х2 + у2 ф 0; 2тг; об-
область не является односвязной. 75. б) 1°) тг/2; 2°) 0; 3°) тг; 4°) 0; в) 1°) в
точке A: i = ер, j = е^, к = ег; в точке В: i = — е^, j = ер, к = ег; 2°) в
точке А: ер = i, е^ = j, ег = к; в точке В: ер = j, е^ = —i, ez = k.
76. б) 1°) тг/2; 2°) 0; 3°) тг; 4°) 0; в) 1°) в точке A: i = er, j = e^,
к = — е#; в точке В: i = — е^, j = er, k = — е#; 2°) в точке A: er = i,
е# = —k, e^ = j; в точке В: er = j, е^ = —к, е^ = —i. 77. gradи = ^ ер +
,. 78.
где а = ар(р, <р) ер + а<р(р, <р) е^. 79. grad^ = |^ ег
80. a) divа(р, ^,^) = 1р \щ(раР) + ^ + Р^], где а = арер
б) div a(r, 6>, ip) = yz^-Q [§р(r2ar sin в) +rj^(a6 sin (9) + r^J, где a = arer +
. 81. a) rot a(p, ^, ^) = (^ - ^)ep + (^ - ^
apep + aipeip + агег; 6) rot a(r, 6>, 9?) =
где a = ar er + a» e* + a^ e^. 82. Au(p, ц>, z) = ~p-§-p(p%) + jz0 + 0-
83. a) C\ Inp + С2; 6) Ci<?> + C2; в) C\z + C2; Ci и С2 — произвольные по-
постоянные. 84. a) Ci/r + C2; 6) Ci In tg | + C2; в) Ciy? + C2; Ci и С2 — про-
произвольные постоянные. 85. m(m+l)rm~2 86. divei = „ ^ „ ^\
П1Д2ЛЗ
dive2 = „ " „ ^"»"^, dive3 = „ " „ "^t}^>- a) divep = ±, dive,, =
= 0, dive^ = 0; 6) diver = -, dive^ = -ctg(9, dive^ = 0. 87. a) rotep = 0,
rot e^ = - ez, rot ez = 0; 6) rot er = 0, rot e^ = - e^, rot e^ = - ctg в, er e#.
p т т т
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аддитивность интеграла 150, 188
Асимптотические формулы 55
Безвихревое поле 388
Бесконечная производная 66
Бесконечно большая последователь-
последовательность 21
более высокого порядка рос-
роста 29
функция при х —>¦ а справа, сле-
слева 42
х —>¦ +оо, х —> —сю 42
— дифференцируемая функция 81
— малая последовательность 21
функция 52, 199
более высокого порядка 52,
199
Бесконечно малые одного порядка 52
Вектор нормали 69, 216
Вектор-функция 68
Векторная линия 384
Векторное поле 384
Векторный потенциал 389
Вертикальная асимптота 130
Верхний интеграл Дарбу 144
Лебега 187
— предел последовательности 34
Верхняя грань функции 108
числового множества 8
— сумма по Лебегу 187
Риману 144
Ветвь кривой 138
Вихрь 387
Внешняя мера 179
Внутренняя точка множества 192
поверхности 346
Возрастание функции в точке 116
на промежутке 116
Возрастающая последовательность 32
Волновое уравнение 406
Вторая производная 80
Второй дифференциал 81, 226
Выпуклая область 233
Выпуклость графика вверх 131
вниз 131
Гармоническая функция 340, 402
Геометрическая интерпретация диф-
дифференциала 77
дифференцируемости функции
двух переменных 215
производной 66
— — равномерной непрерывности
функции 113
теоремы Лагранжа 117
Ролля 117
Геометрические приложения двойно-
двойного интеграла 283
— — определенного интеграла 164,
165, 167, 168, 171
Гиперболический косинус 49
— котангенс 49
— синус 49
— тангенс 49
Гладкая кривая 318
— поверхность 346
Годограф 68
Градиент 385
Граница множества 192
— поверхности 346
Граничная точка множества 192
поверхности 346
Двойной интеграл 279
Двусторонняя поверхность 360
Диаметр множества 279
Дивергенция 387, 410
Дифференциал независимой пере-
переменной 77, 217
— функции 77, 216
— n-го порядка 82, 227
Дифференцирование 65
Дифференцируемая п раз функция
81, 226
— функция 77, 214
Дифференцируемое п раз скалярное,
векторное поле 384
472
Предметный указатель
Длина кривой 165, 317
Дополнение множества 179
Зависимость функций 257
Закон сохранения интенсивности
векторной трубки 410
Замена переменных в выражении, со-
содержащем обыкновенные произ-
производные 269
, — частные производные
270
Замечательные пределы 47, 49
Замкнутая область 193
— поверхность 348
Замкнутое множество 178, 192
Знакоопределенная квадратичная фор-
форма 238
Знакопеременная квадратичная фор-
форма 238
Измеримая на множестве функция 184
Измеримое (по Лебегу) множество 179
Инвариантность формы первого диф-
дифференциала 78, 217
Интеграл Гаусса 379
— Лебега 186
— с переменным верхним пределом
153
Интегральная сумма 143, 279, 295, 312,
317, 325, 353
Интегрирование иррациональных функ-
функций 100
— рациональных функций 96
— тригонометрических функций 106
Интегрируемая по Лебегу функция 187
Риману функция 143
— функция 279, 295
Касательная 66
— плоскость 215
Квадрируемая поверхность 348
— фигура 167
Квантор всеобщности 8
— существования 8
Колебание функции 109, 144
Конвективная производная 392
Коэффициент растяжения объема 300
площади 283
Криволинейные координаты 282, 298
— ортогональные координаты 432
Криволинейный интеграл второго
рода 324
первого рода 317
Критерий Коши сходимости последо-
последовательности 37, 194
— Сильвестра знакоопределенности
квадратичной формы 238
Кубируемое тело 171, 312
Кусочно гладкая кривая 318
— поверхность 346
Кусочно непрерывная функция 145
вдоль кривой 318
Лебеговская интегральная сумма
188
Лебеговское разбиение 187
Левая производная 66
Левый предел 41
Лемма Дарбу 144
Линейность интеграла 87, 149, 188
Линия тока 383
— уровня 383
Локальная производная 392
Локальный максимум 131, 236
— минимум 131, 236
— экстремум 131, 236
Максимальное значение функции 109
Масштабный коэффициент 433
Матрица квадратичной формы 237
Мера (Лебега) 179
Метод вычеркивания 98
— замены переменной 91, 155, 281,
297, 313
— интегрирования по частям 94
— исключения части переменных 261
— Лагранжа 263
— математической индукции 14
— неопределенных коэффициентов 98
Минимальное значение функции 109
Многочлен Тейлора 125, 229
Множества одинаковой мощности 177
Множество меры нуль 182
— мощности континуума 177
— точек площади нуль 280
Монотонная последовательность 32
Наклонная асимптота 130
Невозрастающая последовательность
32
Независимая переменная 40, 198
Независимость интеграла от пути ин-
интегрирования 335
Неограниченная последовательность
16
Неопределенности разных типов 25,
59, 60
Неопределенный интеграл 87
Неособая точка поверхности 347
Непрерывная кривая 193
Непрерывность функции в точке 48,
205
по отдельной переменной
205
Предметный указатель
473
Непрерывность функции в точке по
совокупности переменных 205
слева 48
Непрерывность функции в точке спра-
справа 48
вдоль кривой 318
множестве 206
Неравенство Бернулли 14
— треугольника 195
Неубывающая последовательность 32
Нечетная функция 130
Неявная функция 243
Нижний интеграл Дарбу 144
Лебега 187
— объем тела 312
— предел последовательности 34
Нижняя грань функции 109
числового множества 7, 8
— сумма по Лебегу 187
Риману 144
Нормаль 69, 216
Ньютоновский потенциал поля тяго-
тяготения 386
Область 193
— определения функции 40, 198
Обобщенные полярные координаты 290
— сферические координаты 299
Образ области 281
Общая форма остаточного члена 125
Объединение множеств 177
Объем m-мерного параллелепипеда 312
— тела (по Жордану) 171, 312
Объемно односвязная область 409
Ограниченная последовательность 16,
194
— сверху функция 108
— снизу функция 108
— функция 108, 206
Ограниченное множество 8, 193
— сверху множество 7
— снизу множество 7
Односвязная область 335
Односторонняя поверхность 360
Окрестность 6, 193
Оператор Гамильтона 390
— дифференциала 227
— "набла" 390
— Лапласа 402
— производной по направлению 391
— частной производной 227
Определенный интеграл 143
Определитель Якоби 245
Ориентация поверхности 361
Ориентируемая поверхность 361
Особая точка поверхности 347
Остаточный член асимптотической
формулы 56
формулы Тейлора в форме Ко-
ши и Лагранжа 125
Остаточный член формулы Тейлора
в форме Пеано 125, 229
Открытое множество 178, 192
Открытый m-мерный шар 192
Отрицательно определенная квадра-
квадратичная форма 237
Отрицательное направление обхода
325
Параметр 67, 345
— Ламэ 433
Параметрическое задание поверхнос-
поверхности 345
функции 68
Первообразная 87, 154
Первый дифференциал 77, 216
Переменная дуга 165
Пересечение множеств 177
Периодическая функция 130
Плоская фигура 167
Площадь плоской фигуры (по Жорда-
Жордану) 167
— поверхности 348
Поверхностно односвязная область
369
Поверхностный интеграл второго ро-
рода 361
первого рода 353
Поверхность уровня 383
Повторный интеграл 280, 296, 313
— предел 200
Подпоследовательность 34
Подстановки Эйлера 100
Покоординатная сходимость 194
Полная производная 392
Полное приращение 204
Полный дифференциал 335, 369
Положительно определенная квадра-
квадратичная форма 237
Положительное направление обхода
325, 367
Последовательность 16
— точек пространства 193
Потенциал электрического поля 383
Потенциальное поле 386
Поток векторного поля 363, 407
— жидкости 408
Правая производная 66
Правила дифференцирования 66
Правило Лопиталя 122
— построения отрицания 8
— сравнения чисел 5
Правый предел 41
474
Предметный указатель
Предел вектор-функции 68
— длин ломаных 164
— интегральных сумм 143, 279, 295,
317, 325, 348
Предел последовательности 16
точек пространства 193
— функции в точке 40, 199
на бесконечности 41, 199
Предельная точка множества 40, 192
последовательности 34
Представление вещественных чисел
в виде бесконечных десятичных
дробей 5
Приращение функции 65, 205
Произведение вещественных чисел 11
Производная 65
— вектор-функции 68
— по направлению 385
— n-го порядка 80
Прообраз области 281
Простая замкнутая кривая 164, 317
— незамкнутая кривая 164, 317
— область 334, 377
— поверхность 346
Простейшие дроби 97
— элементарные функции 48
Равенство вещественных чисел 5
Равномерная непрерывность функции
112, 206
Разбиение множества 186
Разностное отношение 65
Разность множеств 178
Расстояние между двумя точками 191
Расходящаяся последовательность 16
Ротор 387, 414
Свойство, справедливое почти всюду
184
Связное множество 193
Силовая линия 383
Скалярное поле 383
Скалярный потенциал 386
Сложная функция 48, 206
Смешанная производная 226
Совокупность неявных функций,
определяемых системой уравне-
уравнений 245
Соленоидальное поле 388, 410
Спрямляемая кривая 164, 317
Среднее значение функции 150
Строго монотонная последователь-
последовательность 32
Сторона поверхности 360
Сумма множеств 177
— ряда 178
Суммы Дарбу 144
Сферические координаты 299
Схема построения графика функции
У = /(*) 132
Схема построения кривой, заданной
параметрически 137
Сходящаяся последовательность 16,
193
Сходящийся ряд 178
Счетная аддитивность меры Лебега
179
Счетное множество 177
Таблица основных неопределенных
интегралов 89
— производных простейших элемен-
элементарных функций 65
Телеграфное уравнение 405
Тело 171, 300, 312
Теорема Больцано-Вейерштрасса 34,
194
— Вейерштрасса вторая 109, 206
первая 108, 206
— Кантора 113, 206
— Коши 117
— Лагранжа 117
— Лузина 185
— о вычислении площади поверхнос-
поверхности с помощью двойного интегра-
интеграла 348
— — — поверхностного интеграла
первого рода с помощью двойно-
двойного интеграла 354
дифференцируемости обратной
функции 67
сложной функции 67, 216
локальной ограниченности функ-
функции, непрерывной в точке 108
непрерывности сложной функ-
функции 48, 206
разложении рациональной дро-
дроби на сумму простейших дробей
97
связи между криволинейными
интегралами первого и второго
рода 326
структуре открытых множеств
178
существовании точных граней
числового множества 9
сходимости монотонной огра-
ограниченной последовательности 32
трех последовательностях 25
— об устойчивости знака непрерыв-
непрерывной функции 108
— Ролля 117
Предметный указатель
475
Теоремы о вычислении кратных ин-
интегралов с помощью повторного
интегрирования 280
криволинейных интегралов
с помощью определенного интег-
интеграла 318, 326
дифференцируемых функциях
77, 116, 215
зависимости и независимости
функций 257, 258
замене переменных в интегра-
интегралах 91, 155, 282, 300, 316
направлении выпуклости и точ-
точках перегиба графика функции
131
непрерывных функциях 48, 49,
108, 109, 205, 206
неявных функциях 243-246
первообразных 87, 91, 94, 97,
154, 155
пределах последовательностей
16, 21, 25, 32, 34, 37, 194
функций 41, 199, 200
производных 66, 67
равенстве смешанных производ-
производных 226
— об измеримых функциях 184, 185
интегрируемых функциях 144,
145, 187, 279, 280, 295
условиях независимости криво-
криволинейного интеграла второго ро-
рода от пути интегрирования 335,
369
экстремумах функций 131, 236,
263
Точка возврата 141
— возможного экстремума 131, 237
— перегиба 131
— разрыва 49, 205
I и II рода 49
— устранимого разрыва 49
— m-мерного координатного прост-
пространства 191
Точные верхняя и нижняя грани
множества 8
функции 108, 206
Тройной интеграл 295
Убывание функции в точке 116
на промежутке 116
Убывающая последовательность 32
Угловая точка 134
Угловой минор 237
Упорядоченная совокупность чисел
191
Уравнение касательной 66
плоскости 216
Уравнение Лапласа 235
— теплопроводности 235
— Пуассона 403
Уравнения Максвелла 389
Условия связи 261
Условный максимум 261
— минимум 261
— экстремум 261
Физическая интерпретация вектор-
функции и ее производной 68
дифференциала 77
поверхностного интеграла вто-
второго рода 363
производной 66
теоремы Лагранжа 117
Ролля 117
формулы Остроградского-Гаус-
са 408
Стокса 412
частной производной 213
Формула бинома Ньютона 29
— Грина 334
вторая 338, 425, 426
первая 425, 426
— замены переменной 91, 155
— интегрирования по частям 94, 155
— Коши 118
— Лагранжа конечных приращений
117, 229
— Лейбница 81
— Маклорена 125
— Ньютона-Лейбница 155
— Остроградского-Гаусса 378, 408
— Стокса 368, 411
— Тейлора 125, 228
Формулы для вычисления длин плос-
плоских кривых 165
моментов и координат цент-
центра тяжести 175, 284, 301, 319, 327,
354
Формулы для вычисления объемов
тел 172, 282, 300
площадей 168, 283, 348
— замены переменных 269
в кратных интегралах 281,
297, 313
— среднего значения 150
Фундаментальная последователь-
последовательность 37, 194
Функциональная матрица 257
Функция 40
— Дирихле 44, 146, 151, 185, 189
— Лагранжа 263
— Римана 148
— т переменных 198
— sgnx 88, 154
476
Предметный указатель
Цилиндрические координаты 298
Циркуляция 411
Частичная сумма ряда 178
Частичный предел последовательнос-
последовательности 34
Частная производная 213
n-го порядка 225
Частное значение функции 40, 198
— приращение функции 204
Четная функция 130
Число е 49
Числовая последовательность 16
— прямая 6
Числовой ряд 178
Член последовательности 16
— ряда 178
Эквивалентные бесконечно малые 52
— множества 177
— функции 185
Эквипотенциальная поверхность 387
Экстремум 131, 236
Элемент объема в криволинейных
координатах 300
Элемент объема в прямоугольных
координатах 300
— площади в криволинейных коор-
координатах 283
прямоугольных координатах
283
Элементарная функция 49
Эллиптический интеграл 166
Явная функция 130
Явное задание поверхности 345
Якобиан 245
С-свойство измеримых функций 185
m-кратный интеграл 312
m-мерная сфера 192
т-мерное евклидово пространство 191
— координатное пространство 191
m-мерный параллелепипед 192
— шар 192
"о малое" 52
ж?/?-проектируемая поверхность 368
^-трапециевидная область 280
^-цилиндрическая область 377
^-окрестность 6, 192
ОГЛАВЛЕНИЕ
Предисловие 3
ГЛАВА I
ВЕЩЕСТВЕННЫЕ ЧИСЛА
§ 1. Сравнение вещественных чисел 5
§ 2. Точные грани числового множества. Применение символов мате-
математической логики 7
§ 3. Арифметические операции над вещественными числами 11
§ 4. Метод математической индукции 14
глава п
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
§ 1. Ограниченные и неограниченные последовательности 16
§ 2. Бесконечно малые и бесконечно большие последовательности . . 21
§ 3. Свойства сходящихся последовательностей 24
§ 4. Замечательные пределы 29
§ 5. Монотонные последовательности 32
§ 6. Предельные точки 34
§ 7. Фундаментальные последовательности. Критерий Коши сходи-
сходимости последовательности 37
ГЛАВА III
ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 1. Предел функции. Теоремы о пределах. Бесконечно большие функ-
функции 40
§ 2. Непрерывность функции в точке 48
§ 3. Сравнение бесконечно малых функций. Символ "о малое" и его
свойства 52
§ 4. Вычисление пределов функций с помощью асимптотических фор-
формул. Вычисление пределов показательно-степенных функций ... 58
ГЛАВА IV
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
§ 1. Производная функции. Правила дифференцирования 65
§ 2. Дифференциал функции 77
§ 3. Производные и дифференциалы высших порядков 80
478 Оглавление
ГЛАВА V
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1. Первообразная и неопределенный интеграл 87
2. Простейшие неопределенные интегралы 89
3. Метод замены переменной 91
4. Метод интегрирования по частям 94
5. Интегрирование рациональных функций 96
6. Интегрирование иррациональных функций 100
7. Интегрирование тригонометрических функций 106
ГЛАВА VI
ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ
И ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
1. Теоремы об ограниченности непрерывных функций 108
2. Равномерная непрерывность функции 112
3. Некоторые теоремы о дифференцируемых функциях 116
4. Правило Лопиталя 122
5. Формула Тейлора 125
ГЛАВА VII
ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
И ПОСТРОЕНИЕ ГРАФИКОВ
1. Построение графиков явных функций 130
2. Исследование плоских кривых, заданных параметрически 137
ГЛАВА VIII
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1. Интегрируемость функции (по Риману) и определенный ин-
интеграл 143
2. Свойства определенного интеграла 149
3. Формула Ньютона-Лейбница 153
4. Вычисление длин плоских кривых 164
5. Вычисление площадей плоских фигур 167
6. Вычисление объемов тел 171
7. Физические приложения определенного интеграла 173
ГЛАВА IX
МЕРА И ИНТЕГРАЛ ЛЕБЕГА
1. Мера множества 177
2. Измеримые функции 184
3. Интеграл Лебега 186
Оглавление 479
ГЛАВА X
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Последовательности точек в m-мерном евклидовом пространстве 191
§ 2. Предел функции 198
§ 3. Непрерывность функции 204
§ 4. Частные производные и дифференцируемость функции 213
§ 5. Частные производные и дифференциалы высших порядков .... 225
§ 6. Локальный экстремум функции 236
ГЛАВА XI
НЕЯВНЫЕ ФУНКЦИИ И ИХ ПРИЛОЖЕНИЯ
§ 1. Неявные функции 243
§ 2. Зависимость функций 257
§ 3. Условный экстремум 261
§ 4. Замена переменных 269
ГЛАВА XII
КРАТНЫЕ ИНТЕГРАЛЫ
§ 1. Двойные интегралы 279
§ 2. Тройные интегралы 295
§ 3. m-кратные интегралы 312
ГЛАВА XIII
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. Криволинейные интегралы первого рода 317
§ 2. Криволинейные интегралы второго рода 324
§ 3. Формула Грина. Условия независимости криволинейного интегра-
интеграла второго рода от пути интегрирования 333
ГЛАВА XIV
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
§ 1. Площадь поверхности 345
§ 2. Поверхностные интегралы первого рода 353
§ 3. Поверхностные интегралы второго рода 360
§ 4. Формула Стокса 367
§ 5. Формула Остроградского-Гаусса 377
ГЛАВА XV
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
§ 1. Дифференциальные операции в скалярных и векторных полях . . 383
§ 2. Повторные дифференциальные операции в скалярных и вектор-
векторных полях 402
§ 3. Интегральные характеристики векторных полей 407
§ 4. Основные дифференциальные операции векторного анализа в кри-
криволинейных ортогональных координатах 432
Ответы и указания 437
Предметный указатель 471
Учебное издание
БУТУЗОВ Валентин Федорович
КРУТИЦКАЯ Наталья Чары
МЕДВЕДЕВ Герман Николаевич
ШИШКИН Александр Александрович
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
В ВОПРОСАХ И ЗАДАЧАХ
Редактор Е.Ю. Ходан
Оригинал-макет Н.Л. Ивановой
ЛР №071930 от 06.07.99. Подписано в печать 01.08.02.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 30. Уч.-изд. л. 33. Тираж 3000 экз. Заказ №
Издательская фирма "Физико-математическая литература''
МАИК "Наука/Интерпериодика"
117864 Москва, ул. Профсоюзная, 90
Отпечатано с готовых диапозитивов
в ППП "Типография "Наука"
121099 Москва, Шубинский пер., 6
5-92 1- 284-2
785922'102841