Московский инженерно-физический институт (государственный университет)
Московский городской лицей № 1511 при МИФИ
А.А. Бучин, А.В.Иванищук
Г рафики элементарных функций Для 9-10 классов физико-математических лицеев
Москва 2004 г.

Графики элементарных функций, (для 9-10 классов физико-математических лицеев) А. А. Бунин, А. В. Ивани-щук: Учебное пособие. М: Лицей 1511,2004. - 62 с.
Настоящее учебное пособие составлено в соответствии с программой по математике физико-математических школ и, в частности, физико-математического лицея 1511. Задачи систематизированы по темам, расположены в порядке возрастания трудности, подобраны так, чтобы однотипные задачи можно было решать в аудитории и использовать в качестве домашнего задания. Каждой теме предшествует теоретический материал с большим количеством примеров, разобранных самым подробным образом.
При составлении пособия авторы учитывали опыт работы многих преподавателей математики физико-математического лицея 1511, а также варианты поточных контрольных работ, проводимых в лицее.
Данное пособие предназначено для физико-математических лицеев, классов с углубленным изучением математики и может быть использовано при самостоятельной подготовке к экзаменам в ВУЗ.
© А. А. Бунин, А. В. Иванишук, 2004
СВОДКА ОСНОВНЫХ ОПРЕДЕЛЕНИЙ.
Пусть заданы некоторые множества X и Y.
Функцией f из X в Y называется закон ( правило ), которое каждому элементу х, принадлежащему множеству X ( хеХ ), ставит в соответствие олин и только один элемент yeY.
Обозначение: y=f(x); х - называется аргументом или независимой переменной.
Множество X называется областью определения функции f (обозначение X=D(f)), множество Y называется областью значений функции f ( Y=E(f)).
У нас множества X и Y всегда будут подмножествами действительных чисел R. Такие функции называются числовыми. В подавляющем большинстве случаев функции будут задаваться некоторой формулой, без специального указания области определения, поэтому под D(f) будет пониматься множество всех тех действительных чисел, для которых эта формула имеет смысл.
Графиком функции называется множество всех точек плоскости, координаты которых имеют вид ( х, f(x)).
Координатные оси OX, OY называются, соответственно, осью абсцисс и осью ординат.
Функция у=Дх) называется возрастающей на множестве М, если ЗНсХЧСШигО ЛрГуАЮгяТЗ. COOTo&TOllSjST OOJIdUICv ЗНаЧСгхгтС фуНКЦИг» ( ДНЯ любых X2>X1, XieM, XjeM ) => ( ЦХ1)>Ях2) ).
Функция y=f(X) называется убывающей на множестве М, если большему значению аргумента соответствует меньшее значение функции. ( для любых Х2>Х[, Х[еМ, х2еМ ) => ( f(X])<f(x2)).
Если заменить строгие неравенства на нестрогие, то функция называется неубывающей, соответственно, невозрастающен.
Сумма, композиция возрастающих функций - возрастающая функция.
Заметим, что если функция убывает ( возрастает ) на каждом их двух непересекающихся множеств Mt и М2, то, вообще говоря, неверно, что функция убывает (возрастает) на объединении М(иМ2.
1. ГРАФИКИ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
1) Линейная функция y=kx+b
Графиком линейной функции является прямая.
Благодаря известной аксиоме планиметрии, для его построения достаточно знать две точки: например ( если к*0 ), т. А(О,Ь) и т. В(-~,0), которые, конечно, суть точки пересечения этой прямой с осями координат. Можно взять и любую другую пару точек.
Если к=0, то прямая будет параллельна оси абсцисс.
Если Ь=0, то прямая проходит через начало координат.
Коэффициент к имеет простой геометрический смысл: это тангенс угла а, образованного осью абсцисс и прямой, угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Поясним сказанное рисунками:
Здесь ki>0, кг>0,
Если к>0 - функция у=кх+Ь возрастающая.
Если к<0 — функция у=кх+Ь убывающая.
kj<0, причем кг>к1
Не любую прямую на плоскости можно задать графиком y=kx+b. Исключением являются прямые, параллельные оси ординат (перпендикулярные оси абсцисс). Уравнение таких прямых имеет вид: х=с
Единым же образом уравнение прямой можно записать так:
Ах+Ву=С
„ „ Л	АС
При В*0 получаем: у=-—х+— и
в в
В’
С
В с
При В=0, а^О имеем вертикальную прямую х=—
Наконец, при В=А=0 уравнение Ах+Ву=С превратится либо в тождество, если С=0, либо станет неразрешимым, если С±0. В первом случае графиком будет вся плоскость, во втором - пустое множество, т. е.,
Здесь С1>0, с2<0
К линейным функциям непосредственно примыкает функция у= I х | - модуль числа х.
„	j х, е с ли х> О
11о определению y=i
-х, е с ли х-< О
2) Квадратичная функция у= аз^+Ьх+с (а*0)
Графиком квадратичной функции является парабола, вершина
Ь	Дас—Ь1
которой С имеет координаты х<=----, у.=-------, и обладающая осью
2а 4а
симметрии, параллельной оси ординат и проходящей через вершину С.
Если а>0, то ветви параболы направлены вверх.
Если а<0, то вниз
Парабола может иметь две точки пересечения с осью абсцисс, одну и ни одной, в зависимости от числа решений уравнения ах2+Ьх+с=О Последнее определяется условиями D>0, ГМ), ГКО, соответственно (D=b2-4ac).
При построении графика параболы необходимо отметить следующие b 4ас-Ь2	,п_
точки: вершину С(---,------), точку пересечения с осью ординат (О,С) и
2а 4а
точки пересечения с осью абсцисс ( если они есть ).
Здесь ai>0, а2<0, причем ai<l.
На интервале у=-х2+2х возрастает, на [1;+ оо) убывает
На интервале (-«>; 3/2] у=х2-3х+3 убывает, на [3/2;+ да)- возрастает
Можно доказать, что парабола однозначно определяется тремя различными точками ( см. №39 ) с различными ординатами, не лежащими на одной прямой.
3) Дробно-линейная функция у =
ах + Ь ex + d
(с* 0, ad*be).
Частным случаем дробно-линейной функции является обратная
зависимость у = — ( это получается, если положить a=d=O, b=k,c=l) X
k
График обратной зависимости у = — есть гипербола, ветви которой
находятся в 1 и 3 четвертях, если кХ), и в 2 и 4 четвертях при к<0 ( при к=0 получим прямую у=0, те., ось абсцисс ). Гипербола имеет оси симметрии -
прямую у=х и прямую у=-х и центр симметрии - начало координат.
Гинербола, задаваемая уравнением У= ~ Отмечена ось симметрии -прямая у=х и точки пересечения этой прямой с гиперболой: А(1,1) и В(-1,-1), эти точки называются вершинами гиперболы.
Злесь кг^О, kj>0, к3<0 и кхку Пары (Ai3i), (АгЗг), (Аз,Вз) являются вершинами соответствующих гипербол. tT	л	1
Координаты Af хА1=Уа1=-^= •yKj
и	1
Вь ХВ1=УВ1—“с= з/к,
для пары (Аз,В3) Хдз—удз^-Д=
В общем случае графиком функции у = —(с # 0, ad * be) ex + d v	'
также является гипербола.
Рецепт” ее построения следующий: надо провести вертикальную и d	а
горизонтальную прямые, х = — и у = — , соответственно, и, принимая эти с	с
прямые за новые оси координат О’Х’ и О’Y’, построить относительно этих осей гиперболу:
k , be - ad
—, где к = —-— х'	с
График функции у =	-
Отмечены новые оси: прямые х—1 и у=3; т. О’ - новое начало координат ( в исходной системе ее координаты хо,=-1, Уо,=3 ); и точки пересечения гиперболы с исходными осями координат.
Для данной функции к=-1.
Заметим, что центром симметрии этой гиперболы является точка О’, осями симметрии будут прямые у=х+Ь+ и у=-х+Ь_, где константы и Ь. однозначно определяются из следующего условия: прямые у=+х+Ь± проходят через точку О’. ( В данном примере у=х+4 и у=-х+2)
Вертикальная и горизонтальная прямые, принимаемые за новые координатные оси, называются вертикальной и горизонтальной асимптотами.
Примечание. При построении графиков гипербол указывать точку О’ и находить значения к не обязательно. Чтобы выяснить, в каких четвертях лежат ветви гипербол, надо отметить точки пересечения с осями координат.
Примеры.
На одном чертеже построить графики функций: у^-Зх-З и у=-х-1
Замечание. При решении такого рода задач необходимо указывать точки пересечения графиков.
Для правильного взаимного расположения графиков удобно начинать с их общих точек.
Решая уравнения х2-2х-3—х-1 или х2-х-2=0 находим Х|—1, х2=2 . Подставляя эти значения в одну их функций ( любую!), получим
У 1=0, У2=-3
*3
Добавляя найденные точки к тем, которые необходимы для построения соответствующего графика ( для прямой это точки пересечения с осями координат, для параболы это вершина, пересечение с осью OY и пересечение с осью ОХ, если есть ), легко получить требуемый чертеж.
Решить графически систему неравенств:
Множество точек плоскости, для координат которых выполнено условие у^х2, находится над параболой у^
Аналогично, множество точек плоскости, координаты которых удовлетворяют условию у<5х-6, находятся под прямой у=5х-6
Постройте графики следующих функций:
1)^-2
2) у=2х+3
3) у = —^-х + 2
4) у=-Зх-1
6)2х+3у=6
7)-х+2у=1	8)3х-у=5	9) х=2
10)0*х+Зу=1
11)0*х+0*у=2
12)
у-2

х +1
Решите графически следующие уравнения и системы уравнений
19) -Зх+2=-Зх-1
20)|х|=2х+3
22) 1x1+х=-1- х+6
23) |х|=х-2
25)
2х - Зу = 4 х - у = 3
26)
' х + 2у = -3
-2х - 4у = 6
28)
у-|х| = 0
2у - х = 3
Изобразить точки плоскости, координаты которых удовлетворяют
неравенствам или системам неравенств
57) у!>|х|
58)у<1-|х|
[Зу^З-х
•Ъ-xsl
60)
у + Зх £ 0 2х а 1 + у
61)
у < х1 - х - 2
у > х2 - 2х - 3
62)
у s х! + 4
у > -х2 + 8
«>( ''Vх;5, |у 2. х2 + 4х - 5
Постройте на одной системе координат
64) у=х2-Зх+4
65) у =
х-3 2х-4

Постройте графики следующих функций:
29) у=-х2
30)у=-х2+1
31) у=х2-4х+3
32) у=2х2-Зх-2	33)у=х2+4х+1	3-1) у- 1 ^1x13
По следующим графикам определить знаки а, Ь, с.
38)	Известно, что парабола у=ах2+Ьх+с проходит через точки:
А(0,5), В(1,2), С(2,1). Найти ее уравнение и построить график
. Доказать, что любая тройка различных точек (хь yi), (х2, у2), (х3, 39) уз), не лежащих на одной прямой, где xi, х2, х3 попарно различны однозначно определяет проходящую через них параболу.
По трем точкам А, В и С, лежащим на параболе у=ах2+Ьх+с определить знаки коэффициентов и указать, есть ли у функции корни.
41) В разобранном выше примере найти координаты вершин гиперболы
Построить графики следующих функций и найти координаты вершин:
42) у=-—	43) у= —
X	X
Построить графики и найти уравнения осей симметрии
Найти координаты вершин следующих гипербол и построить график
Зх	ЛОз х-5
47)у = "1ТГ	48)у = -77Г
ю
49)* Доказать, что любая тройка попарно различных точек, не лежащих на одной прямой, однозначно определяют гиперболу, проходящую через эти точки.
4)(х-а)Чу-Ь)М12
Графиком этого уравнения является окружность, центр которой - О -имеет координаты х„=а, у0=Ь, а радиус равен R.
Найти координаты центра, радиус и нарисовать окружность:
50) х2+(у-1)2=1	51) х2-2х+у2-4у=0
52) х2-х+у2+2у-2=0	53) х2-6х+у2-2у-6=О
S)‘ F + ^ = 1
Графиком этого уравнения является эллипс. х?	у2	х2
Поскольку —— = 1-------5— < 1 и, аналогично, -	- = 1---z— < 1, то
a-	b	b2	а1
х2^2 и -b<ySb. Тем самым эллипс целиком находится в прямоугольнике;
Здесь Ь<а
Можно представлять эллипс как “сплюснутую” окружность, в частном случае, при а=Ь получим окружность.
Положим с—Va2 - b2 , точки с координатами х=-с, у=0 и х=с, у=0 ( на рисунке они обозначены F2 и Fi ) называются фокусами эллипса. Число с
е=— ( заметим, что 0<е<1 ) называется эксцентриситетом эллипса. Отрезки Я.
Оа и ОЬ называются соответственно большой и малой полуосью.
С точностью до выбора единицы длины, эллипс полностью определяется своим эксцентриситетом. Например, принимая а за единицу длины ( т е., а=1 и 0<Ь<1 ), при е=0 или получим окружность, при увеличении е ст 0 до 1 ( не включая ) эта окружность будет “сжиматься” в вертикальном направлении, неограниченно приближаясь к отрезку [-а,а].
Отметим без доказательства, что |р2Х|=а+ех, (F|Xl=a-ex, где X -произвольная точка эллипса, ах- абсцисса X
Отрезки F2X и F[X называются радиусами эллипса.
Нарисуйте эллипсы: 54)*
а) 4х2+9у2=36	Ь) 9х2+у2=9
Используя формулу 1 АВ I ^ха-хв^+Суа-Ув)2, где А(ха,Уа) и В(хв,Ув), докажите формулы:
55)* Докажите, что IFjXI+IFjXI не зависит от точки х
(Здесь F) J2 - фокусы эллипса, х - произвольная точка эллипса)
56)* Докажите, что верно и обратное, если для точки X | FjXl +| F2XI =2а ( где F1.F2 - фокусы эллипса, а - большая полуось ), то X принадлежит эллипсу.
Заметим, что две последние задачи вместе означают, что эллипс есть геометрическое место точек X, сумма расстояний от которых до двух заданных точек F, и Fj постоянна.
Аналогичные по форме утверждения можно сформулировать и для параболы и для гиперболы.
6)* У=М, У={*}> У=(*)
[х] - целая часть числа х, {х} - дробная часть числа х, (х) - расстояние от х до ближайшего целого числа.
Каждое число х попадает в один ( и только один! ) из интервалов вида [k,k+l), где keZ (целое число).
По определению: [х]=к, (х}=х-[х], (x}=mm(x-k,k+l-x)
Заметим, что х=[х]+{х}; [х]<х; 0<{х}<1; 0<(х) <1/2
К примеру [11=1, [1/2]=0, [Л- ]=2, т.к. 22=4<7<9=32, [-VT ]=-2, {1,75}=0 75, {Л~{Л"}=2-Л~ Функции {х}, (х) - являются периодическими с периодом 1, что означает просто, что {х+1 }={х}; (х+1)=(х) для любого
2. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ГРАФИКОВ ФУНКЦИЙ
Среди разнообразных способов построения графика функции самым банальным является, конечно, “построение по точкам”.
Суть его в следующем: сначала на координатную плоскость наносится более или менее густая сетка точек, через которые проходит данный график, для чего составляется таблица типа:
	-5	-3	-2	-1	0	1/2	1.5	2	3	4
У	1.1	1.2	1	2	3	11	-0.3	0.3	0.5	0.7
(конкретные числа мы подсчитали, взяв в качестве примера функцию х2~3 .
У —;--------), затем нанесенные точки соединяют “достаточно плавной”
X + X ~ 1
линией - графи»; готов. И графики простейших функций: у=х;	у=—-—
(их вид и основные свойства мы напомнили в части 1), а также графики функций у=зшх; y=cosx; у=2* - о которых вы узнаете позже - строятся именно таким способом. Но для немного более сложных функций, скажем, той, что мы выбрали в качестве примера, попытка построить ее график “по точкам” вряд ли будет сколько-нибудь успешной. На рисунке слева представлен ее график, построенный по точкам, справа - более точными методами (“правильный график”).	ч
Мы выделили три основные причины, объясняющих такую неэффективность метода построения по точкам:
1) Случайность выбора точек.
По тем или иным причинам ( психологическим, удобство счета,...) в качестве значения аргумента выбирают целые, в крайнем случае -рациональные числа, причем небольшие по абсолютной величине. Но на рисунке справа видно, насколько важны для правильного построения графика отдельные “особые” значения аргумента: это точки xtj=	 , где функция не определена, а график имеет разрывы; это
точки хз.^^-Уз-, где функция обращается в ноль, а график пересекает ось абсцисс; это, наконец, точки А(-3;1.2) и В(-1;2), где график имеет “горб”
( такие точки называются локальными экстремумами ). И найти эти точки, ие привлекая дополнительный идей, наобум, конечно, невозможно.
2) "Соединим отмеченные точки плавной линией".
Даже нанеся на координатную плоскость очень густую сетку - что само по себе сопряжено с долгой и трудоемкой работой - как мы можем быть уверены, что некоторая "плавная" линия правильно отражает ход изменения функции? На рисунке слева, по виду графика на интервале (0;1) еще можно догадаться, что что-то не так - график имеет сильный всплеск, но на отрицательной полуоси нет даже намека на существующий разрыв. Здесь нужны другие соображения, связанные с возрастанием или убыванием функции. Наконец, график произвольной функции совсем не обязан быть плавной линией - в отдельный точках он может иметь изломы. 3) Поведение графика функции на "бесконечности".
Как выглядит график функции при значениях аргумента, больших по абсолютной величине ( т.е., далеко влево и вправо от начала координат)? Ведь сколько бы точек мы не отметили - их все равно конечное число, т.е., вся информация, которую мы имеем, относится только к конечной части графика ( в примере - на отрезке [-5,4] ) - как понять, что происходит дальше? Какая закономерность определяет вид график при очень больших по модулю значениях аргумента?
И здесь без дополнительных соображений не обойтись.
Наиболее простой способ построения графиков функций состоит в том, что искомый график строится "по частям" из уже известных, готовых графиков функций, при помощи операций сдвига, растяжений, отражения, сложения или умножения графиков и некоторых других.
1.	Параллельный перенос (сдвиг).
Пусть требуется построить график функции y=f(x)-b.
Ясно, что ордината этого графика для всех значений х на b единиц меньше соответствующих ординат графика y=f(x), при Ь>0, и на |b| единиц больше - при Ь<0. Следовательно, график функции y=f(x}-b можно получить, сдвигая график функции y=f(x) как единое целое на b единил вниз ( параллельно оси OY ), когда Ь>0 или на |b| единиц вверх в противном случае.
Ал алогично, пусть требуется построить график функции y=f(x+a).
Рассмотрим фуНКЦИЮ y=f(x) И ПРОИЗВОЛЬНУЮ ТОЧКУ X], ПУСТЬ ЦХ])^!. Очевидно, что функция y=f(x+a) принимает значение yi в точке х2, определяемой их равенства х2+а=Х], те., x2=xi-a. Это верно для произвольной точки Xi из области определения функции f(x), значит, сдвигая график функции y=f(x) на а единиц влево, если а положительно, или на i at единиц вправо, если а отрицательно, получим график функции у=Цх+а)
Еа рисунке это выглядит так:
Поскольку прямую нарисовать легче, чем кривую, на практике обычно поступают так: переносят не график функции у=Цх), а оси координат, руководствуясь принципом "все относительно" - опустить график на b единиц вниз, это то же самое, что поднять ось ОХ на b единиц вверх, сдвинуть график на а единиц вправо, это то же самое, что сдвинуть ось OY на а единиц влево и т.д.
Наконец, отметим, что график функции y=f(x+a)-b строится последовательным выполнением обеих операций: сначала сдвигаем на |а| единиц вдоль оси ОХ (влево или вправо - в зависимости от знака а), потом на | b| единиц вдоль оси OY. Можно и в обратном порядке - результат будет тот же.
График параболы y=ic-2x-3 получен из графика параболы сдвигом на I вправо и на 4 единицы вниз
Или так, нарисовав параболу у=^, сдвинули оси: ось ОХ на 4 единицы вверх, ось OY на 1 единицу влево.
_	ах+Ъ „ ,	,
Пример. у=------ с^О, bc*ad

у
Проделаем следующие преобразования: а / с(сх + d) + b - ad / с сх + d be - ad
X + — с
a d be -ad Положим А=—, В=-, к=-------—>,
с с с
Л , к
У =-------т
сх + d
a	be - ad
— + '  ----
с	с(сх + d)
Для определенности мы считаем, что к>0; В<0; А<0
_______А
затем
Мы построили график гиперболы
а
к
стаут пупы QCH X	J'
координат: ось ОХ на I А| едшшц вверх, ось OY на IВI единиц влево, в
If новых осях графику гиперболы у=-------- становится графиком гиперболы
ах +Ь
у=-	+~ , старые же оси становятся, соответственно, горизонтальной и
вертикальной асимптотами:
х= -В, у=А
Заметим, что этот пример полностью объясняет принцип построения графика гиперболы в части ч где он был дан без пояснений,
2.	Растяжение и сжатие
График функции y=kf(x), где к>0, получается из графика функции у=Цх) "растяжением" вдаль оси OY в К раз, если к>1, и «сжатием» вдоль
OjBi—2О1А;
О3В3—2О3А3
О2В2-2О1А2
OiB^CXA,
OiBi=2/3OiAt	О2В2=2/ЗО2А2
ОзВ3=2/ЗОзА3	О4В4-2/ЗО4А4
График функции y=f(<ax), где <о>0. получается из графика функции
5’=f(x) "растяжением" вдоль оси ОХ
в — раз, если <в<1, и "сжатием" вдоль
оси ОХ в <а раз, если <п>1
0161=1/20^!	О3Вз=1/2ОзА3
О2В2=1/2О2А2	O4B4-I/2O4A4
OiBi=3O|Ai О2В2=ЗО2А2 ОэВз=ЗОзАз
3.	Отражения.
y=-f(x)
Ординаты графика функции y=-f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y=f(x). Таким образом, для построения графика функции y=-fix) следует построить график функции y=f(x) и отразить его относительно оси абсцисс:
Ясно, что функции f(x) и Ц-х) принимают одинаковые значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Следовательно, для построения графика функции у=Ц-х) нужно построить график функции y=f(x) и отразить его
Замечание 1. График функции y=f(-©x), соХ), строится в два этапа:
сначала "растяжение" в рт раз вдоль оси ОХ
( если |а>|<1 ) или "сжатие" в
|<в| раз ( если |<в|>1 ), затем - отражение полученного графика относительно осиОУ.
Аналогично, для построения графика функции у=-кДх), комбинируются сжатие или растяжение вдоль осн OY ( в зависимости от того |к|<1 или |к|>1 ) и отражение относительно оси ОХ.
Причем в обоих случаях эти операции можно выполнять в любой последовательности.
Замечание 2.
Укажем схему, по которой строится график функции y=kf(ox+a)-b.
y=f(x)----->
Начинаем с графика функции
y=f(|c)|x)-->
Производим растяжение или сжатие вдоль оси абсцисс
y=f(fflx)------> y=[k|fi^jx)
Отражение графика	Сжатие или
относительно оси растяжение вдоль ординат ( этап	оси ординат
выполняется только
прн ш<0)
y=|k|f(cox)-----> y=kf(cax)--------►
Отражение графика относительно оси абсцисс ( этап выполняется только при к<0)
у=кЦф(х+—)------> y=kf(<Dx+a)-b
ш
Сдвиг оси ординат на Сдвиг оси
. а	,	абсцисс на |Ь1
|—] единиц (влево,	1 1
®	единиц ( вниз,
если — <0, вправо,	еслиЬ<0,
в)
вверх, если
если^Х))	ь>о
Второй и третий этапы, по очевидным причинам, опущены.
4.	Графики функций, содержащие знак модуля.
Напомним определение модуля величины ( числа) а: {а, если а > О
-а, еслиа<0
Г рафик функции y=|f(x)|
о	X
График уравнения |y|=f(x).
Непосредственно из определения модуля следует:
J f(x), если f(x) > О Y [- f(x), если f(xj < О Значит, для построения графика функции y=|f(x)| нужно построить график функции y=f(x), затем ту часть графика, которая лежит над осью ОХ ( т.е, f(x)>0 ), оставить без изменений, а часть графика, расположенную под осью ОХ, отразить относительно оси абсцисс.
Поскольку |у]>0 для любого у, а |-у|=|у|, то для построения графика уравнения |y|=f(x) надо построить график функции y=f(x), затем удалить часть графика, лежащую под осью ОХ ( где f(x)<0 и ’/равнение |у|=Цх) не имеет решений ), а к части графика, находящейся над осью ОХ, добавить ее отражение относительно оси абсцисс (т.к. если |y|=f(x), то и 1-уНС*))
Г рафик функции y=f(|x|).
Функция ЗДх|) является четной ( т.к. уже |-х|=|х[ ), поэтому сначала строится график функции у=Цх) на положительной полуоси ОХ ( х>0 ), затем часть графика у=Ц|х|) на отрицательной полуоси получается отражением относительно оси OY.
3) у=хг-4|х|+3 Запишем фукнцию в таком виде:
Заштрихована ненужная часть полуплоскости ( где х<0 )
По определению модуля имеем: а) ||х-1|-2]-|у+2|=5
б) ||х-1|-2|-|у+2|=-5
Значит, требуемый график состоит из двух частей, определяемых уравнениями а) и б)
Займемся уравнением а): |у+2|=||х-1|-2|-5
График правой части мы уже умеем строить:
Заменим у+2 на у’ в осях OX, OY’ получим график:
Поскольку у=у’-2, то наш график получается из построенного
6) ||M+1|-2|=2^
Будем последовательно применять правило построения графика |y|=f(x) (т.е., снимая модули, будем «добираться» до у)
Для этого обозначим yi=||y|+l|-2; У2=1у1+1
Теперь имеем: |yz|=yi+2. Далее
|у|=У2-1 и график построен.
7) (у-пЧу-ЦС^+Зх+г)
Уравнение можно переписать так: |у-1|(|у-1|-х2-Зх-2)=О	( т.к. (у-
-1)2=|у-1|2)
Откуда следует, что график состоит из двух частей: прямая у=1 и
Итак,
Точки пересечения с осью абсцисс находятся из уравнения:
х2+Зх+2=1
х2+Зх+1=0

В общем случае для функции ( уравнения ), содержащей ( его ) знак модуля, график строится так: ось абсцисс ( координатная плоскость ) разбивается на части, на каждой из которых все выражения, стоящие под
знаком модуля, имеют постоянный знак. На каждой из этих частей с тем или иным знаком раскрываются знаки модулей и строится- график получившейся функции ( уравнения ). Совокупность построенных графиков ( каждый на своем участке!) и будет искомым графиком.
Поясним эту процедуру на примерах.
1) у=2х+|х+2|-|2х-1|
Разобьем ось абсцисс на интервалы:	* \/	%
(при х—2 х+2=0, при х=0.5 2х-1=0)	~2	*1
| xg(-°o;2),	y=2x-x-2+2x-l=3x-3
|| хе[-2;0.5), у=2х+х+2+2х-1=5х+1
III хе[0.5;+<ю), у=2х+х+2-2х+1=х+3
На каждом интервале имеется уравнение линейной функции, значит, графиком ее буде часть прямой, лежащей над данным интервалом.

Поэтому достаточно задать две точки на каждом участке, через которые
соответствующая прямая проходит. Например, у(-3)=-14,	у(-2)=-9,
у(1/2)=3.5, у(1)=4
Отметим, что так можно построить график любой функции вида: y=fl(x)+f2(x)+.. .+fk(x)±|gl(x)|±|g2(x)|±...
±Ы*)1
где все f|(x),...,fk(x) и gi(x),...,gn(x) -линейные функции. '
2) у=-|х|х+2|-3|
Сначала строим график функции у=х|х+2|-3
Надо разобрать два случая: а) х>-2, Ь) х<-2
a) x>-2 'xV2x-3 У(-2;3
Окончательный график y=-|xjx+2|-3|
Итоговый график.
Замечание, 'примерах такого рода обязательно надо находить значения (
функций в ьнцах интервала ( во втором примере это была точка х=2, в 3-ем - точка х? ) В разобранных примерах эти значения совпадали, н части
графика «склеивались» вместе без разрыва. Но бывают и противоположные ситуации.
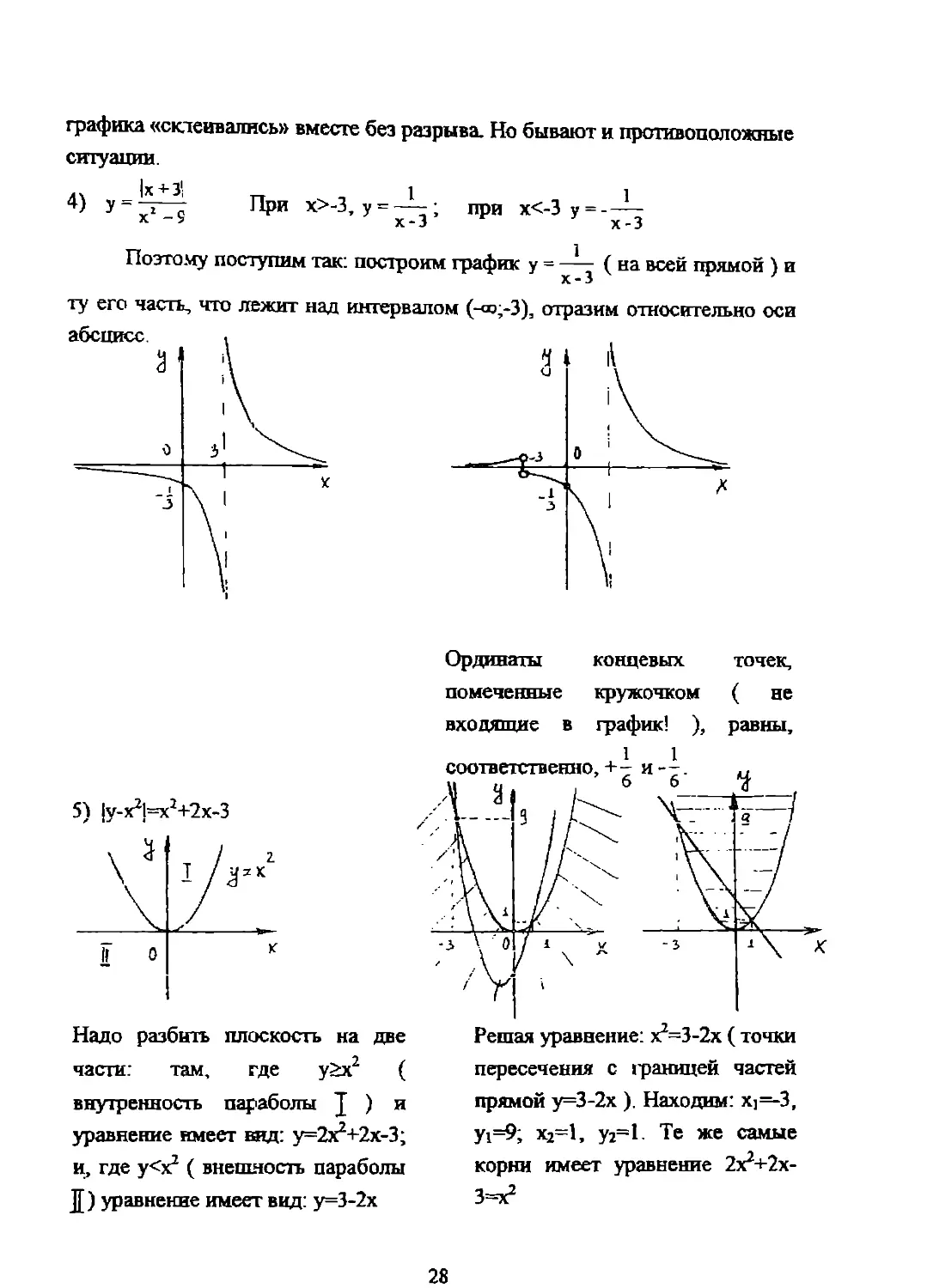
..	|х+3'	1	1
4) y~~i - При х>-3, у = —-; при х<-3 у = -—
х	х-3	х-3
Поэтому поступим так: построим график у = —- ( на всей прямой ) и
ту его часть, что лежит над интервалом (-оо;-3), отразим относительно оси
5) |у-х21=х2+2х-3
Ординаты концевых точек, помеченные кружочком ( не входящие в график! ), равны,
Надо разбить плоскость на две части: там, где у>х2 ( внутренность параболы J ) и уравнение имеет вид: у=2х2+2х-3; и, где у<х2 ( внешность параболы ][) уравнение имеет вид: у=3-2х
Решая уравнение: х2=3-2х ( точки пересечения с 1раницей частей прямой у=3-2х ). Находим: Xj— 3, У1=9; х2=1, у2=1 Те же самые корни имеет уравнение 2х2+2х-3=з?
Соединяя все вместе, получим искомый график:
У +х -2
Заметим, что сомножитель------ равен ±1, в зависимости от того,
’	у + х-2 н
больше нуля у+х-2 или меньше. Итак, над прямой у=2-х уравнение принимает вид:	под прямой у=2-х вид уравнения: у^х2.
Точки пересечения прямой у=2-х с параболой у=^ находим из уравнения 2-х=х2 , xi=-2, yi=4, Х2=1, У2=1, С параболой у=-х2 прямая у=2-х
7) |2|у-х|+|2у-х||=2
Имеем два уравнения: а) 2|у-х|+|2у-х|=2
б) 2|у-х|+|2у-х|=-2
Уравнение б) заведомо не имеет решений и дает пустое множество.
Для построения графика уравнения а) разобьем плоскость на четыре части;
Точки пересечения прямой у=-
1; х?=2, у2=2
и в каждой рассмотрим соответствующее уравнение:
1.	у<х, у>^х=> х=2
2.	y2x,yi|x=>y=jx+|
2	4	2
1
3.	у£х, у<-х х=-2
1	3	1
4.	У<х,у<-Х=>у=-Х--
х+- с границей 2 части - xi=-2, ут
Точки пересечения прямой у=^х-^ с границей 4 части - xi=-2, yi—2;
5.	Г рафик уравнения x=f(y) (График обратной функции)
Чтобы построить график уравнения х=Цу), можно поступить так: выразить у через х ( если получится ), т.е., найти зависимость y=g(x) и построить ее график ( функция g(x) называется обратной функцией ). Но, во-первых, эта зависимость может быть достаточно сложной, во-вторых, может быть, выразить у через х вообще не удастся. Поэтому такой способ не самый лучший.
Проще поступить по-другому.
Сначала в осях ОХ и OY построить график функции y=f(x), после чего отразить его относительно биссектрисы 1 четверти у=х, получится требуемый график. Эго очевидно, потому что при симмекрни относительно биссектрисы у=х оси ОХ и OY переходят друг в друга, и, значит, любая точка М(хо,уо)переходит в точку М’(уоЛ), короче говоря , при такой симметрии х меняется на у и наоборот, и график функции у=т(х) переходит
Пример. х=2у-у2 Сначала (в осях ОХ и OY ) построим [рафик функции
6.	Арифметические действия.
(^Л*)+ё(х).А>)е(х))
__1_
При построении графика у=—— сначала строим график y=f(x), при этом обращая внимание на следующие моменты:
1)	Точки, где f(x) обращается в 0 или стремится в бесконечность.
2)	Интервалы, где Дх)>0, соответственно, Дх)<0.
3)	Интервалы, где 1(х) возрастает, убывает и локальные экстремумы ( если это возможно найти )
4)	Поведение функции Дх) на бесконечности ( т.е., при больших по абсолютной величине значениях аргумента ).
На картинке это выглядит примерно так:
Отметим следующие
закономерности:
1)	Нули f(x) переходят в
1
оесконечносгь —в точках, 1(х)’
где f(x) стремится в
„ 1 бесконечность,	-
f(x)
обращается в ноль, причем
этот воль выкалывается.
2)	Знак Дх) сохраняется у
1
Цх)'
3)	На интервалах, где Дх) имеет постоянный знак,
убывание Дх) переходит в
возрастание
)
Цх)
и наоборот;
локальный минимум Дх)
становится
локальным
1 максимумом и наоборот.
4)	Если на бесконечности график y=f(x) имеет горизонтальную асимптоту 1 у=а, а*0, то график у=—— i(.xj
имеет	горизонтальную
асимптоту у= -. а
Сначала строятся графики функций у=Дх) и y=g(x). График функции y=f(x)+g(x) строится по точкам, складыванием ординат графиков функций f(x) и g(x), соответствующих одному н тому же значению аргумента из общей области определения.
При этом полезно учесть следующее:
1)	Точки, где какая-нибудь из функций обращается в бесконечность.
2)	Поведение на бесконечности обеих функций.
3)	Интервалы, где эти функции сохраняют знак.
4)	Интервалы, где эти функции возрастают или убывают.
Заметим, что функция v=x+—- нечетная, х
поэтому ее график достаточно построить только для положительных значений х
Поскольку в начале координат функция
1
у=- стремится в бесконечность, то
справа, в окрестности 0, основной вклад дает она; т.к. функция х на интервале (0;оо) положительна, то результирующий график будет лежать выше графика гиперболы и убывать до некоторой
точки
На бесконечности график гиперболы приближается к оси ОХ, и основной вклад дает график у=х, результирующий график лежит над прямой у=х ( т.к. — >0 ), приближаясь к ней по мере увеличения х. Точку.
, 1
где функция х+- достигает наименьшего значения, легко найти, используя неравенство: а+Ь>2 Tab, а>0, ЬХ)
( Доказательство, а-2 -Jzb +Ъ=( Та /-2 Та -Th +( Tb )2=( Та - Tb )2Х) и равенство достигается только при а=Ь )
Имеем: х+ - >2 ^х • - =2, причем равенство возможно только при х=-, т.е., х=1 ( хХ) ). Симметрично отражая построенный график относительно начала координат, получим искомый график.
Построение графика функции y=flx)-g(x) сводится к предыдущему, построением графиков у=Дх) и y=-g(x).
Цх)-8<х)
Для построения графика функции f(x)-g(x) надо построить графики функций Ях) и g(x) и перемножить значения ординат, соответствующих одним и тем же значениям аргумента из общей области определения.
При этом полезно учесть точки, где какая-нибудь из функций обращается в ноль или стремится в бесконечность, интервалы, где эти функции сохраняют знак. _	х-2
Пример. у=
Неявное задание (f(x,y)=O ).
В таких ситуациях надо сначала упростить соотношение f(x,y)=O, а затем выразить явно у через х или х через у ( Если это не получится, значит, требуются более серьезные идеи )
Пример. 1)хУ-ху-2=0
Разложим это выражение на множители: х2у2-ху-2=(ху-2Хху+1)
Тем самым надо построить два графика: ху-2=0 и ху+1=Э
у=2/х	у=-1/х
х
у1 ~ 3	1
2)		= у -1 Эго соотношение эквивалентно такому:
уг-3 = (у->:)(у-1)	Гу(х + 1) = х + 3
Находим < у х	к у * х
,	х + 3
ясно, что х*>-1 и, окончательно, у=—-, у*х
’	х + 1
тт -	х + 3
Найдем те значения х, которые не подходят	—- =х
Точки (л/з ,7з ) н (--Тз ,-7з ) выкалывается из графика гиперболы
Могут выпасть и целые участки графика.
|х + 2|-|х|-2
3)	= 2
у + х
Преобразуем, получим 2у=|х+2|-[х|-2х-2; у£-х
Разобьем ось абсцисс на три интервала:
1.	хе(-оо;-2) у=-х-2 у(-4)=2, у(-2)=0
2.	хе[-2;0)	у=0
3.	хе[0;+оо) у=-х Весь промежуток [0;+<ю) выпадает.
Асимптоты, локальные экстремумы.
л.	а,х2+Ь,х + с,
Мы ограничимся функциями вида: у= ---------5----где числитель
а2х + Ь2х+ с2
и знаменатель не имеют общих корней, знаменатель тождественно не равен
О, и теми, которые приводятся к такому виду в результате преобразований.
Вертикальной асимптотой называется прямая х=хо , если хо - корень уравнения ajX2+O2X+C2=0 ( если корней это уравнение не имеет, то, соответственно, нет и вертикальных асимптот )
При приближении х к точке хо слева или справа график функции неограниченно приближается к прямой х=хо .
Наклонные и горизонтальные асимптоты.
Если степень многочлена a^+bix+ci равна степени многочлена a2x2+bix+c2 ( мы считали, что at и а2 могут быть равными 0 ), график имеет
„	а.	_	.
горизонтальную асимптоту. Это прямая у=—. если а2?н? ( и, в2 ’
автоматически, ), илн у=~, если а2=0. Ь2
При больших по абсолютной величине значениях аргумента х график функции неограниченно приближается к данной прямой.
( Пусть, к примеру, а2*0, поделим на х2 и числитель и знаменатель:
Ь. С	.г	с bt bz ct с2
а,+ — -i--v Ясно, что при больших х все дроби -	~т-
1 X Х~	X X X X
У bz с-	а
а2 + ~очень малы, и основной вклад дают а] и а2 , т.е., у® — )
Если же степень числителя меньше степени знаменателя, то график будет иметь горизонтальную асимптоту у=0, т.е., ось ОХ.
Наконец, если степень числителя на единицу больше степени знаменателя, график будет иметь наклонную асимптоту - некоторую прямую y=kx+b, к которой он неограниченно приближается при стремлении х к бесконечности.
2х* - х + 5
Например, у=——	к=2/3 ( к всегда равно отношению
коэффициентов при старших степенях ). Чтобы найти Ь, рассмотрим разность:
2х2 -х + 5 2^_6х2-Зх + 15-бх2 - 8х -Пх + 15	И	-1
Зх+4 ' 3Х" 9х + 12	“ 9х + 12	~9 ИУ~3*'"9 '
наклонная асимптота.
2х' - х+5 2	11	135
Как легко подсчитать, разность —-------------1-х-—)=---------- при
_'х+4 v3 9' 81Х + 108 г
больших по абсолютной величине значениях х становится очень малой, что
и означает, что график -
неограниченно приближается к прямой
2 II
3Х' 9 ’
Локальные экстремумы.
Отыскание локальных экстремумов проводится с помощью производной, но в данной ситуации помогает такое соображение:
ах2 + Ь.х + с
Рассмотрим уравнение ——--------------=Л, где А. - произвольное
а2х + Ь2х + с2
действительное число.
Будучи квадратным ( (aI-^a2)x2+(b|-xb2)x+(Cj-?.ci)=0 ), оно может иметь два, один или ни одного корня.
Геометрически корни этого уравнения - это абсциссы точек .	.	а|х2+Ь]х + с1	_
пересечения графика функции у=---------------с прямой у=А.
а2х +bjX+Cj
Зная X,, нетрудно найти х:
Как нетрудно видеть, тот случай, когда имеется ровно один корень, соответствует локальному экстремуму. Другими словами, надо записать дискриминант квадратного уравнения D=(bi-?.b2)M(ai-Xa2) (d-Xcz) и найти к из квадратного уравнения IX).
х=т^-~г( т.к. 1Х))Пример.
Найдем локальные экстремумы:
х2 -3
к (Х.-1)х2+Лх+3-Х.=О
D=X.2-4(X-1X3-X)=5X.2-16X.+12=O =>^=6/5 ?.2=2
-6/5	,	-2	,
Х,ТТЛ~3 Х!"“1
Найдем асимптоты:
Вертикальные:
х2+х-1=0 Х|Д=—-
Х1=~1~и Х2“
Г оризонтальная	у= 1
Точки пересечения с осями: xi>2=± -Л у(0)=3
4х2 - 4х + 5 2х-1
Пример. у=
4Х2 — 4х 5	,
Локальные экстремумы:	—j— =k 4х-(4+2Х)х+5+Х=0
1/4D=(2+A.)2-4(5+X)=?l2-16=0 => Xu=±4 2+4 .с	2~4 А С
xi=——=1.5	х2=—--=-0.5
4	4
1 Вертикальная асимптота: х=-
,	4х2 - 4х + 5	- 2х + 5
Наклонная асимптота: к=2; ---------------2х=------=> Ь=-1
2х -1	2х-1
Итак, у=2х-1 - наклонная асимптота.
Точки пересечения с осями: у(0)=-5, с осью ОХ - нет.
Задачи.
Постройте графики следующих функций и уравнений.
Условное разбиение по темам: номера 67-96 посвящены графикам кусочно-линейных функций; 37-118 - кусочно-квадратичных; 119-144 - кусочно-дробно-рациональных; 145-161 - арифметические действия с графиками;
162-168 - неявное задание.
67)у=|х-2|	84) ||х|-||у-1|-ЗЦ=1	101) у=-]x2+3ixi-10|
68) у=2-|х+2]	85) ||y|+x|+||yj-x|=y-x	v + 2 '®> ^"х+3
69) у=|3-|х+1||	1у-х| 1х-11 , у-х х-1	103) у=^х2-2х+1 ' } х-2
70)|у|=2-х	йт, 1х-2|	1уИ , 87)	7Тзх = 3	104) |у-х|=х2-2х
71) М+|х|=2	x’-v2 88) -^=|у|+х	1С5) [у-х^-х-г
72) |у+2|+2|х-1|=4	89) |||у-2|-х|-2|=2	106) (х2+4х+2)1у-х|=у2-х1
73) у=|2х-1|+х	90) |]х+1|+]|у-1|-3|-3|=1	ifA У-W	1 у^-х х-2
74)у=|х-1|+2|х+1|	91) |||у|+|х-2|-3|-2|=1	108) х=г-2у
75) у=|х-1^х-2|+2|х+2|-6	92) -2р4=2 у-|х +11	109) ^^-Зу-Л
76) у=Зх-1+|х-2|-|>.-1|	93) y^2-iilx+lj-i-2Hj	110) -)=ix2-9|-jx2-4'|
77) Цу|-|х)|=2	94) |у|=2-|2-|1-|х|||	1И)|х-У'=Г
78) ||у|-1Нх+2|	95) ||х+у|-|х-у||=2	H2)(jx|-l)2=y4
79) у=|||х-11-2|-3|	96) ||х+у|+|х-у||+||х-у|-|х+уЦ=2	П3)у=|х2-2х-3|
80) ||у-2|+1 |=2-|х+1|	97) 1у1=2|х|-х2	114) |у|=х2-Зх+2
81) |у-2х|+[у+2х|=4	98) у=х|х-2|-3	115) |у[=2+х-х2
82) |2у-х|+|у-2х|=3	99) |у|=(х+1)|х+2|+6	116) |у+2|=х2-2|х|+2
83)|у-х+ЗНУ+2х+1|=5	100) у=-|х|х+3|+2]	H7)y=S^^i
118)y.tfoM =
120)y=^±2
121) 1 = ^ у x + 3
122) - = £Ц у H
123>^dh
124) x+y+xy=l
125) x+jy|+xy=l
126) x+(x-l)|y-l|=l
127)	x3-^xJ-4' + 2
~ 3	2(х-1)
/S?;.	х3 - xlx2 —41 + 2
-128)у-1=	L 1
2|Н

129) у=п~4 1уМ
130) y=—
131)y=^±*
33 x + 2 2x-l 1321
. 2x-l 133>yT+i i34)y-bhd!
33 2x-l
оды-^	152)У=^хЛ-3
136)^11=^1	153^774
137)|у|=—Ц- 1+—	154)у=^
X- 1	
|И)Г'-'Й	х3 155) у=~	 ’J xJ-4x + 3 <
139) у- '	,	х3-2х + 5 156) у~
1-		Х-1
Ы-1	
140) х=^ М+1	157) у=—2V3 Х-1
141) х= — У+1	158) у= 2Х'3 33 х2 + 4х+5
142) |х-Ц=^	х2-Зх- 4 159)*= (X.,)2
...	2х-1	16О)у=[^-~--3‘~10 33 |х-2(х + 2)
I44)y.±±fc5	1б1)у=г-^| + .„3
х + 4х +3	|х-1| (2-х)2
’145) У=^	X 1	1 loz) - + -=х+у ух
146) у=Л+х X	163) -Лг+Д =|х|+у-2 у-2 |х!
147) у=^-х* X	164) (у+х)2-2(у+х)-3=0
148)у=Аг + А	165)6х2-х|у|У=0
.	х-2 х-1	
149)у=-Ц--5-	166) (2х+х2-у;2+2(2х+х2-у)-3=0
х-3 х-2	
150) у=-ч—	 3 х3 + 4х + 3	167) (х-1)2(у-1)2+|х-1Ку-1)-2=0
151)y=jj 12		168) 1х|х2-|у|у2+|х|у2-|у|х2+|у|-
xlx| +5х + 6	1*1=0
7. Г рафики иррациональных функций.
Начнем с графика функции у= Jx .
Область определения функции y=Vx есть промежуток [О;+ад) ( т.к. кзадрагный корень существуют только для неотрицательных чисел ).
Область значений, очевидно, (0;+<п).
Поскольку равенство у=д/х эквивалентно условию у2=х и у^О, то график у=7х легко строится, используя способ, изложенный в главе 2.
Нижняя часть параболы (симметричной параболе у=х‘ относительно прямой у=х ) откинута, ввиду условия у£0.
Любой график функции у= Tax + b строится по схеме, изложенной на
странице 20.
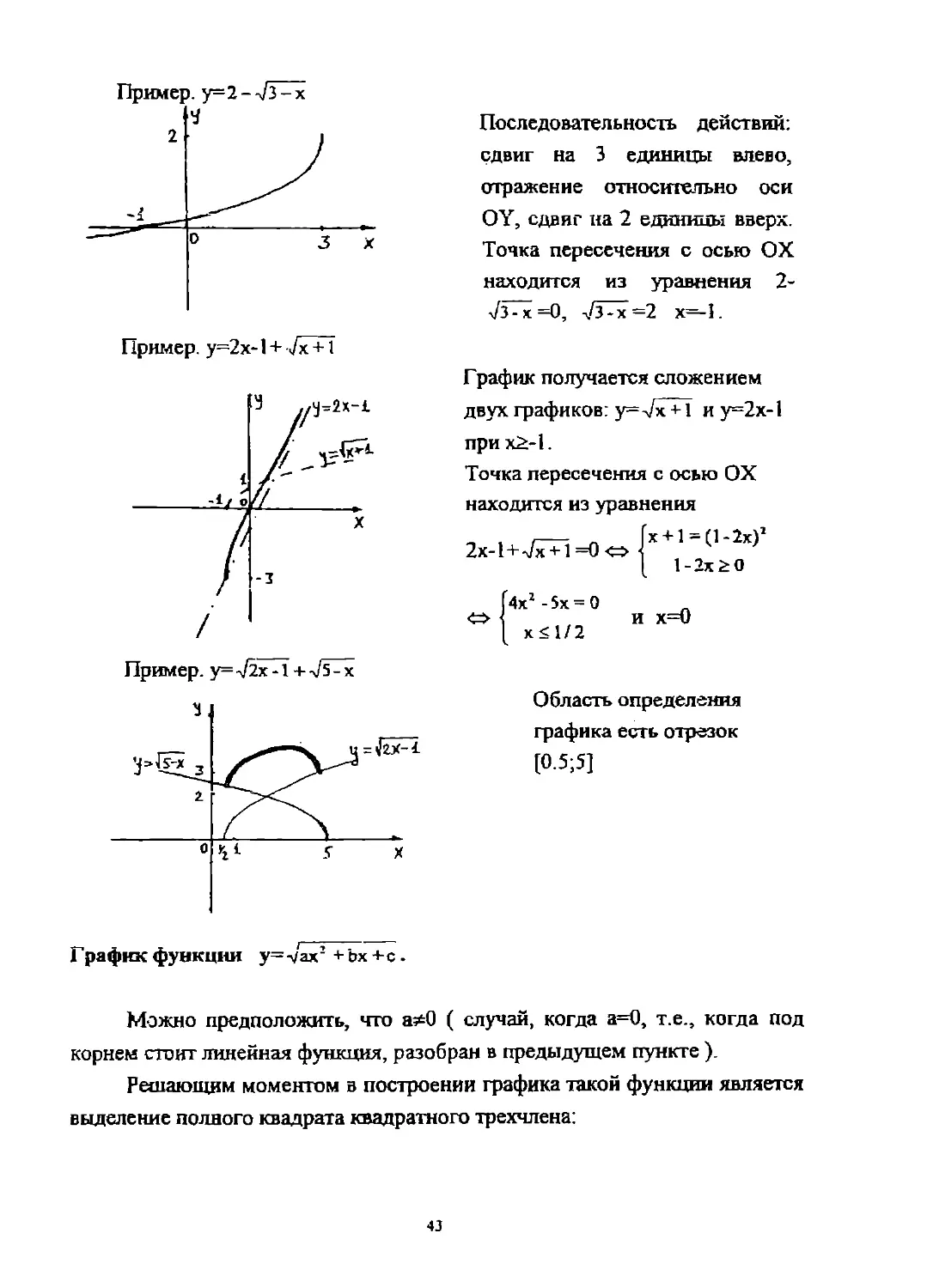
Пример. y=Vx-2
График получается из графика у=7х сдвигом на 2 единицы вправо по оси ОХ.
у= ./2(1/2-х) = -/2^1 /2 - х
График получается из графика у=7х в результате комбинации сдвига ( на 1/2 влево ), отражения относительно осн OY и растяжения вдоль оси OY в J2 раз.
Последовательность действий: сдвиг на 3 единицы влево, отражение относительно оси OY, сдвиг на 2 единицы вверх. Точка пересечения с осью ОХ находится из уравнения 2-у!з-х =0, 73-х =2 х—1.
График получается сложением двух графиков: у= -7х-Н и у=2х-1 при х£-1.
Точка пересечения с осью ОХ находится из уравнения „ . I----- „	Ix + l^l-lx)1
2x-l+-Jx +1 =0 <=> (
1-2x2* О
4хг-5х = 0
И х=0 х<1/2
Область определения графика есть отрезок [О.5;5]
Можно предположить, что а*0 ( случай, когда а=0, т.е., когда под корнем стоит линейная функция, разобран в предыдущем пункте ).
Решающим моментом в построении графика такой функции является выделение полного квадрата квадратного трехчлена:
ь ь2
ax2+bx+c=a(x+—)2+(c— ^a^x-xo^+S,
„	, bZ ч
где мы приняли за S выражение (с-—), за хь - константу 4а
b
2а ‘
Разберем отдельно два случая.
1)а<0
Если дискриминант D квадратного трехчлена ах2+Ьх+с отрицателен, те., для любого xeR ax2+bx+c<0, то область определения функции у=т/ахг +Ьх + с - пустое множество, и графика нет.
Если дискриминант D положителен, и xj, Х2 - корни уравнения ах2+Ьх+с=0, то область определения функции есть отрезок [х^хг], и графиком функции является в общем случае эллипс ( точнее, часть эллипса, лежащая над осью ОХ).
В основном, нас будет интересовать случай а= -1.
Уравнение, задающее функцию, легко переписать в виде: y2+(x-x0)2=S, у2Ю; поскольку S>0, S можно представить как S=R2, и это есть уравнение полуокружности, расположенной над осью ОХ, с центром в точке О(хс;0) н радиусом R.
2)аХ)
Выделим полный разность: А(х)=Л/а(х - х0 )2 + S - Va]x - х,
Преобразуем ее так:
A(x}=^a(x-x0)2 +S - -a(x-x<>)2+S-a(x-xe)
-УаГх-х,,)2 +S + 7а(х-х0)2 J^x-xJ2 +S + т/а(х-х0)
квадрат: ax2+bx+c=a(x-Xo/-S и рассмотрим
|х - х„| =т/а(х - х,)2 +S-^'a(x-x0)2 =
2	S
Наконец, Л(х>п —	-
Ja(l-—)2+—+ Ja(l-—)’ Ч х ' х V х
Ясно, что при больших по абсолютной величине значениях х
Д(х)=Л. Но это означает, что «угол» y=Va jx-xoj - является наклонной асимптотой графика функции y=-Jax2+Ьх+с, т.к. график неограниченно приближается к сторонам угла по мере увеличения значений х.
Заметим также, что при S>0 ( это соответствует тому, что дискриминант уравнения ах2+Ьх+с=0 отрицателен ), Л(х)>0 и, значит, график лежит над асимптотой; при S<0 ( т.е., дискриминант положителен, уравнение ах2+Ьх+с=0 имеет корни Х|,Х2, и область определения есть объединение двух интервалов: (-®;xi]<j[x2;^-«>) ) график состоит из двух частей ( над интервалом (-«рч] и (хг;+®)) и лежит под асимптотой.
Можно показать, используя формулы замены координат, что график гиперболы у=-, повернутый на угол 45° вокруг начала координат против часовой стрелки ( точнее, его часть, расположенная над осью ОХ ), будет графиком функции y=~Jx~ + Г, он же, повернутый на угол 45° по часовой стрелке, будет графиком функции y=-Jx’ -1 ( и, снова, только его часть над осью ОХ).
Общий случай у=7ах2 +Ьх + г получается применением еще операций сдвига и растяжения.
Здесь ax2+bx+c=a(x-xo)2+S;
S<0, X|,x2 - корни уравнения ax2-4jx+c=0
Примеры
1) у=3+л/-х3 +бх - это полуокружность y=3+-j9-(x-3)’
Здесь ах2+Ьх+с=а(х-ХоУ+S; SX)
2) |у|=1+л/х’~-бх+8
Сначала строим график функции у=	-6х + 8
Затем поднимаем его на 1 вверх и отражаем относительно оси ОХ:
3) У=^х2 -4х-5|
Мы должны рассмотреть два случая;
а) х2-4х-5^0, т.е., xe(-<»;-l]Kj[5;+co)
у=л/х2-4х-5 = V(x-2)2-9
b) X^x-ScO, т.е., xe(-l;5) у=л/-хг + 4x + 5 = ,)9- (x- 2)2
Соединяя их вместе, получим искомый график: ‘	у
4) У=2- л/х2 + Зх + 4
Начинаем с графика у=7х2 +Зх + 4 =
Координаты вершины гиперболы
Затем отражаем его относительно оси ОХ и поднимаем на 2 единицы рверх:
Точки пересечения с осью ОХ находим из уравнения: х2+Зх+4=4 => х,— 3,х2=0 ,,	. 3	л/7 ,
Координаты вершины: (- - ,2 - — )
5) y=2x+-j4x2 + 16х +17
Заметим, что если график функции у=у4х2 + 16х + 17=т/(2х+4)2 +1 имеет наклонную асимптоту у=|2х+4|, то график функции у=2х+л/4х2 +16Х + 17 имеет наклонную асимптоту у=2х+|2х+4|, так как ясно, что (2x+j4x2 *16х + 17 )-(2х+|2х+4|) стремится к нулю по мере возрастания аргумента ( 2х просто сокращается ).
Точнее, мы имеем наклонную асимптоту у=4х+4, когда х стремится к +» и горизонтальгрто асимптоту у=М, когда стремится к -=о.
»	Теперь ясно, что графикам на-
шей функции будет гипербола в асимптотах у=4+4х ( х—►+« ) и
<

Задачи.
Постройте графики функций и уравнений.
1МЛ V=.7?7	179)у=|(3-2х-4л/5-х)	189)	-?4x2 + 5x -10
170} y=V^	180) y=x+2+ 7б - x	190)у=л/Зх2 +12x + 16-l
171)y=VR	181) у=)х|+л/2х + 4	191) у=л/-х2 -4x + 12
172) у=3+лАГ2	182) y= л/2х -1 + Jx	192)у=л/-х2 -5x
173)y=-Vf-2x	183) y=|VT7-l|	193) y—^-W^
174) |у-1(=2+уТ1	184) у=л/6-х +Vx + 2	194)у=Л/’4х-21 + 2
175) |y|-l=^2x + 9	185) |y|=V2x + 7 -л/х + 3	195) [y-2|=2-^-x2 +4x-3
Г/ у=х+л/х-2
Г у=2+ д/x+lx-i]
186) у= XX3 - Зх + 2
Гу=-Лх + з|+|х-1|
187) у=Л3-2х+3
188) у= Jx3+|2х + 1|
196) у=-7х3 +xjx^4| + 2
197) |у+2|=|-Л+4х-Х-1|
198) у=
1*М х3 -4

Ответы.
1 к<0, ЬХ). 17. к>0, Ь<0. 19. 0, т.к. прямые параллельны. 21. х=1/2. 23. 0 2 х=1, у=-2. 27. 0 31. С(2;-1); (1ЭО); (3;0); (0;3). 33. С(-2;-3); (-2±7з ;0); (;). 35. аХ), Ъ<0, с<0. 37. а<0, ЬХ), сХ). 41. (0,2), (-2;4). 43. (3;3), (-3;-3).
4 у=х+1,5; у^-х-1/. 47. (0;0), (-6,6). 51. (1;2), R=T5.53. (-3;1), R=4.


93.
97.
99





SR

6Л

СОДЕРЖАНИЕ.
Сводка основные; определений................. 1
I Графики простейших элементарных функций ... 2
1)	Линейная функция.......................... 2
2)	Квадратичная функция..................... 4
3)	Дробно-линейная функция.................... 5
4)	Уравнение окружности..................... 11
5)	Уравнение эллипса........................ 11
6)	Целая и дробная часть..................... 13
II Элементарные методы построения графиков функций 13
1) Параллельный перенос...................... 15
2) Растяжение и сжатие....................... 18
3)Отражения ................................. 19
4)	Графики функций. содержащие знак модуля..	21
5)	График уравнения х =f(y).'............... 30
6)	Арифметические действия................... 31
Разное, а) Неявное задание................... 34
б) Асимптоты, локал ьные экстремумы.......... 35
7) Графики иррациональных функций............ 42
Ответы ...................................... 49