Discrete Mathematics
with Combinatorics
JAMES A. ANDERSON
University of South Carolina, Spartanburg
Prentice Hall, Upper Saddle River, New Jersey

Дискретная математика
и комбинаторика
ДЖЕЙМС А. АНДЕРСОН
Университет Южной Каролины, Спартанбург
Москва • Санкт-Петербург • Киев
2004

ББК 32.973.26-018.2.75
А65
УДК 681.3.07
Издательский дом "Вильяме"
Зав. редакцией СИ. Тригуб
Перевод с английского канд. физ.-мат. наук ММ. Беловой
Под редакцией канд. физ.-мат. наук С.С. Шкильняка и М.Р. Саит-Амепгова
Научный консультант докт. физ.-мат. наук, проф. Ю.В. Казаченко
По общим вопросам обращайтесь в Издательский дом "Вильяме" по адресу:
info@williamspublishing.com, http://www.williamspublishing.com
Андерсон, Джеймс А.
А65 Дискретная математика и комбинаторика. : Пер. с англ. — М. : Издатель-
Издательский дом "Вильяме", 2004. — 960 с. : ил. — Парал. тит. англ.
ISBN 5-8459-0498-6 (рус.)
Эта книга представляет собой современный учебник по дискретной математике.
Кроме таких разделов, как математическая логика, теория множеств, комбинаторика,
теория графов, теория алгоритмов и вычислений, традиционно включаемых в основ-
основной курс дискретной математики, она содержит обширные сведения по теории вероят-
вероятностей, алгебре и теории чисел. Особое внимание уделено теории доказательств. Чте-
Чтение книги требует некоторой математической культуры, хотя для изучения основных
глав достаточно знаний по математике в объеме средней школы. Материал сопрово-
сопровождается многочисленными примерами, в конце каждого раздела приводится большое
количество упражнений.
Книга адресована в первую очередь преподавателям и студентам технических
специальностей. Она будет также полезна тем, кто интересуется дискретной матема-
математикой и желает изучить ее самостоятельно.
ББК 32.973.26-018.2.75
Все названия программных продуктов являются зарегистрированными торговыми марками соответ-
соответствующих фирм.
Никакая часть настоящего издания ни в каких целях не может быть воспроизведена в какой бы то
ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая
фотокопирование и запись на магнитный носитель, если на это нет письменного разрешения издательства
Prentice Hall, Inc.
Authorized translation from the English language edition published by Prentice-Hall, Inc, Copyright ©
2001
All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means,
electronic or mechanical, including photocopying, recording or by any information storagg;;;f^rnj:^alsystem,
without permission from the Publisher.
Russian language edition published by Williams Publishing House according to^b^Agr^nent wf^hu^&I
Enterprises International, Copyright © 2003
ISBN 5-8459-0498-6 (рус.) © ИздательскМ
ISBN 0-13-086998-8 (англ.) © Prentice-Hall

кание
Н
1
2
3
Предисловие ю
Таблицы истинности, логика,
доказательства is
1.1. Высказывания и логические связки 15
1.2. Условные высказывания 23
1.3. Эквивалентные высказывания 27
1.4. Аксиоматические системы: умозаключения
и доказательства 34
1.5. Полнота в логике высказываний 45
1.6. Карты Карно 50
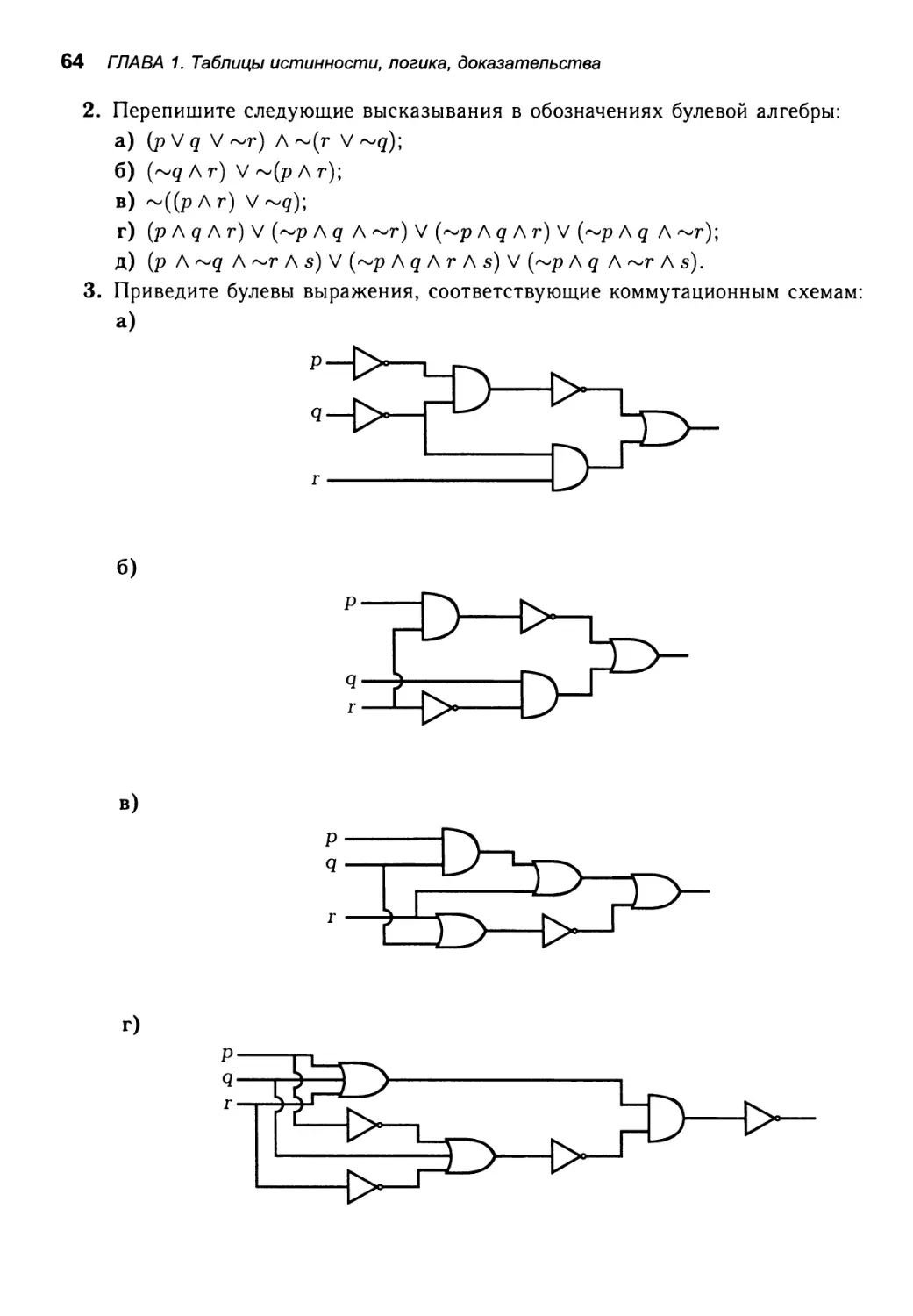
1.7. Коммутационные схемы 56
Теория множеств 67
2.1. Понятие множества 67
2.2. Операции над множествами 71
2.3. Диаграммы Венна 77
2.4. Булевы алгебры 84
2.5. Отношения 90
2.6. Частично упорядоченные множества ЮЗ
2.7. Отношения эквивалентности 106
Логика, целые числа
и доказательства из
3.1. Исчисление предикатов ИЗ
3.2. Основные положения теории доказательств
и теории целых чисел 123
3.3. Математическая индукция 129
3.4. Делимость 139
3.5. Простые числа 144
3.6. Сравнения 149

6 Содержание
4
5
6
7
Функции и матрицы 156
4.1. Функции 156
4.2. Специальные функции 161
4.3. Матрицы 167
4.4. Мощность 177
4.5. Мощность (продолжение) 178
АЛГОРИТМЫ И рекурСИЯ 184
5.1. Циклы и алгоритмы для матриц 184
5.2. Рекурсивные функции и алгоритмы 188
5.3. Сложность алгоритмов 201
5.4. Алгоритмы сортировки 205
5.5. Префиксная и суффиксная записи 214
5.6. Двоичные и шестнадцатеричные числа 219
5.7. Числа со знаком 231
5.8. Дальнейшее изучение матриц 237
Графы, ориентированные
графы и деревья 244
6.1. Графы 244
6.2. Ориентированные графы 252
6.3. Деревья 259
6.4. Мгновенное безумие 267
6.5. Пути и циклы Эйлера 270
6.6. Матрицы инцидентности и смежности 278
6.7. Гиперкубы и код Грея 290
Теория чисел 298
7.1. Решето Эратосфена 298
7.2. Метод выделения множителей Ферма 300
7.3. Алгоритмы деления и алгоритм Евклида 301
7.4. Цепные дроби 306
7.5. Подходящие дроби 310

8
9
10
11
Содержание 7
Комбинаторика и вероятность зш
8.1. Основные комбинаторные принципы 316
8.2. Комбинаторный принцип сложения 324
8.3. Перестановки и сочетания 331
8.4. Формирование перестановок и сочетаний 343
8.5. Введение вероятности 347
8.6. Обобщенные перестановки и сочетания 354
8.7. Перестановки и сочетания с повторением 359
8.8. Принцип клеток 363
8.9. Снова о вероятности 369
8.10. Теорема Байеса 384
8.11. Цепи Маркова 386
Алгебраические структуры 392
9.1. Вновь о частично упорядоченных множествах 392
9.2. Полугруппы и полурешетки 397
9.3. Решетки 403
9.4. Группы 409
9.5. Группы и гомоморфизмы 415
Некоторые специальные вопросы
теории чисел 422
10.1. Целочисленные решения линейных уравнений 422
10.2. Решения сравнений 424
10.3. Китайская теорема об остатках 428
10.4. Свойства функции ф 433
10.5. Порядок целого числа 439
Некоторые специальные вопросы
теории рекурсии 448
11.1. Однородные линейные рекуррентные
отношения 448
11.2. Неоднородные линейные рекуррентные
отношения 460
11.3. Конечные разности 469
11.4. Факториальные многочлены 473
11.5. Суммирование разностей 483

8 Содержание
12
13
14
15
16
Снова о комбинаторных подсчетах 489
12.1. Задачи о размещении 489
12.2. Числа Каталана 495
12.3. Общее включение-исключение
и разупорядочения 502
12.4. Ладейные полиномы и запрещенные позиции 509
ПрОИЗВОДЯЩИе фуНКЦИИ 523
13.1. Определение производящей функции 523
13.2. Производящие функции и рекуррентные
отношения 525
13.3. Производящие функции и комбинаторные
подсчеты 535
13.4. Разбиения 542
13.5. Экспоненциальные производящие функции 549
Некоторые специальные вопросы
теории графов 556
14.1. Алгебраические свойства графов 556
14.2. Планарные графы 580
14.3. Раскраска графов 586
14.4. Пути и циклы Гамильтона 600
14.5. Взвешенные графы и алгоритмы поиска
кратчайшего пути 611
Деревья 624
15.1. Свойства деревьев 624
15.2. Бинарные деревья поиска 631
15.3. Взвешенные деревья 638
15.4. Обход бинарных деревьев 649
15.5. Остовные деревья 658
15.6. Минимальные остовные деревья 682
Сети 691
16.1. Сети и потоки 691
16.2. Паросочетание 707
16.3. Сети Петри 716

Содержание 9
17
18
19
20
21
22
Теория вычислений 725
17.1. Регулярные языки 725
17.2. Автоматы 731
17.3. Грамматики 741
ТеорИЯ КОДОВ 753
18.1. Введение 753
18.2. Порождающие матрицы 757
18.3. Коды Хемминга 767
Перечисление цветов 775
19.1. Теорема Бернсайда 775
19.2. Теорема Пойа 781
Кольца, области целостности
И ПОЛЯ 788
20.1. Кольца и области целостности 788
20.2. Области целостности 797
20.3. Полиномы 801
20.4. Алгебры и полиномы 808
Характеры групп и полугрупп 819
21.1. Комплексные числа 819
21.2. Характеры групп 820
21.3. Характеры полугрупп 825
Приложения теории чисел 829
22.1. Приложение: поиск по образу 829
22.2. Приложение: функции хеширования 837
22.3. Приложение: криптография 843
Литература 850
Ответы к упражнениям 856
Предметно-именной указатель 942
Список обозначений 954

Памяти Эльвуда В. Стоуна и Орвилла Г. Уиби.
Моей семье: Мэрилин, Энди, Кристин и Филу.
Учителям, наставникам и друзьям: Т.Хэду,
Н.Кимура, Л.С.Лоузу и Э.Л.Дубовски.
словие
Несмотря на то, что на рынке учебной литературы на сегодняшний день имеет-
имеется немало книг по дискретной математике, пожалуй, ни одна из них не может
сравниться с этой книгой по размаху и глубине рассматриваемых тем. Отличи-
Отличительной особенностью данной книги является то внимание, которое уделяется в
ней теории доказательств. Понятие доказательства вводится уже в первой главе
и развивается на протяжении всей книги. Дискретную математику изучают, как
правило, на первых курсах математических факультетов и факультетов информа-
информатики. Необходимость изучения техники доказательств для будущих математиков
очевидна. Она также крайне важна для развития логического мышления у бу-
будущих специалистов в области информатики. По сути, правильно составленная
компьютерная программа эквивалентна логическому доказательству. По мнению
автора, использовать то или иное приложение (или, в крайнем случае, не оши-
ошибаться при его использовании) легче, если понимаешь, как оно работает. За ред-
редкими исключениями, материал книги является самодостаточным. Использованию
любого понятия в тексте предшествует его строгое математическое определение.
Материал данной книги не требует от читателя знания математического ана-
анализа. Для понимания основных глав вполне достаточно знакомства со школьным
курсом алгебры. Но, несмотря на самодостаточность книги в целом, отдельные ее
главы все же требуют от читателя определенной математической подготовки.
Книга планировалась как основа семестрового или двухсеместрового кур-
курса по дискретной математике. В первых восьми главах закладываются основы
предмета; их можно использовать при чтении начального курса. Эти главы прак-
практически независимы друг от друга, так что преподаватель сам может выбрать
материал для изложения. Содержание остальных глав соответствует второй ча-
части курса по дискретной математике. В них введенные ранее понятия изучаются
более детально, и рассматриваются темы повышенного уровня сложности. Темы
рассматриваются с различных точек зрения, чтобы показать, как их можно ис-
использовать в зависимости от ситуации. В спектр рассматриваемых тем входят:
Логика, включающая таблицы истинности, логику высказываний, коммутацион-
коммутационные схемы, исчисление предикатов, индукцию и доказательства;
Теория множеств, включающая понятие мощности множеств, отношения, ча-
частично упорядоченные множества, отношения конгруэнтности, графы, ориентиро-
ориентированные графы и функции;
Алгоритмы, включающая понятие сложности алгоритмов, алгоритмы поиска и
сортировки, а также алгоритмы Евклида, Хаффмана, Прима, Уоршолла, Форда-
Фулкерсона, Флойда-Уоршолла и Дейкстры;

Предисловие 11
Теория графов, включающая ориентированные графы, циклы и пути Эйлера, цик-
циклы и пути Гамильтона, плоские и взвешенные графы;
Деревья, включающая бинарные деревья поиска, взвешенные деревья, обход де-
деревьев, коды Хаффмана и остовные деревья;
Комбинаторика, включающая перестановки, сочетания, включение-исключение,
разбиения, производящие функции, числа Каталана, числа Стирлинга, ладейные
многочлены, разупорядочения и перечисления цветов;
Алгебра, включающая полугруппы, группы, решетки, полурешетки, булевы алге-
алгебры, кольца, поля, области целостности, полиномы и матрицы.
Книга содержит обширные сведения по алгебре и теории чисел, что, по мне-
мнению автора, усиливает ее содержание, хотя включать эти темы в курс лекций
вовсе не обязательно. Материал соответствующих глав полностью независим от
остальных частей книги, и в каком объеме его стоит излагать — решать лек-
лектору. Данное пособие содержит также элементы теории вероятностей, сведения
о конечных разностях и другие темы, обычно не рассматриваемые в книгах по
дискретной математике.
СТРУКТУРА КНИГИ
Содержание первых трех глав охватывает логику и теорию множеств. Здесь пози-
позиция автора состоит в том, что понимание основ теории доказательств необходи-
необходимо для логического построения передовых компьютерных технологий. Изложены
основные положения теории доказательств и проиллюстрированы многочисленны-
многочисленными примерами. В главе 2 студенту предлагается самостоятельно доказать неко-
некоторые элементарные утверждения теории множеств. В главе 3 вводится понятие
аксиоматической системы для теории чисел. Студенту предоставляется возмож-
возможность попрактиковаться в доказательстве теорем о хорошо знакомых ему объек-
объектах. В этой же главе вводится метод доказательства по индукции. Далее в книге
приводится множество доказательств, а также посвященных им задач. Сначала
эти задачи довольно просты, но по ходу изложения книги уровень их сложности
постепенно возрастает.
Отношения и графы вводятся в главе 2. В главе 4 из понятия отношения
естественным образом выводится понятие функции. Однако подробное изучение
функций в главе 4 проводится независимо от материала главы 2. Точно так же
в главе 6 графы исследуются вне контекста главы 2, где они рассматриваются в
связи с отношениями.
Матрицы, перестановки и последовательности вводятся в главе 4 как функ-
функции специального вида. Дальнейшее изучение свойств этих функций продолжает-
продолжается в главе 6. Здесь же вводятся алгоритмы операций над матрицами и рассматри-
рассматриваются те свойства матриц, которые используются далее в главах, посвященных
алгебре, комбинаторике и теории кодов.
В главе 8 перестановки используются как инструмент комбинаторных под-
подсчетов. Перестановки также используются в последующих главах, посвященных
прикладным вопросам алгебры и комбинаторики. Глава 8, хотя она и связана с
главой 4, может изучаться независимо.

12 Предисловие
Содержание главы 5 не связано с предыдущими главами ничем, за исклю-
исключением того, что касается матриц. Подробно изучены алгоритмы, в частности,
алгоритмы сортировки. Понятие сложности алгоритмов также рассмотрено в этой
главе. Здесь же даны сведения о префиксной и суффиксной записях. Эта тема
опять обсуждается в главе 15 в связи с обходом бинарных деревьев. В главе 5
вводятся также двоичные и шестнадцатеричные числа.
Многие элементарные понятия, связанные с графами, ориентированными
графами и деревьями, рассматриваются в главе 6. Более глубоко эти вопросы
изучаются в главах 14-16. Содержание главы 6 не зависит от содержания преды-
предыдущих глав.
В главах 7 и 10 получает дальнейшее развитие теория чисел. Материал этих
глав используется в главе 22 при изучении приложений теории чисел. В остальном
они вполне самостоятельны и при желании могут быть опущены.
С главы 8 начинается изучение широкого круга вопросов комбинаторики,
которое затем продолжается во многих других частях книги, включая главы 12,
13 и 17. В той же главе 8 приводятся некоторые сведения из теории вероятностей,
что само по себе весьма необычно для книг по дискретной математике.
Главы 9 и 20 охватывают основные понятия алгебры, включающие полу-
полугруппы, группы, кольца, решетки, полурешетки, области целостности и поля.
При построении примеров групп и колец в этих главах используется материал
разделов 3.6 и 4.3. Материал главы 9 используется далее в приложениях, рас-
рассматриваемых в главах 17-21.
По многим причинам главы И, 12 и 13 можно выделить в отдельную группу.
В главе 11 продолжается изучение рекурсии. Кроме обычных линейных рекур-
рекуррентных отношений, включаемых, как правило, в учебные курсы по дискретной
математике, глава содержит сведения по теории конечных разностей. Если чита-
читатель не имеет хотя бы поверхностного представления о рекурсии, то для понима-
понимания этой главы ему необходимо ознакомиться с материалом главы 6. В главе 12
продолжается изучение комбинаторики, начатое в главе 8. Здесь рассматриваются
такие вопросы, как включение-исключение и задача о размещении. Кроме того,
вводится понятие разупорядочения и ладейного полинома. Главы И и 12 тесно
взаимосвязаны; в них многие темы рассматриваются с различных точек зрения.
Одним из объектов такого разностороннего рассмотрения являются числа Стир-
линга. Тем не менее, каждая из этих глав вполне самостоятельна.
В главе 13 вводится понятие производящей функции, и на его основе про-
продолжается изучение материала глав 11 и 12. В частности, производящие функции
используются для построения эффективного метода решения задач о размещении.
В главах 14-16 продолжается изучение графов и деревьев, начатое в главе 6.
Содержание этих глав очевидным образом зависит от материала главы 6, но с
материалом большинства предыдущих глав практически не связано. Исключение
составляет использование матриц в одном из рассматриваемых алгоритмов. Здесь
изучаются стандартные для теории графов и деревьев объекты: плоские графы,
циклы Гамильтона, бинарные деревья, остовные деревья, минимальные остовные
деревья, алгоритмы нахождения кратчайшего пути и потоки в сетях.
Еше одну группу составляют главы 17-22, посвященные прикладным вопро-
вопросам теории чисел, алгебры и комбинаторики. Глава 17 посвящена теории вычис-

Предисловие 13
лений; в ней рассматриваются коды, регулярные языки, автоматы, грамматики и
связь между ними. Здесь используются полугруппы, введенные в разделе 9.2. В
главе 18 вводятся специальные коды, такие как коды с обнаружением ошибок и
коды с исправлением ошибок. Для понимания материала этой главы требуется
знание теории групп в объеме раздела 9.4 и теории матриц в объеме глав 4 и 5.
Совершенно иное применение теория кодов получает в главе 22, где рассматрива-
рассматриваются вопросы криптографии. Эта глава требует знаний по теории чисел на уровне,
выходящем за пределы данной книги.
В главе 19 при изложении теорем Бернсайда и Пойя для перечисления цве-
цветов используются как алгебра, так и комбинаторика. Здесь, главным образом,
требуется знание перестановок в объеме раздела 9.4.
Глава 21 посвящена простейшим приложениям групп и полугрупп, а так-
также их отображениям на комплексную плоскость. Необходимые предварительные
сведения содержатся в разделах 9.2 и 9.5.
Глава 22 содержит три важных приложения теории чисел. Изучение функций
хеширования и криптографии является для информатики весьма актуальным.
При чтении вводного курса автор, как правило, полностью излагает матери-
материал глав 1-5, разделов 8.1-8.3, а также старается изложить первые три раздела
главы 6. Как отмечалось ранее, материал первых восьми глав составлен так, что-
чтобы обеспечить максимальную гибкость. В следующей таблице указано, какие
предварительные сведения требуются для усвоения материала каждой из глав:
Глава Необходимые главы или разделы
Глава 1 Никакие
Глава 2 Никакие
Глава 3 Разделы 1.1-1.4 и 2.1
Глава 4 Никакие
Глава 5 Разделы 4.1-4.3
Глава 6 Никакие
Глава 7 Глава 3
Глава 8 Никакие
Глава 9 Раздел 3.6
Глава 10 Глава 7
Глава 11 Разделы 5.1-5.3
Глава 12 Глава 8
Глава 13 Главы И и 12
Глава 14 Главы 5 и 6
Глава 15 Главы 5 и 6
Глава 17 Глава 9
Глава 18 Главы 5 и 9
Глава 19 Глава 9
Глава 20 Глава 9
Глава 21 Глава 9
Глава 22 Глава 10

14 Предисловие
ПОДДЕРЖКА
Имеется подробное руководство к решению всех задач, рассмотренных в этой
книге, которое можно заказать в издательстве Prentice Hall. Книга имеет свою
страницу в Интернете; ее адрес: www.prenhall.com/janderson. Здесь вы найдете
ссылки на другие интересные сайты, посвященные дискретной математике, в том
числе содержащие контрольные задания и формулировки интересных проблем
дискретной математики, не вошедшие в данное издание.
БЛАГОДАРНОСТИ
В первую очередь мне хочется поблагодарить Джорджа Лобелла, руководившего
разработкой этой книги, и Барбару Мэк, координировавшую наши усилия. Я бла-
благодарю Кристиана и Филиппа Мусик за мастерски выполненное художественное
оформление. Особую благодарность я приношу Джеймсу Беллу, внесшему огром-
огромный вклад в написание данной книги. Очень жаль, что он не смог выступить в
роли моего соавтора. Мне очень не хватает его партнерской поддержки. Кроме
того, я хочу поблагодарить за помощь моих коллег Дэна Кука, Эда Вайлда, Рика
Чоу, М. Б. Ульмера и Джерома Льюиса. Я благодарен своей студентке Соледад
Шугаи за усилия, приложенные ею при изучении моего курса. Также хочу по-
поблагодарить студентов Джоди Дина, Джессику Доне, Грейса Эллисона, Винни
Чин Фай Ип, Присциллу Лапьер, Эстер Лай, Бадрала Мадани, Джулию Нор-
рис, Трейси Квина и Роберта Вигерта, бывших первыми, кто прослушал данный
материал.
Пожалуйста, присылайте по электронной почте свои замечания и предложе-
предложения по дальнейшему улучшению книги.
Джеймс А. Андерсон
janderson@gw.uscs.edu

ГЛАВА
ТАБЛИЦЫ ИСТИННОСТИ,
ЛОГИКА,
ДОКАЗАТЕЛЬСТВА
1.1. ВЫСКАЗЫВАНИЯ И ЛОГИЧЕСКИЕ СВЯЗКИ
В этом разделе рассматриваются таблицы истинности, знакомство с которыми
будет для нас первым шагом в изучении логики. Далее мы увидим, что табли-
таблицы истинности являются также основным инструментом для определения других
важных понятий дискретной математики. Логика, созданная как наука знамени-
знаменитым Аристотелем C84-322 до н.э.), на протяжении столетий использовалась для
развития многих областей знания, включая теологию, философию, математику.
Она — тот фундамент, на котором построено все здание математики. По сути,
логика — это наука о рассуждениях, которая позволяет определить истинность
или ложность того или иного математического утверждения, исходя из совокуп-
совокупности первичных предположений, называемых аксиомами. Логика применяется
также в информатике для построения компьютерных программ и доказательства
их корректности. Понятия, методы и средства логики лежат в основе современных
информационных технологий. Одна из основных целей этой книги — изложить
основы математической логики, показать, как она используется в информатике, и
разработать методы анализа и доказательства математических утверждений.
Высказывание — это утверждение или повествовательное предложение, о
котором можно сказать, что оно истинно или ложно. Иными словами, утвержде-
утверждение об истинности или ложности высказывания должно иметь смысл. Истинность
или ложность, приписываемые некоторому утверждению, называются его значе-
значением истинности, или истинностным значением.
Вот примеры предложений, не являющихся высказываниями:
Кто вы? (вопрос),
Прочтите эту главу до следующего занятия (приказ или восклицание),
Это утверждение ложно (внутренне противоречивое утверждение).

16 ГЛАВА 1. Таблицы истинности, логика, доказательства
Мы будем обозначать высказывания буквами латинского алфавита р, q, г, ...
Например, р может обозначать утверждение Завтра будет дождь, a q — утвер-
утверждение Квадрат целого числа есть число положительное.
В обыденной речи для образования сложного предложения из простых ис-
используются связки — особые части речи, соединяющие отдельные предложения.
Наиболее часто употребляются связки и, или, нет, если ... то, только если,
и тогда и только тогда. В отличие от обыденной речи, в логике смысл таких
связок должен быть определен однозначно. Истинность сложного высказывания
однозначно определяется истинностью или ложностью составляющих его частей.
Высказывание, не содержащее связок, называется простым. Высказывание, со-
содержащее связки, называется сложным.
Пусть р и q обозначают высказывания
р : Джейн водит автомобиль,
q : У Боба русые волосы.
Сложное высказывание
Джейн водит автомобиль и у Боба русые волосы
состоит из двух частей, объединенных связкой и. Это высказывание может быть
символически записано в виде
pwq
или просто как
рЛд,
где символ Л обозначает слово и на языке символических выражений. Выражение
р Л q называется конъюнкцией высказываний pwq.
Точно так же высказывание
Джейн водит автомобиль или у Боба рыжие волосы.
символически выражается как
р или q
или
pVg,
где V обозначает слово или в переводе на символический язык. Выражение р V q
называется дизъюнкцией высказываний pwq.
Опровержение, или отрицание высказывания р обозначается через
Таким образом, если р есть высказывание Джейн водит автомобиль, то ~р —
это утверждение Джейн не водит автомобиль.
Если г есть высказывание Джо нравится информатика, то Джейн не во-
водит автомобиль и у Боба русые волосы или Джо любит информатику симво-
символически запишется как ((~р) Л q) V г. И наоборот, выражение р Л (~д) Л г — это

РАЗДЕЛ 1.1. Высказывания и логические связки 17
символическая форма записи высказывания Джейн водит автомобиль, у Боба
волосы не русые и Джо нравится информатика.
Рассмотрим выражение р Л q. Если некто говорит: "Джейн водит автомобиль
и у Боба русые волосы", то мы, естественно, представляем себе Джейн за рулем
автомобиля и русоволосого Боба. В любой другой ситуации (например, если Боб
не русоволос или Джейн не водит автомобиль) мы скажем, что говорящий не
прав.
Возможны четыре случая, которые нам необходимо рассмотреть. Высказы-
Высказывание р может быть истинным (Т) или ложным (F) и независимо от того, какое
истинностное значение принимает р, высказывание q может также быть истин-
истинным (Т) или ложным (F). Таблица истинности перечисляет все возможные
комбинации истинности и ложности сложных высказываний.
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
pAq
т
F
F
F
Ранее мы убедились, что только в первом случае высказывание pAq истинно.
В остальных же мы имеем ложное значение pAq. Например, случай 3 описывает
значение истинности для р A q, когда неверно, что Джейн водит автомобиль и у
Боба русые волосы. Если р — высказывание Джон богат, a q — высказывание
Джон красив, то не знакомая с Джоном девушка, которую убедили в том, что
высказывание Джон богат и Джон красив, или Джон богат и красив истинно,
будет представлять себе Джона и богатым, и красивым.
Точно так же рассмотрим высказывание
Джейн водит автомобиль или у Боба русые волосы,
которое символически выражается как р V q. Если некто скажет: "Джейн водит
автомобиль или у Боба русые волосы", то он будет не прав только тогда, когда
Джейн не сможет управлять автомобилем, а Боб не будет русоволосым. Для того
чтобы все высказывание было истинным, достаточно, чтобы одна из двух состав-
составляющих его компонент была истинной. Поэтому р V q имеет таблицу истинности
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
pWq
Т
Т
т
F
Высказывание р V q ложно только в случае 4, когда р и q оба ложны.
Если р — высказывание Джоя богат, a q — высказывание Джон красив, и не
знакомая с Джоном девушка уверена в истинности высказывания Джон богат
или Джон красив, или Джон богат или красив, то она вправе ожидать, что

18 ГЛАВА 1. Таблицы истинности, логика, доказательства
истинно одно из высказываний, но не обязательно оба. Девушка почувствует себя
введенной в заблуждение, только если обнаружит, что Джон беден и уродлив.
Таблица истинности для отрицания р имеет вид
Случай р
1 Т
2 F
F
Т
Истинностное значение ~р всегда противоположно истинностному значе-
значению р. В таблицах истинности отрицание всегда оценивается первым, если только
за знаком отрицания не следует высказывание, заключенное в скобки. Поэтому
~pVg интерпретируется как (~р) Vg, так что отрицание применяется только к р.
Если мы хотим отрицать все высказывание pAq, то это записывается как ~(pVg).
Символы Л и V называют бинарными связками, так как они связывают два
высказывания как, например, в выражениях р Л q и р V q. Символ ~ является
унарной связкой, так как применяется только к одному высказыванию.
Еще одна бинарная связка — это исключающее или, которое обозначается
через V. Высказывание р V q истинно, когда истинно р или q, но не оба одновре-
одновременно. Эта связка имеет таблицу истинности
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
pVg
F
Т
Т
F
Используя слово или, мы можем иметь в виду исключающее или. Например,
когда мы говорим: "Дик сдаст экзамен по логике или он не сдаст этот экзамен",
мы, конечно, предполагаем, что Дик сделает что-то одно. Таким образом, когда
мы говорим, что р — либо истина, либо ложь, то, естественно, предполагаем,
что это не выполняется одновременно. В логике исключающее или используется
довольно редко, и в дальнейшем мы, как правило, будем обходиться без него.
Рассмотрим высказывание
Сэм уплатит налог за машину или Сэм утратит свою
машину и будет ходить на работу пешком.
Пусть р обозначает высказывание Сэм уплатит налог за машину, q — высказы-
высказывание Сэм останется при своей машине, а г — высказывание Сэм будет ходить
на работу пешком. Тогда наше сложное высказывание можно представить в виде
где скобки использованы, чтобы показать, какие именно высказывания являются
компонентами каждой связки.
Таблица истинности дает возможность однозначно указать те ситуации, ко-
когда высказывание р V ((~q) Л г) является истинным; при этом мы должны быть

РАЗДЕЛ 1.1. Высказывания и логические связки 19
уверены, что учтены все случаи. Поскольку сложное высказывание содержит три
основных высказывания p,q и г, то возможны восемь случаев
Случай
1
2
3
4
5
6
7
8
Р
Г
Г
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
~д
F
F
Т
Т
F
F
Т
Т
(~д) Л г
F
F
Т
F
F
F
Т
F
pV(H)Ar)
Т
т
т
т
F
F
Т
F
При нахождении значений истинности для столбца (~д) Л г мы используем
столбцы для (~<?) и г, а также таблицу истинности для Л. Таблица истинности
для Л показывает, что высказывание (~<?) Л г истинно лишь в том случае, когда
истинны оба высказывания (~<?) и г. Это имеет место лишь в случаях 3 и 7.
Заметим, что при определении значений истинности для столбца pV((~g)Ar)
играет роль только истинность высказываний р и (~д) Л г. Таблица истинности
для V показывает, что единственный случай, когда высказывание, образованное
с помощью связки или, ложно, — это случай, когда ложны обе части этого вы-
высказывания. Такая ситуация имеет место только в случаях 5, 6 и 8.
Если Сэм не уплатит налог за машину (т.е. р ложно, или имеет значение F),
лишится своей машины (q имеет значение F) и будет ходить на работу пешком (г
имеет значение Т), то будет иметь место случай 7. Тот, кто скажет: "Сэм уплатит
налог за машину или Сэм утратит машину и будет ходить на работу пешком",
будет абсолютно прав.
Другой, эквивалентный способ построения таблицы истинности состоит в
том, чтобы записывать истинностные значения выражения под связкой. Снова
рассмотрим выражение pV ((~g) Л г). Сначала мы записываем истинностные зна-
значения под переменными р, q и г. Единицы под столбцами истинностных значений
указывают на то, что этим столбцам истинностные значения присваиваются в пер-
первую очередь. В общем случае число под столбцом будет показывать номер шага,
на котором производятся вычисления соответствующих истинностных значений.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
р V
Г
Г
Г
г
F
F
F
F
1
((~ я)
т
т
F
F
Т
Т
F
F
1
Л г)
Т
F
Т
F
Т
F
Т
F
1

20 ГЛАВА 1. Таблицы истинности, логика, доказательства
Затем мы записываем под символом ~ истинностные значения высказывания
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Ч
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
р V
т
т
т
т
F
F
F
F
1
((~
F
F
Т
Т
F
F
Т
Т
2
ч)
Т
т
F
F
Т
Т
F
F
1
Л г)
Т
F
Т
F
Т
F
Т
F
1
Далее записываем истинностные значения (~<?) Л г под символом Л.
Случай
1
2
3
4
5
6
7
8
Р
Г
Т
Г
т
F
F
F
F
Ч
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
р V
Г
т
т
т
F
F
F
F
1
((~
F
F
Т
Т
F
F
Т
Т
2
ч)
т
т
F
F
Т
Т
F
F
1
Л
F
F
Т
F
F
F
Т
F
3
г)
Т
F
Т
F
Т
F
Т
F
1
Наконец, записываем значения высказывания р V ((~<?) Л г) под символом V.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Ч
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Р
Г
т
г
г
F
F
F
F
1
V
г
г
г
г
F
F
Т
F
4
((~
F
F
Т
Т
F
F
Т
Т
2
ч)
т
т
F
F
Т
Т
F
F
1
Л
F
F
Т
F
F
F
Т
F
3
г)
Г
F
Т
F
Т
F
Т
F
1
ПРИМЕР 1.1. Пусть р, q и г обозначают, соответственно, высказывания Фрэд
любит футбол, Фрэд любит гольф, Фрэд любит теннис. Требуется записать
высказывание Фрэд любит футбол и неверно, что он любит гольф или теннис
в символической форме и указать соответствующую ему таблицу истинности.

РАЗДЕЛ 1.1. Высказывания и логические связки 21
Сначала заменим это высказывание эквивалентным — Фрэду нравится фут-
футбол и неверно, что Фрэд любит гольф или теннис. Высказывание Фрэд любит
гольф или теннис в символической форме записывается как q V г. Высказыва-
Высказывание Неверно, что Фрэд любит гольф или теннис, символически записывается
как ~(gVr), поскольку отрицание применяется ко всему высказыванию, которое
следует после "что". Итак, исходное высказывание символически изображается
рА (~(g Vr)). Таблица истинности этого высказывания имеет вид
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
q
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Р
Т
т
т
т
F
F
F
F
1
Л
F
F
F
Т
F
F
F
F
*
(~
F
F
F
Т
F
F
F
Т
3
(gVr))
Т
Т
Т
F
Т
Т
Т
F
2
?
УПРАЖНЕНИЯ
1. Найдите среди указанных ниже предложений высказывания. Укажите их
истинностные значения.
а) Который час?
б) Целое число 1 есть наименьшее положительное целое число.
в) Если х = 3, то х2 = 6.
г) Берегись автомобиля!
д) Южная Дакота — южный штат.
2. Найдите среди указанных ниже предложений высказывания. Укажите их
истинностные значения.
а) Все четные числа делятся на 2.
б) Загрузите пакеты в машину.
в) Это утверждение не может быть истинным.
г) Юпитер — ближайшая к солнцу планета.
д) Не следует хранить компакт-диски в микроволновой печи.
3. Пусть р, q и г обозначают следующие высказывания:
р : Путешествие на Марс является дорогостоящим,
q : Я совершу путешествие на Марс,
г : У меня есть деньги.
Запишите в символической форме такие высказывания:
а) У меня нет денег и я не совершу путешествие на Марс.
б) У меня нет денег и путешествие на Марс является дорогостоящим
или я совершу путешествие на Марс.

22 ГЛАВА 1. Таблицы истинности, логика, доказательства
в) Неверно, что у меня есть деньги и я полечу на Марс.
г) Путешествие на Марс не является дорогостоящим и я полечу на Марс
или путешествие на Марс является дорогостоящим и я не полечу на
Марс.
4. Пусть р, q и г обозначают следующие высказывания:
р : Мой компьютер — быстродействующий,
q : Я окончу проект вовремя,
г : Я сдам экзамен.
Запишите в символической форме такие высказывания:
а) У меня не быстродействующий компьютер или я закончу проект во-
вовремя.
б) Я не закончу проект вовремя и не сдам экзамен.
в) Неверно, что я закончу проект и сдам экзамен.
г) У меня быстродействующий компьютер или я не закончу проект во-
вовремя и сдам экзамен.
5. Постройте таблицы истинности для каждого высказывания в упражнении 3.
6. Постройте таблицы истинности для каждого высказывания в упражнении 4.
7. Пусть р, q и г обозначают следующие высказывания:
р : Эта игра очень трудна,
q : Я играю в шахматы,
г : Игра в шахматы требует времени.
Интерпретируйте следующие выражения как обычные высказывания:
а) q /\г\
б) ~р V ~д;
в) (р V г) Л д;
г) р A q Л г.
8. Пусть р, q и г обозначают следующие высказывания:
р : Доги — большие собаки.
q : У меня маленький дом.
г : У меня есть дог.
Представьте следующие символические выражения как обычные высказыва-
высказывания:
а) р Л q Л ~г;
б) р Л (~q V ~r);
в) (р V ~д) Л г;
г) (р Л г) V (д Л ~г).
9. Постройте таблицы истинности для высказываний в упражнении 7.
10. Постройте таблицы истинности для высказываний в упражнении 8.
11. Постройте таблицы истинности для следующих высказываний:
а) р A (q V ~r);
б) (<?Л~г) V (~рЛг);
в) ~(р Л г) V (~gAr);
г) ~(~pV(gA~r));
д) (pAr) V (pA~q).

РАЗДЕЛ 1.2. Условные высказывания 23
12. Постройте таблицы истинности для следующих высказываний:
а) (pVg)A(rVg);
б) (~дЛг) V~(pAr);
в) ~((рЛг) V ~д);
г) ~(~pA(gV~r));
Д) (Р ^ ~г) Л ~(р V ~#).
1.2. УСЛОВНЫЕ ВЫСКАЗЫВАНИЯ
Допустим, некто утверждает, что если случится одно событие, то случится и
другое. Это утверждение зачастую принимает форму угрозы, но мы рассмотрим
более позитивный пример. Предположим, отец говорит сыну: "Если в этом се-
семестре ты сдашь все экзамены на «отлично», я куплю тебе машину". Заметьте,
что высказывание имеет вид: если р, то q, где р — высказывание В этом се-
семестре ты сдашь все экзамены на «отлично», a q — высказывание Я куплю
тебе машину. Сложное высказывание мы обозначим символически через р —» q.
Спрашивается, при каких условиях отец говорит правду? Предположим, выска-
высказывания р и q истинны. В этом случае счастливый студент получает отличные
оценки по всем предметам, и приятно удивленный отец покупает ему машину.
Естественно, ни у кого не вызывает сомнения тот факт, что высказывание отца
было истинным. Однако существуют еще три других случая, которые необходимо
рассмотреть. Допустим, студент действительно добился отличных результатов, а
отец не купил ему машину. Самое мягкое, что можно сказать об отце в таком
случае, — это то, что он солгал. Следовательно, если р истинно, a q ложно, то
р —> q ложно. Допустим теперь, что студент не получил положительные оценки,
но отец тем не менее купил ему машину. В этом случае отец предстает очень
щедрым, но его никак нельзя назвать лжецом. Следовательно, если р ложно и q
истинно, то высказывание если р, то q (т.е. р —> q) истинно. Наконец, предполо-
предположим, что студент не добился отличных результатов, и отец не купил ему машину.
Поскольку студент не выполнил свою часть соглашения, отец тоже свободен от
обязательств. Таким образом, если р и q ложны, то р —> q считается истинным.
Итак, единственный случай, когда отец солгал, — это когда он дал обещание и
не выполнил его.
Таким образом, таблица истинности для высказывания р —> q имеет вид
Случай
1
2
3
4
Р
Т
Т
F
F
q
т
F
Т
F
р —> я
т
F
Т
Т
Символ —> называется импликацией, или условной связкой.

24 ГЛАВА 1. Таблицы истинности, логика, доказательства
Еще одним примером, который подтверждает таблицу истинности для им-
импликации, является высказывание
Если целое число равно 3, то его квадрат равен 9.
Конечно, желательно, чтобы это высказывание было истинным всегда. Пусть р —
высказывание Целое число равно 3, a q — высказывание Квадрат целого числа
равен 9. Если р и q истинны, то целое число равно 3 и его квадрат равен 9.
Это соответствует первой строке таблицы истинности. Если целое число равно
—3, то его квадрат по-прежнему равен 9. В этом случае р ложно и q истинно,
что совпадает со случаем 3 и подтверждает правильность третьей строки табли-
таблицы. Если целое число равно 4, то ложны и р, и q, что соответствует случаю 4.
Этим подтверждается правильность четвертой строки таблицы. Заметим, что слу-
случай 2 здесь не имеет места, но во всех других случаях эта таблица истинности
обеспечила нам желаемый результат.
Может показаться, что р —> q носит характер причинно-следственной связи,
но это не является необходимым. Чтобы увидеть отсутствие причины и следствия
в импликации, вернемся к примеру, в котором р есть высказывание Джейн управ-
управляет автомобилем, ад — утверждение У Боба русые волосы. Тогда высказыва-
высказывание Если Джейн управляет автомобилем, то у Боба русые волосы запишется
как
если р, то q
или как
p->q.
То, что Джейн управляет автомобилем, никак причинно не связано с тем, что Боб
русоволосый. Однако нужно помнить, что истинность или ложность бинарного
сложного высказывания зависит только от истинности составляющих его частей
и не зависит от наличия или отсутствия между ними какой-либо связи.
ПРИМЕР 1.2. Требуется найти таблицу истинности для выражения
(р -> q) л
г).
Используя таблицу истинности для —>, приведенную выше, построим сначала
таблицы истинности для (р —» q) и (q —> г), учитывая, что импликация ложна
только в случае, когда Г —> F.
Случай
1
2
3
4
5
6
7
8
Р
Т
Г
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(Р
Т
Т
т
т
F
F
F
F
1
-¦
Т
т
F
F
Т
Т
Т
Т
2
ч)
т
т
F
F
Т
Т
F
F
1
Л (д
Г
Т
F
F
Т
Т
F
F
1
Т
F
Т
Т
Т
F
Т
Т
2
г)
Т
F
Т
F
Т
F
Т
F
1

РАЗДЕЛ 1.2. Условные высказывания 25
Теперь используем таблицу для Л, чтобы получить для высказывания
(Р -> Я) A (q -> г)
таблицу истинности
Случай
1
2
3
4
5
6
7
8
Р
Т
Г
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(Р
Т
Т
Т
Т
F
F
F
F
1
Т
т
F
F
Т
Т
Т
Т
2
я)
т
т
F
F
Т
Т
F
F
1
Л
Т
F
F
F
Т
F
Т
Т
*
т
т
F
F
Т
Т
F
F
1
-¦
Т
F
Т
Т
Т
F
Т
Т
2
г)
Т
F
Т
F
Т
F
Т
F
1
?
Высказывание вида (р —¦ q) Л (q —> р) обозначается через р <-» q. Символ «->
называется эквиваленцией. Очевидно, таблица истинности для (р —> q) Л (q —> р)
определяет таблицу истинности для р «-> q.
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
(Р
—>
Т
F
Т
Т
я)
Л
Т
F
F
Т
*
(ч
У
т
т
F
Т
Р)
р *-* г
Т
F
F
Т
*
Непосредственно из определения вытекает, что эквиваленция истинна только
в случае, когда р и q имеют одинаковые истинностные значения.
Может возникнуть вопрос о том, как интерпретировать такие выражения,
как ~рVq,pAq\/r,pAq-+r ирЛд<->д\/г, в которых отсутствуют скобки. Во
избежание неоднозначности лучше всегда использовать скобки. Однако здесь, как
и в алгебре, имеется приоритет выполнения операций. Операции выполняются в
следующей последовательности: ~, Л, V, —> и «->. Поэтому указанные выражения
можно интерпретировать как (~р) V q, (р Л q) V г, {р Л q) —> г и (р Л q) <-+ (q V г).
¦ УПРАЖНЕНИЯ
1. Пусть р, q и г обозначают следующие высказывания:
р : Он купит компьютер,
q : Он будет праздновать всю ночь,
г : Он выиграет в лотерею.
Запишите следующие высказывания в виде символических выражений:
а) Если он выиграет в лотерею, он купит компьютер и будет праздно-
праздновать всю ночь.

26 ГЛАВА 1. Таблицы истинности, логика, доказательства
б) Если он не купит компьютер, то и праздновать всю ночь не будет.
в) Если он выиграет в лотерею, то будет праздновать всю ночь и если
он не выиграет в лотерею, то не купит компьютер.
г) Если он не выиграет в лотерею или не купит компьютер, то празд-
праздновать всю ночь не будет.
2. Пусть р, q и г обозначают следующие высказывания:
Он читает комиксы.
Он любит научную фантастику.
Он — ученый-информатик.
Запишите следующие высказывания в виде символических выражений:
а) Если он читает комиксы и любит научную фантастику, то он —
ученый-информатик.
б) Если он не читает комиксы и не любит научную фантастику, то он
не является ученым-информатиком.
в) Если он читает комиксы, то он любит научную фантастику и если
он не читает комиксы, то он — ученый-информатик.
г) Если он — ученый-информатик, то он читает комиксы или он не
любит научную фантастику.
3. Пусть р, q и г обозначают следующие высказывания:
р : Ему нравятся фиолетовые галстуки,
q : Он популярен,
г : У него странные друзья.
Запишите следующие символические выражения в виде высказываний:
а) (р Л q) -> г;
б) q —> ~г;
в) Р-* (9 Vr);
г) (р-> ~д)Л(д-*г).
4. Пусть р, q и г обозначают следующие высказывания:
р : Он удачлив,
q : Он популярен,
г : Он богат.
Запишите следующие символические выражения как высказывания:
а) r^(p-^q)-
б) (pvr)-+ q\
в) д^(рЛг);
г) (р —* я) л (~г —¦ (~Р v ~Я))-
5. Постройте таблицы истинности для следующих выражений:
а) (р ->q) ~> г\
б) р -> (q -> г);
в) g->(pAr)f4 ((g -> р) Л (q -> г));
г) ((р _> 9) v г)-> (~р V-g).
6. Постройте таблицы истинности для следующих выражений:
а) (р -> д) -> (д -> г)'»

РАЗДЕЛ 1.3. Эквивалентные высказывания 27
б) (р —> q) V ~(r Л д);
в) (р\/г) -> (рЛд);
г) ~((Р ~~* #) л ~r) "^ (P v ~г)*>
Д) ((Р -> «) Л ~(r Vp)) -> (~р V ~g).
7. Постройте таблицы истинности для следующих выражений:
а) (р->д) <-> (~д-*~р);
б) (р Л ~(д V ~г)) ^ (р -^ д);
в) (pVr)-> q\
г) ((р -* д) Л (д -> -г)) -> (г -> р);
Д) (pA(gVr))->((PAg)V(PAr)).
8. Постройте таблицы истинности для следующих выражений:
а) (~(pA~r)Vg)->(gVr);
б) ~((р Л ~g) Vr)b>(r-> g);
в) (~(р -^ д) -> (д -> г));
г) (pVg)A(p-*r);
Д) ({Р Vr)^q)^ ((р -, д) V (р -, г)).
9. Укажите, какие из следующих высказываний являются истинными:
а) Если 22 = 4, то З2 = 9;
б) Если 22 = 5, то З2 = 9;
в) Если 22 = 5, то З2 = 10;
г) Если 22 = 4, то З2 = 10.
10. Таблица истинности простого высказывания содержит две строки. Высказы-
Высказывание, состоящее из двух компонент, имеет таблицу истинности из четырех
строк; сложное высказывание, составленное из трех простых, имеет таблицу
истинности из восьми строк. Сколько строк содержит таблица истинности
высказывания, состоящего из четырех компонент? А если высказывание со-
состоит из п компонент?
1.3. ЭКВИВАЛЕНТНЫЕ ВЫСКАЗЫВАНИЯ
Особый интерес представляют сложные высказывания, имеющие различное стро-
строение, но являющиеся истинными в одних и тех же случаях. Такие высказывания
называются логически эквивалентными. Эквивалентность двух высказываний
легко установить посредством сравнения их таблиц истинности.
Например, пусть р и q обозначают высказывания
р : Сегодня шел дождь,
q : Сегодня шел снег.
Рассмотрим сложные высказывания
Неверно, что сегодня шел дождь или снег,

28 ГЛАВА 1. Таблицы истинности, логика, доказательства
или символически
Сегодня не шел дождь и сегодня не шел снег,
или символически
Л
Построим таблицы истинности для обоих высказываний.
Случай
1
2
3
4
Р
Г
Г
F
Ч
т
F
Т
F
F
F
F
Т
*
(pVq)
Т
Т
Т
F
~р
F
F
Т
Т
Л
F
F
F
Т
#
F
Т
F
Т
Итак, во всех четырех строках истинностные значения для ~(р V q) (обо-
(обозначенные *) и для ~р Л ~q (обозначенные #) совпадают. Это означает, что два
рассматриваемых высказывания логически эквивалентны, т.е.
~(р v я) — ~р л ~я •
Эквивалентность — очень полезное свойство; используя его, можно строить
отрицание высказываний с "или", осуществляя отрицание каждой из его частей
и меняя "или" на "и".
С условным высказыванием — импликацией р —> q — связаны еще три типа
высказываний: конверсия, инверсия и конпграпозиция высказывания р —> q. Они
определяются следующим образом:
р —* q импликация
q —¦ р конверсия высказывания р —> q
~р —> ~д инверсия высказывания р —> q
~q —> ~р контрапозиция высказывания р —> q
Пусть дано высказывание-импликация Если он играет в футбол, то он
популярен. Для этой импликации имеем:
конверсия: Если он популярен, то он играет в футбол
инверсия: Если он не играет в футбол, то он не популярен
контрапозиция: Если он не популярен, то он не играет в футбол
Важно понимать, что высказывания Если он живет в Детройте, то Боб
навестит его и Боб навестит его, если он живет в Детройте по сути являются
одним и тем же высказыванием. Однако высказывание Если Боб навестит его,
то он живет в Детройте не совпадает с предыдущими высказываниями. Не
важен порядок, в котором р и q присутствуют в предложении, а важно, какая

РАЗДЕЛ 1.3. Эквивалентные высказывания 29
часть предложения является частью "если", а какая часть является частью "то".
Может показаться, что при замене если р, то q на q, если р получается конверсия,
но с логической точки зрения последнее высказывание совпадает с исходным.
Часть (ж) теоремы, которая будет сформулирована ниже, говорит о том,
что импликация и ее контрапозиция логически эквивалентны. Эквивалентность
и контрапозиция условных высказываний имеют в математике большое значе-
значение. Зачастую гораздо легче доказать теорему от противного, чем дать ее пря-
прямое доказательство. Используя эквивалентность импликации и ее контрапозиции,
нетрудно показать, что конверсия и инверсия импликации имеют одну и ту же
таблицу истинности. В то же время импликация и ее конверсия (или инверсия)
имеют различные таблицы истинности. Непонимание этого факта — источник
распространенных ошибок в так называемых "логических" рассуждениях.
ТЕОРЕМА 1.3. Используя таблицы истинности, можно доказать следующие ло-
логические эквивалентности:
а) Законы идемпотентности
Р А р = р;
р v р = р.
б) Закон двойного отрицания
~(~р) =р.
в) Законы де Моргана
~(р V q) = ~р Л ~q ;
~(Р Л Я) — ~Р v ~Q •
г) Свойства коммутативности
д) Свойства ассоциативности
pA(qAr) = (pAq)Ar;
р V (q V г) = (р V q) V г .
е) Свойства дистрибутивности
р A (q V г) = (р A q) V (р А г);
р V (q А г) = (р V q) А (р V г).
ж) Закон контрапозиции
р —> q = r^>q —> r^>p.
з) Другие полезные свойства
р-+ q= ~p V q\

30 ГЛАВА 1. Таблицы истинности, логика, доказательства
Отметим, что благодаря свойству ассоциативности высказывания (pAq)Ar и
р A (q Л г) могут быть записаны в виде pAqAr. Аналогично, (р V q) V г и р V (q V г)
можно записать просто как р V g V г.
Высказывание, истинное во всех случаях, называется логически истинным,
или тавтологией] высказывание, построенное так, что оно ложно в каждом слу-
случае, называется логически ложным, или противоречием. Теоремы в математике
являются примерами тавтологий. Было бы неприятно сознавать, что математиче-
математические теоремы справедливы, к примеру, только в 80 процентах случаев. Высказы-
Высказывание Он сдаст или не сдаст экзамен есть пример тавтологии, поскольку либо
одно событие, либо другое обязательно должно иметь место. Каждое высказы-
высказывание вида р V ~р — тавтология. Шекспир должен был бы провозгласить: "Быть
или не быть, это и есть тавтология". Высказывание Если сдаст, то сдаст —
тоже тавтология, хотя оно и не отличается глубиной. Примером тавтологии яв-
является высказывание Если он богат и удачлив, то он удачлив. Высказывание
Она движется в направлении Техаса и она не движется в направлении Техаса
всегда ложно, т.к. нельзя делать одновременно и то, и другое. Следовательно, это
противоречие.
Рассмотрим высказывание вида
(pA(p-+q))-+q.
Ему соответствует таблица истинности
Случай
1
2
3
4
Р
Т
т
F
F
Я
т
F
Т
F
(Р
Т
Т
F
F
Л
Т
F
F
F
(Р - Я))
Т
F
Т
Т
->
т
т
т
т
*
я
т
F
Т
F
Столбец, обозначенный звездочкой, дает истинностные значения исходно-
исходного сложного высказывания. Высказывание истинно во всех четырех возможных
случаях, следовательно, является тавтологией.
Имея логически истинное высказывание-тавтологию, легко построить логи-
логически ложное высказывание-противоречие. Для этого достаточно взять отрицание
логически истинного высказывания. Поэтому высказывание
логически ложно.
Давайте теперь рассмотрим некоторые свойства, связанные с логически ис-
истинными и логически ложными высказываниями. Пусть символ Т обозначает
высказывание, которое есть тавтология, поэтому имеет таблицу истинности, со-
состоящую из одних Т. Символом F обозначим противоречие, т.е. высказывание,
таблица истинности которого содержит F во всех строках. Используя таблицы

РАЗДЕЛ 1.3. Эквивалентные высказывания 31
истинности, можно показать, что
р
р
р
р
р
р
р
л
л
V
V
л
V
->
т
F
т
F
~р
~р
р
= р,
= г,
= Р ,
—- ¦* ?
= Г»
В каждом высказывании можно заменить любую его компоненту на логи-
логически эквивалентное ей высказывание. Полученное в результате такой замены
высказывание будет логически эквивалентно исходному, поскольку истинностное
значение высказывания зависит исключительно от истинностных значений со-
составляющих его компонент (но не от их формы или сложности). Например,
(q V г) V (р Л ~r) = q V (г V (р Л ~г) = свойство ассоциативности
= q V ((г V р) Л (г V ~г)) = свойство дистрибутивности
= q V ((г V р) Л Г) = эквивалентность
= q V(г V р) = эквивалентность
= q V (р V г) = свойство коммутативности
= (q V р) V г = свойство ассоциативности
= (р V д) V г. свойство коммутативности
Здесь мы впервые использовали законы логики и фиксированное множество
"истинных высказываний" для образования новых "истинных" высказываний.
Условные высказывания могут выражаться в виде различных языковых кон-
конструкций, но символически все они записываются как р —»> q. Вот несколько
примеров таких конструкций:
Если р, mo q.
р достаточно для q.
р является достаточным условием для q.
q необходимо для р.
q является необходимым условием для р.
р, только если q (или: только если q, то р).
Таблица для р —> q показывает, что если р —> q истинно и р истинно, тогда
q должно быть истинным, т.е. истинность р достаточна для истинности q. По-
Поэтому р достаточно для q имеет тот же смысл, что и р —> q. Таким образом,
если q ложно и q необходимо для р, тогда р должно быть ложно. Поэтому, если
~д истинно, тогда ~р должно быть истинно и ~д —> ~р. Но последнее выраже-
выражение — контрапозиция для р —> q\ следовательно, q необходимо для р имеет то же
значение, что ир->д.
Анализ значения р только если q проводится аналогично. Получаем, что р
может быть истинным, только если q истинно. Если q не истинно, то р не может

32 ГЛАВА 1. Таблицы истинности, логика, доказательства
быть истинным. Но это эквивалентно утверждению, что если ~q истинно, то ~р
должно быть истинно и ~q —> ~р. Последнее есть контрапозиция высказывания
р —> д, поэтому р только если q имеет то же значение, что и р -+ q.
Ранее было установлено, что порядок простых высказываний в составе услов-
условного высказывания не имеет значения; важно то, какое из простых высказываний
следует за если (или в данном случае только если), а какое следует за то. По-
Поэтому утверждения Только накопив денег, Фрэд сможет поступить в колледж
и Фрэд сможет поступить в колледж, только если накопит денег рассматри-
рассматриваются как одно и то же высказывание.
ПРИМЕР 1.4. Приведите следующие высказывания к виду р —> q или q —> р:
а) Он добьется успеха, только если будет усердно работать.
б) Он счастлив, только если управляет автомобилем.
в) Наличия денег достаточно, чтобы быть счастливым.
г) Наличие денег необходимо, чтобы быть счастливым.
д) Чтобы победить на выборах, нужно набрать достаточно голосов.
Ответ:
а) Если через р обозначить высказывание Он добьется успеха, а через q — Он
будет усердно работать, то высказывание если р, то q, или р —> q примет
вид Если он добивается успеха, то он работает усердно.
б) Если р обозначает Он управляет автомобилем, a q — Он счастлив, то
высказывание q только если р, или q—>p имеет вид Если он счастлив, то
он управляет автомобилем.
в) Пусть р обозначает У него есть деньги, a q есть Он счастлив. Тогда вы-
высказывание р достаточно для q, или р —> q может быть записано как Если у
него есть деньги, он счастлив.
г) Пусть р обозначает У него есть деньги, a q обозначает Он счастлив. Тогда
высказывание р необходимо для q, или q —> р будет иметь вид Если он
счастлив, то у него есть деньги.
д) Пусть р обозначает Он победит на выборах, a q обозначает Он получит
достаточное количество голосов, тогда высказывание q необходимо для р,
или если р, то q, или р —> q может быть записано в виде Если он победит
на выборах, то он получит достаточное количество голосов. ?
Вернемся к рассмотрению логической связки <->. Поскольку высказывания
вида рн^и (р —» q) Л (q —> р) логически эквивалентны, то р «-> q означает
то же, что и р тогда и только тогда, когда q, или р если и только если q.
Пусть, например, р обозначает высказывание Джим будет играть в футбол, а
q — высказывание Джейн организует поддержку зрителей. Тогда р «-> q может
быть выражено как
Джим будет играть в футбол, если и только если
Джейн организует поддержку зрителей.
Следующие языковые конструкции, выражающие эквиваленцию высказыва-

РАЗДЕЛ 1.3. Эквивалентные высказывания 33
ний р «-» q, равносильны:
р если и только если q.
р необходимо и достаточно для q.
р есть необходимое и достаточное условие для q.
Пусть имеется высказывание
Сэм играет в гольф тогда и только тогда, когда тепло,
тогда ожидается, что если будет тепло, то мы увидим Сэма, играющего в гольф,
и если Сэм играет в гольф, то погода, безусловно, теплая.
Точно так же, если имеется высказывание
Быть счастливым является необходимым и достаточным условием, чтобы
быть удачливым,
то имеется в виду, что если Джон счастливчик, то он и удачлив, а если Джону
везет, то он, конечно, счастливчик.
¦ УПРАЖНЕНИЯ
1. Используя таблицы истинности, докажите следующие эквивалентности:
а) Закон де Моргана
б) Свойство ассоциативности связки V
р V (q V г) = (р V q) V г .
в) Свойство дистрибутивности связки или относительно и
р V (q Л г) = (р V q) Л (р V г).
г) Эквивалентность импликации и высказывания со связкой или
р —> q = ~р V q .
2. Используя пункт (г) предыдущего упражнения, покажите, что отрицание
для р —> q эквивалентно р Л ~д.
3. Ранее были рассмотрены связанные между собой условные высказывания,
включающие в качестве компонент высказывания р и q. Ими являлись
р —> q импликация,
q —> р конверсия (для р —¦ д),
~д —> ~р контрапозиция (для р —> q),
~р —> ~д инверсия (для р —> д).
Используя таблицы истинности, докажите, что

34 ГЛАВА 1. Таблицы истинности, логика, доказательства
Импликация эквивалентна своей контрапозиции, но не эквивалентна своей
конверсии. Часто используется выражение если р, то q, и наоборот. На
самом деле это означает если р, то q, и если q, то ру или
(р -> q) Л (q -> р),
что эквивалентно р <-> q, или р, если и только если q. Докажите, что
р —> q = ~q _> ~р, не используя непосредственно таблицы истинности.
На основании этого результата докажите, что инверсия импликации эквива-
эквивалентна ее конверсии.
4. Используя логически эквивалентные высказывания и не применяя непосред-
непосредственно таблицы истинности, покажите, что
а) р = ~(р As)-> (~s Л р).
б) ~(р <-> q) = (р Л ~g) V(gA ~р).
5. Преобразуйте следующие высказывания к виду если р, то q\
а) Он кентавр, только если он имеет шесть ног.
б) Чтобы быть преуспевающим политиком, нужно быть избранным.
в) Достаточно иметь деньги, чтобы быть популярным.
6. Преобразуйте следующие высказывания к виду если р, то q:
а) Необходимо иметь шлем, чтобы играть в американский футбол.
б) Только если я читаю Шекспира, я литературно образован.
в) Для меня сдать этот курс достаточно, чтобы получить диплом.
7. Дано высказывание Если я голосую, то я хороший гражданин.
а) Сформулируйте конверсию этого выражения.
б) Сформулируйте инверсию этого выражения.
в) Сформулируйте контрапозицию этого выражения.
8. Дано высказывание Если я не буду выплачивать ссуду, у меня отберут
участок.
а) Сформулируйте конверсию этого высказывания.
б) Сформулируйте инверсию этого высказывания.
в) Сформулируйте контрапозицию этого высказывания.
1.4. АКСИОМАТИЧЕСКИЕ СИСТЕМЫ: УМОЗАКЛЮЧЕНИЯ
И ДОКАЗАТЕЛЬСТВА
Математики в большинстве своем имеют дело с теоремами и их доказательства-
доказательствами. Теоремы представляют собой "истинные" утверждения относительно рассмат-
рассматриваемых математических систем. Например, утверждение
Гипотенуза прямоугольного треугольника
длиннее любого из катетов
— это известная из геометрии теорема Евклида. Это утверждение считается ис-
истинным, поскольку оно "выводимо" из ранее принятых или выведенных истин
геометрии Евклида.

РАЗДЕЛ 1.4. Аксиоматические системы: умозаключения и доказательства 35
Математическая система начинается с неопределяемых понятий и утвержде-
утверждений, точно описывающих фундаментальные характеристики или истинные утвер-
утверждения относительно этих понятий, которые математики используют для обра-
образования системы. Эти фундаментальные характеристики называются аксиомами
или постулатами. Утверждения, выведенные (доказанные) только на основе этих
фундаментальных свойств (аксиом и постулатов) и ранее доказанных утвержде-
утверждений с помощью логических правил, называются теоремами.
Таким образом, в математических системах вся информация, необходимая
для доказательства теоремы, должна содержаться в аксиомах и ранее доказан-
доказанных теоремах. Развивая конкретный раздел математики, можно не включать в
него все аксиомы и доказанные теоремы. Вместо этого можно принять доказан-
доказанные теоремы в качестве аксиом. Например, аксиомы для целых чисел и аксиомы
Пеано для положительных целых чисел неявным образом предполагают выпол-
выполнение аксиом теории множеств, но, поскольку в теории чисел акцент делается
на свойствах целых чисел, было бы излишним стремиться в ней одновременно к
полному развитию теории множеств.
Важно, что логические правила, которые используются для вывода новых
теорем из аксиом, постулатов и ранее доказанных в данной системе теорем, не
порождают в качестве "теорем" ложные высказывания. Эти логические правила
называются правилами вывода. Умозаключение состоит из совокупности утвер-
утверждений, называемых гипотезами, или посылками, и утверждения, называемого
заключением. Правильным умозаключением называется такое умозаключение,
заключение которого истинно всякий раз, когда истинны его гипотезы. Правила
вывода выбираются так, чтобы они были правильными умозаключениями.
Умозаключения часто представляют в виде
#1
Я2 гипотезы
Яз
л С заключение
Символ л означает "следовательно". Гипотезы представляют собой перечень од-
одного или более высказываний, или посылок. Умозаключение правильно, если
всякий раз, когда ЯЬЯ2, и Яз истинны, то истинно и С или, что равносильно,
всякий раз, когда Hi Л Я2 Л Яз истинно, истинно и С.
Правильность умозаключения можно проверить двумя способами. Во-первых,
мы можем построить таблицу истинности и показать, что всякий раз, когда ги-
гипотезы истинны, истинно и заключение. Во-вторых, мы можем использовать та-
таблицы истинности для обоснования правил вывода, а затем использовать правила
вывода для доказательства справедливости заключения. Длинные умозаключе-
умозаключения, как правило, проще обосновывать при помощи правил вывода. В частности,
используя правила вывода, легко проверить правильность умозаключения
р-> q
q —> г
г —¦ s

36 ГЛАВА 1. Таблицы истинности, логика, доказательства
Проверка того же утверждения с использованием таблиц истинности намного
сложнее. Однако, при помощи таблиц истинности мы можем доказать ложность
утверждения, чего правила вывода сделать не позволяют.
Рассмотрим умозаключение
V
q->r
.'. р Л q Л г
Таблицы истинности для посылок и заключения имеют следующий вид.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
ч
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Р
Т
т
т
т
F
F
F
F
1
р-* q
Т
Т
F
F
Т
Т
Т
Т
2
q —* г
Т
F
Т
Т
Т
F
Т
Т
3
р Л q Л г
Т
F
F
F
Т
F
Т
Т
*
Заметим, что, когда истинны все посылки (что имеет место в случае 1),
истинным также является и заключение, а само умозаключение является пра-
правильным.
Рассмотрим умозаключение
р
q
Построим для него таблицу истинности.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
pAq
Т
т
т
т
т
т
F
F
1
р—> q
Т
F
Т
F
Т
Т
Т
Т
2
q —> г
Т
F
Т
Т
Т
F
Т
Т
3
г
Т
F
Т
F
Т
F
Т
F
*

РАЗДЕЛ 1.4. Аксиоматические системы: умозаключения и доказательства 37
Мы снова приходим к выводу, что, когда все посылки истинны (что имеет
место в случаях 1, 3 и 5), заключение истинно, и умозаключение правильно.
Однако, если рассмотреть следующее умозаключение
Р
Я
г
Я
г
Л р
и посмотреть на его таблицу истинности,
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
p->q
т
т
F
F
Т
Т
Т
Т
1
q -v r
Т
F
Т
Т
Т
F
Т
Т
2
г
Т
F
Т
F
Т
F
Т
F
3
Р
Т
т
т
т
F
F
F
F
*
мы обнаружим, что хотя в случае 1 истинны и посылки, и заключение, в случаях
5 и 7 посылки истинны, а заключение ложно. Следовательно, умозаключение не
является правильным.
Рассмотрим метод проверки правильности умозаключений, альтернативный
методу таблиц истинности. Пока предлагается принять метод на веру, вернувшись
к его обоснованию несколько позже. Это не прямой метод, поскольку он направ-
направлен на доказательство неправильности умозаключения. В случае успеха такого
доказательства это будет свидетельством неправильности умозаключения. Если,
предполагая неправильность умозаключения, мы приходим к противоречию, то
умозаключение является правильным. Например, рассмотрим умозаключение
Если умозаключение неправильное, существуют истинностные значения р, q
и г, для которых посылки истинны, а заключение ложно. Если заключение ложно,
то г ложно. Если q —> г истинно , а г ложно, то q должно быть ложно. Аналогично,
если р —> г истинно, тогда р должно быть ложно. Но тогда р V q ложно, что
приводит к противоречию с утверждением, что заключение ложно, а посылки
истинны. На основании этого делаем вывод, что умозаключение правильно.

38 ГЛАВА 1. Таблицы истинности, логика, доказательства
Рассмотрим умозаключение
p
q
г
s
q
г
s
t
Снова попытаемся свести рассмотрение к случаю, когда заключение ложно, а
посылки истинны. Если р —у t ложно, то р должно быть истинно и t ложно.
Поскольку t ложно, то из истинности s —> t следует, что 5 ложно. Если s ложно
и г —> s истинно, то г ложно. Если г ложно и q —> г истинно, то q должно быть
ложно. Но поскольку р истинно, a q ложно, то р —* q ложно, что невозможно.
Опять приходим к противоречию с тем, что заключение ложно, а все посылки
истинны. Таким образом, умозаключение правильно.
Рассмотрим умозаключение
Р
Я
Я
г
.'. р V г
Если заключение ложно, то и р и г — оба ложны. Однако, если q ложно, то
p—>qHq-*r — оба истинны. Поскольку обе посылки истинны, а заключение
ложно, то умозаключение неправильно. Если посмотреть на таблицу истинности
данного умозаключения,
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
р-* q
Т
Т
F
F
Т
Т
Т
Т
1
q^r
Т
F
Т
Т
Т
F
Т
Т
2
р V г
Т
Т
Т
Т
F
F
Т
F
*
легко заметить, что рассмотренный случай соответствует строке 8 таблицы ис-
истинности, откуда следует неправильность умозаключения.
Рассмотрим умозаключение
Р
Я
г
Я
г
Если заключение ложно, это означает, что р ложно. Но если посылки истин-
истинны, то г истинно. В этом случае р —> q и q —> г истинны вне зависимости от того,

РАЗДЕЛ 1.4. Аксиоматические системы: умозаключения и доказательства 39
истинно q или ложно. Таким образом, имеется два случая, когда можно показать
неправильность нашего умозаключения: A) р ложно, q истинно, г истинно и B)
р ложно, q ложно, г истинно. В этих случаях посылки истинны и заключение
ложно. Из таблицы истинности
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
q
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
р—> я
т
т
F
F
Т
т
т
т
1
q —> г
Т
F
Т
Т
Т
F
Т
Т
2
г
Т
F
Т
F
Т
F
Г
F
3
Р
Т
т
т
т
F
F
F
F
*
легко видеть, что это случаи 5 и 7.
Следует обратить внимание, что любое умозаключение с посылками Н\, Щ,
#з, ..., #п и заключением С является правильным тогда и только тогда, когда
высказывание
(#i Л #2 Л #3 Л ... Л Нп) -* С
есть тавтология. Заметим, что порядок следования посылок не является суще-
существенным, поскольку
Н1АН2 = Н2АН1.
Примем в качестве правила вывода следующее умозаключение, в правиль-
правильности которого легко убедиться.
.'• Я
Это правильное умозаключение называется правилом отделения (modus ponens).
Рассмотрим пример использования правила отделения. Предположим, b —
целое число. Пусть р и q заданы следующим образом
р : b четно
q : b делится на 2,
так что
Правило отделения дает
.'. Я
если b четно, то b делится на 2.
если b четное, то b делится на 2
b четное
b делится на 2

40 ГЛАВА 1. Таблицы истинности, логика, доказательства
Допустим, что высказывание если b четно, то b делится на 2 получено как
свойство целых чисел и b = 12. Тогда обе посылки истинны, так что нет сомнения
в том, что 12 делится на 2. С другой стороны, если b = 13, тогда р ложно, и хотя
умозаключение правильно, нельзя утверждать что-либо о делимости 6 = 13 на
2. Если одна из посылок ложна, то истинность заключения никоим образом не
зависит от правильности умозаключения.
Перечислим некоторые правила вывода, на которые мы будем ссылаться в
дальнейшем:
а) Правило отделения (Modus Ponens)
г) Расширение
.'. Я
б) Силлогизм
g-»r
л р —> г
в) Modus Tollens
Р-+Я
.'. pVq
д) Специализация
pAq
Л р
е) Конъюнкция
Р
Я
.'. pAq
ж) Выбор
Р
р —> (г V s)
r->q
s-> Я
-'. Я
з) Исключающий выбор
pWq
р —* (г Л ~г)

РАЗДЕЛ 1.4. Аксиоматические системы: умозаключения и доказательства 41
и) Сведение к абсурду (Reductio ad Absurdum)
~р —> (г Л ~г)
Л р
Правильность всех перечисленных умозаключений можно показать с помо-
помощью таблиц истинности.
Сведение к абсурду используется в методе доказательства, известном как
доказательство от противного. Он состоит в следующем: мы допускаем, что
истинным является отрицание того высказывания, которое необходимо доказать;
затем пытаемся прийти к противоречию. Если это удается, исходное утверждение
доказано. Обратите внимание, именно такое рассмотрение было основой ранее
упомянутого метода доказательства правильности умозаключения, альтернатив-
альтернативного использованию таблиц истинности. Таким образом, этот альтернативный
метод рассуждения является правильным.
Рассмотрим такое умозаключение:
Если яблоко красное, то оно спелое
Яблоко спелое
Яблоко красное
В обозначениях
р:
Я-
умозаключение принимает вид
яблоко красное
яблоко спелое
Р
л р
Из таблицы истинности
Случай
1
2
3
4
Р
Т
Т
F
F
я
т
F
Т
F
((Р
—¦
Т
F
Т
Т
Я)
Л
Г
F
Т
F
я)
Т
F
Т
F
Т
т
F
Т
*
Р
т
т
F
F
очевидным образом следует неправильность умозаключения. В случае 3 обе по-
посылки р —> q и q истинны; однако, заключение р таковым не является. Таким
образом, умозаключение неправильно. Данный вид неправильного умозаключе-
умозаключение называется ложной конверсией. Точно так же умозаключение

42 ГЛАВА 1. Таблицы истинности, логика, доказательства
является неправильным и называется ложной инверсией.
В большинстве аксиоматических систем теоремы и аксиомы могут быть весь-
весьма сложными, а их переплетение с правилами вывода — весьма запутанным. Сей-
Сейчас мы попытаемся объяснить, что происходит в процессе доказательства и как
доказательства конструируются. Сложные доказательства обычно представляют
собой длинную цепочку правильных умозаключений вышеуказанных типов. По-
Поэтому доказательство можно определить как последовательность утверждений,
каждое из которых истинно в силу одной из следующих причин:
а) по предположению;
б) по аксиоме или определению;
в) по ранее доказанной теореме или лемме;
г) выведено из предыдущих утверждений;
д) логически эквивалентно предыдущему утверждению.
Используя логическую символику, в качестве примера покажем, что
есть правильное умозаключение.
Номер
1
2
3
4
5
6
Утверждение
р-> я
Как получено
предположение
предположение
предположение
2, 3 и правило отделения
1 и эквивалентность р —> q = ~q —> ~р
4, 5 и правило отделения
Итак, из трех посылок следует заключение ~р, и мы доказали ~р.
В большинстве математических доказательств логика "скрыта" в том смысле,
что о ней специально не упоминается. Предполагается, что читатель может отсле-
отслеживать логику без посторонней помощи, а ее рассмотрение неизбежно усложнило
бы сам процесс доказательства. В некоторых доказательствах, которые последу-
последуют ниже, мы заглянем за кулисы с тем, чтобы проиллюстрировать использование
логики.
¦ УПРАЖНЕНИЯ
1. Используя таблицы истинности, докажите правильность следующих умоза-
умозаключений.
а) Правило силлогизма
л р

РАЗДЕЛ 1.4. Аксиоматические системы: умозаключения и доказательства 43
б) Правило выбора
Р
р —> (г V s)
г —> q
s —* q
.'• Я
в) Правило сведения к абсурду (reductio ad absurdum)
~w —* (г Л ~г)
Л w
2. Покажите, что следующее умозаключение не является правильными:
Р-+Я
q —* г
.'. г
3. Определите, какое из следующих умозаключений является правильным:
а) Р ~* Я б) ~р V q
р —> г ~gVr
в) р —> g г) ~р V
р —> г г V ~
.". ~р .'. г V ~р
4. Определите, какое из следующих умозаключений является правильным:
а) ~г б) р V g
р —> г ~g V r
q —+ г ~г
Л ~(рЛд) /. р
в) р —» g г) р V ~q
q —> г г V ~д
q У г ~р
Л р Л ~Г
5. Установите правильность следующих умозаключений, используя метод, аль-
альтернативный применению таблиц истинности:
a) s V t б) р —> q
t —> г q —> г
s —> к; г
ЛrWw Лр
в) р —> g г) ~р V g
~g —> ~s r V~g
5->t p
tVg s
/. p Vs л rVs
6. Установите правильность следующих умозаключений, используя метод, аль-

44 ГЛАВА 1. Таблицы истинности, логика, доказательства
тернативный методу таблиц истинности:
a) s V t б) р -> q
t —> г q —* г
s —> w г
.'. г V w .'. р
в) р -* q г) ~рv q
s-^t р
.'. р V s .'. г V s
7. Покажите правильность следующих умозаключений, используя правила вы-
вывода и эквивалентные высказывания:
a) ~(sA?) б) р —> g
.*. s —> w
в) ~(~р V д) г) ~х —> ~ги
~z —> ~5 (х V ~гу) -
(р Л ~д) —>• 5 ~р —> ~z
-2 V г ю -¦ (~г V '
.*. r .*. ~r V ~s
8. Докажите, что логическая эквивалентность двух высказываний означает,
что эквиваленция двух высказываний есть тавтология. Иными словами, для
высказываний р и q докажите, что
означает то же самое, что и
р <-> q — тавтология.
Вслед за этим докажите, что последнее утверждение эквивалентно утвер-
утверждению:
как р —> q, так и q —> р являются тавтологиями.
В случае, когда импликация р —> q есть тавтология, говорят, что р имеет
следствием q, и часто записывают это как р => q.
9. Найдите среди указанных ниже выражений тавтологии:
а) р-> (рЛд);
б) р-+ (pVg);
в) (p->q) -> (g->p);
г) ((р -> «) л -д) -> -р);
д) ((р->д)лд) ->р).

РАЗДЕЛ 1.5. Полнота в логике высказываний 45
1.5. ПОЛНОТА В ЛОГИКЕ ВЫСКАЗЫВАНИЙ
Кроме использования в логике, одно из важных применений таблиц истинности
состоит в конструировании коммутационных схем. Прежде, чем приступить к изу-
изучению коммутационных схем, мы рассмотрим вопрос о минимальном количестве
логических связок, необходимых для выражения любого высказывания, образо-
образованного с помощью определенных нами выше логических связок. Известно, что
р <-» q можно выразить как (р —> q) Л (q —» р), так что использовать <-> удобно, но
не необходимо. К тому же р v q эквивалентно
(р Л
V
q).
Также р —> q эквивалентно ~р V q, поэтому нет необходимости использовать —>,
если применяется ~ и V. Кроме того, pAq эквивалентно ~(~р V~g) и pVq экви-
эквивалентно ~(~р Л~д). Следовательно, любое высказывание может быть выражено
через пару связок ~ и Л или ~ и V, причем в любом случае необходимы обе
связки. Однако существуют две связки, обладающие тем свойством, что любое
высказывание может быть выражено с использованием только одной из них. Эти
связки: | — так называемый штрих Шеффера и j — так называемая стрелка
Пирса. Свои названия эти связки получили в честь математиков Г.Шеффера и
Ч.Пирса. Этим связкам соответствуют таблицы истинности
Случай
1
2
3
4
Р
Т
т
F
F
я
т
F
Т
F
р\ я
F
Т
Т
Т
Случай
1
2
3
4
Р
Т
т
F
F
Я
т
F
Т
F
Р 1 Я
F
F
F
Т
Для того, чтобы показать, что любую связку можно заменить связкой |, доста-
достаточно показать это для пар связок ~ и Л или ~ и V, поскольку возможность
выразить любую связку одной из этих пар уже показана. Эквивалентность р \ р
и ~р устанавливается при помощи следующей таблицы истинности:
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
Р
Т
т
F
F
1
F
F
Т
Т
*
Р
Т
т
F
F
Точно так же таблица
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
(Р
Т
т
F
F
1
F
F
Т
Т
Р)
Т
т
F
F
1
Т
т
т
F
*
(я
т
F
Т
F
1
F
Т
F
Т
я)
Т
F
Т
F

46 ГЛАВА 1. Таблицы истинности, логика, доказательства
показывает, что (р | р) \ (q \ q) эквивалентно р V q. Можно также показать, что
(р I я) I {Р I я) эквивалентно р A q.
Таким образом, если показать, что ~ и Л или ~ и V можно выразить,
используя только |, тогда и любую связку можно выразить, используя лишь |.
Предоставляем читателю показать, что pip эквивалентно ~р, (р [ р) [ (q [ q)
эквивалентно р A q, а (р | q) [ (р | q) эквивалентно р V q. Заметим, что р \ q
эквивалентно ~(рЛд), а р | q эквивалентно ~(pVg). Поэтому в дальнейшем
связка | будет называться не-и, а связка | будет называться не-или.
Допустим, что задана произвольная таблица истинности. Существует про-
простой способ найти высказывание, которому она соответствует. Например, предпо-
предположим, что имеется таблица истинности
Случай
1
2
3
4
Р
Т
Т
F
F
Я
т
F
Т
F
Т
Т
F
Т
Известно, что pAq истинно в случае 1 и ложно во всех остальных случаях.
Аналогично, рЛ~д истинно только в случае 2, ~pAq истинно только в случае 3,
а ~р Л ~д истинно только в случае 4. Пусть высказывание должно быть истин-
истинным точно в указанных нами случаях. Если для каждого такого случая (строки
таблицы) выбрать высказывание, которое истинно только в этом случае, и свя-
связать эти высказывания связкой V, то мы получим высказывание, истинное только
в требуемых случаях (строках). В приведенном выше примере рассматриваемая
таблица истинности соответствует высказыванию
(р A q) V (р A ~q) V (~р Л ~q) .
В случае таблиц истинности с тремя переменными имеем аналогичную ситу-
ситуацию. Для каждой строки следующей таблицы приведено высказывание, истинное
только для этой строки.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
рЛ
р А
р А
р А
~р
~р
~р
~р
qA
qA
~q
~q
Aq
Aq
r
Ar
Лг
Л ~г
^q Ar
Заметьте, что если в какой-либо строке переменная имеет ложное значение,
то в соответствующем высказывании она использована с отрицанием. Если требу-
требуется построить высказывание, соответствующее конкретной таблице истинности,

РАЗДЕЛ 1.5. Полнота в логике высказываний 47
необходимо выбрать выражения, соответствующие случаям (строкам), где выска-
высказывание истинно, и соединить их связкой V. Например, построение высказывания
с таблицей истинности
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Т
Т
F
F
Т
F
F
Т
дает высказывание
(р Л q Л г) V (р Л q Л ~г) V (~р Л q Л г) V
Построение высказывания с таблицей
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
F
Т
Т
F
F
Т
F
F
дает высказывание
(р Л q Л ~г) V (р Л ~д Л г) V
Л ~г) .
Л
Такая форма выражения высказывания называется дизъюнктивной нор-
нормальной формой. Выражения р Aq Л ~г, р Л ~д Л г и ~р Лд Л~г называются
элементарными конъюнкциями. Дадим более точное определение.
ОПРЕДЕЛЕНИЕ 1.5. Пусть pi.p2.P3i • • •. Рп — простые высказывания. На-
Назовем выражение х\ Л х2 Л ^з Л • • • Л хп, в котором х^ = р^ или я^ = ~pj,
элементарной конъюнкцией. Выражение, представляющее собой дизъюнкцию
элементарных конъюнкций, называется дизъюнктивной нормальной фор-
формой, так что если ть т2, т3, ..., тп есть элементарные конъюнкции, тогда
mi V Ш2 V m3 V • • • V mn есть дизъюнктивная нормальная форма.

48 ГЛАВА 1. Таблицы истинности, логика, доказательства
Хотя любое высказывание может быть выражено в дизъюнктивной нормаль-
нормальной форме, эта форма высказывания не является простейшей. Карты Карно, ко-
которым посвящен следующий раздел, как раз позволяют упростить выражение
высказывания в дизъюнктивной нормальной форме.
Действуя по той же схеме, мы замечаем, что pVgVr ложно, только когда
р, q и г ложны. Вообще, в таблице
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
q
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
~р V
~р V
~р V
~р V
р V-
р V~
pVq
p\Jq
q
q
jq
->q
V
V
,q v ~r
-qWr
V ~r
Vr
V ~r
Vr
~r
r
каждое выражение ложно в строке, где оно расположено, и истинно в любой дру-
другой строке. Если требуется найти высказывание, обладающее данной таблицей
истинности, зная все случаи (строки), где в таблице истинности стоит ложное
значение, то используются высказывания, каждое из которых ложно только в
соответствующей строке, и все эти высказывания объединяются связкой Л. На-
Например, таблице истинности вида
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
ч
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Т
Т
F
F
Т
F
F
Т
соответствует высказывание
(~р V q V ~г) Л (~р V q V г) Л (р V ~q V г) Л (р V q V ~r) .
Такая форма выражения высказывания называется конъюнктивной нормальной
формой. Выражения ~р V q V ~r, ~p V^Vr,pV~gVr npVgV~r носят название
элементарных дизъюнкций. Теперь дадим более формальное определение.
ОПРЕДЕЛЕНИЕ 1.6. Пусть р1э Р2, Рз, • • • > Рп — простые высказывания. Назо-
Назовем выражение х\ VX2N/хз V.. .Vxn,B котором xi = pi или ~рь элементарной
дизъюнкцией.

РАЗДЕЛ 1.5. Полнота в логике высказываний 49
Выражение, представляющее собой конъюнкцию элементарных дизъ-
дизъюнкций, называется конъюнктивной нормальной формой, так что если
mi, ^2» тпз, • • • > ™<п — элементарные дизъюнкции, то rai Лт2 Лшз Л ... Лгап
есть конъюнктивная нормальная форма.
УПРАЖНЕНИЯ
1. Используя таблицы истинности, докажите, что
sl) p I p эквивалентно ~р;
б) (р I p) I (q 1 <?) эквивалентно р Л q\
в) (р I </) I (p I 9) эквивалентно [р V <?).
2. Найдите высказывания, которым отвечают следующие таблицы истинности:
б) Случай р q r
а) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Т
Т
F
F
F
Т
F
Т
1
2
3
4
5
6
7
т т т
Т Т F
Т F Т
Т F F
F Т Т
F T F
F F Т
F F F
Т
F
Т
F
F
Т
F
Т
в) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
q
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Т
F
Т
Т
F
F
F
Т
3. Найдите высказывания, которым отвечают следующие таблицы истинности:
а) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
F
Т
Т
Т
F
F
F
Т
б) Случай
1
2
3
4
5
6
7
8
Р
Г
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
F
F
F
F
Т
Т
F
Т

50 ГЛАВА 1. Таблицы истинности, логика, доказательства
в) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
q
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Т
F
Т
Т
F
F
Т
F
1.6. КАРТЫ КАРНО
Для простых высказываний р\у р2, рз> • • • ирп существует 2П различных элемен-
элементарных конъюнкций. (Это будет показано в главе 8.) Например, для высказываний
р и q элементарными конъюнкциями будут рЛ q, p Л~д, ~рЛд и ~р Л~д. Карта
Карно — это таблица, каждый элемент которой является элементарной конъ-
конъюнкцией. Например, для высказываний р и q карта Карно должна иметь вид,
изображенный на рис. 1.1, а на рис. 1.2 внутри прямоугольников представлены
соответствующие элементарные конъюнкции.
Р
~Р
Рис. 1.1
Я
~р
Рис. 1.2
рЛ q
~РА q
рЛ ~q
~рЛ ~q
Для представления картой Карно высказывания, записанного в дизъюнктив-
дизъюнктивной нормальной форме, необходимо поместить х в прямоугольниках, соответству-
соответствующих элементарным конъюнкциям. Например, высказыванию
(р Л q) V (~р Л ~д)
соответствует карта Карно, изображенная на рис. 1.3.
q ~Q q ~q
P
X
X
~p
X
X
~P
Рис. 1.3
Заметим, что если высказыванию соответствует карта Карно с двумя сосед-
соседствующими в строке или в столбце х, тогда выражение можно упростить, сведя

РАЗДЕЛ 1.6. Карты Карно 51
две элементарные конъюнкции к одной, содержащей на одну компоненту меньше
(т.е. либо р, либо q не будут присутствовать в выражении). Например, высказы-
высказывание (р Л q) V (р Л ~д), которому соответствует карта Карно, изображенная на
рис. 1.4, эквивалентно высказыванию;?, так как (pAq)\/(pA~q) = pA(q\/~g) =
рАТ = р.
Р
~Р
Я
я
~г
. /.5
Карта Карно для р, q и г может иметь вид, изображенный на рис. 1.5, а на
рис. 1.6 в прямоугольниках внутри представлены элементарные конъюнкции.
~Р
Я
р A q A r
~р A q A r
р A q А ~г
~р A q А ~г
"Я
р A ~q А ~г
~р A ~q А ~г
р A ~q Л г
~р Л ~q A r
г
Рис. 1.6
~г
Следовательно, высказыванию
(р Л q Л ~г) V (р Л ~д Л г) V (~р Л q Л ~г)
будет соответствовать карта Карно, изображенная на рис. 1.7.
р
~Р
с
1
X
X
Я
X
~г
Рис. 1.7
Как и прежде, поскольку два знака соседствуют, две элементарные конъ-
конъюнкции могут быть сведены к одной, содержащей на одну из компонент р, q и г
меньше. В данном случае (р Л q Л ~г) V (~р Л q Л ~г) сводится к (дЛ ~г), так
что выражение принимает вид {q Л ~г) V (р Л ~д Л г).
В случае, когда четыре значка расположены в прямоугольнике рядом, как
показано на рис. 1.8
Я
X
X
X
X
~Я
~r
Рис. 1.8

52 ГЛАВА 1. Таблицы истинности, логика, доказательства
или на рис. 1.9,
Р
~Р
г ~г
я
X
X
1?
X
X
Рис. 1.9
тогда четыре элементарные конъюнкции, отмеченные значками, могут быть све-
сведены к одному члену, содержащему только одну из компонент р, q и г. Например,
первая карта Карно представляет
(р A q Л ~г) V (р Л ~д Л г) V (~р A q А ~
что сводится к ~г.
Вторая карта Карно представляет выражение
V
Л
Л
(р A q А г) V (р A q А ~г) V
Л
A
V(p Л ~д Л г),
что может быть сведено к р.
Поскольку г появляется на обоих концах карты Карно, ее можно "скрутить"
и считать, что четыре значка на карте Карно образуют прямоугольник из четырех
значков (см. рис. 1.10), поэтому выражение
(р A q А г) V (~р Л q А г) V (р Л ~д Л г) V
сводится просто к г.
Р
~Р
Л
Л г)
X
X
^ ^-—
Я
Ч
X
X
~г
Выражение
(р Л q А г) V (~р Aq Ar)V (р Aq A
V
Л g Л
Рис. 1.10
V (р Л
Л
представленное на рис. 1.11, может быть преобразовано к gV(pA~gA~r) на основе
правостороннего блока из четырех значков. Более того, благодаря наличию блока
из двух значков в середине первой строки, его можно еще больше упростить,
приведя к виду q V (р Л ~г).
Р
~Р
X
X
Я
X
X
X
s
-г
Рис. 1.11

РАЗДЕЛ 1.6. Карты Карно 53
Перечислим четыре последовательных шага при использовании карты Карно:
1. Для каждой элементарной конъюнкции обозначьте на карте соответствую-
соответствующий прямоугольник.
2. Покройте знаки, используя, по возможности, несколько прямоугольных бло-
блоков.
3. Используйте блоки, максимальные по величине, не меняя числа блоков.
4. Оцените блоки с соответствующими высказываниями, которые описывают
их, и объедините эти высказывания символом V.
Проиллюстрируем этот процесс путем построения карты Карно для четы-
четырех высказываний р, q, г и s, изображенной на рис. 1.12, где во внутренных
прямоугольниках представлены элементарные конъюнкции, составленные из тех
высказываний, расположенных на краях, которые принадлежат строке и столбцу
соответствующих прямоугольников. Например, крайние высказывания, соответ-
соответствующие второй строке и третьему столбцу, есть р, ~д, ~г и ~s, что порождает
элементарную конъюнкцию р Л ~q Л ~г Л ~s.
Рассмотрим выражение
(pAqArAs)V(pAq Л ~г Л s) V (р Л g Л г Л ~s)V
V(p Л q Л ~г Л ~s) V (~р Л q Л г Л ~s) V (~р Л q Л ~г Л ~s)V
V(~p Л q Л г Л s) V (~р Л q Л ~r As) V (р Л ~д Л ~г Л s)V
V(p Л ~g Ar A s) V (р Л ~д Л г Л ~s).
~р
я
2
/./2
Размещая соответствующие значки в карте Карно, получаем карту, изобра-
изображенную на рис. 1.13, которую можно покрыть восьмикратным, четырехкратным
и двукратным блоками. Восьмикратный блок можно описать, используя только
одну из компонент р, g, r или s. В данном случае восьмикратный блок описывает
q. Четырехкратный блок можно описать, используя только два простых высказы-
высказывания. В данном случае этот блок можно описать, используя р Л s. Двукратный
блок можно описать, используя три простых высказывания. В данном случае это
р A~qAr. Следовательно, исходное высказывание можно упростить и привести к
виду q\/(pAs) V (р Л~дЛг). Поскольку г находится на обоих концах строки, a s
находится на обоих концах столбца, "скручивание" карты Карно объединяет эти

54 ГЛАВА 1. Таблицы истинности, логика, доказательства
Я ~Q
~Р
( «
X
[ «
I «
X
X
X
X
X
X
X
~г
Рис. 1.13
случаи, так что верхний край можно считать прилегающим к нижнему, а левый —
прилегающим к правому.
Например, четырехкратный блок на карте Карно на рис. 1.14 можно описать
посредством г Л s.
Я ~Я
~Р
(
X
X
X
~г
Рис. 1.14
УПРАЖНЕНИЯ
1. Упростите высказывания, выраженные следующими картами Карно:
а)
Я ~Я
~Р
X
X
X
X
X
~г
б)
~Р \
X
X
X
X
X
X
X
~s

РАЗДЕЛ 1.6. Карты Карно 55
в)
~Р
Я
х
X
X
X
X
X
~Ч
X
X
-V- ^
~г
2. Упростите высказывания, выраженные следующими картами Карно:
а)
q ~q
Р
~Р
б)
~Р
X
X
X
X
X
~г
X
X
X
X
X
X
X
X
~г
в)
~р
X
X
X
X
Ч
X
X
X
X
s
X
X
X
X
~s
~r

56 ГЛАВА 1. Таблицы истинности, логика, доказательства
3. Используйте карты Карно для упрощения следующих выражений:
а) (pAqAr)V (~р Л q А г) V (~р Л q A ~r)V
V(~p Л ~q A ~r) V (р Л q А ~г);
б) (р Л q А ~г Л 5) V (р Л ~q л ~г Л 5) V (р Л g Л ~г Л ~s)V
V(p Л ~g Л ~г Л ~s) V (~р A q А ~г Л ~s)V
V(~p A q A ~r A s) V (~р Л ~д Л ~r A s) V (~р A q Ar A ~5)V
V(~p Л ~g Л г Л ~5);
в) (р Л g Л г Л 5) V (~р Л g Л г Л s) V (р Л ~<у Л ~г Л ~5)V
V (~р Л ~д Л г Л ~s).
4. Используйте карты Карно для упрощения следующих выражений:
а) (pAqAr)W (~р Л q А ~г) V (~р Л g Л r)V
V(p Л ~g Л ~г) V (~р Л ~д Л г);
б) (р A q А ~г Л s) V (р Л ~д Л ~r A s) V (~р A q Ar A s)V
V(~p Л g Л ~г Л 5) V (~р Л ~<? Л ~г Л s) V (~р Л ~д Л г Л s);
в) (pAqArAs)V(pAqArA ~s) V (~р ЛдЛгЛ ~s)V
V(p Л ~g Л г A s) V (р Л ~д Л г Л ~s) V (~р Л^Лг Л ~s).
1.7. КОММУТАЦИОННЫЕ СХЕМЫ
Высказывания, соответствующие коммутационным (релейно-контактным) схемам,
принято выражать в системе обозначений булевой алгебры, которая будет введена
в разделе 2.4. Поэтому, прежде чем перейти к изучению коммутационных схем,
мы перейдем от обозначений, принятых в логике, к булевой записи. Символы
Л, V и ~ заменяются, соответственно, на -, + и '. Таким образом, (р Л q) V ~r
превращается в (р • q) + г', а
(р A q А ~г) V [р А ~д Л г) V (~р Л q А ~г)
принимает вид
(Р • g • г7) + (р • д' • г) + (р' • g • г').
Как и в обычной алгебре, знак произведения, как правило, опускается, и предпо-
предполагается, что произведение выполняется перед сложением, поэтому приведенное
выше выражение можно переписать в виде
pqr1 + pq'r 4- p'qr'.
В таблицах истинности Т заменяется на 1, a F на 0, так что таблица истин-
истинности

РАЗДЕЛ 1.7. Коммутационные схемы 57
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Р
Т
т
т
т
F
F
F
F
V
Г
Т
Т
Т
F
F
Т
F
((~
F
F
Т
Т
F
F
Т
Т
я)
Т
т
F
F
Т
Т
F
F
Л
F
F
Т
F
F
F
Т
F
г)
Т
F
Т
F
Т
F
Т
F
преобразуется в таблицу
Случай
1
2
3
4
5
6
7
8
Р
1
1
1
1
0
0
0
0
я
1
1
0
0
1
1
0
0
г
1
0
1
0
1
0
1
0
р
1
1
1
1
0
0
0
0
+
1
1
1
1
0
0
1
0
W
0
0
1
1
0
0
1
1
•
0
0
1
0
0
0
1
0
г)
1
0
1
0
1
0
1
0
Рис. 1.15
В 1938 г. Клод Шеннон заметил связь между таблицами истинности и элек-
электрическими цепями. Рассмотрим схему переключения на рис. 1.15, которая состо-
состоит из источника питания (рис. 1.16) и электрической лампочки (рис. 1.17).
Рис. 1.16
Рис. 1.17
Присвоим значение 1 переключателям р и q, если они замкнуты (т.е. элек-
электрический ток проходит через них). В противоположной ситуации присвоим им

58 ГЛАВА 1. Таблицы истинности, логика, доказательства
значение 0. Присвоим значение 1 схеме, когда лампочка светится (т.е. электри-
электрический ток через нее проходит). Заметим, что при последовательном соединении
элементов цепи р и q, как это имеет место на приведенной выше схеме, лампочка
загорается, и значение схемы становится равным 1 только в случае, когда оба
переключателя замкнуты, т.е. и р, и q имеют значение 1. Таким образом, схема
соответствует высказыванию р • q. Такое расположение переключателей называ-
называется логическим элементом р и q, или схемой логического умножения. Этот
логический элемент обозначается символом, изображенным на рис. 1.18.
=D-'«
Рис. 1.18
Теперь рассмотрим схему переключения, показанную на рис. 1.19, где пере-
переключатели р и q соединены параллельно.
1
р
q
\
Рис. 1.19
Отметим, что теперь лампочка загорается, и значение схемы становится равным
1, когда один из двух переключателей р или q замкнут, т.е. либо значение р = 1,
либо q = 1 (либо оба они равны 1). Эта схема соответствует высказыванию
р + q. Такое расположение выключателей называется логическим элементом р
или q, или схемой логического сложения. Этот логический элемент обозначается
символом, изображенным на рис. 1.20.
Рис. 1.20
не р
Предположим, имеется схема (мы не будем пытаться ее изобразить), с одним
переключателем р, который обладает таким свойством, что лампочка загорается
тогда и только тогда, когда р разомкнут. Следовательно, схема имеет значение 1,
когда р имеет значение 0, и имеет значение 0, когда р имеет значение 1. Эта схема
соответствует р', а соответствующий логический элемент называется логическим
элементом не, или инвертором. Логический элемент не обозначается символом,
изображенным на рис. 1.21.

РАЗДЕЛ 1.7. Коммутационные схемы 59
ПРИМЕР 1.7. Схема на рис. 1.22 содержит логический элемент р и q, за которым
следует инвертор, так что схема соответствует выражению (р • q)'. Заметим, что
инвертор отрицает всю предшествующую ему схему.
Рис. 1.22
?
ПРИМЕР 1.8. Схема на рис. 1.23 содержит соединение логического элемента р
или q с логическим элементом не г посредством логической схемы умножения.
Следовательно, она соответствует выражению (p + q) -rf.
Рис. 1.23
?
ПРИМЕР 1.9. Булево выражение, соответствующее схеме на рис. 1.24, имеет вид
Рис. 1.24
?
ПРИМЕР 1.10. Коммутационная схема, соответствующая выражению (р' • q) + г,
показана на рис. 1.25.
я-
г-
Рис. 1.25
?
ПРИМЕР 1.11. Коммутационная схема, соответствующая выражению ((р + q)'
(р + г)) + г;, показана на рис. 1.26.
Рис. 1.26
?

60 ГЛАВА 1. Таблицы истинности, логика, доказательства
ПРИМЕР 1.12. Построим схему трехклавишного переключателя, при помощи ко-
которого свет включается тремя различными двупозиционными переключателями.
Рассмотрим сначала соответствующее булево выражение. Свет должен включать-
включаться, когда все три переключателя замкнуты, т.е. необходимо иметь pqr. Если один
из переключателей разомкнут, то свет должен быть выключен. Однако, если разо-
разомкнуть другой переключатель, то свет должен включиться. Следовательно, иско-
искомое выражение имеет вид pqr Н-pq'r1 -f-p'q1г + p'qr1. Для простоты, вместо схемы,
представленной на рис. 1.27, для выражения pqr мы будем использовать схему,
изображенную на рис. 1.28.
Р
Я
Рис. 1.27 Рис. 1.28
А для выражения р + q + г вместо схемы на рис. 1.29 мы будем использовать
схему, показанную на рис. 1.30.
г-
Рис. 1.29 Рис. 1.30
Тогда искомая схема будет такой, как показано на рис. 1.33. ?
Ранее было отмечено, что штрих Шеффера, обозначаемый через |, имеет ту
же таблицу истинности, что и (pq)' (в булевой записи), поэтому мы и упоминали
его как логическую связку не-и. В свою очередь, стрелка Пирса, обозначенная |,
имеет ту же самую таблицу истинности, что и (p + qI, поэтому она упоминалась
как связка не-или. Логические элементы не-и и не-или обозначаются символами,
показанными на рис. 1.31 и 1.32.
Рис. 1.31 Рис. 1.32
Выражению (p\q) [ (p\r) соответствует схема, изображенная на рис. 1.34.
Рис. 1.34

РАЗДЕЛ 1.7. Коммутационные схемы 61
; i»
¦>
Рис. 1.33
ПРИМЕР 1.13. Полусумматор находит сумму двух двоичных чисел 1 и 0 со-
согласно таблице сложения:
+
0
1
0
0
1
1
1
10
Свое название полусумматор получил в связи с тем, что при сложении дво-
двоичных чисел с более чем одним разрядом (что станет предметом обсуждения в
последующей главе) суммируются только низшие разряды, поскольку нет возмож-
возможности учесть в сумме число, которое "переносится". Для удобства суммирования
одноразрядных двоичных чисел таблица, приведенная выше, преобразована к ви-
ДУ
+
0
1
0
00
01
1
01
10
Пусть р и q обозначают числа, которые требуется сложить, a di,do — первый и
второй разряды суммы, тогда приходим к следующим таблицам истинности:
Случаи
1
2
3
4
P
1
1
0
0
я
l
0
l
0
d0
0
1
1
0
Случаи
1
2
3
4
P
1
1
0
0
Я
1
0
1
0
dx
1
0
0
0

62 ГЛАВА 1. Таблицы истинности, логика, доказательства
Следовательно, do = pqf +p'q, что эквивалентно (p+q)'(pq)''. Это можно показать,
используя таблицы истинности или правило эквивалентности (см. упражнения).
Также d\ =pq. Коммутационная схема для полусумматора приведена на рис. 1.35.
Я-
О
<*,
Рис. 1.35
Поскольку полусумматор дает сумму двух чисел, он обозначается символом,
изображенным на рис. 1.36.
Рис. 1.36
?
ПРИМЕР 1.14. Полный сумматор складывает три одноразрядных двоичных чис-
числа. Следовательно, он может сложить два двоичных числа с тем числом, которое
"переносится". Пока необходимо рассматривать это как сложение трех однораз-
одноразрядных двоичных чисел. Если предположить, что р, q и г обозначают числа,
которые необходимо сложить, a df,df — первый и второй разряды их суммы,
получаем следующие таблицы истинности:
Случай
1
2
3
4
5
6
7
8
Р
1
1
1
1
0
0
0
0
я
1
1
0
0
1
1
0
0
г
1
0
1
0
1
0
1
0
df
1
1
1
0
1
0
0
0
dt
1
0
0
1
0
1
1
0
df действительно есть результат сложения d0 с г, где d0 — второй разряд суммы
р и q. Следовательно, его схему легко описать. Значение df проще получить,
используя приведенную выше таблицу истинности
df = pqr + pqr1 -f pq'r + p'qr .
Воспользовавшись картой Карно для выражения df, получаем следующую карту:
Я ~Q
~Р
X
X
X
X
~г

РАЗДЕЛ 1.7. Коммутационные схемы 63
Таким образом, df = pq+pr + qr = pg + (р 4-g)r, поэтому схема может быть при-
приведена к виду, показанному на рис. 1.37. (Более подробно эта схема представлена
на рис. 1.39, приведенном ниже.)
Рис. 1.37
Поскольку полный сумматор складывает три числа, он будет обозначаться
символом, показанным на рис. 1.38.
Рис. 1.38
?
Рис. 1.39
УПРАЖНЕНИЯ
1. Перепишите следующие высказывания в обозначениях булевой алгебры:
а) (р Л q) Л (q V ~r);
б) (q V ~г) Л (~р V г) Л (q V ~r V s);
в) ~(р Л ~q Л г) V (~q Л г) V (р Л ~g Л ~г);
г) ~(~pV(g Л~г));
д) (р Л г) V (р Л ~д) Л (р V г V ~s).

64 ГЛАВА 1. Таблицы истинности, логика, доказательства
2. Перепишите следующие высказывания в обозначениях булевой алгебры:
а) (р V q V ~г) Л ~(r V ~д);
б) (~д Л г) V~(pAr);
в) ~((р Л г) V ~д);
г) (р Л q Л г) V (~р Л ^ Л ~г) V (~р Л q Л г) V (~р Л g Л ~г);
д) (р Л ~д Л ~г Л s) V (~р A q Ar A s) V (~р A q А ~г Л 5).
3. Приведите булевы выражения, соответствующие коммутационным схемам:
а)
б)
в)
г)

РАЗДЕЛ 1.7. Коммутационные схемы 65
д)
4. Приведите булевы выражения, соответствующие коммутационным схемам:
а)
в)

66 ГЛАВА 1. Таблицы истинности, логика, доказательства
д)
5. Постройте коммутационные схемы, соответствующие булевым выражениям:
а) (р'+ q)(p + (qr));
б) (pq') + ((qr') + (p'r));
в) (q'r') + ((pqy(q'r));
г) (q(r + s))((p'q') + (qr'));
д) (pq) + ((pq'r') + r)'.
6. Постройте коммутационные схемы, соответствующие булевым выражениям:
а) (pq'Y + (,г)';
б) ((Р+ «)*)';
в)
г)
д)
7. Муниципальный совет состоит из пяти членов. Каждый член совета имеет
для голосования кнопку "за" и кнопку "против". Решение принимается, если
за него проголосует большинство. Постройте коммутационную схему устрой-
устройства, сигнализирующего о том, что решение принято, путем высвечивания
индикатора. Указание: при построении схем используйте последовательное
и параллельное соединение переключателей, как показано в начале раздела.
8. Муниципальный совет состоит из пяти членов, включая председателя совета.
Каждый член совета имеет для голосования кнопку "за" и кнопку "против".
Решение принимается, если за него проголосует большинство. Председатель
совета голосует только в том случае, если голоса "за" и "против" раздели-
разделились поровну. Постройте коммутационную схему для определения принятия
или непринятия решения путем высвечивания индикатора. Указание: при
построении схем используйте последовательное и параллельное соединение
переключателей, как показано в начале раздела.
9. Муниципальный совет состоит из пяти членов, включая председателя сове-
совета. Каждый член совета имеет для голосования кнопку "за" и кнопку "про-
"против". Решение принимается, если за него проголосует большинство, исклю-
исключая председателя, который имеет право вето. Постройте коммутационную
схему для определения принятия или непринятия решения путем высвечи-
высвечивания индикатора.
10. Электрическая схема содержит три двупозиционных переключателя. Скон-
Сконструируйте схему для включения и выключения любым переключателем.

ГЛАВА
ТЕОРИЯ МНОЖЕСТВ
2.1. ПОНЯТИЕ МНОЖЕСТВА
Под множеством понимается некоторая, вполне определенная совокупность объ-
объектов или элементов. Это утверждение не следует рассматривать как строгое
определение. Такое "определение" напоминает данное основоположником теории
множеств Георгом Кантором определение множества как "объединения в одно
целое объектов, хорошо различимых нашей интуицией или мыслью". Расплывча-
Расплывчатость, недостаточность этого определения стала понятной, когда в 1879 году ита-
итальянский логик Бурали-Форти, а немного позже выдающийся философ и логик
Бертран Рассел открыли парадоксы, указывающие на внутреннюю противоречи-
противоречивость канторовой теории множеств. Для устранения таких противоречий и пара-
парадоксов для теории множеств были предложены аксиоматические системы. Наи-
Наиболее известны системы Цермело-Френкеля-фон Неймана, Гильберта-Бернайса-
Геделя и Рассела-Уайтхеда. В силу ограниченности объема книги мы не будем
изучать эти системы. Поэтому, по сути, мы оставим понятие множества неопре-
неопределенным и будем считать множество заданным, если его элементы однозначно
определены и это не приводит к каким-либо противоречиям.
Конечные множества можно описывать, перечисляя их элементы. Элемен-
Элементы, принадлежащие конечному множеству, условимся записывать между двумя
фигурными скобками и разделять их запятыми. Например, {1,2,3,4} есть мно-
множество, содержащее натуральные числа 1, 2, 3 и 4. Множество гласных мож-
можно представить как {а, о, у, э, и, ы}. Как правило, для обозначения множеств
будем использовать прописные буквы. А = {Боб, Джейн, Нэнси} есть множе-
множество, состоящее из Боба, Джейн и Нэнси. Множество первых п положительных
целых чисел обозначаем {1,2,3,... ,п}, где точками показано продолжение пере-
перечисления элементов. Это же обозначение можно использовать для некоторых бес-
бесконечных множеств. Например, множество положительных целых чисел можно
обозначить как {1,2,3,4,...}. Часто при перечислении множества используется
описание характеристического свойства элементов этого множества. Например,
С = {1,8,27,..., fc3,...} описывает множество кубов всех положительных чисел,
а 5 = {1,4,9,... ,п2} описывает множество квадратов всех положительных чи-

68 ГЛАВА 2. Теория множеств
сел, которые меньше или равны п. Очевидно, что перечисление элементов удобно
только в том случае, когда множество элементов мало или произвольный элемент
характеризуется свойством, которое легко описать. Используя этот метод, не так
легко описать множество граждан Соединенных Штатов Америки и совершенно
немыслимо описать множество действительных чисел.
В общем случае множество задается путем указания характеристического
свойства, т.е. свойства, которому удовлетворяют элементы данного множества, и
только они. Для задания обычно используются фигурные скобки, а внутри них
приводится характеристическое свойство, описывающее множество. Таким обра-
образом, множество {х : х обладает свойством Р) предполагается содержащим только
те объекты, которые имеют свойство Р. Например, {х : х — футболист, играю-
играющий за Юго-западный колледж} — множество, состоящее из всех футбольных
игроков, выступающих за Юго-западный колледж. Запись {х : х —- гражданин
Англии} описывает множество всех граждан Англии. Способ задания множества
должен быть адекватным, т.е. должен полностью определять множество. Это не
представляет труда, если объекты множества перечислены. Рассмотрим, однако,
множество А = {х : х — высокий студент данной группы} или В = {х : х — хо-
хороший студент данной группы}. Если различным студентам группы предложить
определить множества i и В, они могут сделать это неоднозначно, выбирая в
качестве элементов как множества А, так и множества В не одних и тех же
людей. При рассмотрении множества С = {х : х — привлекательная (или кра-
красивая) студентка группы} выбрать элементы множества С не только трудно, но
не стоит даже пытаться это сделать. Однако, если множество А = {х : х — сту-
студент данной группы, рост которого выше 180см} и В = {х : х — студент данной
группы, средний балл которого не ниже 4}, то можно сказать определенно, явля-
является ли данный студент элементом А или В, так что А и В действительно есть
множества.
Таким образом, мы приходим к следующему формальному определению.
ОПРЕДЕЛЕНИЕ 2.1. Если а есть один из объектов множества А, мы говорим,
что а есть элемент А, или а принадлежит А. Принадлежность элемента а
множеству А записывается как а Е А. Если а не является элементом А, это
записывается как а <? А.
Например, 3 е {1,2,3,4}, но 5 ^ {1,2,3,4}. Если Р есть множество {х : х
был президентом Соединенных Штатов}, то Авраам Линкольн ? Р, а Патрик
Гэнри ? Р.
ОПРЕДЕЛЕНИЕ 2.2. Множество А есть подмножество множества В
(обозначается А С В), если каждый элемент А есть элемент В\ т.е. если
х G А, то х G В. В частности, каждое множество есть подмножество самого
себя. Если А не является подмножеством В, это записывается как А <? В.
Таким образом, A (jL В, если существует элемент А, не принадлежащий В.

РАЗДЕЛ 2.1. Понятие множества 69
Следовательно, {1, 2,3} С {1,2,3,4}, но {1,2,5} ? {1,2,3,4}. Если А = {х :
х — футболист колледжа}, В — {х : х — спортсмен колледжа}, а С = {х : х —
самый сильный математик колледжа}, то А С В, но С ^ J5.
Множества равны, если они содержат одни и те же элементы. Если А есть
множество {2,4,6}, а В есть множество {х : х есть четное положительное целое
число, которое меньше 7}, тогда А и В — равные множества. Таким образом, мы
приходим к следующему определению.
ОПРЕДЕЛЕНИЕ 2.3. Пусть А и В — некоторые множества. Говорят, что А
равно В, и пишут А = В, если для любого х имеем: х е А тогда и только
тогда, когда х Е В. Иначе говоря, А = В тогда и только тогда, когда А С В и
В С А. Если А С В и А ^ В} то это записывают Л С В и говорят, что А есть
собственное подмножество В.
Таким образом, доказательство равенства множеств А и В состоит из двух
этапов:
1) Доказать, что А есть подмножество В.
2) Доказать, что В есть подмножество А.
Поскольку множество однозначно определяется только элементами, которые
оно содержит, порядок их перечисления роли не играет. Например, {1,2,4,6} =
{2,1,6,4}. Кроме того, любой элемент либо принадлежит данному множеству,
либо нет. Каждый элемент может входить во множество не более одного раза.
С этого момента вводится два новых множества: универсальное множество,
или универсум, и пустое множество. В известном смысле они представляют со-
собой противоположности, поскольку пустое множество не содержит элементов, а
универсальное множество содержит "все" элементы.
ОПРЕДЕЛЕНИЕ 2.4. Пустое множество, обозначаемое 0 или {}, есть мно-
множество, которое не содержит элементов. Универсальное множество U есть
множество, обладающее таким свойством, что все рассматриваемые множества
являются его подмножествами.
В теории чисел универсальное множество обычно совпадает со множеством
всех целых или натуральных чисел. В математическом анализе универсальное
множество может быть множеством всех действительных чисел или множеством
всех точек n-мерного пространства. Следует отметить, что универсальное множе-
множество f/, хотя и названо универсальным, однозначно не определено, если точно не
указана область рассмотрения (предметная область). Конечно, любое множество,
содержащее ?/, может быть использовано как универсальное множество.
По определению, каждое множество есть подмножество универсального мно-
множества. Пустое множество есть подмножество любого данного множества А, по-
поскольку каждый элемент пустого множества содержится в А. Можно сказать, что
не существует элементов пустого множества, которые не принадлежали бы А.

70 ГЛАВА 2. Теория множеств
¦ УПРАЖНЕНИЯ
1. Перечислите элементы множества {х : х — целое и х2 < 100}.
2. Перечислите элементы множества {х : х — президент США после 1940
года}.
3. Перечислите элементы множества {х : х — гласный звук}.
4. Перечислите элементы множества {х : х — положительное четное целое
число, меньшее чем 21}.
5. Опишите множество {3,6,9,12, 15,18,21,24} при помощи характеристиче-
характеристического свойства.
6. Опишите множество {а, 6, с, d, e, /, g,h,i,j} при помощи характеристическо-
характеристического свойства.
7. Опишите множество {Огайо, Оклахома, Орегон} при помощи характеристи-
характеристического свойства.
8. Опишите множество {1,4,9,16,25, 36,...} при помощи характеристического
свойства.
9. Перечислите подмножества множества {а}.
10. Перечислите подмножества множества {а, Ь}.
И. Перечислите подмножества множества {а,Ь,с}.
12. Перечислите подмножества множества {а, 6, с, d}.
13. Перечислите подмножества множества 0.
14. Используя результаты пяти предыдущих упражнений, определите число под-
подмножеств для множества, состоящего из п элементов.
15. Установите истинность или ложность каждого из следующих утверждений:
а) 0 С 0;
б) 0 С 0;
в) 0 G 0;
г) 0 С А, где А — произвольное множество;
д) 0 G А, где А — произвольное множество.
16. Установите истинность или ложность каждого из следующих высказываний:
а) {2} G{1,2,3,4,5}; б) {2} С {1,2,3,4, 5};
в) 0 = {0}; г) {1,2,3} ?{1,2,3,{1,2,3}};
д) {1,2,3} С {1,2,3,A,2,3}}.
17. Определите количество элементов в каждом множестве:
а) {0,{0}}: б) {{0,{0}}};
в) {1,2,3,A,2,3}}; г) {0,{0},а,Ь,{а,6},{а,6,{а,6}}};
д) {0,@}, {0,{0}}}.

РАЗДЕЛ 2.2. Операции над множествами 71
2.2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Рассмотренные ниже операции над множествами позволяют строить новые мно-
множества, используя уже существующие.
ОПРЕДЕЛЕНИЕ 2.5. Пересечением множеств А и В называется множество,
состоящее из всех тех и только тех элементов, которые принадлежат и А, и В.
Пересечение множеств Аи В обозначается АпВ. Это определение равносильно
следующему: An В = {х : х € А и х е В}.
Например, если А = {1,2,3,4, 5} и В = {1,3,5,7,9}, тогда А П В = {1,3,5}.
Если С = {х : х имеет рост выше 180см} и D = {х : х любит играть в шахматы},
тогда С П D — {х : х имеет рост выше 180см и любит играть в шахматы}.
Обратите внимание, что в описании пересечения множеств В ПС использована
связка "и". В дальнейшем мы убедимся, что символы П и Л, введенные в главе 1,
связаны между собой и имеют схожие свойства.
Определим пересечение трех и более множеств. Пусть Ль А2 и As — мно-
множества. Их пересечение можно определить следующим образом:
В = Ai П (А2 П Аз) •
Далее будет показано, что А\ П (А2 П Аз) = (А\ П А2) П Лз, поэтому можно
использовать запись
В = Ai П А2 П Аз.
Очевидно, х е J5 тогда и только тогда, когда х е -Ai, x G А2 и х е А3; иными
словами, х е В тогда и только тогда, когда х принадлежит всем трем множествам
Ль А2 и Л3. Пусть J = {1,2,3}. В таком случае х е В тогда и только тогда,
когда х ? Aj для всех j € J, что равносильно записи
В = {х : х € Aj для всех j E J }.
Пересечение множеств в общем случае определяется следующим образом.
ОПРЕДЕЛЕНИЕ
2.6.
Если
iei
I--
=
А\ П
{х:
2,3
А2
х е
п
А
Л3п
г ДЛЯ
, ТО
... п
всех
Ак
г G
=
!}¦
Объединением множеств А и В называется множество, состоящее из всех
тех элементов, которые принадлежат хотя бы одному из множеств А или В.
Объединение множеств А и В обозначается Аи В. Сформулированное выше
определение можно записать так: Аи В = {х : х е А или х е В}.
ПРИМЕР 2.7. Например, если А = {1,2,6,7}, г В = {2,3,5,6}, тогда Аи В =
{1,2,3,5,6,7}. Объединение Аи В образовано из Л и Б путем соединения вместе
элементов Аи В. ?

72 ГЛАВА 2. Теория множеств
Если А = {х : х — политик}, а В — {х : х — выпускник колледжа}, то
Аи В = {х : х — политик или выпускник колледжа}. Обратите внимание, что в
описании объединения Аи В использована связка "или" так же, как в описании
пересечения множеств использована связка "и".
Объединение множеств А\, А2 и Аз определяется следующим образом:
В = A1U(A2UA3).
Далее будет показано, что А\ U (А2 U A3) = (A\ U А2) U Аз, поэтому можно
использовать запись
В = А\ U A2 U Аз .
Очевидно, х Е В тогда и только тогда, когда х € А\ или я Е А2 или х Е Лз;
иными словами, х € В тогда и только тогда, когда х принадлежит хотя бы одному
из трех множеств А\, А2 или Аз. Таким образом, х Е В тогда и только тогда,
когда для некоторого j Е {1,2,3}, х Е Aj, что равносильно записи
В = {х : х ? Aj для некоторого j Е {1,2,3}}.
Объединение множеств в общем случае определим следующим образом.
ОПРЕДЕЛЕНИЕ 2.8.
и*
Пусть / =
= А\ U А2
{1,2,3,.
U A3 U • •
= {х : существует г
..,*;}, тогда
•UAk =
Е I такое, что х Е Ai}.
ОПРЕДЕЛЕНИЕ 2.9. Пусть А и В множества. Разностью множеств А - В
называется множество всех тех и только тех элементов А, которые не содер-
содержатся в В. Или, что то же самое, А — В = {х:хеАих? В}. Симмет-
Симметрическая разность множеств А и В, обозначаемая А Л В, есть множество
(А-В)и{В-А).
Например, если А = {1,2,4,6,7},аВ = {2,3,4, 5,6}, то А - В = {1,7} , а
ААВ есть множество {1, 3, 5, 7}. Симметричная разность множеств А и В состоит
из тех элементов, которые принадлежат в точности одному из двух множеств А
или В. Если А = {х : х играет в теннис}, а В = {х : х играет в гольф}, то
А — В = {х : х играет в теннис, но не играет в гольф}. Множество А Л В =
{х : х играет только в теннис или играет только в гольф}. Обратите внимание на
сходство со связкой "исключающее или" из главы 1.
ОПРЕДЕЛЕНИЕ 2.10. Дополнение множества Л, обозначаемое А\ — это мно-
множество элементов универсума, которые не принадлежат А. Следовательно,
А' = U - А = {х : х Е U и х $ А}.

РАЗДЕЛ 2.2. Операции над множествами 73
Если U — множество положительных целых чисел, а А = {2,4,6,8,...} —
множество всех четных положительных чисел, то А! — {1,3,5,7,...} — мно-
множество всех нечетных положительных чисел. Если U — множество всех букв
английского алфавита, а V = {а, е,г,о, и}, то V — множество всех букв, обо-
обозначающих в английском языке согласный звук. Если А = {х : х — любитель
научной фантастики}, тогда А! — {х : х не любит научную фантастику}. Обратите
внимание, что дополнение множества связано с символом ~ в логике.
В соответствии с определением равенство двух множеств может быть уста-
установлено в два этапа.
Докажите, что первое множество есть подмножество второго.
Докажите, что второе множество есть подмножество первого.
Этот способ используется, например, в доказательствах приведенных ниже тео-
теорем. Первый случай расписан более подробно.
ТЕОРЕМА 2.11. Для произвольных множеств Аи В справедливо равенство
А - В = А П В'.
ДОКАЗАТЕЛЬСТВО. Для доказательства равенства двух множеств нужно пока-
показать, что каждое из множеств является подмножеством другого. Это можно осу-
осуществить, выбирая произвольный элемент одного множества и доказывая, что он
принадлежит другому множеству. Такое доказательство гораздо легче провести,
следуя приведенным ниже рассуждениям, поскольку в них каждый шаг обратим.
а G А - В <=> (а G А) Л (а ? В) <=> определение разности А- В
4Ф (a G А) Л (а Е В') <=> определение дополнения
<=> а G (Ап В'). определение пересечения
Обратите внимание, что при доказательстве следующей теоремы один из
законов логики — закон де Моргана — существенно используется для доказа-
доказательства соответствующего закона де Моргана в теории множеств.
ТЕОРЕМА 2.12. Для произвольных множеств А и В имеет место
а) {АпВ)' = А'иВ'\
б) (АиВ)' = А'ПВ'.
ДОКАЗАТЕЛЬСТВО. Ниже приведено доказательство части (а). Доказательство
части (б) предоставляется читателю.
Как и в предыдущем доказательстве, мы покажем, что каждое из множеств,
входящих в равенство, есть подмножество другого.
a e (An BY ^ a ^ (АП В)' <=$> определение дополнения
<ф ~(а е (АП В)) «Ф определение $
ф> ~((а G А) Л (а е В)) о определение пересечения

74 ГЛАВА 2. Теория множеств
<=> ~(а G А) V ~(а gB)^ закон логики де Моргана
<& (а ? A)V (а ? В) <=> определение ?
<=> (a G А') V (а Е Б') <=> определение дополнения
<ФаЕ (Л' U В'). определение объединения
¦
Обратите внимание, что при доказательстве следующей теоремы логический
закон дистрибутивности существенно используется для доказательства соответ-
соответствующего закона дистрибутивности в теории множеств.
ТЕОРЕМА 2.13. Для произвольных множеств А, В и С справедливы равенства
а) А П (В U С) = (А П В) U (А п С);
б) A U (Б П С) = (Л и #) П (А и С)-
ДОКАЗАТЕЛЬСТВО. Ниже приведено доказательство части (а). Доказательство
части (б) предоставляется читателю. Опять покажем,что каждое из множеств,
входящих в равенство, есть подмножество другого.
а G А П (В U С) ^ (a G A) A (a G (В U С)) <4> определение пересечения
<=> (a G А) А ((а G J5) V а € С) «=> определение объединения
<=> ((а G A) A (a G Б)) V определение пересечения
V ((а G А) /\ (а G С)) <=> закон логики де Моргана
<=> (a G (An Б)) V (а G (А П С)) «=> определение пересечения
<^ а е ((А ПВ)и(АП С)) <=> определение ?
<^(aG Л') U (a G Б'). определение объединения
Мы убедились, что свойства, доказанные в теории множеств, имеют свой
аналог в логике. В разделе 2.4 при рассмотрении булевой алгебры будет дано
обобщение как операций теории множеств, так и логических операций.
ОПРЕДЕЛЕНИЕ 2.14. Множество всех подмножеств множества Л, или бу-
леан множества Л, обозначаемый V(A), есть множество, состоящее из всех
подмножеств множества А.
Следовательно, булеан множества А = {1,2,3} есть множество
V(A) = {0, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
Когда А содержит 3 элемента, V(A) состоит из 23 = 8 элементов или, что то же
самое, А включает 23 = 8 подмножеств. Это будет показано в главе 8. В общем
случае, если А содержит п элементов, множество V(A) включает 2П элементов,
т.к. А имеет 2П подмножеств. По этой причине V(A) часто обозначают через 2А.
Еще одной часто используемой операцией над множествами является декар-
декартово произведение, которое определяется следующим образом.

РАЗДЕЛ 2.2. Операции над множествами 75
ОПРЕДЕЛЕНИЕ 2.15. Декартово произведение множеств А и Б, обозначае-
обозначаемое Ах В, есть множество {(а,6) : а ? А и b e В}. Объект (а,6) называется
упорядоченной парой с первой компонентой а и второй компонентой Ь.
Множество Ах В состоит из всех упорядоченных пар, имеющих в качестве
первой компоненты элемент из Л, а в качестве второй компоненты — элемент из
В. По существу, это та же упорядоченная пара, которую мы обычно использу-
используем в алгебре. Порядок компонент в паре существенен! Например, рисуя график
функции, мы знаем, что точка A,2) не совпадает с точкой B,1).
Пусть А = {1,2,3}, а В = {г, s}. Тогда
АхВ = {(l,r), (l,s), B,г), B,5), C,г), C,5)}.
Если каждое из множеств А и В представляет собой множество действительных
чисел, то А х В представляет собой декартову плоскость, на которой упорядо-
упорядоченные пары чисел используются для графического изображения функций.
Если А содержит п элементов, а В содержит т элементов, тогда Ах В содер-
содержит п-т элементов. В частности, если А пусто или В пусто, то, по определению,
Ах В пусто.
¦ УПРАЖНЕНИЯ
1. Пусть А = {1,2,3,4,5,6,7}, В = {4,5,6,7,8,9,10}, С = {2,4,6,8,10}, а
U = {1,2,3,4,5,6, 7,8,9,10}. Определите следующие множества:
а) Аи С; б) АО В;
в) АП {В U С); г) (АП В) U С;
д) (АпВ)'\ е) А'ПВ'\
ж) А А В\ г) А-В.
2. Пусть А = {1,2,3,4,5,6,7}, В = {4,5,6,7,8,9,10}, С = {2,4,6,8,10}, а
U = {1,2,3,4,5,6,7,8,9,10}. Определите следующие множества:
а) А-С; б) (A-B)U(B-A)',
в) АП(ВПС')\ г) (AUC)-B'\
д) (A-0)U(A-A)\ е) ВАС;
ж) С-А.
3. Пусть А = {1,2,3}, а В = {а,Ь}. Определите
г) Ах В\ б) В х В; в) А х 0.
4. Пусть А = {1,2,3}, а В = {а, 6}. Определите
а) А х А; б) В х А\ в) А А В.
5. Определите V(A), если А = 0.
6. Определите V{A), если А = {0, {0}}.
7. Определите ^(^(Л)), если А = 0.
8. Определите, какие из следующих утверждений истинны, а какие ложны:
а) АП0 = А; б) ЛЛЛ = 0;
в) если АС В, то An В = А; г) если А П В = А, то В С А\
д) Л - А = А\ е) (А х B)f = А' х Б'.

76 ГЛАВА 2. Теория множеств
9. Определите, какие из приведенных утверждений истинны, а какие ложны:
a) AU0 = A; б) АД0 = А;
в) если А С В, то A U В = А; г) если A U В = А, то В С Л;
д) А-0 = А.
10. Докажите, что Аи(ВпС) = (ЛиВ)П(Ли С).
11. Докажите, что (A U В)' = А' П Б'.
12. Определим (а, Ь) как множество {а, {а, Ь}}. Покажите, что при таком опреде-
определении мы вправе называть компоненты "первой" и "второй", т.к. (а, Ь) = (с, d)
тогда и только тогда, когда a = с и 6 = d. Таким образом, это определение
позволяет ввести понятие порядка через понятие множества, в котором по-
порядок следования элементов не играет никакой роли.
13. Наследником множества А называется множество Ли {А}. Определите на-
наследников следующих множеств:
а) 0; б) {0}; в) {0,{0}}-
14. Пусть / — некоторое множество и пусть для каждого г ? / Аг — множество,
обозначенное этим г, тогда
П Ai = {х : х е Ai для всех г G /}.
iei
Множество Р| Ai называется обобщенным пересечением совокупности
iei
множеств {Ai : г е 1} и обозначается иногда в сокращенном виде как {Аг}.
Множество / называется индексным множеством, а совокупность {Аг}
называется индексированной множеством /.
а) Пусть N = {1, 2,3,...}, а I = {?, Л, О}- Пусть
A\j = {х : х = 2/с, где к — некоторое целое число};
Ад = {х : х = ЗА:, где к — некоторое целое число};
Аэ = ix '• х ~ 5^' гДе ^ — некоторое целое число}.
Найдите такое С, что
С = р| Аг = {х : х е А{ для всех г G {П, Л, О}-
iei
б) Пусть/ = N-{1,2,3,...}, а
А,; = {х : х G N и х > г} = {г, г 4- 1, г + 2,...}.
Определите f]ieI А{.
15. Если / — множество, а А^ — множество для каждого г Е /, тогда
^ = {х : существует г ? I такое, что х е Аг}.
Множество U Aj называется обобщенным объединением совокупности мно-
iei
жеств {Аг : г Е /}. Пусть / = N = {1,2,3,...}, а
Аг- = {х : х € JV и х > г} = {г, г + 1, г 4- 2,...}.
Определите \JieIAi.

РАЗДЕЛ 2.3. Диаграммы Венна 77
2.3. ДИАГРАММЫ ВЕННА
Диаграммы Венна — очень удобный инструмент, позволяющий изображать мно-
множества и иллюстрировать операции над ними. Множества в диаграммах Венна
изображаются внутренними частями кругов, их пересечениями, объединениями и
т.д. Прямоугольник изображает универсальное множество. На рис. 2.1 приведена
диаграмма Венна для множества А которое изображено внутренней частью кру-
круга. Внешняя часть круга, находящаяся внутри прямоугольника, изображает А1.
На рис. 2.2 приведена диаграмма Венна для двух множеств, скажем, Aw В,
каждое множество изображено кругом, и круги пересекаются.
А'
Рис. 2.1
Рис. 2.2
Как показывает диаграмма, внутренняя часть прямоугольника разделена на че-
четыре части. Множеству А П В соответствует закрашенная часть диаграммы на
рис. 2.3. Закрашенная область на рис. 2.4 представляет Аи В.
Рис. 2.3
Рис. 2.4
Рис. 2.6
Рис. 2.7

78 ГЛАВА 2. Теория множеств
An В
АиВиС
АпВп С
(А и В)-С
(An С) и В
Рис. 2.5
Закрашенные области на рис. 2.5 изображают множества АпВ, (АиВиС),
(АпВпС), (АиВ) —С и (АпС)иВ. Множество А-В представлено закрашенной
областью на рис. 2.6. Диаграмма Венна для трех множеств, например, Л, В и С,
показана на рис. 2.7. Эта диаграмма состоит из восьми частей.
Используя диаграммы Венна, можно показать равенство двух множеств.
ПРИМЕР 2.16. Покажем, что (АиВ)' = А'ПВ1. Множество (АиВ)' — дополнение
множества A U Б, представленного диаграммой Венна на рис. 2.4, поэтому его
изображает закрашенная область, показанная на рис. 2.8.

РАЗДЕЛ 2.3. Диаграммы Вен на 79
Рис. 2.8
Множеству А' соответствует закрашенная область на рис. 2.9. А множеству
В' — закрашенная область на рис. 2.10.
Рис. 2.9 Рис. 2.10
Множеству А'ПВ' соответствуют части, закрашенные на обеих предыдущих
диаграммах, поэтому на рис. 2.11 оно изображено более темной областью.
Рис. 2.11
Получили, что и (A U В)\ и А' П В' одинаково изображаются на диаграмме
Венна, поэтому (A U В)' = А' П В'. ?
ПРИМЕР 2.17. Покажите, что Ап(ВиС) = (АпВ)и(Ап С). Множество А
представлено закрашенной областью на рис. 2.12. Множеству ВиС соответствует
закрашенная область на рис. 2.13.

80 ГЛАВА 2. Теория множеств
Рис. 2.12
Рис. 2.13
Множество АГ\{ВиС) изображает область, закрашенная на обеих предыду-
предыдущих диаграммах, поэтому оно представлено на рис. 2.14 более темной областью.
Множество АпВ представлено на рис. 2.15 закрашенной областью.
Рис. 2.14
Рис. 2.15
Множество АпС изображено на рис. 2.16 более темной областью, а множе-
множество {А П В) U {А П С) изображено закрашенной областью на рис. 2.17.
Рис. 2.16
Рис. 2.17
Следовательно, Ап{ВиС) и {АпВ)и{АпС) изображаются одинаково на
диаграммах Венна, поэтому АП{В UC) = {An B)U {АПС). ?

РАЗДЕЛ 2.3. Диаграммы Венна 81
Свойства множеств, сформулированные в приведенных ниже теоремах, мо-
могут быть проверены путем формальных доказательств или на диаграммах Венна.
Обратите внимание, что они дублируют соответствующие свойства в исчислении
высказываний (см. теорему 1.3).
ТЕОРЕМА 2.18. Пусть Л, В и С — подмножества универсального множества U.
Тогда справедливы
а) Законы идемпотентности
АГ)А = А;
АиА = А.
б) Двойное дополнение
(А')' = А.
в) Законы де Моргана
{АиВ)' = А'ПВ';
(АПВ)' = А'и В'.
г) Свойства коммутативности
An В = ВпА;
ЛиВ=ВиА
д) Свойства ассоциативности
A U (В U С) = (A U В) U С.
е) Свойства дистрибутивности
А П (В U С) = (А П В) U (А П С);
Л U (Б п С) = (Л U Б) П (А и С).
ж) Свойства тождества
AU0 = А;
з) Свойства дополнения
AUA' = U;
АПА' = 0.

82 ГЛАВА 2. Теория множеств
¦ УПРАЖНЕНИЯ
1. Для каждого из приведенных ниже множеств используйте диаграммы Венна
для двух множеств и заштрихуйте те ее части, которые изображают задан-
заданные множества:
а) А!\ б) (АпВ)'\
в) (Аи В)-АП В; г) А-В'.
2. Для каждого из приведенных ниже множеств используйте диаграммы Венна
для двух множеств и заштрихуйте те ее части, которые изображают задан-
заданные множества:
а) В'\ б) (A U В)'\
в) А-АГ) В; г) А А В.
3. Для каждого из приведенных ниже множеств используйте диаграммы Венна
для двух множеств и заштрихуйте те ее части, которые изображают задан-
заданные множества:
а) А-В\ б) (АпВ)'\
в) (АиВ)-АпВ\ г) Аи (В ПС);
д) {В ПС)-А; е) В-(Аи С);
ж) (АП В ПС)\
4. Для каждого из приведенных ниже множеств используйте диаграммы Венна
для двух множеств и заштрихуйте те ее части, которые изображают задан-
заданные множества:
а) А А В; б) (Аи В)';
в) А-АПВ\ г) (АП В) АС;
д) (АиВиС)-(АпВпСу е) (А П В) U (В П С) U (А П С);
ж) (А-В) U (В-С).
5. Опишите множества, соответствующие закрашенной части каждой диаграм-
диаграммы Венна:
а)

б)
РАЗДЕЛ 2.3. Диаграммы Венна 83
в)
г)
6. Опишите множества, соответствующие закрашенной части каждой диаграм-
диаграммы Венна:
а)

84 ГЛАВА 2. Теория множеств
б)
в)
г)
7. С помощью диаграммы Венна покажите, что (А Г) В)' = A' UB'.
8. С помощью диаграммы Венна покажите, что Au(J3nC) = (АиВ)П(АиС).
2.4. БУЛЕВЫ АЛГЕБРЫ
Сравнение основных свойств множеств и логики высказываний показало, что эти
свойства имеют много общих черт. Данное обстоятельство нашло свое вопло-
воплощение в общей теории, известной как булева алгебра. Свое название теория
получила в честь Дж. Буля, основоположника математической логики. Главное
назначение данной главы состоит в установлении основных аксиом булевой ал-
алгебры и их использовании для доказательства теорем, справедливых для любой
системы, обладающей подобными свойствами. В задачах и примерах этой главы

РАЗДЕЛ 2.4. Булевы алгебры 85
предполагаются известными элементарные свойства целых чисел, хотя формально
их изучению будет посвящена следующая глава.
ОПРЕДЕЛЕНИЕ 2.19. Операция, заданная на некотором множестве, называ-
называется бинарной, если она действует на два элемента этого множества и ее
результатом является элемент этого же множества.
ОПРЕДЕЛЕНИЕ 2.20. Операция, заданная на множестве, называется унарной,
если она действует на один элемент множества и ее результатом является
элемент этого же множества.
Обозначения, использованные ниже, были введены в главе 1.
ОПРЕДЕЛЕНИЕ 2.21. Булева алгебра есть множество В, содержащее специ-
специальные элементы 1 и 0, на котором заданы
бинарные операции 4- и • и унарная
операция '. Для всех х, у и z из В должны выполняться следующие аксиомы:
а) Законы коммутативности
х-у =
х + у =
б) Законы ассоциативности
x-(y-z) =
x + (y + z) =
в) Законы дистрибутивности
х • (у + z) = (х
x + (y-z) = (x
г) Законы тождества
х + 0
х-1
д) Законы дополнения
х 4- х1
х - х'
у-х;
У 4-х.
(х-у)- z\
(х 4- у) 4- z.
•у)+ (*¦*);
+ у) •(* + *).
= х;
= X.
= 1;
= 0.
Элемент 1 называется единичным элементом, или единицей, элемент 0 назы-
называется нулевым элементом, или нулем; а
х' называется дополнением х. Знак
бинарной операции • часто опускается, и х • у записывается просто как ху.

86 ГЛАВА 2. Теория множеств
Используя приведенные выше аксиомы, легко доказать ряд теорем о булевых
алгебрах, в частности, справедливы приведенные ниже теоремы.
ТЕОРЕМА 2.22. Для всех элементов х и у булевой алгебры выполняются такие
соотношения:
а) Законы идемпотентности
х + х = х;
х - х = х.
б) Свойства констант
х • 0 = 0.
в) Законы поглощения
х + (х • у) = х;
х • (х + у) = х.
ДОКАЗАТЕЛЬСТВО. В каждом случае доказано только первое из утверждений
теоремы. Доказательство второго утверждения предоставляется читателю.
а) х + х = (х + х) • 1 = свойство констант
= (х + х) • (х + х1) = закон дополнения
= х + (х • х1) = закон дистрибутивности
= х + 0 = закон дополнения
= х; закон тождества
б) х + 1 = (х + 1) • 1 = закон тождества
= (х + 1) • (х + х') = закон дополнения
= х + A • х') = закон дистрибутивности
= х + (х' • 1) = закон коммутативности
= х + х1 = закон тождества
= 1; закон дополнения
в) х + (х • у) — (х • 1) + (х • у) = закон тождества
= х • A + у) = закон дистрибутивности
= х • (у + 1) = закон коммутативности
= х•1 = свойство констант
= х. закон тождества
ТЕОРЕМА 2.23. (Закон единственности дополнения) Дополнение произволь-
произвольного элемента х булевой алгебры единственным образом определяется его свой-
свойствами: если х + х1 = 1, х • х1 = 0, х + х* = 1, а х • х* = 0, то х' = х*.

РАЗДЕЛ 2.4. Булевы алгебры 87
ДОКАЗАТЕЛЬСТВО. Если х + х' = 1 и х 4- х* = 1, тогда
х' = х' • 1 = закон тождества
= х1 • (х + х*) = задано
= х' • х + х' • х* — закон дистрибутивности
= х - х' 4- х1 • х* = закон дополнения
-0
= X
= X
X* =Х
= X
+ Х' ¦ X* :
' • X* + 0 :
'•X*
• . 1 —
* ¦ (х + х'
=
') =
задано
закон коммутативности
закон тождества
закон тождества
задано
= х* • х + х* • х' = закон дистрибутивности
= х • х* 4- х' • х* = закон коммутативности
= 0 4- х1 • х* = задано
= ж' • х* 4- 0 = закон коммутативности
= х1 • х*, закон тождества
так что х* = х'х* = х'. ¦
ТЕОРЕМА 2.24. Для всех элементов х и у булевой алгебры имеют место такие
соотношения:
а) Закон инволюции
(х'У = х.
б) Дополнение законов тождества
О' = 1;
1;=0.
в) Законы де Моргана
(х + у)' =х' -у';
(х •?/)'= х'4-</•
ДОКАЗАТЕЛЬСТВО. Для доказательства пункта (а) заметим, что
х1 4- х = х 4- х1 = закон коммутативности
= 1; закон дополнения
х1 • х = х - х1 — закон коммутативности
= 0. закон дополнения

88 ГЛАВА 2. Теория множеств
Следовательно, х есть дополнение х' и в соответствии с законом единствен-
единственности дополнения
Доказательство пункта (б) оставляем читателю. Доказательство пункта (в)
приведено ниже. ¦
Обратите внимание, что каждая аксиома булевой алгебры состоит из пары
равенств, которые являются двойственными в том смысле, что если в одном ра-
равенстве заменить + на •, • на 4- , 0 на 1 и 1 на 0, получим второе равенство.
В результате каждая теорема обладает двойственностью в том смысле, что ес-
если в любой теореме булевой алгебры заменить + на •, • на -Ь, 0 на 1, а 1 на
О, снова получим теорему (хотя она может и не отличаться от исходной). Это
соответствие имеет место, поскольку каждый шаг в доказательстве двойствен-
двойственной теоремы является двойственным соответствующему шагу в доказательстве
исходной теоремы. Для примера рассмотрим приведенные ниже доказательства
первого из законов де Моргана
(х 4- уУ = х'-у'
и двойственное к нему соотношение
(х • у)' = х1 + у'.
Сначала докажем, что (x+y)f = х'-у1. Для этого покажем, что {х+у)+х'-у' =
1 и (х4- у) • (х' -у') = 0. После этого, используя закон единственности дополнения,
приходим к тому, что (х -f у)' = х1 • у1.
(х 4- у) + х' • у' = ((х + у) + х;) • ((х 4- у) 4- у') — закон дистрибутивности
= ((у 4- х) 4- х') • ((х 4- у) 4- у') = закон коммутативности
= (у 4- (х 4- х')) • (х 4- (у 4- у')) = закон ассоциативности
= (у 4-1) • (х 4- 1) = закон дополнения
= 1 • 1 = свойство констант
= 1; закон тождества
(х 4- у) - (х' • у1) = (х' • у1) • (х 4- у) = закон коммутативности
= ((х' • у1) • х) 4- ((х' • у') • у) = закон дистрибутивности
= (х • (х' • у')) 4- ((х' • у') • у) = закон коммутативности
= ((х • х') • у') 4- (х' • {у1 • у)) = закон ассоциативности
= ((х • х1) • у') 4- (х' • (у • у')) = закон коммутативности
= @ • у') 4- (х; • 0) = закон дополнения
= {у1 • 0) + (х' • 0) = закон коммутативности
= 0 4-0= свойство констант
= 0. закон тождества
Теперь докажем, что {х-уI = х;4-у'. Сначала покажем, что (х-у)-(х/4-у/) =
0 и (х • у) 4- (х; 4- yf) — 1. После этого, на основании закона единственности
дополнения, получаем, что (х • у)' = х' 4- у'.

РАЗДЕЛ 2.4. Булевы алгебры 89
(ж • у) • (ж' 4 2/') = ((я • у) • я') 4- -((ж • у) • у') = закон дистрибутивности
= ((у - х) - х') 4 ((ж • у) - у') = закон коммутативности
= (у • (ж • ж')) -Ь (ж • (у • у')) = закон ассоциативности
= (у • 0) • (ж • 0) = закон дополнения
= 0 • 0 = свойство констант
= 0; закон тождества
(ж • у) + (ж' 4- у') = (ж' 4 у') 4 (ж • у) = закон коммутативности
= ((ж' 4 у') 4 ж) • ((ж' 4 у1) 4 у) = закон дистрибутивности
= (ж 4- (ж' 4 у1)) • ((ж7 4- у') 4 у) = закон коммутативности
= ((ж 4 ж') 4 у') • (ж' 4- (у' 4- у)) = закон ассоциативности
= ((ж 4 ж') 4 у1) • (ж' + (у 4 у')) = закон коммутативности
= A4 у1) - (х' 4- 1) = закон дополнения
= (у' 4 1) • (ж' 4-1) = закон коммутативности
= 1 • 1 = свойство констант
= 1. закон тождества
Обратите внимание, что каждая строка второго доказательства двойственна со-
соответствующей строке первого доказательства.
Итак, всякий раз, доказывая теорему относительно булевой алгебры, мы
фактически доказываем две теоремы: саму теорему и двойственную ей (если они
отличаются). Таким образом, доказывая одну теорему, вторую теорему получаем
даром.
Используя правила теории множеств (теорема 2.18), легко можно показать,
что подмножества произвольного множества А образуют булеву алгебру, где П и
U аналогичны бинарным операциям • и 4, соответственно, г А- В соответствует
В'. Множество А является единичным элементом 1, а пустое множество есть
нулевой элемент 0 этой булевой алгебры.
¦ УПРАЖНЕНИЯ
1. Докажите непосредственно, что ж • ж = ж.
2. Докажите непосредственно, что ж • 0 = 0.
3. Докажите непосредственно, что ж • (ж 4 у) = ж.
4. Докажите непосредственно, что 0' = 1.
5. Докажите непосредственно, что V = 0.
6. Найдите выражения, двойственные приведенным ниже:
а) ж • у1 4 ж • z1 4 у • ж';
б) ж • у • z1 4 ж • у' • z\
в) ж-у • (ж 40 4 (z- 1)).
7. Найдите выражения, двойственные приведенным ниже:
а) (* +у')-(*' + »)';
б) A 4 ж) -у 4ж-у' • z\
в) (ж • у 4 1) • @ 4 ж) • z.

90 ГЛАВА 2. Теория множеств
8. Докажите, что если ху = xz и х'у = x'z, то у = z.
9. Сформулируйте задачу, двойственную к предыдущей.
10. Докажите, что ху' = 0 тогда и только тогда, когда ху = х.
11. Сформулируйте задачу, двойственную к предыдущей.
12. Докажите, что нулевой элемент 0 и единичный элемент 1 определены своими
свойствами единственным образом.
13. Множество называется коконечным, если его дополнение конечно. Пусть
универсальное множество U есть множество всех конечных и всех коконеч-
ных подмножеств множества положительных целых чисел. Докажите, что
подмножества U вместе с операциями объединения, пересечения и дополне-
дополнения образуют булеву алгебру.
2.5. ОТНОШЕНИЯ
Среди рассмотренных операций над множествами было декартово произведение
множеств А и В, которое обозначается через А х В. Оно представляет собой
множество {(а, Ь) : а е А и 6 G J5}. Таким образом, множество Ах В состоит из
всех упорядоченных пар, имеющих в качестве первой компоненты элемент из А,
а в качестве второй компоненты — элемент из В.
ОПРЕДЕЛЕНИЕ 2.25. Отношением R множеств А и В называется произволь-
произвольное подмножество Ах В. Если (а, 6) е R, это записывают как аИЬ\ при этом
говорят, что а и Ь находятся в отношении R, или просто, что а относится
к 6. Если А = В, то отношение есть подмножество А х А\ такое отношение
называют бинарным отношением на А.
В дальнейшем на множестве будем обычно рассматривать бинарные отноше-
отношения, поэтому вместо термина "бинарное отношение" будем употреблять термин
"отношение".
Если А = {1,2,3}, а В = {г, s}, так что
А х В - {A,г), (М), B, г), B,s), C,r), C,s)},
тогда R — {(l,r), (l,s), C,5)} есть отношение множеств А и В. Можно также
записать 3i?s, поскольку C, s) G R. Множество Ах В содержит шесть элементов,
поэтому существует 26 = 64 подмножества множества А х В. Следовательно,
существует 64 различных отношения на Ах В.
В примерах и упражнениях, приведенных ниже, предполагаются известными
элементарные свойства действительных и целых чисел, а также заданных на этих
числах функций.
Вот несколько примеров отношений:
1. Все множество Ах В есть отношение множеств А и В.
2. Если А — множество действительных чисел, то {(х,у) Е А х А : х2 + у2 = 4}
есть бинарное отношение на А.

РАЗДЕЛ 2.5. Отношения 91
3. Пусть А — множество товаров в магазине, а В — множество действительных
чисел. Тогда {(х,у) Е Ах В : у — цена х} — отношение множеств А и В.
4. Пусть А —- множество женщин, а В — множество мужчин, тогда {(х,у) :
у является мужем х} есть отношение множеств А и В.
5. Если А — множество людей, то {(х,у) Е Ах А : у является родственником х}
есть бинарное отношение на А.
ОПРЕДЕЛЕНИЕ 2.26. Область определения отношения R на А и В есть мно-
множество всех х Е А таких, что для некоторых у Е В имеем {х,у) Е R. Другими
словами, область определения R есть множество всех первых координат упо-
упорядоченных пар из R. Множество значений отношения R на А и В есть
множество всех у Е В таких, что (х, у) Е R для некоторого х Е А. Други-
Другими словами, множество значений R есть множество всех вторых координат
упорядоченных пар из R.
В примерах отношений, приведенных выше, в частности, в A), область опре-
определения есть все множество А, а множество значений — все множество В. В B)
как область определения, так и множество значений совпадают с множеством
{t : — 2 < t < 2}. В C) область определения есть множество А, а множество зна-
значений есть множество всех действительных чисел, каждое из которых совпадает
с ценой некоторого товара в магазине. В D) область определения есть множе-
множество всех замужних женщин, а множество значений — множество всех женатых
мужчин. В E) область определения и множество значений есть множество всех
людей, имеющих родственников.
С каждым отношением R на А х В связано отношение Я на В х А.
ОПРЕДЕЛЕНИЕ 2.27. Пусть R С А х В есть отношение на А х В. Тогда
отношение R~l на В х А определяется следующим образом:
Другими словами, (Ь, а) Е R~l тогда и только тогда, когда (a, b) E R или, что
равносильно, bR~la тогда и только тогда, когда aRb. Отношение R~l называ-
называется обратным отношением к данному отношению R.
Пусть Я = {A, г), A, s), C, s)}, тогда Я = {(г, 1), E,1), (s,3)}. Пусть Я -
отношение {(х,у) : у является мужем х}, тогда Я г — отношение {(х,у) : у —
жена х}. Пусть Я — отношение {(х,у) : у является родственником х} либо Я —
отношение {(х, у) : х2 + у2 = 4}, тогда Я = Я.
Имея два заданных отношения, можно образовать новые отношения указан-
указанным ниже способом.

92 ГЛАВА 2. Теория множеств
ОПРЕДЕЛЕНИЕ 2.28. Пусть RCAx В - отношение на А х В, а 5 С В х С
— отношение на В х С. Композицией отношений 5 и Д называется отношение
Т С А х С, определенное таким образом:
Т = {{а, с) : существует такой элемент Ъ из В, что (а, Ъ) Е R и F, с) Е 5}.
Это множество обозначается Т = S о R.
ПРИМЕР 2.29. Пусть А = {1,2,3}, В = {х,у}, а С = {П,Д,О,*}„ и пусть
отношения ДнаАхВи5наВхС заданы в виде:
Тогда
5оД = {A,?), A,Л), A,0), A,•), C,?), C,Л)},
поскольку
из A, х) € R и (х, ?) Е 5 следует A, ?) Е 5 о Д;
из A, х) Е 7? и (ж, Л) Е 5 следует A, Л) Е S о Д;
из A, у) Е Д и (у, О) ? 5 следует A, О) G 5 о Д;
из C, ж) Е Д и (х, Л) Е 5 следует C, А) Е 5 о Д.
?
ПРИМЕР 2.30. Пусть Д и 5 — бинарные отношения на множестве положительных
целых чисел, заданные в виде 5 = {(х,х 4- 2) : х — положительное целое число}
и Д = {(х,х2) : х — целое положительное число}. Тогда SoR = {(х,х2 + 2) : х —
положительное целое число} и Д о S = {(х, (х + 2J) : х — положительное целое
число}. ?
ТЕОРЕМА 2.31. Композиция отношений ассоциативна; т.е., если Л, В и С —
множества и если ДСАхВ,5СВхСиТССхД тогда To(SoR) = (ToS)oR.
ДОКАЗАТЕЛЬСТВО. Покажем сначала, что Г о E о Д) с (Т о 5) о Д. Пусть
(a, d) Е Т о E о Д), тогда существует такое с Е С, что (а, с) Е 5 о Д и (с, d) E Т.
Поскольку (а, с) Е 5 о Д, существует такое Ь Е В, что (а, 6) Е Д и (Ь, с) Е 5.
Поскольку (Ь,с) Е 5 и (c,d) E T, F,d) Е Г о 5. Поскольку (М) € То 5 и
(а, 6) Е Д, (а, d) Е (Г о 5) о Д. Таким образом, Т о (S о Д) С (Т о 5) о Д. Вторая
часть доказательства, показывающая, что (Т о 5) о Д С Т о (S о Д), аналогична и
предоставляется читателю как упражнение. ¦
Теперь рассмотрим специальные свойства отношений на А.

РАЗДЕЛ 2.5. Отношения 93
ОПРЕДЕЛЕНИЕ 2.32. Отношение R на А х А называется рефлексивным, если
(а, а) принадлежит R для всех а из А. Отношение R называется антирефлек-
антирефлексивным, если из (а, Ь) ? R следует а фЬ. Отношение R симметрично, если
для всех аиб, принадлежащих А, из (а, Ъ) ? R следует, что F, а) ? R. Отно-
Отношение R транзитивно, если для всех а, Ь и с из А из того, что (а, 6) ? R и
(Ь, с) ? R, следует, что (а, с) ? R. Отношение R называется антисимметрич-
антисимметричным, если для всех а и 6 из Л, из принадлежности (а, Ь) и F, а) отношению R
следует, что а = Ь.
ПРИМЕР 2.33. Пусть А = {1,2,3,4,5,6} и пусть отношение Ri С А х А есть
множество fli = {A,1), B,2), C,3), D,4), E,5), F,6), A,2), A,4), B,1), B,4),
C,5), E,3), D,1), D,2)}. Отношение R\ рефлексивно, т.к. для каждого а ? А,
{а,а)еЯг.
Рассмотрев все возможные случаи и показав, что в каждом из них из
(a,b) ? R\ следует F,а) ? R\, можно показать, что отношение R\ является
симметричным.
Случай
1
2
3
(а,
Ь)
A,
A,
B,
G Яг
2)
4)
1)
(Ъ,
B,
D,
A,
а)
1)
1)
2)
(Ь,
а) G Й1?
Да
Да
Да
Можно также показать, что R\ транзитивно, используя метод прямого пере-
перебора, как показано на примере следующей таблицы.
Случай
1
2
3
4
5
(а, Ь) е Ri
A,2)
A,2)
A,2)
A,4)
A,4)
(Ь,с)б Дх
BД)
B,2)
B,4)
D,1)
D,2)
•
F, с)
AД)
A,2)
A,4)
A,1)
A,2)
(а, с) ЕЙ!?
Да
Да
Да
Да
Да
Проанализировав каждый возможный случай, когда (а, Ь) ? i?x и F, с) ? /2Ь
получаем, что (а, с) ? Дх.
Ri не является антисимметричным, поскольку A,2) ? i?i и B,1) ? Ль но
1^2. ?
ПРИМЕР 2.34. Пусть А = {?, Л, О, *} и пусть J?2 Q А х А определено в виде
Дз = {(?,?), (ЦЛ), (?,•), (л,п), (*,?), (*,*), (о,*), (О,О)}.

94 ГЛАВА 2. Теория множеств
J?2 не является рефлексивным, т.к. Д Е А, но (А, А) ^ Д2. #2 не является
симметричным, поскольку (О?*) ? #2, но (*'О) ^ -^2- #2 не является анти-
антисимметричным, поскольку (А,П) Е Д2 и (?, А) Е Д2, но А 7^ П. Д2 не является
транзитивным, т.к. (Л,П) ЕЙ2и (?,*) € Д2, но (А,*) ? Д2. ?
ПРИМЕР 2.35. Пусть А — множество положительных целых чисел. Определим
отношение Д, задавая (х,у) Е Д условием: у кратно х. R рефлексивно, поскольку
для каждого положительного целого числа п, и = 1-п и (n, n) Е R. R не является
симметричным, т.к B,4) Е Д, но D,2) ^ Д; однако, Д антисимметрично, т.к.,
если (га, n) Е R и (n, m) Е Д, тогда п кратно шит кратно п, так что т — п.
R транзитивно, потому что если (т,п) Е R и (n,p) E Д, тогда п кратно тир
кратно п, так что р кратно m и (га,р) e R. О
ОПРЕДЕЛЕНИЕ 2.36. Пусть R — бинарное отношение на множестве А. Ре-
Рефлексивное замыкание R есть наименьшее рефлексивное отношение на А,
содержащее R как подмножество. Симметричное замыкание R есть наи-
наименьшее симметричное отношение на А, содержащее R как подмножество.
Транзитивное замыкание R есть наименьшее транзитивное отношение на А,
содержащее R как подмножество.
ТЕОРЕМА 2.37. Пусть R — отношение на множестве А и / = {х : х = (а, а) для
некоторого а е А}. Тогда
sl) RU I есть рефлексивное замыкание R\
б) йий есть симметричное замыкание R\
в) если А — конечное множество, содержащее п элементов, то отношение
R U R2 U R3 U • • • U Rn есть транзитивное замыкание R.
ДОКАЗАТЕЛЬСТВО. Доказательство утверждений (а) и (б) предоставляется чи-
читателю. Обозначим транзитивное замыкание R через R. Для доказательства
утверждения (с) сначала покажем, что R U R^_U R3 U • • • U Rn С ~R. Прове-
Проведем индукцию по п. Для и = 1 имеем_Я С Ry что достоверно истинно. До-
Допустим, что R U i?2JJ Д3 U • • • U Rk С Д. Необходимо доказать, что ДиД2и
Д3 U ... U Rk+l С Д или, что то же самое, Rk+1 С Д. Пусть (а,с) Е Я*+1.
Тогда существует b такое, что (a, b) e Rk и (Ь, с) Е Д. Но, согласно индуктив-
индуктивному предположению, (а, 6) и F, с) Е Д. Поскольку Д транзитивно, (а, с) Е Д.
Поэтому Д U Д2 U Д3 U • • • U Д^4 С Д. Для того, чтобы показать, что Д С
ДиД2иД3и---иД*:+1, просто покажем, что ДиД2иД3и- • •иД/с+1 транзитивно.
Пусть (а, Ь) Е Д7 и F, с) Е Д^. Тогда (а, с) Е R^k. Если а = с, утверждение
доказано. В противном случае существуют Ь2,Ь^,Ь^... ,bj+fc-i ^ ^ такие, что
(a,62),(b2,b3),(b3,b4),...,(bi+ib-2,bbi+fc_1),(bJ-+fc-i,c) Е Д. Обозначим а через Ьь
а с через 6jH_a:. Если некоторые из 6* равны, например, Ьр = bqi из указанной вы-
выше последовательности упорядоченных пар, находящихся в отношении Д, можно
удалить Fp,bp+i),(bp+i,bp+3),...,Fg_i,bg) и после этого получить последова-
последовательность а, Ь2,Ьз,Ьр-1,Ья,... ,6j+fc-i,c, в которой каждый предыдущий элемент
находится в Д-отношении к последующему. Так можно продолжать до тех пор,
пока все элементы окажутся отличными, но при этом каждый из них будет нахо-

РАЗДЕЛ 2.5. Отношения 95
диться в Д-отношении к последующему. Поскольку во множестве А существует
только и различных элементов, получаем, что (а, с) Е Rn и RuR2UR3U- • -Ui?fc+1
транзитивно. ¦
Одним из наглядных способов представления конечного антирефлексивного
симметричного отношения является граф. В дальнейшем мы убедимся, что легко
установить связь между конечными антирефлексивными симметричными отно-
отношениями и графами. Однако, помимо этого конкретного использования, графы
получили самостоятельное развитие, и в настоящее время теория графов являет-
является одной из важных областей математики.
ОПРЕДЕЛЕНИЕ 2.38. Граф есть конечное множество V, называемое множе-
множеством вершин, на котором задано симметричное антирефлексивное отношение
R и выделено множество Е двухэлементных подмножеств V, определяемое как
{а, Ь) ? Е тогда и только тогда, когда (а, 6) € R и а ф Ь. Множество Е на-
называется множеством ребер. Всякий элемент Е называется ребром. Граф
обозначается G(V,E). Говорят, что элементы а и Ь графа V соединены или
связаны ребром {а,6}, если {а, Ь) е Е.
Конечный граф обычно изображается при помощи диаграммы, в которой
вершины представлены точками, а ребра, соединяющие две вершины, — линиями
между этими точками.
ПРИМЕР 2.39. Граф, в котором множество вершин V = {а, 6, с}, a E = {{а, 6}, {Ь, с}},
может иметь вид, как на рис. 2.18 или рис. 2.19.
Т с
• а а с
Рис. 2.18 Рис. 2.19
Д = {(а,Ь), F,^,F,0), (с, Ь)}. ?
ПРИМЕР 2.40. Граф, в котором множество вершин V = {а, 6,с, d, e}, a
имеет диаграмму, изображенную на рис. 2.20.
с
R = {(а,Ь), F,о), (е,а), (а,е), (е,6), (Ь,е), F,d), (d,6), (Ь,с), (с,6), (d,c), (c,d)}.
D

96 ГЛАВА 2. Теория множеств
Мы видели, что граф описывал симметричное отношение R на множестве
V, в котором никакой элемент не находился в отношении с самим собой. Для
отношения R более общего вида необходимо представление элемента (а, Ъ) Е
R, для которого возможно (Ь, а) ф. R. Необходимо также иметь возможность
представлять элемент (а, а) ? R. Все сказанное можно осуществить с помощью
ориентированного графа.
ОПРЕДЕЛЕНИЕ 2.41. Ориентированный граф, или орграф G, обозначаемый
G(V, Е), состоит из множества V вершин и отношения Е на V, называемого
множеством ориентированных ребер, или просто ребер, если понятно, что
граф ориентирован. Элемент множества Е называется ориентированным ре-
ребром. Если (а, Ъ) е Е, тогда а называется начальной вершиной (а,6), а Ь —
его конечной вершиной.
Обратите внимание, что, в отличие от неориентированного графа, в случае
ориентированного графа мы допускаем наличие петель. Причин этому две. Во-
первых, ориентированные ребра естественным образом включаются в наше опре-
определение, поскольку петля при вершине а есть просто ребро (а, а). Этого нельзя
было сделать в случае неориентированного графа, поскольку его ребра имеют вид
{а, 6}, так что петля имела бы вид {а,а}. Во-вторых, вообще говоря, элементы
могут находиться в отношении к самим себе, что для множеств не имеет смысла,
поскольку любой элемент присутствует во множестве только один раз. Тем не
менее, дальнейшее рассмотрение покажет, что петли в ориентированных графах
встречаются чаще, чем в неориентированных.
Ребро (а, Ь) орграфа обозначается на диаграмме стрелкой от а к Ь. Заме-
Заметим, что в простом графе ребро представляется двухэлементным подмножеством,
чтобы подчеркнуть, что ребро как отношение симметрично, тогда как в оргра-
орграфе ребро представлено упорядоченной парой, чтобы подчеркнуть то, что порядок
имеет значение, и то, что (а, Ь) может быть ребром диаграммы, а F, а) — нет.
ПРИМЕР 2.42, Орграф с вершинами
и ребрами
Е = {(а, а), (а, Ь), (Ь, с), (с, 6), (с, а)}
показан на рис. 2.21.
Ь
с Рис. 2.21 ?
ПРИМЕР 2.43. Орграф с вершинами
V = {a,b,c,d}

РАЗДЕЛ 2.5. Отношения 97
и ребрами
Е = {(а, Ь), F, с), (с, с), (Ь, d), (d, b), (с, d), (d, a)}
показан на рис. 2.22.
Рис. 2.22
П
УПРАЖНЕНИЯ
1. Найдите область определения и множество значений отношений:
а) {(а, 1), (а, 2), (с, 1), (с, 2), (с, 4), (d, 5)};
б) {A,2), B,4), C,6), D,8),...};
в) {(х,у) :х,у € Д и х = у2}.
2. Найдите область определения и множество значений отношений:
а) {(а, 1), (а, 2), (а, 3), (а, 4), (а, 5), (а, 6)};
б) {(х,у):х,у€/их2 + у2<16};
в) {(я, у) : 0 < х, у < 10 и х > 2у}.
3. Пусть А = {1,2,3,4,5};
В = {6, 7,8,9};
С = {10,11,12,13};
?> = {П,Д,О,*}-
Пусть й С Л х В, SCBxChTCCxD определены следующим образом
Я = {A,7), D,6), E,6), B,8)};
5 = {F,10), F,11), G,10), (8,13)};
Т = {A1, Л), A0, Д), A3, *), A2, D), A3,0)}-
Определите отношения:
а) R'1 и S;
в) SoS

д) To(SoR);
ж) (Т о 5) о Д.
4. Пусть А = {(Ь, а), (с, е), (d, г), (/, о){д, и)} и
В = {(v, а), (го, е), (х, г), (у, о)(г, и)}.
а) Опишите отношение А~г.
б) Опишите отношение В.
в) Опишите отношение А~1 о В.
г) Опишите отношение В~1 о А.
б) SoR-
г) R-io
е) То 5;

98 ГЛАВА 2. Теория множеств
5. Пусть отношения ?/, V С R x R определены указанным ниже способом
U = {(х,у) : у = х2 + 5)} и У = {(х,у) : у = Зх}.
а) Опишите отношение U о V.
б) Опишите отношение V о U.
в) Опишите отношение U~l.
г) Опишите отношение У.
д) Найдите область значений U.
6. Пусть А = {a,b,c,d,e}. Опишите наименьшее рефлексивное отношение на
множестве Л.
7. Пусть А = {а, Ь, с, d, е} и 5 = {(а, а), (а, Ь), F, с), F, d), (с, е), (е, d), (с, 6)}.
а) Опишите наименьшее симметричное отношение на Л, содержащее 5.
б) Опишите наименьшее рефлексивное и симметричное отношение на А,
содержащее S.
в) Опишите наибольшее симметричное отношение, содержащееся в 5.
г) Опишите наименьшее транзитивное отношение на Л, содержащее 5.
8. Пусть А = {а, 6, с, d, e}, a 5, Т, 17 и У — отношения на Л, где
5 = {(а, а), (а, 6), (Ь, с), F, d), (с, в), (е, d), (с, а)};
Т = {(а, 6), F, а), (Ь, с), F, d), (e, e), (d, e), (с, 6)};
С/ = {(а, Ь), (а, а), F, с), F, Ь), (е, с), F, а), (с, Ь), (с, с), (d, d), (а, с), (с, а)};
V = {(а, 6), F, с), (Ь, Ь), (е, е), F, а), (с, 6), (d, d), (а, с), (с, а)}.
а) Какое из отношений является симметричным?
б) Какое из отношений является рефлексивным?
в) Какое из отношений является транзитивным?
г) Какое из отношений является антисимметричным?
9. Пусть А = {а, 6, с, d, e}, a 5, Т, U и V — отношения на Л, где
5 = {(а, а), (а, Ь), (Ь, с), (Ь, d), (с, е), (е, d), (с, а)};
Г = {(а, 6), F, а), (Ь, с), F, d), (e, e), (d, e), (с, 6)};
С/ = {(а, Ь), (а, а), F, с), (Ь, 6), (е, е), (Ь, а), (с, 6), (с, с), (d, d), (а, с), (с, а)};
У = {(а, 6), F, с), F, 6), (е, е), F, а), (с, 6), (d, d), (а, с), (с, а)}.
а) Опишите UnV.
б) Опишите S U Т.
в) Опишите U — Т.
г) Опишите С/Д 5.
10. Докажите, что пересечение рефлексивных отношений рефлексивно.
11. Докажите, что пересечение симметричных отношений симметрично.
12. Пусть Л = {а, 6, с, d, e}.
а) Опишите отношение на Л, которое рефлексивно, но не является ни сим-
симметричным, ни транзитивным.
б) Опишите отношение на Л, которое симметрично, но не является ни ре-
рефлексивным, ни транзитивным.

РАЗДЕЛ 2.5. Отношения 99
в) Опишите отношение на А, которое транзитивно, но не является ни ре-
рефлексивным, ни симметричным.
13. Пусть А = {а, 6, с, d, е}.
а) Опишите отношение на А, которое рефлексивно и симметрично, но не
является транзитивным.
б) Опишите отношение на А, которое симметрично и транзитивно, но не
является рефлексивным.
в) Опишите отношение на А, которое рефлексивно и транзитивно, но не
является симметричным.
14. Установите истинность или ложность каждого из приведенных ниже выска-
высказываний. Для каждого ложного высказывания приведите контрпример.
а) Если отношения Ru S рефлексивны, то отношение RnS рефлексивно.
б) Если отношения RuS рефлексивны, то отношение RuS рефлексивно.
в) Если отношения R к S рефлексивны, то отношение RoS рефлексивно.
г) Если отношения R и S рефлексивны, то отношение R — S рефлексивно.
д) Если отношения R и 5 рефлексивны, то отношение RAS рефлексивно.
15. Установите истинность или ложность каждого из следующих высказываний.
Для ложных высказываний приведите контрпример.
а) Если отношения Д и S симметричны, то отношение RnS симметрично.
б) Если отношения RuS симметричны, то отношение Ru S симметрично.
в) Если отношения R S симметричны, то отношение RoS симметрично.
г) Если отношения R и 5 симметричны, то отношение R — S симметрично.
д) Если отношения RuS симметричны, то отношение RAS симметрично.
16. Установите истинность или ложность приведенных ниже высказываний. Для
ложных высказываний приведите контрпример.
а) Если отношения RuS антисимметричны, то отношение RnS антисим-
антисимметрично.
б) Если отношения Ru S антисимметричны, то отношение RuS антисим-
антисимметрично.
в) Если отношения RuS антисимметричны, то отношение RoS антисим-
антисимметрично.
г) Если отношения RuS антисимметричны, то отношение R — S антисим-
антисимметрично.
д) Если отношения RuS антисимметричны, то отношение RAS антисим-
антисимметрично.
17. Установите истинность или ложность приведенных ниже высказываний. Для
каждого ложного высказывания приведите контрпример.
а) Если отношения RuS транзитивны, то отношение RnS транзитивно.
б) Если отношения RuS транзитивны, то отношение RuS транзитивно,
в) Если отношения RuS транзитивны, то отношение До 5 транзитивно.
г) Если отношения RuS транзитивны, то отношение R- S транзитивно.
д) Если отношения RuS транзитивны, то отношение RAS транзитивно.

100 ГЛАВА 2. Теория множеств
18. Постройте граф для каждого из приведенных ниже отношений на А.
а) А = {a,b,c,d,e};
R = {(а, Ь), (Ь, а), F, с), (с, 6), (с, а), (а, с), (d, e), (e, d)};
б) A = {a,b,c,d,e};
R = {(а, 6), (Ь, а), F, с), (с, 6), (с, d), (d, с), (с, а), (а, с)};
в) Л = {a,6,c,d,e};
Д = {(а, 6), F, а), F, с), (с, 6), (с, d), (<*, с), (d, e), (e, d),
F,e),(e,6),(b,d),(d,6)};
г) Л = {a,b,c,d};
Д = {(а, 6), F, а), F, с), (с, Ь), (с, d), (d, с), (d, a), (a, d),
F,d),(d,b),(o,c),(c,a)}.
19. Постройте граф для каждого из приведенных ниже отношений на А.
а) А = {a,b,c,d,e};
Д = {(a, 6), F, а), F, с), (с, 6), (с, d), (d, с), (d, a), (a, d)};
б) A = {a,&,c,d,e,/};
Д - {(а, 6), F, а), F, с), (с, Ь), (с, а), (а, с), (d, e), (e, d)};
в) Л = {o,6,c,d,e};
Д = {(а, 6), F, а), F, с), (с, 6), (с, d), (d, с), (d, e), (e, d),
(a,d),(d,a)};
г) А = {a,b,c,d,e,f};
R = {(a, b), (b, a), F, с), (с, 6), (с, а), (а, с), (а, е), (е, а),
F, е), (е, 6), F, /), (/, Ь), (с, d), (d, с), (с, /), (/, с),
(d,/),(/,d),(e,/),(/,e)}.
20. Найдите множество вершин, ребер и соответствующее симметричное отно-
отношение для графов, изображенных на нижеследующих рисунках.
а) „ б)
в)
а
г)
а Ь
с.
d f e

РАЗДЕЛ 2.5. Отношения 101
21. Найдите множество вершин, ребер и соответствующее симметричное отно-
отношение для графов, изображенных на нижеследующих рисунках.
а)
б)
в)
г)
22. Постройте орграфы со следующими свойствами:
а) Множество вершин {а, 6, с, d, е,/} и отношение R для ребер имеет вид
Я = {(а, Ь), F, с), (а, с), (Ь, е), (с, /), (с, d), (d, /), (/, е)}.
б) Множество вершин {а, 6, с, d} и отношение Я для ребер имеет вид R =
{(ft, с), (а, d), (ft, а), (d, с), (ft, d), (с, а)}.
в) Множество вершин {a,b,c,d} и отношение Д для ребер имеет вид R =
{F, а), (а, а), F, с), (с, d), (d, с), (d, 6), (d, а)}.
г) Множество вершин {а, ft, с, d, e} и отношение Л для ребер имеет вид
Л = {(а, ft), (а, с), (а, d), (с, а), (d, e), (е, d)}.
23. Постройте орграф со следующими свойствами:
а) Множество вершин {а, 6, с, d, e,/} и отношение i? для ребер имеет вид
Л = {(а, ft), (ft, с), (d, с), (d, e), (/, е), (/, а), (ft, e)}.
б) Множество вершин {a,b,c,d} и отношение R для ребер имеет вид R =
{(а, с), (а, ft), (d, с), (d, ft), (а, d), (ft, с), (а, а), (с, с)}.
в) Множество вершин {а,Ь,с} и отношение R для ребер имеет вид R =
{(а, ft), (а, а), (ft, с), (ft, ft), (с, с), (с, а)}.
г) Множество вершин {а, ft, с, d, e) и отношение Л для ребер имеет вид
R = {(a, ft), (а, с), (а, d), (с, d), (d, e), (ft, e)}.
24. Найдите вершины и ориентированные ребра приведенных ниже орграфов.

102 ГЛАВА 2. Теория множеств
а)
i ъ
о с
б)
в)
а Ъ с d e
">•t > # >*
г)
¦о
25. Найдите вершины и ориентированные ребра приведенных ниже орграфов.
а) б)
в)
г)
26. Приведенное ниже доказательство предположительно показывает, что если
отношение R симметрично и транзитивно, то оно и рефлексивно. Является
ли это доказательство правильным? Если нет, то почему?

РАЗДЕЛ 2.6. Частично упорядоченные множества 103
ДОКАЗАТЕЛЬСТВО. Пусть R — симметричное и транзитивное отношение
на множестве А. Пусть a ? А и (а, 6) Е R. Поскольку (а, Ь) Е R и R
симметрично, (Ь, а) Е R. Поэтому, в силу транзитивности Д, имеем (a, a) E
Я, откуда следует, что R рефлексивно. ¦
27. Докажите теорему 2.31.
28. Докажите теорему 2.37.
2.6. ЧАСТИЧНО УПОРЯДОЧЕННЫЕ МНОЖЕСТВА
При изложении оставшейся части этой главы будем предполагать известными
элементарные свойства целых чисел, действительных чисел и заданных на них
функций, хотя формально до настоящего времени они не обсуждались.
ОПРЕДЕЛЕНИЕ 2.44. Отношение R на А есть отношение частичного поряд-
порядка, если оно рефлексивно, симметрично и транзитивно. Если отношение R на
А является отношением частичного порядка, то (Л, R) называют частично
упорядоченным множеством, или ЧУ-множеством с порядком R. Если от-
отношение порядка R предполагается по умолчанию, то (A, R) можно обозначать
просто через А.
В примере 2.35 было показано, что если А — множество положительных
целых чисел и отношение R определено условием (х,у) е Я, если х делит у
нацело, то R есть отношение частичного порядка, a (A, R) — ЧУ-множество.
ПРИМЕР 2.45. Пусть С = {1,2,3}, а X — множество всех подмножеств множе-
множества С:
X = Р(С) = {0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.
Определим отношение R на X посредством (Т, V) € i?, евли Т С V. Таким
образом, ({2},{1,2}) € Д, поскольку {2} С {1,2} и ({2,3},{3}) ? Л, поскольку
{2,3} ? {3}. Можно легко проверить, что Д — отношение частичного порядка, а
(Д i?) — ЧУ-множество. ?
ПРИМЕР 2.46. Пусть 5 — множество действительных чисел, г R\ — отноше-
отношение, определенное условием (х,у) Е Яь если х < у. Легко показать, что R\ —
отношение частичного порядка, a (S,R\) — ЧУ-множество. ?
Частичное упорядочение принято обозначать через <, а частично упорядо-
упорядоченное множество — через E, <), где < — частичный порядок на множестве 5.
Если (а, Ь) ?<, то, согласно введенным ранее обозначениям для отношений, а <Ь.

104 ГЛАВА 2. Теория множеств
ОПРЕДЕЛЕНИЕ 2.47. Два элемента а и Ь частично упорядоченного множества
E, <) сравнимы, если а < b или b < а. Если каждые два элемента частич-
частично упорядоченного множества E, <) сравнимы, то E, <) называется вполне
упорядоченным множеством, или цепью.
ПРИМЕР 2.48. Пусть Т — множество положительных делителей числа 30 и <i
есть отношение га <i n, если га делит п нацело. Целые числа 5 и 15 сравнимы,
поскольку 5 делит 15 нацело, а 5 и б — нет. ?
ПРИМЕР 2.49. Пусть А — множество целых чисел и R =<2 — отношение х <2 у,
если х меньше или равно у. Упорядоченное множество (Д <2) является цепью. ?
ПРИМЕР 2.50. Пусть 5 — множество всех подмножеств множества {а,Ь,с}, а <з
есть отношение частичного порядка, определенное в примере 2.45. Множества
{а, 6}, 0 и {а, 6, с} сравнимы, но {а, 6} и {6,с} таковыми не являются. Таким
образом, E, <з) — ЧУ-множество, однако цепью не является. ?
Для изображения частично упорядоченных множеств имеется графический
аппарат, известный как диаграммы Гессе. Для заданного ЧУ-множества (Л, <г)
диаграмма Гессе состоит из совокупности точек и линий, в которой точки пред-
представляют элементы А, и если а < с для элементов а и с множества Л, тогда а
помещено ниже с, и они соединены линией, если не существует такое b ф а, с,
что а < b < с. Если рассмотрение отношений ограничено отношениями частичного
порядка, для них диаграммы Гессе представляют собой просто ориентированный
граф, в котором петли не указаны; и если а < b < с, тогда линия от а к с не указа-
указана. Например, диаграмма Гессе, соответствующая множеству (Т, <i), описанному
выше, показана на рис. 2.23.
Диаграмма Гессе, представляющая E, <з), показана на рис. 2.24. А на
рис. 2.25 представлена диаграмма Гессе для цепи с четырьмя элементами.
10
15
Рис. 2.23

{a,b,c}
fa,b)
РАЗДЕЛ 2.6. Частично упорядоченные множества 105
{Ъ,с}
{с}
Рис. 2.24
и С
а
Рис. 2.25
УПРАЖНЕНИЯ
1. Какое из приведенных ниже отношений Д является отношением частичного
порядка на Л = {а, Ь, с, d}?
а) R = {(а, а), F, 6), (с, с), (d, d), (а, с), F, с), (с, d), (а, d), F, d)};
б) Д = {(а, а), (Ь, 6), (с, с), (d, d), (а, 6), F, с), (с, d), (d, а)};
в) R = {F, Ь), (с, с), (d, d), (а, с), (Ь, с), (с, d), (а, d), F, d)};
г) i2={(a,a),F,b),(c,c),(d,d),(a,b),(b,c)s(a,c),(a1d),F1d),(c,d)}.
2. Какое из приведенных ниже отношений Д является отношением частичного
порядка на Л = {а, 6, с, d} ?
а) А — множество всех людей, а отношение Д определено условием: xRy,
если х старше у.
б) А — множество всех граждан Соединенных Штатов, и Д определено
условием: xRy, если х имеет больший номер карточки социального стра-
страхования, чем у.
в) А — множество целых чисел, Д определено условием: xRy, если х > 2у.
г) А — множество всех людей, и Д определено условием: xRyy если х и у
являются братом и сестрой.
д) А — множество всех упорядоченных пар положительных целых чисел, и
(а, Ь)Д(с, d), если а < с, и если а = с, то 6 < d.
3. Постройте диаграммы Гессе для следующих ЧУ-множеств (А, <), где
а) А = {a,6,c,d} и
< = {(а, а), F, Ь), (с, с), (d, d), (а, с), (Ь, с), (с, d), (a, d), F, d)};
б) Л = {а, Ь, с, d} и < = {(а, а), F, 6), (с, с), (d, d), (а, с), F, с)};
в) A = {a,b,c,d}H< = {(a,a),(b,6),(c,c),(d,d)};
г) А = {а, 6, с, d} и
< = {(а, а), F, Ь), (с, с), (d, d), (а, Ь), (Ь, с), (а, с), (с, d), (a, d), F, d)}.
4. Постройте диаграммы Гессе для следующих ЧУ-множеств (Л, <), где
а) Л = {1,2,3,4, 5,6, 7,8, 9,10,11} и х < у, если х делит у нацело.

106 ГЛАВА 2. Теория множеств
б) А = В х J3, где В = {1, 2,3,6, }. Определим а <\ 6, если а делит Ь нацело,
и (а, 6) < (с, d), если а <i с, и если а = с, то Ъ <i d.
в) А — множество положительных целых чисел, которые делят 27 нацело,
и х < у, если х делит у нацело.
г) А — множество положительных целых чисел, которые делят 54 нацело,
и х <у, если х делит у нацело.
5. Перечислите элементы множества А и выразите < как множество упорядо-
упорядоченных пар для каждой из приведенных ниже диаграмм Гессе:
а) . б)
в)
г)
а Ь с
Д)
a b
6. Для каждого частичного порядка из предыдущего упражнения перечислите
элементы:
а) не сравнимые с а;
б) не сравнимые с Ь\
в) не сравнимые с с;
г) не сравнимые с d.
7. Опишите симметричные отношения, которые являются отношениями частич-
частичного порядка.
2.7. ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ
В разделе 2.5 были определены следующие свойства бинарных отношений. Отно-
Отношение R на А рефлексивно, если (а, а) принадлежит R для всех а из А. Отноше-
Отношение R симметрично, если для всех а и b из А из того, что (а, 6) принадлежит R,

РАЗДЕЛ 2.7. Отношения эквивалентности 107
следует, что (Ь, а) принадлежит it. Отношение R транзитивно, если для всех а,
b и с из А таких, что (а, 6) и F, с) принадлежат R, (а, с) также принадлежит R.
Эти свойства объединены в приведенном ниже определении.
ОПРЕДЕЛЕНИЕ 2.51. Отношение it на А есть отношение эквивалентности,
если оно рефлексивно, симметрично и транзитивно.
Пусть А = {1,2,3,4,5,6}. В примере 2.33 уже было установлено, что отно-
отношение iti на А, определенное как
Ri = {A,1), B,2), C,3), D,4), E,5), F,6), A,2),
A,4), B,1), B,4), C,5), E,3), D,1), D,2)},
рефлексивно, транзитивно и симметрично, поэтому iti есть отношение эквива-
эквивалентности на множестве А.
ПРИМЕР 2.52. Пусть А — множество целых чисел. Определим отношение Дз С
А х А посредством R$ = {(а, Ь) : а - b = 5 • к для некоторого целого числа к}.
Например, G,2) е R3, поскольку 7-2 = 5 = 5-1, и (-11,4) € R$, так как
(-11)-4 = -15 = 5(-3).
Отношение R3 рефлексивно. Если а — целое число (т.е. а € А), то а — а =
0 = 5 • 0 = 5 • к для к = 0, так что (а, а) G Дз.
Отношение R$ симметрично. Допустим, (а, b) e R$. Тогда существует такое
целое число т, что а — b = 5 • т и
b — а = — (а — Ь) =
= -E-т) =
= 5 • (-т)
для целого числа —in. Таким образом, F, а) € R$.
Отношение Rs транзитивно. Предположим, что a, b и с — целые числа,
(а, 6) G it3 и F,с) G i?3- По определению, если
(а, Ь) G Дз, тогда а - b = 5 • к для некоторого целого числа к,
и если
(Ь, с) G из, тогда Ь — с = 5 • т для некоторого целого числа т.
Суммирование левых и правых частей этих двух равенств дает
(а - Ь) + (Ь - с) = 5 • к Н- 5 • т
или
а — с = 5 • (к -f т)
для целого числа fc + m. По определению Дз, (а, с) е Rs, поэтому Rs транзитивно.
Поскольку Дз рефлексивно, симметрично и транзитивно, оно является отношени-
отношением эквивалентности. ?

108 ГЛАВА 2. Теория множеств
Отношение эквивалентности R на множестве А разбивает его на подмноже-
подмножества, элементы которых эквивалентны друг другу и не эквивалентны элементам
других подмножеств. В контексте отношений эквивалентности эти подмножества
называются классами эквивалентности по отношению R.
Это разбиение можно представлять себе следующим образом. Пусть мно-
множество А — это набор разноцветных шаров, а отношение R задается условием:
(а, 6) е R тогда и только тогда, когда а и b имеют одинаковый цвет. Поскольку
R — отношение эквивалентности, каждый класс эквивалентности будет состоять
из шаров, имеющих одинаковый цвет. Если определить отношение R условием:
(а, 6) G R тогда и только тогда, когда шары а и b имеют одинаковый диаметр, то
каждый класс эквивалентности будет состоять из шаров одинакового размера.
ОПРЕДЕЛЕНИЕ 2.53. Пусть а Е А, и R — отношение эквивалентности на
А х А. Пусть [а] обозначает множество {х : xRa} = {х : (я, a) Е i?}, назы-
называемое классом эквивалентности, содержащим а. Символ [A]r обозначает
множество всех классов эквивалентности множества А по отношению R.
ПРИМЕР 2.54. Ранее было показано, что отношение Дь определенное выше, есть
отношение эквивалентности на множестве А = {1,2,3,4,5,6}. Классы эквива-
эквивалентности по отношению R\ были получены путем определения класса эквива-
эквивалентности каждого элемента множества А:
[1] = {х : (х, 1) Е Rx} = {х : xRxl} = {1,2,4},
где 1 е [1], поскольку A,1) е Дь 2 € [1], т.к. B,1) е Дь 4 € [1], поскольку
D,1) Е i?i, и не существует никакого иного х из А такого, что (х, 1) € R\. Точно
так же, получаем
[2] = {х:(х,2)€Д1} = {2,1,4};
Итак, имеется только три различных класса эквивалентности:
[1] = й = [4] = {1,2,4},
[3] = [5] = {3,5}
[6] = {6},

РАЗДЕЛ 2.7. Отношения эквивалентности 109
так что
Этот пример показывает, что любой элемент класса эквивалентности порождает
класс эквивалентности; другими словами, если be [а], то [а] = [Ь]. На основании
этого свойства говорят, что любой элемент класса эквивалентности представляет
класс.
Каждый класс эквивалентности содержит по крайней мере один элемент,
поэтому, в силу рефлексивности отношения, множество всех элементов, эквива-
эквивалентных элементу а, должно содержать а. С другой стороны, никакой элемент не
может принадлежать двум различным классам эквивалентности. ?
ПРИМЕР 2.55. Рассмотрим отношение эквивалентности R$ из примера 2.52. Для
множества А всех целых чисел R3 Q А х А было определено посредством Д3 =
{(а, Ь) : a — b = 5 • к для некоторого целого числа к}. Поскольку
[а] = {х : (ж, а) G Д3} = {х : xR3a} =
= {х : х — a = 5 • к для некоторого целого числа к} =
= {х : х = a + 5 • к для некоторого целого fc},
получаем, что классы
[0] = {..., -15, -10, -5,0, 5,10,15, 20,25,...} =
[1] = {...,-14,-9,-4,1,6,11,...} =
= ... = [-9] = h4] = [l] = [6] = ..
[2] = {...,-13,-8,-3,2,7,12,...} =
= ... = [_3] = [-2] = [7] = [12] = .
[3] = {...,-12,-7,-2,3,8,13,...} =
[4] = {...,-11,-6,-1,4,9,14,...} =
... = [-6] = [-!] = [4] = [9] = .-.
представляют собой различные классы эквивалентности по отношению Дз- Таким
образом,
[А]Яз = {[0], [1], [2], [3], [4]}.
Элементы [0] "похожи" в том смысле, что каждый из них кратен пяти. Элементы
любого другого класса эквивалентности также "похожи" в том смысле, что имеют
один и тот же остаток при делении на пять. ?

110 ГЛАВА 2. Теория множеств
Как отмечалось выше, совокупность классов эквивалентности разделяет все
множество А на непустые взаимоисключающие, или непересекающиеся подмно-
подмножества, в том смысле, что никакие два из них не имеют общих элементов. Такое
разделение множества называется его разбиением.
ОПРЕДЕЛЕНИЕ
J непусто, есть
2.56. Пусть Аи I —
множества и пусть (А) =
~-{Аг
множество непустых подмножеств множества А.
(А) называется разбиением А, если
a) Ai nAj = ?
б) А = U Ai,
некоторого
5 для всех г Ф j ;
т.е. а принадлежит
iel.
выполнены два условия:
А тогда и только тогда,
когда
: г Е /}, где
Множество
а Е А{ для
ТЕОРЕМА 2.57. Непустое множество подмножеств (А) множества А есть раз-
разбиение А тогда и только тогда, когда (А) = [A]r по некоторому отношению
эквивалентности R.
ДОКАЗАТЕЛЬСТВО. Пусть (А) = {Аг : г ? /} есть разбиение А. Определим
отношение R на А х А таким образом: aRb тогда и только тогда, когда а и b
принадлежат одному и тому же подмножеству Ai для некоторого г. Несомненно,
что для всех а из Л имеем aRa, поэтому R рефлексивно. Если а и b принадлежат
одному подмножеству А{, тогда b и а также принадлежат этому подмножеству Ai,
поэтому R симметрично. Если элементы а и b принадлежат одному подмножеству
и элементы бис принадлежат одному подмножеству, то а и с тоже находятся в
одном подмножестве, в силу условия А{ П Aj = 0 для г ф j. Следовательно, R
транзитивно и представляет собой отношение эквивалентности.
Обратно, предположим, что R — отношение эквивалентности. Необходимо
показать, что [А]ц = {[а] : а Е А} есть разбиение А. Очевидно, [а] непусто
для всех а, т.к. а ? [а]. Очевидно также, что А есть объединение [а], так что
а ? А. Допустим, что пересечение [а] П [Ь] непусто и х ? [а] П [Ь]. Тогда xRa и
xRb, и, в силу симметричности отношения, aRx. Но поскольку aRx и xRb, то,
в силу транзитивности отношения, aRb. Поэтому, а ? [Ь]. Если у Е [а], то yRa,
а поскольку aRb, то yRb, в силу транзитивности отношения. Поэтому [а] С [6].
Аналогично можно показать, что [Ь] С [а], поэтому [а] = [Ь] и [A]r представляет
собой разбиение А. Ш
ПРИМЕР 2.58. Пусть А = {?, Д,О>*}- Рассмотрим разбиение
Согласно доказательству предыдущей теоремы, необходимо определить R таким
образом: R = {(а, Ь) : а Е Ai и b E А{ для некоторого г}. Итак,
R = {(?, ?), (*, Л), (*, О), (*, •), (О, А),
(О, О), (О,*), (А, А), (А, О), (А,*)}
есть отношение, соответствующее заданному разбиению. П

РАЗДЕЛ 2.7. Отношения эквивалентности 111
УПРАЖНЕНИЯ
1. Установите, является ли каждое из перечисленных ниже отношений на А
отношением эквивалентности. Для каждого отношения эквивалентности по-
постройте классы эквивалентности.
а) А — множество целых чисел, и Д есть отношение, заданное условием:
(а, 6) G Д, если а + b = 0;
б) А — множество целых чисел, и Д есть отношение вида (а, Ь) € Д, если
а + b = 5;
в) А — множество высказываний, и R есть отношение вида (р, q) G Д, если
р логически эквивалентно q\
г) А — множество упорядоченных пар целых чисел, и (а,6)Д(с, d), если
ad = bc\
д) А = {-10, -9, -8, -7,... 0,1,..., 9,10}, и (а, Ь) е Д, если а2 = Ъ2\
е) А = {-10, -9, -8, -7,... 0,1,..., 9,10}, и (а, Ъ) ? Д, если а3 = б3.
2. Пусть А = {1,2,3}. Установите, является ли каждое из приведенных ни-
ниже отношений на А отношением эквивалентности. Для каждого отношения
эквивалентности постройте классы эквивалентности.
а) Д1 = {B,2),A,1)};
б) Л2 = {A,1),B,2),C,3)};
в) Дз = {A,1), B,2), C,3), A,2), B,1), C,1), A,3)};
г) Д4 = {A,1), B,2), C,3), A,2), C,2), B,1)};
д) Д5 = {A,1), B,2), C, 3), A, 2), B,1), B,3), C,2), A, 3), C,1)}.
3. Установите, является ли каждое из приведенных ниже отношений на А от-
отношением эквивалентности. Для каждого из отношений эквивалентности
постройте классы эквивалентности.
а) А — множество всех подмножеств множества {а, 6, с, d}, отношение Д
определяется следующим образом: $Д?, если s и t содержат одинаковое
количество элементов;
б) А = {1,2,3,4,5,6,7,8,9,10}, отношение Д определяется следующим об-
образом: аДЬ, если а 4- b положительно;
в) А = {1,2,3,4,5,6,7,8,9,10}, отношение Д определяется следующим об-
образом: by аД6, если а + Ь четное;
г) А — множество прямых в плоскости, отношение Д определяется следу-
следующим образом: nRm, если пит пересекаются;
л) А — множество прямых в плоскости, отношение Д определяется следу-
следующим образом: nRm, если пит параллельны;
е) А — множество компьютерных программ, написанных для NASA, отно-
отношение Д определяется следующим образом: pRq, если р и q написаны на
одном и том же языке программирования.
4. Пусть А = {?, Л, О>w, ?> г, /г, *}. Отношение Д на А определено, как:
Я = {(?, ?), (А, А), (О, О), К «;), (t, 0, (^ z), (Л, /г), (*, *), (П, О),
(О, г), К /г), (*, *), (?, *), (г, ?), (г, О), (Л, tu), (*, t), (О, ?)}•
а) покажите, что Д является отношением эквивалентности на А\

112 ГЛАВА 2. Теория множеств
б) постройте все классы эквивалентности по отношению R.
5. Пусть f(x) = rr2 + 1, где х ? [—2,4] = {х : х действительное число и
-2 < х < 4} = А. Определим отношение R на А х А следующим образом:
(a, b) e R тогда и только тогда, когда f(a) = f(b).
а) покажите, что R является классом эквивалентности на А = [—2,4];
б) определите классы эквивалентности:
6. Для X ф 0 определим отношение I как / = {х : х = (а, а) для некоторого
а € X} = {(а,а) е X х X : а G X}. / представляет собой отношение
эквивалентности на X и называется отношением тождества на X. Пусть
i? — отношение на X. Докажите, что
а) R рефлексивно тогда и только тогда, когда /Си;
б) R симметрично тогда и только тогда, когда R = R~~l\
в) R транзитивно тогда и только тогда, когда RoR'1 С R.
7. Установите, какие из приведенных ниже совокупностей элементов составля-
составляют разбиение множества А = {1,2,3,4,5,6,7}. Если некоторая из совокуп-
совокупностей не входит в разбиение, объясните, почему. Для всех совокупностей,
входящих в разбиение, перечислите элементы соответствующего отношения
Д, и если это перечисление представляется слишком длинным, опишите
множество упорядоченных пар, не перечисляя их.
а) {{1,2},0,{3,4,5}{6,7}}; б) {{1,2}, {3,4,5}{6,7}};
в) {{1,7},{3,4,6}}; г) {{1,5},{3,4,5}{2,6,7}};
д) {{1,2,3,4,5,6,7}}.
8. Установите, какие из приведенных ниже совокупностей элементов составля-
составляют разбиение множества А = {1,2,3,4,5,6,7}. Если некоторая совокупность
не входит в разбиение, объясните, почему. Для совокупностей, входящих в
разбиение, перечислите элементы соответствующего отношения i?, и если
это перечисление представляется слишком длинным, опишите множество
упорядоченных пар, не перечисляя их.
а) {{1},{2},{3},{4},{5}Д6},{7}}; б) {{1,4}, {3,5,8}{6,2,7}};
в) {{1,6},{3,4},{5,2}}; г) {{1,7},{3,5},{2,4},{6}};
д) {{1,2,3,4}, {4,5,6, 7}}.
9. Пусть А — множество неотрицательных целых чисел, В — множество по-
положительных целых чисел. Определим отношение R на А х В следующим
образом: (a, 6)i?(c, d), если ad = be. Является ли это отношением эквивалент-
эквивалентности? Если это так, докажите. Если нет, объясните почему. Какие элементы
множества Ах В находятся в отношении с A,2)?

ГЛАВА
ЛОГИКА, ЦЕЛЫЕ ЧИСЛА
И ДОКАЗАТЕЛЬСТВА
3.1. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
Многие утверждения, имеющие форму высказываний, на самом деле таковыми не
являются, так как содержат переменные, конкретные значения которых не указа-
указаны. Поскольку такое утверждение при одних значениях переменных может быть
истинным, а при других — ложным, ему не может быть предписано истинностное
значение. Такие утверждения, примерами которых являются
Р{х) : 3 + х = 5;
Q(x,y,z): x2+y2>z2-
R(x,y): z2+y2>0;
S(x) : - 1 < sin(x) < 1,
называются предикатами. Предикат с одной переменной называется одномест-
одноместным предикатом. Предикат, имеющий две переменные, называется двуместным
предикатом, а предикат, содержащий п переменных, называется п-местным
предикатом. Предикат Р{х) — одноместный, поскольку имеет одну переменную.
Предикат Q(x,y,z) является трехместным предикатом. Предикаты становятся вы-
высказываниями, когда их переменным присваивается значение. Например,
РB) : 3 + 2 = 5
является высказыванием, и это высказывание истинно.
РG) : 3 + 7 = 5
тоже является высказыванием, и это высказывание ложно. Говорят, что набор
значений переменных удовлетворяет предикату, если на этом наборе предикат
принимает значение "истина", т.е. становится истинным высказыванием. Напри-
Например, 2 удовлетворяет Р(х), поскольку РB) истинно, а 7 не удовлетворяет Р(т),
поскольку РG) ложно.

114 ГЛАВА 3. Логика, целые числа и доказательства
Некоторые предикаты истинны для каждого возможного набора значений
переменных, взятых из данного множества. Среди примеров, приведенных выше,
S(x) — предикат —1 < sin(x) < 1, где х принадлежит множеству действительных
чисел. Тот факт, что для любого значения х
-1 < sin(x) < 1,
дает основание сказать, что
для любого х истинно S(x),
что символически изображается как
VxS(x)
или
Vx(-1 < sin(x) < 1).
Символ Vx называется универсальным квантором, или квантором всеобщно-
всеобщности, и читается "для любого х" или "для всех х". Множество значений, которое
может принимать х, называется универсом, или предметной областью. В част-
частности, предметной областью может являться множество действительных чисел,
множество целых чисел или другие подобные множества. Вообще говоря, ис-
истинность утверждения с квантором всеобщности зависит от предметной области.
Например, высказывание
Vx(x2 > 5)
не истинно, если универсом (предметной областью) является множество целых
чисел; однако, оно было бы истинным, если в качестве предметной области взять
множество целых чисел, больших чем 2. Точно так же высказывание
Vx(x2 > 0)
истинно, если предметная область — множество действительных чисел, но ложно,
если предметная область содержит комплексное число г, т.к. г2 = — 1.
Квантифицированный предикат
VxP(x),
где Р(х) : 3+х = 5, не является истинным, если предметная область — множество
целых чисел, потому что имеются значения х из этой области (например, х — 4)
такие, что Р(х) ложно. Для истинности УхР(х) Р{х) должно быть истинным
для каждого значения х из предметной области. Таким образом, VxP(x) имеет
конкретное истинностное значение, поэтому является высказыванием.
Предикат VxVy R(x,y) читается как "для каждого х, для каждого у имеет
место Д(х, у)" или "для каждого х и для каждого у имеет место i?(x, у)". Предикат
\/х\/уR(x,y) истинный только тогда, когда для любого набора значений х и у
из соответствующей предметной области х2 + у2 > 0 истинно. Если предметной
областью для х и для у является множество действительных чисел, то
Vx\/yR(x,y)

РАЗДЕЛ 3.1. Исчисление предикатов 115
истинно. Рассматривая приведенный выше предикат Q{x,y,z) : х2 + у2 > г2, мы
находим, что
не является истинным, когда предметная область для х, у и z — множество целых
чисел, поскольку высказывание
«A,2,3)
ложно. Для ясности будем иногда заключать квантор в скобки, записывая (Vx)P(x)
вместо VxP(x) и (Vx)(Vy)i?(x,y) вместо VxVyi?(x,y).
Хотя VxP(x), вообще говоря, не истинно, Р(х) истинно по крайней мере
для одного значения х, а именно, х = 2. Поэтому существует х такой, что Р(х)
истинно. Символически это записывается как
ЗхР(х).
Символ Зх называется квантором существования. Здесь, как и в случае Vx,
выражение Зх относится к значению х из предметной области.
Высказывание
Зх(х2 = 4)
истинно, если предметной областью есть множество действительных чисел, т.к.
х2 = 4 истинно для х = 2. Высказывание
Зх(х2 = 5)
также истинно, если предметной областью есть множество действительных чи-
чисел; однако, оно не является истинным, если предметная область есть множество
целых чисел, так как не существует целого числа, квадрат которого равен 5.
Поскольку для предиката Q(x,t/, z) высказывания Q(l,2,0) и Q(-3,4, 5) ис-
истинны, то высказывание
3x3y3zQ(x,y, z)
истинно.
Чтобы предикат был высказыванием, все его переменные должны иметь кон-
конкретные значения или быть связаны соответствующим квантором. Например,
Cx)(Vz)Q(x,y,z)
не является высказыванием, т.к. переменная у не связана никаким квантором.
Если D{x) — предикат, то высказывание VxD(x) истинно только тогда, когда
высказывание -D(x) истинно для любого х. Когда же высказывание \/xD(x) будет
ложным? Отрицание VxJ9(x) может быть записано как
~Vx?>(x).
Чтобы доказать ложность высказывания VxD(x), достаточно найти только одно
значение х, для которого D(x) ложно (или, что равносильно, ~D(x) истинно).
Таким образом, VxD(x) ложно тогда и только тогда, когда
3x(~D(x))

116 ГЛАВА 3. Логика, целые числа и доказательства
истинно, т.е. существует такое значение х (из предметной области), что ~D(x)
истинно (или D(x) ложно). Например, высказывание
Vx(x2 > 0)
не является истинным, если предметная область — множество целых чисел, т.к.
х2 не больше, чем 0, если х = 0. Таким образом, Vx(x2 > 0) ложно, потому
что Зх(х2 ^ 0) истинно. Но это означает, что Vx(x2 > 0) ложно, потому что
Зх(~(х2 > 0)) истинно.
Аналогично, если G{x) — предикат, отрицание существования такого х,
что G(x) истинно, записывается в виде
~(ЗхОД).
Очевидно, если не существует значения х, при котором G(x) истинно, то G(x)
ложно для любого х. В этом случае ~G(x) будет истинным для всех значений х
или, что равносильно,
Vx(~G(x)).
Результат проведенных рассуждений может быть сформулирован в виде тождеств:
~3x(G(x))=Vx(~G(x)).
Для образования отрицания с навешенным квантором всеобщности нужно
заменить Vx на Зх и взять отрицание предиката, следующего за квантором. А
для формирования отрицания предиката с навешенным квантором существования
нужно заменить Зх на Vx и взять отрицание предиката, следующего за квантором.
Отрицание высказывания, содержащего более одного квантора, осуществля-
осуществляется путем последовательного рассмотрения каждого квантора, начиная с первого.
Например, для отрицания (Vx)(\/y)R(x,y) имеем
y) = Эх~(Уу)Д(:г,у) =
ее(Зх)CУ)~Д(х,у).
Аналогично,
~Cx)(Vy) Cz) Q(x, у, z) = (Vx)~(Vy) Cz) Q(x, y, z) =
Следовательно, для отрицания высказывания, содержащего кванторы, 3 заменя-
заменяется на V и наоборот, после чего берется отрицание предиката, связанного с этой
последовательностью кванторов.
Существует связь между квантифицированными предикатами и предиката-
предикатами, в которых используются конкретные значения переменных. Рассмотрим, на-
например, предикат вида
Vx5(x)

РАЗДЕЛ 3.1. Исчисление предикатов 117
в форме высказывания
для каждого х верно, что — 1 < sin(x) < 1.
Предположим, что это высказывание истинно. Применим это к конкретному зна-
значению х, равному 8. Тогда
5(8).
Если Vx5(x) истинно и а —- конкретное значение х (из предметной области), то
S(a)
истинно. Таким образом, для случая х равно 8 истинным является
-1 <sin(8) < 1.
Обратно, если 6 — произвольно выбранное значение из универса (т.е. единствен-
единственным известным и допускаемым свойством 6 есть принадлежность предметной
области), и мы покажем, что 5F) истинно, то
для любого х имеем 5(х)
или
Vx5(x).
Следующие два правила устанавливают связь между предикатами с наве-
навешенным квантором всеобщности и предикатами, примененными к произвольным
константам (элементам) из универса.
Из истинности Vx5(x) следует, что S(a) истинно для произвольного
(т.е. произвольно выбранного) элемента а из универса.
Из истинности 5F) для произвольной константы 6 из универса следует,
что Vx5(x) истинно.
Пусть дано высказывание Зх(х2 + 2х - 3 = 0), отсюда заключаем, что су-
существует значение а (а именно, а = 1) такое, что а2 + 2а — 3 = 0. Обратно, если
для конкретного значения а имеем а2 + 2а — 3 = 0, можно сделать вывод, что
2
Следующие два правила дают возможность установить связь между пре-
предикатами с конкретными значениями переменных и предикатами с навешенным
квантором существования.
Из истинности 3xS(x) следует, что S(a) истинно для некоторого а из
универса.
Из истинности 5F) для некоторого 6 из универса следует, что 3xS(x).
Суммируя вышесказанное, получаем такие соотношения:
1) Универсальная конкретизация
Из истинности VxP(x) следует истинность Р(а) для произвольного а из
универса.

118 ГЛАВА 3. Логика, целые числа и доказательства
2) Универсальное обобщение
Если произвольное а из универса обеспечивает истинность Р{а), делаем
вывод, что Vx(P(x) истинно.
3) Экзистенциональная конкретизация
Из истинности ЗхР(х) следует, что существует конкретное b такое, что
РF) истинно.
4) Экзистенциональное обобщение
Из существования конкретного с из универса, для которого Р(с) истинно,
можно сделать вывод, что ЭхР(х).
На основе этих соотношений можно доказать следующие утверждения.
ТЕОРЕМА 3.1. Для произвольных предикатов Р(х) и Q(x), имеющих одну пред-
предметную область,
а) Vx(P(x) Л Q(x)) = VxP(x) Л VxQ(x);
б) 3x(P(x)vQ(x)) = 3xP(x)v3xQ(x);
в) из VxP(x) WxQ(x) следует, что Vx(P(x) V Q(x))\
г) из Зх(Р(х) A Q(x)) следует, что ЗхР(х) A 3xQ(x).
ДОКАЗАТЕЛЬСТВО. Чтобы доказать
Vx(P(x) Л Q(x)) = VxP(x) Л VxQ(x),
сначала предположим, что Vx(P(x) AQ(x)), откуда следует, что VxP(x) AVxQ(x).
Из Vx(P(x) Л Q(x)), используя универсальную конкретизацию, заключаем, что
для произвольного а имеет место Р(а) AQ(a). Следовательно, согласно правилу
специализации (логики высказываний) можно сделать вывод, что для произволь-
произвольного а имеет место как Р(а), так и Q(a). На основе универсального обобще-
обобщения делаем вывод, что \/хР(х) и VxQ(x). Таким образом, можно заключить, что
\/хР(х) Л VxQ(x), в силу правила конъюнкции (логика высказываний). Обратно,
предположим, что VxP(x) Л \/xQ(x). На основе правила специализации можно
сделать вывод, что VxP(x) и MxQ{x). Из правила всеобщей конкретизации следу-
следует, что для произвольного а имеют место Р(а) и Q(a). Следовательно, используя
правило конъюнкции, можно сделать вывод, что Р(а) Л Q(a) для произвольно-
произвольного а. На основе универсального обобщения делаем вывод, что Vx(P(x) Л Q(x)).
Оставшуюся часть доказательства предоставляем провести читателю. ¦
Если р(х) — утверждение "х — студент", а утверждение q(x) — "x учится
усердно", то утверждение Vx(p(x) —> q(x)) может быть интерпретировано как
"Все студенты учатся усердно". Точно так же, если р(х) — утверждение "х —
слон", a q(x) — утверждение "х предпочитает арахис в шоколаде", то выражение
Зх(р(х) Aq(x)) может быть сформулировано как "Некоторые слоны предпочитают
арахис в шоколаде". Утверждение "Все люди смертны" логически может быть
выражено как Vx(p(x) —> q(x)), где р(х) — утверждение "х — человек", a q(x)
— утверждение "х смертен". Аналогично, утверждение "Некоторые целые числа
делятся на 5" может быть записано Зх(р(х) Лд(х)), где р(х) — утверждение "х
— целое число", a q(x) — утверждение "х делится на 5". Обычно логические
выражения, содержащие Vx, можно превратить в утверждения, содержащие "для

РАЗДЕЛ 3.1. Исчисление предикатов 119
всех", а логические выражения, содержащие Эх, можно обратить в утверждения,
содержащие "для некоторого".
В силу такого характера перевода с языка логики на естественные языки
и обратно, отрицание утверждения типа "для всех" есть утверждение типа "для
некоторого", а отрицание утверждения типа "для некоторого" есть утверждение
типа "для всех". Например, отрицание утверждения
Все целые числа являются простыми
есть утверждение
Некоторые целые числа не являются простыми,
а отрицание утверждения
Некоторые люди любят есть репу
есть утверждение
Все люди не любят есть репу.
Для неформальной проверки правильности умозаключений, включающих
утверждения типа "для всех" и "для некоторого", используются так называемые
диаграммы Эйлера, которые состоят из кругов, изображающих множества. На-
Например, утверждению "Все р есть q" соответствует диаграмма, приведенная на
рис. 3.1, где круг, изображающий множество р, содержится в круге, изображаю-
изображающем множество q. Утверждение "Некоторые р есть q" представляется диаграммой
на рис. 3.2, где мы видим, что пересечение кругов, изображающих множества
р и q, непусто. Для проверки умозаключения необходимо попытаться построить
диаграмму Эйлера, в которой посылки истинны, а заключение ложно. Если такое
построение осуществимо, то умозаключение неправильно, если же нет, то это
доказывает правильность нашего умозаключения.
Рис. 3.1 Рис. 3.2
ПРИМЕР 3.2. Рассмотрим умозаключение
Все студенты колледжа выдающиеся
Все выдающиеся люди — ученые
л Все студенты колледжа — ученые

120 ГЛАВА 3. Логика, целые числа и доказательства
В соответствии с посылками круг, изображаю-
изображающий студентов колледжа (СК), должен быть внутри
круга, изображающего выдающихся людей (ВЛ), ко-
который, в свою очередь, должен быть внутри круга (У),
изображающего ученых. Следовательно, круг студен-
студентов колледжа должен находиться внутри круга уче-
ученых, и умозаключение является правильным. ?
ПРИМЕР 3.3. Рассмотрим умозаключение
Все поэты счастливы
Некоторые поэты ленивы
.-. Некоторые ленивые люди счастливы
В соответствии с посылками круг, изображаю-
изображающий поэтов (П), должен быть внутри круга, изобра-
изображающего счастливых людей (СЛ), а пересечение по-
поэтов и ленивых людей (ЛЛ) должно быть непусто. Но
это пересечение содержится в круге, изображающем
поэтов, так что пересечение ленивых и счастливых
людей непусто. Умозаключение правильно. ?
ПРИМЕР 3.4. Рассмотрим умозаключение
Некоторые поэты неудачники
Некоторые атлеты неудачники
.*. Некоторые поэты являются атлетами
Соответствующая диаграмма Эйлера изображена на рис. 3.3.
Рис. 3.3
Мы видим, что возможно построить такую диаграмму Эйлера, в которой
пересечение кругов поэтов (П) и неудачников (Н) непусто и пересечение кру-
кругов атлетов (А) и неудачников непусто, так что посылки истинны, но при этом
круги поэтов и атлетов не пересекаются, так что следствие не является верным.
Следовательно, умозаключение не является правильным. ?
ПРИМЕР 3.5. Рассмотрим умозаключение
Все гении нелогичны
Некоторые политики нелогичны
.*. Некоторые политики гении

РАЗДЕЛ 3.1. Исчисление предикатов 121
На рисунке слева круг для гениев (Г) со-
содержится внутри множества нелогичных людей
(НЛ), а пересечение круга политиков (П) и кру-
круга нелогичных людей непусто, но круги поли-
политиков и гениев не пересекаются. Следовательно,
посылки истинны, но заключение ложно. Поэто-
Поэтому умозаключение не является правильным. ?
¦ УПРАЖНЕНИЯ
1. Заданы предикаты
Р(х,У,
Q(x,
R(x,
S(n,
T(a,b,
z):
у)--
г):
У):
с):
х2 +у2 > z
2.
у = (х-4)/(х +
\х-1\ <г;
У = п\;
а нравится
Запишите следующие высказывания:
a) PC,4,5);
в) ДC,7);
д) Т(Джон, Сью, Мэри)
2. Заданы предикаты
б)
г)
b бол
Q(8,
5D,
4);
[ьше
2);
24);
Г1Х) Уч z) • х * У — z ?
Q(x, у) : если у2 = х2, то х = у\
R(x): [[x\\ = [х\;
5(а,Ь,х): а < х2 < 6;
Т(а, Ь) : а играет в теннис лучше, чем Ь.
Запишите следующие высказывания:
а) РC,4,5); б) Q(-2,2);
в) ЯC.1416); г) 5@,4,-3);
д) Т(Джон, Фред).
3. Используя Р, Q,i?, 5 и Г из упражнения 1, запишите высказывания:
а) (Эх)(Э2/)Р(х,2/,25); б) Cx)Q(x,7);
в) (Vr)Cx)i?(x,r); г) Cn)(VyM(n,y);
д) (Ус)Т(Джон, Сью, с).
4. Используя Р, Q,i?, 5 и Т из упражнения 1, запишите высказывания:
a) (Vz)(V2/)Cz)P(z,y,2); б) (Vx)(Vy)Q(x,y);
в) (Ух)Д(х); г) (Vx)Ca)CbM(a,6,x);
д) (Уа)Г(а,Тед).

122 ГЛАВА 3. Логика, целые числа и доказательства
5. Запишите приведенные ниже утверждения в символической форме, введя
предикаты. В случае необходимости укажите предметную область.
а) На каждой улице будет праздник.
б) Некоторые машины умнее людей.
в) Любой играет в теннис лучше Фрэда.
г) Для каждого действия существует равное и противоположно направлен-
направленное противодействие.
д) Каждый игрок в гольф, в конце концов, будет обыгран более сильным
игроком.
6. Запишите приведенные ниже утверждения в символической форме, введя
предикаты. В случае необходимости укажите предметную область.
а) Некоторые композиторы пишут симфонии лучше, чем другие.
б) Для каждого п существует три целых числа таких, что n-я степень одного
из них равна сумме n-ых степеней двух других.
в) Существуют лошади, которые могут обогнать некоторых людей.
г) Он лучший атлет в мире.
д) Не существует совершенных героев.
7. Ранее было показано, что если Q(x,y,z) : х2 + у2 > г2, то утверждение
VxVyVzQ(x,y,z)
ложно. Если универс — множество положительных целых чисел, то что
можно сказать об истинности
а) VxVy3zQ(x,y,2)?
б) Vx3y3zQ(x,y,z)?
в) 3xiy3zQ(x,y,z)->
г) 3x3y3zQ(x,y,z)?
д) 3x3yVzQ(x,y,z)'?
8. Пусть известно, что
Уп(п нечетно —> Cfc)(n = 2fc + 1)).
а) Какое из этих утверждений истинно?
7 нечетно -* Cfc)G = 2k + 1),
6 нечетно -> Cfc)F = 2fc + 1).
б) Какое из этих утверждений истинно и почему?
Cfc)G = 2fc + l),
Cfc)F = 2fc + l).
9. Докажите, что из Vx P(x) Wx Q{x) следует, что Vx (Р(х) V Q(x)).
10. Докажите, что из Зх (Р(х) Л Q(x)) следует, что Зх Р(х) Л Зх Q(x).

РАЗДЕЛ 3.2. Основные положения теории доказательств и теории целых чисел 123
11. Проверьте правильность умозаключений при помощи диаграмм Эйлера.
Все адвокаты богаты Некоторые адвокаты богаты
Все богатые едят омаров Некоторые врачи богаты
л Все адвокаты едят омаров .*. Некоторые врачи — адвокаты
12. Проверьте правильность умозаключений при помощи диаграмм Эйлера.
Некоторые марсиане зеленые Все мужчины любят мясо
Все елки зеленые Некоторые учителя — мужчины
л Некоторые марсиане — елки .*. Некоторые учителя любят мясо
13. Проверьте правильность умозаключений при помощи диаграмм Эйлера.
Все врачи любят музыку Некоторые врачи умные
Все поэты любят музыку Все умные люди поэты
.-. Все врачи — поэты л Некоторые врачи — поэты
14. Проверьте правильность умозаключений при помощи диаграмм Эйлера.
Все машины дорогие Все мужчины смотрят телевизор
Велосипед недорогой Некоторые слесари — мужчины
.*. Велосипед — не машина .*. Некоторые слесари смотрят телевизор
15. Проверьте правильность умозаключений при помощи диаграмм Эйлера.
Все люди смертны Некоторые гуси — мужчины
Гуси — не люди Некоторые мужчины играют в гольф
л Гуси бессметрны л Некоторые гуси играют в гольф
3.2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ДОКАЗАТЕЛЬСТВ
И ТЕОРИИ ЦЕЛЫХ ЧИСЕЛ
В данном разделе рассматриваются некоторые свойства целых чисел, которые
докажут свою полезность в дальнейшем. Возможно, более важная цель — ис-
использовать множество целых чисел как хорошо известную предметную область
для развития и применения на практике техники доказательства теорем. Пер-
Первая проблема —- с чего начать. Что можно считать известным и, следовательно,
использовать в доказательстве теорем? В общем курсе по теории чисел можно
было бы начать с основных аксиом теории чисел и развивать изложение в этом
направлении. В нашем случае это не совсем целесообразно. Вторая проблема —
решить, какие детали включать в рассмотрение. Нужно ли объяснять, почему
в одном месте доказательства имеем 4 4- х + 5 = у, а в другом — у = х 4- 9?
Если обращать внимание на все несущественные детали, то основные моменты
доказательства затеряются в таком хаосе. Обычно предполагается, что все дета-
детали читателю понятны и в случае необходимости он может сам их воспроизвести.
Не существует точных правил, которые бы говорили, о чем нужно упомянуть, а
что можно опустить. Изящное изложение доказательства теоремы — искусство.
В дальнейшем мы будем предполагать, что большинство аксиом, перечисленных
в этом разделе, известны и могут использоваться без подробных разъяснений.
Для начала примем следующие аксиомы равенства. Они распространяются
на элементы любого множества, в том числе и множества Z целых чисел.

124 ГЛАВА 3. Логика, целые числа и доказательства
(Е1) Для любого a, a = a.
(Е2) Для любых а и 6, если а = 6, то b = а.
(ЕЗ) Для любых а, 6 и с, если а = Ъ и Ь = с, то а = с.
Аксиомы El, E2 и ЕЗ говорят о том, что равенство на любом множестве
обладает свойствами отношения эквивалентности. Эти аксиомы распространяются
на все математические формы, а не только на теорию чисел.
Примем также следующие свойства сложения, вычитания и умножения на
множестве Z целых чисел.
(И) Если а и Ь — целые числа, то а + b и а-b — целые числа. Множество целых
чисел замкнуто относительно операций сложения и умножения.
A2) Если а = b и с = d, то а + с = b -\- d и а • с — b • d.
A3) Для любых целых чисел а и b имеют место равенства а 4- 6 = Ь 4- а и
ab = b-а. Множество целых чисел коммутативно относительно операций
сложения и умножения.
A4) Для любых целых чисел а, 6 и с имеют место равенства (а-Ьб)+с = а + (Ь+с)
и а- (Ь- с) = (а-Ь) • с. Множество целых чисел ассоциативно относительно
операций сложения и умножения.
A5) Для любых целых чисел а, 6 и с имеет место равенство a-(b+c) = (a-b)-f(a-c).
Умножение целых чисел дистрибутивно относительно сложения.
A6) Существуют единственные целые числа 0 и 1 такие, что a4-0 = 0 + a = a
HQ'l = l-o = o для любого целого числа а. Целое число 0 называется
нейтральным элементом сложения, или нулем множества целых чисел,
целое число 1 называется нейтральным элементом умножения.
A7) Для каждого целого числа а существует единственное целое число —а,
называемое его обратным элементом относительно сложения, такое, что
a + (-a) = (-a) + a = 0.
A8) Если b и с — целые числа и для некоторого ненулевого числа а имеем
a • Ъ = а - с, то b = с. Это утверждение называется мультипликативным
свойством сокращения.
Как уже отмечалось, в математике принято доказывать теоремы без излиш-
излишнего формализма, поскольку предполагается, что читателю известны многие де-
детали, поэтому нет необходимости излагать их явно. Для иллюстрации такого
подхода сначала будет дано формальное доказательство того, что квадрат четно-
четного числа есть число четное. Поскольку предметная область — множество целых
чисел, формально утверждение теоремы имеет вид
Vn (п — четное —> п2 — четное).
Формальное доказательство теоремы изложено ниже. Для доказательства истин-
истинности утверждения с навешенным квантором всеобщности одновременно исполь-
используется принцип универсального обобщения.

РАЗДЕЛ 3.2. Основные положения теории доказательств и теории целых чисел 125
1.
2.
3.
4.
5.
б.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
а — целое число
а — четное
Vn(n — четное —> Cfc)(n = 2A;))
а — четное —> (Bk)(a = 2k)
(ЗА;) (а = 2*:)
a — 2L для некоторого L
2 = s2
— s
(a = 2L)-+
2
2 =
= S2)
= BLJ
()
BLJ = 2BL2)
(x = у и у = г)
а2 = BLJ и BLJ = 2BL2)
-+ а2 = 2BL2)
а2 = BLJ и BLJ = 2BL2)
а2 = 2BL2)
{3k)(a2=2k)
Vx(Cfc)(x = 2k)
—* x — четное)
а — четное
<r — четное
а — четное -
а* — четное
20. \/п(п — четное —> п2 — четное)
фиксированный элемент универса
задано (предположение)
определение четного числа
1, 3 и универсальная конкретиза-
конкретизация
2, 4 и правило отделения
5 и экзистенциональная конкрети-
конкретизация
следует из аксиомы 12, известно
7 и универсальная конкретизация
6, 8 и правило отделения
9 и свойство ассоциативности це-
целых чисел
(шаги опущены для краткости)
свойство транзитивности равенства
9, 11 и универсальная конкретиза-
конкретизация
9, 10 и закон конъюнкции
12, 13 и правило отделения
14 и экзистенциональное обобще-
обобщение для фиксированного значения
BL2)
определение четного целого числа
16 и универсальная конкретизация
для фиксированного значения а2
15, 17 и правило отделения
2, 18 и то, что ((р Л q) —> (р —> q)
есть тавтология)
1, 19 и универсальное обобщение
Приведенные выше рассуждения выписаны более формально, чем это приня-
принято в курсах математической логики. Этот пример иллюстрирует, как в конкретном
случае взаимодействуют законы логики, кванторы, правильные умозаключения и
вывод. Более типичное для данной книги математическое доказательство приве-
приведено ниже.
ТЕОРЕМА 3.6. Если п четно, то п2 тоже четно.
ДОКАЗАТЕЛЬСТВО. Предположим, что п — (произвольное) четное целое число.
По определению четного целого числа существует целое число L такое, что
Если целые числа равны, то равны квадраты этих чисел, так что
п2 = BХJ .
Но

126 ГЛАВА 3. Логика, целые числа и доказательства
поэтому п2 = 2BL2) и n2 = 2J для некоторого целого числа J (а именно J =
2L2). По определению четного целого числа п2 — четное число. ¦
В качестве другого примера рассмотрим утверждение, обратное предыдуще-
предыдущему.
ТЕОРЕМА 3.7. Если п2 четно, то и п четно.
ДОКАЗАТЕЛЬСТВО. Доказательство этой теоремы будет примером доказатель-
доказательства методом контрапозиции вместо прямого доказательства самой теоремы.
Этот метод доказательства возможен, т.к.
Это означает, что доказательство ~д —> ~р эквивалентно доказательству р —¦ q.
Утверждение
r^>q —> г^р
означает следующее:
Если п не является четным, то п2 тоже не является четным.
Пусть п — целое число, которое не является четным (напомним, что четные
целые числа имеют вид 2К, а нечетные целые числа имеют вид 2L + 1, и целое
число является либо четным, либо нечетным, но не может быть и тем, и другим
одновременно). Необходимо показать, что число и2 — нечетное. Поскольку п
нечетное, существует целое число L такое, что
п = 2L + 1.
Возводя в квадрат обе части соотношения, получаем
п2 = BL 4-1J =
= 4L2 + 4L + 1 =
- 2BL2 + 2L) + 1.
Так что, если J = 2L2 + 2L, имеем
п2 = 2 J + 1.
По определению нечетного числа число п2 нечетно, и теорема доказана. ¦
Доказательство следующей теоремы предоставляем читателю.
ТЕОРЕМА 3.8. Пусть a, b и с — целые числа.
а) Если Ь + а = с 4- а, то b = с.
б) Для любого целого числа а имеет место равенство а • 0 = 0.
в) Для любого целого числа а имеет место равенство —(—а) = а.
г) a-{-b) = -(ab).
д) (-а) • (-6) =а.Ъ.
е) -(а + Ь) = (-а) + (-Ь).

РАЗДЕЛ 3.2. Основные положения теории доказательств и теории целых чисел 127
Множество целых чисел Z содержит подмножество N положительных це-
целых чисел.1 Примем в качестве аксиом следующие утверждения относительно
множества N.
(N1) Целое число 1 есть положительное целое число.
(N2) Множество положительных целых чисел замкнуто относительно сложения
и умножения, т.е. если а и b — положительные целые числа, тоа + биа-6 —
положительные целые числа.
(N3) (Аксиома трихотомии) Для каждого целого числа а истинным является
одно и только одно из перечисленных ниже утверждений:
а) а — положительное целое число;
б) а = 0;
в) —а — положительное целое число.
Далее приведено частичное упорядочение целых чисел, в котором целые
числа расположены по принципу "большее за меньшим". Обычно целые числа
"упорядочены" следующим образом:
...,-4,-3,-2,-1,0,1,2,3,4,5,...,
где все положительные числа "идут за" нулем, а нуль "идет за" или "больше,чем"
любое отрицательное число. Трихотомия позволяет установить, является ли число
положительным, поэтому отношение > на множестве Z x Z можно определить
так: а > b тогда и только тогда, когда а—Ь положительно. В силу трихотомии, a—b
либо положительно, либо нуль, либо отрицательно. Поэтому можно объединить
две из этих возможностей в одну и говорить, что а > b тогда и только тогда, когда
а > b или а = Ь. Сказанное выше формализуем в виде следующего определения.
ОПРЕДЕЛЕНИЕ 3.9. Для целых чисел а и b имеем: а > b тогда и только тогда,
когда а — Ь положительно; а > b тогда и только тогда, когда а > b или а = Ь.
Кроме того, b < а равносильно а > b и b < а равносильно а> Ь.
Очевидно, а > 0 равносильно утверждению, что а положительное, потому
что а > 0 тогда и только тогда, когда а — 0 = а положительное. Аналогично, а < 0
равносильно утверждению, что а отрицательно.
Хотя приведенные ниже утверждения хорошо известны и могут рассматри-
рассматриваться как предположения, они приведены для практики доказательства теорем.
ТЕОРЕМА 3.10. Для целых чисел а и 6:
а) (a>b)A(b>a)^a = b;
б) (а > Ь) А (Ь > с) -> а > с.
ДОКАЗАТЕЛЬСТВО, а) Здесь мы используем принцип сведения к абсурду. Если,
предположив, что утверждение в части (а) ложно, мы получим противоречие, то
!В отечественной литературе положительные целые числа принято называть числами нату-
натуральными. — Прим. ред.

128 ГЛАВА 3. Логика, целые числа и доказательства
истинность этого утверждения будет доказана. Предположим, что утверждение в
части (а) ложно. Тогда, если а > ft, 6 > а и а / Ь, то а > 6 и 6 > а. Но в этом
случае а — ft положительно и ft — a = —(а — ft) положительно, что противоречит
аксиоме трихотомии N3. Так как мы пришли к противоречию, должен иметь место
случай a = ft. б) Если a > ft и ft > с, то a —ft и Ъ — с положительны. Следовательно,
согласно N2 число (а - Ъ) + (Ь — с) = a - с положительно, и а > с. ¦
ТЕОРЕМА 3.11. Пусть а,Ь,сис!- целые числа. Тогда
а) (а > ft) Л (с > d) -» а + с > Ь + d;
б) (а > 0) Л (с > d) —> ac> ad;
в) (а > Ь > 0) Л (с> d > 0) -¦ ас> bd;
г) (а > Ъ > 0) Л (с > d > 0) -> ас > bd.
ДОКАЗАТЕЛЬСТВО, а) Если а > 6 и с > d, то числа a-b и c-d положительны.
Следовательно, (а-6) + (c-d) положительно. Но (a-6) + (c-d) = (a+c)-F+d), и
поэтому a -he > c + d. б) Если с > d, то разность с — d положительна. Поскольку
а положительно, а(с — d) = ас — ad также положительно, и ас > ad. в) Если
а > b > 0 и с > d > 0, то ас > be и 6с > bd. Поэтому ас > bd. г) Доказательство
этой части предоставляется читателю. ¦
Далее иллюстрируется применение доказательства перебором. Выбор из
трех возможностей обычно имеет вид
Р
р -> (г V s V t)
г —> q
s->q
ТЕОРЕМА 3.12. Пусть п — целое число. Тогда п2 > 0.
ДОКАЗАТЕЛЬСТВО. Поскольку п — целое число, согласно аксиоме трихотомии
оно либо положительно, либо отрицательно, либо равно 0. Если п положительно,
топ-п положительно по аксиоме N2, и п2 > 0. Если п отрицательно, то п = -т
для некоторого положительного целого числа т. Поэтому п2 = (—га)(—т) = га2
опять является положительным, и п2 > 0. Если п — 0, то п2 = 0, так что п2 > 0.
Следовательно, п2 > 0. ¦
¦ УПРАЖНЕНИЯ
1. Пусть a, b и с — целые числа. Докажите, что
а) если b + a = с + а, то Ь = с;
б) a • 0 = 0 для любого целого числа а;
в) —(—а) = а для любого целого числа а;
г) а.(-6) = -(а6);
д) (-а) • (-6) = а • 6;
е) _(а + Ь) = (-а) + (-Ь).

РАЗДЕЛ 3.3. Математическая индукция 129
2. Докажите, что если a + b = а, то Ь = 0.
3. Докажите, что если a > Ь > 0 и с > d > 0, то ас > bd.
4. Докажите, что а2 > а для любого целого числа а.
5. Докажите неравенство а2 4- Ь2 > 2ab для целых чисел а и Ь.
3.3. МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ
Одна из наиболее сложных проблем теории чисел состоит в доказательстве ис-
истинности утверждений для всех положительных целых чисел. Если утверждение
истинно для первых десяти положительных чисел или даже для первых десяти
биллионов положительных чисел, то из этого еще не следует, что утверждение
истинно для всех положительных целых чисел. Обычно легко доказать, что утвер-
утверждение не является истинным для всех положительных целых чисел. В самом
деле, используя тот факт, что отрицание (Ух)Р(х) есть (Зх)~Р(х), необходимо
найти только одно положительное целое число, для которого утверждение Р(х)
не является истинным. Эта процедура известна как нахождение контрпримера.
Инструментом для доказательства истинности утверждений относительно всех
положительных чисел является принцип индукции, который будет нашей послед-
последней аксиомой для множества положительных чисел N. Это вовсе не означает, что
доказательство любого утверждения относительно положительных чисел требует
индукции. Многие теоремы могут быть доказаны на основе других теорем и акси-
аксиом. Тем не менее, в основе доказательств многих рассматриваемых ниже теорем
лежит принцип индукции. В дальнейшем принцип индукции будет сформулиро-
сформулирован в другой, эквивалентной форме.
(N4) (Принцип математической индукции) Пусть Р(п) есть такое утверждение,
что
а) РA) истинно, и
б) для каждого А;, если Р(к) истинно, то Р{к + 1) истинно.
Тогда Р(п) истинно для любого целого положительного числа п.
В символической записи принцип математической индукции имеет вид
(РA) Л ((Vfc) Р(к) - Р{к + 1)) - (Vn) P(n).
Математическую индукцию можно сравнить с бесконечным рядом костяшек до-
домино. Свойство выстроенных в ряд домино состоит в том, что если опрокинуть
одну костяшку, падает следующая. Пусть утверждение Р(п) состоит в том, что па-
падает n-я костяшка. Опрокидывание первой костяшки домино обозначим РA), т.е.
истинность РA) состоит в том, что первая костяшка падает. Поскольку каждая
костяшка опрокидывает следующую, то из истинности Р(к) следует истинность
Р(к + 1). Поскольку падают все костяшки, Р{п) истинно для каждого поло-
положительного целого числа п. В дальнейшем, проводя доказательство при помощи
описанного выше принципа математической индукции, мы будем просто говорить,
что доказываем утверждение по индукции.

130 ГЛАВА 3. Логика, целые числа и доказательства
ПРИМЕР 3.13. Допустим, необходимо найти формулу для вычисления суммы пер-
первых п положительных целых чисел, l + 2-f Зн \-п. Такая формула была бы по-
полезна, если надо было бы, например, найти сумму первых 100000 положительных
целых чисел, не выполняя для этого 99 999 операций сложения. Предположим,
у нас имеются основания полагать, что сумма первых п положительных чисел
равна n\n+li. Докажем это утверждение по индукции.
Пусть Sn есть утверждение
1 + 2 + 3 + ... + п=^±И. A)
Сначала покажем, что S\ истинно. При п = 1 левая часть равенства 1-1-2Н-ЗЧ \-п
равна 1. Справа получаем
п(п 4-1) _ 1A + 1)
2 ~ 2 '
так что Si истинно. Затем предполагаем, что для любого положительного числа к
Sk истинно, т.е. равенство A) истинно для п = к. Это означает, что
Теперь необходимо доказать, что S^+i истинно, т.е. равенство Sn истинно для
п = к + 1. Другими словами, требуется доказать, что
Используя предположение
и сравнивая это равенство с предыдущим, мы замечаем, что, добавив к + 1 к
обеим частям последнего равенства, получим левую часть искомого равенства:
« о , Цк + 1)
1 + 2 + 3 + • • • + к = -Ц—*•;
Итак, доказано равенство
которое означает, что соотношение A) справедливо для п = к +1. Этот результат
обеспечивает истинность S/c+ь Следовательно, в силу аксиомы N4, Sn истинно
для любого положительного целого числа п. ?

РАЗДЕЛ 3.3. Математическая индукция 131
ПРИМЕР 3.14. Требуется доказать, что
l2 + 22 + 3* + ... + n2 = n(n + 1)ftBn + 1). B)
О
Пусть 5П обозначает утверждение, что равенство в уравнении B) выполня-
выполняется. Сначала покажем, что утверждение Sn истинно для и = 1. Подставляя 1 в
обе части равенства, получаем
л2_ 1A
что дает нам 1 = 1 и обеспечивает истинность утверждения Sn при п — 1.
Затем мы предполагаем, что равенство Sn истинно для п = к. То есть,
Теперь требуется доказать, что равенство Sn истинно для и = fc + 1. Иначе говоря,
требуется доказать, что
_ (к + 1){к + 2){2к + 3)
6
Используя предположение
6
замечаем, что, прибавив к обеим частям последнего равенства (fc-4-lJ, мы полу-
получим левую часть искомого равенства. Таким образом,
к(к + 1)Bк + 1) 6(fc
+
+ 6
l)+6(fc +

132 ГЛАВА 3. Логика, целые числа и доказательства
Итак, доказано равенство
которое означает, что равенство Sn выполняется для п = к + 1. Следовательно,
Sn истинно для каждого положительного целого числа п. D
ПРИМЕР 3.15. Требуется показать, что для любого положительного целого чис-
числа п, число п3 — п делится на 3. (Заметим, что положительное целое число t
делится на 3 при условии, что существует положительное целое число га такое,
что t = 3m.) Доказательство будет проведено индукцией. Пусть Sn — утвер-
утверждение "п3 - п делится на 3". Покажем, что Si истинно. Для и — 1 имеем
п3 — п = 13 — 1 = 1 — 1 = 0, поэтому п3 — и при п — 1 делится на 3, т.к. 0 = 3-0.
Таким образом, S\ истинно.
Теперь покажем, что для любого положительного числа к, если Sk истинно,
то Sfc+i истинно. Допустим, что Sk истинно. Иначе говоря, к3 — к делится 3,
поэтому к3 — к = Зга для некоторого положительного целого числа га. Требуется
доказать, что Sfc+i истинно. Последнее означает, что (fc-hlK — (fc-fl) делится на
3, т.е. существует положительное целое число w такое, что (fc-flK — (к + 1) = 3w.
Обратим внимание на положительное целое число (к + IK - (к + 1). В данном
случае стратегия состоит в том, чтобы преобразовать (к + IK - (к + 1) таким
образом, чтобы была возможность использовать наши знания о к (а именно, что
к3 - fc = 3m). Итак,
{к + IK - (fc + 1) = (fc3 + 3fc2 + 3fc + 1) - (fc + 1) =
= (fc3 _ к) + (ЗА:2 + 3fc) =
= 3 • га + 3(fc2 + к) =
где w = ra-f (к2+к). Таким образом, (fc+lK-(fc+l) делится на 3, и, следовательно,
истинно. Поэтому, по индукции, Sn истинно для всех п. ?
ПРИМЕР 3.16. Требуется показать, что плоскость, разделенная на области любым
числом различных прямых линий, может быть раскрашена черной и белой краской
таким образом, что любые две области, имеющие общую границу, будут окрашены
в различные цвета, как изображено на рис. 3.4.
Рис. 3.4. Закрашенные области

РАЗДЕЛ 3.3. Математическая индукция 133
Поскольку в формулировке задачи спрашивается о всех возможных случа-
случаях расположения областей и линий, это приводит к бесконечно большому числу
возможностей. Принцип индукции является наиболее подходящим для решения
задач указанного типа. У нас имеется выбор: либо показать, что любые га та-
таких областей может быть раскрашено указанным образом, либо показать, что
любое число областей, образованных при помощи га прямых линий, может быть
раскрашено нужным образом. В любом из этих случаев покажем, что чертеж
может быть раскрашен нужным образом. В первом случае скажем, что доказа-
доказательство индукцией проводится по числу областей. Во втором случае мы скажем,
что доказательство индукцией проводится по числу прямых линий. Далее будем
использовать число линий, имеющихся на чертеже.
Пусть Р(т) — утверждение, что чертеж, выполненный с использованием га
линий, может быть раскрашен требуемым образом (т.е. при помощи черного и
белого цветов, и при этом никакие соседние области, имеющие общий участок
границы, не будут окрашены в один и тот же цвет).
Выбираем
М = {т : Р(га) истинно} =
= {га : чертеж, выполненный га линиями, может быть раскрашен}.
Таким образом, если М = N, то чертеж, образованный любым числом линий,
может быть требуемым образом раскрашен. М С N по определению,
(а) Покажем, что 1 Е М. Это равносильно тому, что РA) истинно, т.е. чертеж,
сделанный при помощи только одной линии, может быть раскрашен. Из геометрии
известно, что линия, проведенная в плоскости, делит ее на две области. Окрасим
одну из них в черный цвет, а другую — в белый, как показано на рис. 3.5. Таким
образом, показано, что 1 Е М.
Рис. 3.5. Раскрашено в соответствии с
наличием одной линии в плоскости
(б) Покажем, из га Е М следует га + 1 Е М. Предположим, что га — поло-
положительное целое число из М. Это означает, что Р(т) истинно, и любой чертеж,
выполненный при помощи га линий, может быть нужным образом раскрашен. Рас-
Рассмотрим положительное целое число га + 1. Необходимо показать, что Р(т + 1)
истинно, или, что эквивалентно, чертеж, выполненный с использованием га 4-1
линии, может быть нужным образом раскрашен. Для этого можно использовать
"индуктивную гипотезу", а именно: предположение о том, что любой чертеж, вы-
выполненный с использованием га линий, может быть нужным образом раскрашен.

134 ГЛАВА 3. Логика, целые числа и доказательства
Рис. 3.6. Множество линий
Рассмотрим чертеж, выполненный с использованием т+1 линии, как изображено
на рис. 3.6.
Теперь нам нужно создать ситуацию, в которой мы сможем использовать тот
факт, что т Е М, или что любой чертеж, выполненный с использованием га ли-
линий, может быть раскрашен нужным образом. Для этого выберем одну из линий,
например, линию L, и удалим ее. Полученный в результате чертеж содержит
только т линий, поэтому в силу индуктивного предположения, что любой чер-
чертеж, состоящий из т линий, может быть требуемым образом раскрашен, можно
нужным образом раскрасить чертеж на рис. 3.7.
Рис. 3.7. Раскрашено в соответствии с наличием т линий
Теперь вернем линию L на прежнее место и изменим цвет каждой области с
одной стороны линии L на противоположный (черные области станут белыми, а
белые — черными), как показано на рис. 3.8. Этот чертеж раскрашен требуемым
образом, т.к. каждые две соседние области, которые находились по ту сторону от
L, где цвета были изменены, имели различные цвета по разные стороны линии,
поэтому если цвета были изменены на противоположные, то цвета по разные
стороны любой такой границы остались различными. Изменения вносят только
те границы, которые находятся вдоль линии L, но если L делила область, то

РАЗДЕЛ 3.3. Математическая индукция 135
цвет был изменен по обе стороны от L, делая цвета различными по обе стороны
от такой границы. Таким образом, этот чертеж, выполненный с использованием
га 4-1 линии, может быть требуемым образом раскрашен. Полученный результат
означает, что Р(т + 1) истинно, т.е. га + 1 G М.
Рис. 3.8. Раскрашено в соответствии с наличием т + 1 линии
Итак, мы доказали части (а) и (б) принципа индукции. Таким образом,
М = N. В таких случаях, как правило, говорят, что индукцией установлено ра-
равенство М и N. Таким образом, чертеж, выполненный с использованием любого
(конечного) числа линий, может быть раскрашен требуемым образом. ?
Существует два других эквивалентных определения принципа математиче-
математической индукции. Они эквивалентны исходному определению в том смысле, что
любая из трех форм может быть использована для доказательства двух дру-
других. Рассмотрим множество А = {3,7,8}. Целое число 3 обладает в отношении
множества А уникальным свойством, а именно: число 3 принадлежит А и оно
меньше или равно каждому элементу множества А. При этом говорят, что 3 —
наименьшее целое число множества А. Не каждое множество целых чисел име-
имеет наименьшее целое число. Пустое множество 0 не имеет наименьшего целого
числа, поскольку оно пусто и не содержит целых чисел вообще. Множество
С = {п: п е Z и п = 5/с для некоторого целого числа к} =
= {...,-15,-10,-5,0,5,10,15,20,...}
не имеет наименьшего целого числа, т.к., если т — наименьшее целое число
множества С, то т = 5 • к для некоторого целого числа fc. Но целое число
s = 5(fc — 1) также принадлежит С и, естественно, s — Ъ{к — 1) < 5 • к — т, так
что s < га, и это противоречит предположению о том, что га — наименьшее целое
число множества С.
ОПРЕДЕЛЕНИЕ 3.17. Пусть А — множество целых чисел. Целое число а есть
наименьшее целое число множества А тогда и только тогда, когда
а) а принадлежит А, и
б) если 6 принадлежит А, то а < Ь.

136 ГЛАВА 3. Логика, целые числа и доказательства
ТЕОРЕМА 3.18. Если множество целых чисел имеет наименьшее целое число, то
такое число единственно.
ДОКАЗАТЕЛЬСТВО. Допустим, что числа а и b оба являются наименьшими эле-
элементами множества А. По определению наименьшего элемента a < Ъ и Ъ < а.
Следовательно, a = Ъ. Ш
Теперь сформулируем два утверждения, эквивалентные принципу индукции.
(N5) (Принцип полного упорядочения) Каждое непустое множество положи-
положительных целых чисел содержит наименьший элемент.
(N6) (Второй принцип индукции) Пусть Р{п) — утверждение. Если
а) РA) истинно, и
б) для произвольного к из истинности Р(т) для всех т < к следует
истинность Р(к),
то Р(п) истинно для всех положительных целых чисел п.
В символической форме принцип индукции имеет вид
(РA) Л ((Vfc)(Vm < к)Р(т)) -+ Р(к)) -> (Vn) P(n).
Пример использования второго принципа индукции N6 будет приведен ниже при
доказательстве того, что каждое целое число представляет собой произведение
простых чисел. Следующая теорема — пример утверждения, которое может по-
показаться слишком очевидным для проведения его доказательства, но поскольку
рассматриваемая модель целых чисел определена совокупностью правил, для на-
наших "целых чисел" эти утверждения могут не оказаться столь очевидными или
даже истинными. Мы можем установить это, доказывая соответствующую тео-
теорему с использованием имеющихся правил. Доказательство является хорошим
примером использования принципа полного упорядочения N5. Оно является так-
также примером использования принципа сведения к абсурду.
ТЕОРЕМА 3.19. Не существует такого положительного целого а, что 0 < а < 1.
ДОКАЗАТЕЛЬСТВО. Предположим, что такое число существует, и пусть 5 —
множество всех положительных целых чисел между 0 и 1. Поскольку 5 непу-
непусто, по аксиоме N5 множество 5 имеет наименьшее положительное целое число,
скажем, а. Умножая неравенство 0 < a < 1 на а, получаем 0 < а2 < а. Те-
Теперь, поскольку а < 1, имеем а2 < 1. Но это противоречит тому факту, что a —
наименьшее положительное целое число, которое меньше 1. Следовательно, 5 —
пустое множество, и не существует положительное целое число между 0 и 1. ¦
СЛЕДСТВИЕ 3.20. Если Ъ — целое число, то не существует целое число а, обла-
обладающее свойством Ъ < a < Ъ 4-1.
Аксиомы N4 и N6 сформулированы для целых чисел, начиная с 1, с про-
продолжением условий на целые числа, большие 1. Аналогичные теоремы индукции
верны для целых чисел, не меньших некоторого целого j, которое может не сов-
совпадать с 1. Следующая теорема служит обоснованием индукции по подмножеству
целых, не обязательно положительных, чисел.

РАЗДЕЛ 3.3. Математическая индукция 137
ТЕОРЕМА 3.21. (Принцип индукции для целых чисел) Пусть Р(п) — выска-
высказывание, обладающее свойствами
а) P(j) истинно и
б) для произвольного fc > j, если P(k) истинно, то P(fc 4-1) истинно.
Тогда Р{п) истинно для каждого п> j.
ДОКАЗАТЕЛЬСТВО. Доказательство следует из аксиомы N4. Для этого доста-
достаточно положить n — t — j 4-1. ¦
Далее в примере доказывается утверждение, включающее неравенство. Ча-
Часто в такой ситуации приходится использовать следующее свойство, сформулиро-
сформулированное в теореме 3.11:
(а > Ь > 0) Л (с> d > 0) -> ac> bd.
ПРИМЕР 3.22. Используя принцип индукции для целых чисел, нужно доказать,
что для любого целого числа п > 4 имеет место неравенство п! > 2П. При ис-
использовании индукции по п, в данном случае нельзя начинать сп = 1, поскольку
утверждение для п = 1 неверно. Начальной точкой должно быть п = 4, т.к.
утверждение неверно также для п = 2 и п = 3. Согласно обозначениям, введен-
введенным для принципа индукции для целых чисел, имеем: j = 4, Р(п) — утверждение
"п! > 2П". Сначала докажем утверждение для п = 4. При п = 4 имеем 4! = 24 и
24 = 16, так что 4! > 24.
По индуктивному предположению имеем fc! > 2k. Нам нужно доказать, что
(fc4-l)! > 2/с+1. Заметим, что желаемый результат можно получить, если умножить
левую часть неравенства на (fc + 1), а правую — на 2. Поэтому, если мы покажем,
что (fc 4- 1) > 2, то получим fc! > 2k и (fc 4-1) > 2 и сможем сделать вывод, что
(fc 4-1)! > 2/c+1. Поскольку fc > 4, то fc > 2. Следовательно, (fc 4-1) • fc! > 2 • 2k и
(fc 4-1)! > 2fc+1. Таким образом, n! > 2n для каждого п > 4. ?
¦ УПРАЖНЕНИЯ
1. Докажите, что 1 + 4 4- 7 + 10 н + Cn - 2) = ~ .
о гт 1111 1 U
2. Докажите, что —- + —- 4- 7—= + тг^ Н +
3-55-77-9 Bп-1)Bп
3. Докажите, что 1 4- 2 4- 22 4- 23 4- • • • 4- 2п~1 = 2п - 1.
1 — гп
4. Докажите, что 1 + г4-г24-г34----4- гп~1 = .
1 - г
5. Докажите, что 1 4- 3 4- 5 4- 7 + • • • 4- Bп - 1) = п2.
6. Докажите, что У]г = — —.
г = 1 4
п n(n + l)(n + 2)
Y1 г(г + *) ^
3
7. Докажите, что Y1 г(г +
г=1
8. Для положительного целого числа п определим ап как а1 = а и afc+1 = ак -а.
Докажите, что am+n = aman.
9. Используя математическую индукцию, докажите, что (ab)k = akbk.

138 ГЛАВА 3. Логика, целые числа и доказательства
10. Используя математическую индукцию, докажите, что п2 > 2п-Ы для п > 3.
11. Используя математическую индукцию, докажите, что 2П > п2 для п > 5.
12. Найдите наибольшее множество положительных целых чисел, для которых
2П > п\ истинно. Докажите истинность утверждения.
13. Докажите, что каждое целое число п > 8 может быть записано как п =
ЗА: + 5га для некоторых неотрицательных целых чисел кит.
14. Докажите, что для каждого положительного целого числа п > 2
4П Bп)!
п + 1 (п!J '
15. Докажите, что для любого целого числа а и положительных целых чисел т
и п имеет место равенство amn = (am)n.
16. Используя математическую индукцию, докажите, что п\ > п3 для всех п > 6.
17. Используя математическую индукцию, докажите, что
18. Докажите, что если W — непустое подмножество множества Z и существует
целое число х такое, что х < w для всех к; из W% то W имеет наименьший
элемент.
19. Найдите ошибку в доказательстве того, что все лошади имеют одну и ту же
масть.
ДОКАЗАТЕЛЬСТВО. Для доказательства утверждения покажем, что любые
п лошадей имеют одну и ту же масть. При п = 1 имеется одна лошадь,
которая, естественно, имеет такую же масть, как она сама. Для п = к пред-
предположим, что любые данные к лошадей имеют одинаковую масть. Предполо-
Предположим, что в загон помещена к 4- 1-я лошадь. Выведем из загона одну лошадь.
Теперь в загоне к лошадей, поэтому они имеют одну и ту же масть. Вернем
выведенную лошадь в загон и выведем другую лошадь. Опять в загоне к
лошадей, поэтому все они имеют одну масть. Итак, все лошади имеют ту же
масть, что и те лошади, которые были выведены. Поэтому все fc + 1 лошадей
имеют одну и ту же масть. Таким образом, все лошади имеют одну и ту же
масть. ¦
20. Определим U?=i ^ следующим образом: [j]=l Ai = A\ и \Jl=l -A» =
() л+1. Определим f]7=iAi как П!=Иг = А1 и flj^1 A{ =
(l)ki=iAi)
Докажите, что
а) (\JAl)nA=\J(AinA)] б) (
\г=1 / г=1 \г=1
21. Используя приведенные выше определения, докажите, что
а) (г\Аг)пА= (SiAnA); б) (Г) Аг) = \J A[.
\г=1 / г=1 \г=1 / г=1
22. Докажите, что из первого принципа индукции вытекает принцип полного
упорядочения.

РАЗДЕЛ 3.4. Делимость 139
23. Докажите, что из принципа полного упорядочения вытекает второй принцип
индукции.
24. Докажите, что из второго принципа индукции вытекает первый принцип
индукции.
25. Метод "бесконечного спуска" используется иногда для доказательства то-
того, что никакое положительное целое число не может обладать некоторым
заданным свойством. Метод заключается в следующем. Предположим, что
существует положительное целое число, скажем, а\% обладающее каким-то
свойством. Теперь образуем второе положительное целое число, скажем, а2,
тоже обладающее этим свойством, но такое, что п2 < а\. Аналогично, обра-
образуем положительное целое число аз, обладающее нашим свойством, и такое,
что аз < а2, и так далее. Таким образом, получаем "бесконечно убывающую"
последовательность а\ > а2 > аз > • • • положительных чисел. Очевидно,
что такая последовательность не может существовать. Эта последователь-
последовательность возникла из предположения о том, что существует положительное це-
целое число, которое меньше произвольного фиксированного числа и обладает
заданным свойством. Таким образом, наше предположение ошибочно. До-
Докажите следующее утверждение, которое подтверждает приведенное выше
рассуждение. Предположим, что
а) Т — подмножество N.
б) Если п Е Т, то существует га Е N такое, что га < п и га Е Т.
Тогда Т = 0.
26. Используя метод бесконечного спуска, докажите, что не существуют по-
положительные целые числа р и q такие, что р2 = Зд2, путем нахождения
положительного числа р' < р такого, что для некоторого положительного
числа qr имеем (р1J = 3(о'J. Можно считать известным тот факт, что, если
а и b — положительные целые числа такие, что б2 = 3 • а, то существует
положительное целое число fc, обладающее свойством Ь — 3 • к.
3.4. ДЕЛИМОСТЬ
Многие целые числа можно представить как произведение меньших чисел. Важ-
Важные характеристики и отношения целых чисел могут быть получены на основе
анализа их структуры с точки зрения составляющих множителей.
ОПРЕДЕЛЕНИЕ 3.23. Целое число а есть кратное числа Ь, если а = Ът для
некоторого целого числа га. Ненулевое целое число b делит целое число а,
что обозначается как Ъ \ а, если а есть кратное Ь. Целое число 6, которое делит
целое число а, называется делителем числа а.
По определению, 9 | 27, поскольку 27 = 9 • 3, но 5 не делит 12, т.к. не
существует целого числа га такого, что 12 = 5 • га. Целые числа 1,2,3,4,6 и 12,
и только они, являются положительными делителями числа 12. Целые числа — 1,
-2, -3, -4, -6 и -12 также являются делителями числа 12.

140 ГЛАВА 3. Логика, целые числа и доказательства
ТЕОРЕМА 3.24. Пусть а, 6 и с — целые числа. Тогда
а) а | а для любого а.
б) Для любых а, 6исиза|ЬиЬ|с следует а | с.
в) Для любых а, 6 и с имеем: Ъ \ а и 6 | с тогда и только тогда, когда
Ь | (m-o + n-c) для всех целых чисел тип.
ДОКАЗАТЕЛЬСТВО.
а) a = a • 1.
б) Если а | 6 и 6 | с, то6 = а-7тгис = 6-п. Следовательно, c = b-n = (a-m)-n =
а • (ш • п) и а | с.
в) Допустим, что 6 | а и 6 | с. Тогда a = b-pnc = b-q для некоторых целых
чисел р и q. Следовательно, т • a -f n • с = т • F • р) + п • F • q) = b • (m • р + n • g)
и Ь | (m • a -f n • с). Обратно, предположим, что Ъ \ (т • а + п • с) для всех
целых чисел тип. Тогда, если m = 1 п = 0, имеем b | а. Если т = 0 и
п = 1, имеем 6 | с.
¦
ТЕОРЕМА 3.25. Если а и b — положительные целые числа и а | 6, то а < 6.
ДОКАЗАТЕЛЬСТВО. Доказательство следует из пункта (г) теоремы 3.11. ¦
СЛЕДСТВИЕ 3.26. Если для положительных целых чисел аи b имеем а \ b и b \ а,
то а = Ъ.
ТЕОРЕМА 3.27. Для целых чисел а и Ь, если а \Ь и b \ а, то а = b или а = —Ь.
ДОКАЗАТЕЛЬСТВО. Если а > 0 и Ь > 0, то в силу следствия 3.26 имеем а = Ъ.
Если а < 0 и Ь > 0, то —а > 0 и (—а) | 6, и 6 | (—а), так что b = —а или а = —Ь.
Справедливость утверждения теоремы в случае а > 0 и b < 0 является следствием
симметрии. Доказательство случая а < 0 и b < 0 предоставляется читателю. ¦
Из приведенных выше теорем следует, что для положительных целых чисел
отношение "делит" рефлексивно, антисимметрично и транзитивно, поэтому оно
является частичным порядком на множестве положительных целых чисел. Обра-
Обратите внимание, что отношение делимости не является отношением частичного
порядка на множестве целых чисел, т.к. "делит" не является на множестве целых
чисел антисимметричным отношением.
Следующая теорема объясняет действие, которое встречается в элементар-
элементарной арифметике. Положительное целое число а можно разделить на положитель-
положительное целое число b и получить остаток г, который меньше, чем Ь. Например, если
31 делить на 9, получим частное 3 и остаток 4. К примеру, 31 = 3-94-4, где 4 < 9.
Доказательство следующей теоремы также является иллюстрацией принци-
принципа полного упорядочения.
ТЕОРЕМА 3.28. (Алгоритм деления) Для положительных целых чисел а и b
существуют единственные неотрицательные целые числа q и г, где 0 < г < b
такие, что а = bq -f г. Такие целые числа г и q называются, соответственно,
остатком и частным от деления а на Ь.

РАЗДЕЛ 3.4. Делимость 141
ДОКАЗАТЕЛЬСТВО. Пусть а и Ь — положительные целые числа. Рассмотрим
множество 5 всех неотрицательных целых чисел, имеющих вид a—bq' для неотри-
неотрицательного целого числа q', т.е.
5 = {х : х = а - bq', х > 0, и q' > 0} .
Множество 5 непусто, поскольку для q1 — 0 имеем a—bq' = a—b-0 = а > 0, так что
а Е 5. Множество 5 имеет наименьший элемент, скажем, г', В самом деле, если
0 Е 5, он и является наименьшим элементом. В противном случае S содержит
только положительные целые числа и, следовательно, согласно принципу полного
упорядочения N5 имеет наименьший элемент. Поскольку г' принадлежит 5, пусть
q' — неотрицательное целое число такое, что г' = а — bq'.
Если г' > Ь, то г" = г' - Ъ > 0 и
а — bq' = г',
а - bq' - Ъ = г' - 6,
a-b(q' + l)=r",
так что г" принадлежит 5. Кроме того, г" < г', так как
6>0,
-6<0,
г' - ь < г' + 0 = г'.
Но г" < г' и то, что г" G 5, противоречит предположению, что г' является
наименьшим элементом множества 5. Таким образом, 0 < г' < Ь.
Чтобы показать единственность, предположим, что а = bq + г = Ьр + 5, где
0 < г < s < Ь. Поскольку г > 0, то -г < 0. Следовательно, s-r<b-bO = 6.
Но s - г = b(q - р), и по теореме 3.25, если q - р не равно 0, то 5 - г > Ь.
Следовательно, q — р = 0, q = р и г = s. Ш
Если а < Ь, то q должно быть равно 0, чтобы выполнялось а = bq + r, где
0<г<Ьи<7>0. Например, для а = 4 и b = 7 алгоритм деления дает q = 0 и
г = а = 4, так что 4 = 7-0 + 4.
В силу единственности q и г, если можно получить q и г каким-нибудь
другим способом, причем а = bq + r, 0<г<Ьид>0, то эти q и г должны
совпадать с теми, которые существуют согласно теореме.
Поскольку любой положительный делитель положительного целого числа п
не может быть больше самого этого числа, все положительные делители числа п
можно найти, перебирая все целые числа от 1 до п и проверяя, не делят ли они п.
Так, например, мы определили, что положительными делителями числа 12 явля-
являются числа 1, 2, 3, 4, 6 и 12. Точно так же можно показать, что положительными
делителями числа 90 являются 1, 2, 3, 5, 6, 9,10, 15, 18, 30, 45 и 90.
Проверка показывает, что числа 1, 2, 3 и 6 являются делителями как 12,
так и 90. Числа 1, 2, 3 и 6 называются общими делителями чисел 12 и 90.
Более того, 6 есть наибольший из этих общих делителей. Обратим внимание,
что общие делители 1, 2, 3 и 6 являются также делителями наибольшего общего
делителя 6. В контексте наибольших общих делителей рассматриваются только
положительные делители.

142 ГЛАВА 3. Логика, целые числа и доказательства
ОПРЕДЕЛЕНИЕ 3.29. Положительное целое число d называется общим дели-
делителем чисел а и Ь, если d \ a и d \ b.
ОПРЕДЕЛЕНИЕ 3.30. Положительное целое число d называют наибольшим
общим делителем целых чисел а и 6, если
а) d | а и d | 6, и
б) из с | а и с | Ь следует с | d.
Наибольший общий делитель чисел а и Ъ обозначается через НОД(а, Ъ).
Алгоритм нахождения наибольшего общего делителя приведен в главе 7.
ТЕОРЕМА 3.31. Если d и с — наибольшие общие делители целых чисел а и 6, то
с = d\ другими словами, существует единственный общий делитель для целых
положительных чисел а и 6.
ДОКАЗАТЕЛЬСТВО. По определению наибольшего общего делителя d \ с и с \ d.
Следовательно, с — d или с = — d. Поскольку end — оба положительные, то
c = d. Ш
ТЕОРЕМА 3.32. Наибольший общий делитель положительных целых чисел а и b
существует. Такой наибольший общий делитель может быть записан в виде
и • a -f v • Ь
для некоторых целых чисел и и v. Кроме того, наибольший общий делитель —
это наименьшее положительное целое число такого вида.
ДОКАЗАТЕЛЬСТВО. Пусть 5 — множество всех положительных целых чисел,
имеющих форму па + mb. Пусть d = иа + vb — наименьший элемент множества
5. Тогда d < а, т.к. а = 1 • а 4- 0 • 6 принадлежит 5. Кроме того, а = qd -f r
для некоторых q и г, где д>0и0<г<А Итак, а = q(ua + vb) -f г. Решая
относительно г, получаем, г = A - gn)a + (—v)gb, так что г принадлежит S
или г = 0. Но г меньше, чем d, которое, в свою очередь, является наименьшим
элементом множества S, так что г — 0. Поэтому d | а. Аналогично, d | 6. Если с —
произвольный делитель чисел а и 6, то по теореме 3.24 часть (в) с \ d, поскольку
d = иа + vb. Следовательно, d — наибольший общий делитель чисел а и Ь. Ш
Алгоритм нахождения и и v приведен в главе 7.
Свойства наибольшего общего делителя, которые сформулированы в следу-
следующей теореме, будут использованы в дальнейшем.
ТЕОРЕМА 3.33. Если а = bq + с, то НОД(а,Ь) = НОДF, с); другими словами,
каждый делитель а и b является делителем бис, и обратно.
ДОКАЗАТЕЛЬСТВО. Пусть е = НОД(а,6) и / = НОД(Ь,с). Поскольку е \ а и
е | 6, то по теореме 3.24(в) имеем е | с, т.к. с = а - bq. Тогда, по определению
наибольшего общего делителя е | /.
Обратно, поскольку / | b и / | с, то по теореме 3.24(в) / | а. По определению
наибольшего общего делителя / | е. Следовательно, е = f. Ш

РАЗДЕЛ ЗА. Делимость 143
ТЕОРЕМА 3.34. Если а, Ъ и с — целые числа, НОД(а, Ъ) = 1 и а | 6с, то а | с.
ДОКАЗАТЕЛЬСТВО. Поскольку НОД(а, 6) = 1, то существуют целые числа и и v
такие, что аи + bv = 1. Умножим каждое слагаемое на с, получая саи + cbv = с.
Тогда а \ саи и а \ cbv, т.к. а \ be. Следовательно, а \ с. Ш
ОПРЕДЕЛЕНИЕ 3.35. Если наибольший общий делитель а и 6 есть 1, то числа
а и b называются взаимно простыми.
Непосредственно из определения следует, что если а и b — взаимно простые
числа, то существуют целые числа и и v такие, что аи 4- bv — 1.
Заметим, что если а и b — положительные целые числа, то ab кратно и а, и 6.
Если рассматривать множество всех чисел, кратных а и 6, то согласно принципу
полного упорядочения существует наименьшее кратное чисел а и Ь. Если с —
наименьшее кратное чисел а и 6, a d — другое кратное чисел а и Ь, то с \ d. Иначе
говоря, существуют q и г такие, что d = qc + г, где г < с. Поскольку и а, и 6
делят числа d и с, они также делят г. Но тогда г было бы кратным а и Ь, которое
меньше, чем с, что приводит к противоречию. Таким образом, мы приходим к
следующим определениям.
ОПРЕДЕЛЕНИЕ 3.36. Положительное целое число т называется общим
кратным целых чисел а и Ь, если а | т и b \ т.
ОПРЕДЕЛЕНИЕ 3.37. Положительное целое число m называется наименьшим
общим кратным целых чисел а и 6, если
а) а | т и b \ m, и
б) если а | п и Ъ \ п, то га | п.
Наименьшее общее кратное чисел а и 6 будем обозначать НОК(а, 6).
Использование наибольшего общего делителя оказывается полезным при на-
нахождении решений уравнений вида ах-{-by = с или для доказательства, что такие
решения не существуют. Это вытекает из приведенной ниже теоремы.
Алгоритм для нахождения х и у приведен в главе 7.
ТЕОРЕМА 3.38. Уравнение ах + by = с, где а,Ьис- целые числа, имеет цело-
целочисленное решение (т.е. существуют целые числа х и у такие, что ах + by = с)
тогда и только тогда, когда с делится на НОД(а, 6). Если с делится на НОД(а, 6),
то решение ах -\-Ъу = с имеет вид
и • с v • с
Х° = НОД(а,6) Уо = НОД(а,Ь) '
где и и v — любые решения уравнения НОД(а, b) = cm Ч- 6г>.

144 ГЛАВА 3. Логика, целые числа и доказательства
ДОКАЗАТЕЛЬСТВО. Известно, что существуют целые числа и и v такие, что
аи 4- bv = НОД(а, Ь). Если с делится на НОД(а, Ь), то с = е • НОД(а, 6) для
некоторого целого числа е. Следовательно, аие + bve = е • НОД(а, 6) = с, так что
х = и-е и у = v-e — решения уравнения. Обратно, если существуют х и у такие,
что ах + by = с, то, поскольку НОД(а, 6) делит как а, так и 6, он делит ах Н- by
и, следовательно, делит с. ¦
¦ УПРАЖНЕНИЯ
1. Найдите положительные делители каждого из следующих целых чисел:
а) 54; б) 63; в) 72; г) 73; д) 74.
2. Для положительных целых чисел а и b найдите неотрицательные целые
числа q и г, где 0 < г < b таковы, что а = bq + г.
а) а = 54, 6 = 27; б) а = 47, Ь = 47; в) а = 93, Ь = 17;
г) а = 43, 6 = 8; д) а = 33, Ь = 1.
3. Для положительных целых чисел а и b найдите НОД(а, Ь), НОК(а,Ь) и
НОД(а,Ь) • НОК(а, 6), если они определены.
а) а = 54, Ъ = 27; б) а = 17, 6 = 0; в) а = 6, 6 = 15;
г) а = 12, Ь = 16; д) а = 33, 6 = 1.
4. Докажите или опровергните утверждение: для положительных целых чисел
а и Ъ НОД(а,6) < НОК(а,Ь).
5. Если а = 0 или 6 = 0, то что можно было бы принять в качестве НОК(а,6)?
Ответ обоснуйте.
6. Докажите, что для взаимно простых чисел а и b и заданного целого числа
и существуют целые числа х и у такие, что ах + by = п.
7. Докажите, что для положительных целых чисел а и 6, если а > 6, то
НОД(а,6) = НОД(а-6,Ь).
8. Рассмотрим теорему: если целые числа а и b таковы, что а \ b и b \ а, то
а = b или а = -Ь. Докажите, что эта теорема также справедлива в случае,
когда а < 0 и b < 0.
3.5. ПРОСТЫЕ ЧИСЛА
Очевидно, что каждое целое число а делится само на себя и на 1, т.к. а = 1 • а.
Каждое целое число делит 0, но 0 не делит никакое целое число. Для некоторых
задач теории чисел необходимо знать, имеет ли некоторое конкретное целое число
делители, отличные от него самого и 1. Некоторые целые числа не могут быть
разложены в произведение целых чисел, исключая тривиальный способ. Такие
целые числа называются простыми.
ОПРЕДЕЛЕНИЕ 3.39. Целое число, большее 1, называется простым, если оно
не имеет положительных делителей, кроме 1 и самого себя. Положительное
целое число, большее 1, называется составным, если оно не является простым.

РАЗДЕЛ 3.5. Простые числа 145
Среди первых 10 положительных целых чисел имеется четыре простых чис-
числа: 2, 3, 5 и 7. Целые числа 4 = 2-2, 6 = 2-3, 8 = 2-4, 9 = 3-3и 10 = 2-5
являются составными. Итак, если п = г • s, где 1 < г < п и 1 < 5 < п, топ —
составное число. По определению, целое число 1 не является ни простым, ни
составным. Число 2 — единственное четное простое число. Определить, является
ли небольшое целое число простым, пытаясь разделить его на меньшие простые
числа, сравнительно легко, т.к. количество возможных вариантов невелико. Од-
Однако, вопрос о том, является ли простым большое целое число, может оказаться
достаточно сложным.
Следующая теорема показывает, что существует бесконечно много простых
чисел. Доказательство теоремы является классическим примером использования
принципа сведения к абсурду.
ТЕОРЕМА 3.40. (Евклид) Существует бесконечно много простых чисел.
ДОКАЗАТЕЛЬСТВО. Допустим, что существует только конечное число простых
чисел, например, pi, pi, • • •, Рк- Рассмотрим целое число (р\Р2 • • 'Рк) + 1. Пред-
Предположим, что рг — некоторое простое число, и рТ | ((р\Р2 • • -Рк) + 1)- Но тогда
Pr I (piP2- 'Рк), откуда следует, что рт | 1, а это приводит к противоречию, т.к.
рг > 1. Следовательно, (р\Р2'—Рк) + 1 — простое число, что, в свою очередь,
также является противоречием, т.к. этого числа нет среди указанной конечной
совокупности простых чисел. Таким образом, наше предположение о том, что су-
существует конечное число простых чисел, ложно, поэтому простых чисел должно
быть бесконечно много. ¦
Поскольку разложение целых чисел на простые множители является важной
задачей, необходимо иметь быстрый и простой способ определения, является ли
данное положительное целое число простым или составным. Следующая теоре-
теорема показывает, что для проверки простоты числа необходимо определить только
некоторые из его возможных делителей.
ТЕОРЕМА 3.41. Если положительное целое число п является составным, то п
имеет простой делитель р такой, что р2 < п.
ДОКАЗАТЕЛЬСТВО. Пусть р — наименьший простой делитель числа п. Если п
раскладывается на множители г и s, то р < г и р < s. Следовательно, р2 <rs = п.
Например, чтобы определить, является ли п = 521 простым, необходимо
рассмотреть только простые числа, которые меньше или равны 22, потому что
222 = 484, а 232 = 529. Простые числа, меньшие или равные 22, — это 2, 3, 5, 7,
11, 13, 17 и 19. Проверяя каждое из них, находим, что ни одно из них не делит
521. Поэтому 521 является простым числом в силу предыдущей теоремы.
Как покажет следующая теорема, простые числа образуют множество своего
рода строительных блоков для целых чисел.
ТЕОРЕМА 3.42. Каждое положительное целое число либо равно 1, либо простое,
либо может быть записано как произведение простых чисел.

146 ГЛАВА 3. Логика, целые числа и доказательства
ДОКАЗАТЕЛЬСТВО. В доказательстве этой теоремы использован второй прин-
принцип индукции. Несомненно, теорема справедлива для га = 1. Допустим, что она
справедлива для всех положительных целых чисел га, меньших, чем /с. Если к —
простое, то теорема справедлива также и для к. Если к не является простым, то
оно делится на некоторое простое число р и к = pq, где и р, и q не могут быть
равными к или 1. Поскольку согласно теореме 3.25 числа р и q меньше, чем fc, то
по индуктивному предположению они либо простые, либо могут быть записаны
как произведение простых чисел. Следовательно, к = pq может быть записано
как произведение простых чисел. ¦
Целое число 37 — простое. Целое число 1554985071 = 3 • 3 • 4463 • 38713 —
произведение четырех простых чисел, два из которых совпадают.
Следующая теорема показывает, что если некоторое целое число п делится
на простое число р, то невозможно разложить п на множители таким образом,
чтобы р не был делителем по крайней мере одного из этих множителей.
ТЕОРЕМА 3.43. Если р — простое число и р \ ab, где а и Ъ — положительные
целые числа, то р \ а или р \ Ь.
ДОКАЗАТЕЛЬСТВО. Если р | а, то утверждение теоремы имеет место. С другой
стороны, предположим, что р не делит а. Поскольку р и а — взаимно простые,
то существуют u,v такие, что ри + av = 1. Поэтому pub + avb = 6. В силу того,
что р | pub и р | abv (т.к. р \ ab), имеем р\Ь. Ш
ЛЕММА 3.44. Если простое число р делит произведение положительных целых
чисел q\q2 • • • qn> то р делит qi для некоторого г, 1 < г < гг.
ДОКАЗАТЕЛЬСТВО. В доказательстве леммы использована индукция по п, чис-
числу множителей в произведении. Если п = 1, правильность леммы очевидна. До-
Допустим, что лемма верна для п = к. Это означает, что если р делит произведение
любых к целых чисел, то р делит один из к множителей. Предположим, что
р делит произведение к + 1 целых чисел, скажем, р \ q\q2 • • -фсфс+ь так что
Р I (<7i<72 • • -qk)qk+\- Если р делит <?fc+i, то доказательство завершено. Если р не
делит qk+1, то по теореме 3.43 имеем р \ (q\ • • • qk). Но поскольку q\ • • • qk — произ-
произведение к целых чисел, то по индуктивному предположению р \ qi для некоторого
1 < i < к. Следовательно, р \ qi для некоторого г, 1 < г < fc + 1. ¦
ЛЕММА 3.45. Если простое число р делит произведение простых чисел gb q2,
... t qnt то р = qi для некоторого г, 1 < г < п.
ДОКАЗАТЕЛЬСТВО. Согласно лемме 3.44, р делит qi для некоторого 1 < г < п.
Поскольку числа р и ^ — простые, то р = qi. Ш
Из совокупности теорем, приведенных выше, получаем главный результат
этой главы, который известен как основная теорема арифметики, или теорема о
единственности разложения на простые множители.
ТЕОРЕМА 3.46. (Основная теорема арифметики) Любое положительное целое
число, большее, чем 1, либо является простым, либо может быть записано в виде
произведения простых чисел, причем это произведение единственно с точностью
до порядка сомножителей.

РАЗДЕЛ 3.5. Простые числа 147
ДОКАЗАТЕЛЬСТВО. Допустим, что q\q2 • • • qn и р\Р2 • • -р8 — два способа записи
положительного целого числа т как произведения простых чисел. В доказатель-
доказательстве теоремы будет использована индукция по п, числу простых сомножителей в
первом произведении. Если п = 1, теорема тривиально верна. Сформулируем ин-
индуктивное предположение: пусть теорема верна, когда qiq2"-qk = Р\Р2'"Рз\
т.е., если т = q\q2---qk = P\P2-'Ps, то к = s и произведение единствен-
единственно с точностью до порядка простых сомножителей. Предположим теперь, что
т = QiQ2 --qk+\ = PiP2'-Psf- Поскольку qk+i делит piP2-"Ps', отсюда сле-
следует, что <7fc+i = pi для некоторого 1 < г < s'. Разделим оба произведения
на qk+\ или используем свойство сокращения (аксиому 18). Тогда q\q2--qk =
Р\Р2 '' -Pt-iPi+i * • 'Psf- Но по индукции к = s' — 1, и произведение единственно
с точностью до порядка простых сомножителей. Следовательно, к + 1 = s', и
разложение на множители числа га единственно с точностью до порядка простых
сомножителей. ¦
Например,
п = 39616304 =
= 2 • 13 • 7 • 2 • 23 • 13 • 2 • 13 • 2 • 7 =
= 2 • 2 • 2 • 2 • 7 • 7 • 13 • 13 • 13 • 23
представляют собой два разложения на множители числа п; однако, в каждом из
произведений одно и то же простое число использовано одинаковое число раз.
Различается только порядок записи простых чисел. Фактически имеется 12,600
различных способов разложения на множители числа п с использованием 10
простых сомножителей, однако, каждое такое разложение содержит ровно четыре
двойки, две семерки, три множителя, равных 13, и один, равный 23. Обычно
простые множители группируют, используя экспоненциальную запись. Например,
п = 2472133231.
СЛЕДСТВИЕ 3.47. Каждое положительное целое число, большее 1, может быть
записано единственным образом с точностью до порядка в виде qx q2 * * • qn ,
где fc(l), fcB), ... и fc(n) — положительные целые числа.
Теперь понятно, почему 1 не входит во множество простых чисел. В против-
противном случае теорема о единственности разложения на простые множители была бы
неверна. При изучении разложения различных целых чисел, используя их пред-
представление, данное в предыдущем следствии, зачастую для удобства обозначения
допускается нулевая степень простого сомножителя. Обычно такая практика не
приводит к путанице, т.к. при q® = 1 всегда qi > 1. Если разложение на простые
множители известно, то простые числа, формирующие разложение на простые
множители любого делителя этого числа, образуют подмножество соответствую-
соответствующего множества для делимого.
Доказательство двух следующих теорем предоставляется читателю.
ТЕОРЕМА 3.48. Если a = р?A) • • -рак{к) и Ъ \ а, то Ь = p\W • • -pbk{k\ где 0 < b(i) <
a(i) для всех г; и обратно.

148 ГЛАВА 3. Логика, целые числа и доказательства
ТЕОРЕМА 3.49. Пусть а = rf^^-P?4 и Ъ = P*A)pf Vf> • • -Р%к).
где pi — простые числа, которые делят либо а, либо Ь, и некоторые показатели
степени могут быть равны 0. Пусть га(г) = тт(а(г),Ь(г)) и М(г) = тах(а(г),Ь(г))
для 1 < г < к. Тогда
НОК(а, 6) = РГA)р2МB)РзМC) • • -Pf(fc)-
Применим теорему 3.49 в случае, когда a = 195000 и 6= 10435750. Разло-
Разложения на простые множители чисел а и Ъ имеют вид
a = 233154131 и Ь = г^З^Э1.
Таким образом,
НОДA95000,10435750) = 2minC'1KminA'0MminD'3I3minA'3I9min@'1) =
= 213°5313119° = г^З1 = 3250,
НОКA95000,10435750) = 2maxC'1KmaxA'0MmaxD>3I3maxA>3I9max@»1) =
= 233154133191 = 626145000.
Следующая теорема вытекает из теоремы 3.49. Доказательство предостав-
предоставляется читателю.
ТЕОРЕМА 3.50. Если а и b — положительные целые, то НОД(а, 6)-НОК(а, 6) = ab.
¦ УПРАЖНЕНИЯ
1. Разложите каждое из следующих целых чисел на простые множители.
а) 728
б) 1599 (используйте равенство 1599 = 1600 - 1)
в) 4899 г) 131 д) 523
2. Используйте теоремы данной главы для нахождения НОД и НОК следующих
пар чисел:
а) 162 и 12 б) 71 и 23 в) 72 и 30
г) п! и (п + 2)! д) 75 и 99
3. Два простых числа а и Ъ называются числами-близнецами, если разность
между ними равна 2, т.е. если а+ 2 = 6. Например, 3 и 5 являются числами-
близнецами. Найдите три другие пары чисел-близнецов.
4. Является ли среднее арифметическое двух простых чисел-близнецов про-
простым числом?
5. Если а и Ь — простые числа, следует ли отсюда, что а2 + Ь2 — простое число?
6. Объясните, почему для любого положительного целого числа п все числа
п! + 1, п! + 2, п! 4- 3, п! + 4, ... ,п\ + п являются составными. Что данный
факт говорит о расстоянии между простыми числами?

РАЗДЕЛ 3.6. Сравнения 149
7. Покажите, что числа 479001603 и 479001607 не являются простыми, исполь-
используя предыдущее упражнение и калькулятор.
8. Если рь р2> рз, • • • > Рп — первые п последовательных простых чисел, то
следует ли отсюда, что р\ -рч -рз • • • • 'Рп +1 (произведение первых п простых
чисел плюс единица) есть простое число. Обоснуйте свой ответ.
9. Покажите, что не существует троек последовательных нечетных чисел, каж-
каждое из которых является простым, за исключением тройки C,5,7).
10. Докажите, что если р и q — простые числа, большие или равные 5, то р + q
или р — q делится на 3 и, следовательно, р2 — q2 делится на 24. (Указание:
р + 2 или р — 2 делится на 3 и q — 2 или q 4- 2 делится на 3.)
11. Докажите, что если а = р\^ • • -ра^ и Ь | а, то b = р\^ • • -р^к\ где 0 <
Ь{г) < а{г) для всех г, и обратно.
12. Пусть а = pfW2V™ ¦ ¦ -rffc> и Ь = р^р^А™ • • -pf \ где ft - про-
стые числа, которые делят или а, или 6, и некоторые показатели степени
могут быть равны 0. Пусть т(г) = min(a(z),b(z)) и М(г) = тах(а(г),6(г))
для 1 < г < к. Затем докажите, что
HOK(a,b) =
3.6. СРАВНЕНИЯ
В примере 2.52 изучалось отношение Rs на множестве целых чисел, определен-
определенное как Дз = {(а>Ь) : а — Ь = 5 • /с}. Отношение эквивалентности, порожденное
таким разбиением, называется "сравнением по модулю 5". Фактически такие раз-
разбиения можно построить для любого положительного целого числа п, как это
было сделано для и = 5.
ОПРЕДЕЛЕНИЕ 3.51. Пусть п — положительное целое число. Целое число а
сравнимо с целым числом 6 по модулю п, что обозначается а = b (mod n),
если п делит (a- 6).
Следующая теорема доказывается по аналогии с примером 2.52.
ТЕОРЕМА 3.52. Отношение = для фиксированного п является отношением экви-
эквивалентности на множестве целых чисел. Это означает, что
а) а = a (mod n) для каждого целого числа а;
б) если a = b (mod n), то Ъ = a (mod n) для целых чисел а и 6;
в) если а = Ъ (mod n) и 6 = с (mod n), то а = с (mod n).
ОПРЕДЕЛЕНИЕ 3.53. Пусть п — положительное целое число. Множество всех
классов эквивалентности по модулю п обозначается Zn и называется множе-
множеством классов вычетов по модулю п.

150 ГЛАВА 3. Логика, целые числа и доказательства
Классы вычетов по модулю п представляют собой новые объекты. Они яв-
являются классами эквивалентности. Элементы каждого класса эквивалентности
сравнимы между собой по модулю п. Например, пусть п = 3. Имеется три класса
эквивалентности по модулю 3, так что множество
содержит три элемента. Элементы Z$ — классы эквивалентности и, следовательно,
множества. Эти три множества содержат 0, 1 и 2, соответственно, как свои имена.
В каждом из этих классов эквивалентности все элементы сравнимы между собой
по модулю 3, так что a = b (mod 3) тогда и только тогда, когда аи Ь принадлежат
одному и тому же классу эквивалентности — классу вычетов. Таким образом,
[0] = {...-6,-3,0,3,6,9...};
[1] = {...-8,-5,-2,1,4,7...};
[2] = {... -7, -4,-1,2, 5,8...}.
Теперь нам нужно определить операции между классами вычетов по мо-
модулю п. Отношение сравнимости =, как подсказывает само обозначение, имеет
много общего с отношением равенства. Но с отношением сравнимости по модулю
п связано больше ограничений, чем с аналогичным ему отношением равенства.
ТЕОРЕМА 3.54. Отношение сравнимости обладает следующими свойствами:
а) если a = b (mod п) и с = d (mod n), то a + c = b + d (mod и) и
ac = bd (mod n);
б) если a = b (mod ran), то a = b (mod га) и a = b (mod n).
ДОКАЗАТЕЛЬСТВО. Мы докажем пункт (а); часть (б) предлагаем доказать чи-
читателю. По определению, если a = b (mod n) и с = d (mod n), то a — b = un и
с — d = vn для некоторых целых чисел и к v. Таким образом,
(а 4- с) — (Ь 4- d) = (а — Ь) + (с — d) = и - п -f v • п = (и -f v) • п
для некоторых целых чисел и н v, иа-Ьс = &4-с? (mod п). Кроме того, а = Ь + ип
и с = d 4- vn, так что
ас — F 4- (un))(d 4- (vn)) =
= bd 4- b(vn) 4- d(un) 4- uvn2 =
= bd 4- (Ьг> 4- ltd 4- uvn) n .
Таким образом, ас — bd = (bv 4- ud 4- vun)n к ac = bd (mod n). ¦
ПРИМЕР 3.55. Пусть п = 3.
1 = 7 (mod 3),
2 = -4 (mod 3).
Из теоремы 3.54 (а) следует, что
14-2 = 7 +(-4) (mod3),
а также, что
A)B) = G)(-4) (mod3),
что верно, поскольку 2 - (-28) = 30 = 3-10 = 3-fc. ?

РАЗДЕЛ 3.6. Сравнения 151
ТЕОРЕМА 3.56. Для произвольного положительного целого числа п,
а) если г = r' (mod п), 0 < г < п и 0 < г' < п, то г = г';
б) если a — любое целое число и п — положительное целое число, то имеется
целое число г, где 0 < г < п такое, что a = r (mod п). Целое число г —
остаток от деления а на п, поэтому a = nq -f r.
ДОКАЗАТЕЛЬСТВО. Утверждения теоремы следуют непосредственно из алгорит-
алгоритма деления. ¦
Часть (а) утверждения теоремы гарантирует, что классы вычетов по моду-
модулю п обладают тем свойством, что классы вычетов, порожденные неотрицательны-
неотрицательными целыми числами, меньшими, чем п, различны. Таким образом, [0], [1], [2],...,
[п — 2], [п — 1] — различные множества относительно сравнимости по модулю п.
Часть (б) показывает, что каждое целое число а сравнимо по модулю п с
одним из целых чисел 0,1,2,... ,п — 1. Итак, любое целое число а принадлежит
одному из п различных классов эквивалентности [0], [1],..., [п — 1]. Проведенное
рассмотрение служит объяснением к следующей теореме.
ТЕОРЕМА 3.57. Пусть п — произвольное положительное целое число. Тогда Zn,
множество классов вычетов по модулю п, состоит точно из п различных классов
вычетов
представленных различными остатками, которые могут быть получены при деле-
делении на п. Кроме того, для 0 < г < п, класс вычетов [г] состоит точно из тех
целых чисел а, для которых a = r (mod n).
Следующая теорема является простым следствием предыдущих теорем, ко-
которое, тем не менее, часто оказывается полезным.
ТЕОРЕМА 3.58. Если a = nq + г и b = nq1 + г' для 0 < г < п и 0 < г' < п, то
г — г1 тогда и только тогда, когда a = b (mod n).
В целом, при работе с классами вычетов по модулю п желательно для его
представления выбрать в классе наименьшее неотрицательное целое число. Это
особенно важно для сложения и умножения классов вычетов в Zn, поскольку
необходимо, чтобы сумма и произведение все еще представлялись целыми числа-
числами, которые находятся между 0 и п— 1. Это приводит к следующему определению.
ОПРЕДЕЛЕНИЕ 3.59. Пусть Zn — множество классов вычетов по модулю п.
Для любого заданного целого числа т существует целое число г такое, что
0 < г < п - 1 и [т] = [г] или т = г (mod п). При этом говорят, что [[т]]п = г.
ПРИМЕР 3.60. Для п = 5 получаем

152 ГЛАВА 3. Логика, целые числа и доказательства
На множестве Zn можно определить операции сложения и умножения. Если
[а] — класс вычетов по модулю п, содержащий а, и [Ь] — класс вычетов по модулю
п, содержащий Ь, то сложение и умножение определим соотношениями
где сложение и умножение в центре и справа осуществляется между целыми
числами, а сложение и умножение по левую сторону выполняется между классами
эквивалентности.
Использование предыдущей теоремы показывает, что операции сложения и
умножения таких классов эквивалентности — классов вычетов — определены пра-
правильно; т.е. определение не зависит от представителей классов вычетов. Напри-
Например, если [а] = [с], то результат сложения не должен зависеть от того, используем
мы [а] или [с]. Иначе говоря, если [а] = [с] и [b] = [d], то [а] 0 [Ь] = [с] 0 [d] и
[а] О [6] = [с] ©И.
ПРИМЕР 3.61. Для п = 5 и Z5 = {[0], [1], [2], [3], [4]} находим, что
[2] е [4] = [2 + 4] = [6] = [1], поскольку 6 = 1 (mod 5);
[2] © [4] = [2 • 4] = [8] = [3], поскольку 8 = 3 (mod 5).
Вычисляя все возможные суммы и произведения, можно создать таблицы "сло-
"сложения" и "умножения" для классов вычетов по модулю 5.
[а] © [Ь]
[0]
[1]
[2]
[3]
[4]
[0]
[01
[1]
[2]
[31
[4]
[1]
[11
[2]
[3]
[4]
[0]
[2]
[21
[31
[4]
[0]
[1]
[3]
[31
[4]
[0]
[11
[2]
[4]
[41
[0]
[11
[21
[3]
[а] © [Ь]
[01
[1]
[2]
[3]
[4]
[0]
[01
[01
[01
[01
[01
[1]
[01
[11
[21
[31
[4]
[2]
[01
[21
[41
[11
[3]
[01
[31
[11
[41
[2]
[4]
[01
[41
[31
[21
[1]
?
Теорема 3.57 показывает, что для произвольного положительного целого чис-
числа п множество целых чисел может быть разбито на п непересекающихся мно-
множеств, или классов эквивалентности. В дальнейшем мы часто будем возвращаться
к этим множествам, интересуясь их представителями.

РАЗДЕЛ 3.6. Сравнения 153
ОПРЕДЕЛЕНИЕ 3.62. Если Ъ = г (mod n) для положительного целого числа п,
то говорят, что г есть вычет числа Ь по модулю п. Полная система вычетов
по модулю п есть множество 5 = {ri,r2,... , гп}, где пересечение множества 5
с каждым классом вычетов по модулю п содержит точно одно целое число, т.е.
S содержит одного и только одного представителя из каждого такого класса
вычетов. Полная система вычетов {0,1,2,..., (п — 1)} называется первичной
системой вычетов. Если Ь — целое число, Ъ = г (mod п)иО<г<п— 1,
то этот единственный первичный вычет по модулю п обозначается через г =
[[Ь)]п. Приведенная система вычетов по модулю п есть подмножество полной
системы вычетов, состоящее только из тех целых чисел, которые являются
взаимно простыми с п, т.е. {г : г е 5 и НОД(г, п) = 1}.
Полная система вычетов получается путем выбора одного целого числа из
каждого класса вычетов [0], [1],..., [п — 1] множества Zn. Итак, для п = 6,
{24,7,-58,40,113} — полная система вычетов по модулю 6, так как
24 = 0
7=1
-58 = 2
15 = 3
40 = 4
113 = 5
(mod
(mod
(mod
(mod
(mod
(mod
6),
6),
6),
6),
6),
6),
поэтому
поэтому
поэтому
поэтому
поэтому
поэтому
24
7
-58
15
40
113
е
€
€
И;
[1];
И;
И;
И];
[5].
Очевидно, что {0,1,2,3,4,5} является полней (и притом первичной) системой
вычетов по модулю 6. По определению, [[24]]в = 0 и [[-58]]6 = 2.
Поскольку все элементы любого класса вычетов по модулю п сравнимы один
с другим, но не являются таковыми по отношению к элементам другого класса
вычетов, каждое целое число сравнимо ровно с одним элементом полной системы
вычетов. Проведенные рассуждения приводят к следующей теореме.
ТЕОРЕМА 3.63. Если п — положительное целое число, {ri,r2,... ,гп} — полная
система вычетов по модулю п и а — некоторое целое число, то а = r^ (mod n)
для одного и только одного fc, 1 < к < п.
Элементы полной системы вычетов {24,7, —58,15,40,113} и первичной (пол-
(полной) системы вычетов {0,1,2,3,4,5} по модулю 6, которые являются взаимно
простыми с п = 6, содержат в себе, соответственно, множества {7,113} и {1,5}.
Поэтому оба последних множества являются приведенными системами вычетов
по модулю 6. При этом говорят, что {1,5} является первичной приведенной си-
системой вычетов по модулю 6.
Следующая теорема показывает, что приведенная система вычетов содержит
больше существенной информации о целых числах из Z, чем система чисел,
взаимно простых с п. Доказательство теоремы предоставляется читателю.
ТЕОРЕМА 3.64. Пусть п — положительное целое число и {п,г2,... ,г^} — при-
приведенная система вычетов по модулю п. Если а — целое число, взаимно простое
с п, то а = rj (mod n) для одного и только одного j, I < j < к.

154 ГЛАВА 3. Логика, целые числа и доказательства
Если дана одна система вычетов, имеется несколько способов воспроизве-
воспроизвести другие системы вычетов. Один из способов состоит в прибавлении одного и
того же целого числа к каждому вычету в полной системе вычетов. Иной способ
демонстрирует следующая теорема. Доказательство предоставляется читателю.
ТЕОРЕМА 3.65. Пусть и — положительное целое число и {гь г2,..., г*} — полная
[приведенная] система вычетов по модулю п. Если a — целое число, взаимно
простое с п, то {ari, ar2,..., ar^} — также полная [приведенная] система вычетов.
Поскольку НОДF,35) = 1, имея полную систему вычетов {0,1,2,3,4,5} и
приведенную систему вычетов {1,5} по модулю 6, получаем, что {35 • 0,35 • 1,35 •
2, 35-3,35-4,35-5} и {35-1,35-5} являются, соответственно, полной и приведенной
системами вычетов. Но
[[0JJ6
№
[[2]]б
№
= 0 и
= 1
= 2
= 3
= 4
= 5
[[35-
[[35-
[[35-
[[35-
[[35-
O]Je =
2]]е =
3]]е =
4]]е =
5]]б =
[[35]]6
[[70]]в
[[Ю7]]6
[[140]]6
[[175]]6
= 0
= 5
= 4
= 3
= 2
= 1
Таким образом, в результате умножения каждого элемента Т{ полной или приве-
приведенной системы вычетов по модулю п на целое число а, взаимно простое с п,
получаем представителей тех же классов вычетов, возможно, в другом порядке.
¦ УПРАЖНЕНИЯ
1. Вычислите
а) [[37]]4; б) [[93]]5; в) [[48]]23; г) [[149]]27;
2. Вычислите
а) [[33]]; б) [[47]]9; в) [[49]]17; г) [[146]]21;
3. Вычислите
а) [[8!]]6;
б) [[1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10]]3;
в) [[12 + 22 + 32 + ---252]]2;
г) [[A46J]]21.
4. Покажите, что а2 = Ь2 (mod п) не имеет следствием а = Ь (mod и).
5. Покажите, что если a — нечетное целое число, то a2 = I (mod 8).
6. Постройте таблицу сложения для классов вычетов по модулю 4.
7. Постройте таблицу умножения для классов вычетов по модулю 4.
8. Постройте таблицу сложения для классов вычетов по модулю 7.
9. Постройте таблицу умножения для классов вычетов по модулю 7.
10. Используя таблицы сложения и умножения для классов вычетов по модулю
5, приведенные ранее, найдите в Z5 решения следующих уравнений:
а) х + [3] = [5]; б) [3]-х = [2];
в) [4].* = [3]; г) [2] ¦* = [!].

РАЗДЕЛ 3.6. Сравнения 155
11. Используя таблицы сложения и умножения для классов вычетов по модулю
4 из приведенных выше упражнений, найдите в Z± решения следующих
уравнений:
а) х + [3] = [2]; б) [3].х = [2];
в) [2]-х = [2]; г) [2].* = [0].
12. Используя таблицы сложения и умножения для классов вычетов по модулю
7 из приведенных выше упражнений, найдите в Zr решения следующих
уравнений:
а) х + [5] = [2]; б) [3]-х = [4];
в) [2].х = [5]; г) [4]-* =[6].
13. Докажите, что если a = b (mod ran), то a = Ъ (mod га) и a = b (mod n).
14. Докажите, что если ас = be (mod n) и целые числа сип — взаимно простые,
то a = b (mod n).
15. Докажите теорему 3.64. Пусть п — положительное целое число, и {гх,Г2,
• • • ,^fc} — приведенная система вычетов по модулю п. Если a — целое число,
взаимно простое с п, то a = Vj (mod n) для одного и только одного j,
1 < j < fc.
16. Докажите теорему 3.65. Пусть п — положительное целое число, и {ri,r2,
. ..,гл} — полная [приведенная] система вычетов по модулю п. Если a —
целое число, взаимно простое с п, то {ari,ar2,... ,ark} — тоже полная [при-
[приведенная] система вычетов.

ГЛАВА
ФУНКЦИИ И МАТРИЦЫ
4.1. ФУНКЦИИ
Функция из множества А в множество В представляет собой специальное отно-
отношение на А х В, обладающее следующими свойствами:
1. Областью определения отношения является все множество А. Следователь-
Следовательно, для каждого элемента а из А существует элемент Ь из В такой, что а и
Ь связаны данным отношением.
2. Если а относится к b и а относится к У, то Ъ = У. В терминах упорядо-
упорядоченных пар это утверждение означает, что если (а, Ь) и (а, У) принадлежат
отношению, то Ь = У'. Дадим более формальное определение функции.
ОПРЕДЕЛЕНИЕ 4.1. Отношение / на А х В называется функцией из Л в В и
обозначается через f : А—> В, если для каждого а Е А существует единствен-
единственный элемент b е В такой, что (а,Ь) € /. Если / : А —> В — функция, и (а, 6) ?
/, то говорят, что b = /(а). Множество А называется областью определения
функции /, а множество В называется областью потенциальных значений.
Если Е С А, то множество f(E) = {b : /(a) = b для некоторого а из Е} назы-
называется образом множества Е. Образ всего множества А называется областью
значений функции /. Если F С В, то множество f~l(F) = {а : /(а) € F}
называется прообразом множества F. Функция f : А -> В называется также
отображением ; при этом говорят, что / отображает А б В. Если (а,Ь) € /,
так что Ь = /(а), то говорят, что элемент а отображается в элемент Ь.
ПРИМЕР 4.2. Пусть А = {-2, -1, 0, 1, 2}, а В = {0,1,2,3,4,5}. Определим
отношение / С А х В как / = {(-2,5), (-1,2), @,1), A,2), B,5)}. Отношение /
— функция из Л в В, так как / С А х В, и каждый из элементов А присутствует
в качестве первой компоненты упорядоченной пары из / ровно один раз. ?

РАЗДЕЛ 4.1. Функции 157
ПРИМЕР 4.3. Пусть А = {-2, -1, О, 1, 2} и В = {0,1,2,3,4,5}. Функция / :
А-> В определена соотношением f(x) = х2 + 1. Если Е = {1,2}, то
f(E) = {b : (a, b) Е / для некоторого а из Е} =
= {Ь: Ь = /(а) для некоторого а из Е} =
= {2,5}
является образом Е при отображении /. Если F = {0,2,3,4,5} С J9, то
f~1(F) = {b : существует а е А такое, что /(а) = 6} =
= {-1,1,-2,2}
является прообразом F, где -1 Е /"НЛ. т-к- /(-1) = 2, 1 € f~l(F), т.к. /A) =
2, -2 Е f~x(F)y т.к. Д-2) = 5 и 2 Е /"HF), т.к. /B) = 5. Заметим, что элементы
0, 3 и 4 не вносят никаких элементов в /~1(F), поскольку они не принадлежат
области значений функции /. Прообраз может быть пустым. Так, например, в
случае W = {0,3} прообраз f~l{W) пуст, поскольку не существует такого а е А,
для которого f(a) = 0 или /(а) = 3.
Область значений функции / имеет вид
= {Ь : /(а) = 6 для некоторого а е А} =
= {1,2,5}.
Элементами f(A) являются те и только те элементы области потенциальных зна-
значений Б, которые "используются" функцией /. ?
Мы уже отмечали, что если R — отношение на А х В, а 5 — отношение на
ВхС, то можно определить отношение SoR на Ах С, называемое композицией S
и R. Если R и S — функции, то 5 о R — тоже функция, называемая композицией
5 и R. Следующая теорема описывает некоторые полезные свойства композиций.
ТЕОРЕМА 4.4. Пусть д : А -> В и / : В -> С. Тогда
а) композиция / о р есть функция из Л в С, что может быть записано как
fog:A->C;
б) если а е А, то (/ о g)(a) = f(g(a)).
ДОКАЗАТЕЛЬСТВО, а) Если д : А-> В и f : В-+С, то д С А х В и f С В х С.
По определению композиции отношений / од С А х С. Пусть (а,с) е / од и
(а,с') € f °д. Требуется показать, что с = с'. Поскольку (а,с) € f од, существует
такой элемент 6 Е В, что (а, Ъ) Е # и F, с) Е /. Точно так же, поскольку (а, с') Е
/ о д, то существует такой элемент Ъ' Е Б, что (а, Ъ1) Ери (Ь7,^) Е /. Но
д является функцией, так что (a,b) E g и (а, 6') Е #, откуда следует равенство
b = Ъ1. Следовательно, (Ъ',с') = F, с') Е / и F, с) Е /. Поскольку / также является
функцией, то с = с'. Поэтому fog — функция из А в С.
б) Если д : А —> В и a G Л, тогда существует такое b из В, что b = g(a).
Поскольку 6 Е В f : В —> С, имеется некоторое се С, для которого F,с) Е /, т.е.
с = /F). Но Ь = д(а), так что f(g(a)) = f(b) = c=(fog)(a), поэтому (a,b) E д и
(Ь, с) Е /, откуда следует, что (а, с) Е / о д. Ш

158 ГЛАВА 4. Функции и матрицы
Поскольку композиция отношений обладает свойством ассоциативности (см.
теорему 2.31), то, в частности, имеет место следующая теорема.
ТЕОРЕМА 4.5. Пусть / : А -+ В, д : В -» С и h : С -> D. Тогда ho (go f) =
(hog) о /, т.е. композиция функций ассоциативна.
ПРИМЕР 4.6. Пусть f(x) = у/х и д(х) = х + 3 — функции, заданные на мно-
множестве действительных чисел. Функция f(g(x)) = f(x + 3) = у/х 4- 3. Функция
Функция / из А в В может быть классифицирована в зависимости от то-
того, существуют ли элементы из В, связанные данным отношением с более чем
одним элементом из А, и связан ли каждый элемент из области значений В с
соответствующим элементом области определения А.
ОПРЕДЕЛЕНИЕ 4.7. Функция f : А —> В называется инъективной, или инъ-
инъекцией, если из f(a) = f(a') следует a = a'. Функция / называется отображе-
отображением "на", или сюръективной функцией, или сюръекцией, если для каждого
6 Е В существует некоторое а ? А такое, что f(a) = b. Функция, которая
является одновременно и инъективной, и сюръективной, называется взаимно
однозначным соответствием, или биекцией. Если А = Ви/:А^>В яв-
является взаимно однозначным соответствием, то / называется перестановкой
множества А.
ПРИМЕР 4.8. Пусть А и В — множества действительных чисел и / : А —> В
определена таким образом: f(x) = Зх 4- 5. Функция / инъективна, т.к. если
f(a) = f(a'), тогда За + 5 = За' + 5 и, следовательно, а = а'. Функция / является
также сюръекцией. Для любого действительного числа Ь требуется найти такое
а, что f(a) = b = За 4- 5. Решая это уравнение относительно а, находим, что
если а = A/3)F - 5), тогда f(a) = Ъ. Поэтому / представляет собой взаимно
однозначное соответствие, а в силу А = В, f является также перестановкой. ?
ПРИМЕР 4.9. Пусть А и В — множество действительных чисел, и функция
/ : А —» В определена как f(x) = х2. Функция / не является инъективной,
т.к. /B) = /(—2), но 2 ф —2. Функция / не является также и сюръективной, по-
поскольку не существует такого действительного числа а, для которого f(a) = —1.
Заметим, что если А и В — множество неотрицательных действительных чисел,
тогда / является как инъективной, так и сюръективной. ?
Пусть / — функция из множества А во множество В, т.е. / : А —> В.
Очевидно, / С А х В, так как / является отношением на А х В. Обратное
отношение f~l С В х А определяется как f~l = {F,а) : (а,6) е /}. При этом
отношение f~l может не быть функцией из В в А, даже если / является функ-
функцией из А в В. В следующей теореме сформулированы условия, при которых f~l
является функцией. Если f~l действительно является функцией, то ее называют
обращением функции /, или ее обратной функцией.
ТЕОРЕМА 4.10. Если функция / : А —> В является биекцией, то обратное отноше-
отношение f~l является функцией из В в А, причем биекцией. Обратно, для / : А —> В,
если f~l — функция из В в А, то / является биекцией.

РАЗДЕЛ 4.1. Функции 159
ДОКАЗАТЕЛЬСТВО. Для доказательства того, что f~l — функция из В в А,
необходимо убедиться, что областью определения f~l является В, и что если
F, а) и F, а') ? Z, то а = о!. Для доказательства того, что область определения
f~l совпадает с В, возьмем произвольное b ? В. Поскольку / сюръективна, то
существует а Е А такое, что /(а) = Ъ или (а, Ь) ? /. Поэтому F, а) Е /~* и
В является областью определения 7. Пусть F, а) и F, а') ? /-1. Тогда (а, Ь) и
(а', 6) Е /. Поскольку / инъективна, то а = о!. Поэтому f~l — функция. При этом
она сюръективна, т.к. если а Е А, то в силу того, что / — функция, существует
некоторое Ь такое, что /(а) = Ь, т.е. (а, Ъ) Е /. Поэтому F, а) Е У, и элемент
а принадлежит области значений функции f~l. Следовательно, А представляет
собой область значений /-1, а сама функция f~l — сюръективна. Для доказа-
доказательства инъективности функции f~l предположим, что F, а) и F',а) Е Z, т.е.
f~x(b) = а и f~l(b') = а. Тогда (а, 6) Е / и (а, 6х) Е / (или, что эквивалентно,
/(а) = 6и /(а) = 6'). Поскольку / — функция, то b = b'. Для доказательства
обратного утверждения следует в последнем рассуждении f~l заменить на /. ¦
ТЕОРЕМА 4.11. Если / : А —> В — биекция, то
а) /(/~1(Ь)) = b для любого b из В;
б) /~1(/(а)) — а Для любого а из Л.
ДОКАЗАТЕЛЬСТВО. Пусть b E В и а = f'1^). Тогда /(а) = 6. Но поскольку
а = f~l(b), то f(f~l(b)) = f(a) = b. Аналогично доказывается, что /~1(/(а)) =: а
для любого а из А. Ш
ПРИМЕР 4.12. Требуется найти обратную функцию для у = Зх + 6. Обращая
функцию, получаем
{(у,ж) :у = 3х + 6}.
Но это то же самое, что
{(ж, у) : х = 3у + 6}.
Решая уравнение относительно у, получаем
?
ОПРЕДЕЛЕНИЕ 4.13. Пусть I: А-+ А определено соотношением 1(а) = а для
всех а Е А. Функция / называется тождественной функцией на А.
Предлагаем читателю доказать следующую теорему.
ТЕОРЕМА 4.14. Если / : А —+ А и / — тождественная функция на А, то / о / =
/ о / = /. Если для / существует обратная функция, то / о /-1 = f~l о / = /.
ТЕОРЕМА 4.15. Пусть р : А -> Б и / : Б -¦ С. Тогда
а) если g и f — сюръекции Л на Б и В на С соответственно, то / о g есть
сюръекция А на С. Другими словами, композиция двух сюръекции — сюръ-
екция;
б) если g и / — инъекции, то fog — также инъекция; иными словами, компо-
композиция двух инъекций — инъекция;

160 ГЛАВА 4. Функции и матрицы
в) если д и / — биекции, то fog — также биекция; иными словами, композиция
двух биекций — биекция;
г) (fogr^g-'of-K
¦ УПРАЖНЕНИЯ
1. Пусть / С R х i?, где R — множество действительных чисел. Найдите
область значений и область определения следующих функций:
a) Дх) = х2 + 4; б) Дх) =
в) /(*) = -Д==; г) /(*)=
Ь4'
д) /(*) = -Л*
2. Какие из приведенных ниже отношений являются функциями, если х и у —
действительные числа, х принадлежит области определения, а у —- области
значений?
в) у = 5; г) х = 7;
д) у = л/х2 - 2 .
3. Для функций /ид, заданных на множестве действительных чисел, найдите
f(g(x)) и g(f(x)), если:
а) Дх) = х2 4-1 и д(х) = х + 3;
б) Дх) = yjx2 +2 и #(х) = х2 + 3;
в) /0е) — "~ и р(х) = 2х -f 3.
х
4. Найдите обратную для каждой из следующих функций:
ч х + 4 _ з ч х~2
а) у = —77—-; б) у = х; в) у = —— .
Z X -г о
5. Выясните, какие из приведенных ниже функций, у которых область опре-
определения и область значений совпадают с действительной числовой осью,
являются инъективными, сюръективными, имеют обратную функцию.
а) Дх) = |х|;
б) дх) = х2 + 4;
в) Дх) = х3 + 6;
г) Дх) = х + |х|;
д) f(x) =x(x- 2)(х + 2).
6. Пусть / : А —> В, А\ и А2 — подмножества А, а В\ и ?2 — подмножества
В. Докажите, что
а) если А\ С Аг, то /(^i) Q /(^2);
б) если Bi С В'2, то f~1(B\) С /~1(B2)i
г) /"H^i U В2) = /"^i) u f~l(B2)\
Д) /(AinA2)C/(Ai)n/(A2);
е) /"H^i П В2) = f~l{B\) П f~l{B2)\

РАЗДЕЛ 4.2. Специальные функции 161
ж) Г1(В[) = (Г1(В1))>.
з) Приведите пример функции / и множеств А\ и А2 таких, что
f(A1nA2)^f(A1)Df(A2).
7. Пусть / : А —> В — биекция, а д : В —> А — функция, обладающая следую-
следующими свойствами:
(9 ° /)(а) = a Для всех а G Л;
(/ ° #)(^) = Ь для всех b e В .
Докажите, что д = Z. Заметим, что данное утверждение говорит о том, что
/-1 — функция из В в А, при этом /о/ = /Б и f~l о f = IAt где /^ и /б
являются тождественными функциями на А и В соответственно. {Указание:
используйте свойство ассоциативности композиции.)
8. Пусть / : А —> В. Докажите, что / инъективна тогда и только тогда, когда
для всех подмножеств X и Y множества А имеем f(X П У) = f(X) П f(Y).
9. Для функции / : А —» В докажите, что
а) / инъективна тогда и только тогда, когда (Z о f)(W) = W для любого
W С А, где f~l(K) обозначает прообраз множества К\
б) / сюръективна тогда и только тогда, когда (/ о /""^(V) = V для любого
VCB.
10. Пусть ^:А->Ви/:В->С. Докажите, что
а) если д и / — сюръекции, то / о д — сюръекция;
б) если д и / — инъекции, то / од — инъекция;
в) если д и / — биекции, то / о д — биекция;
г) (fogr^g-iof-K
11. Докажите, что если / : А —> А и I — тождественная функция на А, то
/о/ = /о/ = /. Если / имеет обратную функцию, то /о f~l = f~l о f = I.
4.2. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Перестановка была определена как функция, которая на множестве устанавли-
устанавливает взаимно однозначное соответствие. Если / — перестановка на множестве
{1,2,3,..., п}, она может быть представлена в виде
1 2 ... п
/A) /B) ... /(п)
Напомним, что нам известна еще одна специальная функция — тождественная
функция /, определенная соотношением 1(а) = а для всех а е А. Она может быть
представлена в виде
1 2 ... п
1 2 ... п
ПРИМЕР 4.16. Если А — {1,2,3} и функция / : А —¦ А определена соотношени-
соотношениями /A) = 3, /B) = 2и /C) = 1, то / может быть представлена как
1 2 3 \
3 2 1 )• ?

162 ГЛАВА 4. Функции и матрицы
Если д : А —> А определена соотношением дA) = 2, дB) — 3 и дC) — 1, то
д можно изобразить в виде
12 3
2 3 1
Композиции этих функций имеют вид
, /123\/123\ /123
*°9={з 2 1 )°{2 3 1 ) = {2 1 3
,/123\/123\ /123
9°f={2 3 1 )°{3 2 1 ) = { 1 3 2
В предыдущих примерах было показано, что перестановка
2 3
1 ~ ! "¦ 2 3
также является тождественной функцией в том смысле, что Iof = fol = f для
любой перестановки / на множестве А. Чтобы построить обратную перестановку,
нужно найти число, стоящее над 1, и поместить его под 1; затем найти число,
стоящее над 2, и поместить его под 2; наконец, найти число, стоящее над 3, и
поместить его под 3. Таким образом, обращение перестановки
1 2 3 \ /12 3
2 3 1 У еСТЬ V, 3 1 2
Введем еще три специальные функции.
ОПРЕДЕЛЕНИЕ 4.17. Функция / : А —» В, где А — множество действитель-
действительных чисел, а В — множество целых чисел, называется нижним округлением
и обозначается /(ж) = |_^_|, если она каждому a e А ставит в соответствие наи-
наибольшее целое число, меньшее или равное а. Функция / : F —» В называется
верхним округлением и обозначается /(х) = |"х], если она каждому a e A
ставит в соответствие наименьшее целое число, большее или равное а.
Например, [2.99J = 2, [4J = 4, [-4J = -4 и [-4.1J = -5. Точно также,
[2.99] = 3, [4] = 4, [-4"! = -4 и [-4.1] = -4.
ОПРЕДЕЛЕНИЕ 4.18. Пусть Аи В совпадают со множеством неотрицательных
целых чисел. Факториалом назовем функцию / : А —> В, обозначаемую через
/(п) = п! и определяемую следующими соотношениями:
О! = 1
1! = 1 =1-0!
2! = 1-2 =2=2-1!
3! = 1-2-3 =6 =3-2!
4! = 1-2-3-4 = 24 = 4-3!
к\ = 1-2-3-4 к = fc-(fc-l)!

РАЗДЕЛ 4.2. Специальные функции 163
П
' ?
Операции сложения, вычитания, умножения и деления также являются при-
примерами функций. В случае вычитания целых чисел 5 — 3 означает, что операция
вычитания ставит целое число, а именно, 2, в соответствие числам 5 и 3. Чтобы
подчеркнуть функциональную природу операции вычитания, можно было бы за-
записать — (E,3)) = 2. Вычитание каждой паре целых чисел (г, s) ставит в соответ-
соответствие целое число. Функция двух переменных такого частного вида называется
бинарной операцией и определяется следующим образом.
ПРИМЕР
ПРИМЕР
4.19.
4.20.
12!
10!
12-
7!
4!-3!
11 • 10!
10!
7-6-
4!-3
5-
•2
4!
•1
ОПРЕДЕЛЕНИЕ 4.21. Бинарной операцией на множестве А называется функ-
функция b : А х А —> А. Образ пары (г, s) при отображении 6 записывается как
b((r,s)), или как rbs.
Поскольку область значений бинарной операции на А по определению есть
подмножество А, то множество А обладает свойством замкнутости относительно
бинарной операции (в том смысле, что значение операция на двух элементах г и
s множества А также является элементом А).
Последовательности также являются частными видами функций, область
определения которых есть начальное подмножество множества положительных
или неотрицательных целых чисел. Полагаем, что читатель знаком с такими по-
последовательностями, как 1, 2, 4, 9, 16, ... или 2, 4, 6, 8, 10, ..., хотя, может быть,
никогда и не думал о них, как о функциях.
ОПРЕДЕЛЕНИЕ 4.22. Конечной последовательностью назовем функцию из
{1,2,3,4, ...,п} в некоторое множество 5. Бесконечной последовательно-
последовательностью назовем функцию из {1,2,3,4,...} в некоторое множество 5. Любая
конечная или бесконечная последовательность может быть названа просто
последовательностью.
В большинстве случаев 5 представляет собой множество положительных це-
целых, целых, рациональных или действительных чисел. Последовательность обыч-
обычно изображают списком или перечислением элементов. Если А — функция, то
значение АA) можно обозначить через А\, значение АB) — через А2 и так далее.
Поэтому, если А — конечная последовательность, она может быть представлена
как
или

164 ГЛАВА 4. Функции и матрицы
Если же А — бесконечная последовательность, она может быть представлена как
ИЛИ
Ai,A2,A3,... .
Например, последовательности 1,4,9,16,... соответствует запись А{ = г2. Здесь
А(\) = 1, АB) = 4, АC) = 9, АD) = 16 и т.д. Заметьте, что 1,4,9,16 и 1,9,4,16 -
это две разные последовательности.
ПРИМЕР 4.23. Пусть А(п) = п + 5. Запишем первые пять членов последователь-
последовательности: А{\) = 1 + 5 = 6, А{2) = 2 + 5 = 7, АC) = 3 + 5 = 8, А{4) = 4 + 5 = 9 и
ЛE) = 5 + 5 = 10. ?
ПРИМЕР 4.24. Пусть А(п) = п2 — 3. Запишем первые пять членов последователь-
последовательности: ЛA) = 12-3 = -2, А{2) = 22-3 = 1, АC) = 32-3 = 6, 4D) = 42-3 = 13
и 4E) = 52 - 3 = 22. П
ПРИМЕР 4.25. Заданы первые пять членов последовательности: 1,6,11,16,21.
Требуется описать ее как функцию. Поскольку каждый член последовательно-
последовательности больше предыдущего на 5, то А(п) = 1 + 5(п - 1), где 1 < п < 5. ?
ПРИМЕР 4.26. Заданы первые пять членов последовательности: 0,3,8,15,24, и
требуется описать ее как функцию. Поскольку первые пять членов последова-
последовательности В(п) = п2 совпадают с 1,4,9,16,25, эта последовательность может
быть задана формулой А(п) = п2 - 1. ?
ПРИМЕР 4.27. Заданы первые пять членов последовательности: 1,-2,3,-4,5.
Эта последовательность может быть описана формулой А(п) = (—1)п+1п. Если
бы знакопеременная последовательность начиналась с отрицательного числа, то
вместо (—l)n+1 мы бы подставили (—l)n . D
Два вида последовательностей — арифметическая прогрессия и геомет-
геометрическая прогрессия — представляют особый интерес. Каждый член арифметиче-
арифметической прогрессии может быть получен из предыдущего прибавлением константы с.
Таким образом, арифметическая прогрессия имеет вид а + (п — 1)с, где а — пер-
первый член прогрессии. Последовательность 3, 5, 7, 9, 11, ... представляет собой
арифметическую прогрессию с а = 3 и с = 2.
В геометрической прогрессии каждый член может быть получен из преды-
предыдущего путем умножения на константу г. Таким образом, геометрическая про-
прогрессия имеет вид А(п) — аАп~1\ где а — первый член прогрессии. Последова-
Последовательность 4, 12, 36, 108, 324, ... является геометрической прогрессией, в которой
а = 4 и г = 3. Последовательность 32, 16, 8, 4, 2, ... — геометрическая прогрес-
прогрессия, где а = 32 и г = ^.
ОПРЕДЕЛЕНИЕ 4.28. Сумма Аг + Аг+г + Аг+2 4- Д.+3 Н Ь Ar+k может быть
Т + к
записана с использованием знака суммирования как YL Ai-

РАЗДЕЛ 4.2. Специальные функции 165
Например, 7
г=3
г=4
4
5^г = 1 + 24-34-4;
г=1
3
]Г(г + 3) = A + 3) + B 4- 3) 4- C + 3).
г=1
п
Часто требуется найти сумму Yl Ai первых п членов последовательности А.
Выведем формулу суммы первых п членов арифметической прогрессии
5 = a + (а 4 с) + (а 4 2с) 4-... 4 (а + (п - 2)с) 4 (а 4 (п - 1)с).
Для этого запишем 5 в обратном порядке и сложим саму с собой, так что
5 = a 4 (а 4 с) 4 (а 4 2с) 4 Ь [а + (п - 1)с],
5 = [а 4 (п - 1)с] 4 [а 4 (п - 2)с] 4 [а 4 (п - 2)с] 4 • • • 4 а,
25 = [а 4 (а 4 (п - 1)с)] 4 [а 4 (а 4 (п - 1)с)] 4 [а 4 (а 4 (п - 1)с]L
4 • • • 4 [а 4 (а 4 (п - 1)с] =
= [2а 4 (п - 1)с] 4 [2а 4 (п - 1)с] 4 [2а + (п - 1)с] 4 • • • 4 [2а 4 (п - 1)с].
Таким образом, имеем
2S = nBa4(n- l)c),
так что
5 = -Ba4(n-l)c)).
Поскольку А\ = а и An = a 4 (п — 1)с), то
ПРИМЕР 4.29. 5 = 3 4 5 4 7 4 9 4 11 4 13 = -C 4 13) = 48. ?
Теперь выведем формулу для вычисления суммы геометрической прогрессии
5 = а 4 аг 4 аг2 4 аг3 4 аг4 4 ... 4 агп~2 4 агп~1.
Заметим, что rS = ar 4 аг2 4 аг3 4 аг4 4 аг54 4 ... 4 агп~1 4 агп. Вычитая 5 из
rS, получаем rS - S = агп - а, так что
а{гп - 1)
~ г- 1
ПРИМЕР 4.30. 2 4 6 418 4 54 4162 = 2^_ ^ = 2^ ^ = 243, так как здесь
a = 2, г = 3ип = 5. ?

166 ГЛАВА 4. Функции и матрицы
¦ УПРАЖНЕНИЯ
1. В приведенных ниже упражнениях для перестановок fug найдите переста-
перестановки /
«О / =
НОВКИ fog, до f, f 'hj *.
г) / =
12 3
2 3 1
12 3 4
2 14 3
12 3 4
4 2 13
12 3 4
3 2 14
9 =
9 =
9 =
12 3
3 1 2
12 3 4
4 3 2 1
12 3 4
3 2 4 1
12 3 4
12 3 4
2. Вычислите значения следующих выражений:
, 10! .. 12!
Е) ~8\' б) 8!~4Г
г) -L-2.999J; д) [1-001J;
ж) [-4.01].
3. Вычислите значения следующих выражений:
. 14! 15!
а) -.о, л,; б)
п\
е) Г3.51;
5!-4!-6!'
д) L-1-001J;
в) L^J;
е) Г-3.71;
13!-О!'
г) - [2.999J;
ж) [4.01].
4. Найдите первые пять членов следующих последовательностей:
п!'
(п + 3)!
а) Ап = п3 + 3;
б)
.>*
.-[=!=
г)
5. Найдите первые пять членов следующих последовательностей:
п , п п! '
'1'
в) Ап =
г)
п
6. Определите по первым пяти членам последовательности А формулу для Ап.
а) 3, 8, 13, 18, 23; б) \, -§, \, -|, |;
в) 4, 12, 36, 78, 144; г) 2, 2, 4, 12, 48.
7. Определите по первым пяти членам последовательности А формулу для Ап.
а) 2, 8, 18, 32, 50; б) I, -I, I, -I, ^
в) 1, -1, 2, -2, 3; г) 3, 6, И, 18, 27.

РАЗДЕЛ 4.3. Матрицы 167
4.3. МАТРИЦЫ
До сих пор мы рассматривали лишь "функции одной переменной". Они, как пра-
правило, обозначаются через /(х), где х — так называемая "переменная". Например,
/(х) = х2 с областью определения R есть функция одной переменной. Если об-
область определения / представляет собой декартово произведение двух множеств,
скажем, С х D, то функцию / : С х D —> В называют "функцией двух пере-
переменных" и обычно обозначают через /(х,у), где х и у называются переменными,
причем значение х берется из области С, а значение у — из области D. Если
(с, d) е С х D, то пишут f((c,d)) или просто f(c,d). Например, /(х, у) — х2 +у2
с областью определения Дхй- это функция двух переменных. Бинарные опе-
операции также являются функциями двух переменных. Точно так же, если область
определения / — множество CxDx?,a/:CxDx?->B, то/ называется
"функцией трех переменных". Например, /(х,у, z) = x2 4- у2 +2yz с областью
определения R x R x R есть функция трех переменных.
Дадим описание специальной функции двух переменных, называемой мат-
матрицей или массивом. Информация в компьютере обычно хранится в виде матриц.
ОПРЕДЕЛЕНИЕ 4.31. Для положительных целых чисел тип матрицей
т х п, или массивом т х п, называется функция
где D — это, как правило, множество действительных, комплексных, рацио-
рациональных или целых чисел. Элементы D называются скалярами. Таким обра-
образом, для каждого г, 1 < г < га, и каждого j, 1 < j < n, имеется элемент
A(i, j) из Z), который находится в г-ой строке и в j-ом столбце соответствую-
соответствующей прямоугольной таблицы. Образ A(i,j) элемента (i,j) области определения
сокращенно обозначается через Aij. Таким образом, п х т матрица А изобра-
изображается прямоугольной таблицей, где образы (г, j) Е {1,2,... ,т} х {1,2,... ,п}
при отображении А могут быть перечислены следующим образом:
In А12 А13 ••• Aln
I21 A22 Л23 • * • A2n
A =
где первая строка таблицы состоит из A\j для j = 1 до п, вторая строка состоит
из A2j для j = 1 до и и т.д. При этом говорят, что А содержит т строк и п
столбцов и является матрицей размера тхп. Иногда заЬисывают сокращенно
А = [А^] или даже А = [а^\. Значение А^ называется компонентой, или
элементом матрицы А.
Матрица размера 1 х т называется матрицей-строкой, а матрица размера
nxl называется матрицей-столбцом. Если в матрице число строк и чис-
число столбцов совпадает, она называется квадратной матрицей. Если А —
матрица-строка, индекс строки обычно опускают и пишут

168 ГЛАВА 4. Функции и матрицы
А=[Ап А12 ¦¦¦ Aim] = [Ai A2 •¦¦ Ат].
Точно так же, если А — матрица-столбец, то мы опускаем индекс столбца:
А =
Г Аи
А21
А2
Ап
2 17
Например, А = | , ~ fi | — это матрица 2 х 3, а В =
-2 5 7
-3 9 0
25 2 9
представляет собой квадратную матрицу 3x3. По определению, А\з = 7, А21 = 4,
??12 = 5 и Вз1 = 25. Матрица С = Q o есть квадратная матрица 2x2.
«5 У
ОПРЕДЕЛЕНИЕ 4.32. Говорят, что две матрицы А = [Aij] и В = [B{j] размера
га х п равны, если равны их соответствующие элементы; т.е. А = В тогда и
только тогда, когда А^ = Bij для всех г, 1 < г < т, и всех j, 1 < j < п.
Ац
А21
Аз1
А\2 А\з
А22 А2з
Азч Азз
В2\
В 31
В\2
в22
Вз2
Например,
Взз
тогда и только тогда, когда Aij = Bij для 1 < i,j < 3. Заметим, что это определе-
определение равенства матриц является всего лишь переформулировкой условия равенства
двух функций А и В: A((i,j)) = B((i,j)) для всех (г, jf).
В данном разделе некоторые определения и теоремы будут сформулированы
только для матриц 2 х 2 и 3 х 3; более общая их формулировка будет дана в
последующих главах. Для упрощения выкладок, а также для удобства и опреде-
определенности, большинство теорем будет доказано только для матриц 2 х 2 и 3 х 3.
ОПРЕДЕЛЕНИЕ 4.33. Если d — скаляр, а А = [А^\ — матрица т х п, то dA
есть матрица D = [Dij] размера тхп, где Dij = dAij, т.е. каждая компонента
D есть произведение соответствующей компоненты А на d. Произведение числа
d и матрицы А называется умножением матрицы на скаляр.
ПРИМЕР 4.34. Пусть А =
q -2
Т°ГДа
1 -3 5
6 0 -2
_ [ G)A) G)(-3) G)E) 1 _
7 -21 35
42 0-14
?

РАЗДЕЛ 4.3. Матрицы 169
ОПРЕДЕЛЕНИЕ4.35. Если А — [Ац] и В = [Вц] — тхп матрицы, тогда А+В
есть тхп матрица С = [С^], где CV,- = Aij + Bij, другими словами, матрицы
складываются покомпонентно. Матрица С называется суммой матриц А и В.
Запись А - В означает А + (—1)В.
ПРИМЕР 4.36. Пусть А-
-1 3
2 7
4 -5
А--
4-
3
-5
8
-1
2
4
11
4
2
3
7
-5
-
и В =
2+ (-5)
4 + 8
3 11
-5 4
8 2
3 + 11
7 + 4
(-5)+2
Тогда
2 14
-3 11
12 -3
?
ОПРЕДЕЛЕНИЕ 4.37. Произведение двух матриц определяется следующим
образом:
а) Пусть V — матрица-строка или матрица-столбец с п элементами, и W —
матрица-строка или матрица-столбец с п элементами:
V =
W =
v2
vn
w2
wn
или
v = [ v, v2
2
Vn ],
или
W2
Тогда скалярным произведением, или внутренним произведением V и W
называется число ViH^ + V^V^H HVnWn, которое обозначается через V»W.
б) Пусть
An ¦•• Aip
An ¦¦¦ А2р
есть матрица т х р, а
-6
22
В1п
в2п
ВР2 ¦¦ ¦ В
ipn _
есть матрица р х п.

170 ГЛАВА 4. Функции и матрицы
Тогда (матричное)
С = [С^] размера
матрицы А и j-ro <
с* = [;
произведение А
т х п, где С^ -
:толбца матрицы
Lii Ai2
Ai3 .-
и В, обозначаемое через АВ, есть матрица
- это скалярное произведение г-ой строки
В. То есть,
• Aip]m
в1]
- ВРЗ -
р
ПРИМЕР 4.38. Пусть
о J
и JB =
-2408
3-1-2 1
0 5 7 0
Вычислим матричное произведение С = [С^] = АВ следующим образом. Мат-
Матрица А имеет размер 2 х 3, а матрица В — размер 3x4, так что произведение
АВ = С определено и будет представлять собой матрицу размера 2 х 4. Сц есть
скалярное произведение первой строки матрицы А и первого столбца матрицы В,
я Огз — скалярное произведение второй строки матрицы А и третьего столбца
матрицы В. Таким образом,
-2
3
О
О
-2
7
= [ 1 -3 5 ] <
С23 = [ 6 0 -2 ]
Продолжая вычисления в том же духе, получаем
АВ
_Г1 -3 5 1
~ [6 0 -2 J
-2408
3-1-2 1
0 5 7 0
-11 32 41 5
-12 14 -14 48
?
Доказательство следующей теоремы можно найти в любой книге по линей-
линейной алгебре.
ТЕОРЕМА 4.39. Для любых матриц Л, В и С размера п х и и действительных
чисел г и s справедливы следующие утверждения:
а) А + В = В + А (свойство коммутативности сложения);
б) А + (В + С) = (А + В) + С (свойство ассоциативности сложения);
в) А - (В • С) = (А - В) • С (свойство ассоциативности умножения);
г) А - (В 4- С) = (А • В) + (А • С) (свойство дистрибутивности матриц);
д) А - (гВ 4- sC) = г (А • В) + s(A • С) (свойство линейности матриц ).

РАЗДЕЛ 4.3. Матрицы 171
ОПРЕДЕЛЕНИЕ 4.40. Пусть А — матрица п х га. Ее транспонированной
матрицей называется матрица А1 размера га х п такая, что А1^ = Aji, где
Aij — элемент г-ой строки и j-ro столбца матрицы А. Если А — матрица пхп
и А^ = Aji для всех 1 < г, j < п, то матрица А называется симметричной.
Иными словами, матрица А симметрична тогда и только тогда, когда А = Аг.
ПРИМЕР 4.41. Пусть А = fi ~ _о г ^огда ^ ~~ матРии>а размера 3x2,
полученная из А заменой строк на столбцы:
Аг =
1-3 5
6 0-2
1 6
-3 0
5 -2
?
ТЕОРЕМА 4.42. Пусть А и В —- матрицы, произведение которых определено.
Тогда (АВУ = ВгАь.
Доказательство этой теоремы мы предоставляем читателю.
ОПРЕДЕЛЕНИЕ 4.43. Пусть А = {аьа2,... ,ап} и В = {6Ь62,... ,6т}, и
пусть R — отношение на Ах В. Матричным представлением R называется
матрица М = [Mij] размера п х га, определенная соотношениями
L, если (ai,bj) e i?;
), если (o>i,bj) ? R.
ПРИМЕР 4.44. Пусть А = {ai,a2,a3} и В = {61,62}- Пусть i? — отношение
i, 61), (a2,6i), (a2,62), (аз,62)}. Тогда матричное представление имеет вид
' 1
1
0
0
1
1
D
ПРИМЕР 4.45. Наименьшее рефлексивное отношение на А = {ai,a2,a3} есть
отношение {(ai,ai), (a2la2), (a3,a3)}. Матричное представление этого отношения
имеет вид
0 0
0 10
0 0 1
Наибольшее отношение на А есть Ах А. Его матричное представление имеет вид
1 1 1
1 1 1
1 1 1
?

172 ГЛАВА 4. Функции и матрицы
ОПРЕДЕЛЕНИЕ 4.46. Определим булевы операции V и Л на множестве {0,1}
следующим образом:
V
0
1
0 1
0 1
1 1
Л
0
1
0 1
0 0
0 1
Булевой матрицей называется матрица, каждый элемент которой есть 0 или 1.
Пусть А и В — булевы матрицы размера т х п, а С — булева матрица размера
п х р. Тогда
а) U = А V В определяется соотношением
Uij = Aij V Bij, где 1 < i < га, 1 < j < п;
б) I = АаВ определяется соотношением
Iij = А^ Л Bij, где 1 < г < т, 1 < j < п;
в) D = А 0 С определяется соотношением
Л Bxj) V (Ai2 Л B2j) V
j), где 1<г<
ПРИМЕР 4.47. Пусть А = {аиа2,а3}у R = {(abai), (аьа2), (a2,ai), (а2,а2),
(a3,ai)} и 5 = {(ai,ai),(ai,a3),(a3,ai),(a2,a2), (а2,а3),(а3,а2)}. Матричными
представлениями отношений R и 5, соответственно, являются
Тогда
1
1
0
1
1
0
1
1
0
1
1
1
1
1
0
1
1
0
1
1
0
1
1
0
1 ¦
0
0
1 ¦
0
0
1 "
0
0
0
0
0
Л
V
©
" 1
0
1
¦ 1
0
1
¦ 1
0
1
и
0
1
1
0
1
1
0
1
1
1"
1
0
1"
1
0
1 ¦
1
0
1
0
1
0
1
1
" 1
0
0
" 1
1
1
¦ 1
1
0
1
1
0
0
1
0
1
1
1
1
1
0
1 ¦
0
0
1 ¦
1
0
1 ¦
1
0
?

РАЗДЕЛ 4.3. Матрицы 173
ТЕОРЕМА 4.48. Пусть R и S — отношения на конечном множестве А = {ai,a2,
...,ап} и им соответствуют матричные представления М и N.
а) Если R рефлексивно, то Мц = 1 для 1 < г < п.
б) Если R симметрично, то Mij = Mji для 1 < г, j < п; поэтому М = М1У
и М — симметричная матрица.
в) Пусть М02 = М0 М. Если J? транзитивно, то, как только М{02 = 1, мы
имеем Mik — 1 для 1 < г, к < п.
г) MvTV является матричным представлением R\JS.
д) МЛ iV является матричным представлением RD S.
ДОКАЗАТЕЛЬСТВО, а) Поскольку отношение R рефлексивно, то (ai,ai) G R для
всех 1 < г < п. Поэтому Мц = 1 для всех 1 < г < п.
б) Если М^ = 1, то (ai,aj) ЕЙ,а поскольку R симметрично, то (а^,^) е
Д, так что Mji = 1. Обратно, если Mji — 1, то (%,аг) G Д, а поскольку R
симметрично, то (аг,%) € R, так что М^- = 1. В силу того, что М^ = 1 тогда и
только тогда, когда Mji = 1, М = М*, М — симметричная матрица.
в) Допустим, что Мг^2 = 1. Поскольку Мг^2 = (АцААцс) V (А^ЛА^) V • • • V
(AinAAnk), то существует такое т, что (АгтЛАпг/с) = 1. Поэтому Aim = 1 и
Атк = 1. По определению матричного представления (di,am) e i? и (am,afc) G i?.
Поскольку i? транзитивно, то (a^a^) € R и М^ = 1.
Оставшуюся часть доказательства предоставляем читателю. ¦
Доказательство следующей теоремы мы также предоставляем читателю.
ТЕОРЕМА 4.49. Пусть R — отношение на А х В и 5 — отношение на В х С.
Если М и N — матричные представления R и S соответственно, то М © N —
матричное представление S о R.
ПРИМЕР 4.50. Пусть А = {0,^0,2}, В = {bub2,b3} и С = {ci,c2,c3,c4}. Пусть
R = {(abbi),(abb2),(a2,63)} и 5 = {Fbci), Fьс2), (Ь2,с3), F3,ci), F3,с2)}. То-
Тогда матричными представлениями R и S являются, соответственно,
Далее, имеем
1 1 О
О 0 1
110 0
0 0 10
110 0
1 1 0
0 0 1
О
110 0
0 0 10
110 0
1110
110 0
D
и 5 = {(ab ci), (a1,c2), (auc3), (a2, ci), (a2, c2)}.
Следующее утверждение является следствием теорем 4.48, 4.49 и 2.37.
ТЕОРЕМА 4.51. Пусть А — матричное представление отношения R.
а) Рефлексивное замыкание R имеет матричное представление Аи I.
б) Симметричное замыкание R имеет матричное представление Аи А*.
в) Если А — конечное множество, содержащее п элементов, тогда транзитивное
замыкание R имеет матричное представление A U A02 U A03 U • • • U А°п.

174 ГЛАВА 4. Функции и матрицы
ОПРЕДЕЛЕНИЕ 4.52. Пусть М — матрица размера п х п, в каждой строке и в
каждом столбце которой только один элемент равен 1, а все остальные равны
0. Такая матрица М называется матрицей перестановок.
ТЕОРЕМА 4.53. Пусть М — матрица перестановок, г I — матрица размера nxl
с различными элементами. Тогда Ml — матрица размера nxl, элементы которой
образуют перестановку элементов матрицы /.
ДОКАЗАТЕЛЬСТВО. Пусть / =
Поскольку
«2
и Г = Ml. Рассмотрим aj в j-ой строке.
Mi2 Mi3
Min ]
«2
и имеется одна строка р, в которой MPj = 1 и Mpk = 0 для к ф j, то р-я строка
матрицы Г есть aj. Далее, поскольку Mkj — 0 для всех к ф р, aj не может
появиться ни в какой другой строке матрицы /'. ¦
ПРИМЕР 4.54. Пусть М =
0
1
0
0
0
1
1 ¦
0
0
и / =
«1
а2
аз
. Тогда Ml —
?
УПРАЖНЕНИЯ
1. Вычислите:
а)
в)
Д) (-2)
3 -1
2 7
-5 О
1
3
4
5 _
" -5
-1
1
О
3
[-23-50
1
6 -7
2. Пусть А =
а) А1;
3. Пусть А =
а) АВ;
б)
1
3
6
-1
1
-1
г) [ -2 3
е)
-2
6
2
-3
7
б)
4
1
3
2 '
5
В
7
5
—4
б)
1
ВЫЧР
АА*;
Г 4
[-2
в)
1СЛИТ
1]
9J
АВ1;
2 '
4
5
" 2
5
0
-5 0 ]
-2
5
6
¦ 1 ¦
3
4
. 5 .
8 '
1
4
;
-8
в) А1 Ах.
Вычислите:
г) А1 В; д)
{АВУ;

РАЗДЕЛ 4.3. Матрицы 175
е)
В1А1;
Пусть А =
а)
г)
АВ;
В*;
ж) А
0
-4
-В;
J
б)
д)
з)
=
ВА
АгЬ
В-
' -1
3
10
А;
2 "
9
0
и) ЪА;
. Вычислите:
в) Л(;
е) (BAY.
к) 2В-ЗА
5. Докажите справедливость или постройте контрпример для высказывания Ес-
Если для матриц А, В и С имеет место АВ = АС, то В = С.
6. Докажите справедливость или постройте контрпример для высказывания Ес-
Если для матриц А и В произведение АВ равно нулевой матрице, то либо
А, либо В является нулевой матрицей.
7. Докажите, что если произведение матриц А и В определено, то (АВI =
В1Аг.
8. Докажите, что для отношений Йи5на конечном множестве А = {ai, а^,...,
ап} с матричными представлениями MhJV, соответственно, MvN является
матричным представлением отношения Ди S.
9. Докажите, что для отношений Ди5на конечном множестве А = {аь а2,...,
ап} с матричными представлениями М и ЛГ, соответственно, MAN является
матричным представлением отношения R.
10. Докажите, что если R — отношение на А х В, а S — отношение на J5 х С
и если М и N — матричные представления й и S, соответственно, тогда
М Q N является матричным представлением отношения S о R.
11. Пусть Л = {1,2, 3,4, 5}, В = {6,7,8,9}, С = {10,11,12,13}, D = {?, Л, О, *}•
Отношения RC. А х В, SCBxCnTCCxD определены как
Д = {A,7), D,6), E,6), B,8)},
S -{F,10), F,11), G,10), (8,13)},
Г = {A1, Л), A0, Л), A3, *), A2, D), A3,0)}-
Найдите матричные представления отношений й, S и Т, затем найдите
матричные представления отношений
а) Д-1 и S; б) 5ой; в) S о S и S о S;
г) Д-1о5~1; д) ТоEой); е) Т о 5;
ж) (Г о 5) о R.
12. Пусть А = {F,а),(с,е),(с/,г),(/,о),(^,гг)} иВ = {(г;, a), (w, e), (х,г), (у, о),
(z, и)}. Найдите матричные представления Аи В. Затем найдите матричные
представления отношений
а) А-1; б) В; в) А о В; г) В о А
13. Пусть А = {а, 6, с, d, е} и 5, Г, U и У — отношения на А, где
5 = {(а, а), (а, Ь), (Ь, с), F, d), (с, е), (е, d), (с, а)},
Т = {(а, 6), F, а), F, с), F, d), (e, e), (d, e), (с, Ь)},
?/ = {(а, Ь), (а, а), F, с), (Ь, 6), (е, е), F, а), (с, 6), (с, с), (d, d), (а, с), (с, а)},
V = {(а, 6), (Ь, с), F,6), (е, е), (Ь, а), (с, Ь), (d, d), (а, с), (с, а)}.
Найдите матричные представления 5, Г, U V. Затем, используя эти матри-

176 ГЛАВА 4. Функции и матрицы
цы, определите какие из этих отношений
а) симметричны;
б) рефлексивны;
в) транзитивны;
г) антисимметричны.
14. Пусть А = {а, 6, с, d, е} и 5, Т, U и V — отношения на А, где
5 = {(а, а), (а, 6), (Ь, с), F, d), (с, е), (е, d), (с, а)},
Т = {(а, 6), (Ь, а), (Ь, с), F, d), (e, e), (d, e), (с, 6)},
С/ = {(а, Ь), (а, а), F, с), (Ь, 6), (е, е), F, а), (с, 6), (с, с), (d, d), (а, с), (с, а)},
У - {(а, 6), F, с), F, Ь), (е, в), F, а), (с, 6), (d, d), (а, с), (с, а)}.
а) Найдите матричное представление 5, Т, С/ и У.
б) Найдите матричное представление отношений S оТ и U oV.
в) Найдите матричное представление отношений 5 П Т и С/ П V.
г) Найдите матричное представление U A S.
15. Пусть А = {1,2,3,4,} В = {a,b,c}. Найдите отношение на А х В с матрич-
матричным представлением
а)
0 1
0 1 О
0 0 1
1 1 О
б)
в)
1 0 1
0 1 О
1 0 1
О 1 О
0 1 1
1 1 О
1 0 1
1 0 1
16. Пусть А — {a,b,c,d,e}. Найдите отношение на Л с матричным представле-
представлением
Г 1 0 0 1 О
0 10 0 0
0 0 10 0
10 0 11
0 0 10 1
а)
в)
1000
10 0 0 0
0 10 10
0 10 0 1
0 0 10 0
б)
г)
0 0 10 1
0 10 10
10 10 1
0 10 10
10 10 0
Г 1 0 0 0 1
0 10 10
10 10 0
0 10 10
10 10 1
17. Пусть А = {a,b,c,d,e}. Постройте графы со следующими матричными пред-
представлениями:
а)
Г 1 0 1 1 О
0 0 0 0 0
10 10 1
10 0 0 1
0 0 111
б)
Г 0 0 1 0 1
0 10 10
10 10 1
0 10 10
10 10 0
в)
1001
10 110
0 10 11
0 110 1
10 110
18. Пусть А = {о, Ь, с, d, e}. Постройте орграфы со следующими матричными
представлениями:

а)
10 110
0 10 10
10 0 0 0
110 0 1
0 110 1
б)
0 0 10 1
10 0 10
1110 1
0 10 0 0
10 10 0
РАЗДЕЛ 4.4. Мощность 177
в)
0 0 0 0 0
10 0 10
0 10 10
0 10 0 1
10 0 0 0
19. Для каждого отношения R, заданного в предыдущем упражнении матрич-
матричным представлением, найдите йой, используя соответствующее матричное
представление.
4.4. МОЩНОСТЬ
В этом разделе мы обсудим понятие мощности множества. Если множество ко-
конечно, то его мощность есть просто количество содержащихся в нем элементов.
Таким образом, для определения мощности множества нам достаточно подсчитать
количество содержащихся в нем элементов. Сформулируем сказанное формально
в виде следующего определения.
ОПРЕДЕЛЕНИЕ 4.55. Пустое множество есть конечное множество мощно-
мощности О. Если существует взаимно однозначное соответствие между множеством
А и множеством {1,2,3,... п}, то А есть конечное множество мощности п.
ПРИМЕР 4.56. Множество {а,р, г, x,z} имеет мощность 5, т.к. существует вза-
взаимно однозначное соответствие: {1,2,3,4,5} —> {а,р, г, х, г}, определяемое равен-
равенствами 0A) = а, 0B) = р, 0C) = г, 0D) = ж, 0E) = z. ?
ОПРЕДЕЛЕНИЕ 4.57. Множество А называется счетно бесконечным, если
существует взаимно однозначное соответствие между множеством А и множе-
множеством положительных целых чисел {1,2,3,..., п,...}. Множество называется
счетным, если оно конечно или счетно бесконечно.
ТЕОРЕМА 4.58.
а) Пусть А и В — непересекающиеся конечные множества. Тогда множество
Аи В конечно. Если А имеет мощность п и В имеет мощность га, то Аи В
имеет мощность т + п.
б) Пусть А и В — непересекающиеся счетно бесконечные множества. Тогда
A U В — счетно бесконечное множество.
в) Пусть А и В — непересекающиеся счетные множества. Тогда АиВ — счетное
множество.
ДОКАЗАТЕЛЬСТВО, а) Поскольку множества А и В конечны, то для положи-
положительных целых чисел пит существуют взаимно однозначные соответствия
01 : {1,2,3, ...,п} —¦ А и 02 : {1,2,3,... ,т} —> В. Определим отображение
0 : {1,2,3,..., m + п} —> A U В посредством равенств ф[к) — ф\(к) для 1 < к <п

178 ГЛАВА 4. Функции и матрицы
и ф(п-\-г) = 4>2{i) для 1 < i < га. Функция ф устанавливает взаимно однозначное
соответствие между множествами {1,2,3,..., т + п) и Аи В.
б) Поскольку А и В — счетно бесконечные множества, то существуют взаим-
взаимно однозначные соответствия ф\ : {1,2,3,... п, ...}—> А и ф2 : {1,2,3,... га, ...}—>
В. Определим функцию ф : {1,2,3,...} —> Аи В посредством равенств </>(п) =
0i((n + l)/2) в случае, когда п нечетно, и ф(п) — ф2 (п/2) в случае, когда п
четно. Функция ф устанавливает взаимно однозначное соответствие между мно-
множествами {1,2,3,...} и A U В.
в) Пусть А и В — непересекающиеся счетные множества. Единственный
случай, который остался не рассмотренным в пунктах (а) и (б), — это когда одно
из множеств А или В конечно, а другое счетно бесконечно. Предположим, что
А — конечное множество. Тогда существует взаимно однозначное соответствие
ф\ : {1, 2,3,... ,п} —» А. А поскольку В — счетно бесконечное множество, то
существует ф2 : {1,2, 3,... ,га,...} —> В. Определим ф : {1,2,3,...} —> Аи В
следующим образом: ф(к) = ф\(к) для 1 < к < п и ф{к) = ф2(к - и) для к > п.
Функция ф устанавливает взаимно однозначное соответствие между множествами
{1,2,3,...} и ЛиВ. ¦
Доказательство следующей теоремы предоставляется читателю.
ТЕОРЕМА 4.59. Множество неотрицательных целых чисел и множество целых
чисел являются счетно бесконечными.
Дальнейшие свойства мощности будут рассмотрены в следующем разделе.
Будет показано, что существуют множества, которые не являются счетными, и
что имеется бесконечно много различных бесконечных мощностей.
¦ УПРАЖНЕНИЯ
1. Используя определение, найдите мощности следующих множеств:
а) {a,6,c,d,e,/,#};
б) {3, б, 9,12,15,18,21, 24,27,30, 33};
в) {5,10,15,20,25,30,...}.
2. Покажите, что множество неотрицательных целых чисел счетно бесконечно.
3. Покажите, что множество отрицательных целых чисел счетно бесконечно.
4. Покажите, что множество целых чисел счетно бесконечно.
5. Покажите, что множество { — 10, —9, —8,..., —2, —1,0,1,2,3,...} счетно бес-
бесконечно.
4.5. МОЩНОСТЬ (ПРОДОЛЖЕНИЕ)
Исследуем теперь понятие мощности множества более основательно. Прежде все-
всего, покажем, что подмножество счетного множества счетно. Отсюда будет следо-
следовать, что всякое множество, для которого существует взаимно однозначное соот-
соответствие с подмножеством счетного множества, счетно.
ТЕОРЕМА 4.60. Подмножество счетного множества счетно.

РАЗДЕЛ 4.5. Мощность (продолжение) 179
ДОКАЗАТЕЛЬСТВО. Покажем, что если В — счетное множество и А С В, то
множество А также счетно. Предположим, что В — конечное множество. По-
Покажем, что в таком случае А тоже конечно. Поскольку В конечно, для неко-
некоторого положительного целого числа и существует взаимно однозначное соот-
соответствие ф между {1,2,3,... ,п} и В. Следовательно, В можно представить в
виде {Ь1,Ь2»Ьз,...,Ьп}. где 6; = 0@- Теперь построим взаимно однозначное со-
соответствие ф между {1,2,3,... ,т} и А, где т < п. Начинаем с 6Х и находим
первое biy скажем, 6Ql, в последовательности 6Ь Ь2, 63, ..., Ьп такое, что bi Е А.
Пусть 0A) = bai. Просматривая последовательность, находим в ней следующее
bi, скажем, Ьа2 такое, что bi Е А. Пусть 0B) = Ьп2. Продолжаем процесс, пока
не достигнем Ьп. Пусть т — наибольшее целое число, которое ф отображает в
элемент А. Поскольку г < ai для всех г, то т < п и поэтому, несомненно, ф
отображает {1,2,3,..., га} в А.
Теперь предположим, что В — счетно бесконечное множество. Если А —
конечное, то оно счетное, поэтому предположим, что оно не является конечным.
Поскольку В —- счетно бесконечное, существует взаимно однозначное соответ-
соответствие ф между {1,2,3,...} и В. Следовательно, В можно представить в виде
{&1,&2,6з,...}, Где ^ = 0@- Используя принцип вполне упорядочения, находим
наименьшее г такое, что Ь{ Е А. Пусть 0A) = bi и В\ = В — {6;}. Очевид-
Очевидно, что 1 < г. Предположим, что мы определили 0A), 0B), 0C),... ,0(fc) E А,
Вк = В_- {0A), 0B), 0C),..., 0(fc)}, 0(г) < Ъ для всех 1 < г < к и всех Ь Е Вк,
и если ф{к) = Ьг, то к < г. Выберем наименьшее j такое, что bj E А П Вк. Пусть
ф(к) = bj и Bk+\ = Bk - {bj}. Очевидным образом получаем последовательность
0(l),0B),0C),...,0(fc)^
1)}, 0@ < Ь для всех 1<г</с-|-1и всех 6 Е Вк+\, и если ф{к + 1) = 6Г,
то к Ч- 1 < г. Итак, функция ф определена по индукции, при этом очевидно,
что 0(г) Е А для всех г и 0(г) ф 0(j), если г ф j. Остается только показать,
что отображение ф сюръективно. Пусть а Е А, тогда а = Ьп для некоторого п.
Следовательно, для некоторого га < п имеем 0(га) = Ъп. Ш
ТЕОРЕМА4.61. Пусть 5 — счетно бесконечное множество, тогда множество SxS
также счетно бесконечно.
ДОКАЗАТЕЛЬСТВО. Сначала покажем, что если iV — множество положительных
целых чисел, то N х N счетно. Рассмотрим следующий рисунок:
Рис. 4.1
Двигаясь по диагональным стрелкам, начиная с верхней, мы определяем
отображение ф следующим образом: 0A) = A,1), 0B) = A,2), 0C) = B,1),

180 ГЛАВА 4. Функции и матрицы
0D) = A,3,), 0E) = B,3) и т.д. Функция ф устанавливает искомое взаимно
однозначное соответствие. Упорядоченная пара (т, п) лежит на т + п — 1-ой по
порядку диагонали и является га-ым элементом вдоль этой диагональной линии.
Следовательно, множество, изображенное на рис. 4.1, счетно. Таким образом,
множество N х N счетно. Поскольку S — счетно бесконечное множество, то су-
существует взаимно однозначное соответствие в : N —> 5. Определим соответствие
exd:NxN->SxS следующим образом: в х 0(а, 6) = @(а), в(Ь)). Легко пока-
показать, что функция в х в устанавливает взаимно однозначное соответствие между
множествами N х N и 5 х 5. ¦
ТЕОРЕМА 4.62. Множество Q+ положительных рациональных чисел является
счетно бесконечным.
ДОКАЗАТЕЛЬСТВО. Рассмотрим подмножество М множества NxN вида {(а, Ь) :
(а, b) G N х N, при этом целые числа а и Ь — взаимно простые}. Очевидно, функ-
функция ф : Q+ —> М, определенная соотношением ф(а/Ь) = (а, 6), — это и есть ис-
искомое взаимно однозначное соответствие. Поскольку множество NxN — счетно
бесконечное, множество М также является счетно бесконечным. Следовательно,
Q+ — счетно бесконечное множество. ¦
ТЕОРЕМА 4.63. Если А и В — счетные множества, то множество A U В также
счетно.
ДОКАЗАТЕЛЬСТВО. Множество А — В счетно, как подмножество счетного мно-
множества А. Но множества А — В и В не пересекаются, поэтому по теореме 4.58 (в)
множество (А- В)и В = Аи В является счетным. ¦
Приведенные выше теоремы могут навести на мысль, что все множества
счетны. Однако, как показывает следующая теорема, существуют бесконечные,
но несчетные множества.
ТЕОРЕМА 4.64. Пусть R — множество действительных чисел. Множество / вида
I = {x:x?RhO<x<1} не является счетным.
ДОКАЗАТЕЛЬСТВО. Применим метод сведения к абсурду. Предположим, что
множество / счетно. Тогда / можно представить в виде {аьа2,аз,а4,а5,...},
где ai — образ i при взаимно однозначном соответствии между N и I. Пусть
.anai2aisai4ui5 . •. — это запись в виде десятичной дроби числа а,{. Тогда мы
имеем таблицу
а2 =
«5 = .«51^52^53^54^55 • • •
Определим элемент Ь Е /, где Ъ = .b^bsb^s ..., следующим образом: Ь{ = 5, если
ац ф 5, и bi = 8, если ац = 5. Рассмотрим конкретный пример:
аг = .5135897623...

РАЗДЕЛ 4.5. Мощность (продолжение) 181
а2 = .1425958273...
а3 = .2837462982...
а4 = .1985723986...
а5 = .2309847621...
Имея an = 5, а22 = 4, азз = 3, а44 = 5, аъъ = 8и т.д., получаем Ъ\ = 8, Ъ2 = 5,
Ьз = 5, ЬА = 8, Ь5 = 5 и т.д. Таким образом,
Ь = .85585...
Число Ь не принадлежит множеству {ai,a2,a3,a4,a5,. •.}, т.к. для каждого
т число 6 не может совпадать с am. В самом деле, 6т ф атт, поэтому Ьиат
не совпадают в m-ой цифре. Но это противоречит предположению о том, что / =
{ai,a2,a3,a4,a5, • • •}» так как b е I, но b <? {ai,a2, a3,a4,a5,...}. Следовательно,
предположение о счетности / является ложным, и множество / — несчетное. ¦
ТЕОРЕМА 4.65, Множество действительных чисел R несчетно.
ДОКАЗАТЕЛЬСТВО. Если бы R было счетным, то множество /, как подмноже-
подмножество Д, было бы счетным, однако, / — несчетно. Следовательно, множество R —
несчетное. ¦
В дальнейшем мы опишем метод построения бесконечного числа бесконеч-
бесконечных множеств, никакие два из которых нельзя связать взаимно однозначным
соответствием.
ТЕОРЕМА 4.66. Не существует взаимно однозначного соответствия между мно-
множеством 5 и его булеаном V(S).
ДОКАЗАТЕЛЬСТВО. Очевидно, не существует взаимно однозначного соответ-
соответствия между пустым множеством 0 и его булеаном {0}, содержащим один эле-
элемент — 0. Снова воспользуемся методом сведения к абсурду. Предположим, что
взаимно однозначное соответствие ф между 5 и его булеаном существует. Это
значит, что функция ф биективно отображает элементы множества S на подмно-
подмножества множества 5. Например, пусть S — множество положительных целых
чисел, и пусть
0A) = {2, 5, 7,9,10},
0B) = {2,4,6,8,...},
0C) = 0,
0D) = {1,2,3,4,5,6,...},
0E) = {1,2},
В некоторых случаях г Е 0(г). В нашем примере 2 G 0B) и 4 Е 0D). Однако,
0A), 3 ^ 0C) и 5 ^ 0E). Понятно, что любой элемент г, который функция ф

182 ГЛАВА 4. Функции и матрицы
отображает в пустое множество, будет обладать свойством г $. 0(г), а всякий эле-
элемент j, который функция ф отображает в 5, будет обладать свойством j e 0(j).
Пусть W = {x:x€Shx? ф(х)}. Поскольку отображение ф сюръективно, то
существует элемент a ? S такой, что 0(а) = W. Принадлежит ли а множеству
W? Если a g W, то а принадлежит множеству тех элементов 5, которые ф не
отображает на множества, их содержащие. Следовательно, а ? ф(а) = W. Таким
образом, мы приходим к противоречию. Если же а ф W, то а ? ф(а) = W. Поэто-
Поэтому а удовлетворяет условию принадлежности множеству W, т.е. a G W. Снова
получаем противоречие. Итак, в любом случае мы приходим к противоречию. Сле-
Следовательно, утверждение о существовании взаимно однозначного соответствия ф
между S и его булеаном неверно. ¦
ПРИМЕР 4.67. Пусть 5 = {1,2,3,4} и
= {2,4},
0B) = {1,2,3,4},
0C) = {1,3},
0D) = 0.
Тогда W = {1,4} — множество из доказательства теоремы, и в него не отобра-
отображается никакой элемент. ?
Примером рассуждения, очень похожего на доказательство предыдущей те-
теоремы, является парадокс Рассела. Он показывает нам, что при определении мно-
множеств нужно быть очень осторожным. Иначе в своей математической системе мы
можем получить внутреннее противоречие. Особое внимание следует обращать
на то, чтобы множества не становились "слишком большими".
ПРИМЕР 4.68. (Парадокс Рассела) Пусть 5 — множество всех множеств. Пусть
W = {х : х ? х}. Пустое множество принадлежит W, т.к. оно не принадлежит
самому себе. На самом деле, большинство известных нам множеств принадлежит
W. Однако, 5 не принадлежит W, т.к. 5 € 5. А вот принадлежит ли множе-
множеству W само W? Если W E W, то оно принадлежит множеству всех множеств,
которые сами себе не принадлежат. Следовательно, W ? W. Однако, если пред-
предположить, что W ф W, то W принадлежит множеству всех множеств, которые
не принадлежат сами себе. Но таким множеством является W, так что W e W.
В любом случае мы приходим к противоречию. ?
¦ УПРАЖНЕНИЯ
1. Пусть S = {1,2,3,4,5,6} и ф — инъективная функция из S в его булеан
V(S), определенная следующим образом:
0A) = {1,2,3,4},
0B) = {1,4},
0C) = {2,3,4},
0D) = 0,

РАЗДЕЛ 4.5. Мощность (продолжение) 183
0E) = {1,2,3,4,5,6},
0F) = {1,3,6}.
Опишите множество, отсутствие отображения на которое гарантирует нам
теорема 4.66.
2. Пусть S = {1,2,3,4,5,6} и ф — инъективная функция из S в его булеан
V(S), определенная следующим образом:
= {2, 3,4},
0B) = {1,4},
0C) = {2,4},
0D) = 0,
0E)-{1,2,3,4,6},
0F) = {1,3}.
Опишите множество, отсутствие отображения на которое гарантирует нам
теорема 4.66.
3. Пусть 5 — {1,2,3,4,5,6} и 0 — инъективная функция из 5 в его булеан
V(S), определенная следующим образом:
= {1,2,3,4},
0B) = {1,2,4},
0C) = {2,3,4,5},
0D) = {4},
0E) = {1,2,3,4,5,6},
0F) = {1,3,6}.
Опишите множество, отсутствие отображения на которое гарантирует нам
теорема 4.66.
4. Докажите, что множество неотрицательных рациональных чисел счетно.
5. Докажите, что множество рациональных чисел счетно.
6. Пусть 5 = {а 4- Ы : а, 6 Е Z}, где г = у/^Л. Докажите, что 5 счетно.
7. Докажите, что множество всех полиномов 5-ой степени с целыми коэффи-
коэффициентами счетно.
8. Докажите, что множество всех полиномов степени не выше п с целыми
коэффициентами является счетным.

ГЛАВА
АЛГОРИТМЫ И РЕКУРСИЯ
5.1. ЦИКЛЫ И АЛГОРИТМЫ ДЛЯ МАТРИЦ
Алгоритмом называется совокупность инструкций о том, как решить некоторую
задачу. Множество зачастую непонятных руководств, прилагаемых ко всевоз-
всевозможным устройствам и обучающих нас, как устанавливать и использовать их,
являются примерами алгоритмов. Компьютеру необходимы инструкции, объясня-
объясняющие, как выполнить задание, поэтому любая компьютерная программа также
представляет собой алгоритм. Всегда желательно, чтобы алгоритм носил макси-
максимально общий характер. Например, существенно, что алгоритм умножения двух
матриц работает в случае любых двух матриц, для которых операция умножения
определена. Как мы увидим в дальнейшем, многие алгоритмы содержат периоди-
периодически повторяющиеся процессы. Например, при умножении двух матриц разме-
размера и х и используется определенная процедура нахождения элементов матрицы-
произведения, которая повторяется п2 раз. Вообще, важность алгоритмов, содер-
содержащих повторяющиеся процедуры, для решения задач при помощи компьютеров
трудно переоценить.
Введенная нами ранее операция суммирования последовательности, по су-
сути, представляет собой определенный алгоритм. Знак суммы ]СГ=1Р(О говорит о
том, что мы должны вычислить элемент р(г) при г = 1, затем положить г = 2,
вычислить p(i) и прибавить его к предыдущей сумме. Далее мы увеличиваем г
на единицу и повторяем описанную процедуру до тех пор, пока г не превзойдет
п. По аналогии с описанным процессом вводится следующая процедура "цикла
перечислением". В соответствии с приведенным ниже набором инструкций, тре-
требуется положить г = 1 и выполнить шаги с A)-го по (ш)-ый. Затем положить
г = 2 и повторить процесс.
Цикл по г от 1 до п:
Шаг A);
Шаг B);
Шаг (т);
Конец цикла.

РАЗДЕЛ 5.1. Циклы и алгоритмы для матриц 185
Выполнив процесс для г = /с, нужно положить г = к + \ к повторять процесс до
тех пор, пока не выполним его для г = п.
Таким образом, для того чтобы вычислить сумму 5 = 53Г=1Р(О» мы должны:
Положить 5 = 0;
Цикл по г от 1 до п:
Заменить значение S на 5 + р(г);
Конец цикла.
В итоге получим значение 5, равное Ym=\P^)-
ПРИМЕР 5.1. Вычислить М = гп.
Положить М = 1;
Цикл по г от 1 до п\
Заменить значение М на М * г;
Конец цикла.
ПРИМЕР 5.2. Вычислить р(а), где р(х) — полином, используя схему Горнера.
Сначала заметим, что
4 азх3 + п2Х2 4- сцх 4- uq = х(х{х(а±х + аз) + «2) + ai) + ao •
Используя этот факт, построим алгоритм вычисления 5 = р(а), где р(х) = апхп +
ап-\хп~1 + • • • 4- а>2Х2 4- а\х 4 а0. Алгоритм имеет вид:
Положить S = ап\
Цикл по г от 1 до п\
Заменить S на aS 4- an_i;
Конец цикла.
ОПРЕДЕЛЕНИЕ 5.3. Даны частичные упорядочения, <i и <2, упорядочение <2
называется топологической сортировкой упорядочения <ь если <2 является
полным упорядочением, и всякий раз, когда а <\ 6, тогда a <2 6.
Опишем достаточно простой алгоритм нахождения топологической сортиров-
сортировки для упорядочения <i на множестве 5. Он состоит в следующем: мы находим
произвольный минимальный элемент частичного упорядочения и объявляем его
минимальным элементом полного упорядочения; затем выбираем другой мини-
минимальный элемент и объявляем его следующим элементом в полном упорядочении
и т.д. Это действие повторяется, пока все элементы множества не будут выбраны.
Мы всегда выбираем минимальный элемент, поэтому если в исходном упорядо-
упорядочении а < 6, то это соотношение будет иметь место и в новом упорядочении, так
как а будет выбрано первым. Теперь опишем алгоритм формально:
Процедура ТСE, <i):
Выбрать минимальный элемент s из E, <i);
Удалить s из 5;
Выполнять следующие шаги до тех пор, пока 5 не пусто;
Выбрать минимальный элемент t из (S, <i) и удалить его;
Положить s <\ t\
Переименовать t в s;
Конец процедуры.

186 ГЛАВА 5. Алгоритмы и рекурсия
Если А = [Aij] — матрица размера га х п, то произведение этой матрицы на
скаляр а есть матрица [Bij] = a[Aij] (см. главу 4). Алгоритм нахождения этого
произведения можно описать следующим образом:
Процедура Скаляр(а, А, т, п):
Цикл по г от 1 до га:
Цикл по j от 1 до п:
В^ = aAij ;
Конец цикла;
Конец цикла;
Конец процедуры.
Имя этой процедуры состоит из собственного имени "Скаляр" и входных
данных, каковыми являются скалярная величина а и матрица А размера га х п.
Если А = [А^] и В = [В^] — матрицы размера га х п, то сумма А 4- В,
определенная в главе 4, есть матрица С = [С^] размера гахп, где С^ = Aij + Bij.
Алгоритм нахождения суммы двух матриц А и В размера гахп может быть
описан следующим образом:
Процедура Сложение матриц(А, JB, m, п):
Цикл по г от 1 до га:
Цикл по j от 1 до п:
Конец цикла;
Конец цикла;
Конец процедуры.
Напомним, что если
А =
— матрица размера п х р, и
В =
Ац А12
А21 А22
Ап\ Ап2
В\\ В\2
В2\ В22
p
А2р
АПг
В
Вр1 В
Р2
2гп
Jpm Л
— матрица размера р х т, то произведение матриц А и В, обозначаемое через
ЛВ, есть матрица С = [Cij] размера пхт, где С^ — точечное произведение г-ой
строки матрицы А и j-oro столбца матрицы В. То есть,
'ij = [ Ац Ai2 A
гЗ
Bij
B2j
Д
PJ -I

РАЗДЕЛ 5.1. Циклы и алгоритмы для матриц 187
Опишем алгоритм умножения матриц А и В размера п х р и р х т.
Процедура Умножение матриц(.А, В,т,р, п):
Цикл по г от 1 до т:
Цикл по j от 1 до п:
Сц = 0;
Цикл по А; от 1 до р:
Значение С^ заменить на C,j + AjfcB/y;
Конец цикла;
Конец цикла;
Конец цикла;
Конец процедуры.
УПРАЖНЕНИЯ
1. Опишите алгоритм нахождения транспонированной матрицы.
2. Вычислите:
1 -1
а)
б)
в)
3 4
0 -5
1 -1 2
3 1 4
4-15
3 0-12
3 1 5 0
2-2 3
5 3 1
0 0 4
1
-2
3
-5
[4 3 -5 0 ];
г) [ -4 3 -5 0 ]
1
2
4
3
Д) (-4)
-3 1
2 -4
е)
-1 3
3 2
-3
3. Пусть А =
а) А1;
4. Пусть А =
а) АВ;
е) В*А1\
-2
1
1 4
-2 1
4 3
1 7
Вычислите:
2 -4 1
б)
и В =
1 2
4 5
б) ВА\
ж) А- В;
в) А1 А.
4 1
-2 -3
в) АВе;
з) В - А;
. Вычислите:
г) А1В;
и) ЪА;
Д)
к) 2В-ЗА

188 ГЛАВА 5. Алгоритмы и рекурсия
5. Пусть -А = о _4 пи^= ^ 4 . Вычислите:
L ^ 4 и J [ 6 О
а) АВ\ б) ВА; в) Аь\
г) В'; д) А'Б<; е) {ВА)г.
6. Постройте алгоритм нахождения наибольшего элемента последовательности.
7. Постройте алгоритм нахождения наименьшего элемента последовательности.
8. Постройте алгоритм нахождения наименьшего и наибольшего элементов по-
последовательности.
9. Постройте алгоритм для проверки, является ли матрица А симметричной.
10. Постройте алгоритм для проверки рефлексивности отношения, используя его
матричное представление.
11. Постройте алгоритм нахождения среднего арифметического для п чисел.
12. Напишите алгоритм сложения двух целых чисел.
13. Напишите алгоритм вычитания двух целых чисел.
14. Напишите алгоритм умножения двух целых чисел.
15. Напишите алгоритм деления одного целого числа на другое целое число.
5.2. РЕКУРСИВНЫЕ ФУНКЦИИ И АЛГОРИТМЫ
Непосредственное задание функции при помощи формулы, как правило, является
предпочтительным. Однако, иногда функцию бывает удобно или даже необходи-
необходимо задавать при помощи так называемого "рекурсивного метода". Из принципа
индукции следует, что если
а) функция задана для некоторого данного начального значения а (обычно О
или 1), и
б) когда функция задана для некоторого значения fc, большего а, она задана
также для значения fc 4-1,
то, тем самым, функция определена для всех целых чисел, больших а.
Вероятно, правильнее говорить не о рекурсивной функции, а о функции,
допускающей рекурсивное определение, поскольку многие функции могут быть
заданы как рекурсивно, так и непосредственно.
Заметим, что такая форма рекурсивного определения применима лишь к
функциям, заданным на множестве неотрицательных целых чисел. В дальней-
дальнейшем мы рассмотрим возможность рекурсивного определения для более широкого
класса функций. Кроме того, заметим, что возможность рекурсивного опреде-
определения функции не всегда очевидна. Например, рассмотрим функцию, заданную
как
Г /@) = 2,
| /(* + !) =
fc! '
Может показаться, что такое определение соответствует приведенным выше пунк-
пунктам (а) и (б) и задает рекурсивную функцию на множестве неотрицательных це-

РАЗДЕЛ 5.2. Рекурсивные функции и алгоритмы 189
лых чисел. Мы видим, однако, что /A) = 2, /B) = 1, /C) = |, а значение /D)
не определено, т.к. запись (^)! не имеет смысла.
Аналогично, если алгоритм может быть выполнен для фиксированного зна-
значения а и если из выполнимости алгоритма для значения /с, большего а, следует
выполнимость алгоритма для значения к + 1, то такой алгоритм выполним для
всех значений п> а.
Для начала рассмотрим несколько примеров рекурсивных функций.
Рассмотрим функцию /(п) = ап, определенную на множестве неотрицатель-
неотрицательных целых чисел. Ее можно задать как произведение п чисел, каждое из которых
равно а. Функция допускает также и рекурсивное определение, а именно:
/@) = 1;
ПРИМЕР 5.4. Рассмотрим функцию /(п) = п!, называемую "факториалом". Эту
функцию легко выразить посредством соотношения
п! = 1-2-3 п.
Но компьютеру, выполняющему вычисления, невозможно объяснить, что означает
троеточие. Однако мы можем составить процедуру, или алгоритм непосредствен-
непосредственного вычисления п!. Вот один из возможных вариантов такого алгоритма:
Процедура Факториал(п):
Если п = 0, то Факториал(п) = 1;
Положить Факториал(п) = 1;
Цикл по /с от 1 до п:
Значение Факториал(п) заменить на к- (Факториал(п));
Конец цикла;
Конец процедуры.
При переходе к рекурсивному определению функция "факториал" принимает
вид
Факториал(О) = 1;
Факториал (к + 1) = (fc + 1) • Факториал(/с).
Соответствующая компьютерная программа может быть описана как
Процедура Факториал(п):
Если п = 0, то Факториал(п) = 1;
Если п > 0, то Факториал(п) = п • Факториал(п - 1);
Конец процедуры.
Заметим, что в этой программе процедура Факториал(п) вызывает саму се-
себя, что допустимо в большинстве языков программирования. Когда процедура
Факториал(п) вызывается при п > 1, она выполняется до тех пор, пока не встре-
встретится Факториал(п — 1). Тогда выполнение процедуры приостанавливается (с со-
сохранением всей информации), и вызывается процедура Факториал(п - 1). Если
п-1 > 0, то выполнение процедуры Факториал(п-1) продолжается до тех пор, по-
пока в программе не появится Факториал(п-2). Тогда выполнение программы вновь

190 ГЛАВА 5. Алгоритмы и рекурсия
приостанавливается (с сохранением всей информации), и вызывается процедура
Факториал(п - 2). Процесс продолжается до момента, пока не будет достигнуто
и вычислено значение Факториал(О). Это дает возможность продолжить выпол-
выполнение процедуры ФакториалA) и вычислить соответствующее значение. Это, в
свою очередь, дает возможность продолжить процедуру ФакториалB) и вычис-
вычислить соответствующее значение. Процесс продолжается, пока не будет вычислен
Факториал(п- 1), после чего, наконец, вычисляется Факториал(п). ?
ПРИМЕР 5.5. Еще одним примером функции, которую обычно задают рекурсив-
рекурсивно, является последовательность чисел Фибоначчи. Первый и второй элементы
последовательности равны 1, а каждый следующий элемент последовательности
равен сумме двух предыдущих. Таким образом, первые десять членов последова-
последовательности представляют собой числа 1,1,2,3,5,8,13,21,34 и 55.
Приведенная ниже процедура Фиб(п) описывает программу вычисления зна-
значения n-го члена последовательности чисел Фибоначчи:
Процедура Фиб(п):
Если п = 1, то Фиб(п) = 1;
Если и = 2, то Фиб(п) = 1;
Если и > 2, то Фиб(п) = Фиб(п - 1) + Фиб(п - 2);
Конец процедуры.
Процедура крайне неэффективна, хотя имеет простой вид, т.к. на каждом
шаге к она вычисляет Фиб(&—1), начинает снова вычислять Фиб(А;-2), игнорируя
тот факт, что значение Фиб(/с —2) уже найдено при вычислении Фиб(/с — 1). Чита-
Читателю будет полезно проследить этот процесс и вычислить Фиб(п) для небольших
значений п, таких как 5 или 6. ?
ПРИМЕР 5.6. Последовательность чисел Каталана задается формулой
iz / n Bп)!
Кат(п) = -—v y .
Если последовательность начинается с 0-го члена, то первые 11 элементов по-
последовательности суть числа 1,1,2, 5,14,42,132,429,1430,4862 и 16796. Функция
Кат может быть задана рекурсивно как
Кат(О) = 1;
+ 1) { ^
О!
Чтобы доказать это, вычислим сначала Кат(О) = -— = 1. Затем покажем,
что имеет место равенство
2Bга + 1
Упрощая левую часть равенства, получаем

РАЗДЕЛ 5.2. Рекурсивные функции и алгоритмы 191
2Bп
(п + 2)
Кат(п) =
2Bп
Bп)!
(п
2) (п
1JBп +
1)!(п!)
_ Bn + 2)Bn+l)Bn)! _
_ Bn + 2)! _
~ (n + 2)!(n + l)! ~
= Кат(п + 1).
Рассмотрим теперь две задачи, в которых возникают числа Каталана.
1. Пусть задан выпуклый (п + 2)-угольник. Число способов разбиения такого
многоугольника на треугольники, путем соединения вершин многоугольника
с использованием п — \ отрезка, равно значению Кат(п). Для треугольника
(п = 1) существует только один способ образовать треугольник с использо-
использованием 0 линий, и КатA) = 1. Для четырехугольника (п = 2), как показано
на рис. 5.1, существует только два способа разбиения с использованием од-
одной линии.
Рис. 5.1
Отметим, что КатB) = 2. Для пятиугольника (п = 3), как показано на
рис. 5.2, существует пять различных способов разбиения на треугольники с
использованием двух линий.
Рис. 5.2
В этом случае мы имеем Кат(З) = 5.
2. Число способов, которыми можно расставить п пар скобок в выражении

192 ГЛАВА 5. Алгоритмы и рекурсия
• -anan+i так, чтобы получить п произведений пар чисел, равно
Кат(п). При и — 1 имеется один и только один способ, а именно: (а^).
При п = 2 имеем {(aia2)as) и (ai(a2a3)), так что существует два способа.
Для п = 3 имеем (((aia2)a3)a4), (ai(a2(a3a4))), ((aia2)(a3a4)), ((ai(a2a3))a4)
и (ai((a2a3)a4)), так что существует пять способов расстановки скобок. ?
ПРИМЕР 5.7. Еще одним важным примером является функция Аккермана —
Аккер: N х N —> N. Функция определена рекурсивно на N х JV, где iV — мно-
множество целых неотрицательных чисел, следующим образом:
Аккер@, п) = п + 1;
Аккер(т, 0) = Аккер(т - 1,1), если т > 0;
Аккер(т, п) = Аккер(т — 1, Аккер(т, п — 1)), если п, т > 0.
Процедуру вычисления функции Аккермана можно описать следующим образом:
Процедура Аккер(т, п):
Если т = 0, то Аккер(т, п) = п + 1;
Если га > 0 и п = 0, то Аккер(т, п) = Аккер(т - 1,1);
Если т > 0 и п > 0, то Аккер(т, п) = Аккер(т - 1, Аккер(т, п - 1));
Конец процедуры.
Попробуйте вычислить вручную значение АккерC,2). ?
ПРИМЕР 5.8. Приведем еще один пример рекурсивного определения функции.
Рассмотрим функцию, которая выражает величину ежегодной ренты, когда сумма
Р инвестируется в течение п периодов с процентной ставкой г за один период,
причем подсчет производится в конце каждого периода. Для начала заметим, что
если сумма Р, которая инвестируется на некоторый период с процентной ставкой
г, выражается десятичным числом, то в конце периода объем инвестиции будет
равен основной сумме плюс начисленные проценты. Проценты, начисляемые за
первый период, составляют гР, так что общий объем инвестиции будет равен
Р-f гР = A + г)Р. Например, если $1000 инвестировано на год под 5%, то г = .05.
Тогда в конце года общий объем вклада будет равен $1000 инвестированных
плюс .05 х $1000 = $50. Если другие деньги не вкладываются, то в конце второго
периода вклад составит A 4- г)Р + гA 4- г)Р = A4- гJР, где гA 4- г)Р — проценты
от вложенния A 4- г)Р. К концу второго периода сумма инвестиции составит
A 4- гJР. В нашем примере по прошествии двух лет инвестиция в $1000 даст
сумму $1050 плюс проценты, которые составят .05A050). По прошествии п лет
начальная инвестиция вырастет до A 4- г)пР.
Теперь предположим, что сумма Р инвестируется в конце каждого периода в
течение п периодов с процентной ставкой г за каждый период, и подсчет произво-
производится в конце каждого периода. На только что вложенную сумму Р проценты не
начисляются, поэтому она остается равной Р. Вклад Р, инвестированный в пре-
предыдущий период, вместе с начисленными процентами составляет теперь (l-M)-R
Вклад, инвестированный в позапрошлый период, вместе с процентами за два пе-
периода составляет A-ИJР. Продолжая подсчет, находим, что общая сумма вклада,
накопленная за п периодов, равна
Р 4- A 4- г)Р + A + г?Р + ••• + (! + г)п~1Р = Р • 5(п, г),

(i + On-i (H
r
r
-г)"
— 1
- 1
- 1
РАЗДЕЛ 5.2. Рекурсивные функции и алгоритмы 193
где S(n, г) = 1 + A 4- г) + A + гJ + • • • + A 4- i)n~l и представляет собой геомет-
геометрическую прогрессию
Следовательно,
Очевидно, более эффективно вычислять функцию S(n, г) непосредственно,
но она может быть вычислена и рекурсивно. Заметим, что
S(n + 1, г) = 1 + A + г) + A + гJ + ¦ • • + A + г)" + A + *)" =
= 1 + A + »)A + A + 0 + A + гJ + • • • + A + г)") =
= 1 + A + гM(п,г).
Следовательно, рекурсивное определение функции S(n, г) имеет вид:
5A,0 = 1;
S(n, г) = 1 + A + i)S(n — 1, г) для п > 1. q
Теперь рассмотрим рекурсивный алгоритм, который не является определени-
определением рекурсивной функции. Согласно старой легенде, в задаче о Ханойской башне
фигурируют три стержня и набор дисков разного диаметра. Диски нанизаны на
один из стержней в порядке убывания их диаметра, причем диск наибольшего
диаметра находится в самом низу, а диск наименьшего диаметра — самый верх-
верхний. Задача состоит в том, чтобы переместить все диски на другой стержень с
сохранением порядка. При этом диски можно перемещать со стержня на стержень
по одному за раз, и диск большего диаметра нельзя помещать над диском мень-
меньшего диаметра. Очевидно, что мы имеем дело с рекурсивной задачей, поскольку,
если на стержне имеется, например, шесть дисков и известно, как переместить
пять из них, то пять верхних дисков можно переместить на средний стержень,
затем переместить последний диск на свободный стержень, а затем поместить
пять дисков со среднего стержня поверх самого большого диска. Эта ситуация
проиллюстрирована на рис. 5.3.
Опишем алгоритм перемещения п дисков с первого стержня на третий. Пе-
Перенумеруем стержни от 1 до 3 и, кроме того, отождествим их с переменными А,
Б и С, которые могут принимать значения от 1 до 3.
Процедура Хан(Л, С, п):
Если п = 1, переместить единственный диск со стержня А на С;
Положить В = 6 — А — С;
Если и > 1, то
Сместить верхние п—\ дисков на В, используя Хан(ДБ,п— 1);
Сместить последний диск с А на С, используя Хан(Д С, 1);
Сместить верхние п — 1 дисков на С, используя Хан(Б,С, п — 1);
Конец процедуры.

194 ГЛАВА 5. Алгоритмы и рекурсия
Рис. 5.3
Например, если п = 3, начинаем с ХанA, 3,3), так что А = 1}В = 2иС = 3.
Находясь внутри процедуры ХанA,3,3), мы вызываем процедуру ХанA,2, 2), ко-
которая должна переместить два верхних диска на стержень 2. Для ХанA,2,2)
имеем: А = 1, В = 3 и С = 2. Из процедуры ХанA,2,2) мы вызываем про-
процедуру ХанA,3,1), которая должна переместить верхний диск со стержня 1 на
стержень 3. Далее вызываем ХанA,2,1), чтобы переместить второй диск на стер-
стержень 2. Затем вызываем ХанA,3,1), чтобы переместить второй диск со стержня 1
на стержень 3. Затем вызываем ХанC,2,1), перемещая верхний диск со стерж-
стержня 2 поверх второго диска на стержне 3. Возвращаемся к ХанA,3,3) и вызываем
ХанA,3,1), перемещая тем самым самый нижний диск со стержня 3 на стер-
стержень 1. Затем вызываем ХанB,3,2) для перемещения двух дисков со стержня 2
на стержень 3. В этот момент А = 2, В = 1 и С = 3. Из процедуры ХанB,3,2)
вызываем ХанB,1,1) для перемещения верхнего диска со стержня 2 на стер-
стержень 1. Далее вызываем ХанB,3,1) для перемещения второго диска со стержня
2 на стержень 3. Наконец, вызываем ХанA,3,1) для перемещения верхнего диска
со стержня 1 поверх всех дисков на стержне 3. Этим мы завершаем выполнение
процедур ХанB,3,2) и ХанA,3,3), и игра заканчивается.
Легенда гласит, что на один из трех бриллиантовых стержней нанизаны 64
золотых диска. Некий монах перемещает диски согласно правилу, приведенному
выше, со скоростью одно движение за секунду. Согласно легенде, когда монах
выполнит эту миссию, наступит конец света. Спрашивается, как долго продлит-
продлится этот процесс? Построим функцию для вычисления количества движений (и,
следовательно, количества секунд), необходимых для переноса п дисков с одно-
одного стержня на другой. Обозначим эту функцию Н. Известно, что если п = 1,
то для переноса диска с одного стержня на другой требуется одно движение.
Следовательно, НA) = 1. Допустим, что Н(к — 1) известно. Тогда Н(к), количе-
количество движений, необходимых для переноса к дисков со стержня 1 на стержень 3,

РАЗДЕЛ 5.2. Рекурсивные функции и алгоритмы 195
складывается из Н(к - 1) движений, необходимых для переноса к - 1-го диска
со стержня 1 на стержень 2, одного движения по переносу нижнего диска со
стержня 1 на стержень 3 и Н(к — 1) движений, необходимых для переноса к — 1-
го диска со стержня 2 на стержень 3. Таким образом, рекурсивное соотношение
Н(к) = 2Н(к — 1) + 1 задает искомую рекурсивную функцию.
Попробуем задать эту функцию непосредственно. С этой целью вычислим
несколько первых значений Н и попытаемся найти общее выражение для Н{п).
ЯB) = 2-1 + 1 = 3;
ЯC) = 2-3 + 1 = 7;
ЯD) = 2-4 + 1 = 15;
ЯE) = 2-15 + 1 = 31.
Если к каждому члену последовательности 1, 3, 7, 15, 31 прибавить 1, полу-
получим 2, 4, 8, 16, 32. Поэтому можно предположить, что Н(п) = 2П —1. Докажем это
по индукции. Очевидно, утверждение справедливо для п = 1. Предположим, что
оно справедливо для п = /с, т.е. Я(/с) = 2fc — 1. Нужно показать, что утверждение
справедливо для п = fc + 1, т.е., что i/(fc + 1) = 2fc+* — 1. Но
fi{k-\-l) = 2 • /з [к) + 1 = z-(z — 1) + 1 = 2 —1.
Следовательно, наше предположение верно. Предлагаем читателю определить,
когда, если верить легенде, наступит конец света.
Ранее в этом разделе мы осуществляли переход от рекурсивного описания
функции к непосредственному. Для этого мы вычисляли несколько первых зна-
значений функции и по ним пытались определить вид выражения, задающего функ-
функцию непосредственно. Такая процедура называется исключением рекурсии, или
решением рекурсивной функции. Давайте рассмотрим еще несколько примеров
исключения рекурсии, а также примеры перехода от непосредственного задания
функции к рекурсивному.
ПРИМЕР 5.9. Исключим рекурсию из следующего рекурсивного определения:
/A) = 1;
f(k) = f(k -1) + k.
Имеем
1-2

196 ГЛАВА 5. Алгоритмы и рекурсия
Разумно предположить, что функция имеет вид
Чтобы доказать справедливость этой формулы, нужно показать, что данная
функция удовлетворяет нашему рекурсивному определению, т.е. показать, что
функция f(n) = п(п+1) удовлетворяет соотношениям
Сначала покажем, что /A) = 1:
Затем покажем, что f(k) = f(k — 1) -f k:
k2-k 2k
2 + 2
k2 + k _
2
fe(fc + 1) _
_ , ,, . n(n + 1)
Таким образом, f(n) = —^——- удовлетворяет рекурсивному определению. П
ПРИМЕР 5.10. Исключите рекурсию для функции, заданной соотношением
fc) = 2-fe-/(fc-l).
Имеем следующие равенства:
/A) = 2 = 21 • 1!;
/B) =2-2-2 = 22-2!;
/C) = 2-2-2-2-3 = 23-3!;
/D) = 2-2-2-2-3-2-4 = 24-4!
/E) = 2-2-2-2-3-2-4-2-5 =

РАЗДЕЛ 5.2. Рекурсивные функции и алгоритмы 197
Отсюда можно предположить, что искомая функция задается выражением /(п) =
2П • п!. Чтобы это доказать, нам нужно показать, что данная функция удовле-
удовлетворяет приведенному выше рекурсивному определению. Иными словами, нужно
показать, что функция /(п) = 2п • п! удовлетворяет соотношениям
Проверим сначала, что /A) = 2:
/A) = 21 • 1! = 2.
Далее покажем, что f(k) = 2kf(k - 1). Но
= 2k - k\ .
Итак, функция f(n) = 2n • n! удовлетворяет рекурсивному определению. ?
ПРИМЕР 5.11. Для функции /(n) = n(n+1NBn+1) найдем задающие ее рекурсив-
рекурсивные соотношения. Имеем
Д1) = 1 =12;
/B) = 5 =12 + 22;
/C) = 14 = 12 + 22 + 32;
/D) =30 = 12+22 + 32+42;
/E)-55 = 12 + 22+32 + 42 + 52.
Поэтому можно предположить, что
Для доказательства применим индукцию. Очевидно, что /A) = 1. Допустим, что
_ 1) = (t-i)(*)P*-0 , „ покаже„, что тогда /(It) =
6
(fc - l)Bfc - 1) + 6k
6
- 4k +
6
l)Bfe
= /(fe). ?

198 ГЛАВА 5. Алгоритмы и рекурсия
¦ УПРАЖНЕНИЯ
1. Найдите /A), /B), /C) и /D) для приведенных ниже рекурсивных функ-
функций:
а) { № = 3, . f /@) = 1,
' \ № = 3/(fc - 1). °' \ f(k) = 2f(k - 1) + 3fe.
в) / /@) = 2' г) I /@) = X'
' I f(k) = (f(k-l))\ r) \ /(fc) = fc2/(fc-l).
лч Г /@) = i,
д) \ ^
f(k) =
2. Найдите /A), /B), /C) и /D) для следующих рекурсивных функций:
- 0
= 4'
/@) = 2
/(*) = 8'^ - (/(fc -1)J г)
/@) = 2,
3. Найдите /B), /C), /D) и /E) для следующих рекурсивных функций:
/(о) -1,
а) { 1A) = 3,
/@) - О,
б) { /A) = 1,
/@) = 1,
в) { /A) = 2,
/@) = 1,
г)
/@) = -1,
д)
4. Найдите /B), /C), /D) и /E) для следующих рекурсивных функций:
/@) - 2,
а)
/(/с) = 3/(fc - 1) - 2/(fc - 2).
/@) = 1,
б)

РАЗДЕЛ 5.2. Рекурсивные функции и алгоритмы 199
о,
в) { /A) = 2,
-2))!.
/@) = Ю,
/@) = -1,
д) { /A) = 1,
5. Найдите явные выражения для /(п), исключив рекурсию из следующих
определений:
а) \ '<°> = *' б) / /@) = Х'
' I /(*) = 2/(* - 1). &) \ /(fc) = 1 + /(*: - 1).
г)
д) I /@) = Х
/(*) = 5/(fc - 1).
6. Найдите явные выражения для /(п), исключив рекурсию из следующих
определений:
Г /@) = 2,
а)
, /@) = -1,
в) ffM _ -1 г)
ДО) = -1,
/@) = 1, е) J /A) = 1?
"/(fc-2)"
7. Докажите, что ап = 7 - 2й4 удовлетворяет рекурсивному определению
а0 = 5,
ак = 2o>k-i — 7 при к > 0.
8. Докажите, что an = 3n — n3n+1 удовлетворяет рекурсивному определению
а0 = 1,
а\ = —6,
а^ = 6а&_1 — 9а^_2 при к > 1.
9. Докажите, что ап = -1 - 2n+1 удовлетворяет рекурсивному определению
а0 = -3,
аг = -5,
пк = 6а?_1 — 8а^_2 — 3 при к > 1.

200 ГЛАВА 5. Алгоритмы и рекурсия
- rn+1
1 r
10. Докажите, что ап = — удовлетворяет рекурсивному определению
1 — v
f а0 = 1,
\ dk = cik-i
гк при fc > 0.
11. Докажите, что ап = (п2 4- п 4-1) удовлетворяет рекурсивному определению
ai=3,
a/c = afc_i 4- 2fc при fc > 1.
12. Докажите, что ап = n2(n 4- IJ удовлетворяет рекурсивному определению
1=4,
,к = a/c-i 4- 4fc3 при fc > 1.
13. Докажите, что ап = —2(—1)п 4-2 • Зп удовлетворяет рекурсивному определе-
определению
а0 = 0,
ai=8,
ajt = 2a^_i 4- 3a^_2 при fc > 2.
14. Докажите, что ап = 2(—3)n4-5-2n удовлетворяет рекурсивному определению
а0 = 7,
ak = —ак—\ 4- 6afc_2 при fc > 1.
15. Докажите, что ап = 3(-2)п + 2 • Зп - 3 • B)п удовлетворяет рекурсивному
определению
&о = 2,
о>1 = -6,
afc = afc-i 4- 6afc_2 4- 3 • B)к при fc > 1.
16. Докажите, что
удовлетворяет рекурсивному определению
ai = 1,
^2 = 1,
ak = afc_i 4- а^_2 при fc > 1.
17. Как скоро, согласно легенде о Ханойской башне, наступит конец света после
того, как монах начнет перекладывать диски?

РАЗДЕЛ 5.3. Сложность алгоритмов 201
5.3. СЛОЖНОСТЬ АЛГОРИТМОВ
В примере с Ханойской башней нам требовалось 2П — 1 отдельных перемеще-
перемещений дисков, чтобы переложить п дисков с одного стержня на другой. Зачастую
важно иметь возможность оценивать число элементарных операций или время,
необходимое компьютеру для выполнения всего алгоритма. Это не всегда одно
и то же, поскольку выполнение одних операций длится дольше, чем выполнение
других. Необходимо учитывать и другие факторы, такие как требуемый для вы-
выполнения алгоритма объем памяти компьютера, точность вычислений и многое
другое. Очевидно, что на самом деле это важно только для программ, требующих
для выполнения значительного времени. Время выполнения зачастую зависит от
такого фактора, как объем входных данных. В вышеупомянутом примере таковым
является и — количество дисков. Время или число операций, необходимых для
выполнения процедуры, увеличивается по мере увеличения п.
ОПРЕДЕЛЕНИЕ 5.12. Пусть область определения функций / и д — множе-
множество целых положительных чисел, а множество их значений — множество
действительных чисел. Говорят, что функция д мажорирует функцию /, если
существует действительное число к и целое положительное число га такое, что
|/(п)| < к\д(п)\ для всех п > га. Если д мажорирует /, это обозначается как
f{n) = О(д(п)). Символ О(д(п)) читается как "О большое" от д(п)\ при этом
говорят, что /(п) имеет порядок О большое от д{п).
Для положительных целых чисел г и s следующую теорему можно доказать
методом индукции. Справедливость утверждения теоремы для положительных
рациональных чисел г и s можно показать, не используя логарифмы (см. упраж-
упражнения).
ТЕОРЕМА 5.13. Если г и s — действительные числа, г < s и п > 1, тогда пг < п3.
Следовательно, пТ — O(ns).
ДОКАЗАТЕЛЬСТВО. Функция 1п(х) — возрастающая, поэтому а < Ь тогда и
только тогда, когда 1п(а) < 1п(Ь). Отсюда nr < ns тогда и только тогда, когда
ln(nr) < ln(n5), что, в свою очередь, выполняется тогда и только тогда, когда
rln(n) < sln(n), т.е. тогда и только тогда, когда г < s, поскольку 1п(п) для
п > 1 — величина положительная. ¦
Следующая теорема показывает, что свойство функции иметь порядок О(д(п))
замкнуто относительно операций сложения и умножения на скаляр. Это значит,
что рассматриваемые функции образуют векторное пространство, хотя изучение
подобных вопросов выходит за рамки данной книги.
ТЕОРЕМА 5.14. Если f(n) = О{д(п)), то cf(n) = О(д(п)).
ДОКАЗАТЕЛЬСТВО. По определению, |/(п)| < А:|^(гг)| для некоторого постоян-
постоянного действительного числа к и всех п, больших или равных некоторому целому
числу т. Поэтому
\cf(n)\<k\c\\g(n)\
ис/(п)=О(9(п)). ¦

202 ГЛАВА 5. Алгоритмы и рекурсия
ТЕОРЕМА 5.15. Если /(п) = О(д(п)) и h(n) = О(д(п))у то (/ 4- h)(n) = О(д(п)).
ДОКАЗАТЕЛЬСТВО. По определению, для некоторого постоянного к и некото-
некоторого целого числа mi имеем |/(n)| < fc|g(n)| для всех п > mi. Опять же по
определению, для некоторой постоянной I и некоторого целого числа т2 имеем
|Л(п)| < 1\д{п)\ для всех и > т2. Пусть m = max(mim2). Следовательно, для
всех п > т
\f(n) + h(n)\<\f(n)\ + \h(n)\<
<к\д(п)\+1\д(п)\ =
= (к + 1)\д(п)\
ТЕОРЕМА 5.16. Если /(п) = О(д(п)) и h(n) = О(е(гг)), то (/-Л)(п) = О((д-е)(п)).
ДОКАЗАТЕЛЬСТВО. По определению, для некоторого постоянного А; и некото-
некоторого целого числа mi имеем |/(n)| < /c|g(n)| для всех п > mi. Также по опре-
определению, для некоторого постоянного I и некоторого целого числа тп2 имеем
\h(n)\ < 1\е(п)\ для всех п > т,2. Пусть т — max(mim2). Поэтому для всех
п > т
\f(n)-h(n)\ = \f(n)\-\h(n)\<
<к\д(п)\1\е(п)\ =
= kl\g(n).e(n)\
и (/•/i)(n) = О((9 • е)(п)). ¦
Следующая теорема утверждает, что степень полинома единственным обра-
образом определяет его мажоранту.
ТЕОРЕМА 5.17. Если р(п) — а,кпк + а.к-\пк~1 + • • • + а2п2 + ахп + а<э, то р(п) =
О{пк).
ДОКАЗАТЕЛЬСТВО.
\{)\ \к 4- ak-ink~l Н h а2п2 + ain + ао\ <
< \акпк\ + Idfc-ink-1! H Ь |а2п2| + \ain\ 4- |ао| <
(в силу неравенства треугольника: \А 4- В\ < \А\ 4- \В\)
< \ак\пк + \ak-i\nk~1 +••• + |a2|n2 + |ai|n4-|a0| <
< \ак\ пк + |afc_i| пк 4- • • • 4- \а2\ пк 4 \аг\пк 4- \ао\ пк =
по теореме 5.13
= (\ак\ + |afc_i| + • • • 4- \а2\ + \аг\ + \ао\)пк
и р[п) = О(пк). Ш
ТЕОРЕМА 5.18. Для целых чисел а и 6, больших единицы, loga(n) = O(log6(n)).

РАЗДЕЛ 5.3. Сложность алгоритмов 203
ДОКАЗАТЕЛЬСТВО. Следует непосредственно из равенства loga(n) = -—^j^-. ¦
l°ga(o)
ТЕОРЕМА 5.19. Пусть п — неотрицательное целое число. Тогда и < 2п и, следо-
следовательно, п = ОBП).
ДОКАЗАТЕЛЬСТВО. Воспользуемся индукцией, имея для п = 0, 0 < 2° = 1.
Допустим, что к < 2к, тогда
и, по индукции, п < 2п. Ш
Пусть R — отношение на множестве функций со значениями во множестве
целых положительных чисел, определенное как fRg, если f(n) = O(g(n)). Оче-
Очевидно, отношение R рефлексивно. Приведенная ниже теорема утверждает, что
это отношение также и транзитивно. Доказательство теоремы предоставляется
читателю.
ТЕОРЕМА 5.20. Если /(п) = О(д(п)) и д(п) = O(h(n))9 то /(n) = O(h(n)).
Следующая теорема дает ответ на вопрос о том, какие функции могут вы-
выступать в роли мажорант для других функций.
ТЕОРЕМА 5.21. Для целых чисел а, больших единицы, loga(n) = О(п).
ДОКАЗАТЕЛЬСТВО. Согласно теореме 5.19, имеет место неравенство п < 2п.
Поэтому Iog2(n) < Iog2Bn) — nw Iog2(n) = О(п). Поскольку loga(n) = O(log2(n)),
то по теореме 5.18 имеем loga(n) = О(п). Ш
Доказательство сформулированных ниже теорем предоставляем читателю.
ТЕОРЕМА 5.22. Пусть п — неотрицательное целое число, тогда п\ < пп и, сле-
следовательно, п! = О(пп).
ТЕОРЕМА 5.23. Пусть a > 1 и п — неотрицательное целое число, тогда loga(n!) <
nloga(n), следовательно, loga(n!) = O(nloga(n)).
Ранее, при решении задачи о Ханойской башне, определялось число шагов,
необходимых для перемещения дисков. В примере, приведенном ниже, определя-
определяется число арифметических операций, необходимых, соответственно, для сложе-
сложения двух матриц и умножения двух матриц.
ПРИМЕР 5.24. Рассмотрим алгоритм сложения матриц:
Процедура Сложение матриц(А, В, т, п):
Цикл по г от 1 до т:
Цикл по j от 1 до п:
Cij = Aij + B{j;
Конец цикла;
Конец цикла;
Конец процедуры.
Как видим, сложение выполняется для каждого г и каждого j. Поскольку г при-
принимает т значений, а j принимает п значений, то выполняется тп операций
сложения. Пусть iV = max(m, n). Тогда число выполняемых арифметических опе-
операций имеет порядок O(N2). ?

204 ГЛАВА 5. Алгоритмы и рекурсия
ПРИМЕР 5.25. Алгоритм умножения матрицы А размера га х р и матрицы В
размера р х п имеет вид:
Процедура Умножение матриц( A, J3, т, р, п):
Цикл по г от 1 до га:
Цикл по j от 1 до п:
Cxj = 0;
Цикл по к от 1 до р:
Значение С^ заменить на Qj + AikB^j ;
Конец цикла;
Конец цикла;
Конец цикла;
Конец процедуры.
Поскольку к принимает значения от 1 до р, то выполняется р операций сложения
и р операций умножения. Величина к изменяется от 1 до р для каждого г и каждо-
каждого j, поэтому к пробегает значения от 1 до р тп раз. Таким образом, выполняется
тпр операций сложения и тпр операций умножения. Следовательно, всего вы-
выполняется 2тпр операций. Пусть N = тах(га, п,р). Тогда число выполняемых
арифметических операций имеет порядок O(NS). ?
ПРИМЕР 5.26. Сравним количество операций, которое требуется для непосред-
непосредственного вычисления значения р(с), где р(х) = апхп + an-ixn~l -\ + а2х2 +
а\х + ао, с количеством операций, которое потребуется для вычисления того же
значения при помощи схемы Горнера.
Если р(с) вычисляется непосредственно, то для подсчета ск требуется вы-
выполнить к — 1 операций умножения. Еще одна операция нужна для умножения
на аь так что вычисление akCk требует к операций умножения. Таким образом,
нужно выполнить 1-ь2 + 3 + ---+п= n(n2+1) умножений. Для того чтобы найти
сумму и 4- 1 слагаемых, требуется выполнить п сложений, так что общее число
арифметических операций равно n ^ *' -f n и имеет порядок О(п2).
Если мы вычисляем р(а), где р(х) — полином, используя схему Горнера, то
прежде всего замечаем, что выражение а4х4Н-азх34-а2Х2+а1Х+ао = x(x(x(a4x +
^з) + а2) + Q>i) + ^o включает четыре операции сложения и четыре операции
умножения. Далее мы определяем, что в общем случае р(х) = х(х(- • -х((апх +
an_i) 4- an-2) H h a2) + ai) -f a0 включает п операций сложения и п операций
умножения. Таким образом, общее число арифметических операций равно 2п и
имеет порядок О(п). ?
¦ УПРАЖНЕНИЯ
1. Сколько нужно выполнить перемещений в задаче о Ханойской башне, если
число дисков равно восьми?
2. Как говорилось ранее, существует древняя легенда (начала девятнадцатого
века) о том, что на один из трех бриллиантовых стержней нанизано 64
золотых диска, которые некий монах перемещает со стержня на стержень со
скоростью одно движение за секунду. Согласно легенде, по окончании этой
миссии наступит конец света. Как скоро это произойдет?

РАЗДЕЛ 5.4. Алгоритмы сортировки 205
3. Оцените количество арифметических операций, необходимых для вычисле-
вычисления указанных ниже значений полиномов (i) при непосредственном вычис-
вычислении, (и) при помощи схемы Горнера.
а) /C), где f(x) = Зх2 + 4х + 5;
б) /B), где /(я) = 2х4 + 4х3 + Зх2 + 2х + 3;
в) /D), где f(x) = хъ 4- 4х4 + 2х3 4- 6х2 4- х 4- 3.
4. Оцените количество арифметических операций, необходимых для вычисле-
вычисления следующих произведений:
а)
в)
3 -1
2 7
-5 О
2 -1
5 1
б)
1
3
6
-1
1
-1
2
4
5
2
5
0
-2
5
6
8
1
4
1
3
4
5
[ -2 3 -5 0 ].
5. Какие из приведенных ниже функций имеют порядок Ofa3)}
а) п4-Зп4-5; б) п2 - 6п 4-5; в) Aп(п)K;
г) n(ln(n)J; д) n2ln(n).
6. Какие из приведенных ниже функций имеют порядок О(п3)?
a) 6n3 + 3n2 + 2n + 5; б) n3ln(n); в) ln(nnln<n));
г) loga(n!); д) п\.
7. Пусть п — некоторое неотрицательное целое число. Докажите, что п! < пп
и, следовательно, п\ = О(пп).
8. Докажите, что для а > 1 и п е N справедлива оценка loga(n!) < nloga(n),
поэтому loga(n!) = O(nloga(n)).
9. Докажите, что если /(п) = О(д(п)) и д{п) = O(h(n)), то /(п) = О(/г(п)).
10. Докажите, что для целого числа а, большего единицы, loga(n) = О(п).
11. Используя индукцию, докажите, что если г и s — положительные целые
числа, г < s и п > 1, то nr < ns. Отсюда пТ = O{ns).
12. Используя результаты предыдущих задач, докажите, что для положительных
рациональных чисел г и s, г < s и п > 1, из неравенства пг < п3 следует,
что пг = О(п3).
5.4. АЛГОРИТМЫ СОРТИРОВКИ
В этом разделе мы рассмотрим некоторые методы сортировки данных. В даль-
дальнейшем мы будем считать выполненными два условия. Во-первых, будем считать,
что данные пронумерованы так, что имеется первый элемент данных, второй эле-
элемент, и так далее до n-го. Такая организация данных может быть реализована
при помощи массива, указателей или еще каким-либо образом. Конкретный ме-
метод реализации списка нас не интересует. Второе предположение состоит в том,
что на множестве данных введено полное упорядочение, и мы хотим расположить

206 ГЛАВА 5. Алгоритмы и рекурсия
данные в соответствии с этим порядком. Это может быть лексикографическое упо-
упорядочение (т.е. упорядочение по алфавиту) или же упорядочение в соответствии
с числовыми значениями, которые приписываются элементам данных. Опять же,
нас не интересует, что это за упорядочение, лишь бы оно было задано. В дальней-
дальнейшем запись а < b будет означать, что в нашем упорядочении а предшествует 6.
Для начала рассмотрим сортировку выбором (СВ). Пусть а\, а2, ..., ап —
элементы, подлежащие сортировке. Сам процесс сортировки очень прост. Мы
фиксируем элемент а\, находим наименьший элемент и меняем местами этот
элемент и а\. Затем переходим к а2. Рассматриваем все элементы, начиная с а2,
находим среди них наименьший и меняем местами этот элемент и а2. Процесс
продолжаем до завершения. Более строго: пусть мы находимся на этапе, когда
необходимо заменить а;. Введем переменную ram, для того чтобы отслеживать
индекс наименьшего элемента среди а* и всех тех элементов, которые за ним
следуют. Сначала полагаем ram = г и начинаем сравнивать оставшиеся элементы
с dmin. Если находим элемент, который меньше am{n, скажем аь полагаем ram =
к и продолжаем поиск наименьшего элемента, сравнивая его с am{n. Если таковой
находится, процесс повторяем. Дойдя до n-го элемента, меняем местами а* и amin
и переходим к a.i+\. Теперь мы можем записать алгоритм.
Процедура СВ:
Цикл по г от 1 до и — 1:
Положить ram = г;
Цикл по j от 1 до п:
Если uj < amin, то пусть ram = j\
Конец цикла;
Поменять местами а^ и amin;
Конец цикла;
Конец процедуры.
ПРИМЕР 5.27. Пусть с, 6, a, v, /г, d — список для сортировки. Начинаем с с на
позиции 1 и полагаем ram = 1. Сравниваем с с b и, поскольку Ъ < с и b находится
на второй позиции, полагаем min = 2. Далее сравниваем b с а и, поскольку а < Ь,
полагаем ram = 3. Букв, меньших а, не находим, поэтому меняем местами а и Ь,
получая в результате а, 6, с, v, /i, d. Повторяем процесс, начиная с Ь, поэтому ram =
2. Сравнение b с оставшимися буквами показывает, что ни одна из них не меньше
Ь, так что ram остается равным 2, и мы меняем местами b с самим собой. Далее
переходим к с и полагаем ram = 3. Опять ни один элемент не меньше с, поэтому
с остается на том же месте. Переходим к г; и полагаем ram = 4. Поскольку h < v,
то ram = 5. Затем сравниваем h и d. Поскольку d < v, полагаем min = 6. Меняем
местами d и v, получая последовательность а, 6, c,d, /г, v. Продолжаем процесс для
h, а так как h < v, то сортировка закончена. ?
Рассмотрим число сравнений, которое производится согласно этому методу,
для списка из п элементов. Первый элемент сравнивается с остальными п — 1
элементами. Второй элемент сравнивается с п — 2 элементами и так далее до
(п — 1)-го элемента, который сравнивается только с одним элементом. Таким

РАЗДЕЛ 5.4. Алгоритмы сортировки 207
образом, имеем
так что число сравнений имеет порядок О(п2).
Теперь рассмотрим весьма популярный алгоритм сортировки, очень напоми-
напоминающий сортировку выбором. Он называется пузырьковой сортировкой (ПС),
так как в нем меньшие числа поднимаются вверх, как пузырьки в воде. (В дан-
данном случае "вверх" означает налево.) Процесс начинают с правого конца списка и
сравнивают два последних элемента, сдвигая меньший влево. Затем сравнивают
этот меньший с элементом, стоящим слева от него, и опять передвигают мень-
меньший из них влево. Процесс продолжают, пока не будет достигнут первый элемент.
В результате наименьший элемент становится первым элементом. Затем процесс
повторяется до тех пор, пока он не вернется ко второму по величине элемен-
элементу. Теперь второй по величине элемент располагается на втором месте. Процесс
повторяется до тех пор, пока все элементы не будут рассортированы.
На данном этапе новым является то, что при такой сортировке движение
происходит с двух сторон. Процесс начинается справа, движется влево вплоть
до первого элемента. Затем опять начинается справа, движется влево вплоть
до второго элемента. Всякий раз движение влево осуществляется вплоть до j-
го элемента данных, при этом значение j возрастает. Для описания такого рода
перемещений нам понадобится новая разновидность цикла перечислением. Говоря
"цикл по г от п до к с шагом —1", где п > fc, мы будем иметь в виду, что, начиная
с г — п, мы будем шаг за шагом уменьшать значение г на 1, вплоть до г = к.
Процедура ПС:
Цикл по г от 2 до гг:
Цикл по j от и до г с шагом —1:
Если clj < dj-i, то поменять местами dj и a^-i;
Конец цикла;
Конец цикла;
Конец процедуры.
ПРИМЕР 5.28. Пусть, как и ранее, с, Ь, a, v, /г, d — список для сортировки. Сначала
меняем местами h и d, поскольку d меньше, чем /г. Затем меняем местами d и
v, т.к. d меньше, чем v. На данный момент список выглядит таким образом:
с, 6, a, d, г>,/г. Поскольку d не меньше, чем а, мы не меняем местами and. Теперь
меняем местами b и а, поскольку а меньше, чем Ь. Наконец, меняем местами а и
с, т.к. а меньше, чем с. Состояние списка на данном этапе — а, с, 6, d, v, h.
Повторяя процесс, меняем местами h и v, поскольку h меньше и. Оставляем
d на своем месте, т.к. h не меньше d. Теперь список имеет вид а, с, 6, d, /г, v. Также
на своих местах остаются d и 6, поскольку d не меньше Ь. Элемент b меньше с,
поэтому бис меняются местами, и мы получаем а, 6, с, d, h,v. Несмотря на то, что
процесс повторялся трижды, лишние перестановки не потребовались, сортировка
закончилась. ?
Если проанализировать процесс сравнения в этом просмотре п элементов,
то в первом цикле он включает гг — 1 операцию, во втором — п — 2 операции.

208 ГЛАВА 5. Алгоритмы и рекурсия
Процесс завершается выполнением одного сравнения в последнем цикле. Отсюда
получаем
так что общее число сравнений имеет порядок О(п2). Таким образом, получен-
полученное значение совпадает с соответствующей величиной для сортировки выбором.
Несмотря на то, что число операций сравнения этих двух методов имеет один и
тот же порядок, их скорости в реальных случаях могут различаться.
Теперь рассмотрим алгоритм сортировки, который называется быстрой сор-
сортировкой (БС). Это первый метод сортировки, который будет определен рекур-
рекурсивно. Процесс быстрой сортировки состоит с следующем: мы берем аь первый
элемент списка данных, затем каждый элемент (исключая ах) помещаем слева от
аь если он меньше или равен а\. Назовем этот список S\. Затем поместим справа
от а\ каждый элемент, который больше а\. Назовем этот список 52. Теперь при-
применим этот же процесс к S\ и S^- Процесс продолжаем до тех пор, пока в каждом
списке не останется по одному элементу. Затем собираем новый список, каждый
раз производя конкатенацию Sj, a;, S^+i в список SidiSi+i, где а^ — элемент,
который послужил основой для создания Si и Si+i. Более формально алгоритм
описывается следующим образом:
Процедура БСA,п):
Положить I = 1 и г = п\
Если I ф г, то
Положить га = I и разбить список (а/,а/_|_1,а/+2, • • • ,flr) на 5Ь
полученный как {а; : а^ < а/, г ф /},
и 52, полученный как {а* : а; > а/, }, так что
S\ = (a/,af+i,aj+2,...,aj) и 52 = (aj+i,aj+2,aj+3, • • • ,ar)
после переобозначения;
Произвести конкатенацию БСA, j), am и BC{j -f l,r);
Конец процедуры.
ПРИМЕР 5.29. Пусть, как и ранее, d, 6, с, г, г;,/г, a —- список для сортировки. По-
Поскольку d — первый элемент списка, разбиваем список на два подсписка: Ь,с,а —
элементов, меньших d, и г, v, h — список элементов, больших d. Далее, соглас-
согласно процедуре БС первым рассматриваем левый из вновь созданных подсписков,
там мы используем Ь для разделения с и а на списки, где а будет слева, ас-
справа. После конкатенации получаем а, 6, с и возвращаемся к первому шагу, где
процедура БС вызывается для списка справа от d, а именно, г, v,h. Буква г ис-
используется для разделения v и h в списки h и v. После конкатенации имеем
h,r,v. И, наконец, последняя конкатенация дает список а, 6, с, d, h, r, v. ?
Теперь оценим количество операций сравнения, используемых в этом про-
процессе. Быстрая сортировка реализуется наиболее оптимально, когда п = 2т для
некоторого т, и каждое разбиение делит список элементов ровно пополам. Пред-
Предположим, что это так. Если Qn — число сравнений в быстрой сортировке для
списка из п элементов, тогда имеется и операций сравнения для определения,
в какой из списков попадет тот или иной элемент. Далее будет уже два списка

РАЗДЕЛ 5.4. Алгоритмы сортировки 209
оставшихся п — 2 элементов, каждый из которых потребует Q* операций сравне-
сравнения, поэтому Qn = 2Q™ +п. Но п = 2т, так что
__,-i+2m.
Поэтому
2m 2m~l
= 2rn~2 + ~*~ =
2 =
2m—2
""""' +3 =
2т—3
2rn~r
+ т =
Поскольку п = 2т, то т = Iog2(n), поэтому Qn = n(Qi + Iog2(n)), что приблизи-
приблизительно равно nln(n). Таким образом, число сравнений имеет порядок О(пIog2(n)).
Самый неблагоприятный случай и наибольшее число операций сравнения реали-
реализуются, когда элемент, который обычно разделяет множество элементов, всегда
остается в конце списка. В этом случае число операций сравнения совпадает с
тем, которое требуется в рассмотренных ранее алгоритмах сортировки, поэтому в
самом неблагоприятном случае число сравнений имеет порядок О(п2).
Аналогичной, но более простой для понимания процедурой, является сорти-
сортировка слиянием (СС). Процедура состоит в разделении элементов, подлежащих
сортировке, пополам или почти пополам. Затем каждый из списков опять делит-
делится пополам. Процесс продолжается до тех пор, пока каждое множество не будет
содержать только один элемент. После этого процесс обращается, списки соби-
собираются вместе таким же способом, как они разделялись, но при этом происходит
их слияние. Сначала мы опишем собственно процедуру сортировки слиянием, а
затем приведем пример, иллюстрирующий, как ее применять. В большинстве слу-
случаев, использующих рекурсию, процедура вызывает себя через свое имя в теле
процедуры. Чтобы явно указать тот факт, что процедура вызывает сама себя, мы
будем использовать команду "вызов". В приведенной процедуре переменные /, т
и г представляют левый, центральный и правый элементы в текущем списке.
Процедура CC(J,r):
Если I < г, то
-т
Вызов CC(Z,m);
Вызов СС(т + 1,г);
Слияние(/,т, г);
Конец процедуры.
Положить т

210 ГЛАВА 5. Алгоритмы и рекурсия
Прежде чем перейти к объяснению процедуры СС, нам нужно описать про-
процедуру "Слияние". Процедура "Слияние" просто берет два уже упорядоченных
списка и сравнивает их первые элементы. Меньший из этих двух элементов уда-
удаляется из своего списка и помещается в некий новый список в качестве первого
элемента. Затем процедура повторяется, и всякий раз удаляемый элемент дописы-
дописывается в конец нового списка. Это продолжается до тех пор, пока один из списков
не опустеет. Затем остаток другого списка дописывается в конец нового списка.
Полученный таким образом список и есть результат сортировки. Мы не будем
формализовать процедуру "Слияние", т.к. метод ее практической реализации бу-
будет зависеть от используемой вычислительной техники.
Процедура Слияние(/, т, г):
Пусть А = (a/,aj+i,a*+2,... ,ат), В = (ат+1,ат+2,ат+;,... ,аг),
и С — новый список, результат слияния;
Если А и В содержат в списках элементы данных, то
Сравнить первые элементы А и В и удалить меньший
элемент из его множества;
Добавить удаленный элемент в конец списка С;
Если А или В не содержат элементов, то
добавить остаток другого списка в конец списка С;
Переобозначить список С как (а/,а/+ьа/+2,.. • ,ar);
Конец процедуры.
Пусть с, Ь, a,t;,h, d, x,e — список для сортировки, и символ | обозначает раз-
разбиение. На первом шаге список разбивается так: с, 6, a, v\h, d, х,е. Затем, посколь-
поскольку в начале каждой записи стоит команда "вызов СС", мы снова вызываем про-
процедуру СС для левой части, получая разбиение с, Ъ\а, v\h, d, x, e. Следующий вы-
вызов процедуры СС для левой части дает разбиение с|6|а, г;|/г, d, x, е. Левую часть
мы больше разбивать не можем, поэтому пытаемся разбить правую часть, че-
чего опять-таки сделать не можем. Тогда мы производим слияние с и 6, получая
6, c|a,v|/i, d, x, е. Далее возвращаемся к вызову процедуры СС, в котором разде-
разделяются Ь, с и a,v. Вызов СС(/,га) для левой части полностью завершен, поэтому
переходим к вызову процедуры СС(т, г) для правой части, получая разбиение
b,c\a\v\h,d,x,e. He имея более возможности вызвать процедуру СС, производим
слияние а и v. В результате получаем разбиение bc\a,v\h,d, x,e. Затем возвраща-
возвращаемся на тот уровень СС, где разделяются Ь,си a,v. Итак, мы завершили вызовы
СС(/,т) и СС(га, г) и можем произвести слияние 6, с и а, г;, получая разбиение
а, 6, с, и, |/i,d, x,e. Теперь возвращаемся на тот уровень СС, где было получено
разбиение на с, 6,a, v и /г, d, х,е. Завершив, таким образом, вызов СС(/,т), акти-
активизируем вызов СС(ш, г), получая разбиение а, Ь, с, v, |/г, d\x,e. Снова вызываем
СС для разделения h и d\ получаем разбиение а, 6, с, г>, |/i|d|x, е. Поскольку мы
больше не можем использовать процедуру СС, то производим слияние h и d,
получая а, 6, с, и, |d, /г|х, е. Затем возвращаемся на уровень СС, где разделяются
/г, d и х,е. Дальнейшее использование процедуры CC(Z,m) невозможно, поэтому
мы переходим к вызову СС(т, г), получая разбиение а, 6, с, v, |d, h\x\e. Теперь пе-
переходим к процедуре "Слияние" для осуществления слияния х и е, после чего
получаем а, 6, с, и, |d, /i|e,z. Опять возвращаемся на тот уровень СС, где разделя-

РАЗДЕЛ 5.4. Алгоритмы сортировки 211
ются Ми х,е. Обе команды СС выполнены, поэтому производим слияние d,h
и е,х, получая а,Ь, с, v\d, e, /г, х. В конечном счете мы возвращаемся на уровень
СС, где разбиение проходит между с, 6, а, г; и /i, d, x,e. Ha этом уровне выполнены
обе команды СС, поэтому мы производим слияние а, 6, с, г> и d, е,/г, х, получая
а, Ь, с, d, e, /i, г?, 5. На этом процедура завершена.
По количеству операций сравнения процедура СС относится к числу наибо-
наиболее эффективных. Для доказательства этого факта предположим, что п = 2т для
некоторого значения т. Отсюда т = log2 п. Для фиксированного га это самый
неблагоприятный случай. Если рассмотреть слияние, выполняемое начальным вы-
вызовом процедуры сортировки, то проводится слияние 2 (= 21) списков, каждый
из которых содержит 2ТП~1 элементов. Эта ситуация соответствует первому уров-
уровню. Вообще, на fc-ом уровне имеется 2к списков, в каждом по 2тп~к элементов.
Необходимо провести 2/с~1 сравнений пар списков, по 2тп~к элементов в каждом.
Каждое сравнение пар списков требует не более 2m~fc+1-l сравнений, поскольку
один оставшийся элемент не должен сравниваться с каким-либо. Следовательно,
на fc-ом уровне будет не более
2^—1 . Bтп
операций сравнения. Поэтому общее число операций сравнения не превышает
тп т— 1
fc=l i=0
m-1
= ^Г 2m - 2i = ra2m - Bm - 1) = n log2 n - (n - 1),
i=0
и поэтому в самом неудачном случае число сравнений имеет порядок O(nlnn).
Последней рассмотрим сортировку, которая называется сортировка встав-
вставками. Процедура для этой сортировки действительно очень простая. При этом
методе сортировки элементы данных выбираются по одному и помещаются во
вновь создаваемом списке на соответствующее место. При этом, если место эле-
элементу найдено, то все другие вставляемые элементы располагают левее, если они
меньше, и правее, если они больше. Опять рассмотрим тот же список для сор-
сортировки с, 6, а,г>, /г, d, x,e. Первым выбираем с и помещаем его в новом списке.
Далее, поскольку b меньше с, помещаем его перед с, формируя Ь, с. Следующим
выбираем а. Поскольку оно меньше 6, помещаем его перед Ь, формируя а,Ъ,с. Да-
Далее выбираем у. Оно больше с, поэтому помещаем его после с, формируя а,Ъ,с,у.
Поскольку h меньше, чем г>, и больше, чем с, помещаем его между сиу, форми-
формируя список а, 6, с, /г, у. Теперь рассматриваем d. Оно больше, чем с, и меньше, чем
/i, поэтому помещаем его между с и /г, что дает а, 6, с, d,/г, г;. Поскольку х больше
г;, помещаем его после у, получая а, Ь, с, d, /i, г;,х. Наконец, поскольку е больше,
чем d, и меньше, чем /г, помещаем его между d и /г, формируя рассортированный
список а, 6, с, d, е, /г, г>, х.
В самом плохом варианте число операций сравнения на каждом этапе такое
же, как в пузырьковой сортировке, т.е. имеет порядок О(п2).

212 ГЛАВА 5. Алгоритмы и рекурсия
И быстрая сортировка, и сортировка слиянием рекурсивно определяют раз-
разбиение множества на меньшие множества, сортировку этих меньших множеств и
последующую сборку этих рассортированных множеств. Такой метод разбиения
множества на подмножества, выполнения операций над ними и обратной сборки
множеств вместе называется методом "разделяй и властвуй". Как правило, это
весьма эффективный подход к решению задач.
Очень часто процедуры типа "разделяй и властвуй", такие как приведенная
выше, удовлетворяют рекурсивному соотношению вида Qn = CQ™ 4- /(^), где
Qn может характеризовать число операций, число сравнений, затрачиваемое вре-
время или другие параметры. В данном разделе в качестве такой характеристики
будем рассматривать число операций. Функция /(п) описывает число операций,
затрачиваемых на разделение множества на два множества и последующую сбор-
сборку этих двух подмножеств в целое. Когда используется запись ^ как индекс в
формуле, это предполагает, что множество данных, над которым производится
действие, разбивается на две равные части. Это достаточно распространенная
ситуация, т.к. наиболее часто используются бинарные деревья или другие поня-
понятия, содержащие бинарные операции. Если бы множество делилось на к равных
частей, была бы использована запись ^. Предполагается также, что п является
некоторой степенью числа 2. Нас, в основном, будут интересовать случаи, когда
/(п) равно константе и когда /(n) = Dn для некоторого постоянного D. Исполь-
Использование записи f(n) = Dn равносильно предположению, что число операций для
разбиения и последующего соединения п объектов прямо пропорционально коли-
количеству элементов множества. При изучении эффективности быстрой сортировки
было показано, что решение рекурсивного соотношения Qn = 2Q* -f п, где п —
степень числа 2, имеет вид n{Q\ 4- Iog2(n)). Это частный случай решения для
соотношения Qn = CQ% + Dn, когда С = 2 и D = 1. Для С > 2 решением
рекурсивного соотношения будет Qn = Anlogic + [j^j n, где А выбрано таким
образом, что Qi = A 4- -%Вс-
Если /(n) = D, где D — некоторая константа, то решением рекурсивного
соотношения Qn = CQ* +D для С ф 1 будет Qn = °<<Сп^1 ~1К В частном слу-
случае, когда С = 2, решение упрощается до Qn = DBn - 1). Изучение такого рода
рекурсивных соотношений будет продолжено при решении конкретных задач. К
сожалению, целое число п в общем случае не является степенью числа 2. Однако,
если предположить, что Qn — возрастающая функция и п меньше некоторого а,
где а — степень числа 2, то Qn < Qa, т.е. функция Qn ограничена сверху.
¦ УПРАЖНЕНИЯ
1. Рассортируйте последовательность 7,11,4,0,3,1,9,4,2,8, используя:
а) сортировку выбором;
б) пузырьковую сортировку;
в) быструю сортировку;
г) сортировку слиянием;
д) сортировку вставками.

РАЗДЕЛ 5.4. Алгоритмы сортировки 213
2. Рассортируйте последовательность 12,50,-1,-10,10,11,52,30,2,8,-12, ис-
используя:
а) сортировку выбором;
б) пузырьковую сортировку;
в) быструю сортировку;
г) сортировку слиянием;
д) сортировку вставками.
3. Рассортируйте последовательность х, а, с, у, р, г, /, ?, га, у, и, 6, d, n, 5, г, исполь-
используя:
а) сортировку выбором;
б) пузырьковую сортировку;
в) быструю сортировку;
г) сортировку слиянием;
д) сортировку вставками.
4. Рассортируйте последовательность Джонсон, Браун, Блэк, Джексон, Мэр-
Мэрфи, Смит, Джонс, используя:
а) сортировку выбором;
б) пузырьковую сортировку;
в) быструю сортировку;
г) сортировку слиянием;
д) сортировку вставками.
5. Постройте самый неблагоприятный вариант последовательности для осуще-
осуществления каждой из перечисленных ниже сортировок:
а) сортировка выбором;
б) пузырьковая сортировка;
в) быстрая сортировка;
г) сортировка слиянием;
д) сортировка вставками.
6. Покажите, что для слияния двух уже рассортированных списков длины п
требуется не более п — 1 операций сравнения.
7. Напишите компьютерную реализацию алгоритма сортировки выбором.
8. Напишите компьютерную реализацию алгоритма пузырьковой сортировки.
9. Напишите компьютерную реализацию алгоритма быстрой сортировки.
10. Напишите компьютерную реализацию алгоритма сортировки слиянием.
11. Напишите компьютерную реализацию алгоритма сортировки вставками.
12. Покажите, что Qn = An — D удовлетворяет рекурсивному соотношению
Qn = 2Qt+?>.
13. Покажите, что Qn = Dn(\og2 n + А) удовлетворяет рекурсивному соотноше-
соотношению Qn = 2Q» + Dn.
14. Покажите, что Qn = Anlog^c 4- (^г^) п Для С > 2 удовлетворяет рекурсив-
рекурсивному соотношению Qn = CQ% + Dn.

214 ГЛАВА 5. Алгоритмы и рекурсия
15. Восстановив пропущенные выкладки, докажите, что
является решением Qn = CQ* 4- Dn для С > 2, если А выбрано так, что
Qi = А + j^g. Мы предполагаем, что п = 2т.
16. Получите решение вида Qn = — для рекурсивного соотноше-
соотношения Qn = CQ™ 4- D, когда С ф 1.
5.5. ПРЕФИКСНАЯ И СУФФИКСНАЯ ЗАПИСИ
В арифметике, как и в логике, существуют определенные правила, касающиеся
приоритета выполнения операций над целыми числами, что дает возможность, не
приводя к путанице, сокращать число используемых в выражении скобок. Неко-
Некоторые свойства целых чисел также позволяют уменьшить потребность в скобках.
Например, известно, что благодаря закону ассоциативности сложения выраже-
выражение 3 + 5 + 7 не требует скобок, т.к. C + 5) + 7 = 3 + E 4- 7). Понятно также,
что операции возведения в степень должны быть выполнены первыми, за ними
следуют умножение и деление и, наконец, сложение и вычитание. Но даже при
таком соглашении необходимо использовать скобки. Например, нельзя выразить
(а4-ЬJD-Ь56), не используя скобок. Исключить скобки можно, применив префикс-
префиксную или суффиксную форму записи. Чтобы подчеркнуть их отличие от обычной

РАЗДЕЛ 5.5. Префиксная и суффиксная записи 215
для арифметики формы записи, в которой знак бинарной операции записывает-
записывается между операндами, назовем обычную форму записи инфиксной. Например,
выражения 3 + 4 и 6 -=- 3 записаны в инфиксной форме.
ОПРЕДЕЛЕНИЕ 5.30. Выражение находится в префиксной (польской) запи-
записи, если в нем знак операции непосредственно предшествует операндам, на
которые она действует. Выражение находится в суффиксной (постфиксной,
или обратной польской записи), если в нем знак операции следует непо-
непосредственно за операндами, на которые она действует. Выражение находится
в инфиксной записи, если в нем знак операции находится между операндами,
на которые она действует.
Например, инфиксное выражение a + fc в префиксной записи имело бы вид
+ab, а в постфиксной записи, соответственно, вид ab+. Инфиксное выражение ах
(Ь+с) имело бы в префиксной записи вид ха+bc, а в постфиксной, соответственно,
вид аЬс + х. Обратите внимание, что постфиксную запись следует "читать" слева
направо, а "читать" префиксную запись необходимо справа налево. Операцию
возведения в степень для удобства будем обозначать символом \ Таким образом,
а5 будет записываться как сГ5. Выражение (a + Ь) x (c + d) в префиксной записи
имеет вид x+ab~ +cd3, а в постфиксной записи, соответственно, вид ab+cd+3~ х.
В данном разделе рассмотрены алгоритмы перехода от инфиксной записи
к постфиксной и от постфиксной — к инфиксной. Подобные алгоритмы для пе-
перехода от инфиксной записи к префиксной и наоборот могут быть построены
аналогичным образом.
ОПРЕДЕЛЕНИЕ 5.31. Арифметическое выражение находится в полной ско-
скобочной записи, если каждому оператору в нем соответствует пара скобок, в
которые заключены оператор и те операнды, на которые он действует.
Упрощенно можно сказать, что арифметическое выражение — полноскобоч-
полноскобочное, если скобки в нем присутствуют всюду, где это возможно по смыслу. Напри-
Например, (ах (Ь + с)) и ((a + b) x ((c+d)"x)) являются полноскобочными выражениями,
а выражения а + (Ь х с) и (а-^ЪУс полноскобочными не являются.
Переход от инфиксного выражения к постфиксному может быть осуществлен
посредством следующей процедуры:
1. Добавлять скобки в выражение, пока оно не станет полноскобочным.
2. Начиная с самых внутренних скобок, удалить пару скобок и поместить на-
находящийся внутри скобок оператор на место соответствовавшей ему правой
скобки. При наличии более одной самой внутренней пары скобок начинать
нужно с левой пары.
3. Перейти к следующей паре скобок, удалить ее и поместить оператор, нахо-
находившийся внутри скобок, на место соответствовавшей ему правой скобки.
4. Продолжать шаг C), пока все скобки не будут удалены.

216 ГЛАВА 5. Алгоритмы и рекурсия
ПРИМЕР 5.32. Пусть дано инфиксное выражение (а + b) x (c + d)~x. Добавляем
скобки, пока выражение не станет полноскобочным. Получаем выражение ((а +
Ь) х ((c + d)~x)). Выполнив шаг B), получим (ab+x (cd+"x)). Выполнив шаг C),
получим (ab+ х cd + х~). Повторяя шаг C), приходим к записи ab + cd + x~x. ?
ПРИМЕР 5.33. Пусть дано инфиксное выражение а х b + c x d. Добавляем скобки,
пока не получим полноскобочное выражение, т.е. выражение ((а х 6) + (с х d)).
Выполнив шаг B), получим (abx + cdx). Повторяя шаг C), получаем abxcdx+.
?
Неформально стек определяется как область памяти, из которой данные
извлекаются в порядке, обратном порядку их ввода. Такой способ организации
памяти часто называют LIFO.1 Добавление в стек и удаление из него элемента
обычно называют операциями вталкивания и выталкивания, соответственно.
Постфиксное выражение может быть заменено инфиксным посредством сле-
следующей процедуры:
1. Начинать считывание выражения слева направо.
2. Если считанный символ не является символом операции, то поместить его в
стек и продолжать чтение.
3. Если считанный символ является символом операции, то:
а) вытолкнуть из стека два верхних элемента;
б) поместить символ операции между вторым и первым элементом из сте-
стека и поставить скобки;
в) поместить выражение, полученное на шаге (б), обратно в стек.
4. Продолжать чтение слева направо и выполнять шаги B) и C) до завершения.
ПРИМЕР 5.34. Пусть дано выражение abcx +. Вначале считываем а и, поскольку
это не символ операции, помещаем этот элемент в стек, как показано на рис. 5.4.
Затем считываем Ъ и, т.к. это не символ операции, помещаем его в стек, как
показано на рис. 5.5.
Эсх-f
(а)Ь с x-f
Рис. 5.4 Рис. 5.5
Далее считываем с и, т.к. это не символ операции, помещаем его в стек,
как показано на рис. 5.6. Затем считываем х и, поскольку это символ операции,
выталкиваем из стека (удаляем) с (верхний элемент) и Ь (следующий элемент),
помещаем х между бис, как показано на рис. 5.7.
Ют англ. last-in-first-out — "последним вошел, первым вышел". — Прим. перев.

РАЗДЕЛ 5.5. Префиксная и суффиксная записи 217
(х>
с
Ь
а
Рис. 5.6
Рис. 5.7
Помещаем F х с) в стек, как показано на рис. 5.8. Далее считываем 4-
и, поскольку это символ операции, выталкиваем из стека (удаляем) (b x с) и a
(следующий элемент). Помещаем 4- между а и F х с), как показано на рис. 5.9.
Рис. 5.8
Рис. 5.9
Помещаем (a + (bx с)) в стек, как показано на рис. 5.10. Получаем искомое
выражение. Очевидно, лишние скобки можно удалить.
Рис. 5.10
?
ПРИМЕР 5.35. Пусть дано выражение a6 + cd + 3~x. Сначала считываем а и, т.к.
это не символ операции, помещаем его в стек. Следующим считываем Ь и, т.к.
это не символ операции, помещаем его в стек. Далее считываем + и, поскольку
это символ операции, выталкиваем из стека (удаляем) Ъ (верхний элемент) и a
(следующий элемент) и помещаем + между а и 6. Переносим (а + Ь) в стек.
Далее считываем с. Поскольку с не является символом операции, то помещаем
его в стек. Далее считываем d и, поскольку это не символ операции, переносим
его в стек. Затем считываем + и, поскольку это символ операции, выталкиваем
из стека (удаляем) d (верхний элемент) и с (следующий элемент), помещаем +
между end. Переносим (с + d) в стек. Далее считываем 3 и, поскольку это не
символ операции, помещаем 3 в стек. Затем считываем символ Л и, поскольку это
символ операции, выталкиваем из стека 3 (верхний элемент) и (c+d) (следующий
элемент), после чего помещаем символ Л между (c + d) и 3. Переносим ((c + d))
в стек. Считываем х и, т.к. это символ операции, выталкиваем ((c-f d)) и (a-f b)
из стека. Помещаем х между (a + b) и ((c + d)A3), образуя (a + b) x ((c + d)A3).
Переносим ((а + 6) х ((с + d)~3)) в стек. Это и есть искомый результат. Очевидно,
лишние скобки можно удалить. ?

218 ГЛАВА 5. Алгоритмы и рекурсия
¦ УПРАЖНЕНИЯ
1. Замените следующие инфиксные выражения постфиксными:
а) аА2 + 6Л2;
б) сГЗ + 3 аЛ2-Ь 7;
в) (<Г2 + Ь)(с + сГ2);
г) (<Г2 + 6Л3)Л4;
д) <Г2F + с).
2. Замените следующие инфиксные выражения постфиксными:
а) (с + <*)-(а + Ь)Л2;
б) ((а + 6)-с)Л3;
в) (а + Ь)Л2-(с + <*)Л2;
г) (а-6)(а + Ь);
д) а-У (с Л- d).
3. Замените следующие постфиксные выражения инфиксными:
а) аЪ + cd - 4-;
б) аЬ2Л +Ы2Л 4- х;
в) ЗаЬ х х4Ы2Л х х+;
г) а&+ Л2сс/А -f-r;
д) а2Л6 + сй2Л 4- х.
4. Замените следующие постфиксные выражения инфиксными:
а)
б)
в) ЗаЬ х x4cd2~ x x-h;
г) аб-f Л2ссГ +-Г-;
д) а2Лб4-с4-ссг2Л 4-4-.
5. Замените следующие инфиксные выражения префиксными:
а) бГ2 + 6Л2;
б) аГ3 4-3 аА2 + 7;
в) (аЛ2 + Ь)(с +d^2);
г) (аЛ2 + ЬЛ3)Л4;
д) аЛ2F + с).
6. Замените следующие инфиксные выражения префиксными:
а) (с + ?*)-(а4-Ь)Л2;
б) ((а + Ь)-с)Л3;
в) (а4-6)Л2-(с4-й)Л2;
г) (a-b)(a + b);
д) а-ЬЛ(с4-^).
7. Замените следующие префиксные выражения инфиксными:
а) 4- 4- ab — cd\
б) ^ + a2~d2 + ЛС2Л62;
в) 4- х хЗаб 4- х х Acd x x5ad;

РАЗДЕЛ 5.6. Двоичные и шестнадцатеричные числа 219
г) л + ла2 + лЬ2Ас23;
д) х + сГ26 + ссГ2.
8. Замените следующие префиксные выражения инфиксными:
а) Л 4- хабсЗ;
б) х + +abc 4- +cde;
в) Ч х х Заб х x4cd2;
г) Л ^-+аЛЬ2 + сЛ^22;
д) х И—аЬс abc.
9. Напишите процедуру для перехода от инфиксной формы записи выражения
к префиксной.
10. Напишите процедуру для перехода от постфиксной формы записи выражения
к инфиксной.
5.6. ДВОИЧНЫЕ И ШЕСТНАДЦАТЕРИЧНЫЕ ЧИСЛА
Использование цифры 0 для обозначения разрядов в записи числа привело к боль-
большому прорыву в развитии математики. Оно дало возможность различать такие
числа, как 47, 4700, 4007 и 4070. В данном примере значение четверки и семерки
определяется позицией, которую они занимают в записи числа. Например, в числе
47 цифры 4 и 7 находятся в таких позициях, что цифра 4 обозначает 4 десятка, а
цифра 7 обозначает 7 единиц. В числе 4700 цифра 4 обозначает 4 тысячи, а цифра
7 обозначает 7 сотен. Таким образом, число 47 можно записать как 4 • 10 4- 7, а
число 4700 — как 4 • 1000 + 7-100 или 4 • 103 + 7 • 102. Точно так же, число 4007
можно записать как 4 • 103 4-7-1, а число 4070 — как 4 • 103 + 7-10. В общем
случае, если число п представляется в десятичной системе счисления, в основе
которой лежит число 10, как amam_iam_2 • • -e^aiao, то
п = amA0)m 4- а^Ю)™-1 + • • • + a2A0J 4- aiA0) + a0,
где п{ — целые числа между 0 и 9 для всех 0 < г < га. Например, 3124 = 3A0K 4-
1A0J 4-2A0) +4. Аналогично, если число п представлено в двоичной системе
счисления, в основе которой лежит число 2, то каждая цифра должна быть либо 1,
либо 0, и ее значение определяется занимаемой позицией. Таким образом, 1101 =
1BK 4- 1BJ 4- 0B) 4- 1 = 13, где число 13 представлено в десятичной системе.
Первые 20 положительных целых чисел, записанные в двоичной системе, имеют
вид: 1, 10, 11, 100, 101, ПО, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111,
10000, 10001, 10010, 10011 и 10100. В общем случае, двоичному представлению
п — amam_iam_2 • • -a2aia0 соответствует десятичное представление
п = amB)m 4- am_1B)m -f - - - 4- a2BJ + аг{2) 4- a0,
где a; равно либо 1, либо 0 для всех 0 < г < т. Для исключения возможной
путаницы двоичное число, например, 1101101, будем обозначать как 11011012, а
десятичное число, например, 312, будем обозначать как 312ю.

220 ГЛАВА 5. Алгоритмы и рекурсия
Когда на одометре машины достигается число 9999 и добавляется еще одна
миля, то все девятки сбрасываются и получается 10,000. Аналогично, если к
числу 111112 прибавить 1, то все единицы сбрасываются и получается число
ЮОООО2. Таким образом, если прибавить 1 к 101112, получим ПООО2. Для того
чтобы перевести двоичное число amam_iam_2 • • • a2aiao в десятичное, нам просто
нужно вычислить значение этого числа, равное amB)m + am_iB)m + ••• +
a2BJ + aiB) + a0, в обычной десятичной системе счисления. Например, 11010112
записывается в виде
26 2\ 2°4 2Хз 2°2 21 1 = 1BN + 1BM+0BL + 1BK +
+ 0BJ + 1BI + 1 =
= 64 + 32 + 8 + 4 + 1 =
= 109.
Точно так же находим
10101 = 1BL + 0BK + 1BJ + 0BI + 1 = 16 + 4 + 1 = 21.
Этот метод нахождения значения двоичного числа часто называют "подсчет
обмена", поскольку он аналогичен подсчету наличных денег, если имеется монета
в 25 центов, монета в 10 центов и пенни. Сначала мы опишем метод перехода
от десятичного числа к двоичному, который часто называют "разменом". Если
необходимо определить, какие монеты отдать в обмен за 42 цента, первой будет
выбрана монета в 25 центов, поскольку это наибольшая монета, которая меньше
42 центов. Если вычесть 25 центов, то необходимо еще 17 центов. Теперь выбира-
выбираем монету в 10 центов, поскольку это наибольшая монета, которая меньше, чем
17 центов. Вычитаем 10 центов из 17 центов и находим, что необходимо еще 7
центов. Следующей выбираем монету в 5 центов и 5 центов вычитаем, остается
еще 2 цента, которые необходимо добавить. Подобным образом, если имеется,
например, число 83ю, которое нужно перевести в двоичное, то сначала выбира-
выбирается наибольшая степень 2, которая не превосходит 83ю. В данном случае это
26 = 64ю. Помещаем 1 в колонку, соответствующую 26. Теперь вычитаем 64ю из
83ю и получаем 19ю:
1
2б суъ 2^ 23 22 2* 1
Нам не нужно использовать 25 = 32ю, т.к. это число слишком велико, поэтому в
колонке, соответствующей 25, помещаем 0:
1 0
2б <уь 2^ 23 22 2* 1
Но 24 = 16ю нам нужно, поэтому помещаем 1 в колонку, соответствующую 24:
1 0 1
2б 25 94 23 22 21 1

РАЗДЕЛ 5.6. Двоичные и шестнадцатеричные числа 221
Вычитаем 16ю из 19юи получаем Зю. Нам не нужно использовать 23 = 8ю или
22 = 4ю, т.к. они слишком велики, поэтому помещаем 0 в соответствующие ко-
колонки. Но 2 и 1 нам нужны, поэтому мы помещаем по единице в соответствующие
колонки:
10 10 0 11
2б 25 24 23 22 21 1
Следовательно, искомым числом является 10100112.
Аналогично, 199ю = 11000111, т.к. для этого необходимо одно 27 = 128ю,
одно 26 = 64ю, одно 22 = 4ю, одно 2ю и одно 110.
Можно получить другой способ преобразования десятичного числа в дво-
двоичное, если проанализировать такой процесс: при делении 234 на 10 обычным
арифметическим способом получаем частное 23 и остаток 4. Если теперь делить
23 на 10, частным будет 2, а остатком — 3. Наконец, если разделить 2 на 10,
получаем частное 0 и остаток 2. Обратите внимание, что расположение остатков
в обратном порядке дает исходное число. Используя приведенный ниже алгоритм,
целое десятичное число п можно преобразовать в то же самое по значению, но
двоичное число п.
1. Разделить п на 10, получив частное q\ и остаток г\.
2. Разделить q\ на 10, получив частное q2 и остаток г2.
3. До тех пор, пока qk не равно 0, делить q^ на 10, получая частное qk+i и
остаток r/fc+i-
4. Если qn = 0, тогда rnrn_i • • • r3r2ri = п.
Использование приведенного выше алгоритма в двоичной системе счисления, где
10 соответствует десятичному числу 2, обеспечит такой же результат. Но, по-
поскольку 102 есть десятичное число 2, деление на 10 в двоичной системе должно
давать такие же остатки, как и деление на 2 в десятичной арифметике. Рас-
Рассмотрим приведенные ниже соответствующие операции для преобразования де-
десятичного числа 57 в двоичное число, в которых все числа одни и те же, за
исключением того, что в первом столбце они выражены в двоичной форме, а во
втором — в десятичной форме.
двоичная запись десятичная запись
Разделить 111001 на 10; qi = 11100, п = 1. Разделить 57 на 2; q\ = 28, п = 1.
Разделить 11100 на 10; q2 = 1110, r2 = 0. Разделить 28 на 2; q2 = 14, r2 = 0.
Разделить 1110 на 10; <?з = 111, гз = 0. Разделить 14 на 2; д3 = 7, гз = 0.
Разделить 111 на 10; q± = 11, га = 1. Разделить 7 на 2; q± = 3, г 4 = 1.
Разделить 11 на 10; q$ = 1, г5 = 1. Разделить 3 на 2; qs = 1, г5 = 1.
Разделить 1 на 10; qe = 0, re = 1. Разделить 1 на 2; qe — 0, г& = 1.
111001 = 111001. 57 = 111001.
Следующий алгоритм должен переводить число п из десятичной системы
счисления в двоичную:
1. Разделить и на 2, получив частное q\ и остаток т\.
2. Разделить q\ на 2, получив частное <?2 и остаток г2.

222 ГЛАВА 5. Алгоритмы и рекурсия
3. До тех пор, пока qk не равно 0, делить qk на 2, получая частное qk+i и
остаток rfc+i-
4. Если qn = О, тогда (rnrn-i • • • r3r2r1J = п10.
Для того чтобы записать целое положительное число в шестнадцатерич-
ной системе счисления, в основе которой лежит число 16, нам понадобятся но-
новые символы, поскольку все неотрицательные целые числа, меньшие 16, должны
представляться одной цифрой. Иными словами, 10i6 эквивалентно 16 в десятич-
десятичной форме. Вводим "цифры" А, Ву С, D, Е и F для обозначения чисел 10, 11,
12, 13, 14 и 15. Таким образом, первые 20 целых положительных чисел в шест-
надцатеричной форме имеют вид 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F,
10, 11, 12, 13 и 14. Если число п в шестнадцатеричной форме представлено как
amam_iam_2 • • • 0,20,10,0, то ему соответствует представление в десятичной форме,
п = amA6)m + ат.^Щ™-1 + • • • + а2A6J + aiA6) + а0,
где для всех 0 < г < т, 0 < а* < 16. Поэтому числу и = 2АЗВ4\е соответство-
соответствовало бы десятичное число п = 2A6L + АA6K + 3A6J 4- ВA6) + 4. Используем
следующую таблицу:
2A6L = 2 х 65536 - 130072
ЛA6K = 10 х 4096 = 40960
3A6J = 3 х 256 = 768
ВA6) = 11 х 16 = 176
4=4x1 =4
Сумма = 171980
и 2АЗВ4гб = 171980ю.
Аналогично, 3C9i6 = 3A6J + 12A6) + 9 = 3 х 256 + 12 х 16 + 9 = 969ю.
Способом, аналогичным "сбрасыванию" для двоичных чисел, после прибавления
1 к FFFFF получаем 100000. Поэтому, если прибавить 1 к 23CFFFF, получим
23D0000.
Первый способ перевода десятичного числа в шестнадцатеричное аналогичен
способу перевода десятичного числа в двоичное. Если дано десятичное число,
например, 530328, наибольшей степенью числа 16, которая разделит 530328 с
ненулевым частным, будет 164 = 65536. Поскольку частное от деления 530328 на
66536 равно 8, запишем 8 в первом столбце:
8
65536 4096 256 16 1
164 163 162 161 16°
Разделим разность 530328 - 8F5536) = 6040 на 4096. Частное от деления
равно 1, остаток равен 1944, поэтому помещаем 1 во второй столбец:
8 1
66536 4096 256 16 1
164 163 162 161 16°

РАЗДЕЛ 5.6. Двоичные и шестнадцатеричные числа 223
и делим 1944 на 256. Поскольку частное от деления равно 7, а остаток равен 152,
помещаем 7 в третий столбец:
8 1 7
66536 4096 256 16 1
164 163 162 161 16°
и делим 152 на 16.
Частное от деления равно 9, остаток равен 8, поэтому помещаем 9 в четвер-
четвертом участке, а 8 — в последнем столбце:
8 17 9 8
66536 4096 256 16 1
164 163 162 161 16°
Следовательно, 530328ю = 81798i6.
Для использования альтернативного метода перевода шестнадцатеричного
числа в десятичное необходимо делить на 16ю = Юхв вместо деления на 2ю =
102 аналогично предыдущему алгоритму перевода десятичного числа в двоичное.
Таким образом, имеем следующий алгоритм:
1. Разделить п на 16, получив частное q\ и остаток г\.
2. Разделить q\ на 16, получив частное q2 и остаток г2.
3. До тех пор, пока qk не равно 0, делить qk на 16, получая частное qk+\ и
остаток rfc+i.
4. Если qn = 0, то (rnrn_i • • • r3r2riJ =
ПРИМЕР 5.36. Снова рассмотрим преобразование 530328 в шестнадцатеричное
число. Поскольку 530328 = 16C3145) + 8, то qx = 33145 и гг = 8. Поскольку
33145 = 16B071) + 9, то q2 = 2071 и г2 = 9. Поскольку 2071 = 16A29) + 7, то
<7з = 129 и г3 = 7. Поскольку 129 = 16(8) +1, то q± = 8 и г4 = 1. Следовательно,
г5 = 8 и 530328ю = 81798i6. ?
Рациональное число в десятичной системе счисления, например, 326.149,
представляется в виде
3A0J + 2A0)х + 6A0)° + l(lO) + 4A0)~2 + 3A0)-3,
или
3 2 6 1 4 3
A0J A0I A0)° (И)) A0)-2 A0)-3.
Аналогичным образом рациональное число в двоичной системе счисления,
например, 1011.0111, представляется в виде
1BK + 0BJ + Ц2I 4-1B)°
или
1
BK
0
BJ
1
BI
1
B)°
0
B)
1
B)
1
B)-3
1
B)

224 ГЛАВА 5. Алгоритмы и рекурсия
Поэтому для преобразования двоичной записи рационального числа в десятичную
необходимо каждый разряд числа преобразовать в десятичную систему счисления
и результаты сложить.
ПРИМЕР 5.37. Преобразовать IOII.IIII2 в десятичную форму.
= 1BK + 0BJ 4- Ц2I + 1B)°
= 11 + .5 + .25 + .125 + .0625 =
= 11.9375. ?
ПРИМЕР 5.38. Преобразовать 1010.01012 в десятичную форму.
1010.01012 = 1BK + 0BJ + Ц2I + 0B)° + 0B)"Ч
+ 1B)-2+0B)-3 4
=
= 10
= 10
<
1- + .
+ .25
.3125.
1 -+
+
-0+ +
.0625 =
lf
4+С
, , 1
)+16
?
Заметим, что .3729, умноженное на 10, дает 3.729, где первая цифра справа
от десятичной точки передвигается на позицию слева от десятичной точки. Если
после этого число .729 умножить на 10, то 7 передвинется на позицию слева от
десятичной точки. Умножая теперь .29 на 10, мы передвинем 2 в позицию сле-
слева от десятичной точки. Наконец, если умножить .9 на 10, то 9 переместится в
позицию слева от десятичной точки. Удалив эту цифру, мы получим 0. Цифры, по-
последовательно перенесенные слева направо относительно десятичной точки, вновь
образуют исходное число .3729. Таким образом, если для заданного десятично-
десятичного числа, меньшего единицы, последовательно повторять процесс, состоящий в
умножении числа на десять, выборе цифры, стоящей слева от десятичной точки,
и последующем ее удалении, до тех пор, пока не останется ни одной цифры, то
мы выберем все цифры, входящие в десятичную запись исходного числа.
Тот же самый процесс применим и в случае, если задано двоичное число,
меньшее единицы. Пусть, например, задано двоичное число .1101. Умножая его
на 102, т.е. на два, получаем 1.101. Запомнив и удалив 1, мы умножаем .101
на 10, получая 1.01. Вновь запомнив и удалив 1, умножаем .01 на 10, получая 0.1.
Наконец, запомнив и удалив 0, умножаем .1 на 10; получаем и запоминаем 1.
Перемещенные и сохраненные в памяти цифры — это цифры, образующие ис-
исходную двоичную запись. Если десятичное число, меньшее 1, умножить на 2, то
слева от десятичной точки должна появляться та же цифра, что и при умножении
этого числа в двоичной записи на 102, и которая является первой цифрой числа
в двоичной форме записи. Таким образом, если умножать числа в десятичной
системе счисления на 2, запоминать и удалять цифры слева от десятичной точ-
точки, то, продолжая этот процесс, мы должны получить цифры, которые образуют

РАЗДЕЛ 5.6. Двоичные и шестнадцатеричные числа 225
число в двоичной записи. Ниже приведены соответствующие операции, преоб-
преобразующие .125 в двоичное число. В них фигурируют одни и те же числа, но в
первом столбце они выражены в двоичной, а во втором — в десятичной форме:
двоичная запись десятичная запись
Умножим .001 на 10 и получим 0.01. Умножим .125 на 2 и получим 0.250.
Удалим 0 и запомним как 1-ю цифру. Удалим 0 и запомним как 1-ю цифру.
Умножим .01 на 10 и получим 0.1. Умножим .250 на 2 и получим 0.500.
Удалим 0 и запомним как 2-ю цифру. Удалим 0 и запомним как 2-ю цифру.
Умножим .1 на 10 и получим 1.0. Умножим .500 на 2 и получим 1.000.
Удалим 1 и запомним как 3-ю цифру. Удалим 1 и запомним как 3-ю цифру.
.0012 = .0012. Л25ю = .0012.
ПРИМЕР 5.39. Заменить десятичную запись числа .875 двоичной. Сначала умно-
умножаем .875 на 2, получаем 1.750. Удаляем 1, сохраняя 1 как первую цифру дво-
двоичного числа. Умножаем .750 на 2, получаем 1.500. Удаляем 1, сохраняя 1 как
вторую цифру двоичного числа. Умножаем .500 на 2, получаем 1.000. Удаляем
1, сохраняя 1 как третью цифру двоичного числа. Следовательно, наше число в
двоичной форме записи имеет вид .111.
В приведенной ниже таблице первый столбец содержит этапы умножения на
2, второй — результаты умножения, а третий — те цифры, которые нужно удалить
и запомнить для формирования двоичной записи исходного десятичного числа.
.875 х 2 1.750 1
.750 х 2 1.500 1
.500 х 2 1.000 1
Таким образом, .87510 = .ИЬ- ?
ПРИМЕР 5.40. Десятичную форму записи числа .4 заменить двоичной формой
записи. Используя приведенную выше процедуру, получаем
.4
.8
.6
.2
.4
.8
.6
.2
X
X
X
X
X
X
X
X
2
2
2
2
2
2
2
2
0.8
1.6
1.2
0.4
0.8
1.6
1.2
0.4
0
1
1
0
0
1
1
0
Заметим, что когда 0.8 повторяется во втором столбце, повторяется и весь про-
процесс, так что представление числа 0.8 в двоичной форме состоит из повторяю-
щихся цифр 0110. Следовательно, .4ю = .0110011001100110- • • = .ОНО ?
Действуя способом, подобным преобразованию двоичного числа в десятич-
десятичное, замечаем, что 32F.12 в шестнадцатеричной системе счисления записывается
в виде
3A6J + 2A6I + FA6)° + Ц16)-1 + 2A6),

226 ГЛАВА 5. Алгоритмы и рекурсия
что эквивалентно
о(До) -f- ^(loj -Ь 15(loj -f- Ц1о) -+¦ ^(lbj ,
ИЛИ
3 x 256 + 2 x 16 4-15 + Л + 7TZ = 815 + 0625 + 0078125 =
16 256
= 815.0703125ю.
Поэтому 32F.12i6 = 815.0703125ю. Как видим, для чисел, меньших единицы, в
шестнадцатеричной системе счисления умножение на 16 — это то же самое, что
умножение на 10 в десятичной. Поэтому, по аналогии с переходом от десятичного
числа к двоичному, где производилось умножение на 2(= 102), мы теперь умно-
умножаем на 16(= 10i6), запоминаем и удаляем цифру слева от десятичной точки и
используем ее как первую цифру. Далее, умножая на 16, используем цифры сле-
слева от десятичной точки как очередные цифры записи числа в шестнадцатерич-
шестнадцатеричной форме. Например, рассмотрим число .0703125ю. Умножая на 16, получаем
1.1250000, так что первой цифрой шестнадцатеричной записи будет 1. Умножая
далее .125 х 16, получаем 2.0. Поэтому .0703125ю = .12i6:
.0703125 х 16 1.125 1
.125 х 16 2.0 2
ПРИМЕР 5.41. Требуется заменить десятичную запись числа .875 шестнадцате-
шестнадцатеричной. Умножая .875 на 16, получаем 14 = E\q. Поэтому .875ю = -E\q. ?
ПРИМЕР 5.42. Требуется заменить десятичную запись числа .0078125 шестна-
шестнадцатеричной. Имеем
.0078125 х 16 0.125 0
.125 х 16 2.0 2
и .0078125ю = .02ie ?
ПРИМЕР 5.43. Преобразуем десятичное число .8 в шестнадцатеричное. Имеем
.8 х 16 12.8 С
.8 х 16 12.8 С
.8 х 16 12.8 С
и, таким образом, .8ю = .СССС • • • = .С. ?
Приведенные выше примеры показывают, что периодичность или конечность
представления рационального числа является функцией основания соответствую-
соответствующей системы счисления, а не самого рационального числа.
В информатике зачастую важно иметь возможность переходить от шест-
шестнадцатеричной формы записи числа к двоичной и обратно. Заметим, что для
представления в двоичной форме записи • • • а\\а\^а^а^а^а^аг)а^а^а2С1\Aо имеем

РАЗДЕЛ 5.6. Двоичные и шестнадцатеричные числа 227
= • • • an2n + aiO210 4- а929а8284-
+ а?27 + а626 + а525 + а4244-
+ а323 4- а222 + а^1 4- а0 =
= • • • (ац23 4- аю22 4- а921а8J8 +
+ (а723 + а622 4- а52х 4- а4J44-
4- а323 4- а222 4- а^1 4- а0 =
= • • • (ац23 4- аю22 4- a921asI62+
4- (а723 4- а622 4- a52l 4- а4I6 4-
4- а323 4- а222 4- аг21 4- а0.
Тогда, если • • • aii234-ai0224-a9214-a8, a7234-a6224-a5a24-a4 и a3234-a222+ai214-a0
преобразованы, соответственно, в шестнадцатеричные числа • • • h2i hi и h0, полу-
получаем число bft2A6J+/iiA6)-f/io, которое представляет собой шестнадцатерич-
ное число • • • h2/ii/io. Поэтому объединение двоичных цифр в группы по четыре и
преобразование их в шестнадцатеричные числа дает преобразование всего числа
из двоичной формы в шестнадцатеричную. Например, рассмотрим двоичное чис-
число 1010011001010111. Первые четыре цифры 1010 формируют шестнадцатеричную
цифру А, следующие четыре цифры ОНО формируют шестнадцатеричную цифру
6, следующие четыре цифры 0101 дают шестнадцатеричную цифру 5, последние
четыре цифры 0111 дают шестнадцатеричную цифру 7. Поэтому шестнадцатерич-
ное представление рассматриваемого числа А657 имеет вид:
1010 ОНО 0101 0Ш
Л 6 5 7
Если количество цифр в двоичном представлении не кратно четырем, необ-
необходимо впереди дописать нули так, чтобы количество цифр в двоичном представ-
представлении стало кратно четырем. Например, пусть дано двоичное число 1010011110.
Дописываем впереди 00 и получаем 001010011110, после чего делаем следующее
преобразование:
0010 ОНО 1001 1110
2 6 9 Е
Пусть задано двоичное представление рационального числа, такое, напри-
например, как 101100.0111101. Начиная с десятичной точки и двигаясь от нее в каж-
каждом направлении, формируем группы по четыре двоичных цифры, дописывая нули
в конце каждой группы, если это необходимо. Затем преобразовываем каждую
группу из четырех двоичных цифр (двоичных разрядов) в шестнадцатеричную
цифру (шестнадцатеричный разряд). Полученное шестнадцатеричное число явля-
является представлением исходного числа. Отсюда имеем:
0010 1100 .0111 1010
2 С .7 А

228 ГЛАВА 5. Алгоритмы и рекурсия
Таким образом, 101100.01111012 = 2C.7Ai6. Точно так же получаем 011100.112 =
00011100.1100 = 1С.С1в.
Строим обратный процесс, преобразуя шестнадцатеричные числа в двоич-
двоичные. Пусть дано шестнадцатеричное число 72F5. Поскольку 7i6 = ОШ2, 2i6 =
ООЮ2, Fie = IIH2 и 5ie = OIOI2, то 72F5i6 = 01110010111101012. Аналогично,
2А.ЗС = 00101010.00111100 = 101010.001111.
Для чисел, представленных в двоичной форме, справедливы те же правила
сложения, вычитания, умножения и деления, как и для чисел, представленных в
десятичной форме, исключая тот факт, что сложение и вычитание производится
согласно приведенным ниже таблицам:
+
0
1
0
0
1
1
1
10
X
0
1
0
0
0
1
0
1
При вычитании важно помнить, что если 1 "занято" из 10, то остается только 1,
т.к. Юг в действительности есть число 2.
ПРИМЕР 5.44. Требуется выполнить следующие операции в двоичной системе
счисления:
а) 1011 б) 1100 в) 1101
ОНО -1001 х101
+0101 011 1101
10110 0000
1101
1000001 ?
Аналогично, для шестнадцатеричных чисел правила сложения, вычитания,
умножения и деления остаются теми же, за исключением того, что для выполне-
выполнения сложения и умножения должны быть использованы таблицы, представленные
на рис. 5.11 и 5.12.
ПРИМЕР 5.45. Требуется выполнить следующие операции в шестнадцатеричной
системе счисления:
а)
F051
315А
+4163
1630Е
б)
FD32
-475Л
B5D8
в)
28
х34
АО
78.
820
?
УПРАЖНЕНИЯ
1. Запишите числа от 1 до 25 в двоичной системе счисления.
2. Запишите числа от 1 до 25 в шестнадцатеричной системе счисления.
3. Преобразуйте следующие десятичные числа в двоичные:
а) 45; б) 86;
в) 243; г) 194;
Д) 312.

РАЗДЕЛ 5.6. Двоичные и шестнадцатеричные числа 229
+
1
2
3
4
5
6
7
8
9
А
В
С
D
Е
F
1
2
3
4
5
6
7
8
9
А
В
С
D
Е
F
10
2
3
4
5
6
7
8
9
А
В
С
D
Е
F
10
11
3
4
5
6
7
8
9
А
В
С
D
Е
F
10
11
12
4
5
6
7
8
9
А
В
С
D
Е
F
10
11
12
13
5
6
7
8
9
А
В
С
D
Е
F
10
11
12
13
14
6
7
8
9
А
В
С
D
Е
F
10
11
12
13
14
15
7
8
9
А
В
С
D
Е
F
10
11
12
13
14
15
16
8
9
А
В
С
D
Е
F
10
11
12
13
14
15
16
17
9
А
В
С
D
Е
F
10
11
12
13
14
15
16
17
18
А
В
С
D
Е
F
10
11
12
13
14
15
16
17
18
19
В
С
D
Е
F
10
11
12
13
14
15
16
17
18
19
1Л
С
D
Е
F
10
11
12
13
14
15
16
17
18
19
\А
\В
D
Е
F
10
11
12
13
14
15
16
17
18
19
1Л
1В
1С
Е
F
10
11
12
13
14
15
16
17
18
19
\А
\В
1С
ш
F
10
11
12
13
14
15
16
17
18
19
\А
\В
1С
Ш
\Е
Рис. 5.11
X
1
2
3
4
5
6
7
8
9
А
В
С
D
Е
F
1
1
2
3
4
5
6
7
8
9
А
В
С
D
Е
F
2
2
4
6
8
А
С
Е
10
12
14
16
18
\А
1С
2Е
3
3
6
9
С
F
12
15
18
1В
IE
21
24
27
2Л
2D
4
4
8
С
10
14
18
1С
20
24
28
2С
30
34
38
ЗС
5
5
А
F
14
19
\Е
23
28
2D
32
37
ЗС
41
46
АВ
6
6
С
12
18
\Е
24
2А
30
36
ЗС
42
48
АЕ
54
ЪА
7
7
Е
15
1С
23
2А
31
38
3F
46
4D
54
ЪВ
62
69
8
8
10
18
20
28
30
38
40
48
50
58
60
68
70
78
9
9
12
1В
24
2D
36
3F
48
51
ЪА
63
6С
75
7Е
87
А
А
14
\Е
28
32
ЗС
46
50
ЪА
64
6Е
78
82
8С
96
В
В
16
21
2С
37
42
AD
58
63
6?
79
84
8F
9А
АЪ
С
С
18
24
30
ЗС
48
54
60
6С
78
84
90
9С
Л8
?4
D
D
1А
27
34
41
АЕ
ЪВ
68
75
82
8F
9С
А9
Б6
СЗ
Е
Е
1С
2Л
38
46
54
62
70
7Е
8С
9Л
Л8
В6
СА
D2
F
F
IE
2D
ЗС
АВ
ЪА
69
78
87
96
АЪ
ВА
СЗ
D2
Е\
Рис. 5.12
4. Преобразуйте следующие десятичные числа в двоичные:
а) 53; б) 99;
в) 287; г) 186;
Д) 334.
5. Преобразуйте следующие двоичные числа в десятичные:
а) 1011; б) 11010;
в) 100100; г) 111011;
д) 110101.

230 ГЛАВА 5. Алгоритмы и рекурсия
6. Преобразуйте следующие двоичные числа в десятичные:
а) 1101; б) 10110;
в) 101101; г) 110101;
д) 1010101.
7. Преобразуйте следующие десятичные числа в шестнадцатеричные:
а) 63; б) 116;
в) 376; г) 734;
д) 5246.
8. Преобразуйте следующие десятичные числа в шестнадцатеричные:
а) 183; б) 297;
в) 458; г) 861;
д) 36304.
9. Преобразуйте следующие шестнадцатеричные числа в десятичные:
а) 4?; б) 2F3;
в) 4FA; г) 41FD;
д) D1E3.
10. Преобразуйте следующие шестнадцатеричные числа в десятичные:
a) AF] б) ЗЛ4;
в) АВ2; г) D13A-,
д) 21F2D.
11. Преобразуйте следующие десятичные числа в двоичные:
а) 23.875; б) 43.75;
в) 86.125; г) 94.4;
д) 52.3.
12. Преобразуйте следующие десятичные числа в двоичные:
а) 3.1875; б) 22.625;
в) 87.71875; г) 16.53125;
д) 34.28125.
13. Преобразуйте следующие двоичные числа в десятичные:
а) 1110.11; б) 1010.101;
в) 100.1001; г) 11.0111;
д) 1101.0101.
14. Преобразуйте следующие двоичные числа в десятичные:
а) 101.01011; б) 11100.1010;
в) 1011.01110; г) 1101.1011;
д) 10101.01111.
15. Преобразуйте следующие десятичные числа в шестнадцатеричные:
а) 36.625; б) 161.78125;
в) 592.15625; г) 1876.54625;
д) 5246.34765625.
16. Преобразуйте следующие десятичные числа в шестнадцатеричные:
а) 273.9375; б) 349.796875;

РАЗДЕЛ 5.7. Числа со знаком 231
в) 576.640625; г) 1997.35;
д) 36304.140625.
17. Преобразуйте следующие шестнадцатеричные числа в десятичные:
а) 5С.ЗЛ; б) F12.AE;
в) 4AF.C48; г) 32АВ.С11;
д) 13CE.D24.
18. Преобразуйте следующие шестнадцатеричные числа в десятичные:
a) 14.D2; б) 11F.E33;
в) 47F.344; г) 237F.755;
д) 233В.FDA.
19. Преобразуйте следующие двоичные числа в шестнадцатеричные:
а) 101.1010; б) 110111.010101;
в) 110110110.011011111; г) 1110101110.0011011011;
д) 1111010100.001000101.
20. Преобразуйте следующие двоичные числа в шестнадцатеричные:
а) 110.11001; б) 100101.011110;
в) 101110101.010101011; г) 11010101010.11001101101;
д) 10001010111.1101001010101.
21. Преобразуйте следующие шестнадцатеричные числа в двоичные:
а) 2САВ\ б) 1F2.A3C;
в) AF8A8C\ г) А12Е.11С;
д) CUA.2D4.
22. Преобразуйте следующие шестнадцатеричные числа в двоичные:
a) CE.2D5; б) F\A.E3D\
в) В7Е.ЗС4; г) FA31.2Eb\
д) С46В.АС4.
5.7. ЧИСЛА СО ЗНАКОМ
В предыдущем разделе мы рассматривали представления в двоичной и шестна-
дцатеричной форме только для положительных рациональных чисел. В данном
разделе мы покажем, как строить двоичные и шестнадцатеричные представления
положительных и отрицательных целых чисел при помощи метода двоичного
дополнения. Этот метод требует, чтобы целые числа были записаны с использо-
использованием фиксированного количества битов (двоичных разрядов). Поэтому число
в двоичной системе будет всегда записываться с использованием одного и того
же количества разрядов. Если используется 8 двоичных разрядов, то двоичное
представление числа 3 будет иметь вид 00000011. Для представления целого по-
положительного числа с помощью 8 бит перед ним при необходимости дописывается
нужное количество нулей. До конца этого раздела будем использовать 8 бит для
чисел в двоичной форме и 16 бит для чисел в шестнадцатеричной форме. Сначала
рассмотрим случай использования 8 бит.

232 ГЛАВА 5. Алгоритмы и рекурсия
Целое положительное число должно начинаться с 0, а целое отрицательное
число будет начинаться с 1. Поэтому 10110011 будет представлять целое отрица-
отрицательное число, а 01110101 будет представлять целое положительное число. По-
Поскольку при таком способе записи наибольшее возможное целое положительное
число есть 01111111, то всего имеется 127 целых положительных чисел. Пусть
дано положительное целое число, представленное с использованием п бит. Тогда
соответствующее ему отрицательное число находят путем вычитания этого числа
из 2П, выраженного в двоичной форме. Это осуществляется вычитанием числа из
2П — 1 (что называется нахождением 1-го дополнения) и последующим прибавле-
прибавлением 1. Поэтому в случае, когда используется 8 бит, положительное целое число
вычитается из
Т - 1 = 11111111,
а затем прибавляется 1. Например, чтобы найти отрицание числа 00101011, мы
вычитаем его из 11111111:
11111111
-00101011 ,
11010100
а затем к полученному числу 11010100 прибавляем 1. Таким образом, отрицанием
числа 00101011 будет число 11010101.
Заметим, что вычитание 00101011 из 11111111 просто меняет нули на едини-
единицы, а единицы — на нули. Всегда ли это справедливо, когда 8-битовая двоичная
строка вычитается из 11111111?
ПРИМЕР 5.46. Найти представление числа —56 в 8-битовом двоичном дополне-
дополнении. Сначала число 56 представляется как 00111000. Вычитая его из 11111111,
получаем 11000111. Прибавление 1 дает 11001000, так что —56 имеет представ-
представление 11001000. ?
Если задано целое отрицательное число, можно найти целое положитель-
положительное число, для которого данное число является отрицанием, просто выполняя те
же самые операции с отрицательным числом. Например, чтобы найти то поло-
положительное число, для которого 10110111 представляет отрицание, просто вычтем
его из 11111111, получая 01001000. После прибавления 1 получаем 01001001, что
является двоичным представлением числа 72. Отсюда 10110111 изображает —72.
Отрицательные двоичные дополнения изменяются от 11111111 до 10000000, так
что их имеется 128. Таким образом, если использовать 8 двоичных разрядов,
можно представить все числа от -128 до 127. В общем случае, если имеется п
двоичных разрядов, можно представить все целые числа от -2й до 2П~1 - 1.
Если для представления целых чисел используется 16 (или больше) бит, то
удобнее всего пользоваться шестнадцатеричной системой счисления. Поскольку
каждый шестнадцатеричный разряд состоит из четырех двоичных, то для 16 бит
необходимо 4 шестнадцатеричных разряда. Таким образом, 21А5, F9AB и 004F
являются примерами шестнадцатиразрядных целых чисел со знаком, представлен-
представленных в шестнадцатеричной системе счисления. Поскольку двоичное представление
целого положительного числа должно начинаться с 0, то наибольшее число, кото-
которое может стоять в первом разряде его шестнадцатеричного представления, это 7

РАЗДЕЛ 5.7. Числа со знаком 233
(= 01112). Поэтому 691F, 7FFF и 0031 изображают целые положительные чис-
числа, а 8124, А105 и FFF1 изображают целые отрицательные числа. Как и ранее,
если целое положительное число представлено с использованием п битов, отрица-
отрицание числа находят путем его вычитания из 2П. В случае использования 16 битов
это осуществляется путем вычитания целого положительного числа в шестнадца-
шестнадцатеричной форме из FFFF и последующего прибавления 1. Как и раньше, для
преобразования отрицательного числа обратно в его положительного двойника
выполняем операцию дополнения, вычитая его из
216 - 1 = FFFF,
а затем прибавляя 1.
ПРИМЕР 5.47. Найти представление в шестнадцатеричной системе счисления от-
отрицания шестнадцатеричного числа 78F с использованием 16 бит. Сначала за-
заменим запись числа на 16-битовое шестнадцатеричное число 078F. Затем вычтем
078F из FFFF, получив F870, и далее прибавляем 1. В итоге получаем пред-
представление F871. ?
ПРИМЕР 5.48. Найти 16-битовое представление в шестнадцатеричной форме чис-
числа — 1158ю. Поскольку 1158ю = 486i6 = 0486, представленное в 16-битовой
шестнадцатеричной форме, вычитаем 0486 из FFFF, получая FB79, после че-
чего, прибавляя 1, получаем FBI А. Следовательно, 16-битовое шестнадцатеричное
представление числа — 1158ю есть FBI А. ?
Сложение чисел фиксированной длины со знаком на основе двоичного или
шестнадцатеричного представления ничем не отличается от обычного сложения
двоичных и шестнадцатеричных чисел, за исключением того, что если сумма
порождает дополнительный разряд, тогда первый разряд удаляется. Например,
если 0111 и 1011 складываются как двоичные числа:
0111
1011 ,
[1] 0010
то цифра 1 слева удаляется. Если шестнадцатеричные числа со знаком FF14 и
0FIA складываются как шестнадцатеричные:
FF14
0FL4,
[1] 0Е2Е
то цифра 1 слева также удаляется.
Если попытаться сложить 7F14 и 6F23, то получаем
7F14
6Д23 .
ED37
т.е. сложив два положительных числа, получили отрицательное число. В таком
случае говорят, что имеет место переполнение. Значение суммы слишком велико

234 ГЛАВА 5. Алгоритмы и рекурсия
для представления с использованием 16 бит. Числа со знаком, выражаемые с ис-
использованием 16 двоичных разрядов или 4 шестнадцатеричных разрядов, должны
находиться между -32768 и 32767.
В десятичной арифметике, чтобы вычесть 25 из 75, к 75 прибавляют —25.
Во многих учебниках пишут: "измените знак вычитаемого [того числа, которое
вычитается] и выполните сложение". При сложении чисел со знаком необходимо
действовать таким же образом. При вычитании одного целого числа из друго-
другого находим двоичное дополнение числа, которое нужно вычесть, и производим
сложение.
Например, для нахождения разности
01010110
- 01110001
мы сначала находим двоичное дополнение числа 01110001, которое равно 10001111,
после чего выполняем сложение:
01010110
+ 10001111 .
11100101
Как и следовало ожидать, результат — отрицательное число.
Используя тот же самый подход при решении следующей задачи:
01010001
- 11101001 .
мы сначала находим двоичное дополнение числа 11101001, которое равно 00010111,
после чего выполняем сложение:
01010001
+ 00010111 .
01101000
В данном случае отрицательное число вычиталось из положительного, поэтому
отрицательное число мы заменили положительным и произвели сложение.
ПРИМЕР 5.49. Вычесть 56 из 23, используя 8-битовые числа со знаком. Поскольку
56 = 00111000 и 23 = 00010111, имеем
00010111
- 00111000 .
Сначала находим двоичное дополнение числа 00111000, которое равно 11001000,
а затем выполняем сложение:
00010111
+ 11001000 .
11011111
Так как двоичным дополнением числа 11011111 является 00100001, которое равно
33, число 11011111 равно -33. ?

РАЗДЕЛ 5.7. Числа со знаком 235
ПРИМЕР 5.50. Вычесть 7328 из 3614, воспользовавшись 16-битовыми шестна-
дцатеричными числами со знаком. Поскольку 7328ю = ICAOiq и 3614 = ElEie,
0Е1Е
- 1С АО .
Сначала находим двоичное дополнение числа 1С АО, которое равно E35F, а затем
выполняем сложение:
0Е1Е
+ ?360 .
F17E
Поскольку двоичным дополнением числа F1E является 0?"82 и 0Е82 = 3714ю,
то 3614 - 7328 = -3714. ?
¦ УПРАЖНЕНИЯ
1. Найдите двоичное дополнение приведенных ниже 8-битовых чисел в двоич-
двоичной форме:
а) 01110110; б) 10110101;
в) 00110111; г) 11101011.
2. Найдите двоичное дополнение приведенных ниже 8-битовых чисел в двоич-
двоичной форме:
а) 01100100; б) 11011001;
в) 00111011; г) 10010000.
3. Выразите следующие десятичные числа как 8-битовые двоичные числа со
знаком:
а) 73; б) -101;
в) -37; г) -14.
4. Выразите следующие десятичные числа как 8-битовые двоичные числа со
знаком:
а) 48; б) -33;
в) -58; г) -114.
5. Выполните следующие операции, используя 8-битовые двоичные числа со
знаком:
10110100 00110100
а) 4- 01110010 ; б) + 01001010 ;
00110101 00110101
в) - 01110110 ; г) - 01110110 .
6. Выполните следующие операции, используя 8-битовые двоичные числа со
знаком:
11001001 00101001
а) + 01011110 ; б) + 01010011 ;
01011100 01101101
в) - 01110111 ; г) - 01111000 .

236 ГЛАВА 5. Алгоритмы и рекурсия
7. Превратите следующие числа в 8-битовые двоичные числа со знаком и вы-
выполните указанные операции:
43 12
а) + 28 ; б) + 81 ;
43 86
в) - 67 ; г) - 73 .
8. Превратите следующие числа в 8-битовые двоичные числа со знаком и вы-
выполните указанные операции:
29 34
а) + 61 ; б) - 56 ;
13 22
в) - 87 ; г) - 98 .
9. Найдите двоичное дополнение следующих чисел со знаком, выраженных в
шестнадцатеричной форме:
а) 723А; б) АВ20\
в) FA12; г) 23ВС.
10. Найдите двоичное дополнение приведенных ниже чисел со знаком, выра-
выраженных в шестнадцатеричной форме:
a) 23CF; б) 1В5С;
в) FF13; г) 1020.
11. Выразите следующие десятичные числа как 16-битовые числа со знаком в
шестнадцатеричной форме:
а) 270; б) -893;
в) -17; г) -9872.
12. Выразите следующие десятичные числа как 8-битовые двоичные числа со
знаком:
а) 48; б) -237;
в) -8858; г) -12499.
13. Выполните следующие операции, используя 16-битовые числа со знаком в
шестнадцатеричной форме:
ЗС14 C12F
а) + S9AC ; б) + 359Л ;
В127 34С5
в) - С1АВ ; г) - FF12 .
14. Выполните следующие операции, используя 16-битовые числа со знаком в
шестнадцатеричной форме:
4713 5379
а) + 0F23 ; б) + FA12 ;

РАЗДЕЛ 5.8. Дальнейшее изучение матриц 237
37В4 С129
в) - АА44 ; г) - D48A .
15. Переведите следующие числа в 16-битовые шестнадцатеричные числа со зна-
знаком и выполните указанные операции:
936 1639
а) + 258 ; б) + 3926 ;
8836 994
в) - 19923 ; г) - 1713 .
16. Переведите следующие числа в 16-битовые шестнадцатеричные числа со зна-
знаком и выполните указанные операции:
829 778
а) + 1499 ; б) - 569 ;
13 19237
в) - 87 ; г) - 18 .
17. Найдите диапазон целых чисел, который может быть выражен числами со
знаком с использованием 32 бит.
18. Найдите диапазон целых чисел, который может быть выражен числами со
знаком с использованием 64 бит.
5.8. ДАЛЬНЕЙШЕЕ ИЗУЧЕНИЕ МАТРИЦ
Детерминант является важной функцией, отображающей множество матриц с
элементами из множества действительных чисел во множество действительных
чисел. Детерминант используется при решении систем уравнений (метод Краме-
Крамера), а также при определении обратной матрицы (если она существует).
Пусть дана п х п матрица
А2\ А22 ••• А2п
А =
Символом Aij обозначим матрицу размера (п — 1)х(гг — 1), полученную удалением
в исходной матрице г-ой строки и j-ro столбца.
ПРИМЕР 5.51. Пусть
. _ Г Ап Ап 1
Тогда ~М{ = [А22], АЦ = [^2i], ^21 = [Аи] и!^= [Ап]. ?

238 ГЛАВА 5. Алгоритмы и рекурсия
ПРИМЕР 5.52. Пусть
А =
Тогда
Г А22 А
= [
23
п
А32
Г Ап
= [
' и
^22 ^
22 ^23
?
ОПРЕДЕЛЕНИЕ 5.53. Детерминант матрицы размера п х п
А =
-422
. АП1 А
п2
обозначается через det(A), |Л| или
Аи А12 •
-422 •
Ап2 '
и определяется следующим образом:
а) если и = 1, то det(A) = |Ац| = Ац\
п
б) если п > 2, то det(A) = J2 A\j{
А2п
А2п
Пусть Mij = det(Aij). Число Mij называется минором элемента Ai
Cij = (—l)t+J det(Aij) — алгебраическим дополнением элемента A
вательно, det(A) = J2 A1:j(-l)l+j f
, а число
ij. Следо-
СледоОбратите внимание, что в приведенном выше определении \Ац\ не является
абсолютным значение Ли, хотя обозначение кажется таким же.
Давайте теперь составим алгоритм для вычисления детерминанта. Прежде
всего отметим, что детерминант порядка и х п определен через детерминанты
порядка (п - 1) х (п - 1). Здесь мы сталкиваемся с примером рекурсивного ал-
алгоритма. В дальнейшем мы рассмотрим алгоритмы такого типа более подробно.
Процедура вычисления детерминанта имеет следующий вид:

РАЗДЕЛ 5.8. Дальнейшее изучение матриц 239
Процедура Детерминант(Л, п):
Цикл по г от 1 до гг:
Если п = 1, то det(A) = \Ац\ = Ац\
Если п > 2, то det(A) = 0;
Цикл по j от 1 до п:
Значение det(.A) заменить на
det(A) + А^(-1I"Ь:;'Детерминант(А17,п - 1);
Конец цикла;
Конец цикла;
Конец процедуры.
Поскольку детерминант (А,п) определен через детерминанты (Aij,n— 1),
для вычисления детерминанта (А, п) прежде необходимо определить детерминан-
детерминанты (Aij,n — 1). Многие компьютерные программы обладают свойством "вызывать"
саму себя. Это дает возможность написать компьютерную программу, очень похо-
похожую на приведенную выше процедуру. В более полном объеме этот вопрос будет
рассмотрен в последующих разделах.
Следовательно, если
то det(-A) = An
Если
*21 ^22
\А2\\ = An • A22 -
An Ai2
A2i A22 А2з
Аз2 Азз
TO
A22
det(A) = An
ПРИМЕР 5.54. Пусть А =
-A12
A22
A31 A33
A2i A22
A31 AS2
2 3
. Тогда
det(A) =
2 3
1 2
= 2 |2| + 3(- |1|) = 2x2-3x1 = 1.
В общем случае, если А — \ , , то det(A) = ad — be.
ПРИМЕР 5.55. Пусть А =
1 2 0
1 1 2
3 0 1
. Тогда
det(A) =
1 2 0
1 1 2
3 0 1

240 ГЛАВА 5. Алгоритмы и рекурсия
= 1
-2
1 2
3 1
+ 0
1 2
3 1
= 1A х 1 - 2 х 0) - 2A х 1 - 2 х 3) + 0 =
= 1-2(-5) = 11.
?
Определим 6ij как
если г = j ;
если г ф j .
ОПРЕДЕЛЕНИЕ 5.56. Пусть 1п есть матрица [Uj] размера пхп, где 1^= 6ij,
т.е. на диагонали матрицы 1п стоят единицы, а все остальные ее элементы
равны нулю. Матрица 1п называется единичной матрицей размера пхп, или
просто единичной матрицей. Единичная матрица обладает тем свойством, что
для любой матрицы А размера пхп имеет место равенство А1п = 1пА = А.
ПРИМЕР 5.57. Единичными матрицами размера 2 х 2 и 3 х 3 являются
1
0
0
0
1
0
0
0
1
?
ОПРЕДЕЛЕНИЕ 5.58. Пусть А — матрица размера пхп. Мультипликатив-
Мультипликативно обратной, или просто обратной к матрице А называется матрица А~1,
обладающая (если она существует) тем свойством, что АА~1 = А~1А = 1п.
2 5
ПРИМЕР 5.59. Матрица - Q является обратной к 1 о , т.к.
1 о —1 Z
3 -5
2 5
1 3
3
-1
ПРИМЕР 5.60. Матрица
поскольку
2 1 0
-12 2
0 1 1
0 -1
1 2
-1 -2
2 1 0
-12 2
0 1 1
2
-4
5
0
1
-1
3 -5
-1 2
2 5
1 3
1 0
0 1
?
является обратной к
0
1
-1
2
-4
5
2
-2
2
-4
5
2
-1
0
1
2
1
0
2
1
1 0 0
0 10
0 0 1
?

РАЗДЕЛ 5.8. Дальнейшее изучение матриц 241
Ниже приводится алгоритм нахождения матрицы, обратной к матрице А
размера п х п:
1. Найти det(^l). Если он равен нулю, обратная матрица не существует.
2. Для каждого Aij найти алгебраическое дополнение Cij и сформировать мат-
матрицу С — [С^]у называемую матрицей алгебраических дополнений.
3. Найти матрицу С1, транспонированную к матрице С, так что С*. = Cji.
Матрица С1 называется сопряженной к матрице А и обозначается adj(-A).
4. Разделить каждый элемент сопряженной матрицы adj(A) на det(A).
1 adj(A).
5. А'1 =
det(A)
Следовательно, если В =
а Ъ
с d
то
-Ь
det(B) det(B)
—с
L det(B) det(B) J
где det(jB) = ad - be. Путем прямых вычислений можно показать, что ВВ~1 =
В~1В = /2. Аналогично, для нахождения матрицы, обратной к матрице А, где
А =
Ап
А2\
А12 А13
А22 А2з
А32
определяем матрицу алгебраических дополнений С = [Cij], где С^ — детерми-
детерминанты матриц, полученных из А = [А^] удалением строки и столбца, содержащих
Aij, умноженные на соответствующий знак, а именно, (-1)г+:7. Наконец, для по-
получения А~1 матрица С транспонируется и делится на det(^), после чего
det(A)
А22
А32
А21
Азх
А21
А23
Азз
А2з
Азз
А32
-
—
А12
Аз2
Аи
Аз1
Ап
Аз1
Ап
А33
А13
Азз
А12
Аз2
-
А22
Ап
Ап
А23
Al2
А22
ПРИМЕР 5.61. Пусть А =
3 -5
_1 2
Тогда det(A) = 1. Матрицей алгебраиче-
ских дополнений для матрицы А будет
2 -(-1) 1 _
-(-5) 3
2 1
5 3

242 ГЛАВА 5. Алгоритмы и рекурсия
Матрицей, сопряженной к матрице А, будет
Обратной к матрице А будет матрица
2 5
1 3
ПРИМЕР 5.62. Пусть А =
0-1 2
1 2 -4
-1 -2 5
det(A) = 0 •
2 -4
-2
-(-!)¦
2 5
1 3
. Тогда
1 -4
-1
+ 2
1 2
-1 -2
= 0 + 1 + 0 = 1.
Матрицей алгебраических дополнений для матрицы А будет
С =
2 -4
-2 5
-1 2
-2 5
-1 2
2 -4
-
1 -4
-1 5
0 2
-1 5
0 2
1 -4
1 2
-1 -2
0 -1
-1 -2
0 -1
1 2
2-10
1 2 1
0 2 1
Таким образом, матрицей, сопряженной к А, будет
adj(A) = С =
2 1 О
-12 2
О 1 1
а обратной
A"-i
2
-1
О
1
2
1
О "
2
1
2 10
-12 2
0 11
?

РАЗДЕЛ 5.8. Дальнейшее изучение матриц 243
УПРАЖНЕНИЯ
1.
2.
3.
4.
Вычислите
а)
в)
1 3
2 5
3
-6
2
Вычислите
а)
в)
" 1 3
2 5
3
-6
9
Вычислите
Найдите А
а)
в)
2 3
5 7
4
-3
2
детерминанты матриц:
];
-2
1
0
-3 '
0
-1
детерминанты матриц:
];
-2
1
0
-1 ¦
2
-3
;
детерминант
]=
-1
1
0
если А =
3 '
-3
1
»
матрицы
¦ о
0
0
. 1
0
0
1
0
б)
г)
б)
г)
1
0
0
0
б)
г)
3
-4
" 6
1
3
3
-4
1
-6
3
0 "
1
0
0 .
3
-4
' 7
4
2
б]
-4
-11
-1
б]
-6
-1
2
-5
7
-7
-3
_2
-5
2
1
3
2
1
]'
3 "
2
1
5. Понятие матрицы перестановок было дано в определении 4.52. Докажите,
что если А — матрица перестановок, то А~г = А*.
6. В предположении, что если А и В — матрицы, то det(AB) — det(A)det(jB),
а) докажите, что детерминант единичной матрицы равен 1;
б) докажите, что если матрица А имеет обратную матрицу, то
det(A) '
в) докажите, что матрица А имеет обратную тогда и только тогда, когда
det(A) ф 0.

ГЛАВА
ГРАФЫ,
ОРИЕНТИРОВАННЫЕ
ГРАФЫ И ДЕРЕВЬЯ
6.1. ГРАФЫ
В главе 2 графы использовались для представления отношений. Однако теория
графов имеет свою собственную проблематику и является важным разделом мате-
математики. В данной главе мы определим понятие графа непосредственно, вне связи
с отношениями.
ОПРЕДЕЛЕНИЕ 6.1. Граф есть конечное множество V, называемое множе-
множеством вершин, и множество Е двухэлементных подмножеств множества V.
Множество Е называется множеством ребер. Элемент множества Е называ-
называется ребром. Граф обозначается G(V, E). Элементы а и b множества V назы-
называются соединенными, или связанными ребром {а, 6}, если {а, 6} Е Е.
Обычно конечный граф изображают в виде диаграммы, на которой вершины
обозначаются точками, а ребра, соединяющие две вершины,— линиями между
этими точками.
ОПРЕДЕЛЕНИЕ 6.2. Если {а, Ь) — ребро, тогда вершины а и Ъ называются
концами ребра {а, Ь). Ребро {а, Ь} называют также инцидентным к вершинам
а и 6. Обратно, говорят, что вершины а и b инцидентны к ребру {а, Ь}. Две
вершины называются смежными, если они являются концами ребра, или, что
то же самое, если они инцидентны к одному ребру. Два ребра называются
смежными, если они инцидентны к общей вершине.
ПРИМЕР 6.3. Граф с множеством вершин V = {а,Ь,с} и множеством ребер Е
{{а, Ь}, {Ь, с}} может быть изображен, как показано на рис. 6.1 или рис. 6.2.

РАЗДЕЛ 6.1. Графы 245
Рис. 6.1
а с
Рис. 6.2
?
ПРИМЕР 6.4. Граф, у которого V = {a,6,c,d,e} и
Е = {{а, Ь}, {а, е}, {Ь, е}, {6, d}, {Ь, с}, {с, d}},
может быть изображен диаграммой, показанной на рис. 6.3.
Рис. 6.3
?
Во многих книгах по математике графы, определенные выше, называют про-
простыми графами. Тем не менее, в теории графов чаще всего используются струк-
структуры именно такого типа. Ограничение на существование только одного ребра
между двумя вершинами дает возможность представлять любое ребро как мно-
множество из двух элементов, а именно, вершин ребра. Перечислим теперь основные
типы графов, которые будут использоваться в других главах. Заметим, что мно-
многие теоремы этой главы будут справедливы для графов более общего вида. Ребро,
которое соединяет вершину саму с собой, называется петлей. Если в графе до-
допускается наличие петель, то он называется графом с петлями. Если в графе
допускается наличие более одного ребра между двумя вершинами, то он называ-
называется мультиграфом. Если каждая вершина графа отмечена, то граф называется
размеченным. Если же допускается как наличие петель, так и существование
более одного ребра между двумя вершинами, то мы будем называть такой объект
псевдографом.
Теория графов берет начало с решения знаменитым математиком Эйлером
задачи о кенигсбергских мостах в 1736 году. Существуют две внешне различ-
различные версии этой задачи. Задача возникла в прусском городке Кенигсберг на реке
Прегал. Жителям Кенигсберга нравилось гулять по дорожке, которая включала
семь мостов через реку Прегал. Люди интересовались, могут ли они, начав путь
с одного участка суши, обойти все мосты, посетив каждый лишь однажды, и
вернуться в точку начала пути, не переплывая реки. Различие между двумя вер-
версиями задачи — чисто географическое. Согласно первой версии на реке Прегал
был остров Кнайпхоф и участок суши, возникший в результате разветвления реки
Прегал на рукава. Этот район и семь мостов показаны на рис. 6.4.

246 ГЛАВА 6. Графы, ориентированные графы и деревья
река Прегал ( КнайРпхоф ^ZX^ Участок суши d
b
Рис. 6.4
Согласно второй версии на реке Прегал было два острова, один из которых
остров Кнайпхоф. Эта ситуация изображена на рис. 6.5.
d Рис. 6.5
Точная версия авторам не известна. К тому же это не имеет значения для
математической формулировки задачи. Эйлер построил мультиграф, показанный
на рис. 6.6, который пригоден для каждого из этих случаев. В этом мультиграфе
участки суши Эйлер изобразил как вершины, а дорожки через мосты — как ребра.
В таком случае задача приобретает следующую формулировку: начиная с любой
вершины, проходя по каждому ребру только один раз, вернуться в исходную вер-
вершину. Далее будет показано, как на основе понятия мультиграфа Эйлер решил
эту задачу. Приведенный пример иллюстрирует полезность математических аб-
абстракций, по крайней мере, в двух аспектах. Во-первых, абстракция устраняет в
содержании проблемы несущественные детали и концентрирует внимание на тех
понятиях, которые действительно важны. Во-вторых, абстракция часто выявляет
кажущееся различие задач, совпадающих по сути или, по крайней мере, имеющих
сходные решения. Сказанное особо справедливо для теории графов.
Рис. 6.6
Решение задачи о кенигсбергских мостах будет рассмотрено в разделе 6.2.
Примером другой проблемы, которую можно промоделировать на основе тео-
теории графов, является задача о снабжении трех домов тремя видами коммунальных
услуг. Согласно условию задачи к каждому из трех домов необходимо подключить
три вида коммунальных услуг, например, воду, газ и электричество, посредством
подземных линий труб и кабелей. Вопрос состоит в том, можно ли обеспечить
эти три дома коммунальными услугами без пересечения линий снабжения. Граф,
моделирующий данную задачу, показан на рис. 6.7

РАЗДЕЛ 6.1. Графы 247
Дом1 Дом 2 ДомЗ
вода
электричество рис $ у
Аналогичная задача более практического характера возникает при создании
микросхем. В них пересечение проводов на каждом уровне является нежелатель-
нежелательным. Такого рода задачи будут рассмотрены в одной из последующих глав при
изучении планарных графов.
ОПРЕДЕЛЕНИЕ 6.5. Степенью вершины г;, обозначается deg(i;), называется
количество ребер, инцидентных этой вершине. Вершина степени 0 называется
изолированной.
ПРИМЕР 6.6. В графе, показанном на рис. 6.8, вершины а и с
и ез - смежные ребра.
смежные, a ei,e2
Рис. 6.8
Однако, вершины аи/ смежными не являются, а е2 и е5 не являются смежными
ребрами. Вершины 6, с и d имеют степень 2, в то время как вершины аи/ имеют
степень 3. ?
ТЕОРЕМА 6.7. Сумма степеней вершин графа всегда четная.
ДОКАЗАТЕЛЬСТВО. Поскольку каждое ребро графа имеет два конца, степень
каждого конца увеличивается на 1 за счет одного ребра. Таким образом, в сумму
степеней всех вершин каждое ребро вносит 2 единицы, поэтому сумма долж-
должна в два раза превышать число ребер. Следовательно, сумма является четным
числом. ¦
Теперь воспользуемся этой теоремой для доказательства следующего утвер-
утверждения.
ТЕОРЕМА 6.8. В любом графе количество вершин нечетной степени четно.
ДОКАЗАТЕЛЬСТВО. Доказательство проведем методом от противного: предпо-
предположив, что теорема не верна, найдем противоречие, из которого будет следовать,
что теорема справедлива. Если теорема не верна, то имеется нечетное количество
вершин, степени которых нечетны. Но сумма степеней вершин с четными степеня-
степенями четна. Сумма степеней всех вершин есть сумма степеней вершин с нечетными

248 ГЛАВА 6. Графы, ориентированные графы и деревья
степенями плюс сумма степеней вершин с четными степенями. Поскольку сум-
сумма нечетного числа и четного числа есть число нечетное, сумма степеней всех
вершин нечетная. Но это противоречит теореме 6.7, поэтому мы пришли к про-
противоречию. Следовательно, делаем вывод, что теорема справедлива. ¦
ОПРЕДЕЛЕНИЕ 6.9. Граф G'(V',E') называется подграфом графа G(V,E),
обозначается G'(V\E') ^ G(V,E), если V С V и Е1 С Е. Таким образом,
каждая вершина в G1 является вершиной в G, и каждое ребро в G' является
ребром в G.
ПРИМЕР 6.10. Графы, изображенные на рис. 6.9, 6.10 и 6.11,
а е
Рис. 6.9
d e
Рис. 6.10
являются подграфами графа на рис. 6.12.
D
Путь (маршрут) в графе — это просто совокупность ребер, которые объ-
объединены вместе вершинами так, что вдоль них можно двигаться по графу. В
определении, приведенном ниже, свойства пути очерчены более формально. Для
удобства договоримся в оставшейся части этого раздела использовать символы
^о,^ь^2,^з, • • • ,Vk,u и v для обозначения вершин.
ОПРЕДЕЛЕНИЕ 6.11. Пусть G = G(V,E) — граф с вершинами v0, vi, v2,
Щ> • • •, Vk € V и ребрами ei, б2, ез,..., е^ G Е. Путем длины k из г;о в Vk (или
между г;о и Vk) называется последовательность у^е\У\е2У2^Щ • • -VkekVk такая,
что ei = {vi-\,Vi}. Таким образом, путь длины к имеет к ребер. По причине
избыточности обозначений в этом определении для графа в общем случае путь
будет обозначаться через г^г^г^з • • >Vk- Каждые два последовательных ребра
пути имеют общую вершину, поэтому являются смежными. Простым путем
из vq в Vk называется путь, в котором нет повторяющихся вершин.

РАЗДЕЛ 6.1. Графы 249
ПРИМЕР 6.12. В графе, изображенном на рис. 6.13,
3 V4
PUC. 6.13
ИЗ V0 В V7 Ведут ПуТИ VoViV2V5V7, V0ViV2V5V4ViV2V5V7i V0ViV4V5V^V5V7 И VqV3V4V6V7
длины 4, 8, 6 и 4 соответственно. Пути vov\v2v^v7 и voVsV4Vqv7 являются про-
простыми. ?
ОПРЕДЕЛЕНИЕ 6.13. Граф G называется связным, если имеется путь между
любыми двумя его различными вершинами.
ПРИМЕР 6.14. Граф на рис. 6.14 не связный. Например, нет пути из г;0 в г;3 и
Между 1J И D4-
4 Рис. 6.14
?
Возвращаясь к рассмотрению графа на рис. 6.13, следует отметить, что путь
voViv2v5V4Viv2v5v7 можно сократить до voviv2v5v7. Поскольку вершина v\ повто-
повторялась, необходимо удалить часть пути между двумя появлениями вершины v\
и после первого появления вершины v\ переходить сразу к v2. Аналогично, путь
voViV4V5V4V$v7 можно сократить до vqV\v^v^v7. Таким образом, если путь вклю-
включает какую-либо вершину Vi более чем один раз, его можно сократить, удалив
Vi и вершины, лежащие на пути между двумя появлениями вершины v». Мож-
Можно продолжать действовать таким образом, пока не будет исключено повторение
любой из вершин. Проведенные рассуждения дают возможность сформулировать
следующую теорему.
ТЕОРЕМА 6.15. Пусть G = G(V,E) — граф. Если существует путь из вершины
V{ в вершину vj, тогда существует простой путь из вершины Vi в вершину Vj.
Комбинируя определение 6.13 и теорему 6.15, приходим непосредственно к
такому следствию (следствием называется теорема, которая непосредственно вы-
вытекает из другой теоремы).
СЛЕДСТВИЕ 6.16. Граф G является связным тогда и только тогда, когда между
любыми двумя его вершинами существует простой путь.

250 ГЛАВА 6. Графы, ориентированные графы и деревья
ОПРЕДЕЛЕНИЕ 6.17. Пусть G = G(V,E) — граф. Подграф G' графа G назы-
называется компонентой графа G, если выполнены следующие два условия:
1. G' — непустой связный граф.
2. G" — связный подграф графа G к G' < G", тогда G' = G". Отсюда G' —
максимальный связный подграф графа G.
ПРИМЕР 6.18. Графы, изображенные на рис. 6.15 и 6.16, являются компонентами
графа, представленного на рис. 6.14.
Рис. 6.15
Рис. 6.16
?
ОПРЕДЕЛЕНИЕ 6.19. Пусть G = (V,E) — граф. Циклом называется путь
ненулевой длины, соединяющий вершину саму с собой и не содержащий по-
повторяющихся ребер. Простым циклом называется цикл, соединяющий вер-
вершину v саму с собой и не содержащий повторяющихся вершин, кроме v. Цикл
называется п-циклом, если он содержит п ребер и п различных вершин.
ПРИМЕР 6.20. Если опять рассмотреть граф на рис. 6.13, то в нем пути
vqV\v^v^v7vqv^v^vq, viV2V5v7v6V4Vi и г^г^г^г^т^б^^з^о являются циклами. При
этом все циклы , кроме vqViv^vsVjVgv^vsVq, простые. ?
Давайте теперь определим графы специального вида, которые пригодятся
нам в следующих разделах.
ОПРЕДЕЛЕНИЕ 6.21. Граф называется полным, если любые две его вершины
соединены ребром. Полный граф с п вершинами обозначается через Кп.
ПРИМЕР 6.22. На рис. 6.17 показаны, соответственно, графы К2, К$, К4 и К5.
Рис. 6.17
?
ОПРЕДЕЛЕНИЕ 6.23. Граф G = (V, Е) называется двудольным, если V можно
представить как объединение непересекающихся множеств, скажем, V = АиВ,
так что каждое ребро имеет вид {а,Ь}, где а Е А и b E В. Таким образом,
каждое ребро связывает вершину из А с вершиной из В, но никакие две вер-

РАЗДЕЛ 6.1. Графы 251
шины из А или две вершины из В не являются связанными. Двудольный граф
называется полным двудольным графом ifm,n, если А содержит т вершин,
В содержит и вершин и для каждого a e A, b G В имеем {а, 6} G Е. Таким
образом, для каждого a € А и Ь € В имеется связывающее их ребро.
ПРИМЕР 6.24. Графы
, ^2,2 и Х3,з приведены по порядку на рис. 6.18.
Рис. 6.18
?
УПРАЖНЕНИЯ
1. Что из приведенного ниже является путем в графе на рис. 6.19? Которые из
них являются простыми путями? Приведите длину каждого из путей.
a) aebfcd\ б) aecdaec;
в) aebecfbd; г) aecfbdafc.
2. Что из приведенного ниже является путем в графе на рис. 6.20? Которые из
них являются простыми путями? Приведите длину каждого из путей.
a) abcabcd\ б) bcdeca\
в) debace\ г) decab.
bee
Рис. 6.20
3. Что из приведенного ниже является циклом в графе на рис. 6.21? Которые из
них являются простыми циклами? Для каждого n-цикла приведите значение
п.
a) dabefbed; б) bfeedbfeb;
в) abcfebfca\ г) aeefbda.
4. Что из приведенного ниже является циклом в графе на рис. 6.22? Которые из
них являются простыми циклами? Для каждого n-цикла приведите значение
п.
a) abcdbaea\ б) ebcdbcdae\
в) adcbea\ г) adbedea.

252 ГЛАВА 6. Графы, ориентированные графы и деревья
а Ь с а Ъ
5. Нарисуйте следующие графы:
а) К6; б) ЛГ1>3; в) К1л\ г) КЗА.
6. Докажите, что если граф содержит цикл от вершины v к самой себе, то он
содержит простой цикл от вершины v к самой себе.
7. В игре "вытягивание палочек" некоторое множество их подбрасывается над
столом. Содержание игры — вытащить из образовавшейся груды палочки
по одной, не нарушая положение других. Представьте себе, что "палочки" —
вершины графа. Между двумя вершинами имеется ребро, если одна палочка
касается другой. Что представляют собой компоненты этого графа?
8. Покажите, что каждому рефлексивному отношению соответствует граф с
петлями и обратно, граф с петлями в каждой вершине описывает рефлек-
рефлексивное отношение. Верно ли, что каждому графу с петлями соответствует
рефлексивное отношение?
6.2. ОРИЕНТИРОВАННЫЕ ГРАФЫ
Во многих случаях необходимы графы, у которых ребра, по существу, представ-
представляют собой улицу с односторонним движением. Это означает, что если рассматри-
рассматривается ребро, выходящее из вершины а в вершину 6, то его нельзя рассматривать
выходящим из вершины Ь в вершину а. Например, если граф моделирует поток
нефти в трубопроводе, и если нефть течет из пункта а в пункт 6, нам не хоте-
хотелось бы, чтобы поток был и в обратном направлении, из пункта Ъ в пункт а. В
последующих главах мы встретим применение ориентированных графов в сетях
и теории автоматов.
ОПРЕДЕЛЕНИЕ 6.25. Ориентированный граф или орграф G, который обо-
обозначается через G(V, Е)у состоит из множества V вершин и множества Е упо-
упорядоченных пар элементов из У, называемого множеством ориентированных
ребер или просто ребер, если понятно, что граф ориентирован. Элемент множе-
множества Е называется ориентированным ребром. Если (а, Ь) € -Б, то а называется
начальной вершиной ребра (а, 6), a b называется конечной вершиной.
Заметим, что понятие ориентированного графа допускает наличие петель,
чего не было в случае простых графов. Тому есть, в основном, две причины.
Во-первых, определение ориентированного ребра естественным образом включа-
включает понятие петли, т.к. петля у вершины а есть просто ребро (а, а). В случае

РАЗДЕЛ 6.2. Ориентированные графы 253
неориентированных графов это нельзя было сделать, так как ребро неориентиро-
неориентированного графа имеет вид {а,6}, поэтому петля должна была бы иметь вид {a,a}.
Во-вторых, когда речь идет об отношениях, элемент может находиться в отноше-
отношении с самим собой, что не имеет смысла для множеств, так как любой элемент
присутствует во множестве только один раз. И еще, понятие петли в большей
степени присуще ориентированным графам.
Ребро (а, Ь) ориентированного графа обозначается на диаграмме стрелкой
из а в Ь. Отметим, что в простом графе ребро представляется двухэлементным
подмножеством, чтобы подчеркнуть, что отношение симметрично, в то время как
в ориентированном графе ребро представлено упорядоченной парой, чтобы акцен-
акцентировать важность порядка и то, что (а, Ъ) может быть ребром в орграфе, а (Ь, а)
— нет.
ПРИМЕР 6.26. Орграф, у которого V = {а, 6, с} и Е = {(а, 6), (Ь, с), (с, 6), (с, а)},
изображен на рис. 6.23. ?
ПРИМЕР 6.27. Орграф, у которого V = {а, 6, с, в] и Е = {(а, Ь), (Ь, с), (с, с), F, d),
(d,b),(c,d),(d,a)}, изображен на рис. 6.24. ?
Рис. 6.23
Рис. 6.24
ОПРЕДЕЛЕНИЕ 6.28. Если (a,b) — ребро ориентированного графа G(V,E),
так что a — начальная вершина, а 6 — конечная вершина ребра (а, Ь), тогда
вершины а и 6 инцидентны ребру (а, 6). Вершина а называется смежной к
вершине Ь. Вершина Ь называется также смежной от вершины а.
ОПРЕДЕЛЕНИЕ 6.29. Степенью выхода вершины v называется количество
ребер, для которых v является начальной вершиной, обозначается outdeg(t>).
Степенью входа вершины v называется количество ребер, для которых v явля-
является конечной вершиной, обозначается indeg(v). Если indeg(i>) = 0, то вершина
v называется источником. Если outdeg(i;) = 0, то вершина v называется сто-
стоком.
ПРИМЕР 6.30. В ориентированном графе на рис. 6.25 indeg(vo) = 0, indeg(t;i) = 1,
indeg(i;3) = 2, indeg^) = 2 и indeg^) = 3. Также outdeg(i;o) = 3, outdeg(i;i) =
2, outdeg(t>2) = 2, outdeg(i>3) = 1 и outdeg^) = 0. Таким образом, вершина v0 —
источник, а вершина v± — сток.

254 ГЛАВА 6. Графы, ориентированные графы и деревья
Рис. 6.25
Обратим внимание, что, хотя согласно определению ориентированного гра-
графа он может иметь петли, до настоящего момента не рассматривалась ситуация,
когда из вершины а в вершину b может выходить более чем одно ребро. Ори-
Ориентированный граф с более чем одним ребром из одной вершины в другую на-
называется мультиграфом, или, более точно, ориентированным мультиграфом.
Если каждое ребро помечено, будем говорить, что это размеченный ориентиро-
ориентированный, или просто размеченный граф, с пониманием того, что это ориентиро-
ориентированный граф. Поскольку в действительности не имеет смысла иметь два ребра из
вершины а в вершину 6, если нет возможности их отличать, обычно их каким-то
образом нумеруют. Формально размеченный граф можно определить следующим
образом.
ОПРЕДЕЛЕНИЕ 6.31. Размеченный граф G = G(V,L,E) представляет собой
множество вершин V, множество меток L и множество Еу которое является
подмножеством V х L xV. Таким образом, ребро е графа G имеет вид (а,/, 6),
где I — метка, а а, Ь — вершины.
Графически ребро е = (а,/,Ъ) размеченного графа обозначается, как на
рис. 6.26, или, как на рис. 6.27, если ребро — петля.
Рис. 6.26
Рис. 6.27
Рис. 6.28
Графы, представленные на рис. 6.28 и 6.29, являются примерами типичных
размеченных графов, называемых автоматами.
Рис. 6.29
К этим вопросам мы вернемся в главе 17.

РАЗДЕЛ 6.2. Ориентированные графы 255
ОПРЕДЕЛЕНИЕ 6.32. Ориентированный граф G'(V',Ef) называется ори-
ориентированным подграфом ориентированного графа G(V, E), обозначается
G'(V\E') ^ G(V,E), если V CV и Е' С Е. Таким образом, каждая вершина
в G1 является вершиной в G и каждое ориентированное ребро в G' является
ориентированным ребром в G.
Понятие ориентированного пути в ориентированном графе вводится по ана-
аналогии с понятием пути в графе. Разница лишь в том, что, перемещаясь вдоль
ориентированного пути, двигаться нужно в направлении, задаваемом ориентаци-
ориентацией ребер.
ОПРЕДЕЛЕНИЕ 6.33. Ориентированный путь из а в 6 задается последова-
последовательностью вершин г^г^г^з • • • vnt где а = vo> b = vn и (v»-i> v%) Для 1 < г < n
— ориентированное ребро. Длиной ориентированного пути называется количе-
количество ориентированных ребер, входящих в путь.
ПРИМЕР 6.34. Для графа G, изображенного на рис. 6.30,
Рис. 6.30
графы на рис. 6.31 и 6.32 являются подграфами. Ориентированные пути в G
ВКЛЮЧаЮТ VoV\V2V4j У\У2^А И VQV3V4.
Рис. 6.31 Рис. 6.32 П
Теперь для заданного ориентированного графа G будет построен неориенти-
неориентированный граф Gs такой, что каждое ориентированное ребро G (исключая петли)
станет неориентированным ребром графа Gs.
Пусть для каждого ориентированного графа G(V, Е) Е' = E—{(v, v) : v e V},
так что G'(V,?") — ориентированный подграф графа G(V, E), в котором уда-
удалены петли. Пусть R — симметричное замыкание множества ?", так что если
(а, Ь) е Е\ то (а, 6), F, а) G R, a Es — множество ребер, представляющих от-
отношение R. В таком случае граф GS(V,Es) называется соотнесенным графом

256 ГЛАВА 6. Графы, ориентированные графы и деревья
ориентированного графа G(V, E). Упрощая формулировку, можно сказать, что
множество ребер Е3 неориентированного графа GS(V,Es) можно определить та-
таким образом: {а, 6} Е Es тогда и только тогда, когда для различных вершин а и
b ребро (a, 6)eG или F, а) Е G.
ОПРЕДЕЛЕНИЕ 6.35. Ориентированный граф G(V, E) называется связным,
если его соотнесенный граф является связным. Ориентированный граф назы-
называется сильно связным, если для любой пары вершин a, b Е V существует
ориентированный путь из а в Ъ.
ПРИМЕР 6.36. Для ориентированного графа на рис. 6.30 соотнесенным будет
граф, показанный на рис. 6.33.
Рис. 6.33
Ориентированный граф является связным, поскольку его соотнесенный граф связ-
связный. Рассматриваемый граф однако не является сильно связным, поскольку из v\
в vs не существует ориентированного пути. ?
УПРАЖНЕНИЯ
1. Найдите вершины и ориентированные ребра для приведенных ниже оргра-
орграфов. Для каждой вершины определите степень входа и степень выхода. Име-
Имеются ли здесь источники и стоки?
а) 6)
О
• a
± Ь
I c

в)
РАЗДЕЛ 6.2. Ориентированные графы 257
г)
а Ь с d e
-*>*: > • > •
•о
2. Найдите вершины и ориентированные ребра для приведенных ниже оргра-
орграфов. Для каждой вершины определите степень входа и степень выхода. Име-
Имеются ли здесь источники и стоки?
а)
б)
в)
г)
3. Для каждого графа из предыдущего упражнения постройте четыре подграфа.
4. Найдите вершины и ориентированные ребра для приведенных ниже оргра-
орграфов. Для каждой вершины определите степень входа и степень выхода. Име-
Имеются ли здесь источники и стоки?
а)
б)
О,
• с

258 ГЛАВА 6. Графы, ориентированные графы и деревья
в) г)
ЛЛ
Р
5. Для каждого графа из предыдущего упражнения постройте четыре подграфа.
6. Определите простой ориентированный путь.
7. Определите ориентированный цикл.
8. Определите простой ориентированный цикл.
9. Который из приведенных ниже орграфов является связным? Какой из них
является сильно связным?
а)
в)
,* .*
V 1
г)
10. Для каждого графа из предыдущего упражнения найдите, если возможно,
ориентированный путь длины 2, ориентированный путь длины 3, ориентиро-
ориентированный путь длины 4 и ориентированный путь длины 5. Приведите пример
пути максимальной длины. Какой самый длинный простой цикл (если тако-
таковой существует) может быть построен?
11. Который из приведенных ниже орграфов является связным? Какой из них
является сильно связным?
а)
б)

РАЗДЕЛ 6.3. Деревья 259
в)
12. Для каждого графа из предыдущего упражнения найдите, если возможно,
ориентированный путь длины 2, ориентированный путь длины 3, ориентиро-
ориентированный путь длины 4 и ориентированный путь длины 5. Приведите пример
пути максимальной длины. Какой самый длинный простой цикл (если тако-
таковой существует) может быть построен?
6.3. ДЕРЕВЬЯ
Когда Джойс Килмер (Joyce Kilmer, 1886-1918) писал: "Нет, не увижу, это ясно,
поэмы дерева прекрасней", — вряд ли он имел в виду деревья, которые мы будем
рассматривать. Разрешим, однако, наши сомнения в пользу автора этих строк.
Дерево — это граф без циклов. Лес — это граф, компоненты которого являются
деревьями (почему бы и нет!). Понятие дерева широко используется во многих
областях математики и информатики. Например, они используются как инстру-
инструмент при вычислениях, как удобный способ хранения данных, способ сортировки
или поиска данных. Некоторые из этих приложений будут рассмотрены в после-
последующих разделах. Дерево и названо деревом, поскольку, будучи нарисованным,
выглядит как дерево, только перевернутое "вверх ногами". Граф, изображенный
на рис. 6.34, является примером дерева.
Рис. 6.34
В одной из последующих глав будет показано, что это дерево можно исполь-
использовать для демонстрации результатов трехкратного подбрасывания монеты. Граф
на рис. 6.35 не является деревом, поскольку содержит цикл. Граф на рис. 6.36 —
это лес.
Рис. 6.35
Рис. 6.36

260 ГЛАВА 6. Графы, ориентированные графы и деревья
Достаточно развитое генеалогическое дерево образует дерево. Если начать с кон-
конкретной (хорошо известной) личности и провести ребра между каждым из ро-
родителей и каждым сыном или дочерью, это сформирует дерево. При построении
генеалогического дерева, однако, необходимо быть очень осторожным, чтобы бра-
браки между дальними родственниками не образовывали циклов. Другим примером
дерева может служить организационный устав. Дерево на рис. 6.37 — типич-
типичное частичное организационное дерево для университета. В этом разделе, тем не
менее, деревья будем рассматривать как графы.
Ректор
Проректор по
учебной работе
Проректор по
административно-
хозяйственной части
Декан по Декан по Декан по Зам. по Зам. по Зам. по
бизнес-циклу педагогике гуманитарным коммерческой строительству студенческим
и точным деятельности и эксплуатации вопросам
дисциплинам зданий
Зам. по Зав. Зав. Зав. кафедрой
научной кафедрой кафедрой математики и
работе прикладного общественных информатики
искусства наук
Методист
Преподаватели
Рис. 6.37
Ориентированное дерево Т представляет собой свободный от петель ори-
ориентированный граф, соотнесенный граф которого является деревом; так что если
существует путь от вершины а к вершине 6, то он единственный. Сначала заме-
заметим, что если в ориентированном дереве имеется ребро (а, Ь), тогда не существует
ребро (Ь, а), в противном случае путь aba был бы циклом, и путь из а в Ь не был
бы единственным. Таким образом, множество Е, которое для дерева представляет
собой как множество ребер, так и отношение, обладает таким свойством, что если
(а, 6) G Е, то F, а) ф Е. Такое отношение называется асимметричным.
Возвращаясь к (неориентированным) деревьям, сначала отметим, что если
дерево имеет хотя бы одно ребро, оно имеет хотя бы две вершины со степенью
1. Чтобы убедиться в этом, рассмотрим для заданного дерева Т возможные пути.
Если у дерева п вершин, тогда длина пути не может превысить п - 1, так как
каждую вершину можно использовать только один раз. В противном случае по-
получились бы циклы, а у дерева нет циклов. Поэтому существует максимальный
путь, который нельзя продлить, чтобы получить более длинный путь. Предполо-
Предположим, что путь начинается в вершине а и заканчивается в вершине 6. Как а, так и b

РАЗДЕЛ 6.3. Деревья 261
должны иметь степень 1, поскольку в противном случае путь можно было бы про-
продолжить. Но это противоречит тому, что путь максимальный. Вершины степени 1
называются листьями. Другие вершины называются внутренними вершинами.
Максимальный путь не обязательно совпадает с самым длинным путем в дере-
дереве. Например, в дереве на рис. 6.38 путь V0V2V5 является максимальным путем.
Вершины ^з, ^4, ^5, ^8 и v-j представляют собой листья.
v* Рис. 6.38
Деревья обладают одним весьма интересным свойством, которое мы сейчас
докажем.
ТЕОРЕМА 6.37. Для любых двух вершин а и Ъ дерева Т существует единствен-
единственный путь из а в 6.
ДОКАЗАТЕЛЬСТВО. Для доказательства используется тот факт, что контрапо-
зиция утверждения логически эквивалентна самому утверждению. Поэтому пред-
предположим, что для некоторых вершин а и Ь дерева Т путь из а в Ъ не является
единственным, и покажем, что в таком случае Т не будет деревом. Допустим, что
существуют два различных пути: vqV\V2 • • • vn длины п и vqv'^ • • • v^ длины га,
где а = vq и Ъ = vn = v^. В каждом пути должна существовать первая верши-
вершина, начиная с которой соответствующие вершины не совпадают, скажем V{ ф v\,
и в каждом из путей должна существовать точка, начиная с которой вершины
опять одни и те же, скажем, Vj = v'k. Тогда Vi-\ViVi+\Vi+2''' vjvkvk-ivk-2vivi-i
является циклом, поэтому граф Т не является деревом. ¦
На основании следующей теоремы можно убедиться в том, что верна также и
обратная теорема. Поэтому дерево можно определить как граф, в котором между
двумя его вершинами имеется только один путь.
ТЕОРЕМА 6.38. Если для любых двух вершин графа G существует единственный
путь из вершины а в вершину 6, тогда G — дерево.
ДОКАЗАТЕЛЬСТВО. Опять покажем справедливость теоремы, доказывая контра-
позицию исходного утверждения. Предположим, что G не является деревом. Тогда
либо G не является связным, либо содержит цикл. Если граф G не связный, то
существуют вершины a,b e G, для которых не существует пути из а в 6. В таком
случае, очевидно, не существует и единственного пути из а в Ь. Если G содержит
цикл vqV\V2V2V^ • • • Vk-\Vk> то как г>2^з * • • ^fc-i^fc^o» так и V2V\Vq являются путями
из г>2 в vq. Положив а = v2 и Ъ = v0> видим, что путь между вершинами а и 6 не
является единственным. ¦

262 ГЛАВА 6. Графы, ориентированные графы и деревья
Предположим, что дерево представляет собой физический объект, подвиж-
подвижный в вершинах, и подвесим дерево за одну из его вершин так, что остальная его
часть повиснет ниже этой вершины. Например, пусть задано дерево на рис. 6.39.
8 Рис. 6.39
Если подвесить его за вершину г>3, получим дерево, представленное на рис. 6.40.
Если подвесим дерево за вершину г>4, оно будет выглядеть так, как показано на
рис. 6.41.
Рис. 6.40
Рис. 6.41
Вершина в самой верхней части каждого из изображений называется корнем
дерева. Если корень дерева определен, дерево называется корневым деревом. При
необходимости можно заменить корневое дерево Т на ориентированное Т", при
этом дерево на рис. 6.42 будет заменено деревом на рис. 6.43.
Рис. 6.42
Рис. 6.43
Такое дерево называется корневым ориентированным деревом, V поро-
порожденным корневым деревом Т. При этом следует помнить, что это дерево отли-
отличается от неориентированного дерева и что вид ориентированного дерева зависит
от выбора корня.
Если корень выбран, уровень вершины v определяется длиной единственного
пути из корня в вершину v. Высотой дерева называется длина самого длинного
пути от корня дерева до листа. Если рассматривается корневое ориентированное
дерево Т", порожденное данным корневым деревом Т, тогда вершина и называ-
называется родителем вершины г;, a v называется сыном вершины и, если существует

РАЗДЕЛ 6.3. Деревья 263
ориентированное ребро из и в v. Если и — родитель v и t/, тогда v и г/ на-
называются братьями. Если существует ориентированный путь из вершины tx в
вершину г% тогда и называется предком вершины v, a v называется потомком
вершины и. Если наибольшая из степеней выхода для вершин дерева равна га,
тогда дерево называется т-арным деревом. В частном случае, когда га = 2,
дерево называется бинарным деревом. В каждом бинарном дереве каждый сын
родителя обозначается либо как левый сын, либо как правый сын (но не то и
другое одновременно).
ПРИМЕР 6.39. Граф на рис. 6.44 — бинарное дерево. Уровень вершины vQ равен 2,
уровень вершины v$ равен 3. Высота дерева — 3, поскольку длина пути i^ii^s
равна 3 и не существует более длинного пути от корня к листу. Вершина v\
является родителем для ^ и v4.
Рис. 6.44
Вершины vz и vi — братья. Таковыми же являются вершины v\ и v2, v5 и ve и v7
и v8. Вершина v\ — предок вершин г>3, v7, v8f a v3i v7 и г>8 — потомки вершины vi.
Вершина v$ — левый сын вершины г>з, а г;4 — правый сын вершины v\. ?
Теперь докажем, что в каждом дереве число вершин на единицу больше
числа ребер. Предположим, что имеется дерево Т. Ранее уже показано, что любое
дерево можно представить как корневое дерево, и это никоим образом не меняет
ни числа ребер, ни числа вершин. Рассмотрим теперь ориентированное дерево
Т', порожденное деревом Т. У каждого ребра Т одна и только одна конечная
вершина. Следовательно, число ребер и вершин одно и \о же, исключая корневую
вершину. Если учесть корневую вершину, получим, что вершин на одну больше,
чем ребер. Таким образом, нами доказана следующая теорема.
ТЕОРЕМА 6.40. Если у дерева Т имеется е ребер и v вершин, тогда v = е + 1.
Справедлива также и обратная теорема.
ТЕОРЕМА 6.41. Если в связном графе G, содержащем е ребер и v вершин, имеем
v — е + 1, тогда G — дерево.
ДОКАЗАТЕЛЬСТВО. Если G содержит цикл, то, как было установлено при до-
доказательстве теоремы 6.38, если ребро {vi,Vj} входит в цикл, существуют два
пути из Vi в Vj. Таким образом, ребро {^ь^} можно из цикла удалить, а путь
из вершины V{ в вершину Vj будет существовать. Пусть а и b — любые точки в
G. Поскольку граф G — связный, существует путь из а в Ъ. Если ребро {vi,Vj}
удалено, все равно существует путь из а в Ь, поскольку ребро {vi,Vj}, входящее
в путь, можно заменить альтернативным путем из Vi в Vj. Удалим ребро {v^Vj}
из G и, если оставшийся граф все еще содержит цикл, удалим другое ребро, ис-
используя ту же процедуру. Будем продолжать, пока все циклы не будут удалены. В

264 ГЛАВА 6. Графы, ориентированные графы и деревья
результате получим связный граф, скажем, G', без циклов. Поэтому G' является
деревом, и по теореме 6.40 число вершин v = е' + 1, где е' — число ребер графа
G'. Поскольку ни одна из вершин не была удалена, число вершин остается таким,
которое было раньше. Если было удалено и ребер, тогда е = e'4-n. Но поскольку
г> = е + 1иг> = е' + 1, то е = е' и п = 0. Следовательно, ни одно ребро не было
удалено, поэтому G — дерево. ¦
Дерево С, построенное из G в процессе приведенного выше доказатель-
доказательства, называется остовным (или каркасным) деревом графа G. Дадим более
формальное определение.
ОПРЕДЕЛЕНИЕ 6.42. Дерево Т называется остовным деревом графа G, если
Т —- подграф графа G и каждая вершина в G является вершиной в Т.
Итак, доказана следующая теорема.
ТЕОРЕМА 6.43. У каждого связного графа существует подграф, который явля-
является остовным деревом.
До сих пор рассматривались ориентированные деревья, образованные из кор-
корневых (неориентированных) деревьев. Ориентированное дерево называется кор-
корневым ориентированным деревом, если существует единственная вершина vq
такая, что indeg(i;o) = 0, и существует путь из vo в каждую другую вершину де-
дерева. Заметим, что ориентированные деревья, которые были рассмотрены до сих
пор, в действительности соответствуют этому определению. Рассмотрим, однако,
ориентированное дерево на рис. 6.45.
:°
A V3 A
v,- v; v- •, •,,
Это ориентированное дерево, но оно не является корневым ориентирован-
ориентированным деревом. Большинство ориентированных деревьев, которые мы рассмотрим в
дальнейшем, будут, тем не менее, корневыми ориентированными деревьями.
¦ УПРАЖНЕНИЯ
1. Которые из приведенных ниже графов являются деревьями?
а) б)

РАЗДЕЛ 6.3. Деревья 265
в)
г)
2. Для каждого дерева из предыдущего упражнения
а) используйте в качестве корня вершину v2 и нарисуйте корневое дерево;
б) нарисуйте порожденное корневое ориентированное дерево;
в) используйте в качестве корня вершину v$ и нарисуйте корневое дерево;
г) нарисуйте порожденное корневое ориентированное дерево.
3. Которые из приведенных ниже графов являются деревьями?
а)
б)
в)
д)
4. Для каждого дерева из предыдущего упражнения
а) используйте в качестве корня вершину v2 и нарисуйте корневое дерево;
б) нарисуйте порожденное корневое ориентированное дерево;
в) используйте в качестве корня вершину г;з и нарисуйте корневое дерево;
г) нарисуйте порожденное корневое ориентированное дерево.
5. Покажите, что если лес содержит га компонент, то v = е + тп.
6. Которые из приведенных ниже графов являются корневыми ориентирован-
ориентированными деревьями?

266 ГЛАВА 6. Графы, ориентированные графы и деревья
а)
vo у, Ь
• v.
А''А
б)
V0 *l
-. л л
л -'• А
V5 *6
7 r8
Д)
в)
"о •-
7. Для корневого ориентированного дерева, показанного на рис. 6.46,
а) найдите потомков вершины г?з;
б) найдите предков вершины у&\
в) найдите родителя вершины v*>\
г) определите уровень вершины vq\
д) найдите сыновей вершины г>3;
е) найдите высоту дерева;
ж) найдите листья дерева;
з) определите, является ли это дерево бинарным?
л«л
.Л
Рис. 6.46
Рис. 6.47
8. Для корневого ориентированного дерева, показанного на рис. 6.47,
а) найдите потомков вершины v2\
б) найдите предков вершины г;5;
в) найдите родителя вершины v\\

РАЗДЕЛ 6.4. Мгновенное безумие 267
г) определите уровень вершины v5\
д) найдите сыновей вершины v2\
е) найдите высоту дерева;
ж) найдите листья дерева.
9. Нарисуйте генеалогическое дерево, начиная с одного из своих прадедушек.
10. Нарисуйте генеалогическое дерево, начиная с одной из своих прабабушек
(но не с жены прадедушки из предыдущей задачи).
11. Используя индукцию, докажите теорему 6.40, которая утверждает, что если
у дерева Г имеется е ребер и v вершин, то v = е + 1.
6.4. МГНОВЕННОЕ БЕЗУМИЕ
В игру мгновенное безумие играют с помощью четырех кубиков, каждая из ше-
шести граней которых окрашена в один из четырех цветов: красный, синий, зеленый
или желтый (набор четырех цветов может быть произвольным). Цель игры —
составить из кубиков столбик так, что каждая сторона столбика будет окрашена
в один из четырех цветов. Решения (если они существуют) зависят от выбора
цветов для граней кубика. Решение может быть одно, их может быть несколько,
или решение может вообще не существовать. Обозначим грани кубика, показан-
показанные на "развертке" на рис. 6.48, как фронтальную (ф), заднюю (з), верхнюю (в),
нижнюю (н), левую (л) и правую (п).
Ф
П I 3
Рис. 6.48
Части кубика, которые должны образовывать сторону столбика, назовем Ле-
Левой, Правой, Фронтальной и Задней (чтобы отличать их от граней кубика, перво-
первоначально фигурирующих в головоломке). Таким образом, Фронтальная и Задняя,
а также Левая и Правая части кубика — противоположны друг другу. Предполо-
Предположим, что для заданной игры имеются кубики, показанные на рис. 6.49.
Рис. 6.49
Теперь покажем относительно простой способ нахождения решения, осно-
основанный на использовании графов. Перед началом, однако, важно уяснить, что
выбор противоположных граней кубика как Фронтальной и Задней никоим обра-
образом не определяет, какая другая пара граней может быть Левой и Правой, или
какая сторона выбранной пары будет Левой, а какая — Правой. Возможно, в этом
легче убедиться, если захватить кубик за противоположные стороны (Фронталь-
(Фронтальную и Заднюю) и вращать его. Как легко убедиться, четыре вращения реализуют
все возможные, упомянутые выше ситуации для других двух сторон (Левой и

268 ГЛАВА 6. Графы, ориентированные графы и деревья
Правой). Таким образом, если Фронтальная и Задняя грани для каждого куби-
кубика определены, имеется полная свобода выбора пары противоположных граней
как Левой и Правой, соответственно. Создаваемый нами граф имеет в качестве
вершин четыре цвета. Ребра графа связывают цвета на противоположных гранях
кубика. Для первого блока необходимо иметь по одному ребру
Рис. 6.50
от зеленого к синему, от зеленого к красному и от красного к желтому, что изоб-
изображено на рис. 6.50. Граф для совокупности четырех блоков показан на рис. 6.51.
ж
Рис. 6.51
Переупорядочение вершин на диаграмме зачастую позволяет привести граф
к более аккуратному виду.
Теперь построим подграф, чтобы иметь возможность выбрать фронтальную
и заднюю грань для каждого кубика. Нам нужен такой подграф, что
A) каждая вершина графа является вершиной подграфа;
B) грань каждого кубика присутствует в подграфе;
C) порядок каждой вершины равен 2.
Каждая вершина должна присутствовать, потому что все четыре цвета по-
появляются на фронтальной и задней сторонах. Ребро от каждого кубика должно
присутствовать, чтобы мы получили фронтальную и заднюю сторону каждого
кубика. Порядок каждой вершины равен двум, потому что каждый цвет появля-
появляется один раз на фронтальной поверхности и один раз — на Задней. Примеры
возможных подграфов показаны на рис. 6.52.
Рис. 6.52
(Попытайтесь найти и другие такие подграфы.) Итак, начинаем с испытания
первого из показанных подграфов. Изображая его как ориентированный граф,
образующий цикл, можно рассматривать начальную вершину как фронтальную
грань, а конечную грань — как заднюю. Таким образом, получаем таблицу

РАЗДЕЛ 6.4. Мгновенное безумие 269
Фронтальная
с
3
ж
к
Задняя
3
ж
к
с
Теперь нам нужен другой подграф с такими же свойствами. Единственное
ограничение для второго подграфа — он не должен содержать ребра первого
подграфа. Эти ребра уже были использованы как Фронтальные и Задние грани
для блоков, поэтому не могут фигурировать как боковые. Для упрощения графа
удалим использованные ребра, после чего получаем рис. 6.54. По этому графу
строим подграф, показанный на рис. 6.53, который можно использовать.
Рис. 6.53
Рис. 6.54
В результате получаем цвета для Левой и Правой частей, показанные в
таблице, что и приводит нас к решению.
Левая
к
с
3
ж
Правая
3
с
ж
к
Если граф, выбранный для Фронтальной и Задней частей, не дает результата,
или желательно найти другое решение, то необходимо испытать другие варианты
выбора Фронтальных и Задних частей. Для поиска иных вариантов полезным
будет замечание о том, что такие подграфы должны иметь одну из базисных
форм, показанных на рис. 6.55.
00
Рис. 6.55

270 ГЛАВА 6. Графы, ориентированные графы и деревья
Ш УПРАЖНЕНИЯ
1. Найдите решение (если оно существует) для следующих наборов кубиков:
а)
к\ж\з\с\ \K\K\a\c\ \к\с\ж\к\ \с\к\ж\к
3\Ж\С\К\ \C\K\3\K\ \C\C\3\K\ \K\3\C\C
6.5. ПУТИ И ЦИКЛЫ ЭЙЛЕРА
ОПРЕДЕЛЕНИЕ 6.44. Пусть G = (V, JS) — граф. Цикл, который включает все
ребра и вершины графа G, называется эйлеровым циклом. Если это условие
выполняется, говорят, что граф G имеет эйлеров цикл.
Если теперь вернуться к задаче о кенигсбергских мостах, легко убедиться,
что она сводится к попытке определить, содержит ли граф, изображающий за-
задачу, эйлеров цикл. Для этой цели нам потребуется приведенная ниже теорема.
Эта теорема справедлива также для мультиграфов и псевдографов, исключая тот
случай, когда псевдограф имеет только одну вершину. Более того, доказательство
теоремы остается тем же. Для ясности будем использовать термин граф, понимая,
что каждое утверждение справедливо для мультиграфов и псевдографов.
ТЕОРЕМА 6.45. Граф с более чем одной вершиной имеет эйлеров цикл тогда и
только тогда, когда он связный и каждая его вершина имеет четную степень.

РАЗДЕЛ 6.5. Пути и циклы Эйлера 27Л
ДОКАЗАТЕЛЬСТВО. Предположим, что граф G имеет эйлеров цикл. Граф яв-
является связным, т.к. каждая вершина принадлежит циклу. Для всякой вершины
v графа G каждый раз, когда эйлеров цикл проходит через v, он вносит 2 в
степень v. Поэтому степень v четная.
Обратно, нужно показать, что каждый связный граф, у которого степени
вершин четные, имеет эйлеров цикл. Докажем эту теорему, используя индук-
индукцию по числу вершин. Поскольку теорема тривиально справедлива при п < 3,
начнем индукцию сп = 3. Предположим, что каждый связный граф, имеющий
менее к вершин, и все вершины которого обладают четной степенью, содержит
эйлеров цикл. Пусть G — связный граф, содержащий к вершин, степени кото-
которых четные. Допустим, что v\ и v2 — вершины графа G. Поскольку граф G —
связный, существует путь из v\ в v2. Поскольку степень v2 — четная, существует
неиспользованное ребро, по которому можно продолжить путь. Поскольку граф
конечный, то путь, в конце концов, должен вернуться в ^, и эйлеров цикл С\
можно считать построенным. Если С\ является эйлеровым циклом для G, тогда
доказательство закончено. Если нет, то пусть G1 — подграф графа G, полученный
удалением всех ребер, принадлежащих С\. Поскольку С\ содержит четное число
ребер, инцидентных каждой вершине, каждая вершина подграфа G' имеет четную
степень.
Пусть е — ребро графа С, пусть Ge — компонента графа С, содержащая е.
Поскольку G' имеет менее, чем fc, вершин, и у каждой вершины графа G' четная
степень, граф G' имеет эйлеров цикл. Пусть это С2. Далее, у С\ и С2 имеется
общая вершина, скажем, а. (Почему?) Теперь можно продолжить эйлеров цикл,
начиная его в а, пройти Сь вернуться в а, затем пройти С2 и вернуться в а.
Если новый эйлеров цикл не является эйлеровым циклом для G, продолжаем
использовать этот процесс, расширяя наш эйлеров цикл, пока, в конце концов, не
получим эйлеров цикл для G. ¦
ПРИМЕР 6.46. Граф на рис. 6.56 имеет эйлеров цикл, поскольку степень каждой
его вершины четная. ?
ПРИМЕР 6.47. Граф на рис. 6.57 не имеет эйлерова цикла, поскольку степени
вершин v2 и V4 — нечетные. ?
Рис. 6.56
Рис. 6.57
Возвращаясь к задаче о кенигсбергских мостах, обнаруживаем, что муль-
тиграф на рис. 6.58, построенный Эйлером для описания кенигсбергских мостов,

272 ГЛАВА 6. Графы, ориентированные графы и деревья
имеет нечетные степени всех его вершин. Итак, этот мультиграф не имеет эйлеро-
эйлерова цикла, поэтому невозможно пройти каждый мост по одному разу и вернуться в
исходную точку пути. Необходимо также отметить, что хотя задача была решена
с использованием мультиграфа, ее можно решить, используя простой граф. Когда
имеется более одного
Рис. 6.58
ребра между вершинами, нужно к исходному мультиграфу просто добавить вер-
вершину для представления середины каждого моста. Тогда получится простой граф,
показанный на рис. 6.59, который также описывает задачу о кенигсбергских мо-
мостах.
Рис. 6.59
Что касается кенигсбергских мостов, можно также задать вопрос: "Возмож-
"Возможно ли не проходить каждый мост по одному разу и не возвращаться обязательно
в исходную точку маршрута?". Это предположение приводит к следующему опре-
определению и теореме.
ОПРЕДЕЛЕНИЕ 6.48. Пусть G = (V,E) — граф. Путь, который включает
каждое ребро графа G только один раз называется эйлеровым путем. В этом
случае говорят, что граф G имеет эйлеров путь.
Теперь нас будет интересовать случай, когда эйлеров путь не является эй-
эйлеровым циклом. Такой путь будем называть собственным эйлеровым путем.
Предоставляем читателю доказать следующую теорему.
ТЕОРЕМА 6.49. Граф (мультиграф или псевдограф) имеет собственный эйлеров
путь тогда и только тогда, когда он связный и ровно две его вершины имеют
нечетную степень.
Поскольку граф для кенигсбергских мостов имеет четыре вершины с нечет-
нечетными степенями, можно сделать вывод о невозможности пройти каждый мост по
одному разу, даже если не нужно возвращаться в исходную точку маршрута.
ПРИМЕР 6.50. Граф на рис. 6.60 имеет собственный эйлеров путь, т.к. ровно две
его вершины имеют нечетную степень. ?
ПРИМЕР 6.51. Граф на рис. 6.61 не имеет собственного эйлерова пути, т.к. четыре
его вершины имеют нечетную степень. ?

РАЗДЕЛ 6.5. Пути и циклы Эйлера 273
Рис. 6.60
Рис. 6.61
ОПРЕДЕЛЕНИЕ 6.52. Пусть G = (V,E) — ориентированный граф. Ориен-
Ориентированным циклом называется ориентированный путь ненулевой длины из
вершины в ту же вершину без повторения ребер.
ОПРЕДЕЛЕНИЕ 6.53. Пусть G = (V,E) — ориентированный граф. Ориенти-
Ориентированный цикл, который включает все ребра и вершины графа G, называется
эйлеровым циклом. В этом случае говорят, что ориентированный граф G име-
имеет эйлеров цикл.
Доказательство следующей теоремы предоставляется читателю.
ТЕОРЕМА 6.54. Ориентированный граф имеет эйлеров цикл тогда и только тогда,
когда он связный и степень входа каждой вершины равна ее степени выхода.
ПРИМЕР 6.55. Ориентированный граф на рис. 6.62 имеет эйлеров цикл, так как
степень входа каждой вершины равна степени выхода. ?
ПРИМЕР 6.56. Ориентированный граф на рис. 6.63 не имеет эйлерова цикла, так
как степень входа вершины v\ не равна ее степени выхода. ?
Рис. 6.62
Рис. 6.63
УПРАЖНЕНИЯ
1. Среди приведенных ниже графов найдите те, которые имеют эйлеров цикл.

274 ГЛАВА 6. Графы, ориентированные графы и деревья
а)
б)
в)
2. Среди приведенных ниже графов найдите те, которые имеют эйлеров цикл.
а)
V
б)
в)
г)
3. Среди приведенных ниже графов найдите те, которые имеют собственный
эйлеров цикл.

РАЗДЕЛ 6.5. Пути и циклы Эйлера 275
а)
в)
б)
г)
4. Среди приведенных ниже графов найдите те, которые имеют собственный
эйлеров цикл.
а) б)
т
>¦¦
в)
5. Какие из следующих графов являются сильно связными?
а) б)
ь

276 ГЛАВА 6. Графы, ориентированные графы и деревья
в) г)
6. Какие из следующих графов являются сильно связными?
а) б)
a
a
>? i
в)
г)
7. Какие из следующих ориентированных графов имеют эйлеровы циклы?
а)
б)

РАЗДЕЛ 6.5. Пути и циклы Эйлера 277
в)
г)
8. Какие из следующих ориентированных графов имеют эйлеровы циклы?
а) б)
в)
г)
9. Докажите теорему 6.49. Граф (мультиграф или псевдограф) имеет собствен-
собственный эйлеров путь тогда и только тогда, когда он связный и ровно две его
вершины имеют нечетную степень.
10. Докажите, что если граф содержит цикл от вершины v к ней самой, то он
содержит простой цикл от вершины v к ней самой.
11. Докажите, что ориентированный граф является сильно связным, если в гра-
графе существует вершина v такая, что каждая другая вершина графа дости-
достижима из v и вершина v достижима из любой другой вершины графа.
12. Докажите теорему 6.54. Ориентированный граф имеет эйлеров путь тогда
и только тогда, когда он сильно связный и степень входа каждой вершины
равна ее степени выхода.

278 ГЛАВА 6. Графы, ориентированные графы и деревья
6.6. МАТРИЦЫ ИНЦИДЕНТНОСТИ И СМЕЖНОСТИ
В этом разделе будут определены две матрицы, связанные с графами: матрицы
инцидентности и матрицы смежности. Будет показано, что задание любой из
этих матриц дает возможность восстановить граф. Фактически будет показано,
что матрица смежности совпадает с матрицей отношения, определенного этим
графом. Как и в случае матрицы отношения для графа, все эти матрицы содержат
в качестве элементов 1 или 0, поэтому такие матрицы удобно хранить в памяти
компьютера.
ОПРЕДЕЛЕНИЕ 6.57. Пусть G — граф. Пусть В — матрица, строки которой
обозначены вершинами графа, а столбцы обозначены ребрами графа. Будем
считать, что вершины и ребра графа пронумерованы. Элемент г-ой строки и j-ro
столбца матрицы J9, обозначаемый Bij, равен 1, если г-ая вершина инцидентна
j-ому ребру, и равен 0 в противном случае. Матрица В называется матрицей
инцидентности графа G.
ПРИМЕР 6.58. Пусть G — граф, изображенный на рис. 6.64, тогда его матрица
инцидентности имеет вид, изображенный на рис. 6.65.
Рис. 6.64
1110
10 0 0
0 0 11
0 10 1
Рис. 6.65
?
Легко видеть, что степень вершины равна сумме элементов строки, обо-
обозначенной этой вершиной, так как каждая единица в этой строке представляет
инцидентность этой вершины ребру. В каждом столбце также будут две единицы,
так как каждое ребро инцидентно двум вершинам.
Можно также включить в рассмотрение матрицы инцидентности для графов
с петлями. Вид матрицы инцидентности непосредственно показывает, является
ли данное ребро петлей, так как ребро представляет собой петлю тогда и только
тогда, когда соответствующий столбец содержит только одну единицу. Заметим,
что в матрице инцидентности для графа с петлями сумма элементов строки, со-
соответствующей данной вершине, не представляет собой степень вершины, если в
ней имеются петли.
ПРИМЕР 6.59. Пусть G — граф, изображенный на рис. 6.66, его матрица инци-
инцидентности изображена на рис. 6.67.

РАЗДЕЛ 6.6. Матрицы инцидентности и смежности 279
Рис. 6.66
_е,е2е3еАе5
1110 0
10000
0 0 110
0 0011
Рис. 6.67
Обратите внимание, что наличие петель в2 и е5 приводит к тому, что в столбцах,
обозначенных этими ребрами, содержится только по одной единице. ?
Матрицы инцидентности не имеют большого значения при рассмотрении
ориентированных графов, т.к. они не содержат информации о том, как ребро
ориентировано. Поэтому, используя матрицу инцидентности, нельзя восстановить
ориентированный граф. Такую возможность обеспечивает матрица смежности,
определение которой будет сейчас дано.
ОПРЕДЕЛЕНИЕ 6.60. Пусть G — граф (ориентированный граф). Пусть В —
матрица, строки которой обозначены вершинами графа и столбцы обозначе-
обозначены теми же вершинами в том же самом порядке. Элемент г-ой строки и j-ro
столбца матрицы В, обозначаемый Bijy равен 1, если имеется ребро (ориен-
(ориентированное ребро) из г-ой вершины в j-ую вершину, и равен 0 в противном
случае. Матрица В называется матрицей смежности графа G.
Заметим, что свойства матриц смежности в точности совпадают со свойства-
свойствами матриц отношения из раздела 4.3. Единственное отличие состоит в том, что
используется терминология теории графов, и смысл матрицы смежности интер-
интерпретируется для графов. Для матриц смежности включен в рассмотрение также
алгоритм Уоршолла.
ПРИМЕР 6.61. Пусть G — граф, изображенный на рис. 6.68. Его матрица смеж-
смежности приведена на рис. 6.69.
Рис. 6.68
^V1V2V3V4
0 111
10 0 0
10 0 1
10 10
Рис. 6.69
?
Поскольку петли отсутствуют, все элементы диагонали матрицы равны 0.
Матрица смежности симметрична, так как граф представляет симметричное от-
отношение.
ПРИМЕР 6.62. Пусть G — ориентированный граф, изображенный на рис. 6.70.
Его матрица смежности показана на рис. 6.71.

280 ГЛАВА 6. Графы, ориентированные графы и деревья
• с
а Ь с
0 1 1
1 1 1
0 0 0
Рис. 6.70
Рис. 6.71
?
Очень часто обозначения вершин несущественны. В таких случаях матрицы
будут приводиться без обозначений. Например, матрица
Г 1 0 0 1 1
10 10
0 0 0 1
1110
является матрицей смежности для ориентированного графа, у которого четыре
вершины и восемь ребер.
Важным применением матрицы смежности является возможность находить
путь фиксированной длины к. Следующий пример дает ключ к пониманию, как
это можно сделать.
Пусть матрица
А =
1
1
0
1
0
0
0
1
0
1
0
1
1 -
0
1
0
представляет собой матрицу смежности ориентированного графа G с вершинами
^1,^2,^3 и г»4. Рассмотрим матрицу
10 0 11
10 10
0 0 0 1
1110
©
Г 1 0 0 1
10 10
0 0 0 1
1110
и вычислим, например, элемент
А?22 = (An Л А12) V (А12 Л А22) V (А13 Л А32) V (Аи Л А42) =
= A Л 0) V @ Л 0) V @ Л 0) V A Л 1) =
= OVOVOV1 =
= 1.
Обратите внимание, что значение Af2 равно 1, так как А\4 и Aj2 оба равны 1,
что означает наличие ребра из вершины г>1 в вершину г>4 и из vA в вершину v2.
Поэтому из вершины vi в вершину v2 имеется путь длины 2. В общем случае
получаем, что Af? = 1 тогда и только тогда, когда имеется такое число к, что
Aikf\ Akj — 1, или, другими словами, имеется ребро из вершины Vi в вершину vt-

РАЗДЕЛ 6.6. Матрицы инцидентности и смежности 281
и из Vk в вершину Vj. Поэтому существует путь длины 2 или 2-путь из вершины
V{ в вершину Vj. Но для Af2 имеем
А3? = (^31 Л Аы) v (А32 Л А24) v (А33 Л АЗА) v (Л34 л ААА) =
= (О Л 1) V (О Л 0) V (О Л 1) V A Л 0) =
=ovovovo=
= 0,
так что Af2 = О, потому что не существуют ребра из v3 в v^ и от г>; к v4 ни при
каком фиксированном г. Другими словами, не существует 2-путь из вершины v\
в вершину v2. Отсюда следует, что Af? = 1, если имеется 2-путь из вершины Vi в
вершину Vj, и Afj2 = О, если такой 2-путь не существует. Аналогичным образом,
можно убедиться в том, что если использовать обычное умножение матриц, то
A?j равно числу значений к таких, что Aik и Akj оба равны 1, поэтому оно равно
числу путей из вершины г>» в вершину Vj длины 2.
Просим читателя, используя индукцию, доказать следующие теоремы.
ТЕОРЕМА 6.63. Пусть G — (ориентированный) граф с вершинами v\, V2, v3,
..., vn и матрицей смежности А. Путь длины fc, или fc-путь из г>; в Vj для
1 < к < п существует тогда и только тогда, когда Afjk = 1.
ТЕОРЕМА 6.64. Пусть G — (ориентированный) граф с вершинами v\, V2, v3,
..., vn и матрицей смежности А. Из вершины v{ в вершину Vj имеется т путей
длины /с, где 1 < к < п тогда и только тогда, когда А^ = т.
Предлагаем читателю, воспользовавшись теоремой 6.63, доказать следующее
утверждение.
ТЕОРЕМА 6.65. Пусть G — (ориентированный) граф с вершинами v\, v2, v3,
..., vn и матрицей смежности А. Пусть А = А V А®2 V Л°3 V А04 V • • • V А0П.
Тогда Aij = 1 тогда и только тогда, когда существует путь из г>; в vj.
Справедливость теоремы, приведенной ниже, следует непосредственно из
определения связности графов или сильной связности ориентированных графов.
По сути это та же теорема 6.65.
ТЕОРЕМА 6.66. Пусть G — (ориентированный) граф с вершинами v\% v2, v3y
..., vn и матрицей смежности А. Пусть А1 = / V А V А°2 V Аез V А°4 V • • • V Л0П,
где / — мультипликативная единичная матрица. Тогда А1- = 1 для всех г и j
тогда и только тогда, когда граф G (сильно) связный.
Из теоремы 6.65 следует, что если R — отношение, задаваемое (ориентиро-
(ориентированным) графом G, и А — матрица смежности графа G, тогда А представляет
собой матрицу смежности графа, который описывает транзитивное замыкание R.
В более общем случае, когда G — граф, который не обязательно связный,
для матрицы А1 справедлив следующий результат.

282 ГЛАВА 6. Графы, ориентированные графы и деревья
ТЕОРЕМА 6.67. Пусть G — граф с вершинами v\, v2, г?з, ..., vn и матрицей
смежности А. Как и ранее, пусть А1 = I V А V А®2 V А03 V Л04 V • • • V А°п.
Тогда (если необходимо) вершины могут быть упорядочены таким образом, что
А1 будет иметь вид
0
0
где каждое А{ представляет собой квадратную матрицу, главная диагональ кото-
которой направлена вдоль главной диагонали А1 и содержит все ее элементы, равные
1. Как указано, любой элемент А1, который находится вне всех матриц А{, равен
0. Матрица А также может быть разбита на блоки такого же размера, что и А1,
при этом А будет иметь вид
¦ Аг
Здесь каждое А{ имеет такую же форму, как и Aiy и представляет собой матрицу
инцидентности компоненты графа G, а любой элемент матрицы А, находящийся
вне всех матриц А;, равен 0.
ДОКАЗАТЕЛЬСТВО. Если все вершины G, которые принадлежат одной и той же
компоненте, помещены вместе, тогда, поскольку между двумя любыми такими
вершинами существует путь, блок матрицы А1, состоящий только из строк и
столбцов, обозначенных этими вершинами, содержит в качестве элементов только
единицы. Далее, любой элемент А в этой же строке или столбце, обозначенных
указанными вершинами, должен быть равен нулю, поскольку не существует пути
из любой другой вершины в вершину, принадлежащую компоненте.
Поскольку для блоков Ai вершины, обозначающие его строки и столбцы,
принадлежат одной и той же компоненте, соответствующий блок А; в матрице А
представляет граф — компоненту графа G. Как и ранее, и по той же причине,
все другие элементы той же строки или столбца матрицы А, обозначенных этими
вершинами, должны быть равны нулю. ¦
Матрица А может быть вычислена как А = А V А02 V А03 V А04 V • • •
но такой способ не очень эффективен. Намного лучший метод обеспечивает ал-
алгоритм Уоршолла, известный также как алгоритм Роя-Уоршолла. Чтобы понять,
как он работает, рассмотрим матрицу смежности, изображенную на рис. 6.72.

РАЗДЕЛ 6.6. Матрицы инцидентности и смежности 283
A=
1 О О
0 1
1 О
О 1 О
Рис. 6.72
Матрица А представляет множество всех 1-путей. Теперь необходимо найти
все 2-пути, где средней вершиной является vb чтобы скомбинировать 1-пути, ко-
которые уже имеются. Начинаем с первого столбца. Игнорируем 1 в первой строке,
если имеется 1 в г-ой строке первого столбца, так как в этом случае существует
1-путь из Vi в vi. Поскольку 1 имеется в строке 3, существует 1-путь из v3 в
v\. Теперь посмотрим на первую строку. Игнорируем 1 в первом столбце, если
имеется 1 в j-ом столбце, так как в этом случае существует ребро, или 1-путь из
vi в Vj. Поскольку 1 имеется в четвертом столбце, существует ребро из vi в vA.
Таким образом, имеется 2-путь из v$ через v\ в г>4. Обозначим это, поместив 1 в
третьей строке четвертого столбца, и получим матрицу, показанную на рис. 6.73.
V1
1
0
1
0
V2
0
1
0
1
V3
0
1
1
0
V4
1
0
1
0
Рис. 6.73
Поскольку в первом столбце и в первой строке нет других единиц, этот шаг
закончен. Если бы в любой другой строке первого столбца имелась 1, скажем,
в г-ой строке, или в любом другом столбце первой строки имелась 1, скажем, в
j-ом столбце, тогда нам нужно было бы поместить 1 в г-ой строке j-oro столбца.
В нашем примере, использовав V как сложение, мы фактически просуммировали
первую строку с третьей. В общем случае, если имеется 1 в г-ой строке первого
столбца, то первая строка прибавляется к г-ой строке.
Теперь необходимо найти все пути длины не больше 3, проходящие через
v\ и/или г>2 (если такие имеются). Рассмотрим второй столбец. Игнорируя 1 во
второй строке, ищем 1 в любой другой строке столбца 2. Поскольку имеется 1 в
строке 4, то существует 1-путь из г;4 в г>2 или 2-путь из г>4 через v\ в г>2, так как
это единственный способ, которым мы можем получить единицу.
Игнорируя 1 во втором столбце, ищем другие 1 в любом другом столбце
строки 2. Поскольку имеется 1 в столбце 3, существует 1-путь из V2 в г>з, или
2-путь из г>2 через v\ в v%. В любом случае существует путь из г>4 в vs такой, что
он проходит только через вершины v\ и^. Опять обозначаем это, помещая 1 в
четвертой строке третьего столбца, и получаем матрицу, показанную на рис. 6.74.
10 0 1
0 110
10 11
0 1 1 °
Рис. 6.74
То же самое можно выполнить, прибавляя вторую строку к четвертой строке.
Если бы 1 находилась в г-ой строке столбца 2 и 1 находилась бы в j-ом столбце
второй строки, нам надо было бы прибавить строку 2 к строке г.

284 ГЛАВА 6. Графы, ориентированные графы и деревья
Аналогично, теперь нам необходимы все пути длины 4 или менее, прохо-
проходящие через vi и/или v2i и/или г>з (если такие имеются). Рассмотрим третий
столбец и третью строку. Если имеется 1 в г-ой строке столбца 3 и 1 имеется в
j-ом столбце строки 3, то существует путь из Vi в ^, который проходит только
через вершины v\ и/или v2 (если таковой имеется) и путь из г>3 в Vjy проходящий
только через вершины vi и/или v2 (если таковой имеется). Поэтому существует
путь из V{ в Vj, и 1 нужно поместить на (г, j)-ou позиции. Это равносильно сложе-
сложению строки 3 с любой строкой, содержащей 1 в столбце 3. Поскольку 1 имеется
в третьем столбце первой и четвертой строк, строка 3 прибавляется к каждой из
этих строк. Это дает матрицу, показанную на рис. 6.75.
2
V3
V4
1
1
1
1
0
1
0
1
0
1
1
1
1
1
1
1
Рис. 6.75
Окончательно, нам необходимы все пути длины 4 или менее, проходящие
через v\ и/или v2, и/или v^, и/или v± (если таковые существуют). Прибавляем
четвертую строку к любой другой строке, в которой 1 появляется в столбце 4.
Ниже приведены два алгоритма вычисления А. Оба алгоритма следуют из
способа, которым проводились вычисления в нашем примере. Первый способ —
самый удобный для счета вручную. Следует помнить, что в алгоритме сложение
означает булево сложение.
АЛГОРИТМ УОРШОЛЛА 1
1) Просмотреть столбец 1 матрицы А. Найти строку этого столбца, в которой
имеется 1, и прибавить строку 1 к этой строке.
2) Просмотреть столбец 2 матрицы, построенной в пункте A). Найти строку
этого столбца, в которой имеется 1, и прибавить строку 2 к этой строке.
3) Просмотреть столбец 3 матрицы, построенной в пункте B). Найти строку
этого столбца, в которой имеется 1, и прибавить строку 3 к этой строке.
4) Продолжать процесс просмотра следующего по счету столбца матрицы,
построенной на предыдущем шаге; искать строку, содержащую 1; прибав-
прибавлять строку, соответствующую исследуемому столбцу, к строке, в которой
имеется 1.
5) Продолжать, пока не будут рассмотрены все столбцы.
Второй метод использует тот факт, что процесс начинается с первой строки
и первого столбца, и если 1-цы имеются в г-ой строке первого столбца и в j-
ом столбце первой строки, тогда 1-ца помещается в г-ой строке j-ro столбца
матрицы. Другими словами, если Ац = 1 и Aij = 1, тогда полагаем Aij = 1.
Если А^ уже было равно 1, тогда оставляем его равным 1. Это эквивалентно
следующему: "для всех г А^ = А^ V (Ац A Aij), поскольку Ац A A\j равно 1
тогда и только тогда, когда Ац = 1 и A\j = 1, и равно 0 в противоположном
случае". Используя вторую строку и второй столбец, можно было бы получить

РАЗДЕЛ 6.6. Матрицы инцидентности и смежности 285
новые значения для А^, положив А^ = А^ V (А{2 Л A2j). Продолжая процесс,
приходим к следующему алгоритму в псевдокодах.
АЛГОРИТМ УОРШОЛЛА 2
Цикл по к от 1 до п:
Цикл по г от 1 до п:
Цикл по j от 1 до гг:
Aij = Ai:i V (Aik A Akj);
Конец цикла;
Конец цикла;
Конец цикла.
УПРАЖНЕНИЯ
1. Найдите матрицы инцидентности следующих графов:
а) б)
es
e2
/
/
/
i
«7
e3
, eio
i
e
\ 1
An
'7 е12
В)
Г)
2. Найдите матрицы инцидентности следующих графов:
а) б)

286 ГЛАВА 6. Графы, ориентированные графы и деревья
в)
г)
3. Найдите матрицы смежности для графов из упражнения 1.
4. Найдите матрицы смежности для графов из упражнения 2.
5. Для заданной матрицы инцидентности
Г 1 0 1 0 0 1 О О
0 10 10 0 10
01101001
10011000
0 0 0 0 0 111
найдите соответствующий граф.
6. Для заданной матрицы инцидентности
Г101010000001
010101010000
010000101000
100010000100
001000110010
000100000000
000001000010
000000001101
найдите соответствующий граф.
7. Для заданной матрицы смежности
Г 0 0 1 0 1 О
0 0 10 11
110 10 0
0 0 10 11
110 10 0
0 10 10 0
найдите соответствующий граф.
8. Для заданной матрицы смежности
Г 0 1 0 0 1 О
10 110 0
0 10 10 0
0 110 11
10 0 10 1
0 0 0 110

РАЗДЕЛ 6.6. Матрицы инцидентности и смежности 287
найдите соответствующий граф.
9. Для графа, показанного на рис. 6.76,
а) найдите матрицу смежности;
б) используя матрицу смежности, найдите все пути длины 2;
в) используя матрицу смежности, найдите все пути длины 3.
10. Для графа, показанного на рис. 6.77,
а) найдите матрицу смежности;
б) используя матрицу смежности, найдите все пути длины 2;
в) используя матрицу смежности, найдите все пути длины 3.
Рис. 6.76
Рис. 6.77
11. Для графа, показанного на рис. 6.78,
а) найдите матрицу смежности;
б) используя матрицу смежности, найдите все пути длины 2;
в) используя матрицу смежности, найдите все пути длины 3.
12. Для графа, заданного на рис. 6.79,
а) найдите матрицу смежности;
б) используя матрицу смежности, найдите все пути длины 2;
в) используя матрицу смежности, найдите все пути длины 3.
Рис. 6.79
13. Используя тот факт, что А = А V Л°2 V Аег V А°4 V • • • V А°п, определите
транзитивное замыкание отношения, представленного графом на рис. 6.80.
14. Используя тот факт, что А = А V А°2 V А°3 V А®4 V • • • V А°п, определите
транзитивное замыкание отношения, представленного графом на рис. 6.81.

288 ГЛАВА 6. Графы, ориентированные графы и деревья
Рис. 6.80
15. Используя тот факт, что А = А V А®2 V Л°3 V Ао4 V • • • V Л0П, определи-
определите транзитивное замыкание отношения, представленного ориентированным
графом на рис. 6.82.
16. Используя тот факт, что А = А V Ае2 V Аез V Ае4 V • • • V Л°п, определи-
определите транзитивное замыкание отношения, представленного ориентированным
графом на рис. 6.83.
Рис. 6.82
Рис. 6.83
17. Используя алгоритм Уоршолла, определите транзитивное замыкание отно-
отношения, представленного графом на рис. 6.84.
18. Используя алгоритм Уоршолла, определите транзитивное замыкание отно-
отношения, представленного графом на рис. 6.85.
Рис. 6.84
Рис. 6.85
19. Используя алгоритм Уоршолла, определите транзитивное замыкание отно-
отношения, представленного графом на рис. 6.86.
20. Используя алгоритм Уоршолла, определите транзитивное замыкание отно-
отношения, представленного ориентированным графом на рис. 6.87.

РАЗДЕЛ 6.6. Матрицы инцидентности и смежности 289
Ъ
Рис. 6.87
21. Используя алгоритм Уоршолла, определите транзитивное замыкание отно-
отношения, представленного ориентированным графом на рис. 6.88.
22. Используя алгоритм Уоршолла, определите транзитивное замыкание отно-
отношения, представленного ориентированным графом на рис. 6.89.
Рис. 6.88 Рис. 6.89
23. Матрицы инцидентности для мультиграфов можно определить таким же спо-
способом, как и для обыкновенных графов. Как по матрице инцидентности мож-
можно судить о том, имеют ли два ребра мультиграфа общие вершины? (Такие
ребра называются кратными.)
24. Если рассматривается матрица инцидентности для мультиграфа, дает ли
сумма элементов строки, обозначенной данной вершиной, степень данной
вершины? Что означает сумма элементов строки?
25. Используя индукцию, докажите теорему 6.63. Пусть G — (ориентированный)
граф с вершинами i>i, г>2, г>з, ..., vn и матрицей смежности А. Из вершины vi
в вершину Vj тогда и только тогда существует путь длины fc, где 1 < к < п,
когда Aff = 1.
26. Используя индукцию, докажите теорему 6.64. Пусть G — (ориентированный)
граф с вершинами v\, v2, г?з, ..., vn и матрицей смежности А. Из вершины
vi в вершину Vj тогда и только тогда существует т путей длины /с, где
1 < к < п, когда А^л = т.
27. Используя теорему 6.63, докажите теорему 6.65. Пусть G — (ориентирован-
(ориентированный) граф с вершинами vi, v2i vSi ..., vn и матрицей смежности А. Если
А = А V Л02 V Л03 V Л04 V • • • V А0П, то Aij = 1 тогда и только тогда, когда
имеется путь из вершины V{ в вершину Vj.
28. Опишите матрицу смежности для дерева.
29. Опишите транзитивное замыкание для дерева.

290 ГЛАВА 6. Графы, ориентированные графы и деревья
6.7. ГИПЕРКУБЫ И КОД ГРЕЯ
ОПРЕДЕЛЕНИЕ 6.68. Расстоянием между двумя вершинами графа называ-
называется длина самого короткого пути между этими двумя вершинами.
ОПРЕДЕЛЕНИЕ 6.69. Диаметром графа называется наибольшее расстояние
между двумя любыми его вершинами.
Во многих случаях вместо использования одиночных процессоров, способ-
способных выполнять только одну программу, несколько процессоров соединяется для
выполнения программ в параллельном режиме. При этом обеспечивается обмен
информацией между процессорами, и различные программы выполняются одно-
одновременно. Одним из способов связи компьютеров есть соединение их сериями
в кольцо. Указанный метод обладает тем недостатком, что для передачи инфор-
информации от одного процессора к другому потребуется прохождение ее через зна-
значительное число процессоров. В самой неблагоприятной ситуации информация
должна будет пройти через половину процессоров. Незначительное улучшение
дает использование сетки, или прямоугольного массива процессоров, когда они
помещены в каждой точке сетки. Пример такой сетки показан на рис. 6.90.
Рис. 6.90
Таким способом достигается лишь некоторое улучшение, так как прохожде-
прохождение информации через значительное число процессоров остается необходимым. В
случае сетки 4x5, показанной выше, может возникнуть необходимость прохо-
прохождения информации через восемь процессоров, включая конечные процессоры. В
общем случае сетки т х п возможна ситуация прохождения информации через
га 4- п — 1 процессор.
Намного лучшей конфигурацией является гиперкуб. В частности, п-гиперкуб
может быть использован для соединения вплоть до 2П компьютеров. Граф п-
гиперкуба строится рекурсивно следующим образом. Для п = 1 одну вершину
представляем посредством 1, а другую — посредством 0, так что получаем граф,
изображенный на рис. 6.91.
1.
0* Рис. 6.91
Таким образом, вершины графа состоят из всех строк длины 1, содержащих
0 и 1. Для и = 2 вершины представляем посредством 11, 10, 01 и 00, так что
получаем граф, изображенный на рис. 6.92.
Таким образом, вершины представлены строками длины 2, содержащими 0
и 1. Для п = 3 вершины представлены посредством 111, 110, 101, 100, 011, 010,
001, 000, так что получаем граф, изображенный на рис. 6.93.

РАЗДЕЛ 6.7. Гиперкубы и код Грея 291
@,0) <
A.0) *
Рис.
> <
6.92
' @,1)
1 (U)
@,0,0)
@,1,0)
@,С
,1)
(III)
@,1,1)
Рис. 6.93
Таким образом, вершины этого графа описывают строки длины 3, состоящие
из 0 и 1. Заметим, что две вершины являются смежными, если одна переходит в
другую при замене одного символа в строке.
В главе 1 при построении таблиц истинности был составлен список всех
возможных комбинаций утверждений.
Если использовать систему обозначений булевой алгебры и заменить Т на 1
и F на 0, то обнаружим, что образованы вершины гиперкубов порядка 1, 2, 3 и
4, которые в сокращенном виде можно записать следующим образом:
порядок 1
1
0
порядок 2
И
10
01
00
порядок 3
111
110
101
100
011
010
001
000
порядок 4
1111
1110
1101
1100
1011
1010
1001
1000
0111
оно
0101
0100
ООП
0010
0001
0000
Что означает для этих точек быть смежными, уже было определено для п = 2, 3
и 4. Рассмотрим следующую карту Карно:
11
01
10
00
р
~р
Нас интересует, какие блоки являются смежными. Если опять заменить Т
на 1, F на 0 и придать первой переменной значение р, а второй переменной —
значение </, тогда внутренние значения в таблице покажут, где находятся соседние

292 ГЛАВА 6. Графы, ориентированные графы и деревья
блоки. Следовательно, каждая вершина является смежной к другой вершине, если
они смежные как вершины куба порядка 2.
Аналогично, для трех переменных, где значения р, q и г даны по порядку,
получаем таблицу
q q ~ q ~ q
Р
111
011
110
010
100
000
101
001
Вспоминая теперь, что в случае карты Карно таблица скручена так, что два края
рассматриваются как смежные, приходим к выводу, что две вершины являются
смежными, если они смежные как вершины куба порядка 3.
Рассматривая карту Карно для четырех переменных и присваивая перемен-
переменным значения р, qy r и s по порядку, аналогичным образом получаем
р
р
р
р
q
nil
1110
оно
0111
q
1101
1100
0100
0101
1001
1000
0000
0001
~ q
1011
1010
0010
ООП
Вспоминая, что в случае карты Карно таблица скручена так, что два края рас-
рассматриваются как смежные, и смежными являются также верх и низ таблицы,
снова приходим к выводу, что две вершины являются смежными в таблице только
тогда, когда они смежные как вершины куба порядка 4.
Используя приведенный выше метод, построим последовательность вершин
для к -Ь 1-мерного куба, используя последовательность вершин /с-мерного куба
следующим образом:
1) Поместить 1 перед каждой вершиной в последовательности вершин fc-
мерного куба. Вершины, которые были смежными в fc-мерном кубе, с
приставленной единицей остаются смежными в к 4- 1-мерном кубе.
2) Поместить 0 перед каждой вершиной в последовательности вершин к-
мерного куба. Вершины, которые были смежными в А:-мерном кубе, с
приставленным нулем остаются смежными в к 4- 1-мерном кубе.
3) Поместить последовательность, построенную в B), вслед за последова-
последовательностью, построенной в A).
Нами предложен метод для построения вершин гиперкубов, причем для
п = 1, 2, 3 и 4 можно использовать карты Карно, чтобы показать, когда вершины
являются смежными. При п > 4 для образования вершин можно использовать
приведенные выше шаги A)-C).
Предположим, что имеется вращающийся диск, разделенный на секторы, и
серия щеток или лазерных лучей, возвращающих информацию о том, на какой

РАЗДЕЛ 6.7. Гиперкубы и код Грея 293
угол диск успел повернуться на текущий момент. Если двоичные строки, которы-
которыми пронумерованы соседние секторы, существенно различны в том смысле, что
при переходе от одного сектора к другому многие цифры в них изменяются, то
устройство, считывающее эту информацию непосредственно в процессе враще-
вращения, может выработать число, совершенно не похожее ни на одно из чисел. В
данном случае желательно пронумеровать секторы так, чтобы двоичные строки,
нумерующие соседние секторы, различались только одной цифрой.
В общем случае, однако, вершины в приведенном выше списке не являют-
являются смежными. Можно, тем не менее, изменить ситуацию, внеся незначительные
исправления в приведенной выше части B). Для формирования списка вершин
k -f 1-мерного куба, до того как помещать 0 перед элементами списка для к-
мерного куба, реверсируем список вершин для fc-мерного куба, т.е. порядок вер-
вершин в списке изменим на обратный. Например, при формировании списка вершин
2-мерного куба помещаем 1 перед столбцом для 1-мерного куба:
1
О
Затем меняем порядок элементов в столбце:
О
1
Наконец, помещаем 0 перед каждым элементом, имея в итоге
1 1
1 О
О О
О 1
Чтобы получить вершины 3-мерного куба, помещаем 1 перед приведенным
выше списком для 2-мерного куба и помещаем 0 перед реверсированным списком
для 2-мерного куба. В итоге для 3-мерного куба получаем
1 1 1
1 1 О
1 О О
1 0 1
О 0 1
0 0 0
0 1 0
0 1 1
Легко доказать, что приведенная процедура всегда будет давать последова-
последовательность вершин для fc-мерного куба, которую назовем к-списком. В таком к-
списке A) каждая вершина последовательности является смежной для следующей
вершины и B) первая вершина последовательности является смежной к послед-
последней вершине последовательности. Используя индукцию, начнем с констатации

294 ГЛАВА 6. Графы, ориентированные графы и деревья
того, что последовательность вершин для 1-мерного куба очевидным образом об-
обладает перечисленными свойствами. Предположим, что fc-список для fc-мерного
куба обладает этими свойствами. Если поместить 1 перед каждым элементом
fc-списка вершин fc-мерного куба, то каждая вершина последовательности будет
очевидным образом смежной к последующей. Также при реверсировании, т.е. при
изменении на обратный порядка вершин в fc-списке для fc-мерного куба, каж-
каждая вершина остается смежной к последующей вершине. И после помещения О
перед каждым элементом реверсированного списка вершин каждая вершина в но-
новом списке остается смежной к последующей. Первый элемент реверсированного
списка для fc-мерного куба совпадает с последним элементом исходного fc-списка
для fc-мерного куба, поэтому когда первый элемент реверсированного списка с
О впереди следует за последним элементом исходного fc-списка с 1 впереди, они
отличаются только первой цифрой и, следовательно, являются смежными. Анало-
Аналогичным образом, последний элемент в реверсированном fc-списке равен первому
элементу в fc-списке, так что при помещении 0 перед последним элементом в
реверсированном fc-списке и помещении 1 перед первым элементом fc-списка эти
две вершины получаются смежными. Таким образом, рассматриваемый fc + 1-
список обладает требуемыми свойствами. Эта последовательность, построенная
для n-мерного куба, называется кодом Грея для п.
Итак, правила построения кода Грея для fc + 1 состоят в следующем:
1) Поместите 1 перед каждой вершиной в fc-списке fc-мерного куба. Вер-
Вершины, смежные в fc-мерном кубе, с приставленной впереди 1 остаются
смежными в fc + 1-мерном кубе.
2) Поместите 0 перед каждой вершиной в реверсированном fc-списке fc-мерного
куба. Вершины, смежные в fc-мерном кубе, с приставленным впереди О
остаются смежными в fc 4- 1-мерном кубе.
3) Разместите последовательность, сформированную в B), после последова-
последовательности, сформированной в A).
4) Каждая последовательная пара вершин в fc+1-мерном списке fc+1-мерного
куба является смежной. Первая вершина fc + 1-списка также является
смежной к последней вершине списка.
Например, 3-список и реверсированный 3-список представляют собой, соот-
ветственно,
1
1
1
1
0
0
0
0
1
1
0
0
0
0
1
1
1
0
0
1
1
0
0
1
и
0
0
0
0
1
1
1
1
1
1
0
0
0
0
1
1
1
0
0
1
1
0
0
1
Заметим, что первый элемент каждого списка равен последнему элементу другого
списка. Дописывая 1 перед каждой вершиной в первом списке и 0 перед каждой
вершиной во втором списке и помещая второй список в конце первого списка,

РАЗДЕЛ 6.7. Гиперкубы и код Грея 295
получаем
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
0
0
1
1
0
0
1
1—1
0
0
1
1
0
0
1
Таким образом, мы построили код Грея для п = 4.
Ранее упоминалось соединение компьютеров в конфигурацию сетки или ре-
решета. Под сеткой понимают граф, вершины которого заданы массивом размерно-
размерности га х п, и для которого две вершины, соседствующие в одной и той же строке
или столбце массива, являются смежными как вершины графа. Возможно ли для
га < 2к и п < 21 построить подграф к + /-мерного куба, т.е. сетку размера га х п?
Это уже делалось при построении карт Карно. Указанное легко сделать, обозна-
обозначая строки согласно первым т элементам кода Грея для к и обозначая столбцы
согласно первым и элементам кода Грея для /. Элемент на позиции (г, j) сетки
есть метка г-ой строки, за которой следует метка j-ro столбца. Таким образом,
если необходимо построить сетку 3 х 7, то она будет иметь вид
11
10
00
111
110
100
101
001
000
010
11111 11110 11100 11101 11001 11000 11010
10111 10110 10100 10101 10001 10000 10010
00111 00110 00100 00101 00001 00000 00010
Здесь (г, j)-bifi элемент сетки является (г, ^)-ым элементом таблицы. Проведенные
рассмотрения доказывают следующую теорему.
ТЕОРЕМА 6.70. Каждая сетка размера т х п представляет собой подграф г -f j-
мерного куба, где га < Т и п < У.
Предоставляем читателю доказать следующую теорему.
ТЕОРЕМА 6.71. Каждый гиперкуб для п > 1 является двудольным графом, в
котором непересекающиеся множества вершин состоят из множества тех вершин,
которые изображаются строками, содержащими четное число единииц, и мно-
множества вершин, которые изображаются строками, содержащими нечетное число
единиц.

296 ГЛАВА 6. Графы, ориентированные графы и деревья
¦ УПРАЖНЕНИЯ
1. Найдите диаметр следующих графов:
а) Кп б) Кт,п
в) г)
Ь
2. Найдите диаметр следующих графов:
а) б)
в)
г)
@,0,0)
A,
@,1,0)
@,1
A,0,1)
,1)
A,1,1)
@,1,1)
д) 4-гиперкуб.
3. Постройте код Грея для 5.
4. Постройте код Грея для 6.
5. Постройте сетку 4x5.
6. Постройте сетку 3x8.
7. Постройте сетку 5x6.
8. Докажите теорему 6.71. Каждый гиперкуб для п > 1 является двудольным
графом, в котором непересекающиеся множества вершин состоят из мно-

РАЗДЕЛ 6.7. Гиперкубы и код Грея 297
жества тех вершин, которые изображаются строками, содержащими четное
число единиц, и множества вершин, которые изображаются строками, со-
содержащими нечетное число единиц.
9. Докажите, что если т = Т и п = 2J, то построенная сетка га х п обладает
свойством, что соответствующие вершины в первой и последней строке сетки
являются смежными, и соответствующие вершины в первом и последнем
столбце являются смежными.

ГЛАВА
ТЕОРИЯ ЧИСЕЛ
7.1. РЕШЕТО ЭРАТОСФЕНА
В предыдущей главе отмечалось, что алгоритм представляет собой конечное
множество правил для чисто механического решения задач. Первым примером
алгоритма в теории чисел будет древний метод нахождения простых чисел, на-
называемый "решетом Эратосфена", который представляет собой алгоритм опреде-
определения простых чисел, меньших заданного целого числа. Проиллюстрируем этот
метод, определяя простые числа в интервале от 1 до 100. Прежде всего перечис-
перечислим целые числа от 1 до 100:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100.
Начиная с 2, которая является первым простым числом, выделим жирным
шрифтом все числа, кратные 2. Эта процедура очень проста, так как отмеченным
должно быть каждое второе целое число, больше 2.
1, 2, 3, 4, 5, 0, 7, 8, 9, 10, И, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 11, 78, 79, 80,
81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100
Следующее простое число равно 3. Продолжая процедуру, отметим все чис-
числа, кратные 3. Эта процедура также является простой, так как должно быть
отмечено каждое третье целое число, больше 3.

РАЗДЕЛ 7.1. Решето Эратосфена 299
1, 2, 3, 4, 5, 6, 1, 8, 9, /О, 11, 12, 13, /4, /5, 16, 17, /«, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 50, 31, 32, 33, 34, 35, 36, 37, 3«, 39, 40,
41, 42, 43, 44, 45, 46, 47, 45, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, б*, 69, 70, 71, 72, 73, 74, 75, 76, 11, 78, 79, «О,
81, 82, 83, 54, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 95, 99, /00
Теперь отмечаем все числа, кратные простому числу 5.
1, 2, 3, 4, 5, б, 7, 8, 9, 10, 11, /2, 13, 14, 15, 16, 17, 18, 19, 20,
2/, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 41, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 11, 78, 79, 80,
81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99,100
Далее отмечаем все числа, кратные простому числу 7.
1, 2, 3, 4, 5, 6, 7, «, 9, 10, 11, /2, 13, /4, 15, 16, 17, /«, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 3*, 39, 40,
41,42, 43, 44, 45, 46, 47, 4*, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, «О,
81, 82, 83, «4, *5, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100
Поскольку 7 — наибольшее простое число, квадрат которого меньше или равен
100, по теореме 3.41 продолжать процесс нет необходимости. Числа, большие 1
и не отмеченные жирным шрифтом, представляют собой простые числа, которые
не превышают 100.
УПРАЖНЕНИЯ
1. Постройте решето Эратосфена для положительных целых чисел, меньших
200.
2. Используйте решето Эратосфена и калькулятор для разложения на простые
множители числа 1726.
3. Используйте решето Эратосфена и калькулятор для разложения на простые
множители числа 481.
4. Используйте решето Эратосфена и калькулятор для разложения на простые
множители числа 2502.
5. Используйте решето Эратосфена и калькулятор для разложения на простые
множители числа 1739.
6. Используйте решето Эратосфена и калькулятор для разложения на простые
множители числа 391.
7. Используйте решето Эратосфена и калькулятор для разложения на простые
множители числа 3901.

300 ГЛАВА 7. Теория чисел
7.2. МЕТОД ВЫДЕЛЕНИЯ МНОЖИТЕЛЕЙ ФЕРМА
Следущая теорема является основой алгоритма разложения на простые множите-
множители, названного методом выделения множителей Ферма. Метод используется
для определения того, является ли число простым.
ТЕОРЕМА 7.1. Целое нечетное число п > 1 не является простым тогда и только
тогда, когда существу]
и при этом р — q > 1.
тогда, когда существуют неотрицательные целые числа р и q такие, что п = p2—q2
Очевидно, если п можно представить как разность квадратов двух неотри-
неотрицательных целых чисел, скажем, п — р2 — q2, тогда п = (р — q)(p + q). Поскольку
р — q > 1, то также р + q > 1; и п не является простым числом.
Обратно, если п = rs, где г > s > 1, тогда п можно представить как
((r + s)/2J-((r-s)/2J. Поскольку и нечетное, г и s также являются нечетными
и, следовательно, r+s и r—s — четные числа. Положив р = (r+s)/2 и q = (r—s)/2,
находим, что р и q — целые неотрицательные числа и р — q = s > 1. При п = 1
положим р = 1, a q = 0. ¦
Применение этого метода состоит в попытке найти целые числа р и q такие,
что п = р2 - q2 или, что эквивалентно, р2 = п 4- д2, или q2 = р2 - п. Если
используется первое уравнение, полагаем q = 1,2,... до тех пор, пока n + g2
не станет полным квадратом. Если до значения q = (п — 1)/2 полный квадрат не
достигнут, рассмотрим ситуацию, когда q = (n—1)/2, что дает n+q2 = ((n-f l)/2J
и приводит к разложению п на множители п-1. Поскольку q имеет вид (r — s)/2,
где г и 5 — делители п, то очевидно, что q не может превысить (п - 1)/2.
Следовательно, если до значения q = (п — 1)/2 полный квадрат не достигнут,
число п является простым.
При использовании второго уравнения, т.е. q2 = р2 - п, берем в качестве
т наименьшее целое число такое, что га2 > п, и последовательно полагаем,
р = ш, т-Ы,... до тех пор, пока р2—п не станет полным квадратом. Как и прежде,
q не может превысить (п — 1)/2, так что если до значения р = (п + 1)/2 полный
квадрат не получен, число п является простым. Преимущество использования
второго соотношения состоит в том, что проверке на полный квадрат подлежит
меньшее количество чисел.
Например, рассмотрим применение записи р2 = n+q2 для проверки, является
ли простым число п = 527. Рассмотрим q = 1, 2,..., (п — 1)/2.
я
1
2
3
4
5
6
7
527 Н
527 Н
527^
527-
527-
527-
527-
п + Я*
h 1 = 528
h4 = 531
h 9 = 536
h 16 = 543
h 25 = 552
h 36 = 563
\- 49 = 576 = B4J

РАЗДЕЛ 7.3. Алгоритмы деления и алгоритм Евклида 301
Итак, п = 527 является составным, и его делители легко вычисляются:
527 = B4J - 72 =
= B4-7)B4 + 7) =
= 17-31.
Решение вопроса о том, является ли число п простым, не всегда требует проверки
всех значений q от 1 до (га — 1)/2.
¦ УПРАЖНЕНИЯ
Воспользовавшись методом выделения множителей Ферма, определите, являются
ли следующие числа простыми.
1. 1001
2. 1349
3. 4851
4. 1079
5. 8051
6. 567
7. 7931
7.3. АЛГОРИТМЫ ДЕЛЕНИЯ И АЛГОРИТМ ЕВКЛИДА
Ранее была доказана теорема, названная алгоритмом деления. Теорема гласила,
что для положительных целых чисел а и b существуют единственные неотрица-
неотрицательные числа q и г такие, что 0<г<Ьиа = bq+r. Это утверждение не является
алгоритмом, но алгоритмы для нахождения q и г существуют. Если числа а и b
велики, число q можно "угадать". Если умножить b на q и результат слишком
велик, следует q заменить на q - 1 и повторять процесс, пока не получим bq < a,
после чего положить г = а — bq. Однако, если bq < а, но а — bq > 6, то следует
заменить q на q +1 и повторять процесс, пока не получим a-bq < 6, после чего
положить г = а — bq. Более системно метод описывается следующим образом:
1. Положить q = lnr = a — bq.
2. Если г > b, положить q = q + 1 и г = а — bq.
3. Продолжать процесс, пока г < Ь.
Изложенное представляет собой алгоритм нахождения наибольшего общего
делителя больших чисел, названный алгоритмом Евклида. Нахождение наиболь-
наибольшего общего делителя необходимо при сложении дробей, а также при решении
уравнений в целых числах.
ТЕОРЕМА 7.2. (Алгоритм Евклида) Допустим, что а и b — положительные
целые числа, и последовательное применение алгоритма деления приводит к по-
последовательности следующего вида:

302 ГЛАВА 7. Теория чисел
а = bq0 + г0 0 < г0 < Ь
Ь = roqi + т\ 0 < г\ < г0
7*0 = П<?2 + 7*2 0 < Г2 < Г\
П = г2Яз 4- г3 0 < г3 < г2
7*2 = 7*3^4 +7^4 0 < Г4 < Г3
Г/с = Tk+iqk+2 + T^fc+2 0 < Tk+2 < 7*A:-hl
Существует r^ = 0. Пусть 5 — первое целое число такое, что rs = 0. Тогда
rs_i = НОД(а, 6), если s > 0, и 6 = НОД(а, 6), если 5 = 0.
ДОКАЗАТЕЛЬСТВО. Пусть 5 = {ro,ri,...}. Если г0 = 0, тогда результат очеви-
очевиден, поэтому предположим, что г0 > 0. Согласно принципу полного упорядочения
множество 5 содержит наименьшее положительное целое число, скажем, г^. Но
О < ri+i < ri, и поэтому г»+1 = 0. Положим s = i 4- 1.
По теореме 3.33,
НОД(а,6) = НОДF,г0) = НОД(го,п) = ... = Н0Д(г5_ьгД
но поскольку rs = 0, НОД(гв_1,гв) = rs_b так что НОД(а, b) = rs_b ¦
ПРИМЕР 7.3. Используя алгоритм Евклида для нахождения НОДB03,91), дей-
действуем следующим образом. Сначала делим 203 на 91 нацело и получаем
203 = 91-2 + 21;
а = b • qo + tq.
Теперь делим 91 на остаток 21 нацело:
91 = 21-4 +7;
Разделяя 21 на 7 нацело, получаем
21 = 7-3 + 0;
7*0 = 7*1 • <?2 +7*2.
Итак, 5 = 2 и НОДB03,91) = НОД(91,21) = НОДB1,7) = 7 = гв_1 =гь ?

РАЗДЕЛ 7.3. Алгоритмы деления и алгоритм Евклида 303
ПРИМЕР 7.4. Найти НОД(99,205). Действуя вышеуказанным образом, делим 205
на 99 нацело, получая
205 = 99 • 2 + 7.
Теперь делим 99 нацело на остаток 7, получая
99 = 7-14 4-1.
Далее делим 7 на 1 и получаем
7 = 1-7 + 0.
Таким образом, НОД(99,205) = 1. ?
Алгоритм Евклида позволяет находить такие значения и и v, что НОД(а, Ь) =
rt, аи Л-vb — НОД(а, 6). Используя обозначения теоремы 7.2, запишем г*_2 =
rt-i • qt + rt. Отсюда rt = rt_2 - rt-\ • qt- Аналогично, rf_i = rt_3 - rt-2 • qt-\-
Подстановка в предыдущее уравнение дает
ft = rt-2 ~ (rt-з ~ rt-2 • qt-i) - qt-
Аналогичным образом можно выразить rt_2 через rt-s и 7-t_4 и, подставив в пре-
предыдущее уравнение, исключить г?_2. Продолжая в том же духе, можно исключить
все Г{ и вернуться обратно к а и 6, получив НОД(а, Ь) в виде иа + vb.
ПРИМЕР 7.5. Выразить НОД(85,34) в виде 85г* + 34г;. Для использования алго-
алгоритма Евклида сначала разделим 85 на 34 нацело:
85 = 34 ¦ 2 + 17.
Разделяя 34 на 17 нацело, получаем
34 = 17 • 1 + 0.
Таким образом, НОД(85,34) = 17 и НОД(85,34) = 17 = (85)A) + C4)(-2). ?
ПРИМЕР 7.6. Выразить НОДB52,580) в виде 2Ъ2и + 580и. Делим 580 на 252
нацело, получая
580 = 252 • 2 + 76;
о> — b • ^о ~Ь t*q.
Теперь делим 252 нацело на 76:
252 = 76 • 3 + 24;
Продолжая процесс, получаем
76 = 24 • 3 + 4;
^о = П • ^2 4- г2

304 ГЛАВА 7. Теория чисел
и
24 = 4 • 6 + 0;
Обратная подстановка дает
4 = 76-24-3 =
= 76 - [252 - 76 • 3] • 3 =
= 76 -10 + 252 -(-3) =
= [580 - 252 • 2] • 10 + 252 • (-3) =
= 580-10 4-252-(-23).
где гi выделены подчеркиванием. ?
ПРИМЕР 7.7. Выразить НОДB52,576) в виде 252и4-576г>. Сначала разделим 576
на 252 нацело:
576 = 252 • 2 + 72.
Теперь разделим 252 нацело на 72:
252 = 72 • 3 4- 36.
После обратной подстановки получаем
36 = 252-723 =
= 252 - [576 - 252 • 2] • 3 =
= G)B52L-(-3)E76). ?
В примере 7.3 показано, что НОД(91,203) = 7. Если разделить числа 91 и
203 на их наибольший общий делитель 7, получим Щ- = 13 и ^ = 29. Легко
видеть, что целые числа 13 и 29 — взаимно простые; т.е. НОДA3,29) = 1. Таким
образом, оказалось, что результаты деления двух целых чисел на их наибольший
общий делитель не имеют общих делителей, за исключением 1. Доказательство
следующей теоремы предоставляем читателю.
ТЕОРЕМА 7.8. Пусть заданы целые числа а и 6, не равные нулю, тогда числа
нода(о,ь) и нодкь) являются взаимно простыми, т.е. НОД (Н0Да(аЬ) , НодЬ(а,ь)) = L
Было определено ранее, что положительное целое число га представляет
собой наименьшее общее кратное целых чисел а и b при условии, что (а) а | га
и b | га, и (б) если п — любое общее кратное чисел а и 6, то га | п. Наименьшее
общее кратное чисел а и b обозначим НОК(а, Ь).
Необходимо построить алгоритм нахождения наименьшего общего кратного
двух целых чисел. Цель достигается определением наибольшего общего делителя
этих чисел (алгоритм нахождения которого уже имеется) и использованием тео-
теоремы 3.50. Указанная теорема утверждает, что для положительных целых чисел
а и b НОД(а, Ь) • НОК(а, b) = ab.

РАЗДЕЛ 7.3. Алгоритмы деления и алгоритм Евклида 305
Для нахождения НОК(91,203) сначала определим НОД(91,203), воспользо-
воспользовавшись алгоритмом Евклида, как это было сделано ранее, а затем разделим на
него произведение чисел 91 и 203. Поскольку НОД(91,203) = 7, находим
НОК(91,203) = (91)B°3) = 2639.
¦ УПРАЖНЕНИЯ
1. Задан алгоритм деления a = bq 4- г. Найдите q и г для указанных ниже
значений а и 6:
a) a = 75, Ь = 8; б) a = 102, Ь = 5;
в) a = 81, Ъ = 9; г) a = 16, Ь = 25.
2. Найдите наибольший общий делитель для следующих пар чисел:
а) 75, 25; б) 27, 18;
в) 621, 437; г) 289, 377;
д) 822, 436.
3. Найдите наименьшее общее кратное для пар чисел из упражнения 2.
4. Для приведенных ниже пар чисел а и 6 найдите и, v и d такие, что au + bv =
d, где d — наибольший общий делитель чисел а и Ь:
а) 83,17; б) 361,418;
в) 25,15; г) 81,9;
д) 216,324.
5. Докажите, что если НОД(а,Ь) выражен как ах + by, то х и у — взаимно
простые числа.
6. Докажите, что для целых чисел а и 6, не равных нулю, НОда(а Ь\ и НОдЬ(а ь)
ВЗаИМНО ПрОСТЫ, Т.е. НОД ( Н0Д(а Ь) ' НОШ а Ь) ) = 1 (теоРема 7.8).
7. Запишите в псевдокодах процедуру нахождения согласно алгоритму деления
величин диг, когда произвольное положительное целое число а делится на
произвольное положительное целое число Ь.
8. Запишите в псевдокодах процедуру для алгоритма Евклида.
9. Задано целое число а и положительное целое число Ь. Докажите, что целые
числа, произведение которых равно а и наибольший общий делитель которых
равен 6, существуют тогда и только тогда, когда b2 \ а.
10. Предполагая, что
F(k) = 22" + 1 при к > 0,
а) докажите, что F(m + 1) = F@)F(l)FC) • • • F(ra) + 2 для каждого т > 0;
б) докажите, что F(m) и F(n) — взаимно простые числа, если тфп.
11. Покажите, что если НОД(а, 6) выражен как ах+Ъу, то х и у не определяются
единственным образом.
12. Докажите, что если НОД(а,6) = 1, то НОД(а + пЬ,6) = 1.
13. Докажите, что п • НОД(а,6) = НОД(па,п6).
14. Пусть S — множество всех целых чисел вида ах+by. Покажите, что НОД(а, Ь)
делит все элементы множества 5.

306 ГЛАВА 7. Теория чисел
7.4. ЦЕПНЫЕ ДРОБИ
В данной главе алгоритм деления и алгоритм Евклида будут применяться доста-
достаточно часто. Рассмотрим сначала рациональные числа а/b, где а и 6 — целые
числа и b > 0. Если алгоритм деления применен к целым числам а и 6, где b > О,
то существуют единственные целые числа t (частное) и г (остаток) такие, что
a = b-t + r при 0 < г < Ь.
Для а = —124 и b — 35 имеем
-124 = C5)(-4) + 1б.
Переписав последние два равенства и перейдя к рациональным числам, получаем
а г -124 А 16
"^ I г» р» ''' ел *
Воспользовавшись функцией целой части числа, отношения можем переписать в
таком виде
при этом дробный остаток r/b обладает свойством 0 < r/b < 1. Если г ф 0,
равенства можно переписать следующим образом:
а 1 -124 А 1
t + = -4 +
b b/r 35 35/16 '
где b/r > 1. Алгоритм деления можно применить снова и получить b = rt' + r' и
35 = A6)B) + 3. Таким образом, обращая дробный остаток и применяя алгоритм
деления снова и снова, указанным способом получаем выражение рационального
числа -124/35:
-124 16 1
= -4 + — = -4 +
35 35 /35
ie
24-
16 /16
3
= -4 +
Поскольку дробь 1/3 имеет числителем 1, нельзя далее сокращать 3/1, используя
алгоритм деления. Выражение
-4+ К

РАЗДЕЛ 7.4. Цепные дроби 307
называется цепной дробью и представляет собой альтернативный способ запи-
записи рационального числа -124/35. В связи с тем, что цепная дробь имеет ре-
регулярную структуру и числители всегда равны 1, для точного задания цепной
дроби необходимо упомянуть только числа —4, 2, 5 и 3, поэтому записыва-
записываем -124/35 = [-4; 2,5,3]. Числа -4, 2, 5 и 3 называются элементами цеп-
цепной дроби или неполными частными, поскольку порождены алгоритмом деле-
деления. Точка с запятой отмечают особую природу первого члена —4. Например,
[3; 7] = 3 + 1/7 = 22/7, но
[0; 3,7]= 0 +—Ц_
Возвращаясь к цепной дроби —124/35 — [—4; 2,5,3], замечаем, что
3 = C — 1) + 1 = C — 1) + 1/1. Таким образом, можно записать
-124 , 1
4 +
35
так что запись —124/35 = [—4; 2, 5,2,1] тоже имеет место, однако в ней на послед-
последнем шаге алгоритм деления не использован. Пример подсказывает, что каждое
рациональное число имеет два различных представления в виде цепной дроби с
целыми числами в качестве элементов: в одном представлении последний элемент
больше 1, а в другом — равен 1.
Если х — действительное, но не рациональное число, алгоритм деления не
применим; однако, используя функцию целой части, можно получить представ-
представление х в виде цепной дроби длины п способом, аналогичным рациональному
случаю. Таким образом, для действительного, но не рационального числа х име-
имеется единственное число t0, где t0 < х < ?0 + 1 такое, что t0 = [x\. Тогда
1 > у\ = х — [х\ = х — to > 0
есть так называемая дробная часть х. Если х\ = 1/уъ тогда
х = [х\ + ух = t0 + 2/1 = t0 + —
Х\
и X! > 1. Пусть ti = [zij , У2 = х\ - [xi\ и х2 = l/j/2. т-к- 2/2 > 0. Тогда
х\ =t\-\ , где Х2 > 0. Сочетание этих равенств дает
х2
1
х = t0 + — = t0 +
., + ¦!-¦

308 ГЛАВА 7. Теория чисел
Продолжая в том же духе, получаем
х = t0 H
1
+ • • • +
tk-1 + —
Xfc
где U — целое число для каждого г, ?» > 0 для г > 1, х& — иррациональное
действительное число и х* > 1. Можно также записать
Например, пусть х = л/3 = 1.7320508 •••. Построим представление числа
в виде цепной дроби следующим образом:
t0 = |sj =
где
У\ = х - [х\ = х - t0 = \/3 - 1;
X! = 1/У1 = 1/(л/3 - 1) = (л/3 + 1)/2;
где
У2 = хг- LxiJ = xi - ti = (>/3 + 1)/2 - 1 = (л/3- 1)/2;
х2 = 1/1/2 =2/(>/3-1) = >/3 + 1;
t2 = [x2j = 2,
где
уг = х2- [х2\ = х2 - t2 = (v/3 + 1) - 2 = V3 - 1;
хз = 1/уз = 1/(л/3 - 1) = (\/3 Ч-1)/2,
таким образом,
= [to\tux2] = [to;[*i;*2]] = [l;l, (л/3 + 1)] =
= [to;tut2,x3] = [to;*i, [t2;x3]] = [1; 1,2,(л/з
Но поскольку x3 = хь структура повторяется , поэтому
л/3 = [1; 1,2,1,2,1,2, (л/3 + 1)/2]
и т.д.
Отсюда выводим следующее рекурсивное определение цепной дроби.

РАЗДЕЛ 7.4. Цепные дроби 309
ОПРЕДЕЛЕНИЕ 7.9. Для конечной последовательности t0, ti, ^2, • • • , tn дей-
действительных чисел, где п > 0 и t{ > 0 для г > 1, определим конечную цепную
дробь [t0] ?ь ?2,..., *п] следующим образом:
[to;] = ^о;
[*o;ti,t2,...,tfc]; = [to;[ti;t2,...,tfc]] для 1 < к < п.
Числа to,ti,... , tn называются неполными частными, или элементами цеп-
цепной дроби. Цепная дробь [to;ti,t2,... ,tn] называется простой, если ?; — це-
целое число для каждого г, т.е. каждый элемент цепной дроби есть целое число.
Числа [t0;], [*o;*i], [to;ti,t2], ••• > [to;tb t2,... ,tfc], ••• > [to;tbt2, • • • ,tn] называ-
называются подходящими дробями цепной дроби [to;ti,t2, • • • 5tn]. [to;ti,t2, • • • ?tfc]i
где есть А:-я подходящая дробь при 0 < к < п. Для удобства обозначения
запись [*о;*ь*2, •-.»**]. использованная при А: = 0, будет означать [?0;]. Бу-
Будем говорить, что две цепные дроби [to; ti, ?2, • • •, *п] и [Ьо; bi, 62,..., Ьт] равны
почленно, если п = т и ti = bi при 0 < г < п. Если х — действительное
число и х = [*o;*i,*2?...?*n]i тогда будем говорить, что [*о;*ь*2? • •. 5^п] есть
представление цепной дробью числа ж. Два представления называются
падающими, или равными, если они равны почленно.
Следующая теорема дает иной способ разложения цепной дроби на подхо-
подходящие дроби.
ТЕОРЕМА 7.10. Если п — положительное целое число и [?о;?ь*2> • • • ^п] — цепная
дробь, тогда для каждого к, 1 < к < п,
ДОКАЗАТЕЛЬСТВО. Равенство докажем методом математической индукции. Ес-
Если п = 1, по определению, [to; *i] = [*o; [*i; ]]. Предположим, что утверждение
теоремы выполняется при и = га, т.е. для любой цепной дроби [Ьо; Ьь ..., Ьт]>
[Ьо; &ь &2, • • •, Ьт] = [Ьо; bi, Ь2,..., Ь^_1, [fy; 6j+b ..., 6т]]
для 1 < j < т. Рассмотрим п = т -Ь 1. Пусть [to] ti, t2,..., tm+i] — цепная дробь
и 1 < к < т -f 1. Тогда
[to;*i,...,Wi] = [*o;[ti;*25...,*m+i]] (по определению) =
полагая по индуктивному предположению bi = t^+i и j = fc - 1. Таким образом,
[to;ti,... ,tm+i] = [to;ti,t2,... ,tfc_i, [tjt;
согласно определению цепной дроби. Следовательно, по методу индукции теорема
справедлива. ¦

310 ГЛАВА 7. Теория чисел
¦ УПРАЖНЕНИЯ
1. Найдите два представления цепной дробью, [*о;*ь • • • >*п]> Для каждого из
приведенных ниже рациональных чисел:
а) 37/11; б) 48/1003; в) -257/2003;
г) 11/37; д) -5/44; е) 5.
2. Вычислите приведенные рациональные числа и выразите их в виде p/q, где
р и q — целые числа:
а) [3;5,2]; б) [0;3,5,2]; в) [-10; 1,4,3];
г) [6; 4, 7, 3,5]; д) [2; 5,3]; е) [5; 3,7,4,6].
3. Найдите представление числа х конечной цепной дробью в виде х = [*о;*ь
*2,*3,*4,*5,^б] ДЛЯ
а) х = >/5;
б) х = у/2]
в) х = 7г;
г) х = A + >/5)/2.
4. Пусть [*о;*ь • • • ,*п] — конечная цепная дробь, где U > 0 для 1 < г < гг.
Докажите, что если Ь > 0, то
а) [*о;*ь*2,..-,*п] > [*о;*ъ*2,---,*п + Ь1' если п нечетно'
б) [*о;*ь*2,...,*п] < [*о;*ь*2,...,*п + Ь], если п четно.
7.5. ПОДХОДЯЩИЕ ДРОБИ
Вполне очевидно, что [t0; ^i, ^2, • • •, ?fc] Д-^я каждого /с представляет собой дей-
действительное число. Запишем первые четыре подходящие дроби и упростим их,
выразив каждую как отношение двух действительных чисел, где как числитель,
так и знаменатель выражены через t{. Особый интерес будут представлять чис-
числитель и знаменатель каждой из подходящих дробей.
где мы положили ро = *о и до = 1.
= ?0
где pi = toti + 1 и gi = ti.
[*;t*] [*;[*;*]] * + t +t+ 2
*1 г
*2
*2 _ (*0*l + 1)*2 + *O
*1*2 + 1 *i*2 + 1

РАЗДЕЛ 7.5. Подходящие дроби 311
где р2 = Р\^2 +Ро и q2 = 91^2 4- 9о- Подобным образом вычисляем
4- ?о^з + ^2^з 4- 1
4- 91 9з
где рз = Р2^з 4- Pi и дз = 92^з 4-9ь В каждом случае число [to; t\, t2,..., tk]
"переформировывается" из представления цепной дробью без какого-либо "сокра-
"сокращения" и образует отношение двух полиномов Р и Q в переменных ?о,?ъ • • • >^ь
т.е.
Справедливым является и то, что до?#ь<72 и дз положительны, поскольку получе-
получены путем умножения и сложения положительных чисел. Рассмотренные примеры
дают основание сформулировать следующую теорему.
ТЕОРЕМА 7.11. Пусть п — неотрицательное целое число и [?о;?ъ*2? • • • ?*п] —
конечная цепная дробь, которая рекурсивно определяет конечные последователь-
последовательности рсьРь • • - ,Рп и go, 9i» • • • iQn следующим образом:
а) ро = *oi
go = 1.
б) pi = *o*i 4-1,
в) Р/с = Pk-ltk 4" Pfc-2i
9fc = 9fc-i*A: 4- 9fc-2 при 2 <к <п.
Тогда g*; > 0 и [*o;*i>*2, • • • Лк] = — при 0 < к < п.
Як
ДОКАЗАТЕЛЬСТВО. Не представляет труда методом математической индукции
показать, что qk > 0 при 0 < к < п. Эту часть теоремы предоставляем доказать
читателю. Выше было показано, что теорема справедлива при к = 0,1 и 2, т.е.
[*о;] = Ро/Яо> [to\ti] = pi/qi и [to\ti,t2} = p2/q2- Предположим, что 2 < к < п,
и для любой цепной дроби [Ьо;&ь • • • >bfc] и любого j 0 < j < к справедливо
утверждение о том, что [60;6i,... ,6j] = p'j/q'j, где р^ и <^ определены способом,
аналогичным (а)-(с), но для цепной дроби [6О;ЬЬ... ,6*.]. Тогда
[t0] tu ..., tk, tk+i] = [to] tu ..., tfc-i, [tk] tk+i}} (по теореме 7.10) =
где 6i = U при 0<г</с-1ибА; = [tfc;tfc+i] = tk H . Таким образом, в силу
индуктивного предположения /с+1
q>k_lbk+q>_2

312 ГЛАВА 7. Теория чисел
Поскольку bi = ti при 0 < г < к — 1, имеем, что для таких г pi = p^ и ^ = <7г'-
Подставляя соответствующие выражения для &ь р\ и q[, получаем
Pk-i
1
(qk-itk + 9fc-2) + Як-i/tk+i
Pktk+i
4- g/b-i
Следовательно, по индукции,
= Рк/Як при 0 < /с < п.
Числа рк и qk (теорема 7.11) определены вне зависимости от того, что они
могут быть использованы как числитель и знаменатель выражения, равного к-ой
подходящей дроби. Рекурсивное отношение, заданное теоремой 7.11, обеспечива-
обеспечивает быстрый способ вычисления подходящих дробей для заданной цепной дроби,
поскольку числитель pi и знаменатель qi можно вычислить одновременно и до-
достаточно просто. Например, для х = [—4; 2,5,2,1] = [t0;^1,^2,^3,^4] подходящие
дроби можно вычислить согласно приведенной ниже таблице:
к
0
1
2
3
4
tk
-4
2
5
2
1
(-4)(
(-7)E)
-39)B)
(-85)A)
Рк
-4
2) + 1 =
+ (-4) =
+ (-7) =
+ (-39)
-7
= -39
= -85
= -124
B)E)
(П)B]
B4)A)
Як
1
2
+
+
+
1 =
2
11
= 11
= 24
= 35
Рк/Як
-4/1
-7/2
-39/11
-85/24
-124/35
Так что х = —124/35, т.е. числу, породившему цепную дробь [—4; 2, 5,2,1] (см.
раздел 5.1).
Благодаря рекурсивному способу задания цепных дробей, имеется значи-
значительное количество соотношений, связывающих подходящие дроби через числи-
числители и знаменатели, рк и </&, введенные теоремой 7.11. Чтобы запись этих соотно-
соотношений сделать справедливой при к = 0, зачастую удобно определять рк и qk при
к = —1, положив
р-1 = 1;
4-1=0.
Таким образом, р\ — p§t\ +p_i = t§t\ 4-1 и </i = q§t\ + q-\ = 1 • ?1 4-0 = ?ь как в
теореме 7.11.
ТЕОРЕМА 7.12. Если [to;?1,... ,tn] — конечная цепная дробь, где ti — действи-
действительные числа, pk и qk — заданы теоремой 7.11, тогда
а) РкЯк-i ~Рк-\Як = (-l)* при 0 < к < п\

РАЗДЕЛ 7.5. Подходящие дроби 313
б) pg.-Ptzi^W-1 n?Ki<k<n.t
Як Як-\ ЧкЧк-i
v Pk Pk-2 (-l)fc^ о / 7 /
в) = при 2 < к < п.
qk qk-2 ЯкЯк-2
г) Подходящие дроби четного порядка образуют возрастающую последователь-
последовательность, т.е.
El < El < Е± <
Яо Q2 Яа
а подходящие дроби нечетного порядка образуют убывающую последова-
последовательность, т.е.
Кроме того,
El > El > El >
Яг Яз Яъ
92j
при 0 < j < [п/2\ и 0 < г < [{п - 1)/2J, где слева равенство имеет место,
когда п четное, а справа равенство имеет место, когда п нечетное.
д) Если дробь [to; *i,..., tn] — простая, то Як > к при 0 < к < п.
е) Если дробь [*о;*ь • • ч*п] — простая, то д^ < g^+i при 1 < к < п-1 и д0 < <7ь
ДОКАЗАТЕЛЬСТВО, а) При к = lpigo-pogi = (*o*i4-1)A) — to*i = 1 = (-1I
по теореме 7.11. Пусть 2 < т < п и допустим, что формула в части (а) справедлива
при к = т. Показано, что формула имеет место при к = т + 1. Опять, используя
теорему 7.11, имеем
Рт+\Ягп -РтпЯтп+\ = (Pmtm+1 + Ргп-1)Ягп ~ Ртп{Я
= Ргп-\Ятп - РтЯгп-1 =
q^-i -Рт-1Ятп) =
Таким образом, формула в части (а) имеет место при 1 < к < п. Также роЯ-i —
qop_i = to •0 — 1-1 = —1 и формула справедлива при к = 0.
б) Утверждение теоремы следует из части (а), если в соответствующем
равенстве при к > 1 произвести деление на qkqk-i-
в) Если к > 2, то по теореме 7.11
Pk = Рк-ltk +Рк-2\
qk = qk-itk + qk-2-
Умножение первого из равенств на qk-2, & второго — на pk-2
Pkqk-2 = Pk-iqk-2tk +Рк-2Як-2',
ЯкРк-2 = Як-\Рк-2^к + Як-2Рк-2-
Вычитая второе равенство из первого, получаем
РкЯк-2 - ЯкРк-2 = {Рк-\Як-2 - Рк-2Як-\)^к-

314 ГЛАВА 7. Теория чисел
Теперь, учитывая утверждение в части (а), получаем
РкЯк-2 ~ QkPk-2 = (-l)(fc-lbltifc = (-l)fc(-l)-2ifc - (-1L-
Разделив на ЯкЯк-2 > 0> получаем желаемый результат:
Pfc _ Рк-2 _ (~l)ktk
Як qk-2 ЧкЯк-2
г) Если 2 < к <п и к — четное, то к - 2 тоже четное и /с - 2 > 0. Поэтому
{—1)к = 1 и из утверждения в части (в) вытекает, что
tffc <?fc-2 ЯкЯк-2
поскольку ?fc и ЯкЯк-2 положительные при к > 1. Если 3</с<пи/с — нечетное,
то /с — 2 также нечетное и /с — 2 > 1. В этом случае (—l)fc = —1, так что из
утверждения в части (в) вытекает, что
Як Як-2 ЯкЯк-2
так как tk и ЯкЯк-2 положительны при к > 3.
Если п нечетное, то согласно (б) — > п~1, так что [?0;?ь ^2, • • •, tn] =
Яп Яп-1
Рп/Яп больше, чем наибольшая подходящая дробь четного порядка, Рп-г/Яп-i-
Если п четное, то — < , так что [to; ti, ^2,..., tn] = рп/яп меньше, чем
Яп Яп-1
наименьшая подходящая дробь нечетного порядка, pn_i/gn_i.
Доказательство пунктов (д) и (е) оставляем за читателем. ¦
Подходящие дроби для х = [—4; 2,5,2,1] вычислены ранее в данном разделе
и приведены в таблице. Подводя итог этим результатам в контексте части (г),
находим, что
Ро/Яо < Р2/Я2 < Ра/Яа = х < p3/q3 < pi/яи
-4/1 < -39/11 < -124/35 = х < -85/24 < -7/2.
Непосредственным вычислением определяем также, что
РЗЯ2-Р2ЯЗ = (-85)A1) - (-39)B4) = (-935) - (-936) = 1.
Значение теоремы 7.12 состоит в том, что она точно устанавливает, что
последовательные и взаимно исключающие подходящие дроби могут отличать-
отличаться не более, чем на величину, обратно пропорциональную "знаменателям" под-
подходящих дробей, а также, что подходящие дроби альтернативно больше, чем
[?о;*ь*2,...,*Л], и меньше> чем [*о;*ь*2,...,*п].
Практический интерес представляют некоторые отношения Рк/Як числите-
числителей и знаменателей подходящих дробей. Эти отношения приведены в следующей
теореме, доказательство которой предоставляется читателю.

РАЗДЕЛ 7.5. Подходящие дроби 315
ТЕОРЕМА 7.13. Для конечной цепной дроби [?о;?ь^2, • • • , ^п]
а) qic/qk-i = [**;**-ъ • • ¦ ,*2,*i] при 1 < к < п.
б) Если t0 ф 0, то Pk/Pk-i = [t/k;*fc-i,-..i*b*o] при 1 < fe < n.
в) Если t0 = О, то pk/pk-i = [**;**-ь• • •, *2,*i] при 2 < к < п.
I УПРАЖНЕНИЯ
1. Докажите теорему 7.11 при условии, что qk > 0 при 0 < к < п.
2. Вычислите подходящие дроби для
а) [2; 5,1,2,4]; б) [2; 5,1,2,3,1]; в) [5; 1,2,3];
г) [0;5,1,2,3]; д) [-5;3,8,2].
3. Вычислите подходящие дроби pk/qk, определяя рк и qk при 0 < к < 5
для х = [*о;*1,*2?*з?*4>*51?б] и для следующих значений х (см. упражнения
раздела 7.1):
а) х = \/5;
б) х = \/2;
в) х = 7г;
г) х = A + \/5)/2.
4. Докажите утверждения (д) и (е) теоремы 7.12.
5. Докажите теорему 7.13. Указание: используйте теорему 7.11.
6. Пусть для цепной дроби [?о;?ь*2,... ,?п] величины Рк и qk определены тео-
теоремой 7.11. Докажите, что
Рк Pk-i
= (-l)k+1 при 0 < к < п,
где левая часть равенства записана с помощью определителя.
7. В теореме 7.11 показано, что если р-\ — 1 и g_i = 0, утверждение (в)
справедливо при к — 1. Какие значения должны иметь р-2 и д_2, чтобы
утверждение (в) было справедливо для к = 0?

ГЛАВА
КОМБИНАТОРИКА
И ВЕРОЯТНОСТЬ
8.1. ОСНОВНЫЕ КОМБИНАТОРНЫЕ ПРИНЦИПЫ
Как говорил Альберт Эйнштейн: "Не все, что можно сосчитать, сосчитано, и не
все, что сосчитано, можно сосчитать". Хотя это высказывание не очень воодушев-
воодушевляет, все же попытаемся заняться подсчетами. Фактически, очень много проблем
в данной книге начинается со слова "сколько". Сколько в этой книге проблем
начинается со слова "сколько"? Мы не задаем этот вопрос по нескольким при-
причинам, поскольку не знаем, будет ли ответ содержать сам вопрос? Возможно,
главная причина, что вопрос остается без ответа, это отсутствие схемы, по кото-
которой на него можно было бы ответить. В действительности, важнее нахождение и
использование общих схем для подсчетов, чем решение отдельных задач. Наша
цель — избегать простого перечисления элементов с последующим подсчетом,
в особенности, если таких элементов очень много. Однако, данный метод мож-
можно использовать для небольшого количества объектов, если это поможет найти
общую схему.
Представьте себе, что человек, которому нечем больше заняться, подбрасы-
подбрасывает монету и кость (в виде игрального кубика). На монете может выпасть "орел"
(Я) и "решка" (Т). При падении кости возможные исходы представляют собой
1, 2, 3, 4, 5 и 6. Возможными исходами обоих событий являются (Я, 1), (Я, 2),
(Я,3), (Н,4), (Я, 5), (Я, 6), (НЛ), (Я, 2), (Я,3), (Г,4), (Г, 5) и (Г,6). Один из
возможных способов представить эти события — построить дерево подсчета,
изображенное на рис. 8.1.
Рис. 8.1
Для нахождения исхода (Я, 2) идем по левой ветке к Я, а затем по ветке
к 2. Очевидно, что таким образом представлены все исходы событий, и каждое

РАЗДЕЛ 8.1. Основные комбинаторные принципы 317
из обведенных чисел изображает единственный исход. Если на монете выпал Я,
то существуют шесть возможных исходов для кубика; и те же шесть возможных
исходов, если выпала "решка" Т. Таким образом, можно найти общее количество
исходов, умножая 2x6, т.е. умножая число возможных исходов для подбрасы-
подбрасывания монеты на число возможных исходов для подбрасывания игральной кости.
Следует обратить внимание, что исход подбрасывания монеты не влияет на воз-
возможный исход подбрасывания кости.
Можно представить, что игрок подбрасывает две кости. Существуют шесть
исходов выпадений первого кубика и шесть — второго. Поэтому существует
6 х 6 = 36 возможных исходов выпадения при подбрасывании двух кубиков. По
желанию можно снова нарисовать дерево подсчета. Аналогичным образом пред-
предположить, что выбирается сначала одна буква из 26-символьного алфавита, а
затем — вторая, причем вторая буква может совпадать с первой. Для нахождения
общего числа буквенных пар важно заметить, что имеются 26 вариантов выбора
первой буквы, и для каждой выбранной первой буквы существуют 26 вариантов
выбора второй. Следовательно, существуют 26 х 26 = 676 возможных способов
выбора из алфавита буквенных пар. Если вторая буква не должна совпадать с
первой, то после выбора первой буквы имеется только 25 вариантов выбора вто-
второй. Поэтому всего имеются 26 х 25 = 650 возможных вариантов выбора. Другой
способ решения этой же задачи: вычесть из 676, общего числа возможных вари-
вариантов выбора буквенных пар из алфавита, число всех вариантов, в которых обе
буквы совпадают. Их, понятно, 26, поэтому, вычитая 26 из 676, снова получаем
650.
Предположим, что номерной знак автомобиля содержит три буквы алфавита,
за которыми следуют три десятичные цифры. Если повторения разрешены, то
существуют 26 вариантов выбора каждой буквы и 10 вариантов выбора каждой
цифры. Таким образом, общее число номерных знаков составит
26 х 26 х 26 х 10 х 10 х 10 = 17,576,000.
Допустим, что по какой-то причине буквы и цифры не могут повторяться. Тогда,
после выбора первой буквы имеются 25 вариантов выбора второй и 24 варианта
выбора третьей буквы. Аналогично имеем 10 вариантов выбора первой цифры,
9 вариантов выбора второй и 8 вариантов выбора третьей цифры номера. Таким
образом, общее число номерных знаков составит
26 х 25 х 24 х 10 х 9 х 8 = 11,232,000.
Выразим данный метод в приведенной ниже теореме, которую примем в
качестве аксиомы.
ТЕОРЕМА 8.1. (Комбинаторный принцип умножения) Пусть задана последо-
последовательность событий
El,E2,Es, . . . , Em
таких, что событие Е\ осуществляется щ способами, и если события Е\,Е2,Ез,
...,?fc_i осуществились, то событие Ek может осуществиться rtk способами.
Тогда существует п\ х n<i х пз х • • • х nm способов осуществления всей последо-
последовательности событий.

318 ГЛАВА 8. Комбинаторика и вероятность
ПРИМЕР 8.2. Сколько существует функций, задающих взаимно однозначное со-
соответствие между множеством 5, содержащим п элементов, и множеством Т,
содержащим т элементов? Если п > га, то такие функции не существуют, по-
поэтому предположим, что п < т. Не уменьшая общности, допустим, что элементы
множества 5 обозначены ai,a2,a3,... ,an. Существует га вариантов отображения
элемента а\. Если образ а\ определен, то имеется га — 1 вариантов отображе-
отображения элемента а2, поскольку он не может быть отображен в образ элемента а\.
Аналогично, существует га — 2 вариантов отображения аз и т — 3 вариантов
отображения а4, и т.д. Руководствуясь этой схемой, получаем, что существует
га — г + 1 вариантов отображения а;- Поэтому, в соответствии с комбинаторным
принципом умножения, имеется
(га)(га - 1)(га - 2)(га - 3) • • • (га - п + 1)
способов отображения множества S на множество Т, при котором никакие два
элемента множества S не будут отображены в один и тот же элемент множе-
множества Т. Таким образом, существует
(га)(га - 1)(га - 2)(га - 3) • • • (га - п + 1)
взаимно однозначных функций из 5 в Т. ?
ПРИМЕР 8.3. Сколько существует функций из множества 5, содержащего п эле-
элементов, в множество Т, содержащее га элементов? На этот раз любой из п элемен-
элементов множества 5 может быть отображен в любой из га элементов множества Т.
Следовательно, существует (га)(га)(га)(га) • • • (га) = тп функций из 5 в Т. ?
ПРИМЕР 8.4. Битовая строка — это строка, состоящая из элементов, каждый
из которых имеет значение 1 или 0. Сколько существует битовых строк, имеющих
длину 5? Сколько существует битовых строк длины А;? Поскольку каждый символ
строки может иметь значение 1 или 0, то существует два варианта выбора для
каждой позиции. Следовательно, существует 2x2x2x2x2 = 25 битовых строк
длины 5. По аналогичным соображениям, имеется 2к битовых строк длины к. ?
ПРИМЕР 8.5. Сколько существует подмножеств множества 5, содержащего пять
элементов? Сколько подмножеств имеет множество, содержащее к элементов?
Имеется несколько способов подсчета подмножеств. Укажем два из них. Рассмот-
Рассмотрим первый способ. Пусть ai,a2,a3,a4,a5 — элементы множества 5. Определим
взаимно однозначное соответствие между множеством 5 и множеством битовых
строк длины 5, при котором каждому подмножеству s множества 5 соответству-
соответствует строка, в которой г-ый бит равен 1, если а{ G 5, и равен 0, если at <? S.
Таким образом, подмножество {ai,a2,a4} соответствует строке 11010, подмноже-
подмножество {a2,a5} соответствует строке 01001, 0 соответствует строке 00000, а мно-
множество S соответствует строке 11111. Итак, установлено взаимно однозначное
соответствие между подмножествами множества S и битовыми строками длины
5. Из предыдущего примера известно, что существует 25 битовых строк длины
5. Поэтому существует 25 подмножеств множества из пяти элементов. Исполь-
Используя аналогичные рассуждения, можно показать, что существует 2к подмножеств
/с-элементного множества.

РАЗДЕЛ 8.1. Основные комбинаторные принципы 319
Второй метод подсчета состоит в том, чтобы для каждого подмножества
s e S определить функцию fs из 5 в множество {0,1}. Функция fs определена
соотношениями /Да*) = 1, если а^ G s, и Л («г) = 0, если а* ^ s. Обратно,
пусть задана функция / из множества 5 в множество {0,1}. Если положить 5 =
{а; : f(ai) = 1}, то функция / является функцией fs. Поэтому имеется взаимно
однозначное соответствие между подмножествами множества 5 и функциями из 5
в {0,1}. Но, согласно примеру 8.3, существует 25 функций из 5 в {0,1}. Подобным
образом, если множество S содержит к элементов, то имеется 2к функций из S
в {0,1}, и поэтому существует 2* подмножеств множества 5. ?
Предположим, что на собрании присутствуют 10 мужчин и 15 женщин, и
кого-то одного нужно выбрать председателем. Существует 10 + 15 = 25 спосо-
способов выбора председателя. Предположим, что человек направляется в ресторан, в
котором предлагаются 15 блюд из говядины, 8 блюд из свинины и 12 блюд из
морских продуктов. Посетителю ресторана предложен выбор из 15 4- 8 + 12 = 35
различных блюд. Предположим теперь, что студент выбирает книгу на полке, где
находятся 25 различных учебников по математике, 30 учебников по информатике
и 15 — по химии. Существует 25 + 30 + 15 = 70 различных вариантов выбора кни-
книги студентом. Заметим, что в каждом случае множества, из элементов которых
делается выбор, не пересекаются. Эти примеры приводят к следующей теореме,
которая формулируется без доказательства.
ТЕОРЕМА 8.6. (Комбинаторный принцип сложения) Пусть 5Ь 52,53,..., 5т —
попарно непересекающиеся множества (т.е. Si П Sj = 0 для всех г ф j), и пусть
для каждого г, множество Si содержит щ элементов. Количество вариантов вы-
выбора из S\ или 52 или 5з или ... или Sm равно rii + П2 + пз Н Ь nm. На языке
теории множеств утверждение теоремы имеет вид
\S1 U 52 U 53 U ... U Sm\ = |5i| + \S2\ + \S3\ + ... + |5m|,
где \S\ обозначает количество элементов множества 5.
ПРИМЕР 8.7. Сколько существует целых чисел между 0 и 1000, содержащих
ровно одну цифру 6? Пусть 5 будет множеством целых чисел между 0 и 1000,
содержащих ровно одну цифру 6. Пусть S\ — подмножество множества 5, ко-
которое содержит число, состоящее из одной цифры, и эта цифра равна 6. Пусть
52 — подмножество множества 5, содержащее двузначные числа ровно с одной
цифрой, равной 6. Пусть 5з — подмножество множества S, содержащее трехзнач-
трехзначные числа ровно с одной цифрой, равной 6. Множество Si содержит только один
элемент — число 6. В S2 каждый элемент, содержащий 6, имеет ее либо пер-
первой, либо второй цифрой. Если 6 — вторая цифра, то существуют 8 различных
чисел, поскольку первое число не может быть 0 или 6. Если 6 — первая цифра,
то таких чисел 9, поскольку вторая цифра не может быть 6. Таким образом, 52
содержит 8 -f 9 = 17 элементов. Элемент из 53 содержит 6 как первую, вторую
или третью цифру. Если 6 — первая цифра, то существуют 9 вариантов выбора
второй цифры и 9 вариантов выбора третьей цифры. Согласно комбинаторному
принципу умножения, 5з содержит 9 х 9 = 81 чисел с 6 как первой цифрой. Если
6 — вторая цифра, то имеются 9 вариантов выбора третьей цифры и 8 вариантов

320 ГЛАВА 8. Комбинаторика и вероятность
выбора первой цифры, поскольку первая цифра не может быть нулем. Следова-
Следовательно, 5з содержит 9 х 8 = 72 чисел, у которых 6 — вторая цифра. Аналогично,
5з содержит 72 числа, у которых 6 — третья цифра. Следовательно, всего S3 со-
содержит 81 4- 72 4- 72 = 225 элементов. Поскольку 5 = S\ U S2 U S3, то 5 содержит
1 + 17 + 225 = 243 элементов. ?
ПРИМЕР 8.8. Сколько существует целых чисел между 0 и 1000, содержащих хо-
хотя бы одну цифру 6? Для решения этой задачи положим 5 множеством целых
чисел от 0 до 1000, не содержащих цифру 6 ни в одном из разрядов. Пусть Si —
подмножество множества S, содержащее однозначные числа; S2 — подмножество
множества S, содержащее двузначные числа; S3 — подмножество множества S,
содержащее трехзначные числа; и54- подмножество множества S, содержащее
четырехзначные числа. Множество Si содержит девять чисел без цифры 6, по-
поскольку только число 6 исключено. Множество S2 содержит числа, имеющие 8
вариантов выбора первой цифры и 9 вариантов выбора второй цифры, поскольку
первая цифра не может быть ни 6, ни 0, а вторая цифра не может быть 6. Поэтому
S2 содержит 8 х 9 = 72 элементов без цифры 6. Множество S3 содержит числа,
имеющие 8 вариантов выбора первой цифры, 9 вариантов выбора второй цифры и 9
вариантов выбора третьей цифры. Поэтому множество S3 содержит 8x9x9 = 648
элементов без цифры 6. Множество S^ содержит только число 1000. Следователь-
Следовательно, S содержит 9 + 72 + 648-1-1 = 730 элементов. Пусть Г — множество всех чисел
между 0 и 1000. Тогда Т — S — множество всех целых чисел между 0 и 1000,
содержащих хотя бы одну цифру 6. Более того, S и Т — S — непересекающиеся
множества. Следовательно, |S| + |T-S| = |Г|, так что 730 + |T-S| = 1001. Значит,
\Т — S\ = 271, поэтому между 1 и 1000 существует 271 целое число, содержащее
хотя бы одну цифру 6. ?
ПРИМЕР 8.9. Сколькими способами можно выбрать две книги по разным темам,
когда на полке находятся 15 книг по информатике, 12 книг по математике и 10
книг по химии? Если выбирать книгу по информатике и книгу по математике, то
существуют 15 вариантов выбора книги по информатике и 12 вариантов выбора
книги по математике, поэтому существует 12 х 15 = 180 возможностей. Если
выбирать книги по информатике и по химии, то имеются 15 вариантов выбора
книги по информатике и 10 вариантов выбора книги по химии, поэтому суще-
существует 15 х 10 = 150 возможностей. Если выбирается книга по математике и
книга по химии, то имеются 12 способов выбора математической книги и 10 —
книги по химии, поэтому имеется 12 х 10 = 120 возможностей. Следовательно,
существуют 180 + 150 + 120 = 450 возможных способов выбора двух книг. ?
ПРИМЕР 8.10. Сколько нечетных целых чисел находятся между числами 100 и
1000? Один из способов решения этой задачи состоит в следующем. Пусть S
— множество нечетных целых чисел между 100 и 1000. Для г е {1,3,5,7,9}
пусть Si — подмножество множества S такое, что г является последней цифрой
его элементов. Для каждого i существуют 9 вариантов выбора первой цифры и
10 вариантов выбора второй цифры, так что каждое множество 5» содержит 90
элементов. Поскольку S = Si U S3 U S5 U S7 U S9, имеем

РАЗДЕЛ 8.1. Основные комбинаторные принципы 321
= 90 4- 90 + 90 + 90 + 90 =
= 450,
поэтому между числами 100 и 1000 находятся 450 нечетных целых чисел.
Данную задачу можно решить, используя также комбинаторный принцип
умножения. Существуют 5 вариантов выбора последней цифры, поскольку она
должна быть нечетной. Существуют 10 вариантов выбора средней цифры и 9
вариантов выбора первой цифры. Таким образом, имеем 9 х 10 х 5 = 450 нечет-
нечетных чисел между 100 и 1000. Этот пример показывает, каким образом принцип
комбинаторного умножения следует из комбинаторного принципа сложения. ?
Рис. 8.2
Наконец, вернемся к тому, с чего начали, — к использованию деревьев.
Предположим, что команды А и В играют между собой в турнире по бейсболу.
Для победы в турнире команде необходимо выиграть три игры из пяти. Все воз-
возможные результаты игр представлены деревом на рис. 8.2, где буква в каждой
вершине обозначает команду, победившую в игре. Обведенная кружком буква
обозначает команду, победившую в турнире. Обратите внимание, что всего име-
имеется 20 возможных исходов: 10 возможных побед у команды А и 10 — у команды
В. Предположим, известно, что команда В выиграла первую игру, что оставляет
для рассмотрения только правую сторону дерева, начиная с вершины В. Сторона
обведена пунктирной линией. Обратите внимание, что имеются четыре исхода, в
которых побеждает команда А, и шесть исходов с победой команды В. Предполо-
Предположим, что первую игру выигрывает команда А, вторую — команда В и команда А
выигрывает третью игру. Результат игры отображен на дереве (часть дерева, об-
обведенная сплошной линией). Обратите внимание, что имеются два исхода, когда
побеждает команда А, и только один исход с победой команды В.
ПРИМЕР 8.11. Предположим, что команды Aw В участвуют в ежегодном чемпи-
чемпионате США по бейсболу, для победы в котором командам необходимо выиграть
четыре игры из семи возможных. Если команда А выигрывает первые две игры,

322 ГЛАВА 8. Комбинаторика и вероятность
то сколько вариантов победы есть у команды А и сколько у команды В? Дерево
на рис. 8.3 показывает возможные исходы. Имеются десять исходов с победой
команды А и пять возможных исходов с победой команды В. ?
Рис. 8.3
УПРАЖНЕНИЯ
1. Сколько положительных целых чисел, меньших 700, делятся на 5? Сколько
таких чисел делятся на 3? А сколько таких чисел делятся и на 5, и на 3?
2. Если авиакомпания осуществляет 15 рейсов из Сан-Франциско в Чикаго и
20 рейсов из Чикаго в Нью-Йорк, то сколько всего рейсов из Сан-Франциско
в Нью-Йорк проходит транзитом через Чикаго?
3. Сколько существует способов избрания президента, вице-президента, секре-
секретаря и казначея среди членов клуба, включающего 8 студентов последнего
курса, 10 студентов предпоследнего курса, 15 второкурсников и 20 перво-
первокурсников, если
а) отсутствуют какие-либо ограничения?
б) президентом должен быть студент последнего курса?
в) студент последнего курса не может быть вице-президентом?
г) первокурсники могут быть избраны только на должность секретаря?
4. В ресторане из напитков предлагают кофе, чай, молоко или колу. Пред-
Предлагают на выбор суп или салат. Имеются 10 различных бифштексов и 5
разнообразных куриных блюд. На гарнир можно выбрать картофель фри,
печеный картофель, макароны с сыром или рис. На десерт подают сладкий
пирог, мороженое или то и другое вместе.
а) Сколько можно составить различных меню?
б) Сколько можно составить различных меню, включающих бифштекс?
в) Сколько можно составить различных меню, если клиент выбирает биф-
бифштекс и картофель или не выбирает ни то, ни другое?

РАЗДЕЛ 8.1. Основные комбинаторные принципы 323
5. Сколько существует различных четырехзначных положительных чисел, ес-
если, по крайней мере, две цифры в числе совпадают?
6. Если каждый элемент матрицы размерности 4x5 — неотрицательное одно-
цифровое число, то сколько существует таких матриц?
7. Сколько существует вариантов ответа на тест из 30 вопросов, если на каж-
каждый вопрос требуется ответ да или нет?
8. Если часы показывают часы, минуты, секунды и ам-рм, то сколько различ-
различных моментов времени они могут показать?
9. Позывные американских радиостанций состоят из трех или четырех букв и
начинаются с к или w. Сколько существует различных позывных?
10. Сколько существует номерных знаков для автомобилей, состоящих из двух
букв и последующих четырех цифр?
11. Если имеются высказывания р, q, r и s, то
а) сколько строк содержит соответствующая таблица истинности?
б) в скольких строках все р, q, r и s имеют истинное значение?
в) в скольких строках хотя бы одно из четырех высказываний ложно?
12. Сколько существует номерных знаков для автомобилей, состоящих из двух
букв с последующими четырьмя цифрами, если буквы могут повторяться, а
цифры — нет?
13. Сколько существует различных номеров карточек социального страхования?
14. Сколько существует номерных знаков для автомобилей, состоящих из двух
букв с последующими четырьмя цифрами, если ни одна из букв не может
быть гласной? Если хотя бы одна из букв должна быть гласной?
15. Сколько существует функций из 6-элементного множества в 3-элементное?
16. Сколько существует инъективных функций из 3-элементного множества в
б-элементное?
17. Сколько положительных целых чисел, меньших 700, не делятся на 8?
18. Сколько положительных целых чисел, меньших 1000, не делятся на 5? Ко-
Которые не делятся на 5?
19. Сколько существует двубуквенных или трехбуквенных инициалов для лю-
людей?
20. Сколько существует различных двубуквенных или трехбуквенных инициа-
инициалов для людей, если никакие буквы не могут повторяться?
21. Сколько существует битовых строк длины 7?
22. Сколько существует битовых строк длины 7, если первый и последний биты
совпадают?
23. Сколько существует битовых строк длины 7-элементных строк битов, содер-
содержащих две или более единиц?
24. Если телефонный номер не может начинаться с 0, 1 или 8, то сколько суще-
существует различных 7-значных телефонных номеров?
25. Сколько существует четырехзначных чисел, содержащих хотя бы одну цифру
7?
26. Сколько существует четырехзначных чисел, которые не содержат цифру 7?
27. Если компьютерный пароль содержит семь символов, которые могут быть
цифрой или буквой, то сколько существует паролей, начинающихся с буквы?

324 ГЛАВА 8. Комбинаторика и вероятность
8.2. КОМБИНАТОРНЫЙ ПРИНЦИП СЛОЖЕНИЯ
До настоящего момента непересекающиеся множества рассматривались только в
связи с комбинаторным принципом сложения. Предположим, что множества 5
и Т не являются непересекающимися и требуется найти |5иТ|. Когда количе-
количество элементов множества 5 суммируется с количеством элементов множества Т,
элементы, принадлежащие SnT, учитываются дважды. Поэтому количество эле-
элементов, принадлежащих множеству 5 П Г, нужно из суммы вычесть. Отсюда
получаем следующую теорему.
ТЕОРЕМА 8.12. Пусть 5 и Т — множества. Количество элементов, которое можно
выбрать из S или Т, равно |5| 4- |Г| - \S П Т\. Иными словами, \SuT\ = \S\ +
\T\-\SnT\.
ДОКАЗАТЕЛЬСТВО. Множество 5 U Г = E - Т) U (Т - 5) U E П Т), где 5 - Т,
Т — S и S ПТ — попарно непересекающиеся множества. Поэтому \SUТ\ = \S —
Г| + |Г-5| + |5пГ|. Имеем также, что 5 = (S-T)u(SnT) и Г = (T-S)U(SnT),
откуда \S\ = \S - Т\ + \S П Г| и |Г| = \Т - S\ -f \S П Г|. Следовательно,
\S\ + |Г| - \S П Т\ = \S - Т\ + \Т - 5| + 2|5 П Т\ - \S П Г| =
= |S-T| + |r-S| + |Snr| =
= |5UT|. ¦
ПРИМЕР 8.13. Предположим, что в группе из 100 студентов 60 человек изучают
математику, 75 — историю, а 45 человек — и то, и другое.
а) Сколько студентов изучают математику или историю?
б) Сколько студентов не изучают ни математику, ни историю?
а) Пусть универсум U — группа из 100 студентов, М — множество сту-
студентов, изучающих математику, Н — множество студентов, изучающих историю.
Тогда количество студентов, изучающих математику или историю, равно
\м и н\ = \м\ + \н\ -\мпн\ =
= 60 + 75 - 45 =
-90.
б) Количество студентов, не изучающих ни математику, ни историю, равно
\М' П Н'\. Но М'пЯ' = (Ми Я)', поэтому
\М'ПН'\ = |(MUtf)'| =
= 100 - 90 =
= 10. ?
ПРИМЕР 8.14. Найдем количество положительных целых чисел, меньших 1001,
которые делятся на 3 или на 5. Количество элементов множества 5 положитель-
положительных целых чисел, меньших 1001, которые делятся на 3, равно [hfJ или 333.
Количество элементов множества Т положительных целых чисел, меньших 1001,
которые делятся на 5, равно [Щр"\ или 200. Элементами множества SOT явля-
являются целые числа, меньшие 1001, которые делятся на 5 и на 3, и поэтому делятся
на 15. Следовательно, \Sr\T\ = [Щ±\ или 66. Значит
\S U Т\ = 333 4- 200 - 66 = 467. ?

РАЗДЕЛ 8.2. Комбинаторный принцип сложения 325
ПРИМЕР 8.15. Сколько существует способов разместить цифры
0,1,2,3,4,5,6,7,8,9
так, чтобы первая цифра была больше единицы, а последняя — меньше семи?
Пусть U — множество всех возможных способов размещений цифр, г S — мно-
множество всех размещений цифр таких, что первая цифра больше единицы, а по-
последняя — меньше 7. Для нахождения \U\ заметим, что существуют десять спо-
способов выбора первой цифры, девять способов выбора второй, восемь способов
выбора третьей цифры, ... , два способа выбора девятой и один способ выбо-
выбора десятой цифры. Поэтому в соответствии с комбинаторным принципом умно-
умножения имеются 10! = 3 628 800 возможных способов размещения цифр, значит
\U\ = 3 628800. Как и в первом примере, воспользуемся "остаточным" принципом
и найдем количество размещений цифр, которые не входят в 5, после чего вы-
вычтем это количество из \U\. Пусть А — множество всех таких размещений цифр,
где первая цифра меньше или равна 1. Подсчитывая количество элементов из А,
обнаруживаем, что имеются два варианта выбора первой цифры, а именно, 0 и
1. Существуют девять вариантов выбора второй цифры, восемь вариантов выбора
третьей цифры, ... , два варианта выбора девятой цифры и один вариант выбора
десятой цифры. Таким образом, множество А содержит 2x9! = 725760 элемен-
элементов. Пусть В — множество всех таких размещений цифр, что последняя цифра
больше или равна 7. Подсчитывая количество элементов В, заметим, что имеются
три варианта выбора последней цифры, и, следуя схеме, использованной для мно-
множества А, получаем, что существуют 9! вариантов выбора остальных цифр. Таким
образом, |В| = 3 х 9! = 1088 640. Множество АГ)В состоит из таких размещений
цифр, в которых первая цифра больше или равна 1, а последняя цифра больше
или равна 7. Подсчитывая количество элементов множества АГ\В, находим, что
существуют два способа выбора первой цифры и три способа выбора последней
цифры. Используя процедуру, аналогичную предыдущей, получаем 8! способов
размещения оставшихся цифр. Таким образом,
\АПВ\ = 3х 2 х 8! = 241920
и
\AUB\ = 725760 + 1088640 - 241920 = 1572480.
Все размещения целых чисел такие, что первая цифра больше единицы, а послед-
последняя цифра меньше семи, описывают множество А!С\В' = (АиВ)'. Поэтому число
таких размещений равно \U\ - \(А U В)'\ = 3628800 - 1572480 = 2056320. ?
Рассмотрев случай двух множеств, переходим к изучению случая трех мно-
множеств. Пусть заданы множества А, В и С, требуется определить \А U В U С|,
количество элементов множества АиВиС, в случае, когда эти множества могут
пересекаться. Если составить сумму количества элементов в каждом множестве
А, В и С, то согласно диаграмме Венна, изображенной на рис. 8.4, некоторые
подмножества при подсчете будут учтены дважды. Если теперь вычесть |АпВ|,
|АПС| и |J3nC|, т.е. количество элементов множества АпВ, множества АГ\С
и множества В Г) С соответственно, то, как следует из диаграммы Венна, изоб-
изображенной на рис. 8.5, элементы множества АпВпС совсем не будут учтены.

326 ГЛАВА 8. Комбинаторика и вероятность
Рис. 8.4
Рис. 8.5
Поэтому добавляем |АП J3nC|, после чего каждый элемент множества АиВиС
учтен в сумме ровно один раз. Это дает следующую формулу:
|A U В U С\ = \А\ + \В\ + \С\ - \А П В\ - |А п С\ - \В П С\ + \А П В П С\.
ПРИМЕР 8.16. Предположим, что, согласно исследованию, из 200 людей, смот-
смотрящих телевизор, 110 человек смотрят спортивную передачу, 120 — комедии, 85
предпочитают драмы, 50 смотрят драмы и спорт, 70 — комедии и спорт, 55 смот-
смотрят комедии и драмы и 30 человек смотрят все три вида передач. Сколько человек
смотрят спорт, комедии или драмы? Сколько человек не смотрят ничего из вы-
вышеперечисленного? Пусть U — множество 200 людей, среди которых проводился
опрос. Пусть 5 — множество людей, которые смотрят спорт, D — множество
людей, которые смотрят драмы, и С — множество людей, предпочитающих коме-
комедии. Тогда первое задание — найти \SuDuC\. Это можно сделать, используя
непосредственно формулу, приведенную выше:
\S U D U С\ = \S\ + \D\ + \C\ - \S П D\ - \D n C\ - \S n C\ + \S П D П C\ =
= 110 + 85 + 120 - 50 - 55 - 70 -f 30 = 170,
так что 170 человек смотрят спорт, комедии или драмы. Второе задание требует
найти |E U D U С)'\ = \U\ - \(S U D U C)\ = 200 - 170 = 30. Итак, 30 человек не
смотрят по телевидению ни спорт, ни драмы, ни комедии. ?
Существует альтернативный метод решения приведенной выше задачи, кото-
который является более информативным. Известно, что 30 человек смотрят по телеви-
телевидению спорт, комедии и драмы. Поскольку 50 человек смотрят спорт и драмы, то
20 человек должны смотреть спорт и драмы, но не смотреть комедии. Аналогич-
Аналогично, 55 смотрят комедии и драмы, поэтому 25 человек должны смотреть комедии
и драмы, но не смотреть спорт. К тому же 70 человек смотрят спорт и комедии,
поэтому 40 из них смотрят спорт и комедии, но не смотрят драмы. Таким образом,
получаем следующие диаграммы Венна, изображенные на рис. 8.6.
д/
s—
10
X25
\
20^
\30j
25
К
20 \
у зо
Рис. 8.6
Рис. 8.7

РАЗДЕЛ 8.2. Комбинаторный принцип сложения 327
Известно, что 85 человек предпочитают смотреть драмы. Поскольку 75 из
них уже перечислены, остальные 10 должны смотреть только драмы. Рассуждая
аналогичным образом, получаем, что из 110 тех, кто смотрит спорт, уже пере-
перечислены 90 человек, поэтому оставшиеся 20 должны смотреть только спорт. И
наконец, замечаем, что из 120 тех, кто смотрит комедии, 95 уже учтены. Таким
образом, 25 человек смотрит только комедии. Если подсчитать количество людей
в непересекющихся подмножествах, то получим число 170. Поэтому 30 человек
не смотрят ни спорт, ни комедии, ни драмы (диаграмма Венна, рис. 8.7).
Используя эту диаграмму, можно, например, установить следующие факты:
35 человек смотрят драмы, но не спорт; 50 человек смотрят спорт или драму, но
не комедии; 55 человек предпочитают только одну из трех программ; 85 предпо-
предпочитают две программы из трех; 85 человек смотрят комедии или спорт, но только
не драмы.
ПРИМЕР 8.17. Предположим, что из 100 опрошенных студентов 50 изучают хи-
химию, 53 — математику, 42 — физику, 15 — химию и физику, 20 занимаются
физикой и математикой, 25 — математикой и химией и 5 студентов изучают все
три предмета.
а) Сколько студентов изучают хотя бы один из трех перечисленных предметов?
б) Сколько студентов не изучают ни один из трех перечисленных предметов?
в) Сколько студентов изучают только математику?
г) Сколько студентов изучают физику или химию, но не изучают математику?
д) Сколько студентов не изучают ни математику, ни химию?
Поскольку 5 человек изучают все три предмета, а 15 человек — химию и физику,
остаются 10 человек, изучающих химию и физику, но не изучающих математику.
Аналогично, 25 — 5 = 20 человек занимаются математикой и химией, но не физи-
физикой, и 20 — 5 = 15 человек изучают математику и физику, но не изучают химию.
Данную ситуацию изображает диаграмма Венна, приведенная на рис. 8.8.
Рис. 8.8
Рис.
Поскольку 50 студентов изучают химию, и 35 из них уже учтены, то остав-
оставшиеся 15 изучают только химию. Аналогично, 53 студента занимаются матема-
математикой, и 40 из них уже учтены, поэтому 13 человек изучают только математику.
Наконец, 42 студента изучают физику, и 30 из них уже учтены, поэтому 12 чело-
человек изучают только физику.
а) Суммируя количество людей, принадлежащих семи непересекающимся под-
подмножествам, получаем 90 тех, кто изучает хотя бы один из трех предметов.

328 ГЛАВА 8. Комбинаторика и вероятность
б) Поскольку 90 из 100 студентов изучают хотя бы один предмет, то 100-90 =
10 человек не изучают ни один из этих трех предметов.
в) Из диаграммы Венна следует, что 13 человек изучают только математику.
г) Тридцать семь студентов занимаются химией или физикой, но не изучают
математику.
д) Из диаграммы Венна, изображенной на рис. 8.9, следует, что 75 человек изу-
изучают математику или физику. Поэтому 100 — 75 = 25 студентов не изучают
ни математику, ни физику. ?
ПРИМЕР 8.18. Сколько положительных целых чисел, меньших 1001, делятся на
2, 3 или 5? Сколько положительных целых чисел, меньших 1001, не делятся на
2, 3 или 5? Имеется всего
целых чисел, которые делятся на 2. Имеется всего
целых числа, которые делятся на 3. Имеется всего
TJ-»
целых чисел, которые делятся на 5. Если целое число делится на 2 и на 3, то оно
делится на 6, поэтому существует
целых чисел, которые делятся на 2 и на 3. Если целое число делится на 2 и 5, то
оно делится на 10, поэтому существует
целых чисел, которые делятся на 2 и на 5. Если целое число делится на 3 и на 5,
то оно делится на 15, поэтому имеется
1001
15
= 66
целых чисел, которые делятся на 3 и на 5. Наконец, если целое число делится на
2, 3 и 5, то оно делится на 30, и существует
целых числа, которые делятся на 2, 3 и 5. Следовательно, количество чисел,
которые делятся на 2, 3 или 5, равно 500 + 333 + 200 - 166 - 100 - 66 4- 33 = 734.
Количество положительных чисел, которые не делятся ни на одно из указанных
целых чисел, равно 1001 - 734 = 267. ?

РАЗДЕЛ 8.2. Комбинаторный принцип сложения 329
ПРИМЕР 8.19. Сколько неотрицательных целых чисел, меньших 100000, содер-
содержат цифры 3, 6 и 9? Пусть универсум U будет множеством всех неотрицательных
целых чисел, меньших 100 000. Следовательно, \U\ = 100000. Пусть 53 — мно-
множество всех целых чисел, меньших 100000, которые не содержат цифру 3. Пусть
5б — множество всех целых чисел, меньших 100000, которые не содержат циф-
цифру 6. Пусть Sg — множество всех целых чисел, меньших 100000, не содержащих
цифру 9. Нас интересует \Sf3 nS'6nS'Q\t но
\S3US6US9\ =
= |S3| + |S6| + |S9| - |53 П S6\ - \S3 П S9\ - \S6 П 59| 4- \S3 П S6 П Sg\.
Для S3 существуют девять вариантов выбора каждой из пяти цифр, посколь-
поскольку только цифра 3 исключена. Поэтому |S3| = 95. Аналогично, \Sq\ = \Sg\ = 95.
Поскольку каждая цифра числа из множества 53 П Sq может быть любой, за
исключением 3 и 6, то существуют восемь вариантов выбора каждой цифры, по-
поэтому |5з П Se\ = 85. Аналогично, |53 П S9\ = \S6 П Sg\ — 85. Каждая цифра числа
из S3 П 5б П Sg может быть любой, исключая 3, 6 и 9, поэтому существуют семь
вариантов выбора каждой цифры. Отсюда |53 П56П Sg\ = 75. Следовательно,
|53 U 56 U S9\ = 95 + 95 + 95 - 85 - 85 - 85 + 75 = 95 650
S3nSf6nSg = \U\ - E3 U 56 U Sg) = 100000 - 95 650 = 4350. ?
УПРАЖНЕНИЯ
1. В классе из 200 студентов 120 человек изучают историю Канзаса 1995-96 гг.,
ПО занимаются тестированием продукта "Йогурт II", а 80 студентов делают
и то, и другое. Сколько студентов изучают хотя бы один из этих курсов?
Сколько студентов не изучают ни одного из них?
2. Сколько целых чисел между 1 и 401 делятся на 5 или на 7?
3. Сколько целых чисел между 1 и 401 делятся на 7 или на 11?
4. Сколько целых чисел между 1 и 401 делятся на 6 или на 10?
5. Сколько целых чисел между 1 и 401 делятся на 10 или на 15?
6. Сколько целых чисел между 1 и 1001 делятся на 10, но не делятся на 40?
7. Сколько целых чисел между 1 и 1001 делятся на 10, но не делятся на 14?
8. Год является високосным, если (а) количество дней в нем делится на 4, но
не делится на 100, или (б) если он делится на 400. Сколько високосных
годов было между 1001 и 2001 годами?
9. Сколькими способами можно разместить положительные целые числа, мень-
меньшие 10, так чтобы 4 было расположено сразу после 5 или 5 было расположено
сразу после 4? Сколько существует размещений, в которых 4 и 5 не стоят
рядом?

330 ГЛАВА 8. Комбинаторика и вероятность
10. Сколькими способами можно разместить положительные целые числа, мень-
меньшие 10, так что 4 было бы расположено сразу после 3 или 7 было бы распо-
расположено сразу после 6?
11. Сколько существует положительных целых чисел, содержащих не более пяти
цифр, в которых
а) первой цифрой является 3?
б) последней цифрой является 5?
в) первой цифрой является 3 или последней цифрой является 5?
г) ни первая цифра не равна 3, ни последняя цифра не равна 5?
12. Сколько целых чисел между 1 и 2003 делится на 3, 5 или 7?
13. Сколько целых чисел между 1 и 2003 делится на 5, 7 или 11?
14. Сколько целых чисел между 1 и 2003 делится на 4, 5 или 6?
15. Сколько целых чисел между 1 и 2003 делится на 6, 7 или 8?
16. В группе из 200 студентов 75 изучают математику, 70 — историю, 75 —
социологию, 35 изучают математику и социологию, 20 — историю и социо-
социологию, 25 изучают математику и историю, 15 студентов — все три предмета.
а) Сколько студентов изучают хотя бы один из трех предметов?
б) Сколько студентов изучают только один из трех предметов?
в) Сколько студентов изучают историю или математику, но не изучают со-
социологию?
г) Сколько студентов не изучают ровно два из трех предметов?
д) Сколько студентов не выбрали историю или математику?
17. Согласно опросу 250 телезрителей, 95 из них нравится смотреть новости, 125
предпочитают смотреть спорт, 125 — комедии, 25 — новости и комедии, 45 —
спорт и комедии, 35 — новости и спорт, 5 любят все три вида программ.
а) Сколько телезрителей смотрят новости, но не смотрят спорт?
б) Сколько телезрителей смотрят новости или спорт, но не любят комедии?
в) Сколько телезрителей не любят смотреть ни новости, ни спорт?
г) Сколько телезрителей смотрят не только спорт?
д) Сколько телезрителей смотрят спорт и комедии, но не смотрят новости?
18. Сколько пятизначных целых чисел имеют одной из цифр 3, 5 или 7?
19. Сколько пятизначных целых чисел начинаются с 3 и заканчиваются на 5
или содержат цифру 7 ?
20. В группе из 100 студентов 35 изучают французский язык, 42 — испанский,
43 — немецкий, 17 изучают французский и испанский, 15 — испанский и
немецкий, 13 — французский и немецкий, и 20 студентов не изучают ни
один из трех языков.
а) Сколько студентов изучают французский или немецкий язык, но не изу-
изучают испанский?
б) Сколько студентов изучают только один из трех языков?
в) Сколько студентов изучают два из трех языков?
г) Сколько студентов не изучают ни испанский язык, ни французский?
д) Сколько студентов изучают только испанский?

РАЗДЕЛ 8.3. Перестановки и сочетания 331
8.3. ПЕРЕСТАНОВКИ И СОЧЕТАНИЯ
Переставляя объекты некоторого набора, мы обычно располагаем их в различном
порядке. В этом смысле перестановка — это переупорядочение набора объек-
объектов, или функция, которая задает такое переупорядочение (см. главу 4, раздел
4.2.). Теперь будем исследовать, сколько существует способов переупорядочения
набора объектов. Все необходимое для этого уже имеется. Для подсчета переста-
перестановок достаточно воспользоваться правилом умножения. Рассмотрим количество
возможных способов формирования числа, переставляя цифры 1, 2, 3, 4 и 5.
Варианты возможных перестановок — это, например, числа 12345, 15342, 32415
и 32415. Для нахождения количества возможных размещений или перестановок
заметим, что первую цифру можно выбрать пятью способами, вторую — четырь-
четырьмя способами, третью — тремя способами, четвертую — двумя, и только один
вариант остается для выбора пятой цифры. Поэтому существует 5! возможных
перестановок. Точно так же, если необходимо переупорядочить п объектов, то
для этого существует п! способов. В перестановках важен порядок. Числа 51342
и 32415, образованные перестановкой цифр 1, 2, 3, 4 и 5, не совпадают. Кроме
того, поскольку перестановки рассматриваются как переупорядочения, то каждый
объект можно использовать только один раз. Если бы повтор цифр допускался,
то при формировании числа для каждой цифры существовало бы пять вариантов
выбора, поэтому существовало бы 55 возможных чисел.
Мы будем также рассматривать перестановки, когда объектов больше, чем
мест для их размещения. Это обобщает сформулированное выше понятие переста-
перестановки, так как в этом случае нельзя рассматривать перестановку как переупоря-
переупорядочение. Предположим, например, что в организации — 20 человек и из них тре-
требуется выбрать президента, вице-президента, секретаря и казначея. Имеются 20
вариантов выбора президента, 19 вариантов выбора вице-президента, 18 способов
выбора секретаря и 17 — казначея. Таким образом, получаем 20x19x18x17 спосо-
способов выбора должностных лиц. Заметьте, что порядок все еще остается существен-
существенным. Есть разница, является ли Мэри Браун президентом, вице-президентом, се-
секретарем или казначеем. Каждое из размещений на должностях четырех выбран-
выбранных лиц представляет собой различную организацию руководства. По-прежнему,
любого человека можно избрать только один раз. Если Мэри Браун выбрана
президентом, то ее нельзя избрать ни на одну из остальных трех должностей.
Заметим также, что
20 х 19 х 18 х 17 - ^ = 20!
16! B0-4)!'
поскольку все множители в числителе, не превышающие 16, сокращаются с мно-
множителями знаменателя, входящими в 16!.
Предположим, имеется п человек. Требуется выбрать г из них и расположить
в определенном порядке. Существует и способов выбрать первого человека, п— 1
способов выбора второго, и - 2 способов выбора третьего, п — j + 1 способов
выбора j-ro ип-r + l способов выбора r-го человека. Следовательно, существует
(п)(п - 1)(п - 2)(п - 3) • • • (п - г + 1) • • • (п - г + 1)

332 ГЛАВА 8. Комбинаторика и вероятность
способов выбрать г человек из п. Но
(п)(п - 1)(п - 2)(п - 3) • • • (п - г + 1) • • • (п - г + 1) = . П' Ч| .
(п-г)!
Сформулируем вышесказанное в виде следующей теоремы.
ТЕОРЕМА 8.20. Количество способов выбрать г объектов с учетом порядка из п
объектов равно
п!
(п)(п - 1)(п - 2)(п - 3) • • • (п - г +1) • • • (п - г + 1) =
(п - г)! *
п!
ОПРЕДЕЛЕНИЕ 8.21. Пусть Р(п,г) = - —— . Р(п,г) называется числом
(п — г у.
перестановок из п объектов по г.
Заметим, что если выбирать все и объектов и размещать их в определенном
порядке, то г = п и, поскольку 0! = 1, имеем
(п — п)\ 0!
Таким образом, приходим к уже известному результату для случая перестановок
п элементов.
ПРИМЕР 8.22. Сколько различных четырехзначных чисел можно образовать из
цифр 1, 2, 3, ..., 9, если все цифры в каждом четырехзначном числе различны?
Для формирования каждого четырехзначного числа выбираем четыре цифры из
девяти, поэтому существует
таких различных чисел. ?
ПРИМЕР 8.23. Сколькими способами можно расставить в ряд для фотографиро-
фотографирования пять мальчиков и шесть девочек, если ни две девочки, ни два мальчика не
должны стоять рядом? Мальчиков меньше, чем девочек, поэтому первой долж-
должна стоять девочка, а дальше мальчики и девочки должны чередоваться. Итак,
ряд должен иметь вид ДМДМДМДМДМД. Существуют 6! способов расположить
девочек на позициях Л и 5! способов расположить мальчиков на позициях М.
Следовательно, имеется 6! х 5! способов расставить детей. ?
ПРИМЕР 8.24. Сколькими способами можно расположить для фотографирования
пять мальчиков и пять девочек, если ни две девочки, ни два мальчика не должны
стоять рядом? В данной ситуации первым в ряду может быть либо мальчик,
либо девочка. Если первой стоит девочка, то ряд имеет вид ДМДМДМДМДМ.
Имеются 5! способов расставить девочек на позициях Д и 5! способов расставить
мальчиков на позициях М. Поэтому, существуют 5! х 5! способов расположить
детей в ряд, если первой стоит девочка. Аналогично, существуют 5! х 5! способов
расположить детей в ряд, если первым стоит мальчик. Таким образом, имеются
2 х 5! х 5! способов расположить детей в ряд для фотографирования. ?

РАЗДЕЛ 8.3. Перестановки и сочетания 333
ПРИМЕР 8.25. Сколькими способами можно рассадить 10 человек за круглым
столом, если имеет значение только порядок соседей. Существует несколько ва-
вариантов решения данной задачи. Первым делом, отметим, что вращение людей
вокруг стола не меняет их взаимного расположения, поскольку соседи справа и
слева остаются прежними. Предположим, что место за столом уникально. Тогда
существует 10! способов рассадить людей за столом. Считаем, что при вращении
места остаются теми же, так как соседи не меняются. Существует десять таких
вращений, поэтому делим 10! на 10, что дает 9! способов расположить людей за
столом, если имеет значение только порядок соседей.
Иной подход к решению задачи состоит в том, чтобы сначала усадить одного
человека. Этим исключается вращение, а оставшихся 9 человек можно рассадить
9! способами. ?
ПРИМЕР 8.26. На книжной полке требуется расположить 15 различных книг по
математике, 12 различных книг по физике и 16 различных книг по информатике.
Сколькими способами это можно сделать, если
а) не существует никаких ограничений?
б) все книги по одному и тому же предмету должны стоять вместе?
в) все книги по одному и тому же предмету должны стоять рядом, но матема-
математические книги и книги по информатике не должны стоять рядом?
а) Всего имеется 43 книги, поэтому существуют 43! различных способа распо-
расположить их на полке.
б) Предположим, что первыми на полке помещаем книги по математике, кни-
книги по физике помещаем вторыми и последними располагаем книги по ин-
информатике. Обозначим это расположение МФИ. Существуют 15! различных
способов расставить книги по математике, 12! — по физике и 16! — по
информатике. Следовательно, имеются 15! х 12! х 16! способов разместить
книги. Если первыми поставить на полку книги по физике, затем книги по
информатике и, наконец, книги по математике, что можно обозначить как
ФИМ, то опять получили бы 15! х 12! х 16! способов разместить книги. Лю-
Любая перестановка Я, М и Ф даст 15! х 12! х 16! способов размещения книг.
Поскольку существуют 3! способа переставить Я, М и Ф, то существуют
3! х 15! х 12! х 16! различных способов расставить книги на полке.
в) Поскольку книги по физике следует расположить посередине, книги по ин-
информатике должны стоять либо первыми, либо последними. Поэтому един-
единственными возможными конфигурациями являются ИФМ и МФИ. Посколь-
Поскольку для каждой из них существуют 15! х 12! х 16! различных способов раз-
разместить книги, то в итоге получаем 2 х 15! х 12! х 16! различных способов
разместить книги. ?
ПРИМЕР 8.27. Сколько существует перестановок букв w, e, d, г, д, га, а, ?, /г, в ко-
которых последовательности букв не образуют слова "we", "dig", и "math"? Напри-
Например, перестановка с/, д, г, ги, е, ?, /г, а, т не подходит, поскольку включает сочета-
сочетание букв "we". Пусть универсум U будет множеством всех перестановок букв
w,e,d,iig,m,a,t,h. Тогда \U\ = 9! = 362 880. Пусть S\ — множество всех пере-
перестановок, в которых встречается слово "we". Пусть 5г — множество всех переста-

334 ГЛАВА 8. Комбинаторика и вероятность
новок, в которых встречается слово "dig", и 5з - множество всех перестановок,
которые включают слово "math". В задаче требуется найти \S[ Г) S'2 Г\ S'3\ или
|l/|-|SiUS2US3|. Но
|5i U 52 U 53| = |5i| + \S2\ + \S3\ - |Si П S2\ - \S1 П S3| - |S2 П S3| +
+ |Sins2ns3|.
Поскольку буквы "-ш,е" должны стоять вместе, множество Si состоит из
всех перестановок восьми символов we,d,i,g,m,a,t,h. Поэтому |Si| = 8!. Мно-
Множество S2 состоит из всех перестановок семи символов w, е, dig, т, a, t, h. Следо-
Следовательно, IS2I = 7!. Множество S3 состоит из всех перестановок шести символов
w, е,d, г,д, math. Поэтому |5з| = 6!. Множество Si П S2 составляют все пере-
перестановки шести символов we,dig,m,a,t,h. Поэтому |Si П S2\ = 6! Множество
S2 П S3 составляют все перестановки четырех символов w,e, dig, math. Поэтому
|S2 nS3| = 4! Множество Si П S3 составляют все перестановки пяти символов
we,d,i,g,math. Поэтому |Si П S2| = 5! Наконец, множество Si П S2n S3 состав-
составляют все перестановки трех символов we, dig, math. Поэтому |Si П S2 nS3| = 3!
и
|Si U S2 U S3| = 8! -h 7! + 6! - 6! - 5! - 4! + 3! =
= 45 222,
так что
IS^nS^nS^I = |f/|-|SiUS2US3| =
= 362 880 - 45 222 =
= 317658. ?
Вернемся к задаче выбора президента, вице-президента, секретаря и казна-
казначея в группе из 20 человек. Известно, что существуют
20!
16!
различных способов сделать выбор. В этом случае избрание Мэри Браун прези-
президентом, Джорджа Смита вице-президентом, Джейн Джонс — секретарем и Джо
Джексона — казначеем отличается от избрания Джейн Джонс президентом, Джо
Джексона — вице-президентом, Джорджа Смита — секретарем и Мэри Браун
— казначеем. Допустим, что вместо выборов президента, вице-президента, секре-
секретаря и казначея избирается просто комитет из четырех членов. В этом случае
избрание в комитет Мэри Браун, Джорджа Смита, Джейн Джонс и Джо Джек-
Джексона ничем не отличается от избрания в комитет Джейн Джонс, Джо Джексона,
Джорджа Смита и Мэри Браун. Теперь порядок больше не дает различий в спо-
способах выбора. При выборе четырех должностных лиц любая перестановка Мэри
Браун, Джорджа Смита, Джейн Джонс и Джо Джексона была бы различной, но
при избрании комитета они различаются. Поскольку существует 4! перестановки
четырех должностных лиц, которые не меняют состав комитета, для нахождения
числа комитетов необходимо Щ разделить на 4!. Используя те же аргументы при
выборе г объектов из п без учета порядка, получаем следующую теорему.

РАЗДЕЛ 8.3. Перестановки и сочетания 335
ТЕОРЕМА 8.28. Количество способов выбора г объектов из п объектов без учета
порядка равно
п!
(п-г)\г\
ОПРЕДЕЛЕНИЕ 8.29. Для 0 < г < п положим С(п,г) = (Л = -—^—-.
\rj (n — r)\r\
С(п,г) называется числом сочетаний из п объектов по г.
ТЕОРЕМА 8.30. Для 0 < г < п имеем С(п, г) - С(п, п - г).
ДОКАЗАТЕЛЬСТВО.
с(пг)_ п!
(п — г)\г\
(п — г)\(п — (п — г))!
= С(п,п-г). ¦
Обратите внимание, что в случае сочетаний, как и в случае перестановок,
при выборе г объектов каждый объект может быть выбран не более одного раза.
Если выбираются все п объектов без учета порядка, то г = п. Поскольку
0! = 1, имеем
L,[n,n)- (n_n)!(n!) - @!)(n!) -i,
поэтому существует только один способ выбрать и элементов: просто взять их
все.
ПРИМЕР 8.31. Если множество содержит десять элементов, то сколько оно имеет
трехэлементных подмножеств? Поскольку множество не упорядочено, выбирают-
выбираются три элемента из десяти, поэтому всего имеется
)=~
различных подмножеств. ?
ПРИМЕР 8.32. Сколько строк длины девять содержат ровно 5 единиц и 4 нуля?
Несмотря на то, что строки сами по себе — упорядоченные объекты, эту задачу
можно решить, используя сочетания. В строке имеется девять мест для размеще-
размещения 1 и 0. Можно выбрать любые пять из девяти мест для размещения единицы.
Поэтому имеется
мест для размещения единицы. Как только единицы вставлены, остальные места
заполняются нулями. И хотя для строки важен порядок элементов, порядок за-
заполнения пяти мест единицами не существенен; как только эти места выбраны,
их порядок уже не имеет значения. ?

336 ГЛАВА 8. Комбинаторика и вероятность
ПРИМЕР 8.33. Сколькими способами можно выбрать комитет, включающий 6
мужчин и 8 женщин, из группы, состоящей из 12 мужчин и 20 женщин? Суще-
Существует
19!
СA2'6> =
способов выбора мужчин и
способов выбора женщин. Поэтому, согласно комбинаторному принципу умноже-
умножения, имеется
ш.х ш =116396280
способов выбрать комитет. ?
ПРИМЕР 8.34. Сколько существует вариантов выбора 5 карт из стандартной ко-
колоды, содержащей 52 карты? Поскольку порядок карт не имеет значения, речь
идет о выборе 5 объектов из 52, поэтому существует
52'
СE2, 5) = ^= 2598960
возможных комбинаций. ?
ПРИМЕР 8.35. Сколькими способами можно вытянуть 5 карт трефовой масти из
стандартной колоды, содержащей 52 карты? В колоде имеется 13 треф, из которых
выбираются 5, поэтому существует
СA3,5) =
возможных 5-карточных раскладов пяти треф. ?
ПРИМЕР 8.36. Говорят, что 5-карточный расклад содержит каре, если четыре из
них являются либо тузами, либо королями, либо дамами и т.д. Эти четыре карты
называются картами одного ранга. Сколько существует раскладов, при которых
пятерка карт содержит каре? Существуют 13 способов выбрать каре и 48 способов
выбрать пятую карту. Поэтому существует 13 х 48 = 624 различных раскладов,
включающих каре. ?
ПРИМЕР 8.37. "Фулл хаус" содержит три карты одного ранга и две карты другого
ранга. Например, расклад, содержащий три короля и две шестерки представляет
собой "фулл хаус". Сколько существует 5-карточных раскладов с "фулл хаус"?
Предположим, что "фулл хаус" составили три короля и две шестерки. Три короля
выбираются из четырех, поэтому существуют СD,3) = 4 способа выбрать трех
королей. Две шестерки выбираются из четырех, поэтому существуют СD,2) = 6
способов выбрать две шестерки. Поэтому, согласно комбинаторному принципу
умножения существуют 4 х 6 = 24 способа выбрать трех королей и две шестерки
или три карты одного ранга и две карты другого ранга. Существуют 13 способов
выбрать три карты одного ранга и 12 способов выбрать две карты одного ранга.
Поэтому существуют 13 х 12 = 156 различных способов сочетания рангов. Следо-
Следовательно, существуют 156 х 24 = 3744 возможных 5-карточных раскладов с "фулл
хаус". ?

РАЗДЕЛ 8.3. Перестановки и сочетания 337
Рассмотрим разложение
(а + ЬM = (а + b)(a + b)(a + 6)(а + Ь)(а 4- 6).
Каждое слагаемое в разложении является результатом выбора а или Ь в каждом
сомножителе (а + Ь) и последовательного их перемножения. Например, а5 по-
получено путем выбора а из каждого сомножителя. Если из первого сомножителя
выбрано а и b выбрано из остальных сомножителей, то в результате получим ab4.
Предположим, что требуется найти коэффициент при a3b2. Слагаемое a3b2 полу-
получается при выборе трех а и двух b из пяти сомножителей. Поскольку существует
3! х 2!
способов выбора трех а, то коэффициент при а3Ь2 равен f ].
Обобщая результат, получаем следующую теорему.
ТЕОРЕМА 8.38. (Биномиальная теорема) Для произвольного положительного
целого числа п справедливы равенства
г=0 ^ ^ г=0
ДОКАЗАТЕЛЬСТВО. Поскольку arbn~r получено в результате r-кратного выбора
а и n-r-кратного выбора b из п сомножителей в выражении (а + 6)п, то коэффи-
коэффициент при arbn~r равен числу способов r-кратного выбора а из и сомножителей
Второе равенство следует из того факта, что
„ = „
г I \п — г
ПРИМЕР 8.39. Построим разложение Bх + 3у2L. Используя биномиальную тео-
теорему, находим
= Ba:L + 4BxKCt/2) + 6BxJCy2J + 4Bx)Cy2K + (Зу2L =
= 16x4 + 96z3y2 + 216x2y4 + 216xj/6 + 81y8. П

338 ГЛАВА 8. Комбинаторика и вероятность
ПРИМЕР 8.40. Найдем коэффициент при х4у6 в разложении (Зх4-4уI0. Исполь-
Используя биномиальную теорему находим, что слагаемое, содержащее х4у6, имеет вид
= 210 • З4 • 46zV =
= 69672960х4у6,
поэтому коэффициент при х4у6 равен 69672960. ?
ПРИМЕР 8.41. Покажем, что для любого положительного целого числа п,
Пусть a = b = 1, тогда по биномиальной теореме
г=О х 7
и результат очевиден. ?
Следующая теорема имеет весьма широкое применение. Теорема, в частно-
частности, дает возможность построить треугольник Паскаля. В доказательстве, при-
приведенном ниже, использована комбинаторная техника. Читателю предлагается
доказать теорему, используя метод математической индукции.
ТЕОРЕМА 8.42. Для всех целых чисел г и п таких, что 1 < г < п,
С(п, г) = С(п - 1, г - 1) + С(п - 1, г).
ДОКАЗАТЕЛЬСТВО. Пусть т — один из п объектов, из которых требуется вы-
выбрать г объектов. Из С(п,г) способов, которыми можно выбрать г объектов,
рассмотрим то количество случаев, когда т является одним из выбранных объек-
объектов, и количество случаев, когда т выбранным объектом не является. Их сумма
должна равняться С(п,г). (Почему?) Сначала рассмотрим количество случаев,
когда m — один из выбранных объектов. Поскольку т уже выбрано, требуется
выбрать г —1 объект из п—1 объектов. Существует С(п—1,г— 1) способов сделать
этот выбор. Далее рассмотрим количество способов, при которых т не являет-
является одним из выбранных объектов. По-прежнему требуется выбрать г объектов,
но теперь из п — 1 объектов, учитывая, что т не может быть выбран. Другими
словами, существует только п — 1 объектов, из которых выбираются г объектов.
Таким образом, существуют С(п — 1,г) способов сделать такой выбор. Складывая
количество способов выбора в обоих случаях, получаем
С(п, г) = С(п - 1, г - 1) + С(п - 1, г). ¦

РАЗДЕЛ 8.3. Перестановки и сочетания 339
о
Ш (!)
E) (?) E)
С) (?) Ш С)
(!) С) (!) ID B)
(!) «).(;) E)
(г)
Рис. 8.10
Диаграмма, изображенная на рис. 8.10, известна как треугольник Паска-
Паскаля. Каждый из внутренних элементов треугольника равен сумме двух элементов,
расположенных над ним, что является прямым следствием доказанной выше тео-
теоремы. Имеем
В первом случае п = 2 и г = 1, а во втором случае п = 3 и г = 2. Можно
заметить, что (п 4- 1)-ый ряд состоит из коэффициентов разложения (а 4- Ь)п.
Например,
Эти коэффициенты приведены в пятом ряду треугольника. На рис. 8.11 изображен
треугольник Паскаля с вычисленными элементами.
1
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
•
Рис. 8.11

340 ГЛАВА 8. Комбинаторика и вероятность
ПРИМЕР 8.43. Найдем разложение (a + bM. Используя шестой ряд треугольника
Паскаля, получаем
(а + бM = а5 + 5а46 + 10а3Ь2 + Юа263 + 5аЬ4 + б5. ?
Приведенная ниже теорема важна сама по себе и, кроме того, включает один
весьма интересный частный случай.
ТЕОРЕМА 8.44. (Вандермонд) Пусть га, п и г — положительные целые числа
такие, что г < min(ra,n). Тогда
k=z0\kJ\r-
ДОКАЗАТЕЛЬСТВО. Левая часть равенства выражает количество способов вы-
выбора г объектов из га + n объектов. Каким бы образом мы не выбирали г объектов
из га 4- п объектов, для некоторого 0 < к < г всегда к объектов выбираются из
га объектов и г - к объектов выбираются из п объектов. Для этого существуют
га\ / п
к)\т-к
способов. Обратно, если к объектов для любого 0 < к < г выбираются из га
объектов и г - к объектов выбираются из п объектов, то при этом г объектов
выбираются из га -h n объектов. Следовательно,
га + п\ ^^ /^г\ / п
Следующее утверждение позволяет находить сумму квадратов чисел, обра-
образующих строку треугольника Паскаля.
СЛЕДСТВИЕ 8.45. Для любого положительного целого числа п
2п\ A /n^ 2
ДОКАЗАТЕЛЬСТВО. Полагая в предыдущей теореме п = тп = г, получаем
или
так что
к) \п - к)'

РАЗДЕЛ 8.3. Перестановки и сочетания 341
I УПРАЖНЕНИЯ
1. Вычислите
а) Р(8,5); б) РA1,8); в) СA2,7); г) СA4,2); д) СA4,12).
2. Вычислите
а) Р(8,3); б) РA1,4); в) СA5,5); г) СA2,7); д) СA2,5).
3. Сколько трехзначных чисел можно образовать, используя цифры 2, 3, 4, 5,
6, 8 и 9? А сколько таких трехзначных чисел меньше 450? Сколько среди
них четных чисел? Сколько из них делятся на 4?
4. Сколькими способами девять человек могут расположиться в ряд?
5. К несчастью, судья на выставке цветов не разбирается в орхидеях. Если он
выбирает победителей случайным образом среди 18 участниц, то сколько
имеется способов вручить первый, второй и третий приз?
6. В скачках участвуют десять лошадей. Сколько существует вариантов призо-
призовой тройки лошадей?
7. Пять пар идут в кино. Сколькими способами они могут занять места, если
а) они могут сидеть в любом порядке?
б) все пять пар сидят подряд?
8. Шесть мальчиков и шесть девочек идут на концерт вместе. Сколькими спо-
способами они могут занять места, если
а) мальчики не будут сидеть рядом?
б) ни мальчики, ни девочки не будут сидеть все вместе?
в) все мальчики сядут вместе?
г) два мальчика сядут по краям?
д) один мальчик и одна девочка откажутся сесть вместе?
9. Сколько имеется шестизначных чисел, если первая цифра разряд может быть
нулем, цифры не должны повторяться и
а) последние две цифры должны быть 7 или 8?
б) первая цифра должна быть 1, а последние цифры не могут быть 7 или 8?
в) цифры 7 и 8 должны стоять рядом?
г) число должно делиться на 4?
д) число должно делиться на 8?
е) в числе должны присутствовать цифры 5 и 6?
10. Сколько существует перестановок букв a,c, f,m,p,r,t и х, если
а) нет никаких ограничений?
б) между а и с должны стоять две или три буквы?
в) буквы а и с не должны быть разделены двумя или тремя буквами?
г) первые четыре буквы должны быть выбраны из a,c,f и га?
д) буквы а, с, f и га должны стоять рядом?
11. Сколько существует способов рассадить за круглым столом пятерых мужчин
и пятерых женщин, если двое мужчин не должны сидеть рядом?
12. Сколько существует способов выбрать комитет из 5 человек в клубе, насчи-
насчитывающем 25 членов?

342 ГЛАВА 8. Комбинаторика и вероятность
13. Сколько существует способов составить комитет из 6 мужчин и 7 женщин,
если организация состоит из 15 мужчин и 20 женщин?
14. Сколько существует 8-битовых строк, содержащих 3 нуля и 5 единиц?
15. Сколько существует способов вытащить 13 карт из стандартной колоды, со-
содержащей 52 карты?
16. Сколько существует способов вытащить из колоды 13 карт, содержащих 6
карт одной масти?
17. Сколько существует способов вытащить из колоды 13 карт, содержащих 7
карт одной масти?
18. Сколько существует способов вытащить из колоды 13 карт, содержащих 8
карт одной масти?
19. Сколько существует способов вытащить из колоды 13 карт, содержащих 9
карт одной масти?
20. Сколько существует способов получить в 5-карточной раздаче ровно две
пары (две карты одного ранга и две карты другого ранга, например, два
туза и два короля)?
21. Сколько существует способов получить в 5-карточной раздаче три карты
одного ранга (например, три десятки)?
22. Сколько существует способов получить в 5-карточной раздаче пять карт
одной масти (флеш)?
23. Сколько существует способов разделить 10 человек на две команды по 5
человек для игры в баскетбол?
24. Пусть А = {а, 6, с, d, е, /, д, h}. Сколько существует
а) трехэлементных подмножеств множества А?
б) пятиэлементных подмножеств множества А, содержащих Ь?
в) пятиэлементных подмножеств множества А, не содержащих 6?
г) пятиэлементных подмножеств множества А, содержащих с, но не содер-
содержащих d и е?
д) подмножеств множества А, содержащих хотя бы три элемента?
е) подмножеств множества А, содержащих не более шести элементов?
25. Если монета подброшена 10 раз, то сколько существует способов выпадения
четырех "решек" и шести "орлов"? Сколько существует способов выпадения
не менее трех "решек"?
26. В зоомагазине продаются 5 черепах, 7 ящериц и 12 мышей. Сколько суще-
существует способов выбрать себе 2 черепахи, 3 ящерицы и 5 мышей?
27. Известно, что ответ на тест, состоящий из 30 вопросов, содержит 20 утвер-
утвердительных ответов и 10 отрицательных. К сожалению, больше ничего не
известно. Сколько существует вариантов ответа на тест, содержащих 20
утвердительных ответов на вопросы?
28. Если многоугольник имеет п сторон, то сколько у него диагоналей?
29. В команде из 20 человек каждый игрок одинаково хорошо играет на всех
позициях. Сколько существует способов выбрать для начала игры команду
из 9 человек?
30. Сколькими способами можно расставить игроков в предыдущей задаче?
31. Найдите разложение (a + b)8, используя треугольник Паскаля.

РАЗДЕЛ 8.4. Формирование перестановок и сочетаний 343
32. В разложении Bх + 3уI0 найдите коэффициент при х6у4.
33. В разложении (Зх — АуI3 найдите коэффициент при х8у5.
34. В разложении (х-f 2y2I3 найдите коэффициент при х5у16.
35. В разложении (х3 — Зу2I0 найдите коэффициент при хдуы.
36. Попытайтесь найти числа Фибоначчи в треугольнике Паскаля и описать
их местоположение. Указание: посмотрите на второй элемент второго ряда и
первый элемент третьего ряда; затем посмотрите на второй элемент третьего
ряда и первый элемент четвертого ряда. Наконец, посмотрите на третий
элемент третьего ряда вместе со вторым элементом четвертого ряда и первым
элементом пятого ряда.
8.4. ФОРМИРОВАНИЕ ПЕРЕСТАНОВОК И СОЧЕТАНИИ
Пусть множество 5, содержащее п элементов, линейно упорядочено, например,
как целые числа или буквы алфавита, и требуется найти все перестановки данного
множества. Это означает, что нас интересует множество строк, которые включа-
включают каждый элемент множества 5, причем, только один раз. Для начала введем
понятие лексикографического порядка. Лексикографическим порядок называет-
называется потому, что он лежит в основе упорядочения слов в словаре. Например, слово
able в английском словаре стоит перед словом gray, так как в алфавите буква
а стоит перед буквой д. Слово goose стоит перед словом gray, потому что, хотя
первые буквы совпадают, вторая буква слова goose стоит в алфавите перед второй
буквой слова gray. Слово seconded предшествует слову seconds, потому что, хотя
первые шесть букв совпадают, седьмая буква слова seconded стоит в алфавите
перед седьмой буквой слова seconds. Точно так же число 12346 предшествует
числу 12349.
ОПРЕДЕЛЕНИЕ 8.46. Для заданного линейно упорядоченного множества S
лексикографический порядок ^ на строках элементов множества 5 опреде-
определяется следующим образом: а -<Ъ, если а = сг^аз ... ат, b = 616263 • • • Ьп, и
выполнено одно из условий:
а) а\ < Ъ\\
б) а; = Ь{ для всех 1 < г < к и а^+i < 6^+1;
в) а; = bi для всех 1<г<гаига<п.
Теперь будем формировать множество всех перестановок элементов линейно
упорядоченного множества. Для простоты рассмотрим только перестановки пер-
первых п целых чисел, отметив, что метод справедлив и для прочих случаев. Пусть
строка aia2a3 .. .ап обозначает перестановку
1 2 3 ... п
а1 а2 аЗ • • • ап

344 ГЛАВА 8. Комбинаторика и вероятность
Таким образом, 51342 представляет перестановку
12 3 4 5
5 13 4 2
Для нахождения всех перестановок необходимо иметь возможность сформи-
сформировать перестановку, следующую за данной согласно лексикографическому поряд-
порядку. Поскольку нас интересуют лишь строки одной длины, пункт (в) определения
лексикографического порядка можно опустить. При лексикографическом поряд-
порядке увеличение второй цифры изменит расположение строки в большей мере, чем
изменение в пятой цифре. Аналогично, увеличение первой цифры изменит распо-
расположение строки в большей степени, чем изменения в седьмой цифре. Например,
если начать со слова dare, то слово read находится от него дальше, чем слово
dear. Поэтому для формирования следующей строки необходимо менять те сим-
символы, которые ближе всего к концу. Предположим, что а; > ai+i для т < а; < п.
Если бы это условие выполнялось для всех неотрицательных га, то мы имели бы
лексикографически наибольшую строку, что означало бы завершение процесса.
Поэтому допустим, что существует такое га, что а* > а^\ для га < г < п, но
ат < am+i. Если переупорядочить все а*, где г > т, то мы создадим строку, кото-
которая будет лексикографически меньше. Например, любая перестановка последних
четырех цифр в строке 12348765 создаст лексикографически меньшее число. Та-
Таким образом, следует увеличивать цифру ат, не меняя при этом никакое а^, где
г < га, т.е. нужно увеличивать ат, оставляя без изменения все а;, где i < т.
Поэтому выберем наименьшее число а; такое, что г > га и ат < а^. Меняем
местами ат и а;. Затем переставляем в возрастающем порядке все а*, следующие
за новым ат. Так мы получим наименьшее из чисел, больших исходного числа.
Например, рассмотрим число 12348765. Для получения следующего числа
меняем местами 4 и 5, получая 12358764. Затем переставляем 8, 7, 6 и 4 в воз-
возрастающем порядке и получаем 12354678.
Пусть задано число 1437652. Для нахождения следующего числа меняем
местами 3 и 5, получая 1457632. Теперь переставляем 7, 6, 3, 2 в возрастающем
порядке, получая 1452367. Обратите внимание, что перестановка последних цифр
свелась к записи их в обратном порядке, поскольку до этого они находились в
убывающем порядке. Таким образом, приходим к следующей процедуре:
Процедура Формирование перестановки (ai,..., an)
Найти га такое, что a; > a;+i для га < а* < п, но am < ат+ъ
Выбрать наименьшую цифру ait такую что i > га и am < a*;
Поменять местами am и а*;
Переупорядочить все а;, стоящие после нового ат,
в возрастающем порядке;
Конец процедуры.
Теперь рассмотрим метод формирования всевозможных сочетаний из п эле-
элементов множества 5. Мы не будем использовать лексикографический порядок
элементов множества 5, а воспользуемся лексикографическим порядком на стро-
строках бинарных чисел. Напомним, что любому сочетанию элементов из п элемен-
элементов соответствует бинарная строка длины п. Если множество 5 задано в виде

РАЗДЕЛ 8.4. Формирование перестановок и сочетаний 345
{а1,<22,аз,... ,ап}, то единица на месте fc-ro бита в бинарной строке показывает,
что ak присутствует в выбранном подмножестве, в то время как 0 в том же ме-
месте бинарной строки показывает, что а^ не включено в выбранное подмножество.
Например, если множество 5 представляет собой {а\,02,03,^4,^5}» то 10110 со-
соответствует выбору подмножества {ai,a3,a4}, а 10001 — выбору подмножества
{ai,a5}. Таким образом, для формирования всех сочетаний из множества и эле-
элементов достаточно сформировать все бинарные строки длины п. С этой целью
проще всего сосчитать от 0 до 2П — 1, используя бинарные строки длины п.
Эквивалентный метод состоит в том, чтобы показать, как по данной бинар-
бинарной строке длины п построить следующую бинарную строку такой же длины. Для
этого достаточно найти в строке первый 0 справа, заменить его на 1, а все элемен-
элементы справа от новой единицы заменить на 0. Как говорилось ранее, формирование
сочетаний не является лексикографическим упорядочением объектов множества,
а представляет собой лексикографическое упорядочение бинарных строк.
ПРИМЕР 8.47. Пусть 5 = {а, 6, с, d, e}. Найдем сочетание, следующее за {a,d, е}.
Поскольку сочетанию {a, d, e) соответствует бинарная строка 10011, следующей
строкой будет 10100. Поэтому следующим сочетанием будет {а,с}. ?
Рассмотрим, наконец, как сформировать все сочетания по г элементов, вы-
выбранных из элементов линейно упорядоченного множества S. Снова воспользуем-
воспользуемся лексикографическим упорядочением элементов множества S. Как и ранее, не
ограничивая общности, можем положить 5 = {1,2,3,... п}. Будем предполагать,
что сочетания перечислены в возрастающем порядке. Как и для перестановок,
покажем, как по данному сочетанию найти следующее согласно лексикографи-
лексикографическому порядку. Предположим, что п = 5 и г = 3. Если можно увеличить
последнюю цифру, то так и будем делать. Поэтому, если имеем число 123, то
его можно заменить на 124. Если имеем 125, то последнюю цифру увеличивать
нельзя. Отсюда переходим к следующей цифре и смотрим, можно ли ее увели-
увеличить. В данном случае это можно сделать, поменяв 2 на 3. Однако мы стремимся
построить наименьшее число из тех, которые больше 125. Поэтому увеличиваем
последнюю цифру на 1. Имеем первые две две цифры 1 и 3, значит, следующее
число — 134. Предположим, что имеется число 145. Последнюю и предпослед-
предпоследнюю цифры нельзя увеличивать. Однако, 1-ю цифру увеличить можно, поэтому
1 увеличиваем до 2. Чтобы сделать число минимальным, в качестве последних
цифр возьмем 3 и 4. В результате получаем число 234.
Если начинать справа, то значение последней цифры будет наибольшим воз-
возможным, если оно равно п = п — г + г. Если последняя цифра — наибольшая
возможная, то предыдущая цифра будет наибольшей возможной, если она рав-
равна п — г + (г — 1) или п — г 4- г, где г = г — 1 — позиция предыдущей цифры.
В общем случае, значение каждой г-ой цифры будет наибольшим возможным,
если цифры справа — наибольшие возможные, и это значение равно п - г + г.
Для формирования максимальной перестановки идем справа налево и проверяем,
равно ли значение г-ro элемента величине п — г 4- г. Первое значение, которое
не удовлетворяет этому условию, можно увеличить. Например, это значение т
на j-ом месте. Увеличиваем т на 1 и затем увеличиваем значение каждого эле-
элемента, стоящего после j-ro, на 1 значения предыдущего элемента. В результате

346 ГЛАВА 8. Комбинаторика и вероятность
приходим к следующей процедуре:
Процедура r-сочетание (п, г)
Начиная справа, найти первую цифру со значением а*,
таким что a,i^n — r + i\
Прибавить единицу к этому значению сц\
Начиная с а»+1. увеличиваем его значение на 1;
Конец процедуры.
¦ УПРАЖНЕНИЯ
1. Определите перестановку, следующую за 21435.
2. Определите перестановку, следующую за 621435.
3. Определите перестановку, следующую за 21453.
4. Определите перестановку, следующую за 416532.
5. Пусть 5 = {а, 6, с, d, е}. Определите сочетание, следующее за {a,c,d}.
6. Пусть 5 = {а, 6, с, d, e}. Определите сочетание, следующее за {а, с, d, e}.
7. Пусть S = {1,2,3,4,5}. Определите сочетание, следующее за {1,4,5}.
8. Пусть 5 = {1,2,3,4,5,6}. Определите сочетание, следующее за {1,3,5,6}.
9. Пусть 5 = {1,2,3,4,5,6}. Определите сочетание, следующее за {1,6}.
10. Пусть 5 = {1,2,3,4,5,6}. Определите трехэлементное сочетание, следующее
за {1,5,6}.
11. Пусть 5 = {1,2,3,4,5,6}. Определите трехэлементное сочетание, следующее
за {1,4,6}.
12. Пусть 5 = {1,2,3,4,5,6}. Определите четырехэлементное сочетание, следу-
следующее за {1,4,5,6}.
13. Пусть 5 = {1,2,3,4,5,6}. Определите четырехэлементное сочетание, следу-
следующее за {1,3,4, 5}.
14. Перечислите все перестановки 1,2,3,4 в лексикографическом порядке.
15. Перечислите все перестановки х,у, z в лексикографическом порядке.
16. Сформируйте все трехэлементные подмножества множества {1,2,3,4,5}.
17. Сформируйте все трехэлементные подмножества множества {a,b,c,d,e}.
18. Найдите первый и последний элементы в списке перестановок целых чисел
{1,2,3,4,5,6,7}.
19. Найдите первый и последний элементы в списке перестановок букв англий-
английского алфавита.
20. Найдите первый и последний элементы в списке трехэлементных подмно-
подмножеств множества целых чисел {0,1,2,3,4,5,6,7,8,9}.
21. Найдите первый и последний элементы в списке пятиэлементных подмно-
подмножеств множества букв английского алфавита.
22. Найдите первый и последний элементы в списке пятиэлементных подмно-
подмножеств множества букв английского алфавита.
23. Используя алгоритмы данного раздела, разработайте алгоритм формирова-
формирования Р(п,г) всех перестановок г из п элементов.
24. Используя алгоритмы предыдущего упражнения, сформируйте перестановки
трехэлементных подмножеств множества {а, 6, с, d, e}.

РАЗДЕЛ 8.5. Введение вероятности 347
8.5. ВВЕДЕНИЕ ВЕРОЯТНОСТИ
Много лет назад студент Стэнфордского университета послал письмо в бюро
погоды города Сан-Франциско с вопросом, что они имели в виду, прогнозируя
выпадения дождя с вероятностью 60%. Означает ли это, что дождь будет идти на
60% всей площади? Означает ли это, что дождь будет идти 60% времени? "Это
означает, — ответило бюро, — что из десяти сотрудников шесть человек утвер-
утверждали, что пойдет дождь". Вскоре мы увидим, что все на самом деле зависит от
выборочного пространства. Многие задачи теории вероятностей и комбинатори-
комбинаторики сконцентрированы вокруг азартных игр. Одна из причин заключается в том,
что математики, разработавшие значительную часть данной теории, были наняты
компаниями, контролировавшими игорный бизнес, для расчетов вероятностей вы-
выигрыша или проигрыша в тех или иных азартных играх. Многие из этих игр слу-
служат замечательным примером использования вероятности. Вероятность позволит
читателю оценить, как много он может потерять, если будет неверно выполнять
свое домашнее задание.
Наша концепция вероятности будет зависеть от того, что мы понимаем под
экспериментом. Оставив термин "эксперимент" неопределенным, зададимся це-
целью, чтобы он отвечал следующим условиям:
а) эксперимент дает более одного исхода;
б) исход точно не известен;
в) конечное множество всех исходов может быть определено до начала экспе-
эксперимента;
г) эксперимент можно повторить при тех же условиях.
Примером эксперимента является подбрасывание двух монет. В этом случае
множество исходов
5 = {(Я, Я), (Я, Г), (Г, Я), (Г, Г)},
где Я обозначает падение монеты вверх "орлом", а Т — падение монеты "решкой"
вверх. Другим примером эксперимента служит подбрасывание монеты и играль-
игральной кости. В этом случае множество результатов
5 = {(Я, 1), (Я, 2), (Я, 3), (Я, 4), (Я, 5), (Я, 6), (Т, 1), (Т, 2), (Г, 3),
(Г, 4), (Г, 5), (Г, 6)},
где за результатом выпадения монеты обозначен результат выпадения кости.
ОПРЕДЕЛЕНИЕ 8.48. Выборочное пространство, или множество элемен-
элементарных событий — это множество всех исходов эксперимента. Событие —
подмножество выборочного пространства.
Таким образом, в каждом из приведенных выше примеров множество S —
это выборочное пространство. На языке теории множеств выборочное простран-
пространство 5 является универсом.

348 ГЛАВА 8. Комбинаторика и вероятность
Интуитивно, вероятность события — это вероятность того, что событие на-
наступит. Если эксперимент повторяется несколько раз, то вероятность события —
это частота наступления события. В этом и следующих разделах будем пред-
предполагать, что все исходы эксперимента равновозможны. Заметим, что это вовсе
не означает, что все события в мире равновозможны. Просто такое предполо-
предположение дает нам возможность использовать комбинаторные принципы, поскольку
вероятность — одно из основных приложений комбинаторики. С учетом этого
предположения сформулируем определение вероятности.
ОПРЕДЕЛЕНИЕ 8.49. Пусть 5 — множество всех возможных исходов экспе-
эксперимента. Вероятность Р(А) наступления события А определяется как отно-
отношение
Р(А) - J4
ПА) \S\'
ПРИМЕР 8.50. Пусть S — множество всех исходов подбрасывания двух костей.
Пусть А — множество всех исходов, при которых сумма показаний двух костей
равна 6. Таким образом,
А = {A,5), B,4), C,3), D,2), E,1)}.
так что \А\ = 5. Как было показано выше, если существуют шесть возможных
исходов выпадений для первой кости и шесть возможных исходов выпадений для
второй кости, то множество 5 содержит 6x6 возможных исходов. Поэтому
\S\ 36 п
ПРИМЕР 8.51. Пусть 5 — множество всех исходов при подбрасывании двух мо-
монет. Пусть А — множество исходов, когда обе монеты выпадают одинаково. Таким
образом, Л = {(Я, Я), (Г, Г)}, 5 = {(Я, Я), (Я, Г), (Г, Я), (Г, Г)} и
И _ 2 _ 1
\S\ ~ 4 - 2 • п
Означает ли это, что если мы подбросим две монеты четыре раза, то на двух
монетах выпадут одновременно "орлы" или "решки" точно два раза? Конечно, нет.
Однако, если мы подбросим две монеты 400 раз, то можно ожидать, что монеты
выпадут надлежащим образом порядка 200 раз.
Предположив опять, что все исходы равновозможны, и воспользовавшись
приемами комбинаторики, можем доказать приведенные ниже теоремы.
ТЕОРЕМА 8.52. Если А и В — непересекающиеся множества исходов экспери-
эксперимента, то Р(А U В) = Р(А) + Р(В).

РАЗДЕЛ 8.5. Введение вероятности 349
ДОКАЗАТЕЛЬСТВО. Используя принцип сложения, имеем
\A\JB\
Р(А U В) =
\S\
\А\ + \В\
\S\
\S\ + |5|
Следующая теорема определяет некоторые из свойств вероятности события.
ТЕОРЕМА 8.53. Если S — выборочное пространство, А' — дополнение множества
А до множества 5 как универса, то
а) P(S) = 1.
б) Р(А') = 1-Р{А).
в) Р@) = 0.
г) Для каждого события А имеем Р(А) > 0.
д) Если Л С В, то Р(А) < Р(В).
е) Для каждого события А имеем 0 < Р{А) < 1.
ДОКАЗАТЕЛЬСТВО, a) P(S) = Щ = 1.
б) Согласно пункту (а) и предыдущей теореме имеем
U А') =
Поэтому Р(А') = \-Р(А).
в) Согласно пункту (б) имеем Р@) = 1 - Р@') = 1 - РE) = 1-1 = 0.
г) Поскольку должно существовать не менее двух исходов, то \S\ > 0. Кроме
того, \А\ > 0, учитывая, что множество А содержит некоторое число элементов.
Следовательно,
д) Если А С В, то В = А + (В - А). Поэтому
Р(В) = Р{А 4- (В - А)) =
= Р(А) + Р(В - А)
и
Р(В)-Р(А) = Р(В-А).
Однако, согласно пункту (г),
Р(В -А)>0.

350 ГЛАВА 8. Комбинаторика и вероятность
Поэтому
Р(В) - Р(А) > 0
Р(А) < Р(В).
е) Поскольку А С 5, то Р(А) < P(S) = 1. Объединяя с пунктом (г),
получаем
0 < Р{А) < 1. ¦
ПРИМЕР 8.54. Найдем вероятность того, что при подбрасывании двух монет обе
они не выпадут "решкой". Пусть А — множество исходов, когда обе монеты вы-
выпадают не "решкой". Тогда А! — множество исходов, когда обе монеты выпадают
"решкой". Поскольку существуют четыре возможных исхода, и только при одином
из них выпадает две "решки", то
"х~4- ?
ПРИМЕР 8.55. Найдем вероятность того, что при подбрасывании двух костей
сумма показаний не равна семи. Пусть А — множество результатов, когда сумма
показаний не равна семи. Тогда А' — множество исходов, когда сумма показаний
равна семи. Общее число исходов при подбрасывании двух костей равно 6x6.
Исходы, при которых сумма равна семи, включают A,6), B,5), C,4), D,3), E,2)
и F,1). Таким образом \А'\ = 6, так что
?
Для полноты изложения приведем следующую теорему. Принципы, лежащие
в основе этой теоремы, более подробно рассмотрены в разделе, посвященном
принципу включения-исключения. Данная теорема представляет собой обобщение
теоремы 8.6.
ТЕОРЕМА 8.56. Если А и В — множества исходов эксперимента, то
Р(А UB) = Р(А) + Р(В) - Р(А П В).
ДОКАЗАТЕЛЬСТВО. На рис. 8.12 показано, что
А = (А-В)и(АпВ),
В = (В-А)и{АпВ),
и A U В = (А - В) U (А П В) U (В - А),
где (А — Б), (АпВ) и (В — А) — попарно непересекающиеся множества.
Рис. 8.12

РАЗДЕЛ 8.5. Введение вероятности 351
Поэтому, по теореме 8.6 имеем
Р(А) = Р{(А -В) U (АП В)) = Р(А - В) + Р(А П В),
Р{В) = Р((В -Л)и(ЛП В)) = Р(В -А) + Р(А П Б),
Р(А U В) = Р((А - В) U (А П В) U (В - А)) =
= Р(А - В) + Р(А п В) + Р(В - А).
Следовательно,
Р(Л) + Р(В) = (Р(А - В) + Р(А П В)) + (Р(В -А)+ Р{А п В)) =
= (Р(А - В) 4- Р(А ПВ) + (Р(В - А)) + Р(А П В) =
так что Р(А U В) = Р(А) + Р{В) - Р(А П В). ¦
ПРИМЕР 8.57. Найдем вероятность того, что при случайном выборе номерного
знака для автомашины, содержащего три буквы и три цифры, совпадут три буквы
или совпадут три цифры. Пусть S — множество всех номерных знаков, содержа-
содержащих три буквы и три цифры. Пусть А — множество исходов, когда три буквы
совпадают, а В — множество исходов, когда совпадают три цифры. Если три
буквы совпадают, то существует 26 способов выбора букв и
10 х 10 х 10 = 1000
способов выбора цифр. Следовательно, \А\ = 26000. Если цифры совпадают, то
существует
26 х 26 х 26 = 17576
способов выбора букв и 10 способов выбора цифр. Поэтому \В\ = 175760. Если
все буквы одинаковые и все цифры одинаковые, то существует 26 способов выбора
букв и 10 способов выбора цифр. Поэтому |АпВ| = 260. Уже было показано, что
существуют
26 х 26 х 26 х 10 х 10 х 10 = 17576000
различных способов создать номерной знак для автомашины, включающий три
буквы и три цифры. Следовательно,
26,000 _ 175,760 _ 260
( }~ 17 576 000' ( }~ 17 576 000 И ( ° } ~ 17 576 000 '
так что
26 000 175 760 260
17 576 000 17 576 000 17 576 000
201 500
17 576 000 ~
П

352 ГЛАВА 8. Комбинаторика и вероятность
¦ УПРАЖНЕНИЯ
1. Подбрасываются две игральные кости. Найдите вероятность того, что сумма
выпавших очков равна
а) 4; б) 7; в) 8; г) 9;
д) 10 или больше.
Найдите вероятность того, что на обеих костях выпадет одинаковое коли-
количество очков. Найдите вероятность того, что сумма выпавших очков будет
четна.
2. Карта вытягивается из стандартной колоды, содержащей 52 карты. Найдите
вероятность вытягивания
а) валета, королевы, короля или туза (картинка);
б) пиковой карты;
в) королевы или пиковой карты;
г) картинки или червовой карты.
3. Из урны, в которой лежат 12 красных, 8 синих, 6 белых и 10 желтых шаров,
вытягивается шар. Найдите вероятность вытягивания
а) красного шара;
б) белого или желтого шара;
в) не белого шара;
г) шара, который не будет ни синим, ни белым.
4. Буква случайным образом выбирается из английского алфавита. Какова ве-
вероятность выбора гласной буквы?
5. Положительное целое число, меньшее 302, выбирается случайным образом.
Найдите вероятность того, что это число
а) делится на 3;
б) делится на 3 и на 7;
в) делится на 3 или на 7;
г) не делится на 3 или на 7.
6. Положительное целое число, меньшее 101, выбирается случайным образом.
Найдите вероятность того, что это число
а) делится на простое число;
б) есть произведение двух (не обязательно различных) простых чисел;
в) есть произведение двух различных простых чисел;
г) есть произведение трех различных простых чисел.
7. Пять положительных целых чисел, меньших 10, выбираются случайным об-
образом. Какова вероятность того, что все они различны ?
8. Если номерной знак автомобиля содержит три буквы и последующие три
цифры, то какова вероятность, что сумма трех цифр четна? Какова вероят-
вероятность, что все буквы гласные? Какова вероятность, что хотя бы одна из букв
не является гласной?
9. После опроса 250 телезрителей оказалось, что 86 человек любят смотреть
новости, 100 человек предпочитают спорт, 90 человек — комедии, 23 человека
любят смотреть новости и комедии, 35 смотрят спорт и комедии, 33 человека

РАЗДЕЛ 8.5. Введение вероятности 353
смотрят новости и спорт, 10 человек смотрят все три вида передач. Для
интервью телезритель выбирается случайным образом.
а) Какова вероятность, что он смотрит новости, но не смотрит спорт?
б) Какова вероятность, что он смотрит новости или спорт, но только не
комедии?
в) Какова вероятность, что он не смотрит ни новости, ни спорт?
г) Какова вероятность, что он смотрит новости и спорт, но только не коме-
комедии?
10. Если у игрока на руках 13 карт, то какова вероятность того, что он имеет
а) 5 карт одной масти?
б) 6 карт одной масти?
в) 7 карт одной масти?
г) 8 карт одной масти?
д) 9 карт одной масти?
11. У игрока на руках пять карт. Какова вероятность того, что среди них
а) две карты одного ранга (например, два короля)?
б) три карты одного ранга (например, три туза)?
в) на руки стрит-флэш (например, 2,3,4,5,6 одной масти)?
г) на руки флэш-рояль (например, А, К, Q, J, 10 одной масти )?
д) на руки флэш (например, пять червей)?
е) на руки стрит (например, 2,3,4,5,6 одной масти)?
12. В группе из 100 студентов, 40 изучали французский, 50 — испанский, 40 —
немецкий, 12 студентов изучали французский и испанский, 13 — испанский
и немецкий, 15 — французский и немецкий, и 10 студентов не изучали ни
один из трех языков. Если студент выбран случайным образом, то
а) какова вероятность, что он изучал только французский?
б) какова вероятность, что он изучал испанский или немецкий?
в) какова вероятность, что он не изучал французский?
г) какова вероятность, что он изучал немецкий, но не изучал испанский?
д) какова вероятность, что он не изучал ни один из трех языков?
13. В трех урнах находятся: четыре красных шара и пять синих, шесть красных
шаров и три синих, пять красных шаров и два синих, соответственно. Если
из трех урн случайным образом выбран один шар, то какова вероятность,
что этот шар будет красным?
14. Какова вероятность того, что четырехзначное число, не начинающееся с ну-
нуля, имеет среди цифр 3, 5 или 7?
15. Какова вероятность того, что четырехзначное число, не начинающееся с ну-
нуля, начинается с цифры 3, заканчивается на 5 или одна из его цифр — 7?
16. Произвольно выбирается трехбуквенное слово, буквы не повторяются. Како-
Какова вероятность, что буквы расположены в алфавитном порядке?
17. Какова вероятность того, что произвольное четырехзначное число содержит
цифру 7? Какова вероятность того, что оно содержит цифру 4 или 9?

354 ГЛАВА 8. Комбинаторика и вероятность
8.6. ОБОБЩЕННЫЕ ПЕРЕСТАНОВКИ И СОЧЕТАНИЯ
Рассмотрим теперь разновидность подсчетов, которые представляют собой нечто
промежуточное между перестановками и сочетаниями. На самом деле это обоб-
обобщение и того, и другого. Предположим, что требуется определить различные
размещения букв в слове миссиссиппи. Проблема состоит в том, что некоторые
буквы повторяются. Метод подсчета количества различных размещений букв бу-
будет весьма похож на метод подсчета количества сочетаний. Предположим сначала,
что все буквы различны. В таком случае существовало бы 11! способов размеще-
размещения 11 букв. Теперь обратим внимание, что буква "и" встречается четыре раза.
Допуская, что все буквы различны, мы предположили, что каждое размещение
букв "и", которое оставляет все другие буквы на своих местах, отличается от
других таких размещений. Теперь все такие размещения нужно считать одинако-
одинаковыми. Таким образом, 4! размещения четырех букв "и" на самом деле являются
одним размещением. Для подсчета количества размещений 11 букв, когда 4 бук-
буквы "и" уже не рассматриваются как различные, нужно 11! разделить на 4!. Точно
так же, для подсчета количества размещений, когда четыре буквы "с" не рассмат-
рассматриваются как различные, нужно еще раз разделить на 4!. Осталось рассмотреть
две буквы "п". Как и предыдущих случаях, каждое размещение букв "п", которое
оставляло все прочие буквы на своих местах и рассматривалось как уникальное,
теперь рассматривается как одно и то же размещение. Поскольку существуют 2!
способов размещения двух V, то для подсчета количества размещений, когда две
буквы "п" не различаются, нужно разделить еще на 2!. Таким образом, получаем
11!
4!4!2!
различных размещений.
Заметим, что делая буквы неразличимыми, мы игнорируем их порядок, как
это было в сочетаниях.
ТЕОРЕМА 8.58. Пусть множество 5 содержит п объектов к таких различных
типов, что имеется nx неразличимых объектов типа 1, п2 неразличимых объектов
типа 2, пз неразличимых объектов типа 3 и, вообще, п; неразличимых объекта
типа г. Пусть Р(п; п\, гг3, п3,... ,п^) — количество различных размещений эле-
элементов множества 5. Тогда
Р(П] ПЬ П2, . . . , Пк) = С(П, 7li)C(n - 71Ь П2)С{п - П! - П2, П3)
• • • С(п -п\-п2 nk-i,nk)
п\
ni\n2\n3\ " - пк\ '
ДОКАЗАТЕЛЬСТВО. Рассмотрим первое уравнение. Имеется п мест, которые
можно заполнить элементами из S. Существует C(n,ni) способов выбрать места
для п\ неразличимых объектов типа 1. Если эти места выбраны, то для запол-
заполнения останется п — п\ мест, поэтому имеются С(п — п\,п2) способов выбрать
места для п2 неразличимых объектов типа 2. Если объекты типа 1 и типа 2 вы-
выбраны, то для заполнения остается п — п\ — п2 мест, поэтому объекты типа 3

РАЗДЕЛ 8.6. Обобщенные перестановки и сочетания 355
можно разместить С(п — п\ — П2,пз) способами. Аналогично, объекты типа г для
2 < г < к можно выбрать С(п — п\ — П2 — пз щ-1,щ) способами. Используя
комбинаторный принцип умножения, имеем
С(п, П\)С(п — П\, 7l2)C(n — 71i — 712, П3) * • * С(п — П\ — П2 ~ ' ' ' ~ 71/с-Ь
способов выбора различных размещений элементов из S.
Чтобы показать, что
п!
P(n;ni,n2,...,nk) =
воспользуемся рассуждением, которое использовалось неоднократно. Сначала пред
положим, что все п объектов из 5 различны. Если это так, то имеется п! способов
разместить данные объекты. Для 1 < г < к, щ объектов являются неразличи-
неразличимыми. Поэтому способы расположения таких объектов, при которых остальные
объекты остаются на своих местах, неразличимы. Поскольку имеется п*! таких
расположений, то для нахождения количества различных размещений, когда все
щ объектов типа г являются неразличимыми, необходимо п! разделить на nj для
каждого г. Это дает
п\
что и требовалось доказать. ¦
ПРИМЕР 8.59. Предположим, что 12 книг, включающих 4 одинаковых учебника
по математике, 6 одинаковых учебников по информатике, 2 одинаковых учебника
по химии, следует расставить на полке. Сколькими способами это можно сделать?
Используя предыдущую теорему, имеем
= 13860. ?
ПРИМЕР 8.60. Сколькими различными способами можно расставить буквы в сло-
слове succeeded? Девять букв образуют пять типов неразличимых объектов, вклю-
включающих: A) букву 5, B) букву и, C) два вхождения буквы с, D) три вхождения
буквы е и E) два вхождения буквы d. Следовательно, количество неразличимых
объектов равно
Р(9; 1,1,2,3,2) = ш||^ = 15120.
Заметим, что типы, состоящие только из одного объекта, не влияют на конеч-
конечный результат. Поэтому следует рассматривать типы, содержащие более одного
объекта. ?
Теперь обобщим биномиальную теорему на случай нахождения коэффици-
коэффициентов разложения {х\ + х2 + х3 Н Ь zm)n. Рассмотрим
(а + Ь 4- сL = (а + Ь + c)(a + b + с)(а + Ъ + с)(а + Ь + с).
Для нахождения коэффициента при ab2c необходимо найти все способы выбора
а, двух бис, где буквы выбираются из каждого из сомножителей. Возможные

356 ГЛАВА 8. Комбинаторика и вероятность
варианты: abbe, ebba, abeb, dbab, babe, beba, bbac, bbca, cabb, aebb, bacb, bcab. Но это
только размещения а, двух b и одного с. Таким образом, количество размещений,
которое является коэффициентом при ab2c, равно
2'1) = ТШ = 12-
Аналогично, коэффициент при Ь2с2 равен
22) 6
ТЕОРЕМА 8.61. Для заданного положительного числа п
/ I I I I \П \ ^ * rp^l rr'ri2 /^^3 rr^m
^-^ Т1\\Т12\Т1^\ ' ' • 7Ът!
где сумма взята по всем неотрицательным целым числам ni,n2,--- ,nm, таким,
что ni + п2 + пз 4- • • • + nm = п.
ДОКАЗАТЕЛЬСТВО. Поскольку (xi +х2 Н hxm)n = (х! +х2н hxm)(xi +
х2 Н hxm) • • • (xi +x2H hxm), то каждое слагаемое в разложении получено
путем выбора Х{ из каждого сомножителя в произведении и их перемножения.
Для нахождения коэффициента при x^x^Xg3 • • -x^m необходимо найти все воз-
возможные способы выбора х\ в количестве nb х2 в количестве п2, ... и хт в
количестве nm. Но это есть не что иное, как число размещений х\ в количестве
гсь х2 в количестве п2, ... и хт в количестве nm, которое равно
п\ __
Р{щ щ, п2, п3, • • • , nm) = —¦—— '
•n
ПРИМЕР 8.62. Найдем коэффициент при ab2c3 в разложении (а 4- b 4- сN. Этот
коэффициент равен
ПРИМЕР 8.63. Найдем коэффициент при a3b2c3 в разложении Bа 4- 36 + с)8.
Слагаемое имеет вид
Р(8; 3,2, 3)BаKC6Jс3 = 560 • 23 • 32а362с3 = 4320а362с3,
поэтому коэффициент равен 4320. ?
Предположим, что имеются семь различимых шаров, и требуется положить
три шара в первую коробку, два шара — во вторую и два шара — в третью коробку.
Сколькими способами можно это сделать? Существует СG,3) способов выбрать
три шара для первой коробки. После того, как шары выбраны, остается четыре
шара, два из них выбираются для второй коробки. Для этого существуют СD,2)
способов. Наконец, остается два шара, которые мы кладем в последнюю коробку.

РАЗДЕЛ 8.6. Обобщенные перестановки и сочетания 357
Это может быть сделано СB,2) или одним способом. Таким образом, количество
способов размещений шаров равно СG,3) • СD,2) • СB,2). Но по теореме 8.58
это равно
22)
Как видим, существует связь между размещениями неразличимых объектов
и разбиением множества, что, по сути, мы и делали с шарами и коробками. Для
того, чтобы выявить эту связь, рассмотрим следующий пример. Предположим,
что имеются два красных, три зеленых и четыре синих шара, которые отличают-
отличаются только цветом. Требуется найти все возможные различные размещения данных
шаров. Пусть si,s2,S3,S4,s5,S6,s7,S8,sg — позиции, в которые шары могут быть
помещены. Допустим, красные шары располагаются в позициях s2 и s7. Отожде-
Отождествим такое размещение с помещением s2 и s7 в коробку R. Предположим, что
зеленые шары находятся в позициях si, S3 и sg. Отождествим это с помещением
si, S3 и sg в коробку G. Предположим, наконец, что синие шары располагаются в
позициях s4, s5, sq и s8. Отождествим это с помещением s4, s5, s6 и s8 в короб-
коробку В. Обратно, если sx и sg помещены в коробку Д, s2 s7 и s8 — в коробку G, а
S3, s4, s5 и s6 — в коробку 5, мы отождествим это с помещением красных шаров
в позиции si и sg, зеленых шаров — в позиции s2, s7 и s8, а синих шаров — в
позиции S3, s4, s5 и sq. Таким образом, задача о размещении неразличимых ша-
шаров свелась к задаче о помещении шаров в коробки. В общем случае справедлива
следующая теорема.
ТЕОРЕМА 8.64. Пусть С(п;п1,п2,пз,... ,гат) — количество разбиений множе-
множества 5, содержащего га элементов на га множеств 5Ь 52, 53, ... и 5т, содержа-
содержащих гаь га2, га3, ... и гат элементов соответственно. Тогда
га!
С(га; гаь га2, га3,..., пт) = Р(щ п\, га2, га3,..., пш) = —:—;—: .
ДОКАЗАТЕЛЬСТВО. Существуют С(га,rai) способов выбора элементов для S\.
Как только эти элементы выбраны, остается п — п\ элементов, из которых необ-
необходимо выбрать га2 элементов для 52. Последнее можно осуществить С(га — ni,n2)
способами. Если эти элементы выбраны, остаются га - rai - п2 элементов, из ко-
которых необходимо выбрать га3 элементов для 53. Предположим, что множества
5ь $2, 5з, ... и Si-i уже выбраны, тогда для выбора щ элементов для множества
Si остается га — rai — га2 — • • • — ra^_i элементов. Этот выбор можно осуществить
С{п — п\—П2 ra;_i,ra;) способами. Используя принцип умножения, получаем
C(ra;rab...,ram) = C(ra, rai)C(n- rabra2)C(ra-rai - ra2,ra3) •••
• • • С(га - rai rik-i,nk) =
- га! _
rai!ra2!ra3!---ram!
= Р(га; гаь га2, га3,..., гат).
Заметим, что сочетание С(п,к) = С(п\к,п — к) является частным случаем разби-
разбиения га-элементного множества на множество, содержащее к элементов (которые

358 ГЛАВА 8. Комбинаторика и вероятность
мы выбираем), и множество, содержащее п — к элементов (которые остаются).
Важно отметить, что множество разбивается в последовательность подмножеств
с заданным количеством элементов. При этом мы подсчитывем количество разби-
разбиений множества в последовательность подмножеств заданных размеров. Один из
способов убедиться в этом — заметить, что С(п, к) = С{п\ к,п — к) —- количество
способов выбрать к объектов из и объектов. Мы не включаем сюда количество
способов выбрать и - к объектов и, следовательно, оставляем к объектов, что
также дает разбиение множества 5, содержащего и объектов, на подмножества,
содержащие к и и — к объектов. Для этого также существуют С(п\ к,п — к) спо-
способов, поэтому существуют 2C(n;fc,n- к) способов разбиения множества 5 на
множества, содержащие к объектов и и — к объектов. Другой способ представить
себе содержание теоремы — это рассматривать ее как описание раскладывания
различимых шаров в разные коробки. ¦
ПРИМЕР 8.65. Сколькими способами можно выбрать четыре набора по пять карт
из колоды, содержащей 52 карты? По сути, колода разбивается на пять множеств:
четыре набора по пять карт и 32 оставшихся карты. Поэтому количество таких
наборов равно
52!
55532)
УПРАЖНЕНИЯ
1. Сколько различных размещений можно образовать, используя буквы в слове
seceeded?
2. Сколько различных размещений можно образовать, используя буквы в слове
unsuccessful?
3. Сколько различных размещений можно образовать, используя буквы в слове
Sussex?
4. Сколько различных размещений можно образовать, используя буквы в слове
Tallahassee?
5. Предположим, что нужно расставить на полке 26 книг, среди которых 8 оди-
одинаковых учебников по математике, 6 одинаковых учебников по информатике,
9 одинаковых учебников по физике и 3 — по химии. Сколькими способами
это можно сделать?
6. В урне находятся 6 синих, 5 красных и 14 желтых шаров. Если шары одного
цвета неразличимы, то сколько существует способов одновременно вытащить
из урны шары одного цвета?
7. Тест содержит 35 вопросов, каждый вопрос имеет пять вариантов ответа:
а, б, в, г и д. Сколько может быть различных ответных листов, в которых
выбрано равное количество ответов а, б, в, г и д.
8. У профессора Кренка в группе 20 студентов. Согласно критерию, известному
лишь ему одному, он решил поставить две оценки А, три оценки В, десять
С, три D и две оценки F. Сколькими способами он может поставить оценки
студентам?
9. В бейсбольной команде 24 игрока. В гостинице они остановились в шести
четырехместных номерах. Сколькими способами можно расселить игроков?

РАЗДЕЛ 8.7. Перестановки и сочетания с повторением 359
10. Чему равен коэффициент при x2y3zA в разложении (х 4- у 4- z)9?
11. Чему равен коэффициент при x3y6z3 в разложении (х + 2у + )
12. Чему равен коэффициент при w3x2y5z7 в разложении (ги -I- х 4- у ¦+- гI7?
13. Чему равен коэффициент при w4x5y6z3 в разложении Bw + Ах + у + 5zI8?
14. Чему равен коэффициент при xsy6z12 в разложении (я + 2у2 +4г3I0?
15. Чему равен коэффициент при wl0x12y4z3 в разложении Dw5+2x3+y2+5z)n?
8.7. ПЕРЕСТАНОВКИ И СОЧЕТАНИЯ С ПОВТОРЕНИЕМ
Идея перестановки с повторением может показаться бессмысленной, поскольку
перестановки ассоциируются с перегруппировками, которые, похоже, не допус-
допускают повторений. Если допустить повторение, то необходимо пересмотреть наше
представление о перестановке. Главным свойством перестановки является поря-
порядок. Строка cab отличается от строки abc. Если опять рассмотреть задачу о номер-
номерных знаках автомобилей с тремя буквами, за которыми следуют три цифры, и не
допускать повторений, то получим 26x25x24x10x9x8 различных номерных зна-
знаков. Существует РB5,3) способов выбора букв и РA0,3) способов выбора цифр.
Таким образом, существуют РB5,3) х РA0,3) различных номерных знаков. В
этом и состоит обычное представление о перестановках. Заметим, что допуская
повторение, мы не отказываемся от понятия порядка. Номерной знак ФПФ 199
отличается от номерного знака ПФФ919. Говоря о перестановках с повторением,
имеется в виду, что этот порядок сохраняется. Вспомним, что если в номерном
знаке разрешить повторения букв и цифр, то существуют 26 возможных способов
выбора для каждой буквы и 10 возможных способов выбора для каждой цифры.
Таким образом, если разрешить повторение, то будут существовать 263 х 103 воз-
возможных номерных знаков. В общем случае, если имеется к упорядоченных мест,
для каждого из которых можно выбрать любой из п объектов, существуют пк
способов выбора объектов. Таким образом, число перестановок с повторением,
когда к объектов выбираются из и объектов, равно пк. Наверное, идея повто-
повторения, использованная здесь, требует разъяснений. Один из способов трактовки
повторения — это думать, что повторение предполагает возвращение объекта и
повторное его использование. Другой способ трактовки данного типа повторения
состоит в том, что имеется столь достаточное количество объектов каждого типа,
которое нельзя исчерпать. Например, в случае с номерными знаками требует-
требуется теперь только три копии каждой буквы и каждой цифры. Приведенная ниже
теорема сформулирована для такого представления о повторении.
ТЕОРЕМА 8.66. Пусть 5 — множество, содержащее п неразличимых объектов.
Тогда количество различных перестановок, образованных выбором к элементов с
повторением, равно пк.
ПРИМЕР 8.67. Лототрон содержит 500 шаров с номерами. Из него выбирают шар,
номер которого записывают. Шар возвращают в лототрон и процедура повторяет-
повторяется. Так продолжается до тех пор, пока не наберется комбинация из пяти номеров.

360 ГЛАВА 8. Комбинаторика и вероятность
Подсчитаем количество возможных комбинаций чисел. Для каждого из пяти чи-
чисел имеется 500 способов выбора. Следовательно, число различных комбинаций
составляет 5005. ?
ПРИМЕР 8.68. Сколько существует индивидуальных номеров карточек социаль-
социального страхования?
Поскольку номер следует выбирать из неотрицательных целых чисел, мень-
меньших десяти, то выбираются девять цифр, причем каждая выбирается из десяти
цифр с повторением, поэтому имеются 109 различных номеров карточек социаль-
социального страхования. ?
Предположим, что комитет состоит из восьми человек. При принятии реше-
решения они голосуют "за", "против" или воздерживаются от голосования. Сколько
возможных исходов голосования по данному решению? Если интересует вопрос,
кто и как голосовал, тогда речь идет о числе перестановок, когда для каждого
голосующего имеются три варианта ответа, что дает З8 возможных исходов го-
голосования. Допустим, что нас интересует только общий результат голосования.
Таким образом, четыре голоса "за", три голоса "против" и один воздержавший-
воздержавшийся — это один из возможных исходов. Таким же возможным исходом является
вариант: два голоса "за", четыре голоса "против" и два воздержавшихся. Для
удобства перечислим сначала голоса "за", затем "против" и, наконец, голоса воз-
воздержавшихся. Таким образом, голосование можно изобразить, например, в виде
ЗЗППВВВВ, где два голоса "за", два "против" и четыре воздержавшихся. Далее
можно строить разбиение голосов, например, 33\ПП\ВВВВ. Поскольку порядок
расположения голосов понятен, можно перейти к записи хх\хх\хххх, изобража-
изображающей 33\ПП\ВВВВ. Таким образом, запись хх\\хххххх будет представлять два
голоса "за" и четыре воздержавшихся, а запись хххххххх\\ будет соответство-
соответствовать голосованию "за" всех восьми членов комитета. Таким образом, установлено
взаимно однозначное соответствие между возможными исходами голосования и
различными способами размещения восьми знаков х и двух знаков |. Но это ни
что иное, как количество способов выбора двух мест из десяти для размещения
знака | или, что эквивалентно, количество способов выбора восьми мест из десяти
для размещения знака х. Следовательно, существуют
способов разместить х и |. А значит, существуют
возможных исходов голосования.
Предположим, что и объектов выбираются из к типов объектов с неограни-
неограниченным повторением. Пусть а; — объект типа г, тогда пхах+^е^+пзазН Ьп^аь
где щ > 0 для всех г, a n\ Ч-П2 + п^-\ \-rik = п представляет выбор щ объектов
типа г. Как и прежде, это можно записать в виде
- a2\ • • • \akdkak • • -а^,

РАЗДЕЛ 8.7. Перестановки и сочетания с повторением 361
где каждое а; повторено щ раз. Поскольку место расположения каждого типа
понятно, то выборку можно записать в виде
ххх - • • х\ххх • • • х\ - • • \ххх - х.
Заметим, что разделителей | на один меньше количества типов. Таким обра-
образом, имеем п объектов плюс к - 1 разделителей, образующих и 4- к - 1 мест для
размещения х или |. Каждое расположение знаков х и | дает новый способ вы-
выбора п объектов из к типов объектов с неограниченным повторением. Поскольку
существует С(п + к - 1, п) = С(п 4- к - 1, к - 1) способов выбора места для знака
х или, что эквивалентно, для знака |, то существуют
C(n -f к - 1, и) = С(п + к - 1, к - 1)
различных способов выбора п из к типов объектов с неограниченным повто-
повторением. Такие выборки будем называть сочетаниями из к объектов no n с
повторением. Получаем следующую теорему.
ТЕОРЕМА 8.69. Количество различных сочетаний из к объектов по п равно
С(п + к - 1, п) = С(п + к - 1, к - 1) = {Пп^кк^'
ПРИМЕР 8.70. Если в булочной продается 10 различных видов пончиков, то
сколькими способами можно выбрать дюжину пончиков? Поскольку 12 пончи-
пончиков выбираются из 10 различных типов с повторением, то имеются
A0 + 12-1)! 21!
1)!! 12!9!
различных способов выбрать дюжину пончиков. ?
ПРИМЕР 8.71. Сколько решений имеет уравнение
Щ 4- п2 4- п3 + п4 4- п5 = 25,
где каждое щ — неотрицательное целое число? Это эквивалентно вопросу о том,
сколько существует различных выборок вида
4" Tl2Q>2 4" 72за3 4~ 714*24 4~
где имеется щ объектов типа аг и
Щ 4- п2 4- пз + 7i4 4- пъ = 25,
но количество таких выборок — это количество различных сочетаний из 5 эле-
элементов по 25 с повторениями. Итак, существуют
B5 4-5-1)! 29!
25!E-1)Н 25!4!
различных решений уравнения п\ 4- П2 4- 713 4- п^ 4- тг5 = 25. ?

362 ГЛАВА 8. Комбинаторика и вероятность
Было показано, что число различных сочетаний из к объектов по п объектов
с повторением равно
С(п + к - 1, п) = С(п + fc - 1, к - 1) =
Если необходимо выбрать хотя бы по одному объекту каждого типа, то имеются
п-к выборов из к различных объектов. Следовательно, имеем C(n—fc+fc-1, fc-1)
или С(п — 1, fc — 1) способов выбора.
ТЕОРЕМА 8.72. Количество различных сочетаний из к объектов по п объектов
с повторением, когда необходимо выбрать хотя бы по одному объекту каждого
типа, равно
С{п - 1, п - к) = С{п - 1, к - 1) = ^ " ^! .
ПРИМЕР 8.73. Если в булочной продается 10 различных видов пончиков, то
сколькими способами можно выбрать две дюжины пончиков, если необходимо
выбрать хотя бы по одному пончику каждого вида? Если бы не было послед-
последнего ограничения, то для выбора двух дюжин пончиков из 10 различных видов
существовало бы
СB4 + 10-1,24) = СC3,24)
различных способов. Однако, учитывая ограничение, можно выбрать только 24 —
10 = 14 пончиков из 10 различных видов, что дает
СA4 + 10-1,14) = СC3,14)
различных вариантов выбора. ?
ПРИМЕР 8.74. Найдем количество различных целочисленных решений уравнения
I I I I О С%
если rii > 1, п2 > 1, п3 > 2, п4 > 2 и пъ > 2. Представим эту задачу, как подсчет
количества выборок вида
7120,2 + П3С13
где
пЪ = 25,
причем следует выбрать, по крайней мере, одно а\, одно а2, два аз, два а4 и два
а5. Это оставляет для выбора только 25 — 8 = 17 элементов из пяти типов, что
дает
A7 + 5-1)! _ 21!
17! " 17!
решений для
п\ + п2 + п3 + п4 + п5 = 25. ?

РАЗДЕЛ 8.8. Принцип клеток 363
I УПРАЖНЕНИЯ
1. Сколько существует решений уравнения п\ 4- Н2 -I- пз 4- п^ 4- п$ = 17 таких,
что каждое и; — неотрицательное целое число?
2. Сколько существует решений уравнения их + п2 4- пз + п4 = 23 таких, что
каждое п; — неотрицательное целое число?
3. Сколько существует решений уравнения п\ 4- П2 4- из 4- Н4 = 23 таких, что
rci > 2, п2 > 3, п3 > 4, п4 > 5?
4. Сколько существует решений уравнения ni 4- н2 + п3 + п4 = 21 таких, что
rci > 2, и2 > 3, п3 > 4, п4 > 5?
5. Сколько различных коллекций из десяти монет можно собрать из монет
стоимостью 1 цент, 5 центов, 10 центов, 25 центов и 50 центов?
6. В киоске продаетея мороженое 21 вида. Фрэд хочет купить пять порций
мороженого. Если мороженого одного вида может быть более одной порции,
то сколько существует способов сделать покупку?
7. Если в урне имеются 20 красных, 20 зеленых и 20 синих шаров, то сколькими
различными способами можно выбрать 10 шаров?
8. Цветочник продает 10 видов цветов. Сколько различных букетов из 12 цвет-
цветков он может сделать?
9. Сколько существует чисел, меньших 10000 и таких, что сумма цифр равна
12?
10. Сколько существует бриджевых раздач (из 13 карт), содержащих три трефо-
трефовые, четыре червовые, пять пиковых карт и одну карту бубей?
11. Если не делать различий между картами одной масти, то сколько может
быть типов бриджевых раздач?
12. Человек покупает 12 различных игрушек для своих четырех детей. Сколь-
Сколькими способами он может распределить игрушки? А сколькими способами,
если игрушки делить поровну?
8.8. ПРИНЦИП КЛЕТОК
Принцип клеток, известный также как принцип Дирихле, — это очень простая, но
тем не менее очень мощная идея. Она особенно полезна в теории чисел. Данный
раздел состоит из двух довольно простых теорем и нескольких не совсем простых
примеров. Начнем с наиболее известной формы принципа клеток.
ТЕОРЕМА 8.75. Если поместить п 4-1 голубей в п клеток, то, по крайней мере,
в одной клетке будет находится более одного голубя.
ДОКАЗАТЕЛЬСТВО. Если в каждой клетке не более одного голубя, то голубей
не может быть больше, чем клеток. Тогда во всех клетках должно быть не более,
чем п голубей, что противоречит условию. ¦
Из теоремы следует, что если т > и и требуется га голубей разместить в п
клетках, то в одной клетке находится более одного голубя.
ПРИМЕР 8.76. В списке, содержащем m + 1 положительных целых чисел, по
крайней мере, два числа имеют один и тот же остаток при делении на га. Пусть

364 ГЛАВА 8. Комбинаторика и вероятность
ai,a2>a3, ¦•• , am,am+i — перечень положительных целых чисел. Предположим,
что для 1 < г < га 4- 1 имеем п{ = о^га -f г;, где 0 < Т{ < тп. Следовательно,
П,Г2,г3,... ,rm,rm+1 — список, содержащий га 4- 1 положительных целых чисел,
меньших т. Но существует только га различных неотрицательных чисел, мень-
меньших га. Поэтому два числа из Г{ должны быть равны. ?
ПРИМЕР 8.77. Если \А\ > \В\, то не может существовать инъективная функция
/ : А —> В. Пусть |В| = п. Существует п множеств /~1F) = {х : f(x) = 6} для
b е В и А = [jbeB /~1F). Но А содержит больше п элементов. Поэтому не менее
двух элементов, например, а и а', должны быть в одном множестве. Но тогда
/(а) = /(а') и / не является инъективной функцией. ?
ПРИМЕР 8.78. Если в прямоугольнике со сторонами 6 и 8 дюймов помещены пять
точек, то существуют две точки, расстояние между которыми не более 5 дюймов.
Разделим исходный прямоугольник на четыре прямоугольника, размером 3 на 4
дюйма каждый. Поскольку пять точек должны находиться либо внутри, либо на
границах четырех прямоугольников, то хотя бы две точки должны быть либо
внутри, либо на границе одного и того же прямоугольника размера 3 х 4. Но
любые такие точки находятся на расстоянии не более 5 дюймов. ?
ПРИМЕР 8.79. В последовательности a\, а2, аз,..., аю из десяти целых чисел су-
существует последовательность идущих подряд элементов am, am+i, ат+2, • • •, а<т+п,
сумма которых делится на 10. Рассмотрим числа s\ = ab $2 = а\ 4- а2, $з =
^1 4- а2 4- аз, «4 = о>\ 4- а2 4- а3 4- а4, ..., «ю = а>\ 4- а2 4- аз 4- а4 4- • • • 4- аю.
Если одна из этих сумм делится на 10, то процесс завершен, элементы суммы
образуют искомую последовательность. Если нет, то каждое Si = IOoj -f r;, где
1 < п < 9. Имеется десять г*, и только девять значений, которые они могут при-
принимать. Поэтому существуют два г с одинаковыми значениями, например, rj = г^
для некоторого j < k. Тогда
sk - Sj = 10qk +rk- (lOqj + rj) =
= 10qk - Wqj =
= 10(qk-qj)
кратно 10. Но это не что иное, как сумма aJ+i + aJ+2 4- a^+з Н + а&, элементы
которой образуют искомую последовательность. ?
ПРИМЕР 8.80. (Эрдош и Шекерес) Пусть 5 — подмножество множества {1,2,3,
..., 2п}, содержащее n-Ы элемент, где п — некоторое положительное целое число.
Существуют два элемента, принадлежащие множеству 5 такие, что один элемент
делит другой элемент. Любое положительное целое число можно представить в
виде Tqi, где q{ — положительное нечетное число. Запишем каждый элемент
множества 5 в таком виде. Множество {gbg2,... ,gn,gn+1,} содержит п + 1 по-
положительных нечетных целых чисел, при том что имеется только п нечетных
чисел, которые меньше или равны 2п. Поэтому qi = qj при г ф j. Таким образом,
множество 5 содержит два различных целых числа вида a = 2rOj и b = 2sq{
соответственно. Если г < 5, то а делит 6, и если г > 5, то 6 делит a. D

РАЗДЕЛ 8.8. Принцип клеток 365
А теперь приведем более сильные формы принципа клеток.
ТЕОРЕМА 8.81.
а) Пусть т> п голубей помещены в п клеток, тогда некоторая клетка содержит
не менее — голубей.
I п I
б) Пусть т = mi 4- ^2 4- ^з 4- * • • + ™<п — п 4- 1 голубей помещены в п клеток,
где гп{ — положительное целое число для каждого 1 < г < п. Тогда, для
некоторого г, г-ая клетка содержит не менее га* голубей.
ДОКАЗАТЕЛЬСТВО, а) Пусть каждая клетка содержит меньше [^] голубей.
Тогда, поскольку нас интересуют целые голуби, каждая клетка содержит меньше
^ голубей. Поэтому общее количество голубей меньше пх ^ = тп, что противо-
противоречит условию.
б) Пусть г-ая клетка содержит меньше, чем rrii голубей. Тогда количество
голубей в г-ой клетке меньше или равно ш» — 1. Просуммировав по всем клеткам,
получаем, что всего голубей не более, чем
(mi — 1L- (m2 — 1L- (m3 — 1) Н h (mn - 1) = mi 4- m2 + m3 H h mn - n,
что противоречит условию. ¦
ПРИМЕР 8.82. Пусть в урне находятся 10 красных, 10 синих и 10 зеленых ша-
шаров. Сколько шаров нужно взять из урны, чтобы с уверенностью иметь хотя бы
4 красных или 5 синих, или 6 зеленых шаров? Мы знаем, что 12 шаров недоста-
недостаточно, поскольку можно выбрать 3 красных, 4 синих и 5 зеленых шаров. Если
отождествить шары одного цвета с голубями, находящимися в одной клетке, то,
согласно части (б) сильной формы принципа клеток, имеем и = 3, mi = 4, m2 = 5
и тз = 5. Поэтому искомое количество шаров равно
7п = тп\ 4- 77i2 4- тз + • • • 4- тп — и 4- 1 =
= 44-54-6-3 + 1 =
= 13. ?
ПРИМЕР 8.83. (Эрдош и Шекерес) Конечная последовательность целых чисел
«ь «2, а3, ..., а/с возрастающая, если каждое число последовательности больше
предыдущего. Иначе говоря, если г > j, то а» > a,j. Конечная последовательность
целых чисел аь а2, а3, ..., а^ убывающая, если каждое число последователь-
последовательности меньше предыдущего. Иначе говоря, если г > j, то а; < aj. Любая по-
последовательность из п2 4- 1 различных целых чисел содержит либо убывающую
подпоследовательность, включающую не менее п4-1 членов, либо возрастающую
подпоследовательность, включающую не менее n-fl членов. Для доказательства
предположим, что S{ — количество чисел в самой длинной возрастающей после-
последовательности аь п2, аз, ..., ап2+ъ начинающейся с а^. Если S{ > n + 1 для
некоторого г, то процесс завершен. Если нет, то для каждого г, 1 < Si < п. По-
Поэтому для всех п2 4 1 штук si, где 1 < i < п2 4-1, имеется п значений. Согласно
части (а) сильной формы принципа клеток получаем, что
п
> п

366 ГЛАВА 8. Комбинаторика и вероятность
штук S{ равны. Поэтому, по крайней мере, п + 1 чисел из s* равны. Пусть
все они равны s. Рассмотрим подпоследовательность длины и + 1, состоящую
из таких а;, что S; равны s. Эта последовательность — убывающая, потому что
если п{ > a,j для г > j, то, добавляя п{ в начало последовательности длины s,
начинающейся с а,, можно получить возрастающую последовательность длины
s + 1, начинающуюся с а*. Но это противоречит тому факту, что самая длинная
возрастающая последовательность, начинающаяся с а*, имеет длину s. Таким
образом построена убывающая последовательность длины и + 1. ?
ПРИМЕР 8.84. Предположим, что в комнате находятся шесть человек, и каждые
два из них либо друзья, либо враги. Тогда есть три человека, которые дружат
между собой, или есть три человека, которые враждуют между собой. Выберем
одного человека, назовем его А и поставим в середине комнаты. Разместим всех
его врагов вдоль южной стены, а всех друзей — вдоль северной стены. Согласно
части (а) сильной формы принципа клеток либо не менее трех человек стоят вдоль
южной стены, либо не менее трех человек стоят у северной стены. Если у южной
стены стоит не менее трех человек, то или трое из них — взаимные друзья, что
и требовалось доказать, или двое из них — враги. Тогда эти люди вместе с А —
трое взаимных врагов. Аналогично, если не менее трех человек стоят у северной
стены, то или трое из них — взаимные враги, что и требовалось доказать, или
двое из них — друзья. Тогда они вместе с А — трое взаимных друзей. ?
Рассмотренный выше пример является характерным, хотя и довольно про-
простым примером задач из раздела комбинаторики, который носит название теория
Рамсея. Можно считать, что нам повезло, поскольку в теории Рамсея очень мало
простых примеров. Почти все ее проблемы по сей день не решены. Поясним тео-
теорию Рамсея на примере полного графа с раскрашенными ребрами. Предположим,
что в предыдущем примере вершины графа — аналоги людей. Образуем граф сле-
следующим образом: если двое людей — друзья, то соответствующие им вершины
соединяет красное ребро. Если двое людей — враги, то соответствующие вершины
соединяет синее ребро. Поскольку каждые двое — либо друзья, либо враги, то
ребро существует между двумя любыми вершинами графа. Следовательно, этот
граф — граф Ке, полный граф с шестью вершинами.
В рассмотренном выше примере, утверждалось, что если все ребра графа
Kq раскрашены либо красным, либо синим цветом, то в графе К6 имеется ли-
либо красный треугольник, либо синий треугольник, каждый из которых является
подграфом графа Kg, по сути, просто графом К$. Граф К$ не обладает таким
свойством, что если его ребра раскрашены либо красным, либо синим цветом, то
он содержит красный или синий подграф К$. Это доказывает граф, изображенный
на рис. 8.13, где пунктиром изображены красные ребра, а синей линией — синие
ребра.
Рис. 8.13

РАЗДЕЛ 8.8. Принцип клеток 367
Теперь дадим определение свойства Рамсея для двух цветов на примере
графов. Существует обобщение свойства Рамсея для произвольного числа цветов.
ОПРЕДЕЛЕНИЕ 8.85. Полный граф Кп обладает (р, q) свойством Рамсея,
если в случае, когда он раскрашен двумя цветами, например, красным и синим,
он содержит либо подграф Кр с красными ребрами, либо подграф Кя с синими
ребрами.
ОПРЕДЕЛЕНИЕ 8.86. Число Рамсея, R(p,q) — это наименьшее число и
такое, что граф Кп имеет (р, q) свойство Рамсея.
Вполне очевидно, что R(p,q) = R(q,p), поскольку можно заменить красный
цвет на синий, а синий — на красный. Также, если т > R{p,q) = п, то, поскольку
Кп — подграф графа Km, граф Km также обладает свойством Рамсея.
Относительно чисел Рамсея будут доказаны только две теоремы. Эти теоре-
теоремы интересны сами по себе, но более важным является то, что они доказывают
существование чисел Рамсея.
ТЕОРЕМА 8.87. Для всех р > 2 Д(р, 2) = ДB,р) = р.
ДОКАЗАТЕЛЬСТВО. Рассмотрим граф Кр. Если одно ребро раскрашено красным
(или синим) цветом, то существует красный (или синий) граф К2. Если нет, тогда
все ребра раскрашены синим (красным ) цветом, и мы получаем синий (красный)
граф Кр. Ш
ТЕОРЕМА 8.88. (Эрдош и Шекерес) Для всех р, q > 3
ДОКАЗАТЕЛЬСТВО. Предположим, что К — полный граф, имеющий Д(р—
R(p,q- 1) вершин, ребра которого раскрашены в красный или синий цвет. Пусть
v —• выбранная вершина графа К. Пусть N — полный подграф графа К, вершины
которого Удг связаны с вершиной v красным ребром. Пусть S — полный подграф
графа К, вершины которого Vs связаны с вершиной v синим ребром. Поскольку
Vn U Vs содержит
R(p - l,g) + Я(р,9 - 1) - 1 = R(p - 1,9) + Д(р,9 - 1) - 2 + 1
вершин, разделенных на п = 2 множества, то либо V}v имеет R(p — 1,9) вершин,
либо Vs имеет R(p,q — 1) вершин. Поэтому, либо N — полный граф, имеющий
Д(р—1,9) вершин, либо S — полный граф, имеющий R(p,q-l) вершин. Если N —
полный граф, имеющий R(p — 1,9) вершин, то он содержит либо подграф Кр-\
со всеми красными ребрами, либо подграф Kq со всеми синими ребрами. Если он
содержит граф Kq со всеми синими ребрами, то доказательство завершено. Если
он содержит граф Кр-\ со всеми красными ребрами, то, добавив вершину v и
все красные ребра из г; в вершины подграфа Кр-\, получим полный граф Кр со
всеми красными ребрами, что и требовалось доказать.

368 ГЛАВА 8. Комбинаторика и вероятность
Аналогично, если 5 — полный граф, имеющий R(p,q — 1) вершин, то он
содержит либо подграф Кр со всеми красными ребрами, либо подграф Кя-\ со
всеми синими ребрами. Если он содержит граф Кр со всеми красными ребрами,
то доказательство завершено. Если он содержит граф Кя-\ со всеми синими
вершинами, то если добавить вершину v и все синие ребра из вершины v во
все вершины подграфа Kq-i, получим полный граф Кя с синими ребрами, что и
требовалось доказать. ¦
Основываясь на результатах двух приведенных выше теорем и используя
индукцию или принцип полного упорядочения для положительных целых чисел,
а также технику доказательства второй теоремы, можно доказать еще один ре-
результат, сформулированный в виде следующей теоремы
ТЕОРЕМА 8.89. (Рамсей) . Если целые числа р и q больше единицы, то число
Рамсея, i?(p, g), существует.
¦ УПРАЖНЕНИЯ
1. Сколько людей нужно выбрать из группы, включающей 40 человек — жен-
женщин и их мужей, чтобы наверняка выбрать супружескую пару?
2. Сколько чисел нужно выбрать из первых 210 положительных целых чисел,
чтобы наверняка выбрать четное число?
3. Покажите, что в компании из 30 человек существуют двое, имеющие одина-
одинаковое количество взаимных друзей.
4. Если группа людей приехала из пяти различных стран, то насколько велика
должна быть эта группа, чтобы она гарантированно включала трех человек,
приехавших из одной страны?
5. Если на кухне имеется 7 банок супа с лапшой, 10 банок овощного супа,
14 банок супа с моллюсками, 18 банок лукового супа и 20 банок томатного
супа, то сколько банок нужно взять, чтобы наверняка иметь 12 банок супа
одного вида?
6. Сколько человек должно быть в группе людей, чтобы, по крайней мере, у
двоих дни рождения были в одном месяце?
7. Сколько человек должно быть в группе людей, чтобы, по крайней мере, у
троих дни рождения были в одном месяце?
8. Сколько человек должно быть в группе людей, чтобы, по крайней мере, двое
родились в один день недели?
9. Докажите, что в произвольном списке из п положительных целых чисел
всегда существует последовательность идущих последовательно чисел, сум-
сумма которых делится на п.
10. Сколько нужно выбрать слов, чтобы, по крайней мере, два начинались с
одной и той же буквы?
11. Сколько нужно выбрать слов, чтобы, по крайней мере, два начинались с
одной и той же буквы и оканчивались одной и той же буквой?
12. Анкета разослана 13 первокурсникам, 5 второкурсникам, 15 студентам пред-
предпоследнего курса и 20 выпускникам. Сколько анкет нужно собрать, чтобы
наверняка получить 9 анкет от студентов одной категории?

РАЗДЕЛ 8.9. Снова о вероятности 369
13. Сколько чисел нужно выбрать из последовательности {1,2,3,4,..., 19,20},
чтобы два из них давали в сумме 21?
14. Покажите, что любое подмножество, содержащее не менее п различных це-
целых чисел, находящихся между числами 2 и 2п, всегда содержит два взаимно
простых числа.
15. Пусть в ресторане 14 столов и 170 стульев, и п — наибольшее количество
стульев за столом. Определите наименьшее возможное значение числа п?
16. Докажите, что десятичное разложение рационального числа имеет период.
17. Докажите, что если каждое из п +1 различных положительных целых чисел
не превышает число 2п, то два из них отличаются на единицу.
18. Покажите, что если сумма 10 положительных чисел равна 151, то сумма
трех из этих чисел должна быть не меньше 46.
19. Покажите, что если т шаров положить в п коробок и
то, по крайней мере, в двух коробках будет находиться одинаковое число
шаров.
20. Покажите, что если сумма п + 1 положительных целых чисел равна 2п,
то для любого положительного целого числа /с, меньшего 2п, существует
подмножество этих п + 1 целых чисел, сумма которых равна к.
8.9. СНОВА О ВЕРОЯТНОСТИ
В предыдущем рассмотрении вероятности предполагалось, что все результаты
эксперимента равновозможны. Теперь мы снимем это ограничение и дадим более
общее понятие вероятности, для чего наш подход должен быть более аксиомати-
аксиоматическим; при этом некоторые теоремы станут аксиомами и определениями.
ОПРЕДЕЛЕНИЕ 8.90. Вероятностной функцией на выборочном пространстве
(множестве элементарных событий) 5 называется такая функция Р из подмно-
подмножеств множества 5 на действительную числовую ось, что
1. Р(А) > 0 для всех ACS.
2. P(S) = 1.
3. Если ДВС5не имеют общих исходов, то Р(А U В) = Р(А) + Р(В).
Доказательства приведенных ниже теорем аналогичны тем, которые даны
в разделе 8.2. Единственное отличие состоит в том, что три сформулированных
выше условия для вероятностной функции были доказаны в теореме 8.53 в пред-
предположении, что все исходы эксперимента равновозможны. Необходимо соблюдать
осторожность при использовании такой комбинаторной техники, как подсчет чис-
числа сочетаний и перестановок, чтобы не допустить по умолчанию равновозмож-
ность исходов эксперимента.

370 ГЛАВА 8. Комбинаторика и вероятность
ТЕОРЕМА 8.91. Пусть S — множество исходов, множество S также будет уни-
версом. Пусть А! — дополнение множества А, тогда
а) Р(А') = 1 - Р(А)\
б) Р@) = 0;
в) для любого события А имеем Р(А) > 0;
г) если АС В, то Р(А) < Р(В)\
д) для любого события А имеем 0 < Р(А) < 1.
Читателю предлагается доказать следующую теорему, используя принцип
индукции.
ТЕОРЕМА 8.92. Пусть А\, А2, Аз,..., Аш — попарно непересекающиеся события.
Тогда
Р{АХ U A2 U A3 U • • • U Am) = Р(Аг) + Р(А2) + Р(А3) + • ¦ • 4- Р(Ат).
Доказательство следующей теоремы аналогично доказательству соответству-
соответствующей теоремы 8.56.
ТЕОРЕМА8.93. Для событий A,BCS имеем Р(АиВ) = Р(А)+Р{В)-Р(АГ)В).
Мы имели возможность убедиться, что для вероятности существует теоре-
теорема, аналогичная комбинаторному принципу сложения. Представляется разумным
задать вопрос, существует ли для вероятности теорема, аналогичная комбина-
комбинаторному принципу умножения. Так оно и есть, но сначала необходимо тщатель-
тщательно разобраться в формулировке комбинаторного принципа умножения. Принцип
гласит: "Пусть задана последовательность событий Е1,Е2,Ез,...,Егп таких, что
событие Е\ осуществляется п\ способами, и если события Е\, Е2,Е%,... ,Ek-i
осуществились, то событие Ek может осуществиться rik способами. Тогда суще-
существуют п\ х П2 х пз х • • • х rtk способов осуществления всей последовательности
событий". Количество способов осуществления события Ek зависит от того, про-
произошли ли события Е\,Е2,Е$,.. .,Ek-i- Таким образом, может оказаться, что
число способов осуществления события Ek не реализуется само по себе и может
зависеть от предыдущих событий.
Рис. 8.14
Сходным образом дадим определение условной вероятности. Предположим,
что имеются два события А и В. Требуется определить вероятность того, что
событие В произойдет, если событие А произошло или наверняка произойдет.
Сокращенно будем называть это вероятностью события В при условии А или

РАЗДЕЛ 8.9. Снова о вероятности 371
относительно события А. Интуитивно понятно, что предположение о том, что
событие А произошло или наверняка произойдет, ограничивает выборочное про-
пространство до Л, как показано на рис. 8.14, поэтому событие В ограничено теперь
р( г>\ P( A n R}
исходами из АпВ, и вместо Р(В) — , получаем
г\Ь)
ОПРЕДЕЛЕНИЕ 8.94. Вероятность В при условии А, обозначаемая Р(В\А),
Р(АпВ)
равна
Это можно также записать в виде Р(АГ)В) = Р(А)Р(В\А).
ПРИМЕР 8.95. Предположим, что из колоды вытягивают карту, затем возвращают
ее в колоду и вытягивают вторую карту. Какова вероятность того, что обе карты
пиковой масти? Какова вероятность того, что хотя бы одна из карт будет пиковой?
Пусть А — множество исходов, когда первая карта — пиковая, а В — множество
исходов, когда вторая карта — пиковая. Для ответа на первый вопрос необходимо
найти Р(АПВ). Заметим, что
Н - I
52 ~ 4 '
так как 13 из 52 карт — пиковые. Поскольку первая карта возвращена в колоду,
то также имеем
Следовательно, вероятность того, что обе карты — пиковые, равна
Р{АПВ) = Р(А)Р(В\А) =
_ 1 1 _
~ 4 ' 4 ~
_ 1
~ 16'
Для ответа на второй вопрос необходимо найти Р(АиВ), но
поэтому вероятность того, что, по крайней мере, одна из карт — пиковая, равна
Р(А UB) = Р(А) + Р(В) - Р(А Г\В) =
_ 1 1 _ J_ _ 7_
~ 4 + 4 16 ~ 16 ' п

372 ГЛАВА 8. Комбинаторика и вероятность
ПРИМЕР 8.96. Предположим, что карту вытягивают из колоды, но в колоду не
возвращают, затем вытягивают вторую карту. Какова вероятность того, что обе
карты — пиковые? Какова вероятность того, что хотя бы одна из карт будет
пиковой? Пусть А — множество результатов, когда первая карта — пиковая, а
В — множество результатов, когда вторая карта — пиковая. Для ответа на первый
вопрос необходимо найти Р(АГ)В). Заметим, что
поскольку 13 из 52 карт — пиковые. Для нахождения Р(В\А) заметим, что од-
одну пиковую карту вытянули, но не вернули. Теперь в колоде 51 карта, 12 из
которых — пиковые, поэтому
Следовательно, вероятность того, что обе карты — пиковые, равна
Р(А П В) = Р(А)Р(В\А) = \ • g = 1.
Чтобы ответить на второй вопрос нужно найти Р(АиВ). Известно, что
\ ¦
Теперь задача состоит в том, чтобы найти Р{В). Если событие В произошло,
то либо две пиковые карты были вытянуты подряд, либо первая карта не была
пиковой, а вторая карта была пиковой. Поэтому
Р(В) = Р(А П В) + Р(А' П В).
Согласно предыдущей теореме
Р(А'ПВ) = Р(А')Р{В\А').
Поскольку 39 карт не являются пиковыми, то
После выбора первой карты среди 51 карты все еще остается 13 пиковых, так что
Следовательно,
1 + Н = НЛ
17 68 68 4

РАЗДЕЛ 8.9. Снова о вероятности 373
Теперь видно, что когда А неизвестно, то Р(В) является таким же, как если бы
В осуществилось без реализации события А. Можем определить теперь, что
Р(А U В) = Р{А) + Р(В) - Р(А ПВ) =
_ 1 1 __1_ _ 15
~ 4 + 4 ~ 17 ~~ 34' ?
ПРИМЕР 8.97. Предположим, что из стандартной колоды, содержащей 52 карты,
последовательно вытягиваются 6 карт. Какова вероятность того, что шестая кар-
карта — это третья вытянутая карта пиковой масти? Пусть А — событие, при котором
две пиковые карты вытянуты за первые пять шагов, а В — событие, при кото-
котором пиковая карта вытянута на шестом шаге. Требуется найти Р(АГ\В). Опять
воспользуемся тем фактом, что
Р(АПВ) = Р(А)Р(В\А).
Количество способов осуществления события А равно количеству способов осу-
осуществления того, что вытянуты 2 пиковые карты из 13 возможных, а 3 карты
вытянуты из 39 карт, которые не являются пиковыми. Таким образом,
'52^
Всего имеется ( ] способов выбора 5 карт из 52. Поэтому
5
Для определения Р(В\А) заметим, что поскольку две пиковые карты были вы-
выбраны, то существуют 11 способов выбора пиковой карты. Для выбора шестой
карты в колоде осталось 47 карт, поэтому
Р(В\А) = Н
и
'39^
D
Ранее было отмечено, что если первую карту вытянули и вернули в колоду,
то вероятность, что вторая вытянутая карта — пиковая, не зависит от выбора
первой карты. Когда исход первого события не влияет на исход второго события,
говорят, что второе событие независимо от первого события.

374 ГЛАВА 8. Комбинаторика и вероятность
ОПРЕДЕЛЕНИЕ 8.98. Если Р(В) = Р(В\А), то событие В называется неза-
независимым от события А.
Поскольку Р(АПВ) = Р(А)Р(В\А), то для случая Р{В\А) = Р{В) получаем
следующую теорему.
ТЕОРЕМА 8.99. Если событие В независимо от события А, то Р(А П В) =
Р(А)Р(В).
ПРИМЕР 8.100. Предположим, что монету подбрасывают десять раз. Пусть А —
событие, при котором монета падает "решкой" вверх первые девять раз, а В —
событие, при котором на десятом шаге монета падает "решкой" вверх. Покажем,
что событие В является независимым от события А. Вероятность Р(АпВ) — это
вероятность, что десять подбрасываний монеты дадут десять выпадений "решкой"
вверх. Всего существует 210 = 1024 равновозможных исходов, и только в одном
из них "решка" выпадает вверх десять раз. Поэтому
Р(АПВ) =
1024'
Событие А может осуществиться двумя способами. Все десять выпадений монеты
будут "решкой" вверх или первые девять выпадений будут "решкой" вверх, а
последнее выпадение будет "орлом" вверх. Следовательно,
Р(А) =
1024
1024
Значит, событие В не зависит от события А. ?
Если монета подбрасывается и раз, можно считать, что результат каждого
подбрасывания не зависит от результатов прочих подбрасываний. Например, на
результат третьего подбрасывания никоим образом не влияют результаты первых
двух подбрасываний. Такое событие будем называть повторением независимых
испытаний. Предположим, что в эксперименте, состоящем из повторения п неза-
независимых испытаний, каждое испытание имеет два возможных исхода: успех и
неудача. Пусть р — вероятность успеха и q = 1 — р — вероятность неудачи. Тре-
Требуется найти вероятность к успехов в п независимых испытаниях. Если вернуться
к нашему примеру с монетой и рассматривать выпадение "решки" как успех, то
р = q = ^. Если п = 5 и к = 3, то вопрос стоит о вероятности получить три
"решки" после пяти подбрасываний монеты.
В случае заданного эксперимента с повторением п независимых испытаний
для нахождения вероятности к успехов предположим сначала, что они осуще-
осуществляются в определенном порядке. Например, первыми реализуются к успехов,
а вторыми — п - к неудач. Поскольку испытания независимые, то вероятность
осуществления к успехов с последующей реализацией и-к неудач равна pkqn~k.

РАЗДЕЛ 8.9. Снова о вероятности 375
Фактически, каждое осуществление к успехов в п независимых испытаниях бу-
будет иметь вероятность pkqn~k. Поскольку существуют (?) способов получения к
успехов в п независимых испытаниях, то вероятность к успехов в п испытаниях
равна (r]c)pkqn~k. Таким образом, приходим к следующей теореме.
ТЕОРЕМА 8.101. В эксперименте с п независимыми испытаниями, называемыми
испытаниями Бернулли, где каждое имеет два исхода, успех с вероятностью р и
неудачу с вероятностью q = 1 - р, вероятность осуществления к успехов равна
Говорят, что такой эксперимент имеет биномиальное распределение по-
поскольку
к=0
ПРИМЕР 8.102. Дана монета с равновозможным выпадением обеих сторон. Како-
Какова вероятность выпадения трех "решек" в результате пяти подбрасываний монеты?
Поскольку р — q = ^, вероятность выпадения трех "решек" после пяти подбрасы-
подбрасываний равна
1\3 /1\2 _ 10
Ы Ы 2* П
ПРИМЕР 8.103. Предположим, что правильная игральная кость подбрасывается
десять раз. Какова вероятность трехкратного выпадения шестерки? Вероятность
р выпадения шестерки равна ^. Следовательно, вероятность q выпадения не ше-
шестерки равна 1 —^ = |. Поэтому вероятность выпадения шестерки равно три раза
равна
©'(!)'¦
Предположим, что в выборочном пространстве каждому исходу поставлено в
соответствие действительное число. Например, если подбрасываются две играль-
игральные кости, то таким числом может быть сумма показаний на обеих костях. Если
монета подбрасывается десять раз, то таким числом может быть общее количе-
количество выпадений "решки". Такое число назовем случайной величиной и определим
следующим образом.
ОПРЕДЕЛЕНИЕ 8.104. Случайной величиной называется функция из выбо-
выборочного пространства во множество действительных чисел.
Если задана случайная величина на выборочном пространстве, можно рас-
рассматривать вероятность того, что случайная величина будет равна заданному
значению. Например, пусть монета подбрасывается семь раз и R(x) — число вы-
выпаданий "решки". Тогда вероятность, что R(x) = 5, равна

376 ГЛАВА 8. Комбинаторика и вероятность
Если игральная кость подбрасывается десять раз и R(x) — количество выпаданий
пятерки, то вероятность, что R(x) = 4, равна
-|Г)\ /i\4 /г\6
4
Предположим, что мы играем в игру, в которой, подбрасывая игральную
кость, получаем количество долларов, равное выпавшему числу. Таким образом,
если выпадает число 5, мы получаем $5. Сколько нам следовало бы заплатить за
участие в игре? Это количество называется ожидаемым значением. Оно находится
суммированием произведений количества долларов, которое должно быть полу-
получено, на вероятности получения таких сумм. В данном случае эта вероятность
равна | для каждого значения, поэтому ожидаемое значение равно
и справедливая цена за участие в игре должна быть $3.50.
В рассмотренном выше примере случайная величина R(x) принимает зна-
значение х, которое выпадает на кости. Таким образом, i?(l) = $1, RB) = $2, ...,
ДF) = $6. В общем случае, пусть R — случайная величина, определенная на ре-
результатах хх,Х2,хз,.. .,хп, которые осуществляются с соответствующими веро-
вероятностями Pi, P2, Р3,..., Рп- Ожидаемое значение, или математическое ожи-
ожидание E{R) = ]Г*=1 R(xi)Pi} Пусть
— значения, которые может принимать случайная величина R (т.е. множество
результатов функции R). Множество всех результатов, для которых R имеет
фиксированное значение aiy обозначается R = а*. Вероятность того, что X при-
принимает значение P(R — а*), обозначается через pi. Если использовать данное
обозначение, то эквивалентной, но более удобной формой записи математическо-
математического ожидания E(R) будет E(R) = Y^iLi aiPi-
В приведенных ниже примерах будут определены две случайные величины
для рулетки.
ПРИМЕР 8.105. Предположим, что колесо рулетки в равномерно расположенных
по колесу ячейках имеет числа от 0 до 36. Заплатив $1, игрок выбирает число.
Если он выигрывает, то получает $36. В случае проигрыша — не получает ниче-
ничего. Пусть R\ — случайная величина, равная количеству денег, которые получит
игрок. Пусть е\ — событие R = 36, a e<i — событие R = 0. Тогда рь вероятность
выигрыша, равна ^, а р2 — вероятность проигрыша, равна Щ. Поэтому,
_ 36 _
~ 37 ~
« .973.
Поскольку игрок платит $1, то в среднем, за попытку он теряет около $0.027. ?
'В отечественной литературе принято обозначение M(R). — Прим. ред.

РАЗДЕЛ 8.9. Снова о вероятности 377
ПРИМЕР 8.106. Предположим, что мы играем в ту же самую игру, но теперь
R2 — случайная величина, равная сумме выигрыша или проигрыша. Пусть е\ —
событие R = 35, а е2 — событие R2 = — 1. Тогда р\, вероятность выигрыша, равна
-у, а р2, вероятность проигрыша, равна ||. Поэтому
= 35.1 + (-i).p =
1
= 7*
« -.027.
Поскольку R2 представляет сумму выигрыша или проигрыша, то в среднем за
попытку игрок теряет $0.027, что согласуется с результатом первого примера. ?
ПРИМЕР 8.107. Представим себе ту же самую рулетку, на которой нечетные
числа от 1 до 36 — черные, а четные числа от 1 до 36 — красные. Игрок платит
$1 и выбирает цвет. Если он выигрывает, то получает $2. Если проигрывает, то
не получает ничего. Пусть Д3 — случайная величина, равная выигрышу. Пусть
е\ — событие /?з = 2, а е2 — событие Rs = 0. Тогда р\, вероятность выигрыша,
равна ||, а р2, вероятность проигрыша, равна Щ. Поэтому,
~ 37 ' 37
_ 36 _
~ 37 ~
и .973.
Поскольку игрок платит $1, то в среднем за попытку он теряет около $0.027. ?
ПРИМЕР 8.108. Предположим, что мы играем в ту же самую игру, но теперь
Д4 — случайная величина, равная выигрышу или проигрышу. Пусть е\ — событие
R = 1, а е2 — событие R2 = —1. Тогда рь вероятность выигрыша, равна ||, а р2,
вероятность проигрыша, равна Щ. Поэтому
"~37 ~
« -.027.
Поскольку Д4 представляет сумму выигрыша или проигрыша, то в среднем игрок
теряет за попытку $0.027, что согласуется с результатом первого примера. ?
Снова вернемся к испытаниям Бернулли, где случайная величина дает число
успехов в п испытаниях. Покажем, что в данном случае математическое ожидание
есть произведение количества испытаний на вероятность успеха.
ТЕОРЕМА 8.109. Пусть в эксперименте с п независимыми испытаниями каждое
имеет два исхода: успех с вероятностью р и неудачу с вероятностью q = 1— р\ слу-
случайная величина R представляет число успехов. Тогда математическое ожидание
E{R) = пр.

378 ГЛАВА 8. Комбинаторика и вероятность
ДОКАЗАТЕЛЬСТВО. Поскольку вероятность к успехов равна
к) к\(п — к\\
и первое слагаемое в приведенной ниже сумме равно 0, математическое ожидание
равно
п .
п
(п-1)!
= пр ж v ;
Положив т = к — 1, получаем
п-1
E(R) =nPJ2 , _pmgn-(m+l) =
71— 1 / i \ I
rn (n-l)-m _
q
= пр,
поскольку р -f q = 1. ¦
ПРИМЕР 8.110. Монету подбрасывают 20 раз. Игрок получает $1 за каждое вы-
выпадание "решки". Справедливая цена за участие в игре будет пр = 20 • \ = 10
долларов. ?
Теперь рассмотрим дальнейшие свойства математического ожидания, кото-
которые вскоре нам пригодятся.
ТЕОРЕМА 8.111. Пусть R и S — случайные величины, определенные на исходах
#ъ #2» #з» • • •» #п> которые осуществляются с соответствующими вероятностями
Pi, Р2, Р3,..., Рп.
а) Пусть с — константа. Тогда E{cR) = с • E(R).
б) Пусть с — константа. Тогда Е(с) = с.
в) E(R + S) = E(R)+ E(S).
ДОКАЗАТЕЛЬСТВО. Для исходов хьх2,х3,... ,жп, которые осуществляются с
соответствующими вероятностями Pi, Р2, Р3,..., Рп, математичесткое ожидание
= J2 ЩХг)Рг И ?(S) = ? 5(Xi)P». ПОЭТОМУ
г=1 г=1

РАЗДЕЛ 8.9. Снова о вероятности 379
а) E(cR) = ? сЩх{)Р{ = с ? Я(х,)Рг = с • Я(Д).
г=1 г=1
б) ?(с) = ]Г сРг =cf2Pi=C> ПОСКОЛЬКУ ? Рг = 1.
в) Я(Д + S) = ?(д'Й) + 5(^))^ =
г = 1
п
= J2 R(Xi)Pi + S(Xi)Pi =
г=1 г=1 i=l
= E(R) + E(S). "
В случайных выборках мы интуитивно думаем о среднем значении как о
некоторой середине или о наиболее вероятном значении случайной величины. В
некотором смысле, это ее усредненное значение. Можно заметить, что если каж-
каждое значение случайной величины равновероятно, тогда математическое ожидание
будет "средним арифметическим" значений случайной величины.
Приведенное ниже определение интуитивно выглядит вполне логичным.
ОПРЕДЕЛЕНИЕ 8.112. Среднее значение \х случайной величины R — это ее
математическое ожидание E(R).
Дисперсия случайной величины R показывает, насколько велик разброс или
насколько широко распределены значения случайной величины.
ОПРЕДЕЛЕНИЕ 8.113. Дисперсия а2 случайной величины есть E((R-fiJ) =
E{(R-E(R)J).
Используя теорему 8.111, получаем важное свойство дисперсии.
ТЕОРЕМА 8.114. Пусть R — случайная величина, тогда а2 = E{R2) - ц2
E(R2) - (E(R)J.
ДОКАЗАТЕЛЬСТВО.
- E{R2 -
= E(R2) — 2piE{R) + Е{ц2) = по теореме 8.111, поскольку /х — константа.
= E(R2) — 2/i2 + ц2 = по теореме 8.111, поскольку /i — константа.
= E(R2) - f. ¦
Важно отметить, что и среднее значение, и дисперсия — теоретические по-
понятия, и их не следует путать со средним значением и разбросом множества
данных.
Для примера выберем опять биномиальное распределение. Будем также пред-
предполагать, что случайная величина R указывает количество успешных испытаний.
Известно уже, что
/i = E(R) = пр.

380 ГЛАВА 8. Комбинаторика и вероятность
Поскольку a2 = E(R2) — (E(R)Ji то теперь попытаемся найти E(R2). По опре-
определению,
711
Расписывая к2 = к(к — 1) + к и учитывая тот факт, что первые два слагаемых в
приведенной ниже сумме равны 0, получаем
=2 v
п-2
'Е-
п-2
/с—U
2{р + q)n~2
= п(п — 1)р (р + q)n +np =
= п(п — \)р2 +пр =
= п2р2 — пр2 + пр =
= п2р2 4- прA -р) =
Таким образом,
= п2р2 + npq.
E(R2) - (E{R)J = п2р2 + npq - (прJ =
= npq,
что приводит к следующей теореме.
ТЕОРЕМА 8.115. Пусть в эксперименте с п независимыми испытаниями каждое
имеет два исхода: успех с вероятностью р и неудачу с вероятностью q = 1 - р\
случайная величина R описывает число успехов. Тогда дисперсия а2 = npq.

РАЗДЕЛ 8.9. Снова о вероятности 381
ПРИМЕР 8.116. В эксперименте игральную кость подбросили 72 раза. Пусть слу-
случайная величина R представляет количество выпаданий числа 1, так что р = ^ и
q = |. Тогда
E(R) = \х = пр = 72 • - = 12
6
= 72 = 10. п
6 6 '—'
Уже было отмечено, что дисперсия — мера разброса значений случайной
величины. Неравенство Чебышева дает более точное соотношение между диспер-
дисперсией и распределением случайной величины. Перед тем как сформулировать и
доказать неравенство Чебышева, рассмотрим следующую лемму.
ЛЕММА 8.117. Пусть R — случайная величина, определенная на выборочном
пространстве 5. Тогда
Р(|Л|>О)<?Ш = 2!.
ДОКАЗАТЕЛЬСТВО.
Р(\Щ >с) =
|
\R{xt)\>c
< i
Подставляя R — fi вместо Д, получаем неравенство Чебышева.
ТЕОРЕМА 8.118. (Неравенство Чебышева) Пусть R — случайная величина, опре-
определенная на выборочном пространстве 5. Тогда
УПРАЖНЕНИЯ
1. В партии из пяти автомобилей один имеет дефект. Два человека собирались
приобрести автомобили. Какова вероятность того, что вторая из покупаемых
машин будет исправна, если известно, что первая машина была без дефекта.
2. Подбрасываются две кости. Какова вероятность того, что на первой выпало
5, если известно, что сумма равна 8?
3. Подбрасываются две кости. Какова вероятность того, что сумма значений на
кубике равна 7, если известно, что сумма нечетная?

382 ГЛАВА 8. Комбинаторика и вероятность
4. Подбрасываются две кости. Какова вероятность того, что сумма значений на
кубике равна 8, если известно, что сумма больше или равна 7?
5. В урне содержится восемь белых и семь черных шаров. Вынимается четыре
шара без возвращения. Какова вероятность, что первый шар белый, если
известно, что было вытянуто два белых шара? Какова вероятность, что пер-
первый шар белый, если известно, что было вытянуто два белых шара (шары
вытягивались с возвращением)?
6. Четыре туза из стандартной колоды перетасованы и разложены на столе
картинкой вниз. Две карты, не раскрывая, убирают. Какова вероятность,
что третья карта — туз пик?
7. Монету подбрасывают три раза. Какова вероятность того, что "решка" выпа-
выпадет три раза, если известно, что, по крайней мере, один раз выпала "решка"?
8. Пусть А и В — независимые события. Пусть Р(А) = .7 и Р(В) = .6, найдите
Р(В\А).
9. Из трех урн вынимают по одному шару. В первой урне находятся три белых
и два черных шара. Во второй — два белых и три черных шара. Третья урна
содержит три белых и три черных шара. Если известно, что два из трех
вынутых шаров белые, то какова вероятность, что белый шар был вынут из
первой урны?
10. Из стандартной колоды с 52 картами вытягивают две карты. Какова вероят-
вероятность того, что вторая карта — король, если известно, что первая карта —
туз? Какова вероятность того, что вторая карта — король, если известно, что
первая карта — туз пик?
11. Шесть шаров пронумерованы числами 0, 1, 1, 2, 5 и 10 и помещены в урну.
Произвольным образом выбирается один шар, и если он имеет номер п, то
игрок получает п долларов. Каково математическое ожидание выигрыша?
12. Шесть шаров пронумерованы числами 0, 0, 0, 0, 10 и 20 и помещены в
урну. Произвольным образом выбирается один шар, и если этот шар имеет
номер п, то игрок получает п долларов. Каково математическое ожидание
выигрыша?
13. Восемь шаров пронумерованы числами 0, 1, 1, 2, 2, 2, 5 и 10 соответственно.
Шары помещены в урну, и три из них произвольно вытягиваются. Игрок
получает сумму в долларах, равную сумме чисел на трех шарах. Каково
математическое ожидание выигрыша?
14. Восемь шаров пронумерованы числами 0, 0, 0, 2, 3, 3, 7 и 10, соответственно.
Шары помещены в урну, и три из них произвольно вытягиваются. Игрок
получает сумму в долларах, равную сумме чисел на трех шарах. Каково
математическое ожидание выигрыша?
15. В игре подбрасывают два кубика. Игрок получает сумму в долларах, равную
сумме значений на кубиках. Сколько может стоить участие в этой игре?
16. Предположим, что картам присвоены такие стоимости: туз имеет стоимость 1,
двойка — 2, ..., десятка — 10, валет — 11, дама — 12, король — 13. Игрок
вытягивает карту. Если вытянута карта червовой масти, то игрок получает
удвоенную стоимость карты. Если это карта бубей, он получает стоимость
карты. Если карта черной масти, то игрок платит $10. Каково математиче-
математическое ожидание в этой игре?

РАЗДЕЛ 8.9. Снова о вероятности 383
17. Фирма "Асе Cleaning House" учредила главный приз в размере $10 миллио-
миллионов участнику конкурса. Если человек платит 33 цента за марку (фирма "Асе
Cleaning House" предоставляет конверт и анкету участника) и 50 миллио-
миллионов человек участвуют в тотализаторе, то каково математическое ожидание
победы в конкурсе?
18. Допустим, что вероятность рождения девочки 0.51, а мальчика — 0.49. Если
в семье Джонс пятеро детей, то какова вероятность, что в ней три девочки?
Какова вероятность, что в семье не менее четырех девочек?
19. Если бейсбольная команда выигрывает с вероятностью 60%, то какова веро-
вероятность, что команда одержит победу в трех из последующих пяти игр?
20. Две бейсбольные команды, участвующие в турнире, имеют равные шансы
на выигрыш. Если команда А проиграла две первые игры, то какова вероят-
вероятность, что команда А выиграет турнир?
21. Если монету подбрасывают семь раз, то какова вероятность выпадания че-
четырех "решек"?
22. Если игральную кость подбрасывают семь раз, то какова вероятность того,
что шестерка выпадет равно два раза?
23. Если 10% продукции составляют брак, то какова вероятность получить два
бракованных изделия среди выбранных десяти изделий?
24. Сэм попадает по мячу один раз из трех. Какова вероятность, что он попадет
три раза из десяти?
25. Если десять карт последовательно вытягиваются из колоды, то какова веро-
вероятность, что две карты будут червовыми?
26. Если две игральные кости подбрасывают 12 раз, то какова вероятность, что
6 выпадет ровно 3 раза?
27. Предположим, что мы играем в рулетку, и рассматриваемая случайная ве-
величина такая же, как в примере 8.105, за исключением того, что имеется
дополнительная ячейка, обозначенная 00. Найдите математическое ожида-
ожидание случайной величины R\.
28. Предположим, что мы играем в рулетку, и рассматриваемая случайная ве-
величина такая же, как в примере 8.106, за исключением того, что имеется
дополнительная ячейка, обозначенная 00. Найдите математическое ожида-
ожидание случайной величины /?2-
29. Предположим, что мы играем в рулетку, и рассматриваемая случайная ве-
величина такая же, как в примере 8.107, за исключением того, что имеется
дополнительная ячейка, обозначенная 00. Найдите математическое ожида-
ожидание случайной величины R%.
30. Предположим, что мы играем в рулетку, и рассматриваемая случайная ве-
величина такая же, как в примере 8.108, за исключением того, что имеется
дополнительная ячейка, обозначенная 00. Найдите математическое ожида-
ожидание случайной величины R4.
31. Пусть в эксперименте с 10 независимыми испытаниями каждое имеет два
исхода: успех с вероятностью 0.3 и неудачу; случайная величина R описы-
описывает число успехов. Каково математическое ожидание эксперимента? Какова
дисперсия?

384 ГЛАВА 8. Комбинаторика и вероятность
8.10. ТЕОРЕМА БАЙЕСА
Теорема Байеса названа в честь Реверенда Томаса Байеса, министра и матема-
математика. Его теория, изложенная в работе Essay towards Solving a Problem in the
Doctrine of Chances, была опубликована в 1764 году, через четыре года после его
смерти, в журнале Philosophical Transactions, издаваемом Лондонским Королев-
Королевским обществом. У многих людей возникали проблемы с пониманием теоремы
Байеса. Казалось, что она меняет местами причину и следствие. Изучая след-
следствие, можно определять вероятность причины. Теорема Байеса весьма полезна
для определения причин заболеваний, таких как рак. Она также полезна при
изучении воздействия лечения на заболевание.
Предположим, что имеется п непересекающихся событий В\,В2, ?3, • • • -> Вп,
которые разбивают выборочное пространство, и известно, что событие А осуще-
осуществилось. По определению, Р(В{\А) равна P<"pPR^'. Но
А = (А П Bi) U (А П В2) U (А П В3) U • • • U (А П Вп),
так что
Р(А) = Р(А п Вг) + Р(А П В2) + Р{А П В3) 4- • • • + Р(А П Вп)
Р{ЩА) Р(А п в^ + Р(А п в^ + р(А п 5з) + ... + Р(А п Вп)
Поскольку P(AnBi) = P(A\Bi)P{Bi), имеем
Р(Вг\А) =
Р(А\В2)Р(В2) + • • • + Р(А\Вп)Р(Вп) '
откуда следует, что если известны вероятности Р{В{) и Р(Л|В») для каждого г, то
можно определить Р(В»|А). Таким образом, мы "обратили" условную вероятность.
Например, предположим, что Сэм вышел из дому, чтобы купить замок для
гаража. Вероятность того, что он пойдет в "Andy's Automatic Unopeners" равна
0.3; вероятность того, что он пойдет в "Ben's Best Buys" равна 0.2; и вероятность
того, что за покупкой он пойдет в "Cheap Charley's Cash and Credit" равна 0.5.
Если он пойдет в "Andy's Automatic Unopeners", то вероятность, что он купит
высококачественный автоматический гаражный замок, равна 0.2. Если он пойдет
в "Ben's Best Buys", то вероятность сделать такую же покупку равна 0.4. Если
он пойдет в "Cheap Charley's Cash and Credit", то вероятность купить высокока-
высококачественный автоматический гаражный замок равна 0.3. Если Сэм приобрел такой
замок, то какова вероятность, что он купил его в "Ben's Best Buys"?
Пусть В\ — событие, что необходимый замок был куплен в "Andy's Automatic
Unopeners", B2 — событие, что этот замок был куплен в "Ben's Best Buys", иВ3-
событие, что этот замок был куплен в "Cheap Charley's Cash and Credit". Пусть
A — событие, которое состоит в том, что Сэм купил необходимый замок. Тогда
P(Bi) = .3, P(A|Bi) = .2, Р(В2) = .2, Р{А\В2) = .4, Р(В3) = .5 и Р(А\В3) = .3.
Поэтому
р(в ш = (-2)(.4) = А ^ 98
^ 2| ; C)B) + B)D) + (.5)(.3) 29 ~' *

РАЗДЕЛ 8.10. Теорема Байеса 385
Если события В\,В2, Б3,..., Вп равновозможны, то
Р(Вг) = Р(В2) = Р(В3) = ¦ • ¦ = Р(Вп).
Тогда соотношение для Р(В{\А) сводится к
Р{А\Вг)
P(Bi\A) =
Р{А\В,) + Р(А\В2) + Р(А\В3) + ¦¦¦ + Р(А\Вп) •
Например, предположим, что урна 1 содержит три красных, четыре синих
и шесть белых шаров, урна 2 содержит пять красных, три синих и два белых
шара, а урна 3 содержит четыре красных, два синих и четыре белых шара. Из
произвольным образом выбранной урны выбран шар. Если этот шар красный, то
какова вероятность, что выбрана урна 1? Пусть В\ — событие, что была выбрана
урна 1, В2 — событие, что была выбрана урна 2, а В3 — событие, что была выбрана
урна 3. Пусть R — событие, что был выбран красный шар. Поскольку выбор
урны носит случайный характер, то предположим, что Р(В\) = Р(В\) = P(Bi).
Следовательно, можно использовать упрощенную формулу. Имеем P(R\B\) = .3,
P{R\B2) = .5 и P(R\B3) = .4. Поэтому
УПРАЖНЕНИЯ
1. Компания производит автопокрышки на трех заводах. Сорок пять процентов
покрышек производится на заводе А, 25% — на заводе В и 30% производятся
на заводе С. Предположим, что 5% автопокрышек, произведенных на заводе
А, бракованные; на заводе В брак составляет 10%; а на заводе С бракован-
бракованные автопокрышки составляют 2%. Если купленная автопокрышка оказалась
бракованной, то какова вероятность, что она была произведена на заводе В?
2. Коробка 1 содержит три красных, четыре белых и один синий шар. Коробка 2
содержит два красных, четыре белых и два синих шара. Коробка 3 содержит
два красных, три белых и три синих шара. Если произвольным образом
выбранный шар оказался синим, то какова вероятность, что он был вынут
из коробки 3?
3. В коробке лежат три монеты. У одной монеты на обеих сторонах — "решки",
одна монета правильная, и еще одна монета выпадает "решкой" вверх в 70%
случаев. Монету выбирают случайным образом и подбрасывают. Если монета
выпадет "решкой", то какова вероятность того, что была выбрана правильная
монета?
4. Анализ крови является на 90% эффективным при диагнозе некоторого забо-
заболевания. В 4% случаев анализ ошибочно устанавливает болезнь у здорового
человека. Если 10% людей имеют это заболевание, то какова вероятность,
что человек, получивший результат анализа, подтверждающий болезнь, в
действительности имеет это заболевание?
5. Студент с одинаковой вероятностью может выбрать один из трех курсов
из блока социально-гуманитарных дисциплин. Если он выберет "Историю

386 ГЛАВА 8. Комбинаторика и вероятность
Канзаса, 1995-1997", то вероятность сдачи экзамена составит 40%. Если он
выберет "Курс устного счета повышенного типа II", то вероятность сдать
экзамен — 30%. При выборе курса под названием "Телевидение III: выбор
каналов", вероятность сдачи экзамена составит 60%. Если студент сдаст
экзамен, то какова вероятность того, что он выбрал "Историю Канзаса, 1995—
1997"?
6. В процессе производства 80% изделий получаются высококачественными.
Из тех, что проверены, 10% изделий признаны бракованными и не подлежа-
подлежащими продаже. Только 5% бракованных изделий улучшены и отправлены в
продажу. Если изделие поступило в продажу, то какова вероятность того,
что изделие имеет брак?
7. Допустим, что страховая компания классифицирует водителей как умелых,
неумелых и нормальных. Предположим, что 25% водителей являются уме-
умелыми, 50% — нормальными и 25% — неумелыми. Предположим также, что
у умелого водителя вероятность аварии в следующем году составит 10%,
вероятность аварии у нормального водителя — 20%, а вероятность аварии
у неумелого водителя составит 30%? Если в прошлом году у Сэма была
авария, то какова вероятность того, что он умелый водитель?
8. Подбрасывают правильную монету. Если она падает "решкой" вверх, то под-
подбрасывают две игральные кости. Игрок получает сумму в долларах, равную
выпавшей на кубиках. Если монета падает вверх "орлом", то подбрасывают
три монеты, и за каждую выпавшую "решку" игрок получает $4. Если игрок
выиграл $8, то какова вероятность, что первая монета выпала "решкой"?
8.11. ЦЕПИ МАРКОВА
Предположим, что проводится серия экспериментов с возможными исходами
si, 52,5з,..., sn. Назовем эти исходы состояниями. Предположимь, что мы начи-
начинаем в одном из этих состояний и что р-0^ — вероятность того, что мы начинаем
в состоянии Si. Далее будем предполагать, что вероятность данного исхода в те-
текущем эксперименте зависит только от исхода предыдущего эксперимента. Пусть
Pij — вероятность того, что в результате эксперимента состояние было изменено
от состояния Si к состоянию Sj. Таким образом, эксперимент начался в состоя-
состоянии Si и закончился в состоянии Sj. Пусть р\ ' — вероятность того, что исходом
эксперимента будет состояние sit Тогда
A) (о) , (о) , (о) , (о)
Pi = Pi Pit + Р2 P2i + Рз РЗг + ' ' ' + р\ 'Pit,
а это означает, что вероятность исхода в состоянии Si равна сумме вероятностей
начать эксперимент в некотором другом состоянии и окончить в состоянии Si.
Если эксперимент был начат в состоянии Sj, то в результате эксперимента исходом
должно стать некоторое состояние. Поэтому для каждого 0 < j < п имеем
РЯ + Pj2 + Pj3 + • • • + pjn = I-

РАЗДЕЛ 8.11. Цепи Маркова 387
= (р1 ,Р2 ?Рз ? • • • »Рп )• Предпо-
Предположим для простоты, что существуют три возможных состояния, поэтому р(°) —
(Р1°\р20)'Рз0))- Пусть Т — матрица
ПустьР(°) = (pj°\,40),Р<°\...,р<0)) и
Pll Pl2 Pl3
Р21 Р22 Р23
Р31 Р32 РЗЗ
Матрица Т называется матрицей перехода. В общем случае, матрица Т имеет
вид
~ Pll Р\2 Р\3 • • • Pin
Р21 Р22 Р23 • • • Р2п
Р31 Р32 РЗЗ • • • РЗп
. Рп\ Рп2 РпЗ
Пусть
/ l \ / @)
(а,Ь,с) = (р\ \
• Рп
Pll Р\2 Р\3
Р21 Р22 Р23
Р31 Р32 РЗЗ
тогда
@) , @) ,
= Pi JPl3 + р\ }Р23 +
@) A)
з РЗЗ = Рз ,
так что
Pll Pl2 Pl3
Р21 Р22 Р23
Р31 Р32 РЗЗ
ПРИМЕР 8.119. Погода классифицируется в прогнозах как ясная, умеренно пас-
пасмурная и пасмурная. Если погода ясная, то вероятность, что она будет ясной на
следующий день, составляет 0.5; вероятность, что она будет умеренно пасмурной,
составляет 0.4; а вероятность пасмурной погоды на следующий день составляет
0.1. Если погода умеренно пасмурная, то вероятность, что на следующий день она
будет ясной, равна 0.3; вероятность, что погода останется умеренно пасмурной,
равна 0.5; и вероятность, что погода станет пасмурной, равна 0.2. Если погода
пасмурная, то вероятность, что на следующий день она останется пасмурной, со-
составляет 0.4; вероятность, что она станет умеренно пасмурной, составляет 0.4; и
вероятность, что она станет ясной, составляет 0.2. Если вероятность ясной погоды
в воскресенье равна 0.6, а вероятность умеренной пасмурности — 0.4, то какова
вероятность, что погода в понедельник будет ясной? Какова вероятность, что во
вторник погода будет умеренно пасмурной?

388 ГЛАВА 8. Комбинаторика и вероятность
Если порядок, в котором перечисляются погодные условия, таков: ясно, уме-
умеренно пасмурно и пасмурно, то
Т =
.5 .4 .1
.3 .5 .2
.2 .4 .4
Следовательно,
= (.6, .4,0)
.5 .4 Л
.3 .5 .2
.2 .4 .4
= (.42, .44,.14),
и вероятность, что в понедельник будет ясная погода, равна 0.42.
Пусть р\ * — вероятность того, что во вторник будет ясная погода, р2 —
вероятность того, что во вторник будет умеренно пасмурно и р3 вероятность
того, что во вторник будет пасмурно. Пусть рB) = (р*2\ р?\р^)- Тогда
= (.42, .44,. 14)
.5 .4 Л
.3 .5 .2
.2 .4 .4
= (.37, .444, .186).
Следовательно, вероятность того, что во вторник будет умеренно пасмурная по-
погода, равна 0.444. ?
Пусть р;т) — вероятность, что исходом m-го проведения эксперимента будет
состояние sit и р<»*> = (р<Г\р{Г\р(Г\ ¦ ¦ -J^).
ТЕОРЕМА 8.120. Для любого положительного целого числа га имеем р(тп) =
@)
ДОКАЗАТЕЛЬСТВО. Докажем теорему, используя индукцию. Было показано, что
для га = 1 утверждение справедливо. Предположим, что оно справедливо для
п = к, так что pW = p(°^Tk. Поскольку
то
ПРИМЕР 8.121. В процессе опроса владельцев автомобилей трех американских
марок: марки Л, марки В и марки С, им был задан вопрос о том, какую торговую
марку они бы выбрали для следующей покупки. Среди владельцев автомобилей

РАЗДЕЛ 8.11. Цепи Маркова 389
марки А 20% в сказали, что они опять выбрали бы марку А, в то время как
50% ответили, что они бы перешли на марку В, а 30% заявили, что предпочли
бы марку С. Среди владельцев автомобилей марки В 20% сказали, что перейдут
на марку А, в то время как 70% заявили, что приобрели бы опять автомобиль
марки В, а 10% заявили, что в следующий раз предпочли бы марку С. Среди
владельцев автомобилей марки С, 30 процентов ответили, что перешли бы на
марку Л, 30% сказали, что перешли бы на марку В, а 40% заявили, что остались
бы верны той же торговой марке С.
(а) Если для первой машины некто приобрел автомобиль марки А, то какова
вероятность, что его второй машиной будет автомобиль марки С?
(б) Если при покупке первой машины покупатель подбросил монету, выбирая
между маркой В и маркой С, то какова вероятность, что его третьей машиной
будет автомобиль марки А?
(в) Если все три марки автомобилей равновозможны для покупки перво-
первого автомобиля, то какова вероятность, что третьей машиной станет автомобиль
марки В?
Матрица перехода для этого события имеет вид
.2 .5 .3
.2 .7 .1
.3 .3 .4
Для случая (а) имеем р@) = A,0,0), поэтому
РA) = A,0,0)
.2 .5 .3
.2 .7 Л
.3 .3 .4
Вероятность того, что вторая машина будет марки С, равна 0.3. Для случаев
(б) и (в) требуется найти
Т2 =
.23 .54 .23
.21 .62 .17
.24 .48 ..28
Для (б) имеем р<°) = @, .5, .5) и
.23 .54 .23
.21 .62 .17
.24 .48 ..28
= (.225, .55, .225),
поэтому вероятность того, что третий автомобиль будет марки А, равна 0.225. ?
ПРИМЕР 8.122. Для случая (в) имеем р<°) = (.333, .333, .333) и
р{2) = (.333, .333, .333)
.23 .54 .23
.21 .62 .17
.24 .48 ..28
= (.227, .547, .227),
где все числа округлены до трех цифр после десятичной точки. Поэтому вероят-
вероятность выбора марки С для третьей машины равна 0.227. ?

390 ГЛАВА 8. Комбинаторика и вероятность
¦ УПРАЖНЕНИЯ
1. Пусть осуществление событий А% В и С представлено состояниями s\, s2 и
s3 соответственно. Пусть переход осуществляется каждый день, и матрица
перехода имеет вид
" .2 .5 .3
.3 .6 Л
.2 .3 ..5
а) Какова вероятность того, что если событие А произошло в первый день,
то оно произойдет снова на третий день?
б) Какова вероятность того, что если событие В произошло в первый день,
то событие С произойдет на четвертый день?
в) Какова вероятность того, что если событие А произошло в первый день,
то событие В произойдет на пятый день?
2. Пусть осуществление событий А, В и С представлено состояниями sb s2 и
S3, соответственно. Пусть переход осуществляется каждый день, и матрица
перехода имеет вид
" .3 .4 .3
.4 .2 .4
.2 .5 .3
а) Какова вероятность того, что если событие А произошло в первый день,
то событие В произойдет на третий день?
б) Какова вероятность того, что если событие А произошло в первый день,
то событие С произойдет на четвертый день?
в) Какова вероятность того, что если событие С произошло в первый день,
то событие С произойдет на пятый день?
3. Аптека продает средство от изжоги трех торговых марок: Л, В и С Поку-
Покупатели меняют марки препарата согласно матрице перехода
.7 .2 .1
.2 .6 .2
.1 .1 .8
Если препарат приобретается ежемесячно, то:
а) Какова вероятность того, что если в этом месяце приобретен препарат
марки А, то через три месяца будет приобретен препарат марки С?
б) Какова вероятность того, что если в этом месяце приобретен препарат
марки В, то через два месяца будет приобретен препарат марки ?
в) Какова вероятность того, что если в этом месяце приобретен препарат
марки С, то через три месяца будет опять приобретен препарат марки С?
Предположим, что Конгресс объявил о возможном сокращении налогов, и
это сообщение распространяется от человека к человеку. Если сокращение

РАЗДЕЛ 8.11. Цепи Маркова 391
налогов состоится, то вероятность того, что сообщение будет передано сле-
следующему человеку правильно, составляет 0.6. Если сокращения налогов не
будет, то вероятность правильности передачи информации составит 0.7.
а) Если сокращение налогов состоится, то какова вероятность, что четвер-
четвертый человек, услышавший эту новость, услышал ее правильно?
б) Если сокращение налогов не состоится, то какова вероятность, что третий
человек, услышавший эту новость, услышит ее правильно?
в) Если сокращение налогов не состоится, то какова вероятность, что пя-
пятый человек, услышавший эту новость, поймет, что сокращение налогов
состоится?
5. Команда А и команда В участвуют в ежегодном чемпионате США по бейс-
бейсболу. Каждая команда имеет равные шансы выиграть первую игру. Если
команда А выиграет первую игру, то вероятность ее победы в следующей
игре равна 0.6. Если первую игру выиграет команда В, то вероятность ее
победы в следующей игре равна 0.7. Какова вероятность, что команда В вы-
выиграет третью игру? Какова вероятность, что команда А выиграет четвертую
игру?
6. У самолета четыре мотора. Для выполнения боевого задания ему необходимо
оставаться в воздухе в течение часа. Если из-за вражеского обстрела веро-
вероятность выхода из строя одного из моторов в любой 15-минутный период
времени равна 0.25 и для продолжения полета самолету нужны, по край-
крайней мере, два мотора, то какова вероятность, что самолет вернется на базу?
Предполагается, что вероятность того, что самолет с тремя поврежденными
моторами будет оставаться в воздухе настолько долго, что может выйти из
строя четвертый мотор, равна 0.
7. В колледже 80% первокурсников становятся второкурсниками. 10% бросают
учебу или переводятся. 90% в второкурсников на следующий год становят-
становятся студентами предпоследнего года обучения. 5% второкурсников бросают
учебу или переводятся. 95% студентов предпоследнего курса становятся на
следующий год старшекурсниками. 2% студентов предпоследнего курса бро-
бросают учебу или переводятся. 1% старшекурсников бросают учебу или перево-
переводятся, а 98% заканчивают колледж. Те, кто не заканчивают, бросают учебу,
переводятся или остаются на второй год обучения. Какова вероятность, что
поступивший в колледж в течение четырех лет бросит учебу или переве-
переведется? Если 1000 новичков стали студентами, то сколько из «их закончат
обучение через четыре года? Сколько закончат обучение через пять лет?

ГЛАВА
АЛГЕБРАИЧЕСКИЕ
СТРУКТУРЫ
9.1. ВНОВЬ О ЧАСТИЧНО УПОРЯДОЧЕННЫХ МНОЖЕСТВАХ
Согласно определению 2.44, отношение R на множестве А есть отношение частич-
частичного порядка, если оно рефлексивно, антисимметрично и транзитивно. Множество
А в этом случае назывется частично упорядоченным множеством или ЧУ-
множеством с порядком R. Отношение частичного порядка будем обозначать
символом < (или >, где а > b если а < Ь). Частично упорядоченное множество
А с порядком < будем обозначать через (А, <).
Согласно определению 2.47, два элемента а и b частично упорядоченного
множества (ЧУ-множества) E, <) сравнимы, если а < b или b < а. Если каждые
два элемента частично упорядоченного множества E, <) сравнимы, тогда E, <)
называется вполне упорядоченным множеством, или цепью.
ОПРЕДЕЛЕНИЕ 9.1. Для подмножества В ЧУ-множества А элемент а из А
назывется верхней гранью В, если b < а (или а > Ь) для всех b из В.
Элемент а называется наименьшей верхней гранью (нвг) подмножества В,
если (а) а — верхняя грань В и (б) если любой другой элемент а1 множества
А является верхней гранью В, то а < а'. Наименьшая верхняя грань для всего
ЧУ-множества А (если она существует) называется наибольшим элементом
A. Для подмножества В ЧУ-множества А элемент а из А называется нижней
гранью Б, если а < Ъ (или Ъ > а) для всех b из В. Элемент а называется
наибольшей нижней гранью (ннг) подмножества В, если (а) а — нижняя
грань В] (б) если любой другой элемент о! из А является нижней гранью
B, то а > о!. Наибольшая нижняя грань всего ЧУ-множества А (если она
существует) называется наименьшим элементом А.
ОПРЕДЕЛЕНИЕ 9.2. Элемент а подмножества В ЧУ-множества А называется
максимальным элементом В, если для каждого элемента b E В из того, что
b > а, следует b = а. Другими словами, во множестве В нет элемента, который

РАЗДЕЛ 9.1. Вновь о частично упорядоченных множествах 393
был бы "больше", чем а. Элемент а подмножества В ЧУ-множества А называ-
называется минимальным элементом В, если для каждого элемента Ь е В из того,
что b < а, следует b = а. Другими словами, в В нет элемента, который был бы
"меньше", чем а. Обычно термины "минимальный" и "максимальный" элемент
относятся ко всему множеству, т.е. А = В.
ПРИМЕР 9.3. Пусть, как в примере 2.45, С = {1,2,3} и X — булеан множества
С:
X = Р(С) = {0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.
Определим отношение < на множестве X таким образом: Т < V, если Т С V. По
определению, {1,2} есть наибольшая нижняя грань для {0, {1}, {2}}, а также
для {0, {1}, {2}, {1,2}}. Множество {1,2,3} — наименьшая верхняя грань для X.
Элемент 0 является наибольшей нижней гранью для всех трех множеств. ?
ПРИМЕР 9.4. Рассмотрим множество X = {0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}} с
таким же отношением порядка, как и в примере 9.3. В этом случае множества
{1,2}, {1,3}, и {2,3} являются максимальными элементами множества X, но в
X нет наибольшего элемента. Такая ситуация возможна, потому что данные три
максимальных элемента не сравнимы между собой. D
ПРИМЕР 9.5. Рассмотрим множество X = {{1}, {2}, {3}, {1,2}, {1,3}, {2,3},
{1,2,3}} с тем же отношением порядка, как и в примере 9.3. В этом случае
{1}, {2} и {3} — минимальные элементы множества X, но наименьшего элемен-
элемента множество X не имеет. ?
ПРИМЕР 9.6. Пусть Т — множество всех положительных делителей числа 30
и <i есть отношение порядка, которое задается таким образом: га <i n, если
m делит п. Наименьшая верхняя грань для {3,5} — число 15. Понятно, что
наименьшая верхняя грань, 30, и наибольшая нижняя грань, 1, множества Т
сравнимы. Понятно, что 5 <i 15, поскольку 15 делится на 5, но 5 и 6 не сравнимы.
?
ПРИМЕР 9.7. Наименьшая верхняя грань и наибольшая нижняя грань множества
не обязательно являются элементами этого множества. Пусть Q — множество
рациональных чисел и пусть < — обычное отношение "меньше или равно", и < —
отношение "меньше" для рациональных чисел. Тогда для множества А = {х Е
Q : 0 < х < 1} с частичным порядком < имеем 0 = ннг(Л) и 1 = нвг(А), однако
0,1 g A. ?
Если для каждого двухэлементного подмножества ЧУ-множества А суще-
существует наименьшая верхняя грань, принадлежащая А, то на множестве А можно
определить следующее бинарное отношение. Если а и b принадлежат А, то пусть
aVfc = нвг{а,6}. Если используются обозначения булевой алгебры, то вместо aV6
записывают а + 6.
ОПРЕДЕЛЕНИЕ 9.8. ЧУ-множество Л, все двухэлементные подмножества ко-
которого имеют наименьшую верхнюю грань, принадлежащую А, называется
верхней полурешеткой и обозначается (A,V) или (А, +).

394 ГЛАВА 9. Алгебраические структуры
Если для каждого двухэлементного подмножества ЧУ-множества А суще-
существует наибольшая нижняя грань, принадлежащая А, то на множестве А можно
определить следующее бинарное отношение. Если а и b принадлежат А, то пусть
a/\b = ннг{а, Ь}. Если используются обозначения булевой алгебры, то вместо a/\b
записывают a • 6.
ОПРЕДЕЛЕНИЕ 9.9. ЧУ-множество А, все двухэлементные подмножества ко-
которого имеют наибольшую нижнюю грань, принадлежащую А, называется
нижней полурешеткой и обозначается (А, Л ) или (Д •).
В примере 9.3 {1,2} V {1,3} = {1,2,3} и {1,2} Л {1,3} = {1}. В этом случае
наименьшая верхняя грань и наибольшая нижняя грань — объединение и пе-
пересечение множеств соответственно, и обозначения совпадают с обозначениями
теории множеств.
В примере 9.6 6 V 15 = 30 и 6 Л 15 = 3. В этом случае наименьшая верхняя
грань и наибольшая нижняя грань — это наименьшее общее кратное и наиболь-
наибольший общий делитель соответственно.
Доказательство приведенной ниже теоремы, в которой сформулированы ал-
алгебраические свойства полурешеток, предоставляется читателю.
ТЕОРЕМА 9.10.
а) Пусть А — верхняя полурешетка. Тогда для всех а,Ъ,с € А а V (Ь V с) =
(aV b)V с, а V а = а и a\/b = bV а.
б) Пусть А — нижняя полурешетка. Тогда для всех а, 6, с Е А а Л F Л с) =
(a Ab) Ас, а Л а = а и a Ab = b Ла.
УПРАЖНЕНИЯ
1. Постройте диаграмму Гессе (см. раздел 2.6) для ЧУ-множества из приме-
примера 9.3.
2. Постройте диаграмму Гессе для ЧУ-множества из примера 9.6.
3. Постройте диаграмму Гессе для ЧУ-множества из примера 9.4.
4. Постройте диаграмму Гессе для ЧУ-множества из примера 9.5.
5. По диаграмме Гессе для ЧУ-множества, изображенной на рис. 9.1, опреде-
определите:
а) наибольший элемент ЧУ-множества (если он существует);
б) наименьший элемент ЧУ-множества (если он существует);
в) максимальный и минимальный элементы ЧУ-множества;
г) является ли рассматриваемое ЧУ-множество верхней или нижней полу-
полурешеткой (или и тем, и другим)?

РАЗДЕЛ 9.1. Вновь о частично упорядоченных множествах 395
f.
Рис. 9.1
6. По диаграмме Гессе для ЧУ-множества, изображенной на рис. 9.2, опреде-
определите:
а) наибольший элемент ЧУ-множества (если он существует);
б) наименьший элемент ЧУ-множества (если он существует);
в) максимальный и минимальный элементы ЧУ-множества;
г) является ли рассматриваемое ЧУ-множество верхней или нижней полу-
полурешеткой (или и тем, и другим)?
d Рис. 9.2
7. По диаграмме Гессе для ЧУ-множества, изображенной на рис. 9.3, опреде-
определите:
а) наибольший элемент ЧУ-множества (если он существует);
б) наименьший элемент ЧУ-множества (если он существует);
в) максимальный и минимальный элементы ЧУ-множества;
г) является ли рассматриваемое ЧУ-множество верхней или нижней полу-
полурешеткой (или и тем, и другим)?
ьЬ Рис. 9.3
8. По диаграмме Гессе для ЧУ-множества, изображенной на рис. 9.4, опреде-
определите:
а) наибольший элемент ЧУ-множества (если он существует);
б) наименьший элемент ЧУ-множества (если он существует);
в) максимальный и минимальный элементы ЧУ-множества;
г) является ли рассматриваемое ЧУ-множество верхней или нижней полу-
полурешеткой (или и тем, и другим)?

396 ГЛАВА 9. Алгебраические структуры
Рис. 9.4
9. По диаграмме Гессе для ЧУ-множества, изображенной на рис. 9.5, опреде-
определите:
а) наибольший элемент ЧУ-множества (если он существует);
б) наименьший элемент ЧУ-множества (если он существует);
в) максимальный и минимальный элементы ЧУ-множества;
г) является ли рассматриваемое ЧУ-множество верхней или нижней полу-
полурешеткой (или и тем, и другим)?
a Рис. 9.5
10. Основываясь на диаграммах Гессе из предыдущих упражнений, опишите их
характерные свойства, которые гарантируют, что
а) ЧУ-множество имеет максимальный элемент;
б) ЧУ-множество имеет наименьшую верхнюю грань (или наибольший эле-
элемент);
в) ЧУ-множество имеет минимальный элемент;
г) ЧУ-множество имеет наибольшую нижнюю грань (или наименьший эле-
элемент).
11. Докажите следующее:
а) пусть А — верхняя полурешетка. Тогда а V F V с) = (а V 6) V с для всех
а, 6, с Е A, a V а = а для всех a ? А и aV b = b\/ a для всех а, Ь Е А\
б) пусть А •— нижняя полурешетка. Тогда а Л (Ь Л с) = (а Л 6) Л с для всех
а, 6, с е А, а Л а = а для всех a e А и a Ab = b Aa для всех a,b e А.
12. Докажите, что в каждом конечном ЧУ-множестве имеются максимальный и
минимальный элементы.
13. Докажите, что в каждой конечной верхней полурешетке имеется наимень-
наименьшая верхняя грань (или наибольший элемент).

РАЗДЕЛ 9.2. Полугруппы и полурешетки 397
14. Докажите, что в каждой конечной нижней полурешетке имеется наибольшая
нижняя грань (или наименьший элемент).
15. В главе 2 булевы операции V и Л на множестве {0,1} определены таблицами:
V
0
1
0
0
1
1
1
1
Л
0
1
0 1
0 0
0 1
Была введена также булева матрица как матрица, у которой все элементы О
или 1. Если А = [Aij] и В = [Bij] — булевы матрицы размерности га х п, то
U — А У В определяется как
V = АаВ определяется как
V В^ при 1 < г < га, 1 < j < п\
ЛВ^ при 1 < г < га, 1 < j < п.
Пусть 5 — множество всех булевых матриц размерности пхп. На множестве
5 определим отношение < следующим образом: А < В для А, В Е 5, если
А^ < В^ при 1 < г, j < п.
а) Докажите, что множество 5 с этим отношением представляет собой ЧУ-
множество.
б) Докажите, что Av В — наименьшая верхняя грань для {А,В}.
в) Докажите, что А/\В — наибольшая нижняя грань для {А,В}.
г) Докажите, что 5 является и верхней, и нижней полурешеткой.
д) Что является наибольшим и наименьшим элементом для множества 5?
9.2. ПОЛУГРУППЫ И ПОЛУРЕШЕТКИ
В определении 4.21 бинарная операция на множестве 5 определена как функция
Ь : 5 х 5 —> 5. Поскольку множество значений бинарной операции на множестве
5 является подмножеством множества 5, то, по определению, бинарная операция
обладает свойством замыкания, когда результат операции над двумя элементами
г и s множества 5 также является элементом S. Существует достаточно много
примеров бинарных операций.
Например, если 5 — множество положительных целых чисел, то произве-
произведение и сумма — бинарные операции, поскольку и произведение, и сумма по-
положительных целых чисел есть положительное целое число. Во многих случаях
такие операции являются еще и ассоциативными, например, как для сложения
положительных целых чисел (a + b)+c = a + (b + c) и умножения положительных
целых чисел (а • 6) • с = а • F • с). Пусть S — множество матриц размерности пхп,
элементы которых — целые числа. Сумма и произведение элементов из 5 сно-
снова являются элементами S. Более того, если Л, В и С — матрицы размерности
п х п, то (А • В) • С = А • {В • С) и (А + В) + С = А + (В + С). В приведенном
ниже определении бинарным операциям с такой структурой даны специальные
названия.

398 ГЛАВА 9. Алгебраические структуры
ОПРЕДЕЛЕНИЕ 9.11. Множество 5 с такой бинарной операцией * на 5 х 5,
что для всех а, Ь и с из 5 имеет место (a*b) * с = a* (b* с), называется по-
полугруппой и обозначается E,*), или просто 5, если понятно, какая операция
имеется в виду. Если, в дополнение к этому, для всех а и b из 5 выполня-
выполняется а * Ъ = Ь * а, то множество 5 с оператором * называется абелевой, или
коммутативной полугруппой. Если в E,*) существует элемент / такой, что
1*а = а*1 = а для всех а из А, то такое I называется единицей полугруп-
полугруппы E,*), а E,*) называется полугруппой с единицей, или моноидом. Если
E,*) — полугруппа, и 5 С 5, то 5_ называется подполугруппой полугруппы
5, если * — бинарная операция на 5. Это эквивалентно следующему:^,*) —
подполугруппа полугруппы E,*), если 5 С 5, и для каждых a,b € S имеем
а * b ? 5.
Отметим еще раз: тот факт, что * является бинарной операцией на множестве
S x S, означает, что если s, 5' Е 5, то s * s' Е S. Указанное свойство называется
замкнутостью.
ПРИМЕР 9.12. Множество 5 матриц размерности пхп является моноидом E, •).
Единицей в данном случае будет матрица / с единицей в качестве элементов
главной диагонали и нулем в качестве прочих элементов, так что
j = (l, если г = j;
13 | 0, если г ф j.
Следовательно, единичная матрица размерности 3x3 имеет вид
?
1 О О
0 10
0 0 1
ПРИМЕР 9.13. Если E,-) — полугруппа матриц размерности пхп, элементами
которых являются рациональные числа с операцией матричного умножения и если
E, •) -^полугруппа матриц размерности пхп, элементы которых — целые числа,
тогда E,-) — подполугруппа полугруппы E,-). ?
ПРИМЕР 9.14. Для положительного целого числа п положим S° = {х : х целое
число и х ^ п} U {0}. Полугруппа 5° — коммутативный моноид с операцией
сложения целых чисел и нулем в качестве единицы. Пусть 5^ = {х : х целое
число и х ^ п) U {1}. Полугруппа 5^ — коммутативный моноид с операцией
умножения целых чисел с единицей в качестве единицы. Если т > п, то 5^ —
подполугруппа полугруппы 5^ и 5^ - подполугруппа полугруппы 5^ ?
ПРИМЕР 9.15. Пусть 5 — множество всех функций из непустого множества А в
само множество А с бинарной операцией композиции. Таким образом, для /, g e 5
результат операции fog определяется как (/ о g)(a) = f(g(a)) для всех а Е А.
Поскольку для f,g,h ? 5 имеет место {(f°g)°h)(a) = (f°(g°h))(a) = f(g(h(a)))
для всех а ? А, то (fog) oh — fo(goh), поэтому 5 — полугруппа. Далее функция
/ : А —> А, определенная как 1(а) = а для всех а ? А, является единицей в 5 и,
следовательно, 5 — моноид. ?

РАЗДЕЛ 9.2. Полугруппы и полурешетки 399
ПРИМЕР 9.16. Пусть А — конечный набор символов. Такое множество символов
называется алфавитом. Например, А могло бы быть подмножеством английского
алфавита или просто множеством {0,1}. Строка или слово символов из множе-
множества А имеет вид а^аз^... ап, где п{ е А. Таким образом, если А = {0,1}, то
1, 100, 101, 11011 и 0001 — возможные строки символов из множества А. Кроме
того, определим пустую строку, которая обозначается А и не содержит никаких
символов. Пусть Л* обозначает множество всех строк алфавита А. Введем бинар-
бинарную операцию о, называемую конкатенацией на А*, следующим образом: если
... an и ЬхЬ2Ь^ЬА • • • bm E А*, то
• • • an ° ^162^3^4 . . . Ьт = aiB2a3a4 • • • йтА^^З^ • • • bm.
Например, если А = {0,1}, то 11011 о 100010 = 11011100010. В частности, если
и — строка в А*, то Aoai = u;oA = w, и это говорит о том, что если строке
предшествует пустая строка или пустая строка следует за ней, то в результате
конкатенации получаем ту же самую строку.
Пусть п\п2 ... an, 6162 ... bra и с\С2 . •. ср Е А*. Тогда
... an о b\b2 ... Ъш) о с\с2 .. .ср = {а\п2 ... an о b\b2 ... bm) ° с\с2 ... ср =
... anbib2 ... bm о с\С2 . ..ср =
... an о
... an о (bib2 ... bm о cic2 ... cp),
и бинарная операция конкатенации ассоциативна на А*, так что множество А*
вместе с операцией конкатенации представляет собой полугруппу. Далее, по-
поскольку А — это единица, то А* —- моноид. Заметим, что этот моноид с оче-
очевидностью некоммутативен. Если А С А, то А* — подполугруппа полугруппы
А*. Полугруппа Л*называется свободной полугруппой над алфавитом А. ?
ПРИМЕР 9.17. Пусть Zn = {[0], [1], [2],..., [п - 1]} — множество классов вычетов
по модулю и (см. раздел 3.6). Согласно теореме 3.54 (Zn,+) и (Zn,-) вполне
определены. Предоставляем читателю доказать, что (Zn,+) и (Zn,-) являются
полугруппами. ?
Пусть E, •) — полугруппа, и а Е 5. Определим an рекурсивно, полагая
а0 = 1 и ап = а • ап~1. Отсюда непосредственно следует, что а1 = а. Предлагаем
читателю, используя метод индукции, показать, что ак • am = afc+m для всех
целых чисел fc, m > 0. Множество
является подполугруппой полугруппы 5.
ОПРЕДЕЛЕНИЕ 9.18. Полугруппа (а) называется циклической полугруппой.
Точнее, она называется циклической полугруппой, порожденной а.

400 ГЛАВА 9. Алгебраические структуры
Доказательство следующей теоремы оставляем читателю.
ТЕОРЕМА 9.19. Пусть E,-) — полугруппа и аьа2,аз, • • • >afc € S- Пусть А =
{ai,a2,a3,... ,afc} и А* = (^1,^2,^3, • • • ,a/c) — множество, состоящее из всех
конечных произведений ai,a2,a3,afc. Тогда А* — полугруппа. Более того, А* —
наименьшая подполугруппа полугруппы 5, содержащая А.
ОПРЕДЕЛЕНИЕ 9.20. Полугруппа А* называется полугруппой, порожденной
множеством А. Если для каждого собственного подмножества В множества А
имеем В* ф Л*, то А называется минимальным порождающим множеством
для полугруппы А*.
ОПРЕДЕЛЕНИЕ 9.21. Пусть E, •) и (Г, о) — полугруппы и / : 5 -> Т — такая
функция, что f(s • sf) = f(s) о f(sf). Функция / называется гомоморфизмом
из 5 в Т.
ТЕОРЕМА 9.22. Пусть E,-) и (Т, о) — полугруппы и / : S -> Т — гомоморфизм
из S в Т. Если 5 — подполугруппа полугруппы 5, то /E) — подполугруппа
полугруппы Т.
ДОКАЗАТЕЛЬСТВО. Пусть t,t' G /E). Существуют такие s,s' G 5, что f(s) = t
и f(s') = t'. По определению полугруппы s-s' E 5. По определению гомоморфизма
f(s • s') = f(s) о f(s') = t-t\ т.е. t -11 G /E) и /E) — полугруппа. ¦
Доказательство приведенной ниже теоремы оставляем читателю.
ТЕОРЕМА 9.23. Пусть E,-) и (Т, о) — полугруппы и / : 5 -»• Т — гомоморфизм
из S в Т. Если Т — подполугруппа полугруппы Т, то f~1(T) — подполугруппа
полугруппы 5.
ОПРЕДЕЛЕНИЕ 9.24. Пусть E, •) — полугруппа и R — отношение эквивалент-
эквивалентности на 5. Если R обладает свойством, что если siRs2 и 53Д54, то выпол-
выполняется S1S3RS2S4 для всех si,s3,s2,s4 ^ ^' тогда ^ называется отношением
конгруэнтности.
ТЕОРЕМА 9.25. Пусть E,-) и (Т, о) — полугруппы и / : 5 -> Т — гомоморфизм
из 5 в Т. Определим отношение R на множестве S таким образом: si?s', если
/E) = /(s'). Тогда отношение R — отношение конгруэнтности.
ДОКАЗАТЕЛЬСТВО. Для всех s G 5 f(s) = /E), поэтому Д — рефлексивно.
Если f(s) = /(s;), то /(s;) = /E), и R — симметрично. Если /(s) = /(s') и
/(s') = /(s"), то /(s) = /(s")> поэтому Д транзитивно. Допустим, siRs2 и s3i?s4.
Следовательно, /(si) = /(^2) и /($з) = /(^4). Учитывая, что / — гомоморфизм,
получаем
f(Sl ¦ S3) = /(Si) О /(S3) = /Ы О /(в4) = /(«2
поэтому 5i • ssRs2 • 54.

РАЗДЕЛ 9.2. Полугруппы и полурешетки 401
ОПРЕДЕЛЕНИЕ 9.26. Коммутативная полугруппа E, *) называется полуре-
полурешеткой, если а * а = а для всех а Е S. Элемент а полугруппы называется
идемпотентом, если а* а = а. Таким образом, полурешетка — это коммута-
коммутативная полугруппа, в которой каждый элемент является идемпотентом. Если
E, *) — полурешетка и 5 С 5, то_5 будет подполурешеткой полурешетки E, *),
если * — бинарная операция на 5. Эквивалентно, E, *) — подполурешетка по-
полурешетки E, *), если 5 С 5, и для всех а, 6 Е 5 имеем а * b E S.
Из теоремы 9.10 следует, что верхние и нижние полурешетки являются полу-
полурешетками. Более того, каждую полурешетку можно рассматривать как верхнюю
или как нижнюю полурешетку.
ТЕОРЕМА 9.27. Пусть 5 — полурешетка. Определим на 5 отношение < таким
образом: а < 6, если а * 6 = 6 для а, Ь Е 5. Тогда E, <) — это ЧУ-множество,
и а * b — наименьшая верхняя грань для а и Ь. Следовательно, E, *) — верхняя
полурешетка. Аналогично, E, *) можно рассматривать как нижнюю полурешетку.
ДОКАЗАТЕЛЬСТВО. Поскольку а* а = а для всех а Е 5, а < а, поэтому E, <)
рефлексивна. Если а < b и b < а, тоа*Ь = Ьиа*Ь = 6*а = а. Поэтому b = а и
E, <) антисимметрична. Допустим, что а < b и b < с. Имеем а*Ь = 6и6*с = с.
Получаем
а*с = а*(Ь*с) =
= (а * 6) * с =
= b * с =
= с
и а < с. Следовательно, E, <) транзитивна и является ЧУ-множеством.
Теперь покажем, что а*Ь — наименьшая верхняя грань для а и Ь. Поскольку
а * (а *Ь) = (а * а) * b =
= а * Ь,
то а < а * Ь. Точно так же,
b * (а * Ь) — b * F * а) =
= (Ь * 6) * а =
= b * а =
= а * 6,
так что 6 < а*6. Поэтому а*6 — верхняя грань для а и 6. Предположим, что с —
тоже верхняя грань для а и Ь, тогда а*с = си6*с = с. Следовательно,
(а * Ь) * с = а * (Ь * с) =
= а * с =
= с
и а * b < с. Поэтому а * b — наименьшая верхняя грань для а и Ь, и E, <) —
верхняя полурешетка. ¦

402 ГЛАВА 9. Алгебраические структуры
¦ УПРАЖНЕНИЯ
1. Пусть E, U) — полурешетка всех подмножеств множества {а, 6, с} с операци-
операцией объединения. Найдите три разные подполурешетки полурешетки E, и).
2. Пусть E, •) — полурешетка на множестве всех матриц, элементы которых —
вещественные числа, а операция — матричное умножение. Найдите пять
подполугрупп полурешетки E,-).
3. Докажите, что множество положительных целых чисел вида 4fc + l, где к —
неотрицательное целое число, образует полугруппу с операцией умножения.
4. Найдите пять подполугрупп множества положительных рациональных чисел
с операцией сложения.
5. Докажите, что (Zn,+) и (Zn,-) являются полугруппами для любого целого
числа и > 1.
6. Докажите по методу индукции, что если S — полугруппа и a e 5, то ^-а171 =
ак+т для всех целых чисел га, n > 0.
7. Докажите теорему 9.19. Пусть E,-) — полугруппа и ai,a2,a3,... , а* Е 5.
Пусть А = {ai,a2,a3,... , a/J и А* = (ai,a2,a3,... ,а^> — множество всех
конечных произведений а1,а2,аз,а?. Тогда А* — полугруппа. Более того,
А* — наименьшая подполугруппа полугруппы 5, содержащая А.
8. Докажите теорему 9.23. Пусть E, •) и (Г, о) — полугруппы, и / : 5 —> Т —
гомоморфизм из 5 в Т. Если Т — подполугруппа полугруппы Т, то f'1^) —
подполугруппа полугруппы S.
9. Пусть E, о) — полугруппа всех функций на множестве А с операцией ком-
композиции.
а) Покажите, что множество взаимно однозначных соответствий образует
подполугруппу полугруппы 5.
б) Если / Е 5 — идемпотент, то / о / = /. Такая функция называется ре-
тпракционным отображением. Образ / называется ретрактором. По-
Покажите, что ретракционное отображение является взаимно однозначным
отображением на свой образ.
в) Покажите, что функции f(x) = |х|, д(х) = |_?j и h(x) = [x], заданные на
множестве действительных чисел, являются ретракционными отображе-
отображениями. Что представляют собой соответствующие ретракторы?
г) Коммутируют ли функции из пункта (в)? Иначе, верно ли, что fog = go/?
д) Образуют ли функции из пункта (в) полурешетку?
10. Пусть 5 — множество действительных чисел и * — бинарный оператор,
определенный соотношением а* 6 = т&х(а,6). Покажите, что E,*) — полу-
полугруппа. Является ли E, *) полурешеткой?
11. Пусть E, *) — множество матриц размерности и х п с операцией умножения
в качестве бинарной операции. Известно, что для (n x п)-матриц А и В
выполняется det(A) • (detB) = det(AB). Используя этот факт, покажите,
что матрицы, у которых det ф 0, образуют моноид. Что можно сказать о
матрицах, у которых определитель равен О?
12. Приведите пример бинарной операции * на множестве вещественных чисел,
относительно которой они не образуют полугруппу.

РАЗДЕЛ 9.3. Решетки 403
13. Покажите, что единица в моноиде единственна в том смысле, что существует
только один элемент, например, / такой, что а*1 = 1*а = а для всех а в
моноиде.
14. Пусть 5 — множество. Определим операцию * на 5 таким образом: а*6 = Ъ
для всех a,b e S. Докажите, что E,*) — полугруппа, в которой каждый
элемент является идемпотентом. Почему E,*) не является полурешеткой?
9.3. РЕШЕТКИ
В предыдущем разделе были рассмотрены множества с одной бинарной операцией.
В данном разделе рассматриваются множества с двумя бинарными операциями.
ОПРЕДЕЛЕНИЕ 9.28. ЧУ-множество E, <), которое является и нижней, и
верхней полурешеткой, называется решеткой.
В решетке E, <) будем обозначать наименьшую верхнюю грань а, 6 Е S че-
через а V6 (называемое соединением а и 6), а наибольшую нижнюю грань a,b E S
через аЛЬ (называемое пересечением а к Ъ). Решетка будет обозначаться че-
через E,V,A), чтобы подчеркнуть используемые бинарные операции. На основе
свойств наименьшей верхней грани и наибольшей нижней грани докажем следу-
следующие свойства решетки, которые можно использовать в качестве альтернативного
определения.
ТЕОРЕМА 9.29. Пусть E, V, Л) — решетка, тогда следующие свойства имеют
место для всех a,b,ce S.
а) Коммутативность
а ЛЬ = b Л а;
б) Ассоциативность
(а Л Ь) Л с = а Л (Ь Л с);
в) Поглощение
а Л (а V 6) = а;
а V (а Л 6) = а.
ДОКАЗАТЕЛЬСТВО. Для доказательства пунктов (а) и (б) см. теорему 9.10 и
упражнения в конце раздела. Покажем, что аЛ(а\/ Ь) = а:
а < а по определению частичного порядка ;
а < a V b по определению наименьшей верхней грани.

404 ГЛАВА 9. Алгебраические структуры
Поэтому а есть нижняя грань для {o,aVb}. Допустим, что с — нижняя грань
для {a,aVb}. Тогда с< а, так что а — наибольшая нижняя грань для {а,а\/Ь} и,
следовательно, а = а Л (а V 6). Доказательство того, что a V (а Л 6) = а оставляем
читателю. ¦
ПРИМЕР 9.30. Пусть 5 — булеан (множество всех подмножеств) множества А с
частичным порядком U <Vy если U С V для всех С/, V е S. Тогда нвг{С/, V} =
U U V и ннг{?У, V} = U П V, поэтому E, U, П) является решеткой. ?
ПРИМЕР 9.31. Пусть 5 — множество положительных целых чисел с частичным
порядком: п < га, если га делит п. Тогда нвг{т, п} = Н0К(т, и) и ннг{т, п) =
НОД(т, п) для всех т,п € S. Поэтому 5 с бинарными операциями НОК и НОД
является решеткой. ?
ПРИМЕР 9.32. Рациональные, действительные и целые числа с обычным ча-
частичным порядком образуют решетку, где нвг{т,п} = тах(т, п) и ннг{т, п)
= min(ra, n). ?
ОПРЕДЕЛЕНИЕ 9.33. Непустое подмножество^ решетки^ E, V, Л) называется
подрешеткой решетки 5, если для всех a.b^SaAbESnaVbeS.
Следовательно, в примере 9.30, если В — подмножество множества А и 5 —
булеан множества В, то (S, и,П) будет подрешеткой решетки E,и,П). В приме-
примере 9.31, если S — _множество всех положительных делителей фиксированного
целого числа п, то 5 с бинарными операциями НОК и НОД будет подрешеткой
решетки S. В примере 9.32 целые числа образуют подрешетку рациональных чи-
чисел, а рациональные числа, в свою очередь, образуют подрешетку действительных
чисел.
ОПРЕДЕЛЕНИЕ 9.34. Решетка E, V,A) называется ограниченной, если мно-
множество 5, как ЧУ-множество, имеет наименьшую верхнюю грань и наиболь-
наибольшую нижнюю грань. Наименьшая верхняя грань обозначается через 1, а наи-
наибольшая нижняя грань — через 0. Эквивалентно, решетка ограничена, если
существуют элементы 0,1 е5 такие, что 0Ла = 0 и lVa= 1 для всех а ? S.
Поскольку 0 — наименьший элемент множества, и 1 — наибольший элемент
множества, получаем следующий результат.
ТЕОРЕМА 9.35. В ограниченной решетке 1Ла= 1 и OVa = a для всех а из
решетки.
ПРИМЕР 9.36. Решетка в примере 9.30 ограничена, А — максимальный элемент
решетки и 0 — минимальный элемент. ?
ПРИМЕР 9.37. В примере 9.31, если 5 — полурешетка всех положительных де-
делителей фиксированного целого числа п, то 5 ограничена с максимальным эле-
элементом п и минимальным элементом 1. ?

РАЗДЕЛ 9.3. Решетки 405
В главе 2 отмечалось, что для множеств А, В и С выполняются соотношения
АП(ВиС) = (А П В) U {А ПС) и A U (В П С) = (ЛиВ)П(ЛиС). Эти
соотношения были названы свойством дистрибутивности для множеств. Далее
будет дано определение аналогичных свойств для решеток.
ОПРЕДЕЛЕНИЕ 9.38.
кои, если для всех а,
Решетка E, V,
6, с Е 5 имеем
а Л F V с) =
aV (ЬАс) =
Л)
(а
(а
называется дистрибутивной решет-
Л
V
Ь)
V
Л
(а
(а
Л
V
с);
с).
В качестве упражнения предлагаем читателю доказать, что решетки, изоб-
изображенные на рис. 9.6, не дистрибутивны.
Рис. 9.6
Хотя подобное утверждение выходит за рамки данной книги, однако можно
показать, что решетка дистрибутивна тогда и только тогда, когда она не содержит
ни одну из этих двух решеток в качестве подрешеток. Следовательно, решетки
на рис. 9.7 не являются дистрибутивными.
Рис. 9.7
Булева алгебра, о которой шла речь в разделе 2.3, является специальным
случаем ограниченной дистрибутивной решетки. Теперь перейдем к системе обо-
обозначений булевой алгебры из раздела 2.3, заменив бинарную операцию V на +, а
бинарную операцию Л на •. Далее решетка будет обозначаться как E, +, •). Для
удобства приведем определение булевой алгебры еще раз. Более подробно данный
вопрос рассмотрен в разделе 2.4.

406 ГЛАВА 9. Алгебраические структуры
ОПРЕДЕЛЕНИЕ 9.39. Булева алгебра — это ограниченная дистрибутивная
решетка E, +, •), в которой имеется унарная операция ' на множестве 5 такая,
что х + х1 = 1 и х - х' = 0. Для х Е 5 х1 называется дополнением х. Следова-
Следовательно, булева алгебра, обозначаемая как E, +, •/ , 1,0), обладает следующими
свойствами, которые выполняются для всех x,y,z e S.
1. Законы ассоциативности
х + (у + z) = (х + у) + z\
х - (у • z) = (х-у) • z.
2. Законы коммутативности
х + у = у + х;
х-у = у-х.
3. Законы дистрибутивности
X • (у + 2) = (X ¦
* + B/ • 2) = (х •
4. Законы дополнения
5. Законы тождества
х • х; = 0.
X • 1 = X.
УПРАЖНЕНИЯ
1. Какое изображение из приведенных ниже представляет собой решетку?
а) б)

РАЗДЕЛ 9.3. Решетки 407
в)
г)
Д)
2. Покажите, что приведенные ниже решетки не дистрибутивны.
е
3. Покажите, что решетка, изображенная на рис. 9.8, не дистрибутивна.
4. Покажите, что решетка, изображенная на рис. 9.9, не дистрибутивна.
d
Ь
Рис. 9.8
Рис. 9.9
5. Какие из приведенных ниже решеток являются дистрибутивными?

408 ГЛАВА 9. Алгебраические структуры
а) б)
в)
г)
Д)
е)
6. Докажите, что для всех а, Ь, принадлежащих решетке, a\/ (aAb) = a.
7. Атомом в булевой алгебре называется ненулевой элемент х, обладающий
таким свойством, что для каждого у из алгебры либо ху = х, либо ху = 0.
а) Пусть 5 — булеан (множество всех подмножеств) множества {а,Ь,с}.
Пусть
E,и,П/,0) — булева алгебра на 5 с обычным определением пересе-
пересечения и объединения. Что является атомами данного множества?
б) Пусть S — множество всех высказываний, полученных из р, q и г с
использованием обычных пропозициональных связок Л, V и ~. Покажи-
Покажите, что в булевой алгебре E, V,A, ~,T, F) атомы — это элементарные
конъюнкции, определенные в разделе 1.5.
в) Найдите атомы булевой алгебры, изображенной на рис. 9.10.

РАЗДЕЛ 9.4. Группы 409
г) Найдите атомы булевой алгебры, изображенной на рис. 9.11.
а
Рис. 9.10
Рис. 9.11
9.4. ГРУППЫ
Ранее отмечалось, что множество неотрицательных целых чисел с операцией -Ь
образуют моноид. Однако, если включить в рассмотрение множество всех целых
чисел с той же операцией +, то опять получим моноид, но обладающий свой-
свойством, которое отсутствовало в первоначальном моноиде, а именно: для каждого
целого числа а существует целое число -а такое, что а + (-а) = (-а) + а = 0,
единице моноида. Аналогичным образом, если рассмотреть множество положи-
положительных рациональных чисел с операцией умножения, то снова получим моноид,
и для каждого рационального числа ? существует рациональное число ? такое,
что ?.? = 1, единице моноида. Рассмотрим свойства, фигурирующие при решении
уравнения 2х + 3 = 7. Сначала прибавляем —3, — элемент, обратный к 3 относи-
относительно сложения, к обеим частям уравнения, и получаем Bx-f 3)-Ь(—3) = 7+(—3).
После использования ассоциативности получаем уравнение 2х-ЬC — 3) = 4. Затем
применяем свойство обратного элемента и получаем 2х + 0 = 4. Используя свой-
свойство нейтральности 0 относительно сложения, имеем 2х = 4. Затем для получения
окончательного решения применяем свойства нейтральности и ассоциативности.
Группы — это нечто большее, чем только абстракция множества действи-
действительных чисел с операцией сложения или множества положительных целых чисел
с операцией умножения. Далее показано, что множество перестановок п элемен-
элементов образует группу. Группы имеют важное применение в физике и во многих
других областях. Они используются в теории чисел, теории кодов, в комбинато-
комбинаторике.
Любой моноид E, о), обладающий свойством, что для каждого элемента
моноида s существует элемент моноида s~l такой, что s о s = s о s = /,
единице моноида, называется группой. Более формально понятие группы может
быть определено следующим образом.

410 ГЛАВА 9. Алгебраические структуры
ОПРЕДЕЛЕНИЕ 9.40. Группа представляет собой множество G вместе с би-
бинарной операцией (или произведением) о на G x G, обладающей следующими
свойствами:
1. а о F о с) = (а о Ь) о с для всех а, 6 и с из G (т.е. операция о на 5
ассоциативна).
2. В G существует элемент 1, называемый единицей, который обладает свой-
свойством aol = 1оа = а для всех а из G.
3. Для каждого элемента а из множества G существует элемент а из
множества G, который называется обратным элементом для а и такой,
что а о а = а о а = 1.
Если группа G обладает таким свойством, что aob = bo а для всех а, 6 из G,
то она называется коммутативной, или абелевой группой.
Снова наблюдается ситуация, что поскольку о — бинарная операция на G,
то отсюда вытекает, что если g,g' E G, то g о gr e G. Это свойство называется
замкнутостью.
ПРИМЕР 9.41. Примеры групп включают следующее:
1. Четные целые числа с операцией сложения.
2. Множество (n x т)-матриц с действительными элементами и бинарной опе-
операцией сложения.
3. Классы вычетов по модулю некоторого положительного целого числа п, об-
образующие Zn с бинарной операцией сложения. ?
ОПРЕДЕЛЕНИЕ 9.42. Если G — группа с п элементами, то п называется
порядком группы G.
Пусть 5 = {г, -г, -1,1}, где г = yf-l. Легко убедиться, что это множество
вместе с операцией умножения образует группу порядка 4.
Заметим, что всякая группа является полугруппой. Обратное, вообще говоря,
неверно.
ТЕОРЕМА 9.43. Единица группы G единственна.
ДОКАЗАТЕЛЬСТВО. Допустим, что 1 и е — единицы группы G. Тогда 1 = loe = e
по определению единицы. ¦
ТЕОРЕМА 9.44. В каждой группе обратный элемент для каждого элемента един-
единственный.
ДОКАЗАТЕЛЬСТВО. Пусть а — элемент группы G, и оба элемента 6 и с —
обратные к элементу а, тогда
ТЕОРЕМА 9.45. Для каждого элемента а группы G имеем (а) = а.

РАЗДЕЛ 9.4. Группы 411
ДОКАЗАТЕЛЬСТВО. Поскольку а о а = а о а = 1, то а удовлетворяет опреде-
определению обратного элемента для а. Поскольку обратный элемент единственный,
то а и является элементом, обратным к а. ¦
ТЕОРЕМА 9.46. Для элементов а и b группы G имеем (а о Ъ)~1 = Ь~г о а.
ДОКАЗАТЕЛЬСТВО, (а о Ъ) о (Ъ~1 о а) = (а о (Ь о б)) о а = (а о 1) о а =
а о а = 1. Аналогично, (Ь о а) о (а о 6) = 1, и по определению обратного
элемента, и вследствие его единственности имеем (а о б) = Ь о а. ¦
Если а — элемент группы G, то обозначим (а)^ = а~к. Пусть а0 обозначает
единицу 1.
Доказательство приведенных ниже теорем оставляем читателю.
ТЕОРЕМА 9.47. Пусть G — группа и а — элемент группы G.
а) ап о а~п = 1 для всех положительных целых чисел п.
б) a(m+n) =amoan для всех целых чисел пит.
в) (am)n = ашп для всех целых чисел тип.
г) (а~п)~1 = ап для всех целых чисел п.
ТЕОРЕМА 9.48. Если а — элемент группы (G, о) и а о а = а, то а = 1, единице
группы G.
ЛЕММА 9.49. Если G — конечная группа и а — элемент G, то а3 — 1 для
некоторого положительного целого числа s.
ДОКАЗАТЕЛЬСТВО. Если G — конечная группа и а — элемент G, то известно,
что aj = ак для некоторых положительных целых чисел j и fc, поскольку только
конечное число степеней может быть различно. Пусть j < fc, тогда a~jak =
a~iai = 1 и ak~i = 1. Пусть s = к — j. Ш
Пусть р — наименьшее целое число, которое больше 1 и такое, что ар = 1.
Элементы 1,а, а2,... ,ар-1 различны, т.к. если аг = а3 для 0 < г, s < р и г > s,
то ar~s = 1, что противоречит тому факту, что р — наименьшее положительное
целое число такое, что ар = 1. Также, если п > ру то ап = аг для некоторого
О < г < р, поскольку если п = pq + r для некоторого 0 < г < р, то
ап = apq+r = apq oar = ^py oar = 1qoar = loar =аг
ТЕОРЕМА 9.50. Пусть G — группа и а — элемент G такой, что а3 = 1 для
некоторого s. Если р — наименьшее положительное целое число такое, что ар = 1,
то р | s. Целое число р называется порядком а.
ДОКАЗАТЕЛЬСТВО. Пусть р — наименьшее положительное целое число такое,
что ар = 1. Как это было сделано выше, положим s = pq + r для некоторого 0 <
г < р, тогда а3 = аРЯ+г = apqar = (ap)qar = (l)qar = ar. Следовательно, а3 = 1
тогда и только тогда, когда г = 0, потому что р — наименьшее положительное
целое число, обладающее свойством ар — 1. ¦
Снова рассмотрим множество 5 = {г,—г,—1,1} с операцией умножения.
Каков порядок г? Каков порядок —1?

412 ГЛАВА 9. Алгебраические структуры
ОПРЕДЕЛЕНИЕ 9.51. Подмножество Я группы G является подгруппой G,
если Я с той же самой операцией, что и G, также является группой.
ПРИМЕР 9.52. Пусть (Z, +) — группа целых чисел с операцией сложения. Для
положительного целого числа т пусть (mZ,+) — группа всех чисел, кратных га.
Понятно, что это группа, поскольку если сложить два числа, кратных га, то снова
получим число, кратное га. Элемент, обратный rai, это — гаг = га(—г). ?
ПРИМЕР 9.53. Пусть (Д, +) — группа действительных чисел с операцией сложе-
сложения. Тогда группа (Q, +) — рациональные числа со сложением, является подгруп-
подгруппой группы (Д,+). ?
ПРИМЕР 9.54. Пусть (Д+, •) — группа положительных действительных чисел с
умножением. Группа (Q+,-) положительных рациональных чисел с умножением
является подгруппой группы (Д+,-). ?
ПРИМЕР 9.55. Легко проверить, что E,+), где 5 = {[0], [2], [4]} — подгруппа
группы (Z6, +). ?
Чтобы определить, является ли подмножество группы подгруппой, не требу-
требуется проверять ассоциативность, поскольку она наследуется от исходной группы.
Необходимо проверить наличие обратного элемента и то, что произведение двух
элементов из множества принадлежит множеству. Необходимо убедиться в том,
что единица содержится во множестве, но это, как показывает доказательство
приведенной ниже теоремы, следует из свойства замкнутости и свойства обрат-
обратного элемента. Теорема дает альтернативный метод проверки того, что некоторое
подмножество группы является подгруппой.
ТЕОРЕМА 9.56. Непустое подмножество Я группы (G, •) будет подгруппой тогда
и только тогда, когда для всех hi,h2 G Н имеем h\ • h^1 G Я.
ДОКАЗАТЕЛЬСТВО. Сначала предположим, что Я — группа и hi,h2 G Я. То-
Тогда h^1 принадлежит группе, поскольку элемент, обратный элементу группы, то-
тоже принадлежит группе. Следовательно, по замыканию, hih^1 принадлежит Я.
Обратно предположим, что для всех hi,h2 G Н имеем hi • h^1 G Н. Если h\ G Я,
то /ii/ij G Я, поэтому единица I € Н. Следовательно, для всех h2 G Я имеет ме-
место I-h^1 G Я и /i^1 G Я. Наконец, если /ii,/i2 G Я, то hi • (h^1)'1 = hi -h2 G Я.
Поэтому Я — группа. ¦
Доказательство приведенной ниже теоремы оставляем читателю.
ТЕОРЕМА 9.57. Если g — элемент группы G такой, что дп = 1 для некоторого п,
и р — наименьшее положительное целое число такое, что др = 1, тогда множество
{0102>--ч5р} является подгруппой группы G.
ОПРЕДЕЛЕНИЕ 9.58. Множество {д, д2,..., др} называется циклической
группой или, точнее, циклической группой, порожденной д. Она обозначается
через (д).

РАЗДЕЛ 9.4. Группы 413
Еще раз рассмотрим множество S = {г,—г,—1,1} с умножением. Это цик-
циклическая группа. Что может быть использовано в качестве д? Найдите две под-
подгруппы группы S. Являются ли они циклическими?
Доказательство приведенной ниже теоремы оставляем читателю.
ТЕОРЕМА9.59. Пусть (G, •) — группа и ai,a2,a3,... ,a^ Е G. Пусть А = {ai,a2,a3,
..., a/c} Hj4* = (ai, a2, a3,..., a^) — множество всех конечных произведений эле-
элементов ai,a2,a3,... ,а* и обратных к ним. Тогда А* —• группа. Более того, А* —
наименьшая подгруппа группы G, содержащая А.
ОПРЕДЕЛЕНИЕ 9.60. Подгруппа А* называется группой, порожденной мно-
множеством А. Если для каждого собственного подмножества В множества А
имеем В* ф А*, тогда А называется порождающим множеством для А*.
Если множество А порождает группу G и никакое собственное подмножество
множества А не порождает G, тогда А называется минимальным порождаю-
порождающим множеством для группы G.
В циклической группе порождающее множество может быть образовано од-
одним элементом. Возможно ли иметь минимальное порождающее множество более
чем из одного элемента?
ОПРЕДЕЛЕНИЕ 9.61. Для подгруппы Я группы G и произвольного а из G
aoH = {x:x = aoh для некоторого h из Я} называется левым смежным
классом подгруппы Я группы G.
ПРИМЕР 9.62. Ранее было показано, что множество Z целых чисел с бинарной
операцией сложения, -Ь, является группой. Пусть
Н = {п : и G Z и п = 5fc для некоторого целого числа к} =
= {...,-10,-5,0,5,10,15,20,...}.
Покажем, что Н является подгруппой группы Z. Понятно, что Н С Z. Множество
Н замкнуто относительно сложения, поскольку если s € Н и t Е Н, то s = 5г
и t = 5j для соответствующих целых чисел г и j. Таким образом, s 4-1 = 5г -Ь
5j = 5(г + j) = 5к для к = г + j, так что s + ? принадлежит Я. Единичный
элемент Я является единичным элементом G, а именно, 0. Каждый элемент Н
имеет обратный элемент относительно |вЯ, потому что если t = Бк Е Я, то
t = 5(-fc).
Теперь рассмотрим левые смежные классы подгруппы Я, генерируемые раз-
различными элементами множества Z. Пусть aoH = a + H = {x:x = a + h для
некоторого h Я}, тогда
0 + H = {x:x = 0 + h для некоторого h из Я} =
-{...,-10,-5,0,5,10,15,20,...};

414 ГЛАВА 9. Алгебраические структуры
1 + H = {x:x = l + h для некоторого h из Я} =
= {...,-9,-4,1,6,11,16,21,...};
2 + H = {x:x = 2 + h для некоторого h из Я} =
= {...,-8,-3,2,7,12,17,22,...};
3 + H = {x:x = 3 + h для некоторого h из Я} =
= {...,-7,-2,3,8,13,18,23,...};
4Ч-Я = {х:х = 4 + /г для некоторого h из Я} =
= {...,-6,-1,4,9,14,19,24,...}.
Таким образом, снова получен класс вычетов Zs, поскольку a + Н = [а], и пять
левых смежных классов подгруппы Я образуют разбиение исходной группы Z. ?
ЛЕММА 9.63. Для фиксированной подгруппы Я группы G левые смежные классы
подгруппы Я группы G образуют разбиение группы G.
ДОКАЗАТЕЛЬСТВО. Каждый левый смежный класс непустой, поскольку для ле-
левого смежного класса аоН\ элемент а — aol находится в аоЯ. Предположим, что
пересечение а о Я и bo H непустое; пусть элемент с принадлежит пересечению.
Следовательно, c = aoh = boh' для некоторых h и Ы из Я. Умножая обе части
уравнения на h~~l, получаем ао ho h~l = b о h! о h~l\ поэтому по определению
обратного элемента имеем а = b о (h! о /г). Поскольку Ы о h~l принадлежит Я,
то элемент а содержится в b о Я. Следовательно, ао h содержится в 6 о Я для
всех h из Я, поэтому а о Я С 6 о Я. Аналогично, bo Н С ао Н и 6 о Я = а о Я.
Следовательно, левые смежные классы образуют разбиение группы G. Ш
ЛЕММА 9.64. Если G — конечная группа и Я — подгруппа группы G, то все
левые смежные классы подгруппы Я группы G содержат одно и то же количество
элементов, а именно, количество элементов, которое находится в подгруппе Я.
ДОКАЗАТЕЛЬСТВО. Пусть а о Я — левый смежный класс подгруппы Я из G.
Определим / : Я —> аоЯ таким образом: /(/г) = ао/г. Читателю остается показать,
что / представляет собой взаимно однозначное соответствие, или биекцию. ¦
ТЕОРЕМА 9.65. (Лагранж) Если G — конечная группа и Я — подгруппа группы
G, то порядок Я делит порядок G.
ДОКАЗАТЕЛЬСТВО. Если р — порядок Я, q — количество левых смежных клас-
классов Я в G и п — порядок G, то согласно двум предыдущим леммам п = pq. Ш
ТЕОРЕМА 9.66. Если G — группа порядка и и д приналежит G, то дп = 1.
ДОКАЗАТЕЛЬСТВО. Пусть р — наименьшее положительное число такое, что
др = 1 и Я = {д, д2,... ,др}. Тогда Я — подгруппа с р элементами и, следо-
следовательно, р делит п. Пусть и = pq, таким образом, дп = дря = (#р)9 = Iя = 1.

РАЗДЕЛ 9.5. Группы и гомоморфизмы 415
¦ УПРАЖНЕНИЯ
1. Составьте таблицу сложения и умножения для Z^.
2. Составьте таблицу сложения и умножения для Z-j.
3. Вычислите [1] о [2] о [3] в ZA.
4. Вычислите [1] о [2] о [3] о [4] в Z7.
5. В Zio найдите элемент, обратный [7] относительно умножения.
6. В Zi2 найдите все такие а, что [а] о [6] = [0].
7. Пусть Zn — {[0], [1], [2],..., [п — 1]} для некоторого целого числа п. Пусть
5 = {[к] : fc положительное и взаимно простое с п). Является ли 5 группой
с операцией умножения?
8. При выполнении каких условий Zn будет группой с операцией умножения?
9. Докажите, что числа, кратные 3, образуют подгруппу целых чисел с операци-
операцией сложения. Опишите соответствующие смежные классы этой подгруппы.
10. Докажите, что числа, кратные 3, образуют полугруппу целых чисел с опе-
операцией умножения. Почему они не образуют группу?
11. Докажите, что множество классов вычетов по модулю 6 образует группу
относительно сложения. Будут ли они образовывать группу относительно
умножения?
12. Докажите теорему 9.47. Пусть G — группа и а — элемент группы G.
а) ап о а~п = 1 для всех положительных целых чисел п.
б) a(rn+n) = а771 о ап для всех целых чисел пит.
в) (am)n = amn для всех целых чисел тип.
г) (а"") = ап для всех целых чисел п.
13. Докажите теорему 9.57. Если д — элемент группы G такой, что дп = 1
для некоторого п, и р — наименьшее положительное целое число такое, что
др = 1, тогда множество {д,д2,... ,др} является подгруппой группы G.
14. Докажите теорему 9.48. Если а — элемент группы (G, о) и а о а = а, то
а = 1, единице группы G.
9.5. ГРУППЫ И ГОМОМОРФИЗМЫ
Существуют специальные функции на множестве групп такие, что некоторые
свойства области определения сохраняются в образе функции. Например, образы
подгрупп из области определения являются подгруппами в области значений.
Такие функции называются гомоморфизмами. Обратите внимание, что группы
являются полугруппами, и это определение гомоморфизма пригодно также для
полугрупп.
ОПРЕДЕЛЕНИЕ 9.67. Пусть (G, •) и (Я, *) — группы, где • и * — операции на
G и Н соответственно. Пусть / : G —> Н — функция. Функция / называется
гомоморфизмом, если f(g*g') = f(g)*f(g') для всех д и д' из G. Гомоморфизм
/ назывется мономорфизмом, если функция / — инъекция, эпиморфизмом,
если функция / — сюръекция, и изоморфизмом, если функция / — биекция.

416 ГЛАВА 9. Алгебраические структуры
ПРИМЕР 9.68. В примере 9.62, где Я = {га : га е Z и га = Бк для некоторого цело-
целого числа к} является подгруппой группы Z, множество левых смежных классов
подгруппы Я имеет вид
W = {0 4- Я, 1 + Я, 2 + Я, 3 + Я, 4 + Я}.
Определим сложение левых смежных классов следующим образом:
(а + Я) 0 (Ь + Я) = (а + Ь) + Я,
где сложение (а 4- Ь) есть сложение целых чисел а и Ь. Несложно показать, что
определение операции 0 не зависит от представления a + Я и b 4- Я.
Легко показать, что для группы (Z5,+) классов вычетов по модулю 5 функ-
функция / : Z5 —¦> W, определенная соотношением
является гомоморфизмом между группами (Zs,+) и (IV,©) и также является
изоморфизмом.
Рассмотрим две группы (Z, +) и (Zs,+) и функцию g : Z —> Z5, определен-
определенную таким образом:
Я(а) = [а].
Функция д является гомоморфизмом, поскольку д(а 4- Ь) = [а + Ь] = [а] 4- [6] =
д(а) 4- дF). Гомоморфизм д является эпиморфизмом, поскольку ясно, что для
любого заданного элемента [с] из группы Z$ имеем д(с) = [с]. ?
ПРИМЕР 9.69. В одной из задач, рассмотренных в разделе 5.8, показано, что
(га х га)-матрица имеет обратную тогда и только тогда, когда ее детерминант не
равен 0. Хотя этот вопрос выходит за рамки данной книги, можно показать,
что функция вычисления детерминанта представляет собой гомоморфизм из мно-
множества (га х га)-матриц с действительными (или рациональными) элементами с
операцией умножения на множество действительных (или рациональных) чисел
с умножением. Следовательно, если определитель каждой из матриц не равен
нулю, то определитель их произведения тоже не равен нулю. Отсюда следует, что
произведение двух матриц, каждая из которых имеет обратную, также обрати-
обратимо. Следовательно, множество таких (га х га)-матриц образует группу с операцией
умножения, которая называется группой несингулярных матриц. Если опреде-
определитель матрицы М имеет ненулевое значение г, то чему равен определитель
матрицы М? ?
Доказательство приведенных ниже теорем оставляем читателю.
ТЕОРЕМА 9.70. Пусть / : G —> Я — гомоморфизм из группы G в группу Я и 1
— единица группы G. Тогда /A) — единица группы Я.
ТЕОРЕМА 9.71. Пусть / : G —> Я — гомоморфизм из группы G в группу Я и д1 —
элемент, обратный элементу д из G. Тогда /(#') есть элемент, обратный элементу
f(g) из Я.
ТЕОРЕМА 9.72. Если / : G —> Я — гомоморфизм из группы G в группу Я и К —
подгруппа группы Я, то f~l(K) — подгруппа группы G.
ТЕОРЕМА 9.73. Если f : G —> Н — гомоморфизм из группы G в группу Я и К —
подгруппа G, то f(K) — подгруппа группы Я.

РАЗДЕЛ 9.5. Группы и гомоморфизмы 417
ОПРЕДЕЛЕНИЕ 9.74. Для подмножеств Я и К группы (G, о) пусть Я о К =
{ho к : h G Н,к е К}. Если Я = {/i}, то Н о К обычно записывают как hK.
Доказательство приведенной ниже теоремы оставляем читателю.
ТЕОРЕМА 9.75. Если Я, J и К — подмножества группы (G, о), то (Я о J) о К =
ffo(JoX).
В примере 9.68 показано, что группа делится на классы и эти смежные
классы можно "перемножать" (в том случае умножением групп было сложение
целых чисел). В общем случае это не всегда возможно. Тем не менее, будет по-
показано, что если подгруппа, которая используется для формирования смежных
классов, обладает определенными свойствами, то имеется возможность перемно-
перемножения смежных классов.
ОПРЕДЕЛЕНИЕ 9.76. Если Я — подгруппа группы (G, о), обладающая свой-
свойством дНд = Я для всех д Е G, то такая группа Я называется нормальной
подгруппой.
ОПРЕДЕЛЕНИЕ 9.77. Пусть / : G —> Я — гомоморфизм из группы G в группу
Я. Ядром гомоморфизма / называется множество {х : х Е G и f(x) = 1} =
Z ({!})' гДе 1 "" единица группы Н.
Доказательство приведенной ниже теоремы оставляем читателю.
ТЕОРЕМА 9.78. Ядро гомоморфизма / : G -> Н есть нормальная подгруппа
группы G.
ТЕОРЕМА 9.79. Подгруппа Н группы (G, о) является нормальной подгруппой
тогда и только тогда, когда дН = Нд для всех д Е G.
ДОКАЗАТЕЛЬСТВО. Предположим, что подгруппа Я нормальна в группе G, так
что дНд~1 = Я для всех д е G. Пусть gh E #Я. Поскольку дНд~1 = Я, то
g/ig = Ы для некоторого /г' Е Я. Следовательно, р/г = Ъ!д и gh € Нд, поэтому
дН С Нд. Аналогично, Нд С дН. Доказать утверждение в обратную сторону
предоставляется читателю. ¦
ТЕОРЕМА 9.80. Если Я — подгруппа группы (G, о), то Я о Я = Я.
ДОКАЗАТЕЛЬСТВО. Предположим, что Я — группа. Тогда по определению за-
замыкания Я о Я С Я. Поскольку Я — группа, то для h E Я имеем h = ho I, где
/ — единица группы G, а значит, и группы Я. Поэтому /гЕЯоЯиЯСЯоЯ.
Таким образом, Я = Я о Я. ¦
Обратная теорема неверна. Однако, если Я — множество положительных
целых чисел с обычным умножением, то Я = Я о Я, но Я не является группой.
ТЕОРЕМА 9.81. Если Я — нормальная подгруппа группы (G, о), то аЬЯ =
(аЯ)FЯ) для всех a,b €G.

418 ГЛАВА 9. Алгебраические структуры
ДОКАЗАТЕЛЬСТВО. Для a,beG,
аЬН = а(ЬН) = по теореме 9.75
= а(Ъ(НН) = по теореме 9.80
= а(ЬН)Н = по теореме 9.75
= а(НЬ)Н = по теореме 9.79
= (аН)(ЬН). по теореме 9.75 ¦
СЛЕДСТВИЕ 9.82. Если Я — нормальная подгруппа группы (G, о), то смеж-
смежные классы подгруппы Я в группе G образуют группу относительно операции
(аН)(ЬН) = аЬН. Эта группа называется фактор-группой и обозначается G/H.
СЛЕДСТВИЕ 9.83. Если f : G —> G/H определить соотношением f(a) = aH, то
/ — гомоморфизм.
Доказательство приведенных ниже теорем предоставляется читателю.
ТЕОРЕМА 9.84. Если / : G —> G1 — гомоморфизм из группы (G, о) в группу
(С, о), то Я = {х : f(x) = 1, единице группы G'} будет подгруппой группы G.
ТЕОРЕМА 9.85. Если / : G —> Н — гомоморфизм из группы G в группу Н и К —
подгруппа группы Я, то /-1 ({!})» гДе 1 ~ единица группы Я, есть нормальная
подгруппа группы G.
В разделе 4.2 показано, что перестановки на конечном множестве замкнуты
относительно бинарной операции композиции. Было также показано, как найти
перестановку, обратную данной. Как и другие функции, эти перестановки ассо-
ассоциативны относительно композиции. Следовательно, множество всех перестано-
перестановок фиксированного конечного множества образует группу относительно бинар-
бинарной операции композиции. Множество всех перестановок п элементов называется
симметрической группой и обозначается Sn.
ПРИМЕР 9.86. Вспомним, что если / перестановка на множестве {1,2,3,... ,п},
то ее можно представить в виде
2 ... и \
... /(п) ;•
/B)
Рассмотрим следующую подгруппу симметрической группы 54, основанную на
квадрате, изображенном на рис. 9.12.
1 2
3 Рис. 9.12
Перестановка
12 3 4
3 2 14

РАЗДЕЛ 9.5. Группы и гомоморфизмы 419
меняет местами 1 и 3. Геометрически — это отражение квадрата относительно
диагонали между вершинами 2 и 4. Аналогично, перестановка
¦О
2 3 4
4 3 2
меняет местами 2 и 4. Геометрически — это отражение квадрата относительно
диагонали между вершинами 1 и 3. Перестановка
12 3 4
4 3 2 1
геометрически отражает квадрат относительно горизонтальной оси, проходящей
через центр квадрата. Перестановка
02 =
1 2 3 4
2 1 4 3
)
геометрически отражает квадрат относительно вертикальной оси, проходящей че-
через центр квадрата. Пусть р\, р2, и рз — вращения квадрата по часовой стрел-
стрелке на 90°, 180° и 270° соответственно. Следовательно, Pi = ( о Ч 4 1 )'
/1 2 3 4\ /1 2 3 4\ п т
Р2 = ( з 4 1 2/H/93=V4 1 2 3/ ПУСТЬ * ~~ тождественная пере-
перестановка. Все результаты умножения этих элементов содержит приведенная ниже
таблица.
о
/
Pi
Р2
Рз
Si
s2
Ф\
Фг
I
I
Pi
Pi
Рз
Si
s2
4>i
ф2
Pi
Pi
P2
Рз
I
ф2
Ф\
Si
s2
P2
P2
Рз
I
Pi
s2
Si
ф2
ф\
Рз
Рг
I
Pi
P2
Ф\
Ф2
s2
Si
Si
Si
Ф1
s2
ф2
I
P2
Pi
Pz
s2
s2
ф2
Si
Ф1
Pi
I
P3
Pi
Ф\
Ф1
s2
ф2
Si
Рз
Pi
I
P2
Ф2
ф2
Si
Ф1
s2
Pi
Рз
P2
I
Эта группа называется оптической группой, или группой симметрии квадра-
квадрата. Множество Н = {/, рьР2>Рз} — подгруппа октической группы. Посколь-
Поскольку Н содержит четыре элемента, и число элементов в смежном классе должно
делить порядок группы, то существует только один смежный левый класс, аН
для любого а ? Н. Этот класс состоит из всех элементов октической группы,
которые не попали в Я. Но он должен совпадать с На для любого а ? Н, по-
поскольку существует только один другой правый смежный класс. Следовательно,
Я — нормальная подгруппа октической группы. Читателю остается показать, что
{/, р2} — нормальная подгруппа октической группы. D

420 ГЛАВА 9. Алгебраические структуры
Пусть А — конечное множество из и элементов и пусть Sn — группа пере-
перестановок на А. Поскольку имеется п\ перестановок элементов множества А, то
Sn содержит п! элементов. Пусть, для удобства, 1, 2, ..., п — элементы из А.
Для фиксированной перестановки а определим отношение R на А таким образом:
aRb, если Ь = crk(a) для некоторого неотрицательного целого числа fc.
ТЕОРЕМА 9.87. Отношение R есть отношение эквивалентности на А.
ДОКАЗАТЕЛЬСТВО. Поскольку группа Sn конечна, то ат = 1, единице группы
Sn для некоторого неотрицательного целого числа га. Следовательно, сгт(а) = а
и aRa. Пусть aRb, тогда Ъ — crk(a) для некоторого неотрицательного целого
числа fc. Поскольку akam~k = am = 1, то am~k — обратный элемент для ак,
так что <тт~к(Ь) = а и bRa. Следовательно, R симметрично. Пусть aRb и bRc.
Тогда b = aj(a) для некоторого неотрицательного целого числа j и с = сг^б) для
некоторого неотрицательного целого числа fc. Следовательно, с = aj+k(a), и R
транзитивно. Поэтому R — отношение эквивалентности. ¦
Поскольку R является отношением эквивалентности, оно делит множество
{1,2,3,..., п} на классы эквивалентности. Например, пусть А={1,2,3,..., 8} и
_/12345678\
"^43278615 у
Легко видеть, что множество классов эквивалентности имеет вид {{1,4,7}, {2,3},
{5,8}, {6}}. Множество классов эквивалентности, созданное таким образом, на-
называется орбитой перестановки а.
Теперь определим специальный вид перестановки, называемый циклом. Ес-
Если обозначить сгс = (ах,а2,аз,... ,afc) как цикл, тогда (Tc(a>i) = ^i+i Для г < fc, и
ac(ak) = а\. Например, если ас = A,3,5,7) — цикл в 58, то
¦(i
2 3 4 5 6 7 8
'c~l32547618
Данную перестановку а можно записать как произведение циклов, которые не
имеют общих элементов. Для этого сначала необходимо разделить множество А
на классы эквивалентности. Выбираем элемент а и образуем цикл (а, сг(а),<т2(а),
сг3(а),... ,afc(a)), где crfc+1(a) = а. Эти циклы не содержат общих компонент,
поскольку классы эквивалентности не пересекаются. Назовем эти циклы непере-
непересекающимися.
Например, в перестановке
12345678\
СГ~143278615
с множеством классов эквивалентности {{1,4,7}, {2,3}, {5,8}, {6}} циклами яв-
являются A,4,7), B,3), E,8) и F). Поскольку каждый цикл двигает только числа
из цикла, а циклы непересекающиеся, то а — A,4,7)B,3)E,8)F). Поскольку
циклы не пересекаются, то порядок циклов не меняет перестановку. По жела-
желанию, одноэлементные циклы можно опускать, поскольку они реально ничего не
меняют. Поэтому можно записать а = A,4,7)B,3)E,8). Если использовать од-
одноэлементные циклы, то тождественную перестановку в Sg можно записать как

РАЗДЕЛ 9.5. Группы и гомоморфизмы 421
¦ УПРАЖНЕНИЯ
1. Докажите теорему 9.70. Пусть / : G —> Я — гомоморфизм из группы G в
группу Я и 1 — единица группы G. Тогда /A) — единица группы Я.
2. Докажите теорему 9.71. Пусть / : G —> Я — гомоморфизм из группы G
в группу Я и д' — элемент, обратный элементу д из G. Тогда f(g') есть
элемент, обратный элементу f(g) из Я.
3. Следуя доказательству теоремы 9.64, пусть а о Я — левый смежный класс
подгруппы Я группы G. Определим / : Я —* аоЯ соотношением f(h) = ао/г.
Покажите, что функция / — биекция.
4. Докажите теорему 9.78. Ядро гомоморфизма / : G —> Я есть нормальная
подгруппа группы С
5. Пусть Z^ = {[1], [2], [3], [4]} — множество элементов Z5 без элемента [0].
Эти элементы соответствуют целым числам, которые дают при делении на 5,
соответственно, остатки 1,2,34. Вместе с операцией умножения, •, введенной
для Z5, получаем группу (Z^,-). Покажите, что (Zl*,-) изоморфна (Z4,+),
непосредственно указав изоморфизм / : Zl* —> Z4.
6. Покажите, что {/, рг} — нормальная подгруппа октической группы.
7. Найдите двухэлементную подгруппу октической группы, которая не являет-
является нормальной подгруппой.
8. Докажите теорему 9.72. Если / : G —+ Я — гомоморфизм из группы G в
группу Я и К — подгруппа группы Я, то /~г(К) — подгруппа группы G.
9. Докажите теорему 9.73. Если / : G —> Я — гомоморфизм из группы G в
группу Я и К — подгруппа G, то f(K) — подгруппа группы Я.
10. Запишите приведенные ниже перестановки как произведение непересекаю-
непересекающихся циклов:
1
3
1
2
1
2
1
3
2
9
2
4
2
4
2
4
3
4
3
7
3
1
3
5
4
7
4
8
4
7
4
6
5
8
5
3
5
3
5
1
6
6
6
6
6
6
6
2
7
1
7
9
7
5
•
8
5
8
1
V
У
9
2
9
5
б)
в)
г)
11. Найдите а о т, где
а)<7 = A,3,4)B,5)ит =
б) а = A,2)C,4)E,6) и т = A,2)C,4)E,6);
в) а = A,2,3)D,5,6) и г = A,2)C,4)E,6);
г) а = A,2,3,8)D,5,6)G) и г = A,2)C,8)D,5)F,7).
12. Докажите теорему 9.75. Если Я, J и К — подмножества группы (G, о), то
(Я о J) о К = (Я о (J о #)
13. Докажите теорему, обратную теореме 9.79. Если для заданной подгруппы Я
группы (G, о) имеет место дН = Нд для всех д е G, то Я — нормальная
подгруппа.

ГЛАВА
НЕКОТОРЫЕ
СПЕЦИАЛЬНЫЕ
ВОПРОСЫ
ТЕОРИИ ЧИСЕЛ
10.1. ЦЕЛОЧИСЛЕННЫЕ РЕШЕНИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ
В данной главе рассмотрены некоторые положения теории чисел, которые явля-
являются в большей степени алгебраическими. Начнем с нахождения решений алге-
алгебраических уравнений.
Используя алгоритм Евклида, можно найти целочисленные решения уравне-
уравнения ах+by = с, если они существуют. Приведенное ниже утверждение было ранее
доказано как теорема 3.38 и приводится здесь еще раз для удобства изложения.
ТЕОРЕМА 10.1. Уравнение ах + by = с, где a, b и с — целые числа, имеет цело-
целочисленное решение (т.е. существуют целые числа х и у такие, что ах Л-by = с)
тогда и только тогда, когда с делится на НОД(а, Ъ).
Если с делится на НОД(а, Ь), то решением уравнения ах -{-by = с является
пара чисел
и • с v • с
Хо = НОД(а,Ь) ' Уо = НОДМ) '
где и и v — любое решение уравнения НОД(а, Ь) = аи + bv.
ПРИМЕР 10.2. Найти решение уравнения 85х + 34у = 51. В примере 7.5 показано,
что НОД(85,34) = 17 и (85)A) + C4)(-2) = 17. Поэтому решение имеет вид
и - с 1-51
НОД(а,6)
Уо НОД(а,Ь) 17
Для проверки вычислим
ах0 + Ьу0 = 85 • 3 + 34 • (-6) = 255 + (-204) = 51.

РАЗДЕЛ 10.1. Целочисленные решения линейных уравнений 423
Иной способ построения решения состоит в непосредственном использовании
уравнения аи + bv = НОД(а, 6). Поскольку
аи + bv = НОД(а, Ь)
или
а.A) + Ь-(-2) = 17,
то, умножая на 3, получаем
а-C)+6-(-6) = 51.
Замечая, что при х = 5 к у = -11
85 • 5 + 34 • (-11) = 425 4- (-374) = 51,
приходим к выводу, что может существовать более одного решения. ?
ПРИМЕР 10.3. Решить уравнение 252х + 580у = 20.В примере 7.6 показано, что
НОДB52,580) = 4 и B52)(-23) + E80)A0) = 4. Умножая каждое слагаемое на
5, получаем B52)(—115) + E80)E0) = 20. Следовательно, х = -115 и у = 50
являются решением. ?
Теперь у нас есть возможность определять, существует ли решение, и на-
находить частное решение для уравнения ах + by = с, если решение существует.
Теорема, приведенная ниже, дает возможность находить все решения уравнения.
ТЕОРЕМА 10.4. Если а и b — ненулевые целые числа и (хо,уо) — решение
уравнения ах + Ьу = с, тогда любое другое решение (х, у) имеет вид
Ъ
где t — произвольное целое число, a d = НОД(а,Ь).
ДОКАЗАТЕЛЬСТВО. Если (х,у) и (хо,уо) являются решениями уравнения ах +
6у = с, то ах Л-by = ах0 + Ьу0. Поэтому ах - ах0 = byQ -by и а(х - х0) = Ь(уо — у)-
Разделив обе части соотношения на d = НОД(а,Ь), имеем §(х — х0) = |(уо - 2/).
Поскольку по теореме 7.8 НОД (§, ^) = 1, получаем, что §(уо — у) и §(ж - х0),
скажем, х - х0 = гх (^) и (у0 - у) = v (§). Тогда (§) г/ (^) = (^) v (§), и отсюда
после сокращения и = v. Положив t = и = v, получаем х = х0 4- (^) * и у =
Уо - (§)*• Необходимо еще показать, что пара (х0 + (jj)*i Уо - (§) *) является
решением уравнения ах -f by = с. Но
= ах0 + Ьуо =
-с

424 ГЛАВА 10. Некоторые специальные вопросы теории чисел
Возвращаясь к примеру 10.2, мы видим, что общее решение уравнения 85x4-
34у = 51 имеет вид х = 3 + 2t и у == -6 - 5?. В примере 10.3 общим решением
уравнения 252х + 580г/ = 20 является х = —115 -4-145? и у = 50 — 63?.
¦ УПРАЖНЕНИЯ
1. Найдите решение каждого из приведенных ниже уравнений:
a) 24x + 81t/ = 6; б) 803х + 154?/ = 33; в) 73х + 151у = 3;
г) 165х + 418у = 121; д) 27х + 78у = 12.
2. Найдите общее решение каждого из уравнений упражнения 1.
3. Найдите (если оно существует) решение каждого из приведенных ниже урав-
уравнений:
а) 23х + 18у = 4; б) 299х + 533у = 52; в) 39х + 299у = 27;
г) 272х 4- Ю2г/ = 68; д) 27х + Шу = 33.
4. Найдите общее решение каждого из уравнений упражнения 3, если оно
существует.
5. Напишите в псевдокодах процедуру для нахождения целочисленных реше-
решений линейных уравнений.
10.2. РЕШЕНИЯ СРАВНЕНИИ
В предыдущем разделе рассматривались уравнения вида ах + Ьу = с, имеющие в
качестве решений целые числа х и у. В частном случае 6 = 0 можно находить
решения уравнения ах = с. Теперь будем искать решения сравнений ах = с
(mod n) в том смысле, что требуется найти такое целое число х, при котором
целое число ах сравнимо с с по модулю п. Или, на языке классов эквивалентности,
для классов эквивалентности [а] и [с] по модулю п, найти класс эквивалентности
[х] такой, что [а] 0 [х] = [с], где равенство означает равенство множеств.
Используя таблицу умножения для Zs (см. раздел 3.6),
[а] О [6]
[0]
[1]
И
[3]
[4]
И
[0]
[01
[0]
[0]
[0]
[1]
[0]
[11
[2]
[3]
И]
[2]
[0]
[21
[4]
[1]
[3]
[3]
[0]
[31
[1]
[4]
[2]
[4]
[0]
[41
[3]
[2]
[1]
можно найти решение сравнения
Зх = 1 (mod 5),
рассматривая (по модулю 5)
[3] О [*] = [1].

РАЗДЕЛ 10.2. Решения сравнений 425
Анализ таблицы умножения показывает, что [х] = [2] будет решением, т.к. [3] О
[2] = [1]. Поэтому можно положить х = 2. Поскольку [2] = {...,—8,-3,2,7,12,
...}, отмечаем, что каждое число из совокупности х = —3, х = 7 и х = — 8 является
тем значением х, которое удовлетворяет
Зх = 1 (mod 5).
В теореме, приведенной ниже, сформулированы важные свойства сравнимости.
Части (а) и (г) доказаны в теореме 3.54. Доказательство остальных пунктов
предоставляется читателю.
ТЕОРЕМА 10.5.
а) Если a = b (mod n) и с = d (mod n), то a + с = b 4- d (mod n) и ac = bd
(mod n).
б) Если ac = be (mod n) и НОД(с, п) = 1, то а = b (mod n).
в) Если a = b (mod n), то am = bm (mod n) для всех целых положительных
чисел га.
г) Если a = 6 (mod тип), то a = 6 (mod m) и a = b (mod n).
д) Для сф 0 соотношение ac = be (mod n) имеет место тогда и только тогда,
когда a = Ь ( mod ЦГ|П, г ).
V НОД(с, п))
е) Если a = b (mod m), a = b (mod n) и НОД(т, n) = 1, to a = b (mod mn).
В следующих двух теоремах формулируются условия, при которых решение
ах = с (mod n) существует, и указывается явный вид решения.
ТЕОРЕМА 10.6. Сравнение ах = с (mod m) имеет решением целое число х тогда
и только тогда, когда НОД(а, га) | с. Все целочисленные решения имеют вид
t • m
х = +
НОД(а,га)'
где t — любое целое число, и для х0 существует такое уо, что (хо,уо) является
решением уравнения ах 4- ту = с.
ДОКАЗАТЕЛЬСТВО. По определению, ах = с (mod га) тогда и только тогда,
когда ах- с делится на га, т.е. существует целое число j такое, что ах- с = jm.
Это справедливо тогда и только тогда, когда
ах 4- ту = с
имеет решение. Целые числа а, га и с фиксированы, и требуется найти целые
числа х и у такие, что ах 4- ту = с. По теореме 10.1 ах 4- ту = с имеет целочис-
целочисленное решение тогда и только тогда, когда НОД(а, га) | с. Также согласно этой
теореме, решение имеет вид
и • с v • с
х0 =
НОД(а,га)' *и НОД(а,га)'

426 ГЛАВА 10. Некоторые специальные вопросы теории чисел
где и и v выбраны таким образом, что au + mv = НОД(а, m). По теореме 10.4 все
решения имеют вид
? • 771 ? • ТП
+
х =
НОД(а,га)' » уи НОД(а,га)'
где ? — произвольное целое число. В данном случае необходимо решение только
для х. Таким образом, все целочисленные решения ах = с (mod га) имеют вид
? • га
Х = Х° + НОД(а,га) '
где ? — любое целое число. ¦
Следующая теорема предоставляет различные решения сравнений ах = с
(mod га). Поскольку существует конечное число классов эквивалентности по мо-
модулю га, может существовать только конечное число различных решений по мо-
модулю га. Все они даны в приведенной ниже теореме. Доказательство теоремы
предоставляется читателю.
ТЕОРЕМА 10.7. Если НОД(а,га) | с, то ах = с (mod га) имеет конечное число
различных решений по модулю га. Эти решения имеют вид
? • га ГГ ? • га ]]
х° + ИгшТ 7 по М°ДУЛЮ т = \\хо + TTTTiTT Г
НОД(а,га) [[ НОД(а,га)_|_|т
для ? = 1,2,3,..., НОД(а, га), где для хо существует такое уо, что (хо,?/о) явля-
является решением уравнения ах + ту = с.
ПРИМЕР 10.8. В силу того, что НОДC5,84) = 7 и 7 | 14, сравнение
35 • х = 14 (mod 84)
имеет в точности 7 различных решений по модулю 84, которые имеют вид
х0 + -у- = х0 + 12 • ?,
где ? = 1,2,3,..., 7 и (хо, уо) является решением
35х 4- 84у = 14,
которое равносильно
5х + 12у = 2.
Проверка дает в качестве решения хо = — 2 и уо = 1. Семь различных решений
по модулю 84 имеют следующий вид.
t
1
2
3
4
5
6
7
-2
-2
-2
-2
-2
-2
-2
+
+
+
+
+
+
+
12 • 1 = 10
12 • 2 = 22
12 • 3 = 34
12 • 4 = 46
12 • 5 = 58
12 • 6 = 70
12 • 7 = 82

РАЗДЕЛ 10.2. Решения сравнений 427
Когда НОД(а, га) = 1, существует единственное решение сравнения ах = с
(mod m). Например, рассмотрим сравнение
6х = 7 (mod 55),
НОДF,55) = 1, и, очевидно, 1 делит 7. Поэтому существует только одно решение
по модулю 55, которое имеет вид
tm 1-55 rr
+ + 55
где (хо,уо) — решение уравнения ах + my = с или 6х + 55у = 7. Для нахожде-
нахождения х0 и г/о начнем перебор с возвратом по алгоритму Евклида, как показано в
примерах, следующих за теоремой 7.2, получая при этом 6(-9) + 55A) = 1 =
НОДF, 55). Умножая каждое слагаемое на 7, получаем 6(—63) + 55G) = 7, так
что х0 = -63 и х = -63 + 55 = -8. ?
ПРИМЕР 10.9. Решить сравнение
623х = -406 (mod 84).
Число 623 больше, чем модуль сравнения 84, а —406 является отрицательным.
Поскольку разыскиваются решения по модулю 84, выбираем целые числа в диа-
диапазоне 0,1,2,..., 83, т.к. они являются возможными остатками при делении на 84
и простейшими представителями классов эквивалентности, порожденных сравни-
сравнимостью по модулю 84. Используя алгоритм деления, получаем
623 = 84 • 7 + 35, так что 623 = 35 (mod 84);
-406 = 84(-5) + 14, так что - 406 = 14 (mod 84).
Таким образом,
35х = 14 (mod 84)
равносильно исходному 623х = —406 (mod 84). Решение сравнения 35х = 14
(mod 84) было найдено в предыдущем примере. ?
Доказательство следующей теоремы предоставляется читателю.
ТЕОРЕМА 10.10. Если а = Ь (mod щ), а = Ь (mod 712), ..., а = 6 (mod
п = HOK(ni, 7i2, • • • 1 ttfc)i то а = 6 (mod n), и обратно.
УПРАЖНЕНИЯ
1. Для каких значений п справедливо 75 = 35 (mod n)?
2. Найдите решения следующих сравнений:
а) 4х = 3 (mod 7); б) 27х = 12 (mod 15); в) 28х = 56 (mod 49);
г) 24х = 6 (mod 81); д) 91х = 26 (mod 169).
3. Докажите, что если а — целое нечетное число, то а2 = 1 (mod 8).
4. Перечислите все положительные целые числа, которые одновременно срав-
сравнимы с 5 по модулю 3 и сравнимы с 5 по модулю 2.

428 ГЛАВА 10. Некоторые специальные вопросы теории чисел
5. Докажите, что если a = Ъ (mod ni), a = b (mod 712), ..., a = b (mod n^), и
n = HOK(ni,n2,... ,nfc), то а = b (mod n).
6. Докажите, что если ас = be (mod n) и НОД(с, и) = 1, то a = b (mod n).
7. Докажите, что если a = b (mod n), то am = bm (mod n) для всех положи-
положительных целых чисел га.
8. Докажите, что если a = b (mod га), a = b (mod n), и НОД(га, n) = 1, то
a = b (mod ran).
9. Докажите, что для с ^ 0 ас = be (mod n) тогда и только тогда, когда а =
Ъ [ mod тт^„.— ч
V НОД(с,п)>
10.3. КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ
В предыдущем разделе рассматривались сравнения вида
ах = с (mod га),
где целые числа а и с, а также положительное целое число га были заданы, и
требовалось найти целое число х, удовлетворяющее сравнению. Теперь переходим
к рассмотрению системы сравнений:
х = а\ (mod rai)
х = a2 (mod 7712)
x = an (mod ran),
где числа га* — попарно взаимно простые. То есть, требуется найти целое число х,
которое при делении на га; дает остаток а;, если HOJ\(rrii,mj) = 1 при i ф j.
Еще в древние времена люди рассматривали системы сравнений и успешно
их решали. Очень часто ставились задачи на устный счет, наподобие следующей.
Представьте, что группа обезьян пытается разложить по кучкам груду кокосовых
орехов. Если обезьяны разложат орехи в кучки по пять штук, то останется че-
четыре ореха. Если разложат в кучки по четыре, останутся три ореха. Кучки по
семь дадут остаток два. Кучки по девять — остаток шесть. Каково минимальное
возможное число орехов?
Если х — возможное число орехов в кучке, тогда наличие четырех в остатке
при раскладке в кучки по пять можно выразить как
х = 4 (mod 5).
Аналогично, другие условия имеют вид
х = 3 (mod 4);
х = 2 (mod 7);
х = 6 (mod 9).
Наименьшее целое положительное число х, удовлетворяющее четырем сравнени-
сравнениям, и является искомым решением. Решение таких задач дает следующая теорема.

РАЗДЕЛ 10.3. Китайская теорема об остатках 429
ТЕОРЕМА 10.11. (Китайская теорема об остатках) Пусть гаь га2, ..., тп —
попарно взаимно простые числа , т.е. Н0Д(тг,т^) = 1 для всех г и j, меньших
или равных п, где г ^ j. Тогда система сравнений
х = a\ (mod mi)
х = п2 (mod ГП2)
x = an (mod тпп)
одулю
п
{[ГГЦ
имеет решение, которое единственно по модулю, равному целому числу raira2 • • • mn
Далее, если
и Zj — решение сравнения MjZj = cij (mod rrij) для каждого j, тогда решение
имеет вид
п
х = Y^
1ТП2"'ТПп
ДОКАЗАТЕЛЬСТВО. Пусть х определено согласно теореме. Тогда при любом к,
1 < к < п,
X =
так что
x = ^ Mj Zj j mod Yl mi
jZj (mod mjt), по теореме 10.5(г)
(mod mk)
= a^ (mod mfc),
поэтому x удовлетворяет n сравнениям, х = ak (mod m^) при 1 < k < п. Если х'
также удовлетворяет п сравнениям, тогда
x — x' = 0 (mod га;) при 1 < г < гг.
Поскольку НОД(гПг,т^) = 1 при г ^ j, получаем
х = х1 j mod J^[ mi I,
V t=i /
n
т.е. решение х единственно по модулю П тг-
г=1

430 ГЛАВА 10. Некоторые специальные вопросы теории чисел
ПРИМЕР 10.12. Найти решение системы сравнений
х = 5 (mod 4);
х = 7 (mod 11).
Поскольку числа 4 и 11 — взаимно простые, существует целое число, а именно,
10 такое, что D)A0) = 7 (mod 11), и существует целое число (а именно, 3) такое,
что A1)C) = 5 (mod 4). Следовательно, D)A0) + A1)C) = 73, которое сравнимо
с 29 по модулю 44, удовлетворяет обоим вышеприведенным сравнениям. ?
ПРИМЕР 10.13. Найдем ответ на вопрос об обезьянах и орехах, решая систему
сравнений
х = 4 (mod 5);
х = 3 (mod 4);
х = 2 (mod 7);
х = 6 (mod 9).
Имеем Mi = 4 • 7 • 9 = 252, M2 = 5 • 7 • 9 = 315, M3 = 180 и М4 = 140.
Поскольку числа 5 и 252 — взаимно простые, существует целое число z\ такое,
что 252^1 = 4 (mod 5) или, что то же самое, 1z\ = 4 (mod 5), или z\ = 2 (mod 5).
Следовательно, z\ может быть равно 7.
Поскольку числа 4 и 315 — взаимно простые, существует целое число 22 та-
такое, что 315^2 = 3 (mod 4) или, что то же самое, 3z2 = 3 (mod 4). Следовательно,
22 может быть равно 1.
Поскольку числа 7 и 180 — взаимно простые, существует целое число 23 та-
такое, что I8O23 = 2 (mod 7) или, что то же самое, 5z3 = 2 (mod 7). Следовательно,
23 может быть равно 6.
Поскольку числа 9 и 140 — взаимно простые, существует целое число 24
такое, что 140г4 = 6 (mod 9) или, что то же самое, 5z4 = 6 (mod 9). Следова-
Следовательно, 24 может быть равно 3.
Отсюда х = G)B52) + A)C15) + F)A80) + C)A40) (mod 5 • 4 • 7 • 9) или
х = 3579 (mod 1260) и х = 1059 — наименьшее положительное целочисленное
решение. ?
Китайскую теорему об остатках можно следующим образом обобщить на
случай модулей ть т2, ..., тп, которые не являются взаимно простыми.
ТЕОРЕМА 10.14. Система сравнений
х = a\ (mod mi)
х = п2 (mod ГП2)
x = an (mod mn)
имеет решение тогда и только тогда, когда Н0Д(шг,т^) делит а* — a,j при всех
г и j, где 1 < г < j < п. Если решение существует, оно единственно по модулю
H0K(mi,m2,...,mn).

РАЗДЕЛ 10.3. Китайская теорема об остатках 431
ДОКАЗАТЕЛЬСТВО. Для и = 1 справедливость теоремы очевидна. Покажем тех-
технику доказательства, рассматривая случай п = 2. Пусть заданы уравнения
х == a\ (mod тп\)\
х = п2 (mod 7712).
Имеем
х = п\ Н- ктп\.
Подставляя это значение во второе уравнение, получаем
п\ -4- кш\ = а2 (mod m-2)
или
fcmi = а2 — a\ (mod 7712).
Поскольку Н0Д(т1,т2) делит ai-a2, существует решение для fc, a x+fcm! явля-
является решением для обоих уравнений. Поскольку mi и т2 делят HOK((mi,m2)),
то
х + krni + НОК((шь т2))
также является решением. Если как хь так и Х2 — решения обоих сравнений, то
#1 — ^2 делится как на т\, так и на Ш2, и поэтому делится на H0K((mi,ra2)).
Теперь предположим, что имеется система сравнений
х = a\ (mod mi)
х = п2 (mod 777,2)
x = ak (mod
x = afc+i (mod mfc+i)
и есть значение х такое, что х = a^ (mod m^) при 1 < г < fc. Поэтому каждое
решение сравнения х = a; (mod m^) при 1 < г < fc имеет вид х -f uMk, где
Mfc = HOK(mi,m2, ...,
Подставляя это значение в последнее сравнение, имеем
(mod
Если существует решение для и, тогда х 4- t/M/t есть решение для всех к + 1
сравнений. Решение этого сравнения существует, если Н0Д(М?,т?+1)|(х—
Но для всех г
х -
а поскольку х — a^ делится на т^ и а* — afc+i делится на НОД(тг,т*.+1), то
Н0Д(тг,тЛ:4.1)|(х-аЛ:+1) для всех г. Таким образом, Н0Д(М/с,тЛ;+1)|(х-аЛ:Ч.1).
(Чтобы убедиться в этом, подберите наивысшую степень простого числа, которая
делит Mk и mfc+i. Покажите, что это число делит т» и mfc+i для некоторого г.)
Мы показали, что решение существует. Предоставляем читателю доказательство
единственности решения по модулю HOK(mi, m2,..., тп). ¦

432 ГЛАВА 10. Некоторые специальные вопросы теории чисел
Приведенный ниже пример демонстрирует алгоритм решения таких задач.
ПРИМЕР 10.15. Найти решение:
х = 5 (mod 6);
х = 3 (mod 10);
х = 8 (mod 15).
Решение сравнения
х = 5 (mod 6)
имеет вид 5 + 6?. Подставляя эту величину во второе сравнение, получаем 54-6? =
3 (mod 10). Поэтому 6t = 8 (mod 10) и
t = 3 (mod 10).
Поэтому, t = 3 4- 10u. Подставляя ? в третье уравнение, имеем
3 + 10и = 8 (mod 10).
Поэтому 10u = 5 (mod 10) и и = 2 (mod 15). Отсюда w = 2 + 15i> для некоторого
vy и
t = 3 + 10B 4- 15v) = 150u + 23,
a
x = 5 + 6A50г; + 23) = 203 4- 6 • 10 • 15v,
так что х = 203 является решением. ?
¦ УПРАЖНЕНИЯ
1. Решите приведенные ниже системы сравнений:
а) х = 9 (mod 12); б) х = 3 (mod 4);
х = 6 (mod 25). х = 5 (mod 9);
х = 10 (mod 35).
в) х = a (mod 15); r) x = 5 (mod 7);
x = b (mod 16). x = 12 (mod 15);
x = 18 (mod 22).
2. Решите приведенные ниже системы сравнений:
а) х = 2 (mod 13); б) х = 7 (mod 17);
х = 5 (mod 21). х = 9 (mod 13);
х = 3 (mod 12).
в) х = a (mod 15); r) x = 5 (mod 9);
x = b (mod 16). x = 13 (mod 11);
x = 7 (mod 5).

РАЗДЕЛ 10.4. Свойства функции 433
3. Если в игре с разноцветными шариками в мешочке располагать их по 15 в
ряд, в мешочке останутся 4 шарика. Если шарики располагать по 8 в ряд,
то 3 шарика останутся в мешочке. Если каждый ряд будет содержать 23
шарика, то 10 шариков останется в мешочке. Какое наименьшее количество
шариков первоначально могло находиться в мешочке? Какое было при этом
количество рядов по 15, 8 и 23 шарика в каждом?
4. Предположим, имеются две шестерни: одна (шестерня А) — с 25 зубьями,
другая (шестерня В) — с 54 зубьями. У шестерни А поврежден зубец, а у
шестерни В повреждена секция между двумя зубцами. Шестерни сцеплены
вместе, при этом шестерня А находится слева. Шестерня А вращается по
часовой стрелке, а шестерня В — против часовой стрелки. Перед началом
вращения зубец шестерни А точно захвачен шестерней В, поврежденный зу-
зубец шестерни А находится за три зубца до места сцепления, а поврежденная
секция — на 20 секций вперед от места сцепления. После какого количества
захватов зубьев поврежденный зубец впервые попадет в поврежденную сек-
секцию? Как часто после этого поврежденные части будут вновь сталкиваться?
5. Найдите, если это возможно, решение каждой из приведенных ниже систем
сравнений:
а) х = 21 (mod 36); б) х = 8 (mod 12); в) х = 19 (mod 49);
х = 5 (mod 8). х = 5 (mod 9); х = 10 (mod 14).
х = 14 (mod 15).
10.4. СВОЙСТВА ФУНКЦИИ ф
Пусть п = р^Р21 - • *Pfcfc — разложение на простые множители числа п. Каждый
положительный делитель числа и либо равен 1, либо делится на pi при неко-
некотором г, и каждое целое число, взаимно простое с п, не имеет ни одного из
указанных чисел в качестве делителя. Некоторые свойства числа п зависят от
количества целых чисел s, 1 < s < n, не содержащих ни одно из pi в качестве
делителя. Например, если п = 40 = 23 • 5, тогда целые числа 5, 1 < 5 < п, и их
разложения на множители имеют вид
1 = 1
2 = 2
3 = 3
4 = 22
5 = 5
6 = 2-3
7 = 7
8 = 23
9 = 32
11 = 11
12 = 22 • 3
13 = 13
14 = 2 • 7
15 = 3 • 5
16 = 24
17 = 17
18 = 2 • З2
19 = 19
21 = 3 7
22 = 2-11
23 = 23
24 = 23 • 3
25 = 52
26 = 2 • 13
27 = 33
28 = 22 • 7
29 = 29
31 = 31
32 = 25
33 = 3 11
34 = 2 • 17
35 = 5 • 7
36 = 22 • З2
37 = 37
38 = 2 • 19
39 = 3 13
10 = 2-5 20 = 22-5 30 = 2-3-5 40 = 23 • 5
Каждое из целых чисел, выделенных жирным шрифтом, не делится ни на 2, ни на

434 ГЛАВА 10. Некоторые специальные вопросы теории чисел
5, и является числом, взаимно простым с п = 40. Количество чисел s, I < s < n,
взаимно простых с п, обозначается 0D0) = 16.
ОПРЕДЕЛЕНИЕ 10.16. Пусть ф{п) — количество положительных целых чисел,
меньших п и взаимно простых с п, т.е. ф(п) — количество приведенных вы-
вычетов по модулю п. Функция ф называется тотиент-функцией Эйлера, или
функцией Эйлера ф.
Из приведенной выше таблицы разложения на множители следует, что
0A) = 1; 0E) = 4; 0(9) = 6;
0B) = 1; 0F) = 2; 0A0) = 4;
0C) = 2; 0G) = 6; 0A1) = 10;
0D) = 2; 0(8) = 4; 0A2) = 4.
Любое положительное целое число и может быть выражено с помощью по-
положительных целых чисел, не превосходящих и взаимно простых с каждым де-
делителем числа п. Например, 6 = 2-3 имеет четыре делителя: 1, 2, 3 и 6. Из
приведенной выше таблицы следует, что
0A) 4- 0B) + 0C) + 0F) = 1 + 1 + 2 + 2 = 6.
Это свойство сформулировано в следующей теореме.
ТЕОРЕМА 10.17. (Гаусс) Если п — положительное целое число, то
d\n
где делители d являются положительными делителями числа п.
ДОКАЗАТЕЛЬСТВО. Пусть d — положительный делитель числа п. Пусть C(d) —
множество положительных целых чисел 1 < т < п, для которых НОД(т,п) = d.
C(d) и C(d') не пересекаются, если d ф d', поскольку произвольное целое число
может иметь с числом п только один наибольший общий делитель. Согласно
теореме 7.8, C(d) является также множеством положительных целых чисел т,
1 < т < п, для которых HOJX(m/d,n/d) = 1. Но количество положительных
целых чисел, меньших n/d и взаимно простых с n/d, совпадает со значением
функции 0(n/d). Поскольку объединение этих множеств есть множество целых
чисел между 1 и п, то п — Y^^n^i71/^)- ^° для кажД°Г0 d, которое делит п,
имеется соответствующее n/d, которое делит п. Следовательно, Yld\n Ф(п/^) =
5Z<f|n Ф№) = п, что и доказывает теорему. ¦
ПРИМЕР 10.18. Пусть п = 12. Делителями 12 являются 1, 2, 3, 4, 6 и 12. Согласно
приведенной выше таблице значений функции Эйлера ф
0A) + 0B) + 0C) + 0D) + 0F) + 0A2) = 1 + 1 + 2 + 2 + 2 + 4 = 12.
Для иллюстрации доказательства теоремы 10.17 в частном случае d = 1, 2, 3,
4, 6 и 12 находим, что соответствующие значения n/d равны, соответственно,
n/d = 12, 6, 4, 3, 2 и 1, так что две упомянутые суммы равны. ?

РАЗДЕЛ 10.4. Свойства функции 435
Теперь перейдем к способам вычисления ф(п) для любого целого положи-
положительного числа п. Решить указанную задачу помогут три следующие теоремы.
ТЕОРЕМА 10.19. Если числа тип — взаимно простые, то
ф(тп) = ф(т)ф(п).
ДОКАЗАТЕЛЬСТВО. Пусть числа тип — взаимно простые. Целое число яв-
является взаимно простым с ran, тогда и только тогда, когда оно взаимно простое
и с га, и с п. Пусть число a — взаимно простое с га и пусть a < га. Рассмот-
Рассмотрим последовательность а, а 4- га, а + 2га,..., а 4- (п — 1)га. Никакие два из этих
чисел не сравнимы по модулю п, поскольку, если a + jm = a + km (mod n), то
n | (jm — km). Отсюда n | m(j — k). Поскольку числа тип — взаимно простые, то
711 (j — ^)» что невозможно. Следовательно, рассматриваемая последовательность
представляет собой полную систему вычетов по модулю п, и каждый элемент
данной последовательности сравним по модулю п с целым положительным чис-
числом, меньшим п. Следовательно, количество этих элементов, взаимно простых с
п, равно ф(п). Поскольку существуют ф(т) таких последовательностей, то су-
существует ф(т)ф(п) чисел, взаимно простых одновременно и с га, и с п, которые
меньше ran и взаимно простые с ran. Поэтому ф(тп) — ф(т)ф(п). Ш
Например, пусть га = 8 и п = 15. Тогда ф(8) = 4, поскольку только 1, 3,
5 и 7 — положительные целые числа, которые меньше 8 и взаимно простые с 8.
Также 0A5) = 8, поскольку только 1, 2, 4, 7, 8, 11, 13 и 14 — положитель-
положительные целые числа, которые меньше 15 и взаимно простые с 15. Следовательно,
0A20) = 0(8HA5) = 32, что можно проверить непосредственно. В соответствии
с утверждением теоремы 10.19 говорят, что ф — мультипликативна относительно
взаимно простых множителей. В следующей главе рассматриваются другие муль-
мультипликативные функции. Теперь покажем, как вычислять 0(п), когда п представ-
представляет собой степень единственного простого числа.
ТЕОРЕМА 10.20. Если р — простое число, то ф(рк) —рк -рк~1.
ДОКАЗАТЕЛЬСТВО. Числа, не превышающие рк и не являющиеся взаимно про-
простыми с рк, имеют вид р, 2р, Зр,..., (рк~1)р. Поскольку имеются рк~1 таких целых
чисел, то существует рк —рк~1 целых чисел, взаимно простых с рк. Следователь-
Следовательно, 0(р/с) = рк - рк~1. Ш
СЛЕДСТВИЕ 10.21. Целое положительное число р является простым тогда и
только тогда, когда ф(р) = р - 1.
ДОКАЗАТЕЛЬСТВО. Если р — простое число, то из теоремы 10.20 непосред-
непосредственно следует, что ф(р) = р - 1. С другой стороны, если число р не является
простым, у него есть делитель d, отличный от р и от 1. Поскольку, по опреде-
определению, ф(р) < р — 1 и d являются одним из р — 1 положительных целых чисел,
меньших р, имеем ф[р) < р — 2, что составляет противоречие. ¦
СЛЕДСТВИЕ 10.22. 0B*) = 2к~1.

436 ГЛАВА 10. Некоторые специальные вопросы теории чисел
На основе свойства мультипликативности ф{тп) = ф(т)ф(п) для взаимно
простых чисел т и п в сочетании с соотношением ф(рк) = рк - рк~1 можно
для любого целого положительного числа п получить явное выражение для ф(п),
используя разложение п на простые множители. Эта формула приведена в сле-
следующей теореме, доказательство которой предоставляется читателю в качестве
упражнения.
ТЕОРЕМА 10.23. Если п — целое положительное число с разложением на простые
множители вида
то
г=1 г=1
ПРИМЕР 10.24. Поскольку и = 40 = 23 • 5, 0D0) = 40A - 1/2)A - 1/5) =
40A/2)D/5) = 16, что совпадает со значением, полученным в одном из примеров
в начале этого раздела. Кроме этого, в главе 3 показано, что п = 39616304 =
24-72-133-231, поэтому
0C9616304) = 23B - 1OХG - 1I32A3 - 1J3°B3 - 1) =
= 8 • 1 • 7 • 6 • 169 • 12 • 1 • 22 = 14990976. ?
Существуют ограничения, касающиеся количества целых чисел s, I < s <
п, взаимно простых с п. Одну из таких ограничивающих связей устанавливает
следующая теорема.
ТЕОРЕМА 10.25. Если целое число и больше 2, то ф(п) — четное.
ДОКАЗАТЕЛЬСТВО. Если п = 2кту где т — целое нечетное число и к > 1,
то фBкт) = фBк)ф(т) = 2к~1ф(т) и, следовательно, ф(п) — четное. Если п =
ркту где р — нечетное простое число и числа рк и т — взаимно простые, тогда
ф{ркт) = ф{рк)ф(т) = (рк - рк-1)ф{т). Но рк - рк~1 = рк~1{р - 1) и р - 1 -
четное число, поскольку р — нечетное. Следовательно, ф{п) — четное. ¦
Приведенный ниже результат нами уже упоминался, но здесь он излагается
формально.
ТЕОРЕМА 10.26. Если и — целое число, тогда ненулевой класс приведенных
вычетов образует группу относительно умножения по модулю п.
ДОКАЗАТЕЛЬСТВО. Если числа а и Ъ — взаимно простые с п, то, очевидно,
число ab — также взаимно простое с п, поэтому наш класс вычетов замкнут
относительно умножения. Если число a — взаимно простое с п, то сравнение ах =
1 (mod n) имеет единственное решение, и, следовательно, существует величина,
обратная к а. ¦

РАЗДЕЛ 10.4. Свойства функции 437
Пусть число р — простое. Поскольку {1,2,... ,р — 1} — множество приведен-
приведенных вычетов по модулю р, то [1], [2],..., [р — 1] образуют, как это было показано
в разделе 3.6, группу относительно умножения. Следующая теорема показывает,
что произведение [1] © [2] 0 • • • © [р - 1] всех ненулевых классов вычетов всегда
является классом вычетов [р- 1] = [—1]. На языке сравнимости это эквивалентно
утверждению, что 1-2 (р - 1) = -1 (mod p).
ТЕОРЕМА 10.27. (Уилсон) Целое положительное число р является простым
тогда и только тогда, когда (р — 1)! = — 1 (mod p).
ДОКАЗАТЕЛЬСТВО. Если число р — простое, то р = 0 (mod р)ир-1 = -1
(modp). Когда р — простое, ненулевой класс вычетов по модулю р образует
группу относительно умножения, так что каждый класс вычетов является спа-
спаренным со своим обращением и дает в произведении [1]. Таким образом, если
I < и < р — 1, то существует единственное целое число и~г, 1 < и~1 < р — 1
такое, что и • и~1 = 1 (mod p). Имеем и — и'1 или и ф и~1. Очевидно, что для
и = 1 имеем и~1 = 1, а также и2 = ии~1 = 1 (modp). Если существует целое
число а, 1 < а < р - 1 такое, что а2 = 1 (mod р), то а2 - 1 = (а - 1)(а + 1) = 0
(mod р) и р | (а — 1)(а + 1). Таким образом, р | (а — 1) или р | (а + 1). Поскольку
а — 1^0иа<р, получаем, что р \ (а — 1). Таким образом, р \ (а 4- 1), откуда
р < а + 1; и поскольку а < р — 1, это имеет следствием а + 1 < р. Получаем,
что р = а + 1 или а = р — 1. Таким образом, для 1 < и < р — 1 только и = 1
и и = р — 1 обладают таким свойством, что и2 = 1 (modp). Итак, получаем
(р - 1)! = lfait^XuauJ1) • • • (uku^)(p — 1) = 1 -1 -1 1 • (р - 1) = р - 1 = -1
(mod р), где tzj — одно из целых чисел 2, 3, ..., (р — 2), и к = (р — 3)/2.
Если число р не является простым, то р = г • s, где 1 < г, 5 < р. Поскольку
(р - 1)! делится на г, то (р - 1)! = 0 (mod г), так что (р - 1)! ф -1 (mod r).
Поэтому р должно быть простым. ¦
Например, пусть р = 5. Тогда (р — 1)! = 4! = 24 = — 1 (mod 5). Заметим, что
в теореме говорится о том, что произведение (р — 1)! не может быть сравнимо с
— 1, если число р не является простым. Посредством теоремы можно проверять
простоту числа р, устанавливая, справедливо ли сравнение (р-1)! = -1 (mod p).
Однако, такой критерий не используется для больших значений р, т.к. вычисление
(р- 1)! (modp) практически нецелесообразно.
Теперь рассмотрим теорему Уилсона с алгебраической точки зрения. Уже
известно, что Zp-{[0]} образует группу относительно умножения. Поэтому каж-
каждый ненулевой элемент из Zv имеет мультипликативную инверсию — обратный
элемент относительно умножения. Доказательство приведенной выше теоремы
Уилсона показывает, что только [1] и [р — 1] совпадают со своими обратными
элементами. Следовательно, в произведении [1][2][3] • • • [р - 1] каждый элемент
является спаренным со своим обратным элементом, так что [1][2][3] • • • [р — 1] =
[1][р - 1] = [р - 1] или, что то же самое,
1-2-3 (р-1) = Р-1 (modp) = -1 (modp).
Легко показать, что в циклической группе четного порядка существуют толь-
только два элемента, которые совпадают со своими обратными элементами. Этими
элементами в данном случае являются [1] и [р- 1].

438 ГЛАВА 10. Некоторые специальные вопросы теории чисел
Рассматриваемая нами функция ф названа в честь Леонарда Эйлера, перу
которого принадлежит наибольшее количество математических трудов. Многие
из доказанных им теорем встречаются на страницах этой книги. Творческое на-
наследие Эйлера могло бы составить более 75 объемных томов. Ему принадлежат
открытия практически во всех областях математики. Только в теории чисел ему
принадлежит более 140 оригинальных работ, включая доказательства целого ря-
ряда малых теорем Ферма. Он считается основоположником топологии, а также
целых разделов математического анализа. Престижную премию Парижской Ака-
Академии наук, присуждаемую раз в два года, Эйлер получал 12 раз. Многие из ныне
существующих систем математических обозначений введены Эйлером.
Леонард Эйлер (Leonard Euler, 1707-1783) был сыном лютеранского священ-
священника в Швейцарии. Его отец был его первым учителем. Он хотел, чтобы сын
также пошел в духовенство, но Эйлеру посчастливилось стать учеником Иоган-
Иоганна Бернулли (Jean Bernoulli), одного из лучших европейских математиков того
времени. Не найдя в Швейцарии условий для научной деятельности, он вместе
с другими европейскими математиками уехал работать в Россию, где незадолго
до этого была основана Санкт-Петербургская Академия наук. Во время пребыва-
пребывания в России он ослеп на один глаз. Вскоре после прибытия Эйлера в Россию
в стране начались политические репрессии, и после 14 лет жизни в России он
уехал в Германию, чтобы возглавить математический отдел Берлинской Академии
наук. По-видимому, в этот период жизни в Германии на вопрос королевы-матери
о том, почему он такой неразговорчивый, Эйлер ответил, что только что приехал
из страны, где вешают всякого, кто разговаривает.
Тем не менее, Эйлер оставался весьма уважаемым в России. Когда в 1760
году началась война между Россией и Германией, дом, где жил Эйлер, был раз-
разрушен, и когда об этом узнали в России, материальный ущерб был моментально
возмещен, а императрица сделала ему подарок. После 25 лет пребывания в Герма-
Германии, по причине разногласий с королем Фридрихом II, Эйлер вернулся в Россию,
приняв великодушное приглашение Екатерины И. Через четыре года после воз-
возвращения Эйлер ослеп на второй глаз и оставался слепым последние 17 лет своей
жизни, однако занятий математикой не прекращал. В 1771 году в доме Эйлера
случился пожар. Его слуга-швейцарец, Петр Гримм, храбро ринулся в пылающий
дом и вынес слепого Эйлера. Императрица Екатерина вскоре выстроила Эйлеру
новый дом. Говорят, что 18 сентября 1783 года, проведя вечер за вычислением
законов для описания подъема воздушных шаров и наметив в общих чертах вы-
вычисление орбиты открытой незадолго до того планеты Уран, Эйлер курил трубку
и играл со своим внуком, когда его хватил удар. Трубка вывалилась изо рта, он
произнес слова: "Я умираю", и эпоха Эйлера закончилась.
Существует целый ряд занимательных историй об Эйлере. Говорят, он мог
декламировать слово в слово Энеиду Вергилия, хотя читал ее лишь в детстве.
Тьебо (Thiebault) рассказывает, что к Российскому двору был пригашен Дидро,
который, будучи атеистом, стал распространять свои идеи. Чтобы заставить его
замолчать, был придуман план. Эйлер, истинно верующий христианин, подошел
к Дидро и провозгласил по-французски: "(а + bn)/n = x, следовательно, Бог
существует! Отвечай!" Дидро не знал математики, поэтому молчал. Поднялся
хохот, отчего Дидро смутился настолько, что немедленно вернулся во Францию.

РАЗДЕЛ 10.5. Порядок целого числа 439
Другая история повествует о том, как Эйлер, будучи в почтенном возрасте,
слепой, был приглашен княгиней Дашковой посетить ее выступление в связи со
вступлением княгини в должность директора Императорской Академии наук в
Санкт-Петербурге. Эйлер, в сопровождении сына и внука, приехал вместе с кня-
княгиней в ее экипаже. После выступления, в котором Эйлеру была воздана высокая
хвала, княгиня села на место, предполагая, что Эйлер займет почетное место ря-
рядом с ней. Высокомерный профессор Штелин занял это место до того, как Эйлера
к нему подвели. Дашкова обратилась к Эйлеру с предложением занять любое ме-
место, сделав его тем самым почетным. Этот жест княгини произвел благоприятное
впечатление на всех присутствовавших.
¦ УПРАЖНЕНИЯ
1. Найдите такие целые положительных числа тип, что ф(тп) =? ф(т)ф(п).
2. Докажите, что если число р — простое и р > 2, то (р - 2)! = 1 (mod p).
3. Докажите, что 1 • 2 • 3 1007 = 1 (mod 1009).
4. Пусть
S(n) = sin 7г
L
п
Покажите, что число п — простое тогда и только тогда, когда S(n) = 0.
5. Докажите теорему 10.23.
6. Постройте таблицу значений ф(п) при 1 < п < 50.
7. Вычислите значение 0B025).
8. Докажите, что если число п — составное и п > 4, то (п — 1)! = 0 (mod n).
9. Докажите, что число п — простое тогда и только тогда, когда п делит
10.5. ПОРЯДОК ЦЕЛОГО ЧИСЛА
В этом разделе будут рассмотрены такие целые числа j, что а-7 = 1 (mod m). В
частности, нас будет интересовать наименьшее из этих положительных чисел j.
ТЕОРЕМА 10.28. (Эйлер) Если т — целое положительное число и НОД(а, т) =1,
то а^т) = 1 (mod m).
ДОКАЗАТЕЛЬСТВО. Пусть т — целое положительное число и a — число, вза-
взаимно простое с т. Если {xi,X2,... ,x^} — приведенная система вычетов по моду-
модулю т, то, поскольку числа а и т — взаимно простые, {axi,ax2,... ,ахь) также
является системой приведенных вычетов. Следовательно, каждое Х{ сравнимо по
модулю т только с одним axj. Поэтому
(mod m)
или
a<?(m)XiX2 ... Хк= х\Хч - - • Xk (mod m),
и, поскольку числа т и x\X2"-Xk взаимно просты, то на Х{ можно сокращать,
что дает a^m) = I (mod га). ¦

440 ГЛАВА 10. Некоторые специальные вопросы теории чисел
Например, при a = 3, т = 4 имеем фD) = 2, так что З2 = 9 = 1 (mod 4).
Если в теореме 10.28 т — простое число, то каждое целое положительное
число, которое меньше га, является взаимно простым с га, так что ф(т) = га —
1. Случай простого числа га рассмотрен как следствие к теореме 10.20. Таким
образом, как частный случай, справедлива следующая теорема.
ТЕОРЕМА 10.29. (Малая теорема Ферма) Если р — простое число, то для
каждого такого целого числа а, что 0 < а < р, имеем ap~l = 1 (mod р).
Например, если р = 7, то р— 1 = 6. В таком случае шестая степень каждого
целого положительного числа, которое меньше р = 7, должна быть сравнима с 1
по модулю 7:
I6 = 1 = 1 (mod 7),
26 = 64=1 (mod 7),
З6 = 729 = 1 (mod 7),
46 =4096 ее 1 (mod 7),
56 = 15625 = 1 (mod 7),
б6 = 46656 = 1 (mod 7),
76 = 117649 = 0 (mod 7).
Утверждение, обратное малой теореме Ферма, неверно. Например, З90 = 1 (mod 91)
однако, 91 = 7-13 — составное число. С другой стороны, если р — целое положи-
положительное число и 0 < a < р таково, что ар ф 1 (mod p), тогда р не может быть
простым. Таким образом, малая теорема Ферма содержит частичный критерий
простоты числа, поскольку с ее помощью можно показать, что целое положи-
положительное число не является простым без определения нетривиального делителя
числа р. Составные положительные числа и таковы, что an~l = 1 (mod n) для
некоторого а, 1 < а < п, до определенной степени схожи с простыми числами; по
этой причине такого рода составное число и называют псевдопростым числом по
основанию а. Таким образом, число п = 91 — псевдопростое по основанию a = 3.
Однако, если выбрать a = 2, то получим 290 = 64 ф 1 (mod 91); то есть, число
п — 91 не является псевдопростым по основанию 2. Итак, 91 — псевдопростое
число по основанию 3, но не является псевдопростым по основанию 2.
ОПРЕДЕЛЕНИЕ 10.30. Пусть п — целое положительное число и a — целое
число такое, что НОД(а,п) = 1. Порядком числа а по модулю п называется
наименьшее целое положительное число к такое, что ak = I (mod n). Это
число обозначается через ordna.
ТЕОРЕМА 10.31. Пусть п — целое положительное число, НОД(а, п) = 1 и к =
ordn а. Тогда
а) если а171 = 1 (mod n), где т — целое положительное число, то к \ га;
б) к | ф(п)\
в) для целых г и s, ar = as (mod п) тогда и только тогда, когда г = s (mod fc);

РАЗДЕЛ 10.5. Порядок целого числа 441
г) никакие два из целых чисел a,a2,a3,... ,ак не являются сравнимыми по
модулю к\
д) если га — целое положительное число, то порядок числа а171 по модулю п
к
Щ
е) порядок числа ат по модулю п равен к тогда и только тогда, когда числа га
и fc — взаимно простые.
ДОКАЗАТЕЛЬСТВО.
а) Если а171 = 1 (mod п) для целого положительного числа га, то согласно
алгоритму деления га = kq + г, где 0 < г < к. Следовательно, а171 = akq+r —
akqar, так что ar = I (mod n). Но это противоречит определению порядка
числа а, если не г = 0. Следовательно, А: | га.
б) Поскольку по теореме 10.28 имеем аф^ = 1 (mod n), из части (а) следует,
что к | 0(п).
в) Предположим, что г > s. Поскольку числа а и п — взаимно простые, аг =
as (mod n) тогда и только тогда, когда ar~s = I (mod n); следовательно,
согласно части (а) к делит г — 5, и г = s (mod к).
г) Справедливость утверждения непосредственно следует из части (в).
д) Пусть d = НОЩк, т), так что к = ud и т = vd. (а™)*/ нод(/с,т) = ^myd/d =
aUTn = auvd = aSud}v = akv = 1 (mod n). Допустим, что число t таково, что
(а171I = 1 (mod n). Тогда amt = 1 (mod n), так что fc | mt, потому что
ordn а = к. Следовательно, ud \ vdt и, поскольку числа и и v — взаимно
простые, и | t. В силу того, что А: = ud, (k/d) = /с/НОД, (fc,m) делит ?,
поэтому /с/ НОД(/с, га) и является порядком числа а171 по определению.
е) Это утверждение следует непосредственно из части (д).
ПРИМЕР 10.32. Для иллюстрации теоремы 10.31 предположим, что п = 14 = 2-7,
так что (/>(п) = B — 1)G — 1) = 6. Первичная приведенная система вычетов для
п = 14 есть множество {1,3,5,9,11,13}. Рассмотрим приведенную ниже таблицу
вычетов для степеней числа а = 5,
m
1
2
3
4
5
6
7
[Kiln
5
11
13
9
3
1
5
m
8
9
10
11
12
13
[Kiln
11
13
9
3
1
5
из которой видно, что после га = 6 идет повторение одной и той же схемы. Таким
образом, к = ordi4 5 = 6. Для га = 12, аш = 512 = 1 (mod 14) и к \ тп, что
согласуется с утверждением теоремы 10.31(а). Также ordi4 5 | 0A4), поскольку
6 | 6 [теорема 10.31F)]. Кроме того, 2 = 8 = 14 (mod 6) и 52 = 58 = 514 = 11

442 ГЛАВА 10. Некоторые специальные вопросы теории чисел
(mod 14) [теорема 10.31(в)]. Согласно таблице никакие два из чисел 51, 52, 53,
54, 55 и 56 не являются сравнимыми по модулю 14 [теорема Ю.ЗЦг)]. Поскольку
ordn Ь | ф(п) для любого целого числа Ь и ф(п) = 6 для и — 14, порядок каждого
Ь в {1,3,5,9,11,13} можно легко подсчитать, как это было сделано для a = 5.
6
1
3
5
9
11
13
ordn 6
1
6
6
3
3
2
Если га = 4, то 5т = 9 (mod 14), но ordi4 5/HQfl(ordi4 5,4) = 6/НОДF,4) =
6/2 = 3. Согласно таблице порядков ordi4 54 = 3 [теорема 10.31 (д)].
Только 6 = 3 и 6 = 5 имеют порядок 6 по модулю 14. Показателями степени
т в таблице, приведенной выше, определяющими значение ат, которое сравнимо
либо с числом 3, либо с числом 5, являются т = 1,5,7,11, и 13. Это только
такие значения га, которые являются взаимно простыми с числом и = 14 [теоре-
[теорема Ю.ЗЦе)]. ?
ТЕОРЕМА 10.33. Если НОД(а, п) = НОДF, п) = 1 и ordn а является взаимно
простым с ordn Ь, то ordn (ab) — (ordn a) • (ordn b).
ДОКАЗАТЕЛЬСТВО. Пусть ordn а = R и ordn 6 = 5, тогда
(ab)RS = aRSbRS = (aR)s(bs)R = 1-1 = 1 (mod n).
По теореме 10.31, ordn (ab) \ RS. Поскольку числа R и S — взаимно простые, то
существуют целые числа г и 5, для которых ordn (ab) = rs1r-w = Rns'X = S.
Покажем теперь, что г = R и s = S. По определению г и s,
(ab)rs = arsbrs = 1 (modn);
(arsbr3)w = lw = 1 (mod n);
(arw)s • (brw)s = 1 (mod n).
Но поскольку arw = 1 (mod n) и rw = i?, имеем
bRs = 1 (mod n).
По теореме Ю.ЗЦа) имеем ordn b \ Rs или, что то же самое, S \ Rs. В силу того,
что НОД(Я, S) = 1, имеем S \ s, но также s \ 5, так что S = s. Аналогично,
R = г. Таким образом, ordn (ab) = (ordn a) • (ordn b). Ш

РАЗДЕЛ 10.5. Порядок целого числа 443
ПРИМЕР 10.34. Если п = 11, то все приведенные вычеты являются взаимно
простыми с п. Таблица порядков по модулю 11 имеет вид
Вычет
1
2
3
4
5
Порядок
1
10
5
5
5
Вычет
6
7
8
9
10
Порядок
10
10
10
5
2
Если a = 3 и Ь = 10, то ab = 30 = 8 (mod 11). Таким образом, ordu (ab) =
ordnC0) = ordn 8 = 10 = (ordu 3) • (ordn 10). Безусловно, НОДC,11) =
НОДA0,11) = 1, ordn 3 = 5 и ordn 10 = 2 — взаимно простые. Заметим, что
если a = 3 и с = 7, то ordn 3 = 5 не является взаимно простым с ordn 7 = 10. В
этом случае ordn (ас) = ordn 21 = ordn 10 = 2 / (ordn 3) • (ordn 7) = 50. ?
ПРИМЕР 10.35. Порядок a = 5 по модулю п = 14 был получен в примере 10.32
при вычислении ат для т = 1,2,3,..., ф(п) вплоть до нахождения того, что
а171 = 1 (mod n). Из теоремы 10.31F) следует, что порядок а по модулю п дол-
должен делить ф{п)\ поэтому вместо проверки по одному каждого га, 1 < га < ф(п),
тестируются только те значения га, которые делят ф(п). Для п = 14 ф[п) = 6,
единственными положительными делителями которого являются 1, 2, 3 и 6. В
данном случае работа по определению ordi4 5 сокращается незначительно, по-
поскольку в примере 10.32 значения т = 4 и 5 были уже протестированы.
Однако, для п = 58 и а = 25, используя теорему 10.31F), легко получаем
ord58 25 = 7. 0E8) = фB • 29) = B - 1)B9 - 1) = 28 = 22 • 7. Единственными
положительными делителями числа 22-7 являются 1, 2, 4, 7, 14 и 28. Приведенную
ниже таблицу легко построить:
т [[25™]]58
1
2
4
7
25
45
53
1
Поэтому ord5e 25 = 7, и нет необходимости проверять п = 14 и 28. ?
Результаты, полученные в теоремах 10.31 и 10.36, приводят к формулировке
критерия, названного критерием простоты числа Лукаса.
ТЕОРЕМА 10.36. (Лукас) Если п — целое положительное число, и существует
такое целое число а, что
а71 = 1 (mod n)
ар ф\ (mod n)
для каждого простого числа р, которое делит п — 1, тогда п — простое число.

444 ГЛАВА 10. Некоторые специальные вопросы теории чисел
ДОКАЗАТЕЛЬСТВО. Из соотношения an~l = 1 (mod n) следует, что НОД(а,п) =
1, а также, по теореме Ю.ЗЦа), что ordn a \ (п - 1). Если число р — простое и
такое, что р | (п - 1), тогда из сравнимости aSn~lVp ф 1 (mod га) следует, что
ordn a \[{n - 1)/р], потому что, если ordna | [(га — 1)/р], это противоречило бы
aordn a = 1 (mod га). Ho ordn a | (n - 1) и ordn a\[(n- l)/p) для всех р, которые
делят га- 1, откуда следует, что ordn a = га- 1. По теореме 10.31F), c/>(n) = n— 1.
Поэтому, согласно следствию 10.21, п — простое число. ¦
Для того чтобы использовать критерий Лукаса для проверки га, необходимо
уметь раскладывать на множители число га - 1, что само по себе может пред-
представлять трудности. Более того, требуется находить соответствующее а. Целое
число а, введенное в теореме 10.36, называется примитивным корнем числа
п. Используя критерий с числом a = 7, можно показать, что число Мерсенна
п = 231 — 1 является простым, поскольку га — 1 = 2 • З2 • 7 • 11 • 31 • 151 • 331.
Смотрите упражнения в конце данного раздела.
Если НОД(а, п) = 1 и число и — простое, теорема Ферма утверждает, что
an-i ^ ^ (mod n). Ее обобщение, теорема Эйлера, для любого положительно-
положительного числа п дает а^п^ = 1 (mod n). Исключая эти и некоторые другие случаи,
вычисление ае по модулю и или, более точно, вычисление [[ae]]n, т.е. остатка
от деления ае на п, для большого значения е может представлять значительные
трудности, поскольку само вычисление ае в таких случаях и деление его на п
практически нецелесообразно.
В предыдущих примерах мы использовали запись е = е\ + в2 4- • • • 4- е^ с
соответствующими е*, вычисляли [[aei]]n, перемножали результаты и приводили
произведение по модулю п. Этот метод работает, поскольку
Nil» = [[[[«]]„ •[[*]]„]]„•
При этом значения е^ были выбраны специальным образом.
Более эффективный алгоритм вычисления подобен рассмотренному выше, но
использует двоичное представление показателя степени е, т.е. представление на
основе числа 2. А именно,
е = 6m2m 4- 6m_i2m-1 + • • • 4- &121 4- b0 =
— [bmbm-l ' ' ' Ь\Ь()\дво
где bi = 0 или 1 и 6m = 1. Таким образом,
Если в выражении для показателя степени сделать перегруппировку с тем, чтобы
сократить количество сомножителей, получим представление в соответствии с
правилом Горнера:
е = (• ¦ • (Fт • 2 4- bm-i) • 2 4- Ьт_2) • 2 4- • • • 4- Ьг) • 2 + Ьо,
так что
ае = (• • • ((а6™'2 • а6—1J • а6—2J а61J • аъ°.

РАЗДЕЛ 10.5. Порядок целого числа 445
Мы можем найти значение [[ае]]п, последовательно вычисляя выражения в скоб-
скобках в порядке их вложения, начиная с внутренних, и приводя каждое произведе-
произведение по модулю п. Таким образом, для е = [6mbm_i • • • bibo\deou4HOe, начинаем с
Рт = [И]„ ¦
Затем для к = т — 1, т — 2, ..., 2, 1 и 0 вычисляем
если bk = 0;
если bk = 1.
Окончательным результатом является ро = [[ав]]п- Более подробно, начиная с
Рт = [[а]]П' получаем следующее произведение рь возводя в квадрат предыдущее
произведение и приводя полученное по модулю п, когда bk = 0; возводя в квадрат
предыдущее произведение, умножая его на а и приводя полученное по модулю п,
когда bk = 1. Алгоритм работает, поскольку если а возводится в квадрат к раз,
результатом будет а2 ; а если а2 Ь возводится в квадрат j раз, в результате
получится a2 +Jb2J.
ПРИМЕР 10.37. Предположим, что необходимо вычислить[[3103]]41. Поскольку
103 = 26 + 25 4- 22 + 21 4-1 =
= 1100111
и т = 6, получаем
к
6
5
4
3
2
1
0
ьк
1
1
0
0
1
1
1
Рк = [[р1+1
3 =
32-3 -
B7J =
C2J =
D0J • 3 =
CJ-3 =
B7J . з =
•аЧ]
J J n
3
27
729 = 32
1024 = 4
4800 = 3
27
2187 = 14
Поэтому [[3103]]41 = 14. Используя сравнимость по модулю 41 специальным об-
образом, получаем
З10 = 57049 = 9;
З50 = (З10M = 95 = 59049 = 9;
З103 = З50 • З50 • З3 = 9 • 9 • 27 = 2187 = 14. ?
УПРАЖНЕНИЯ
1. Докажите малую теорему Ферма в такой формулировке. Если р — простое
число иа^О (mod р), то ap~l = 1 (mod p).

446 ГЛАВА 10. Некоторые специальные вопросы теории чисел
2. Докажите, что если НОД(а, га) = 1, то сравнение ax = b (mod га) имеет
решение х = a^Tn^~1b (mod га).
3. Пусть р — простое число, р > 2 и J = 0 (mod (p - 1)). Докажите, что
1J + 2J + 3J + • • • 4- (р - 1)J = -1 (mod p).
4. Пусть НОД(га, n) = 1 и пусть множества {ri,r2,... ,rm} и {si,$2, • •• >5n} —
полные системы вычетов по модулю тип соответственно. Докажите, что
множество ran целых чисел {п • n + га • Sj : 1 < г < га и 1 < j < п}
представляет собой полную систему вычетов по модулю ran.
5. Восполните все детали доказательства малой теоремы Ферма, используя
формулу бинома Ньютона и индукцию по а.
6. Используйте метод упражнения 2 для решения таких сравнений:
а) Ъх = 8 (mod 11); б) 7х = 8 (mod 25); в) 9х = 13 (mod 25).
7. Докажите, что для каждого простого числа р
(а + Ъ)р = а? + ЬР (modp).
8. Докажите теорему, обратную к теореме 10.31(а): если п — целое положи-
положительное число, НОД(а, п) = 1, k = ordn а и к \ га, то а171 = 1 (mod га).
9. Определите ordn а для 1 < а < п — 1, если
a) n = 9; б) п = 20; в) п = 27.
10. Покажите, что
а) Ь10 - 1 делится на 11, если b и 11 — взаимно простые числа;
б) 610fc - 1 делится на 11, если НОДF,11) = 1;
в) Ь7 — Ь делится на 42 при любом целом Ъ.
11. Покажите, что
а) 74 = 1 (mod 5);
б) 74 = 1 (mod 2);
в) 74 = 1 (mod 10);
г) 74fc = I (mod 10) для любого положительного целого числа к.
Что представляет собой последний десятичный разряд числа 74000?
12. Покажите, что
а) 720 = 1 (mod 25); б) 72 = 1 (mod 4);
в) 720 = 1 (mod 4); г) 720 = 1 (mod 100).
Что представляет собой последний десятичный разряд числа 7500?
13. Подсчитайте следующие вычеты :
а) [[3275]]100 б) [[65И]10оо
в) [[И24681]]83 г) [[3497^0]]1234
д) ^72.8».7.11.31.331]]^_1 = [[714221746]]214748зе47 (Для выполнения этого
задания вам, вероятно, потребуется использовать компьютер.)
14. Покажите при помощи критерия Лукаса, что следующие числа являются
простыми:
а) 37; б) 199.

РАЗДЕЛ 10.5. Порядок целого числа 447
15. Докажите следующие утверждения.
а) Пусть и — нечетное положительное целое число. Если существует такое
положительное целое число а, что
(i) оГ^~ = —1 (mod n) и
(ii) a~p~ ф 1 (mod n) для каждого нечетного простого числа р, которое
делит (п — 1),
топ- простое число.
б) Воспользовавшись критерием части (а) вместо критерия Лукаса, докажи-
докажите, что целые числа в упражнении 14(а) и (б) являются простыми.
16. Докажите, что если F(n) = 22П + 1 — число Ферма и существует целое
положительное целое число а такое, что а2 =1 (mod F(n)) и а2 ф\
(mod F(n)), то F(n) — простое число.
17. Используйте упражнение 16 для доказательства, что приведенные ниже це-
целые числа являются простыми:
a) FC) = 257; б) FD) = 65537.

ГЛАВА
НЕКОТОРЫЕ
СПЕЦИАЛЬНЫЕ
ВОПРОСЫ
ТЕОРИИ РЕКУРСИИ
11.1. ОДНОРОДНЫЕ ЛИНЕЙНЫЕ РЕКУРРЕНТНЫЕ ОТНОШЕНИЯ
В главе 5 было начато рассмотрение в общих чертах методов исключения рекур-
рекурсии, или решения рекурсивных функций. Под решением рекурсивной функции мы
понимали следующее: рассматривали функцию а(п) или апу заданную рекурсивно
на множестве положительных или неотрицательных целых чисел, и заменяли ее
функцией, заданной в явном виде, когда функция ап была выражена непосред-
непосредственно как функция от п. Например, функция, заданная рекурсивно согласно
соотношениям
ai = 1,
ак = ak-i + fc,
может быть задана непосредственно в виде
_ п(п + 1)
ап- - .
Использовался метод, который заключался в вычислении функции ап для
нескольких первых значений п из ее области определения с последующим поиском
выражения для непосредственного задания ап как функции п. Вообще, решение
произвольных рекуррентных отношений представляет большие трудности, иногда
фактически непреодолимые.
В этом разделе рассматривается широкий класс рекурсивных функций, для
которых решения известны.
Сначала определим класс рекурсивных функций, известный как класс ли-
линейных рекурсивных функций.
ОПРЕДЕЛЕНИЕ 11.1. Рекурсивное отношение вида
ап = ci(n)an_i + c2(n)an_2 4- с3(п)ап-3 + • • • + ср(п)ар + f(n)
называется линейным рекуррентным отношением порядка р.

РАЗДЕЛ 11.1. Однородные линейные рекуррентные отношения 449
ОПРЕДЕЛЕНИЕ 11.2. Линейное рекуррентное отношение вида
а>п = ci(n)an_i 4- с2(п)ап-2 + с3(п)ап-3 4 Ь ср(п)ап-р
называется линейным однородным рекуррентным отношением порядка р.
Рассматриваемое отношение названо линейным рекуррентным отношением,
поскольку показатель степени каждого а* равен единице. Другими словами, ни
одно из п{ не возводится в какую-либо степень, кроме первой. Таким образом,
отношение ап = За^_х + 4an_2 не будет линейным, т.к. an_i возведено в третью
степень. Однако, отношение ап = 3n3an_i 4- nan_2 линейно. К сожалению, рас-
рассматриваемое множество линейных рекуррентных отношений необходимо огра-
ограничить еще в большей степени. Дополнительно требуется, чтобы коэффициенты
Ci(n) для каждого г были константами.
ОПРЕДЕЛЕНИЕ 11.3. Линейное рекурсивное отношение вида
ап = cian_i 4- c2an_2 4- сзап-3 Н h срап-р + /(п), ср ф О
с постоянными коэффициентами с» при 1 < i < p называется линейным ре-
рекуррентным отношением с постоянными коэффициентами порядка р.
Далее будем рассматривать некоторые линейные рекурсии такого вида, но
даже при указанных выше ограничениях возможности решения задачи будут за-
зависеть от выбора функции f(n). Линейные рекуррентные отношения с постоян-
постоянными коэффициентами общего вида рассматриваются в следующем разделе. Но
прежде, чем решать задачи такого типа, требуется ввести еще одно ограничение
на рассматриваемый класс линейных рекурсий.
ОПРЕДЕЛЕНИЕ 11.4. Линейное рекуррентное отношение вида
ап = cian_i -f c2an_2 4- c3an_3 H Ь срап-р, ср ф О
с постоянными коэффициентами с; при 1 < i < p называется линейным од-
однородным рекуррентным отношением с постоянными коэффициентами
порядка р.
Такое отношение является частным случаем линейного рекуррентного отно-
отношения с постоянными коэффициентами, когда f(n) = 0. Один из известных при-
примеров — последовательность Фибоначчи: 1,1,2,3,5,8,13,21,..., в которой каж-
каждый элемент после первых двух равен сумме двух предшествующих элементов
последовательности. Рекурсивно это условие определено следующим образом.
ФибA) = 1;
ФибB) = 1;
Фиб(п) = Фиб(п - 1) 4- Фиб(п - 2) для п > 2.

450 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Таким образом, в этом случае р = 2, с\ — 1 и с2 = 1. Далее в разделе приводится
решение этой рекурсивной функции.
Для начала давайте рассмотрим случай р = 1. Допустим, что рекурсивная
функция имеет вид
ао = с;
ап — 6an_i при п > 0.
Отсюда получаем последовательность
а\ = be
а2 = Ь2с
а3 = Ь3с
B4 = Ь4С
ап = Ьпс,
в которой значение с определяется через значение, присвоенное а0. Легко заме-
заметить, что отношение an = 6an_i имеет решение вида ап = Ьпс. Далее убедимся,
что для любого и > 1 решение можно представить в виде ап = Ьпс. Но если пред-
предположить, что мы с самого начала рассматривали рекурсивную функцию вида
а-п = ban-i при п > 1,
то получим последовательность вида
аг=с
п2 = Ьс
а3 = 62с
а4 = Ь3с
а5 = Ь4с
ап = b" *c.
Можно ли по-прежнему использовать запись ап = с'Ьп, если это действи-
действительно существенно? Ответ утвердительный, поскольку ап = bn~1c = bn(c/b).
Если положить с' = (с/6), то ап = dbn. Допустим, мы начали действовать иначе
и, в силу таинственных причин, например, посоветовавшись с оракулом, предпо-
предположили, что ап имеет вид ап = гп для некоторого значения г. Тогда, учитывая
соотношение ап = Ьап_ь получаем гп = 6гп~1. Если разделить обе части равен-
равенства на гп~~\ имеем г = Ь, так что ап = Ьп. Заметим далее, что если умножить

РАЗДЕЛ 11.1. Однородные линейные рекуррентные отношения 451
обе части равенства гп = Ьгп~1 на константу с, получим сгп = Ьсгп~1у так что
если ап = гп есть решение для ап = 6ап_ь то решением является и ап = сгп.
Поэтому получаем, что общее решение имеет вид сЬп. Но в таком случае, задав
значение а\% можно определить значение с.
Например, если
а0 = 4;
ап = 5an_i при и > 1,
то ап = сБп. Но а0 = с5° = 4, поэтому с = 4. Вообще говоря, отношение ап =
6an_i имеет решение с6п, где с = а0.
Если же
ai =4;
ап = 5an_i при п > 1
и ап = с5п, то ai = сЪ1 = 4 и с = 4/5.
Причиной морочить читателю голову очевидными вещами и придавать им
вид непонятных, рассматривая случай р = 1, является переход к обсуждению
ситуации р = 2, когда
Опять предположим, что имеется решение вида ап — гп, и в этом случае получаем
Если разделить обе части равенства на гп~2, получим
Г2 = С\Г 4" С2-
Таким образом, величину г можно найти, решая квадратное уравнение г2 =
2. Это характеристическое уравнение описывает характеристический мно-
мно2
гочлен г2 — с\г — С2 отношения ап = с\ап-\ +
Например, предположим, что ап = an_i +6an_2- Тогда характеристический
многочлен задает характеристическое квадратное уравнение г2 = г — 6 или г2 —
г - 6 = 0. Раскладывая на множители, получаем (г — 3)(г + 2) = 0, так что
решениями характеристического уравнения являются г = -2 и г = 3. Поскольку
решения данного рекуррентного отношения имеют вид an = rn, где г — решение
уравнения г2 — г — 6 = 0, то отсюда следует, что ап = Зп и an = (—2)п — решения
рассматриваемого отношения.
Предположим, найдены два различных действительных решения уравнения
г2 = с\г + С2, например, г = а и г = 6, так что для уравнения an = cian_i +
c2an_2 имеем решения an = ап и an = Ьп, поэтому an = cia71 + c2an~2 и
bn = cib71 4- c2bn~2. Но если умножить ап = cian~1 4- с2ап~2 на константу с,
то получим сап = c\can~l +C2can~2, так что ап = сап также является решением
для ап = cian_i 4-
Далее, если сложить ап = с\ап~1 4- C2an~2 и 6n = cib71 4- С2бп~2, получим
an + Ъп = Clan-1 4- сгЬп'1 + c2an + c2bn =
= с^а"-1 + б") + c2(an + Ьп),

452 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
так что ап = ап -\-Ьп является решением для ап = cian_i -f c2an_2. Подводя итог
сказанному выше, получаем, что поскольку умножение на константу решения
для ап = cian_i + C2an_2 также дает решение, поэтому если ап и Ьп — решения,
то для некоторых констант end решениями являются также сап и dbn. Но
поскольку сумма решений для ап = cian_i + c2an_2 есть решение, то сап + dbn
для констант end также является решением. Таким образом, общее решение для
ап = cian_i + c2an-2 имеет вид сап + dbn, где с и d — константы, аг = аиг = 6
— решения уравнения г2 = cir + с2.
Например, известно, что ап — an_i + 6an_2 имеет решения ап = Зп и
an = (-2)п. Поэтому an = c3n + d(-2)n общее решение для ап — an_i + 6an_2.
Если было бы необходимо полностью определить решение ап = an_i H-6an_2 как
рекурсивной функции, то следовало бы задать первые два значения последова-
последовательности. Например, если а0 = 1 и а\ — 8, то а0 = сЗ° + d(-2)° = c + d=l и
аг = сЗ1 + d{-2I = Зс - 2d = 8. Решая систему уравнений
Зс - 2d = 8,
находим, что с = 2 и d = — 1, поэтому решением рекурсивной функции
а0 = 1,
ai=8,
ап = ап_х + 6ап-2 при п > 2
является ап = 2 • Зп - (-2)п.
ПРИМЕР 11.5. Решим рекурсивную функцию
ai=2;
а2 = 10;
an = 5an_i — 6ап_2 при п > 2.
Сначала запишем характеристическое уравнение г2 = Ъг — 6 или г2 — Ъг + 6 = 0.
Раскладывая на множители, получаем (г — 2)(г — 3) = 0, так что г = 2 и г = 3.
Поэтому общее решение отношения ап = 5an_i— 6an_2 имеет вид an = c2n-f d3n.
Но ai = c2l + с/31 = 2c + 3d = 2 и a2 = c22 + d32 = 4c + 9d = 10. Решая систему
УРЗВНеНИЙ 2с + 3d = 2,
4c + 9d = 10,
получаем с = -2 и d = 2, поэтому an = (-2) ¦ 2n + 2 • 3n. D
ПРИМЕР 11.6. Найти решение для последовательности Фибоначчи, заданной со-
соотношениями
ФибA) = 1;
ФибB) = 1;
Фиб(п) = Фиб(п — 1) + Фиб(п — 2) при п > 2.

РАЗДЕЛ 11.1. Однородные линейные рекуррентные отношения 453
Предупреждение: в некоторых книгах последовательность Фибоначчи определя-
определяется иначе, и поэтому имеет другое решение.
Характеристическим уравнением для Фиб(п) = Фиб(п —1) 4-Фиб(п —2) при
и > 2 будет г2 = г + 1 или г2 — г — 1 = 0. Используя формулу корней квадратного
уравнения, находим, что
_1±у/Е
поэтому общее решение для Фиб(п) = Фиб(п — 1) + Фиб(п — 2) имеет вид
Фиб(п) = с ' А ' v " х . ., i 1 - >/5
Чтобы упростить решение уравнения, положим ао = 0. По-прежнему, каждый
член последовательности равен сумме двух предшествующих ему, если они су-
существуют. Решая относительно сие/, получаем
Фиб@) = с^—j +^-2-J =c + d = 0
Поскольку c+d = 0, то с = —d. Поэтому второе уравнение может быть переписано
как
Так что
фиб(п) = —=
v /Е \ 2
есть последовательность Фибоначчи. ?
Изучив ситуацию, в которой имелось два различных действительных корня,
рассмотрим случай совпадающих корней. Итак, пусть задано рекурсивное отно-
отношение ап = cian_i +c2an_2, и характеристическое уравнение г2 = с\г + с2 имеет
равные корни, например, г = а. Будем утверждать, что ап = ап и ап = пап
— оба являются решениями для ап = cian_x + с2ап-2- Известно, что ап = ап
— решение, но необходимо убедиться в том, что ап = пап также является ре-
решением. Поскольку оба корня уравнения г2 = с\г + с2 равны а, то уравнение
г2 = cir + C2 в действительности имеет вид (г — аJ = 0 или г2 = 2ar — а2, так
что с\ = 2а и С2 = -а2. Поэтому рассматриваемое рекуррентное отношение есть

454 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
an = 2aan_i - a2an_2- Необходимо показать, что an = nan является решением.
Подставив это выражение в отношение, получаем
nan = 2a(n - l)an~l - a2(n - 2)an =
= 2nan - 2an - nan 4- 2an =
= nan,
так что an = nan в действительности удовлетворяет рекуррентному отношению.
ПРИМЕР 11.7. Найдем общее решение рекуррентного отношения an = 6an_i -
9an_2. Характеристическое уравнение имеет вид г2 = 6г - 9 или г2 - 6г 4- 9 = 0.
Раскладывая на множители, получаем (г - ЗJ = 0, поэтому г = 3 — корень крат-
кратности два. Следовательно, общим решением данного рекуррентного отношения
является an = c3n + dn3n. ?
ПРИМЕР 11.8. Найдем решение рекурсивной функции
an = 4an_! - 4ап_2 при п > 2.
Характеристический многочлен для an — 4an_i — 4an_2 имеет вид г2 — 4r +
4, он задает уравнение г2 — 4г + 4 = 0. Раскладывая на множители, получаем
(г - 2J = 0, так что г = 2 — двойной корень. Поэтому общим решением для
рекурсивной функции является an = c2n + dn2n, a0 = c2° 4- d@J° = с = 2,
ai = С21 -f d(lJ1 = 2c 4- 2d = 6. Поэтому с = 2 и d = 1. Следовательно, an =
2-2n + n2n = (n + 2Jn. П
Осталось рассмотреть случай, когда оба корня характеристического урав-
уравнения — комплексные числа. Для этого нам понадобится одно важное свойство
комплексных чисел, которое выводится из свойств тригонометрических функций.
ТЕОРЕМА 11.9. Для углов аи/?
(cos(a) 4- isin(a))(cos(/3) 4- isin(/3)) = (cos(a + /3) 4- isin(a 4- /?)).
ДОКАЗАТЕЛЬСТВО.
(cos(a) 4- isin(a))(cos(/3) 4- isin(/3)) =
= cos(a) cos(/3) 4- i2 sin(a) sin(^3) 4- isin(a) cos(/?) 4- isin(/3) cos(a) =
= cos(a) cos(/3) - sin(a) sin(/3) 4- z(sin(a) cos(/3) 4- cos(a) sin(/3)) =
= cos(a 4- C) 4- г sin(a 4-/3). ¦
Из этой теоремы следует, что (cos@) 4- ismF)J = cosB0) 4- isinB0).
Попробуйте доказать следующую теорему, используя метод индукции.
ТЕОРЕМА 11.10. (Муавр) Для произвольного угла в имеет место равенство (cos@L-
isin@))* = cos(fc0) 4-isin(fe0).

РАЗДЕЛ 11.1. Однородные линейные рекуррентные отношения 455
Нам необходимо еще одно свойство комплексных чисел. Рассмотрим ком-
комплексное число а + Ы, как изображено на рис. 11.1.
(a+bt)
Рис. 11.1
По теореме Пифагора р = \/а2 + б2. По определению cos@) = -, a sin@) = - ,
поэтому
а + Ы = р(- + г-) = p(cos@) 4- г sin@)).
Р Р
Таким образом, любое комплексное число может быть преобразовано к виду
p(cos@) +isin@)). Из приведенной выше теоремы далее следует, что (а + Ы)п =
(p(cos@) + isin@)))n = pn(cos(n6) -f isin(n0)).
Рассмотрим рекуррентное отношение ап = an_i - an_2, которое имеет ха-
характеристический многочлен г2 — г 4- 1, и соответствующее характеристическое
уравнение г2 — г 4-1 = 0. По формуле корней квадратного уравнения находим, что
г = 1 ± гл/1 — 4 =
= 1 ± \/Зг.
Как и ранее, предположим, что искомое общее решение имеет вид сг\ 4- dr\, где
т\ и Г2 — корни характеристического уравнения. Таким образом,
ап =
\/Зг)п
— 2nc (cos(-) + isin( —Л" 4- 2nd (cos(-) — isinf-^" —
= 2n f с ( cos(n • —) 4- i sin(n • —) J + d f cos(n • —) — г sin(n *¦"))) =
= 2n((c 4- d) cos(n • —) 4- i(c — d) sin(n • —)).
Если положить fci = с 4- d и к2 — г(с - d), то
7Г 7Г
an = 2 (к\ cos(n • —) 4- к2 sm(n • —)).
Здесь может показаться, что ловкостью рук удален какой-либо след ком-
комплексных чисел. И это действительно так. Предположим, например, что а$ = 1 и
ai = 4. Тогда
a0 = 2°(fci cos@ • -г) +k2 sin@ • —)) = fci cos(O) 4- k2 sin(O) = fci

456 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
и ао = кг = 1. К тому же
1 7Г 7Г 7Г 7Г
аг = 2 (fci cos(l • —) + fc2sin(l • —)) = 2((cos(—) + fc2sin(—))
3 3 3 3
= 2 ^2+/C2"J =l + fc2V3
и oi = 1 + А:2>/3 = 4. Решая относительно fc2, получаем
так что
Л2л/3 = -т= = л/3
v3
an = 2n(cos(n • |) + л/3вт(п • |)).
Вообще, если корни характеристического уравнения равны г\ = a + Ы и
Г2 = а — Ы, то
ап = pn{k\ cos(n6) + /с2 sin(n^)),
а ь
где р — у/а2 Ч-62, cos@) = - и sin@) = - .
Р Р
ПРИМЕР 11.11. Решить рекурсивную функцию, заданную следующим образом:
а0 = 1;
аг =2;
ап = 2\/2ап_1 - 4ап_2.
Характеристический многочлен имеет вид г2 — 2у/2г 4- 4. Используя формулу
корней квадратного уравнения, находим г = у/2 ± >/2*. так что р = 2и cos@) =
sin@) = —. Поэтому в = — и
7Г 7Г
an = 2n(fci cos(n • —) + /с2 sin(n • —)).
Следовательно,
a0 = 2°(fei cos@ • —) + fc2 sin(O • -)) = fci cos(O) + fc2 sin(O) = fci
и ao = fci = 1. К тому же,
ai = 21(A:icos(l • ^) + fe2sin(l- 7)) = 2((cos(^) + fc2sin(^)) =

РАЗДЕЛ 11.1. Однородные линейные рекуррентные отношения 457
и а\ = 2 = \/2 4- &2\/2- Решая относительно &2, получаем
an = 2n(cos(n • j) + (v/2 - 1) sin(n • J)). П
Теперь рассмотрим линейные рекуррентные отношения вида
ап = cian_i + c2an_2 + c3an_3 И h срап-р,
где р>2. Например, рассмотрим рекуррентное отношение
ап = -6an_i - 5an_2 + 24an_3 + 36an_4.
Ему соответствует характеристическое уравнение
г4 + 6г3 + 5г2 - 24г - 36 = 0.
Раскладывая на множители, получаем
(r-2)(r + 2)(r + 3J = 0.
В таком случае общее решение имеет вид
ап = а- B)п + Ъ • (-2)п + с • (-3)n + d • n(-3)n.
Следующая формула общего решения приводится без доказательства.
ТЕОРЕМА 11.12. Пусть рекуррентное отношение
ап = cian_i + c2an_2 + c3an_3 H h cpap
имеет характеристическое уравнение
rn - cirn~l - c2rn~2 - с3гп~3 сргп~р = 0.
Если Г{ — корень характеристического уравнения кратности qi, так что (г — r;)9i
является множителем характеристического многочлена, то
aar? + ai2nr^ + ai3n2r? 4- ai4nsr? + ••-+ aiq. n^r?
включается в общее решение для ап.
ПРИМЕР 11.13. Пусть рекуррентное отношение для ап имеет характеристическое
уравнение
(r_lK(r_2J(r_ зJ=0.
Тогда
ап = а + Ъп 4- сп2 + d • B)п + е • пB)п + / • 3n + g • nC)n
есть общее решение для ап. П

458 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Определение чисел Каталана в разделе 5.2 является примером задания од-
однородного линейного рекуррентного отношения, хотя его коэффициенты не явля-
являются постоянными. Напомним, что они были определены следующим образом.
Кат(О) = 1;
УПРАЖНЕНИЯ
1. Найдите среди приведенных ниже линейные рекуррентные отношения:
a) an = n2an_i ~ y/nan-2\ б) an = al_x - an_2;
в) an = an_i + \/3an_2 4- sin(n); r) an = an_! 4- 3an_2an_3;
д) an = an_i-f 3an_2 — пап_з.
2. Найдите среди рекуррентных отношений предыдущего упражнения однород-
однородные линейные рекуррентные отношения.
3. Найдите общее решение для приведенных ниже рекуррентных отношений:
а) ап - 3an_i = 0; б) an + 3an_i = 0;
в) an = -an_i 4- 6an_2; г) an = an_i + 3an_2.
4. Найдите общее решение для приведенных ниже рекуррентных отношений:
а) ап 4- 7an_! = 0; б) an - 5an_i = 0;
в) an = 4-2an_i 4- 8an_2; г) an = 4-3an_i - 2an_2.
5. Решите приведенные ниже рекуррентные функции:
а) а0 = 1; б) аг = 1;
an = -4an_i при и > 1; an = 6an_i;
в) a0 = 2; г) a0 = 2;
ai = 5; ax =4;
an = 5an_i - 6an_2 при n > 2; an = 7an_i - 12an_2 при n > 2.
6. Решите приведенные ниже рекуррентные функции:
а) а0 = 0; б) а0 = 2;
ai =5; ai = 5;
an = 9an_i - 20an_2 при n > 2; an = 7an_i - 12an_2 при n > 2;
в) a0 = 2; r) a0 = 4;
ai = 1; ai = 2;
an = 2an_! 4- 2an_2 при n > 2; an = -an_i 4- an_2 при n > 2.
7. Решите приведенные ниже рекуррентные функции:
а) а0 = 3; б) а0 = 2;
ai = 21; ai = 6;
an = 6an_i - 9an_2 при n > 2; an = 4an_i - 4an_2 при n > 2;

РАЗДЕЛ 11.1. Однородные линейные рекуррентные отношения 459
в) а0 = 1; г) а0 = -3;
а\ = —8; а\ = 1;
ап = -4an_i - 4ап_2 при п > 2; ап = 2an_i - ап_2 при п > 2;
д) а0 = 2;
ai = 6;
ап = —2an_i — ап_2 при и > 2.
8. Решите приведенные ниже рекуррентные функции:
а) ао = 3; б) а0 = 1;
ах =4; ai = 2;
ап = -4ап_2 при и > 2; ап = an_i - ап_2 при п > 2;
в) а0 = 5; г) а0 = 1;
ai =4; ai = О;
ап = -16ап_2 при п > 2; an = _2v/2an_i - 4ап_2 при п > 2;
д) а0 = 2;
а1 = 1 - ^3;
а2 = 1 - 2\/3;
ап = ап_3 при п > 3.
9. Найдите общее решение для приведенных ниже рекуррентных отношений:
а) ап - 5an_2 4- 4an_4 = 0;
б) an - 2an_i + 2an_2 - 2an_3 + an-4 = 0;
в) an = an_4;
r) an = + 3an_i — 3an_2 + an-3 — ^n_4 + 3an_5 — 3an_6 + an_7.
10. Покажите, что последовательность
удовлетворяет рекуррентному отношению для чисел Фибоначчи и, следова-
следовательно, является альтернативным представлением чисел Фибоначчи.
11. Общая последовательность Лукаса Ln задается рекурсивной функцией
Li =a,
Ln = Ln_i + Ln_2 при n > 2,
где р и q — целые числа. Заметим, что если L\ = L2 = 1, то имеем последова-
последовательность Фибоначчи Фиб(п). Покажите, что Ln = 6Фиб(п-1)+аФиб(п-2)
для всех и > 2.
12. Используя теорему 11.9 и индукцию, докажите теорему 11.10. Для заданного
угла в (cos@) + isin@))* = cos(fc0) + isin(fc0).

460 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
11.2. НЕОДНОРОДНЫЕ ЛИНЕЙНЫЕ РЕКУРРЕНТНЫЕ ОТНОШЕНИЯ
Рассмотрим рекурсивную функцию ап, заданную соотношениями
an = a- an_i + 6,
где аф\. Сразу получаем, что
а\ = с;
п2 = ас 4- Ь;
а3 = а2с 4- аЬ + Ь;
а4 = а3с 4- a2b 4- аб 4- Ь;
as = а4 с 4- a3b 4- а26 4- at 4- Ь;
ап = ап-1с + ап~2Ь 4- ап~36 4- • • • 4- a2b 4- ab + Ь =
= ап~1с + 6(ап 4- ап~3 + • • • + а2 + а 4- 1 =
'а"-Г
= Ic4
а- 1
b
a-lj a-1
Ь \ ._п 6
= (с-
1-a/ 1-a
Заметим, что данную рекурсивную функцию можно записать в более общем виде
an = 4/()
где с\ — а и /(п) = Ь. Будем стремиться решить эту задачу с помощью методов,
использованных для однородных рекурсий. Для этого необходима следующая те-
теорема.
ТЕОРЕМА 11.14. Пусть а^ = Рп удовлетворяет уравнению
ап = С1ап-1 + С2«2 + С3«3 + • • • + Са
иап = Qn есть частное решение уравнения
an = cian_i 4- c2an_2 4- c3an-3 + • • • 4- cpan-p 4- /(n).
Тогда an = Pn 4- Qn также является решением уравнения
an = Cian_x 4- c2an_2 4- c3an_3 H h cpan-p 4- /(^)-
ДОКАЗАТЕЛЬСТВО. Поскольку a? = Pn удовлетворяет уравнению
a°n = cia^.j 4- c2a°n_2 4- c3a^_3 + • • • 4- cpa°n_p,

РАЗДЕЛ 11.2. Неоднородные линейные рекуррентные отношения 461
имеем
Pn = ciPn_i 4- c2Pn_2 4- сзРп-з Н Ь cpPn-p.
Поскольку an = Qn удовлетворяет уравнению
ап = c\an-i 4- с2ап_2 4- с3ап_3 4- • • • 4- срап-р + f{i
имеем
Qn = ClQn-l + C2Qn-2 + C3Qn-3 + • • ' + CpQn-p 4- /(n).
Складывая
Pn - CiPn_i + C2Pn-2 + C3Pn-3 + • ' '
Qn = ciQn_i + c2Qn-2 + csQn-з 4- • • • + cpQn-p 4- /(n),
получаем
Pn + Qn =
Cl(Pn-l + Qn-l) + C2(Pn-2 + Qn-2) + * ' ' + Cp(Pn_p + Qn_p) + /(n),
так что ап = Pn 4- Qn удовлетворяет уравнению
a>n = cian_i -f c2an_2 -f c3an_3 + • • • + cpan_p + /(n). I
ТЕОРЕМА 11.15. Пусть Qn есть решение уравнения
ап = cian_i 4- c2an_2 4- c3an_3 H + cpan.p + f(n).
Тогда каждое решение уравнения
an = cian-i 4- c2an-2 + с3ап-3 Н h cpan-p 4- /(n)
имеет вид Pn 4- Qn, где Рп является решением уравнения
fl°n = cia°.! 4- c2a«_2 + c3a^_3 + • • • + cpa°n_p.
ДОКАЗАТЕЛЬСТВО. Известно, что Рп 4- Qn ~ решение уравнения
an = Cian_i 4- c2an-2 + Сзап-з Н h cpan-p 4- /(n).
Предположим, что Qn и i?n являются решениями уравнения
ап = cian_i + с2ап-2 + с3ап-3 4- Ь cpan_p 4- /(п).
Поэтому
n = ciQn_i 4- c2Qn-2 + c3Qn_3 + • • • 4- cpQn_p 4- /(n)
_2 4- c3Rn-3 + • • • + cpi?n-P + /(n).

462 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Вычитая первое уравнение из второго, получаем
Rn~Qn = Ci(i?n_i - Qn_!) + C2(#n_2 - Qn_2) + ¦ . ¦ + Cp(#n_p - Qn_p),
так что Rn — Qn — решение уравнения
fln = cia°n-i + c2a°n_2 + c3a^_3 + • • • + cpa°n_p.
Обозначим Rn — Qn = Pn. Тогда i?n = Qn 4- Pn» где Рп удовлетворяет уравнению
a° = cia^_! + c2a°n_2 + c3a°n_3 4- • • • + cpa°_p.
и теорема доказана. ¦
Известно, что рекуррентное отношение an = a • an_i имеет общее решение
an = fcian, где fci — константа. Поэтому, если можно было бы найти частное
решение Qn рекуррентного отношения an = a-an_i +6, тогда его общее решение
имело бы вид Rn = Qn + k\an.
ЗАМЕЧАНИЕ 11.16. Будем предполагать, что частное решение Qn для
ап = Cian_i + с2ап-2 + сзап_3 Н h cpan-p + f(n)
имеет такой же вид, как и функция /(п).
Например, если f(n) = а • Ьп, то предполагаем, что частное решение Qn
имеет вид к2 -6П, а если /(п) — многочлен третьей степени, то предполагаем, что
Qn имеет вид к2 • п3 4- fc3 • п2 4- fc4 • п + къ.
В рассматриваемом частном случае /(п) — константа, поэтому предполагаем,
что константа к2 является решением для an = a • an_i -h 6. Поэтому, подставляя
к2 в уравнение, получаем
к2 = a • к2 4- Ь,
так что
1-а
Поэтому рекуррентное отношение имеет вид
b
an = fcian 4-
1-а
Поскольку в частном случае а\ — с, то имеем
Ъ \ ( Ь
с — к\а 4- fci = — I с — -—
так что
1 / Ъ \ п Ь ( Ь \ п, b
ап = - [с- ап 4- = с - ]а 4- ,
а\ \ — а) \ — а \ \ — а) \ — а
что согласуется с решением, приведенным в начале этого раздела.

РАЗДЕЛ 11.2. Неоднородные линейные рекуррентные отношения 463
В начале раздела была рассмотрена рекурсивная функция ап вида
ai =с,
ап = a- an_i 4- Ь,
где аф\. Предположим, что а = 1, поэтому
ai =с,
ап = ап_х + Ь.
Уравнение ап = an_i имеет характеристическое уравнение г — 1 = 0, поэтому
общее решение для ап = an_i имеет вид
Следует искать частное решение для ап = an_i+b в виде ап = к2, поскольку
/(п) = Ь, т.е. равно константе. Но ап = к2 удовлетворяет уравнению ап = an_i,
так что если Ь ф 0, оно не может удовлетворять ап = an_i + Ь. Поэтому повторим
рассмотренную выше процедуру для кратных корней и положим ап = п-/с2- Если
подставить это выражение в уравнение ап = an_i +Ь, получим
п • к2 = (п — 1)к2 + Ь,
или
Поэтому
an = fci + nb.
Поскольку а\ = с,
с = fci 4- 6
fci = с — Ь.
Следовательно,
an = с — 6 + nb =
= с+(п-1)Ь.
ЗАМЕЧАНИЕ 11.17. Допустим, имеется рекуррентное отношение
Q<n = cian_i + c2an_2 + c3an_3 + • • • + cpan_p + /(n).
Если f(n) = aP(n) и общим решением для однородного рекуррентного отно-
отношения
! + c2an_2 + c3an_3 H Ь cpan_p
является b\f{n) + b2nf(n) + 63n2/(n) H h bjnjf(n), но bjnjf(n) решением не
является, то Qn = knj+1f(n).

464 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Например, если an = 4an_i — 4an_2 4- 3 • 2П, то характеристическим много-
многочленом является г2 - 4г + 4, и однородное рекуррентное отношение имеет вид
an = a • 2n + b • n2n, поэтому предположим, что частное решение для an =
4an_i — 4an_2 4- 3 • 2n имеет вид к • n22n.
ПРИМЕР 11.18. Пусть an = 5an_i - 4an_2 + 3 • 2n. Характеристическим много-
многочленом является г2 - 5г + 4, и однородное рекуррентное отношение имеет вид
an = a 4- 6 • 4П. Поэтому предположим, что Qn имеет вид к • 2П. Подставляя это
выражение в рекуррентное отношение, получаем
к • Т = 5fc • 271-1 - 4А: • 2П + 3 • 2П
или
4fc • 2П = 10к • 2П - 4fc • 2П + 12 • 2П,
так что
4fc = 10fc - 4fc 4-12
и fc = -6. Следовательно, общее решение для an = 5an_i - 4an_2 4- 3 • 2П имеет
вид an = a + 6-4n-6-2n. D
ПРИМЕР 11.19. Пусть an = 5an_i - 6an_2 4- 6 • 3n. Характеристическим мно-
многочленом будет г2 - Ъг 4- 6, и однородное рекуррентное отношение имеет вид
an = a • 2n 4- Ь • Зп. Поэтому предположим, что Qn имеет вид /с • пЗп. Подставляя
это выражение в рекуррентное отношение, получаем
кпТ = 5fc(n - 1KП - 6к(п - 2KП + 6 • Зп
или
9fcn3n = 1Щп - 1KП - 6fc(n - 2KП + 54 • Зп,
так что
9fcn = 15fc(n - 1) - 6к(п - 2) + 54
и к = 18. Поэтому общим решением рекуррентного отношения an = 5an_i —
6an_2 4- 6 • Зп будет an = a • 2n 4- b • 3n 4- 18n3n. П
ПРИМЕР 11.20. Решим рекурсивную функцию:
ai = 1,
an = ^n-i 4- n.
Учитывая, что an равно сумме первых п положительных целых чисел, фактиче-
фактически требуется найти формулу для суммы первых п положительных целых чисел.
Характеристическим уравнением будет
г - 1 - 0,
поэтому решение однородного отношения имеет вид an = к\. Поскольку /(п) =
п, естественно предположить, что частное решение для an = an_i 4- и имеет
вид fc2n -f ^з- Поскольку константа является решением однородного отношения,

РАЗДЕЛ 11.2. Неоднородные линейные рекуррентные отношения 465
частное решение для ап = an_x + п следует искать в виде ап = k2n2 + fc3n.
Подставляя это выражение в рекуррентное отношение ап = an_i +ny получаем
k2n2 + k3n = k2(n - IJ + А:3(п - 1) + n
или
fc2n2 + fc3n = k2(n2 - In + 1) + fc3(n - 1) + n.
Приравнивая коэффициенты при п, получаем
fc3 = -2fc2 -f /сз + 1
или
Приравнивая константы, получаем
k2-k3 = О,
так что
Поэтому общее решение для an = an_i 4- п имеет вид
1 о 1
an = fci 4- -тг 4- 2n-
Поскольку ai = 1, имеем
п1 = 1 = кг + - + - ,
так что fci = 0 и
1 о 1 п(п +1) __
= 2 + 2П = 2 в
ПРИМЕР 11.21. Найдем решение рекуррентного отношения
an = 3an_i - 2an_2 + 3sin f-yj
при п > 2. Однородное отношение легко решается. Характеристическое уравнение
имеет вид
г2 - Зг + 2 = О
или
так что общим решением для однородного отношения будет

466 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Учитывая, что /(n)=3sin ( —) и решение однородного рекуррентного отношения
с квадратичным характеристическим многочленом, имеющим комплексные корни
a 4- Ы и a — Ыу имеет вид bi cos(n0) + 62 sin(ra0), частное решение для
an = 3an_i - 2an_2 + 3sin (—J
, /П7Г\ . /П7Г\ _
будем искать в виде fci cos ( — ) + 62sin ( — J. После подстановки этого выраже-
выражения в рекуррентное отношение имеем
/П7Г\ . . /П7Г\ /(П1OГ\ .
61COS IT/ + 2 8Ш vTJ = г °OS 2 + 2 8Ш
/(П-1OГ\
2
2
, /(п-2)тг\ , /(п-2)тг\ /птг\
- 2 cos 6i (^ 2 ) " 2Ь2 sin f 2 ) + 3 sin (^") •
Так как это должно выполняться для всех п > 2, подставляем п = 2и получаем
&i cosGr)-fb2 sinGr) = 3&i cos (J^j +362 sin E) -2bi cos @)-262 sin @L-3 sin Gт),
или
или
bi = 362.
Если подставить п = 3, получим
ЗтЛ
L . /Зтг\
+62sin( — \ =
= 36i cos (тг) + 362 sin Gг) - 2 cos bi (-) - 2b2 sin (-] + 3 sin [ -^ ),
или
_62 = —3bi - 262 - 3,
или
36i + b2 = -3.
Подставляя в это уравнение b\ = ЗЬ2, получаем
962 + 62 = -3
или
62 = -^'
так что

РАЗДЕЛ 11.2. Неоднородные линейные рекуррентные отношения 467
и искомое общее решение имеет вид ап = а 4- b • 2П — ^ cos (^f-) — ^ sin (Ij-).
Заметьте, мы показали, что это общее решение, если оно существует, поскольку
справедливость этого показана только для п = 2 и п = 3. В общем случае будем
предполагать, что решение существует, и использовать изложенный метод. Одна-
Однако, для того чтобы правильно показать, что это решение, следует взять исходное
уравнение
/П7Г\ , . /П7Г\ Л1 (Ы— 1OГ\ Л, . ({и— 1)тг\
bl cos (—J + Ь2 sm (—J = 3bi cos {^J~ J + 3b2 sin ^V 2 j -
- 2cosb! f v 2 ; j - 2b2sin f v 2 ; j 4- 3sin ^J
и, используя тригонометрические тождества, выразить все слагаемые в виде
^^^J или sin МП~2?7ГV
Рассматривая каждое слагаемое отдельно, находим
/птг\
cos ^—J = &i cos
/(п-2)тг\ . /(п-2)тг\ .
I ^—y^ \ cos(tt) - bi sin ( ^ ) sinGr) =
= -bicos( ^—Y^Y
, . (n'K\ , /(п-2)тг\ . , ч , . /(п-2)тг\ , ч
02 Sin I — ) = 62 COS I 1 SinGT) + O2 Sill I 1 COSGr) =
= -b2sin^^— J;
/(п-1)тг\ L /(п-2)тг\ /тг\ nL . /(п-2)тг\
3bi cos ^ 2 ; j = 36i cos ^ 2 ; j cos (-) - 3bi sin [ 2 J
(n-2Or
v
J sin (^) =
(Ы— 1OГ\ , /(п — 2)?г\ /7Г\ /(п — 2)тг\ /7Г\
Зо2 sm ( 1 = Зо2 cos ( -— 1 sin ( — J 4- sin I -— j cos ( — J =
'(п-2)тгч
= ЗЬ2 cos
3sin (— ) = 3cos f -——— j sinGr) + 3sin f -— j cos(tt) =
= -38in^(n-2)'r
2
Подставляя эти слагаемые в
/ШГ\ . /727Г\ /(п— 1)ТГ\ . /(п— 1)?Г
Oi cos I — 1 4- о2 sm ( — J = 3oi cos I 1 4- 3o2 sin (
f V 2 ; j -262sinf v 2 y j +3sin^—J,

468 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
имеем
- bx cos \^ 2 J ~ Ь2 sin у 2 ) =
OL . /(п-2)тг\ oL /(п-2)тг\ ль /(п-2)тг\
- -3&! sin ( V 2 M 4- ЗЬ2 cos ( 2 ) - 2bi cos ( 2 )
/(п-2)тг\ /(п-2)тг
- 2Ь2 sin ^ i- - 3sin ' v y
Приравнивая коэффициенты при cos f -— j, имеем
—Ьх =r 362 — 2&i при bi = 3&2.
Приравнивая коэффициенты при sin f -— j, имеем
-62 = -36i - 262 - 3 при 3bi 4- b2 = 3,
что совпадает с уравнениями, полученными ранее. Следовательно, теперь мы убе-
убедились, что решение действительно существует. ?
¦ УПРАЖНЕНИЯ
1. Найдите общее решение для приведенных ниже рекуррентных отношений:
a) an = 2an_i+5; б) ап = -3an_i 4- Щ
в) an = -an_i + 12an_24-2n; г) ап --Зап_! - ап_2 + Зп;
д) an = 4an_i - 4ап_2 4- п2.
2. Найдите общее решение для приведенных ниже рекуррентных отношений:
а) an = -2an_i 4- п2; б) an = 4an_i 4- 4n;
в) an = 6an_!+9an_2 + (-2)n; г) an =-9an_2 + 3n;
д) an = -4an_i - 2an_2 4- 5.
3. Найдите общее решение для приведенных ниже рекуррентных отношений:
а) an = 2an_!4-2n; б) an = -6an_i - 9an_2 + (-3)n;
в) an = 3n_i - 2an_2 + 5; г) an = an_i 4- 6an_2 4- 3n;
д) an = 2\/3an_i - 4an_2 + 3.
4. Найдите общее решение для приведенных ниже рекуррентных отношений:
ч /П7Г\ /П7Г\
а) an = an_2 + cos \^—J; 6) an = -an_2 4- cos \^—j;
в) an = 6an_i-12an_2+8an_34-3n; r) an = 6an_1-12an_2+8an_34-2n;
д) an = -an_3 4- n.
5. Найдите приведенные ниже суммы, используя рекуррентные отношения:
а) 12 + 22 + 324---- + п2; б) 1 + 4 + 7 + • • • + Зп - 2;
Используйте соотношение Используйте соотношение
an — an-i 4- ft2. an = an_i 4- 3n — 2.

РАЗДЕЛ 11.3. Конечные разности 469
в) 21+22 + 23 + 24 + --- + 2П; г) 1-2 + 2-3 + 3-4 + -•-+п. (п
Используйте соотношение Используйте соотношение
ап = an_i + 2П. ап = an_i +n-(n + l).
6. Найдите приведенные ниже суммы, используя рекуррентные отношения:
а) 13 + 23 + 33 + ..- + п3; б) 12-2+22.3+32.4+-. .+п2-(
Используйте соотношение Используйте соотношение
ап = an_i + n3. ап = an_! + п2 • (n -f 1).
в) 1-2°+2-21+3-22 + -.-+п-2(п-1);
Используйте соотношение
<1)
11.3. КОНЕЧНЫЕ РАЗНОСТИ
Для студентов, прослушавших курс математического анализа, многие результа-
результаты, изложенные в данном разделе, покажутся хорошо известными. Фактически,
конечные разности можно рассматривать как бесконечно малые без предельных
переходов. Аналогично исчислению бесконечно малых, теория конечных разно-
разностей имеет широкое применение в таких разнообразных областях, как инфор-
информатика, актуарная математика, экономика, психология и социология. Сфера их
использования включает обнаружение случайных погрешностей, построение по-
полиномов, аппроксимирующих функциональную зависимость по результатам изме-
измерений, экстраполирование и интерполирование функций, суммирование функций,
дифференцирование комбинаторных функций, аппроксимацию площадей и мно-
многое другое. Конечные разности — одно из базовых средств численного анализа.
Следует, однако, подчеркнуть, что изучение данного раздела не требует знания
математического анализа. В этом разделе мы только вводим понятие о конечных
разностях и показываем некоторые их элементарные свойства.
Первая разность, или разность первого порядка функции /, обозначаемая
Л/, определена следующим образом
Д/(х) = /(х + 1)-/(х).
Вторая разность, или разность второго порядка функции /, обозначаемая
Л2/, определена следующим образом
А2/(х) =
Поэтому,
= (f{x + 2) - f{x + 1)) - (/(* + 1) - /(*)) =
В общем случае n-ая разность функции /, обозначаемая А"/, индуктивно
определена выражением

470 ГЛАВА 11. Некоторые специальные еопросы теории рекурсии
Далее приводится формула, выражающая Дп/(х) через f(x). Приведенная
ниже таблица иллюстрирует разностную функцию:
X
1
2
3
4
5
6
1
8
27
64
125
216
Д/(х)
7
19
37
61
91
Л2/(*)
12
18
24
30
А3/(х)
6
6
6
Д4Я*)
0
0
Заметим, что в данном случае /(х) = х3 и Л4/(х) = 0 для всех значений х.
Оператором называется функция, которая отображает функции в функции.
Следовательно, Л является оператором. Определим также другой оператор Е
согласно выражению E(f(x)) = fix -f 1). Таким образом,
Л/(х) = E(f(x))-f(x) = (E-I)(f(x)),
где использовано обозначение (F + G)(u) = F(u)-f G(u). Оператор / представляет
собой тождественный оператор. Поэтому Л = (Е — I) и ? = / +Л.
Используя запись Л = (Е - I) и полагая Е° = /, получаем
Дп(/(х)) = (Е - /)n(
x)) = En(f(x)) - и
• En~k(f(x)) + .
= /(x + гг) - гг • /(гг - 1)
(/(x + r. - /с))
ПРИМЕР 11.22. A3(/(x)) = f(x + 3) - 3/(x + 2) + 3/(x + 1) - f(x).
ТЕОРЕМА 11.23. Операторы Л и Е обладают следующими свойствами.
Для действительного числа а и функций / и д
а) Д(/ + д) = Д(/) + А(д); E(f + д) = E(f) + E(g);
б) Л(а/) = aA(f); E(af) = aE(f);
в) ЕА = АЕ;
г) Л(а) = 0; Е(а) = а.
ДОКАЗАТЕЛЬСТВО. Докажем пункт (а).
) = A(f(x)+g(x)) =
= f(x + 1) + д(х + 1) - (/(х) + д(х)) =
= f(x + l)-f(x)+g(x + l)-g(x) =
П
= (Af + Ag)(x)

РАЗДЕЛ 11.3. Конечные разности 471
и
Д((а/)(х)) = Л(а/(х)) =
= а/(х + 1) + а/(х) =
= а(/(х + 1)-/(х)) =
= аД/(х).
Доказательство пунктов (б) и (в) предоставляется читателю. ¦
ПРИМЕР 11.24.
ЛCх4 + 2х3 + 5х + 4) = ЛCх4) + АBх3) + ДEх) + ЛD) =
= ЗЛ(х4) + 2Л(х3) + 5Л(х). П
Теперь необходимо найти Л(хп). К сожалению, здесь все не так просто.
Имеем
Л(х) = (х + 1) - х - 1
и
Д(х2) = (х + 1J-х2 = х2 + 2х + 1-х2 = 2х + 1.
В общем случае имеем
Д(х") = (х + 1)" -хп = хп + пхп~1 +¦¦¦ + Ц)хк + ¦ ¦ ¦ + 1 - х" =
= пхп-1 + --- + {Ч)хк--- + 1.
Теперь введем два свойства оператора Л, которые знакомы студентам, про-
прослушавшим курс математического анализа. Они называются соответственно пра-
правило произведения и правило частного.
ТЕОРЕМА 11.25. Для функций fug
д Л =g.A{f)-f.{A{g))
9-(E(g))
ДОКАЗАТЕЛЬСТВО.
A(fg(x)) = A(f(x)-g(x)) =
= /(x + l)-<7(x + l)-/(x)-5(x) =
= /(x + 1) • g(x + 1) - /(x) • g(x + 1) + /(x) • g(x + 1) - f(x) ¦ g(x)
= {f{x + 1) - f{x)) ¦ g{x + 1) + f{x) ¦ {g{x + 1) - -<?(x)) =
= A/(x) • E{g{x)) + f{x) ¦ Ag{x)
= f{x) ¦ Ag{x) + Eg{x) ¦ Af{x) =
= {f ¦ Ag + Eg ¦ Af){x).
Доказательство второй части предоставляется читателю.

472 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
ПРИМЕР 11.26.
Д((х2 + 6х)Bх2 + 5) = (х2 + 6х)АBх2 + 5) + ?Bх2 + 5)А(х2 + 6х) =
= (х2 + 6х)BА(х2) + ДE)) + ?Bх2 + 5)(Д(х2) + 6А(х)) =
= (х2 + 6х)Dх + 2) + ?Bх2 + 5)Bх + 1 + 6) =
= (х2 + 6х)Dх + 2) + B((х + IJ + 5)Bх + 7) =
= (х2 + 6х)Dх + 2) + Bх2 + 4х + 7)Bх + 7). ?
ПРИМЕР 11.27.
д/ х2 + 2 \ _ Bх2 + 6х + 5)- Д(х2 + 2) - (х2 + 2) • АBх2 + 6х + 5)
Bх2 + 6х + 5) • ЕBх2 + 6х + 5)
_ Bх2 + 6х + 5) • (А(х2) + АB)) - (х2 + 2) • BЛ(х2) + 6А(х) + АE)) _
Bх2 + 6х + 5) • B(з + IJ + 6(х + 1) + 5)
_ Bх2 + 6х + 5) • Bх + 1) - (х2 + 2) • BBх + 1) + 6) _
Bх2 + 6х + 5) • B(х2 + 2х + 1) + 6х + 11)
= Bх2 + 6х + 5) • Bх + 1) - (х2 + 2) • Dх + 8)
Bх2 + 6х + 5) • Bх2 + Юх + 13) ' ?
Как показывает приведенная ниже теорема, находить А/(х) для /(х) = ах
гораздо легче.
ТЕОРЕМА 11.28. Если /(х) = ах, то А/(х) = ах(а - 1). В частности, если
fix) = 2х, то А/(х) = 2х.
ДОКАЗАТЕЛЬСТВО. А(ах) = ах+1 - ах = ах(а - 1). ¦
ПРИМЕР 11.29.
Д(х2 + Зх + 4 + 2х + 4х) = А(х2) + ЗА(х) + АD) + АBХ) + АDХ) =
П
УПРАЖНЕНИЯ
1. Найдите Д2(х3), вычисленное при х = 1.
2. Найдите Д3BХ), вычисленное при х = 1.
3. Найдите Д2Е2(х4), вычисленное при х — 4.
4. Найдите А2Е(п\), вычисленное при п = 1.
5. Найдите Д(Cх + 2)(х - 3)).
6. Найдите Д(Dх - 2)(х + 5)).
/х-6
7. Найдите Д
V3x
8. Найдите Д
ч4х + 1у
9. Покажите, что Д(х!) = х • х!

РАЗДЕЛ 11.4. Факториальные многочлены 473
10. Докажите части (б), (в) и (г) теоремы 11.23 для действительного числа а и
функций / и д
а) Д(а/) = аД(/); б) E(af) = aE(f); в) ЕА = Д?;
г) А(а) = 0; д) Е(а) = а.
11. Докажите вторую часть теоремы 11.25.
ДА =
11.4. ФАКТОРИАЛЬНЫЕ МНОГОЧЛЕНЫ
Ранее была возможность убедиться в том, что нахождение конечных разностей
функции хп довольно запутанно. Это — неблагоприятный момент, поскольку по-
полиномиальные функции весьма распространены. Для решения данной проблемы
рассмотрим факториальную задачу. Пусть при х > п > О
(п) _ J х(х ~ 1)(х ~ 2) • • • (х — п 4-1), если п > 0;
1 1, если п = 0.
К счастью,
Д(х(п)) = (х + 1)(х)(х - 1) • • • (х - п + 2) - х(х - 1)(х - 2) • • • (х - п + 1) =
= (х)(х - 1)(х - 2) • • • (х - п + 2)((х 4- 1) - (х - п + 1) =
= (х)(х - 1)(х - 2) • • • (х - п 4- 2)(п) =
= п(х)(х - 1)(х - 2) • • • (х - (п - 1) + 1) = пх^п-1\
так что теперь имеется функция с очень хорошими разностями. В действитель-
действительности те, кто изучал математический анализ, возможно, надеялись на такой хо-
хороший результат для х^п\ Заметим также, что х^1) = х. Таким образом, если
то
Дх) = 5х<4> + 6х<3> - ЗхB) 4- 2Х*1) 4- 7,
Д/(х) = E • 4)хC) 4 F • 3)х<2> - 3 • 2х^) 4 2 = 20х^ + 18х^2) - 6х^ + 2.
Если /(х) = апх(п) 4 an^ix^n~^ Н п2Х^ 4- сцх + а$ для некоторого п, то
/ называется факториальным многочленом. Очевидно, что вычислять разности
факториального многочлена очень просто. Задача состоит в том, чтобы обычный
многочлен записать в виде факториального. Ниже будет дан алгоритм решения
этой задачи. Читатель может заметить, что здесь используется техника, подобная
одной из тех, которые применялись в разделе 5.6 для перехода от представления
числа на основе 10 к представлению числа на основе п.
Начнем с примера. Предположим, что обычный многочлен
Зх4 - 19х3 4- 34х2 - 21х + 5

474 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
необходимо записать в виде факториального многочлена
а4хD) 4- а3хC) + а2хт + п\Х + а0.
Напомним, что оба многочлена задают одну и ту же функцию. Они являются
только ее разными представлениями.
Если разделить
Зх4 - 19х3 + 34х2 - 21х - 5
на х, то получим частное Зх3 — 19х2 4- 34х — 21 с остатком —5. Если разделить
а4хD) 4- а3хC) + а2хB) 4- агх + а0
на х, то получим
а4(х - 1)(х - 2)(х - 3) 4- а3(х - 1)(х - 2) 4- а2(х - 1) + <ц
с остатком ао. Следовательно, ао = — 5 и
Зх3 - 19х2 4- 34х - 21 =
= а4(х - 1)(х - 2)(х - 3) + а3(х - 1)(х - 2) + а2(х - 1)
Если
Зх3 - 19х2 4- 34х - 21
разделить на х - 1, то получим частное Зх2 - 16х 4-18 с остатком -3.
Если
а4(х - 1)(х - 2)(х - 3) 4- а3(х - 1)(х - 2) 4- а2(х - 1) 4- ах
разделить на х - 1, получим частное
а4(х - 2)(х - 3) 4- а3(х - 2) 4- а2
с остатком а\. Поэтому ах = -3 и
Зх2 - 16х + 18 = а4(х - 2)(х - 3) 4- а3(х - 2) 4- а2.
Если разделить
Зх2 - 16х 4-18
на х - 2, то получим частное Зх - 10 с остатком -2. Если разделить
а4(х - 2)(х - 3) 4- а3(х - 2) 4- а2
на х — 2, то получим частное а4(х — 3) 4- а3 и остаток а2. Следовательно,
а2 = -2
и
Зх- 10 = а4(х-3) +а3.

РАЗДЕЛ 11.4. Факториальные многочлены 475
Разделив Зх — 10 на х — 3, получаем 3 и остаток —1.
Разделив а±(х — 3) + аз на х — 3, получаем а^ и остаток аз. Поэтому
п4 = 3 и аз = —1.
Итак, искомый факториальный многочлен имеет вид
_ ,,.C) _ 2хB) _ Зх + _5.
Окончательно для нахождения коэффициента ао факториального многочлена
делим на х и берем остаток. Для нахождения коэффициента а\ факториального
многочлена делим частное на х— 1 и берем остаток. Продолжаем процесс деления
полученного каждый раз частного нах-2, х-Зих-4 для нахождения остатков
а2, а3 и а4 соответственно.
Теперь представим алгоритм нахождения факториального многочлена апх^-
an-iz^") Н Ь a2zB) A)
Ь a2zB) + aixA) + аох.
Алгоритм Факториальный многочлен:
Шаг 1. Для заданного многочлена f(x) степени и положить к = 0.
Шаг 2. Разделить f(x) на х — к, получив остаток г и частное д(х).
Шаг 3. Положить а^ = ги /(х) = q(x).
Шаг 4. Если fc = п, то процесс завершен. В противном случае
положить к = к + 1 и вернуться к шагу 2.
Простейший способ реализовать этот процесс — использовать сокращенное
деление. Проиллюстрируем его на примере, положив f(x) = х4—8х3+21х2—6х+3.
0
1
2
3
4
1
1
1
1
1
[1]
-8
0
-8
1
_7
2
-5
3
[-2]
21
0
21
-7
14
-10
[4]
-6
0
-6
14
[8]
3
0
[3]
Это дает факториальный многочлен х^ — 2х^ + 4х^ -Ь 8х + 3.
Существуют несколько способов перехода от факториального многочлена к
обычному. Один из них — просто раскрыть каждое слагаемое и собрать члены с
одинаковыми степенями х. Другой метод мог бы состоять в вычислении факто-
факториального многочлена вп + 1 точке, где п — степень многочлена, с последующей
аппроксимацией этих значений многочленом степени п.
Третий метод представляет собой обратную форму сокращенного деления.
Чтобы показать, как работает этот метод, рассмотрим факториальный многочлен
_ Зх - 5.

476 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Раскрыв каждое слагаемое, имеем
Зх(х - 1)(х - 2)(х - 3) - х{х - 1)(х - 2) - 2х(х - 1) - Зх - 5.
Раскрыв (х — 3) в первом члене, оставив х с первым членом и присоединив —3 ко
второму члену, получаем
Зх2(х - 1)(х - 2) + C(-3) - 1)х(х - 1)(х - 2) - 2х(х - 1) - Зх - 5.
Теперь, раскрыв (х — 2) во втором члене, оставив х со вторым членом и присо-
присоединив —2 к третьему члену, получаем
Зх2(х - 1)(х - 2) - 10х2(х -
-2) - 2)х(х - 1) - Зх - 5.
Теперь раскрытие (х — 1) в третьем члене, присоединение х к третьему члену, а
— 1 — к четвертому члену дает
Зх2(х - 1)(х - 2) - 10х2(х - 1) + 18х2 + (-18 - 3)х - 5
или
Зх2(х - 1)(х - 2) - 10х2(х - 1) + 18х2 - 21х - 5,
что совпадает с рассматриваемым многочленом после стадии 1. Заметим, что,
используя приведенный ниже процесс, мы бы получили тот же самый результат
в таблице
3
2
1
3
3
-1
-9
-10
2
20
18
-3
-18
-21
-5
Заметим, что числа в верхней строке являются коэффициентами факториально-
го многочлена, а числа в первом столбце — целые числа, начинающиеся с 3, на
единицу меньше, чем степень многочлена. Переносим вниз 3, как при сокращен-
сокращенном делении, и умножаем на 3 первое число столбца. Но вместо сложения с —1,
следующим числом строки, вычитаем 9 из —1, получая —10. Теперь берем —10,
умножаем на 2, следующее число в столбце, и вычитаем из -2, следующего числа
в строке. Получаем 18. Продолжаем процесс, умножая 18 на 1 и вычитая резуль-
результат из —3, получаем —21. Последнее число в строке не используется и остается
неизменным. Легко видеть, что числа в третьей строке вместе с последним числом
в первой строке являются коэффициентами многочлена на стадии 1.
Теперь берем многочлен на первой стадии
Зх2(х - 1)(х - 2) - 10х2(х - 1) + 18х2 - 21х - 5

РАЗДЕЛ 11.4. Факториальные многочлены 477
и повторяем процесс. Раскрываем х - 2, оставляем х с первым членом, присоеди-
присоединяем -2 ко второму члену, после чего получаем
Зх3(х -
-2) - 10)х2(х - 1) + 18х2 - 21х - 5.
Теперь раскрываем х — 1 во втором члене, оставляя х со вторым членом, присо-
присоединяя -1 к третьему члену, что дает
Зх3(х - 1) - 16х3 + A6 + 18)х2 - 21х - 5
или
Зх3(х - 1) - 16х3(х - 1) + 34х2 - 21х - 5
для многочлена второй стадии. Обратите внимание, что каждая стадия повышает
степень х в том слагаемом, в котором раскрывается множитель.
Снова, возвращаясь к таблице, повторяем процесс за исключением того, что
сносим 3, первый элемент строки, умножаем на 2 и вычитаем результат из —10,
числа во втором столбце. Это дает —16. Умножаем —16 на 1 и вычитаем резуль-
результат из 18, получая 34. Опять —21, последнее число в строке, не используется.
Снова замечаем, что оставшаяся строка вместе с числами —21 и —5 формирует
многочлен второй стадии:
3
3
3
-1
-9
-10
-6
_2
20
18
16
_з
-18
—5
-21
2 3 -16 34
Теперь берем многочлен второй стадии
Зх3(х - 1) - 16х3 + 34х2 - 21х - 5
и раскрываем х — 1 в первом члене. Это дает
Зх4 - 19х3 + 34х2 - 21х - 5,
что является искомым многочленом.
Снова, глядя на таблицу, сносим 3 и умножаем на 1. Вычитаем результат
из -16. Это оставляет неиспользованным -19. Наконец, сносим 3. Замечаем, что

478 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
числа в скобках являются искомыми коэффициентами.
3
2
1
3
3
3
3
[3]
-1
-9
-10
-6
-16
-3
[-19]
-2
20
18
16
[34]
-3
-18
[-5]
[-21]
Продемонстрировав этот процесс, предоставляем читателю четко сформули-
сформулировать алгоритм перехода от факториального многочлена к обычному.
ПРИМЕР 11.30. Заменим многочлен хD) - 2хC) +4хB) 4-бх + З обычным много-
многочленом. Используя обратное сокращенное деление, имеем
3
2
1
1
1
1
1
[1]
-2
-3
-5
-2
-7
-1
[-8]
4
10
14
7
[21]
6
-14
[3]
[-8]
В результате получаем многочлен f(x) = х4 - 8х3 + 21х2 - 8х + 3.
Было показано, что
z(n> = х(х - 1)(х - 2) • • • (х - (п - 1) + 1)(х - п + 1) =
= (х-п + 1)х(х - 1)(х - 2) • • • (х - (п - 1) + 1) =
= (х-п + 1)х(п-1\
Решая относительно х^'1'1, имеем
?
х — и -f 1
Теперь имеется способ определить х^п\ когда п — отрицательное целое число.

РАЗДЕЛ 11.4. Факториалычые многочлены 479
Положив п = 1, имеем
х-1+1
Положив п = 0, имеем
1
х-0 + 1 х4-1
Теперь воспользуемся индукцией и соотношением
х - п4-1'
чтобы показать, что
(—гг>\ 1
для всех т > 1, при которых знаменатель не равен нулю.
Было показано, что
х
Предположим, что
(x + k)W
Тогда
хЫк+1)) = x(-*-U) = ^1 :
1 1
(х
(X
(х
+
+
+
*)<*> X
к)(х + fc
fc + l)(x
1
+ к + 1
1
_!)..
1
+ к)(х
•(х +
+ А:-
1)(х
¦1).-
+ к
•(х
+
+
1)
1))
Теперь необходимо найти Л(х~п). По определению
1 \ 1 1
Л(х"п) = А
1 1
(х + п + 1)(х + п)(х + п - 1) • • • (х + 2) (х + п)(х + п - 1) • • • (х + 1)
Х + 1-(х + П + 1) — П _п-1
(х -f n 4- 1)(х 4- п)(х 4- п - 1) • • • (х 4-1) (х + п

480 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
поэтому для каждого целого числа п, не равного нулю, имеем А(х^) — nz^).
Теперь есть возможность обобщить одну из комбинаторных теорем. Для
положительного целого числа п пусть
га! '
Когда х — целое число, это обычное определение числа сочетаний.
Взяв разность, находим
{х\ пх^) гг^-1) ( х
п\ (п - 1)! \п -
Но
поэтому имеем
или
(х+1) = (*) + ( х\
V п ) \п) \n-lj
Положив у = х + 1, получаем
а(х)(х + 1)-(х\
\nj \ п ) \п)
х - 1\ _ /х + 1\ (х
га — 1/ \ га / \п
в более привычной форме, которая ранее была доказана для случая, когда у
целое число.
ОПРЕДЕЛЕНИЕ 11.31. Числа Стирлинга первого рода определены соотно-
соотношениями / ч
5q = 0 при всех га > 1;
s^ = 1 при всех п > 0.
>+1) _ »
_
— S
/с-]
ОПРЕДЕЛЕНИЕ 11.32. Числа Стирлинга второго рода определены соотно-
соотношениями / ч
5q = 0 при всех га > 1;
5^п) = 1 при всех га > 0.

РАЗДЕЛ 11.4. Факториальные многочлены 481
Покажем, что числа Стирлинга первого и второго рода могут быть описа-
описаны на основе многочленов. Числа Стирлинга первого рода равны абсолютным
значениям коэффициентов многочлена, равного х^п\ для п = 1,2,3,...
ТЕОРЕМА 11.33. Пусть
х(п) = s(n)xn _ 8WiXn-l + S{n%X«-2 - .-.
Коэффициенты s\n' являются числами Стирлинга первого рода.
ДОКАЗАТЕЛЬСТВО. По определению, Sq1^ = 0 для всех п > 1 и s^ = 1 для
всех и > 0. Чтобы показать, что s\n' — числа Стирлинга первого рода, требуется
(п+1) (п) . (п) 1 ^ . ^
показать, что s\ ' — s]_\ + n • s\ ' для 1 < г < п.
По определению, z(n+1) = (х - п)х^ = х « х^ - п • х^п\ Следовательно,
г=0
n
x • У^(-1)П~'
i=0
n
y^(-i)n~'5-n
i=0
n+1
x%Jrl — n •
n
• Yj
n
vv
i=0
n
i=l i=0
Увеличивая г на 1 в первой сумме, получаем
г = 1 г=0
Приравнивая коэффициенты при хг для 1 < г < п, имеем s\n~*~ ' = 5г-_х + ns[n\
что и требовалось доказать. ¦
Покажем, что числа Стирлинга второго рода есть не что иное, как коэффи-
коэффициенты факториальных многочленов, равных хп для п = 1,2,3, • • -.
ТЕОРЕМА 11.34. Пусть
хп = S(n)x(n) + 5H,(n-l) + 5W2l(-2) + . . . 5(n)xB) + s(n)x + 5(n)e
Коэффициенты s± являются числами Стирлинга второго рода.

482 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
ДОКАЗАТЕЛЬСТВО. По определению, 5^п) = 0 для всех и > 1 и sin) = 1 для
всех п > 0. Требуется показать, что для 1 < г < и
По определению,
n+1 n
V^ c(n+!) (i) _ n+1 _ n _ ~ . V^
г=0 г=0
г=О
= г • ^ 5|п)а:^ + (ж - г)
г=О г=О
г=О г=0
г=0 t=0
t=0 j=l
Приравнивая коэффициенты при xl для 1 < г < п, получаем 5t-+ = i-S\n'+Si_x,
что и требовалось доказать. ¦
¦ УПРАЖНЕНИЯ
1. Найдите Д2Cх<3> - Ьх™ + 4).
2. Найдите Д4Dх<5) - Зх<4> + 6хC) + х™ - Зх + 4.
3. Найдите Д3(х<5) + Зх<4> - Зх^3) - 2х<2) + 4х - 1.
4. Найдите ДCхB) + 2х- 5)(х^ + 4х<3> + 2хB').
5. Найдите Д(хC> - 2х^2) - 4)(х^4) + 2х<3) - 6х^2) + х - 3).
а и - л /хC)+6хB)+3х\
6. Найдите Д ( т^т——щ— 1.
\ /
/ /v»D) о B) | о
7. Найдите Д
8. Упростите выражение
n+lj iT1 V"
9. Найдите Д3((х - 3)(х - 5)(х - 7)).
/X
10. Найдите А3

РАЗДЕЛ 11.5. Суммирование разностей 483
/х\
11. Найдите Д4( I при х = 0.
12. Преобразуйте хА — 2х3 4- Зх2 4-5 в факториальный многочлен.
13. Преобразуйте х4 — 6х3 -f 4х2 — 4х -Ь 5 в факториальный многочлен.
14. Преобразуйте х4 — х3 -Ь х2 — х + 1 в факториальный многочлен.
15. Преобразуйте х5 — х4 -f х3 — х2 4- х — 1 в факториальный многочлен.
16. Преобразуйте х^4) — х^3) + х^ — х + 1 в обычный многочлен.
17. Преобразуйте х^4) 4- Зх^3) — 4х^2^ — 2х -Ь 1 в обычный многочлен.
18. Преобразуйте 4х^4^ — 2х^3^ + Зх^2^ — 4х + 1 в обычный многочлен.
19. Преобразуйте хE) - хD) + хC) - хB) + х - 1 в обычный многочлен.
20. Постройте алгоритм перехода от факториальных многочленов к обычным.
21. Найдите Д3( ], вычисленное при х = 0.
W
11.5. СУММИРОВАНИЕ РАЗНОСТЕЙ
Мы знаем, что
п
Поэтому, если х принимает только целочисленные значения, любое разностное
отношение может быть представлено в виде рекуррентного отношения. Например,
может быть записано как
fix + 3) - 3/(х + 2) + 3/(х + 1) + Дх)-
- 3(/(х + 2) - 2/(х + 1) + fix)) = 2(/(х + 1) - fix)),
так что
fix + 3) = 6fix + 2) - 7(/(х + 1) - 4/(х),
что является записью в рекурсивной форме. Поэтому для решения этого отноше-
отношения можно использовать результаты первых трех разделов данной главы.
В этом разделе мы используем несколько иной подход. Определим J2 как
оператор, обратный разностному. То есть, желательно, чтобы из AF{x) = /(х)
следовало Х^/(х) — F(X)- Мы установим, однако, что на самом деле, если
AF(x) = /(х), то J2f(x) — F{X) + с> гДе с "~ константа, так как A(F(x) + с) =
AF(x) + А(с) = AF(x). Те, кто знаком с математическим анализом, без труда
узнают в этом аналог первообразной функции или неопределенного интеграла.
Из того, что A(F(x)) = 0, вообще говоря, не следует, что F(x) — константа.
Рассмотрим, например, F(x) = sinB7rx):
AF(x) = sinB7r(x + 1)) - sinB7rx) =

484 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
= sinB7rx + 2тг) — sinB7rx) =
= sinB7rx) — sinB7rx) = 0.
Это объясняется тем, что sin(x) — периодическая функция. Но в дальнейшем
мы ограничимся рассмотрением многочленов, рациональных и экспоненциальных
функций. Для таких функций, если A(F(x)) = 0, то F(x) — константа.
ПРИМЕР 11.35. Используя разностные формулы предыдущего раздела, находим,
что если f(x) = —, то
п -Ь 1
Д/(х) = Д-
п+1
- —!— Д(х(п+1>) = по теореме 11.23
п + 1
= -(п + 1)х(п) = поскольку Д(х(п)) = nx{n~l)
так что
х(п) = + с.
Пусть
D) ^ 6жB) + 4х^) + 5,
тогда
+ 2х<4)
Далее, мы видим, что если f(x) = ( ), то
¦с. ?
= Аах = по теореме 11.23
а — 1
= -(ах)(а — 1) = показано в предыдущем разделе
так что У2(ах) = [ ) + с.
\a-lj
ПРИМЕР 11.36. Пусть Д/(х) = 15х^ + Зх^ + 2х + 8 • Ъх. Тогда
_ 8 • 5х

РАЗДЕЛ 11.5. Суммирование разностей 485
= ЗхE) + хC) + 2х + 2 • 5х + с. ?
Также пусть
как показано в предыдущем разделе, так что
ПРИМЕР 11.37. Пусть Д/(х) = Ъх^ + 6 • 4х + 6 • (г5°). Тогда
/(х) = хE) + 2 • 4х + 6 • A0 J + с. П
Наконец, рассмотрим /(х) = х^~п+1К
д/(х) = д^ =
= Дх(-п+1) = по теореме 11.23
1 — п
= - \п "т~ 1)^ == ^
1 - П
Следовательно, Vx^"^ = — +с.
—и 4-1
ПРИМЕР 11.38. Пусть Д/(х) = х^ + 2х + 5х + х^) + х(\ тогда
Теперь рассмотрим метод, который называется суммированием по частям.
ТЕОРЕМА 11.39. ?/(х)Д<7(х) = f(x)g(x) -J2E(g(x))Af(x)+c.
ДОКАЗАТЕЛЬСТВО. Из теоремы 11.25 имеем
A(fg) = f • А(д) 4- Е{д)
Поэтому
так что

486 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
Рассмотрим теперь суммы, которые являются аналогом определенных инте-
интегралов в математическом анализе. Пусть
/(*) = AF(x) = F(x + 1) - F(x),
тогда
X=l
1=1
Обозначим F(n + 1) - F(l) через F(z)|"+1.
ПРИМЕР 11.40. Пусть f(x) = х^3) + 3х + х(
7
\ тогда
7
Е
Х=1
/(х) =
X=l
ПРИМЕР 11.41. Найти сумму I2 4- 22 + 32 -f • • • + n2.
П
хC) хB)ч 'n+1
3 2
пример
11.42. у; гх = —
x=o г - 1
- iB(n + IK - 3(n + IJ + (n + 1)) - 0 =
= in(n + l)Bn + l).
rn+i _
r- 1
D
П
ПРИМЕР 11.43. ? x = ^r-
x=i 2
x(x — 1
n+1
(n + l)n
П

РАЗДЕЛ 11.5. Суммирование разностей 487
ПРИМЕР 11.44. Как упоминалось выше,
Поэтому
Х=1
(*) ¦ А(д(х))
Х=1 Х=1
ИЛИ
(f(x)g(x))\n1+1 = ?/(я) • А(д(х))
х=1
Следовательно,
х=1
Х=1
ПРИМЕР 11.45.
Х=1
n+1
= (f(x)g(x))\n1+1 -
1=1
Х=1
хЗх
2
(n +
n-м
1K'
2
2
Bn -1):
" Зх-f
x = l
i+i з
2
l+l 3
Jn+1 + 3
1
(
((
\\
Л т
jx+14
'gn+2 N
¦ A(f(x)).
D
УПРАЖНЕНИЯ
1. Найдите сумму разностей первого порядка для функции 3х - х3 + х2 - х + 5
от х = 1 до х = 9.
2. Найдите сумму разностей первого порядка для функции 2х — Зх3 + 2х2 от
х = 1 до х = 5.
3. Найдите ? 2х - 12х<3).
г=4
10
4. Найдите X] 3х -h
7
5. Найдите Y1
i=4
11 /х\
6. Найдите ? + 3 • 5х + 14хF).
г=6 VV

488 ГЛАВА 11. Некоторые специальные вопросы теории рекурсии
п
7. Покажите, что YL %г = п(п + 1).
о г, 'Я ч п2(п + 1J
8. Покажите, что }2 г = —~т— •
о гг ^ ¦/¦ , 14 n(n + l)(n + 2)
9. Покажите, что 22 г(г + 1) — •
п
10. Покажите, что 5Z 4г — 2 = 2п2.
г = 1
8
11. Используя суммирование по частям, найдите ^Bx4- 3KХ.
х=1
10
12. Используя суммирование по частям, найдите ]Г) 4Cх — 6LХ.
х=2
8
13. Используя суммирование по частям, найдите ^ (^)(^ — 1JХ.
х=0
8
14. Используя суммирование по частям, найдите Y1 (х)(х ~ 1JХ.
х=0
8
15. Используя суммирование по частям, найдите Y
х=0
ю
16. Используя суммирование по частям, найдите ^
х=0
ю
17. Используя суммирование по частям, найдите ^
х=0
9
18. Используя суммирование по частям, найдите ^ х
х=0
9
19. Используя суммирование по частям, найдите ]Г) х
х=0
20. Докажите, что А ?) /(г) = fix + 1).
г=с
с
21. Докажите, что A Y1 /(г) = —/(ж).

ГЛАВА
СНОВА О
КОМБИНАТОРНЫХ
ПОДСЧЕТАХ
12.1. ЗАДАЧИ О РАЗМЕЩЕНИИ
В этом разделе мы займемся подсчетом числа способов размещения объектов в
ящики или урны. Подобные задачи нами уже рассматривались. Так, в разделе 8.3
было показано, что число способов поместить го из п различимых объектов в
один ящик, а остальные п — га — в другой, равно
С(п,т) =
т\{п — га)!
Более того, мы показали, что если имеется п различимых объектов и к
различимых ящиков, то число способов поместить щ объектов в г-ый ящик для
всех 1 < г < /с, где п = п\ -f п2 -Ь гг3 + • • • 4- пь определяется по формуле
п!
C(n;ni,n2,n3, • • • )
Отметим, что в каждом из этих случаев ящик может быть пуст, а объекты
и ящики являются различимыми.
Рассмотрим теперь количество способов размещения п различимых объек-
объектов в к различимых ящиках при условии, что некоторые из ящиков могут быть
пустыми. Отметим, что количество объектов, помещаемых в каждый ящик, не
фиксировано, поэтому существуют к возможностей выбора ящика для размеще-
размещения каждого из п объектов. Согласно комбинаторному принципу умножения су-
существуют кп способов разместить объекты в ящиках. Это число совпадает с ко-
количеством функций из множества 5, содержащего п объектов, во множество Г,
содержащее А: объектов, что нетрудно понять, если отождествить отображение
объекта s из множества 5 в объект t из множества Т с размещением объекта s в
ящик t.
ТЕОРЕМА 12.1. Существуют кп способов размещения п различимых объектов
в к различимых ящиках, когда некоторые из ящиков могут быть пустыми.

490 ГЛАВА 12. Снова о комбинаторных подсчетах
Задача значительно усложняется в ситуации, когда ни один ящик не может
быть пустым, поэтому мы отложим ее рассмотрение на потом.
В разделе 8.6 было показано, что число способов размещения га неразличи-
неразличимых объектов в к различимых ящиках, некоторые из которых могут быть пусты-
пустыми, равно
С(п + к - 1, п) = С(п + к - 1, fc - 1) = ^^f •
Кроме того, показано, что число способов размещения га неразличимых объектов
в к различимых ящиках, ни один из которых не может быть пустым, равно
Подсчитаем теперь количество способов размещения га различимых шаров
в к неразличимых ящиках. Сначала рассмотрим случай, когда ни один из ящиков
не может быть пустым. Это также будет числом способов разбиения множе-
множества, содержащего п объектов на к непересекающихся подмножеств.
ТЕОРЕМА 12.2. Существуют S^ способов размещения п различимых шаров в
к неразличимых ящиках, когда ни один из ящиков не может быть пустым, где
{s?n) : 0 < fc < п} — множество чисел Стирлинга второго рода.
ДОКАЗАТЕЛЬСТВО. Требуется показать, что если /(n, fc) — количество способов
размещения п различимых шаров в fc неразличимых ящиках, когда ни один из
ящиков не может быть пустым, то /(п,п) = 1 для всех п > 0, /(п,0) = 0 для
всех п > 1 и /(га + 1, fc) = /(га, fc - 1) + fc/(n, fc). Очевидно, что для га > 1 имеется
только один способ размещения п шаров в п ящиках, так что ни один из ящиков
не будет пуст. Поэтому /(га, и) = 1 для всех п > 1. Случай га = 0 несколько
надуманный, но представляется разумным предположить, что существует только
один способ разместить 0 объектов в 0 ящиках. Поэтому положим /@,0) = 1.
Очевидно, что для га > 1 не существует способа разместить 0 объектов в га
ящиках и не оставить ни один ящик пустым, поэтому /(га,0) = 0 для всех га > 1.
Чтобы доказать соотношение /(га + l,fc) = /(га, fc — 1) 4- fc/(n,fc), предполо-
предположим, что га объектов размещены в fc ящиках и нужно поместить в ящик (ra-f 1)-ый
объект. Имеются две возможности: либо положить объект в пустой ящик, либо —
в уже занятый. В первом случае остальные га объектов должны быть размещены
в оставшихся ящиках. Поскольку имеется fc — 1 таких ящиков, то га объектов
следует поместить в fc— 1 ящик. Существует /(га,fc — 1) способов такого размеще-
размещения. Если (га -f 1)-ый объект помещается в уже занятый ящик, то предыдущие га
объектов были размещены в fc ящиках. Это возможно сделать /(га, fc) способами.
Следующий, (?г + 1)-ый, объект может быть помещен только в один из fc ящиков,
поэтому существуют fc- /(га, fc) способов размещения объектов при условии, что
ни один из fc ящиков не пуст. Следовательно, существуют /(га, fc — 1) -f fc/(ra, fc)
способов разместить п + 1 объектов в fc ящиках, и
/(га + 1, fc) = /(га, fc - 1) + fc/(ra, fc).
Отсюда, /(га, fc) = s? , где {S^ : 0 < fc < га} — множество чисел Стирлинга
второго рода. ¦

РАЗДЕЛ 12.1. Задачи о размещении 491
Теперь, используя свойство 5^.n+1^ = S%!}1 + kS^\ можно сформировать
таблицу чисел Стирлинга второго рода аналогично тому, как это было сделано в
случае треугольника Паскаля.
п
0
1
2
3
4
5
6
7
8
9
10
gin)
1
0
0
0
0
0
0
0
0
0
0
5
1
1
1
1
1
1
1
1
1
1
Треугольник для чисел
in) gin)
1
3
7
15
31
63
127
255
511
g(n)
1
6
25
90
301
966
3025
9330
gin)
1
10
65
350
1701
7770
34105
Стирлинга второго
gin)
1
15
140
1050
6951
42525
gin)
1
21
266
2646
22827
gin)
1
28
462
5880
рода
gin) gin)
1
36 1
750 45
gin)
1
ТЕОРЕМА 12.3. Снимем ограничение на то, что ни один из ящиков не может
быть пустым. Возможны ситуации: A) все п объектов помещены в один ящик,
что можно осуществить s[n>} способами; B) все и объектов помещены в два
ящика, что можно осуществить S^ способами, ..., (к) все п объектов помещены
в к ящиков, что можно осуществить S^ способами, и т.д. Итого, имеется
s[n)
-(n)
способов размещения п объектов в к ящиках при условии, что ящики могут быть
пустыми.
Используя тот факт, что S^ "~ число возможных способов размещения п
различимых объектов в к неразличимых ящиках, ни один из которых не может
быть пустым, мы можем найти количество способов размещения и различимых
объектов в к различимых ящиках, ни один из которых не может быть пустым.
По сути, нам нужно перейти от неупорядоченных ящиков к упорядоченным. При
переходе от упорядоченных ящиков к неупорядоченным нужно делить соответ-
соответствующее количество способов размещения на fc!, как было сделано при переходе
от перестановок к сочетаниям. Поэтому при обратном переходе нужно умножать
на к\. Таким образом, существуют k\S^ способов размещения п различимых
объектов в к неразличимых ящиках, ни один из которых не может быть пустым.
Пусть S — множество, содержащее п объектов, и Т — множество, содержа-
содержащее к объектов. Ранее было подсчитано количество всех функций из 5 в Т, а
также количество биективных функций из 5 в Т. Теперь мы можем подсчитать
количество сюръективных функций из S в Т. Представляя к объектов множества
Т как ящики, отображение элемента s из S в элемент t из Г можно отождествить
с размещением объекта s в ящик ?. Поскольку функция сюръективна, то ни один

492 ГЛАВА 12. Снова о комбинаторных подсчетах
из ящиков не будет пустым. Следовательно, существуют k\S^ сюръективных
функций из n-элементного множества в k-элементное множество.
Теперь мы можем построить следующую таблицу:
A)
B)
C)
D)
E)
F)
G)
Размещение п объектов в к ящиках
объекты — различимые, ящики — различимые,
rii объектов в г-ом ящике
объекты — различимые, ящики — различимые,
ящики могут быть пустыми
объекты — различимые, ящики — различимые,
ящики не могут быть пустыми
объекты — неразличимые, ящики — различимые,
ящики могут быть пустыми
объекты — неразличимые, ящики — различимые,
ящики не могут быть пустыми
объекты — различимые, ящики — неразличимые,
ящики могут быть пустыми
объекты — различимые, ящики — неразличимые,
ящики не могут быть пустыми
Количество способов
С(п;п1,П2,713,--- ,пк)
кп
k\S[n)
С{п + к- 1,п)
C(n- l,fc- 1)
с-(п) , сB) , , rr(n)
°1 + °2 Н г °/с
ТЕОРЕМА 12.4. Завершив рассмотрение размещений объектов в ящики, перей-
перейдем к нахождению количества способов разделения п объектов на fc-циклы при
условии, что никакие два из fc-циклов не имеют общих элементов. Цикл из га
объектов имеет вид aia2as • • -am, где am считается соседом аь так что
Следовательно,
Можно представить себе n-цикл как п человек, сидящих за круглым столом. В
главе 8 было установлено, что существуют (га — 1)! способов рассадить га человек
за круглым столом. Следовательно, если дано га объектов, то существуют (га—1)!
способов построить га-цикл.
Теперь подсчитаем количество способов разделения п объектов на fc-циклы
при условии, что никакие два из fc-циклов не имеют общих элементов.
ТЕОРЕМА 12.5. Количество возможных способов разделения п объектов на fc-
циклы так, что никакие два из fc-циклов не имеют общих элементов, равно s), ,
где {Sfc : 0 < fc < n} — множество чисел Стирлинга первого рода.
ДОКАЗАТЕЛЬСТВО. Пусть /(n, fc) — количество возможных способов разделе-
разделения и объектов на fc-циклы, когда никакие два из fc-циклов не имеют общих эле-
элементов. Чтобы доказать справедливость соотношения /(гг,fc) = s^\ необходимо
сначала показать, что /(п, 0) = 0 для всех п > 1. Но если и > 1, то невозможно

РАЗДЕЛ 12.1. Задачи о размещении 493
сформировать 0 циклов и использовать все п объектов. Следовательно, /(п, 0) = 0
для всех п > 1. Теперь покажем, что /(п, п) = 1 для всех п > 0. Если п > 1, то
можно построить п циклов длины 1, т.е. 1-циклов. Очевидно, сделать это мож-
можно единственным образом, поскольку порядок записи цикла несущественен. Если
и — 0, то представляется разумным считать, что существует единственный спо-
способ построить цикл, не используя объекты, — просто не строить его. Поэтому
/(п, и) — 1 для всех п > 0. Далее необходимо показать, что
f(n + 1, fc) - /(п, к - 1) 4- n/(n, к).
Каждое размещение п + 1 объектов сводится либо к размещению п + 1-го объекта
в новый цикл, либо к добавлению его в уже существующий цикл. Если п + 1-ый
объект размещен в новый цикл, то остальные и объектов размещены в к — 1 цик-
циклах. Последнее можно осуществить f(n,k — 1) способами. Если п + 1-ый объект
размещен в уже существующий цикл, содержащий, например, га объектов, то
п + 1-ый объект может быть помещен вслед за любым из га объектов в цикле.
Следовательно, можно построить га различных циклов, если n-fl-ый объект раз-
размещать в цикле, содержащем га объектов. Допустим, что имеются циклы ci, С2,
..., сь где С{ является щ циклом и п\ + n<i 4- • • • + п\~ = п. Тогда, если an+i
размещен в цикл с;, то можно построить щ новых циклов. Следовательно, путем
добавления n-hl-ro элемента в фиксированное множество fc-циклов, содержащих
п элементов, можно образовать ni-hn2H Vrik = n новых циклов. Поскольку су-
существуют /(п,/с) способов размещения п элементов в fc-циклах, имеется nf(n,k)
способов образовать fc-цикл с п + 1 объектами, если в цикл добавлен п + 1-ый
объект. Следовательно, существуют
/(n,fc- I) +nf(n,k)
способов разбиения п + 1 объектов по fc-циклам и /(гг, fc — 1) = s^. Ш
Используя соотношение s^n = 5^1 + nsk » можно построить таблицу
чисел Стирлинга первого рода аналогично тому, как была построена таблица
чисел Стирлинга второго рода.
ТЕОРЕМА 12.6. Треугольник для чисел Стирлинга первого рода
п
0
1
2
3
4
5
6
7
8
9
10
i
0
0
0
0
0
0
0
0
0
0
s[n)
1
1
2
6
24
120
720
5040
40320
362880
l
3
li
50
274
1764
13068
109584
1026576
<s(n)
S3
1
6
35
225
1624
13132
118124
1172700
„(")
S4
1
10
85
735
6769
67284
723680
4n)
l
15
175
1960
22449
269325
1
21
322
4536
63273
4n)
l
28
546
9450
(n) (n) (n)
S8 S9 S1O
1
36 1
870 45 1

494 ГЛАВА 12. Снова о комбинаторных подсчетах
¦ УПРАЖНЕНИЯ
1. Сколькими способами можно разместить 7 объектов в 3 ящиках, если
а) объекты различимы, ящики различимы и ящики могут быть пустыми?
б) объекты различимы, ящики различимы и ящики не могут быть пустыми?
в) объекты неразличимы, ящики различимы и ящики могут быть пустыми?
г) объекты неразличимы, ящики различимы и ящики не могут быть пусты-
пустыми?
д) объекты различимы, ящики неразличимы и ящики могут быть пустыми?
е) объекты различимы, ящики неразличимы и ящики не могут быть пусты-
пустыми?
2. Сколькими способами можно разместить 10 объектов в 4 ящиках, если
а) объекты различимы, ящики различимы и ящики могут быть пустыми?
б) объекты различимы, ящики различимы и ящики не могут быть пустыми?
в) объекты неразличимы, ящики различимы и ящики могут быть пустыми?
г) объекты неразличимы, ящики различимы и ящики не могут быть пусты-
пустыми?
д) объекты различимы, ящики неразличимы и ящики могут быть пустыми?
е) объекты различимы, ящики неразличимы и ящики не могут быть пусты-
пустыми?
3. Заполните следующие два ряда треугольника для чисел Стирлинга второго
рода.
4. Заполните следующие два ряда треугольника для чисел Стирлинга первого
рода.
5. Сколькими способами можно разместить 12 объектов в 4 ящиках, если
а) объекты различимы, ящики различимы и ящики могут быть пустыми?
б) объекты различимы, ящики различимы и ящики не могут быть пустыми?
в) объекты неразличимы, ящики различимы и ящики могут быть пустыми?
г) объекты неразличимы, ящики различимы и ящики не могут быть пусты-
пустыми?
д) объекты различимы, ящики неразличимы и ящики могут быть пустыми?
е) объекты различимы, ящики неразличимы и ящики не могут быть пусты-
пустыми?
6. Сколькими способами можно разместить 14 объектов в 6 ящиках, если
а) объекты различимы, ящики различимы и ящики могут быть пустыми?
б) объекты различимы, ящики различимы и ящики не могут быть пустыми?
в) объекты неразличимы, ящики различимы и ящики могут быть пустыми?
г) объекты неразличимы, ящики различимы и ящики не могут быть пусты-
пустыми?
д) объекты различимы, ящики неразличимы и ящики могут быть пустыми?
е) объекты различимы, ящики неразличимы и ящики не могут быть пусты-
пустыми?

РАЗДЕЛ 12.2. Числа Каталана 495
7. Пусть S(n, k) = ± Е-=о(-1){ (*) (Л - 0" •
а) Покажите, что 5(п, 0) = 0 для всех п > 1.
б) Покажите, что 5(п, к) удовлетворяет рекурсивному отношению
S(n + 1, к) = S(n, к - 1) + fcS(n, fc).
12.2. ЧИСЛА КАТАЛАНА
В этом разделе рассмотрены три различные задачи, но в процессе их решения
понятно, что это, по сути, одна и та же задача.
12.2.1 Задача 1
Человек идет на место работы, которое находится в десяти кварталах к северу
и десяти кварталах к востоку от его дома. По диагонали, соединяющей его дом
и место работы, течет река. К сожалению, на этом участке реки нет мостов, так
что при достижении диагонали человек также достигает и реки. Следовательно,
он может попасть на диагональ, но после этого должен повернуть направо. Если
улицы проходят по квадратной сетке, так, что в каждом квартале есть улицы в
направлении север-юг и улицы в направлении восток-запад, то сколькими спо-
способами человек может попасть на работу, не возвращаясь и не пересекая реку.
Примеры его возможных маршрутов показаны на рис. 12.1.
/
л . . ,
л
f.
Рис. 12.1
Если обозначить продвижение человека на один квартал на восток через Е, а
его продвижение на один квартал на север через N, то первый из приведенных
маршрутов можно обозначить как
ENEENEENNNEEEENNNNEN.
Второй маршрут можно обозначить как
ENEEEENNNNEENNENENEN
и третий — как
EEEENNNNEEEEEENNNNNN.
Заметим, что любой маршрут должен начинаться с Е, и в любой точке маршрута
количество продвижений Е должно быть не меньше количества продвижений N,
иначе человек попадет в реку.

496 ГЛАВА 12. Снова о комбинаторных подсчетах
12.2.2 Задача 2
Сколькими способами можно сложить последовательность из десяти чисел 1 и де-
десяти чисел —1 так, что если Sk — сумма первых к элементов последовательности,
то Sk > 0 для всех 1 < к < 20. Возможными последовательностями являются
1,-1,1,1,-1,1,1,-1,-1,-1,1,1,1,1,-1,-1,-1,-1,1,-1;
1, -1,1,1,1,1, -1, -1, -1, -1,1,1, -1, -1,1, -1,1, -1,1, -1
и
1,1,1,1, -1, -1, -1, -1,1,1,1,1,1,1, -1, -1, -1, -1, -1, -1.
Заметим опять, что в любой точке вдоль любой из последовательностей количе-
количество 4-1 должно быть не меньше количества —1.
12.2.3 Задача 3
Задано 11 чисел и бинарные операции между ними. Сколькими способами в этом
выражении можно вставить 10 пар круглых скобок? Эта проблема выглядит похо-
похожей на предыдущую, поскольку при движении слева направо закрывающих (пра-
(правых) скобок должно быть не больше, чем открывающих (левых) скобок. Однако,
проблемой остается их размещение. Оказывается, что лучше использовать левые
(открывающие) скобки и первые 10 чисел, чем левые и правые скобки, поскольку
чисел не может быть больше, чем левых скобок. Например, рассмотрим
34-4-8x24-4-7 + 4x5^6-2x4.
Согласно последовательности
1,-1,1,1,-1,1,1,-1,-1,-1,1,1,1,1,-1,-1,-1,-1,1,-1
разместим левые скобки там, где имеется 1, а символ — там, где имеется —1,
после чего получим
C + (D - ((8 х 2) ч- 4)) - (((G + 4) х 5)Л6) - B х 4)))).
Левые скобки размещены в паре с правыми скобками. Теперь рассмотрим
1,-1,1,1,1,1,-1,-1,-1,-1,1,1,-1,-1,1,-1,1,-1,1,-1,
что соответствует
C + (((D - 8) х 2) ч- 4) - (G + 4) х E"F - B х 4)))))),
и наконец
1,1,1,1,-1,-1,-1,-1,1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,
что соответствует
(((C + 4) - 8) х 2) ч- (((((D - 7) + 4) х 5)'6) - 2) х 4)).

РАЗДЕЛ 12.2. Числа Каталана 497
Формулировке задач мы уделили достаточно много времени. Теперь присту-
приступим к их решению. Для начала найдем решение при п = 10, чтобы окончательно
разобраться с нашим примером, а затем выведем формулу для произвольного
п. Вернемся к человеку, идущему на работу. Для начала рассмотрим все пути,
по которым он может добраться до работы мокрым или сухим, не возвращаясь.
Ему следует в некотором порядке пройти 10 кварталов на север и 10 на восток.
Поскольку рассматриваются все пути, включая те, которые пересекают реку, то
десять Е и десять N могут быть в любом порядке. Если рассмотреть строку из
десяти Е и десяти N как строку из 20 пробелов, то необходимо выбрать 10 из
них, в которых разместить Е. Таким образом, общее количество путей к месту
работы равно количеству способов выбрать 10 пробелов из 20, в которых будут
размещены Е. Это число равно С^, или (^) = г™01. Теперь воспользуемся до-
довольно распространенным в подсчетах приемом. Подсчитаем количество путей,
при прохождении которых наш персонаж будет мокрым, и вычтем это число из
общего количества путей. Иными словами, найдем количество путей, которые
нам не подходят, и вычтем его из общего количества путей, чтобы получить ко-
количество путей, по которым наш персонаж может безопасно добраться до места
работы. Наш герой оказывался в реке всякий раз, когда, достигнув какой-либо
точки маршрута, он проходил на север больше кварталов, чем на восток. Иными
словами, если в некоторой точке продвижений N у него на одно больше, чем
продвижений Е, то он попадает в реку. Например, в строке
EENNNEENENENEENNNENE A)
знак N показывает точку, в которой человек попадает в реку. К моменту попада-
попадания в реку было сделано два продвижения Е и три продвижения ЛГ, после чего
осталось еще 8 Е и 7 N. Заменим теперь все Е, расположенные в строке после
ЛГ, на Лг, а все N — на Еу после чего получаем строку
EENNNNNENENENNEEENEN. B)
На новом пути (который не приведет человека к месту работы) имеется 2 Е и 3 ЛГ,
за которым следует 8 N и 7 Е, что в сумме даст 9 Е и И N. Это понятно, если
учесть, что при попадании в реку в пройденном пути было на одно N больше,
поэтому в оставшейся части пути на одно Е было больше. После изменения
остатка пути в нем оказалось на одно N больше. Следовательно, во всем пути
продвижений N стало на два больше, чем продвижений Е. Попробуем еще раз.
В строке
ENENENENNENENEENENNE C)
человек попадает в реку после 5 продвижений N и 4 продвижений Е. После N
осталось 5 N и 6 Е продвижений. Опять заменяем каждое Et стоящее в строке
после N, на ЛГ, а каждое N — на Е, после чего получаем 6 N и 5 Е, стоящие в
строке после ЛГ,
ENENENENNNENENNENEEN. D)
Поэтому новая строка имеет в сумме 9 Е и 11 N продвижений.
Обратно, если имеется строка, в которой 9 Е и 11 ЛГ, то в некоторой точ-
точке строки продвижений ЛГ должно быть больше, чем продвижений Е. Выбираем

498 ГЛАВА 12. Снова о комбинаторных подсчетах
первую такую точку и меняем первое такое N на N. Далее снова изменяем остав-
оставшуюся часть строки, меняя каждое N на Е и каждое Е — на N. Например, пусть
дана строка
ENENEENENENNNENENNNE, E)
которая содержит 9 Е и 11 JV. Выберем первое место в последовательности, в
котором количество продвижений N больше, чем количество продвижений Е, и
заменим TV в этой точке на N. На данный момент в строке имеется 6 Е и 7 N,
включая N. Остаток строки содержит 3 Е и 4 N. Меняем все N, стоящие после
N, на Е, а все Е, стоящие после N, на N. В результате получаем
ENENEENENENNNNENEENN, F)
в которой после N стоит 4 Е и 3 N. В сумме получаем 10 Е и 10 N. Опять
получили путь, который приводит нашего героя в реку, и это произойдет в точке
N. Это понятно, поскольку мы начали с момента 9 Е и И N, и до момента N, и
включая его, у нас продвижений N было на одно больше, чем продвижений Е.
Следовательно, оставшаяся часть строки, стоящая после N, также имеет на одно
iV больше, чем Е. После изменения остатка строки в ней продвижений Е на одно
больше, чем продвижений N. Следовательно, во всей новой строке всегда будет
равное количество Е и N, а начальная часть строки, включая N, всегда будет
содержать на одно N больше, чем Е. При этом N — то лишнее продвижение на
север, которое и приводит нашего героя в реку. Легко заметить, что каждая стро-
строка, которая "окунает" наш персонаж в реку, может быть преобразована в строку
с 9 Е и 11 iV, и обратно, каждая строка, содержащая 9 Е и 11 N, может быть
преобразована в строку, которая приводит нашего героя в реку. Отсюда количе-
количество строк, приводящих в реку, равно количеству способов сформировать строку,
содержащую 9 Е и 11 N. Таким образом, 9 мест для Е выбираются из 20 мест, и
для этого существуют СB0,9) = (9°) = щуу способов. Поэтому количество спо-
способов добраться до места работы сухим равно числу, полученному при вычитании
из общего числа способов количества путей, при которых персонаж попадает в
реку. Обозначим это число Сю, так что Сю = зшш ~~ ШТТ* ^то число можно бы-
было бы подсчитать, но настоящие математики никогда не используют числа, когда
можно оперировать символами, чтобы избежать арифметических ошибок.
Предположим, что имеется и кварталов на север и п на восток, т.е. в рас-
рассмотренном выше примере п = 10. Теперь используем строку длины 2п, половину
которой составляют символы Е, а вторую половину — символы N. Во избежание
попадания человека в реку, нежелательно, чтобы число символов N превышало
число символов Е. Как и ранее, рассмотрим все возможные пути попасть к месту
работы сухим или мокрым без возвращений. Выбираем из 2п возможных мест и
мест для размещения Е. Как было показано, существуют СBп, и) = B^) = ^г
таких размещений. Далее опять находим пути, которые нам не подходят, по-
поскольку приводят нашего героя в реку. Используя процедуру, описанную выше,
находим, что количество таких путей равно количеству строк, в которых символ
Е появляется га— 1 раз, символ N появляется п + 1 раз. Число таких строк равно
количеству способов выбрать и — 1 место из 2п возможных для размещения сим-
символов Е. Таких размещений будет СBп,п— 1) = (J2^) = (n-nun+i)!' так что ^«'

РАЗДЕЛ 12.2. Числа Каталана 499
количество безопасных путей добраться до места работы, равно ^^ *—^~
Теперь можно осуществить подсчет. Итак, получаем
(п-1)!(п+1)Г
Сп =
Bп)!
Bп)!
п\п\
= 1-
п
п
. Bп)!
п\п\
Bп)!
п\п\
n-h 1
Bп)!
п!п!
Bп)!
п!п!
2п
п
Прежде чем оставить это путешествие, снова вернемся к случаю п = 10.
Рассмотрим иной способ подсчета подходящих путей, т.е. Сп, а также случай,
когда наш герой достигает реки, пройдя один километр на восток и один на север.
Считаем, что дом нашего героя находится в начале координат @,0), так что он
достигает точки A,1) и продолжает путь к месту работы. Этот путь изображен
на рис. 12.2.
Рис. 12.2
Сколько существует таких путей? Очевидно, попасть в точку A,1) по суше
можно только одним способом. Легко видеть, что задача о том, как попасть из
точки A,1) в точку A0,10), т.е. к месту работы, ничем не отличается от исходной,
за исключением того, что теперь нужно, не угодив в реку, пройти 9 кварталов на
восток и 9 на север. Это можно сделать Сд способами. Поскольку Со = 1, мы
говорим, что имеются Со • С9 способов попасть к месту работы, проходя через
точку A,1). Это соответствует обозначениям, которые мы введем в дальнейшем.
Теперь предположим, что наш герой по пути на работу первый раз достигает
берега реки в точке (/с,/с), где 1 < к < 10. Для начала подсчитаем, сколько путей,
не достигающих берега реки, вплоть до точки (к, к), ведут из точки @,0) в точку
(к,к). Любой из путей должен начинаться с движения на 2 квартала на восток,
иначе персонаж достигнет реки в точке A,1). Закончить путь персонаж должен
движением на 2 квартала на север, иначе ему следовало бы достигнуть реки в
точке (к — l,fe — 1). Как видно из рис. 12.3, если провести линию, параллельную
реке и проходящую на один километр южнее между точками A,0) и (к,к- 1), то
путь не пересечет эту линию. Следовательно, можно использовать любой путь,
который начинается в точке A,0), проходит к — 1 блоков на север и к — 1 блоков на
восток и достигает точки (к, к — 1), не пересекая новую диагональ. Существуют
Ck-i способов провести такой путь. Следовательно, имеются Ck-\ путей из точки
@,0) в точку (fc,/c), которые до достижения точки (fc, к) не приводят к реке.

500 ГЛАВА 12. Снова о комбинаторных подсчетах
Теперь рассмотрим пути, которые по суше ведут из точки (к, к) в точку места
работы. Но эта задача эквивалентна задаче о перемещении посуху на 10 - к
кварталов на север и 10 - к кварталов на восток, а значит, число путей равно
Сю-*. Поскольку существуют Ck-\ способов попасть в точку (к,к) и Сю-*
способов попасть из точки (fc, к) к месту работы, то существуют Ck-\ • Сю-*
способов попасть на работу, достигнув реки первый раз в точке (к,к). Более
того, для каждого пути существует только одно значение /с, поскольку место, где
он первый раз достигает реки, только одно. Рассмотрим случай, когда наш герой
попадает к месту работы, не достигая реки. Иными словами, рассмотрим случай
к = 10. Используем вышеприведенные аргументы, чтобы показать, что количество
путей на работу в этом случае равно Ck-\, т.е. С9, но в этом случае, в отличие
от предыдущих, нет второй части путешествия. Для удобства записи, исходя из
того, что Со = 1, запишем, что число способов дойти до работы, не достигая
реки, равно С$ • Со. Если просуммировать количество путей для всех возможных
значений fc, 1 < к < 10, то получим количество всех возможных путей от дома к
месту работы. Следовательно,
ю
/с = 1
Как легко видеть, рассуждения не связаны с использованием числа 10. Если
взять п вместо 10, то получим
Сп =
Пусть задан n + 2-сторонний выпуклый многоугольник; требуется разделить
многоугольник на треугольники, проводя прямые из вершины в вершину, причем
прямые не должны пересекаться. Сколько существуют способов такого разбие-
разбиения? Обозначим это число через Тп. Например, для п = 4 возможная триангуля-
триангуляция (разбиение на треугольники) показана на рис. 12.4. Для удобства обозначим
вершины через г;о, г>а, vi, г>2, г>з, • • •, vn. Предположим, что проведена линия из вер-
вершины v0 в вершину v\. Сколько треугольников можно начертить? (См. рис. 12.5.)
Рис. 12.4
Рис. 12.5
Теперь для триангуляции остался многоугольник vqV\V2V^. . ,vn. Поскольку
у него п + 1 сторон, то имеется Tn_i способов триангуляции этого многоуголь-
многоугольника. Предположим, что мы начали триангулировать исходный п + 2-сторонний
многоугольник, нарисовав прямую из вершины v0 в вершину г>ь где 1 < к < п,

РАЗДЕЛ 12.2. Числа Каталана 501
и запретили рисовать прямые из вершины v0 в любую другую вершину viy где
г < к, так что к — наименьшее целое число, для которого существует отрезок из
вершины v0 в вершину с таким нижним индексом. Но тогда должен существо-
существовать отрезок из вершины Vk в вершину va, образующий треугольник VkVavo. В
результате для триангуляции остается многоугольник vav\V2Vs.. . г^. Поскольку
в этом многоугольнике fc + 1 сторон, то существуют Tk-\ способов разбиения его
на треугольники. (См. рис. 12.6.)
Рис. 12.6 Рис. 12.7
Для триангуляции остается также многоугольник v0VkVk+iVk+2Vk+3 • • -vn. В
нем n-fc+2 сторон, поэтому его можно разбить на треугольники Tn_fc способами.
Следовательно, многоугольник справа от линии, соединяющей вершины v0 и v^,
можно триангулировать Tk-\ способами, а многоугольник слева от этой линии
можно триангулировать Тп_^ способами. Поэтому весь многоугольник вместе с
линией от вершины г;о к вершине Vk можно триангулировать Tk-\ -Tn-k способа-
способами. Рассмотрим случай, когда первой линией будет линия из вершины vo в вер-
вершину vn, что можно интерпретировать как отсутствие прямых, выходящих из vo
к любым другим вершинам. Но в таком случае должна быть прямая, выходящая
из вершины vn в вершину va, и многоугольник vaviv2vs.. .vn триангулирован.
(См. рис. 12.7.)
Но этот многоугольник имеет гг + 1 сторон и поэтому может быть триангули-
триангулирован Tk-\ способами. Принимая во внимание, что суммирование по к от 1 до п
учитывет все возможные разбиения на треугольники исходного п 4- 2-стороннего
многоугольника и, полагая То = 1, получаем
тп =
что совпадает с определением чисел Каталана, поэтому Тп = Сп,
¦ УПРАЖНЕНИЯ
1. Вычислите С5, Cq и С7.
2. Во время перерыва 20 человек выстроились у автомата по продаже напитков.
Любой напиток стоит 50 центов. В автомате нет монет для сдачи, но как
только автомат получает монету, он может возвращать ее как сдачу. Если
10 человек могут заплатить без сдачи, а 10 человек имеют только купюры
в один доллар, то сколькими способами они могут выстроиться в очередь,
чтобы каждый, кто нуждается в сдаче, мог ее получить.

502 ГЛАВА 12. Снова о комбинаторных подсчетах
3. Сколькими способами можно расставить в очереди 15 мужчин и 15 женщин,
если в любом месте очереди женщин впереди должно быть не меньше, чем
мужчин?
4. Пусть имеется последовательность из 12 чисел. Сколькими способами можно
перемножить эти числа, не меняя их порядка записи.
12.3. ОБЩЕЕ ВКЛЮЧЕНИЕ-ИСКЛЮЧЕНИЕ И РАЗУПОРЯДОЧЕНИЯ
Ранее мы уже обсуждали принцип включения-исключения для трех или менее
множеств. В этом разделе мы рассмотрим принцип включения-исключения для
конечного числа конечных множеств. Для начала докажем следующую теорему.
ТЕОРЕМА 12.7. Пусть А\, А2, Аз,..., Ап — совокупность конечных множеств.
Количество элементов во множестве A1UA2UA3U.. .иАп определяется формулой
|Ai u A2 U A3 и ... и Ап\ = 2^ \Аг\ - 2^ \А{ П А,| -f
+ (-l)n+1|Ai П А2 П А3 П ... П An\.
ДОКАЗАТЕЛЬСТВО. Необходимо показать, что в правой части приведенного вы-
выше равенства каждый элемент множества А\ U А2 U А3 U ... U Ап подсчитан и
учтен ровно один раз. Предположим, что элемент а принадлежит в точности р
множествам совокупности А\, А2: Аз,..., Ап. В сумме Х^|А;| элемент а учтен
р раз. В сумме ^2i<\Ai П Aj\ элемент а учтен всякий раз, когда выбраны два
множества, содержащие элемент а. Существуют (?) способов выбрать такие два
множества. Следовательно, в сумме 5Z;<j \А{ П Aj\ элемент а учтен (?) раз. В
сумме ^2i<j<k\Ai П Aj П Afc| элемент а учтен всякий раз, когда выбраны три
множества, содержащие элемент а. Существуют (?) способов выбрать такие три
множества. Следовательно, в сумме Yli<j<k \AiDAjnAk\ элемент а учтен (?) раз.
В сумме элементов всех возможных пересечений г множеств, где г < р, элемент a
учтен (^) раз. Следовательно, в сумме
+ (-1)п+1\А1ПА2ПА3П...ПАп\
элемент а учтен р - (ij) + (§) + (-l)i+1(?) + • • • + (~l)p+1 раз. Но
0 = A - 1)р = 1 - р + Q - Q + • • • + (-1)",
и получаем, что элемент а учтен в точности один раз.

РАЗДЕЛ 12.3. Общее включение-исключение и разупорядочения 503
На основании этой теоремы докажем утверждение, известное как теорема о
включении-исключении.
ТЕОРЕМА 12.8. (о включении-исключении) Пусть Аь А2, А3,..., Ап — набор
конечных множеств. Количество элементов множества А[ П А2 П А3 П ... П А!п
определяется формулой
ДОКАЗАТЕЛЬСТВО. Из теории множеств известно, что
А\ П А!2 П А3 П ... n A'n = (Ai U А2 U A3 U ... U Ап)' =
= U-(j4i U A2 U Аз U ... U Ап),
так что имеем соотношение
\А[ П А2 П А'3 П ... П Л^| = |U| - |Ai U A2 U А3 U ... U Ап\,
подстановка которого в
\Аг U А2 U А3 U ... U Ап\ = ^ |Ai| - ^ |Ai П А,-| +
4- ^ |АгПА,-пА^| + (-l)n+1|AinA2nA3n...nAn|
дает требуемый результат. ¦
ПРИМЕР 12.9. Сколько положительных чисел, меньших 2003, делятся на 2, 3, 5
или 7? Сколько положительных чисел, меньших 2001, не делятся на 2, 3, 5 или 7?
Имеются [^р-\ = 1001 целых чисел, делящихся на 2; [^f^J = 666 целых чисел,
делящихся на 3, |_^pj = ^ целых чисел, делящихся на 5, и |_^PJ = 286 целых
чисел, делящихся на 7. Выбирая по два, получаем, что [^pj — 333 целых числа
делятся на 2 и 3, [nirJ = 200 и>елых чисел делятся на 2 и 5, |_niPJ = 133 Целых
числа делятся на 3 и 5, [^pj = 143 целых числа делятся на 2 и 7, |_^pj = 95
целых чисел делятся на 3 и 7, и |_^§rpj = 57 целых чисел делятся на 5 и 7.
Выбирая по три, получаем, что L^§?rJ = 66 целых числа делятся на 2, 3 и 5,
L^i!rJ = 47 целых чисел делятся на 2, 3 и 7, [^JJrJ = ^8 целых чисел делятся
на 2, 5 и 7, и [^fj = 19 целых чисел делятся на 3, 5 и 7. Наконец, имеются
J = 9 целых чисел, которые делятся на 2, 3, 5 и 7. Итак, существуют

504 ГЛАВА 12. Снова о комбинаторных подсчетах
1001 + 666 + 400 + 286 - C33 + 200 +133 +143 + 95 + 57) + +66 4- 47 + 28 +19 - 9
или 2353 - 961 + 160 - 9 = 1543 целых числа, которые делятся на 2, 3, 5 или 7.
Соответственно, существуют
2001 - 1543 = 458
целых чисел, которые не делятся на 2, 3, 5 или 7. ?
Воспользуемся теперь теоремой о включении-исключении для подсчета ко-
количества разупорядочений.
ОПРЕДЕЛЕНИЕ 12.10. Разупорядочением называется перестановка и различ-
различных упорядоченных символов, при которой ни один из символов не остается
на своем месте. Количество разупорядочений на и различных упорядоченных
символах обозначается через Dn.
Для удобства обозначим рассматриваемые п символов как 1,2,3,... ,п. Для
и = 1 величина D\ = 0, поскольку перестановка одного элемента оставляет его
на месте. Для и = 2 единственным разупорядочением будет
1 2
2 1
поэтому D2 = 1. Для п = 3 разупорядочениями будут перестановки
1 2 3 \ /12 3
2 3 1 ) и ^312
так что Ds = 2. Существует 9 разупорядочений, если п = 4. Предлагаем читателю
найти эти перестановки самостоятельно.
Попробуем найти количество разупорядочений для и — 4, используя технику
подсчетов. Пусть U — множество всех перестановок на множестве {1,2,3,4}.
Таким образом, \U\ — 4!. Пусть А\ — множество перестановок, оставляющих на
месте символ 1, А2 — множество перестановок, оставляющих на месте символ 2,
Аз — множество перестановок, оставляющих на месте символ 3 и Л4 — множество
перестановок, оставляющих на месте символ 4. В таком случае, множество А[ П
А'2 П A3 П А'А — множество перестановок, не оставляющих на месте ни один из
символов. По теореме о включении-исключении
J2 \AiC\Aj\-
г<4 i<j<4
\Ai n Aj П Ak\ + \Аг П А2 П Аз П
Пусть Aij = Ai П Aj, Aijk = А{ П Aj П^и А1234 = A\ П А2 П A3 П А4. Таким
образом, Aij — множество всех перестановок, оставляющих на месте символы г
и j, A^k — множество перестановок, оставляющих на месте символы г, j и fc, и

РАЗДЕЛ 12.3. Общее включение-исключение и разупорядочения 505
множество Аиз4 содержит только тождественную перестановку, которая остав-
оставляет на месте все четыре символа. Для нахождения суммы ]С;<4 I^M требуется
найти количество перестановок, оставляющих на месте символ Г.
Рассмотрим, в частности, А\. Любая перестановка из А\ оставляет символ
1 на месте и переставляет символы 2, 3 и 4. Следовательно, множество А\ содер-
содержит 3! перестановки. По аналогичным соображениям, множество Ai содержит 3!
элемента. Следовательно,
\Аг\ + \А2\ + \А3\ + \А4\ = 4 х 3! = 4! = 4! х ± .
Найдем теперь
Рассмотрим частный случай |^4i2|- Чтобы принадлежать множеству А^, пе-
перестановка должна оставлять на месте символы 1 и 2 и переставлять символы
3 и 4. Для этого существует 2! способа. Таким образом, \Ai2\ = 2. Аналогично,
\Aij\ — 2 при всех 1 < г < j < 4. Теперь возникает вопрос, сколько имеется
таких множеств Л^? Поскольку символы г и j выбираются из 4 элементов, то
существуют (*) множеств вида Aij. Следовательно,
Далее найдем
Сначала рассмотрим Аиз- Поскольку символы 1, 2 и 3 не меняют своих
мест, то остается только 4. Отсюда, множество А^з содержит только 1 элемент.
Аналогично, множество А^ при l<i<j<fc<4 содержит только 1 элемент.
Поскольку символы г, j и к выбираются из 4 элементов, то существуют (^)
множеств вида А^. Следовательно,
Е
Наконец, множество Аизл, как уже отмечалось, состоит из 1 элемента, но
4! 1
Сводя вместе полученные результаты, получаем
\А\ПАЪпА'3ПА'А\=4\-4\х± + 4\±-4\±+4\х± =
В более общем виде можно сформулировать следующую теорему.

506 ГЛАВА 12. Снова о комбинаторных подсчетах
ТЕОРЕМА 12.11. Для п > 1 величина Dny количество разупорядочений на и
символах 1,2,3,..., п, вычисляется по формуле
ДОКАЗАТЕЛЬСТВО. Для доказательства этого утверждения рассмотрим А\ П
А2 П Аз П... п Ak при 1 < fc < п. Любой элемент множества А\ П А2 П Л3 П... П А*
оставляет на месте символы 1,2,3,... fc, поэтому он переставляет п - к символов.
Следовательно, \А\ П А2 П Аз П ... П <А&| = (n - fc)!. Аналогично, для любых
фиксированных mi,m2, m3,... га* имеем
|Ami П Ат2 П Лтз П ... П Amfc | = (n - fc)!.
Поскольку fc символов выбираются из п символов, то существуют (?) множеств
вида Ami n ^m2 ^ ^m3 П ... П Amfc. Следовательно,
Ьпц ПЛт2 ПАтз n...nAmJ = (ТУ) х (n-fc)! =
Снова предположив, что U — множество всех перестановок п объектов, так
что \U\ = п!, получаем
Dn = \А[ П А'2П А'3П ... П А'п\ = \U\ -
i.n! + i.n!-in! + ... + (-iri
4 + + + A)П)
В математическом анализе показано, что это разложение в ряд Тейлора
функции е имеет вид
1 , 1 1 1 1 1
p—i — 1 | I и...
1Г 2! 3! 4! 5! *
Следовательно, Dn w n\e~l.
ПРИМЕР 12.12. Неопытный официант подает 10 различных блюд, обслуживая 10
клиентов. Сколькими способами он может сделать так, чтобы ни один клиент не
получил свой заказ? В данном случае имеет место хаотическая перестановка 10
объектов, поэтому количество таких перестановок равно
111111111 1Ч

РАЗДЕЛ 12.3. Общее включение-исключение и разупорядочения 507
ПРИМЕР 12.13. Матрицей перестановок размерности 8x8 является матрица,
в каждой строке и в каждом столбце которой только один элемент равен 1, а
все остальные равны 0. Сколько существует матриц перестановок размерности
8x8, содержащих на главной диагонали только нули? Такие матрицы являют-
являются матричными представлениями перестановок 8 символов, которые и являются
разупорядочениями. Следовательно, имеется
11111111,
^ + ^
таких матриц. ?
ПРИМЕР 12.14. В шахматах две ладьи (туры) могут атаковать друг друга, ес-
если они расположены на одной вертикали (столбце) или на одной горизонтали
(строке). Следовательно, неатакующие ладьи — это те, которые расположены в
разных столбцах или в разных строках. Очевидно, что восемь неатакующих ладей
можно расположить на стандартной (8 х 8)-клеточной шахматной доске. Сколь-
Сколькими способами это можно сделать? Поскольку размещение на шахматной доске
неатакующих ладей эквивалентно размещению единиц в перестановочной матри-
матрице, и существуют 8! перестановок на 8 объектах, то существуют 8! различных
перестановочных матриц размерности 8x8.
Если не привязываться к перестановочным матрицам, то расположение ла-
ладьи в г-ой строке и в j-ом столбце можно идентифицировать с упорядоченной
парой чисел (г, j). Если это сделано для каждой ладьи, то в результате имеем
8 упорядоченных пар,что дает перестановку, в которой первый элемент каждой
упорядоченной пары отображен на второй элемент. В данном случае имеем стан-
стандартное представление функции как множества упорядоченных пар. ?
ПРИМЕР 12.15. Сколькими различными способами можно расположить на стан-
стандартной (8х8)-клеточной шахматной доске 8 неатакующих ладей, чтобы у каждой
номер строки и номер столбца не совпадали? Итак, ладья, расположенная в г-ой
строке, не может находиться в г-ом столбце. Количество таких размещений равно
количеству перестановочных матриц, у которых отсутствуют единицы на главной
диагонали (там только нули). В терминах перестановок это означает, что ни один
элемент не отображается сам на себя. Следовательно, существуют
1 1 1 1 1 1 1 1
1! + 2!~3! + 4!~5! + 6! 7! + 8!}
различных способов разместить ладьи. ?
¦ УПРАЖНЕНИЯ
1. Докажите, что для любого положительного целого числа п
2. У преподавателя обучаются 25 студентов. Преподаватель проводит тест, а
затем просит студентов обменяться бумагами так, чтобы никто не проверял
свой ответ. Сколькими способами это можно сделать?

508 ГЛАВА 12. Снова о комбинаторных подсчетах
3. Студент сдает экзамен, в процессе которого на каждый из 15 вопросов он
должен выбрать один из 15 ответов. Если никакие два вопроса не имеют
совпадающих ответов, то сколькими способами студент может дать непра-
неправильный ответ?
4. Пусть А = {1,2,3,4,5,6,7,8,9} и В = {-1, -2, -3, -4, -5, -6, -7, -8-, 9}.
Каждому элементу из первого множества нужно поставить в соответствие
единственный элемент из второго множества. Элементы каждой пары сум-
суммируются. Сколькими способами можно образовать пары, так чтобы ни одна
из сумм не равнялась нулю?
5. Неграмотный почтальон должен доставить по одному письму каждому из 7
своих клиентов.
а) Сколькими способами он может доставить письма, так чтобы ни один из
клиентов не получил свою почту?
б) Сколькими способами он может доставить письма, так чтобы хоть один
клиент получил свою почту?
в) Сколькими способами он может доставить письма, так чтобы только один
клиент получил свою почту?
г) Сколькими способами он может разнести письма, так чтобы только один
клиент не получил свою почту?
6. Пусть множество А содержит 12 элементов, и <р — перестановка элементов
множества А. Пусть S = {в : в — перестановка на множестве А и в(а) ф ip(a)
дя всех а е А}. Найдите |5|.
7. Семь джентльменов отправляются на вечеринку и сдают там свои шляпы.
Сколькими способами непутевый гардеробщик может вернуть шляпы, так
чтобы
а) ни один из джентльменов не получил свою шляпу?
б) только один из джентльменов получил свою шляпу?
в) хоть один из джентльменов получил свою шляпу?
г) хотя бы двое джентльменов получили свои шляпы?
8. Сколько существует перестановок элементов множества {1,2, 3,4, 5,6,7,8,9}
таких, что
а) в каждой перестановке ни один элемент не остается на своем месте, т.е.
перестановка не отображает ни одно из чисел само в себя?
б) перестановка не оставляет ни одно четное число на своем месте?
в) перестановка оставляет на своем месте хотя бы одно четное число?
г) в результате перестановки в точности четыре числа остаются на своем
месте?
9. Используя предыдущую задачу в качестве схемы, определите количество
перестановок на и элементах, в результате которых в точности к элементов
остаются на своих местах.
10. Найдите количество положительных целых чисел, меньших или равных чис-
числу 2300, взаимно простых с числом 700.
11. Найдите количество положительных целых чисел, меньших или равных чис-
числу 5460, взаимно простых с числом 700.

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 509
12.4. ЛАДЕЙНЫЕ ПОЛИНОМЫ И ЗАПРЕЩЕННЫЕ ПОЗИЦИИ
В приведенных выше примерах на (8 х 8)-клеточной шахматной доске было изуче-
изучено расположение неатакующих ладей, а также расположение ладей на шахматной
доске, когда они не могут находиться на пересечении строки и столбца, номера
которых совпадают. Клетки шахматной доски, на которых ладья не может быть
расположена, можно представить себе как запрещенные позиции. Рассмотрим
теперь шахматную доску или часть шахматной доски с запрещенными позиция-
позициями. При использовании такой (n x п)-клеточной шахматной доски ситуация так-
также описывается как перестановки с запрещенными позициями по аналогии с
перестановками неатакующих ладей. До того, как у читателей, не играющих в
шахматы, возникнет желание пропустить этот раздел или отложить книгу в сто-
сторону, заметим, что шахматы и шахматная доска используются только потому, что
они хорошо иллюстрируют то, что мы собираемся делать.
Начнем с введения ладейного полинома.
ОПРЕДЕЛЕНИЕ 12.16. Пусть С — произвольная доска с т квадратами, кото-
которая для некоторого целого числа и является частью nxn-клеточной шахматной
доски. Для 0 < k < m целое число г^(С) равно количеству способов, которыми
к ладей могут быть размещены на доске С в неатакующих позициях. Ладей-
Ладейным полиномом R(x, С) на С называется производящая функция для чисел
гь{С), так что
R{x, С) = ro{C) +
+ г2(С)х2 + г3(С)х3 + • • • +
ПРИМЕР 12.17. Пусть С — доска, изображенная на рис. 12.8. Всегда имеется
способ разместить 0 ладей на доске, поэтому го(С) — 1 для любой доски С. В этом
случае имеются три способа разместить на С одну ладью, поскольку ее можно
расположить в любой клетке доски С. Расположить две ладьи в неатакующей
позиции можно только одним способом. Следовательно,
Я(ж,С) =
?
Рис. 12.8
Рис. 12.9
ПРИМЕР 12.18. Пусть С — доска, изображенная на рис. 12.9. Доска состоит из
8 блоков, поэтому имеются 8 способов расположить одну ладью на доске С. Для
размещения двух ладей в неатакующей позиции имеются 4 способа выбора на
верхней горизонтали и три места для размещения ладьи на второй горизонтали,
поскольку ладьи не могут располагаться друг под другом. Значит, существует
всего 12 возможных способов расположения двух неатакующих ладей. Следова-
Следовательно,
?

510 ГЛАВА 12. Снова о комбинаторных подсчетах
ПРИМЕР 12.19. Пусть С — доска, изображенная на рис. 12.10. Чтобы упростить
задачу, заметим, что доску С можно представить состоящей из двух частей, С\
и С2, как показано на рисунке. Поскольку обе части не имеют ни общих строк,
ни общих столбцов, то размещение ладей в одной части не влияет на размещение
ладей в другой части.
2 Рис. 12.10
Для размещения одной ладьи на С нужно разместить ее либо на Сь либо на
С2. Имеются 3 способа размещения одной ладьи на С\ и 4 — на С2, поэтому есть
7 способов размещения ладьи на доске С. Для размещения двух неатакующих
ладей на доске С можно размещать их в части С\, одну ладью - в Ci и одну
ладью — в С2 или обе - в Сг. Имеется 1 способ разместить две ладьи в части
С\ и 3 способа размещения ладьи в части С\ и 4 — в части С2, что дает 12
способов размещения 1 ладьи в части С\ и одной ладьи в части С2. Есть 2 способа
размещения двух неатакующих ладей в части С2. Таким образом, существуют
1 + 12 + 2 = 15 способов размещения двух неатакуюших ладей на доске С.
Чтобы разместить 3 ладьи на доске С, можно две ладьи разместить в части С\
и одну ладью — в части С2, или наоборот. Имеется 1 способ размещения двух
неатакующих ладей в части С\ и 4 способа размещения одной ладьи в части С2,
что дает 4 способа размещения двух ладей в части С\ и одной ладьи — в части
С2. Есть 3 способа размещения одной ладьи в части С\ и 2 способа размещения
двух неатакущих ладей в части С2, поэтому существуют 6 способов размещения
двух ладей в части С2 и одной ладьи — в части С\. Это даст всего 4 + б = 10
способов размещения 3 ладей на доске С. И наконец, чтобы разместить четыре
неатакующие ладьи на доске С, можно две неатакующие ладьи разместить в
части С\ и две — в части С2. Имеется 1 способ размещения двух неатакующих
ладей в части С\ и 2 способа размещения двух неатакующих ладей в части С2.
Поэтому есть 2 способа размещения четырех неатакующих ладей на доске С.
Таким образом, ладейный полином для доски С имеет вид
R{x, С) = 1 + 7х + 15х2 + Юх3 + 2х4.
?
ПРИМЕР 12.20. Пусть С — доска, изображенная на рис. 12.11. Как и в предыду-
предыдущем примере, доску С можно представить состоящей из двух частей, С\ и С2,
как показано на рисунке. Поскольку обе части не имеют ни общих строк, ни
общих столбцов, то размещение ладей в одной части не влияет на размещение
ладей в другой части.

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 511
X
.-.—
.
С2
Рис. 12.11
Имеются 5 способов размещения ладьи в части С\ и 8 — в части С2. Поэтому
существуют 13 способов размещения ладьи на доске С. Отметим, что г\[С) =
ri{C\) + ri(C2). Учитывая, однако, что ro(Ci) = ro(C2) = 1, можно положить
ri(C) = ri(Ci)ro(C2)+ro(Ci)ri(C2).
При выборе двух неатакующих ладей можно выбрать две ладьи из части С\, одну
ладью из части С\ и одну — из части С2 или выбрать две ладьи из части С2.
Имеются 4 способа выбора двух неатакующих ладей из части С\. Есть 5 способов
выбора одной ладьи из части С\ и 8 способов выбора одной ладьи из части С2.
Следовательно, имеются 5 х 8 = 40 способов выбора 1 ладьи из части С\ и 1 —
из части С2. Имеются 12 способов выбора двух неатакующих ладей из части С2.
Следовательно, существуют 5 -f 40 + 12 = 56 способов расположения двух неата-
неатакующих ладей на доске С. Согласно методу выбора имеем, что
г2(С) = r2(Ci) +ri(C1)r1(C2) +г2(С2),
и это можно переписать в виде
r2(C) = r2(Ci)r0(C2) + r^d)^^) + rotCOr^Cs).
Далее, чтобы получить 3 неатакующие ладьи на доске С, можно попробо-
попробовать получить 3 неатакующие ладьи из части С\, но такой возможности нет.
Можно получить одну ладью из части С\ и две неатакующие ладьи из части С2.
Имеются 5 способов получить одну ладью из части С\ и 12 способов получить
две неатакующие ладьи из части С2. Это дает 5 х 12 = 60 способов получить
три неатакующие ладьи, располагая одну ладью в части С\ и две неатакующие
ладьи в части С2. Также можно получить две неатакующие ладьи из части С\
и одну ладью из части С2. Имеются 4 способа получить две неатакующие ла-
ладьи из части С\ и 8 способов получить одну ладью из части С2. Следовательно,
существуют 4 х 8 = 32 способа получить три неатакующие ладьи, располагая
две неатакующие ладьи в части С\ и одну ладью в части С2. Снова можно по-
попробовать расположить три неатакующие ладьи в части С2, но такого способа
нет. Следовательно, существуют гз(С) = 60 4- 32 = 92 способа расположить три
неатакующие ладьи на доске С. В соответствии с методом выбора можно также
записать
г3(С) =

512 ГЛАВА 12. Снова о комбинаторных подсчетах
Наконец, чтобы расположить четыре неатакующие ладьи на доске С, нужно
две неатакующие ладьи получить из части С\ и две неатакующие ладьи — из
части С2. Имеются 4 способа получить две неатакующие ладьи из части С\ и
12 способов получить две неатакующие ладьи из части С2. Таким образом, есть
4 х 12 = 48 способов получить четыре неатакующие ладьи на доске С. Можно
записать, что
r4(C)=r2(Ci)r2(C2).
Таким образом,
Д(х, С) = 1 + 13х 4- 56х2 4- 92х3 4- 48х4.
А также
R(x,C) = ro(Ci)ro(C2) + (г!(С1)го(С2) +ro(C1)r1(C2))z+
+ (r2(Ci)r0(C2) + nCCOnCCa) -f ro(Ci)r2(C2))x2 +
+ (r2(Ci)n(C2) + nCCOraCCaJJx3 4- r2(d)r2(C2)x4 =
a: + (r2(C1)x2)((r0(C2) + (n(C2)x + (r2(C2)x2) =
Следовательно, можно было бы получить ладейный полином для С, пере-
перемножая ладейный полином для части С\ и ладейный полином для части С2.
Действительно,
R(x,C1) = 1 + 5х + 4х2
Щх,С2) = 1 + 8х
а их произведение
, С2) = A + 5х 4- 4х2)A 4- 8х 4- 12х2) =
= 1 4- 13х 4- 56х2 4- 92х3 + 48х4 =
= Д(х,С). П
На основе изложенного выше примера приходим к следующей теореме.
ТЕОРЕМА 12.21. Если доска С состоит из двух частей, С\ и С2, не имеющих ни
общих строк, ни общих столбцов, то R(x,C) = R(x, C\)R(x, C2).
ДОКАЗАТЕЛЬСТВО. Рассмотрим коэффициент гь(С) при хк в полиноме R(x,C).
Для выбора к неатакующих ладей на доске С следует выбрать / из них из части С\
и к — I — из части С2. Существуют r/(Ci) способов выбора I неатакующих ладей
из части С\ и г/с_/(С2) способов выбора к — I неатакующих ладей из части С2.
Это дает n(Ci)r/c_/(C2) способов выбора I неатакующих ладей из части С\ и
к — I неатакующих ладей из части С2. Если предположить, что I принимает все
значения от 0 до /с, получим
rib (С) = ro(Ci)rfc(C2) 4-
• • • 4- п(С1)г*_/(С2) 4- • • • 4- rfc(Ci)r0(C2).

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 513
Но это не что иное, как коэффициент при хк в произведении
R(x, d)R(x, C2) = (го(С0 + r,(d)x + • • ¦
¦ + rm(C2)xm). Ш
rm(C1)xm)(r0(C2) + Г1(С2)х
ПРИМЕР 12.22. Снова рассмотрим доску, изображенную на рис. 12.12.
Рис. 12.12
R(x,C1) =
Имеем
Следовательно,
-Ь2х4. ?
Существует еще один способ нахождения Д(х, С) путем разбиения С на
доски. В этом случае доски могут иметь общие строки и столбцы.
ТЕОРЕМА 12.23. Пусть задана доска С, пусть s — квадрат доски С. Пусть
Cs — доска С, в которой удален квадрат s. Пусть Cf — доска С, в которой
удалены строка и столбец, содержащие удаленную клетку s. Тогда Д(х, С) =
= A 4- Зх + х2)A + 4х + 2х2) =
ДОКАЗАТЕЛЬСТВО. Пусть к — положительное целое число. Если к неатакую-
щих ладей помещены на доске С и она имеет т клеток, то на клетке s либо есть
ладья, либо ее нет. Если ладья помещена на клетке 5, то остальные к — 1 ладей
должны быть выбраны из доски Cf, что можно осуществить rk-\(Cf) способа-
способами. Если ладья не помещена на клетке 5, то к ладей должны быть выбраны из
доски Cs, что можно осуществить г^{С8) способами. Следовательно,
и поскольку го (С) = ro(Cs) = 1,
/с=0
к=0

514 ГЛАВА 12. Снова о комбинаторных подсчетах
Но
ТП-1
m— 1 m
поскольку rm(Cf) = 0, что должно равняться 0, т.к. Cf содержит менее m
клеток. Следовательно,
ПРИМЕР 12.24. Пусть С — доска, изображенная на рис. 12.13, где s — отмеченная
клетка. В таком случае Cs — доска, изображенная на рис. 12.14, и доска Cf —
фигура, изображенная на рис. 12.15.
S
Рис. 12.13 Рис. 12.14
Ладейные полиномы имеют вид
R(x,Ca) = l +
Рис. 12.15
Следовательно,
(х, Cf ) =
4z + 2x2)
6x + 6x2 =
П
ПРИМЕР 12.25. Пусть С — доска, изображенная на рис. 12.16, где s — отме-
отмеченная клетка. Тогда Cs — доска, изображенная на рис. 12.17, и Cf — доска,
изображенная на рис. 12.18.
5
i
i
i
i
Рис. 12.16
Рис. 12.17
Рис. 12.18

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 515
R(x,Ca) = R(x,C's)R(x,C'a'),
где C's — верхний левый прямоугольник и С" — нижний правый квадрат.
Следовательно,
R(x,Cs) = A4-2х)A+4х4-2х2) = 1 + 6х + 10х2 + 4х3.
Легко заметить, что
R(x,Cf) = l + 3x + 2x2.
Следовательно,
= хA 4- Зх + 2х2) + 1 + 6х 4- Юх2 + 4х3 =
= 1 + 7х4-13х24-6х3. П
Изучению ладейных полиномов было уделено достаточно времени, поэтому
представляется разумным теперь указать на некоторое их применение. Вспомним
перестановочные матрицы. Каждая из них имеет только по одной единице в каж-
каждой строке и в каждом столбце, и нули — во всех остальных позициях. Если
ладьи отождествлять с единицами, то перестановку п элементов можно отожде-
отождествить с размещением п неатакующих ладей на шахматной доске размером пхп.
Если рассматривать перестановку ф на и элементах как функцию, то ее можно
представить как множество упорядоченных пар {(/с, ф(к)) : к = 1,2, 3,... п). Если
отождествить упорядоченную пару (к,ф(к)) с клеткой шахматной доски, лежа-
лежащей на пересечении строки к и столбца ф(к), то опять приходим к размещению п
неатакующих ладей на шахматной доске размером пхп. Поэтому различные пе-
перестановки на п элементах можно отождествлять с различными расположениями
п неатакующих ладей на шахматной доске размером пхп.
Предположим, что студент хочет прослушать 5 различных дисциплин в те-
течение пяти различных лекционных часов. Если изобразить ситуацию с помощью
шахматной доски, то ее заштрихованные области могут изображать лекционные
часы, когда требуемые дисциплины не читаются. Пусть ф отображает каждую
дисциплину на период, когда ее читают. Как и ранее, будем рассматривать ф как
перестановку. В таком случае, у нас имеются те значения fc, которые не должна
принимать функция ф(к). Например, предположим, что п — 5, и 0A) не должно
принимать значения 2, 3 или 5; фB) не должно равняться 1, 2 или 3; фC) не
должно равняться 1, 3 или 5; ф(А) не должно принимать значения 1, 2 или 5
и фE) не должно быть равно 1, 3 или 4. Перестановки, удовлетворяющие этим
ограничениям, называются допустимыми размещениями на доске. Запрещенная
область, или запрещенные позиции, — это то, что принадлежит заштрихованной
области шахматной доски, изображенной на рис. 12.19.

516 ГЛАВА 12. Снова о комбинаторных подсчетах
12 3 4 5
Рис. 12.19
Рис. 12.20
Вполне очевидно, что допустимыми размещениями являются
2 3 4 5
5 4 3 2
2 3 4 5
4 2 3 5
Предположим теперь, что клеток в запрещенной области сравнительно ма-
мало. Пусть имеется доска, запрещенная область которой изображена на рисун-
рисунке 12.20. Работать с запрещенной областью, которая весьма мала, гораздо проще.
Предположим, что имеется доска размером n x п, у которой запрещенная об-
область А относительно мала. Пусть А{ — множество всех перестановок ф таких,
что ф{г) принадлежит запрещенной области А. В таком случае нас интересует
|А/1пА/2П...пА;|. Но
\А[ ПА'2П...П A'n\ = n\-
i П Aj\ -
поэтому необходимо найти значения всех членов, входящих в правую часть урав-
уравнения. Рассмотрим \Ai\ для фиксированного значения г. Пусть щ — количество
клеток запрещенной области, которые находятся в строке г. Тогда существуют
щ способов выбора ф(г) таких, что ф{г) принадлежит А{. Но для к ф г функ-
функция ф(к) может принимать любое значение, поскольку ф является перестановкой.
Следовательно, имеются (п — 1)! способов выбора других значений функции ф.
Следовательно, и в области А{ существуют щ(п — 1)! перестановок. Суммируя,
получаем
= ?>(n- 1)! =
г
Но (]Ctn*) = ri(^)' количеству клеток в запрещенной области А. Следовательно,
n-1I
Теперь рассмотрим J2i<j \А% П Aj\. Пусть г и j — фиксированы. Чтобы ф
принадлежало Ai nAj, требуется, чтобы ф(г) и ф{^) — принадлежали области А
и находились в различных столбцах. Пусть Let n^ — количество способов таких,

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 517
что ф{г) и ф{^) — принадлежат области А и не находятся в одном и том же столб-
столбце. Поэтому существуют п^ способов выбора ф{г) и ф(э). Для к ф г, j значение
ф(к) может быть любым, поскольку ф является перестановкой. Следовательно,
имеются (п - 2)! способов выбора другого значения функции ф. Следовательно,
Ai П Aj содержит riij(n — 2)! перестановок. Суммируя по г и j, получаем
Ho Yli<j nij ~~ всего лишь количество способов, которыми можно расположить
две неатакующие ладьи в области А. Поэтому Yli<jnij —
Аналогично, для нахождения ]?ti<i2<-<im \Ач ^ Ai2 П • - • П Airn\ положим
niii2-im равным количеству способов таких, что ф{г\), Ф{г2), • • •, Ф(^т) все при-
принадлежат области Л и не находятся в одном столбце. Поэтому имеются nili2...irn
способов выбора 0(ii),0(i2),... ,ф(гш). Для к ф гьг2,.. .,гт значение ф(к) может
быть любым, поскольку ф — перестановка. Следовательно, имеются (п —га)! спо-
способов выбора другого значения для ф, и А^ПА^П- • '^Aim содержит nili2...iTn(n-
т)\ перестановок. Суммируя по гь г2, ..., гт, имеем
Е
ii<i2<--<in
niii2..Arn{n- mV- =
E
п
ii г2 ...гг
(n — га)!.
\ii<*2<--<in
^° Ylil<i2<...<iri niii2...irn ~" всего лишь количество способов размещения га
неатакующих ладей в области А. Следовательно, X^i<i2< -<гт пп '2 ...гт = гт(А)
и
Y^ г2 П-'-nAiJ =rm(i4)(n-m)!.
Поэтому
|Л; П Л;2 П ... П A'n\ = n! - п(Л)(п - 1)! 4- r2(A)(n - 2)! + • • • + (-l)nrn(A),
где ладейный полином для области А, Д(х, А) = ^Z^=zOrk(A)xk.
ПРИМЕР 12.26. Рассмотрим доску, изображенную на рис. 12.21, где заштрихован-
заштрихованная область А — запрещенная зона. Найдем количество допустимых размещений.
Рис. 12.21

518 ГЛАВА 12. Снова о комбинаторных подсчетах
Требуется найти
\А[ П А!2 Г)А'3ПА'4ПА'5П А'6\ = 6! - п(А) • 5! + г2(Л«) • 4! + •. • + (-1Nг6(А).
Уже известно, что полином ладьи для области А имеет вид
Д(х, А) = 1 + 7х + 15х2 + 10х3 + 2х4,
поэтому количество допустимых размещений определяет соотношение
\А[ П А!2 П Аз П Л4 П Л'5 П Лв| = 6! - 7 • 5! + 15 • 4! - 10 • 3! + 2 • 2! = 184. ?
ПРИМЕР 12.27. Рассмотрим доску, изображенную на рис. 12.22, где заштрихован-
заштрихованная область А — запрещенная зона. Найдем количество возможных размещений.
Рис. 12.22 Рис. 12.23
Требуется найти
\А\ П Л'2 П • • • П А!7\ = 7! - п(А) • 6! + г2(А.) • 5! + • • • + (-1Oг7(А),
поэтому нужен ладейный полином для области А. Заметим, что на доске, изоб-
изображенной на рис. 12.23, заштрихованная область В имеет такой же ладейный
полином, как и область А. Заштрихованная область В состоит из областей В\,
В2 и J33, У которых нет общих строк и столбцов. Поэтому
(х, А) = Д(х, В) =
(х, В2) • Д(х, В3).
Поскольку
Л(х, В2) = 1 + Зх;
Д(ж, В3) = 1 + 2х,
то имеем
Д(х, А) = A + 4х + 2х2)A + Зх)A + 2х) =
= 1 + 9х + 28х2 + 34х3 + 12х4.
Следовательно,
|Л; П А'2 П • • • П Л'7| = 7! - 9 • 6! + 28 • 5! - 34 ¦ 4! + 12 • 3! = 1176,
так что количество возможных размещений равно 1176.
?

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 519
¦ УПРАЖНЕНИЯ
1. Найдите ладейный полином для доски, изображенной на рис. 12.24.
2. Найдите ладейный полином для доски, изображенной на рис. 12.25.
Рис. 12.24
Рис. 12.25
3. Найдите ладейный полином для доски, изображенной на рис. 12.26.
4. Найдите ладейный полином для доски, изображенной на рис. 12.27.
Рис. 12.26
Рис. 12.27
5. Найдите ладейный полином для доски, изображенной на рис. 12.28.
6. Найдите ладейный полином для доски, изображенной на рис. 12.29.
Рис. 12.28
Рис. 12.29
7. Найдите ладейный полином для доски, изображенной на рис. 12.30.
8. Найдите ладейный полином для доски, изображенной на рис. 12.31.
Рис. 12.30
Рис. 12.31

520 ГЛАВА 12. Снова о комбинаторных подсчетах
9. Найдите ладейный полином для доски, изображенной на рис. 12.32.
10. Найдите ладейный полином для доски, изображенной на рис. 12.33.
Рис. 12.32
Рис. 12.33
11. Найдите ладейный полином для доски, изображенной на рис. 12.34.
12. Найдите ладейный полином для доски, изображенной на рис. 12.35.
Рис. 12.34
Рис. 12.35
13. Для заданной доски, изображенной на рис. 12.36, где заштрихованная об-
область А — запрещенная зона, найдите количество допустимых размещений.
14. Для заданной доски, изображенной на рис. 12.37, где заштрихованная об-
область А — запрещенная зона, найдите количество допустимых размещений.
Рис. 12.36
Рис. 12.37
15. Для заданной доски, изображенной на рис. 12.38, где заштрихованная об-
область А — запрещенная зона, найдите количество допустимых размещений.
16. Для заданной доски, изображенной на рис. 12.39, где заштрихованная об-
область А — запрещенная зона, найдите количество допустимых размещений.

РАЗДЕЛ 12.4. Ладейные полиномы и запрещенные позиции 521
Рис. 12.38
Рис. 12.39
17. Для заданной доски, изображенной на рис. 12.40, где заштрихованная об-
область А — запрещенная зона, найдите количество допустимых размещений.
18. Для заданной доски, изображенной на рис. 12.41, где заштрихованная об-
область А — запрещенная зона, найдите количество допустимых размещений.
Рис. 12.40
Рис. 12.41
19. Найдите количество допустимых перестановок на доске размером 4x4, когда
запрещенные позиции — клетки вдоль обеих диагоналей.
20. В футбольной команде, состоящей из шести игроков, игрок А не может
играть на позициях 1 и 3, игрок В — на позициях 2 и 4, игрок С — на
позиции 6, игрок D не может играть на позициях 5 и 6, игрок Е не может
играть на позициях 5 и 6, а игрок F не может играть на позициях 1 и 3.
Найдите количество возможных способов заполнить все позиции игроками.
21. Шестеро мужчин арендуют дом с шестью спальнями. Первый мужчина не
хочет спать в спальнях 4 и 6. Второй не хочет спать в спальнях 4, 5 и
6. Третий мужчина не может спать в спальне 3. Четвертому мужчине не
подходят спальни 1 и 2. Пятый не хочет спать в спальнях 1 и 2. Шестой
мужчина не может спать в спальнях 1, 2 и 3. Сколькими способами жильцы
могут распределить между собой спальни?
22. Футбольный тренер купил шесть новых автомобилей для шести лучших иг-
игроков. Он приобрел Volvo, Mercedes, BMW, Lexus, Lincoln и Cadillac. Первый
игрок не хочет управлять Cadillac или Lincoln. Второй игрок не будет управ-
управлять Cadillac или Lincoln. Третий не будет управлять Lexus. Чевертый игрок
не будет управлять Mercedes. Пятый игрок не будет управлять Volvo или
BMW. Шестой не будет управлять Volvo или BMW. Сколькими способами
тренер может раздать машины?
23. Латинский квадрат размером n x n — это квадратная таблица, в которой
элементы каждой строки и элементы каждого столбца являются перестанов-
перестановкой первых п положительных целых чисел. Таким образом, каждое число
появляется один раз в каждой строке и в каждом столбце. Предположим,
что первые две строки чисел латинского квадрата размером 4x4 имеют
вид 1,4,3,2 и 4,1,2,3. Сколько можно образовать различных третьих строк?

522 ГЛАВА 12. Снова о комбинаторных подсчетах
Указание: в первой строке таблицы вычеркните позицию, на которой при-
присутствует 1, и т.д.
24. Предположим, что первые две строки латинского квадрата размером 4x4
имеют вид 4,3,1,2 и 3,4,2,1. Сколько можно образовать различных третьих
строк?
25. Предположим, что первые две строки латинского квадрата размером 5x5
имеют вид 1,3,2,4,5 и 2,1,3,5,4. Сколько можно образовать различных
третьих строк?
26. Предположим, что первые две строки чисел латинского квадрата размером
5x5 имеют вид 1,2,3,4,5 и 3,4,5,2,1. Сколько можно образовать различных
третьих строк?
27. Предположим, что первые две строки чисел латинского квадрата размером
5x5 имеют вид 1,2, 3,4,5 и 2, 3,4,5,1. Сколько можно образовать различных
третьих строк?

ГЛАВА
ПРОИЗВОДЯЩИЕ
ФУНКЦИИ
13.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ
В этом разделе вводится абстрактное определение производящей функции. Чи-
Читатель, не желающий выходить на такой уровень абстракции, может пропустить
этот раздел, не теряя нити изложения.
В дальнейшем мы убедимся, что производящие функции, которые мы сей-
сейчас определим, являются основой эффективных методов решения рекуррентных
отношений и выполнения комбинаторных подсчетов.
Пусть ao,ai,a2,a3,a4,... ,an,... — последовательность действительных чи-
чисел. Запишем ее в виде (ao,ai,a2,a3,a4,... , an,...). Сумма двух последователь-
последовательностей определяется следующим соотношением:
(ao,ai,a2,a3,«4,... ,an,...) + (bo,bi,62,b3,64,... ,6n,...) =
= (a0 4- bo,ai + bi,a2 + b2,a3 + b3,a4 + fc4,... ,an 4- bn,...).
Для действительного числа с введем операцию
со (ao,ai,a2,a3,a4,... ,an,...) = (са0,са\,са2,са^,са±,... ,шп,...).
Кроме того, определим операцию
х о (ao,ai,a2,a3,a4,... ,an,...) = @, ao,ai,a2,a3, a4,... ,an,...),
где х сдвигает каждый элемент последовательности на одну позицию вправо, а в
оставшуюся свободной помещает 0. Наконец, определим
xkJrl о (a0, ai,a2, а3, а4,..., ап,...) = х о (хк о @, а0, аь а2, а3, а4,..., ап,...)),
так что
хоA,0,0,0,0,...)-@,1,0,0,0,...);
х2 о A,0,0,0,0,...)= х о @,1,0,0,0,...} = @,0,1,0,0,...);

524 ГЛАВА 13. Производящие функции
х3оA,0,0,0,0,...)=хо(х2оA,0,0,0,0,...)) =
= хо@,0,1,0,0,...) = @,0,0,1,0,...).
Методом индукции можно доказать, что хк о A,0,0,0,0,...) — последова-
последовательность, в которой после к нулей стоит единица, а оставшаяся часть последова-
последовательности состоит из нулей. Поскольку A,0,0,0,0,...) — это последовательность
1,0,0,0,... , ее можно отождествить с числом 1. Таким образом,
х = х-1 = хоA,0,0,0,0,...) =@,1,0,0,0,...);
х2=х2-1 = х2оA,0,0,0,0,...) = @,0,1,0,0,...);
х3 = х3 • 1 = х3 о A,0,0,0,0,...) = @,0,0,1,0, 0,...);
х4=х4-1 = х4о A,0,0,0,0,...) = @,0,0,0,1,0,0,...),
и хк = хк о A,0,0,0,0,...) — последовательность, в которой после к нулей стоит
единица, а оставшаяся часть последовательности состоит из нулей. Понятно, что
(а0,а1,а2,а3,а4,0,0,0,0,...)=а0оA,0,0,0,0,0,...) +
+ 010@,1,0,0, 0,0,...) +
+ а2о@,0,1,0,0,0,...) +
+ а3о@,0,0,1,0,0,...) +
+ а4о@,0,0,0,1,0,...) =
\- апхп.
(ao,ai,a2,a3,a4,...,an,...) = a0 + a\x + a2x2 + a3x3 + а4х4 + ••• + апх
r\
(ao,ai,a2,a3,..
В общем случае
0,
0,
0,
о,...;
—
) = a0 +
a0 +
¦aix
alX +
+ a2x2
a2x2 + a
+ a3x3 -
3x3 +
Ь a4x4
a4x4
+ ••
Выражение ао + а\х + а2х2 + а3х3 + а4х4 Н Ь апхп • • • называется произ-
производящей функцией последовательности а0, аь а2, а3,...
В разделе 13.5 используются производящие функции несколько иного типа,
называемые экспоненциальными. Для обычной производящей функции
A,1,1,1,1,1,...) = 1 + х + х2 + х3 + х4 + х5 + • • • ,
(ao,ai,a2,a3,a4, • • •) = a0 + a\X + a2x2 + a3x3 + а4х4 Н
и
2 + а3х3 ЛЬ ахп
(а0, аь а2, а3,..., ап, 0,0,0,0,...) = а0 + а\х + а2х2 + а3х3 Л Ь апхп,
а для экспоненциальной производящей функции мы полагаем
/Т* ГТ% Т* /Т*
+ +
A,1,1,1,1,1,...) = 1+- + -+ - + - + - + -+

РАЗДЕЛ 13.2. Производящие функции и рекуррентные отношения 525
Тогда
(ao,ai,a2,a3,a4,---) = а0 4- «i — 4- а2 —
X X2 X3 X4
х2
(ао,аьа2,аз,...,ап,0,0,0,0,...) =ao + ai~ -f- a2— + аЗ"зГ
13.2. ПРОИЗВОДЯЩИЕ ФУНКЦИИ И РЕКУРРЕНТНЫЕ ОТНОШЕНИЯ
В этом разделе рассматривается использование производящей функции для ре-
решения рекуррентных отношений. В следующих трех разделах рассматривает-
рассматривается применение производящих функций для комбинаторных подсчетов. Назовем
а0 4- а\х 4- а2х2 + а3х3 + а4х4 Н 1" an^n 4—• производящей функцией после-
последовательности a0, oi, а2, аз, ...
/(х)
Пусть /(х) и д(х) — многочлены. Определим отношение ——г как
9{х)
~7-~ = a0 4- aix -f a2x2 4- a3x3 4- a4x4 H h anxn • • •
тогда и только тогда, когда
f(x) = g(x)(a0 4- axx 4- a2x2 4- a3x3 4- a4x4 + • • • 4- anxn
ОПРЕДЕЛЕНИЕ 13.1. Если Щ- = a0 4- aix 4- a2x2 4- a3x3 4- • • • 4- anxn • • •, то
f(x\
ao4a1x4-a2x2+a3x34-a4x4H \-anxn-\ называется разложением
—7—7.
9\x)
ТЕОРЕМА 13.2. Для любого га имеет место разложение
1
A-ах)™ VI/ V 2
(т 4- 2\ 3 3 /га 4- п - 1
3 / Х V п
ДОКАЗАТЕЛЬСТВО. Используя метод индукции, покажем для га = 1, что
= 1 4- ах 4- а2х2 4- а3х3 4 Ь апхп -\ ,
A - ах)
что эквивалентно
1 = A - ах)A 4- ах 4- а2х2 4- а3х3 4- • • • 4- апхп 4- • • • )•

526 ГЛАВА 13. Производящие функции
Но
A - ах)A 4- ах 4- а2х2 + а3х3 + h anxn + •••) =
= 1 4- ах 4- а2х2 Н Ь anxn H ax(l 4- ax + а2х2 Н Ь апхп Н ) =
= 1 4- ах + а2х2 + • • • + апхп 4- ах - а2х2 апхп = 1.
Таким образом, для т = 1 теорема справедлива.
Предположим, что теорема справедлива для m = /с, то есть, что
1
1
Требуется доказать, что
A -ах)^1 V 1 /— V 2
+С:
Поскольку
1 1 1
A - ax) A - ax)k'
имеем
A )
Поэтому приведенное выше выражение для производящей функции после-
последовательности n_ag)fc+i верно тогда и только тогда, когда после умножения на
A — ах) мы получаем производящую функцию последовательности ц_!д)Ь •
Но
A - ах)A + (k+^ax + (*+2)а2х2
= 1 + (*| V + (к?)а2х2 + v з ;- *
(пт\(Л i (к+1\пт 4- (к+2\п2т2
= 1 + (fc+V + (fc+2)a2x2 + (fc+3 )a3x3 + • ¦ ¦ + (fe+n)a"xn + • • • -
- ах - (fe+1)a2x2 - (fc+2)a3x3 (^"I1)*"*"
= 1 + Cl)ax + (fc+1)a2x2 + (fc+2)a3x3 + ¦ • ¦ + f+J-'Jo"!" + • • ¦ ,
поскольку, согласно тождеству Паскаля, имеем
к 4- п - 1\ /fc 4- п - 1\ _ /А: 4- п
п ) \ п—1 ) \ п

РАЗДЕЛ 13.2. Производящие функции и рекуррентные отношения 527
так что
(к + п\ _ /к + п - 1\ _ /А; + п - 1\
\ п )~\ п-1 )~\ п )¦
Следовательно,
A - ax)fe+1(l + (Ч^ах + (fc+2)a2x2 + (fc+3)a3z3 + • • • + (fc+n)a"xn + •••) =
= {l-ax)k(l + С[)ах +
Но, по индуктивному предположению,
— ax) \\ -f y^jax -\- у 2 )a x ¦ v з /
что и требовалось доказать.
Из доказанной теоремы следует, что
7 l—-z = 1 + 2ах -f За2х2 + 4a3x3 + • • • + (n -f l)anxr
A - axJ
и
A — ахN 2
Из математического анализа известно, что любая дробь вида
Ах + В
(l-Cx)(l-DxY
где константы С и D различны, равна
а Ь
1-Сх l-Dx
для некоторых постоянных а и Ъ. Такое представление называется разложением
на элементарные дроби.
Более того, любая дробь вида
Ах2 + Вх + С
(l-DsXl-JSxXl-Fx)'
где константы Dy E и F различны, равна
a b с
1 - Dx + 1 - Ex + 1-Fx
для некоторых постоянных a, 6 и с. Также, если константы D и Е различны, то
Ах2 + Бх + С a 6 с
(l-DxJ 1-Ех

528 ГЛАВА 13. Производящие функции
для некоторых постоянных a, b и с, и если константы Е и F различны, то
Ах3 4- Вх2 + Cx + D a b с d
(l-?xK(l-Fx) 1-?х A-ЕхJ (\-Exf 1-Fx
для некоторых постоянных а, Ь, с и d.
Предположим, что требуется найти разложение производящей функции
15х 15х
1 4- Зх - 4х2 = A4-4х)A-х) *
Пусть
15х a b
х) 14-4х 1-х
для некоторых а и 6. Умножая обе части равенства на A 4-4х)A — х), получаем
Полагая х = 1, приходим к уравнению
15A) = аA - 1) + ЬA + 4),
решая которое, получаем Ъ = 3. Полагая х = —-, приходим к уравнению
11 1
4 4 4
решая которое, получаем а = —5, поэтому
15х _ -5 3
A +4х)A -х) ~~ 14-4х + 1-х'
Применяя формулу
г = 1 4- ах 4- а2х2 4- а3х3 4 Ь апхп 4 ,
A - ах)
при а = — 4 и а = 1, получаем
= 14- (-4)х 4- (-4Jх2 4- (-4Kх3 + • • • + (-4)пхп 4- • • •
и
A-х)
так что
-5 3
* -I,. 2 . 3 , _|_ п
= -5A 4- (-4)х + (-4Jх2 + (-4Kх
2^2 , / лчЗ^З
1 + 4х 1-х
• •. + (-4)пхп + • • •) 4- 3A + х + х2 + х3 + • • • + хп + • • •) =
= -2 + 23х - 77х2 + 323х3 + • • • + (-5(-4)п + 3)хп + • • • .
В дальнейшем нам понадобится еще одна теорема о производящих функциях.
1 _ xn+i
ТЕОРЕМА 13.3. При всех п > 0 имеем = 1 + х 4- х2 4- х3 И Ь хп.
1-х

РАЗДЕЛ 13.2. Производящие функции и рекуррентные отношения 529
ДОКАЗАТЕЛЬСТВО.
A х)A +х + х
1-х
4- х + х2 4- • • • 4- хп + •••)- хA + х + х + --.+х+ •••) =
= A 4- х + х2 4- • • • + хп + xn+1 +-..)" (xn+1 + хп+2 + хп+2 + •••) =
= 1 4- х + х2 4- х3 Н Ь хп. Ш
Теперь рассмотрим применение производящих функций для решения ре-
рекуррентных отношений. Сначала проиллюстрируем метод на простом примере.
Рассмотрим рекуррентное отношение ап = 3an_i или ап — 3an_i = 0. Пусть
/(х) = а0 4- а\х -f a2x2 + a3x3 H h anxn H .
Умножим обе части равенства на Зх, помня о том, что умножение на х сдвигает
каждый элемент последовательности вправо, так что
Зх/(х) = Заох + 3aix2 + За2х3 4- За3х4 + • • • 4- 3an_ixn 4- 3anxn+1 + • • ¦ .
Вычитая Зх/(х) из /(х), получаем
/(х) - Зх/(х) = а0 4- (ai - Зао)х + (а2 - 3ai)x24-
4- (аз - За2)х3 + • • • + (а„ - 3an_i)xn -\ .
Но ап — 3an_i = 0 при всех п > 1, поэтому
/(х) - Зх/(х) = а0.
Таким образом,
A - Зх)/(х) = а0
= аоA 4- Зх 4- 32х2 4- 33х3 4- • • • 4- Зпхп + •••) =
= ао + Заох 4- 32аох2 4- 33а0х3 -f h 3naoxn + • • • .
Следовательно, ап = 3nao. Заметим, что мы умножали обе части равенства на
Зх, поэтому, вычитая, должны получить an-3an_i. Но, по определению данного
рекуррентного отношения, это выражение равно 0.
ПРИМЕР 13.4. Найдем функцию, заданную рекуррентными отношениями
а0 = 5;
ak = ak-i 4-3.
Второе уравнение можно переписать в виде а^ - пк-\ -3 = 0.

530 ГЛАВА 13. Производящие функции
Снова положим
/(х) = а0 4 а\х 4 а2х2 + а3х3 4 h anxn 4 .
Поскольку коэффициент при а^-i равен 1, то теперь требуется найти
xf(x) = аох 4- aix2 + a2x3 + а3х4 + • • • 4 anxn+1 + • • • .
Кроме того, нам потребуется производящая функция, у которой при каждом члене
стоит коэффициент 3, т.е.
3
= 3A 4- х 4 х2 4 х3 4 • • • 4 хп 4 • • •) =
1-х
= 3 4 Зх 4 Зх2 4 Зх3 4 h Зхп + • • .
Теперь
3
/(х) - х/(х) - = а0 - 3 4 (ai - a0 - 3)х4
1-х
4- (a2 - ai - 3)х2 4 h (an - an_! - 3) 4 • • • .
Ho a/c - dk-i -3 = 0 при всех к > 1, так что
/(х) - xf(x) - = a0 - 3 = 2.
1-х
Решая это уравнение относительно /(х), получаем
3 2
= 3A 4 2х 4 Зх2 + • • • 4 (п 4 1)хп 4 • • • L
4 2A 4 х 4 х2 4 • • • 4 хп 4 • • •) =
= 5 4 8х 4 Их2 4 14х3 4- • • • 4 (Зп 4 5)хп 4 • • • ,
так что ап = Зп 4 5. ?
ПРИМЕР 13.5. Найдем функцию, заданную рекуррентными отношениями
а0 = 1;
Q>i = 4;
Как и ранее, положим
/(х) = а0 4- aix 4 а2х2 4- а3х3 4 Ь апхп 4
Поскольку коэффициент при a^_i равен 1 и коэффициент при а^_2 равен 6, нужно
найти
х/(х) = аох 4- aix2 4 a2x3 4- a3x4 4 4- anxn+1 4 • • •

РАЗДЕЛ 13.2. Производящие функции и рекуррентные отношения 531
и
6х2/(х) = 6аох2 4 6aix3 4- 6а2х4 4- 6а3х5 + • • • 4- 6anxn+2 4 • • • .
Поэтому
/(х) - xf(x) - 6х2/(х) = a0 4 (ai - ao)x 4 (a2 - a* - 6ao)x2 4
4 (a3 - a2 - 6ai)x3 H h (an - an_i - 6an_2)xn H .
Ho anxn — an_i — 6an_2 = 0 для всех п > 1, так что
/(x) - x/(x) - 6x2/(x) = a0 4 (ai - ao)x = 1 4 3x.
Решая уравнение относительно /(х), получаем
_ 1 + Зх _ 14 3х
J[X)~ l-x-бх2 " A-Зх)A4 2х)*
Полагая
14 3x a 6
4
и умножая обе части равенства на A — Зх)A 4 2х), получаем
1 4 Зх = а{\ 4 2х) 4 6A - Зх).
Полагая х = — - , получаем
так что b = -- . Полагая х = -, получаем
О о
так что а = - . Следовательно, имеем
о
6 1
5j\(l-3x)
так что
а„=(|)F.(ЗГ-(-2)п). D

532 ГЛАВА 13. Производящие функции
ПРИМЕР 13.6. Найдем функцию, заданную рекуррентными отношениями
а0 = 1;
ak =3afc_! +4n.
Как и ранее, пусть
/(х) = а0 + ецж 4- а2х2 4- а3х3 Н 4- апхп + • • • .
Поскольку коэффициент при ак-\ = 3, найдем
Зх/(х) = Заох 4- 3aix2 + 3a2x3 + 3a3x4 + • • • + 3anxn+1 + • • • .
Так как
= A4- 4х 4- 42х2 4- 4V 4- • • • 4- Апхп + ---),
A - Ах)
это даст 4пхп. Поэтому
Дх) - Зх/(х) - ^
= ао — 1 4- (ai — Зао — 4)х 4- (а2 — За\ — 42)х2 +
+ (аз - За2 - 42)х3 + ... + (ап - ап_! - 4п)хп +
Поскольку ап — За^_х — 4П = 0 при всех п > 1, имеем
/(х) - Зх/(х) - _Х = ао - 1 = 0.
Решая уравнение относительно /(х), имеем
/(х) = 1 .
у J (I -4x)(l -Зх)
Пусть
1 а Ь
Умножая обе части равенства на A — 4х)A — Зх), имеем
1 = (l-3x)a + (l-
Полагая х = -, получаем
о
так что Ъ = -3. Полагая х = - , имеем
4

РАЗДЕЛ 13.2. Производящие функции и рекуррентные отношения 533
поэтому а = 4. Следовательно, имеем
= 4A 4- 4х 4- 42х2 4- 43х3 4- • • • 4- 4пхп 4- • • •) -
- 3A 4- Зх 4- 32х2 4- 33х3 4- • • • 4- Зпхп 4- • • • ,
поэтому
ап = 4 • 4П - 3 • 3n = 4n+1 - 3n+1. D
ПРИМЕР 13.7. Найдем функцию, заданную рекуррентными отношениями
CLq == 3]
ап = 2an_i 4- п.
Второе уравнение также можно переписать в виде ап - 2an_i - п = 0.
Опять положим
/(х) = а0 4- а\х + а2х2 4- а3х3 Н Ь апхп -\ .
Поскольку коэффициент при а^_х равен —2, найдем
2х/(х) = 2аох 4- 2aix2 -f 2a2x3 4- 2а3х4 Н + 2anxn+1 Н- • • • .
Кроме того, нам нужна производящая функция, каждый член которой имеет мно-
множителем п, но это есть
= хA + 2х 4- Зх2 4- Ь пхп~1 + ...) =
= х 4- 2х2 4- Зх3 Н h пхп Н .
Теперь
f(x) - 2х/(х) - Х = а0 + (ах - 2а0 - 1)х +
A-хJ
4- (а2 - 2а\ — 2)х2 И 4- (ап - 2an_i - п) -\ .
Но а/с - 2а/с_1 - к = 0 для всех к > 1, поэтому
/(х) - 2х/(х) - ^ = а0 = 3.
Решая уравнение относительно /(х), получаем
х 3 3 - 5х 4- Зх2
f (Х) ~
. т\2 (Л _ От\ (
Л R (~*
A - х) + A - хJ + A - 2х) '

534 ГЛАВА 13. Производящие функции
так что
3 - 5х + Зх2 = ЛA - х)A - 2х) + В{\ - 2х) + СA - хJ =
= ЛA - Зх + 2х2) + ВA - 2х) + СA - 2х + х2).
Приравнивая коэффициенты при х2, х и 1, получаем соответственно
3 = 2А + С;
-5 = -ЗА -2В- 2С;
Решая эти уравнения, получаем А = —1, В — — 1 и С = 5. Следовательно,
U \ - -1 _ l j. _5
= -A + х + х2 + • • • + хп + • • •) - A + 2х + Зх2 + • • •
• • • + (п + 1)хп + ...) + 5A + 2х + BхJ + ••- + Bх)г
УПРАЖНЕНИЯ
1. Выразите приведенные ниже дроби через элементарные дроби:
' (х + 4)(х + 3) ' ; (х-2)(х-3) '
х2 + 2х + 3 х
В) (х-1J(х-2) ; Г) (х-1)(х-2)(х-3)
Зх2 + 1
А) (х-1J(х-2J*
2. Выразите приведенные ниже дроби через элементарные дроби:
2х 4-1 . 2х - 3
а* (х-4)(х4-2) ' J (x-2)(x-f 4) '
х2 -h 2х + 3 х2
в) 7 i TT7 гГГ9 » г^
-1)(х + 3)(х-5)'
. Зх2 + 1
Д) т Туг ¦
(х - 1)л
3. Найдите разложения приведенных ниже производящих функций:
а) к 1
х + 4' ' (х-2J'
.1 X
в) 7- 7^< г)
(х-1K' ' (х-1)(х-2)'
Зх2 + 1
?

v X Х_
В/ / 1\q » * ) / | 1\/
РАЗДЕЛ 13.3. Производящие функции и комбинаторные подсчеты 535
4. Найдите разложения приведенных ниже производящих функций:
1 х_
х — 3 ' (х —
А) (х-1J(х + 2J*
5. Используя производящие функции, решите следующие рекуррентные отно-
отношения:
а) а0 = 1; б) а0 = 2;
an = 2an_i + Зп при n > 0. an = 3an_i 4- n при n > 0.
в) a0 = 8; r) a0 = 1;
d\ = 16; ai = 0;
an = 2an_i + 3an_2 при n > 1. an = 4an_i - 4an_2 при n > 1.
Д) a0 = 4;
an = 2an_i — 3 при n > 0.
6. Используя производящие функции, решите следующие рекуррентные отно-
отношения:
а) а0 = 1; б) а0 = 3;
an = 2an_i при п > 0. an = 4an_i + 2n при n > 0.
в) a0 = 1; г) a0 = 1;
an — 5an_i — 6an_2 при n > 1. an = 7an_i — 10an_2 при n > 1.
Д) ao = 1;
an = 2an_i -f n — 1 при n > 0.
7. Используя производящие функции, решите следующие рекуррентные отно-
отношения:
а) а0 = 1; б) а0 = 2;
an = an_i + n при n > 0. an = 3an_i + 2n при n > 0.
в) a0 = 1; r) a0 = 1;
an = 2an_i -f 2n при n > 0. ai = 8;
an = 6an_i - 9an_2 + 2n при n >
13.3. ПРОИЗВОДЯЩИЕ ФУНКЦИИ И КОМБИНАТОРНЫЕ ПОДСЧЕТЫ
В настоящем разделе речь пойдет о применении производящих функций для
комбинаторных подсчетов. Это превосходный метод, который оценит каждый, кто
столкнется с его использованием. Ранее мы рассматривали производящие функ-
функции как формальные ряды, не касаясь таких понятий анализа, как сходимость,
ряды Тейлора, интегрирование и дифференцирование.

536 ГЛАВА 13. Производящие функции
Для начала рассмотрим функцию A4- х)п. Известно, что по формуле бинома
Ньютона
(l + xr^QxO+^ + QK + .-. + Ox",
так что коэффициент при хк равен количеству способов выбора к объектов из и
объектов без учета порядка. Следовательно, производящая функция вида A4х)п
является производящей функцией для числа сочетаний из п объектов по к.
По теореме 13.2
V + Гз+V
поэтому коэффициент при хк есть число сочетаний из га объектов по к с повто-
повторениями. Следовательно, производящая функция цДлт является производящей
функцией, которая применяется для определения числа сочетаний из т объектов
по к с повторениями.
Теперь рассмотрим произведение
Aа + ха)Aь 4 х6)Aс + хс + x2c)(ld + xd 4 x2d),
где нижние индексы отслеживают только "происхождение" каждого х и никак не
влияют на его значение. Таким образом, ха, хь, хс и xj — это х, где нижний
индекс — просто метка. Если положить х° = U при г = а, 6, с и d и рассмотреть
слагаемое х4, то мы увидим, что оно представляет собой сумму
СГ О 2_2 , „О 1 2,1 , ^l^O 2„1 , 112-1 „О ,
XaXbXcXd + XaXbXcXd + XaXbXcXd + XaXbXclXd +
Сумма степеней в каждом слагаемом равна четырем, значит, имеются все воз-
возможные решения уравнения
еа 4- еь 4- ес + е^ = 4
при 0 < еа < 1, 0 < еь < 1, 0 < ес < 2 и 0 < е^ < 2. В общем случае, при
О < г < 6 коэффициент при хг равен количеству решений уравнения
еа 4- еь 4- ес + е^ = г
при 0 < еа < 1, 0 < еъ < 1, 0 < ес < 2 и 0 < ed < 2.
Предположим, имеется множество А, содержащее 1 объект типа а, 1 объект
типа Ь, 2 объекта типа с и 2 объекта типа d. Пусть х^ представляет j объектов
типа г. Таким образом, la обозначает 0 элементов типа а, хь обозначает 1 элемент
типа b и х2 обозначает 2 элемента типа с. Например, x^x^x^lx^ представляет
выбор 1 объекта типа а, 1 объекта типа Ь и 2 объектов типа с. Тогда коэффициент
при х4 равен количеству способов выбора 4 объектов среди объектов 4 типов,
принадлежащих множеству А. Легко представить, что 1с4хс4х^ означает выбор
О, 1 или 2 объектов типа с.
A 4- х)A + х 4- х2)A + х + х2 + х3)A + х 4 х2 4 х3 4 х4 + х5).

РАЗДЕЛ 13.3. Производящие функции и комбинаторные подсчеты 537
Коэффициент при хг представляет количество способов выбора г объектов из
множества, содержащего 1 элемент типа а, 2 элемента типа 6, 3 элемента типа с
и 5 элементов типа d, если нижние индексы в произведении опущены, а также
количество решений уравнения
еа + еь + ес 4- е<* = г
при 0 < еа < 1, 0 < еь < 2, 0 < ес < 3 и 0 < ed < 5.
ПРИМЕР 13.8. В урне находятся 4 красных, 5 синих и 2 зеленых шара, (а) Сколь-
Сколько существует способов выбора 7 шаров из урны? (б) Сколько существует спосо-
способов выбора из урны 7 шаров, если 1 шар красный и 2 синие.
Для части (а) производящая функция имеет вид
A 4- х + х2 + х3 -4- х4)A + х + х2 + х3 4- х4 4- х5)A + z + х2),
и количество способов выбора 7 шаров равно коэффициенту при х7 в разложении
этой производящей функции.
В части (б) нужно учесть, что 1 вытянутый шар красный, соответствующий
многочлен имеет вид (х 4- х2 + х3 4- х4), что представляет вытягивание 1, 2,
3 или 4 красных шаров. Точно так же, учитывая, что 2 вытянутых шара синие,
соответствующий многочлен должен иметь вид (х2-Ьх3+х44-х5), что представляет
вытягивание 2, 3, 4 или 5 синих шаров. Таким образом, производящий многочлен
имеет вид
(х 4- х2 + х3 4- х4)(х2 4- х3 + х4 4- х5)A + х 4- х2),
и количество способов выбора 7 шаров равно коэффициенту при х7 в разложении
производящей функции. ?
ПРИМЕР 13.9. Допустим, в урне находятся 3 красных, 8 зеленых, 9 оранжевых
и 2 белых шара. Сколько существует способов выбора 12 шаров из урны, если
1 выбранный шар — красный, количество выбранных зеленых шаров — четное,
а количество оранжевых — нечетное? Учитывая, что хотя бы 1 выбранный шар
должен быть красным, то могут быть выбраны 1, 2 или 3 таких шара, поэтому
многочлен, представляющий красные шары, имеет вид
х + х2 + х3.
Поскольку количество выбранных зеленых шаров четное, выбранными могут быть
О, 2, 4, 6 или 8 таких шаров, поэтому многочлен, представляющий зеленые шары,
имеет вид
1 + х2 4-х4 4-х6 4-х8.
Количество выбранных оранжевых шаров должно быть нечетным, поэтому вы-
выбранными могут быть 1, 3, 5, 7 или 9 таких шаров, так что многочлен, представ-
представляющий оранжевые шары, имеет вид
х + х3 4-х5 4-х7 + х9.
Следовательно, производящей функцией для рассматриваемой задачи будет
(х 4- х2 4- х3)A 4- х2 4- х4 4- х6 + х8)(х 4- х3 4- х5 + х7 4- х9)A 4- х 4- х2),
а ответ на вопрос даст коэффициент при х12. ?

538 ГЛАВА 13. Производящие функции
Для нахождения коэффициентов некоторых полиномиальных производящих
функций введем в рассмотрение производящие функции из предыдущего раздела.
ПРИМЕР 13.10. Найдем коэффициент при х24 в разложении производящей функ-
функции (х3 + х4 + х5 + х6 + • • • L.
()\+ + ++ + )
= (х12) ( ] = по теореме 13.2
\l-xj
по теореме 13.2.
Следовательно, чтобы найти коэффициент при хт в разложении этой производя-
производящей функции, необходимо найти коэффициент при хг~12 в разложении произво-
производящей функции
1 + 4x4-
п
так что коэффициент при хг равен
'4 + г - 12 - 1\ _ / г - 9
г-12 )~\т-12)'
а коэффициент при х24 равен
24-
24-127 V12/' °
ПРИМЕР 13.11. Выясним, сколько существует способов выбора 12 объектов из
совокупности объектов пяти типов, если необходимо выбрать не более 2 объектов
первых трех типов и неограниченное количество объектов остальных двух типов.
Производящая функция имеет вид
Но по теореме 13.3
Поэтому

РАЗДЕЛ 13.3. Производящие функции и комбинаторные подсчеты 539
Поскольку
A - х3K = 1 - Зх3 4- Зх6 - х9
+ п-1
то, согласно правилу умножения полиномов, коэффициент при х12 в произведении
n
равен
ПРИМЕР 13.12. Сколько существует способов выбора 20 объектов из множества
объектов пяти типов, если количество выбранных объектов первого типа кратно
5, количество выбранных объектов второго типа кратно 3, объектов третьего типа
следует выбрать не более 4, объектов четвертого типа — не менее 3, а объектов
пятого типа — не более 2?
Производящая функция имеет вид
и может быть представлена в виде выражения
L] 1-х5 х3 1 - х3 х3
_ _
1 - х5 ' 1 - х3 ' 1-х " 1 - х ' 1-х ~ A - хK '
исходя из этого, производящая функция имеет вид
(г - 1\ /19\
Коэффициент при хг равен ( 1, а коэффициент при х20 равен ( 1. ?
\т - 3/ V17/
ПРИМЕР 13.13. Найдем производящую функцию, n-ый коэффициент которой да-
дает количество неотрицательных целочисленных решений уравнения е\ + 4е2 +
без + Зв4 = п, что эквивалентно нахождению количества способов выбора и объ-
объектов, когда объекты второго типа выбираются по 4 за один раз, объекты третьего
типа выбираются по 5, а объекты четвертого типа выбираются по 3 за раз. Сле-
Следовательно, производящая функция имеет вид
),
п
A +
но это
х 4- х2 4- • •
равно
•)A +
х4
4-
х8
н- ••
0A
1
4-
х5
4-
х10
4- ...
)A4-х
¦3 4-
х6
4-

540 ГЛАВА 13. Производящие функции
¦ УПРАЖНЕНИЯ
1. Найдите производящую функцию, в которой коэффициент при хг описывает
количество решений уравнения
а) ei 4- е2 4 е3 4 е4 = г, где 0 < е2 < 2 и 0 < е4 < 4;
б) ei 4- б2 4- ез = г, где 0 < ei < 3 и ез четно;
в) ei 4- е2 4- ез 4- е4 = г, где ei нечетно, е2 четно и е4 > 4;
г) ei 4- е2 4- е3 4 е4 = г, где е; > г для всех г;
д) ei 4 2е2 4- Зе3 4- 4е4 = г.
2. Найдите производящую функцию, r-ый коэффициент которой дает количе-
количество решений уравнения
а) ех 4- е2 4- е3 4- е4 = г, где ei > 2 и 0 < е3 < 3;
б) в\ 4- е2 4 ез = г, где 0 < е» < 3 для всех г;
в) е\ 4- е2 4- ез 4- е4 = г, где в\ нечетно, е2 и е3 четны и е4 > 2;
г) в\ 4- е2 + ез 4- е4 = г, где е* > 3 для всех г;
д) ei + 2е2 4- е3 4- 2е4 = г.
3. Найдите производящую функцию, которую можно использовать для нахо-
нахождения количества способов выбора г элементов из
а) 4 красных, 3 синих, 6 оранжевых и 2 зеленых шаров;
б) 2 красных, 5 зеленых, 4 оранжевых и 3 зеленых шаров, если необходимо
выбрать не менее 1 шара каждого цвета;
в) 6 красных, 12 черных, 7 белых и 10 синих шаров, если необходимо вы-
выбрать не менее 4 черных шаров и четное количество синих шаров;
г) 6 красных, 12 черных, 7 белых и 10 синих шаров, если необходимо вы-
выбрать не менее 1 шара каждого типа, четное количество красных шаров
и нечетное количество белых шаров.
4. Найдите производящую функцию для нахождения количества способов вы-
выбора г элементов из
а) 6 красных, 5 синих, 4 оранжевых и 3 зеленых шаров;
б) 7 красных, 5 зеленых, 8 оранжевых и 4 белых шаров, если необходимо
выбрать нечетное количество зеленых и красных шаров и четное количе-
количество оранжевых и белых шаров;
в) 5 красных, 4 фиолетовых, 6 белых и 8 черных шаров, если необходимо
выбрать не менее 2 черных шаров, 1 оранжевого, 3 красных и четное
количество синих шаров;
г) 9 красных, 7 черных, 6 белых и 11 синих шаров, если необходимо выбрать
не менее 2 шаров каждого типа, нечетное количество красных шаров и
нечетное количество белых шаров.
5. Найдите производящую функцию для определения количества способов со-
составить к центов, используя монеты стоимостью 1, 5, 10 и 25 центов.
6. В маленьком городке 50 зарегистрированных избирателей, каждый из них
либо голосует дважды, либо остается дома, за исключением мэра города,
который голосует либо три раза, либо пять. Используя производящую функ-
функцию, определите, сколько существует способов собрать и голосов.

РАЗДЕЛ 13.3. Производящие функции и комбинаторные подсчеты 541
7. Для всех п > 8, почтовое отправление стоимостью п центов оплачивается
марками стоимостью 5 и 3 цента. Используйте производящую функцию для
описания количества способов оплаты почтового отправления стоимостью к
центов, используя исключительно марки по цене 5 и 3 центов.
8. Найдите производящую функцию, которая используется для нахождения ко-
количества способов разложения к различных типов шоколадок в 6 коробок,
если в первую коробку помещать четное количество шоколадок, во вторую —
нечетное количество, не менее 3 шоколадок помещать в третью коробку, не
более 3 — в четвертую коробку и любое их количество — в оставшиеся две
коробки.
9. Подбрасывание к игральных кубиков дает в сумме п. Используйте произво-
производящую функцию для определения количества способов подбрасывания.
10. Найдите коэффициент при х7 в разложении производящей функции
И. Найдите коэффициент при х10 в разложении производящей функции
12. Найдите коэффициент при х17 в разложении производящей функции
"*' ~ 1 - х5 ¦
13. Найдите коэффициент при х19 в разложении производящей функции
J к"' ~ 1 - х5 •
14. Найдите коэффициент при х20 в разложении производящей функции
15. Найдите коэффициент при х12 в разложении производящей функции
16. Найдите коэффициент при х10 в разложении производящей функции
f{x) = (х2 + х3 + х4 4- х5)(х + х5 + х10).
17. Найдите коэффициент при х12 в разложении производящей функции
/(Х) 1-2х + х2 •
18. Найдите коэффициент при х12 в разложении производящей функции
г3 -
х
(x\ -

542 ГЛАВА 13. Производящие функции
19. Найдите коэффициент при х12 в разложении /(х) = A — Зх)~4.
20. Найдите коэффициент при х12 в разложении производящей функции
21. Используйте производящую функцию для нахождения количества способов
выбора 10 шаров из 20 красных, 20 белых и 20 синих шаров, если
а) следует выбрать не менее одного шара каждого цвета;
б) следует выбрать четное количество красных шаров и четное количество
синих шаров.
22. Используя производящую функцию, определите, сколько существует спосо-
способов распределения 15 игрушек между 5 детьми, если ни один ребенок не
может получить более 4 игрушек?
23. Используя производящую функцию, определите, сколькими способами мож-
можно разложить в коробки шестнадцать конфет, если имеется 4 вида конфет и
нужно выбирать не более 4 конфет каждого из первых трех видов.
24. Используя производящую функцию, определите, сколько имеется способов
раскладывания 16 одинаковых предметов в 5 различных ящиков, если каж-
каждый ящик может содержать не менее 2 и не более 6 предметов?
25. Пусть F(x) — производящая функция, коэффициенты которой являются чис-
числами Фибоначчи. Используя рекуррентное отношение для F(x), покажите,
что х
F{X) = A-(х + х2)) '
Используя это выражение, постройте разложение производящей функции
F(x). Покажите, что коэффициент при xn+1 равен
и - 1\ (п- 2
поэтому
13.4. РАЗБИЕНИЯ
В этом разделе при помощи производящих функций описывается число распре-
распределений множества, содержащего п неразличимых объектов, по заданному числу
неразличимых ящиков. Это эквивалентно описанию количества способов разбие-
разбиения положительного целого числа п на группы, содержащие заданное количество
положительных целых чисел, сумма которых равна п; при этом группы, которые
отличаются только порядком элементов, являются неразличимыми.
Если противное не оговорено, то под числом в этом разделе мы будем
подразумевать положительное целое число.

РАЗДЕЛ 13.4. Разбиения 543
Например, число 3 можно выразить как сумму 1 + 1 + 1 и как 14-2. Число 4
можно выразить как 1 + 14-1 + 1, 1 + 1+2, 1+3, 2+2 и 4. Способы выражения числа
4 в виде суммы двух чисел сводятся к1 + Зи2 + 2. Таких способов два, поэтому
существует два способа разложить 4 неразличимых объекта по двум неразличи-
неразличимым ящикам так, чтобы ни один ящик не был пустым. Способы выражения числа
4 в виде суммы двух или менее чисел таковы: 1 + 3, 2 + 2 и 4. Таких способов
три, поэтому существует три способа разложить 4 неразличимых объекта по 2
неразличимым ящикам, так что некоторые из этих ящиков могут быть пустыми.
Сначала рассмотрим количество способов, благодаря которым п неразличи-
неразличимых объектов раскладывается по п ящикам при условии, что некоторые ящики
могут быть пустыми. Это то же самое, что искать число способов разбиения
числа и на группы из п или менее чисел, сумма которых равна п. Последнее
представляет собой число неотрицательных целочисленных решений уравнения
е\ + 2е2 + Зе3 4 Ь пеп = п.
Если п фиксировано, то количество решений находится как коэффициент
при хп в разложении производящей функции
1
A - х){1 - х2)A - х3) • • • A - хп) '
Последний пример предыдущего раздела показывает, что количество реше-
решений эквивалентно нахождению количества способов выбора п объектов при усло-
условии, что объекты первого типа выбираются по одному, объекты второго типа —
по два, объекты третьего типа — по три и т.д. Именно это то мы и делаем, по-
поскольку каждая выбранная единица вносит в сумму показателей степеней 1, и
эти единицы суммируются вплоть до п в хп\ каждая выбранная двойка вносит в
сумму степеней 2, и эти двойки суммируются вплоть до п и т.д. По мере увеличе-
увеличения п требуется все больше членов в произведении. Поскольку мы хотим, чтобы
наша производящая функция описывала число решений для всех п, то искомая
производящая функция имеет вид
A - х){1 - х2)A - х3) • • • A - хк) • • • '
в результате приходим к следующей теореме.
ТЕОРЕМА 13.14. Производящая функция, n-ый коэффициент которой равен ко-
количеству способов, которыми можно разложить п неразличимых объектов по п
ящикам при условии, что некоторые ящики могут быть пустыми, или, что эквива-
эквивалентно, равен количеству разбиений числа п на группы, содержащие п или менее
чисел, сумма которых равна п, имеет вид
1
A - х)A - х2)A - х3) • • • A - хк) • • • '
ПРИМЕР 13.15. Покажем, что любое число можно выразить следующим образом
2° + 21 + 22 + 23 + • • • + 2*.

544 ГЛАВА 13. Производящие функции
Из данного выражения следует, что любое число можно записать в двоичной
системе счисления, что является весьма важным моментом при использовании
целых чисел в компьютерных приложениях,
(а) Убедимся сначала, что для всех п
Используем метод индукции по п. Вполне очевидно, что утверждение спра-
справедливо при п = 0. Предположим, что оно выполняется для п = к, так что
но
Отсюда
поэтому утверждение справедливо для п = к + 1 и для всех п.
(б) Покажем далее, что A — х)A + х)A + х2) • • • A — х2") •.. = 1. Согласно
части (а) для любого к > 1 в левой части равенства коэффициент при хк равен
0. Поэтому производящая функция 1 4- Ох + Ох2 Н = 1.
(в) Согласно части (б) получаем, что
A + х)A + х2) • • • A + х2") • • • = —— = 1 + х + х2 + х3 + • • • .
1-х
(г) Левая часть равенства в части (в) есть производящая функция после-
последовательности, состоящей из степеней числа 2, где каждая степень появляется
только раз. Правая часть равенства представляет собой производящую функцию
множества всех положительных целых чисел. Следовательно, любое число есть
сумма степеней числа 2. ?
ПРИМЕР 13.16. Рассмотрим количество способов разбиения числа п на группы,
содержащие п или менее различных чисел. Таким образом, каждое число может
войти в заданную сумму только один раз. Например, число 4 можно представить
либо как 4, либо как 1 -f 3. В каждом представлении числа п в виде суммы
различных чисел любое число, меньшее или равное п, может входить в сумму
или не входить. Поэтому производящая функция имеет вид
(l + x)(l + x2)(l + x3)...(l + xfc)... . ?
ПРИМЕР 13.17. Количество способов разбиения числа п на группы, содержащие
п или менее различных чисел, равно количеству способов разбиения числа п на
группы, содержащие п или менее нечетных чисел, сумма которых равна п.

РАЗДЕЛ 13.4. Разбиения 545
Сначала найдем производящую функцию, при помощи которой сможем опре-
определить количество способов разбиения числа п на группы, содержащие п или ме-
менее нечетных чисел, сумма которых равна п. Исходя из теоремы 13.14, находим,
что производящая функция имеет вид
1
Из предыдущего примера следует, что производящая функция, используемая для
нахождения количества способов разбиения числа и на группы, содержащие п
или менее различных чисел, имеет вид
A + х)A + х2)A 4- х3) • • • A + хк) • • • .
Но
так что
1-х2 1-х4 1-х6 1-х8 1-х
10
1-х 1 - х2 1 - х3 1 - х4 1-х5
Но fc-ый член в числителе сокращается с 2/с-ым членом в знаменателе, а в зна-
знаменателе остается только Bfc + 1)-ый член. Поэтому имеем
что является производящей функцией, используемой для определения количества
способов разбиения числа п на группы, содержащие п или менее нечетных чисел,
сумма которых равна п. ?
Следующая цель — описать количество способов разложения и неразличи-
неразличимых предметов по к неразличимым ящикам. Для этого понадобится простой, но
удобный метод, состоящий в использовании так называемых диаграмм Ферре.
Будем использовать одну из модифицикаций этого метода, где простоте отдается
предпочтение над строгим алгебраическим описанием. В данной версии начнем с
описания распределения предметов по ящикам, используя строки возрастающей
длины. Например, распределение 12 предметов по 4 ящикам можно изобразить
так, как показано на рис. 13.1.
Рис. 13.1

546 ГЛАВА 13. Производящие функции
Если судить по строкам, то видно, что в первый ящик помещен 1 пред-
предмет, во второй — 3 предмета, в третий ящик — 4 предмета и в четвертый — 4
предмета. Если же судить по столбцам, то в первом ящике находится 4 пред-
предмета, во втором — 3 предмета, в третьем — 3 предмета и в четвертом — два
предмета. В столбцах ящики расположены в порядке убывания их размера. Но
это несущественно, т.к. ящики неразличимы. В частности, легко заметить, что
каждому распределению по строкам соответствует некоторое распределение по
столбцам, и наоборот. Следовательно, существует взаимно однозначное соответ-
соответствие между распределениями по строкам, содержащим ящики возрастающего
размера, и распределениями по столбцам, содержащим ящики уменьшающегося
размера. Рассмотрим произвольное распределение 12 предметов по 4-м ящикам.
Допустим, что в первом ящике — 1 предмет, во втором — 2 предмета, 4 пред-
предмета — в третьем ящике и 6 предметов — в четвертом ящике. Соответствующая
диаграмма Ферре приведена на рис. 13.2.
Рис. 13.2
Если теперь посмотреть на распределение предметов по столбцам, то можно
увидеть, что в первом ящике находятся 4 предмета, во втором ящике — 3 предме-
предмета, в третьем и четвертом ящиках — по 2 предмета и по 1 предмету — в пятом и
шестом ящиках. Однако, поскольку в распределении по строкам с самого начала
использовались 4 ящика, то в распределении по столбцам нельзя поместить в
каждый ящик более 4 предметов. И наоборот, если в распределении по столб-
столбцам класть в каждый ящик не более 4-х предметов, то при переходе к строкам
понадобятся не более четырех ящиков. Более того, в распределении по строкам
4 непустых ящика будут только тогда, когда в распределении по столбцам бу-
будет один ящик, содержащий в точности 4 предмета. Таким образом, существует
взаимно однозначное соответствие между распределениями 12 предметов по 4
ящикам, где некоторые пусты, и такими распределениями 12 предметов, когда в
каждом ящике находятся не более 4 предметов. Кроме того, существует взаимно
однозначное соответствие между распределениями 12 предметов по 4 ящикам,
при которых в каждый ящик попадает хотя бы один предмет, и такими распреде-
распределениями 12 предметов, при которых хотя бы 1 ящик содержит 4 предмета. Такие
же рассуждения с п предметами и к ящиками приводят к следующей теореме.
ТЕОРЕМА 13.18. Количество способов размещения п предметов в к ящиках при
условии, что некоторые ящики могут быть пустыми, равно количеству размеще-
размещений п предметов по ящикам при условии, что в каждом ящике будет находится не
более к предметов. Кроме того, количество способов размещения п предметов в к
ящиках, где ни один ящик не может быть пустым, равно количеству размещений
и предметов по ящикам при условии, что в каждом ящике может находиться не
более к предметов и хотя бы один ящик содержит к предметов.

РАЗДЕЛ 13.4. Разбиения 547
Сформулируем эквивалентную теорему в терминах разбиений числа п.
ТЕОРЕМА 13.19. Количество способов разбиения числа п на группы, содержащие
к или менее чисел, равно количеству способов разбиения числа и на группы, со-
содержащие п или менее чисел, при которых ни одно число из группы не превышает
к. Кроме того, количество способов разбиения числа п на группы, содержащие
ровно к чисел, равно количеству способов разбиения числа п на группы, содер-
содержащие п или менее неотрицательных целых чисел, когда наибольшее число в
каждой группе равно к.
Поскольку количество способов разбиения числа п на группы, содержащие
п или менее чисел при условии, что никакое число в группе не превышает /с,
равно количеству неотрицательных целочисленных решений уравнения
ei 4- 2е2 + Зез Н h кеь — п,
то производящая функция имеет вид
1111
1-х 1-х2 1-х3 1 - хк '
ТЕОРЕМА 13.20. Производящая функция, описывающая количество способов
разбиения числа п на группы из к или менее неотрицательных целых чисел,
имееет вид
A + х + х2 + • • • )A + х2 + х4 + • • • )A + х3 + х6 + • • •) • • • A + хк + х2к + • • •)
или
1-х 1-х2 1-х3 1 — хк
Теперь сформулируем эквивалентную теорему в терминах распределения
неразличимых объектов.
ТЕОРЕМА 13.21. Производящая функция, описывающая количество способов
размещения п неразличимых объектов по к ящикам при условии, что некоторые
из ящиков пустые, имеет вид
111
1-х 1-х2 1-х3 1 — хк '
Теперь рассмотрим случай с количеством способов разбиения числа п на
группы из к чисел, сумма которых равна п. По теореме 13.19 это есть количе-
количество способов разбиения числа п на группы из п или менее неотрицательных
целых чисел, когда наибольшее число в каждой группе равно к. В этом случае
производящая функция имеет вид

548
что
хк
или
ГЛАВА
равно
A+S +
13.
х2
Производящие функции
+ •••)(! + х2 + х4+ ¦¦¦)(!
хк
+ х3 + х6 4- • • •) • • • A + х + х2к 4- • • •)
Этот результат можно получить иначе, воспользовавшись производящей функ
цией, описывающей количество способов разбиения числа п на группы из к или
менее чисел, сумма которых равна п, и вычесть из нее производящую функцию,
описывающую количество способов разбиения числа п на группы из к — 1 или
менее чисел, сумма которых равна п. В результате получим производящую функ-
функцию, где число и разбито на группы, содержащие ровно А: чисел, сумма которых
равна п. Исходя из вышеизложенного, имеем
= -A + х + х2 + • • • )A 4- х2 4- х4 + • • •) • • •
...A+^-1+^-1)+...) =
= A + х + х2 + • • • )A + х2 + х4 4- • • •) • • •
... A + хк~1 4- я2**) 4- • • • )(A 4- хк 4- х2к + • • •) - 1) =
= A + х 4- х2 4- • • • )A + х2 + х4 4- • • •) • • •
... A + х*-1 + х2**-1* + • • • )((хк + х2к 4- • • •).
Таким образом, мы получили следующую теорему.
ТЕОРЕМА 13.22. Производящая функция, описывающая количество способов
разбиения числа п на группы, содержащие ровно к неотрицательных целых чисел,
сумма которых равна п, имеет вид
хкA 4- х + х2 + • • • )A + х2 4- х4 4- • • • )A 4- х3 4- х6 4- • • •) • • • A 4- х 4- х2к + • • •)
или
хк
Следующая теорема содержит равносильное утверждение.
ТЕОРЕМА 13.23. Производящая функция, описывающая количество способов
размещения п неразличимых предметов в к ящиках таким образом, что ника-
никакой из ящиков не будет пустым, равна
xfc(l 4- х + х2 Н )A + х2 4- х4 Н )A + х3 4- х6 Н ) • • • A 4- хк + x2fc H )
или
х^_
A - х)A - я2)A - х3) • • • A - хк) ¦

РАЗДЕЛ 13.5. Экспоненциальные производящие функции 549
I УПРАЖНЕНИЯ
1. Найдите количество разбиений числа 7.
2. Найдите количество разбиений числа 5.
3. Найдите производящую функцию, описывающую количество способов раз-
размещения 10 неразличимых объектов в 6 неразличимых ящиках.
4. Найдите производящую функцию, описывающую количество способов раз-
разбиения числа и на различные нечетные числа.
5. Найдите производящую функцию, описывающую количество способов раз-
разбиения числа п на различные четные числа.
6. Предположим, что атлет участвует в соревнованиях по 3 видам спорта. В
каждом из состязаний он может выиграть 1, 2, 3, 4 или 5 очков. Найди-
Найдите производящую функцию, показывающую, сколько существует различных
способов набрать п очков.
7. При помощи диаграммы Ферре покажите, что количество разбиений числа
на четные части равно количеству разбиений этого числа на части так, что
каждая часть присутствует четное количество раз.
8. При помощи диаграммы Ферре покажите, что количество разбиений числа
п на 3 части равно количеству разбиений числа 2п на 3 части меньшего раз-
размера, чем п. Что можно сказать о количестве разбиений числа п на 4 части
и числа Зп на 4 части меньшего размера, чем п? Можно ли это утверждение
обобщить?
9. При помощи диаграммы Ферре покажите, что число разбиений числа п равно
количеству разбиений числа 2п на п частей.
10. При помощи диаграммы Ферре покажите, что число разбиений числа 2n + k
нап + fc частей одинаково для всех к.
11. Пусть несчастные случаи классифицированы в соответствии с днем неде-
недели, в который они произошли. Найдите производящую функцию, описываю-
описывающую количество различных способов, которыми можно классифицировать п
несчастных случаев.
13.5. ЭКСПОНЕНЦИАЛЬНЫЕ ПРОИЗВОДЯЩИЕ ФУНКЦИИ
В данном разделе будут использованы производящие функции вида
Для начала положим
х х2 х3 хп
х х2 х3 х4 х5 х6
+ + + + +
е = е(х) = 1 + - + -+зГ + - + - + - + ....
Единственное свойство этой функции, которое нам понадобится, сформулировано
в следующей теореме. Ее доказательство мы предоставляем читателю.
ТЕОРЕМА 13.24. Для любого неотрицательного числа п справедливо (ех)п = епх.

550 ГЛАВА 13. Производящие функции
Известно, что
и
поэтому при использовании обычных производящих функций A + х)п является
производящей функцией для числа сочетаний. Однако,
П\ п\ п\ 2 п\ к п\ п _
0!(п)! + 1!(п - \)\Х + 2!(п - 2)\Х + + к\(п-к)\Х + + 0!(п)!
п\ п\ х п\ х2 п\ хк п\
Ы + (п - 1)! ' 1! + (п - 2)! " 2f + ' " + (п - fc)! "к\ + ' " + 0!
так что A + х)п является экспоненциальной производящей функцией, описываю-
описывающей количество перестановок.
Итак, коэффициенты экспоненциальной производящей функции не равны
количеству сочетаний, как в случае обычной производящей функции, а равны
количеству перестановок. Теперь переходим к подсчетам объектов с учетом их
порядка.
Предположим, что имеется неограниченное количество красных, зеленых,
белых и синих предметов. Известно, что производящая функция, описывающая
количество способов выбора п предметов при условии, что необходимо выбрать
хотя бы 2 зеленых и 3 синих предмета, имеет вид
A + х + х2 Н )(х2 + хг + х4 Н )A + х 4- х2 + • • • )(х3 + х4 + хъ + • • •).
Например, если выбираются 12 предметов, то х2х3х4х3 описывает выбор 2 крас-
красных, 3 зеленых, 4 белых и 3 синих предметов. Предположим, однако, что вы-
выбираются не красные, зеленые, белые и синие предметы, а буквы /с, з, б и с, и
спрашивается, сколько слов можно из них составить. Нам нужно получить не
один из возможных результатов — 2/с, Зз, 46 и Зс, а число
12!
2!3!4!2! '
выражающее количество способов перегруппировки 2/с, Зз, 46 и Зс. Заметим,
что, если вместо использования приведенного выше произведения производящих
функций использовать
то вместо х2х3хлх3, как одного из сомножителей, дающих х12, можно получить
х2 х3 х4 х3 _ х12 _ 12! х^_
2! 3! 4! 3! ~ 2!3!4!2! ~ 2!3!4!2! ' 12! "

РАЗДЕЛ 13.5. Экспоненциальные производящие функции 551
Коэффициент при ^т Равен 2!3!4!!2! * Таким образом, если требуется количество
способов, которыми можно переупорядочить предметы, а не выбрать их, то вме-
вместо обычных производящих функций необходимо использовать экспоненциальные
производящие функции.
При использовании обычных производящих функций коэффициент при хп
даст общее количество способов, которыми можно выбрать п предметов. Если ис-
использовать экспоненциальную производящую функцию, то коэффициент при ^
даст количество способов, которыми п предметов можно выбрать и переупорядо-
переупорядочить. Напомним, что в разделе 8.6 приводилось равенство
Р( ) С( )
(\и2Г ,к) , ,. , (]и2Г ,Пь),
определяющее количество перестановок и предметов при условии, что имеется г*
предметов типа г, при этом
П 4- r2 Ч + rk = п,
и количество разбиений множества, содержащего и неразличимых предметов, по
к неразличимым ящикам, когда п предметов попадает в г-ый ящик, и
П 4- г2 Ч h г к = п.
Следовательно, экспоненциальную производящую функцию можно использовать
для решения задач обоих типов.
ПРИМЕР 13.25. Сколько последовательностей длины и можно сформировать из
целых чисел 1,2,3 и 4, если должно быть не менее одной цифры 1, двух цифр 2,
нечетное количество цифр 3 и четное количество цифр 4?
Если бы мы просто выбирали объекты, производящая функция имела бы вид
(х Ч- х2 Ч- х3 • • • )(х2 + х3 Ч- х4 + • • • )(х 4- х3 Ч- х5 • • • )(х2 Ч- х4 Ч- х6 Ч- • • •).
Учитывая, что требуется количество последовательностей, порядок элементов име-
имеет значение, поэтому соответствующая экспоненциальная функция имеет вид
х х2 \ (х2 х3 х4 \(х х3 х5
п
ПРИМЕР 13.26. Найдем производящую функцию, описывающую количество спо-
способов размещения п человек в трех комнатах при условии, что в каждой комнате
должно быть не менее двух и не более десяти человек. Используя основное свой-
свойство обычных экспоненциальных функций, определяем, что искомая экспоненци-
экспоненциальная производящая функция имеет вид
2 х3 х10\ /х2 х3 х10\ (х2 х3 х10

552 ГЛАВА 13. Производящие функции
или
/ г2 ^3 т10\3
?
ПРИМЕР 13.27. Из объектов п типов требуется найти количество различных пе-
перестановок к объектов при условии, что имеется неограниченное количество объ-
объектов каждого типа. Из вышеизложенного исследования перестановок с неогра-
неограниченным числом повторений известно, что ответом является число пк (см. раз-
раздел 8.7). Попытаемся применить экспоненциальную производящую функцию. В
данном случае экспоненциальная производящая функция имеет вид
/ х х2 х3
— %JL/ JU JU JU JU %JU
так что
xr
так что коэффициент при —, как и ожидалось, равен пк. П
АС.
Доказательство следующей теоремы предоставляем читателю.
ТЕОРЕМА 13.28.
ч X X2 X3
а)б -1=1! + 2! + 3!+---;
, х2 х4 х6
1
2!? ?
х х3 х5 х7
б)
в) 2 1! ' 3! ' 5! ' 7! '
ПРИМЕР 13.29. Найдем экспоненциальную функцию для описания количества
способов размещения п гостей в трех комнатах при условии, что в первой комна-
комнате находится хотя бы один гость, нечетное количество гостей находится во второй
комнате и четное количество — в третьей комнате. Производящая функция зада-
задается выражением
х х2 х3 \ (х х3 хъ \ (х2 х4 х6
2х _ -2х
е 6
х 1
поэтому коэффициент при — равен т(C)п ~ (-!)n ~ B)п + (-2)п) •
п\

РАЗДЕЛ 13.5. Экспоненциальные производящие функции 553
Теперь имеются средства для нахождения количества способов размещения
п различимых объектов в к различимых ящиках при условии, что ни один из ящи-
ящиков не будет пустым, и количество способов размещения п различимых объектов
в fc неразличимых ящиках, когда ни один из ящиков не будет пустым.
ТЕОРЕМА 13.30. Количество способов размещения п различимых объектов в fc
различимых ящиках при условии, что ни один из ящиков не будет пустым и
1 < fc < п, равно
г=1
ДОКАЗАТЕЛЬСТВО. Экспоненциальная производящая функция, описывающая ко-
количество размещений п различимых объектов в fc различимых ящиках при усло-
условии, что ни один из ящиков не будет пустым, имеет вид
х х2 х3
Но
2 3
1
по теореме 13.28
по формуле бинома Ньютона.
По определению,
так что
2!
3!
4- -
п!
и коэффициент при — равен
гг!
X7
—
гг!
Теперь мы готовы доказать следующую теорему.
ТЕОРЕМА 13.31. Количество способов размещения п различимых объектов в к
неразличимых ящиках при условии, что ни один из ящиков не будет пустым и
1 < fc < п, равно
п :
где {5д.п : 0 < fc < п} — множество чисел Стирлинга второго рода.

554 ГЛАВА 13. Производящие функции
ДОКАЗАТЕЛЬСТВО. Поскольку TJ^ равно количеству способов размещения п
неразличимых объектов в к различимых ящиков, то при переходе от множества с
различимыми объектами ко множеству с неразличимыми объектами приходится
делить на /с!, т.к. все к\ перестановок к ящиков тождественны. Следовательно,
с(п) т>(п)
Sk =fc!Tfc =l
УПРАЖНЕНИЯ
1. Найдите разложение соответствующей производящей функции, чтобы опре-
определить, сколько кодов из десяти цифр в каждом можно образовать из цифр
О, 1 и 2, если
а) цифра 0 должна встречаться в коде хотя бы дважды;
б) цифра 1 может встречаться не более трех раз, а цифра 2 — не более
четырех раз;
в) цифра 1 может встречаться четное, а цифра 0 — нечетное число раз.
2. Двенадцать воздушных шаров должны быть привязаны к 12 фонарным стол-
столбам по маршруту парада. Найдите разложение соответствующей производя-
производящей функции для определения количества способов развешивания красных,
синих, желтых и зеленых шаров при условии, что
а) использован хотя бы один шар каждого цвета;
б) использовано не более 4 красных, 3 желтых, 7 зеленых и 6 синих шаров;
в) использовано не более 2 красных шаров, не более 3 зеленых шаров, от 1
до 5 зеленых шаров и четное количество синих шаров.
3. Найдите производящую функцию последовательности факториалов 0!,1!,2!,
3!....
4. Найдите производящую функцию, описывающую количество способов рас-
раскрашивания 8 х 8-клеточной шахматной доски, используя красный, белый и
синий цвета, при условии, что четное количество клеток — красные.
5. Используя производящую функцию, определите количество чисел, состоя-
состоящих из п цифр, все цифры в которых нечетные, а цифры 1 и 3 присутствуют
в них не менее одного раза.
6. Воспользуйтесь производящей функцией для нахождения количества чисел,
состоящих из п цифр, все цифры которых нечетные, при условии, что все
цифры присутствуют хотя бы один раз, а цифра 5 появляется четное число
раз.
7. Воспользуйтесь производящей функцией для нахождения количества спосо-
способов размещения 30 человек в 3 комнатах гостиницы, если в каждой комнате
находится хотя бы по одному человеку.
8. Воспользуйтесь производящей функцией для нахождения количества спосо-
способов размещения 30 человек в 3 комнатах гостиницы, если в каждой комнате
находится четное количество людей.

РАЗДЕЛ 13.5. Экспоненциальные производящие функции 555
9. Используйте производящую функцию для определения количества способов
размещения 25 объектов четырех типов по порядку, если количество объек-
объектов первого типа — четное, количество объектов второго типа — нечетное,
и хотя бы по одному объекту третьего и четвертого типа.
10. Используя производящую функцию, определите, сколько существует спосо-
способов распределения 9 кусков торта между 4 детьми при условии, что каждый
ребенок из первых двух получает кусок торта.
11. Найдите производящую функцию для вычисления количества упорядочений
монет стоимостью 1 цент, 5 центов, 10 центов и 25 центов, которые в сумме
дадут и центов.
12. Покажите, что л^п — экспоненциальная производящая функция, описы-
описывающая количество способов выбора некоторого, возможно пустого, подмно-
подмножества из к объектов. Распределите их по п ящикам, учитывая порядок в
подмножестве.
13. Найдите экспоненциальную производящую функцию, описывающую коли-
количество способов разбиения числа и на к частей, учитывая порядок.
14. Используя метод индукции, докажите теорему 13.24. епх = (ех)п для любого
неотрицательного целого числа п.
15. Докажите теорему 13.28.
9 Ч
ОС ОС ОС
а)еХ-1=1!+2Г+зГ + ---;
^ ех+е~х х2 х4 х6
б) 1+ + + +
ех — е х х х3 х5 х7

ГЛАВА
НЕКОТОРЫЕ
СПЕЦИАЛЬНЫЕ ВОПРОСЫ
ТЕОРИИ ГРАФОВ
14.1. АЛГЕБРАИЧЕСКИЕ СВОЙСТВА ГРАФОВ
В этом разделе рассматриваются отношения между графами. Если два графа на-
находятся в данном отношении, то свойства, которыми обладает один граф, присущи
и другому графу. Материал раздела представлен так, что большая часть понятий
может быть обобщена на случай мультиграфов и псевдографов.
ОПРЕДЕЛЕНИЕ 14.1. Функция / из графа G(V,E) в граф G'{V',E') называ-
называется гомоморфизмом из G в С и обозначается / : G —> G', если обладает
следующими свойствами.
а) Если е G Е, то /(е) е Е'. (/(?) С Е').
б) Если v € V, то f(v) e V. (/(V) С V).
в) Если вершины и и v инцидентны ребру е графа G, то вершины f(u) и
f(v) инцидентны ребру /(е) графа G'.
Доказательство приведенных ниже теорем предоставляется читателю.
ТЕОРЕМА 14.2. Если функция / — гомоморфизм из G в С, то f(G) — подграф
ТЕОРЕМА 14.3. Если граф G связный и / — гомоморфизм, то граф f(G) связный.
ТЕОРЕМА 14.4. Если граф G полный и / — гомоморфизм, то f(G) полный.
Из примеров увидим, что многие свойства графа G не являются инвариант-
инвариантными относительно /.
ОПРЕДЕЛЕНИЕ 14.5. Гомоморфизм f : G —> G' является изоморфизмом, если
f : V —> V w f \ Е -+ Ег представляют собой взаимно однозначные соответ-
соответствия. Если / : G —> G' — изоморфизм, то G и G1 называются изоморфными.

РАЗДЕЛ 14.1. Алгебраические свойства графов 557
Таким образом, изоморфизм, по сути, является переименованием вершин и
ребер графа V, которое сохраняет свойство гомоморфности, так что если вершины
и и v инцидентны ребру е графа G, то вершины f(u) и f(v) инцидентны ребру
/(е) графа G'. Инварианты изоморфизмов приведены в задачах.
Вполне очевидно, что практически все свойства графов инвариантны отно-
относительно изоморфизма. Отсюда следует, что простейший способ показать неизо-
неизоморфность двух графов — установить свойство, которым обладает один граф и не
обладает другой.
ОПРЕДЕЛЕНИЕ 14.6. Если граф G(V, Е) содержит ребро е = {vi,v2} и граф
G'(V',E') получен из графа G(V,E) добавлением новой вершины v в множе-
множество V и заменой ребра {^i,^} ребрами {vi,v} и {v,v2}, то граф G'(V',E')
называется расширением графа G(V, Е). Если графы d, G2, G3,... Gn таковы,
что G*+i является расширением графа G{, то граф Gn назовем производным
от графа G\.
Если граф G'(V',Er) — расширение графа G(V,E)> то посредине одного из
ребер множества V появляется вершина, а исходное ребро делится на два но-
новых ребра, которые соединяют вершины, инцидентные исходному ребру, и новую
вершину.
ОПРЕДЕЛЕНИЕ 14.7. Графы G и G' называются гомеоморфными, если су-
существует граф G" такой, что оба графа, G и G', являются производными от
графа G".
ПРИМЕР 14.8. Граф, изображенный на рис. 14.1, является расширением графа,
изображенного на рис. 14.2.
?
ПРИМЕР 14.9. Граф, изображенный на рис. 14.3, является производным от графа,
изображенного на рис. 14.4.

558 ГЛАВА 14. Некоторые специальные вопросы теории графов
Рис. 14.3
Рис. 14.4
О
ПРИМЕР 14.10. Граф, изображенный на рис. 14.5, является производным от гра-
графа, изображенного на рис. 14.6.
Рис. 14.5
Рис. 14.6
?
ПРИМЕР 14.11. Граф, изображенный на рис. 14.7, является гомеоморфным графу,
изображенному на рис. 14.8.
Рис. 14.7
Рис. 14.8
?
Приведенные ниже определения введены, главным образом, для рассмотре-
рассмотрения планарных графов в следующем разделе. Они демонстрируют, каким образом
свойства графов остаются инвариантными для отношений между графами.
Если граф G'(V',Ef) — расширение графа G(V,i?), то новая добавленная
вершина имеет степень 2. Степени других вершин не изменились. Отсюда выте-
вытекает следующая теорема.
ТЕОРЕМА 14.12. Если графы G и G' — гомеоморфны, то у них одинаковое
количество вершин нечетной степени.
Из данной теоремы и теорем 6.45 и 6.49 непосредственно вытекает следую-
следующая теорема.
ТЕОРЕМА 14.13. Если графы G и G гомеоморфны, то граф G имеет эйлеров
цикл (собственный путь) тогда и только тогда, когда граф G' имеет эйлеров цикл
(собственный путь).
Если G' — подграф графа G, то это обозначается как G' •< G.

РАЗДЕЛ 14.1. Алгебраические свойства графов 559
ОПРЕДЕЛЕНИЕ 14.14. Пусть G = G(V,E) - граф и GbG2,G3,... ,Gn -
подграфы графа G. Подграф G1 графа G называется объединением графов
п
Gi, G2, G3,..., Gn и обозначается (J G*, если
г=1
1. Вершина v e G1 тогда и только тогда, когда v € Gi для некоторого 1 <
г < п.
2. Ребро е € G1 тогда и только тогда, когда е ? Gi для некоторого 1 < г < п.
ОПРЕДЕЛЕНИЕ 14.15. Пусть G = G(V,E) - граф и Gi,G2,G3,... ,Gn -
подграфы графа G. Подграф G' графа G назывется пересечением графов
п
Gi, G2, G3,..., Gn и обозначается П G*, если
г=1
1. Вершина v ? G' тогда и только тогда, когда v G Gi для всех 1 < г < п.
2. Ребро е eG' тогда и только тогда, когда е ? Gi для всех 1 < г < п.
ОПРЕДЕЛЕНИЕ 14.16. Пусть G = G(V,E) - граф и GbG2,G3,... ,Gn под-
подграфы графа G. Подграфы Gi, G2, G3,..., Gn являются попарно непересекаю-
непересекающимися, если Gi n Gj = 0 для всех 1 < i < j < п.
Доказательство приведенных ниже теорем предоставляется читателю.
ТЕОРЕМА 14.17. Если Gi и G2 — различные компоненты графа G, то G\ и G2 —
попарно непересекающиеся.
ТЕОРЕМА 14.18. Граф G является объединением попарно непересекающихся ком-
компонент.
ОПРЕДЕЛЕНИЕ 14.19. Пусть G(V,E) — граф. Дополнением графа G, обозна-
обозначаемым Gc(Vr, Е')у называется граф такой, что для всех вершин и, v ? V ребро
между и и v в графе Gc существует тогда и только тогда, когда в графе G
отсутствует ребро, соединяющее и и v.
ОПРЕДЕЛЕНИЕ 14.20. Подграф G'(V\Ef) является остовным графом для
графа G = (V, ?), если V = V.
ПРИМЕР 14.21. Для заданного графа, изображенного на рис. 14.9,
a b с
е f Рис. 14.9

560 ГЛАВА 14. Некоторые специальные вопросы теории графов
графы, изображенные на рис. 14.10-14.12, — остовные графы.
d e f
Рис. 14.11
d e f
Рис. 14.12
В то же время графы, изображенные на рис. 14.13-14.15, остовными не яв-
являются.
d e f
Рис. 14.13
?
Определение остовного дерева дано в главе 6 и приводится здесь для удоб-
удобства изложения. В главе 6 было показано также, что каждый связный граф имеет
остовное дерево.
ОПРЕДЕЛЕНИЕ 14.22. Дерево называется остовным деревом графа G, если
оно является остовным графом графа G.
Доказательство приведенных ниже теорем предоставляется читателю.
ТЕОРЕМА 14.23. Если T(V, Е') — остовное дерево графа G = (V,E), то для
любого цикла vo^i^2^3^4, • • -^о, по крайней мере, одно из ребер принадлежит
Е-Е'.
Предположим, что компания создает коммуникационную сеть (рис. 14.16).
Сан-Франциско
Лос-Анджелес
Бостон
Нью-Йорк
Майами
Хьюстон Атланта
рис J4.16
Для компании важно знать, сколько городов окажутся не связанными между
собой, если удалить некоторые линии. В частности, сколько линий требуется
удалить, чтобы города оказались не связанными.

РАЗДЕЛ 14.1. Алгебраические свойства графов 561
ОПРЕДЕЛЕНИЕ 14.24. Множество ребер С связного графа G = (V,E) на-
называется разрезающим множеством, если удаление ребер из множества С
нарушает связность графа, а удаление собственного подмножества множества
С оставляет граф связным. Если множество С состоит из одного ребра, то это
ребро называется разрезающим ребром.
Иной способ описания разрезающего множества — это определение его как
минимального множества ребер, удаление которых нарушает связность графа.
ПРИМЕР 14.25. Для графа, изображенного на рис. 14.17, е5 и е6 - разрезающие
ребра.
* Рис. 14.17
ПРИМЕР 14.26. Для графа, изображенного на рис. 14.18,
,^з}, {^6,^7}} — разрезающие множества.
?
К{^б}} И
7 Рис. 14.18
U
Доказательства приведенных ниже теорем предоставляются читателю.
ТЕОРЕМА 14.27. Если T(V,E') — остовное дерево графа G = (V,E) и С —
разрезающее множество графа G, то СП Е1 ф 0.
ТЕОРЕМА 14.28. Ребро е графа G является разрезающим ребром графа G тогда
и только тогда, когда оно не входит в цикл графа G.
Другая важная задача: сколько городов лишится связи, если коммуникаци-
коммуникационная сеть выйдет из строя в определенном городе (города представлены верши-
вершинами). Вопрос сводится к следующему: "Что произойдет, если удалить вершину
графа"?
ОПРЕДЕЛЕНИЕ 14.29. Вершина а € V связного графа G = (V,E) является
разрезающей вершиной, или точкой сочленения, если удаление этой верши-
вершины и инцидентных ей ребер приводит к нарушению связности графа.

562 ГЛАВА 14. Некоторые специальные вопросы теории графов
ОПРЕДЕЛЕНИЕ 14.30. Граф G(V, E) называется двусвязным, если не содер-
содержит точек сочленения.
ТЕОРЕМА 14.31. Вершина а графа G = (V,E) является точкой сочленения тогда
и только тогда, когда существуют различные вершины v и w такие, что каждый
путь из v в w проходит через а.
ДОКАЗАТЕЛЬСТВО. Сначала докажем достаточность. Предположим, что каж-
каждый путь из вершины v ъ w проходит через вершину а. Тогда, если вершина а
удалена, то не существует более пути из вершины г; в it;, и граф G становится
несвязным. Следовательно, вершина а — точка сочленения.
Для доказательства необходимости в утверждении теоремы используется
метод доказательства от противного. Предположим, что для каждой пары раз-
различных вершин v и w существует путь, который не проходит через а. В этом
случае при удалении вершины а для всех v,w € V всегда остается путь из вер-
вершины v в w, и граф G остается связным. Следовательно, вершина а не является
точкой сочленения. ¦
ПРИМЕР 14.32. В графе, изображенном на рис. 14.19, вершины г>з, г>4 и vq —
разрезающие вершины.
Рис. 14.19
?
ТЕОРЕМА 14.33. Для связного графа G = (V, Е) определим отношение R на Е:
eii?e2, если е\ = е2 или в графе G существует простой цикл, содержащий е\ и е2
в качестве ребер. Тогда отношение R является отношением эквивалентности.
ДОКАЗАТЕЛЬСТВО. Свойства рефлексивности и симметричности очевидны.
Предположим, что eii?e2 и e2J?e3. Если е\ = е2 или е2 = е3, то результат очеви-
очевиден. В противном случае существует цикл, содержащий в качестве ребер е\ и е2, и
цикл, содержащий в качестве ребер е2 и ез. Если оба цикла содержат е\ и ез, до-
доказательство завершено. Если нет, то существуют различные циклы, содержащие
ребро е2 и, возможно, другие ребра вместе с ним. Пусть vqV\V2V$ • • • VmVo — цикл,
содержащий ei, и Voviv2v3 ''' vnvb ~~ Дикл> содержащий ез. Пусть г^+х^+г • • • Vj
и v'kv'k+\v'k+2 "' v'i "" ПУТИ максимальной длины в циклах vqV\V2V$ • • 'Ушу0 и
vbviv2v3 "'vnvo> соответственно такие, что е\ — ребро пути ViVi+iVi+2---Vj, a
ез — ребро пути vkvk+lvk+2 • • -v[, причем Vi = vk и Vj = v[, но пути не имеют
других общих точек. Значит путь ViVi+\Vi+2 ' * * vovi-ivi-2 '"vk является простым
циклом, содержащим ребра е\ и е3. Следовательно, отношение R транзитивно. ¦

РАЗДЕЛ 14.1. Алгебраические свойства графов 563
ОПРЕДЕЛЕНИЕ 14.34. Пусть для каждого класса эквивалентности Ei и от-
отношения эквивалентности R V* — множество вершин, инцидентных ребрам из
множества Ei, и Gi(Vi,Ei) — подграф графа G(V, E) с вершинами Vi и ре-
ребрами Ei. Подграф Gi(Vi,Ei) называется компонентой двусвязности графа
G(V,E).
ТЕОРЕМА 14.35. Если (а, Ь) и (c,d) — различные ребра из компоненты двусвяз-
двусвязности Gi(Vi,Ei), то в подграфе Gi(V^Ei) существует простой цикл, содержащий
в качестве ребер (а, Ь) и (с, d).
ДОКАЗАТЕЛЬСТВО. Если (а, 6) и (с, d) — различные ребра из компоненты дву-
двусвязности Gi(yi,Ei)y то в графе G(V, E) существует простой цикл, содержащий в
качестве ребер (а, Ь) и (с, d). Но если существует ребро (с, d) из этого цикла, не
принадлежащее классу эквивалентности 25», то существуют два ребра из разных
классов эквивалентности, которые входят в один простой цикл, что противоречит
принципу построения классов эквивалентности. ¦
Доказательство приведенных ниже теорем предоставляется читателю.
ТЕОРЕМА 14.36. Если компонента двусвязности diy^Ei) состоит из единствен-
единственного ребра е*, то ei — разрезающее ребро графа G.
ТЕОРЕМА 14.37. Если каждые два различных ребра входят в общий простой
цикл графа G(V,E)y то граф G(V,E) — двусвязный.
ДОКАЗАТЕЛЬСТВО. Предположим, что каждые два различных ребра входят в
один и тот же цикл. Если G(V,E) содержит единственное ребро е*, то результат
очевиден. В противном случае, пусть и и v — вершины графа G и a — вершина
на пути из вершины и в вершину v. Пусть {с, а} и {а, 6} — различные ребра из
этого пути. Тогда {с, а}и {а, 6} —• ребра, входящие в один и тот же простой цикл,
поэтому существует путь из Ь в с, который не проходит через вершину а. Согласно
теореме 14.28 вершина а не может быть точкой сочленения. Следовательно, граф
G(V,E) двусвязный. ¦
СЛЕДСТВИЕ 14.38. Подграф Gi(VuEi) - двусвязный.
ТЕОРЕМА 14.39. Если Gi(Vi,Ei) и Gj(Vj,Ej) — компоненты двусвязности графа
G(V,E)t то Vi П Vj содержит не более одной вершины.
ДОКАЗАТЕЛЬСТВО. Если VJ П Vj содержит две вершины а и 6, то существуют
два ребра {а, с} и {Ь,d}, принадлежащие классу эквивалентности Ei. По опре-
определению Ei, в Gi(Vi,Ei) существует простой цикл, содержащий {а,с} и {6, d}.
Следовательно, в графе Gi(Vi,Ei) существует путь из вершины а в 6. Аналогич-
Аналогично, в графе Gj(Vj,Ej) существует путь из Ь в а. Но поскольку графы Giiy^Ei)
и Gj(Vj,Ej) не имеют общих ребер, то путь из вершины а в 6 в графе Gt(VJ, ??»),
за которым следует путь из вершины b в а в графе Gj(Vj,Ej), является циклом,
который содержит простой цикл. Но тогда в общем простом цикле существуют
ребра из графов Gi(V^Ei) и Gj(Vj,Ej), что противоречит принципу построения
графа Gi(Vi,Ei) и графа Gj(Vj,Ej). Ш

564 ГЛАВА 14. Некоторые специальные вопросы теории графов
ТЕОРЕМА 14.40. Вершина а является точкой сочленения тогда и только тогда,
когда для некоторого i ф j эта вершина принадлежит Vi П Vj для компонент
двусвязности Gi(Vi,Ei) и Gj(Vj,Ej)
ДОКАЗАТЕЛЬСТВО. Если a — точка сочленения, то существуют ребра {а, 6} и
{а, с} такие, что не существует пути из вершины 6 в с, не проходящего через а.
(См. доказательство теоремы 14.37.) Следовательно, ребра {а, 6} и {а, с} не входят
в один и тот же простой цикл и, значит, принадлежат различным компонентам
двусвязности, например, Gi(Vi,Ei) и Gj(Vj,Ej). Поэтому а е ViDVj. Обратно,
если а е ViHVj, то существует ребро {а,6} из класса эквивалентности Е{ и ребро
{а, с} из класса еквивалентности Ej. Но при этом не существует другого пути из
b в с, кроме как через а. Иначе {а, 6} и {а, с} были бы ребрами одного и того же
простого цикла, что противоречит построению множеств Е{ и Ej. Следовательно,
а — точка сочленения. ¦
ТЕОРЕМА 14.41. Граф G(V,E) является двусвязным тогда и только тогда, когда
любые два различных ребра входят в один и тот же простой цикл графа G(V, E).
ДОКАЗАТЕЛЬСТВО. Половина утверждения теоремы является переформулиров-
переформулировкой теоремы 14.37. Предположим, что в графе G(V, E) имеются два различных
ребра, которые не входят в общий простой цикл графа G(V, E). Тогда они при-
принадлежат различным компонентам двусвязности. Следовательно, соединяющий их
путь должен проходить через вершину, которая, согласно предыдущей теореме,
является точкой сочленения, общей для этих компонент двусвязности. Поэтому
граф G(V,E) не является двусвязным. ¦
ТЕОРЕМА 14.42. Если Gi(Vi,Ei) — компонента двусвязности графа G(V, E) и
Gi(Vi,Ei) ¦? G(V,E), то существует, по крайней мере, одна несовпадающая ком-
компонента двусвязности Gj(Vj,Ej) такая, что VJfiVj содержит ровно одну вершину.
ДОКАЗАТЕЛЬСТВО. Согласно теореме 14.39, для любых двух различных ком-
компонент двусвязности Vi и Vj, пересечение множеств V{ П Vj содержит не более
одной вершины. Однако, если а € Vi и 6 ^ Vi, существует путь из вершины а
в 6, и последняя вершина v по ходу пути, принадлежащая Vit является элементом
пересечения множеств V{ и Vj для некоторого j. Ш
¦ УПРАЖНЕНИЯ
1. Для каждой приведенной ниже пары графов найдите гомоморфизм из пер-
первого графа во второй, если он существует.
а)

б)
РАЗДЕЛ 14.1. Алгебраические свойства графов 565
в)
г)
Д)
е)
а* • Ъ
v2 a
*г ь

566 ГЛАВА 14. Некоторые специальные еопросы теории графое
2. Для каждой приведенной ниже пары графов опишите изоморфизм или пока-
покажите, что вследствие нарушения инвариантности графы не изоморфны.
а)
б)
в)
\ i
г)
Д)
L
a b

РАЗДЕЛ 14.1. Алгебраические свойства графов 567
е)
3. Для каждой приведенной ниже пары графов опишите изоморфизм или пока-
покажите, что вследствие нарушения инвариантности графы не изоморфны.
а)
а bed*
в)
 d

568 ГЛАВА 14. Некоторые специальные вопросы теории графов
г)
Д)
е)
4. Для каждой приведенной ниже пары графов опишите изоморфизм или пока-
покажите, что вследствие нарушения инвариантности графы не изоморфны.
а)

б)
РАЗДЕЛ 14.1. Алгебраические свойства графов 569
г)
Д)
а Ь с
d e f
в)
ё d

570 ГЛАВА 14. Некоторые специальные вопросы теории графов
е)
5. Какой из приведенных ниже графов является производным от графа, изоб-
изображенного на рис. 14.20?
а)
в)
г)
6. Какой из приведенных ниже графов является производным от графа, изоб-
изображенного на рис. 14.21?
d e Рас. 14.21

а)
РАЗДЕЛ 14.1. Алгебраические свойства графов 571
б)
в)
г)
7. Какие из приведенных ниже пар графов гомеоморфны?
б)
в)
ащ\—~f^
c/-\d

572 ГЛАВА 14. Некоторые специальные вопросы теории графов
г)
п о
\ "О
Я г
д)
е)
а Ъ
с d e
f
8. Какие из приведенных ниже пар графов гомеоморфны?
а)
а Ъ S h
f
б)

РАЗДЕЛ 14.1. Алгебраические свойства графов 573
в)
Ъ f
г)
Д)
е)
d e
f j
9. Найдите объединение и пересечение приведенных ниже множеств графов.
а)
Ъ с Ъ с
d e

574 ГЛАВА 14. Некоторые специальные вопросы теории графов
б)
д)
d с
Ъ al
в)
а Ь с а Ъ с
d e f d e f
г)
с a
¦* е<
d g
f
е)

РАЗДЕЛ 14.1. Алгебраические свойства графов 575
10. Найдите дополнения приведенных ниже графов.
а)
б)
в)
г)
Д)
е)
11. Найдите дополнения приведенных ниже графов.
а) б)

576 ГЛАВА 14. Некоторые специальные вопросы теории графов
в) г)
Д)
е)
У
V3.
t,
Л
V7 е12
12. Задан граф G, изображенный на рис. 14.22. Какие из приведенных ниже
графов являются его остовными графами?
а)
с d
J
'/ Рис. 14.22
б)
в)
С
г)
13. Задан граф G, изображенный на рис. 14.23. Какие из приведенных ниже
графов являются его остовными графами?

а)
dm
e*
РАЗДЕЛ 14.1. Алгебраические свойства графов 577
Ь
б)
h Рис. 14.23
в)
г)
а ш
c{
, f
14. Покажите, что любой гомоморфизм из графа, изображенного на рис. 14.24,
на граф G является изоморфизмом.
к' У2 Рис. 14.24
15. Покажите, что если G и G — графы, / : G —> G' — гомоморфизм, а граф G
связный, то граф G1 может быть несвязным.
16. Докажите теорему 14.3. Если граф G связный и / — гомоморфизм, то граф
f(G) тоже связный.
17. Докажите теорему 14.4. Если граф G полный и / — гомоморфизм, то граф
f(G) тоже полный.
18. Докажите теорему 14.17. Если графы G\ и G<i являются различными компо-
компонентами графа G, то графы G\ и С?2 попарно непересекающиеся.
19. Докажите теорему 14.18. Граф G — объединение попарно непересекающихся
компонент.
20. Докажите теорему 14.23. Если T(V, E') — остовное дерево графа G = (V, ?"),
то для любого цикла г^о^1^2^з^4, • • -^о в графе G, по крайней мере, одно
ребро должно принадлежать множеству Е - Е'.
21. Докажите, что если граф G связный и / — гомоморфизм, то граф f(G) тоже
связный.
22. Покажите, что если G(V,E) и G'(V\E') - графы, / : G -> G1 - изомор-
изоморфизм, и вершина v e V имеет степень п, то в графе f(G) вершина f(v)

578 ГЛАВА 14. Некоторые специальные вопросы теории графов
необязательно имеет степень п. Что можно сказать о степени вершины f(v)
как о вершине графа /(G)? Что можно сказать о степени вершины f(v) как
о вершине графа С?
23. Покажите, что если графы G и G' — изоморфны, то они имеют одинаковое
количество вершин и ребер.
24. Покажите, что если / — изоморфизм из графа G в граф С, то граф G
связный тогда и только тогда, когда граф G связный.
25. Покажите, что если / — изоморфизм из графа G в граф G' и Н — компонента
графа G, то f(H) — компонента графа G'.
26. Покажите, что если / — изоморфизм из графа G в граф G' и вершина v e V
имеет степень п в графе G, то вершина f(v) имеет степень и в графе G'.
27. Покажите, что если / — изоморфизм из графа G в граф G1 и граф G имеет
эйлеров цикл, то граф G' тоже имеет эйлеров цикл.
28. Покажите, что если / — изоморфизм из графа G в граф G' и граф G имеет
собственный эйлеров путь, то граф G1 тоже имеет собственный эйлеров путь.
29. Покажите, что если / — изоморфизм из графа G в граф G' и граф G является
двудольным, то граф G' тоже является двудольным.
30. Покажите, что если / — изоморфизм из G в G' и граф G является полным
двудольным графом Kmn, то граф G' является полным двудольным графом
ТУ"
¦Гъ-тп-
31. Докажите, что пересечение графа G = (V, Е) и его дополнения представляет
собой граф, состоящий только из вершин графа G и не содержащий ребер.
32. Докажите, что объединение графа G = (V, Е) и его дополнения является
полным графом.
33. Покажите, что если / — изоморфизм из графа G в граф Сие — разрезаю-
разрезающее ребро графа G, то /(е) — разрезающее ребро графа G'.
34. Граф G — самодополнительный граф, если он изоморфен своему дополне-
дополнению (см. определение 14.19). Приведите пример самодополнительного графа.
35. Какая связь между матрицами смежности графа и его дополнения?
36. Покажите, что граф G\ изоморфен графу G тогда и только тогда, когда граф
G\ изоморфен графу Gc.
37. *Пусть G и G' — графы, а В и В' — соответственно их матрицы смежности.
Докажите, что граф G изоморфен графу G' тогда и только тогда, когда
существует перестановка Р такая, что В1 = РВР1 = РВР~1.
38. Найдите три разрезающих множества в графе, изображенном на рис. 14.25.
Найдите точку сочленения. Имеются ли разрезающие ребра?
Рис. 14.25
39. Найдите три разрезающих множества в графе, изображенном на рис. 14.26.
Найдите точки сочленения. Найдите разрезающие ребра.

РАЗДЕЛ 14.1. Алгебраические свойства графов 579
Рис. 14.26
40. Найдите три разрезающих множества в графе, изображенном на рис. 14.27.
Найдите точки сочленения. Найдите разрезающие ребра.
Ь
Рис. 14.27
41. Докажите теорему 14.28. Ребро е графа G является разрезающим ребром
графа G тогда и только тогда, когда оно не входит в цикл графа G.
42. Докажите теорему 14.27. Если T(V, Ef) — остовное дерево графа G = (V,E)
и С — разрезающее множество графа G, то С П Е' ^ 0.
43. Докажите теорему 14.36. Если компонента двусвязности Gi(Vi,Ei) состоит
из единственного ребра е», то е; — разрезающее ребро графа G.
44. Дано следующее определение. Пусть G = G(V, Е) — граф и Gi, G2, G3,..., Gn
подграфы графа G. Подграф G' графа G называется пересечением графов
п
G\, ^2, ?*з,..., Gn и обозначается f] Gi, если
г=1
1. Для всех iG' <G{.
2. Для всех г G" < G? < G, то
G'.
Покажите, что это определение эквивалентно определению пересечения, при-
приведенному в данном разделе.
45. Дано следующее определение. Пусть G = G(V, Е) — граф и Gi, G2, G3,..., Gn
подграфы графа G. Подграф G' графа G называется объединением графов
п
3,.. .,Gn и обозначается (J
г=1
если
1. Для всех г G^ < Gf.
2. Для всех г Gf ^ G" ^ G, то G' ^ G".
Покажите, что данное определение эквивалентно определению объединения,
приведенному в данном разделе.

580 ГЛАВА 14. Некоторые специальные вопросы теории графов
14.2. ПЛАНАРНЫЕ ГРАФЫ
Интегральная микросхема состоит из слоев миниатюрных микросхем, впечатан-
впечатанных в пластину. В такой ситуации крайне важно исключить пересечение проводов
в местах, не предназначенных для соединений. Если изобразить места указанных
соединений вершинами графа, то возникнет задача построения графа с непересе-
непересекающимися ребрами. Важно отметить, что нас интересует возможность постро-
построения графа с непересекающимися ребрами. Например, граф, изображенный на
рис. 14.28, изображается также другим способом (рис. 14.29). Граф, изображен-
изображенный на рис. 14.30, может быть изображен, как показано на рис. 14.31.
Рис. 14.28
Рис. 14.29
а Ъ
Рис. 14.30
Рис. 14.31
Если бы проблема, рассмотренная нами в разделе 6.1, заключалась в предо-
предоставлении двух видов коммунальных услуг трем домам или трех видов комму-
коммунальных услуг двум домам, то ее можно было бы решить, используя в каждом
случае граф, изображенный на рис. 14.32, согласно которому линии снабжения
не будут пересекаться.
Рис. 14.32
Чтобы решить задачу о предоставлении коммунальных услуг трем домам,
потребуются некоторые определения и методы. Начнем с наименования графов,
обладающих указанными свойствами.
ОПРЕДЕЛЕНИЕ 14.43. Планарным графом называется граф, который может
быть изображен в плоскости, так что его ребра не пересекаются. Граф, который
не является планарным, называется не планарным.

РАЗДЕЛ 14.2. Пленарные графы 581
Рассмотрим граф как рисунок, изображенный на листе бумаги. Если граф
планарен и нарисован так, что никакие линии не пересекаются, и его необхо-
необходимо разрезать вдоль ребер, то граф окажется разделенным на части, включая
внешнюю часть. Такие части называются гранями. Заметим, что граница каждой
грани является циклом.
ОПРЕДЕЛЕНИЕ 14.44. Грань планарного графа — максимальный участок
плоскости такой, что любые две точки этого участка могут быть соединены
кривой, не пересекающей ребро графа.
Теперь докажем теорему, называемую формулой Эйлера, с помощью которой
можно определять, является ли граф планарным.
ТЕОРЕМА 14.45. Если G — связный планарный граф, содержащий v вершин, е
ребер и / граней, то v - е 4- / = 2.
ДОКАЗАТЕЛЬСТВО. Докажем утверждение, используя индукцию по числу ре-
ребер. Если е = 0, то имеется одна вершина, нет ребер и есть одна грань, которая
составляет всю плоскость. Поэтому имеем 1 — 0 + 1 = 2, и теорема верна, если
е = 0. Отметим также, что если имеется одно ребро, то существуют две вершины
и одна грань. Поэтому имеем 2 - 1 4- 1 = 2; и теорема верна для е = 1.
Предположим, что теорема верна для произвольного связного планарного
графа, у которого к ребер, и имеется планарный граф Gk+i, у которого к + 1
ребер. Теперь удалим ребро, так что останется связный планарный граф G^, у
которого к ребер, поэтому формула v — е 4- / = 2 для него верна. После этого
докажем, что формула также верна и для связного планарного графа Gfc+i.
Предположим, что граф G^+i не имеет циклов. Движемся вдоль пути до тех
пор, пока не достигнем вершины, из которой нет другого выходящего ребра. Это
произойдет, если граф Gk+1 не содержит циклы. Найденная вершина будет иметь
степень 1. Удалим эту вершину и ребро, инцидентное ей. Количество граней не
изменится. При этом граф останется связным и планарным и будет иметь к ребер,
значит формула v — е 4- / = 2 верна. Поскольку количество ребер и количество
вершин уменьшилось на 1, то значение выражения v — е 4- / после процедуры
удаления останется неизменным, поэтому v — е 4- / = 2 для связного планарного
графа Gfc+i.
Далее предположим, что граф Gk+i содержит цикл. Удалим из цикла ребро
в{ с инцидентными вершинами щ и V{, но сами вершины оставим. Согласно теоре-
теореме 14.28 известно, что все еще имеется путь из вершины щ в вершину г?», так что
граф остается связным. Граф также остается планарным и будет иметь к ребер,
так что выполняется формула v — e + f = 2. Поскольку ребро е» входит в цикл, оно
разделяет две грани. Следовательно, удаление ребра равноценно удалению грани.
Таким образом, удалены одно ребро и одна грань. Поэтому значение выражения
v — е 4- / не изменилось, и формула v — е 4- / = 2 справедлива для графа Gfc+i- ¦
Теперь имеется все необходимое для доказательства того, что граф, описы-
описывающий проблему предоставления трех видов коммунальных услуг трем домам,
является полным двудольным графом Кз,з и его нельзя изобразить без пересека-
пересекающихся ребер.

582 ГЛАВА 14. Некоторые специальные вопросы теории графов
ТЕОРЕМА 14.46. Полный двудольный граф К^,з не является планарным.
ДОКАЗАТЕЛЬСТВО. Используем метод приведения к абсурду и предположим,
что граф Яз,з ~ планарный. Если Кз,з планарный граф, и поскольку имеется
девять ребер и шесть вершин, то 6 — 9 -f / = 2, поэтому / = 5. Пусть А и
В — непересекающиеся трехэлементные множества вершин, формирующие мно-
множество V вершин графа Кз,з- Если начать путь из одного из непересекающихся
множеств, например, А, и не повторять ребра, то можно попасть в вершину из
множества В, вернуться в вершину из множества А, вернуться в вершину из
множества В и, наконец, вернуться в вершину из множества Л, прежде чем за-
завершить цикл. Каждый цикл в /Сз,з представляет собой путь, длина которого, по
меньшей мере, равна 4. Поэтому каждая грань определена циклом, в котором не
менее четырех ребер. Следовательно, сумма ребер всех граней больше, чем 4/.
Но каждое ребро подсчитывается не более двух раз, поскольку оно может слу-
служить границей только для двух граней. Значит, сумма ребер всех граней должна
быть меньше, чем 2е. Объединяя эти неравенства, получаем, 4/ < 2е, поэтому
4/ < 18. Но это противоречит тому, что / = 5. Следовательно, мы пришли к
противоречию, и граф Яз,з не является планарным. ¦
Теперь докажем, что полный граф Къ, изображенный на рис. 14.33, не яв-
является планарным. Для этого нам необходима лемма (так называется теорема,
которую используют для доказательства другой теоремы).
Рис. 14.33
ЛЕММА 14.47. В произвольном связном планарном графе G с количеством вершин
не менее трех имеет место неравенство Зг> — е > 6.
ДОКАЗАТЕЛЬСТВО. Если граф G не имеет циклов, то в нем количество ребер
меньше количества вершин: е < v. Учитывая также, что v > 3, 2v — 6 > О,
получаем, е < v + 2v — 6 = Зг; — 6 или 3v — е > 6. Если граф G содержит
цикл, опять суммируем ребра, ограничивающие грани. Поскольку граница каждой
грани включает не менее трех ребер, то сумма ребер всех граней должна быть
больше 3/. Но каждое ребро может быть границей не более двух граней (см.
предыдущее доказательство), поэтому количество ребер должно быть меньше 2е.
Следовательно, 3/ < 2е и 2 = v—e+f, откуда 6 = Зи-Зе+3/ < Зг>-3е4-2е = 3v-e
и Зг; - е > 6. ¦
ТЕОРЕМА 14.48. Полный граф К$ не является планарным.
ДОКАЗАТЕЛЬСТВО. Граф Кь имеет пять вершин и десять ребер, Зг; — е = 3 • 5 -
10 = 5, поэтому, согласно предыдущей лемме, граф Къ не является планарным.¦

РАЗДЕЛ 14.2. Пленарные графы 583
Используя предыдущую лемму, докажем еще одну теорему, которая будет
использована в следующем разделе для доказательства того, что планарный граф
можно раскрасить, используя не более пяти цветов.
ТЕОРЕМА 14.49. Каждый планарный граф G содержит вершину степени 5 или
менее.
ДОКАЗАТЕЛЬСТВО. Для каждого ребра имеется две вершины (см. главу 2),
каждое ребро вносит число 2 в сумму степеней вершин. Поэтому сумма степеней
вершин равна 2е. Если в графе G не более двух вершин, то, очевидно, вершины
имеют степень 5 или менее. Отсюда предположим, что имеются три и более
вершин. Тогда по предыдущей лемме имеем е < 3v — 6, поэтому 2е < 6v — 12. Но
если степень каждой вершины больше или равна 6, то сумма степеней вершин
больше или равна бг;. По условию сумма степеней вершин равна 2е, поэтому
2е ^ бг;. А это невозможно, поскольку 2е < 6v — 12. Следовательно, существует
вершина со степенью не более 5. ¦
Доказательство следующей теоремы предоставляется читателю.
ТЕОРЕМА 14.50. Если два связных графа гомеоморфны, то они либо оба планар-
ны, либо оба непланарны.
Из этой теоремы вытекает непосредственно следующая теорема.
ТЕОРЕМА 14.51. Произвольный граф, гомеоморфный графу Кз,з или К$, не яв-
является планарным.
Поскольку любой граф, содержащий непланарный подграф, является непла-
нарным, это доказывает часть приведенной ниже теоремы. Остальную часть утвер-
утверждения примем без доказательства.
ТЕОРЕМА 14.52. (Куратовский) Граф является планарным тогда и только тогда,
когда он не содержит подграф, гомеоморфный /С3,з или К5.
ПРИМЕР 14.53. Покажем, что граф, изображенный на рис. 14.34, является пла-
планарным. Учитывая, что граф состоит из двух компонент, можем отделить их и
образовать граф, изображенный на рис. 14.35, который, очевидно, является пла-
планарным.
Рис. 14.34 Рис. 14.35 ?
ПРИМЕР 14.54. Покажем, что граф, изображенный на рис. 14.36, является пла-
планарным. Передвигая вершину d, получаем более простой граф, изображенный на
рис. 14.37. Передвигая вершину с, получаем граф (рис. 14.38), который, очевидно,
является планарным.

584 ГЛАВА 14. Некоторые специальные вопросы теории графов
е d
Ш •
d
Рис. 14.37
?
ПРИМЕР 14.55. Покажем, что граф Петерсена, изображенный на рис. 14.39, не
является планарным. Покажем, что граф содержит подграф, гомеоморфный ^з,з-
Единственная трудность — выбрать правильное множество вершин. Если в ка-
качестве верхних вершин выбрать е, / и д, а в качестве нижних — j, а, и г и
соединить каждую верхнюю вершину с каждой нижней вершиной, получим граф,
изображенный на рис. 14.40. Отсюда видим, что вершина с не нужна, поэтому
вершину и все ребра, инцидентные ей, удаляем. Все остальные ребра пока при-
присутствуют. Теперь можем удалить вершины h, b и d, формируя ребра {/, j}, {a,g},
{е,г}, соответственно, и получить граф, изображенный на рис. 14.41, который яв-
является гомеоморфным предыдущему графу. Но этот граф может быть изображен
как Кз,з- Следовательно, граф Петерсена содержит подграф, гомеоморфный /^з,з,
и поэтому не является планарным.
Рис. 14.39
УПРАЖНЕНИЯ
1. Каждый из приведенных ниже графов проверить на планарность. Ответ ар-
аргументируйте.
а) б)
Ь с V е
<*<,:

РАЗДЕЛ 14.2. Пленарные графы 585
в)
г)
Д)
2. Для каждого планарного графа из предыдущего упражнения проверить, что
v-e + / = 2.
3. Каждый из приведенных ниже графов проверить на планарность. Аргумен-
Аргументировать решение.
а)
б)
abed
/
е f g h
в)
abed
г)

586 ГЛАВА 14. Некоторые специальные вопросы теории графов
д)
4. Для каждого планарного графа из предыдущего упражнения проверить, что
v-e + / = 2.
5. Если планарный граф содержит 12 вершин со степенью 3, то сколько у него
ребер и граней ?
6. Если планарный граф имеет вершины со степенями 2, 2, 2, 3, 3, 3, 4, 4, 4 и
5, соответственно, то сколько у него ребер и граней?
7. Найдите значение величины v - e + f для графа, у которого
а) две компоненты;
б) три компоненты;
в) к компонент.
8. Если G — планарный граф, у которого п вершин и каждая грань графа G
ограничена циклом длины 3, найдите зависимость количества граней и ребер
от числа п.
9. Докажите, что произвольный граф с четырьмя вершинами является планар-
ным.
10. Докажите, что граф с пятью вершинами, одна из которых имеет степень 2,
является планарным.
11. Используя метод индукции, докажите, что дерево является планарным гра-
графом.
12. Докажите теорему 14.50. Если два связанных графа гомеоморфны, то они
или оба планарны, или оба непланарны.
14.3. РАСКРАСКА ГРАФОВ
Одной из наиболее известных нерешенных проблем на протяжение многих лет
оставалась так называемая проблема четырех красок. Она возникла в связи с
раскрашиванием географических карт и заключается в следующем: карту нужно
раскрасить, используя только четыре цвета, так, чтобы любые две граничащие
страны были раскрашены разными цветами. Известно, что для раскрашивания
карты пяти красок достаточно, а трех — нет. Для карты, нанесенной на тор,
минимальное количество красок было определено, но проблема четырех красок
оставалась нерешенной. На сегодняшний день она решена, но, возможно, не са-
самым лучшим способом. Решение потребовало длительной проверки компьютером
огромного числа случаев, которые иначе проанализировать не удавалось. Хотя
сам по себе метод является выдающимся достижением и вполне достаточен, что-
чтобы прекратить поиски контрпримера, было бы неплохо, если бы кому-то удалось

РАЗДЕЛ 14.3. Раскраска графов 587
найти более элегантное доказательство гипотезы. Самое замечательное в этом
доказательстве — то, что оно расширило наше представление о математическом
доказательстве.
Рассмотрим карту, изображенную на рис. 14.42.
Рис. 14.42
Если левая часть карты закрашена красным цветом, то при закрашивании примы-
примыкающих центральных граней чередуются синий и зеленый цвета. Правую грань
снова можно закрасить красным цветом, поскольку, как следует из рис. 14.43, она
не граничит с левой гранью.
Рис. 14.43
При изображении карты с помощью графа естественно использовать ребра
в качестве границ, а грани — в качестве стран, так что карта, изображенная на
рис. 14.44,
Рис. 14.44
превращается в граф, изображенный на рис. 14.45.
Рис. 14.45
Однако, вместо использования такого графа лучше сделать некоторые изме-
изменения. Гораздо удобнее работать с двойственным графом G' планарного графа
G, который формируется путем замены граней (или стран) вершинами и соедине-
соединения их ребрами, если грани в исходном графе смежные. Следовательно, в двой-
двойственном графе G' вершины являются смежными тогда и только тогда, когда
соответствующие грани являются смежными в исходном графе G. Таким обра-
образом, двойственным к рассматриваемому графу становится граф, изображенный
на рис. 14.46. Внешняя грань будет включаться как вершина в том случае, если
она раскрашена.
Рис. 14.46

588 ГЛАВА 14. Некоторые специальные вопросы теории графов
ПРИМЕР 14.56. Для графа G, изображенного на рисунке 14.47, двойственным
является граф G (рис. 14.48), поэтому в данном случае граф G изоморфен графу
G.
Рис. 14.47
Рис. 14.48
?
Поскольку грани графа G стали вершинами G', раскрашиваем теперь вер-
вершины графа G'. Исходная проблема раскрашивания стран на карте при условии,
чтобы никакие две страны, имеющие общую границу, не были окрашены в один
цвет, стала теперь проблемой раскрашивания вершин графа при том же условии.
А теперь рассмотрим новую задачу. Зафиксируем для графа количество цве-
цветов и попытаемся определить, сколько существует способов раскрашивания вер-
вершин при условии, что никакие две смежные не будут одного цвета. Эта концепция
принадлежит Г.Д. Биркгофу (G. D. Birkhoff) [И]. Предположим, например, что
имеется пять цветов и необходимо раскрасить граф, изображенный на рис. 14.49.
Рис. 14.49
Для раскрашивания первой вершины имеется пять цветов, и только четыре цвета
для раскашивания второй. Необходимо учесть, что вторая вершина отличается
по цвету от первой. Следовательно, существует 5 • 4 = 20 способов раскрашива-
раскрашивания графа. Заметим, что данный метод использовался в разделе 8.1 для подсчета
количества перестановок, а также и в других случаях, при использовании комби-
комбинаторного принципа умножения.
Предположим, что имеются четыре цвета и необходимо раскрасить граф G,
изображенный на рис. 14.50
в с Рис. 14.50
Для раскрашивания первой вершины а имеются четыре цвета. Далее, имеются
три цвета для раскрашивания вершины Ь.Только два цвета остается для раскра-
раскрашивания вершины с, поскольку она смежная саиб, цвет ее вершины должен
отличаться от цвета вершин а и Ь. Для раскрашивания вершины d также имеют-
имеются два цвета. Цвет вершины d может совпадать с цветом вершины 6, но должен
отличаться от цвета смежных вершин а и с. Таким образом, имеем 4-3-2-2 = 48
способов раскраски графа G. Важно не раскрашивать вершины 6 и d до определе-
определения количества цветов для вершины с, иначе потребуется разбить подсчет на два

РАЗДЕЛ 14.3. Раскраска графов 589
случая: когда b и d — одного цвета и когда b и d по цвету не совпадают. Пред-
Предположим, что имеется А цветов для раскрашивания графа G. Имеются А цветов
для раскрашивания вершины а, А— 1 цветов для раскрашивания вершины Ь, А —2
цветов для раскрашивания с и А —2 цветов для раскрашивания d. Следовательно,
имеются (А)(А — 1)(А — 2)(А — 2) способов раскраски графа G. Обозначим эту
величину через Сс(А). Таким образом, Сс(А) — число способов раскраски графа
G с использованием А цветов. Заметим, что Cg@) = CgA) = CgB) = 0.
Функция Cg(A) предполагается полиномиальной при формулировке ниже-
нижеприведенного определения. На интуитивном уровне это кажется верным и будет
доказано позже.
ОПРЕДЕЛЕНИЕ 14.57. Пусть G — граф. Раскраской графа G называется окра-
окрашивание вершин графа G такое, что никакие две смежные вершины не имеют
один цвет. Пусть Cg(A) обозначает количество способов раскраски графа G с
использованием А цветов, так что никакие две смежные вершины не имеют
один цвет, т.е. Cg(A) — количество способов раскраски графа G. Для фик-
фиксированного графа G функция Cg(A) является полиномиальной функцией от
А, называемой хроматическим многочленом графа G. Хроматическое число
графа — это наименьшее число цветов, которое используется для раскраски
графа. Это наименьшее положительное число п такое, что Сс(п) Ф 0.
ПРИМЕР 14.58. Пусть граф G состоит из пяти изолированных вершин, так что в
нем нет ребер, поэтому нет смежных вершин. Если раскрашивать граф А цветами,
то будем иметь А вариантов для каждой вершины, поэтому будет существовать
А • А • А • А • А = А5 способов раскраски графа и Cg(A) — А5. Очевидно, что если
граф G состоит из к изолированных вершин, то Cg(A) = Afc, а хроматическое
число равно 1. ?
ПРИМЕР 14.59. Пусть G — граф К$, так что каждая из пяти его вершин яв-
является смежной с остальными четырьмя вершинами. Если раскрашивать этот
граф А цветами, то для первой вершины имеется А вариантов цвета. Поскольку
вторая вершина смежная с первой, то имеем А — 1 вариантов выбора цвета для
следующей вершины. Третья вершина является смежной с первой и со второй,
поэтому для нее имеется А — 2 вариантов выбора. Четвертая вершина — смежная
с каждой из первых трех раскрашенных, поэтому для нее имеется А — 3 вари-
вариантов выбора цвета. И, наконец, пятая вершина является смежной с каждой из
первых четырех окрашенных вершин, поэтому имеется А - 4 вариантов выбора
цвета для этой вершины. Таким образом, Cg(A) = (А)(А-1)(А - 2)(А-3)(А-4).
Отметим, что этот граф не может быть раскрашен четырьмя цветами, посколь-
поскольку CgD) = 0, но учитывая, что граф G не является планарным, этот факт не
противоречит утверждению, что планарный граф может быть окрашен четырь-
четырьмя цветами. Используя рассмотренный выше частный случай графа К$ в каче-
качестве ориентира для изучения графа G = Кп, находим, что если G = Кп, то
Cg(A) = (А)(А - 1)(А - 2)(А - 3) • • • (А - (п - 1)). Таким образом, хроматическое
число для графа G равно п. ?

590 ГЛАВА 14. Некоторые специальные вопросы теории графов
Раскраска одной компоненты графа не ограничивает раскрашивание другой
компоненты, поскольку никакая из вершин одной компоненты не является смеж-
смежной с вершиной другой компоненты. Следовательно, имеем следующую теорему.
ТЕОРЕМА 14.60. Если G = Gl U G2 U G3 U • • • U Gn, где Gb G2, G3,..., Gn -
компоненты графа G, то Gg(A) = Cq^X) • Gg2(A) • Gg3(A) Gcn(A).
Из теоремы следует, что Gg(A) = 0 тогда и только тогда, когда С^ДА) = 0
для некоторого 1 < i < п. Отсюда вытекает приведенное ниже следствие.
СЛЕДСТВИЕ 14.61. Если для раскраски графа G требуется к цветов, то и для
одной из его компонент требуется для раскраски к цветов.
Учитывая этот результат, рассмотрим раскрашивание только связных графов.
Теперь на основе заданного графа G(V, E) сформируем два специальных
графа. Пусть е = {а, 6} — ребро графа G. Пусть Ge — граф G, в котором удалено
ребро е, но сохранены вершины а и Ь. Пусть G/е — граф Ge с отождествленными
(склеенными) вершинами а и 6.
Отметим, что граф G/e, фактически, является гомоморфным образом графа
Ge, где гомоморфизм / : Ge —> G/e определен на вершинах графа Ge таким
образом: f(a) = /F) и f(v) = v для всех v из V — {a,b}. Для ребер имеем
f({u,v}) = {f(u),f(v)}. Также отметим, что / = / о/, поскольку для вершин
и ребер графа G/e функция / представляет собой тождественное отображение.
Функция с такими свойствами называется стягивающим отображением.
ПРИМЕР 14.62. Пусть G — граф, изображенный на рис. 14.51. Тогда граф Ge
изображен на рис. 14.52, a G/e — на рис. 14.53.
a e Ь
Рис. 14.51
Рис. 14.52
Рис. 14.53
?
ПРИМЕР 14.63. Пусть G — граф, изображенный на рис. 14.54. Тогда Gg — граф
на рис. 14.55, a G/e — на рис. 14.56.
а с
Рис. 14.54
а с
Рис. 14.55
Рис. 14.56
?
Введенные специальные графы используем для доказательства следующей
теоремы.
ТЕОРЕМА 14.64. Для произвольного планарного графа G с ребром е имеет место
равенство CGe(X) = CG(X) + CG/e(X).

РАЗДЕЛ 14.3. Раскраска графов 591
ДОКАЗАТЕЛЬСТВО. Предположим, что имеется раскраска графа G^ Если цвет
вершины а не совпадает с цветом вершины 6, то эта раскраска будет также рас-
раскраской графа G и наоборот. Если цвет вершины а совпадает с цветом вершины
Ь, в таком случае имеем раскраску графа G/е и наоборот. Поэтому произвольная
раскраска графа Ge является либо раскраской графа G, либо раскраской графа
G/e, но не обоих одновременно. Следовательно, количество раскрасок графа G«s
равно количеству раскрасок графа G плюс количество раскрасок графа G/e, или
() () ()
Интуитивно понятно, что для произвольного планарного графа Gen вер-
вершинами Cg(A) — многочлен степени п, поскольку всякий раз в примерах при
построении Cg(A) формировалась для каждой вершины величина А -к для неко-
некоторого целого числа 0 < к < п. Фактически, это предположение было использо-
использовано при определении хроматических многочленов. Теперь докажем это, строго
используя предыдущую теорему и метод индукции по числу ребер.
ТЕОРЕМА 14.65. Для произвольного планарного графа Gen вершинами функция
Cg(A) представляет собой многочлен n-ой степени.
ДОКАЗАТЕЛЬСТВО. Пусть т — количество ребер в планарном графе Gen
вершинами. Если т = О, тогда согласно примеру 14.58 функция Gg(A) = Ап,
т.е. является многочленом n-ой степени. Предположим, что теорема верна для
всех планарных графов, у которых п вершин и к ребер. Напомним, что к —
фиксированное число, an — нет. Пусть граф G имеет п вершин и fc + 1 ребер. По
теореме 14.64, функция Gg(A) = Ссё(А) — С<з/е(А). Но граф Gi имеет п вершин и
к ребер, и граф G/e имеет п—1 вершину и к ребер. К тому же оба графа планарны.
Следовательно, по индуктивному предположению функции С^ДА) и Сс/е(А) —
многочлены степени п и п-1 соответственно. Поэтому Gg(A) = Ссё(А)-Сс/е(А)
— многочлен степени п. Ш
Из доказанной теоремы вытекает следующая теорема.
ТЕОРЕМА 14.66. Для произвольного непустого планарного связного графа G
постоянный член в Сс(А) равен 0. Если граф G имеет две или более вершин, то
сумма коэффициентов многочлена С^(А) равна 0.
ДОКАЗАТЕЛЬСТВО. Поскольку непустой планарный граф G не может быт рас-
раскрашен 0 цветами, то Gg@) = 0. Если граф G имеет две или более вершин,
то поскольку граф G связный, существуют две смежные вершины и граф G не
может быть раскрашен одним цветом. Поэтому GgA) = 0. Но значение GgA)
равно сумме коэффициентов многочлена Gg(A), поэтому сумма коэффициентов
многочлена Gg(A) равна 0. ¦
Использование равенства Ссё(А) = Сс(А)+Сс/е(А) используется двумя спо-
способами. Предположим, имеется граф Ge, тогда можно найти многочлен Ссё(А),
выраженный как сумма многочленов Cg(A) и Сс/е(А). Но граф G по сравнению
с Ge имеет дополнительное ребро и, таким образом, увеличивает количество ре-
ребер, а граф G/e, в котором две вершины графа Gg отождествлены, уменьшает
количество вершин. В конце концов получим полные графы. Теоретически — это
ответ, но, возможно, не самый простой.

592 ГЛАВА 14. Некоторые специальные вопросы теории графов
Предположим, например, что требуется найти хроматический многочлен для
графа, изображенного на рис. 14.57. Если положить е = {а, 6}, a Gi будет вы-
вышеупомянутым графом, в этом случае G — граф, изображенный на рис. 14.58, а
G/e — граф, изображенный на рис. 14.59.
а
с
Рис. 14.59
Рис. 14.57
Рис. 14.58
Следовательно, Ссё (А) = Cq (A) + G/e. Если / — ребро {с, d} и G = G'-,
тогда G1 — граф, изображенный на рис. 14.60, G/f — граф, изображенный на
рис. 14.61,
Рис. 14.60 Рис. 14.61
и C'G, (A) = Cg'(A) + CG> (А). Но G' является графом К4, поэтому
CG/(A) = A(A-l)(A-2)(A-3).
Граф G/f является графом К$} поэтому
СО//(Л) =
Следовательно,
СС(А) -
- Сс(Х) + CG//(A) =
= А(А - 1)(А - 2)(А - 3) + А(А - 1)(А - 2) =
= А(А-1)(А-2)(А-2).
Пусть д = {с, d} и G/e — граф G'!. Тогда граф G" изображен на рис. 14.62, граф
G/f — на рис. 14.63,
Рис. 14.62
Рис. 14.63

РАЗДЕЛ 14.3. Раскраска графов 593
и C'G,,(\) = Сс(А) 4- Сс/в(А). Но G" является графом Кз, поэтому
G/g является графом К2, поэтому
GG//(A) =
Следовательно,
CG/c = C'G,,(X) = CG"(X) + CG/g(X)
= А(А-1)(А-2) +
Таким образом,
= А(А - 1)(А - 2)(А - 2) + А(А - 1)(А - 1) =
= А(А-1)[(А-2)(А-2) + (А-1)] =
= А(А-1)(А2-ЗА + 3).
Второй метод использования равенства GGJA) = GG(A) + GG/e(A) явля-
является рекурсивным, в котором данное равенство записывется в виде GG(A) =
Ссг(А) — Сс/е(А). Согласно этому методу удаляем ребра и склеиваем вершины,
уменьшая количество ребер и вершин в графе до тех пор, пока это возможно,
и, если необходимо, получаем изолированные вершины. Рассмотрим тот же граф
на рис. 14.64. Если предположить, что G является этим графом, и удалить ребро
{a,d}, то Ge — граф, изображенный на рис. 14.65, а G/e — на рис. 14.66.
d а d
LJ aVb
с с b с
Рис. 14.64 Рис. 14.65 Рис. 14.66
Если для раскраски графа Gg используется А цветов, то и для раскраски
вершины а можно использовать А цветов, а для раскраски любой другой вершины
можно использовать А —1 цветов, поскольку каждая из оставшихся вершин может
быть окрашена в любой цвет, отличный от цвета предыдущей вершины. Таким
образом,
Граф G/e = Кз, так что
GG/e(A) = A(A-l)(A-2)

594 ГЛАВА 14. Некоторые специальные вопросы теории графов
= А(А- 1K + А(А-1)(А-2) =
А(А-1)(А2-ЗА + 3),
и этот результат, к счастью, совпадает с вычисленным ранее.
Проблема четырех красок эквивалентна утверждению, что для каждого пла-
нарного графа G значение CgD) ^ 0. Как уже отмечалось, проблема четырех
красок в течение долгого времени оставалась нерешенной. На это были две ве-
весомые причины. С одной стороны, проблема столь проста, что ее можно было
объяснить любому, и все же она оставалась нерешенной. Проблема впервые была
сформулирована в 1852 Фрэнсисом Гутерье (Francis Gutherie), учеником Огюста
де Моргана (Augustus De Morgan). Некоторые математики посвятили жизнь ре-
решению этой проблемы. Существовало достаточно много "доказательств" пробле-
проблемы четырех красок, найденных любителями и профессиональными математиками.
В 1880 году казалось, что Альфред Бэй Кэмпе (Alfred Bay Kempe) [60] решил
проблему. Однако, в 1890, П. Дж. Хивуд (P. J. Heawood) [42] нашел в его до-
доказательстве ошибку. Модифицировав доказательство Кемпе, П. Дж. Хивуд смог
доказать, что произвольную плоскую карту можно раскрасить пятью цветами.
ТЕОРЕМА 14.67. Произвольный планарный граф G можно раскрасить, используя
только пять цветов.
ДОКАЗАТЕЛЬСТВО. В соответствии с доводами, принятыми ранее, предполо-
предположим, что граф G связный. Помимо этого будем считать, что граф G изображен
так, что никакие из его ребер не пересекаются. В доказательстве использует-
используется индукция по количеству вершин. Если граф включает только одну вершину
(фактически пять или менее), то, несомненно, такой граф можно раскрасить, ис-
используя только пять цветов. Предположим, что при раскрашивании произвольного
графа с к вершинами используются только пять цветов. Пусть G — граф с к + 1
вершиной. По теореме 14.49 граф имеет вершину степени 5 или менее. Пусть
v — такая вершина. Пусть G' — подграф графа G, в котором удалена верши-
вершина v и все инцидентные ей ребра. Поскольку в графе G' только к вершин, то
по индуктивному предположению граф G' можно раскрасить, используя только
пять цветов. Если степень вершины v меньше пяти, тогда в графе G она явля-
является смежной с четырьмя или менее вершинами и, следовательно, может быть
раскрашена цветом, отличным от цветов смежных вершин. Раскраска завершена.
Поэтому предположим, что степень вершины v равна 5. В этом случае верши-
вершина v смежная с пятью вершинами графа G, назовем их ^1,^2,^3,^4 и ^5- Если
какие-либо вершины из этих пяти имеют одинаковый цвет, то для их окраски ис-
использовано только четыре цвета, и можно снова выбрать неиспользованный цвет
для окрашивания вершины v, в результате раскраска завершена. Поэтому пред-
предположим, что вершины ^1,^2,^3,1*4 и v$ окрашены различными цветами. Пусть
1,2,3,4 и 5 — номера красок, которыми окрашены вершины у\,У2,Щ,Щ и ^5 со-
соответственно. Предположим для определенности, что вершины vi,V2,уз,у4 и v5

РАЗДЕЛ 14.3. Раскраска графов 595
расположены по часовой стрелке вокруг вершины v. Начиная с вершины v\ графа
С, будем строить подграф Gi3 графа G следующим образом : множество вершин
подграфа Vi3 графа Gi3 состоит из вершины v\ и всех вершин графа G', которые
могут быть связаны с v\ путями, проходящими только через вершины с цветом
1 или 3. Предположим сначала, что г;3 ? Vi3. По построению графа Gi3 граф G
не содержит вершины, которые имеют цвет 1 или 3, не принадлежат множеству
Vis и являются смежными с вершинами из Vi3. Поэтому в графе Gi3 цвета 1 и
3 можно поменять местами, не меняя цвета остальных вершин. Теперь вершины
vi и vs окрашены одним цветом и, согласно результатам, полученным ранее, граф
G можно раскрасить. Если г>3 € Vi3, то существует путь из vi в г>36, который
проходит только через вершины, окрашенные цветом 1 или 3. Назовем этот путь
Pi3. Тогда путь vviPisVsv является циклом и имеет форму, изображенную на
рис. 14.67 или рис. 14.68. В первом случае вершина V2 находится внутри цикла,
а вершина v4 — вне цикла.
Рис. 14.67
Рис. 14.68
Во втором случае вершина v^ находится внутри цикла, а вершина V2 —
вне цикла. В каждом из случаев в графе G не существует путь от вершины
V2 к вершине г>4, проходящий через вершины цвета 2 или 4. Дело в том, что
граф G планарный, поэтому его вершины не пересекаются, и переход из вершины
V2 в вершину 1>4 требует прохождения через вершину цикла vviPisvsv, а все
эти вершины окрашены цветом 1 или 3, за исключением, возможно, вершины г;,
которая не принадлежит графу G. Поэтому можно повторить изложенную выше
процедуру, формируя граф G24 вместо Gi3, и раскрасить вершину v. Ш
УПРАЖНЕНИЯ
1. Найдите графы, двойственные данным :
а) б)

596 ГЛАВА 14. Некоторые специальные вопросы теории графов
в) г)
Jl <
«9 «10
«12
«14
\ > (
i \\
«n
«13 "
«15 «16
д)
2. Найдите графы, двойственные данным:
а) б)
в)
г)

д)
РАЗДЕЛ 14.3. Раскраска графов 597
3. Определите хроматическое число приведенных ниже графов.
а)
a • <
-• с
б)
а Ъ
с >
в)
с dy
f
г)
с dy
f
Д)
a b с
d e f
4. Определите хроматическое число приведенных ниже графов.

598 ГЛАВА 14. Некоторые специальные вопросы теории графов
а) б)
я 1
с d e f
в)
а Ь
с d e f
г)
а Ъ
с d e f
Д)
5. Покажите, что двудольный граф ifm,n всегда можно раскрасить двумя цве-
цветами. Определите хроматический многочлен графа /fm,n?
6. Чему равно хроматическое число гиперкуба?
7. Используя теорему14.64, найдите хроматический многочлен каждого из при-
приведенных графов:
а)

РАЗДЕЛ 14.3. Раскраска графов 599
в)
г)
а с b
Д)
8. Используя теорему 14.64, найдите хроматический многочлен каждого из при-
приведенных графов:
а)
б)
в)
г)

600 ГЛАВА 14. Некоторые специальные вопросы теории графов
Д)
с d
9. Докажите, что если произвольный планарный граф с и вершинами изомор-
изоморфен своему двойственному графу, то он имеет 2п — 2 ребер.
10. Докажите, что если хроматическое число связного графа, имеющего, по
крайней мере, одно ребро, равно 2, то он является двудольным.
14.4. ПУТИ И ЦИКЛЫ ГАМИЛЬТОНА
В 1857 году математик Уильям Роуэн Гамильтон (William Rowan Hamilton) при-
придумал игру. Существует несколько версий того, как это произошло. По одной
из версий он описал эту игру в письме к другу. Согласно другой, он действи-
действительно изобрел игру и продал ее производителю игрушек. В любом случае она,
по-видимому, включала додекаэдр, т.е. правильный многогранник, 12 граней ко-
которого представляли собой конгруэнтные правильные пятиугольники. В каждом
из 20 углов, или вершин тела, просверливалась дырка, в которую вставлялся ко-
колышек, изображавший город. Используя веревку, требовалось найти путь через
города, посетив каждый город один раз, и вернуться в исходный город. Додекаэдр
на плоскости изображается так, как показано на рис. 14.69.
Рис. 14.69
Проблема в таком случае сводится к нахождению цикла в графе, проходяще-
проходящего через каждую вершину, исключая начальную, только один раз. Отсюда любой
цикл графа, обладающий таким свойством, назывется гамильтоновым циклом.
Этот цикл в некотором смысле противоположен эйлерову циклу, который прохо-
проходит через все ребра только один раз. До определенного момента оба цикла могут
показаться похожими, но дальнейшее изучение покажет, что цикл Гамильтона
намного сложнее.
Формально путь Гамильтона и цикл Гамильтона (гамильтонов цикл) описы-
описываются следующим образом.

РАЗДЕЛ 14.4. Пути и циклы Гамильтона 601
ОПРЕДЕЛЕНИЕ 14.68. Пусть G — граф. Гамилыпонов путь — это простой
путь, который проходит через каждую вершину графа G. Гамилыпонов цикл
— это простой цикл, который проходит через каждую вершину графа G.
Убедимся, что граф для игры Гамильтона действительно имеет гамильто-
нов цикл, оправдывающий свое название. Один из таких циклов изображен на
рис. 14.70.
d Рис. 14.70
ПРИМЕР 14.69. Граф на рис. 14.71 имеет гамильтонов цикл, изображенный на
рис. 14.72.
Рис. 14.71
?
ПРИМЕР 14.70. Гиперкуб порядка п при п > 3 имеет гамильтонов цикл. Его
описывет код Грея для п (см. раздел 6.7). Таким образом, гамильтонов цикл для

602 ГЛАВА 14. Некоторые специальные вопросы теории графов
гиперкуба порядка 4 имеет вид
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
?
ПРИМЕР 14.71. Полный граф Кп при п > 3 имеет гамильтонов цикл. Пусть v\, V2,
vs,...,vn — вершины графа Кп. Поскольку между двумя любыми вершинами
имеется ребро, то всегда существует ребро из v» в vi+i и, наконец, существует
ребро из последней вершины vn обратно в v\. ?
Для следующего примера необходима теорема, приведенная ниже.
ТЕОРЕМА 14.72. Для любой вершины из цикла Гамильтона существует ровно
два ребра из этого цикла, инцидентные данной вершине.
ДОКАЗАТЕЛЬСТВО. По ходу цикла для каждой вершины V имеется ребро к
циклу и ребро из цикла. Если бы существовало еще одно ребро цикла, инцидент-
инцидентное вершине V, то цикл вернулся бы в вершину V, и она опять появилась бы
в цикле, что противоречит определению гамильтонова цикла. Следовательно, су-
существует ровно два ребра, которые инцидентны вершине V из цикла Гамильтона.
Заметим, что граф, у которого есть гамильтонов цикл, называют гамильто-
новым графом. И как следствие приведенной выше теоремы, получаем, что любой
граф, содержащий вершину степени 1, не может быть гамильтоновым.
ПРИМЕР 14.73. Граф Петерсена, изображенный на рис. 14.73, имеет гамильтонов
путь, но не имеет гамильтонова цикла. Путь показан на рис. 14.74.

РАЗДЕЛ 14.4. Пути и циклы Гамильтона 603
Рис. 14.73
Рис. 14.74
Доказательство, что граф Петерсена не имеет гамильтонова цикла, потре-
потребует некоторого количества проб и ошибок. Попытаемся построить гамильтонов
цикл. Всякий раз мы будем попадать в тупик. Для начала припомним, что звезда
в центре должна соединяться с внешним пятиугольником, поэтому, не нарушая
общности, можно предположить, что {а,/} — ребро в цикле. Из вершины / цикл
должен идти к вершине г или вершине /i, но, в силу симметрии, это не имеет
значения, поэтому предположим, что {/, г} — ребро из цикла. Согласно преды-
предыдущей теореме ребро {/, h) не может входить в цикл, поскольку тогда будут три
ребра, инцидентных вершине /. Значит, ребра {j, k] и {h, с} должны входить
в цикл, поскольку это единственно возможные ребра, инцидентные вершине h.
Если ребро {i,d} принадлежит циклу и ребро {/, г} входит в цикл, получаем,
что ребро {i,g} не может принадлежать циклу, поскольку согласно предыдущей
теореме только два ребра могут быть инцидентными вершине г. Поэтому ребра
{j,g} и {Ь, д} должны находится в цикле, поскольку только два ребра могут быть
инцидентными вершине д. Поскольку ребра {j, h} и {j,g} принадлежат циклу,
ребро {j, e) не может находиться в цикле, поскольку тогда будут три ребра, ин-
инцидентных вершине j. Поэтому ребра {d, e) и {е,а} должны входить в цикл,
поэтому имеется два ребра, инцидентных вершине е. В результате имеем части
цикла, изображенные на рис. 14.75.
Рис. 14.75
Поскольку ребра {i,d} и {d, e} находятся в цикле, то ребро {d, с} не мо-
может входить в цикл, т.к. в противном случае было бы три ребра, инцидентных
вершине d, поэтому ребро {с, Ь) должно быть в цикле, чтобы было два ребра, ин-
инцидентных вершине с. Поскольку ребра {Ь,д} и {с, 6} находятся в цикле, то ребро
{а, Ь} не может входить в цикл, и в результате получаем граф, изображенный на
рис. 14.76, в котором больше нет ребер, чтобы добавить в цикл. Таким образом,
этот путь не может породить гамильтонов цикл.
Если вернуться к рассуждениям, согласно которым ребра {а,/}, {/,г}, {j,h}
и {/г, с} входят в цикл, а ребро {/, h} не входит в цикл, поскольку {г,й} не может
быть в цикле, ребро {i,g} должно быть в цикле, поэтому имеется два ребра, ин-
инцидентных вершине г. Ребра {e,d} и {d, с} должны быть в цикле, так что имеется

604 ГЛАВА 14. Некоторые специальные вопросы теории графов
два ребра, инцидентных вершине d. Поскольку ребра {/г, с} и {d, с} принадлежат
циклу, ребро {Ь, с} не может входить в цикл, поскольку тогда будут три ребра,
инцидентные вершине с. Поэтому ребра {а, 6} и {д,Ь} должны быть в цикле, что-
чтобы было два ребра, инцидентных вершине Ъ. Учитывая, что ребра {г,д} и {д,Ь}
должны быть в цикле, ребро {j, g} не может входить в цикл, поскольку тогда бу-
будут три ребра, инцидентные вершине д. На этом этапе имеем граф, изображенный
на рис. 14.77.
Рис. 14.77
Рис. 14.78
Ребро {е, j} должно входить в цикл, чтобы было два ребра, инцидентных
вершине j. Поскольку ребра {e,d} и {e,j>} должны входить в цикл, то ребро
{е,а} не может входить в цикл. В результате получаем граф, изображенный на
рис. 14.78, в котором не осталось свободных ребер и который не является гамиль-
тоновым циклом. Поскольку исчерпаны все возможности построения, приходим к
выводу, что граф Петерсона не имеет цикла Гамильтона. ?
Рассуждения, приведенные выше, убеждают в следующем: чтобы граф имел
гамильтонов цикл, степень каждой вершины должна быть не меньше двух. Оче-
Очевидно также, что граф должен быть связным, чтобы иметь гамильтонов цикл.
Приведенная ниже теорема содержит дополнительную информацию по этому во-
вопросу. Доказательство теоремы предоставляется читателю.
ТЕОРЕМА 14.74. Если граф G имеет разрезающее ребро, то он не может иметь
гамильтонов цикл. Если компоненты графа, полученные путем удаления разреза-
разрезающего ребра, имеют гамильтонов цикл, то граф G имеет гамильтонов путь.
Ранее нами были найдены весьма изящные критерии существования у гра-
графа эйлерова цикла. К сожалению, никому не удалось установить необходимые
и достаточные условия существования у графа гамильтонова цикла. Тем не ме-
менее, в следующей теореме приводятся некоторые условия существования у графа
гамильтонова цикла. Очевидно, чем больше ребер при фиксированном числе вер-
вершин имеет граф, тем выше степень вершин и более вероятно, что имеется цикл,
проходящий через все вершины, без повторения вершин. На интуитивном уровне
понятно, что если одна вершина имеет более низкую степень, то это компенси-
компенсируется более высокой степенью другой вершины, что отображено в приведенной
ниже теореме.
ТЕОРЕМА 14.75. Если G(V, Е) — связный граф с п вершинами, где п > 3, и для
каждой пары различных несмежных вершин и, v ? V, deg(u) -f deg(t;) > n, тогда
граф G имеет гамильтонов цикл.

РАЗДЕЛ 14.4. Пути и циклы Гамильтона 605
ДОКАЗАТЕЛЬСТВО. Пусть у\у2уз • • • ^т — максимальный простой путь в графе
G. Пусть a = deg(t>i) и b = deg(z;Tn). Сначала покажем, что перестановка вершин,
входящих в путь, предоставляет возможность формирования простого цикла. Ес-
Если ВерШИНЫ Vi И Vm — СМеЖНЫе, ТО V1V2V3 . . . VmVi — ЦИКЛ, И ИСКОМЫЙ ЦИКЛ
найден. Если v\ и vm смежными не являются, то a + 6 > п. Мы хотим показать,
что в данном случае существуют вершины Vi и Vi+i, входящие в путь при усло-
условии, что вершина vi является смежной с г^+ъ а вершина г;т является смежной
к Vi. Если это сделано, то начинаем путь с viv2vs ... г^+i • • -Vm- Удаляем ре-
ребро между Vi и г>;+1. Затем начинаем новый путь с вершины г;*+ь продолжаем
его до вершины v\, поскольку вершины Vi+i и v\ являются смежными. Продол-
Продолжаем далее и, поскольку вершины Vi и vm являются смежными, получаем путь
.ViVm, как показано на рис. 14.79.
Рис. 14.79
Движемся в обратном направлении вдоль пути vrnvrn-ivrn-2 ... Vi+2Vi+\ и
ПОЛучаеМ ИСКОМЫЙ ЦИКЛ Vi+iViV2V3 . . .ViVTnVrn-iVTn-2 • • .Vi+2^i + l-
Теперь требуется показать, что существуют вершины Vi и v»+i» входящие
в путь такие, что вершина v\ — смежная с вершиной vi+1, а вершина г>т —
смежная с вершиной г^. Предположим обратное. В таком случае вершина v\ не
является смежной ни к одной из вершин, которые не входят в путь, поскольку
если существует вершина ги, не входящая в путь и смежная с вершиной v\% то
.У™, — простой путь, а это противоречит предположению о том, что
m — максимальный простой путь в графе G, и тогда существует a
вершин, входящих в путь v\v2v^.. .vmi смежных с вершиной v\. Аналогично,
существует Ъ вершин, входящих в путь v\v2v^... vm, смежных с вершиной vm.
Если включить вершину v\, то путь v\v2v^.. .vm будет содержать a 4-1 вершин,
совпадающих с вершиной v\ или смежных с ней. Существует также Ь вершин,
входящих в путь г^г^з • • • Vm и смежных с вершиной vm. Если для каждой вер-
вершины Vi, входящей в путь, смежной с вершиной vm, вершина vi+i не является
смежной с вершиной v\, то путь содержит a -f 1 вершин, совпадающих с верши-
вершиной v\ или смежных с ней, и b вершин, входящих в путь, которые не совпадают
с вершиной v\ и не смежные с ней. Таким образом, путь v\v2v$.. .vrn содержит
a + b -f +1 различных вершин, что невозможно. Следовательно, сделанное пред-
предположение было неверным, и существуют вершины Vi и Ui+i, входящие в путь и
такие, что вершина v\ — смежная с вершиной г>г+ь а вершина vm — смежная с
вершиной Vi. Таким образом, искомый цикл получен. Предположим для простоты,
что вершины переобозначены, так что цикл имеет вид v\v2v^.. .vmvi.
Покажем теперь, что этот цикл содержит все вершины множества V. Если
это не выполняется и вершина г/ не совпадает ни с одной из вершин v», то,
поскольку граф G связный, существует путь из вершины v' в одну из вершин
Vi, и существует вершина w, которая не входит в путь v\v2v$.. .г;т и является
смежной с одной из вершин Vj. Но тогда
WVjVj + iVj+2 • • • VmViV2V3 . . . Vj-i

606 ГЛАВА 14. Некоторые специальные вопросы теории графов
простой путь, который длиннее, чем путь v\V2Vz.. . г;т, что является противоре-
противоречием. Следовательно, цикл v\V2Vz---vrnv\ является гамильтоновым циклом. ¦
Из теоремы непосредственно вытекает следствие, которое получено раньше
и является более известным, чем сама теорема.
СЛЕДСТВИЕ 14.76. Если G(V, Е) — связный граф, имеющий и вершин, где п > 3,
и если для каждой вершины v ? V выполняется deg(i;) > §, то граф G имеет
гамильтонов цикл.
При доказательстве теоремы 14.75 был использован только тот факт, что
сумма степеней вершин v\ и vm максимального пути v\V2Vs -- -Ущ больше, чем
число вершин. Поэтому получаем такое развитие теоремы 14.75.
ТЕОРЕМА 14.77. Пусть G(V,E) — связный граф с и > 3 вершинами и пусть и
и v — несмежные вершины графа G такие, что deg(it) + deg(v) > п. Отсюда
граф Ge, состоящий из графа G с присоединенным ребром е = {и, v}, имеет
гамильтонов цикл тогда и только тогда, когда граф G имеет гамильтонов цикл.
ДОКАЗАТЕЛЬСТВО. Если граф G имеет гамильтонов цикл, то и граф Ge имеет
гамильтонов цикл, т.к. для него используется тот же самый цикл. Обратно, пред-
предположим, что граф Ge имеет гамильтонов цикл. Если ребро е не входит в цикл, то
вполне очевидно, что граф G имеет гамильтонов цикл. Если ребро е не принадле-
принадлежит циклу, то гамильтонов цикл в графе Ge записывается в виде uv\V2Vz • • • vmvu.
Но в этом случае uviv2v3 • • • v-mV — гамильтонов путь в графе G и, следовательно,
является максимальным путем, и, кроме того, deg(u)+deg(t;) > п. Согласно до-
доказательству предыдущей теоремы вершины этого пути можно переставить так,
что они образуют цикл в графе G. Поскольку этот цикл содержит все вершины
графа G, то это гамильтонов цикл. ¦
Пусть имеется граф Gen вершинами. Добавляем ребра к несмежным вер-
вершинам и и v графа G, для которых
deg(u) + deg(i>) > n,
до тех пор, пока это возможно. По завершении процесса полученный граф назовем
замыканием графа G.
ОПРЕДЕЛЕНИЕ 14.78. Пусть G — граф с п вершинами. Замыканием гра-
графа G, обозначаемым cl(G), называется граф, полученный из графа G рекур-
рекурсивным добавлением ребер к несмежным вершинам и и v графа G, для которых
deg(u)+deg(i>) > n до тех пор, пока это возможно.
Таким образом, cl(G) обладает свойством, что если в графе cl(G) есть две
несмежные вершины и и vy для которых deg(tx)+deg(v) > n, то между этими вер-
вершинами существует ребро. Необходимо показать, что cl(G) определено корректно.
Это означает, что если получить граф G' из графа G путем рекурсивного добавле-
добавления ребер к несмежным вершинам и и v графа G, для которых deg(tx)+deg(i;) > п,
пока это возможно, и граф G" из графа G путем рекурсивного добавления ребер

РАЗДЕЛ 14.4. Пути и циклы Гамильтона 607
к несмежным вершинам и и v графа G, для которых deg(u)+deg(i>) > n, пока
это возможно, но другим рекурсивным способом, то G' = G". Для доказатель-
доказательства данного утверждения предположим, что е[,е'2,е'3,... ,е[ — ребра, рекурсивно
добавленные к графу G для построения графа G', а е", е^', е%,..., е^ — ребра, ре-
рекурсивно добавленные к графу G для построения G" Если ребра не совпадают, то
существует, например, ребро в графе G', которое не принадлежит графу G". Пусть
e'j — первое ребро, рекурсивно добавленное для получения графа G', которое не
принадлежит графу G", и пусть e'j = {u,v}. Тогда с ребрами е^е^е^,...,е^-р
добавленными к графу G, deg(u)+deg(v) > п. Но поскольку e'j — первое ребро,
рекурсивно добавленное для получения графа С, которое не входит в граф G",
то ребра е[,е'2,е'3,... ,е^-_1 входят в граф G". Следовательно, deg(tx)+deg(t;) > п
в графе G", но между вершинами и и v не существует ребро, что и приводит
к противоречию. Следовательно, G' = G", поэтому замыкание cl(G) определено
однозначно.
Отметим, что для произвольного графа G cl(cl(G)) = cl(G).
ПРИМЕР 14.79. Если G — граф, изображенный на рис. 14.80, то cl(G) — граф,
изображенный на рис. 14.81.
Рис. 14.80
Рис. 14.81
ПРИМЕР 14.80. Если G — граф, изображенный на рис. 14.82, то cl(G)
изображенный на рис. 14.83.
?
граф,
Рис. 14.83
?
ПРИМЕР 14.81. Если G — полный двудольный граф КШ)ГП при т > 1, то cl(G) —
полный граф Кгп+т. ?
Предлагаем читателю доказать приведенную ниже теорему, используя метод
индукции и теорему 14.77.
ТЕОРЕМА 14.82. Граф G имеет гамильтонов цикл тогда и только тогда, когда
граф cl(G) имеет гамильтонов цикл.

608 ГЛАВА 14. Некоторые специальные вопросы теории графов
На основе теоремы и примера, приведенных выше, получаем, что при т > 1
полный двудольный граф ifm?m имеет гамильтонов цикл.
УПРАЖНЕНИЯ
1. Найдите гамильтонов цикл, если он существует, для каждого из приведен-
приведенных ниже графов.
а) б)
а а \
-^и,
в)
г)
Д)
2. Найдите гамильтонов цикл, если он существует, для каждого из приведен-
приведенных ниже графов.
а) б)

в)
РАЗДЕЛ 14.4. Пути и циклы Гамильтона 609
г)
е f
д)
3. Найдите гамильтонов путь, если он существует, для каждого из приведен-
приведенных ниже графов.
а) б)
d
в)
о t
г)
Д)

610 ГЛАВА 14. Некоторые специальные вопросы теории графов
4. Найдите гамильтонов путь, если он существует, для каждого из приведен-
приведенных ниже графов.
а) б)
а Ь a
в)
Д)
a 1
е
) С
i • /
1 щ J
» •
g h i
г)
5. Докажите теорему 14.74. Если граф G имеет разрезающее ребро, то граф G
не может иметь гамильтонов цикл. Если компоненты графа, полученные при
удалении разрезающего ребра, имеют гамильтоновы циклы, то граф G имеет
гамильтонов путь.
6. Нарисуйте граф с шестью вершинами, который имеет гамильтонов цикл, но
не имеет эйлерова цикла.
7. Нарисуйте граф с шестью вершинами, который имеет эйлеров цикл, но не
имеет гамильтонова цикла.
8. Используя теорему 14.77 и метод индукции, докажите теорему 14.82. Граф
G имеет гамильтонов цикл тогда и только тогда, когда его замыкание cl(G)
имеет эйлеров цикл.

РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 611
14.5. ВЗВЕШЕННЫЕ ГРАФЫ И АЛГОРИТМЫ ПОИСКА
КРАТЧАЙШЕГО ПУТИ
До сих пор при рассмотрении графов нас интересовали вершины и ребра, по
которым можно перемещаться. Теперь нас интересует не только перемещение из
точки А в точку В, но и то, как это сделать наилучшим способом. Первый вопрос
состоит, конечно, в том, что означает "наилучшим способом". Это может быть са-
самый дешевый путь, самый безопасный путь, кратчайший путь или тот, который
требует минимум энергии, или путь, выбранный в соответствии с каким-то иным
критерием. Для определения наилучшего пути присвоим каждому ребру вес или
меру. Если пытаться найти кратчайшее расстояние между двумя городами, то их
необходимо представить в виде вершин, а вес, присвоенный ребрам, — это рас-
расстояние между городами. Если пытаться найти самый дешевый способ перелета
из одного города в другой, то вес ребер между вершинами, представляющими го-
города, будет стоимостью перелета из города в город. Если прямого перелета между
городами нет, то не будет ребра между соответствующими вершинами. Хотя вес
или мера, присвоенные ребрам, могут иметь различные значения, для упрощения
будем рассматривать вес ребра как расстояние, а наилучший путь из точки А в
точку В как кратчайший путь между точками А и В. Это всего лишь вопросы
терминологии, и они ни в коей мере не ограничивают использование теории или
общность результатов. Тем не менее, одно важное ограничение будет введено.
Предположим, что вес или мера, названные теперь расстоянием и приписыва-
приписываемые ребрам между двумя различными точками, положительные. Существуют
алгоритмы, которые с некоторыми ограничениями допускают отрицательные зна-
значения веса ребер. Например, алгоритм Флойда-Уоршолла, приведенный в данном
разделе, можно использовать для ребер с отрицательным весом.
В оставшейся части раздела будем использовать символ оо. Для упрощения
рассмотрения предположим, что все целые числа меньше оо, так что min(a, оо) =
а для каждого неотрицательного целого числа а и min(oo,oo) = оо. Примем
также, что a-boo = oo-foo = oo. Это — для удобства обозначений.
Для улучшения системы обозначений используется следующее определение.
ОПРЕДЕЛЕНИЕ 14.83. Пусть А = {aua2, а3,...,а„)иВ = FЬ Ь2, Ь3,..., Ьп) -
матрицы-строки, где каждое из а; и bi — неотрицательные целые числа или
ос. Тогда
А А В = (min(ab 6i), min(a2, Ь2), min(a3, Ь3), • •, min(an, bn))
ОПРЕДЕЛЕНИЕ 14.84. Пусть с — число, а А = {аиа2, а3,..., ап) — матрица-
строка. Тогда
Первый алгоритм, который будет описан, назывется алгоритмом Дейкстры.
Существует несколько версий этого алгоритма. Первым будет приведен ориги-
оригинальный алгоритм, а затем его улучшенная версия, которая является более эф-

612 ГЛАВА 14. Некоторые специальные вопросы теории графов
фективной. Кроме того, алгоритм обладает дополнительным свойством, которое
позволяет определить не только длину кратчайшего пути, но и сам путь. Это
достигается с помощью указателя, который для каждой вершины из кратчайшего
пути указывет предыдущую вершину пути. Таким образом, если найдена длина
кратчайшего пути между А и В, то двигаясь вдоль кратчайшего пути в обратном
направлении от В к Д можно найти сам путь. Далее будет продемонстрирована
улучшенная версия алгоритма Дейкстры вместе с возможностью находить путь.
Прежде, чем начать, сформулируем теорему, которая может показаться ин-
интуитивно очевидной. Доказательство предоставляется читателю.
ТЕОРЕМА 14.85. Пусть a = viub = vn. Если v\,v2,..., v», и»+ь • • • ^j^j+b- • • ->vn
есть кратчайший путь между а и 6, то v», г>;+ь ..., Vj, часть этого пути между вер-
вершинами V{ и Vj, является кратчайшим путем между V{ и Vj.
Начнем с формулировки первого алгоритма Дейкстры, а затем дадим пример
его использования. Согласно алгоритму отыскивается кратчайшее расстояние от
вершины г>1 к вершине vn. Начинаем с вершины v\ и находим расстояние от v\ до
каждой из смежных с ней вершин. Выбираем вершину, расстояние от которой до
вершины г>1 наименьшее, пусть это будет вершина Vi. Далее находим расстояние
от вершины v\ до каждой вершины, смежной к V{ вдоль пути, проходящего через
вершину Vi. Если это расстояние меньше, чем текущее расстояние, присвоенное
каждой из вершин, то заменяем им текущее расстояние. Снова выбираем вершину,
ближайшую к vi, но не совпадающую с выбранной ранее, и процесс повторяется.
Алгоритм ДейкстрыA)
Для данного взвешенного графа алгоритм дает кратчайшее расстояние
от вершины vi к вершине vn. Каждой вершине поставим в соответствие
упорядоченную пару (оо,0). Первая координата вершины Vi(m,vr) будет
означать присвоенное расстояние от вершины v\ к вершине г>;, а вторая
координата — предыдущую вершину пути от v\ к v{.
A) Начать в вершине ui(oo,0), заменить ее на i>i@,0) и сделать постоянной.
Остальные вершины на этот момент оставить временными.
B) Когда вершина Vk{rn,vr) станет постоянной, для каждой вершины Vj,
смежной к Vk, прибавить величину т к расстоянию от вершины Vk к
вершине Vj. Если это значение меньше, чем текущее расстояние, присво-
присвоенное вершине Vj, заменить текущее расстояние этой суммой и заменить
вторую координату на Vk.
C) Найти минимум из расстояний, приписанных временным вершинам. Пер-
Первую из вершин с таким расстоянием делаем постоянной.
D) Если vn — не постоянная вершина, то возвращаемся к пункту B).
E) Если vn — постоянная вершина, то расстояние, присвоенное вершине vni
является кратчайшим расстоянием от v\ к vn.
F) Для нахождения пути начать в вершине vny найти предшествующую ей
вершину пути (вторая координата). Для каждой вершины пути Vj нахо-
находить предшествующую ей вершину пути, пока не будет достигнута верши-
вершина v\. Перестановка вершин в обратном порядке даст кратчайший путь.

РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 613
ПРИМЕР 14.86. Пусть граф, изображенный на рис. 14.84, — взвешенный граф, в
котором отыскивается кратчайшее расстояние от вершины А к вершине F. Поста-
Поставив в соответствие каждой вершине упорядоченную пару (оо,0), рассматриваемый
граф приводим к виду, показанному на рис. 14.85.
D
В
DK0)
Рис. 14.84
А(оо,0)
Рис. 14.85
F(oo,0)
С(оо,0) 7 Е(оо,0)
Приступим к построению путей от вершины А к другим вершинам. Пер-
Первая компонента упорядоченной пары покажет длину кратчайшего пути к вер-
вершине в момент достидения, а вторая компонента укажет на предыдущую вершину
кратчайшего пути. Первая компонента будет содержать оо, а вторая — 0 до тех
пор, пока путь не найден. Вершина, которая стала постоянной, будет выделена
жирным шрифтом. Выполнив шаг 1 алгоритма, получаем граф, изображенный на
рис. 14.86.
Поскольку вершины В и С — смежные с вершиной А, выполняем шаг 2 и
упорядоченной паре для вершины В присваиваем значение E, А), а упорядочен-
упорядоченной паре для вершины С присваиваем значение F, А). (Фактичестки, изменения
вносятся, тогда и только тогда, когда новые расстояния меньше старых, но по-
поскольку старые расстояния до вершин В и С равны оо, в данном случае это не
имеет значения.) Выполнив шаг 3, выбираем наименьшее из временных присво-
присвоенных значений. В данном случае это расстояние до вершины А, равное 5, и
вершину ВE, А) делаем постоянной. Таким образом, получаем рис. 14.87.
D(oo,0)
D(oo,0)
А@,0)
Рис. 14.86
F(oo,0)
С(оо,0)
А@,0)
Рис. 14.87
F(oo,0)
СF,А)
Возвращаясь к шагу 2, рассмотрим временные вершины С, D, Е и F, смеж-
смежные с вершиной В. В каждом случае прибавляем расстояние от вершины А к
вершине В к расстоянию от вершины В к данным вершинам. Таким образом, для
вершины С это будет 5 + 3 = 8. Для вершины D имеем 5 + 7 = 12. Для верши-
вершины Е имеем 5 + 2 = 7. Для вершины F получаем 5 + 10 = 15. Поскольку новое

614 ГЛАВА 14. Некоторые специальные вопросы теории графов
расстояние до вершины С не меньше, чем уже присвоенное, упорядоченную пару
СF, А) оставляем без изменения. Новые расстояния до вершин Д Е и F меньше
уже присвоенных, поэтому им задаем значения, которые получены для пути из
вершины В, т.е. меняем их на -0A2, В), ЕG,В) и FA5, В). Выполнив шаг 3,
находим наименьшее из расстояний, присвоенных временным вершинам, поэтому
берем min{6,12,15,7} = 6, и поскольку вершина С имеет это расстояние, делаем
вершину СF, А) постоянной. Таким образом, получаем рис. 14.88.
DA2,B)
А@,0)
FA5,B)
СF,А)
ЕG,В)
Рис. 14.88
?
Теперь берем новую постоянную вершину С. Выполнение шага 2 не приводит
к изменениям. Выполнив шаг 3, делаем вершину Е{1,В) постоянной. Получаем
в результате рис. 14.89.
А@,0)
FA5,B)
СF,А)
ЕG,В)
Рис. 14.89
Берем новую постоянную вершину Е и, используя шаг 2, меняем FA5, В) на
). Выполнив шаг 3, делаем вершину F(l\,E) постоянной. Таким образом,
получаем рис. 14.90.
DA2,B)
ВE,А)
F(H,B)
А@,0)
6
СF,А) -*'>«/ Рис М90
Вершина F стала постоянной, поэтому процесс завершен и 11 — это крат-
кратчайшее расстояние от вершины А к вершине F. Если бы совокупность вершин,
смежных с постоянной вершиной, была исчерпана до того, как мы достигли вер-
вершину F, то задача не имела бы решения, поскольку не было бы пути от вершины
А к вершине F. Для нахождения кратчайшего пути заметим, что вершине F
предшествует вершина Е, вершине Е предшествует вершина В, а вершине В
предшествует вершина А. Поэтому кратчайшим путем является ABEF. О

РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 615
Сформулируем теперь второй алгоритм Дейкстры, в котором для нахождения
кратчайшего расстояния между двумя вершинами использованы матрицы. Пусть
п — количество вершин в графе. Матрица W — матрица размерности n x п, в
которой значение W(i, j) равно расстоянию между вершинами Vi и vj, если они
смежные, или полагается равным оо в противном случае. Обозначим г-ю строку
матрицы W через W(i). Используем вспомогательные матрицы Р, Г, Sum и pred
размерности lxn и переменную V. Матрица-строкаpred(i) содержит индекс вер-
вершины, которая предшествует вершине V{ в кратчайшем пути к V{. Матрица-строка
Р(г) хранит постоянное расстояние от вершины v\ к вершине V{, если вершина Vi
выбрана как постоянная вершина. Матрица-строка Т(г) содержит значения вре-
временного расстояния от вершины v\ к вершине V{. Переменная V отслеживает
последнюю постоянную вершину. Матрица-строка Sum используется просто для
временного хранения значений P(V) + W(V).
Алгоритм ДейкстрыB)
A) Установить РA) = О, ТA) = оо и Wj\ = оо при 1 < j < 5. Положить
V = 1.
B) Добавить P(V) к каждому элементу W(V). Более точно, пусть Sum =
P(V) -f W(V). Для Sum(j) < T(j) положить pred(j) = V. Далее, поло-
положить T = Т Л Sum, и для наименьшего г такого, что Т(г) = min{T(j) :
1 < j < ™} положить Р(г) = Т(г), Г(г) = оо и Wji = оо для 1 < j < п.
Положить V = г.
C) Если г ф п, вернуться к шагу 2.
D) Если г = п, то Р(г) — кратчайшее расстояние от v\ к vn.
E) Для нахождения пути использовать pred(n) и найти вершину, которая
предшествует п. Для каждой вершины пути Vj использовать pred(j) и
находить предшествующую ей вершину, пока не будет достигнута вершина
vi. Перестановка вершин в обратном порядке даст кратчайший путь.
ПРИМЕР 14.87. Определим кратчайший путь от вершины ^i к вершине v& для
графа, изображенного на рис. 14.91.
Продемонстрируем алгоритм Дейкстры с использованием матриц и покажем
соответствующий граф. Упорядоченные пары, связанные с вершинами, введем
аналогично предыдущему примеру, после чего получим рис. 14.92.
2 I
•—
Рис.
V2
Лч
Г?
6
14.91
8
-Ы
1
V5
4
%~—
v/oo,0) б
Рис. 14.92
8
6
V/OO.0)
\4
v/00,0)
Вместо того, чтобы использовать предыдущую вершину г>; в качестве второй
координаты для вершины, принадлежащей пути, для представления вершины Vi

616 ГЛАВА 14. Некоторые специальные вопросы теории графов
используем только индекс г. Таким образом, вместо записи Vj(m,Vi), где га —
присвоенное расстояние от вершины v\ к Vj, a V{ — предыдущая вершина пути,
используем запись Vj(m,г).
Первоначально установим pred(i) = 0 для 1 < г < 5, т.к. в данный момент
ни одна из вершин не имеет предшественника. Положим РA) = О, ТA) = оо и
Wji = оо для 1 < j < 5. Это делает вершину v\ постоянной вершиной и приводит
к ситуации, изображенной на рис. 14.93.
v/oo,0)
v/0,0) ^-,„, рис }4дз
Прибавляем РA) = 0 к каждому элементу матрицы-строки
Via, ^15) = @0,2,00,6,00).
Точнее, полагаем Sum = P(l) + Щ1). Для Sum(j) < T(j), полагаем pred(j) = 1.
Затем полагаем T = T A Sum, так что Т = (оо, 2, оо, 6, оо). Это не что иное, как
присваивание расстояния вершинам, смежным с вершиной v\. Для наименьшего
г такого, что Т(г) = min{T(j) : 1 < j < 5}, полагаем Р{г) = Т(г), Г(г) = оо
и Wji = оо при 1 < j < 5. Этим определяется выбор вершины v^ как второй
постоянной вершины. Полагаем V = 2. (Переменная У отслеживает последнюю
постоянную вершину.) Таким образом, Т= (оо, оо, оо,6, оо), Р = @,2, оо, оо, оо)
и pred = @,1,0,1,0). Матрица W имеет вид
W =
Получаем граф, изображенный на рис. 14.94.
00
00
00
00
00
00
00
00
00
00
00
4
0
6
2
6
00
6
0
4
00
8
2
4
0
v/0,0) ,^., рис 14д4
Теперь прибавляем РB) = 2 к каждому элементу матрицы-строки
Щ2) = (W2U W22,W2z, W2A, W25) = @0,00,4,00,8)
Точнее, пусть Sum = РB) + WB), что дает расстояние от вершины v\ к каж-
каждой вершине, смежной с вершиной v2i вдоль пути, проходящего через v2. Для

РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 617
Sum(j) < T(j) полагаем pred(j) = 2. Далее, пусть Т — Т Л Sum, так что Г =
(оо,оо,6,6,10), и для наименьшего г такого, что Т(г) = min{T(jf) : 1 < j < 5}, по-
полагаем P(i) = Т(г), Т(г) = оо и Wji = оо при 1 < j < 5. Таким образом, уз выбра-
выбрана как постоянная вершина. Полагаем V = 3. В результате Г = (оо, оо,оо,6,10),
Р = @,2,6, оо, оо) и pred = @,1,2,1,2). Матрица W имеет вид
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
6
оо
6
0
4
оо
8
2
4
0
Получаем граф, изображенный на рис. 14.95.
v/10,2)
v/0,0)
-/6,1)
Рис. 14.95
Теперь прибавляем РC) = 6 к каждому элементу матрицы-строки
ЩЗ) = (W3l,W32, W33, W34, W35) = (оо, оо, оо, 6,2).
Точнее, полагаем Sum = PC) 4-WC), что дает расстояние от вершины v\ к каж-
каждой вершине, смежной с вершиной vs, вдоль пути, проходящего через вершину
г>з. Для Sum(j) < T(j) полагаем pred(j) = 3. Далее полагаем Т = Т Л Sum, так
что Т = (оо, оо,оо,6,8), и для наименьшего г такого, что T(i) = min{T(j) : 1 <
j < 5}, полагаем P(i) = Т(г), Т(г) = оо и Wji = оо при 1 < j < 5. Это определяет
выбор вершины г>4 как постоянной вершины. В результате Т = (оо, оо,оо,оо, 10),
Р = @,2,6,6, оо), pred = @,1,2,1,3), а
W =
оо оо оо оо оо
оо оо оо оо 8
оо оо оо оо 2
оо оо оо оо 4
оо оо оо оо О
Имеем граф, изображенный на рис. 14.96.
8 v/8,3)
v/0,0)
Наконец, прибавляем РD) = 6 к каждому элементу матрицы-строки
Щ4) = (W4b W42,VF43,^44, W45) = @0,00,00,00,4).

618 ГЛАВА 14. Некоторые специальные вопросы теории графов
Точнее, полагаем Sum = PD)-fVKD). Это дает расстояние от вершины v\ к каж-
каждой вершине, смежной с вершиной г>4, вдоль пути, проходящего через вершину
V4. Для Sum(j) < T(j) полагаем pred(j) = 4. Далее полагаем Т = Т Л Sum,
так что Т = (оо,оо,оо, оо,8), и для наименьшего г такого, что Т(г) = min{T(j) :
1 < 3 < 5}> полагаем Р{г) = Г(г), Т(г) = оо и И^ = оо для 1 < j < 5. Это
определяет выбор вершины уъ как последней постоянной вершины. В результате
имеем Т = (оо, оо, оо, оо, оо), Р = (О,2,6,6,8), pred = @,1,2,1,3), а
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
оо
Таким обраазом, мы получили граф, изображенный на рис. 14.97, и завершили
алгоритм. Длина пути равна 8. Отслеживая путь, как в первом примере, находим,
что У\У2УзУ5 — кратчайший путь.
"AD
2
,0)
8
6
1
v/8,3
^6,1)
Рис.
14.97
?
Теперь рассмотрим алгоритм Флойда-Уоршолла. Этот алгоритм обладает пре-
преимуществом большей эффективности по времени и объему требуемой памяти.
Используя алгоритм, также можно найти кратчайшее расстояние между двумя
вершинами. Данный алгоритм очень напоминает алгоритм Уоршолла, который
использовался для нахождения всех путей в графе путем определения матрицы
А где Aij = 1 тогда и только тогда, когда существует путь из вершины v{ в
вершину Vj. В предыдущем случае мы отыскивали все пути длины 1. Далее —
множество всех 2-путей, в которых серединной вершиной была вершина v\% и
множество комбинировались затем со всеми путями длины 1. Затем отыскивали
все пути длины 3 или менее, проходящие через вершину v\ и/или v2 и/или г»з
(если такие существовали), и продолжали процесс до тех пор, пока не находили
все пути длины п или менее, проходящие через любую из и вершин.
На этот раз, вместо нахождения путей из вершины V{ к вершине Vj, на
каждом этапе находим длину пути и сравниваем ее с найденной ранее длиной
кратчайшего пути из вершины г/» в Vj (если он существует) и заменяем преды-
предыдущее значение в г-ой строке и j-ом столбце новой длиной, если найден более
короткий пути из Vi к Vj. Очевидно, что на этот момент имеется две длины. Одна
длина определена суммированием длин всех ребер, входящих в путь. Другая —
нормальная длина пути, равная числу ребер пути. Надеемся, что удастся избе-
избежать путаницы, если говоря о длине ребра, иметь в виду его вес, как это было
при рассмотрении алгоритмов Дейкстры.

РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 619
Ниже приведены два алгоритма вычисления А. Первый алгоритм более удо-
удобен при вычислениях вручную. Второй — для реализации на компьютере. Он
приводится в конце раздела.
1-й алгоритм Флойда-Уоршолла
A) Посмотрим на столбец 1 матрицы А. Если в j-ой строке столбца имеется
положительное целое число, добавить его к строке 1, чтобы сформировать
Aj. Положить Aj равной j-ой строке матрицы А и заменить j-ую строку
матрицы Л на Л] Л Aj. Назвать эту матрицу А^\
B) Рассмотреть столбец 2 матрицы А^1\ построенной на шаге 1. Если в j-ой
строке столбца имеется положительное целое число, добавить его к строке
2, чтобы сформировать А?. Положить Aj равной j-ой строке матрицы А и
заменить j-ую строку матрицы А^ на A2jAAj. Назвать эту матрицу А^2\
C) Рассмотреть столбец 3 матрицы А^2\ построенной на шаге 2. Если в j-ой
строке столбца имеется положительное целое число, добавить его к строке
3, чтобы сформировать А*. Положить Aj равной j-ой строке матрицы А и
заменить j-ую строку матрицы А^ на A^AAj. Назвать эту матрицу А^К
D) Продолжать процесс, рассматривая следующий, например, г-ый столбец
матрицы, построенной на предыдущем шаге. Если в j-ой строке этого
столбца имеется положительное целое число, добавить его к соответству-
соответствующей строке, чтобы сформировать Л*-. Положить Aj равной j-ой строке
матрицы А и заменить j-ю строку матрицы А^г~^ на AjAAj. Назвать эту
матрицу А^.
E) Продолжать, пока все столбцы не будут проверены.
ПРИМЕР 14.88. Задан граф, изображенный на рис. 14.98.
v< Рис. 14.98
Пусть А — матрица, где Aij — вес ребра {vi,Vj}, если ребро существует и оов
противном случае. В рассматриваемом случае
А =
"О 2 оо 3 оо
2 0 4 оо 1
оо 4 0 6 2
3 оо 6 0 3
оо 1
О
Найдем вес всех путей длины 2, или 2-путей, в которых средней вершиной
является вершина v\. Начинаем с первого столбца. Находим первую строку в
столбце 1, в которой имеется положительное целое число. В данном случае это

620 ГЛАВА 14. Некоторые специальные вопросы теории графов
число 2 в строке 2. Таким образом, существует ребро из вершины v2 к вершине v\
весом 2. Если в строке 1 на позиции A, j) имеется целое число га, то существует
ребро из вершины v\ к вершине Vj весом га. Тогда 2 + ш- вес 2-пути из вер-
вершины v2 в вершину Vj. Таким образом, если прибавить 2 к каждому элементу в
строке 1, то получим строку, которую следует рассматривать как матрицу-строку,
обозначая ее А\ = B,4,оо, 5,оо), так что A2(j) — вес пути длины 2, или 2-пути
из вершины v2 к вершине Vj. Если рассматривать А2 = B,0,4, оо, 1), строку 2
матрицы А как матрицу-строку, тогда A2(j) — вес пути длины 1 из вершины v2 к
вершине Vj. Поскольку нас интересует кратчайший путь для каждого j, заменя-
заменяем строку 2 матрицы А на А\ Л А2 = B,4, оо, 5, оо) Л B,0,4, оо, 1) = B,0,4,5,1).
Аналогичным образом, в строке 4 первого столбца находится число 3. Таким об-
образом, существует ребро из вершины v4 к вершине v\ весом 3. Если в строке 1
на позиции (l,j) имеется целое число га, то существует ребро из вершины v4
к вершине Vj весом га. Тогда 3 + т - вес 2-пути из вершины v4 к вершине
Vj. Следовательно, если прибавить 3 к каждому элементу в строке 1, то полу-
получим строку, которую следует рассматривать как матрицу-строку, обозначая ее
А\ = C,5, оо,6, оо), так что A\(j) — вес 2-пути из v4 к Vj. Если рассматри-
рассматривать А4 = C,оо,6,0,3), строку 4 матрицы А как матрицу-строку, тогда A4(j)
— вес пути длины 1, или 1-пути из вершины v4 к вершине Vj. Поскольку нас
интересует кратчайший путь для каждого j, заменяем строку 4 матрицы А на
А\лА4 = C,5, оо, 6, оо) Л C,оо,6,0,3) = C,5,6,0,3). И т.к. в других строках
столбца 1 больше нет положительных целых чисел, первый этап завершен, в
результате которого имеем
0
2
оо
3
оо
2
0
4
5
1
оо
4
0
6
2
3
5
6
0
3
оо
1
2
3
0
Теперь используем второй столбец матрицы А^\ Если в строке г столбца
2 имеется число fc, то существует ребро из вершины V{ к вершине v2 весом к.
Если в строке j на позиции B,jf) имеется целое число т, то существует ребро
из вершины v2 к вершине Vj весом т. Тогда к 4- т — вес пути из Vi к Vj. Сле-
Следовательно, если прибавить число к к каждому элементу в строке 2, то получим
строку, которую следует рассматривать как матрицу-строку, обозначая ее Af, так
что Af(j) — длина 2-пути из вершины v» к вершине Vj. Если рассматривать Aiy
строку г матрицы А^ как матрицу-строку, тогда Ai(j) — длина пути из вершины
Vi к вершине Vj. Поскольку нас интересует кратчайший путь для всех j, заменяем
строку г матрицы А^ на Af Л А{. Во втором столбце имеется число 2 в строке
1, число 4 — в строке 3, число 5 — в строке 4 и число 1 — в строке 5. Используя
этот процесс для каждой из указанных строк, получаем
0 2 6 3 3
2 0 4 5 1
А{2) = 6 4 0 6 2
3 5 6 0 3
3 12 3 0

РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 621
Рассмотрим теперь третий столбец матрицы А^2\ Для каждой позиции C,.7)
матрицы А^2\ на которой имеется положительное целое число, прибавляем это
число к третьей строке матрицы А^2\ получая матрицу-строку А*, после чего по-
положим Aj равной j-ой строке матрицы А^2\ Далее заменяем j-ю строку матрицы
^ на А? Л Aj и получаем
Г 0 2 6 3 3
2 0 4 5 1
6 4 0 6 2
3 5 6 0 3
3 12 3 0
Теперь рассмотрим четвертый столбец матрицы А^3К Для каждого поло-
положительного элемента на позиции D, j) матрицы А^ добавляем это значение к
четвертой строке матрицы А^3\ чтобы получить А* и положить Aj, равной j-ой
строке матрицы А^3К Далее заменяем j-ю строку матрицы А^ на А1- Л Aj и
получаем
Г 0 2 6 3 3
2 0 4 5 1
6 4 0 6 2
3 5 6 0 3
3 12 3 0
Наконец, рассмотрим пятый столбец матрицы А^4К Для каждого положи-
положительного элемента на позиции E,j) матрицы А^ прибавляем это значение к
пятой строке матрицы А^А\ получая А^, и полагаем Aj, равной j-ой строке мат-
матрицы А^А\ Далее заменяем j-ю строку матрицы А^ на А^ /\Aj и получаем
0 2 5 3 3
2 0 3 4 1
5 3 0 5 2
3 4 5 0 3
3 1 2 3 0 J ?
Второй метод использует то же самый процесс, записанный в псевдокоде,
включая соглашения относительно оо, принятые выше. Единственная разница
состоит в том, что в отличие от метода, изложенного выше, в данной ситуации
допускается, что А{к может не быть положительным целым числом.
И-й алгоритм Флойда-Уоршолла
Цикл по к от 1 до п:
Цикл по г от 1 до п:
Цикл по j от 1 до п\

622 ГЛАВА 14. Некоторые специальные вопросы теории графов
¦ УПРАЖНЕНИЯ
1. Используйте алгоритм Дейкстры для нахождения в приведенных ниже гра-
графах кратчайшего расстояния между вершинами vq и v.
а)
У2 4 Уз 3 *0
1
6 V.
б)
в)
v, 6 v2
г)
д)
2. Используйте алгоритм Флойда-Уоршолла для нахождения кратчайшего рас-
расстояния между вершинами каждого графа из упражнения A).
3. Используйте алгоритм Дейкстры для нахождения в приведенных ниже гра-
графах кратчайшего расстояния между вершинами vq и у.

а)
РАЗДЕЛ 14.5. Взвешенные графы и алгоритмы поиска кратчайшего пути 623
б)
в)
Д)
v. 2 v.
V» • 1
4. Используйте алгоритм Флойда-Уоршолла для нахождения кратчайшего рас-
расстояния между вершинами каждого графа из упражнения 3.

ГЛАВА
ДЕРЕВЬЯ
15.1. СВОЙСТВА ДЕРЕВЬЕВ
В разделе 6.3 дерево определяется как связный граф без циклов. Следующая
теорема обобщает свойства деревьев, приведенные в разделе 6.3.
ТЕОРЕМА 15.1. Следующие утверждения эквивалентны.
а) Граф G — дерево.
б) Граф G — связный и v = е + 1, где v — количество вершин, а е — количество
ребер графа G.
в) Для каждой пары различных вершин а и Ъ существует единственный путь
из а в Ъ.
г) Граф G — ацикличный (не имеет циклов) и v = е -Ь 1.
ДОКАЗАТЕЛЬСТВО. Эквивалентность пунктов (а) и (б) доказана в теоремах 6.37
и 6.38 раздела 6.3. Эквивалентность пунктов (а) и (в) доказана в теоремах 6.40
и 6.41. Пункт (г) есть прямое следствие пунктов (а) и (б). Для доказательства
того, что утверждение (а) следует из утверждения (г), предположим, что граф
G — ацикличный. В этом случае все компоненты Gi,G2,C?3,... ,Gm графа G —
деревья. Для каждого Gi имеем Vi = в{ + 1, где vi — количество вершин, а е* —
количество ребер графа Gi. Поэтому Y^L\ v* = Y;T=iei + m- Но г; = YlT=ivi и
е — YlTLi ег» так что v = е + т. Следовательно, т = 1, поэтому есть только одна
компонента, и граф G — связный. Таким образом, граф G — дерево. ¦
В главе 6 определено, что ориентированное Т — это ориентированный граф
без петель, соотнесенный граф которого является деревом, так что если существу-
существует путь из вершины а в вершину Ь, то он единственный. Ориентированное дерево
Т является корневым ориентированным деревом, если существует единствен-
единственная вершина г;о такая, что indeg(i;o) = 0, и существует путь из вершины v0 в
каждую другую вершину дерева Г. Как и в случае деревьев, представим несколь-
несколько эквивалентных описаний корневых ориентированных деревьев. В приведенном
ниже доказательстве, если р и q обозначают пути, то pq обозначает путь р, за
которым следует путь q.

РАЗДЕЛ 15.1. Свойства деревьев 625
ТЕОРЕМА 15.2. Для ориентированного графа G следующие утверждения экви-
эквивалентны.
а) G — корневое ориентированное дерево.
б) G имеет единственный такой элемент г>о, что для любой вершины а графа
G существует единственный ориентированный путь из vq в а.
в) Соотнесенный граф графа G связен, и G содержит единственный элемент г/
такой, что indeg(t>') = 0, и для любой другой вершины а графа G имеем,
indeg(a) = 1.
г) Соотнесенный граф графа G связен, и G содержит единственный элемент
vq такой, что для любой вершины а графа G существует единственный путь
из vq в а.
ДОКАЗАТЕЛЬСТВО, (а) —> (б) Поскольку G — корневое ориентированное дерево,
то существует ориентированный путь из корня vq в любую заданную вершину а,
и в силу того, что G — ориентированное дерево, этот путь единственный. Корень
только один, и если вершина v'Q обладает тем же свойством, тогда существует
путь р из vq в Vq и путь р' из v'o в vq. Но в таком случае путь рр'р — еще один
путь из vq в v'o, и между vq и v'o существует более чем один путь.
(б)—>(в) Пусть v1 — тот единственный элемент vq, о котором идет речь в
пункте (б). Тогда indeg(t/) = 0, но если indeg(v') ^ 0, для некоторой вершины a
существует ребро (а, г/). Отсюда существует также путь р из г/ в а, и p(a,v')p
также является путем из р в а, поэтому между р и а существует более одного
пути. Вершина v1 — единственная вершина, степень входа которой равна 0. Если
существует другая вершина г>, у которой indeg(i;) = 0, тогда между г/ и v не
существовало бы пути, что противоречит пункту (б). Каждая другая вершина
имеет степень входа 1, потому что если вершина v имеет степень входа больше
чем 1, тогда для двух различных вершин а и 6 существует ориентированное ребро
из а в г; и ориентированное ребро из Ъ в v. Но существует путь р из г/ в а и путь
q из v1 в Ь, так что p(a, v) и д(Ь, г;) — различные пути из vf в г;, что противоречит
пункту (б). Соотнесенный граф графа G связный, поскольку для заданных вершин
а и b существует путь из г/ в а и из г/ в Ь, и, следовательно, в соотнесенном графе
существует путь из а в г/ и путь из г/ в 6, т.е. существует путь из а в Ь.
(в) —> (г) Очевидно, v0 = v'. Согласно пункту (в) для любой вершины графа
а существует путь из vq в а. Предположим, что для некоторой вершины а суще-
существует два пути из vq в а. Пусть Ь — первая вершина, начиная с которой оба пути
из b в а совпадают. Ею может быть и сама вершина а. В этом случае indeg(t) > 1,
что противоречит пункту (в).
(г) —> (а) Предположим, что соотнесенный граф G' содержит два неориенти-
неориентированных пути из вершины г;* в вершину а. Если оба пути ориентированы из г/*
в а, это противоречит гипотезе. Если один путь есть ориентированный путь р
из а в и*, а другой путь — ориентированный путь q из v* в а, то qpq — так-
также ориентированный путь из v* в а, что противоречит условию единственности
пути. Остается только предположить, что один из связных путей из и* в а не
является ориентированным путем. В этом случае в одном из путей для некоторой
вершины с существует ребро F, с) и ребро (d, с). Но поскольку существует ори-
ориентированный путь р' из v* в b и ориентированный путь р" из v* в dy существуют

626 ГЛАВА 15. Деревья
различные пути р'(Ь,с) и p"(d,c) из г;* в с, что опять является противоречием.
Поэтому неориентированный путь из вершины v* в вершину а единственный.
Неориентированный путь из любой вершины а в любую вершину 6 должен быть
единственным, так как если бы существовали два пути из а в 6, то существовали
бы два различных пути из v* в а и в Ъ или, другими словами, два различных
пути из г;* в 6, что неверно. Поэтому G — ориентированное дерево и, поскольку
v* удовлетворяет определению корня, G — корневое ориентированное дерево. ¦
В оставшейся части книги рассматриваются только корневые ориенти-
ориентированные деревья; следовательно, под всеми ориентированными деревьями
следует понимать корневые ориентированные деревья.
Некоторые из приведенных ниже определений для удобства изложения по-
повторены. Обращаем внимание читателя, что во многих учебниках эти определения
сформулированы по-другому.
ОПРЕДЕЛЕНИЕ 15.3. В ориентированном дереве уровень вершины v — это
длина пути от корня дерева до вершины v. Высота ориентрованного дерева
— это длина самого длинного пути от корня до листа.
ОПРЕДЕЛЕНИЕ 15.4. т-арным ориентированным деревом назывется такое
ориентированное дерево, в котором outdeg(v) < га для каждой его вершины v.
Таким образом, родитель имеет не более га сыновей. Полным т-арным ори-
ориентированным деревом назывется такое ориентированное дерево, в котором
outdeg(i;) = га для каждой его вершины v, не являющейся листом, и каждый
лист находится на одном и том же уровне. Таким образом, каждый родитель
имеет в точности га сыновей.
ОПРЕДЕЛЕНИЕ 15.5. m-арное ориентированное деревом высоты h назывет-
назывется сбалансированным {полным, или почти полным), если уровень каждого
листа равен h или h — 1.
ТЕОРЕМА 15.6. Если полное m-арное ориентированное дерево имеет п вершин и
г внутренних вершин, то и = mi 4- 1. Решая относительно г, получаем г = .
т
ДОКАЗАТЕЛЬСТВО. Каждая вершина, за исключением корня, является сыном
внутренней вершины. Поскольку имеется г внутренних вершин и каждая внутрен-
внутренняя вершина имеет т сыновей, всего имеется гт сыновей. Если учесть корень,
то общее число вершин равно mi + 1. ¦
ТЕОРЕМА 15.7. Если полное m-арное ориентированное дерево имеет и вершин,
г внутренних вершин и I листьев, то I = (га — 1)г 4- 1. Решая относительно г,
/-1
получаем г = .
га - 1
ДОКАЗАТЕЛЬСТВО. По предыдущей теореме число вершин равно п = гаг + 1.
Вычитая г внутренних вершин из и — mi + 1, получаем I = п — г = гаг 4-1 — i =
(га — 1)г 4-1 листьев. ¦

РАЗДЕЛ 15.1. Свойства деревьев 627
ТЕОРЕМА 15.8. Полное m-арное ориентированное дерево высоты h имеет mm_~1
вершин и mh листьев. В частности, полное бинарное ориентированное дерево
высоты h имеет 2/l+1 — 1 вершин и 2h листьев.
ДОКАЗАТЕЛЬСТВО. Поскольку число вершин на каждом уровне в т раз больше,
чем на предыдущем, это приводит к геометрической прогрессии, поэтому т-арное
ориентированное дерево высоты h имеет
2 3 н 1 к mh+1 ~ *
1 + га + га2 + га Н 1- mn~l + mn =
771—1
вершин. Поскольку листьями являются только те вершины, которые находятся на
уровне /г, их насчитывается mh. Ш
Доказательство следующей теоремы предоставляется читателю.
ТЕОРЕМА 15.9.
а) Если полное m-арное дерево высоты h имеет / листьев, то h = logm(Z).
б) Если m-арное дерево высоты h имеет / листьев, то h > logm(Z).
в) Если полное бинарное дерево высоты h имеет v вершин, то h = Iog2(i>+1)-1.
г) Если бинарное дерево высоты h имеет v вершин, то h > Iog2(t; + 1) - 1.
Напомним, что функция / из графа G(V,E) в граф G'{Vl,E') назывется
гомоморфизмом из G в С, обозначается / : G —> G\ если она обладает следую-
следующими свойствами.
ОПРЕДЕЛЕНИЕ 15.10.
а)
б)
в)
Если
Если
Если
ребру
е € Е, то
v € V, то
вершины
Де) в G
fie)
fiv)
и и v
f
е
е
Е1
V
(f(E)
(f(V)
С
с
инцидентны
Е').
V).
ребру
е в G, то f(u)
и f(v) инцидентны
Напомним также, что гомоморфизм / : G —> G' является изоморфизмом,
если / : V —> V и / : Е —> Е1 являются взаимно однозначными соответствиями.
Если / : G —> G' изоморфизм, то говорят, что G и G' изоморфны.
ОПРЕДЕЛЕНИЕ 15.11. Два корневых бинарных дерева T(E,V) и T'{E',V)
изоморфны, если существует изоморфизм / из Т в Т' такой, что
а) V{ — левый сын вершины Vj тогда и только тогда, когда f(vi) — левый
сын вершины f{vj).
б) Vi — правый сын вершины Vj тогда и только тогда, когда f(vi) — правый
сын вершины f(vj).
в) / отображает корень г дерева Т в корень г1 дерева Т".
Любителям заниматься подсчетами предлагаем следующую теорему.
ТЕОРЕМА 15.12. Число неизоморфных корневых бинарных деревьев с п верши-
вершинами равно числу Каталана Сп.

628 ГЛАВА 15. Деревья
ДОКАЗАТЕЛЬСТВО. Пусть 1п — число изоморфных корневых бинарных деревьев
с п вершинами. Если п = О, имеем пустое дерево и полагаем Iq = 1. Если п = 1,
имеем одну вершину и, очевидно, только одно дерево, поэтому 1\ = 1. Если и = 2,
имеем два корневых бинарных дерева, изображенных на рис. 15.1. Если п = 3,
имеем пять корневых бинарных дерева, изображенных на рис. 15.2.
/ \ л
Рис. 15.1 Рис. 15.2
Предположим, что п > 3, и выберем такое к, что 1 < к < п. Пусть Тп обозна-
обозначает дерево с п вершинами и пусть Тп^ — дерево с и вершинами, определенное
следующим образом. Поскольку одна вершина является корнем, предположим,
что имеются правое поддерево Tk-i с к — 1 вершиной и левое поддерево Тп-к с
п- к вершинами, как показано на рис. 15.3.
Рис. 15.3
Тогда по определению число способов, которыми можно построить дерево Tk-i,
равно ifc-ъ а число способов, которыми можно построить дерево Тп_ь равно
In-к- Таким образом, число способов построения Тп^ равно h-i-In-k- Суммируя
по fc, получаем число всевозможных способов построения дерева Тп. Итак,
что совпадает с определением числа Каталана Сп. Поэтому
Bп)!
In = Сп =
п 4-1 п\ • п\
УПРАЖНЕНИЯ
1. Найдите неизоморфные корневые бинарные деревья с п вершинами: когда
а) п = 2; б) п = 3; в) п = 4.
2. Сколько существует неизоморфных корневых бинарных деревьев с и верши-
вершинами:
а) п = 5; б) п = 6; в) п = 8;
г) п = 10; д) п = 20.

РАЗДЕЛ 15.1. Свойства деревьев 629
3. Сколько в полном m-арном дереве высоты h имеется листьев, вершин и
внутренних вершин при условии:
а) га = 2 и h = 5; б) т = 3 и h = 4;
в) m = 2 и h = 8; г) га = 4 и /i = 3;
д) га = 1 и h = 10.
4. Для дерева, изображенного на рис. 15.4, определите:
(i) высоту корневого дерева;
(и) уровень вершины е;
(iii) уровень вершины д\
(iv) уровень вершины а;
(v) какая вершина является родителем г;
(vi) какие вершины являются сыновьями вершины b
а) если корнем выбрана вершина d\
б) если корнем выбрана вершина /;
в) если корнем выбрана вершина с;
г) если корнем выбрана вершина j\
д) если корнем выбрана вершина Ъ.
Рис. 15.4
5. Для дерева, изображенного на рис. 15.5, определите:
(i) высоту корневого дерева;
(ii) уровень вершины е;
(iii) уровень вершины д\
(iv) уровень вершины а;
(v) какая вершина является родителем г;
(vi) какие вершины являются сыновьями вершины Ь
а) если корнем выбрана вершина d\
б) если корнем выбрана вершина /;

630 ГЛАВА 15. Деревья
в) если корнем выбрана вершина с;
г) если корнем выбрана вершина j\
д) если корнем выбрана вершина 6.
6. Какие из приведенных ниже деревьев являются сбалансированными? Какие
из них являются полными?
а) б) в)
г)
д)
d e
е f g
7. Какие из приведенных ниже деревьев являются сбалансированными? Какие
из них являются полными?
а) б) в)
X
с d
е
е f g hi j
г)
Д)
8. При условии, что полное бинарное дерево имеет 32 листа, определите:
а) высоту этого дерева;
б) количество вершин.
9. При условии, что полное бинарное дерево имеет 128 листьев, определите:
а) высоту этого дерева;
б) количество вершин.
10. Докажите, что
а) для полного m-арного дерева высоты h с I листьями h — logm(/);
б) для полного m-арного дерева высоты h с I листьями h > logm(Z);
в) для полного бинарного дерева высоты h с числом вершин, равным v,

РАЗДЕЛ 15.2. Бинарные деревья поиска 631
11. Докажите теорему 15.9
а) для полного m-арного дерева высоты h с / листьями h = logm(Z).
б) для полного m-арного дерева высоты h с I листьями h > logm(Z).
в) для полного бинарного дерева высоты h с числом вершин, равным v,
h = log2(v + l) - 1.
г) для бинарного дерева высоты /г, имеющего v вершин, h > Iog2(i; +1) — 1.
12. Докажите, что дерево с двумя или более вершинами является двудольным
графом.
13. Докажите, что связный граф является деревом тогда и только тогда, когда
добавление нового ребра между вершинами графа всегда приводит к возник-
возникновению цикла.
14. Докажите или опровергните, что связный граф является деревом тогда и
только тогда, когда каждое его ребро является разрезающим ребром.
15. Докажите или опровергните, что связный граф является деревом тогда и
только тогда, когда каждая его вершина является разрезающей вершиной.
16. Какие вершины в корневом дереве являются разрезающими?
17. Пусть G — связный граф. Сформулируйте необходимые и достаточные усло-
условия того, что удаление из графа G любого ребра превращает его в дерево.
18. Пусть T(V, E) — корневое дерево. Определим отношение < на V как а < 6,
если a = b или а — потомок Ь. Покажите, что отношение < есть частичный
порядок. Определим произведение a • Ъ = нвг(а, 6), так что (V,-) — верхняя
полурешетка. Опишите a • b в терминах путей из вершин а и b в корень.
19. Пусть T(V, E) — корневое дерево. На V определено умножение, как в пре-
предыдущем упражнении. Для заданной вершины а из V определим a : V —> V
как a(v) = av. Докажите, что a — гомоморфизм полугрупп.
15.2. БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА
Бинарное корневое дерево, которое назовем просто бинарным деревом, обеспе-
обеспечивает прекрасный метод организации данных, при котором любые конкретные
данные можно легко найти или установить их отсутствие. Очевидно, что самый
неэффективный способ поиска — последовательный просмотр всех данных, так
как если необходимые данные отсутствуют, то для установления этого факта нуж-
нужно просмотреть весь список. Бинарное дерево поиска позволяет избежать этого.
Единственным требованием является введение на данных некоторого линейного
порядка. Этим порядком может быть, к примеру, алфавитный или числовой по-
порядок. Линейный порядок может быть на теге, указателе, файле или некотором
другом ключе, определяющем данные. Но нас будет интересовать только нали-
наличие некоторого линейного порядка. Для простоты примем расположение имен в
алфавитном порядке. Бинарное дерево поиска — это прежде всего бинарное де-
дерево, в каждом узле которого находится имя (или другой ключ). Рассмотрим
построение бинарного дерева поиска. В процессе построения станет понятно, как
использовать это дерево. Предположим, что необходимо запомнить имена: Петер-
сон, Джонсон, Смит, Вейл, Спенсер, Рассел, Бауэр, Мартин, Уилсон и Лайман.

632 ГЛАВА 15. Деревья
Начинаем с имени Петерсон и помещаем его в корень дерева. Поскольку следую-
следующее имя, Джонсон, в алфавитном порядке стоит перед именем Петерсон, делаем
Джонсона левым сыном Петерсона, как показано на рис. 15.6. Следующее имя,
Смит, в алфавитном порядке стоит после имени Петерсон, поэтому имя Смит
становится правым сыном имени Петерсон, как показано на рис. 15.7.
Петерсон
Петерсон
[Дж
онсон
Рис. 15.6
Джонсон
Рис. 15.7
Смит
Теперь рассмотрим имя Вейл. В алфавитном порядке имя Вейл стоит перед
(или меньше, чем) именем Петерсон, спускаемся к левому сыну, Джонсону, и
поскольку в алфавитном порядке имя Вейл расположено перед именем Джонсон,
делаем Вейла левым сыном Джонсона, как показано на рис. 15.8.
Далее рассматриваем имя Спенсер. Поскольку в алфавитном порядке имя
Спенсер идет после имени Петерсон, спускаемся к правому сыну, Смиту. Но так
как в алфавитном порядке имя Спенсер расположено после имени Смита, делаем
Спенсера правым сыном Смита, как показано на рис. 15.9.
IПетерсон |
Смит
Спенсер
Следующее имя Рассел. Поскольку по алфавиту имя Рассел стоит после
имени Петерсон, спускаемся к правому сыну, Смиту. Имя Рассел по алфавиту
расположено перед именем Смит; делаем Рассела левым сыном Смита, как пока-
показано на рис. 15.10.
Петерсон
Джонсон
Смит
Рассел
Спенсер
Рис. 15.10
Надеемся, что теперь схема начинает проясняться. Предположим, что есть
имя, которое необходимо поместить в дерево. Если в вершине дерева уже есть
имя и вставляемое имя в алфавитном порядке стоит после этого имени, то следует
спуститься к левому сыну, а если оно стоит до этого имени, то нужно спуститься

РАЗДЕЛ 15.2. Бинарные деревья поиска 633
к правому сыну. Если в вершине нет имени, то имя, которое нужно вставить,
помещается в данную вершину.
Используя эту процедуру, доведем до конца рассмотрение нашего списка.
Следующее имя — Бауэр. По алфавиту оно стоит перед именем Петерсон, поэтому
спускаемся к левому сыну, Джонсону. По алфавиту имя Бауэр стоит перед именем
Джонсон, поэтому спускаемся к левому сыну, Вейлу. В алфавитном порядке имя
Бауэр располагается перед именем Вейл, поэтому спускаемся к левому сыну.
Поскольку там нет имени, делаем Бауэр левым сыном, как показано на рис. 15.11.
Петерсон
[Джонсон] | Смит
|Вейл
Рассел
Спенсер
Рис. 15.11
Следующее имя, которое необходимо сохранить, — Мартин. Это имя по ал-
алфавиту стоит перед именем Петерсон, поэтому спускаемся к левому сыну, Джон-
Джонсону. Но имя Мартин в алфавите следует после имени Джонсон, отсюда спуска-
спускаемся к правому сыну и, поскольку там нет имени, делаем Мартина правым сыном,
как показано на рис. 15.12.
Петерсон
Джонсон
Смит
Вейл 11 МартинI Рассел | Спенсер
Бауэр
Рис. 15.12
Далее имя, которое необходимо сохранить, — Уилсон. Поскольку в алфа-
алфавитном порядке оно стоит после имени Петерсон, спускаемся к правому сыну,
Смиту. Но имя Уилсон расположено после имени Смит, значит, спускаемся к
правому сыну, Спенсеру. Поскольку имя Уилсон стоит по алфавиту после имени
Спенсер, и у Спенсера нет правого сына, делаем Уилсона правым сыном Спенсера,
как показано на рис. 15.13.
[?тётерсон|
|Дж>
онсон
Вейл
/
Бауэр
Мартин
Рассел
Спенсер
\
Уилсон
Рис. 15.13

634 ГЛАВА 15. Деревья
Последним по счету, но не по значению, помещаем на свое место имя Лай-
ман. Имя Лайман по алфавиту стоит перед именем Петерсон, спускаемся к левому
сыну, Джонсону. Поскольку по алфавиту имя Лайман стоит после имени Джон-
Джонсон, спускаемся к его правому сыну, Мартину. Так как имя Лайман по алфавиту
стоит перед имением Мартин, спускаемся к его левому сыну. Но там имени нет,
поэтому делаем Лаймана левым сыном Мартина.
При достижении левого (или правого) сына, который еще не определен, ве-
вероятно, точнее было бы сказать: "Если левый (правый) сын не существует, то
создаем вершину и сохраняем имя", вместо: "Если там нет имени, то сохраняем
имя". Но в данной ситуации внимание сосредотачивается, в основном, на концеп-
концепции, а не на технических деталях. Теперь приведем алгоритм вставки имени в
дерево поиска, который реально создает дерево поиска, за исключением размеще-
размещения имени в корне дерева. Используя < и >, следует иметь в виду, что сказанное
применимо для любого упорядочения.
Вставка(элемент)
A) Начинаем с корня.
B) Если элемент < объекта в вершине, переходим к левому сыну.
C) Если элемент > объекта в вершине, переходим к правому сыну.
D) Повторяем шаги 2 и 3, пока не достигнем вершины, которая не определена.
E) Если достигнутая вершина не определена, то определяем вершину и встав-
вставляем элемент.
Поскольку метод создания дерева поиска описан, легко понять, как произ-
производить поиск элемента в дереве. Используется, в основном, тот же самый подход,
кроме проверки, является ли данное имя больше или меньше имени в вершине,
проверяется также несовпадение этого имени с именем в вершине. Если последнее
выполняется, процесс поиска завершен. В противном случае повторяются преды-
предыдущие действия. Если достигается вершина, которая не определена, это означает,
что данное имя не хранится в дереве. Предположим, например, что в рассмотрен-
рассмотренном выше дереве разыскивается имя Дженкинс. Поскольку оно "меньше, чем имя
Петерсон", идем к левому сыну, Джонсону. Но так как имя Дженкинс "меньше,
чем имя Джонсон", идем к левому сыну, Вейлу. Поскольку данное имя "больше,
чем Вейл" (на самом деле нет имени больше, чем Вейл), идем к правому сыну.
Но он не определен, поэтому данное имя отсутствует в списке. Далее приведен
алгоритм поиска имени в дереве поиска.
Поиск(элемент)
A) Начинаем с корня.
B) Если элемент < объекта в вершине, идем к левому сыну.
C) Если элемент > объекта в вершине, идем к правому сыну.
D) Если элемент = объекту в вершине, то имя найдено; выполняем соответ-
соответствующие действия и выходим.
E) Повторяем шаги 2, 3 и 4, пока не достигнем вершины, которая не опреде-
определена.

РАЗДЕЛ 15.2. Бинарные деревья поиска 635
F) Если достигнутая вершина не определена и в дереве нет имени, то выпол-
выполняем соответствующие действия и выходим.
Вполне очевидно, что длина пути поиска элемента не может превышать
высоту дерева. Поэтому, если дерево полное, то по теореме 15.9 в самом неблаго-
неблагоприятном варианте длина пути имеет порядок ОAп(п)), где п — число элементов
в дереве. Следовательно, если дерево сбалансированное, самый неблагоприятный
случай имеет порядок ОAп(п)).
В заключение рассмотрим, как удалять вершину из дерева. Предлагается
один из методов. При изложении будут опущены все технические детали, касаю-
касающиеся его фактической реализации.
Метод резюмирован в приведенном ниже алгоритме.
Удаление(элемент)
A) Если вершина vo не имеет сыновей, просто удаляем ее.
B) Если вершина vo имеет одного сына, удаляем v0 и заменяем ее сыном.
C) Если vo имеет двух сыновей, находим правого сына v\ вершины г>о, а
затем находим левого сына вершины v\ (если он существует). Продолжаем
выбирать левых сыновей каждой найденной вершины, пока не найдется
такая вершина v, у которой не будет левого сына. Заменим v0 на v и
сделаем правого сына вершины v левым сыном родителя вершины v.
ПРИМЕР 15.13. Рассмотрим дерево, изображенное на рис. 15.14. Если удалить
вершину х, то получится дерево, изображенное на рис. 15.15. Если же удалить
вершину /с, то получится дерево, изображенное на рис. 15.16.
Р е Р е Р
k w k w * w
\ /\ \ / /\
I s х Is s х
/\ /\ /\
q t q t q t
\ \ \
г г г
Рис. 15.14 Рис. 15.15 Рис. 15.16
Если в исходном дереве удаляется вершина /г, нужно спуститься к правому
сыну р, а затем к левому сыну к. Поскольку к не имеет левого сына, это искомый
элемент для замены. Итак, меняем h на к и делаем / левым сыном р. В результате
получаем дерево, изображенное на рис. 15.17.
Если вместо этого необходимо удалить вершину р, следует идти вправо к
вершине ги, затем влево к 5, затем влево к q. Поскольку q не имеет левого сына,

636 ГЛАВА 15. Деревья
это искомая вершина для замены. Поэтому заменяем р на q и делаем г левым
сыном вершины s. В результате получаем дерево, изображенное на рис. 15.18.
w
X
г г' Ч
Рис. 15.17 Рис. 15.18 П
УПРАЖНЕНИЯ
1. Задано дерево (рис. 15.19).
а) Вставьте букву j.
б) Вставьте букву и.
в) Вставьте букву т.
2. Задано дерево из предыдущего упражнения.
а) Сколько требуется сравнений для определения того, что г отсутствует?
б) Сколько требуется сравнений для определения того, что и отсутствует?
в) Сколько требуется сравнений для определения того, что / отсутствует?
е Р
/ \
У \
к w
/ \
q t
\
Рис. 15.19
3. Задано дерево (рис. 15.20).
а) Вставьте букву е.
/
(
Рис.
m
/\
/ \
'\ /\
\ / \
/ \
о г
15.20

РАЗДЕЛ 15.2. Бинарные деревья поиска 637
б) Вставьте букву п.
в) Вставьте букву и.
4. Задано дерево из предыдущего упражнения.
а) Сколько требуется сравнений для определения того, что и отсутствует?
б) Сколько требуется сравнений для определения того, что и отсутствует?
в) Сколько требуется сравнений для определения того, что Ь отсутствует?
5. Опишите бинарное дерево с пятью вершинами, которое дает наихудший ва-
вариант для поиска?
6. Постройте бинарное дерево для следующих имен, хранящихся в алфавитном
порядке, если данные вводились в таком порядке: Говард, Джеймс, Аарон,
Спенсер, Джексон, Мэдисон, Винес, Кальхаун, Варне, Макдав и Петерсон.
7. Постройте бинарное дерево для имен президентов Соединенных Штатов,
хранящихся в алфавитном порядке, если имена вводились в том порядке, в
котором президенты находились на своем посту первый срок.
8. Постройте бинарное дерево для приведенных ниже чисел, хранящихся в
обычном порядке, если они вводились в следующем порядке: 25, 35, 15, 25,
48, 36, 22, 44, 18, 30, 42, 11, 39, 32.
9. Постройте бинарное дерево для приведенных ниже букв, хранящихся в алфа-
алфавитном порядке, если они вводились в следующем порядке: m,a,r,i,g,o,l,d,
s,t,u,l,i,p,s.
10. Постройте бинарное дерево для приведенных ниже марок автомобилей, хра-
хранящихся в алфавитном порядке, если данные поступили в следующем по-
порядке: Бэнсон, Крайслер, Шевроле, Додж, Мэркьюри, Нэш и Олдсмобил.
11. Постройте бинарное дерево высоты 4 для букв английского алфавита.
12. Задано дерево (рис. 15.21).
с h r w
/V /\ /\ /\
a d g к р t v z Рис.
а) Удалите а.
б) Удалите /.
в) Удалите т.
г) Удалите и.
д) Удалите г.
13. Задано дерево (рис. 15.22).
a d m t
./\
A/ s "
f l Puc. 15.22

638 ГЛАВА 15. Деревья
а) Удалите а.
б) Удалите е.
в) Удалите г.
г) Удалите т.
д) Удалите t.
14. Напишите программу для алгоритма Вставка (элемент) в псевдокодах или
на заданном языке.
15. Напишите программу для алгоритма Поиск (элемент) в псевдокодах или на
заданном языке.
16. Напишите программу для алгоритма Удаление (элемент) в псевдокодах или
на заданном языке.
15.3. ВЗВЕШЕННЫЕ ДЕРЕВЬЯ
В этом разделе рассматриваются две проблемы, имеющие одно и то же решение.
В компьютере все буквы и другие символы хранятся в виде строк из единиц
и нулей. Например, если символы хранятся как ASCII-символы, они состоят из
строк длины 7 плюс восьмой символ, который используется для контроля четно-
четности. Пусть А — множество всех символов, которые необходимо сохранить. Всегда
есть возможность сохранить А в виде строк некоторой фиксированной длины п,
состоящих из единиц и нулей. Это дает существенное преимущество при "деко-
"декодировании" строки обратно в символы из А. Первые п байтов (единиц и нулей в
строке) образуют первый символ из А, вторые п байтов — второй символ и т.д.
Однако, если данных достаточно много, всегда желательно провести их ком-
пактификацию, т.е. использовать для их хранения как можно меньше места. Оче-
Очевидный способ компактно скомпоновать данные — изменять длину строк, ис-
используемых для их хранения, так чтобы более короткие строки хранили часто
используемые символы, а более длинные строки — редко используемые симво-
символы. И здесь возникает проблема: если строки, представляющие разные символы,
имеют разную длину, то как узнать, где заканчивается строка одного символа и
начинается строка другого? Например, если Ъ представлено как 101, е как 11, а
как 10, q как 1011 и w как 110, то строка 1011110 представляет Ьеа или qw?
Определим однозначно декодируемый код для языка как такое множество,
что каждая строка в языке может быть задана однозначно как конкатенация
элементов С. В этом случае строки из единиц и нулей, представляющие элемен-
элементы из А, будут нашим кодом. Если эти строки образуют однозначно декодируе-
декодируемый код, то, по крайней мере, разделяя строки на элементы, представляющие А,
мы знаем, что представление однозначно и, следовательно, декодированные слова
правильные. Хотелось бы это как-то улучшить. Определим код С как префикс-
префиксный код, если он обладает тем свойством, что никакой элемент кода не может
быть начальной строкой другого элемента кода. Таким образом, прочитав строку
из единиц и нулей, представляющую символ из А, мы знаем, что это искомый
символ, а не начало другого символа. Поэтому следующие 1 или 0 должны на-
начинать строку для следующего символа, который декодируется. Например, если

РАЗДЕЛ 15.3. Взвешенные деревья 639
строки 111, 1011, 1001, 110 и 01 представляют в пятибуквенном алфавите соот-
соответственно буквы а, е, г, о и и и в качестве первых трех знаков строки имеются
цифры 110, это означает представление буквы о, поскольку никакая другая буква
не начинается с этих цифр. Аналогично, если следующие три цифры 011, это
означает, что 01 представляет букву и, а 1 — начало следующей буквы.
Рассмотрим бинарное дерево с листьями
^ь t>2<> ^з, ?4, ?5 и t6, изображенное на рис. 15.23.
Если рассматривать путь от корня дерева к лю-
любому из листьев, то каждое ребро вдоль пути
должно вести к правому или левому сыну пре-
предыдущей вершины. Если ребро ведет к левому
сыну, обозначим его через 0, а если к право-
правому сыну, то пометим его 1. Поскольку путь к
листу vi есть путь к левому сыну, а затем к рис. 15.23
другому левому сыну, то путь к v\ обозначаем
через 00. Аналогично пути к v2, v3, v4, vb и v6 обозначаются через 010, 011, 10,
ПО и 111. Строку, соответствующую данному листу, назовем путевым кодом.
Заметим, что строки, соответствующие этим листьям, образуют префиксный код.
Строка, соответствующая каждому листу, определяется однозначно, так как к
каждому листу ведет единственный путь. Обобщая вышеизложенное, приходим
к следующей теореме. Доказательство оставляем читателю.
ТЕОРЕМА 15.14. В любом бинарном дереве путевые коды для листьев дерева
являются префиксным кодом.
Предположим, что имеется бинарное дерево и для каждого символа в алфа-
алфавите А, который требуется представить с помощью двоичной строки, на дереве
имеется лист. Присвоим каждой букве алфавита А путевой код соответствующего
листа на бинарном дереве. Таким образом, если буквы а, е, г, о, и и w связаны
соответственно с листьями v\, V2, г?3, v±, ^5 и vq в упомянутом выше дереве, то
буквам а, е, г, о, и и w соответствуют строки 00, 010, 011, 10, 110 и 111. Первона-
Первоначальная формулировка задачи содержала требование, чтобы часто встречющиеся
символы имели более короткие строки. В рамках изложенного выше метода это
означает, что часто встречающимся символам должен соответствовать более ко-
короткий путь от корня или, что равносильно, они должны находиться на более
низком уровне. Для того чтобы оценить, насколько близки мы от цели поставить
в соответствие часто встречающимся буквам более короткие строки, т.е. миними-
минимизировать коды, необходим некоторый критерий. Предположим, что каждая буква
at в алфавите символов А появляется с относительной частотой /» и представля-
представляющая ее двоичная строка имеет длину /;. Тогда величина
W = hfl + /2/2 + /3/3 + /4/4 + ' • • + L
называется весом кода. Если листья взвешенного дерева представляют знаки
кода, вес листа равен частоте появления буквы, а расстояние от корня до вершины
равно длине двоичного кода для символа в листе. Определим вес дерева как

640 ГЛАВА 15. Деревья
величину
+ /2/2 + /з/з + /4/4 + • • • +
В более общем виде вес дерева определяется как
w =
l2w2 4-
H К
г=1
где ^ — вес, приписанный вершине viy и /; — длина пути от корня до вершины.
Данное понятие не следует путать с понятием взвешенного графа, включающего
деревья, где вес приписывается ребрам. Эти вопросы мы обсудим в разделе 15.6.
Чем меньше вес дерева, тем в большей степени достигнута поставленная
цель. Таким образом, чтобы найти наилучший код для минимизации данных,
необходимо найти код с минимальным весом. Процесс построения такого дерева
называется алгоритмом Хаффмана. Код, приписываемый символам согласно их
путевому коду, называется кодом Хаффмана. Прежде чем излагать алгоритм,
следует разобраться в механизме его работы. Предположим, имеются следующие
буквы и соответствующие им частоты:
символ
а
е
w
к
т
#
%
частота
7
10
3
5
8
2
1
А
% #
Рис. 15.24
Для начала разместим частоты в возрастающем по-
порядке: A,2,3,5,7,8,10). Затем формируем дерево, исполь-
используя две буквы с наименьшими частотами в качестве вер-
вершин и сумму частот в качестве их родителя. Помещаем
0 на ребре к левому сыну и 1 на ребре к правому сыну,
после чего получаем дерево, изображенное на рис. 15.24.
В списке частот заменяем значения двух наимень-
наименьших частот их суммой, после чего имеем C,3,5,7,8,10).
Если бы полученная сумма оказалась больше одной или
нескольких частот в списке, его надо было бы отсортиро-
отсортировать так, чтобы частоты снова располагались в возраста-
возрастающем порядке. Опять выбираем две вершины или деревья
в соответствии с наименьшими числами в списке частот
и формируем дерево с этими вершинами или деревьями в качестве сыновей и
их суммой в качестве родителя. В данном случае это дерево со значением 3 и
буква w со значением 3 в качестве сыновей и их суммой 6 в качестве родителя.
Рис. 15.25

РАЗДЕЛ 15.3. Взвешенные деревья 641
Помещаем 0 на ребре к левому сыну и 1 на ребре к правому сыну, после чего
получаем граф (рис. 15.25).
Теперь заменим в списке частот значения двух наи-
наименьших частот их суммой, 6, и расположим значения
в возрастающем порядке. В результате получим список
E,6,7,8,10). Во всех случаях значения вершин или дере-
деревьев, использованных в качестве сыновей, удаляются из
списка частот и из строящегося дерева. Мы формируем
дерево, выбирая две вершины или два дерева с наимень-
наименьшими числами в списке частот и используя их как сыно-
сыновей, а их сумму в качестве частоты родителя. В данном
случае это вершина к со значением 5 и дерево со значе-
значением 6. Помещаем 0 на ребро к левому сыну и 1 на ребро
к правому сыну, после чего получаем дерево, изображенное на рис. 15.26.
В списке частот опять заменяем значения двух наименьших частот их сум-
суммой, 11, и располагаем значения частот в возрастающем порядке, после чего по-
получаем список G,8,10,11). Продолжая процесс, получаем следующие деревья и
списки частот: рис. 15.27 A0,11,15) и рис. 15.28 A5,21).
15
к 0/\1 а т
к 0/\1 а т
Л
Рис. 15.27
Рис. 15.28
Наконец, соединяем два оставшихся дерева, поместив 0 на ребро к левому
сыну, 1 на ребро к правому сыну, в результате получаем дерево, изображенное на
рис. 15.29.
Рис. 15.29
Помещать сумму в корень нет необходимости. Заметим, что числами кода
Хаффмана для а, е, w, fc, га, # и % являются 00, 10, 1111, 01, ПО, 11101 и 11100
соответственно. Ниже представлен алгоритм Хаффмана построения дерева для
символов si, 52,... 5П, имеющих соответствующие частоты /i, /2,..., /п.

642 ГЛАВА 15. Деревья
Алгоритм Хаффмана ((si, Д), (s2, /2),..., (sn, fn))
A) Расположить частоты в возрастающем порядке в таблице частот.
B) Если fi и fj — две наименьшие частоты, то сформировать бинарное дерево
с Si и Sj в качестве сыновей, где Si — левый, a fi + fj — частота родителя.
Поместить 0 на ребро к левому сыну, а 1 — на ребро к правому сыну.
C) Удалить fi и fj из таблицы частот и заменить суммой /» + fj.
D) Снова расположить частоты в возрастающем порядке.
E) Удалить две наименьшие частоты из таблицы частот и сформировать дере-
дерево, используя в качестве сыновей символы или деревья, соответствующие
этим частотам, когда меньший символ или дерево — левый, а сумма их ча-
частот — частота родителя. Если какой-либо из сыновей — дерево, удалить
метку его частоты из построенного дерева.
F) Заменить значение двух наименьших частот их суммой.
G) Повторять шаги 4-7, пока в таблице частот не останется только один
элемент.
(8) Удалить частоту из корня дерева и из таблицы частот.
(9) Сформировать код Хаффмана для элемента, составляя строку из единиц
и нулей на ребрах пути из корня к заданному элементу.
Рассмотрим вторую из упомянутых выше задач с таким же решением. Пред-
Предположим, имеется и элементов данных и известна частота использования каждого
из них. Требуется сохранить их как листья бинарного дерева так, чтобы наиболее
часто используемые элементы были более доступны при обратном поиске. Но это
означает, что наиболее часто используемым элементам должны соответствовать
самые короткие пути от корня. Это как раз то, что делалось до сих пор, поскольку
наиболее часто используемые символы имеют самые короткие двоичные строки
и, следовательно, самые короткие пути от корня.
ПРИМЕР 15.15. Предположим, имеются следующие буквы и их частоты:
символ
А
В
С
D
Е
F
частота
15
25
10
30
15
5
Построим такое бинарное дерево, чтобы наиболее часто используемые эле-
элементы были возможно ближе расположенны к корню. Более точно, требуется
найти такое дерево, что вес дерева
+ /2/2 + hfs + /4/4 + • • • 4- lnfn =
i=\

РАЗДЕЛ 15.3. Взвешенные деревья 643
минимален, где U и fa — уровень и частота заданного элемента. Сначала упоря-
упорядочим частоты, приведенные в списке частот E,10,13,17,25,30). Воспользовав-
Воспользовавшись приведенным выше алгоритмом, получаем следующие деревья и списки ча-
частот: рис. 15.30, A3,15,17,25,30); рис. 15.31 A7,25,28,30); рис. 15.32 B8,30,42);
рис. 15.33 D2,58).
0/
•
F
Рис.
15
\l
•
С
15.30
28
л
А
е А
• •
F С
Рис. 15.31
28
А
Е «Д,
• •
F С
Рис. 15.32
С
/
4
А
42
Д/
Ъ
В
В заключение объединяем два дерева и формируем искомое дерево, которое
изображено на рис. 15.34.
42
i D Л
А В
?
Теперь необходимо показать, что дерево Хаффмана — это дерево с мини-
минимальным весом. Начнем с доказательства серии лемм.
ЛЕММА 15.16. Для заданного множества из п символов и их частот существует
бинарное дерево минимального веса с символами в качестве листьев.
ДОКАЗАТЕЛЬСТВО. Существует только конечное число бинарных деревьев с п
листьями. Для каждого из них подсчитаем
iv = hfi 4- /2/2 + /з/з + Uh
г=1
и выберем дерево, которое обеспечивает наименьшее значение. ¦
ЛЕММА 15.17. В дереве с минимальным весом на максимальном уровне листья
присутствуют в парах, т.е. везде, где есть левый сын, имеется и правый сын и
наоборот.

644 ГЛАВА 15. Деревья
• ДОКАЗАТЕЛЬСТВО. Допустим, что на максимальном
• уровне имеется единственный сын; пусть это будет ле-
левый сын, помеченный символом s. Правого сына нет,
поэтому имеем дерево, изображенное на рис. 15.35.
Если мы теперь удалим левого сына и обозначим
родителя меткой s, то в результате получим дерево с
меньшим весом, а это противоречит предположению о
том, что дерево имеет минимальный вес. ¦
ЛЕММА 15.18. В дереве с минимальным весом два символа с минимальными
частотами расположены на максимальном уровне.
ДОКАЗАТЕЛЬСТВО. Если теорема не верна, то имеется символ а на уровне U с
частотй fi и символ 6 на уровне lj с частотой fj, где U > lj и fi > fj. В общий вес
дерева эти два символа вносят величину Ufi +ljfj. Если эти символы поменять
местами, то их вклад в общий вес дерева составит Ufj +ljfi. Но
hfi + hfj ~ (hfj + hfi) = Ufi + hfj ~ hfj ~ hfi =
= (h - lj)(fi ~ fj) >
поскольку U — lj > 0 и fi — fj > 0. Таким образом, hfi + ljfj > hfj+ljfi, поэтому
перестановка символов приводит к уменьшению веса дерева, что противоречит
предположению о том, что дерево имеет минимальный вес. ¦
ЛЕММА 15.19. Существует дерево с минимальным весом, в котором два символа
с наименьшими частотами имеют одного родителя.
ДОКАЗАТЕЛЬСТВО. По лемме 15.17 каждый лист на максимальном уровне имеет
брата. По лемме 15.18 оба символа с минимальным весом, к примеру, а и 6,
находятся на одном уровне. Если они не братья, то поскольку находятся на одном
уровне, замена а на 6 не повлияет на вес дерева. ¦
Теперь все готово для формулировки основной теоремы.
ТЕОРЕМА 15.20. Для заданного множества символов с соответствующими ча-
частотами дерево Хаффмана является деревом с минимальным весом.
ДОКАЗАТЕЛЬСТВО. Докажем теорему, используя индукцию по числу символов.
Для двух символов, скажем, а и 6, дерево Хаффмана изображено на рис. 15.36 и
действительно является деревом с минимальным весом.
Таким образом, теорема верна для и = 2. Предполо-
Предположим, что утверждение теоремы справедливо для дерева с п
символами. Пусть Tn+i — дерево минимального веса, содер-
содержащее п 4- 1 символ. Предположим, что а и 6 с частотами
fa и fb являются символами с самыми низкими частотами.
Рис. 15.36 Тогда по лемме 15.18 они могут быть братьями на самом вы-
высоком уровне / + 1. Теперь удалим аибиз дерева и присвоим
их родителю символ с с частотой /а +Д. Назовем это дерево Тп. Поскольку в де-
дереве только п символов, то по индуктивному предположению существует дерево
л

РАЗДЕЛ 15.3. Взвешенные деревья 645
Хаффмана с минимальным весом с этими символами. Назовем дерево Т^. По-
Поскольку Т'п имеет минимальный вес, то вес Т'п меньше или равен весу дерева Тп.
Теперь заменим с с частотой Д + Д на родителя с сыновьями а и 6, образуя дере-
дерево Т'п+1. Другими словам, для перехода от дерева Tn+i к дереву Тп используется
обратный процесс. Но это совпадает с построением дерева Хаффмана с п + 1 сим-
символом, поскольку для построения дерева Хаффмана сп + 1 символом следовало
бы начать саиби образовать дерево с родителем, имеющим частоту Д + Д, так
что если рассматривать с как представителя этого дерева, то построение дерева
Хаффмана Т'п является продолжением дерева Хаффмана Г^+1.
Теперь имеются четыре дерева: деревья Хаффмана Т'п и T^+i» г^е ^п ~" дере-
дерево с минимальным весом, и деревья Тп и Тп+ь где Tn+i — дерево с минимальным
весом. Мы перешли от дерева Т'п к дереву T'nJrl и от дерева Тп к дереву Тп+ь
заменяя с с частотой Д + Д на вершины а и 6 с частотами Д и Д и их родителя.
Теперь рассмотрим, каким образом это влияет на вес дерева. При переходе от
дерева Тп к дереву Tn+i вершина с с частотой Д + Д, длиной Z, общим весом
Kfa+fb)
заменяется вершиной а с частотой Д, длиной / + 1 и вершиной b с частотой Д,
длиной Z 4-1, общий вес которых равен
fa{l + 1) + ЛС + 1) = К/а + Л) + fa + Л-
Таким образом, увеличение веса дерева составило Д 4- Д. Аналогично при
переходе от дерева Т'п к дереву Т^+1 увеличение веса дерева также равно Д + Д.
Поскольку вес дерева Т^ меньше или равен весу дерева Тп и увеличение веса
при переходе от дерева T'nJrl и Tn+i одно и то же, то вес дерева Т^+1 меньше или
равен весу Tn+i. Таким образом, дерево Т^+1 — дерево минимального веса. ¦
УПРАЖНЕНИЯ
1. Заданы следующие символы и их коды:
символ
с
d
е
г
s
и
код
111
101
01
11001
0010
1101
а) закодируйте слово discuss-,
б) закодируйте слово suede;
в) декодируйте слово 101011111100110101101;
г) декодируйте слово 11001001000101101010010.

646 ГЛАВА 15. Деревья
2. Заданы следующие символы и их коды:
символ
а
с
е
г
9
h
т
s
t
код
111
101
01
11011
0010
1001
0001
10001
11001
а) закодируйте слово mathematics',
б) закодируйте слово mammals;
в) декодируйте слово 11100101111000111001;
г) декодируйте слово 100101110110010100111001.
Заданы следующие символы с их частотами и три множества кодов.
символ
с
d
е
г
s
и
частота
7
8
10
2
9
4
код 1
111
101
01
11001
0010
1101
код 2
010
11
001
101
011
000
код 3
111
101
001
10001
011
100011
Найдите вес каждого кода и выберите наиболее подходящий для компакт-
компактного хранения данных.
4. Заданы следующие символы с их частотами и три множества кодов.
символ
а
с
е
i
9
h
т
s
t
частота
8
4
13
9
5
2
3
7
11
код 1
111
101
01
11011
0010
1001
0001
10001
11001
код 2
1111
1110
1100
1001
1011
1000
1010
ООП
0111
кодЗ
111
011
101011
11011
001
000
100
10111
10110
Найдите вес каждого кода и выберите наиболее подходящий для компакт-
компактного хранения данных.

РАЗДЕЛ 15.3. Взвешенные деревья 647
5. Заданы следующие символы с их частотами:
а) постройте дерево Хаффмана;
б) определите код Хаффмана;
в) найдите вес кода;
г) закодируйте слово crab\
д) закодируйте слово bar;
е) декодируйте 1100111;
ж) декодируйте 10011110.
6. Заданы следующие символы с их частотами:
а) постройте дерево Хаффмана;
б) определите код Хаффмана;
в) найдите вес кода;
г) закодируйте слово break;
д) закодируйте слово barber;
е) декодируйте 11011011000;
ж) декодируйте 11110110111101101.
7. Заданы следующие символы с их частотами:
а) постройте дерево Хаффмана;
б) определите код Хаффмана;
в) найдите вес кода;
г) закодируйте слово eraser;
д) закодируйте слово darker.
е) декодируйте 10010110001100;
ж) декодируйте 0011011001111001.
8. Заданы следующие символы с их частотами:
а) постройте дерево Хаффмана;
б) определите код Хаффмана;
в) найдите вес кода;
г) закодируйте слово ghost;
д) закодируйте слово choose;
е) декодируйте 100010010000111101;
ж) декодируйте 10001001110111101;
з) декодируйте 11100010000100110001.
символ
а
Ъ
с
г
частота
8
6
3
4
СИМВОЛ
а
Ъ
е
к
г
частота
8
5
10
1
3
символ
а
d
е
к
г
s
частота
8
7
12
1
4
6
символ
с
е
9
h
о
г
S
t
и
частота
7
12
3
2
9
4
5
8
1

648 ГЛАВА 15. Деревья
9. Заданы следующие символы с их частотами:
символ
а
с
е
г
9
частота
8
4
13
9
5
символ
h
т
s
t
частота
2
3
7
И
а) постройте дерево Хаффмана;
б) определите код Хаффмана;
в) найдите вес кода.
10. Заданы следующие символы с их частотами:
символ
а
d
е
г
9
h
1
частота
19
8
20
11
3
1
5
символ
т
п
о
г
S
t
частота
7
9
12
11
16
14
а) постройте дерево Хаффмана;
б) определите код Хаффмана.
в) найдите вес кода;
г) закодируйте слова moonlightandroses;
д) закодируйте слово roosters.
11. Заданы следующие символы с их частотами:
символ
а
d
е
f
9
h
I
т
частота
20
9
25
4
8
2
6
10
символ
п
о
Т
S
t
и
W
частота
7
13
15
11
5
14
1
а) постройте дерево Хаффмана;
б) определите код Хаффмана;

РАЗДЕЛ 15.4. Обход бинарных деревьев 649
в) найдите вес кода;
г) закодируйте слова eastofthesunandwestofthemoon;
д) закодируйте слово sweater.
12. Заданы следующие символы с их частотами:
символ
a
Ь
е
9
h
i
I
частота
25
10
30
7
6
18
8
символ
п
о
г
S
t
и
У
частота
12
20
9
11
15
3
13
а) постройте дерево Хаффмана;
б) определите код Хаффмана;
в) найдите вес кода;
г) закодируйте слова eastofthesunandwestofthemoon\
д) закодируйте слова lightsout.
13. Докажите теорему 15.14: В любом бинарном дереве путевые коды для ли-
листьев дерева являются префиксным кодом.
15.4. ОБХОД БИНАРНЫХ ДЕРЕВЬЕВ
В данном разделе рассматриваются три способа обхода бинарного дерева, при
которых каждая вершина посещается в точности один раз. Внимание будет со-
сосредоточено на деревьях, изображающих арифметичесткие выражения, хотя такие
обходы имеют также другое использование. Сначала представим арифметические
выражения с помощью деревьев, а затем рассмотрим способы их обхода.
Деревья, изображающие арифметические выражения, обладают тем свой-
свойством, что все их внутренние вершины являются бинарными операторами. Рас-
Рассмотрим выражение А+В. Соответствующее ему дерево изображено на рис. 15.37.
А В
Рис. 15.37
А+В C+D
Рис. 15.38
Воспользуемся нисходящим принципом обработки, который продемонстри-
продемонстрируем на примере. Рассмотрим выражение (А + В) х (С + D). Оно представляет
собой произведение А 4- В и С + Д поэтому сначала формируем дерево, изобра-
изображенное на рис. 15.38. Далее, поскольку выражение А + В — это сумма А и В, г
С + D — сумма С и D, то мы формируем дерево, изображенное на рис. 15.39.

650 ГЛАВА 15. Деревья
Рис. 15.39 Рис. 15.40
Каждое арифметическое выражение, содержащее бинарный оператор, по су-
сути является бинарной операцией над двумя арифметическими выражениями (ко-
(которые могут и не содержать арифметические операции). Начинаем с корня и,
если выражение в вершине имеет вид Е\ о Е2, где о — бинарная операция над
выражениями Е\ и E2i заменяем вершину деревом, изображенным на рис. 15.40.
Повторяем тот же процесс для вершин Е\ и Е2. Продолжаем действовать та-
таким образом, пока не останется вершин, содержащих бинарные операции. Теперь
покажем три способа обхода дерева, которое задает арифметическое выражение.
В каждом случае используем команду обработать (п), где и — узел. Оставим этот
термин пока неопределенным, поскольку его значение будет зависеть от того, че-
чего мы хотим достичь при прохождении вершин. Для наших целей достаточно
рассмотреть обычную команду печати символа. Начнем с обхода дерева в цен-
центрированном порядке. При таком обходе мы обращаем процесс, использованный
при создании дерева. Если задано дерево, изображенное на рис. 15.40, где о — би-
бинарная операция над выражениями Е\ и Е2, обрабатываем (или печатаем) это как
Е\ о Е2. В результате получается выражение в инфиксной записи, как описано
в разделе 5.5.
Приведенный ниже алгоритм описывает процедуру обхода дерева в цен-
центрированном порядке (ОЦП). Обозначим левого сына вершины v аббревиатурой
лс(г>), а правого сына вершины v — аббревиатурой пс(г>).
Алгоритм обхода дерева в центрированном порядке — ОЦП (корень)
A) Если лс(корень) существует, то О1\П(лс(корень)).
B) Обработать(/соре^б).
C) Если пс(корень) существует, то ОЦП(пс(/сореяь)).
Рис. 15.41
Рассмотрим дерево, изображенное на рис. 15.41. Начнем с ОЦПD-); первая
инструкция вызывает ОЦП(х). Первая инструкция команды в ОЦП(х) вызывает

РАЗДЕЛ 15.4. Обход бинарных деревьев 651
ОЦП(Л). Поскольку А не имеет левого сына, то переходим к шагу 2 команды
ОЦП(Л) и обрабатывем (печатаем) А. Переходим к шагу 3 в ОЦП(А) и, по-
поскольку ОЦП(А) не имеет правого сына, обработка ОЦП(А) закончена, и мы
возвращаемся к шагу 2 в ОЦП(х). Здесь обрабатывается (печатается) х, а на
шаге 3 вызывается ОЦП(В). Заметим, что результатом вызова ОЦП(А) была об-
обработка (печать) листа А и возврат к родителю. Поэтому впредь, если имеется
ОЦПA/), где L — лист, то три шага соответствующего алгоритма будем сокращен-
сокращенно описывать как обработать лист L. Используя это обозначение, печатаем В и
возвращаемся к ОЦП(х). Теперь выполнена команда "обработать" (напечатать)
Ах В.
Команда ОЦП(х) выполнена, поэтому возвращаемся к ОЦП(+). (К настоящему
моменту общая концепция уже вполне ясна, в дальнейшем будем говорить про-
просто "обработать", понимая под этим "печатать". Находясь на шаге 2 в ОЦП(+),
обрабатываем -f и переходим к шагу 3 в ОЦП(+). На этом этапе вызываем ко-
команду ОЦП(-^). На первом шаге ОЦП(ч-) вызываем ОЦП(С), обрабатываем лист
С и возвращаемся на шаг 2 в ОЦП(-ь). Теперь обрабатываем -г-, после чего уже
обработано
Ах B + C-f.
Возвращаемся на шаг 3 в ОЦП(^) и вызываем ОЦП(—). На шаге 1 в ОЦП(—) вы-
вызываем OUJ\(D) и обрабатывем лист D. Затем возвращаемся на шаг 2 в ОЦП(—)
и вызываем ОЦП(?). Обрабатываем лист Е, после чего возвращаемся к коман-
команде ОЦП(-). Однако, команда ОЦП(-) уже выполнена, поэтому возвращаемся к
ОЦП(-!-). Но эта команда тоже закончена, поэтому возвращаемся к ОЦП(+). На-
Наконец, в завершение всего процесса выполняем команду ОЦП(+). Итак, получено
выражение
Ах В + С + D- Е.
Это выражение, согласно изложенному в разделе 5.5, имеет инфиксную запись.
К сожалению, в отсутствие скобок выражение в том виде, в каком получено, не
имеет смысла. Если вспомнить содержание раздела 5.5, то именно такая ситуа-
ситуация была основанием для перехода к префиксной (польской) или постфиксной
(польской инверсной) записи выражений. К счастью, два следующих способа
обхода бинарных деревьев порождают именно такие формы записи выражений.
Следует отметить, что инфиксный способ обхода в применении к бинарному де-
дереву поиска дает обработку элементов в алфавитном порядке.
Теперь рассмотрим обход в прямом порядке. Такой
обход осуществим, например, для дерева, изображенного
на рис. 15.42, где о — бинарная операция над выраже-
выражениями ?i и ^2- Эту операцию будем обрабатывать (или
печатать) как 0Е1Е2. В результате получим выражение в е[ ?
префиксной форме. Такая форма записи широко исполь-
используется в логике и хороша тем, что в ней не используются "ис- ^42
скобки.
Приведенный ниже алгоритм описывает процедуру обхода в прямом порядке
(ОПП). Как и раньше, будем сокращенно обозначать левого сына вершины v
аббревиатурой лс(г;), а правого сына вершины v — аббревиатурой пс(г;).

652 ГЛАВА 15. Деревья
Алгоритм обхода дерева в прямом порядке — ОПЩкорень)
A) Обработать (корень).
B) Если лс(корень) существует, то ОПЩлс(корень)).
C) Если пс(корень) существует, то ОПП(пс(корень)).
В С
Рис. 15.43
Снова рассмотрим дерево (рис. 15.43). Начнем с ОПП(+); первая инструкция
обрабатывает 4-. Шаг 2 вызывает ОПП(х). Первая инструкция ОПП(х) обраба-
обрабатывает х. Затем вторая инструкция вызывает (А). На шаге ОПП(А) обрабатываем
А. На этом этапе уже обработано
+ х А.
Поскольку А не имеет левого сына, переходим к шагу 3 в ОПП(Л); так как нет
и правого сына, возвращаемся к ОПП(х). Опять замечаем, что, как и в случае
ОЦП(Л), результатом вызова ОПП(А) является обработка (печать) листа А и
возврат к родителю. Поэтому впредь, если имеется ОПП(Ь), где L — лист, то три
шага соответствующего алгоритма будем сокращенно описывать как обработать
лист L. Находясь на шаге 3 в ОПП(х), вызываем ОПП(В). Обрабатываем лист
В и возвращаемся к ОПП(х). Это завершает ОПП(х), поэтому возвращаемся к
ОПП(+). К этому моменту обработано (уже напечатано)
+ х АВ.
Затем на шаге 3 в ОПП(+) вызываем ОПП(ч-). Первый шаг ОПП(ч-) обрабаты-
обрабатывает -г. Второй шаг вызывает ОПП(С). Обрабатываем лист С и возвращаемся на
шаг 3 в ОПП(^). Эта инструкция вызывает ОПП(—). Первый шаг в ОПП(—) об-
обрабатывает —. Шаг 2 вызывает ОПП(?>). Обрабатываем лист D и возвращаемся
на шаг 3 в ОПП(—). На данном этапе уже обработано
-fx AB + C-D.
Шаг 3 в ОПП(-) вызывает ОШ\(Е). Обрабатываем лист Е и возвращаемся к
ОПП(-). Но ОПП(-) завершено, поэтому возвращаемся к ОПП(ч-). Однако,
ОПП(ч-) также завершено, поэтому возвращаемся к ОПП(+). Наконец, ОПП(+)
тоже завершен, и мы получаем результат
+ х АВ ч- С - DE,
который, согласно изложенному в разделе 5.5, выражен префиксной, или поль-
польской записью.

РАЗДЕЛ 15.4. Обход бинарных деревьев 653
О
El "г Рис. 15.44
И, наконец, рассмотрим обход в обратном порядке. Этот обход осуществим
для дерева, изображеного на рис. 15.44, где о — бинарная операция над выраже-
выражениями Е\ и ?2, которую будем обрабатывать (или печатать как Е1Е2О. В резуль-
результате получим выражение в постфиксной, или польской инверсной записи, как
описано в разделе 5.5. Всякий, кто пользовался калькулятором, знаком с пост-
постфиксной, или польской инверсной записью. Она обладает тем преимуществом,
что позволяет без скобок, чем и объясняется ее популярность.
Приведенный ниже алгоритм описывает процедуру обхода в обратном поряд-
порядке (ООП). Как и раньше, будем сокращенно обозначать левого сына вершины v
аббревиатурой лс(г>), а правого сына вершины v — аббревиатурой пс(г>).
Алгоритм обхода дерева в обратном порядке — ООЩкорень)
A) Если лс(корень) существует, то ООЩлс(корень)).
B) Если пс(корень) существует, то ООП(пс(корень)).
C) Обработать(/сореяь).
Снова рассмотрим дерево, изображенное на рисунке 15.45.
Рис. 15.45
Начинаем с ООП(-Ь); первая инструкция вызывает ООП(х). Первая инструкция
в ООП(х) вызывает ООП(А). Поскольку А не имеет левого сына, переходим к
шагу 2 в ОПП(А). Но так как нет и правого сына, переходим к шагу 3 в ОПП(А),
на котором обрабатываем А и возвращаемся к ООП(х). Опять замечаем, что, как
и в случае ОЦП(Л) и ОПП(А), результатом вызова команды ООЩА) является
обработка (печать) листа А и возврат к родителю. Поэтому впредь, если имеется
команда ООПA/), где L — лист, то три шага соответствующего алгоритма будем
сокращенно описывать как обработать лист L. Находясь на шаге 2 команды
ООП(х), вызываем ООП(В). Обрабатываем лист В и возвращаемся на шаг 3
в (х). Обрабатываем х и, поскольку это завершает ООП(х), возвращаемся к
ООП(+). На этом этапе имеем обработанным
АВ х .
Теперь мы на шаге 2 в ООП(+) вызываем ООП(ч-). Первый шаг ООП(ч-) вызы-
вызывает ООП(С). Обрабатываем лист С и возвращаемся на шаг 2 в ООП(ч-). Эта

654 ГЛАВА 15. Деревья
инструкция вызывает 00П(—). Певый шаг команды ООП(—) вызывает OOU(D).
Обрабатываем лист D и возвращаемся на шаг 2 в ООП(-). Второй шаг в ООП(-)
вызывает ООЩЕ). Обрабатываем Е и возвращаемся на шаг 3 в ООП(-). Обра-
Обрабатываем — и возвращаемся на шаг 3 в ООП(-г). На этом этапе результатом
обработки является
АВ х CDE - .
На шаге 3 в ООП(-т-) обрабатываем ~ и возвращаемся на шаг 3 в (+). Обраба-
Обрабатываем + и завершаем процесс. В качестве результата обработки имеем
АВ х CDE - -Т-+,
т.е. выражение, преобразованное в постфиксную запись.
Умение обходить дерево дает возможность легко устанавливать изоморф-
ность двух деревьев. Проходя два дерева одновременно, можно проверять наличие
вершины у одного дерева при условии наличия ее у другого. При одновременном
прохождении двух деревьев обработка вершин будет означать проверку обоих де-
деревьев на наличие соответствующих вершин. В данном случае для прохождения
деревьев представляется разумным использовать префиксный обход, так как это
позволяет не интересоваться наличием сыновей, если один из родителей отсут-
отсутствует. При обработке вершины V будем присваивать переменной наличие(У)
значение N, если вершина V отсутствует, и значение У, если вершина имеется.
Последующая проверка соответствующих вершин покажет, что если для одной
вершины значение переменной наличие(У) равно У, а для другой вершины оно
равно N, то два дерева не изоморфны.
Введем переменную, названную Изо, которая будет принимать значения Т и
F. Изначально ей присваивается значение Т, но если на каком-то этапе выявля-
выявляется, что деревья не изоморфны, то этой переменной присваивается значение F.
Итак, имеем следующий алгоритм для двух деревьев Т\ и Т2 с корнями т\ и г2
соответственно.
Пусть Изо = Г.
Алгоритм проверки изоморфности бинарных деревьев — ИБД(гх,г2)
A) Обработать т\ и т^.
B) Если наличие(г{) = У и наличие{г2) = N или наличие(г\) = N и
наличие(г2) = У, то Изо = F.
C) Если Изо = F, то завершить ИБД(г1,г2).
D) Если наличие{г{) = У и наличие(г2) = У, то ИБД(лс(г1), лс(г2)).
E) Если наличие{г\) = У и наличие(г2) = У, то ИБД(пс(г1),пс(г2)).
Испытаем этот алгоритм на деревьях Т\ и Г2, изображенных на рис. 15.46.
т, т2
Рис. 15.46

РАЗДЕЛ 15.4. Обход бинарных деревьев 655
Обрабатываем г\ и г2. Поскольку наличие{г{) — У и наличие(г2) = У,
переходим к шагу 3 ИБД(гх,г2). Здесь вызываем ИБД(лс(г1),лс(г2)), т.е. обра-
обрабатываем ai и а2. Поскольку наличие(а{) = У и наличие(а2) = У, переходим к
шагу 3 алгоритма ИБД(аьа2). Здесь вызываем ИБД(лс(а1), лс(а2)), т.е. обраба-
обрабатываем Ь\ и Ь2. Поскольку наличие(Ъ\) = У и наличие^) = У, переходим к шагу
3 алгоритма ИБД (ai,a2). Здесь вызываем ИБД(лс(Ь1), лс(б2)), т.е. обрабатываем
лс(&1) и лс(Ь2)« А так как наличие(пс(Ь{)) = N и наличие(лс(Ь2)) = N, возвра-
возвращаемся к шагу 4 алгортма ИБД(аьа2), который вызывает ИБД(пс(а1),пс(а2)).
Обрабатываем с\ и пс(а2). Но наличие(с\) = У и наличие(пс(а,2)) = iV, поэтому
Язо = F, и процесс прекращается. Таким образом, два рассмотренных дерева не
изоморфны.
¦ УПРАЖНЕНИЯ
1. Для дерева, изображенного на рис. 15.47,
а) приведите инфиксную запись вершин дерева;
б) приведите префиксную запись вершин дерева;
в) приведите постфиксную запись вершин дерева.
х
d e
Рис. 15.47 Рис. 15.48
2. Для дерева, изображенного на рис. 15.48,
а) приведите инфиксную запись вершин дерева;
б) приведите префиксную запись вершин дерева;
в) приведите постфиксную запись вершин дерева.
3. Для дерева, изображенного на рис. 15.49,
а) приведите инфиксную запись вершин дерева;
б) приведите префиксную запись вершин дерева;
в) приведите постфиксную запись вершин дерева.
А X
X Xj N
а Ь рис. 15.49
4. Для дерева, изображенного на рис. 15.50,
а) приведите инфиксную запись вершин дерева;

656 ГЛАВА 15. Деревья
б) приведите префиксную запись вершин дерева;
в) приведите постфиксную запись вершин дерева.
А ¦/'
ab/m
Рис. 15.50 Рис. 15.51
5. Для дерева, изображенного на рис. 15.51,
а) приведите инфиксную запись вершин дерева;
б) приведите префиксную запись вершин дерева;
в) приведите постфиксную запись вершин дерева.
6. Для дерева, изображенного на рис. 15.52,
а) приведите инфиксную запись вершин дерева;
б) приведите префиксную запись вершин дерева;
в) приведите постфиксную запись вершин дерева.
а b Xj m n Puc I552
7. Дана инфиксная запись (а + b) х с:
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения;
в) укажите постфиксную запись этого выражения.
8. Дана инфиксная запись (a + b) x (c + d):
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения;
в) укажите постфиксную запись этого выражения.
9. Дана инфиксная запись ((а + Ь) х с) -f- (с + d)\
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения.
в) укажите постфиксную запись этого выражения.
10. Дана инфиксная запись (а ч- Ь) + (с х (d + e)):
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения;
в) укажите постфиксную запись этого выражения.

РАЗДЕЛ 15.4. Обход бинарных деревьев 657
11. Дана инфиксная запись (а х F + (d - (е + /)))) -f- ((g + К) х (г + j)):
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения;
в) укажите постфиксную запись этого выражения.
12. Дана инфиксная запись (а + Ь) х ((((е — /) + д) ч- h) — г):
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения;
в) укажите постфиксную запись этого выражения.
13. Дана инфиксная запись (((а + Ъ) — с) х d) -f- (e — (/ х (д 4- /г))):
а) найдите бинарное дерево, задающее это выражение;
б) укажите префиксную запись этого выражения;
в) укажите постфиксную запись этого выражения.
14. Найдите такое бинарное дерево, обход которого в центрированном порядке
дает acbde, а обход в обратном порядке дает abced.
15. Найдите такое бинарное дерево, обход которого в центрированном порядке
дает acbde, а обход в обратном порядке дает acedb.
16. Найдите такое бинарное дерево, обход которого в центрированном порядке
дает acbdefg, а обход в обратном порядке дает dcbfeg.
17. Найдите такое бинарное дерево, обход которого в центрированном порядке
дает acbdefg, а обход в обратном порядке дает edcabfg.
18. Найдите дерево, содержащее не менее трех вершин, инфиксная запись ко-
которого совпадает с префиксной.
19. Найдите дерево, содержащее не менее трех вершин, инфиксная запись ко-
которого совпадает с постфиксной.
20. Постройте три неизоморфных бинарных дерева, которые при обходе дают
постфиксное выражение abed.
21. Постройте три неизоморфных бинарных дерева, которые при обходе дают
префиксое выражение abed.
22. Докажите, что задание для дерева инфиксного и постфиксного выражений
однозначно определяет его структуру.
23. Если все арифметические операции бинарные, то какое из приведенных ниже
выражений истинно для дерева, задающего данное арифметическое выраже-
выражение?
а) Бинарное дерево сбалансировано.
б) Бинарное дерево полное.
в) Лист может быть арифметическим выражением.
г) Внутренняя вершина должна быть арифметическим выражением.
24. Напишите алгоритм, который правильным образом расставляет скобки в ин-
инфиксном арифметическом выражении, полученном при обходе дерева в цен-
центрированном порядке.
25. Сформулируйте необходимые и достаточные условия, при выполнении кото-
которых выражение было бы постфиксным арифметическим выражением.
26. Арифметическая операция возведения в степень является бинарной или унар-
унарной? Почему? Приведите пример унарной арифметической операции.

658 ГЛАВА 15. Деревья
27. Опишите, где и каким образом алгоритм ИБД покажет, что деревья, изоб-
изображенные на рис. 15.53, не изоморфны.
Рис. 15.53
15.5. ОСТОВНЫЕ ДЕРЕВЬЯ
В разделе 6.3 остовное дерево было определено как дерево Т, которое является
подграфом графа G и таким, что каждая вершина в G является вершиной в Г;
показано также, что каждый связный граф имеет остовное дерево.
В данном разделе рассматриваются два метода построения остовного дерева.
Первый — метод поиска в ширину, а второй — метод поиска в глубину. Начнем
с метода поиска остовного дерева в ширину. Согласно методу произвольную вер-
вершину vq графа G выбираем в качестве корня дерева Г. Для каждой вершины v
графа G, смежной с вершиной г;о, в дерево Т добавляется вершина v и ребро
{v,vo}- Это вершины уровня 1. Затем берем каждую вершину V{ уровня 1 и для
каждой вершины Vj графа G, смежной с вершиной V{ из тех, что еще не выбраны,
добавляем в дерево Т вершину Vj и ребро {v{,Vj}. Вершины, добавленные на
этом этапе, — это вершины уровня 2. Продолжаем процесс, пока в графе G не
останется вершин, которые можно было бы добавить в дерево. По построению
Т является деревом. Если расстояние от vq до вершины v графа G равно п, то
эта вершина будет добавлена в дерево на уровне п. Следовательно, Т несомненно
является остовным деревом.
При построении алгоритма требуется наверняка знать, что некоторые верши-
вершина и ребро уже были добавлены в дерево, с тем чтобы, с одной стороны, описывать
дерево, а с другой стороны, — исключать возможность повторного использования
вершин, так как в противном случае мы не получим дерево. Требуется также знать
уровень, на котором добавляется вершина, поскольку для определения листьев на
следующем уровне эффективнее использовать только вершины, добавленные на
последнем уровне. При определении новых вершин для добавления в дерево необ-
необходимо также иметь возможность выбора вершин по одной. Существует несколь-
несколько способов решения такого рода задач, в том числе решения с использованием
массивов и очередей, поэтому мы не будем подробно останавливаться на том, как
определить "следующую" вершину. Можно считать, что вершины графа G предва-
предварительно упорядочены. Пусть V и Е обозначают множество вершин и множество
ребер графа G, и пусть VT и Ет обозначают множество вершин и множество
ребер дерева Т. При добавлении в дерево вершины v мы будем обозначать через
L(v) уровень, на котором она добавляется.

РАЗДЕЛ 15.5. Остовные деревья 659
Алгоритм поиска остовного дерева в ширину — ПОДШ(С)
A) Выбрать произвольный элемент vo графа G. Пусть vo E VT и L(vq) = 0.
B) Для всех v Е V — VT таких, что v смежна с vo, положить v € VT,
{г;0,г;} е ЕТ и L(v) = l.
C) Пусть г = 1.
D) Выбрать Vj G VT такое, что L(vj) = г.
E) Выбрать v G V - VT. Если v смежна с Vj, положить v € VT, {vo,v} e ET
и L{v) = г + 1.
F) Продолжать шаг 5, пока все элементы множества V - VT не будут рас-
рассмотрены. (Обратите внимание, что V — VT постоянно меняется.)
G) Повторять шаги 4, 5, и 6, пока все Vj такие, что L(vj) = г, не будут
выбраны.
(8) Положить г = г + 1.
(9) Повторять шаги 4-8 до V = VT.
ПРИМЕР 15.21. Рассмотрим граф, изображенный на рис. 15.54. Предположим,
что вершина vo выбрана в качестве первой вершины. Тогда L(vq) = 0 и г>о Е VT.
Поскольку v\ является смежной с г>0, положим v\ e VT, {vo,vi} е Ет и L[v\) = 1.
Вершина v2 также смежна с v0, поэтому положим v2 G V^, {^0,^2} Е Ет и
Ь(у2) = 1. Наконец, вершина г>з тоже смежна с vo, поэтому полагаем г;з G VT,
{^0,^3} ? Ет и L(vz) = 1. На данный момент имеем дерево, изображенное на
рис. 15.55.
Рис. /5.55
Теперь рассматриваем вершины v такие, что L{v) = 1. Начинаем cwi и на-
находим неиспользованные вершины, смежные с v\. Поскольку вершина г;5 смежна
с v\% полагаем v$ е ^т, {vi, vs} € ?т и 1/(^5) = 2. Больше нет неиспользованных
и смежных с v\ вершин, поэтому переходим к v2. Поскольку v^ смежна с v2y
полагаем г;4 G VT, {^2,^4} € ?"т и L(t>4) = 2. Теперь все вершины использованы,
процесс завершен. В результате имеем дерево, изображенное на рис. 15.56.
Рис. 15.56
?

660 ГЛАВА 15. Деревья
ПРИМЕР 15.22. Рассмотрим граф, изображенный на рис. 15.57.
12
Рис. 15.57
Как и раньше, выберем v$ как начальную вершину. Тогда L{vq) = 0 и
г;0 Е VT. Поскольку у\,У2,уз,у±,уъ являются смежными с г;0, положим vi E VT,
{уо,У{} G Ет и L(vi) = 1, где 1 < г < 5. После этого получаем дерево, изобра-
изображенное на рис. 15.58.
"' v* У' '* "* Рис. 15.58
Теперь начинаем на уровне 1 с вершины v\. На этом уровне находятся:
вершина vq, смежная с г>ь вершина г>ю, смежная с г?з, вершины уц и г>14, смежные
с г>4, и i;i5, vis, смежные с v5. Поэтому V6,vio,vn,vi4,vi5?vi8 ^ ^Т» ^(^б) =
= Цуп) = Ь(уы) = L{yib) = L(vis) = 2 и {vi,v6}, {v3, v10}, {г;4,г7ц},
{г>5,1;15}, {i;5,i;i8} G ?т В результате получаем дерево, изображенное на
рис. 15.59.
Теперь начинаем на уровне 2. На этом уровне: вершины г;7,^85^9. смежные
с Уб* г>12. смежная с г/ц, vi3, смежная с vu, г;^, смежная с vi5, и г>17, смежная
с г>18. Поэтому v7, г;8, г>9, vi2, vi3, vie, V17 € VT, {г;6, г;7}, {f6, г>8}, {г;6,
13}, {^16, V13}, {V17, Vie} G ?T, И L(V7) = L(V8) = L(Vg) ( (
= L(vn) = 3. В результате получаем дерево, изображенное на рис. 15.60.

РАЗДЕЛ 15.5. Остовные деревья 661
v'7 Рис. 15.60 П
При поиске в ширину первым делом отыскиваются все вершины, смежные
с заданной вершиной, а потом осуществляется переход на следующий уровень.
При поиске в ширину усилия направлены на построение для дерева как можно
более длинного пути. Когда путь заходит в тупик и формирует лист, необходимо
возвращаться к родителю листа и пытаться сформировать другой путь. Возврат к
родителю происходит только после попытки построить все возможные пути от сы-
сына этого родителя. В образах создаваемого дерева это означает, что мы пытаемся
достичь самый глубокий, или самый большой уровень, какой только возможен.
Алгоритм начинается у заданной вершины графа, которую будем считать корнем.
Выбираем вершину, смежную с корнем, и формируем ребро дерева. Затем выби-
выбираем вершину, смежную с ранее выбранной вершиной, и формируем новое ребро.
По ходу процесса необходимо помечать использованные вершины, с тем чтобы
каждая вершина использовалась один раз. Если, находясь в вершине v, мы вы-
выбираем другую вершину w и обнаруживаем, что вершина w уже была добавлена
в дерево, то ребро {v,w} между этими вершинами не может быть добавлено в
дерево. Такое ребро назовем обратным ребром, и будем хранить его след для
дальнейшего использования. Прежде, чем объявить ребро обратным, нужно тща-
тщательно проверить, не является ли вершина w родителем вершины v, поскольку
в этом случае ребро {v,w} уже присутствует в дереве. По существу, при выбо-
выборе w как возможной новой вершины следует избегать ситуации, когда вершина w
является родителем v. Если {v,w} — обратное ребро, то мы остаемся в г> и выби-
выбираем новую смежную вершину, если это возможно. По определению, любое ребро
графа, в конечном счете, — либо ребро дерева, либо обратное ребро.
В рассматриваемом алгоритме множество ребер дерева назовем РЕБРА ДЕ-
ДЕРЕВА, а множество обратных ребер — ОБРАТНЫЕ РЕБРА. В самом начале пред-
предположим, что для "новых" вершин использованы метки "нов", а после добавления
вершины в дерево эти метки меняются на "исп" — "использованные".
Алгоритм поиска остовного дерева в глубину — ПОДГ(С)
A) Пометить каждую вершину графа G символом п.
B) Выбрать произвольный элемент v0 графа G и назвать его корнем дерева.
C) Заменить метку вершины vq с "нов" на "исп" и положить v = vo
D) Пока имеются невыбранные вершины, смежные с v, выполнять следующие
действия:
а) Выбрать вершину w, смежную с v.

662 ГЛАВА 15. Деревья
б) Если w имеет метку "нов", добавить (v,w) в РЕБРА ДЕРЕВА, поме-
поменять метку w на "исп", положить w = v и повторить шаг 4.
в) Если w имеет метку "исп" и не является родителем v, добавить (г;, w)
в ОБРАТНЫЕ РЕБРА и повторить шаг 4.
E) Если v ф а, положить v = (v) и повторить шаг 4.
Заметим, что пока для вершины v имеется смежная с ней неиспользованная
вершина w, мы продлеваем путь от v к w. Только в том случае, когда двигаться
дальше нельзя, переходим к шагу 5, возвращаемся к родителю вершины v.
ПРИМЕР 15.23. Рассмотрим граф, изображенный на рис. 15.61.
Рис. 15.61
Произвольным образом выбираем вершину а в качестве корня. Меняем мет-
метку а с "нов" на "исп". Поскольку вершина b смежна с а и имеет метку "нов",
добавляем ребро {а, Ь} в РЕБРА ДЕРЕВА и меняем метку вершины b на "исп",
как показано на рис. 15.62.
От вершины b переходим к вершине d, поскольку она является смежной с 6.
Вершина d имеет метку "нов", поэтому добавляем ребро {6, d} в РЕБРА ДЕРЕВА
и меняем метку вершины d на "исп", как показано на рис. 15.63.
Рис. 15.62
Теперь выбираем вершину, смежную с вершиной d. Можно выбрать a, f
или д. Выбор определит форму дерева, поэтому поиск в глубину не продуцирует
дерево единственным образом. Предположим, что следующей вершиной выбира-
выбираем д. Вершина д имеет метку "нов", поэтому добавляем ребро {d,g} в РЕБРА
ДЕРЕВА и меняем метку вершины д на "исп", как показано на рис. 15.64.
Из вершины д выбираем вершину /, так как она является смежной с д.
Вершина / имеет метку "нов", поэтому добавляем ребро {д, /} в РЕБРА ДЕРЕВА
и меняем метку вершины / на "исп", как показано на рис. 15.65.

РАЗДЕЛ 15.5. Остовные деревья 663
Рис. 15.64
Рис. 15.65
Из вершины / выбираем вершину d, так как она является смежной с верши-
вершиной /. Однако вершина d уже имеет метку "исп", поэтому добавляем ребро {d, /}
в ОБРАТНЫЕ РЕБРА, как показано на рис. 15.66.
Поскольку больше нет ребер для проверки на смежность с вершиной /,
кроме родителя, возвращаемся к вершине д. (Далее не будем упоминать родителя
как возможную смежную вершину.) Но иных ребер для проверки на смежность
с вершиной д тоже нет, поэтому возвращаемся к вершине d. Здесь единственной
вершиной для проверки является а, но вершина а уже имеет метку "исп", поэтому
ребро {d, /} добавляем в ОБРАТНЫЕ РЕБРА и возвращаемся в вершину 6, как
показано на рис. 15.67.
Ребер для проверки на смежность с вершиной b больше нет; возвращаемся
к вершине а. Заметим, что если бы была возможность достичь каждую вершину,
построив путь из 6, то пока дерево не построено полностью, нам не надо было бы
возвращаться в вершину а. Вернувшись в вершину а, можем выбирать с или е.
Предположим, что выбрана вершина с. А так как вершина с имеет метку "нов",
добавляем ребро {а, с} в РЕБРА ДЕРЕВА и меняем метку вершины с на "исп",
как показано на рис. 15.68.
Вершина е смежна с вершиной с и имеет метку "woe"; добавляем ребро
{с, е) в РЕБРА ДЕРЕВА и меняем метку е на "исп", как показано на рис. 15.70.
Допустим теперь, что выбрана вершина а, потому что она является смежной с
вершиной е. Но вершина а уже имеет метку "ucri\ поэтому добавляем ребро {е,а}
в ОБРАТНЫЕ РЕБРА и возвращаемся в вершину е, как показано на рис. 15.70.
Поскольку вершина h смежна с е, добавляем ребро {е, К) в РЕБРА ДЕРЕВА
и меняем метку вершины h на "wen", как показано на рис. 15.71.

664 ГЛАВА 15. Деревья
Больше нет вершин для проверки из вершины Л, поэтому возвращаемся в
вершину е. Но больше нет вершин для проверки из вршины е, поэтому возвра-
возвращаемся в вершину с. Поскольку нет больше вершин для проверки из вершины
с, возвращаемся в вершину а. Других вершин для проверки из вершины а тоже
нет, поэтому процесс завершен. ?
ПРИМЕР 15.24. Найти остовное дерево графа, изображенного на рис. 15.72.
12
Рис. 15.72
Предположим, что все вершины графа имеют метку "woe". Пусть vq — первая вы-
выбранная вершина. Добавим ребра (vo,v5), (t;5,i;18), (vi8,vu), (^17,^16) и (vi6,vis)
в РЕБРА ДЕРЕВА и заменим метки вершин ^0,^5,^18,^17,^16 и vi5 на и. Из вер-
вершины vis находим, что вершины г;5 и v\s — смежные с вершиной г>15, но они уже
отмечены меткой "исп", поэтому ребра (vi5, vis) и (^15,^5) добавляются в ОБРАТ-
ОБРАТНЫЕ РЕБРА. Теперь последовательно возвращаемся в v\q, уц, затем в у\$ и, на-
наконец, в уъ. Находясь в г;5, добавляем ребра (уь,у\а), (^i4,^i3), (^13,^12), (^12,^11)
и (уц^щ) в РЕБРА ДЕРЕВА и меняем метки вершин Vi4,i>i3?vi2,i>n и у± на и.
Вершины г?о и уц — смежные с вершиной г;4, но они уже имеют метку "wen",
поэтому ребра (г;4, г;0) и (^4,^14) добавляются в ОБРАТНЫЕ РЕБРА. Возвраща-
Возвращаемся в вершину vi 1, откуда находим, что вершина уц является смежной с г>ц. Но
у\4 уже отмечена меткой "исп", поэтому добавляем ребро (уп,уы) в ОБРАТНЫЕ
РЕБРА. Осуществляем возврат, пока не достигаем вершины уо. На этот момент
имеем дерево с обратными ребрами, изображенное на рис. 15.73.

РАЗДЕЛ 15.5. Остовные деревья 665
'* Рис. 15.73
Находясь в вершине г/0, выбираем вершину, смежную с г/0, например, г/3,
добавляем ребро (г;0,г/3) в РЕБРА ДЕРЕВА и меняем метку вершины г/3 на "wen".
Продолжаем процесс, добавляя (г;3,г/6), (v6,v9), (г;9,г/ю) и (г/ю,г>8) в РЕБРА ДЕ-
ДЕРЕВА, и меняем метки вершин г/б,г/д,г/ю и г>8 на "исп". Теперь мы находимся
в вершине i>g. Вершина vq является смежной с у&, но vq уже отмечена меткой
"исп", поэтому добавляем ребро (г/8,г/б) в ОБРАТНЫЕ РЕБРА. Возвращаясь в
vio, находим, что вершина v7 — смежная с г>ю, поэтому добавляем (г/ю,г>7) в
РЕБРА ДЕРЕВА, меняя метку вершины v7 на и. Вершина г/7 — смежная с вер-
вершиной г/6, но г/6 уже отмечена меткой "исп", поэтому добавляем ребро (г/7,г/6) в
ОБРАТНЫЕ РЕБРА. Возвращаясь в вершину г/ю, находим, что г;3 — смежная
с г;ю. Вершина г;3 уже отмечена меткой и, поэтому добавляем ребро (^ю,г/з) в
ОБРАТНЫЕ РЕБРА. Осуществляем возврат в вершину vq. Вершина v\ — смеж-
смежная с г>б, добавляем ребро (ve,vi) в РЕБРА ДЕРЕВА, меняя метку вершины v\
на "исп". Находясь в вершине v\, определяем, что вершина v0 — смежная с v\, и
поскольку г;0 уже отмечена меткой "исп", добавляем ребро (v\,vo) в ОБРАТНЫЕ
РЕБРА. Возвращаясь в г>6, находим, что вершина v2 — смежная с v6, поэтому
добавляем ребро (г>6,г/2) в РЕБРА ДЕРЕВА и меняем метку вершины v2 на "исп".
Из вершины г>2 находим, что вершина г/о — смежная с вершиной г/2 и отмечена
меткой "исп", добавляем ребро (v2,vo) в ОБРАТНЫЕ РЕБРА. Построение дерева
закончено, и на рис. 15.74 оно изображено вместе с обратными ребрами.
Рис. 15.74
?
Если граф не связный, то алгоритм ПОДГ будет применяться не ко всему
графу, а только к его компоненте, содержащей вершину, выбранную в качестве
корня. По этой причине алгоритм поиска остовного дерева в глубину можно ис-
использовать для проверки связности графа, для чего необходимо просто реализовы-
вать алгоритм. Если какая-либо вершина не достижима, то рассматриваемый граф

666 ГЛАВА 15. Деревья
не является связным. Алгоритм также может быть использован для построения
остовного дерева каждой компоненты несвязного графа. Следует, как и прежде,
выбрать вершину для корня первого дерева и построить остовное дерево. Затем
выбрать одну из недостижимых вершин и построить второе дерево. Продолжать
процесс, пока не останется вершин. Лес остовных деревьев, построенных таким
образом, называется остовным лесом.
Алгоритм построения остовного дерева в глубину можно также использо-
использовать для проверки графа на наличие точек сочленения. Для этого потребуется
следующая теорема.
ТЕОРЕМА 15.25. Если Т — глубинное остовное дерево графа G(V, E) и {а, 6} —
ребро графа G(V, E), то либо а является потомком 6, либо b — потомком а.
ДОКАЗАТЕЛЬСТВО. Если {а, 6} — ребро дерева Т, то вывод очевиден. Если это
не так, то одна из вершин, например, а, должна быть помещена в дерево первой.
Но поскольку вершина b не была помещена в дерево на шаге 4 алгоритма ПОДГ,
то поиск продолжается из вершины а до тех пор, пока не будет найдена вершина Ь.
Поэтому вершина b является потомком а. ¦
ТЕОРЕМА 15.26. Пусть Т — глубинное остовное дерево графа G(V, E). Вершина
a G V является точкой сочленения графа G(V, E) тогда и только тогда, когда
вершина а A) либо является корнем дерева Т и имеет более одного сына, либо
B) вершина а не является корнем дерева Т, и существует такой сын с, что между
с, или одним из его потомков, и собственным предком вершины а не существует
обратного ребра.
ДОКАЗАТЕЛЬСТВО. A) Если а — корень дерева Т и имеет только одного сына с,
то между любой вершиной дерева Т и вершиной с существует путь. Поэтому для
двух вершин v и w, ни одна из которых не совпадает с а, существует путь из
v в с в w, который не проходит через а, и, следовательно, а не является точкой
сочленения. Если корень а имеет двух сыновей, с и с', и если поиск в глубину
начинается от с, он может достичь с' только путем возврата в вершину а; поэтому
не существует пути из с в с', который не проходит через а.
B) Предположим, что существует сын с вершины а такой, что между с
или одним из его потомков и собственным предком вершины а не существует
обратное ребро. Пусть р — родитель а. Поскольку не существует обратного ре-
ребра между с или одним из его потомков и собственным предком вершины а, по
предыдущей теореме каждое ребро из а или одного из ее потомков должно идти
в а или одного из ее потомков. Таким образом, каждый путь, имеющий начало в
вершине с, должен заканчиваться в с или в одном из ее потомков либо проходить
через а. Поэтому единственный путь из с в р проходит через а, и а является
точкой сочленения. Обратно, предположим, что для всех сыновей с вершины а
существует обратное ребро из с в собственного предка вершины а. Пусть с и с' —
сыновья вершины a, a b и bf — собственные предки вершины а, так что е = {d,b}
и е = {d! ,Ъ'} — обратные ребра, где d и d! — потомки вершин сие' соответ-
соответственно. Таким образом, существует путь рс?ь из с в d в b и путь рс^у из d в d1
в Ъ''. Поскольку существует путь р из b в Ь\ который не проходит через а, путь
рс^ь , за которым следует путь р и путь, обратный к рс/,ь', является путем из с

РАЗДЕЛ 15.5. Остовные деревья 667
в с', который не проходит через а. Пусть v и w — две вершины графа G(V,E).
Если v и w — потомки вершины а, то из вершин v и w в с и d соответственно
существуют пути, которые не проходят через а, где с и с' — сыновья вершины а.
Поскольку существует также путь из с и с', который не проходит через а, то
существует путь из г; в с, далее в с' и далее в w, который не проходит через а.
Если v — потомок вершины о, aw- нет, то поскольку существует путь из г; к
сыну с вершины а, путь рс^ из с в Ь, где 6 — собственный предок вершины а,
и путь вдоль дерева из вершины 6 в ад, и ни один из этих путей не содержит а,
то существует путь из v в w, не содержащий а. Если ни vy ни w не являются
потомками вершины а, то существует путь вдоль дерева из v в w, не содержащий
а. Таким образом, всегда существует путь из v в w, не содержащий а, и поэтому
а не является точкой сочленения. ¦
Для нахождения точек сочленения графа G используем предыдущую теоре-
теорему и попытаемся выяснить, имеется ли в дереве Г сын с такой, что между с или
одним из его потомков и собственным предком вершины а не существует обрат-
обратного ребра. Прежде всего нам нужен такой способ упорядочения вершин, при
котором если вершина а является собственным предком вершины Ь, то значение,
приписываемое а, больше значения, приписываемого Ъ. Это можно сделать путем
присваивания вершинам порядкового номера их поступления в дерево. Тогда, ес-
если с является п-ой вершиной, попавшей в дерево, то ей будет присвоено значение
счета п, которое мы обозначим через ЗС(с). Используя это упорядочение, при-
присвоим с наименьшее значение вершины а такой, что между а и с или одним из
ее потомков существует обратное ребро. Обозначим это значение через ОР(с) и
назовем его ОЯ-значением вершины с. Как отмечалось раннее, при поиске в глу-
глубину, пока у вершины v имеется смежная с ней неиспользованная вершина w} мы
проходим путь от v в w. И только в случае, когда нельзя продвигаться дальше, мы
покидаем шаг 4. Желательно, чтобы новый алгоритм делал то же самое, но, кроме
того, по мере добавления в дерево новой вершины w присваивал новое значение
счета величине 3C(w). Временно положим OP(w) — 3C(w). Будем определять ОР-
значения для вершины w по восходящему принципу. Дойдя до листа /, сравним
его ОЯ-значение со значением счетчика или ЗС-значения всех вершин, смежных
с Z, исключая его родителя, и присвоим ОРA) значение, минимальное из всех
перечисленных. При возврате к родителю р сравним его текущее ЗС-значение с
ОЯ-значением того сына с, от которого произошел возврат. Если ОР(с) > ЗС(р),
то никакой потомок вершины с не имеет обратного ребра к собственному предку
вершины р, и согласно предыдущей теореме р является точкой сочленения.
Далее, положим ОР(р) равным минимуму из его текущего значения и значе-
значения ОР(с). Если новых ребер из р больше нет, положим ОР(р) равным минимуму
из его текущего значения и ЗС-значений всех вершин таких, что между р и этими
вершинами существует обратное ребро. Продолжаем, пока не завершится поиск
в глубину.
Заметим, что если достигнута точка сочленения а, и мы удалим те (еще
неудаленные) ребра, вершиной которых является а и ее потомки, но оставим вер-
вершину а, то получим остовное дерево одной из компонент двусвязности графа G.
Формально процедура выражается следующим алгоритмом. Используем ре-
рекурсивное свойство, позволяющее алгоритму вызывать самого себя. Используем

668 ГЛАВА 15. Деревья
счетчик, изначально установленный на 0. Как и ранее, предположим, что началь-
начальной меткой для каждой вершины будет метка "нов".
Алгоритм поиска точек сочленения — ПТС(*;)
A) Пометить v символом "исп".
B) Присвоить г значение г 4-1.
C) Положить OP(v) = ЗС(у) = L
D) Пока имеется невыбранная вершина, смежная с v, выполнять следующее:
(а) Выбрать вершину w, которая является смежной с v.
(б) Если w имеет метку "нов", то:
(i) добавить (v, tu) в РЕБРА ДЕРЕВА;
(ii) положить v = parent(w)\
(iii) вызвать ПТС(ги);
(iv) если OP(w) > 3C(v), то v — точка сочленения. Ребра, ниже v,
которые охватывают компоненту, удаляются;
(v) положить OP(v) = mm@P(v),0P(w)).
(г) Если w имеет метку "исп" и w не является parent(ги), то OP(v) =
min(OP(v),3C(w)).
ПРИМЕР 15.27. Рассмотрим граф, изображенный на рис. 15.75, и соответствую-
соответствующее дерево (рис. 15.76).
Рис. 15.75
Рис. 15.76
Из пути abdgf дерева определяем, что ОР(а) = ЗС(а) = 1, ОР(Ь) = ЗС(Ь) =
2, OP(d) = 3C(d) = 3, ОР(д) = ЗС(д) = 4 и OP(f) = 3C(f) = 5. Из вершины / на-
находим обратное ребро из / в d и присваиваем OP(f) = 3C(d) = 3. Возвращаемся в
вершину д, поскольку / — сын д, то ОР(д) = min@P(/), ОР(д)) = minD,3) = 3.
Поскольку ОР(д) = 3 > 3C(d) и д — сын вершины d/d — точка сочленения, а
дерево на рис. 15.77, сформированное ребрами {/,#} и {d,g}, охватывает компо-
компоненту двусвязности (рис. 15.78).
Рис. 15.77
Г
Рис. 15.78

РАЗДЕЛ 15.5. Остовные деревья 669
Возвращаемся в вершину d, поскольку g — сын вершины d, полагаем OP(d) =
min(@P(<7), OP(d)) = minC,3) = 3. Затем, так как существует обратное ребро из
d в а, присваиваем OP(d) — ЗС(а) = 1. Возвращаемся в 6. Поскольку d — сын
вершины Ь, присваиваем OP(b) = min(OP(d),OP(ft)) = min(l,2) = 1. Потому что
ОЯF) > ЗС(а), вершина а — точка сочленения (а — корень с двумя сыновья-
сыновьями), и дерево (рис. 15.79), сформированное ребрами {d, 6} и {6, а}, охватывает
компоненту двусвязности, изображенную на рис. 15.80.
Рис. 15.79 Рис. 15.80
Возвращаемся в вершину а; поскольку b — сын вершины а, сравниваем
их ОР-значения и находим, что ОР{а) = min((ОЯ(а), ОЯ(Ь)) = min(l, 1) = 1,
поэтому ОР(а) остается неизменным. Из того, как сформирован путь aceh дерева,
находим ОР(с) = ЗС(с) = 6, ОР(е) = ЗС(е) = 7 и ОР(/г) = 3C(/i) = 8. А так как
вершина h не имеет обратных ребер, OP(h) остается неизменным. Из того, что
OP(h) > ЗС(е) и h — сын вершины е, следует, что е — точка сочленения и ребро
{e,/i} — остовное дерево компоненты двусвязности, изображенной на рис. 15.81.
Возвращаемся в е; поскольку h — сын вершины е, имеем ОР(е) = min(OP(e),
OP(h)) minG,8) = 7, поэтому ОР(е) остается неизменным. Но существует обрат-
обратное ребро из е в а, значит ОР{е) = ЗС(а) = 1. ОР(с) = min(OP(c),OP(e)) =
min(l,6) = 1. Поскольку ОР(е) > ЗС(а), то, как и ожидалось, вершина а — опять
найдена как точка сочленения, дерево (рис. 15.82), сформированное ребрами {а, с)
и {с, е}, охватывает бикомпоненту, изображенную на рис. 15.83.
Рис. 15.81 Рис. 15.82 Рис. 15.83
Наконец, возвращаемся в вершину а, и процесс завершен. ?
Заметим, что множество из п вершин размечено, если каждой вершине при-
приписано единственное целое число между 1 и п. Таким образом, имеем вершины
^1^2,^3, ••• ,vn. Если рассмотреть все графы, имеющие п размеченных вершин,
то сколько остовных деревьев можно построить? Другими словами, сколько име-
имеется остовных деревьев для п размеченных вершин? Ответ на этот вопрос дает
формула Кэли. Это число остовных деревьев для Кп.
ТЕОРЕМА 15.28. (Формула Кэли для дерева) Число остовных деревьев для п
размеченных вершин равно пп~2.

670 ГЛАВА 15. Деревья
ДОКАЗАТЕЛЬСТВО. Для доказательства утверждения покажем, что каждое остов-
ное дерево однозначным образом можно представить в виде последовательности
ai, a2, аз,..., ап_2 длины п — 2 такой, что для 1 < к < п — 2 элемент последова-
последовательности ak может быть любым целым числом между 1 и п, и обратно, каждой
последовательности а\, а2, аз,..., ап_2 длины п — 2 такой, что для 1 < к < п — 2
выполняется 1 < а^ < п, соответствует единственное остовное дерево. Если это
сделать, то вопрос сведется к тому, сколькими способами можно заполнить п-2
пробела, если имеется п способов заполнения каждого пробела, а таких спосо-
способов, как известно, существует пп~2. Вместо формального доказательства приве-
приведем алгоритм построения указанной последовательности по остовному дереву и
алгоритм построения остовного дерева по соответствующей последовательности.
Далее покажем на примере, что если начать с остовного дерева и использовать
алгоритм построения последовательности, а затем применить к ней алгоритм по-
построения остовного дерева, то получим исходное остовное дерево.
Начнем с алгоритма преобразования остовного дерева в последовательность.
Алгоритм перевода дерева в последовательность — ДвП(Т) для п > 3
A) Для выбора а\ взять лист Vj с наименьшим значением j. Всегда существу-
существует единственное к такое, что {vj,Vk} является ребром дерева. Удалить это
ребро и положить а\ = к.
B) Если выбрано ai_i, то для выбора а; из оставшегося дерева взять лист Vj
с наименьшим значением j. Всегда существует единственное к такое, что
{vj,Vk} является ребром дерева. Удалить это ребро и положить ai = к.
C) Продолжать, пока не будет выбрано an_2. ¦
ПРИМЕР 15.29. Пусть Т — дерево, изображенное на рис. 15.84. Вершина г;2 —
лист с наименьшим индексом, поэтому удаляем ребро {^2,^i} и полагаем а! = 1,
как показано на рис. 15.85. Поскольку в оставшемся дереве вершина г;3 — лист с
наименьшим индексом, удаляем ребро {г^,!^} и полагаем а2 = 4 (рис. 15.86).
Рис. 15.85
Рис. 15.86
Далее, г»5 — лист с наименьшим индексом, удаляем ребро {vs,vi} и полагаем
а3 = 1, как показано на рис. 15.87. Поскольку в оставшемся дереве вершина v\ —
лист с наименьшим индексом, удаляем ребро {г^г/б} и полагаем а4 = 6, как
показано на рис. 15.88. В оставшемся дереве вершина vj — лист с наименьшим
индексом, поэтому удаляем ребро {v-j,vq} и полагаем а5 = б (рис. 15.89).

РАЗДЕЛ 15.5. Остовные деревья 671
Рис. 15.87
Рис. 15.88
Рис. 15.89
Наконец, поскольку в оставшемся дереве v6 — лист с наименьшим индексом,
удаляем ребро {^г^} и полагаем а6 = 4. Осталось только ребро, изображенное
на рис. 15.90. Поэтому искомая последовательность имеет вид
1,4,1,6,6,4. v,
Отметим, что происходит число вхождений в последователь-
последовательность индекса каждой вершины на единицу меньше ее степени.
Это потому, что при удалении ребра вершина-лист не учиты-
вется, а вторая его вершина учитывается как вершина в ребре, v*
которое остается как лист, или как вершина в ребре, которое Рис. 15.90
остается. ?
ПРИМЕР 15.30. Пусть Т — дерево, изображенное на рис. 15.91. Поскольку v2 —
лист с наименьшим индексом, удаляем ребро {v2,v§} и полагаем а\ = 9, как
показано на рис. 15.92. В оставшемся дереве v% — лист с наименьшим индексом,
удаляем ребро {vs,vg} и полагаем а2 = 8, как показано на рис. 15.93.
vio
Рис. 15.91
Рис. 15.92
Рис. 15.93
Поскольку вершина vA стала листом с наименьшим индексом, удаляем ребро
{^4,^io} и полагаем аз = 10 (рис. 15.94). Теперь вершина v$ стала листом с
наименьшим индексом, удаляем ребро {г^^ю} и полагаем а^ = 10, как показано
на рис. 15.95. Далее, поскольку вершина v6 стала листом с наименьшим индексом,
удаляем ребро {v6,vi} и полагаем а5 = 1 (рис. 15.96).

672 ГЛАВА 15. Деревья
V1O
V,
Рис. 15.94
Рис. 15.95
Рис. 15.96
Поскольку в оставшемся дереве вершина v7 стала листом с наименьшим
индексом, удаляем ребро {v7^vg} и полагаем clq = 8, как показано на рис. 15.97.
Теперь вершина vs стала листом с наименьшим индексом, поэтому удаляем ребро
{vs,vq} и полагаем а7 = 9, как показано на рис. 15.98. Наконец, оставшаяся
вершина г;9 стала листом с наименьшим индексом, и мы удаляем ребро {vg,i>i} и
полагаем а8 = 1. В результате осталось только ребро, изображенное на рис. 15.99.
Рис. 15.97 Рис. 15.98 Рис. 15.99
Таким образом, искомая последовательность имеет вид
9,8,10,10,1,8,9,1.
Теперь нам нужен обратный алгоритм.
Алгоритм перевода последовательности в дерево —
ПвД(ах, а2,..., ап_2) для п > 3
A) Для каждого viy если г появляется в последовательности П{ раз, положить
deg(vi) = щ + 1.
B) Прочитать а\ и сформировать ребро {vai,Vj}, где j — наименьшая метка,
такая что deg(vj = 1).
C) Уменьшить deg(vai) и deg(vj) на 1.
D) Предположим, что a;_i прочитано, читать а; и формировать ребро {vai,Vj},
где j — наименьшая такая метка, что deg(i;j) = 1.
E) Уменьшить deg(t;aJ и deg(vj) на 1.
F) После того, как an_2 прочитано, создать ребро между двумя оставшимися
вершинами степени 1.
ПРИМЕР 15.31. Рассмотрим последовательность
1,4,1,6,6,4
и воспользуемся ею для восстановления исходного дерева из примера 15.29.

РАЗДЕЛ 15.5. Остовные деревья 673
Поскольку 1, 4 и 6 появляются в последовательности дважды, то
deg(vi) = deg(u4) = deg(v6) = 3.
А так как 2, 3 и 5 не встречаются вообще, то
deg(i;2) = deg(u3) = deg(y5) = deg(i;7) = deg(ys) = 1.
Запишем их с помощью восьмерки из чисел C,1,1,3,1,3,1,1), которую назовем
восьмеркой степеней.
Теперь считываем а\ = 1 и, поскольку уъ среди всех вершин степени 1 имеет
наименьший индекс, создаем ребро \y\,y<i\ (рис. 15.100). Положим deg(^i) = 2
и deg(t>2) = 0, поэтому восьмерка степеней теперь имеет вид B,0,1,3,1,3,1,1).
Далее считываем а2 = 4 и, потому что уз среди всех вершин степени 1 имеет
наименьший индекс, создаем ребро {г;3,^4}, после чего получаем граф, изобра-
изображенный на рис. 15.101.
Полагаем deg(i>4) = 2 и deg(i;3) = 0, поэтому восьмерка степеней теперь
имеет вид B,0,0,2,1,3,1,1). Второе ребро наклонено в другую сторону, потому
что я смошенничал и посмотрел на дерево, которое пытаюсь воссоздать. Теперь
считываем а3 = 1 и, поскольку уъ среди всех вершин степени 1 имеет наимень-
наименьший индекс, создаем ребро {у\,у$}, после чего получаем граф, изображенный на
рис. 15.102.
Рис. 15.100 Рис. 15.101 Рис. 15.102
Полагаем deg(vi) = 1 и deg^) = 0, поэтому восьмерка степеней теперь име-
имеет вид A,0,0,2,0,3,1,1). Считываем а4 = б и, поскольку у\ среди всех вершин
степени 1 имеет наименьший индекс, создаем ребро {у\,уъ}, после чего получаем
граф, изображенный на рис. 15.103.
Полагаем deg(vi) = 0 и deg(i>6) = 2, поэтому восьмерка степеней теперь
имеет вид @,0,0,2,0,2,1,1). Считываем а$ = 6 и, потому что уг среди всех вер-
вершин степени 1 наименьшую степень, создаем ребро {г>7,г;б}, после чего получаем
граф, изображенный на рис. 15.104.
Полагаем deg(t>7) = 0 и deg(i;6) = 1, поэтому восьмерка степеней теперь име-
имеет вид @,0,0,2,0,1,0,1). Считываем а^ = 4 и, поскольку Ув среди всех вершин
степени 1 наименьший индекс, создаем ребро {и^^б}, после чего получаем граф
изображенный на рис. 15.105.

674 ГЛАВА 15. Деревья
Рис. 15.103 Рис. 15.104 Рис. 15.105
Полагаем deg(t;4) = 1 и deg(t;6) = 0, поэтому восьмерка степеней теперь име-
имеет вид @,0,0,1,0,0,0,1). Наконец, поскольку все последовательности прочитаны
и deg(v^) = deg(t>s) = 1, формируем ребро {v^v%} и получаем искомое дерево из
примера 15.29. ?
ПРИМЕР 15.32. Теперь рассмотрим последовательность
9,8,10,10,1,8,9,1
и воспользуемся ею для воссоздания исходного дерева из примера 15.30.
Поскольку 10, 9, 8 и 1 появляются в последовательности по два раза, то
= deg(i;9) = deg(v8) = deg(vi) = 3.
А так как 2, 3 и 5 не встречаются в последовательности вообще, то
= deg(v4) = deg(u5) = deg(v6) = deg(v7) = 1.
Запишем их с помощью десятки чисел C,1,1,1,1,1,1,3,3,3), которую будем
называть десяткой степеней.
Считываем а\ = 9 и, поскольку v2 среди всех вершин степени 1 имеет
наименьший индекс, создаем ребро {^9,^2}, как показано на рис. 15.106.
Полагаем deg^g) = 2 и deg(i>2) = 0, поэтому десятка степеней имеет вид
C,0,1,1,1,1,1,3,2,3). Считываем а2 = 8 и, потому что г;3 среди всех вершин
степени 1 имеет наименьший индекс, создаем ребро {г>8,г>3}, как показано на
рис. 15.107. Полагаем deg(z;8) = 2 и deg(v3) = 0; десятка степеней теперь имеет
вид C,0,0,1,1,1,1,2,2,3). Считываем а3 = 10 и, поскольку vA среди всех вершин
степени 1 имеет наименьший индекс, создаем ребро {г^о,^}, как показано на
рис. 15.108.
'У у о У в 4
v/ v2* v/ v/v/ v/
Рис. 15.106 Рис. 15.107 Рис. 15.108
Полагаем deg(i;io) = 2 и deg(i;4) = 0; десятка степеней теперь имеет вид
C,0,0,0,1,1,1,2,2,2). Считываем а4 = 10 и, так как v$ среди всех вершин

РАЗДЕЛ 15.5. Остовные деревья 675
степени 1 имеет наименьший индекс, создаем ребро {viq,vs}, как показано на
рис. 15.109. Полагаем deg(i;io) = 1 и deg(t>5) = 0, поэтому десятка степеней теперь
имеет вид C,0,0,0,0,1,1,2,2,1). Считываем а5 = 1 и поскольку v6 среди всех
вершин степени 1 имеет наименьший индекс, создаем ребро {vi,v6} рис. 15.110.
. /./ У . /./ У „
V2 V3 VW V2 V3 V10 Vl V6
Рис. 15.109 Рис. 15.110
Полагаем deg(v1) = 2 и deg^) = 0, поэтому десятка степеней имеет вид
B,0,0,0,0,0,1,2,2,1). Считываем а6 = 8 и, поскольку v7 среди всех вершин
степени 1 имеет наименьший индекс, создаем ребро {^3,^7}, как показано на
рис. 15.111.
Полагаем deg(i>8) = 1 и deg(i;7) = 0; десятка степеней теперь имеет вид
B,0,0,0,0,0,0,1,2,1). Считываем а7 = 9 и, потому что v% среди всех вершин
степени 1 имеет наименьший индекс, создаем ребро {^з,^}, как показано на
рис. 15.112.
Рис.
V9
А
4 •
V3 V7
15.112
VS V4
V _
Рис. 15.111
Полагаем deg(v9) = 1 и deg^s) = 0, поэтому десятка степеней теперь имеет
вид B,0,0,0,0,0,0,0,1,1). Считываем ag = 1 и, поскольку vq среди всех вершин
степени 1 имеет наименьший индекс, создаем ребро {vi,vg}, как показано на
рис. 15.113.
v
Рис. 15.113
Полагаем deg(vi) = 1 и deg(i>9) = 0, поэтому десятка степеней теперь
имеет вид A,0,0,0,0,0,0,0,0,1). Наконец, вся последовательность прочитана и
deg(i>i) = deg(vio) = 1; формируем ребро {vi,vio} и получаем искомое дерево из
упражнения 15.30. ?

676 ГЛАВА 15. Деревья
Предыдущая теорема дает количество различных остовных деревьев на п
размеченных вершинах, но не рассматривает конкретный граф с этими вершина-
вершинами. Когда рассматривается определенный граф, то количество различных остов-
остовных деревьев для этого графа уменьшается, так как используются только ребра
графа. Данный раздел завершает метод определения количества остовных дере-
деревьев для графа с п размеченными вершинами.
ОПРЕДЕЛЕНИЕ 15.33. Пусть G — граф с п размеченными вершинами
vi,V2,V3,...,vn. Матрицей степеней графа G называется пхп матрица Д
определенная следующим образом: Dij = О, если г ф j, и Da равно степени
вершины vi.
Используя это определение, сформулируем следующую, весьма впечатляю-
впечатляющую теорему, которую приведем без доказательства.
ТЕОРЕМА 15.34. (Матричная формула Кирхгофа) Пусть G — связный граф
с помеченными вершинами. Пусть К = D — А, где А — матрица смежности
графа G, a D — матрица степеней графа G. Число остовных деревьев графа G
равно любому из алгебраических дополнений матрицы К.
ПРИМЕР 15.35. Найдем количество остовных деревьев графа, изображенного на
рис. 15.114.
Поскольку
Матрица А имеет вид
rz J Рис. 15.114
2 и deg(i;2) = deg(i>4) = 3,
Г 2 О О О 1
0 3 0 0
0 0 2 0
0 0 0 3
0 10 1
10 11
0 10 1
1110
К=С-А=
Г 2 0 0 0
0 3 0 0
0 0 2 0
0 0 0 3
Г 0 1 0 1
10 11
0 10 1
1110
2
-1
0
-1
-1
3
-1
-1
0
-1
2
-1
-1
-1
-1
3

РАЗДЕЛ 15.5. Остовные деревья 677
Алгебраическое дополнение К\\ есть
det
3 -1 -1
-1 2 -1
-1 -1 3
= 3det
2 -1
-1 3
-(-l)det
-1 -1
-1
+ (-l)det
Значит, существует восемь остовных деревьев.
-1 2
-1 -1
= 3E) -4-3 = 8.
?
УПРАЖНЕНИЯ
1. Задан граф (рис. 15.115), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
Рис. 15.115
Рис. 15.116
2. Задан граф (рис. 15.116), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
3. Задан граф (рис. 15.117), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
гг v
Рис. 15.117
Рис. 15.118

678 ГЛАВА 15. Деревья
4. Задан граф (рис. 15.118), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
5. Задан граф (рис. 15.119), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
6. Задан граф (рис. 15.120), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
7. Задан граф (рис. 15.121), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
Рис. 15.122
8. Задан граф (рис. 15.122), вершины которого упорядочены так, как помечены.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.

РАЗДЕЛ 15.5. Остовные деревья 679
9. Задан граф К$.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
10. Задан граф /Сз,4-
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
11. Задан граф Петерсена.
а) Найдите остовное дерево, удаляя ребро из каждого цикла.
б) Найдите остовное дерево поиском в ширину.
в) Найдите остовное дерево поиском в глубину.
12. Используя алгоритм ПТС поиска точек сочленения, найдите точки сочлене-
сочленения и компоненты двусвязности для графа, изображенного на рис. 15.123.
Рис. 15.123
Рис. 15.124
13. Используя алгоритм ПТС поиска точек сочленения, найдите точки сочлене-
сочленения и компоненты двусвязности для графа, изображенного на рис. 15.124.
14. Используя алгоритм ПТС поиска точек сочленения, найдите точки сочлене-
сочленения и компоненты двусвязности для приведенных ниже графов.
а)
б)

680 ГЛАВА 15. Деревья
в)
12
15. Для графа G, представляющего собой простой цикл, опишите его остовные
деревья, полученные поиском в ширину и в глубину. Если G имеет п вершин,
то сколько у него остовных деревьев?
16. Если G —- граф, представляющий собой цикл, но необязательно простой,
изменится ли описание его остовных деревьев? Почему? Может ли граф G
иметь точку сочленения?
17. Докажите, что ребро графа G принадлежит всем его остовным деревьям
тогда и только тогда, когда это разрезающее ребро.
18. Найдите для графа G необходимые и достаточные условия равенства остов-
остовных деревьев, полученных поиском в глубину и в ширину?
19. Покажите, что остовное дерево, полученное поиском в глубину для Кп при
п > 3, является простым путем, а остовное дерево, полученное поиском в
ширину, таковым не является.
20. Найдите такое а, что если п > а, то Кп имеет два остовных дерева без
общих ребер.
21. Докажите, что если Е' — разрезающее множество графа G, то каждое остов-
остовное дерево содержит ребро из Е1.
22. Сколько остовных деревьев имеет граф К$? Сколько остовных деревьев име-
имеет К? Сколько остовных деревьев имеет Кп?
23. Сколько остовных деревьев имеет граф i^2,n?
24. Если G — граф с v вершин и е ребер, то сколько ребер можно удалить, не
нарушив связности оставшегося графа?
25. Пусть Т и Т" — различные остовные деревья графа G. Пусть е — ребро
дерева Г, которое не является ребром дерева Т', и Те — это дерево Т, из
которого удалено ребро е. Докажите, что в дереве Т" имеется такое ребро е',
добавив которое в Те, получим граф, который будет опять остовным деревом
графа G.
26. Используя алгоритм преобразования дерева в последовательность, определи-
определите соответствующие последовательности для каждого из приведенных ниже
деревьев.

РАЗДЕЛ 15.5. Остовные деревья 681
а)
б)
в)
г)
27. Используя алгоритм преобразования дерева в последовательность, определи-
определите последовательности, соответствующие каждому из следующих деревьев.
а) б)
в)
г)
28. Используя алгоритм перевода дерева в последовательность, постройте соот-
соответствующие деревья для приведенных ниже последовательностей.
а) 1,2,3,3,2,3.
б) 1,3,3,5,5,4,4.
в) 1,2,2,2,5,4,5,6.
29. Используя алгоритм перевода дерева в последовательность, постройте соот-
соответствующие деревья для приведенных ниже последовательностей.
а) 1,4,2,3,2,3.
б) 1,4,3,3,4,4,4.
в) 1,5,2,5,3,6,5,5.

682 ГЛАВА 15. Деревья
30. Используя матричную формулу Кирхгофа, определите число остовных дере-
деревьев для каждого из приведенных ниже графов.
а) б) в)
31. Используя матричную формулу Кирхгофа, определите число остовных дере-
деревьев для каждого из приведенных ниже графов.
а) б) в)
32. Сколько остовных деревьев имеет граф KniTl?
15.6. МИНИМАЛЬНЫЕ ОСТОВНЫЕ ДЕРЕВЬЯ
Взвешенный граф определен в предыдущей главе как граф, каждому ребру ко-
которого приписано положительное число, назывемое весом. Этот вес может опи-
описывать расстояние, стоимость или другие данные. Например, если бы вершины
представляли города, то вес мог бы быть расстоянием между городами или сто-
стоимостью перелета из одного города в другой. Вес остовного дерева взвешенного
графа G равен сумме весов, приписанных ребрам остовного дерева. Минималь-
Минимальным остовным деревом назывется такое остовное дерево графа G, что вес Г
меньше или равен весу любого другого остовного дерева графа G.
Мы рассмотрим два способа построения минимального остовного дерева
взвешенного графа G. Первый называется алгоритмом Крускала. Идея метода
состоит в том, чтобы формировать дерево Т(Е, V), выбирая ребра с наименьшим
весом так, чтобы не возникал цикл.
Алгоритм Крускала
A) Выбрать в графе G ребро е минимального веса, не принадлежащее мно-
множеству Е и такое, что его добавление в Е не создает цикл в дереве Т.
B) Добавить это ребро во множество ребер Е.
C) Продолжать, пока имеются ребра, обладающие указанными свойствами.
ПРИМЕР 15.36. Рассмотрим взвешенный граф, изображенный на рис. 15.125.

РАЗДЕЛ 15.6. Минимальные остовные деревья 683
Ь
7
Рис. 15.125
Выберем ребро {6, d} и добавим его в Е. Далее — ребро {d, е}, так что Е =
{{Ь, d}, {d, е}}. Затем добавим ребро {а, е}, после чего ? = {{Ь, d}, {d, e}, {а, е}}.
Ребро {а, 6} добавить нельзя, так как это приведет к образованию цикла, поэтому
добавим ребро {/, <?}, так что Е = {{6, d}, {d, e}, {а, е}, {/,#}}. Следующим можно
добавить {е,/}, и Е = {{b,d},{d,e},{a,e},{f,g},{e,f}}. Наконец, добавляем
ребро {c,d}, после чего Е = {{b,d},{d,e},{a,e},{/,g},{e,/}},{c,d}. Больше не
осталось ребер, которые можно добавлять, поэтому искомое дерево выглядит, как
изображенное на рис. 15.126.
Рис. 15.126 ?
ТЕОРЕМА 15.37. Алгоритм Крускала создает минимальное остовное дерево.
ДОКАЗАТЕЛЬСТВО. Алгоритм Крускала дает минимальное остовное дерево по
построению. Пусть
ei,e2,e3,e4, • •., еп
— ребра дерева Т в том порядке, в котором их выбирает алгоритм Крускала.
Пусть к — наибольшее целое число такое, что в1,е2,ез,е4,..., е^ — ребра мини-
минимального остовного дерева, и пусть Т" является этим деревом. Если к ф п, то
присоединим ребро ek+i к дереву Т'. Теперь дерево Т" с присоединенным ребром
содержит цикл. Удалим из этого цикла е, где е ф е;, для 1 < г < fc + 1, и обозна-
обозначим полученное дерево Т". Вес ребра е не может быть меньше веса е^+ь если бы
это было так, то ребро уже было бы выбрано алгоритмом Крускала или создавало
бы цикл, поэтому ребра {е1,е2,ез,е4,... ,е^,е} не могут составлять часть ребер
дерева. Но это невозможно, поскольку данное множество ребер является частью
дерева V. Таким образом, поскольку дерево Т" создано из дерева V заменой
ребра е на ребро, которое не тяжелее, то вес дерева Г" меньше или равен весу
дерева V. Поэтому Т" — минимальное остовное дерево, которое как часть сво-
своего множества ребер содержит {е1,е2,ез,е4,... ,efc,efc+i}« Но это противоречит
определению числа к. Поэтому к = и и Т — минимальное остовное дерево. ¦

684 ГЛАВА 15. Деревья
Второй и последний из представленных алгоритмов построения минималь-
минимального остовного дерева называется алгоритмом Прима. Принципиальное отличие
алгоритма состоит в том, что всегда имеется дерево, к которому ребра добавляют
до тех пор, пока не получится остовное дерево. Используя алгоритм Прима, сна-
сначала выбираем вершину v0 графа G, а затем выбираем ребро с наименьшим весом
ei = {^1,^0}, инцидентное к вершине vOi и формируем дерево Т\. Следующим вы-
выбираем ребро с наименьшим весом е^ такое, что одна вершина ребра принадлежит
дереву Ti, а вторая — нет, и добавляем его в дерево, после чего получаем дерево
Г2 с двумя ребрами. Сформировав дерево Ть формируем дерево Т*+1, выбирая
ребро с минимальным весом e^+i такое, что одна его вершина принадлежит де-
дереву Т^, а другая — нет, и добавляем это ребро в дерево. Продолжаем процесс
до тех пор, пока дерево не будет содержать все вершины графа G.
Теперь опишем алгоритм формально.
Алгоритм Прима нахождения минимального остовного дерева
A) Выбрать вершину v0 графа G и ребро с наименьшим весом еь для кото-
которого vo — одна из вершин, и сформировать дерево Т\.
B) Для заданного дерева Tk с ребрами ei, б2, ез,..., е*, если имеется верши-
вершина, не принадлежащая Ть выбрать ребро с наименьшим весом, смежное с
ребром дерева Tk и имеющее вершину вне дерева Tk. Добавить это ребро
в дерево Tk, формируя дерево Tk+i.
C) Продолжать, пока имеются вершины графа G, не принадлежащие дереву.
ПРИМЕР 15.38. Снова рассмотрим дерево (рис. 15.127).
Рис. 15.127
Начав с вершины а, первым выбираем ребро {а, е}, поскольку оно имеет ми-
минимальный вес. Таким образом, дерево 7\ состоит из ребра {а, е}. Теперь выбира-
выбираем ребро {e,d}, так как это ребро с минимальным весом из тех, что имеют только
одну вершину в дереве Ti. Получаем дерево Т2, изображенное на рис. 15.128.
Далее выбираем ребро {d, 6}, поскольку это ребро с минимальным весом из
тех, что имеют только одну вершину в Т2. Получаем Тз — дерево, изображенное
на рис. 15.129. Теперь, так как имеется два ребра с одинаковым весом и одной
вершиной в Тз, имеем выбор. Предположим, выбрано ребро {d,c}, поэтому дерево
Т4 имеет следующий вид (рис. 15.130).

РАЗДЕЛ 15.6. Минимальные остовные деревья 685
а <
е «
d*
>
Рис. 15.128
е <
Рис. 15.129
а
е (
d.
К
Рис. 15.130
Следующим выбираем ребро {е, /}. Это ребро имеет минимальный вес из
тех, что имеют только одну вершину в дереве Т4; отсюда Т5 — дерево на рисун-
рисунке 15.131.
Рис. 15.131
Наконец, выбираем ребро {/,д}. Поскольку это ребро минимального веса
из тех, что имеют одну вершину в Т4, а вершина д —- последняя из оставшихся
вершин, имеем дерево Тб, которое является искомым остовным деревом. ?
Теперь докажем, что данный алгоритм в действительности создает мини-
минимальное остовное дерево.
ТЕОРЕМА 15.39. Для заданного взвешенного графа G дерево, создаваемое в
соответствии с алгоритмом Прима нахождения минимального остовного дерева,
является минимальным остовным деревом.
ДОКАЗАТЕЛЬСТВО. Из построения дерева следует, что оно остовное. Доказа-
Доказательство того, что оно является минимальным остовным деревом, аналогично
доказательству подобного утверждения для алгоритма Крускала. Пусть
— ребра дерева Т в том порядке, в каком они выбраны согласно алгоритму При-
Прима нахождения минимального остовного дерева, и к — наибольшее целое число
такое, что ei,e2,e3,e4,..., е/с являются ребрами минимального остовного дере-
дерева, и V является этим деревом. Пусть Tk — дерево, сформированное ребрами
ei,e2, ез,е4,... ,efc. Если к Ф п, присоединяем ребро e^+i к дереву Т". Теперь V
с новым присоединеннным ребром содержит цикл. В цикле содержится другое
ребро е, имеющее только одну вершину в дереве 7^. Удалим ребро е из дере-
дерева V U {efc+i}, формируя дерево Т" с ребром e^+i вместо ребра е. Поскольку
e/c+i — ребро с наименьшим весом среди тех, что имеют одну вершину в дере-
дереве Ть вес efc+i меньше или равен весу е. Поэтому вес Т" меньше или равен
весу Т\ так что Т" также является минимальным остовным деревом с ребрами
б1,е2,ез,б4,.. .,е/^е*;+1| но это противоречит определению к. Поэтому к = п, и
алгоритм Прима нахождения минимального остовного дерева создает минималь-
минимальное остовное дерево. ¦

686 ГЛАВА 15. Деревья
Алгоритм Прима можно также реализовать с помощью матриц. Для графа G
с п вершинами требуется матрица размерности (п+1)х(п+1). Сначала определим
п х п весовую матрицу W, где W^ — вес ребра из V{ в Vj, если ребро из V{ в Vj
существует, и 0, если такого ребра нет. После этого добавим п + 1-ую строку и
п + 1-ый столбец, которые пока будут пустыми. Новую матрицу обозначим через
W*.
Формально изложим следующий алгоритм.
Матричный алгоритм Прима
A) Создать весовую матрицу W.
B) Добавить дополнительную строку и столбец, чтобы создать матрицу W*.
C) В строке 1 матрицы W* поместить * в последнем столбце. В столбце 1
заменить все числа на 0 и поместить U в последней строке.
D) Выбрать наименьшее число, так что строка с этим числом имеет * в столб-
столбце п + 1, а столбец с этим числом не содержит U в строке п + 1.
E) Если число выбрано в строке г и столбце j, то поместить * в последний
столбец строки j, заменить оставшиеся числа в столбце j на 0, поместить
U в строке п + 1 столбца j и добавить ребро (vi,Vj) в остовное дерево.
F) Продолжать выполнение шагов 4 и 5, пока не останется чисел, которые
можно выбирать.
ПРИМЕР 15.40. Предположим, что имеется граф, изображенный на рис. 15.132
Рис. 15.132
поэтому матрицы W и W* имеют, соответственно, вид
3002
0 3 0 0 2 0 8
3 0 6 10 0 0
0 6 0 4 0 5 0
0 14 0 2 0 0
2 0 0 2 0 4 0
0 0 5 0 4 0 3
8 0 0 0 0 3 0
Сначала выбираем строку 1, что означает выбор первой вершины травной 0,
так как не собираемся больше возвращаться к вершине v\, и помещаем U в
восьмой ((п + 1)-ой) строке столбца 1, чтобы показать, что столбец 1 не будет
больше использован. Помещаем * в строке 1, тем самым указывая, что можно
3
0
0
2
0
8
0
6
1
0
0
0
6
0
4
0
5
0
1
4
0
2
0
0
0
0
2
0
4
0
0
0
5
0
4
0
3
8 '
0
0
0
0
3
0
и

РАЗДЕЛ 15.6. Минимальные остовные деревья 687
выбирать значения из этой строки, поскольку она содержит значения ребер из
в соседние вершины. Отсюда имеем
¦ о
0
0
0
0
0
0
и
3
0
6
1
0
0
0
0
6
0
4
0
5
0
0
1
4
0
2
0
0
2
0
0
2
0
4
0
0
0
5
0
4
0
3
8 * "
0
0
0
0
3
0
Выбираем наименьшее ненулевое значение в этой строке (т.е. выбираем ре-
ребро с наименьшим весом, смежное с v\). В данном случае это значение равно 2 и
находится в столбце 5. Таким образом, в качестве первого ребра выбрано ребро
(^1,^5)- Все другие значения в столбце 5 полагаем равными 0 и в восьмой строке
этого столбца устанавливаем значение, равное С/, поэтому данную строку уже
не будем использовать и не будем больше возвращаться к вершине v5. Помеща-
Помещаем * в восьмом столбце строки 5, показывая, что элементы в строке 5 можно
теперь использовать так же, как элементы первой строки, поскольку эти строки
представляют ребра из v\ и v$ в смежные вершины. Имеем
0
0
0
0
0
0
0
и
3
0
6
1
0
0
0
0
6
0
4
0
5
0
0
1
4
0
2
0
0
2
0
0
0
0
0
0
и
0
0
5
0
4
0
3
8 *
0
0
0
0 *
3
0
Далее выбираем наименьшее ненулевое значение в строке 1 или в строке 5.
В данном случае это значение 2 в столбце 4 строки 5. Таким образом, в каче-
качестве следующего ребра выбрано (^5,^4)- Остальные значения в данном столбце
полагаем равными 0 и в восьмой строке данного столбца устанавливаем значе-
значение, равное С/, поэтому строку не будем больше использовать и не будем больше
возвращаться к вершине v±. Помещаем * в восьмом столбце строки 4, показывая,
что элементы в этой строке можно теперь использовать так же, как и элементы
строки 1 и строки 5, поскольку эти строки представляют ребра из v\v^^ и v$ в
смежные вершины. Имеем
0
0
0
0
0
0
0
и
3
0
6
1
0
0
0
0
6
0
4
0
5
0
0
0
0
0
2
0
0
и
2
0
0
0
0
0
0
и
0
0
5
0
4
0
3
8 *
0
0
0 *
0 *
3
0

688 ГЛАВА 15. Деревья
Теперь выбираем наименьшее ненулевое значение из 1-ой, 4-ой или 5-ой
строки. В данном случае это значение, равное 1 в столбце 2 строки 4. Таким
образом, в качесте следующего ребра выбрано (г>4,г>2). Остальные значения в
столбце полагаем равными 0 и в восьмой строке этого столбца устанавливаем
значение, равное U. Помещаем * в восьмом столбце строки 2, показывая, что эти
элементы можно теперь использовать, как и элементы строк 1, 4 и 5, поскольку
эти строки представляют ребра из v\V2V±, и^в смежные вершины. Имеем
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
6
0
4
0
5
0
0
0
0
0
2
0
0
2
0
0
0
0
0
0
0
0
5
0
4
0
3
8 *
0 *
0
0 *
0 *
3
0
и и
и и
Используя ту же процедуру, выбираем значение 4 в строке 4 столбца 3 и
значение 4 в строке 5 столбца 6, что дает ребра (и^^з) и (г>5,^б)> соответственно,
и матрицы
0000208*
0000000*
0000050*
0 14 0 0 0 0*
0002040*
0 0 0 0 0 0 3
0 0 0 0 0 3 0
и и и и и
0
0
0
0
0
0
0
1
0
0
0
4
0
0
0
0
2
0
0
0
0
0
0
0
8 *
0 *
0 *
0 *
0 0 0 2 0 4 0
0 0 0 0 0 0 3
0 0 0 0 0 0 0
и и и и и и
Наконец, выбираем значение 3 в строке 6 столбца 7, что дает ребро
и матрицу
0000200
0000000
0000000
0140000
0002040
0000003
0 0 0 0 0 0 0
и и и и и и
а также остовное дерево, изображенное на рис. 15.133.

РАЗДЕЛ 15.6. Минимальные остовные деревья 689
7 Рис. 15.133
?
УПРАЖНЕНИЯ
1. Заданы взвешенные графы, изображенные на рис. 15.134 и 15.135, найдите
минимальные остовные деревья, воспользовавшись:
а) алгоритмом Крускала;
б) алгоритмом Прима.
в) матричным алгоритмом Прима;
Рис. 15.135
2. Заданы взвешенные графы, изображенные на рис. 15.136 и 15.137, найдите
минимальные остовные деревья, воспользовавшись;
а) алгоритмом Крускала;
б) алгоритмом Прима;
в) матричным алгоритмом Прима.
2 h
Рис. 15.136
3. Заданы взвешенные графы, изображенные на рис. 15.138 и 15.139, найдите
минимальные остовные деревья, воспользовавшись:
а) алгоритмом Крускала;
б) алгоритмом Прима;

690 ГЛАВА 15. Деревья
в) матричным алгоритмом Прима.
4. Заданы взвешенные графы, изображенные на рис. 15.140 и 15.141, найдите
минимальные остовные деревья, воспользовавшись:
а) алгоритмом Крускала;
б) алгоритмом Прима;
в) алгоритмом Прима с матрицами.
4 b l
3
10
/6
л
4
| 4
4
Рис. 15.140
g 3 h 2
Рис. 15.141

ГЛАВА
СЕТИ
16.1. СЕТИ И ПОТОКИ
Сеть можно представить как систему, транспортирующую некий продукт из одной
точки в другую. Этим продуктом могут быть люди, электроэнергия, природный
газ, нефть и многое другое. Примером может служить система нефтепровода, где
нефть течет из одной точки к другим точкам системы. Наша терминология будет
соответствовать данной концепции. Используя такое представление, рассмотрим
сеть как ориентированный граф, ребра которого — трубы между точками системы,
а они, в свою очередь, представлены вершинами графа. Каждому ребру е = (г^, Vj)
соответствует положительное целое число с(е), называемое пропускной способ-
способностью е. Если между двумя вершинами не существует ребра, то пропускную
способность полагаем равной нулю. В примере с нефтяными сетями пропускная
способность связана с количеством нефти, проходящей через трубу (ребро).
Перед тем как определить сеть, ограничим определение ориентированного
графа. Наличие петель у графа недопустимо, поскольку рассматриваемые задачи
связаны только с транспортировкой продукта между различными точками. Бу-
Будем считать, что если существует ребро из Vi в Vj, то нет ребра из Vj в vit
Таким образом, рассматривается поток продукта только в одну строну. Необходи-
Необходимое требование: ориентированный граф должен быть связным, т.к. если имеется
путь из а в z, нас будет интересовать только компонента, содержащая а и z.
Если между а и z не существует пути, то и определять нечего. Ориентирован-
Ориентированный граф, удовлетворяющий этим условиям, часто называется простым связным
ориентированным графом. Назовем такой граф ориентированным графом, имея в
виду, что он удовлетворяет упомянутым выше ограничениям. Рассмотрим также
особую вершину а, называемую источником, и особую вершину z, называвемую
стоком. Степень входа вершины а равна 0, так что в источник ничто не втекает.
Степень выхода вершины z равна 0, так что из стока ничто не вытекает. Таким
образом, продукт перевозится из а и имеет местом назнанчения z. Более точно
определим сеть следующим образом.

692 ГЛАВА 16. Сети
ОПРЕДЕЛЕНИЕ 16.1. Сеть — это ориентированный граф (G, V, JS) вместе с
весовой функцией С : Е —> ЛГ и выделенными вершинами а, г, такими что
(i) indeg(a) = 0;
(ii) outdeg(z) = 0.
Например, граф, изображенный на рис. 16.1, является примером сети, где
числа на каждом ребре обозначают пропускную способность.
Рис. 16.1
Для этой сети, которая представлена как нефтепровод, введем понятие потока
(количество нефти, проходящее через трубы нефтепровода). Таким образом, для
каждого ребра е имеется значение /(е), которое является потоком через конкрет-
конкретное ребро или трубу. Очевидно, величина потока не может превысить пропускную
способность трубы. Потребуем также, чтобы поток, входящий в вершину, был ра-
равен потоку, выходящему из вершины, за исключением вершин а и z.
Это называется сохранением потока. Пусть in(i>) — множество ребер, для
которых v — конечная вершина, и out(i>) — множество ребер, для которых v —
начальная вершина. Таким образом, out(i;) — множество ребер, выходящих из
вершины vy и in(x;) — множество ребер, входящих в вершину v. Следовательно,
имеем следующее определение.
ОПРЕДЕЛЕНИЕ
(i) для всех е €
(ii) для всех v e
16.2.
Е,0
Поток
< Не) <
V таких, что
в сети —
с(е);
v ^ a, z,
это
Ее
функция
Ein(.)/(e)
f:E-*
Л^и{0} такая, что
>ut(u)/(e).
Допустим, имеется фиксированный поток. Пусть поток(а) = 5Zeeout(a) Де)'
т.е. поток(а) — поток, вытекающий из источника а, и nomoK(z) = YLee'm(z) /(e)>
т.е. nomoK(z) — поток, втекающий в сток z. Пример потока в сети, где первый
элемент упорядоченной пары на каждом ребре — пропускная способность, а вто-
второй — поток, демонстрирует рис. 16.2.
Рис. 16.2

РАЗДЕЛ 16.1. Сети и потоки 693
Поток через каждое ребро меньше, чем его пропускная способность. Обра-
Обратите внимание, что для вершины Ь поток, втекающий в Ь, равен 4 и поток, вы-
вытекающий из Ь, равен 4. Таким образом, оба потока совпадают, и в вершине Ь
имеет место сохранение потока. Это верно также и для всех других вершин, за
исключением вершин а и z. Воспользуемся принципом сохранения потока для
доказательства того, что интуитивно кажется очевидным. А именно, поток из а
равен потоку в г, т.е. поток(а) = поток(г), что и утверждает приведенная ниже
теорема. Рассмотрим сначала конкретную сеть.
Заметим, что для потока на рис. 16.2 выполняется равенство поток(а) =
потоках) = 6. Пусть S — множество вершин {6,с,с?}, аТ = У-5- множество
вершин {a,/, z}. Если просуммировать потоки в 5, то согласно приведенной ниже
таблице получим, что входящий поток равен 9 и выходящий поток равен 9. Таким
образом, разность потоков равна 0.
вершина
b
с
d
сумма
входящий поток
4
3
1
1
9
ребро
(а, Ь)
F, с)
(e,d)
(b,d)
выходящий поток
3
1
3
2
9
ребро
F, с)
(М)
{с, г)
(d,z)
Если во множество S добавить вершину а, получим, что разность 15 (выхо-
(выходящий поток) и 9 (входящий поток) равна 6 = поток{а).
вершина
6
с
d
а
сумма
входящий поток
4
3
1
1
0
9
ребро
(а, Ь)
F, с)
(e,d)
(b,d)
выходящий поток
3
1
3
2
4
2
15
ребро
F, с)
(М)
(c,z)
(d,z)
(a,b)
(а,е)
Заметим, что ребра (а, 6), F, с) и (b, d) присутствуют в колонке для входя-
входящего и выходящего потока, потому что обе вершины каждого ребра принадлежат
5. При вычитании эти ребра сокращаются, поэтому, удалив их из обеих частей,
получаем

694 ГЛАВА 16. Сети
вершина
b
с
d
а
сумма
входящий поток
1
0
1
ребро
(e,d)
ВЫХОДЯЩИЙ ПОТОК
3
2
2
7
ребро
(с, z)
(d,z)
(а,е)
Снова разница входящего и выходящего потока равна 6. Но поскольку ребра, обе
вершины которых принадлежат 5, удалены, то выходящий поток — это сумма
потоков ребер, которые идут из 5 в Г, а входящий поток — это сумма потоков
ребер, которые идут из Т в 5. Аналогичные рассуждения будут использованы в
приведенной ниже теореме.
ТЕОРЕМА 16.3. Для любого фиксированного потока /
поток(а) =
eGout(a) eEin(z)
ДОКАЗАТЕЛЬСТВО. Пусть 5 — подмножество множества V, содержащее а, но
не содержащее zt а Т = V — S. Для v ф a,z из условия сохранения потока
имеем J2ee'm{v) f(e) = Yleeout(v) f(e)- Следовательно, суммирование по вершинам,
принадлежащим 5 — {а}, дает
Е
vES-{a}
= E E
vES-{a} e€out(r)
?
E E /oo- E E
veS-{a} eeout(v) veS-{a}
или
Поэтому, если включить а, получим
Е Е Ле)-Е Е /(*)= Е /(«)•
vES eEout(v) veS e?in(v) eGout(a)
Пусть E, T) — множество всех ребер из S в Т, т.е. E, Т) = {е : начальная
вершина е принадлежит 5, а конечная вершина е принадлежит Г}. Аналогично,
пусть (Т, 5) — множество всех ребер из Т в 5. Рассмотрим опять
У! У /(е)-Е Е /(е)-
in(v)

РАЗДЕЛ 16.1. Сети и потоки 695
В случае, когда начальная и конечная вершины ребра е принадлежат 5, е появ-
появляется в обеих суммах и, следовательно, взаимно сокращается. Если исключить
такие ребра, то слева получим только ребра, идущие из S в Т, а справа — только
ребра, идущие из Г в 5. Таким образом, имеем
Е Е /(е)-Е Е /(«)= Е /(<о- Е Я6)-
ee(S,T) еб(Т,5)
Следовательно,
Е /(«о- Е /(*)= Е
e<E(S,T) e€(T,5) e€out(a)
т.е. для любого заданного множества вершин 5, содержащего а, но не содержа-
содержащего г, разность выходящего из 5 и входящего в S потоков равна поток(а), т.е.
потоку, выходящему из источника а. Теперь пусть 5 = V — {z}, так что Т = {z}.
Тогда Y2ee(s,T) Де) есть ПРОСТО поток, вливающийся в г, так что
Е ^е)= Е f(e) = nomoK{z)
ee(S,T) eein(z)
и 2Zee(TS)/(e) = 0» поскольку это поток, вытекающий из г. Следовательно,
Е Яе)" Е Яе)= Е /(е)
е€(Г,5) e6inB)
и поток(а) = nomoK(z). Ш
При доказательстве теоремы попутно доказано такое следствие.
СЛЕДСТВИЕ 16.4. Пусть 5 — подмножество множества У, содержащее а, но не
содержащее z, и Т = V - S. Тогда
5Z ^^е) = nomoK{a) —
е€E,Т)
ОПРЕДЕЛЕНИЕ 16.5. Величина потока /, обозначаемая как val(f), равна
поток(а) — nomoK(z).
ОПРЕДЕЛЕНИЕ 16.6.
Тогда {е : е е E,Г)}
Пусть 5 —
называется
называется a — z сечением.
подмножество
сечением. Если
множества
a E 5 и 2
G
и
Т
т =
, то
: V ~ S.
сечение
ОПРЕДЕЛЕНИЕ 16.7. Величина C(S,T) = ]?ee(ST)c(e) называется пропуск-
пропускной способностью сечения.

696 ГЛАВА 16. Сети
ОПРЕДЕЛЕНИЕ 16.8. Поток / в сети называется максимальным потоком,
если val(f) > val(f) для любого возможного потока / в сети.
ОПРЕДЕЛЕНИЕ 16.9. a — z сечение E, Г) называется минимальным сече-
сечением, если C(S, Г) не больше пропускной способности любого другого а - z
сечения.
ТЕОРЕМА 16.10. Пусть 5 — подмножество множества V, содержащее а, но не
содержащее z, и Т = V — S. Тогда
val(f)<C(S,T).
ДОКАЗАТЕЛЬСТВО.
val(f)=
- У" f(e)
ee(T,S)
< V fie
eE(S,T)
0 < V
-' - Z^
e€E,T)
ee(S,T)
СЛЕДСТВИЕ 16.11. Если val(f) = C(S,T) для некоторого потока /, а а - z
сечения E,Т), то / — максимальный поток, а С — минимальное сечение.
СЛЕДСТВИЕ 16.12. Для некоторого потока / и а — z сечения E, Т) равенство
val(f) — C(S,T) имеет место тогда и только тогда, когда /(е) = с(е) для всех
е е E, Т) и /(е) = 0 для всех е <Е (Г, 5).
Опишем способы определения максимального потока сети. Рассмотрим сеть,
изображенную на на рис. 16.3.
Рис. 16.3
Максимальный поток (не обязательно единственный) легко найти способом, про-
проиллюстрированным на рис. 16.4.
16А
В данном случае известно, что поток максимальный, потому что величина
потока, выходящего из а, не может превысить сумму пропускных способностей
ребер, выходящих из а.
Рассмотрим сеть, изображенную на рис. 16.5.

РАЗДЕЛ 16.1. Сети и потоки 697
D,4)
Кажется, что у этой сети максимальный поток, потому что не существует
ориентированного пути, по которому можно увеличить поток. Заметим, однако,
что сеть на рис. 16.6 имеет больший поток, и, фактически, он максимальный.
Рис. 16.6
Следует обратить внимание, что если поток из источника равен сумме про-
пропускных способностей ребер, выходящих из источника, или поток, втекающий в
сток, равен сумме пропускных способностей ребер, входящих в сток, то поток
максимальный. Однако, поток может быть максимальным и без удовлетворения
какого-либо из этих признаков. Например, сеть на рис. 16.7 имеет максимальный
поток.
Рис. 16.7
Итак, как же находить максимальные в смысле потока сети? Для этого
сформируем пути изавг, не обращая внимания на направление ребер. Такие пути
назовем цепями. Рассмотрим снова сеть с потоком, изображенную на рис. 16.5.
Одним из таких путей является
(8,6) C,3) (9,6)
а —> Ь —> с —> z.
Очевидно, что нет возможности увеличить поток по этому пути, поскольку ребро
из Ъ в с наполнено до его пропускной способности. То же самое верно и для цепи
(8,6) E,3) G,7)
а —> о —> е —* z.
Однако, при рассмотрении цепи
(8,6) E,3) D,4) E,3) (9,6)

698 ГЛАВА 16. Сети
видим: если увеличить поток на 2 для стрелок, имеющих то же самое направле-
направление, что и цепь, и уменьшить поток на 2 для стрелок, имеющих противоположное
направление, то получим
(8,8) E,5) D,2) E,5) (9,8)
а—» о —>е<— а —> с —> z,
что увеличивает поток на 2. Первый вопрос, который следовало бы задать: "Поче-
"Почему выбираем 2?". Вполне очевидно, что поток желательно увеличить как можно
больше. Но он не может превысить пропускную способность ни одного из задан-
заданных ребер. Именно по этой причине мы ограничены величиной 2. Кроме того,
если ребро имеет направление, противоположное цепи, то нельзя уменьшить по-
поток через это ребро более, чем на текущую величину потока через него, иначе
получим отрицательный поток. Поэтому, если бы не было других ограничений,
то
D,4)
е <— а
ограничило бы изменение потока до 4. Второй вопрос: "Как это влияет на сохране-
сохранение потока?". Убедимся, что условие сохранения потока выполняется. Рассмотрим,
например, изменение
(8,6) E,3)
а —> о —> е
на
(8,8) E,5)
а —> о —> е.
Поток, выходящий из вершины 6, увеличен на ту же самую величину, что и поток,
входящий в вершину Ь. Поэтому чистый поток через b остается прежним. При
изменении
E,3) D,4)
о —> е <r- a
на
E,5) D,2)
о —> е <— а
поток из вершины Ъ в вершину е увеличен на ту же величину, на которую умень-
уменьшен поток из вершины d в вершину е, поэтому чистый поток в вершине е остался
тем же. Наконец, рассмотрим изменение
D,4) E,3)
е <r— a —> с
на
D,2) E,5)
е <— а —> с
Поток из d в е уменьшен на ту же величину, на которую увеличен поток из d в с.
Поэтому чистый поток и вершины d остался неизменным.
Процесс увеличения потока в сети чрезвычайно прост. Формируем цепь из а
в z. Если возможно, то увеличиваем поток, определяя наибольшую величину,
которую можно добавить к каждому из ребер, имеющих то же самое направле-
направление, что и цепь, чтобы поток не превысил пропускную способность, и которую
можно вычесть из каждого ребра, имеющего противоположное направление, не

РАЗДЕЛ 16.1. Сети и потоки 699
создавая отрицательный поток. Поскольку последнее ребро, входящее в z, име-
имеет то же самое направление, что и цепь, то поток в z возрастает. Аналогично,
ребро, выходящее из а, имеет то же самое направление, что и цепь, поэтому,
как и ожидалось, поток из а возрастает. Так и должно было быть, потому что
поток(а) = потоках). Потому что пропускная способность — конечная величи-
величина, а общая величина потока увеличивается, неизбежно наступает момент, когда
наращивать поток далее нельзя. Когда это происходит, получаем максимальный
поток. До сих пор рассматривался способ увеличения уже существующего потока.
А с какого потока начинать? Ответ прост. Следует начинать с нулевого потока,
т.е. когда поток через каждое ребро равен 0, а затем наращивать его. Теперь пе-
перейдем к изложению систематического алгоритма для нахождения максимального
потока. Каждой вершине поставим в соответствие упорядоченную пару. Первый
элемент пары — предшествующая вершина в рассматриваемой цепи предназначе-
предназначена для того, чтобы можно было найти обратный путь. Второй элемент пары —
резерв, т.е. величина, на которую можно увеличить поток на каждом ребре вдоль
пути, если ориентация ребра совпадает с направлением цепи (такую ориентацию
назовем правильной), или уменьшить поток, если ребро ориентировано непра-
неправильно. Проще говоря, резерв заданной вершины равен максимальной величине,
на которую поток вдоль цепи до этой вершины можно увеличить без нарушения
самого потока. Рассмотрим также множество 5, содержащее все вершины, не за-
задействованные при построении цепи в z. Если S окажется пустым, до того как
будет достигнута вершина zt то больше не будет вершин, которые можно испы-
испытать на пути к z, поэтому нет иного пути в z и нет более возможности увеличить
поток, значит поток максимален.
Алгоритм (Форда-Фалкерсона) нахождения максимального потока
A) Установить предшественника каждой вершины и резерв равными сим-
символу — (непомечено). Вершина помечена, когда ее резерв не обозначен
символом -. Установить резерв вершины а равным оо, с тем чтобы она
не ограничивала резерв других вершин. Положить S = {а}.
B) Если 5 — пустое множество, то поток максимизирован. Если 5 не явля-
является пустым, то выбираем любой элемент из 5 и удаляем его. Полагаем
этот элемент равным v.
C) Если w не помечена, (v,w) является ребром и f((v,w)) < c((v,w)). Поло-
Положить резерв вершины w равным минимуму величины c((v,w)) — f((v,w))
и резерва вершины v. Установить предшественника вершины w в v. Если
w ф г, добавить w ъ S.
D) Если w не помечена, (w,v) является ребром и f((v,w)) > 0. Положить
резерв вершины w равным минимуму из f((v,w)) и резерва вершины v.
Установить предшественника вершины w в v. Добавить w во множество 5.
E) Если z помечена, то, используя функцию предшествования, вернуться в
вершину а и для каждого ребра цепи добавить резерв вершины z к потоку
каждого правильно ориентированного ребра, и вычесть резерв z из потока
каждого неправильно ориентированного ребра. Вернуться к шагу 1.
F) Вернуться к шагу 2.

700 ГЛАВА 16. Сети
Требуется еще доказать, что алгоритм действительно определяет максималь-
максимальный поток, но сначала посмотрим, как он работает.
ПРИМЕР 16.13. Найдем максимальный поток для сети, изображенной на рис. 16.8.
> z
Рис. 16.8
На шаге 1 для каждой вершины устанавливаем предшественника и резерв
равными символу -, для вершины а устанавливаем резерв, равный оо, и полагаем
S = {а}. После чего получаем сеть, изображенную на рис. 16.9.
(-,-) B,0)
Рис. 16.9
На шаге 2 проверяем, не пусто ли множество 5, и выбираем из него вершину
а. На шаге 3 полагаем резерв вершины b равным minG, оо) = 7 и устанавлива-
устанавливаем вершину а в качестве предшественника вершины Ь. Помещаем вершину b во
множество S. Устанавливаем резерв вершины d равным minF, оо) = 6 и устанав-
устанавливаем вершину а в качестве предшественника вершины d. Помещаем вершину d
во множество S. Шаги 4 и 5 не применяем, поэтому возвращаемся к шагу 2.
Проверяем, не является ли множество 5 пустым, и выбираем из него вер-
вершину, например, Ь. Теперь множество S содержит только вершину d. На шаге 3
полагаем резерв вершины с равным minC, 7) = 3 и устанавливаем вершину b в
качестве предшественника вершины с. Помещаем вершину с во множество 5, так
что 5 = {с, d}. Опять шаги 4 и 5 не применяем и возвращаемся к шагу 2.
Проверяем, не является ли множество 5 пустым, и выбираем из 5 вершину,
например, с. Множество S опять содержит только вершину d. На шаге 3 полагаем
резерв вершины z равным minC, 5) = 3 и устанавливаем вершину с в качестве
предшественника вершины z. He помещаем z во множество S. На шаге 4 следует
пометить вершину d, но она уже помечена.
На шаге 5 видим, что вершина z уже помечена, и, используя функцию пред-
предшествования, находим цепь
G,0) C,0) E,0)
а —> о —> с —> z.
Добавляя 3 (резерв вершины z) к потоку каждого ребра, получаем
а ™ Ь CА3) с EА3) х,
что дает сеть, изображенную на рис. 16.10.

РАЗДЕЛ 16.1. Сети и потоки 701
(а,6) B,0)
z(c,3)
Рис. 16.10
Теперь возвращаемся к шагу 1, где переустанавливаем метки и предшествен-
предшественников и полагаем 5 = {а}. На шаге 2 выбираем вершину а из множества 5. На
шаге 3 устанавливаем резерв вершины Ь равным min(oc,7 —3) = 4 и устанавлива-
устанавливаем а в качестве предшественника вершины Ь. Помещаем вершину Ь во множество
5. Полагаем также резерв вершины d равным б и устанавливаем вершину а в
качестве предшественника вершины d. Помещаем вершину d во множество 5.
Шаги 4 и 5 не применяем, поэтому возвращаемся к шагу 2. Выбираем вершину b
из множества S. Поскольку поток из 6 в с равен пропускной способности из 6 в с,
то вершину с не помечаем. Выбираем вершину d из множества S и продолжаем
процесс, после чего получаем цепь
F,0) B,0)
а —> а —> z
и, добавляя 2 (резерв вершины z) к потоку каждого ребра, получаем цепь
F,2) B,2)
а —> а —> z.
Текущая ситуация изображена на рис. 16.11.
(а,6) B,2)
z(d,2)
Снова возвращаемся к шагу 1 и повторяем процесс, пока не получим цепь
F,2) B,0) E,3)
а —+ d —> с —> z.
Добавляя 2 (резерв вершины z) к потоку каждого ребра, получаем
z.
Ситуация изображена на рис. 16.12.

702 ГЛАВА 16. Сети
B,2)
Рис. 16.12
Возвращаемся к шагу 1, переустанавливаем метки предшественника и по-
полагаем 5 = {а}. На шаге 2 выбираем вершину а из множества S. Как и ранее,
на шаге 3 полагаем резерв вершины b равным 4 и устанавливаем вершину а в
качестве предшественника вершины Ь. Помещаем вершину b во множество 5.
Устанавливаем также резерв вершины d равным 6 —4 = 2 и помещаем вершину d
во множество 5. Возвращаемся к шагу 2. Выбираем вершину b из множества 5.
Поскольку поток из вершины b в вершину с равен пропускной способности из b
в с, пометить с нельзя, поэтому, в конце концов, возвращаемся к шагу 2. Выби-
Выбираем вершину d из множества S. Поскольку поток из вершины d в вершину с
и вершину z равен их пропускным способностям, нельзя помечать сиг. Опять
возвращаемся к шагу 2, но множество 5 пусто. Процесс закончен. Окончательный
поток изображен на рис.16.13.
(a.z) B'2) Рис. 16.13 П
ПРИМЕР 16.14. Найдите максимальный поток для сети, изображенной на рис. 16.14.
9 Рис. 16.14
Первые несколько проходов ничем не примечательны, поэтому опишем их
вкратце. На первом проходе помечаем а(—,оо), 6(а, 9), d(a, 8), сF,4), е(Ь,4) и
г (с, 4). Это дает a — 2 путь
(9,0) D,0) (8,0)
а -^ о -* с -+ z,
и поскольку резерв вершины z равен 4, добавляем 4 к каждому потоку, получая
что изображено на рис. 16.15.
(9,4) D,4) (8,4)
а —+ о —> с —>

РАЗДЕЛ 16.1. Сети и потоки 703
z(c,4)
d
(а%(9,0)
Рис. 16.15
На втором проходе помечаем а(—,оо), 6(а, 5), d(a, 8), c(d, 4), e(d, 8) и z(e, 7).
Это дает а — z путь
„ ^ d (9А0) е GА0) г,
и поскольку резерв вершины z равен 7, добавляем 7 к каждому потоку, получая
(8,7) (9,7) G,7)
а —¦> d —> е —> z,
что изображено на рис. 16.16.
C,(d.4)
z(e,7)
(а,8) (9,7)
Pwc. /6.
На третьем проходе помечаем а(-, оо), Ь(а, 5), d(a, 1), c(d, 1), e(d, 1) и z(c, 1).
Это дает а - z путь
(8,7) D,0) (8,4)
a —> a —> с —> z,
и поскольку резерв z равен 1, добавляем 1 к каждому потоку, получая
(8,8) D,1) (8,5)
а -^ d —> с —> z,
что изображено на рис. 16.17.
Теперь начинается кое-что поинтересней, поэтому дальнейшее описание бу-
будет более подробным. Пометим 6(а, 5), но d пометить нельзя; помещаем b в 5.
При выборе вершины Ъ из множества 5 нельзя пометить вершину с, но можно

704 ГЛАВА 16. Сети
пометить еF,5); помещаем вершину с во множество 5. Выбирая е из S, нельзя
пометить вершину zy но т.к. d еще не помечена, ее можно пометить. Посколь-
Поскольку ребро (d, e) ориентировано неправильно, полагаем резерв вершины d равным
minG, 5) = 5. Устанавливаем е в качестве предшественника вершины d и поме-
помещаем вершину d во множество S. Выбирая вершину d из множества 5, имеем
единственную возможность — пометить вершину c(d, 3) и поместить с в S. Вы-
Выбираем вершину с из множества S и помечаем z(c, 3). Это дает а — z путь
(9,4) F,0) (9,7) D,1) (8,5)
а—> о —> е *— а—> с —» 2,
и поскольку резерв z равен 3, прибавляем 3 к каждому потоку, исключая ребро
(d, е). Это ребро ориентировано неправильно; вычитаем 3 из его потока, получая
(9,7) F,3) (9,4) D,4) (8,8)
а -+ о -* е <— d —> с —* z,
что изображено на рис. 16.18.
z(c,3)
Начинаем последний проход. Сначала 5 = {а}. Удаляем вершину а из мно-
множества 5, помечаем вершину 6(а, 2) и помещаем 6 в 5. Удаляем вершину Ь из
множества 5, помечаем еF,2), сF,2) и помещаем вершины с, е во множество 5.
Удаляем е из 5, помечаем d(e,2), поскольку резерв d равен минимуму из потока
ребра (d, e) и резерва вершины d. Помещаем d в 5. Затем из 5 удаляем d, но ни
один из оставшихся шагов нельзя выполнить, поэтому возвращаемся к шагу 2.
Следующим из 5 удаляем с, но мы не можем выполнить ни один из оставшихся
шагов и возвращаемся к шагу 2. Множество 5 пусто, поэтому алгоритм завершен.
Результат изображен на рис. 16.19.
e(b,2)
Рис. 16.19 U
ТЕОРЕМА 16.15. Алгоритм максимального потока строит максимальный поток
для сети.

РАЗДЕЛ 16.1. Сети и потоки 705
ДОКАЗАТЕЛЬСТВО. Пусть S — множество всех вершин, помеченных во время
последнего прохода алгоритма, и Г = V - 5. Множество 5 не пусто, поскольку
а 6 5. Если е — ребро из 5 в Т, например, е = (s,?), так что t не помечено,
то /(е) = с(е), так как иначе t могла быть помечена. Если е — ребро из Т в 5,
скажем, е = (?, s), так что ? не помечена, то /(е) = 0, так как в противном случае t
могла быть помечена. Согласно следствиям 16.11 и 16.12 поток / — максимальный,
и E, Т) — минимальное сечение. ¦
Следствие 16.12 утверждает, что если val(f) = C(S,T) для некоторого по-
потока / и а — z сечения E, Т), то / — максимальный поток, а С — минимальное
сечение. В изложенном выше алгоритме показано, как находить минимальное се-
сечение E,Т), так что / — максимальный поток, val(f) = СE, Т). Соединяя все
вместе, приходим к теореме.
ТЕОРЕМА 16.16. Поток / на заданной сети N является максимальным тогда и
только тогда, когда существует сечение E, Т) такое, что val(f) = C(S,T).
Заметим, что в примере 16.13 множество 5 состоит из всех вершин, которые
можно пометить при последнем проходе, поэтому S = {а, 6, d} и Т = {с, z}.
В примере 16.14 S = {а, Ь, с, d, е) и Т = {z}.
УПРАЖНЕНИЯ
1. Для сети, изображенной на рис. 16.20,
а) проверить сохранение потока в вершинах 6, с и d\
б) найти val(f), величину потока;
в) найти значение C(S,T), где S = {а, 6, с, d}\
г) найти значение C(S,T), где S = {a,d, е};
д) найти значение СE, Г), где S = {a,b,d}.
Рис. 16.20
2. Для сети, изображенной на рис. 16.21,
а) проверить сохранение потока в вершинах Ь, d и е;
б) найти val(f), значение потока;
в) найти значение C(S,T), где S = {а, Ь, с, d};
г) найти значение C(S, Г), где 5 = {a,b,d, е};
д) найти значение СE, Г), где 5 = {а, 6, е}.

706 ГЛАВА 16. Сети
A0,5)
B,1)
Рис. 16.21
3. Дополнить поток в сети, изображенной на рис. 16.22, так чтобы имело место
сохранение потока.
4. Дополнить поток в сети, изображенной на рис. 16.23, так чтобы имело место
сохранение потока.
Ь-Ш+с,
Ъ F,1) с
E,3)
*¦ z
(и)
Рис. 16.22
d A,D
Рис. 16.23
5. Найти максимальный поток в сети, изображенной на рис. 16.24.
6. Найти максимальный поток в сети, изображенной на рис. 16.25.
Рис. 16.24
Рис. 16.25
7. Найти максимальный поток в сети, изображенной на рис. 16.26.
8. Найти максимальный поток в сети, изображенной на рис. 16.27.
F,1) ^ с
Рис. 16.26
am-
\
d (И)
Рис. 16.27
->• z

РАЗДЕЛ 16.2. Паросочетание 707
9. Найти минимальное сечение для потока в сети из упражнения 5.
10. Найти минимальное сечение для потока в сети из упражнения 6.
11. Найти минимальное сечение — разрез для потока в сети из упражнения 7.
12. Найти минимальное сечение — разрез для потока в сети из упражнения 8.
16.2. ПАРОСОЧЕТАНИЕ
Теория потоков в сети имеет непосредственное применение в теории графов. Вспо-
Вспомним, что граф G = (V,E) назывется двудольным графом, если V можно выра-
выразить как несвязное объединение непустых множеств, например, V = A U J5, так
что каждое ребро имеет вид {a,b}, где a e А и b e В. Таким образом, каждое
ребро соединяет вершину из А с вершиной из В, и не существует двух вершин
из одного и того же множества (А или В), которые соединены друг с другом.
Подмножество М множества Е называется паросочетанием, если никакие два
ребра из М не имеют общей вершины. Таким образом, никакие два ребра не
являются инцидентными. Если {а, 6} — ребро в паросочетании, тогда как а, так
и Ъ имеет паросочетающие ребра. При этом вершины а и b называются паро-
сочетанными. Например, для двудольного графа, изображенного на рис. 16.28,
паросочетающие ребра, обозначенные на рисунке жирной линией, образуют паро-
паросочетание.
Рис. 16.28
Наглядным примером может служить соответствие между множеством ра-
работников и множеством заданий для них. Ребра графа показывают, какие зада-
задания может выполнить тот или иной работник. Еще один пример — паросочетание
множества юношей и множества девушек. Паросочетающие ребра соединяют сов-
совместимые пары.(Будем считать, что эти множества образуют двудольный граф, и
воздержимся от дальнейших комментариев.)
ОПРЕДЕЛЕНИЕ 16.17. Паросочетание М на двудольном графе G = (V,E) на-
назывется максимальным, если никакое другое паросочетание на G не содержит
ребер больше, чем М.
ОПРЕДЕЛЕНИЕ 16.18. Паросочетание М на двудольном графе G = {V,E), где
V = A U Б, называется полным, если для каждого а ? А существует Ъ е В
такое, что {а, Ь} Е М.

708 ГЛАВА 16. Сети
ПРИМЕР 16.19. Граф, изображенный на рис. 16.29, максимальный, но не полный.
Рис. 16.29
?
Очевидно, нам нужен метод нахождения максимального паросочетания. Для
упрощения задачи заменим рассматриваемый двудольный граф ориентированным
графом, ребра которого имеют начало в вершинах множества А и заканчиваются
в вершинах множества В. Добавим также две новые вершины а и z и ребра
из вершины а в каждую вершину множества А, и ребра из каждой вершины
множества В в вершину z. Граф, изображенный на рис. 16.30, превратится в
граф, изображенный на рис. 16.31.
Рис. 16.30
Рис. 16.31
Теперь двудольный граф превращен в сеть. Такая сеть называется сетью
паросочетаний. Для каждого а; € А обозначим через е^ ребро из а в а;. По-
Положим пропускную способность с(е*) = 1 для всех вг. Аналогично, для каждого
bi G В обозначим через Е{ ребро из bi в z и положим пропускную способность
с(ег) = 1 для всех е». Для ребра kij из а; в bj положим c(fc^) = |Л| + 1, так
что пропускная способность больше, чем количество вершин в А. Причину объ-
объясним позже. Заметим, т.к. поток в каждую вершину <ii не может превысить 1,
поток через каждое ребро к^ из а; в bj должен быть 1 или 0 независимо от
пропускной способности c(k{j). Для ребра к^ из а* в bj определим поток f(kij)
равным 1, если имеется паросочетающее ребро между ai и bj, и равным 0 в про-
противном случае. Величина потока, val(f), в таком случае равна количеству ребер
в паросочетаний между А и В. Максимальный поток имеет место, когда имеется
максимальное паросочетание. Таким образом, задача нахождения максимального
паросочетания сведена к задаче построения максимального потока.
Воспользуемся алгоритмом нахождения максимального потока, описанным
в предыдущем разделе. Начнем с ребра е^, ведущего в вершину а^, которое не

РАЗДЕЛ 16.2. Паросочетание 709
является паросочетающим, в противном случае /(е;) = с(е*) = 1. Затем движемся
по ориентированному ребру kij к вершине bj множества В. Если вершина bj не
паросочетается, создаем паросочетающее ребро между а; и bj, увеличивая поток.
Если вершина bj паросочетается, нужно вернуться по неправильно ориентирова-
ному ребру. Поэтому его поток должен быть равен 1, и мы продолжаем цепь назад
во множество А по паросочетающему ребру. Снова, возвращаясь в J3, выбираем
ребро, которое не является паросочетающим. Продолжаем цепь, пока не достиг-
достигнем вершины во множестве В, которая не паросочетается. В цепи необходимо
добавить 1 к потоку правильно ориентированных ребер из А в В и вычесть 1 из
потоков неправильно ориентированных ребер из В в А. В результате паросочетаю-
щими ребрами станут те, которые ими не были, а прежние паросочетающие ребра
будут удалены. Это добавит одно паросочетающее ребро двудольному графу, и
мощность паросочетания увеличится на 1. Таким образом, алгоритм нахождения
максимального потока позволяет найти максимальное паросочетание.
Начать можно с пустого паросочетания, как того требует алгоритм нахо-
нахождения максимального потока. В этом случае используем алгоритм построения
паросочетающих ребер, а затем увеличим их число, чтобы найти максимальное
паросочетание. В следующих примерах мы предполагаем, что изначально имеется
некоторое паросочетание, которое будем увеличивать до максимального.
Мы видим, что при использовании этого метода нет необходимости забо-
заботиться о вершинах а и z. Мы просто начинаем с вершины из множества А,
которая не паросочетается, и продолжаем движение назад и вперед, пока оно не
закончится в вершине множества В, у которой нет паросочетающего ребра.
ПРИМЕР 16.20. Для графа, изображенного на рис. 16.32, найти максимальное
паросочетание.
Рис. 16.32
Начинаем в вершине а4, поскольку она не имеет паросочетающего ребра.
По ориентированному ребру попадаем в вершину Ь4, т.к. ребро (а4,64) не при-
принадлежит начальному паросочетанию. Продолжаем цепь назад в а2, посколь-
поскольку ребро (а2,Ь4) принадлежит текущему паросочетанию. Из а2 цепь продол-
продолжаем в &ь поскольку (a2,&i) — не паросочетающее ребро. Из Ь\ цепь продол-
продолжаем в аз, поскольку (a3,&i) — паросочетающее ребро. Из аз цепь продолжа-
продолжаем в вершину Ь3> т.к. (а3,&з) не принадлежит паросочетанию. Из Ь3 Цепь про-
продолжаем назад в аь поскольку (аь63) — паросочетающее ребро. Из а\ цепь
продолжаем в 62, поскольку (ai,b2) не принадлежит паросочетанию. Из 62 не
выходит ни одно паросочетающее ребро, поэтому цепь построена и имеет вид:
а4 -» 64 <— а2 —> 6i <r- а3 —> 63 ¦— а\ —> 62. После этого удаляем из исходного

710 ГЛАВА 16. Сети
паросочетания ребра, имеющиеся в цепи, и добавляем ребра из цепи, которые в
нем отсутствуют. Получаем граф, изображенный на рис. 16.33.
Рис. 16.33
Построенное паросочетание является максимальным и, к тому же, полным
паросочетанием, потому что количество ребер в паросочетании равно количеству
вершин в А. П
ПРИМЕР 16.21. Для графа, изображенного на рис. 16.34, найти максимальное
паросочетание.
Рис. 16.34
Рис. 16.35
Начинаем в вершине а5, поскольку у нее нет просочетающего ребра. По
ориентированному ребру попадаем в вершину Ь5, т.к. (а5,65) — не паросочетающее
ребро. Затем продолжаем цепь назад в а3, потому что (а3,Ь5) — паросочетающее
ребро. Из аз продолжаем цепь в Ь±, поскольку @3,64) — не паросочетающее ребро.
Далее продолжаем цепь назад в аь т.к. (ах,Ь4) — паросочетающее ребро. Из а\
продолжаем цепь в 6з, потому что (а\,Ъъ) — не паросочетающее ребро. После
этого возвращаем цепь в <22, поскольку (а2,Ьз) — паросочетающее ребро. Из п2
продолжаем цепь в 62» (^2,^2) — не паросочетающее ребро. Из 62 не выходит ни
одно паросочетающее ребро, поэтому цепь построена и имеет вид:
Удаляем из исходного паросочетания ребра, имеющиеся в цепи, и добавляем ребра
из цепи, которые в нем отсутствуют. Получаем граф, изображенный на рис. 16.35.
Поскольку количество ребер в паросочетании равно количеству вершин в Л,
имеем максимальное паросочетание, которое является полным. ?

РАЗДЕЛ 16.2. Паросочетание 711
ОПРЕДЕЛЕНИЕ 16.22. Для подмножества X множества А введем множество
R(X) = {b : b Е В и b смежная с вершиной из X). R(X) называется множе-
множеством значений X.
Это определение согласовано с определением множества значений, которое
представлено в главе 2 при изучении отношений. Теперь можно сформулировать
необходимые и достаточные условия полноты паросочетания.
ТЕОРЕМА 16.23. (Теорема Холла) Двудольный граф G(E, V), в котором V =
Аи В, имеет полное паросочетание тогда и только тогда, когда для каждого
подмножества X С А выполняется \Х\ < \R(X)\.
ДОКАЗАТЕЛЬСТВО. Очевидно, что если граф G(E, V) — полный, тогда необхо-
необходимо |Х| < |Д(Х)| для каждого подмножества X множества А, т.к. в противном
случае не для всех элементов из X и, следовательно, не для всех элементов из А
существует паросочетающее ребро. В частности, каждый элемент из А смежен с
элементом из В и \А\ < \В\.
Обратно, предположим, что \Х\ < \R(X)\ для каждого подмножества X мно-
множества А. Согласно теореме 16.16 существует разрез E, Г) такой, что val(f) =
C(S,T). Известно, что val(f) равно количеству вершин в максимальном паро-
сочетании, поэтому C(S,T) тоже равно количеству вершин в макисимальном
паросочетании. Пусть \А\ = п. Тогда C(S,T) < п, поскольку количество элемен-
элементов в максимальном паросочетании не может превысить количество вершин в А.
Вспомним, что C(S,T) равно сумме пропускных способностей всех ребер меж-
между 5 и Г. Известно также, что этот разрез не может содержать ребро k{j между
вершиной п{ из А и вершиной bj из В, т.к. c(k{j) = п 4-1. Поэтому, если а* Е 5,
то R({a}) С 5. Отсюда следует, что R(AnS) С S. Между каждой вершиной из
R(A П S) и z существует ребро. Кроме того, каждое из этих ребер принадлежит
разрезу E, Т), поскольку z Е Т и вносит 1 в C(S,T). Множество А — несвязное
объединение множеств AnS и АпТ. Следовательно, п = \А\ = \AC\S\ + |АпГ|.
Между элементом а и каждым элементом множества АпТ существует ребро.
Поскольку а Е 5, каждое из этих ребер принадлежит разрезу E, Т) и вносит 1 в
СE,Г). Поскольку по предположению |ЛП5| < \R(AnS)\, отсюда следует, что
C(S, Т) > \R(A П 5)| + |А п Г| > \А П S\ + |А П Т\ = \А\ = п.
Вспомним, однако, что C(S,T) равно количеству ребер в максимальном паросоче-
паросочетании. Поэтому C(S,T) < п, откуда следует, что C(S,T) = п, т.е. максимальное
паросочетание является полным. ¦
Теперь представим другой алгоритм нахождения максимального паросочета-
паросочетания. На этот раз используем матрицы. Начнем с модифицированной матрицы ин-
инцидентности. Поскольку имеются ребра только из А в Б, то необходима та часть
матрицы А, в которой строка соответствует элементу из А, а столбец соответ-
соответствует элементу из В. Строки именуем вершинами из А, столбцы — вершинами
из В. Как и раньше, помещаем 1 в г-ую строку j-oro столбца, если существует
ребро из п{ в bj. Начнем с расстановки скобок вокруг каждой 1 в г-ой строке и
j-ом столбце, если существует паросочетающее ребро из а; в bj. Проиллюстри-
Проиллюстрируем этот процесс для паросочетания из примера 16.20. Помещаем символ # в

712 ГЛАВА 16. Сети
конец строки, соответствующей сц, чтобы отметить, что в строке нет [1] и, следо-
следовательно, для а4 нет паросочетающего ребра. Считаем строку, содержащую такой
символ в конце, помеченной. Точно так же считаем помеченным каждый столбец,
содержащий в конце указанный символ. На этом этапе матрица имеет следующий
вид:
сц
а2
а3
а4
0
1
Ш
0
1
0
0
0
Ьг | Ь4
11] 0
1 [1]
1 1
0 1
1
#
Поскольку строка, содержащая а^, помечена, то везде, где имеется 1 без скобок,
помещаем а4 под каждым столбцом, содержащим 1. Числа внизу и справа помогут
найти обратный путь. Переход по 1 в столбце 64 равносилен переходу из а4 в 64
по непаросочетающему ребру. В столбце, соответствующем 64, выберем строку,
содержащую [1], которая встречается вог, и поместим 64 в правый столбец этой
строки, что эквивалентно построению паросочетающего ребра из 64 в а2. На этом
этапе имеем следующую матрицу:
а>2
^3
а4
0
1
[1]
0
ъ2
1
0
0
0
Ьз
llj
1
1
0
64
0
11]
1
1
а4
#
Теперь ищем вхождение единиц в строке а2 и помещаем а2 внизу каждого столб-
столбца. В данном случае единицы имеются в столбцах 6i и 63. Имеем, таким образом,
две возможности для непаросочетающего ребра. В столбцах, соответствующих b\
и 6з, находим строки, содержащие [1]. Ими являются строки, соответствующие а3
и а\. Помещаем Ь\ в правый столбец строки аз и 6з — в правый столбец строки
а\. Получаем матрицу вида
аз
0,4
bi
0
1
[1J
0
а2
\ ь2
1
0
0
0
1
11]
1
1
0
| а2
Ь4
0
[1]
1
1
а4
Ьз
Ь4
h
#
В строке а\ отыскиваем 1 в одном из столбцов. Таким столбцом является 62.
Под ним помещаем а\. В строке а3 отыскиваем 1 в столбцах. Ими являются
столбцы Ьз и Ь±, но они уже помечены. В столбце 62 нет ни одной [1], поэтому
вершина из В, не имеющая паросочетающего ребра, найдена. Следовательно,

РАЗДЕЛ 16.2. Паросочетание 713
искомая цепь построена. Теперь имеем матрицу.
0-1
а2
аз
а4
bi | b2
0
1
11J
0
а2
1
0
0
0
ai
bz
[1]
1
1
0
а2
Ьа
0
[IJ
1
1
а4
h
Ьа
bi
#
Используя метки ребер внизу и в самом крайнем столбце таблицы, возвращаемся
назад и восстанавливаем цепь
а2
а1
Заметим, что цепь не совпадает с построенной в примере 16.20. Она короче.
Изменение статуса ребер (паросочетающие — на непаросочетающие и наоборот),
как в примере 16.20, дает паросочетание, изображенное на рис. 16.36.
Рис. 16.36
Для получения новой матрицы каждую 1 по ходу движения меняем на [1], а
каждую [1] — на 1. В результате получаем такую матрицу.
<*2
аз
аА
Ь\ | Ь2 Ь3
64
0 [1] 1 0
1 0 [1] 1
[1] 0 1 1
0 0 0 [1]
1 1
Используя приведенную выше процедуру для паросочетания из примера 16.21,
начинаем с матрицы
0.1
0.2
аз
а4
а5
б! | 62 | 63 | Ь4
h
1 11]
[1] 1
1 [1]
[1] 1
1
1 1 1

714 ГЛАВА 16. Сети
и в конце приходим к матрице
«3
a4
b\ \ i>2 \ 63
1
[1]
a | a2
1
[1J
ai
64
[1]
1
1
аз
1
[1J
1
1
a5
b4
Ьз
#
Используя метки ребер внизу и в самом крайнем столбце таблицы, возвра-
возвращаемся назад и восстанавливаем цепь
которая совпадает с полученной в примере 16.21. Матрица нового паросочетания
имеет следующий вид.
CL2
аз
а4
UJ
а
ь2
11J
«2
6з
[1J
1
«I
64
1
[1]
1
аз
Ьь
1
1
1
11]
64
63
Ьъ
#
УПРАЖНЕНИЯ
1. Для приведенных ниже двудольных графов найдите максимальное паросо-
четание, используя методы, изложенные в этой главе. Является ли каждое
паросочетание полным?
а)
б)
• е
• е

РАЗДЕЛ 16.2. Паросочетание 715
в)
г)
2. Выполните задание предыдущего упражнения для следующих графов.
а)
б)
• f
•g
• h
i
• i
•j
• k
b\/
c\ A
d//
/
^/
•i
в)
• г

716 ГЛАВА 16. Сети
3. Шесть человек ищут работу. Человек а готов выполнять работы A, D и F.
Человек b готов выполнять работу С. Человек с готов выполнять работы В
и D. Человек d готов выполнять работы А и Е. Человек е готов выполнять
работы В и D. Человек / — работу Е. Найдите паросочетание, согласно
которому наибольшее количество людей получит работу, которую они готовы
выполнять. Все ли получат работу?
4. Шестеро девушек хотят выбрать партнера для танцев. Элис нравятся Чарльз
и Эдвард; Бетти нравятся Альберт и Дэн; Клара предпочитает Чарльза и Эд-
Эдварда; Донна любит танцевать с Дэном; Элизабет нравятся Барт и Эдвард.
Подберите как можно большему числу девушек пару для танцев, которая бы-
была бы им по душе. Возможно ли каждой девушке подобрать парня, который
ей нравится?
5. Эмми входит в состав комитетов а и Ь. Брюс — комитетов а и с. Чарльз —
член комитета Ь. Дэнис — член комитетов 6, с и е. Эллен входит в состав
комитетов d и е. Председатель студенческого совета планирует пригласить
на совещание пятерых членов совета, входящих в различные комитеты. Воз-
Возможно ли это?
6. Шестеро друзей собираются на маскарад. Все хотят быть в разных костю-
костюмах. Анне нравится костюм клоуна; Бену нравятся костюмы приведения и
Франкенштейна; Кортни — клоуна и костюмы из вестернов; Денис хотел бы
нарядиться приведением, Дракулой или Франкенштейном; Эллен предпочи-
предпочитает костюм клоуна, костюм из вестернов или Шерлока Холмса; Френк —
костюм Дракулы и клоуна. Есть ли возможность для всех пойти на маскарад
в разных костюмах, причем в тех, которые им нравятся?
7. Составьте формальный алгоритм для нахождения максимального паросоче-
тания М на двудольном графе G = (V,E) без использования матриц.
8. Составьте формальный алгоритм для нахождения максимального паросоче-
тания М на двудольном графе G = (V, Е) с использованием матриц.
16.3. СЕТИ ПЕТРИ
В этом разделе продолжается рассмотрение двудольных графов с ориентирован-
ориентированными ребрами. Однако, в отличие от предыдущего раздела ориентация ребер
допускается в обоих направлениях. Пусть G(V,E) — двудольный ориентирован-
ориентированный граф, в котором V = Р и Т. Множество Р называется множеством пози-
позиций, а множество Т — множеством переходов. Е — множество ориентированных
ребер между Р и Т. В рассмотрение включено также множество функций М
таких, что каждая функция \х € М ставит в соответствие неотрицательное це-
целое число каждому элементу множества Р. Функция \i называется разметкой
графа G. Ориентированный граф, обладающий такими свойствами, называется
сетью Петри.
Сети Петри используются главным образом для моделирования параллель-
параллельных процессов: для моделирования компонентов компьютера, параллельных вы-
вычислений, в робототехнике и даже для описания музыкальных структур (см. [41]).
Вообще, сети Петри используются для нахождения дефектов в проекте системы,

РАЗДЕЛ 16.3. Сети Петри 717
хотя имеют и многие другие применения. Они обладают многими свойствами
блок-схем и конечных автоматов, речь о которых пойдет дальше. Более подробно
см. [85].
Каждая позиция в сети Петри обозначена кружком, а каждый переход —
вертикальной линией. Если р — позиция, то f(p) называется разметкой позиции р.
Разметка множества G показана на графе с помощью больших черных точек,
называемых метками, помещенных в кружки, которые обозначают позиции. Если
кружок позиции р пуст, это означает, что в р меток нет, поэтому f(p) = 0.
Рассмотрим граф, изображенный на рис. 16.37. В этой сети Петри р\ и р^
— позиции, a t\ — переход. Позиция р\ содержит одну метку, а ръ меток не
содержит.
Pi
о-
р2
о
Рис. 16.37
Срабатывание перехода t — это удаление по одной метке из каждой пози-
позиции pi} так что имеется ориентированное ребро из pi в ?, и добавление метки
в каждую позицию pj, так что имеется ориентированное ребро из t в pj. На-
Например, срабатывание t\ в приведенном выше примере приводит к сети Петри,
изображенной на рис. 16.38.
о-
р2
©
Рис. 16.38
В сети Петри, изображенной на рис. 16.39, срабатывание перехода t\ даст в
результате сеть Петри, изображенную на рис. 16.40.
*©
р,0'
Рис. 16.39
О
¦©*,
Рис. 16.40
В сети Петри, изображенной на рис. 16.41, срабатывание перехода t\ даст в
результате сеть Петри, изображенную на рис. 16.42.
Pi
©•
.о
Pi
о
•0*
Рис. 16.41
Рис. 16.42

718 ГЛАВА 16. Сети
В сети Петри, изображенной на рис. 16.43, срабатывание перехода t\ даст в
результате сеть Петри, изображенную на рис. 16.44, поскольку имеется ориенти-
ориентированное ребро из t\ обратно в р\.
Pi
р2
о
Р2
0
ti
Рис. 16.43
Рис. 16.44
Переход t может сработать, когда каждая позиция pi такая, что имеется
ориентированное ребро из pi в t, содержит метку. Когда такая ситуация имеет
место, говорят, что переход t разрешен. Переход ti в сети Петри, изображенной
на рис. 16.45, не может сработать, поскольку в р2 нет метки.
¦©
Рис. 16.45
В некоторых случаях необходимо, чтобы при срабатывании перехода удаля-
удалялась или прибавлялась более чем одна метка. Если при срабатывании перехода t
из позиции р необходимо удалить более чем одну метку, то ориентированное ре-
ребро из р в t помечается таким количеством меток, которое следует удалить из р.
Если меток нет, то их количество по умолчанию предполагается равным 1. Если
при срабатывании перехода t в позицию р необходимо добавить более чем одну
метку, то ориентированое ребро из t в р помечается таким количеством меток,
которое нужно добавить в р. Если меток нет, то количество опять предполагается
равным 1. Если при срабатывании перехода t из позиции р следует удалить п
меток, то р должна содержать, по крайней мере, и меток, чтобы переход t был
разрешен. В сети Петри, изображенной на рис. 16.46, срабатывание перехода t\
дает в результате сеть Петри, изображенную на рис. 16.47. Переход t\ не может
сработать снова, поскольку в р\ нет достаточного количества меток.
S^
¦о
¦©*
Рис. 16.46
Рис. 16.47
Срабатывание перехода предполагается мгновенным и может произойти в
любой момент, когда переход разрешен. Порядок срабатывания перехода огра-
ограничен только наличием достаточного количества меток, необходимых для разре-
шенности перехода. Вполне возможно, что в некоторый момент времени более

РАЗДЕЛ 16.3. Сети Петри 719
чем один переход будет разрешен. В этом случае любой из них может сработать
первым. Например, если моделируются несколько процессоров, имеющих общие
данные и периферию, то неизвестно, когда одному из процессоров понадобится
принтер или данные. Сети Петри используются для проверки работоспособности
системы даже в условиях такой неопределенности системы.
Состоянием s сети Петри называется количество меток в каждой позиции,
определяемое функцией /х; € М. Таким образом, состояние сети Петри — это
то же самое, что и разметка сети Петри. Термин "состояние" используется при
рассмотрении автоматов и других машин с конечным количеством состояний.
Поскольку fii полностью определяют состояние, будем их отождествлять. Сраба-
Срабатывание перехода изменяет текущее состояние на состояние, определяемое другой
функцией tij из М. Поэтому новое состояние сети Петри зависит от текущего
состояния и сработавшего перехода. Таким образом, \ij — 5(//г,?)» ГДе ^(МьО —
состояние, полученное из состояния /х;. Если в некоторый момент времени не су-
существует разрешенного перехода, то функция состояния более не определяется,
и процесс, описывающий сеть Петри, завершается.
Рассмотрим сеть Петри, изображенную на рис. 16.48. При срабатывании
перехода t\ сеть Петри переходит в состояние, показанное на рис. 16.49. При
срабатывании перехода ?4 имеем сеть Петри, изображенную на рис. 16.50.
Pi
Pi
Pi\
'O-hO
Pi
Рис. 16.48
Рис. 16.49
Вполне очевидно, что в конце концов все метки переместятся в р$, и про-
процесс завершится. Процесс в сети Петри, изображенной на рис. 16.51, никогда не
завершится, поскольку переход t\ всегда разрешен.
Pt (I
Рз
„-ОЛ
Рис. 16.50
Рис. 16.51
Сеть Петри на рис. 16.52 выполняет вычисления (а + b) x (c + d). Каждый из
переходов t\ или t<i может сработать первым; однако переход ?з не будет разрешен,
пока оба перехода t\ и ^ не сработают.

720 ГЛАВА 16. Сети
ex
ex
0
. a+b
-о-
, c+d
-о
(a+b) (c+d)
-о
Рис. /6.52
Состояние Hj называется непосредственно достижимым из состояния //;,
если срабатывание какого-либо перехода ? в то время, пока сеть находится в со-
состоянии fii, приводит к состоянию Hj. Более формально, состояние fij непосред-
непосредственно достижимо из состояния /ii, если существует переход t такой, что fij =
?(//{, ?). Состояние /xj достижимо из состояния /i;, если, начиная из состояния ^;,
срабатывание последовательности переходов производит состояние \ij. Состояние
/iim достижимо из состояния /i^, если существуют состояния /Xj2,/ij3, • • • ,Aiim_1
и переходы ?b?2, • • • ,*m-i такие, что /i;fc+1 = 6(fiik,tk) для fc = 1,2,... ,m - 1.
В частности, состояние, изображенное на рис. 16.53, непосредственно достижимо
из состояния, изображенного на рис. 16.54, поскольку оно производится срабаты-
срабатыванием перехода t\.
Pi
Т\ 2,
:O-
-o-
Рис. 16.53
Рис. 16.54
Состояние сети Петри, изображенное на рис. 16.55, достижимо из состояния
сети Петри, изображенного на рис. 16.56, поскольку оно производится срабаты-
срабатыванием перехода t\, а затем срабатыванием перехода t±.
Pi
©¦
Рз
Pi
0-
Pi
p> (::)
О-
Рз
Рис. 16.55
Рис. 16.56

РАЗДЕЛ 16.3. Сети Петри 721
Сеть Петри называется живой, если для любого состояния /i и любого пе-
перехода t существует состояние //', достижимое из состояния /i, так что переход
t в состоянии // является разрешенным. Таким образом, каким бы ни было те-
текущее состояние, существует такая последовательность срабатывания переходов
с началом в текущем состоянии, что любой заданный переход может сработать.
Очевидно, что сеть на рис. 16.57 является живой.
Рис. 16.57
Одно из определений тупиковой сети Петри — сеть не живая. Следователь-
Следовательно, существует такое состояние, что если сеть Петри находится в этом состоянии,
то один или более переходов могут никогда не сработать. Назовем это состояние
частичным тупиком. Будем говорить, что сеть Петри находится в тупике,
если имеется состояние, в котором ни один из переходов не может сработать.
Таким образом, существует такое состояние /х, когда 5(/х, t) не определена для
всех переходов t. Рассмотрим стандартный пример, когда два процессора исполь-
используют совместно два ресурса, например, принтер и память, каждый из которых не
может быть использован ими одновременно. Если один процессор имеет доступ к
принтеру, а другой — к памяти, то оба не могут завершить задания. Они также
не могут освободить используемый ресурс, поэтому система находится в тупике.
Эта ситуация показана на рис. 16.58.
ресурс I
задание а
допуск допуск
обработка
задание b
обработка
допуск у^допуск
ресурс II
Рис. 16.58
Еще один пример, проблему обедающих философов, мы рассмотрим в
упражнениях.
Другая, с которой приходится сталкиваться при использовании сети Петри
для совместного использования файлов, — это проблема взаимного исключения.
Предположим, что одновременный доступ двух людей к одним и тем же данным

722 ГЛАВА 16. Сети
нежелателен. Так, недопустимо, чтобы один человек читал данные, а другой в это
же время их изменял. Эта проблема решается путем взаимного исключения. Пока
один человек работает с данными, для другого доступ закрыт. Такая ситуация
проиллюстрирована на рис. 16.59. Единственная метка в позиции с препятствует
допуску другого субъекта до тех пор, пока метка не будет перемещена.
субъект А
субъект В
Рис. 16.59
Сеть Петри называется безопасной, если каждая позиция содержит не бо-
более одной метки. Когда сеть Петри безопасна, в каждой позиции имеется либо
одина метка, либо они отсутствуют вообще, поэтому помещение метки в пози-
позицию является бинарной операцией. Для большинства моделей контроля необходи-
необходима безопасная сеть Петри, поскольку наличие метки может означать протекание
процесса, а ее отсутствие — сигнал о его остановке.
Сеть Петри называется ограниченной, если количество
меток в каждой позиции не превышает некоторое целое чис-
число к. Ограниченная сеть Петри предоставляет возможность
контроля проблемы переполнения. Очевидно, что безопасная
цепь Петри — ограниченная. Сеть Петри, изображенная на
рис. 16.60, ограниченной не является.
В некоторых сетях Петри на вместимость позиций на-
накладываются ограничения, и по условию количество меток не
может превышать эту вместимость.
Сеть Петри называется консервативной, если общее чис-
число меток во всех позициях всегда постоянно. В этом случае
количество меток на входе каждого перехода равно количеству меток на выходе
перехода. Если метки описывают ресурсы, то консервативная сеть Петри гаран-
гарантирует, что никакой ресурс не будет ни создан, ни утерян. Консервативная сеть
Петри является очевидным образом ограниченной. Сеть Петри, изображенная на
рис. 16.61, консервативна.
Рис. 16.60
Рис. 16.61

РАЗДЕЛ 16.3. Сети Петри 723
УПРАЖНЕНИЯ
1. Какие из приведенных ниже сетей Петри
а) являются безопасными?
б) являются консервативными?
в) являются ограниченными?
г) имеют достижимым каждое состояние?
д) являются живыми?
е) имеют все текущие переходы разрешенными?
ж) имеют переходы, которые могут быть разрешены в некотором состоянии,
достижимом из текущего состояния?
(О (Н)
«з
о:
(ш)
(iv)
0 - О-
о ©
(v)
0 - О

724 ГЛАВА 16. Сети
2. В сетях Петри (упражнение 1) найдите:
а) все возможные состояния сети Петри;
б) состояние после срабатывания перехода t\\
в) состояние после последовательного срабатывания переходов t\ и ^;
г) любое тупиковое состояние;
д) любое частично тупиковое состояние.
3. Постройте пример сети Петри, в которой два перехода разрешены, но сраба-
срабатывание каждого из них блокирует другой.
4. Постройте пример сети Петри, которая является безопасной, но не является
живой.
5. Постройте пример сети Петри с ограничением 4.
6. Постройте пример сети Петри, которая является безопасной, но не является
ограниченной.
7. Постройте пример сети Петри, которая является консервативной, но не яв-
является безопасной.
8. Постройте сеть Петри, которая эквивалентна сети, изображенной на рис. 16.58,
но не является тупиковой.
9. Может ли консервативная сеть Петри быть тупиковой?
10. Приведите пример сети Петри, которая имеет состояние, недостижимое из
исходного состояния.
11. Постройте сеть Петри, которая частино тупиковая, но не тупиковая.
12. Проблема обедающих философов формулируется следующим образом: пять
философов сидят за столом, чтобы есть и размышлять. В любой заданный
промежуток времени они могут делать что-то одно. Философы едят китай-
китайское блюдо, используя палочки, поэтому для еды каждому необходимо иметь
две палочки. Когда философы размышляют, палочки не нужны. На столе
между двумя сидящими лежит одна палочка, т.е. всего пять палочек. Оче-
Очевидно, что если философы одновременно возьмут правую палочку, то каж-
каждый будет лишен пищи. Постройте сеть Петри, моделирующую эту задачу,
которая не была бы тупиковой, т.е. когда философ будет приниматься за еду,
у него для этого будут две палочки по обе стороны от него.

ГЛАВА
ТЕОРИЯ ВЫЧИСЛЕНИЙ
17.1. РЕГУЛЯРНЫЕ ЯЗЫКИ
В примере 9.16 приведены следующие определения.
ОПРЕДЕЛЕНИЕ 17.1. Пусть А — конечное множество символов. Такое мно-
множество символов называется алфавитом. Например, А может быть подмноже-
подмножеством английского алфавита или просто множеством {0,1}. Строка или слово
символов из А имеет вид aia2a3a4 ... an, где a; G A.
Если А = {0,1}, то 1, 100, 101, 11011 и 0001 - строки символов из А.
Определим также пустую строку — А, не содержащую ни одного символа.
ОПРЕДЕЛЕНИЕ 17.2. Пусть А* обозначает множество всех строк алфавита А.
Определим бинарную операцию о, называемую конкатенацией на А*, следу-
следующим образом: если а^аз^ ... ап и 61&263&4 ''' ^т ^ ^*' Т0
... ап о
Если А = {0,1}, то 11011 о 100010 = 11011100010. В частности, если и —
строка из Л*, то А о и = и о А = и, и это свидетельствует о том, что если строке
предшествует или следует за ней пустая строка, то в результате конкатенации
получаем ту же самую строку.
ОПРЕДЕЛЕНИЕ 17.3. Пусть А* обозначает множество всех строк алфавита А.
Подмножество L множества А* называется языком.
Если А — множество букв английского алфавита, то L могло бы быть множе-
множеством слов английского языка. Если А — множество букв греческого алфавита,
то L могло бы быть множеством слов греческого языка. Если А — множество
символов языка программирования, то L — множество слов этого языка.

726 ГЛАВА 17. Теория вычислений
Если алфавит А={1,0}, то следующие множества являются языками.
L1== {0,1,00,11,000,111,...};
L2 = {w : w G А* и содержит точно одну цифру 1} ;
?,3 = {w : w E А* и содержит точно две цифры 1};
L4 = {w : w e А* и содержит не мене двух цифр 1}.
Если алфавит А = {а,Ь,с}, то следующие множества являются языками.
L\ — {acb, aacbb, aaacbbb,...} ;
L2 = {w : w = anbn для п > 1} ;
L3 = {w : w € апЪш для m, n > 1};
L4 = {u;: w G Л* и не содержит последовательных одинаковых букв}.
ОПРЕДЕЛЕНИЕ 17.4. Пусть 5 — подмножество множества А*. Тогда 5* —
множество всех строк или слов, образованных конкатенацией слов из множе-
множества 5, т.е. S* = {wiW2 .. .wn : Wi e S}. Символ * называется звездой Клини в
честь математика и логика Стивена Коула Клини.
Заметим, что данное определение согласовано с определением множества А*.
ОПРЕДЕЛЕНИЕ 17.5. Пусть А — алфавит. Выражением над А называется
строка символов, которая представляет собой подмножество множества Л*.
Регулярное выражение состоит из символов *, V, Л, (, ) и а для каждого
элемента а из А. Класс регулярных выражений определяется следующими
правилами.
i) Символ А является регулярным выражением и для каждого а Е А сим-
символ а — регулярное выражение.
И) Если wi и W2 — регулярные выражения, то w\W2, w\ V w2, w\ и (w\) —
регулярные выражения.
iii) Все регулярные выражения образуются по правилам (i) и (и).
Каждому выражению сопоставляется множество согласно соответствию ?,
определенному следующим образом:
?(Х) = А
?(&) — {а} для всех а е А
?(у) = U
?(•)='
?@ = (
?{))=)

РАЗДЕЛ 17.1. Регулярные языки 727
Поэтому
?(аа*) = {а} о {а}* = {а, аа, ааа, аааа, аааа,...};
?(a(bVc)d) = {а} о {{Ъ} U {с}} о {d} = {abd, acd}\
jC((a V b)*) ={aU b}* = {A, a, b, ab, ba, abb, aba,...} =
= все строки, состоящие из 0 или более
символов аиЬ;
?(ab*c) = {а} о {Ь}* о {с} = {ас, abc, abbe, abbbc,...};
?(aVbVc) = {а} U {b} U {с} ={а,Ь,с}.
Образ регулярного выражения является регулярным языком. Регулярные языки
можно определить следующим образом.
ОПРЕДЕЛЕНИЕ 17.6. Класс R называется регулярным языком, если обладает
следующими свойствами.
i) Пустое слово, А е R, и если а ? А, то {а} е R.
И) ЕСЛИ 5i И 52 € i?, TO 5i U 52, S\ О 52, 5^ € R.
iii) Только множества, образованные согласно (i) и (ii), принадлежат R.
Хотя следующие утверждения здесь и не доказываются, но пересечение ре-
регулярных множеств является регулярным множеством и дополнение регулярного
множества является регулярным множеством.
ОПРЕДЕЛЕНИЕ 17.7. Пусть 5 и Т — подмножества множества А*. Если
5 = Т*, то S называется множеством, порожденным множеством Т.
Если множество 5 порождено множеством Т, то каждый элемент из множе-
множества 5 является конечной конкатенацией элементов множества Т. Однако, эле-
элементы конкатенации, образующие данное слово, необязательно являются одно-
однозначно определимыми. Если Г = {а,Ь}, то Т* состоит из пустого слова и всех
возможных конечных строк из символов а и Ь. Если Т = {a,ab,6}, то Г* = Г*,
но хотя каждая строка в Г* может выражаться единственным об?азом конка-
конкатенацией элементов из Т, это неверно для элементов множества Т, поскольку
выражение abab можно записать как (a)(b)(a)(b), а также как (a)(b)(ab) и как
<аЬ)(аЬ).
ОПРЕДЕЛЕНИЕ 17.8. Пусть 5 и С — подмножества множества А*. Если
5 = С*, то каждая строка в 5 может выражаться конкатенацией элемен-
элементов множества С, и будем говорить, что С является кодом. Код С называется
однозначно декодируемым, если каждую строку из 5 можно однозначно вы-
выразить конкатенацией элементов из С.

728 ГЛАВА 17. Теория вычислений
Поэтому {ba,ab,c}, {ade,ddbee:dfc,ddd} и {а, 6, с, de} являются однозначно
декодируемыми кодами, хотя {a,ab,bc,c}, {ab,abc,cde,de} и {a,bc,abc} однознач-
однозначно декодируемыми не являются.
ПРИМЕР 17.9. Функция на множестве 5 называется ретракционным отобра-
отображением, или ретракцией, если / о / = /. Образ при отображении / называется
ретрактом. Пусть R — ретракт при ретракционном отображении / : А* —> А*.
Том Хэд (Tom Head) показал, что ретракт порождается конечным кодом, обла-
обладающим таким свойством: каждое слово кода содержит элемент из А, который
встречается в этом слове только один раз и не встречается ни в каком другом
слове кода. Такие коды называются ключевыми кодами. Следовательно, {а,Ь,с},
{а, бе, се}, {ade,ddbee,caa} и {ad,bdde,cede} являются ключевыми кодами, по-
порождающими ретракты, поскольку каждый из элементов а, 6 и с встречаются
точно в одном слове и при этом только один раз. Однако, {ba,ab,c}, {ab,abc,cde}
и {а, аб, 6с, d} тоже являются кодами, но не порождают ретракты. Пересечение
ретрактов необязательно является ретрактом. На усмотрение читателя оставим
доказательство, что пересечение множеств {ac,bc,d}* и {a,cb,cd}* порождено
кодом, который можно описать выражением ac(bc)*d. ?
ОПРЕДЕЛЕНИЕ 17.10. Пусть А — алфавит. Код С С А* называется префикс-
префиксным кодом, если для всех слов и,v ? С; если и = vw для w € А*, то и = v
и w = А. Это означает, что одно слово кода не может быть начальной строкой
другого слова кода. Код С С А* называется суффиксным кодом, если для
всех слов u,v Е С; если u — wv для w Е Л*, то и = v и w = А. Это означает,
что одно слово кода не может быть конечной строкой другого слова кода.
Множество {a,ab,ac} является кодом, но не является префиксным кодом,
так как а является начальной строкой как для ab, так и для ас. Однако, данное
множество — суффиксныи код. Множество {а,Ьа,са} является префиксным ко-
кодом, но суффиксным не является, поскольку а — конечная строка для Ьа и для
са. Множество {ad,ab,ac} — одновременно префиксный и суффиксныи код.
¦ УПРАЖНЕНИЯ
1. Найдите регулярные множества, соответствующие приведенным ниже выра-
выражениям. Если множество бесконечное, перечислите десять его элементов.
а) a(bVcVd)a;
б) а*Ь*с;
в) (aVb)(cVd);
г) (ab*A)v(cd)*;
Д) a(bc)*d.
2. Найдите регулярные множества, соответствующие приведенным ниже выра-
выражениям. Если множество бесконечное, перечислите десять его элементов.
а) Ьс(Ьс)*;
б) (aVb* VA)(cVd*);

РАЗДЕЛ 17.1. Регулярные языки 729
в) (aVbcVd)*;
г) (aVb)(cVd)b;
д) a*(bVcV)d*.
3. Найдите регулярные выражения, соответствующие приведенным ниже регу-
регулярным множествам.
а) {ab,ac,ad}\
б) {ab,ac,bb,bc]\
в) {а, ab, abb, abbb, abbbb,...};
г) {ab, abab, ababab, abababab, ababababab,...};
д) {ab, abb, aab, aabb}.
4. Найдите регулярные выражения, соответствующие приведенным ниже регу-
регулярным множествам.
а) {ab,acb,adb}\
б) {ab, abb, abbb, abbbb,...}]
в) {ad, ae, af, bd, be, bf, cd, ее, с/};
r) {abed, abebed, abebebed, abcbcbcbcd,...};
д) {abcd,abef,cdcd,cdef}.
5. Пусть А = {a, b, c].
а) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, содержащих точно два символа 6.
б) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, содержащих точно два символа b и два символа с.
в) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, содержащих точно два или более символов 6.
г) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, которые начинаются и оканчиваются символом а и содержат, по
крайней мере, один символ Ъ и один символ с.
д) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, которые состоят из одного или более символов а, за которым
следует один или более символов Ь, а затем один или более символов с.
6. Пусть Л = {а,Ь}.
а) Постройте регулярное выражение для множества всех элементов мно-
множества Л*, содержащих в точности два символа b или в точности два
символа а.
б) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, содержащих четное число символов Ь.
в) Постройте регулярное выражение для множества всех элементов множе-
множества Л*, которые начинаются и оканчиваются символом а и содержат не
менее одного символа 6.
г) Постройте регулярное выражение для множества всех элементов множе-
множества Л* таких, что количество символов а в каждой строке кратно 3, а
количество символов b кратно 5.

730 ГЛАВА 17. Теория вычислений
д) Постройте регулярное выражение для множества всех элементов множе-
множества А* таких, что длина каждой строки кратна 3.
7. Какое из приведенных ниже выражений является однозначно декодируемым
кодом?
а) {ab,ba,a,b}\
б) {аб, acb, accb, acccb,...};
в) {a,6,c,6d};
г) {ab,ba,a}\
д) {a,ab,ac,ad}.
8. Какие из приведенных ниже выражений описывают однозначно декодируе-
декодируемые коды?
а) аЬ*;
б) ab*Vbaaa;
в) ab*cVbaaac;
г) (avb)(bva);
д) (aVbvA)(b V aVA).
9. Какое из перечисленных ниже выражений является однозначно декодируе-
декодируемым кодом? Какое является суффиксным кодом?
а) {аЬ,6а,};
б) {ab,abc,bc}\
в) {а,Ь,с,М};
г) {aba,ba,c}\
д) {ab, acb, accb, acccb}.
10. Какие из приведенных ниже выражений описывают префиксные коды? Какие
из них описывают суффиксные коды?
а) ab*;
б) ab*c;
в) а*Ьс*;
г) (aVb)(bVa);
Д) а*Ь.
11. Какие из приведенных ниже кодов являются однозначно декодируемыми?
Обоснуйте свой ответ.
а) 1110,111,1011,11,0101;
б) 10,110,1110,0101;
в) 010,101,0101,1010,10101;
г) 0101,1001,011,11, 10011, 00101;
д) 101,1001,10001,11011,11001,00111.
12. Какие из приведенных ниже кодов являются однозначно декодируемыми?
Обоснуйте свой ответ.
а) 110,1110,11110,111110,10;
б) 1011,1010,1100,0101, ООП, 1100,1100,1111,0000;
в) 101,010,11,10101,1011,1010;

РАЗДЕЛ 17.2. Автоматы 731
г) 110,101,1001,11101,0101, ОНО, 0111,10001;
д) 11011,101,010100,11,1011,1110.
13. Какие из приведенных ниже кодов являются префиксными кодами?
а) 101,1101,0101,001,1001,11101, ОНО, 01001;
б) 1101, ООП, 1010,1110,1010,0101,1100,1111;
в) 101,1100,01010,10101, ООН, ОНО;
г) 1011,10101,10110,0101,01100,111000;
д) 1101,10001,1001,01110,10110,110110.
14. Какие коды в упражнении 1 являются префиксными кодами?
15. Какие коды в упражнении 2 являются префиксными кодами?
16. а) Какие коды в упражнении 1 являются суффиксными кодами?
б) Какие коды в упражнении 2 являются суффиксными кодами?
в) Какие коды в упражнении 3 являются суффиксными кодами?
17. Код называется инфиксным кодом, если никакая строка кода не является
подстрокой другой строки кода. Всегда ли суффиксный и префиксный коды
являются инфиксными кодами? Докажите или постройте контрпример.
18. Всегда ли инфиксный код является префиксным и суффиксным кодом одно-
одновременно? Докажите или постройте контрпример.
19. Какие коды в упражнении 1 являются инфиксными кодами?
20. Какие коды в упражнении 2 являются инфиксными кодами?
21. Какие коды в упражнении 3 являются инфиксными кодами?
22. Существует ли префиксный код, состоящий из слов длины 1,2,3,3?
23. Существует ли префиксный код, состоящий из слов длины 1, 3, 3, 3, 4, 5,
5, 5?
24. Существует ли инфиксный код, состоящий из слов длины 1,3,3,3?
25. Докажите, что ключевой код является префиксным и суффиксным кодом
одновременно.
17.2. АВТОМАТЫ
По сути, автомат представляет собой устройство, распознающее, воспринимаю-
воспринимающее или допускающее определенные элементы множества А*, где А — конечный
алфавит. Различные автоматы (совокупность автоматов) распознают или допуска-
допускают различные элементы множества А*. Подмножество элементов множества А*,
допускаемое автоматом М,— это язык, который называется языком над алфави-
алфавитом Л, допускаемым автоматом М, и обозначается M(L).
Для заданного конечного алфавита автомат состоит из множества 5 — мно-
множества состояний и функции F : А х 5 —> 5, называемой функцией переходов.
Множество 5 содержит элемент s0 и одно или более финальных состояний. Ав-
Автомат М обозначается через (Д 5, so,T, F)9 где А — алфавит, 5 — множество
состояний, so — начальное или исходное состояние, Г — множество финальных
состояний и F — функция перехода. Обратите внимание, что входом для F яв-
является буква из Л и состояние, принадлежащее множеству 5. Выходом является

732 ГЛАВА 17. Теория вычислений
состояние из S (возможно, то же самое состояние). Если автомат находится в со-
состоянии s и "читает" букву а, то (а, s) является входом для F, и F(a, s) — следую-
следующее состояние. Для автомата в качестве "начала" можно рассматривать начальное
состояние 50. Если автомат "читает" букву а алфавита А, то он "переходит" в со-
состояние s = F(a,so). Если теперь автомат "читает" букву из А, например, 6, то
он переходит в состояние s' = F(a,s). Следовательно, по мере "прочтения" букв
алфавита автомат переходит из одного состояния в другое. Пусть М — автомат
с алфавитом А = {а, 6}, множеством состояний 5 = {so,si,S2}, a ФУНК1*ия F
задана таблицей
F
а
Ь
so
si
S2
si
si
S2
S2
Si
Предположим, что М "читает" букву а, за которой следуют буквы b и а. По-
Поскольку автомат начинает функционировать в состоянии so, и буква, которую он
читает, это а, то F(a,s0) = sb поэтому теперь автомат находится в состоянии s\.
Следующей буквой для чтения является Ь и F(b,s\) = 52. Наконец, читается
последняя буква а, и так как F(a,S2) = $2, автомат остается в состоянии s2.
Функцию перехода F можно задать также совокупностью правил.
Если автомат находится в состоянии sq и читает а , то он переходит в состояние s\.
Если автомат находится в состоянии s\ и читает а , то он переходит в состояние s\.
Если автомат находится в состоянии 52 и читает а , то он переходит в состояние s2.
Если автомат находится в состоянии so и читает 6, то он переходит в состояние s2.
Если автомат находится в состоянии si и читает 6, то он переходит в состояние s2.
Если автомат находится в состоянии s2 и читает 6, то он переходит в состояние s\.
Такой автомат лучше всего изображать графически с помощью диаграммы со-
состояний, являющейся ориентированным графом, у которого состояния представ-
представлены вершинами, а ориентированное ребро из вершины s в вершину s' помечено
буквой из алфавита А, например, буквой а, если F(a,s) = s'. Направленная
стрелка, помеченная буквой а, будет называться а-стрелкой. Поэтому приведен-
приведенный выше автомат можно представить графически, как показано на рис. 17.1.
"^. *r
•fI
Рис. 17.1
(Отметим, что хотя диаграмма состояний на рис. 17.1 и является ориентиро-
ориентированным графом, тем не менее, исходя из условий задания некоторых автоматов,
соответсвующие диаграммы могут не быть ориентированными графами, посколь-
поскольку из одного состояния в другое может вести не одно ориентированное ребро.

РАЗДЕЛ 17.2. Автоматы 733
Более точным названием таких диаграмм является мультиграфы, или помечен-
помеченные орграфы.
Слово или строку aoaia2 .. . ап из Л* автомат "читает" следующим образом:
сначала читается а0, затем а\ и так до тех пор, пока не будет прочитано ап. Как
отмечалось выше, некоторые состояния определены как финальные состояния.
Автомат допускает или распознает строку, a0aia2 .. . ап, если после прочтения
ап он останавливается в финальном состоянии. Если 5 — начальное состояние,
то соответствующая вершина обозначается схемой, изображенной на рис. 17.2.
Если s — финальное состояние, то соответствующая вершина обозначается, как
изображена на рис. 17.3.
Рис. 17.2 Рис. 17.3
Например, для автомата, диаграмма состояний которого изображена на рис. 17.4,
состояние sq —- начальное, а состояние s^ — финальное.
Автомат допускает слово baa, поскольку после прочтения Ь он переходит в
состояние 52', после прочтения а — в состояние s\\ после прочтения второго а,
он переходит в состояние s3, которое является финальным состоянием. Можно
убедиться, что автомат допускает также слова abbba и bb, но не распознает слова
bbb, abab или abb. Как отмечалось выше, множество слов, допускаемых автоматом,
назывется языком, допускаемым автоматом.
ПРИМЕР 17.11. Рассмотрим автомат с диаграммой состояний, изображенной на
рис. 17.5.
О'
Рис. 17.5
Очевидно, что автомат допускает слово bb. Для слова а в каждом состоянии
имеется петля, поэтому при чтении а состояние не меняется, что дает возмож-
возможность до прочтения следующего слова b читать любое необходимое количество

734 ГЛАВА 17. Теория вычислений
слов а. Таким образом, автомат читает aababaaa, baabab, baaab, babaaa, aabaabaa
и может фактически прочесть любое слово языка, заданного регулярным выраже-
выражением a*ba*ba*. Поскольку А = {а,Ь}, то такой язык можно описать также как
множество всех слов, содержащих точно два 6. Состояние S4 является примером
состояния зацикливания. Попав в состояние зацикливания, автомат никогда не
сможет из него выйти. ?
ПРИМЕР 17.12. Рассмотрим автомат с диаграммой состояния, изображенной на
рис. 17.6 (упрощенный вид — на рис. 17.7).
а,Ь,с
Рис. 17.6
Рис. 17.7
Автомат допускает, очевидно, только слова аЪ и ас. Этот язык можно задать
с помощью регулярного выражения a(bVc). ?
ПРИМЕР 17.13. Рассмотрим автомат с диаграммой состояний, изображенной на
рис. 17.8.
а,Ь, с
Рис. 17.8
Каждое слово следует начинать с аЪ и заканчивать на с. Однако петлю
aabc можно повторять требуемое количество раз, поскольку она начинается и
заканчивается в S3. Поэтому регулярным выражением для этого автомата будет
abc(aabc)*. ?
ПРИМЕР 17.14. Рассмотрим автомат с диаграммой состояний, изображенной на
рис. 17.9.
а,Ь
о
Рис. 17.9

РАЗДЕЛ 17.2. Автоматы 735
Автомат при чтении трех последовательных b переходит в состояние s3,
которое является состоянием зацикливания. Это единственный способ попасть в
состояние S3, и все другие состояния являются финальными состояниями. Таким
образом, язык, который допускает автомат, состоит из вех слов, не включающих
три последовательных Ъ. ?
Рассмотренные автоматы часто называются детерминированными автома-
автоматами, так как в любом состоянии и для любого значения из алфавита, которое
подается в автомат для чтения, существует одно и только одно состояние. Иными
словами, такая ситуация обусловлена тем, что F : Ах S —> 5 является функцией.
Зачастую удобно ослабить правила таким образом, чтобы F была не функцией,
а отношением. Если опять рассмотреть F как множество правил для а е А и
s ? 5, то могут существовать правила, предоставляющие возможность перехо-
перехода из данного состояния в некоторые другие состояния, или такие правила не
могут существовать. В последнем случае автомат, как говорят, "зависает" и не
может далее функционировать. Автоматы, для которых F не обязательно являет-
является функцией, называются недетерминированными автоматами. Рассмотрим,
например, приведенную ниже диаграмму состояний, изображенную на рис. 17.10.
Рис. 17.10
Если в состоянии so прочитывется слово, символ а, то автомат переходит в
состояние s\ или S2. Однако, если автомат находится в состоянии s\ и прочитыва-
прочитывается слово, символ Ь, то автомат "зависает", поскольку нет 6-стрелки, выходящей
из состояния si. Отметим, что в соответствии с приведенным выше определением
множество детерминированных автоматов принаждлежит множеству недетерми-
недетерминированных автоматов.
ПРИМЕР 17.15. Легко убедиться, что автомат с диаграммой состояний, изобра-
изображенной на рис. 17.11, допускает язык, задаваемый регулярным выражением ab*c.
Рис. 17.11
?
ПРИМЕР 17.16. Автомат с диаграммой состояний, изображенной на рис. 17.12,
допускает язык, задаваемый регулярным выражением aVb.
Рис. 17.12
?

736 ГЛАВА 17. Теория вычислений
ПРИМЕР 17.17. Автомат с диаграммой состояний, изображенной на рис. 17.13,
допускает язык, задаваемый регулярным выражением aa*bb*.
Рис. 17.13 ?
ПРИМЕР 17.18. Автомат с диаграммой состояний, изображенной на рис. 17.14,
допускает язык, состоящий их строк, содержащих не менее двух символов а.
Рис. 17.14 П
Преимущество недетерминированных автоматов состоит в том, что нет необ-
необходимости включать в них несущественные ребра. Поэтому в некоторых дальней-
дальнейших построениях будет намного проще использовать недетерминированные ав-
автоматы. Любой язык, который допускается детерминированным автоматом, оче-
очевидно, допускается и недетерминированным автоматом, так как множество неде-
недетерминированных автоматов включает в себя множество детерминированных ав-
автоматов. Следующая теорема показывает, что любой язык, который допускается
недетерминированным автоматом, допускается и детерминированным автоматом.
ТЕОРЕМА 17.19. Для каждого недетерминированного автомата существует эк-
эквивалентный детерминированный автомат, который допускает тот же язык.
Вместо формального доказательства продемонстрируем построение детерми-
детерминированного автомата, который допускает язык, допускаемый недетерминирован-
недетерминированным автоматом. Пусть S — множество состояний недетерминированного автомата.
Используем элементы V(S), т.е. элементы подмножества множества 5 в качестве
состояний для создаваемого детерминированного автомата. Рассмотрим недетер-
недетерминированный автомат N, изображенный на рис. 17.15.
о-
©¦
Рис. 17.15
Пусть {so} — начальное состояние. Построим а-стрелку из {s0} во множе-
множество всех таких состояний, что существует а-стрелка из sq в это состояние. В
данном случае имеется а-стрелка из sq в so и а-стрелка из 5о в 5Ь т.е. постро-
построена а-стрелка из {so} в {so,si}. He существует 6-стрелки из so B любое другое
состояние, поэтому строим 6-стрелку из {s0} в пустое множество 0. Теперь рас-
рассмотрим состояние {so, si}. Строим а-стрелку из {so, $1} во множество всех таких
состояний, что существует а-стрелка либо из so, либо из s\ в это состояние. В
данном случае строим а-стрелку из {so,si} B самое себя. Строим 6-стрелку из

РАЗДЕЛ 17.2. Автоматы 737
{s'o.si} во множество всех таких состояний, что существует 6-стрелка из s0 или
из 5i в это состояние. В данном случае строим b-стрелку из {so,si} в {52}« По-
Поскольку не существует ни а-стрелки, ни Ь-стрелки из любого состояния в пустом
множестве ни в какое другое состояние, строим а-стрелку и 6-стрелку из пустого
множества в себя. Теперь рассмотрим {52}. Поскольку не существует а-стрелки
из $2 ни в какое другое состояние, строим а-стрелку из {52} в пустое множество.
Учитывая, что только 6-стрелка ведет из 82 в себя, строим 6-стрелку из {52} в
себя. Финальное состояние (состояния) состоит из всех множеств, содержащих
элемент финального множества автомата N. В данном случае {S2} — единствен-
единственное финальное состояние. Итак, построена диаграмма состояний, изображенная
на рис. 17.16, которая является диаграммой состояний детерминированного ав-
автомата. Этот автомат допускает тот же язык, что и автомат iV, а именно, язык,
заданный выражением a*abb*.
Рис. 17.16
В общем случае имеется следующая процедура для построения детермини-
детерминированного автоматата из недетерминированного.
1. Начать из состояния {s0}, гДе so ~ начальное состояние недетерминирован-
недетерминированного автомата.
2. Для каждого сц € А построить а^-стрелку из {$о} во множество всех состо-
состояний таким образом, что имеется а^-стрелка из so в это состояние.
3. Для каждого вновь построенного состояния Sj и для каждого а* е А постро-
построить ai-стрелку из Sj во множество всех таких состояний, что существует
ai-стрелка из элемента множества Sj в это состояние.
4. Продолжать процесс, пока есть возможность создавать новые состояния.
5. Преобразовать все множества состояний Sj, содержащие элемент финально-
финального множества недетерминированного автомата, в финальное состояние.
ПРИМЕР 17.20. Построим детерминированный автомат, соответствующий неде-
недетерминированному автомату, изображенному на рис. 17.17.
Рис. 17.17

738 ГЛАВА 17. Теория вычислений
Поскольку имеется а-стрелка из so в si, строим а-стрелку из {s0} в {s\}. Так
как не существует 6-стрелки из so в любое иное состояние, строим 6-стрелку из so
в пустое множество 0. Имеется а-стрелка из s\ в $з, поэтому строим а-стрелку
из {$i} в {$з}- Поскольку имеется 6-стрелка из si в so и из si в S2, строим
6-стрелку из {s\} в {50,52}. Стрелок из 5з в другое состояние не существует,
поэтому строим а-стрелку и 6-стрелку из 5з в пустое множество. Имеются а-
стрелки из so в si, из 52 в 5i и из 52 в S3, поэтому строим а-стрелку из {so,S2} в
{si,s3}. He существует 6-стрелок ни из состояния s0, ни из состояния s2, поэтому
строим 6-стрелку из {so,S2} в пустое множество. Так как имеется а-стрелка из si
в S3, строим а-стрелку из {si,s3} в {s3}. Имеются 6-стрелки из si в s0 и из si в
S2, поэтому строим 6-стрелку из {si,S3} в {so,S2}. Этим завершается построение
детерминированного автомата, изображенного на рис. 17.18.
Рис. 17.18
?
Проведенное нами исследование регулярных языков и автоматов подытожи-
подытоживает следующая теорема, которая приводится без доказательства.
ТЕОРЕМА 17.21. (Клини) Язык является регулярным тогда и только тогда, когда
он допускается автоматом.
УПРАЖНЕНИЯ
1. Какие из перечисленных ниже слов допускаются автоматом, изображенным
на рис. 17.19?
а) абба
б) aabbb
в) babab
г) aaabbb
д) bbaab
Ъ(
Рис. 17.19

РАЗДЕЛ 17.2. Автоматы 739
2. Какие из перечисленных ниже слов допускаются автоматом, изображенным
на рис. 17.20?
а) aaabb
б) abbbabbb
в) bababa
г) aaabab
д) bbbabab <у^
Рис. 17.20
3. Составьте выражение для языка, который допускается автоматом, изобра-
изображенным на рис. 17.21.
4. Составьте выражение для языка, который допускается автоматом, изобра-
изображенным на рис. 17.22.
т
so
Рис. 17.22
Рис. 17.21
5. Составьте выражение для языка, который допускается автоматом, изобра-
изображенным на рис. 17.23.
5?
Рис. 17.23
6. Составьте выражение для языка, который допускается автоматом, изобра-
изображенным на рис. 17.24.
Рис. 17.24
7. Найдите детерминированный автомат, который допускает язык, заданный
выражением aa*bb*cc*.

740 ГЛАВА 17. Теория вычислений
8. Найдите детерминированный автомат, который допускает язык, заданный
выражением (a*ba*ba*b)*.
9. Найдите детерминированный автомат, который допускает язык, заданный
выражением (a*(ba)*bb*a)*.
10. Найдите детерминированный автомат, который допускает язык, заданный
выражением (a*b)V(b*a)*.
11. Найдите недетерминированный автомат, который допускает язык, заданный
выражением aa*bb*cc*.
12. Найдите недетерминированный автомат, который допускает язык, заданный
выражением (a*b)V(c*b)V(ac)*.
13. Найдите недетерминированный автомат, который допускает язык, заданный
выражением (aVb)*(aaVbb).(aVb)*
14. Найдите недетерминированный автомат, который допускает язык, заданный
выражением ((aa*b)vbb*a)ac*
15. Найдите детерминированный автомат, который допускает тот же язык, что
и недетерминированный автомат, изображенный на рис. 17.25.
JbL
а,Ь
Q
Рис. 17.25
Рис. 17.26
16. Найдите детерминированный автомат, который допускает тот же язык, что
и недетерминированный автомат, изображенный на рис. 17.26.
17. Найдите детерминированный автомат, который допускает тот же язык, что
и недетерминированный автомат, изображенный на рис. 17.27.
Рис. 17.27
18. Найдите детерминированный автомат, который допускает тот же язык, что
и недетерминированный автомат, изображенный на рис. 17.28.
Рис. 17.28

РАЗДЕЛ 17.3. Грамматики 741
17.3. ГРАММАТИКИ
Грамматика — это совокупность правил, которые используются для построения
языка. Правила позволяют заменять символы или строки символов другими сим-
символами или строками символов. Допустим, имеется начальное слово add, которое
можно заменить на А + В, а А и В можно заменить любым неотрицательным
целым числом, меньшим 10. Пользуясь этим правилом, А можно заменить на 3
и В — на 2, получив 3 4-2. Если А заменить на 5, а В — на 6, то получим 5 + 6.
При вводе дополнительного правила о возможности замены А на А + В
появится возможность начать с замены add на А + В. Если после этого заменить
А на А+В, получим А+В+В. Заметим следующее: поскольку А можно заменить
как на А + В, так и на целое число, то при замене символов однозначности не
требуется. Кроме того, и одно, и второе В в выражении А + В + В не обязательно
заменять одним и тем же значением. Если А заменить на 3, первое В заменить
на 5, а второе В — на 7, то получим 3 + 5 + 7. С другой стороны, можно снова
было бы заменить А на А + В, получить А + В + В + В и продолжать строить
суммы произвольной длины.
Отметим, что в приведенных выше правилах символы add, А и В можно
заменять другими символами, в то время как символ + и целые числа заме-
заменять нельзя. Символы, которые можно заменять другими символами, называются
нетерминальными символами, а символы, которые нельзя заменять другими
символами, называются терминальными символами. Правила, указывающие,
как заменять символы, называются продукциями. Обозначим продукцию (или
правило), смысл которой состоит в том, что add можно заменить на А + В, через
add -» А + В.
Таким образом, продукция для первого из приведенных выше примеров имеет вид:
add-* А + В
А->0 В -+0
Л->1 В-+1
А — 2 В-> 2
А-+9 В-+9
Если добавить правило, состоящее в том, что А можно заменить на А + В,
то продукции будут иметь вид:
add-* А + В А-> А + В
А-+ О В -> О
А-> 1 В-> 1
А-+2 В -+2
Формально грамматика определяется следующим образом.

742 ГЛАВА 17. Теория вычислений
ОПРЕДЕЛЕНИЕ 17.22. Формальная грамматика, или грамматика непо-
непосредственных составляющих состоит из конечного множества нетерминаль-
нетерминальных символов N, конечного множества терминальных символов Т, элемента
S e N, называемого начальным символом, и конечного множества продук-
продукций Р, которое является отношением в (iVuT)*, таким что каждый первый
элемент упорядоченной пары из Р содержит символ из N и, по крайней мере,
один первый элемент некоторого правила является начальным элементом 5.
Если W и W — элементы из (N U Г)*, W = uvw, W = uv'w, a v —» v' —
продукция, то непосредственный вывод W из W обозначается W => W. Если
Wi => W2 => W3 => • • • =» Wn
для п > 0, то говорят, что Wn выводится из W\. Обозначается это следую-
следующим образом: W\ =»•* Wn. Формальная грамматика Г обозначается четверкой
(N,T,S,P). Множество всех строк элементов из Т, которые можно породить с
помощью множества продукций Р, называется языком, порождаемым грам-
грамматикой Г, и обозначается
При порождении слова в грамматике Г для вывода новых строк продолжаем
использовать продукции до тех пор, пока не получим строку, содержащую только
терминальные элементы.
Таким образом, для последнего из приведенных выше примеров имеем:
N = {add, Л, В} ,
Г = {+,0,1,2, 3,4, 5, 6,7,8,9},
Р = {(add, А+В), (Л, А+В), (А, 0), (А, 1),..., (А, 9), (В, 0), (В, 1),..., (В, 9)} ,
где (add, А 4- В) обозначено через add —+ А + В, (А, А + В) обозначено через
А —> А + В и т.д. Язык, порожденный грамматикой Г, —- это множество всех
формальных выражений конечных сумм неотрицательных целых чисел, меньших,
чем 10.
ПРИМЕР 17.23. В описанной выше грамматике выведем выражение 3 + 2 + 4.
Начнем с продукции
add-* A + B,
чтобы вывести
А + В.
Затем применим продукцию
А->А + В,
чтобы вывести

РАЗДЕЛ 17.3. Грамматики 743
Далее применим продукции
Л->3 В-^2 В->4,
чтобы вывести
+2 + 4. ?
ПРИМЕР 17.24. Пусть требуется построить грамматику, позволяющую вывести
арифметические выражения для множества целых чисел {0,1,2,3,4,5,6,7,8,9}.
Язык, порожденный этой грамматикой, есть множество всех конечных арифме-
арифметических выражений для множества целых чисел {0,1,2,3,4,5,6,7,8,9}. При-
Примерами служат выражения 3 х E 4- 4) и D 4- 5) -г- CЛ2), где символ Л обо-
обозначает показатель степени. Понятно, что желательно исключить такие выра-
выражения, как 3 4- хб и 3 + -гб х 4 - 5. Пусть множество N = {5, А, В} и Т =
{4, -, х,4, А,0,1,2,3,4,5,6,7,8,9, (,)}. Нам понадобятся следующие продукции:
S -»
5 -»
S ->
5 ->
S -»
А -»
А -»
А -»
Л ->
(А + В)
{А-В)
{Ах В)
(А + В)
(Л'В)
{А + В)
{А-В)
{Ах В)
(А + В)
В ->
В -н.
в -»
в -¦
в -»
л -»
в -¦
(А + В)
(А-В)
{Ах В)
(А + В)
(А'В)
0
9
0
А -+ {А'В) : ': ':
В -> 9
Используем грамматику для вывода арифметического выражения (B+3) х D+5)).
Начнем с продукции
S-»(AxB).
Затем применим продукции
А -> (А + В)
В -» (Л + В),
чтобы получить
{(А + В) х {А + В)).
Продукции
Л->2 и В->3
дают
(B + 3)х(А
Наконец, применим продукции
Л-+4 и В->5,

744 ГЛАВА 17. Теория вычислений
чтобы вывести
(B + 3) х D + 5)).
Теперь применим грамматику для вывода арифметического выражения (C*2)
E + 7). Начнем с продукции
S^(A + B).
Затем применим продукции
А-*(А~В) и В^(А + В),
чтобы получить
Продукции
Л — 3 и В-+2
дают
(C*2)ч-(Л + В)).
Наконец, применяя продукции
А-+5 и В ->7,
выводим (
CЛ2) + E + 7)). D
ПРИМЕР 17.25. Аналогичным образом формируются арифметические выражения
в постфиксной форме. Пусть множество N = {5, А, В} и
Г = {+,-,х, //,0,1,2,3,4,5,6,7,8,9}.
Нам потребуются следующие продукции:
A->AB+ В^>АВ+ А->0
s —»
s->
5-*
AB-
ABx
AB+
A -» AB-
A-^ABx
A —> ЛВч-
B^AB-
B^ABx
В —> АВч-
^9
В-+АВ*
Рассмотрим выражение 32 + 47+ х. Поскольку все рассматриваемые целые числа
меньше, чем 10, то 32+ представляет собой символ целого числа 3, за которым
следует символ целого числа 2 и символ +. Для построения этого выражения
начнем с продукции
5 -> АВ х .
Затем воспользуемся продукциями
А^> А + В и В -* Л + Б,

РАЗДЕЛ 17.3. Грамматики 745
чтобы вывести
АВ + АВ + х .
Продукции
Л-+2 и В->3
дают
23 4- ЛБ 4- х .
Наконец, применияя продукцию
А->4 и Б -> 7,
выводим
3 4- 47 + х . ?
ПРИМЕР 17.26. Грамматику можно также использовать для вывода истинных
выражений. Такие выражения истинны в том смысле, что они грамматически
правильны, хотя даже лишены смысла. Предположим, что нужно построить грам-
грамматику, которая наряду с другими выводит следующие утверждения:
Джо преследует Фреда.
Большой пес прыгает через старый забор.
Том исчезал медленно за горизонт.
Перед началом фактического построения грамматики выберем ее структуру. В
каждом из рассматриваемых предложений имеется именная группа (им. гр.), гла-
глагольная группа (гл. гр.) и еще одна именная группа. Кроме того, два последних
предложения содержат предлог (предл.). Поэтому, пусть первой продукцией будет
S —> (им. гр.)(гл. гр.)(предл.)(им. гр.).
В нашем примере наиболее общей формой именной группы является прилагатель-
прилагательное (прил.), за которым следует существительное (сущ.). Следующим правилом
будет
(им. гр.) —> (прил.)(сущ.).
Наиболее общей глагольной формой является глагол (гл.), за которым следует
наречие (нар.). Поэтому пусть следующей продукцией будет
(гл. гр.)-+(нар.)(гл.).
Заранее известно, что финальное множество имеет вид Г = {Джо, преследует,
Фреда, большой, пес, прыгает, через, старый, забор, Том, исчезал, медленно, за,
горизонт}. Нетерминальное множество имеет вид N = {5, (им. гр.), (гл. гр.),
(прил.), (сущ.), (нар.), (гл.), (предл.)}.
Теперь понадобятся продукции, приписывающие значения для (прил.), (сущ.),
(нар.), и (гл.). В некоторых из приведенных предложений не нужны (прил.),
(предл.) и (нар.). Для решения этой задачи введем продукции
(прил.) —> А (нар.) —> А (предл.) —> А.

746 ГЛАВА 17. Теория вычислений
Поставив в соответствие этим символам пустое множество, мы можем вычерки-
вычеркивать их за ненадобностью. Оставшаяся часть продукций включает следующее:
(сущ.) —»Фред (сущ.) —> забор (наР-) —»медленно
(прил.) —>большой (сущ.) —>пес (гл.) —> преследует
(прил.) —> старый (сущ.) —>Том (гл.) —> прыгает
(сущ.) —>Джо (сущ.) —> горизонт (предл.) —>за
(гл.) —> исчезает (предл.) —> через
Для вывода предложения "Джо преследует Фреда" начнем с
5 —> (им. гр.)(гл. гр.)(предл.)(им. гр.),
чтобы вывести
(им. гр.)(гл. гр.)(предл.)(им. гр.).
Используя продукцию
(им. гр.) -> (прил.)(сущ.),
выводим
(прил.)(сущ.)(гл. гр.)(предл.)(им. гр.).
Применив
(прил.) -> А,
выводим
(сущ.)(гл. гр.)(предл.)(им. гр.).
Повторяя процесс для второй именной группы (им. гр.), выводим
(сущ.)(гл. гр.)(предл.)(сущ.).
Применив
(гл. гр.) -> (нар.)(гл.),
выводим
(сущ.)(нар.)(гл.)(предл.)(сущ.).
Применив
(предл.) -> А,
выводим
(сущ.) (гл.) (сущ.).
Воспользовавшись
(сущ.) —>Джо (сущ.) —>Фред (гл.) —>преследует,
выводим
Джо преследует Фреда.

РАЗДЕЛ 17.3. Грамматики 747
Выведем предложение: "Большой пес прыгает через старый забор". Как и в
предыдущем случае, начнем с продукции
5 —> (им. гр.)(гл. гр.)(предл.)(им. гр.),
чтобы вывести
(им. гр.)(гл. гр.)(предл.)(им. гр.).
Применив продукцию
(им. гр.) —> (прил.)(сущ.),
выводим
(прил.)(сущ.)(гл. гр.)(предл.)(им. гр.).
Используя
(прил.) —> большой (сущ.) —» пес ,
выводим
Большой пес (гл. гр.)(предл.)(им. гр.).
Применив
(гл. гр.) -> (нар.)(гл.),
выводим
Большой пес(нар.)(гл.)(предл.)(им. гр.).
Используя
(нар.) —» А (гл.) —> прыгает,
выводим
Большой пес прыгает(предл.)(им. гр.).
Применив
(предл.) —> через,
выводим
Большой пес прыгает через(им. гр.).
Используя продукцию
(им. гр.) —> (прил.)(сущ.),
получаем
Большой пес прыгает через(прил.)(сущ.).
Применив
(прил.) —> старый (сущ.) —>забор,
выводим
Большой пес прыгает через старый забор.
Вывод последнего предложения предоставляем читателю. ?
ОПРЕДЕЛЕНИЕ 17.27. На рис. 17.29 изображено соответствующее дерево
ДЛЯ ПРОДУКЦИИ Р —> W\W2Ws . . • Wn.

748 ГЛАВА 17. Теория вычислений
//К
"/W»". Рис. 17.29
Таким образом, соответствующим деревом для S —> А + В является дерево,
изображенное на рис. 17.30.
А
А + в Рис. 17.30
ОПРЕДЕЛЕНИЕ 17.28. Если соответствующие деревья продукций, использо-
использованных для вывода данного выражения, связны, то они формируют дерево с
корнем 5, называемое деревом грамматического разбора или деревом выво-
вывода. Листья дерева при чтении слева направо формируют выражение.
ПРИМЕР 17.29. В примере 17.23 продукции использовались для вывода 3-f 2-f 4.
Для построения дерева начнем с первой использованной продукции
add -> A -f В,
чтобы сформировать соответствующее дерево, изображеное на рис. 17.31.
Ж А
А + В А + В
Рис. 17.31 Рис. 17.32
Затем воспользуемся деревом, изображенным на рис. 17.32, которое соответ-
соответствует продукции
А^А + В,
чтобы сформировать дерево, изображенное на рис. 17.33.
Далее воспользуемся деревьями, соответствующими следующим продукциям
А->3, В->2, В ->4,
чтобы сформировать дерево грамматического разбора, изображенное на рис. 17.34.
А
4 А + В
А А + Л
А + В / \ 4
/\\ А + В
/1\ I I
А + В 3 2
Рис. 17.33 Рис. 17.34 П

РАЗДЕЛ 17.3. Грамматики 749
ПРИМЕР 17.30. В примере 17.25 для вывода выражения (B 4-3) х D4-5)) исполь-
использовались продукции
S-^(AxB), А-+(А + В), А->2, В-> 3,
В->(Л + В), А—4, В->5.
Поэтому дерево грамматического разбора — это дерево, изображенное на рис. 17.35.
(А+В) (А+В)
1111
2 3 4 5 рис. U.35 ?
ПРИМЕР 17.31. В примере 17.26 для вывода выражения "Большой пес прыгает
через старый забор" использовались продукции
5 —> (им. гр.)(гл. гр.)(предл.)(им. гр.) (им. гр.) —> (прил.)(сущ.)
(им. гр.) —> (прил.)(сущ.) (прил.) —^большой (сущ.) —>пес
(гл. гр.) —¦ (нар.)(гл.) (нар.) —> ^ (гл.) —>прыгает
(предл.)через
(прил.) -^старый (сущ.) -^забор
Соответствующее дерево грамматического разбора изображенно на рис. 17.36.
(им. гр.)
/ \
(прилаг.) (сущ.)
\ 1
Большой пес
(гл. гр.)
/
(нар.)
{
'Х
\
(гл.)
1
(предл.)
1
через
прыгает
(им. гр.)
/ \
(прилаг.) (сущ.)
i i
старый забор рпс. 17.36
Во всех грамматиках данного раздела продукции имели вид А —> W, где
А — нетерминальный символ. Следовательно, эти продукции можно использо-
использовать всюду, где возникает А> невзирая на его расположение в выражении. Такие
грамматики назывются контекстно-свободными грамматиками. Если грамма-
грамматика содержит продукцию вида аАЬ —> W\ где А — нетерминальный символ, и а
либо b не являются пустым словом, то эту продукцию можно использовать только
тогда, когда а находится слева от А, а 6 — справа. Поэтому такую продукцию
нельзя применять непосредственно к А, и, следовательно, грамматика зависит от
контекста, в котором находится А. Такая грамматика называется контекстно-
зависимой, или контекстной грамматикой. D

750 ГЛАВА 17. Теория вычислений
В приведенных ниже примерах рассматриваются контекстно-свободные грам-
грамматики, порождающие более абстрактные языки.
ПРИМЕР 17.32. Пусть Г = (N,T,S,P) — грамматика, определенная с помощью
N = {5, Д В}, Т = {а, 6} и множества продукций Р.
S->AB, Л->а, В->ВЪ, В->А.
Применив продукцию 5 —> АВ, выводим АВ. Далее с помощью продукций А —> а
и В —> А выводим а. Если теперь последовательно использовать продукции
S-+AB, А->а, Б —В6, В->А,
то получим аЪ. Можно породить также аббб, abbbb и abbbbb. Фактически, для
любых неотрицательных чисел п можно породить abn. Следовательно, язык, по-
порожденный грамматикой Г, задается выражением ab*. О
ПРИМЕР 17.33. Пусть Г' = (N,T,S,P) — грамматика, определенная с помощью
N = {5, А}, Т = {а, 6} и множества продукций Р.
S -> аАЬ, А -> аАЪ, А -> А.
Применив продукции 5 —> аЛ6 и А —> А, выводим аЬ. Применяя последовательно
продукции
5 —> аАЬ, А —> аЛ6, Л —» А,
получаем aabb, или а2Ь2. Воспользовавшись последовательно продукциями
, А —у аАЬ , А —> аЛЬ , Л —¦ аб,
выводим aaabbb, или а363. Легко показать, что язык, порожденный грамматикой
Г', — это {anbn : п — положительное целое число }. Отметим, что это не то же
самое, что а*6*, поскольку последнее может включать также am6n, где числа m
и и не обязательно равны. ?
ПРИМЕР 17.34. Пусть Г" = (iV, Г, 5, Р) — грамматика, определенная с помощью
N = {5, А, В}, Т = {а, 6} и множества продукций Р.
S-+ABABABA, А->Аа, А -» А, В-*Ь.
Можно показать, что язык, порожденный грамматикой Г", задается выражени-
выражением а*6а*6а*6а*. Это язык, состоящий из всех слов, содержащих в точности три
символа 6. ?
В примере 17.33 порожден язык {an6n : п — положительное целое число}.
Интуитивно понятно, что это не регулярный язык, поскольку единственный спо-
способ построения бесконечного регулярного языка на основе конечного алфавита
состоит в использовании звезды Клини *. В данном случае единственной возмож-
возможностью является а*6*, но, как отмечалось ранее, эта возможность не реализуема,
так как сюда включаются и слова am6n, где числа m и п не обязательно равны.
Возникает вопрос, существует ли такая грамматика, которая порождает толь-
только регулярные языки. Ответ положительный.

РАЗДЕЛ 17.3. Грамматики 751
ОПРЕДЕЛЕНИЕ 17.35. Контекстно-свободная грамматика Г = (N,T,S,P) на-
называется регулярной грамматикой, если каждая продукция р € Р имеет вид
п —¦ w, где строка w содержит не более одного нетерминального символа,
который встречается только в конце строки.
Следовательно, w может иметь вид aacA, ab или ЬА, где a, b и с — терми-
терминальные символы, а символ А — нетерминальный. Однако, строка w не может
иметь вид аАЬ, аАВ или Аа. Продукцию п —» абсЛ можно заменить продукцией
п->аВ, В -> 6С, С -> сА.
Возможно также, что строка ги не содержит ни одного терминального символа
и один нетерминальный, поэтому имеем В —> С, но если за этим следует С —*
?С, где t — терминальный символ, то можно скомбинировать две продукции и
получить В —> ?С. Поэтому нет необходимости вводить ограничение на то, чтобы
каждая продукция имела одну из следующих форм:
где А, В и С — нетерминальные символы, а символы а и 6 — терминальные.
Приведенная ниже теорема объединяет понятия регулярных грамматик, ре-
регулярных языков и автоматов. Теорема сформулирована без доказательства.
ТЕОРЕМА 17.36. Язык является регулярным тогда и только тогда, когда он по-
порожден регулярной грамматикой.
¦ УПРАЖНЕНИЯ
1. Воспользовавшись грамматикой из примера 17.32, постройте дерево грамма-
грамматического разбора для строки abbb.
2. Воспользовавшись грамматикой из примера 17.33, постройте дерево грамма-
грамматического разбора для строки aaabbb.
3. Воспользовавшись грамматикой из примера 17.34, постройте дерево грамма-
грамматического разбора для строки babaab.
4. Найдите язык, порожденный грамматикой Г = (ЛГ,Г,5, Р), определенной с
помощью N = {5, А, В}, Т = {а, Ь} и заданного множества продукций Р:
S->AB, А->аА, А -> А, В -> ?6, ?->А.
5. Найдите язык, порожденный грамматикой Г = (N,T,S,P), определенной с
помощью N = {5, Л, В}, Т = {а, 6} и заданного множества продукций Р:
S ->аВ, В -> ЬД А -> аВ, В -> Ь.
6. Найдите язык, порожденный грамматикой Г = (N, Т, 5, Р), определенной с
помощью N = {5, Л, Б}, Т = {а, Ь) и заданного множества продукций Р:
5 —> аД В —> аА, S —+ 6J3, А —> а?,
В -*ЪВ, А -> 6Д В -¦ Ь, А -> а.

752 ГЛАВА 17. Теория вычислений
7. Найдите язык, порожденный грамматикой Г = (N,T,S,P), определенной с
помощью N = {5, Л, Б}, Г = {а, 6} и заданного множества продукций Р:
S -> С, А -> аБ, С -> ЬС, Б -> 6Б,
С —> аЛ, Б —> аЛ, Л —* 6А, Б —* А.

ГЛАВА
ТЕОРИЯ КОДОВ
18.1. ВВЕДЕНИЕ
Когда речь идет о кодах, как правило, имеются в виду секретные коды. Боль-
Большинство читателей наверняка вспомнят, как в детстве придумывали свои коды,
непонятные взрослым. Проблема передачи информации, которая должна быть по-
понятна только тому, для кого она предназначена, весьма важна для военных целей,
для обеспечения конфиденциальности переписки и в других случаях, когда ин-
информация может попасть в руки посторонних лиц. Параллельно с разработкой
кодов идет работа по их взламыванию. Имеется в виду перехват и декодирование
сообщений упомянутыми выше посторонними лицами. Это серьезная задача для
военных и всех, кто заинтересован в защите целостности своих кодов и взламыва-
взламывании чужих. В наши дни взламывание кодов стало весьма популярным увлечением.
Существует своего рода состязание между теми, кто создает коды, и теми, кто их
взламывает. Одним из наиболее примечательных случаев взлома была разгадка
секретного кода Германии в период Второй мировой войны (см. [54], [55]). Раздел
теории кодов, посвященный этим вопросам, называется криптологией.
В данном разделе рассматриваются различные типы кодов. Как и в раз-
разделе 15.3, мы определим код как представление множества символов строками,
состоящими из единиц и нулей. Это множество символов обычно включает бук-
буквы алфавита, цифры и, как правило, определенные контрольные символы. Коды
представляются бинарными строками с целью использования их компьютерами
для хранения и передачи данных. Желательно, чтобы коды обладали некоторыми
свойствами. Мы увидим, однако, что некоторые из этих свойств несовместимы.
Наиболее важное свойство кода состоит в том, что когда сообщение кодируется
как двоичная строка, состоящая из конкатенации элементов кода, эта конкатена-
конкатенация однозначна. При декодировании сообщения не должно возникать проблем с
тем, какую букву представляет элемент кода. Такой код назовем однозначно деко-
декодируемым кодом (см. определение 17.8). Существует несколько способов достиже-
достижения этой цели. Один из них — кодирование всех символов двоичными строками
одной длины. Такой код называется блоковым. Например, если для кодирования
каждого символа используется 8 бит, то известно, что каждые восемь бит пред-

754 ГЛАВА 18. Теория кодов
ставляют один символ передаваемого сообщения. Блоковый код особенно полезен
при ограничении длины кода для каждого посланного символа или буквы. Дру-
Другим способом построения однозначно декодируемого кода является использование
префиксного кода, который рассматривался в разделе, посвященном взвешенным
деревьям. Согласно определению 17.10, код С является префиксным, если обла-
обладает тем свойством, что элемент кода не может быть начальной строкой другого
элемента кода. Таким образом, при чтении строки из единиц и нулей, изобра-
изображающей символ А, всегда известен момент завершения строки. Префиксный код
называют также мгновенным кодом.
Разновидностью префиксного кода является кома-код. При его использова-
использовании каждый символ кодируется строкой из единиц, в конце которой стоит нуль.
Значит, множество строк кода имеет вид {0,10,110,11110,111110,...}. Этот код
имеет явный недостаток: элементы кода могут быть очень длинными и занимать
большой объем памяти.
Часто необходимо сжимать данные, чтобы минимизировать объем памяти
для их хранения или время для передачи данных. Что касается минимизации
объема памяти, то наиболее эффективным является код Хаффмана. Кодирова-
Кодирование при помощи кода Хаффмана описано в разделе 15.3. Преимущество кода
Хаффмана состоит также в том, что это мгновенный код.
Хорошо известным примером кода, минимизирующего время передачи, яв-
является код Морзе. В кодах Хаффмана и Морзе буквы или символы, которые
встречаются наиболее часто, имеют более короткий код. В коде Морзе буквы
разделены "пробелами", а слова — тремя "пробелами". В данном случае "пробе-
"пробелы" — это единицы времени.
А
В
С
D
Е
F
G
Я
/
Код Морзе
J
К
L
М
N
О
Р
Q
R
S
Т
и
V
W
X
Y
Z
В процессе передачи данных могут возникать ошибки. Все, что может стать
причиной ошибок, называется неопределенным термином "шум". Например, дан-
данные, полученные от такого отдаленного космического корабля, как "Voyager" или
"Galileo", наверняка подвержены различного рода шумам. В некоторых случа-
случаях интерес представляет только определение наличия ошибки, что соответствует
ситуации передачи данных еще раз. Коды, обладающие свойством определения
наличия ошибок, называются кодами, обнаруживающими ошибки.
В другом случае, когда данные не могут быть переданы еще раз (например,
данные от удаленного космического корабля), требуется дополнительная инфор-

РАЗДЕЛ 18.1. Введение 755
мация о данных с целью не только обнаружения, но и исправления ошибки.
Коды, позволяющие исправлять ошибки, называются кодами, исправляющими
ошибки. Может показаться разумным всегда использовать коды с исправлени-
исправлением ошибок. Проблема использования кодов с исправлением ошибок и кодов с
обнаружением ошибок состоит в том, что они должны включать в себя дополни-
дополнительную информацию, поэтому они являются менее эффективными в отношении
минимизации объема памяти. К сожалению, использование кодов с исправлением
ошибок и кодов с обнаружением ошибок не дает абсолютной гарантии того, что
ошибка будет исправлена или обнаружена. Проблема заключается в возможности
многих ошибок. Несомненно, ошибку можно исправить или обнаружить, если она
одна. Все, что мы можем сделать, — это уменьшить вероятность того, что ошиб-
ошибки останутся необнаруженными и неисправленными. Но проблема, опять-таки, в
том, что чем в большей степени будет уменьшена эта вероятность, тем больше
информации потребуется переслать, и тем менее эффективным будет наш код.
Прежде чем начать изучение кодов с исправлением ошибок и кодов с обна-
обнаружением ошибок, необходимо ввести еще один тип кодов. Существует классиче-
классический пример, демонстрирующий применение такого кода. Предположим, имеется
вращающийся диск, разделенный на секторы, и серия щеток или лазерных лучей,
выделяющих информацию о скорости вращения диска. Если двоичные строки, за-
записывающие нумерацию соседних секторов, существенно различаются в отдель-
отдельных цифрах при переходе от одного сектора к следующему, тогда считывающее
устройство воспримет это так, чтобы измененный сектор мог выработать число,
совершенно отличное от числа, выработанного любым из секторов. В данном слу-
случае желательно пронумеровать секторы таким образом, чтобы двоичные строки,
определяющие соседние секторы, различались только одной цифрой. Код, обла-
обладающий таким свойством, называется кодом Грея. Его построению посвящен
раздел 6.7.
В качестве первого метода обнаружения ошибок рассмотрим бит контро-
контроля четности. Продемонстрируем этот метод на примере кода ASCII. ASCII-код
является блоковым кодом, который использует 7 битов, поэтому любой закоди-
закодированный символ изображается строкой из семи символов 1 и 0. Восьмой бит
добавляется таким образом, чтобы количество единиц было четным. Поэтому,
если код переданной строки получен с единственной ошибкой, то количество
единиц будет нечетным, и получатель информации поймет, что произошла ошиб-
ошибка. К сожалению, если произошло две ошибки, их нельзя будет обнаружить, по-
поскольку количество единиц опять будет четным. Предположим, что вероятность
ошибки при передаче равна 0.01 как для изменения 1 на 0, так и для изменения
0 на 1. Предположим далее, что вероятность ошибки не зависит от расположения
ошибки и от того, что является ошибкой: изменение 1 на 0 или наоборот. Предпо-
Предположим также, что появление одной ошибки не влияет на вероятность появления
другой.
Из биномиальной теоремы для вероятности (теорема 8.101) известно, что ве-
вероятность появления в точности одной ошибки равна (^)(.01)(.99O, что прибли-
приблизительно равно 0.07. Вероятность же появления в точности двух ошибок равна
B)(.01J(.99N, что приблизительно равно 0.002 и является существенно меньшей
величиной.

756 ГЛАВА 18. Теория кодов
код
00000000
10000001
10000010
00000011
10000100
00000101
00000110
10000111
10001000
00001001
00001010
10001011
00001100
10001101
10001110
00001111
10010000
00010001
00010010
10010011
00010100
10010101
10010110
00010111
00011000
10011001
10011010
10011011
10011100
00011101
00011110
10011111
символ
NUL
SOH
STX
ЕТХ
EOT
ENQ
АСК
BEL
BS
нт
LF
VT
FF
CR
SO
SI
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
Код ASCI
код
10100000
00100001
00100010
10100011
00100100
10100101
10100110
00100111
00101000
10101001
10101010
00101011
10101100
00101101
00101110
10101111
00110000
10110001
10110010
00110011
10110100
00110101
00110110
10110111
10111000
00111001
00111010
10111011
00111100
10111101
10111110
00111111
с битом
символ
SP
I
#
$
%
&
1
(
)
*
+
—
/
0
1
2
3
4
5
6
7
8
9
<
=
>
?
контроля четности
код
11000000
01000001
01000010
11000011
01000100
11000101
11000110
01000111
01001000
11001001
11001010
01001011
11001100
01001101
01001110
11001111
01010000
11010001
11010010
01010011
11010100
01010101
01010110
11010111
11011000
01011001
01011010
11011011
01011100
11011101
11011110
01011111
символ
@
А
в
с
D
Е
F
G
н
I
J
к
L
м
N
о
р
Q
R
S
т
и
V
W
X
Y
Z
[
\
код
01100000
11100001
11100010
01100011
11100100
01100101
01100110
11100111
11101000
01101001
01101010
11101011
01101100
11101101
11101110
01101111
11110000
01110001
01110010
11110011
01110100
11110101
11110110
01110111
01111000
11111001
11111010
01111011
11111100
01111101
01111110
11111111
символ
а
b
с
d
е
f
g
h
i
j
k
1
m
n
о
p
q
r
s
t
u
V
w
X
У
z
{
}
DEL
Поскольку З ошибки будут обнаружены, вероятность не обнаружить более
двух ошибок меньше, чем вероятность наличия четырех или более ошибок, по-
поскольку любое нечетное количество ошибок будет обнаружено. Эта вероятность
пренебрежимо мала по сравнению с вероятностью одной или менее ошибок.
Рассмотрим код, в котором для кодирования используется простое повто-
повторение кодируемой строки заданное число раз. Например, если при кодировании
каждую строку кода нужно повторить один раз, то 10110 будет закодировано как
1011010110. Если при кодировании каждую строку кода нужно повторить два-
дважды, то 10110 будет закодировано как 101101011010110. Если при кодировании
каждая строка повторена один раз, то в результате получаем код с обнаружением

РАЗДЕЛ 18.2. Порождающие матрицы 757
ошибок. Если произошла ошибка, то соответствующие позиции не будут совпа-
совпадать. Например, если закодированная строка имеет вид 111111010110111011, то
ошибки имеются в третьем и в последнем битах. Исправить ошибки мы не мо-
можем, поскольку не знаем, в какой из копий какая ошибка присутствует. Если
кодируемая строка повторяется дважды, то лучше всего выявить ошибку. Если
имеются три копии строки, то можно исправить код при наличии единственной
ошибки. Если имеется отличие в битах в соответствующих позициях строк, то
выбирается значение, которое встречается дважды. Например, если строка имеет
длину 4 и нам передано 110110011101, то во второй позиции мы два раза полу-
получим 1 и один раз 0. Таким образом, предполагаем, что правильное значение равно
1, и правильным вариантом закодированной строки является 1101. Конечно, если
ошибка появляется в одной и той же позиции строки более одного раза, возника-
возникает проблема. Если строка повторена так, что имеется п ее копий, то исправление
ошибки дает правильный результат, если при повторении ошибка встречается в
одной и той же позиции менее, чем [^J раз.
18.2. ПОРОЖДАЮЩИЕ МАТРИЦЫ
С этого момента мы будем предполагать, что все строки кода имеют фиксирован-
фиксированную длину п, и будем трактовать эти строки как векторы или A х п)-матрицы.
Следовательно, можно использовать сложение векторов. Мы, однако, определим
сложение по модулю 2, так что 1 + 1 = 0. Таким образом,
11110001 + 10100111 = 01010110.
Коды, представленные в данном разделе, называются линейными кодами. Они
известны также как групповые коды. Как уже упоминалось, строками кода С
будут двоичные строки длины п, которые мы будем рассматривать также как
векторы или A х п)-матрицы. Если Вп — множество всех двоичных строк дли-
длины п, то С — подмножество множества Вп. Предлагаем читателю доказать, что
множество Вп вместе с указанной выше операцией сложения образует группу
относительно сложения. Каждая строка из Вп совпадает со своим обратным эле-
элементом, так что в этом смысле сложение и вычитание — это одно и то же. Если в
некоторых ситуациях покажется, что следует вычитать, а не складывать, то нуж-
нужно помнить, что это не имеет значения. Код С называется линейным, если С —
подгруппа группы Вп. Если вспомнить линейную алгебру, то можно заметить, что
в действительности С — линейное векторное пространство, и многие из свойств
линейной алгебры могут оказаться здесь полезными. Однако, рассматривая код
С, мы будем использовать здесь только те свойства, что С является группой и что
элемент из С — вектор, поэтому может быть умножен на матрицу соответству-
соответствующего размера. Будет использован также закон дистрибутивности для матриц,
согласно которому
А(В + С) = АВ + АС
для любых матриц А, В и С, произведение которых определено. Читатель может
вспомнить, что если и = (tzi,n2,tx3,.. .,ип) и v = (vi,V2,v$,... ,г;п), то скалярное

758 ГЛАВА 18. Теория кодов
произведение векторов и и vy обозначаемое и • vy равно
ЩУ1 + u2v2 + U3V3 Н h ^n^n •
Весом строки кода с, обозначаемым wt{c), называется количество единиц в стро-
строке. Например, если с = 1011010, то wt(c) = 4.
Предположим, что имеется такая (Агхп)-матрица G, что ее первые к столбцов
и строк образуют единичную матрицу Ik размера (к х /с), все столбцы которой
различны. Таким образом, матрица G имеет вид [Д|АП_^]. Например,
10 0 10 1
0 10 110
0 0 10 11
является такой матрицей. Матрица G называется порождающей матрицей. Рас-
Рассмотрим строки порождающей матрицы как векторы или строки кода. Обозначим
это множество строк 5. Например, для матрицы, приведенной выше,
5 = {100101,010110,001011}.
Пусть С — код, образованный всеми векторами, которые являются конечными
суммами строк из 5. Предлагаем читателю доказать, что С — подгруппа Вп. В
нашем примере получаем 110011, складывая первые две строки из 5, поэтому
110011 будет принадлежать С. Говорят, что группа С порождена множеством 5.
Это 5 является также минимальным множеством, порождающим код С, посколь-
поскольку никакие элементы из 5 не являются суммами других элементов из 5. То, что
группа С порождена множеством 5, обозначим С = S*. Код С вида [ifc|An_fc]
(т.е. порожденный строками [Jfc|j4n_fc]) называется [п, /с]-кодом.
ТЕОРЕМА 18.1. [п, fcj-код С содержит 2к строк.
ДОКАЗАТЕЛЬСТВО. Первые к битов строки С определяют элементы С. Пози-
Позиции, в которых находятся единицы в первых к битах строки из С, показывают,
какие строки из 5 были просуммированы. Например, если единицы находятся в
первом и третьем битах строки из С, то эта строка получена в результате сложе-
сложения первой и третьей строк кода G. Поскольку существует 2к различных способов
сформировать первые к битов, то в коде С имеется 2к строк. ¦
Если необходимо передать строки сообщения длины /с, то мы кодируем их,
умножая справа на матрицу G. Таким образом, если w = wiw2w3 • • -wk или
(wi,w2,W3,... ,ги/с), то мы кодируем это строкой wG. В нашем примере закодиру-
закодируем ПО или A,1,0) как
A,1,0)
10 0 10 1
0 10 110
0 0 10 11
= A,1,0,0,1,1)
или 110011. Заметим, что строка сообщения совпадает с первыми тремя бита-
битами закодированной строки. В общем случае строка сообщения длины к будет

РАЗДЕЛ 18.2. Порождающие матрицы 759
совпадать с первыми к битами закодированной строки, поскольку единичная мат-
матрица /ь образующая первые к столбцов матрицы G, просто повторяет исходную
строку. Поэтому мы можем осуществлять декодирование, взяв первые к битов
закодированной строки. Заметим также, что выше, при умножении A,1,0) на G,
мы получили
A,1,0,0,1,1) = 1.A,0,0,1,0,1L-1 -@,1,0,1,1,0) +0-@,0,1,0,1,1),
так как для любого вектора v имеем 1 • v — v и 0 • v = @,0,0,0,0,0). Таким
образом, закодированная строка является суммой векторов из множества 5 и,
следовательно, принадлежит С, поскольку С — группа. В общем случае, ес-
если S = (si,S2?S3,...,Sfc) — множество строк порождающей матрицы и w =
(^1,^2,^3,... ,Wk) — код сообщения, то закодированная строка имеет вид
Она представляет собой сумму строк из 5, так как каждое Wi равно либо 1,
либо 0 и, следовательно, принадлежит С, поскольку С — группа, порожденная
множеством 5.
Отметим, что G имеет вид [ifc|An_fc] и что /*. передает сообщение. А что
делает Ап_а? Рассмотрим тот же пример. Если (wi,w2,ws) — строка сообщения,
то закодированная строка имеет вид
10 0 10 1
0 10 110
0 0 10 11
Таким образом, четвертый бит закодированной строки должен быть равен w\+W2,
пятый бит должен быть равен W2 + W3 и шестой бит должен быть равен w\ 4-ги3.
Следовательно, если закодированная строка имеет вид (wi,W2, г^з,^, ^5,^б), то
W4 — w\ 4- W2, уоъ = ^2 + ^з и we = w\ 4- w%. Если любая закодированная
строка после передачи не удовлетворяет этим соотношениям, то понятно, что при
передаче произошла ошибка. Например, если получена закодированная строка
101100, то, учитывая, что w\ = 1, W2 = 0 и ги3 = 1, должны иметь w4 = 1 =
1 4- 0, w5 = 0 = 04-1 и w6 = 0 = 14-1. Поскольку соотношение для w5 не
выполняется, становится понятным, что имеется ошибка. Таким образом, матрица
Ап-к служит для контроля точности передачи данных так же, как ранее это делал
бит контроля четности. В общем случае, если имеется закодированная строка
wn и
R =
0 0
0 10
0 0 1
0
0
0
L 0 0 0 0 1 Ak,k+i Ак,к+2
Ак,п .
то для г > к имеем Wi =
строка должна удовлетворять всем этим п — к соотношениям.
з,; 4 ЬWkAk,i, и закодированная

760 ГЛАВА 18. Теория кодов
Следующая проблема — исправление ошибки, если известно, что произо-
произошла единственная ошибка. Изложенный ниже метод известен как использование
лидеров смежных классов. Метод будет проиллюстрирован нашим примером, в
котором
0 0 10 1
R= 0 10 110
0 0 10 11
Известно, что
S = {100101,010110,001011},
так что
С = {000000,100101,010110,001011,110011,011101,101110,111000}.
Теперь, как это описано в разделе 9.4, сформируем для С смежные классы в Вп.
Первым смежным классом является сам С. Для формирования следующего смеж-
смежного класса выберем элемент из Вп, который имеет минимальный вес и не при-
принадлежит С. Например, можно выбрать Ь\ — 100000. Смежный класс
Ъх + С = {100000,000101,110110,101011,010011,111101,001110,011000}.
Опять выбираем элемент из Впу который имеет минимальный вес и не принад-
принадлежит ни одному из предыдущих смежных классов. Например, можно выбрать
Ь2 = 010000. Смежный класс
Ь2 + С = {010000,110101,000110,011011,100011,001101,111110,101000} .
Продолжая этот процесс, получаем следующую таблицу для ВП1 разделенного на
смежные классы, где элемент с минимальным весом выписан первым. Элементы
первого столбца называются лидерами смежных классов.
000000
100000
010000
001000
000100
000010
000001
100010
100101
000101
110101
101101
100001
100111
100100
000111
010110
110110
000110
011110
010010
010100
010111
110100
001011
101011
011011
000011
001111
001001
001010
101001
110011
010011
100011
111011
110111
110001
110010
010001
011101
111101
001101
010101
011001
011111
011100
111111
101110
001110
111110
100110
101010
101100
101111
001100
111000
011000
101000
110000
111100
111010
111001
011010
В последнем смежном классе необходимо использовать строки веса 2. Можно
выбрать одну из строк 100010, 010001 или 001100. Откровенно говоря, нам повез-
повезло, что мы нашли хотя бы одну. Процесс работает следующим образом. Получив
закодированную строку, ищем ее в таблице. Предположим, например, что полу-
получена строка 110110. Смотрим на первый столбец строки, содержащей 110110, и
получаем 100000, поэтому предполагаем, что ошибка возникла в первом бите,

РАЗДЕЛ 18.2. Порождающие матрицы 761
поскольку 100000 была добавлена каждому элементу С при построении этого
смежного класса. Смотрим на первую строку столбца, содержащего 110110, и
получаем 010110, что, по нашему предположению, является правильной строкой
кода С Теперь предположим, что получена строка 001010. Смотрим на первый
столбец строки, содержащей 001010, и получаем 000001, поэтому предполагаем,
что ошибка возникла в шестом бите. Смотрим на первую строку столбца, со-
содержащего 001010, и находим 001011, что, по нашему предположению, является
правильной строкой кода С.
Теперь поищем более простой способ обнаружения ошибок. Пусть v и w —
векторы (или строки) длины п. Вектор v называется ортогональным вектору w,
если их скалярное произведение v • w = 0. Пусть задан код С. Двойственным
кодом к коду С, обозначаемым С-1, называется множество всех строк из Бп, ор-
ортогональных каждой строке из кода С. Предоставляем читателю доказать, что Сх
— подгруппа группы Вп. Если код С является [п, А:]-кодом, так что он порожден
к строками, то CL порожден п — к строками. Поскольку доказательство этого
утверждения требует знания линейной алгебры, то доказывать его не будем, а
просто примем на веру. Следующую теорему, однако, мы докажем.
ТЕОРЕМА 18.2. Пусть С — групповой код, а С1- — двойственный ему код. Строка
t принадлежит коду С1- тогда и только тогда, когда она ортогональна каждой
строке из 5, множества порождающих элементов кода С.
ДОКАЗАТЕЛЬСТВО. Очевидно, что если строка t принадлежит коду С-1, то она
ортогональна каждой строке из множества 5, поскольку она ортогональна каждой
строке из кода С и S С С. Предположим, что 5 = {s\,s2,S3, * • * Sk^y и стРока *
ортогональна строке Si для всех S{ Е 5, так что tmsi =0 для всех S* Е 5. Каждый
элемент из С имеет вид
w2s2 4-
где каждое w\ равно 1 или 0. Согласно свойству линейности матриц имеем
t • (wisi -f w2s2 + ... 4- WkSk) = wi(t • si) 4- w2(t • s2) 4-... 4- Wk(t • sk) =
= 04-04-04-...4-0 =
= 0.
Вспомним, что в рассматриваемом примере
G =
Определим теперь
10 0 10 1
0 10 110
0 0 10 11
110 10 0
0 110 10
10 10 0 1

762 ГЛАВА 18. Теория кодов
где А\ — транспозиция матрицы Аз, полученная заменой строк матрицы As на
столбцы. Матрица G-1 называется матрицей контроля четности.
Перебирая все возможные варианты, можно показать, что скалярное произ-
произведение любой строки из G с любой строкой из G1- равно 0. Отсюда получаем,
что
G^l = 0,
где г\ — транспозиция г-ой строки матрицы G. По определению транспозиции т\
является г-ой строкой матрицы G, преобразованной в столбец. Мы превращаем
строку в столбец, чтобы на него можно было умножить матрицу G1:
w2r\
w2G±
rt2 4-
=0+0+0=
= 0.
Таким образом, если умножить матрицу
из С, то получим 0.
В общем случае, если
на транспозицию любого элемента
= [Ik\An.k} =
1 0 0 ••• 0
0 1 0 ••• 0
0 0 1'-.:
:::*-. 0
0000 1
то
= [А*п_к\1п-к] =
4fc,fc+l
Ak,k+2
Ак,к+з
0
1
о
о
0 0 1
0 0 0 0
Скалярное произведение г-ой строки матрицы G на j-ю строку матрицы
0 4- 0 4-... 0 + Aij -f 0 + ... 0 4- Aij + ...4-04-0 = 0,
равно
так что в общем случае
Gxrl = 0,
где г\ — транспозиция г-ой строки матрицы R. Если умножить матрицу Gx на
транспозицию любого элемента из С, то, используя те же самые рассуждения,
имеем в результате 0. Мы также получаем еще один замечательный результат.
Если два элемента &i и Ь2 из Вп принадлежат одному и тому же смежному классу,
образованному вВпс использованием группы С, как это было сделано выше, то
G±b\ = G±bt2 .

РАЗДЕЛ 18.2. Порождающие матрицы 763
Для доказательства воспользуемся тем фактом, что если Ьг и Ь2 принадлежат
одному смежному классу, то Ь\ = Ь2 4- с для некоторого с € С. Следовательно,
Ь\ = Ьь2 + с1 и
GLb\ = G±(bt2+ct) =
= G4\ + G±ct =
= G±bt2+0 =
= G b2 ,
т.к.
c1 = 0
для всех с е С.
Поскольку G±bt одно и то же для всех b из класса смежности, то можно
выбрать любое b из класса смежности и определить это значение. Таким обра-
образом, в каждую строку приведенной выше таблицы можно добавить это общее
значение образа С?-1, т.к. элементы каждой строки определяют класс смежности.
Мы выбираем лидера смежного класса, потому что он простейший, и помещаем
значение его образа во второй столбец. Эти значения называются синдромами.
" 0 ~
Уже известно, что первый синдром есть
О
О
Находим, что
поэтому
поэтому
1
1
О
110 10 0
0 110 10
10 10 0 1
— второй синдром, и
110 10 0
0 110 10
10 10 0 1
— третий синдром.
1
0
0
0
0
0
1
0
1
" 0
1
о
о
о
о
1
1
о
Продолжая процесс, получаем следующую таблицу.

764 ГЛАВА 18. Теория кодов
000000
100000
010000
001000
000100
000010
000001
100010
0
0
0
1
0
1
1
1
0
0
1
1
1
0
0
0
1
0
0
0
1
1
1
1
100101
000101
110101
101101
100001
100111
100100
000111
010110
110110
000110
011110
010010
010100
010111
110100
001011
101011
011011
000011
001111
001001
001010
101001
110011
010011
100011
111011
110111
110001
110010
010001
011101
111101
001101
010101
011001
011111
011100
111111
101110
001110
111110
100110
101010
101100
101111
001100
111000
011000
101000
110000
111100
111010
111001
011010
¦ 1"
0
1
1
0
0
" 0 "
1
0
Заполнив таблицу, предположим, что получена переданная строка 101100.
Умножение матрицы G-1 на транспозицию строки дает
110 10 0
0 110 10
10 10 0 1
Отсюда следует, что 101100 находится в строке 6. Лидер смежного класса —
000010, элемент крайнего левого столбца строки, содержащей 101100. Элемент С,
расположенный в верхней строке столбца, содержащего 101100, равен 101110.
Согласно способу построения таблицы имеем 101100 = 101110 + 000010, поэтому
можем предположить, что переданная строка 101100 должна иметь вид 101110, и
в пятом бите была ошибка.
Этот метод намного быстрее, поскольку требует только умножить матри-
матрицу G1- на транспозицию строки-сообщения, найти строку, содержащую синдром,

РАЗДЕЛ 18.2. Порождающие матрицы 765
и найти переданное сообщение. Лидер для этого сообщения — индикатор ошиб-
ошибки, а элемент кода С, расположенный в первой строке столбца, содержащего
переданное сообщение, есть исправленное сообщение.
Заметим, однако, что процесс можно сделать еще быстрее. При этом потре-
потребуются только два первых столбца приведенной выше таблицы. Предположим,
что получено сообщение 110000. Умножение матрицы G-1 на его транспозицию
дает
1
0
1
1
1
0
0
1
1
1
0
0
0
1
0
0
0
1
¦ 1 "
1
0
0
0
0
" 0 "
1
1
поэтому синдром —
о
1
1
, а лидер смежного класса — 001000. Поскольку лидер
указывает, что ошибка появилась в третьем бите, то, добавляя 001000 к 110000,
получаем 111000, исправленный код. Таким образом, этот метод прост. Умно-
Умножить транспозицию сообщения на матрицу G±, чтобы найти синдром. Для этого
нужно найти лидера смежного класса и прибавить его к сообщению, чтобы полу-
получить исправленный код. Обратите внимание, что используются только первые два
столбца таблицы. Однако, теперь возникла еще одна проблема. Если полученным
1 "
сообщением будет строка 101001, то синдром будет
и в соответствующей
строке будет три элемента с весом 2. Вспомним, что строка 100010 была выбра-
выбрана произвольно. Любая из таких строк равновероятно может содержать ошибку,
поэтому в данном случае совершенно безнадежно использовать синдромы для ис-
исправления ошибки. Кроме того, мы пытаемся в данном случае исправить строку
с двумя ошибками вместо одной.
УПРАЖНЕНИЯ
1. Какие из приведенных ниже матриц в действительности являются порожда-
порождающими? Если нет, то почему?
а)
10 0 111
0 0 10 11
0 10 110
10 0 111
в) 0 10 10 1
0 0 1110
2. Для заданной порождающей матрицы
б)
г)
10 0 110
0 10 0 11
0 0 1110
10 0 10 1
0 10 0 0 1
0 0 110 0
10 0 111
0 10 0 11
0 0 1110

766 ГЛАВА 18. Теория кодов
а) найдите GL\
б) закодируйте 111,011,101,110;
в) декодируйте 111011,110100,010010,011110;
г) используя С?-1, определите, какие из строк пункта (с) являются правиль-
правильными кодированными строками.
3. Для заданной порождающей матрицы
10 0 0 111
0 10 0 110
0 0 10 10 0
_ 0 0 0 1 0 1 1
а) найдите G±\
б) закодируйте 1111,0101,1001,1010;
в) декодируйте 1111110,0111010,0111101,1011110;
г) используя G±, определите, какие строки из пункта (с) являются пра-
правильными закодированными строками.
4. Для заданной порождающей матрицы
Г 1 0 0 0 0 1 1
0 10 0 10 1
0 0 10 110
_ 0 0 0 1 1 О О
а) найдите GL\
б) постройте таблицу смежных классов вместе с лидерами;
в) используйте эту таблицу для исправления ошибок (если они имеются) в
переданных строках 1111100, 1111000, 0110101 и 1011000.
5. Для заданной порождающей матрицы
10 0 10 1
0 10 0 11
1 0 0 1 1 1 1
а) найдите G1-;
б) найдите синдромы для смежных классов;
в) используйте эти синдромы для исправления ошибок (если они имеются)
в переданных строках 111101, 111001, 110010, 101001.
6. Для заданной порождающей матрицы
10 0 110
0 10 0 11
0 0 10 11
а) найдите G-1;

РАЗДЕЛ 18.3. Коды Хемминга 767
б) найдите синдромы для смежных классов;
в) используйте эти синдромы для исправления ошибок (если они имеются)
в переданных строках 111101, 111001, 110101, 101001.
7. Для заданной порождающей матрицы
Г 1 0 0 0 0 1 1
0 10 0 10 1
0 0 10 110
_ 0 0 0 1 0 0 1
а) найдите G1-;
б) постройте таблицу смежных классов вместе с лидерами;
в) используйте эту таблицу для исправления ошибок (если они имеются) в
переданных строках 1110011, 1111000, 1101001, 1011101.
8. Объясните, что случится при использовании порождающей матрицы в упраж-
упражнении 7, если будут две или более ошибок.
9. Используя порождающую матрицу из упражнения 5, найдите другие строки,
отличные от строк матрицы GL, которые принадлежат CL, и, используя эти
строки, постройте матрицу контроля четности.
10. Используя порождающую матрицу из упражнения 4, найдите другие строки,
отличные от строк матрицы G^, которые принадлежат С-1, и, используя эти
строки, постройте матрицу контроля четности.
И. Докажите, что Вп, множество всех двоичных строк длины п, — группа
относительно сложения, введенного в этой главе.
12. Пусть С — код, образованный с помощью всех векторов, которые являются
конечными суммами строк из S. Докажите, что С — подгруппа Вп относи-
относительно сложения.
13. Докажите, что двойственный код для кода С, обозначаемый CLy является
подгруппой группы Вп относительно сложения.
18.3. КОДЫ ХЕММИНГА
В конце предыдущего раздела было показано, что существовали определенные
трудности при попытке исправить код для некоторых строк, поскольку все ли-
лидеры имели вес 1. Эти трудности устраняются путем использования матрицы,
называемой матрицей Хемминга, в качестве порождающей матрицы. Перед тем
как перейти к рассмотрению матрицы Хемминга G#, посмотрим на матрицу кон-
контроля четности Gjj. Пусть Gjj — матрица, в которой г таких строк, что столбцы
состоят из всевозможных строк длины г, за исключением строки, состоящей толь-
только из нулей. Предположим, что г > 3. Существует 2Г — 1 таких строк, поэтому
Gjj есть (г х п)-матрица, где п = 2Г - 1. Будем использовать столбцы с весом
1 как последние г столбцов, формирующих единичную матрицу, так что матрица
Gj^ имеет вид [Л*|/г], где А1 — (г х (п — г))-матрица. Матрица Хемминга

768 ГЛАВА 18. Теория кодов
— это ((п — г) х п)-матрица вида [Jn_r|j4], где А — ((п — г) х г)-матрица. Код,
образованный строками матрицы Хемминга, называется кодом Хемминга.
Например, пусть г = 3 и Gfj — матрица
110 110 0
0 1110 10
1 0 1 1 0 0 1
Тогда Gh — матрица
10 0 0 10 1
0 10 0 110
0 0 10 0 11
0 0 0 1111
Для изучения матриц Хемминга необходимо понятие расстояния и его связь с
весом каждой из строк. Начнем с теоремы о весах строк.
ТЕОРЕМА 18.3. Для строк end вес wt(c + d) < wt(c) 4- wt(d).
ДОКАЗАТЕЛЬСТВО. Пусть с = cic2c3 ... сп и с' = с[с^с'3 ... с'п. Если с{ + с[ = 1,
то либо Ci = 1, либо с'{ = 1. Поэтому существованию каждой единицы в с + с'
соответствует существование единицы либо в с, либо в d. Ш
Расстояние Хемминга, или просто расстояние между двумя строками ко-
кода с и с', имеющими одинаковую длину, — это число соответствующих битов в
строке, где одна строка имеет цифру 1, а другая имеет цифру 0. Будем обозначать
функцию расстояния через 5(c,d). Например, если с = 101011 и с1 = 110010, то
8(с,с') = 3, так как две строки отличаются во второй, третьей и шестой позициях.
Очевидно, что чем больше расстояние между двумя строками кода, тем больше
ошибок можно обнаружить. Поскольку S названа функцией расстояния, мы долж-
должны показать, что она обладает основными свойствами функции расстояния.
ТЕОРЕМА 18.4. Функция расстояния Хемминга имеет следующие свойства:
а) для строк си d расстояние 5{с,с') = 0 тогда и только тогда, когда с = с'\
б) для строк сие' расстояние 5(с,с') = S(cf\c)\
в) для строк с, с' и с" выполняется соотношение 5(с, с") < 6(с,с') +5(с',с").
ДОКАЗАТЕЛЬСТВО. Пункты (а) и (б) следуют непосредственно из определения,
и их доказательство оставляем читателю. Для доказательства части (в) заметим,
что для строк с и с" вес wt(c-f с") = J(c, с"), а также, что если с = с\С2С$ ... сп и
с" = с'/с'з'сз ... с^, то Ci 4- с" вносит 1 в вес wt(c + с") тогда и только тогда, когда
а = 0 и с" — 1 или Ci — 1 и с" = 0. Но это верно в том и только том случае, если
Ci и с" различны, что вносит 1 в 5(с,с"). Заметим также, что для любой строки с'
строка с1 4- с' состоит только из нулей. Назовем такую строку О. По определению
сложения 0 4-е = с для каждой строки с. Следовательно,
с, с") = wt(c 4- с") = гу*(с 4- О 4- с") = w?(c 4- d 4- с' 4- с") <
< wt(c 4- с') 4- wt(d + с") = 5(с, с') 4- <
с', с").

РАЗДЕЛ 18.3. Коды Хемминга 769
Важно знать минимальное расстояние между двумя строками кода. Если
С — код, то минимальное расстояние кода С, обозначаемое D(C), равно наи-
наименьшему расстоянию между двумя строками из С. В приведенной ниже теореме
сформулирован важный критерий для определения числа ошибок, которые могут
быть исправлены или обнаружены с использованием кода.
ТЕОРЕМА 18.5. Для кода С,
а) если D(C) = к + 1, то использование кода позволяет обнаружить вплоть до
к ошибок;
б) если D{C) = 2к + 1, то использование кода позволяет исправить вплоть до
к ошибок.
ДОКАЗАТЕЛЬСТВО, (а) Если D{C) = fc + 1, то для данной строки се С. Отсюда
следует, что с отличается от любой другой строки кода по крайней мере в к + 1
позициях. Поэтому, если переданная строка с имеет к или менее ошибок, то она
не может быть другой строкой кода, и ошибка определена.
(б) Если строка с передана как с' о, к или менее ошибками, то для любой
строки с е С имеем 6(с,с') < к. Если для некоторой строки с" из С расстояние
5(с',с") < fc, то 6(с,с') + 6(с',с") < 2fc. Но 5(с',с") < 6(c,d)+ 6(c',c") и 5(с,с") >
2к 4- 1, что приводит к противоречию. Следовательно, с' можно исправить на с,
единственную строку, расстояние которой от d меньше, чем к + 1. ¦
Возникает проблема определения D(C)y наименьшего расстояния между лю-
любыми двумя строками из кода С. Для решения задачи нам сначала потребуется
следующая теорема.
ТЕОРЕМА 18.6. Минимальное расстояние D{C) кода С равно W{C) = min{it;?(c) :
се С и
ДОКАЗАТЕЛЬСТВО. По определению D(C), существует w,w' E С такое, что
8{w,w') = D(C). Но 6(c,d') = wt(c + d') и, поскольку с + с" е С, то W{C) <
wt(c + c"). Следовательно, W(C) < D(C). Обратно, для с е С имеем wt(c) =
wt(c+O) = 5(c,0) > D(C). Следовательно, W[C) > D[C). Отсюда W(C) = D{C).
Покажем, что для кода Хемминга С выполняется соотношение W(C) > 3.
Прежде всего, не существует с е С с весом 1. Если бы такая строка с существо-
существовала, то она содержала бы нули во всех позициях, за исключением позиции j, в
которой стояла бы единица; в силу ортогональности строки с к каждой строке
матрицы Gjj имели бы, что j-ый столбец матрицы Gjj содержит только 0, что
противоречит построению матрицы Gjj. He существует также с е С с весом 2.
Если бы такие с е С существовали, то с была бы строкой, состоящей только из
нулей, за исключением двух единиц, например, в позициях i и j. Из ортогональ-
ортогональности строки с к каждой строке матрицы Gjj следует, что г-ый и j-ый столбцы
каждой строки матрицы Gjj должны быть одновременно 1 или 0. Но тогда г-ый
и j-ый столбцы матрицы Gjj должны совпадать, что опять же противоречит по-
построению матрицы Gjj. Следовательно, W(C) > 3, и код С можно использовать
для исправления единственной ошибки.

770 ГЛАВА 18. Теория кодов
Теперь необходимо показать, что в каждом смежном классе, за исключе-
исключением самого С, имеется один элемент с весом 1. Доказательство этого факта
значительно упростит проблему декодирования. По теореме 18.1, [п, /с]-код С со-
содержит 2к строк. Поскольку Gh имеет вид [/П_Г|А], то код Хемминга С является
[п, и—г]-кодом, поэтому код С содержит 2п~г элементов. Множество Вп содержит
2П элементов. Следовательно, существует
On —1
= 2Г
смежных классов, включая С. Строка из С имеет длину Т - 1. Поэтому суще-
существует 2Г —1 строк с весом 1. Теперь нужно показать, что никакой смежный класс
не содержит две строки с весом 1. Предположим, что строки s и s' принадлежат
одному смежному классу, и каждая из них имеет вес 1. Тогда, согласно опреде-
определению смежного класса, s = s' + с для некоторой строки с е С. Следовательно,
с = s + s\ поэтому, по теореме 18.3,
wt(c) < wt(s) + wt(s') < 1 + 1 = 2.
Но wt(c) > 3, что противоречит полученному. Поэтому каждый смежный класс
содержит ровно одну строку с весом 1, за исключением С, который содержит
строку с весом 0.
Вернемся к нашему примеру, в котором матрица Gjj имеет вид
110 110 0
0 1110 10
1 0 1 1 0 0 1
а матрица
имеет вид
Г 1 0 0 0 1 0 1
0 10 0 110
0 0 10 0 11
0 0 0 1111
Учитывая, что каждый смежный класс содержит лидера с весом 1, рассмотрим
строку 0010000. Если умножить ее на матрицу Gjj, получим
110 110 0
0 1110 10
10 110 0 1
0
0
1
0
0
0
0
=
' 0 "
1
1
поэтому синдром равен
0
1
1
, что совпадает с третьим столбцом матрицы Gjj.
По сути, если 1 встречается в j-ой позиции строки с весом 1, то синдром по-
после умножения матрицы Gjj на транспозицию строки становится j-ым столбцом

РАЗДЕЛ 18.3. Коды Хемминга 771
матрицы Gjj. Поэтому всякий раз, когда мы получаем правильную строку пе-
переданного сообщения, умножаем на ее транспозицию матрицу G#, то получаем
синдром со всеми нулями. Если имеется единственная ошибка, то мы получим
один из столбцов матрицы Gjj, поскольку строка переданного сообщения должна
быть в одном из смежных классов, поэтому существует лидер смежного класса
с весом 1. Следовательно, если г-ый столбец матрицы Gjj является синдромом,
это говорит о том, что лидер смежного класса имеет 1 в г-ом столбце, поэтому
ошибка имеется в г-ом столбце или в г-ом бите строки. Например, предположим,
получена строка 1110110 переданного сообщения. Умножение матрицы Gjj на
транспозицию этой строки дает
110 110 0
0 1110 10
10 110 0 1
¦ 1 ¦
1
1
0
1
1
0
=
¦ 1"
1
0
что совпадает со второй строкой матрицы Gjj. Следовательно, ошибка во втором
бите, и переданным сообщением должна быть строка 1010110.
Оставшуюся часть этого раздела посвятим небольшому обзору других кодов.
Первый из них — код Голе. Коды Хемминга были открыты независимо Хеммингом
в 1950 г. и Голе в 1949 г. Не будем пытаться объяснить, почему они названы
именно кодами Хемминга. Это длинная и запутанная история, о которой подробно
можно прочитать у Томпсона [112]. Тем не менее, существует и код Голе. Он был
описан в работе Голе в 1949 г. Речь идет о разработанной им модели B3,12, 7), где
цифры означают, что используется порождающая матрица размерности B3,12)
с минимальным расстоянием 7 между строками кода С. Этот код Голе имеет
порождающую матрицу G = [1ц\А], где
А =
100111000111
101011011001
101101101010
101110110100
110011101100
110101110001
110110011010
111001010110
111010100011
111000001101
0 11111111111
Эта матрица имеет геометрическую интерпретацию с использованием пяти пря-
прямых в плоскости (см. [112]). Код легче изучить, используя расширенную поро-

772 ГЛАВА 18. Теория кодов
ждающую матрицу G = [1п\А] с параметрами B4,12,8), где
0 11111111111
111011100010
110111000101
101110001011
111100010110
111000101101
110001011011
100010110111
100101101110
101011011100
110110111000
101101110001
(см. [44]). Матрица получена путем перестановок в порождающей матрице Голе
и добавления бита четности. Симметричность матрицы упрощает ее изучение.
Легко видеть, что GL = [-A|/i2], поскольку А = А1. Голе ввел еще несколько
кодов, среди которых D096,244,8)-код, использованный космическим кораблем
"Voyager" для передачи изображений планет Юпитер, Уран и Нептун.
Для заданной строки s длины п положим s = s-hl, где 1 — строка длины п,
состоящая только из единиц. Для заданной строки 5 положим
Plot(S) = {ss : s e S} U {ss : s G 5}.
Для заданного множества
S = {0000, ООП, 1100,1111}
положим: Si = Plot(S), S2 = Plot(Si), 53 = Plot(S2) и 5n = Plot(Sn-i). Кон-
Конструкция Plot названа в честь разработавшего ее М. Плоткина (см. [88]). Коды,
порождаемые множествами Si, S2, S3, ..., называются кодами Рида-Мюллера.
Множество S3 — это F4,32,16)-код, который использовался для исправления
ошибок на изображении, переданном космическим кораблем "Mariner 9". В част-
частности, матрицу Рида-Мюллера часто называют матрицей Адамара, определение
которой будет дано ниже.
Рассмотрим матрицы, определенные рекурсивно следующим образом:
А2п =
= [0];
А А
А А
где матрица Ап определена соотношением
тельно,
Ai =
для 1 < г, j < п. Следова-

СледоваРАЗДЕЛ 18.3. Коды Хемминга 773
А4 =
0 0 0 0
0 10 1
0 0 11
0 110
Пусть Нп обозначает матрицу, полученную из матрицы Ап заменой 0 на 1, а 1
на -1, для каждого элемента Aij для 1 < г, j < п. Таким образом,
Н2 =
1 1
1 -1
Матрица Нп обладает свойством: НпН^ — nl, где I — единичная матрица. Мат-
Матрицы, обладающие таким свойством, называются матрицами Адамара. Поро-
Порождаемый ими код называется кодом Адамара.
¦ УПРАЖНЕНИЯ
1. Пусть Gjj — матрица
10 1110 0
1110 0 10
1 1 0 1 0 0 1
Найдите
2. Пусть Gjj — матрица
0 1110 0
0 1110 10
u 1 1 0 1 0 0 1
Найдите матрицу Gh-
3. Найдите расстояние между строками 110010101 и 010101111.
4. Найдите расстояние между строками 110011001 и 111100001.
5. Найдите три строки, ортогональные к строке 110011001.
6. Найдите три строки, ортогональные к строке 010101111.
7. Для заданной порождающей матрицы
Г 1 0 0 0 1 1 1
0 10 0 0 11
0 0 10 110
_ 0 0 0 1 1 0 1
а) найдите матрицу Gjj\
б) используя только матрицу Gjj, исправьте ошибки (если они имеются) в
переданных сообщениях 1110110, 1011000, 1101100 и 1111110.
8. Для заданной порождающей матрицы
10 0 0
0 10 0
0 0 10
0 0 0 1
1
0
1
1
1
1
1
0
1
1
0
1

774 ГЛАВА 18. Теория кодов
а) найдите матрицу
б) используя только матрицу Gjj, исправьте ошибки (если они имеются) в
переданных сообщениях 1111110, 1011001, 1101100 и 1111101.
9. Для каждой матрицы Хемминга из упражнений 7 и 8, если строка 1001110
передана как 1011010, то каков исправленный код? Как это повлияло на
исходное закодированное слово?
10. Какие из приведенных ниже матриц являются матрицами Хемминга?
10 0 0 111
0 10 0 0 11
0 0 10 110
10 0 0 111
0 10 0 0 11
0 0 10 111
0 0 0 110 1
10001111
0 10 0 0 11
0 0 10 110
0 0 0 10 0 0
11. Докажите теорему 18.4: Функция расстояния Хемминга обладает следую-
следующими свойствами:
а) для строк с и с' расстояние 5(с, с') = 0 тогда и только тогда, когда с = с'\
б) для строк сие' расстояние 5(с,с') = 5(с',с).
12. Постройте код Рида-Мюллера, Si.
13. Постройте матрицы Адамара Я2, Я4, Я8 и #i6.

ГЛАВА
ПЕРЕЧИСЛЕНИЕ ЦВЕТОВ
19.1. ТЕОРЕМА БЕРНСАЙДА
Вначале рассмотрим количество способов раскраски вершин правильного гг-уголь-
ника с помощью т цветов. Поскольку случай т = 1 не представляет интереса,
начнем с двух цветов, например, красного (/?) и синего (В). Сначала рассмотрим
квадрат, т.е. будем раскрашивать двумя цветами вершины квадрата. Назовем рас-
раскрашивание вершин просто раскраской. Таким образом, если выкрасить верхнюю
левую вершину красным цветом, а все остальные —- синим, то это будет примером
раскраски. Если не допускать движений квадрата, то имеем два способа выбора
для каждой из вершин, поэтому существует 24 = 16 способов раскрасить квад-
квадрат. Чтобы усложнить задачу, разрешим вращение квадрата и поворот вокруг
осей, проходящих через противоположные вершины или середины противолежа-
противолежащих сторон. Первый класс движений назовем вращениями, а второй класс —
отражениями. Все раскраски, которые можно получить из данной раскраски
вершин квадрата путем вращения и отражения, будем считать эквивалентными.
Таким образом, все раскраски, изображенные на рис. 19.1, эквивалентны, посколь-
поскольку каждая может быть получена из другой вращением.
R
В В
R В
В
В
В
с,
» 4
I {
с2
| <
с,
с4
В В В В В R R В рис \91
Это также справедливо для раскрасок, изображенных на рис. 19.2.
В R R В R R R R
с5
с6
) i
> 4
1 <
Су
с,
R
R R
R R
В В
R Рис. 19.2

776 ГЛАВА 19. Перечисление цветов
Раскраска, изображенная на рис. 19.3, эквивалентна только самой себе, т.к.
любое вращение или отражение дает в результате ту же раскраску. Аналогично,
раскраска, изображенная на рис. 19.4, эквивалентна только самой себе.
R
Следующие две раскраски на рис. 19.5 эквивалентны, поскольку каждая
получена из другой вращением на 90°, и никакие другие раскраски в результате
вращения или отражения не могут быть получены.
в Рис. 19.5
Наконец, легко видеть, что все раскраски множества на рис. 19.6 эквива-
эквивалентны, так как каждая раскраска может быть получена из другой вращением.
Рис. 19.6
Можно заметить, что в случае двухцветных раскрасок квадрата отражения
фактически не нужны, т.к. всевозможные эквивалентные раскраски можно полу-
получить в результате одних лишь вращений.
Вспомним раздел 9.4, в котором вращения и отражения квадрата описаны
подгруппой 54 (группой перестановок четырех элементов). Эта группа называется
оптической группой, или группой симметрии квадрата.
Для квадрата, изображенного на рис. 19.7,
12 3 4
3 2 14
12 3 4
14 3 2
являются отражениями, которые меняют местами вершины 1 и 3 и вершины 2 и
4, соответственно.

РАЗДЕЛ 19.1. Теорема Бернсайда 777
Перестановки
12 3 4
4 3 2 1
Рис. 19.7
02 =
12 3 4
2 14 3
отражают квадрат относительно горизонтальной оси, проходящей через центр
квадрата, и относительно вертикальной оси, проходящей через центр квадрата.
Перестановки pi, р2 и рз вращают квадрат по часовой стрелке соответственно на
90°, 180° и 270°.
Р\ =
12 3 4
2 3 4 1
Р2 =
Рз =
12 3 4
4 12 3
— тождественная перестановка
12 3 4
3 4 12
12 3 4
12 3 4
Заметим, что группа симметрии правильного n-угольника всегда содержит 2п
преобразований. Всегда имеется п вращений. Если число п нечетное, то имеется
п отражений относительно осей, проходящих через каждую вершину и середину
противоположной стороны. Если число п четное, то имеется | отражений от-
относительно осей, проходящих через противоположные вершины, и ^ отражений
относительно осей, проходящих через середины противоположных сторон много-
многоугольника. В каждом случае получаем п вращений и п отражений.
Возвращаясь к двухцветным раскраскам квадрата, отметим, что для каждой
перестановки а можно образовать перестановку а раскрасок, такую что а(С;) =
Cj, где Cj — раскраска, полученная в результате того, что квадрат с раскраской
С{ преобразуется перестановкой о. Например, р\{С{) — С2 и р\(Сц) = С\2. Для
простоты будем писать вместо д просто о и использовать а как для обозначе-
обозначения перестановок вершин, так и для обозначения перестановок цветов. Ранее мы
говорили об эквивалентных раскрасках. Теперь, согласно такой эквивалентности
раскрасок, введем отношение эквивалентности.
Определим отношение R на множестве раскрасок соотношением CiRCj, ес-
если в циклической группе существует перестановка а такая, что а(С{) = Cj.
Покажем, что R — отношение эквивалентности. Рефлексивность отношения R
очевидна, поскольку /(С*) = С{ для любой раскраски С{. Если CiRCj, то су-
существует перестановка о такая, что о{С?) = Cj. Но поскольку перестановка а
принадлежит октической группе и a~l(Cj) = Ciy то CjRCi. Если CiRCj и CjRCk,
то существуют такие перестановки а и а', что o{Ci) — Cj и o{Cj) = C^. Сле-
Следовательно, o'o{Ci) = С/с, и, поскольку о'о также является перестановкой из

778 ГЛАВА 19. Перечисление цветов
группы симметрии квадрата, имеем CiRCk- Следовательно, R — отношение экви-
эквивалентности, которое можно аналогичным образом получить для произвольного
множества К раскрасок на множестве 5 и группы перестановок S. Это дает нам
следующую теорему.
ТЕОРЕМА 19.1. Пусть К — множество раскрасок на множестве 5, и G — груп-
группа перестановок 5. Пусть отношение R на К определено следующим образом:
CiRCj, если существует перестановка jgG такая, что сг(С{) = Cj. Отношение
R есть отношение эквивалентности.
Возвращаясь к двухцветным раскраскам квадрата, отметим, что когда впер-
впервые упоминалась эквивалентность раскрасок, мы имели в виду, что одна раскраска
может быть получена из другой посредством вращения и отражения. Говоря об эк-
эквивалентных раскрасках в упомянутой выше теореме, мы имеем в виду, что одна
раскраска может быть получена из другой посредством перестановки. Поскольку
каждую перестановку можно рассматривать как вращение или отражение, стано-
становится очевидным, что это, по сути, одна и та же эквивалентность.
Необходимо помнить, что наша цель — найти количество "различных" рас-
раскрасок, где раскраски, принадлежащие одному классу эквивалентности, считают-
считаются "одинаковыми". Следовательно, нас фактически интересует количество классов
эквивалентности, поскольку оно совпадает с количеством "различных" раскрасок.
Например, рассмотрим круглый стол, за которым сидит п человек. Предположим,
что оба способа разместить людей являются одинаковыми, если у каждого из
сидящих тот же сосед справа и тот же сосед слева. Следовательно, если стол
вращать, то взаимное расположение людей за столом при этом не меняется. Мы
не будем рассматривать отражения, т.к. в результате сосед слева и сосед спра-
справа поменяются местами, а вся еда окажется на полу. Существует п\ способов
разместить п человек за столом. Поскольку два способа размещения людей эк-
эквивалентны, или одинаковы, если один способ получен из другого вращением и
всего имеется п вращений, то количество различных способов разместить лю-
людей равно количеству классов эквивалентности. Но число классов эквивалентно-
эквивалентности равно п\ (число способов разместить п человек за столом), деленному на п
(число таких размещений в каждом классе эквивалентности), и поэтому равно
^ = (п — 1)!. Такой метод подсчета оправдывает себя, потому что каждое враще-
вращение дает новый элемент в классе эквивалентности. На вопрос, куда подевались
цвета, ответим, что каждого человека можно рассматривать как представителя
своего собственного цвета, поэтому фактически рассматривается n-угольник, в
котором все вершины окрашены в различные цвета.
Снова, возвращаясь к двухцветной раскраске квадрата, заметим, что не каж-
каждая перестановка дает другую раскраску. Например, р2(Сц) = Сп = 6\(Сц) =
<b(Cii). На самом деле нам уже известно, что классы эквивалентности различны
по размеру. Поэтому нужен иной подход.
Для фиксированной раскраски С пусть Gc = {& : сг(С) = С}, так что
Gc — множество всех перестановок в G, которые не меняют С. Множество Gc
называется стабилизатором, или стационарной подгруппой С.
ТЕОРЕМА 19.2. Для фиксированной раскраски С стабилизатор Gc есть подгруп-
подгруппа группы G, группы перестановок.

РАЗДЕЛ 19.1. Теорема Бернсайда 779
ДОКАЗАТЕЛЬСТВО. Для доказательства, что Gc — группа, покажем сначала,
что если (Ji,(Jj Е Gc, то Oi о gj е Gc. Но <7;(C) = С и <tj{C) = С, а значит,
G, О aj(C) = (ТгЫС)) = Gi{C) = С
и Oi ogj е Gc. Очевидно, что тождественная перестановка / принадлежит
поскольку 1{С{) = С{ для каждой раскраски С;. Если a E Gc, то <т(С) = С и,
следовательно, сг~1(С) = С, т.к.
С = /(С) = а о сг(С) = a" V(C)) = а'1 (С).
Следовательно, о~г Е Gc. Отсюда Gc — группа.
Пусть С и С' принадлежат одному классу эквивалентности. Количество пе-
перестановок в G, которые отображают С в С", равно \Gc\- Для доказательства
положим сго(С) = С1 и сг(С) = С. Тогда
сто о о(С) = <то(<т(С)) = <70(С) = С'.
Таким образом, при фиксированном gq для каждой перестановки а такой, что
<у(С) = С, имеется перестановка ао о <т, которая переводит С в С". Для каждой
сг такой, что сг(С) = С, положим /(сг) = сто о а. Тогда / отображает каждую
перестановку, переводящую С в саму себя, в перестановку, которая переводит С
в С. Более того, если о\ и оъ — две перестановки, которые переводят С в себя,
И (То О G\ = (Jq О G2, ТО
&Q1 о (а0 о <7i) = Gq1 ° (ао ° СГ2) •
Поэтому
(СГ^1 О СГ0) О G1 = (О^1 О G0) О G2 ,
что дает
J о Gi = I О G2
и
G1 = G2 .
Следовательно, функция / инъективна. Пусть <т переводит С в С Тогда
/((Jq1 о а) = G0 о (а^1 о а) = (а0 о а^1) оо = I оо = о,
так что / — сюръекция. Следовательно, / — взаимно однозначное соответствие,
поэтому существует одинаковое количество перестановок, которые переводят С в
С", и тех, которые отображают С в себя. Следовательно, если С\ и С2 принад-
принадлежат Е, тому же классу эквивалентности, что и С, то количество перестановок,
которые переводят С в Сь равно количеству перестановок, которые переводят С
в Сг, а именно, \Gc\- Это число называется кратностью класса эквивалентности
Е. Отсюда следует, что |б?|, количество перестановок в G, равно \Gc\ • \Щ, где
\Е\ — количество раскрасок в Е, или
\GC\-\E\ = \G\.

780 ГЛАВА 19. Перечисление цветов
Последнее соотношение можно также переписать в виде
сеЕ
и тогда, если N — количество классов эквивалентности,
е сеЕ сек
где К — множество раскрасок. Следовательно, количество различных раскрасок,
т.е. число N классов эквивалентности, дает следующая формула
? \Gc\ .
N = ?$? = — V \Gc\
\G\ \G\^] c|"
Для каждой перестановки а пусть <р(сг) равно количеству раскрасок, которые а
не изменяют. Заметим, что если для каждой раскраски найти число перестановок,
не изменяющих ее, и просуммировать эти числа по всем раскраскам, то получим
тот же результат, как если бы мы находили количество раскрасок, которые не
изменяет каждая перестановка. Поэтому, суммируя по перестановкам, получаем
сек
Подведем итог в приведенной ниже теореме.
ТЕОРЕМА 19.3. (Лемма Бернсайда о подсчете) Если К — число раскрасок над
множеством 5, G — группа перестановок на множестве 5 и N — число классов
эквивалентности (т.е. различных раскрасок), то
УПРАЖНЕНИЯ
1. Определите группу симметрии равностороннего треугольника.
2. Определите группу симметрии правильного пятиугольника.
3. Определите группу симметрии правильного восьмиугольника.
4. Определите группу симметрии тетраэдра.
5. Если стержень украшен пятью полосками, каждая из которых может быть
одного из двух цветов, то сколькими способами можно раскрасить стержень?
(Напомним, что стержень можно перевернуть.)
6. Сколькими способами можно раскрасить равносторонний треугольник, ис-
используя два цвета?
7. Сколькими способами, используя два цвета, можно раскрасить прямоуголь-
прямоугольник, который не является квадратом?

РАЗДЕЛ 19.2. Теорема Пойа 781
19.2. ТЕОРЕМА ПОЙА
Сделав первый шаг, будем развивать дальше теорию подсчета числа раскрасок.
С этой целью рассмотрим теорему Пойа, которая дает производящую функцию
для нахождения числа раскрасок неориентированной фигуры с использованием
заданного количества цветов. При этом нам будет особенно полезна последняя
часть уравнения Бернсайда. Если удастся найти простой способ определения ко-
количества раскрасок, которые остаются неизменными при каждой перестановке, то
мы сможем просуммировать эти числа и разделить сумму на число перестановок.
В разделе 9.5 показано, что каждую перестановку можно представить как про-
произведение непересекающихся циклов. Если вернуться к двухцветной раскраске
квадрата, то
ф1=
4 3 2 1
можно выразить как
В цикле раскраска будет оставаться неизменной, если цвет каждой вершины бу-
будет совпадать с цветом той вершины, в которую она переходит. Поэтому все
вершины в цикле должны быть одного цвета. Если ф\ должна оставить раскрас-
раскраску неизменной, то вершины 1 и 4 должны быть одного цвета и вершины 2 и 3
должны быть одного цвета. Следовательно, вершины 1 и 4 могут быть красными
или синими, и вершины 2 и 3 могут быть красными или синими. Это значит,
что есть четыре раскраски, которые остаются неизменными при перестановке ф\.
Это раскраски Cg,Cio,Ci4 и C\q. Поскольку для каждого цикла есть выбор из
двух цветов, то в общем случае число раскрасок, которые не меняются при пе-
перестановке а, равно 2Су(а\ где Су(а) — количество циклов в перестановке сг,
включая циклы длины 1. Тождественную перестановку / можно представить в
виде A)B)C)D). Она имеет четыре цикла, поэтому оставляет неизменными 24
раскрасок. В приведенной ниже таблице указана каждая перестановка, ее выра-
выражение через циклы, ее цикловая структура, количество циклов (iVi), раскраски,
которые она не меняет (инвариантные раскраски), и количество таких раскрасок
(N2). Для записи цикловой структуры будем использовать обозначение с^, где
и — число циклов длины т в перестановке. Таким образом, цикловая структура
для ф\ имеет вид с\, т.е. ф\ выражается через два цикла длины 2.
Перестановка
5Х = A3)B)D)
52 = A)C)B4)
0! = A4)B3)
ф2 = A2) C4)
Р\ = A234)
р2 = A3)B4)
Рз = A432)
/ = A)B)C)D)
Всего
Цикловая структура
с[с2
с\с2
4
4
СА
4
с4
4
с\ + 2с\с2 + Зс2 + 2с4
Ni
3
3
2
2
1
2
1
4
Инвариантные раскраски
С*2, С4, С6, С8, Cg, Сю, СцС\2
Ci, Сз, С5, С7, Cg, Сю, С\\С\2
Cg, Cio,Ci4Ci6
Cg, Сю, С13С15
Cg, Сю
Cg, Cio,CnCi2
Сд,Сю
Ci, C2, C3, C4,... ,Ci6
N2
8
8
4
4
2
4
2
16
48

782 ГЛАВА 19. Перечисление цветов
Как отмечалось ранее, для определения количества раскрасок, инвариантных
относительно перестановки сг, достаточно найти 2Су^\ где Су (а) — количество
циклов в перестановке сг. Затем нужно просуммировать по всем перестановкам и
найти ^ZaeGlP(<T)- Другой метод — взять цикловую форму и присвоить каждому
циклу значение 2. Например, 52 = с\с2 оставляет неизменными 22 • 2 = 8 раскра-
раскрасок. Затем нужно найти сумму X^reG^C0")- Третий метод — сложить вместе все
цикловые формы. Согласно таблице имеем
с\ + 2с\с2 + Зс| 4- 2с4 .
Если теперь присвоить каждому циклу значение 2, то получим
24 + 2 • 22 • 2 + 3 • 22 + 2 • 2 = 48.
Итак, всего имеется 48 раскрасок, которые не меняются при перестановках. Если
теперь это число разделить на 8, количество перестановок, то получим
/ ч 48 п
ром-т-"
различных раскрасок.
Далее предположим, что имеется три цвета. Используя аналогичные рассу-
рассуждения и таблицу, можно вычислить 3^у^\ где Су(а) — количество циклов в
перестановке сг, чтобы найти количество раскрасок, которые остаются неизмен-
неизменными при перестановке сг, а затем просуммировать эти числа и найти YlaeG^^)-
Затем снова можно разделить на 8 и получить количество различных раскрасок.
Второй метод: учитывая, что уже имеется
с\ + 2с\с2 + Scl + 2с4 ,
присвоим каждому циклу значение 3, так что сумма всех раскрасок, которые не
меняются при перестановках, равна
З4 + 2 • З2 • 3 + 3 • З2 + 2 • 3 = 168 .
Разделив теперь на 8, получаем
1 v^ / ч 168
1 ' aEG
различную раскраску. Пусть имеется т цветов, тогда
Поскольку в общем случае нам нужна величина щ Y^ 4>(а)> которую можно
aEG
получить из
D

РАЗДЕЛ 19.2. Теорема Попа 783
то положим
, с2, с3, с4) = —(с\ + 2с\с2
14
2с4)
где Ci — цикл длины г, и назовем Pg(ci,C2,C3,c4) цикловым индексом.
ПРИМЕР 19.4. Ранее отмечалось, что для двухцветных раскрасок квадрата до-
достаточно одних вращений. Предположим, что G = {/,
получим таблицу.
- В таком случае
Перестановки
Рх = A234)
р2 = A3) B4)
Рз = A432)
/ = A)B)C)D)
Всего
Цикловая структура
с4
с\
с4
4
с\+с\ + 2с4
Ni
1
2
1
4
Инвариантные раскраски
Cg,Cio,CnCi2
Cg^ClO
Сь Сг? Сз^ С4, • • •, Ci6
N2
2
4
2
16
24
(Здесь N\ — количество циклов, N2
Тогда
1
количество инвариантных раскрасок.)
ч 24 п
И 6
и, как и ранее, получаем шесть различных раскрасок. Опять, если присвоить
каждому циклу значение 2 в выражении
;<
то получим
lt
и снова получаем шесть различных раскрасок.
?
Рассмотрим общий случай, когда группа перестановок G содержит \G\ эле-
элементов раскрашивание проводится с помощью т красок, и сумма циклов равна
+ a^c\3 + • • • -f anc^n. Цикловой индекс в этом случае равен
a\c\l 4-
+a2c\2
а количество различных раскрасок равно Рс(гп,т,т,... ,т). Теперь перейдем
от подсчета структур к рассмотрению структуры раскрасок, сохраняющихся при
конкретных перестановках. Опять начнем с двухцветной раскраски квадрата. Рас-
Рассмотрим цикловую стркутуру с\с2 перестановки 5\ = A3)B)D). Сначала посмот-
посмотрим на элемент структуры с\, который представляет два цикла длины 1. Для
двух циклов имеется четыре способа выбора цветов, при которых раскраска не
будет меняться: вершины в обоих циклах могут быть окрашены только в крас-
красный или только в синий цвет, вершины в одном цикле могут быть окрашены в

784 ГЛАВА 19. Перечисление цветов
красный, а в другом — в синий, и наоборот. Очевидно, существует только один
способ раскраски вершин в обоих циклах красным и один способ раскрасить их
в обоих циклах синим. Если вершины в одном цикле красные, а в другом — си-
синие, то имеются две возможности выбора синих вершин; тогда в другом цикле
вершины должны быть красные. Запишем эту структуру в форме ЬЬ + 26г + гг
(Ь — синий, г — красный), где знак + можно читать как "или". Для удобства
запишем эту структуру как b2 + 2br + г2. Заметим, что алгебраически это F-hrJ.
Другой цикл задается С2, что представляет один цикл длины 2. Поскольку это
единственный цикл длины 2, то в нем обе вершины должны быть окрашены в
красный или обе — в синий. Запишем эту структуру как bb + rr, или Ь2 + г2.
Поскольку структура раскраски двух вершин есть F 4- гJ, а для других двух
вершин эта структура есть 62Ч-г2, то структура раскрасок, не изменяющихся при
перестановке <5ь может быть описана как (b + rJ(b2 +r2).
Допустим, что имеется цикл с^. Это произведение п циклов длины га. Пусть
R представляет раскраску цикла красным, а В представляет раскраску цикла
синим. Таким образом, R3Bn~i представляет раскраску j циклов красным и п — j
циклов — синим. Количество способов раскраски j циклов красным и п—j циклов
синим равно количеству вариантов выбора j циклов из п циклов для окраски
в красный цвет. Это равно C(n,j) = (п). Поэтому будем использовать запись
(")RjBn~j для обозначения раскрасок с j красными и п- j синими циклами. Но
это не что иное, как коэффициент при R^Bn~3 в разложении (R + B)n. Таким
образом, можно представить раскраски цикла с7^ как (i?+B)n. Поскольку каждая
раскраска цикла состоит из раскраски га вершин, положим R = г™ и В = Ьт.
Теперь структуры раскрасок для с7^ можно описать выражением (rm -hbm)n. В
результате для каждой перестановки получим следующее множество раскрасок,
которое назовем перечнем раскрасок для перестановки.
Перестановка
6г = A3)B)D)
62 = A)C)B4)
ф, = A4)B3)
ф2 = A2)C4)
Рх = A234)
р2 = A3) B4)
Рз = A432)
/ = A)B)C)D)
Всего
Цикловая структура
с\с2
с\с2
4
4
сА
4
с4
г4
с\ + 2с\с2 + Зс2, + 2с4
Перечень инвариантных раскрасок
(г + 6J(г2 + 62)
(г + 6J(г2+62)
(Г2 + б2J
(Г2 + б2J
(г4+64)
(Г2 + 62J
(г4 + б4)
(г + 6L
8г4 + 8г36 + 16г262 + 8г63 + 864
Последняя строка в столбце перечней раскрасок получается, если раскрыть скоб-
скобки в выражениях для всех перечней и результаты сложить.
Ранее было показано, что для раскраски С количество перестановок в G,
обозначенное |G|, равно \Gc\ • \Е\, где \Е\ — количество раскрасок в классе эк-
эквивалентности Е, содержащем С, и |б?с| — количество перестановок, которые не

РАЗДЕЛ 19.2. Теорема Попа 785
меняют С. Поскольку каждая перестановка переводит раскраску в раскраску с
той же цикловой структурой, то в сумму наших перечней раскраски, эквивалент-
эквивалентные С и описываемые той же структурой, вошли \G\ раз. Таким образом, для
определения перечня неэквивалентных структур раскрасок мы определяем общий
перечень инвариантных раскрасок как |G| = 8 и для нашего перечня структур
раскрасок получаем
1(8г4 + 8гЧ + 16г2Ь2 + 8гЬ3 + 864) = г4 + г36 + 2г2Ь2 + гб3 + Ь4 .
8
Для получения полного перечня структур мы брали инвариантные раскраски
из цикловой структуры каждой перестановки, а затем суммировали их. Можно
было сначала сложить цикловые структуры, как в колонке 2 приведенной выше
таблицы, а затем для получения такого же результата перевести циклы в раскрас-
раскраски. Таким образом, для суммы
с\ + 2с\ с2 + 3cl + 2с4
получаем полный перечень структур
(г4 + Ь4) + 2(г + ЪJ(г2 + Ь2)(г + ЪJ + 3(г2 + Ъ2J + 2(г4 + Ь4),
что после раскрытия скобок и приведения подобных членов равно
8г4 + 8г36 + 16г262 4- Srb3 + 864 .
Таким образом, если сумма циклов имеет вид a\c\l + c^c^2 + a^c\3 -+-••• + anc^n,
то перечень неэквивалентных структур раскрасок имеет вид
Если бы мы использовали три цвета: красный (г), белый (ю) и синий (Ь), то
перечень неэквивалентных структур раскрасок имел бы вид
PG(r + w + 6, г2 + w2 + Ь2,..., rn + wn 4- Ьп).
В общем случае имеет место следующая теорема.
ТЕОРЕМА 19.5. (Теорема Пойа о подсчете) Если задано множество 5, цикловой
индекс Pg(ci,C2, ... ,сп) и цвета /ci,fc2, ^'з5 • • •, ^т, то перечень неэквивалентных
структур раскрасок имеет вид
г=1 г=1
ПРИМЕР 19.6. Снова рассмотрим двухцветные раскраски квадрата с использо-
использованием только вращений. Пусть G = {/, рьР2,рз}- В таком случае получаем
таблицу

786 ГЛАВА 19. Перечисление цветов
Перестановка
Р1 = A234)
р2 = A3)B4)
Рз = A432)
/ = A)B)C)D)
Всего
Цикловая структура
с4
4
с4
с\
С1 + С2 + 2с4
Перечень инвариантных раскрасок
(г4 + Ь4)
(г2 + 62J
(г4+64)
(г + 6L
4г4 + 4г36 + 8г262 + 4г63 + 464
PG(r + 6, г2 + Ь2,г3 + Ь3,г4 + Ь4) = ±((г 4- бL + (г2 + б2J + 2(г4 + Ь4)) =
что дает совпадение перечня неэквивалентных структур раскрасок с уже рассмот-
рассмотренным случаем, в котором была использована вся группа симметрии. ?
ПРИМЕР 19.7. Пусть 5 — вершины треугольника, a G — группа симметрии тре-
треугольника. Найдем перечень неэквивалентных структур раскрасок. Пусть р\ =
A23) и р2 = A32) - вращения вершин. Пусть 5Х = A)B3), 62 = A3)B) и
6s = A2)C) — отражения, а / = A)B)C) — тождественное преобразование. В
таком случае имеем таблицу
Перестановка
Pi = A23)
Р2 = A32)
<5i = A)B3)
<52 = A3)B)
*2 = A2)C)
/ = A)B)C)D)
Всего
Цикловая структура
сз
сз
С\С2
С\С2
С\С2
с\ 4-3cic2 +2с3
Перечень инвариантных раскрасок
(г3+Ь3)
(г3 + 63)
(г + 6)(г2+ б2)
(г + 6)(г2+Ь2)
(г + 6)(г2+Ь2)
(г + 6K
6г3 + 6г26 4- бгб2 + 6Ь3
2 г3
PG(r + 6, г2 + б2, г
= -((г + бK + 3(г2 + 62)(г 4- Ъ) + (г3 4- б3)) -
п
¦ УПРАЖНЕНИЯ
В приведенных ниже заданиях допускается, что все вращения и отражения воз-
возможны.
1. На браслете пять бусинок. Если их нужно раскрасить двумя цветами, то
сколько раскрасок существует? Сколько существует трехцветных раскрасок?
2. Сколькими способами можно раскрасить клетки шахматной доски 3x3?
3. Сколько существует способов раскраски равностороннего треугольника тре-
тремя цветами?

РАЗДЕЛ 19.2. Теорема Пойа 787
4. Сколько существует способов раскраски куба двумя цветами?
5. Сколько существует способов раскраски правильного пятиугольника двумя
цветами?
6. Сколько существует способов раскраски правильного пятиугольника тремя
цветами?
7. Сколько существует способов раскраски правильного восьмиугольника дву-
двумя цветами?
8. Найдите структурный перечень двухцветных раскрасок браслета с семью
бусинками.
9. Найдите структурный перечень двухцветных раскрасок прямоугольника, ко-
который не является квадратом.
10. Найдите структурный перечень трехцветных раскрасок равностороннего тре-
треугольника.
11. Найдите структурный перечень двухцветных раскрасок пятиугольника.
12. Найдите структурный перечень двухцветных раскрасок тетраэдра.
13. Найдите структурный перечень двухцветных раскрасок шахматной доски
размера 3x3.
14. Найдите структурный перечень двухцветных раскрасок восьмиугольника.
15. Десять кеглей выставлены в треугольник стандартным образом. Найдите
структурный перечень двухцветных раскрасок этих кеглей без ограничений
на движения. Найдите структурный перечень при условии, что разрешены
только вращения.

ГЛАВА
КОЛЬЦА, ОБЛАСТИ
ЦЕЛОСТНОСТИ И ПОЛЯ
20.1. КОЛЬЦА И ОБЛАСТИ ЦЕЛОСТНОСТИ
В разделах, посвященных решеткам и булевым алгебрам, рассматривались две
бинарные операции и были описаны некоторые связи между ними. Здесь мы будем
действовать по той же схеме, но обобщим понятие целого числа. Фактически
речь пойдет об операциях + и •. Мы выделим определенные свойства целых
чисел, и любое множество с указанными двумя операциями, удовлетворяющее
этим свойствам, назовем кольцом. Определив кольца, на некоторое время снова
вернемся к целым числам.
ОПРЕДЕЛЕНИЕ 20.1. Кольцом называется непустое множество R вместе с
бинарными операциями, называемыми умножением и сложением, которые обо-
обозначаются соответственно • и -f и удовлетворяют следующим условиям.
1. Множество R замкнуто относительно сложения, т.е., если х Е R и у Е Д,
то х + у Е R.
2. Сложение в R ассоциативно, т.е. х 4- (у + z) — (х + у) 4- z для всех я, у и
z из R.
3. Множество R содержит аддитивную единицу (нейтральный элемент от-
относительно сложения, обозначаемый 0), так что х + 0 = 0-f x = i для
всех х из R.
4. Для каждого элемента х из R множество R содержит элемент —х, обрат-
обратный х относительно сложения, так что х + -х = -х + х = 0.
5. Сложение в R коммутативно, т.е. х -Ь у = у + х для всех х и у из R.
6. Множество R замкнуто относительно умножения, т.е., если х е R и
у Е -R, то х • у Е R.
7. Умножение в R ассоциативно, т.е. х • (у • z) = (х • у) • z для всех х, у и z
ИЗ i?.

РАЗДЕЛ 20.1. Кольца и области целостности 789
8. Для всех х, у и z из R выполняются следующие законы дистрибутивности:
x-(y + z) = (x-y) + (x-z)
и
(у + 2) -Ж = (у - X) + (Z - X).
Если во множестве R существует элемент 1 (мультипликативная единица, или
нейтральный элемент относительно умножения) такой, что 1 • г = г • 1 = г для
всех г из Д, то множество R называется кольцом с единицей. Если г-г' = г' -г
для всех г и г' из R, то множество R называется коммутативным кольцом.
Заметим, что кольцо R является группой относительно сложения и полу-
полугруппой относительно умножения. Примером колец относительно обычных опера-
операций сложения и умножения могут служить целые, действительные, рациональные
и комплексные числа. Другими примерами колец являются множество (n x п)-
матриц для фиксированного целого числа п и множество полиномов — оба отно-
относительно обычных операций сложения и умножения. Среди перечисленных выше
колец только матрицы не образуют коммутативное кольцо.
ОПРЕДЕЛЕНИЕ 20.2. Областью целостности называется коммутативное
кольцо с единицей, не совпадающей с 0, так что из условия ab = 0 следу-
следует а = 0 или 6 = 0.
Множества целых, рациональных и действительных числа являются обла-
областями целостности. Множество Bх2)-матриц не является областью целостности,
поскольку
 1 1 Г 1 0 1 Г 0 0
0 0 J [ 0 0 J
т.е. произведение двух ненулевых матриц может быть нулевой матрицей.
Области целостности обладают свойством сокращения относительно умно-
умножения, которое означает, что если ab = ас и а ^ 0, то Ъ = с. Это очень важно,
т.к. кольца не обязательно содержат взаимно обратные элементы, поэтому не все-
всегда возможно умножить обе части уравнения ab = ас на а~1 и получить b = с.
Доказательство следующей теоремы оставляем читателю.
ТЕОРЕМА 20.3. Пусть R — коммутативное кольцо с единицей. Кольцо R является
областью целостности тогда и только тогда, когда из ab = ас следует, что b = с
для всех 6, с и ненулевых элементов а из R.
Теперь проверим, является ли множество классов вычетов Zn кольцом или
областью целостности. Нетрудно убедиться, что Zn всегда является кольцом. Ра-
Ранее было показано, что Zn удовлетворяет всем законам кольца, за исключением
законов дистрибутивности. Выполнение законов дистрибутивности также легко
показать. Рассмотрев, однако, Zq, можно обнаружить, что [3] 0 [2] = [0], и, следо-
следовательно, множество Zq не является областью целостности. На самом деле, если

790 ГЛАВА 20. Кольца, области целостности и поля
число п не простое, например, n = pq, то [р] 0 [q] = [0], поэтому Zn не будет
областью целостности.
Если п — простое число, то для заданного целого числа а ф 0 (mod п),
не равного нулю, из теоремы 10.6 следует, что сравнение ax = I (mod n) име-
имеет решение, например, а'. Следовательно, имеем [а] 0 [а'] = [1], и для каждо-
каждого элемента существует обратный элемент. Поэтому, если аЪ — 0 и а ф 0, то
Ь = a~lab = а~10 = 0. Таким образом, если п — простое число, то множество
Zn — область целостности.
В случае, когда число п не является простым, рассмотрим подмножество
R = {[х] : х — взаимно простое с и). Легко показать, что это множество образует
группу относительно умножения. Произведение двух целых чисел, взаимно про-
простых с п, является числом, взаимно простым с п. Единица, 1, есть число, взаимно
простое с п\ и если число Ь — взаимно простое с п, то сравнение Ъх = 1 (mod и)
имеет единственное решение, поэтому для элемента [Ь] существует обратный эле-
элемент. Однако, относительно сложения множество R не образует даже полугруппу,
поскольку сумма двух чисел, взаимно простых с п, не обязательно является чис-
числом, взаимно простым с п.
ОПРЕДЕЛЕНИЕ 20.4. Пусть йий'- кольца и пусть / : R -> R1 - функция
из Д в R'. Функция / называется гомоморфизмом колец тогда и только тогда,
когда
f(a + 6) = /(а) + /F),
/(а • 6) = /(а) • /(Ь)
для всех a,b € R. Сложение и умножение в соответствующих кольцах одина-
одинаково определены. Если гомоморфизм колец f : R—> R' — инъекция, то его на-
называют мономорфизмом. Если гомоморфизм колец / : R —> R' — сюръекция,
то его называют эпиморфизмом. Гомоморфизм колец / : R —> R' называют
изоморфизмом, если функция / : R —> R' — биекция. Обычно при описании
гомоморфизма из кольца R с единицей в кольцо R' с единицей требуется, что-
чтобы мультипликативная единица кольца R отображалась на мультипликативную
единицу кольца R1.
Например, рассмотрим кольцо целых чисел Z и кольцо
классов вычетов по модулю 7. Предположим, что функция / : Z —> Z-j определена
соотношением f(a) = [а]; другими словами, /(а) — класс эквивалентности целых
чисел, сравнимых с а по модулю 7. Если каждое из чисел аиЬ является целым, то,
используя определение умножения и сложения классов эквивалентности Z7, полу-
получим, что f(ab) = [ab] = [a][b] = f(a)f{b) и f(a + b) = [а + Ь] = [а} + [Ь] = f(a) + /F).
Таким образом, функция / — гомоморфизм. Ясно, что / представляет собой эпи-
эпиморфизм, потому что /(г) = [г] для 0 < г < 6. Функция / не является инъекцией,
поскольку 7 = 0 (mod 7) и, следовательно, /G) = [7] = [0] = /@). Поэтому

РАЗДЕЛ 20.1. Кольца и области целостности 791
функция / не является ни мономорфизмом, ни изоморфизмом. Те же самые рас-
рассуждения, несомненно, применимы к кольцам Z и Zn для любого положительного
целого числа п > 1.
Изоморфные кольца имеют одинаковую алгебраическую структуру и отли-
отличаются только именованием своих элементов.
ТЕОРЕМА 20.5. Для всех а из кольца R выполняется соотношение a • 0 = 0.
ДОКАЗАТЕЛЬСТВО. Доказательство теоремы оставляем читателю. ¦
ОПРЕДЕЛЕНИЕ 20.6. Подмножество R! кольца R называется подкольцом
кольца Д, если R! — это кольцо с той же самой операцией.
Например, целые числа образуют подкольцо кольца рациональных чисел.
Рациональные числа образуют подкольцо кольца действительных чисел. Дей-
Действительные числа образуют подкольцо кольца комплексных чисел. Множество
(пхп)-матриц с целочисленными элементами образуют подкольцо кольца (пхп)-
матриц с рациональными элементами. Можно легко проверить, что {[0], [2], [4]} —
это подкольцо кольца Z6.
Дадим теперь определение поля, хотя само понятие будет использовано лишь
в следующей главе.
ОПРЕДЕЛЕНИЕ 20.7. Полем называется коммутативное кольцо с единицей, не
совпадающей с 0, каждый ненулевой элемент которого имеет обратный элемент
относительно умножения.
Множества рациональных, действительных и комплексных чисел являются
полями. Если рассмотреть только положительные действительные числа и по-
положительные рациональные числа, то получим области целостности. Во многих
случаях область целостности не является полем, но образует подкольцо поля. Ра-
Ранее было показано, что в случае простого числа п каждый элемент множества
классов вычетов Zn имеет обратный элемент, поэтому Zn — поле.
Приведенная ниже теорема устанавливает связь между областью целостно-
целостности и полем.
ТЕОРЕМА 20.8. Поле является областью целостности. Конечная область целост-
целостности является полем.
ДОКАЗАТЕЛЬСТВО. Если F — поле и ab = 0 для а, Ъ е F, и если а ф 0, то
Но a~lab = 6, поэтому b — 0 и F — область целостности. Обратно, если D —
конечная область целостности с элементами 0,l,ai,a2,a3,... ,ап и а = а; для
некоторого 0 < г < п, то все элементы а-0, а-1,аа1,аа2,ааз,... ,аап являются
различными. Если а • a,j = a • аь то а • (a.j - а*) = 0, no3TO\fy (a,j - а*) = 0 и
dj = dk. Следовательно, а-0, а-1,а-а1,а-а2,а-аз,... ,a-an — в tO4HOCTH элементы
области D, так что a • а^ = 1 для некоторого /с, где 0 < к < п, поэтому а имеет
обратный элемент. Таким образом, область целостности D является полем. ¦

792 ГЛАВА 20. Кольца, области целостности и поля
Заметим, что целые числа образуют область целостности, но не являются
полем. Следовательно, не каждая область целостности является полем. Тем не
менее, будет показано, что каждая область целостности вкладывается в поле.
Это означает, что для заданной области целостности А существует поле F и
мономорфизм из А в F.
Пусть А — область целостности. В частности, А может быть множеством
целых чисел Z. Рассмотрим множество упорядоченных пар
Р={(а,Ь) : (а, 6) еАхАиЬ^О}
и определим отношение ~ на Р следующим образом.
ОПРЕДЕЛЕНИЕ 20.9. Если пары (а, Ь) и (c,d) принадлежит Р, то (a, b) ~ (c,d)
тогда и только тогда, когда ad = be.
Например, если А = Z, то класс эквивалентности [B,3)] содержит такие упо-
упорядоченные пары: B,3), D,6), F,9),..., (—2, —3), (—4, —6),..., которые соответ-
соответствуют представлениям рациональных чисел в виде 2/3,4/6,6/9,..., (—2)/(—3),
(—4)/(—6), Все они являются различными представлениями одного и того же
рационального числа, [B,3)].
ТЕОРЕМА 20.10. Отношение ~ на множестве Р есть отношение эквивалентности.
Доказательство этой теоремы тривиально и предоставляется читателю.
Обозначим через а/Ъ класс эквивалентности, содержащий (a,b) G Р, т.е.
[(а, Ь)], а через F — множество классов эквивалентности на множестве Р.
ОПРЕДЕЛЕНИЕ 20.11. Для заданных элементов а, 6, с и d из области целост-
целостности А сложение на F определено соотношением a/b + c/d = (ad + bc)/bd, a
умножение на F — соотношением (a/b)(c/d) = ac/bd.
Покажем, что операции сложения и умножения на F определены корректно,
т.е. не зависят от выбора представителей классов эквивалентности.
ТЕОРЕМА 20.12.
а) Сложение в F определено корректно.
б) Умножение в F определено корректно.
ДОКАЗАТЕЛЬСТВО. Пусть а/b = а1/V и c/d = с'jdl. Имеем непосредственно,
что ab' = а'Ъ и cd! = c'd.
а) По определению сложения имеем а/Ь -4- c/d = (ad + bc)/bd и a'/b' + с'/d' =
(a'df + b'cf)/bfd'. Необходимо показать, что (ad + bc)/bd = (a'd' + b'c')/b'd'
или, что равносильно, b'd'(ad + be) = bd(a'df + Ус1), но
b'd'(ad + be) = У add1 + cd'bb' =
= a!bdd! + c'dbb' =
= bd(a'd' + b'c'),
где второе равенство выполняется, поскольку ab' = а'Ъ и cd' = c'd.

РАЗДЕЛ 20.1. Кольца и области целостности 793
б) Из определения умножения следует, что (a/b)(c/d) = ac/bd и (a'/6')(с'/df) =
dd jb'd!. Необходимо показать, что ac/bd = a'c1/b'd' или, что равносильно,
acb'd' = a'c'bd. Ho acb'd' = ab'cd' = a'bc'd = a'c'bd.
¦
ТЕОРЕМА 20.13. Множество классов эквивалентности F является коммутатив-
коммутативным кольцом с аддитивной единицей 0/1 и мультипликативной единицей 1/1.
Доказательство этой теоремы тривиально и предоставляется читателю.
ЛЕММА 20.14. Для а и b из А имеем a/b = 0/1 тогда и только тогда, когда a = 0.
ДОКАЗАТЕЛЬСТВО. Очевидно, что равенство a/b = 0/1 имеет место тогда и
только тогда, когда a = аA) = 6@) =0. ¦
ТЕОРЕМА 20.15. Коммутативное кольцо F является полем.
ДОКАЗАТЕЛЬСТВО. Если a/b ф 0, то а ф 0 и b/a G F. Но
(a/b)(b/a)=ab/ab= 1/1 = 1.
Следовательно, для каждого ненулевого элемента из F существует обратный эле-
элемент, поэтому F — поле. ¦
Пусть f : А —* F определено соотношением /(а) = а/1. Имеем f(ab) =
ab/1 = (а/1)F/1) = f(a)f(b) и f{a + b) = (а + Ь)/1 = (аA)+ЬA))/1 = а/1+6/1 =
/(а) 4-/F). Кроме того, функция / — инъекция, потому что если /(а) = /F), то
а/1 = 6/1 иа = а-1 = 6-1 = 6. Следовательно, / — мономорфизм, и элементу
а из Л однозначно соответствует элемент {а/1 : а е А} из F. Таким образом,
область целостности А можно рассматривать как подкольцо поля F.
ТЕОРЕМА 20.16. Отображение / : А —> F, определенное соотношением /(а) =
а/1, является мономорфизмом, при этом говорят, что область целостности А вло-
вложена в поле F или что поле F содержит область целостности А.
Легко показать, что это поле F есть наименьшее поле, в которое область
целостности А может быть вложена.
ОПРЕДЕЛЕНИЕ 20.17. Поле F называется полем частных области целостно-
целостности А. Если А — множество целых чисел Z, то поле F — множество рацио-
рациональных чисел, обозначаемое, как правило, через Q.
В этом разделе развиваются алгебраические структуры целых чисел, и целые
числа алгебраически определяются с точностью до изоморфизма. Отметим, что
из такого рассмотрения не следует существование целых чисел, а только наличие
присущих им алгебраических свойств, если сами эти числа существуют.
ОПРЕДЕЛЕНИЕ 20.18. Подмножество / кольца R называвется идеалом коль-
кольца R, если
а) / — подкольцо кольца R\
б) если х принадлежит /иг принадлежит R, то х • г и г • х принадлежат /.

794 ГЛАВА 20. Кольца, области целостности и поля
Например, в кольце целых чисел множество всех чисел, кратных фиксиро-
фиксированному целому числу р, образует идеал.
ОПРЕДЕЛЕНИЕ 20.19. Пусть R — коммутативное кольцо. Идеал / кольца R
называется главным идеалом, порожденным элементом а, если / состоит из
всех произведений а на элементы кольца R, т.е. I = (а) = {аг : г е R}.
ТЕОРЕМА 20.20. Каждый непустой идеал / кольца целых чисел является главным
идеалом.
ДОКАЗАТЕЛЬСТВО. Для / Ф {0} пусть р — наименьшее положительное целое
число в идеале / и пусть т принадлежит /. Согласно алгоритму деления, га =
pq + r, где 0 < г < р. Поскольку г = т — pq, то г принадлежит /. Таким образом,
поскольку г < р и р — наименьшее положительное целое число в идеале /, то
г = 0. Следовательно, каждое целое число в идеале / кратно числу р и / = (р). ¦
Заметим, что при доказательстве этой теоремы используется принцип вполне
упорядочения и алгоритм деления, каждый из которых выполняется для целых
чисел.
ПРИМЕР 20.21. Рассмотрим кольцо Z целых чисел и два главных идеала, поро-
порожденных целыми числами 8 и 12:
(8) = {Sr:reZ} =
= {...,-24,-16,-8,0,8,16,24,...};
A2) = {12s :seZ} =
= {...,-24,-12,0,12,24,...}.
Пересечение множеств (8) П A2) есть множество
{...,-48,-24,0,24,48,...},
которое является главным идеалом, порожденным целым числом 24. Заметим, что
24 — наименьшее общее кратное чисел 8 и 12. Вообще,
(а)П(Ь> = (НОК(а,Ь)> .
Результаты, имеющие отношение к этому примеру, сформулированы в приведен-
приведенной ниже теореме. Доказательство предоставляется читателю. ?
ТЕОРЕМА 20.22. Если s и t — ненулевые целые числа и (s) и (t) — соответству-
соответствующие главные идеалы в кольце Z, то
а) если (s) С (?), то t \ s;
б) (s) П (t) = (и), где и = НОК(М).
ПРИМЕР 20.23. Если (а, Ь) — наименьший идеал, содержащий а и 6, то
(а,Ь) = (НОД(а,Ь)>.

РАЗДЕЛ 20.1. Кольца и области целостности 795
Например,
(8,12) = {-16, -12, -8, -4,0,4,8,12,16,...} = (НОД(8,12)) ,
поскольку НОД(8,12) = 4 и
Пусть / — наименьший идеал, содержащий целые числа а и Ь. Тогда каждый
элемент идеала / имеет вид am + Ъп, где тип — целые числа. При этом
говорят, что идеал / порожден элементами а и 6. По теореме 20.22 идеал I
порожден наименьшим положительным целым числом такого вида. Но это число,
как упоминалось ранее, является наибольшим общим делителем чисел а и Ь.
Эту идею можно обобщить на случай идеала, порожденного любым конечным
множеством положительных целых чисел. И опять этот идеал будет порожден
наибольшим общим делителем всех этих чисел. ?
Доказательство следующей теоремы предоставляется читателю.
ТЕОРЕМА 20.24. Идеал / кольца R с единицей совпадает с R тогда и только
тогда, когда 1, мультипликативная единица кольца R, принадлежит идеалу /.
ТЕОРЕМА 20.25. Поле не содержит собственных идеалов.
ОПРЕДЕЛЕНИЕ 20.26. Идеал / коммутативного кольца R называется про-
простым идеалом, если ab E / имеет следствием, что а е I или b Е /.
ТЕОРЕМА 20.27. В кольце целых чисел идеал (а) является простым идеалом
тогда и только тогда, когда а — простое число.
ДОКАЗАТЕЛЬСТВО. Предположим, что число а не является простым, например,
а = rs, где г и s — целые числа, каждое из которых больше 1. Тогда число а
принадлежит идеалу (а), однако, числа г и s этому идеалу не принадлежат. Если
число а — простое и rs E (а), то а делит rs; следовательно, по теореме 3.43, а
делит г или а делит s. Поэтому либо г принадлежит идеалу (а), либо s принад-
принадлежит (а). ¦
ОПРЕДЕЛЕНИЕ 20.28. Область целостности D является областью главных
идеалов, если каждый идеал в области D является главным идеалом.
Было уже показано, что Z, область целостности целых чисел, является об-
областью главных идеалов.
ОПРЕДЕЛЕНИЕ 20.29. Если А — коммутативное кольцо с единицей, то пусть
Л* обозначает множество {а е А : существует b е А такое, что ab = 1}.
Подмножество А* является группой относительно умножения, которая назы-
называется группой делителей единицы кольца А. Каждый элемент множества
А* называется делителем единицы кольца А. В кольце с единицей элемент s
называется неприводимым, если он ненулевой, не равен единице и не может
быть выражен как произведение двух элементов, не являющихся делителями
единицы.

796 ГЛАВА 20. Кольца, области целостности и поля
В области целостности Z имеем ab = 1 только тогда, когда a = b = 1 или
a = b = -1, поэтому 1 и -1 — делители единицы области целостности Z. В поле
каждый ненулевой элемент является делителем единицы, поскольку a • а = 1
для а^О.
ПРИМЕР 20.30. Множество Z6 = {[0], [1], [2], [3], [4], [5]} — коммутативное кольцо
с единицей [1] и нулем [0]. Таблица умножения в Z6 имеет вид
0
[0]
[1]
[2]
[3]
[4]
[5]
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[1]
[0]
[1]
[2]
И
[4]
[5]
[2]
[0]
[2]
[4]
[0]
[2]
[4]
И
[0]
[3]
[0]
[3]
[0]
[3]
14]
[0]
[4]
[2]
[0]
[4]
12]
[5]
[0]
[5]
[4]
[3]
И
[1]
Таблица показывает, что [3] 0 [2] = [0], но [3] | [0] и [2] | [0], так что [3] и
[2] — ненулевые делители элемента [0]. Таким образом, Zq не является областью
целостности. ?
Как показывает предыдущий пример, в Z6 свойство сокращения не удовле-
удовлетворяется, поскольку [3] 0 [1] = [3] = [15] = [3] 0 [5] и, хотя [3] ф [0], имеем
[1] ф [5]. Делители единицы Zq соответствуют целым числам, взаимно простым
с 6; поэтому, как следует из приведенной выше таблицы умножения, делителями
единицы кольца Z6 являются [1] и [5].
В кольце Z5 = {[0], [1], [2], [3], [4]} с единицей [1] и нулем [0] каждый нену-
лувой элемент Z5 представляет собой делитель единицы, поскольку является
взаимно простым с простым числом 5. Следовательно, каждый элемент имеет
обратный элемент, поэтому Z5 — поле. Таблица результатов операций для Z5
дана в примере 3.61.
¦ УПРАЖНЕНИЯ
1. Докажите, что если F — поле, то уравнение ax = b имеет в поле единствен-
единственное решение.
2. Элемент а кольца R называется делителем нуля, если в кольце R суще-
существует такой элемент Ь, что ab = 0. Докажите или опровергните, что сумма
двух элементов, каждый из которых не является делителем нуля, не будет
делителем нуля.
3. Докажите или опровергните, что в кольце R произведение двух элементов,
каждый из которых не является делителем нуля, не будет делителем нуля.
4. Что представляют собой делители нуля в Zio?
5. Что представляют собой делители нуля в Z7?
6. Докажите теорему 20.25. Поле не содержит собственных идеалов.
7. Докажите теорему 20.3. Пусть R — коммутативное кольцо с единицей. Коль-
Кольцо R является областью целостности тогда и только тогда, когда из того, что
ab = ас, следует, что b = с для всех 6, с и ненулевых а из R.

РАЗДЕЛ 20.2. Области целостности 797
8. Пусть М — кольцо BхJ-матриц вида ~ . Докажите, что множество
\ а Ъ ] ..
всех матриц вида а п является идеалом кольца М.
9. Докажите, что сумма идеалов I и J коммутативного кольца R, определен-
определенного соотношением / + J = {г + j | г е / и j G J}, является идеалом кольца
R.
10. Пусть А = A4) и В = A6). Найдите АпВ и А + В.
11. Опишите наименьший идеал целых чисел, содержащих числа 6, 9 и 12.
12. Докажите, что если / — идеал кольца R и — 1 е /, то / = R.
13. Пусть f : R—> R' — гомоморфизм колец. Докажите, что f(R) — кольцо.
14. Пусть / : R —> R' — гомоморфизм колец. Докажите, что если R — поле, то
f(R) — поле.
15. Пусть f : R —> R' — гомоморфизм колец. Если R — область целостности, то
является ли областью целостности /(Д)?
16. Пусть f : R —> R' — гомоморфизм колец. Докажите, что {х Е R | f(x) = 0}
— идеал кольца R.
17. Докажите или опровергните, что делители нуля коммутативного кольца R
образуют идеал кольца R.
18. Образует ли множество полиномов с целыми коэффициентами область це-
целостности?
19. Элемент а кольца R называется идемпотентом, если а2 = а. Докажите, что
если R — область целостности, то идемпотентами будут только элементы О
и 1.
20. Докажите теорему 20.24. Идеал / кольца R совпадает с R тогда и только
тогда, когда 1, мультипликативная единица кольца Д, принадлежит /.
21. Докажите, что для любых элементов а, Ь кольца R имеют место равенства
а(-Ь) - -(ab) = (-a)b и (-а)(-6) = ab.
20.2. ОБЛАСТИ ЦЕЛОСТНОСТИ
ОПРЕДЕЛЕНИЕ 20.31. Говорят, что область целостности D является гауссо-
гауссовым кольцом, если выполнены следующие условия:
а) если элемент области D не нуль и не делитель единицы, то его можно
представить в виде произведения конечного числа неприводимых элемен-
элементов;
б) если элемент области D имеет разложения р\ • • -рг и q\ - • -qs в виде про-
произведения неприводимых элементов, то г = s и qj можно перенумеровать,
так что pi и qi для всех г будут отличаться делителем единицы, т.е.
Pi = aiqi для некоторого делителя единицы п{.

798 ГЛАВА 20. Кольца, области целостности и поля
Известно, что множество целых чисел является гауссовым кольцом. Простое
число было определено как число, у которого нет нетривиальных множителей.
Иными словами, простое число неприводимо. Альтернативное определение про-
простого числа сводится к тому, что р — простое число тогда и только тогда, когда
из того, что р | аб, следует, что р \ а или р | Ь. Для целых чисел эти определе-
определения эквивалентны, но в случае произвольных областей целостности это неверно.
Например, пусть А — множество всех комплексных чисел вида
a +
Легко показать, что А — область целостности и что
21 = 3 • 7 = A + 2y/bi){\ ~
Все эти множители неприводимые, и, следовательно, А не является гауссовым
кольцом. Однако, ни один из этих множителей не является простым согласно
альтернативному определению простого числа.
ОПРЕДЕЛЕНИЕ 20.32. Коммутативное кольцо А с единицей назывется упоря-
упорядоченным кольцом тогда и только тогда, когда существует непустое подмно-
подмножество А+ кольца А, называемое подмножеством положительных элементов
кольца А таких, что
а) если a,b e A+, то a 4- b Е A+\
б) если a,b Е А+, то а • b Е А+;
в) для заданного элемента а е А выполняется одно и только одно из перечис-
перечисленных ниже альтернативных условий:
(i) aGi+;
(ii) a = 0;
(iii) -a ? A+.
Говорят, что коммутативное кольцо с единицей, которое содержит такое мно-
множество А+, удовлетворяет аксиоме трихотомии. Если а Е А+, то будем говорить,
что а > 0. Если —а Е А+, то будем говорить, что а < 0.
Доказательство приведенной ниже теоремы предоставляется читателю.
ТЕОРЕМА 20.33. Каждое упорядоченное кольцо является областью целостности.
Для любого заданного а^0 имеем а2 > 0. В частности, I2 > 0 и, следовательно,
ОПРЕДЕЛЕНИЕ 20.34. Упорядоченная область целостности А называется
вполне упорядоченной тогда и только тогда, когда любое непустое подмно-
подмножество S множества А+ имеет первый элемент, т.е. существует такой элемент
s Е 5, что если t < 5, то t ? S.

РАЗДЕЛ 20.2. Области целостности 799
Было уже показано, что целые числа образуют вполне упорядоченную об-
область целостности.
ТЕОРЕМА 20.35. Если А — вполне упорядоченная область целостности, то не
существует такой элемент с области А, что 0 < с < 1.
ДОКАЗАТЕЛЬСТВО. Пусть S — подмножество всех таких элементов с из мно-
множества Л, что 0 < с < 1. Если S не пусто, то существует наименьший элемент s
из 5. Но 52 принадлежит А\ и учитывая, что s > 0, получаем s2 > 0. Поскольку
из условий s < 1, 0 < s следует, что s2 < s, то имеем 0 < s2 < s. Поэтому s2 G S
и 52 < 5, что противоречит тому факту, что s — наименьший элемент множества
5. Следовательно, S — пустое множество. ¦
ОПРЕДЕЛЕНИЕ 20.36. В упорядоченной области целостности пусть п + 1 =
п + 1, где 1 — мультипликативная единица.
ТЕОРЕМА 20.37. В любой упорядоченной области целостности А для подмноже-
подмножества положительных элементов А+ следующие утверждения эквивалентны:
1) Первый принцип индукции.
2) Принцип полного упорядочения.
3) Второй принцип индукции.
ДОКАЗАТЕЛЬСТВО. A) -+ B). Пусть S = {п ? А+: если п е Т, где Т -
подмножество множества А+, то Т имеет наименьший элемент }. Необходимо
показать, что 5 = А+. Очевидно, 1 е 5, так как если 1 G Т, то 1 — наименьший
элемент множества Т. Предположим, что к е S и пусть к + 1 е Т. Требуется
показать, что множество Т содержит наименьший элемент. Если 1 е Т, то Г
содержит наименьший элемент, что и требовалось доказать. Предположим, что
1 ? Г. Пусть V = {s : s + 1 G Г}. Поскольку /с е Г', то V имеет наименьший
элемент, например, г. По определению, r + 1 G Т. Кроме того, г + 1 — наименьший
элемент множества Т. В противном случае, если ugTh u<r + l, то в силу
того, что u = v + 1 для некоторого г> G Т', получаем, что v < г, что является
противоречием. Следовательно, множество Т имеет наименьший элемент, fc + lE
5 и 5 = А+.
B) —> C). Предположим, что 5 — подмножество множества А+, обладающее
следующими свойствами:
а) 1 е 5;
б) если к G А+ и s G 5 для всех s < к, то к Е 5.
Требуется показать, что 5 = А+. Выберем подмножество 5 с перечисленными
выше свойствами. Пусть Т = {п : п е А+ и п ? S}. Теперь необходимо показать,
что множество Т пустое. Если Т не пусто, то по принципу вполне упорядоче-
упорядочения Т содержит наименьший элемент, например, ?, причем t ф 1, потому что 1
принадлежит множеству 5, a t ему не принадлежит. Следовательно, t = г + 1
для некоторого г. Множество всех таких х е А+, что х < ?, не пусто, т.к. ему
принадлежит г. Все эти элементы принадлежат 5, поскольку t — наименьшее

800 ГЛАВА 20. Кольца, области целостности и поля
положительное целое число, которое не принадлежит 5. Следовательно, соглас-
согласно пункту (б) имеем t e S, что является противоречием, поэтому множество Т
пусто.
C) —> A). Пусть S — подмножество А+. Пусть рA) есть утверждение: "га Е 5
имеет следствием (га + 1) Е 5", а рB) есть утверждение: "Если для всех га < и
имеем га Е 5, то га Е 5". Очевидно, что из рA) вытекает рB). Второй принцип
индукции можно сформулировать так: "Если 1 Е S и рB), то 5 = Л+", а первый
принцип индукции можно сформулировать таким образом: "Если 1 Е 5 и рA),
то 5 = А+". Поскольку 1 Е 5 и рA) имеет следствием 1 е 5 и рB), то из
утверждения:  € 5 и рB) имеет следствием 5 = А+" вытекает утверждение
 Е 5 и рA) имеет следствием 5 = А4")". (Это верно, потому что (р —> q) =^
((Я - г) -+ (р -> г)).) ¦
ТЕОРЕМА 20.38. Любые две вполне упорядоченные, упорядоченные области це-
целостности являются изоморфными, поэтому они изоморфны Z.
ДОКАЗАТЕЛЬСТВО. Пусть А — вполне упорядоченная, упорядоченная область
целостности и N — множество положительных целых чисел. Пусть / — муль-
мультипликативная единица области целостности А. Определим f : N -+ Л+ соотно-
соотношением /A) = /, и если f(k) = К, то f(k + 1) = К + I. Легко показать, что
f(N) удовлетворяет первому принципу индукции и, следовательно, f(N) = Л+.
Необходимо показать, что /(га + п) = /(га) + /(п) и /(га • и) = /(га)/(п).
Используя индукцию по п, покажем сначала, что /(га + га) = /(га) + /(п).
Для га = 1, /(га 4-1) = /(га) + / по определению функции /, поэтому /(га Ч-1) =
/(га) + /A). Предположим, что /(га + fc) = /(га) + f(k). Тогда
/(га + (к + 1)) = /((га + к) + 1) =
= /(га + *;) + / =
= /(т)+ /(*:)+/ =
и для любых га, га Е N
/(т + п) = /(т) + /(п).
Индукцией по га покажем, что /(га • га) = /(га)/(га). При га = 1
Предположим, что f(m ¦ к) = f(m)f(k). Тогда
/(т ¦ (fc + 1)) = /((т • к) +т) =
= f{m ¦ к) + /(т) =
- /(m)/(fc) + /(т) =
= f(m)S(k) + S(m)I =
и /(га • га) = /(га)/(га) для всех га, га Е N. Поэтому функция / — изоморфизм.
Этот изоморфизм легко расширить до изоморфизма из Z в А. Ш

РАЗДЕЛ 20.3. Полиномы 801
ОПРЕДЕЛЕНИЕ 20.39. Область целостности называется минимальной обла-
областью тогда и только тогда, когда она не содержит никакой подобласти, кроме
самой себя.
Минимальную область можно найти, построив пересечение всех подобластей
области целостности. Доказательство следующей теоремы оставляем читателю.
ТЕОРЕМА 20.40. Любые две упорядоченные минимальные области целостности
изоморфны. Они изоморфны целым числам и, следовательно, вполне упорядоче-
упорядочены.
¦ УПРАЖНЕНИЯ
1. Докажите, что пересечение всех подобластей произвольной области целост-
целостности является областью целостности, и используйте этот факт для дока-
доказательства того, что каждая область целостности содержит минимальную
область целостности.
2. Докажите, что любые две упорядоченные минимальные области целостности
изоморфны. Докажите, что они изоморфны множеству целых чисел, поэтому
вполне упорядочены.
3. Докажите, что в упорядоченной области целостности для любого ненулевого
элемента а имеем а2 > 0. В частности, 1 > 0 (теорема 20.33).
20.3. ПОЛИНОМЫ
В этом разделе будут формально определены полиномиальные формы и изучены
некоторые их алгебраические свойства. Полиномиальные функции f(x) и д(х)
равны при условии, что /F) = д(Ь) для всех b из их общей области определения.
Полиномиальные формы / и д равны при условии, что равны коэффициенты при
соответствующих степенях х. Для полиномов над целыми числами эти два по-
понятия совпадают; однако, в общем случае коммутативных колец с единицей это
неверно. В конце раздела будет показана согласованность этих двух понятий ра-
равенства. Большинство из приведенных ниже рассуждений изложено в терминах
коммутативных колец с единицей и областей целостности, однако, использовать-
использоваться будут, как правило, кольца целых или рациональных чисел. Для простоты, в
большей части последующего изложения можно представлять себе А как множе-
множество целых чисел.
В дальнейшем станет понятно, что фактически полиномы определяются как
производящие функции.
ОПРЕДЕЛЕНИЕ 20.41. Пусть А — коммутативное кольцо с единицей и пусть
S — множество всех последовательностей (ao,ai,a2,...) элементов кольца А
таких, что если / е 5, то существует целое число N/, так что aj = 0 для
всех j > N/. Если / е 5, то говорят, что / — полином, или полиномиальная
форма над кольцом А.

802 ГЛАВА 20. Кольца, области целостности и поля
Например,
A,0,0,0,0,...) и A,1,1,0,0,0,...)
принадлежат 5, но
A,1,1,1,1,1,1,1,...) и A,0,1,0,1,0,1,0,1,...)
множеству S не принадлежат. Если А = Z, то
@,-5,2,0,0,...) и C,7,5,8,0,0,...)
являются полиномами из 5.
ОПРЕДЕЛЕНИЕ 20.42. Пусть А — коммутативное кольцо с единицей и пусть
/ = (а;)* = (ао,аьа2,...), и д = F*)* = (Ьо, Ьи Ь2,...) принадлежат 5, мно-
множеству полиномов над кольцом А. Определим сумму полиномов / и д как
последовательность / -4- д = (а; 4- &;)* = (а0 4- fro, «i + Ьь • • •) и произведение
полиномов / и g как последовательность fg = (с^)*, где с^ =
= ]Г
ТЕОРЕМА 20.43. Пусть f,g € S, где 5 — множество полиномов над коммутатив-
коммутативным кольцом А с единицей. Тогда f + geSufgeS.
ДОКАЗАТЕЛЬСТВО. Случай суммы / + g мы оставляем читателю. Для доказа-
доказательства того, что fg G S, заметим, что для любого к > Nf + Ng + 1, если i+j = fc
и г < iV/, то j > ЛГр +1, и если j < Ng, то г > N/ 4-1. Следовательно, с^ = 0 для
любого к > Nf + Ng +1, поскольку в выражении для с^ либо а^ = 0, либо bj = 0.
¦
Доказательство следующей теоремы оставляем читателю.
ТЕОРЕМА 20.44. Если S — множество полиномов над коммутативным кольцом
А с единицей, то 5 — также коммутативное кольцо с единицей. Его единицей
является A,0,0,0,...), а нулевым элементом — @,0,0,...).
ОПРЕДЕЛЕНИЕ 20.45.
а) Пусть А — коммутативное кольцо с единицей, пусть / Е S и / = (а*)*.
Для / ф 0 пусть deg(/) равно наибольшему целому числу к такому, что
ак ф 0. Функция deg(/) называется степенью полинома /. Множество
S называется кольцом полиномов над кольцом А. Множество 5 обо-
обозначается через А[х]. Произвольный элемент множества А[х] называется
полиномом над кольцом А. Любой полином степени 0 или равный нулю
называется константой.
б) Пусть / = (ao,aba2,...) принадлежит А[х]. Члены последовательности
ai называются коэффициентами полинома /. Если f ф 0 и п = deg(/),
то ап называется старшим коэффициентом полинома /. Если ап = 1,
то полином / называется нормированным. Если / ф 0 обладает таким
свойством, что наибольший общий делитель всех его ненулевых коэффи-
коэффициентов равен единице, то / называется примитивным полиномом.

РАЗДЕЛ 20.3. Полиномы 803
в) Два элемента / и д множества А[х] равны (/ = д), если равны их соответ-
соответствующие коэффициенты; т.е. если / = (ао, ах, а2,...) и д = (Ьо, 61,62,.. .)>
то / = д тогда и только тогда, когда а* = bi для любого неотрицательного
целого числа г.
г) Полином / делит полином g в том случае, если существует такой поли-
полином /г, что fh = g.B этом случае говорят, что / и h являются делителями
полинома д.
Например, если
/ = @,1,1,0,1,0,0,...),
то deg(/) = 4. Если
то deg(#) = 0 и д — константа. Тождественно нулевой полином
@,0,0,...)
не имеет степени. Предоставляем читателю доказать, что равенство есть отноше-
отношение эквивалентности на множестве А[х].
ТЕОРЕМА 20.46. Пусть А — коммутативное кольцо с единицей, пусть А[х] —
кольцо полиномов над кольцом А и пусть / и д принадлежат А[х].
а) Если f,g ф 0, то deg(/ + д) < max(deg(/),deg(p)).
б) Либо fg = 0, либо deg(fg) < deg(/) + deg(g).
в) Если А — область целостности, то либо fg = 0, либо deg(fg) = deg(/) 4-
г) Если А — область целостности, то А[х] — также область целостности.
ДОКАЗАТЕЛЬСТВО.
а) Пусть / = (ао,ах,а2,...) и д = (Ь0,Ьх,Ь2,...). ГД^ п = deg(/) и т = deg(g).
Поскольку а{ = 0 для г > п и bj = 0 для j > m, то если к > max(m, n), то
ак+Ьк = 0 и deg(/ + ^) < max(deg(/), deg(y)).
б) Пусть п = deg(/), т = deg(g) и fg = (с0, сь с2,...), так что ск = Yl a*bj-
i+j=k
Произведение aibj = 0, когда i > п, поскольку а^ = 0. Если i <n w i + j >
т + п, то j > т + (п — г), поэтому bj = 0 и, в любом случае, с^ = 0.
Следовательно, deg(fg) < deg(/) -hdeg(p).
в) Согласно пункту (б) deg(/#) < deg(/) + deg(^). Однако, поскольку ап и
Ьт не равны 0, то cn+m = anbm не равно 0. Следовательно, deg(fg) >
deg(/) 4-deg(^), и требуемое равенство доказано.
г) Пусть / и д — ненулевые элементы множества А[х] степени пит, соответ-
соответственно. Поскольку А — область целостности, то deg(/p) = deg(/) + deg(#)
и fg не равно 0.

804 ГЛАВА 20. Кольца, области целостности и поля
ТЕОРЕМА 20.47. Существует мономорфизм из Л в А[х], кольцо полиномов над
кольцом А, для которого образ кольца А является подкольцом кольца А[х]. Если
А — область целостности, то каждый делитель единицы в А[х] соответствует
делителю единицы в А согласно мономорфизму.
ДОКАЗАТЕЛЬСТВО. Определим функцию ф : А —> А[х] следующим образом:
если a G А, то пусть ф(о) = (а, 0,0,0,...). Если а и 6 принадлежат А, то
ф(а + Ь) = (а+ 6,0,0,0,0,...) =
= (а,0,0,0,0,...) + (Ь,0,0,0,0,...) =
= ф(а) + ф{Ь),
ф(а.Ь) = (а- 6,0,0,0,...) =
= (а, 0,0,0,...).F,0,0,0,...) =
= 0(а) • Ф(Ь).
Кроме того, ф{\) = A,0,0,0,...) = 1. Следовательно, ф — гомоморфизм из Л в
А[х].
Если (с, 0,0,0,...) = ф(с) = 0 = @,0,0,0,...), то с = 0. Если ф(а) = ф(Ь),
то ф(а) — ф(Ь) = 0; т.е. ф(а — 6) = 0 и а — 6 = 0. Поэтому а = 6, и функция 0 —
инъекция.
Напомним, что делитель единицы кольца — это элемент, который имеет
обратный элемент; т.е. если 6 — делитель единицы, то существует такой элемент
б, что 6-б = 1.
Предположим, что А — область целостности и / — делитель единицы в А[х].
Пусть д — соответствующий обратный элемент, поэтому fg = l = A,0,0,0,...).
Но 0 = deg(fg) = deg(f) + deg(g), откуда следует, что deg(/) и deg(#) — обе
равны 0. Таким образом, / = (а, 0,0,0,...) и д = F,0,0,0,...) для некоторых
а, 6 G А. Поскольку
ф(а. 6) = /fl = A,0,0,0,...) = 0A)
и, учитывая, что ф — инъекция, получаем, что аЪ = 1, поэтому а и 6 — делители
единицы области целостности А.
Поскольку мономорфный образ ф{А) в кольце А[х] является кольцом, изо-
изоморфным кольцу А, то А можно отождествить с ф(А) как подкольцом кольца
А[х] и считать А подкольцом кольца А[х]. Ш
ОПРЕДЕЛЕНИЕ 20.48. Символ Кронекера — Sij — для целых чисел г и j
определяется соотношениями:
l,
0, если г ф j.

РАЗДЕЛ 20.3. Полиномы 805
Например, если / = (а0, аь а2,...), гДе ai = из, то
/ = @,0,0,1,0,0,...).
5
Если д= 52 (Sij)*, то
3 = 1
^ = @,1,1,1,1,1,0,0,...).
ТЕОРЕМА 20.49. Если х = @,1,0,0,0,...) = (с»)*, где а = 8цу то для каждого
к > 0 имеем хк = (ao,ai,a2,...), где а* = 5^.
ДОКАЗАТЕЛЬСТВО. При к = 1 теорема, очевидно, справедлива. Предположим,
что теорема справедлива для к = п. Поскольку xn+1 = х -хп, то простое умноже-
умножение показывает, что г-ый член в последовательности xn+1 равен <^}П+1- ¦
Если a G А и / = (ао,ах,а2,...)» то а/ — (аао,аа!,аа2,...). В частности,
если а € Л, то ахк = @,0,0,... ,а,0,0,0,...), где а находится на (/с-Ы)-ом месте.
Пусть / G А[х] имеет степень п. Тогда
/ = (ао,аьа2,...,ап,0,0, •••) =
= а0 4- а\х + а2х2 Н Ь апхп .
ОПРЕДЕЛЕНИЕ 20.50. Пусть А — коммутативное кольцо с единицей и пусть
А[х] — множество полиномов над кольцом А. Символ х назовем переменной
над кольцом А. С каждым полиномом
/ = а0 + aix + а2х2 Н Ь ап^п € Л[х]
связана функция из Л в А вида
/(х) = ао 4- а\х -Ь а2х2 4- • • • + апхп
или
f(x) = апхп Н Ь а2х2 4- а^ 4- а0,
которая называется полиномиальной функцией. Пусть А{х) = {/(х) : f ? S}.
Степень функции /(х) совпадает со степенью соответствующего полинома
/ Е А[х]. Элементы / множества А[х] будем называть полиномиальными
формами, чтобы иметь возможность отличать их от полиномиальных функ-
функций.
Определим функцию в : А[х] —> А(х) соотношением #(/) = /(х). Легко
показать, что отображение в, которое устанавливает соответствие между эле-
элементами множества А[х] и соответствующими полиномиальными функциями из
А(х), представляет собой гомоморфизм. Поскольку отображение в — сюръекция,
оно является также эпиморфизмом. Таким образом, все свойства множества А[х],

806 ГЛАВА 20. Кольца, области целостности и поля
сохраненные гомоморфизмом, перенесены на коммутативное кольцо полиномиаль-
полиномиальных функций А(х). Вскоре будет показано, что если А — бесконечная область
целостности, то в : А[х] —> А(х) — изоморфизм.
ОПРЕДЕЛЕНИЕ 20.51. Пусть А — коммутативное кольцо с единицей. Если
/(ж) = anxn Н Ь а2х2 + aYx + а0
и
д(х) = bnxn + -•• + b2x2 + Ьхх + Ь,
где некоторые из а{ и 6; из А могут быть 0, включая ап или Ьп, то
/(ж) + д(х) = (ап + Ъп)хп + ... + (п1+ Ьг)х + (а0 + 60)
и
f{x)g(x) = cmxm H + с2х2 + cix + с0,
Будем говорить, что /(ж) = д(х) тогда и только тогда, когда f(b) = g(b) для
всех b е А. Решением уравнения /(ж) = 0 называется элемент а ? А такой,
что /(а) = 0.
На основании вышесказанного мы можем сформулировать следующую тео-
теорему относительно полиномиальных функций над областью целостности А.
ТЕОРЕМА 20.52. Если /(ж) и д(х) — полиномиальные функции над областью
целостности А, степень /(ж) равна п, а степень р(ж) равна т, то
а) степень /(ж) -f #(ж) меньше или равна, чем max{m,n};
б) степень f(x)g(x) равна т Н- п.
Согласно определению две полиномиальные формы f и д равны тогда и толь-
только тогда, когда равны их коэффициенты. Две полиномиальные функции f(x) и
д(х) по определению равны тогда и только тогда, когда /(Ь) = д(Ь) для всех b e А.
В следующем разделе для полинома / степени п будет показано, что уравнение
/(ж) = 0 имеет не более п решений. Сейчас без доказательства сформулиру-
сформулируем теорему, утверждение которой используем для доказательства более слабого
результата.
ТЕОРЕМА 20.53. Если / — полином степени п над бесконечной областью це-
целостности и /(ж) — соответствующая полиномиальная функция, то уравнение
/(ж) = 0 имеет не более п решений.
СЛЕДСТВИЕ 20.54. Пусть /(ж) = апхп Н Ь а2х2 + агх + а0 — полиномиальная
функция над бесконечной областью целостности А. Если /(а) = 0 для всех а € А,
то ао — а\ = а2 = - - - = ап = 0.
ТЕОРЕМА 20.55. Пусть /ид — полиномы над бесконечной областью целостности
А. Тогда f = g тогда и только тогда, когда соответствующие полиномиальные
функции /(ж) и д(х) обладают таким свойством, что f(b) = д(Ь) для всех b e А.

РАЗДЕЛ 20.3. Полиномы 807
ДОКАЗАТЕЛЬСТВО. Если / и д — полиномы над областью целостности А такие,
что / = д, то очевидно, /(&) = д(Ь) для всех Ь ? А. Пусть
f{x) = апхп -Ь • • • + d2# -f- ^ix -f cio
р(х) = 6пхп 4- h
— полиномиальные функции степени пит, соответственно, и /(с) = д(с) для
каждого с е А. Пусть f и д — соответствующие полиномы. Тогда полиномиальная
функция h(x) = csxs -f • • • + с2х2 -f с\х -f с, где s = max(n,m) и с* = а; -
6i, обладает свойством: /i(c) = /(с) — #(с) = 0 для всех с € А. Но, согласно
предыдущему следствию, если h(c) = 0 для всех с из Л, то /i(rr) должен быть
нулевым полиномом. Поэтому с» = а* — Ь» = 0 или а* = 6i для г> 1 и f = д. Ш
Из предыдущей теоремы непосредственно следует теорема, упоминавшаяся
нами ранее.
ТЕОРЕМА 20.56. Пусть А — бесконечная область целостности, определим в :
А[х] —> А(х) соотношением 0(/) = f(x). Тогда функция 0 является изоморфизмом.
Следующий пример демонстрирует, что для справделивости приведенных вы-
выше следствия и теоремы существенно, чтобы область целостности А была беско-
бесконечной.
ПРИМЕР 20.57. Множество Z5 = {[0], [1], [2], [3], [4]} классов вычетов по модулю 5
является полем, поэтому по теореме 20.8 представляет собой область целостности.
По теореме Ферма, если для простого числа р имеем а ф 0 (modp), то ар~1 =
1 (modp). Тогда ар = a (mod p) для любого целого числа а, даже если а =
0 (modp). Для р = 5 имеем а5 = a (mod 5) для всех а G Z. Это сравнение
равносильно [а]5 = [а] или [а]5 - [а] = [0] для любого целого числа а. Таким
образом, если д(х) = хъ—х, то д(х) = [0] выполняется для любого х из Z5. Однако,
если h — полином, равный нулю, то h(x) = [0] для всех х из Z$. Полиномы
д и h не равны, но g(b) = h(b) для всех Ь из области целостности Z. Таким
образом, над конечной областью целостности равенство полиномиальных форм не
эквивалентно равенству полиномиальных функций. С другой стороны, поскольку
множество целых чисел бесконечно, то понятия равенства для полиномиальных
форм и полиномиальных функций над Z совпадают. ?
¦ УПРАЖНЕНИЯ
1. Докажите теорему 20.44.
2. Покажите, что равенство на множестве 5 в определении 20.45 есть отноше-
отношение эквивалентности.
3. Докажите или опровергните: пусть /ид — полиномы над коммутативным
кольцом А. Если /, д ф 0, то
deg(/ + g) = max (deg(/), deg(g)) .

808 ГЛАВА 20. Кольца, области целостности и поля
4. Найдите такие два полинома из множества полиномов над областью целост-
целостности Z\2 (т.е. коэффициенты полиномов принадлежат Z12), что deg(fg) <
deg(/) + deg(#).
5. Докажите или опровергните: для множества полиномиальных функций над
областью целостности Z6, если /(х) = д(х) для всех х, то соответствующие
полиномы равны.
20.4. АЛГЕБРЫ И ПОЛИНОМЫ
В этом разделе рассматриваются особые подкольца и подполя комплексных чи-
чисел. Они состоят из комплексных целых чисел, алгебраических целых чисел и
алгебраических чисел. В данном разделе будут изучены также другие свойства
полиномов, и для заданного поля F будут найдены такие расширения поля, что
полиномы, которые не могут быть разложены на множители в поле F, могут
быть разложены на множители в расширении этого поля. Напомним, что дели-
делитель единицы является делителем числа 1; т.е.элемент и — делитель единицы
при условии, что существует такой элемент и', что ии' — 1. Напомним также, что
каждый ненулевой элемент поля является делителем единицы.
В дальнейшем будет построена алгебраическая структура, которую мы за-
затем применим к полиномам. Все рассматриваемые кольца будут предполагаться
коммутативными.
ОПРЕДЕЛЕНИЕ 20.58. Поле F называется подполем поля F', если оно содер-
содержится в F' и имеет те же самые операции. Поле F1 называется расширением
поля F. В общем случае, поле F' называется расширением поля F, если су-
существует изоморфизм г) : F —> Е, где Е — подполе поля F'.
ОПРЕДЕЛЕНИЕ 20.59. Пусть А — область целостности. Ненулевой элемент а
из А называется неприводимым, если из того, что а = be, следует, что b
или с является делителем единицы; в противном случае элемент а называется
приводимым. Пусть А[х] обозначает множество полиномов с коэффициентами
из А. Полином / из А[х] с ненулевой степенью называется неприводимым,
если из того, что f = g-h, следует, что g или h — элемент области целостности
А\ в противном случае полином / называется приводимым.
Таким образом, если полином / приводимый, то существуют полиномы нену-
ненулевой степени g и h такие, что / = g • h.
Далее покажем, что определения неприводимости для областей целостности
и полиномов совпадают, если А — поле или рассмотрение ограничено нормиро-
нормированными полиномами.

РАЗДЕЛ 20.4. Алгебры и полиномы 809
ОПРЕДЕЛЕНИЕ 20.60. Полином / из множества А[х] называется простым,
если его степень больше 0, и всякий раз, когда / | д • h, то или / | д, или / | h.
Вообще, элемент р интегральной области является простым, если из того, что
р | ab, следует, что р \ а или р \ Ь.
Во множестве целых чисел простые числа и неприводимые числа совпадают.
Однако для некоторых колец полиномов это неверно.
ТЕОРЕМА 20.61. В области целостности простой элемент всегда неприводим.
ДОКАЗАТЕЛЬСТВО. Предположим, что р — простой элемент и р = аЬ\ тогда,
по определению, р \ а или р \ Ь. Предположим, что р \ а; тогда а = тр для
некоторого га. Далее, р — mpb = mbp, поэтому тЪ = 1 и b — делитель единицы.
Следовательно, элемент р — неприводимый. ¦
ОПРЕДЕЛЕНИЕ 20.62. Пусть А0 обозначает ненулевые элементы области це-
целостности А. Тогда А называется евклидовым кольцом, если существует такая
функция 0 : Л0 —> N, где N — множество положительных целых чисел, что
1. Если a,!) G А0, то ф(а) < ф(аЬ), или, что эквивалентно, если а \ с, то
ф(а) < ф(с).
2. Если а,Ь ? А0, то существуют q,r е А® такие, что а — bq + r и либо г = 0,
либо ф{г) < ф(Ь).
В евклидовом кольце А величина ф(а), где а е А0, называется нормой элемен-
элемента а.
ТЕОРЕМА 20.63. Пусть F — поле. Тогда F[x] — евклидово кольцо с нормой
ф(/) = deg(f) яля f e F[x].
ДОКАЗАТЕЛЬСТВО. Пусть Л0 = F[x] - {@)*}. Определим ф : А0 -» TV соотно-
соотношением </>(/) = deg(f), когда / ^ 0. Часть (а) следует из теоремы 20.46. Для
доказательства части (б) пусть / G F[x] — полином степени n, a g —- поли-
полином степени к. Пусть 5 — множество полиномов вида / — q • g. Если окажется,
что произвольный элемент множества 5 равен 0, то доказательство завершено.
В противном случае выберем один элемент с наименьшей степенью, например, г,
и пусть q — соответствующее частное. Степень этого элемента меньше, чем п,
потому что если старший коэффициент полинома b равен v, то выберем полином
степени п- к со старшим коэффициентом, равным с, так что vc — старший коэф-
коэффициент полинома а. В таком случае степень / — qg меньше, чем п. Аналогично,
если deg(r) не меньше, чем degF), то
где deg(r/) меньше, чем deg(r), поэтому

810 ГЛАВА 20. Кольца, области целостности и поля
где deg(r') < deg(r). Но это противоречит определению элемента г. Следователь-
Следовательно, deg(r) < deg(b). ¦
Следующая теорема является частным случаем теоремы 20.89, которая будет
доказана далее.
ТЕОРЕМА 20.64. Пусть F — поле и р Е F[x] — полином степени п. Тогда для
произвольного a Е F полином х — а будет делителем полинома р тогда и только
тогда, когда р(а) = 0.
ДОКАЗАТЕЛЬСТВО. Если х—а — делитель полинома р, то, несомненно, р(а) = 0.
Обратно, предположим, что р(а) = 0. По предыдущей теореме р = (х - а) • q + г,
где г е F. Поэтому р(а) = (а - а) • д + г = г и г = 0. Следовательно, (х — а) —
делитель полинома р. Ш
Использя две предыдущие теоремы и принцип индукции, приходим к следу-
следующему утверждению.
ТЕОРЕМА 20.65. Пусть F — поле ирЕ F[x] — полином степени п. Тогда урав-
уравнение р(х) = 0 имеет не более п решений.
Поскольку область целостности можно вложить в поле, то приходим к тако-
такому следствию.
СЛЕДСТВИЕ 20.66. Пусть А — область целостности и р Е А[х] — полином
степени п. Тогда уравнение р(х) = 0 имеет не более п решений.
ТЕОРЕМА 20.67. Любое евклидово кольцо А есть кольцо главных идеалов.
ДОКАЗАТЕЛЬСТВО. Пусть / — ненулевой идеал евклидового кольца А. Пусть d
— ненулевой элемент идеала / с минимальным значением нормы и пусть р ? I.
Однако, р = dq+r, где норма элемента г меньше, чем норма элемента d. Поскольку
г Е /, то элемент d имеет минимальную норму, а норма г меньше, чем норма d,
имеем г = 0 и р = dq. Следовательно, элемент d порождает I. Ш
СЛЕДСТВИЕ 20.68. Пусть F — поле, тогда F[x] — кольцо главных идеалов.
ОПРЕДЕЛЕНИЕ 20.69. Идеал / называется максимальным в кольце Д, если
для любого идеала J из того, что / С J С R, следует, что I = J или J = R.
ТЕОРЕМА 20.70. Идеал / из кольца главных идеалов является максимальным,
тогда и только тогда, когда р, порождающий элемент идеала /, является непри-
неприводимым над полем F.
ДОКАЗАТЕЛЬСТВО. Предположим, что идеал / — максимальный, и элемент р не
является неприводимым, например, р = rs. Тогда элемент р принадлежит идеалу
J, порожденному элементом г(или s), и / С J, что является противоречием.
Обратно, если элемент р приводимый и идеал / — не максимальный, напри-
например, / С J и элемент г порождает J, то р = rs для некоторого элемента 5, что
невозможно, поскольку элемент р — неприводимый. ¦

РАЗДЕЛ 20.4. Алгебры и полиномы 811
ТЕОРЕМА 20.71. Пусть / — идеал, принадлежащий кольцу R. Определим отно-
отношение ~ на R таким условием: а ~ 6 тогда и только тогда, когда a — b E /. В этом
случае отношение ~ есть отношение эквивалентности.
ДОКАЗАТЕЛЬСТВО. Отношение ~ имеет следующие свойства:
а) рефлексивность: а ~ а, поскольку 0 € /;
б) симметричность: если а ~ 6, то а-b е 1\ следовательно, Ь — а = —{а-Ъ) е /,
поскольку / — группа относительно сложения. Поэтому Ъ ~ а\
в) транзитивность: пусть а ~ Ъ и Ъ ~ с, так что a- b е I к b - с е I. Поэтому
(а - 6) + (Ь - с) = а - се I.
Таким образом, а ~ с. ¦
ТЕОРЕМА 20.72. Если а ~ Ь и с ~ d, то а + с~ b + d и ас ~ bd.
ДОКАЗАТЕЛЬСТВО. Если а ~ b и с ~ d, то a-beluc-del, тогда
(а - Ь) + (с - d) = (а + с) - (Ь + rf) G /
и а4-с ~ 6-f d. Кроме того, с(а-Ъ) = ас —be e / и b(c-d) = bc-ad e /, поскольку
/ — идеал. Следовательно, (ас — be) + Fс — 6d) = ас — bd G I и ас ~ bd. Ш
Теперь можно определить сложение и умножение между классами отноше-
отношения эквивалентности. Если а +1 обозначает класс эквивалентности, содержащий
элемент а, и если b + I — класс эквивалентности, содержащий элемент 6, то
определим
Когда есть возможность умножать и складывать классы эквивалентности,
то, как отмечалось ранее, отношение называется отношением конгруэнтности.
Кольцо классов эквивалентности обозначается через R/I. Заметим, что 0 4- / —
это нулевой элемент кольца, а 1 + / — мультипликативная единица. Класс экви-
эквивалентности а + I называется левым смежным классом идеала /, точнее говоря,
левым смежным классом, порожденным элементом а. Следовательно, различные
левые смежные классы идеала / — это именно классы эквивалентности в R/I.
ТЕОРЕМА 20.73. Пусть R — коммутативное кольцо с единицей и/- идеал коль-
кольца R. В этом случае R/I — поле тогда и только тогда, когда / — максимальный
идеал.
ДОКАЗАТЕЛЬСТВО. Предположим, что идеал / — максимальный и пусть а +1 ?
R/I, где а ? I. Пусть М — {га + 6|гейибЕ/}. Можно непосредственно
показать, что М ¦— идеал. Поскольку а ? /, получаем, что М с I и М = R.
Следовательно, 1 е М и существуют элемент b из R и элемент с из / такие, что
1 = ab + с. Таким образом, 1+/ = а6 + /=(а + /)F -h /) и элемент а + I имеет
обратный элемент. Следовательно, R/I — поле.

812 ГЛАВА 20. Кольца, области целостности и поля
Обратно, предположим, что R/I — поле. Допустим, что существует такой
идеал J, что I с J С. R. Рассмотрим элемент a 4- /, где элемент а принадлежит
J, но не принадлежит /. Тогда существует такой элемент о! из Д, что о! 4- / —
элемент, обратный элементу a 4- /, откуда получаем, что aa' + / = 1 4- /. Более
того, поскольку J — идеал, то aa' Е J. Кроме того, 1 = aa! Л-с для некоторого с из
/. Поскольку aa! и с принадлежат J, то 1 принадлежит J. Но если 1 принадлежит
J, то rl принадлежит J для всех г, и J = Я. ¦
ТЕОРЕМА 20.74. Пусть i? — коммутативное кольцо с единицей. В этом случае
R/I — область целостности тогда и только тогда, когда I — простой идеал.
ДОКАЗАТЕЛЬСТВО. Если R/I — область целостности и ij — элемент идеала /,
то ij 4- / = 0 4- /. Следовательно, (г 4- I)(j -f /) = 0 -f I. Но поскольку R/I —
область целостности, то либо г -f /, либо j + / равняется 0 + /. Следовательно,
либо г G /, либо j ? I, и I — простой идеал.
Обратно, если / — простой идеал и (г + I)(j -f /) = 0, то ij 4- / = 0 и ij G /.
Но поскольку / — простой идеал, то г Е / или j Е /; поэтому, г + / = 0 или
j 4- / = 0, и / — область целостности. ¦
ТЕОРЕМА 20.75. Любой максимальный идеал является простым идеалом.
ДОКАЗАТЕЛЬСТВО. Доказательство следует непосредственно из теорем 20.73
и 20.74. ¦
ТЕОРЕМА 20.76. В кольце главных идеалов А каждый неприводимый элемент
является простым.
ДОКАЗАТЕЛЬСТВО. Пусть р — неприводимый элемент кольца А и пусть (р) —
главный идеал, порожденный элементом р. Поскольку элемент р неприводим,
то по теореме 20.70 (р) — максимальный идеал и, вследствие теоремы 20.75,
является простым идеалом. Поэтому, если р | (ab), то ab E (р). Таким образом,
а Е (р) или 6 Е (р), так что р \ а или р \ 6, и элемент р — простой. ¦
Комбинируя следствие 20.68 и теорему 20.76, получаем следующий резуль-
результат.
СЛЕДСТВИЕ 20.77. Если F — поле, то каждый неприводимый элемент множества
F[x] является простым.
Следующая теорема является аналогом принципа единственности разложе-
разложения целого числа на простые множители.
ТЕОРЕМА 20.78. Если F — поле, то каждый неконстантный полином из множе-
множества F[x] можно единственным образом представить в виде произведения непри-
неприводимых полиномов в том смысле, что множители являются единственными с
точностью до умножения на делитель единицы.

РАЗДЕЛ 20.4. Алгебры и полиномы 813
ДОКАЗАТЕЛЬСТВО. Воспользовавшись индукцией по степеням полинома, пока-
покажем, что любой полином степени п, не равный константе, можно единственным
образом разложить на неприводимые элементы. Для и = 1 имеем полином ви-
вида ах + 6, который уже является неприводимым, поскольку в противном случае
ах + Ъ = fg, но deg(ax + b) = deg(/)+ deg(g) > 2, что составляет очевидное проти-
противоречие. Предположим, что к > 1, и теорема справедлива для всех и < /с, и пусть
полином / имеет степень к. Если полином / — неприводимый, то доказательство
завершено. Если нет, то / можно разложить на полиномы д и h, степень каждого
из которых меньше, чем степень /. Следовательно, каждый из полиномов д и h
можно разложить на неприводимые элементы, поэтому полином / также можно
разложить на неприводимые элементы.
Для доказательства единственности разложения опять воспользуемся индук-
индукцией по числу множителей в разложении. Для п = 1 результат очевиден. Пред-
Предположим, что единственность имеет место для п = к множителей. Предположим,
что / можно разложить на к + 1 неприводимых элементов gi,g2, • •. ,fffc+i и на m
неприводимых элементов д\,д'2, • • • ^д'т- Из fc+1 неприводимых элементов выберем
множитель gi. Поскольку, в силу следствия 20.77, неприводимый элемент являет-
является простым и д\ делит /, то д\ должен делить один из га неприводимых элементов
во втором разложении, например, д'у Но так как д^ — неприводимый элемент, то
#i и g'j отличаются множителем — делителем единицы. Следовательно, делим оба
разложения на д\, оставляя первое разложение полинома / состоящим из к непри-
неприводимых множителей д2,... ,<7/с+ь а второе разложение — состоящим из га — 1
неприводимых множителей д[,... ^«цф+ь... ,д'т и возможного множителя —
делителя единицы. По индуктивному предположению разложение полинома f /д\
единственно, и поэтому разложение полинома / единственно. ¦
Напомним, что полином / = а0 + а\х + ••• + апхп примитивный, если
НОД(а0, аь ..., ап) равен единице.
ТЕОРЕМА 20.79. (Гаусс) Пусть А — область целостности. Произведение двух
примитивных полиномов из множества А[х] является примитивным полиномом.
ДОКАЗАТЕЛЬСТВО. Пусть / = а0 + а\х Л Ь апхп и д = Ьо + Ь\х Н Ь Ь^х™,
и пусть р — неприводимый элемент из А. Поскольку полином / — примитивный,
то существует такой коэффициент а;, что р не делит а;. Пусть аг — первый такой
коэффициент. Аналогичным образом, существует такой коэффициент bj, что р
не делит bj. Пусть bs — первый такой коэффициент. Пусть h = с$ + с\х + • • • +
cm+nxm+n — произведение полиномов /ид. Тогда
s + • • • + ar_i&s_|_i 4- arbs + ar+i65_i H 4- ar+sfro-
Hop делит a0,... ,ar_i, поэтому р делит aobr+s-\ bar_ibe+i; при этом р делит
bo,... ,6s_i, поэтому р делит ar+i6s_i H \-ar+sb0. Но р не делит arbSi поэтому
p не делит h. Следовательно, полином h — примитивный. ¦
Может показаться, что полином, неприводимый над полем целых чисел, мо-
может и не быть неприводимым, если допустить разложение на полиномы с раци-
рациональными коэффициентами. Приведенная ниже теорема, однако, показывет, что
это не так.

814 ГЛАВА 20. Кольца, области целостности и поля
ТЕОРЕМА 20.80. Пусть А — область единственности разложения на множители,
т.е. область целостности, в которой разложение на простые множители единствен-
единственно, и пусть F — его поле частных. Если р Е А[х] и если многчлен р приводимый
в F[x], то он приводимый в А[х]. Если полином р — примитивный в А[х], то он
приводимый в F[x] тогда и только тогда, когда он приводимый в А[х].
ДОКАЗАТЕЛЬСТВО. Пусть полином р € А[х] — приводимый в F[x]f например,
р = fg. Пусть и — наименьшее общее кратное знаменателей коэффициентов
полиномов / и д. Тогда up = f'g\ где /' и д1 принадлежат множеству А[х]. Но
/' = а/" и д' = bg"', где /" и д" примитивные полиномы, ир = ср\ где с —
примитивный полином. Следовательно, иср1 • f"g". Но поскольку f"g" — также
примитивный полином, то легко показать, что два выражения для примитивного
полинома отличаются множителем — делителем единицы. Итак, ucv = aby где
v — делитель единицы. Следовательно, иср' = ucvf'g". Поэтому
up = ucvf'g"
или
p = cvf"g",
и мы получили разложение полинома р на множители в А[х].
Очевидно, что если полином разлагается на множители в А[х]9 то он разла-
разлагается на множители в F[x], но если полином р не является примитивным в А[х],
то он приводимый в А[х], потому что он является произведением целого числа
и полинома. Однако, в поле F[x] полином может быть неприводимым, поскольку
целое число может быть делителем единицы. ¦
ТЕОРЕМА 20.81. Область целостности А является областью единственности раз-
разложения тогда и только тогда, когда таковой является область А[х].
ДОКАЗАТЕЛЬСТВО. Пусть F — поле частных области целостности А и р —
полином из А[х]. Тогда полином р разложим на неприводимые множители в
F[x], следовательно, р разложим на неприводимые множители в А[х], где каждый
неприводимый множитель разложения в F[x] равен соответствующему неприво-
неприводимому множителю разложения в A[x]t умноженному на элемент поля F.
Пусть d равно наибольшему общему делителю коэффициентов полинома р,
так что р = dp1\ где р' — примитивный полином. Поскольку полином d разло-
разложим единственным образом, то необходимо только показать, что р' разложим
единственным образом. Поэтому предположим, что полином р — примитивный.
Поскольку, по теореме 20.78, поле F[x] — область единственности разложения на
множители, то пусть
Р* =Г1Г2--ГП = SiS2'"Sn.
Допустим, что после перегруппировки имеем, что г; и s; отличаются только нену-
ненулевым множителем из F. Например, г; = (a/b)siy поэтому Ьг{ = asi, но поскольку
г; и S{ примитивные полиномы, то а и Ь отличаются множителем — делителем
единицы из А[х], поэтому разложение будет единственным.
Обратно, поскольку область целостности А — подмножество множества А[х],
то если А[х] — область единственности разложения на множители, то каждый
элемент из А должен раскладываться на множители единственным образом, по-
поэтому А — область единственности разложения на множители. ¦

РАЗДЕЛ 20.4. Алгебры и полиномы 815
ТЕОРЕМА 20.82. Пусть А — область единственности разложения на множители,
тогда два полинома из А[х] имеют наибольший общий делитель.
ДОКАЗАТЕЛЬСТВО. Пусть р и q — полиномы из А[х]. Поскольку А[х] — область
единственности разложения на множители, то разложим р и q на неприводимые
множители. Тогда НОД(р, q) равен произведению множителей, которые присут-
присутствуют в разложениях как р, так ид, в самых низких степенях. ¦
ТЕОРЕМА 20.83. Пусть А — кольцо главных идеалов и/- идеал, порожденный
элементами р и q. Если d порождает /, то d = НОД(р, q) и d можно записать в
виде up + vq.
ДОКАЗАТЕЛЬСТВО. Вполне очевидно, что d делит р и q. Поскольку d E /, то d
можно записать в виде up + vq. Если с делит рис делит qt то с делит up + vq к
с делит d. Таким образом, d = НОД(р, q). Ш
Начиная с области целостности А, такой как целые числа, несомненно, мож-
можно найти поле частных области целостности А, например, поле F, и сформировать
множество F[x]. Поскольку А[х] — область целостности, то можно сформировать
поле частных области целостности А[х], порождая, по существу, элементы вида
p/q, где р и q принадлежат А[х]. Поскольку F[x] — также область целостности,
то можно сформировать поле частных области целостности F[x], которое состоит
из элементов вида p/q, где р и q npHHa&ne>KaTF[z]. Это поле называется полем
рациональных функций над полем F.
ОПРЕДЕЛЕНИЕ 20.84. Элемент с е С, множеству комплексных чисел, назы-
называется алгебраическим целым числом, если он является нулем некоторого
нормированного полинома р из Z[x], т.е. р(с) = 0.
ОПРЕДЕЛЕНИЕ 20.85. Элемент а поля Е — расширения поля F — называ-
называется алгебраическим над полем F, если /(а) =0 для некоторого ненулевого
полинома / G F[x].
ОПРЕДЕЛЕНИЕ 20.86. Элемент с G С, алгебраический над полем рациональ-
рациональных чисел Q, называется алгебраическим числом; т.е. с € С — алгебраическое
число, если существует такой полином р ? Q[x]t что р(с) = 0.
ОПРЕДЕЛЕНИЕ 20.87. Пусть А — область целостности. Элемент а е А назы-
называется корнем полинома р, если р(а) = 0
Далее в абстрактной форме покажем, как по заданному полю и неприво-
неприводимому полиному над этим полем можно найти расширение поля, содержащее
корень неприводимого полинома. Затем сравним это расширение поля с таким,
которое было бы сформировано расширением поля корнем неприводимого поли-
полинома в комплексных числах.

816 ГЛАВА 20. Кольца, области целостности и поля
ТЕОРЕМА 20.88. Пусть F — поле ир- неприводимый полином над полем F.
Тогда F изоморфно подполю поля F[x]/{p), и существует такой элемент / поля
F[*]/(p), чтор(/)=0.
ДОКАЗАТЕЛЬСТВО. Согласно теоремам 20.70 и 20.73, множество F[x]/(p) пред-
представляет собой поле. Поле F можно отождествить с подполем F' поля F[x]/(p)
следующим образом: пусть д : F —> F' определено соотношением д(а) = а 4- (р).
Функция д является мономорфизмом (т.е. инъекцией), поскольку если д(а) =
д(Ь), то а + (р) = b 4- (р), и р делит а — Ь. Поскольку р — полином, и полиномы а
и b принадлежат F, то а - 6 = 0 и а = Ь.
Пусть / = х 4- (р) и р = ао -f ai# 4- • • • 4- апхп. Тогда
• • • 4- ап(х 4- (р))п =
= а0 4- ахх Н 4- ап^п 4- (р) =
= Р + (р) =
= 0 4- (р> =
= 0
ТЕОРЕМА 20.89. Пусть р — неприводимый полином из F[x] и р(а) = 0 в расши-
расширении поля F. Если д(а) — 0 для полинома д из F[x], то р делит д.
ДОКАЗАТЕЛЬСТВО. Можно показать, что / = {д : д Е F[x] и g(a) = 0} —
идеал. Вполне очевидно, что этот идеал порожден элементом р, так как р —
неприводимый элемент. Следовательно, если д Е /, т.е. д(а) = 0, то полином д
должен быть кратным полиному р. ¦
ТЕОРЕМА 20.90. Пусть F — поле и р Е F[x] — неприводимый полином. Если
К — расширение поля F, содержащее корень а полинома р, т.е. р(а) = 0, то F[a]
изоморфно F[x]/(p).
ДОКАЗАТЕЛЬСТВО. Определим h : F[x]/{p(x)) -> F[a] соотношением h(f 4-
(р)) = /(а). Вполне очевидно, что h — гомоморфизм. Если h(f + (p)) = h(g + (p)),
то /(a) = д{а) и (/ — д)(а) = 0. Следовательно, по теореме 20.89 полином р делит
f — дн/ + (р)=д + (р), поэтому функция h — инъекция. Пусть / Е F[a], тогда
h(f + (р)) = /(а), поэтому /г — сюръекция и, следовательно, /г — изоморфизм. ¦
Пусть F — поле действительных чисел и р = х2 + 1, и пусть /С — расширение
поля F, содержащее элемент г — корень полинома р(х), т.е. г2 + 1 = 0. По
теореме 20.89 поле F[x]/(p) изоморфно полую F[i]. Поскольку р(х) имеет степень
2, необходимо рассматривать только / Е F[i] степени 1. Следовательно, каждый
элемент поля F[i] будет иметь вид a + Ьг, где а и b — действительные числа. Итак,
мы создали комплексные числа.
Подкольцо, состоящее из элементов поля F[i], где а и 6 — целые числа,
называется множеством комплексных целых чисел, или множеством гауссовых
чисел. Его можно также рассматривать как наименьшее подкольцо комплексных
чисел, содержащее целые числа и число г. Очевидно, что число 5 не является
неприводимым в этом кольце, поскольку 5 = A — 2г)A+2г). Пусть норма элемента

РАЗДЕЛ 20.4. Алгебры и полиномы 817
по на множестве комплексных целых чисел определена соотношением пс{а+Ы) =
а2 +Ь2. Тогда
nG{(a + Ы)(с + di)) = nG((ac - bd) + (ad + bc)i) =
= (ac-bdJ + (ad + bcJ =
= a2c2 - 2abcd + b2d2 + a2d2 + 2abcd + b2c2 =
= пс(а + bi)nc(c 4- di),
так что uq — мультипликативный гомоморфизм из множества Гауссовых чисел
во множество целых чисел. Поскольку псA — 2г) = пс{1 4- 2г) = 5, то 1 — 2г и
1 + 2г — неприводимые элементы в кольце комплексных целых чисел. Произве-
Произведение неприводимых комплексных целых чисел 2 -f г и 2 — г есть также число 5.
Следовательно, единственность разложения на неприводимые множители не име-
имеет места. Обратите внимание, что неприводимые множители в данном примере не
являются простыми.
Еще один пример. Пусть F — поле рациональных чисел, и р(х) = х2 — 2.
Тогда F[x]/(p) = F[y/2]. Опять достаточно рассмотреть полиномы степени 1, и
F[x]/(p) — поле, состоящее из рациональных чисел вида а 4- Ь>/2, где а и 6 —
рациональные числа. Мы можем рассмотреть подкольцо, состоящее только из
элементов множества F[x]/(p) вида а + 6\/2, где а и b — целые числа. Но
C 4- \/2)C — %/2) = 7, поэтому число 7 не является неприводимым в этом множе-
множестве.
Мы предположили, что, начиная с рациональных чисел, все алгебраические
целые числа являются подмножеством множества комплексных чисел. В рамках
такого предположения докажем следующую теорему.
ТЕОРЕМА 20.91. Множество А всех алгебраических чисел над полем рациональ-
рациональных чисел Q является подполем поля комплексных чисел.
ДОКАЗАТЕЛЬСТВО. Пусть а и b — ненулевые алгебраические числа. Если чис-
число а не является рациональным, то существует такой неприводимый полином р
степени 2 или выше, что а — корень полинома р. Пусть F — Q[x]/(p). Если число
b не принадлежит F, то в F существует такой неприводимый полином, скажем,
q, степени выше 2, что b — корень полинома q. Пусть G = F[x]/(q). Тогда G —
поле, которое содержит элементы а и Ь, поэтому оно содержит а 4- Ь, а - 6, ab и
а/Ъ. Поскольку поле G содержится в А, то все эти элементы принадлежат А, и
поэтому А — поле. ¦
¦ УПРАЖНЕНИЯ
1. Докажите, что множество Гауссовых чисел образует подкольцо множества
комплексных чисел.
2. Докажите или опровергните, что множество Гауссовых чисел является об-
областью целостности.
3. Докажите, что sin(a:) нельзя выразить полиномом.

818 ГЛАВА 20. Кольца, области целостности и поля
4. Докажите или опровергните, что произведение двух простых полиномов бу-
будет простым полиномом.
5. Докажите или опровергните, что сумма двух простых полиномов будет про-
простым полиномом.
6. Найдите порождающий элемент наименьшего главного идеала, содержащего
полиномы х2 - 4 и х2 + 4х + 4, где полиномы рассматриваются над кольцом
целых чисел.
7. Докажите или опровергните, что любое комплексное целое число является
алгебраическим числом.
8. Найдите идеал целых чисел, который не является максимальным идеалом.
9. Опишите наименьшее подполе поля действительных чисел, содержащее корни
полинома х2 — 5 = 0.
10. Опишите наименьшее подполе поля действительных чисел, содержащее корни
полинома х2 + 5 = 0.
11. Опишите наименьшее подполе поля действительных чисел, содержащее корни
полинома х3 - 1 = 0.
12. Опишите наименьшее подполе поля действительных чисел, содержащее корни
полинома х4 — 1 = 0.

ГЛАВА
ХАРАКТЕРЫ ГРУПП И
ПОЛУГРУПП
21.1. КОМПЛЕКСНЫЕ ЧИСЛА
В предыдущей главе комплексные числа рассматривались как корни многочленов.
Теперь мы введем их формально и рассмотрим с различных точек зрения.
ОПРЕДЕЛЕНИЕ 21.1. Пусть R — множество действительных чисел и С —
множество вида
{(г,s) :r,sGK} = KxK,
так что каждый элемент множества С — упорядоченная пара действительных
чисел. Определим сложение на С соотношением
а умножение определим соотношением
(а, Ь) • (с, d) = (ас — 6d, ad -f be).
Множество С называется множеством комплексных чисел.
Легко показать, что С — поле. Отображение / : R —> С, определенное со-
соотношением f(a) = (а, 0), является мономорфизмом и изоморфизмом в подполе
{(а,0) : a G R}. Поэтому будем считать, что поле действительных чисел R содер-
содержится в поле комплексных чисел, и называть поле R подполем поля С. Далее,
@,1)-@,1) = (—1,0) = -1. Если определить г = @,1), то г2 = —1. Следовательно,
элемент (а, 6) можно записать в виде (а,0) + F,0) • @,1) = а + Ы. Таким образом,
определения операций сложения и умножения принимают вид
(а + Ы) + (с + ей) = (а + с) 4- (Ь + d)i
и
(а + Ы) • (с + di) = (ас - bd) + (ad + bc)i.

820 ГЛАВА 21. Характеры групп и полугрупп
Пусть z = a 4- Ы = (a,b) — комплексное число. Тогда а называют его дей-
действительной частью и записывают Re(z) = Re(a 4- Ы) = а, а 6 называют его
мнимой частью и записывают Im(z) = Im(a + 6i) = b. Поскольку упорядоченная
пара действительных чисел обычно изображается в виде точки на плоскости с
введенной на ней декартовой системой координат, то комплексное число а 4- Ы
также можно изобразить точкой плоскости, как и пару чисел (а, 6). В этом слу-
случае горизонтальня ось называется действительной осью, а вертикальная ось на-
называется мнимой осью. Таким образом, действительная часть числа а + Ы (т.е.
Re(a + bi) = а) измеряется вдоль горизонтальной оси, а мнимая часть числа а + Ы
(т.е. 1т(а + Ьг) = Ь) измеряется вдоль вертикальной оси. Когда плоскость с декар-
декартовой системой координат используется таким образом, ее называют комплексной
плоскостью.
ОПРЕДЕЛЕНИЕ 21.2. Пусть С — множество комплексных чисел. Для с = а+Ы
из С величина \с\ = \Ja2 + Ъ2 называется абсолютным значением, или длиной
числа с.
В комплексной плоскости величина \с\ равна расстоянию от точки с = а + Ы
до начала координат. Легко показать, что для комплексных чисел end имеем
\с\ \d\ = \cd\ и \c + d\ < \c\ 4- |rf|. Пусть г — комплексное число, которое являет-
является корнем п-ой степени из 1, т.е. тп = 1, тогда \г\п = \гп\ = |1| = 1. Поэтому
число г имеет длину 1 и находится на единичной окружности с центром в нача-
начале координат, т.е. окружности, состоящей из всех точек комплексной плоскости,
расстояние от которых до начала координат равно 1. Следующая теорема, форму-
формулируемая нами без доказательства, устанавливает важное свойство комплексных
чисел.
ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ. (Гаусс) Для любого многочлена р положи-
положительной степени с коэффициентами из множества действительных чисел R или
множества комплексных чисел С существует такой элемент b из С, что р(Ь) = 0.
Поэтому, в частности, каждый многочлен над Z имеет, по крайней мере,
один корень во множестве комплексных чисел.
21.2. ХАРАКТЕРЫ ГРУПП
ОПРЕДЕЛЕНИЕ 21.3. Характер группы коммутативной группы G — это го-
гомоморфизм из G во множество ненулевых комплексных чисел с операцией
умножения.
ОПРЕДЕЛЕНИЕ 21.4. Числом, сопряженным с данным комплексным числом
с = а 4- Ьг, называется число а - 6г, которое обозначается через с.

РАЗДЕЛ 21.2. Характеры групп 821
В оставшейся части этого раздела ограничимся рассмотрением характеров
коммутативных конечных групп. Пусть х ~~ характер группы. Таким образом,
существует такой элемент д € G, что х(#) Ф 0. Поскольку группа G конечная, то
существует такое п, что дп = 1. Следовательно, х{дп) = (х(#))п = 1> хЫ являет-
является корнем n-ой степени из 1, и элемент д отображен на единичную окружность.
Таким образом, характер группы отображает группу G в единичную окружность.
Доказательство приведенной ниже теоремы предоставляем читателю.
ТЕОРЕМА 21.5. Если х(<?) — a + bi, то х(д~г) является сопряженным к х(<?)> т-е-
l) = a-bi.
ОПРЕДЕЛЕНИЕ 21.6. Первообразным корнем n-ой степени г комплексного
числа а называется такой корень n-ой степени из а, что rk ф а для 0 < к < п.
ОПРЕДЕЛЕНИЕ 21.7. Характер группы хь определенный соотношением
Xi(g) = 1 для всех д из группы Gy называется главным характером груп-
группы G. Группа характеров группы G состоит из множества характеров группы
G вместе с операцией (х • х')(#) = х(у)х'(#) Для характеров групп х и х'«
ОПРЕДЕЛЕНИЕ 21.8. Пусть Gb G2,..., Gm — подгруппы группы G. Группа G
назывется прямой суммой подгрупп Gi, G2,..., Gm, обозначается Gi © G2 0
• • • 0 Gm, если каждый элемент группы G может быть единственным образом
записан в виде a\a<i • • • am, где а^ ? Gk.
ТЕОРЕМА 21.9. Любая конечная абелева группа есть прямое произведение цик-
циклических подгрупп. Таким образом, если G — G\ © G2 0 G3 0 • • • 0 Gm для
циклических групп Gi с порождающим элементом gi порядка /с(г), тогда каждый
элемент д G G можно единственным образом записать в виде:
где 0 < j(i) < к(г).
ДОКАЗАТЕЛЬСТВО. Покажем, что существует целое число т такое, что
G = Gi ф G2 ф G3 Ф • • • Ф Gm ,
и каждый элемент группы G может быть единственным образом записан в виде
0i(i:]932{2]]93з3) • • • 2mm), где 0 < j(i) < k(i). Пусть дг е G имеет порядок /сA), и
G\ — подгруппа, порожденная элементом д\. Если G\ = G, то т — 1, и до-
доказательство завершено. Если нет, то выберем элемент д2 из G - Gb и пусть
G2 — группа, порожденная элементом д2. Тогда д% = 1 для некоторого п, по-
поскольку группа G конечная. Следовательно, некоторая степень элемента д2 при-
принадлежит G\. Пусть кB) — наименьшая степень элемента д2 такая, что д2
принадлежит G\. Если G\ UG2 = G2, то переобозначим G\ = G2 и начнем снова.
Если G\ U G2 ф G2, то в этом случае легко показать, что каждый элемент из

822 ГЛАВА 21. Характеры групп и полугрупп
G\ UG2 может быть единственным образом записан в виде д^д^ где 0 < j < fc(l),
О < s < fcB). Если выбрать элемент д$ из G — (G\ ©G2) и продолжить процесс, то
получим G1G2G3 • • • GrGr+i • • •. А поскольку группа G конечная, то существует
число га такое, что G = G = G\ ® G2 Ф G% Ф • • • Ф Gm, и каждый элемент группы
G может быть единственным образом записан в виде д{^gJ2^9з^ ''' gU^K где
0<j(i)<k(i). Ш
ТЕОРЕМА 21.10. Группа характеров группы G изоморфна группе G.
ДОКАЗАТЕЛЬСТВО. Пусть G = Gx ф G2 Ф • • • Ф Gm, где элемент д{ порождает
группу G;, и пусть п{ — первообразный корень щ-ои степени из единицы, где G;
имеет порядок щ. Для каждого элемента д Е G определим х^ соотношением
где элементы д \\Ъ группы G имеют представления через прямые суммы
где 0 < j(i) < щ и О < h(i) < щ. Можно показать, что для любого д G G
отображение \д является гомоморфизмом из G в корень n-ой степени из единицы.
Далее, если д ф д\ то Хд Ф Хд^ поэтому существуют П1^1 пг = п характеров
группы, когда группа G содержит п элементов. Определим отображение г\ из G в
группу характеров группы G следующим образом:
= (xgiYw (х92У{2) • • • (х9тУ{тп) •
Легко показать, что отображение rj является изоморфизмом.
Кроме того, если А — матрица, где Aij = XgAQj), T0
2i 1 1 ••• 1
1
1 1 1 ••• ак
ПРИМЕР 21.11. Рассмотрим множество G$ = {[1], [2], [3], [4]}, которое состоит из
ненулевых элементов множества Z5. Поскольку число 5 простое, то классы приве-
приведенных вычетов как раз являются ненулевыми классами в Z5, а ненулевые классы,
соответствующие приведенным вычетам, образуют группу относительно умноже-
умножения. Таким образом, G5 — группа относительно умножения. Таблица умножения
для G5 имеет вид
0
[11
[2]
[31
[4]
[11
[11
[2]
[31
[4]
[2]
[21
[4]
[11
[3]
[3]
[31
[1]
[41
[2]
[4]
[41
[3]
[21
[1]

РАЗДЕЛ 21.2. Характеры групп 823
Чтобы сделать более понятным приведенное ниже построение характеров
групп, будем использовать обозначения, введенные при доказательстве теоре-
теоремы 21.10.
Комплексное число
2*«/Л /2тгЛ . . 2тг?
e2nti/n = cos -f г sin
V n J n
находится на единичной окружности, потому что
Для любого целого числа t число e2ntl/n является корнем n-ой степени из едини-
единицы, поскольку
y 7rt) + isinB7rt) = 1.
Фактически, множество
является совокупностью и различных комплексных корней n-ой степени из еди-
единицы.
Для п = 4, порядка группы G5, приведенная выше формула дает четыре
корня четвертой степени из единицы.
t
0
1
2
3
еBтг«)/4
1
г
-1
—г
Подсчитывая I4 = г4 = (—IL = (—гL = 1. проверяем, что 1, г, —1 и —г являются
корнями четвертой степени из единицы.
Если положить д\ = [3], то
д\ = И2 = [4],
я\ = И3 = и,
д! = И4 = [1] = з?.
Следовательно, fc(l) = 4 и G\ = G, так что ш=1в обозначениях доказательства
теоремы 21.10. Для д\ = [3] выберем корень четвертой степени г\ — г. Поскольку
г\ = —1, rj = -г и г4 = 1, то корень г\ = г является первообразным. С помощью
этого первообразного корня можно определить характер для каждого элемента д
группы G5. Следующая таблица дает определение всех характеров группы G5.

824 ГЛАВА 21. Характеры групп и полугрупп
Л1)
0
3
i
2
9 = 9iW
[1]
И
[3]
[4]
Хд(Ь) = Xg(9iW)
3/i(l) _ -Щ1)
' 1 — '
lh(l) _ .fc(i)
'l — *
r2-Ml) = f2fc(l)
Следовательно, четыре элемента группы характеров для G5 дает следующая та-
таблица, в которой Ь = #1 :
9
[1]
И
[3]
[4]
Х9(Ь)
Х[1]{Ь)
Х[2](Ь)
Х[з](Ь)
Х[4](Ъ)
ь
/1A) =
=
=
=
[1]
0
1
1
1
1
[2]
3
1
г
—i
-1
[3]
1
1
—г
г
-1
[4]
2
1
-1
-1
1
Очевидно, X[i] = 1 — это главный характер.
Для иллюстрации гомоморфной природы характеров групп рассмотрим Х[2]:
Xt2]([3][4]) = X
Остальные 15 произведений для \[2] можно проверить аналогичным образом.
Используя таблицу определений характеров групп, приведенную выше, легко
построить таблицу умножения для группы характеров.
Х[1]
Х[2]
Х[з]
Х[4]
Х[1]
Х[11
Х[2]
Х[3]
Х[4]
Х[2]
Х[2]
Х[4]
Xli)
Х[з]
Х[з]
Х[з]
Х[1]
Х[4]
Х[2]
Х[4]
Х[4]
Х[з]
Х[2]
Х[Ц
п
УПРАЖНЕНИЯ
1. Докажите теорему 21.5.
2. Докажите, что если Ъ — элемент коммутативной группы G и 6 Ф е, еди-
единичному элементу группы G, то существует такой характер группы х. что
Х(Ь) ф 1.

РАЗДЕЛ 21.3. Характеры полугрупп 825
3. Пусть д и д' — элементы конечной коммутативной группы G такие, что
д ф д'. Докажите, что \д Ф Хд'-
4. Завершите доказательство теоремы 21.10.
21.3. ХАРАКТЕРЫ ПОЛУГРУПП
ОПРЕДЕЛЕНИЕ 21.12. Пусть 5 — конечная коммутативная полугруппа.
Характером полугруппы на S называется гоморфизм из 5 в множество ком-
комплексных чисел с операцией умножения. Как и для случая групп, в данном
разделе будем предполагать, что все рассматриваемые полугруппы являются
коммутативными и конечными.
Пусть s е 5, где 5 — конечная коммутативная полугруппа. Если |хE)| >
то
что невозможно, поскольку полугруппа S конечна. Точно так же, если 0 |хE)| < 1>
то
о < |x(*fc+1)| < |х(**)| < < |х(*2)| < IxWI < 1,
что опять-таки невозможно. Следовательно, либо |хE)| = 0» либо |хE)| = 1 Для
каждого элемента s из полугруппы S.
ОПРЕДЕЛЕНИЕ 21.13. Подполугруппа / коммутативной полугруппы 5 назы-
называется идеалом полугруппы 5, если из того, что г ? I и s € 5, следует, что
s - г € /. Идеал / назывется простым идеалом, если S — I — полугруппа.
Доказательство следующей теоремы оставляем читателю.
ТЕОРЕМА 21.14. Если S — конечная коммутативная полугруппа их — характер
полугруппы 5, то / = {5 : \x(s)\ = 0} является идеалом. Обратно, если / — любой
идеал в S и существует такой характер х> что xis) Ф 0 Для некоторого s из 5 - /,
то существует такой ненулевой характер хь ч™ Х/@ = 0 тогда и только тогда,
когда г принадлежит /.

826 ГЛАВА 21. Характеры групп и полугрупп
Теперь рассмотрим множество Zn классов вычетов по модулю п. Напомним,
что множество элементов Zn, состоящее из классов эквивалентности, содержащих
целые числа, взаимно простые с п, называется множеством приведенных классов
вычетов. Множество приведенных классов вычетов образует группу относительно
умножения в классе. Обозначим эту группу через Gn. Множество Zn является
полугруппой относительно умножения в классе. Множество Zn - Gn является
идеалом полугруппы, поскольку произведение любого целого числа и целого чис-
числа, не взаимно простого с п, не является взаимно простым с п. Следовательно,
можно сформировать характеры Zni которые являются характерами группы Gn, и
отобразить все элементы группы Zn-Gn в 0. Эти характеры называются харак-
характерами Дирихле. Известно, что количество характеров Дирихле по модулю и
равно количеству характеров группы Gn. Поскольку множество характеров груп-
группы Gn изоморфно Gn и существуют ф(п) элементов в Gn, то существует ф(п)
характеров Дирихле по модулю п. Итак, мы приходим к следующей теореме.
ТЕОРЕМА 21.15. Существует ф(п) различных характеров Дирихле по модулю
положительного целого числа п.
ЛЕММА 21.16. Пусть G — конечная группа, д' — произвольный элемент группы
G и G' = {х : х = д'д для д из G}. Тогда G = G'.
ДОКАЗАТЕЛЬСТВО. Предположим, что G' = {х : х = д'д для д из G}. Вполне
очевидно, что G' С G. Пусть gi и д2 — элементы группы G. Тогда д'д\ и д'д2
принадлежат G1. Если д'д\ = д'д2> то д\ = {д')~1д'д\ — д2- Следовательно, в G'
имеется столько же элементов, сколько и в G; и поскольку группа G конечная,
то G = G1. Ш
ТЕОРЕМА 21.17. Пусть G -— конечная коммутативная группа порядка п. Если
X — характер группы, то
^0, еслих^Хь
ДОКАЗАТЕЛЬСТВО. Поскольку xi(<?) = 1 Для всех элементов д из G, то первая
часть утверждения очевидна. Если х Ф Xi и Q1 ~ такой элемент группы G, что
х(д') ф 1, то
= по лемме 21.16
geG
)
geG
так что
geG
и, поскольку 1 — х(#') т^ 0, то ]Г х(д) = 0.
geG

РАЗДЕЛ 21.3. Характеры полугрупп 827
ТЕОРЕМА 21.18. Если G — конечная коммутативная группа порядка п и д е G,
то
I п, если з = е;
\0, если^е,
где е — единичный элемент группы, и суммирование осуществляется по всем
характерам группы х-
ДОКАЗАТЕЛЬСТВО. Если д — е, то х(е) = 1 Для всех Х> так как каждый харак-
характер х является гомоморфизмом. Таким образом, сумма равна п. Предположим, что
д ф е и Ха — такой характер, что Ха(д) ф 1. Такой характер существует, потому
что д = 01 ^02 #з ''' 9™ , где 0 < j(i) < /с(г), как показано в доказательстве
теоремы 21.10. Далее, поскольку д ф е, то j(s) ф 0 для некоторого s. Теперь
можем положить Ха(д) равным Xgs(d) по т°й причине, что х^(^) = Н3 Ф 1» гДе
rs — первообразный корень /с($)-ой степени из единицы. Тогда
согласно лемме 21.16
Поскольку Ха(д) ф 1, получаем ^x(fl) = °- ¦
х
Следующая теорема формулирует два полезных свойства ортогональности
характеров групп. Доказательство теорем оставляем читателю.
ТЕОРЕМА 21.19. Пусть G — конечная коммутативная группа порядка п, пусть
gi,gj € G, пусть Ха и хь — характеры группы G. Тогда
если ov = Qi'j
п, если Ха = Хь;
О, если Ха Ф Хь-
ТЕОРЕМА 21.20. Предположим, что группа G имеет порядок п и а — (п)-
матрица, в которой <т^ = Xi(gj)> где ХьХ2,Хз, • • • ,Хп — характеры группы G.
Если а1 — матрица, в которойЬ о'- = Щ1, то
п 0 0 ••• 0
0 п 0 ••• О
0 0 п ••• 0
0 0 0 ••• п
= аа

828 ГЛАВА 21. Характеры групп и полугрупп
ДОКАЗАТЕЛЬСТВО. Пусть С = [Су] = о1 о. Тогда
/c=l
поэтому первое утверждение теоремы следует из теоремы 21.19. Доказательство
второго утверждения предоставляем читателю. ¦
ТЕОРЕМА 21.21. Всего существует ф(т) различных характеров Дирихле по
модулю положительного целого числа га. Каждый характер Дирихле является
вполне мультипликативным и обладает тем свойством, что х([а + т]) = х([а])>
где [а] — класс вычетов по модулю га, содержащий а, или, что эквивалентно,
х(а +га) = х(а).
Замечание: поскольку сложение и умножение в Zm не зависят от выбора
представителя класса из Zm, то, как правило, вместо х([а + т}) используется
запись х(а + т)- Таким образом, область определения функции х расширена до
Z. Именно в этом обобщенном смысле мы говорим о том, что каждый характер
является вполне мультипликативным.
ДОКАЗАТЕЛЬСТВО. Поскольку каждый характер Дирихле является единствен-
единственным расширением характера группы из группы приведенных классов вычетов по
модулю т, то первая часть утверждения теоремы следует из того факта, что
количество характеров группы совпадает с количеством элементов в группе. По-
Поскольку каждое "целое" в образе характера Дирихле на самом деле представляет
класс сравнимости по модулю т, то [а] = [а + га] и х([а + т]) = х([а])-
Характер х является вполне мультипликативным, так как если элементы а и
Ъ — взаимно простые с га, то [а] и [6] принадлежат группе приведенных вычетов,
и х — гомоморфизм на эту группу. Если а или Ъ не является взаимно простым с
га, то таковым не является и их произведение, поэтому оба х([а])х(М) и х([аЧ)
равны 0 или, что эквивалентно, оба х(а)х(^) и х(а^) равны 0. ¦
¦ УПРАЖНЕНИЯ
1. Докажите теорему 21.14.
2. Докажите теорему 21.19.
3. Завершите доказательство теоремы 21.20.

ГЛАВА
ПРИЛОЖЕНИЯ ТЕОРИИ
ЧИСЕЛ
22.1. ПРИЛОЖЕНИЕ: ПОИСК ПО ОБРАЗУ
В компьютерных приложениях часто возникает задача поиска по образу. Простой
пример такой задачи можно найти в компьютерных программах обработки тек-
текстов, когда при написании или редактировании документа в нем требуется опреде-
определять местоположение конкретного слова или фразы, например, слова "effect". Если
документ содержит несколько разделов, то визуальный поиск отнимает много вре-
времени, это весьма скучное занятие, и возможны ошибки. Более сложным примером
является ситуация, когда объект представлен двумерным прямоугольным изобра-
изображением или картинкой, которая в рамках компьютерного приложения имеет вид
двумерного массива нулевых или единичных битов, указывающих на белый или
черный цвет. Такое цифровое изображение может иметь размер 1024 х 1024 битов
и быть выведено на экран компьютера. В этом случае задача может состоять в
поиске некоторой специальной формы или конкретного изображения белого или
черного цвета, например, креста — >Ь.
Метод прямого поиска предполагает сравнение образца с каждым возмож-
возможным претендентом. В примере с поиском слова "effect" мы бы сравнивали шесть
букв слова "effect" с каждой последовательностью шести символов из текста до-
документа. Эта операция потребовала бы в худшем случае сравнения шести букв с
каждым шестисимвольным словом документа. Для коротких образов и коротких
текстов этот метод может быть достаточно эффективен. Однако, как правило,
тексты бывают весьма объемными, а образы — достаточно длинными, что делает
метод прямого поиска непрактичным. Эффективным будем называть такой ме-
метод, который для решения задачи требует относительно "короткого" времени или
относительно "небольшого" числа сравнений или вычислений. Более конкретно,
нам нужен алгоритм поиска, использующий минимум памяти, для которого чис-
число требуемых сравнений/вычислений линейно зависит от длины образа и текста
поиска, и который, что может быть важно для некоторых приложений, функцио-
функционирует в реальном времени (считывает текст поиска по одному символу, не зная
всего текста заранее, и требует для обработки каждого символа текста одно и
то же время). Желательно также, чтобы помимо эффективности алгоритм был

830 ГЛАВА 22. Приложения теории чисел
применим ко многим типам поисковых контекстов. Ниже мы приводим достаточ-
достаточно общий алгоритм поиска по образцу, разработанный Ричардом М. Карпом и
Майклом О. Рабином [56], в основе которого лежит выбор случайных простых
чисел. Этот алгоритм обладает описанными выше свойствами и является приме-
примером использования вероятностных методов.
Все числа и символы (цифры и буквы алфавита) представлены в компьютере
как последовательности нулей и единиц. Например, представлением буквы "е" на
основе ASCII 8-битовой кодировки является последовательность битов
[01100101],
которая трактуется как двоичное целое число
0 • 27 + 1 • 26 + 1 • 25 + 0 • 24 + 0 • 23 + 1 • 22 + 0 • 21 + 1 • 2°.
Слово "effect" можно представить в виде
[[01100101][01100110][01100110][01100101][01100011][01110110].
Рассматривая эту последовательность как битовую строку, мы можем трактовать
ее как двоичное целое число
0 • 247 + 1 • 246 + 1 • 245 + • • • + 1 • 21 + 0 • 2°.
Строка битов [01100101] для буквы "е" может быть представлена в шестнадцате-
ричной системе счисления как 65i6 или в восьмеричной — как 1458. При прак-
практической реализиции алгоритма можно выбирать более естественную систему
счисления, но при описании алгоритма Карпа и Рабина мы будем рассматривать
"образ" и "текст" как битовые строки. Пусть X — образ и У — текст, тогда
X = [xi х2 х$ • • • жп], где Xi = 0 или 1;
У = [у\ Уч Уз * • • Ут], где у» = 0 или 1.
Образ имеет длину п битов и текст имеет длину га битов, где га > п. Пусть
У(г) — подстрока из п последовательных битов строки У, которая начинается с
позиции г, 1 < г < га — n-fl, так что
У (г) = [Уг Уг+1 Уг+2 ' * ' Уг+n-l].
Очевидно, для всякого г такого, что X = У (г), имеется соответствие между обра-
образом и частью текста. Заметим, что X и У (г) можно рассматривать как элементы
множества {0,1}п = {0,1} х {0,1} х • • • х {0,1} — декартовой n-степени множе-
множества {0,1}, или множества n-элементных наборов с элементами из {0,1}. Пусть
N(X) и N(Y(i)) — целые двоичные числа, которые имеют представления:
ЩХ) = хх2п-1 + х22п~2 + • • ¦ + Хп-121 + хп;
N(Y(i)) = у{2П-1 + Уг+12П-2 + • • • + Уг+п-221 + Jfc+n-Ь
при этом соответствие имеет место тогда и только тогда, когда N(X) = N(Y(i)).

РАЗДЕЛ 22.1. Приложение: поиск по образу 831
Сравнение N(X) и N(Y(i)) потребует не меньше усилий, чем сравнение
X и У(г). Поэтому необходимо "сжать" информацию, содержащуюся в N(X) и
N(Y(i)), с тем, чтобы это сравнение требовало меньше работы. Одним из спо-
способов осуществления такого сжатия является отображение целых чисел N(X) и
N(Y(i)) на меньшие целые числа, используя модульную арифметику. Пусть р —
простое число из интервала 1 < р < М, где М — некоторое достаточно большое
положительное целое число, которое будет определено ниже. Пусть Np — отоб-
отображение множества битовых строк длины п на множество первичных вычетов по
модулю р, {0,1,2,..., (р — 1)}, определенное соотношением
так что NP{X) = [[N(X)]]P и Np(Y(z)) = [[N{Y(i))]]p. В типичных приложениях
величина п может быть порядка 200, а р может находиться в диапазоне от 216
до 264. Большинство компьютеров могут эффективно сравнивать 16-битовые це-
целые числа с 64-битовыми. Функция Np вырабатывает "доверенное" число NP(W)
для N(W), которое будет использоваться в сравнениях вместо W или N(W).
Такую функцию часто называют идентифицирующей функцией, a NP(W) назы-
называют идентификатором для W. Заметим, что в этом случае идентифицирующая
функция Np не является однозначной, поэтому можно иметь две битовые строки
W и V длины и с одним и тем же идентификатором, т.е. NP(W) = NP(V). Если
NP(W) = NP(V), но W ф V, то в этом случае будем говорить, что имеет место
коллизия — ошибочное соответствие. В дальнейшем мы решим эту проблему. Ес-
Если N(W) сводить по модулю р до NP(W), начиная с N(W) для каждого новой
строки W, то это преобразование потребует значительного количества времени. К
счастью, имеется возможность находить последовательность ЛГр(УA)), NP(YB)),
ЛГр(УC)), ... без лишних вычислений. Сведение N(W) к NP(W) может быть
выполнено постепенно. Заметим, что
N(W) = Wl2n~l + w22n~2 + • • • + Wn-121 -f wn =
= (••• ((wl • 2 + w2) - 2 + w3) • 2 + • • • + Wn-i) -2 + wn.
Порядок выполнения операций в последнем выражении определен однозначно.
Согласно теореме 3.54, если а = Ь (modp), то 6 можно подставить вместо а в
любом выражении, содержащем умножение, сложение и вычитание, не меняя при
этом вычет выражения по модулю р. Будем говорить, что операция а©Ь для целых
чисел а и Ъ выполнена по модулю р, если после выполнения операции результат
сведен по модулю р до наименьшего неотрицательного вычета; т.е. подставляем
первичный вычет [[а © Ъ]]р вместо а 0 Ь. Для сокращения записи иногда будем
писать а 0Р 6 вместо [[а 0 6]]р, чтобы подчеркнуть, что сведение по модулю р
должно быть выполнено после выполнения операции. Например, если подставить
w\ -р 2 вместо w\ -2, г затем подставить (w\ -р 2) +р w2 вместо (wl -р 2) + W2, то в
результате получим
NP{W) = (-¦- ({wi 'р 2 +р w2) -Р 2 +р гуз) 'р 2 +р • • • +р tyn-i) .р 2 +р wn.
Таким образом, приведение N(W) к его первичному вычету по модулю р, iVp(VK),
может выполняться по одной операции, начиная с самых внутренних круглых ско-
скобок. Остается еще необходимость сравнивать X и У(г) для каждого г, сравнивая

832 ГЛАВА 22. Приложения теории чисел
для каждого i "доверенные" целые числа NP(X) и Np(Y(i))', таким образом, хотя
Np(Y(i)) может быть вычислено эффективно для каждого г, алгоритм поиска мо-
может оказаться в целом неэффективным. Однако, это тот случай, когда Np(Y(i+1))
можно получить из Np(Y(i)) и т/;+ъ выполнив несколько арифметических опера-
операций, без полного пересчета Np(Y(i + 1)) из рабочего файла. Поскольку
N(Y(i + 1)) = (N(Y(i)) - 2"-1 • и) • 2 + yi+n,
то, используя только операции по модулю р, имеем
Np(Y(i + 1)) = (Np(Y(i)) -р [[2п-% -р уг) -р 2 +р yi+n.
Такая формула, как описанная выше, позволяющая легко вычислять "следующее"
значение по текущему, называется корректирующей формулой. Таким образом,
можно сказать, что Np(Y(i)) легко корректируется. Основная идея алгоритма
Карпа и Рабина состоит в выборе случайным образом простого числа р из со-
соответствующего множества 1 < р < М и вычислении идентификатора NP(X)
битовой строки образа X. Далее, необходимо сравнивать NP(X) с идентифика-
идентификатором Np(Y(i)) каждой последовательности Y(i) из п последовательных битов
в текстовой строке битов Y для г = 1,2,3,... , га — п + 1. Если случается так,
что NP(X) = Np(Y(k)) для некоторого /с, то имеем доказательство того, что
X = Y(k), и процесс завершен. Обычно, если алгоритм применяется с одним про-
простым числом р, необходимо проверять, выполняется ли соотношение X = Y(k),
поскольку функция Np не является однозначной. Если X ф Y(k), необходи-
необходимо продолжить алгоритм для г = к + 1; вскоре мы увидим, что использование
нескольких простых чисел и нескольких идентифицирующих функций иллюстри-
иллюстрирует сущность вероятностной методологии.
АЛГОРИТМ ПОИСКА ПО ОБРАЗУ (Карп и Рабин) Предположим, что битовой
строкой X длины п задан образ; битовой строкой У длины т, где т > п, за-
задан текст; задано целое положительное число М, которое будет зависеть от т
и п. Пусть S = {р : р простое число и 1 < р < М]. Для простого числа р из
множества S пусть Np : {0,1}П —> {0,1,2,..., (р - 1)} — идентифицирующая
функция. Выберем случайным образом к простых чисел рь рч, .. •, Рк из мно-
множества {1,2, ...,М}, выбирая случайным образом целые числа из совокупности
{1,2,3,... ,М}, проверяя, являются ли они простыми, и останавливая процесс
поиска, когда к простых чисел найдены. Процедура поиска состоит в следующем.
Для каждого г, 1 < г < m-n+1 = ty сравнить Np^(X) с Np^)(Y(i)) для каждого
простого числа pj = p(j), где 1 < j < к, пока не найдется такое г, что
Np{j){X) = NpU)(Y{i)) для всех j, 1 < j < к,
и тогда объявляется, что "соответствие" имеет место, или пока г не достигнет
значения г — t, что будет означать, что "соответствие" не найдено.
Отметим, что для полного соответствия необходимо, чтобы все к иденти-
идентифицирующих функций давали соответствие. Другим важным моментом является
выбор простых чисел р\,Р2, • • • ,Рк случайным образом из достаточно большого
множества. При этом наличие ошибочного соответствия все еще возможно, а

РАЗДЕЛ 22.1. Приложение: поиск по образу 833
именно, когда NP^(X) = Л^)(У(г)) для всех j, но X ф Y{i). Суть, однако,
заключается в том, что вероятность или возможность ошибочного соответствия
может быть сделана сколь угодно малой. Эта последняя особенность воплощает
в себе то, что понимают под вероятностным алгоритмом.
ПРИМЕР 22.1. Чтобы лучше понять идею приведенного выше алгоритма, рассмот-
рассмотрим в качестве примера небольшую задачу, предназначенную для иллюстрации
применения метода. Предположим, что
X = [10011011] где п = 8
и
У = [1011011001101100 • • • 0], где т = 300.
Пусть t = т - п + 1 = 293 и М = nt2 = 686792. Предположим, что fc = 2
и случайным образом получены простые числа р\ = 47 и р2 = 31. Вычисляя
первичные вычеты, получим сначала идентификаторы строки X
NpW(X) = [[N(X)]]pW = [[15510]]47 = 14;
Np{2)(X) = [[N(X)}}p{2) = [[15510]]з1 = 0.
Начиная с г = 1, вычислим идентификаторы (строки) У(г), взамно простые с
простыми числами 47 и 31, и проверим на соответствие. Соответствия с каждым
из двух идентификаторов отмечены звездочкой (*).
i
1
2
3
4
5
6
7
Y(i)
[10110110]
[01101100]
[11011001]
[10110011]
[01100110]
[11001101]
[10011011]
N(Y(i))
182
108
217
179
102
205
155
N47{Y(i))
41
14 *
29
38
8
17
14 *
ЛГз1(У(г))
27
15
0 *
24
9
19
0 *
Соответствует?
Нет
Нет
Нет
Нет
Нет
Нет
Да
Первое соответствие наблюдается на позиции 7 в битовой строке У. Следует
отметить, что в этом примере мы провели прямое вычисление вычетов, поскольку
числа достаточно малы. Компьютерная реализация потребовала бы использования
модулярных операций и корректирующей формулы, описанных выше. ?
Следуя Карпу и Рабину, получим теперь предельное значение вероятности
ошибочного соответствия при использовании этого алгоритма. Для начала нам
потребуются два понятия: вероятности и теоретико-числовой функции.
Пусть Г — непустое множество "возможностей", и любая из этих возмож-
возможностей может быть выбрана. Пусть подмножество А множества Г содержит ин-
интересующие нас возможности. Выберем один элемент из Т. Вероятность выбора
элемента из А определена соотношением
^лг^т^ / .ч Количество элементов в А
PROB (А) = .
Количество элементов в Т

834 ГЛАВА 22. Приложения теории чисел
В такой ситуации будем говорить, что элемент выбран случайным образом из
множества Т (каждый элемент множества Т имеет такую же возмножность быть
выбранным, как и любой другой ) и событие А имеет место, если выбранный эле-
элемент принадлежит множеству А. Формула, приведенная выше, дает вероятность
события А. Например, предположим, что Т — множество граней игрального ку-
кубика, так что Т = {1,2,3,4,5,6}, и мы бросаем кубик один раз (выбираем сторону
случайным образом). Пусть А — событие (множество возможных исходов), состо-
состоящее в получении числа точек, выраженного простым числом. А = {2,3,5}. Тогда
PROB(A) = 3/6 = 0.5. Очевидно, вероятность любого события лежит между 0 и
1 включительно.
Пусть тг(ги) количество простых чисел, которые меньше или равны w. Таким
образом, тгA) = 0, 7гB) = 1, тгE) = 3 и тгB0) = 8.
Сформулируем два результата, полученные Дж. Россером и Л. Шонфилдом
в работе [103].
ТЕОРЕМА 22.2. Если w > 29, то
PlP'-'Pn(w) > 2™,
где рьР2,Рз, • • • ,Pn(w) -~ простые числа, которые меньше или равны w.
ТЕОРЕМА 22.3. Если w > 17, то
w 1.25506w
log(iy) W log(w)
ТЕОРЕМА 22.4. Если w > 29 и b < 2W, то b имеет менее, чем тг(г^) простых
делителей.
ДОКАЗАТЕЛЬСТВО. Допустим, что w > 29 и b < 2W, но Ъ имеет не менее тг(гу)
простых делителей. Пусть d\ < d,2 < • • • < dr — простые делители числа Ь, так
что г > 7г(ги). Пусть р\ < р2 < - - • < Рк — первые к простых чисел для любого к.
Тогда
2W > Ь дано
b > did2ds • • • dr, поскольку d^ • • -dr \b
d\d2 - • - dr > P1P2 - -pr, поскольку di > pi для каждого г
P\Pi "Pr> PlP2 ' • ' Pn(w), ПОСКОЛЬКУ Г > 7T(w)
P1P2 • - -Pn{w) > 2W по теореме 22.2.
Ho 2W > 2W является противоречием. Таким образом, Ь должно иметь менее, чем
tt(w) простых делителей. ¦
Как упоминалось выше, рассмотренный алгоритм поиска имеет возможность
завершения с ошибочным соответствием. От этого алгоритма мало пользы, если
ошибочное соответствие будет наблюдаться часто. Приведенная ниже теорема
утверждает, что вероятность получения ошибочного соответствия в результате
применения алгоритма не превышает некоторое определенное значение.

РАЗДЕЛ 22.1. Приложение: поиск по образу 835
ТЕОРЕМА 22.5. Если алгоритм применен к задаче поиска для X и Y с характе-
характеристиками n, m, tt M, k n 5, то вероятность ошибочного соответствия меньше
или равна
(^)k прип>29.
ДОКАЗАТЕЛЬСТВО. Допустим, что п > 29, 1 < г < t и X ф Y(r). Поскольку
О < ЩХ) < 2П и 0 < N(Y{r)) < 2П, то \N(X) - N(Y(r))\ < 2П. По теореме 22.4
количество простых чисел, которые делят \N(X) - N(Y(r))\9 меньше, чем 7r(n);
следовательно, для любого j, I < j < fc, учитывая, что простое число pj выбрано
случайным образом из множества 5, в котором имеется тг(М) элементов, имеем
PROB (р,- делит \ЩХ) - N(Y(r))\) < ^
Поскольку к простых чисел pi,p2,... ,Pk выбраны случайно и независимо, то по
свойству вероятности пересечения к таких событий имеем
делит \ЩХ) - N(Y(r))\ для всех j) < (^Щ)
Поскольку имеется t взаимоисключающих событий для г, то по свойству вероят-
вероятности все простые числа р\,р2,...,Рк делят \N(X) — N(Y(r))\ для некоторого г,
и сама вероятность меньше или равна t • / . ¦
\7T(M)J
ТЕОРЕМА 22.6. При выполнении предположений теоремы 22.5, если М = nt2,
где п > 29, то вероятность ошибочного соответствия меньше или равна
A.25506)fc t-Bfc-1} (I 4- 0.6 \og(t))k.
ДОКАЗАТЕЛЬСТВО. Из теоремы 22.5 следует, что
/ ( \ \ ^
PROB (ошибочного соответствия) < t • [ . _ _ч ) .
Из теоремы 22.3 следует, что
су
тг(п) < cr-^-г, где с - 1.25506, и " < 7r(nt2).
log(n) log(nt2)
Таким образом,
Г 1 ( f2\ "I ^
PROB (ошибочного соответствия) < ? • -—г-т * — о =
~ [log(n) nt2 J
Но для п > 29 имеем log(n) > logB9). Следовательно, теорема верна, поскольку
2 2
непосредственное вычисление показывает, что ;—т—- < -—-—г < 0.6. ¦
log(n) ~ logB9)

836 ГЛАВА 22. Приложения теории чисел
Для иллюстрации теоремы 22.6 предположим, что имеется задача сопостав-
сопоставления строк с образом X длины пО, которая соответствует 25 в 8-битовой ASCII-
кодировке, с текстовой строкой Y длины 32000, соответствующей 4000 в кодиров-
кодировке ASCII. Тогда t = 31801 и М = nt2 < 200C2000J = 211 • 108 « 211 • 2266 < 238,
так что компьютерные представления простых чисел pi и соответствующих выче-
вычетов в двоичной системе счисления будут иметь менее 38 битов. Если к = 4, то
вероятность ошибочного соответствия не будет превосходить величину 2 • 10~28.
Алгоритм Карпа и Рабина является алгоритмом, выполняющимся в реаль-
реальном времени и требующим одинакового времени вычисления для каждого символа
текста. Он также требует постоянного количества памяти, зависящего только от
п, к и t. Можно доказать, что алгоритм имеет малую вероятность ошибки. Бо-
Более того, метод можно леко обобщить для применения в многомерных задачах.
Помимо Np этот метод может использовать и другие "идентифицирующие" функ-
функции. Заметим, что Карпу и Рабину принадлежат другие подобные, но отличные
от вероятностных алгоритмы поиска по образцу, которые можно найти в ссылках,
приведенных ранее. Информацию о некоторых эффективных невероятностных ал-
алгоритмах поиска для сравнения можно найти в работах A) Fast Pattern Matching
in Strings, авторы Д. Э. Кнут, Дж. X. Моррис и В. Р. Пратт [65]; B) A Fast
String Searching Algorithm, авторы Р. С. Боер и Дж. С. Мур [12]; C) Pattern
Matching Alternatives: Theory vs. Practice, автор Джек Пардум [93] и D) A Very
Fast Substring Search Algorithm, автор Даниэль М. Сандей [111].
¦ УПРАЖНЕНИЯ
1. Докажите, что если W и V — битовые строки длины и, то
\N(W)-N(V)\ <2n.
2. В теореме 22.2 было показано, что произведение всех простых чисел, кото-
которые меньше или равны w, превышает величину 2W, если w > 29. Определите,
для какого положительного целого числа w < 29 также выполняется утвер-
утверждение этой теоремы.
3. В теореме 22.3 были показаны два неравенства, которые имеют место для
каждого положительного числа w > 17. Используя непосредственные вычис-
вычисления, покажите, какое положительное целое число w < 17 также удовле-
удовлетворяет этим неравенствам.
4. Для образа X длины п — 0 и текста длины rnOOO, используя теорему 22.6,
определите верхнюю границу вероятности ошибочного соответствия для к =
1,2,3 и 4.
5. Предположим, что задан образ длины п битов, количество простых чисел
к и такое число М, что все идентифицирующие простые числа и их вы-
вычеты имеют не более, чем 32 бита. Кроме того, будет использована опи-
описанная в данном разделе корректировка. Определите количество 32-битовых
компьютерных слов информационной памяти, необходимых для реализации
алгоритма Карпа и Рабина.

РАЗДЕЛ 22.2. Приложение: функции хеширования 837
22.2. ПРИЛОЖЕНИЕ: ФУНКЦИИ ХЕШИРОВАНИЯ
В компьютерных приложениях часто возникает ситуация, когда имеется п набо-
наборов информации Ii,l2,...,In, где каждый набор идентифицирован ключом, на-
например, fci,/с2, • • • ,кп, соответственно. При этом желательно иметь возможность
быстро находить информацию Ij, если известен ключ kj. Ключи можно рассмат-
рассматривать как целые числа, хотя они могут иметь вид конечных последовательностей
символов алфавита. Просмотр списков ключей может занимать достаточно много
времени; более того, если поиск с использованием ключей необходимо проводить
неоднократно, то вычислительные затраты могут быть значительными. Компи-
Компилятор — это компьютерная программа, преобразующая другую компьютерную
программу, написанную на языке программирования высокого уровня (напрмер,
ФОРТРАН или Паскаль), в эквивалентную программу на машинном языке. В
течение процесса трансляции компилятор должен генерировать таблицы и неод-
неоднократно обращаться к ячейкам таблиц для получения информации. Важным
моментом здесь является то, что поисковая таблица создается один раз, а ис-
используется многократно. Поскольку таких таблиц может быть достаточно много,
необходимо также использовать как можно меньше памяти для хранения.
Одно из решений проблемы "размещения" состоит в использовании функции
хеширования h : К —> {0,1,..., га}, где К = {/сь /с2, • • •, кп} и га + 1 > п. Таким
образом, мы обеспечиваем т + 1 компьютерных ячеек для хранения п наборов
информации. Итак, чтобы найти Ij, нужно вычислить h(kj) и перейти в ячей-
ячейку /i(fcj), где хранится Ij. Вообще, найти идеальную функцию хеширования, т.е.
такую что h(kr) ф h(ks), когда kr ф ks и т 4- 1 = п, достаточно трудно. Наи-
Наиболее широко используемые функции хеширования отображают множество К во
множество, содержащее более, чем п элементов, поэтому не являются инъектив-
ными. Для функции h, которая не является взаимно однозначным отображением,
должно быть выработано соглашение поведения при возникновении коллизии, т.е.
в ситуации, когда kr и ks — разные ключи, но h(kr) = h(ks). Дональд Э. Кнут в
томе 3 книги Искусство программирования [64] рассматривал различные спосо-
способы выбора функций хеширования и методы разрешения коллизий. Яэшке в книге
Reciprocal Hashing: A Method for Generating Minimal Perfect Hashing Functions
[51] описывает особый тип минимальной функции хеширования, т.е. такой функ-
функции хеширования, которая является инъективной и использует минимальный объ-
объем памяти {минимальная совершенная функция хеширования) . Для функции
хеширования, которую ввел Яэшке, необходима возможность отображения клю-
ключей {fci, /с2,..., /сп}, которые могут не быть попарно взаимно простыми, во множе-
множество попарно взаимно простых целых чисел {/(fci),/(fc2),..., f(kn)}. Он доказал
следующую теорему.
ТЕОРЕМА 22.7. Пусть К = {kuk2,... ,А:П} — множество п различных положи-
положительных целых чисел. Пусть существуют целые числа D и Е такие, что если
функция f(x) определена соотношением f(x) = Dx + Е, то элементы набора
положительных целых чисел {/(fci),/(/c2), • • •,/(^п)} являются попарно взаимно
простыми. Таким образом, целые числа Dki+Е, Dk2 + E, v. и Dkn + E являются
попарно взаимно простыми.
ДОКАЗАТЕЛЬСТВО. Доказательство теоремы является слишком длинным и при-

838 ГЛАВА 22. Приложения теории чисел
водиться не будет (см. [51]). Тем не менее, далее рассмотрим специальный случай,
вполне адекватный нашим целям. ¦
Основной результат, который получил Яэшке, сформулирован в приведен-
приведенной ниже теореме. В ней [w\ — набольшее положительное целое число, которое
меньше или равно w.
ТЕОРЕМА 22.8. Если множество К = {/сь fc2, • • •, кп) содержит различные целые
положительные ключи, то в нем существуют целые числа С, D и Е такие, что
где х ? К является минимальной совершенной функцией хеширования.
ДОКАЗАТЕЛЬСТВО. Пусть к\ < к2 < • - • <кп\\ пусть целые числа D и Е заданы
в соответствии с теоремой 22.7, так что f(kj) = Dkj +E и HOJ\(f(ki),f(kj)) = 1
для г ф j. Поскольку D и Е могут быть выбраны таким образом, что f(kj) > п
для каждого j, имеется возможность выбрать п целых чисел аьа2,... ,ап таких,
что п{ ф uj (mod n) и таких, что
(г - 1) • (Dki + Е)<а{<1' (Dki + Е).
Тогда, согласно обобщенной китайской теореме об остатках, применимой к моду-
модулям, не являющимся взаимно простыми (теорема 10.14), существует такое чис-
число С, что
С = а2 (mod n(Dk2 + ??)),
С = ап (mod n(Dkn + E)).
Поэтому, существуют целые числа qi такие, что С = qi[n(Dki + E)}+ai для всех г.
Следовательно,
I Г* I
= 4%п 4- (г — 1) = г — 1 (mod п).
ki + Е
Из этого следует, что функция /г, определенная в теореме, обладает тем свой-
свойством, что h(ki) ф h(kj), когда г ф j, поэтому функция h является инъективной.
Более того, множеством значений функции h является {0,1,..., (п — 1)}. ¦
Яэшке привел алгоритмы вычисления чисел С, D и Е\ однако, эти методы
не являются конструктивными. С другой строны, Чанг и Ши в работе Pairwise
Relatively Prime Generating Polynomials and Their Applications [19] дают способ
вычисления требуемых многочленов вида f(x) = Dx -f 1, где Е = 1. Доказатель-
Доказательство приведенной ниже леммы предоставляется читателю.
ЛЕММА 22.9. Если а и b положительные целые числа, а > b и d кратно а - 6, то
d(a - Ъ) и da + 1 — взаимно простые числа.

РАЗДЕЛ 22.2. Приложение: функции хеширования 839
ТЕОРЕМА 22.10. Пусть К = {/сь fc2, • • •, kn} — множество, содержащее п различ-
различных положительных целых чисел, для которых /с* < ki+\. Если {t\,t2,... ,ts} =
{k{ — kj : 1 < j < i < n} — множество, содержащее s = n(n — l)/2 разностей,
то D = w • H0K(ti,^2,..., ts), где w — произвольное положительное целое чис-
число, обладает тем свойством, что Dki + 1, Dk2 -hi,..., Dkn + 1 являются попарно
взаимно простыми числами.
ДОКАЗАТЕЛЬСТВО. Поскольку НОД(а,Ь) = НОД(а-Ь,а), где а и 6 - це-
целые числа, для которых НОД(а, 6) и НОД(а — Ь, Ь) определены, получаем, что
HOR{Dki +1, Dkj +1) = HOJX(D(ki - kj), Dk{ +1) для i > j, где D задано соглас-
согласно теореме. По определению, D кратно (ki - kj), следовательно, из леммы 22.9
следует, что HOR(Dki + 1, Dkj + 1) = 1 для i> j. Ш
Заметим, что для доказательства теоремы требуется только, чтобы D было
кратно всем ti, ^2,..., ts. Естественно, можно было бы выбирать D как можно
меньшим {w = 1); однако, для доказательства теоремы 22.8 необходимо, чтобы D
было таким, чтобы f(ki) = Dki 4-1 > п. Такое D может быть всегда получено за
счет выбора w достаточно большим.
ПРИМЕР 22.11. Предположим, что К = {3,6,7,12}. Тогда
{к{ -kj'.l<j<i<4} = {6 - 3, 7 - 3,12 - 3, 7 - 6,12 - 6,12 - 7} =
= {3,4,9,1,6,5},
так что D = НОКC,4,9,1,6,5) = 180. Таким образом, f(x) = 180х 4-1 и
i
1
2
3
4
ki
3
6
7
12
/(*<) = Dki + 1
180 • 3 + 1 = 541
180 • 6 + 1 = 1081
180 • 7 + 1 = 1261
180 • 12 + 1 = 2161
Проверка показывает, что любые два из чисел 541, 1081, 1261 и 2161 являются
взаимно простыми. ?
Для реализации алгоритма обратного хеширования, предложенного Яэшке,
необходимо иметь возможность вычислять целое число С. К счастью, Чанг и Ши
в работе A Fast Algorithm for Constructing Reciprocal Hashing Functions [18]
представили алгоритм вычисления целого числа С.
В оставшейся части этого раздела мы будем использовать как функцию це-
целой части |_tuj, описанную ранее, так и функцию округления рш], равную наимень-
наименьшему положительному целому числу, большему или равному w. Таким образом,
[5.231 = 6 и [81 = 8.
ТЕОРЕМА 22.12. Если
а) mi,77i2,... ,mn — попарно взаимно простые целые числа;
б) Ш{ > п для всех г, 1 < г < п;

840 ГЛАВА 22. Приложения теории чисел
в) М= ftm,;
г) Mi = nYl Wsj = для всех г;
д) bi является таковым, что М{Ъ{ = п (mod пга*), и
ч _. Г(г-1)шЛ
е) Л^г = — для каждого г,
I п I
тогда
п
i-^i j 3 3
1.
= (г - 1) (mod n) для всех г,
2. С = Sj=i MjbjNj — наименьшее положительное целое число такое,
\ \ п
\ с \
что — = (г — 1) (mod n) для всех г.
ДОКАЗАТЕЛЬСТВО. Пусть ai = Ni - п, тогда ai — наименьшее число, кратное п,
так что (i — 1) - mi < ai < i • 7П{ для всех i иа^ ау (mod n), когда г ^ j. Сумма
]Cj=i MjbjNj является решением п сравнений
х = а\ (mod
х = п2 (mod n/77>2);
х = ап (mod nran),
потому что, если j ф i, то Mj содержит множитель пгп{. Поэтому MjbjNj = 0
(mod птпг) и
MjbjNj = MibiNi (mod пт^) =
= nTVi = a^ (mod nm^).
Поэтому,
TTT-i 771i 771^ TTlj
для соответствующего целого числа J;. Поскольку М& = п (mod пт^), то су-
существует целое число U такое, что М& = ti(nmi) 4- п, поэтому
пдг.
i H -.
ттг

РАЗДЕЛ 22.2. Приложение: функции хеширования 841
Таким образом, учитывая (г — 1) • га; < п{ < г • га^, имеем
• I = I ^11 = (г _ 1) (mod n),
что доказывает часть 1.
Пусть С = ]Cj=i MjbjNj . Нам нужно показать, что U^L = (г-1) (mod n)
для 1 < г < п. Согласно алгоритму деления, существует целое число J такое, что
п
53 MjbjNj = J(nM) -f С Для 1 < г < п, опять согласно алгоритму деления,
i=i
существуют целые числа qi и г;, где 0 < ri < m* такие, что
j =qimi+ri,
поэтому
3 = 1
Согласно результату части 1 существует целое число ti такое, что
q{ = (г - 1) + Un\
qirrii +n = (i —
J(nM) + С = (г —
4- r^,
поэтому
ч
= (г - 1) 4-
\
JM\
U
J
i J
4
так что
— = (г — 1) (mod n).
Читателю остается доказать, что если С — любое другое положительное целое
число такое, что —¦ = (г - 1) (mod п) для всех г, 1 < г < п, то С > С. Ш

842 ГЛАВА 22. Приложения теории чисел
Объединяя последние несколько результатов, получаем следующую теорему.
ТЕОРЕМА 22.13. Пусть К = {fci, &2,. •. ,fcn} — множество, содержащее п раз-
различных положительных целых чисел; пусть D и Е — целые числа и пусть/(х) =
Dx 4- Е — функция, описанная в теоремах 22.8 22.10. Предположим также, что
число С задано согласно части 2 теоремы 22.12, где mi = /(&;). Тогда
h{x) =
Dx + E
является минимальной совершенной функцией хеширования.
ДОКАЗАТЕЛЬСТВО. Если гп{ = /(&»). то из теоремы 22.12 следует, что
С
f(ki)
= (г - 1) для 1 < г < гг.
Следовательно, h является биекцией на {0,1,..., (п — 1)}.
ПРИМЕР 22.14. Вернемся к примеру 22.11, в котором К = {/^1,^2,^
{3,6,7,12} и /(*) = 180х + 1. Было показано, что {f{k1)J(k2)J{k3)J(k4)} =
{541,1081,1261,2161}. Пусть mi — f(k{). Числа га; являются попарно взаимно
простыми и rrii > п = 4. Используя теорему 22.12, получаем следующую таблицу
г
1
2
3
4
541
1081
1261
2161
Mi
11782990804
5896945444
5055192724
2949837124
ь,
235
12
172
1303
Ni
0
273
631
1621
MJiNi
0
19318393274544
548650176721168
6230536829339212
h{ki)
0
1
2
3
Например, чтобы найти 6з, решаем сравнение 5055192724 Ьз = 4 (mod 5044), что
эквивалентно решению сравнения 1263798181 • 63 = I (mod 1261) или решению
сравнения 22 • 6з = 1 (mod 1261). Следовательно, требуется найти Ьз и у такие,
что 2263 + 1261?/ = 1. Используя алгоритм Евклида и обратную подстановку,
приходим к результату 22 • 172 + (-3) • 1261 = 1. Таким образом,
С =
з=\
= [[6798505399334924]] пМ 183904723300.
пМ
Далее используем С, / и h для хеширования /с3 = 7.
3183904723300
h(k3) =
1261
= [[2524904618]]4 = 2.
П
Обратные функции хеширования, введенные Яэшке, порождают большие це-
целые числа. Вычислительные затраты, необходимые для реализации этого, должны
быть соизмеримы с ресурсами, необходимыми для использования неминимальной
и несовершенной функции хеширования: A) максимально возможные затраты па-
памяти, B) возможность разрешения коллизий и C) использование алгоритмов по-
поиска для нахождения элементов данных в таблице.

РАЗДЕЛ 22.3. Приложение: криптография 843
УПРАЖНЕНИЯ
1. Докажите, что если оиб- целые числа, для которых определены НОД(а, Ъ)
и НОД(а-Ь,а), то НОД(а,6) = НОД(а-6,а).
2. Для каждого из приведенных ниже множеств найдите многочлен f(x) =
Dx + l, который биективно отображает это множество на множество попарно
взаимно простых чисел:
а) {12,15,18,24};
б) {5,15,20,25}.
3. Пусть ai,a2,... ,ап являются и различными положительными целыми числа-
числами. Докажите или опровергните утверждение: НОД(ах, с&2,..., ап) = 1 тогда
и только тогда, когда НОД (a^a^) — 1 для всех i ф j.
4. В доказательстве теоремы 22.12 покажите, что а; = Л^п является наимень-
наименьшим числом, кратным числу п, так что (г — 1) • m» < a» < г • т».
5. Проверьте числа в таблице примера 22.14.
6. Для
а) К = {12,15,18,24} из упражнения 2(а);
б) К = {5,15,20,25} из упражнения 2F).
вычислите, используя теорему 22.12, целое число С и, соответственно, ми-
минимальную совершенную обратную функцию хеширования из теоремы 22.13.
Проверьте тот факт, что h(k{) = г — 1 при любом г.
22.3. ПРИЛОЖЕНИЕ: КРИПТОГРАФИЯ
Во всем мире правительства, компании и обычные люди хотят отправлять сооб-
сообщения таким образом, чтобы прочитать их мог только адресат. Военные посылают
приказы, банки передают информацию о движении капиталов, люди делают по-
покупки, используя кредитные карточки. Сообщения, посланные по телефонным
линиям, по радио, через спутник или через компьютерные сети могут быть пе-
перехвачены посторонними, возможно, враждебными лицами. Чтобы не допустить
возможности получения информации или ее изменения посторонними лицами, со-
сообщения изменены таким образом, что оригинал скрыт. Процесс засекречивания
информации называется шифрованием или кодированием, а процесс рассекре-
рассекречивания — дешифровкой или декодированием. Исходное сообщение называется
открытым или незашифрованным текстом, а засекреченное сообщение — зашиф-
зашифрованным текстом (см. рис. 22.1).
Конечно, и отправитель, и получатель сообщения должны согласовать про-
процедуру шифрования и дешифровки. Эта процедура обычно состоит из общего
метода и "ключа". Ключ обеспечивает специфическую информацию, что вместе
с общим методом позволяет отправителю легко зашифровать, а получателю -—
легко дешифровать сообщение. Однако, в отсутствие ключа любой, перехватив-
перехвативший сообщение, не может за приемлемое время, используя самые мощные вы-
вычислительные ресурсы, получить исходный текст сообщения, даже зная общий
метод шифрования. Например, восстановление сообщения при использовании са-
самого быстродействующего компьютера потребовало бы, скажем, миллион лет или

844 ГЛАВА 22. Приложения теории чисел
Шифрование
М *• С *• Канал передачи
Исходное с = Е(м) Зашифрованный
сообщение, текст
или
открытый текст
Перехват
Дешифровка
М"
Криптоанализ
М = D(C)
Несанкционированное
восстановление М Восстановление
сообщения сообщения
Рис. 22.1
исследования всех возможных сообщений на основе полного перебора, используя
метод проб и ошибок. Попытка расшифровать открытый текст по зашифрованному
тексту без использования общего метода или ключа называется криптоанализом.
Рис. 22.1, на котором Е — функция шифрования, a D — функция дешифровки,
иллюстрирует механизм поиска. Таким образом, D(E(M)) = М. Криптография —
это наука, которая изучает методы шифрования и криптоанализа этих методов.
Шифрование и дешифровка обычно выполняются компьютерами, поэтому со-
сообщение М сначала преобразуется в целое число или в последовательность целых
чисел с тем, чтобы появилась возможность преобразовывать эти числа, используя
компьютерную арифметику. Таким образом, будем считать, что М — целое число.
Сообщение в виде целого числа М обычно делят на блоки МьМг, Мз,..., М&,
так что каждый блок представляет собой целое число Mi, где 0 < Mi < и, и число
п выбрано заранее. В таком случае шифрование выполняется блок за блоком как
E(Mi) = Ci, и дешифровка проводится аналогично относительно D(Ci) = Mi. На-
Например, можно следующим образом использовать 8-битовые компьютерные коды
ASCII для каждого символа алфавита:
М 010011012 = 77ю,
О 010011112 = 79ю,
iV 010011102 = 78io,
Е 010010102 = 69ю,
Y 010110012 = 891О.
Тогда Mi могло бы соответствовать группам из двух букв, что дает
"Л/О" -> Mi = 01001101OIOOIIH2 = 19791io,
так что 0 < Mi < и = 216 = 65536. Конечно, полное сообщение можно было бы
рассматривать как единую строку двоичных цифр, которые затем можно группи-
группировать в последовательность блоков любого удобного размера.
Р. Л. Райвест, А. Шамир и Л. Адлеман в работе Method for Obtaining
Digital Signatures and Public Key Cryptosystems [98] представили общий метод

РАЗДЕЛ 22.3. Приложение: криптография 845
шифрования, известный по фамилиям авторов как RSA-метод. Метод обладает
многими хорошими характеристиками.
Пусть р и q — два достаточно больших числа, каждое из которых имеет,
например, 100 разрядов, и пусть и = р • q. Для шифрования и дешифровки будут
использованы два целых числа end, которые связаны с числами р, q и п. Оба
числа end будут определены ниже. Для шифровки сообщения М — Mi вычислим
а для дешифровки вычислим
M = D(C)=[[Cd]]n.
Поскольку произведения Ме и Cd приведены по модулю п, то зашифрованный
текст и блоки исходного текста — это целые числа в диапазоне от 0 до (п - 1).
Ключ для шифрования — пара целых чисел (п, е), и ключ для дешифровки —
пара целых чисел (n, d).
Сначала выберем в качестве d "большое" целое число, взаимно простое с
произведением (р - 1) • (q - 1). Затем определим целое число е, 0 < е < п, т.е.
единственное решение (теорема 3.65) сравнения
d-x = l (mod (p- l)(q- 1)).
Следовательно, учитывая соотношение ф(п) = <j>{p)(t>(q) = (р — l)(q — 1), имеем
d • е = 1 (mod ф(п)).
ТЕОРЕМА 22.15. Если
а) п — р • д, где р и q — различные простые числа;
б) НОД(^0(п)) = 1;
в) d • е = 1 (mod ф(п))\
г) для 0 < J < п, определим функции
тогда для 0 < J < п
D{E(J)) = J и E(D(J)) = J.
ДОКАЗАТЕЛЬСТВО. Пусть 0 < J < п. Из соотношения А = В (mod n) следует,
что \[А))п = [[В]]п. Поэтому
= D([{Je})n)=[[[[r}}dn]}n =
= [[(Je)d]}n=[[Jed]}n =
потому что по теореме 10.31 соотношения d-e = l (mod ф{п)) и г = s (mod ф(п))
имеют место тогда и только тогда, когда xr = xs (mod n). Результат E(D(J)) = J
может быть доказан аналогично. ¦

846 ГЛАВА 22. Приложения теории чисел
ПРИМЕР 22.16. Предположим, что мы решили использовать 8-битовый код ASCII
для символов алфавита с размером блока, равным одному символу или букве.
Нам потребуется п > 28 = 256. Пусть р = 41 и q = 73, так что п = р • q = 2993,
ф(п) = 40-72 = 2880 = 26-32-5. Пусть d = 217 = 31-7, так что НОДB17,2880) = 1.
Используя алгоритм Евклида, в качестве решения сравнения 217х = 1 (mod 2880)
получаем е = 1513. В таком случае, слово "MONEY", зашифрованное с исполь-
использованием RSA-метода с ключом (п, е) = B993,1513), имеет вид, приведенный в
следующей таблице
г
1
2
3
4
5
Блок
"М"
"О"
"N"
"Е"
"Y"
М{
77
79
78
69
89
E(Mi) = \[щ]]п = а
1683
79
2560
872
2571
Для эффективного вычисления Mf по модулю п был использован алгоритм из
раздела 3.6. Можно показать также, что D(Ci) = М{, используя в каждом случае
тот же самый алгоритм с ключом (n, d) = B993,217). Сравнительно небольшая
величина числа п в этом примере не позволяет полностью раскрыть возможно-
возможности шифровальной функции Е, поскольку малое п можно легко разложить на
множители. Кроме того, размер блока, как правило, выбирается большим, чем
один символ, иначе мы бы имели шифр простой замены, который легко поддается
криптоанализу. ?
RSA-метод используют следующим образом. Оба простых числа р и q, ко-
которые дают п = pq, а также целое число dy взаимно простое с ф(п), сохраняются
в тайне. Вместе с тем, целые числа п и е становятся общедоступными; известен
также и общий метод. Поэтому всякий, знающий ключ шифрования (п, е), может
зашифровать сообщение М, получив в результате зашифрованное сообщение С,
прочесть которое может только тот, кто обладает ключом (n, d). Каждый может
иметь собственный набор ключей криптосистемы RSA. Ключ общего пользования
каждого человека, (п, е), может быть внесен в список, например, в регистр, как
это сейчас сделано для телефонных номеров. Если некая особа, например, Алиса,
хочет послать Бобу тайное послание Мд, то Алисе необходимо найти его ключ
общего пользования, {пв,ев) в общедоступном регистре. Затем Алисе нужно
зашифровать сообщение Мд следующим образом:
Зашифрованное сообщение С а следует передать Бобу любым удобным способом.
Всякий, помимо Боба, перехвативший сообщение С^, не сможет за приемлемое
время восстановить сообщение Ма- Получив зашифрованное сообщение СА, Боб
сможет восстановить оригинал, воспользовавшись своим личным ключом
следующим образом:
[[^]] =мА.
nD

РАЗДЕЛ 22.3. Приложение: криптография 847
Особенность RSA, отличающая этот метод от обычных криптосистем, заключа-
заключается в том, что часть ключа является общеизвестной. Такие методы назывеются
криптосистемами с ключами общего пользования. Они были введены У. Диффи
и М. Э. Хеллмэн в работе New Directions in Cryptography [28].
Согласно теореме 22.15 D(E(J)) = J и E(D(J)) = J, поэтому криптосисте-
криптосистема RSA обладает очень полезной характерной особенностью, на которую указали
Диффи и Хеллмэн. Ключ Боба общего пользования (пв,ев) доступен для каждо-
каждого, поэтому каждый может послать ему собщение; поэтому, если Алиса посылает
Бобу сообщение, то как он может быть уверен, что сообщение пришло от Али-
Алисы, а не от кого-то другого? Алиса может набрать подписанное сообщение SA>
содержащее ее имя и другую идентифицирующую информацию. Далее, Алиса
использует собственный секретный дешифрирующий ключ (па,с1а)
= ТА
1A
и включает ТА вместе или как часть основного зашифрованного текста СА сооб-
сообщения МА. Когда Боб получает сообщение Алисы, он выделяет ТА и применяет
ключ шифрования общего пользования Алисы, (пА,еА), что дает
ЕА(ТА) = EA(DA(SA)) = SA.
Учитывая, что, по-видимому, только Алиса могла создать сообщение ТА, кото-
которое преобразуется в SA при помощи ключа общего пользования Алисы {пА,еА)у
соответствующее сообщение МА является подлинным. Инструмент установления
подлинности для такого применения не должен зависеть от сообщения и подпи-
подписывающего лица. Простой способ реализации такого определения подлинности
сообщения Алисы для Боба, состоящего из блоков МЬМ2,... ,М/с, мог бы со-
состоять в том, что Алиса создаст подпись 5, состоящую из блоков 5Ь52,..., S^,
которая преобразуется в Т; = DA(Si) путем использования дешифрующего ключа
Алисы. Можно даже положить Si = Mi, после чего Т; = DA(Mi). Комбинация су-
суперблоков TiMi,T2M2,... ,TkMk шифруется ключом Боба общего пользования.
Может возникнуть необходимость переписать целые числа TiMi,T2M2,... ,TkMk
в виде Ji, J2,..., Jm, где 0 < J; < п^, чтобы они удовлетворяли модулю Боба,
пв. Таким образом, имеем
Ui = ЕВЩ.
Получив последовательность f/i, ?/2,..., С/ь Боб воспользуется своим секретным
ключом и получит
что может быть разблокировано и снова даст TiMi,T2M2,... ,TkMk. Затем Боб
сверит подпись с
ЕА(Тг) = М{
в предположении, что было использовано Si = Mi. Поскольку Т;, преобразуемое в
Mi = EA(Ti), могло быть создано только Алисой, сообщение является подлинным.
Безопасность криптосистемы RSA зависит от того, насколько сложно найти
разложение на множители n = p- q, получая посредством этого р и q. Поскольку

848 ГЛАВА 22. Приложения теории чисел
е общеизвестно, то d можно определить, решая, при условии, что известны р и q,
сравнение ех = 1 (mod (р — l)(q — 1)). Безопасность метода зависит также от
сложности определения индексов. Если М известно, то С = [[Ме]]п можно вы-
вычислить, используя общедоступную информацию. Криптоаналитику потребуется
решить сравнение М = Cd (mod n), если d = indcM no модулю п, что также
является непростым делом. Кроме того, р и q — случайным образом выбранные
большие простые числа, что делает разложение на множители числа п трудно-
трудновыполнимым. Более того, d выбирается случайным образом так, чтобы оно было
взаимно простым с ф(п) и достаточно большим, чтобы сделать быстрый полный
перебор при малых d неэффективным.
Традиционные методы шифрования требуют, чтобы обе стороны, и только
они, владели одинаковым ключом. Примером является 56-битовый ключ, исполь-
используемый в стандарте кодировке данных DES — The United States Data Encryption
Standard (см. работу Мейера и Матиаса Cryptography: A New Dimension in
Computer Data Security [71]). Для передачи сообщений большого объема ис-
использование DES может быть предпочтительнее, чем использование метода RSA,
т.к. DES требует меньших вычислительных затрат. Вопрос состоит в том, как
стороны могут сообщать ключ друг другу? Диффи и Хелмэн [28] предложили
следующий метод обмена ключами.
Предположим, что р — простое число и д — первообразный корень простого
числа р. Числа р и д могут быть общеизвестны. Предположим, что Алиса и
Боб хотят пользоваться одним ключом. Алиса выбирает случайное целое число
а такое, что I < а < р — 2, и Боб выбирает случайное целое число b такое, что
1 < Ь < р — 2. Числа а и 6 хранятся в секрете и известны только Алисе и Бобу,
соответственно. Алиса вычисляет
л = [[<?%
и передает А Бобу любым удобным способом. Со своей стороны, Боб вычисляет
В =[[9%
и передает В любым способом Алисе. Алиса вычисляет
и Боб вычисляет
Но К\ = К2, потому что
[[А%=[[(9а)%= [№)% = №%.
Таким образом, Боб и Алиса имеют теперь один и тот же ключ, К = К\ = К2.
Поскольку В, А,р и д могут быть известны, криптоаналитик может взломать
шифр, решая сравнение А = да (mod р) для а или решая В = дь (mod p) для 6,
т.е. нужно иметь возможность вычислить тАд А или indy В по модулю р, что в
каждом случае связано с большими вычислительными трудностями. Сложность

РАЗДЕЛ 22.3. Приложение: криптография 849
этого вычисления, согласно обсуждениям, проведенным в разделе 3.14, имеет
порядок у/р, поэтому р должно быть большим простым числом, а р- 1 должно
иметь в разложении хотя бы один большой простой множитель.
Общие сведения о криптографии можно найти в работе Дэвида Кана The
Codebreakers: The Story of Secret Writing [54]. Вопросы криптографии с ключами
общего пользования рассмотрены в работе М. Э. Хеллмэна The Mathematics of
Public-Key Cryptography [43]. RSA-метод был запатентован Райвестом, Шамиром
и Адлеманом в 1983 году; срок патента истек осенью 2000 года.
¦ УПРАЖНЕНИЯ
1. В примере 22.16 проверьте, что D(J) = [[^21?]]2993 ДешиФРУет сообщение
1683,79,2560,872,2571.
2. Создайте RSA-криптосистему, используя п = 83 • 107, путем нахождения
ключа общего пользования (п, е) и личного ключа (n, d).
а) Используйте эти ключи, чтобы зашифровать сообщения "HELP"'.
б) Пусть RSA-ключи из примера 22.16 принадлежат Алисе, а ключи для
п = 83 • 107 принадлежат Бобу. Используйте метод подписей, описанный
в этом разделе, для пересылки Бобу подписанного сообщения "MONEY"
от Алисы.
в) Используя личный ключ Боба и ключ Алисы общего пользования, де-
дешифруйте сообщение из части (б) и проверьте, что оно пришло от Алисы.
3. Покажите, что в RSA-криптосистеме с ключом общего пользования (п,е),
если ф(п) может быть найдено, то криптосистема может быть взломана по-
посредством вычисления d.
4. Рассмотрите RSA-криптосистему, когда п = р • q и ф(п) — известны, но
простые числа р и q — неизвестны.
а) Покажите, что р + q можно выразить через и и ф{п).
б) Покажите, что если q > р, то q — р = \/(р + qJ — 4п.
в) Определите р и q.
г) Выполните пример 22.16 в предположении, что п = 2993 и ф(п) = 2880.
Используйте метод, приведенный выше, для нахождения р и q.

атура
[I] Jiff Adamek, Foundations of Coding, Wiley, New York, 1991.
[2] L. M. Adleman, "A Subexponential Algorithm for the Discrete Logarithm
Problem with Applications to Cryptography," Proc. 20th IEEE Found. Comput.
Sci. Symp. A979), 55-60.
[3] W. R. Alford, A. Granville, and C. Pomerance, "There Are Infinitely Many
Carmichael Numbers," Ann. Math., Volume 140 A994), 703-722.
[4] Ian Anderson, A First Course in Combinatorial Mathematics, Oxford
University Press, New York, 1995.
[5] James A. Anderson and James M. Bell, Number Theory With Applications,
Prentice-Hall, Upper Saddle River, NJ, 1997.
[6] E. T. Bell, The Development of Mathematics, 2nd ed., McGraw-Hill, New
York, 1945.
[7] E. T. Bell, Men of Mathematics, Simon & Schuster, New York, 1965.
[8] C. Berge, Principles of Combinatorics, Academic Press, New York, 1971.
[9] Jean Berstel and Dominique Perrin, Theory of Codes, Academic Press, New
York, 1985.
[10] Norman Biggs, Algebraic Graph Theory, Cambridge University Press,
Cambridge, 1993.
[II] G. D. Birkhoff, A Determinant Formula for the Number of Ways of Coloring
a Map. Ann. of Math., 14 A912) 42-46).
[12] R. S. Boyer and J. S. Moore, "A Fast String Searching Algorithm," Commun.
ACM, Volume 20, No. 10 A977), 762-772.
[13] R. P. Brent, "Irregularities in the Distribution of Primes and Twin Primes,"
Math. Comput., Volume 29 A975), 43-56.
[14] R. P. Brent and J. M. Pollard, "Factorization of the Eighth Fermat Number,"
Math, of Comput., Volume 36, No. 154 A981), 627-630.
[15] Richard A. Brualdi, Introductory Combinatorics, Prentice-Hall, Upper Saddle
River NJ, 1999.
[16] F. Cajori, A History of Mathematics, 2nd ed., Macmillan, New York, 1961.
[17] R. D. Carmichael, "On Composite Numbers P Which Satisfy the Fermat
Congruence ap~l = 1 modP," Amer. Math. Monthly, Volume 19, No. 2 A912),
22-27.

Литература 851
[18] С. С. Chang and J. С. Shieh, "A Fast Algorithm for Constructing Reciprocal
Hashing Functions," Proc. Internat. Symp. New Directions Comput. A985),
232-236.
[19] С. С Chang and J. C. Shieh, "Pairwise Relatively Prime Generating
Polynomials and Their Applications," Proc. Internat. Workshop Discrete
Algorithms Complexity, November A989), 137-139.
[20] Nan-xian Chen, "Modified Mobius Inversion Formula and Its Application to
Physics," Phys. Rev. Lett., Volume 64, No. 11 A990), 1193-1195.
[21] L. W. Cohen and G. Ehrlich, The Structure of the Real Number System, Van
Nostrand Reinhold, New York, 1963.
[22] H. Cohn, Advanced Number Theory, Dover, New York, 1980.
[23] D. Coppersmith, "Cryptography," IBM J. Res. Develop., Volume 31, No. 2
A987), 244-248.
[24] R. Crandall, J. Doenias, C. Norrie, and J. Young, "The Twenty-Second Fermat
Number Is Composite," Math. Comput., Volume 64 A995), 863-868.
[25] T. Dantzig, Number: The Language of Science, 4th ed., Macmillan, New York,
1954.
[26] H. Davenport, The Higher ABithmetic, 6th ed., Cambridge University Press,
New York, 1992.
[27] L. E. Dickson, Studies in the Theory of Numbers, Chelsea, New York, 1957.
[28] W. Diffie and M. E. Hellman, "New Directions in Cryptography," IEEE Trans.
Inform. Theory, Volume IT-22, No. 6 A976), 644-654.
[29] H. W. Eves, In Mathematical Circles, Quadrants I and II, Prindle, Weber &
Schmidt, Boston, 1969.
[30] William Feller, An Introduction to Probability Theory and its Applications,
Wiley, New York, 1950.
[31] G. S. Fishman and L. R. Moore, "A Statistical Evaluation of Multiplicative
Congruential Random Number Generators with Modulus 231 - 1," /. Amer.
Statist. Assoc, Volume 77 A982), 129-136.
[32] G. S. Fishman and L. R. Moore III, "An Exhaustive Analysis of Multiplicative
Congruential Random Generators with Modulus 231 - 1," SI AM J. Sci. Statist.
Comput., Volume 7, No. 1 A986), 24-45.
[33] M. Gardner, "Through the Looking Glass," by Lewis Carroll, from The
Annotated Alice, Bramhall House, New York, 1960.
[34] С W. Gear, Computer Organization and Programming, 2nd ed., McGraw-Hill,
New York, 1974.
[35] Samuel Goldberg, Introduction to Difference Equations, Dover, New York,
1986.
[36] Edgar G. Goodaire and Michael M. Paramenter, Discrete Mathematics with
Graph Theory, Prentice-Hall, Upper Saddle River NJ, 1998.

852 Литература
[37] Ronald Gould, Graph Theory, Benjamin/Cummings, Menlo Park, 1988.
[38] Ronald R. Graham, Donald E. Knuth, and Oren Patashnik, Concrete
Mathematics, Addison Wesley, New York, 1994.
[39] E. Grosswald, Representations of Integers as Sums of Squares, Springer-
Verlag, New York, 1985.
[40] Richard Hamming, Coding and Information Theory, Prentice-Hall, Upper
Saddle River NJ, 1986.
[41] Goffredo Haus and Sametti ScoreSnyth: A System for the Synthesis of Music
Scores Based on Petri Nets and a Music Algebra Readings in Computer-
Generated Music Denis Baggi ed. pp 53-77.IEEE Computer Press Society Los
Alamitos, California, 1992
[42] P. J. Heawood, Map-Color Theorem, Quart. J. Math., 23A890), 332-339)
[43] M. E. Hellman, "The Mathematics of Public-Key Cryptography," Sci. Amer.,
Volume 241, August A979), 146-157.
[44] Raymond Hill, A First Course in Coding Theory, Oxford University Press,
1993).
[45] F. S. Hillier and G. Lieberman, Operations Research, 2nd ed., Holden-Day,
San Francisco, 1974.
[46] Paul G. Hoel, Introduction to Mathematical Statistics, Wiley, New York.
[47] Robert V. Hogg and Allen T. Craig, Introduction to Mathematical Statistics,
Macmillan, New York, 1965.
[48] Ellis Horowitz and Sartaj Sahni, Fundamentals of Data Structures in Pascal,
Computer Science Press, Rockville MD, 1984.
[49] John M. Howie, Automata and Languages, Oxford University Press, New
York, 1991.
[50] A. E. Ingham, The Distribution of Prime Numbers, Cambridge University
Press, New York, 1992.
[51] G. Jaeschke, "Reciprocal Hashing: A Method for Generating Minimal Perfect
Hashing Functions," Commun. ACM, Volume 24, No. 12 A981), 829-833.
[52] Richard Johnsonbaugh, Discrete Mathematics, Prentice-Hall, Upper Saddle
River NJ, 1997.
[53] Charles Jordan, Calculus of Finite Differences, Chelsea, New York, 1979.
[54] D. Kahn, The Codebreakers: The Story of Secret Writing, Macmillan, New
York, 1968.
[55] David Kahn, Kahn on Codes, MacMillan, New York, 1983).
[56] R. M. Karp and M. O. Rabin, "Efficient Randomized Pattern-Matching
Algorithms," IBM J. Res. Develop., Volume 31, No. 2, March A987), 249-
260.
[57] Steven G. Kellison, Fundamentals of Numerical Analysis, Richard D. Irwin,
Homewood IL, 1975.

Литература 853
[58] John G. Kemeny and J. Laurie Snell, Mathematical Models in the Social
Sciences, Blaisdell, Waltham, 1962.
[59] John G. Kemeny, J. Laurie Snell, and Gerald L. Thompson, Introduction to
Finite Mathematics, Prentice-Hall, Upper Saddle River NJ, 1966.
[60] Alfred Bay Kempe, On the Geographical Problem of the Four Colors Amer. J.
Math., 2A879),193-200.
[61] A. Ya. Khinchin, Continued Fractions, The University of Chicago Press,
Chicago, 1964.
[62] H. A. Klein, The Science of Measurement: A Historical Survey, Dover, New
York, 1988.
[63] M. Kline, Mathematical Thought from Ancient to Modern Times, Oxford
University Press, New York, 1972.
[64] D. E. Knuth, The Art of Computer Programming, 2nd ed., Volumes 2 and 3,
Addison-Wesley, Reading, Mass., 1981 and 1973.
[65] D. E. Knuth, J. H. Morris, and V. R. Pratt, "Fast Pattern Matching in Strings,"
SIAM J. Comput., Volume 6, No. 2, June A977), 323-350.
[66] P. L'Ecuyer, "Efficient and Portable Combined Random Number Generators,"
Commun. ACM, Volume 31 A988), 742-774.
[67] A. K. Lenstra and H. W. Lenstra, Jr., editors, The Development of the Number
Field Sieve, Springer-Verlag, New York 1993.
[68] H.Levy, and F. Lessman, Finite Difference Equations, Dover, New York, 1992.
[69] Harry Lewis and Christos H. Papadimitriou, Elements of the Theory of
Computation, Prentice Hall, Upper Saddle River NJ, 1981
[70] G. Marsaglia, "Random Numbers Fall Mainly in the Planes," Proc. Nat. Acad.
Sci. U.S.A., Volume 61 A968), 25-28.
[71] C. H. Meyer and S. M. Matyas, Cryptography: A New Dimension in Computer
Data Security, Wiley, New York, 1982.
[72] R. P. Millane, "A Product Form of the Mobius Transform," Phys. Lett. A,
Volume 162 A992), 213-214.
[73] R. P. Millane, "Mobius Transform Pairs," /. Math. Phys., Volume 34 A993),
875-877.
[74] L. M. Milne-Thompson, The Calculus of Finite Differences, Chelsea, New
York, 1981.
[75] O. Neugebauer, The Exact Sciences in Antiquity, 2nd ed., Dover, New York,
1969.
[76] O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts, American
Oriental Society, New Haven, Conn. 1945.
[77] J. R. Newman, The World of Mathematics, Simon & Schuster, New York,
1956.

854 Литература
[78] В. W. Ninham et al., "Mobius, Mellin, and Mathematical Physics," Physica
A, Volume 186 A992), 441-481.
[79] J. M. H. Olmsted, The Real Number System, Appleton-Century-Crofts, New
York, 1962.
[80] G. Ottewell, The Astronomical Companion, Astronomical Workshop, Furman
University, Greenville, S.C., 1979.
[81] R. E. A. C. Paley, "On Orthogonal Matrices," J. of Math. Phys., Volume 12
A933), 311-320.
[82] B. K. Parady, J. R. Smith, and S. Zarantonello, "Largest Known Twin Primes,"
Math. Compute Volume 55 A990), 381-382.
[83] S. K. Park and K. W. Miller, "Random Number Generators: Good Ones Are
Hard to Find," Commun. ACM, Volume 31 A988), 1192-1201.
[84] Emanuel Parzen, Modern Probability Theory and its Application, Wiley, New
York, 1960.
[85] James L. Peterson, Petri Net Theory and the Modeling of Systems, Prentice
Hall, Upper Saddlle River NJ, 1981.
[86] R. L. Plackett and J. P. Burman, "The Design of Optimum Multifactorial
Experiments," Biometrika, Volume 33 A946), 305-325.
[87] Vera Pless, Introduction to the Theory of Error-Correcting Codes, Wiley, New
York, 1998.
[88] M. Plotkin, Binary codes with specified minimal distance, IEEE Trans. Info.
Theory, 6, 445-450).
[89] S. Pohlig and M. Hellman, "An Improved Algorithm for Computing
Logarithms over GF(p) and Its Cryptographic Significance," IEEE Trans.
Inform. Theory, Vol. IT-24, No. 1 A978), 106-110.
[90] J. M. Pollard, "Theorems on Factorization and Primality Testing," Proc.
Cambridge Philos. Soc, Volume 76 A974), 521-528.
[91] J. M. Pollard. "A Monte Carlo Method for Factorization," Bit, A975), 331-334.
[92] C. Pomerance, Lecture Notes on Primality Testing and Factoring, The
Mathematical Association of America, Washington, D.C., 1984.
[93] J. Purdum, "Pattern Matching Alternatives: Theory vs. Practice," Comput.
Language, November A987), 33-44.
[94] M. Rabin, "Probabilistic Algorithm for Testing Primality," /. Number Theory,
Volume 12 A980), 128-138.
[95] F. Reid and K. Honeycutt, "A Digital Clock for Sidereal Time," Sky &
Telescope, July A976), 59-63.
[96] S. Y. Ren and J. D. Dow, "Generalized Mobius Transforms for Inverse
Problems," Phys. Lett. A, Volume 154 A991), 215-216.
[97] P. Ribenboim, The Little Book of Big Primes, Springer-Verlag, New York,
1991.

Литература 855
[98] R. L. Rivest, A. Shamir, and L. Adleman, "A Method for Obtaining Digital
Signatures and Public Key Cryptosystems," Commun. ACM, Volume 21, No. 2
A978), 120-126.
[99] Fred S. Roberts, Applied Combinatorics, Prentice-Hall, Upper Saddle River
NJ, 1984.
[100] Steven Roman, Introduction to Coding and Information Theory, Springer-
Verlag, New York, 1991.
[101] Gian-Carlos Rota, Studies in Combinatorics, Mathematical Association of
America, 1978.
[102] Joseph J. Rotman, An Introduction to the Theory of Groups, Springer Verlag,
New York, 1995.
[103] J. B. Rosser and L. Schoenfeld, "Approximate Formulas for Some Functions of
Prime Numbers," Illinois J. Math., Volume 6 A962), 64-94.
[104] A. Schimmel, The Mystery of Numbers, Oxford University Press, New York,
1993.
[105] M. R. Schroeder, Number Theory in Science and Communication, 2nd ed.,
Springer-Verlag, Berlin, 1986.
[106] Robert Sedgewick, Algorithms, Addison Wesley, New york, 1988.
[107] R. W. Sinnott, Sky & Telescope, January A989), 80-82.
[108] D. E. Smith, History of Mathematics, Dover, New York, 1958.
[109] D. E. Smith, A Source Book in Mathematics, Dover, New York, 1959.
[110] R. Solovay and V. Strassen, "A Fast Monte-Carlo Test for Primality," SIAM J.
CompuL, Volume 6, No. 1 A977), 84-85. "Erratum: A Fast Monte-Carlo Test
for Primality," SIAM J. Comput., Volume 7, No. 1 A978), 118.
[Ill] D. M. Sunday, "A Very Fast Substring Search Algorithm," Commun. ACM,
Volume 33, No. 8 A990), 132-142.
[112] Thomas M. Thompson, From Error-Correcting Codes through Sphere
Packings to Simple Groups, Mathematical Mathematical Association, 1983.
[113] J. A. Todd, "A Combinatorial Problem," /. Math. Phys., Volume 12 A933),
321-333.
[114] Alan Tucker, Applied Combinatorics, Wiley, New York, 1984.
[115] Lekh R. Vermani, Elements of Algebraic Coding Theory, Chapman and Hill,
New York, 1996.
[116] B. L. van der Waerden, Science Awakening, Vol. I, 3rd ed., Oxford University
Press, New York, 1971.
[117] Douglas B. West, Introduction to Graph Theory, Prentice-Hall, Upper Saddle
River NJ, 1996.
[118] A. E. Western and J. С Miller, Tables of Indices and Primitive Roots, Royal
Society Mathematical Tables, Vol. 9, Cambridge University Press, Cambridge,
1968.

>i к упражнениям
Раздел 1.1.
1. а) нет;
3. а) ~ гЛ ~ q\
в) ~ (г Aq)\
Случай
1
2
3
4
Я
Т
Т
F
F
г
Т
F
Т
F
F
Т
F
Т
г
Г
F
Т
F
л
F
F
F
Т
F
F
Т
Т
Я
Т
Т
F
F
б) да, истинное; в) да, ложное; г) нет;
б) (~ г Л р) V q\
г)
б)
д) да, ложное.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
F
Т
F
Т
F
Т
F
Т
г
Т
F
Т
F
Т
F
Т
F
Л
F
Т
F
Т
F
F
F
F
р)
Т
Т
т
т
F
F
F
F
V
Т
Т
F
Т
Т
Т
F
F
Я
т
т
F
F
Т
Т
F
F
в)
Случай
1
2
3
4
Я
Т
Т
F
F
г
Т
F
Т
F
F
Т
Т
Т
(г
Т
F
Т
F
Л
Г
F
F
F
я)
т
т
F
F
Случай
1
2
3
4
Р
Т
Т
F
F
Я
Т
F
Т
F
F
F
Т
Т
Р
Т
Т
F
F
л
F
F
Т
F
я)
т
F
Т
F
V
F
Т
Т
F
(Р
Т
т
F
F
Л
F
Т
F
F
F
Т
F
Т
я)
т
F
Т
F
7. а) я играю в шахматы, и игра в шахматы требует времени;
б) эта игра не очень трудна, или я не буду играть в шахматы;
в) эта игра очень трудна, или игра в шахматы требует времени, и я играю в шахматы;
г) эта игра очень трудна, и я играю в шахматы, и игра в шахматы требует времени.
9. а) Случай
1
2
3
4
в) Случай
1
2
3
4
5
6
7
8
Я
Т
т
F
F
Р
Т
Т
Т
Т
F
F
F
F
г
Т
F
Т
F
Я
Т
Т
F
F
Т
Т
F
F
(я
т
т
F
F
г
Т
F
Т
F
Т
F
Т
F
Л
Т
F
F
F
(Р
Т
Т
т
т
F
F
F
F
г)
Т
F
Т
F
V
т
т
т
т
т
F
Т
F
г)
Т
F
Т
F
Т
F
Т
F
Л
т
т
F
F
Т
F
F
F
Я
т
т
F
F
Т
Т
F
F
б) Случай р q ~ p V ~ q
1 Т Т F T F F Т
2 Т F F T T T F
3 F T T F T F Т
4 F F T F T T F
г)
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(Р
Т
т
т
т
F
F
F
F
Л
Т
Т
F
F
F
F
F
F
я)
т
т
F
F
Т
Т
F
F
Л
Т
F
F
F
F
F
F
F
г
Т
F
Т
F
Т
F
Т
F

Ответы к упражнениям 857
11. а) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
Т
Т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Р
Т
Т
Т
Т
F
F
F
F
Л
т
т
F
Т
F
F
F
F
(я
т
т
F
F
Т
Т
F
F
V
Т
т
F
Т
Т
Т
F
Т
F
Т
F
Т
F
Т
F
Т
г)
Т
F
Т
F
Т
F
Т
F
в) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
F
Т
F
Т
Т
Т
Т
Т
(Р
т
т
т
т
F
F
F
F
Л
Т
F
Т
F
F
F
F
F
г)
Т
F
Т
F
Т
F
Т
F
V
F
Т
Т
Т
Т
Т
Т
Т
F
F
Т
Т
F
F
Т
Т
Я
Т
Т
F
F
Т
Т
F
F
л
F
F
Т
F
F
F
Т
F
г)
Т
F
Т
F
Т
F
Т
F
д) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(Р
Т
т
т
т
F
F
F
F
Л
Т
F
Т
F
F
F
F
F
г)
Т
F
Т
F
Т
F
Т
F
V
Т
F
Т
Т
F
F
F
F
(Р
Т
т
т
т
F
F
F
F
Л
F
F
Т
Т
F
F
F
F
F
F
Т
Т
F
F
Т
Т
я)
Т
т
F
F
Т
Т
F
F
б) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
Т
Т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
F
(я
т
т
F
F
Т
Т
F
F
Л
F
Т
F
F
F
Т
F
F
F
Т
F
Т
F
Т
F
Т
г)
Т
F
Т
F
Т
F
Т
F
V
F
Т
F
F
Т
Т
Т
F
(~
F
F
F
F
Т
Т
Т
Т
Р
Т
Т
Т
Т
F
F
F
F
Л
F
F
F
F
Т
F
Т
F
г)
Т
F
Т
F
Т
F
Т
F
г) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
Т
Т
F
F
F
F
Я
Т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Т
F
Т
Т
F
F
F
F
F
F
F
F
Т
Т
Т
Т
Р
Т
Т
Т
Т
F
F
F
F
V
F
Т
F
F
Т
Т
Т
Т
*
(я
т
т
F
F
Т
Т
F
F
Л
F
Т
F
F
F
Т
F
F
F
Т
F
Т
F
Т
F
Т
г)
Т
F
Т
F
Т
F
Т
F
Раздел 1.2.
1. а) г —> (р Л q)\ б) ~ р —*~ q\
в) (г —¦ q) Л (~ г —>~ р); г) ~(rV р) —>~ q.
3. а) если ему нравятся фиолетовые галстуки и он популярен, то у него странные друзья;
б) если он популярен, то у него нет странных друзей;
в) если ему нравятся фиолетовые галстуки, то он популярен, или у него странные друзья;
г) если ему нравятся фиолетовые галстуки, то он не популярен, и если он популярен, то
у него странные друзья.
5. а) Случай р q г \ (р —» q) —> г б) Случай р д г \ р —> (д —>• г)
1
2
3
4
5
6
7
8
Т
Т
т
т
F
F
F
F
Т
Т
F
F
Т
Т
F
F
Т
F
Т
F
Т
F
Т
F
Т
Т
Т
Т
F
F
F
F
Т
Т
F
F
Т
Т
Т
Т
Т
Т
F
F
Т
Т
F
F
Т
F
Т
Т
Т
F
Т
F
Г
F
Т
F
Т
F
Т
F
1
2
3
4
5
6
7
8
Т
Т
т
т
F
F
F
F
Т
Т
F
F
Т
Т
F
F
Т
F
Т
F
Т
F
Т
F
Т
Т
Т
Т
F
F
F
F
Т
F
Т
т
т
т
т
т
г
т
F
F
Т
Т
F
F
Т
F
Т
Т
Т
F
Т
Т
Т
F
Т
F
Т
F
Т
F

858 Ответы к упражнениям
в) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(я
т
т
F
F
Т
Т
F
F
Т
F
Т
Т
F
F
Т
Т
(р
Т
т
т
т
F
F
F
F
Л
Т
F
Т
F
F
F
F
F
г))
Т
F
Т
F
Т
F
Т
F
4—>
т
т
т
т
т
т
т
т
((я
т
т
F
F
Т
Т
F
F
->
т
т
т
т
F
F
Т
Т
р)
т
т
т
т
F
F
F
F
Л
Т
F
Т
Т
F
F
Т
Т
(я
Т
Т
F
F
Т
Т
F
F
—
Т
F
Т
Т
Т
F
Т
Т
г))
Т
F
Т
F
Т
F
Т
F
г) Случай
1
2
3
4
5
6
7
8
Р
Г
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
((Р
Т
т
т
т
F
F
F
F
—¦
Т
т
F
F
Т
Т
Т
Т
я)
Т
т
F
F
Т
Т
F
F
V
Г
Т
т
F
Т
Т
Т
F
г)
Т
F
Т
F
Т
F
Т
F
—>
F
F
Т
т
т
т
т
т
(~
F
F
F
F
Т
Т
Т
Т
Р
Т
Т
Т
Т
F
F
F
F
V
F
F
Т
Т
Т
Т
Т
Т
F
F
Т
Т
F
F
Т
Т
я)
т
т
F
F
Т
Т
F
F
Случай
1
2
3
4
Р
Т
Т
F
F
Я
Т
F
Т
F
(Р
Г
т
F
F
—>
Т
F
Т
Т
я)
т
F
Т
F
Т
т
т
т
(~
F
Т
F
Т
Я
Т
F
Т
F
—
т
F
Т
Т
F
F
Т
Т
Р)
Т
т
F
F
б) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(Р
Т
т
т
т
F
F
F
F
Л
F
F
Т
F
F
F
F
F
F
F
Т
F
F
F
Т
F
(я
Т
т
F
F
Т
Т
F
F
V
Т
Т
F
Т
Т
Т
F
Т
F
Т
F
Т
F
Т
F
Т
г))
Т
F
Т
F
Т
F
Т
F
F
F
F
Т
F
F
F
F
(Р
Т
Т
т
т
F
F
F
F
-*
Т
т
F
F
Т
Т
Т
Т
я)
т
т
F
F
Т
Т
F
F
в) Случай
1
2
3
4
5
6
7
8
Р
Г
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
(Р
Т
т
т
т
F
F
F
F
V
т
Т
т
т
т
F
Т
F
г)
Т
F
Т
F
Т
F
Т
F
—>
Г
т
F
F
Т
Т
F
Т
Я
Т
Т
F
F
Т
Т
F
F

Ответы к упражнениям 859
г) Случай
1
2
3
4
5
6
7
8
Р
Г
Т
Т
Т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
«Р
Т
т
т
т
F
F
F
F
—>
Т
т
F
F
Т
Т
Т
Т
я)
т
т
F
F
Т
Т
F
F
л
F
Т
F
F
F
Т
Т
Т
(я
т
т
F
F
Т
Т
F
F
—¦
F
Т
Т
Т
F
Т
Т
Т
F
Т
F
Т
F
Т
F
Т
г))
Т
F
Т
F
Т
F
Т
F
—>
Т
т
т
т
т
т
F
Т
(г
Т
F
Т
F
Т
F
Т
F
—*
Т
т
т
т
F
Т
F
Т
Р)
т
т
т
т
F
F
F
F
д) Случай
1
2
3
4
5
6
гг
(
8
Р
Т
Т
т
т
F
F
Г
F
Я
Т
т
F
F
Т
Т
Г
F
г
Т
F
Т
F
Т
F
гр
1
F
(Р
Г
Т
т
т
F
F
I?»
Г
F
Л
Т
Т
т
F
F
F
тр
Г
F
(я
т
т
F
F
Т
Т
гр
Г
F
V
Т
Т
т
F
Т
Т
гр
1
т
г))
т
F
Т
F
Т
F
гр
1
F
—>
Т
Т
т
т
т
т
X
1
т
((р
т
т
т
т
F
F
тр
Г
F
Л
Т
Т
F
F
F
F
F
я)
Т
Т
F
F
Т
Т
F
V
Т
Т
т
F
F
F
F
(Р
Т
т
т
т
F
F
F
Л
Г
F
Т
F
F
F
F
г))
Т
F
Т
F
Т
F
гр
1
F
9. а) Т;
б)Т;
в)Т;
г) F.
Раздел 1.3.
Случай
1
2
3
4
Р
Т
Т
F
F
q
Т
F
т
F
~ (
F
Т
Т
Т
pAq)
Т
F
F
F
~Р
F
F
Т
Т
V
F
Т
т
т
~ я
F
Т
F
Т
б) Случай р g r
(р V (q V г)) (р V q) V г))
Т Т Т
Т Т F
Т F Т
Т F F
F Т Т
F T F
F F Т
F F F
Т Т Т Т
Т Т Т Т
Т Т F Т
Т Т F F
F 1 Т Т
F Т Т Т
F Т
F F
F Т
F F
Т Т Т Т
Т Т Т Т
Т Т F 1
Т Т F Т
F Т Т Т
F Т Т 1
F F F Т
F F F F
в) Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
V
Т
Т
Т
Т
F
F
F
F
V
Т
т
т
т
т
F
F
F
*
(9 Л г)
Г
F
F
F
Т
F
F
F
pV q
т
Т
Т
т
т
т
F
F
Л
т
т
т
т
т
F
F
F
*
(pVr)
Т
т
т
т
т
F
Т
F

860 Ответы к упражнениям
Случай
1
2
3
4
Р
Т
Т
F
F
Я
Т
F
Т
F
Р-* Я
т
F
Т
Т
~ р
F
F
Т
Т
V
Т
F
Т
Т
Я
т
F
Т
F
3. Случай
1
2
3
4
Р
Т
Т
F
F
Я
Т
F
Т
F
Р-+Я
т
F
Т
Т
Я
т
F
Т
F
—
Т
т
F
т
р
т
т
F
F
Таблицы истинности не совпадают, поэтому высказывания не эквивалентны.
p—+q = ~p\/q = теорема 1.3(з)
= qV ~ р = закон коммутативности
= ~~ gv ~ p = двойное отрицание
= ~ q —>~ р теорема 1.3(з)
Следовательно, ~ р —>~ q = q —> р, и инверсия высказывания эквивалентна конверсии.
5. а) если он кентавр, то у него шесть ног;
б) если он преуспевающий политик, то он избран;
в) если он имеет деньги, то он популярен.
7. а) если я хороший гражданин, то я голосую;
б) если я не голосую, то я не являюсь хорошим гражданином;
в) если я не являюсь хорошим гражданином, то я не голосую.
Раздел 1.4.
Случай
1
2
3
4
5
6
7
8
Р
Т
Т
т
т
F
F
F
F
Я
Т
Т
F
F
Т
Т
F
F
г
Т
F
Т
F
Т
F
Т
F
Р — Я
т
г
F
F
Т
т
т
т
q -> г
Т
F
Т
Т
т
F
Т
т
р-+т
т *
F
Т
F
Т *
т
т *
т *
б) Случай
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Р
Т
Т
Т
Т
Т
т
т
т
F
F
F
F
F
F
F
F
Я
Т
Т
Т
Т
F
F
F
F
Т
Т
Т
Т
F
F
F
F
г
Т
Т
F
F
Т
Т
F
F
Т
Т
F
F
Т
Т
F
F
s
Т
F
Т
F
Т
F
Т
F
Т
F
Т
F
Т
F
Т
F
Р Р-*
Т
Т
Т
Т
Т
Т
Т
Т
F
F
F
F
F
F
F
F
(TVs)
Т
Т
т
F
Т
Т
Т
F
т
т
т
т
т
т
т
т
г -> q
т
т
т
т
F
F
Т
Т
т
т
т
т
F
F
Т
Т
s -> q
Т
т
т
т
F
Т
F
Т
т
т
т
т
F
Т
F
Т
Я
т *
т *
т *
т
F
F
F
F
Т *
т *
т *
т *
F
F
F
F

Ответы к упражнениям 861
в)
Случай
1
2
3
4
г
Т
Т
F
F
w
Т
F
Т
F
~ w —¦+ (гЛ
Г
F
Т
F
-г)
w
Т *
F
Т *
F
3. а)
5. а)
7. а)
б)
в)
г)
неправильное;
правильное;
1.
2.
3.
4.
5.
6.
1.
2.
3.
4.
5.
6.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
1.
2.
3.
4.
5.
6.
7.
8.
9.
~(вЛ*)
~ w —> t
~ sV ~ ?
~ ? —> w
s —> w
Р —<7
~ г —>~ q
~ г
~q
~ я —>~ р
~Р
~(~pV9)
~ 2 —>~ S
(рЛ ~ (?) ->
~~ рЛ ~ q
рЛ ~ (^
5
S —> 2
2
2 —> Г
Г
~ х —> ~ гу
(xV ~ w) —¦
О ~~^ (/^4*1 7*V r
xV ^^ г/;
2
2— р
Р
~ rV ~ s
б) правильное; в) правильное;
б) неправильное; в) неправильное;
дано
дано
1 закон де Моргана
3 и теорема 1.3(и)
2 и контрапозиция
силлогизм;
дано
дано
дано
2, 3 и modus ponens
1 и контрапозиция
4, 5 и modus ponens;
дано
дано
• s дано
дано
1 и закон де Моргана
5 и двойное отрицание
3, 6 и modus ponens
2 и контрапозиция
7, 8 и modus ponens
4 и теорема 1.3(и)
9, 10 и modus ponens.
дано
2 дано
дано
~ s) дано
1 и теорема 1.3(h)
2, 5 и modus ponens
3 и контрапозиция
6, 7 и modus ponens
4, 8 и modus ponens.
г) правильное
г) правильное
9. а) нет;
б) да;
в) нет;
г) да;
д) нет.

862 Ответы к упражнениям
Раздел 1.5.
1. а) Случай р q
1 Т Т
2 Т F
3 FT
4 FF
Р I Я
TFT F
TFT F
FTF T
FTF T
в)
Случай
1
2
3
4
P
T
T
F
F
T
F
T
F
(P
T
T
F
F
1
F
F
F
T
9)
T
F
T
F
1
T
T
T
F
(P
T
T
F
F
1
F
F
F
T
9)
T
F
T
F
pvg
T
T
T
F
б)
Случай
1
2
3
4
Р
Т
Т
F
F
Я
Т
F
Т
F
(Р
Т
т
F
F
1
F
F
Т
Т
Р)
Т
т
F
F
1
Т
F
F
F
(я
т
F
Т
F
I
F
Т
F
Т
я)
т
F
Т
F
pAq
т
F
F
F
3. а) (р Л q Л ~г) V (р Л ~д Лг) V (р Л ~q Л ~г) V (~р Л ~q Л ~г);
б) (~р Л q Л г) V (~р Л g Л ~г) V (~р Л ~д Л ~г);
в) (р Л <? Л г) V (р Л ~q Л г) V (р Л ~q Л ~г) V (~р Л ~д Л г).
Раздел 1.6.
1. а) г V (рЛ~д);
б) (г Л s) V (р Л ~д Л ~s) V (р Л ~
в) (р Л ~г) V (~г Л s) V (~g Л г Л
3. а)
б)
в)
P
P
P
P
P
P
P
P
P
P
X
X
r
X
r
Я
X
X
X
X
r^ Г
Я
X
X
X
X
Я
~ <?
X
~ Я
X
X
X
~q
X
X
~q
r
X
r
X
X
q V (~рЛ ~ r);
(рЛ ~ г) V (qA ~ r)V
V(~ рЛ ~ г Л s) V (~ рЛ
V (д Л г Л s).
Раздел 1.7.
1. а) р<?(<7 + гх);
в) (pgVy+g'r + pgV
д) рг -Ьр<?/(Р + Г + 5').
3. а)(рУУ+^г;
в) (pq 4- г) + (д + г)';
б) (9+ 0(^ +
г) (р' + яг'У;
б) (рг)' + qr'\
г)
в);

Ответы к упражнениям 863
5. а)
Раздел 2.1.
1. {-9, -8, -7, -6, -5, -4, -3, -2, -1,0,1,2,3,4, 5,6,7,8,9}.
3. {а,е,г,о, it}.

864 Ответы к упражнениям
5. {х : 0 < х < 24 и х кратно 3}.
7. {х : х — название американского штата, которое начинается с буквы "О"}.
9. 0,{а}.
И. 0, {а}, {6}, {с}, {а, 6}, {а, с}, {6, с}, {а, 6, с}.
13. 0.
15. а) истинно; б) ложно; в) ложно; г) истинно; д) ложно.
17. а) 2; б) 1; в) 4; г) 6; д) 3.
Раздел 2.2.
1. а) {1,2,3,4,5,6,7,8,10}; б) {4,5,6,7};
г) {2,4,5,6,7,8,10}; д) {1,2,3,8,9,10};
ж){1,2,3,8,9,10}; з) {1,2,3}.
3. а) {A, а), B, а), C, а), A,6), B,6), C,6)};
б) {(а, а), (а, 6), F, а), F, 6)};
в) 0.
5. {0}.
7. {
в) {2,4,5,6,7};
е) 0;
9. а) Т;
И. х € (Л U В)'
д) Т.
13.
15.
а)
N.
Раздел
1.
а)
{0};
2.3.
б) Т; в) F; г) Т;
х ? (Л U В) определение дополнения
~ (х € (Аи В)) определение ^
~ ((х ? А) V (х е В)) определение объединения
~ (х е А)/\ ~ (х G В) закон де Моргана;
(х ? А) Л (х ? В) определение ^
х ? An В определение пересечения.
б) {0, {0}}; в) {0, {0}, {0, {0}}}.
^

Ответы к упражнениям 865
3. а)
5. а) А';
б) {{A U В) - С) U {А П Б);
в) ((Л П Б) U (Л П С) U (Б П С))';
г) ((Л П Б) U (А П С) U (Б П С))
7.
В П С).

866 Ответы к упражнениям
Раздел 2.4.
1. х-х = х-х4-0 = закон тождества
= х • х -f х • х = закон дополнения
= х • (х + ж') = закон дистрибутивности
= х • 1 = закон дополнения
= а: закон тождества
3. х • (х + ?/) = (х + 0) • (х 4- у) = закон тождества
= х + @ • у) = закон дистрибутивности
= х + 0 = свойства констант
= х закон тождества.
5. 1 + 0 = 1 закон тождества
1-0 = 0 закон тождества.
Следовательно, 0 удовлетворяет закону дополнения для 1 и, согласно закону единственно-
единственности дополнения, является единственным элементом, который обладает таким свойством.
7. а) ху' 4- (z'y)'\ б) (@ • х) + у){х + у' + z)\
в) ((х 4 у) • 0) + A • х) 4- z.
9. Если х + у = х -f z и х' 4- у = х' -f z, то у = z.
11. х + у = 1 тогда и только тогда, когда х -\- у = х.
13. Объединение и пересечение двух конечных множеств является конечным множеством.
Объединение и пересечение двух коконечных множеств коконечно. Объединение конечно-
конечного множества и коконечного множество коконечно. Пересечение конечного множества и
коконечного множества конечно. Поэтому свойство объединения и пересечения определе-
определено для всех рассматриваемых множеств. Для множеств было показано выполнение зако-
законов коммутативности, ассоциативности и дистрибутивности. Пустое множество конечно,
а множество U коконечно. Поэтому они относятся к рассматриваемым множествам. До-
Дополнение конечного множества коконечно, а дополнение коконечного множества конечно.
Следовательно, дополнение определено для всех рассматриваемых множеств. Справедли-
Справедливость законов тождества и законов дополнения для множеств была доказана ранее.
Раздел 2.5.
1. а) область значений = {1,2,4,5}; область определения = {a,c,d}\
б) область значений = {2,4,6,...}; область определения = {1,2,3,....
в) область значений = R\ область определения = {х:хб#их>0}.
3. а) Я = {G,1), F,4), F,5), (8,2)},
5 = {A0,6), A1,6), A0,7), A3,8)};
б) 5 о R = {A,10), D,10), D,11), E,10), E,11), B,13)};
в) SoS~l = {A0,10), A0,11), A1,10), A1,11), A3,13)},
5-1о5 = {F,6),F,7),G,6),G,7),(8,8)};
г) R^oS'1 = {A0,4), A0,5), A1,4), A1,5), A0,1), A3,2)};
д) Т о (S о R) = {A, А), D, Л), E, Л), B, *), B,0)};
е) Т о S = {F, Л), G, Л), (8, *)(8,0)};
ж) (Т о 5) о R = {A, Л), D, Л), E, Л), B, *), B,0)}.
5. а) {(х,2/):у = 9х24-5};
б) {(х,2/):у = Зх2 + 15};
в) {(х, у) :у = ±у/х - 5;
г) {(х,2/):2/=|х;

Ответы к упражнениям 867
Д) {</:</> 5}.
7. а) {(а, а), (а, 6), (Ь, а), F, с), (с, 6), F, d), (d, 6), (с, е), (е, с), (е, d), (d, e)};
б) {(а, а), (а, 6), F, а), (Ь, с), (с, 6), F, d), (d, Ь), (с, е), (е, с), (е, d), (d, e), F, 6), (с, с),
(d,d),(e,e)};
в) Л х Л;
г) {(а, а), (а, 6), F, с), (Ь, d), (с, е), (е, d): (с, Ь), (а, с), (а, d), (Ь, е), (Ь, Ь), (с, d), (с, с)}.
9.а)(/ПК = {(а,Ь), F, с), F, Ь), (е, е), F, а), (с, Ь), (d, d), (а, с), (с, а)};
б) S U Т = {(а, а), (а, Ь), F, с), F, d), (с, е), (е, d), (с, а), F, а), (е, е), (d, e), (с, Ь)};
в) l/-r = {(a,a),Flb)l(clc),(d,d)l(alc),(c,a)};
г) С/ Л 5 = {F, 6), (е, е), F, а), (с, Ь), (с, с), (d, d), (а, с), (Ь, d), (с, е), (е, d)}
11. Пусть Я и S — симметричные отношения и (а, Ь) ? Я П S. Поскольку Я симметрично, то
(Ь,a) G Я. Поскольку 5 симметрично, то F,а) е S. Следовательно, F,a) e Rn S и ЯП 5
симметрично.
13. a) {(a,a),F,b),(c,c),(d,d),(e,e),(a,b),F,a),(c,6),F,c)};
6){(a,a),(b,6),(c,c),(d,d)};
в) {(a,a),F,6),(c,c),(d,d),(e,e),(a,6)}.
15. а) истинно; б) истинно;
в) ложно. Пусть R = {(Ь, с), (с, 6)} и S = {F, a), (a, 6)}, тогда (а, с) G R о S, но (с, а) ?
Я о 5.
д) истинно.
г) истинно;
17. а) истинно;
б) ложно. Пусть Я = {(Ь,с)} и 5 = {(а, 6)}, тогда Я и 5 транзитивны, но Я U 5 =
{(а, 6), F, с)} не транзитивно;
в) ложно. Пусть Я = {(с, а)F,6)} и 5 = {(а, Ь), F, с), (а, с)}, тогда Я и 5 транзитивны, но
Я о 5 = {(а, 6), (Ь, а), (а, а)} не транзитивно;
г) ложно. Пусть Я = {(а, 6), F, с), (а, с)} и S = {(а, с)}, тогда Я и 5 транзитивны, но
Я - S = {(а, Ь), F, с)} не транзитивно;
д) Я = {(а, 6), F, с), (а, с)} и 5 = {(а, с)}, тогда Я и S транзитивны, но Я AS = {(a, 6), F, с)}
не транзитивно.
19. а)
f •

868 Ответы к упражнениям
21. а) V = {a,b,c,d};
Е = {{а, 6}, {а, d}, {b, d}, {с, d}, {а, с}};
R = {(а, 6), (Ь, а), (а, d), (d, а), (Ь, d), (d, b), (с, d), (d, с), (а, с), (с, а)}.
б) V = {a,b,c,d};
Е = {{а, Ь}, {a, d}, {Ь, d}, {с, d}, {а, с}, {Ь, с}};
Д = {(а, 6), F, a), (a, d), (d, а), (Ь, d), (d, b), (с, d), (d, с), (а, с), (с, а), (Ь, с), (с, Ь)}.
в) V = {a,6,c,d,e,/};
? = {{а, с}, {a, d}, {а, е}, {а, /}, {Ь, с}, {Ь, d}, {Ь, е}, {Ь, /}};
R = {(а, с), (с, a), (a, d), (d, а), (а, е), (е, а), (а, /), (/, а), (Ь, с), (с, 6), F, d);
г) K = {a,6,c,d,e,};
Я = {(а, Ь), (Ь,а), (с, d), (d, с), (d, e), (e, d), (с, е), (е,с)}.
23. а)
е •
25. а) V = {a,b,c,d,e,};
Е = {(а, Ь), (Ь, а), (а, е), (Ь, е), (с, d), (d, с), (d, e), (с, е)}.
б) V = {a,b,c,d};
E = {(d,6),(d,a),(c,d),(b,c)}.
в) V = {a,6,c,d,e,};
Е = {(а, Ь), (Ь, с), (с, d), (d, е), (е, а), (Ь, d), (Ь, е), (с, е), (d, a)}.
г) K = {a,6,c,d,e,};
Е = {(а, Ь), F, с), (с, d), (d, е), (е, а), (Ь, d), F, е), (с, е), (е, d), (а, с)}.
27. Покажите, что (Т о 5) о Я С Т о E о Я). Пусть (a, d) € (Т о S) о Я, тогда существует be В
такое, что (а, 6) е Я и (Ь, d) G Т о 5. Поскольку F, d) G Т о 5, то существует с е С такое,
что (Ь,с) е S и (c,d) G Т. Поскольку (a,b) G Я и F, с) € 5, то (а, с) е S о К Поскольку
(b,d) € ToS и (а,6) G Я, то (a,d) € (ToS)oR. Таким образом, To(SoR) С (ToS)oR.
Раздел 2.6.
1. (а), (г).

Ответы к упражнениям 869
3. а)
б)
в)
• • • •
abed
г)
• d
о С
5. а) {(а, а), F, 6), (с, с), (d, d), (e, e), (d, а), (d, с), (d, 6), (d, e), (а, 6), (с, 6)};
б) {(а, а), (Ь, Ь), (с, с), (d, d), (e, e), (d, Ь), (d, а), (d, e), (с, е), (с, а), (с, 6), (е, а), (е, 6)};
в) {(а, а), F, Ь), (с, с), (d, d), (e, e), (/, /), (а, 6), (а, с), (/, Ь), (/, с), (/, d), (e, d), ; (e, с)}
г) {(а, а), F,6), (с, с), (d, d), (е, е), (е, а), (е, 6), (е, с), (е, d), (d, а), (d, Ь), (d, с)};
д) {(а, а), F,6), (с, с), (d, d), (e, e), (с, а), (с, 6), (е, а), (е, 6)}.
7. Никакие два элемента не сравнимы.
Раздел 2.7.
1. а) нет; б) нет.
в) да, \р] = {q : q имеет такую же таблицу истинности, как и р}\
г) да, \(а,Ъ) = {(c,d) : ad = be};
д) да, [п] = {п, -п};
е) да, [п] = {п}.
3. а) да, [Б] = {С : С содержит такое же количество элементов, как и В}\
б) да, [1] = Л;
в) да, [1] = {1,3,5,7,9}, [2] = {2,4,6,8,10};
г) нет;
д) Да, [п] = {т : т параллельно п};
е) Да, [р] = {q : р написано на том же языке программирования, что и q).
5. а) для всех а е А имеем /(а) = /(а), поэтому R рефлексивно. Если /(а) = /F), то
/F) = /(а), поэтому R симметрично. Если /(а) = /F) и /F) = /(с), то /(а) = /(с),
поэтому R транзитивно. Следовательно, R — отношение эквивалентности;
б) [1] = {1, -1}; [2] = {2, -2}; [0] = {0}; [3] = {3}; [-1] = {I; -1}; [4] = {4}.
7. а) нет;
б) R = {A,1), A,2), B,1), B,2), C,3), D,4), E,5), C,4)D,3), C,5), E, 3), D,5), E,4), F,6),
F, 7), G,6), G, 7)};
в) нет; г) нет; д) А х А.
9. Да. Покажем, что R рефлексивно. Имеем, что (а, 6)Я(а, 6) тогда и только тогда, когда
ab = ab. Покажем, что R симметрично. Допустим, что (a,b)R(c,d). Но (a,b)R(c,d) тогда
и только тогда, когда ad = be. Также (с, d)R(a, b) тогда и только тогда, когда cb = ad. Сле-
Следовательно, (c,d)R(a,b). Покажем, что R транзитивно. Пусть (a,b)R(c,d) и (c,d)R(e,f).
Следовательно, ad = be и с/ = ed. Из первого равенства adf = bcf. Подставляя с/ = ed в
это равенство, получаем adf = bed. Разделив на d, получаем а/ = be и (а, b)R(e, /).
Раздел 3.1.
1. аK2 + 42>52; б) 2 = |=J;
д) Джон любит Сью больше, чем Мэри.
г) 24 = 4!.

870 Ответы к упражнениям
3. а) существуют х и у такие, что х2 + у2 > 252;
б) существует х такое, что 7 = §^|;
в) для каждого г существует х такое, что \х — 1| < г;
г) существует п такое, что для всех у выполняется у = п!;
д) Джон любит Сью больше, чем кого-либо.
5. а) предметная область для х — множество всех улиц. Область для у — множество всех
праздников. R(x,y): x имеет свой у.
Vx3yR(x,y);
б) предметная область для х — множество всех машин. Область для у — множество всех
людей. S(x,y) : x умнее, чем у.
в) предметная область — люди. Т(х,у) : х играет в теннис лучше, чем у.
г) предметная область для х — множество всех действий. Область для у — множество
всех противодействий. U(x, у) : х имеет равное и противоположно направленное у.
д) предметная область — игроки в гольф. V(x,y) : x будет в конце концов обыгран более
сильным у.
Vx3yV(x,y).
7. а) истинно; б) истинно; в) истинно; г) истинно; д) ложно.
9. VxP(x) WxQ(x) дано
Р(а) V VxQ(x) для произвольного а универсальная конкретизация
Р(а) V QF) для произвольного 6 универсальная конкретизация
Р(а) V Q(a) поскольку 6 произвольно, выберем Ь = а
Vx(P(x) V Q(x)) универсальное обобщение.
11. а) б)
12. а)
14. а)
б)

Ответы к упражнениям 871
Раздел 3.2.
1. а) 6 + а = с + а дано
F + а) + (-а) = (с + а) + (-а) 12
6 + (а + (-а)) = (с + а) + (-а) закон ассоциативности
Ь + 0 = с + 0 17 аддитивно обратный элемент
6 = а 16 аддитивно нейтральный элемент;
б) а • 0 = а • @ 4- 0) = 16 аддитивно нейтральный элемент
= а • @) + а •@) закон дистрибутивности.
Таким образом,
а • 0 — а • 0 = (а • @) 4- а • @)) — а • 0 = аддитивно обратный элемент
а • 0 — а • 0 = а • @) 4- (а • @)) — а • 0) = закон ассоциативности
О = а • @) 4- 0 = аддитивно обратный элемент
= а • @) аддитивно нейтральный элемент;
в) поскольку —а является обратным к а, имеем а 4- (—а) = (—а) 4-а. Но это удовлетворяет
требованию, при котором а является обратным к —а. Следовательно, а = —(—а);
г) а • (—6) 4- а • Ь = а • (—6 4- 6) = согласно закону дистрибутивности
= а • 0 = по определению обратного элемента
= 0 согласно пункту (б).
Аналогично, а Ъ + а- (—6) = 0, поэтому, по определению, а • (—6) является аддитивно
обратным элементом для а • Ь, поэтому а • (—6) = —аЬ\
д) а • (—6) 4- (—а) • (—Ь) = (—Ь) • а 4- (—6) • (—а) = закон коммутативности
= (—Ь) • (а 4- (—а)) = закон дистрибутивности
= (-6) • 0 = определение обратного элемента
= 0 согласно пункту (б).
Аналогично, (—а) • (—6) 4- а • (—6) = 0, поэтому (—а) • (—6) — обратный элемент для
а • (-6). Но а • Ь — элемент, обратный для а • (—6). Следовательно, а • Ъ = (—а) • (—6).
3. Учитывая, что если а > Ь > 0 и с > d > 0, то ас > bd. Требуется рассмотреть только
случай, когда а = с или с = d. Если а = b и с > d, то ас > ad. Следовательно, ас > bd.
Случай с = d аналогичен.
5. Поскольку (а — ЬJ > 0, имеем
(а - ЬJ = (а - Ь)(а - Ь) = а(а - Ъ) 4- (-Ь)(а - 6) > 0,
согласно закону дистрибутивности. Используя совместно закон дистрибутивности, пункты
(д) и (е) задачи 1 и закон коммутативности, получаем а(а—ЬL-(—Ь)(а—6) = a2—ab—ab+b2.
Следовательно, а2 — 2аЬ 4- Ь2 > 0. Прибавляя 2ab к обеим частям неравенства, получаем
а2 4- b2 > 2ab.
Раздел 3.3.
1. Для п = 1 имеем 1 = г2 ' , поэтому утверждение истинно. Предположим, что утвержде-
утверждение истинно для п = /с, так что 1 4- 4 4- 7 Н h C/с - 2) = fcC^~^ . Теперь необходимо
доказать, что утверждение истинно для п — к 4-1, так что

872 Ответы к упражнениям
Если прибавитьC(/с + 1) — 2) = 3/с 4- 1 к обеим частям утверждения, записанного для
п = /с, имеем
1 4- 4 + 7 + • • • + C/с - 2) 4- C(/с 4- 1) - 2) =
_ k{3k - 1) _ 3/с2 4- 5/с + 2 _ (fc + l)Cfc + 2)
" 2 + ** + 1- 2 " 2 '
и справедливость утверждения для n = k + 1 доказана.
3. Для п = 1 имеем 1 = 2—1, поэтому утверждение истинно для п = 1. Предположим, что оно
истинно для п = к, поэтому 1 + 2 + 22Н \-2к~х = 2к — 1. Мы хотим доказать истинность
утверждения для п = /с + 1, т.е. 1 + 2 + 22Н ^2fc~1+2/c = 2fc+1-l. Прибавляя 2к к обеим
частям утверждения, записанного для п = /с, имеем 1+ 2 + 22Н b2fc~1+2fc = 2fc — l + 2fc.
Но 2fc-l4-2fc = 2-2fc-l = 2fc+1 -1. Таким образом, истинность утверждения для п = /с + 1
доказана.
5. Для п = 1 имеем 1 = I2, поэтому утверждение истинно. Предположим, что оно истинно
для п = /с, поэтому имеем 1 + 34-54 \- Bп - 1) = п2. Мы хотим доказать истинность
утверждения для п = к 4- 1, т.е. равенство 1 4- 3 4- 5 + • • • 4- Bп — 1) 4- Bп + 1) =
(п 4- IJ. Прибавляя 2п 4- 1 к обеим частям равенства, записанного для п = /с, имеем
1+ 3 4- 5 Н Ь Bп - 1) 4- Bп + 1) = п2 4- Bп 4-1) = (п 4-1J, что доказывает истинность
утверждения для п = к 4-1.
7. Для п = 1 имеем 1A 4- 1) = — ^ или 2 = 2, поэтому утверждение истинно.
о
Предположим, что оно истинно для и = /с, поэтому имеем 1-24-2-34 h /с(/с 4- 1) =
А:(А:4-1)(/с4-2) АЯ . л
—^ ^ -. Мы хотим доказать, что утверждение истинно для п = к4-1, т.е. равенство
о
1-2 + 2-3 + -.. + *(* + !) + (*+!)(* + 2) = (fc
Прибавляя (к + l)(fe + 2) к обеим частям равенства, записанного для п = к, имеем
1 . 2 + 2 • 3 + • • • + к(к + 1) + {к + l)(fc + 2) = fc(fc + У + 2) + (к + l)(fc + 2),
НО
к(к 4- l)(fe 4- 2) 4- 3(/с + l)(fc -f 2) = (/с + 3)(/с 4-1)(/с 4-2)
= =
3 3
что доказывает истинность утверждения для п = к + 1.
9. Пусть п = 1. Тогда ah = ab, что и требовалось. Предположим истинность утверждения
для п = /с, согласно которому (a6)fc = akbk.
Мы хотим доказать, что (a6)fc+1 = afc+16/c+1. Но
(ab)fc+1 = (ab)k{ab)= согласно определению, введенному в предыдущей задаче
= акЪк(аЪ) — согласно индуктивному предположению
= акакЬкЪ = согласно коммутативности умножения
= ak+1bk+1 согласно определению, введенному в предыдущей задаче.

Ответы к упражнениям 873
11. В этой задаче используются результаты предыдущей задачи. Пусть п = 5, тогда 2° > 52,
что и требовалось. Предположим, что утверждение истинно для п = к, поэтому 2к > к2.
Мы хотим доказать, что 2fc+1 > (к 4- IJ. Но по индуктивному предположению 2к > к2
и согласно результату предыдущей задачи 2к > 2к + 1. Поэтому, складывая, получаем
2к + 2к > к2 + 2к 4- 1 или 2fc+1 > (к 4- IJ.
13. Для п = 8 имеем 8 = 3A) 4- 5A). Предположим истинность утверждения для п = к,
поэтому к = Зг 4- 55. Если г > 3, то /с 4- 1 = 3(г - 3) 4- 5(s + 2). Если г < 3, то s > 1,
поэтому /с + 1 = 3(г 4- 2) + 5E - 1). Так или иначе, мы выразили к 4-1 в надлежащем виде.
15. Для п = 1 имеем ат = ат, поэтому равенство истинно для п = 1. Предположим истин-
истинность для п = /с, поэтому amfc = (am)fc. Используя затем индуктивное предположение,
имеем
flm(fc+l) = amfc+m = amfc # flm = ^mjfc . flm = (a™}k+l
17. Для n = 2 имеем 1 - \ = 2±! или f = f, поэтому утверждение истинно. Предположим
истинность для п = /с, поэтому
2k '
Мы хотим показать, что
к 4-2
" 2/с 4-2'
Умножая на A — *1J) обе части равенства, записанного для п = /с, имеем
Но
/с 4- 1 Л 1 \ к 4- 1 / (к 4- IJ - 1 \ /с2 4- 2А: А; 4- 2
/с 4-1 Л _ _1_\ = fe4-l ((k + 1J -1\ =
2к V (^ + 1JУ 2/с V (А: + 1J У
2(/с4-1)
и утверждение истинно для п = к 4-1.
19. Некорректный переход от/с = 1 к/с4-1 = 2.
21. а) для п = 1 имеем А\Г\А = А\Г\А. Предположим истинность утверждения для п — /с, так
что (П?=1 Лг)ПА = П^=1(^п^)- Мы хотим показать, что (fj^1 At)nA = C\i=i(AinA)-
Но
к
Л?) п А = ((Р| Ai) П Afc+i) П А = определение из предыдущей задачи
U) П Afc+i) ПЛПЛ= поскольку АПА = Л
= ((р| Ai) П А)Г\ A/c+i П А = закон коммутативности
к
= (Р| (А» П А)) П (Afc+i п А) = индуктивное предположение
= (Р| (Ai П А)) определение из предыдущей задачи;

874 Ответы к упражнениям
б) для п = 1 имеем А[ = А\, поэтому равенство справедливо. Предположим истинность
утверждения для п = к, поэтому имеем f П?=1 ^*) = Ui=i М- Мы хотим доказать,
что (n^i1 Ai)' = Ufoi1 A5. По закону де Моргана (flfi1 Л<)' = (ft=i ^ П Afc+1)' =
(П?=1 Ai) Ui4fc+1. Воспользовавшись индуктивным предположением, имеем f П?=1 ^i) U
А'к+г = (JiLsi AjUi4fc+1 = \Ji*j A'i. Следовательно, утверждение истинно для п = fc + 1.
23. Предположим, что Т удовлетворяет условиям (а) и (б) второго принципа индукции. Пусть
Т' — множество всех целых чисел, для которых утверждение Т не является истинным.
Если Т не пусто, тогда, согласно принципу полного упорядочения, Т" содержит наимень-
наименьшее положительное целое число, например, п. Но поскольку п — наименьший элемент в
Т" для всех m таких, что m < п, утверждение Т истинно. Это противоречит (б), поэтому
Т" пусто и Т истинно для всех п.
25. Предположим, что Т не пусто. Тогда, согласно принципу вполне упорядочения, это мно-
множество имеет наименьший элемент, например, п. Но по условию 2 существует m < п,
которое принадлежит Т. Это является противоречием, поэтому Т пусто.
Раздел 3.4.
I. а) 54,27,18,9,6,3,2,1; б) 63,21,9, 7,3,1;
в) 72,36,18,9,24,12,6,3, 8, 4, 2,1; г) 73,1;
д) 74,37,2,1.
3. а) НОДE4,27) = 27, НОКE4,27) = 54; б) НОД и НОК не определены;
НОДE4,27) • НОКE4,27) = 1458;
в) НОДF,15) = 3, НОКF,15) = 30; г) НОДA2,16) = 4, НОКA2,16) = 48;
НОДF,15) • НОКF,15) = 90; НОДA2,16) • НОКA2,16) = 192;
д) НОДC3,1) = 1, НОКC3,1) = 33;
НОДC3,1) • НОКC3,1) = 33.
5. В качестве НОК(а,0) можно было бы взять 0. Число 0 является кратным для а и для 0.
Если некоторое число делит а и 0, то оно делит 0.
7. НОД (а, 6) делит а и 6, поэтому он делит а — Ъ. Следовательно, НОД (а, 6)| НОД (а — 6,6).
Обратно, если любое целое число делит а — b и 6, то оно делит а. Поэтому НОД(а —
6,6)| НОД (а, 6). Следовательно, НОД (а - 6, 6) = НОД (а, 6).
Раздел 3.5.
1. a) 7-23 • 13;
б) 1599 = 1600 - 1 = D0 - 1)D0 4- 1) = 3 • 13 • 41;
в) 3-23-71; г) 131; д) 523.
3. 5 и 7, 11 и 13, 17 и 19.
5. Если одно из простых чисел не равно 2, то сумма а2 +Ъ2 никогда не будет простым числом,
поскольку она делится на 2.
7. 479001603 = 12! + 3 и 479001603 = 12! + 7.
9. Пусть р, р + 2ир + 4 — три последовательных нечетных числа. Число р может быть
записано как Зт, Зт + 1 или Зт + 2. Если оно имеет вид Зт, то оно делится на 3. Если
оно имеет вид Зт + 1, то р + 2 делится на 3. Если оно имеет вид Зт + 2, то р + 4 делится
на 3. Поскольку одно из трех чисел должно делиться на 3, эти числа не могут быть все
простыми.
II. Если 0 < 6(г) < а(г), то р^(г)|р°(г) для всех г, поэтому Ь\а. Если 6|а, то р^(г)|а. Учитывая
единственность разложения целого числа на простые множители, можем утверждать, что
рь^ является частью единственного разложения числа а, поэтому P;(l)|p°(l).

Ответы к упражнениям 875
Раздел 3.6.
1. а) 1; б) 3; в) 2;
3. а) 0; б) 1; в) 1;
5. Если а — нечетное целое число, тогда а = 2к + 1 для некоторого к.
Следовательно,
г) 14.
г) 1.
а2 = B/с + IJ = 4/с2
-I- 1 =
+ к) + 1,
так что
а2 -I = 4(/с2 + А:) = 4fc(fc + 1),
и поскольку либо fc, либо А: + 1 — четно, то о2 - 1 делится на 8, и а2 = 1 (mod 8).
7.
0
1
2
3
[0]
[0]
1] [2] [3]
0] [0] [0]
[0] 1] [2] [3
[0] [2] [0] [2]
[0] [3] [2] [1]
9.
0]
1
2
3]
4
5
6
[0] [1] I И |
[0] [0] [0]
3
0
[4] [5
[Р] [0
|
6]
0]
[0] [1] [2] [3] [4] [5] [6]
[0] [2] [4] [6] [1] [3] [5]
[0] [3] [6] [2] [5] [1] [4]
[0] [4] [1] [5] [2] [6] [3]
[0] [5] [3] [1] [6] [4] [2]
[0] [6] [5] [4] [3] [2] [1]
П. а) [3]; б) [2]; в) [1]; г) [3]; д) [0], [2].
13. Если а = Ь (mod ran), то а — 6 равно ктп для некоторого к. Учитывая, что а — b равно
(кп)т, имеем а = b (mod га). Аналогично, а = b (mod n).
15. Уже известно, что существует одно и только одно г, где 0 < г < п такое, что а = г
(mod n). Мы должны показать, что г является также взаимно простым с п. Поскольку
а = nq + г для некоторого q, и если г не является взаимно простым с п, то существует
целое число га такое, что п = cm и г = dm для целых чисел cud. Следовательно,
а = cmq + dm = (cq -f d)m,
так что га также является множителем а, что противоречит предположению о том, что а
и п — взаимно простые числа.
Раздел 4.1.
1. а) область определения / — множество R\ область значений / — {у : у > 4};
б) область определения / — {х : х > 2}; область значений / — {у : у > 0};
в) область определения / — {х : х > 2}; область значений / — {у : у > 0};
г) область определения / — множество Я; область значений / — {у : 0 < ?};
д) область определения / — множество R - {2, -2}; область значений / — {у : у <
-T}U{t/:y>0};
е) область определения / — множество R\ область значений / — {у : у > 0}.
3. a) f(g(x)) = (х + 3J + 1, g(f(x)) = х2 + 1 + 3 = х2 + 4;
б) f(g(x)) = д/(*2+3J + 2, g(f(x)) = х2 + 5;

876 Ответы к упражнениям
)
5. а) не удовлетворяет ни одному из условий;
б) не удовлетворяет ни одному из условий;
в) инъективна, сюръективна, имеет обратную функцию;
г) не удовлетворяет ни одному из условий;
д) сюръективна.
7. Г1 = ГЧВ = ГЧ/Р) = (Г7)<7 = 1л 9 = 9-
9. а) предположим, что / не инъективна, тогда существуют a, a' e А такие, что /(а) =
/(а') = b для некоторого b e В. Следовательно, f~1(f{a}) = f~l{b} = {а,а}, поэтому
неверно, что /~X(/(W) = W для всех W С А. Предположим, что существует W С А
такое, что f~l{f(W) ф W. Пусть а е f~l(f(w) и а $ W. Но /(а) е f(W) по
определению /~\ например, /(а) = 6. Поскольку 6 е /(ИО, то существует а1 € W
такое, что /(а') = Ь, и / не является инъекцией.
б) если / не является сюръекцией, то существует b € В такое, что оно не принадлежит
f(A). Следовательно, ff~l(A\J{b}) ф AL){b}. С другой стороны, предположим, что / —
сюръекция. По определению функции f~l соотношение ff~l(W) С W выполняется
всегда. Пусть w e W. Поскольку / — сюръекция, то существует а ? А такое, что
/(а) = w, и при этом а е /~1(VV). Следовательно, /(а) € //~1(И/), поэтому w ?
//-1(И0 и 1У С ff~l(W). Таким образом, 1У = ff'^W).
11. Пусть а 6 Л и /(а) = а', /(/(а)) = /(а') = а' = /(а) = /(/(а)). Если / имеет обратную
функцию, то Z /(а) = f~l(a) = а = /(а). Пусть а G А и а" = /~:(а)» тогда ff~l(a) =
f(a")=a = I(a).
Раздел
i
l.
3.
5.
7.
а)
в)
а)
д)
а)
в)
а)
в)
4.3.
J °9 -
9° f -
= 1
-1 _ [
/ °9 =
1 /
-1 /
9 - \
14;
-2;
6,11,18
-4,-2,
А(п) =
А{п) =
/ 1
V 1
/ 1
^ 1
' 1
3
1
2
/ 1
\^ 1
A
f 1
ч 3
' 1
ч 4
2
2
2
2
2
1
2
3
2
2
to to
2
2
2
2
, 2738;
-1,-
2п2;
(-1)
-1,<
п + 1
3
3
3
3
3
2
3 <
1
3
3
со со
3
4
3
1
0;
1"
>
4 \
4 J '
4 \
4 J '
4 \
1 у '
4 \
з у ;
б) 630630;
е) -3;
±!|;
б)
_\
г)
в)
/ °9
9° I
*
9
J °9
9°f
*
9
-9;
ж) 5.
г)
г)
2,3,2
А{п)
А(п)
/ 1
= V 3
/ 1
= \ 3
/ 1
= V 2
/ 1
= V 4
/ 1
= \ 3
<1
( 1
= \ 3
/ 1
= v 1
• ? I-
3' ~4'
= 1(-
= п2Ч
2
4
2
4
2
1
2
3
2
2
to to
2
2
2
2
i
5"
-2.
3
1
3
1
3
4
3
2
3
1
3
1
3
1
3
3
-1.
4 \
2 )
4 \
2 J
4 \
з у;
4 \
1 у;
4 \
4 у
4 \
4 у
4 \
4 у '
:)¦
г) -2

Ответы к упражнениям 877
Раздел 4.3.
1. а)
в)
Д)
1 -4 -3 12
39 5 21 8
-10 5 0 -20
-2 3-5 0
-6 9 -15 О
-8 12 -20 О
-10 15 -25 О
10 -2
-12 14
б)
-3 5 15
11 23 41
7 13 67
г) [ -13 ] ;
е)
-25 -29
66 -1
„ ч Г -16 15 1 _ Г -5 13 1 ч Г -10 24 1 ч Г -26 60 1
3- а) [ 18 42 J ; б) [ 69 41 J ; В) [ 33 31 J ; Г) [ -2 47 J ;
Д)
и)
-16 18
15 42
е)
-16 18
15 42
в)
ж)
33 31
-7 1
9 -4
г)
з)
7 -1
-9 4
Г —15 10 1 Г 17 -4 1
|_ 35 25 J ; К) [-25 3 J
В =
и С =
Тогда АВ = AC =
но
5. Пусть А =
ВфС.
7. Предположим, что А и В — матрицы, и их произведение АВ определено. Пусть С = АВ,
так что dj = ^AikBkj. При этом, в матрице (АВ)г элемент C)i — ^AikBkj или
C\j = ^AjkBki. Пусть С = В1А\ тогда Сц = Yl^kiAjk = ^AjkBki. Следовательно,
В1 А1 = (АВУ.
9. Пусть R и S — отношения с матричными представлениями М и ЛГ, соответственно. Пусть
А = М AN. Если {ai,aj)y e RnS, то (ai,aj)t e R и (ai,aj)t € S. Поэтому M»j = Nijt = 1,
так что Aij — Mij A Nij = 1. Следовательно, если Ai
так что (а»,^), € R и (a»,aj)t € 5. Следовательно,
является матричным представлением для Rn S.
0 10 0
i л Nij = 1, то Mij = ATij = 1,
G Я П 5. Поэтому Mij Л Nij
11. R =
Т =
а) Я =
в)
0 0 0 11
10 0 0 0
0 10 0 0
0 0 0 0 0
110 0
10 0 0
0 0 0 0
0 0 10
110 0
110 0
0 0 0 0
0 0 0 1
б) S о R =
0
0
1
0
1
0
0
1
1
1
1
0
0
0
0
0
1
1
0
0
0
1
0
0
0
0
0
0
0
0
1
0
1
0
0
0
г) S~loS =
110 0
110 0
0 0 10
0 0 0 0

878 Ответы к упражнениям
д)
ж) Т о S =
10 0 11
0 0 0 11
0 0 0 0 0
0 10 0 0
0 10 0
0 10 0
0 0 11
0 0 0 0
13. 5=
U=
а)
110 0 0
0 0 110
10 0 0 1
0 0 0 0 0
0 0 0 10
1
11
11
11
0 0
10 0
10 0
0 0 0 10
0 0 0 0 1
(У, V\
Т =
V =
б) U\
е) To{SoR) =
з) (ToS)oR =
0 10 0 0
10 110
0 10 0 0
0 0 0 0 1
0 0 0 0 1
0 110 0
1110 0
110 0 0
0 0 0 10
0 0 0 0 1
в) U-
15. а) {A,а),A,с),B,Ь),C,с),D,а),D,Ь)};
в) {(l! а)' A, с)' (i Ь), (з', а)' C, с)\ D, &)}.
17. а) б)
*• О
0 10 0
0 0 11
0 0 0 0
0 10 0
0 10 0
0 10 0
0 0 11
0 0 0 0
0 10 0
0 10 0
г) S.
19. а)
11111
110 11
10 110
11111
11111
Раздел 4.4.
1. а) 7;
3. 1
1
-1
а(п) = — п
5. 1 2
I 1
-10 -9
а(п) = п — 11
4
I
-7
б)
1110 1
0 110 1
11111
10 0 10
1110 1
б) И;
-2 -3 -4 -5
5
1
-6
11
I
0
12
1
1
в)
0 0 0 0 0
0 10 0 1
110 11
10 0 10
0 0 0 0 0
в) счетно бесконечное.

Ответы к упражнениям 879
Раздел 4.5.
1. {2,4}.
3. 0.
5. Согласно теореме 4.51 множество положительных рациональных чисел счетно бесконеч-
бесконечное. Поскольку существует взаимно однозначное соответствие между положительными
рациональными числами и отрицательными рациональными числами, то множество отри-
отрицательных рациональных чисел счетно. Поэтому по теореме 4.52 их объединение счетно.
Поскольку множество {0} счетно, то его объединение с ненулевыми рациональными чис-
числами счетно. Поэтому множество рациональных чисел счетно.
7. Используя индукцию, покажем сначала, что если А счетно, то Ах Ах Ах- • -х А, декартово
произведение п копий множества А, счетно. Существует взаимно однозначное соответствие
между многочленами пятой степени с целыми коэффициентами uZxZxZxZxZxZ,
где пэХ5+ а,4Х4 + азх3+а,2Х2+ aix + ao соответствует (а5,а4,аз,а2,аьао). Следовательно,
множество многочленов пятой степени с целыми коэффициентами счетно.
Раздел 5.1.
1. Процедура Транспонирование матрицы (Л, m,n):
Цикл по г от 1 до га:
Цикл по j от 1 до п:
Конец цикла;
Конец цикла;
Конец процедуры.
Г -2 1 2 ]
3. а) 4 1-4;
3 7 1
5. а)
Г -31 2].
[ -14 -12 J '
г)
-1
2
б)
б)
Д)
29
23
-17
3
И
6
3
-8
5
23
51
5
-8
-16
0
11
-16
-15
-17
5
11
5
-15
-30
6
0
-30
в)
в)
е)
9
15
3
1
0
5
3
8
5
-15
33
15
21
-4
oj
11
-16
-15
3
15
59
6
0
-30
7. Процедура Наименьшее целое число (oi, аг, аз,..., аъ
(находит наименьшее значение а*):
Положить к = 1;
Цикл по г от 2 до п;
Если а{ <ак, то положить к = г;
Конец цикла;
Конец процедуры.
9. Процедура Проверка симметричности матрицы (Л, тг):
Положить Т = 1;
Цикл по г от 1 до п:
Цикл по j от г до п:
Если Aij Ф Aji, то положить Т = 0;
Конец цикла;
Конец цикла;
Конец процедуры.

880 Ответы к упражнениям
11. Процедура Среднее арифметическое(ai,a2,O3,...,on):
Положить 5 = 0;
Цикл по г от 1 до п:
Заменить S на S -f а,;
Конец цикла;
Положить А = —;
п
Конец процедуры.
13. Следующая процедура вычитает 6 из а, где 6 имеет размерность m, a имеет размерность
п, га < п и 6 < а. Предположим, что 6 = 616263 • • • 6П и а = а^аз • • • а„, где 6* = 0 для
i < п — т. Кроме того, предположим, что у нас имеется процедура Сложение (а, 6), по-
построенная в предыдущей задаче, которая складывает числа а и 6. Пусть 6(fc) = 616263 • • • 6^.
Процедура Вычитание (a,b,m,n):
Цикл по г от 1 до п:
Условие: если 6„_г+1 < an-i+i, то положить cn-i+i = an_i+i - 6„_г+ь
Условие: если 6n-i+i > ап-г+ь то
ПОЛОЖИТЬ Сп-г+1 =10 + ап-*+1 - 6п_г+Ь
заменить 6(п~7) на Сложение F(n-i), 1);
Конец цикла;
Конец процедуры.
15. Следующая процедура делит а на 6, определяя частное q и остаток г.
Процедура Деление (atb):
Если 6 > а, положить q = 0 и г = а;
Положить г = 1;
Условный цикл: до тех пор, пока г > 6,
положить г = а — (г • 6);
положить ^ = г;
положить г = г + 1;
Конец условного цикла;
Конец процедуры.
Раздел 5.2.
1. а) /A) = 9 /B) = 27 /C) = 81 /D) = 243;
б) /A) = 5 /B) = 16 /C) = 41 /D) = 94;
в) /A) = 4 /B) = 16 /C) = 256 /D) = 65536;
г) /A) = 1 /B) = 4 /C) = 36 /D) = 576;
д) /A) = 2 /B) = 4 /C) = 16 /D) = 65536.
3. а) /B) = 5 /C) = 7 /D) = 9 /E) = 11;
б) /B) = 1 /C) = 0 /D) = -1 /E) = 1;
в) /B) = 7 /C) = 56 /D) = 3145 /E) = 9890994;
г) /B) = 2 /C) = 0 /D) = -48 /E) = -5760;
= -1 ДЗ) = -1 Д4) = 1 Д5) = -1.
5. а) /(п) = 2"; б) /(п) = п + 1; в) /(п) = 1;
г) Дп) = 1 + 2п; д) Дп) = 5п.
7. ао = 7 - 20+1 = 5. Требуется показать, что 7 - 2fc+1 = 2G - 2k) - 7. Подставляя в
рекурсивную функцию, имеем
2G - 2к) - 7 = 7 - 2 • 2к = 7 - 2fc+1.

Ответы к упражнениям 881
9. ао = — 1 - 20+1 = —3. а\ = — 1 — 21+1 = —5. Подставляя в рекурсивную функцию, имеем
-1 - 2k+l = 6(-1 - 2к) - 8(-1 - 2к~1) - 3.
Но
6(-l-2fc)-8(-l-2fc)-3 = -l-6'2k+8'2k~l = -l-3-2fc+1+2-2fc+1 = -l-2fc+1.
11. ai = I2 -h 1 + 1 = 3. Подставляя в рекурсивную функцию, имеем
(/с _ IJ + к - 1 + 1 4- 2к = к2 - 2к + 1 4- ЗА: = к2 + к 4- 1.
13. ао = -2(-1)° + 2-3° = 0, ai = -2(-1)х +2-31 =8. Подставляя в рекурсивную функцию,
имеем
с-гс-г)*1-1 + 2 • з*) + 3(-2(-i)fc~2 + 2 • з*) =
4 • З*" + 6 • 3fc~2 =
= 4(-l)fc - 6(-l)fc 4- 4 • З* + 2 • З* = -2(-l)fc + 2 • 3\
15. a0 = 3(-2H + 2-3°-3.2° = 2, <ц = 3(-2)х + 2-31 -3-21 = -6. Подставляя в рекурсивную
функцию, имеем
3(_2)fc 4- 2 • 3fc - 3 • 2к = Ц-2)к-г + 2 • 3fc-1 - 3 •
4- 6C(-2)fc 4- 2 • З*-2 - 3 • 2fc) + 3 • 2к =
= C - 9)(-2)fc + B 4- 4Kfc 4- (-3 - 9Jfc 4- 3 • 2k =
= 3(-2)fc 4- 2 • 3fc - 6 • 2k + 3 • 2k = 3(-2)fc 4- 2 • 3fc - 3 • 2k.
17. « 5.8 x 1011 лет.
Раздел 5.3.
1. 28 - 1 = 255.
3. а) (а) 5 (б) 4; б) (а) 14 (б) 8; в) (а) 18 (б) 9.
5. (б), (в), (г).
7. Для п = 1 имеем 1! = 1 = I1, поэтому утверждение истинно. Предположим, что утвержде-
утверждение истинно для п = к, т.е. к\ < кк < (к 4- 1)к поскольку разложение (к 4- 1)к включает
кк как один из множителей. Умножая обе части неравенства к\ < (к 4- l)fc на (к 4- 1),
получаем (к 4-1)! < (/c + l)fc+1.
9. Если f(n) = O(g(n)), то существуют к\,т\ такие, что f(n) < k\g(n) для п > т\.
Если g(n) = O(h(n)), то существуют /с2,Ш2 такие, что g(n) < k2h(n) для п > тг.
Полагая М = max(mi,m2), получаем /(n) < kig(n) < /ci/c2/i(n) для п > М, поэтому
/(п) = O(fc(n)).
11. Пусть Р(т) является утверждением "Если гит — положительные целые числа, г < т
и п > 1, то nr < nm". Утверждение несомненно истинно, если т = 1. Предположим, что
Р(/с) истинно, так что если г < /с, то пг < пк. Нужно доказать, что Р(к) истинно, так
что если г < к 4- 1, то пг < nk+l. Поскольку 1 < п, то nfc • 1 < пк • п. Следовательно,
nk < nk+1. Предположим, что г < к4-1. Если г < А;4-1, то г < к, поэтому nr < nk < nk+l.
Если г = /с 4-1, то nr < nk+1. Таким образом, Р(к 4-1) истинно.

882 Ответы к упражнениям
Раздел 5.4.
1. 0,1,2,3,4,5,7,8,9,11.
3. а, 6, с, d, /, j, га, n, p, r, s, t, и, х, у, z.
5. a) 9,8,7,6,5,4,3,2,1 (для п объектов количество сравнений всегда одинаково);
б) 9,8,7,6,5,4,3,2,1 (для п объектов количество сравнений всегда одинаково);
в) 1,2,3,4,5,6,7,8,9;
г) 5,3,1,2,4,3,7;
д) 1,2,3,4,5,6,7,8,9.
7. 2D(|)(log2(|) + А) + Dn = L>n(log2 n - log2 2 + A) + Dn =
= Dn(\og2 n - 1 + A) + Dn = Dn(\og2 n + A).
рекурсивная формула, деленная на n = 2Л
2.2—1 ¦ -
_ /c\2 Q2m~2 с _ повторное применение рекурсивной
4 2/ 2m + 2 + ~ формулы
2/ 2т~3 формулы
повторное применение рекурсивной
повторное применение рекурсивной
формулы
m = loS2 n- поскольку n = 2"
D = сумма геометрической прогрессии
(
D= поскольку clog2n = nlog2c
I _ ? I (возьмите log2 от обеих частей)
2 /
niog2 с/ 2D\
= Л 4- 4- подставьте значение Q\
n \ 2 — с J
nlog2c nlog2c
A +
2-е n 2-е 2-е n n 2-е
П r7log2c ОП ОП
Следовательно, -^- = A 4- ;f^- и Qn = nlog2 M + т^-п.
n n 2-е 2-е

Ответы к упражнениям 883
б) 4- 4- Ла3 х 3Ла27;
Раздел 5.5.
1. а) а2АЬ2л+; б) аЗлЗа2л х
в) аТЪ 4- а?Г+; г) aThV 4- 4А;
д) а2л6с+ х.
3. а) (а 4- Ь) -f- (с - d), б) (а 4- 6А2) х (с 4- сГ2);
вKхах6 + 4хсх dA2; г)
д) (<Г2 + 6) х (c4-dA2).
5. а) + ла2АЬ2;
в) х 4- ла26 4- cAd2; г) л 4- ла2А634;
д) хла2 4- be.
7. а) (а + Ь) -i- (с - d) б) (ал2 4- dA2) -f (cA2 4- d^2);
в) ЗаЬ 4-4cd + 5ad; г) (ал2 + ЬА2 + сл2)лЗ;
д) (ал2 4- Ь)(с4- dA2).
9. 1. Добавлять скобки в выражение, пока оно не станет полноскобочным.
2. Начиная с самых внутренних скобок, удалить пару скобок и поместить находящийся
внутри скобок оператор на место соответствовавшей ему левой скобки. При наличии
более чем одной самой внутренней пары скобок начинать с правой пары.
3. Перемещаясь к следующей паре скобок, снова удалить их и поместить оператор,
находившийся внутри скобок, на место соответствовавшей ему левой скобки.
4. Продолжать шаг C), пока все скобки не будут удалены.
Раздел 5.6.
1. 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111
10000, 10001, 10010, 10011, 10100, 10101, 1011010111.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
а) 101101;
г) 11000010;
а) 11; б) 26;
а) 3F; б) 74;
а) 74; б) 755;
а) 10111.111;
г) ЮППО.ТТОО;
а) 14.75;
г) 3.4375;
а) 24.Л;
г) 754.8BD7;
а) 92.2265625;
в) 1199.767578125;
д) 5070.821289062.
а) 5.Л;
г) ЗДЯ.36С;
а) 101100.01001011;
б)
д)
б)
д)
б)
д)
б)
д)
б)
д)
в) 101011111000.010010001100;
1010110;
100111000.
в) 36;
в) 178;
в) 1274;
101011.11;
110100.0100ТТ.
10.625;
13.3125.
Л1.С8;
147Я.59.
37.54;
3D4.228.
д) 1100000101001010.001011010100.
Раздел 5.7.
1.
а) 10001010;
в) 11001001;
б)
г)
б)
г)
б)
г)
в) 11110011;
г) 59; д) 53.
г) 2DE\ д) 147?.
г) 16893; д) 53731.
в) 10111010.001;
в) 4.5625;
в) 250.28;
3858.6796875;
12971.75415039;
в) 1?6.6F8;
111110010.101000111100;
1010000100101110.000100011100;
01001011;
00010101.

884 Ответы к упражнениям
3. а) 01001001; б) 10011011;
в) 11011011; г) 11110010.
5. а) 00100110; б) 01111110;
в) 10111111; г) 11000101.
7. а) 01000111; б) 01011101;
в) 11101000; г) 00000110.
9. а) 8?>С6; б) 54F0; в) 05ЕЕ\ г) DC44.
11. а) 010F; б) FC83; в) FFEF\ г) D970.
13. а) С5С0; б) F6C9; в) EF7C\ г) 3563.
15. а) 04АА; б) 15Б?>; в) ?>4Б1; г) FJD31.
17. -2147483648 to 2147483647.
Раздел 5.8.
1. а) -1; б) 22; в) 15; г) -234.
3. -1.
5. Если А — перестановочная матрица, то в каждой строке и в каждом столбце этой матрицы
только один элемент равен 1, а все остальные равны 0. Пусть В = А А1. Пусть Ai — строка
матрицы А и пусть в г-ой строке Агк = 1. Если А] — j-ый столбец в транспонированной
матрице А1, то Bij = 1 тогда и только тогда, когда Akj = 1. В противном случае Bij = 0.
Но Akj = Ajk, поэтому Bij = 1 тогда и только тогда, когда Ajk = 1. Но поскольку
имеется только одна 1 в каждой строке и столбце, то это имеет место, только если г — j.
Следовательно, Bij = 1 тогда и только тогда, когда г = j, поэтому В — единичная матрица.
Раздел 6.1.
1. а) путь, простой путь, длина 5; б) путь, не простой путь, длина 6;
в) путь, не простой путь, длина 7; г) путь, не простой путь, длина 8.
3. а) не цикл; б) цикл, не простой, длина 8;
в) не цикл; г) цикл, простой, длина 6.
5. а)
б)
в)
7. Компонента представляет собой наименьший подграф такой, что если точка, изображаю-
изображающая палочку, принадлежит графу и палочка касается другой палочки, то вершина, изоб-
изображающая вторую палочку, и ребро между ними принадлежат подграфу. Иными словами,
это граф, представляющий совокупность палочек, лежащих одна поверх другой.
Раздел 6.2.
1. а) V = {а, 6, c,d, e}. Вершина а имеет степень входа 2 и степень выхода 1, вершина Ъ —
степень входа 1 и степень выхода 1, вершина с — степень входа 2 и степень выхода 1,
вершины d и е — степень входа 0 и степень выхода 1, вершины d и е — источники;
б) V = {а, 6, c,d, e}. Вершины а, 6, d и с имеют степень входа 0 и степень выхода 1.

Ответы к упражнениям 885
Вершина е имеет степень входа 4 и степень выхода 0. Вершины a,b,d и с — источники.
Вершина е — сток;
в) V = {а, 6, с, d, e,/}. Вершина а имеет степень входа 0 и степень выхода 2. Вершины 6,
си^ имеют степень входа 1 и степень выхода 2. Вершина е имеет степень входа 1 и
степень выхода 1. Вершина / имеет степень входа 5 и степень выхода 0. Вершина a —
источник, а вершина / — сток.
г) V = {а, Ь, с, d, е}. Вершина а имеет степень входа 2 и степень выхода 1. Вершины Ь,
d и е имеют степень входа 1 и степень выхода 1. Вершина с имеет степень входа 1 и
степень выхода 2.
3. а)
7'
в)
d a
d Ч
г)
• с е • <-
</ (/•
5. а)
.d
• С
б) совпадают с построенными в (а)
в)
а Ъ
d di

886 Ответы к упражнениям
г)
• d
7. Ориентированным циклом называется ориентированный путь, который начинается и за-
заканчивается в одной и той же вершине.
9. Орграфы (а), (б), (г) — связные, граф (б) — сильно связный.
11. Орграфы (а), (в), (г) — связные, граф (в) — сильно связный.
Раздел 6.3.
1. (а); (б) и (д).
3. (а); (б) и (в).
5. Поскольку каждая компонента d — дерево, то Vi = е» + 1. Следовательно, для каждого
целого дерева имеем J27Li vi = Sili(e* + *)» поэтому v — е + т.
7. а) г;б, V7, v&, vg\ б) vo, ^з» i^6\ в) v\\
г) 2; д) we, V7\ e) 3;
ж) г?2,г>4,г;5,г>7, ^8,г>д; з) нет, vq имеет степень выхода 3.
9. Воспользуемся индукцией по количеству вершин. Если if v — 1, то е = 0. Таким образом,
теорема верна, если v = 1. Предположим истинность утверждения теоремы для v = к.
Пусть Т — дерево с к + 1 вершинами. Удалим лист и инцидентное ему ребро. Теперь
дерево имеет к вершин. Следовательно, по индуктивному предположению, для этого дерева
v = е + 1. Если возвратить на место лист и ребро, то количество вершин и количество
ребер увеличится на один. Поэтому для дерева с к + 1 вершинами по-прежнему будем
иметь v = е 4- 1.
Раздел 6.4.
1. а) фронтальная задняя левая правая б)
фронтальная
Ж
С
к
3
задняя
с
к
ж
3
левая
к
3
с
ж
правая
3
ж
к
с
•альна
с
к
3
ж
я задняя
ж
3
с
к
левая
3
с
ж
к
правая
с
ж
к
3
в) фронтальная задняя левая правая г) фронтальная задняя левая правая
3
ж
с
к
с
3
к
ж
к
3
ж
с
ж
с
3
к
3
к
ж
с
ж
к
с
3
к
3
ж
с
ж
с
3
к
д) решение отсутствует.
Раздел 6.5.
1. (а).
3. (в).
5. (а), (в).
7. (б).
9. Предположим, что граф G связный и ровно две его вершины имеют нечетную степень.

Ответы к упражнениям 887
Пусть а и 6 — вершины нечетной степени. Если между а и Ь ребро отсутствует, добавим
его. Теперь каждая вершина имеет четную степень, поэтому новый граф имеет эйлеров
цикл. В этом цикле следует проходить и ребро {a,b}. Например, проходя цикл, мы дви-
движемся от а к 6. Если начать с этого ребра и пройти цикл, то легко заметить, что если
ребро удалить, начать путь в вершине Ь и пройти его, следуя циклу, то получим эйлеров
путь из Ь в а. Если между а и b имеется ребро, удалим его. Новый граф имеет эйлеров
цикл, если он по-прежнему связный. Пусть эйлеров цикл начинается и заканчивается в
вершине а. Если мы пройдем этот цикл, а затем проследуем вдоль удаленного ребра от а к
6, то получим эйлеров путь от а к 6. Если новый граф перестал быть связным, то он имеет
эйлеров цикл для компоненты, содержащей вершину а, который начинается и заканчива-
заканчивается в вершине а, а также для компоненты, содержащей вершину 6, который начинается
и заканчивается в вершине Ь. Пройдем эйлеров цикл от а к а, удаленное ребро от а к 6,
затем пройдем эйлеров цикл от 6 к 6. В результате получим эйлеров путь от а к 6.
Предположим, что граф G имеет эйлеров путь. Пусть, например, он начинается в вер-
вершине а и заканчивается в вершине Ь. После первого ребра пути, выходящего из а, для
каждого ребра пути, который ведет в а, должно существовать ребро, выходящее из а. По-
Поэтому вершина а должна иметь нечетную степень. Аналогично, вершина 6 должна иметь
нечетную степень. В любых других вершинах, для любого ребра пути, который ведет в
эту вершину, должно существовать ребро, которое выходит из этой вершины. Поэтому
вершина имеет четную степень.
11. Если граф сильно связный, то для любой его вершины г>, несомненно, любая другая вер-
вершина достижима из вершины v, н v достижима из любой другой его вершины. Обратно,
пусть имеется вершина v, обладающая указанным свойством. Пусть а и Ь — произвольные
вершины. Поскольку существует путь из а в г; и путь из г; в 6, то существует путь из а в
6, поэтому рассматриваемый граф сильно связный.
Раздел 6.6.
1. а)
е\ е2 ез е4 еъ ее
vi 1 О О 1 10
V2 1 1 О О О О
уз О 1 1 О О О
у4 О О О О 1 1
уъ О О 1 1 О 1
в) е\ е2 ез е4 еъ ее
vi 1 0 0 1 О О
v2 1 1 1 О О О
vz 0 1 0 0 1 1
v4 0 0 1 1 1 О
v-o 0 0 0 0 0 1
3. a) V\ V2 V3 t>4 ^5
vi 0 1 0 1 1
v2 1 0 1 О О
v3 0 1 0 0 1
vA 1 0 0 0 1
«510110
б)
е\
ее е-? е% eg ею ец е\2
1100001000
г)
е\ е2 ез
ее е-? ее eg ею
vi 0 0 1 1 0 0 0 1 1 О
v2 1 1 0 0 0 0 0 0 1 1
уз 0 0 1 0 1 1 0 0 0 1
V4 0 1 0 1 0 1 1 О О О
уъ 1000101100
б)
VI
V2
УЗ
V4
v5
ve
vi
0
1
1
0
1
0
V2
1
0
0
1
0
1
уз
1
0
0
1
0
0
V4
0
1
1
0
0
0
УЪ
1
0
0
0
0
1
ve
0
1
0
0
1
0
V7
0
0
1
0
1
0
vs
0
0
0
1
0
1
v7 0 0 1 0 1 0 0 1
v8 0 0 0 1 0 1 10
0
v2 1001100000 0 0
v3 0000001011 О О
V4 0000100001 1 0
уъ 0110000100 0 0
ve 0011010000 О О
v7 0000000110 0 1
v8 0000010000 1 1

888 Ответы к упражнениям
В)
v3 О 1 О 1 1
v4 1 1 1 О О
г>5 О О 1 О О
vi
0
1
V2
1
0
V3
0
1
VA
1
1
V5
0
0
5.
7.
Г) V\ V2 V3 VA Vo
vi 0 1 1 1 1
v2 1 0 1 1 1
v3 1 1 0 1 1
V4 1 1 1 0 1
V5 1 1 1 1 0
9. А =
V\
V\ V2 V3
t>2
^з
f4
ibie
0
1
1
0
0
из
1
0
1
0
0
Vi Bt
1
1
0
0
0
>1 V2
0
0
0
0
1
V3
0
0
0
1
0
ИЗ V2 В
V2
V3
Vo
1
1
1
0
0
0
0
0
1
0
0
0
0
0
1
из г>з в г>1,г>2,г>з, из va в г>4, из v$ в vs.
11. а)
0 0 110
0 0 110
110 0 1
110 0 1
0 0 111
13. R =
б)
110 0 1
110 0 1
0 0 110
0 0 110
110 0 1
в)
0 0 110
0 0 110
110 0 1
110 0 1
0 0 111
15. Ах А.
17. R = {
(г;5, г>5),
19. Ах А.
21. R={(vi,V3),(vi,V2),(Vi,Vi),(Vi,Vs),(v5,V4
23. Ребрам соответствуют одинаковые столбцы.
25. По определению матрицы смежности, теорема верна, когда п = 1. Предположим, что она
верна для п = к. Следовательно, /с-путь из вершины Vi в вершину vj существует тогда и

Ответы к упражнениям 889
только тогда, когда А®к = 1. Теперь,
Aek+1 = W (A°n Л Am ) = 1
тогда и только тогда, когда существует га, так что Af? = 1 и Amj = 1. Но, по индук-
индуктивному предположению, это имеет место тогда и только тогда, когда существует /с-путь
из г в га и 1-путь из га в j. Последнее утверждение истинно тогда и только тогда, когда
существует к + 1-путь из г в j.
27. Путь из вершины t>» в вершину vj существует тогда и только тогда, когда существует
/с-путь из Vi в vj для некоторого 1 < к < га, т.е. тогда и только тогда, когда Afk = 1 для
некоторого 1 < к < га, или тогда и только тогда, когда Atj = 1.
29. Если дерево T(V, E) не является ориентированным, то транзитивным замыканием является
V х V. Если T(V, E) — ориентированное дерево, то aRb, если а — предок 6.
Раздел
1. а)
3. 1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
6.7.
1;
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
б)
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2;
0
1
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
в) 2;
г) 4.
5.
11
10
00
01
111
11111
10111
00111
01111
110
НПО
10110
00110
01110
100
11100
10100
00100
01100
101
11101
10101
00101
01101
001
11001
10001
00001
01001
7.
111
по
100
101
001
111
111111
110111
100111
ЮПИ
001111
по
111110
110110
100110
101110
001110
100
111100
110100
100100
101100
001100
101
111101
110101
100101
101101
001101
001
111001
110001
100001
101001
001001
000
111000
110000
100000
101000
001000
9. Поскольку т = 2\ первые т цифр вершин в каждом столбце образуют код Грея для
т. Следовательно, первые т цифр первой вершины и последней вершины в столбце от-
отличаются ровно одной цифрой. Последние п цифр вершин в каждом столбце совпадают.
Следовательно, первая и последняя вершины в столбце отличаются ровно одной цифрой,
поэтому они являются смежными. Поскольку n = 2J, последние п цифр вершин в каждой

890 Ответы к упражнениям
строке образуют код Грея для п. Таким образом, последние п цифр первой вершины и
последней вершины в строке отличаются ровно одной цифрой. Первые т цифр вершин
в каждой строке совпадают. Вполне очевидно, что первая и последняя вершины в строке
отличаются ровно одной цифрой, поэтому они являются смежными.
Раздел 7.1.
1. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27,
28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73,
74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96,
97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116,
117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135,
136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154,
155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173,
174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192,
193, 194, 195, 196, 197, 198, 199, 200.
3. 37 13.
5. 37-47.
7. 47-83.
Раздел 7.2.
I. 322 = 452 — 1001, поэтому 1001 не является простым числом.
3. 702 — 72 = 4851, поэтому 4851 не является простым числом.
5. 902 — 72 = 8051, поэтому 8051 не является простым числом.
7. 902 - 132 = 7931, поэтому 7931 не является простым числом.
Раздел 7.3.
1. а) 75 = 8 х 9 + 3; б) 102 = 5 х 20 4- 3; в) 81 = 9 х 9 + 0; г) 16 = 25 х 0 + 16.
3. а) 75; б) 54; в) 11799; г) 271377; д) 179196.
5. Если ах 4- by = НОД(а,6), то щ^ух -Ь Н0^а%Ь)у = 1. Любой делитель чисел х и у
должен также делить 1. Поэтому числа х и у — взаимно простые.
7. Процедура Алгоритм деления (а, 6):
Положить q = 0 и г = а;
Условный цикл: до тех пор, пока г > Ь,
Положить q = q 4- 1 и г = г — 6;
Конец условного цикла;
Конец процедуры.
9. Допустим, что существуют такие г и s, что rs = а и НОД(г, s) = b. Тогда г = ub и s = vb,
поскольку НОД(г, s) делит как г, так и s. Таким образом, а = ubvb = uvb2 и б2 | а.
Обратно, если б2 | а, то ub2 = а для некоторого целого и. Положим г = ub и s — 6. Тогда
rs = а и НОД(г, s) = b.
II. НОД(а, 6) = ах 4- by = а(х - Ь) 4- Ъ{х 4- а).
13. (п • НОД(а,Ь)) | па и (п • НОД(а,6)) | пЪ. Таким образом, (п • НОД(а,6)) | НОД(па,пЬ).
п-НОД(а,Ь) = n(ua + vb) при некоторых целых а и Ь. НОД(па,пЬ) | пиа и НОД(па,п6) |
nvb. Таким образом, НОД(па,п6) | п(иа 4- vb), так что НОД(па,пЬ) | п • НОД(а,Ь) и
НОД(па,пЬ) = п- НОД(а,6).
Раздел 7.4.
1. а) [3; 2,1,3], [3; 2,1,2,1]; б) [0; 20,1,8,1,1,2], [0; 20,1,8,1,1,1];
в) [-1;1,6,1,3,1,5,1,1,1,2], [-1; 1,6,1,3,1,5,1,1,1,1,1];

Ответы к упражнениям 891
г) [0; 3,2,1,3], [0; 3,2,1,2,1];
3. а) [2; 4,4,4,4,4,2 + л/5];
в) [3;7,15,1,292,1,1.736...];
д) [-1; 1,7,1,4], [-1; 1,7,1,3,1].
б) [1:2,2,2, 2,2,1 +л/2];
г) [1; 1,1, 1,1, 1,^Ь^].
Раздел 7.5.
1. Доказательство проведем индукцией. Поскольку qo = 1, то qo > 0. Предположим, что
qm > 0 для всех т < к. Но qk = qk-\tk +qk-2- По индуктивному предположению, qk-i и
qk-2 больше, чем 0. По определению конечной цепной дроби, tk положительно. Поэтому
qk положительно.
3. а) к
0
1
2
3
4
5
в) к
0
1
2
3
4
5
Рк
2
9
38
161
682
2899
qk
1
4
17
72
305
1292
Рк
3
22
333
355
103993
104348
* - (Pit/?*)
0.236 • •
-0.0139 •¦•
7.73-.. х 10
-4.31 ••• х 10~5
2.40- •• х 10
-1.33. •• х Ю-7
Як
1
7
106
113
33102
33215
я- (Рк/Як)
0.141 •••
-1.26 ••• х 10~3
8.32- -. х 10~5
-2.66 •• х 10~7
5.77-•• х Ю-10
-3.31 ••• х 100
б) к
0
1
2
3
4
5
г) к
0
1
2
3
4
5
Рк
1
3
7
17
41
99
Рк
1
2
3
5
8
13
qk
1
2
5
12
29
70
Як
1
1
2
3
5
8
я - (Рк/Як)
0.414 •••
-8.57-•• х 10~2
1.42-•• х 10
-2.45 ••• х 10~3
4.20- -. х 10~4
-7.21 ••• х 10
х ~ (Рк/Як)
0.618- ••
-0.381 • • •
0.118-..
-0.0486 • • •
0.0180 •••
-0.00696 • • •
5. По теореме 7.11,
qk-i
Як-ltk +<?fc-2 _ . , qk-2 _ . ,
— tfc "Г — Cfc "Г
tk-i
= tfc
qk-2
tk-i
tk-2
7. p_2=0, 9-2-1.
Раздел 8.1.
1. 139, 233, 46.
3. a) 53 x 52 x 51 x 50 = 7027800;
б) 8 x 52 x 51 x 50 = 1060800;
в) 45 x 52 x 51 x 50 = 5967000;
г) 20 x 33 x 32 x 31 + 33 x 32 x 31 x 30 = 1636800.
5. 104 - 10 x 9 x 8 x 7 = 4960.
7. 230 = 1073741824.
9. 2 x 262 + 2 x 263 = 36504.
11. a) 16; 6) 1;
13. 109.
15. 36.
17. 699 - 87 = 612.
19. 262 + 263 = 18252.
21. 254.
23. 27 - 8 = 120.
25. 104 - 94 = 3439.
27. 26 x 366.
в) 15.

892 Ответы к упражнениям
Раздел 8.2.
1. 120 + 110-80 = 150, 50.
3. 57 + 36 - 5 = 88.
5. 40 4- 26 - 13 = 53.
7. 100 - 14 = 86.
9. 2x8! = 80640.
11. а) 11111; б) 10000; в) 20000; г) 79,999.
13. 400 + 286 + 182 - 57 - 36 - 26 4- 5 = 754.
15. 333 4- 286 + 250 - 47 - 83 - 35 4- 11 = 715.
д) 40.
д) 91.
д) 50400.
17.
19.
а) 60;
38212
Раздел 8.3.
1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29.
31.
33.
35.
а) 6720;
210, 70, 120, 60
18 • 17 • 16 = 4896
а) 10! = 3628800;
а) 3360;
2880.
387897600.
V13;
235237860.
б) 120;
б) 6652800;
б) 8820;
= 22394644272.
58656, включая все "фулл хаус",
252.
210, 968.
30045015.
167960.
a84-8a76 4-28a6b
-8646663168.
-262440.
Раздел 8.4.
1.
3.
5.
7.
9.
11.
13.
15.
17.
21453.
21534.
{а, с, е).
{2,3,4}.
{2,3}.
{1,5,6}.
{1,3,4,6}.
xyz, xzy, yxz, yzx
{a,b,c,d\, {а, 6, с,
в) 65;
в) 792;
б) 25 • 5!
в) 30240;
, или 54912, исключая
г) 200;
г) 91;
= 3840.
г) 36960;
все "фулл хаус
2 4- 56а5Ь3 4- 70а4Ь4 4- 56а3Ь5 4- 28а2Ь6 + 8а67 4- б8.
:, zxy, zyx.
,e},{a,6,d,e},
{a,c,d,e},{6,c,d,e}.

Ответы к упражнениям 893
19. abcdefghijklmnopqrstuvwxyz, zyxwvutsrqponmlkjihgfedcba.
21. {abcde}, {vwxyz}.
23. Цикл по г от 1 до С(п,г):
Использовать процедуру Сочетание (п.г) для образования г-ro г-сочетания
из п элементов;
Использовать процедуру Обобщенная перестановка, чтобы упорядочить
все перестановки из г элементов, образованных процедурой Сочетание (п.г)\
Конец цикла.
Раздел 8.5.
1-
3.
5.
7.
9.
И.
13.
15.
17.
а) 36'
«>&
а) — •
15120
59049•
я\ 53 .
*' 250'
\ 1098240 _ 4о<
Л> 2598960 ~ '**'
т\ 4
*' 2598960'
345
567'
4464
9000-
3168 5146
9000' 9000'
Раздел 8.6.
Q 1
qJ
б)
26;
'М-'
» 105.
1 250'
R^ 5
В' 36'
fi\ 54912 .
"' 2598960»
ч 5148 .
А' 2598960'
В) 36'
в) 129-
\ 97 .
В' 250'
Г' 36'
в)
е)
г)
г)
г)
36
2598960
9216
2598960
л> я-
22
36-
172
301 *
23
250-
1.-5-
4!2!
26!
* 8!6!9!ЗГ
7.
9.
11.
13.
15.
7!7!7!7!"
24!
D!N'
12! л«
4!5!6!3!
33 = 31933440-
241553
2 4 5 •
422453 = 2217600000.
Раздел 8.7.
12'
9!3!
14'
ш
12'
=1001-

894 Ответы к упражнениям
9
ЗЛЯ
" 40 = 415
Раздел 8.8.
1. 21.
3. Если у одного человека 29 взаимных друзей, то каждый имеет 29 взаимных друзей. Если
это не так, то количество взаимных друзей, которое люди могут иметь, изменяется от О
до 28, поэтому существует 29 возможностей. Но в компании имеется 30 человек, поэтому,
по крайней мере, 2 человека должны иметь одинаковое количество взаимных друзей.
5. 51.
7. 25.
9. Пусть ai,<Z2,a3,...,an — последовательность из п положительных целых чисел. Пусть
5i = ai, S2 = а\ 4- a2, $з = ai + <*2 + аз, .... sn = а\ 4- аг + аз + • • • + ап. Каждое s»
эквивалентно г, по модулю п, где 0 < г» < п — 1. Если какое-либо из г* равно 0, то Si
делится на п, и доказательство завершено. Если нет, то существует п — 1 значений для
г, и п штук п. Следовательно, два из г», например, г, и r^, должны иметь одно и то же
значение. Предположим, что j < /с, тогда aJ+i 4- aJ+2 + • • • + a/t делится на п.
11. 262 + 1.
13. 11.
15. fe I = 13.
170] _
14 I"
17. Рассмотрим пары чисел {1,2}, {3,4}, {5,6},... {2п — 1,2п}. Имеется п пар чисел, поэтому
если у нас п + 1 чисел, то два должны принадлежать одной и той же паре. Эти два числа
отличаются на 1.
19. Поскольку 0 + 1 + 2 + ЗН \- п - 1 = п(п - 1)/2, существует только п - 1 различных
целых чисел, сумма которых меньше, чем п(тг — 1)/2. Поэтому m является суммой не более
п — 1 различных целых чисел. Имеется только п — 1 различных целых чисел и и ящиков,
поэтому два ящика должны содержать целые числа, которые не будут различными. Эти
ящики содержат одинаковое количество шаров.
Раздел 8.9.
1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
1
4'
6
18'
1 1
2' 2*
1
7 '
15
19'
19
"б""
483
56 '
252
36 '
-13 центов.
3456.

Ответы к упражнениям 895
21.
23.
25.
27.
29.
31.
35
27 '
/13W394
V2 А в) ^ о
/52} ~ 6'
V10/
36
38 '
36
38'
3, 2.1.
Раздел 8.10.
1.
3.
5.
7.
т - -47.
22 ~ ""'
Тз ^ -51-
125.
Раздел 8.11.
1.
3.
5.
7.
а) .25;
а) .26;
а) .365ь
а) .181632;
Раздел 9.1.
1.
{1,13}
/|\
/ 1 \
{1,2} {1,3} {2,3}
DXX]
{1} {2} {3}
.1937.
б)
б)
б)
.232;
.28;
1000-
б)
.67032 «
.6365.
670;
в)
в)
в)
.4989.
.585.
1000-
3.
{1,2} {1,3} {2,3}
W {2} {3}
5. а) наибольший элемент /;
б) наименьший элемент а;
в) максимальный элемент /, минимальный элемент а;
г) и то, и другое.
7. а) наибольший элемент д\
б) наименьший элемент не существует;
в) максимальный элемент д, минимальные элементы а, 6, с, d\

896 Ответы к упражнениям
г) верхней.
9. а) наибольший элемент г;
б) наименьший элемент а;
в) максимальный элемент г, минимальный элемент а;
г) и то, и другое.
11. а) докажем a V F V с) = (а V Ь) V с
b < (а V 6) < (aV b)V с определение нвг
с < (а V 6) V с определение нвг
Л (Ь V с) < (а V 6) V с определение нвг
a < (aV b) < (aV b)V с определение нвг
.'. aV (bv с) < (а V 6) V с определение нвг
Точно так же, (а V 6) V с < а V F V с) и (aV b)V c = aV (bV с).
Докажем a = aV a. a < a\/ a no определению верхней грани. Поскольку a < a no
определению наименьшей верхней грани, то a V а < а. Таким образом, a = a\/ a.
Докажем aVb = 6Va. a < aV6 по определению наименьшей верхней грани. Точно так
же, b <bvа. Следовательно, по определению наименьшей верхней грани, aVt < bVa.
Точно так же, Ь V а < a V Ь, HaVb = bVa;
б) докажем а Л F Л с) = (а Л 6) Л с.
6 > (а Л Ь) > (а ЛЬ) Ас определение ннг
с > (а ЛЬ) Лс определение ннг
.-.F Л с) > (а Л Ь) Л с определение ннг
а > (а Л Ь) > (аЛЬ) Л с определение ннг
.-. а Л (Ь Л с) > (а Л Ь) Л с определение ннг
Точно так же, (а Л 6) Л с > а Л F Л с) и (а Л 6) Л с = а Л (Ь Л с).
Докажем а = а А а. а > а Ла по определению наибольшей нижней грани. Поскольку
а > а по определению наибольшей нижней грани, то аЛа > а. Таким образом, a = aAa.
Докажем аЛб = Ьл а. а> aAb по определению наибольшей нижней грани. Точно так
же, 6 > 6 Л а. Таким образом, по определению наибольшей нижней грани, aAb>bAa.
Точно так же, b Л a > а Л Ь, иаЛЬ = 6Ла.
13. Доказательство проведем индукцией по числу элементов в полурешетке, имеющей наи-
наименьшую верхнюю грань. Вполне очевидно, что единственный элемент имеет наименьшую
верхнюю грань. По определению полурешетки, это утверждение истинно для любых двух
элементов. Предположим, что любые к элементов имеют наименьшую верхнюю грань. Ес-
Если полурешетка содержит только к элементов, доказательство завершено. В противном
случае, пусть ai,a2,a3,. • .afc,afc+i и оь — наименьшая верхняя грань для ai,a2,a3,.. .a/c-
Тогда (Jk Vafc+i — наименьшая верхняя грань для ai,a2,a3,.. .afc,afc+i. Вполне очевид-
очевидно, di < &k V afc+i для 1 < г < к -f 1. Предположим, что а» < 6 для 1 < г < к + 1.
Поскольку <ii < b для 1 < г < /с, то Gfc < Ь. Поэтому, учитывая, что ak+i < 6 и
сгк < Ь, имеем ак V ak+i < b. Следовательно, Ок V ak+i — наименьшая верхняя грань
для ai,d2,a3,. • .afc,afc+i-
15. а) если А < В и В < С, то Ai3 < Bij для всех 1 < i,j < n и By < Ci3 для всех
1 < h 3 < п. Следовательно, Aij < CV, для всех 1 < г, j < и и А < С\
б) поскольку Aij, Bij < AijV Bij для всех I < i,j < п, то А < Av В и В < Av В.
Следовательно, А V В — верхняя грань для А и В. Предположим, что D — верхняя

Ответы к упражнениям 897
грань для А и В. Тогда Aij,Bij < Dij для всех 1 < i,j < п. Если AijV Bij = 1, то
Aij = 1 или Bij = 1, и Dij = 1. Следовательно, AijV Bij < Dij для всех 1 < г, j < n,
и А V Б < ?>;
в) поскольку Aij ЛБ^ < Aij.Bij для всех 1 < i,j < п, то А Л Б —• нижняя грань для А и
В. Предположим, что D — нижняя грань для А и В. Если AijA Bi3 = 1, то Aij — О или
В^ = 0, и Dij = 0. Следовательно, Dij < AijA Bij для всех 1 < i,j < п, и D < Af\B\
г) поскольку любые два элемента имеют как наименьшую верхнюю границу, так и наи-
наибольшую нижнюю границу, то S является как верхней, так и нижней полурешеткой;
д) наибольший элемент — матрица С/, где Uij = 1 для всех 1 < i,j < п. Наименьший
элемент — матрица L, где Lij = 0 для всех 1 < г, j < п.
Раздел 9.2.
I. {{а}, {а, 6, с}}, {0, {а}, {а, Ь}, {а, Ь, с}}; {{а}, {6}, {а, 6}, {а, Ь, с}}.
3. Требуется только показать, что произведение двух целых чисел вида 4/с + 1 имеет такую
же форму. Пусть а = Am 4-1 и Ь = 4п + 1 — целые числа такого вида. Произведение
ab = Dm + l)Dn + l) =
= 16mn + 4m + 4+l =
= 4Dmn + m -f n) + 1
также имеет вид 4k + 1, где k = 4mn + m -f n.
5. Поскольку [a] 0 [b] = [a + Ь] и [a] О [Ь] = [a + Ь] для всех положительных целых чисел а
и Ь, то имеет место замыкание.
Поскольку
(И е |Ц) е М = [а + це [с] =
= [(а + 6)+с]
= [а] 0 [Ь + с] =
= (W © (И) в [с]),
то сложение ассоциативно.
Поскольку
(И © и) © [с] = и © [с] =
= \(ab)c] =
= КИ] =
= [а] © [be] =
= ([а]©([Ь])©ф[с]),
то умножение ассоциативно.
7. Пусть а и Ь — конечные произведения элементов из {ai, a2, a3,..., afc}. Тогда ab несомнен-
несомненно является конечным произведением элементов из {ai,a2,a3,... ,afc}. Поскольку А* —
подмножество множества 5, то имеет место ассоциативность. Следовательно, А* — под-
подполугруппа полугруппы S. Любая подгруппа А, содержащая все конечные произведения
элементов из Л, следовательно, должна содержать А*.
9. а) в главе 2 было показано, что композиция ассоциативна, поэтому требуется только по-
показать, что если / и g биективны, то fog также является биекцией. Если (f о д)(х) =

898 Ответы к упражнениям
(/ ° Р)Ы. то f(g(x)) = f(g(y)) и д(х) = д(у), поскольку / биективна. Но тогда х = г/,
так как д биективна. Следовательно, /од — инъективна. Пусть г € S. Поскольку / —
сюръекция, то существует у € S такой, что f(y) = 2. Поскольку д — сюръекция, то
существует х е S такой, что у(х) = у. Таким образом,
(/ор)(х) = /(р(*)) =/(у) ==*
и / о д сюръективна;
б) пусть а и Ь принадлежат образу ретракционного отображения / и а ф Ь. Следовательно,
а = /(с) и 6 = /(<?) для c,de А.
/F) = f(f(d)) = /(Ь) = 6,
так что / не только задает взаимно однозначное соответствие, но и является тожде-
тождественным отображением;
в) поскольку |х| положительно, то его абсолютное значение опять равно |х|, и / — ретрак-
ционное отображение. Ретракт — множество неотрицительных действительных чисел.
Поскольку [xj — целое число, то p(|_sj) = [х\, и д — ретракция. Ретракт — множество
целых чисел.
Поскольку \х] — целое число, то h(\x~\) = \х], и h — ретракция. Ретракт — множество
целых чисел;
г) нет;
д) нет.
11. Пусть А и В — (п х п)-матрицы с ненулевым детерминантом. Поскольку
det(AB)=det(A)det(B),
то det(AB) не равен нулю. Множество (пхп)-матриц с ненулевым детерминантом замкну-
замкнуто относительно умножения. Поэтому они образуют полугруппу на множестве (n x п)-
матриц. Поскольку det(/) = 1, где / — единица относительно умножения, то множе-
множество (п х п)-матриц с ненулевым детерминантом образует моноид. Если det(A) = 0 и
det(B) = 0, то det(AB) = 0. Следовательно, множество (n x п)-матриц с нулевым детер-
детерминантом замкнуто относительно умножения и также образует полугруппу.
13. Предположим, что I*a = a = a*I для всех аЕ5ие*а = а = о*е для всех а € S.
Следовательно,
е = / * е = поскольку / — единица
= / поскольку е — единица.
Раздел 9.3.
1. (б); (г).
3. Подрешетка, полученная удалением е, изоморфна первой решетке в упражнении 2.
5. (а); (б); (г); (д).
7. а){а};{Ь};{с};
б) элементарными конъюнкциями являются р A q А г, р Л qA ~ г, рЛ ~ q Л г, рЛ ~ q Л г,
~ р Aq Аг, ~ р A qA ~ г, ~ рЛ ~ q А г, ~ рЛ ~ qA ~ г. Пересечение любых двух из
них порождает противоречие и, следовательно, равно F, нулевому элементу;
в) (б),(в); г) (б),(в),(г).

Ответы к упражнениям 899
Раздел
1.
3. [
©
0]
1]
2]
3]
2].
5. [3].
7. Да.
9.4.
[0]
[0
[1
[2
[3]
[1
[1
[2
[3
[0
©
[0]
[1]
[2]
[3]
0]
0]
0]
0]
0]
[1]
[0]
[1]
B]
[3]
И
[0]
[2]
[0]
[2]
[3]
(о;
[з;
[2]
11]
9. Пусть а = Зт и 6 = Зп. Тогда
а + Ь = ЗА; + Зп = 3(fc + п),
поэтому сумма а и b кратна 3. Несомненно, 0 = 3-0 принадлежит множеству. Обратным
элементом для ЗА; будет (—3)А;. Следовательно, это подгруппа.
11. Согласно задаче 5 раздела 9.2, это полугруппа. Поскольку
то [0] является единицей. Поскольку [а] + [6 - а] = [6] = [0], то каждый элемент имеет
обратный элемент. Следовательно, Z6 — группа относительно сложения. Это множество
не является группой относительно умножения, так как элементы [0], [2], [3] и [4] не имеют
обратных элементов.
13. Элемент др — единица, принадлежит множеству и лучше обозначить ее через д°. Согласно
этим обозначениям дч • дг = д8, где 0 < s<pns=q+r (mod р). Обратным элементом
для дч является др~ч.
Раздел 9.5.
1. Имеем /A) = /A • 1) = /A) • /A), поэтому /A) — идемпотент. Вполне очевидно, это
единица группы Я, поскольку в группе Я только идемпотент является единицей.
3. Если f(h) — f(ti), то ah — ah'. Следовательно, a~lah = a~lah' и h = h'. Таким образом,
функция / — инъекция. Пусть h e H. Тогда /(a-1/i) = aa~lh = h. Следовательно, / —
сюръекция.
б. Определим f : Z* -> Z4 соотношениями /@) = 1, /A) = 3, /B) = 4 и /C) = 2.
Соотношение легко угадать, поскольку мы отображаем 1, что порождает Z* на 3, а это,
в свою очередь, порождает Z4. В изоморфности также легко убедиться, проанализировав
следующие таблицы
ф
0
1
2
3
0
0
1
2
3
1
1
2
3
0
2
2
3
0
1
3
3
0
1
2
0
1
1
3
4
2
3
3
4
2
1
4
4
2
1
3
2
2
1
3
4
7. Пусть = {l,Ei}. pi{l,Ei} = {pi,</>i} и {l,Si}pi = {p\,<fo}y поэтому группа Я не является
нормальной.
9. Было уже показано, что ф(\) — единица группы Я и, следовательно, группы ф(К). Пусть
h,h' G Ф{К). Тогда h = ф(д) и h! = ф{д') для некоторых д,д' G Я.
поэтому h • h' е Ф(К). Далее, Ф(д~1) • Ф(д) = ф(д • д'1) = </>A), поэтому если h e Ф(К),
то h G Ф(К). Следовательно, ф(К) — подгруппа группы Я.

900 Ответы к упражнениям
И. а) A,5,2,3)D); б) /;
в) A,3,5,4X2); г) A,3)B)D,6,7)E)(8).
13. Предположим, что дН = Нд для всех д € G. Пусть h € Н. Поэтому hg e Нд. Посколь-
Поскольку Нд = дН, то существует элемент h! такой, что hg = gh! и h — gh'g~l e дНд'1.
Следовательно, Н С дНд~1. Предположим, что ghg~l e дНд~1 Поскольку Нд = рЯ, то
существует элемент W такой, что gh = p/i' и /i' = ghg~l. Следовательно, ghg~l G Я и
дНд~1 С Я. Таким образом, дНд~1 = Я.
Раздел 10.1.
1. а) х = -20 з/ = 6; б) ж = 15 у = -78;
в) х = 180 у = -87; г) х = -55 у = 22;
д) х = 12 г/ = -4.
3. а) х = -28 у = 36; б) х = -64 у = 36;
в) решение не существует; г) х = — 2 у = 6;
д) решение не существует.
5. Процедура Целочисленное решение (т, п, с):
//Решение уравнения х • т + у • п = с//
Положить ? = т, и = п, х = 0, х' = 1, у = 0, у' = 1;
Условный цикл: до тех пор, пока и ф 0,
q = [? -Ь uj, ? = tz, и = t — qu, x = x', x = x — gx', у = у', у' = у — qy'\
Конец условного цикла;
Положить d = иу е = c + d;
Если е^ [е\, то решения не существует;
Иначе х = ех; у = еу
Конец процедуры.
Раздел 10.2.
1. п= 1,2,4,5,8,10,20,40.
3. Если а нечетное, то а = 2т + 1 для некоторого целого числа т. Следовательно,
а2 = Bт 4-1J = 4т2 + 4т + 1
и
а2 - 1 = 4т2 4- 4т = 4т(т + 1).
Но или т, или т + 1 является четным. Очевидно, а2 — 1 делится на 8.
5. Если а = Ь (mod n), где п = НОК(п1,П2,пз,... ,rifc), то а — Ь делится на НОК(п1,П2,пз,
..., rik)> так что а—Ь делится на п» для 1 < г < к. Таким образом, а = Ъ (mod rij). Обратно,
предположим, что а = Ъ (mod n,), для некоторого 1 < г < к. Тогда а — Ь делится на тц
для некоторого 1 < г < к. По определению НОК, а — Ь делится на HOK(ni, пг, пз,..., njt),
и а = Ь (mod n).
7. Докажем индукцией по т. Несомненно, а = Ь (mod n). Поэтому утверждение истинно
для m = 1. Предположим, что оно истинно для п = /с, поэтому afc = bfc (mod n). По тео-
теореме 3.54, если а = b (mod n) и ак = bfc (mod n), то afc+1 = bfc+1, поэтому утверждение
истинно для п = к 4-1.
9. Если a = Ь (mod щ^у), то a - 6 = /с нод^с п) для некоторого к. Поэтому ас - be =
кнод^с п)с. Поскольку НОД(с, п)|с, то нод^с п) — целое число, скажем, q. Таким образом,
ас — be — kqn и ас — be mod п. Обратно, если ас = be mod n, то ас — be = kn для
некоторого к. Поскольку (а - Ъ)с = кп, (а - Ь) H0Rc{Cyn) = цод?с,п) • Поскольку hoi^c>n) и
ноД?с,п) взаимно простые числа, щд^у Делит (а ~ 6)« поэтому а = 6 (mod )

Ответы к упражнениям 901
Раздел 10.3.
1. а) х = 81 (mod 300);
б) х = 815 (mod 1260);
в) х = 16а - 156 (mod 240);
г) х = 1272 (mod 2310).
3. 1459 разноцветных шариков; 97 рядов по 15 шариков, 182 рядов по 8 шариков и 63 рядов
по 23 шариков.
5. а) х = 21 (mod 72);
б) х = 104 (mod 180);
в) нет решения.
Раздел 10.4.
1. m = 4 п = 2.
3. Поскольку 1009 — простое число, то по теореме Уилсона 1008! = 1 (mod A009). Посколь-
Поскольку 1008 = -1 (mod A009), то 1007! = -1 (mod 1009).
5. Докажем по индукции, что если п = рр%2 • • -р, то ф(п) = ГП^рГ^Чр* — !)- При п =
1 теорема верна в силу теоремы 10.20. Предположим, теорема верна при t — /с, так что, ее-
ли т = рГР22 •••P2fc. то 0(m) = ntiP^'^Pi-l). Допустим, чю n = p^pV "'PlXV -
Тогда 0(п) = Ф(гп)ф(рЦ+11) по теореме 10.19. Но Ф(р?+\г) = Pfc+T'^Pfc+i ~ *) по теоРе"
ме 10.20, поэтому ф(п) = UliP^iPi - Wp&V^iPb+i ~ 1)) = U^i P^iPi ~ *)•
7. 1080.
9. По теореме Уилсона, число р простое тогда и только тогда, когда (р — 1)! = —1 (mod p).
Последнее имеет место тогда и только тогда, когда (р - 1)! -f 1 = 0 (mod p). А это имеет
место тогда и только тогда, когда (р — 1)! 4-1 делится на р.
Раздел 10.5.
1. Если а не равно 0 по модулю р, то а = 6 (mod р), где 1 < Ь < р — 1. По малой теореме
Ферма, cV = 1 (mod р). Но а?~1 = ЬР~1 (mod р). Следовательно, ар~1 = 1 (mod p).
3. Поскольку J = 0 (mod р — 1), J = к(р — 1) для некоторого целого к. Пусть 1 < а < р — 1.
Поскольку
ар-1 = 1 (modp),
aJ = aMP-i) = (a(p-D)fc = 1* = 1 (mod р),
то
1J + 2J + • • • 4- (р - 1)J = 1 4- 1 + • • • + 1 (mod p) =
= р — 1 (mod p) =
= —1 (mod p).
7. Поскольку ар = a (mod р),^ = Ь (mod р) и (а + 6)р = а + Ь (mod р), то
(mod p).
9. а)
б)
в)
а
ordn
а
ordn
а
ordn
а
а
а
1
1
1
1
1
1
2
со со
4
2
4 5
3 6
7 9
4 2
4
18 9
7
3
11
2
5
18
8
2
13
4
7 8
9 6
17
4
10
3
19
2
11
18
13
9
14
18
16
9
17
6
19
3
20
18
22
9
23
18
25
9
26
2

902 Ответы к упражнениям
11. а) 2401 = 1 (mod 5);
б) 2401 = 1 (mod 2);
в) 2401 = 1 (mod 10);
г) поскольку 74 = 1 (mod 10), G4)fc = lfc (mod 10), то 74fc = 1 (mod 10). Последняя
десятичная цифра числа 74000 есть 1.
13. а) 7; б) 376; в) 68; г) 961; д) 535044134.
15. а) Если а1^1" = —1 (mod п), то а11 = 1 (mod n). Поскольку а11^" = —1 (mod п),
оно не сравнимо с 1 по модулю п. Таким образом, все требования критерия Лукаса
удовлетворены, поэтому п — простое число;
б) 218 = -1 (mod 37), 212 = 26 (mod 37), поэтому число 37 простое;
З198 = _1 (mod 199), З66 = 106 (mod 199), З18 = 125 (mod 199), поэтому число 199 -
простое.
17. а) З256 = 1 (mod 257); З128 = -1 (mod 257). Поэтому число 257 простое.
б) З65536 = 1 (mod 65537);
з27б8
Раздел
1. (а)
3. а)
в)
5. а)
в)
7. а)
в)
3 = — 1 (т<
565536 = 1 (mod
5*2768 s _j (m<
¦ (с), (е).
а„ = ci • 3";
а„ = ci • (-3)"
а„ = (-4)";
о„ = Зп + 2П;
а„ = 3 • Зп + 4п
3d 65537);
1 65537);
ad 65537).
+ С2-2П;
•Зп;
ап = (-2)п+Зп-(-2)";
б)
г)
б)
г)
б)
г)
ап=с\- (-3)";
ап = 6П~ ;
ап = 4-Зп-2-4п.
ап = 22п4-п.2п;
ап = -3 4- 4п;
с2
9. a) an = ci -4п+с2;
б) an = ci 4-c2n (^) ()
в) an = ci + с2 • (~1)п + сз cos (^) + с4 sin
г) an = ci -f c2 -n-hc3n2-f (^) (^) (^)
11. Воспользуемся индукцией.
При п = 3 имеем Z/з = а Ц-Ь = аФибB) + 6ФибA)
Допустим, Lfc = аФиб(/с — 1) 4- ЬФиб(/с — 2) для любого 3 < к < т.
L/m = Ldrn — \ 4" L/rn—2 =
= а Фиб(т - 2) + Ь Фиб(т - 3) + а Фиб(т - 3) 4- Ь Фиб(т - 4)
= а(Фиб(т - 2) 4- Фиб(т - 3)) 4- Ь(Фиб(т - 3) 4- Фиб(т - 4))
= аФиб(т- 1) 4-6Фиб(т-2).
Раздел 11.2.
1. a) an = ci • 2П - 5;
6)an = ci.C) + i
в)с1.Зп+с2.(-4)п-|.2п;
() ()
д) an = ci • 2n 4- c2n • 2n -f n2 4- 8n 4- 32.

Ответы к упражнениям 903
3. a) an =ci-2n+n-2n;
б) an=Cl. (-3)п 4- с2п . (-3)п 4- \п2 • (-3)п;
в) an = с\ 4- С2П • 2П — 5п;
г) an = Cl.3
д) an = 2- (C
n(n + l)Bn + l). _
5. a) an = т , o) an =
в) an = 2n+1 - 2; r) an = |n(n + l)(n 4- 2).
11.3.
1. 12.
3. 644.
5. Зх2 4- 8х - 6.
1П
7. т.
:4-4)(Зх + 7)"
9. По определению, А(х!) = (х 4-1)! — х! = х!(х 4-1 — 1) = х • х!.
И. A/(g) = fix + 1) fix) = fjx + l)gjx) - fjx)gjx + 1) =
gix) p(x4-l) p(x) p(x4-l)p(x)
_ /(x 4- l)p(x) — /(x)p(x) 4- /(x)p(x) — /(x)p(x 4- 1) _
~ p(x 4- l)p(x) ~
= jfjx + 1) - /(x))g(x) - /(x)(g(x + 1) - t/(x)) =
= A/(x) .g(x) - fjx) • Ap(x)
p(x 4- l)p(x)
Раздел //.4.
1. 18x-10.
3. 60xB) 4- 72x - 18.
5. (xC) - 2xB) - 4)DxC) 4- 6xB) - 12x 4- 1L-
4-((x 4- IL 4- 2(x 4- 1)C) - 6(x 4-1)B) 4-х - 2)CxB) - 4x).
jx^ - 3x^3> + 6xB>)Dx<3> - 6x -f 3) - (x^4> - 3x<2> + 3x)DxC) - 9x^2> + 12x)
(xD) - 3xC> 4- 6xB))((x 4- 1)D) - 3(x 4-1)C) 4- 6(x 4-
9. 3!.
11. x.
13. xD) - 7xB) - 5x 4- 5.
15. xE) 4- 9x<4> + 20xC> + 10xB> + x - 1.
17. x4-3x3-2x24-2x4-l.
19. x5 - llx4 4- 42x3 - 65x2 -f 34x - 1.
21. -3.
Раздел 11.5.
1. 58137.
3. -8988.
5. 62132.
" гB)
г=1

904 Ответы к упражнениям
9. ]jTi(i + l) =
г=1
И. 177144.
13. 22520.
15. 26106.
17. 6203013120.
19. 28385280.
21. Пусть AF(x)
f=t ??
(n + l)(n)(n-l)
3
= /(х), тогда
+ 2г = гC) + гB)
п + 1
1
/ . -I \ / \ / , е\\
3
с
Д Y, /(*) = MF(c + 1) - F(x)) = A(F(c + 1) - AF{x) = 0 - f(x) = -
/2./.
1. a) kn = 37 = 2187;
б) fc!S?n) = 3!5f > = 6 • 301 = 1806;
в) C(n + fc-l,n) = CG + 3-l,7) = C(9,7) = 36;
r) C(n - 1, k - 1) = CF,2) = 15;
д) S[7) + S^7) + 5^7) = 1 + 63 + 301 = 365;
е) S(kn) =301.
3. n\fc
11
12
0 1 2 3 4567 8 9 10 11 12
0 1 1023 28501 145750 246730 179487 63987 11880 1155 55 1
0 1 2047 86526 611501 1379400 1323652 627396 159027 22275 1705 66
5. a) kn = 412 = 16777216;
б) k\S(kn) = 4!Sf2) = 24 • 611501 = 14676024;
в) C(n + k - 1, n) = CA5,12) = 455;
r) C(n-l,/c-l) = CA1,3) = 165;
д) (e) s[12) + S^12) + S^12) + 5^12) = 1 + 2047 + 86526 + 611501 = 70075;
е) Skn) =SD12) =611501.
7. aM(n,0) = i(-l)°(°)@-0r=0;
6) S(n,fc-l)'

Ответы к упражнениям 905
Раздел 12.2.
Раздел 12.3.
1. о = A -1)" = (?) _
3. I
+ + + + + +
«4.1 х 1OU.
5. а) 7!A -1+1-1+^-^ + ^,-^) = 1854.
б) 7! - 1855 = 3185;
в) 7!A -l + i-i + i-Tl5 + ?i5) = 1855;
гH.
7. а) 7!A -1 + 1-1 + ^-^ + ^-^) = 1854;
6O!A_l + I_i+i__I_
в) 7! - 1855 = 3185;
г) 7! - 1855 - 1854 = 1331.
9.
11. Число, которое делится на 7, 2 или 5, есть 2730 + 1092 + 780-546-390-156 + 78 = 3588.
Число, взаимно простое с 700, равно 5640 - 3588 = 1872.
Раздел 12.4.
1. #(х,С) = 1+6х + 6х2.
3. Я(х,С) = A + 4х + 2х2J.
5. Я(х, С) = A + Зх + х2)A + 2х) + хA + Зх + 2х2).
7. Я(х,С) = A + Зх + х2JA + х).

906 Ответы к упражнениям
9. Я(х, С) = 1 + 8х + 15х2 + 6х3.
11. Я(х, С) = A + 2х)A 4- х)A + 4х + 2х2).
13. Я(х, С) = 1 + 4х + 68х2 + 148х3 4- 144х4 4- 48х5,
количество размещений равно 8! - 14 • 7! 4- 68 • 6! - 148 • 5! 4-144 • 4! - 48 • 3! = 4128.
15. Я(х, С) = 1 4- 6х 4- Их2 4- 6х3,
количество размещений равно 5! - 6 • 4! 4-11 • 3! - 6 • 2! = 30.
17. Я(х, С) = 1 4- 12х 4- 54х2 + 112х3 4- Ю8х4 4- 48х5 4- 8х6, количество
размещений равно 6! - 112 • 5! 4- 54 • 4! - 112 • 3! + 108 • 2! - 48 • 1! + 8 • 0! = 80.
19. Я(х, С) = 1 4- 8х 4- 20х2 4- 16х3 4- 4х4,
количество размещений равно 4! - 8 • 3! 4- 20 • 2! - 16 • 1! 4- 4 • 0! = 4.
21. Я(х, С) = 1 4- 13х 4- 59х2 4- П5х3 + ЮОх4 + 32х5,
количество размещений равно 6! - 13 • 5! + 59 • 4! - 115 • 3! 4-100 • 2! - 32 = 54.
23. Я(х, С) = 1 4- 8х 4- 20х2 4- 16х3 4- 4х4,
количество размещений равно 4! — 8 • 3! 4- 20 • 2! — 16 • 1! 4- 4 = 4.
25. Я(х, С) = 1 4- Юх 4- 35х2 4- 50х3 4- 26х4 4- 4х5,
количество размещений равно 5! - 10 • 4! 4- 35 • 3! - 50 • 2! 4- 26 • 1! - 4 = 12.
27. Я(х, С) = 1 + Юх 4- 35х2 4- 50х3 4- 25х4 4- 2х5,
количество размещений равно 5! - 10 • 4! 4- 35 • 3! - 50 • 2! + 25 • 1! - 2 = 13.
Раздел 13.2.
t , -1 1 g4 -1 , 3 ч -10 6 11
ч \ 2 | ч 14 4 14 , 13
х - 1 х - 2 (х - 3)' х - 1 (х - lJ х - 2 (х - 2J •
3. a)i(l-ix
г) I
5. а) ап = 3n+1 - 2n+1; б) ап = ^Зп - \п - |; в) ап = 6 • Зп 4- 2(-1)п
г) ап = 2п-п2п; д) ап = 2П 4-3.
7. а)ап = п+2П + 2; б) ап = -2 . 2П + 4 • Зп;
в) ап = (п 4- 3JП - п - 2; г) ап = (Зп - 3)Зп 4- 4 • Т.
Раздел 13.3.
1. а) A4-х4-х24----JA + ^ + ^2)A+^ + ^2 + ^3 + х4);
б) A 4- х 4- х2 4- • • • JA -f х 4- х2 4- х3)A 4- х2 + х4 4- х6 4- • • •);
в) (х + х3+х54-х7 + ---)A+х24-х44-х64----)A + ^ + ^2 + ---)(^4+х5 + х6+х7 + ''*);
г) (х + х24-х3 + ...)(^2+х34-х4 + ...)(а:3+х4+х54----)(^4 + х54-х64-х74----);
д) A4-х 4-х2 + •••)(! + x2-hx4 4- •••)(! +^3+х6 4-•••)(! +х44-х8 4----)-
3. а) A4-х4-х24-х3+х4)A4-х + х24-х3)A+х4-х24----4-х6)A4-х4-х2);
б) (х 4- х2)(х + х2 4- х3 + х4 4- х5)(х 4- х2 4- х3 4- х4)(х 4- х2 4- х3);
в) (l-fx4-x2 + ...4-x6)(x44-x54----4-x11)(l+x4-x24----4-x7)(l4-x2-hx44----x10);
Г) (х2+х4 + +х6)((х + 2З 12 З5724 10

Ответы к упражнениям 907
5. A 4-х+ х2-f .-.)A + х5 4-х10 + ...)A+х10 + х20 + •
7. A + х3 + х6 + • • • )A 4- х5 + х10 + • • •).
9. A 4- х 4- х2 -f х3 + х4 4- х5 4- х6)*.
и. Се0)-
13. 1.
«¦ Q.
17. 51.
19. (}?)-312.
21. а) 36;
б) 30.
23. A5)-ЗС7°)+3©.
25. F(x) - xF(x) - x2F(x) = = а0 + сцх 4- а2х2 + а3х3 + а4х4 4- а5х5 Н
— аох — aix2 — агх3 — азх4 — сцхъ -\
— аох — а\х — Q.2X — азх 4- • • • =
= ао 4- (ai - ао)х =
= х,
поскольку а0 = 0 и ai = 1.
Следовательно, A-х — x2)F(x) = х, так что
F(x) =
1 - х - х2 1 - (х 4- х2) '
Воспользовавшись разложением, получаем
= х 4- х2A + х) 4- х3A + хJ 4- х4A 4- хK + х5A + хL 4- • • • .
Коэффициент при xn+1 в выражении xfc+1(l 4- x)fc, если существует, то равен (n!lfc).
Суммируя по к = п, п - 1, п - 2,..., имеем
Раздел
1. 15.
Q J
3' 1-
/3.4
L
-x 1
1
1
-X2
1
1
1
-X3
1
1
1
-X4
1
1
1
—
x5
1
1
1
-x6
1 - х2 1 - х4 ' 1 - х6 ' 1 - х8 ' 1 - х10
7. В строках, начиная с верхней, представим каждую часть разбиения на четные величины.
Теперь, глядя на столбцы, видим, что представленные части разбиения присутствуют па-
парами и убывают по размеру. Поскольку рост в строке влечет за собой увеличение четного
числа, в столбцах это порождает пару или пары одного размера.

908 Ответы к упражнениям
9. Пусть столбцы изображают разбиение 2п объектов на п частей.
Поскольку ни одна из этих частей не пуста, то нижняя строка содержит п элементов.
Если отбросить эту строку, то легко увидеть, что другие строки образуют разбиение п
элементов.
1111111
1-х 1-х2 1-х3 1-х4 1-х5 1-х6 1-х7'
Раздел 13.5.
х5 , х6 , х7 , х10\ Л , х , х2, х3 \ Л , х , х2 , х3 , х4
-5\ + "бГ + 7Г + • • • J / + + + J( + + + +
10\ Л , х , х2, х3
otJ \/ + T!+-2r + ^
\ (л х х2 х10\ ( х3 х5 , х7 х9\ (л х2 х4 х10
3. ех.
5. Производящая функция е5х — 2е4х 4 е3х, количество способов 5П — 2 • 4n -f Зп.
7. Производящая функция е3х - Зе2х -f Зех 4- 1, количество способов З30 - 3 • 230 -I- 3.
9. Производящая функция \ (е4х - 2е3х -f е2х - 1 + 2е~х - Зе~2х) ,
количество способов
iD25 - 2 • З25 -f 225 + 2(-1J5 - (-2J5).
И. ех-е5х-е10х.е25х = е41х.
13. (ех - 1)(е2х - 1)(е3х - 1) • • • (екх - 1).
15. а) (ех - 1) =
\
_ х х2
~ IT ~2\ ;
х I -х I 2
б) 6 6— = -A 4- у} + Ту +
2!?
ч ех -е~х 1., х х2
в) —Т— = 2A+1!+ 2Г
1 х
3 х5
l

Ответы к упражнениям 909
Раздел 14.1.
1. а) /Ы = /Ы = а;
/Ы = /Ы = Ь;
/Ы = с;
в) f(vs) = с;
/Ы = 6;
Д) /Ы = /Ы = с;
= 6;
= а;
б) гомоморфизм не существует;
г) /Ы =/Ы = Д*>з) = а;
/Ы = /Ы = /Ы = Ь;
е)
= /(«ч) = а;
/Ы = f(ve) = Ь.
3. а) графы не изоморфны, разное количество вершин;
б) f(vi) = а; в) f(v6) — а; г)
= с;
/Ы = d;
/Ы = е;
/Ы = Ь;
= с;
= /;
Дг>2) = а;
/(^з) = Ь;
/(we) = d;
/(из) = с;
д) графы не изоморфны, вершина d имеет степень 4, ни одна из вершин первого графа не
имеет степень 4;
е) графы не изоморфны, первый граф несвязный, второй граф — связный.
5. (а), (с).
7. (а), (с), (е).
9. а) объединение; б) объединение;
be e
пересечение;
сщ ft/
а *

910 Ответы к упражнениям
в) объединение; г) объединение;
а Ь с Ь
И. а)
Т\
ь,
V
г)
13. (a); (b).
15. G имеет вид
б)
с d
a b
Д)
С имеет вид
Cm em
д) объединение;
с
пересечение.
с%
е)
Л /1
/ : G —> G1 задана соотношениями f(a) = с; f(b) = d.
17. Пусть f : G —+ Gf. Пусть a,b ? /(V"). Тогда a = /(x), 6 = f(y) для некоторых х, у G К. По-

Ответы к упражнениям 911
скольку граф G полный, то существует е = {х,у}. Поэтому /(е) = {a,b}. Следовательно,
между двумя любыми вершинами графа f(V) имеется ребро, и граф f(G) — полный.
19. Пусть v € V. Имеется наибольший связный граф, содержащий v. Поэтому v принадлежит
компоненте. Пусть е 6 Е. Имеется наибольший связный граф, содержащий е. Поэтому е
принадлежит компоненте. Следовательно, граф G(E, V) — объединение компонент, и, по
теореме 12.17, они являются попарно непересекающимися.
21. Эквивалентно показать, что если G'(E\ V) — расширение графа G(E, V), то один являет-
является связным тогда и только тогда, когда связным является второй. Предположим, что граф
G связный и ребро ab заменено путем acb. Пусть v\ и V2 — вершины в графе G. Поскольку
G связный, то существует путь из v\ в V2. Если ребро ab входит в путь, заменим его на
acb, и v\,v2 остаются связанными в графе G1. Обратно, если G' связный и v\,v2 € G1, то
в графе G' существует путь из v\ в v2. По определению расширения, только ребра, инци-
инцидентные вершине с, являются инцидентными вершинам а и 6. Следовательно, любой путь,
включающий с, должен включать путь acb или bca. В графе G путь acb можно заменить
на ab, а путь bca можно заменить на 6а, так что путь из v\ в V2 по-прежнему существует.
23. Если / : G(E, V) -+ G'(E',V) — изоморфизм, то он задает взаимно однозначное отобра-
отображение из Е на Е' и взаимно однозначное отображениее из V на V. Таким образом, G и
G' содержат одинаковое количество ребер и вершин.
25. Пусть / : G(E, V) —> G'(E' ,V) — изоморфизм. Вершины а и 6 принадлежат одной и той
же компоненте графа G тогда и только тогда, когда существует путь av\v2 • --Vk-ib из a
в 6, тогда и только тогда, когда существует путь f(a)f(vi)f(v2)---f(vk-i)f(b) из /(а) в
f(b) , тогда и только тогда, когда /(а) и /(Ь) принадлежат одной и той же компоненте.
27. Пусть / : G(E, V) -> G'(E',V) — изоморфизм. Поскольку deg(v) = deg(f(v)) для всех
v e V, то все вершины в V имеют четную степень тогда и только тогда, когда все вершины
в f(V) имеют четную степень.
29. Пусть / : G(E, V) -+ G'(E', V) — изоморфизм. Если граф G двудольный, то V = A U В\
при этом не существует ребро между вершиной из Л и вершиной из В. Если существует
ребро е' между /(а) 6 f(A) и f(b) e f(B), то е' = /(с), где е — ребро между а и 6.
Но это противоречит предположению, что граф G двудольный. Следовательно, граф G'
двудольный.
31. По определению, каждая вершина графа G принадлежит его дополнению. Таким образом,
пересечение графа G и его дополнения содержит все вершины графа G. Ни одно из ре-
ребер графа G не принадлежит его дополнению. Следовательно, пересечение графа G и его
дополнения не содержит ни одного ребра графа G. Значит, пересечение графа и его допол-
дополнения представляет собой граф, состоящий только из вершин графа G и не содержащий
ребер.
33. Пусть е — разрезающее ребро графа G и G — граф G с удаленным ребром е. Пусть G1
— граф G с удаленным ребром /(е). Пусть / — изоморфизм из G в G'. По определению
разрезающего множества, существуют вершины а, Ь, которые не связаны в G. Поэтому они
принадлежат различным компонентам графа G. Следовательно, как показано в предыду-
предыдущем упражнении, /(а) и /(Ь) принадлежат различным компонентам графа G', и граф G'
несвязный. Вполне очевидно, что /(е) — разрезающее ребро графа G'.
35. В матрице смежности графа имеется единица, если в матрице смежности его дополнения
имеется нуль.
37. Пусть а1,а2,аз,... ,ап — вершины графа G, и Р — перестановочная матрица размерности
п х п. Пусть vi = A,0,0,... ,0) представляет ai, v2 = @,1,0,... ,0) представляет a2
и ы = @,... ,0,1,0,... ,0) представляет ai, где 1 находится на г-ом месте. Аналогично,
пусть w\ = A,0,0,. ..,0), представляет ab w2 = @,1,0,... ,0), представляет аг и ьл =

912 Ответы к упражнениям
(О,..., 0,1,0,..., 0) представляет а», где 1 находится на г-ом месте. Определим /(сц) = bj,
если Pvi = Wj. Предположим, что /(а*) = bj и f{ak) = Ы. Тогда Pji = 1 и Pik = 1
Рассмотрим произведение РВР1, где Б — матрица смежности графа G. Пусть Т — ВР1.
Тогда, поскольку Pkl = Plk = 1, то BikPkl = Ti*. Пусть Б' = РТ. Поскольку Pji = 1, то
Bji = PjiTu, поэтому число в j-ой строке и в 1-ом столбце матрицы В' равно Bik, и ребро
между bj и bi существует тогда и только тогда, когда существует ребро между а, и ak.
Следовательно, G и С изоморфны. Обратно, если они изоморфны, то матрицы В и ?',
определенные выше, являются матрицами смежности для соответствующих графов.
39. Разрезающие множества включают {{a,d},{a,b}}, {{d, e}, {d, а}}, и {{/, <7}, {/,*}}• Раз"
резающими ребрами являются {6, с}, {е, /}, {г, j}.
41. Пусть е = {v,t/} входит в цикл vv'v\ --vk-\v и пусть а,Ь — вершины графа G. Если
имеется путь из а в 6, который не включает е, то путь из а в 6 существует, если ребро е
удалено. Если е не входит в путь, то заменим ребро vvf путем vvk-\ • • -г^г/, и путь из а в
b по-прежнему существует. Обратно, допустим, что е = {v,v'} не является разрезающим
ребром. В этом случае, если ребро е удалено, то по-прежнему имеется путь vvk-\ • • -v\v'
из v в г>', и t>ffc-i • • -viv't; является циклом.
43. Если Gx(Vi,Ei) состоит из единственного ребра е, то не существует простой цикл графа
G, содержащий е, поэтому е — разрезающее.
45. Если воспользоваться определением объединения, которое дано в определении 14.14, то
вполне очевидно, что любой граф Gj является подграфом объединения U?=i ^*- Также,
согласно этому определению, если любой граф d принадлежит графу G", то каждое ребро
и каждая вершина любого из графов d принадлежат G". Следовательно, каждое ребро
и каждая вершина объединения графов G» принадлежат G". Таким образом, определение
объединения, которое дано в определении 14.14, удовлетворяет определению, данному в за-
задаче. Два определения эквивалентны, если существует только один граф, удовлетворяющий
определению, данному в задаче. Но если имеются два графа G1 и <2", удовлетворяющие
определению, то G' •< G" и G" •< G't поэтому G" = G1.
Раздел 14.2.
1. а) да, граф нарисован так, что линии не пересекаются;
б) нет, граф содержит К3,з как подграф;
в) нет, граф содержит Къ как подграф;
г) да, граф можно изобразить как д) да, граф можно изобразить как
т
3. а) да, граф можно изобразить как
б) нет, граф содержит /Сз.з как подграф.

в) да, граф можно изобразить как
а с
Ответы к упражнениям 913
г) да, граф можно изобразить как
/ h
d i
д) да, граф можно изобразить как
5. Если имеется 12 вершин степени 3, то степень вершин равна 36, поэтому имеется 18 ребер.
Поскольку г> - е + / = 2, то12-18 + / = 2и/ = 8.
7. а) 4;
б) 6;
в) 2/с.
9. Поскольку граф с 4 вершинами не может содержать граф, гомеоморфный подграфу, гомео-
морфному Кь или Кз,з, то он должен быть планарным. С другой строны, легко показать,
что граф К а планарный. Поскольку любой граф с 4 вершинами — подграф графа К*, он
является планарным.
11. Будем использовать индукцию по количеству ребер дерева. Очевидно, что любое дерево с
одним ребром — планарное. Предположим, что любое дерево, имеющее к ребер, планарное.
Пусть Т — дерево, имеющее к 4-1 ребер. Любое дерево имеет вершину степени 1. Выберем
такую вершину и удалим ее и ребро, инцидентное к ней. Оставшееся дерево по индуктив-
индуктивному предположению является планарным. Удаленное ребро и вершина могут быть снова
добавлены так, что ребро не пересечет ни одно из других ребер. Следовательно, дерево
Т — планарный граф.
Раздел 14.3.
1. а)
б)

914 Ответы к упражнениям
г)
3. а) 2; б) 3; в) 4; г) 3; д) 4.
5. Кт,п содержит множество т вершин и множество п вершин. Ребра имеются только между
двумя множествами. Поэтому можно раскрасить одно множество одним цветом, а второе
множество — другим.
7. а) А(А-1)(А-2J;
в) А(А-1)(А-2J(А-3);
д) А(А-1)(А-2J.
9. Если планарный граф изоморфен своему двойственному графу, то количество граней равно
б) А(А-1J(А-2);
г) А(А-1)(А-2J;
количеству вершин. Поскольку v —
= 2, топ —
= 2ие = 2п- 2.
Раздел 14.4.
1. a) acgfedba',
г) не существует;
3. a) abcde\
б) abfecda',
д) не существует.
б) abcdef\
в) abihfdcega\
в) fdcegabih;
г) egacdfhb; д) adbcefgh.
5. Если граф G имеет гамильтонов цикл, то любое ребро является частью цикла. Но разре-
разрезающее ребро не может быть ребром, входящим в цикл. Следовательно, G не содержит
разрезающее ребро. Пусть {а, 6} — разрезающее ребро и компоненты С\ и С2 — компонен-
компоненты, имеющие гамильтоновы циклы, например, av\V2Vz • • • Vk-\a и Ьу[у2уз • • -fm-i^. Тогда
viv2v3 • • • Vk-iabviv^v'z • • • i^n-i — гамильтонов путь.
7.
Ь
с

Раздел 14.5.
Ответы к упражнениям 915
1. а)
ув@,0)
у (9,2)
у,D,3)
б)
vo(O,O)
v,G,5)
в)
ve@,0)
vG,2)
v;C,3)
r)
vo(O,O)
v,B,0)
vE,2)
Д)
v;C,0) 8 v/9,5)
vjE,2)
3. a)
vo(O,O)
v,B,0)
6)
v,D,6)
vE,8)

916 Ответы к упражнениям
в)
vo(O,O)
г)
v,C,2) v,C,2) v7E,4)
vF,4)
v;C,0)
vF,7)
',E,2)
Д)
v;C,0)
I I \ \v.E,3) vE,4)
Раздел 15.1 .
1. a)
/
\
3. a) 63 вершины, 32 листа и 31 внутренняя вершина;
б) 141 вершина, 81 лист и 60 внутренних вершин;
в) 511 вершин, 256 листьев и 255 внутренних вершин;
г) 85 вершин, 64 листа и 21 внутренняя вершина;
д) 10 вершин, 1 лист и 9 внутренних вершин.
5. a) (i) 5, (И) 2 (iii) 4, (iv) 2, (v) dy (vi) e,a;
б) (i) 5, (ii) 4 (iii) 2, (iv) 2, (v) d, (vi) e,d;
в) (iL, (iiK(iii) 1, (iv) 1, (v)d, (vi)e,d;
r) (i) 6, (ii) 5 (iii) 3, (iv) 3, (v) d, (vi) e,d;
д) (i) 4, (ii) 1 (iii) 3, (iv) 1, (v) d, (vi) a,e,d.
7. а) сбалансированное; б) сбалансированное; в) сбалансированное.
9. а) 7; б) 127.
И. а) / = 2\ Поэтому log2 Z = log2 2h = h\
б) поскольку количество листьев меньше или равно 2h, и равно 2h только в том случае,
когда дерево полное, то
2" >/
.Iog22h>log2/
и h > log2 Z
поскольку / — возрастающая функция

Ответы к упражнениям 917
в)
v = 2h+1 - 1;
И h = Iog2(t; + 1) - 1;
v < 2h+l - 1,
поскольку полное дерево имеет
максимальное количество вершин;
поскольку / — возрастающая функция;
поскольку / — возрастающая функция
.\v + l <2h+\
Л Iog2(t;+1) < h + 1,
и /i > Iog2(t; + 1) - 1.
13. Предположим, что граф G — дерево. Пусть ребро {а, 6} добавлено к дереву. Поскольку
дерево было связным, уже существовал путь av\V2V3 • • -Vk-\b из а в 6. Таким образом,
av\V2V3 - - - Vk-iba является циклом.
Предположим, что добавление ребра {а, 6} создает два цикла , av\V2V3 • • • vk-\b и
av[v2v3 • • • v'm-ib, тогда av\V2V3 • • • Vk-ibbv'rn_1 • • • у3у2у[а уже является циклом, что про-
противоречит предположению, что G — дерево.
Предположим, что граф G не является деревом. Тогда он уже содержит цикл. Предпо-
Предположим, что ребро {а, 6} добавлено в G. Путь из а в 6 уже существовал, поскольку граф
G связный. Теперь имеются два пути из а в Ь, поэтому {а, 6} — часть цикла, но не часть
исходного цикла, поэтому в графе G с добавленным ребром теперь имеется, по крайней
мере, два цикла.
15. Утверждение ошибочное. На дереве лист не является разрезающей вершиной.
17. G содержит эйлеров цикл.
19. Нужно показать, что a(vv') = a(v)a(vf).
a(yv) = a(vv) —
Раздел 15,2.
1. a)
= (aa)(vv) =
= avav =
= a(v)a(v').
6)
поскольку элементы полурешетки
являются идемпотентами
поскольку решетка ассоциативна и
коммутативна
' /V
I s х

918 Ответы к упражнениям
3. а) б)
m
Л Л
d * р v
\ /\
е о г
в)
m
/( >
О Г U
5. Цепь.
7.
Adams
Jefferson
J.Q. Adams
Jackson
Harrison
Fillmore Hayes
Buchanan Grant Hoover
Arthur Cleveland Garfield B. Harrison
Carter Coolidge Harding
Bush Clinton Eisenhower
Ford
9.
m
1 О S
/
Washington
Madison
Wilson
Lincoln
A. Johnson McKinley Van Buren
Kennedy Tyler
L. Johnson Polk
Pierce Taylor
Nixon T. Roosevelt Truman
F. Roosevelt Taft
Reagan

Ответы к упражнениям 919
П.
b d f i к mo q
13. a)
с г
\ /\
d m t
i
/
/
i >
6)
С Г
\ /\
d m t
/ /\
i s u
в)
с s
/\ /\
a dm t
/\ \
i p u
/\ /\
• v /\
i s u
Д)
a d m u
15. Процедура Поиск (a, r)
Если a = г, то
Положить Найдено = да\
Если а < г, то
Если г имеет левого сына и, то вызвать Поиск(а,г*);
Положить Найдено = нет;
Если а > г, то
Если г имеет правого сына w, то вызвать Поиск(а, w)
Положить Найдено = нет;
Конец процедуры.

920 Ответы к упражнениям
Раздел 15.3.
1. а) 1011100010010111110100100010;
б) 001011010110101;
в) decided;
г) issues.
3. Вес кода 1 равен 127. Вес кода 2 равен 112. Вес кода 3 равен 136. Выбираем код 2.
5. а)
б) а = 0, Ь = 10, с = ПО, г = 111;
в) вес равен 41;
г) 110111010;
д) 100111;
е) саг;
ж) barb.
7. а)
б) а = 01, d = 00, е = 11, к = 1000, г = 1001, s = 101;
в) вес равен 92;
г) 11100101101111001;
д) 000110011000111001;
е) raked;
ж) dearer.
9. а)
б) а = 100; с = 1010; е = 01; г = 111; g = 1100; /i = 10110; m = 10111; 5 = 1101; t = 00;
в) вес равен 118.

11. а)
Ответы к упражнениям 921
б) a = 100; d = 0111; е = 111; / = 00001; д = ОНО; h = 000001; / = 10111; т = 1010;
п = 0001; о = 1101; г = 010; 5 = 1100; t = 10110; и = 001; w = 000000;
в) вес равен 547;
г) 1111001100101101101000011011000000111111
00001000110000010111
0000001111100101101101000011011000000111
11010110111010001
д) 110000000011110010110111010.
13. Рассмотрим два элемента для кодирования. Коды совпадают, пока к элементам ведет один
путь. Если эти пути расходятся на n-ом ребре, то коды отличаются в n-ом двоичном
разряде. Их пути должны разойтись до того, как один путь достигнет листа. В противном
случае они бы достигли одного листа и остановились. Следовательно, ни один элемент
кода не может быть начальной строкой другого элемента кода, и код — префиксный.
Раздел 15.4.
1. a) abdce\
3. a) dacbfegijhkt;
5. a) deacbgfhjlkmi\
7. а)
б) bacde\
б) gfdcabehijki,
б) hgedcabfijklm\
в) adecb.
в) abcdefjilkhg.
в) dabcefglmkjih.
б) х +abc;
9. а)
в) ab + cx.
б)тх +abc + cd\
в) ab + с х cd + -4-.

922 Ответы к упражнениям
11. а)
а +
/\ /\ ,
b - g hi
d +
6) -i-xa + b-
13. a)
+gh 4- ij\ в) abcdef 4 h xp/i 4-1j 4- x 4-.
a b
e x
15.
6)-f x —h a6cd — e x / 4- p/i;
b
/\
с d
в) ab 4- с — d x efgh 4- x — -r .
17.
d f
\
с g
4b

19.
21.
Ответы к упражнениям 923
>
23. (д).
25. Для каждой арифметической операции количество предшествующих ей чисел на два или
больше превышает количество предшествующих ей арифметических операций, и последний
символ должен быть арифметической операцией.
27. После того как вершина 6 была обработана на обоих деревьях, на шаге 4 вызывается ал-
алгоритм ИБД для обработки на обоих деревьях левого сына вершины Ь. На обоих деревьях
это вершина с, и на обоих деревьях у вершины с нет сыновей. ИБД возвращается в обоих
деревьях к вершине Ь, и на шаге 5 вызывается ИБД для обработки правого сына вершины
Ъ. Когда на шаге 2 будет Iso = F, алгоритм установит, что деревья не изоморфны.
Раздел 15.5.
1. а)
б)
в)
3. а)
б)
V5 V6

924 Ответы к упражнениям
5. а)
в)
-о*
Г'тт
7. а)
в)

Ответы к упражнениям 925
9. а)
б)
в)
11. а)
в)
V0 Vl V4 V5 V3 V9 VS V6 V2 V7
13. v8 точка — сочленения; vsvevs,vsvavz,V8V\V2, v0v7V8 — компоненты двусвязности
15. Если V0V1V2 • • -Vk-i — цикл и если начать в вершине г;0, то дерево поиска в ширину будет
состоять из двух простых путей, vqv\vi • • • и VbVk-\Vk-iVk-z • • •, поэтому оно будет иметь
вид • • • V2VivoVk-iVk-2Vk-3 • • • • Дерево поиска в глубину будет иметь вид t;ot;it?2 • • • Vk-i-
Имеется к деревьев. В каждом одно из к ребер удалено.
17. Пусть {а, 6} — ребро графа. Если это не разрезающее ребро, то после удаления {а, 6}
граф остается связным. Следовательно, у графа, не содержащего {a,b}, имеется остовное
дерево. Если {а,6} — разрезающее ребро, то существуют такие вершины vo и v\, что
любой путь из г>о в v\ содержит ребро {а, 6}. Поскольку vq и v\ принадлежат любому
остовному дереву и дерево связно, то на дереве должен существовать путь из vo в г>ь
который должен содержать ребро {a,b}. Следовательно, ребро {а, 6} принадлежит всем
остовным деревьям графа G.
19. Остовное дерево, полученное поиском в глубину для Кп, — это простой путь вида viv? • • • vk
или в любом другом порядке. Поскольку из любой вершины можно попасть в любую дру-
другую вершину, то при поиске в глубину каждая вершина будет в какой-то момент выбрана.
Если при поиске в ширину вершина vi выбрана как начальная, то другие вершины явля-
являются сыновьями этой вершины, поскольку все являются смежными к ней.
21. Пусть Е' — разрезающее множество графа G. Если Е' удалено из графа, то граф пере-
перестает быть связным, и существуют такие вершины а и 6, что путь из а в 6 отсутствует.
Следовательно, в графе G любой путь из а в Ь должен содержать ребро из Е'. Для любого
остовного дерева графа G вершины а и 6 принадлежат дереву. Поскольку остовное дерево
связно, то существует путь из а в Ь. Но этот путь должен содержать ребра из Е''.
23. пх 2й.

926 Ответы к упражнениям
25. Предположим, что граф G имеет п + 1 вершин. Следовательно, Т и Т' — оба имеют
по и ребер. Предположим, что они имеют к общих ребер, так что каждое дерево имеет
п — к ребер, не принадлежащих другому дереву. Пусть G1 — граф, который содержит п
ребер дерева Т" ип-fc-l ребер дерева Те, не принадлежащих Т"'. Граф G' содержит
п + п — к — 1 = 2п — к— 1 ребер. При формировании остовного дерева п — к — 1 ребер могут
быть удалены из цепи. Ни одно из ребер дерева Те не может быть удалено, поскольку в
цепи всегда имеется ребро, не принадлежащее Тс. Поэтому в остовном дереве остаются
все ребра дерева Те и одно ребро из Т".
27. а) 1,1,0,2,2,6,6;
6J,2,3,4,5,4,5;
в) 2,2,3,4,5,4,5;
г) 0,1,1,1,0,3,11,4,14,4,3,0,5,15,5.
29. а) б)
31. а) 4;
б) 8;
в) 24.
Раздел 15.6.
1.

Ответы к упражнениям 927
Раздел 16.1.
1. а) вершина
Ъ
с
d
вход,
поток
2
1
3
3
1
ребро
(а,Ь)
(е,6)
(Ь,с)
(a,d)
(c,d)
ВЫХОД.
ПОТОК
3
2
1
4
ребро
(Ь,с)
(c,z)
(c,d)
(d,e)
6M;
в) 10;
5.
7.
ф>
F,3) >
9. {а}.
П. {a,d}.
г) 10;
Д) П.

928 Ответы к упражнениям
• е
• е
• г
3. Да.
5. Да.
7. Алгоритм (А,В,М):
Отметить все a € А, для которых имеется ребро, инцидентное к а, в паросочетании
М, знаком *. Отметить все Ь Е В такие, что не существует ребро, инцидентное к Ь, в
паросочетании М, знаком #.
1) Для каждого вновь отмеченного а* е Л отметить все bjy для которых существует
ребро из at в fej, знаком г, если они уже не отмечены целым числом.
2) Если некоторое bj, отмеченное знаком #, теперь отмечено целым числом, то паро-
сочетание расширено. Если никакое bj не является вновь отмеченным, то паросоче-
тание максимизировано.

Ответы к упражнениям 929
3) Для каждого вновь отмеченного bj 6 В, если существует сч такое, что существует
ребро из щ в bj в паре, отметьте его знаком j.
4) Вернуться к шагу A).
Раздел 16.3.
1. (О (а), (б), (в);
(«) (б), (в), (е);
(ш) (а), (в), (г), (е), (ж);
(iv) (а), (б), (в), (г), (д), (е), (ж);
(v) (а), (в), (г), (е), (ж)
(vi) (б), (в), (г), (д), (е), (ж);
(vii) (а), (б), (в), (г), (д), (е), (ж).
3.
©'
-о
о
¦о
9. Да.
11.
•О

930 Ответы к упражнениям
Раздел 17.1.
1. a) {aba,aca,ada)\
б) {с, abc, аабс, abbe, aabbc, ас, be, aac, bbc, aaabbbc}\
в) {ас, ad, be, bd}\
r) {a, ab, abb, abbb, A, cd, eded, ededed, cdcdcdcd, abbbb}\
д) {ad, abed, abebed, abebebed, abebebed, abcbcbcbcd, abcbcbcbcbcd, abcbcbcbcbcbcd,
abcbcbcbcbcbcbcbcd}.
3. a) a(bVcVd);
б) (avb)(bvc);
в) abab*;
r) (ab)*;
д) a(AvbVaVab)b.
5. a) (aVc)*b(aVc)*b(aVc)*;
б) a*ba*ba*ca* ca*Va*ba*ca* ba'ca* Va*ca*ba*ba*ca*V
Va*ca*ca*ba*ba* Va*ca*ba*ca* ba*Va*ba*ca* ca*ba*;
в) (avbvc)*b( avbvc)'b(avbvc)*;
r) a(avbvc)*b(avbvc)*c(avbvc)*va(avbvc)*c(avbvc)*b(avbvc)*;
д) aa*bb*ccV
7. (б), (в), (д).
9. Однозначно декодируемые коды (а), (б), (в), (г), (д).
Суффиксные коды (а), (в), (д).
11. а) код не является однозначно декодируемым, т.к. в 111011 за 11 следует 1011 и за 1110
следует 11;
б) однозначно декодируемый префиксный код;
в) код не является однозначно декодируемым, т.к. в 10101010 за 10101 следует 010 и за
1010 следует 1010;
г) код однозначно декодируемый. Предположим, что существует два различных способа
комбинирования кода для образования одной и той же строки. Конечное слово кода
одной строки должно быть заключительной подстрокой конечного слова кода другой
строки. Но тогда слово кода, предшествующее самому короткому слову, должно закан-
заканчиваться на 0, что невозможно;
д) однозначно декодируемый префиксный код.
13. (а), (б).
15. (а), (б), (г).
17. Нет, 110011,1001 является кодом, который является суффиксным и префиксным, но ин-
инфиксным не является.
19. Никакой.
21. (б).
23. Нет.
25. Пусть www' — элементы ключевого кода. Существует элемент алфавита, который принад-
принадлежит w и не принадлежит w . Существует также элемент алфавита, который принадлежит
w и не принадлежит w. Следовательно, ни одна из строк не может быть начальной или
конечной строкой другого элемента кода.
Раздел 17.2.
1. (б), (в), (г).
3. a*b(aa*b)*.
5. (avba)*

Ответы к упражнениям 931
И.
13.
.?©:
О'
15.
a,b
17.
a,b
о
...

932 Ответы к упражнениям
Раздел 17.3.
1.
3.
5.
7.
А
I
л
]
3 А
в
1 Ы
b Aab
I
X
ab(ab)*.
b*i
Раздел
1.
3.
5.
(с)
а)
б)
в)
г)
а)
б)
i b*a (b *
18.2.
r
G±=\
L
1111110,
111, 110,
А В
U
Aab
К
А а
1
X
ab'ab*
1 1
1 1
1 0
А
I
X
У
1 0
0 1
0 1
1 0
0 1
0 0
°1
0 ;
11
0101101, 1001100, 1010011;
010, Oil;
да, нет, нет, нет
Сх =
000000
100000
010000
001000
000100
000010
000001
100100
0 1
1 0
1 1
100011
000011
110011
101011
100111
100001
100010
000111
1 1
1 0
0 0
010101
110101
000101
011101
010001
010111
010100
110001
0 0 "
1 0
0 1
001110
101110
011110
000110
001010
001100
001111
10101С
5
110110
010110
100110
111110
110010
110100
110111
010010
011011
111011
001011
010011
011111
011001
011010
111111
101101
001101
111101
100101
101001
101111
101100
001001
111000
011000
101000
110000
111100
111010
111001
011100;

Ответы к упражнениям 933
в) вместо 011001 должно стоять 011011; 111000 — правильно; вместо 110111 должно
стоять 110110; вместо 101100 должно стоять 101101.
10 110 0 1
7. a) G1- =
б)
0 110 10
1110 0 1
000000
100000
010000
001000
000100
000010
000001
110000
0
0
0
1
0
1
0
1
1
1
1
1
1
0
0
0
1
0
0
0
1
1
1
0
100101
000101
110101
101101
100001
100111
100100
010101
010011
110011
000011
011011
010111
010001
010010
100011
001111
101111
001111
000111
001011
001101
001110
111111
110110
010110
100110
111110
110010
110100
110111
000110
011100
111100
001100
010100
011000
011110
011101
101100
101010
001010
111010
100010
101110
101010
101011
011010
111001
011001
101001
110001
111101
111001
111000
001001
в) вместо 111101 должно стоять 111001; 111001 — правильно; вместо 110010 должно
стоять 110110; вместо 101001 должно стоять 111001.
9. 101101, 011011, 110110;
1 0 1 1 0 1 1
0 110 11.
1 1 0 1 1 0 J
11. Ассоциативность. Пусть а = (ai,a2,--- ,an), 6 = F1,62,-•• ,6П) и с = (ci,C2,--- ,cn) —
элементы из Вп
(а + 6) +с = ((ai,a2,--- ,an) + F1,62,-•• ,6n)) 4- (ci,C2,- •• ,cn) =
= (ai 4- 61,(i2 + 62, • • • ,an 4- 6n) 4- (ci,C2, • • • ,cn) =
• 61) 4- cu (<*2 + 62) 4- c2, • • • , (an 4- 6n) 4- cn) =
F1 4- ci), a2 + F2 + C2), • • • , anD-6n 4- cn)) =
>,••• , an) 4- F1 4-ci,62 4-C2,- •• ,6n 4-cn) =
>, • • • , an) 4- (F1, 62, • • • , 6n) 4- (ci, C2, • • • , cn)) =
Единицей является элемент @,0, ••• ,0). Каждый элемент является своим обратным
элементом. Замкнутость следует из определения сложения. Следовательно, Вп — группа.

934 Ответы к упражнениям
13. Поскольку С1- — подмножество множества Вп, оно ассоциативно. Каждый элемент явля-
является своим обратным элементом. Поэтому необходимо показать только замкнутость. Пусть
u,v е С1-. Тогда иос — voc =0 для всех се С. Поэтому (u+v)oc = uoc+voc =0+0 = 0
для всех сеСии + ибС1. Следовательно, С1- — группа.
Раздел
1. Gh
18.3.
=
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
0
1
1
1
1
1
0
1
1
0
1
3. EA10010101,010101111) = 5.
5. 001100110, 101100111, 100000111.
[10 1110 0]
1110 0 10;
1 1 0 1 0 0 1 J
б) вместо 1110110 должно быть 1110010, вместо 1011001 должно быть 1010001,
вместо 1101100 должно быть 1100100, и вместо 1111110 должно быть 1111111.
9. Порождающая функция в упражнении 7 меняет 1001001 на 1101001. Порождающая функ-
функция в упражнении 8 меняет 1001001 на 1011001. Обе порождающие функции "исправляют"
код, генерируя ошибки.
11. а) если с = с', то нет такой позиции, в которой соответствующие биты отличались бы.
Следовательно, отсутствуют позиции, в которых один бит равен 1, а другой равен 0.
Таким образом, 6(с,с') = 0. Обратно, если 6(с,с') = 0, отсутствует позиция, в которой
один бит равен 1, а соответствующий бит равен 0. Вполне очевидно, что все соответ-
соответствующие биты должны совпадать, и с = с'.
б) пусть 6{с,с') = п. В таком случае имеется п позиций, где соответствующие биты строк
сие' отличаются. Но тогда But имеется п позиций, где соответствующие биты строк
с' и с отличаются, и 5(с',с)=п.
13.
#2 =
Я4 =
1 Ч-
1 -1J'
#8 =
1
1
1
1
1
1
1
1
1
1
1
1
1
-1
1
-1
1
-1
1
-1
1
1
1
-1
1
1
-1
-1
1
1
-1
-1
1
1
-1
-1
1
-1
-1
1
1
-1
-1
1
1
-1
-1
1
1
1
1
1
-1
-1
-1
-1
1
-1
1
-1
-1
1
-1
1
1
1
-1
-1
-1
-1
1
1
1
-1
-1
1
-1
1
1
-1

Ответы к упражнениям 935
#16 =
1 1
1 -1
1 1
1 -1
1 1
1 -1
1 1
1 -1
1 1
1 -1
1 1
1 -1
1 1
1 -1
1 1
1 -1
1
1
-1
-1
1
1
-1
-1
1
1
-1
-1
1
1
-1
1
-1
-1
1
1
-1
-1
1
1
-1
-1
1
1
-1
-1
1
1
1
1
1
-1
-1
-1
-1
1
1
1
1
-1
-1
-1
-1
1
-1
1
-1
-1
1
-1
1
1
-1
1
-1
-1
1
-1
1
1
1
-1
-1
-1
-1
1
1
1
1
-1
-1
-1
-1
1
1
1
-1
-1
1
-1
1
1
-1
1
-1
-1
1
-1
1
1
-1
1
1
1
1
1
1
1
1
-1
-1
-1
-1
-1
-1
-1
-1
1
-1
1
-1
1
-1
1
-1
-1
1
-1
1
-1
1
-1
1
1
1
-1
-1
1
1
-1
-1
-1
-1
1
1
-1
-1
1
1
1
-1
-1
1
1
-1
-1
1
-1
1
1
-1
-1
1
1
-1
— ]
-
L 1
1 -1
L 1
L -1
L -1
L 1
L -1
1 1
L -1
L 1
-1 -1
-1 1
1 1
L -1
L 1
L -1
1
1
-1
-1
1
-1
1
1
-1
-1
1
1
1
1
-1
-1
1
-1
-1
1
-1
1
1
-1
-1
1
1
-1
1
-1
-1
1
Раздел 19.1.
1. Пусть
1 =
1 2 3
1 2 3
\ / 1 2 3 \
) ; pl = { 2 3 1 ) ;
/ 1 2 3 \ / 1 2 3 \
ai = { 1 3 2 ) ; °2 = V 3 2 1 ) ;
В таком случае имеем следующую таблицу умножения.
3.
( 1 2 3 \
р2 = { 3 1 2 )
( 1 2 3 \
аз = [ 2 1 3 )
/
pl
P2
СГ\
02
сгз
j
I
Pl
P2
O\
02
(Уз
Pl
P2
I
02
03
Cf\
\ P2
P2
I
Pl
03
0\
O2
01
01
03
&2
I
P2
Pl
O2
02
01
03
Pl
1
P2
03
03
02
01
P2
Pl
I
1
1
1
2
1
3
1
4
1
5
1
6
2
2
2
3
2
4
2
5
2
6
2
7
3
3
3
4
3
5
3
6
3
7
3
8
4
4
4
5
4
6
4
7
4
8
4
1
5
5
5
6
5
7
5
8
5
1
5
2
6
6
6
7
6
8
6
1
6
2
6
3
7
7
7
8
7
1
7
2
7
3
7
4
8
8
8
1
8
2
8
3
8
5
8
5
)¦¦
) '
>
)¦

936 Ответы к упражнениям
/12345678
78 123456
12345678
/12345678\
1~Д21876543у/;
_/12345678
2~
л_/12345678\
3~V65432187>);
/12345678\
4~V8765432iy;
12345678
18765432
12345678
т
_/12345678\
"^54321876,1'
_/12345678\
~\76543218у*
5. 8.
7. 7.
Раздел 19.2.
1. 8.
3. 4.
5. 18.
7. 39.
9. г4 + г3Ь
П. го + Г4б + 2г3Ь2 + 2г2Ь3 + гЪА + Ьъ.
13. г8 + r7b 4- 4г662 + 5г563 4 8г464 + 5г3Ь5 + 4r266 -f rb7 + b8.
15. г10 + 4rgb + 15r8b2 + 42r7b3 + 72г664 + 84г5Ь5 + 72г466 4 42г367 4 15г268 4 4г69 4- б10.
Раздел 20.1.
1. Если ах = 6, то а~1ах = a~lb и х = a~lb. Если am = b и an = 6, то am = an, поэтому
a~1am = a~lan и m = п.
3. Предположим, что аб — делитель нуля. Тогда (ab)c = 0 для некоторого с. Следовательно,
а(Ьс) = 0. Если be = 0, то 6 — делитель нуля. Если 6с Ф 0, то a — делитель нуля.
5. 0.
7. Предположим, что из ab = ас следует, что 6 = с для всех ненулевых а из R. Если
ad = 0 = аО и а ф 0, то d = 0, и R — область целостности. Обратно, если R — область
целостности и ab = ас для а ф 0, то а(Ь — с) = 0. Следовательно, 6 — с = 0 и Ь = с.
9. Пусть i + j и г' 4 з принадлежат I + J. Тогда i + j + i' + j' = i 4 г 4 j 4 /. Поскольку
г 4- г' € / и j + j' ? J, то г + j 4- г 4- / G / 4- J. Также а(г 4 j) = ai 4- aj. Поскольку аг G /
и aj G J, то а(г + ji) G / -f J.

Ответы к упражнениям 937
11. C).
13. /@) = 0. Поэтому 0 е f(R). Пусть a,be f(R). Тогда а = /(с) и 6 = f(d) для некоторых
c,deR. Поэтому с - d е R и /(с - d) = f(c) - f(d). Следовательно, /(с) - f(d) e f(R).
Аналогично, если а, 6 € /(Я), а = /(с) и 6 = f(d) для некоторых с, d ? Я, то cd ? Я и
/(cd) = f(c)f(d). Таким образом, аб Е /(Я). Следовательно, /(Я) — кольцо.
15. Нет.
17. Неверное утверждение. Элементы [2] и [3] — нулевые делители кольца Zi2- Однако, [2] +
[3] = [5] не является нулевым делителем кольца Zi2.
19. Пусть Я — область целостности. Если а2 = а, то а • а = а • 1 и, согласно результату
предыдущей задачи, а = 1.
21. Для всех а, 6 G Я имеем (—а)(Ь) + аЬ = (—а + а)Ь = 0-6 = 0. Поэтому (—а)F) = —ab.
Аналогично, а(—6) = —аЬ. Для всех a,b e R
(-а)(-Ь) + (-а)(Ь) = (-а)(-Ь + Ь) = (-а) -0 = 0.
Поэтому (-а)(-6) + (-а)(Ь) = аб + (-а)F) и (-а)(-Ь) = аЬ.
Раздел 20,2.
1. Покажем сначала, что пересечение подколец с единицей является кольцом с единицей. По-
Поскольку мультипликативная единица принадлежит всем подкольцам, то она принадлежит
их пересечению. Пусть а, 6 принадлежит пересечению подколец, тогда а, 6 принадлежит
каждому из подколец. Поэтому а — b принадлежит всем подкольцам и, следовательно,
пересечению подколец. Аналогично, ab принадлежит пересечению всех подколец. Следо-
Следовательно, пересечение подколец с единицей есть кольцо с единицей. Далее покажем, что
пересечение областей целостности есть область целостности. Предположим, что а и 6 при-
принадлежат пересечению всех подколец, ab = 0 и а ф 0. Но а и 6 принадлежат каждой из
областей целостности. Поэтому 6 = 0.
3. Или а > 0, или -а > 0. Если а > 0, то, согласно определению упорядочения, а2 > 0. Если
-а > 0, то (-аJ > 0. Но (-аJ = а2, поэтому а2 > 0. Поскольку I2 = 1, то 1 > 0.
Раздел 20.3.
1. Пусть / = (аг)\ g = F;)* и h = (a)*.
f + {9 + h) = (сц)* + (bi + аУ =
= (пг + biY +
поэтому сложение ассоциативно. Аддитивной единицей является (di)*, где di = 0 для
всех г. Обратным элементом относительно сложения для (а»)* будет (—ai)*.
f + g = (<иУ + (ЫУ =
= (а; + bi)* =
= (^ + en)' =
= (Ы + (aiy =

938 Ответы к упражнениям
и сложение коммутативно. Следовательно, множество многочленов — коммутативная груп-
группа относительно сложения.
i+j=k
m+i+j=n
= ( E ( E «~Ь)<*Г =
= {fg)h,
и умножение ассоциативно. Окончательно,
= (Е <*№+<*))* =
= (Е а^^)* + (Е
3. Неверное утверждение. Пусть / = A,1,1,1,0,0,--) и р = A,1, -1, -1,0,0, •••). Тогда
f + g = A,1,0,0,0,0,-..). deg(/) = deg(g) = 3, тогда как deg(/ + g) = 1.
5. В Z5, f(x) = x4 — 1 — нулевая функция, тогда как / имеет степень 4.
Раздел 20А.
1. Пусть г = а + Ы и 5 = c + di — целые комплексные числа. Тогда г — 5 = (а — с) + F — d)i и
rs = (а + Ьг)(с 4- dt) = (ас — bd) 4- (ad 4- Ьс)г — также целые комплексные числа. Поэтому
множество целых комплексных чисел является подкольцом.
3. sin(nTr) = 0 для любого целого числа п. Следовательно, уравнение имеет бесконеное ко-
количество нулей, и sin(x) нельзя представить в виде многочлена.
5. Пусть А = Z и f,g е А[х] определены соотношениями f(x) = х2 4- 1 и д(х) = х2 - 3
соответственно, тогда fug — простые многочлены, но / 4- д простым многочленом не
является, поскольку / 4- д(х) = 2х2 - 2.
7. Пусть с = а 4- bi — комплексное целое число. Тогда
= (х - а) + Ы)(х - а) - Ы) =
= (x-aJ+fc2,
поэтому / € Q[x] и /(с) = 0.

Ответы к упражнениям 939
9. Подкольцо, состоящее из всех чисел вида a + Ь\/5, где а и 6 — рациональные числа.
11. Подкольцо, состоящее из всех чисел вида a + by/bi, где а и 6 — рациональные числа.
13. Подкольцо, состоящее из всех чисел вида a + 6\/3г, где а и Ъ — рациональные числа.
Раздел 21.2.
1- 1 = Х(99'1) = хЫхОГ1) = (а + ИхОГ1). Следовательно, хСр) = ^ = Яф- Но
поскольку а + 6г лежит на единичной окружности, то а2 +Ъ2 = 1, поэтому х(р-1) = а-Ьг.
3. Если р ^ <Д то giA)gii2)gJ3C) • • -^m) и g' = ^'A)й'B)^'C) • • • <^(m), где для некоторого
г имеем pf(i) ^ pf(i). Тогда Х*Ы = a^(i) и Хв'(р<) = ^'(<). Поскольку а?г) ф а{(i), то
Раздел 21.3 .
1. Пусть i G / и s G S. \(} ' s) = xW * x(s) = 0 * xE) = 0 и г • s G /. Следовательно,
/ — идеал. Пусть s, s' € S — I. Тогда xES') = x(s)xE') = 1*1 = 1- Таким образом,
ss' G S — I и S принадлежат идеалу. Следовательно, / — простой идеал. Обратно, если
/ — простой идеал, то искомый характер может быть получен путем отображения. Если
X — отображение из
если s G S — /;
если s G /.
Если х — характер на S — /, то определим х' на 5 соотношениями
л.)-{?•'•
если s € S — I;
если 5 G /.
3. Пусть С = [dj] = aaf. Тогда
fc=l
согласно теореме 21.19.
Раздел 22.1.
1. Пусть N(W) = Xl2n-1 + x22n + • • • + xn-X2l + xn и JV(V) = y^" + 2/22n-2 +
yn-\2l +yn. Тогда
... + |xn_i - yn-i\2l + \(xn - yn)\ =

1L0 Ответы к упражнениям
3. w = 7,8,11,12,13,14,15,16.
5. к слов для хранения к простых чисел;
к слов для хранения NP(X) для к простых чисел р;
к слов для хранения Np(Y(i)) для к простых чисел р;
к слов для хранения [[2П]]Р;
незначительное количество слов для циклов и т.п.;
всего приблизительно 4/с слов.
Раздел 22.2.
1. Если d\a и d\b, то d\a-b. Поэтому d\ НОД(а-Ь, а) и НОД(а, 6)| НОД(а-Ь, а). Обратно, если
d\a и d\a—6, то d\b, и, следовательно, d\ НОД(а, 6). Таким образом, НОД(а—Ь, а)\ НОД(а, 6).
Значит, НОД(а -Ь,а) = НОД(а, Ъ).
3. НОДF,10,15) = 1, однако НОДF,10) ф 1. Фактически, наибольший общий делитель
любой пары этих целых чисел не равен единице.
5. а) г к{ гщ Mi hi Ni MibiNi
1 12 145 26551252 532 0 0
2 14 169 22780660 5 43 4897841900
3 15 181 21270340 711 91 1376212268340
4 18 217 17741620 81 163 234242608860
D = 12; С = 2231403840;
7. a) i ki rrn Mi hi Ni MibiNi
1 5 301 6496934404 1066 0 0
2 15 901 2170452004 232 226 113801139473728
3 20 1201 1628290804 379 601 370890451044316
4 25 1501 1302849604 5832 1126 8555594470734528
D = 60; С = 1607985850884;

Ответы к упражнениям 941
Раздел 22.3.
1.
[[1683217]]2993 = 77;
[[79217]]2993 = 79;
[[2560217]]299з = 78;
[[872217]]2993 = 69;
[[2571217]]2993 = 89.
3. Для шифрования необходимо иметь значения е и п. Если известно ф(п), то, используя
формулы из теоремы 22.15, можно найти d, что обеспечит возможность дешифровки.

тно-именнои указатель
Абсолютное значение — Absolute value,
820
Автомат — Automaton, 731
детерминированный — deterministic,
735
диаграмма состояний — state
diagram, 732
допускаемый язык — accepted
language, 731
допускание — accepting, 733
недетерминированный —
nondeterministic, 735
состояние зацикливания — sink state,
734
функция переходов — transition
function, 731
Адлеман, Л. М. (Adleman, L. М.), 844
Аксиоматическая система — Axiom
system, 67
Гильберта-Бернайса-Геделя —
Godel-Hilbert-Bernays, 67
Рассела-Уайтхеда —
Russell-Whitehead, 67
Цермело-Френкеля-фон Неймана —
Zermelo-Fraenkel-von Neumann,
67
равенство — equality, 123
целые числа — integers, 124
Алгебраический элемент — Algebraic
element, 815
Алгебраическое число — Algebraic number,
815
целое — Algebraic integer, 815
Алгоритм — Algorithm, 184, 298
Горнера — Homer's algorithm, 185
Дейкстры — Dijkstra's algorithm, 612,
615
Евклида — Euclidean algorithm, 302
Крускала — Krushkal's algorithm, 682
Прима — Prim's algorithm, 684, 686
Флойда-Уоршолла — Floyd-Warshall
algorithm, 619, 621
Форда-Фалкерсона — Ford-Fulkerson
algorithm, 699
Хаффмана — Huffman's algorithm,
640, 642
быстрой сортировки — quick sort, 208
деления — Division algorithm, 140,
301
перевода последовательности в
дерево — Sequence to tree
algorithm, 672
поиска дерева в глубину —
Depth-first tree search, 661
поиска дерева в ширину —
Breadth-first tree search, 659
преобразования дерева в
последовательность — Tree to
sequence algorithm, 670
пузырьковой сортировки — bubble
sort, 207
сортировки — sorting algorithm, 205
сортировки вставками — insertion
sort, 211
сортировки выбором — selection sort,
206
сортировки слиянием — merge sort,
209
Алфавит - Alphabet, 399, 725
Бернулли, Иоганн (Bernoulli, Jean), 438
Бесконечный спуск — Infinite descent, 139
Бинарная операция — Binary operation,
163, 397

Предметно-именной указатель 943
Бинарное дерево поиска — Binary search
tree, 631
обход — traversing, 649
Биномиальная теорема — Binomial
theorem, 337
Биномиальное распределение — Binomial
distribution, 375
Битовая строка — Bit String, 318
Блоковый код — Block code, 753
Боер, Р. С. (Воуег, R. S.), 836
Булева алгебра — Boolean algebra, 84, 406
дополнение законов тождества —
complement of identities laws, 87
законы ассоциативности — associative
properties, 85
законы де Моргана — De Morgan's
laws, 87
законы дистрибутивности —
distributive properties, 85
законы дополнения — complement
properties, 85
законы идемпотентности —
idempotent laws, 86
законы инволюции — involution laws,
87
законы коммутативности —
commutative properties, 85
законы поглощения — absorption
laws, 86
законы тождества — identity
properties, 85
свойства констант — null laws, 86
Бурали-Форти (Burali-Forti), 67
В
Вероятность — Probability, 348, 369, 833
биномиальное распределение —
binomial distribution, 375
математическое ожидание —
mathematical expectation, 376
множество элементарных событий —
sample space, 347
независимые события — independent
events, 374
непересекающиеся множества —
disjoint set, 348
ожидаемое значение — expected
value, 376
среднее значение — mean, 379
условная — conditional, 370
Взаимоисключающие множества —
Mutually exclusive sets, 110
Включение-исключение —
Inclusion-exclusion, 502
Внутреннее произведение — Inner product,
169
Вполне упорядоченная область
целостности — Well ordered
integral domain, 798
Выводимость — Deducibility, 34
Выражение — Expression, 726
регулярное — regular, 726
Высказывание — Proposition, 15
Вычет — Residue, 153
Гамильтонов — Hamiltonian
путь — path, 601
цикл — cycle, 601
Гауссово кольцо — Unique factorization
domain, 797
Гиперкуб — Hypercube, 290
Гипотеза — Hypothesis, 35
Гомоморфизм — Homomorphism
колец — ring homomorphism, 790
полугрупп — semigroup
homomorphism, 415
Грамматика — Grammar, 741
контекстная — context-sensitive, 749
начальный символ — start symbol,
742
непосредственных составляющих —
phrase structure, 742
нетерминальные символы —
nonterminal symbols, 741, 742
порождаемый язык — language
generated by, 742
продукции — productions, 741
регулярная — regular, 751
соответствующее дерево —
corresponding tree, 747
терминальные символы — terminal
symbols, 741, 742
формальная — formal, 742
Граф — Graph, 95, 244, 556
Петерсена — Petersen graph, 584
вершина — vertex, 95, 244
взвешенный — weighted, 611
гомеоморфный — homeomorphic, 557

944 Предметно-именной указатель
гомоморфизм — homomorphism, 556
грань — face, 581
двойственный — dual, 587
двудольный — bipartite, 250
двусвязный — biconnected, 562
диаметр — diameter, 290
дополнение — complement, 559
изоморфизм — isomorphism, 556
компонента — component, 250
компонента двусвязности —
bicomponent, 563
матрица инцидентности — incidence
matrix, 278
матрица смежности — adjacency
matrix, 279
мультиграф — multigraph, 245
объединение — union, 559
остовное дерево — spanning tree, 560
остовной граф — spanning graph, 559
пересечение — intersection, 559
планарный граф — planar graph, 580
полный — complete, 250
полный двудольный — complete
bipartite, 251
попарно непересекающиеся —
pairwise disjoint, 559
производный — derived, 557
простой путь — simple path, 248
простой цикл — simple cycle, 250
путь — path, 248
разрезающее множество — cut set,
561
разрезающее ребро — cut edge, 561
раскраска — coloring, 589
расстояние — distance, 290
расширение — extension, 557
ребро — edge, 95, 244
связный — connected, 249
сетка — grid, 295
смежные вершины — adjacent
vertices, 244
смежные ребра — adjacent edges, 244
степень вершины — degree of vertex,
247
точка сочленения — articulation point,
561
хроматический многочлен —
chromatic polynomial, 589
хроматическое число — chromatic
number, 589
цикл — cycle, 250
эйлеров цикл — Euler path, 270
Группа — Group, 410
абелева — abelian, 410
группа симметрии — symmetric
group, 419
единичный элемент — identity, 410
коммутативная — commutative, 410
конечная циклическая — finite cyclic
group, 412
левый смежный класс — left coset,
413
нормальная подгруппа — normal
subgroup, 417
обратный элемент — inverse, 410
подгруппа — subgroup, 412
порядок — order, 410
порядок элемента — order of an
element, 411
прямая сумма — direct sum, 821
симметрии квадрата — symmetries of
the square, 776
смежный класс — coset, 413
фактор-группа — factor group, 418
характер — character, 821
циклическая — cyclic group, 412
ядро — kernel, 417
д
Деление
остаток — remainder, 140
частное — quotient, 140
Делитель единицы — Unit, 795
Дерево - Tree, 259, 624
m-арное — m-агу, 263
бинарный поиск — binary search, 631
братья — sibling, 263
вес — weight, 639
внутренняя вершина — internal
vertex, 261
высота — height, 262
корень — root, 262
корневое — rooted, 262
корневое ориентированное — rooted
directed, 262
лес - forest, 259
листья — leaves, 261
ориентированное — directed, 260, 624
остовное — spanning tree, 264, 658
подсчета — counting tree, 316

Предметно-именной указатель 945
поиск в глубину — depth-first search,
661
поиск в ширину — breadth-first
search, 659
потомок — descendent, 263
предок — ancestor, 263
родитель — parent, 262
сын - child, 262
уровень — level, 262
Детерминированный автомат —
Deterministic automata, 735
Дешифровка — Decryption, 844
Диаграмма — Diagram
Венна — Venn diagram, 77
Ферре — Ferrer's diagram, 545
Эйлера — Euler diagram, 119
Дизъюнктивная нормальная форма —
Disjunctive normal form, 47
Диффи, У. (Diffie, W.), 847
Доказательство — Proof
контрпример — counterexample, 129
перебором — case proof, 128
приведение к абсурду — reductio as
absurdum, 127
Евклид (Euclid)
теорема о простых числах — theorem
on primes, 145
Евклидово кольцо — Euclidean domain, 809
норма — norm, 809
Единичная окружность — Unit circle, 820
Запрещенные позиции — Forbidden
positions, 509
Зашифрованный текст — Ciphertext, 844
И
Идеал - Ideal, 793, 825
максимальный — maximal, 810
простой — prime, 795
Идемпотент — Idempotent, 401
Идентифицирующая функция —
Fingerprint, 831
Изоморфизм — Isomorphism
колец — ring isomorphism, 790
полугрупп — semigroup isomorphism,
415
Импликация — Conditional, 24, 33
Инверсия — Inverse, 33
Инверсная польская запись — Reverse
Polish notation, 651, 653
Индукция — Induction, 136, 137, 799
Инфиксная запись — Infix notation, 215
Инфиксный код — Infix code, 731
Испытания Бернулли — Bernnoulli trials,
377
К
Кан, Дэвид (Kahn, David), 849
Кантор, Георг (Cantor, Georg), 67
Карп, Р. М. (Кагр, R. М.), 830
Карта Карно — Karnaugh map, 50
Квантор — Quantifier, 114, 115
существования — existential, 115
универсальный — universal, 114
Китайская теорема об остатках — Chinese
Remainder Theorem, 429
Класс смежности — Coset, 414
левый - left, 811
Ключ — Key
криптографический — cryptographic,
843
общий шифрующий — enciphering,
847
секретный дешифрирующий —
deciphering, 847
Кнут, Д. Э. (Knuth, D. Е.), 836, 837
Код - Code, 638, 727
ASCII - ASCII code, 756
RSA - RSA code, 845
Адамара — Hadamard code, 773
Голе — Golay code, 771
Грея - Gray code, 294, 755
Морзе — Morse code, 754
Рида-Мюллера — Reed-Muller code,
772
Хаффмана — Huffman code, 754
Хаффмана — Huffman's code, 640
Хемминга — Hamming code, 768
блоковый — block code, 753
вес - weight, 639, 758
групповой — group code, 757
двойственный — dual code, 761
инфиксный — infix code, 731
исправляющий ошибки — error
correcting code, 755

946 Предметно-именной указатель
ключевой — key code, 728
кома-код — comma code, 754
линейный — linear code, 757
мгновенный — instantaneous code, 754
обнаруживающий ошибки — error
detecting code, 754
однозначно декодируемый — uniquely
decipherable, 638, 727
префиксный — prefix, 638
префиксный — prefix code, 728, 754
суффиксный — suffix code, 728
Кольцо — Ring, 788
главный идеал — principal ideal, 794
группа делителей единицы — group of
units, 795
делитель единицы — unit, 795
идеал — ideal, 793
коммутативное — commutative, 789
неприводимый элемент — irreducible
element, 795
подкольцо — subring, 791
полиномов — ring of polynomials, 802
с единицей — ring with unity, 789
упорядоченное — ordered, 798
Комбинаторный принцип
сложения — Addition counting
principle, 319, 324
умножения — Multiplication counting
principal, 317
Коммутационная схема — Circuit Diagram,
56
инвертор — negation gate, 58
логический элемент и — and gate, 58
логический элемент или — or gate, 58
логический элемент не — negation
gate, 58
логический элемент не-и — nand gate,
60
логический элемент не-или — nor
gate, 60
полный сумматор — full-adder, 62
полусумматор — half-adder, 61
схема переключения — switching
circuit, 57
Комплексная плоскость — Complex plane,
820
Комплексное число — Complex number, 819
абсолютное значение — absolute
value, 820
действительная часть — real part, 820
длина — length, 820
мнимая часть — imaginary part, 820
сопряженное — conjugate, 820
Конверсия — converse, 33
Конечные разности — Finite differences,
469
правило произведения — product rule,
471
правило частного — quotient rule, 471
суммирование — summation, 483
суммирование по частям —
summation by parts, 485
факториальный многочлен — factor
polynomials, 473
Конкатенация — Concatenation, 399, 725
Константа — Constant, 802
Контрапозиция — Contrapositive, 29, 33
Конъюнктивная нормальная форма —
Conjunctive normal form, 48
Корректирующая формула — Update
formula, 832
Криптоанализ — Cryptanalysis, 844
Криптография — Cryptography, 844
Криптосистемы с ключами общего
пользования — Public-key
cryptosystems, 847
Критерий простоты Лукаса — Lucas'
Primality Test, 443
Л
Ладейный полином — Rook polynomial,
509
Лексикографический порядок —
Lexicograhical ordering, 343
Лемма Бернсайда о подсчете — Burnside
counting lemma, 780
Линейное рекуррентное отношение —
Linear recurrence relation, 448,
451
неоднородное — nonhomogeneous, 460
одноролное — homogeneous, 449
с постоянными коэффициентами —
constant coefficients, 449
Линейные уравнения — Linear equations,
422
целочисленные решения — integral
solutions, 422
Логическая истинность — Logical truth, 30
Логическая ложность — Logical falsity, 30

Предметно-именной указатель 947
Логическая эквивалентность — Logical
equivalence, 27, 28
закон двойного отрицания — double
negation, 29
закон идемпотентности — idempotent
law, 29
закон контрапозиции —
contrapositive, 29
законы де Моргана — de Morgan's
Laws, 29
свойства ассоциативности —
associative properties, 29
свойства дистрибутивности —
distributive properties, 29
свойства коммутативности —
commutative properties, 29
Логическое умозаключение — Logical
argument, 35
М
Максимальное паросочетание — Maximal
matching, 707
Максимальный идеал — Maximal ideal,
810
Малая теорема Ферма — Fermat's Little
Theorem, 440
Матиас (Matyas, S. M.), 848
Матрица — Matrix, 167, 186
Адамара — Hadamard matrix, 773
Хемминга — Hamming matrix, 767
булева — boolean, 172
детерминант — determinant, 238
единичная — identity, 240
контроля четности — parity check
matrix, 762
матричное представление — matrix
representation, 171
обратная — inverse matrix, 240
перестановок — permutatiom, 174
порождающая — generator matrix, 758
произведение — product, 169, 170, 186
симметричная — symmetric, 171
степеней — degree matrix, 676
сумма — matrix sum, 169, 186
транспонированная — transpose, 171
умножение на скаляр — multiplication
by a scalar, 168
Матричная формула Кирхгофа для дерева
— Kirchoff's matrix tree formula,
676
Мгновенное безумие — Instant insanity,
267
Мейер (Meyer, С. Н.), 848
Метод — Method
Ферма выделения множителей —
Fermat's Factorization, 300
двоичного дополнения — two's
compliment, 231
Минимальное остовное дерево — Minimal
spanning tree, 682
алгоритм Крускала — Krushkal's
algorithm, 682
алгоритм Прима — Prim's algorithm,
684, 686
Множество — Set, 67
всех подмножеств — power set, 74
декартово произведение — Cartesian
product, 75
дополнение — complement, 72
индексированное — indexed, 76
индексное — indexing, 76
пустое — empty set, 69
универсальное — universal, 69
элемент — element of, 68
Моноид — Monoid, 398
Мономорфизм — Monomorphism
колец — ring monomorphism, 790
полугрупп — semigroup
monomorphism, 415
Моррис, Дж. X. (Morris, J. H.), 836
Мощность — Cardinality, 177
счетная — countable, 177, 180
Мур, Дж. С. (Moore, J. S.), 836
H
Наибольший общий делитель — Greatest
common divisor, 142
Наименьшее общее кратное — Least
common multiple, 143, 304
Недетерминированный автомат —
Nondeterministic automata, 735
Неоднородное рекуррентное отношение —
Nonhomogeneous recurrence
relation, 460
Непересекающиеся множества — Disjoint
sets, 110
Неполное частное — Partial quotient, 309
Неприводимый элемент — Irreducible
element, 795

948 Предметно-именной указатель
Неравенство Чебышева — Chebyshev's
inequality, 381
О
Область главных идеалов — Principal ideal
domain, 795
Область значений — Range, 156
Область определения — Domain, 156
Область потенциальных значений —
Codomain, 156
Область целостности — Integral domain,
789
вложенная — embedded, 793
вполне упорядоченная — well-ordered,
798
минимальная область — minimal, 801
неприводимый элемент — irreducible
element, 808
приводимый элемент — reducible
element, 808
Образ — Image, 156
Обратная польская запись — Reverse
Polish notation, 215
Обратное отношение — Inverse relation,
158
Обратное ребро — Back edge, 661
Обход дерева — Transversal, 650
в обратном порядке — postorder
transversal, 653
в прямом порядке — preorder
transversal, 651
в центрированном порядке — inorder
transversal, 650
Однозначно декодируемый код — Uniquely
decipherable code, 727
Однородное рекуррентное отношение —
Homogeneous recurrence relation,
449
Операции над множествами — Set
operations
обобщенное объединение —
generalized union, 76
обобщенное пересечение —
generalized intersection, 76
объединение — union, 71
пересечение — intersection, 71
разность — difference, 72
симметрическая разность —
symmetric difference, 72
Ориентированное дерево — Directed tree,
624
m-арное — m-агу, 626
высота — height, 626
гомоморфизм — homomorphism, 627
изоморфизм — isomomorphism, 627
корневое — rooted directed tree, 624
полное m-арное — full m-ary, 626
сбалансированное — balanced, 626
уровень — level, 626
Ориентированный граф — Directed graph,
96, 252
источник — source, 253
конечная вершина — terminal vertex,
96, 252
начальная вершина — initial vertex,
96, 252
ориентированное ребро — directed
edge, 96, 252
ориентированный путь — directed
graph, 255
ориентированный цикл — directed
cycle, 273
подграф — subgraph, 255
размеченный — labeled, 254
связный — connected, 256
сильно связный — strongly connected,
256
соотнесенный граф — underlying
graph, 255
степень входа вершины — indegree of
vertex, 253
степень выхода вершины — outdegree
of vertex, 253
сток — sink, 253
Основная теорема
арифметики — Fundamental Theorem
of Arithmetic, 146
Основная теорема алгебры — Fundamental
Theorem of Algebra, 820
Остовное дерево — Spanning tree, 560, 658
минимальное — minimal, 682
Открытый текст — Plaintext, 844
Отношение — Relation, 90
антирефлексивное — antireflexive, 93
антисимметричное — antisymmetric,
93
эквивалентность — equivalence, 107
композиция — composition, 92
конгруэнтности — congruence, 811

Предметно-именной указатель 949
множество значений — range, 91
область определения — domain, 91
обратное — inverse, 91, 158
рефлексивное — reflexive, 93
рефлексивное замыкание — reflexive
closure, 94
симметрическое замыкание —
symmetric closure, 94
симметричное — symmetric, 93
транзитивное — transitive, 93
транзитивное замыкание — transitive
closure, 94
частичного порядка — partial
ordering, 103, 392
Отношение конгруэнтности — Congruence
relation, 400
Отношение множеств — Set relation
взаимоисключение — mutual
exclusiveness, 110
непересечение — disjointness, 110
подмножество — subset, 68
равенство — equality, 69
собственное подмножество — proper
subset, 69
функция — function, 156
Отображение — Mapping, 156
инъективное — injective, 158
сюръективное — surjective, 158
П
Парадокс Рассела — Russell's paradox, 182
Пардум, Джек (Purdum, Jack), 836
Паросочетание — Matching, 707
максимальное — maximal, 707
полное — complete, 707
Паросочетающие ребра — Matching edges,
707
Первообразный корень n-ой степени —
Primitive n-th root, 821
Переменная — Indeterminate, 805
Перестановка — Permutation, 161, 331,
332, 418
обобщенная — generalized, 354
орбита — orbit, 420
с запрещенными позициями — with
forbidden positions, 509
с повторением — with repetition, 359
цикл — cycle, 420
Перечень раскрасок — Inventory of
colorings, 784
Планарный граф — Planar graph, 580
По модулю — Modulo, 149
Подграф — Subgraph, 248
Подходящая дробь — Convergent fraction,
309
Поле - Field, 791
подполе - subfield, 808, 819
расширение — extension, 808
рациональных функций — field of
rational functions, 815
частных — field of fractions, 793
Полином — Polynomial, 801, 802
деление — division, 803
делители — factors, 803
коэффициент — coefficient, 802
ладейный — rook polynomial, 509
неприводимый — irreducible, 808
нормированный — monic, 802
приводимый — reducible, 808
примитивный — primitive, 802
произведение — product, 802
простой — prime, 809
равенство — equality, 803
старший коэффициент — leading
coefficient, 802
степень — degree, 802
сумма — sum, 802
функция — function, 805
Полиномиальная форма — Polynomial
form, 801, 805
Полиномиальное уравнение
решение — Solution of a polynomial
equation, 806
Полугруппа — Semigroup, 398
гомоморфизм — homomorphism, 400
замкнутость — closure, 398
идеал — ideal, 825
минимальное порождающее
множество — minimal generating
set, 400
моноид — monoid, 398
свободная полугруппа — free
semigroup, 399
Полурешетка — Semilattice, 401
верхняя — upper semilattice, 393
нижняя — lower semilattice, 394
Польская запись — Polish notation, 215,
652
Порядок целого числа — Order of an
integer, 440

950 Предметно-именной указатель
Последовательность — Sequence, 163
Фибоначчи — Fibonacci sequence,
449, 452
Постфиксная запись — Postfix notation,
215, 653
Посылка — Premise, 35
Поток — Flow, 692
величина — value, 695
максимальный — maximal, 696
алгоритм нахождения — maximum
flow algorithm, 699
сохранение — conservation, 692
Правило Горнера — Homer's rule, 444
Пратт, В. P. (Pratt, V. R.), 836
Предикат — Predicate, 113
п-местный — n-place, 113
двуместный — two-place, 113
одноместный — one-place, 113
Предметная область — Domain of
discourse, 114
Префиксная запись — Prefix notation, 215,
651, 652
Префиксный код — Prefix code, 638, 754
Принцип индукции — Induction principle,
129
второй — second principle, 136, 799
для целых чисел — for integers, 137
первый — first principle, 799
принцип полного упорядочения —
well-ordering principle, 799
Принцип клеток — Pigeonhole principle,
363
сильная форма — strong form, 365
Принцип полного упорядочения —
Well-ordering principle, 136, 799
Проблема обедающих философов — Dining
philosophers' problem, 721
Производящая функция — Generating
function, 523-525
подсчет — counting, 535
разбиения — partitions, 542
рекуррентное отношение —
recurrence relation, 524
рекуррентное отношение —
recurrence relation, 525
экспоненциальная — exponential, 549
Прообраз — Preimage, 156
Прогрессия — Progression
арифметическая — arithmetic, 164
геометрическая — geometric, 164, 193
Простое число — Prime
взаимно простое — relatively prime,
143
псевдопростое — pseudo-prime, 440
целое — integer, 144
Противоречие — Contradiction, 30
Прямая сумма — Direct sum, 821
Рабин, М. О. (Rabin, M. О.), 830
Разбиение — Partition, ПО, 542
Разделяй и властвуй — Divide and conquer,
212
Размещение — Occupancy, 489
Разупорядочение — Derangement, 504
Райвест, Р. Л. (Rivest, R. L.), 844
Раскраска — Coloring, 775
перечень — inventory, 784
Раскраска графа — Coloring of a graph, 589
Рассел, Бертран (Russell, Bertrand), 67
Расстояние Хемминга — Hamming
distance, 768
Рациональные числа — Rational numbers,
793
Регулярная грамматика — Regular
grammar, 751
Регулярное выражение — Regular
expression, 726
Рекуррентное отношение
линейное — linear, 448
производящая функция — generating
function, 524, 525
Рекурсивная функция — Recursive function
решение — solution, 195
Рекурсия — Recursive, 188
определение — definition, 188
решение — solving, 195
Ретракт — Retract, 402, 728
Ретракционное отображение — Retraction
map, 728
Решетка — Lattice, 403
дистрибутивная — distributive, 405
ограниченная — bounded, 404
пересечение — meet, 403
подрешетка — sublattice, 404
соединение — join, 403
Решето Эратосфена — Sieve of
Eratosthenes, 298
Россер, Дж. Б. (Rosser, J. В.), 834

Предметно-именной указатель 951
Сандей, Д. М. (Sunday, D. М.), 836
Свойства множеств — Set properties
двойное дополнение — double
complement, 81
законы де Моргана — de Morgan's
Laws, 81
свойства ассоциативности —
associative properties, 81
свойства дистрибутивности —
distributive properties, 81
свойства дополнения — complement
properties, 81
свойства коммутативности —
commutative properties, 81
свойства тождества — identity
properties, 81
свойство идемпотентности —
idempotent properties, 81
Связка — Connective, 16
дизъюнкция — disjunction, 16
исключающее или—exclusive or, 18
конъюнкция — conjunction, 16
не-и — nand, 46
не-или — nor, 46
отрицание — negation, 16, 18
условная — conditional, 24
эквиваленция — biconditional, 32
эквиваленция — biconditional, 25
Сеть — Network, 692
паросочетаний — matching network,
708
поток — flow, 692
сечение — cut, 695
Сеть Петри — Petri net, 716
безопасная — safe, 722
достижимое состояние — reachable
state, 720
консервативная — conservative, 722
метка — token, 717
непосредственно достижимое
состояние — immediately
reachable state, 720
ограниченная — bounded, 722
переход — transition, 716
позиция — place, 716
разметка — marking, 716
разрешенный переход — enabled
transition, 718
срабатывание — firing, 717
частичный тупик — deadlock, 721
Сечение — Cut, 695
минимальное — minimal, 696
пропускная способность — capacity,
695
Символ Кронекера — Kronecker delta, 804
Синдромы — Syndromes, 763
Система вычетов — Residue system
первичная — primary, 153
полная — complete, 153
приведенная — reduced, 153
Система счисления
двоичная — binary representation, 219
десятичная — decimal representation,
219
шестнадцатеричная — hexadecimal
representation, 222
Скаляр — Scalar, 167
Скалярное произведение — Dot product,
169
Слово — Word, 725
Сложность — Complexity, 201
О большое — big-oh, 201
Случайная величина — Random variable,
375
Смежный класс — Coset, 413
Составное число — Composite number, 144
Сочетание — Combination, 335
обобщенное — generalized, 354
с повторением — with repetition, 361
Сравнение — Congruence, 149, 424
Стабилизатор — Stabilizer, 778
Стек — Stack, 216
вталкивание — push, 216
выталкивание — pop, 216
Стрелка Пирса — Peirce's Arrow, 45
Строка — String, 399, 725
конкатенация — concatenation, 725
Таблица истинности — Truth table, 17
Тавтология — Tautology, 30
Теорема — Theorem, 35
Вандермонда — Vandermonde's
Theorem, 340
Клини — Kleene's Theorem, 738
Куратовского — Kuraotowski's
Theorem, 583
Пойа о подсчете — Polya's Counting
Theorem, 785

952 Предметно-именной указатель
Рамсея — Ramsey's Theorem, 368
Уилсона — Wilson's Theorem, 437
Эйлера — Euler's Theorem, 439
о разложении на простые множители
— Prime Factorization Theorem,
146
Теория Рамсея — Ramsey theory, 366
Тотиент-функция Эйлера — Euler's totient
function, 434
Точка сочленения — Articulartion point,
561, 668
Треугольник Паскаля — Pascal's triangle,
339
Трихотомия
аксиома — Trichotomy Axiom, 127
Умозаключение — Argument, 35
сведение к абсурду — reductio ad
absurdum, 247
modus ponens, 39, 40
modus tollens, 40
выбор — cases, 40
гипотеза — hypothesis, 35
доказательство — proof, 42
исключающий выбор — case
elimination, 40
контрапозиция — contrapositive, 126
конъюнкция — conjunction, 40
ложная инверсия — inverse fallacy, 42
ложная конверсия — converse fallacy,
41
неправильное — invalid, 41
посылка — premise, 35
правило отделения — law of
detachment, 39, 40
правильное — valid, 35
расширение — addition, 40
сведение к абсурду — reductio ad
absurdum, 41
силлогизм — syllogism, 40
специализация — specialization, 40
Универс — Universe, 114
Универсальная конкретизация — Universal
instantiation, 117
Универсальное обобщение — Universal
generalization, 118
Упорядоченная пара — Ordered pair, 75
Ф
Формирование перестановок — Generating
permutations, 344
Формирование сочетаний — Generating
combinations, 344
Функция — Function, 156
Аккермана — Ackerman's function,
192
Сложность — Complexity, 201
Эйлера — Euler's ф function, 434
биекция — bijection, 158
бинарная операция — binary
operation, 163, 397
верхнее округление — ceiling, 162
инъективная — injective, 158
нижнее округление — floor, 162
областью значений — range, 156
область определения — domain, 156
область потенциальных значений —
codomain, 156
образ — image, 156
перестановка — permutation, 158
прообраз — preimage, 156
сюръективная — surjective, 158
тождественная — identity, 159
факториал — factorial, 162
хеширования — hashing function, 837
минимальная совершенная —
minimum perfect, 837
Ханойская башня — Tower of Hanoi, 193
Характер — Character
Дирихле — Dirichlet character, 826
главный — principal, 821
группы — group character, 820
полугруппы — semigroup character,
825
Хеллмэн, М. Э. (Hellman, M. E.), 847, 849
Хроматический многочлен — Chromatic
polynomial, 589
Хроматическое число — Chromatic number,
589
Ц
Целое число — Integer
взаимно простые — relatively prime,
143
гауссовы — Gaussian integers, 816

Предметно-именной указатель 953
делитель — divisor, 139
кратное — multiple, 139
множество классов вычетов по
модулю п — set of integers
modulo n, 149
наибольший общий делитель —
greatest common divisor, 142
наименьшее — least, 135
наименьшее общее кратное — least
common multiple, 143, 304
порядок — order of, 440
простое — prime, 144
простое число — prime, 798
составное — composite, 144
сравнимое — congruent, 149
Цепи Маркова — Markov chains, 386
матрица перехода — transition matrix,
387
состояния — states, 386
Цепная дробь — Continued fraction, 309
конечная — finite continued fraction,
309
простая — simple continued fraction,
309
Цикл — Cycle
гамильтонов — hamiltonian, 601
Цикловый индекс — Cycle index, 783
Чанг (Chang, С. С), 839
Частично упорядоченное множество —
Partially ordered set, 103, 392
вполне упорядоченное — total
ordering, 104, 392
диаграмма Гессе — Hasse diagram,
104
максимальный элемент — maximal
element, 392
минимальный элемент — minimal
element, 393
наибольшая верхняя грань — greatest
lower bound, 392
наименьшая верхняя грань — least
upper bound, 392
наименьший элемент — least element,
392
сравнимое — comparable, 104, 392
топологическая сортировка —
topological sorting, 185
цепь — chain, 104
Частичный порядок — Partial ordering,
103, 392
Числа Каталана — Catalan numbers, 190,
495
Числа Стирлинга — Stirling numbers
второго рода — second kind, 480, 481,
490, 491, 553
первого рода — first kind, 480, 481,
492, 493
Число Рамсея — Ramsay number, 367
ш
Шамир, A. (Shamir, A.), 844
Шекерес (Szekeres), 364, 365, 367
Ши (Shieh, J. С), 839
Шифрование — Encryption, 844
Шонфилд, Л. (Schoenfeld, L), 834
Штрих Шеффера — Sheffer Stroke, 45
Эйлер, Леонард — Euler, Leonard, 438
Эквивалентность — Equivalence
класс — class, 108
отношение — relation, 107
Экзистенциональная конкретизация —
Existential Instantiation, 118
Экзистенциональное обобщение —
Existential Generalization, 118
Экспоненциальная производящая функция
— Exponential generating
function, 549
Элементарная дизъюнкция — Maxterm, 48
Элементарная конъюнкция — Minterm, 47
Элементарные дроби — Partial fractions,
527
Эпиморфизм — Epimorphism
колец — Ring epimorphism, 790
полугрупп — semigroup epimorphism,
415
Эрдош (Erdos), 364, 365, 367
Я
Язык — Language, 725
Яэшке, Г. (Jaeschke, G.), 837

ЕС обозначений
¦ ЛОГИКА
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
И.
12.
13.
14.
pAq
pVq
~р
у
р-+я
р*-+ я
p = q
Т
F
'Г
1
V
3
¦ МНОЖЕСТВА
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
{ai a2 a3
{*:>} '
ае Л
лев
0
и
ЛПВ
лив
л- в
ЛАВ
Л'
V(A)
Лх В
(а, 6)
aRb
R-1
SoR
33.
34.
t=i
р a q стр. 16
р или q стр. 16
не р стр. 16
исключающее или стр. 18
если р, то q стр. 23
р тогда и только тогда, когда q стр. 25 и 32
р логически эквивалентно q стр. 28
утверждение-тавтология стр. 30
логически ложное утверждение стр. 30
следовательно стр. 35
штрих Шефера (не-и) стр. 45
стрелка Пирса (не-или) стр. 45
для всех стр. 114
существует стр. 115
множество элементов ai,a2,a3,..., а„ стр. 67
множество элементов, обладающих свойством Р стр. 68
а есть элемент множества А стр. 68
множество Л есть подмножество множества В стр. 68
пустое множество, или нуль-множество стр. 69
универсальное множество стр. 69
пересечение множеств Л и В стр. 71
объединение множеств Л и В стр. 71
разность множеств Л и В стр. 72
симметрическая разность множеств Л и В стр. 72
дополнение множества Л стр. 72
множество всех подмножеств множества Л стр. 74
декартово произведение множеств Л и В стр. 75
упорядоченная пара стр. 75
а и 6 связаны отношением R стр. 90
отношение, обратное к R стр. 91
композиция отношений 5 и R стр. 92
множество, с отношением частичного порядка < стр. 103
пересечение множеств А\, Л2,..., Лп стр. 138
объединение множеств А\, Л2,..., Лп стр. 138

Список обозначений 955
¦ ФУНКЦИИ
35. f:A-*B
36. /(?)
37. Г\Р)
38. fog
39. /-1
40. f(x) = [x\
41. /(*) = [*!
42. /(*)=*!
43. OE(n))
44. tfy
функция / из А в В
образ ?
прообраз F
композиция функций / и д
обратная функция
нижнее округление
верхнее округление
факториал
О-большое от д(п)
стр. 156
стр. 156
стр. 156
стр. 157
стр. 158
стр. 162
стр. 162
стр. 162
стр. 201
символ Кронекера стр. 240 и 804
¦ КОММУТАЦИОННЫЕ СХЕМЫ
45. D
46. D
47. >
48. D>
49. L>
50. p ¦ q
51. p + q
52. P'
логический элемент и
логический элемент или
логический элемент не
логический элемент не-и
логический элемент не-или
булево произведение (р и q)
булева сумма (р или q)
булево дополнение (не р)
¦ ГРАФЫ И ДЕРЕВЬЯ
53. G(V,E)
54. {a,b}
55. (a,b)
56. deg(y)
57. tfn
58. Km,n
59. ^ot>iU2 • • • г>п
60. GC(V,E')
61. CG(A)
62. Ge
63. G/e
64. с/(С)
65. c(e)
66. /(e)
67. va/(/)
68. E,T)
69. C(S,T)
¦ ТЕОРИЯ ЧИСЕЛ
70. Z
71. N или Z+
72. alb
граф с вершинами V и ребрами Е стр.
ребро между вершинами а и Ъ стр.
ориентированное ребро из вершины а в вершину Ъ
степень вершины v
полный граф с числом вершин п
полный двудольный граф с числом вершин тип
путь длины п из vo в Vn
дополнение к графу G(V, E)
число способов раскраски графа G(V, E) с использо-
использованием А цветов
граф G с удаленным ребром е
граф G с удаленным ребром е = {а,Ъ} и отожде-
отождествленными вершинами а и Ъ
замыкание графа G(V, E)
пропускная способность ребра е
поток через ребро е
величина потока /
сечение сети на подсети S и Т
пропускная способность сечения E, Т)
множество целых цисел
множество целых положительных чисел
а делит b
стр. 58
стр. 58
стр. 58
стр. 60
стр. 60
стр. 56
стр. 56
стр. 56
95 и 244
95 и 244
стр. 252
стр. 247
стр. 250
стр. 251
стр. 248
стр. 559
стр. 589
стр. 590
стр. 590
стр. 606
стр. 691
стр. 692
стр. 695
стр. 695
стр. 695
стр. 123
стр. 127
стр. 139

956 Список обозначений
73.
74.
75.
76.
77.
78.
79.
НОД(а, Ь)
НОК(а,6)
а = Ь (mod n)
[а]
[а]ф[6]
[а] 0 [6]
[[т])п
80. 0
81. ordn а
¦ МАТРИЦЫ
82. [Aij]
83. А + В
84. аЛ
85. ЛБ
86. А1
87. ЛОБ
88. А^
89. |Л| = det(A)
90. In
91. Л
92. adj(^)
наибольший общий делитель чисел а и 6
наименьшее общее кратное
а сравнимо с b по модулю п
класс эквивалентности, содержащий a
сумма классов эквивалентности
произведение классов эквивалентности
наименьшее целое положительное число, сравнимое
С 771 ПО МОДУЛЮ 71
функция Эйлера
порядок а по модулю п
матрица элементов Aij
сумма матриц
умножение матрицы на скаляр
произведение матриц
транспонированная матрица А
булево произведение матриц
матрица, полученная из А удалением г-ой строки и
j-ro столбца
определитель (детерминант) матрицы Л
единичная n x n матрица
матрица, обратная к А
матрица, сопряженная с А
93.
94.
РЕКУРСИЯ И ПОДСЧЕТ
п!
95. P(n,r) = T^
96. 0G1,0 = 0 = ^^7
97. PGi;ni,n2,...,nfc) =
98. C(n;ni,n2,.. .,nfc) =
99. P(A)
100. P(B | Л)
101. Е(Д)
102. /x
103. а2
104. Д(р,9)
105. Фиб(тг)
106. Кат(тг) = С,
107.
тг-факториал
+ a2 -\ \- an
символ суммы
число перестановок объектов из п по г
число сочетаний объектов из тг по г
! обобщенная перестановка
обобщенное сочетание
n ,n, w ,
!
108. A*7(z)
109. Е
ПО. х(п)
111. апх(п) Ч
112.
П1 'тгг'.-.тг^!
вероятность события А
вероятность В при данном А
ожидаемое значение случайной величины R
среднее значение случайной величины R
дисперсия случайной величины R
число Рамсея
п-ое число Фиббоначи
7i-oe число Каталана
стабилизатор раскраски С
к-я разность функции f(x)
оператор, определяемый равенством
я(Я*) = я* + 1)
Ч Ь а\х Ч- а0 факториальный
многочлен
1
стр. 142
стр. 143
стр. 149
стр. 108
стр. 152
стр. 152
стр. 151
стр. 434
стр. 440
стр. 167
стр. 169
стр. 168
стр. 170
стр. 171
стр. 172
стр. 237
стр. 238
стр. 240
стр. 240
стр. 241
стр. 162
стр. 164
стр. 332
стр. 335
стр. 354
стр. 357
стр. 348
стр. 371
стр. 376
стр. 379
стр. 379
стр. 367
стр. 190
стр. 190
стр. 778
стр. 469
стр. 470
стр. 473
стр. 473
стр. 479

Список обозначений 957
из. О
114. s[n)
115. S™
116. Е
117. Ln
118. Dn
119. rfc(c)
120. Д(х,(
121. [to : *]
122. T<n)
¦ АЛГЕБРА
123. (Л,У) или (Л,+)
124. (Л,Л) или (Л,-)
125. (S,V,A)
126. aoH
127. GieG2
128. (а)
129. А[х]
130.x
131.
132. Л*
133. M =
134. МЩ
135. Г = (АГ,Т,5,Р)
¦ КОДЫ
136. wt{c)
137. CL
138. GH
139. G^
140. (с, с')
141. D{C)
^ стр. 480
число Стирлинга первого рода стр. 480
число Стирлинга второго рода стр. 480
оператор суммирования стр. 483
n-ое число Лукаса стр. 459
число разупорядочений п различных упорядоченных стр. 504
символов
число возможных расположений к ладей стр. 509
на доске С в неатакующих позициях
ладейный полином на доске С стр. 509
цепная дробь стр. 309
число способов размещения п различимых объектов стр. 553
в к различимых ящиках при условии, что ни один из
ящиков не будет пустым
верхняя полурешетка Л стр. 393
нижняя полурешетка Л стр. 394
решетка S стр. 403
левый смежный класс стр. 413
прямая сумма групп G\ и Сг стр. 821
главный идеал, порожденный элементом а стр. 794
множество полиномов с коэффициентами в Л стр. 805
характер группы стр. 821
строка символов алфавита Л стр. 725
множество всех строк над алфавитом Л стр. 725
автомат с алфавитом Л, множеством состояний 5, стр. 731
начальным состоянием so, множеством допускающих
состояний Т и функцией переходов F
язык, допускаемый автоматом М стр. 731
грамматика с множеством нетерминальных символов стр. 742
7V, множеством терминальных символов Т, началь-
начальным символом S и множеством продукций Р
число единиц в строке кода с стр. 758
код, двойственный к коду С стр. 761
порождающая матрица Хемминга стр. 767
матрица контроля четности Хемминга стр. 767
расстояние Хемминга между строками кодов сне' стр. 768
наименьшее расстояние между двумя произвольными стр. 769
элементами С

Научно-популярное издание
Джеймс Андерсон
Дискретная математика и комбинаторика
Литературный редактор
Верстка
Художественный редактор
Корректоры
Т. Т. Шматко
М.Р. Саит-Аметов
С.А. Чернокозинский
Л.А. Гордиенко, О.В. Мишутина
Издательский дом "Вильяме".
101509, Москва, ул. Лесная, д. 43, стр. 1.
Изд. лиц. ЛР № 090230 от 23.06.99
Госкомитета РФ по печати.
Подписано в печать 25.08.2004. Формат 70x100/16
Гарнитура AntiquaPSCyr. Печать офсетная.
Усл. печ. л. 77,4. Уч.-изд. л. 63,17.
Доп. тираж 2500 экз. Заказ № 343.
Отпечатано с диапозитивов в ФГУП "Печатный двор"
Министерства РФ по делам печати,
телерадиовещания и средств массовых коммуникаций
197110, Санкт-Петербург, Чкаловский пр., 15.