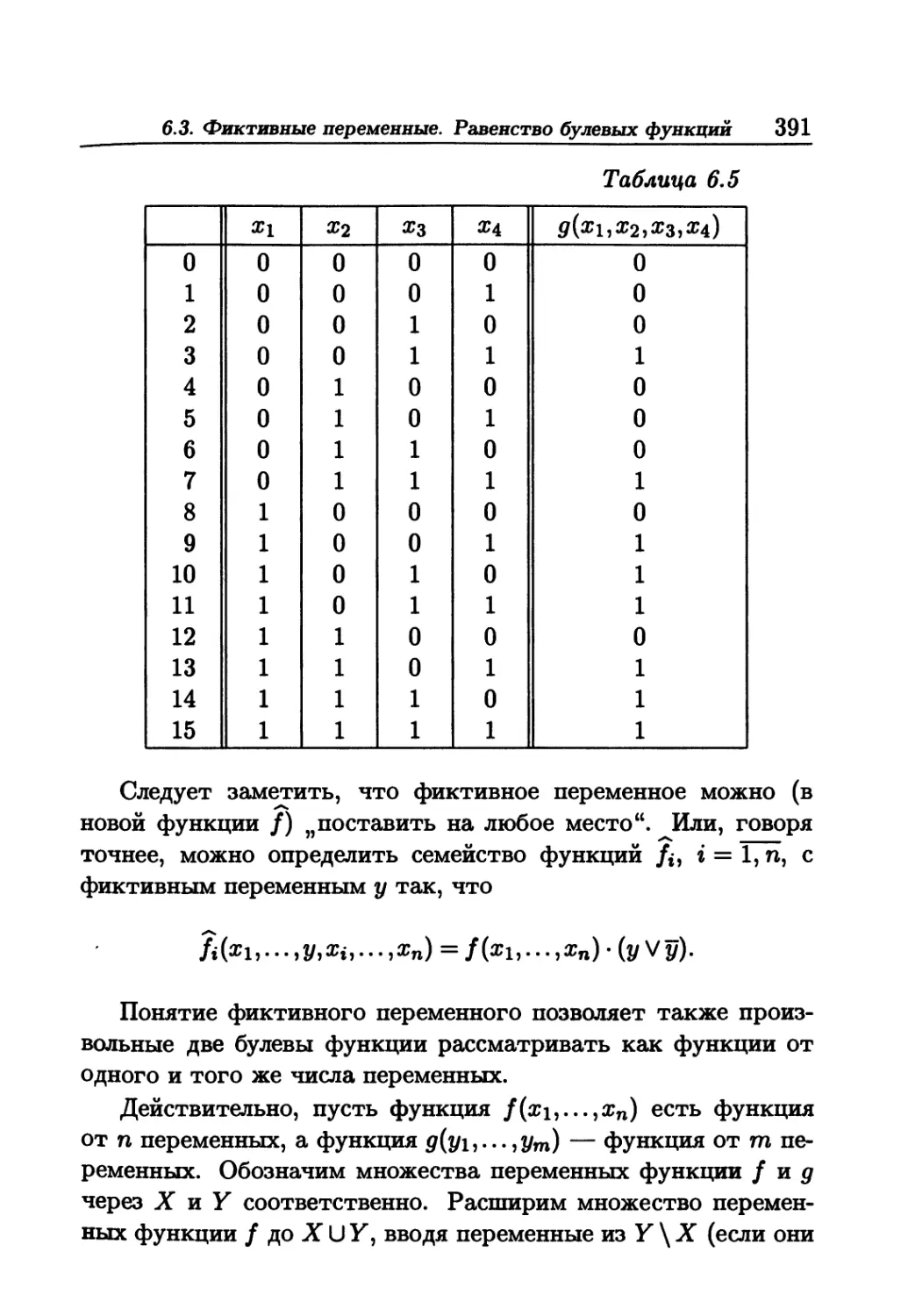
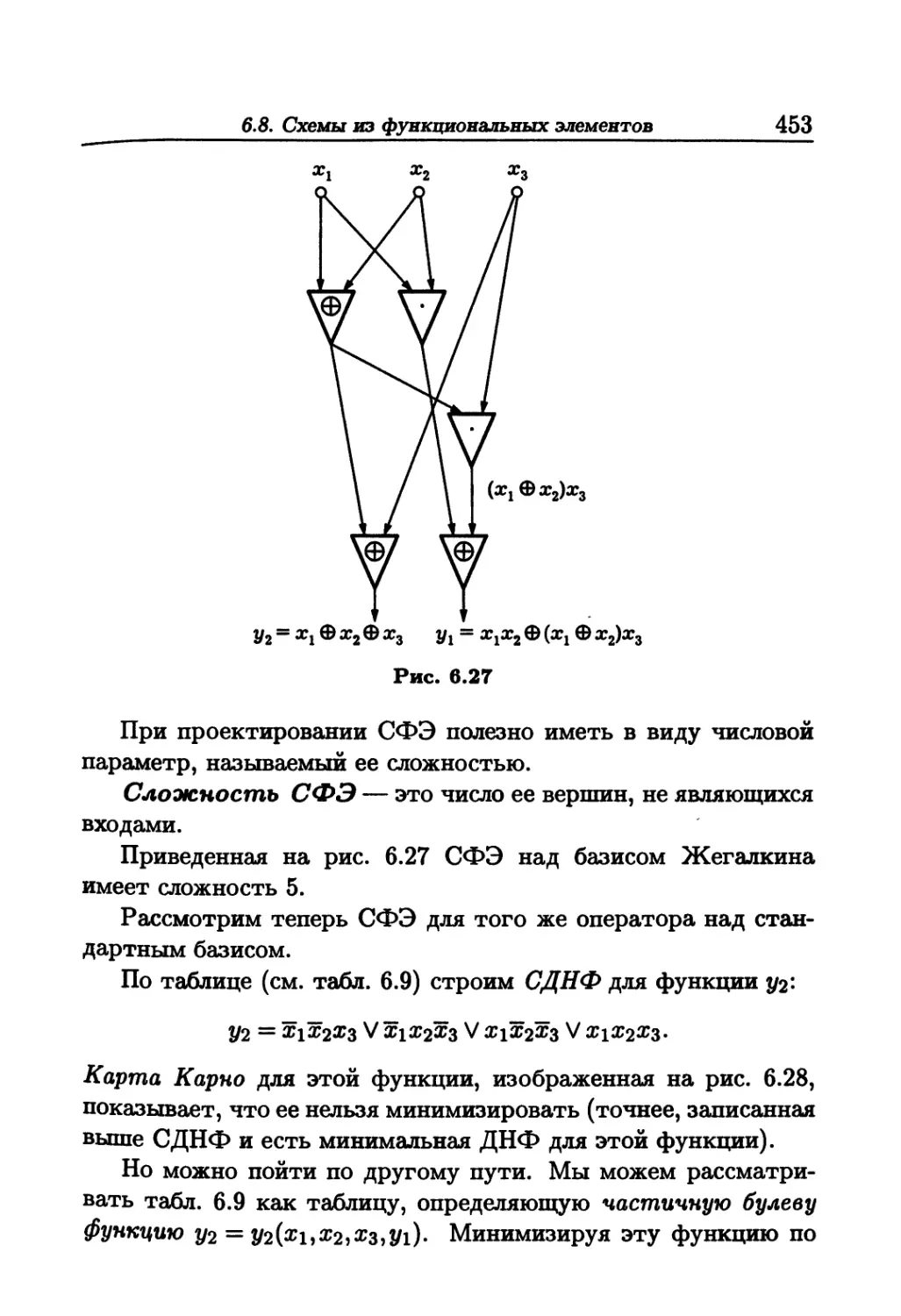
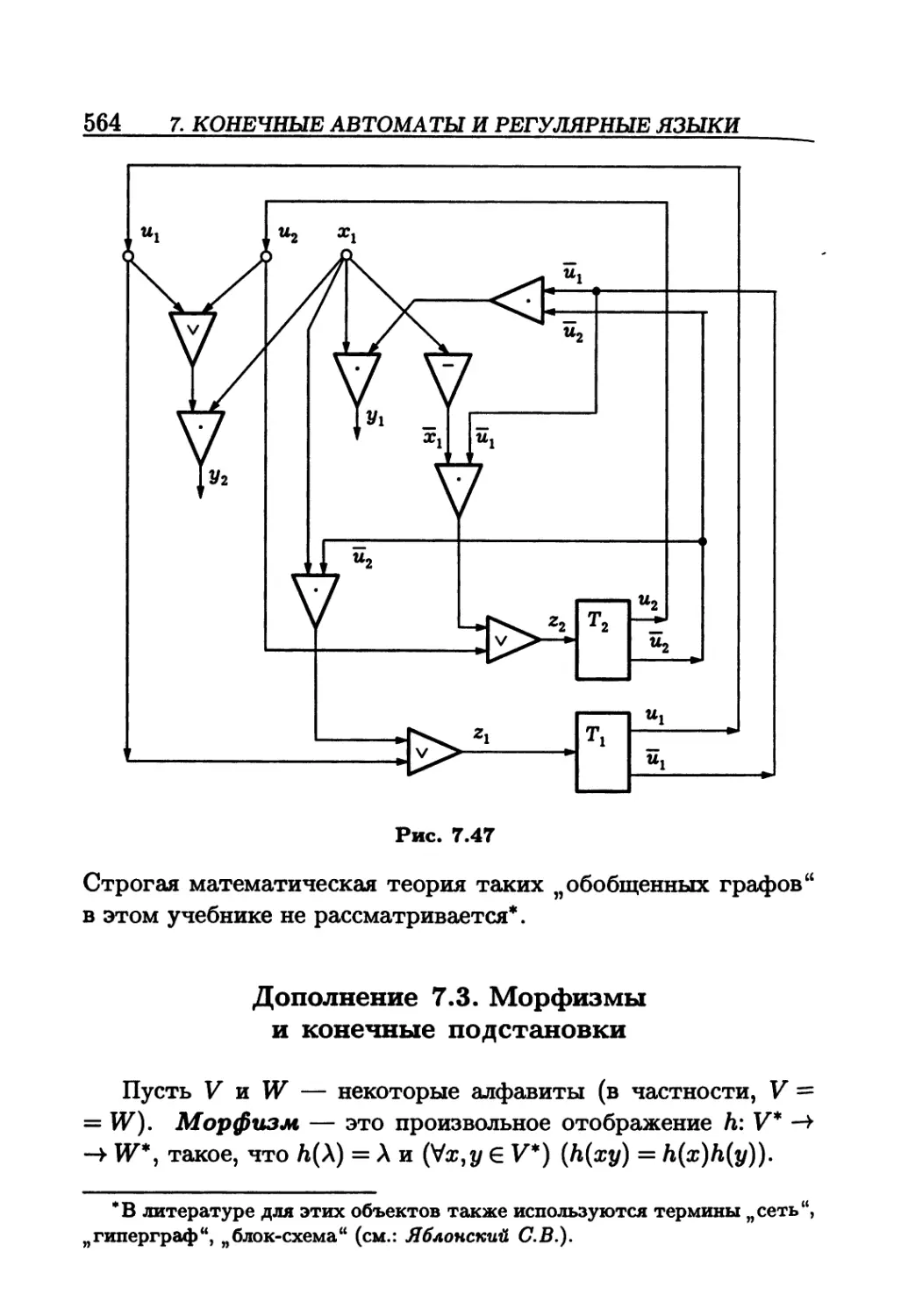
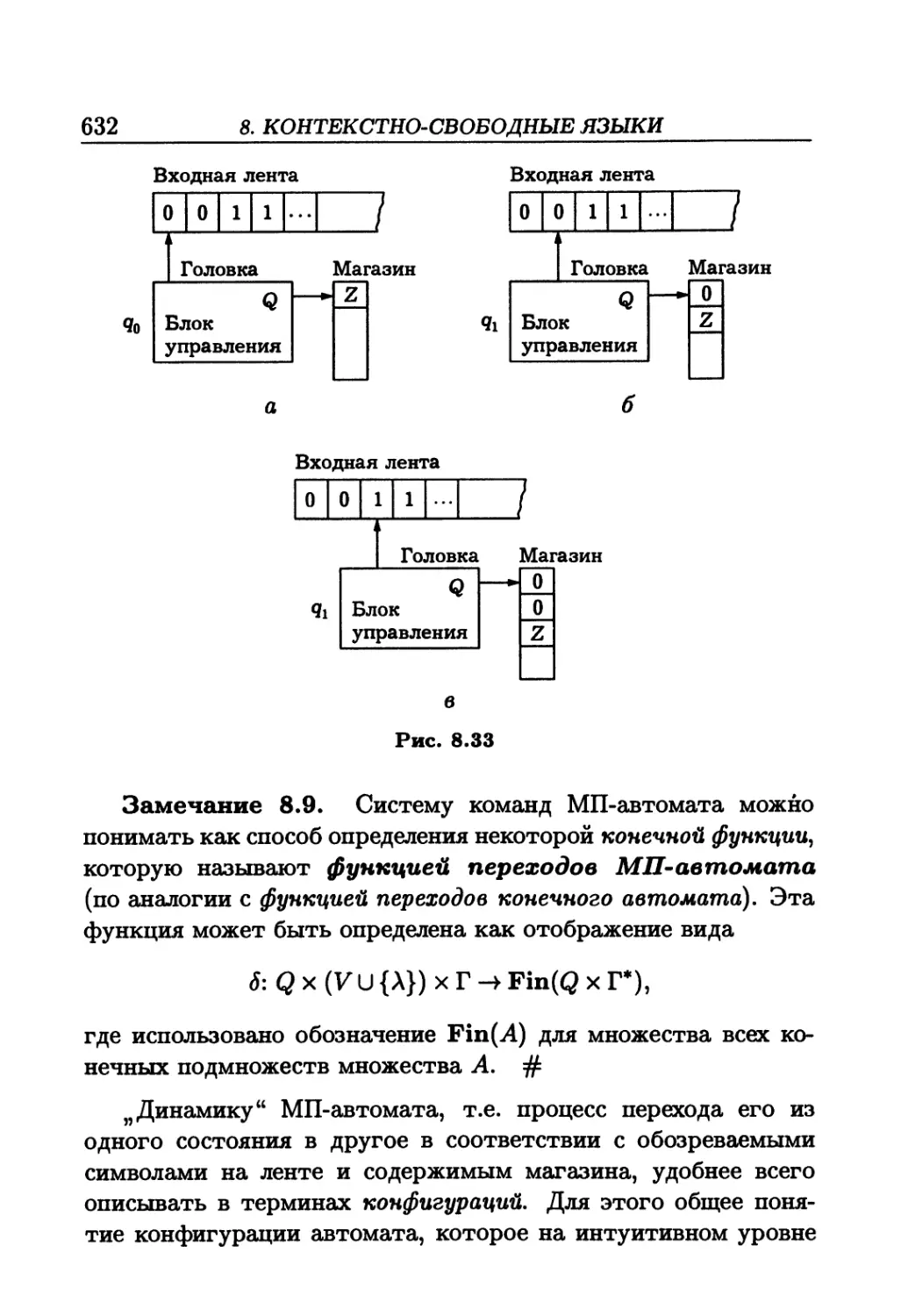
Author: Белоусов А.И. Ткачев СБ.
Tags: алгебра теория вероятностей математическая статистика комбинаторный анализ теория графов высшая математика дискретная математика
ISBN: 5-7038-1769-2
Year: 2004
Математика в техническом
университете
Выпуск XIX
Серия удостоена
Премии Правительства
Российской Федерации
в области науки и техники
за 2003 год
Комплекс учебников из 21 выпуска
Под редакцией B.C. Зарубина и А.П. Крищепко
I. Введение в анализ
II. Дифференциальное исчисление функций
одного переменного
III. Аналитическая геометрия
IV. Линейная алгебра
V. Дифференциальное исчисление функций
многих переменных
VI. Интегральное исчисление функций
одного переменного
VII. Кратные и криволинейные интегралы.
Элементы теории поля
VIII. Дифференциальные уравнения
IX. Ряды
X. Теория функций комплексного переменного
XI. Интегральные преобразования
и операционное исчисление
XII. Дифференциальные уравнения
математической физики
XIII. Приближенные методы математической физики
XIV. Методы оптимизации
XV. Вариационное исчисление и оптимальное управление
XVI. Теория вероятностей
XVII. Математическая статистика
XVIII. Случайные процессы
XIX. Дискретная математика
XX. Исследование операций
XXI. Математическое моделирование в технике
А.И. Белоусов, СБ. Ткачев
ДИСКРЕТНАЯ
МАТЕМАТИКА
Под редакцией
д-ра техн. наук, профессора B.C. Зарубина
и д-ра физ.-мат. наук, профессора А.П. Крищенко
Издание третье, стереотипное
Рекомендовано
Министерством образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Москва
Издательство МГТУ им. Н.Э. Баумана
2004
УДК 512.54-519.1@75.8)
ББК 22.174
Б43
Рецензенты: чл.-корр. РАН Ю.Н. Павловский, проф. А.К. Платонов
Б43 Белоусов А.И., Ткачев СБ. Дискретная математика:
Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. -
3-е изд., стереотип. - М.: Изд-во МГТУ им. Н.Э. Баумана,
2004. -744 с. (Сер. Математика в техническом университете;
Вып. XIX).
ISBN 5-7038-1769-2 (Вып. XIX)
ISBN 5-7038-1270-4
В девятнадцатом выпуске серии „Математика в техническом универ-
университете" изложены теория множеств и отношений, элементы современной
абстрактной алгебры, теория графов, классические понятия теории буле-
булевых функций, а также основы теории формальных языков, куда включены
теории конечных автоматов, регулярных языков, контекстно-свободных
языков и магазинных автоматов. В анализе графов и автоматов особое
внимание уделено алгебраическим методам.
Содержание учебника соответствует курсу лекций, который авторы
читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен пре-
преподавателям, аспирантам и инженерам.
Ил. 200. Табл. 27. Библиогр. 65 назв.
УДК 512.5+519.1@75.8)
ВБК 22.174
© А.И. Белоусов, СБ. Ткачев, 2001
© Московский государственный
технический университет
ISBN 5-7038-1769-2 (Вып. XIX) им НЭ' Баумана> 2001
ISBN 5-7038-1270-4 © Издательство МГТУ
им. Н.Э. Баумана, 2001
К 175-летию
МГТУ им. Н.Э. Баумана
ПРЕДИСЛОВИЕ
Предлагаемая читателю книга является девятнадцатым вы-
выпуском комплекса учебников „Математика в техническом уни-
университете". Она содержит систематическое изложение курса
дискретной математики.
Развитие классической („непрерывной") математики бы-
было обусловлено прежде всего решением задач естествознания,
главным образом физики. „Дискретная" же математика раз-
развивалась в связи с изучением законов и правил человеческого
мышления, что и обусловило ее применение в тех областях
техники, которые так или иначе связаны с моделированием
мышления, и в первую очередь в вычислительной технике и
программировании.
Мышление реализует себя прежде всего в языке. Поэтому
разумно считать, что ядро дискретной математики образует
именно математическая теория языков, точнее, область этой
теории, называемая теорией формальных языков. Слово „фор-
„формальный" подчеркивает, что в этой теории изучаются в основ-
основном искусственные языки, специально созданные для каких-то
целей: языки программирования, языки математики и т.п. Те-
Теория формальных языков является базой теории кодирования,
„криптологии", изучающей методы защиты информации, тео-
теории алгоритмов и в определенном смысле математической ло-
логики. В прикладном аспекте эта теория служит основой разра-
разработки математического обеспечения вычислительных машин.
Доминирующим в современной теории формальных языков
является алгебраический подход, в котором существенно ис-
используется аппарат, базирующийся на понятии алгебраической
структуры полукольца. Этот аппарат во многом похож на ап-
аппарат линейной алгебры. Систематическое изложение теории
ПРЕДИСЛОВИЕ
формальных языков на базе теории полуколец и является одной
из основных задач этой книги. Отметим, что в отечественной
учебной литературе такой подход почти не получил отражения.
Теория формальных языков существенно опирается и на те-
теорию графов. Многие задачи теории языков (например, задача
определения языка конечного или магазинного автомата) сво-
сводится к задаче о путях во взвешенных (размеченных) ориенти-
ориентированных графах, где множество меток имеет алгебраическую
структуру полукольца.
Изложение материала построено следующим образом. Гла-
Глава 1 посвящена множествам и отношениям. Здесь напомина-
напоминаются основы теории множеств, изложенные в первом выпуске
комплекта учебников, причем некоторые вопросы излагаются
более детально. Основное содержание главы составляет теория
отношения. Центральным результатом является теорема о не-
неподвижной точке для индуктивных упорядоченных множеств,
на базе которой строятся методы решения задач о путях в гра-
графах и алгебраические методы в теории формальных языков.
Ввиду важности алгебраических методов в дискретной ма-
математике большое внимание уделяется алгебраической теории:
ей посвящены три главы. В главе 2 излагаются элементы клас-
классической общей алгебры и рассматриваются группы, кольца
и поля. Глава 3 посвящена полукольцам и булевым алгебрам.
Приведенный здесь материал имеет важное значение с точ-
точки зрения приложения алгебраических методов как в теории
формальных языков, так и в теории булевых функций. Особен-
Особенностью изложения является определение булевой алгебры как
частного случая полукольца. В главе 4 приведены некоторые
результаты общей теории алгебраических систем.
Глава 5 посвящена теории графов. Центральное место в гла-
главе занимает изложение алгебраического метода решения задач
о путях в ориентированных графах, размеченных над полуколь-
полукольцами. Этот материал служит, с одной стороны, иллюстрацией
применения алгебраической техники в решении графовых за-
задач, а с другой — основой решения задач в теории формальных
языков. Глава содержит также описание некоторых алгорит-
алгоритмов на графах: алгоритма „поиска в глубину" и „поиска в
ширину", алгоритма Краскала для отыскания остовного дерева
наименьшего веса, алгоритма топологической сортировки. Ко-
Коротко рассматриваются изоморфизм графов, группы автомор-
автоморфизмов графов и элементы цикломатики (анализа структуры
циклов неориентированного графа).
Глава 6 посвящена классическому разделу дискретной ма-
математики — булевым функциям — и включает вопросы мини-
минимизации булевых функций и теорему Поста о функциональной
полноте.
В главах 7 и 8 изложена теория формальных языков. Гла-
Глава 7 содержит „линейную часть" этой теории — теорию ко-
конечных автоматов и регулярных языков, а глава 8 — теорию
контекстно-свободных языков. Это важнейший класс языков,
его теоретический анализ является основой многих информа-
информационных технологий, таких, в частности, как проектирование
компиляторов или разработка лингвистического обеспечения
баз данных. Фундаментальным является понятие магазинно-
магазинного автомата — распознавателя в классе контекстно-свободных
языков. Именно эта модель языка служит математической
основой конкретных технологий разработки синтаксических
анализаторов для языков программирования.
В дополнениях к главе 8 приведены элементарные сведения о
синтаксическом анализе контекстно-свободных языков и введе-
введение в математическую теорию семантики формальных языков
(в частности, языков программирования). Здесь мы пытаемся
перекинуть „мостик" от чистой теории к практической тех-
технологии анализа контекстно-свободных языков, используемой
прежде всего в компиляторах. Этот материал призван проил-
проиллюстрировать связь между изложенои математической теорией
и ее приложениями к разработке математического обеспечения
компьютеров.
В конце каждой главы помещены задачи для самостоятель-
самостоятельного решения. Наиболее трудные задачи снабжены указаниями.
В некоторых задачах содержатся и теоретические результаты,
8 ПРЕДИСЛОВИЕ
дополняющие основной текст. Часть задач придумана автора-
авторами, часть заимствована из других задачников и учебников.
Дискретная математика — бурно развивающаяся область.
К сожалению, в этом учебнике мы не нашли возможности даже
обзорно изложить некоторые результаты, развивающие клас-
классическую теорию графов (гиперграфы, сети Петри, потоко-
потоковые диаграммы) и теорию языков (сверхъязыки, автоматы над
структурами, отличными от слов, теорию алгоритмов как ди-
динамических систем, топологические методы в семантике). Мы
рекомендуем интересующемуся читателю обстоятельно напи-
написанную „Handbook of Theoretical Computer Science", а также
последние выпуски периодического издания „Lecture notes in
Computer Science". Наиболее интересные, с нашей точки зре-
зрения, работы из этого издания указаны в списке литературы.
Для успешного освоения материала книги достаточно зна-
знания традиционных курсов математического анализа и линейной
алгебры, читаемых в техническом университете. Мы в основ-
основном опирались на материал, изложенный в выпусках I-IV на-
настоящего комплекса учебников.
В тексте книги имеются ссылки на другие выпуски комплек-
комплекса учебников. Такой ссылкой служит номер выпуска. Напри-
Например, [I] означает, что имеется в виду первый выпуск. Ссылки
без римских цифр относятся только к этому, девятнадцатому,
выпуску. Так, (см. 1.2) отсылает читателя ко второму пара-
параграфу первой главы, а (см. Д.7.1) — к первому дополнению
седьмой главы этой книги. Ссылки на номера формул и ри-
рисунков набраны обычным шрифтом (например, B.1) — первая
формула в главе 2, (рис. 1.5) — пятый рисунок в главе 1).
Большинство используемых в этой книге обозначений поме-
помещено в перечне основных обозначений, где наряду с их краткой
расшифровкой указаны глава и параграф, в которых можно
найти более подробное объяснение по каждому из обозначений.
Для части обозначений, введенных в первом выпуске, указаны
глава и параграф первого выпуска, а также при необходимости
глава и параграф этой книги. Например, 1-1.3, 1.1 показыва-
показывает, что обозначение введено в третьем параграфе первой главы
9
первого выпуска и пояснения к нему содержатся в первом па-
параграфе первой главы девятнадцатого выпуска. После этого
перечня приведены написание и русское произношение входя-
входящих в формулы букв латинского и греческого алфавитов.
В конце книги помещены список рекомендуемой литературы
и предметный указатель, в котором расположены в алфавитном
порядке (по существительному в именительном падеже) все
выделенные в тексте полужирным курсивом термины с
указанием страницы, где они строго определены или описаны.
Выделение термина светлым курсивом означает, что этот
термин в данном параграфе относится к ключевым словам
и читателю должно быть известно его значение. Значение
этого термина можно уточнить, найдя с помощью предметного
указателя необходимую страницу этого выпуска, на которой
термин определен или описан. Бели термин введен в другом
выпуске, то дана ссылка на этот выпуск (например, III означает
ссылку на третий выпуск), а также указана курсивом страница
предлагаемой книги, на которой имеются некоторые пояснения
к этому термину.
Авторы выражают глубокую благодарность А.А. Кириль-
ченко и М.С. Виноградовой за многочисленные пожелания и
замечания, которые были учтены при подготовке книги.
Перед чтением книги в целях самоконтроля предлагается
выполнить приведенные ниже задания. В тексте заданий пря-
прямым полужирным шрифтом выделены термины, значение
которых должно быть известно читателю, а в конце каждо-
каждого задания указана ссылка на номер выпуска, в котором можно
найти соответствующие разъяснения. В основном тексте книги
эти термины не выделены и не входят в предметный указатель.
Задания для самопроверки
1. Что такое конечное множество, подмножество, эле-
элемент множества? Какими способами можно задать мно-
множество? Приведите примеры конечных и счетных мно-
множеств. [I]
10 ПРЕДИСЛОВИЕ
2. Является ли множество всех рациональных чисел
счетным? [I]
3. Что такое множество всех действительных чисел?
Что понимают под расширенной (пополненной) числовой
прямой? [I]
4. Является ли множество натуральных чисел соб-
собственным подмножеством множества целых чисел? [I]
5. Какие операции над множествами Вы знаете? Перечи-
Перечислите свойства этих операций. [I]
6. В чем заключается принцип двойственности для за-
законов де Моргана? [I]
7. Из каких этапов состоит доказательство по методу ма-
математической индукции? [I]
8. Сформулируйте определение взаимно однозначного
отображения двух множеств. Что такое тождественное
отображение? Чему равна композиция прямого и обрат-
обратного отображений двух множеств? [I]
9. При каких условиях отображение одного множества в
другое называют сюръекцией, инъекцией и биекцией? [I]
10. Что называют неподвижной точкой отображения?
Сколько неподвижных точек у отображения у = sina;? [I]
11. Какие элементарные функции Вы знаете? [II]
12. Что такое область определения и область значения
функции? [I]
13. Приведите примеры функций, непрерывных в интер-
интервале (а,Ь). В чем различие между монотонной и строго
монотонной в некотором промежутке функциями? [I]
14. Что такое последовательность элементов множе-
множества? [I]
15. Какими свойствами обладает предел последователь-
последовательности? [I]
16. Сформулируйте признак Вейерштрасса сходимо-
сходимости ограниченной последовательности. [I]
17. Какова связь между количеством сочетаний и количе-
количеством размещений из п элементов по к? [I]
11
18. Что такое единичная и нулевая матрицы? [III]
19. Что такое диагональная матрица, верхняя тре-
треугольная (нижняя треугольная) матрица? [III]
20. Для матриц каких типов (размеров) определены
операции сложения и умножения? [III]
21. Что такое определитель числовой квадратной ма-
матрицы порядка п? Как связаны операции транспонирова-
транспонирования и вычисления обратной матрицы? [III]
22. Какую квадратную матрицу называют вырожденной,
а какую — невырожденной? [III]
23. Какие свойства имеют операции сложения свободных
векторов в пространстве и умножения вектора на число?
Какими алгебраическими свойствами обладают скалярное и
векторное произведения векторов? [III]
24. Что такое коллинеарные и компланарные векто-
векторы? [III]
25. Что такое линейное пространство? Каковы ак-
аксиомы линейного пространства? Что такое линейное
арифметическое пространство? [IV]
26. Что такое размерность линейного пространства и
базис линейного пространства? [IV]
27. Что такое линейный оператор? [IV]
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
М и > — начало и окончание доказательства
# — окончание примера или замечания
а Е А — элемент а принадлежит множеству А (множество А
содержит элемент а) 1-1.1, 1.1
а ? А — элемент а не принадлежит множеству А (множество
А не содержит элемент а) 1-1.1, 1Л
{а,Ь,с} — множество, состоящее из элементов а, Ь, с 1-1.1,
1.1
А = {х: ...} — множество А состоит из элементов ж, обладаю-
обладающих свойством, указанным после двоеточия 1-1.1,
1.1
0 — пустое множество 1-1.1, 1.1
U — универсальное множество 1.1
А = В — множества А и В равны 1.1
А С -В, В D А — множество А является подмножеством мно-
множества В (А включено в В) 1-1.2, 1.1
А С В, В D А — множество А включено в множество В или
совпадает с ним, 1-1.2, 1.1
АПВ — пересечение множеств Аи В 1-1.4, 1.1
Аи В — объединение множеств А и В 1-1.4, 1.1
А — дополнение множества А до универсального множе-
множества 1-1.4, 1.1
А\В — разность множеств Аи В 1-1.4, 1.1
ААВ — симметрическая разность множеств А и В 1-1.4,
1.1
13
— объединение А; множеств Ai, ..., A* I-1.4, 1.5
— пересечение А: множеств Ai, ..., Ak I-1.4, 1.5
— множество всех подмножеств множества А 1.1
— символы дизъюнкции и конъюнкции 1-1.5, 1.1
— булево объединение 3.4
— булево пересечение 3.4
— символ импликации 1-1.5, 1.1
— символ эквивалентности 1-1.5, 1.1
— отрицание высказывания А 1-1.5, 1.1
— булево дополнение элемента х 3.4
— квантор всеобщности (Уж — для любого х) и кван-
квантор существования (Зх — существует х) 1-1.5,1.1
— упорядоченная пара элементов ж и у 1.2
— прямое (декартово) произведение множества X на
множество Y 1-2.5, 1.2
— n-я декартова степень множества X (декартово про-
произведение п экземпляров множества X) 1-2.5
— число размещений (без повторений) из п элементов
по га 1-2.6, 1.9
— число сочетаний (без повторений) из п элементов по
m I-2.6, 1.9
— число перестановок из п элементов 1-2.6, 1.9
— множество натуральных чисел 1-1.3, 1.9
— множество неотрицательных целых чисел 1.9
— множество целых чисел 1-1.3
— множество рациональных чисел 1-1.3
14 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Ш — множество действительных чисел 1-1.3
[ж, у] — замкнутый промежуток (отрезок) 1-1.3
(я> у) — открытый промежуток (интервал) 1-1.3
[ж, у), (ж, у] — полуинтервалы 1-1.3
/: А -> В — отображение (функция) из множества А в множе-
множество В 1-2.1, 1.3
у = f(x) — элемент у есть образ элемента х при отображении
/ 1-2.1,1.3
/: х н> у — отображение (функция) переводит элемент х в эле-
элемент у, т.е. у = f(x) 1.3
Z" — отображение, обратное отображению / 1-2*3, 1.3
/~Х(у) — полный прообраз элемента у при отображении /
1-2.1, 1.3
/(С) — образ множества С при отображении / 1-2.1, 1.3
f~l(D) — полный прообраз множества D при отображении /
1-2.1, 1.8
ВА — множество всех отображений из Ав В 1.3
р°<т, f°g — композиция соответствий р и сг, композиция ото-
отображений / и д 1.3
р С А\ х А2 — соответствие из множества А\ в множество А%
1.3
D(f) — область определения отображения / 1-2.1, 1.3
D(p) — область определения соответствия р 1.3
R(f) — область значения отображения / 1-2.1, 1.3
R(p) — область значения соответствия р 1.3
р(х) — сечение соответствия р 1.3
р~~1 — соответствие, обратное соответствию р 1.3
Р Я А\ х ... х Ап — n-арное отношение на множествах А\, ...,
Ап 1.3
— диагональ множества А 1.3
15
р* — рефлексивно-транзитивное замыкание бинарного от-
отношения р 1.6
fn(x) — результат n-кратного применения функции / к эле-
элементу я, причем f°(x) = х 1.8
p\c,D — (С, ^-ограничение соответствия р 1.4
р\с — С-сужение соответствия р 1.4
р\оС — строгое С-сужение соответствия р 1.4
р\м — ограничение бинарного отношения р на подмноже-
подмножество М 1.4
(Ai)iei — индексированное семейство множеств (с множест-
множеством индексов /) 1.5
U А{ — объединение индексированного семейства множеств
*' 1.5
П Ai — пересечение индексированного семейства множеств
*€/ 1.5
[х]р — класс эквивалентности элемента х по отношению
эквивалентности р 1.7
А/р — фактор-множество множества А по отношению эк-
эквивалентности р 1.7
a = b (mod к) — числа а и 6 равны по модулю к 1.7
=(modife) — бинарное отношение равенства по модулю А; 1.7
^> ^, Е)^ — стандартные обозначения различных отноше-
отношений порядка 1.8
^, >:, 3) ^ — обозначения отношений порядка, двойственных
соответственно к ^, ^, С, ^ 1.8
<, X, Е — обозначения отношений строгого порядка, опреде-
определяемых соответственно ^, ^, С 1.8
>, >-, ID — обозначения отношений строгого порядка, двой-
двойственных соответственно к <, ^, С 1.8
< — обозначения отношения доминирования, определяе-
определяемого отношением порядка ^ 1.8
16 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
sup В (inf J5) — точная верхняя (точная нижняя) грань множе-
множества В 1-2.7, 1.8
supXn (inf-Yn) — точная верхняя (точная нижняя) грань по-
последовательности Хп 1.8
lim хп — предел последовательности хп при п -> оо 1-6.3
п—>оо
О — наименьший элемент индуктивного частично упоря-
упорядоченного множества 1.8
А ~ В — множество А эквивалентно множеству В 1.9
\А\ — мощность множества А 1.9
No — мощность счетного множества 1.9
с — мощность континуума 1.9
0 — нуль относительно операции 2.1
1 — единица относительно операции 2.1
а — элемент, обратный элементу а при мультипликатив-
мультипликативной записи группы 2.2
—а — элемент, противоположный элементу а при аддитив-
аддитивной записи коммутативной группы 2.2
Sn — симметрическая группа степени п (группа подста-
подстановок n-элементного множества) 2.2
аН (На) — левый (правый) смежный класс подгруппы Н (ка-
(какой-либо группы G), определяемый элементом а Е G
2.7
G/H — фактор-группа группы G по нормальной подгруппе
Я 2.8
Zjfe — кольцо вычетов по модулю к 2.3
Z? — аддитивная группа вычетов по модулю к 2.3
Z* — мультипликативная группа вычетов по модулю р
(для простого р) 2.3
В — полукольцо ({0,1}, +, •, 0, 1) (двухэлементное полу-
полукольцо) 3.1
17
TV" — полукольцо (R+, min, +, +00, 0) (полукольцо неот-
неотрицательных действительных чисел вместе с +оо с
операциями взятия наименьшего элемента и сложе-
сложения) 3.1
Sa — полукольцо B^, U, П, 0, А) (полукольцо всех под-
подмножеств множества А) 3.1
TZa — полукольцо BЛхЛ, U, о, 0, id^) (полукольцо всех
бинарных отношений на множестве А) 3.1
N — полукольцо (No, +, •, 0, 1) (полукольцо неотрица-
неотрицательных целых чисел с обычными операциями сло-
сложения и умножения) 3.1
3[ауъ] — полукольцо ([а, 6] CR, max, min, а, Ь) (полукольцо
чисел из отрезка числовой прямой с операциями взя-
взятия максимума и минимума из двух чисел) 3.1
Matr(«S) — множество всех матриц с элементами из полуколь-
полукольца S 3.3
Mn(«S) — полукольцо квадратных матриц порядка п с элемен-
элементами из полукольца S 3.3
Vn — полукольцо всех делителей натурального числа п
3.4
S хпч Ylxn — точная верхняя грань бесконечной последова-
neN тельности х\, ..., жп, ... элементов замкнутого по-
полукольца 3.2
а* — итерация (замыкание) элемента а замкнутого полу-
полукольца (или полукольца с итерацией) 3.2
В — двухэлементная булева алгебра (то же, что полу-
полукольцо В) 3.4
Л = (A, ft, П) — алгебраическая система с носителем А, сиг-
сигнатурой, состоящей из множества операций Q и
множества отношений П 4.1
Л = (А, ?2) — алгебра с носителем А и сигнатурой (множе-
(множеством операций) п 4.1
18 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Л = (А, П) — модель с носителем А и сигнатурой (множе-
(множеством отношений) П 4*1
[В]п — замыкание множества В по операциям сигнатуры С1
($~2-замыкание множества В) 4.2
h: Л —У В — гомоморфизм h алгебраической системы Л в ал-
алгебраическую систему В 4.4
КегЛ — ядро гомоморфизма h одной алгебраической систе-
системы в другую 4.4
h(A) — гомоморфный образ алгебраической системы Л (от-
(относительно гомоморфизма h) 4.4
= — символ изоморфизма алгебраических систем 4.4
Л/р — фактор-система алгебраической системы Л по кон-
конгруэнции р 4.3
v — вершина и соединена ребром с вершиной v в неори-
неориентированном графе G (имя графа часто опускает-
опускается) 5.1
^ — существует дуга в ориентированном графе G с на-
началом и и концом t; (имя графа часто опускается)
5.1
?v — из вершины и (неориентированного графа G) до-
достижима вершина v (имя графа часто опускается)
5.1
и w+ v — существует цепь ненулевой длины, соединяющая
вершины и и v (неориентированного графа) 5.1
v — существует цепь длины п, соединяющая вершины и
и v (неориентированного графа) 5.1
и =>* v — из вершины tx (некоторого ориентированного гра-
графа) достижима вершина v 5.1
и =Ф-+ v — существует путь ненулевой длины из вершины и в
вершину v (в ориентированном графе) 5.1
19
и =ФП v — существует путь длины п из вершины и в вершину
v (в ориентированном графе) 5.1
dg(f) — степень вершины v (в неориентированном или ори-
ориентированном графе) 5.1
dg+(v) — полустепень исхода вершины v (в ориентированном
графе) 5.1
dg~ (v) — полустепень захода вершины v (в ориентированном
графе) 5.1
T(v) — множество всех таких вершин и (ориентированн-
го или неориентированного графа), что и -? v (для
ориентированного графа) или г*»-чг; (для неориенти-
неориентированного графа) 5.1
Г~~г(у) — множество всех таких вершин и (ориентированного
графа), что и -» v 5.1
L[v] — список смежности вершины v (в неориентированном
или ориентированном графе) 5.2
d(v), /i(v), l{v) — глубина, высота и уровень соответственно
узла v дерева 5.3
кт — высота дерева Т 5.3
G\ = G2 — графы G\ и С?2 изоморфны 5.7
G — дополнение графа G 5.7
V* — множество всех слов в алфавите V 7.1
V* — множество всех непустых слов в алфавите V 7.1
Vn — множество всех слов длины п в алфавите V 7.1
Л — пустое слово 7.1
х (г) — г-я буква слова х 7.1
х(\)х{2)... х(к) — побуквенная запись слова х 7.1
(и, ж, v) — вхождение слова х в слово у = uxv 7.1
uQv — слово и входит в слово v 7.1
Li-L2 — соединение (конкатенация) языков Ь\ и L*i 7.1
20 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
L* — итерация языка L 7.1
L+ — позитивная итерация языка L 7.1
C(V) — полукольцо всех языков в алфавите V 7.1
а -> Р — правило вывода (продукция) в грамматике 7.2
7 Ьз & — цепочка S непосредственно выводима в грамматике
G из цепочки j (имя грамматики часто опускается)
7.2
71~р 8 — цепочка S непосредственно выводима в грамматике
G из цепочки 7 применением правила р 7.2
7 Ь~Ь & — цепочка 8 выводима в грамматике G из цепочки 7
(имя грамматики часто опускается) 7.2
7 Ьq S — существует вывод ненулевой длины цепочки 6 в
грамматике G из цепочки 7 (имя грамматики часто
опускается) 7.2
7 Ь^ S — существует вывод длины п цепочки S в грамматике
G из цепочки 7 (имя грамматики часто опускается)
7.2
Oi -> Pi | #21 • • • | Рп — запись множества правил грамматики с
одной и той же левой частью а 7.2
TZ(V) — полукольцо регулярных языков в алфавите V 7.4
(а + Р) — сумма регулярных выражений 7.4
(а • Р) — произведение регулярных выражений 7.4
а*, а+ — итерация и позитивная итерация регулярного выра-
выражения соответственно 7.4
q —»а г — из состояния q конечного автомата возможен пере-
переход в состояние г по символу (или пустой цепочке)
а 7.5
qa—tr — запись команды конечного автомата (по символу
или пустой цепочке а разрешен переход из состояния
q в состояние г) 7.5
21
Я ^х г — цепочка х читается на некотором пути из состояния
q в состояние г конечного автомата 7.5
L(M) — язык конечного автомата М 7.5
= — символ эквивалентности конечных автоматов 7.5
qaZ -> rj — запись команды МП-автомата (из состояния q с
верхним символом в магазине Z по входному симво-
символу или пустой цепочке а разрешен переход в состо-
состояние г с заменой символа Z цепочкой 7) 8.4
\~~м> ^м? 1~д^, Ьд^ — отношения непосредственной выводимо-
выводимости, выводимости, выводимости за ненулевое число
шагов и выводимости за п шагов соответственно на
множестве конфигураций МП-автомата М 8.4
L(M) — язык МП-автомата М 8.4
<S(L,Li,...,Ln) — суперпозиция (подстановка) языков Li, ...,
Ln в язык L 8.5
А\\Х\Х2-..Хт — упорядоченное дерево, корень которого
помечен символом Л, а листья имеют метки Х\, ...,
Хт 8.1
'ХШ — куст упорядоченного дерева, корень кото-
которого помечен символом А, а листья имеют метки
Ai, ..., Хт 8.1
22
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Буквы латинского алфавита
Начертание
А а
В Ъ
С с
D d
Б е
F f
G g
Н h
I i
Jj
К k
L 1
M m
A a
В b
С с
D d
E e
F f
G g
H h
I i
Jj
К к
L I
M m
Произно-
Произношение
a
бэ
цэ
ДЭ
e
эф
же
аш
и
йот
ка
эль
эм
Начертание
N п
О о
РР
Qq
Rr
S s
T t
U u
V v
W w
X x
Yy
Z z
N n
О о
Рр
Qq
R r
S s
T t
U и
V v
W w
X x
У У
Z z
Произно-
Произношение
эн
0
пэ
ку
эр
эс
тэ
У
вэ
дубль-вэ
икс
игрек
зэт
Представлен наиболее употребительный (но не единствен-
единственный) вариант произношения (в частности, вместо „йот" иногда
говорят „жи").
Буквы греческого алфавита
Начер-
Начертание
А а
в р
Г 7
Д S
Е е
z С
Н г,
в дв
Произно-
Произношение
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тэта
Начер-
Начертание
I ь
К н
Л Л
М /i
N v
О о
П тг
Произно-
Произношение
йота
каппа
ламбда
ми
ни
кси
омикрон
пи
Начер-
Начертание
р р
S a
Т т
Т v
Ф <р
х х
ф ф
?2 ш
Произно-
Произношение
ро
сигма
тау
ипсилон
фи )
хи
пси
омега
Наряду с указанным произношением также говорят „лямб-
„мю" и „ню"
1. МНОЖЕСТВА И ОТНОШЕНИЯ
1.1. Множества
Элементы теории множеств изложены в [I]. Напомним здесь
основные понятия и обозначения.
Понятие множества является исходным не определяемым
строго понятием*. Приведем здесь определение множества (точ-
(точнее, пояснение идеи множества), принадлежащее Г. Кантору**:
„Под многообразием или множеством я понимаю вообще все
многое, которое возможно мыслить как единое, т.е. такую
совокупность определенных элементов, которая посредством
одного закона может быть соединена в одно целое".
Множества будем, как правило, обозначать большими бу-
буквами латинского алфавита, а их элементы — малыми, хотя
иногда от этого соглашения придется отступать, так как эле-
элементами некоторого множества могут быть другие множества.
Тот факт, что элемент а принадлежит множеству А, записыва-
записывается в виде аЕ А.
В математике мы имеем дело с самыми различными мно-
множествами. Для элементов этих множеств мы используем два
основных вида обозначений: константы и переменные.
Индивидная константа (или просто константа) с
областью значений А обозначает фиксированный элемент мно-
множества А. Таковы, например, обозначения (записи в опреде-
*Это имеет место в так называемой „наивной" теории множеств. В
современной математической литературе фигурируют различные постро-
построения теории множеств, в которых понятие множества строго определя-
определяется посредством набора аксиом (аксиоматические теории множеств), но
при этом используются уже другие неопределимые понятия. В рамках
курса дискретной математики нам достаточно ограничиться „наивным"
подходом.
*Т. Кантор A845-1918) — немецкий математик, основатель теории
множеств.
24 1. МНОЖЕСТВА И ОТНОШЕНИЯ
ленной системе счисления) действительных чисел: 0; 2; 7,34.
Для двух констант а и 6 с областью значений А будем писать
а = ft, понимая под этим совпадение обозначаемых ими элемен-
элементов множества А.
Индивидное переменное (или просто переменное) с
областью значений А обозначает произвольный, заранее не
определенный элемент множества А. При этом говорят, что
переменное х пробегает множество А или переменное х прини-
принимает произвольные значения на множестве А. Можно фиксиро-
фиксировать значение переменного ж, записав х = а, где а — константа
с той же областью значений, что и х. В этом случае говорят,
что вместо переменного х подставлено его конкретное значе-
значение а, или произведена подстановка а вместо ж, или переменное
х приняло значение а.
Равенство переменных х = у понимается так: всякий раз,
когда переменное х принимает произвольное значение о, пере-
переменное у принимает то же самое значение а, и наоборот. Таким
образом, равные переменные „синхронно" принимают всегда
одни и те же значения.
Обычно константы и переменные, область значений кото-
которых есть некоторое числовое множество [I], а именно одно
из множеств N, Z, Q, R и С, называют соответственно на-
натуральными, целыми (или целочисленными), рациональными,
действительными и комплексными константами и переменны-
переменными. В курсе дискретной математики мы будем использовать
различные константы и переменные, область значений которых
не всегда является числовым множеством.
Для сокращения записи мы будем пользоваться логической
символикой [I], позволяющей коротко, наподобие формул, запи-
записывать высказывания. Понятие высказывания не определяется.
Указывается только, что всякое высказывание может быть ис-
истинным или ложным (разумеется, не одновременно!).
Для образования из уже имеющихся высказываний новых
высказываний используются следующие логические опера-
операции (или логические связки).
1.1. Множества 25
1. Дизъюнкция V: высказывание PV Q (читается: „Р или
Q") истинно тогда и только тогда, когда истинно хотя бы одно
из высказываний Р и Q.
2. Конъюнкция Л: высказывание PAQ (читается: „Р и Q")
истинно тогда и только тогда, когда истинны оба высказыва-
высказывания Р и Q.
3. Отрицание -»: высказывание ->Р (читается: „не Р") ис-
истинно тогда и только тогда, когда Р ложно.
4. Импликация =$>: высказывание Р =Ф- Q (читается: „если Р,
то Q" или „Р влечет Q") истинно тогда и только тогда, когда
истинно высказывание Q или оба высказывания ложны.
5. Эквивалентность (или равносильность) <&: высказы-
высказывание P&Q (читается: „Р, если и только если Q") истинно
тогда и только тогда, когда оба высказывания Р и Q либо од-
одновременно истинны, либо одновременно ложны. Любые два
высказывания Р и Q, такие, что истинно Р <Ф Q, называют ло-
логически эквивалентными или равносильными.
Записывая высказывания с помощью логических операций,
мы предполагаем, что очередность выполнения всех операций
определяется расстановкой скобок. Для упрощения записи
скобки зачастую опускают, принимая при этом определенный
порядок выполнения операций („соглашение о приоритетах").
Операция отрицания всегда выполняется первой, и потому
ее в скобки не заключают. Второй выполняется операция конъ-
конъюнкции, затем дизъюнкции и, наконец, импликации и эквива-
эквивалентности. Например, высказывание (~»Р) V Q записывают так:
-iPVQ. Это высказывание есть дизъюнкция двух высказыва-
высказываний: первое является отрицанием Р, а второе — Q. В отличие
от него высказывание ->(Р V Q) есть отрицание дизъюнкции
высказываний Р и Q.
Например, высказывание
26 1. МНОЖЕСТВА И ОТНОШЕНИЯ
после расстановки скобок в соответствии с приоритетами при-
примет вид
Сделаем некоторые комментарии по поводу введенных выше
логических связок. Содержательная трактовка дизъюнкции,
конъюнкции и отрицания не нуждается в специальных разъяс-
разъяснениях. Импликация Р => Q истинна, по определению, всякий
раз, когда истинно высказывание Q (независимо от истинно-
истинности Р) или Р и Q одновременно ложны. Таким образом, если
импликация Р => Q истинна, то при истинности Р имеет место
истинность Q, но обратное может и не выполняться, т.е. при
ложности Р высказывание Q может быть как истинным, так и
ложным. Это и мотивирует прочтение импликации в виде „ес-
„если Р, то Q". Нетрудно также понять, что высказывание Р =>Q
равносильно высказыванию -iP V Q и тем самым содержательно
„если Р, то Q" отождествляется с „не Р или Q".
Равносильность 4Ф> есть не что иное, как „двусторонняя им-
импликация", т.е. Р <& Q равносильно (Р => Q) Л (Q => Р). Это
означает, что из истинности Р следует истинность Q и, наобо-
наоборот, из истинности Q следует истинность Р.
Пример 1.1. Для определения истинности или ложности
сложного высказывания в зависимости от истинности или лож-
ложности входящих в него высказываний используют таблицы
истинности.
В первых двух столбцах таблицы записывают все-врзмож-
ные наборы значений, которые могут принимать высказывания
Р и Q. Истинность высказывания обозначают буквой „И", а
ложность — буквой „Л". Остальные столбцы заполняют сле-
слева направо. Так для каждого набора значений Р и Q находят
соответствующие значения высказываний.
Наиболее простой вид имеют таблицы истинности логиче-
логических операций (табл. 1.1-1.5).
1.2. Множества
27
р
л
л
и
и
Таблица 1.1
Q
л
и
л
и
PVQ
л
и
и
и
р
л
л
и
и
Таблица 1.2
Q
Л
и
л
и
PAQ
Л
Л
Л
и
Таблица 1.3
Р
Л
И
-.р
и
л
Таблица 1.4
Р
Л
Л
и
и
Q
л
и
л
и
P=>Q
И
И
Л
И
Таблица 1.5
Р
Л
Л
И
И
Q
Л
и
л
и
P&Q
И
Л
л
и
Рассмотрим сложное высказывание
Для удобства вычислений обозначим высказьюание ->Р Л Q че-
через А, высказывание -»Q Л Р через В, а исходное высказывание
запишем в виде А=> В. Таблица истинности этого высказыва-
высказывания состоит из столбцов Р, Q, Л, В и А =>> В (табл. 1.6). #
Таблица 1.6
р
л
л
и
и
Q
л
и
л
и
А
л
И
л
л
в
л
л
и
л
А=>В
И
л
и
и
Сложные высказывания образуются не только посредством
логических связок, но и с помощью предикатов и кванторов.
Предикат есть высказывание, содержащее одно или не-
несколько индивидных переменных. Например, пх есть четное
28 1. МНОЖЕСТВА И ОТНОШЕНИЯ
число" или пх есть студент МГТУ им. Баумана, поступив-
поступивший в 1999 г.". В первом предикате х есть целочисленное
переменное, во втором — переменное, пробегающее множество
„человеческих индивидов". Примером предиката, содержаще-
содержащего несколько индивидных переменных, может служить: „# есть
сын у", „ж, у и г учатся в одной и той же группе", „ж делится
на у", „х меньше у" и т.п. Предикаты будем записывать в виде
Р(х), Q(x,y), Я(я,у,г), полагая, что в скобках перечислены все
переменные, входящие в данный предикат.
Подставляя вместо каждого переменного, входящего в пре-
предикат Р(ж1,...,хп), конкретное значение, т.е. фиксируя значе-
значения х\ = ai,... ,#n = an, где ai,... ,an — некоторые константы с
соответствующей областью значений, получаем высказывание,
не содержащее переменных. Например, „2 есть четное число",
„Исаак Ньютон есть студент МГТУ им. Баумана, поступив-
поступивший в 1999 г.", „Иванов есть сын Петрова", „5 делится на 7" и
т.п. В зависимости от того, истинно или ложно полученное
таким образом высказывание, говорят, что предикат Р вы-
выполняется или не выполняется на наборе значений переменных
х\ = oi,...,хп = ап. Предикат, выполняющийся на любом набо-
наборе входящих в него переменных, называют тождественно
истинным, а предикат, не выполняющийся ни на одном набо-
наборе значений входящих в него переменных, — тождественно
ложным.
Высказывание из предиката можно получать не только под-
подстановкой значений его переменных, но и посредством кванто-
кванторов. Вводят два квантора — существования и всеобщности,
обозначаемые 3 и V соответственно.
Высказывание (Vs E А)Р(х) („для каждого элемента ж, при-
принадлежащего множеству А, истинно Р(х)", или, более коротко,
„для всех х € А истинно Р(х)") истинно, по определению, тогда
и только тогда, когда предикат Р(х) выполняется для каждого
значения переменного х.
Высказывание (Зх G А)Р(х) („существует, или найдется, та-
такой элемент х множества А, что истинно Р{х)", также „для
1.1. Множества 29
некоторого х Е А истинно Р(х)") истинно, по определению, то-
тогда и только тогда, когда на некоторых значениях переменного
х выполняется предикат Р{х).
При образовании высказывания из предиката посредством
квантора говорят, что переменное предиката связывается кван-
квантором. Аналогично связываются переменные в предикатах,
содержащих несколько переменных. В общем случае исполь-
используют формы высказываний вида
(Qixi Е Ai)(Q2x2 Е А2)...(Qnxn € Ап)Р(хих2,...,жп),
где вместо каждой буквы Q с индексом может быть подставлен
любой из кванторов V или 3.
Например, высказывание (Уж Е А)Cу Е В)Р{х^у) читается
так: „для всякого х€А существует у Е В, такой, что истинно
Р(ж,г/)". Бели множества, которые пробегают переменные
предикатов, фиксированы (подразумеваются „по умолчанию"),
то кванторы записываются в сокращенной форме: (Уж)Р(ж) или
Заметим, что многие математические теоремы можно запи-
записать в форме, подобной только что приведенным высказывани-
высказываниям с кванторами, например: „для всех / и для всех а истинно:
если / — функция, дифференцируемая в точке а, то / непре-
непрерывна в точке а".
Обсудив особенности употребления логической символики,
вернемся к рассмотрению множеств.
Два множества А и В считают равными, если любой эле-
элемент х множества А является элементом множества В и наобо-
наоборот. Из приведенного определения равных множеств следует,
что множество полностью определяется своими элементами.
Рассмотрим способы задания конкретных множеств. Для
конечного множества, число элементов которого относительно
невелико, может быть использован способ непосредственного
перечисления элементов. Элементы конечного множества пере-
30 1. МНОЖЕСТВА И ОТНОШЕНИЯ
числяют в фигурных скобках в произвольном фиксированном
порядке {1,3,5}. Подчеркнем, что поскольку множество полно-
полностью определено своими элементами, то при задании конечного
множества порядок, в котором перечислены его элементы, не
имеет значения. Поэтому записи {1,3,5}, {3,1,5}, {5,3,1} и
т.д. все задают одно и то же множество. Кроме того, иногда
в записи множеств используют повторения элементов. Будем
считать, что запись {1,3,3,5,5} задает то же самое множество,
что и запись {1,3,5}.
В общем случае для конечного множества используют фор-
форму записи {ai,..., an}. Как правило, при этом избегают повто-
повторений элементов. Тогда конечное множество, заданное записью
{ai,...,an}, состоит из п элементов. Его называют также
поэлементным множеством.
Однако способ задания множества путем непосредственного
перечисления его элементов применим в весьма узком диапа-
диапазоне конечных множеств. Наиболее общим способом задания
конкретных множеств является указание некоторого свойства,
которым должны обладать все элементы описываемого множе-
множества, и только они.
Эта идея реализуется следующим образом. Пусть пере-
переменное х пробегает некоторое множество С/, называемое уни-
универсальным множеством. Мы предполагаем, что рассматри-
рассматриваются только такие множества, элементы которых являются
и элементами множества U. В таком случае свойство, кото-
которым обладают исключительно элементы данного множества А,
может быть выражено посредством предиката Р(я), выполня-
выполняющегося тогда и только тогда, когда переменное х принимает
произвольное значение из множества А. Иначе говоря, Р(х)
истинно тогда и только тогда, когда вместо х подставляется
индивидная константа а€А.
Предикат Р называют в этом случае характеристичен
ским предикатом множества А, а свойство, выражаемое с
помощью этого предиката, — характеристическим свой-
свойством или коллективизирующим свойством [I].
1.1. Множества 31
Множество, заданное через характеристический предикат,
записывается в следующей форме:
А = {х:Р(х)}. A.1)
Например,
А = {х: х есть четное натуральное число}
означает, что пА есть множество, состоящее из всех таких
элементов #, что каждое из них есть четное натуральное
число".
Термин „коллективизирующее свойство" мотивирован тем,
что это свойство позволяет собрать разрозненные элементы в
единое целое. Так, свойство, определяющее множество
G = {х: х есть студент 2-го курса специальности
ИУ5 МГТУ им. Баумана, поступивший в 1999 г.},
в буквальном смысле слова формирует некий „коллектив".
Бели мы вернемся к канторовскому определению множе-
множества, то характеристический предикат множества и есть тот
закон, посредством которого совокупность элементов соединя-
соединяется в единое целое. Предикат, задающий коллективизирую-
коллективизирующее свойство, может быть тождественно ложным. Множество,
определенное таким образом, не будет иметь ни одного элемен-
элемента. Его называют пустым множеством и обозначают 0.
В противоположность этому тождественно истинный харак-
характеристический предикат задает универсальное множество.
Обратим внимание на то, что не каждый предикат выража-
выражает какое-то коллективизирующее свойство (см. Д.1.1).
Замечание 1.1. Конкретное содержание понятия универ-
универсального множества определяется тем конкретным контекстом,
в котором мы применяем теоретико-множественные идеи. На-
Например, если мы занимаемся только различными числовыми
32 1. МНОЖЕСТВА И ОТНОШЕНИЯ
множествами, то в качестве универсального может фигури-
фигурировать множество R всех действительных чисел. В каждом
разделе математики рассматривается относительно ограничен-
ограниченный набор множеств. Поэтому удобно полагать, что элементы
каждого из этих множеств суть также и элементы некоторого
„объемлющего" их универсального множества. Зафиксировав
универсальное множество, мы тем самым фиксируем область
значений всех фигурирующих в наших математических рас-
рассуждениях переменных и констант. В этом случае как раз
и можно не указывать в кванторах то множество, которое
пробегает связываемое квантором переменное. В дальнейшем
изложении мы встретимся с разными примерами конкретных
универсальных множеств. #
Рассмотрим операции над множествами, которые позволя-
позволяют из уже имеющихся множеств образовывать новые множе-
множества [I].
Для любых двух множеств А и В определены новые мно-
множества, называемые объединением, пересечением, разностью и
симметрической разностью:
А\В = {х: х Е АЛх ? В},
= (A\B)U(B\A),
т.е. объединение А и В есть множество всех таких х, что х
является элементом хотя бы одного из множеств A, JB; пересе-
пересечение А и В — множество всех таких х, что х — одновременно
элемент А и элемент J5; разность А \ В — множество всех та-
таких х, что х — элемент А, но не элемент 2?; симметрическая
разность ААВ — множество всех таких х, что х — элемент А,
но не элемент В или х — элемент В, но не элемент А,
Кроме того, фиксируя универсальное множество U, мы
можем определить дополнение А множества А следующим
1.1. Множества 33
образом: A = U\A [I]. Итак, дополнение множества А —
это множество всех элементов универсального множества, не
принадлежащих А.
Полезно разобраться в том, как операции над множества-
множествами, введенные выше, соотносятся с логическими операциями.
Пусть А = {х: Р(х)}, В = {х: Q(a;)}, т.е. множество А задано
посредством характеристического предиката Р, а множество
В — посредством характеристического предиката Q.
Легко показать, что
= {x:P(x)VQ(x)},
= {x:P(x)AQ(x)},
= {x:P(x)A-*Q(x)}.
Следующие процедуры получения новых множеств связаны
с понятием подмножества. Говорят, что В есть подмножество
множества А, если всякий элемент В есть элемент А. Для
обозначения используют запись: В С А. Говорят также, что
В содержится в А, В включено в А, А включает В (имеет
место включение В С А). Считают, что пустое множество
есть подмножество любого множества и, если фиксировано
некоторое универсальное множество, каждое рассматриваемое
множество есть его подмножество. Нетрудно проверить, что
если А = {х: Р(я)}, В = {х: Q(x)}, то В С А тогда и только
тогда, когда высказывание Q(x) =Ф- Р(х) тождественно истинно.
Сопоставляя определение подмножества и определение ра-
равенства множеств, мы видим, что множество А равно множе-
множеству В тогда и только тогда, когда А есть подмножество В и
наоборот, т.е.
А = В^((ЛСВ)Л(ВС А)). A.2)
Формула A.2) является основой для построения доказа-
доказательств о равенстве множеств. Ее применение состоит в следу-
следующем. Чтобы доказать равенство двух множеств X и У, т.е.
9 _ 1ПП61
34 1. МНОЖЕСТВА И ОТНОШЕНИЯ
что X = У, достаточно доказать два включения X С У и У С X,
т.е. доказать, что из предположения х ? X (для произвольного
х) следует, что жЕУ, и, наоборот, из предположения х Е У
следует, что а; Е X. Такой метод доказательства теоретико-
множественных равенств называют методом двух включе-
включений. Примеры применения этого метода мы дадим позже.
Замечание. Равенство множеств {х: Р(х)} и {х: Q(x)}
означает, что предикаты Р(х) и Q(x) эквивалентны, т.е. пре-
предикат Р(х) <=> Q(x) является тождественно истинным. #
Бели В С А, но В ф А, то пишут В С А и В называют стро-
строгим подмножеством (или собственным подмножеством)
множества А, а символ С — символом строгого включе-
включения.
Для всякого множества А может быть образовано множе-
множество всех подмножеств множества А. Его называют булеаном
множества А и обозначают 2Л:
2А = {Х:ХСА}.
Для булеана используют также обозначения V(A)j B(A) и
ехр(А).
Пример, а. Булеан множества {а, 6} состоит из четырех
множеств 0, {а}, {Ь}, {а, Ь}, т.е. 2^6> = {0, {а}, {6}, {а, 6}}.
б. Булеан 2N состоит из всех возможных, конечных или
бесконечных, подмножеств множества N. Так, 0 6 2N, {5} G
G 2N, вообще для любого п множество {п} Е 2N, множество
{l,...,n}€2N, {n:n = 2fc,fe = l,2,..}E2NHT.n. #
Для булеана 2А мы можем рассматривать произвольные его
подмножества. Таким подмножеством, например, будет рдно-
элементное множество {J5}, где В — произвольное подмноже-
подмножество А. Подчеркнем, что единственным элементом множества
{В} является, в свою очередь, некоторое множество. Вообще
же образование булеана открывает путь для построения мно-
множеств, элементами которых являются множества, элементами
1.1. Множества 35
которых, в свою очередь, являются некоторые множества, и
т.д. Так можно определить множества 22 , 22 и т.д.*
Введенные выше операции над множествами обладают сле-
следующими свойствами:
2) АПВ = ВПА;
3) AU(ВUС) = (ЛиВ)UС;
4) АП(ВПС) = (АПВ)ПС;
5)
S) А~ПВ = A\JB;
9) 4110 = А;
10) АП0 = 0;
И)
12)
13)
14) АПА =
15)
16)
17I = А;
18) Л\В =
19) ААВ = (АиВ)\(АПВ);
20)
22)
'"Применяя теорию множеств, часто выстраивают подобные „башни"
булеанов, начиная этот процесс с элементов, не рассматриваемых как мно-
множества. Такие элементы называют праэлементами. Далее в качестве
праэлементов берутся любые числа, а также такие объекты, как констан-
константы, переменные, буквы какого-нибудь алфавита и т.п.
2*
36 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Каждое из написанных выше равенств, верное для любых
входящих в них множеств, часто называют теоретико->м,но-
жественным тождеством. Любое из них может быть до-
доказано методом двух включений. Докажем этим методом то-
тождество 19.
Пусть х € АДВ. Тогда, согласно определению симметри-
симметрической разности, х ? (А\В) U (В\ А). Это означает, что х ?
е (А \ В) или х е (В \ А). Если х € (А \ В), то х € А и х & В,
т.е. х Е A U В и при этом х & А П В. Если же х G (В \ А), то
х Е В и х & А, откуда х Е Аи В и х 0 АПВ. Итак, в любом
случае из хе (A\B)U(B\A) следует xeAUB их&АПВ, т.е.
х Е (A U В) \ (А П JB). Таким образом, доказано, что
Покажем обратное включение (АиВ)\(АГ)В) СААВ.
Пусть хЕ(ЛиВ)\(АПБ). Тогда xeAUB и Ж0АПЯ.
Из х € AUB следует, что a; G А или х € В. Если ж G -А, то с
учетом х & АПВ имеем х & В, и поэтому жЕА\В. Если же
х Е J5, то опять-таки в силу гг 0 А П J3 получаем, что х & А и
ж€?\А Итак,ж€А\?илияеВ\;4, т.е. s€ (A\B)U(?\A).
Следовательно,
{АиВ)\{АПВ)СААВ.
Оба включения имеют место, и тождество 19 доказано.
Метод двух включений является универсальным и наибо-
наиболее часто применяемым методом доказательства теоретико-
множественных тождеств. Помимо метода двух включений
для доказательства теоретико-множественных тождеств могут
быть использованы другие методы, например метод характе-
характеристических функций (см. Д. 1.2). '
Кроме того, теоретико-множественные тождества можно
доказывать, используя ранее доказанные тождества для пре-
преобразования левой части к правой или наоборот. Такой метод
1.2. Кортеж. Декартово произведение 37
доказательства часто называют методом эквивалентных
преобразований.
Докажем этим методом тождество 22, пользуясь тождества-
тождествами 1-19. Преобразуем левую часть к правой:
= ((АПВI)(АПС))П(АПВ)П(АПС) =
= (АП(ВиС))П((АПВ)и(АПС)) =
= (An(BUC))n(AUB)U(AuC) =
= (АП(ВиС))П(Аи(ВиС)) =
= ((АП(ВиС))ПА)и((АП(ВиС))П(ВиС)) =
= 0U((An(BUC))n(An(BUC))) =
= (АП (В U С)) П (АП (В ПС)) =
= АП((ВиС)\(ВПС)) =
Тождество доказано.
1.2. Кортеж. Декартово произведение
Пусть Аи В — произвольные множества. Неупорядочен-
Неупорядоченная пара на множествах Аи В — это любое множество {а, Ь},
где а € А, Ь G В или аеВ,ЬеА.
Если А = Б, то говорят о неупорядоченной паре на мно-
множестве А. Исходя из понятия равенства множеств, можно
утверждать, что неупорядоченная пара {а, 6} равна неупорядо-
неупорядоченной паре {с, d} если и только если а = с и b = d или a = d
и Ь = с. Заметим, что равенство элементов множества понима-
понимается здесь (и далее в аналогичных ситуациях) как равенство
индивидных констант.
В том случае, когда в неупорядоченной паре {а, Ь) элементы
аиЬ совпадают, получаем, что {а, 6} = {а, а}. Но такая запись,
как мы условились выше, задает то же самое множество, что
и {а}. Таким образом, при а = Ъ неупорядоченная пара {а, 6}
38 1. МНОЖЕСТВА И ОТНОШЕНИЯ
„вырождается" в одноэлементное множество {а}. При а ф Ь
неупорядоченная пара будет двухэлементным множеством.
Упорядоченная пара на множествах А и 23, обозначаемая
записью (а, 6), определяется не только самими элементами а Е А
и 6 6 В, но и порядком, в котором они записаны. И в этом
состоит ее существенное отличие от неупорядоченной пары.
Если А = J3, то говорят об упорядоченной паре на множестве А.
Существенная роль порядка, в котором перечисляются эле-
элементы упорядоченной пары, фиксируется определением равен-
равенства упорядоченных пар.
Определение 1.1. Две упорядоченные пары (а, 6) и (а', Ь')
на множествах Аи В называют равными, если а = а' и Ь = 6'.
Замечание 1.2. Упорядоченную пару (а, 6) не следует
связывать с множеством {а, 6}, так как упорядоченная пара
характеризуется не только составом, но и порядком элементов
в ней. Более того, определение этого объекта вообще не по-
позволяет рассматривать его как множество. Но упорядоченную
пару можно определить и как множество, полагая, что упоря-
упорядоченная пара (а, Ь) есть неупорядоченная пара {{а}, {а, Ь}},
включающая в себя одноэлементное множество {а} и неупо-
неупорядоченную пару {а, 6}. При а = Ь получаем (о, а) = {{а}}.
Такое определение не изменит сути понятия, но тогда следует
не определять явно равенство упорядоченных пар, а доказывать
теорему о равенстве упорядоченных пар как определенного ви-
вида множеств. #
Простейший и важнейший пример использования упорядо-
упорядоченных пар дает аналитическая геометрия [III]. Если на плос-
плоскости введена некоторая прямоугольная система координат,
то каждая точка плоскости однозначно задается упорядоченцои
парой действительных чисел — координатами этой точки. Ни
у кого не возникает сомнений в том, что порядок, в котором пе-
перечисляются координаты точки, является существенным: точ-
точка, заданная координатами A, 3), совсем не то же самое, что
точка с координатами C, 1).
1.2. Кортеж. Декартово произведение 39
Обобщением понятия упорядоченной пары является упоря-
упорядоченный п-набор*, или кортеж. В отличие от конечно-
конечного множества {ai,...,an} кортеж (ai, ..., ап) на множествах
А\, ..., Ап характеризуется не только входящими в него эле-
элементами а\ Е А\, ..., ап е Ап, но и порядком, в котором они
перечисляются. Как и для упорядоченных пар, роль порядка в
кортеже фиксируется определением равенства кортежей.
Определение 1.2. Два кортежа (ai, ..., ап) и Fi, ..., bn)
на множествах А\, ..., Ап равны, если сц = hi, % = 1,п.
Число п называется длиной кортежа (или размерно-
размерностью кортежа), а элемент а, — г-й проекцией (компонен-
(компонентой) кортежа. Для двух кортежей одинаковой размерности
их компоненты с одинаковыми номерами называют одноимен-
одноименными компонентами. Определение 1.2 равенства кортежей
можно переформулировать так: два кортежа одинаковой раз-
размерности равны тогда и только тогда, когда их одноименные
компоненты совпадают.
Простейшим примером кортежа является арифметический
вектор.
Определение 1.3. Множество всех кортежей длины п
на множествах А\, ..., Ап называют декартовым (пря-
(прямым) произведением множеств А\, ..., Ап и обозначают
Ai х... хАп.
Таким образом,
i4iX...Xi4n = {(ab ..., an):aieAu...,aneAn}.
Бели все множества А{, t = l,n, равны между собой, то
указанное декартово произведение называют n-й декартовой
степенью множества А и обозначают Ап. В частности, при
п = 2 получаем декартов квадрат, а при п = 3 — декартов
куб множества А.
*Говорят также: упорядоченная п-ка (например, упорядоченная трой-
тройка, четверка, пятерка и т.д.)-
40 1. МНОЖЕСТВА И ОТНОШЕНИЯ
По определению полагают, что первая декартова степень
любого множества А есть само множество А, т.е. А1 = А.
Декартово произведение имеет следующие свойства:
1) А х (BUC) = (А х В) и (А х С);
2) А х (В П С) = (А х В) П (А х С);
3)Ах0 = 0хА = 0.
Эти свойства нетрудно доказать методом двух включений.
Докажем, например, первое тождество. Если (ж, у) Е А х (В U
U С), то ж ? А и у € В U С. Из того, что у G В U С, следует
у € В или у ?С. Если у € В, то (ж, у) € А х В, а если у €С,
то (ж, у) е А х С. Итак, (ж, у) € А х I? или (ж, у) 6 А х С,
т.е. (ж, у) Е (А х В) U (А х С). Следовательно, А х (В U С) С
С (АхВ)U(Ах С).
Доказательство обратного включения аналогично.
Обратим внимание на последнее из записанных выше трех
тождеств. Из него вытекает, что пустое множество при по-
построении декартовых произведений множеств играет ту же
роль, что и нуль при умножении чисел. Докажем справедли-
справедливость этого тождества. В самом деле, множество 0 х А (для
любого А) есть множество всех упорядоченных пар (ж, у), та-
таких, что ж Е 0 и у Е А. Но таких элементов ж, что ж Е 0, не
существует, и, следовательно, упорядоченных пар (ж, у), при-
принадлежащих декартову произведению 0 х А, не существует, т.е.
0 х А = 0. Аналогично доказывается, что и А х 0 = 0.
1.3. Соответствия и бинарные отношения
Отображение / из множества А в множество В считается
заданным, если каждому элементу ж € А сопоставлен един-
единственный элемент у ? В. Отображение / из множествау А в
множество В обозначают записью /: А —> В. Элемент у G В,
который отображением / сопоставляется элементу ж G А, на-
называют образом элемента ж при отображении f и обознача-
обозначают /(ж).
1.3. Соответствия и бинарные отношения 41
Каждое отображение однозначно определяет множество упо-
упорядоченных пар {(х,у): х Е А, у = /(ж)}, являющееся подмноже-
подмножеством декартова произведения Ах В множества А на множе-
множество В и называемое графиком отображения /.
Наоборот, пусть в декартовом произведении Ах В задано
такое подмножество /, что: 1) для любого х Е А существует
у Е В, для которого (ж, у) Е /; 2) для любых двух пар (ж, у)
и (х', yf) множества / из равенства х = х1 следует равенство
у = у1. Тогда множество / единственным образом определяет
некоторое отображение из А в В. Это отображение, обозна-
обозначаемое также /, элементу х Е А сопоставляет элемент у ? В,
удовлетворяющий условию (#, у) Е /. Таким образом, мы мо-
можем отождествить отображения с их графиками и считать, что
отображение есть подмножество декартова произведения.
Отображение / множества А в себя называют тождест-
тождественным, если f(x) = х при всех х из А.
В общем случае для отображения /: А —> В может суще-
существовать несколько различных элементов множества А, образы
которых совпадают. Множество всех элементов х € А, для ко-
которых f(x) = уо? называют прообразом элемента уо Е В при
отображении /.
Так, прообраз числа а, \а\ ^ 1, при отображении у = sins
есть множество всех решений уравнения sina; = а, т.е. множе-
множество
{х: х = arcsina + 2тгп, n G Z} U {х: х = 7г - arcsina + 2тгп, п 6 Z}.
Прообраз элемента уо Е В может быть пустым множе-
множеством. Это имеет место, например, для числа 2 при отображе-
отображении у = sina;.
Множество всех у ЕВ, таких, что найдется х Е А, для кото-
которого y~f(x), называют областью значений отображения
/. Область значений отображения / будем обозначать R(f)>
Отображение f: A-+ В называют инъективным (инъек-
(инъекцией), если каждый элемент из области его значений имеет
единственный прообраз, т.е. из f(x\) = /(а^) следует х\ = а?2-
42 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Отображение f: A-+ В называют сюръективным (сюръ-
екцией), если его область значений совпадает со всем множе-
множеством В. Сюръективное отображение из А в В называют также
отображением множества А на множество В,
Отображение /: А -> В называют биективным (биекцией),
если оно одновременно инъективно и сюръективно.
Таким образом, если отображение /: А-> В биективно, то
каждому элементу множества А отвечает единственный эле-
элемент множества В и наоборот. Тогда говорят, что множества
А и В находятся между собой во взаимно однозначном со-
соответствии.
Биекцию множества А на себя называют автоморфизмом
множества А. Используют также термин* „ подстановка
множества".
Пример 1.2. а. Отображение, заданное равенством и(п) =
= п +1, есть, как нетрудно показать, биекция множества нату-
натуральных чисел N на его подмножество N\ {1}.
б. Отображение и:п^2п есть биекция множества всех
натуральных чисел на множество всех четных натуральных
чисел.
в. Любая показательная функция у = аж, а > О, есть биекция
множества R всех действительных чисел на множество М+ всех
положительных действительных чисел.
г. Функция у = arctga; есть биекция множества К на интер-
интервал (-тг/2, тг/2).
д. Поворот окружности на заданный угол а, т.е. отобра-
отображение, сопоставляющее каждой точке окружности точку, в
которую она перейдет при повороте всей окружности вокруг ее
центра на угол а, есть автоморфизм множества точек окруж-
окружности. #
Пусть задано отображение f: A-+ В и С С А — некото-
некоторое множество. Множество f(C) элементов у G 23, таких, что
* Иногда этот термин употребляют только для автоморфизма конечного
множества.
1.3. Соответствия и бинарные отношения 43
у = /(ж), х € С, называют образом множества С при ото-
отображении /. Например, при отображении у = sin а: отрезок
[0,1] является образом множества (отрезка) [0, тг], равно как и
любого объединения отрезков вида [2тгЛ, B& + 1)тг] (для произ-
произвольного целого к). При А; = 0 это можно записать следующим
образом: sin([0, тг]) = [0,1].
Заметим, что для любого отображения /: А -> В образ f(A)
всего множества А есть область значений данного отобра-
отображения.
Для произвольного множества D С В множество всех эле-
элементов х € А, таких, что f(x) E «D, называют прообразом мно-
множества D при отображении /.
Например, для любого действительного числа а € [0,1) мно-
множество, которое является объединением всех отрезков вида
[arcsina + 2тг&, тг — arcsina + 2тгЛ], к Е Z, есть прообраз отрезка
[а, 1] при отображении у = sinx.
Прообраз области значений произвольного отображения
/: А-> В совпадает со всем множеством А.
Множество всех отображений из А в В будем обозначать
как ВА.
Понятие отображения можно обобщить. Обобщение может
проходить по двум позициям. Во-первых, можно отказаться от
полной определенности отображения, полагая, что образ опре-
определен не для каждого элемента множества А, а для некоторых
элементов этого множества. Тогда придем к понятию частич-
частичного отображения. При этом подмножество всех элементов
Л, для которых определен образ, называют областью опре-
определения данного частичного отображения.
Многие элементарные функции являются частичными ото-
отображениями множества R всех действительных чисел в себя.
Например, функция у = tgs есть частичное отображение с обла-
областью определения R\ lx: x = ^ + тг&,к € Z|.
Во-вторых, можно отказаться от однозначности отображе-
отображения, полагая, что данному х€А сопоставлен не один, а несколь-
44 1. МНОЖЕСТВА И ОТНОШЕНИЯ
ко образов (множество образов) в множестве В. В этом случае
говорят, что задано соответствие* из множества А в мно-
множество В.
Примером могут служить обратные тригонометрические
функции: скажем, „большой" арксинус [I], сопоставляющий ка-
каждому х ? R множество всех таких чисел у, что siny = ж, т.е.
множество, являющееся прообразом элемента х при отображе-
отображении, определяемом графиком функции у = sinar.
Если задано соответствие р из А в 5, будем использовать
обозначение р(х) по аналогии с обозначением f(x) для ото-
отображений, понимая при этом, что р(х) есть уже не элемент
множества В, а его подмножество.
Аналогично графику отображения можно определить гра-
график соответствия р из множества А в множество В как
множество Ср упорядоченных пар (#,у), таких, что х Е А, у Е В
и элементы х, у связаны соответствием р, т.е. у 6 р(х). Ука-
Указанное множество Ср упорядоченных пар есть подмножество
декартова произведения Ах В.
Обратно, фиксируя на декартовом произведении А х В
какое-либо подмножество С, мы тем самым однозначно опре-
определяем некоторое соответствие рс из А в В, а именно рс(%) =
= {у: У € -S Л (ж,у) € С}. Нетрудно заметить, что графиком со-
соответствия рс будет как раз множество С, а соответствием, от-
отвечающим графику Су,, будет р. Поэтому можно отождествить
соответствие с его графиком и считать, что соответствие из
множества А в множество В есть некоторое подмножество р
декартова произведения ЛхВ, т.е. р С А х В. В частности,
при р = 0 получаем пустое соответствие, а при р, со-
совпадающем со всем указанным декартовым произведением, у-
универсальное соответствие.
При этом будем писать (ж, у) € р для упорядоченных пар,
связанных соответствием р.
* Используют также термины „частичное мультиотображение", „ча-
„частичная многозначная функция".
1.3. Соответствия и бинарные отношения 45
Пример 1.3. Рассмотрим множество программистов А =
= {Я, Я, С} и множество программ В = {ni, П2, пз, 7Ц, П5}. За-
Зададим соответствие т из А в J3, связывающее программистов
и разрабатываемые ими программы:
г = {(Я, щ), (Я, пз), (Я, п5), (Я, п2),
(Я, п4),(С,п2),(С,п5)}СЛхВ. #
Область определения соответствия р С А х В из
множества А в множество В — это множество всех первых
компонент упорядоченных пар из р:
D(p) = {x:CyeB)(x,y)ep}.
Область значения соответствия р — это множество
всех вторых компонент упорядоченных пар из р:
R(p) = {y:Cx?A)(x,y)€p}.
Из определения вытекает, что D(p) С A, R(p) С В. Соот-
Соответствие из А в В называют всюду определенным, если его
область определения совпадает с множеством A: D(p) = A.
Сечением соответствия рСАхВ для фиксированного
элемента х?А будем называть множество р(х) = {у: (х, у) 6 р}.
Можно сказать, что сечение соответствия р(х) есть множество
всех „образов" элемента х при данном соответствии.
Сечением соответствия р по множеству С С А
будем называть множество р(С) = {у: (ж, у) G p, a; G С}.
Пример 1.4. Область определения соответствия г из
примера 1.3есть все множество А, а область значения — все
множество В. Сечением соответствия г по элементу Я будет
множество т(П) = {пг, щ}. #
Соответствие р С А х А из множества А в себя, т.е. подмно-
подмножество множества А2, называют бинарным отношением на
множестве А.
46 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Пример 1.5* Простейшим примером бинарного отноше-
отношения является отношение нестрогого неравенства на множестве
действительных чисел R. Здесь каждому х ? R поставлены в
соответствие такие у Е R, для которых справедливо х ^ у. #
Для произвольного бинарного отношения на некотором мно-
множестве часто используют запись хру вместо (#, у) € р, говоря
при этом об элементах, связанных бинарным отноше-
отношением р. Это согласуется с традиционной формой записи неко-
некоторых часто используемых бинарных отношений. Так, пишут
х ^ у, а не (#, у) Е ^. Для таких бинарных отношений употре-
употребляют устоявшиеся словосочетания. Например, запись х < у
читается так: пх не больше у".
Бинарное отношение на множестве А, состоящее из всех пар
(я, я), т.е. пар с совпадающими компонентами, называют диа-
диагональю множества* А и обозначают icU. Нетрудно понять,
что диагональ А есть тождественное отображение А на себя.
Для наглядного изображения соответствий из А в В (би-
(бинарных отношений, в частности) будем использовать два спо-
способа. Первый из этих способов состоит в интерпретации соот-
соответствия как подмножества декартова произведения, которое
можно изображать примерно так же, как на плоскости можно
изображать подмножества декартова квадрата числовых мно-
множеств. Второй способ, применяемый для конечных множеств
А и J3, — построение так называемого графа соответст-
вил. В этом случае элементы множеств А и В изображаются на
плоскости кружочками. Бели и только если пара (u, v) принад-
принадлежит соответствию р, то в графе соответствия из кружочка,
обозначающего элемент wG-A, проводим стрелку к кружочку,
обозначающему элемент v € В. Для бинарного отношения на
конечном множестве А часто удобнее использовать граф дру-
другого вида. Элементы множества А изображаются кружочками
только один раз, а стрелки проводятся по тем же правилам,
* Иногда говорят о диагонали в множестве А, хотя правильнее было бы
называть это отношение диагональю декартова квадрата множества А.
1.3. Соответствия и бинарные отношения
47
что и в графе соответствия. Заметим, что при таком постро-
построении возможно соединение кружочка стрелкой с самим собой
(петля).
Пример 1*6. а. На рис. 1.1, а изображены график и граф
бинарного соответствия из примера 1.3.
п,
и п с
1О
12 3 4
»О4
б
Рис. 1.1
б. Пусть А = {1,2,3,4}. Бинарное отношение р на А опреде-
определим как множество всех упорядоченных пар (я, у), таких, что
ж^у. Тогда
р={A, 1),B, 1),B, 2),C, 1),C, 2), C,3),
D,1), D, 2), D,3), D, 4)}.
Область определения отношения D(p) = {1,2,3,4}, область зна-
значений R(p) = {1,2,3,4}. График и два варианта графа отноше-
отношения р изображены на рис. 1.1, б.
48 1. МНОЖЕСТВА И ОТНОШЕНИЯ
в. Множество точек окружности х2 + у2 = 1 есть гра-
график бинарного отношения на множестве действительных чи-
чисел, состоящего из всех таких упорядоченных пар (ж, у), что
у = ±у/A — х2), или, что равносильно, компоненты пары удо-
удовлетворяют уравнению х2 + у2 = 1. Область определения бинар-
бинарного отношения есть отрезок [—1,1], область значения — также
отрезок [—1,1]. #
Соответствие р С А х В называют функциональным по
второй (первой) компоненте, если для любых двух упорядо-
упорядоченных пар (ж, у) 6 р и (ж;, у1) ? р из равенства x = xf следует
у = у' (и из у = у' следует ж = ж'). Функциональность соответ-
соответствия по второй компоненте означает, что, фиксируя в любой
упорядоченной паре, принадлежащей данному соответствию,
первую компоненту, мы однозначно определяем и вторую ком-
компоненту. Таким образом, мы можем сказать, что соответствие,
функциональное по второй компоненте, есть отображение (воз-
(возможно, частичное).
Поэтому соответствие fCAxB является отображением из
А в В, если и только если оно всюду определено (т.е. D(f) = A)
и функционально по второй компоненте. Отметим также, что
отображение из А в В является инъекцией тогда и только
тогда, когда оно функционально по первой компоненте.
В заключение обобщим понятие соответствия, определив
отношения произвольной арности.
Определение 1.4. Произвольное подмножество р де-
декартова произведения А\ х ... х Ап называют (п-арным или
п-местным) отношением на множествах А\9 ..., Ап.
В случае если все множества Ai, ..., Ап совпадают, т.е.
А\ = ... = Ап = А, говорят об п-арном отношении на мно-
множестве А.
Бели р — n-арное отношение на множествах Ai, ..., Ап и
(oi, ..., ап) € р, то говорят об элементах ai, ..., ап, связан-
связанных отношением р.
1.3. Соответствия и бинарные отношения
49
Замечание 1.3. При п = 2 получаем бинарное отноше-
отношение на множествах Ai, A<i- Это не что иное, как соответствие
из А\ в Аг, где множества А\ и Лг, вообще говоря, различны.
При j4i = A2 = А получаем введенное ранее бинарное отно-
отношение на множестве, т.е. подмножество декартова квадрата А.
Таким образом, в общем случае (при произвольном п ^ 2)
следует, строго говоря, различать термины „п-арное отноше-
отношение" и
, п-арное отношение на множестве
п-арное
отношение
на множествах
L1 = ... = An=Ay/
n-арное
отношение
на множестве
А
на
\„.2
Бинарное
отношение
множествах А*, А2
(или соответствие из Ах в А2)
п=2 /А=А=А
Бинарное
отношение
на множестве
А
Функциональность ^^
по 2-й компоненте^-—
1' <4*****^
Частичное
отображение
множества А
в себя
N. Полная
N. определенность
Отображение
множества А
в себя
\
Функциональность
по 2-й компоненте
Частичное
отображение
из Ах в А2
Ах А2 А
Полная
определение
Отображение
из Ах в А2
/
Рис. 1.2
50 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Связь между введенными понятиями отношения, соответ-
соответствия и отображения проиллюстрирована на рис. 1.2. #
Пусть n-арное отношение р С А\ х ... х Ап удовлетворяет
условию: для любых двух кортежей (х\, ..., ж», ..., хп) Е р
и (yi, ..., у%, ..., Уп) € Р из выполнения равенств хк = г/ib для
любого Л ^ г @ ^ к < п) следует, что и Х{ = од. Тогда отношение
р называют (^унк^ионольнылс по г-й компоненте A < г < п).
Другими словами, функциональность п-местного отноше-
отношения по г-й (г ^ п) компоненте равносильна условию, что, фик-
фиксируя все компоненты, кроме г-й, мы однозначно определяем и
г-ю компоненту.
Пример 1.7. а. Представим строку учебного расписания
как кортеж вида
(преподаватель, группа, дисциплина, аудитория, день, час).
Тогда расписание можно рассматривать как секстарное (ше-
(шестиместное) отношение на соответствующих множествах. Оно
будет функционально по первой компоненте, если, конечно,
предположить, что два преподавателя или более не проводят
одно и то же занятие одновременно в одном и том же ме-
месте (хотя, например, на лабораторных работах это возможно).
Оно также функционально по третьей компоненте (один пре-
преподаватель не может вести одновременно занятия по разным
дисциплинам), по четвертой (преподаватель со своей группой
не могут находиться в разных аудиториях) и не будет, вообще
говоря, функционально по второй, пятой и шестой компонен-
компонентам.
б. Рассмотрим на множестве V3 геометрических векторов в
пространстве тернарное (трехместное) отношение р, состоящее
из всех упорядоченных троек (х, у, z) компланарных векто-
векторов. Это отношение не является функциональным ни по одной
компоненте, так как любым двум векторам соответствует бес-
бесконечно много векторов, образующих с ними компланарную
тройку.
1.4. Операции над соответствиями 51
1.4. Операции над соответствиями
Поскольку соответствия можно считать множествами, то
все операции над множествами (пересечение, объединение, раз-
разность, дополнение и т.д.) можно применить и к соответствиям.
Заметим, что, говоря о дополнении соответствия из Л в В, мы
имеем в виду дополнение до универсального соответствия из
Л в В, т.е. до декартова произведения Ах В. Естественно,
что и равенство соответствий можно трактовать как равен-
равенство множеств.
В то же время на соответствия можно распространить
операции, определяемые для отображений. Мы рассмотрим
здесь две такие операции.
Композиция соответствий. Следуя аналогии с компози-
композицией отображнений, композицией (произведением) соот-
соответствий рСАхВисгСВхС называют соответствие
рос = {(я, у): CzeB)((x, z)ep)A((z, у) Ест)}. A.3)
Поясним построение композиции двух соответствий. Обра-
Обратимся сначала к отображениям (как частным случаям соответ-
соответствий). Пусть заданы отображения (возможно, частичные):
/ из А в В и g из В в С. Композиция* fog определяется
как отображение из А в С, задаваемое формулой у = g(f(x)).
Тем самым задается график отображения /од, т.е. множество
упорядоченных пар (ж, у), таких, что у = g(f(x)). При этом
упорядоченная пара (ж, у) будет принадлежать графику ото-
отображения / о 0, если и только если найдется элемент z € В,
* Необходимо заметить, что в [I] запись g° f(x) означает g(f(x))y т.е.
отображения в композиции пишутся в порядке, обратном тому, в каком они
применяются. Мы же будем везде использовать запись / о д, полагая, что
fog(x) = g(f(x)) и порядок записи отображений в композиции совпадает с
порядком их применения. Это обусловлено тем, что композиция отображе-
отображении определяется нами как частный случай композиции соответствий, при
записи которой естественным оказывается именно такой порядок.
52 - 1. МНОЖЕСТВА И ОТНОШЕНИЯ
такой, что z = f(x) и у = g(z). Таким образом, график ком-
композиции отображений /ид есть
fog = {(x, у): Cz)(z = f{x) и y = giz))} =
= {(*, У): У = »(/(*))}¦ A-4)
Легко видеть, что A.4) есть частный случай A.3). Отметим,
что при построении композиции отображений обычно пред-
предполагают, что пересечение области значений отображения / и
области определения отображения д не пусто (R(f) П D(g) ф 0),
поскольку в противном случае композиция была бы пуста. Для
отображений, не являющихся частичными, R(f) С D(g), так
как D(g) = В. Поэтому в данном случае пересечение R(f) П
flD(g) всегда не пусто.
Полезно отметить также, что если /ид — биекции, то и
композиция их тоже будет биекцией.
Вернемся к рассмотрению композиции соответствий роа.
Полагая, что область определения D(p) соответствия р не пу-
пуста, возьмем произвольный элемент х Е D(p). Пусть сечение
р(х) С В соответствия р не пусто и найдется такой элемент
z Е р(ж), что сечение a(z) CC также не пусто. Тогда непустое
множество {(ж, t): tEa(z)} будет подмножеством сечения со-
соответствия роа в точке х. Сечением соответствия роа в точке
х будет непустое в силу сделанных предположений множество
всех таких упорядоченных пар (ж, t) Е А х С, что х Е D(p), a
t E cr(z) для некоторого z E р(х). Говоря неформально, нуж-
нужно перебрать все элементы z из сечения р{х). Таким образом,
различие в построении композиции соответствий и компози-
композиции отображений заключается в том, что „промежуточный"
элемент z в общем случае не единственный и каждому тако-
такому элементу также ставится в соответствие не единственный
элемент у еС.
Пример 1.8. Соответствие р возьмем из примера 1.3.
Соответствие а зададим как соответствие из множества про-
1.4. Операции над соответствиями 53
грамм {ni, п2, пз, гц, пь} в множество заказчиков программно-
программного обеспечения {Зх,32,3з,34}. Пусть
а = {(пь 33), (щ, 34), (n2, 3i), (n3, 32), (п4, 34), (п5, 33)}.
Рассмотрим процесс построения композиции соответствий
р и а. Начнем с элемента И. Имеем р{И) = {ni, пз, П5},
= {Зз, 34}, сг(п3) = {32} и а(п5) = {33}. Отсюда получаем
сечение композиции по элементу И. Рассуждая аналогично,
получим (роа)(Я) = {3Ь34} и (роа)(С) = {3Ь33}.
Построение графа композиции роа проиллюстрировано на
рис. 1.3. #
ро(Г
Рис. 1.3
Отметим, что область определения композиции соответ-
соответствий содержится в области определения первого соответ-
соответствия, а область значений композиции соответствий — в обла-
области значений второго соответствия. Из приведенных рассу-
рассуждений следует, что для того, чтобы композиция соответствий
была отлична от пустого соответствия, необходимо и достаточ-
достаточно, чтобы пересечение области значений первого соответствия
и области определения второго соответствия было не пусто.
К определению композиции соответствий можно подойти с
более общих позиций. Пусть pCAxBnaCCxD. При этом
54 1. МНОЖЕСТВА И ОТНОШЕНИЯ
на множества A, J3, С и D априори не накладывается ника-
никаких органичений. Композиция р о а соответствий р и а в этом
случае также определяется соотношением A.3). Чтобы такая
композиция была отлична от пустого соответствия, необходимо
и достаточно выполнение условия R(p) DD(a) ф 0. В частно-
частности, р о а = 0 всякий раз, когда В П С = 0.
Пример 1.9. Рассмотрим соответствие
т = {A, а), B, а),C, d)}
из множества А = {1,2,3} в множество В = {а, Ь, d} и соответ-
соответствие
из множества С = {6, с, d} в множество D = {е, /}. В данном
случае В П С Ф 0, но г о <р = 0, поскольку Д(т) = {a, d}, -D(v?) =
= {Ь,с}иЛ(г)П%)=0. #
Заметим, что композиция соответствий рСАхВиаССх
х D не коммутативна, т.е. в общем случае рост ф а ор, поскольку
Бинарное отношение на множестве является частным слу-
случаем соответствия. Для двух бинарных отношений риа,
заданных на множестве Л, их композиция рост A.3) как соот-
соответствий является бинарным отношением на том же множестве
А. В этом случае говорят о композиции бинарных отно-
отношений на множестве А.
Композицию pop бинарного отношения р на некотором
множестве с самим собой называют квадратом бинарного
отношения р и обозначают р2.
Рассмотрим пример построения композиции бинарных от-
отношений на множестве и покажем, что в общем случае для двух
бинарных отношений т и (р также имеет место неравенство
г о ср ф (р о г, хотя обе композиции, в отличие от аналогичных
композиций двух произвольных соответствий, заданы на одном
и том же множестве.
1.4. Операции над соответствиями 55
Пример 1.10. а. Зададим на множестве А = {1,2,3,4} би-
бинарные отношения г = {(ж, у): х +1 < у}, <р = {(ж,у): |дг — j/| = 2}
и найдем композицию тыр.
Имеем тA) = {3,4}, <рC) = {1} и <рD) = {2}. Следовательно,
(г о V)(i) = ^C) U VD) = {1,2}. Далее гB) = {4}, рD) = {2} и
(г °(р)B) = {2}. Так как тC) = тD) = 0, то в итоге получим
г otp = {A, 1), A? 2), B, 2)}. Построение композиции проиллю-
проиллюстрировано на рис. 1.4, а.
1
2о *О2
ЗО ОЗ
4о О4
(fT
10 01
20 02
¦«ЮЗ
40 *с>4
Найдем композицию (рот. Поскольку <рA) = {3}, а тC) =
= 0, то ((рот)A) = 0. Аналогично у?B) = {4}, а тD) = 0,
поэтому (<роГ)B) = 0. Далее у>C) = {1}, гA) = {3,4}, поэтому
(vr)C) = {3,4}, a VD) = {2}, тB) = {4} и (*>оГ)D) = {4}.
Построение композиции проиллюстрировано на рис. 1.4, б.
Легко видеть, что
56 1. МНОЖЕСТВА И ОТНОШЕНИЯ
б. Пусть отношение р на множестве действительных чисел
определено как функция у = ах + Ь. Найдем квадрат этого
отношения (линейной функции от одного переменного).
Согласно A.4), это будет функция Л, такая, что h(x) =
= а(ах + Ь) + с, т.е. h(x) = а?х + (ab + с). Это тоже линейная
функция, но с другими коэффициентами. #
Приведем некоторые свойства композиции соответствий:
1) ро(аот) = (ро(т)от;
2) для любого соответствия р имеет место ро0 = 0ор = 0;
3) po(aUr) = (poa)U(por);
4) для любого бинарного отношения на множестве А имеет
место равенство р о id^ = icU °p = р.
Эти свойства нетрудно доказать методом двух включений.
Рассмотрим в качестве примера доказательство свойства 3.
Пусть некоторая упорядоченная пара (ж, у) принадлежит ком-
композиции po(aUr). Тогда, согласно A.3), найдется такой эле-
элемент я, что (ж, z) G р и (я, у) ? a U г. Последнее означает,
что (z, у) G а или (г, у) G т. Таким образом, для элемента z
имеем (ж, г) 6 р и (z, у) € о или (ж, г) Е р и (г, у) G т. Пер-
Первая альтернатива имеет место при (ж, у) € р о а, а вторая —
при (ж, у) Е р°т, что означает (ж, у) G ростUрот. Тем самым
включение po(a\Jr)Cpoa\Jpor доказано.
Доказательство включения poaUporCpo^aUr) запишем
коротко, используя логическую символику:
(ж, у) GpoaUpor=> (Эи)(((ж, и)ер)Л((щ y)E
(Э*)(((ж, z)ep)A (((*, у) G a) V ((*, у) G г))) =>
*) €р)Л((*, у)
В данном случае доказательства двух включений не совсем
симметричны: элементы и и v во второй части доказательства
не обязаны совпадать.
1.4. Операции над соответствиями 57
Замечание 1.4. В тождестве, выражающем свойство 3,
нельзя вместо объединения поставить пересечение, так как
в этом случае тождество нарушится. Можно доказать, что
сохранится лишь включение
а обратное включение в общем случае не имеет места. #
Анализ свойств 2 и 4 показывает, что роль пустого со-
соответствия аналогична роли нуля при умножении чисел, а
диагональ множества А играет роль, аналогичную роли еди-
единицы, на множестве всех бинарных отношений на А.
Обратное соответствие. Соответствие, обратное
к соответствию р С А х В, есть соответствие из В в А, обозна-
обозначаемое р и равное, по определению, р" = {(у, х): (ж, у) Е р}.
Для соответствия г из примера 1.3
r-^ttm, Я),(П2, Я),(п2, С),
(п3, Я), (п4, Я), (п5, Я), (п5, С)}.
Обратное соответствие обладает следующими легко прове-
проверяемыми свойствами:
1) (Р~1)-1 = П
2) (роа)-1=а-1ор-\
Для бинарного отношения р на множестве А обратное со-
соответствие есть бинарное отношение на том же множестве. В
этом случае говорят о бинарном отношении р~1 на мно-
множестве А, обратном к р.
Заметим, что соответствия р°р~1 и р~1°р в общем случае
не совпадают. Даже для бинарного отношения р на множестве
А р°р"х Фр~~1°р) а также р°р ^icU и p"lop^idA-
Например, для бинарного отношения р= {C,1), D,1), D,2)}
на множестве А = {1,2,3,4} графы самого отношения, обрат-
обратного отношения р", композиций рор"ир"ор представлены
на рис. 1.5.
58
1. МНОЖЕСТВА И ОТНОШЕНИЯ
Pop''
Ю
2o
01 l
02 2
2
3o^——эоЗ зо
4O
03
O4
Рис. 1.5
Бели /: А-> В — отображение, то оно является соответ-
соответствием. Обратное к / соответствие из В в А в общем случае
не является отображением. Действительно, соответствие /""*,
обратное к /, состоит из всех упорядоченных пар вида (/(#), ж),
хеА. Поскольку в общем случае могут найтись такие два раз-
различных элемента х и я', что f(x) = /(ж')? то соответствие Z" в
общем случае не будет функционально по второй компоненте и
поэтому не будет отображением. Бели отображение f инъек-
тивно, то обратное соответствие есть частичное отображение
из В в А. Бели отображение f биективно, то обратное соот-
соответствие является отображением из В в А, причем имеют место
равенства
Отображение /-1 в этом случае называют отображением,
обратным к /.
Ограничение соответствия. Пусть р С А х В — соответ-
соответствие из А в В и С С A, D Q В. Ограничением соответст-
соответствия р на подмножества С и D (или (С, D)~ограничением
соответствия р) называется соответствие изСв Д обозначае-
обозначаемое р|с,?>) такое, что
(*, у) е p\c,d ^ ((^, у) е р) л (х е С) л (у е D).
Таким образом, (С, 1?)-ограничение соответствия р есть
„то же самое" соответствие р, но из последнего берутся только
1.4. Операции над соответствиями 59
упорядоченные пары, первая компонента которых принадле-
принадлежит подмножеству С, а вторая — подмножеству D. Можно
записать
Так, „малый" арксинус, т.е. функция у = arcsinz, есть огра-
ограничение „ большого" арксинуса у — Arcsin x, который является
соответствием на подмножества [—1,1] и [—-,—].
Рассмотрим некоторые важные частные случаи ограниче-
ограничений соответствий (в частности, бинарных отношений и ото-
отображений).
Всякое (С, В)-ограничение соответствия р С А х В будем
называть сужением соответствия р на подмножество
С (коротко — С-сужением соответствия р), а всякое
(С, /9(С))-ограничение соответствия р — строгим сужением
соответствия р на подмножество С {строгим С-су-
жением соответствия р). С-сужения соответствия р бу-
будем обозначать р|с, а строгое сужение — р\ос соответственно.
Полезно заметить, что для любого отображения /: А ->
-> В строгое сужение /|од есть сюръекция А на f{A). Бели,
сверх этого, / является инъекцией, то /|ол есть биекция А
на f(A). Допуская некоторую вольность речи*, можно ска-
сказать, что любое отображение сюръективно отображает свою
область определения на свою область значений, в частности,
любая инъекция устанавливает взаимно однозначное соответ-
соответствие между областью определения и областью значений. Так,
функция у = sinrr сюръективно отображает множество R всех
действительных чисел на отрезок [—1,1], а любая показатель-
показательная функция биективно отображает R на подмножество всех
положительных действительных чисел.
Для бинарного отношения р С А2 и любого подмножества
М С А (М, М)-ограничение бинарного отношения называют
* Вольность состоит в ТОМ) что мы отождествляем функцию / с функ-
функцией /|од.
60 1. МНОЖЕСТВА И ОТНОШЕНИЯ
ограничением бинарного отношения р на подмноже-
подмножество М и обозначают р\м• Можно записать р\м = рПМ2.
Рассмотрим, например, отношение естественного порядка
< на множестве действительных чисел [I]. Тогда отношение
^ |z = {(^ь n):m^n;m,nGZ} есть ограничение этого поряд-
порядка на подмножество целых чисел. Но ни в коем случае нельзя
путать это отношение с Z-сужением отношения ^! Это по-
последнее состоит из всех таких упорядоченных пар (т, ж), что
m e Z, ж Е R и m ^ ж, т.е. вторая компонента пары может быть
произвольным действительным числом, не меньшим заданного
целого т.
1.5. Семейства множеств
Рассматриваемое ниже понятие семейства множеств обоб-
обобщает аналогичное понятие, сформулированное в [I].
Пусть U — универсальное множество. Если каждому нату-
натуральному числу п взаимно однозначно сопоставлено некоторое
подмножество Ап С [7, то тем самым определена последова-
последовательность множеств Ai, ..., -АЛ, ..., или, в короткой записи,
(<^n)n€N- Предположим теперь, что вместо множества N на-
натуральных чисел задано произвольное множество / и каждому
элементу i EI взаимно однозначно сопоставлено подмножество
Ai С U. Тогда говорят, что задано (индексированное) се-
семейство множеств {Ai)i<zj. Множество / называют мно-
множеством индексов, а множества Ai — элементами семейства
В случае J = N получаем последовательность множеств, или
счетное семейство множеств; если множество / конеч-
конечно, получаем конечное семейство множеств. Таким обра-
образом, семейство (Ai)iei определено, если задано отображение
v:I-+2u.
Отметим, что любое множество, элементы которого есть
некоторые подмножества универсального множества G, т.е.
любое множество А С 2и, можно считать семейством (Ai)i€/,
1.5. Семейства множеств 61
где / = -A, a v — тождественное отображение множества А на
себя.
Пример 1.11. Рассмотрим в качестве множества ин-
индексов множество точек некоторой гладкой плоской кривой
[II] (рис. 1.6) и каждой точке сопоста-
сопоставим касательную, проведенную к кривой
в этой точке (которая будет единствен-
ной в силу гладкости). Тогда получаем
семейство множеств, элементами которого
служат множества точек различных каса-
касательных. # Рис1'6
Операции объединения и пересечения множеств можно рас-
распространить на произвольные семейства множеств [I].
1. Объединение семейства множеств:
2. Пересечение семейства множеств:
iei
Методом двух включений можно доказать следующие то-
тождества:
iei iei iei
Аналогично можно доказать тождества
iei iei iei iei
Тождества A.5) выражают свойство бесконечной дистри-
дистрибутивности операций пересечения и объединения, а тожде-
тождества A.6) называют бесконечными законами де Моргана.
62 1. МНОЖЕСТВА И ОТНОШЕНИЯ
1.6. Специальные свойства
бинарных отношений
В этом параграфе дана определенная классификация бинар-
бинарных отношений на множестве. В основе этой классификации
лежат специальные свойства отношений.
Бинарное отношение р на множестве А называют рефлек-
рефлексивным, если диагональ множества А содержится в р: id а Я р,
т.е. х р х для любого элемента х множества А.
Если же icUflp = 0, то бинарное отношение р на множестве
А называют иррефлексивным.
Указанные свойства бинарных отношений на множестве А
называют рефлексивностью и иррефлексивностью.
Бинарные отношения равенства и подобия на множестве
геометрических фигур рефлексивны: каждый треугольник ръ,-
вен самому себе и подобен самому себе. На самом деле рефлек-
рефлексивны все отношения равенства: равенство чисел, равенство
векторов, равенство множеств и т.п. Также рефлексивны-
рефлексивными являются, например, бинарное отношение нестрогого не-
неравенства на множестве действительных чисел, поскольку для
любого числа х всегда х < ж, и отношение С включения мно-
множеств, так как для любого множества X всегда X СХ.
Напротив, бинарное отношение на множестве действитель-
действительных чисел, задаваемое строгим неравенством х < у, иррефлек-
сивно, равно как я отношение С строгого включения множеств.
Не следует путать иррефлексивное отношение с нерефлек-
нерефлексивным, т.е. не являющимся рефлексивным, отношением. Ирре-
Иррефлексивное отношение нерефлексивно, но не всякое нерефлек-
нерефлексивное отношение иррефлексивно. Иррефлексивному отноше-
отношению на А не принадлежит ни один элемент диагонали icU,
а нерефлексивное отношение может содержать некоторые (но
не все!) элементы диагонали. На рис. 1.7 приведены приме-
примеры графиков иррефлексивного и нерефлексивного отношений
(пунктиром указаны диагонали множеств).
1.6. Специальные свойства бинарных отношении
63
Рис. 1.7
Бинарное отношение р на множестве А называют:
1) симметричным, если для любых хуу€Аюхру следует
2) антисимметричным, если для любых ж, у G А из одно-
одновременной справедливости х руту рх следу-
следует, что х = у.
Соответствующие свойства бинарных от-
отношений на множестве А называют симме-
симметричностью и антисимметричностью.
График симметричного бинарного отно-
отношения на множестве А симметричен относи-
относительно диагонали (рис. 1.8).
А
Рис. 1.8
Теорема 1.1. Бинарное отношение р на множестве А сим-
симметрично, если и только если бинарное отношение на множе-
множестве А, обратное к р, совпадает с р: р~х = р.
< Пусть (ж, у) G р", т.е. (у, х) € р. Тогда, в силу симме-
симметричности р, (ж, у) € р. Следовательно, р" С р. Аналогично
доказывается включение р С р".
Теперь пусть р = р""*1. Тогда (ж, у) G р и (ж, у) G р". Из
определения обратного отношения вытекает, что (у, х) 6 р.
Следовательно, р — симметричное бинарное отношение. >
Теорема 1.2* Бинарное отношение р на множестве А
антисимметрично, если и только если рПр" С icU.
< Действительно, если (ж, у) G рПр", то (#, у) € р и (ж, у) G р"
(т.е. (у, х)€р). Но из выполнения соотношений хруиурх вви-
ввиду антисимметричности р следует, что а; = у, т.е. (ж, у) G ic
64 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Обратно, пусть рПр" С icU. Предположим, что (х, у) G р
и (у, х) € р, причем а; Ф у. Тогда (х, у) € р и (х, у) € рПр",
но (ж, у) ^ icU. Получаем противоречие. >
Отметим, что для антисимметричного бинарного отноше-
отношения на множестве А может иметь место равенство рПр" = 0.
Все бинарные отношения в геометрии типа равенства или
подобия симметричны. Так, если треугольник ABC подо-
подобен треугольнику А'В'С, то и второй из этих треугольников
подобен первому. Бинарные отношения неравенства чисел и
включения множеств, как строгие, так и не строгие, антисим-
антисимметричны.
Бинарное отношение р на множестве А называют транзи-
транзитивным, если для любых х, у, z Е А из того, что хру и у рz,
следует х р z. Соответствующее свойство бинарного отношения
называют транзитивностью. \
Пример 1.12. а. Пусть М — некоторое множество насе-
населенных пунктов. Зададим на нем бинарное отношение дости-
достижимости: из пункта А достижим пункт J5, если есть дорога, по
которой можно доехать из Л в В. Это отношение транзитивно,
поскольку если из пункта А можно доехать до пункта 23, а из
В есть дорога до С, то из А можно проехать в С.
б. Бинарные отношения равенства и подобия в геометрии
являются транзитивными: если треугольник ABC подобен
треугольнику А\В\С\, а этот последний подобен треугольнику
Аг^Сг, то первый треугольник подобен третьему.
в. Бинарное отношение неравенства на множестве действи-
действительных чисел не транзитивно, так как из того, что х фу и
у Ф z, вовсе не следует, что хф z. Аналогично, если х друг у, а
у друг г, то — вопреки известной поговорке — это не означает,
что х друг z. #
Докажем следующее важное свойство транзитивного бинар-
бинарного отношения.
1.6. Специальные свойства бинарных отношении 65
Теорема 1.3. Бинарное отношение р на множестве А тран-
зитивно тогда и только тогда, когда его квадрат содержится
в нем, т.е. р ° р С р.
-4 Пусть бинарное отношение р на множестве А транзитивно
и (ж, z) G р2 = р о р. В силу определения композиции бинарных
отношений на множестве А существует такой элемент у, что
х руту pz, откуда ввиду транзитивности р получаем х р z, т.е.
(ж, z) Е р, а значит, р2 С р.
Обратно, пусть бинарное отношение р на множестве Л
таково, что р2 С р, а (ж, у)бр и (у, г) ? р. Тогда в силу
определения композиции бинарных отношений на множестве А
(ж, z) € р2. Поскольку р2 С р, то (#, z) 6 р. Таким образом,
из того, что (ж, у) € р и (у, г) G р, следует, что (x,z) € р, т.е.
бинарное отношение р на множестве А транзитивно. >
Доказанное свойство целесообразно использовать для про-
проверки транзитивности бинарного отношения р на некотором
множестве в тех случаях, когда построение квадрата р являет-
является более легкой задачей по сравнению с исследованием свойства
транзитивности р на основе определения.
Бинарное отношение р на множестве А называется плот-
ным, если для любых я, у Е Л, отличных друг от друга и таких,
что хру, найдется z, отличный и от re и от у, такой, что хpz
nzpy.
Образно говоря, для любой пары элементов, связанных
плотным отношением, всегда найдется третий элемент, кото-
который „встраивается между ними" и связан с каждым из них
тем же отношением. Так, отношения неравенства (строгого
и нестрогого) на множествах рациональных и действительных
чисел плотны, но аналогичные отношения на множествах целых
и натуральных чисел плотными не являются. В самом деле, ка-
каковы бы ни были рациональные (или действительные) числа х
и у, из того, что х < у, следует, что существует число z, от-
отличное как от ж, так и от у, такое, что х < z < у. Например,
66 1. МНОЖЕСТВА И ОТНОШЕНИЯ
подходит число z = (х + у)/2. Но для целых чисел т и т + 1
такого „промежуточного" целого числа нет.
Бели р — плотное бинарное отношение на множестве А и
для некоторых х,у Е А имеет место х ру, то найдется z 6 А,
такой, что хфг,уфгъхpz,zру. Отсюда в силу определения
композиции отношений следует, что хр2у. Значит, из (х, у) € р
следует (х, у) е р2, т.е. р С р2.
Итак, если р плотно, то оно содержится в своем квадрате.
Напомним, что для транзитивного бинарного отношения р2 С р.
Следовательно, если бинарное отношение р одновременно плот-
плотно и транзитивно, то р = р2.
Среди всех бинарных отношений на произвольном множе-
множестве выделяют классы отношений в зависимости от свойств,
которыми эти отношения обладают.
Бинарное отношение на некотором множестве называют^
1) эквивалентностью, если оно рефлексивно, симмет-
симметрично и транзитивно;
2) толерантностью, если оно рефлексивно и симмет-
симметрично;
3) порядком (или частичным порядком), если оно ре-
рефлексивно, антисимметрично и транзитивно;
4) предпорлдком (или квазипорядком), если оно рефлек-
рефлексивно и транзитивно;
5) строгим порядком, если оно иррефлексивно, антисим-
антисимметрично и транзитивно;
6) строгим предпорядком, если оно иррефлексивно и
транзитивно.
Определенные выше бинарные отношения называют от-
отношениями эквивалентности, толерантности, поряд-
порядка {частичного порядка), предпорядка (квазипорядка),
строгого порядка, строгого предпорядка.
Пример 1.13. а. Бинарное отношение параллельности
двух прямых или двух плоскостей в евклидовой геометрии, если
1.6. Специальные свойства, бинарных отношении 67
считать каждую прямую (плоскость) параллельной самой себе,
есть отношение эквивалентности.
б. Бинарное отношение р на множестве всех непустых
подмножеств некоторого множества С/", для
которого А р В тогда и только тогда, когда
А П В ф 0, является толерантностью. Это
отношение рефлексивно и симметрично, но
не транзитивно. Действительно, из того,
что АПВф0 иВПСф0, никак не следует, рис. i.g
чтоАПСф0 (рис. 1.9).
в* Примером отношения порядка является естественный
числовой порядок*, т.е. отношение неравенства на любом
числовом множестве.
г. На множестве натуральных чисел N зададим бинарное
отношение а|6, означающее, что а делит Ь (а является дели-
делителем 6). Это отношение рефлексивно, поскольку любое число
является делителем самого себя. Покажем антисимметричнсть.
Пусть а делит 6 и в то же время Ь делит а. Тогда найдется на-
натуральное число <i, такое, что Ь = ati, и найдется <2> такое, что
a = 6*2- Отсюда Ь = 6*2*1, что на множестве натуральных чисел
возможно только при *i = *2 = 1- Следовательно, a = 6. Пока-
Покажем транзитивность. Бели а делит 6, а 6 делит с, то найдутся
натуральные числа *i, *2> такие, что 6 = at\ и с = 6*2- Отсюда
имеем с = a*i<2? т.е. a — делитель с. Таким образом, „отноше-
„отношение делимости" на множестве N является отношением порядка.
Бели распространить это отношение на множество целых
чисел, то оно будет уже только предпорядком, поскольку те-
теряется свойство антисимметричности. Например, 2 делится на
—2 и —2 делится на 2, однако 2 ф —2.
*В [I] это отношение названо просто естественным порядком. По-
Поскольку в дискретной математике нам приходится иметь дело со многими
порядками на нечисловых множествах, мы все время будем говорить „есте-
„естественный числовой порядок", подчеркивая тем самым, что речь идет об
отношении порядка на множестве действительных чисел (или об его огра-
ограничении на множества рациональных, целых или натуральных чисел).
68
1. МНОЖЕСТВА И ОТНОШЕНИЯ
д. Рассмотрим множество 2А всех подмножеств множества
А. Покажем, что отношение включения С на множестве 2А
есть порядок. Это отношение рефлексивно, так как для любого
множества X справедливо включение X С X. Поскольку для
любых двух множеств X и У из ХСУ и УСХ следует,
что X = У, рассматриваемое отношение антисимметрично. Из
определения включения вытекает, что если X С У и Y С Z, то
X С Z. Следовательно, отношение транзитивно.
е. Отношение строгого неравенства на числовом множе-
множестве, равно как и отношение строгого включения множеств,
есть отношение строгого порядка.
ж. В качестве примера отношения строгого предпорядка
можно привести отношение пстрогой достижимости" на неко-
некотором множестве населенных пунктов: пункт А считаем строго
достижимым из отличного от него пункта J5, если есть дорога
(автомобильная, железная и т.п.) из А в .В, причем принимает-
принимается, что никакой пункт не является строго достижимым из себя
самого. #
Бинарные отношения
на множестве
Рефлексивность
и
симметричность.
Рефлексивность
и
транзитивность
Отношения
толерантности
Транзитивность
Отношения
предпорядка
Симметричность
Отношения
эквивалентности
Антисимметричность
Отношения
порядка
Рис. 1.10
Отношения толерантности, эквивалентности, предпорядка
и порядка — важнейшие в современной математике. Связь
1.6. Специальные свойства бинарных отношении 69
между этими четырьмя классами бинарных отношений пока-
показана на рис. 1.10. Можно сказать, что эквивалентность есть
транзитивная толерантность или симметричный предпорядок.
Порядок же есть антисимметричный предпорядок.
Для любого бинарного отношения р С А2 можно построить
отношение р* следующим образом: х р* у тогда и только тогда,
когда х = у или существует последовательность #о, #ъ • ••»
#n, n ^ 1, такая, что жо = х> хп = У и для каждого г = 0, п—1
выполняется Xipxi+\. В частности, если (ж, у) Е р, т.е. х ру, то
это означает, что приведенное условие выполняется при п = 1.
Следовательно, (ж, у) Е р*, т.е. р С р*.
Отношение р* называют рефлексивно-транзитивным
замыканием бинарного отношения р на соответствующем
множестве.
Можно также обозначить
и тогда
00
г=0
Отношение р* является рефлексивным, так как icU С р*.
Докажем его транзитивность. Пусть для каких-то x,y,z вы-
выполняется х р* у и у р* z. Докажем, что я; р* z. Будем считать,
что элементы х, у, z попарно различны (так как при х = у или
У = г доказывать нечего). Тогда существуют последователь-
последовательности ж = ж0, хи ..., ffn = 2/ и у = уо, yi, ..., ут=г, такие,
нто Xf р #j+i для каждого г = 0, п—1 и у^ р yj+i для каждого
В итоге получаем последовательность го, ..., 2:n, ^n+i> •••»
zn+m. Где г0 = X, Zn = у, ^n-bm = г, *г = ^г ДЛЯ ВСЯКОГО % = 1, П-1,
zn+j = yj для всякого j = 1, m—1, такую, что г* р Zj+i для любого
г = 0, n+m—1, т.е. ж р* г.
70 1. МНОЖЕСТВА И ОТНОШЕНИЯ
1.7. Отношения эквивалентности
Пусть А — произвольное множество. Семейство
непустых и попарно не пересекающихся множеств называют
разбиением множества А, если объединение множеств семей-
семейства (Bi)i?i равно А, т.е. [jBi = А.
i6/
Сами множества Вг называют элементами (или члена-
членами) разбиения (Д)г€/.
Например, множества [0,1/3), [1/3, 2/3) и [2/3,1] образуют
разбиение отрезка [0,1]. Тривиальными разбиениями А
являются, по определению, разбиение {А}, состоящее только
из самого А, и разбиение, состоящее из всех одноэлементных
подмножеств множества А.
Пусть р — эквивалентность на множестве А и х Е А. Мно-
Множество всех элементов А, эквивалентных х, т.е. множество
{у: у рж}, называют классом эквивалентности по отноше-
отношению р и обозначают [х]р. Отметим, что в силу рефлексивности
для любого элемента х Е А класс эквивалентности не пуст, так
как х Е [х]р.
Теорема 1.4. Для любого отношения эквивалентности
на множестве А множество классов эквивалентности образует
разбиение множества А. Обратно, любое разбиение множества
А задает на нем отношение эквивалентности, для которого
классы эквивалентности совпадают с элементами разбиения.
<4 Покажем, что отношение эквивалентности р на множестве
А определяет некоторое разбиение этого множества. Убедимся
вначале, что любые два класса эквивалентности по отношению
р либо не пересекаются, либо совпадают.
Пусть два класса эквивалентности [х]р и [у]р имеют общий
элемент z Е [х]р П [у]р. Тогда z px и z py. В силу симметрич-
симметричности отношения р имеем хрz, и тогда хрz и zpy. В силу
транзитивности отношения р получим х ру. Пусть h € [#]р,
тогда h р х. Так как х р у, то h р у и, следовательно, h E [у]р.
1.7. Отношения эквивалентности 7\_
Обратно, если h ? [у]р, то в силу симметричности р получим
Нру,У рхив силу транзитивности — hрх, т.е. h € [х]р. Таким
образом, [х]р = [у]р.
Итак, любые два не совпадающих класса эквивалентности
не пересекаются. Так как для любого х € А справедливо х Е [х]р
(поскольку х рх), т.е. каждый элемент множества А принадле-
принадлежит некоторому классу эквивалентности по отношению р, то
множество всех классов эквивалентности по отношению р обра-
образует разбиение исходного множества А. Таким образом, любое
отношение эквивалентности однозначно определяет некоторое
разбиение.
Теперь пусть (Sj)^/ — некоторое разбиение множества А.
Рассмотрим отношение р, такое, что х ру имеет место тогда
и только тогда, когда х и у принадлежат одному и тому же
элементу В{ данного разбиения:
х р у & (Эг е I)(х е Вг) л (у е в{).
Очевидно, что введенное отношение рефлексивно и симметрич-
симметрично. Бели для любых х,уъг имеет место хру и у pz, то ж, у и
z в силу определения отношения р принадлежат одному и тому
же элементу В% разбиения. Следовательно, хpz та. отношение р
транзитивно. Таким образом, р — эквивалентность на А. >
Теорема 1.4 позволяет отождествлять отношения эквива-
эквивалентности и разбиения: любая эквивалентность определяет
единственное разбиение и наоборот.
Множество всех классов эквивалентности по данному от-
отношению эквивалентности р на множестве А называют фак-
тпор-множеством множества А по отношению р и обознача-
обозначают А/р.
Пример 1.14. а. На множестве целых чисел Z определим
отношение равенства по модулю /с, где k G N. Положим
ж==(тос1А:)У> если и только если х — у делится на к.
* Традиционное обозначение: т = n(mod&).
.*
72 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Легко проверяется, что это отношение эквивалентности.
Действительно, рефлексивность следует из того, что для любо-
го m E Z га — т = 0и делится на &; симметричность — из того,
что если га — п делится на А;, то и п — га делится на к. Для до-
доказательства транзитивности заметим, что если т — п делится
на А;, п — р делится на А:, то и их сумма (га — п) + (п—р) =т—р
делится на к. Другими словами, для любых целых m, n, p из
™=(mod*)tt и n=(modA.)p следует m=(modA.)p, что доказывает
транзитивность отношения =(modfc)-
Равенство чисел га и п по модулю & означает, что при деле-
делении на к эти числа дают одинаковые остатки. Действительно,
для каждого х Е Z имеем # = m • fe + г, где г — остаток от деле-
деления х на А:. Следовательно, х — г = m • А;, т.е. tf=(m0(jA;) г. Таким
образом, каждое число попадает в тот же класс эквивалентно-
эквивалентности по отношению =(modA:)> что и остаток от деления его на к.
Поскольку всего различных остатков может быть ровно к\\О,
1, ..., А; — 1, получаем ровно к попарно различных классов экви-
эквивалентности по данному отношению: [0]=(mod/k), [l]=(mod4), -.,
[fc" 1]=(modfc)' ГДе КЛаСС M=(mod*) СОСТОИТ ИЗ ВСвХ ЦвЛЫХ ЧИСвЛ,
дающих при делении на к остаток г.
Отметим, что мы установили взаимно однозначное соот-
соответствие между фактор-множеством Z/=(mod^.) и множеством
Zfc, состоящим из чисел 0, 1, ..., А; — 1.
Второе множество дает нам как бы „наглядный образ" по-
построенного фактор-множества. Нельзя считать, что фактор-
фактормножество Z/=(modfc) равно множеству {0,1,..., к — 1}. Нет,
указанное фактор-множество состоит из к элементов, каждый
из которых есть не число, а множество всех целых чисел, при
делении на к дающих фиксированный остаток. Но каждому
такому классу эквивалентности однозначно сопоставляется це-
целое число от 0 до А; — 1, и, наоборот, каждому целому числу
от 0 до к — 1 соответствует единственный класс эквивалентно-
эквивалентности по отношению =(modA;)- Заметим, что в математике часто
используется прием сопоставления фактор-множеству такого
1.7. Отношения эквивалентности 73
находящегося с ним во взаимно однозначном соответствии мно-
множества, которое легко представить и описать.
б. На множестве R действительных чисел зададим отно-
отношение а=(тосц)Ь, полагая, что числа а и Ь равны по модулю
1 тогда и только тогда, когда число a — b является целым. Из
определения следует, что каждое число по модулю 1 равно своей
дробной части*.
Так как отношение =(mOd i) определено через равенство, то
легко понять, что все свойства отношения эквивалентности для
него выполняются. Каждый класс эквивалентности будет со-
содержать числа с равными дробными частями. Это значит, что
каждый класс эквивалентности по данному отношению одно-
однозначно определяет некоторое число из полуинтервала [0,1) и,
наоборот, каждому числу j ? [0,1) однозначно сопоставляется
класс эквивалентности, состоящий из всех действительных чи-
чисел, дробная часть которых равна 7* Таким образом, фактор-
фактормножество K/=(modi) и полуинтервал [0,1) на числовой прямой
находятся во взаимно однозначном соответствии. Этот полуин-
полуинтервал можно рассматривать как представление определенного
выше фактор-множества. #
Установим теперь связь между понятиями эквивалентности
и отображения. Заметим, что для любого отношения эквива-
эквивалентности р на множестве А можно определить отображение
fp: А -> А/р, положив fp(x) = [ж]р, т.е. сопоставив каждому
х ? А содержащий его класс эквивалентности. Это отобра-
отображение сюръективно, так как каждый элемент множества А
принадлежит некоторому классу эквивалентности, т.е. для ка-
каждого [х]р е А/р справедливо [х]р = fp(x).
Отображение /р, определенное таким образом, называют
канонической сюръекцией множества А.
"Под дробной частью <а> числа а понимается число из полуинтервала
[0,1), такое, что а = п + <а> для некоторого целого п. Поэтому дробной
частью отрицательного числа —о, где о > 0, будет число 1 — <о>. Так,
Дробной частью -1,23 будет не 0,23, а 0,77 = 1 - 0,23.
74 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Покажем, что любое отображение однозначно определяет
некоторое отношение эквивалентности.
Теорема 1.5. Пусть /: А —> В — произвольное отображе-
отображение. Отношение р/ на множестве А, для которого х р/ у, если
и только если f(x) = /(у), является отношением эквивалентно-
эквивалентности, причем существует биекция фактор-множества А/р/ на
множество f(A).
<4 Рефлексивность, симметричность и транзитивность отноше-
отношения pf следуют непосредственно из его определения, т.е. pf —
эквивалентность.
Зададим отображение (р фактор-множества Ajpj в множе-
множество f(A) следующим образом: <p{[x]Pf) = /(ж). Из способа
задания отношения р следует, что отображение определено кор-
корректно, т.е. каждому классу эквивалентности поставлен в со-
соответствие единственный элемент у Е f(A).
Докажем, что <р — биекция, для чего убедимся в том,
что это инъекция и сюръекция одновременно. Пусть классы
эквивалентности [x]Pf и [у]Р/ не совпадают. В силу теоремы 1.4
это означает, что они не пересекаются, т.е. х не эквивалентно
у. Из определения отношения р/ следует, что f(x) ф /(у).
Таким образом, (р — инъекция. Бели элемент и Е /(А), то
найдется такой элемент х Е А, что и = f(x) = <p([x]Pf), т.е. (р —
сюръекция фактор-множества А/р/ на множество f(A). Итак,
(р — биекция. >
Следовательно, в силу доказанных теорем 1.4 и 1.5 суще-
существует связь между тремя понятиями — отображением мно-
множества, отношением эквивалентности на множестве и разбие-
разбиением множества. Но неверно, что существует взаимно одно-
однозначное соответствие между отображениями и отношениями
эквивалентности*. Два разных отображения могут определять
одно и то же разбиение отображаемого множества, тем самым
задавая на нем одно и то же отношение эквивалентности. Так,
'"Заметим, что теорема 1.5 этого и не утверждает.
1.8. Упорядоченные множества 75
например, любое биективное отображение /: А -> В задает на
Л одно и то же разбиение — тривиальное разбиение на одно-
одноэлементные множества.
1.8. Упорядоченные множества.
Теорема о неподвижной точке
Множество вместе с заданным на нем отношением порядка
называют упорядоченным множеством.
Отношение порядка будем, как правило, обозначать < (или
значками г$, С и т.п., похожими на ^). При этом следует пони-
понимать, что даже на некотором множестве S С R рассматриваться
может любое отношение порядка, а не только естественный
числовой порядок. Множество М с заданным на нем отноше-
отношением порядка ^ будем записывать как пару (М,^). Записывая
х ^ у, мы будем говорить, что элемент х не больше элемента у.
Каждому отношению порядка ^ на множестве М можно
сопоставить следующие отношения.
1. Отношение, которое будем обозначать <, получается из
исходного отношения порядка < выбрасыванием всех элементов
диагонали idM> т.е. х < у для любых х,у€М тогда и только то-
тогда, когда х ^ у и х Ф у. Записывая х < у, мы будем говорить,
что элемент х строго меньше элемента у. Из определения следу-
следует, что отношение < есть иррефлексивное, антисимметричное
и транзитивное бинарное отношение на множестве М, т.е. оно
является отношением строгого порядка.
2. Двойственный порядок. Это бинарное отношение
на множестве М, называемое также и отношением, двой-
двойственным к отношению порядка <, определяется как би-
бинарное отношение на множестве М, обратное к отношению
<. Его обозначают ^. Тогда для любых ж, у условие х ^ у
равносильно тому, что у < х. Можно без труда доказать, что
отношение ^ тоже является отношением порядка.
Записывая х^у, мы будем говорить, что элемент х не мень-
меньше элемента у. Отношение строгого порядка, ассоциированное
76 1. МНОЖЕСТВА И ОТНОШЕНИЯ ___
с ^, договоримся обозначать >, говоря при этом, что элемент
х строго больше элемента у, если х ^ у и х Ф у.
3. Отношение доминирования. Для двух элементов х и у,
по определению, х < у тогда и только тогда, когда х строго
меньше у и не существует такого элемента z, что х < z < у.
Отношение < называют отношением доминирования (или
просто доминированием), ассоциированным с отношением
порядка ^. Бели имеет место х < у, то говорят, что элемент у
доминирует над элементом х.
Из определения следует, что отношение доминирования ир-
рефлексивно, антисимметрично, но не транзитивно. Оно может
быть и пусто. Например, легко видеть, что пустым будет
отношение доминирования, если исходный порядок является
плотным бинарным отношением на соответствующем множе-
множестве.
Пример 1.15. а. Рассмотрим множество действительных
чисел с естественным числовым порядком. Пусть а < с. Из-
Известно, что для любых аи с найдется такое 6, что а<Ь<с, т.е.
это отношение порядка на множестве действительных чисел
является плотным. Поэтому отношение доминирования будет
пустым.
По той же причине будет пустым отношение доминирова-
доминирования, ассоциированное с естественным числовым порядком на
множестве рациональных чисел. Но на множестве целых чисел
(опять-таки с естественным числовым порядком) отношение
доминирования не пусто. Так, 1 < 2, —5 < —4, но, конечно,
неверно, что 1 < 3, поскольку между единицей и тройкой су-
существует wпромежуточный" элемент — двойка.
б. На множестве всех подмножеств трехэлементного мно-
множества {а, 6, с}, где в качестве отношения порядка взято отно-
отношение теоретико-множественного включения С, подмножество
{а, 6} доминирует над подмножествами {а} и {Ь}, но не домини-
доминирует над пустым множеством. В свою очередь, все множество
1.8. Упорядоченные множества 77
{а, Ь, с} доминирует над любым своим двухэлементным подмно-
подмножеством, но не доминирует над одноэлементным и над пустым.
в. По отношению делимости на множестве натуральных
чисел 15 доминирует над 3 и 5, но 20 не доминирует над 5,
так как существует япромежуточный" элемент — 10, делитель
20, который делится на 5, но не равен ни 20, ни 5. #
Рассмотрим упорядоченное множество (М, ^) и его произ-
произвольное непустое подмножество В С М. Упорядоченное мно-
множество (JB, ^|в), где ^\в — ограничение отношения ^ на под-
подмножество В, называют упорядоченным подмножеством
упорядоченного множества (М, ^).
Таким образом, можно переносить отношения порядка на
непустые подмножества исходного упорядоченного множества.
Как правило, вместо ^ \в будем писать просто ^ (если ясно,
о каком подмножестве В идет речь). Порядок ^ \в на под-
подмножестве В называют также порядком, индуцированным
исходным порядком < на всем множестве А. Часто прибегают
к такому выражению: „рассмотрим подмножество В упоря-
упорядоченного множества (М, ^) с индуцированным порядком",
понимая под этим порядок ^ |в-
Элементы х и у упорядоченного множества (М, ^) назы-
называют сравнимыми по отношению порядка ^, если х ^ у или
у ^ х. В противном случае элементы хиу называются несрав-
несравнимыми.
Упорядоченное множество, все элементы которого попарно
сравнимы, называют линейно упорядоченным, а соответ-
соответствующее отношение — отношением линейного порядка
(или просто линейным порядком). Бели индуцированный
порядок на подмножестве упорядоченного множества является
линейным, то это линейно упорядоченное подмножество на-
называют цепью. Любое подмножество попарно не сравнимых
элементов данного упорядоченного множества называют ан-
антицепью.
78 J. МНОЖЕСТВА И ОТНОШЕНИЯ
Замечание 1*5. Обратим внимание на то, что термину
„упорядоченное множество" (в смысле приведенного определе-
определения) в [I] отвечает термин „частично упорядоченное множе-
множество", а то, что мы называем линейно упорядоченным мно-
множеством, в [I] называется просто упорядоченным множеством.
Терминология этого вьшуска более принята в алгебраической
литературе и литературе по дискретной математике. Упо-
Употребление в [I] термина „частично упорядоченное множество"
мотивировало желанием подчеркнуть, что в общем случае в
упорядоченном множестве существуют не сравнимые элементы.
Пример 1.16. а. Отношение естественного числового
порядка на множестве Е действительных чисел является от-
отношением линейного порядка, поскольку для любых двух чисел
а, Ь имеет место или неравенство а ^ Ь, или неравенство Ь^а.
б. Отношение делимости (см. пример 1.13.г) на множестве
N и отношение включения С на В (А) (см. пример 1.13.д) не
являются линейными порядками, за исключением случая, когда
А — одноэлементное множество. #
Пусть (А, <) — упорядоченное множество. Элемент а € А
называют наибольшим элементом множества А, если для
всех х G А выполняется неравенство х < а.
Элемент Ъ называют максимальным элементом множе-
множества А, если для всякого х ЕА имеет место одно из двух: или
х ^ Ь, или х и 6 не сравнимы.
Аналогично определяются наименьший и минимальный
элементы упорядоченного множества, а именно: наименьший
элемент упорядоченного множества А — это такой его элемент
а, что а^х для каждого х ? Ау а минимальный элемент — это
такой элемент Ь G А, что для любого х G А элементы 6 и х не
сравнимы или Ъ ^ х.
Покажем, что наибольший (наименьший) элемент множе-
множества, если он существует, является единственным. Действи-
Действительно, полагая, что а и а1 — наибольшие элементы А по
1.8. Упорядоченные множества 79
отношению порядка ^, получаем, что для всякого х € А выпол-
выполняется х < а и х ^ а'. В частности, о! < о и а < а', откуда ввиду
антисимметричности любого отношения порядка следует, что
a = а;. Аналогично доказывается единственность наименьшего
элемента.
Замечание 1.6. Поскольку на одном и том же множестве
могут быть определены разные отношения порядка (например,
на множестве натуральных чисел — естественный числовой
порядок и отношение делимости), то, когда это необходимо,
мы будем говорить о наибольших, наименьших (соответственно
максимальных и минимальных) элементах по данному отноше-
отношению порядка, уточняя тем самым, о каком отношении порядка
идет речь. #
Следующие примеры показывают, что максимальных (ми-
(минимальных) элементов может быть сколько угодно*.
Пример 1.17. Рассмотрим множество точек плоскости с
некоторой фиксированной прямоугольной декартовой систе-
системой координат. Координаты каждой точки плоскости зада-
задаются упорядоченной парой (ж, у) действительных чисел. Отно-
Отношение порядка на множестве точек плоскости определим следу-
следующим образом: (а, Ь) < (c,d), если и только если а < с и Ь ^ d.
Рассмотрим множество точек треугольника ОАВ (рис. 1.11, а).
Точка с координатами @, 0) является наименьшим элементом
этого множества. Максимальными элементами являются все
точки, лежащие на стороне АВ. Наибольшего элемента нет. #
Пусть (А, ^) — упорядоченное множество и В С А. Эле-
Элемент а 6 А называется верхней (соответственно нижней)
гранью множества 2?, если для всех элементов х G В име-
имеет место (х ^ а) (соответственно (х ^ а)).
*Но заметим, что если у множества есть наибольший (соответственно
наименьший) элемент, то он является единственным максимальным (соот-
(соответственно минимальным) элементом данного множества.
80
J. МНОЖЕСТВА И ОТНОШЕНИЯ
Максимальные
элементы
supD€D
Б
О\ В
Наименьший
элемент
О\ С
inf D€D
а б в
Рис. 1.11
Наименьший элемент множества всех верхних граней (соот-
(соответственно наибольший элемент множества всех нижних гра-
граней) множества В называют точной верхней гранью В
(соответственно точной нижней гранью В) и обозначают
supjB (infB).
Множество всех верхних (нижних) граней множества В
называют верхним (нижним) конусом В и обозначают Bv
(соответственно ВА).
В отличие от наибольшего и наименьшего элементов мно-
множества В элементы sup В и inf В не обязаны принадлежать
множеству В. Точная верхняя (нижняя) грань множества су-
существует не всегда.
Пример 1.18. а. Рассмотрим множество D точек пря-
прямоугольника ОАВС (рис. 1.11, б) с заданным в примере 1.17
отношением порядка. Точка О является точной нижней гра-
гранью, а точка В — точной верхней гранью этого множества.
Обе точки принадлежат множеству.
Бели рассмотреть множество F (рис. 1.11, б) с тем же
отношением порядка, то увидим, что точная нижняя грань
(точка О) и точная верхняя грань (точка Е) множества F
существуют, но не принадлежат множеству.
б. На числовой прямой с „выколотой" точкой Ь для по-
полуинтервала [а, Ь) множество верхних граней есть (Ь, +оо), но
точной верхней грани нет. #
1.8. Упорядоченные множества 81
Упорядоченное множество (М, <) называют вполне упо-
упорядоченным, если его любое непустое подмножество имеет
наименьший элемент.
Множество натуральных чисел с отношением естественно-
естественного числового порядка вполне упорядоченное. Множество целых
чисел не вполне упорядоченное, поскольку оно не имеет наи-
наименьшего элемента. Аналогично множества рациональных и
действительных чисел не являются вполне упорядоченными.
Можно показать, что справедлив принцип двойствен-
двойственности для упорядоченных множеств. Пусть (М, ^) —
произвольное упорядоченное множество. Тогда любое утвер-
утверждение, доказанное для порядка ^, останется справедливым
для двойственного порядка ^, если в нем:
1) порядок < заменить на порядок ^ и наоборот;
2) наименьший (минимальный) элемент заменить наиболь-
наибольшим (максимальным) элементом и наоборот;
3) inf заменить на sup и наоборот.
Например, если для некоторого a € М и для В СМ мы
доказали, что a = sup В при заданном отношении порядка, то
для двойственного порядка a = inf В.
Говорят также и о взаимно двойственных определе-
определениях: если в любом определении, связанном с упорядоченным
множеством, произвести взаимные замены согласно принципу
двойственности, то получится новое определение, называемое
двойственным к исходному. Так, определение наибольшего
(максимального) элемента множества двойственно к определе-
определению наименьшего (минимального) элемента, и наоборот. Часто
употребляют оборот речи: „двойственным образом..." (или
„двойственно..."), понимая под этим переход к утверждению
или определению, которое двойственно к исходному.
Рассмотрим теперь некоторые способы наглядного предста-
представления упорядоченных множеств.
Конечное упорядоченное множество можно графически изо-
изобразить в виде так называемой диаграммы Хассе. На этой
Диаграмме элементы множества изображаются кружочками.
82 1. МНОЖЕСТВА И ОТНОШЕНИЯ
2
о
О
1
2"
При этом если элемент Ь доминирует над элементом а, то
кружочек, изображающий элемент Ь, располагается выше кру-
кружочка, изображающего элемент а, и соединяется с ним прямой
линией. Иногда для большей наглядности из а в & ведут стрел-
стрелку. На рис. 1.12 изображены диаграммы Хассе для упорядочен-
упорядоченных множеств делителей чисел 2, 6, 30 и 36 по рассмотренному
выше отношению делимости (см. пример 1.13.г).
На рис. 1.13 приведена диаграм-
диаграмма Хассе для упорядоченного множе-
множества всех подмножеств трехэлемент-
трехэлементно} < А|а'с)> {Ь,с} ного множества (°> ь> с> по отноше-
отношению включения (см. пример 1.13.д).
Последовательность {rPt}teN эле-
элементов упорядоченного множества
называют неубывающей, если для
каждого г € N справедливо неравен-
неравенство Xi ^Xi+\.
Элемент а упорядоченного мно-
множества (М, ^) называют точной верхней гранью после-
последовательности {fft}»€N? если он есть точная верхняя грань
множества всех членов последовательности*.
* Другими словами, точная верхняя грань последовательности есть
точная верхняя грань области ее значений как функции натурального
аргумента.
1.8. Упорядоченные множества 83
Двойственно определяется точная нижняя грань после-
дователъности.
Упорядоченное множество (М, ^) называют индуктив-
индуктивным, если:
1) оно содержит наименьший элемент;
2) всякая неубывающая последовательность элементов этого
множества имеет точную верхнюю грань.
Например, множество всех подмножеств некоторого мно-
множества по отношению включения будет индуктивным. Наи-
Наименьший элемент — пустое множество, а точной верхней гра-
гранью произвольной неубывающей последовательности множеств
будет объединение всех членов этой последовательности (наи-
(наименьшее по включению множество, содержащее в качестве под-
подмножества любой член последовательности).
Определение 1.5. Пусть (Mi, ^) и (Мг, =^) — индук-
индуктивные упорядоченные множества. Отображение /: Mi -* Mi
одного индуктивного упорядоченного множества в другое на-
называют непрерывным, если для любой неубывающей после-
последовательности а\) ..., ап, ... элементов множества Mi образ
ее точной верхней грани равен точной верхней грани после-
последовательности образов /(ai), ..., /(an), ..., т.е. справедливо
равенство /(supan) =sup/(an).
Определение 1.6. Отображение /: Mi -> M*i упорядочен-
упорядоченных множеств (Mi, ^) и (М2, ^0 называют монотонным,
если для любых a, b ? Mi из о ^ Ь следует /(а) ^ /F).
Теорема 1.6. Всякое непрерывное отображение одного
индуктивного упорядоченного множества в другое монотонно.
Ч Пусть / — непрерывное отображение индуктивного упоря-
упорядоченного множества (Mi, <) в индуктивное упорядоченное
множество (Мг, =4). Пусть а,Ъ е М\ и а < Ь. Образуем последо-
последовательность {xn}neNj где х\ = а, а хп = 6, п > 2. Эта последова-
последовательность неубывающая. Для нее supa:n = sup {a, 6} = b. В силу
84 1. МНОЖЕСТВА И ОТНОШЕНИЯ
непрерывности отображения /
f(b) = /(sup*n) = /(sup{a, b}) = sup{/(a), /F)},
откуда следует, что f(a) *4f(b). >
Заметим, что функция /: R —> R, непрерывная в смысле
определений математического анализа, не обязана быть моно-
монотонным отображением упорядоченных множеств R с естествен-
естественным числовым порядком, т.е. приведенное выше определение 1.5
непрерывности не вполне аналогично определению непрерывно-
непрерывности в анализе [I]. Например, рассмотрим непрерывное в смысле
определений математического анализа отображение у = —х чи-
числовой прямой с естественным числовым порядком на себя. Это
отображение не является монотонным в смысле данного выше
определения 1.6, поскольку, например, 0^1, однако неравен-
неравенство /@)=0^/A) = —1 не выполняется.
В общем случае монотонное в смысле определения 1.6 ото-
отображение не является непрерывным в смысле определения 1.5.
Приведем пример, показывающий, что утверждение, обратное
теореме 1.6, неверно.
Пример 1.19. Рассмотрим множество всех точек отрезка
[0,1] числовой прямой с порядком, индуцированным естествен-
естественным числовым порядком. Это множество индуктивно: его
наименьший элемент — 0, а любая неубывающая последователь-
последовательность элементов ограничена сверху и по признаку Вейерштрас-
са [I] имеет предел, который и будет ее точной верхней гранью.
Любая кусочно непрерывная (но не непрерывная!) и монотон-
монотонная в смысле обычных определений из курса математического
анализа функция [I], отображающая этот отрезок на любой
отрезок с порядком, индуцированным естественным числовым
порядком, дает пример монотонного в смысле определения 1.6,
но не непрерывного в смысле определения 1.5 отображения
между индуктивными частично упорядоченными множества-
1.8. Упорядоченные множества 85
ми. Например, пусть функция / имеет вид
0,5х, 0 ^ х < 0,5;
Г
Это отображение монотонно. Для последовательности {хп} =
= I n >, n Е N, точная верхняя грань равна 0,5. Точная верх-
верхняя грань последовательности {f(xn)} равна 0,25, a f(s\xpxn) =
~ /@,5) = 0,75. Следовательно, отображение не является непре-
непрерывным в смысле определения 1.5. #
Не следует путать отображение, монотонное в смысле опре-
определения 1.6, с монотонными функциями из курса математиче-
математического анализа. Функция /: R -> Ш будет монотонной в смысле
определения 1.6 тогда и только тогда, когда она является не-
неубывающей [I].
Для приложений особенно важны непрерывные отображе-
отображения индуктивного упорядоченного множества в себя.
Определение 1.7. Элемент а множества А называют
неподвижной точкой отображения /: А -> А, если /(а) = а.
Элемент а упорядоченного множества М называют паи-
меньшей неподвижной точкой отображения f: М -> М,
если он является наименьшим элементом множества всех непо-
неподвижных точек отображения /.
Теорема 1.7 (теорема о неподвижной точке). Лю-
Любое непрерывное отображение / индуктивного упорядоченно-
упорядоченного множества (М, ^) в себя имеет наименьшую неподвижную
точку.
<4 Обозначим через О наименьший элемент множества М.
Полагаем f°{x) = x и fn(x) = f{fn~l(x)) для любого п > 0,
т.е. fn(x) означает результат n-кратного применения / к х.
Рассмотрим последовательность элементов М
{/"(О) Wo = {О, /(О),..., Г (О),...}. A.7)
86 J. МНОЖЕСТВА И ОТНОШЕНИЯ
Докажем, что последовательность A.7) неубывающая. Ис-
Используем метод математической индукции. Для элемента О,
как наименьшего элемента множества М, имеем О = /°(О) <
^ /(О). Пусть для некоторого натурального п верно соотноше-
соотношение /П"(О) ^ /П(О). Согласно теореме 1.6, отображение / мо-
монотонно, и поэтому /П(О) = /(/""^О)) < /(/П(О)) = /П+1(О),
т.е. соотношение верно и для номера п+ 1. Согласно методу
математической индукции, /П(О) ^ /П+1(О) для любого n € No,
т.е. последовательность A.7) неубывающая. Следовательно,
по определению индуктивного упорядоченного множества, она
имеет точную верхнюю грань. Обозначим ее через а:
a = sup/n(O). A.8)
Докажем теперь, что если у неубывающей последовательно-
последовательности отбросить любое конечное число начальных членов, то ее
точная верхняя грань не изменится.
Действительно, если а есть точная верхняя грань неубываю-
неубывающей последовательности {лп}п^сь то а ^ хп для всякого п ^ 0. В
частности, фиксируя произвольно к > 0, для любого п ^ к име-
имеем а ^ хп, т.е. а будет верхней гранью подпоследовательности
Докажем, что а является точной верхней гранью этой под-
подпоследовательности. Пусть Ь — какая-то ее верхняя грань, т.е.
Ь^хп для любого п ^ к. Так как последовательность {хп}п^о
неубывающая, то хр < з& для каждого р = 0, к—1. Поскольку
Xk < Ь, то в силу транзитивности отношения порядка хр ^ Ъ и
тем самым Ь ^ хп для любого п ^ 0, т.е. Ь есть верхняя грань
всей последовательности {#п}п>о- Поскольку о = supa;n, то а < Ь
и а = sup хп. Следовательно, а — точная верхняя грань под-
последовательности ^
В силу непрерывности / получаем
/(а) = /(8ирГ(О)) =sup/(/"(O)) =suPr+1(O).
1.8. Упорядоченные множества 87
Но
sup/n+1(O) =sup{/1(O),/2(O),...} = sup/n(O) =o.
Таким образом, доказано, что а является неподвижной
точкой отображения /.
Покажем теперь, что найденная неподвижная точка явля-
является наименьшей. Пусть для некоторого у ? M /(у) = у. Так
как О ^ у, а отображение /, будучи непрерывным, монотонно,
то /(О) ^ f(y) = у, /(/(О)) ^ /(/(у)) = у и т.д. Следователь-
Следовательно, для любого п ^ О /П(О) < у, т.е. элемент у есть верхняя
грань последовательности {/п@)}п^о- Поскольку элемент a
(как точная верхняя грань) есть наименьший элемент на мно-
множестве всех верхних граней этой последовательности, то у ^ а.
Таким образом, мы доказали, что произвольная неподвижная
точка отображения / не меньше элемента а, т.е. а — наимень-
наименьшая неподвижная точка отображения /. >
Поиск неподвижной точки отображения f:M-±M можно
рассматривать как задачу решения уравнения
x = f(x). A.9)
Теорему о неподвижной точке можно трактовать таким
образом: для непрерывного отображения / индуктивного упо-
упорядоченного множества в себя уравнение х = f(x) имеет реше-
решение, т.е. существует такой xq Е М, что выполняется равенство
xq = /(жо), причем множество всех решений этого уравнения
имеет наименьший элемент. Этот элемент и будет наименьшей
неподвижной точкой отображения /.
Отметим, что доказательство теоремы о неподвижной точ-
точке конструктивное: оно дает метод получения неподвижной
точки. Для ее нахождения надо построить последовательность
вида A.7) и найти ее точную верхнюю грань.
Пример 1.20. Приведем простой пример вычисления наи-
наименьшей неподвижной точки. В качестве индуктивного упоря-
упорядоченного множества М возьмем отрезок [0,1] с естественным
88 1. МНОЖЕСТВА И ОТНОШЕНИЯ ___
числовым порядком ^. Согласно примеру 1.19, это индуктив-
индуктивное упорядоченное множество.
Рассмотрим на этом множестве уравнение х = -х + j. Мож-
Можно показать, что для индуктивного упорядоченного множества
М любая монотонная функция /: [0,1] -> [0,1], непрерывная в
смысле определения из курса математического анализа, непре-
непрерывна и в смысле данного выше определения. Действительно,
для любой неубывающей последовательности {хп} на множе-
множестве [0,1] справедливо равенство sup{#n} = lim xn [I]. В си-
п—юо
лу непрерывности функции / в смысле определения из курса
математического анализа имеем /(lim xn) = lim f(xn). Так
хп-юо ' n-юо
как функция / монотонна, то {/(яп)}п^о — неубывающая по-
последовательность и lim f(xn) = sup/(a;n). В итоге получаем
п—юо
f(supxn) = /(lim xn) = lim f(xn) = sup/(xn). Следовательно,
n—>oo n—>oo
правая часть данного уравнения непрерывна.
Заметим, что если бы в правой части стояла линейная функ-
функция с отрицательным коэффициентом при х, то условие непре-
непрерывности функции в смысле приведенного выше определения
было бы уже нарушено, поскольку такая функция не является
монотонной в смысле определения 1.6.
Наименьшим элементом рассматриваемого множества явля-
является число 0. Вычисляем:
/»=о,
/х@) = 1/4,
/3@) = A/2) -C/8) + 1/4 = 7/16,
получая последовательность приближений к наименьшей непо-
неподвижной точке.
Можно проверить (например, с помощью метода матема-
2П — 1
тической индукции), что /п@) = , п G N. Предел этой
1.9. Мощность множества 89
последовательности равен 1/2. Таким образом, наименьшая не-
неподвижная точка отображения /, определяемого правой частью
уравнения, равна 1/2. Это единственная в данном случае непо-
неподвижная точка отображения /, что, конечно, очевидно и без
теоремы 1.7 о неподвижной точке. Но здесь мы нарочно рас-
рассмотрели простой пример, показав, как можно решать подоб-
подобные уравнения, основываясь на доказательстве теоремы. Мы
не будем пока приводить более сложные примеры, так как ин-
интересные приложения теоремы о неподвижной точке имеются в
теории графов и теории автоматов, и вернемся к этой теореме
при решении задачи о путях в ориентированных графах.
1.9. Мощность множества
Некоторые сведения о мощности множества приведены в [I].
Здесь мы рассмотрим это понятие более подробно.
Множество А равномощно множеству J5, если существует
биекцил f:A->B.
Из того, что существует биекция /: А —? J5, следует, что
соответствие f~l есть биекция В на А (см. 1,4). Поэтому если
А равномощно В, то и В равномощно Л, и мы можем говорить,
что множества Аи В равномощны.
Факт равномощности множеств А и В будем записывать
так: А~В.
Из определения равномощности и свойств биекции также
следует, что для любого множества А имеет место А ~ А
(тождественное отображение есть биекция множества А на
себя); а для любых множеств А, В, СизА~ВиВ~С следует
А~С {композиция биекций есть биекция).
Таким образом, отношение равномощности множеств есть
отношение эквивалентности*, заданное на „множестве всех
"Зачастую в литературе по теории множеств равномощные множества
и называют „эквивалентными множествами". Однако следует различать
общее понятие отношения эквивалентности и его частный случаи — экви-
эквивалентность, или равномощность, множеств.
90 1. МНОЖЕСТВА И ОТНОШЕНИЯ
множеств" (на самом деле на множестве всех подмножеств
некоторого универсального множества).
Если мы обозначим через \А\ класс эквивалентности мно-
множества А по отношению ~, то утверждение о равномощности
множеств Аи В можно записать так: \А\ = \В\.
Этот класс эквивалентности \А\ называют мощностью
множества А.
Конечные множества А = {а\1..., ап} и В = {&i,..., bm} рав-
номощны тогда и только тогда, когда множества Аи В состоят
из одного и того же числа элементов, т.е. п = т. Отсюда, в
частности, следует, что конечное множество не является рав-
номощным никакому своему собственному подмножеству. Это
свойство конечных множеств можно сформулировать так.
Теорема 1.8. Бели А — конечное множество и /: А ->
-* А — инъекция, то она является сюръекцией и, следовательно,
биекцией. #
В силу приведенных выше соображений мощностью конеч-
конечного множества А = {ai, ...,an} можно считать натуральное
число п, так как, задавая такое число, мы задаем и класс всех
(попарно равномощных) множеств вида {ai,..., an}. Обратно,
каждый такой класс однозначно определяет натуральное число
п как число элементов в каждом множестве данного класса.
Естественно считается, что мощность пустого множества рав-
равна нулю.
Перейдем теперь к исследованию мощности бесконечных
множеств. Таковы хорошо известные нам числовые множества
N, Z, Q, R и С.
Любое множество, равномощное множеству всех натураль-
натуральных чисел, называют счетным. Мощность счетного множества
обозначают No (читается „алеф нуль").
Любую биекцию v\ N -> М называют нумерацией счетно-
счетного множества М; если элемент М есть v(n) для некоторого
п G N, то этот элемент М обозначаем через an, называя на-
1.9. Мощность множества
туральное число п номером элемента ап относительно данной
нумерации v.
Таким образом, элементы счетного множества можно пе-
перенумеровать, записав их в виде последовательности а\, ...,
ап, ... или {an}neN« Другими словами, счетное множество есть
область значений некоторой функции натурального аргумента.
Пример 1.21. а. Множество всех нечетных натуральных
чисел счетно. Нумерацию v можно задать так: и{п) = 2п — 1,
б. Множество всех натуральных чисел, делящихся на за-
заданное число к ^ 2, счетно. Нумерацию v можно задать так:
и(п) = fcn, n E N. В частности, при к = 2 получаем, что мно-
множество всех четных чисел счетно. Этот и предыдущий приме-
примеры показывают, что бесконечное (счетное) множество может
иметь собственное равномощное ему подмножество.
в. Множество Z всех целых чисел счетно. Нумерацию
можно установить так:
2-1, n = 2fc (четно);
-, п = 2fc - 1 (не четно). #
Рассмотрим свойства счетных множеств.
Теорема 1.9. Любое бесконечное множество содержит
счетное подмножество.
< Пусть Мо — бесконечное множество. Значит, оно не пусто
и существует элемент а\ Е Мо. Положим М\ = Мо \ {ai}.
Множество М\ не пусто, так как в противном случае имело бы
место равенство Мо = {ai}, что противоречит предположению
о бесконечности Мо. Выберем элемент а^ Е М\ и положим
Мг = М\ \ {аг} = Мо \ {ai, аг}. Множество Мг также не пусто,
поскольку иначе мы бы имели Мо = {аьаг} и множество
было бы конечным.
92 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Методом математической индукции можно показать, что
для любого п ^ 1 множество Мп = Mo \ {ai,..., an}, где а\ Е
бМо, ..., on € Mn-i, не пусто. Тогда существует элемент
an+i еМп и an+i <? Mn+i = Мп \ {ап+г}. Таким образом, все
элементы оп, п 6 N, попарно различны и множество {ап: п ? N}
счетно, а его нумерация может быть задана так: v(n) = on. >
Теорема 1.10. В любом бесконечном множестве можно
выделить два не пересекающихся между собой счетных под-
подмножества.
<4 Разобьем множество натуральных чисел на два подмноже-
подмножества: Ni = {п: п = 2к — 1, к G N} (множество нечетных чисел),
и N2 = {ты п = 2fc, к 6 N} (множество четных чисел). Оба эти
множества счетны (см. пример 1.21).
Согласно теореме 1.9, бесконечное множество содержит
некоторое счетное подмножество А. Пусть установлена не-
некоторая его нумерация. Разобьем это подмножество на два
подмножества: всех элементов с четными и всех элементов с
нечетными номерами. По построению эти подмножества не пе-
пересекаются и являются счетными, поскольку счетны множества
четных и нечетных чисел. >
Теорема 1.11. Любое подмножество счетного множества
конечно или счетно.
А Пустое подмножество конечно по определению. Пусть М —
счетное множество, а В — его некоторое непустое подмноже-
подмножество. Поскольку множество М счетно, можно считать, что
задана некоторая его нумерация. Следовательно, каждый эле-
элемент подмножества В имеет свой номер. Запишем номера
элементов множества В в порядке возрастания: ti, ..., in, ...
Бели среди них есть наибольший номер гр, то подмножество
В конечно. В противном случае получим счетное подмноже-
подмножество {aix, a,i2,..., ain,...}, нумерация которого установлена так:
v(n) = ain. >
1.9. Мощность множества 93
Бели множество конечно или счетно, его называют не бо-
более чем счетным. Семейство (А;)^/ множеств называют
не более чем счетным, если множество (индексов) / не более
чем счетно.
Теорема 1.12. Объединение любого не более чем счетного
семейства счетных множеств счетно.
<4 Пусть (Ai)i?i — конечное или счетное семейство счетных
множеств. Рассмотрим сначала случай, когда множества А{
попарно не пересекаются.
В этом случае нумерация объединения конечного семейства
счетных множеств может быть проведена по схеме, изображен-
изображенной на рис. 1.14, а нумерация объединения счетного семейства
счетных множеств — по схеме, приведенной на рис. 1.15.
а11 а12-***" а1п-^-'- а11"^а12 а13-^а14 — п1п'~
VI I Оляь* О.льлш ?L. ДЛ. • • • Д— • • •
"I I ^4sl 22 ^лЗ 24 2ti
^*21 22 * * * 2ti * * * X J* ^f J*
Iff а31 а32 а33 аз4*"а2п*"
; ! ; у
\ \ t ап1 ап2 ап3 ап4 опп...
ап1 * ап2 ''" * апп " * • • • • •
Рис. 1.14 Рис. 1.15
Пусть теперь (-An)n€N — произвольное счетное семейство
счетных множеств, т.е. множества А% могут пересекаться. В
этом случае, применяя указанные на рис. 1.14 и 1.15 схемы
нумерации к конечному или счетному объединению счетных
множеств, следует пропускать каждый раз элементы, которые
уже получили номера. >
Полезно отметить также и следующий факт.
Теорема 1.13. Объединение конечного и счетного мно-
множеств счетно. #
94 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Теорема 1.14. Пусть М — бесконечное множество, а N —
его не более чем счетное подмножество. Бели множество M\N
бесконечно, то оно равномощно множеству М.
< По теореме 1.10 в множестве M\N, поскольку оно беско-
бесконечно, можно выбрать счетное подмножество N'. Ясно, что
Nf)Nf = 0. Множество NUN* является счетным как объедине-
объединение двух счетных множеств или объединение счетного и конеч-
конечного множеств. Поэтому существует биекция /: NUNf -> N'.
Поскольку (M\(NUN'))U(NUN')=M, M\ (NUNf) UN' =
= M\N, то требуемую биекцию М на М\N строим так: на
подмножестве М \ (N U iV7), общем для М \ N и М, эта биекция
совпадает с тождественным отображением; на подмножестве
NUNf эта биекция есть биекция /. >
Следствие 1.1. Бели М — бесконечное множество, а N —
не более чем счетное множество, то М ~ М U N.
Существуют бесконечные множества, не являющиеся счет-
счетными. Это вытекает из следующих рассуждений.
Рассмотрим множество всех последовательностей нулей и
единиц, т.е. последовательностей вида {c*i,a2, ...,an,...}, где
cti G {0,1} для каждого г ^ 1.
Обозначим множество таких „двоичных" последовательно-
последовательностей через {0,1}^.
Теорема 1.15 (теорема Кантора). Множество {0,1}ш
не есть счетное множество.
<4 Пусть множество {0,1}^ счетное. Тогда существует биекция
ср: N-> {0,1}ш. Выпишем все последовательности <р(п):
<рA) = {an, ai2,..., ain,.• •},
= {a2i,
(р{п) = {anb an2
1.9, Мощность множества 95
Построим последовательность /3 = {/?i,..., /?п,...}: положим
/% = 1, если ац = 0, и ft = 0, если ац = 1. Ясно, что эта после-
последовательность не совпадает ни с одной из последовательностей
у?(п), а это противоречит допущению, что любая последователь-
последовательность из {0,1}W есть <р(к) для некоторого к.
Итак, N не равномощно {О, I}***.
В то же время {0,1}и содержит подмножество последова-
последовательностей, в каждой из которых только один член отличен
от нуля. Это подмножество равномощно множеству всех одно-
одноэлементных подмножеств N и, следовательно, самому N. Сле-
Следовательно, множество {0,1}и бесконечно, но не равномощно
счетному множеству и потому не является счетным. >
Теорема 1.16. Множество 2N всех подмножеств множества
натуральных чисел и множество {0,1}ш равномощны.
<4 Определим отображение (р множества 2N на множество
{0,1}и следующим образом: если X С N, то <р(Х){ = 1 при г Е X
и (p(X)i = 0 при г ? X.
Тем самым подмножеству X ставится в соответствие по-
последовательность (р(Х), г-й член которой равен единице тогда
и только тогда, когда число г есть элемент множества X. До-
Докажем, что ip — биекция 2N на {0,1}ш.
Покажем, что отображение (р — инъекция. Пусть X и Y —
различные подмножества N. Тогда найдется число i € X \ Y или
число j EY\X. В первом случае в последовательности <р(Х) г-й
член будет равен единице, а в последовательности <p{Y) — нулю.
Таким образом, (р(Х) ф (p(Y). Во втором случае <p{Y)j = 1,
(p(X)j = 0 и опять (р(Х) ф (p(Y). Следовательно, отображение
(р — инъекция.
Покажем, что <р — сюръекция. Возьмем произвольную
последовательность а Е {0,1}W. Образуем множество Ха =
= {г: а» = 1}. Ясно, что <р(Ха) = а. Таким образом, для лю-
любой последовательности а 6 {0,1}^ существует подмножество
Ха Е 2N, такое, что <р(Ха) = а. Следовательно, <р — сюръек-
сюръекция.
96 I, МНОЖЕСТВА И ОТНОШЕНИЯ
Таким образом, мы показали, что <р — биекция, а множества
2N и {0,1}Ш равномощны. >
Мощность множества 2N обозначают с и называют мощ-
мощностью континуума, а любое множество, эквивалентное
множеству 2N, называют множеством мощности конти-
континуума ниш континуальным множеством.
Теорема 1.17. Множество действительных чисел отрезка
[0,1] равномощно множеству всех последовательностей нулей и
единиц {0,1}".
<4 Каждое действительное число из отрезка [0,1] представим в
виде бесконечной дроби в двоичной системе счисления. Число 1
представим в виде периодической дроби, содержащей беско-
бесконечное число единиц — 0,1A). Конечные рациональные дроби
представим как бесконечные, дополнив справа бесконечным чи-
числом нулей. Таким образом, каждое число из [0,1] представлено
в виде последовательности нулей и единиц. Кроме этого, вы-
выбросим счетное множество всех периодических дробей вида
O,aoai...a&O(l), поскольку каждая такая дробь представляет
то же самое число, что и дробь O,aoai...a* 1@), где a* G {0,1}
для всякого г = 1, к. Легко видеть, что полученное таким
образом множество двоичных дробей равномощно множеству
{о, 1Г. >
Следствие 1.2. [0,1] ~ 2N.
4 Выше была доказана равномощность множеств @, 1)" и 2N.
Тогда имеем [0,1] ~ {0,1}" - 2N. >
Теорема 1.18. Следующие множества равномощны:
1) множество действительных чисел отрезка [0,1];
2) множество действительных чисел интервала @,1);
3) множество действительных чисел отрезка [а, Ь];
4) множество действительных чисел интервала (а, Ь);
5) множество действительных чисел (числовая ось) R;
1.9. Мощность множества 97
6) множество всех подмножеств множества натуральных
чисел 2N.
4 Покажем равномощность множеств [0,1] и @,1). Из мно-
множества действительных чисел отрезка [0,1] выделим двухэле-
двухэлементное подмножество {0,1}. Разностью этих множеств будет
множество действительных чисел интервала @,1), и, согласно
теореме 1.14, [0,1] ~ @,1).
Отображение у = F — о)х + а задает биекцию множества
[0,1] на множество [а, Ь]. Следовательно, эти множества рав-
номощны. Заметим, что аналогично доказывается равномощ-
равномощность @,1) и (а, Ь).
Покажем, что @,1) ~ R. Биекцию можно установить, на-
например, с помощью функции у = -arctgx + -.
Поскольку равномощность [0,1] и 2 ранее доказана, имеем
[0,1] ~ @,1) ~ [а, 6] - (а, Ь) ~ R - 2N. >
Замечание 1.7. Заметим, что если в условиях теоремы 1.14
множество М несчетно, а N — его счетное подмножество, то
множество M\N бесконечно, ибо иначе получилось бы, что
множество М = (М \ N) U N счетно как объединение конечного
и счетного множеств.
Таким образом, можно утверждать, что для любого несчет-
несчетного множества М и его не более чем счетного подмножества
N имеет место равенство \М \ N\ = \М\. #
До сих пор речь шла о равенстве мощностей. Однако
мощности разных множеств можно в определенном смысле
сравнивать, говоря о большей или меньшей мощности.
Считают, что мощность множества А не превышает мощ-
мощность множества В (\А\ ^ |В|), если А равномощно некоторому
подмножеству множества В. Можно показать, что из соотно-
соотношений |Л| ^ |В| и |В| < |А| следует, что |Л| = |J5|.
Мощность множества А считается строго меньшей мощно-
мощности множества В (\А\ < \В\), если множества А и В неравно-
98 1. МНОЖЕСТВА И ОТНОШЕНИЯ
мощны и существует собственное подмножество С множества
В, равномощное множеству А, т.е. (А </ В) и (ЗС СВ)(А~С).
Можно доказать, что из \А\ ^ \В\ и \В\ < \С\ следует \А\ <
< \С\. Таким образом, на множестве всех мощностей (т.е.
на множестве всех классов эквивалентности по отношению ~)
установлено отношение порядка.
Из определения сразу следует, что мощность любого ко-
конечного множества строго меньше мощности Но, а из дока-
доказательства теоремы 1.15 вытекает, что No < с. Кроме того,
согласно теореме 1.9, мощность счетного множества No являет-
является наименьшей на множестве всех бесконечных мощностей (т.е.
мощностей бесконечных множеств). Можно сказать, что вся-
всякое бесконечное множество не менее чем счетно.
Без доказательства приведем две важные теоремы.
Теорема 1.19 (теорема Кантора — Бернштейна}.
Для любых двух множеств А и В имеет место в точности одно
из следующих трех условий: либо \А\ < |J5|, либо \В\ < |А|, либо
1*1 = 14- #
Таким образом, любые два множества сравнимы по мощно-
мощности. Другими словами, „шкала мощностей" линейно упорядо-
упорядочена.
Теорема 1.20. Для любого множества А верно неравенство
|Л|. #
В силу теоремы 1.20 нет наибольшей мощности, так как для
любого множества А существует множество большей мощно-
мощности — его булеан. Заметим, что для счетного множества А
теорема 1.20 сводится к теореме Кантора 1.15.
Теорема 1.21 (теорема о квадрате). Для любого бес-
бесконечного множества М его декартов квадрат М х М равно-
мощен самому множеству М.
Ч Доказательство проведем для частных случаев счетного и
континуального множеств.
1.9. Мощность множества 99
Сначала обратимся к счетному множеству. Для доказатель-
доказательства утверждения достаточно показать, что N х N ~ N, т.е.
задать на N х N некоторую нумерацию. Рассмотрим множество
Ai = {(г, j): j G N} упорядоченных пар. Это множество счетно
по построению. Легко видеть, что справедливо равенство
откуда, согласно теореме 1.12, вытекает счетность декартова
квадрата N х N множества N как счетного объединения счет-
счетных множеств.
Перейдем к континуальному множеству. Докажем, что мно-
множество всех упорядоченных пар двоичных последовательностей
эквивалентно множеству всех таких последовательностей, т.е.
2Nx2N~2N.
Паре последовательностей (а, /3) поставим в соответствие
последовательность ао, #о, ai, /?i, ..., ап, /?п, ... Это соот-
соответствие будет взаимно однозначным, т.е. установлена биекция
между 2N х 2N и 2N. >
Получается, что — как это ни удивительно — в квадрате
„столько же" точек, сколько и в каждой его стороне. Можно
обобщить это утверждение для произвольной конечной декар-
декартовой степени множества М.
Следствие 1.3. Множество рациональных чисел Q счетно.
< Каждому рациональному числу, представленному несократи-
несократимой дробью ?, однозначно соответствует упорядоченная пара
(а, Ь), и, напротив, любая упорядоченная пара (а, Ь) взаимно
простых целых чисел а и 6 однозначно определяет несократи-
несократимую дробь 7 и> значит, рациональное число. Следовательно,
множество Q эквивалентно некоторому бесконечному подмно-
подмножеству множества Z x Z. Поскольку множество Z x Z счетно,
из теоремы 1.11 вытекает, что любое его бесконечное подмно-
подмножество счетно. Таким образом, множество Q счетно. >
100 1. МНОЖЕСТВА И ОТНОШЕНИЯ
В заключение приведем сводку результатов по мощностям
некоторых конечных множеств.
Теорема 1.22. Бели М и N — конечные множества и
\М\ = m, a |iV| = п, то:
1) мощность множества всех отображений М в N равна nm;
2) мощность множества всех биекций из N на себя равна
3) мощность множества всех инъекций из М в N (т ^ п)
0
10^
4) мощность множества всех подмножеств множества N
равна 2П;
5) мощность множества всех /с-элементных подмножеств
множества N равна С* = . ^,ч,;
6) мощность прямого произведения М х N равна тп. #
Напомним [I], что в комбинаторике число Рп называют чи-
числом перестановок п элементов, число AJJ1 — числом размеще-
размещений без повторений из п элементов по т, число С* (обозначае-
(обозначаемое также (?)) — числом сочетаний из п элементов по к. Эти
числа называются также биномиальными коэффициентами, по
п
скольку (а + Ь)п = УС*ап b (формула бинома Ньютона).
к=о
Дополнение 1.1. Об одном
парадоксе теории множеств
Задавая с помощью коллективизирующих свойств множе-
множества, следует иметь в виду, что не каждое высказывание опре-
определяет коллективизирующее свойство. Попробуем определить
множество Y = {X: X ? X} — множество всех множеств, не
являющихся элементами самих себя. Это множество не пу-
пусто. Те пнормальные" множества, с которыми мы привыкли
иметь дело, например числовые, как раз не являются элемента-
Д. 1.1. Об одном парадоксе теории множеств 101
ми самих себя: множество R всех действительных чисел не есть
действительное число! Однако попытка определить множество
всех множеств, которые не являются элементами самих себя,
приводит к противоречию. В самом деле, пусть У не является
элементом самого себя, т.е. У ? У. Тогда, поскольку Y есть
множество всех множеств, не являющихся элементами самих
себя, Y € У. В то же время, если Y Е У, оно должно обладать
свойством, которое указано в определении У как коллективи-
коллективизирующее, т.е. должно выполняться Y ?Y. Следовательно, мы
доказали, что У ^ У «Ф» У € У! Это противоречие показывает,
что высказывание о множествах X ? X не задает коллективи-
коллективизирующее свойство.
Указанный парадокс, называемый парадоксом Рассела,
приводится иногда в такой псказочно-шутливой" редакции:
„В некоторой деревне живет брадобрей, который по долгу
службы должен брить тех и только тех, кто не бреет себя
сам". Брадобрей оказывается в незавидном положении: если
он не будет себя брить, то тотчас окажется, что он должен
себя брить, а следуя неумолимой инструкции, он немедленно
должен прекратить бриться, ибо он будет брить себя сам, что
запрещено.
Парадокс Рассела показывает, что интуитивное понимание
множества и коллективизирующего свойства позволяет трак-
трактовать идею множества настолько широко и расплывчато, что
может привести к противоречиям.
Замечание 1.8. Не следует путать высказывание, опре-
определяющее пустое множество (например, пх есть четное число,
не делящееся на два"), и высказывание, не задающее коллек-
коллективизирующего свойства. Первое коллективизирует, определяя
пустое множество, а второе приводит к противоречию, не опре-
определяя никакого множества, в том числе и пустого. #
Обсуждение возможных путей выхода из противоречий, по-
подобных парадоксу Рассела, не является предметом данного
102 1. МНОЖЕСТВА И ОТНОШЕНИЯ
учебника*. Мы же только заметим, что ввиду парадокса Рас-
Рассела мы не можем мыслить конструкции, подобные множеству
всех множеств, которые не являются элементами самих себя, в
законченном виде, т.е. считать, что нам сразу, одновременно
представлены в наличии все мыслимые множества указанного
вида. Вместо этого следует представлять себе процесс (обра-
(обратим внимание на это слово!) порождения новых множеств
(назовем их допустимыми), исходя из определенного набора
„исходных" допустимых множеств. К ним, в частности, можно
отнести известные числовые множества, все конечные множе-
множества. Важно понимать также, что указанный выше процесс
никак не влияет на „объем" уже имеющихся допустимых мно-
множеств: все они жестко зафиксированы и „состав" их элементов
никак не меняется. Всякое уже имеющееся допустимое мно-
множество всегда „равно самому себе". Но совокупность всех
допустимых множеств меняется при порождении новых допу-
допустимых множеств из уже имеющихся, и именно поэтому она
не может считаться множеством, ибо состав ее элементов не
зафиксирован.
Считая, что исходные допустимые множества как-то зада-
заданы, мы должны регламентировать операции, которые позво-
позволяют из уже имеющихся допустимых множеств строить новые
допустимые множества.
Такими операциями являются рассмотренные в главе 1 опе-
операции над множествами, в частности образование неупорядо-
неупорядоченной и упорядоченной пары, булеана и фактор-множества.
Дополнение 1.2. Метод
характеристических функций
Доказательство сложных теоретико-множественных тож-
тождеств методом двух включений часто бывает довольно гро-
громоздким, и при построении доказательства ход рассуждений
*См.: Архангельский А.А.\ Шенфилд Дж.\ Куратовский К., Мостов-
ский А.\ Кон П.
Д. 1.2. Метод характеристических функций 103
не всегда очевиден. Одним из методов, не требующих „уга-
„угадывания" пути доказательства, является метод характери-
характеристических функций.
Характеристическая функция ха множества ACU
есть функция, отображающая универсальное множество U в
двухэлементное множество {0,1}:
Из определения характеристической функции множества А
вытекает справедливость тождества
Выразим характеристическую функцию пересечения множеств
А и В через характеристические функции ха(х) и Хв(х) этих
множеств. Из определения пересечения следует, что искомая
характеристическая функция должна принимать значение 1 для
тех элементов ж, которые принадлежат множествам А и В
одновременно, и значение 0 в противном случае. Легко видеть,
что функция
удовлетворяет этому требованию.
Можно предположить, что характеристическая функция
объединения множеств А и В будет равна сумме характеристи-
характеристических функций множеств. Однако так ее определить нельзя,
поскольку для элементов х ? А П В такая сумма будет иметь
значение 2. Введем „поправку" и в результате получим иско-
искомую формулу:
ХАив(х) = Ха(х)+Хв(х)~Ха(х)хв{х).
Непосредственно из определения А — дополнения множе-
множества А — следует, что
104 i. МНОЖЕСТВА И ОТНОШЕНИЯ
Для разности А\В характеристическая функция имеет вид
Ха\в(х) = Ха{х) - Ха{х)хв(х),
а для симметрической разности ААВ —
Хаав(х) = ха(х) +хв(х) -
Отметим, что последнюю формулу можно получить, опираясь
на свойство 19 (см. с. 35) и тождество A.10), а также на
характеристические функции для пересечения, объединения и
разности:
ХААв(х) = Х(АиВ)\(АПВ)(х) =
= ХАив(х) - ХАив(х)хАпв(х) =
= Ха(х) + хв(х) - Ха(х)хв(х)-
- (ха(х) +Хв{х) -Ха{х)хв{х))ха{х)хв{х) =
= Ха(х) + хв{х) - ха{х)хв(х)~
- (ха(х)хв{х) + Ха(х)хв(х) ~Ха{х)хв(х)) =
= Ха(х) + хв(х) - 2ха(х)хв{х).
С учетом равенства A.10) полученную формулу можно запи-
записать в виде
Хаав{х) = (ха(х) - Хв(х)J.
Метод характеристических функций доказательства спра-
справедливости теоретико-множественного тождества заключается
в выражении характеристических функций обеих его частей
через характеристические функции входящих в него множеств.
Тождество верно тогда и только тогда, когда характеристиче-
характеристические функции левой и правой частей совпадают.
Пример 1.22. Используя метод характеристических функ-
функций, выясним, справедливо ли тождество
(ААВ) Г)С = (АП С)А(В П С).
Д. 1.2. Метод характеристических функции 105
С одной стороны,
X(AAB)nc(x) = ХЛДВХс(я) =
= (ха(х) + хв(х) - 2ха(х)хв(х))хс(х) =
= Ха{х)хс(х) + Хв(х)хс(х) -
С другой стороны,
= ХАпс(х) + Хвпс(х) - 2хапс{х)хвпс{х) =
= ХА(х)хс(х) + Хв (х)хс(х) - 2ха (х)хв(х)хс(х).
Характеристические функции левой и правой частей тожде-
тождества совпадают. Следовательно, тождество верно.
Пример 1.23. Выясним, является ли тождеством следую-
следующее выражение:
А\(В\С) = (А\В)\С.
С одной стороны,
Ха\(в\с)(х) = Ха{х) -
= Ха(х) -
= Ха(х) -
С другой стороны,
Х(а\в)\с(х) = Ха\в(х) - Ха\в(х)хс(х) =
= Ха(х) - ха(х)хв(х) - (ха(х) - Ха(х)хв(х))хс(х) =
= Ха{х) - ха{х)хв(х) - ха(х)хс(х) + ха(х)хв{х)хс(х).
Легко видеть, что получены разные характеристические
функции. Например, при хеА, х$В л х€С Ха\(В\С)(х) = 1>
а Х(а\в)\с(х) = 0- Таким образом, доказано, что А \ (В \ С) Ф
Ф{А\В)\С. #
106 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Отметим, что метод характеристических функций не явля-
является универсальным. Так, его нельзя использовать при до-
доказательстве тождеств, содержащих декартово произведение
множеств, в частности, тождеств для соответствий (бинарных
отношений).
Вопросы и задачи
00
1.1. Найти f) Хп, если: а) Хп = [-1, I]; б) Хп = [о, I];
1.2. Используя методы двух включений и характеристиче-
характеристических функций, доказать свойства 1-18 (см. с. 35).
1.3. Доказать тождества:
а) А х (ВПС) = (А х В) П (А х С);
б) (АПВ) х (СПЯ) = (А х С) П (В х D).
Проиллюстрировать графически, приняв в качестве мно-
множеств Ау J5, С и D отрезки числовой прямой.
1.4. Доказать, что если (АСХ) и (В С У), то (Ах В) С
С(Хх У).
1.5. Показать, что DхВ)^1хВ. Вывести соответству-
соответствующее тождество.
1*в. Используя ранее доказанные тождества, показать спра-
справедливость тождества (А\В) х С = (Ах С)\(В х С).
1.7. Доказать, что для любой функции / и любых множеств
А и В имеют место соотношения:
a) f{AUB) = f(A)Uf(B); б) /(АПВ) С/(А) П/(Я);
»)f(A)\f(B)Cf(A\B).
При каких условиях включения б) и в) превращаются в равен-
равенство?
Вопросы и задачи 107
1.8. Доказать, что для любой функции / и любых множеств
А и В имеет место равенство:
б) Г1(ЛиВ)=/-1(Л)и/-1(В);
1.9. Построить графики и графы следующих бинарных
отношений, заданных на множестве X = {1,2,3,4,5,6}:
а) х\ у #2, если х\ < x<i +1; в) х\ ра?2, если |rri — #2! ^ 3;
б) х\ г Х2, если xi < Х2\ г) {(а, Ь): а + Ь — четное}.
1.10. Определить, какими свойствами (рефлексивность, ир-
иррефлексивность, симметричность, антисимметричность, тран-
транзитивность) обладают следующие бинарные отношения:
а) (р = {(а, а), (а, 6), (с, а), (Ь, d), (а, d), (Ь, с)} на множестве
М = {а, Ь, с, d};
б) рп, такое, что т pn fc, если т — к делится на п, где ш,
fcGZ, anGZn фиксировано;
в) у?, такое, что х </? у, если ж — у ^ 2, а; Е R, у € R.
1.11. Пусть р = {(ж, у): х <у иу + х < 1,5} — бинарное от-
отношение на множестве X = [0,1]. Построить графики отноше-
отношений р и р2. Исследовать свойства отношений рир2.
1.12. Найти D(p), R(p), /Г1, pop, p^op, pop-1 для
бинарных отношений:
а) р={(х, з/):ж,у€[0,1],ж + у<1};
б) р = {(х, у): х,у е [0,1], 2х ^ Зу}.
1.13. Доказать, что для любого бинарного отношения р С
QAx А имеют место равенства:
а) D^1) = Д(р); в) D(Pl ^
б) Л(/9-1) = 1)(р); г)
108 1. МНОЖЕСТВА И ОТНОШЕНИЯ
1.14. Доказать, что для любых бинарных отношений pi, P2,
рзЕАх А имеют место равенства:
а) pinpi=piUpi=pi; д) (piUp2)=Pr1|J/921;
б) р\ о (р2 ор3) = (pi °Р2) °Рз; е) (р)~1 = (р);
в) pi°idi4 = idAop1=p1; ж) (Р1°Р2)=Р^1°рГ1-
г) (pll
1.15. Доказать, что для бинарных отношений т и р*, i Е /,
справедливы равенства:
a) ro(Urt)=(J(i"eA); б) Г
1.16. Доказать, что для бинарного отношения р на А имеет
место равенство рор~~1=р~1ор = id^, если и только если р —
биекция А на А.
1.17. Найти необходимые и достаточные условия односто-
односторонней обратимости бинарного отношения р на множестве Л,
т.е. условия того, что p°p~l = icU (или р" op = icU).
1.18. Построить бинарное отношение, которое является:
а) рефлексивным, симметричным, но нетранзитивным;
б) рефлексивным, антисимметричным, но нетранзитивным;
в) рефлексивным, транзитивным, но несимметричным;
г) антисимметричным, транзитивным, но нерефлексивным.
1.19. Доказать, что для любых рефлексивных отношений р
и а на произвольном множестве A pUaCpoa.
1.20. Пусть А и В — конечные множества, содержащие т
и п элементов. Сколько существует различных соответствий
из А в В? Сколько можно задать функций из А в J5, а среди
последних — инъекций? При каких тип существуют биекции
и сколько их?
1.21. Пусть в R3 задана плоскость ах + by + cz = 0. Точ-
Точки с радиус-векторами г\ и Г2 связаны отношением т, если
Вопросы и задачи 109
— Г2),п) = 0, где п — нормаль к плоскости, а (•, •) — ска-
скалярное произведение векторов. Показать, что т — отношение
эквивалентности. На какие классы эквивалентности разбивает-
разбивается Е3? Указать фактор-множество множества R3 по данному
отношению эквивалентности.
1.22. Пусть А — конечное множество. Какое отношение
эквивалентности на нем дает наибольшее число классов эквива-
эквивалентности? Сколько классов эквивалентности при этом будет?
Сколькими способами можно задать отношение эквивалентно-
эквивалентности, разбивающее А на два класса?
1.23. Доказать, что число различных отношений эквива-
эквивалентности на n-элементном множестве удовлетворяет формуле
г=0
где pi — число различных отношений эквивалентности на г-эле-
ментном множестве.
1.24. Доказать, что композиция piop2 двух эквивалентно
стей рх и рг является эквивалентностью тогда и только тогда,
когда pi<>p2=p2°pi.
1.25. Описать наименьшее по включению отношение экви-
эквивалентности, содержащее данные эквивалентности р и а на А.
Каким будет это отношение, если р о a = а о р?
1.26. Пусть бинарное отношение v определено на множе-
множестве положительных рациональных чисел следующим образом:
(a/b) v (c/rf), если ad ^ be. Показать, что v является отношением
линейного порядка.
1.27. Пусть А — произвольное множество и р, a — бинар-
бинарные отношения на множестве 2А х 2А: (Р, Q) a (X, У), если
Р Я X и Q С У, а (Р, Q) р (X, У), если (PAQ) С (XAY). Явля-
Являются ли р и а отношениями порядка?
110 1. МНОЖЕСТВА И ОТНОШЕНИЯ
1.28. Пусть М — множество квадратных матриц типа
2x2, элементами которых являются целые числа. Выяснить,
является ли бинарное отношение г, заданное на множестве М,
отношением порядка или отношением линейного порядка:
а) А т 2?, если а^ < Ъц, i, j = 1, 2, А, В € М;
б) А г В, если aij < b«j, г, j = 1,2 и хотя бы для одной пары
элементов неравенство строгое, А В € М.
1.29. Пусть F — множество функций, непрерывных на
отрезке [а, 6]. Проверить, является ли заданное отношение
отношением указанного вида:
ь ь
а) /(х)тд(х)у если / f(x)dx= I g{x)dx\ отношение эквива-
а а
лентности;
б б
б) f(x) т д(х)у если / f(x)dx < / g(x)dx; отношение поряд-
а а
ка и отношение предпорядка.
1.30. Пусть р\ и р2 — линейные порядки на множестве А.
Когда рг°р2 — линейный порядок?
Указание: докажите, что если р\фрг, то р\°рг не
является линейным порядком.
1.31. Всегда ли транзитивна композиция транзитивных
бинарных отношений?
Указание: постройте пример конечного упорядоченного
множества, в котором композиция исходного и двойственного
порядка не является транзитивным отношением.
1.32. Пусть Аи В — конечные множества. Используя метод
математической индукции, доказать, что \А х В\ = |А||В|.
Пусть Ai, ..., Ап — конечные множества. Доказать, что
1.33. Какую мощность имеет множество простых чисел?
Вопросы и задачи 111
1.34. Пусть А — множество всех многочленов степени не
выше п, имеющих коэффициенты заданного вида. Определить
мощность этого множества, если: а) все коэффициенты много-
многочленов рациональные; б) свободный член действительный, а все
остальные коэффициенты рациональные.
1.35. Доказать счетность следующих множеств:
а) множества всех многочленов с рациональными коэффи-
коэффициентами;
б) множества всех попарно непересекающихся открытых
шаров в Rn;
в) множество всех цифр 8, расположенных на плоскости так,
что ни одна пара цифр не имеет общих точек, кроме, может
быть, точек касания.
1.36. Определить мощность множество всех точек плоско-
плоскости, у которых:
а) обе координаты рациональные;
б) первая координата рациональная, а вторая — иррацио-
иррациональная.
1.37. Доказать, что следующие множества имеют мощность
континуума:
а) множество N" всех бесконечных последовательностей на-
натуральных чисел;
б) множество №° всех последовательностей натуральных
чисел;
в) множество А°° всех (конечных или бесконечных) после-
последовательностей элементов из конечного множества А.
1.38. Доказать, не используя теорему 1.20, что множество
2[°jll имеет мощность большую, чем мощность континуума.
Указание: установите биекцию множества 2(°'Ч на мно-
множество всех функций из [0,1] в @, 1) (характеристических
функций подмножеств отрезка [0,1]), а затем обобщите „диа-
„диагональную" конструкцию из доказательства теоремы 1.15.
2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Предметом рассмотрения в абстрактной алгебре являют-
являются произвольные множества с заданными на них операциями.
При этом природа множеств и операций может существенно
отличаться от привычных числовых множеств и известных опе-
операций над числами. Мы уже сталкивались с операциями над
множествами и бинарными отношениями (см. 1), которые ока-
оказались в чем-то похожими на операции над числами, но в то же
время проявились и их существенные отличия.
В дискретной математике разрабатываются алгоритмы и
вычислительные методы, позволяющие манипулировать сложно
организованными нечисловыми структурами. Проблема рабо-
работы с такими объектами возникла в связи с развитием современ-
современных информационных технологий и переходом от собственно
вычислений (т.е. операций над числами) к обработке слож-
сложных структур данных. Так, проблемы программирования и
машинного перевода привели к задачам работы с языковыми
структурами, проблемы автоматизации проектирования — к
задачам обработки графических объектов.
Современная дискретная математика проникнута алгебра-
алгебраическим духом, поскольку оказалось, что именно на алгебраи-
алгебраической базе наиболее удобно разрабатывать общие подходы к
работе с объектами различной природы.
2.1. Операции. Понятие
алгебраической структуры
Множество векторов в пространстве с операцией сложения
векторов, операцией векторного умножения, множество ква-
квадратных матриц с операциями сложения или умножения, мно-
множество функций с операцией сложения — вот примеры некото-
2.1. Операции. Понятие алгебраической структуры 113
рых множеств с операциями, рассматривающихся в различных
разделах математики. Выясним, что общего есть в свойствах
операций на этих множествах и в чем их различие.
Определение 2.1. Пусть А — произвольное непустое
множество и п — натуральное число. Любое отображение
называют n-арной (или n-местной) операцией на множе-
множестве А.
Таким образом, согласно приведенному определению, п-ар-
ная операция и каждому кортежу (ai, ..., ап)€Ап однозначно
сопоставляет элемент 6 Е А. Компоненты кортежа называют
при этом аргументами операции о;, а Ь — результатом
применения операции ш к аргументам ai, ..., an.
Для га-арной операции используют обозначение
6 = a;(ai, ..., ап)
или
Ь = а\... апь).
Обычно, если га = 2, пишут а\и)а2>
При п = 1 и п = 2 говорят соответственно об унарной
операции и бинарной операции.
Специально вводят понятие нулъарной операции (т.е. для
п = 0). Под нульарной операцией на множестве А понимают
произвольный фиксированный элемент множества А. Нульар-
ные операции позволяют фиксировать элементы множества А,
обладающие некоторыми специальными свойствами. Примером
выполнения нульарной операции является, например, фикси-
фиксирование нуля в множестве целых чисел с операцией сложе-
сложения. Примером унарной операции служит дополнение задан-
заданного множества до универсального множества.
Наиболее важными в алгебре и, следовательно, наиболее
исследованными являются бинарные операции. Примерами
114 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
таких операций могут служить сложение и умножение чисел,
сложение и умножение матриц, сложение векторов линейного
пространства.
Рассмотрим бинарную операцию на множестве А, обозначив
ее звездочкой (*).
Эту операцию называют:
1) ассоциативной, если (х * у) * z = х * (у * z) для любых х,
у, zeA\
2) коммутативной, если х * у = у * х для любых ж, у € А\
3) идемпотентной, если х*х = х для любого xGA
Ассоциативность операции ¦ позволяет для любых элемен-
элементов oi, a2, ..., ап? А однозначно трактовать результат выра-
выражения а\ * п2 *... * ап, так как
*... * an = ai * (а2 *... * ап) =
Операция сложения, заданная на множестве натуральных
чисел, является ассоциативной и коммутативной. Операция
умножения матриц ассоциативна, но не коммутативна. Идем-
потентными являются операции объединения и пересечения
множеств.
Элемент 0 множества А называют левым (правым) нулем
относительно данной операции *, если 0*ж = 0 (ж*0 = 0) для
любого х 6 А.
Если 0; — левый нуль, а 0" — правый нуль, то они со-
совпадают. Действительно, если (У и 0/; существуют, то они
совпадают, так как 0' = 0; * 0" = 0", и в этом случае говорят
просто о нуле относительно операции. Из приведенных
равенств следует, что нуль единственный и для него одновре-
одновременно выполнены оба равенства О*х = Оиа;*О = О.
Пример 2Л. а. На множестве целых чисел нулем относи-
относительно операции умножения будет число 0.
2.1. Операции. Понятие алгебраической структуры 115
б. На множестве квадратных матриц вида ( , ], где эле-
элементы а и 6 — действительные числа, любая матрица вида
() будет правым нулем относительно операции умноже-
d \)
ния, поскольку
(а 0\ /0 0\ _ /0 0\
[b l)[d l)-\d I)'
Однако левого нуля в этом множестве нет, так как иначе он
совпадал бы с правым нулем и был бы единственным. Но
правых нулей имеется больше одного. #
Элемент 1 множества А называют левым {правым) ней-
нейтральным элементом относительно операции *, если 1*х =
— х (х * 1 = х) для любого элемента х € А. Для левого V и
правого 1" нейтральных элементов, если они оба существуют,
выполнены равенства 1/ = 1' * 1" = 1", согласно которым они
совпадают. В этом случае элемент 1, который является и ле-
левым нейтральным, и правым нейтральным, единственный, и его
называют просто нейтральным элементом.
Пример 2.2. Нейтральным элементом относительно опе-
операции умножения на множестве натуральных чисел является
число 1. На множестве целых чисел нейтральным элементом
относительно операции сложения будет число 0.
На множестве квадратных матриц вида [ , Л ], где элемен-
\ь оу
ты а и о — действительные числа, любая матрица вида I , n I
будет правым нейтральным элементом по операции умножения,
ибо
fa 0\/l OWa 0\
\ъ о) \d о) \ь о)'
Поскольку правых нейтральных элементов несколько, то левого
нейтрального элемента по этой операции нет, так как иначе
116 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
существовал бы единственный нейтральный элемент (левый и
правый). #
Следует заметить, что не для всякой бинарной операции
нули и нейтральные элементы (левые и правые, в частности),
существуют.
Рассмотрим некоторые примеры бинарных операций на
множествах.
Пример 2*3. а. Пусть U — универсальное множество.
Теоретико-множественные операции U, П на множестве 2и
являются идемпотентными, ассоциативными и коммутативны-
коммутативными, причем пустое множество является нулем относительно
пересечения и нейтральным элементом относительно объедине-
объединения @П-А = л4П0 = 0, 0Ui4 = i4U0 = A), тогда как универ-
универсальное множество есть нуль относительно объединения и ней-
нейтральный элемент относительно пересечения
Операция \ (разность множеств) не является ассоциатив-
ассоциативной, так как А \ (В \ С) ф (А \ В) \ С.
б. На множестве всех бинарных отношений на множестве А
операция композиции отношений является ассоциативной, но
не коммутативной, а диагональ множества А будет нейтраль-
нейтральным элементом относительно этой операции (см. 1.4).
в. Пусть X — произвольное множество, содержащее не ме-
менее двух элементов. На множестве всех отображений из X в
X с операцией композиции отображений постоянное отобра-
отображение фа, переводящее любой элемент х Е X в фиксированный
элемент a ? X, будет правым нулем, но не будет нулем относи-
относительно композиции отображений.
Действительно, для любого отображения /: X —> X и любого
х е X имеем / о (ра(х) = <pa(f(x)) = а = (ра(х), т.е. / о (ра = <ра,
что и означает, что (ра — правый нуль относительно операции
композиции на множестве отображений из -X" в X. Однако для
любого хеХ (ра° f(x) = f{<Pa{x)) = /(а), Т.е. (fa о / = <р/(а) —
отображение, которое любой элемент X переводит в элемент
2.1. Операции. Понятие алгебраической структуры 117
f(a). Поскольку /(а) в общем случае не равно а, то <ра о f ф сра.
Значит, (ра не является левым нулем относительно операции
композиции. #
Рассмотренные выше примеры множеств с операциями при-
приводят к следующим определениям.
Определение 2.2. Алгебра (универсальная алгебра,
П-алгебра) считается заданной, если заданы некоторое мно-
множество А, называемое носителем данной алгебры, и неко-
некоторое множество операций п на А, называемое сигнатурой
данной алгебры. Алгебру, носитель которой есть конечное
множество, называют конечной алгеброй.
Поскольку алгебра задается ее носителем и сигнатурой, мы
будем в записи обозначать алгебру как упорядоченную пару
множеств А = (-А, Q), полагая, что первая компонента этой
пары есть носитель, а вторая — сигнатура. Подчеркнем, что
алгебра — это не просто носитель и не просто сигнатура, а
„синтез" этих двух объектов.
Замечание 2.1. Операции, включенные в сигнатуру, за-
заданы как некоторые специальные отображения. Однако при
этом не оговариваются свойства, которыми обладают опера-
операции на носителе. Например, они могут быть ассоциативными,
коммутативными и т.д. При задании алгебр свойства операций
обычно указывают дополнительно.
Бели существует нейтральный элемент относительно опера-
операции, то его можно задать как нульарную операцию на носителе
и включить в сигнатуру, а можно не включать и описать как
свойство соответствующей операции.
Таким образом, одну и ту же алгебру можно задавать
по-разному. Ниже приведены примеры различных описаний
конкретных алгебр.
В ряде случаев указание носителя алгебры предполагает и
задание определенной сигнатуры. В этом случае для упрощения
118 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
пишут не А = (A, ft), а просто ,А = А
алгебры А'\ имея в виду элемент носителя этой алгебры.
Пример 2.4. а. Рассмотрим алгебру
Л = BМ, {и,П,\,Д,-0,М}).
Ее носителем является множество всех подмножеств произ-
произвольно фиксированного множества М, а сигнатура состоит из
следующих операций над множествами: объединения, пересече-
пересечения, разности, симметрической разности, дополнения, пустого
множества и множества М (последние два элемента сигнатуры
определяют нульарные операции).
б. Для любого множества М можно определить алгебру
носителем которой является множество всех подмножеств мно-
множества упорядоченных пар на М, т.е. множество всех бинарных
отношений на множестве М, а сигнатура состоит из опера-
операций объединения, композиции бинарных отношений и взятия
обратного отношения.
в. На множестве К действительных чисел можно, например,
определить такую алгебру:
Из = (*,{+,-,0,1}),
сигнатура которой состоит из операций сложения, умножения,
а также двух нульарных операций, обозначающих два особых
числа 0 и 1. Обратим внимание на то, что числа 0 и 1 в данном
случае являются соответственно нулем и нейтральным элемен-
элементом относительно умножения, а число 0 также играет роль
нейтрального элемента относительно сложения. Мы примени-
применили понятие нульарной операции, чтобы в обозначении алгебры
отразить элементы со специальными свойствами.
г. Все предыдущие примеры алгебр были алгебрами с ко-
конечной сигнатурой, т.е. с сигнатурой, состоящей из конечного
2.1. Операции. Понятие алгебраической структуры 119
числа операций. Однако несложно построить пример алгебры
с бесконечной сигнатурой. Например, алгебра
на множестве действительных чисел R с операцией tn возве-
возведения в натуральную степень п ^ 2 имеет счетную сигнатуру.
Далее будут приведены примеры алгебр и с несчетными сигна-
сигнатурами. #
Определяя алгебру, следует помнить, что результат приме-
применения любой операции обязательно должен принадлежать тому
же множеству, что и ее аргументы. Например, пару из мно-
множества Vz всех свободных векторов в пространстве и операции
скалярного умножения векторов нельзя рассматривать как ал-
алгебру, так как скалярное произведение двух векторов не есть
вектор. Заменив скалярное умножение векторным, получим ал-
алгебру.
Кроме того, нельзя забывать, что n-арная операция, как
и всякое отображение, должна быть определена для любого
кортежа длины п элементов множества. Поэтому не являет-
является алгеброй множество всех матриц с операциями сложения
и умножения матриц, так как эти операции определены не
для любой упорядоченной пары матриц. Бели же при тех же
операциях ограничиться множеством квадратных матриц фик-
фиксированного порядка п, то получим алгебру.
Точно так же множество действительных чисел К с опе-
операцией : деления действительных чисел не является алгеброй,
поскольку результат деления не определен при нулевом делите-
делителе. Пара же (R\{0}, {:}) есть алгебра.
Договоримся, определяя конкретную алгебру, записывать
ее сигнатуру без фигурных скобок, перечисляя после обозначе-
обозначения носителя все операции. Так, в примере 2.4.а первая алгебра
может быть записана как Л\ = Bм,и,П,\, Д,"~~,0,М).
Для алгебры Л = (А, ?1) обозначим через п^ подмножество
сигнатуры ?2, состоящее из всех n-арных операций. Тогда п =
120 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
= U п(п\ Так, для алгебры Л\ в примере 2.4.а будем иметь:
ft(n) = 0 при п > 2.
Определение 2.3. Две алгебры Л\ = (А\, fii) и Лг =
= (^2, ?2г) называют однотипными, если существует такая
биекция п\ на 1^2, при которой n-арная операция из Oi для
любого п переходит в n-арную из ffe-
Пример 2.5. Алгебра Bм, U, П, 0, М), заданная на
множестве всех подмножеств множества М, и алгебра Аз =
= (R, +, •, 0, 1) (см. пример 2.4.в), заданная на множестве дей-
действительных чисел, однотипны. Биекцию (взаимно однознач-
однозначное соответствие) между их сигнатурами, которая сохраняла
бы арность операций, можно определить и так: U »->>+, П »-> •,
0i-»O, Мн>1. Указанный способ задания биекции не един-
единственный. Например, ее можно определить так: Uн* •, Пн>+,
0h>1,Mi->O.
Алгебра Bм, U, П, 0, М) и алгебра Л\ в примере 2.4.а
не являются однотипными, тале как их сигнатуры состоят из
разного числа операций и между ними установить взаимно
однозначное соответствие нельзя.
Не являются однотипными и алгебры Bм, ) и (N, +), ибо
в первой алгебре единственная операция ее сигнатуры является
унарной, а во второй — бинарной. #
Нередко сигнатуры однотипных алгебр и элементы этих
сигнатур — операции — обозначают одинаково. Так, мы пи-
пишем (R, +, •, 0, 1) и (Q, +, •, 0, 1), хотя первая алгебра задана
на множестве всех действительных чисел, а вторая — на мно-
множестве рациональных чисел, и, например, сложение в первой
алгебре, строго говоря, не есть та же самая операция, что4шо-
жение во второй алгебре. В общем случае мы часто будем
2.2. Группоиды, полугруппы, группы 121
говорить о различных (но однотипных) ?2-алгебрах, заданных
на разных носителях, понимая, что п есть общее для всех этих
алгебр обозначение их сигнатур.
2.2. Группоиды, полугруппы, группы
Рассмотрим алгебры, сигнатуры которых состоят из одной.
бинарной операции. Эту операцию будем обозначать точкой (•)
и условно называть в этом случае умножением.
Группоидом называют любую алгебру Q = (G, •), сигнату-
сигнатура которой состоит из одной бинарной операции. В группоиде
на бинарную операцию нет никаких ограничений.
Группоид (G, •) называют полугруппой, если его операция
ассоциативна, т.е. для любых элементов а, 6, с носителя G
выполняется равенство а • F • с) = (а • Ъ) • с.
Пример 2.6. а. Множество % свободных векторов вместе
с операцией векторного умножения является группоидом, но не
полугруппой, так как векторное умножение не ассоциативно.
б. Множество натуральных чисел вместе с операцией воз-
возведения в степень также будет только группоидом, так как
в. Множество 2А всех подмножеств множества А вместе
с операцией \ (разность множеств) тоже только группоид,
поскольку указанная операция не ассоциативна.
г. Множество натуральных чисел N вместе с операцией
сложения будет полугруппой. #
Группоид Q = (G, •) называют моноидом, если его опера-
операция ассоциативна и относительно операции существует ней-
нейтральный элемент. Его называют нейтральным элемен-
элементом моноида Q или единицей моноида и обозначают 1.
Таким образом, моноид Q = (G, •) есть полугруппа, в кото-
которой для любого а имеют место равенства а • 1 = 1 • а = а, где
1 — нейтральный элемент (единица) моноида.
122 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Поскольку нейтральный элемент относительно любой би-
бинарной операции является единственным (см. 2.1), мы можем
рассматривать моноид как алгебру (G, •, 1), сигнатура кото-
которой состоит из двух операций: бинарной операции • (умноже-
(умножение) и нульарной операции 1 (нейтрального элемента). Вве-
Введение 1 в сигнатуру моноида удобно тем, что зачастую при
рассмотрении конкретных примеров моноидов целесообразно
явно указать нейтральный элемент относительно его операции.
Например, алгебра BЛхЛ, о? id^) есть моноид всех бинарных
отношений на множестве А с операцией композиции бинарных
отношений, в котором нейтральным элементом является диа-
диагональ множества А.
Среди полугрупп выделяют полугруппы с коммутативной
операцией — коммутативные полугруппы.
Пример 2.7. а. Множество всех бинарных отношений на
произвольном множестве А с операцией композиции отноше-
отношений будет моноидом, нейтральным элементом которого служит
диагональ множества А, поскольку для любых бинарных отно-
отношений р, т и а на множестве А имеют место равенства (см. 1.4)
ро(тоа) = (рот)оа и idU°р = р°icU = р-
б. Множество всех отображений некоторого множества А
в себя по операции композиции отображений есть моноид.
Напомним, что композиция отображений снова есть ото-
отображение и операция композиции имеет нейтральный элемент:
тождественное отображение А на себя. Поскольку любое
отображение множества А в себя можно рассматривать как би-
бинарное отношение на этом множестве, а композицию отображе-
отображений — как частный случай композиции отношений, требуемые
свойства операции композиции отображений выполняются (см.
пример 2.7.а). При этом тождественному отображению соот-
соответствует диагональ icU множества А. Этот моноид называют
часто симметрическим моноидом или симметрической
полугруппой множества А.
2.2. Группоиды, полугруппы, группы 123
в. Алгебра (No, +), где носитель — множество No неотри-
неотрицательных целых чисел, а сигнатура состоит из одной операции
сложения, есть коммутативный моноид, в котором нейтраль-
нейтральный элемент — это число 0. Действительно, сумма двух на-
натуральных чисел есть натуральное число, операция сложения
ассоциативна, коммутативна и для любого натурального числа
п имеет место равенство п + 0 = п.
Обратим внимание на то, что свойства нейтральных элемен-
элементов и нулей ассоциируются со свойствами чисел 1 и 0 относи-
относительно операций умножения и сложения чисел.
г. Алгебра (Z, •), у которой носителем является множество
целых чисел, а сигнатура состоит из одной операции умноже-
умножения, есть коммутативный моноид. Нейтральным элементом
этого моноида является число 1.
д. Пусть А — конечное множество, а Ап — множество
кортежей длины п. На множестве всех кортежей А+ = (J Ап
определим операцию соединенил (конкатенации) корте-
кортежей следующим образом:
(ai, ..., am)-(bi, ..., Ь*) = (ai, ..., am, 6i, ..., &*).
Можно видеть, что введенная операция ассоциативна, но не
имеет нейтрального элемента. Таким образом, построена по-
полугруппа, но не моноид.
Чтобы превратить эту полугруппу в моноид, расширим
носитель полугруппы, введя понятие нулевой декартовой
степени А0 произвольного множества А. Под А0 понимают
одноэлементное множество {Л}, единственный элемент которо-
которого называют пустым кортежем. Такое определение мно-
множества А0 объясняется следующим: мощность положительной
декартовой степени Ап конечного множества равна \А\п. При
п = 0 должно быть \А°\ = \А\° = 1, откуда заключаем, что А° —
одноэлементное множество.
Обозначив А* = A0 U А+, по определению для любого х € А*
полагаем х • Л = А • х = х. В результате получим алгебру
124 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
(А*, •), являющуюся моноидом, с нейтральным элементом Л.
Его называют свободным моноидом, порожденным множе-
множеством А. #
Полугруппу, операция которой коммутативна и идемпо-
тентна, называют полурешеткой.
Пример 2.8. а. Алгебры BА, и), BЛ, fl) (для произволь-
произвольного фиксированного множества А) являются полурешетками,
поскольку операции U и П ассоциативны, коммутативны и
идемпотентны.
б. Алгебра (N, НОК), где НОК — операция вычисления наи-
наименьшего общего кратного двух чисел, является полурешеткой.
Покажем, что указанная операция ассоциативна. Рассмотрим
произвольные натуральные числа m, n и 1, Каждое из этих
чисел можно разложить на произведение простых чисел и пред-
представить в виде
где набор простых чисел pi, ..., pk выбран одинаковым для
всех трех чисел, а некоторые из показателей од, Д и 7ь * = 1? &>
могут быть равными нулю. Тогда для чисел тип имеем
HOK(n,m) = pp("b/?i) epm«(o* А).
Таким образом, ассоциативность операции НОК сводится к
ассоциативности операции max вычисления наибольшего из
двух натуральных чисел. Ассоциативность последней вытекает
из очевидного тождества max(a,max(fe,c)) = max(max(a,6),c),
верного для любых чисел а, 6 и с.
Поскольку HOK(n,m) = HOK(m,n), операция НОК комму-
коммутативна, а так как для любого натурального числа справедливо
равенство НОК(п,п) = п, то операция идемпотентна.
в. Алгебра (N, НОД), где НОД — операция вычисления наи-
наибольшего общего делителя двух целых чисел, также является
полурешеткой. # \
2.2. Группоиды, полугруппы, группы 125
Группоид Q = (G, •) называют группой, если операция ас-
ассоциативна, существует нейтральный элемент (единица) 1 от-
относительно умножения и для каждого х € G существует такой
элемент х1 Е G, называемый обратным к ж, что х-х' = х'-х = 1.
Таким образом, группа — это алгебра Q = (G, •), в которой
для всех a, b, c€G выполняется равенство а• F• с) = (а• 6) • с,
существует единственный элемент 1 Е G, такой, что а • 1 = 1 •
а = а для любого а Е G, и для каждого a EG существует такой
элемент а', что а • а' = а' • а = 1. Короче говоря, группа — это
моноид, в котором для каждого элемента существует обратный
элемент.
Отметим, что задать группу как алгебру можно нескольки-
несколькими способами в зависимости от состава операций, включенных
в сигнатуру.
Во-первых, в сигнатуру может быть включена единственная
бинарная операция. В этом случае пишут Q = (G, •), а все
свойства операции описывают дополнительно.
Во-вторых, в сигнатуру может быть включена нульарная
операция — нейтральный элемент группы. В этом случае
пишут Q — (G, •, 1) и дополнительно указывают существование
обратного элемента относительно бинарной операции для всех
элементов носителя.
Третий способ задания группы как алгебры вытекает из
следующей теоремы.
Теорема 2.1. В любой группе Q = (G,-) для каждого о € G
элемент, обратный к а, единственный.
< Пусть в группе (G, •) с единицей 1 для некоторого а существу-
существуют два элемента а1 и а;/, обратных к а. Тогда а1 = а! • 1 в силу
свойства единицы. Так как 1 = а• а", то о! = а! -(а-а"). Исполь-
Используя ассоциативность и учитывая, что о; — элемент, обратный
к а, получим
а' ¦ (о-о") = (а'-а)-а" = 1 а" = а". >
126 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Единственность для каждого элемента а обратного элемен-
элемента а' группы Q позволяет обозначать его как а и операцию
-1: а ь-> а"*1 вычисления (или взятия) обратного элемента ввести
в сигнатуру группы. Таким образом, группу можно рассма-
рассматривать и как алгебру Q = (G, •, -1, 1), сигнатура которой
состоит из бинарной операции умножения, унарной операции
взятия обратного элемента и нульарной операции — единицы
группы (нейтрального элемента).
В дальнейшем в зависимости от контекста будем использо-
использовать все указанные варианты задания группы.
Среди групп также выделяют те, бинарная операция в ко-
которых коммутативна, — коммутативные (абелевы*) груп-
группы. В коммутативных полугруппах и группах бинарную опе-
операцию часто обозначают знаком + и называют сложением.
Уместно здесь рассмотреть вопрос о двух формах записи
бинарной операции группы. В аддитивной записи операции
ее обозначают знаком +, нейтральный элемент — знаком 0, а
элемент, обратный к а относительно операции +, записывают
в виде —а, называя его при этом противоположным к а.
В мультипликативной записи операцию обозначают
знаком •, нейтральный элемент — знаком 1, а элемент, обрат-
обратный к а, записывают в виде а. В этом случае бинарную опе-
операцию группы часто называют умножением (также умно-
умножением группы или групповым умножением), а элемент
а • Ь, как правило записываемый в виде аЪ, — произведением
элементов а и Ь.
В алгебраической литературе сложилась такая традиция,
что аддитивная запись используется преимущественно для ком-
коммутативных групп. Поскольку одним из самых простых, рас-
распространенных и вместе с тем важных примеров коммутатив-
коммутативной группы служит аддитивная группа целых чисел, то обозна-
обозначения и термины для произвольной аддитивно записываемой
коммутативной группы „скопированы" с терминов для группы
*Н. Абель A802-1829) — норвежский математик.
2.2. Группоиды, полугруппы, группы 127
(Z, +, 0). Аналогично мультипликативная запись произволь-
произвольной группы „позаимствована" у мультипликативных групп ра-
рациональных и вещественных чисел.
Пример 2.9* а. Алгебра (Z, +) — коммутативная группа,
поскольку на множестве целых чисел операция сложения ассо-
ассоциативна и коммутативна, число 0 есть нейтральный элемент, и
для каждого целого числа п существует обратный по сложению
элемент, а именно число —п, противоположное п. Рассматрива-
Рассматриваемую группу называют аддитивной группой целых чисел.
б. Множество всех биекций некоторого множества А на себя
с операцией композиции отображений есть группа.
Это следует из того, что композиция двух биекций есть
биекция, операция композиции ассоциативна, ее нейтральный
элемент — тождественное отображение icU — есть биекция,
для всякой биекций f: A-* А отображение /"*, обратное биек-
биекций /, определено, является биекцией и выполнены равенства
Эту группу называют симметрической группой мно-
множества А, а в том случае, когда множество А конечно, —
группой подстановок множества А. Бели множество А со-
состоит из п элементов, группу подстановок этого множества
называют также симметрической группой степени п или
группой подстановок п-в степени и обозначают Sn (см. при-
пример 2.10).
в. Алгебры (Q\{0}, •) и (R\{0}, •) есть коммутативные
группы. Их называют мультипликативной группой ра-
рациональных чисел и мультипликативной группой дей-
действительных чисел соответственно. В каждой из них чи-
число 1 есть нейтральный элемент (единица) группы, а обрат-
обратный к числу х по операции умножения элемент х~1 есть число
х = 1/х.
г. Для произвольно фиксированного множества А рассмо-
рассмотрим алгебру BА, Д), где Д — операция вычисления симме-
симметрической разности множеств. Операция Д ассоциативна и
128 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
коммутативна (см. 1.1). Для любого X С А имеем X Д0 = X.
Кроме того, X = Y тогда и только тогда, когда X Д У = 0. По-
Поэтому алгебра BЛ, Д) является абелевой группой, в которой
каждый элемент обратен сам себе, а нейтральный элемент —
пустое множество.
д. Рассмотрим алгебру Ъ\ = ({0,1,..., к — 1}, ©*), в кото-
которой операция ф& (сложения по модулю к) определяется так:
для любых двух тип число га 0* п, называемое суммой чисел
тип по модулю к, равно остатку от деления арифметиче-
арифметической суммы т + п на к. Можно проверить, что эта алгебра
является коммутативной группой. Бе называют аддитивной
группой вычетов по модулю к. Нейтральным элементом
служит число 0, а обратным к числу п будет к — п, поскольку
п ®к (к - п) = 0.
е. Множество всех невырожденных (т.е. имеющих ненуле-
ненулевой определитель) числовых квадратных матриц порядка п с
операцией умножения матриц является группой. Действитель-
Действительно, произведение двух невырожденных матриц снова есть невы-
невырожденная матрица [III]; единичная матрица порядка п невы-
невырожденная, и матрица, обратная к невырожденной, также явля-
является невырожденной. Эту группу будем обозначать Мп- if"
Из рассмотренных четырех видов алгебр — группоида,
полугруппы, моноида и группы — последняя обладает наиболее
интересными свойствами. Изучим более подробно операцию
вычисления обратного элемента.
Теорема 2,2. Пусть Q = (G, •) — группа. Для любых эле-
элементов а, 6 G G верны тождества
В силу ассоциативности умножения группы имеем
2.2. Группоиды, полугруппы, группы 129
Используя еще раз ассоциативность, определение элемента,
обратного к данному, и свойства единицы, получим
Итак, (а-Ь) - (б • оГ1) = 1. Точно так же доказывается, что
(Ь" • а~г)(а • 6) = 1. Поэтому элемент б" • о" является обрат-
обратным к элементу а-Ь. Согласно теореме 2.1, обратный элемент
единственный, и поэтому (а • Ь)~1 = Ь • а. Второе из доказы-
доказываемых равенств следует непосредственно из определения эле-
элемента, обратного к данному. Действительно, определение эле-
элемента а, обратного к а, равенством а -а = а-а~1 = 1 можно
рассматривать как определение (а") — обратного элемента
к а"*1, которым является, согласно этим равенствам, элемент а.
В силу теоремы 2.1 он единственный, т.е. а = (а")". >
Таким образом, мы установили, что элемент, обратный
к произведению а • 6, равен Ь" -о, а элемент, обратный к
элементу, обратному к а, равен а.
Теорема 2.3. В любой группе Q = (G, •, 1) справедливы
левый и правый законы сокращения: если а-х = о• у, то
х = у, и если х • а = у • а, то х = у.
Ч Пусть а • х = а • у. Умножая обе части этого равенства слева
на элемент о, получаем
а-(а-х) =а~1-(а-у).
В силу ассоциативности групповой операции последнее равен-
равенство можно записать так:
Поскольку а • а = 1, то 1 • х = 1 • у, откуда х = у. Тем самым
доказан левый закон сокращения. Аналогично доказывается и
правый закон. >
«к S — 10061
130 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Пусть G = (G, •, 1) — группа, а, Ь — фиксированные эле-
элементы G. Рассмотрим задачу решения уравнений
а-х = Ь, B.1)
х-а = Ь B.2)
в группе G, т.е. поиска всех таких элементов х € G, для которых
уравнение B.1) (или B.2)) превращается в тождество.
Теорема 2.4. В любой группе Q уравнения вида B.1) и
B.2) имеют решения, и притом единственные.
< Покажем, что ж = а"*1 -Ь есть решение B.1). Действительно,
а.(а-1'Ь) = {а-а~1-Ь) = Ь.
Докажем единственность решения. Пусть для фиксирован-
фиксированных а и 6 и некоторого х выполнено равенство а • х = Ь. В
группе для любого а существует и однозначно определен эле-
элемент а~х, обратный к а. Умножив на него обе части равенства,
получим a~l -(a-x) = a~l -b. В силу ассоциативности преобра-
преобразуем последнее равенство к виду (а" • а) • х = а" • 6. Поскольку
а • а = 1, то 1 • х = а" • Ь, откуда х = а • 6. Это решение
единственное в силу единственности обратного элемента.
Аналогично из х-а^Ь получаем х = Ь• а", и это решение
также единственное. >
Замечание. При использовании аддитивной записи опера-
операции для коммутативной группы Q = (G, +, 0) оба написанных
выше уравнения сводятся к одному:
а + х = 6,
а его решение есть х = Ь+ (—а). Правую часть этого равенства
в коммутативной группе называют разностью элементов Ь
и а и обзначают Ь — а. Саму же операцию, сопоставляющую
упорядоченной паре (а,Ь) разность 6— а, называют операцией
вычитания. С учетом введенных обозначений решение урав-
уравнения в коммутативной группе можно записать так: х = Ь — а.
2.2. Группоиды, полугруппы, группы 131
В случае коммутативной группы при употреблении для би-
бинарной операции мультипликативной записи решения обоих
уравнений имеют вид х = &• а". Выражение Ь- а в комму-
коммутативной группе называют частным от деления & на а и
обозначают - (или b/а), а саму операцию называют операцией
деления. Решение уравнения в этом случае записывают в виде
х = - (или х = Ь/а).
a v ' '
Пример 2.10. Рассмотрим группу подстановок n-й сте-
степени Sn всех биекций n-элементного множества {1,2, ...,п}.
Произвольную биекцию а из Sn обычно записывают в виде
/1 2 ... п\
\<*1 а2 ... апу'
обозначая тем самым, что образ 1 (при отображении а) есть
o?i, образ 2 есть <*2, ..., образ п есть ап. Биекцию множества
{1, ...,п} на себя называют подстановкой этого множества.
Подстановку, которая отображает щ ваг, аг в аз, ..., <*к-1
в а&, a c*k в c*i, где 1 < ах, с*2, ..., а/ь < п и все ау попарно раз-
различны, а все элементы, отличные от c*i, ..., а*, отображаются
сами в себя, называют циклом длины к и записывают ее в виде
(ai c*2 ... од). Например, подстановку из группы S*
A 2 3 4\
\3 2 A 1J
можно записать в виде A3 4).
Цикл длины 2 называют транспозицией. Транспозиция
представляет такое отображение множества {1, ...,п} в себя,
при котором два элемента меняются местами, а остальные
остаются на своих местах. Так, полная запись транспозиции
C 4) в S4 будет иметь вид
1 2 3 4
1 2 4
132 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Подстановка, обратная подстановке
A 2 ... п\
\аг а2 ... ап>/'
есть подстановка, которая отображает а\ в 1, с*2 в 2, ... ап в
п. Отметим, что при записи обратной подстановки элементы
первой строки тем не менее записываются в обычном порядке:
1, ...,п.
В группе 6з решим следующее уравнение:
1 2 3\ v /1 2 3\ Л 2 3
з 1 2j°X42 3 lJ = V3 2
Умножив обе части уравнения слева на
-1
/1 2 3\ _ /1 2 З
V3 1 ,2/ \^2 3 l
получим
2 ЗЛ /12 3
3
Далее, умножив полученное уравнение справа на
-1
/1 2 3\ =/1 2 3\
V2 3 I/ "" \3 1 2)
окончательно получим
G l ))- *
В полугруппе в общем случае законы сокращения и разре-
разрешимость уравнений типа B.1) и B.2) могут не иметь места.
Например, в полугруппе квадратных матриц фиксированного
порядка с операцией умножения матриц из матричного равен-
равенства АХ — АУ, вообще говоря, не следует, что X = У. Это
2.2. Группоиды, полугруппы, группы 133
можно утверждать лишь при дополнительном предположении,
что det-4 ф 0. Можно доказать, что в свободном моноиде,
порожденном некоторым конечным множеством, оба закона
сокращения справедливы, но никаких обратных элементов не
существует.
В полугруппе можно умножать любой элемент а сам на себя,
причем в силу ассоциативности операции полугруппы элемент
а-а*...'О определен однозначно. Этот элемент называют п-й
п раз
степенью элемента а и обозначают ап. При этом а1 = а,
ап = а-ап-1, п = 2, 3, ...
В моноиде вводят также нулевую степень элемента, полагая
а° = 1.
Если (А, •, 1) — группа, то можно ввести и отрицательные
степени элемента согласно равенству аГп = (а""*1O1, п = 1, 2, ...
Без доказательства сформулируем утверждения о свойствах
степеней.
Теорема 2.5. Для любой полугруппы ат • ап = am+n,
(am)n = amn (m, n€N).
Теорема 2.6. Для любой группы оГп = (an)-1 (n G N),
ат.ап = aw+n, (am)n = awn (m, nG Z).
Определение 2.4. Полугруппу (в частности, группу) (Л,-)
называют циклической, если существует такой элемент а,
что любой элемент х полугруппы является некоторой (целой)
степенью элемента а. Элемент а называют образующим
элементом полугруппы (группы).
Пример 2.11. а. Полугруппа (No, +, 0) циклическая, с
образующим элементом 1. При аддитивной записи бинарной
операции возведение элемента а в положительную степень п
есть сумма п этих элементов, и это записывают п • а (или па,
без знака умножения).
б. Группа (Z, +, 0) также циклическая. Для нее образую-
образующими элементами могут быть 1 и —1. Рассмотрим элемент 1.
134 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Тогда 0-1 = 0, п-1 = 1 + ... + 1 = п (п>0) и (-1) • 1 =-1,
п раз
(-п) • 1 = п• (-1) = (-1) +... + (-1) = -п(п>0).
п раз
Если в качестве образующего взять элемент — 1, то 0 • (—1) =
= 0, отрицательные целые числа получаются как положитель-
положительные „степени" —1, а положительные — как отрицательные
„степени" -1. Например, (-2) • (-1) = 2, 4 • (-1) = -4.
в. Группа (Z3, 0з» 0) вычетов по модулю 3 циклическая,
причем любой ее ненулевой элемент является образующим.
Действительно, для 1 имеем 1 Фз 1 = 2, 1 Фз 1 ®з 1 =: 0, а для 2
получим 22 = 2 Фз 2 = 1, 2 Фз 2 Фз 2 = 0. #
Изучим подробнее строение конечных циклических групп,
используя мультипликативную запись бинарной операции. На-
Напомним, что конечная алгебра (конечная группа, в частно-
частности) — это алгебра, носитель которой — конечное множество.
Порядком конечной группы называют количество эле-
элементов в этой группе.
Так, например, аддитивная группа вычетов по модулю к
имеет порядок к. Симметрическая группа степени п, т.е.
группа подстановок 5П, имеет порядок п!. Мультипликативная
группа вычетов по модулю р, где р — простое число, имеет
порядок р — 1.
Порядок элемента а циклической группы — это наи-
наименьшее положительное п, такое, что ап = 1.
Теорема 2.7. Порядок образующего элемента конечной
циклической группы равен порядку самой группы.
< Пусть Q = (<3, •, 1) — конечная циклическая группа с обра-
образующим элементом а и п > 0 — порядок этого элемента.
Тогда все степени а0 = 1, а1 = а,..., а71 попарно различны.
Действительно, если ак = а1, 0 < / < к < п, то ак~1 = ак+(~1) =
= ака~1 = а1 а = al~l = 1. Поскольку к — / < п, получено про-
противоречие с выбором п как порядка элемента а (ибо найдена
2.3. Кольца, тела, поля 135
степень, меньшая п, при возведении в которую элемента а по-
получится единица).
Осталось доказать, что любая степень элемента а принад-
принадлежит множеству {1, а,..., ап~~1}. Для любого целого т суще-
существуют также целые п, к, такие, что га = fcn + g, где q — целое
иО<?<п. Тогда ат = акп+* = а*п • cfl = (ап)* • а9 = 1 • а* =
= ая € {1, а,..., а71"}. Поскольку каждый элемент группы Q
есть некоторая степень элемента а, то G = {1,а, ..^а""} и
порядок группы равен п. >
Из доказанной теоремы следует, что в бесконечной цикличе-
циклической группе не существует такого п > 0, что для образующего
элемента а группы выполняется равенство оп = 1.
2.3. Кольца, тела, поля
Определение 2.5. Кольцом называют алгебру
П=(Я, +, .,0, 1),
сигнатура которой состоит из двух бинарных и двух нульарных
операций, причем для любых a,b,c?R выполняются равенства:
1)
2)
3) а + 0 = о;
4) для каждого а Е R существует элемент а;, такой, что
5) а-(Ь-с) = (а-Ь)-с]
6) а • 1 = 1 • а = а;
7) а-(Ь + с) =а-Ь + а-с, (Ь + с) • а = 6• а + с• а.
Операцию + называют слоэюениелс кольца, операцию
умножением кольца, элемент 0 — нулем кольца, элемент
1 — единицей кольца.
Равенства 1-7, указанные в определении, называют акси-
аксиомами кольца. Рассмотрим эти равенства с точки зрения
понятия группы и моноида.
136 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Аксиомы кольца 1-4 означают, что алгебра (J?, +, 0), сиг-
сигнатура которой состоит только из операций сложения кольца +
и нуля кольца 0, является абелевой группой. Эту группу назы-
называют аддитивной группой кольца TZ и говорят также, что
по сложению кольцо есть коммутативная (абелева) группа.
Аксиомы кольца 5 и 6 показывают, что алгебра (Я, •, 1),
сигнатура которой включает только умножение кольца • и еди-
единицу кольца 1, есть моноид. Этот моноид называют муль-
мультипликативным моноидом кольца TZ и говорят, что по
умножению кольцо есть моноид.
Связь между сложением кольца и умножением кольца уста-
устанавливает аксиома 7, согласно которой операция умножения
дистрибутивна относительно операции сложения.
Учитывая сказанное выше, отметим, что кольцо — это
алгебра с двумя бинарными и двумя нульарными операциями
Я= (Я, +, •, 0, 1), такая, что:
1) алгебра (i?, +,0) — коммутативная группа;
2) алгебра (Л, •, 1) — моноид;
3) операция • (умножения кольца) дистрибутивна относи-
относительно операции + (сложения кольца).
Замечание 2.2. В литературе встречается иной состав
аксиом кольца, относящихся к умножению. Так, могут отсут-
отсутствовать аксиома 6 (в кольце нет 1) и аксиома 5 (умножение не
ассоциативно). В этом случае выделяют ассоциативные коль-
кольца (к аксиомам кольца добавляют требование ассоциативности
умножения) и кольца с единицей. В последнем случае добавля-
добавляются требования ассоциативности умножения и существования
единицы.
Определение 2.6. Кольцо называют коммутативным,
если его операция умножения коммутативна.
Пример 2.12. а. Алгебра (Z, +, •, 0, 1) есть коммута-
коммутативное кольцо. Отметим, что алгебра (No, +, •, 0, 1) кольцом
2.3. Кольца, тела, поля 137
не будет, поскольку (No, +) — коммутативный моноид, но не
группа.
б. Рассмотрим алгебру Z* = ({0,1,..., к - 1}, ©*, ©*, 0,1)
(к^1) с операцией ф& сложения по модулю к и ©* (умножения
по модулю к). Последняя аналогична операции сложения по
модулю к: mQkn равно остатку от деления на к числа тп • п.
Эта алгебра есть коммутативное кольцо, которое называют
кольцом вычетов по модулю к.
в. Алгебра BЛ, Д, П, 0, А) — коммутативное кольцо, что
следует из свойств пересечения и симметрической разности
множеств (см. с. 35).
г. Пример некоммутативного кольца дает множество всех
квадратных матриц фиксированного порядка с операциями сло-
сложения и умножения матриц. Единицей этого кольца является
единичная матрица, а нулем — нулевая.
д. Пусть С — линейное пространство. Рассмотрим множе-
множество всех линейных операторов, действующих в этом простран-
пространстве.
Напомним, что суммой двух линейных операторов А и В
называют оператор А + В, такой, что
(А + В)х = Ах + Вх, хеС.
Произведением линейных операторов А и В называют линей-
линейный оператор АВ, такой, что (АВ)х = А(Вх) для любого
хеС.
Используя свойства указанных операций над линейными
операторами, можно показать, что множество всех линейных
операторов, действующих в пространстве ?, вместе с операци-
операциями сложения и умножения операторов образует кольцо. Нулем
этого кольца служит нулевой оператор, а единицей — тожде-
тождественный оператор.
Это кольцо называют кольцом линейных операторов в
линейном пространстве С. #
Аксиомы кольца называют также основными тожде-
тождествами кольца. Тождество кольца — это равенство, справед-
138 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
ливость которого сохраняется при подстановке вместо фигури-
фигурирующих в нем переменных любых элементов кольца. Основные
тождества постулируются, и из них затем могут быть выведе-
выведены как следствия другие тождества. Рассмотрим некоторые из
них.
Напомним, что аддитивная группа кольца коммутативна и
в ней определена операция вычитания.
Теорема 2.8. В любом кольце выполняются следующие
тождества:
() ()
3) (a — b)-c = a-c — b-c, c-(a — b)=c-a — c-b.
-4 Докажем тождество 0 • а = 0. Запишем для произвольного а:
Итак, а + 0 • а — а. Последнее равенство можно рассматривать
как уравнение в аддитивной группе кольца относительно неиз-
неизвестного элемента 0 • а. Так как в аддитивной группе любое
уравнение вида а + х = b имеет единственное решение х — Ь — а,
то 0-а = а — а = 0. Тождество а• 0 = 0 доказывается анало-
аналогично.
Докажем теперь тождество —(a-b) = a-(—b). Имеем
откуда а • (—6) = —(а • Ь). Точно так же можно доказать, что
(-о).Ь = -(оЬ).
Докажем третью пару тождеств. Рассмотрим первое из
них. С учетом доказанного выше имеем
а -F -с) =a-(b+(—c)) =a-b + a-(-c) =ab — a-c,
т.е. тождество справедливо. Второе тождество этой пары
доказывается аналогично. >
2.3. Кольца, тела, поля 139
Следствие 2.1. В любом кольце справедливо тождество
(_1).х = ж.(-1) = -ж.
4 Указанное следствие вытекает из второго тождества теоре-
теоремы 2.8 при о = 1иЬ = ж>
Первые два тождества из доказанных в теореме 2.8 выража-
выражают свойство, называемое аннулирующим свойством нуля
в кольце. Третья же пара тождеств указанной теоремы выра-
выражает свойство дистрибутивности операции умножения кольца
относительно операции вычитания. Таким образом, произво-
производя вычисления в любом кольце, можно раскрывать скобки и
менять знаки так же, как и при сложении, вычитании и умно-
умножении действительных чисел.
Ненулевые элементы аиЬ кольца К называют делителями
нуля, если а • b = 0 или Ь • а = 0. Пример кольца с делителем
нуля дает любое кольцо вычетов по модулю Л, если к —
составное число. В этом случае произведение по модулю к
любых тип, дающих при обычном перемножении число,
кратное к, будет равно нулю. Например, в кольце вычетов по
модулю 6 элементы 2 и 3 являются делителями нуля, поскольку
2 ©в 3 = 0. Другой пример дает кольцо квадратных матриц
фиксированного порядка (не меньшего двух). Например, для
матриц второго порядка имеем
Vo о) [р о) [о о)'
При отличных от нуля а и Ь приведенные матрицы являются
делителями нуля.
По умножению кольцо является только моноидом. Поставим
вопрос: в каких случаях кольцо по умножению будет группой?
Прежде всего заметим, что множество всех элементов кольца, в
котором 0 Ф 1, не может образовывать группы по умножению,
так как нуль не может иметь обратного. Действительно, если
предположить, что такой элемент О' существует, то, с одной
140 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
стороны, 0 • 0' = 0' • 0 = 1, а с другой — 0 • 0' = О' • 0 = О, откуда
0 = 1. Это противоречит условию 0^1. Таким образом,
поставленный выше вопрос можно уточнить так: в каких
случаях множество всех ненулевых элементов кольца образует
группу по умножению?
Если в кольце имеются делители нуля, то подмножество всех
ненулевых элементов кольца не образует группы по умноже-
умножению уже хотя бы потому, что это подмножество не замкнуто
относительно операции умножения, т.е. существуют ненулевые
элементы, произведение которых равно нулю.
Кольцо, в котором множество всех ненулевых элементов по
умножению образует группу, называют телом, коммутатив-
коммутативное тело — полем, а группу ненулевых элементов тела (поля)
по умножению — мультипликативной группой этого те-
тела (поля). Согласно определению, поле есть частный случай
кольца, в котором операции обладают дополнительными свой-
свойствами. Выпишем все свойства, выполнение которых требуется
для операций поля. Их еще называют аксиомами поля.
Поле есть алгебра F = (F, +, •, 0, 1), сигнатура которой
состоит из двух бинарных и двух нульарных операций, причем
справедливы тождества:
2)
3)
4) для каждого а € F существует элемент —а, такой, что
(-а) = 0;
5) о • F • с) = (а • 6) • с;
6) а-6 = Ь-а;
7) а • 1 = 1 • а = а;
8) для каждого аЕ F, отличного от 0, существует элемент
а, такой, что а • а = 1;
9)
Пример 2.13. а. Алгебра (Q, +, •, 0, 1) есть поле, назы-
называемое полем рациональных чисел.
2.4. Области целостности 141
б. Алгебры (Е, +, •, О, 1) и (С, +, •, О, 1) есть поля, на-
называемые полями действительных и комплексных чисел
соответственно.
в. Примером тела, не являющегося полем, может служить
алгебра кватернионов (см. Д.2.1). #
Итак, мы видим, что известным законам сложения и умно-
умножения чисел соответствуют аксиомы поля. Занимаясь число-
числовыми расчетами, мы „работаем в полях", а именно имеем дело
преимущественно с полями рациональных и вещественных чи-
чисел, иногда „переселяемся" в поле комплексных чисел.
2.4. Области целостности
Областью целостности называют коммутативное коль-
кольцо без делителей нуля. Так, кольцо целых чисел есть область
целостности.
Теорема 2.9. Конечная область целостности является
полем.
< Поле — это кольцо, умножение которого коммутативно, а
каждый ненулевой элемент а имеет обратный элемент относи-
относительно умножения. Так как область целостности, по опреде-
определению, является коммутативным кольцом, то достаточно дока-
доказать, что для конечной области целостности любой ненулевой
элемент обратим, т.е. для всякого а ф О существует единствен-
единственный #, такой, что а - х = 1.
Фиксируем произвольный элемент а^Ои определяем ото-
отображение fa множества всех ненулевых элементов в себя по
формуле fa(x)=a-x (а•хфО в области целостности при аФ О
и х ф 0). Отображение fa является инъекцией, поскольку из
равенства а-х = а-у вытекает равенство а • (х — у) = 0, откуда
ввиду отсутствия делителей нуля х — у = Оих = у. Так как но-
носитель по условию теоремы конечен, то, согласно теореме 1.8,
/а также и биекция. Поэтому для любого у существует един-
единственный элемент ж, такой, что у = а-х. В частности, при у = 1
142 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
равенство а • х = 1 выполнено для некоторого однозначно опре-
определенного х, т.е. х = а. >
Доказательство теоремы 2.9 опирается на условие конечно-
конечности кольца. Это условие действительно важно. Пример кольца
целых чисел показывает, что бесконечная область целостности
может и не быть полем.
Теорема 2.9 имеет интересные следствия. Рассмотрим коль-
кольцо Ър вычетов по модулю р.
Следствие 2.2. Кольцо Ър вычетов по модулю р является
полем тогда и только тогда, когда р — простое число.
М Пусть Ър является полем. Покажем, что в этом случае число
р простое. Предположим, что оно составное. Тогда найдутся
такие числа Ли/, 0 < &, / < р — 1, чтор = fc • /. Поскольку в этом
случае к -1 = O(modp), по крайней мере числа к и I являются
в кольце Ър делителями нуля и Ър — не поле. Следовательно,
число р не может быть составным.
Пусть р — простое число. Предположим, что элементы т
и п кольца Ър будут делителями нуля, т.е. т- п = O(modp).
При простом р равенство произведения га • п нулю по модулю
р означает, что либо т делится на р, либо п делится на р, т.е.
либо т = O(modp), либо п = O(modp). Учитывая неравенства
О^т^р — 1 и 0 < п < р — 1, заключаем, что либо т = О,
либо п = 0. Таким образом, при простом р делителей нуля
нет и кольцо Zp, как конечная область целостности, является
полем. >
Мультипликативную группу поля Ър вычетов по мо-
модулю р обозначают Z* и называют мультипликативной
группой вычетов по модулю р.
Для произвольного р легко видеть, что ненулевые элементы
тип кольца Ър будут делителями нуля тогда и только тогда,
когда произведение т • п делится на р (т.е. га • n = 0(modp)).
Например, в кольце Z\2 делителями нуля будут элементы 2 и 6,
3 и 4, 3 и 8, 4 и 6, 4 и 9, 6 и 6, 6 и 8, 6 и 10, 8 и 9.
2,4. Области целостности
143
Замечание 2.3. Следствие 2.2 допускает интерпретацию с
точки зрения теории чисел: каково бы ни было простое число р,
для всякого ненулевого т<р найдется единственное ненулевое
п <р, такое, что тп = 1 (modp). Этот результат имеет место
именно в силу того, что для каждого элемента поля Zp есть
обратный элемент относительно умножения. Это — один из
примеров применения общей алгебры к теории чисел.
Пример 2.14. В заключение приведем „таблицу сложения"
(табл. 2.1) и „таблицу умножения" (табл. 2.2) для поля Z5
ф5
0
1
2
3
4
0
0
1
2
3
4
Таблица
1
1
2
3
4
0
2
2
3
4
0
1
3
3
4
0
1
2
2.1
4
4
0
1
2
3
©5
0
1
2
3
4
0
0
0
0
0
0
Таблица
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
2.2
4
0
4
3
2
1
Таблицы, подобные приведенным выше, которые определя-
определяют операции в конечных алгебрах, носят название таблиц
Кэли. Из таблиц Кэли для поля вычетов по модулю 5 следует,
что в этом поле выполняются слегка шокирующие при первом
взгляде равенства: 4 = —1, 2 = З, 4 = 4" и т.п. Но ни о каких
„отрицательных" числах и ни о каких „дробях" тут речи нет,
поскольку расматриваются другие объекты — остатки при де-
делении на 5. Просто равенство 4 = —1 означает, что элемент
1 есть элемент, противоположный 4 в аддитивной группе вы-
вычетов по модулю 5: 4 ©5 1 = 0. Аналогично по умножению —
в мультипликативной группе вычетов по модулю 5 элемент 3
есть обратный к 2 , так как 3 ©5 2 = 1, а элемент 4 обратен к
себе самому.
Пример 2.15. Рассмотрим пример решения системы ли-
линейных алгебраических уравнений в поле Z5. При записи урав-
144 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
нений будем опускать знак ©5 умножения там, где это не
приводит к недоразумениям. Будем решать систему
( хг ©5 2х2 05 Зх3 = 1,
< 2Ж1 05 2х2 05 4х3 = 3,
[ 4X1 05 3X2 ©5 ЯЗ = О,
V
используя метод Гаусса [III]. Домножив первую строку на 3 и
прибавив ее ко второй строке, получим
C ф5 2)xi ф5 C ©5 2 ф5 2)х2 ©5 C ©5 3 05 4)х3 = 3 Ф5 3.
Воспользовавшись таблицами Кэли, вычислим коэффициенты
при переменных. В итоге имеем
О ©5 Xi ф5 Зх2 ©5 Зх3 = 1.
Прибавив к третьей строке первую, получим
A ©5 4)Х1 ф5 B Ф5 3)Х2 ©5 C Ф5 1)ЯЗ = 1,
откуда 4х3 = 1.
Система привелась к виду
i ©5 2х2 ©5 ЗХ3 = 1,
Зх2 ©5 ЗХ3 = 1,
4х3 = 1.
Из последнего уравнения находим хз = 4" 05 1 = 4 ©5 1 = 4.
Подставив хз = 4 во второе уравнение, будем иметь
т.е. 3x2 = 1 ©5 (—2) = —1 = 4. Отсюда
2.5. Модули и линейные пространства 145
Из первого уравнения после подстановки найденных значений
переменных получим
откуда х\ ©5 1 Фб 2 = 1 и х\ = — 2 = 3.
Таким образом, х\ = 3, Х2 = 3 и жз = 4 — решение системы
линейных уравнений. #
Заметим в заключение, что известная из [III] техника ре-
решения систем линейных алгебраических уравнений в полях дей-
действительных или комплексных чисел может быть без изменения
перенесена на любое поле.
2.5. Модули и линейные пространства
Рассмотрим абелеву группу Q = (G, +, 0) и кольцо 1Z =
= (J?, +, •, 0, 1). Пусть каждому элементу а кольца % сопо-
сопоставлено отображение и>а носителя группы Q в себя так, что
для любых а, /3? R и любых x,y?G выполняются равенства:
2) ша+р{х) = ша{х
3)u>ap(x)=Wa(up(x))l
4) u)\{x) = х.
Последнее равенство означает, что отображение o;j, сопо-
сопоставленное единице кольца 7?, является тождественным ото-
отображением множества G на себя.
Тогда абелева группа Q называется левым модулем над
кольцом И.
Если равенство 3 в определении модуля переписать так:
У)иа.р(х)=Шр(иа(х))у
то получим определение правого модуля над кольцом TZ.
Для коммутативного кольца К левый и правый модули
совпадают, так как ua(vp(x)) =<*>/?-а(я) =^(а;а(а;)).
146 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Заметим, что модуль можно рассматривать как алгебру с
бесконечной сигнатурой, если множество R бесконечно:
? = (?, +, 0, {иа:аеП}).
Следует подчеркнуть, что модуль есть именно абелева груп-
группа с дополнительными операциями, отображениями и>а, соиоу
ставленными элементам кольца И. Носитель модуля есть носи-
носитель G группы Q.
Теорема 2.10. В любом fc-модуле имеют место тожде-
тождества:
Решая уравнение х + шо(х) =х относительно (Jq(x), получа-
получаем шо(х) = х — х = 0.
2) x + u^i(x)=ui(x)+U-i(x)=LO1+(^1)(x)=ui(x) = 0. Та-
Таким образом, х+ш-х(х) = 0, откуда в силу определения проти-
противоположного элемента получаем u>_i(a;) = —x. >
Пример 2.16. а. Пусть И = (Я, +, •, 0, 1) — произволь-
произвольное кольцо. В качестве группы Q возьмем аддитивную группу
этого кольца, а отображение cja, a € R, определим так, что
u)Q(x) = а-х, х € R. Это отображение называют левым сдви-
сдвигом на а. Тогда равенства 1-4 выполнены в силу аксиом
кольца. Таким образм, получаем левый модуль, носитель ко-
которого — аддитивная группа кольца, а отображение иа есть
левый сдвиг произвольного элемента кольца на заданное а.
Бели теперь задать для каждого aGR отображение и>а: R —>
-* R так, что ша(х) = я • а (правый сдвиг на а), то получим
правый модуль с тем же носителем, но сигнатура его (помимо
операции сложения исходного кольца R) будет состоять из
всевозможных правых сдвигов и>а.
б. Пусть Q есть аддитивная группа векторов какого-либо
линейного пространства L, а 1Z — кольцо линейных операторов
2.6. Подгруппы и подкольца 147
из L в L. Тогда, полагая для произвольных линейного опера-
оператора А и вектора х пространства L u>a(x) = Ах, получаем, как
нетрудно проверить, левый модуль над кольцом 11.
в. Пусть 1Z — кольцо квадратных числовых матриц порядка
п с обычными операциями сложения и умножения матриц (см.
пример 2.12.г), a Q — группа матриц-столбцов типа n x 1 по
сложению. Отображение иа определим по правилу и)а(Х) = АХ,
где А — квадратная матрица, а X — вектор-столбец. Легко
видеть, что равенства 1-4 вытекают из свойств умножения
матриц и линейных операций над матрицами [III].
В результате получим левый модуль над кольцом квадрат-
квадратных матриц.
Аналогично, взяв в качестве Q аддитивную группу матриц-
строк типа 1 х п и определив отображение ша(У) = Y А, где
А — квадратная матрица порядка га, a Y — матрица-строка,
получим правый модуль над кольцом квадратных матриц. #
Если рассматривается левый 7^-модуль, то отображение ша
называют левым умножением на элемент а кольца К и
применяют обозначение ша(х) =аож. Для правого 7^-модуля
отображение ша называют правым умножением на элемент
а кольца 11 и пишут ша(х) = х © а.
7?-модуль, у которого кольцо 1Z является полем, называют
линейным пространством над полем 1Z. Бели кольцо 1Z
является полем действительных чисел (или полем комплекс-
комплексных чисел), то мы получаем действительное (соответственно
комплексное) линейное пространство.
2.6. Подгруппы и подкольца
Пусть Q = (G, *) — произвольный группоид и Н С G —
некоторое подмножество множества G. Рассмотрим свойства
бинарной операции * группоида Q на подмножестве Н.
Говорят, что множество Н С G замкнуто относи-
относительно операции *, если х*у Е Н для любых #, у G Н. В
148 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
этом случае подмножество Н с операцией ¦ будет группоидом
% = (if, *). Его называют подгруппоидом группоида Q.
Бели подмножество Н замкнуто относительно бинарной
операции * и эта бинарная операция ассоциативна на множе-
множестве G, то легко убедиться, что операция останется ассоциатив-
ассоциативной и при ее ограничении на подмножество Н. Таким образом, v
если группоид Q является полугруппой, то и всякий его под-
подгруппоид будет полугруппой, называемой подполугруппой
полугруппы Q.
Однако в случае, когда группоид является моноидом {груп-
{группой), уже нельзя утверждать, что любой подгруппоид являет-
является также моноидом (группой). Например, в качестве исход-
исходного группоида рассмотрим аддитивную группу целых чисел
(Z, +). Выделим в множестве целых чисел подмножество N
натуральных чисел. Поскольку это подмножество замкнуто
относительно операциии сложения +, группоид (N, +) будет
подгруппоидом группоида (Z, +). Так как операция сложения
чисел ассоциативна, (N, +) будет подполугруппой. Однако в
множестве N отсутствует нейтральный элемент О относитель-
относительно операции сложения. Следовательно, (N,+) даже не моноид.
Пусть Л4 = (М, •, 1) — моноид. Бели Р есть подмножество
М, замкнутое относительно бинарной операции • моноида Л4 и
содержащее нейтральный элемент (единицу) 1 этого моноида,
то V = (Р, •, 1) также есть моноид. Его называют подмонои-
дом моноида Л4.
Полагая, по определению, что замкнутость подмножества
В С А относительно нульарной операции а на Л равносильна
соотношению oGB, получаем, что моноид V = (Р, •, 1) есть
подмоноид моноида М = (М, •, 1) тогда и только тогда, ко-
когда множество Р замкнуто относительно бинарной операции •
моноида Л1, а также относительно его нульарной операции 1.
Пусть Q = (G, •, ~х, 1) — группа, а Н есть подмножество
G, замкнутое относительно операции • группы С/, содержащее
нейтральный элемент (единицу) 1 этой группы и вместе с ка-
каждым элементом х G Н содержащее элемент ж, обратный
2.6. Подгруппы и подкольца 149
к #, т.е. замкнутое относительно унарной операции ~* взятия
обратного, которая здесь включена в сигнатуру группы. Тогда
% = (ДГ, •, -*1, 1) также есть группа, которую называют под'
группой группы Q.
Пусть ш — унарная операция на множестве G моноида G,
aW — некоторый его подмоноид. Естественно подмоноид Н
моноида G назвать замкнутым относительно унарной операции
а;, если для каждого х ? Н имеет место ш(х) Е Н. Тогда группа
Н = (Я, •, -1, 1) есть подгруппа группы Q = (G, •, "~1, 1) в
том и только в том случае, когда множество Н замкнуто
относительно всех операций •, ", 1 сигнатуры группы Q.
Замечание 2.4. Подмножество ЯСб, замкнутое относи-
относительно группового умножения • группы Q и содержащее вместе
с каждым элементом х обратный к нему элемент ж", будет со-
содержать и нейтральный элемент (единицу) группы, поскольку
в силу замкнутости Н относительно операции умножения из
х ? Н и х G Н следует, что х • ж" = х~1 х = 1еН. #
Используя факт единственности нейтрального элемента (еди-
(единицы) любого моноида и только что сформулированное опре-
определение, можно легко доказать, что единица моноида (группы,
в частности) служит одновременно единицей любого его под-
моноида (любой подгруппы). Заметим, что подмоноид, носи-
носитель которого содержит только единицу исходного моноида
(Р = {1}), а также подмоноид, носитель которого совпадает с
носителем исходного моноида (Р = М), называют тривиаль-
тривиальным подмоноидом (в частности, тривиальной подгруп-
подгруппой). Подмоноид, не являющийся тривиальным, называют
нетривиальным подмоноидом (в частности, нетривиаль-
нетривиальной подгруппой). Подгруппоид (подполугруппу, подмоноид,
подгруппу) (G, *) называют собственным подгруппоидом
(подполугруппой, подмоноидом, подгруппой) группоида
(полугруппы, моноида, группы) (К, *), если его носитель G
есть собственное подмножество множества К.
150 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Пример 2.17. Рассмотрим аддитивную полугруппу нату-
натуральных чисел вместе с нулем (No, +). Подмножество всех по-
положительных четных чисел замкнуто относительно сложения,
и поэтому на нем может быть определена подполугруппа полу-
полугруппы (No, +). Но аддитивная полугруппа натуральных чисел
с нулем является также и моноидом с нейтральным элементом1
0. Тогда построенная выше подполугруппа всех положитель-
положительных четных чисел не будет подмоноидом моноида (No, +,0),
так как ее носитель не содержит нуля — единицы моноида
(No, +, 0).
Подмножество всех натуральных чисел вместе с нулем,
делящихся на заданное число к > 1, замкнуто относительно
операции сложения; на нем может быть определен подмоноид
моноида (No, +, 0).
Мультипликативная группа поля рациональных чисел,
является подгруппой группы (R\ {0}, •, 1) (мультипликативной
группы поля действительных чисел). Но алгебра (Z\{0},-,l)
не является подгруппой последней группы. Несмотря на то
что множество всех отличных от нуля целых чисел замкнуто
относительно операции умножения и содержит единицу, оно не
содержит вместе с каждым целым числом т обратного к нему
числа —. #
т
Пусть Q = (<?, •, -1, 1) — группа. Как следует из теорем
2.5 и 2.6, произведение любых степеней элемента а есть снова
некоторая степень элемента а, нулевая степень дает единицу
группы, а обратным к элементу ак является элемент а~к. Таким
образом, множество всех степеней фиксированного элемента а
группы Q является подгруппой группы Q.
Определение 2.7. Подгруппу группы <?, заданную на мно-
множестве всех степеней фиксированного элемента а, называют
циклической подгруппой группы ?7, порожденной эле-
элементом а.
2.6. Подгруппы и подкольца 151
Пример 2.18. В группе Ъ\г (мультипликативной группе
вычетов по модулю 13) построим циклическую подгруппу,
порожденную элементом 5. Имеем: 5° = 1, 51 = 5, 52 = 5©1з 5 =
= 12, 53 = 5 013 12 = 8, 54 = 5 ©13 8 = 1. Отсюда следует,
что порядок этой циклической подгруппы в силу теоремы 2.7
равен 4. Она состоит из элементов: 1, 5, 8 и 12. #
Рассмотрим кольцо TZ = (Я, +, •, 0, 1). Если множество
Q есть подмножество множества Я, замкнутое относительно
операций сложения и умножения кольца 7?, содержащее нуль и
единицу кольца 1Z, а также вместе с каждым х Е Q содержащее
противоположный к нему элемент —ж, то Q = (Q,+,-,0,1)
также есть кольцо. Его называют подкольцом кольца Q.
Другими словами, кольцо Q = (Q, +, •, 0, 1) — это подколь-
цо кольца TZ = (Я, +, •, 0, 1), если его аддитивная группа есть
подгруппа аддитивной группы кольца 7?, а его мультиплика-
мультипликативный моноид — подмоноид мультипликативного моноида
кольца TZ.
Аналогично определяется понятие подполя (какого-либо
поля). Единственное по сравнению с определением подкольца
дополнительное требование состоит в том, что носитель подпо-
подполя должен вместе с каждым элементом х содержать обратный
к нему по умножению поля элемент х. Это значит, что
мультипликативная группа подполя должна быть подгруппой
мультипликативной группы всего поля. Естественно, что точ-
точно так же обстоит дело и с понятием подтела.
Пример 2.19. Кольцо целых чисел (Z, +, •, 0, 1) есть
подкольцо кольца действительных чисел (Е, +, -, 0, 1). При
этом, несмотря на то что кольцо действительных чисел есть
поле, кольцо целых чисел не является его подполем, поскольку
в последнем для любого целого числа отсутствует обратный к
нему по умножению элемент.
Поле рациональных чисел является подполем поля действи-
действительных чисел, которое, в свою очередь, есть подполе поля
152 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
комплексных чисел. Алгебра (No, +, •, 0, 1) на множестве на-
натуральных чисел вместе с нулем не является подкольцом ни
одного из перечисленных выше колец, так как ее носитель не
содержит ни обратных относительно сложения, ни обратных
относительно умножения элементов.
2.7. Теорема Лагранжа
Пусть Q = (G, •, 1) — группа, а,Н = (Я, •, 1) — ее подгруппа.
Левым смежным классом подгруппы % по элементу
а ? G называют множество
аН = {у: у = a-h, h Е Н}.
Соответственно правый смежный класс подгруппы Н
по элементу a EG — это множество
На = {у: у = h • a, h G Я}.
Очевидно, что в коммутативной группе аН = На.
Замечание* При использовании аддитивной записи груп-
групповой операции смежные классы записываются в виде а + Н
(или Я + а). #
Рассмотрим левые смежные классы. Прежде всего заметим,
что если аЕ Н, то аН = Я. Действительно, если х Е аН, то
для некоторого h € Я х = ah, а так как a G Я и множество
Я замкнуто относительно умножения группы Q, то х G Я.
Обратно, если х G Я, то х = аа"^ = аЛ, где h = а"^ Е Я.
Поэтому х G аЯ. Окончательно получим Я = аЯ.
Введем теперь бинарное отношение ~# на множестве G
следующим образом: элементы а и Ь связаны отношением ~н
(а~нЬ), если и только если левые смежные классы подгруппы
% по элементам а и Ь совпадают (аН = ЬЯ).
2.7. Теорема Лагранжа 153
Теорема 2.11. Бинарное отношение ~# есть эквивалент-
эквивалентность на G, причем класс эквивалентности произвольного
элемента a€G совпадает с левым смежным классом аН.
<4 Докажем, что ~н является эквивалентностью на G. Посколь-
Поскольку аН = аН для любого а ? G, т.е. а~но>, то бинарное отноше-
отношение ~# рефлексивно. Бели а~#Ь, то aff = 6Я, следовательно,
6Я = аЯ и b~H<ii T«e. бинарное отношение ~# симметрично.
Наконец, из того, что а~нЬ и Ъ~нс, следует аЯ = ЬН и ЬЯ = сЯ,
т.е. аН = сЯ и а~нс> откуда вытекает, что бинарное отноше-
отношение ~н транзитивно. Итак, ~# есть эквивалентность.
Докажем, что класс эквивалентности произвольного элемен-
элемента а равен аН. Воспользуемся методом двух включений.
Пусть х Е [а]~#> т.е. #~#а, тогда хН = аН. Последнее
означает, что любой элемент вида a/i, h E Я, может быть
представлен в виде xh\y где h\ G Я, т.е. ah = a;hi. Отсюда
получаем х = ahfv[l. Поскольку % — подгруппа, Л, /ii G Я,
то Лг = hK[l Е Я. Следовательно, ж = ah<i € аЯ и [а]~н С аЯ.
Покажем второе включение, т.е. докажем, что аН С [а]^я.
Пусть х € аН, тогда х = ah для некоторого h € Н. Отсюда
получаем, что жЯ = ahH. Поскольку для всякого h E Я, как
доказано выше, ЛЯ = Я, справедливо равенство хН = аЯ,
откуда х~на> и ж Е [а]^я- ^
Теорема 2.12. Всякий левый смежный класс подгруппы Я
равномощен Н.
< Для произвольного фиксированного a E G зададим отобра-
отображение (ра: Я ->> аЯ следующим образом: ^о(Л) = aft. Во-первых,
отображение у?а есть сюръекция, так как если х Е аЯ, то х =
= aft для некоторого heH, откуда д: = (pa(h). Во-вторых, <ра —
инъекция, поскольку из равенства afti = aft2 в силу законов со-
сокращения в группе Q следует fti = Л2. Следовательно, (ра —
биекция и |аЯ| = |Я|. >
Из доказанных теорем о свойствах левых смежных классов,
справедливых — подчеркнем это — для любой группы, выте-
вытекает простой, но очень важный результат для конечных групп.
154 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Теорема 2.13 (теорема Лагранжа). Порядок конечной
группы делится на порядок любой ее подгруппы.
< Согласно теореме 2.11, все левые смежные классы образуют
разбиение множества G на подмножества, равномощные в силу
теоремы 2.12 подгруппе Н. Так как группа Q конечна, то число
элементов разбиения конечно. Обозначив это число через fc,
заключаем, что \G\ = k\H\. Следовательно, порядок группы \G\
делится на порядок группы \Н|. >
Число всех левых смежных классов подгруппы И конечной
группы Q называют левым индексом подгруппы Н в груп-
группе д.
Рассмотрим некоторые следствия теоремы Лагранжа.
Следствие 2.3. Любая группа простого порядка является
циклической.
< Возьмем в группе, порядок которой есть простое число,
какую-то ее циклическую подгруппу, образующий элемент
которой отличен от единицы (нейтрального элемента) группы.
Тогда эта подгруппа содержит не менее двух элементов и ее
порядок, согласно теореме Лагранжа, должен быть делителем
порядка группы. Поскольку порядок всей группы — простое
число, а порядок подгруппы не меньше 2, то он совпадет с
порядком всей группы. >
Замечание. Группа, порядок которой не является простым
числом, может быть циклической, т.е. утверждение, обратное
следствию 2.3, не имеет места. Так, например, циклической
является Ъ\ — аддитивная группа вычетов по модулю 4. Ее
образующий элемент — 1. Можно доказать, например, что
любая группа порядка 15 является циклической*. #
Группу называют неразложимой, если она не имеет не-
нетривиальных подгрупп.
*См.: Каргополов М.И., Мерзляков Ю.И.
2.7. Теорема, Лагранжа 155
Следствие 2.4. Конечная группа неразложима тогда и
только тогда, когда она является циклической группой, поря-
порядок которой есть простое число.
^ Бели группа циклическая и ее порядок — простое число,
то, согласно теореме Лагранжа, каждая ее подгруппа имеет
порядок, равный либо единице, либо порядку всей группы, и
группа неразложима.
Обратно, пусть конечная группа Q = (G, •, 1) неразложима.
Покажем, что \G\ — простое число. Выберем элемент а ф 1.
Тогда циклическая подгруппа с образующим элементом о сов-
совпадает с Q. Допустим, что \G\ — составное число, т.е. |G| =
= kl для некоторых натуральных А; и /, отличных от 1 и \G\.
Тогда циклическая подгруппа с образующим элементом Ь = ак
не совпадает с С?, так как Ь1 = akl = 1 ив этой подгруппе не
более I элементов, что противоречит неразложимости группы
Q. Следовательно, порядок группы Q есть простое число. >
Следствие 2.5. В конечной группе Q для любого элемента
aEG имеет место равенство a'G' = 1.
М Если группа Q циклическая и элемент a — ее образующий
элемент, утверждение очевидно. Бели же элемент а являет-
является образующим элементом некоторой циклической подгруппы
группы Q порядка к < |G|, то в силу теоремы Лагранжа |G| = kl
для некоторого натурального /. Отсюда получаем a'Gl = ам =
= (акI = 1* = 1. >
С помощью теоремы Лагранжа (точнее, следствия 2.5) мож-
можно доказать, что если целое число п не делится на простое число
р, то пр""х — 1 делится на р. В теории чисел это утверждение
известно как малая теорема Ферма.
Действительно, пусть п = гр + к, где г — целое, а 0 < к < р
(остаток от деления п нар). Тогда ясно, что пр~1 = кр (modp)
(достаточно разложить (гр + к)р~1 по формуле бинома Нью-
Ньютона). Рассмотрим группу Z* (мультипликативную группу
156 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
вычетов по модулю р) и в этой группе элемент к. Порядок
группы Z* = р — 1. Если к = 1, то
п?-1 - 1 = (I* - 1) (modp) = 0 (modp)
и утверждение очевидно. Согласно следствию 2.5, в группе
Z* справедливо равенство кр~1 = 1, т.е. кр~г = l(modp), и,
следовательно, кр~1 — 1 = 0(modp), т.е. число кр~1 равно 1 по
модулю р. Поэтому np~~l = kp~l = I (modp).
Малая теорема Ферма дает возможность доказывать утвер-
утверждения о делимости очень больших чисел. Например, из нее
следует, что при р = 97 число 97 является делителем п96 — 1 для
любого п, не делящегося на 97. Подобного рода заключения
важны при разработке алгоритмов защиты информации.
Кроме того, используя малую теорему Ферма, можно вычи-
вычислять в полях вычетов по модулю р(р — простое число) элемен-
элементы, обратные к заданным относительно умножения. Действи-
Действительно, если a Е Zp, то, так как ар~1 = 1, умножая последнее
равенство на а", получим ар =а~1. Таким образом, для
того чтобы вычислить элемент, обратный к а по умножению,
достаточно возвести его в степень р — 2 или, что равносильно,
в степень, равную остатку от деления числа р — 2 на порядок
циклической подгруппы группы Z*, порожденной элементом а
(см. теорему 2.7).
Пример 2.20. Рассмотрим, как вычислить элемент, обрат-
обратный к а по умножению в поле Z17. Согласно полученному выше
результату, для вычисления обратного к а элемента нужно най-
найти а17" = а15. Однако объем вычислений можно сократить,
если порядок циклической подгруппы, порожденной элементом
а, меньше порядка группы.
Порядок группы Щ7 равен 16, следовательно, порядок ци-
циклической подгруппы, порожденной элементом а, может со-
составлять, согласно теореме Лагранжа, 2, 4, 8, 16 (т.е. быть
каким-то из делителей числа 16). Поэтому при поиске обратно-
обратного элемента достаточно проверить следующие степени а (кроме
2.8. Гомоморфизмы групп 157
15-й): 1 (остаток от деления 15 на 2), 3 (остаток от деления 15
на 4) и 7 (остаток от деления 15 на 8).
Найдем элемент, обратный к 2. Очевидно, что 2 ф 2, так
как 2 ©17 2 = 4^1. Далее получим 23 = 4 ©п 2 = 8. Поскольку
2 ©17 8 = 16 Ф 1, то 23 = 8 также не является обратным к 2.
Вычислим 27 = 23 ©it 23 ©i7 2 = 8 ©i7 8 ©гг 2 = 9. Поскольку
9 ©i7 2 = 1, в итоге получаем 2" = 9.
Найдем элемент, обратный к 14. Так как 14 ©17 14 = 9, то
14 ф 14. Вычисляем 143 = 14 ©гг 9 = 7, но 14 ©i7 7 = 13, т.е.
143^i4-i. Далее,
147 = 143 ©и 144 = 7 ©17 13 = 6,
14 ©17 6 = 16 = -1.
Мы видим, ч*о и 147 ф 14. Следовательно, остается вычи-
вычислить 14 = 1415. Однако в этом случае вычисления можно
сократить, заметив, что 14 ©17 147 = 14 ©17 6 = —1. Из послед-
последнего равенства, согласно следствию 2.1, получим
1 = 14017 (-6) = 14017 11,
откуда 14 = 11.
Отметим, что 1416 = 1, т.е. порядок циклической подгруп-
подгруппы, порожденной элементом 14, совпадает с порядком всей
группы ZJ7, и, следовательно, эта группа является циклической,
порожденной элементом 14 (хотя и не только им).
2.8. Гомоморфизмы групп
и нормальные делители
Пусть заданы группы Q\ = (Gi, •, 1) и <?2 = (Сг, •, 1). Ото-
Отображение /: G\ -> G2 называют гомоморфизмом группы Q\ в
группу </2 (гомоморфизмом групп), если для любых #, у € G\
выполняется равенство f(x • у) = f(x) • /(у), т.е. образ произве-
произведения любых двух элементов группы G\ при отображении f
равен произведению их образов в группе G2-
158 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Бели отображение / сюръективно (биективно), то его на-
называют эпиморфизмом (изоморфизмом) групп. В этом
случае говорят также об эпиморфизме (изоморфизме) группы
Q\ на группу (?2-
Замечание 2.5. Мы обозначили операции групп Q\ и С/2
одинаково, как это обычно и делается для однотипных алгебр,
хотя, конечно, это разные операции разных групп.
Пример 2.21. Пусть Q\ = (Z, +, 0) — аддитивная группа
целых чисел, а ?/2 = Z? — аддитивная группа вычетов по
модулю к.
Зададим отображение / так: для всякого целого т образ
f(m) равен остатку от деления т на А;. Можно проверить,
что для любых целых тип имеет место равенство f(m + n) =
= /(wi) ©fc /(n), т.е. для целых чисел остаток от деления суммы
на к равен сумме по модулю к остатков от деления на к каждого
слагаемого.
Следовательно, данное отображение есть гомоморфизм груп-
группы Q\ в группу С/2- Далее, поскольку любое целое число от 0 до
к — 1 есть остаток от деления на к какого-то числа, то отобра-
отображение / является и эпиморфизмом группы Q\ на группу С/2.
Теорема 2.14. Пусть Q\, G2 — произвольные группы. Бели
/: Q\ -> G2 — гомоморфизм, то:
1) образом единицы (нейтрального элемента) группы Q\ при
отображении / является единица группы С/2, т.е. /A) = 1;
2) для всякого элемента х группы Q\ образом элемента
ж является элемент [/(я?)], обратный элементу f(x), т.е.
/(Х-1) = [/(*)]-!.
¦4 Согласно определению гомоморфизма, для произвольного
xeGi имеем /(х) • /A) = /(х • 1). Далее, /(х • 1) = /(х), т.е.
/(*) • /A) = Дх). Следовательно, /A) = (/(х)) • /(х) = 1, т.е.
Докажем второе утверждение теоремы. Используя опре-
определение гомоморфизма и уже доказанное первое утверждение
2.8, Гомоморфизмы групп 159
теоремы, получаем
т.е. /(аг1) = [/(х)]. >
Множество f{Gi) — образ носителя группы G\ при го-
гомоморфизме / — замкнуто относительно умножения группы
<?2- Действительно, если д2, д2 € /((/1), то существуют такие
01,01' € Gu чт<> f(9i) = 92 и f(gif) = g2'. Тогда
W = /Ы/Ы = /(W) € №).
Из теоремы 2.14 следует, что f(G\) содержит единицу этой
группы и вместе с каждым элементом обратный к нему эле-
элемент. Это значит, что можно определить подгруппу группы <?2>
носителем которой будет множество f(Gi). Эту группу назы-
называют гомоморфным образом группы Gi при гомоморфизме /.
Группу /С называют просто гомоморфным образом груп-
группы G, если существует гомоморфизм группы G на группу
/С. Так, группа Ъ*к при любом А; > 1 является гомоморфным
образом аддитивной группы целых чисел (см. пример 2.21).
Обратимся к следующему примеру.
Пример 2.22. Рассмотрим мультипликативную группу
(С\ {0}, •, 1) комплексных чисел с обычной операцией умноже-
умножения комплексных чисел. Легко понять, что эта группа не что
иное, как мультипликативная группа поля комплексных чисел.
Рассмотрим также группу М2 невырожденных квадратных
матриц второго порядка с операцией умножения матриц (см.
пример 2.9.е).
Определим отображение / множества С комплексных чисел
в множество квадратных матриц второго порядка, положив для
произвольного ненулевого комплексного числа а + Ьг, что
На + Ы)
\-Ь а)
160
2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Покажем, что / — гомоморфизм групп. С одной стороны,
ас — bd ad + bc\
ad — be ас — bd) '
(
С другой стороны,
(
ас — bd ad + bc\
—ad — be ас — bd)
Следовательно,
Таким образом, отображение / — гомоморфизм групп, а
гомоморфный образ мультипликативной группы комплексных
чисел при / — это подгруппа /С группы матриц Л<2> состоящая
из матриц вида I , 1. Здесь мы учли, что любая матри-
ца вида I , 1 является образом некоторого комплексного
числа (а именно а + Ы) при отображении /. Группа /С — соб-
собственная подгруппа группы М.2- #
Сформулируем без доказательства одно важное свойство
гомоморфизмов групп.
Теорема 2.15. Если / — гомоморфизм группы Q в группу
/С, a g — гомоморфизм группы /С в группу ?, то композиция
отображений fog есть гомоморфизм группы Q в группу С. #
Рассмотрим некоторые свойства изоморфизмов групп.
Теорема 2.16. Если /: Q\ -> Q2 — изоморфизм группы Q\
на группу (?2> то отображение Z, обратное к отображению /,
есть изоморфизм группы G2 на группу Q\.
2.8. Гомоморфизмы групп 161
4 Пусть х и у — произвольные элементы группы (?2, пусть
также х = f(u), а у = /(v), где и и v — элементы группы Q\.
Тогда
Г\ху) = rl(fHf(v)) = rl(f(uv)) = uv = Г1(*)Г1(У),
т.е. отображение /~* — гомоморфизм второй группы в первую.
Но так как отображение, обратное к биекции, есть биекция, то
/~х — изоморфизм группы Qi на группу Q\. >
Группы Q и 1С называют изоморфными, если существует
изоморфизм одной из них на другую. При этом используют
обозначение Q = /С.
Изоморфные группы с точки зрения их алгебраических
свойств совершенно одинаковы, хотя их элементы могут иметь
различную природу. Вернемся в этой связи к примеру 2.22.
Легко убедиться в том, что определенное там отображение
/ множества комплексных чисел на множество квадратных
матриц специального вида является биекцией. Следователь-
Следовательно, мультипликативная группа комплексных чисел и группа
матриц указанного вида с операцией умножения матриц изо-
изоморфны, хотя элементы этих групп на первый взгляд не имеют
между собой ничего общего.
Определение 2.8. Ядром гомоморфизма f группы Q
в группу К называют прообраз Кег/ единицы группы Q при
гомоморфизме /: Кег/ = /"хA) С G.
Пример 2.23. Ядром гомоморфизма, рассмотренного в
примере 2.21, служит множество всех целых чисел, делящихся
на к.
Теорема 2.17. Ядро Кег/ гомоморфизма /: Q -> /С есть
подгруппа группы Q.
< Нужно убедиться в том, что множество Кег/ замкнуто
относительно умножения группы Q, содержит единицу этой
группы и вместе с каждым элементом содержит обратный к
нему элемент.
162 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Если a, be Ker/, т.е. /(a) = f(b) = 1, то f(ab) = f(a)f(b) =
= 1 и аб Е Кег/. Ясно, что 1 € Ker/, так как /A) = 1 (см.
теорему 2.14). Если а € Кег/, то /(а") = [/(а)]" = I = 1,
т.е. и о" Е Кег/. >
Ядро гомоморфизма, приведенного в примере 2.21, пред-
представляет собой подгруппу аддитивной группы целых чисел,
состоящую из всех чисел, кратных к.
Подгруппа Н группы Q называется нормальной подгруп-
подгруппой {нормальным делителем) группы {/, если аН = На для
любого aeG.
В коммутативной группе, как было отмечено выше, аН =
= На. Следовательно, в этом случае любая подгруппа является
нормальным делителем.
Пусть И — (Я, •, 1) — подгруппа группы Q = (G, •, 1). Для
фиксированных элементов a, b Е G через аНЪ обозначим мно-
множество всех произведений вида ahb, где h G Н. В силу ассоци-
ассоциативности групповой операции это обозначение корректно.
Теорема 2.18. Подгруппа И — (Я, -, 1) является нормаль-
нормальным делителем группы Q = (G, •, 1) тогда и только тогда, когда
аНа~1 С Н для любого а Е G.
< Если Н — нормальный делитель, то для любого а Е G аН =
= На, т.е. для любого h? H найдется такое h\ € Я, что аЛ =
= h\a. Пусть элемент х Е аНа~1, т.е. ж = aha~l для некоторого
he Н. Так как a/i = /ца, то х = /iiaa" = Лх Е Я и поэтому
аЯа С Я.
Обратно, если аНа~1 С Я, то любой элемент х = aha"'1,
где he Н, принадлежит и множеству Я, т.е. aha = /ц для
некоторого h\ E Я. Отсюда, умножая последнее равенство на a
справа, получим ah = /iia, т.е. элемент ah из левого смежного
класса аН принадлежит и правому смежному классу На. Итак,
аН С На.
Теперь возьмем для произвольного aeG обратный к а эле-
элемент а" и для него запишем включение а На С Я (напомним,
2.8. Гомоморфизмы групп 163
что (а") = а). Рассуждая как и выше, получим, что для не-
некоторых Л, h\ Е Я имеет место равенство a~lh = /iio, т.е.
ha = ah\ и На С аЯ. Итак, аН = #а иИ — нормальный дели-
делитель. >
Оказывается, существует связь между понятием нормально-
нормального делителя и понятием гомоморфизма, которая продолжает и
углубляет на новом уровне уже известную нам из главы 1 связь
между понятиями отображения и класса эквивалентности.
Теорема 2.19. Ядро гомоморфизма / группы Q в группу
/С является нормальным делителем группы Q.
Л Для любого у ЕКег/ и любого aEG имеем
1) = f(a)f(y)f(a-1) = /(a) • 0. /(а) - /(^/(а) = 1.
Это значит, что для любого а Е G выполняется соотношение
а(Кег/)а~1 С Кег/, а, согласно теореме 2.18, Кег/ — нормаль-
нормальный делитель. >
Пусть К = (Я, •, 1) — нормальный делитель группы Q =
= (G, •, 1). Рассмотрим множество всех левых смежных клас-
классов {аН: a€G}. Это будет не что иное, как фактор-множе-
фактор-множество множества G по определенному выше (см. теорему 2.11)
отношению эквивалентности ~#.
Введем операцию умножения на множестве всех левых смеж-
смежных классов следующим образом: произведением аН • ЬН клас-
классов аН и ЬН назовем класс аЬН.
Это определение корректно, так как множество аН • ЬН,
т.е. множество всех произведений вида ahbh\ для различных /г,
h\ Е Я, в силу того что ЯЪ = ЬЯ для всякого Ь Е G, совпадает с
левым смежным классом аЬЯ. Действительно, поскольку hb =
= Wi' для некоторого h1 G Я, то ahbh\ = abh'hi € аЬЯ.
Теперь рассмотрим некоторый х G а&#, т.е. я = abh для
некоторого Л € Н\. Поскольку bh = Л'Ь для некоторого h1 E Я,
то х = аЛ'6 = a/i;61 E аЯЬЯ. Следовательно, аЯ • ЬН = оЬЯ.
164 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Можно далее легко показать, что для каждого a ? G имеют
местоаНН = НаН = аНиаНа-1Н = а-1НаН = Н. Тем
самым определена группа, носителем которой является фактор-
фактормножество G/~h множества G по отношению эквивалентности
~я с операцией умножения левых смежных классов, причем
нейтральным элементом относительно этой операции служит
носитель подгруппы W, а обратным к левому смежному классу
аН будет левый смежный класс аГ1Н. Эту группу называют
фактор-группой группы Q по нормальному делителю %
и обозначают Q/H. Можно указать естественный гомомор-
гомоморфизм / группы G в фактор-группу Qjit, который вводится
согласно правилу: (\/х Е G)(f(x) = хН). Так как хН • уН = хуН,
то для любых x,yeG f(xy) = xyH = хН• уН = f(x)f(y) и / —
действительно гомоморфизм. Его называют каноническим
гомоморфизмом группы Q в фактор-группу Я/Н.
Пример 2.24. а. Рассмотрим аддитивную группу R =
= (R, +, 0) действительных чисел. Эта группа коммута-
коммутативна. Напомним, что в коммутативной группе любая подгруп-
подгруппа будет нормальным делителем. Поэтому для нее нормальным
делителем является подгруппа целых чисел Z = (Z, +, 0) {ад-
{аддитивная группа целых чисел). (Для этих групп мы приняли
такие же обозначения, как и для их носителей: Е и Z соответ-
соответственно.)
Выясним смысл отношения экивалентности ~z> определяе-
определяемого через равенство левых смежных классов*, по подгруппе Z
в этом случае.
Равенство левых смежных классов а + Z = Ь + Z означает,
что для любого целого т найдется такое целое п, что а + т =
¦=¦ Ь + п, т.е. a-i = n-mEZ. Обратно, если разность а — Ь
есть целое число, т.е. a —6 = nGZ, то a + Z = F + n) + Z = 6 + Z.
Итак, a ~z b тогда и только тогда, когда а — Ь € Z, или, иначе
*Мы можем говорить в данном случае просто о смежных классах, не
различая левых и правых, так как для нормального делителя эти классы
равны, тем более что мы „работаем" сейчас в коммутативной группе.
2.8. Гомоморфизмы групп 165
говоря, действительные числа а и 6 ^-эквивалентны тогда и
только тогда, когда их дробные части равны.
Аддитивная группа смежных классов, т.е. фактор-группа
R/Z группы R по нормальному делителю Z строится так: сумма
классов а + Z и Ь + Z равна классу (а + Ь) + Z. Вводя обозначе-
обозначение а + Z = [а], получаем [а] + [Ь] = [а + 6]. При этом [0] = Z
(т.е. единица фактор-группы — это смежный класс нуля —
множество всех целых чисел), причем —[а] = [—а] = (—а) +Z.
Обратим внимание на то, что смежный класс числа х однознач-
однозначно определяется его дробной частью <х> (см. пример 1.14.6),
т.е. [х] = [<#>]. Канонический гомоморфизм в данном случае
задается так: х »-> [х].
б. Рассмотрим теперь аддитивную группу действи-
действительных чисел по модулю 1, т.е. группу S1 = ([0,1), ©i, 0),
заданную на полуинтервале [0,1), сложение в которой опре-
определяется так: х ©1 у = <х + у> (дробная часть суммы х + у).
Другими словами,
[х + у-1,
Докажем, что группа S1 изоморфна фактор-группе R/Z,
т.е.
Зададим отображение (р множества {[о]: а 6 R} смежных
классов в полуинтервал [0,1) тале, что <р([х]) = <х>. Поскольку
[х] = [<ж>], то <р — биекция и, кроме того,
?>(И + Ы) = <р([х + У]) = <х + у> = «д:> + <у» =
= <х> ©1 <у> = <р([х]) ©1 <р(\у]).
Это значит, что ц> — изоморфизм R/Z на S1.
Группу S1 можно воспринимать как „наглядный образ" фак-
фактор-группы R/Z. Довольно абстрактная идея фактор-группы
кристаллизуется в виде группы с носителем [0,1) и операци-
операцией сложения неотрицательных действительных чисел, строго
166 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
меньших единицы, с отбрасыванием в результате целой части.
Здесь хорошо видна „польза" понятия изоморфизма. То, что
само по себе не очень наглядно, становится наглядным через
свой изоморфный образ.
2.9. Гомоморфизмы колец
Рассмотрим очень коротко вопрос о гомоморфизмах колец
и полей.
Пусть П\ = (Дх, +, •, 0, 1) и К2 = (Дг, +, -, 0, 1) — кольца.
Определение 2.9. Отображение /: Ri -> R2 называют
гомоморфизмом колец (кольца И\ в кольцо Т^), если
f(x + y) = /(я) + /(у), f{x-y) = f{x) • f(y) для любых ж, у в Ru
т.е. образ суммы и произведения любых двух элементов кольца
%\ при отображении / равен соответственно сумме и произве-
произведению их образов в кольце 7^2-
Бели отображение / сюръективно (соответственно биек-
биективно), то его называют эпиморфизмом (соответственно
изоморфизмом) колец (кольца К\ на кольцо
Пример 2.25. Рассмотрим TZ\ = (Z, +, •, 0, 1) — кольцо
целых чисел — и Z* = (Z*, ©*, ©*, 0, 1) — кольцо вычетов по
модулю к. Зададим отображение /: Z -> Z* так: для всякого
целого т образ f(m) равен остатку от деления т на fc. Ранее
мы уже доказали (см. пример 2.21), что для любых целых т и
п имеет место равенство f(m + n) = f(m) ф* f(n). Рассуждая
аналогично, можно показать, что для любых целых тип
также верно равенство /(га • п) = /(га) 0* /(п). С учетом того
что отображение / сюръективно, приходим к выводу, что оно
является гомоморфизмом кольца целых чисел на кольцо Z&
вычетов по модулю А:. #
Без доказательства сформулируем некоторые теоремы о го-
гомоморфизмах и изоморфизмах колец (и полей). Все эти утвер-
утверждения могут быть доказаны по аналогии с соответствующими
теоремами о гомоморфизмах и изоморфизмах групп.
2.9. Гомоморфизмы колец 167
Теорема 2.20. Пусть TZ\ и 7^2 — произвольные кольца.
Бели /: И\ -> 7^2 — гомоморфизм, то
1) образ нуля кольца И\ при отображении / есть нуль
кольца 7^2, т.е. /@) = 0;
2) образ единицы кольца И\ при отображении / есть едини-
единица кольца 7^2, т.е. /A) = 1;
3) для всякого элемента х кольца И\ образ элемента, проти-
противоположного элементу ж, равен элементу, противоположному
образу элемента ж, т.е. /(—ж) = — /(#);
4) если кольца 7Z\ и 7^2 являются полями, то для всякого
элемента х кольца И\ образ элемента, обратного к элементу х
по умножению, равен элементу, обратному к образу элемента
Теорема 2.21. Бели / — гомоморфизм кольца 11 в кольцо
/С, a g — гомоморфизм кольца /С в кольцо ?, то композиция
отображений fog есть гомоморфизм кольца V, в кольцо С.
Теорема 2.22. Бели /: 7?i —> К2 — изоморфизм кольца TZ\
на кольцо 7^2? то отображение f~l есть изоморфизм кольца 7^2
на кольцо К\. #
Как и в случае групп, определяются понятия гомоморфно-
гомоморфного образа кольца и изоморфных колец. А именно кольцо К
называют гомоморфным образом кольца К, если существу-
существует гомоморфизм кольца % на кольцо /С. Два кольца И и /С
называют изоморфными и пишут TZ = /С, если существует изо-
изоморфизм одного из них на другой.
Так, например, кольцо вычетов по модулю к есть гомоморф-
гомоморфный образ кольца целых чисел при гомоморфизме, задаваемом
отображением, которое каждому целому т сопоставляет оста-
остаток от деления т на к.
Рассмотрим один интересный пример изоморфизма полей.
Пример 2.26. Так же как и в примере 2.22, поставим в
соответствие комплексному числу а + Ы матрицу f(a + Ы) =
. 1. Получим отображение /, которое, как уже было
WU1,
¦(-
168 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
доказано, является инъекцией, причем /@) = /@ + 0 • г) = 0, где
О — нулевая матрица. Заметим, что, поскольку определитель
матрицы указанного вида равен а2 + б2, среди всех таких
матриц только нулевая будет иметь нулевой определитель.
Далее, легко проверить, что множество таких матриц за-
замкнуто относительно операций сложения и умножения ма-
матриц, содержит (как уже было отмечено) нулевую и единичную
матрицы, а также вместе с каждой матрицей А матрицу —А и
вместе с каждой ненулевой матрицей обратную к ней матрицу.
Это значит, что множество матриц вида ( , ], а, 6 € R, с
операциями сложения и умножения матриц образует поле. Обо-
Обозначим его М2-
Из примера 2.22 следует, что мультипликативная группа
поля комплексных чисел изоморфна мультипликативной группе
поляЛ4в'Ь). Так как
Ь\ ( с d\_
-d c
f[(a + Ы) + (с + di)] = /[(
а + с b + d_(
-b~d а + с) \-Ь
то и аддитивная группа поля комплексных чисел изоморфна
аддитивной группе поля М2 • Итак, мы получаем, что
поле комплексных чисел изоморфно полю матриц Л<2 • Этот
изоморфизм лежит в основе матричного представления алгебры
комплексных чисел, что имеет значение для компьютерных
реализаций этой алгебры.
Дополнение 2.1. Кватернионы
Примером тела, не являющегося полем, может служить
алгебра кватернионов (пчетырехмерных чисел").
Сначала напомним, как строится алгебра комплексных чи-
чисел. Комплексное число определяется как упорядоченная пара
Д.2.1. Кватернионы
169
действительных чисел, причем сложение пар вводится поком-
покомпонентно:
(а, Ь) + (с, d) = (a + cy b + d),
B.3)
а умножение — согласно формуле
(а, 6) • (с, d) = {ac-bd, ad + bc).
Заметим, что покомпонентное определение умножения не
дало бы требуемых свойств этой операции (таких же, как у
умножения действительных чисел), поскольку при покомпо-
покомпонентном умножении имеются делители нуля:
(а,
= (а-О,О-Ь) =
При стандартном определении умножения согласно B.3)
можно доказать, что алгебра комплексных чисел является по-
полем.
Кватернионы определяются как упорядоченные пары ком-
комплексных чисел. Сложение кватернионов вводится снова как
покомпонентное, а умножение — следующим образом:
(а, Ь) • (с, d) = (ас-ЬЗ, ad + bc),
где х — число, комплексно сопряженное с х.
Таблица 2.3
•
1
i
3
к
1
1
i
3
к
i
г
-1
-к
3
3
3
к
-1
—i
к
к
-з
i
-1
Можно показать, что каждый
кватернион однозначно представля-
представляется в виде
где х, у, г, h — действительные
числа, а г, j и А: — кватернионы,
называемые мнимыми единицами. Правила умножения мни-
мнимых единиц вместе с обычной единицей задаются табл. 2.3.
Можно заметить, что умножение попарно различных мни-
мнимых единиц совершается по тем же правилам, что и векторное
умножение ортов г, j, к в векторной алгебре [III].
170 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Сопряженный с a = x + iy + jz + kh кватернион, по
определению, равен а = х — гу — jz — kh. Имеют место следу-
следующие тождества:
Действительное число аа, обозначаемое п(а), называется
нормой кватерниона а.
Построенная таким образом алгебра кватернионов облада-
обладает следующими свойствами:
1. Умножение кватернионов ассоциативно, но не коммута-
коммутативно.
Это свойство непосредственно выводится из табл. 2.3. На-
Например, пусть а = 0 + f I + jO + fcO, а 0 = 0 + гО + jl + kO. Тогда
2. В алгебре кватернионов нет делителей нуля.
Действительно, п(а) = 0 тогда и только тогда, когда a = 0,
т.е. нулевому кватерниону 0 + гО + jO + fcO, и можно показать,
что n(ctf3) = п(а)п(/3).
Тогда, если а ф 0, то
Таким образом, по умножению все ненулевые кватернионы
образуют группу и алгебра кватернионов оказывается телом,
не будучи полем.
Из кватернионов можно также строить упорядоченные па-
пары, вводя операции сложения и умножения как описано выше,
а операцию сопряжения согласно формуле (а,6) = (а,— 6) (а
и Ъ — кватернионы). Полученная таким образом алгебра
называется алгеброй Кэли, а ее элементы — числами Кэли
или октавами. Умножение в алгебре Кэли уже не будет даже
Вопросы и задачи 171
ассоциативным, однако ассоциативный закон имеет место в
частном случае — для любых двух чисел Кэли а и /3:
aifia) = (aP)a.
Кроме того, каждое ненулевое число Кэли имеет обратное.
Другими словами, в алгебре Кэли любое уравнение ах — C (или
ха = /3) имеет единственное решение. Таким образом, алгебра
Кэли также является алгеброй без делителей нуля. Можно
доказать, что, кроме алгебры комплексных чисел, алгебры
кватернионов и алгебры Кэли, не существует „многомерных"
числовых алгебр без делителей нуля.
Вопросы и задачи
2.1. Ассоциативна ли операция © на множестве М, если:
а) Af = N,
б) M = Z,
в) М = R, х © у = sinxsiny;
г)М = Е\{0}, '
д) M = R,
(X Т1\
2.2. Пусть 5 — полугруппа матриц вида I п * 1, где ж, у G
ЕЕ, с операцией умножения. Существуют ли в ней левые или
правые нейтральные элементы?
2.3. На множестве М определена бинарная операция о по
правилу х о у = х. Доказать, что (М, о) — полугруппа. Что
можно сказать о нейтральных элементах этой полугруппы? В
каких случаях она является группой?
2.4. Пусть М — произвольное множество. На множестве
определена операция © по правилу (ж, у) о (г, t) = (ж, t).
172 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
Является ли алгебра (М2, о) полугруппой? Существует ли в
ней нейтральный элемент?
2.5. Привести пример полугруппы с левой единицей (ней-
(нейтральным элементом), не являющейся моноидом.
2.6. Какие из указанных множеств квадратных действи-
действительных матриц одного порядка образуют группу:
а) множество невырожденных матриц относительно умно-
умножения;
б) множество невырожденных матриц относительно сложе-
сложения;
в) множество диагональных матриц относительно сложе-
сложения;
г) множество диагональных матриц относительно умноже-
умножения?
2.7. Доказать, что если в группе Q для любого х Е G
выполняется тождество х2 = 1, то группа Q коммутативна.
2.8. В группе S4 решить уравнения:
2 3 4\ /1 2 3
,4 2 1 ЗУ V3 2 1 4,
2 1
2.9. Является ли полем множество чисел вида х + у/2у, где
xi У 6 Q? с обычными операциями сложения и умножения?
2.10. Доказать, что множество всех верхних треугольных
матриц фиксированного порядка п является подкольцом кольца
всех квадратных матриц порядка п. Верно ли это утверждение
для диагональных и нижних треугольных матриц?
2.11. Построить пример кольца с одним элементом, т.е.
такого, в котором 0 = 1.
Вопросы и задачи 173
2.12. Кольцо К= (Д, +, •, О, 1) называется булевым, если
его умножение идемпотентно, т.е. х • х = х для любых х Е R.
Доказать, что:
а) для любого элемента х булева кольца имеет место равен-
равенство х + х = 0, т.е. —х = ж;
б) любое булево кольцо коммутативно;
в) в любом булевом кольце, имеющем более двух элементов
(\R\ > 2), существуют делители нуля.
2.13. Доказать, что Bм, Д, П, 0, М) — булево кольцо
(см. задачу 2.12). Доказать, что оно изоморфно Z2 при \М\ = 1.
2.14. Показать, что множество остатков от деления много-
многочленов от переменной х на х2 + х + 1 с операциями сложения
и умножения многочленов является кольцом. Является ли это
кольцо полем?
2.15. Элемент х кольца называют обратимым, если су-
существует элемент х\ такой, что х • х' = х' • х = 1. Элемент х
кольца называют обратимым слева (справа), если существует
#', такой, что х' • х = 1 (х • х1 = 1). Элемент кольца называется
односторонне обратимым, если он обратим слева или справа.
Элемент х^О кольца называется левым (правым) делителем
нуля, если существует ненулевой элемент кольца у, такой, что
х • у = 0 (у • х = 0); элемент, являющийся левым и правым
делителем нуля одновременно, называется делителем нуля.
Доказать, что:
а) элемент конечного кольца обратим (слева, справа) тогда
и только тогда, когда он не является делителем нуля (правым,
левым);
б) в конечном кольце и в кольце без делителей нуля любой
односторонне обратимый элемент обратим;
в) элемент кольца вычетов по модулю к обратим тогда и
только тогда, когда он взаимно прост с к.
2.16. Пусть R — кольцо. Доказать, что:
а) если произведения ху и ух обратимы, то элементы х ту
тоже обратимы;
174 2. АЛГЕБРЫ: ГРУППЫ И КОЛЬЦА
б) если в R нет делителей нуля и произведение ху обратимо,
тожиу обратимы;
в) если R конечно и произведение ху обратимо, то х и у
обратимы.
Указание: использовать результаты задачи 2.15.
2.17. Доказать, что множество всех обратимых элементов
кольца (см. задачу 2.15) образуют группу по умножению.
2.18. Решить систему уравнений
а) в поле Z3; б) в поле Z5.
2.19. Выяснить, разрешима ли в кольце Z21 система урав-
уравнений
Г5х + 2у = 1,
\ у-lls = 13.
2.20. Введем группу S „движений" (поворотов) окружности
как группу, элементами которой являются всевозможные пово-
повороты, измеряемые в радианах, причем поворот на любой угол,
кратный 2тг, отождествляется с нулевым поворотом (тожде-
(тождественным отображением множества точек окружности в себя).
Доказать, что группа S изоморфна фактор-группе IR/Z, ко-
которая, в свою очередь, изоморфна аддитивной группе S1 дей-
действительных чисел по модулю 1.
2.21. Пусть М = (G, +, 0, {иа- а € R}) —левый модуль над
кольцом 7?= (jR, +, •, 0, 1). Является ли соответствие между
элементами а кольца И и отображениями ша взаимно однознач-
однозначным? В частности, всегда ли нулевое отображение определяет-
определяется только нулем кольца 7??
Указание: рассмотреть левый модуль матриц-столбцов
вида (х 0) , х € Я, над кольцом верхнетреугольных матриц вто-
второго порядка и показать, что ответы на поставленные вопросы
отрицательны.
3. ПОЛУКОЛЬЦА
И БУЛЕВЫ АЛГЕБРЫ
Полукольцо является одной из важнейших алгебр в совре-
современной дискретной математике. Эта глава посвящена рассмо-
рассмотрению полуколец и булевых алгебр. Изучаемые здесь методы,
прежде всего метод решения систем линейных уравнений в по-
полукольцах, имеют первостепенное значение для теории графов,
булевых функций и теории формальных языков.
3.1. Полукольца. Основные примеры
Определение 3.1. Полукольцо — это алгебра с двумя
бинарными и двумя нульарными операциями
5 = E,+,-,0, 1),
такая, что для произвольных элементов а, 6, с множества S
выполняются следующие равенства, называемые аксиомами
полукольца:
2)
3) а + 0 = а;
4) а • F • с) = (а • Ь) • с;
5) а • 1 = 1 • а = а;
6) а-
7)
8) а • 0 = 0 • а = 0.
Первую операцию + называют сложением полукольца, а
вторую операцию — умножением полукольца «S; элементы
0 и 1 называют соответственно нулем и единицей полуколь-
полукольца S.
176 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Аксиомы полукольца называют также основными то-
ждествами полукольца.
Таким образом, из определения следует, что операция сло-
сложения полукольца ассоциативна и коммутативна, а нуль полу-
полукольца является нейтральным элементом относительно опера-
операции сложения; операция умножения полукольца ассоциативна
и единица полукольца является нейтральным элементом от-
относительно операции умножения. Кроме этого имеет место
свойство дистрибутивности (двусторонней) операции умноже-
умножения относительно сложения полукольца. Аксиому 8 полукольца
называют аннулирующим свойством нуля в полукольце.
Используя понятие моноида, определение 3.1 можно пере-
переформулировать так. Полукольцо S = E, +, •, 0, 1) — это ал-
алгебра с двумя бинарными и двумя нульарными операциями,
такая, что:
1) алгебра (?, +, 0) является коммутативным моноидом
(его называют аддитивным моноидом полукольца);
2) алгебра E, •, 1) является моноидом (его называют муль-
мультипликативным моноидом полукольца);
3) имеют место свойства (двусторонней) дистрибутивности
операции сложения относительно операции умножения;
4) выполняется аннулирующее свойство нуля.
Сравнивая определение полукольца с определением 2.5 коль-
кольца, мы видим, что кольцо есть частный случай полукольца:
если кольцо по сложению является абелевой группой, то полу-
полукольцо — лишь коммутативный моноид.
Выделим два вида полуколец: коммутативное полу-
полукольцо с коммутативной операцией умножения и идемпотен-
тное полукольцо с идемпотентной операцией сложения.
Пример 3.1. Рассмотрим алгебру
П+ = (R+ U{+oo}, min, +, +оо, 0),
где R+ — множество неотрицательных действительных чисел,
min — операция взятия наименьшего из двух данных чисел,
3.1. Полукольца. Основные примеры 177
+ — операция сложения действительных чисел, +оо — „плюс
бесконечность" (в том же смысле, что и в математическом
анализе), 0 — число „нуль".
Эта алгебра — полукольцо, носителем которого является
полуось R+ = {х: х ^ 0}, пополненная элементом +оо (множе-
(множество всех неотрицательных действительных чисел вместе с
плюс бесконечностью44).
Необычность полукольца 7?+ состоит в том, что в качестве
его умножения взято сложение действительных чисел, тогда
как в качестве сложения выбрана операция взятия наименьшего
из двух чисел. Согласно сигнатуре, элемент +оо рассматри-
рассматривается как нуль полукольца. Действительно, min(x, +оо) = х
для любого xGR+U {+oo}, т.е. элемент +оо есть нейтраль-
нейтральный элемент относительно операции min (операции сложения
в полукольце). Элемент +оо также обладает аннулирующим
свойством относительно операции сложения чисел (операции
умножения в полукольце): х + (+оо) = +оо. Следовательно, вы-
выполняются аксиомы 3 и 8 полукольца.
Остальные аксиомы полукольца также выполнены.
Легко убедиться, что алгебра (R+U{+oo}, min, +oo) —
коммутативный моноид и алгебра (R+ U {+оо}, +, 0) — также
коммутативный моноид. Проверим свойства дистрибутивно-
дистрибутивности, которые в данном случае запишутся так:
Имеем
В то з
a + minF,
a + min F
ке время
min(a + b, <
Таким образом,
a + minF,
с)
= min (a + Ь,
, C) = J°'
J-f
с)
- с) = <
\а + с,
= min(a + b,
a + c).
b>c.
6<c;
b>c.
a + c).
178
3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Заметим, что в рассматриваемом полукольце умножение +
коммутативно, а сложение min идемпотентно. Следовательно,
7?+ — идемпотентное коммутативное полукольцо.
Пример 3.2. Рассмотрим алгебру #= ({0,1}, +, •, 0, 1),
в которой операции + и ¦ заданы таблицами Кэли (табл. 3.1
и 3.2).
Таблица 3.1
Таблица 3.2
+
0
1
0
0
1
1
1
1
•
0
1
0
0
0
1
0
1
Проверка аксиом полукольца основана на этих таблицах и
легко выполняется. Обратим внимание, что два элемента О
и 1, из которых в данном случае состоит носитель полуколь-
полукольца, одновременно являются соответственно нулем и единицей
данного полукольца. Легко видеть, что рассматриваемое полу-
полукольцо коммутативное и идемпотентное.
Интересно то, что операции полукольца В можно тракто-
трактовать как логические связки „или" и „и", а элементы 0 и 1 —
как „ложь" и „истина" соответственно.
Пример 3.3. Рассмотрим еще несколько различных алгебр,
являющихся полукольцами. Выполнение аксиом полукольца для
всех приведенных алгебр легко проверяется.
а. Алгебра N = (No, +, •, 0, 1) с носителем — множеством
неотрицательных целых чисел и операциями сложения и умно-
умножения чисел есть коммутативное полукольцо. Оно не является
идемпотентным.
б. Алгебра Sa = BA, U, П, 0, А) с носителем — множест-
множеством всех подмножеств некоторого множества А и операция-
операциями объединения и пересечения есть полукольцо. Оно является
идемпотентным и коммутативным.
3.1. Полукольца. Основные примеры 179
в. Алгебра На = BАхА, U, о, 0, %d^) с носителем — мно-
множеством всех бинарных отношений на множестве А — и опе-
операциями объединения и композиции отношений является полу-
полукольцом. Оно идемпотентное, но не коммутативное.
г. Алгебра <5[в,ь] = ([а> Ч> naax, min, а, Ь), носителем кото-
которой служит отрезок числовой прямой, с операциями взятия
максимума и минимума из двух чисел есть идемпотентное и
коммутативное полукольцо. #
В дальнейшем нас будут интересовать только идемпотент-
ные полукольца, поскольку именно на их основе разрабатыва-
разрабатываются алгебраические методы анализа ориентированных графов
и конечных автоматов.
На носителе идемпотентного полукольца S = E, +, •, 0, 1)
может быть введено отношение порядка, которое, естественно,
согласуется со свойствами операций полукольца: для произ-
произвольных ж, у Е S положим х < у тогда и только тогда, когда
я + У = У, т.е.
х^у&х + у = у. C.1)
Проверим, что таким образом действительно определено от-
отношение порядка. Для этого нужно показать, что введенное
бинарное отношение рефлексивно, антисимметрично и тран-
зитивно.
Поскольку для любого х в силу идемпотентности сложения
имеет место равенство х + х = ж, то, согласно C.1), имеем х < ж,
т.е. введенное отношение рефлексивно.
Соотношения х^у иу^х означают, что х + у = у иу + х =
= х. Поскольку сложение коммутативно, то из этих равенств
следует, что ж = у. Значит, рассматриваемое отношение анти-
антисимметрично.
Соотношения х < у и у < z означают, что х + у = у и у + z = z.
Тогда
откуда следует, что х ^ z. Таким образом, введенное отношение
транзитивно.
180 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Итак, отношение ^ на носителе произвольного идемпотент-
идемпотентного полукольца есть отношение порядка. Будем называть его
естественным порядком идемпотентного полукольца
и говорить, что он задан в этом полукольце.
Мы установили очень важный факт: всякое идемпотентное
полукольцо можно рассматривать как упорядоченное множе-
множество, причем отношение порядка определяется через сложение
этого полукольца согласно C.1). Введенное отношение порядка
можно интерпретировать так: „большее при сложении погло-
поглощает меньшее" (как, скажем, при объединении множества и
некоторого его подмножества).
Поскольку для любого элемента х произвольного идемпо-
идемпотентного полукольца S = E, +, •, 0, 1) имеет место 0 + х = я,
то для любого х Е S выполняется неравенство 0 ^ #, т.е. нуль
идемпотентного полукольца есть наименьший элемент относи-
относительно естественного порядка идемпотентного полукольца.
Объясним, как интерпретируется естественный порядок
идемпотентных полуколец, рассмотренных в приведенных вы-
выше примерах.
Пример 3.4. В полукольце В (см. пример 3.2) выполняется
равенство 0 +1 = 1 и, следовательно, 0^1.
В полукольце И+ (см. пример 3.1) х < у, если и только если
Обозначим через ^к естественный числовой порядок на
множестве действительных чисел. Тогда для произвольных эле-
элементов ж, у полукольца И+ соотношение х < у означает, что
х ^r у, т.е. число х не меньше числа у относительно естествен-
естественного числового порядка. Таким образом, порядок в полукольце
И+ — это двойственный порядок для отношения <ц. В по-
полукольце есть наименьший элемент относительно введенного
порядка — элемент +оо, поскольку для любого элемента х
имеем тт(ж, +оо) = х. Существует и наибольший элемент —
единица полукольца, т.е. число 0. Не следует путать число 0 с
нулем данного полукольца, а именно с элементом +оо.
3.1. Полукольца. Основные примеры 181
В полукольце Sa (см. пример З.З.б) получаем в качестве от-
отношения естественного порядка полукольца отношение вклю-
включения С . Действительно, для любых двух множеств X, У Е 2А
из X U Y = Y вытекает X С Y и наоборот. Наименьшим эле-
элементом является нуль полукольца — 0 (пустое множество), а
наибольшим — единица полукольца (множество А).
В полукольце На (см. пример З.З.в) отношение естественно-
естественного порядка полукольца также совпадает с отношением включе-
включения для бинарных отношений. В этом полукольце существуют
наименьший элемент — пустое отношение 0 и наибольший
элемент — универсальное отношение. Однако в отличие от
полукольца Sa наибольший элемент не совпадает с единицей
полукольца.
В полукольце 5[а,ь] (см. пример З.З.г) имеем естественный
числовой порядок, определенный на множестве действительных
чисел отрезка [а, Ь]. Наименьшим элементом является число
а (нуль полукольца), а наибольшим — число 6 (единица полу-
полукольца).
Теорема 3.1. Если А — конечное подмножество (носителя)
идемпотентного полукольца, то sup Л относительно естествен-
естественного порядка этого полукольца равен сумме всех элементов
множества А.
< Пусть А = {ai,..., an} и а = а\ +... + ап. Для произвольного
элемента a*, i = 1, п, в силу коммутативности и идемпотентно-
идемпотентности сложения имеем
а{ + а = ai + (ах +... + п{ +... + ап) =
= а\ +... + ai + ai +... + an =
= а\ +... + ai +... + an = a,
т.е. ai ^ о, и поэтому а есть верхняя грань множества А.
Покажем, что это точная верхняя грань множества. Возьмем
произвольную верхнюю грань Ь множества А и рассмотрим
182 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
сумму b + а. Так как для каждого г = 1, п имеет место а; ^ 6,
т.е. а{ + b = Ь, то
6 + а = Ь + (а\ + а.2 +... + ап) =
Следовательно, аО и поэтому а — тонная верхняя грань
множества А. >
3.2. Замкнутые полукольца
При изучении колег* большое внимание было уделено полям.
Связано это прежде всего с тем, что в полях разработана тех-
техника решения систем линейных уравнений. Оказывается, мож-
можно выделить специальный класс идемпотентных полуколец, в
которых также удается находить решения систем уравнений,
рассматриваемых в качестве аналогов систем линейных алге-
алгебраических уравнений [III].
Определение 3.2. Полукольцо S = (S, +, -, 0, 1) называ-
называют замкнутым, если:
1) оно идемпотентно;
2) любая последовательность элементов множества S имеет
точную верхнюю грань относительно естественного порядка
^ этого идемпотентного полукольца]
3) операция умножения полукольца S сохраняет точные
верхние грани последовательностей, т.е. для любого а 6 S и
любой последовательности X = {хп}пещ элементов множества S
a sup X = sup aX, (sup X)a = sup(Xa).
Замечание ЗЛ. Условие 3 определения 3.2 можно сформу-
сформулировать иначе и говорить о сохранении точной верхней грани
любого не более чем счетного подмножества множества S. Од-
Однако в дальнейшем такие подмножества часто будут строить-
строиться как множества элементов некоторых последовательностей.
3.2. Замкнутые полукольца 183
Кроме того, из элементов не более чем счетного множества
всегда можно образовать последовательность, используя неко-
некоторую нумерацию этого множества.
Теорема 3.2. Любое конечное идемпотентное полукольцо
замкнуто.
М Поскольку носитель S идемпотентного полукольца
5 = E,+,-,0,1)
есть конечное множество, то множество элементов любой по-
последовательности в этом полукольце конечно. Для нахождения
точной верхней грани такой последовательности нужно найти
точную верхнюю грань множества Р= {pi, -.-,Pn} ее членов,
т.е., согласно теореме 3.1, вычислить некоторую конечную сум-
сумму, которая всегда существует. Таким образом, в конечном
идемпотентном полукольце любая последовательность имеет
точную верхнюю грань.
Условия сохранения точных верхних граней имеют вид
(pi +... + pn)a = pia +... + pna
и выполняются в силу аксиом полукольца.
Таким образом, полукольцо S замкнуто. >
Мы доказали (см. 3.1), что в любом идемпотентном полу-
полукольце сумма произвольного конечного множества элементов
является его точной верхней гранью.
В силу этого в замкнутом полукольце естественно точную
верхнюю грань последовательности {#n}n€N называть суммой
элементов последовательности, полагая, по определе-
определению,
оо
? хп = sup {xn: n G N}. C.2)
п=1
184 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
оо
Согласно условию 2 определения 3.2, всегда J2 хп есть элемент
п=1
множества S. Иногда, если это не приводит к недоразуме-
недоразумению, „пределы суммирования" будем опускать и писать просто
^п. Также будем использовать обозначение ^^хп- Под-
черкивая, что в C.2) множество элементов хп в общем случае
бесконечно, будем сумму, стоящую в левой части C.2), назы-
называть бесконечной суммой. Заметим, что в частных случаях
бесконечная сумма может свестись к конечной (если множество
всех элементов последовательности {хп} конечно).
Итак, согласно определению 3.2, замкнутое полукольцо яв-
является индуктивным упорядоченным множеством, в котором
наименьшим элементом служит нуль полукольца, точной верх-
верхней гранью произвольной (в частности, неубывающей) последо-
последовательности {жп}пен является бесконечная сумма J^#n, причем
операция умножения на произвольный фиксированный элемент
а непрерывна в смысле определения 1.5, поскольку, согласно
определению 3.2, сохраняет точные верхние грани. Заметим,
что это свойство умножения в замкнутом полукольце можно
рассматривать как аналог дистрибутивности (седьмой аксио-
аксиомы полукольца, см. определение 3.1) для бесконечной суммы:
Xn и
Для бесконечной суммы также справедливы аналоги свойств
идемпотентности и коммутативности.
Действительно, для последовательности {#n}n€N? такой, что
хп = а для любого п € N, имеем X^#n = sup{a} = a, т.е. бес-
бесконечная сумма, все слагаемые которой одинаковы и равны
некоторому а, равна а. В этом состоит свойство идемпотент-
идемпотентности бесконечной суммы (или, как иногда говорят, свойство
бесконечной идемпотентности).
Так как точная верхняя грань последовательности любо-
любого упорядоченного множества равна, по определению, точной
3.2. Замкнутые полукольца 185
верхней грани множества всех элементов этой последователь-
последовательности, то при любом расположении слагаемых в бесконечной
сумме мы получим один и тот же результат. Это свойство есть
свойство бесконечной коммутативности, или коммутативности
бесконечной суммы.
Сложнее обстоит дело с аналогом ассоциативности для бес-
бесконечной суммы. Такая ассоциативность означает, что резуль-
результат не изменяется при произвольной группировке слагаемых
бесконечной суммы.
Для некоторой последовательности {xn}n€N элементов замк-
замкнутого полукольца и произвольной последовательности {rik}keN
натуральных чисел образуем последовательность {sjfe}*eN> где
Тогда бесконечная ассоциативность состоит в выполнении
для любой последовательности {#n}n€N равенства
Свойство бесконечной ассоциативности C.3) удобнее не до-
доказывать непосредственно, а вывести из более общих результа-
результатов. Один из них касается характеристики замкнутых полуко-
полуколец в терминах точных верхних граней счетных подмножеств.
Теорема 3.3. Идемпотентное полукольцо S = E, +,-,0,1)
замкнуто тогда и только тогда, когда любое счетное подмно-
подмножество X CS имеет точную верхнюю грань и для любого a E S
верны равенства
a • supX = sup(a • X), (supX) • a = sup(X • a).
186 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
< Справедливость утверждения теоремы немедленно вытекает
из определения точной верхней грани последовательности эле-
элементов упорядоченного множества как точной верхней грани
множества этих элементов. >
Теорема 3.4. Пусть S = E, +, •, 0, 1) — замкнутое полу-
полукольцо, X — не более чем счетное подмножество множества 5,
a (Bi)i?j — не более чем счетное семейство подмножеств мно-
множества X, такое, что объединение семейства совпадает с X,
т.е. (J Bi = X. Тогда
supX = sup {supВ», i € /}. C.4)
<4 Поскольку множества Хи/не более чем счетны, то, согласно
определению 3.2, все точные верхние грани из C.4) существуют
и принадлежат S. Обозначим левую часть равенства C.4) через
а, а правую — через Ь.
Так как а есть точная верхняя грань множества Л", то
для любого х Е X справедливо неравенство х ^ а (где ^ —
естественный порядок идемпотентного полукольца S). В част-
частности, для любого подмножества Bi и любого его элемента
у получаем у ^ а, откуда следует, что элемент а есть верх-
верхняя грань каждого подмножества В%. Значит, этот элемент
не меньше чем точная верхняя грань каждого из этих подмно-
подмножеств, т.е. для любого i G J a ^ sup Д. Последнее означает, что
а есть верхняя грань множества всех точных верхних граней
supJSi, г € J, т.е. а > Ь.
В то же время, поскольку объединение всех подмножеств
В{ равно X, для любого хЕХ найдется такое г Е /, что а:€ fit-
Поэтому х < sup В* < Ь, это означает, что элемент Ь является
верхней гранью множества X, и тогда Ъ ^ а, так кале а есть
точная верхняя грань X.
Итак, а^Ьиб^а, откуда а = Ь, и равенство C.4) доказа-
доказано. >
3.2. Замкнутые полукольца 187
Следствие 3.1. Бели семейство подмножеств из теоре-
теоремы 3.4 (-Bj)ie/ конечно, т.е. / = {1,2,..., п}, то
*=i
Следствие 3.2. Пусть {xn}n^ — произвольная после-
последовательность элементов замкнутого полукольца и (#*)*€/ —
не более чем счетное семейство подмножеств N, такое, что
U Ni = N. Тогда
n€N t€/
xm- #
i
В частности, из следствия 3.2 при условии, что множества
Ni, % € /, попарно не пересекаются, получаем свойство ассоци-
ассоциативности бесконечной суммы C.3). Отсюда же при N\ = {1},
N2 = {1,2} и т.д., т.е. при определении для любого натурально-
натурального k множества Nk в виде Nk = Nfc-i U {fe}, получаем равенство
т.е. точная верхняя грань последовательности {zn}n€N равна
точной верхней грани последовательности частичных сумм
{sjfebeN, где sk = si +... + а*.
Пусть {sn}n€N и {ym}m€N — произвольные последователь-
последовательности в замкнутом полукольце S. Образуем последователь-
последовательность, членами которой являются все произведения хпут при
независимом пробегании индексами пит множества нату-
натуральных чисел*. Эту последовательность будем записывать
* Такую последовательность называют произведением Коши исходных
последовательностей [IX].
188 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
как {xnym}n,meN, а ее точную верхнюю грань обозначим как
Е хпУт-
Теорема 3.5. В любом замкнутом полукольце верно то-
тождество
Е *пут=A
n,mGN n€N
М Ввиду непрерывности умножения в замкнутом полукольце
правую часть тождества C.7) можно переписать в виде
(ЕЖ") (Е *») = Е (?
n€N m€N m€N n€N
Еще раз используя непрерывность умножения и внося со-
сомножитель ут под знак внутренней суммы, получаем
m€N nGN m€N
В правой части последнего равенства каждое слагаемое
внешней суммы (по т) есть точная верхняя грань подпоследо-
подпоследовательности {хпут}пещ при фиксированном т. Поскольку все
эти подпоследовательности в совокупности дают всю последо-
последовательность {xnj/m}n,m€N> TO> согласно следствию 3.2, получаем
()
m€N n€N n,m€N
что и доказывает тождество C.7). >
Следующая теорема устанавливает связь между конечной и
бесконечной суммами.
Пусть {a;n}n€N и {j/n}n€N — произвольные последовательно-
последовательности в замкнутом полукольце S. Образуем последовательность
{#n + 2/n}neN> называемую суммой исходных последовательно-
последовательностей.
3.2. Замкнутые полукольца 189
Теорема 3.6. В любом замкнутом полукольце точная
верхняя грань суммы двух произвольных последовательностей
равна сумме точных верхних граней этих последовательностей,
т.е.
А Обозначим через X множество всех членов последователь-
последовательности {жп}п€н> а через У — множество всех членов последова-
последовательности {yn}n€N- В силу следствия 3.2
sup(X U Y) = supX + sup Y = ^2 xn +
Осталось тогда доказать, что
?>» + !*») =eup(XUY). C.9)
Обозначим через а левую, а через Ь правую часть доказы-
доказываемого равенства C.9). Для любого натурального п имеем
a^xn + yn. Согласно теореме 3.1, хп + уп ^ хп и хп + уп > уп.
Следовательно, для любого п выполняются неравенства а^хпи
а^Уп, т.е. а ^ и для любого и G X U Y. Таким образом, элемент
а является верхней гранью множества X U Y, откуда а^Ь.
В то же время элемент 6 не меньше любого из элементов
множества ХиУ, и, стало быть, для любого натурального
п имеет место Ь^хп и b^yn, т.е. Ь ^ sup{xn, yn} = хп + уп.
Это значит, что Ь есть верхняя грань последовательности
{хп + Уп}пбН, а потому 6 ^ а.
Итак, а = Ь, и равенство C.9) доказано. >
Бели в C.8) уп = а для всех п, то получаем следствие.
Следствие 3.3. Для любой последовательности {хп}п^
элементов замкнутого полукольца и любого элемента а этого
полукольца выполняется равенство
»)- #
190 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Тождество C.10) можно рассматривать как свойство непре-
непрерывности операции сложения в замкнутом полукольце. Это
свойство совершенно аналогично свойству непрерывности опе-
операции умножения, которое имеет место по определению.
Одним из важнейших понятий в замкнутых полукольцах
является понятие итерации (или замыкания) элемента
замкнутого полукольца. Итерация х* элемента х определяется
как точная верхняя грань последовательности всех степеней
элемента х, т.е.
00
** = ?*">
п=0
где, по определению, х° = 1, а хп = xn~lx, n = 1,2,...
Пример 3.5. а* Из теоремы 3.2 сразу получаем, что
идемпотентное полукольцо В (см. пример 3.2) замкнуто, причем
точная верхняя грань любой последовательности элементов
этого полукольца равна 1, если хотя бы один ее член равен 1,
и равна 0 в противном случае. В частности, итерация любого
элемента полукольца В равна 1. Для 1* это очевидно, а для О*
имеем
б. В идемпотентном полукольце К+ (см. пример 3.1) любая
последовательность есть последовательность неотрицательных
действительных чисел. Такая последовательность ограничена
снизу и, как известно из курса математического анализа, имеет
точную нижнюю грань относительно естественного числового
порядка [I], которая, согласно примеру 3.4, представляет собой
точную верхнюю грань относительно естественного порядка
идемпотентного полукольца 7?+. Напомним, что этот порядок
является двойственным к естественному числовому порядку.
Итак, для любой последовательности хп элементов полу-
полукольца 7?+ точная верхняя грань существует. Непрерывность
операции умножения в этом полукольце также можно доказать,
3.2. Замкнутые полукольца 191
опираясь на естественный числовой порядок, для которого она
эквивалентна выполнению равенства
a + infX = infXa, C.11)
где a — неотрицательное действительное число, а X (соот-
(соответственно Ха) — множество элементов последовательности хп
(соответственно хп + а). Равенство C.11) следует из известных
результатов математического анализа.
Таким образом, рассматриваемое идемпотентное полуколь-
полукольцо 7?+ является замкнутым.
Итерация х* элемента х в полукольце 7?+ есть точная верх-
верхняя грань последовательности степеней элемента х. Поскольку
в этом полукольце операция умножения определена как опера-
операция сложения действительных чисел, то х° = 0, так как чи-
число 0 есть единица полукольца 7?+. Далее, х2 = х + х = 2х, ...,
хп = пх. Очевидно, что для каждого n ^ О выполняется не-
неравенство жпHв смысле естественного числового порядка.
Таким образом, число 0 есть наименьший в смысле естествен-
естественного числового порядка член последовательности {жп}п€н и>
следовательно, inf{a;n}nGN = 0. Переходя к двойственному по-
порядку — естественному порядку полукольца 7?+, получим, что
число 0 является точной верхней гранью последовательности
{#n}n€N? т.е. х* = 0. Таким образом, в полукольце И+ итера-
итерация произвольного элемента также равна единице полукольца,
т.е. числу 0.
в. Замкнутость идемпотентного полукольца Sa (cm. при-
пример З.З.б) можно обосновать следующим образом. Отношение
естественного порядка этого полукольца — это отношение
включения (см. пример 3.4). Рассмотрим произвольную после-
последовательность подмножеств J?i, ..., 2?п, ... множества А. В
данном полукольце бесконечная сумма есть объединение после-
последовательности подмножеств множества А.
Докажем, что объединение В = (J Вп и есть supl?n. Оче-
n€N
видно, что для каждого г справедливо включение В» С В, т.е.
192 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
объединение есть верхняя грань последовательности {В
Покажем, что В будет точной верхней гранью. Рассмотрим
произвольную верхнюю грань С последовательности Вп. Тогда
BnQC для каждого п Е N (см. 1.5) и поэтому
т.е. ВСС. Следовательно, В = (J J5n = supBn.
n€N
Непрерывность умножения полукольца 5д, в качестве кото-
которого взято пересечение множеств, эквивалентна тождеству
n€N n€N
(дистрибутивности пересечения относительно произвольного
объединения, см. 1.5). В этом полукольце умножение — это
пересечение множеств. Поэтому любая положительная степень
множества X есть само X. Нулевая же степень Х° равна
единице полукольца, т.е. множеству А. Поэтому итерация X*
равна
т.е. также равна единице полукольца.
г. Рассмотрим идемпотентное полукольцо На (см. при-
пример З.З.в) бинарных отношений на множестве А. Можно до-
доказать, что точной верхней гранью любой последовательности
отношений, как и в полукольце 5д, служит объединение элемен-
элементов этой последовательности (см. пример 3.4).
Аналогично доказательству дистрибутивности композиции
бинарных отношений на множестве относительно конечного
объединения (см. 1.4) можно доказать, что для любых бинар-
3.2. Замкнутые полукольца 193
ных отношений р и an на множестве А справедливы тождества
PoU<7n==
Таким образом, идемпотентное полукольцо На замкнутое.
Итерация бинарного отношения р есть
где рп, п ^ 1, — n-кратная композиция р с самим собой:
рп = ро...ор. Как видно, в общем случае р* ф id^, т.е. в
п раз
этом полукольце итерация элемента, вообще говоря, не равна
единице полукольца. #
Выше было показано, что всякое замкнутое полукольцо
является индуктивным упорядоченным множеством. Следова-
Следовательно, согласно теореме 1.7, любое непрерывное отображение
f замкнутого полукольца в себя имеет наименьшую неподвиж-
неподвижную точку, т.е. в любом замкнутом полукольце всякое уравне-
уравнение вида х = /(ж), где / — непрерывное отображение носителя
этого полукольца в себя, имеет наименьшее решение.
Особенно важными для приложений являются линейные
уравнения в замкнутом полукольце, имеющие вид
C.12)
или
C.13)
В силу непрерывности операций сложения полукольца (см.
тождество C.10)) и умножения полукольца (см. определение 3.2)
правые части уравнений C.12) и C.13) есть непрерывные ото-
отображения. Поэтому, согласно теореме 1.7 о неподвижной точ-
точке, существуют наименьшие решения этих уравнений.
7 — 10061
194 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Теорема 3.7. Наименьшими решениями уравнений C.12) и
C.13) в замкнутых полукольцах являются соответственно
х = а*Ь C.14)
и
х = Ьа\ C.15)
где а* — итерация элемента а.
< Используя формулу A.8) для вычисления наименьшей непо-
неподвижной точки и записывая sup в случае замкнутого полуколь-
полукольца как бесконечную сумму, для уравнения C.14) получаем
где 0 — нуль полукольца, a f(x) — ax + b.
Учитывая, что
/°@) = О,
получаем
п=0 п=1
Используя непрерывность умножения, вынесем Ь (вправо) за
знак бесконечной суммы и получим
n=l Si=l
3.3. Решение систем линейных уравнений 195
Сумма 1 + a +... + an~l есть частичная сумма последователь-
последовательности {а"}п^о- Используя равенство C.6), можем написать
п=1 п=0
Окончательно получаем
П=1
Аналогично доказывается равенство C.15). >
Формулы C.14) и C.15) дают именно наименьшие решения
уравнений C.12) и C.13), а не все возможные их решения.
Приведем в этой связи простой пример. В полукольце В (см.
пример 3.2) можно определить только два уравнения: х = х +1
и х = х + 0. Второе уравнение переписывается совсем просто:
х = х] его решением является любой элемент полукольца — как
0, так и 1. Но по формуле C.14) получим х = 1*0 = 0, что, как
и доказано выше, есть наименьшее решение уравнения.
Заметим еще, что в полукольце, в котором итерация любо-
любого элемента равна единице полукольца, формулы C.14) и C.15)
дают один и тот же результат: х — Ь, т.е. в данном случае наи-
наименьшее решение совпадает со свободным членом уравнения.
3.3. Решение систем линейных уравнений
Полученные выше результаты (см. 3.2) можно распростра-
распространить на системы линейных уравнений вида
Х\ = 0>\\Х\ + ... + CL\nXn •
C.16)
-...+annsn + ftn,
где все элементы a*j, 1 < % < п, 1 < j < n, и Ь», 1 ^ г ^ п, суть
элементы некоторого замкнутого полукольца, и речь идет о
решении системы C.16) в этом полукольце.
7*
196 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Для этого введем в рассмотрение множество ШтХп(8) пря-
прямоугольных матриц типа тхпс элементами из произвольного
идемпотентного полукольца S = E,+,-,0,1). Множество всех
квадратных матриц порядка п с элементами из полукольца S
обозначим МпE). Через Matr(«S) обозначим множество всех
матриц любого типа с элементами из S.
Операции сложения и умножения матриц определяют точно
так же, как и в числовом случае [III], — с учетом того, что
сложение и умножение элементов матриц понимаются в смысле
данного идемпотентного полукольца S, а именно:
1) суммой матриц А = (ау) иВ = (Ьу) типа тхп называют
матрицу С = (cij) того же типа с элементами су = ay + by,
г = 1, га, j = l,n, и используют обозначение С = А + В;
2) произведением АВ матриц А = (оу) типа тхпиВ = (Ьу)
типа пхр называют матрицу С = (су) типа т х р с элементами
к=1
Нулевая (О) и единичная (Е) матрицы любого порядка
определяются с помощью единицы и нуля полукольца.
На множестве Mn(<S) всех квадратных матриц фиксирован-
фиксированного порядка п можно определить алгебру
Теорема 3.8. Алгебра Mn(«S) есть идемпотентное полу-
полукольцо. Бели полукольцо S замкнуто, то полукольцо Mn(«S)
тоже замкнуто.
< Операции суммы и произведения матриц определены таким
образом, что все свойства операций сложения и умножения в
полукольце сохраняются и для соответствующих операций над
матрицами. Поэтому для суммы и произведения матриц из
Mn(«S) выполнены аксиомы полукольца, и, кроме того, опера-
операция сложения матриц идемпотентна. Следовательно, Mn(«S) —
идемпотентное полукольцо.
3.3. Решение систем линейных уравнении 197
Выясним смысл отношения порядка в этом идемпотент-
ном полукольце. В силу определения естественного порядка
идемпотентного полукольца неравенство А ^ В для матриц А
и В означает, что А + В = J3, или для всех г, j справедливо
dij + bij = by. Следовательно, А ^ В тогда и только тогда, ко-
когда для всех г, j справедливо ay ^ Ьу.
Пусть S — замкнутое полукольцо. Докажем замкнутость
идемпотентного полукольца Mn(«S) и существование точной
верхней грани у любой последовательности матриц в Mn(«S).
Пусть {Ат}тещ — произвольная последовательность ква-
квадратных матриц Ат = (а^) порядка п. Рассмотрим матрицу
В=[ ^2 аШ- Каждый элемент Ьу = ^ а$ этой матрицы есть
точная верхняя грань последовательности элементов а^. Эти
точные верхние грани существуют, поскольку а^ — элементы
замкнутого полукольца S. Так как сложение матриц и отноше-
отношение порядка в полукольце матриц определяются поэлементно,
то матрица В и будет точной верхней гранью последователь-
последовательности матриц Ат.
Докажем теперь непрерывность умножения в Mn(«S), т.е.
что для любой последовательности {-Am}meN матриц и произ-
произвольной матрицы В имеет место
Матрица С = (су) = 5Z^m есть точная верхняя грань последо-
последовательности {Ат}т?щ. Тогда имеем
Элемент сщ есть точная верхняя грань последовательности
элементов матриц Ат, т.е.
m€N
198 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Используя непрерывность умножения в исходном полуколь-
полукольце «S, получаем
? = (Е Е
Следовательно,
m€N
Используя непрерывность сложения, получаем
Е ) (
k=l m€N m€N Jk=
Аналогично доказывается, что
Полукольцо МпE) будем называть полукольцом матриц
над полукольцом S. Доказанная теорема позволяет нам
применять к замкнутым полукольцам матриц над некоторым
замкнутым полукольцом S теорему 3.7 и решать произвольные
уравнения вида
Х = АХ + В C.17)
или
Х = ХА + В C.18)
относительно неизвестной матрицы X.
Наименьшие решения этих уравнений есть
X = А* В C.19)
и
Х = ВА* C.20)
соответственно, где А* — итерация матрицы А в Mn(«S).
Итерация А* матрицы А играет в теории линейных уравнений в
3.3. Решение систем линейных уравнений 199
замкнутых полукольцах такую же роль, как обратная матрица
в классической линейной алгебре.
Основную роль при решении задач теории ориентированных
графов и теории формальных языков играют праволиней-
ные уравнения вида C.17), поэтому мы будем, как правило,
рассматривать только их. Леволинейное уравнение C.18)
может быть проанализировано аналогично.
Мы доказали существование решений матричных уравнений
в матричном полукольце над замкнутым полукольцом. Теперь
нам необходимо разработать технику поиска их решений и
применить ее к решению систем вида C.16).
Полагая, что f j — j-й столбец матрицы X, a /3j — j-й стол-
столбец матрицы В, уравнение C.17) можно переписать как систему
уравнений относительно неизвестных столбцов матрицы X:
tj = Mj + fa O^j^n. C.21)
Каждая система вида C.21) есть матричная форма записи
указанной выше системы C.16). Поэтому наименьшее решение
этой системы, как следует из C.19), есть
Ь = А*%. C.22)
Для поиска решения системы вида C.21) можно воспользо-
воспользоваться методом последовательного исключения неиз-
неизвестных, аналогичным классическому методу Гаусса.
Поскольку система уравнений вида C.16) имеет решение,
мы можем подставить его в систему и работать с уравнениями
как с тождествами.
Рассмотрим процедуру решения системы уравнений C.16).
Запишем первое уравнение системы так:
х\ = ацх\ + (аиХ2 +... + а\пхп + Ь\).
Из первого уравнения системы выразим х\ через остальные
неизвестные, воспользовавшись формулой C.14):
... + ainxn + Ьх). C.23)
200 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
В формуле C.23) выражение в скобках не содержит неизвест-
неизвестного х\. Подставляя C.23) вместо х\ в остальные уравнения,
получаем систему из п — 1 уравнений, которая уже не содер-
содержит Х\\
... + агпхп
C.24)
• • • + 0>nnXn + Ьп.
Приводя подобные члены в каждом уравнении системы, полу-
получаем:
... + (апа^ахп + аЪп)хп + az\a\xbi + 63, C.25)
+ апп)хп
Первое уравнение этой системы перепишем так:
Х2 = @>21а,па>12+а22)Х2+'У2,
где
72 = Q>2\a\i{aibXz + ... + ainxn + bx) + 0,23X3 +... + а2пхп
Заметим, что 72 не содержит х\ ИХ2. Воспользовавшись соот-
соотношением C.14), будем иметь
Я2=С*272, C.26)
где О.2 = <b2\Q\\Q»\2 + ^22 не содержит неизвестных. Используя
полученное выражение, исключаем Х2 из остальных уравнений.
3.3. Решение систем линейных уравнении 201
Действуя подобным образом, на г-м шаге A ^ i < n) полу-
получаем
Xi = a\lu C.27)
где выражение а* не содержит неизвестных, а выражение 7t
может содержать только неизвестные, начиная с (г + 1)-го, т.е.
#г+Ъ •••> хп-
При г = п имеем
«п = <7п, C.28)
где выражения а* и jn не содержат неизвестных. Таким обра-
образом, исходная система C.16) преобразована к ятреугольному"
виду: правая часть уравнения C.28) не содержит неизвестных,
уравнение C.27) при г = п — 1 в правой части содержит толь-
только одно неизвестное xn_i и каждое следующее уравнение при
просмотре „снизу вверх" на одно неизвестное больше, чем пре-
предыдущее. Первое уравнение системы — уравнение C.23) — в
правой части содержит все неизвестные от Х2 до хп. На этом
завершается первый этап алгоритма, который называют пря-
прямым ходом метода Гаусса.
Второй этап алгоритма, называемый обратным ходом ме-
метода Гаусса, состоит в последовательном нахождении значения
всех неизвестных х\, ..., #п-ъ начиная с жп-1- Подставив в вы-
выражение для хп-\ вместо хп правую часть C.28), найдем агп-1-
Затем определим жп_2> подставив полученные значения хп и
жп_1 в правую часть выражения C.27) при г = п — 2, и так да-
далее до тех пор, пока не найдем х\.
Замечание 3.2. Положив В = Е в уравнении C.17), полу-
получим X = А*Е = А*. Таким образом, чтобы вычислить итерацию
матрицы А, достаточно решить матричное уравнение C.21) для
всех j = 1, п при /3j, равном j-му столбцу единичной матрицы Е.
Пример 3.6. Проиллюстрируем приведенную схему реше-
решения системы из двух линейных уравнений. Имеем
202 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Из первого уравнения выразим х\\
Подставляя это выражение во второе уравнение, получаем
Подставляя этот результат в написанное выше выражение для
xi, находим окончательное решение:
Особенно просто решение выглядит в случае тривиальной
итерации, т.е. тогда, когда в полукольце итерация любого
элемента равна единице полукольца (как в полукольцах В, ТС+,
Sa, <->[a,6])* В этом случае для системы из двух уравнений
решение равно
ibi + 62) + &ъ
Пример 3.7. Рассмотрим в полукольце 5[Од] (см. при-
пример З.З.г) систему линейных уравнений
! + 0,2,
= 0,3xi+0,9x2 + 0,6.
Решим эту систему уравнений, следуя общему алгоритму.
Из первого уравнения получаем
хг = 0,5* @,4x2 + 0,2) = 1@,4x2 + 0,2) = 0,4х2 + 0,2.
Далее,
х2 = 0,3@,4x2 + 0,2) + 0,9x2 + 0,6 = 0,Зх2 + 0,2 + 0,9х2 + 0,6.
Отсюда х2 = @,3 + 0,9)х2 + 0,6 = 0,9х2 + 0,6 = 0,9*0,6 = 0,6.
3.3. Решение систем линейных уравнении 203
Подётавляя #2 — 0,6 в полученное вьфажение для х\, нахо-
находим, что
хг = 0,4 • 0,6 + 0,2 = 0,4 + 0,2 = 0,4. #
Не всякое бесконечное идемпотентное полукольцо является
замкнутым. Однако можно заметить, что при решении линей-
линейных уравнений и систем требовалось вычисление точной верх-
верхней грани последовательностей специального вида, а именно
нахождение итерации элементов. Поэтому помимо замкнутых
полуколец интерес для приложений представляют так называе-
называемые полукольца с итерацией.
Под полукольцом с итерацией в данном контексте мы будем
понимать идемпотентное полукольцо, которое является под-
полукольцом* некоторого замкнутого полукольца и вместе с
каждым элементом содержит его итерацию. Важнейшим при-
примером такого полукольца является полукольцо регулярных язы-
языков (см. 7).
Рассматривая в полукольце с итерацией произвольное ли-
линейное уравнение, т.е. уравнение вида C.12) или C.13), полу-
получаем следующие результаты. Во-первых, это уравнение имеет
наименьшее решение, так как полукольцо с итерацией содер-
содержится в некотором замкнутом полукольце в качестве подполу-
кольца. Во-вторых, это наименьшее решение снова окажется в
этом же полукольце, поскольку носитель полукольца с итераци-
итерацией замкнут относительно итерации. Таким образом, носитель
полукольца S с итерацией замкнут относительно операции на-
нахождения наименьшей неподвижной точки любого линейного
отображения ах + b (или ха + 6), где а и Ь — элементы S.
Не составляет труда распространить этот результат на про-
произвольные матричные уравнения. Можно доказать следующее
утверждение.
* Полукольцо Q= (Q, +, •, 0, 1) называют подполукольцом полуколь-
полукольца 7?= (Я, +, *, 0, 1), если множество Q есть подмножество множества
R, замкнутое относительно операций сложения и умножения полукольца
Я, а также содержащее нуль и единицу полукольца К.
204 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Теорема 3.9. Если А — матрица, все элементы которой
принадлежат некоторому полукольцу с итерацией, то все эле-
элементы ее итерации А* также принадлежат этому полукольцу с
итерацией.
3.4. Булевы алгебры
Теория булевых алгебр является классическим разделом дис-
дискретной математики. Булевы алгебры возникли в трудах ан-
английского математика Дж. Буля в 50-х годах XIX века как
аппарат логики. При этом элементы булевой алгебры тракто-
трактовались как высказывания, а операциями являлись дизъюнкция,
конъюнкция и отрицание.
Существуют различные подходы к определению булевой
алгебры. Мы определим булеву алгебру как частный случай
идемпотентного полукольца.
Определение 3.3. Полукольцо S = E, +, •, 0, 1) называ-
называют симметричным (или взаимным), если оно идемпотентно
и в нем выполнены следующие тождества:
1) а-а = а ( идемпотентность операции умножения полу-
полукольца);
2) а-Ь = Ьа (коммутативность операции умножения полу-
полукольца);
3) а + (Ь-с) = (а + Ь) • (а + с) (дистрибутивность операции
сложения полукольца относительно умножения);
4) 1 + а = 1 (аннулирующее свойство единицы полукольца
относительно сложения).
Можно дать определение, равносильное определению 3.3.
Идемпотентное полукольцо S = E, +, •, 0, 1) называется сим-
симметричным (или взаимным), если алгебра Sf = E, •, +, 1, 0)
также является идемпотентным полукольцом. При этом будем
говорить, что идемпотентное полукольцо S' есть полукольцо,
двойственное к идемпотентному полукольцу S.
3.4. Булевы алгебры
205
Из определения следует, что в двойственном идемпотент-
ном полукольце операция сложения — это операция умножения
в исходном полукольце и наоборот; нуль двойственного полу-
полукольца — это единица исходного полукольца и наоборот. Легко
видеть, что полукольцо «S", двойственное к двойственному по-
полукольцу <S', есть исходное полукольцо S.
Запишем полностью все аксиомы (основные тождества) сим-
симметричного полукольца, объединяя двойственные аксиомы в
пары (табл. 3.3).
Таблица 3.3
п/п
1
2
3
4
5
6
Аксиома
а + (Ь + с) = (а + Ь) + с
а+Ь=Ь+а
а + а = а
а + 0 = а
а-(Ь + с) =
= (а-Ь) + (а-с)
о-0 = 0
п/п
7
8
9
10
11
12
Аксиома
а-(Ь'с) = (а-Ь)-с
a-b — b-a
а-а = а
а-1 = о
а + (Ь-с) =
= (а + Ь)-(а + с)
а + 1 = 1
В табл. 3.1 можно увидеть, что в симметричном полукольце
операции сложения и умножения, равно как и элементы 0 и 1,
полностью „взаимозаменяемые", или взаимно двойственные.
Таким образом, справедлив принцип двойственности
для симметричных полуколец: любое тождество в симметрич-
симметричном полукольце остается верным, если в нем операцию сло-
сложения заменить операцией умножения и наоборот, а единицу
заменить нулем и наоборот.
Пример 3.8. а. Полукольцо В (см. пример 3.2) симмет-
симметричное.
б. Полукольцо 7?+ (см. пример 3.1) не является симметрич-
симметричным в силу неидемпотентности умножения полукольца, хотя в
206 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
нем единица полукольца (число 0) имеет аннулирующее свой-
свойство, поскольку min@, x) = 0.
в. Полукольцо Sa (см. пример З.З.б) симметрично в силу
известных свойств операций пересечения и объединения мно-
множеств.
г. Полукольцо Ид (cm. пример З.З.в) не является симмет-
симметричным.
д. Полукольцо <S[a,6] (см. пример З.З.г) симметрично.
Пример 3.9. Рассмотрим алгебру
2>» = (Дед(п), НОК,НОД, 1, п),
где Дел(п) — множество всех делителей натурального числа п;
НОК — операция вычисления наименьшего общего кратного;
НОД — операция вычисления наибольшего общего делителя
двух чисел. Эта алгебра является симметричным полукольцом.
Действительно, для любых двух натуральных чисел тир
верно представление
m = 2ai3a2...p?* и р = ^,
где pk — наибольший простой множитель в разложении тир.
Тогда
НОК(т,р) =
НОД(га,р) =
Таким образом, свойства операций НОК и НОД определя-
определяются свойствами операций max и min. В силу этого рассма-
рассматриваемая алгебра и является симметричным полукольцом (см.
пример З.З.г). #
Рассмотрим некоторые свойства симметричного полуколь-
полукольца, вытекающие из его аксиом.
3.4. Булевы алгебры 207
Свойство 3.1. Для любых элементов симметричного полу-
полукольца выполняются равенства
<4 Имеем х(х + у) = хх + ху = х + ху = хA + у) = х-1 =ж. >
Равенства, приведенные в формулировке свойства 3.1, на-
называют тождествами поглощения.
Свойство 3.2. В симметричном полукольце неравенство
х < у имеет место тогда и только тогда, когда ху = х.
< Вспомним, что по определению естественного порядка про-
произвольного идемпотентного полукольца х^у&х + у = у.
Пусть х ^ у. Тогда ху = х(х + у)=х (по свойству 3.1).
Пусть теперь ху = х. Тогда х + у = ху + у = у. Следователь-
Следовательно, х < у. >
Свойство 3.2 выражает связь умножения с естественным
порядком идемпотентного полукольца: меньший сомножитель
поглощает больший, т.е. порядок в двойственном полукольце
Sf является порядком, двойственным к порядку в полукольце
S. Но, как известно, при переходе к двойственному порядку
наибольший (максимальный) элемент становится наименьшим
(минимальным) элементом, а точная верхняя грань — точной
нижней гранью.
Свойство 3.3. В симметричном полукольце произведение
ху есть точная нижняя грань последовательности {я, у}:
Свойство 3.4* Для любого элемента х симметричного
полукольца имеет место неравенство 0 < х < 1.
< Первое неравенство 0 < х равносильно равенству 0 + х = ж,
верному для любого х. Второе неравенство х < 1 вытекает из
четвертого тождества определения 3.3. >
208
3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Таким образом, в симметричном полукольце единица A)
является наибольшим элементом.
Определение 3.4. Булева алгебра — это симметричное
полукольцо, в котором для каждого х существует элемент ж,
называемый дополнением х, такой, что
r l «-1 (О OQ\
X пГ *ь — JL, \О.?%3)
Обычно сложение в булевой алгебре называют булевым
объединением и обозначают V, а умножение — булевым
пересечением и обозначают Л.
Запишем аксиомы булевой алгебры в виде табл. 3.4, объеди-
объединяя „двойственные пары" (как это мы уже сделали, записывая
аксиомы симметричного идемпотентного полукольца).
Таблица 3.4
п/п
1
2
3
4
5
6
7
Аксиома
oVFVc) = (oV6)Vc
аУЪ=ЪУа
aVa = a
aV0 = o
oAFVc) =
= (aA6)V(oAc)
оЛ0 = 0
oVa = l
n/n
8
9
10
11
12
13
14
Аксиома
аЛ(ЬЛс) = (оЛЬ)Лс
оЛЬ=бЛо
аЛа — а
аЛ1 =а
aVFAc) =
= (aV6)A(aVc)
aVl = l
аЛо = 0
Рассмотрим некоторые важные свойства булевых алгебр,
вытекающие из определения.
Свойство 3.5 (единственность дополнения). В булевой
алгебре для любого х его дополнение х единственное.
4 Пусть для элемента х найдется еще одно такое о, что а Л х = О
и
ЗА. Булевы алгебры 209
Имеем a = aVO. Воспользовавшись свойством C.29), по-
получим a = a V (х Ах). В силу дистрибутивности и с учетом
свойств элемента а имеем a = (a V х) Л (а V х) = 1 Л (а V х). С
учетом свойств дополнения преобразуем последнее выражение
следующим образом: a = (х V х) Л (а V х) = (х Л а) V х. Поскольку
# Л а = О, то а = О V ж = 5?. Таким образом, элемент а совпадает
с дополнением х. >
Свойство 3.6 („симметричность" операции дополне-
дополнения). В булевой алгебре выполняется тождество
f = х.
<4 Так как х является дополнением к of, то ofЛж = 0 и 5Vx = 1.
В то же время жЛж = 0 и 5Va: = l. В силу единственности
дополнения к элементу х имеем W = ж. >
Свойство 3.7. В булевой алгебре верны следующие тожде-
тождества:
C.31)
< В силу свойств 3.5 и 3.6 для доказательства первого закона
достаточно показать, что (х Л у) V (а; V у) = 1 и (х Л у) Л (х V у) =
= 0.
Преобразуя выражения в левых частях, получаем
(х Ay)V (xV у) = (sV aV у) Л (yV zV у) = 1Л1 = 1,
Первое тождество доказано. Второе тождество следует из
принципа двойственности. >
Тождества C.31) называют законами де Моргана.
Единственность дополнения означает, что в булевой алгебре
возникает унарная операция — переход от элемента к его
дополнению. Эту операцию можно ввести в сигнатуру алгебры,
т.е. рассматривать булеву алгебру как алгебру вида
В = (В, V, Л,"", 0, 1)
210 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
с двумя бинарными, одной унарной и двумя нульарными опе-
операциями, такую, что:
1) («В, V, Л, 0, 1) — симметричное полукольцо;
2) а V а = 1 и а Л а = 0 (для любого а).
Дополнение в булевой алгебре называют булевым допол-
дополнением, а все операции булевой алгебры — булевыми опера-
операциями.
Рассмотрим теперь некоторые примеры булевых алгебр.
Пример 3.10* Полукольцо В (см. пример 3.2) является бу-
булевой алгеброй. Эта булева алгебра — важнейшая структура.
Мы назовем ее двухэлементной булевой алгеброй и обо-
обозначим В. Видно, что в В
0 = 1, Т = 0.
Пример 3.11. На множестве {0,1}п определим структуру
булевой алгебры, положив для произвольных 5 = (од, ..., ап),
0 = (А, ...,/?„) из {0,1}Л, что
i, ..., апЛ/?п),
2=Ci, ...
0 = @, ...,
Можно без труда показать, что все аксиомы булевой ал-
алгебры выполняются. Носитель определенной таким образом
булевой алгебры называют булевым кубом размерности п,
а его элементы — булевыми векторами (или булевыми
наборами) размерности п. Вектор 0 называют при этом ну-
левым булевым векторомлиш нулевым набором, а вектор
1 — единичным булевым вектором или единичным на-
набором. Заметим, что случаи п = 0ип = 1 включаются в эту
конструкцию. При п = 1 получаем уже рассмотренную двух-
двухэлементную булеву алгебру В, а при п = 0 — так называемую
3.4. Булевы алгебры 211
одноэлементную булеву алгебру, в которой 0 = 1. Но эта
структура малоинтересна.
Итак, булевы операции над булевыми векторами выполня-
выполняются покомпонетно — так же, как сложение векторов или
умножение вектора на число в линейной алгебре. Отношение
порядка здесь определено также покомпонентно, т.е. для произ-
произвольных 5 = (ai, ..., ап), /3 = (/3i, ..., (Зп) е {0,1}П неравенство
5 ^ /3 означает, что а» < /%, i = l,n. Так, например,
(О, 1, 0, 0, 1) ^ A, 1, 0, 0, 1),
а векторы @, 1, 0, 0, 1) и @, 1, 0, 0, 0) не сравнимы.
Пример 3.12. Полукольцо Sa (см. пример З.З.б) — буле-
булева алгебра, в которой все булевы операции суть не что иное,
как обычные теоретико-множественные операции, т.е. буле-
булево объединение есть обычное объединение множеств, булево
пересечение — пересечение множеств, булево дополнение — до-
дополнение множества.
Пример 3.13. а. Рассмотрим полукольцо Vq делителей
числа 6 с операциями НОК и НОД. Из примера 3.9 следует,
что это полукольцо симметричное. Нуль этого полукольца есть
число 1, а единица — число 6. Убедимся, что каждый элемент
полукольца имеет дополнение. Начнем с числа 1. Дополнение х
должно удовлетворять равенствам 1\/х = 6и1Ла; = 1. Первое
равенство означает, что НОКA,а?) = 6, а второе — НОДA,ж) =
= 1. Легко видеть, что х = Т = 6. Рассуждая аналогично,
получим 2 = 3. Следовательно, рассматриваемое полукольцо
есть булева алгебра.
б. Полукольцо 2>i2 делителей числа 12 не является булевой
алгеброй, так как, например, из 2 V х = НОКB, х) = 12 = 1 сле-
следует, что х = 12, но 2 Л12 = НОДB,12) = 2 Ф 1 = 0, и элемент 2
не имеет дополнения. #
Теория булевых алгебр имеет многочисленные приложения:
в математической логике, в теории вероятностей. Она позволя-
позволяет, в частности, рассматривать с единой точки зрения операции
212 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
над множествами, над высказываниями, над случайными собы-
событиями. В этой книге мы используем изложенные здесь факты
в главе в, посвященной булевым функциям.
3.5. Решетки
Напомним, что полурешеткой называют полугруппу, опера-
операция которой коммутативна и идемпотентна.
Таким образом, полурешетка — это алгебра С = (L, V), в
которой для любых a, b, c?L выполнены равенства
а\/а = а.
В каждой полурешетке может быть определено естествен-
естественное отношение порядка аналогично тому, как это определялось
для (идемпотентного) полукольца. По определению полагаем
для произвольных a, b€L
a<6^aVb = b. C.32)
Из определения C.32) отношения порядка в полурешетке
следует, что элемент aVb есть точная верхняя грань двухэле-
двухэлементного множества {a, b}.
Действительно,
(в силу ассоциативности и идемпотентности операции V). Ана-
Аналогично Ь V (а V Ъ) = а V 6 (с использованием и коммутативности
операции V). Итак, aMb есть верхняя грань множества {а,Ь}.
Полагая, что с есть какая-то верхняя грань данного множества,
вычислим (аУЬ)У с. Используя ассоциативность и то, что в си-
силу b < с выполняется равенство bVc = c, получим
3.5. Решетки 213
Но так как и < с, то а Vс = с. Итак, (а V6) Vс = с, т.е.
и поэтому элемент а V Ь есть точная верхняя грань множества
{а, Ь}.
Отношение порядка, определенное в произвольной полуре-
полурешетке согласно условию C.32), будем называть естествен-
естественным порядком данной полурешетки.
Таким образом, в полурешетке любое двухэлементное (и,
следовательно, любое конечное) подмножество имеет точную
верхнюю грань (по естественному порядку полурешетки).
Можно доказать, что имеет место и обратное.
Теорема ЗЛО. Любое упорядоченное множество С =
= (L, ^), в котором всякое двухэлементное подмножество име-
имеет точную верхнюю грань, является полурешеткой, естествен-
естественный порядок которой совпадает с отношением <.
< Определим операцию V так: а V Ь = sup {a, 6}. Комму-
Коммутативность и идемпотентность операции V следует сразу из
определения точной верхней грани множества. Действитель-
Действительно, aW a = sup {а, а} = sup {а} = а, и так как {а, 6} = {Ь, а}, то
а V Ь = sup {а, Ь) = sup {6, а} = Ь V а.
Докажем ассоциативность операции V. Для этого нужно по-
показать, что для произвольных а, 6, с G L имеет место равенство
sup {sup {а, 6}, с} = sup {а, sup{6, с}}. C.33)
Обозначим левую часть равенства C.33) через di, а пра-
правую — через с?2- Элемент d\ является точной верхней гранью
множества, элементы которого суть sup{a,6} и с. Поэтому
d\ ^ sup {a, b} и d\ ^ с. Из первого неравенства следует, что
d\ ^ a is. d\ ^ 6. Тогда, поскольку d\ ^ Ь и d\ ^ с, то d\ есть верх-
верхняя грань множества {6, с}, т.е. d\ ^ sup{6, с}. Так как d\ ^ a,
то d\ ^ sup {a, sup{6, с}} = cfe- Аналогично доказывается, что
^2 ^ di, т.е. d\ = cfe, что и требовалось доказать.
Поскольку для любых элементов а, Ь упорядоченного мно-
множества (L, ^) согласно условию теоремы соотношение а ^ Ъ
214 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
эквивалентно тому, что sup {а, Ь} = 6, то исходное отношение
порядка ^ совпадает с естественным порядком полурешетки
(L, sup). >
Из принципа двойственности для упорядоченных множеств
следует, что точная верхняя (нижняя) грань любого подмноже-
подмножества упорядоченного множества (L, ^) является одновременно
точной нижней (верхней) гранью этого подмножества в смы-
смысле двойственного порядка ^. Отсюда получаем утверждение,
двойственное теореме 3.10.
Теорема 3.11. Любое упорядоченное множество С = (L, ^),
в котором всякое двухэлементное подмножество имеет точную
нижнюю грань, является полурешеткой, причем естественный
порядок этой полурешетки является порядком, двойственным
к исходному порядку ^.
< Доказательство дословно повторяет доказательство теоре-
теоремы 3.10, но операция Л полурешетки определяется так:
a Ab = inf {а, Ь}. >
Полурешетку (L, sup), определенную теоремой 3.10, назы-
называют верхней полурешеткой, а полурешетку (L, inf), опре-
определяемую теоремой 3.11, — нижней полурешеткой.
Замечание 3.3. Обратим внимание на то, что понятия
„верхний" и „нижний" имеют смысл относительно фиксиро-
фиксированного отношения порядка и при переходе к двойственному
порядку „верх" превращается в „низ" и наоборот.
Пример 3.14. а. Отрезок [а, Ь] числовой прямой (с есте-
естественным числовым порядком), согласно теоремам 3.10 и 3.11,
является и верхней и нижней полурешеткой. Более того, по-
поскольку на числовой прямой любое двухэлементное подмноже-
подмножество имеет как точную верхнюю, так и точную нижнюю грань,
то любое подмножество множества действительных чисел R (в
частности, само R) является и верхней и нижней полурешеткой.
3.5. Решетки
215
В
Е
Рис. 3.1
Рис. 3.2
б. Бели на множестве точек плоскости (на которой задана
некоторая декартова система координат и точка рассматрива-
рассматривается как упорядоченная пара действительных чисел) опреде-
определить отношение порядка так, что (#, у) < (u, v) тогда и только
тогда, когда х^ииуО (см. пример 1.17 и рис. 1.11), то
множество точек любого прямоугольника [a, b] x [с, d\ (с ука-
указанным отношением порядка), согласно теоремам ЗЛО и 3.11,
есть и верхняя и нижняя полурешетка (рис. 3.1). Бели же мы
„срежем" у этого прямоугольника углы и рассмотрим, напри-
например, множество точек многоугольника ABCDEF на рис. 3.2, то
это множество не будет ни верхней, ни нижней полурешеткой,
так как, скажем, множество {A, F} не имеет inf, а множество
{С, D} не имеет sup. Бели мы „срежем" только один угол,
левый нижний или правый верхний, то получим верхнюю или
нижнюю полурешетку соответственно.
в. На рис. 3.3 изображена диаграмма Хассе множества,
не являющегося ни верхней, ни нижней полу-
полурешеткой. Действительно, множество {d, e} d
не имеет точной верхней грани, хотя имеет
точную нижнюю грань: inf {d, e} = с. Анало-
Аналогично множество {а, 6} не имеет точной ниж-
нижней грани, хотя имеет точную верхнюю грань:
sup{a,6} = c. # Рис. 3.3
216 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Полурешетка, как полугруппа, может быть моноидом, т.е.
может иметь нейтральный элемент. Нейтральный элемент
верхней полурешетки (L, V) называют нулем полурешетки
и обозначают 0, называя при этом саму полурешетку верхней
полурешеткой с нулем. Двойственным образом нейтральный
элемент нижней полурешетки (L, Л) называют единицей по-
лурешетки, используя обозначение 1 и называя эту полуре-
полурешетку нижней полурешеткой с единицей.
Для нуля полурешетки (L, V, 0) имеем а V 0 = а для всякого
а е L, т.е. нуль полурешетки есть ее наименьший элемент.
Двойственным образом единица полурешетки (L, Л, 1) есть ее
наибольший элемент.
Пример 3.15. а. Прямоугольник [а, Ь] х [с, d] (см. при-
пример 3.14.6 и рис. 3.1) — одновременно и нижняя полурешетка с
единицей, которой служит точка F, rf), и верхняя полурешет-
полурешетка с нулем, которым является точка (а, с). Прямоугольник со
„ срезанныма правым верхним углом — нижняя полурешетка,
но без единицы полурешетки.
б. Отрезок [а, Ь]сК (при любых его границах) есть одно-
одновременно и нижняя полурешетка с единицей, которой является
число Ь, и верхняя полурешетка с нулем. Им служит число а.
Полуинтервалы (а, 6] и [а, Ь) суть соответственно нижняя по-
полурешетка с единицей и верхняя полурештка с нулем. Заметим,
что одновременно первый полуинтервал есть верхняя полуре-
полурешетка, не имеющая нуля, а второй полуинтервал — нижняя
полурешетка без единицы.
Интервал (а, Ь) есть одновременно и нижняя и верхняя полу-
полурешетка, но ни та, ни другая не имеет нейтральных элементов.
в. Индуктивное упорядоченное множество в общем случае
не является верхней полурешткой с нулем, хотя и имеет наи-
наименьший элемент. Дело в том, что двухэлементное подмноже-
подмножество этого множества, состоящее из несравнимых элементов,
может и не иметь точной верхней грани, поскольку точную
верхнюю грань имеет в этом множестве любая неубывающая
3.5. Решетки 217
последовательность и, как можно показать, любая конечная или
счетная цепь.
Индуктивное линейно упорядоченное множество является
верхней полурешеткой с нулем. Обратное неверно. Так, множе-
множество всех неотрицательных вещественных чисел (с естествен-
естественным числовым порядком) есть верхняя полурешетка с нулем, но
ни одна возрастающая последовательность в этом множестве не
имеет точной верхней грани. #
Рассмотренные выше примеры показывают, что существу-
существуют упорядоченные множества, являющиеся нижней и верхней
полурешетками одновременно. Бели такая „ связка" полуре-
полурешеток имеет определенные дополнительные свойства, то она
называется решеткой.
Определение 3.5. Решетка — это алгебра С = (L, V, Л)
с двумя бинарными операциями, такая, что каждая из алгебр
(L, V) и (L, Л) является полурешеткой и выполняются следую-
следующие тождества поглощения:
aV(aAb)=a, aA(aVb)==a.
Операции решетки V и Л называют решеточным объ-
объединением и решеточным пересечением соответственно.
Операции решетки называют также решеточными опера-
циями.
Другими словами, решетка — это алгебра с двумя бинар-
бинарными операциями, обозначаемыми V и Л, такими, что выпол-
выполняются тождества
c, аЛ(бЛс) = (аЛЬ)Лс,
= 6Ла,
Из определения решетки следует, что всякое симметричное
полукольцо и, значит, любая булева алгебра являются решет-
решетками, т.е. сложение и умножение симметричного полукольца.
218 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
равно как и булево объединение и булево пересечение, есть при-
примеры решеточных операций. Тогда и булева алгебра Sa всех
подмножеств некоторого множества -А, и полукольцо Vn всех
делителей натурального числа п — примеры решеток.
Приведем пример решетки, не являющейся полукольцом.
Пример 3*1в. Алгебра ((a, Ь), max,min), носитель кото-
которой — открытый интервал на числовой прямой, а операции —
взятие наибольшего и наименьшего из двух чисел (относитель-
(относительно естественного числового порядка), есть решетка. Однако
отсутствие нейтральных элементов по данным операциям не
позволяет считать данную алгебру полукольцом. #
Заметим, что решеточные операции в общем случае и не
дистрибутивны (хотя в только что рассмотренном примере 3.16
дистрибутивность каждой операции относительно другой име-
имеет место). Конкретные примеры недистрибутивных решеток
будут приведены ниже.
Выясним теперь связь между понятием решетки и понятием
упорядоченного множества. Каждая решетка, как следует из
определения, есть „связка" двух полурешеток, но априори со-
совсем не очевидно, что естественные порядки этих полурешеток
суть взаимно двойственные порядки, т.е. для любых а, 6 Е L не-
неравенство а < 6, равносильное равенству а V Ь = 6, имеет место
если и только если aAb = a. Такую связь между решеточными
операциями устанавливает следующая теорема.
Теорема 3.12. В любой решетке С = (L, V, Л) естествен-
естественный порядок ^ полурешетки (L, V) есть порядок, двойствен-
двойственный к естественному порядку полурешетки (L, Л), т.е. для
любых а, Ь € L имеет место равенство
т.е. о V Ь = sup {a, 6} и а Л Ь = inf {о, Ь}.
< Согласно определению естественного порядка полурешетки,
для любых а, Ь 6 L выполняется условие a^6^aV6 = 6. Мы
3.5. Решетки 219
должны доказать, что двойственный порядок > совпадает с
естественным порядком полурешетки (L, Л), т.е. нужно дока-
доказать, чтоа^Ь«?>аЛЬ = 6или, что равносильно,
Для этого достаточно показать, что a\/b = b
Имеем: если а V Ь = 6, то аЛЬ = аЛ(aV Ь). Согласно второму
тождеству поглощения, а Л (а V 6) = а, и поэтому о Л Ь = а; если
же а Л Ь = о, то с учетом первого тождества поглощения будем
иметь а V Ь = (а Л 6) V Ь = Ь.
Итак, естественные порядки полурешеток (L, Л) и (L, V)
взаимно двойственные. Так как в силу теоремы 3.10 sup {a, 6} =
= а V 6 для любых а, Ь € L, то, согласно принципу двойственно-
двойственности, inf {a, 6} = а Л Ь. >
Обратим внимание на использование тождеств поглощения
при доказательстве теоремы 3.12. Именно они делают есте-
естественные порядки полурешеток (L, V) и (L, Л) взаимно двой-
двойственными.
Таким образом, любая решетка С = (L, V, Л) есть в то же
время упорядоченное множество (L, ^), где отношение поряд-
порядка < совпадает с естественным порядком полурешетки (L, V),
которая тогда будет верхней полурешеткой. Полурешетка же
(L, Л) оказывается (относительно этого же отношения поряд-
порядка) нижней полурешеткой. Первую полурешетку поэтому часто
называют верхней полурешткой решетки ?, а вторую полуре-
полурешетку — нижней полурешеткой той же самой решетки. Само
же отношение порядка < называют естественным поряд-
порядком решетки С.
Можно доказать утверждение, обратное к теореме 3.12.
Теорема 3.13. Любое упорядоченное множество С = (L, <),
в котором всякое двухэлементное подмножество имеет точную
верхнюю и точную нижнюю грани, т.е. для любых а, 6 € L
существуют sup {а, 6} и inf {а, 6}, является решеткой в смысле
определения 3.5, в которой решеточные операции определяются
так:
= sup {a, Ь}, о Л 6 = inf {a, 6}.
220 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
При этом естественный порядок решетки (L, sup, inf) совпада-
совпадает с исходным порядком <.
< То, что каждая из алгебр (L, sup) и (L, inf) является полуре-
полурешеткой, равно как и то, что естественный порядок первой по-
полурешетки совпадает с исходным порядком ^, а естественный
порядок второй полу решетки двойствен к порядку <, следует
из теорем 3.10 и 3.11. Остается доказать тождества поглоще-
поглощения. Достаточно доказать одно из них, так как второе будет
выполняться в силу принципа двойственности (для упорядочен-
упорядоченных множеств).
Итак, докажем, что для любых a, b Е L выполняется равен-
равенство
inf {a, sup {а, Ь}} = а. C.34)
Равенство C.34) следует из того, что для любых элементов
c,d€ L из того, что с < d, следует, что с = inf {с, d}. Тогда в
силу неравенства а ^ sup {а, 6} имеем C.34). >
Важность последнего результата состоит в том, что по-
полурешетку можно задавать как упорядоченное множество с
точными верхними и точными нижними гранями для любой па-
пары элементов. Иными словами, для того чтобы убедиться, что
перед нами решетка, достаточно проверить это свойство.
Пример 3.17. а. Рассмотренный в примере 3.14.6 прямо-
прямоугольник [а, Ь] х [с, d\ есть решетка (см. рис. 3.1), но если мы
срежем" у этого прямоугольника углы и рассмотрим, напри-
например, множество точек многоугольника ABCDEF на рис. 3.2,
то это множество уже не будет решеткой, так как, скажем,
множество {A, F} не имеет inf, а множество {С, D} не имеет
sup.
б. Не является решеткой и конечное упорядоченное мно-
множество, диаграмма Хассе которого изображена на рис. 3.3.
Здесь sup {а, 6} = с, но inf {а, 6} не существует. Аналогично
inf {d, e} = с, но sup{rf, e} не существует.
3.5. Решетки
221
в. Декартов квадрат множества целых чисел 1? — решет-
решетка, где упорядоченные пары целых чисел упорядочиваются ана-
аналогично точкам плоскости (см. пример 3.17.а). Относительно
этого же отношения порядка решеткой
будет и любой „целочисленный прямо-
прямоугольник" [а...6] х [c...d], где [m...n]
обозначает множество всех целых чи-
чисел р, таких, что т ^р ^п (т ^ п).
Этот „прямоугольник" и графически
выглядит как „решетка", что видно
на рис. 3.4, на котором изображено
множество [1... 5] х [1...4]. #
1
| Л
1 1
1 i
1 1
12 3 4
Рис. 3.4
Бели верхняя полурешетка решетки С = (L, V, Л) есть по-
полурешетка с нулем, то этот нуль является наименьшим эле-
элементом решетки С. Тогда ее называют решеткой с нулем, а
нуль полурешетки (L, V) — нулем решетки С. Двойствен-
Двойственным образом единица нижней полурешетки (L, Л), если она
существует, является наибольшим элементом решетки С. Эту
единицу тогда называют единицей решетки ?, а саму ре-
решетку — решеткой с единицей.
Таким образом, решетка с нулем имеет нейтральный эле-
элемент по операции решеточного объединения (и ее верхняя полу-
полурешетка превращается в моноид), а решетка с единицей имеет
нейтральный элемент по операции решеточного пересечения (и
моноидом становится уже ее нижняя полурешетка). Кроме то-
того, из теоремы 3.12 следует, что а Л 0 = 0 для любого о G L
(соответственно а V1 = 1 для любого a G L ), т.е. выполняются
аналоги аннулирующих свойств в симметричных полукольцах.
Симметричное полукольцо является примером решетки с нулем
и единицей.
Пример 3.18. На рис. 3.1 прямоугольник [а, 6] х [с, d\
является решеткой с нулем и единицей, причем 0 = (а, с), 1 =
222
3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Рассмотрим теперь вместо отрезка [а, Ь] промежуток А =
= {х: х < 6} « означает здесь естественный числовой порядок).
Тогда множество А х [с, d] при сохранении того же отноше-
отношения порядка на М2, что и в примере 3.17, будет решеткой с
единицей, равной F, d). Нуля у этой решетки не будет (ес-
(если рассматривать, конечно, нерасширенную числовую прямую,
точнее, не включать в нее —оо). Бели же вместо отрезка [а, Ь]
взять также неограниченный промежуток В = {х: х^а}, то
Bx[c,d\ будет решеткой с нулем, равным (а)с. Если опять-таки
считать, что элемент +оо не принадлежит R, то эта решетка
не будет иметь единицу. #
В общем случае в решетке не имеет места дистрибутив-
дистрибутивность одной из операций относительно другой. На рис. 3.5
и 3.6 приведены диаграммы Хассе решеток, называемых со-
соответственно Пентагоном и диамантом. В каждой из них
ни одна из операций не является дистрибутивной относительно
другой. Так, например, в первой из них а Л (Ь V с) = а Л1 = а,
но (а Л Ь) V (а Л с) = Ь V 0 = 6. Для второй решетки аЛ(Ь\/с) =
= аЛ1 = а, тогда как (аЛЬ) V(а Ас) = О V0 = 0.
Определение 3*6. Решетку С = (L, V, Л) называют дис-
дистрибутивной, если для любых a,b, c€L имеют место равен-
равенства
() (
aA(bVc)==(aAb)V(aAc).
Теперь мы можем дать в терминах решеток характеристику
симметричных полуколец и булевых алгебр.
Вопросы и задачи 223
Теорема 3.14. Симметричное полукольцо — это дистри-
дистрибутивная решетка с нулем и единицей.
Булева алгебра — это дистрибутивная решетка с нулем
и единицей, в которой для каждого элемента х существует
дополнение, т.е. такой элемент а?, что а; V я = 1 и а; Л а; = 0.
Доказательство теоремы 3.14 мы не приводим, так как
оно является непосредственным следствием определений 3.3, 3.4
и 3.6.
Теория решеток находит многочисленные применения в те-
теории графов и теоретическом программировании. В специ-
специальной литературе на базе теории решеток развиты стройная
концепция типов данных в языках программирования и теория
типов данных*, хорошо изложены общая теория решеток** и ее
приложения к теории графов***.
Вопросы и задачи
3.1. Проверив аксиомы, убедиться, что алгебры, приведен-
приведенные в примере 3.3, являются полукольцами.
3.2. Выяснить, является ли алгебра ([0,1], шах, •) полуколь-
полукольцом.
3.3. В полукольце ?[o,i] (см. пример З.З.г) решить систему
линейных уравнений
+ 0,5ж2 + 0,1ж3 + 0,2,
х2 = 0,6xi + 0,8а?2 + 0,4ж3 + 0,6,
+ 0,4я?2 + 0,25ж3 + 0,1.
3.4* Привести примеры замкнутых полуколец из 4, 8 и 16
элементов.
*См.: Скотт Д. Теория решеток, типы данных и семантика
**См.: Гретцер Г.
***См.: Евстигнеев В.А.
224 3. ПОЛУКОЛЬЦА И БУЛЕВЫ АЛГЕБРЫ
Указание: рассмотреть алгебру Bм, U, П, 0, М), где
множество М конечно.
3.5. Доказать теорему 3.9.
3.6. Описать одноэлементную булеву алгебру. Доказать,
что булева алгебра одноэлементна тогда и только тогда, когда
в ней 0 = 1.
3.7. Доказать, что полукольцо Т>т является булевой алге-
алгеброй тогда и только тогда, когда т есть произведение попарно
различных простых чисел.
3.8. Пусть В = (В, V, Л, "", 0, 1) — булева алгебра. Опре-
Определим на носителе В операции 0 и • так:
Доказать, что 7?в = E, ©, •, 0, 1) — булево кольцо. Доказать,
что
3.9. Пусть TZ = (Я, ©, •, 0, 1) — булево кольцо (см. зада-
задачу 2.12). Определим на его носителе R операции V, Ли"" так:
Доказать, что Вя. = (R, V, Л, ~~, 0, 1) — булева алгебра. Пока-
Показать, что В%2 = В.
3.10. Показать, что для любых булевой алгебры В и булева
кольца П (см. задачу 2.12) ftg = П и ВПъ = В.
3.11. На носителе произвольного (т.е. не обязательно идем-
потентного) полукольца S = E, +, •, 0, 1) определим бинарное
отношение •< так, что х ^ у Ф> (Эг)(г/ = х + z). Является ли это
бинарное отношение порядком или предпорядком? Как интер-
интерпретируется это отношение для кольца?
3.12. Пусть полукольцо S = E, +, •, 0, 1) таково, что в его
аддитивном моноиде справедлив закон сокращения, т.е. для
Вопросы и задачи 225
любых ж, у, a Е S из равенства ж + а = у + а следует равенство
х = у, а также для любых а, 6 € 5 из того, что а + Ь = О,
следует а = Ъ = 0. Доказать, что тогда бинарное отношение ^,
введенное в задаче 3.11, является порядком. Привести пример
такого полукольца. При каких условиях полукольцо с такими
свойствами будет идемпотентным?
3.13. Доказать, что в полукольце бинарных отношений на
n-элементном множестве итерация любого бинарного отноше-
отношения равна сумме всех его степеней, начиная с нулевой и кон-
п
чая n-й, т.е. р* = (J р . Доказать, что аналогичное свойство
справедливо для полукольца квадратных матриц над полуколь-
полукольцом В.
3.14. Доказать подробно, что метод последовательного ис-
исключения неизвестных при решении систем линейных уравне-
уравнений в замкнутых полукольцах (или в полукольцах с итерацией)
действительно дает наименьшее решение системы.
Указание: воспользоваться методом математической ин-
индукции и доказать, что на каждом шаге прямого хода метода
Гаусса мы получаем очередную компоненту наименьшего реше-
решения; при этом использовать непрерывность (и, следовательно,
монотонность) операций сложения и умножения.
3.15. Доказать, что идемпотентность решеточных опера-
операций вытекает из тождеств поглощения.
3.16. Доказать, что алгебра (А, V, Л) является решеткой
тогда и только тогда, когда (Ау V) и (-А, Л) — полурешетки, и
равенство a = aAb равносильно равенству 6 = aVЬ.
3.17. Пусть алгебры (А, Л, Vi) и (А, Л, N/г) (с одним и
тем же носителем) являются решетками. Доказать, что тогда
операции Vi и V2 совпадают.
3.18. Нарисовать диаграммы Хассе всех решеток, состоя-
состоящих не более чем из шести элементов.
4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
При решении многих математических задач (задач дискрет-
дискретной математики, в частности) используются более сложные
структуры, чем „множества с операциями". Например, изучая
множество действительных чисел, мы имеем дело не только с
операциями над числами, но и с определенными отношения-
отношениями на множестве действительных чисел, такими, как, скажем,
естественный числовой порядок. Важейшая структура — упо-
упорядоченное множество — вообще определяется без каких-либо
операций. Таким образом, мы приходим к необходимости изу-
изучения „множеств с операциями и отношениями", в частности
„множеств с отношениями" (примерами которых служат упоря-
упорядоченное множество, индуктивное упорядоченное множество,
множество, на котором задано некоторое отношение предпо-
рядка, эквивалентности и т.п.). Это приводит нас к понятиям
„алгебраической системы" и „модели".
В этой главе изучаются некоторые результаты общей тео-
теории алгебраических систем, в том числе обобщаются конструк-
конструкции, которые были введены в двух предшествующих главах.
Материал этой главы будет использован затем в теории гра-
графов, булевых функций и языков.
4.1. Модели и алгебры
Алгебраическая система — это упорядоченная тройка
Л= (А, пу П), где А — некоторое множество, называемое но-
носителем алгебраической системы; Q — некоторое множество
операций на -А, П — некоторое множество отношений на А.
Упорядоченную пару (ft, П) называют сигнатурой алгебраи-
алгебраической системы.
4.1. Модели и алгебры 227
Алгебраическую систему называют конечной, если ее но-
носитель — конечное множество.
Обозначая через ft(n) подмножество всех п-арных операций
в ft, цолучим ft = (J п(п\ Точно так же П = (J П(п), гдеП<п)—
подмножество всех п-арных отношений.
Алгебраическая система, у которой множество П отноше-
отношений пусто (П = 0), есть не что иное, как п-алгебра (см. 2).
Алгебраическую систему, у которой пусто множество опера-
операций (ft = 0), называют моделью.
Замечание 4.1. Докажем, что n-арная операция на мно-
множестве А есть частный случай отношения на этом множе-
множестве. Действительно, если и: Ап -> А — n-арная операция,
то определим (п + 1)-арное отношение рш С An+1 так, что
кортеж, (oi, ..., ап, 6) Е рш тогда и только тогда, когда Ь =
= o;(ai, ..., an). Понятно, что это отношение функционально
по (п + 1)-й компоненте. С учетом этого любая алгебраиче-
алгебраическая система может рассматриваться как модель. #
Мы рассмотрели много примеров алгебр (см. 2 и 3). В
некоторых из них были введены отношения, например есте-
естественный порядок полукольца, естественный порядок булевой
алгебры, естественный порядок решетки. Эти отношения ра-
разумно ввести в сигнатуру и рассматривать указанные алгебры
как алгебраические системы, тем более что указанные отноше-
отношения определяли важнейшие свойства названных алгебр.
Пример 4.1. а. Одной из основных моделей в математике
является упорядоченное множество. Сигнатура этой модели
состоит из единственного отношения порядка. Важным част-
частным случаем служит индуктивное упорядоченное множество.
б* Как уже было замечено, любое полукольцо, в частно-
частности замкнутое полукольцо, является алгебраической системой,
сигнатура которой помимо операций полукольца содержит от-
отношение естественного порядка полукольца.
228 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Рассмотрим теперь некоторое поле Т = (F, +, •,0,1), множе-
множество всех ненулевых элементов которого разбито на подмноже-
подмножества Р и N. Другими словами, по определению полагаем, что
для каждого а Е F выполняется в точности одно из трех усло-
условий: а€ Р, а = О или a G N. Элементы Р назовем (условно)
положительными, а элементы N — отрицательными элемен-
элементами данного поля. При этом, по определению, выполняются
следующие условия:
1) для каждого a€F а отрицательно тогда и только тогда,
когда —а положительно, т.е. —a Е Р;
2) если а, б€Р, то а + бЕРиа&Е Р.
Введенные условия вполне естественны: первое означает,
что элемент, противоположный к отрицательному, является по-
положительным и наоборот, а второе — что сумма и произведение
положительных элементов положительны.
Введем теперь на множестве F бинарное отношение < так,
что a<b<&b — aeP (читается: а „меньше" 6, по определению,
если разность Ь — а есть положительный элемент). Естествен-
Естественно, полагаем, что а ^ Ь означает а <Ь или а = Ь. Можно по-
показать, что введенное таким образом отношение ^ на носителе
поля Т является отношением линейного порядка, т.е. для любых
двух элементов a,b€ F или а < 6, или Ь < а.
Поле вместе с отношением порядка, введенным указанным
образом, называют упорядоченным полем. Таким обра-
образом, упорядоченное поле можно рассматривать как алгебра-
алгебраическую систему То = (Р? +5 •> 0, 1, <), в которой алгебра
T=(Fy +, •, 0, 1) является полем, а отношение порядка ^ опре-
определено так, как сказано выше.
Пусть, кроме этого, отношение порядка в упорядоченном
поле обладает следующим свойством непрерывности: ка-
каковы бы ни были непустые множества AcFaBcF^y которых
для любых двух элементов а Е А и b E В выполняется а ^ Ь, суще-
существует такой элемент а, что для всех а Е А и b E В выполняется
двойное неравенство а ^ а ^ 6. Тогда получаем алгебраиче-
АЛ. Модели и алгебры 229
скую систему, называемую непрерывным упорядоченным
полем. Важнейший пример непрерывного упорядоченного по-
поля — поле действительных чисел.
Заметим, что поле рациональных чисел, являясь упорядочен-
упорядоченным псцем, уже не будет непрерывным. Это вытекает из того,
что можно построить такие два собственных подмножества
А,В С Q, что для всех о ? А и для всех b ? В будет иметь ме-
место а < Ь, но нельзя найти такое рациональное число г, чтобы
выполнялось (VaЕ j4)(V6€B)(a^r^b). Такими двумя подмно-
подмножествами А и В в множестве рациональных чисел могут быть,
например, В = {q: q2 > 2}, А = Q\ В. Дело в том, что, как мож-
можно убедиться, не существует наибольшего рационального числа
в множестве А. В множестве же R наибольшее из всех чисел,
квадрат которых не больше 2, существует и равно у/2. #
Две алгебраические системы
Лг = (Аи Пь ПО иЛ2 = (А2, П2, П2)
называют однотипными, если между множествами операций
fti и U2 существует взаимно однозначное соответствие, ото-
отображающее fli в ^2> ^ ^ 0, а между множествами отношений
111 и Пг можно установить взаимно однозначное соответствие,
при котором III соответствует Щ f n ^ 0.
Таким образом, для однотипных алгебраических систем
*Ai = (Ai, ^ъ Hi) и Дг = (^2? ^2) Пг) любой n-арной опера-
операции из О,\ (любому n-арному отношению из ГЦ) может быть
однозначно сопоставлена n-арная операция из 0,2 (n-арное от-
отношение из Пг).
Например, алгебраическая система (Z, —, +, •, <) с опе-
операциями — (унарный минус — переход к противоположному
числу), + (сложения), • (умножения) и отношением ^ естествен-
естественного числового порядка однотипна с алгебраической системой
(Q) —, +, •, ^) с теми же операциями, а также с алгебраиче-
алгебраической системой Bм, "", U, П, С) (для некоторого множества М)
с операциями дополнения, объединения, пересечения множеств
230 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
и отношением включения. В первом случае операции и отноше-
отношения, заданные на разных множествах (целых и рациональных
чисел), обозначены одинаковыми символами; во втором случае
однотипные алгебраические системы имеют разные обозначе-
обозначения операции и отношении.
В то же время две модели (А, р) и (J5, а), в которых р —
n-арное отношение на А, а а — m-арное отношение на В, при
п^тне будут однотипными.
Зачастую, если это не вредит точности, соответствующие
друг другу операции и отношения однотипных алгебраических
систем будем обозначать одинаковыми символами.
4.2. Подсистемы
Выше (см. 2) введены понятия подгруппы, подкольца, под-
поля, которые можно объединить в рамках общего понятия
подсистемы произвольной алгебраической системы, а также
понятия подалгебры произвольной С1-алгебры.
Пусть Л = (A, ft, П) — произвольная алгебраическая систе-
система и В С А — непустое множество.
Множество В называют замкнутым относительно опе-
операций из П (П-замкнутым множеством), если результат
применения любой п-арной операции из 17 к любым элементам
из В принадлежит В, т.е. для любой n-арной операции и и
любых элементов а\, ..., ап 6 В элемент и>{а\, ..., ап) Е В.
Например, в полугруппе (N, +) подмножество четных чи-
чисел замкнуто относительно операции сложения, а подмножество
нечетных чисел не замкнуто. В кольце целых чисел подмно-
подмножество натуральных чисел замкнуто относительно операциий
сложения и умножения, но не замкнуто относительно операции
взятия противоположного элемента.
Алгебраическую систему В = (J5, ?2, П|я), где В С А, назы-
называют подсистемой алгебраической системы Л, если В
П-замкнуто иИ\в есть множество ограничений на В всех от-
отношений из П: П|в = {р\в- Р € П}.
4.2. Подсистемы 231
Очевидно, что алгебраические системы Л и В однотипны,
и часто вместо П|# будем в таком случае писать просто П.
Если Л — алгебра, то любую ее подсистему называют ее
подалгеброй (точнее, П-подсмгеброй).
Замечание 4.2. В определении ft-подалгебры требует-
требуется лишь замкнутость относительно операций из п. Бели же
мы хотим, чтобы при переходе к подалгебре „наследовались"
какие-либо специальные свойства операций исходной алгебры,
то это нужно специально оговаривать. Именно так мы и по-
поступали, определяя понятия подгруппы, подкольца, подполя и
т.п. Впрочем, подгруппу можно определить и через свойство
замкнутости, но лишь в том случае, если в сигнатуру группы
включить не только одну бинарную операцию „умножения" (ко-
(которая обладает специальными „групповыми свойствами", см.
2.2), но также унарную операцию взятия обратного элемента
и нульарную операцию — единицу группы.
Аналогично, исключительно через требование замкнутости,
можно определить понятие подмоноида. Следовательно, таким
образом можно определить и подкольцо.
Сложнее обстоит дело с телом и полем. Мы не можем опре-
определить поле как алгебру с сигнатурой {+,*,—,~х,0,1}, где
операция — есть операция вычисления противоположного эле-
элемента (обратного по сложению), а операция ~х — операция
вычисления обратного элемента по умножению, так как послед-
последняя операция есть частичное отобраоюение и не определена для
элемента 0. Поэтому она не может быть введена в сигнатуру
алгебры, по определению содержащей только всюду определен-
определенные операции.
Обратим внимание и на то, что переходя к ^-замкнутому
подмножеству, мы можем получить алгебру как обогащенную
новыми свойствами операций сигнатуры Я, так и утратившую
некоторые из свойств. Например, моноид (No, +, 0) будет
только подмоноидом группы (Z, +, 0) (но не подгруппой), а
подмоноид биекций в симметрическом моноиде некоторого
232 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
бесконечного множества будет уже группой (это не подгруппа,
а именно подмоноид, являющийся группой!). #
В следующей теореме сформулировано простое, но очень
важное свойство замкнутых подмножеств.
Теорема 4.1. Непустое пересечение произвольного семей-
семейства ft-замкнутых подмножеств B-замкнуто.
4 Для простоты рассмотрим доказательство для пересечения
двух П-замкнутых подмножеств.
Пусть в алгебре (А, ?2) fi-замкнутые подмножества В\ и
i?2 имеют непустое пересечение. Тогда для любого п ^ 0, а
также любых (не обязательно различных) <*i, ..., ап Е В\ П 2?2
элемент a;(oi, ..., ап), какова бы ни была операция ш € п^п\
снова будет принадлежать пересечению В\ П 1?2, так как в
силу замкнутости каждого из множеств В\ и 2?2 одновременно
..., ап)еВх ии(аи ..., ап)еВ2 >
Рассмотрим алгебру Л = (А, О) и подмножество J5 С Л, не
обязательно П-замкнутое.
Из теоремы 4.1 следует, что существует ?2-замкнутое под-
подмножество, совпадающее с пересечением всех Г2-замкнутых
подмножеств, содержащих В. Его называют замыканием
подмножества В относительно операций из Q (или Ct-за-
мыканием подмножества В) и обозначают [B]q. Хотя бы
одно fi-замкнутое подмножество, содержащее В, обязательно
найдется — весь носитель А. В том случае, когда [В]п = А,
подмножество В называют системой образующих алгебры
А=(А,?1), а ее саму называют алгеброй, порожденной
множеством В. Алгебру, которая имеет конечную систему
образующих, называют конечно порожденной.
Замечание 4.3. Определение замыкания можно предста-
представить и в несколько иной форме, которая содержательно ассо-
ассоциируется с некоторой процедурой построения множества [B]q
по шагам.
4.2. Подсистемы 233
Определим семейство множеств (В$)^о> полагая Во = В, а
Таким образом, множество В\ состоит из всех элементов
Во = В* и к ним добавляются все элементы, которые могут
быть получены как результат применения операций сигнатуры
12 к аргументам операции из Во. Множество 2?2 точно так
же содержит все элементы множества В\ плюс все результаты
применения операций из п к аргументам из В\ и т.д. По
определению, В = Bq С В\ С 2?2 С ... С В% С Bj+i С ..., т.е. для
любого j; ^ О имеют место включения J3j С Sj+i и В» С [B]q С А.
Можно показать, что [B]q = |J B{.
Замкнутость В означает с точки зрения такого определе-
определения, что все множества В% совпадают с множеством В. Кроме
того, может оказаться, что процесс образования множеств В{
„оборвется на некотором шаге", т.е. найдется такое г, что
Д-+1 = Д. Тогда В{ = [В]п.
Для конечной алгебры описанную выше процедуру можно
рассматривать как алгоритм построения замыкания исходного
множества (при том, что каждой операции сопоставлен некий
алгоритм ее вычисления). На первом шаге алгоритма в за-
замыкание [B]q помещают все элементы множества В, а затем
применяют операции сигнатуры ?1 к исходным и вновь полу-
получаемым элементам до тех пор, пока не перестанут появляться
новые элементы.
Иначе это можно описать так:
1) все элементы множества Во считаются и элементами
замыкания [В]п;
2) каковы бы ни были элементы 6i, ..., 6П, относительно ко-
которых известно, что они принадлежат [B]q (т.е. какому-то мно-
множеству В{ из определенного выше семейства), к имеющимся эле-
элементам замыкания [В]п добавляют все элементы cjFi, ..., 6П)
для произвольной n-арной операции ш сигнатуры ft.
234 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Никакие другие элементы, кроме тех, что могут быть
получены рассмотренным выше способом, замыканию [B]q не
принадлежат.
Образно говоря, В — это „детали конструктора", a [B]q —
все, что можно собрать из этих деталей по некоторым заранее
оговоренным „правилам сборки" (каковыми являются операции
сигнатуры U). #
Рассмотрим примеры построения ft-замыкания.
Пример 4.2. а. В алгебре (N, +) возьмем одноэлементное
множество В = {1} = Во. Тогда Вх = {1,2}, В2 = {1,2,3,4},
В$ = {1, 2,3,4,5,6,7,8} и т.д. Множество В{ при г ^ 1 состоит
из всех сумм вида т + п, где m, n Е В%-\. Несложно заметить,
что Bi = {1,2,..., к,..., 2fc}, где к = 2*, % ^ 0. Ясно, что в
данном случае (J J5» = N, и, таким образом, множество {1}
является системой образующих этой алгебры.
б. В мультипликативной группе вычетов по модулю 23
(т.е. в группе Z^) построим замыкание множества В = {3},
полагая, что сигнатура группы состоит из единственной опе-
операции умножения (по модулю 23).
Поскольку в этой алгебре сигнатура состоит из одной опе-
операции, а исходное множество В также одноэлементно, то за-
замыкание В будет состоять из всех степеней элемента 3. Итак,
для построения замыкания множества В в данном случае до-
достаточно вычислять последовательно степени (по модулю 23)
элемента 3. Имеем
32 = 9, 33 = 4, 34 = 4-3 = 12, 35 = 123 = 13,
З6 = 13 • 3 = 16, 37 = 16-3 = 2, З8 = 2-3 = 6,
З9 = 6-3 = 18, 310 = 18-3 = 8, З11 =8-3 = 1.
Так как получена единица, то „круг замкнулся", и тем самым
вычислено замыкание множества {3}. Заметим, что в этом
случае множество В\ состоит из всех степеней тройки, начиная
с первой и кончая второй, множество В2 — из всех степеней,
начиная с первой и кончая четвертой, множество Вз — из
4.2. Подсистемы 235
всех степеней с первой по восьмую, а множество В± — из всех
степеней с первой по 16-ю, но поскольку начиная с 12-й степени
элементы повторяются, т.е. З12 = 3, З13 = З2, З14 = З3, З15 = З4 и,
наконец, З16 = З5, то уже множество В$ совпадет с множеством
J?4, так что в данном случае [#]{.} = В\.
Порожденная множеством {3} группа совпала с циклической
подгруппой группы Z23 с образующим элементом 3. Этот ре-
результат легко обобщить, доказав, что для произвольной конеч-
конечной группы G = (G, ), рассматриваемой как алгебра с сигнату-
сигнатурой, состоящей только из операции умножения, ее циклическая
подгруппа с образующим элементом а совпадает с подгруппой,
порожденной множеством {а}. #
Циклическая группа есть один из важнейших примеров
конечно порожденной алгебры.
В этой связи обратим внимание на одну тонкость. Бели
Q — циклическая группа с образующим элементом а, то ее,
вообще говоря, нельзя рассматривать как алгебру с системой
образующих {а}. Все зависит от конкретной сигнатуры груп-
группы. Действительно, если в сигнатуру группы включить только
умножение, то для бесконечной циклической группы 1 ф ап для
любого положительного п. Поэтому замыкание множества {а}
относительно умножения не содержит единицу. Если же сигна-
сигнатуру группы как алгебры дополнить унарной операцией взятия
обратного, т.е. возведения в степень —1, то циклическая группа
с образующим элементом а будет алгеброй с системой обра-
образующих {а}. При таком подходе аддитивная группа целых
чисел, рассматриваемая как алгебра (Z, +, —, 0), есть беско-
бесконечная циклическая группа, порожденная множеством {1}.
Пример 4*3. а. Алгебра (Z, *, 1) (мультипликативный
моноид кольца целых чисел) не является конечно порожденной.
Действительно, в этом моноиде в систему образующих необхо-
необходимо включить все простые числа, поскольку ни одно из них
нельзя представить как произведение других чисел. Но множе-
множество простых чисел бесконечно.
236 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
б. Любая конечная алгебра будет, разумеется, и конечно по-
порожденной. В частности, любое кольцо вычетов по модулю к
(поле вычетов при простом к) — конечно порожденная алге-
алгебра, даже если в сигнатуре нет операции нахождения обратного
элемента.
в. Свободный моноид, порожденный конечным множеством
(алфавитом) А есть конечно порожденная (и бесконечная)
алгебра, система образующих которой равна Аи {Л}, где А —
пустой кортеж.
г. Хорошим примером замыкания служит линейная обо-
оболочка заданного множества векторов произвольного линейного
пространства [IV]. Как известно, линейная оболочка V мно-
множества векторов xi, ..., хт линейного пространства L есть
т
множество всех линейных комбиниций вида ]Г) сад, где Х{ Е V,
i
% = 1, m, т ^ 1. Линейная оболочка замкнута относительно опе-
операций сложения векторов и умножения вектора на число, так
как линейная оболочка множества векторов является линейным
подпространством. Более того, линейная оболочка V множе-
множества векторов #1, ..., хт — это наименьшее (относительно
отношения включения множеств) замкнутое множество, содер-
содержащее заданное множество векторов, поскольку любое замкну-
замкнутое множество, содержащее векторы a?i,..., xm, содержит и все
их линейные комбинации, т.е. включает в себя V. Отметим, что
конечномерное линейное пространство — конечно порожденная
алгебра, так как оно является линейной оболочкой любого из
своих базисов.
4.3. Конгруэнции и фактор-системы
В этой главе нам будет удобно использовать п бесскобоч-
бесскобочную" запись для обозначения результата применения п-арной
операции и к элементам ai, ..., ап и писать а\...апи вместо
..., ап).
4.3. Конгруэнции и фактор-системы 237
Отношение эквивалентности р на носителе алгебраиче-
алгебраической системы Л называют конгруэнцией на алгебраической
системе Л, если выполняются условия:
1) для любой n-арной (п ^ 1) операции и и любых элементов
аь ..., an, 6i,..., Ьп Е Л из того, что щ рbi для каждого г = 1,п,
следует (аг... ano;) p (&i... Ьпи)\
2) для любого n-арного (п ^ 1) отношения тг и для любых
элементов ai, ..., an, &i, ..., bn ? А из того, что щрЬ^ для
каждого i = Т~п и (аь ..., ап) € тг, следует (Ьь ..., 6n) G тт.
Первое условие означает, что результаты применения любой
операции из С1 к попарно эквивалентным аргументам должны
быть эквивалентными, а второе — что любое отношение из П
содержит или не содержит кортеж (&i, ..., bn) независимо от
того, какие именно элементы Ь{ выбираются в соответствую-
соответствующем классе эквивалентности по отношению р.
Пример 4.4. а. Рассмотрим (R, +, •, 0, 1) — поле дей-
действительных чисел. Докажем, что отношение равенства по
модулю 1 (см. пример 1.14) не является конгруэнцией на этом
поле, но является конгруэнцией на (Е, +, 0) — его аддитивной
группе, т.е. на аддитивной группе действительных чисел.
Докажем сначала второе утверждение.
Пусть а = Ъ (mod 1) и с = d (mod 1). Тогда числа а — Ъ и с — d
являются целыми. Следовательно, и их сумма
тоже целое число, т.е. a + c = b + d (mod 1). Это и означает, что
отношение равенства по модулю 1 является конгруэнцией на
аддитивной группе действительных чисел.
Пусть, как и выше, а = b (mod 1) и с = d (mod 1). Бели бы
(для любых а, Ь, с, d) отсюда следовало, что a-c = b-d (mod 1), то
тогда дробная часть а • с всегда совпадала бы с дробной частью
Ь • d. Но каждое число равно по модулю 1 своей дробной части.
Следовательно, тогда дробная часть произведения любых двух
238 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
чисел должна была бы равняться произведению дробных частей
этих чисел. Простой пример, приведенный ниже, показывает,
что это не так.
При Ь = а = 1,1 имеем а = 0,1 (mod 1), Ь = 0,1 (mod 1) и 0,12 =
= 0,01. Так как аЬ = 1,12 = 1,21, то аЬ = 0,21 (modi). Это и
означает, что равенство по модулю 1 не есть конгруэнция на
поле действительных чисел (R,+,-,0,l).
б. Пусть (Z, +, •, 0, 1) — кольцо целых чисел. Отношение
равенства по модулю &, введенное в разд. 2*3, будет конгруэн-
конгруэнцией на данном кольце.
Действительно, пусть т = п (modfc) и г = s (mod А;). Тогда
существуют такие целые числа 1\ и fe
m-n = /i-A;, r-s = l2-k. D.1)
Складывая уравнения системы D.1), получаем
т.е. га + г = n + s (modк). Умножая первое уравнение системы
D.1) на г, второе — на п и складывая результаты, получаем
mr — ns =
т.е. mr = ns (mod к), что и доказывает сформулированное выше
утверждение.
в. Рассмотрим алгебраическую систему (Z, +, •, 0, 1, ^),
образованную из кольца целых чисел добавлением отношения ^
(естественного числового порядка). Тогда равенство по мо-
модулю к уже не будет конгруэнцией на данной алгебраической
системе. Действительно, если, скажем, а и Ь при делении на к
дают один и тот же остаток /, а с и d — один и тот же остаток
р, то из а ^ с не следует, вообще говоря, что Ъ < d. Например,
5 = 17 (mod4), б = 10 (mod4), 5 < 6, но 17 > 10. Таким образом,
отношение равенства целых чисел по модулю к не „сохраняет"
отношения <, т.е. справедливость неравенства а < Ь зависит от
4.3. Конгруэнции и фактор-системы 239
того, какие элементы а и Ь в соответствующих классах эквива-
эквивалентности выбраны.
г. Пусть в линейном пространстве L фиксировано линей-
линейное подпространство V. Рассмотрим L как модуль над полем
действительных чисел (R, +, •, 0, 1). На множестве векторов L
зададим отношение ~v так: а ~у Ьоа — bEV. Нетрудно пока-
показать, что это отношение экивалентности. Далее, если а ~у Ь и
c~vd> то а + с—F+d) = (a —6) + (c —d) € F, поскольку каждое
слагаемое в последней сумме есть вектор из подпространства
V. Для произвольного действительного а из а ~у Ь следует,
что аа ~v <*Ь, так как аа — ab = а(а — b) E V. Таким образом,
введенное отношение есть1 конгруэнция на линейном простран-
пространстве L.
Напомним, что множество векторов линейного простран-
пространства по сложению есть абелева группа. Следовательно, рас-
рассмотренное отношение эквавалентности ~у есть конгруэнция
на этой группе. Покажем, что указанную конгруэнцию можно
распространить на произвольную абелеву группу. Пусть Q =
= (G, +, 0) — некоторая абелева группа, а Н = (Я, +, 0) —
произвольная подгруппа группы Q. Зададим отношение ~я
так: а~нЬ&a — b€H. Рассуждая так же, как и в случае мно-
множества векторов линейного пространства, можно показать, что
отношение ~я является конгруэнцией.
д. Пусть Л = (-А, ^) и В = {Ву -<) — упорядоченные мно-
множества. Зададим отображение /: А-> В так, чтобы оно было
монотонно, т.е. чтобы для любых а, Ь € А из а ^ 6 следова-
следовало /(а) г< /(Ь). Введем отношение эквивалентности ~/ на А
(см. 1.7), положив a~fb&f(a) = f(b). Выясним, будет ли это
отношение конгруэнцией на модели Л = (А, <).
Пусть а\ ~f 61, с*2 ~/ 02 и а\ ^ a*i. Тогда в силу монотонности
отображения / имеем f(ai) -< /(аг), а так как f(ai) = f(b\)
и /(аг) = /(Ьг), то и f(b\) X /(Ьг). Отсюда, однако, нельзя в
общем случае сделать вывод, что Ь\ < Ьг- На рис. 4.1 /B) ^ /D),
но элементы 2 и 4 не сравнимы. Данное отображение (как
240
4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Д1)=/B)=/C)
В
Рис. 4.1
нетрудно понять, монотонное) не будет конгруэнцией хотя бы
потому, что 1 ~f 2, но 1 < 4, а 2 и 4 не сравнимы.
Бели же отображение / таково, что а ^ Ь <^ f(a) ^ /(Ь), то
~f будет конгруэнцией. Например, если на диаграмме Хассе
для множества Л на рис. 4.1 добавить „ребро", соединяющее
элемент 2 с элементом 4 (см. штриховую линию), т.е. считать,
что 2 < 4, то можно будет получить конгруэнцию ~/ на множе-
множестве А. #
Согласно определению конгруэнции, на алгебраической си-
системе Л классы эквивалентности [ai]p, ..., [ап]р вместе с любой
n-арной (n ^ 1) операцией и однозначно определяют класс экви-
эквивалентности элемента [а\,.. апш]р. Другими словами, для любых
элементов х\ Е [ai]p, ..., хп € [ап]р класс эквивалентности эле-
элемента х\... япо; зависит только от классов эквивалентности эле-
элементов ж», t = l,n, но не зависит от выбора элемента в классе.
Таким образом, мы можем „перенести" операцию ш на
классы эквивалентности, положив
[ai)p... [ап]рш = [ах... апш].
Аналогично для любого n-арного (п ^ 1) отношения, по
определению, полагаем (для любого п ^ 1, любого тг ? П(п) и
любых ai, ..., an)
([ai]p, ..., [ап]р) G тг 4^ (ab ..., an) G тг,
4.3. Конгруэнции и фактор-системы 241
поскольку, согласно определению конгруэнтности, для любых
xi G [ai]p, ..., хпе [ап]р условие (х\, ..., хп) € тг зависит лишь
от классов эквивалентности элементов х^ ъ = 1, п.
Заметим, что в этом случае мы использовали одинаковые
символы (а; и 7г) для соответствующих операций и отношения
на разных множествах, опираясь на соглашение о сигнатурах
однотипных алгебраических систем.
Итак, операции и отношения исходной сигнатуры можно
перенести на множество классов эквивалентности по конгруэн-
конгруэнции р согласно приведенным выше формулам. Получаемая при
этом алгебраическая система {однотипная с исходной) имеет
в качестве носителя фактор-множество А/р. Ее называют
фактор-системой алгебраической системы А по конгру-
конгруэнции р и обозначают Л/р. В том случае, когда исходная
алгебраическая система Л является алгеброй (моделью), ее
фактор-систему А/р называют фактор-алгеброй (фактор-
моделью соответственно).
Пример 4.5. Вернемся к примеру 4.4.а. Конгруэнция,
определенная в этом примере, — не что иное, как отношение
~z (напомним, что для действительных чисел #, у х ~% у 4Ф
^ж-j/GZ, см. 2.6). Следовательно, фактор-алгебра (R, +, 0)
аддитивной группы целых чисел по конгруэнции равенства
по модулю 1 — это фактор-группа M/Z аддитивной группы
действительных чисел по нормальному делителю Z, т.е. по
подгруппе целых чисел. #
Пример 4.5 есть проявление общей связи между понятиями
конгруэнции и нормального делителя группы. Рассмотрим
этот вопрос подробно.
Пусть Q = (G, •, 1) — группа, а Ч = (Я, •, 1) — ее под-
подгруппа, являющаяся нормальным делителем. Отношение ~#>
определенное на носителе G исходной группы так, что
а~нЬ <& аН = Ь#,
242 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
есть, согласно теореме 2.11, эквивалентность. Докажем, что
~я является конгруэнцией. Для этого достаточно доказать,
что для любых а, 6, с, d € G из а~нс и b~#d следует ab~Hcd-
Имеем а~нс, и это означает, что аН = сН. Точно так же
ЬН = dH в силу b~nd. Так как Н — нормальный делитель,
то аЬН = аНЬН. Далее, аНЬН = cHdH, и, снова используя
свойство нормального делителя, получаем cHdH = cd#, откуда
Фактор-алгебра группы Q по конгруэнции ~я совпада-
совпадает (подчеркнем — не просто изоморфна, а именно совпада-
совпадает) с фактор-группой группы Q по нормальному делителю Н
(см. 2.8).
Ниже (см. 4*4) показано, что и, наоборот, фактор-алгебра
любой группы по произвольной конгруэнции есть ее фактор-
факторгруппа по некоторому нормальному делителю. Мы продолжим
обсуждение идеи фактор-системы и поймем ее глубже, когда
свяжем понятие фактор-системы с общим понятием гомомор-
гомоморфизма, знакомого нам пока только по частным случаям гомо-
гомоморфизмов групп и колец.
4.4. Гомоморфизмы
Пусть Л = (-А, fi, П) и В = (В, П, П) — две однотипные
алгебраические системы.
Отображение h: А-± В называют гомоморфизмом алге-
алгебраической системы Л в алгебраическую систему в, если вы-
выполняются следующие условия:
1) для любой п-арной операции ш (п ^ 0) и любых элементов
ль ..., апеА
h(ai... апш) = h(ai)... h(an)u>]
2) для любого п-арного отношения тг (n ^ 1) и любых эле-
элементов oi, ..., ап е А из того, что (ai, ..., ап) G 7г, следует, что
), ..., h(an))en.
4.4. Гомоморфизмы
243
Мы будем использовать обозначение h: А-*В для отобра-
отображения Л, являющегося гомоморфизмом алгебраической систе-
системы Л = (-А, ?2, П) в алгебраическую систему В = (В, П, П).
Рис. 4.2
В определении гомоморфизма первое условие, которое мож-
можно рассматривать как условие „сохранения операций", означает
следующее. Бели отображение h — гомоморфизм, то, вычисляя
образ результата применения любой операции и € Л к любо-
любому кортежу аргументов из носителя алгебраической системы
Л, т.е. образ произвольного элемента а\...апш, мы можем сна-
сначала определить образ каждого из аргументов и уже к ним,
т.е. к элементам h(a\), ..., h(an), на носителе алгебраической
системы В применить рассматриваемую операцию (точнее, опе-
операцию второй алгебраической системы, которая соответствует
операции о;; напомним, что соответствующие друг другу опе-
операции и отношения однотипных алгебраических систем мы
договорились обозначать одинаково). Эта ситуация проиллю-
проиллюстрирована на рис. 4.2.
Второе условие в определении гомоморфизма выражает „со-
„сохранение отношений": если элементы oi,..., ап первой алгебра-
алгебраической системы связаны отношением р, т.е. (ai, ..., ап) G тг,
то их образы /i(ai), ..., h(an) при гомоморфизме h связаны
„тем же"* отношением во второй алгебраической системе, т.е.
), ..., h{an))En.
* Точнее, так же обозначенным. Заключая слова „тем же" в кавычки,
мы еще раз подчеркиваем условность одинакового обозначения операций и
отношений однотипных алгебраических систем.
244 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Заметим сразу, что из того, что (/i(ai), ..., h(an)) ? тг, не
следует, вообще говоря, что (oi, ..., ап) € тг. Если же это
имеет место, т.е. для всякого n-арного отношения тг (n ^ 1)
и любых ai, ..., апе A (oi, ..., an) ? тг тогда и только тогда,
когда (Л(ах), ..., h(an)) € тг, то такой гомоморфизм называют
строгим гомоморфизмом.
Если строгий гомоморфизм алгебраической системы А в
алгебраическую систему В является биекцией А -+ В, то его
называют изоморфизмом. Из определения изоморфизма сле-
следует, что для изоморфизма h: A-* В обратное отображение
Л": В-+А также является изоморфизмом. В этом случае алге-
алгебраические системы Л и В называют изоморфными и пишут
А = В. Если алгебраические системы интересуют нас лишь со
стороны свойств их операций и отношений, то изоморфные ал-
алгебраические системы в этом смысле не различимы, и тогда
говорят о совпадении алгебраических систем с точностью до
изоморфизма.
Если гомоморфизм является инъекцией, то его называют
мономорфизмом или вложением. В том случае, когда суще-
существует вложение алгебраической системы А в алгебраическую
систему #, которое является также строгим гомоморфизмом,
то говорят, что первая алгебраическая система изоморфно
вкладывается во вторую.
Если гомоморфизм h: A-* В является сюръекцией, то его
называют эпиморфизмом А на В. При эпиморфизме носи-
носитель алгебраической системы В совпадает с образом носителя
алгебраической системы А при отображении Л, т.е. В = h(A).
В этом случае говорят также, что алгебраическая система В
является гомоморфным образом системы Л при гомомор-
гомоморфизме Л, и записывают это как В = h(A).
Гомоморфизм алгебраической системы Л в себя называют
эндоморфизмом алгебраической системы Л. Эндоморфизм,
являющийся изморфизмом, называют автоморфизмом.
Легко доказать следующее утверждение.
4.4. Гомоморфизмы 245
Теорема 4.2. Если h: Л-> В и д: B-+V — гомоморфизмы,
то композиция h°g: A-+V — тоже гомоморфизм. #
Ранее (см. 2 и 3) мы достаточно подробно обсудили по-
понятие гомоморфизма для алгебр — групп и колец. Заметим,
что для алгебр любой гомоморфизм является строгим, так как
сигнатура алгебры включает только операции и условие 2 в
определении гомоморфизма для нее не рассматривается. При-
Приведем некоторые дополнительные примеры гомоморфизмов.
Пример 4.6. а. Рассмотрим левый %-модулъ
М = (М, +, {ua:aeR}, 0)
как алгебраическую систему, сигнатура которой помимо груп-
групповой операции сложения и нуля группы 0 содержит и унарные
операции умножения элементов группы на элементы кольца TZ
(мощность множества этих операций равна мощности \R\ носи-
носителя R кольца 1Z). Гомоморфизм h: Mi -> M2 этих 7^-модулей
есть такое отображение, чт© для всех гг, у 6 М и всех а Е R
h(u>a{x))=U>a{h{x)).
Используя вместо выражения ооа(х) более привычную зались
а о х, приведенные выше условия представим в виде
h(aox) =aoh(x).
В случае линейного пространства над полем отображение,
удовлетворяющее этим условиям, есть не что иное, как ли-
линейный оператор. Таким образом, линейные операторы суть
гомоморфизмы линейных пространств.
б. Для линейного пространства отображение, сопоставля-
сопоставляющее каждому вектору х вектор х + а для фиксированного
ненулевого вектора а, не является линейным оператором и, сле-
следовательно, не является гомоморфизмом заданного линейного
246
4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Рис. 4.3
пространства в себя. Действительно, для любого гомомор-
гомоморфизма модулей (и линейных пространств, в частности) образ
нулевого вектора есть нулевой вектор. Здесь же 0 н-> а Ф 0.
в. Пусть Л = (А, р)иВ = B?, р) — модели с одним бинар-
бинарным отношением. Отображение h: A -* В будет гомоморфиз-
гомоморфизмом первой модели во вторую, согласно с общим определением,
тогда и только тогда, когда для любых а:, у Е А из х р у следу-
следует h(x) ph(y). В частности, если р — отношение порядка, то
получаем х ^ у =^ h(x) ^ h(y).
Таким образом, гомоморфизмы упорядоченных множеств —
это монотонные отображения. На рис. 4.3 в виде диаграмм
Хассе изображены четыре упорядоченных множества. Множе-
Множество В является гомоморфным образом множества А, но не
является его строгим гомоморфным образом; множество С есть
строгий гомоморфный образ множества А\ наконец, множество
D не является гомоморфным образом множества А. #
4.4. Гомоморфизмы 247
Установим теперь связь между понятием гомоморфизма и
понятием фактор-системы. Доказываемые ниже результаты
конкретизируют для алгебраических систем связь между по-
понятием отображения и понятием отношения эквивалентности
(см. 1.7).
Теорема 4.3. Для любой конгруэнции р на алгебраической
системе Л = (А, ft, П) каноническая сюръекцил hp множества
А является строгим эпиморфизмом алгебраической системы Л
на ее фактор-систему Л/р.
< Для канонической сюръекции задается hp. Имеем hp(x) = [х]р
(для произвольного х Е А). В силу определения конгруэнции
для произвольных n-арной операции ш и n-арного отношения
тг и любых ai, ..., ап € А, согласно определению операций и
отношений на фактор-множестве А/р (см. 4.3), имеем
hp(ai... апш) = [ai... апи]р = [ai]p... [ап]ри = hp{ai)...
(ab ..., an) G тг Ф> ([ai]pi ..., [an]p) € тг,
>
откуда и следует, что hp — строгий гомоморфизм. >
Ввиду теоремы 4.3 каноническую сюръекцию hp (для кон-
конгруэнции р) можно назвать каноническим гомоморфизмом
алгебраической системы Л.
Справедлива теорема, обратная теореме 4.3.
Теорема 4.4. Для любого строгого гомоморфизма h: Л ->-
-* В отношение рь на носителе А алгебраической системы Д,
определенное тале, что хр^у <& h(x) = Л(у) для любых ж, у G
Е А, является конгруэнцией, причем имеет место изоморфизм
< Пусть h: Л —> В — гомоморфизм, тогда рд — эквивалент-
эквивалентность (см. 1.7).
Введем отображение г: A/ph -> Л(-А), полагая i([a]Ph) = h(a).
Это действительно отображение, так как эквивалентные эле-
элементы множества А имеют один и тот же образ. Поскольку
248 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
неэквивалентные элементы имеют разные образы, то г — инъ-
инъекция. Очевидно, что г является сюръекцией. Следовательно,
г — биекция.
Далее, если аг phbu ..., ап ph 6n, то
h(ai... апи>) = h{ai)... h(an)u = /i(&i)... h(bn)u = h(bi...
т.е. a\... anu> рн b\... bnu; для любой п-арной операции ш.
Точно так же
(аь ...,
причем последняя импликация справедлива в силу того, что h —
строгий гомоморфизм.
Итак, ph — конгруэнция на А. Остается доказать, что
имеет место изоморфизм h(A) ^
Далее, если и G п^п\ то
... апш) =
"
т.е. г „сохраняет" операции.
Рассуждая аналогично, можно доказать, что i „сохраняет"
и отношения как любой гомоморфизм, и, более того, поскольку
h — строгий гомоморфизм, то для любого отношения тг
..., [an]Ph) e тг,
и, следовательно, г — изоморфизм Л/рн на Л(Д) (и вложение
A/ph в Б). >
Таким образом, любой гомоморфный образ алгебраической
системы совпадает с точностью до изоморфизма с некоторой
ее фактор-системой.
4.4. Гомоморфизмы 249
Пример 4.7. Требование строгости гомоморфизма в тео-
теореме 4.4 является существенным. В примере 4.4.д монотонное
отображение / не определяет конгруэнции на упорядоченном
множестве Д, так как не является строгим гомоморфизмом (см.
пример 4.6.в). #
Из теоремы 4.4 вытекает, что любой строгий гомоморфизм
h: A-+B можно разложить в композицию канонического гомо-
гомоморфизма А на А/рн и мономорфизма А/рн в В (который будет
изоморфизмом А/рн — h(A)).
Применяя доказанные теоремы 4.3 и 4.4 к частному случаю
алгебраических систем — алгебрам, получаем следствие.
Следствие 4.1. 1. Любой гомоморфизм h алгебры А —
= (А, О) однозначно определяет конгруэнцию рь на Л, такую,
что h(A)^ A/ph.
2. Любая конгруэнция р на алгебре А = (А, О) однозначно
определяет некоторый гомоморфизм hp данной алгебры на
фактор-алгебру А/р.
Применим полученные результаты к теории групп. До-
Докажем, что фактор-группа заданной группы по нормальному
делителю (см. 2) совпадает с фактор-алгеброй указанной груп-
группы по некоторой конгруэнции.
Прежде всего заметим, что поскольку фактор-алгебра лю-
любой группы (по любой конгруэнции) изоморфна некоторому го-
гомоморфному образу этой группы, а гомоморфный образ всякой
группы является группой (см. 2.8), то фактор-алгебра группы
по любой конгруэнции есть группа.
Докажем теперь следующую теорему.
Теорема 4.5. Пусть Q = (G, •, 1) — произвольная группа и
р — конгруэнция на ней. Тогда фактор-группа Qjp совпадает
с фактор-группой Q/И по некоторому нормальному делителю
И группы Q.
Ч Рассмотрим канонический гомоморфизм hp группы Q. Его
ядром является множество всех элементов, эквивалентных (по
250 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
конгруэнции р) единице группы. Но поскольку, согласно тео-
теореме 2.19, ядро каждого гомоморфизма групп есть нормальный
делитель^ то множество [1]р (класс эквивалентности единицы
группы) является нормальным делителем*. Этот нормальный
делитель, обозначаемый далее %, будучи классом эквивалентно-
эквивалентности единицы группы (/, является единицей фактор-группы Q/p
и фактор-группы Q/H. Осталось показать, что произвольный
левый смежный класс а[1]р совпадает с классом эквивалентно-
эквивалентности элемента a 6 G. Для всякого элемента у этого класса имеем
у = ах для некоторого xpl. Тогда, так как р - конгруэнция,
получим
Ыр = [ах]р = [а]р[х]р = [а]р[1]р = [а]р,
откуда а[1]р = [а]р. Итак, каждый левый смежный класс по
нормальному делителю И является одновременно классом экви-
эквивалентности по исходной конгруэнции р, а группы Q/p и Q/H
совпадают. >
Таким образом, имеет место взаимно однозначное соответ-
соответствие между конгруэнциями на группе и нормальными дели-
делителями этой группы, и каждая фактор-группа по конгруэнции
является в то же время и фактор-группой по нормальному де-
делителю, и наоборот.
Важным результатом для групп является и следующая тео-
теорема.
Теорема 4.6. Ядрами гомоморфизмов групп служат нор-
нормальные делители, и только они.
< То, что ядро гомоморфизма групп есть нормальный дели-
делитель, доказано выше (см. 2,8). Наоборот, если % — нормаль-
нормальный делитель ?, то отношение ~# — конгруэнция (см. 4.3), а
множество Н — ядро соответствующего канонического гомо-
гомоморфизма. >
* Точнее, нормальным делителем будет подгруппа, носителем которой
является множество [1]р.
4.4. Гомоморфизмы 251
В силу установленной связи между фактор-системами и го-
гомоморфизмами можно утверждать, что фактор-алгебра любого
кольца по любой конгруэнции на этом кольце является кольцом.
Естественно назвать его фактор-кольцом (по заданной кон-
конгруэнции).
Пример 4.8. Как уже было показано в примере 4.4.6, от-
отношение ==* есть конгруэнция на кольце целых чисел. Можно
доказать, что фактор-кольцо кольца целых чисел по этой кон-
конгруэнции изоморфно кольцу Zfc вычетов по модулю Л, посколь-
поскольку соответствующий канонический гомоморфизм сопоставляет
каждому целому числу т ? Z его класс эквивалентности [ш]=А.
и существует естественное, сохраняющее операции взаимно од-
однозначное соответствие между множеством этих классов (т.е.
фактор-множеством Z/ =(modfc)) и множеством {0,1,..., к — 1}
остатков от деления на к (см. также пример 2.25). #
В заключение докажем три теоремы, которые описывают с
точностью до изоморфизма все полугруппы, группы и кольца.
Будем говорить, что полугруппа S = E, •) изоморфно вкла-
вкладывается в моноид М = (М, •, 1), если существует мономор-
мономорфизм S в Му т.е. если образ полугруппы S при этом мономор-
мономорфизме является некоторой подполугруппой (но, вообще говоря,
не подмоноидом) моноида Л4.
Например, полугруппа (@,1), •) изоморфно вкладывается в
моноид (@,1], •, 1), где операция — обычное умножение чисел.
Теорема 4.7. Любая полугруппа изоморфно вкладывается
в некоторый моноид.
< Пусть S = E, •) — полугруппа, не являющаяся моноидом
(так как иначе она тривиально вкладывается сама в себя).
Пусть {е} — произвольное одноэлементное множество, не пе-
пересекающееся с S. Определим на множестве S U {е} операцию
• следующим образом: на S операция • совпадает с операцией
полугруппы 5, а для каждого а Е S U {е} она удовлетворяет со-
252 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
отношениям а-е = е-а = а. Очевидно, что М = (SU?, •, е) —
требуемый моноид. >
Теорема 4.8. Любой моноид изоморфно вкладывается в
симметрический моноид некоторого множества А.
< Пусть S = E, •, 1) — моноид. Сопоставим каждому а Е S
преобразование /а: ж ь» ж • а (правый сдвиг на а) множества 5.
Отображение a4/fl множества S в множество всех преобра-
преобразований S инъективно, поскольку если а ф 6, то /a(l) ф /ьA) и
fa Ф h- Далее, если с = а-Ь, то
fab(x) = х ¦ с = х(аЬ) = (ха)Ь = fb(fa(x)) = (Д о Д)(ж).
Итак, a i-+ fa есть мономорфизм S в симметрический моноид
множества А. >
Теорема 4.9 (теорема Кэли). Любая группа изоморфно
вкладывается в симметрическую группу некоторого множе-
множества А.
Л Бели S = E, •, 1) — группа, то введенное в доказательстве
теоремы 4.8 преобразование fa:x^x-a множества S будет
уже биекцией. Чтобы это доказать, достаточно построить
отображение, обратное fa. Действительно, сдвиг /a-i на а"
будет отображением, обратным сдвигу на а:
Точно так же и faifa-1^)s== х- Из доказанного следует, что
множество всех правых сдвигов множества 5 образует по опе-
операции композиции группу, являющуюся подгруппой симметри-
симметрической группы множества S.
Из доказательства теоремы 4.8 заключаем, что отображе-
отображение аи/о, сопоставляющее каждому элементу а множества S
(носителя моноида S) сдвиг на а, инъективно и является, бо-
более того, мономорфизмом моноида S в симметрический моноид
множества S. Но поскольку, как мы только что показали, в том
4.5. Прямые произведения алгебраических систем 253
случае, когда моноид S является группой, для любого aES вы-
выполняется равенство fa-i(x) = /^(x), то данный мономорфизм
отображает элемент, обратный к а, в сдвиг, обратный сдви-
сдвигу fa- Тем самым он оказывается уже мономорфизмом группы
S в группу всех подстановок множества 5 (и изоморфизмом на
подгруппу всех правых сдвигов множества 5), т.е. изоморфным
вложением первой группы во вторую. >
Пусть /С=(#, +, 0) — абелева группа. На множестве End(/C)
всех эндоморфизмов группы /С можно определить структуру
кольца следующим образом. Умножение эндоморфизмов опре-
определим как их композицию, а сложение — так, что для любого
х Е К выполнено равенство (/ + g)(x) = f(x) +g{x).
Введем также нулевой эндоморфизм О, для всех х положив
О(х) = 0, и каждому эндоморфизму / сопоставим противопо-
противоположный эндоморфизм —/, для каждого х положив (—f){x) =
=-/(*)•
Можно доказать, что тем самым действительно определено
кольцо (проверив все аксиомы кольца, см. 2.3). Его называют
кольцом эндоморфизмов абелевой группы /С.
Теорема 4.10. Любое кольцо изоморфно вкладывается в
кольцо эндоморфизмов некоторой абелевой группы. #
Доказательство этой теоремы проводится по аналогии с
доказательствами теорем 4.8 и 4.9. Искомое вложение опреде-
определяется следующим образом: пусть 1Z = (Д, +, •, 0, 1) — кольцо.
Для любого г ? R положим fr (х) = х • г. Тогда отображение
г »-> /г и есть требуемое вложение, причем в качестве абелевой
группы выступает аддитивная группа кольца 11.
4.5. Прямые произведения алгебраических систем
Часто возникает необходимость, имея некоторые исходные
однотипные алгебраические системы, определенным образом
распространить" их операции и отношения на декартово
п
254 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
произведение их носителей: например, определить структуру
группы (кольца, поля) на декартовом произведении носите-
носителей некоторых групп (колец, полей) или перенести структуру
индуктивного упорядоченного множества на декартово про-
произведение носителей заданных индуктивных упорядоченных
множеств и т.п. Выясним, как осуществляется такой пере-
перенос операций и отношений, а также сформулируем некоторые
условия, при которых все свойства исходных алгебраических
систем сохраняются в их декартовом произведении.
Пусть Л\ = (А\, ft, П), ..., Ап = (Ап, ft, П) — однотипные
алгебраические системы (их сигнатурьц как и элементы этих
сигнатур, обозначаются одинаково). Рассмотрим декартово
произведение В = А\ х ... х Ап их носителей и перенесем на В
операции и отношения исходной сигнатуры следующим обра-
образом.
1. Для любой т-арной (т ^ 1) операции о; € ft и произволь-
произвольных кортежей Х{ = (хц, ..., х%п) G В, г = 1, ш, положим
Для любых нульарных операций а\, ..., ап алгебраических
систем Ль ..., Ап определим кортеж а = (ai, ..., ап) как
нульарную операцию на множестве В.
2. Для любого s-арного отношения 7г Е П (s ^ 1) и про-
произвольных кортежей ж» = (хц, ..., Х{п) € В, i = 1,5, положим
(а?х, ..., xs) Е 7г тогда и только тогда, когда (жу, ..., xsj) € тг
для каждого j = 1, п.
Полученную таким образом алгебраическую систему В на
множестве В — А\Х .,.х Ап называют прямым (декартовым)
произведением алгебраических систем Ль •••? Ai и обо-
обозначают Дх х ... х Лп.
В том случае, когда А\ =... = Ап = Л, получаем n-ю декар-
тову степень алгебраической системы Л, обозначаемую Л171.
Замечание 4.4. Несколько особняком стоит случай п = 0.
Как известно (см. 2.2), нулевая декартова степень произвольно-
4.5. Прямые произведения алгебраических систем 255
го множества А есть, по определению, одноэлементное множе-
множество {Л} и его элемент Л называется пустым кортежем. Тогда
нулевая декартова степень Л° алгебраической системы Л есть
алгебраическая система ({Л}, ft, П), где А...Ао; = А для всех
и € ft и (Л, ..., А) 6 тг для всех тг Е П. #
Итак, операции и отношения исходных однотипных алге-
алгебраических систем переносятся на декартово произведение их
носителей покомпонентно.
Пример 4.9. Рассмотрим алгебраическую систему % =
= (R, +, •, 0, 1, О, сигнатура которой состоит из обычных
операций сложения, умножения (бинарные операции), 0 и 1
(нульарные операции) и естественного числового порядка (би-
(бинарное отношение). Распространим эти операции и отношения
на декартов квадрат Ш х Ш = R2 множества действительных чи-
чисел согласно определению, данному выше.
Сложение упорядоченных пар действительных чисел опреде-
определяется тогда равенством
(аь bi) + (а2, Ьг) = (аг + а2, h + 62),
а умножение — равенством
(аи h) • (a2, 62) = (qi • a2, bi • 62).
При этом легко понять, что упорядоченная пара @, 0) будет
нейтральным элементом по сложению в Е2, а упорядоченная
пара A,1) — нейтральным элементом по умножению. Кроме
того, для любых действительных чисел а, Ь будем иметь (а, Ь) •
@, 0) = @, 0), т.е. пара @, 0) играет роль нуля относительно
умножения в К2.
Отношение порядка на множестве упорядоченных пар вво-
вводится по правилу*
(аи bi) < (a2, h) <* Ы ^ о2 и 6i < Ьг).
* Нужно, разумеется, проверить, что построено действительно отноше-
отношение порядка, но эта проверка легко выполняется.
256 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Заметим, что мы уже ранее многократно пользовались подоб-
подобным определением отношения порядка на множестве упорядо-
упорядоченных пар (и, в более общем случае, кортежей). #
Для каждого г = 1, п определим проекцию рг^: В -» А^ пола-
полагая ргДж) = Xi. Можно показать, что рг^ есть строгий гомо-
гомоморфизм, называемый проектирующим гомоморфизмом.
Из определения декартова произведения алгебраических си-
систем априори не следует, что в нем сохраняются все свойства
операций и отношений перемножаемых алгебраических систем.
Разберем в этой связи такой пример.
Пример 4.10. Пусть К\ и /Сг — поля. Их произведение
К\ х К>2 не будет полем, так как в этом произведении возникают
делители нуля. В самом деле, если а € К\ \ {0}, Ъ ? K<i \ {0}, то
(а,0) • @,6) = @,0) — элемент, являющийся нулем произведения
К\ х /Сг. Таким образом, алгебра К\ х /Сг будет, как нетрудно
убедиться, только кольцом. #
Этот пример показывает, что в декартовом произведении
могут теряться некоторые свойства исходных алгебраических
систем. В частности, декартово произведение полей не будет
полем. Здесь уместно вспомнить о поле комплексных чисел,
носителем которого является декартов квадрат R2. Но если
сложение в этом поле определяется покомпонентно, т.е. по пра-
правилам декартова произведения алгебр, то умножение введено
по более сложному правилу, позволяющему сохранить аксиомы
поля.
Теорема 4.11. 1. Прямое произведение полугрупп (монои-
(моноидов, групп) есть полугруппа (моноид, группа).
2. Прямое произведение полуколец (идемпотентных по-
полуколец, колец) есть полукольцо (идемпотентное полукольцо,
кольцо).
3. Прямое произведение полурешеток, решеток, симметрич-
симметричных полуколец, булевых алгебр есть соответственно полурешет-
полурешетка, решетка, симметричное полукольцо, булева алгебра.
4.5. Прямые произведения алгебраических систем 257
4. Прямое произведение (индуктивных) упорядоченных
множеств есть (индуктивное) упорядоченное множество.
М Для простоты будем рассматривать доказательство для про-
произведения двух алгебраических систем.
1. Если S\ = (Si, •) и 62 = ($2, ') — Две полугруппы, то,
вводя на множестве S\ x S2 операцию • так, что для любых ai,
Ь\ € Si, a2, &2 € S2 справедливо
(аь а2) • (Ьь 62) = («1 • &ъ «2 • Ы>
получим полугруппу, поскольку в силу ассоциативности опера-
операции • на множествах Si и S2 будем иметь
(ai, a2) • ((bu Ы ¦ (ci, c2)) = (ai, a2) • F1 • сь 62 • c2) =
i, (a2-62)^2) =
c2).
Если в каждой из указанных выше полугрупп существует
нейтральный элемент е\ и ег соответственно, то легко прове-
проверить, что упорядоченная пара (ei, ег) является нейтральным
элементом по операции • на декартовом произведении Si x S2.
Если же моноиды S\ и #2 суть группы, то элемент из Si x S2,
обратный к (ai, 02), равен (ах х, а^).
2. Доказательство для полукольца и кольца проводится
аналогично предыдущему.
3. Точно так же, совершенно аналогично доказательству
для групп, проводится доказательство для полурешеток, реше-
решеток, симметричных полуколец и булевых алгебр.
4. Пусть теперь М\ = (Mi, <) и M.*i — (М2, <) — индуктив-
индуктивные упорядоченные множества, наименьшие элементы которых
суть Oi и О2.
Определяя отношение порядка ^ на декартовом произведе-
произведении Mi х М2 покомпонентно, так же как это сделано в примере
4.9, получаем, что упорядоченная пара (Oi, O2) является на ука-
указанном произведении наименьшим элементом.
Q - 10061
258 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Далее, произвольной неубывающей последовательности упо-
упорядоченных пар
(аь 6i) ^ (а2, h) < ... ^ (ап, Ьп) < ...
соответствуют две неубывающие последовательности
о>\ < а2 < ... < ап < ... и bi < Ьг ^ • • • < Ьп < •
в множествах М\ и Мг, каждая из которых имеет
верхнюю грань — элементы с\ и С2. Нетрудно показать, что
упорядоченная пара (ci, C2) есть точная верхняя грань запи-
записанной выше последовательности упорядоченных пар. >
Рассмотрим теперь конструкцию, во многом аналогичную
прямому произведению алгебраических систем.
Пусть Л = (A, ft, П) — некоторая алгебраическая система,
а X — произвольное множество. Распространим операции и
отношения алгебраической системы Л на множество Ах всех
отображений из X в А.
Это осуществляется следующим образом:
1) для любого п ^ 0, любой операции ш € ?l'n) и любых
отображений /i, ..., fn G А* полагаем
(Л-/»W)(X) =/!(»).../п(х)«,
где х ? Х\ тем самым определено отображение f\... /no; E -А*
как результат применения операции и к отображениям /i, ...,
fn (в частности, для нульарной операции а€ А соответствую-
соответствующая нульарная операция на Ах есть отображение /а, такое, что
fa(x) = а для любого я G X);
2) для любого п ^ 1, любого отношения тг € П(п) и любых
отображений /i, ..., fn G А* полагаем
(/ь -, /n)e7r^(VxGX)((/i(*), ..., /»(*))€*).
Построенную таким образом алгебраическую систему с
носителем Ах\ однотипную с Л, обозначим Лх. Докажем, что
4.5. Прямые произведения алгебраических систем 259
в случае конечного множества X = {1, ...,п} алгебраическая
система Ах изоморфна алгебраической системе Ап.
Действительно, в этом случае каждому отображению / Е
? Ах можно однозначно сопоставить кортеж (oi, ..., an) G An
таким образом, что сц = /(г), г = 1, п. В то же время каждый
кортеж (oi, ..., ап) € Ап однозначно определяет отображение
/ G -А*, для которого /(г) = а*, г = 1,гс. Тем самым построена
биекция <р множества А* на множество Ап. Докажем, что
она „сохраняет" операции и отношения (в том смысле, как это
определено выше, см. 4*4). Для произвольных отображений
/ъ • • • ? /т ? -4х и произвольной операции a; Е п^ имеем
), ..., /m(n))ui =
что и требовалось доказать.
„Сохранение" отношений доказывается аналогично. Тем
самым изоморфизм Ах = Ап доказан полностью.
Пример 4.11. а. Для аддитивной группы действительных
чисел на множестве всех функций из Е в R по приведенной выше
конструкции строится аддитивнак группа функций из R в R. В
этой группе сумма функций f ид есть функция f+g, такая, что
для любого х € R выполняется равенство (/+д)(х) = f(x)+g(x).
Функция, противоположная к /, определяется так: (—/)(ж) =
= —/(ж). Нейтральный элемент есть нулевая функция 0, т.е.
для любого жЕК имеет место 0 (ж) = 0.
Аналогично можно построить кольцо функций из R в R на
базе кольца действительных чисел. Несмотря на то что дей-
действительные числа образуют поле, кольцо функций, как можно
легко показать, полем не будет. Этот „отрицательный" резуль-
результат вполне соответствует ранее доказанному результату, со-
согласно которому прямое произведение полей не является полем.
260 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
б. Бели Л = (А, <) — упорядоченное множество, то упо-
упорядоченное множество всех функций из X в А строится так:
полагаем / ^ д тогда и только тогда, когда f(x) ^ д(х) для лю-
любого х ? X. Если порядок на А индуктивен, то и порядок на Ах
индуктивен, что доказывается так же, как в п. 4 теоремы 4.11.
4.6. Конечные булевы алгебры
Покажем применение понятия прямого произведения алге-
алгебраических систем к теории булевых алгебр. Мы докажем
здесь интересный факт, состоящий в том, что мощность лю-
любой конечной булевой алгебры есть некоторая степень двойки.
Отсюда будет следовать, например, что в конечной булевой
алгебре может быть 1, 2, 8, 16, 32, 64 и т.д. элементов, но
не может быть, скажем, 100 или 75 элементов. Чтобы до-
доказать сформулированное утверждение о конечных булевых
алгебрах, необходимо ввести некоторые вспомогательные опре-
определения и доказать некоторые утверждения. Напомним, что
мы определили булеву алгебру Вп булевых векторов размер-
размерности п (см. пример 3.11). Эта алгебра есть не что иное,
как п-я декартова степень двухэлементной булевой алгебры
В =({0,1}, V, Л, 0, 1) (см. 4.5).
Пусть С = {L, V, Л, 0,1} — симметричное полукольцо. Рас-
Рассмотрим произвольные элементы а, Ь Е L, такие, что а ^ Ь.
Множество [а, Ь] = {х: а < х < 6} будем называть отрезком,
элемент а — левым, а элемент Ь — правым концом отрезка.
Замечание 4.5. Напомним, что в симметричном полуколь-
полукольце нуль полукольца является наименьшим, а единица полуколь-
полукольца — наибольшим элементом в данном полукольце относитель-
относительно естественного порядка этого идемпотентного полукольца.
Поэтому для любого элемента х симметричного полукольца
справедливо неравенство 0 ^ х ^ 1, и тем самым все симме-
симметричное полукольцо можно рассматривать как отрезок [0,1]
симметричного полукольца. #
4.6. Конечные булевы алгебры 261
Любой отрезок [а, Ь] симметричного полукольца замкнут
относительно операций V и Л, но не является, вообще говоря,
подполукольцом ?, так как не содержит 0 (если а ф 0) и
не содержит 1 (при Ь ф1). Но поскольку элемент а будет
наименьшим, а элемент b — наибольшим элементом отрезка
[а, 6], алгебра
([а, Ь], V, Л, а, Ь)
будет симметричным полукольцом с нулем а и единицей Ь,
которое мы будем обозначать тоже через [а, Ь].
Для произвольно фиксированного элемента а симметрич-
симметричного полукольца С зададим отображение ва, сопоставляющее
каждому х € L упорядоченную пару (х Л а, х V а) € L2. Так как
О^яЛа^а и o^xVa^l для любого х Е L (в силу свойств
симметричного полукольца), то тем самым задано отображение
6а носителя полукольца С в декартово произведение отрезков
[0,a]x[a,l]:
ee:L->[0,a]x[a,l].
Каждый из отрезков есть симметричное полукольцо. В
силу теоремы 4.11 их декартово произведение также является
симметричным полукольцом.
Теорема 4,12. Пусть L — носитель симметричного полу-
полукольца С = (L, V, Л, 0, 1). Для любого a € L отображение ва
есть мономорфизм полукольца С в полукольцо [0, a] x [а, 1].
< Докажем, что 6а — гомоморфизм. Имеем ва@) = @, а), и
эта упорядоченная пара и является наименьшим элементом, т.е.
нулем, полукольца [0,а] х [а,1]. Точно так же 6аA) = (а,1) —
наибольший элемент, т.е. единица того же полукольца.
Далее,
= ((х Л а) V (у Л а), (х V а) V (у V а)) = ва(х) V 0в(у).
Аналогично доказывается, что
262 '4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Итак, 6а — гомоморфизм С в [0, а] х [а,1].
Теперь надо доказать, что 0а — инъекция. Для этого нужно
показать, что из равенства 0а(#) = ва(у) вытекает х = у. Если
ва(а;) = во(у), то верны равенства
хАа = уЛаих\/а = у\/а, D.2)
так как равенство упорядоченных пар означает равенство их
одноименных компонент.
Теперь, используя равенства D.2) и аксиомы симметричного
полукольца (см. 3,4), получим
х = х Л (х V а) = х Л (у V а) =
= (х Л у) V (х Л а) = (у Л х) V (у Л а) =
= у Л (у V а) Л (х V у) Л (х V а) =
= yA(xVy)A(yVa)=yA(yVa)=y.
Таким образом, если ва(х) = 0а(у), то х = у, и 6а — инъек-
инъекция. >
Теорема 4.13, Если симметричное полукольцо
C = (L, V, Л, 0, 1)
есть булева алгебра, то для любого а € L полукольца [0, а] и
[а, 1] тоже булевы алгебры.
4 Поскольку [0, а] и [а, 1] — симметричные полукольца, то
достаточно доказать, что в каждом из отрезков [0, а] и [а, 1]
любой элемент имеет дополнение.
Для произвольного и G [0, а] определим элемент иа равен-
равенством иа = и Л а. Докажем, что этот элемент и есть дополнение
и в полукольце [0, а]. Для этого, как следует из свойства
единственности дополнения в булевой алгебре, достаточно убе-
убедиться в том, что weVw = a, а иа Л и = 0.
4.6. Конечные булевы алгебры 263
Действительно,
Так как и^ а, тоа\/гх = а, и1Л(а\/и) = 1Ла = а. Итак, waVit =
= а. Аналогично ua Л и = (п Л а) Л и = 0. Таким образом, ип
действительно является дополнением элемента и в полукольце
IP, a].
Теперь для произвольного v Е [а, 1] определим элемент Vй
равенством va = v V а. Как и выше, аналогично доказывается,
что va Vv = I, va Av = a. Следовательно, элемент va является
дополнением v в полукольце [а, 1]. >
Теорема 4,14. Бели в условиях теоремы 4.12 полукольцо
С является булевой алгеброй, то ва — изоморфизм булевых
алгебр С til [0, a] x [a, 1].
< В силу теоремы 4.12 достаточно доказать, что 6а — эпимор-
эпиморфизм, сохраняющий дополнение, т.е.
1) для любой пары (у, г), где у ^ a, z ^ а, существует
элемент x?L, такой, что 6a(#) = (j/,z)\
2) ea(x) =
Докажем первое утверждение. Убедимся, что указанный в
нем элемент х может быть определен равенством х =
Имеем
ж Л а = [у V (г Л а) ] Л а = (у V г) Л (у V а) Л а =
Поскольку у ^ а ^ z, то
(у V z) Л а = (у Л а) V (z Л а) = у V а = а.
Следовательно, xha = aA(y\/a) = aAy = y (так как у ^ а).
Аналогично доказывается, что ж V a = z. Таким образом,
®а{х) = (у, z).
264
4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Второе утверждение следует из того, что элемент хЛа есть
дополнение элемента и = х Л а в булевой алгебре [0, о], а элемент
ж V а — дополнение элемента v = х V а в булевой алгебре [а, 1].
Действительно, согласно теореме 4.13,
иа = (х Л а)а = (хЛа) Л а =
Согласно принципу двойственности, va = (жVа)а =
Итак,
ва(х) = ((хЛа)а,(х Уа)а) = (xAa.xWa) = ва(х). >
В силу доказанных теорем имеем следующий результат.
Следствие 4.2. Любая булева алгебра изоморфна прямому
произведению некоторых двух булевых алгебр. #
(а,1) ь Ь1 (ЬД)
(а, а)
(ОД)
Ь 1
Q О
6
О
(b, b)
6
b
(ОД)
@,b)
Ha рис. 4.4 представлены все возможные способы пред-
представления четырехэлементной булевой алгебры (ее элементы
обозначены 0, 1, а, Ь) в виде прямого произведения двух двух-
двухэлементных булевых алгебр. Эти представления определяются
изоморфизмами 0а и 0&. Изоморфизм Оа есть изоморфизм
исходной четырехэлеменнои булевой алгебры на декартово про-
произведение ее отрезков [0, а] и [а, 1], каждый из которых изо-
изоморфен двухэлементной булевой алгебре В. Вместе с тем
декартово произведение указанных отрезков дает (см. 4.5) че-
тырехэлементную булеву алгебру, элементами которой служат
4.6. Конечные булевы алгебры 265
упорядоченные пары @, а), (а, а), (а, 1) и @, 1), причем па-
пара @, а) будет нулем, а пара (а, 1) — единицей этой булевой
алгебры, которая изоморфна исходной. Аналогично рассматри-
рассматривается изоморфизм @ь-
Интересно отметить, что могут быть заданы и изоморфиз-
изоморфизмы вд и 6j, но каждый из них определяет тривиальное разло-
разложение исходной булевой алгебры в виде ее прямого произведе-
произведения на одноэлементную булеву алгебру, т.е. в виде [0,1] х [0, 0]
или в виде [0,1] х [1,1]. Интерес представляют, следовательно,
такие изоморфизмы 0а, где элемент а не является ни нулем, ни
единицей исходной булевой алгебры.
Теперь, наконец, мы докажем основной результат.
Теорема 4.15. Любая конечная булева алгебра изоморфна
булевой алгебре Вп для некоторого п.
<4 Доказательство проведем методом математической индук-
индукции по числу элементов булевой алгебры Л = (А, V, Л, 0, 1).
Одноэлементная булева алгебра изоморфна нулевой степени
алгебры В (см. замечание 4.4). Для самой алгебры В, содер-
содержащей два элемента, доказывать нечего.
Пусть утверждение теоремы доказано для всех булевых
алгебр с числом элементов, не большим некоторого к ^ 2.
Рассмотрим произвольную булеву алгебру Л, содержащую А; +1
элемент, т.е. \А\ = к + 1, и пусть a Е А. Поскольку число
элементов в данной алгебре не меньше трех, то, во-первых,
0^1 (нуль совпадает с единицей только в одноэлементной
булевой алгебре), а во-вторых, можно выбрать элемент а так,
что 0 < а < 1 (т.е. а отлично и от нуля и от единицы).
Тогда по теореме 4.14 Л = [0, а] х [а, 1]. Так как элемент а
отличен от единицы алгебры Л, то отрезок [0, а] не содержит
единицы 1, а так как а ф 0, то отрезок [а, 1] не содержит
нуля алгебры А Следовательно, число элементов в каждом из
отрезков не превышает к.
266 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
В соответствии с предположением индукции найдутся такие
неотрицательные целые числа г и 5, что [0, а] = Вг, а [а, 1] = В8.
Поэтому В й Вг х В* й Вг+8. >
Следствие 4.3. Мощность конечной булевой алгебры есть
некоторая степень двойки.
4.7. Многосортные алгебры
Среди всех алгебр, рассмотренных выше, несколько особое
положение занимает модуль (и, как частный случай, линейное
пространство). Модуль был определен как алгебра, в сигнату-
сигнатуру которой входят бинарная операция сложения и бесконечное
(в общем случае) множество унарных операций. Относитель-
Относительно операции сложения модуль является абелееой группой, а
множество унарных операций имеет структуру кольца. Ка-
Каждая унарная операция рассматривается как умножение (левое
или правое) элементов модуля на тот или иной элемент этого
кольца. Проще было бы интерпретировать такое умножение
как бинарную операцию, но это не вписывается в определение
бинарной операции, поскольку аргументами умножения оказы-
оказываются элементы двух разных алгебр. Модуль представляет
собой как бы „ симбиоз " двух алгебр: абелевой группы и кольца.
Это обстоятельство наводит на мысль ввести алгебраические
системы с несколькими носителями. Так возникает идея мно-
многосортной алгебры.
Многосортная алгебра — это упорядоченная пара
(№ш, ft),
где элементы семейства множеств (Aiji^i называют сорта-
сортами, а множество Q, называемое многосортной сигнатурой,
состоит из многосортных операций — отображений вида
u)\Aix x...xAin->Aio.
4.7. Многосортные алгебры 267
Операцию ш называют при этом п-арной операцией типа
(го, *ь •••» *п)«
Задавая конкретную многосортную алгебру, условимся, что
будем записывать ее в виде кортежа, в котором сначала пере-
перечисляется семейство сортов (как правило, конечное), а затем —
многосортные операции, образующие сигнатуру, причем после
обозначения каждой операции пишется ее тип (в виде корте-
кортежа). Обратим еще раз внимание на то, что в типе операции
первая компонента указывает на сорт результата операции,
следующие компоненты суть номера сортов аргументов опера-
операции. Заметим, что тип нулъарной операции в многосортной
алгебре есть однокомпонентный кортеж: нульарная операция
типа (г) — это фиксированный элемент, принадлежащий сор-
сорту Аг.
В свете определения многосортной алгебры левый модуль
над кольцом 71 может быть описан как многосортная алгебра
М = ((АиА2), +A,1,1), 0A),
0B,2,2), .B,2,2), 0B), 1B), оA,2,1)),
где А\ = G — носитель абелевой группы Q = (G, +, 0), Л2 = R —
носитель кольца TZ = (Д, ф, •, 0, 1), а ©: R x G —>• G — много-
многосортная операция левого умножения элементов группы Q на
элементы кольца К. Ее тип указывает на то, что первым аргу-
аргументом является элемент кольца, вторым — элемент абелевой
группы, а результат принадлежит абелевой группе.
Правый модуль описывается аналогично, но тип операции
правого умножения элемента группы на элемент кольца будет
равен A,1,2).
Условимся о следующей терминологии для модуля. Элемен-
Элементы группы Q будем называть векторами модуля (элемен-
(элементами „первого сорта"), а элементы кольца И — скалярами
данного модуля (элементами vвторого сорта").
Многосортные алгебры
) и В =
268 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
называют однотипными, если существует биекция сигнату-
сигнатуры п на сигнатуру S, сопоставляющая n-арной операции неко-
некоторого типа n-арную операцию того же типа.
Сигнатуры однотипных многосортных алгебр и соответ-
соответствующие друг другу элементы этих сигнатур (т.е. многосорт-
многосортные операции) обычно обозначают одинаково.
Пример 4.12. Алгебра
, +A,1,1), -A,2,1), 0B,1,1), хA,1,1), оB,1,1,1))
имеет в качестве первого сорта множество V$ свободных гео-
геометрических векторов (в трехмерном пространстве)[III], а в
качестве второго сорта — множество действительных чисел.
Первая операция — бинарная операция + (сложения векто-
векторов). Результатом операции является вектор, аргументами —
также векторы, поэтому она имеет тип A,1,1).
Вторая операция — бинарная операция • (левого умножения
вектора на число). Результат операции — вектор, первый
аргумент — число, второй аргумент — вектор, поэтому тип
операции — A,2,1).
Третья операция — бинарная операция (•) (скалярного умно-
умножения векторов). Ее результатом является число, и ее тип есть
B,1,1).
Четвертая операция — бинарная операция х (векторного
умножения векторов), а ее тип — A,1,1).
Последняя, пятая операция — тернарная операция смешан-
смешанного умножения векторов. Результатом операции является
число, и соответственно сорт операции — B,1,1,1). #
Обычная fi-алгебра есть многосортная алгебра с одним сор-
сортом. Покажем, что и любая алгебраическая система может
быть описана как многосортная алгебра. Сигнатура алгебраи-
алгебраической системы кроме операций содержит и отношения.
Каждому отношению тг € П алгебраической системы Л =
= (A, ft, П) сопоставим характеристическую функцию: ото-
4.7. Многосортные алгебры 269
бражение ?п: Ап -> {0,1}, такое, что
Тогда алгебраическую систему можно задать как много-
многосортную алгебру с двумя сортами: носителем А и „логическим
(булевым)" сортом В = {0,1}, а вместо каждого n-арного от-
отношения рассматривать его характеристическую функцию как
многосортную n-арную операцию типа B, 1, ..., 1) (номер 1
приписан сорту А, а номер 2 — сорту В).
Рассмотрим теперь, как на многосортные алгебры распро-
распространяются понятия подалгебры и гомоморфизма.
Семейство (#i)ie/ называют подсемейством семейства
(^i)ie/ (для одного и того же множества индексов J), если
(Vie 7) (В* с л*)-
Семейство (Ci)iei называют объединением (пересечени-
(пересечением) семейств (Ai)iej и (JSj)^/, если (Vi € J) (С* = A{ U Bi)
(соответственно (Vz E /) (Ci = А{ П Bf)).
Пусть Л = ((Aj)i€/, li) — многосортная алгебра и (Bi)ie/ —
подсемейство семейства (Aj)j€/.
Подсемейство (J9i)ie/ называют П-залскнутылс (или за-
замкнутым относительно операций многосортной сигнатуры ?}),
если Ь{х ...binu G Bi0 для всякой n-арной операции и) €п типа
(io, ii, ..., in) (при произвольных п, го, ti, ..., гп) и любых
ъг1евг1,...,ъ1пеВгп.
Для fi-замкнутого подсемейства (Д)гб/ можно тогда опре-
определить однотипную с Л многосортную алгебру В = (B?{)«е/> О),
которую называют многосортной подалгеброй алгебры Л,
Можно показать, что пересечение любого семейства fi-замк-
нутых подсемейств есть также fi-замкнутое подсемейство.
Следовательно, для произвольного подсемейства (Ci)i?i семей-
семейства (Ai)i?i существует наименьшее относительно включения
fi-замкнутое подсемейство Eг)ге/, содержащее подсемейство
(Сг)г€/ и называемое тогда ft-замыканием этого подсемей-
подсемейства. Если fi-замыкание подсемейства (Ciji^j совпадает со
270 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
всем семейством (А*)^/? то первое подсемейство называют си-
системой образующих многосортной алгебры А.
Семейство отображений (/ii)ie/, ГДе ^i: М ~* &и * € Л Для
однотипных многосортных алгебр
и в =
называют многосортным гомоморфизмом алгебры А в
алгебру Б, если для каждой n-арной операции и Е Q типа
(г'о, *ь •••» in) (при произвольных га, г'о, г'ъ ..., гп) и любых
xix ...xinu>) = hh(xix)...hin(x
in)ш.
Многосортный гомоморфизм, все отображения которого
суть биекции, называют многосортным изоморфизмом ал-
алгебры А на алгебру В. Очевидно, что если существует изомор-
изоморфизм А на #, то существует и изоморфизм В на А. Алгебры А
и В называют в этом случае изоморфными многосортными
алгебрами.
Аналогично обычным алгебрам в многосортных алгебрах
вводят понятия многосортного моно- и эпиморфизма.
В качестве простого примера сошлемся на понятие линей-
линейного оператора (для линейных пространств над одним и тем
же полем), известного из курса линейной алгебры [IV]. Оно
является не чем иным, как многосортным гомоморфизмом, где
отображение носителя одного поля в носитель другого является
тождественным отображением.
Более сложными будут следующие примеры.
Пример 4.13. а. Рассмотрим модуль С\ над кольцом
Z целых чисел и модуль ?2 над кольцом вычетов по модулю
к (для некоторого целого к ^ 2). Отображение h\ определим
как произвольный гомоморфизм аддитивной группы векторов
первого модуля в аддитивную группу векторов второго, т.е.
для любых векторов ж, у первого модуля имеет место равенство
4.7. Многосортные алгебры 271
Отображение h2 зададим как канонический гомоморфизм коль-
кольца Z в фактор-кольцо Z&. Тогда, если для любого вектора х
первого модуля и любого целого а выполняется равенство
hi(aoX) = h2(a)ohi(x), D.3)
семейство (Лх, h2) есть многосортный гомоморфизм первого
модуля во второй.
В частности, пусть группа векторов модуля С\ есть п-я
декартова степень аддитивной группы целых чисел (т.е. груп-
группа целочисленных арифметических векторов размерности п по
операции сложения); группу же векторов модуля С2 зададим
как n-ю декартову степень аддитивной группы вычетов по
модулю к (т.е. как группу по операции сложения по моду-
модулю к целочисленных арифметических векторов размерности
п, каждая компонента которых принимает значения от 0 до
к — 1). Обозначая через [x]k остаток от деления х на А: (х Е Z),
гомоморфизм h\ зададим равенством hi(x) = [ж]^, где ж =
По определению, Лг(^) = М*> а 6 Z. Умножение вектора на
скаляр в каждом из модулей определим стандартно через умно-
умножение в соответствующем кольце, т.е. для первого модуля по-
положим
где а G Z, ж € Zn, a для второго —
где а 6 {0,1,..., А;-1}, ж Е {0,1, ...,*-1}п. Тогда
hi (а о х) = [а • ж]* = [а]* О* [ж]* = h2(a) о hx (ж),
и равенство D.3) выполняется.
В то же время если бы гомоморфизм h\ мы задали как
проектирующий, т.е. положили бы
272 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
(для некоторого фиксированного г, 1 < i ^ п), тогда h\(a°x) =
= a-Xi, а
h2(a) о hi {x) = [а]к Qk Ык = [a • х{]к фа-хг.
Таким образом, в этом случае семейство (/ii, h2) не будет мно-
многосортным гомоморфизмом, при том что каждое отображе-
отображение семейства будет гомоморфизмом соответственно группы
и кольца.
Заметим, что, если группы векторов рассмотренных моду-
модулей взять соответственно как аддитивную группу целых чисел
и аддитивную группу вычетов по модулю fc, многосортный
гомоморфизм превращается в обычный канонический гомомор-
гомоморфизм кольца Z.
б. Пусть векторами левого модуля Mi являются векторы
какого-то конечномерного линейного пространства С над по-
полем действительных чисел [IV], а скалярами модуля служат ли-
линейные операторы, действующие в этом пространстве. Пусть
размерность пространства С равна п. В качестве векторов
модуля М2 рассмотрим линейное пространство действитель-
действительных матриц-столбцов типа п х 1, а скаляров — квадратные
матрицы n-го порядка (см. пример 2.12.г). Зафиксировав в
пространстве С базис, зададим отображение hi так, чтобы оно
каждому вектору из С сопоставляло столбец его координат в
данном базисе, а отображение h2 пусть для каждого линейного
оператора, действующего в пространстве ?, дает его матрицу
в том же базисе. Основываясь на известных результатах линей-
линейной алгебры [IV], можно утверждать, что тем самым определен
многосортный изоморфизм модуля Mi на модуль М2.
Замечание 4.6. Как и для обычного „односортного" слу-
случая, в теории многосортных алгебр можно доказать теоремы,
аналогичные теоремам 4.3 и 4.4 и связывающие понятия много-
многосортного гомоморфизма и многосортной фактор-алгебры.
Не рассматривая этот вопрос подробно, заметим, что переход
от многосортной алгебры А = ((Aj)^/, il) к ее фактор-алгебре
Вопросы и задачи 273
осуществляется на основе многосортной конгруэнции —
такого семейства отношений эквивалентности (р$ С А?)^, что
для любых попарно эквивалентных элементов a*, bitAi, i Е J,
т.е. таких, что п{ pi 6», имеет место также и эквивалентность
{aix ...uinu) pi0 (Ь{1...Ь{пш)^ какова бы ни была n-арная опера-
операция и Ей типа (t(hHi--•)*'*»)- Тогда любая такая операция
может быть распространена на семейство фактор-множеств
согласно равенству
Определенную таким образом многосортную алгебру называ-
называют фактор-алгеброй исходной алгебры Л = ((Ai)iej, $}) относи-
относительно МНОГОСОРТНОЙ КОНГруЭНЦИИ (pi)i€/- #
Многосортные алгебры широко используются в современ-
современном теоретическом программировании*.
Вопросы и задачи
4.1. Показать, что отношение ^ (см. пример 4.1 [б]) на
носителе поля Т является отношением линейного порядка, т.е.
для любых двух элементов a,beF имеет место а^Ь или b < a.
4.2. Доказать следующие изоморфизмы: Bn = Vqi%,,qn =<5д,
гДе 9i? •••> Qn — попарно различные простые числа, а \А\ = п
(см. примеры З.З.б, 3.9 и 3.11).
4.3. Установить, сохраняет ли отношение, введенное в при-
примере 4.4.а, на множестве Z отношение делимости: т \ п (т
делит п).
4.4. На множестве всех отображений множества М в себя
определено отношение т: / г д, если и только если R{f) = R(d).
*Об использовании понятия многосортной алгебры в программировании
см.: Гоген Дж.А., Мезегер Ж.
274 4. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Доказать, что в общем случае это отношение, будучи эквива-
эквивалентностью, не является конгруэнцией относительно компози-
композиции отношений. Построить пример.
4.5. Имеет ли место изоморфизм ZJ? = Z^n?
4.6. Определить группы движений цилиндра и тора, рассу-
рассуждая так же, как и при решении задачи 2.20. Доказать, что
первая изоморфна группе K2/Z, а вторая — R2/Z2 =
4.7. Доказать, что полукольцо бинарных отношений на
n-элементном множестве {ai,...,an} изоморфно полукольцу
квадратных матриц порядка п над полукольцом В (см. 3).
4.8. Найти все разложения булевой алгебры В3 в виде
В3 S В х В2 S* В2 х В.
4.9. Доказать, что любой гомоморфный
образ решетки, диаграмма Хассе которой
изображена на рис. 4.5, изоморфен либо ей
Рис. 4.5 самой, либо одноэлементной решетке.
4.10. Найти все гомоморфные образы решетки, диаграмма
Хассе которой изображена на рис. 3.5, которые не изоморфны
ей самой, а также не изоморфны одноэлементной решетке.
5. ТЕОРИЯ ГРАФОВ
Неформально граф можно рассматривать как множество
точек и соединяющих эти точки линий со стрелками или без
них.
Первой работой теории графов как математической дисци-
дисциплины считают статью Эйлера A736 г.), в которой рассматри-
рассматривалась задача о Кёнингсбергских мостах. Эйлер показал, что
нельзя обойти семь городских мостов и вернуться в исходную
точку, пройдя по каждому мосту ровно один раз. Следующий
импульс теория графов получила спустя почти 100 лет с разви-
развитием исследований по электрическим сетям, кристаллографии,
органической химии и другим наукам.
С графами, сами того не замечая, мы сталкиваемся посто-
постоянно. Например, графом является схема линий метрополитена.
Точками на ней представлены станции, а линиями — пути дви-
движения поездов. Исследуя свою родословную и возводя ее к
далекому предку, мы строим так называемое генеалогическое
древо. И это древо — граф.
Графы служат удобным средством описания связей меж-
между объектами. Ранее мы уже использовали графы как спо-
способ наглядного представления конечных бинарных отношений
(см. 1.3). Но граф используют отнюдь не только как иллю-
иллюстрацию. Например, рассматривая граф, изображающий сеть
дорог между населенными пунктами, можно определить марш-
маршрут проезда от пункта А до пункта Б. Бели таких маршру-
маршрутов окажется несколько, хотелось бы выбрать в определенном
смысле оптимальный, например самый короткий или самый бе-
безопасный. Для решения задачи выбора требуется проводить
определенные вычисления над графами. При решении подоб-
подобных задач удобно использовать алгебраическую технику, да и
само понятие графа необходимо формализовать.
276
5. ТЕОРИЯ ГРАФОВ
Методы теории графов широко применяются в дискрет-
дискретной математике. Без них невозможно обойтись при анализе
и синтезе различных дискретных преобразователей: функцио-
функциональных блоков компьютеров, комплексов программ и т.д.
В настоящее время теория графов охватывает большой ма-
материал и активно развивается. При ее изложении ограничим-
ограничимся только частью результатов и основной акцент сделаем на
описании и обосновании некоторых широко распространенных
алгоритмов анализа графов, которые применяются в теории
формальных языков.
5.1. Основные определения
Графы, как уже отмечалось в примерах, есть способ „ви-
„визуализации" связей между определенными объектами. Связи
эти могут быть „направленными", как, например, в генеало-
генеалогическом древе, или "ненаправленными" (сеть дорог с двусто-
двусторонним движением). В соответствии с этим в теории графов
выделяют два основных типа графов: ориентированные (или
направленные) и неориентированные.
Построение математического определения графа осущест-
осуществляется путем формализации и „объектов", и „связей" как
элементов некоторых (как правило, конечных) множеств.
Основные понятия для неориентированных и ориентирован-
ориентированных графов удобно вводить „параллельно". Такое изложение
позволит наглядно сопоставить соответствующие понятия.
Неориентированные
графы
Неориентированный граф G
задается двумя множествами
G = (V, JS),
где V — конечное множество,
элементы которого называют
вершинами или узлами] Е —
Ориентированные
графы
Ориентированный граф G
задается двумя множествами
G = (V,E),
где V — конечное множество,
элементы которого называют
вершинами или узлами; Е —
5.1. Основные определения
277
множество неупорядоченных пар
на V, т.е. подмножество мно-
множества двухэлементных подмно-
подмножеств V, элементы которого на-
называют ребрами. Для каждого
ребра {и, v} Е Е считаем, что и
и и — различные вершины.
множество упорядоченных пар
на V, т.е. подмножество множе-
множества V х V, элементы которого
называют дугами.
Если ребро е = {щ v}, то гово-
говорят, что ребро е соединяет вер-
вершины и и v, и обозначают это
wmv; если необходимо, указы-
указывают имя графа G: и м<з v.
Бели дуга е = (и, v), то говорят,
что дуга е ведет из вершины и
в вершину v, и обозначают это
и ->• v; если необходимо, указы-
указывают имя графа G: м
Вершины и и v, соединеные ре-
ребром (uhhv), называют смеж-
смежными, а также концами ре-
ребра {и, v}. Если whhv, гово-
говорят, что вершины и и v свя-
связаны отношением непосред-
непосредственной достижимости.
Вершины и и v, такие, что из
вершины it в вершину i> ведет
дуга (u->v), называют смеж-
смежными, причем и называют на-
началом, а г? — концом дуги
(и, v). Дугу, начало и конец ко-
которой есть одна и та же вер-
вершина, называют петлей. Ес-
Если и -* v, то говорят, что вер-
вершины иии связаны отноше-
отношением непосредственной до-
достижимости.
Ребро е называют инцидент-
инцидентным вершине v, если она явля-
является одним из его концов.
Дугу (u,v) называют заходящей
в вершину v и исходящей из
вершины и. Дугу называют ин-
инцидентной вершине v, если она
заходит в v или исходит из v.
Степенью вершины v назы-
называют число dgv всех инцидент-
инцидентных ей ребер.
Полустепенью захода вер-
вершины v называют число dg~(v)
заходящих в нее дуг, а по-
полустепенью исхода вершины
v — число dg+(v) исходящих из
нее дуг. Степень вершины
г;, обозначаемая dg(v), — это
сумма полустепеней захода и ис-
исхода.
278
5. ТЕОРИЯ ГРАФОВ
Для вершины v множество
T(v) = {х:
называют множеством смежных
с v вершин. Справедливо равен-
равенство
Для вершины v множество
T(v) = {х: v -> х}
называют множеством преем-
преемников вершины v, а множество
множеством предшественни-
предшественников вершины v. Справедливы
равенства
Цепь в неориентированном гра-
графе G — это последовательность
вершин (конечная или бесконеч-
бесконечная) vOi v\, ..., vn, ..., такая,
что Vi»-HVi+i для любого г, если
Vi+i существует. (Под конечной
последовательностью понимает-
понимается кортеж вершин.)
Путь в ориентированном гра-
графе G — это последовательность
вершин (конечная или бесконеч-
бесконечная) vo, vi,..., vn,..., такая, что
V{ -» Vi+i для любого г, если
существует.
Для конечной цепи vo, v\, ..., vn
число n (n ^ 0) называют дли-
длиной цепи. Таким образом, дли-
длина цепи есть число ее ребер, т.е.
всех ребер, соединяющих вер-
вершины V{ и Vi+i (г = 0, п—1). Цепь
длины 0 — это произвольная
вершина графа.
Для конечного пути vo, vi, ...,
vn число п называют длиной
пути (п ^ 0). Тем самым дли-
длина пути есть число его дуг, т.е.
всех дуг, которые ведут из вер-
вершины V{ в вершину Vj+i (г =
= 0,п-1). Путь длины 0 — это
произвольная вершина графа.
Говорят, что вершина v неори-
неориентированного графа G дости-
достижима из вершины и этого гра-
графа и обозначают и м* v, если
существует цепь vo, «i, ..., vn,
такая, что и = vo, vn = v (при
этом говорят также, что дан-
данная цепь соединяет вершины и и
v, которые называют концами
цепи). Таким образом, задано
Говорят, что вершина v ори-
ориентированного графа G дости-
достижима из вершины и этого гра-
графа и обозначают и =>* г>, если
существует путь v0, vi, ..., vn,
такой, что и = vo, v = vn (при
этом говорят, что данный путь
ведет из вершины и в верши-
вершину v, называя первую вершину
началом, а вторую — концом
5.1. Основные определения
279
отношение достижимости
«* в неориентированном гра-
графе. Оно является рефлексивно-
транзитивным замыканием от-
отношения ни непосредственной
достижимости.
данного пути). Таким обра-
образом, задано отношение до-
достижимости =Ф>* в ориенти-
ориентированном графе. Оно является
рефлексивно-транзитивнглм за-
замыканием отношения —> непо-
непосредственной достижимости.
Отношение достижимости в не-
неориентированном графе рефлек-
рефлексивно^ симметрично и транзи-
тивно% т.е. является отношени-
отношением эквивалентности.
Отношение достижимости в ори-
ориентированном графе рефлексив-
рефлексивно и транзитивно, но в общем
случае не антисимметрично: ес-
если две вершины ориентирован-
ориентированного графа достижимы одна
из другой, то из этого вовсе
не следует, что они совпадают.
Таким образом, отношение до-
достижимости в ориентированном
графе есть отношение предпо-
рлдка.
Бели существует цепь ненулевой
длины, соединяющая « и и, то
пишут
+ v.
Если необходимо явно указать
длину цепи, то пишут
и говорят, что существует цепь
длины п, соединяющая и и v.
Если существует путь ненуле-
ненулевой длины, ведущий из и в v, то
пишут
и =?•"*" v.
Если необходимо явно указать
длину пути, то пишут
и говорят, что существует путь
длины п, ведущий из и в v.
Простая цепь — это цепь, все
вершины которой, кроме, быть
может, первой и последней, по-
попарно различны и все ребра по-
попарно различны.
Простой путь — это путь,
все вершины которого, кроме,
быть может, первой и послед-
последней, попарно различны.
Простую цепь ненулевой длины
с совпадающими концами назы-
называют циклом.
Простой путь ненулевой длины,
начало и конец которого совпа-
совпадают, называют контуром.
280
5. ТЕОРИЯ ГРАФОВ
Произвольную цепь ненулевой
длины с совпадающими конца-
концами, все ребра которой попарно
различны, будем называть за-
замкнутой цепью.
Произвольный путь ненулевой
длины, начало и конец которо-
которого совпадают, будем называть
замкнутым путем.
Неориентированный граф, не
содержащий циклов, называют
ациклическим графом.
Ориентированный граф, не со-
содержащий контуров, называют
бесконтурным графом.
Замечание 5.1. Требование, чтобы все ребра простой цепи
неориентированного графа были попарно различными, суще-
существенно. Если его снять, то цепь вида u, v,
и, где tzi-HV, будет циклом, в котором одно
и то же ребро {м, г;} проходится дважды в
противоположных направлениях, хотя та-
такую цепь естественно циклом не считать.
Не будет эта цепь в соответствии с приня-
принятой терминологией и замкнутой цепью.
В неориентированном графе на рис. 5.1
цепь аьнЬысьчйь—• е»—icho является при-
примером замкнутой цепи.
Рис. 5.1
Замечание 5.2. В общем случае в ориентированном графе
пересечение множества преемников Г(г>) вершины v и множе-
множества F"(v) ее предшественников будет не пусто, если есть
петля (г;, v): Г{и)ПГ-г(у) ф 0.
Пример 5.1. Расмотрим неориентированный граф, изо-
изображенный на рис. 5.2. Он задается множеством вершин
V =
и множеством неупорядоченных пар
Е =
, v7}
В этом графе последовательность вершин vi, V3, V4 есть простая
цепь, а последовательность vi, V3, v2, vi, ^3, V4 — цепь, не являю-
5.1. Основные определения 281
щаяся простой, поскольку в ней есть со-
совпадающие ребра. Последовательность
вершин т>з, vi, ^2, v± не является цепью,
поскольку в графе нет ребра {v2^v^}.
Последовательность «i, V3, V2, vi есть
цикл, а последовательность v4, г>з? ^ъ ^2>
^з, v4 — цепь с совпадающими концами,
но не цикл, поскольку эта цепь не является простой. Эта цепь
не будет и замкнутой, так как в ней есть повторяющееся ребро
Степени вершин графа следующие: dg(vi) = dg(^2) = 2,
= 3, dg(v4) = dg(v5) = dg(v6) = 1, dg(v7) = 0.
Вершины vi, ^2, V3, V4 попарно достижимы (vjt=i* Vj, t,j6
G {1,2,3,4}) и образуют класс эквивалентности по отношению
достижимости. Для вершин v$ и vq имеет место t>5 w* vq, и они
также образуют класс эквивалентности. Заметим, что вершина
V7, по определению, образует цепь длины 0 и эквивалентна по
отношению достижимости только самой себе.
Пример 5.2. Обратимся к ориентированному графу, изо-
изображенному на рис. 5.3. Он задается множеством вершин
V = {vi, г>2, ^з, V4, V5, vq} и множеством дуг
={(vi, V2), (Vi, V3), (V2, Vl), (V2, V3), (V2, W
l), (i73, V4), (V5,
В этом ориентированном гра-
графе последовательность вершин vi,
V2? ^з, v4 есть простой путь, а
последовательность вершин vi, V2,
V3» vi, v3, w4 — путь, не являющий-
являющийся простым, поскольку в нем, на-
например, два раза встречается вер- Рис# 5#3
шина г;з, не служащая началом и концом пути.
Последовательность вершин г;з, vi, ^2, ^3 есть контур, а
последовательность v3, vi, V2, vi, v3 — замкнутый путь, но не
282 5. ТЕОРИЯ ГРАФОВ
контур, поскольку вершина vi, не являющаяся началом пути,
встречается два раза. Последовательность вершин vi, v3, v4, г^
не задает путь, так как в рассматриваемом ориентированном
графе нет дуги (v4, vq).
Полустепени захода, полустепени исхода и степени у вер-
вершин следующие: у vi и v3 — dg~(vi) = dg~(v3) = 2, dg+(vi) =
= dg+(v3) = 2, dg(vi) = dg(v3) = 4; у v2 — dg~(v2) = 1, dg+(v2) =
= 3, dg(v2) = 4; у v4 — dg-(t74) = 3, dg+(v4) = 0, dg(v4) = 3; у
*>5 — dg-(v5) = 0, dg+(v5) = 1, dg(v5) = 1; у v6 — dg""(v6) = 1,
+ = 2. #
Отношение достижимости в неориентированных и ориенти-
ориентированных графах обладает следующим важным свойством.
Теорема 5.1. Для любой цепи, соединяющей две вершины
неориентированного графа, существует простая цепь, соединя-
соединяющая те же вершины. Для любого пути, ведущего из вершины
и в вершину v ориентированного графа, существует простой
путь, ведущий из и в v.
<4 Проведем доказательство для неориентированного графа
(для ориентированного графа доказательство проводится ана-
аналогично).
Пусть вершины и и v неориентиро-
с\/\л/\/*о ванного графа таковы, что и w* v. Если
эти вершины являются концами цепи ну-
нулевой длины, то утверждение теоремы
тривиально. Пусть и и+ v, т.е. суще-
существует цепь ненулевой длины, соединя-
соединяющая и и v. Рассмотрим какую-либо из
таких цепей (рис. 5.4). Обозначим ее С.
Рис. 5.5 Если цепь С простая, то доказывать не-
нечего. Пусть существует внутренняя (не
^Ч/ЧА/Ч/^ЛАААА^ совпадающая ни с одним из концов) вер-
вершина w цепи G, которая повторяется в
Рис. 5.6 этой цепи, т.е. и t=i* w *==*+ w и* v. Это
5.1. Основные определения 283
значит, что вершина w содержится в некоторой цепи С не-
ненулевой длины (подцепи цепи С) с совпадающими концами
(рис. 5.5). Удалим все вершины и ребра цепи С", кроме вершины
w (служащей ее началом и концом одновременно). После этого
получим новую цепь Ci, соединяющую вершиы и и v (рис. 5.6),
в которой число повторений вершины w будет по крайней мере
на единицу меньше, чем в цепи С. Если цепь С\ простая, то
утверждение доказано. В противном случае поступаем с ней
так же, как и с цепью С. В силу конечности множества вершин
и ребер графа после конечного числа шагов получим простую
цепь, соединяющую вершиы и и v. >
Следствие 5.1. Бели вершина неориентированного графа
содержится в некоторой замкнутой цепи, то она содержится
и в некотором цикле. Бели вершина ориентированного графа
содержится в некотором замкнутом пути, то она содержится и
в некотором контуре.
Замечание 5.3. Следствие 5.1 перестает быть верным для
произвольной цепи с совпадающими концами. Например, для
неориентированного графа, состоящего из двух вершин vi, V2
и единственного ребра («i, V2) цепь vi, V2> v\ с совпадающими
концами не содержит цикла. #
Перейдем теперь к понятию подграфа. Формулируется это
понятие одновременно для неориентированных и ориентиро-
ориентированных графов (с учетом различий в терминологии).
Определение 5.1. Неориентированный (ориентирован-
(ориентированный) граф G\ = (Vi, E\) называют подграфом неориентиро-
неориентированного (ориентированного) графа G = (V, J5), если Vi С V и
ЕХСЕ.
Будем использовать обозначение 6?i С G, аналогичное обо-
обозначению включения для множеств.
Замечание 5.4. Так как в определении 5.1 пара Gi = (Vi,f?i)
есть неориентированный (ориентированный) граф, то для лю-
284
5. ТЕОРИЯ ГРАФОВ
бого ребра {и, г;} Е Е\ (дуги (u, v) ЕЕ\) предполагается, конеч-
конечно, что и, v E Vi, поскольку иначе пару (Vi, i?i) нельзя будет
считать неориентированным (ориентированным) графом. #
Если хотя бы одно из указанных двух включений в опреде-
определении 5.1 строгое, то G\ называют собственным подграфом
графа G; если Vi = V, то G\ называют остовным подграфом
графа G.
Подграф G\ неориентированного (ориентированного) гра-
графа G называют подграфом, порожденным множеством
вершин V\ С Vj если каждое ребро (дуга) тогда и только то-
тогда принадлежит Е\ С Е, когда его (ее) концы принадлежат V\.
Часто в случае, если множество вершин Vi подразумевается, го-
говорят просто о порожденном подграфе.
Отметим, что подграф графа G, порожденный множеством
вершин Vi, в отличие от произвольного подграфа графа G с
множеством вершин Vi, должен включать все ребра (дуги),
концы которых принадлежат множеству V\.
Подграф G\ С G называют максимальным подграфом,
обладающим данным свойством Р, если он не является соб-
собственным подграфом никакого другого подграфа графа G,
обладающего свойством Р.
Например, на рис. 5.7 подграфы Gi, G2, G3 являются мак-
максимальными ациклическими подграфами графа G. Отметим,
что они также являются собственными и остовными подгра-
подграфами указанного графа.
¦¦¦ о о о о
G3 G
Рис. 5.7
Следующее важное понятие снова введем параллельно для
рассматриваемых двух видов графов.
5.1. Основные определения
285
Неориентированные
графы
Неориентированный граф назы-
называют связным, если любые две
его вершины unv соединены це-
цепью (uw* г;).
Компонента связности (или
просто компонента) неориен-
неориентированного графа — это его
максимальный связный подграф.
Ориентированные
графы
Ориентированный граф называ-
называют связным, если для любых
двух его вершин и, v вершина
v достижима из вершины и или
вершина и достижима из верши-
вершины v (и =>* v или v =Ф>* и).
Компонента связности (или
просто компонента) ориенти-
ориентированного графа — это макси-
максимальный связный подграф.
В неориентированном графе две вершины, соединенные
цепью, связаны отношением достижимости, которое является
эквивалентностью. Поэтому компонента такого графа — это
подграф, порожденный некоторым классом эквивалентности
вершин по отношению достижимости.
Поскольку каждая компонента неориентированного графа
порождается некоторым классом эквивалентности вершин, то
две различные компоненты не пересекаются, т.е. не имеют ни
общих вершин, ни общих ребер.
Так как отношение достижимости в ориентированном гра-
графе не является эквивалентностью, то компоненты ориентиро-
ориентированного графа могут пересекаться.
Пример 5.3. Граф, изображенный на рис. 5.2, не является
связным. Он состоит из трех компонент. Эти компоненты
порождены тремя классами эквивалентности по отношению
достижимости, указанными в примере 5.1.
Связными являются все графы, изобра-
изображенные на рис. 5.7.
Ориентированный граф на рис. 5.8 связ-
связный, а ориентированные графы на рис. 5.3
и 5.9 не являются связными. В ориентиро-
ориентированном графе на рис. 5.3 вершины v<i и v&
не достижимы одна из другой, а в ориенти-
Рис. 5.8
286
5. ТЕОРИЯ ГРАФОВ
Рис. 5.9
рованном графе на рис. 5.9 взаимно не достижимы, например,
вершины V2 и vq. В ориентированном графе, изображенном на
рис. 5.9, имеются две компоненты связности: С\ и Сг, которые
пересекаются. #
Для ориентированного графа можно определить также по-
понятия сильной и слабой связности.
Определение 5.2. Ориентированный граф называют силь-
сильно связным^ если для любых двух его вершин и иу вершина v
достижима из вершины и и вершина и достижима из вершины v
(и =Ф-* v и v =Ф* и). Бикомпонента ориентированного графа —
это его максимальный сильно связный подграф.
Бели и =И v и v =Ф>* г*, то говорят, что и и v связаны от-
ногиением взаимной достижимости. Это бинарное отно-
отношение рефлексивно, симметрично и транзитивно, т.е. является
отношением эквивалентности. Следовательно, две различные
бикомпоненты не пересекаются, т.е. не имеют ни общих вер-
вершин, ни общих ребер.
Пример 5*4. а. В ориентированном графе, изображенном
на рис. 5.3, бикомпонентой является подграф Gi, порожденный
множеством вершин {^1,^2,^3}. Действительно, эти вершины
взаимно достижимы, поэтому ориентированный граф G\ силь-
сильно связный. Так как из вершин v±, V5, ^б ни одна из вершин v\,
5.1. Основные определения
287
г>2, из не достижима, то выделенный сильно связный подграф
G\ является максимальным.
б. В ориентированном графе, представленном на рис. 5.9,
имеются четыре бикомпоненты В\у 2?2, В$ и В±. Это подгра-
подграфы, порожденные соответственно множествами вершин {t>i},
{^2>^з}, {^4?^б} и {ve, V7}. Отметим, что подграф, порожден-
порожденный множеством {^i}, не содержит ни одной дуги. Тем не менее
этот подграф — бикомпонента, поскольку каждая вершина до-
достижима сама из себя (по пути длины 0).
Определение 5.3. Неориентированный граф G\ = (Vi, E\)
называют ассоциированным с ориентированном графом G =
= (F, 25), если его множество вершин совпадает с множеством
вершин ориентированного графа G, а пара {щ v} образует
ребро тогда и только тогда, когда ифуиизивь или из v
в и ведет дуга, т.е. V\ = V и
Ei = {{u,v}: {щ у)€Еили (v, и) € Е, иф v}.
Таким образом, переход от ориентированного графа к ас-
ассоциированному с ним неориентированному графу состоит в
„стирании" ориентации дуг ориентированного графа с учетом
того, что все петли исчезают, а дуги (гх, v) и (г;, и) при и Ф v
переходят в одно и то же ребро {и, v}.
Для ориентированного графа, изображенного на рис. 5.10, а,
ассоциированный с ним неориентированный граф приведен
на рис. 5.10, б. Отметим, что дуги (vi, V2) и (г>2, vi) переходят
в ребро {vi, ^г}> а петля (г;б, г>б) исчезает.
б
Рис. 5.10
288 5. ТЕОРИЯ ГРАФОВ
Определение 5.4. Ориентированный граф называют ела-
бо связным, если ассоциированный с ним неориентированный
граф связный. Компонентой слабой связности (слабой
компонентой) ориентированного графа называют его макси-
максимальный слабо связный подграф.
Ориентированные графы, представленные на рис. 5.3, 5.9
и 5.8, являются слабо связными. Ориентированный граф, изо-
изображенный на рис. 5.10, не является слабо связным, поскольку
не является связным ассоциированный с ним неориентирован-
неориентированный граф. Ориентированный граф на рис. 5.10, а имеет две
компоненты слабой связности. Соответственно ассоциирован-
ассоциированный с ним неориентированный граф на рис. 5.10, б имеет две
компоненты связности.
5.2. Способы представления
До сих пор мы задавали ориентированные и неориенти-
неориентированные графы, изображая их с помощью рисунков. Можно
задать граф как пару множеств, следуя определению, однако
этот способ довольно громоздкий и представляет, скорее, те-
теоретический интерес. Развитие алгоритмических подходов к
анализу свойств графов требует иных способов описания гра-
графов, более пригодных для практических вычислений, в том
числе с использованием ЭВМ. Рассмотрим три наиболее рас-
распространенных способа представления графов.
Предположим, что все вершины и все ребра неориентиро-
неориентированного графа или все вершины и все дуги (включая петли)
ориентированного графа пронумерованы начиная с единицы.
Граф (неориентированный или ориентированный) может быть
представлен в виде матрицы типа пхт, где п — число вершин,
am — число ребер (или дуг). Для неориентированного графа
элементы этой матрицы задаются следующим образом:
Г 1, для г-й вершины j-e ребро инцидентное;
%3 I 0, иначе.
5.2. Способы представления 289
Для ориентированного графа элементы матрицы задаются так:
{1, для г-й вершины j-я дуга выходящая]
—1, для г-й вершины j-я дуга заходящая;
О, иначе.
Матрицу (aij) типа пхт, определенную указанным обра-
образом, называют матрицей инциденции.
Пример 5,5. Для ориентированного графа, представлен-
представленного на рис. 5.8, нумерация вершин уже задана. Зададим
нумерацию дуг следующим образом: дуге (vi, v2) присвоим но-
номер 1, дуге (vi, V3) — 2, дуге (v2, v3) — 3 и дуге (v3, v2) — 4.
Матрицу инциденции удобно заполнять по столбцам, запи-
записывая для к-и дуги (vj, Vj) 1 в г-й и —1 в j-й строках fc-ro столбца
и 0 во всех остальный строках fc-ro столбца. В результате по-
получим матрицу
#
Несмотря на то что представление графа в виде матрицы
инциденции играет весьма большую роль в теоретических ис-
исследованиях, практически этот способ весьма неэффективен.
Прежде всего, в матрице в каждом столбце только два нену-
ненулевых элемента, что делает этот способ представления графа
неэкономным при большом количестве вершин. Кроме того,
решение практических задач с помощью матрицы инциденции
весьма трудоемко.
Оценим, например, временные затраты на решение с помо-
помощью матрицы инциденции такой простой задачи в ориенти-
ориентированном графе: для данной вершины и& найти ее „окруже-
„окружение" — множество преемников и множество предшественников
вершины Vk, т.е. множество всех вершин, непосредственно до-
достижимых из vj;, и множество всех вершин, из которых она
непосредственно достижима.
10 - 10061
290 5. ТЕОРИЯ ГРАФОВ
Для решения этой задачи на матрице инциденций ориен-
ориентированного графа нужно идти по строке с номером к до
появления ненулевого элемента (+1 или —1). В случае если об-
обнаружена +1, в соответствующем столбце надо найти строку,
в которой записано число —1. Номер строки, в которой стоит
это число, дает номер вершины, непосредственно достижимой
из данной вершины. Бели обнаружена — 1, в столбце надо най-
найти строку, в которой записана 1, и получить номер вершины,
из которой непосредственно достижима данная вершина. Для
получения всего „окружения" надо проделать указанный поиск
для всех ненулевых элементов fc-й строки. Наиболее трудоемкой
процедурой является поиск ненулевого элемента в столбце. Чи-
Число таких процедур поиска равно степени вершины и&. Будем в
этом случае говорить, что сложность алгоритма анализа
окружения вершины и* составляет O(dgVk) (порядка dgv*).
Можно увидеть, что поиск „ окружения" всех вершин займет
время порядка произведения числа вершин ориентированного
графа на сумму степеней всех вершин, которая, как можно
показать, пропорциональна числу дуг ориентированного гра-
графа. Таким образом, сложность алгоритма поиска „ окружения"
составляет О(пт), т.е. поиск занимает время порядка произве-
произведения числа вершин на число дуг.
Более эффективной матричной структурой, представляю-
представляющей граф, служит матрица смежности вершин, или бу-
булева матрица графа. Это квадратная матрица В порядка п,
элементы которой определяют следующим образом:
для неориентированного графа
Г 1, г-я и j-я вершины смежные;
J 10, иначе;
для ориентированного графа
из г-й вершины в j-ю ведет дуга;
иначе.
5.2. Способы представления 291
Заметим, что в fc-й строке матрицы ориентированного гра-
графа количество единиц равно полустепени исхода dg+ од верши-
вершины од, а количество единиц в fc-м столбце — полустепени захода
Для неориентированного графа матрица смежности вершин
симметрическая.
Для ориентированного графа, изображенного на рис. 5.8,
матрица смежности вершин имеет вид
Рассмотрим решение задачи поиска „окружения" с исполь-
использованием матрицы смежности вершин. Для определения „ окру-
окруженияu вершины од нужно сначала идти по fc-й строке матрицы
и искать ненулевые элементы. Бели элемент од = 1, то вершина
Vi достижима из вершины од. После просмотра fc-й строки надо
просмотреть Л-й столбец. Бели элемент а^ = 1, то вершина од
достижима из вершины Vj.
Можно показать, что с использованием матрицы смежно-
смежности вершин решение задачи поиска „ окруженияu всех вершин
ориентированного графа будет иметь сложность порядка п2,
что эффективнее предыдущей оценки пга, если число дуг ори-
ориентированного графа превышает число его вершин, а это часто
бывает в практических задачах.
Матрица смежности верпган является достаточно эффек-
эффективным способом представления графов. Однако эту матрицу
удобно строить по графу, уже заданному каким-либо спосо-
способом, например рисунком. Во многих задачах граф создается
динамически, т.е. в ходе решения задачи меняется множество
вершин и множество ребер (или дуг). В этом случае эффек-
эффективным способом машинного представления графа являются
списки смежности (или списки инцидентности).
Рассмотрим ориентированный граф. Для задания множе-
множества вершин, непосредственно достижимых из вершины v, ис-
292 5. ТЕОРИЯ ГРАФОВ
пользуют линейный однонаправленный список*. Каждый эле-
элемент такого списка включает данные (например, некоторое
число) и указатель на следующий элемент списка. Список в це-
целом задается указателем на его первый элемент (голову спис-
списка). Последний элемент списка содержит „пустой" указатель
(рис. 5.11).
Рис. 5.11
Задать для вершины v ее список смежности означает в
произвольном порядке поместить в данные элементов списка
номера вершин и, для которых в ориентированном графе есть
дуга из v в и (v —> и). Список смежности вершины v
обозначают L(v).
Отметим, что список смежности вершины может при не-
необходимости дополняться. Для этого в последнем элементе
списка ппустой" указатель заменяется указателем на добавляе-
добавляемый элемент, который становится последним элементом списка
с „пустым" указателем.
Бели количество вершин ориентированного графа известно
заранее, то ориентированный граф удобно задавать в виде
структуры, называемой массивом лидеров.
Под массивом мы понимаем матрицу-столбец, элементами
которой могут быть некоторые объекты (например, элементы
списка смежности). Их называют элементами массива.
Число элементов массива лидеров равно числу вершин графа.
Элементами массива лидеров являются первые элементы
списков смежности вершин ориентированного графа. Пример
представления ориентированного графа списками смежности,
собранными в массив лидеров, представлен на рис. 5.12.
* Подробное описание обработки списков и всей „программистской"
терминологии, использованной в этом абзаце, см.: Вирт Н.
5.2. Способы представления
293
Рис. 5.12
С использованием списков смежности совсем просто реша-
решается задача поиска преемников данной вершины: для этого
достаточно просмотреть список смежности вершины, затратив
на это время, пропорциональное ее полустепени исхода. Тогда
на решение этой задачи для всего ориентированного графа по-
потребуется время порядка числа его дуг.
Менее эффективно решается задача поиска предшествен-
предшественников вершины, так как в этом случае необходимо, вообще
говоря, просмотреть списки смежности всех вершин с целью
поиска в них данной вершины.
Таким образом, задача поиска я окружения" с использовани-
использованием списков смежности является более трудоемкой, чем в случае
использования матриц. Однако удобство динамического фор-
формирования описания ориентированного графа в данном случае
перевешивает. Бели задача поиска предшественников возника-
возникает часто, можно использовать двусторонние списки смежности,
сопоставляя каждой вершине уже два списка — преемников и
предшественников.
Описанные способы представления графа списками не ис-
исчерпывают всех возможных вариантов, и в литературе по
программированию можно найти разнообразные варианты ор-
294 5. ТЕОРИЯ ГРАФОВ
ганизации списков. Поскольку эти особенности относятся к
технологии программирования, мы не будем в них углубляться
и в дальнейшем для простоты при описании различных алго-
алгоритмов будем считать, что (односторонние) списки смежности
собраны в массив лидеров, так как в рассматриваемых ниже
алгоритмах анализа графов именно анализ множества преем-
преемников вершины наиболее важен.
Неориентированный граф задать с помощью списков смеж-
смежности можно так же, как и ориентированный. Здесь в список
смежности вершины v войдут все вершины, смежные с ней, а
списки смежности могут быть собраны в массив лидеров. Для
неориентированого графа задача поиска „ окружения" одной
вершины требует однократного просмотра ее списка смеж-
смежности, и затраты времени на это пропорциональны степени
вершины. На решение задачи поиска „окружения" для всего
неориентированного графа потребуется время, пропорциональ-
пропорциональное произведению числа вершин графа на число его ребер.
В заключение рассмотрим еще одну матрицу, характеризу-
характеризующую граф, — так называемую матрицу достижимости.
Это квадратная матрица С порядка |V|, каждый элемент c%j
которой равен 1, если j-я вершина достижима из i-й верши-
вершины, и равен 0 если иначе. Отметим, что, согласно определению
достижимости, элементы сц = 1.
Метод вычисления матрицы достижимости ориентирован-
ориентированного графа по его матрице смежности будет рассмотрен в 5.6.
Матрица достижимости несет очень важную информацию
об ориентированном графе. Бе анализ позволяет, например,
найти его бикомпоненты и компоненты.
По определению, в бикомпоненту входят взаимно дости-
достижимые вершины. Для двух таких вершин с номерами % и j
должно выполняться равенство Cjj = Cji = 1. Поэтому, что-
чтобы найти бикомпоненту, в которую входит г-я вершина ори-
ориентированного графа, нужно просмотреть г-ю строку и г-й
столбец матрицы достижимости С и сформировать множество
Pi = {р- (Ир = Cpi = 1} номеров вершин, порождающих искомую
5.2. Способы представления
295
бикомпоненту. Из определения матрицы достижимости выте-
вытекает, что в Pi содержатся номера всех вершин данной биком-
поненты. Поскольку две различные бикомпоненты не пересека-
пересекаются, вершины с номерами из множества Р% при поиске других
бикомпонент из рассмотрения можно исключить. Процесс по-
поиска целесообразно начать с первой вершины. Он закончится,
когда для каждой вершины будет найдена содержащая ее би-
компонента. При этом может оказаться, что некоторые (а
может быть, и все) бикомпоненты содержат только по одной
вершине, поскольку каждая вершина, по определению, дости-
достижима сама из себя.
Поиск компонент ориентированного графа сложнее, так
как в компоненту входят вершины с номерами г и j, для
которых cij — 1 или Cji = 1. Кроме того, одна и та же вершина
может входить в несколько различных компонент. Отметим,
что любая бикомпонента или не пересекается с некоторой
компонентой, или целиком в нее входит.
Мы не будем приводить общий алгоритм поиска компонент,
а рассмотрим его на примере.
Пример 5.6. Для ориентированного графа, изображенного
на рис. 5.9, имеем матрицу достижимости
(\
0
0
0
0
0
^0
1
1
1
0
0
0
0
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
1
1
0
0
0
0
1
1 1
Начнем с поиска бикомпонент. Для первой вершины множе-
множество Pi = {1} включает только ее саму. Для второй вершины
имеем Р2 = {2,3}, для четвертой — Р± = {4,5} и для шестой —
^6 = {6,7}. Соответственно полученные множества вершин по-
порождают бикомпоненты В\, Дг? -Вз и В^ изображенные на
рис. 5.9.
296 5. ТЕОРИЯ ГРАФОВ
Перейдем к поиску компонент. Используя матрицу С, выпи-
выпишем для каждой вершины v^ г = 1, 7, множество К{, состоящее
из тех вершин, которые достижимы из г-й вершины или из ко-
которых достижима она.
В рассматриваемом ориентированном графе для вершины v\
в множество К\ входят вершины, для которых c\j = 1 или Cj\ =
= 1, т.е. К\ = {vi, V2, V3, V4, V5}. Для вершин V2 и v$ множества
K<i и К$ совпадают с множеством К\. Поскольку все элементы
четвертого и пятого столбцов матрицы С равны единице, то
для вершин ^4 и v$ имеем К\ = К$ = {vi, t>2, V3, ^4) ^5, ve, v-j}.
Для вершин ve и v-j получим i^e = ^7 = {^4, V5, V6, V7}.
Отметим, что множество Ki построено так, что любая
компонента, содержащая вершину v», может содержать только
вершины из множества К{.
Кроме того, если некоторая компонента Ср содержит вер-
вершины Vi и Vj, то вершина vm будет принадлежать этой компо-
компоненте в том и только в том случае, если vm G Ki П Kj.
Действительно, пусть вершина vm принадлежит компоненте
Ср вместе с вершинами Vi и Vj. Тогда либо вершина vm дости-
достижима из вершины Vi, либо, наоборот, V{ достижима из vm, и,
следовательно, vm G К^ Из аналогичных рассуждений выте-
вытекает, что vm G Kj. Таким образом, вершина vm принадлежит
пересечению множеств Ki и Kj.
Пусть теперь вершины Vi и Vj принадлежат компоненте
Ср и vm E KiC\Kj. Тогда вершина vm также принадлежит
компоненте Ср, поскольку либо вершина Vi достижима из vm,
либо vm достижима из Vj, и для вершин Vj и vm ситуация
аналогична.
Начнем строить компоненты, содержащие вершину v\. Рас-
Рассмотрим множество К\. Так как вершина г>2 принадлежит
множеству ifi, найдется по крайней мере одна компонента, в
которую входят обе эти вершины. Обозначим ее через С\. Вер-
Вершина vs будет принадлежать этой компоненте в том и только
в том случае, если ^з € К\ П-Кг- Непосредственная проверка
показывает, что последнее условие выполняется.
5.3. Деревья 297
Можно заметить, что
Кг ПК2 Г)К3 Г)К4 ПКЬ = Ки
поэтому компонента С\ (см. рис. 5.9) есть подграф, поро-
порожденный множеством К\, и вершина v\ не может входить в
какую-либо другую компоненту, отличную от С\. Поскольку в
компоненту С\ вошли все вершины из множеств К2 и Кз, то
вершины v2 и г;з также не входят ни в какие другие компо-
компоненты.
Перейдем к поиску компонент, отличных от Ci, в которые
входит вершина v±. В множестве К\ содержится вершина v$.
Пересечению множеств К± и К$ принадлежат вершины vq и
^7, не вошедшие в выделенную компоненту С\. Рассуждая
аналогично и учитывая, что v± и у$ принадлежат бикомпоненте
Вз, a vq и vj — бикомпоненте В^ получаем, что компонента С2
порождается множеством вершин
и других компонент в рассматриваемом ориентированном гра-
графе нет.
5.3. Деревья
Определение 5.5. Неориентированным деревом на-
называют связный и ациклический неориентированный граф.
Определение 5.6. Ориентированным дерев ом называ-
называют бесконтурный ориентированный граф, у которого полусте-
полустепень захода любой вершины не больше 1 и существует ровно
одна вершина, называемая корнем ориентированного де-
дерева, полустепень захода которой равна 0.
Опираясь на данное определение, можно доказать, что в
ориентированном дереве любая вершина достижима из корня.
298
5. ТЕОРИЯ ГРАФОВ
Отметим, что из определения 5.6 не-
нельзя убрать требование бесконтурности
ориентированного графа, поскольку бес-
контурность не вытекает из других усло-
условий. Например, на рис. 5.13 изображен
ориентированный граф, не являющийся
ориентированным деревом, хотя полу-
полустепени захода всех вершин не больше 1 и ровно одна вершина
имеет полустепень захода, равную 0.
Определение 5.7. Вершину v ориентированного дерева
называют потомком (подлинным потомком) вершины и,
если существует путь из и в г; (путь ненулевой длины из и в v).
В этом же случае вершину и называют предком (подлинным
предком) вершины v, а если длина пути из и в v равна 1,
то вершину v называют сыном вершины гх, которая при этом
вполне естественно именуется отцом вершины v. Вершину, не
имеющую потомков, называют листом.
На рис. 5.14 вершины v± и v$ есть сыновья вершины V2, кото-
которая, в свою очередь, является сыном вершины vq — корня дере-
дерева. Вершины V4 и V5 являются подлинными потомками вершин
Уровень 3
Уровень 2
Уровень 1
Уровень 0
v4 vs v6 v7 v8
Рис. 5.14
5.3. Деревья
299
vo и t>2, которые соответственно будут их подлинными предка-
предками. Вершины vi, V4, t>5, ve, V9, ve — листья дерева. Взаимно
недостижимые вершины ориентированного дерева (например,
такие, как V2 и vq) не являются ни предком, ни потомком од-
одна другой. Каждая вершина будет сама для себя предком и
потомком, но не подлинным.
Определение 5.8. Произвольный ациклический граф на-
называют неориентированным лесом. Бели каждая слабая
компонента ориентированного графа является ориентирован-
ориентированным деревом, то такой граф называют ориентированным
лесом.
На рис. 5.15, а даны примеры неориентированного леса, а на
рис. 5.15, б — примеры орентированного леса.
VS "в
V14 V13
300 5. ТЕОРИЯ ГРАФОВ
Определение 5.9. Подграф неориентированного (ориен-
(ориентированного) дерева, являющийся неориентированным (ориен-
(ориентированным) деревом, называют поддеревом исходного де-
дерева.
Из определения следует, что неориентированный лес —
это неориентированный граф, каждая компонента которого
является неориентированным деревом.
На рис. 5.14 подграф, порожденный множеством вершин
{^з, V6? ^7? ^8, V9}, является поддеревом изображенного на ри-
рисунке ориентированного дерева.
Определение 5.10. Ориентированное дерево, у которого
каждая вершина, отличная от корня, есть лист, называют
кустом.
На рис. 5.13 граф, изображенный слева, является кустом.
Рассмотрим теперь некоторые числовые параметры, кото-
которыми характеризуется ориентированное дерево.
Определение 5.11. Высота ориентированного дере-
дерева — это наибольшая длина пути из корня в лист; глубина
d(v) вершины ориентированного дерева v — это дли-
длина пути из корня в эту вершину; высота h(v) вершины
ориентированного дерева v — это наибольшая длина пу-
пути из данной вершины в лист и, наконец, уровень вершины
ориентированного дерева — это разность между высотой
ориентированного дерева и глубиной данной вершины.
Уровень корня равен высоте ориентированного дерева, но
уровни различных листьев, так же как и их глубины, мо-
могут быть различными; высота любого листа равна нулю (см.
рис. 5.14).
Определение 5.12. Ориентированное дерево называют
бинарным, если полустепень исхода любой его вершины не
больше 2; бинарное ориентированное дерево называют пол-
полным, если из любой его вершины, не являющейся листом, исхо-
исходят ровно две дуги, а уровни всех листьев совпадают.
5.3. Деревья
301
Примеры различных бинарных ориентированных деревьев
приведены на рис. 5.16: ориентированные деревья на рис. 5.16, а
и б неполные, а ориентированное дерево на рис. 5.16, в полное.
vo
Используя индукцию по высоте ориентированного дерева,
можно показать, что в полном бинарном ориентированном де-
дереве высоты h ровно 2h листьев. Действительно, ориентиро-
ориентированное дерево высоты 0 имеет 2° = 1 лист. Полное бинарное
ориентированное дерево высоты 1 имеет 21 = 2 листа.
Пусть полное бинарное ориентированное дерево имеет высо-
высоту к и соответственно 2k листьев. Рассмотрим полное бинарное
ориентированное дерево высоты к + 1. Поскольку в полном
бинарном ориентированном дереве уровни всех листьев совпа-
совпадают, легко видеть, что ориентированное дерево высоты А; +1
можно получить из полного бинарного ориентированного де-
дерева высоты к, если из каждого листа последнего провести по
две дуги. Тогда количество листьев в ориентированном дереве
высоты к +1 будет в 2 раза больше, чем в ориентированном
дереве высоты fc, т.е. 2к • 2 = 2*+1.
Отсюда следует, что в произвольном бинарном дереве вы-
высоты h не более 2h листьев. Таким образом, мы получаем
следующий простой, но важный результат.
302 5. ТЕОРИЯ ГРАФОВ
Теорема 5.2 (теорема о высоте бинарного ориенти-
ориентированного дерева с заданным числом листьев). Бинар-
Бинарное ориентированное дерево с п листьями имеет высоту, не
меньшую log2 п. #
Эта теорема имеет одно весьма интересное приложение.
Предположим, что необходимо расположить строго по возра-
возрастанию элементы конечного линейно упорядоченного множе-
множества {ai, ...,an}. Эту задачу называют задачей сортиров-
сортировки, а любой алгоритм, ее решающий, — алгоритмом сорти-
сортировки. С математической точки зрения алгоритм сортиров-
сортировки должен найти такую перестановку {п{х ,..., a»n } элементов
множества, которая была бы согласована с заданным на нем
отношением < линейного порядка, т.е. для любых fc, l из спра-
справедливости неравенства г* < ц должно следовать а,{к ^ пц .
Первоначально сортируемые элементы могут быть распо-
расположены в произвольном порядке, т.е. исходной может быть
любая перестановка элементов сортируемого множества, и мы
не имеем никакой априорной информации об этой переста-
перестановке. Единственный способ получить такую информацию —
проводить попарные сравнения элементов а* (относительно рас-
рассматриваемого линейного порядка) в какой-либо последова-
последовательности. Заметим, что при этом совершенно не обязательно
проводить все возможные сравнения, т.е. сравнивать а% с a,j для
всех % ф j. Например, можно использовать транзитивность от-
отношения порядка.
Все сравнения, которые в принципе могут быть проведе-
проведены в процессе работы некоторого алгоритма, изображаются
наглядно в виде ориентированного дерева, называемого дере-
деревом решений. На рис. 5.17 приведено дерево решений для
трехэлементного множества {а, Ь, с}. Вершины ориентирован-
ориентированного дерева, не являющиеся листьями, помечены проверяемы-
проверяемыми неравенствами, а множество листьев находится во взаимно
однозначном соответствии с множеством всех перестановок
исходного множества.
5.3. Деревья 303
Да / \ Нет
Да
Нет
а<с<Ь с<а<Ь Ь<с<а с<Ь<а
Рис. 6.17
Поскольку в результате сортировки может получиться лю-
любая перестановка исходного множества и каждой такой пере-
перестановке соответствует лист дерева решений, в общем случае
количество листьев будет равно п! — количеству перестановок
n-элементного множества.
Следовательно, сортируя входную последовательность, ал-
алгоритм обязательно пройдет какой-то путь от корня дерева
решений к одному из листьев, и, таким образом, число операций
сравнения (число шагов алгоритма сортировки) будет величи-
величиной, пропорциональной высоте дерева решений, не меньшей чем
log2n!, в силу теоремы 5.2.
Используя для оценки факториала при больших п формулу
Стирлинга
получаем, что дерево решений имеет высоту порядка nlog2n.
Таким образом, в общем случае задачу сортировки с по-
помощью попарных сравнений нельзя решить быстрее, чем за
указанное число шагов. Безусловно, конкретный путь в дере-
дереве решений из корня к одному из листов зависит от исходной
перестановки. Например, в дереве решений, приведенном на
304 5. ТЕОРИЯ ГРАФОВ
рис. 5.17, есть два „коротких" пути длины 2, однако остальные
пути имеют длину 3.
Заметим, что в общем случае ориентированное дерево —
это не связный ориентированный граф. Компонентами ори-
ориентированного дерева являются его подграфы, порожденные
множеством вершин, расположенных на некотором пути из кор-
корня в лист.
Остовным лесом (деревом) неориентированного (ориен-
(ориентированного) графа называют любой его остовный подграф,
являющийся лесом (деревом).
Теорема 5.3. У всякого неориентированного графа суще-
существует максимальный остовный лес.
«* Поскольку неориентированный лес — это произвольный аци-
ациклический граф, то достаточно показать, что всякий неориен-
неориентированный граф содержит максимальный остовный ацикли-
ациклический подграф.
Рассмотрим произвольный неориентированный граф Go =
= (V, Е). Если он ациклический, то утверждение очевидно. В
противном случае в нем есть хотя бы один цикл. Выберем
один из циклов графа и обозначим его С\. Удалим из цикла
С\ какое-нибудь ребро. Обозначим его е\. Так как цикл —
это простая цепь, то удаление ребра е\ приводит к подгра-
подграфу G\ = (V, Е\{е\}) графа Go, в котором будет по крайней
мере одним циклом меньше, чем в графе Go- В то же вре-
время любые две вершины, соединенные цепью в исходном графе,
будут соединены цепью и в подграфе G\. Если граф G\ аци-
ациклический, то он и будет искомым максимальным остовным
лесом исходного графа, так как возвращение удаленного ре-
ребра е\ приведет к появлению цикла. Если же граф G\ имеет
циклы, то поступим с ним точно так же, как с графом Go, a
именно, выбрав какой-нибудь его цикл Сг, удалим из него од-
одно ребро — обозначим его ег- В силу конечности множеств
ребер исходного графа через конечное число n ^ 1 шагов, на
каждом из которых удаляется ровно одно ребро некоторого
5.3. Деревья 305
цикла графа G, получим некоторый его ациклический подграф
Gn = (V, Т), где Т = Е \ {еь ..., еп}, причем подграф Gn_i =
= (V, Е\{е\, ...,en_i}) содержит цикл, проходящий по ребру
еп. Покажем, что добавление к множеству ребер Т хотя бы од-
одного ребра из ранее удаленных, т.е. любого ребра из множества
{ei,..., еп}, приведет к появлению цикла.
Действительно, на каждом шаге описанной выше процедуры
происходит удаление нового цикла графа Go, т.е. все циклы Си
Сг, • • •» Сп попарно различны. Для каждого г = 1, п рассмотрим
два случая: 1) цикл Ci содержит только одно из удаленных
ребер, а именно ребро е^; 2) цикл Ci содержит не менее двух
удаленных ребер, т.е. вместе с ребром ег- он содержит по
крайней мере еще одно ребро ej 6 {ei,..., en}.
Очевидно, что в первом случае добавление ребра е* к мно-
множеству ребер Т приведет к появлению цикла, а именно цикла
С{. Рассмотрим второй случаи. Для простоты будем считать,
что есть только одно ребро е7, отличное от ребра е*, которое
содержится в цикле С{ (случай нескольких таких ребер анализи-
анализируется аналогично). Так как ребро ej содержится в некотором
цикле Cj, отличном от С», то, добавляя ребро е* к множеству
ребер Т, все равно получим цикл (рис. 5.18). Действительно, ес-
если ребро е{ не содержится в цикле Cj, то, как видно на рис. 5.18,
концы ребра е* соединены цепью, не содержащей этого ребра.
Тогда, согласно теореме 5.1, существует простая цепь (не со-
содержащая ребра ег), соединяющая его концы. Добавляя к ней
Рис. 5.18
306 5. ТЕОРИЯ ГРАФОВ
ребро е,-, получим цикл. Бели же ребро е,- содержится в цикле
Cjy то удаление этого ребра приведет к исчезновению вместе с
циклом С{ и цикла Cj, что невозможно, так как С» и Cj — ци-
циклы, удаляемые на разных шагах описанной выше процедуры
(на самом деле можно показать, что в рассматриваемой ситуа-
ситуации ребро ej, а вместе с ним и цикл Cj, удаляется позже ребра
е,). Таким образом, всегда найдется цепь, соединяющая кон-
концы ребра вг (и не содержащая этого ребра). Следовательно,
существует и цикл, содержащий ребро е% (но не содержащий
ребра ej).
Итак, добавляя к подграфу Gn = (V, Т) произвольное ребро
из множества {ei,...,en}, получим цикл. Следовательно, этот
подграф и будет искомым максимальным остовным лесом гра-
графа G. >
Утверждение теоремы сохраняет силу и для ориентирован-
ориентированных графов. Доказательство в этом случае будет несколько
более сложным, и мы его не приводим.
Далее в этой главе мы опишем некоторые способы нахожде-
нахождения множества циклов неориентированного графа и способы
построения максимальных остовных лесов. Эти задачи реша-
решаются на основе приведенных ниже алгритмов поиска в глубину.
5.4. Остовное дерево наименьшего веса
Следующая задача известна в теории графов под названи-
названием задачи Штейнера: на плоскости заданы п точек; нужно
соединить их отрезками прямых таким образом, чтобы сум-
суммарная длина отрезков была наименьшей.
В процессе поиска решения разрешено вводить новые точки;
„длина" отрезка, соединяющего две заданные точки, не обя-
обязательно понимается буквально геометрически — это может
быть некоторая количественная оценка „цены" прохождения из
точки в точку по какой-то ломаной линии.
5.4. Остовное дерево наименьшего веса 307
Можно дать следующую графовую интерпретацию задачи
Штейнера. Дан неориентированный граф Gq = (%, 0) без
ребер. Требуется найти неориентированый граф G = (F, Т) со
специальными свойствами.
Мы предполагаем, что каждому ребру любого неориентиро-
неориентированного графа, получаемого в процессе решения задачи, можно
сопоставить неотрицательное число, называемое весом этого
ребра. При этом, во-первых, искомый граф G должен быть
неориентированным деревом, во-вторых, его множество вер-
вершин должно включать множество вершин исходного графа, т.е.
Vq С V, и, в-третьих, сумма весов его ребер должна быть наи-
наименьшей.
Требование, чтобы искомый граф G был неориентирован-
неориентированным деревом, вызвано тем, что в нем любую пару вершин
должна соединять единственная цепь, так как в противном
случае граф не будет иметь наименьшую сумму весов. Дей-
Действительно, если существуют хотя бы две цепи, соединяющие
какую-то пару вершин, то выбирается та, сумма весов ребер
которой меньше. Бели же предположить, что в рассматривае-
рассматриваемой ситуации имеются хотя бы две цепи с одинаковым весом,
то все равно для оптимального решения выбирается какая-то
одна цепь (и тогда оптимальное решение не единственно).
Эффективных алгоритмов*, дающих точное решение зада-
задачи Штейнера, не существует. Однако известны эффективные
алгоритмы, находящие некоторые приближения точного реше-
решения. Одно из таких решений дает алгоритм Краскала.
Неориентированный (ориентированный) граф, у которого
каждому ребру (дуге) сопоставлено некоторое действительное
число, называют взвешенным или размеченным графом.
Это число называют весом или меткой ребра (дуги). Как
* Алгоритм считают эффективным, если сложность алгоритма выра-
выражается функцией, ограниченной сверху некоторым полиномом от параме-
параметра, характеризующего „объем" исходных данных. Для задачи Штейнера
этим параметром является число вершин графа Go.
308 5. ТЕОРИЯ ГРАФОВ
правило, мы рассматриваем граф с натуральными метками
ребер (дуг).
Алгоритм Краскала вычисляет для заданного взвешенного
неориентированного графа G остовное дерево с наименьшей
суммой весов ребер — остовное дерево наименьшего веса.
Существенное отличие только что сформулированной задачи
от задачи Штейнера (в ее графовой постановке) состоит в том,
что в новой задаче множество вершин при поиске остовного
дерева наименьшего веса не меняется. Поэтому алгоритм
Краскала и дает лишь некоторое приближение решения задачи
Штейнера.
При описании алгоритма будем использовать способ хра-
хранения данных, называемый очередью. Элементы данных в
очереди упорядочиваются по времени поступления. Элементы
можно добавлять в очередь и извлекать из очереди. В каждый
момент времени доступен только один элемент, который был
помещен в очередь раньше других, — „голова" очереди. При
добавлении новый элемент помещается в „хвост" очереди, т.е.
работа ведется по обычному для очереди правилу — „первым
пришел — первым вышел". Чтобы извлечь из очереди некото-
некоторый элемент, не доступный в текущий момент, надо извлечь
все ранее поступившие элементы, начиная с „головы" очереди.
Рассмотрим алгоритм нахождения остовного дерева наи-
наименьшего веса (алгоритм Краскала). Пусть дан связный неори-
неориентированный граф G = (V, Е) с числовыми неотрицательными
весами ребер. Вес ребра е обозначим (р{е).
В результате работы алгоритма получим остовное дерево
Т = (V, Я) графа С?, такое, что сумма J2 ^(е) является наи-
еен
меньшей.
Отсортируем все ребра исходного графа по возрастанию
весов и сформируем из них очередь так, чтобы в „голове"
очереди находилось ребро с наименьшим весом, а в „хвосте" —
с наибольшим и веса ребер не убывали от „головы" очереди к
„хвосту".
5.4. Остовное дерево наименьшего веса 309
Метод состоит в исшивании" искомого дерева из компонент
остовного леса. Первоначально остовный лес представляет со-
собой множество изолированных вершин исходного графа, т.е.
его множество ребер пусто. На первом шаге из очереди из-
извлекается ребро наименьшего веса и добавляется к множеству
ребер исходного дерева.
На последующих шагах алгоритма из очереди извлекается
по одному ребру. Если это ребро соединяет вершины, при-
принадлежащие разным компонентам текущего остовного леса, то
оно добавляется к текущему множеству ребер искомого дере-
дерева, а указанные компоненты сливаются в одну. Иначе ребро
отбрасывается. Процесс повторяется до тех пор, пока число
компонент остовного леса не окажется равным 1. Можно пока-
показать, что эта компонента и будет искомым остовным деревом
наименьшего веса.
Переходим к формальному описанию алгоритма.
Алгоритм Краскала
1. Множество ребер Н искомого остовного дерева полагаем
пустым (Я = 0).
2. Формируем множество Vs = {{^i},..., {vn}}? элементами
которого являются множества вершин, соответствующих ком-
компонентам исходного остовного леса. Каждая такая компонента
состоит из единственной вершины.
3. Сортируем множество ребер Е исходного графа по воз-
возрастанию весов и формируем очередь Q, элементами которой
являются ребра графа G.
4. Если множество Vs содержит более одного элемента (т.е.
остовный лес состоит из нескольких компонент) и очередь Q не
пуста, переходим на шаг 5, если иначе — на шаг 7.
5. Извлекаем из очереди Q ребро е. Если концы ребра е
принадлежат различным множествам вершин V{ и Vjиз Vs, то
переходим на шаг 6, если иначе, то отбрасываем извлеченное
ребро и возвращаемся на шаг 4.
310
5. ТЕОРИЯ ГРАФОВ
6. Объединяем множества вершин V* и Vj (полагая W =
= Vi U Vj), удаляем множества V% и Vj из множества Vs и
добавляем в V$ множество W. Добавляем ребро е в множество
Н. Возвращаемся на шаг 4.
7. Прекращаем работу. Множество Н есть множество
ребер полученного остовного дерева.
Доказательство корректности алгоритма Краскала, т.е. до-
доказательство того факта, что выдаваемое алгоритмом остов-
ное дерево действительно является остовным деревом наимень-
наименьшего веса, мы не приводим.
На рис. 5.19, а-д для неориентированного графа показана
последовательность построения остовного дерева наименьшего
веса. Заметим, что результат работы алгоритма в общем
случае зависит от порядка следования ребер одинакового веса
в очереди. Предположим, что после сортировки первым в
очереди находится ребро {vq, v\} с весом 2.
5.5. Методы обхода вершин 311
Исходный граф изображен на рис. 5.19, а. На рис. 5.19,5
проиллюстрирован результат выполнения первого шага алго-
алгоритма. На рис. 5.19, в показан результат добавления следующе-
следующего ребра {vi, V2) с весом 2 из очереди. На рис. 5.19, г приведен
результат добавления ребра {vq, V4} с весом 3. Если следующим
в очереди ребром будет {v\, V4}, оно будет отброшено. Дальней-
Дальнейший ход работы алгоритма зависит от того, в каком порядке
в очереди размещены ребра {v2, г>з} и {г>з, v^} с весами 4. Лю-
Любое из них может быть добавлено в множество ребер остовного
дерева, и на этом алгоритм закончит работу. На рис. 5.19, д
приведено остовное дерево, полученное после добавления ребра
Отметим, что для приведенного графа оба ребра с весом 2
войдут в остовное дерево независимо от порядка их расположе-
расположения в очереди после сортировки, а ребро {v\, V4} не войдет ни
в какое остовное дерево наименьшего веса.
Можно доказать, что наиболее трудоемким шагом в алго-
алгоритме Краскала является сортировка ребер графа по возраста-
возрастанию весов. Как мы уже знаем, задачу сортировки п элементов
нельзя решить быстрее, чем за время O(nlog2n). Следова-
Следовательно, сложность алгоритма Краскала оценивается числом
О(\Е\ log2 \Е\), где \Е\ — мощность множества ребер графа. По-
Поскольку справедливо неравенство \Е\ log2 \E\ < \Е\2, то алгоритм
Краскала можно считать эффективным.
5.5. Методы систематического
обхода вершин графа
Важными задачами теории графов являются задачи гло-
глобального анализа как неориентированных, так и ориентиро-
ориентированных графов. К этим задачам относятся, например, задачи
поиска циклов или контуров, вычисление длин путей между
парами вершин, перечисление путей с теми или иными свой-
свойствами и т.п. Глобальный анализ графа следует отличать от
312 5. ТЕОРИЯ ГРАФОВ
локального, примером которого может служить задача опреде-
определения множеств предшественников и преемников фиксирован-
фиксированной вершины ориентированного графа.
Базой для решения многих задач глобального анализа явля-
являются так называемые алгоритмы обхода или поиска.
Необходимо уметь обходить все вершины графа таким обра-
образом, чтобы каждая вершина была отмечена ровно один раз.
Обычно такое „путешествие" по графу сопровождается нуме-
нумерацией вершин графа в том порядке, в котором они отмеча-
отмечаются, а также определенной „маркировкой" ребер (или дуг)
графа.
Существуют две основные стратегии таких обходов: поиск
в глубину и поиск в ширину. Эти стратегии можно описать
так.
При поиске в глубину, отправляясь в „путешествие" по гра-
графу из некоторой начальной вершины г>о, мы действуем следую-
следующим образом. Пусть, „путешествуя", мы достигли некоторой
вершины v (в начале „путешествия" v = vq). Отмечаем вершину
v и просматриваем вершины из ее списка смежности L[v].
При условии, что в этом списке существует хотя бы одна
неотмеченная вершина, продолжаем „путешествие" из первой
такой вершины w, действуя как описано выше — „ныряем"
вглубь, т.е. просматриваем вершины списка смежности L[w]
вершины w, откладывая анализ других элементов L[v] как
возможных продолжений поиска „на потом".
Бели же неотмеченных вершин в L[v] нет, то возвращаемся
из г; в ту вершину, из которой мы в нее попали, и продолжаем
анализировать список смежности этой вершины.
„Путешествие" прекратится в тот момент, когда мы вер-
вернемся в начальную вершину vq и либо все вершины будут отме-
отмеченными, либо окажется, что неотмеченные вершины есть, но
из vq больше никуда пойти нельзя. В последнем случае возмож-
возможны продолжение поиска из новой вершины или остановка, что
определяется конкретной версией алгоритма.
5.5. Методы обхода вершин
313
Заметим, что результат поиска в глубину зависит от по-
порядка вершин в списках смежности, представляющих граф, а
также от выбора начальной вершины vq.
На рис. 5.20 показаны примеры поиска в глубину на неори-
неориентированном и ориентированном графах.
Рис. 5.20
Рассмотрим неориентированный граф, изображенный на
рис. 5.20, о. Списки смежности вершин графа удобно задать
кортежами:
E.1)
Здесь запись V{ -> (vfc,...,vm) означает, что кортеж (v/k,..
задает список смежности вершины V{.
Результаты работы алгоритма с использованием приведен-
приведенных списков смежности проиллюстрированы графически. При
поиске отмечаем вершины, присваивая им номера. При этом
каждая новая вершина получает номер, на единицу больший,
чем текущая. Вершине vo присвоим номер 1. Номера осталь-
остальных вершин, присвоенные им в процессе поиска, приведены на
графе. Ребра, по которым из текущей вершины переходим к
новой, изображены более толстыми линиями.
Прокомментируем поиск в глубину в ориентированном гра-
графе, изображенном на рис. 5.20, б. Пусть списки смежности
314 5. ТЕОРИЯ ГРАФОВ
вершин имеют следующий вид:
v3->(vi, v4), v4-
V5 -> (*>3> V6, V7), V6 -> (), V7 -> ().
„Путешествие" начинается в вершине vo, и ей присваивается
номер 1. Первой в списке смежности вершины vq стоит верши-
вершина v\. Даем ей номер 2 и продолжаем поиск из этой вершины.
В списке смежности последней только одна вершина v2. Даем
ей номер 3 и, так как ее список смежности пуст, возвращаемся
в вершину vi. В списке смежности вершины vi нет других вер-
вершин, кроме вершины v2, уже помеченной номером 3, поэтому
возвращаемся в вершину v<>.
Второй элемент списка смежности вершины vo — вершина
V3- Эта вершина новая. Помечаем ее номером 4 и переходим
к рассмотрению ее списка смежности. Первая в списке смеж-
смежности вершина v\ уже получила номер 2. Поэтому переходим
в новую вершину v4 и помечаем ее номером 5. Единственный
элемент ее списка смежности, вершина v2, уже отмечена. Воз-
Возвращаемся в вершину v$. Здесь тоже нет никаких „отложенных
продолжений", и мы снова оказываемся в стартовой верши-
вершине vo. Все вершины из списка смежности стартовой вершины
уже отмечены, т.е. все возможные пути поиска из этой верши-
вершины пройдены. Тем не менее в графе остались непосещенные
(непронумерованные) вершины. Следующей по исходной нуме-
нумерации вершин графа является вершина v$. Продолжим поиск
из этой вершины и пометим ее номером 6. Первая вершина
ее списка смежности —вершина V3 — уже отмечена. Посе-
Посещаем следующую вершину — вершину ve — и помечаем ее
номером 7. Ее список смежности пуст. Возвращаемся в вер-
вершину V5. Посещаем последнюю неотмеченную вершину из ее
списка смежности — вершину v7 — и помечаем ее номером 8.
Поскольку все вершины из списка смежности вершины vs от-
отмечены, поиск в глубину закончен.
5.5. Методы обхода вершин
315
На рис. 5.20, б более толстыми стрелками изображены дуги,
по которым из очередной текущей вершины мы переходили к
новой.
Рассмотрим теперь поиск в ширину. При поиске в ширину
„правила игры" такие: достигнув некоторой вершины w, от-
отмечаем ее. Затем просматриваем ее список смежности L[v] и
отмечаем все ранее не отмеченные вершины списка (при старте
поиска v = vo). После того как отмечены все вершины из L[v],
вершину v считаем полностью обработанной и продолжаем об-
обработку вершин из списка L[v) по очереди согласно описанным
правилам.
Именно в обработке сразу всего списка смежности текущей
вершины заключается принципиальное отличие поиска в шири-
ширину от поиска в глубину: там мы „ныряли" как можно „глубже",
а здесь идем с „бреднем", „загребая" сразу все, что можно.
Поиск в ширину заканчивается, когда все вершины полно-
полностью обработаны или продолжение поиска невозможно.
Для сравнения возьмем неориентированный и ориентиро-
ориентированный графы предыдущего примера и рассмотрим для них
поиск в ширину (рис. 5.21).
Рис. 5.21
Для неориентированного графа (см. рис. 5.21, а) поиск из
стартовой вершины vo будем осуществлять так. Стартовой
вершине присвоим номер 1. Затем пронумеруем все вершины
из списка смежности стартовой вершины в порядке следования
316 5. ТЕОРИЯ ГРАФОВ
их в списке. При этом вершина v\ получит номер 2, а вер-
вершина vs — номер 3. Теперь, когда все вершины из списка
смежности вершины vo отмечены, перейдем в первую по оче-
очереди вершину v\. В ее списке смежности только одна ранее
не отмеченная вершина — V2- Присвоим ей номер 4 и перей-
перейдем в вершину г;з- На этом этапе номер 5 получит вершина
v±, а номер 6 — вершина v^. Затем перейдем в вершину V2-
Поскольку все вершины из списка смежности вершины V2 уже
отмечены, перейдем в вершину v±. Здесь также все вершины
из списка смежности отмечены, поэтому перейдем в вершину
V5. Просмотрим неотмеченные вершины из ее списка смежно-
смежности и отметим вершины vq и V7, присваивая им номера 7 и 8
соответственно. Теперь, когда список смежности вершины v$
обработан полностью, перейдем в вершину vq. Так как в ее
списке смежности нет неотмеченных вершин, перейдем в вер-
вершину vj. Здесь также в списке смежности нет неотмеченных
вершин. Все вершины обработаны, и поиск в ширину для графа
закончен.
Результаты поиска в ширину из вершины vq в ориентиро-
ориентированном графе представлены на рис. 5.21, б.
Обратим внимание на то, что нумерация вершин при поиске
в ширину отличается от нумерации вершин при поиске в глу-
глубину. Так, в ориентированном графе на рис. 5.21, б мы сразу
отмечаем оба элемента списка смежности вершины vq. Поэтому
вершине, получившей при поиске в глубину номер 4, при поиске
в ширину присваивается номер 3.
Перейдем теперь к подробному описанию алгоритмов поис-
поиска в глубину и поиска в ширину.
Рассмотрим алгоритм поиска в глубину в неориентирован-
неориентированном графе. Будем считать, что граф задан списками смежно-
смежности, собранными в массив лидеров.
При поиске вершины графа нумеруются в порядке их посе-
посещения. Номер вершины v графа, присваиваемый ей при поиске
в глубину, обозначим D[v] и будем называть D-номером.
5.5. Методы обхода вершин 317
В процессе обхода будем находить фундаментальные ци-
циклы графа. Понятие фундаментального цикла в неориенти-
неориентированном графе вводится следующим образом. Пусть в не-
неориентированном графе G = (V, Е) произвольно фиксирован
максимальный остовный лес (см. теорему 5.3). Для связного
графа это будет максимальное остовное дерево. Множество
его ребер обозначим Т. Все ребра из Г назовем древесными,
а ребра исходного графа G, не принадлежащие Т, — обрат-
обратными. Таким образом, фиксируя в графе G максимальный
остовный лес, мы тем самым фиксируем разбиение множества
его ребер на подмножества древесных и обратных ребер. В си-
силу максимальности остовного леса любая пара вершин графа G,
принадлежащих одной и той же компоненте связности, соеди-
соединена цепью, все ребра которой являются древесными. Возьмем
теперь произвольно две вершины и к v, принадлежащие одной
и той же компоненте связности графа G. Пусть эти вершины
соединены обратным ребром. Поскольку они также соединены
цепью, содержащей исключительно древесные ребра, то суще-
существует цикл, содержащий эти две вершины, в котором будет
единственное обратное ребро {u, v}. Любой цикл графа G,
содержащий только одно обратное ребро, назовем фундамен-
фундаментальным.
Докажем, что не существует двух различ-
различных фундаментальных циклов, содержащих
одно и то же обратное ребро (рис. 5.22). Дей-
Действительно, если предположить противное, то
возникает цикл С, содержащий лишь древес-
древесные ребра, что невозможно. ис"
Итак, фиксируя в графе максимальный остовный лес, мы
тем самым фиксируем взаимно однозначное соответствие меж-
между множеством обратных ребер и множеством фундаменталь-
фундаментальных циклов.
Одним из способов построения максимального остовного
леса может служить поиск в глубину. Именно при поиске в
глубину всякое ребро, по которому из текущей вершины мы
318 5. ТЕОРИЯ ГРАФОВ
попадаем в неотмеченную ранее вершину, будет древесным.
Каждое ребро, не являющееся древесным, будет обратным.
Максимальный остовный лес, находимый с помощью алгоритма
поиска в глубину, называют остовным лесом поиска в
глубину или глубинным остовным лесом.
Заметим, что классификация ребер зависит от хода работы
алгоритма, который определяется стартовой вершиной и рас-
расположением вершин в списках смежности.
Таким образом, алгоритм поиска в глубину в неориентиро-
неориентированном графе может быть использован для вычисления мно-
множества фундаментальных циклов графа, т.е. решения одной из
задач глобального анализа.
Отметим, что не всякий максимальный
остовный лес может быть получен с помо-
помощью алгоритма поиска в глубину. Напри-
Например, для графа, изображенного на рис. 5.23,
выделенный максимальный остовный лес
нельзя получить при поиске в глубину, из
какой бы вершины мы не начинали поиск.
Для организации работы алгоритма поиска в глубину ис-
используется способ хранения данных, называемый стеком.
Элементы в стеке упорядочиваются в порядке поступления. В
стек можно добавлять новые элементы и из него можно извле-
извлекать элементы. При этом доступен только последний добавлен-
добавленный элемент — вершина стека, чем и определяется режим
работы стека (последним пришел — первым ушел). Образно
стек можно представить в виде стопки тарелок. Из стопки
можно взять только верхнюю тарелку и только наверх можно
добавить новую. Обычно стек реализуется в виде списка.
В алгоритме поиска в глубину используется стек вершин.
Мы будем считать, что из стека можно считывать информацию
без изменения его содержимого, но в том порядке, в каком
ее удаляли бы из стека. Указанная операция считывания
понадобится нам для поиска фундаментальных циклов.
5.5. Методы обхода, вершил 319
Алгоритм поиска в глубину
Вход. Граф G = (У, Е), заданный списками смежности.
Выход. Множества Tree древесных и Back обратных ре-
ребер соответственно; множество Fc фундаментальных циклов,
массив D, содержащий JD-номера вершин.
0. Просмотреть массив лидеров и сформировать множество
Vb вершин графа. Это множество используется для хранения
новых (не обработанных алгоритмом) вершин. В ходе работы
алгоритма обработанные вершины будут удаляться из этого
множества.
В процессе работы алгоритма для каждой вершины v не-
необходимо знать, какие вершины из ее списка смежности L[v]
обработаны на предыдущих шагах работы алгоритма. Для
этого формируется массив Lp размера |Vb|, в котором хранят-
хранятся номера первых еще не обработанных алгоритмом вершин
списка смежности L[v] каждой вершины v. Первоначально все
элементы массива Lp полагают равными 1.
Стек вершин STACK и список вершин фундаментального
цикла Cycle положить пустыми (STACK = 0, Cycle = 0).
Множества Tree древесных ребер, Back обратных ребер
и Fc фундаментальных циклов положить пустыми (Tree = 0,
Back = 0, Fc = 0). Массив D-номеров D обнулить.
Задать начальную вершину для поиска (v = vo). (Обычно
это первая вершина массива лидеров.) Счетчик D-номеров
вершин count положить равным 1 (count = 1).
1. Бели множество Vo не пусто (Vb Ф 0), перейти на шаг 2,
если иначе — на шаг 8 (выход).
2. Бели стек пуст (STACK = 0) и алгоритм стартует из
вершины vo (count = 1), то перейти на шаг 3, если иначе, то
выбрать из множества Vo произвольную вершину, из которой
поиск в глубину будет продолжен (v = u, и G Vb), и перейти на
шаг 3.
3. Поместить текущую вершину v в стек STACK. При-
Присвоить вершине v ?)-номер (D[v] = count). Увеличить счетчик
320 5. ТЕОРИЯ ГРАФОВ
D-номеров на 1 (count = count +1). Удалить вершину v из мно-
множества Vb новых вершин. Перейти на шаг 4.
4. Проверить по элементу Lp[v], что не достигнут конец
списка смежности L[v] текущей вершины v. Бели в списке
смежности есть еще не обработанные вершины, получить из
списка смежности очередную вершину до, увеличить Lp[v] на 1
и перейти на шаг 6.
Бели список смежности L[v] вершины v обработан полно-
полностью, удалить вершину v из стека STACK и перейти на шаг 5.
5. Если стек STACK пуст, вернуться на шаг 1, если иначе,
то в качестве текущей вершины v взять вершину, находящуюся
в вершине стека, и перейти на шаг 4.
6. Бели вершина w новая (w Е Vo), то добавить ребро {v, w}
в множество древесных ребер
(Tree = TreeU{{v,w}}),
сделать вершину w текущей (v = w) и вернуться на шаг 3.
Бели вершина w не новая (w ? Vo), то перейти на шаг 7.
7. Если ребра {v, w} нет среди древесных ({v, w} ^ Tree),
поместить ребро в список обратных ребер
(Back = Back U {{v, w}}).
Поместить вершину w в список Cycle. Читать содержи-
содержимое стека STACK, начиная с вершины стека, до появления
вершины w и помещать в список Cycle (включая вершину ги),
т.е. формировать фундаментальный цикл, соответствующий
обратному ребру {v, w}.
Добавить список Cycle в множество фундаментальных ци-
циклов Fc
(FC = FCU {Cycle}).
Список Cycle положить пустым (Cycle = 0).
Вернуться на шаг 4.
8. Закончить работу.
5.5. Методы обхода вершин 321
Пусть для неориентированного графа, изображенного на
рис. 5.20, а, списки смежности имеют вид E.1). При выполне-
выполнении поиска в глубину выделенные ребра являются древесными,
остальные — обратными. Около каждой вершины указан при-
присвоенный ей JD-номер. Фундаментальные циклы — в порядке
их нахождения — таковы: vi, U2, V4, V3, *>1 и vo, vi, ^2, V4, г>з, vq.
Поиск в глубину в неориентированном графе можно исполь-
использовать и для нахождения числа его компонент. Очевидно, что
это число равно числу опустошений стека от начала до конца
поиска в глубину. Регистрируя удаляемые из стека вершины,
можно после очередного его опустошения распечатать номера
вершин, принадлежащих данной компоненте.
В ориентированном графе поиск в глубину реализуется во
многом аналогично поиску в глубину в неориентированном гра-
графе. В этом случае возникает остовный ориентированный лес
поиска в глубину, дуги которого — это в точности те ду-
дуги, по которым в процессе работы алгоритма переходят от
очередной вершины к новой, еще не отмеченной вершине. Мож-
Можно показать, что это максимальный остовный лес исходного
графа.
Слабыми компонентами этого глубинного остовного леса
будут некоторые ориентированные деревья: поэтому, исполь-
используемая далее терминология из теории деревьев относится к
той или иной слабой компоненте глубинного остовного леса. В
ориентированном графе вершинам также присваиваются D-но-
мера. Но классификация дуг при поиске в глубину в ориентиро-
ориентированном графе сложнее по сравнению с аналогичной классифика-
классификацией ребер при поиске в глубину в неориентированном графе.
Различают четыре класса дуг:
1) древесные дуги — каждая такая дуга ведет от отца к
сыну в глубинном остовном лесу;
2) прямые дуги — каждая такая дуга ведет от подлинного
предка к подлинному потомку (но не от отца к сыну) в глубин-
глубинном остовном лесу;
322 5. ТЕОРИЯ ГРАФОВ
3) обратные дуги — от потомков к предкам (включая все
петли);
4) поперечные дуги — все дуги, не являющиеся ни дре-
древесными, ни прямыми, ни обратными.
Следовательно, в результате работы алгоритма будут по-
получены множества Tree — древесных дуг, Back — обратных
дуг, Forward — прямых дуг, С — поперечных дуг и массив D,
содержащий D-номера вершин.
В процессе работы алгоритма по сравнению с алгоритмом
поиска в глубину в неориентированном графе имеется ряд
особенностей. Так, если очередная вершина w, извлеченная из
списка смежности текущей вершины v, новая, т.е. w € Vo, то
дуга (v, w) является древесной. Следует добавить дугу (v, w)
в множество древесных дуг (Tree = TreeU{(v, ги)}), сделать
вершину w текущей (v = w) и начать ее обработку.
Бели вершина w не новая (w ? Vo), то дуга (v, w) будет либо
прямой, либо обратной, либо поперечной.
Бели jD-номер вершины v строго меньше D-номера вершины
w (D[v] < D[w]), то дуга (v, w) является прямой. Добавляем ее в
множество прямых дуг Forward (Forward = Forward U {(v, w)}).
Бели D-номер вершины v не меньше D-номера вершины w
(D[v] > Z)[ty]), необходимо проверить, есть ли в стеке STACK
вершина w. Бели вершина w находится в стеке, то дуга (v, w)
является обратной и ее следует добавить в множество обратных
дуг Back (Back = Back U {(v, w)}). Бели вершины w в стеке
нет, то дуга является поперечной. Тогда нужно добавить
ее в множество поперечных дуг С (С = CU{(v, w)}). Далее
следует перейти к рассмотрению очередной вершины из списка
смежности текущей вершины (если он не пуст).
Бели стек пуст, но не все вершины ориентированного гра-
графа обработаны, поиск продолжают из любой необработанной
вершины.
В случае ориентированного графа поиск контуров на базе
поиска в глубину существенно сложнее, чем в случае неориен-
неориентированного графа, и здесь он не рассматривается. Однако
5.5. Методы обхода вершив 323
можно доказать следующий критерии бесконтурности ориен-
ориентированного графа: ориентированный граф является бескон-
бесконтурным тогда и только тогда, когда при поиске в глубину от
некоторой начальной вершины множество обратных дуг ока-
оказывается пустым.
Заметим также, что для ориентированного графа нет такой
простой связи между числом опустошений стека и числом
компонент, как для неориентированного графа.
На базе алгоритма поиска в глубину может быть разработан
эффективный алгоритм поиска бикомпоненгп в ориентирован-
ориентированном графе. Однако здесь мы не будем останавливаться на
задаче поиска бикомпонент, так как эта задача обсуждается
в рамках общей задачи о путях в графах (см. 5.6).
Можно показать, что алгоритм поиска в глубину имеет
сложность порядка тах(|У|,|2?|).
Пример 5.7. Проведем поиск в глубину на ориентиро-
ориентированном графе, представленом на рис. 5.24. Поиск начнем из
вершины vq. Пусть списки смежности вершин имеют следую-
следующий вид:
3, Vi), VX -> (V?), V2
Щ ~> (vi), V5 ~> (vi), E.2)
5), V7 —V (V5, Ve).
Результаты выполнения поиска в глубину представлены на
рисунке: около каждой вершины указан ее D-номер, все дре-
в
324 5. ТЕОРИЯ ГРАФОВ
весные дуги выделены более толстыми стрелками, а прямые,
обратные и поперечные помечены буквами F, J5, С соответ-
соответственно.
Первое опустошение стека происходит после обработки пер-
первых пяти вершин (в порядке обхода): vo, t>2> V4, V3, v\.
После опустошения поиск продолжается из вершины vj, ко-
которой присваивается 15-номер 6. (Напомним, что в приведен-
приведенном выше алгоритме после опустошения стека для продолжения
поиска выбирается любая из необработанных вершин.) #
В отличие от алгоритма поиска в глубину, алгоритм поис-
поиска в ширину использует не стек, а очередь вершин. Мы дадим
здесь вариант поиска в ширину, когда, начиная поиск в неко-
некоторой начальной вершине г>о, мы останавливаемся при первом
же опустошении очереди. Это значит, что некоторые из вер-
вершин могут остаться неотмеченными. Таким образом может
быть решена задача распознавания достижимости от заданной
вершины. Мы совместим также поиск в ширину с вычислени-
вычислением длины кратчайшего пути от vq до любой вершины графа.
Будем предполагать, что вершины графа пронумерованы без
пропусков числами от 0 до N: V = {vf. г = О, N}.
Поиск в ширину рассматриваем только для ориентирован-
ориентированного графа.
Алгоритм поиска в ширину
в ориентированном графе
Вход. Граф G = (V, Е), заданный списками смежности;
vq — начальная вершина (не обязательно первый элемент мас-
массива лидеров).
Выход. Массив М меток вершин, где каждая метка равна
длине пути от vq до v.
0. Очередь Q положить пустой (Q = 0). Все вершины поме-
пометить как недостижимые из вершины vo, присваивая элементам
массива М значение +оо (М[и*] = +00, i = 1, N).
5.5. Методы обхода вершин 325
Стартовую вершину vo пометить номером 0, т.е. длину пути
от стартовой вершины vq до самой себя положить равной О
(M[t>o] = 0). Поместить вершину vo в очередь Q. Перейти на
шаг 1.
1. Бели очередь Q не пуста (Q Ф 0), то из „головы" очереди
извлечь (с удалением из очереди) вершину и и перейти на шаг 2.
Бели очередь пуста, перейти на шаг 3.
2. Если список смежности L(u) вершины г* пуст, вернуться
на шаг 1.
Бели список смежности L(u) вершины и не пуст, для каждой
вершины w из списка смежности, где M[w] = +оо, т.е. вершины,
которую еще не посещали, положить длину пути из стартовой
вершины vq до вершины w равной длине пути от vq до вершины
и плюс одна дуга (М[w] = М[и] +1), т.е. отметить вершину w и
поместить ее в очередь Q. После просмотра всех вершин списка
смежности L(u) вернуться на шаг 1.
3. Распечатать массив М. Закончить работу.
Алгоритм поиска в ширину может быть дополнен процеду-
процедурой „обратного хода", определяющей номера вершин, лежащих
на кратчайшем пути из вершины vq в данную вершину и. Для
этого необходимо завести массив PR размера |V|, каждый эле-
элемент РД[гу] которого содержит номер той вершины, из которой
был осуществлен переход в вершину w при ее пометке.
Если вершина w находится в списке смежности L(u) вер-
вершины и, заполнение элемента массива PR[w] происходит при
изменении метки вершины w M[w] с +оо на единицу. При этом
в элементе PR[w] сохраняется номер вершины и (PR[w] = и).
Для начальной вершины PR[vo] можно положить равным 0, в
предположении, что начальная вершина vo имеет номер 0 и
остальные вершины пронумерованы от 1 до N.
Сложность рассмотренного алгоритма поиска в ширину,
известного под названием „Алгоритм волнового фронта", со-
составляет O(max(\Vl \E\))-
326
5. ТЕОРИЯ ГРАФОВ
Пример 5.8. На рис. 5.25 дан пример работы алгоритма
волнового фронта (при поиске из вершины vo) для ориентиро-
ориентированного графа, изображенного на рис. 5.24. Списки смежности
ориентированного графа имеют вид E.2).
Рис. 5.25
Около каждой вершины Vi поставлена метка M[vj], кото-
которую получает вершина при поиске в ширину. Выделены дуги,
составляющие кратчайшие пути из вершины vq в остальные.
Отметим, что вершины V5, ve, и vj не достижимы из vq и их
начальные метки +оо остались без изменения. При рассмотрен-
рассмотренном ходе алгоритма массив PR будет содержать следующие
номера вершин: PR[vQ] = 0, PR[vi] = 0, PR[v2] = 0, РЛ[г;3] = О,
PiJ[v4] = 2. Для остальных вершин соответствующие значения
не определены, поскольку они не „посещались".
Используя массив PR, восстановим кратчайший путь из
вершины vo в вершину v±. Поскольку Pi?[v4] = 2, a Pi?[v2] = О,
искомый путь есть vo, V2, гл*.
5.6. Задача о путях во взвешенных
ориентированных графах
Среди задач анализа ориентированных графов весьма важ-
важны следующие задачи.
1. Вычисление для заданного ориентированного графа его
матрицы достижимости. Эту задачу будем называть зада-
задачей построения транзитивного замыкания ориентиро-
5.6. Задача о путях 327
ванного графа. Такое название связано с тем, что матрицу
достижимости можно рассматривать как матрицу транзитив-
транзитивного и рефлексивного замыкания бинарного отношения непо-
непосредственной достижимости в ориентированном графе.
2. Вычисление наименьших расстояний между всеми парами
вершин в ориентированном графе. Эту задачу будем называть
задачей о кратчайших расстояниях.
Задачу о кратчайших расстояниях можно сформулировать
так. Пусть задан взвешенный ориентированный граф и пусть
из вершины v достижима вершина w. Фиксируем какой-либо
путь ?, ведущий из v в w. Расстоянием от вершины v до
вершины w по пути S называют сумму меток дуг, входящих в
этот путь, а наименьшим — минимальное из расстояний между
вершинами v и w по всем возможным путям.
Отметим, что задача о кратчайших расстояниях не всегда
имеет решение. Например, если в ориентированном графе есть
петля, метка которой — отрицательное число, то по этой петле
можно проходить сколько угодно раз и тем самым уменьшать
сумму меток дуг пути, включающего эту петлю, до любого
наперед заданного значения.
3. Перечисление всех путей между двумя произвольными
вершинами. Эту задачу будем называть задачей о перечи-
перечислении путей. При ее решении требуется для любой заданной
пары вершин и и v ориентированного графа получить все пути,
для которых и является началом, а г; — концом.
Все указанные задачи (перечисленные в порядке возраста-
возрастания сложности) можно решить в рамках единого подхода, суть
которого сводится к следующему.
Ранее мы ввели понятие взвешенного неориентированного
(ориентированного) графа и метки ребер (дуг) определили как
числа, поставленные в соответствие ребру (дуге). Обобщим
это понятие для ориентированного графа.
Определение 5.13. Взвешенным (или размеченным)
ориентированным графом называют пару W = (G, ср), где
328 5. ТЕОРИЯ ГРАФОВ
G = (F, Е) — обычный ориентированный граф, а <р: Е -* TZ —
весовая функция (или функция разметки) со значениями
в некотором идемпотентном полукольце TZ = (Я, +, •, 0, 1),
причем (Ve € Е)(ср(е) ф 0).
Мы будем в этом случае также говорить, что ориентирован-
ориентированный граф размечен над идемпотентным полукольцом И. Часто
полукольцо 71 является замкнутым, хотя это требование необя-
необязательно. Будем, однако, везде в этом пункте предполагать,
что TZ — полукольцо с итерацией.
Пусть вершины ориентированного графа каким-либо обра-
образом пронумерованы. Тогда взвешенный ориентированный граф
может быть задан матрицей А, элемент которой a%j равен зна-
значению <р((г, ])) весовой функции на дуге (г, j), если из вершины
г ведет дуга в вершину j, или нулю полукольца в противном слу-
случае. Эту матрицу будем называть матрицей меток дуг.
Оказывается, что вычисление итерации А* матрицы А дает
решение всех сформулированных выше задач, если для каждой
задачи выбирать соответствующее полукольцо. А именно в слу-
случае полукольца В (см. пример 3.2) получаем решение задачи о
транзитивном замыкании, в случае полукольца 1Z* (см. при-
пример 3.1) — решение задачи о кратчайших расстояниях*.
Будем называть задачу вычисления матрицы А* для ориен-
ориентированного графа, размеченного над произвольным полуколь-
полукольцом с итерацией, в частности над замкнутым полукольцом,
общей задачей о путях во взвешенных ориентированных
графах.
В такой общности подхода, когда множество, казалось бы,
не связанных друг с другом задач решается единым алгорит-
алгоритмом, „настраиваемым" на разные задачи выбором соответству-
соответствующего идемпотентного полукольца (т.е. разных областей зна-
значений весовой функции), состоит несомненное преимущество
*О методе решения третьей из сформулированных выше задач см.
задачу 7.36.
5.6. Задача о путях 329
абстрактно-алгебраического подхода к решению таких задач
на графах.
Рассмотрим теперь решение общей задачи о путях для
произвольного замкнутого полукольца TZ.
Метка пути, ведущего из вершины V{ в вершину Vj, есть
произведение в полукольце И меток входящих в путь дуг в
порядке их следования (для пути ненулевой длины) и есть 1
(единица полукольца It) для пути нулевой длины.
Стоимость прохождения из вершины Vi в вершину Vj
(или между 1-й и j-й вершинами) — это сумма в полукольце 11
меток всех путей, ведущих из вершины Vi в вершину Vj.
Заметим, что сумма, определяющая стоимость прохожде-
прохождения, вообще говоря, есть бесконечная сумма замкнутого по-
полукольца, т.е. точная верхняя грань соответствующей после-
последовательности меток. Это связано с тем, что множество всех
путей, ведущих из одной вершины графа в другую, в общем слу-
случае бесконечно (но, как можно доказать, не более чем счетно).
Аналогично можно определить стоимость прохождения из
вершины в вершину по какому-либо множеству путей. Отме-
Отметим, что если стоимость прохождения между парой вершин по
какому-либо множеству путей равна 0, то это означает, что не
существует пути, принадлежащего данному множеству путей,
ведущего из первой вершины рассматриваемой пары во вторую
вершину.
Матрица меток дуг является элементом полукольца матриц
над полукольцом TZ. В этом полукольце определены операции
сложения и умножения матриц, а также возведение матрицы в
неотрицательную степень. Докажем следующее утверждение.
Лемма 5.1. Элемент a\j матрицы А', I ^ 0, равен стоимо-
стоимости прохождения из вершины vi в вершину Vj по всем путям
длины /.
< Доказательство проведем индукцией по /. При / = 0 утвер-
утверждение очевидно, так как А0 = Еу где Е — единичная матрица,
330 5. ТЕОРИЯ ГРАФОВ
которая будет матрицей стоимости прохождения по всем путям
длины 0.
При / = 1 утверждение также очевидно. Далее,
Согласно предположению индукции, элемент а\^ ' равен стои-
стоимости прохождения из вершины V{ в вершину Vk по всем путям
длины 1-1. Множество всех путей длины I из вершины г;,* в вер-
вершину Vj, проходящих через фиксированную к-ю вершину так,
что вершина v^ связана дугой с вершиной Vj (vk -> Vj,) обра-
образуется путем присоединения дуги (г;*, Vj) к каждому из путей,
ведущих из Vi в Vk и имеющих длину / - 1.
Тогда видно, что написанное выше выра-
выражение для элемента а\) дает стоимость
прохождения из вершины V{ в вершину Vj
по всем путям длины / (рис. 5.26). >
Так как стоимость прохождения между парой вершин (vi,Vj)
равна сумме меток всех путей, ведущих из первой вершины во
вторую, а указанную сумму можно можно получить, суммируя
последовательно метки путей длины 0, длины 1, длины 2 и т.д.,
то матрица стоимостей взвешенного ориентированного графа с
учетом доказанной леммы 5.1 может быть представлена в виде
До сих пор мы рассматривали матрицы над замкнутым
полукольцом. Однако, если элементы матрицы А принадлежат
некоторому полукольцу с итерацией, из теоремы 3.9 следует,
что и все элементы матрицы стоимостей С = А* останутся в
этом же полукольце. Таким образом, полученные результаты
можно перенести на произвольное полукольцо с итерацией.
5.6. Задача о путях 331
Теорема 5.4. Матрица стоимостей ориентированного гра-
графа G, размеченного над полукольцом с итерацией 11 (в частно-
частности, над замкнутым полукольцом), равна итерации матрицы А
меток дуг ориентированного графа G. #
Для вычисления С = А* достаточно решить (т.е. найти
наименьшее решение) в % при всех j = 1, п систему уравнений
где €j € TZn — j-й единичный вектор, т.е. вектор, все элементы
которого, кроме j-ro, равны 0, a j-й равен единице полукольца
%. Наименьшее решение имеет вид ? = A*€j (см. 3.3). Тогда
столбец ? = A*6j есть j-й столбец матрицы А*. Такой метод
вычисления матрицы А* аналогичен известному из линейной
алгебры методу элементарных преобразований при вычислении
обратной матрицы.
Выясним теперь смысл матрицы стоимостей С = А* для
полуколец В и 7?+.
В первом из этих полуколец метка отдельного пути всегда
равна 1 (так как метка дуги в размеченном над полукольцом
графе не может, согласно определению, быть нулем полуколь-
полукольца). Следовательно, стоимость с^ = 1, если существует хотя бы
один путь из г-й вершины в j-ю, и Cij = 0, если иначе. Други-
Другими словами, для полукольца В матрица стоимостей совпадает с
матрицей достижимости ориентированного графа.
В полукольце И+ метка пути — это арифметическая сумма
меток его дуг, так как умножение в К+ — это обычное ариф-
арифметическое сложение. Поскольку сложение в IVе — это взятие
наименьшего из слагаемых, то стоимость с# — это наимень-
наименьшая из меток пути среди всех путей, ведущих из г-й вершины
в j'-ю, т.е. это и есть наименьшая длина пути между указан-
указанными вершинами. Таким образом, в полукольце 7?+ матрица
стоимостей является матрицей кратчайших расстояний, т.е.
наименьших длин путей между всеми парами вершин ориен-
ориентированного графа.
332
5. ТЕОРИЯ ГРАФОВ
Пример 5.9. Рассмотрим граф, изображенный на рис. 5.27,
и решим для него задачу вычисления матрицы достижимости.
На числовые метки дуг внимания пока не обращаем, считая,
что ориентированный граф размечен над
полукольцом В и метка каждой дуги равна
1, т.е. ориентированный граф задан матри-
матрицей
/О
О
.А =
Рис. 5.27
1
1
1
О
0
О О
1 о;
Запишем систему уравнений в полукольце В для определения
первого столбца матрицы А*:
XI =
Х2 =
! + Ж3 + Ж4 + 1,
х2
+ 0,
+ 0.
E.3)
Отметим, что часто нулевые слагаемые не записывают, как и
в системах уравнений в поле действительных чисел.
Воспользуемся методом последовательного исключения не-
неизвестных (см. 3.3). Поскольку в правой части первого урав-
уравнения нет переменной х\, можно исключить эту переменную из
системы, подставив в остальные уравнения. С учетом идемпо-
идемпотентности сложения получим
+0,
+0,
Из второго уравнения имеем х*ъ = 1*(жз + 0)- В полукольце В
итерация любого элемента равна единице полукольца. Поэтому
Х2 = #з + 0- Исключив Х2 из системы, получим
+ 0,
#4= #3+^4
5.6. Задача о путях
333
Далее вычислим хз = 1*0 = 1-0 = 0. Подставив хз = 0 в послед-
последнее уравнение, найдем Х4 = 1*1 = 1.
Итак, первый столбец А* есть
0
0
Второй столбец определяется из системы
XI =
Х2+Х3
Х2
+ 1,
+ 0,
+ 0.
Исключая xi, получаем
= ^2 + #3
+ 1,
+ 0,
+ 0.
Из второго уравнения имеем Х2 = 1*(#з + 1) = яз + 1- flflJ&e
находим
j = хз +1,
Отсюда хз = 1*1 = 1 и а?4 = а?4 +1. В итоге Ж4 = 1*1 = 1, «2 =
= 1 + 1 = 1, Ж1 = 1 + 1 + 1+0 = 1. Таким образом, второй столбец
А* есть
334
5. ТЕОРИЯ ГРАФОВ
Аналогично вычисляем третий и четвертый столбцы и в
результате получаем матрицу А*:
А* =
П 1 1
0 110
0 110
VI 1 1 \)
Анализ этой матрицы показывает (см. 5.2), что данный
граф связен и имеет две бикомпоненты: {vi, V4} и {^2, из}-
Заметим, что в полукольце В можно упростить решение
систем уравнений, воспользовавшись свойствами полукольца.
Легко видеть, что наименьшее решение уравнения
есть Xk = 1 и не зависит от значений переменных в правой части
уравнения. С учетом этого решение системы E.3) упростится.
Так, из первого уравнения сразу получаем х\ = 1. Тогда
четвертое уравнение принимает вид х\ = жз +1, откуда х\ = 1.
Поскольку х\ и х\ не входят в оставшиеся два уравнения, их
решение нужно искать, используя метод исключения.
Пример 5.10. Для графа, изображенного на рис. 5.27, вы-
вычислим матрицу кратчайших расстояний, перейдя к полукольцу
И+. Договоримся, что для упрощения записи оо здесь будем
понимать как +оо.
Наш взвешенный ориентированный граф задается теперь
следующей матрицей:
оо 5 10 1
оо 2 3 оо
оо 1 оо оо
\3 оо 4 оо/
E.4)
5.6. Задача о путях 335
Система для вычисления первого столбца матрицы А* имеет
вид
'Х\ = ЪХ2 + Юяз + 1X4 + О,
Х2 = 2#2 + Зжз + ОО,
+оо.
Обратим внимание на нюансы, связанные с работой в по-
полукольце R+: элементы 1 и 0 не являются единицей и нулем
полукольца, т.е. х^ж + Оиж^Ьжв общем случае. Напомним,
что сложение в полукольце 7?+ — взятие наименьшего из двух
чисел, а умножение — обычное арифметическое сложение. За-
Заметим, что наличие слагаемого 0 в любой сумме (в полукольце)
означает, что вся сумма равна 0; слагаемое +оо можно не за-
записывать (как нуль полукольца).
Из первого уравнения системы сразу следует, что х\ = О,
так как одно из слагаемых в правой части есть элемент 0.
Напомним, что итерация любого элемента в рассматриваемом
полукольце равна единице полукольца. Учитавая этот факт, из
второго уравнения получаем
Исключая Х2 из остальных уравнений системы и учитывая,
что xi = 0, получаем
оо,
Далее, из второго уравнения имеем
#3 = A • 3)хз + оо = 4хз +
откуда хз = 4* • оо = оо, и поэтому
336
5. ТЕОРИЯ ГРАФОВ
Подставляя найденное значение х$ в выражение для #2? полу-
получаем Х2 = оо. Первый столбец искомой матрицы вычислен:
/0\
00
оо
W
Этот столбец содержит кратчайшие расстояния от всех вершин
графа до вершины v\. Наличие в нем нулей полукольца во
второй и третьей строках говорит о том, что вершина v\ не
достижима из вершин г>2 и г>з-
Аналогично вычисляются остальные столбцы матрицы А*.
Результат будет следующим:
/О 5 5 1>
оо О 3 оо
оо 1 0 оо
^3 5 4 0/
Для данного простого ориентированного графа легко сопо-
сопоставить полученный алгебраический результат с результатом
„визуального" анализа ориентированного графа. Рассмотрим,
например, пару вершин (vi, из). В ориентированном графе есть
различные пути из вершины v\ в вершину v$. Легко видеть,
что заведомо „не выгодны" пути, содержащие контуры и пе-
петли, поэтому их рассматривать не будем и вычислим метки по
простым путям. По пути v\ -> v± -> v$ сумма меток равна 5,
по пути v\ -> vs — 10, а по пути v\ -» V2 —> v$ — 8. Кратчайшее
расстояние — 5, что совпадает с ответом, полученным алге-
алгебраически: элемент а\3 также равен 5. #
Помимо изложенного есть еще один способ вычисления за-
замыкания матрицы с элементами в замкнутом полукольце. Он
основан на понятии пути ранга к из вершины V{ в вершину Vj.
Пусть в ориентированном графе выбрана и зафиксирована
нумерация вершин. Будем полагать, что все вершины прону-
пронумерованы подряд натуральными числами, начиная с 1.
5.6. Задача о путях 337
Путь V{0 -> Vix ->...-> Vim длины m называют путем ранга к
при га > 1, если к — наибольшее среди чисел t'i, ..., im-i? и
путем ранга 0 при га = 1. Путь нулевой длины также считают
путем ранга 0. Таким образом, ранг пути — это максималь-
максимальный номер вершины, в которую разрешено заходить по пути из
Vi в Vj (исключая вершины Vi и Vj). Путь ранга 0 не содержит
промежуточных вершин. Максимальный ранг пути в ориенти-
ориентированном графе при указанном выше способе нумерации равен
числу его вершин.
Пример 5.11. В ориентированном графе, изображенном
на рис. 5.27, путь v\ -> v± -> v\ имеет ранг 4, путь u* -* v\ ->¦
-> V2 — ранг 1, путь V4 -> v\ -> vz ~> щ — ранг 3. Пути
Щ ~> ^з -> ^2? Щ -> v\ -> V3 -> ^2 и V4 -> ^2 -> ^2 ~> V3 ->• ^2 также
имеют ранг 3. #
Обозначим через С'*' матрицу стоимостей прохождения
между различными парами вершин по всем путям ранга, не
превосходящего к. Ее элемент Су содержит стоимость прохо-
прохождения из вершины Vi в вершину Vj по всем путям рангов О,
Выведем формулу для вычисления элемента Су матрицы
. Для этого заметим следующее. По пути ранга, не боль-
большего /с, из вершины Vi в вершину Vj можно пройти следующими
способами:
1) идя из вершины Vi в вершину Vj по некоторому пути
ранга, не превосходящего к — 1, т.е. минуя вершину г;*;
2) сначала идя из Vi в Vk по пути ранга,
не большего к — 1, затем „покрутившись" v c<jf-l> v
любое число раз (а может быть, и ни ра-
разу) по какому-либо контуру или любому
замкнутому пути из Vk в Vk ранга, не
большего к — 1, и, наконец, идя из вер-
вершины Vk в вершину Vj по пути ранга, не
большего к - 1 (рис. 5.28). Рис# 5'28
338 5. ТЕОРИЯ ГРАФОВ
При первом способе следования стоимость прохождения из
вершины Vi в Vj по всем путям ранга, не большего к — 1,
составит Су .
При втором способе следования стоимость прохождения из
Vi в Vk по всем путям ранга, не большего к — 1, будет равна
с\к~ К Стоимость прохождения из v* в v* по всем замкнутым
путям ранга, не большего к — 1, составит (cjj.fc~~ )*.
Поясним это в частном случае, когда вершина Vk содержит-
содержится в каком-то одном контуре. Пусть Г — такой контур, а /хг —
метка этого контура. Тогда очевидно, что метка пути, обра-
образованного нуль-кратным прохождением по контуру Г, равна
единице полукольца (как метка всякого пути длины 0), мет-
метка же пути, образованного m-кратным прохождением по Г при
т ^ 1, равна ц™. Следовательно, стоимость прохождения по
всем путям, которые получаются при произвольном числе про-
прохождений по контуру Г, составит ]? /хр = /ip.
Стоимость прохождения из вершины и* в вершину Vj по
пути ранга, не большего к — 1, равна cL~~ ' (см. рис. 5.28).
Таким образом, стоимость прохождения по пути ранга, не
большего к, при указанном способе следования составит
гк \скк ) Ckj '
Таким образом, словесное описание п путешествия" из ^ в vj
по путям ранга, не большего к, приводит к следующей формуле
для вычисления элемента матрицы С^:
кк ) ckj • \°'°)
Пусть aij — элементы матрицы меток дуг ориентирован-
ориентированного графа. Поскольку каждый путь ранга 0 между несовпа-
5.6. Задача о путях 339
дающими вершинами состоит из одной дуги, а каждая вершина
достижима сама из себя по пути нулевой длины с меткой 1 или
по петле с меткой ац, то элементы матрицы С(°) имеют вид
Тогда матрицу стоимостей С = А* можно найти, вычисляя
последовательно матрицы С^к\ к = 0, п, по формулам E.5)
и E.6).
Вычисления по формулам 5.5 и 5.6 образуют алгоритм
Флойда — Уоршелла — Клини определения стоимости
прохождения между любыми парами вершин.
Для полуколец В и TZ+ в силу того, что в них итерация любо-
любого элемента х равна единице полукольца, получим упрощенный
вариант формулы E.5):
Ckj '
Вычисления по формуле E.7) начинают с матрицы
определяемой соотношением E.6). Все дальнейшие вычисления
удобно также проводить в матричном виде. Для нахождения
матрицы С^ удобно определить сначала матрицу D^k\ эле-
элементы которой вычисляются по формуле
cik ckj '
Чтобы найти j-й столбец матрицы D^k\ достаточно &-й столбец
матрицы С^*") умножить (в смысле соответствующего полу-
полукольца) на j-й элемент k-и строки этой же матрицы.
Решим описанным способом задачу о кратчайших расстоя-
расстояниях в графе, изображенном на рис. 5.27. Для него С^ = А,
где матрица А имеет вид E.4). Используя формулу E.7), по-
340
5. ТЕОРИЯ ГРАФОВ
следовательно находим
/0
-
оо
оо
\з
/0
C)
оо
оо
< з
5
0
1
8
5
0
1
5
10
3
0
4
8
3
0
4
1\ /0
оо
оо
0 ,
сB) _ оо
оо
\з
1 \ /0
оо
оо
0 /
ОО
оо
5
0
1
8
5
0
1
5
8
3
0
4
5
3
0
4
1\
оо
оо
о)
1\
оо
оо
о/
•
Например, матрица С^ по матрице С^ вычисляется так.
Сначала выделим в С^ вторую строку и второй столбец:
/0
00
оо
\з
5
0
1
8
10 1 \
3 оо
0 оо
4 0 /
Затем, чтобы вычислить первый столбец матрицы С^2\ бе-
берем второй (выделенный) столбец матрицы С^ и умножаем (в
полукольце 7?+) его элементы по очереди на первый элемент
второй (выделенной) строки той же матрицы С^1\ Каждое
такое произведение складываем в полукольце с одноименным
элементом первого столбца матрицы С^1\ Поскольку умно-
умножение в полукольце TZ+ — это арифметическое сложение, а
сложение — взятие наименьшего из двух чисел, мы получим
следующие элементы первого столбца матрицы С^:
с}? = min {eft, eft + 4? } = min {0, оо} = О,
4? = min{41i), 4з + 4?} = nrin{oo, оо} = оо,
= min
= min
ei21)=min{ei11),c512)+eft}=mm{3,oo} =
5.7. Изоморфизм графов 341
Как видим, первый столбец матрицы С^ не изменился по
сравнению с первым столбцом матрицы С^1\ Это означает, что
нельзя уменьшить стоимость прохождения в первую вершину
из других вершин графа, идя через вторую вершину (см.
рис. 5.27).
Точно так же для вычисления второго столбца матрицы С®
умножаем второй столбец С^ на второй элемент второй стро-
строки той же матрицы, для вычисления третьего столбца — на
третий элемент второй строки и т.д. Не выписывая подробно
всех вычислений, отметим характерный момент — изменение
элемента q3 = 8 по сравнению с q3 = 10, связанное с тем, что
стоимость прохождения из v\ в ^з по пути ранга 2 оказалась
меньше, чем стоимость прохождения по пути ранга 1. Мини-
Минимальная же стоимость прохождения с[% = 5 получена по пути
ранга 4.
5.7. Изоморфизм графов
Для ориентированного графа (У, Е) множество Е дуг мож-
можно рассматривать как график бинарного отношения непосред-
непосредственной достижимости, заданного на множестве вершин.
В неориентированном графе (V, Е) множество Е ребер явля-
является множеством неупорядоченных пар. Для каждой неупоря-
неупорядоченной пары {и, v} 6 Е можно считать, что вершины и и v
связаны симметричным бинарным отношением р, т.е. (и, v) Е р
и (и, и) Е р.
Таким образом, с каждым неориентированым и ориентиро-
ориентированным графом связано бинарное отношение р. Это отношение
будем называть отношением смежности.
С алгебраической точки зрения как ориентированный, так
и неориентированный граф можно рассматривать как модель,
сигнатура которой состоит из одного бинарного отношения:
G = (V, р). В классической теории графов изучаются преиму-
преимущественно конечные модели такого рода.
342 5. ТЕОРИЯ ГРАФОВ
При указанном подходе различия между ориентированным
и неориентированным графами проявляется только в свойствах
отношения смежности р. Бели это отношение симметрично,
то граф называют неориентированным, и с этой точки зре-
зрения неориентированный граф можно считать частным случаем
ориентированного*.
Применяя к данному частному случаю моделей общие поня-
понятия гомоморфизма и изоморфизма (см. 4.4), мы можем сфор-
сформулировать следующие определения.
Определение 5.14. Отображение h: V\ -> V2 множества
вершин графа G\ = (Vi, р\) в множество вершин графа G2 =
= (^2, р2) называют гомоморфизмом графов (графа G\ в
граф G2), если для любых двух вершин, смежных в первом
графе, их образы при отображении h смежны во втором графе,
т.е. если
(Vi/,v e Vi)(upi v =» h{u) p2 h(v)).
Биективный гомоморфизм Л, такой, что любые две верши-
вершины смежны в первом графе тогда и только тогда, когда их
образы смежны во втором графе, т.е.
(Vu,v e Vi)(u piv<* h(u) p2 h(v)),
называют изоморфизмом графов G\ и G*i (графа G\ на граф
), а графы G\ и G*i — изоморфными, что записывают в виде
Гомоморфизм графов, который является эпиморфизмом, на-
называется также гомоморфизмом одного графа на другой.
Возвращаясь к нашему определению графа посредством
двух множеств: множества вершин V и множества ребер (дуг)
Е, получим следующие варианты определений гомоморфизма и
изоморфизма.
*При таком подходе в неориентированном графе могут быть петли,
если отношение р содержит некоторые элементы диагонали, в частности
является рефлексивным.
5.7. Изоморфизм графов 343
Гомоморфизм неориентированного графа G\ = (Vi, E\) в не-
неориентированный граф С?2 = (V2, -Бг) есть такое отображение
h: V\ -> V2, что для любых двух вершин первого графа, соеди-
соединенных ребром, их образы при отображении h также соединены
ребром, т.е.
(VujV € Vi)({ti, v] € Ek =» {ЛЫ, Л(«)} 6 Я2).
Гомоморфизм ориентированного графа Gi = (Vi, J5i) в ори-
ориентированный граф С?2 = (^2, J5?2) есть такое отображение
h: V\ —> V2, что для любых двух вершин щ v первого графа,
таких, что есть дуга, ведущая из и в v, из вершины h(u) тоже
ведет дуга в h(v)y т.е.
(Vu,v e vi)((u, v) е Ех => (Л(и), ад) € ??2).
Изоморфизм неориентированного графа Gi на неориенти-
неориентированный граф (?2 есть такал биекция h: V\ —У V2, при которой
две вершины гх и г; графа Gi соединены ребром тогда и только
тогда, когда соединены ребром их образы h(u) и h(v), т.е.
Аналогично изоморфизм ориентированного графа Gi на
ориентированный граф G2 есть такая биекция h: V\ -* \^, при
которой в ориентированном графе Gi из вершины и ведет дуга
в вершину v тогда и только тогда, когда в ориентированном
графе <?2 из образа /i(u) вершины и ведет дуга в образ h(v)
вершины v, т.е.
(Vtx,v e vx){u -+v& h(u) -> ад).
Пример 5.12. а* На рис. 5.29 отображение /г, где /i(vi) =
= tui, /1(^2) = ьJ, h(vz) = /1(^4) = гуз, есть гомоморфизм ориен-
ориентированного графа G\ в ориентированный граф G<i*
344
5. ТЕОРИЯ ГРАФОВ
w<
Рис. 5.29
Обратим внимание на петлю (гиз, ^з)« эта петля является
образом дуги (г>4, г;з), так как h(v4) = гиз и h(vs) = г#з. В
противоположность этому петля (гух, w\) не имеет прообраза
bGi.
На этом же рисунке более толстыми стрелками выделен
подграф G'2 графа Сг, порожденный подмножеством вершин
{iui, W2,ws}. Этот подграф будет гомоморфным образом графа
G\. Удаляя петлю в вершине tui, получим (для того же подмно-
подмножества вершин) порожденный подграф, являющийся строгим
гомоморфным образом графа G\. Отметим, что каждая дуга в
строгом гомоморфном образе ориентированного графа G\ име-
имеет прообраз в G\.
б. На рис. 5.30 неориентированный граф G2 есть строгий
гомоморфный образ графа G\ (если рассматривать неориенти-
неориентированные графы без петель).
Рис. 5.30
в. На рис. 5.31 отображение h не является гомоморфизмом
G\ на #2, поскольку v\ -> V2, но h{v\) -* /1(^2) (петли (twi, w\)
5.7. Изоморфизм графов
345
нет); h{v2) -* Л(^з), хотя V2 -> v$ и т.д. Легко сообразить,
что любой двухвершинный гомоморфный образ графа Gi на
рис. 5.31 должен иметь петлю, и, следовательно, G<i не является
гомоморфным образом Gi ни при каком отображении.
го.
го,
го,
го2
Рис. 5.31
Рис. 5.32
г. На рис. 5.32 изображен один граф из множества двух-
двухвершинных гомоморфных образов G\.
д. Графы, изображенные на рис. 5.33, изоморфны, и изо-
изоморфизмом является, например, отображение Л, такое, что
h(vi) = U7i, h(v2) = w4, h(vs) = w2, h(v4) = tu
= tl76. #
Рис. 5.33
Зачастую для того, чтобы распознать изоморфизм графов,
удобно перейти от исходных графов к их дополнениям.
346
5. ТЕОРИЯ ГРАФОВ
Определение 5.15. Неориентированный (ориентирован-
(ориентированный) граф G = V;E называют дополнением неориентиро-
неориентированного (ориентированного) графа G = (У, J5), где 2? —
дополнение множества Е до множества всех неупорядоченных
(упорядоченных пар) на V.
Можно доказать, что графы изоморфны тогда и только то-
тогда, когда изоморфны их дополнения. Например, перейдем к
дополнениям графов, изображенных на рис. 5.33. Анализ ука-
указанных дополнений (рис. 5.34) позволяет сразу обнаружить их
изоморфизм, а следовательно, и изоморфизм исходных графов.
Рис. 5.34
Более сложные случаи распознавания изоморфизма (глав-
(главным образом, для неориентированных графов) будут рассмо-
рассмотрены в 5.9.
Определение 5.16. Автоморфизм графа G = (V, р) —
это любая подстановка множества его вершин, являющаяся
изоморфизмом G на себя.
Можно показать, что композиция двух любых автоморфиз-
автоморфизмов графа снова есть автоморфизм этого графа, а подстановка,
обратная к автоморфизму, опять-таки есть автоморфизм. Та-
Таким образом, множество всех автоморфизмов данного графа
образует группу по операции композиции, которая является
подгруппой симметрической группы множества вершин гра-
графа. Бе называют группой автоморфизмов данного графа.
5.7. Изоморфизм графов
347
Рассмотрим некоторые примеры групп автоморфизмов.
Рис. 5.35
Для графа, изображенного на рис. 5.35, а, группа автомор-
автоморфизмов порождается транспозициями A 4) и B 3), что легко
усматривается из анализа дополнения этого графа (рис. 5.35, б).
Очевидно, что группа автоморфизмов графа есть подгруппа
группы перестановок множества его вершин. Поэтому, со-
согласно теореме 2.13 Лагранжа, порядок группы автоморфизмов
графа есть делитель факториала числа его вершин. В част-
частности, для графа на рис. 5.35, а группа автоморфизмов имеет
порядок 4 и состоит из тождественной подстановки е и подста-
подстановок A 4), B 3), A 4) B 3). Очевидно, что 4! делится на 4.
Можно доказать, что автоморфизмы неориентированно-
неориентированного графа сохраняют степени, а ориентированого графа —
полустепени исхода и захода всех его вершин. Это свойство
позволяет упростить описание автоморфизмов графа.
Пример 5.13. Найдем нетривиальные
(т.е. отличные от тождественной подста-
подстановки) автоморфизмы неориентированного
графа, изображенного на рис. 5.36. Так как
среди вершин графа лишь одна вершина v\
имеет степень 1 и лишь одна вершина v±
имеет степень 2, то при любом изоморфиз-
изоморфизме эти вершины перейдут в себя. Значит,
при изоморфизме возможны лишь переста-
перестановки вершин V2, v$ и v$.
Рис. 5.36
348
5. ТЕОРИЯ ГРАФОВ
Итак, для любого автоморфизма h этого графа h(v\) = tii.
Поскольку v\ ьн^, то h(v\) »-h/i(v2), и, следовательно, поскольку
V2 — единственная вершина, смежная с vi, всегда hfo) = г>2, т.е.
вершина v<i переходит в себя. Таким образом, единственным
нетривиальным автоморфизмом данного графа будет транс-
транспозиция C 5) — „отражение" квадрата V2V3V4V5 относительно
диагонали V2V\. #
Иногда группу автоморфизмов графа легко найти именно
из чисто геометрических соображений при удачном изображе-
изображении графа. Автоморфизм есть не что иное, как преобразование
графа (геометрической фигуры), при котором граф совмеща-
совмещается с самим собой. Поэтому группу автоморфизмов графа
можно изучать, анализируя его как геометрическую фигуру.
Пример 5.14. Для графа, изображенного на рис. 5.37,
из геометрических соображений вытекает, что автоморфизм
<р сводится к повороту графа на 60° по часовой стрелке вокруг
центра тяжести треугольника
Рис. 5.37
Следовательно, группа автоморфизмов порождается под-
подстановкой (р, являющейся композицией трех циклов:
<р = A 2 3)D 6 8)E 7 9).
Заметим, что ни один цикл, входящий в <р, сам по себе не будет
автоморфизмом данного графа. Так, если мы рассмотрим цикл
h = A 2 3), то ЛC) = 1, ЛD) = 4, и ЛC) нчЛD), но vs 0v4. #
5.8. Топологическая сортировка 349
В заключение сформулируем без доказательства теорему,
доказанную Фрухтом в 1938 г. и характеризующую все ко-
конечные группы в терминах групп автоморфизмов конечных
неориентированных графов.
Теорема 5.5 (теорема Фрухта). Каждая конечная груп-
группа изоморфна группе автоморфизмов конечного неориентиро-
неориентированного графа.
5.8. Топологическая сортировка
Определение 5.17. Ориентированной сетью (или про-
просто сетью) называют бесконтурный ориентированный граф*.
Поскольку сеть является бесконтурным графом, можно по-
показать, что существуют вершины (узлы) сети с нулевой по-
лустепенью исхода, а также вершины (узлы) с нулевой полу-
степенью захода. Первые называют стоками или выходами
сети, а вторые — источниками или входами сети.
Определение 5.18. Уровень вершины сети — это нату-
натуральное число, определяемое следующим образом:
1) если полустепень захода вершины равна 0, то ее уровень
равен 0 и наоборот (т.е. нулевой уровень Щ — это множество
всех входов);
2) если множества Ni вершин уровня г определены для всех
г < fc, то уровень iVfc+i содержит те и только те вершины,
предшественники которых принадлежат любому из уровней с
номером от 0 до fc, причем существует хотя бы один предше-
предшественник уровня Л, т.е.
*В некоторых задачах встречаются бесконтурные ориентированные
графы, имеющие бесконечные множества вершин и дуг. Такие графы
называют бесконечными сетями. Мы рассматриваем только конечные
сети. Кроме того, в литературе по теории графов термин „сеть" иногда
используется в ином смысле — для объекта, более сложного, чем граф (см.:
Яблонский СВ.).
350 5. ТЕОРИЯ ГРАФОВ
где Г l(v) = {х: х -> v} — множество предшественников верши-
вершины V.
Уровень вершины сети можно интерпретировать как длину
максимального пути от входов сети до этой вершины.
Определение 5.19. Порядковой функцией сети G =
= (V, Е) называют отображение ord: V -> N, сопоставляющее
каждой вершине сети номер ее уровня.
Во многих прикладных задачах возникает проблема такого
упорядочения вершин сети, при котором вершины, принадле-
принадлежащие одному уровню, располагаются друг под другом, а дуги
ориентированного графа ведут в его изображении на плоско-
плоскости от вершин с меньшим уровнем к вершинам с большим
уровням слева направо. Подобного рода проблема называется
проблемой топологической сортировки, поскольку необ-
необходимо расположить вершины графа на плоскости так, чтобы
отчетливо было видно распределение вершин по уровням. Само
расположение при этом может быть разным, лишь бы оно имело
„слоистую" структуру, в которой каждый слой составляют вер-
вершины одного уровня. На рис. 5.38 показаны сеть и результат
применения топологической сортировки сети.
Топологическая сортировка применяется в самых разных
ситуациях, например при распараллеливании алгоритмов, ко-
когда по некоторому описанию алгоритма нужно составить граф
зависимостей его операций и, отсортировав его топологически,
определить, какие из операций являются независимыми и могут
выполняться параллельно (одновременно).
Формально топологическую сортировку можно реализовать
по-разному. Мы опишем один из возможных методов*.
Этот метод состоит в вычислении порядковой функции сети
и известен как алгоритм Демукроиа. Предполагается, что
вершины сети пронумерованы от 1 до п.
* Другие методы топологической сортировки см.: Кнут Д.; Вирт Н.
5.8. Топологическая сортировка
351
viz
Рис. 5.38
Наглядно процесс определения уровней вершин можно пред-
представить следующим образом. Нулевой уровень образуют входы
сети — вершины с полустепенью захода, равной 0. Удалив из
сети все вершины нулевого уровня и исходящие из них дуги,
вновь получим сеть, входами которой будут вершины первого
уровня исходной сети. Указанный процесс „послойного" удале-
352 5. ТЕОРИЯ ГРАФОВ
ния вершин следует продолжать до тех пор, пока все вершины
исходной сети не будут распределены по уровням.
Алгоритм Демукрона использует матрицу смежности вер-
вершин В типа п х п в качестве средства представления сети и
основан непосредственно на определении уровня вершины и
свойствах матрицы В. Можно увидеть, что сумма элементов
к-го столбца матрицы В равна полустепени захода вершины
Vk> Поэтому, просуммировав элементы матрицы по всем столб-
столбцам и выбрав вершины, соответствующие столбцам с нулевой
суммой, получим множество вершин нулевого уровня — входы
сети.
Безусловно, „физически" удалять вершины и дуги из сети
и вычеркивать из матрицы В строки, соответствующие уда-
удаляемым вершинам, нет необходимости. Процесс вычисления
порядковой функции можно организовать следующим образом.
Запишем суммы элементов столбцов матрицы В в вектор М
длины п. При этом элемент га* вектора М будет содержать
полустепень захода вершины Vk. Пусть из сети удалены вер-
вершина Vi и все исходящие из нее дуги. Заметим, что элемент
bik равен 1, если из вершины Vi идет дуга в вершину Vk, и ра-
равен 0 в противном случае. Поэтому, чтобы получить новую
полустепень захода вершины v^, необходимо из элемента rrik
вектора М вычесть элемент Ь^ матрицы В. Чтобы пересчи-
пересчитать полустепени захода всех вершин сети, оставшихся в ней
после удаления вершины v^, надо из вектора М вычесть г-ю
строку матрицы В.
Если на очередном шаге входами сети являются вершины
Щ\ > • • ч Щг > т0 Для определения следующего „слоя" вершин нуж-
нужно из вектора М вычесть строки матрицы В с номерами ti,...,
ir и зафиксировать новые нулевые элементы вектора М, появив-
появившиеся после вычитания. Фиксировать следует именно новые
нулевые элементы, поскольку элементы вектора М, соответ-
соответствующие вершинам, лежащим на предыдущих уровнях, стали
равными 0 на предыдущих шагах алгоритма.
5.8. Топологическая сортировка 353
Заметим, что порядковую функцию сети можно задать, ука-
указав множества вершин, принадлежащих каждому уровню, или
сопоставив каждой вершине ее номер уровня. Первый способ
более удобен при теоретических рассуждениях, второй — при
вычислениях.
Алгоритм Демукрона
вычисления порядковой функции сети
Алгоритм обрабатывает матрицу В смежности вершин гра-
графа порядка п. В результате работы алгоритма получаем мас-
массив Ord длины п, г-й элемент которого равен номеру уровня
вершины V{.
0. Сформировать множество V\ вершин сети. Значение
счетчика уровней к положить равным 0. Найти суммы элемен-
элементов по всем столбцам матрицы В (полустепени захода вершин)
и заполнить ими массив М.
1. Бели множество V\ не пусто, перейти на шаг 2, если
иначе, то перейти на шаг 3.
2. Определить множество / номеров всех новых нулевых
элементов массива М, т.е. таких, что соответствующие этим
номерам вершины принадлежат множеству V\.
Присвоить элементам массива Ord с номерами из множества
/ номер уровня к и удалить вершины с этими номерами из мно-
множества V\ („замаскировать" вершины). Вычесть из массива М
строки матрицы В, соответствующие вершинам с номерами из
множества I (т.е. вершинам последнего вычисленного уровня).
Увеличить счетчик уровней на 1 (к = А; + 1). Вернуться на
шаг 1.
3. Закончить работу.
Пример 5.15. Применим алгоритм Демукрона к сети,
представленной на рис. 5.38. Матрица смежности вершин сети
12- 10061
354
5. ТЕОРИЯ ГРАФОВ
имеет следующий вид:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
1
1
23456789 10 11
1
1
1 1 1
1 1
1
1 1 11
1
1
1
1
12 13 14
1
1
1 1
1
1
Приведем последовательность значений массива М, соот-
соответствующую итерациям алгоритма и множества N{ вершин
г-го уровня. Прочерки соответствуют вершинам, не принад-
принадлежащим множеству V\ („замаскированные" вершины) на со-
соответствующем этапе алгоритма.
1
2
2
0
—
—
2
1
0
—
—
—
3
5
4
4
3
3
п
и
4
2
1
1
1
0
5
0
—
—
—
6
2
1
1
0
7
2
1
0
—
8
0
—
—
—
9
1
0
—
—
10
1
0
—
—
11
2
2
2
1
0
12
2
2
1
1
0
13
3
3
2
1
0
14
1
1
0
—
—
No
Ni
N2
N3
N4
N5
= {5,8}
= {2,9,10}
= {1,7,14}
= {6}
= {4,11,12,13}
= {3}
#
Алгоритм Демукрона может быть модифицирован так, что-
чтобы он останавливался, если ориентированный граф, поданный
на вход, не является сетью, и сообщал об этом. Можно увидеть,
5.8. Топологическая сортировка 355
что анализируемый граф не будет сетью тогда и только тогда,
когда при очередном перевычислении массива М не появятся
новые нули.
В заключение рассмотрим вопрос о связи понятий ориенти-
ориентированной сети и упорядоченного множества.
Так как сеть есть бесконтурный граф, то отношение до-
достижимости в нем будет отношением порядка. Действитель-
Действительно, пусть для двух отличных друг от друга вершин щ v сети
вершина и достижима из вершины v (v =>* и) и вершина v дости-
достижима из вершины и (и =4>* v). Тогда существует путь ненулевой
длины из г; в и (v =Ф+ и) и из и в v (и =Ф-+ v). Отсюда вытекает,
что существует путь ненулевой длины из и в и (и =Ф-+ и) и из v в
v (v =Ф>+ v). Следовательно, существует контур, связывающий
вершины и и v, что невозможно.
Обратно, пусть (А, <) — конечное упорядоченное множе-
множество. Сопоставим ему ориентированный граф G = (V, Е) так,
что множество вершин V находится с А во взаимно однознач-
однозначном соответствии, а множество дуг определяется следующим
образом: и -> v тогда и только тогда, когда v доминирует над
и в смысле порядка <.
Построенный таким образом ориентированный граф G бу-
будет сетью. Действительно, предположим, что в нем существует
контур, содержащий некоторую вершину и. Тогда и =Ф-+ и, так
как контур есть путь ненулевой длины. Бели и =П щ то суще-
существует дуга (петля), ведущая из и в щ т.е. и -> и. Но такой
петли в графе G быть не может, так как ни один элемент не
может доминировать над самим собой (отношение доминиро-
доминирования иррефлексивно).
Если же и =ФП г/, где п > 1, то существует вершина v,
отличная от и, такая, что и =^+ v и v =Ф-+ и, откуда, согласно
построению графа G, следует, что и < v и v < щ но это
невозможно. Итак, G — бесконтурный ориентированный граф,
т.е. сеть.
Входы сети G есть минимальные элементы исходного упо-
упорядоченного множества, а выходы — максимальные. Кроме
356 5. ТЕОРИЯ ГРАФОВ
того, каждый уровень сети образует антицепь в упорядочен-
упорядоченном множестве (А, ^).
Построенная сеть G будет обладать еще одним интересным
свойством: для любых трех попарно различных вершин u, v и
w из того, что и —> v и v -> гу, следует и -/> ги. Иначе говоря,
в сети G отсутствуют все „замыкающие дуги", подобные дуге
vi —> ^з для сети, изображенной на рис. 5.39. Такие сети будем
называть простыми.
{а,Ъ}
К
{а,Ь,с}
-о-
Рис. 5.39
Итак, каждому упорядоченному множеству может быть со-
сопоставлена простая сеть согласно описанной выше процедуре.
Эта простая сеть может рассматриваться как вариант нагляд-
наглядного изображения конечного упорядоченного множества и ис-
использоваться как диаграмма Хассе. На рис. 5.40 показана сеть,
сопоставленная множеству всех подмножеств трехэлементно-
трехэлементного множества {а, Ь, с}, упорядоченного отношением включения.
Полезно сравнить эту сеть с диаграммой Хассе, приведенной
на рис. 1.13.
5.9. Элементы цикломатики
При обсуждении алгоритма поиска в глубину в неориенти-
неориентированном графе рассматривался вопрос о поиске так называе-
называемых фундаментальных циклов графа. При этом под фундамен-
фундаментальным понимался цикл, содержащий в точности одно обрат-
обратное ребро, и между фундаментальными циклами и обратными
5.9. Элементы цикломатики 357
ребрами устанавливалось взаимно однозначное соответствие,
фундаментальные циклы возникают всякий раз, как только
фиксировано произвольное разбиение всех ребер неориентиро-
неориентированного графа на древесные (формирующие некоторый макси-
максимальный оспьовный лес исходного графа) и обратные, причем
в общем случае это разбиение может быть задано совершенно
независимо от алгоритма поиска в глубину. Поиск в глубину
есть лишь один из способов реализации такого разбиения.
Теперь рассмотрим вопрос о фундаментальных циклах не-
неориентированного графа с алгебраической точки зрения и по-
покажем, что фундаментальные циклы являются базисом неко-
некоторого линейного пространства, которое содержит все циклы
графа, а алгоритм поиска в глубину вычисляет один из бази-
базисов этого линейного пространства*. Алгебраическое изучение
циклов неориентированного графа важно, в частности, при ис-
исследовании проблемы распознавания изоморфизма двух графов.
Пусть с — некоторая цепь графа G. Через Е(с) обозначим
множество ребер этой цепи. Для любой цепи с множество ее
ребер Е(с) определяется однозначно. Обратно, если фиксиро-
фиксировано какое-то (конечное) множество ребер {ei,...,en} графа
G, то можно доказать следующий факт: если указанное вы-
выше множество ребер формирует цепь, т.е. существует такая
цепь (последовательность вершин графа) vo, i>i, ..., vn, что
{v0, vi} = eix, ..., {vn-ъ vn} = ein, где 1 < iu ..., in ^ n, то эта
цепь при условии, что она не является циклом, определяется
с точностью до порядка расположения ребер в последователь-
последовательности (от vq к vn или наоборот). Бели цепь является циклом,
то она определяется с точностью до порядка расположения ре-
ребер в последовательности и до выбора начальной вершины vo.
Так, на рис. 5.41 множество ребер {{vi,V2}, {*>2>*>з}> {^3,^5},
(V5,v6}} формирует цепь vi, ^2, V3, V5, ve, а также цепь ve,
V5» V3, V2> Щ („инверсия" предыдущей цепи). Множество ре-
* Отметим, что не любой базис может быть вычислен посредством
поиска в глубину (см. граф на рис. 5.23).
358
5. ТЕОРИЯ ГРАФОВ
V2 VA
Рис. 5.41
бер {{vuv2},{v2,V3},{v3,vi}} формирует цикл vu v2, v3,
вместе с ним циклы:
i, a
Множество же ребер {{vi, ^2}, {^2, v3}, {v3, V5}, {^4, vq}} не
формирует никакой цепи.
Тогда, говоря неформально, если не различать цепи, состо-
состоящие из одних и тех же ребер, но проходимые в противополож-
противоположных направлениях, и циклы, состоящие из одних и тех же ребер,
но проходимые в противоположных направлениях и от различ-
различных начальных вершин, можно отождествить цепи (и циклы)
с множествами их ребер. Эти соображения позволяют ввести
операцию сложения цепей как операцию над множествами их
ребер.
Для двух произвольных цепей а, Ь графа G их сумму опре-
определим (с учетом сделанного выше замечания) так:
т.е. сложение цепей сводится к вычислению симметрической
разности множеств их ребер.
Сумма цепей, вообще говоря, не является цепью, т.е. соот-
соответствующее множество ребер в общем случае не формирует
цепь. На рис. 5.41 сумма цепей vi, v3, V4, v^ и V2, v3, 174,
V5, t>6 не есть цепь. Алгебра, системой образующих которой
служит множество всех конечных цепей данного графа G, назы-
5.9. Элементы цикломатики 359
вают алгеброй цепей неориентированного графа G. Эта
алгебра является абелевой группой в силу известных свойств
операции симметрической разности множеств (см. 1 и 2).
Любая абелева группа G = (М, ф, 0) может быть рассмо-
рассмотрена как линейное пространство над полем Ъъ (полем вы-
вычетов по модулю 2). Действительно, определим умножение
элемента g группы на элементы поля Z2: 0-д = 0и1-д = д. Вы-
Выполнение аксиом линейного пространства в этом случае можно
легко проверить. Обратим внимание, что в любой линейной
п
комбинации J2 Afc-efc элементов ei, ..., е* такого линейного
пространства каждый коэффициент А* равен либо 0, либо 1.
Тогда понятно, что нетривиальная линейная комбинация эле-
элементов ei, ..., еп, т.е. линейная комбинация, не все коэффици-
коэффициенты которой равны 0, есть не что иное, как сумма элементов
непустого подмножества множества {ei,..., еп}.
Применив указанное построение к алгебре цепей неориенти-
неориентированного графа, получим линейное пространство цепей дан-
данного графа. Его называют пространством цепей графа.
Заметим, что в этом пространстве каждый элемент противо-
противоположен себе самому, так как для каждого элемента а этого
пространства а ф а = 0 (в силу известных свойств операции
симметрической разности).
Рассмотрим теперь линейное подпространство этого ли-
линейного пространства, порожденное множеством всех конеч-
конечных циклов данного графа. Это линейное пространство будем
называть пространством циклов данного графа.
Пространство циклов неориентированного графа есть тем
самым линейная оболочка в пространстве цепей данного графа
множества всех его конечных циклов (причем, как видно на
рис. 5.42, сумма циклов в общем случае не есть цикл). Бели
граф конечен, то его пространство циклов также конечно.
Теорема 5.6. Множество фундаментальных циклов, вы-
вычисляемое алгоритмом поиска в глубину в неориентированном
графе G, есть базис пространства циклов этого графа.
360
5. ТЕОРИЯ ГРАФОВ
Рис. 5.42
Ч Как следует из описания алгоритма поиска в глубину, ка-
каждый вычисляемый им фундаментальный цикл содержит в
точности одно обратное ребро и каждое обратное ребро при-
принадлежит в точности одному фундаментальному циклу. Таким
образом, каждый фундаментальный цикл содержит ребро, не
принадлежащее остальным циклам, и, следовательно, сумма
элементов любого непустого подмножества множества фунда-
фундаментальных циклов отлична от нуля, т.е. фундаментальные
циклы, вычисляемые алгоритмом поиска в глубину, являются
линейно независимыми.
Теперь докажем, что любой цикл графа G есть линейная
комбинация фундаментальных циклов.
Докажем сначала, что в пространстве циклов сумма любых
двух отличных друг от друга циклов есть либо замкнутая
цепь (в частности, цикл), либо непустое множество попарно
не пересекающихся (т.е. не имеющих один с другим ни общих
ребер, ни общих вершин) циклов4'.
Пусть С\ и (?2 — два цикла графа G. Если они не имеют ни
общих вершин, ни общих ребер, то доказываемое утверждение
*Это выражение есть, разумеется, вольность речи. Строго говоря,
сумму циклов нельзя назвать множеством циклов, но ей в данном случае
можно однозначно сопоставить такое множество. Так, на рис. 5.42 сумме
циклов соответствуют два непересекающихся между собой цикла.
5.9. Элементы цикломатики
361
тривиально. Предположим, что ребра
все ребра, общие для циклов С\ и C*i (рис. 5.43). В каждом из
рассматриваемых циклов для каждого % = 1,п—1 существуют
цепи, соединяющие вершины Ь{ и aj+i. Обозначим их W}
для первого и Wf для второго цикла. Также существуют
цепи, в первом цикле — И^ и во втором — Wq , соединяющие
вершины oi и Ьп. Все эти цепи таковы, что не содержат ни
одного из ребер е*, i = 1, п. Поскольку ребра е$, г = 1, п, —
все ребра, общие для циклов С\ и Сг, то для каждого i =
= 0, п—1 цепи И^1 и И^2 не имеют общих ребер и имеют две
общие вершины (см. рис. 5.43). Это значит, что каждая сумма
Wl © И7/2, i = 0, п—1, есть цикл (в пространстве цепей графа G).
Обозначим его щ.
Рис. 5.43
Докажем, что циклы щ попарно не пересекаются (т.е. не
имеют попарно ни общих вершин, ни общих ребер). Действи-
Действительно, цепи W} и Wj при гфз не могут иметь ни общих
вершин, ни общих ребер, так как вершины а\, Ъ\, а,2, &2) •••?
ап, Ъп — это, по построению, все вершины, общие для циклов
С\ и Сг. В то же время (для фиксированного s € {1,2}) никакие
две цепи W* и W? при i Ф j не могут иметь общих вершин и
362 5. ТЕОРИЯ ГРАФОВ
ребер, так как тогда циклы С\ или C*i не были бы простыми
цепями.
Итак, циклы щ попарно не пересекаются. Тогда
С\ © с2 = х0 е xi е... е xn_i,
причем в том и только в том случае, когда множество ребер
{ei,..., еп} формирует цепь, написанная выше сумма есть цикл.
Аналогично рассматривается случай, когда циклы С\ и Сг,
не имея общих ребер, имеют общие вершины: а\, аг, ..., ап
(рис. 5.44). Тогда, как можно видеть на рис. 5.44, сумма
С\ © Сг будет замкнутой цепью (которая в общем случае не
будет циклом).
Рис. 5.44
Пусть С — произвольный цикл графа, а Д, ..., /т — все
его обратные ребра, и пусть Fi, ..., Fm — фундаментальные
циклы, содержащие ребра /i, ..., /m соответственно.
Рассмотрим суммы (в пространстве циклов):
5.9. Элементы цикломатики 363
Как было доказано выше, каждая из этих сумм есть либо
замкнутая цепь, либо множество попарно не пересекающихся
циклов, причем сумма С», l^i^n-1, содержит обратные
ребра /i+i, ..., /m, и только их, так как при сложении С с F\
исчезает общее для них ребро /i, при сложении С\ с F2 — общее
для них ребро /2 и т.д. Следовательно, последняя из этих сумм
содержит единственное обратное ребро /т. Значит, сумма
Cm-i есть цикл. В самом деле, если бы она была непустым
множеством попарно не пересекающихся циклов, то содержала
бы по крайней мере два таких цикла. Поскольку в Ст-\ только
одно обратное ребро, то по крайней мере один из этих циклов
проходил бы только по древесным ребрам, что невозможно.
Аналогично, предполагая, что Cm_i есть замкнутая цепь,
не являющаяся циклом, получим (с учетом следствия 5.1), что
такая цепь представима в виде суммы по крайней мере двух
циклов, не имеющих общих ребер. Тогда один из этих циклов
содержит только древесные ребра, что невозможно.
Итак, сумма Ст-\ есть цикл, содержащий только одно
обратное ребро. В силу взаимно однозначного соответствия
между множеством обратных ребер и множеством фундамен-
фундаментальных циклов цикл Ст-\ совпадает с фундаментальным ци-
циклом Fm:
m-l — -мп?
ИЛИ
откуда (поскольку каждый элемент пространства циклов про-
противоположен сам себе)
Таким образом, произвольный цикл С представляется в виде
некоторой линейной комбинации фундаментальных циклов. >
Из доказанной теоремы следует, что число фундаменталь-
фундаментальных циклов, находимое алгоритмом поиска в глубину, разно
364 5. ТЕОРИЯ ГРАФОВ
размерности линейного пространства циклов и не зависит от
выбора начальной вершины, поскольку все базисы конечномер-
конечномерного линейного пространства состоят из одного и того же
числа векторов [IV]. Это число называют циклическим ран-
рангом неориентированного графа. Разность числа всех ребер
графа и его циклического ранга называется коциклическим
рангом неориентированного графа. Таким образом, цикличе-
циклический ранг неориентированного графа — это число обратных
ребер при поиске в глубину из любой вершины, а коцикличе-
ский ранг — число древесных ребер при поиске в глубину из
той же вершины.
Выведем формулу, связывающую циклический ранг v, число
ребер т, число вершин п и число компонент связности к
произвольного неориентированного графа G.
Обозначим через /i коциклический ранг графа G. Тогда,
поскольку в неориентированном дереве число ребер на единицу
меньше числа вершин, получим
v = m-(i = m- ((щ - 1) +... + {rik - 1)) = т-п + fc,
где щ — число вершин в г-й компоненте связности графа G.
Итак,
v = т — п + к.
Эта формула выражает циклический ранг неориентирован-
неориентированного графа через характеристики графа, не зависящие от спо-
способа поиска в глубину, и тем самым еще раз подтверждает
инвариантность циклического ранга относительно выбора на-
начальной вершины для поиска. Выбирая различные начальные
вершины в алгоритме поиска в глубину, мы получаем различ-
различные базисы пространства циклов.
Циклический ранг неориентированного графа показывает
„степень цикличности" этого графа: чем больше циклический
ранг, тем больше в графе циклов. Лес, в частности дерево,
имеет нулевой циклический ранг (нуль-мерное пространство
циклов).
5.9. Элементы цикломатики 365
Пример 5.16. Рассмотрим неориентированные графы,
изображенные на рис. 5.41. Предположим, что в списках смеж-
смежности вершины упорядочены по возрастанию номеров. На
рис. 5.41 показаны результаты поиска в глубину из двух разных
вершин: v\ в графе G\ и v± в графе G2- Древесные ребра в гра-
графах выделены. По результатам поиска циклический ранг равен
4, а коциклический ранг — 5. В графе G\ фундаментальными
являются циклы*
С2:
С3:
Циклы пронумерованы в порядке обнаружения.
Для графа G*i фундаментальными будут циклы
Разложение одного и того же цикла С
по двум указанным базисам будет следующим (рис. 5.45):
#
Можно доказать, что изоморфные неориентированные гра-
графы имеют изоморфные линейные пространства циклов, однако
'Записывая циклы (которые, по определению, есть последовательности
вершин), мы .ради наглядности пишем между вершинами значок »—• непо-
непосредственной достижимости.
366
5. ТЕОРИЯ ГРАФОВ
Рис. 5.45
обратное в общем случае неверно. Более того, в изоморфных
графах должны совпадать „тонкие" структуры циклов: любое
утверждение о циклах, истинное в одном графе, останется ис-
истинным в изоморфном ему графе.
Таким образом, анализ циклов может быть использован для
доказательства неизоморфности графов.
Пример 5.17. Рассмотрим графы, представленные на
рис. 5.46. Заметим, что у этих графов одинаковое количе-
количество вершин и ребер, а также одинаковые степени всех вершин.
Поэтому гипотеза об их изоморфности представляется прав-
правдоподобной. Однако для доказательства изоморфизма графов
необходимо явно указать биекцию множества вершин одного
графа на множество вершин второго, при которой сохраняется
отношение смежности. Поиск такой биекции весьма трудоемок,
так как может потребовать полного перебора всех возможных
вариантов. Для доказательства неизоморфности достаточно
показать принципиальную невозможность установления требу-
требуемой биекции. Используем для этого анализ циклов.
Проведем поиск в глубину в каждом из графов. Бели коли-
количество обратных ребер окажется различным, неизоморфность
5.9. Элементы цикломатики
367
ю
Рис. 5.46
графов будет доказана. Для определенности в каждом из гра-
графов начнем поиск с вершины v\ и будем считать, что списки
смежности каждой вершины упорядочены по возрастанию но-
номеров вершин. На рис. 5.46 в графах выделены древесные
ребра, полученные при поиске в глубину. В каждом из графов
оказалось по шесть обратных ребер, и, следовательно, вывод о
неизоморфности сделать нельзя.
Различие можно увидеть в „тонких" стуктурах циклов.
Заметим, что в графе G\ имеются четыре цикла длины 3:
В графе Сг2 таких циклов также четыре:
Однако количество циклов длины 4 в графах различно. В
графе G\ таких циклов шесть:
V2 ьн V4
Vi •—i V2 »-н V5 ы V3 ьн Vi,
Vg нн v-r ы V8 »-H vio ьн V9,
368 5. ТЕОРИЯ ГРАФОВ
а в графе 6г2 — всего два:
V\ ьн Vs »-i V2 ы V4 и Vi,
Следовательно, графы неизоморфны. #
Итак, исследование структуры циклов неориентированного
графа как инварианта, сохраняющегося при изоморфизмах,
позволяет в некоторых случаях быстро находить ответ на
вопрос об изоморфности двух заданных графов.
Заметим, что в общем случае все циклы графа можно по-
получить, рассматривая различные линейные комбинации над 7*2
фундаментальных циклов. При этом следует учесть, что ре-
результатом сложения может быть множество ребер, образующих
несколько непересекающихся циклов.
Вопросы и задачи
5.1. Сколько существует неориентированных графов с п
вершинами?
5.2. Доказать, что сумма степеней всех вершин неориенти-
неориентированного графа равна удвоенному числу ребер (это утвержде-
утверждение известно под названием „леммы о рукопожатиях").
5.3. Доказать, что если число ребер неориентированного
графа с п вершинами при п > 2 больше С\_ъ то он связный.
5.4. Доказать, что не существует неориентированного гра-
графа, степени всех вершин которого попарно различны.
5.5. Найти все попарно неизоморфные неориентированные
графы с четырьмя вершинами и тремя ребрами.
5.6. Установить, какие из изображенных на рис. 5.47 графов
изоморфны, а какие — нет.
5.7. Привести пример неориентированного графа с четырь-
четырьмя вершинами, изоморфного своему дополнению (самодополни-
(самодополнительного). Доказать, что число вершин любого самодополни-
самодополнительного неориентированного графа равно 4Л или 4к +1.
Вопросы и задачи
369
Рис. 5.47
5.8. Найти группы автоморфизмов графов, изображенных
на рис. 5.48.
Рис. 5.48
5.9. Пусть симметрическая матрица А порядка п, в ка-
каждой строке которой находится одинаковое нечетное число
t ненулевых элементов, является матрицей смежности неори-
неориентированного графа. Показать, что число вершин графа п
четное. (Учесть, что ац = 0.)
5*10. Доказать, что отношение взаимной достижимости в
ориентированном графе есть эквивалентность.
5.11. Установить, является ли ориентированный граф, изо-
изображенный на рис. 5.49, связным. Найти все его компоненты и
бикомпоненты.
370
5. ТЕОРИЯ ГРАФОВ
Рис. 5.50
5.12. Конденсация ориентированного графа G = (F, Е) есть
ориентированный граф G' = (F/p, 25'), где р — отношение
взаимной достижимости (см. задачу 5.10), а для любых и1,
(t/, v1) еЕ'<& (Зи е и'), Cv е г/), (it, v) е Е.
Доказать, что G — бесконтурный граф тогда и только тогда,
когда G изоморфен своей конденсации G'.
5.13. Найти все ориентированные графы с двумя верши-
вершинами, являющиеся гомоморфными образами ориентированного
графа, изображенного на рис. 5.50.
5.14. Установить, является ли конденсация ориентирован-
ориентированного графа (см. задачу 5.12) его гомоморфным образом. По-
Построить примеры.
Указание: выяснить, может ли конденсация ориентиро-
ориентированного графа содержать петли.
5.15. Доказать, что ориентированный граф связный тогда
и только тогда, когда в нем есть путь, проходящий через все
вершины. Останется ли это утверждение справедливым, если
потребовать, чтобы существовал простой путь?
5.16. Пусть /: V -» V — биекция множества вершин ориен-
ориентированного графа G = (V, Е) в себя. Сопоставим ей матрицу
S с элементами
= /(*);
иначе.
я I1' j
Вопросы и задачи 371
Доказать:
а) S~l = ST (т.е. 5 — ортогональная матрица);
б) если / — автоморфизм графа G, то матрица смежности
В1 автоморфного образа f(G) есть В' = STBS.
5.17. Доказать, что если неориентированный граф fc-pery-
лярный, т.е. степени всех его вершин одинаковы и равны /с, то
число к есть собственное число матрицы смежности графа.
т
Указание: доказать, что вектор ж = A, 1, ..., 1) раз-
размерности n = \V| есть собственный вектор матрицы смежности
fc-регулярного графа G.
5.18. Написать алгоритм нахождения множества предше-
предшественников F"(v) для каждой вершины графа по спискам
смежности. Оценить сложность алгоритма.
5.19. Что является компонентами связности в ориентиро-
ориентированном дереве?
5.20. Найти остовное дерево наименьшего веса для неори-
неориентированного графа с десятью вершинами, заданного следую-
следующим сциском ребер с метками (вершина, вершина, метка):
(«ь *>2, 1),
5), (г
», 5),
,4),
(, 5),
'8, V9
(«2, 1
(«6, *
(«3, «4
, И), 1
»7, 8),
'7, 6),
b4),
[vg, wi
(t>3, V
(«8, «i
(w4, V5
o, 8),
7,7),
r, 12),
,8),
(^10,'
(«3, V,
(W9, '
(«5, «6
vi, 7),
5,3),
;7, 9).
,3),
5.21. Найти условия, необходимые и достаточные для един-
единственности остовного дерева наименьшего веса.
5.22. Доказать, что сеть является простой, если любой
подграф, порожденный множеством всех вершин, достижимых
из некоторого корня, является деревом. Верно ли обратное?
372
5. ТЕОРИЯ ГРАФОВ
5.23* Используя алгоритм Демукрона, найти порядковую
функцию сети, заданной следующими матрицами смежности:
а)
0
1
1
0
0
0
0
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
и
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
1
0
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
/0
1
0
0
0
1
0
^о
0
0
0
0
0
0
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
1
0
1
о)
5.24* Составить подробное описание алгоритма вычисления
порядковой функции сети, который в случае, если входной граф
есть сеть, работает как алгоритм Демукрона, если же иначе,
то сообщает о наличии в графе контуров и останавливается.
5.25. Эйлеровым циклом в неориентированном графе
называется цикл, в котором каждое ребро графа проходится
ровно один раз. Доказать, что связный неориентированный
граф имеет эйлеров цикл тогда и только тогда, когда степень
каждой его вершины четная.
5.26. Доказать, что ориентированный граф не содержит
контуров тогда и только тогда, когда при поиске в глубину
из некоторой вершины (независимо от ее выбора) множество
обратных дуг пусто.
5.27. Доказать, что в связном ориентированном графе най-
найдется вершина, при поиске в глубину из которой глубинный
остовный лес является деревом. Верно ли обратное?
Указание: используйте результат задачи 5.15.
5.28. Найти все возможные глубинные остовные леса, полу-
получающиеся при поиске из вершины v\\
Вопросы и задачи 373
а) для неориентированного графа с 10 вершинами и множе-
множеством ребер
б) для ориентированного графа с 10 вершинами и множе-
множеством дуг
(O5, V6), (l77, V6), (V7, Vb), (V7, V8), (V8, Vg), (v
Указание: рассмотреть различные порядки расположе-
расположения вершин в списках смежности.
5.29* Выполнить поиск в глубину для неориентированных
графов, изображенных на рис. 5.47, из различных стартовых
вершин.
5*30* Выполнить поиск в ширину из вершины v2 для ориен-
ориентированного графа из задачи 5.28.
5.31. Выполнить поиск в ширину из вершины v$ для ориен-
ориентированного графа, изображенного на рис. 5.38. После оста-
остановки алгоритма продолжить поиск из вершины v8. Сравнить
стоимости прохождения со значениями порядковой функции се-
сети, приведенными на рисунке.
5.32. Для ориентированных графов, заданных множеством
дуг с указанием меток (вершина, вершина, метка), решить
задачу транзитивного замыкания (в полукольце В) и задачу
вычисления кратчайших расстояний (в полукольце if1"):
а) («ь v2, 8), («1, vi, 2), (г>1, v3, 5), (v2, vu 3), (v3, v2, 2);
б) («1, г;2, 2), (t7i, v4, 10), (г>2, v3, 3), A73, u5, 4), (v5, v4, 5),
(v2, v4, 7), (v4, v3, 6);
в) (vi, «2, 10), (t7i, u4, 5), («2, vi, 6); («2, v3, 7), (v2, v4, 2),
(^2, v5, 9), (v3, v3, 8), (v3, v4, 10), (v4, v3, 5), (v4, v5, 4), (v4, i;2, 7),
(v5, vb 8), (v5, v3, 4);
374
5. ТЕОРИЯ ГРАФОВ
г) («ь «2, 2), («1, «з, 3), («2, W3, 6), («з, V2, 5), («2, «4, 6),
(«3, «5, 2), («4) «5, 3), («5, «4, 4), («6, W4, I), (W7, «5, 5), («6, «7, 4),
(«7, «2, 6);
Д) («Ь «2, 1), («2, «з, 3), («з, V4, 4), (V5, «4, 5), (V5, «6, 1),
(V6, «i, 1), (Wb «7, 2), (v2, V7, 1), («4, «7, 1), (W7, «3, 2), (w7) «5, 1),
(u7, u6, 1);
5.33. Ориентированный граф задан матрицей смежности,
содержащей метки соответствующих ребер:
ГО
0
0
0
7
0
-2
-4
-7
8
8
0
-3
-6
9
9
9
0
—о
10>
10
10
10
0)
Решить задачу о кратчайших путях для данного ориентиро-
ориентированного графа, обратив внимание на то, что метки некоторых
дуг равны 0 или отрицательны. Выяснить, применим ли здесь
алгоритм Флойда — Уоршела — Клини.
Можно ли изменить метки дуг таким образом, чтобы алго-
алгоритм Флойда — Уоршела — Клини стал неприменимым?
5.34. Установить, можно ли использовать алгоритм Флой-
Флойда — Уоршела — Клини для вычисления стоимости путей
наибольшей длины во взвешенном графе. Сформулировать
ограничение на граф, при котором такое использование воз-
возможно.
6. БУЛЕВЫ ФУНКЦИИ
6.1. Понятие булевой функции.
Булев куб
В дискретной математике большую роль играют конечные
функции. Конечной функцией называют отображение од-
одного конечного множества в другое. Важный класс таких
функций образуют булевы функции.
Булева функция (от п переменных) — это произвольное
отображение вида
/:{0,1}п->{0,1}, F.1)
т.е. булева функция определена на множестве всех п-элемент-
ных (при п ^ 0) последовательностей (или п-компонентных
кортежей) нулей и единиц и принимает два возможных зна-
значения: 0 и 1.
С понятием булевой функции тесно связаны понятия булевой
константы и булева переменного*.
Булева константа — это индивидная константа с обла-
областью значений {0,1}. Таким образом, существуют две булевы
константы: 0 и 1. По определению принимается, что каждая
булева константа есть также булева функция от 0 переменных
(что вполне аналогично определению нульарной операции).
Булево переменное — это индивидное переменное с обла-
областью значений {0,1}, т.е. это переменное, которое может при-
принимать только два значения: 0 и 1 (подобно тому, как действи-
действительное переменное принимает произвольное действительное
*В литературе по теории булевых функции традиционно употребляется
термин „булева переменная" (в женском роде). Но так как в данном
комплексе учебников принят термин „переменное" (среднего рода), мы
пишем везде „булево переменное".
376 6. БУЛЕВЫ ФУНКЦИИ
значение, а комплексное переменное — произвольное комплекс-
комплексное значение). Тогда с использованием понятия булева пере-
переменного мы можем задать булеву функцию F.1) записью у =
= /(#ъ... ,#п), в которой каждое булево переменное ж», г = 1,п,
и функция / принимают два возможных значения: 0 и 1. Пере-
Переменные #i, ..., хп называют при этом переменными булевой
функции /. Фиксируя значение а* € {0,1} каждого переменно-
переменного ж», получаем кортеж 5 = (o?i, ..., ап) из множества {0,1}п,
называемый набором значений переменных х\, ..., хп, и
соответствующее ему значение функции /(ai,...,an), которое
будет значением переменного у, сопоставленным заданным зна-
значениям переменных xi, ..., хп.
Подчеркнем, что, если специально не оговорено противное,
в выражении у =/(xi,...,xn) все переменные предполагаются
попарно различными, т.е. пробегающими каждое независимо
от других множество {0,1}.
Понятию булевой функции можно придать иной смысл, по-
понимая элементы множества {0,1} как истинностные значения,
а именно понимая единицу как „истину", а нуль как „ложь".
Такие истинностные значения могут быть, как мы знаем, сопо-
сопоставлены каждому высказыванию. Тогда булева функция есть
некоторое правило, позволяющее каждому фиксированному на-
набору истинностных значений, т.е. набору значений булевых
переменных, сопоставить то или иное истинностное значение.
Так может быть вычислено, например, истинностное значение
сложного высказывания, составленного по определенным пра-
правилам из простых высказываний. Подобного рода сложные
высказывания составляются с помощью логических операций:
„или", „и", „если ..., то ..." и т.п. Указанная логическая ин-
интерпретация булевой функции позволяет понять, почему булево
переменное часто называют логическим переменным*, а буле-
булеву функцию — логической функцией (или функцией алгебры
логики).
"Традиционный термин: „логическая переменная".
6.1. Понятие булевой функции. Булев куб 377
Кроме того, согласно определению, булева функция от п пе-
переменных есть отображение n-й декартовой степени множества
{0,1} в множество {0,1}, т.е. не что иное, как п-арная опера-
операция на множестве {0,1}. Тем самым логическая интерпретация
булевой функции согласуется с ее алгебраической интерпрета-
интерпретацией: булева функция есть операция (в алгебраическом смысле
этого слова) на множестве истинностных значений. Тогда
и понятие логической операции, которое было введено ранее
(см. 1.1), оказывается частным случаем общего понятия опера-
операции (см. 2.1).
Будем обозначать через 7*2 множество всех булевых функ-
функций (для всех возможных значений п числа переменных), а
через V*i,n — множество всех булевых функций от п переменных
(для фиксированного п).
Из определения следует, что
Итак, областью определения любой булевой функции от п
переменных является множество {0,1}п, т.е. булев куб? размер-
размерности п. Элементы булева куба {0,1}п называют п-мерными
булевыми векторами (или наборами). Число всех элементов бу-
булева куба {0,1}п составляет 2п. Элементы булева куба будем
также называть его вершинами.
Булев куб {0,1}п является носителем булевой алгебры Вп
(это же обозначение часто будем использовать и для соответ-
соответствующего булева куба). Но в любой булевой алгебре Л =
= (А, V, Л, 0, 1) определяется, как известно, естественное от-
отношение порядка ^ так, что для произвольных а, Ь Е А соотно-
соотношение а ^ Ь выполняется тогда и только тогда, когда о V Ъ = Ь
(или, что равносильно, аЛЬ = а). Напомним (см. 3.4), что буле-
булева алгебра Вп является не чем иным, как n-й декартовой сте-
степенью двухэлементной булевой алгебры В = ({0,1}, V, Л, 0, 1).
* Употребляются также термины: единичный куб размерности п,
п-мерный единичный куб\ вместо слова „куб" говорят также „гиперкуб".
378 6. БУЛЕВЫ ФУНКЦИИ
Согласно общему принципу распространения отношения поряд-
порядка на декартово произведение множеств (см. 4.5), для произ-
произвольных двух наборов а = (ai, ..., ап) и C = (/?i, ..., /Зп) из Вп
имеет место 5^/3 тогда и только тогда, когда а% < /% для ка-
каждого г = 1,п, т.е. щ\/fii= fa.
Другими словами, a ^ /? тогда и только тогда, когда а» = /%
или а{ = 0, a ft = l для каждого i = 1,га. Бели существует
хотя бы одно 1, для которого выполняется ai = О, /% = 1, то
имеет место строгое неравенство a < /3. В частности, если
существует ровно одно такое t, то набор /8 доминирует над
набором 5, так как ясно, что в этом случае нельзя найти такой
набор 7, что a < 7 < Р-
Пример 6Л. В булевом кубе В4
@, 0, 1, 1) < A, 0, 1, 1) < A, 1, 1, 1),
причем второй из этих наборов доминирует над первым, а тре-
третий — над вторым (но, естественно, третий уже не доминирует
над первым, а лишь строго больше его). Наборы же @, 1, 0, 1)
и A, 0, 1, 1) — несравнимые элементы, так как первая ком-
компонента второго набора больше первой компоненты первого
набора, но зато вторая компонента первого набора больше
второй компоненты второго набора. Подчеркнем также, что
описанное сравнение наборов возможно только для фиксиро-
фиксированной размерности и никак нельзя сравнивать наборы разных
размерностей. #
Рассмотренное отношение порядка на Вп будем называть
булевым порядком.
Булев куб как упорядоченное множество, можно изобра-
изобразить в виде диаграммы Хассе. На рис. 6.1 приведены диаграм-
диаграммы Хассе для булевых кубов размерностей от 0 до 4.
Другой способ наглядного изображения булева куба основан
на том, что диаграмма Хассе любого конечного упорядоченно-
упорядоченного множества А может быть задана в виде ориентированной
сети, так что дуга из вершины, сопоставленной элементу х€А,
6.1. Понятие булевой функции. Булев куб
379
11
111
0000
Рис. 6.1
ведет в вершину, сопоставленную элементу у G А, тогда и толь-
только тогда, когда у доминирует над х и каждый уровень сети
состоит из вершин, сопоставленных попарно несравнимым эле-
элементам множества А (т.е. элементам некоторой антицепи в А).
Входы сети сопоставлены минимальным, а выходы — макси-
максимальным элементам А.
Каждый уровень представляющей булев куб Вп сети состоит
из всех вершин, соответствующих наборам, у которых ровно
к @ < к < п) компонент отличны от нуля (множество всех
таких наборов для фиксированного к называют к-слоем булева
куба Вп).
380
6. БУЛЕВЫ ФУНКЦИИ
Сеть, служащую изображением булева куба размерности п,
будем называть булевой п-сетъю или просто булевой се-
тъю, если упоминание о размерности опускается. Так как
булев куб имеет наименьший элемент — нулевой набор и наи-
наибольший элемент — единичный набор, то каждая булева сеть
имеет единственный вход (помеченный нулевым набором) и
единственный выход (помеченный единичным набором).
На рис. 6.2 приведено изображение булева куба В4 в виде
сети.
Помимо булева порядка полезно также ввести на булевом
кубе другое отношение порядка, которое мы будем называть
лексикографическим порядком, используя обозначение :<.
Пусть 5, /3 Е Вп (для произвольного фиксированного п). По
определению, 5 :< /?, если
F.2)
1=1
г=1
6.1. Понятие булевой функции. Булев куб 381
Каждая из сумм в неравенстве F.2) есть не что иное, как пред-
представление некоторого натурального числа (включая и нуль) в
двоичной системе счисления (при числе разрядов, равных фик-
фиксированной размерности п). На каждый булев вектор можно
смотреть как на такое представление (двоичный код) натураль-
натурального числа, и лексикографический порядок на булевом кубе Вп
есть не что иное, как естественный числовой порядок на под-
подмножестве {0,1,..., 2й*} множества NU {0} (при условии, что
числа заданы в двоичной системе счисления)*.
Заметим, что отношение лексикографического порядка яв-
является, в отличие от булева порядка, отношением линейного
порядка.
Пример 6.2. Набор A, 0, 1) как двоичный код числа 5 =
= 1 • 22 + 0 • 21 +1 • 2° лексикографически больше набора @, 1, 1),
служащего двоичным кодом числа 3, но при этом указанные
наборы не сравнимы по отношению булева порядка. #
Однако лексикографический порядок при изучении булевых
кубов играет вспомогательную роль. В частности, при изобра-
изображении булевых кубов (в виде диаграмм Хассе или в виде сети)
принято располагать вершины каждого fc-слоя в лексикографи-
лексикографическом порядке (по возрастанию — слева направо или сверху
вниз). Везде в дальнейшем, рассуждая о булевом кубе как об
упорядоченном множестве, мы имеем в виду булев порядок.
Гранью булева куба размерности п — fc, где п — размер-
размерность булева куба, называют множество наборов, имеющих не
менее к одинаковых компонент.
Грань размерности п — к вШп будет определена, если фик-
фиксировать к номеров 1 ^ i\ ^ ... ^ г* ^ п и к констант а\у ..., а*
из множества {0,1}. Тогда грань, обозначаемая как В^-,*** >
есть множество всех таких a Е Вп, что а^ = <ji, ..., aik = а*.
При этом кортеж номеров (п, ..., г&) называют направление
* Более строго: упорядоченное множество (Вп, •<) изоморфно подмно-
подмножеству {0,1,..., 2П~} С N(J {0} с естественным числовым порядком.
382 6. БУЛЕВЫ ФУНКЦИИ
ем грани В?!*1..'.",'*** • Если число п — А;, определяющее размер-
размерность грани, равно 1 (т.е. к = п — 1), то такую грань называют
ребром булева куба Вп. Таким образом, ребро — это множе-
множество, состоящее из двух наборов, один из которых доминирует
над другим (в смысле булева порядка). Другими словами, эти
два набора отличаются друг от друга значением единственной
компоненты. Для ребра булева куба будем использовать обозна-
обозначение [а, /3], полагая, что второй набор доминирует над первым.
Любая вершина булева куба считается гранью размерности 0.
Можно показать, что число всех граней размерности п — к
составляет 2к • С*.
Пример 6.3. В четырехмерном булевом кубе В4 напра-
направление трехмерной грани задается фиксированием одного из
номеров от 1 до 4 и фиксированием значения соответству-
соответствующей компоненты наборов, принадлежащих этой грани. На
рис. 6.1 выделены ребра грани Bq'1. Эта грань состоит из вось-
восьми наборов:
@,0,0,0), @,0,0,1), @,0,1,0), @,0,1,1),
@,1,0,0), @,1,0,1), @,1,1,0), @,1,1,1).
На рис. 6.1 выделены все ребра булева куба В3, имеющие
направление A, 2). #
Грани булева куба, имеющие одно и то же направление, на-
называют параллельными. Две параллельные грани В??.\',а?* и
Щи»'Якк называют соседними, если один из наборов («п,...
и Gi, ..., 7*) доминирует над другим. На рис. 6.1 грани о
и В*'1 соседние, равно как и грани (ребра) B0'J' и Вдд'2. Но
ребра B^'J'2 и Bq'J'2 не являются соседними.
Нетрудно догадаться, что каждая грань размерности п — к
булева куба Вп сама является булевым кубом размерности п — к
и содержит, следовательно, 2п~~к вершин. Точнее говоря, эта
грань вместе с отношением порядка, индуцированным булевым
6.2. Таблицы булевых функции 383
порядком на Вп, будет упорядоченным множеством, изоморф-
изоморфным булеву кубу Шп~к (с булевым порядком на нем). Поэтому
часто грани булева куба называют его подкубами.
В то же время булев куб Вп изоморфно вкладывается (не-
(несколькими способами) в булев куб большей размерности, а
именно булев куб Вп вкладывается (как грань) в булев куб Вп+*,
к ^ 1, столькими способами, сколько существует разных п-мер-
ных граней в кубе размерности п + к, т.е. 2к • Ск+к способами.
Так, одномерный куб В вкладывается в двумерный В2 четырь-
четырьмя способами — как одна из его четырех одномерных граней
(т.е. как одно из его четырех ребер, см. рис. 6.1).
Договоримся впредь записывать конкретные наборы (эле-
(элементы булева куба соответствующей размерности) без скобок
и запятых, т.е. будем писать не @, 1, 0, 1), а 0101 (если, конеч-
конечно, это не ведет к недоразумениям).
В заключение найдем мощность множества всех булевых
функций от п переменных для фиксированного п. Поскольку
каждая булева функция отображает множество из 2п элементов
в двухэлементное множество, а мощность множества всех ото-
отображений из п-элементного множества в m-элементное равна,
как известно, тп, то мощность множества V*i,n равна 22П. В
частности, при п = 0 получаем две булевы константы: 0 и 1.
Замечание 6.1. Поскольку булева функция от п перемен-
переменных является в то же время и n-арной операцией на множестве
{0,1}, то при п = 0 получаем нульарную операцию. Ясно, что на
множестве {0,1} существуют две нульарные операции: 0 и 1,
которые есть не что иное, как нуль и единица двухэлементной
булевой алгебры.
6.2. Таблицы булевых функций
Булева функция от п переменных может быть задана таб-
таблицей, состоящей из двух столбцов и 2П строк. В первом
столбце перечисляются все наборы из В71 в лексикографиче-
384
б. БУЛЕВЫ ФУНКЦИИ
ском порядке, а во втором — значения функции на наборах.
Форма таблицы произвольной булевой функции приведена ни-
ниже (табл. 6.1).
0.
1.
..хп
..0
••«Jb,n)
"i
Таблица
f(xu..
/(о,..
накл::.
.,0)
)
В (к + 1)-й строке таблицы расположен набор
являющийся двоичным кодом числа к (при 0 < к < 2п — 1).
Рассмотрим некоторые примеры булевых функций, которые
будем задавать посредством таблиц.
При п = 1 имеем четыре булевы функции (табл. 6.2).
Таблица 6.2
X
0
1
Л(*)
0
1
/2(*)
0
0
/з(х)
1
1
h{x)
1
0
Функцию /i называют тождественной функцией, а
функцию /4 — отрицанием. Функции /2 и /з являются функ-
функциями (от одного переменного), принимающими постоянное
значение @ и 1 соответственно). Их также зачастую называют
константой 0 и константой 1. Постоянные функции, разуме-
разумеется, могут быть определены и при любом (большем 1) числе
переменных.
В табл. 6.3 указаны семь (из 22 = 16) наиболее важных для
дальнейшего изложения булевых функций от двух переменных.
6.2. Таблицы булевых функций
385
Таблица 6.3
XI
0
0
1
1
х2
0
1
0
1
Л
0
1
1
1
/2
0
0
0
1
/з
0
1
1
0
/4
1
1
0
1
/б
1
0
0
1
/б
1
1
1
0
/7
1
0
0
0
Поскольку каждая булева функция от двух переменных есть
одновременно и бинарная операция на множестве {0,1}, то
естественно для таких функций использовать запись, принятую
для бинарных операций: хшу вместо ш(х,у).
Для функций, записанных в табл. 6.3, принимаются следую-
следующие обозначения:
= a?i -X2 (или
=#1
Функцию /i называют дизъюнкцией, /г — конъюнкци-
конъюнкцией» /з — сложением по модулю 2 (mod 2), /4 — имплика-
импликацией] Д — эквивалентностью, /в — штрихом Шеффера,
/7 — стрелкой Пирса.
Дизъюнкция и конъюнкция, как видно, — это операции
двухэлементной булевой алгебры — объединение и пересече-
пересечение соответственно (тогда как функция отрицания есть не что
иное, как дополнение в этой булевой алгебре). В то же время
дизъюнкция и конъюнкция — это не что иное, как одноименные
логические операции, введенные в 1.1 (в свете логической ин-
интерпретации булевой функции, см. 6.1). Очевидным образом
с логическими связками, помимо отрицания, соотносятся им-
импликация и эквивалентность (хотя их обозначения как булевых
386
6. БУЛЕВЫ ФУНКЦИИ
функций несколько отличаются от введенных в 1.1). Таблицы
для введенных булевых функций являются тогда не чем иным,
как формой представления таблиц истинности.
Далее, можно заметить, что сложение по модулю 2 совпа-
совпадает с операцией сложения кольца вычетов Ъг по модулю 2,
штрих Шеффера есть отрицание конъюнкции, а стрелка Пир-
Пирса — отрицание дизъюнкции, т.е.
Х\ | Х2 = Х\ •
Приведем для примера таблицу булевой функции от трех
переменных (табл. 6.4).
Таблица 6.4
0
1
2
3
4
5
6
7
Хх
0
0
0
0
1
1
1
1
х2
0
0
1
1
0
0
1
1
хз
0
1
0
1
0
1
0
1
f(xUX2,X3)
0
0
0
1
0
1
1
1
Эта функция называется мажоритарной функцией или
функцией голосования. Заметим, что в первом столбце
табл. 6.4 для каждого набора из {О, I}3 указан его номер, т.е.
число, двоичным кодом которого служит данный набор.
Теоретически таблицей можно задать любую булеву функ-
функцию, но при большом числе переменных этот способ практи-
практически не применим. Далее (см. 6.4) мы рассмотрим способ
задания булевых функций в виде формул, аналогичный анали-
аналитическому заданию элементарных функций в анализе [I]. С
точки зрения логической интерпретации булевой функции ее
6.2. Таблицы булевых функции 387
таблица есть таблица истинности некоторого сложного выска-
высказывания. Переменными функции являются входящие в сложное
высказывание простые высказывания.
Кроме того, полезно иметь в виду, что, записывая таблицу
булевой функции от п переменных, нет необходимости каждый
раз перечислять все наборы длины п — достаточно записать
вектор значений булевой функции, понимая, что г-я ком-
компонента этого вектора есть значение функции на г-м наборе
(двоичном коде числа г).
Тогда мажоритарная функция / может быть задана так:
/ = @,0,0,1,0,1,1,1).
Можно также перечислить номера тех наборов, на которых
функция принимает значение 1:
/ = {3,5,6,7}.
Обобщением понятия булевой функции служит понятие бу-
булева оператора. Булев оператор — это произвольное ото-
отображение вида
/:Bn->Bw F.3)
для произвольных щтЕ NU {0}.
Булев оператор F.3) может быть задан посредством семей-
семейства булевых функций в виде
F.4)
Функции fi в F.4) будем называть координатными функци-
функциями булева оператора F.3). Бели ввести векторы перемен-
переменных у = (j/i, ..., ут) и х = (а?ь ..., жп), то булев оператор F.3),
заданный семейством координатных функций F.4), можно за-
записать в таком виде:
У = /(*). F.5)
388 б. БУЛЕВЫ ФУНКЦИИ
6.3. Фиктивные переменные.
Равенство булевых функций
Ключевым понятием в теории булевых функций является по-
понятие равных булевых функций. Для функций от одного и того
же числа переменных п нет необходимости рассматривать ка-
какое-то специальное определение равенства, ибо такие функции
равны, если они совпадают как отображения булева куба Вп в
В. Проблема состоит в том, чтобы определить равенство буле-
булевых функций независимо от числа переменных.
Пример 6.4. Рассмотрим булевы функции f(x,y) — xWyn
д(х, у, z)=xzVxzVyzV yz.
Можно заметить, используя тождества булевой алгебры,
что
а поскольку z V z = 1, то
s(s,2/,z) = (я V у) = /(ж,у),
и функции / и д естественно рассматривать как равные, несмо-
несмотря на то что они зависят от разного числа переменных. #
В примере 6.4 функция д определена как функция от трех
переменных, но значение переменного z не влияет на значение
функции. Обобщая ситуацию примера, можно ввести понятие
фиктивного переменного булевой функции.
Определение 6.1. Переменное ж* называют фиктив-
фиктивным переменным булевой функции /(si,...,xn), если значе-
значение функции не зависит от значения этого переменного, т.е.
если для любых значений переменных х\, ..., Жг-ъ x%+\i ••> хп
Будем называть переменное х, не являющееся фиктивным
переменным функции /, существенным переменным дан-
данной функции и говорить, что функция / существенно зависит
от переменного х.
6.3. Фиктивные переменные. Равенство булевых функции 389
Пусть дана булева функция у = /(ж1,...,жп) от п перемен-
переменных. Пусть существенными переменными этой функции явля-
являются переменные tf»x, ..., ж*г, где г^пи 1 < *i < ... < tr < п.
Присваивая каждому фиктивному переменному функции / про-
произвольное значение, получим функцию /, такую, что она есть
функция от г переменных, т.е. есть отображение из Вг в В, и
для любого набора ctix, ..., а»г значений переменных Xix, ..., Х{г
имеет место равенство
независимо от значений фиктивных переменных функции /
(т.е. переменных, отличных от ж^, ..., Xir). Тем самым функ-
функция / оказывается уже функцией, определенной на некоторой
r-мерной грани булева куба Вп.
Договоримся только что описанный переход от функции / к
функции /, уже не имеющей фиктивных переменных, называть
удалением фиктивных переменных (функции /).
Замечание 6.2. В качестве упомянутой выше г-мерной
грани может быть взята любая грань с направлением, заданным
номерами фиктивных переменных. Фиксация грани означает
фиксацию конкретного набора значений фиктивных перемен-
переменных. Тогда соответствующая этой грани функция / получается
из исходной функции / в результате подстановки вместо ка-
каждого фиктивного переменного того конкретного значения,
которое задано указанным выше набором.
Вернемся к примеру 6.4. Удаляя фиктивное переменное г,
вместо функции д получим либо функцию ff(#,j/,0), которая
определена на (двумерной) грани Вд'3 булева куба В3, либо
функцию 0(ж,у,1), определенную на грани В3'3. Направлением
каждой из этих граней будет однокомпонентный кортеж C),
определенный номером фиктивного переменного z. #
С использованием понятий фиктивного и существенного пе-
переменного можно дать следующее определение равных булевых
функций.
390 б. БУЛЕВЫ ФУНКЦИИ
Определение 6.2. Булевы функции /ид называют рав-
равными, если их существенные переменные соответственно рав-
равны и на каждом наборе значений этих переменных функции /
и д принимают равные значения.
Чтобы распознать по таблице булевой функции, является
ли переменное Х{ фиктивным, нужно рассмотреть все наборы с
фиксированным значением г-й компоненты (один раз фиксиро-
фиксировав это значение как 0, другой раз — как 1). Из определения 6.1
ясно, что переменное Х{ фиктивно тогда и только тогда, когда
для любых двух наборов, отличающихся только значением г-й
компоненты, функция принимает равные значения.
Пример 6.5. а. Из табл. 6.4 следует, что мажоритарная
функция не имеет фиктивных переменных, так как, например,
/@,0,1) = 0, а /A,0,1) = 1, т.е. переменное х\ существенное.
Далее, /A,0,0) =0, но /A,1,0) = 1, что означает существен-
существенность переменного x*i\ для ггз имеем /A,0,0) = 0, но /A,0,1) = 1,
что означает существенность и этого переменного.
б. Ниже приведена таблица функции д от четырех перемен-
переменных (табл. 6.5). Рекомендуется проверить, что переменное Х2
является фиктивным и что остальные переменные существен-
существенны. Более того, анализ таблицы показывает, что эта функция
есть не что иное, как мажоритарная функция, существенно за-
зависящая от переменных жх, #з и х\. #
Кроме процедуры удаления фиктивных переменных исполь-
используют и процедуру добавления к множеству переменных булевой
функции одной или нескольких фиктивных переменных. Так,
если дана функция /(#1,...,жп) ? V2.n1 то можно ввести новое
фиктивное переменное j/, определив новую, равную исходной,
согласно определению 6.2, функцию от п+1 переменного та-
таким образом:
(см. пример 6.4).
6.3. Фиктивные переменные. Равенство булевых функций 391
Таблица 6,5
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Xi
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
x2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
жз
0
0
1
1—1
0
0
1
1
0
0
1
1
0
0
1
1
Ж4
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
g(xi1x2,x3txA)
0
0
0
1
0
0
0
1
0
1
1
1
0
1
1
1
Следует заметить, что фиктивное переменное можно (в
новой функции /) „поставить на любое место". Или, говоря
точнее, можно определить семейство функций /j, г = 1, п, с
фиктивным переменным у так, что
Понятие фиктивного переменного позволяет также произ-
произвольные две булевы функции рассматривать как функции от
одного и того же числа переменных.
Действительно, пусть функция /(жъ...,#п) есть функция
от п переменных, а функция д{у\,... ,ym) — функция от m пе-
переменных. Обозначим множества переменных функции / и д
через X и У соответственно. Расширим множество перемен-
переменных функции / до X U У, вводя переменные из У \ X (если они
392 6. БУЛЕВЫ ФУНКЦИИ
существуют) как фиктивные. Точно так же поступим с функ-
функцией д, добавляя фиктивные переменные из множества X \ Y
(если, конечно, оно не пусто). Тогда получим функции / и
#, равные, согласно определению 6.2, функциям /ид соответ-
соответственно и определенные как функции от одного и того же числа
переменных, составляющего |JfUY|.
Нетрудно распространить описанную конструкцию на про-
произвольное конечное множество булевых функций и считать тем
самым все функции этого множества функциями от одного и
того же числа переменных.
В заключение рассмотрим понятие проектирующей функ-
функции.
Функцию рг^ от п переменных, такую, что
называют (г-й) проектирующей функцией. В общем случае
нумерация множества переменных может быть явно не зада-
задана, и тогда при определении проектирующей функции следует
указывать не номер соответствующего переменного, а само
переменное. В этом случае проектирующая функция рг* с
множеством переменных X этой функции и выделенным пе-
переменным х Е X определяется так:
г* (...,*,...) =
х
(за многоточиями „скрыты" переменные проектирующей функ-
функции, отличные от переменного х).
Из определения следует, что проектирующая функция
имеет единственное существенное переменное, а именно пере-
переменное х. Все остальные переменные проектирующей функции
являются фиктивными. Поэтому любые две проектирующие
функции рг* и рг^ равны, согласно определению 6.2, при лю-
любых множествах переменных X и У, содержащих переменное х.
Вместе с тем для двух различных переменных х и у про-
проектирующие функции рг* и рг* — разные функции. Так,
6.4. Формулы и суперпозиции 393
— функция, отличная от функции рг2(х1,:г2), по-
поскольку, например, рг1A,0) = 1, рг2A,0) =0.
Впредь договоримся любую из множества равных между
собой проектирующих функций рг* обозначать символом х ее
единственного существенного переменного.
Замечание 6.3. Такое обозначение проектирующих функ-
функций есть условность и определенная вольность, состоящая в
том, что проектирующая функция рг* как бы отождествляется
с самим переменным х. Однако отождествление функции и пе-
переменного недопустимо, так как понятие переменного, хоть и
связано с понятием функции, никак не есть частный случай по-
понятия функции. Переменное — только имя, некое обозначение,
которое используется при аналитическом задании функции, но
никак не сама функция. Тем не менее ради краткости, мы
сохраним обозначение х как обозначение любой из проекти-
проектирующих функций рг* и будем использовать иногда даже вы-
выражение „ функция #", понимая под этим любую из указанного
семейства проектирующих функций.
6.4. Формулы и суперпозиции
Табличный способ задания булевой функции не является
эффективным. Им практически нельзя воспользоваться при
большом числе переменных. Помимо этого способа существует
способ представления булевых функций в виде формул. Этот
способ аналогичен аналитическому способу задания функций
действительного переменного [I].
Как известно, в математическом анализе мы исходили из
определенного множества элементарных функций и строили из
них сложные функции, записывая их в виде формул, например:
y = sin(tga;), у = ln(cosx), у = e~cos(x+tex) и т.п. Аналогично
обстоит дело для булевых функций, но только вместо элемен-
элементарных функций математического анализа мы используем эле-
394 6. БУЛЕВЫ ФУНКЦИИ
ментарные булевы функции — главным образом, те функции
от одной и от двух переменных, которые мы определили в 6.1.
Но в отличие от математического анализа в теории булевых
функций ставится задача представления любой булевой функ-
функции такой формулой, которая содержала бы строго определен-
определенное конечное множество элементарных булевых функций. Эти
функции назовем пока условно „базисными функциями". Мно-
Множества таких базисных функций могут быть разными, но, так
или иначе, мы хотим иметь нечто вроде функционального ба-
базиса (или множества таких базисов), через элементы которого
можно было бы выразить любую булеву функцию. Аналогичная
задача не может быть решена для функций действительно-
действительного переменого. Для булевых же функций задача оказывается
разрешимой, и это обусловлено прежде всего тем, что булева
функция является конечной функцией.
Чтобы математически точно сформулировать и решить по-
поставленную выше задачу, нам необходимо уточнить понятие
формулы. В анализе, поскольку там не возникала задача по-
подобного рода, мы могли ограничиться интуитивной идеей фор-
формулы как некоего способа представления функции. В теории
булевых функций мы хотим доказывать утверждения вида „лю-
„любая булева функция может быть представлена формулой над
заданным множеством базисных функций F". Но тогда нам
нужно дать математическое определение „формулы над задан-
заданным множеством базисных функций «F", а также уточнить, что
значит „булева функция представлена некоторой формулой".
Кроме того, формулы обретают „самостоятельную жизнь" еще
и потому, что одну и ту же булеву функцию можно предста-
представить, вообще говоря, разными формулами (как над одним и
тем же базисом, так и над разными базисами). Тогда необхо-
необходимо иметь механизм эквивалентного преобразования формул,
т.е. перехода от заданной формулы, представляющей некото-
некоторую булеву функцию, к новой, скажем, более простой формуле,
которая представляет ту же самую функцию.
6.4. Формулы и суперпозиции 395
Определение формулы основано на понятии сложной функ-
функции, или суперпозиции.
Пусть булева функция / есть функция от п переменных, а
булевы функции gi, ..., дп — произвольные (и не обязательно
различные) функции от одного и того же числа переменных,
которое обозначим га.
Определим функцию /(si,.-->0n)> называемую суперпози-
суперпозицией функций /, gi, ..., дп так, что для любого S € Вт имеет
место равенство
Таким образом, суперпозиция /(<?ъ--ч9п) есть не что иное,
как композиция булевых операторов до/, где булев оператор
д задается семейством координатных функций </,-, % = 1,п.
Для суперпозиции f(gii--.,gn) используется также обозна-
обозначение <S(/,ffi,...,<7n)- Предположение о том, что все функции
<7i, % = 1,п, — функции от одного и того же числа перемен-
переменных, не ограничивает общности, поскольку, как было показано
(см. 6.3), любое конечное множество булевых функций всегда
можно рассматривать как множество функций от одного и того
же числа переменных.
Замечание 6.4. Обратим внимание на то, что в общем
случае „уравнивание" числа переменных функций ft, % = 1,п,
связано с добавлением фиктивных переменных, а его, как из-
известно, можно осуществлять разными способами. Поэтому
суперпозиция /(#i,... ,рп)? вообще говоря, определена однознач-
однозначно лишь с точностью до равенства булевых функций согласно
определению 6.2. #
Пусть дано некоторое множество булевых функций F. То-
Тогда формулой над множеством F мы считаем любую кон-
константу из F (если она там есть) и любое булево переменное.
Далее, если известно, что Фх, ..., Фп (п ^ 1) — формулы над
множеством F, а / — функция из F от п переменных, то выра-
396 б. БУЛЕВЫ ФУНКЦИИ
жение /(Фь..., Фп) есть формула над множеством F. Никаких
других формул над множеством F, кроме определенных выше,
не существует.
Замечание 6.5. 1. Строго говоря, в формуле /(Ф1,...,ФП)
фигурирует не сама булева функция из множества F, а ее
обозначение, т.е. индивидная константа с областью значений
7^2- Но мы, чтобы не усложнять терминологию, будем ото-
отождествлять обозначения базисных функций, т.е. функций из
заданного множества F, с самими базисными функциями.
2. Обычно предполагают, что рассматриваются переменные
из некоторого заранее фиксированного (и не более чем счетно-
счетного) множества переменных X.
Пример 6.6. а. Пусть F = {V, •,""}. Это множество, со-
состоящее из функций дизъюнкции, конъюнкции и отрицания,
называют стандартным базисом. Формулами над стан-
стандартным базисом будет любое переменное: ж, у, ..., х\, ...,
хп и т.д. Далее, из переменных ж, у как формул и функции V
можно построить новую формулу, например V(a;,y) или -(х,у).
Эти формулы, однако, естественно записывать несколько ина-
иначе. Поскольку каждая булева функция от двух переменных
(каковы, в частности, дизъюнкция и конъюнкция) является од-
одновременно бинарной операцией на множестве В = {0,1}, то
формулы с такими функциями обычно записывают в „ инфикс-
инфиксной форме", т.е. как (#Vy), (х-у) и т.п. Аналогично для
отрицания используют запись ж, а не """(ж).
Кроме того, в формулах над стандартным базисом, во-
первых, опускают скобки, используя ассоциативность булевых
операций V и •, т.е. вместо ((хУу) У z) пишут (хУуУ z)\ во-вто-
во-вторых, опускают, как правило, внешние скобки, записывая фор-
формулу, аналогичную последней, просто как ж V у V z; в-третьих,
используют соглашение о „старшинстве" (или о приоритете)
операций, полагая, что самый высокий приоритет имеет опера-
операция отрицания (т.е. она всегда выполняется перед конъюнкцией
6.4. Формулы и суперпозиции 397
и дизъюнкцией), затем идет конъюнкция и после нее — дизъ-
дизъюнкция.
С учетом сказанного формула ((х Vy) V ((у • z) • и)) может
быть переписана так:
(xVy)Vyz-u. F.6)
Согласно определению формулы, можно представить процесс
построения формулы F.6) следующим образом. Из переменных
я, у и функции V строим формулу Фх = (х V у), затем из нее и
функции отрицания получаем формулу Фг = Фь т.е. формулу
(хУу). Далее из переменных у, z и функции • строим формулу
(у • г), а из нее, переменного и и опять функции • — формулу
ф3 = (у • z) • гх, которую записываем как у • z • и. И наконец,
из формул Фг, Фз и функции V строим формулу Фг V Фз, т.е.
формулу F.6).
Описанный процесс можно наглядно изобразить в виде ори-
ориентированного дерева (рис. 6.3). Листья этого дерева поме-
помечены переменными или константами формулы, а каждый узел,
не являющийся листом, — одной из функций из множества F
(на рисунке эти узлы изображены в виде кружочков, внутри
которых указано имя функции).
398 6. БУЛЕВЫ ФУНКЦИИ
б* Рассмотрим множество булевых функций {ф, •, 1}, кото-
которое называют базисом Жегалкина. При записи формул над
базисом Жегалкина используют те же принципы, что и при за-
записи формул над стандартным базисом. Приоритет операции
конъюнкции считается выше приоритета операции сложения
по модулю 2. Так как последняя ассоциативна, то при записи
формул с этой операцией соответствующим образом опускают
скобки. Так, формулами над базисом Жегалкина будут:
жуфхфу, ж©1, xyz@xy(&xz®yz®x®y®z(Bl.
Процесс построения первых двух формул изображен в виде
деревьев на рис. 6.4.
в. Пусть множество базисных функций F состоит из един-
единственной функции | (штрих Шеффера). Как бинарная опера-
операция, эта функция не ассоциативна, т.е. булева функция (я|у)|г
не равна булевой функции x|(y|z). Поэтому при записи формул
над множеством {|} следует заботиться о расстановке скобок.
Примеры формул над множеством {|}:
(х\х)\(у\у), Ш\Ш, Ш\Ш-
Внешние скобки мы опускаем и в этом случае. Дерево, по-
показывающее процесс построения первой из записанных выше
формул, изображено на рис. 6.5. #
6.4. Формулы и суперпозиции 399
Мы будем использовать запись
ф(#1,...,а;п), указывая тем самым,
что формула Ф содержит перемен-
переменные a?i,..., жп, и только их. Множе-
Множество переменных формулы Ф будем
обозначать через Уаг(Ф).
Нам понадобится также поня-
понятие подформулы.
Из определения и рассмотрен-
рассмотренных примеров следует, что процесс
построения формулы есть процесс
определения некоторой сложной булевой функции, т.е. супер-
суперпозиции. Формула „собирается" из „элементарных формул",
т.е. переменных и базисных функций, так, что на каждом ша-
шаге из уже полученных формул строится новая, более сложная
формула. Естественно назвать эти „промежуточные" форму-
формулы подформулами рассматриваемой формулы. Так, в примере
б.б.а формулы Фь Ф2, Фз (и, конечно, переменные и базисные
функции) — это подформулы формулы F.6).
Строго понятие подформулы может быть введено следую-
следующим образом. Пусть Ф — формула над F. Бели Ф Е F или Ф
есть переменное, то ее единственной подформулой является она
сама. Бели Ф имеет вид /(Фь..., Фп)? где / — функция из F от
п переменных, а Ф», % = 1, п, суть формулы над F, то подфор-
подформулами формулы Ф будут: 1) все формулы Ф»; 2) для каждого
г = 1, п все подформулы формулы Ф».
В дереве, изображающем процесс построения формулы,
каждое поддерево, все листья которого являются также и
листьями всего дерева, определяет некоторую подформулу.
Каждому набору значений переменных, входящих в задан-
заданную формулу, можно определенным образом сопоставить зна-
значение этой формулы. Вычисление этого значения в точности
соответствует процессу построения формулы из подформул (в
конечном счете из переменных и базисных функций).
400 6. БУЛЕВЫ ФУНКЦИИ
Пример 6.7. Полагая в формуле F.6) х = 1, у = 0, z = и = 1,
получим значение формулы F.6), равное
AVO)VO-1-1 = O. #
Таким образом, по каждому набору значений переменных
формулы можно по определенному алгоритму вычислить зна-
значение формулы. Это значит, что каждая формула определяет
(или представляет) некоторую булеву функцию. Введем по-
понятие функции, представляемой формулой над множе-
множеством F. Мы полагаем, что:
1) любая константа из F представляет саму себя;
2) любое переменное х из X представляет проектирующую
функцию х (точнее, любую из множества равных между собой
проектирующих функций существенного переменного ж, см. за-
замечание 6.3);
3) если формулы Фх, ..., Фп над множеством F представля-
представляют соответственно функции gi, ..., </п, а / — функция из F от
п переменных (n ^ 1), то формула /(Фх,...,Фп) представляет
суперпозицию функций /(дь... ,#п);
4) других булевых функций, представляемых формулами
над множеством F, кроме тех, которые могут быть получены
согласно пп. 1-3 данного определения, не существует.
Функцию, представляемую некоторой формулой над мно-
множеством F, называют суперпозицией над множеством F.
Таким образом, суперпозиция над множеством F — это любая
суперпозиция функций вида /(gi,...,<7п)? где / Е F, а каждая из
функций gi, ..., дп есть либо элемент F, либо переменное (точ-
(точнее, проектирующая функция), либо некоторая суперпозиция
над F. Множество всех суперпозиций над F будем обозна-
обозначать [F] и называть замыканием множества F булевых
функций.
Понятия формулы и суперпозиции взаимно предполагают
друг друга. Суперпозиция над множеством F есть некоторая
сложная функция, которая определенным образом построена из
6.4. Формулы и суперпозиции 401
базисных функций — функций фиксированного множества F
(и проектирующих функций). Само „строение" суперпозиции,
т.е. то, из каких именно базисных функций и в какой после-
последовательности образуется результирующая сложная функция
(суперпозиция), и есть формула.
Бели булева функция /(^i,... ,жп) представляется формулой
Ф(я1,...,яп), то будем писать f{xu...,xn) = Ф(я1,...,жп), или,
короче, / = Ф(ж1,...,жп).
Определение 6.3. Множество булевых функций F назы-
называют:
1) замкнутым, если любая формула над F представляет
некоторую функцию из F;
2) полным, если любая булева функция может быть пред-
представлена некоторой формулой над F.
Определение 6.3 равносильно следующему (на „языке су-
суперпозиций"): множество F функций замкнуто, если каждая
суперпозиция над F есть функция из F, т.е. [F] = F, и полно,
если всякая булева функция есть некоторая суперпозиция над
F, т.е. [F] = V2.
Замечание 6.6. Можно заметить, что определение форму-
формулы и суперпозиции над заданным множеством булевых функ-
функций похоже на определение п-замыкания множества в алгебрах
(см. 4.2). Эти определения, равно как и основанные на них
определения замкнутости и полноты множеств булевых функ-
функций, могут быть переведены полностью на алгебраический
язык. Тогда замкнутое множество булевых функций, соглас-
согласно определению 6.3, окажется не чем иным, как замкнутым
подмножеством некоторой алгебры булевых функций, а пол-
полное множество булевых функций — системой образующих этой
алгебры. Однако при попытке чисто алгебраической интерпре-
интерпретации определения 6.3 возникают некоторые технические труд-
трудности, обсуждение которых выходит за рамки этой книги*.
*См., например: Матросов В.Л.> Стеценко В.А.
402 6. БУЛЕВЫ ФУНКЦИИ
Пример 6.8. Для каждой из определенных в 6.1 функций
от двух переменных мы можем записать следующие формулы
над стандартным базисом:
Если мы пополним стандартный базис функцией -> (импли-
(импликацией), то формула для эквивалентности примет вид
XI ~ Х2 = (Ж1 -> Ж2) • (Ж2 "> Xi). #
Тот факт, что одна и та же функция (в данном случае экви-
эквивалентность) может быть представлена по крайней мере двумя
разными формулами над одним и тем же множеством, а именно
над {V, •, ~, ->}, показывает, что соответствие между форму-
формулами над фиксированным множеством и представляемыми ими
функциями не является взаимно однозначным. Эта ситуация
до некоторой степени аналогична разложению по базису векто-
векторов конечномерного линейного пространства [IV]. Формула,
представляющая некоторую булеву функцию, выражает „ раз-
разложение " этой функции по фиксированному „функциональному
базису". Одна и та же функция может иметь несколько таких
разложений. В отличие от линейной алгебры в этом случае
возникает ситуация, когда возможны различные разложения
заданной функции по одному и тому же базису. Например,
формулы (х V у) и х • у над стандартным базисом представляют
одну и ту же функцию.
Назовем эквивалентными формулы, которые представля-
представляют равные функции. Эквивалентным (или тождествен-
тождественным) преобразованием формулы Ф называют переход (по
определенным правилам) к любой формуле Ф, эквивалентной
6.4. Формулы и суперпозиции 403
формуле Ф. Необходимо сделать несколько замечаний относи-
относительно правил, согласно которым осуществляются эквивалент-
эквивалентные преобразования формул.
Введем понятие тождества. Тождеством (над множе-
множеством F С V*i) называют выражение
Ф(*ь...,*п) = *(Уь...,»т), F.7)
где формулы ФиФ — эквивалентные формулы над F. Фор-
Формула Ф называется при этом левой, а формула Ф — правой
частью тождества F.7).
Левая и правая части тождества представляют равные бу-
булевы функции. Поэтому пересечение множеств переменных
Уаг(Ф) = {жь...,жп} и ^аг(Ф) = {уь...,ут} должно содер-
содержать все существенные переменные функций f{x\,...,xn) и
9(У1>«">Ут)) представляемых формулами ФиФ соответствен-
соответственно. В частности, если это пересечение пусто, то обе функции
равны некоторой константе.
Пример 6.9. В тождествах # V а? = у V у, а; V # = 1 пересе-
пересечение множеств переменных в левых и правых частях пусто,
причем во втором тождестве правая часть вообще не содержит
переменных. В тождестве (х V у) • (z V t) = x V у V v • v указанное
пересечение равно {ж, у}.
Все записанные в примере 6.8 выражения являются тожде-
тождествами над множеством {V, -,"",©, -*, ~, |, 4-Ь причем во всех
этих тождествах множества переменных в левой и правой ча-
частях тождества совпадают. Такого же рода тождества —
аксиомы булевой алгебры* (крометождествж\/х = 1иа;Лж = 0)
и вытекающие из них тождества (подобные, например, законам
де Моргана). #
Без доказательства сформулируем следующие правила то-
тождественных преобразований.
* Поскольку все переменные, фигурирующие в этих тождествах, есть
булевы переменные, то речь здесь идет об аксиомах булевой алгебры
применительно к частному случаю — двухэлементной булевой алгебре В.
404 6. БУЛЕВЫ ФУНКЦИИ
Теорема 6Л. 1. Если в тождестве F.7) некоторые пере-
переменные заменить произвольными формулами (над множеством
F), то тождество сохранится, т.е. полученные в результате та-
такой замены новые формулы останутся эквивалентными.
2. Бели в формуле Ф произвольную ее подформулу заменить
любой эквивалентной ей, то получится формула, эквивалентная
формуле Ф. #
Чтобы использовать сформулированные в теореме 6.1 пра-
правила, нужно фиксировать какую-то систему исходных тож-
тождеств. Тогда возникает вопрос: можно ли утверждать, что
при надлежащем выборе исходных тождеств с помощью пра-
правил 1 и 2, сформулированных в теореме 6.1, можно из формулы
Ф получить эквивалентную ей формулу Ф, каковы бы ни были
эти формулы, или, говоря неформально, любые ли две эквива-
эквивалентные формулы над заданным множеством F можно „транс-
„трансформировать" друг в друга, используя фиксированную систему
основных тождеств над F и правила, сформулированные в те-
теореме 6.1?
Рассмотрение этого вопроса выходит за рамки учебника.
Ответ на него зависит от того, какое множество булевых функ-
функций F и какая система исходных тождеств над F выбраны.
Отметим, что для стандартного базиса ответ на вопрос поло-
положителен, причем в качестве исходных тождеств используются
аксиомы булевой алгебры.
В свете изложенного может быть поставлена задача поиска
наиболее простой (в определенном смысле) формулы, среди всех
эквивалентных между собой формул, представляющих данную
булеву функцию. Решение этой задачи для некоторого класса
формул над стандартным базисом будет рассмотрено в 6.6.
Понятие формулы позволяет также взглянуть по-новому на
логическую интерпретацию булевой функции. В силу уста-
установленного в 6.2 взаимно однозначного соответствия между
логическими связками V, Л, -i, =>, Ф* и булевыми функциями
V, •, ~~, —>, ~ любому сложному высказыванию, составленно-
6.5. Дизъюнктивные и конъюнктивные нормальные формы 405
му из некоторых „простых" высказываний с использованием
указанных выше логических связок, однозначно сопоставляется
формула над множеством L = {V, Л,"", ->, ~}, т.е. каждому про-
простому высказыванию сопоставляется булево переменное (так
что разным высказываниям сопоставляются и разные перемен-
переменные), а связки V, Л, -л, =Ф-, <& заменяются соответствующими
функциями из множества L. Тогда, например, высказыванию
(Р => Q) Л (Q =» Р) (читается: „если Р, то Q, и если Q, то Ри)
будет сопоставлена формула (х —> у) • (у —> х).
Таким образом, с логической точки зрения формула над
множеством L есть высказывание. Поскольку мы имеем воз-
возможность вычислять значения формул и проводить их экви-
эквивалентные преобразования (используя, в частности, аксиомы
булевой алгебры), мы получаем алгебраический аппарат для
упрощения сложных высказываний (путем эквивалентных пре-
преобразований) и вычисления их истинностных значений.
Но тогда возникают вопросы: как практически построить
для любой наперед заданной булевой функции представляющую
ее формулу над фиксированным множеством базисных функ-
функций Ft Каковы условия полноты множества F1
Далее (см. 6,5 и 6.6) мы рассмотрим вопрос о представлении
любой булевой функции над стандартным базисом и вопрос
о поиске минимальной (в уточняемом ниже смысле), наиболее
простой формулы над стандартным базисом, представляющей
данную функцию.
6.5. Дизъюнктивные и конъюнктивные
нормальные формы
Любая формула вида х или х над стандартным базисом, где
х — произвольное переменное, называется литералом. Таким
образом, литерал есть обозначение либо самого переменного ж,
либо его отрицания. Часто используют такое обозначение: для
о Е {0,1} пишут ха, понимая под этим само переменное ж, если
406 6. БУЛЕВЫ ФУНКЦИИ
а = 1, и отрицание #, если а = 0, т.е.
<г = 1;
, G = 0. V '
Подставляя в F.8) 0 и 1 вместо ж, получаем
@, <т = 1; ia
0, <т =
Часто используют также обозначение я, понимая под этим
любой из двух литералов — х или х.
Формула вида x\x*i...xm (соответственно вида х\ V#2 V...
... Vxm), где все фигурирующие в ней переменные попарно
различны, называется элементарной конъюнкцией (соот-
(соответственно элементарной дизъюнкцией).
Определение 6.4. Дизъюнктивная нормальном фор-
форма (ДНФ) от переменных a?i, ..., хп — это формула вида
К\ V ... V Кт, где ifi, г = 1, т, — элементарная конъюнкция,
содержащая некоторые из литералов х\, ..., хп. В том слу-
случае, когда в каждую конъюнкцию К{ для каждого номера
j = 1, п входит в точности один из литералов ?}, ДНФ называ-
называется совершенной дизъюнктивной нормальной формой
(СДНФ).
Двойственным образом, т.е. с использованием принципа
двойственности для булевых алгебр, определяются конъюнк-
конъюнктивная нормальная форма (КНФ) и совершенная конъ-
конъюнктивная нормальная форма (СКНФ).
Теорема 6.2. Любая булева функция, отличная от кон-
константы 0 (соответственно от константы 1) представима в виде
СДНФ (соответственно в виде СКНФ).
< Докажем первое из двух (взаимно двойственных) утвержде-
утверждений теоремы. Для функции / ? Р2,п> не равной тождественно
0, рассмотрим множество Cj = {5: /E) = 1}. Каждый набор из
Cj называется конституентой единицы функции /. Так
6.5. Дизъюнктивные и конъюнктивные нормальные формы 407
как по условию / ф 0 тождественно, то множество С) не пусто.
Каждому набору 5 Е Сj поставим в соответствие элементар-
элементарную конъюнкцию К$ = х х%2... х%п, которую также называют
конституентой единицы функции /. Ясно, что К% обращает-
обращается в единицу только на наборе 5. Тогда искомой СДНФ для
функции / будет
/= V **
5ес)
Согласно принципу двойственности, СКНФ для той же
функции будет иметь вид
где множество наборов С9 = {5: /(а) = 0}, и каждый набор 5
из G9 называют конституентой нуля функции /; при этом
элементарная дизъюнкция D% сопоставляется конституенте ну-
нуля 5 по следующему правилу:
Ua —Xi V Х2 V,..VIn ,
т.е. если в наборе г-я компонента равна 0, то в D& ставим
само переменное гг», если иначе — отрицание переменного Х{
(таким образом, дизъюнкция D^ обращается в нуль только на
наборе а). >
Из доказанного следует, что любая булева функция может
быть представлена в виде формулы над стандартным базисом
(СДНФ или СКНФ), и, значит, стандартный базис есть полное
множество булевых функций.
Рассмотрим в качестве примера построение СДНФ и СКНФ
для мажоритатрной функции (см. 6.1). Конституентами еди-
единицы для нее служат наборы: 5i = @, 1, 1), 5г = A, 0, 1),
5з = A, 1, 0) и а4 = A, 1, 1). Им соответствуют элементар-
элементарные КОНЪЮНКЦИИ: К%х = Х\Х2Х^ К^2 = Ж15?2#3? ^5з =
408 б. БУЛЕВЫ ФУНКЦИИ
К%4 = xi#2#3- Тогда СДНФ, представляющая мажоритарную
функцию, имеет вид
Х\Х2Х^ V Ж1^2^3 V X\X2Xs V X\X2Xz- F.9)
Для получения СКНФ для той же функции выпишем все кон-
ституенты нуля данной функции: @, 0, 0), @, 0, 1), @, 1, 0),
A, 0, 0). Сопоставим им элементарные дизъюнкции: х\ У х2 V
V Ж3, #1Vх2 V д?з, х\ V #2 V #з и #1Vх2 V жз соответственно.
В результате получим СКНФ для мажоритарной функции
в виде
(xiV x2V xs)(xi\/ x2Vxs){xiVx2V хз)(хгУ х2У х$). F.10)
Заметим, что если в формуле СКНФ F.10) мы раскроем скобки
и преобразуем полученное выражение согласно законам булевой
алгебры, проведя тем самым эквивалентные преобразования
СКНФ, то придем к формуле СДНФ F.9) .
6.6. Построение минимальных ДНФ
СДНФ, которая строится по таблице булевой функции, за-
зачастую оказывается весьма сложной, т.е. она содержит доста-
достаточно много элементарных конъюнкций и литералов. Необ-
Необходимо уметь находить в определенном смысле минимальную
ДНФ, представляющую исходную функцию.
Уточним задачу.
Определение 6.5. Булеву функцию g называют импли-
кантой* булевой функции /, если для любых наборов значений
переменных из g = 1 следует / = 1-
Замечание 6.7. Напомним, что функции / и g можно рас-
рассматривать как функции от одного и того же числа переменных
(см. 6,3). Обозначая это число через п, можцо так уточнить
"Иногда употребляют и термин „импликант" (мужского рода).
6.6. Построение минимальных ДНФ 409
понятие импликанты: функция д G V2,n есть импликанта функ-
функции / Е Т^гп если для каждого набора а ? Вп из д(а) = 1 следует
/C) = 1. Термин „импликанта" естественным образом ассоци-
ассоциируется и с логической связкой, называемой импликацией, и с
одноименной булевой функцией. Действительно, если д импли-
импликанта /, то из (д -» /) = 1 и д = 1 следует, что и / = 1, т.е.
истинно высказывание
(VS€Bn)((g(«) = l)=M/(a) = l)). #
Бели функция / представлена СДНФ, то любая ее элемен-
элементарная конъюнкция (конституента единицы функции /) будет
ее импликантои. Полезно заметить также, что если g\mg2 —
импликанты /, то дизъюнкция д\ V дъ также является импли-
импликантои /. Действительно, если д\ V #2 = 1> то gi = 1 или дч = 1.
Но тогда, поскольку каждая из этих функций есть импликанта
/, и д\ Vg2 есть импликанта /.
Из определения 6.5 и понятия равных булевых функций (см.
определение 6.2) следует, что булевы функции / и д равны,
если и только если каждая из них служит импликантои другой:
Определение 6.6. ДНФ называют минимальной, если
она содержит наименьшее число литералов среди всех ДНФ,
эквивалентных ей.
Обратим внимание на то, что под числом литералов в ДНФ
понимают число всех подформул этой ДНФ, которые являются
литералами. Так, СДНФ F.9) содержит 12 литералов (по три
литерала в каждой из четырех элементарных конъюнкций).
Пример 6.10. ДНФ х\Х2Ух\Х2 не является минимальной,
так как ее можно преобразовать к эквивалентной ДНФ, не
содержащей ни одного из литералов х\\
= (#1 УХ\)Х2 = Х2-
410 6. БУЛЕВЫ ФУНКЦИИ
Вместо четырех литералов в исходной ДНФ получаем ДНФ,
состоящую из одного литерала.
Определение 6.7. Длиной ДНФ называют число входя-
входящих в нее элементарных конъюнкций.
ДНФ называют кратчайшей, если она имеет наименьшую
длину среди всех эквивалентных ей ДНФ.
Заметим, что кратчайшая ДНФ не обязана быть в то же
время минимальной среди всех ДНФ, эквивалентных исходной
функции. Но поиск минимальных ДНФ, как мы сейчас увидим,
проводится среди кратчайших ДНФ.
Наша задача состоит в том, чтобы описать метод построе-
построения минимальной ДНФ, эквивалентной заданной булевой функ-
функции. Мы рассмотрим простейший метод такого рода, осно-
основанные на алгоритме К в айна — Мак-Клоски. Этот ал-
алгоритм исходит обязательно из СДНФ, которая строится по
таблице функции так, как это было описано ранее (см. 6.5).
Опишем последовательно этапы, составляющие алгоритм
Квайна — Мак-Клоски.
1. Склейка. Пусть Кi и К2 — две элементарные конъ-
конъюнкции, входящие в исходную СДНФ Ф, которая представляет
функцию /, причем для некоторого переменного х и некоторой
элементарной конъюнкции К выполняются равенства К\ = хК
Тогда имеем, согласно тождествам булевой алгебры,
Кх\/К2 = xKVxK = (xVx)K = К.
Мы получаем элементарную конъюнкцию К, которая содержит
на один литерал меньше, чем К\ и К2, и является, как и обе
конъюнкции К\ и^2, импликантой /. Образно говоря, мы
„склеили" две импликанты в одну, в которой число литералов
на единицу меньше.
Операцию получения К по К\ и К2, описанную выше, можно
провести и для любых двух элементарных конъюнкций подоб-
6.6. Построение минимальных ДНФ 411
ного вида, составляющих любую ДНФ, эквивалентную исход-
исходной функции. Такую операцию называют простой склейкой
импликант К\ и К2 по переменному х.
Установим геометрический смысл простой склейки* (с точ-
точки зрения структуры, или „геометрии", булева куба, см. 6.1).
Из доказательства теоремы о представлении булевой функ-
функции в виде ДНФ (см. теорему 6.2) мы знаем, что существует
взаимно однозначное соответствие между множеством эле-
элементарных конъюнкций С ДНФ, представляющей функцию /,
и множеством С) ее конституент единицы. Это соответствие,
напомним, таково, что каждому набору 5 = (c*i, ..., ап) € С\
отвечает элементарная конъюнкция К% = х^1 •... • д;?п, прини-
принимающая значение 1 только на наборе 5. Тогда простая склейка
может быть применена только к таким двум элементарным
конъюнкциям К% и JFCgf, соответствующим наборам а, /? € Су,
что для некоторого % A ^ % < п)
, ..., ап).
Это значит, что наборы 5, /? таковы, что один из них доми-
доминирует над другим (они различаются значением только одной
компоненты), т.е. они образуют ребро булева куба Вп.
Следовательно, простой склейке, применяемой к элементар-
элементарным конъюнкциям исходной СДНФ, представляющей функцию
/, подлежат те и только те элементарные конъюнкции, кото-
которые соответствуют элементам какого-либо ребра булева куба,
на котором функция / принимает единичное значение. Образ-
Образно говоря, две соседние вершины куба, на которых функция
равна 1, ясклеиваются" в ребро, их „соединяющее".
С алгебраической же точки зрения мы из двух элемен-
элементарных конъюнкций jRTg и K-q получаем новую элементарную
конъюнкцию х*1... х^1 х*^1... х%п, лишенную литерала xf{.
"Подробно о геометрической сути минимизации см.: Яблонский СВ.
412 6. БУЛЕВЫ ФУНКЦИИ
Итак, применяя простую склейку к исходной СДНФ Ф, по-
получаем новую ДНФ Фх; к ней также применяем простую склей-
склейку — получаем ДНФ Ф2; продолжаем выполнять эту операцию
до тех пор, пока не окажется, что для некоторого А; в ДНФ
Ф& уже нельзя склеить никакие две элементарные конъюнкции.
Такое к всегда найдется, так как СДНФ Ф состоит из конеч-
конечного числа элементарных конъюнкций, а они, в свою очередь,
состоят из конечного числа литералов. Полученную в резуль-
результате ДНФ Ф& называют сокращенной ДНФ функции /, а
ее элементарные конъюнкции — простыми импликантами
булевой функции /.
Замечание 6.8. Понятие простой импликанты определено
через процедуру многократного повторения простой склейки.
Иногда простую имшгаканту булевой функции / определяют
независимо от понятия о склейке как такую элементарную
конъюнкцию в составе некоторой ДНФ, представляющей функ-
функцию /, что удаление из нее любого литерала лишает ее свойства
„быть импликантой". Например, конъюнкция #1Ж2#з не явля-
является простой импликантой мажоритарной функции, так как из
ее СДНФ F.9) можно удалить литерал я?з и получить конъюнк-
конъюнкцию х\Х2, которая будет снова импликантой функции, но уже,
как будет показано далее, простой.
Можно доказать, что эти два определения простой импли-
импликанты равносильны. #
Геометрия описанного выше многократного повторения про-
простой склейки, как можно показать, состоит в дальнейшем „скле-
„склеивании" каждой пары соседних ребер (граней размерности 1),
на которых значение функции равно 1, в грани размерности 2,
соседних граней размерности 2 в грани размерности 3 и т.д.
Разбираемый ниже пример поясняет эту идею.
Пример 6.11. Зададим функцию / от трех переменных
следующей СДНФ:
/ = Х1Х2Щ VX1X2X3 У Х\Х2ХЪ V Х\Х2Хъ. F.11)
6.6. Построение минимальных ДНФ 413
Подвергнем простой склейке первую и третью, а также вторую
и четвертую элементарные конъюнкции в F.11):
/ = х2ЩУх2х3. F.12)
С геометрической точки зрения склейка первой и третьей конъ-
конъюнкций в формуле F.11) означает, что функция / принимает
единичное значение на ребре [000,100] (рис. 6.6), а склейка
второй и четвертой конъюнкций точ-
точно так же определяет ребро [001,101],
Эти ребра являются соседними, и, кро-
кроме того, оказывается, что функция /
принимает единичное значение и на
другой паре соседних ребер: [000, 001] 001(
и [100,101]. Здесь сказывается суще-
существенное отличие „геометрии" булева
куба от классической: в булевом ку-
кубе ребро — это пара вершин, между Рис# в#6
которыми нет никаких „точек". Тогда любая пара соседних
ребер образует грань размерности 2, любая пара соседних гра-
граней размерности 2 образует грань размерности 3 и т.д. Таким
образом, если функция принимает единичное значение на двух
соседних ребрах булева куба, то она равна 1 в любой точке
образуемой ими грани размерности 2, если она равна 1 на двух
параллельных соседних гранях размерности 2, то она равна 1
на соответствующей грани размерности 3 и т.д.
Применяя простую склейку к F.12) (по переменному жз),
получаем /(#1,Ж2?#з) = ^2* Побочным результатом склейки
явилось и удаление фиктивных переменных функции х\ и х$.
Пример 6.12. Рассмотрим СДНФ мажоритарной функ-
функции F.9).
Имеем следующие склейки:
414
6. БУЛЕВЫ ФУНКЦИИ
В данном случае сразу получаем сокращенную ДНФ:
Для булевых функций от трех и четырех переменных проце-
процедура склейки наглядно и просто выполняется на так называе-
называемых картах Карно. Форма карт Карно, представляющих со-
собой прямоугольные таблицы, для функции от трех переменных
показана на рис. 6.7, а для функции от четырех переменных —
на рис. 6.8. На рис. 6.7 строки отмечены наборами значений
переменного a?i, а столбцы — Х2> #з> а на рис. 6.8 строки —
наборами значений переменных х\, x<i, а столбцы — яз, х±.
0
1
00
01
11
10
00
01
11
10
00
01
11
10
Рис. 6.7
Рис. 6.8
Карта Карно есть не что иное, как форма таблицы для
определения булевой функции. Каждая клетка карты задается
своим набором значений переменных, причем в клетках, со-
соответствующих конституентам единицы данной функции, ста-
ставится единица, тогда как остальные клетки остаются пустыми.
Карта Карно устроена так, что наборы, определяющие любые
две соседние клетки, различаются в точности в одной пози-
позиции (т.е. различаются значениями ровно одной компоненты),
причем клетки (одной и той же строки или одного и того же
столбца), примыкающие к противоположным сторонам прямо-
прямоугольника, также являются соседними в только что опреде-
определенном смысле. Это можно представить себе так, что карта
6.6. Построение минимальных ДНФ
415
язакручивается" в „цилиндр" по обоим направлениям, т.е. в
„тор".
С геометрической точки зрения карта Карно есть способ
изображения булева куба (размерностей 3 и 4)*. Любая пара
соседних клеток (с учетом „закрученности" карты) определяет
некоторое ребро булева куба, а любой прямоугольник, состоя-
состоящий из 2к клеток (или, как говорят, прямоугольник с площадью
2*) для некоторого А;, определяет грань размерности к.
Пусть булева функция / задана таблицей, представленной в
форме карты Карно. Описанный выше итерационный процесс
склейки, в результате которого получается сокращенная ДНФ,
представляющая функцию /, проводится на карте Карно так:
любые две соседние клетки, содержащие единицы, обводятся,
и „поглотивший" их прямоугольник (он и есть обозначение
результата склейки на карте) представляется словом, содержа-
содержащим „О", „1" и „х" („крестик"), причем „крестик" занимает
позицию того переменного, по которому произведена склейка
(рис. 6.9).
xll
Их
Х\ \
0
1
00
01
11
(Т
Ё
10
^^
1x1
Рис. 6.9
С геометрической точки зрения такой прямоугольник пло-
площади 2 соответствует ребру булева куба, в каждой вершине ко-
которого функция принимает значение 1. Запись прямоугольника
в виде слова можно понимать как обозначение соответствующе-
* Можно построить карты Карно и для размерностей 5 и б, но они ис-
используются весьма редко. Может быть построена и простейшая карта
Карно для функции от двух переменных, но для таких функций не возни-
возникает нетривиальных задач построения минимальной ДНФ.
416
6. БУЛЕВЫ ФУНКЦИИ
го ребра. Так, на карте, показанной на рис. 6.9, прямоугольник
Их обозначает ребро [110,111], прямоугольники же 1x1 и
xll — ребра [101,111] и [011,111] соответственно.
По таким обозначениям легко получить и ту импликанту,
которая является результатом простой склейки: для этого
достаточно записать литерал Х{ (соответственно ж»), если в г-й
позиции стоит 1 (соответственно 0), и пропустить литерал х^
если в 1-й позиции стоит „крестик". Так, по слову 1x0 получим
импликанту х\х^.
Наличие на карте Карно двух прямоугольников площади 2,
находящихся в соседних столбцах или строках, показывает, что
функция принимает значение 1 на некоторой паре соседних
ребер, т.е. на некоторой грани размерности 2. Тогда они могут
быть объединены в один большой прямоугольник площади 4
(рис. 6.10).
0
1
00
У
01
У
11
10
хОО хОх х01
Рис. 6.10
Этот прямоугольник можно записать в виде слова хОх,
показывая тем самым, что соответствующая грань (размерно-
(размерности 2) образована любой из двух пар соседних ребер: (хОО, х01)
(два вертикальных прямоугольника площади 2) или @0 х, 10 х)
(два горизонтальных прямоугольника площади 2).
Точно так же можно объединять в один прямоугольник
площади 8 два соседних прямоугольника площади 4 (рис. 6.11).
Если такие большие прямоугольники находить сразу, то
„поглощаемые" ими меньшие прямоугольники уже не рассма-
рассматриваются. Тем самым, находя на карте Карно прямоугольни-
прямоугольники максимальной площади и не содержащиеся друг в друге, мы
6.6. Построение минимальных ДНФ
417
ОхОх
00
01
11
10
00
1
1
1
01
11
/
10
17
1
1
ххОО хххО
Рис. 6.11
\
ххЮ
00
01
11
10
00
1
ш"
(^
01
Г
JT
и
"ЧУ
10
1
[i ^
хОхО
01x1
Рис. 6.12
находим грани максимальных размерностей и максимальные по
включению, такие, на которых заданная функция принимает
единичное значение. Поскольку грань размерности А: имеет
2к вершин, то выделяемые описанным способом прямоуголь-
прямоугольники могут состоять только из 2к клеток (для некоторого fc,
не превышающего числа переменных). Так, на карте, приве-
приведенной на рис. 6.12, получим два прямоугольника площади 4:
хОхОиОхОх, соответствующие граням размерности 2, и один
прямоугольник 01 х 1, отвечающий ребру, которое не содержит-
содержится ни в одной из указанных выше граней. Подчеркнем еще
раз, что соседство клеток, прямоугольников и само выделе-
выделение прямоугольников на карте Карно производится с учетом
ее „закрученности". В этой связи интересен „прямоугольник"
на карте, приведенной на рис. 6.12, обозначенный хОхО. Он
образован двумя парами противоположных угловых клеток.
Таким образом, если на карте Карно сразу выделять все
максимальные (в указанном выше смысле) прямоугольники пло-
площади 2к (для некоторого к > 0 и не превышающего числа
переменных), то тем самым мы „геометрически" реализуем
описанный ранее алгебраический итерационный процесс склей-
склейки и в результате получаем все простые импликанты исходной
функции (составляющие сокращенную ДНФ). Эти импликан-
импликанты восстанавливаются по записям прямоугольников точно так
14 _ 1ПП61
418 6. БУЛЕВЫ ФУНКЦИИ
же, как описано выше для простой склейки. Так, для карты,
приведенной на рис. 6.12, получим сокращенную ДНФ в виде
Х2Х4 V Х\Щ V Х\Х2Х±.
2. Определение ядра. Говорят, что элементарная конъ-
конъюнкция К покрывает элементарную конъюнкцию L (и пишут
К У L), если любой литерал, входящий в К, входит в L. Так,
х\Х2 У х\Х2Хз, Х\х% У х\Х2Х$, но х\х^ )/- х\Х2~хъ, поскольку вто-
вторая конъюнкция содержит литерал х$, отсутствующий в первой
конъюнкции. Легко понять, что если К У L, то К V L — К (со-
(согласно тождествам поглощения).
Каждая входящая в сокращенную ДНФ простая импликан-
та покрывает некоторую элементарную конъюнкцию исходной
С ДНФ. На карте Карно этому отвечает прямоугольник, „за-
„закрывающий" соответствующую единицу.
Простую импликанту называют ядровой, если она покры-
покрывает некоторую элементарную конъюнкцию исходной СДНФ,
не покрываемую никакой другой простой импликантой. На
карте Карно прямоугольник, соответствующий ядровой импли-
канте, отыскивается очень просто: это такой прямоугольник,
удалив который получим единицу, не закрытую никаким дру-
другим прямоугольником. Тогда ни одна ядровая импликанта не
может быть удалена из искомой минимальной ДНФ исходной
функции, т.е. все ядровые импликанты обязательно войдут в
минимальную ДНФ.
Множество всех ядровых импликант (склеек) сокращенной
ДНФ называют ядром.
Пример 6.13. а. У мажоритарной функции все импликан-
импликанты являются ядровыми. Напротив, у функции, изображенной
на карте Карно на рис. 6.13, ядро пусто, т.е. ядровых импли-
импликант нет вовсе.
б. На карте Карно на рис. 6.14 в ядро попадают склейки
Oxxl, Oxlx, 1x00. #
Бели все простые импликанты оказались в ядре, то сокра-
сокращенная ДНФ и есть единственная минимальная и кратчайшая
6.6. Построение минимальных ДНФ
419
Oxxl
00
01
11
10
00
01
11
хОЮ
Oxlx
10x0
1x00
Рис. 6.14
ДНФ для данной функции. Именно так обстоит дело с ма-
мажоритарной функцией (см. пример 6.12). В противном случае
смотрят, не эквивалентна ли ДНФ, построенная как дизъ-
дизъюнкция всех ядровых импликант, исходной СДНФ. Это будет
иметь место тогда и только тогда, когда ядровые импликан-
импликанты покрывают в совокупности все элементарные конъюнкции
исходной СДНФ. На карте Карно тогда каждая клетка, со-
содержащая единицу, должна быть закрыта прямоугольником,
отвечающим некоторой ядровой импликанте. Если это так, то
ДНФ, построенная по ядру, как описано выше, есть минималь-
минимальная и кратчайшая (склейки ядра закрыли все единицы карты
Карно). При этом импликанты, не попавшие в ядро, все оказы-
оказываются „избыточными", т.е. их удаление из сокращенной ДНФ
не приводит к нарушению эквивалентности этой последней с
исходной СДНФ.
В остальных случаях переходят к отысканию так называе-
называемых тупиковых ДНФ.
3. Перечисление тупиковых ДНФ. Простую импли-
канту называют избыточной (относительно некоторой ДНФ,
содержащей только простые импликанты и эквивалентной ис-
исходной СДНФ), если ее можно удалить из этой ДНФ без потери
эквивалентности ее исходной СДНФ. Так, сокращенная ДНФ
14*
420 6. БУЛЕВЫ ФУНКЦИИ
(см. рис. 6.14) содержит избыточные импликанты: импликанта,
соответствующая прямоугольнику 10x0, или импликанта, соот-
соответствующая прямоугольнику хОЮ, может быть удалена (но не
обе сразу!). Это значит, что каждая из этих импликант явля-
является избыточной относительно сокращенной ДНФ, но удаление
одной из них приводит к новой ДНФ, относительно которой
вторая из упомянутых импликант уже не будет избыточной. В
том случае, когда каждую элементарную конъюнкцию исход-
исходной СДНФ покрывает некоторая ядровая импликанта, импли-
импликанты, не вошедшие в ядро, можно удалить одновременно.
Тогда можно представить процесс пошагового удаления из-
избыточных импликант, начиная с сокращенной ДНФ, в резуль-
результате которого получится некоторая ДНФ, уже не содержащая
ни одной избыточной склейки.
Любую ДНФ, эквивалентную исходной СДНФ, содержащую
все ядровые импликанты и не содержащую ни одной избыточ-
избыточной импликанты, называют тупиковой.
Заметим, что в силу конечности множества всех импликант
тупиковая ДНФ обязательно существует, т.е. в упомянутом
выше процессе мы рано или поздно доберемся до такого мо-
момента, когда удаление хотя бы одной склейки приведет к тому,
что „откроется" какая-то единичная клетка на карте Карно и
тем самым будет потеряна эквивалентность полученной таким
образом ДНФ исходной СДНФ.
Для СДНФ, карта Карно которой приведена на рис. 6.14,
имеются две тупиковые ДНФ:
Первые три конъюнкции соответствуют ядру.
В общем случае для перечисления всех тупиковых ДНФ
может быть использован следующий алгоритм. Мы изложим
его в терминах карт Карно и, допуская вольность речи, будем
отождествлять максимальные прямоугольники на карте Карно
с соответствующими простыми импликантами.
\
6.6. Построение минимальных ДНФ 421
Присвоим каждой простой импликанте сокращенной ДНФ
некоторое имя: т.е. обозначим их, например, как К\, К2, ...,
Km- Для любой единицы карты Карно, не покрываемой ядром,
перечислим все простые импликанты, которые ее покрывают,
записав их в виде элементарной дизъюнкции, в которой пе-
переменными считаются введенные выше имена простых импли-
кант. Переменное, именующее данную простую импликанту,
принимает, по определению, значение 1, если данная простая
импликанта выбирается для покрытия рассматриваемой еди-
единицы карты Карно.
Записав все элементарные дизъюнкции, составим из них
КНФ. Рассмотрим карту Карно на рис. 6.13. Обозначив
Ax0),
получим
(KxVKe) A (KiVK2) А (К2УК3) А
. F.13)
Тем самым мы образуем вспомогательную функцию (пред-
(представленную КНФ вида F.13)), называемую функцией Па-
Патрика. Раскрывая скобки в КНФ F.13) и используя тожде-
тождества булевой алгебры (в частности, тождество поглощения),
получим ДНФ, в которой каждая элементарная конъюнкция со-
соответствует некоторой тупиковой ДНФ и, наоборот, каждой
тупиковой ДНФ может быть сопоставлена одна из этих конъ-
конъюнкций.
Для нашего примера поступим так: вычислим конъюнкцию
первой и второй скобки в выражении F.13), а также третьей и
четвертой, пятой и шестой скобок, после чего получим
(Кг V КХК2 V К6Кг V КеК2)А
А (К2К3 V К2К4 УК3У КгК4)А
F.14)
422 6. БУЛЕВЫ ФУНКЦИИ
Используя тождества поглощения, в первой скобке в фор-
формуле F.14) мы можем удалить все члены, содержащие ifi, во
второй скобке — все члены, содержащие Кз, в третьей скоб-
скобке — все члены, содержащие К^. Проделав это, раскрыв все
три скобки и применив еще раз поглощение, окончательно по-
получим
F.15)
Элементарные конъюнкции в F.15) определяют тупиковые
ДНФ. Более того, так как в данном случае отсутствуют ядро-
ядровые импликанты, найденные конъюнкции исчерпывают тупи-
тупиковые ДНФ. Первая тупиковая ДНФ состоит из конъюнкций
К\, K$ и #5, т.е. имеет вид
Точно так же определяются остальные тупиковые ДНФ.
Обоснование описанного выше алгоритма может быть полу-
получено из следующих соображений. Функция Патрика, предста-
представленная КНФ, принимает значение 1 тогда и только тогда, ко-
когда каждая элементарная дизъюнкция принимает значение 1. А
элементарная дизъюнкция принимает значение 1 в том и только
в том случае, когда хотя бы одно ее переменное принимает зна-
значение 1. Согласно определению функции Патрика, это значит,
что хотя бы одна простая импликанта выбрана для покрытия
соответствующей единицы на карте Карно. Поскольку таким
образом перебираются все не покрываемые ядром единицы кар-
карты Карно, то гарантируется эквивалентность искомой ДНФ
исходной СДНФ. Однако, когда функция Патрика представле-
представлена ДНФ и мы выбираем в точности одну из ее элементарных
конъюнкций, полагая, что все входящие в нее переменные рав-
равны 1, мы тем самым из всех возможных вариантов покрытия
каждой единицы на карте Карно выбираем в точности один ва-
вариант. Значит, полученная в результате такого выбора ДНФ
6.6. Построение минимальных ДНФ
423
для исходной (минимизируемой) СДНФ действительно будет
тупиковой.
Но нужно заметить, что перечисление тупиковых ДНФ
является самым неприятным и трудоемким этапом всего ал-
алгоритма минимизации. Если число единичных клеток карты
Карно, не покрываемых ядром, достаточно велико, то функция
Патрика будет весьма сложной и ее упрощение сопоставимо по
трудоемкости со всем процессом минимизации.
4. Отыскание среди тупиковых ДНФ кратчайших
и минимальных. Среди найденных тупиковых ДНФ нахо-
находят кратчайшие и минимальные. Можно легко показать, что
минимальная ДНФ всегда является кратчайшей, но обратное
неверно. Так, х\Х2 V Х2 = х\ V#2 и первая ДНФ кратчайшая,
но не минимальная. Действительно, легко сообразить, что
вторая из записанных ДНФ минимальна. Следовательно, пред-
представляемую ею функцию нельзя представить ДНФ, содержащей
менее двух элементарных конъюнкций. Но в первой ДНФ три
литерала, а во второй — два. Из пяти тупиковых ДНФ, соот-
соответствующих функции Патрика F.15), кратчайшими являются
две. Каждая из них минимальна, так как обе они имеют оди-
одинаковое число литералов.
Пример в, 14. Рассмотрим карту Карно на рис. 6.15.
хООх (К2) xxOl (K3) 11x1 (К4)
Рис. 6.15
424 6. БУЛЕВЫ ФУНКЦИИ
В результате проведения склейки получим следующую со-
сокращенную ДНФ*:
Х\Х$ V Х\Х2 V Х2Х4 V #2#3 V Ж3Ж4
Ядро составляют склейки (простые импликанты) x\x$ и
xi х2.
Шесть клеток, содержащих единицу, на карте Карно оста-
остаются непокрытыми ядровыми склейками. Для неядровых скле-
склеек (обозначенных К\, ..., Kq) составляем функцию Патрика в
виде
Преобразуя ее аналогично функции F.13), получаем
Имеем, следовательно, пять тупиковых ДНФ. Запишем их, для
наглядности, так:
Х2Х4
Х2Х3
Х2Х3 V X3X4 V X1X2X3
ядро
Из этих пяти тупиковых ДНФ кратчайшими являются пер-
первая и вторая. Из них, в свою очередь, минимальной является
первая, так как она содержит на один литерал меньше.
В итоге получаем минимальную ДНФ в виде
"Обратим еще раз внимание на то, что каждый выделяемый прямоуголь-
прямоугольник на карте Карно имеет площадь, равную некоторой степени двойки.
Поэтому, например, три соседние единичные клетки не могут быть объ-
объединены в один прямоугольник, а их „накроют" два прямоугольника пло-
площадью 2, пересекающиеся по одной клетке.
6.6. Построение минимальных ДНФ 425
В данном случае минимальная ДНФ оказалась единственной,
хотя, как это мы видели в ранее разобранных примерах, в
общем случае могут существовать несколько минимальных
ДНФ. #
Техника карт Карно является удобным и наглядным (при
определенных ограничениях на число переменных минимизи-
минимизируемой функции) способом реализации алгоритма Квайна —
Мак-Клоски. Но существуют и другие способы проведения
склейки, т.е. получения сокращенной ДНФ для исходной функ-
функции. Одним из таких способов является чисто алгебраический
метод Блейка, состоящий в том, что к любой ДНФ, предста-
представляющей функцию, применяются следующие тождества:
УхК2 = хКг УхК2УКХК2,
\К\ V К\К2 = К\.
Первое из тождеств F.16) называют тождеством (или
правилом) обобщенного склеивания, второе — тожде-
тождеством (или правилом) поглощения.
„Технология" использования метода Блейка такова: приме-
применяют тождество обобщенного склеивания до тех пор, пока не
перестанут появляться новые элементарные конъюнкции (вида
К\К2). После этого применяют тождество поглощения*.
Как только сокращенная ДНФ тем или иным способом най-
найдена, приступают к нахождению ядра. Ядро можно определить
(без использования карты Карно) с помощью так называемой
таблицы Квайна. Столбцы этой таблицы соответствуют
элементарным конъюнкциям исходной СДНФ, а строки — про-
простым импликантам сокращенной ДНФ. На пересечении строки
и столбца проставляется знак „ + " (плюс), если простая им-
пликанта данной строки покрывает элементарную конъюнкцию
данного столбца. Ядро вычисляется так: отмечаем столбцы с
*См.: Гаврилов Г.П., Сапоженко А.А.
426
6. БУЛЕВЫ ФУНКЦИИ
единственным знаком „ + ", тогда простые импликанты тех и
только тех строк, в которые попал этот знак, образуют ядро.
Для примера 6.13.6 (см. рис. 6.14) получим таблицу Квайна,
изображенную на рис. 6.16.
Oxxi
Oxix
10X0
хою
1X00
0001
+
*
ООП
+
+
0010
+
+
0101
+
*
0111
+
+
оно
+
*
1100
+
*
1000
+
+
1010
+
+
Рис. 6.16
(В целях экономии места элементарные конъюнкции в таблице
заменены цифровыми обозначениями соответствующих вершин
и граней булева куба — точно так же как при обозначении
прямоугольников на картах Карно. Ядровые импликанты
выделены жирным шрифтом.)
По таблице Квайна можно составить и функцию Патрика
для перечисления тупиковых ДНФ. Для этого нужно отметить
все столбцы таблицы, в которых на пересечении со строками,
соответствующими ядровым импликантам, не стоит знак и + ".
Для разбираемого примера таковым является только послед-
последний столбец. Чтобы покрыть соответствующую элементарную
конъюнкцию СДНФ, можно выбрать одну из двух простых им-
пликант: Ж1Ж2Х4 или ?2Жз#4-
В заключение рассмотрим очень кратко применение карт
Карно к построению минимальных ДНФ частичных буле-
булевых функций, т.е. частичных отображений из множества
{0,1}п в множество {0,1}.
6.6. Построение минимальных ДНФ
427
Частичная булева функция может быть задана посредством
карты Карно, в которой кроме клеток с единицами и пустых
клеток будут клетки, заполненные прочерками (-). Такой
прочерк означает, что на соответствующем наборе функция не
определена.
Склейка для частичной функции (заданной картой Карно)
проводится таким образом, что выделяются прямоугольники
максимальной площади (содержащие 2к клеток, для некоторо-
некоторого fc), каждая клетка которых содержит либо единицу, либо
прочерк, причем существует по крайней мере одна единичная
клетка.
Пример 6.15. Пусть частичная функция /(#ъ#2>#з) зада-
задана картой Карно, приведенной на
рис. 6.17. Прямоугольник макси-
максимальной площади (равной 4), со-
состоящий из единицы и прочерков,
записывается как Охх. Следова-
Следовательно, минимальная ДНФ для за-
заданной функции будет Щ. #
По поводу рассмотренного при-
примера возникает такой вопрос: почему не принят во внимание
другой прямоугольник (площади 2), содержащий клетку с еди-
единицей и клетку с прочерком: хОО? Связано это вот с чем.
Перед тем как выделять упомянутые выше прямоугольники,
мы на самом деле доопределяем исходную частичную функцию
(получая обычную булеву функцию) так, чтобы в максималь-
максимальном числе клеток, в которых стоят прочерки (но не нули!),
появились единицы. Точнее говоря, среди прямоугольников
(с прочерками), содержащих данную единицу, выбирают для
замены прочерков единицами такой, который имеет макси-
максимальную площадь. Прочерки же в остальных прямоугольниках
заменяют нулями.
В примере 6.15 мы доопределяем исходную функцию тале,
что получается функция /i, задаваемая картой Карно, приве-
0
1
00
A
-
01
-
/
11
-
10
-J
Охх
Рис. 6.17
428
6. БУЛЕВЫ ФУНКЦИИ
\*2*з
0
1
00
A
01
1
1
f
11
1
1
10
1)
0
1
00
т
1
01
11
10
Охх
Рис. 6.18
хОО
Рис. 6.19
денной на рис. 6.18. Эта функция имеет минимальную ДНФ
х\. Следовательно, и частичная исходная функция может быть
представлена такой ДНФ, поскольку на всех наборах, на кото-
которых она определена, она принимает такое же значение, как и
функция /i.
Конечно, мы могли бы доопределить функцию / по-друго-
по-другому, так, чтобы получилась функция /2, заданная картой Карно,
приведенной на рис. 6.19. Ясно, что /г =^2^з? поэтому и ча-
частичная функция / может быть определена такой ДНФ. Но эта
ДНФ не минимальна для данной частичной (именно частич-
частичной!) функции, поскольку первый способ доопределения дал
ДНФ, содержащую лишь один литерал.
Таким образом, в отличие от минимизации булевых функ-
функций при минимизации частичных булевых функций не следует
выделять все максимальные прямоугольники с прочерками, со-
содержащие данную единичную клетку карты Карно, достаточно
выбрать произвольно любой из таких прямоугольников. Но, ко-
конечно, не нужно забывать о том, что каждая единица на карте
должна быть покрыта некоторой склейкой.
Пример 6.16. Для карты на рис. 6.20 следует взять обе
склейки на четыре позиции: 00х х и х хОО, получив для задан-
заданной этой картой частичной функции минимальную ДНФ в виде
Заметим, что без использования склеек с прочерками мы
вообще не могли бы минимизировать данную функцию. Нуж-
6.7. Теорема Поста,
429
но также отметить, что не все-
всегда использование „частичности"
функции позволяет получить ми-
минимальную ДНФ для нее. Так,
на представленной на рис. 6.20
карте в случае, если мы переме-
переместим нижнюю единицу на стро-
строку выше, обычная склейка на две
позиции дает лучший результат:
Ж1Ж3Ж4, а записанная выше ДНФ
уже не будет минимальной (и да-
даже кратчайшей).
00
01
и
10
00
PI
-
1
Jz
01
-
11
-
\
10
-)
ххОО ООхх
Рис. 6.20
6.7. Теорема Поста
В силу теоремы о представлении любой булевой функции
дизъюнктивной или конъюнктивной нормальной формой стан-
стандартный базис {V,-,""} является полным множеством. По-
Поскольку, согласно законам де Моргана, можно выразить конъ-
конъюнкцию через дизъюнкцию и отрицание, равно как и дизъюнк-
дизъюнкцию можно выразить через конъюнкцию и отрицание, то при
удалении из стандартного базиса одной функции, дизъюнкции
или конъюнкции, при сохранении отрицания, получим снова
полное множество.
Прежде чем рассматривать другие примеры полных мно-
множеств, установим один важный факт.
Теорема 6.3. Пусть F и G — некоторые множества
булевых функций, причем F — полное множество. Тогда, если
каждая функция из F может быть представлена некоторой
формулой над множеством G, то G — полное множество.
М Из условия теоремы следует, что каждая функция / 6 F
может быть представлена некоторой формулой Ф над G, т.е.
F.17)
430 6. БУЛЕВЫ ФУНКЦИИ
Докажем, что всякая формула над F эквивалентна неко-
некоторой формуле над G, т.е. всякая функция <р, представляемая
формулой над F, может быть представлена также и некоторой
формулой над G. Доказательство проведем по такой схеме:
сначала убедимся в справедливости утверждения для „базис-
„базисных" формул, т.е. для переменных и констант из F, а затем в
предположении, что оно уже доказано для формул Фх, ..., Фп,
где п ^ 1, докажем его для любой формулы вида /(Фх,...,Фп),
где / 6 F. Такой метод доказательства называют доказатель-
доказательством индукцией по построению формулы.
Пусть (р — какая-то формула над F. Бели (р = ж, где
х — булево переменное из множества X, то, поскольку каждое
переменное есть, по определению, и формула над G, функция
(р представляется формулой над G.
Если (р есть константа из F, то представляющая <р формула
над G существует ввиду F.17).
Рассмотрим формулу над F вида /(Ф1,...,ФП), где п > 0,
/GF, а Фь ..., Фп — формулы над F. Согласно предпо-
предположению индукции, каждая формула Ф», г = 1, п, может быть
заменена эквивалентной ей формулой в* над G (т.е. имеет ме-
место тождество Ф* = 6* над FUG). Тогда, используя правила
эквивалентных преобразований формул (см. теорему 6.1), по-
получим тождество
а в соответствии с F.17) будем иметь
...,6п). F.18)
Правая часть тождества F.18) и есть формула над G,
эквивалентная исходной формуле над F.
Поскольку в силу полноты множества F любая булева функ-
функция может быть представлена некоторой формулой над F, а
любая такая формула, как мы только что доказали, эквива-
эквивалентна некоторой формуле над G, то любая булева функция
6.7. Теорема. Поста, 431
может быть представлена некоторой формулой над G, что и
доказывает полноту множества G. >
Пример 6.17. Рассмотрим базис Жегалкина {©, •, 1}.
Чтобы доказать полноту этого множества, заметим, что
хУу = х-у®х®у, ж = жф1,
т.е. каждый элемент стандартного базиса может быть пред-
представлен формулой над базисом Жегалкина. Отсюда и следует
(ввиду полноты стандартного базиса и теоремы 6.3) полнота
базиса Жегалкина. #
Любую формулу над базисом Жегалкина называют поли-
полиномом Жегалкина. Полином Жегалкина от п переменных
может быть записан в виде
где коэффициенты полинома Oiii2...im € {0,1} индексированы
всеми возможными подмножествами множества {1, 2, ..., п}
(коэффициент ао соответствует пустому множеству). В част-
частности, при п = 3 будем иметь:
(общий вид полинома Жегалкина от трех переменных). Фор-
Формула вида
п
])Г (mod 2) aiXi ф a0 F.20)
г=1
называется полиномом Жегалкина первой степени от
переменных. В таком полиноме отсутствуют инелинейные"
слагаемые, т.е. все коэффициенты, индексированные более чем
одноэлементными подмножествами, равны 0 (и вместе с ними
равны 0 все слагаемые, содержащие конъюнкции переменных).
432 б. БУЛЕВЫ ФУНКЦИИ
Можно доказать следующее достаточно простое, но важное
утверждение.
Теорема 6.4. Полином Жегалкина для любой булевой
функции определен однозначно.
Для функций от небольшого числа переменных (не пре-
превышающего 4) можно использовать метод неопределенных
коэффициентов, позволяющий получить полином Жегалки-
Жегалкина данной функции. Проиллюстрируем этот метод на примере.
Пример 6.18. Пусть вектор значений булевой функции
/ равен 11001011. Найдем полином Жегалкина, представля-
представляющий /. Поскольку размерность вектора значений / равна
23 = 8, то / задана как функция от трех переменных. Тогда
она представляется некоторым полиномом Жегалкина третьей
степени, общий вид которого дает формула F.19). Наша за-
задача — найти такие значения коэффициентов этого полинома,
при которых он представляет функцию /. Ясно, что значение
функции / на наборе 000 равно коэффициенту оо в формуле
F.19). Но, согласно заданному вектору значений, оно равно 1.
Следовательно, ао = 1. Далее,
/@,0,1) =а
откуда, решая уравнение относительно аз в поле Ъ<ъ, получим
аз = 0;
/@,1,0) =02 01=0,
т.е. п2 = 1;
/A,0,0)= <ц ©1 = 1,
и а\ = 0. Чтобы найти коэффициенты ai2, а\з и агз, нужно
рассмотреть значения функции на наборах 110, 101 и 011
соответственно. Так, для первого набора получим
/A,1,0) = ai2#i#2 © ai^i © a2^2 Ф ao =
© ао = ai2 Ф1Ф1 =
6.7. Теорема Поста 433
(сумма по модулю 2 любого четного числа равных слагаемых
равна 0). Поскольку в то же время /A,1,0) = 1, то аи = 1.
Аналогично
/A,0,1) =
откуда ахз = 1;
/(О,1,1)=а2з0а2еао = О,
и, так как а2 = ао = 1, а2з = 0. Наконец,
/A,1,1) = ai23 0 аг2 © ai3 ф a2 0 a0 = аш = 1.
Итак,
/ = Ж1Ж2#з 0 Я1#2 © Х\Х$ © Х2 © 1. #
Как видно из примера 6.18, суть метода неопределенных
коэффициентов состоит в следующем. Записывая полином Же-
галкина сначала в общем виде, с неопределенными коэффици-
коэффициентами, мы выражаем значение полинома на фиксированных
наборах через коэффициенты и приравниваем его заданному
значению функции. Начинаем с нулевого набора и находим
коэффициент ао, равный значению заданной функции на ну-
нулевом наборе. Зная его, из рассмотрения значений фукнции
на наборах, содержащих в точности одну единицу, находим ко-
коэффициенты а,- при „одиночных" переменных (коэффициенты
„линейной части" полинома). Зная их, из рассмотрения значе-
значений функции на наборах, содержащих в точности две единицы,
находим коэффициенты при конъюнкциях двух переменных и
т.д. При этом выполняются вычисления и решаются простей-
простейшие линейные уравнения в поле вычетов по модулю 2.
Пример 6.19. а. Рассмотрим множество {|}, состоящее
из единственной функции (штриха Шеффера). Полнота этого
множества следует из легко проверяемых тождеств
434 6. БУЛЕВЫ ФУНКЦИИ
б. Полнота множества {4-}, единственным элементом кото-
которого является стрелка Пирса, проверяется аналогично. #
Теперь мы сформулируем и докажем критерий (необходи-
(необходимое и достаточное условие) полноты для произвольного мно-
множества булевых функций. Для этого нам потребуется сначала
рассмотреть некоторые специальные множества функций.
Определение 6.8. Функцию / называют функцией, со-
сохраняющей константу О (соответственно константу 1),
если /@) = 0 (соответственно: /A) = 1), где 0 — нулевой, а 1 —
единичный наборы значений переменных функции /.
Например, мажоритарная функция является функцией, со-
сохраняющей и константу 0, и константу 1. Отрицание не со-
сохраняет ни 0, ни 1, а эквивалентность сохраняет 1, но не
сохраняет 0. Множество всех функций, сохраняющих констан-
константу 0 (константу 1), обозначается Го (соответственно Т\).
Наборы й и 5 из булева куба Шп = {0,1}п (для произвольно-
произвольного фиксированного п) будем называть взаимно противопо-
противоположными, говоря при этом также, что набор а есть инверсия
(или отрицание) набора а (в силу единственности дополне-
дополнения любого элемента булевой алгебры набор 5 будет, очевидно,
инверсией набора S).
Определение 6.9. Функцию g E V<i,n называют двой-
двойственной к функции f ? P2,n) если для всякого 2 ? {0,1}п
(га > 0) имеет место
д(а) = /E).
Полагаем также, что константа 0 является двойственной к
константе 1 и наоборот.
Пример 6.20. а. Стрелка Пирса есть функция, двойствен-
двойственная к штриху Шеффера, так как
х iy = хУ у = х - у = х\у.
6.7. Теорема Поста 435
б. Сумма по модулю 2 двойственна к эквивалентности, так
как
Эти две функции являются и отрицанием друг друга, но
неверно в общем случае, что функция д, будучи отрицанием
функции /, двойственна к /: штрих Шеффера не есть функция,
двойственная к конъюнкции, а стрелка Пирса не есть функ-
функция, двойственная к дизъюнкции, но конъюнкция двойственна к
дизъюнкции и наоборот, а стрелка Пирса двойственна к штри-
штриху Шеффера и наоборот. #
В общем случае в силу уже упомянутого свойства единствен-
единственности дополнения в булевой алгебре функция Л, двойственная
к функции д, которая двойственна к /, равна /.
Определение 6.10. Функцию / ? Т^п называют само-
самодвойственной, если она двойственна к себе самой, т.е.
(V5G{0,l}n)(/E)=7E)),
или
(V5€{0,l}n)(/E) = 7E)).
Таким образом, функция самодвойственна тогда и только
тогда, когда на взаимно противоположных наборах она при-
принимает взаимно противоположные значения. Следовательно,
для того чтобы убедиться в несамодвойственности заданной
функции /, достаточно найти хотя бы одну пару взаимно про-
противоположных наборов а и а, таких, что значения функции на
них совпадают, т.е. /E) = /E). Так, мажоритарная функция
является самодвойственной, а эквивалентность — нет, посколь-
поскольку при 2 = @, 0H~0 = 1и1~1 = 1.
Множество всех самодвойственных функций (при всех п ^ 1)
обозначим S.
Определение 6.11. Функцию / 6 Р2,п называют моно-
монотонной, если для любых наборов 5, /3 Е Вп, таких, что а < /3,
имеет место /E) < /(/?).
436 6. БУЛЕВЫ ФУНКЦИИ
Другими словами, функция монотонна тогда и только то-
тогда, когда для любого набора 5 имеет место следующее свой-
свойство: если значение функции на наборе а равно 1, то оно равно 1
и на всех наборах, строго больших (по отношению булева по-
порядка на Вп) набора 5. Любой минимальный (относительно
того же порядка) набор 5, для которого значение /(а) мо-
монотонной функции / равно 1, называют нижней единицей
функции /. Очевидно, что вектор значений монотонной бу-
булевой функции полностью определяется множеством ее нижних
единиц*. Мажоритарная функция монотонна, и множество ее
нижних единиц есть {011,101,110}. Штрих Шеффера — не-
немонотонная функция, так как 00 < 11, но 0|0 = 1, а 1|1 = 0.
Множество всех монотонных функций принято обозначать че-
через М.
Определение 6.12. Функцию / Е 7*2,п называют линей-
линейной, если она может быть представлена полиномом Жегалкина
первой степени от п переменных, т.е. формулой вида F.20).
Множество всех линейных функций принято обозначать
через L.
Любая булева константа и любая проектирующая функция
х являются линейными функциями. Такова, разумеется, сумма
по модулю 2. Отрицание также линейно, ибо х = х © 1. Конъ-
Конъюнкция и дизъюнкция не являются линейными функциями, так
как не могут быть представлены полиномом Жегалкина первой
степени (см. теорему 6.4).
Определение 6.13. Множества функций То, Ti, 5, М, L
называются классами Поста.
Замечание 6.9. Каждый класс Поста состоит из функций
с соответствующим свойством для любого числа переменных.
'"Нетрудно понять, что множество нижних единиц монотонной функции
/ есть множество всех минимальных элементов множества С} — консти-
тпуентп единицы функции /.
6.7. Теорема Поста 437
Можно доказать также, что если функция / принадлежит како-
какому-то классу Поста С, то и любая функция, равная функции /,
принадлежит этому же классу. Другими словами, добавление
или удаление фиктивных переменных не выводит за пределы
любого из классов Поста.
Полезно еще заметить, что любая проектирующая функция
х принадлежит одновременно всем пяти классам Поста. Дей-
Действительно, если f(x) = х, то /@) = 0 и /A) = 1, т.е. / Е ТоПТ\.
Отсюда же вытекает и самодвойственность функции х. Мо-
Монотонность следует из того, что 0<1 и /@) = 0 < /A) = 1.
Линейность очевидна.
В то же время существуют функции, не принадлежащие ни
одному из классов Поста. Таков, например, штрих Шеффера.
Все свойства, кроме нелинейности, следуют прямо из таблицы
этой функции. Нелинейность же доказывается выводом поли-
полинома Жегалкина для штриха Шеффера:
что не есть полином Жегалкина первой степени. #
Фундаментальным свойством каждого класса Поста являет-
является его замкнутость (в смысле определения 6.3). Это означает
для любого из классов Поста С, что всякая суперпозиция над
С снова есть элемент С.
Теорема 6.5. Каждый класс Поста замкнут.
< Нужно для каждого класса Поста С Е {To, Ti, 5, М, L} дока-
доказать, что замыкание [С] множества булевых функций С совпа-
совпадает с С. Пусть /(gi,...,<7п) — какая-то суперпозиция над С.
Обозначим ее через (р. Без ограничения общности можно счи-
считать, что все функции /, #i, ..., gn Е V<i,n (для некоторого п).
Рассуждаем, используя индукцию по определению суперпо-
суперпозиции. Если для каждого г = 1, п функция gi = ж», где я» —
переменное, то <р = /(#i,...,#n) € С. Предположим, что в су-
суперпозиции (р все функции gi есть элементы класса Поста С
438 6. БУЛЕВЫ ФУНКЦИИ
(в частности, это может быть и соответствующая проектиру-
проектирующая функция, которая ввиду замечания 6.9 принадлежит всем
классам Поста). Докажем, что и ср = /(<7i, • • • >0п) Е С.
1. Если С = Го, то^@) = /(Л@),...,Л@)) = /@1...,0)=0>
так как /, gi, ..., дп Е То. Следовательно, (р Е То.
2. При С = Т\ рассуждаем точно так же.
3. Пусть G = 5. Фиксируем произвольно набор 5 Е {0,1}п.
Вычислим (используя само двойственность всех функций):
Следовательно, (р Е S.
4. С = М. Берем произвольно наборы 5 и /5 так, что S
Докажем, что </? G М. Имеем
так как все функции ft, г = 1, п, монотонны и тем самым вектор
E1 B) > • • • 1 Рп B)) не больше вектора (уi (Д),..., дп (Д)), а функция
/ также монотонна. Тогда ясно, что tpE M.
5. Если же С = X, то очевидно, что при подстановке в линей-
линейную функцию (полином Жегалкина первой степени) вместо ее
переменных произвольных линейных функций получится снова
линейная функция. Итак, мы доказали замкнутость каждого
класса Поста. >
Докажем теперь теорему, характеризующую одно важное
свойство немонотонных функций.
Теорема 6.6. Если функция / не является монотонной, т.е.
М, то найдутся два таких набора S, /?, что
a = (ai, ..., c*i_i, 0, ai+i, ..., an),
6.7. Теорема Поста 439
и /E) = 1, f(/3) = 0, т.е. эти два набора различаются значения-
значениями в точности одной компоненты, а значение функции равно О
на большем наборе и равно 1 на меньшем.
4 Так как функция / не является монотонной, то найдутся
такие два набора у и S, что у < <5, но /G) = 1, f(S) = 0. Строгое
неравенство у < S означает, что найдутся такие номера (не
меньше одного) 1 < %\ < %2 < -.. < t* ^ п, что
7 = GЬ • • •, 7*i-l» 0,7п+Ь • • •»7*2-1» 0» • • • »7*а+1» • • •»
= G1» •••»7u-ii l»7»i+ii •••»7*2-1» 1» •••»7*2+1»
т.е. все компоненты наборов, кроме выделенных, с номерами
*1» ^2? •••? *А; соответственно совпадают, а все компоненты с
выделенными номерами у меньшего набора равны 0, а у боль-
большего равны 1. Построим монотонно возрастающую последова-
последовательность наборов 7 ^ 7о < 7i < 72 < • • • < Ik = ^ так, что для
каждого 5 G {1,2,..., к} набор ys получается из набора 7$-1 за-
заменой нулевого значения компоненты с номером is единичным.
Поскольку /G) = 1, a f(S) = 0, то обязательно найдется такое
5 Е {1,2,..., к}, что /G*-i) = 1, a /Gs) = 0 (на наборе 7*-1 зна-
значение функции еще равно 1, а на наборе ys оно уже равно 0).
Полагая a = 7s-1 и /3 = 7s? получим доказываемое. >
Теорема 6.7 (критерий Поста). Множество F булевых
функций полно тогда и только тогда, когда оно не содержится
целиком ни в одном из классов Поста.
< Необходимость условия теоремы доказывается просто: если
бы для некоторого класса Поста С выполнялось F С С, то вся-
всякая суперпозиция над F, согласно теореме 6.5, снова лежала бы
в С. Между тем существуют функции, не содержащиеся ни в
440 б. БУЛЕВЫ ФУНКЦИИ
одном из классов Поста, например штрих Шеффера (см. при-
пример 6.9). Таким образом, нашлась бы функция, которую нельзя
представить в виде суперпозиции над F, что противоречит
предположению о полноте F.
Переходим к доказательству достаточности условия теоре-
теоремы. Для доказательства полноты множества F, удовлетворяю-
удовлетворяющего условию теоремы, построим формулы над F для функций
отрицания и конъюнкции, поскольку, как было замечено вы-
выше, множество, образованное этими функциями, полно. Тогда
в силу теоремы 6.3 будет полным и множество F.
Для немонотонной функции /м G F\ М, согласно теоре-
теореме 6.6, найдутся два таких набора S и /3, что
5 = (аь ..., а,_1, 0, а*+1, ..., аЛ),
Тогда х = /м(<*1, • • •,oti-i,ж,ai+i,...,а„), т.е. отрицание мо-
может быть получено из немонотонной функции подстановкой
вместо некоторого ее переменного Х{ переменного х, а вме-
вместо остальных переменных констант c*i, ..., а«_1, c*i+i> • • • > ап?
определяемых выбранными выше наборами S и /3. Но, вообще
говоря, система F может и не содержать констант. Поэтому
константы 0 и 1 необходимо представить некоторыми форму-
формулами над F.
Рассмотрим два случая.
Первый случай. В F существует функция /о, не
сохраняющая константу 0, которая сохраняет константу 1;
или существует функция /i, не сохраняющая константу 1, но
сохраняющая константу 0.
Если существует функция /о ^ То и /о Е Ti, то константа 1
представляется формулой
6.7. Теорема Поста 441
так как /о(О,... ,0) = 1 и /оA,..., 1) = 1. Чтобы выразить кон-
константу 0, используем любую функцию д G F, не сохраняющую
константу 1:
0 = 0A,..., 1) = g{fo{x,..., ж),..., /0(х,..., х)).
Если же указанная функция /о не существует, но найдется
функция /i ? То \ Т\, то константы представляем формулами
над F аналогично (двойственным образом).
Второй случай. Любая функция из F, не сохраняющая
константу 0, не сохраняет и константу 1, и, наоборот, любая
функция из F, не сохраняющая константу 1, не сохраняет и
константу 0.
Пусть /о(О,... ,0) = 1, а /оA,..., 1) = 0. Тогда мы получаем
возможность представить отрицание следующей формулой:
Переходим к построению формул для констант, так как они
потребуются нам далее при построении формулы для конъ-
конъюнкции. Чтобы представить константы формулами над F,
воспользуемся несамодвойственной функцией fs из F. Для
этой функции найдется такой набор 5, что /sE) = fs E). Вве-
Введем функцию от одного переменного h(x) = fs(xai,...,xan) (в
предположении, что 5 = (ai, ... r an)). Легко видеть, что h@) =
) = fs(&) = Ml)> так как Д-*101 любого a € {0,1}
* = 0; i<r = /
0, a = l, \0, <r =
Итак, значение /i(x) есть константа. Если она равна 0, то
константу 1 представляем через функцию, не сохраняющую
константу 0; если же h(x) = 1, то константу 0 представляем
через функцию, не сохраняющую константу 1.
Опишем построение формулы для конъюнкции. Берем не-
нелинейную функцию fi из F. В полиноме Жегалкина для этой
442 6. БУЛЕВЫ ФУНКЦИИ
функции выберем произвольное нелинейное слагаемое, содер-
содержащее наименьшее число переменных; пусть это будет слага-
слагаемое Xix, ..., Xik при 2 < к ^ п. Вместо каждого переменного
хт функции /х,, где т ? {гх,..., г&}, подставим константу 0, т.е.
заменим нулем все переменные, которые не вошли в выбранную
ранее конъюнкцию. Получим яредуцированную" функцию
f'L = xix... xik © aix xix®...® aik xik ©o0 =
Заметим, что коль скоро мы уже представили константы фор-
формулами над F, то функция ffL тоже представлена формулой
над F. Разобьем теперь множество переменных {xix,..., xik}
произвольно на две части: {xix,..., xim} и {xim+1,..., xik}, где
l^m^fe — 1, и заменим все переменные первой части пере-
переменным ж, а переменные второй части — переменным у. В
результате получим функцию от двух переменных
Ясно также, что функция х может быть представлена такой
формулой над F:
Х(*, У) = fb @,..., 0,^,0,..., 0,^,0,..., 0,
h im
у ,0,...,0, у ,0,...,0),
гт+1 ik
т.е. функция х получена из нелинейной функции Д G F путем
подстановки на место ее переменных с номерами ii, ..., гт
переменного ж, на место переменных с номерами tm+i, ...,
ifc — переменного у, а на место всех остальных переменных —
константы 0, уже представленной формулой над F (см. выше).
Определим функцию
ф(х,у) = х(х ®Ь,у © а) Ф аЪ® с.
6.7, Теорема, Поста
443
Таблица 6.6
Выразив эту функцию из полинома Жегалкина для х> получим
ф{х,у) = x(z®b,y©a)©ab®c =
= (ж0 Ь)(у © а) ф а(х ф 6) © Ь(у Ф а) © с© аЬф с =
= жу ф ах © 6у ф аб® ах ф абф Ьу ф абф с© аЬ© с = жу,
поскольку сумма по модулю 2 любого четного числа равных
слагаемых равна 0. Итак, функция ф и есть конъюнкция. Так
как прибавление к любой функции константы по модулю 2 есть
либо сама исходная функция, либо ее отрицание, а отрицание
уже представлено формулой над базисом F, то тем самым и
конъюнкция представлена такой формулой. >
Чтобы исследовать полноту конкретного множества функ-
функций F = {/i, /2,..., /п}, нужно построить так называемую кри-
критериальную таблицу (табл. 6.6).
Строки таблицы соответствуют
функциям исследуемого множества,
а столбцы — классам Поста. В ре-
результате анализа функций множе-
множества F клетки таблицы заполняют-
заполняются: если функция fo принадлежит
некоторому классу Поста С, то в
соответствующей клетке критери-
критериальной таблицы ставится знак „ + " (плюс), а если нет, то —
знак „ — " (минус). Множество F тогда полно, если и только
если в каждом столбце таблицы стоит хотя бы один знак „ — ".
Пример 6,21. а. Пусть F = {~, V, 0}. Ниже приведены ре-
результаты исследования элементов этого множества на принад-
принадлежность к классам Поста, а также
заполненная критериальная табли-
таблица (табл. 6.7).
При этом 1 = х ~ ж, так как
функция ~ (эквивалентность) не
сохраняет константу 0, но сохра-
сохраняет константу 1 (т.е. имеет место
/l
/2
1
/п
То
Ti
S
м
L
V
0
Го
—
+
+
Таблица
Ti
+
+
—
S
—
—
—
м
—
+
+
6.7
L
+
—
+
444 6. БУЛЕВЫ ФУНКЦИИ
первый случай из доказательства достаточности условия тео-
теоремы Поста). Константа 0 принадлежит самому множеству F.
Поскольку х = х ~ О, то ввиду полноты множества {V,"""} бу-
будет полным и рассматривамое множество. Конъюнкцию можно
представить формулой над F, следуя доказательтву теоремы
Поста. Берем единственную нелинейную функцию данного
множества, дизъюнкцию, и записываем для нее полином Же-
Жегалкина:
Xi V Х2 = Х\ • Х2 © Х\ © Х2-
Видно, что этот полином есть не что иное, как функция
х(жъ Х2) при а = Ь=1ис = 0. Следовательно,
х\ • х2 = х(#1 © 1>Ж2 ф 1) © 1.
Но так как х = х ~ 0, то х\ • х2 = ((#i ~ 0) V (хг ~ 0)) ~ 0. Этот
же результат (в данном конкретном случае) можно получить и
гораздо проще:
Х\ • Х2 = ^1 V Х2 = ((^1 ~ 0) V (Х2 ~ 0)) ~ 0.
Итак, исходное множество является полным.
Заметим, что это полное множество двойственно к базису
Жегалкина в том смысле, что каждая из его функций двой-
двойственна к соответствующей функции базиса Жегалкина: экви-
эквивалентность двойственна к сумме по модулю 2, дизъюнкция —
к конъюнкции, константа 0 — к константе 1. Полезно заме-
заметить также, что никакое собственное подмножество заданного
множества не будет полным.
б. Функция /i задана картой Карно (рис. 6.21), а вектор
значений функции /2 есть @,1,0,0).
Для функции /2 очень просто находятся ДНФ и полином
Жегалкина:
/2 = XiX2 = (#1 Ф 1)Я2 = XiX2 Ф Х2,
откуда следует нелинейность функции /2. Легко показать
также, что эта функция принадлежит лишь классу Tq.
6.7. Теорема Поста
445
00
01
11
10 "
00
1 1
01
{Г'
11
— —
-
10
¦
и
0x01
ОООх
01x1
^-1x10
^•10x0
хООО
Рис. 6.21
Так как /i@,0,0,0) = 1, a /i(l, 1,1,1) = 0, то функция Д не
сохраняет ни константу 0, ни константу 1. Далее, эта функция
несамодвойственна, поскольку Д@,1,1,1) =/i(l,0,0,0) = 1; не-
немонотонность ее следует из того, что, например, /i @,0,0,0) = 1,
но /i@,1,0,0) = 0. Вопрос о нелинейности функции /i оставим
пока открытым, так как даже из частично заполненной крите-
критериальной таблицы (табл. 6.8) вытекает, что множество {Д, /г}
полно.
Таблица 6.8
Л
/2
То
—
+
—
—
S
—
—
м
—
—
L
?
—
Формулы для отрицания и консталт находятся легко:
Формулу для конъюнкции проще всего построить прямо по
ДНФ для функции Д:
' #2 = /2(^1^2) =
? #2).
446 6. БУЛЕВЫ ФУНКЦИИ
Вернемся теперь к отложенному вопросу о нелинейности
функции /ь По приведенной на рис. 6.21 карте Карно можно
построить одну из минимальных ДНФ, представляющих эту
функцию в виде
Подставляя в последнюю формулу 0 вместо xi, х вместо Х2,
1 вместо #з и у вместо х^ получаем
что доказывает нелинейность функции /i и одновременно пол-
полноту множества {/i}.
Константы же можно представить формулами над базисом
{/i}, используя несамодвойственность функции /i (см. разбор
второго случая в доказательстве достаточности условия тео-
теоремы Поста): мы уже видели, что Д@,1,1,1) = /i(l,0,0,0) = 1,
т.е. набор а из упомянутого места в доказательстве теоремы
Поста есть 0111, и тогда функция Л, фигурирующая в том же
месте доказательства и равная в данном случае константе 1,
будет иметь вид
Но так как х = /i(#,#,?,ж), то получаем
1 = fi(fi{x,x,x,x), х, х, ж),
0 = h{f\{h{x,x,x,x),x,x,x),
Подставив эти формулы в написанную выше формулу для
конъюнкции, получим окончательно формулу над базисом {/i}
для конъюнкции. Мы не выписываем эту формулу ввиду ее
громоздкости.
6.8. Схемы из функциональных элементов 447
6.8. Схемы
из функциональных элементов
Представлению булевых функций формулами можно при-
придать следующий „инженерно-конструктивный" смысл. Будем
рассматривать формулу Ф(ж1,...,жп) над каким-то произволь-
произвольно фиксированным множеством F как „черный ящик", некое
устройство, на вход которого подаются всевозможные наборы
значений переменных, а на выходе появляются соответствую-
соответствующие этим наборам значения функции /, представляемой фор-
формулой Ф (рис. 6.22).
Рис. 6.22
Чтобы понять, как устроен „черный ящик", мы должны ра-
разобрать процесс построения формулы из подформул. Добира-
Добираясь до „базисных" подформул, т.е. элементов множества F, мы
приходим к „кирпичикам", структурным элементам, из кото-
которых собран „черный ящик", вычисляющий функцию /. Каждая
функция „базиса" F вычисляется соответствующим „узлом",
который рассматривается как мельчайшая структурная едини-
единица нашего „черного ящика", и его внутренняя структура уже
не анализируется.
Пример 6.22. Выберем в качестве множества F стан-
стандартный базис. Тогда формула над стандартным базисом,
представляющая функцию ~ (эквивалентность), строится сле-
следующим образом:
F.21)
448 6. БУЛЕВЫ ФУНКЦИИ
Вычисление по этой формуле (и процесс ее построения из
элементов стандартного базиса) можно схематически изобра-
изобразить так, как показано на рис. 6.23.
Рис. 6.23
Переменное х\ (точнее, значение этого переменного) по-
подается на вход структурного элемента, называемого инвер-
инвертором (рис. 6.24, о) и вычисляющего отрицание. Снимаемое
с выхода инвертора отрицание жх, т.е. функция жх, подается
на один из входов конъюнктора (рис. 6.24,5), на второй
вход которого подается переменное Х2* На выходе конъюнк-
конъюнктора появляется функция х\Х2- Аналогично прослеживается
вычисление функции xix2* Обе эти функции подаются на вхо-
входы дизъюнктора (рис. 6.24, в), с выхода которого снимается
функция х\Х2Ух\Х2 (это не что иное, как сумма по модулю 2:
#1 ®Х2). И наконец, эта функция подается на вход инвертора,
на выходе которого уже получается функция ~ (эквивалент-
(эквивалентность). #
а б в
Рис. 6.24
Таким образом, мы приходим к идее „схемы" — математи-
математической модели вычислителя булевой функции, представленной
некоторой формулой, собранного из структурных элементов,
6.8. Схемы из функциональных элементов 449
каждый из которых вычисляет одну из „базисных" булевых
функций. В общем случае „схема" вычисляет булев оператор,
причем каждая координатная функция этого оператора снима-
снимается с одного из выходов схемы.
Математически „схема" определяется как ориентирован-
ориентированный граф специального вида, в котором и вершины, и дуги
снабжены некоторыми метками.
Введем обозначение: если F — какое-то множество булевых
функций, то через F^ обозначаем подмножество F, состоящее
из всех функций от п переменных (n ^ 0).
Определение 6.14. Пусть фиксированы множества: F
(булевых функций) и X (булевых переменных).
Схемой из функциональных элементов над базисом
FUX (СФЭ), или просто схемой над базисом FU-X", так-
также (F,X)-схемой, называют бесконтурный ориентированный
граф (т.е. сеть), каждая вершина которого помечена одним из
элементов множества F U X так, что выполняются следующие
требования:
1) каждый вход сети помечен либо некоторым переменным
из X, либо некоторой константой из F^;
2) если вершина v сети помечена функцией f от п перемен-
переменных (т.е. / ? F(n)), то ее полустепень захода равна п, причем
на множестве дуг, заходящих в вершину
v, задана (взаимно однозначная) нумера-
ция, при которой каждая дуга получает х i4^ Лу
номер от 1 до п.
При изображении схем входы обо-
обозначаются кружочками, а вершины, не
являющиеся входами, — треугольника-
треугольниками, внутри которых записано обозначе-
обозначение функции, помечающей данную вер-
вершину. Выходы отмечаются „выходны-
„выходными" стрелками. На рис. 6.25 приведена рис# 5.25
СФЭ над базисом {|, ж, у}.
IS- 10061
450 6. БУЛЕВЫ ФУНКЦИИ
Бели базис подразумевается, то мы будем говорить просто
„схема". Кроме того, если множество переменных фиксировано
„раз и навсегда" и при рассмотрении различных схем мы меня-
меняем только множество функций F, то, как это мы делали, вводя
понятия формулы и суперпозиции над заданным базисом, будем
говорить о СФЭ над базисом F, полагая каждый раз, что под-
подразумевается однажды фиксированное множество переменных
X, которое (если это не вредит точности) не упоминается.
Определим теперь по индукции понятие булевой функции,
вычисляемой вершиной схемы.
Определение 6.15. Пусть задана СФЭ S над базисом
¦FU-X", множество вершин которой есть V.
1. Принимается, что каждый вход СФЭ вычисляет булеву
функцию, которой он помечен (т.е. некоторое переменное или
константу).
2. Бели вершина v EV помечена функцией / € F^n\ захо-
заходящая в нее дуга с номером г A < i ^ п) исходит из вершины
щ Е V, которая вычисляет функцию <#, то вершина v вычисляет
суперпозицию /(*/ъ... ,sn)-
Таким образом, если каждая вершина СФЭ над F вычисля-
вычисляет некоторую функцию, то порядок, в котором перечисляются
функции pi, ..., 0П, подставляемые на места переменных функ-
функции /, в общем случае существен. Естественно назвать булеву
функцию f от п переменных коммутативной, если она со-
сохраняет значение при произвольной перестановке ее перемен-
переменных. В этом случае мы можем не заботиться о нумерации дуг,
заходящих в вершину схемы, помеченную такой функцией.
Пример 6.23. Рассмотрим СФЭ на рис. 6.25. Вершины v\
и V2 — входы СФЭ. Эти вершины вычисляют соответственно
функции х и у. Тогда вершина г>з, равно как и вершина г>4,
согласно определению 6.15, вычисляет функцию х\у (штрих
Шеффера), а вершина v& (выход сети) — функцию
которая, как известно, равна конъюнкции х • у.
6.8. Схемы из функциональных элементов
451
ху
Рис. 6.26
СФЭ, изображенная на рис. 6.26, имеет два выхода, вычи-
вычисляющие функции (ж|ж)|B/|у) =хУуи (х\у)\(х\у) = х-у.
Определение 6.16. Булева функция, вычисляемая
СФЭ над базисом FU X, — это функция, вычисляемая каким-
либо из ее выходов.
Таким образом, СФЭ вычисляет ровно столько булевых
функций, сколько имеет выходов. СФЭ на рис. 6.25 вычисляет
одну функцию, а СФЭ на рис. 6.26 — две.
В общем случае, если {#i,..., хп} — множество всех пере-
переменных, которые служат метками входов схемы S над базисом
F\JXy имеющей m выходов, СФЭ S определяет отображение
булева куба Шп в булев куб Вт, т.е. булев оператор.
Замечание в. 10. В некоторых случаях функцию, вычисля-
вычисляемую данной СФЭ, определяют несколько иначе, полагая, что
это функция, вычисляемая любой вершиной из подмножества
выделенных вершин СФЭ. В частности, это могут быть и вы-
выходы. В любом случае договоримся из выделенных (в только
нто указанном смысле) вершин схемы проводить я выходную"
стрелку. #
15*
452
6. БУЛЕВЫ ФУНКЦИИ
Таким образом, каждая схема из функциональных элемен-
элементов вычисляет некоторый булев оператор, в частности, если
число выходов схемы равно 1, то она вычисляет некоторую бу-
булеву функцию.
Можно доказать и обратное: по любому булеву оператору
может быть построена СФЭ над базисом F, где F — полное
множество, вычисляющая данный оператор.
Пример 6.24. Зададим таблицей
булев оператор, отображающий В3 в
В2 (табл. 6.9).
Из таблицы легко увидеть, что
Xl
0
0
0
0
1
1
1
1
X2
0
0
1
1
0
0
1
1
Таблица
жз
0
1
0
1
0
i—l
0
1
У\
0
0
0
1
0
1
1
1
6.9
№
0
1
1
0
1
0
0
1
3/1 = Х\Х2
2/2 = Я1 © #2 © #3
(функция 2/1 есть не что иное, как ма-
мажоритарная функция от переменных
яь Х2, ?3) и выше написана минималь-
минимальная ДНФ для нее, см. пример 6.12).
Представим функцию у\ в базисе Жегалкина. Используя
законы де Моргана, получим
Учитывая, что х = х ф 1, будем иметь
Х\Х2 • Х\Хъ • Х2Х$ = (xiX2 Ф 1)(#1Яз © 1)(Я2ЯЗ ф 1) © 1 =
© #1#2 © Х\Х2Х^ Ф
© 1 © 1 =
(напомним, что сумма по модулю 2 любого четного числа
равных слагаемых равна 0).
Итак,
2/1 = Х\Х2 Ф Я1Жз Ф #2^3 = Х\Х2 Ф Яз(#1 Ф ^г).
СФЭ для булева оператора, заданного в табл. 6.9, над
базисом Жегалкина приведена на рис. 6.27.
6.8. Схемы из функциональных элементов
453
ух = ххх2 Ф {хх Ф х2)хг
Рис. 6.27
При проектировании СФЭ полезно иметь в виду числовой
параметр, называемый ее сложностью.
Сложность СФЭ — это число ее вершин, не являющихся
входами.
Приведенная на рис. 6.27 СФЭ над базисом Жегалкина
имеет сложность 5.
Рассмотрим теперь СФЭ для того же оператора над стан-
стандартным базисом.
По таблице (см. табл. 6.9) строим СДНФ для функции у29.
J/2 = Х\Х2Хз УХ\Х2Хъ V Ж1#2#3 V Х\Х2Х$.
Карта Карно для этой функции, изображенная на рис. 6.28,
показывает, что ее нельзя минимизировать (точнее, записанная
выше СДНФ и есть минимальная ДНФ для этой функции).
Но можно пойти по другому пути. Мы можем рассматри-
рассматривать табл. 6.9 как таблицу, определяющую частичную булеву
Функцию у2 = y2(xiiX2,xsyyi). Минимизируя эту функцию по
454
6. БУЛЕВЫ ФУНКЦИИ
Xl \
0
1
00
1
01
1
11
1
10
1
00
01
11
10
00
01
11
xxOl
О -
Рис. 6.28 Рис. 6.29
карте Карно*, изображенной на рис. 6.29, получаем
У2 =
СФЭ над стандартным базисом для рассматриваемого бу-
булева оператора приведена на рис. 6.30. Сложность этой СФЭ
составляет И. Заметим, что вершина, вычисляющая функцию
г/1, не является выходом.
y1(x1va?2vx3)
Уг
Рис. 6.30
"На этой карте мы явно обозначили наборы, на которых функция
принимает значение 0, проставив нули в соответствующих клетках. Тем
самым мы хотим еще раз зафиксировать внимание на том, что не следует
путать нули с прочерками: прочерк в клетке карты, задающей частичную
функцию, означает, что на данном наборе значение функции не определено,
т.е. не равно ни 0, ни 1.
6.8. Схемы из функциональных элементов
455
Булев оператор, рассмотренный в этом примере, вычисля-
вычисляет двухразрядную сумму (по модулю 2) трех одноразрядных
слагаемых. Его можно считать также одноразрядным двоич-
двоичным сумматором — функциональным блоком многоразрядного
двоичного сумматора — для двух слагаемых. Тогда функция
ух интерпретируется как „сигнал переноса" в старший разряд.
На рис. 6.31 изображено wсоединение" трех СФЭ (таких, как
показано на рис. 6.30), с помощью которого вычисляется сумма
двух: трехразрядных двоичных чисел. На третий вход сумма-
сумматора для младшего разряда подается константа 0, а „сигнал
переноса" старшего разряда есть старший разряд суммы, ко-
которая в общем случае будет четырехразрядным числом.
rC)
г?
*<"
11
1 1
I ( ,¦
. 1
1 1 I
. 1
у? s4S)
у? yf
Рис. 6.31
Замечание 6.11. Бели мы проектируем СФЭ над стан-
стандартным базисом и хотим минимизировать ее сложность, то
нам необходимо прежде всего построить соответствующую ми-
минимальную ДНФ. В этом случае мы можем принять во вни-
внимание еще один критерий, по которому минимизируется сама
ДНФ, — число отрицаний. Среди всех минимальных (в смысле
определения 6.6) ДНФ следует отобрать те, в которых число
вхождений переменных под знаком отрицания является наи-
наименьшим. С точки зрения сложности СФЭ, которая будет
456
6. БУЛЕВЫ ФУНКЦИИ
00
01
11
10
00
01
11
щ
ш
10
-—.
^0x10
-011х
-хШ
11x1
Рис. 6.32
построена по минимальной ДНФ, это означает, что в ней мини-
минимизируется число „инверторов" — вершин СФЭ, помеченных
функцией отрицания.
Например, для функции, заданной картой Карно (рис. 6.32),
к ядру, состоящему из простых импликант х\Х2Х\ и
следует добавить простую импликанту Х2Х$х±, а не
поскольку она не содержит отрицаний.
Вопросы и задачи
6Л. Найти число дуг в булевой п-сети.
6.2. Доказать, что объединение двух соседних граней раз-
размерности п — к булева куба Вп является гранью размерности
п — к +1. Как найти направление этой грани?
6.3. Найти число вершин fc-слоя булева куба Вп.
6.4. Построить таблицы для булевых функций, заданных
формулами:
а) (х-+у)У(х-+(х-у)У,
б) {x-+(x.y))-+{xVz);
в) (х-(у-^х))->х;
г) (х -> (у -> z)) -> ({х -> у) -+ (х -> z))\
д) (х.(у V50И(у-> *) Vу).
Вопросы и задачи 457
6.5. Доказать, что если высказывания U и (U => В) тожде-
тождественно истинны, то высказывание В тождественно истинно.
6.6. Доказать, что если формулы (J7 V J3) и (Z7v W) тожде-
тождественно истинны, то формула (В V W) тождественно истинна.
6.7. Найти фиктивные переменные функции /, заданной
вектором значений:
а) / = @,0,1,1,0,0,1,1); б) / = @,0,1,1,1,1,0,0).
6.8. Показать, что х является фиктивным переменным
функции /, представленной формулами:
а)/ = ((*-> V) V*)(V->*)**;
б) / = ((* Vу){х V z) -> (х -> yz))y.
6.9. Доказать, что для любой булевой функции / от п
переменных имеет место следующее равенство:
(Это равенство называют разложением функции / по перемен-
переменному Х{.)
6.10. Пусть булевы функции f ид имеют одно и то же число
существенных переменных, равное г. Тогда каждый набор 5 Е
€ {0,1}г однозначно определяет набор значений существенных
переменных каждой из функций. Пусть для любого такого 5
значения функций / и д на соответствующих наборах своих
существенных переменных равны. Следует ли отсюда, что эти
функции равны?
6.11. Используя алгоритм Квайна — Мак-Клоски, найти
минимальные ДНФ для функций:
а)/ = @,1,1,0,1,0,0,1);
б) / = A,0,0,1,0,0,1,1);
в) / = {1,3,4,7,8,11,14,15};
г) / = {2,4,6,9,10,11,13}.
458 б. БУЛЕВЫ ФУНКЦИИ
6.12. Каждый из четырех членов комитета голосует „за",
нажимая на кнопку. Решение считается принятым, когда не ме-
менее трех членов комитета голосуют „за". Найти минимальную
ДНФ для функции голосования.
6.13. Определить число булевых функций от п переменных:
а) сохраняющих константу @ или 1); б) самодвойственных;
в) несамодвойственных; г) линейных.
6.14. Доказать, что замыкание множества функций, со-
состоящего из дизъюнкции и суммы по модулю 2, совпадает с
классом То.
6.15. Доказать, что множество То Г\Т\ является замыканием
одноэлементного множества {/ = ху ф z © t}.
6.16. Доказать, что число всех монотонных функций от п
переменных равно числу всех антицепей булева куба размерно-
размерности п. Одноэлементное множество считать антицепью.
6.17. Доказать, что сокращенная ДНФ, представляющая
монотонную функцию, является минимальной.
6.18. Доказать, что любая монотонная функция, отличная
от константы, может быть представлена ДНФ без отрицаний.
6.19. Доказать, что в булевом кубе размерности п существу-
существует антицепь, мощность которой составляет Сп - Используя
этот результат, доказать, что число монотонных функций от
-[п/2]
п переменных не меньше 2°п
6.20. Доказать, что число монотонных функций от п пере-
переменных не меньше ( ?} 2С« ) — п.
Указание: используйте результаты задач 6.3 и 6.16.
6.21. Методом неопределенных коэффициентов найти поли-
полином Жегалкина для функций:
а)/ = @, 1,1,0, 1,0, 0,1);
б) f =
Вопросы и задачи 459
в)/ = A,0, 1,0, О, О, 1,1);
г) / = A001110000011000).
6.22. Выяснить, являются ли самодвойственными следую-
следующие функции:
а) xy{z(y^x))->{x~y)]
б) {((xVy)~z)~{y~z))->{xVz);
в) / = @1101001);
г) / = A0101011);
д) / = A100100101101100).
Для несамодвойственных функций найти двойственные функ-
функции.
6.23. Выяснить, полно ли множество булевых функций F:
a) F = {/i = х,/2 = х{у ~z)~yz,/3 = х®у®z}\
б) f = {л = яу ey*ez<, /2 = о, /з = 1, /4 = х vy};
в) F = {/i = ОНО, /2 = A1000011), /3 = A0010110)};
г) F = {Л = ж Vу, /2 = A001101111110110)}.
Для полного множества F построить формулы над F, пред-
представляющие элементы стандартного базиса и базиса Жегал-
кина. Реализовать эти формулы схемами из функциональных
элементов.
6.24. Полное множество булевых функций называют бази-
базисом, если оно не содержит полных собственных подмножеств
(т.е. является минимальным по включению полным множе-
множеством). Найти любой базис, содержащий импликацию (->).
6.25. Проверить полноту множества F, состоящего из функ-
функций /i = ху V xz, /г = х -> у, 0 и х © zy. Выделить в нем
всевозможные базисы.
7. КОНЕЧНЫЕ АВТОМАТЫ
И РЕГУЛЯРНЫЕ ЯЗЫКИ
В этой главе мы начинаем изложение элементов теории
формальных языков.
Говоря „формальный язык", мы имеем в виду то, что при-
приведенные здесь результаты используются прежде всего при
описании искусственных языков, придуманных людьми для
специальных целей, например языков программирования. Но
непреодолимой преграды между специально придуманными ис-
искусственными (формальными) языками и стихийно возникаю-
возникающими и развивающимися естественными языками не существу-
существует. Оказывается, что естественные языки характеризуются
сложными грамматическими правилами, т.е. довольно жестко
формализованы, а даже самый „научно разработанный" язык
программирования содержит „темные места", однозначное по-
понимание которых является проблемой.
Изучая языки, следует иметь в виду три основных аспекта.
Первый из них — синтаксис языка. Язык — это ка-
какое-то множество „слов", где „слово" есть определенная конеч-
конечная последовательность „букв" — символов какого-то заранее
фиксированного алфавита. Термины „буква" и „слово" мо-
могут пониматься по-разному (математическое определение этих
терминов будет дано ниже). Так, „буквами" могут быть дей-
действительно буквы алфавита какого-нибудь естественного или
формального языка, например русского языка или языка про-
программирования „Паскаль". Тогда „словами" будут конечные
последовательности „букв": „крокодил", „integer". Такие сло-
слова называют „лексемами". Но „буквой" может быть „слово"
(„лексема") в целом. Тогда „слова" — это предложения есте-
естественного языка или программы языка программирования. Бс-
461
ли фиксировано какое-то множество „букв", то не каждая их
последовательность будет „словом", т.е. „лексемой" данного
языка, а только такая последовательность, которая подчиня-
подчиняется определенным правилам. Слово „крыкадил" не является
лексемой русского языка, а слово „iff" не является лексемой
в „Паскале". Предложение „Я люблю ты" не является пра-
правильным предложением русского языка, точно так же, как и
запись „x:==t" не есть правильно написанный оператор при-
присваивания „Паскаля". Синтаксис* языка и представляет собой
систему правил, в соответствии с которыми можно строить
„правильные" последовательности „букв". Каждое слово языка
характеризуется определенной структурой, специфичной имен-
именно для данного языка. Тогда необходимо, с одной стороны,
разработать механизмы перечисления, или порождения, слов с
заданной структурой, а с другой — механизмы проверки того,
что данное слово принадлежит данному языку. Прежде всего
именно эти механизмы и изучает классическая теория формаль-
формальных языков.
Второй аспект — семантика языка. Семантика** пред-
предполагает сопоставление словам языка некоего „смысла", „зна-
„значения". Например, записывая математическую формулу, мы
должны соблюдать определенные синтаксические правила (рас-
(расстановка скобок, правописание символов, порядок символов и
т.п.), но, кроме этого, формула имеет вполне определенный
смысл, что-то обозначает.
Язык — это средство общения, передачи информации. Если
мы хотим, чтобы нас поняли, мы должны не только синтаксиче-
синтаксически правильно, соблюдая должный порядок букв в слове и слов в
предложении, строить свою речь, но и заботиться об ее смысле,
о тех идеях, которые мы выражаем в речи. Математические
* Слово „синтаксис" происходит от древнегреческих „syn" — „вместе"
и „taxis" — „порядок, строй". Таким образом, синтаксис можно понимать
как „составление".
**От древнегреческих слов „sema" — „знак, знамение" и „semanticos" —
„ обозначающий ".
462 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
теории „смысла" появились сравнительно недавно, и в допол-
дополнении Д.8.2 к следующей главе мы очень коротко рассмотрим
некоторые подходы к математическому описанию семантики
языков программирования.
Наконец, третий аспект — прагматика языка. Праг-
Прагматика* связана с теми целями, которые ставит перед собой
носитель языка: например, человек произносит речь, имея
перед собой цели, связанные не с синтаксисом, не с семанти-
семантикой языка, на котором он говорит или пишет, а, скажем, с
получением за речь определенной суммы денег. Прагматика
является уже скорее дисциплиной социально-философской, за-
затрагивающей целеполагающую деятельность личности. Мы ни
в малейшей степени не будем ее касаться.
В этой главе вначале будут рассмотрены основные поня-
понятия математической теории формальных языков, важнейшим
среди которых является понятие порождающей грамматики,
а затем — так называемые регулярные языки. Теория регу-
регулярных языков вместе с теорией конечных автоматов образует
фундамент всей теории формальных языков.
7.1, Алфавит, слово, язык
Рассмотрим самое простое понятие теории языков — поня-
понятие алфавита.
Алфавит — это произвольное непустое конечное множе-
множество V = {ai,..., ап}, элементы которого называют буквами
или символами.
Обычно задают определенную нумерацию алфавита (как,
скажем, для русского алфавита: „а" — первая буква, „б" —
вторая и т.д. до 33-й — „я"). Впредь договоримся, фиксируя
алфавит, записывать его буквы в порядке их номеров.
*От древнегреческих „pragma" — „дело, действие" и „pragmateia" —
„деятельность".
7Л. Алфавит, слово, язык 463
Определение 7.1. Словом или цепочкой в алфавите V
называют произвольный кортеж из множества Vk (fc-й декар-
декартовой степени алфавита V) для различных Л = 0,1,2,...
Например, если V = {а,Ь,с}, то (а), (Ь), (с), (а, Ь), (а, 6, с),
(с, Ь, а, а, с) и т.д. есть слова в V.
При & = 0 получаем пустой кортеж, называемый в данном
контексте пустым словом или пустой цепочкой и обозна-
обозначаемый Л. Множество всех слов в алфавите V обозначают У*,
а множество всех непустых слов в V — как V+. Слова, ра-
ради удобства чтения и простоты записи, будем записывать без
скобок и запятых (ср. с записями кортежей в 1.2). Так, для
записанных выше слов получим: а, 6, с, аЬ, abc, cbaac.
Такая запись слова согласуется с его интуитивным понима-
пониманием как цепочки следующих друг за другом символов. Тогда
пустое слово — это слово, не имеющее символов, w пустой лист
бумаги", на котором еще ничего не написано.
По определению, длина слова w — число компонент кор-
кортежа, т.е. если w E Fr, то длина слова w равна г. Длину слова
w договоримся обозначать |гу|. Ясно, что для пустого слова
|Л| = 0. Длину слова тем самым можно понимать как число со-
составляющих это слово букв.
Докажем, что множество V* счетно. Для этого достаточно
построить какую-либо нумерацию этого множества. Рассмо-
Рассмотрим здесь нумерацию, называемую лексикографической.
В данной нумерации пустому слову присваивается номер 0,
а буквам oi, ..., ап алфавита V — номера 1, ..., п соответ-
соответственно. Бели слово х имеет лексикографический номер 1Х, то
слову хп{ присваивается номер nlx + i. Отсюда следует, что
лексикографический номер слова а^а^...aik будет равен
Заметим, что последняя сумма напоминает запись числа в
системе счисления по модулю п (мощности алфавита) с тем
лишь различием, что используется цифра п, но не допускается
464
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
цифра 0. Итак, по любому слову в алфавите V однозначно
вычисляется его лексикографический номер. Обратно, любое
натуральное число однозначно раскладывается по степеням п
указанным выше образом.
Действительно, если дано число iV, то при 0 ^ N ^ п оно
служит номером пустого слова (N = 0) или некоторой буквы
алфавита. Иначе представим N в виде
где 1 < го < п.
Бели к\ ^ п, то N есть номер слова
ваем к\ в виде
. Иначе расклады-
раскладыгде 1
п. Тогда
N = &2П2 + Г\П + Го.
С числом &2 поступаем точно так же, как и с к\. После
конечного числа шагов получим разложение числа N в виде
N = птгт + птгт^ +... + пп + г0,
где каждое число г» @ < г < т) находится в диапазоне от 1 до п.
По полученному разложению N однозначно восстанавливается
слово в У, имеющее номер N:
Пример 7.1. Вычислим номер слова сЪаас в алфавите
{а,Ь,с}. Имеем
Решим обратную задачу, найдя слово в данном трехбуквенном
алфавите, имеющее номер 321.
7.1. Алфавит, слово} язык 465
Согласно приведенному выше алгоритму, получим
321 = 106-3 + 3 = C5-3 + 1K + 3 =
= A1-3 + 2K2 + 1-3 + 3-3° =
= 3-34 + 2-33 + 2-32 +1-3 + 3.
Следовательно, искомое слово есть cbbac. #
Лексикографическая нумерация напоминает способ упоря-
упорядочения слов в словарях: однобуквенные слова следуют в по-
порядке номеров букв в алфавите, среди двух двухбуквенных слов
меньший номер имеет слово, начинающееся буквой с меньшим
номером, и т.д. Но полного совпадения нет, так как в словаре
слова группируются по начальной букве, а не по длине.
Нам будет удобно в дальнейшем использовать следующую
запись непустого слова х в алфавите V по буквам:
где ж(г), 1 < г < А;, — г-я буква слова х.
Определение 7.2. Языком в алфавите V называется
произвольное подмножество множества V*.
Множество всех языков в алфавите V, т.е. множество 2^*,
есть булеан счетного множества, и, следовательно, оно в силу
теоремы 1.15 Кантора имеет мощность континуума.
Наша следующая задача — определить на множестве 2V*
всех языков в произвольном (но фиксированном!) алфавите V
алгебраическую структуру. На множестве 2V* можно опре-
определять различные операции. Прежде всего языки — это мно-
множества, следовательно, над ними можно производить все те
же операции, что и над множествами: объединение, пересе-
пересечение, разность, дополнение и т.п. Универсальное множество
в данном случае есть множество слов F*, которое называют
универсальным языком.
466 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Кроме перечисленных теоретико-множественных операций
можно рассматривать и специальные операции над языками.
Прежде чем обратиться к этим операциям, определим опе-
операцию соединения (или конкатенации) слов. Соединением
слов х = жA)хB)... х(к) и у = уA)уB)... у(т) называют слово
ху = *A)*B)... х{к)у A)</B)... у(т).
По определению, считаем хХ = Хх = х для любого х. Соединение
иногда обозначают точкой (•).
Неформально соединение ху получается приписыванием сло-
слова у справа к слову х. Таким образом, для любых двух слов
х Е Vk и у Е Vm конкатенация ху ? Vk+m (fc,m ^ 0). Следова-
Следовательно, |жу| = |я| + |у|.
Из определения также следует, что соединение слов ассоци-
ассоциативно, т.е. для произвольных трех слов х, у, z имеет место
x(yz) = (xy)z, и поэтому — с учетом написанного выше свой-
свойства пустого слова — множество V* всех слов в алфавите V
с операцией соединения образует моноид (V*, •, Л), Единица
моноида — пустое слово. Этот моноид есть не что иное, как
свободный моноид, порожденный алфавитом V (см. пример 2.7).
Для него используют то же обозначение, что и для самого мно-
множества всех слов в алфавите V, т.е. V*.
На основе понятия соединения слов определим понятие вхо-
вхождения одного слова в другое.
Определение 7.3. Вхождение слова х G V* в слово
у € V* — это упорядоченная тройка слов (tx, rr, v), такая, что
у = uxv.
При этом слово и называют левым, а слово v — правым
крылом указанного вхождения. Слово х называют основой
вхождения.
Говорят, что слово х входит в слово у, если существует вхо-
вхождение х в у. При этом также слово (цепочку) х называют
подсловом (или подцепочкой) слова (цепочки) у. Подцепоч-
Подцепочку х цепочки у называют началом (или префиксом) цепочки
у, если у = xz для некоторой непустой цепочки z\ если же для
7.1. Алфавит, слово, язык
467
некоторой непустой цепочки z имеет место у = zx, то цепочку
х называют концом (или постфиксом) цепочки у.
Заметим, что каждое слово входит в себя само и пустое
слово входит в любое слово.
Например, слова „цикл" и „циклоп" входят в слово „энцикло-
„энциклопедия". Соответствующие вхождения записывают следующим
образом:
(эн, цикл, опедия), (эн, циклоп, едия).
Может существовать несколько разных вхождений одного и
того же слова х в некоторое слово у. Так, слово „абра" дважды
входит в слово „абракадабра". Число вхождений пустого слова
в данное слово р на единицу больше длины слова р. Среди всех
вхождений слбва х в слово у вхождение с наименьшей длиной
левого крыла называют первым или главным вхождением
хву.
Так, вхождение (Л, абра, кадабра) есть первое вхождение
слова „абра" в слово „абракадабра".
Определение 7.4. Говорят, что вхождения (щ х, v) и
(s, z, t) слов х и z в одно и то же слово у не пересекаются,
если существуют такие (может быть, и пустые) слова р и д,
что у = uxpzt (и тогда v = pzt, a s = ихр) или у = szqxv (и тогда
и = szq, a t = qxv) (рис. 7.1). В противном случае говорят, что
указанные вхождения пересекаются.
и
f
s
и
А.
В
р
ИШ
t
J
V
шш
V
= 2/
Рис. 7.1
468 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Так, вхождения слов „цикл" и „циклоп" в слово „энцикло-
„энциклопедия" пересекаются, а два разных вхождения слова „абра" в
слово „абракадабра" не пересекаются. Мы иногда будем ис-
использовать обозначение хЦу для утверждения „слово х входит
в слово у". Можно доказать, что С — отношение порядка.
Определив таким образом операцию соединения слов, вве-
введем теперь операцию с таким же названием, но уже для языков.
Перед этим обратим внимание на то, что всякий раз, говоря о
языках и операциях над ними, мы полагаем фиксированным ка-
какой-то алфавит V. Он не всегда явно упоминается, но нужно
четко усвоить, что нельзя говорить просто о слове, просто о
языке, но всегда — о слове или языке в том или ином алфавите.
Определение 7.5. Соединением (конкатенацией) язы-
языков L\ и 1/2 называют язык L\Li2, состоящий из всех возможных
соединений слов яу, в которых слово х принадлежит первому,
а слово у — второму языку, т.е.
L\L*i = {ху: х Е L\ и у Е Ь%}.
Соединение конечных языков легко вычислить.
Пример 7.2. Бели V = {а, 6, с}, L\ = {аЬ, bec, cab}, L<i =
= {са, bec}, то
L\Li2 = {abca, abbce, becca, becbee, cabca, cabbec},
a
L2L1 = {caab, cabce, cacab, becab, bccbcc, beccab}.
Вычисление конкатенации языков в конечном случае очень
похоже на умножение (раскрытие скобок) в обычной школьной
алгебре. Можно былб бы формально написать так:
(ab + bcc + cab) (са + Ьсс) =
= abca + abbec + becca + bccbcc + cabca + cabbec.
7Л. Алфавит, слово, язык 469
В данном случае плюс (+) — это только соединительный
знак, используемый вместо запятой. Позже мы увидим, что
подобным чисто формальным записям может быть придан
строгий алгебраический смысл. #
Соединение языков не коммутативно, и, как показывает
только что разобранный пример, пересечение L1L2 П L2L1 в
общем случае не пусто. В нашем примере оно содержит одну
цепочку bccbcc.
Операция соединения языков позволяет определить опера-
операцию возведения языка в произвольную натуральную степень.
А именно, по определению, L0 = {Л} для любого L С V*, а 1П =
= Ln~lL при п > 0.
Итерацией языка L называют объединение всех его сте-
степеней:
0
=0
п=0
Рассматривая объединение всех степеней языка L, начиная с
первой, получим позитивную итерацию
П=1
Сформулируем основное алгебраическое свойство множества
всех языков в алфавите V.
Теорема 7.1. Алгебра C(V) = BV\ U, •, 0, {Л}) есть
замкнутое полукольцо.
< Проверка аксиом полукольца (см. 3) сводится к доказатель-
доказательству:
1) того, что по операции объединения множество всех язы-
языков образует коммутативный и идемпотентный моноид (с
пустым множеством в качестве нейтрального элемента (нуль
полукольца)); это тривиально ввиду известных свойств опера-
операции объединения множеств;
470 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
2) того, что по операции конкатенации множество языков
образует моноид (с языком {Л}, состоящим из одного пустого
слова, в качестве нейтрального элемента (единицы полуколь-
полукольца)); для этого достаточно доказать, что операция соединения
языков ассоциативна, а также доказать для любого языка L
тождество
что вытекает из ассоциативности операции соединения слов и
из тождества Хх = х\ = х для любого слова х;
3) следующих тождеств:
(эти тождества определяют свойство дистрибутивности опе-
операции соединения относительно объединения).
Докажем первое из этих тождеств. Пусть слово х принад-
принадлежит его левой части, т.е. языку Li(L2UL^). Тогда, согласно
определению соединения языков, это слово может быть пред-
представлено в виде х = уг, где у G Li, a z G L<i U L3, т.е. z G L2 или
z 6 L3. Если z G 1^2» то yz G L1L2, a если * € Ьз, то yz G Ха^з,
т.е. ж = yz G Lib2 U L\L$. Пусть теперь x G L4L2 U L1L3. То-
Тогда x = j/г, где у € Li, a z G L2 или z G L3, т.е. x G ^1(^2 U?3)»
что и завершает доказательство первого тождества. Второе
доказывается аналогично.
Напомним, что в полукольце S = E, +, -,0,1) отношение по-
порядка вводится следующим образом: для любых ж, у G S по опре-
определению полагают а; < у тогда и только тогда, когда х + у = у.
Так как в полукольце всех языков в алфавите V операция сло-
жения — это операция объединения множеств, то в данном
случае отношение порядка < есть не что иное, как теоретико-
множественное включение С (действительно, включение LQK
равносильно тому, что LUK = К). Тогда замкнутость по-
полукольца C(V) следует из существования объединения любого
7.1. Алфавит^ слово, язык 471
семейства множеств (в частности, бесконечной последова-
последовательности множеств — см. 1.5), служащего точной верхней
гранью этого семейства (относительно теоретико-множествен-
теоретико-множественного включения), а также из следующих тождеств (для любого
языка L и любого семейства языков Р^ iei):
(^ () G.1)
iei iei iei iei
что гарантирует выполнение непрерывности операции умно-
умножения данного полукольца, т.е. непрерывности операции со-
соединения. Эти тождества доказываются точно так же, как
тождества обычной дистрибутивности.
Рассмотрим, например, доказательство второго тождества
из G.1), используя, как и выше, метод двух включений. Бели
х е (\J Pi)L, то х = yz, где у 6 U Р*, a z e L. Согласно
iei ' iei
определению объединения семейства множеств, найдется такое
г € /, что у 6 Р», и тогда yz = х 6 P%L, т.е. х ? (J PiL. Обратное
iei
включение доказываем так: из х Е U PiL следует, что для
iei
некоторого iei х Е P%L, т.е. х = yz, где у EPi, a z E L, откуда
У € U Р», и, следовательно, уг = ж € (|J Pi )L. >
i€/ \ei '
Следствие 7.1* Для любого языка L верно тождество
^ Вычислим соединение LL*: LL* = L( (J Ln). Применяя пер-
00 00 ОО
вое из тождеств G.1), получим L (J Ln = \J LLn = (J Ln, т.е.
n=0 n=0 n=l
i+ = L*L. Тождество L+ = LL* доказывается аналогично. >
Заметим, что в общем случае нельзя утверждать, что пози-
позитивная итерация языка L получается выбрасыванием из обыч-
обычной итерации пустого слова. Это верно в том и только в том
случае, когда язык L не содержит пустого слова. Если же А € Ц
то L+ = L*, так как тогда L0 = {Л} С L.
472 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
7.2. Порождающие грамматики
Как уже отмечалось, классическая теория формальных язы-
языков изучает прежде всего синтаксис языка. Она вводит мате-
математическую модель синтаксиса, которая описывает механизмы
порождения и распознавания „правильно построенных" цепо-
цепочек. В этом разделе мы рассмотрим первый из этих механиз-
механизмов. Задать такой механизм — значит описать некую процеду-
процедуру, позволяющую вывести (или, как обычно говорят, породить)
произвольную цепочку языка согласно определенному конечно-
конечному множеству правил. Последнее очень важно: язык может
быть бесконечным, но множество правил, с помощью которых
выводятся его цепочки, обязано быть конечным. Заметим, что
не каждый язык может быть представлен таким образом, но
мы в рамках этого учебника будем рассматривать только та-
такие языки, т.е. языки, синтаксис которых задается конечным
множеством правил. Эти языки, вообще говоря бесконечные,
но допускающие конечное описание, называют перечислимы-
перечислимыми. Таким образом, мы рассматриваем только перечислимые
языки.
Классическим способом определения языков через порожда-
порождающую процедуру является определение их с помощью поро-
порождающих грамматик, или грамматик Хомского.
Порождающая грамматика позволяет выводить (порождать)
цепочки языка из некоторой начальной цепочки с помощью
определенных правил замены (или правил подстановки, пра-
правил переписывания). Порождение есть пошаговый процесс, в
котором на каждом шаге из цепочки, уже полученной на пре-
предыдущем шаге (в частности, из начальной), можно путем при-
применения к ней правил замены получить новую цепочку. Именно
так мы действуем, решая какую-нибудь математическую за-
задачу, например выполняя дифференцирование и переходя от
одной формулы к другой с помощью таблицы производных.
Порождающая грамматика (далее просто грамматика) за-
задается упорядоченной четверкой G = (V, N, 5, Р), в которой
7.2. Порождающие грамматики 473
V — алфавит, называемый терминальным алфавитом;
N — алфавит, называемый нетерминальным алфавитом,
причем пересечение V и N пусто; S — выделенный символ
нетерминального алфавита, называемый аксиомой; Р — ко-
конечное множество правил вывода, или продукций. Каждое
правило вывода является упорядоченной парой (а,/?) цепочек
в алфавите VUN, причем цепочка а должна содержать вхо-
вхождение хотя бы одного символа нетерминального алфавита;
цепочку а называют левой, цепочку C — правой частью
правила вывода.
Правило вывода принято записывать в таком виде:
разделяя левую и правую части „стрелкой", которая рассма-
рассматривается как „метасимвол" и не принадлежит ни одному из
алфавитов грамматики. Буквы терминального алфавита грам-
грамматики называют терминальными символами (или просто
терминалами); буквы нетерминального алфавита называ-
называют нетерминальными символами (или нетерминалами).
Любую цепочку в терминальном (нетерминальном) алфави-
алфавите называют терминальной (нетерминальной) цепочкой.
Алфавит VUN называют объединенным алфавитом грам-
грамматики G.
Пример 7.3. Четверка
Go = ({а, Ь}, {S, А, В}, S, {S -> аАВЬ, аА -> аВ,
аВ -+ аВа, аА -* аа, аВЬ -> aabb, аВа -» аЬВЬа, ВЬ -> АЬ})
задает грамматику с терминальным алфавитом V = {а,Ь}, с
нетерминальным алфавитом N = {S, А, В}, с аксиомой S и
множеством правил вывода Р, элементы которого перечислены
в фигурных скобках после аксиомы. Обычно ради наглядности
правила вывода грамматики выписывают отдельно:
S-+aABb, аА->аВ, аВ-+аВа, аА->аа,
аВЬ -+ aabb, аВа ->> аЬВЬа, ВЬ -> АЬ.
474 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Замечание 7Л. Нам будет удобно условиться о некото-
некоторых обозначениях, которыми мы все время будем пользоваться,
имея дело с грамматиками. Терминалы будем обозначать ма-
малыми латинскими буквами из начала латинского алфавита: а,
6, си т.д.; нетерминалы — большими латинскими буквами из
начала и середины латинского алфавита: А, В, С, 5, Т и т.д.;
терминальные цепочки (т.е. слова в терминальном алфавите) —
малыми латинскими буквами из середины и конца латинского
алфавита: s, t, p, g, ж, у, z и т.д.; цепочки в объединенном
алфавите — малыми греческими буквами. Наконец, больши-
большими латинскими буквами из конца алфавита будем обозначать
символы объединенного алфавита или пустую цепочку. #
Определение грамматики указывает пока только на то, что
следует фиксировать, чтобы задать какую-либо грамматику. А
именно следует фиксировать два непересекающихся алфавита,
выделив в одном из них символ, названный аксиомой, а также
конечное множество правил вывода. Но мы еще не знаем, каким
образом „работает" грамматика как инструмент порождения
(и преобразования) слов. Чтобы это понять, нужно определить
важнейшее понятие выводимости в данной грамматике.
Неформально каждое правило вывода грамматики тракту-
трактуется как „правило замены", разрешающее произвольное вхо-
вхождение левой части правила в некоторую цепочку в объеди-
объединенном алфавите заменить его правой частью, получив (или
выведя) тем самым новую цепочку. Так, для примера 7.3 мы
можем от цепочки 5, используя правило S -> аАВЬ, перейти к
цепочке аАВЬ. В этой цепочке есть вхождение левой части пра-
правил а А -* аВ и аА —? аа, а также левой части правила ВЬ —> АЬ.
Можно использовать любое из них (но какое-нибудь одно!):
если мы заменим (в данном случае единственное) вхождение
цепочки а А правой частью правила а А —> aJB, то получим це-
цепочку аВВЬ и т.д. Таким образом мы и строим так называемые
выводы — последовательности цепочек, в которых каждый по-
последующий член получается из предыдущего заменой, подобной
только что рассмотренной.
7.2. Порождающие грамматики 475
Определение 7.6. Цепочка 8 непосредственно выво-
выводима в грамматике G из цепочки у (или из 7 непосредственно
выводится 8)> если существуют такие цепочки а и р и такое
правило вывода а -> /3 из Р, что 7 = я^Р (т.е. существует вхо-
вхождение левой части правила вывода в цепочку 7)? a 8 = <т/?р.
Бинарное отношение на множестве цепочек в объединен-
объединенном алфавите, которое состоит из всех упорядоченных пар
G, S), таких, что вторая цепочка непосредственно выводится
из первой, называют отношением непосредственной вы-
выводимости. Его будем обозначать символом \~g , опуская
зачастую имя грамматики: *у\- 8. Ъ этом случае говорят также,
что правило а -+ /5 применяется к цепочке 7 (и что цепочка 8
получена применением правила ач/Зк цепочке 7 или, что рав-
равносильно, в результате замены данного вхождения левой части
правила а —> fi его правой частью).
В общем случае, если левая часть правила вывода входит
в данную цепочку, говорят, что правило применимо к этой
цепочке (или имеет место применимость правила вывода
к цепочке). Бели же левая часть правила вывода не входит
в цепочку, то говорят, что правило не применимо к данной
цепочке.
Рефлексивно-транзитивное замыкание отношения непосред-
непосредственной выводимости обозначаем \-*G (опять-таки опуская имя
грамматики G, если это не приводит к недоразумению: Ь*) и
называем отношением выводимости. Иначе говоря, вы-
выводимость цепочки 8 из цепочки 7) 7 ^Ь ^ в грамматике
G имеет место, по определению, тогда и только тогда, когда
найдутся такие слова <*о = 7? аь • • • ? ап = Л, где n ^ 0, что
<*о Hg oi he - -. Ьо an-i b"G otn.
Для данной цепочки j в объединенном алфавите, если к
ней применимо хотя бы одно правило вывода рассматриваемой
грамматики, существует в общем случае не одна, а много цепо-
цепочек, непосредственно выводимых из нее. Эта неоднозначность
476 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
связана с двумя факторами. Во-первых, может существовать
несколько разных правил вывода, применимых к цепочке 7-
Так, для грамматики примера 7.3 к цепочке аАаВЬ приме-
применимы все правила грамматики, кроме первого. Тогда любая
цепочка, полученная применением к указанной цепочке любого
из этих правил, будет непосредственно выводима из нее. Во-
вторых, если уже фиксировано правило вывода, применимое к
цепочке 7> то существуют, вообще говоря, несколько различ-
различных вхождений левой части этого правила в цепочку j. Тогда
любая цепочка, полученная заменой любого из этих вхождений
правой частью выбранного правила вывода, будет непосред-
непосредственно выводима из 7* Для грамматики примера 7.3, правила
аВ -> Ва и цепочки 7 = ЬаВаВа получим: ЬаВаВа Ь ЬВааВа и
ЬаВаВа Ь ЬаВВаа.
Разные вхождения левой части некоторого правила в задан-
заданную цепочку могут и пересекаться. Так, правило аВа -> ЬВЬ
грамматики примера 7.3 можно к написанному вьппе слову 7
применить двояко: ЬаВаВа Ь ЬЬВЬВа и ЬаВаВа Ь ЬаВЬВЬ.
Заметим, наконец, что множество цепочек, непосредственно
выводимых из данной, пусто тогда и только тогда, когда среди
правил вывода грамматики нет ни одного, применимого к
данной цепочке. Для примера 7.3 в качестве такой цепочки
можно взять хотя бы цепочку аВА.
Определение 7.7. Выводом в грамматике G называют
произвольную, конечную или бесконечную, последовательность
слов о?о, аи •••) «п? .., в которой для любого г ^ 0 a* ha^i,
если цепочка c*i+i существует. Число п ^ О называют длиной
вывода, если указанная последовательность конечна и ап —
ее последний элемент. В этом случае говорят также, что ап
выводится из ао за п шагов. Для положительного п пишем
ao l~+ otn или, если нужно специально оговорить длину вывода
Из определений следует, что выводимость j Ь* S равносиль-
равносильна тому, что существует вывод 7 = ao,ai,... ,an = 5, где п ^ 0.
7.2. Порождающие грамматики 477
Мы будем использовать также термин „фрагмент выво-
да", понимая под этим такую подпоследовательность вывода,
которая сама является выводом. В частности, фрагмент выво-
вывода, состоящий из двух соседних его членов, называется тагом
вывода.
Построение вывода в порождающей грамматике можно
трактовать как „игру", правила которой заданы множеством
Р. Подобно тому как в игре (например, в шахматах) можно
из заданной позиции перейти в одну из множества следующих
позиций, используя правила игры, так и при проведении вы-
вывода в грамматике можно из данной цепочки получить одну
из множества непосредственно выводимых из нее, заменяя в
ней произвольное вхождение левой части правила его правой
частью. При этом мы можем выбрать любое правило, приме-
применимое к очередной цепочке, и среди различных вхождений его
левой части выбрать любое.
На основании сказанного можно предположить, что суще-
существуют несколько различных выводов фиксированной цепочки
C из фиксированной цепочки а. Далее на примерах мы убедим-
убедимся в том, что это действительно так.
Введенные выше понятия непосредственной выводимости,
выводимости и вывода можно уподобить известным из теории
графов понятиям непосредственной достижимости, дости-
достижимости и пути (в ориентированных графах) соответственно.
Мы специально выбирали обозначения выводимости близкими к
тем, которые используют в теории графов. Нужно только заме-
заметить, что множество вершин графа конечно (по крайней мере,
мы в этой книге изучаем только конечные графы), а множество
слов бесконечно. Но графовая аналогия позволяет придать вве-
деным выше понятиям большую наглядность: так, построение
вывода в грамматике можно уподобить ппутешествию" по не-
некоторому пути в ориентированном графе.
Центральным понятием в теории порождающих грамматик
является понятие языка, порождаемого данной грамматикой.
478 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Определение 7.8. Язык, порождаемый грамматикой
(?, — это множество L(G) всех выводимых из аксиомы грамма-
грамматики терминальных цепочек.
L(G) = {x:S\-*Gx,x€V*}.
Продолжая „игровую аналогию", мы можем теперь сказать,
что у „игры", во-первых, появилась выделенная „начальная по-
позиция ", аксиома; во-вторых, возникла „цель" — строя вывод в
согласии с правилами грамматики, получить цепочку, не содер-
содержащую нетерминалов. Так, скажем, и в шахматах, мы начина-
начинаем игру не с произвольной позиции, а со вполне определенной
начальной позиции, предусматривающей строго фиксирован-
фиксированную расстановку фигур, а закончить игру стремимся в любой
позиции, в которой вражескому королю поставлен мат. Но
при этом нужно понимать, что правила вывода грамматики
априори никак не связаны с ограничением строить выводы тер-
терминальных цепочек из аксиомы, а определяют возможность по-
построения любого вывода, даже бесконечного.
Заметим также, что, согласно определению 7.8, нетерми-
нетерминалы не содержатся в цепочках языка, порождаемого грамма-
грамматикой. Это совсем не значит, что нетерминалы „не нужны",
напротив, с их помощью мы организуем вывод и можем по-
получить требуемые терминальные цепочки. Когда мы решаем
математическую расчетную задачу и должны в результате по-
получить число, то это не значит, что мы не должны пользоваться
формулами. Но все буквенные обозначения в окончательном
результате должны исчезнуть, хотя без них этот результат по-
получить невозможно.
Определение 7.9. Две грамматики называются эквива-
эквивалентными, если они порождают один и тот же язык.
Примем соглашение о следующей сокращенной записи пра-
правил с одинаковой левой частью: вместо записи
7.2. Порождающие грамматики 479
будем использовать запись
разделяя разные правые части вертикальной чертой.
Кроме того, рассматривая примеры грамматик, мы зача-
зачастую будем записывать только их множества правил вывода,
избегая скрупулезной записи всего кортежа, определяющего
грамматику. С учетом введенных выше соглашений об обо*
значениях это не должно приводить к недоразумениям.
Пример 7.4, Рассматриваемая ниже грамматика модели-
моделирует простейший фрагмент естественного (русского) языка: ее
терминалы — это некоторые слова русского языка*, нетермина-
нетерминалами являются пграмматические категории", а именно понятия
„предложение", „подлежащее" и „сказуемое" (они даны как сло-
слова, заключенные в угловые скобки):
G\ = ({кот, пес, крокодил, мяукает, лает, плачет},
{(предложение), (подлежащее), (сказуемое)},
(предложение), Pi).
Множество правил Р\ имеет вид
(предложение) -> (подлежащее) (сказуемое),
(подлежащее) —> кот | пес | крокодил,
(сказуемое) -> мяукает | лает | плачет.
Каждое правило вывода грамматики G\ можно трактовать как
определение той или иной грамматической категории: напри-
например, первое правило есть запись такого определения: „предло-
„предложение — это подлежащее, за которым идет сказуемое". Так как
нас интересует только синтаксис языка, то это определение,
*Эти слова рассматриваются как неделимые символы, а именно буквы
данного терминального алфавита. Нас никак не должно это смущать, ибо
алфавит — это любое непустое конечное множество.
480 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
касающееся исключительно записи предложения, есть требова-
требование, согласно которому, записывая предложение, сначала нужно
поставить подлежащее, а после него — сказуемое. Другие пра-
правила грамматики определяют подобным образом „подлежащее"
и „сказуемое". Но тут новых грамматических категорий не
возникает — просто перечисляются те слова, которые могут
быть подлежащим и сказуемым.
Построим какой-нибудь вывод в грамматике G\:
(предложение) Ь (подлежащее) (сказуемое) Ь
Ь кот (сказуемое) Ь кот лает.
Заметим, что „смысл" {семантика) выводимой цепочки нас
никак не интересует. Мы вообще пока не знаем, что такое
„смысл". Так что кот может лаять, крокодил мяукать и т.д. #
Приведенный пример, несмотря на его простоту, позволяет
нам дать еще одну содержательную интерпретацию понятия
грамматики. Грамматику можно рассматривать как „систему
определений" некоторых „терминов", „понятий". Выделяется
самое общее понятие (в данном примере понятие „предложе-
„предложение"), оно сводится к менее общим „понятиям" до тех пор,
пока мы не придем к „конкретным объектам" (в данном случае
к цепочкам в каком-то алфавите), подпадающим под опреде-
определяемые „понятия". Самое общее „понятие" — это аксиома,
другие „понятия" — нетерминалы, „конкретные объекты" —
терминальные цепочки. В подобном духе строится определение
синтаксиса языков программирования с помощью так называе-
называемых форм Бэкуса — Наура. Пример такого описания приведен
ниже (см. Д.8.2). За другими примерами следует также обра-
обратиться к литературе по языкам программирования.
Пример 7.5. а. Грамматика
<?2 = ({аД0,1}, U,D}, /, Р2)
7.2. Порождающие грамматики 481
имеет множество правил Рг-
I-+aD\bD\a\b,
D ^> aD\bD\0D\lD\a\b\0\l.
Нетрудно видеть, что данная грамматика порождает простей-
простейшие „идентификаторы" в алфавите, состоящем из двух „букв"
и двух „цифр", т.е. цепочки, начинающиеся обязательно с „бу-
„буквы".
Примеры выводов в грамматике G^
abOD h abObD h аЬОЫ,
/ha,/hb.
б. Грамматика
Gz = ({(,)}, {S}, S, S-+()\(S)ISS)
порождает множество так называемых „правильных скобочных
структур"*, например S Ь SS h (S)S h (Q)S h (())().
Полезно сопоставить с этой грамматикой индуктивное опре-
определение множества правильных скобочных структур: цепочка
() есть правильная скобочная структура; если известно, что це-
цепочки х и у — правильные скобочные структуры, то цепочку
ху также считаем правильной скобочной структурой; если из-
известно, что х — правильная скобочная структура, то и цепочка
(х) есть правильная скобочная структура; никаких правильных
скобочных структур, кроме определенных выше, не существу-
существует. Видно, что грамматика G$ есть не что иное, как форма
записи сформулированного только что индуктивного опреде-
определения: „правильная скобочная структура" (понятие, обозна-
обозначенное аксиомой S) есть либо цепочка (), либо „правильная
*Мы заключили четверку, задающую грамматику <2з, в угловые, а не
в круглые скобки, чтобы не смешивать их со скобками, являющимися
терминалами данной грамматики.
_ 10061
482 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
скобочная структура" в скобках — E), либо две „правильные
скобочные структуры", записанные одна после другой, — 55.
в. Рассмотрим грамматику
Ь,с}, {S,A,B,C}, S, РА)
с множеством правил вывода Р4:
S^aSBC\abC, A)|B)
СВ-+ВС, C)
ЬВ -+ 66, D)
ЬС-+Ьс, E)
сС->сс. F)
Разберем некоторые примеры выводов: под символом h будем
указывать номер применяемого на данном шаге правила, а над
символом — количество повторений этого правила:
S hi aSBC 1-2 aabCBC h3 ааЬВСС Ь4
1-4 ааЬЬСС h5 aabbcC hs оаббсс;
S hi aSBC hi aaSBCBC h2 aaabCBCBC h3
h3 aaabBCCBC h3 aaabBCBCC h3 aaabBBCCC h4
h4 aaabbBCCC h4 aaabbbCCC h5 aaabbbcCC h| оаобббссс.
Представим теперь вывод произвольной цепочки anbncn:
о5ВС hi aaSBCBC Ь ... ht e"-1^^I1 h2
h2 anbCBCBC...BQ h3 anbBCCBC...BQ h3...
n-l n-2
... h3 о"ЬВ"-1Сп h4 anbbBn-2Cn h4 ...
... h4 a^C1 h5 ontflcCn-1 hg~l on6ncn. G.2)
7.2. Порождающие грамматики 483
Можно заметить, что посредством многократного приме-
применения правила C) в выводе G.2) происходит „перегонка" всех
букв В влево от всех букв С, т.е. из цепочки оРЪСВСВС... BQ
выводится цепочка anbBn~lCn. Бели считать, что правило
C) на каждом шаге соответствующего вывода применяется
так, что происходит замена первого вхождения цепочки СВ
цепочкой ВС, то первый (самый левый) символ В в цепочке
апЬСВСВС...BQ „проходит" через один символ С, следующе-
п-1
му символу В (в цепочке апЬВССPC... ВС) нужно пройти уже
два символа С и т.д. Отсюда следует, что правило C) в ука-
указанном фрагменте вывода G.2) применяется
Тогда последовательность номеров применяемых правил
(протокол вывода) может быть записана так:
(l)n-lB)C)ni?liD)n-1E)F)n-1, n > 1.
Гораздо труднее доказать, что данная грамматика поро-
порождает только цепочки указанного вида. Проанализируем дру-
другие варианты проведения вьгаода после применения правила B)
в выводе G.2).
1. После применения правила B) применяем правило E) и
после многократного применения правила C) получаем
апЬС(ВС)п~1 Ь5 апЬс(ВС)п~1 =
= anbcBCBC...BC\~t anbcBn-lCn~l. G.3)
Цепочка, записанная последней, такова, что, во-первых, она
не является терминальной, а во-вторых, к ней не применимо ни
16*
484 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
одно правило грамматики. Любая такая цепочка называется
тупиковой.
2. Вывод G.2) можно модифицировать, прервав на опреде-
определенном шаге применение правила C) и применив правило D):
= апЪВтСт+1ВС... ВС Ь4 а1
где т < п — 1.
Далее, если посредством применения правила C) мы „пере-
„перегоним" все символы В влево, то получим цепочку anbbBn~2Cn,
из которой легко получается цепочка anbncn. Таким образом,
мы получили другой вариант вывода этой цепочки.
Но если мы будем применять правило D), начиная с цепочки
апЪВтСт+1 ВС. ..Ж7,
n—I—m
до тех пор, пока это возможно, то получим цепочку
Из нее, если не применять сразу правило E), снова полу-
получится цепочка апЪпсп. Применение же правила E) приведет к
тупиковой цепочке.
По аналогии можно рассмотреть произвольное чередование
применения правил C) и D).
Все варианты вывода терминальной цепочки тем самым
разобраны.
В общем же случае строгое доказательство того, что какая-
либо предъявленная нам грамматика не порождает никаких
других цепочек, кроме цепочек определенного вида, может
быть весьма нетривиальным.
7.2. Порождающие грамматики 485
г. Зададим грамматику
Оъ = ({а}, {5, А, С, Я, Я, F}, 5, ft),
множеством Р5 правил
5 -» оСА,
EF -> ,
ED -> Da2E,
Ea -» aU,
Ca -> aC,
CD -> Co,
CF-+A.
Можно доказать, что данная грамматика порождает язык
{ап : п ^ 1}, т.е. все квадраты натуральных чисел, закодиро-
закодированных в однобуквенном алфавите. #
При доказательстве утверждений о грамматиках нам будет
удобно использовать одну процедуру, которую мы назовем
переименованием нетерминалов грамматики.
Пусть дана какая-то грамматика G = (V, JV, 5, Р). Введем
новый алфавит N', не пересекающийся с VUJV, так, что между
алфавитами N и N' установлено взаимно однозначное соответ-
соответствие, при котором каждый символ АЕ N переходит в символ
А' б Nf. Построим новую грамматику G1 = (V, ЛГ;, S", Р'), за-
заменив каждое правило в исходной грамматике новым, в кото-
котором на месте каждого вхождения каждого нетерминала AeN
поставлен нетерминал A' G Nf. Нетрудно доказать, что постро-
построенная таким образом грамматика G1 эквивалентна исходной.
Говоря неформально, описанное преобразование грамматики
состоит в переобозначении ее нетерминалов таким образом,
что вместо каждого нетерминала ставится его п двойник", при-
причем „двойники", соответствующие разным нетерминалам, раз-
различны.
486 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
7.3. Классификация
грамматик и языков
Напомним, что единственное ограничение, накладываемое
на правило вывода любой грамматики, состоит в том, что в ле-
левую часть правила должен входить хотя бы один нетерминал.
В зависимости от дополнительных ограничений, накладыва-
накладываемых на правила вывода грамматики, различают следующие
основные классы грамматик.
1. Грамматики типа О, или грамматики общего ви-
вида. Здесь на правила вывода не накладывается никаких допол-
дополнительных ограничений.
2. Неукорачивающие грамматики. Каждое правило
такой грамматики имеет вид а -»/?, где |ог| ^ |/5|. Таким обра-
образом, длина правой части правила не меньше длины левой. Грам-
Грамматика (?4 из примера 7.5 есть неукорачивающая грамматика,
но грамматика G$ из того же примера таковой не является.
3. Контекстно-зависимые грамматики (КЗ-грамма-
(КЗ-грамматики?). Грамматику называют контекстно-зависимой грамма-
грамматикой (КЗ-грамматикой), если любое ее правило вывода имеет
вид (рАф -»¦ (р?ф, где А — нетерминал, ? — некоторая цепоч-
цепочка, ? ф Л. Каждое такое правило, называемое КЗ-правилом,
позволяет заменить нетерминал А в „контексте", образуемом
цепочками tp и ф в объединенном алфавите, непустой цепоч-
цепочкой f (см. замечание 7.1). Иногда цепочку (р называют левым
контекстом, а цепочку ф — правым контекстом данного
КЗ-правила. Из определения видно, что каждая КЗ-грамма-
КЗ-грамматика является неукорачивающей.
Грамматика G\ из примера 7.5 не является КЗ-грамма-
КЗ-грамматикой, так как правило СВ -> ВС не является КЗ-правилом.
Остальные же правила вывода этой грамматики — КЗ-прави-
КЗ-правила. Грамматика G$ из примера 7.5 не является КЗ-грамматйкой
хотя бы из-за наличия правила вывода с пустой правой частью.
КЗ-грамматикой является грамматика из примера 7.3.
7.3. Классификация грамматик и языков 487
Бели в КЗ-правиле снять требование непустоты цепочки
?, то получим грамматику, которую называют обобщенной
КЗ-грамматикой (или, коротко, О КЗ-грамматикой).
4. Контекстно-свободные грамматики (КС-грамма-
(КС-грамматики). Каждое правило такой грамматики имеет вид А -> а,
т.е. левая часть каждого правила вывода есть нетерминал,
а правая — произвольная (может быть и пустая) цепочка в
объединенном алфавите.
С практической точки зрения это наиболее важный класс
грамматик, поскольку именно в терминах КС-грамматик опи-
описывается синтаксис языков программирования, и этим грамма-
грамматикам будет посвящена отдельная глава. Грамматики &2> ?з>
С?4 из примера 7.5 являются КС-грамматиками.
5. Линейные грамматики. Каждое правило такой грам-
грамматики имеет вид А -> uBv или А -> и, т.е. в правой части
правила может содержаться не более одного вхождения нетер-
нетерминала. Бели во всех правилах вида А -> uBv имеет место v = А,
то грамматика называется праволинейной, а если и = Л —
лее олинейной.
Пример 7.6. Линейной является грамматика
G6 = ({аь...,ап}, {5},5,Р6),
где множество правил вывода Ре есть
5 -> а\ Sai | a2Sa2 |... anSan \ аг \ а2 \... ап \ X.
Можно доказать, что эта грамматика порождает все палин-
палиндромы в алфавите V, т.е. все цепочки, читаемые слева направо
так же, как и справа налево. Например, для V = {а, Ь, с} це-
цепочка acbbca — палиндром. Вывод его в грамматике Gq (для
данного терминального алфавита) будет иметь вид
S Ь aSa Ь acSca Ь acbSbca Ь acbXbca = acbbca.
488 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Замечание 7.2. Формальное определение палиндрома та-
таково. Назовем инверсией непустой цепочки
x = x(l)xB)...x{k-l)x(k)eV
цепочку
Для пустой цепочки Л по определению считаем Ля = Л. Па-
Палиндром в алфавите V — это любая цепочка ж, для которой
xR = x.
6. Регулярные грамматики. У такой грамматики каж-
каждое правило имеет вид А —* аВ или А -> а, где а есть либо
терминал, либо пустая цепочка. Регулярные грамматики —
частный случай праволинейных грамматик.
Эти грамматики подробно будут рассмотрены в 7.4.
Приведем без доказательства некоторые утверждения о
классах грамматик.
Теорема 7.2. 1. Для любой грамматики типа 0 может быть
построена эквивалентная ей ОКЗ-грамматика.
2. Для любой неукорачивающей грамматики может быть
построена эквивалентная ей КЗ-грамматика.
3. Для любой леволинейной грамматики может быть по-
построена эквивалентная ей праволинейная грамматика, и, на-
наоборот, для любой праволинейной грамматики может быть
построена эквивалентная ей леволинейная грамматика.
4. Для любой праволинейной грамматики может быть по-
построена эквивалентная ей регулярная грамматика. #
Отметим, что доказательства первых двух пунктов теоре-
теоремы 7.2 весьма нетривиальны*.
Классификация языков, порождаемых грамматиками, тес-
тесно связана с классификацией самих грамматик, хотя и не
тождественна ей. Язык относят к классу С, если существу-
*См.: Глушков В.М., Цейтлин Г.Е., Ющенко ЕЖ
7.3, Классификация грамматик и языков 489
ет грамматика класса С, порождающая данный язык. Та-
Таким образом определяются языки типа О, неукорачиваю-
щие языки, контекстно-зависимые языки (КЗ-языки),
обобщенные контекстно-зависимые языки (ОКЗ-язы-
ки), контекстно-свободные языки (КС-языки), линей-
линейные языки, право- и леволинейные языки, регулярные
языки.
Так как всякая ОКЗ-грамматика является грамматикой ти-
типа 0, то в соответствии с п. 1 теоремы 7.2 классы языков типа
О и ОКЗ-языков совпадают. В силу п. 2 того же утвержде-
утверждения, а также ввиду того, что любая КЗ-грамматика является
неукорачивающей грамматикой, совпадают классы неукорачи-
вающих и КЗ-языков. В силу пп. 3 и 4 теоремы 7.2 совпадают
классы право-, леволинейных и регулярных языков.
Но можно доказать следующие факты.
Теорема 7*3. 1. Существует ОКЗ-язык, не являющийся
КЗ-языком.
2. Существует КЗ-язык, не являющийся КС-языком.
3. Существует КС-язык, не являющийся линейным языком.
4. Существует линейный язык, не являющийся регулярным
языком. #
Некоторые из утверждений теоремы 7.3 мы докажем позже.
Сейчас заметим только, что языки, порождаемые граммати-
грамматиками G± и G*> из примера 7.5, не являются КС-языками, хотя
для языка, порождаемого грамматикой (?5, можно построить
порождающую его КЗ-грамматику. Язык правильных скобоч-
скобочных структур, порождаемый грамматикой Сз из примера 7.5,
не является линейным языком, а язык палиндромов из примера
7.6 не есть регулярный язык.
Итак, можно утверждать, что имеют место следующие
строгие включения классов языков:
РЕГсЛИНсКСсОКЗ = ТИП0; КЗсОКЗ,
490 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
где РЕГ, ЛИН, КС, КЗ, ОКЗ, ТИП 0 — классы регулярных,
линейных, КС-языков, КЗ-языков, ОКЗ-языков и языков типа
0 соответственно.
Замечание 7.3. В силу п. 1 теоремы 7.3 требование, со-
состоящее в том, чтобы в КЗ-правиле (рАф -> <р?ф цепочка ? была
непустой, является принципиальным. В 8.2 мы докажем, что с
определенными оговорками класс КС-языков можно включить
в класс КЗ-языков, поскольку любую КС-грамматику можно
преобразовать к эквивалентной КС-грамматике, не содержа-
содержащей правила вывода вида А -> Л. #
Принципиальное различие между классификацией грамма-
грамматик и языков состоит в следующем. Чтобы определить класс
грамматики, достаточно посмотреть на множество ее правил
вывода. Чтобы доказать „положительное" утверждение о том,
что заданный язык есть язык такого-то класса, достаточно
придумать любую грамматику из соответствующего класса,
которая его порождает. Но чтобы доказать яотрицательное"
утверждение о классе языка, т.е. доказать, что язык не при-
принадлежит такому-то классу языков, нужно доказать, что не
существует грамматики соответствующего класса, которая его
порождает. Эта задача гораздо труднее. Некоторые методы
построения подобных доказательств будут рассморены далее.
7.4. Регулярные языки
и регулярные выражения
В замкнутом полукольце C(V) всех языков в алфавите V
рассмотрим подалгебру, порожденную множеством, которое
состоит из пустого языка, языка {Л}, всех языков {а}, а Е V
(каждый из которых содержит единственную однобуквенную
цепочку а), и замкнутую относительно итерации. Эта подал-
подалгебра, обозначаемая 7?(V), есть полукольцо с итерацией. Оно
играет важнейшую роль в теории формальных языков. Его
называют полукольцом регулярных языков. Далее будет
7.4. Регулярные языки и регулярные выражения 491
доказано, что элементы полукольца TZ(V) являются в точности
регулярными языками, т.е. языками, порождаемыми регулярны-
регулярными грамматиками.
Теорема 7.4. Язык в алфавите V регулярен тогда и только
тогда, когда он является элементом полукольца TZ(V). #
Здесь мы не будем доказывать эту теорему, а выведем
ее позже, опираясь на другие теоремы о регулярных языках
(см. 7.5).
Таким образом, множество регулярных языков в алфавите
V = {ai,..., оп} есть не что иное, как замыкание конечного мно-
множества {0, {A}, {ai},..., {оп}} относительно операций объеди-
объединения, соединения и итерации. Следовательно, как и всякое
tt-замыкание, оно может быть описано индуктивно (см. 4.1), а
именно:
1) пустое множество 0, множество {А} (состоящее из одной
пустой цепочки) и множество {а} для каждого a € V считаем
регулярным языком в алфавите V;
2) если известно, что PnQ — регулярные языки в алфавите
V, то к множеству регулярных языков в алфавите V следует
добавить объединение PUQ и соединение PQ\
3) если известно, что Р — регулярный язык в алфавите
V, то к множеству регулярных языков в алфавите V следует
добавить его итерацию Р*;
4) никаких других регулярных языков, кроме определенных
в пп. 1-3, не существует.
Из определения регулярного языка, теоремы 7.4 и след-
следствия 7.1 немедленно вытекает, что и позитивная итерация
регулярного языка регулярна.
Далее мы зачастую будем говорить просто о регулярных
языках (или регулярных множествах), подразумевая, что фик-
фиксирован некоторый алфавит V.
Алгебраические операции над регулярными языками удоб-
удобно представлять с помощью так называемых регулярных вы-
выражений. Каждое регулярное выражение представляет (или
492 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
обозначает) некоторый (однозначно определяемый) регуляр-
регулярный язык, причем языки 0, {Л} и {а}, где а € F, обознача-
обозначаются выражениями 0, Л и а соответственно, и если регулярное
выражение р обозначает регулярный язык Р, а регулярное вы-
выражение q обозначает регулярный язык Q, то регулярные вы-
выражения (p + q), (pq) и (р*) обозначают регулярные множества
Р U Q, PQ и Р* соответственно. Таким образом, в регулярных
выражениях для обозначения операции объединения языков ис-
используют знак „+" (плюс).
Условимся также для регулярного выражения аа* или а* а
использовать обозначение а+ и называть это выражение пози-
позитивной итерацией выражения а.
Замечание 7.4. Введенные выше обозначения регулярных
выражений создают при использовании символа Л некий „кон-
„конфликт" обозначений. А именно мы можем, в зависимости от
контекста, понимать этот символ и как обозначение самой пу-
пустой цепочки, и как обозначение языка, состоящего из одной
пустой цепочки (это и будет собственно регулярное вьфажение
Л). Эти интерпретации символа Л следует тщательно разгра-
разграничивать. В то же время (и такова традиция изложения теории
формальных языков) вряд ли целесообразно вводить для регу-
регулярного выражения, обозначающего язык {Л}, какое-то новое
обозначение. #
Можно сократить количество скобок в регулярных выра-
выражениях*, приняв следующее соглашение о приоритетах: самый
высокий приоритет имеет операция итерации, затем — соеди-
соединения и, наконец, — объединения. Так, регулярное выражение
а* + (Ьс)* обозначает множество цепочек, состоящее из цепо-
цепочек вида ап, п ^0, и цепочек вида Fс)п, п^ 0, где а, Ь, се V.
Использование регулярных выражений позволяет получать бо-
более наглядную и простую нотацию для регулярных языков.
*По аналогии с тем, как мы делали это в формулах, представляющих
булевы функции (см. в.4).
7А. Регулярные языки и регулярные выражения 493
Так, вместо рассмотренного выше регулярного выражения мы
должны были бы использовать гораздо менее выразительную и
более громоздкую формулу: {a}* U ({6} • {с})*.
Соответствие между регулярными множествами и регуляр-
регулярными выражениями не является взаимно однозначным: одно и
то же регулярное множество может представляться многими
регулярными выражениями. Продемонстрируем это на таком
примере.
Рассмотрим регулярное выражение
х = (Ь+а)*(Ь+а + Ь*)у а,Ь,с € V.
Используя аксиомы полукольца (см. 3), преобразуем х следую-
следующим образом:
х = (&+а)+ + F+а)*Ь* = (Ь+а)+ + (Ь+а)* + F+а)*Ь+ =
= F+а)* + {Ь+а)*Ь+ = (Ь+а)*Ь*.
Все регулярные выражения, фигурирующие в этих пре-
преобразованиях, эквивалентны, т.е. все они обозначают один
и тот же регулярный язык. Проблемы распознавания эквива-
эквивалентности двух произвольных регулярных выражении, автома-
автоматизации тождественных преобразований регулярных выраже-
выражений и поиск самого короткого („оптимального") регулярного
выражения, обозначающего данный регулярный язык, весьма
трудны и здесь не обсуждаются. В целом соотношение меж-
между регулярными выражениями и регулярными языками вполне
аналогично соотношению между формулами и булевыми функ-
функциями (см. 6.4). В частности, если переход от формулы к
эквивалентной формуле в теории булевых функций совершает-
совершается согласно аксиомам булевой алгебры и другим тождествам,
выводимым из этих аксиом, то переход от заданного регу-
регулярного выражения к эквивалентному регулярному выражению
производится согласно аксиомам полукольца и тождествам, вы-
выводимым из них.
494 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Зачастую в дальнейшем, если это не повлечет непонимания,
мы будем отождествлять регулярный язык с обозначающим его
регулярным выражением (любым!), что позволит не вводить
новых обозначений и пояснений. Так, для рассмотренного вы-
выше примера мы можем написать ЬЬаЬаЬЪЬ ? F+а)*Ь*, что, стро-
строго говоря, обозначает факт принадлежности цепочки bbababbb
языку, обозначенному регулярным выражением F+а)*Ь*. Ра-
Разумеется, следует воздерживаться, например, от употребления
такой записи: Л ? Л, хотя, если подумать, и здесь все понят-
понятно: пустая цепочка Л принадлежит языку {Л}, обозначаемому
регулярным выражением Л.
7.5. Конечные автоматы.
Теорема Клини
Одной из наиболее важных задач, решаемых в теории фор-
формальных языков, является следующая.
Пусть задана некоторая порождающая грамматика G с
терминальным алфавитом V и цепочка х в алфавите V. Спра-
Спрашивается: принадлежит ли цепочка х языку, порождаемому
грамматикой G1 Эту задачу называют проблемой принад-
принадлежности для грамматики G. В теории формальных языков
доказывается, что проблема принадлежности разрешима для
КЗ-грамматик и для КС-грамматик, но в общем случае не
разрешима для грамматик типа 0. Решение проблемы при-
принадлежности состоит в разработке распознающего алгоритма,
который для произвольных грамматики G (из заданного класса
грамматик) и цепочки х за конечное число шагов выдает от-
ответ на поставленный выше вопрос. В основе подобного рода
алгоритмов лежит математическая модель языка, называемая
распознающей моделью или анализирующей моделью и
являющаяся как бы зеркальной к порождающей модели,
примером которой служит порождающая грамматика. Тра-
Традиционно анализирующие модели языков называют автома-
автоматами. В каждом классе языков может быть определена пара
7.5. Конечные автоматы. Теорема Клики
495
порождающая модель — анализирующая модель" или, дру-
другими словами, пара „грамматика — автомат", где автомат в
определенном смысле анализирует (распознает) цепочки, поро-
порождаемые грамматикой.
Неформально автомат можно описать как устройство, со-
состоящее из блока управления, входной ленты, голов-
головки автомата и блока внутренней памяти автомата
(рис. 7.2). На ленте, которая предполагается полубесконечной
(не ограниченной справа) и разделена на ячейки, записываются
цепочки во входном алфавите (обозначаемом далее V) так,
что буквы цепочки занимают последовательно, начиная с пер-
первой и без пропусков, ячейки ленты — по одной букве в каждой
ячейке. Цепочку, записанную таким образом на входной ленте
автомата, будем называть входной цепочкой. Блок управле-
управления может в каждый момент времени находиться в одном из
конечного множества состояний (обозначим его через Q), а
головка может быть установлена в точности на одну ячейку
входной ленты. В таком случае говорят, что автомат обозре-
обозревает данную ячейку.
Автомат, читая входную цепочку, работает по шагам (или
по тактам). Пусть в некоторый момент времени автомат обо-
обозревает какую-то ячейку ленты, а блок управления находится
в некотором состоянии q € Q. Такт работы автомата
Входная
...
а
...
лента
/
Головю
Блок
управления
i автомата
Внутренняя
память
автомата
Рис. 7.2
496 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
состоит в том, что в зависимости от содержимого обозрева-
обозреваемой ячейки, состояния q, а также содержимого внутренней
памяти автомат сдвигает головку вправо или влево на одну
ячейку либо оставляет ее на прежнем месте, его блок управле-
управления переходит в некоторое новое состояние г (возможно, что
это состояние совпадет с исходным состоянием q), а содержи-
содержимое внутренней памяти определенным образом модифицирует-
модифицируется. В общем случае автомат может и поменять содержимое
той ячейки ленты, которую он обозревает (т.е. автомат может
работать с лентой или только в режиме чтения, не меняя ее со-
содержимого, а лишь определенным образом продвигая головку,
или в режиме чтения/записи).
Вводят понятие конфигурации автомата: она определя-
определяется состоянием блока управления, содержимым обозреваемой
ячейки и содержимым внутренней памяти*. Автомат в об-
общем случае не является детерминированным устройством, т.е.
для него из заданной конфигурации возможны переходы в не-
несколько различных конфигураций. Правила, согласно которым
автомат переходит из одной конфигурации в другую, соста-
составляют в совокупности его систему команд автомата. Ка-
Каждая команда разрешает переход из некоторой конфигурации
в какую-то другую конфигурацию. Это напоминает игру, на-
например шахматную, когда из текущей позиции на доске можно,
сделав ход, получить новую позицию — одну из множества всех
позиций, в которые можно попасть из текущей позиции, сделав
ход согласно правилам игры. В данном случае правила игры
аналогичны системе команд, а позиция на доске — конфигура-
конфигурации автомата.
Автоматы классифицируются в соответствии со структу-
структурой своей внутренней памяти, с режимом работы с лентой
(только чтение или чтение/запись), а также с типом движения
*Для автоматов конкретных классов понятие конфигурации несколько
модифицируется: так, например, в конфигурацию входит не только символ
обозреваемой ячейки, но и вся подцепочка входной цепочки, включающая
символ обозреваемой ячейки и все символы справа от него.
7.5. Конечные автоматы. Теорема Клини 497
головки по ленте (одностороннее, двусторонее, число ячеек, на
которые за один такт можно сдвинуть головку). Множество
команд предполагается конечным, т.е. автомат, как и грамма-
грамматика, имеет конечное описание.
Представим теперь следующую ситуацию. Пусть на входной
ленте автомата записана некоторая цепочка х Е V*. Допустим
также, что среди состояний блока управления выделено некото-
некоторое специальное состояние, называемое начальным, а также
некоторое подмножество состояний, которые называются за-
заключительными.
В начальный момент времени блок управления находится
в начальном состоянии, головка обозревает первую (крайнюю
левую) ячейку ленты, в которой записан первый символ вход-
входной цепочки х. Читая цепочку х и делая один такт за другим,
автомат, после того как он прочитает последнюю букву це-
цепочки, окажется в каком-то состоянии q1 (точнее говоря, в
этом состоянии окажется блок управления). Бели это состо-
состояние является заключительным, то тогда говорят, что автомат
допустил цепочку х. Спрашивается: каким образом посред-
посредством грамматики можно описать множество всех цепочек в
алфавите F, которые автомат допускает?
Оказывается, что каждому классу грамматик соответству-
соответствует свой класс автоматов, причем для каждой грамматики соот-
соответствующего класса может быть построен автомат, который
допускает цепочки, порождаемые данной грамматикой, и толь-
только их. Образно говоря, в каждом классе языков возникает пара
„писатель — читатель": грамматика, как „писатель", поро-
порождает определенное множество „текстов" (цепочек в заданном
алфавите), а „читатель" (автомат) проверяет „правильность"
этих текстов, допуская те и только те цепочки, которая по-
порождает „его" грамматика. В качестве „писателя" может
выступать программист, пишущий тексты компьютерных про-
программ, а в качестве „читателя" — системные программы,
обеспечивающие проверку правильности написанного текста
498 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
(соответствия его грамматике того или иного языка програм-
программирования). Тем самым допускающий автомат становится
прообразом некоторого распознающего алгоритма, решающего
проблему принадлежности в том или ином классе грамматик.
Заметим, однако, что автомат сам по себе еще не являет-
является таким алгоритмом и что оказывается, например, в классе
грамматик типа 0 в общем случае построить алгоритм для
решения проблемы принадлежности невозможно, хотя автома-
автоматы, соответствующие грамматикам типа 0, существуют (так
называемые машины Тьюринга, см. Д.7.4). Некоторые вопро-
вопросы, связанные с переходом от анализирующей модели языка
к алгоритму, который решает проблему принадлежности для
грамматики, порождающей этот язык, рассмотрены в Д.8.1.
Мы начинаем с простейших анализирующих моделей — tco-
печных автоматов. Конечные автоматы — это анализиру-
анализирующие модели для регулярных языков. Конечный автомат не
имеет внутренней памяти, головка движется по ленте толь-
только вправо — на одну ячейку за такт. С ленты можно только
читать. Кроме того, автомат может переходить „спонтанно"
из одного состояния в другое, не читая ленту и не продви-
продвигая головку. Такой такт можно рассматривать как переход
из состояния в состояние по пустой цепочке. Его называют
Л-тактом.
Итак, из каждого состояния автомат может переходить в
другое состояние, читая тот или иной символ входной цепочки,
или делать переход по пустой цепочке, причем принимается по
определению, что эти два типа переходов исключают друг дру-
друга. Поведение конечного автомата определяется его системой
команд, в которой каждая команда задается записью
ga->r, G.4)
что означает: „из состояния q по символу а 6 V или по пустой
цепочке (тогда а = Л) можно перейти в состояние г" (возможно,
что g = r).
7.5. Конечные автоматы. Теорема Клини 499
При этом по определению принимается, что переход по пу-
пустой цепочке и переход по входному символу исключают друг
друга. То есть для любой пары (д, г) состояний конечного ав-
автомата имеет место следующее: если существует команда G.4)
при a = Л, то нет ни одной команды (для такой же пары состо-
состояний) при абУи наоборот.
Конфигурация конечного автомата определяется как
упорядоченная пара (q, ay), где q — состояние блока упра-
управления, а — символ в обозреваемой ячейке, у — цепочка во
входном алфавите, расположенная в ячейках справа от обозре-
обозреваемой (цепочку ау принято называть непрочитанной ча-
частью входной цепочки). При этом если обозреваемая ячейка
пуста, т.е. не содержит какого-либо символа входного алфави-
алфавита, то непрочитанная часть входной цепочки считается пустой
цепочкой.
Чтобы дать математическое определение конечного авто-
автомата, нужно заметить, что он, в свете только что изложенного
неформального описания, допускает естественную интерпрета-
интерпретацию в терминах размеченных ориентированных графов. Будем
рассматривать состояния блока управления конечного автома-
автомата как вершины ориентированного графа, множество дуг кото-
которого определяется системой команд следующим образом: дуга
ведет из состояния q в состояние г (для данных состояний q
и г) тогда и только тогда, когда в системе команд автомата
есть команда G.4), т.е. возможен переход из состояния q в со-
состояние г. Каждая дуга имеет метку, которая является либо
множеством букв входного алфавита, либо пустой цепочкой.
Метка дуги (</, г) есть пустая цепочка Л, если из q в г
можно перейти по пустой цепочке; в противном случае метка
дуги (qr, г) есть множество всех входных символов, по которым
возможет переход из состояния q в состояние г.
Пример 7.7. Зададим конечный автомат с входным ал-
алфавитом {а,Ь,с} и множеством состояний {Фь9ъ92?9з} такой
500 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
системой команд:
92&-+91,
92,
> 93-
По этой системе команд построим размеченный ориенти-
ориентированный граф, изображенный на рис. 7.3. Среди состояний
автомата выделены начальное состояние 9о и Два заключи-
заключительных состояния 92 и 9з- На рис. 7.4 показана последова-
последовательность конфигураций, которую
проходит конечный автомат, читая
цепочку abac. Эту цепочку авто-
автомат допускает, так как, читая ее,
он переходит из начального состо-
состояния в одно из заключительных. В
формальной записи последователь-
ность конфигураций на рис. 7.4 вы-
выглядит так: (9о, abac), (91, abac),
(92, Ьас), (9i, ас), (93, с), (93, А).
Этой последовательности отвечает путь в ориентирован-
ориентированном графе, ведущий из вершины 9о в вершину 9з:
Рис. 7.3
9i ~>а 92
9з ->с 9з
(под каждой стрелкой подписана буква, принадлежащая метке
соответствующей дуги и являющаяся очередной буквой чита-
читаемой входной цепочки). Заметим, что, например, находясь в
состоянии 9i и обозревая второй от конца цепочки символ, т.е.
символ а, автомат мог, согласно системе команд, сделать пере-
переход в состояние 92, & не в состояние 9з, но тогда он бы „завис"
7.5. Конечные автоматы. Теорема Клини
501
а
i >
Ъ
а
ъ
с
...
б
a
Ъ
а
с .
Рис.
д
7.'
<
1
••¦/
7з
а
b
а
а
b
с
92
...
...
в
а
с .
.. .
е
*
в состоянии 92 и не смог бы прочитать последний символ запи-
записанной на ленте цепочки, т.е. символ с, так как среди команд
нет такой, которая разрешала бы переход из состояния 92 ку-
куда-либо по символу с.
Эта ситуация демонстрирует как раз недетерминирован-
недетерминированность конечного автомата как распознающего устройства: си-
система команд („правила игры") позволяет автомату допустить
цепочку abac („игроку" найти последовательность ходов, веду-
ведущую к „выигрышу"), но из этого вовсе не следует, что последо-
последовательность конфигураций, которую проходит автомат, читая
записанную на ленте цепочку, является единственной. Автомат
может „ошибиться", сделав „неправильный" ход. Но и последо-
последовательность „правильных" ходов может быть не единственной.
Например, читая последний символ цепочки, т.е. символ с, ав-
автомат мог „выбрать" переход в состояние #2? которое также
является заключительным. Рассматриваемый автомат допус-
допускает не всякую цепочку в алфавите {a,b,c}. Видно, что ни одна
цепочка, которая начинается с префикса са, не будет допущена
автоматом. #
502 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Обозначение пустой цепочки Л, фигурирующей в виде метки
дуги ориентированного графа, который представляет конеч-
конечный автомат, можно интерпретировать как регулярное выра-
выражение, т.е. как регулярный язык, состоящий из одной пустой
цепочки (см. замечание 7.4). Поскольку метка дуги, являю-
являющаяся множеством букв {bi, ...,6m} С V, может быть также
записана в виде регулярного выражения, а именно как сум-
сумма Ь\ + ... + 6W, то метку каждой дуги можно считать ре-
регулярным выражением определенного вида или, так как мы
отождествляем регулярные языки и регулярные выражения, ре-
регулярным языком. Это позволяет нам формально определить
конечный автомат как ориентированный граф, размеченный
над полукольцом %{V) регулярных языков. Такое математиче-
математическое определение конечного автомата весьма удобно: оно дает
нам возможность применить при изучении конечных автоматов
уже изученные нами алгебраические методы анализа размечен-
размеченных ориентированных графов.
Итак, математическое определение конечного автомата фор-
формулируется следующим образом. Конечный автомат — это
ориентированный граф, размеченный над полукольцом TZ(V)
регулярных языков в алфавите V с выделенной вершиной до? ко-
которая называется начальной, и с выделенным подмножеством
вершин F, каждый элемент которого называется заключи-
заключительной вершиной.
На функцию разметки при этом накладываются следующие
ограничения: метка каждой дуги есть либо язык {Л}, либо
непустое подмножество алфавита V.
Вершины графа называют обычно в этом случае состоя-
состояниями конечного автомата, начальную вершину — на-
начальным состоянием, а заключительную вершину — за-
заключительным состоянием конечного автомата.
Замечание 7.5. Если для какой-то дуги е Е Е ее метка
(р(е) есть язык {Л}, то, поскольку этот язык не является под-
подмножеством алфавита V, в этом случае (р(е) % V, и, наоборот,
7.5. Конечные автоматы. Теорема Клики 503
если (р(е) С V, то исключается, что (р(е) = {Л}. Таким образом,
два рассмотренных случая для значений функции разметки ис-
исключают друг друга, на что и было указано в рассмотренном
выше неформальном описании конечного автомата. #
На рис. 7.5 изображен конечный ав- 0+1 0+1
томат, для которого алфавит V = {0,1}.
Начальное состояние показано входной
стрелкой, заключительное — выходной.
Метки дуг обычно пишут без фигурных Рис# 7'5
скобок. Разрешена запись меток дуг и в виде регулярных вы-
выражений (см. рис. 7.5).
Конечный автомат, таким образом, может быть задан как
пятерка:
M = (Q, Я, <р, go, F),
где Q — множество состояний автомата; Е — множество
дуг; <р — функция разметки (весовая функция), причем для
каждой дуги е ? Е ее метка <р(е) = {Л} или (р(е) С V, при этом
подмножество <р(е) не пусто; qo E Q — начальное состояние;
F С Q — подмножество заключительных состояний.
Алфавит V называется входным алфавитом автомата
Му а его буквы — входными символами (или входными
буквами) данного автомата.
Замечание 7.6. Конечный автомат определен как ориен-
ориентированный граф, размеченный над полукольцом регулярных
языков, но метка дуги задается не как произвольный регуляр-
регулярный язык, а как язык, состоящий из одной пустой цепочки,
либо язык, являющийся подмножеством букв входного алфави-
алфавита. Это ни в коей мере не противоречит основному опреде-
определению размеченного ориентированного графа, ибо совершенно
не обязательно, чтобы область значения функции разметки со-
совпадала с носителем полукольца. Чисто формально, конечно,
можно обобщить определение конечного автомата и допустить
в качестве меток дуг произвольные регулярные языки, но, как
504 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
можно показать, это обобщение не является принципиальным, и
такое определение конечного автомата сводится к данному вы-
выше определению (см. задачи в конце этой главы). Немаловажно
и то, что приведенное формальное определение конечного авто-
автомата и задание меток дуг как регулярных языков специального
вида согласуются с интуитивным представлением об автомате
как об устройстве, которое „побуквенно" читает входные це-
цепочки, переходя из одного состояния в другое. Требование,
чтобы такое устройство за один такт анализировало („обозре-
(„обозревало") любое, сколь угодно сложное регулярное выражение, не
отвечает нашей „вычислительной" интуиции, в соответствии с
которой за один такт может быть произведена только простая
операция, каковой и является „реакция" автомата на обозрева-
обозреваемый одиночный символ или на пустую цепочку. #
Бели е = (д, г) — дуга автомата М и ее метка <р(е) есть
регулярное выражение Л, то в этом случае будем говорить,
что в автомате М возможен переход из состояния q в
состояние г по пустой цепочке, и писать q ->д г. Дугу с
меткой Л будем называть ^переходом (или пустой дугой).
Бели же метка дуги е есть множество, содержащее входной
символ а, то будем говорить, что в автомате М возможен
переход из состояния q в состояние г по символу а, и писать
q->ar.
Для конечного автомата удобно ввести в рассмотрение
функцию переходов, определив ее как отображение
6:Qx(VU{\})->2Q,
такое, что
т.е. значение функции переходов на упорядоченной паре (состо-
(состояние, входной символ или пустая цепочка) есть множество всех
состояний, в которые из данного состояния возможен переход
по данному входному символу или пустой цепочке. В частно-
частности, это может быть пустое множество.
7.5. Конечные автоматы. Теорема Клини 505
На рис. 7.5 %о,О) = {9o,9i}, %оД) = {go}, %1,0) = {д2},
S(qul) = 0, 5(92,0) = Ы, 5(92,1) = {ft}.
Понятие функции переходов конечного автомата позволя-
позволяет дать и математическую интерпретацию системы команд. С
этой точки зрения система команд есть просто способ предста-
представления конечной функции, а именно функции переходов.
Система команд есть конечное множество команд вида
qa->r,
где q и г — состояния автомата; а — входной символ или
пустая цепочка, причем указанная команда тогда и только
тогда содержится в системе команд, когда q ->а г.
Содержательная интерпретация команды была приведена
выше. Стрелка (-+), как и в записи правила грамматики, есть
„ метасимволи. Он не содержится ни в одном из алфавитов,
фигурирующих в определении конечного автомата.
Система команд автомата, изображенного на рис. 7.5, при-
приведена ниже:
9оО->9ь
9о1 -> 90,
9iO -> 92,
92O -> 92,
921-+92.
Используя функцию переходов, конечный автомат можно
задавать как упорядоченную пятерку:
где V — входной алфавит; Q — множество состояний; 9о —
начальное состояние; F — множество заключительных состоя-
состояний; S — функция переходов, заданная в виде системы команд.
Как правило, в дальнейшем мы именно так и будем опреде-
определять конечный автомат.
506 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Конечный автомат называют полностью определенным,
если из каждого его состояния по каждому входному символу
возможен переход в некоторое состояние, т.е.
Заметим, что в полностью определенном конечном автомате,
вообще говоря, могут существовать и переходы по пустой
цепочке.
Конечный автомат называется детерминированным, ес-
если в нем нет дуг с меткой Л и из любого состояния по любому
входному символу возможен переход в точности в одно состоя-
состояние, т.е.
(V(/eQ)(Va€F)(|%,a)| = l).
Конечный автомат называется квазидетерминирован-
ным, если в нем нет дуг с меткой Л и из любого состояния
по любому символу возможен переход не более чем в одно со-
состояние, т.е.
Замечание 7.7. Для детерминированного конечного авто-
автомата значением функции переходов для любой пары (состояние,
входной символ) является одноэлементное подмножество мно-
множества состояний. Поэтому естественно понимать функцию
переходов детерминированного конечного автомата не как ото-
отображение множества Q х V в множество 2^, а как отображение
множества Q х V в само множество состояний Q. Впредь так и
будем рассматривать функцию переходов детерминированного
конечного автомата, не оговаривая этого особо. #
Согласно общему определению метки пути в размеченном
ориентированном графе, метка пути в конечном автомате есть
соединение* меток входящих в этот путь дуг (в порядке их про-
прохождения). Таким образом, метка любого пути конечной дли-
длины в конечном автомате есть регулярный язык. Отметим, что
* Умножением полукольца ЩУ) является соединение языков.
7.5. Конечные автоматы. Теорема Клини 507
мы, изучая размеченные ориентированные графы, предполага-
предполагаем, что рассматриваются только пути конечной длины. Так,
для автомата, изображенного на рис. 7.5, метка пути 90)9<h9i)92
равна соединению языков {0,1} • {0} • {0} = {000,100}, что мож-
можно записать в виде регулярного выражения @ +1H0, а метка
пути до? 91) 92) 92) 92 может быть задана таким регулярным
выражением:
00@ +1) @ +1) = 00@0 + 01 +10 +11) =
= 0000 + 0001 + 0010 + ООН,
что означает, что эта метка есть множество цепочек
{0000,0001,0010,0011}.
Метку пути W конечной длины обозначим через (p*(W).
Здесь у>* — это функция, отображающая множество всех путей
конечной длины в размеченном ориентированном графе, в по-
полукольцо 7?(V). Для пути W длины 1 значение <p*(W) = <p(W),
т.е. функция разметки ориентированного графа есть ограниче-
ограничение функции (р* на множество всех путей длины 1.
Бели цепочка х принадлежит метке некоторого пути W —
пути, ведущего из вершины q в вершину г конечного автомата
М, то говорят, что цепочка х читается на пути W в М или
что путь W несет цепочку х. Пишем q =»* г , если х читает-
читается на некотором пути из q в г. В том случае, когда явно надо
указать длину п пути, на котором читается цепочка ж, записы-
записываем q =Ф>5 г. Бели нужно подчеркнуть, что цепочка х читается
на некотором пути ненулевой длины из q в г, то используем
запись q =ФJ г. В терминах неформального описания конечного
автомата любому пути, на котором читается входная цепочка
ж, отвечает последовательность конфигураций, которую прохо-
проходит автомат, читая посимвольно входную цепочку, записанную
на ленте, и продвигая головку на один символ вправо за один
такт.
508 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Стоимость прохождения из состояния q в состояние г есть
(согласно общему определению этого понятия в размеченных
ориентированных графах) объединение меток всех путей*, ве-
ведущих из q в г, т.е. множество всех таких #, что q =Ф-* г. Это
значит, что элемент Cqr матрицы стоимостей есть язык
Говоря об элементе cqr матрицы стоимостей, мы отождествляем
обозначение состояния автомата с его номером в некоторой
нумерации состояний как вершин ориентированного графа.
В частности, язык L(M) конечного автомата М есть
множество всех цепочек во входном алфавите, читаемых в
М на некотором пути из начального состояния в одно из
заключительных состояний. Другими словами,
L(M) = {х: q0 =** qh qf € F} = (J сШр G.5)
где F — множество заключительных состояний.
Таким образом, язык конечного автомата есть объединение
тех элементов матрицы стоимостей автомата, которые нахо-
находятся в строке, соответствующей начальному состоянию ф>> и
в столбцах, соответствующих всем заключительным состояни-
состояниям qf e F.
Замечание 7.8. Необходимо обратить внимание на одну
очень важную вещь. В конечном автомате метка произволь-
произвольного пути конечной длины есть регулярный язык, поскольку
он вычисляется как соединение конечного семейства регуляр-
регулярных языков. Но стоимость прохождения между заданной парой
вершин априори не является регулярным языком, так как мно-
множество путей, ведущих из одной вершины в другую, может
* Здесь объединение понимается как бесконечная сумма замкнутого
полукольца C(V) всех языков в алфавите V, т.е. как точная верхняя
грань последовательности языков относительно теоретико-множественно-
теоретико-множественного включения.
7.5. Конечные автоматы. Теорема Клини 509
быть бесконечным (каждый путь имеет конечную длину, но
множество всех таких путей может оказаться бесконечным,
содержать пути сколь угодно большой длины — простейший
пример дает петля, по которой можно пройти сколько угод-
угодно раз). Поэтому объединение при определении стоимости
прохождения между парой состояний конечного автомата мы
можем сейчас рассматривать только как операцию замкнутого
полукольца всех языков в данном алфавите, а именно опера-
операцию вычисления точной верхней грани („бесконечная сумма"
в замкнутом полукольце). Но коль скоро элементы матрицы
стоимостей уже вычислены, их объединение (в формуле G.5)),
дающее язык конечного автомата, разумеется, конечно. Позже
будет доказано, что на самом деле все стоимости в конечном
автомате также регулярны. #
О языке L(M) говорят, что он допускается (или воспри-
воспринимается) конечным автоматом М. О любой цепочке, при-
принадлежащей языку L(M), говорят, что она допускается (или
воспринимается) конечным автоматом М. Такую цепочку на-
называют также допустимой цепочкой данного конечного
автомата.
Определение 7.10. Два конечных автомата М\ и
называют эквивалентными, если их языки совпадают:
Установим теперь связь между понятиями конечного авто-
автомата и регулярной грамматики.
Теорема 7.5. Язык допускается конечным автоматом то-
тогда и только тогда, когда он порождается регулярной грамма-
грамматикой.
< Чтобы доказать теорему, нужно:
1) указать способ построения регулярной грамматики G
по заданому конечному автомату М, такой, чтобы язык, по-
510 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
рождаемый грамматикой G, совпадал с языком, допускаемым
автоматом М: L(G)=L(M);
2) указать способ построения конечного автомата М по
заданной регулярной грамматике G, такой, чтобы язык, до-
допускаемый автоматом М, совпадал с языком, порождаемым
грамматикой G: L(M) = L(G).
Замечание 7*9. Регулярную грамматику G и конечный
автомат М, такие, что L(G) = L(M), иногда называют эквива-
эквивалентными. #
Рассмотрим эти построения по очереди.
1. Построение регулярной грамматики по конечно-
конечному автомату. Пусть дан конечный автомат
Определим регулярную грамматику G = (V, JV, ?, Р) следую-
следующим образом: терминальный алфавит V совпадает с входным
алфавитом автомата М; нетерминальный алфавит N нахо-
находится во взаимно однозначном соответствии с множеством
состояний Q автомата М, причем состоянию q€Q сопоставлен
нетерминал Sq E N и аксиома сопоставлена начальному состо-
состоянию до? т.е. S = Sqo] множество правил вывода Р строится по
системе команд S так: правило вывода Sq -? aSr, где а Е VU {Л},
принадлежит Р тогда и только тогда, когда в S есть команда
qa -> г; кроме того, если (и только если) состояние г заключи-
заключительное (г € F), то в Р добавляется правило вывода Sq -> a.
Бели же go E F (и только в этом случае), то в Р помещаем пра-
правило вывода Sqo -* Л.
Для конечного автомата на рис. 7.5 получим следующую
регулярную грамматику:
,|05gi,
Я» I о,
7.5. Конечные автоматы. Теорема Клини 511
Заметим, что, читая цепочку в автомате, в грамматике мы
ее выводим (порождаем). Например, до -*о 91 ~~*о 92 —h 92 и
5да1-05^1-005^1-001.
Докажем, что описанное построение корректно, т.е. L(G) =
= L(M). Для этого сначала, используя индукцию по длине п
пути в конечном автомате М, докажем, что из факта дости-
достижимости q =>? г в автомате М (для любого п ^ 0) следует
выводимость Sq \-*G xSr в грамматике G для любых g,r E Q и
x€V*.
Пусть длина пути п = 0, т.е. q =>% г и г = q. Так как метка пу-
пути нулевой длины в ориентированном графе, размеченном над
полукольцом 7?(V), равна единице полукольца — регулярному
выражению Л, то q =*д q при х = А. Но Sq Ь^ Sq выполняется
тривиально.
Пусть для любого А; ^ т — 1 из достижимости q =^* r следует
выводимость Sq Ь* гг5г, и пусть в автомате М существует
путь W длины т, ведущий из вершины q в вершину г, на
котором читается цепочка я;, т.е. q =^J* г. Так как длина
пути W не меньше 1, то в нем есть по крайней мере одна
дуга и существуют такая вершина </ и такое о G V U {Л},
что g -*а ({ ^JJ1"" г, где оу = х (мы выделили первую дугу
пути W). Тогда, согласно построению множества Р правил
вывода грамматики С,вР содержится правило Sq -> aSq^ а, по
предположению индукции, из того, что в М q9 ^J1^1 г, следует,
что Sq> h^ ySr. В итоге получаем Sq h^ aSj Ь? aySr = xSr, т.е.
Sq \-q ж5г, что и требовалось.
Теперь если цепочка х € L(M), то в М существует путь,
ведущий из начального состояния зд в одно из заключительных
состояний д/, на котором читается цепочка ж, т.е. до =^х 9/ Для
некоторого д/ € F. Если 9/ = 9о и тогда д: = Л 6 ?(М), то в
множестве Р правил вывода есть правило Sqo -> Л и Л € ?(&)•
Если же 9/ отлично от <7о, то, какова бы ни была цепочка я,
путь из 9о в д/, на котором она читается, имеет длину, не
меньшую единицы. Выделяя в этом пути последнюю дугу,
получим до =^у 9; ""*а 9/i гДе Уа = х- Но тогда, во-первых,
512 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
как мы только что доказали, в грамматике G имеет место
выводимость Sqo \-q ySqfy а, во-вторых, из того, что q' ->a g/,
согласно построению множества правил вывода грамматики G,
следует, что в ней есть правило 59/ -? а, и окончательно получим
т.е. х е L(G).
Таким образом, мы полностью доказали, что для каждой
цепочки х EV* из того, что х Е Ь(М), следует х Е L(G), т.е.
имеет место включение L(M) С L(G).
Чтобы доказать обратное включение, используя индукцию
по длине п вывода в грамматике G, покажем сначала, что
из факта выводимости Sq Ь? xSr (для любого п ^ 0) следует
достижимость q =>* г в автомате М для любых </,r G Q и а: € V*.
При п = 0 имеем 59 Ь^ 5g, x = Л и тривиально выполняется
Пусть для любого к ^ т — 1 из выводимости 59 h^ ж5г следу-
следует достижимость q =>* г (в автомате М), и пусть в граммати-
грамматике G существует вывод D длины т цепочки xSr из цепочки
Sq, т.е. 5g KJo ж?г. Так как длина вывода D не меньше 1,
то найдется такой нетерминал Sq' и такое a G V U {Л}, что
59 Kg aSq* bjrj aySr, где ау = х (мы выделили первый шаг вы-
вывода D). Непосредственная выводимость Sq^GaSqi означает,
что в множестве правил вывода грамматики G содержится пра-
правило Sq -> aSqt и, следовательно, в системе команд S конечного
автомата М есть команда qa-? q* и тогда q -*a q'- Согласно
предположению индукции, из того, что Sq» Ь^ у?г, следует,
что д' =Ф* г в М. В итоге получаем g ->a g; =Ф* г, т.е., так как
ay = x, q =Ф>* г, что и требовалось.
Бели теперь х ? L(G), то в грамматике G существует вывод
цепочки ж из аксиомы Sqo, т.е. 590 \-*G x. На последнем ша-
шаге этого вывода применяется некоторое правило, правая часть
которого не содержит вхождений нетерминалов, т.е. правило
вида Sq' —> а. Поскольку любая цепочка в выводе в регулярной
7.5. Конечные автоматы. Теорема Клини 513
грамматике может содержать нетерминал только как послед-
последний символ, то Sqo \-q ySq* \~g ya> = #• Отсюда следует, что
до =^у я'- Кроме того, правило вывода Sq* -> а может принад-
принадлежать множеству Р тогда и только тогда (по построению Р),
когда в системе команд автомата М есть команда qfa -> g/,
qj G F. Следовательно, go =>* q' ->a g/, что и означает go =^ж Qf>
т.е. x G L(M).
Итак, доказано включение L(G) С L(M), и L(G) = i(M), т.е.
регулярная грамматика G, построенная, как описано выше, по
конечному автомату М, эквивалентна ему.
2. Построение конечного автомата по регулярной
грамматике. По заданной регулярной грамматике
построим конечный автомат М = (V, Q, go> -F1» ^) так, что вход-
входной алфавит автомата М совпадает с терминальным алфа-
алфавитом грамматики G, множество состояний Q совпадает с
нетерминальным алфавитом грамматики G, пополненным но-
новым состоянием /, не принадлежащим объединенному алфа-
алфавиту грамматики G, т.е. Q = NU {/}; начальное состояние до
совпадает с аксиомой S, множество заключительных состояний
F = {/}. Система команд S определяется следующим образом:
команда Аа -+ В принадлежит 6 тогда и только тогда, когда
в множестве Р правил вывода есть правило А -> аВ, а коман-
команда Аа —> / принадлежит 6 тогда и только тогда, когда правило
вывода А -> а принадлежит множеству Р.
Например, по регулярной грамматике G^ из примера 7.5
строится конечный автомат с входным алфавитом {а, 6,0,1},
множеством состояний {J, D, /}, начальным состоянием /,
единственным заключительным состоянием / и такой системой
команд (рис. 7.6):
D0-+D, Dl^D, Da-+f, Db->f,
?>0->/, ?>l->/, Ia^f, Ib^f.
—*, 17 - 10061
514 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
а,Ь,0,1
Рис. 7.6
Обоснование корректности этого построения может быть
проведено так же, как и построения регулярной грамматики по
конечному автомату (пдвойной" индукцией по длине вывода в
грамматике и по длине пути в автомате), и мы его опускаем. >
Таким образом, конечные автоматы допускают в точности
те же языки, которые порождают регулярные грамматики.
Выше (см. 7.4) без доказательства сформулирована теоре-
теорема 7.4, согласно которой регулярные языки (в алфавите V)
и языки полукольца 1Z(V) — одно и то же. Это позволи-
позволило нам (так сказать, авансом) называть элементы полукольца
TZ(V) регулярными языками. Теперь пришла пора доказать это
подробно. Для этого, опять разделив понятия языка из полу-
полукольца TZ(V) и регулярного языка (т.е. языка, порождаемого
регулярной грамматикой), докажем, что язык допускается ко-
конечным автоматом с входным алфавитом V тогда и только
тогда, когда он есть элемент полукольца H(V). Тогда, с учетом
доказанной теоремы 7.5, будет доказана и теорема 7.4.
Теорема 7.6 (теорема Клини). Пусть V = {ai,..., ап} —
произвольный алфавит. Язык L С V* является элементом
полукольца Tl(V) тогда и только тогда, когда он допускается
некоторым конечным автоматом.
Ч Докажем, что всякий язык из TZ(V) допускается некоторым
конечным автоматом.
Для доказательства этого утверждения мы воспользуемся
методом индукции по построению языка из TZ(V) как элемен-
элемента замыкания множества {0, {Л}, {ai},..., {an}}. Этот метод
7.5. Конечные автоматы. Теорема Клини 515
состоит в следующем: сначала утверждение доказывается для
языков исходного множества (замыкание которого строится), а
затем в предположении, что утверждение доказало для языков
L и К из 7?(V), оно доказывается для LUK, LK и 1Л
Конечные автоматы для языков 0, {А}, {а}, где а € V,
приведены на рис. 7.7.
0 A. a
Рис. 7.7
Пусть конечные автоматы
'01, F\) 8\) и Af2 = (V, Q2, 902? -p2i ^2)
для языков L и К полукольца 7?(F) соответственно уже по-
построены. Обратим внимание на то, что входные алфавиты
этих автоматов совпадают (мы работаем на множестве языков
в произвольном, но фиксированном алфавите V) и автоматы не
имеют ни общих вершин, ни общих дуг.
На рис. 7.8 изображен метод построения конечных автомат
тов для языков LUK, LK и L*. На рисунке видно, что автомат
для объединения (см. рис. 7.8, а) получается при сохранении
всех дуг и вершин автоматов объединяемых языков путем доба-
добавления новой начальной вершины зо> проведения из нее пустых
дуг в каждую из начальных вершин объединяемых автоматов
(?oi и 902) и объявления множеством заключительных вершин
объединения множеств заключительных вершин (i*i и F2) объ-
объединяемых автоматов. Получается „параллельное соединение"
автоматов для языков ЬиК. Любая цепочка ж, читаемая на не-
некотором пути из вершины so в какую-то из вершин множества
^1U F2, может быть представлена так: х = Хх\ = х\ (переход по
пустой цепочке из sq qoi и дальнейшее чтение произвольной це-
цепочки a?i, допускаемой автоматом Mi) или х = Хх2 = х2 (переход
17*
516
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
LUK
по пустой цепочке из sq 902 и дальнейшее чтение произвольной
цепочки #2, допускаемой автоматом* Мг).
Аналогично при построении конечного автомата для соеди-
соединения (см. рис. 7.8, б) достаточно объявить новой начальной
вершиной начальную вершину первого автомата (901)9 a мно-
множеством заключительных вершин — таковое для второго ав-
автомата (F2), после чего из каждой заключительной вершины
первого автомата провести пустую дугу в начальную вершину
второго автомата. Получится „последовательное соединение"
автоматов.
* Новый конечный автомат как некое распознающее устройство может
из своей начальной вершины по пустой цепочке, т.е. не читая ни одного
символа входной ленты, перейти в начальную вершину первого автомата и
потом „работать за него" или „сделать выбор в пользу" второго автомата,
перейдя по пустой цепочке из вершины so в вершину дог-
7.5. Конечные автоматы. Теорема Клини 517
Конечный автомат для итерации (см. рис. 7.8, в) строится
следующим образом. Нужно: а) ввести новые начальную (so) и
заключительную (*) вершины, проведя пустую дугу из первой
в последнюю; б) провести пустые дуги из новой начальной вер-
вершины в прежнюю начальную вершину автомата итерируемого
языка (<?о)> а также из каждой заключительной вершины мно-
множества F автомата языка L в новую заключительную вершину
и прежнюю начальную вершину. Итак, каждый язык полуколь-
полукольца TZ(V) допускается некоторым конечным автоматом.
Докажем теперь, что язык произвольного конечного авто-
автомата есть элемент полукольца 1l(V). Язык конечного автомата,
как следует из формулы G.5), — это конечное объединение язы-
языков, являющихся определенными элементами матрицы стоимо-
стоимостей автомата. Матрица стоимостей есть итерация матрицы
меток дуг, задающей автомат. Метка каждой дуги — регуляр-
регулярное выражение, обозначающее язык из полукольца 7?(V), и ма-
матрица стоимостей, следовательно, является итерацией матри-
матрицы, все элементы которой могут быть определены регулярными
выражениями, т.е. принадлежат полукольцу H(V). Полукольцо
ЩУ) есть полукольцо с итерацией. Поэтому в силу теоремы 3.9
и матрица стоимостей конечного автомата будет состоять из
языков полукольца H(V). Отсюда следует, что язык конечного
автомата есть элемент этого полукольца. >
Замечание 7.10. Обратим внимание на то, что в общем
случае при построении итерации нельзя обойтись без добавле-
добавления новых начальной и заключительной вершин. Рассмотрим в
этой связи построение автомата для итерации языка, допуска-
допускаемого автоматом на рис. 7.9, а.
Если мы построим автомат для итерации так, как показано
на рис. 7.9, б, не вводя новую начальную вершину, то этот ав-
автомат будет допускать, в частности, все цепочки языка @1)*.
Однако эти цепочки не содержатся в итерации исходного язы-
языка. В частности, 01 ^ (@1)* 1)*. Действительно, любая цепочка
языка исходного автомата задается регулярным вьфажением
518
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
@1)* 1 и есть либо 1, либо цепочка, оканчивающаяся подцепоч-
подцепочкой 11. Следовательно, любая цепочка из итерации исходного
языка есть либо цепочка 1П, где п > 0, либо цепочка, оканчива-
оканчивающаяся подцепочкой 11.
Можно построить аналогичный пример и для того, чтобы
убедиться в необходимости добавления новой заключительной
вершины.
На рис. 7.9, в приведен пример правильно построенной ите-
итерации.
Бели при построении конечного автомата для итерации мы
не будем проводить пустую дугу s -* ?, то получим автомат для
позитивной итерации исходного языка. #
Из теорем 7.5 и 7.6 получим следующий результат.
Следствие 7.2. Следующие утверждения о языке L в
алфавите V эквивалентны:
1) L есть элемент полукольца TZ(V);
2) L порождается некоторой регулярной грамматикой;
3) L допускается некоторым конечным автоматом.
Задачу построения конечного автомата по данному регу-
регулярному выражению называют задачей синтеза конечного
7.5. Конечные автоматы. Теорема Клини 519
автомата. Вычисление же языка конечного автомата есть
задача анализа конечного автомата.
Рассмотрим более подробно решение задачи анализа конеч-
конечного автомата.
Как же практически вычислить язык конечного автомата?
Для этого, вообще говоря, достаточно вычислить, как следует
из формулы G.5), матрицу стоимостей автомата (как разме-
размеченного ориентированного графа) любым из способов, кото-
которыми мы анализировали размеченные ориентированные графы
(см. 5). Бели мы выберем для вычисления итерации способ,
связанный с решением систем линейных уравнений, нам пона-
понадобится решить п = |Q| систем вида
где А — квадратная матрица n-го порядка*, элемент aij кото-
которой является регулярным выражением, служащим меткой дуги
из вершины (состояния) qi в вершину (состояние) qj (при не-
некоторой выбранной нумерации состояний!), если такая дуга
существует, и равен регулярному выражению 0, если нет дуги
из q{ в qj] Sj — j-й столбец единичной матрицы, т.е. столбец,
у которого все компоненты, кроме j-й, равны 0 (нулю полу-
полукольца 1Z(V)), a j-я компонента равна Л (единице полукольца
Решив указанные п систем, найдем матрицу стоимостей С —
= А* заданного конечного автомата. Но нам, как правило,
нужна не вся матрица стоимостей, а только элементы вида св*,
где s — номер начального, at — один из номеров заключитель-
заключительного состояния.
Поэтому, вместо того чтобы решать несколько систем ли-
линейных уравнений, достаточно решить одну:
G.6)
*Это не что иное, как матрица меток дуг, определяющая размеченный
ориентированный граф (см. 5).
520 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
где /3 — столбец, все компоненты которого равны 0 (нулю полу-
полукольца ТС(У)), кроме компонент с номерами t\, ..., <m, которые
являются номерами заключительных состояний. Эти компонен-
компоненты равны Л (единице полукольца TZ(V)). Другими словами, ко
всем уравнениям системы, соответствующим заключительным
состояниям, добавляется слагаемое Л.
Действительно, решение системы G.6) будет иметь вид
? = А*р = А*{0, ..., 0, Л, 0, ..., 0, Л, 0, ..., 0)Т G.7)
(элементы А находятся в строках с номерами ti, ..., tm).
Умножая в G.7) матрицу А*, равную матрице С стои-
стоимостей, на столбец /?, получим столбец, 5-я компонента ко-
которого xs будет равна произведению s-й строки матрицы С
(csU ..., cetl, ..., c5tm, ..., с8П) на столбец C в формуле G.7),
т.е.
но это и есть регулярное выражение, обозначающее язык ко-
конечного автомата (ср. с G.5)).
Таким образом, алгебраическая техника анализа ориенти-
ориентированных графов, размеченных над полукольцами (см. 5), дает
возможность чисто алгебраически решать задачи анализа ко-
конечных автоматов.
Пример 7.8. Найдем язык конечного автомата, изобра-
изображенного на рис. 7.10. Запишем для этого автомата матрицу А
меток дуг и систему уравнений:
i = ах\ + 6x2,
А= '
i i ' 1 ~
= ахо + Ьх\ + А
(слагаемое А добавлено в уравнение для Ж2, так
Рис 7.10 как вершина до является заключительной).
7.6. Детерминиэация конечных автоматов 521
Исключая жо, получаем
{Х\ = b(ax\ + Ьх2) + aari,
Х2 = Q>(a>Xi + ЬХ2) + Ьх\ + A,
откуда
{xi = (ba + a)*b2x2,
х2 = (а2 + Ь)(Ьа + а)
Тогда
Отсюда получаем регулярное выражение, обозначающее язык
конечного автомата, как значение переменной xq:
Как видим, полученное регулярное выражение весьма сложно и
найти его, не располагая заранее разработанным алгоритмом,
было бы затруднительно.
7.6. Детерминизация конечных автоматов
Для дальнейшего изучения свойств конечных автоматов
и, в частности, для решения задачи синтеза важное значение
имеет следующая теорема.
Теорема 7.7 (теорема о детерминизации). Для любо-
любого конечного автомата может быть построен эквивалентный
ему детерминированный конечный автомат.
^ Для того чтобы доказать теорему, нужно, во-первых, опи-
описать алгоритм построения детерминированного конечного ав-
автомата по исходному; во-вторых, обосновать этот алгоритм,
строго доказав, что он действительно дает конечный автомат,
522 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
который является детерминированным и эквивалентным исход-
исходному. Здесь мы приведем только сам алгоритм построения
детерминированного автомата. Его обоснование дано в Д.7.1.
Преобразование произвольного конечного автомата к экви-
эквивалентному детерминированному осуществляется в два этапа:
сначала удаляются дуги с меткой А, затем проводится соб-
собственно детерминизация.
1. Удаление Х-переходов (дуг с меткой А).
Чтобы перейти от исходного конечного автомата М =
= (Vj Q, go? F) &) к эквивалентному конечному автомату М' =
= (V, Q', go? F'i &') без А-переходов, достаточно в исходном
графе М проделать следующие преобразования.
а. Все состояния, кроме начального, в которые заходят
только дуги с меткой А, удаляются; тем самым определяется
множество Q' конечного автомата М'. Понятно, что Q1 С Q.
При этом полагаем, что начальное состояние остается преж-
прежним.
б. Множество дуг конечного автомата М1 и их меток (тем
самым и функция переходов М') определяется так: для лю-
любых двух состояний p+r E Q' р ->а г имеет место тогда и только
тогда, когда а Е F, а в графе М имеет место одно из двух: ли-
либо существует дуга изрвг, метка которой содержит символ
а, либо существует такое состояние д, что р =Ф-д q и q ->а г.
При этом вершина ф, вообще говоря, может и не принадле-
принадлежать множеству Q;, т.е. она может
fp^jvvfT) а *Сг) и исчезнУть ПРИ переходе к автома-
K^/SJX/X^\J ^<J ту мг ^рис 7.11). Если же q e Q1,
U то, естественно, в М1 сохранится ду-
/Г\ а г/у\ га (д, г) и символ а будет одним из
Рис. 7.11 символов, принадлежащих метке этой
дуги (рис. 7.12).
Таким образом, в М' сохраняются все дуги М, метки кото-
которых отличны от А и которые соединяют пару (вершин) состоя-
состояний из множества ф;(не удаляемых согласно п. а). Кроме этого,
для любой тройки состояний р,g,r (не обязательно различных!),
7.6. Детерминизация конечных автоматов
523
Рис. 7.12
такой, что р, г е Q1 и существует путь
ненулевой длины изр в д, метка ко-
которого равна Л (т.е. путь по А-пере-
ходам), а из q в г ведет дуга, метка
которой содержит символ а входного
алфавита, в М' строится дуга из р в
г, метка которой содержит символ а
(см. рис. 7.11).
в. Множество заключительных со-
состояний F1 конечного автомата М1
содержит все состояния q E Q', т.е.
состояния конечного автомата М, не
удаляемые согласно п. а, для которых
имеет место q =»д qj для некоторо-
некоторого qj E F (т.е. либо состояние q само
является заключительным состояни-
состоянием конечного автомата М, либо из
него ведет путь ненулевой длины по
дугам с меткой Л в одно из заключительных состояний конеч-
конечного автомата М) (рис. 7.13).
2. Собственно детерминизация.
Пусть М = (Q, V, go? F, 5) — конечный автомат без Л-пе-
реходов. Построим эквивалентный М детерминированный ко-
конечный автомат М\.
Этот конечный автомат определяется таким образом, что
его множество состояний есть множество всех подмножеств
множества состояний конечного автомата М. Это значит, что
каждое отдельное состояние конечного автомата М\ определе-
определено как некоторое подмножество множества состояний конеч-
конечного автомата М. При этом начальным состоянием нового
конечного автомата (т.е. Mi) является одноэлементное подмно-
подмножество, содержащее начальное состояние старого конечного
автомата (т.е. М), а заключительными состояниями нового
конечного автомата являются все такие подмножества Q, ко-
Рис. 7.13
524 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
торые содержат хотя бы одну заключительную вершину исход-
исходного конечного автомата М.
Впредь, допуская некоторую вольность речи, мы будем ино-
иногда называть состояния конечного автомата М\ состояниями-
множествами. Важно, однако, четко усвоить, что каждое такое
состояние-множество есть отдельное состояние нового конеч-
конечного автомата, но никак не множество его состояний. В то
же время для исходного („старого") конечного автомата М
это именно множество его состояний. Образно говоря, каждое
подмножество состояний старого конечного автомата „сверты-
„свертывается" в одно состояние нового конечного автомата*.
Функция переходов нового конечного автомата определе-
определена так, что из состояния-множества S по входному символу а
конечный автомат М\ переходит в состояние-множество, пред-
представляющее собой объединение всех множеств состояний ста-
старого конечного автомата, в которые этот старый конечный
автомат переходит по символу а из каждого состояния мно-
множества S. Таким образом, конечный автомат М\ является
детерминированным по построению.
Приведенное выше словесное описание можно перевести в
формулы следующим образом: строим конечный автомат М\
так, что
где
(VSCQ)(Va€
q€S
'"Формально следовало бы определить множество Qi как множество, на-
находящееся во взаимно однозначном соответствии с множеством 2Q, но
нам все-таки удобнее считать, что Q\ совпадает с 2Q, — ведь множе-
множеством состоянии конечного автомата может быть любое непустое конечное
множество.
7.6. Детерминизация конечных автоматов
525
Обратим внимание на то, что среди состояний нового ко-
конечного автомата есть состояние 0, причем, согласно G.8),
?i@,a) = 0 для любого входного символа а. Это значит, что,
попав в такое состояние, конечный автомат М\ уже его не поки-
покинет. Вообще же любое состояние q конечного автомата, такое,
что для любого входного символа a 8(q,a) = g, называют по-
поглощающим состоянием конечного автомата. Таким
образом, состояние 0 детерминированного конечного автома-
автомата М\ является поглощающим. Полезно заметить также, что
6\(S,a) = 0 тогда и только тогда, когда для каждого q€ S (со-
(состояния старого конечного автомата из множества состояний
S) S(q,a) = 0, т.е. в графе М из каждого такого состояния q не
выходит ни одна дуга, помеченная символом а.
Можно доказать (см. Д.7.1), что полученный по такому
алгоритму конечный автомат эквивалентен исходному. >
Пример 7.9, Детерминизируем конечный автомат, изобра-
изображенный на рис. 7.14.
Рис. 7.14
а,Ъ
Рис. 7.15
Эквивалентный конечный автомат без А-переходов изобра-
изображен на рис. 7.15.
Заметим, что вершина ^2 исчезает, так как в нее заходят
только „пустые" дуги.
Чтобы детерминизировать полученный автомат, совершен-
совершенно не обязательно выписывать все его 23 = 8 состояний, среди
которых многие могут оказаться не достижимыми из началь-
начального состояния {до}- Чтобы получить достижимые из {до}
526
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
состояния, и только их, воспользуемся так называемым мето-
методом вытягивания.
Этот метод в общем случае можно описать так.
В исходном конечном автомате (без пустых дуг) определяем
все множества состояний, достижимых из начального, т.е. для
каждого входного символа а находим множество 6(qo,a). Ка-
Каждое такое множество в новом автомате является состоянием,
непосредственно достижимым из начального.
Для каждого из определенных состояний-множеств S и ка-
каждого входного символа а находим множество |J S(q,a). Все
qes
полученные на этом шаге состояния будут состояниями нового
(детерминированного) автомата, достижимыми из начальной
вершины по пути длины 2. Описанную процедуру повторяем
до тех пор, пока не перестанут появляться новые состояния-
множества (включая пустое!). Можно показать, что при этом
получаются все такие состояния конечного автомата Mi, кото-
которые достижимы из начального состояния {qo}-
Для конечного автомата на рис. 7.15 имеем:
U {91} =
Так как новых состояний-множеств
больше не появилось, процедура „вытяги-
„вытягивания4' на этом заканчивается, и мы полу-
получаем граф, изображенный на рис. 7.16. #
Одним из важных теоретических след-
следствий теоремы о детерминизации являет-
является следующая теорема.
Теорема 7.8. Дополнение регулярного языка есть регуляр-
регулярный язык.
Рис. 7.16
7.6, Детерминизация конечных автоматов 527
<4 Пусть L — регулярный язык в алфавите V. Тогда дополнение
языка L (как множества слов) есть язык L = V* \ L.
Согласно теореме 7.7, для регулярного языка L может быть
построен детерминированный конечный автомат М, допуска-
допускающий L. Поскольку в детерминированном автомате из каждой
вершины по каждому входному символу определен переход в
точности в одну вершину, то, какова бы ни была цепочка
х в алфавите У, для нее найдется единственный путь в М,
начинающийся в начальном состоянии, на котором читается
цепочка х. Ясно, что цепочка х допускается автоматом М,
т.е. х Е ?(М), тогда и только тогда, когда последнее состояние
указанного пути является заключительным. Отсюда следует,
что цепочка х ? L(M) тогда и только тогда, когда последнее
состояние указанного пути не заключительное. Но нам как
раз и нужен конечный автомат М', который допускает цепоч-
цепочку х тогда и только тогда, когда ее не допускает исходный
конечный автомат М. Следовательно, превращая каждое за-
заключительное состояние М в не заключительное и наоборот,
получим детерминированный автомат, допускающий дополне-
дополнение языка L. >
Доказанная теорема позволяет строить конечный автомат,
не допускающий определенное множество цепочек, следующим
методом: строим сначала автомат, допускающий данное мно-
множество цепочек, затем детерминизируем его и переходим к
автомату для дополнения так, как это указано в доказатель-
доказательстве теоремы 7.8.
Пример 7.10. а. Построим конечный автомат, допускаю-
допускающий все цепочки в алфавите {0,1}, кроме цепочки 101.
Сначала построим конечный автомат, допускающий един-
единственную цепочку 101. Этот автомат приведен на рис. 7.17.
Рис. 7.17
528 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Этот автомат квазидетерминированньщ но не детермини-
детерминированный, так как он не полностью определен. Проведем его
детерминизацию и получим детерминированный эквивалент-
эквивалентный конечный автомат, изображенный на рис. 7.18.
И наконец, переходя к дополнению (и переименовывая со-
состояния), получим автомат, изображенный на рис. 7.19.
Обратим внимание, что в полученном автомате все верши-
вершины, кроме вершины вз, являются заключительными.
Заметим также, что переход к дополнению, о котором идет
речь в доказательстве теоремы 7.8, может быть проведен толь-
только в детерминированном автомате. Бели бы мы поменяли
ролями заключительные и незаключительные вершины в ав-
автомате, изображенном на рис. 7.17, то получили бы автомат,
допускающий язык {Л, 1,10}, который не является — как не-
нетрудно сообразить — множеством всех цепочек, отличных от
цепочки 101.
Отметим также, что конечный автомат на рис. 7.19 допус-
допускает все цепочки, содержащие вхождение цепочки 101, но не
совпадающие с самой этой цепочкой. Вот, например, путь, не-
несущий цепочку 1011: so, «i, $2, $з, t.
б. Построим конечный автомат, допускающий все цепочки
в алфавите {0,1}, кроме тех, которые содержат вхождение
цепочки 101. Рассмотрим язык L, каждая цепочка которого
содержит вхождение цепочки 101. Его можно задать так:
L = @ + l)*101@ + l)*.
Нам нужно построить автомат для дополнения языка L.
7.6. Детерминизация конечных автоматов
529
Непосредственно по регулярному выражению в этом слу-
случае легко построить конечный автомат, допускающий язык L
(рис. 7.20).
0,1
Рис. 7.20
Затем методом „вытягивания" проведем детерминизацию.
Результат детерминизации представлен на рис. 7.21.
Рис. 7.21
Для полного решения задачи осталось только на рис. 7.21 по-
поменять ролями заключительные и не заключительные вершины
(рис. 7.22).
Рис. 7.22
в. Обсудим идею построения конечного автомата, допус-
допускающего те и только те цепочки в алфавите {0,1}, которые не
530 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
начинаются цепочкой 01 и не заканчиваются цепочкой 11 (т.е.
не разрешаются цепочки вида 01я? и цепочки вида у 11, каковы
бы ни были цепочки ж, у € {0,1}*).
В этом случае дополнением языка, для которого нужно
построить конечный автомат, является множество всех та-
таких цепочек нулей и единиц, которые начинаются цепочкой
01 или заканчиваются цепочкой 11. Допускающий это множе-
множество цепочек автомат строится как автомат для объединения
01@ +1)* + @ + 1)*11 тем способом, который изложен при до-
доказательстве теоремы Клини (см. теорему 7.6). #
Из свойства замкнутости класса регулярных языков отно-
относительно дополнения (см. теорему 7.8) немедленно вытекает
замкнутость этого класса относительно пересечения, теорети-
теоретико-множественной и симметрической разности.
Следствие 7.3. Для любых двух регулярных языков L\
и 2/2 справедливы следующие утверждения:
1) пересечение L\ П L2 регулярно;
2) разность L\ \ L2 регулярна;
3) симметрическая разность L1AL2 регулярна.
А Справедливость утверждений вытекает из тождеств:
3) LiAL2 = (Li U L2) \ (Li П L2). >
Во-первых, полученные результаты позволяют утверждать,
что класс регулярных языков относительно операций объеди-
объединения, пересечения и дополнения является булевой алгеброй,
в которой единицей служит универсальный язык, а нулем —
пустой язык. Во-вторых, эти алгебраические свойства семей-
семейства регулярных языков позволяют решить важную проблему
распознавания эквивалентности двух произвольных конечных
автоматов.
Согласно определению 7.10, конечные автоматы эквивалент-
эквивалентны, если допускаемые ими языки совпадают. Поэтому, чтобы
7.7. Минимизация конечных автоматов 531
убедиться в эквивалентности автоматов М\ и Мг, достаточ-
достаточно доказать, что симметрическая разность языков L(M\) и
L{M2) пуста. Для этого, в свою очередь, достаточно постро-
построить автомат, допускающий эту разность, и убедиться в том,
что допускаемый им язык пуст. В общем случае проблему
распознавания того, что язык конечного автомата пуст, на-
называют проблемой пустоты для конечного автомата.
Чтобы решить эту проблему, достаточно найти множество
заключительных состояний автомата, достижимых из началь-
начального состояния. Так как конечный автомат — это ориенти-
ориентированный граф, то решить такую проблему можно, например,
с помощью, поиска в ширину (см. 5.5). Язык, допускаемый
конечным автоматом, пуст тогда и только тогда, когда множе-
множество заключительных состояний, достижимых из начального
состояния, пусто. Практически эквивалентность конечных ав-
автоматов предпочтительнее распознавать, используя алгоритм
минимизации (см. 7.7), но сейчас нам важно подчеркнуть, что
принципиальная возможность решить проблему эквивалентно-
эквивалентности вытекает из теоремы 7.7 и ее алгебраических следствий.
7.7. Минимизация конечных автоматов
Может быть поставлен такой вопрос: нельзя ли для произ-
произвольного конечного автомата построить эквивалентный ко-
конечный автомат с меньшим числом состояний! Оказывается,
что ответ на этот вопрос положителен. Более того, мож-
можно построить конечный автомат, эквивалентный исходному и
имеющий наименьшее число состояний (среди всех конечных
автоматов, эквивалентных ему). Процедуру построения такого
автомата называют минимизацией конечного автомата.
В силу теоремы о детерминизации (см. теорему 7.7) можно
считать, что исходный конечный автомат
М = (У, Q, 9o, F, <*)
является детерминированным.
532 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Будем также предполагать, что в исходном конечном ав-
автомате нет состояний, которые не достижимы из начального
состояния. Это предположение мотивировано тем, что если в
М существуют состояния, не достижимые из начального, то их
можно найти (используя, скажем, поиск в ширину на графе М)
и удалить со всеми инцидентными им дугами.
На множестве состояний автомата М зададим семейство
отношений эквивалентности следующим образом:
1) О-эквивалентностъ: для произвольных состояний q\ и
92 полагаем q\ =° q*i тогда и только тогда, когда они оба явля-
являются заключительными или оба не являются заключительными;
2) k-жвивалентностъ: при к ^ 1 полагаем q\ =k 92 то-
тогда и только тогда, когда q\ =Л~1 д2, т.е. состояния q\ и (/2
(к — 1)-эквивалентны, и, кроме того, для любого входного сим-
символа а состояния 6(qi,a) и 5(q2,a) также (А; — 1)-эквивалентны*.
Чтобы понять смысл отношения fc-эквивалентности, обра-
обратимся к рис. 7.23. На этом рисунке q\ и q<i — (к—^-экви-
(к—^-эквивалентные состояния, т.е. они при-
принадлежат одному и тому же клас-
классу (к—1)-эквивалентности С\. Эти
состояния, согласно данному выше
определению, станут А;-эквивалент-
ными, если для любого входного сим-
Рис. 7.23 вола а состояния 5(qi,a) и S(q2,a)
также являются (А; — ^-эквивалент-
^-эквивалентными, содержащимися в некотором классе (к — ^-эквивалент-
^-эквивалентности C<i (возможно, что С\ = Сг). Можно сказать, что
(к — 1)-эквивалентные состояния будут также и А;-эквивалент-
ными, если переход из них по любому входному символу „со-
„сохраняет" (&—1)-эквивалентность состояний, т.е. состояния, в
которые конечный автомат переходит из (к — 1)-эквивалентных
состояний, снова окажутся (& — 1)-эквивалентными.
* Напомним, что функция переходов детерминированного конечного ав-
автомата определена как отображение 6: Q х V —> Q (см. замечание 7.7).
7.7. Минимизация конечных автоматов
533
*od(qva)
+*od(q2,a)
Рис. 7.24
Если же найдется хотя бы один
входной символ а, такой, что состоя-
состояния 8(qi,a) и S(q2,a) окажутся в раз-
разных классах (к—1)-эквивалентности
(рис. 7.24), то состояния q\ и q<i уже
не будут ^-эквивалентными (образ-
(образно говоря, они разойдутся по разным
классам ^-эквивалентности, так как переход из них по некото-
некоторому символу „разрушает" (А;—1)-эквивалентность).
Таким образом, для любого к > 0 отношение эквивалентно-
эквивалентности =fc+1 включается в отношение =*, и, следовательно, любой
класс (к + 1)-эквивалентности включается в некоторый класс
^-эквивалентности (точнее, каждый класс fc-эквивалентности
или разбивается на несколько попарно непересекающихся клас-
классов (к + 1)-эквивалентности, или, если все его состояния оста-
остаются (к + 1)-эквивалентными, не изменяется). Это значит, что
разбиение множества состояний на классы (к + ^-эквивалент-
^-эквивалентности является, не более „крупным", т.е. содержит не меньше
классов эквивалентности, чем разбиение на классы fe-эквива-
лентности.
Минимизация конечного автомата состоит в последователь-
последовательном „измельчении" разбиения множества Q на классы экви-
эквивалентности до тех пор, пока не получится разбиение, кото-
которое уже нельзя измельчить (очевидно, что такое разбиение
для некоторого к < п = |Q| всегда существует). Более стро-
строго: указанные выше отношения эквивалентности строятся до
такого наименьшего &, что отношение =* совпадет с отношени-
отношением =к"г. Это отношение и определяет самое мелкое разбиение
множества состояний. Обозначим его просто =. Тогда ми-
минимальный конечный автомат М = (Vt,Qt^OiFt\6r), т.е.
автомат с наименьшим числом состояний, эквивалентный ис-
исходному, определяется следующим образом:
V = V, Q' = Q/=, <й =
(Va€V)(Vq€QN([q],a) =
' = {[f]:f€F},
534 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
где через [q] обозначен класс эквивалентности состояния q по
отношению =.
Можно доказать вполне строго (аналогично доказательству
корректности алгоритма детерминизации в Д.7.1), что конеч-
конечные автоматы МиМ' эквивалентны.
Резюмируем полученные результаты в виде теоремы.
Теорема 7.9. Для произвольного конечного автомата
может быть построен эквивалентный ему конечный автомат
с наименьшим числом состояний. #
Вытекающий из этой теоремы алгоритм минимизации мо-
может быть описан так:
1) строим эквивалентный исходному детерминированный
конечный автомат;
2) если в полученном конечном автомате остались состоя-
состояния, не достижимые из начальной вершины, удаляем их (для
обнаружения таких вершин может быть использован алгоритм
поиска в ширину, см. 5.5);
3) к полученному конечному автомату применяем изложен-
изложенный выше алгоритм построения разбиения множества состо-
состояний на классы эквивалентности по отношению = и строим
минимальный конечный автомат М', как описано выше.
Замечание 7.11. Если детерминизация конечного авто-
автомата проводится методом „вытягивания", то все вершины в
детерминированном конечном автомате будут достижимы из
начальной вершины.
Кроме того, подчеркнем еще раз, что алгоритм минимиза-
минимизации применяется только к детерминированным конечным ав-
автоматам.
Пример 7.11. Минимизируем конечный автомат, изобра-
изображенный на рис. 7.21.
Введем новые обозначения для состояний автомата:
{go} = S(b {90)9i} = <si, {фь 92} = S2,
{90, q\, qz) = 53, {go, 92,Ы = 54, {go, 93} = 55.
7.7. Минимизация конечных автоматов
535
Полученный автомат изображен на рис. 7.25.
1
Рис. 7.25
Запишем разбиение множества состояний автомата для от-
отношения =°:
Так как состояния 5E2,0) = «о и ?E2>1) = $з не являются
О-эквивалентными состояниями, то в разбиении для 1-эквива-
лентности они „разойдутся" по разным классам; разбиение,
определяемое отношением =*, будет иметь вид
Далее, при переходе к 2-эквивалентности придется „раз-
„развести" состояния sq и si. Поскольку для всех состояний из
множества {53,54,55} конечный автомат переходит в одно из
этих же состояний, то разбиение на классы 2-эквивалентности
и есть искомое пмельчайшее" разбиение:
{5о}, {5i}, {52}, {53,54,55}.
На рис. 7.26 приведен граф минимального конечного авто-
автомата. #
Заметим, что применение рассмотренной процедуры мини-
минимизации может дать два крайних случая:
1) все состояния исходного конечного автомата окажутся
эквивалентными и тогда в минимальном конечном автомате
останется только одно состояние;
536 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Рис. 7.26
2) итоговое разбиение будет состоять из одноэлементных
классов эквивалентности — это означает, что исходный конеч-
конечный автомат нельзя минимизировать, он уже минимален.
Первый случай проиллюстрирован на рис. 7.27. Здесь приве-
приведено построение и минимизация конечного автомата, допуска-
допускающего язык, обозначенный регулярным выражением (а*Ь*)*.
7.7. Минимизация конечных автоматов 537
После удаления Л-переходов получается детерминированный
автомат, все состояния которого заключительные. Значит, ми-
минимальный автомат состоит из одной вершины и допускает
язык (а + Ь)*. Тем самым мы еще и доказали эквивалентность
регулярных выражений (о+ 6)* и (а*6*)* (в алфавите {а, 6}).
Алгоритм минимизации целесообразно использовать и при
распознавании эквивалентности двух заданных конечных авто-
автоматов.
Бели мы хотим выяснить, эквивалентны ли автоматы М\ и
Л/г, то можно минимизировать каждый из них. Бели минималь-
минимальные автоматы М[ и М2 имеют множества состояний с разным
числом вершин, то исходные автоматы заведомо не эквивалент-
эквивалентны. Можно доказать, что исходные автоматы эквивалентны
тогда и только тогда, когда соответствующие им минималь-
минимальные автоматы М[ и М2 изоморфны. Конечные автоматы
М[ и М2 считаются изоморфными, если существует такая би-
екцил h множества состояний первого автомата на множество
состояний второго, которая является изоморфизмом данных
конечных автоматов как ориентированных графов (см. 5.7) и
обладает дополнительно следующими свойствами:
1) если 901 — начальное состояние конечного автомата М{,
то h(qox) = go2 — начальное состояние конечного автомата М'2,
2) если F\ — подмножество заключительных состояний ко-
конечного автомата М{, то h(F\) = F2 — подмножество заключи-
заключительных состояний конечного автомата М2]
3) для любых двух состояний qnr конечного автомата М{ и
любого входного символа a q -?a r тогда и только тогда, когда
*(«)->• МО-
В общем случае проблема распознавания эквивалентности
Л^1 и Mi сводится к проблеме распознавания изоморфизма
минимальных автоматов. Для малого числа вершин (до 10)
этот изоморфизм, как правило, распознается „невооруженным
глазом", но в общем случае нужны специальные алгоритмы*.
*См., например: Кристофидес Я.
538 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
7.8. Лемма о разрастании
для регулярных языков
В теории формальных языков большое значение имеют
утверждения, в которых формулируется необходимое условие
принадлежности языка к тому или иному классу языков. Эти
утверждения известны в литературе под названием лемм о раз-
разрастании (или лемм о „накачке"). С помощью этих лемм удает-
удается доказать, что тот или иной язык не является языком данного
класса, например, не является регулярным, контекстно-сво-
контекстно-свободным и т.п. Доказывать подобного рода „отрицательные"
утверждения гораздо труднее, чем „положительные" (что язык
есть язык данного класса С), ибо в последнем случае требу-
требуется придумать любую грамматику соответствующего класса,
порождающую данный язык, а в первом нужно каким-то обра-
образом доказать, что не существует грамматики этого класса,
порождающей язык. Применение лемм о разрастании состоит
в следующем: доказав, что предлагаемый язык не удовлетво-
удовлетворяет условию леммы о разрастании, мы можем быть уверены
в том, что он заведомо не принадлежит соответствующему
классу языков, и нам нечего и пытаться искать для него грам-
грамматику того же класса.
Мы рассмотрим подобного рода утверждения для классов
регулярных, контекстно-свободных и линейных языков.
Начнем с леммы о разрастании для регулярных языков. Эта
лемма (см. теорему 7.10) утверждает, что любой регулярный
язык допускает представление всех своих достаточно длин-
длинных цепочек в виде соединения трех цепочек, причем средняя
цепочка из этих трех не пуста, ограничена по длине, и ее „на-
„накачка" — повторение любое число раз — или выбрасывание не
выводит за пределы языка (т.е. дает цепочки, принадлежащие
данному регулярному языку).
Теорема 7.10. Бели L — регулярный язык, то существует
натуральная константа ki (зависящая от L), такая, что для
7.8. Лемма о разрастании для регулярных языков
539
любой цепочки ж Е L, длина которой не меньше fcjr,, х допускает
представление в виде х = uvw, где v ф А и \v\ < &?,, причем для
любого п ^ 0 цепочка жп = ш;пги Е L.
<4 Поскольку язык L регулярен, то, согласно теореме Кли-
ни (см. теорему 7.6), существует конечный автомат М =
= (Vj Q, 9o? -F> <J)> допускающий его, т.е. L = L(M) (в силу
теоремы 7.7 о детерминизадии можно считать М детерминиро-
детерминированным автоматом). Положив кь = |Q|, т.е. введя константу кь
как число состояний конечного автомата М, фиксируем произ-
произвольно цепочку х 6 L, длина / которой не меньше ki- Так как
/ > 0, то цепочка х не является пустой, и мы можем положить
х = х{1)...хA), 1>0.
Поскольку конечный автомат М является детерминирован-
детерминированным, то существует единственный путь, ведущий из начально-
начального состояния 9о в одно из заключительных состояний ф/, на
котором читается х (рис. 7.28).
Рис. 7.28
Так как длина I цепочки х не меньше числа состояний М,
т.е. числа всех вершин графа М, то, поскольку число вершин
в любом пути ровно на единицу больше числа дуг в этом пути
(т.е. длины пути), число вершин в рассмотренном выше пути
будет больше, чем число всех вершин графа. Это значит, что
хотя бы одна из вершин данного пути повторяется и она, та-
таким образом, в силу следствия 5.1, содержится в некотором
контуре. Обозначим эту вершину
через р. Тогда путь, несущий це-
цепочку ж, разбивается на три части
(рис. 7.29): 1) путь из q0 вр, 2) кон-
контур, проходящий через р, 3) путь
из р в q*. Рис. 7.29
540 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Обозначая через и цепочку, читаемую на первой части пу-
пути, через v — цепочку, читаемую на контуре, а через w —
цепочку, читаемую на третьей части, получим х = uvw, причем
поскольку любой контур есть простой путь, то \v\ < ki (длина
простого пути не может быть больше, чем число вершин гра-
графа) и v ф А, так как контур имеет ненулевую длину. Но теперь
совершенно очевидно, что контур (на котором лежит вершина
р) можно пройти (по пути из 9о в qj) любое число п (при п > 0)
раз или ни разу. В первом случае на этом пути будет прочи-
прочитана цепочка uvnw при п > 0, а во втором — и цепочка uw.
Таким образом, любая цепочка хп = uvnw (n ^ 0) содержится в
языке L. >
Рассмотрим теперь некоторые примеры доказательств не-
нерегулярности языка с использованием леммы о разрастании.
Стандартный ход рассуждений при решении таких задач со-
состоит в предположении регулярности данного языка и после-
последующем анализе возможности представить любую достаточно
длинную цепочку языка в виде, указанном в условии леммы о
разрастании. Анализируя все возможные случаи размещения
„накачиваемой" подцепочки v, мы должны получить противо-
противоречие.
Пример 7.12. а. Докажем нерегулярность языка
Выбирая п настолько большим, чтобы оно превосходило
&?, (константу леммы), получаем следующие возможные случаи
размещения средней подцепочки v в цепочке апЬп.
1. v = as, s < п, т.е. wнакачиваемая" подцепочка целиком
располагается в „зоне символов а" (рис. 7.30, а).
Ясно, что накачка в этом случае выведет за пределы языка,
так как при повторении цепочки v число символов а будет
неограниченно расти, а число символов Ь будет оставаться
прежним.
7.8. Лемма о разрастании для регулярных языков
541
a ... a
Ь ... b
о ... a
b ... b
a ... а
b ... b
в
Рис. 7.30
2. v = 6s, 5 < n, т.е. „накачиваемая" подцепочка целиком
располагается в „зоне символов 6" (рис. 7.30, б).
Накачка невозможна по той же причине, что и в предыду-
предыдущем случае.
3. v = ар69, где 0 < р < n, 0 < g < п, т.е. „накачиваемая" под-
подцепочка находится „на стыке зон символов а и 6" (рис. 7.30, в).
В этом случае при накачке возникнет вхождение подцепочки
ba в слово, которое, следовательно, уже не принадлежит языку
Li. Таким образом, рассматриваемый язык нерегулярен.
б. Докажем, что язык L<i = LJ, где Li = {anbn: n ^ 0}, нере-
нерегулярный.
Полагая, что язык L2 регулярен, возьмем слово (anbn)m для
достаточно большого п (т ^ 1).
Применяя такую же схему рассуждений, как и выше, легко
убеждаемся в том, что цепочка v не может состоять из одних
символов а или из одних символов 6.
Пусть v = arbs, где r + s<n. Тогда, повторив цепочку v
Два раза, получим слово ...an~rarbsaTbsbn~~s... Если г ф 5, то
цепочка такого вида не может принадлежать языку L2> так
как в любом слове этого языка за подцепочкой символов a
следует подцепочка символов Ъ такой же длины. Но даже если
*" = 5, то получим подцепочку anbs, где s < п (или arbn, г < п),
что также противоречит определению языка L2. Аналогично
рассматривается случай v = 6ras (r + s<n) (рис. 7.31). #
542 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
V
а ... а
V
Ъ ... b
а ... а
Ъ ... b
а ... а
...
Рис. 7.31
Заметим, что в силу ограничения по длине на цепочку v
никакие способы ее размещения в указанной цепочке языка Z/2,
кроме описанных выше, не возможны. #
Полезно иметь в виду следствие из леммы о разрастании.
Следствие 7,4. Бели L — бесконечный регулярный язык,
то в нем найдется последовательность слов, длины которых
образуют возрастающую арифметическую прогрессию.
<4 В качестве такой последовательности можно взять последо-
последовательность слов хп из формулировки леммы о разрастании. Их
длины образуют арифметическую прогрессию со знаменателем
\v\ (длина „накачиваемой" средней подцепочки). >
Отсюда легко получается вывод о том, что не являются
регулярными следующие языки:
1) {ап :п^0} — язык в однобуквенном алфавите, длины
слов которого являются полными квадратами;
2) {ар: р — простое число}.
Можно доказать, что любой конечный язык регулярен и,
более того, допускается конечным автоматом без контуров.
Значит, последовательность цепочек, указанная в формулиров-
формулировке леммы, в таком случае не существует, но утверждение леммы
остается истинным. Нужно всегда помнить простое логическое
правило: утверждение вида „если -А, то Би равносильно утвер-
утверждению вида „не А или Б".
В заключение обсудим еще одну схему доказательства нере-
нерегулярности языка с использованием как леммы о разрастании,
так и алгебраических свойств класса регулярных языков, кото-
которые были установлены в 7.6.
7.8. Лемма о разрастании для регулярных языков 543
Пример 7.13. Докажем нерегулярность языка правильных
скобочных структур, порождаемых КС-грамматикой
<{(,)}, {S}, S, {5-> ()|E)|55}>
(см. грамматику Gs в примере 7.5). Для доказательства посту-
поступим так: рассмотрим пересечение данного языка с регулярным
языком (* )*, который содержит все цепочки вида (m)n для
любых натуральных m, n ^ 0. Поскольку каждая правильная
скобочная структура содержит одинаковое число символов „("
и „)", то указанное пересечение будет языком {(n )n: n ^ 0}. Ес-
Если обозначить через a „открывающую скобку" (символ „("), а
через Ъ „закрывающую скобку" (символ „)"), то получим язык
Li, который, как только что доказано, не является регулярным.
Следовательно, предполагая регулярность языка правильных
скобочных структур, мы вынуждены будем допустить и регу-
регулярность языка Li, так как пересечение регулярных языков
в силу следствия 7.3 регулярно. Полученное противоречие и
доказывает нерегулярность исходного языка. Заметим, что до-
доказательство этого факта с использованием одной лишь леммы
о разрастании было бы весьма затруднительно.
Замечание 7.12. С использованием „техники пересечения"
можно доказать нерегулярность языка L*i из примера 7.12
следующим образом. Так как язык
нерегулярный, то и язык L*i тоже не является регулярным. #
Итак, можно вывести такой „рецепт": если возникают су-
существенные затруднения в доказательстве нерегулярности ка-
какого-либо языка с помощью только леммы о разрастании, то
можно попытаться пересечь этот язык с некоторым регуляр-
регулярным языком так, чтобы нерегулярность пересечения легко до-
доказывалась с использованием леммы о разрастании.
544
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Дополнение 7.1. Обоснование алгоритма
детерминизации конечных автоматов
В этом дополнении мы подробно докажем корректность
приведенного в доказательстве теоремы 7.7 о детерминиза-
детерминизации алгоритма построения по заданному конечному автома-
автомату эквивалентного ему детерминированного конечного авто-
автомата.
Сначала докажем корректность алгоритма удаления А-пе-
реходов, после чего подобное доказательство проведем уже для
самого алгоритма детерминизации.
1. Корректность алгоритма удаления А-переходов.
Пусть М = (V, Q, go? Fy $) — исходный конечный автомат, а
М' = (V,Q'9qDjFf16i) — конечный автомат без А-переходов, по-
построенный согласно алгоритму, описанному в доказательстве
теоремы 7.7 о детерминизации. Мы должны доказать, что
а. Докажем, что для любых цепочки х € V* и состояния
q E Q из того, что в конечном автомате М цепочка х чита-
читается на некотором пути из qo в q, т.е. имеет место qo ^х 9?
следует, что в конечном автомате М1 эта цепочка читается
на некотором пути из qo в такое
состояние р Е Q', что в М имеет
место р =Ф-д д, т.е. либо р = д, ли-
либо в М существует путь ненуле-
ненулевой длины по пустым дугам из р
в Я- Р =^л 9 (на Рис- 7-32 и на ана-
аналогичных следующих рисунках мы
соединяем тонкой штриховой лини-
линией кружки, изображающие одно и
то же состояние, которое остается
после удаления А-переходов).
Возможны два случая для со-
стояния q G Q: оно или остается
м
<!
м
Рис. 7.32
Д.7.1. Обоснование алгоритма детерминизации
545
после удаления А-переходов, т.е. g E Q', либо удаляется в ре-
результате удаления А-переходов, т.е. g ? Q1.
1°. Состояние g остается после удаления А-переходов, т.е.
Проведем индукцию по длине пути в конечном автомате М,
на котором читается цепочка х. Для пути нулевой длины дока-
доказываемое тривиально. Пусть для всех к ^ п — 1 доказываемое
свойство имеет место, и пусть цепочка х читается в М на не-
некотором пути длины п из до в д, т.е. до =>? д. Тогда существует
такое состояние г EQ, что в М имеет место
. П—1 . try t\\
go =>y r ->a g, G.9)
причем x = yanaeVU {A}.
Если а = А, то х = у, и тогда цепочка х читается в конечном
автомате М на некотором пути длины п — 1.
При г € Q* остается только использовать индукционное
предположение, и тогда найдется такое состояние г' Е Q', что
в М1 до =>х г1 и в М г1 =Ф-д г, но так как в М г ->д д, то в М
выполняется г1 =>? д (рис. 7.33). Таким образом, мы, исходя из
условия, что в М до =»? д, нашли такое состояние г' Е Q', что в
М1 имеет место до =>х г;, а при этом в М выполняется г' =>~? д,
что и требовалось доказать.
(%у
X
М'
X
JVbH
М
1 ».
м
(?)
Рис. 7.33
18- 10061
546
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Пусть теперь г ? Q', т.е. состояние г удаляется при удалении
Л-переходов. Это значит, что в состояние г заходят только
дуги с меткой Л. Но поскольку на некотором пути из до в
г в конечном автомате М читается цепочка у, то найдется
такое состояние р Е Q\ что в М до =>™ р =>\ г, и т < п — 1
(в частности, может быть т = 0 и тогда р = до)- Согласно
предположению индукции, отсюда следует, что в М' go =Ф-*=хр',
где р' =>д р в М, а так как в М имеет место р =Фд г —>д д, то в
М р' =Ф-д g (рис. 7.34), и мы снова, исходя из условия, что в М
9о =^2 9? нашли в Q' такое состояние р;, что цепочка а: читается
в М' на некотором пути из начального состояния в р;, при том
что в исходном конечном автомате М из этого состояния р'
ведет путь по пустым дугам в состояние q.
м
! М
1 Я. А, А,
Рис. 7.34
Итак, случай а = А в G.9) проанализирован полностью.
Пусть а ^ А. Если при этом г Е Q', то, согласно предпо-
предположению индукции, существует такое состояние г' Е Q', что в
конечном автомате М; выполняется до =>у г;, при том что в М
При г' = г, ввиду того что дуга (г, д) конечного автомата
М, метка которой содержит символ а, останется и в конечном
автомате М;, получаем, что в М; go =>t г ->а д, т.е. в М' до =»? д.
Д.7.1. Обоснование алгоритма детерминизации
547
При г' Ф г, т.е. в случае, когда г' =»д г в конечном автомате
М, заключаем, что в М существует тройка состояний r;, г, д,
такая, что г' =Ф-д гиг ->а д. По построению конечного автомата
М1 отсюда получаем, что г' -»а g в М'. Тогда в М' будет
выполняться до =*у т* -*а 9? т.е. д0 =*? 9 (рис. 7.35). Случай г Е Q;
тем самым полностью проанализирован.
м1
/
/
/
/
/
/
/
/
: м
Рис. 7.35
Если же г ^ Q;, т.е. состояние г удаляется при переходе к
конечному автомату М;, то тогда существует такое состояние
p€Q', что в М цепочка у читается на некотором пути длины
пкп — 1 из до вр, а из р в г ведет путь ненулевой длины
по пустым дугам, т.е. в конечном автомате М go ^JT^a r
(рис. 7.36). Тогда, согласно предположению индукции, в М1
9о =>у р', где р' =Ф-д рвМ. Тогда опять в М возникает тройка
состояний р;, г, д, такая, что р' =^ г и г ->а q (см. рис. 7.36).
По построению конечного автомата М1 в нем будет выполнено
Р -*в 9- Итак, в М; до =^у Р; —^а 9? т.е. в конечном автомате М'
цепочка х читается на некотором пути из до в д: до =$>? д .
18*
548 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ*
Рис. 7.36
2°. Состояние g удаляется при удалении Л-переходов, т.е.
В этом случае для некоторого г Е Q1 будет выполняться
q0 =ф-* г =>д g в конечном автомате М, откуда, согласно резуль-
результатам, доказанным для случая 1°, go =>? r' B конечном автомате
М' для некоторого г' Е Q', такого, что в М г1 =>\ г. Следо-
Следовательно, г' =Ф-д г =Фд g в М, т.е. г' =Ф-д д, что и требовалось
доказать.
Итак, мы полностью доказали, что любая цепочка ж, чита-
читаемая в исходном конечном автомате М на некотором пути из
начального состояния до в какое-то состояние д, читается так-
также и в автомате М' на некотором пути из начального состояния
до в такое состояние р, что в М имеет место р =Фд д.
б. Докажем, что для любых состояния g G Q' и цепочки
х G V* из того, что в конечном автомате М' цепочка х читается
на некотором пути из начального состояния до в какое-то
состояние д, т.е. имеет место до =$>? д, следует, что в исходном
конечном автомате М цепочка х читается также на некотором
пути из до в д: до =Ф>я Я в М.
Д.7.1. Обоснование алгоритма детерминизации 549
Проведем опять индукцию по длине пути в конечном авто-
автомате М', на котором читается цепочка х. Для пути нулевой
длины доказываемое тривиально. Предполагая, что доказы-
доказываемое верно для любой длины пути, не превосходящей п — 1,
допустим, что в М' до =^2 Я* Тогда для некоторого г Е Q' в М1
имеет место до =>у г -»а 9? причем уа = я, а так как в М' нет
А-переходов, то а Е V, т.е. а не может быть пустой цепочкой.
Согласно предположению индукции, отсюда следует, что в М
q0 =>* г. Далее, из того, что в М1 есть дуга из г в д, на которой
читается символ а, т.е. г —>а q в М;, следует, что либо эта дуга
есть и в исходном конечном автомате М, и тогда г ->а q в М,
либо в М существует такое состояние р, что г =Ф>д р ->а д. Как
в том, так и в другом случае имеем до =^ р =^? 9 в конечном
автомате М, т.е. в М цепочка а: читается на некотором пути
из начального состояния в состояние д: до =>х Я-
в. Пусть цепочка х G Ь(М), т.е. для некоторого заключи-
заключительного состояния f € F цепочка х читается на некотором
пути из начального состояния в состояние /: до =Ф-? /• Тогда из
п. а следует, что в М1 цепочка х читается на некотором пути из
до в такое состояние /;, что /' =>*х / в М. Если /; = /, то /; G F;;
если же /' ф /, т.е. в М существует путь ненулевой длины по
пустым дугам из /; в /, то, согласно определению множества
F'tf'eF'. Итак, xeL(M').
Обратно, если х Е Ь(М;), т.е. в М1 имеет место до =>% /', где
/ Е F', то, согласно п. б, go =>x f и в М. Но так как в мно-
множество F1 попадают либо заключительные вершины конечного
автомата М, либо те его вершины, из которых заключитель-
заключительная вершина достижима по пустым дугам, то найдется такое
/ Е F, что в М /' =>? / и до =>х /' =^д /, т.е. до =*>? / в конечном
автомате М, откуда х Е L(M).
Итак, L(M) = L(M'), что и обосновывает корректность
алгоритма удаления Л-переходов.
2. Корректность алгоритма детерминизации. Пусть
теперь М = (V, Q, go, F, 5) — исходный конечный автомат без
550 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Л-переходов, а М' = (V, Q', g^, F', Sf) — детерминированный
конечный автомат, построенный согласно алгоритму, описан-
описанному в доказательстве теоремы о детерминизации, т.е. Q1 = 2^,
9о = {?o}j F1 = {#: SC\F Ф 0}, и для любого 5CQ и любого
aeV6f(S,a)= \J6(q,a).
qes
Мы должны доказать, что L(M) = L(Mf).
а. Докажем, что для любых цепочки х € V* и состояния
g € Q из того, что в М цепочка х читается на некотором пути
из начального состояния до в какое-то состояние д, т.е. qo =>•* g,
следует, что эта цепочка читается и в М1 на некотором пути из
состояния {qo} в сосшолкгхе-леножесгпво 5, которое содержит д,
т.е. в М' {9о} =*? 5, где q € 5.
Доказательство проводим индукцией по длине пути в ко-
конечном автомате М, на котором читается цепочка х (так как
в автоматах уже нет пустых дуг, т.е. Л-переходов, то длина
пути всегда совпадает с длиной цепочки, читаемой на этом пу-
пути; поэтому индукцию по длине пути в данном случае можно
рассматривать как индукцию по длине цепочки).
Случай пути длины нуль тривиален. Полагая доказываемое
справедливым для всех путей, длина которых не больше п — 1,
допустим, что цепочка х читается в М на некотором пути
длины п из до в д, т.е. до =Ф-? д. Тогда найдется такое г G Q,
что
ft^r-^g, G.10)
где х = уа и а ? V.
Тогда, согласно предположению индукции, в конечном авто-
автомате М' цепочка у читается на некотором пути {до} в такое Я,
что г 6 R: {go} =^y R- Так как конечный автомат М1 является
детерминированным по построению, то из его состояния-мно-
состояния-множества R ведет дуга в некоторое состояние-множество 5 и
метка этой дуги содержит символ а, т.е. R -+а S в М'. До-
Докажем, что S Э д. Состояние S = S'(R,a) есть объединение всех
множеств 6(р,а) при р € R. В частности, при р = г множество
Д.7.1. Обоснование алгоритма детерминизации 551
состояний 6(r,a) в силу G.10) содержит состояние д. Следова-
Следовательно, это состояние принадлежит и множеству 5, и тогда в
М* имеет место {д0} =** R ->a S, т.е. {q0} =>$S3q.
б. Докажем теперь, что для любой цепочки xGV* и любого
состояния 5 G Q' из {до} =>? ^ в М' следует (Vg G 5)(go =^? r)
вАГ.
Проведем индукцию по длине цепочки х. При |#| = 0, т.е.
для пустой цепочки х, утверждение выполняется тривиально.
Пусть оно верно при всех к < п — 1, и пусть {до} =^х & в ^f'-
Отсюда для некоторого R G Q', т.е. Д С Q, в М; выполняется
{^0} =>> у"*1/? ->а 5, причем х = уа и а G V. Тогда, согласно
предположению индукции, в М go =^J г для каждого г € R.
Поскольку 5 = <J;(i?,a), то любой элемент g в S есть элемент
некоторого множества S(r,a) при г ? R, т.е. в М есть дуга
г -+a g. Но, как мы только что доказали, для любого состояния
г € R имеет место до ^у г, т.е. для любого g G S имеем до =Ф*у
г -+а q в конечном автомате М, откуда (Vg G 5)(M: go =^? д), что
и требовалось доказать.
в. Теперь, если х G L(M), т.е. цепочка я читается в М на
некотором пути из начального состояния в одно из заключи-
заключительных, а именно go =^ / /Vй1 некоторого / G F, то, согласно
результатам, доказанным в п. а, в М1 цепочка х читается на
некотором пути из начального состояния в заключительное со-
состояние 5/, содежащее вершину /: {д0} =Ф>* S/ Э /, т.е. S/ G F'
ижб L(M').
Обратно, если х G L(M'), т.е. {д0} =>* 5/ G F' в М;, то для
любого состояния g G 5/ будем иметь в конечном автомате М
9о =^х 9- Но состояние-множество 5/ обязательно содержит
некоторое заключительное состояние исходного конечного ав-
автомата М (состояние из подмножества F). Тогда для любого
такого состояния / G Sff\F получим до =>>? / в М, что и озна-
означает х G L(M).
Итак, L(M) = L(M;), и тем самым вся процедура детерми-
детерминизации конечных автоматов полностью обоснована.
552 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Дополнение 7.2. Конечные автоматы
с выходом. Структурный синтез
Пусть М = (V, Q, go* Fj 8) — детерминированный конечный
автомат. Модифицируем метки его дуг, а именно фиксируем
произвольно алфавит W, который назовем выходным (хотя
он может и совпадать со входным алфавитом V конечного ав-
автомата М), его буквы назовем выходными символами и для
каждой дуги е конечного автомата М проделаем следующее:
каждому входному символу а, принадлежащему метке дуги е,
сопоставим однозначно упорядоченную пару (а,Ь) € V х W.
Полученный таким образом размеченный ориентированный
граф называют конечным автоматом с выходом.
Конечный автомат с выходом может быть определен и
иначе, независимо от понятия детерминированного конечного
автомата.
Конечный автомат с выходом есть упорядоченная семерка
M = (F, W, Q, go, F, S, M),
где V — входной алфавит (его элементы — входные символы);
W — выходной алфавит (его элементы — выходные символы);
Q — конечное множество состояний конечного автома-
автомата с выходом; qo — выделенное состояние, называемое на-
начальным состоянием конечного автомата с выходом;
F — выделенное непустое подмножество состояний, каждый
элемент которого называют заключительным состоянием
конечного автомата с выходом; 5: Q xV -> Q — отобра-
отображение, называемое функцией переходов конечного авто-
автомата с выходом; /л: Q х V -> W — отображение, называемое
функцией выходов конечного автомата с выходом.
Графом (или диаграммой) конечного автомата с
выходом М называют ориентированный граф, множество вер-
шин которого совпадает с множеством состояний Q, а множе-
множество дуг определяется так: из вершины (состояния) q ведет
дуга в вершину (состояние) г тогда и только тогда, когда
Д.7.2. Конечные автоматы с выходом. Структурный синтез 553
г = 5(q,a) для некоторого входного символа а (причем, по-
поскольку S есть отображение, для каждой пары (q,a) указанное
состояние г единственное).
Каждой дуге диаграммы конечного автомата с выходом
М сопоставляется метка, являющаяся конечным множеством
упорядоченных пар из V х W, так, что пара (а,Ь) принадлежит
метке дуги q —> г тогда и только тогда, когда до(д,а) = 6.
Как видно, метка каждой дуги конечного автомата с выхо-
выходом есть конечное соответствие, функциональное по второй
компоненте (т.е. частичное отображение из V в W). Область
определения этого соответствия называется входной мет-
меткой дуги, а область значений — выходной меткой дуги
(диаграммы конечного автомата с выходом).
На рис. 7.37 показана диаграмма конечного автомата с
выходом, у которого входной алфавит V = {а, Ь}, выходной
алфавит W = {0,1}, множество состояний Q = {go? gi, 92} при
начальном состоянии до и заключительном — #2- Функции
переходов и выходов определяются метками дуг. Обычно
при изображении диаграмм упорядоченная пара (г, 0) G V х W
записывается через косую черту: г/0.
Рис. 7.37
Можно показать, что два сформулированных выше опреде-
определения конечного автомата с выходом равносильны и тем самым
существует взаимно однозначное соответствие между конеч-
конечными автоматами с выходом (в смысле второго определения) и
ориентированньюш графами, дуги которых размечены над де-
декартовым произведением двух алфавитов так, как это описано
в пеРвом определении. Исходя из этого, мы можем отожде-
отождествить конечные автоматы с выходом и их диаграммы.
554 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Таким образом, каждому конечному автомату с выходом
М однозначно сопоставляется детерминированный конечный
автомат My = (V, Q, qo, F, J), метки дуг которого получаются
„стиранием" всех выходных символов в упорядоченных парах,
которыми помечены дуги исходного конечного автомата с
выходом (на каждой дуге остается только ее входная метка).
Этот детерминированный конечный автомат будем называть
входной проекцией конечного автомата с выходом
или V-проекцией конечного автомата с выходом М.
Входная проекция конечного автомата с выходом, диаграмма
которого изображена на рис. 7.37, показана на рис. 7.38.
Рис. 7.38
Функцию выходов /л конечного автомата с выходом М мож-
можно доопределить до некоторого отображения /л* из Q х V* в
W*. Для этого фиксируем произвольно состояние q и входную
цепочку х Е V*. Тогда в силу детерминированности конеч-
конечного автомата My существует единственный путь в My (и,
следовательно, в диаграмме М), ведущий из q в некоторое со-
состояние г, на котором читается цепочка ж. Пусть а € V —
входной символ, принадлежащий входной метке некоторой ду-
дуги, исходящей из г. Тогда положим /х*(д,ж) = Л, если х = Л;
(i*(q,xa) = /i*(g,#)/x(r,a) (заметим, что при этом для любых
q e Q и а е V n*(q,a) = /i(?,a), т.е. функция выходов конечного
автомата с выходом есть сужение функции /х* на подмноже-
подмножество Q х V). В частности, для любой входной цепочки #,
допускаемой конечным автоматом My, положим
=М* (<?<),*). G.11)
Д. 7.2. Конечные автоматы с выходом. Структурный синтез 555
функция /м> определенная выражением G.11), называется
функцией, вычисляемой конечным автоматом с выхо-
выходом М.
Так, для конечного автомата на рис. 7.37 имеем, например,
/м(аЬЬа) = 0110. Можно показать, что функция /м, вычисля-
вычисляемая данным конечным автоматом, есть биекцил регулярного
языка (а + Ь)*66(а + Ь)* в алфавите V = {а, 6} на регулярный
язык @ + 1)*11@ + 1)* в алфавите W = {0,1}, такая, что для
каждой цепочки х первого языка цепочка /м(я) получается
заменой каждого вхождения символа а символом 0 и заменой
каждого вхождения символа Ь символом 1.
Функция из V* в W* называется ограниченно детерми-
детерминированной функцией (или ОД-функцией), если она вычи-
вычисляется некоторым конечным автоматом с выходом.
Замечание 7.13. Термин „ограниченно детерминирован-
детерминированная функция" связан с тем, что множество всех функций вида
/: V* —> W*, вычисляемых конечными автоматами с выходом,
есть собственное подмножество множества всех таких функ-
функций, которые вычисляются посредством так называемых ма-
машин Тьюринга. Машина Тьюринга является самой общей ма-
математической моделью „детерминированного преобразователя
слов", т.е. моделью, с помощью которой может быть вычислена
любая функция из множества слов в одном алфавите в множе-
множество слов в другом алфавите (см. Д.7.4). #
Таким образом, каждый конечный автомат с выходом вы-
вычисляет некоторую ОД-функцию. С интуитивной точки зрения
это значит, что конечный автомат с выходом работает как „де-
„детерминированный преобразователь" слов (цепочек) во входном
алфавите в слова (цепочки) в выходном алфавите. В отличие от
обычного конечного автомата, который является чистым „рас-
„распознавателем", конечный автомат с выходом снабжен выходной
лентой, на которую записывается выходная цепочка /м (я) для
заданной входной цепочки х (рис. 7.39).
556
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Входная лента
Выходная
лента
Рис. 7.39
Для конечных автоматов с выходом может быть поставлена
задача структурного синтеза. Содержательно ее можно
представить как задачу, аналогичную задаче реализации буле-
булевой функции или булева оператора схемой из функциональных
элементов. Однако в отличие от СФЭ, реализующей булев
оператор, „схема", которая реализует ОД-функцию (или, что
то же, вычисляющий ее конечный автомат с выходом), долж-
должна помимо функциональных элементов, каждый из которых
вычисляет некоторую булеву функцию из заданного конечно-
конечного множества функций, содержать так называемые элементы
задержки, позволяющие хранить информацию о текущем со-
состоянии автомата.
Чтобы объяснить это, представим себе (на интуитивном
уровне) процесс работы конечного автомата с выходом во
времени.
В начальный момент времени (время дискретно!) t = 0 блок
управления конечного автомата с выходом находится в началь-
начальном состоянии q@) = qo. Предположим, что в произвольный
момент времени t ^ О состояние есть q(t). Пусть в этот мо-
момент времени конечный автомат считывает с входной ленты
символ x(t). Тогда в этот же момент времени t на выходной
ленте появится выходной символ у(?), а его устройство управ-
Д.7.2. Конечные автоматы с выходом. Структурный синтез 557
ления перейдет в состояние q(t+ 1), в котором и останется до
следующего момента времени t +1.
При этом выполняются соотношения
G.12)
Эти соотношения называют каноническими уравнениями
данного конечного автомата с выходом.
Из канонических уравнений G.12) вытекает, что „схема",
реализующая конечный автомат с выходом, должна иметь „па-
„память" о состоянии устройства управления в предыдущий мо-
момент времени. Эта „память" реализуется с помощью так назы-
называемых элементов задержки, или триггеров.
Конструированию „схемы" предшествует двоичное коди-
кодирование входных и выходных символов, а также состояний
устройства управления. Это значит, что каждому состоянию
или символу однозначно сопоставляется булев вектор (набор)
соответствующей размерности. В общем виде искомая „схема"
должна содержать два блока: назовем их комбинационной
частью (КЧ) и запоминающей частью C4) (рис. 7.40). На
вход комбинационной части поступают в каждый момент вре-
времени t двоичный код входного
символа (булев вектор X(t)) и
двоичный код состояния от за-
поминающей части (булев век-
тор U(t)), а с выхода комбина-
комбинационной части снимается двоич-
двоичный код выходного символа (бу-
(булев вектор Y(t)) и двоичный код следующего состояния (булев
вектор U{t + 1)).
Если через F и G обозначить булевы операторы, сопоста-
сопоставленные в результате указанного выше двоичного кодирования
\Y(t)
КЧ
Рис
Z(t)
U(t)
. 7.40
34
558
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
функциям перехода и выхода соответственно, то канонические
уравнения примут вид
G.13)
17@) = С/о,
Таким образом, комбинационная часть строится как некая
схема из функциональных элементов, реализующая булев опе-
оператор, определяемый первыми двумя уравнениями G.13), тогда
как запоминающая часть содержит необходимое число тригге-
триггеров и релизует „задержку" U(t+ I) = Z(t). Каждый триггер
есть устройство преобразования „одноразрядного двоичного
сигнала" (с математической точки зрения булева вектора раз-
размерности 1), состоящего в задержке этого сигнала „на один
такт". Иначе говоря, если в момент времени t на вход тригге-
триггера Г поступает сигнал х(?), в момент t + 1 с выхода триггера
снимается сигнал y(t +1) = x(t). Обычно рассматривают триг-
триггеры с двумя выходами: прямым и
L инверсным. Прямой выход работает
так, как описано выше, а инверсный
I выдает сигнал, являющийся отрицани-
отрицанием сигнала прямого выхода (рис. 7.41).
Теперь обсудим вопрос о размер-
размерности булевых векторов, кодирующих состояния и символы
обоих алфавитов. Произвольное непустое конечное множество
5 = {si,..., sp} может быть „закодировано" двоичными числа-
числами таким образом: нумеруем элементы S от 0 до р — 1 и эти
номера записываем в двоичной системе счисления. Нетрудно
сообразить, что тогда разрядность этих чисел (или, что то же
самое, размерность соответствующих булевых векторов) соста-
составит ]log2p[ (ближайшее целое, большее log2p). Так, если р = 15,
Д.7.2. Конечные автоматы с выходом. Структурный синтез 559
то для того, чтобы закодировать числа от 0 до 14, нужны четы-
четырехразрядные двоичные коды, поскольку ] log215[ = 4. Заметим,
что в общем случае, поскольку число log2P не будет целым, не
все двоичные числа соответствующей разрядности будут ис-
использованы. Так, при р = 15 не будет использовано число 1111
(двоичный код числа 15).
Тогда размерности булевых векторов X (кодов входных
символов), Y (кодов выходных символов), U и Z (кодов теку-
текущего и нового состояний) соответственно будут равны: п =
Предлагается следующий алгоритм определения булевых
операторов F и G в G.13).
1. Составляется таблица для функций переходов и выходов
исходного конечного автомата с выходом (табл. 7.1).
Таблица 7Л
Текущее
состояние
•
q
Входной
символ
•
а
i
Выходной
символ
b = n(q,a)
•
Новое
состояние
":
r = 8(q,a)
i
2. По составленной таблице (см. табл. 7.1) строят так
называемую структурную таблицу (табл. 7.2), в которой
каждый символ (входной и выходной) и каждое состояние
заменяются их двоичным кодом, причем так, что если набор
Таблица 7.2
и
I
til, ...,Ujb
•
X
i
XJ, . . * , Xjj
Y
I
УЬ ...,Ут
•
z
zu...,zk
•
560 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
(г/1, ..., щ) есть код текущего состояния д, набор (a?i, ..., хп)
есть код входного символа а, то
(Уъ •.., ym) = G((ui, ..., и*),(жь ..., хп))
тогда и только тогда, когда набор (j/i, ..., ут) есть код выход-
выходного символа 6 = /i(g,a), а
, ..., гх*),(яь ..., хп))
тогда и только тогда, когда набор (zi, ..., ^) есть код состоя-
состояния г = (J(g,a).
Структурная таблица есть не что иное, как таблица, зада-
задающая некоторый булев оператор (вообще говоря, частичный,
так как не все векторы соответствующей размерности служат
кодами элементов множеств V,W,Q) из Bfc+n в Вт+*. Этот
оператор может быть реализован некоторой схемой из функци-
функциональных элементов (как правило, над стандартным базисом).
Вектор Z поступает (в некоторый момент времени t) на вхо-
входы к триггеров, с прямых выходов которых (в момент времени
t +1) снимается вектор С/, т.е. U(t +1) = Z(t). Таким образом,
если в начальный момент времени t = 0 с выхода запоминаю-
запоминающей части снимается вектор Е/о, код начального состояния qo
и на вход комбинационной части поступит вектор -Х"@), то на
вход запоминающей части в этот же момент времени поступит
вектор Z@) = F(l7@),X@)) = GA) и триггеры запоминающей
части будут хранить уже информацию о новом состоянии до
момента времени t = 1 и т.д.
В этом небольшом дополнении мы никак не можем сколько
нибудь подробно и строго обсуждать математическую теорию
реализации ОД-функций „схемами" с элементами задержки*.
Разумеется, нет и речи о каких-либо доказательствах. Также
мы не решаем „инженерно-технические" проблемы структур-
структурного синтеза, в частности проблемы „аппаратной реализации"
*См., например: Яблонский СВ.; Гаврилов Г.П., Сапоженко А.А.
Д.7.2. Конечные автоматы с выходом. Структурный синтез 561
триггеров. Наша цель здесь — показать в рамках самого
элементарного изложения связь между теорией конечных ав-
автоматов и теорией булевых функций. Эта связь состоит в том,
что теория булевых функций дает аппарат для структурного
синтеза конечных автоматов (с выходом), т.е. для перехода от
описания функции, вычисляемой конечным автоматом, к его
структуре, реализующей его „схеме", построенной на функци-
функциональных элементах и элементах задержки.
В заключение разберем простой пример структурного син-
синтеза.
Пример 7.14. Конечный автомат с выходом задан диа-
диаграммой, изображенной на рис. 7.42. С содержательной точки
зрения этот автомат работает как простейший „лексический
анализатор", распознавая все це-
почки во входном алфавите V =
= {а, Ь, 0,1}, которые начинаются а/0, Ь/0
с „буквы", т.е. с символа а или 6,
как „правильные", тогда как це-
цепочки, начинающиеся с „цифры"
(т.е. с 0 или 1), классифицируются \-/О O/l' l/l'
как „неправильные", о чем выда-
выдается сообщение в виде выходного
символа „?«. рис 7 42
Кодируя входной и выходной
алфавиты, а также состояния, получим следующие двоичные
коды:
1) входной алфавит: a — 00, Ъ — 01, 0 — 10, 1 — 11;
2) выходной алфавит: 0 — 00, 1 — 01, ? — 10, код 11 не
используется;
3) множество состояний: qo — 00, q\ — 01, (ft — Ю, код 11
не используется.
Так как рассматриваемый автомат простой, мы сразу со-
составим структурную таблицу (табл. 7.3).
562
7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
щ
0
0
0
0
0
0
0
0
1
1
1
1
«2
0
0
0
0
1
1
1
1
0
0
0
0
XI
0
0
1
1
0
0
1
1
0
0
1
1
Х2
0
1
0
1
0
1
0
1
0
1
0
1
У\
0
0
1
1
0
0
0
0
0
0
0
0
Таблица
У2
0
0
0
0
0
0
1
1
0
0
1
1
z\
0
0
1
1
0
0
0
0
1
1
1
1
7.3
*2
1
1
0
0
1
1
1
1
0
0
0
0
Для частичных булевых функций у\ =yi(#i,?2>t*bt*2)» у2 =
= У2(жьЖ2,^1,и2), Z\ = Zi{xi,X2,UUU2), Z2 = Z2{xi,X2,Ui,U2) CO-
ставим карты Карно и найдем для каждой из них минимальную
ДНФ.
Для функции у\ карта Карно изображена на рис. 7.43.
Единственная склейка дает у\ = u\u2x\.
OOlx
xllx
00
01
11
10
00
-
01
-
11
-
10
-
ttiV\
00
01
11
10
00
-
01
-
11
s
1
V
10
N
J
Рис. 7.43 Рис. 7.44
Для второй функции получим (рис. 7.44)
У2 = '
Д.7.2. Конечные автоматы с выходом. Структурный синтез 563
•xOlx
00
01
11
10
00
-
1
01
-
1
11
1
-
1
10
ч
1'
00
01
11
10
00
т~
-
01
-
11
——-*
1
-
10
.——
1 '
-
xlxx
Рис. 7.45 Рис. 7.46
Для функции z\ имеем (рис. 7.45) минимальную ДНФ
Наконец, для функции Z2 по карте Карно, изображенной на
рис. 7.46, находим Z2 = щ УхгЩ.
Структурная схема автомата представлена на рис. 7.47.
Обратим внимание на то, что вместо инверторов для сигна-
сигналов u\ и щ мы используем сигналы, снимаемые с инверсных
выходов триггеров Т\ и Гг. Заметим также, что переменная Х2
оказалась фиктивной. Действительно, тип входного символа
(„буква", т.е. а или Ь, и „цифра", т.е. 0 или 1) распознается по
первому разряду входного вектора X: при х\ = 0 имеем „бу-
„букву", а при xi = 1 — „цифру".
Наконец, следует заметить, что синтезированная „струк-
„структурная схема", строго говоря, не является графом (поскольку
содержит, например, „кратные дуги", т.е. допускает несколь-
несколько разных дуг между одной и той же парой вершин). Даже
комбинационная часть этой схемы не может быть уже назва-
названа схемой из функциональных элементов, так кале в вершины,
помеченные переменными ui,it2) заходят некоторые дуги. Это
будет, говоря неформально, схема из функциональных элемен-
элементов, „вставленная" в некий более общий „графовый объект".
564 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Рис. 7.47
Строгая математическая теория таких „обобщенных графов"
в этом учебнике не рассматривается*.
Дополнение 7.3. Морфизмы
и конечные подстановки
Пусть V и W — некоторые алфавиты (в частности, V =
= W). Морфизм — это произвольное отображение h: V* -»
-> W\ такое, что Л(Л) = Л и (Vx,y € V*) (h(xy) = h(x)h(y)).
*В литературе для этих объектов также используются термины „сеть",
„гиперграф", „блок-схема" (см.: Яблонский СВ.).
Д.7.3. Морфизмы и конечные подстановки 565
Иначе говоря, морфизм (в данном контексте) — это гомо-
гомоморфизм свободного моноида V* в свободный моноид W* (см.
пример 2.7.д).
Теорема 7.11. Любой морфизм h: V* —> W* однозначно
определяется конечным отображением
{(aMa)):aeV,h(a)eW*}. #
Обычно такое отображение задается в форме, напоминаю-
напоминающей запись правил вывода порождающей грамматики:
ai->/i(ai), ..., an-+h(an),
где V = {ai,..., an}. Чтобы найти образ некоторого непустого
слова х Е V+, достаточно вместо каждой буквы x(i) подставить
слово h(x{i)) e W*.
Например, если h задается в виде
а —> abcba, b —> 6a, с —> А,
то h(abbc) = abcbababa,
h{h{abbc) = h2(abbc) = h{abcbababa) =
= abcba ba ba abcbaba abcba ba abcba =
= abc(baKabc(baJabc(baJabcba.
Морфизм h называется Х-свободным морфизмом, если
для всякого слова х ф A h(x) ф А. Морфизм предыдущего
примера не является А-свободным.
Если h: V* -> W* — морфизм, то соответствие h~l (обрат-
(обратное к h) из W* в V* называют инверсным морфизмом (ин-
(инверсией морфизма, обратным морфизмом).
Таким образом, из определений сразу следует, что Vy E W*
^ (у) = {%' h(x) = у}. Для рассмотренного выше примера
Л" (abcbaba) = {abcn: n ^ 0} = abc\
566 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Определение 7.11. Пусть h: V* -> W* — морфизм. Тогда
для языка L С F* язык h(L) = {у: у = h(x), х Е V*} называют
морфизмом языка L, а для языка К С W* язык Л" (К) =
= {х: h(x) ? К, х Е V*} — инверсным морфизмом языка L.
Таким образом, язык h(L) есть не что иное, как образ языка
L при отображении h, a hrl(K) — прообраз языка К при
отображении h (см. 1.3).
Соответствие а С V* х W* называют конечной подста-
подстановкой, если:
1) а(Х) = {Л};
2) для каждого а € V множество а (а) конечно;
3) для любых цепочек #, у G V* сг(жу) = <т(х)а(у) (т.е. мно-
множество слов сг(ху) есть соединение языков (т(х) и сг(у)).
Иначе говоря, конечная подстановка — это своего рода мно-
многозначный морфизм, на любой букве алфавита принимающий
лишь конечное множество значений.
Точно так же как и для морфизма, легко показать, что
конечная подстановка полностью определяется своими значе-
значениями на буквах алфавита V и, следовательно, может быть
задана, как и морфизм, в виде системы „правил замены", в
которой одной и той же букве алфавита V сопоставляется, во-
вообще говоря, несколько цепочек в алфавите W. Например:
а —У abcba, a —> ас,
Ъ-*Ъа, Ь —> cab,
c-taa, с -> А, с -» bab,
или в более короткой записи:
о -> abcba | ас, Ь —> ba \ cab, с -> аа \ Л | bob,
как мы записывали правила вывода грамматик и системы
команд конечных автоматов.
Для нашего примера
а(аЪ) = {abcbaba, abcbacab, acba, accab}.
Д. 7.3. Морфизмы и конечные подстановки 567
Если а С V* х W* — конечная подстановка, то обратное со-
соответствие о~х С W* х V* называется инверсной (обратной)
конечной подстановкой (или инверсией конечной под-
становки).
Заметим, что для фиксированного у Е W*, согласно опреде-
леням обратного соответствия и сечения соответствия,
а~1(у) = {х: (ж,у) € с) = {я: у € а(ж)}.
Бели L С V*, а С V* х W* — конечная подстановка, то
o{L) = {y:CxeL)yea(x)}.
Если же К С W*, то
Нетрудно заметить, что, согласно определению области
определения и области значения соответствия, a(L) С Л(а),
a a~1(L) С i)(a) = R(a~~l). Подчеркнем, что не все цепочки
множества а(х) при х € <х~1(К) содержатся в языке К, но
найдется хотя бы одна цепочка в а(ж), которая принадлежит К.
Формулируемая далее теорема связывает конечную подста-
подстановку с основными операциями над языками: объединением
языков, соединением языков и итерацией языка.
Теорема 7Л2. Если К и L — языки в алфавите V, а
и С V* х W* — конечная подстановка, то
#
Основной результат, рассматриваемый в этом дополнении,
составляет следующая теорема.
Теорема 7.13, Если L С V* и К С W* — регулярные языки,
° С V* х W* — конечная подстановка, то a(L) и а (К) —
Регулярные языки в алфавитах W и V соответственно.
568 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
<4 Регулярность языка a(L) легко доказывается индукцией по
построению регулярного выражения с привлечением теоремы
7.12, и детали этого доказательства нетрудно восстановить.
Доказательство регулярности языка а (К) значительно
труднее. Мы используем „технику буферов", которая оказыва-
оказывается полезной в теории формальных языков при доказательстве
многих утверждений. Пусть М = (Q, W, go> F, 6) — конечный
автомат, допускающий язык К. Построим конечный автомат
М' = (Q', V, so, F'i &') следующим образом.
где fc= max M, s0
У€<г(о)
С интуитивной точки зрения множество Q1 состояний ко-
конечного автомата М' включает „новое" состояние sq и конечное
множество упорядоченных пар из Q x W^k\ где к — наиболь-
наибольшая длина среди всех длин слов из образов букв алфавита V
по подстановке а. Образно говоря, каждое состояние нового
автомата определяется состоянием старого автомата (допуска-
(допускающего К) и содержимым „буфера" конечной длины к для слов
из W*, длина которых не превышает к.
2.F' = {[qf,\}:qfeF}.
3. Система команд <$' содержит команды следующих видов:
(г) soa -» [go,s], где a G V U {Л}, х G а(а);
(п) [q,ax] -> [р,#] в том и только в том случае, когда S
содержит команду qa ->p, a G VF, x G W(fc);
(ш) [д,Л]а -+ [д,ж], где ж 6 а(а), а G V, g G Q.
Неформально работа конечного автомата М' может быть
описана следующим образом.
Если входная цепочка у = Л, то М1 допускает цепочку
AGa"(A). Это соответствует команде вида (г) при а = А
(при условии, конечно, что qo G F, т.е. что X G К). Если
у т^ А, то М; прочитает символ уA) и по команде вида (t)
„заполнит буфер" какой-то цепочкой из множества сг(уA)), т.е.
перейдет в одно из состояний [go^i]» где х\ G <т(у{1)). Далее
М; начинает „моделировать" работу конечного автомата М
Д.7.4. Машины Тьюринга 569
(согласно командам вида (и)), „читая содержимое буфера" и
не обращая внимания на вход, т.е. делая \-такты. Исчерпав
цепочку х\, М1 перейдет в состояние [п,А], где qo =>** г\ в М.
XI
Если у = уA) и ri e Fy то а(у) ПК ^0 и уе а (К). Иначе
автомат может допустить другую цепочку из сг(уA)) и т.д. В
том случае, если ни из одного состояния [go>?i] нельзя попасть
в состояние [?/, A], qj G F, однобуквенная цепочка у ? сг~1(К) и
М1 .зависает" в незаключительном состоянии.
77
Бели цепочка у имеет второй символ уB), то по команде
вида (itt) будет обеспечена „подкачка буфера" некоторой це-
цепочкой Х2 € а(уB)) и М1 опять начнет работать за конечный
автомат М, читая буфер, и т.д.
Нетрудно видеть, что
[«b*i] =** [ri,A] =* [ri,a?2] =^* [га,А] =» ... =Ф* [rm,A],
rm€ F при ж» G 0-(у(г)) для всех г = 1,... ,т и |у| = т тогда и
только тогда, когда цепочка х\Х2... жт читается на некотором
пути из qo в rm, т.е. когда сг(у) ПК ^0 иуЕ а (К).
Строгое доказательство равенства L(Mf) = а (К) основа-
основано на индукции по длине пути в графе автомата. Это доказа-
доказательство мы не приводим. >
Следствие 7.5. Бели L CV* и К С W* — регулярные
языки, h: V* -> W* — морфизм, то h(L) и hrl{K) — регулярные
языки в алфавитах W и V соответственно. #
С интуитивной точки зрения доказанные результаты озна-
означают „устойчивость" множества регулярных языков относи-
относительно преобразований, задаваемых конечными подстановками
(в частности, морфизмами).
Дополнение 7.4. Машины Тьюринга
В этом дополнении мы рассмотрим автомат, называемый
^томатом Тьюринга, или машиной Тьюринга, который являет-
является анализирующей моделью для языков типа 0. Одновременно
570 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
машина Тьюринга является одним из математических опреде-
определений алгоритма.
Определение 7.12. Машина Тьюринга определяется
кортежем вида
T=(Q, V,*, О, S, L, Д, до, 9/, *),
где Q — конечное множество состояний; V — конечный
входной алфавит; • $ V — символ, называемый маркером
начала ленты; П ? V — символ, называемый пустым (или
пробелом); 5, L, R ? V — символы, называемые символами
направления движения головки; до € Q — начальное со-
состояние; g/ Е Q — заключительное состояние; S — функция
переходов, являющаяся отображением вида
6: Q х (VU {*,
причем значение ?(д,а), коль скоро оно определено, есть конеч-
конечное (возможно, и пустое) множество упорядоченных троек из
соответствующего декартова произведения.
Функция переходов может быть записана в виде системы
команд. Каждая команда есть слово вида
где а, Ь G V U {*, ?}, М б {5, L, Д}, -> ? V U {*, П, 5, L, Д}.
Слово да (до стрелки) называется левой частью коман-
команды, а слово rb,M (после стрелки) — правой частью коман-
команды.
Неформально работу машины Тьюринга можно предста-
представить следующим образом. Машина имеет устройство упра-
управления, которое может находиться в одном из состояний мно-
множества Q, полубесконечную ленту, разделенную на ячейки, в
каждой из которой может быть записан символ из алфавита
V U {•,?}, причем крайняя левая ячейка хранит символ *, и го-
головку чтения-записи, которая в каждый момент дискретного
Д. 7.4. Машины Тьюринга, 571
времени обозревает какую-то одну ячейку ленты. Символ ?
(пробел) не следует путать с пустой цепочкой — это специаль-
специальный символ, означающий пустую, т.е. не хранящую символов
алфавита VU{*}, ячейку ленты. Команда, записанная выше,
разрешает машине Тьюринга, устройство управления которой
находится в состоянии д, а головка обозревает ячейку, храня-
хранящую символ а, перевести устройство управления в состояние
г, записав в обозреваемую ячейку символ Ь (который может
и совпадать с а), и оставить головку на прежнем месте, если
М = 5, сдвинуть ее на одну ячейку влево, если М = L, или на
одну ячейку вправо, если М = R.
Таким образом, в отличие от конечных автоматов маши-
машина Тьюринга может модифицировать содержимое ленты (т.е.
является преобразователем), а также передвигать головку в
любом направлении. Впредь условимся говорить о состоя-
состоянии машины Тьюринга, подразумевая состояние ее устройства
управления, и об обозреваемом символе, подразумевая под этим
символ той ячейки ленты, которая обозревается в данный мо-
момент головкой.
Формально поведение машины Тьюринга описывается в
терминах конфигураций.
Определение 7.13. Конфигурация машины Тьюринга
Т есть кортеж
(q, x,y)GQx(VU{*, D})* x(FU{*, ?})*.
Из конфигурации С = (g, x, ay) непосредственно выводится
конфигурация С" = (г, ж, Ьу), если qa -+rh, S ? S.
Из конфигурации С = (g, xc, ay) непосредственно выводит-
выводится конфигурация С" = (г, ж, сбу), если qa ->rb, Le S.
Из конфигурации С = (g, ж, асу) непосредственно выводит-
выводится конфигурация С" = (г, жб, q/), если qa -* rb, R 6 S.
Выводом на множестве конфигураций машины Тьюрин-
Тьюринга называется произвольная последовательность конфигураций
572 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Со, С\, ..., Сп, ..., такая, что (Vi ^ 0)(C{ Ь Cj+i, если d+\ су-
существует).
Конфигурация С" выводима из конфигурации С, если суще-
существует вывод С = Со Ь ... Ь Сп = С. Число п называется при
этом длиной вывода. Все обозначения, касающиеся выводимо-
выводимости на множестве конфигураций машин Тьюринга, остаются
такими же, как в случае конечных и магазинных автоматов.
Конфигурация есть тройка (состояние, часть цепочки на
ленте до головки, часть цепочки на ленте, первый символ
которой обозревается головкой). При этом, по соглашению,
любая цепочка из множества хП* (для фиксированного х Е
Е (V U {•,?})*) отождествляется с цепочкой ж, т.е. можно
отбрасывать любое число пробелов в конце слова.
Определение 7.14. Машина Тьюринга называется де-
детерминированной, если из каждой конфигурации этой ма-
машины непосредственно выводится не более чем одна конфигу-
конфигурация.
Нетрудно видеть, что машина Тьюринга является детерми-
детерминированной тогда и только тогда, когда в ее системе команд не
существует двух разных команд с одной и той же левой частью.
Далее будем рассматривать только детерминированные ма-
машины Тьюринга, называя их просто машинами Тьюринга.
Определение 7.15. Словарная (вербальная) функция
в алфавите V есть произвольное частичное отображение мно-
множества слов в алфавите V в себя.
Определение 7.16. Будем говорить, что машина Тьюрин-
Тьюринга Т применима к слову р Е V*, если из конфигурации (до, А, *р)
выводится конфигурация (<j/, Л, *s) для некоторого s E V*.
Слово s будем называть в этом случае результатом при-
менения машины Тьюринга Т к слову р и обозначать его
Т(р). Факт применимости машины Т к слову р будем обо-
обозначать \Т(р); если же Т не применима к р, то будем запи-
записывать -i!T(p).
Д. 7.4. Машины Тьюринга 573
Множество всех слов р, таких, что !Т(р), называется обла-
областью применимости магиины Тьюринга Т.
Определение 7.17. Словарная функция (р в алфавите V на-
называется вычислимой по Тьюрингу, если существует такая
машина Тьюринга Ту с входным алфавитом V\ содержащим V,
что
() !T^(z) Л (Т^(а;) = </>(*)).
Пример 7.15. Рассмотрим натуральное число п как слово
0|п в алфавите {0, |}, а сложение двух натуральных чисел
зададим как словарную функцию ADD в алфавите {0, |,f}>
преобразующую слово 0|nf0|m в слово 0|n+m. Тогда функция
ADD вычислима по Тьюрингу, поскольку приведенная ниже
система команд определяет машину Тьюринга для сложения
двух натуральных чисел:
где система команд S имеет следующий вид:
A)
B)
qo\->qo\,R, C)
9ot~^9i|>-R> D)
E)
F)
G)
(8)
(9)
A0)
(И)
A2)
A3)
A4)
A5)
A6)
574 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Определенная таким образом машина Тьюринга, получая
„на вход" слово 0|n fO|m, где п,т ^ 0, оставаясь в состоянии
#0? „бежит" вдоль ленты слева направо до тех пор, пока не
встретит символ f (играющий роль „разделителя" двух слага-
слагаемых). „Увидев" этот символ, машина перейдет в состояние
qij заменив символ f „палочкой" (|). Следующий затем символ
О (первый символ второго слагаемого) заменяется „палочкой".
Таким образом, после „пробега" второго слагаемого в резуль-
результирующем слове будет на две „палочки" больше, чем следует.
Если второе слагаемое не равно 0, то после выполнения коман-
команды E) будет применима команда F), а после нее — команда G).
Тем самым будет прочитано второе слагаемое до ближайше-
ближайшего пробела, затем применением команд (8)-A0) будут стерты
лишние „палочки", машина вернется к маркеру начала ленты
и остановится в заключительной конфигурации. Если же вто-
второе слагаемое равно 0 (есть однобуквенное слово 0), то после
выполнения команды E) применяется команда A4), и затем по-
посредством применения команд A5) и A6) машина сотрет две
„палочки" и перейдет в заключительную конфигурацию.
Запишем тогда последовательность конфигураций для при-
прибавления нуля к произвольному числу:
Разумеется, предложенная машина Тьюринга для сложения
двух натуральных чисел не обязана быть единственной, но это
и не требуется по определению вычислимости — достаточно,
чтобы нашлась хотя бы одна машина, вычисляющая данную
функцию. #
Д.7.4. Машины Тьюринга 575
Итак, используя понятие машины Тьюринга, можно дать
строгое определение функции как процедуры (правила,
алгоритма) вычисления значения функции по известным зна-
значениям ее аргументов. Тем самым понятие машины Тьюринга
есть одно из возможных математически точных определений
алгоритма.
До построения какого-либо математического определения
алгоритма мы имеем дело с интуитивным представлени-
представлением об алгоритме. Это интуитивное понятие, не являющееся
математически строгим (подобно тому как в рамках „наивной"
теории множеств не является таковым понятие множества), мо-
может быть охарактеризовано следующими признаками:
1) признак детерминированности алгоритма — ал-
алгоритм есть пошагово реализуемая процедура, на каждом шаге
которой однозначно определено ее продолжение (другими сло-
словами, алгоритм не допускает произвола в выборе очередного
шага — в определении алгоритма через машину Тьюринга этот
принцип реализуется через понятие детерминированной маши-
машины Тьюринга);
2) признак результативности алгоритма — процесс
работы алгоритма с исходными данными должен завершаться
через определенное конечное число шагов;
3) признак массовости алгоритма— алгоритм должен
быть применим к определенному достаточно широкому множе-
множеству входных данных.
Наряду с машиной Тьюринга известны и другие уточнения
понятия яалгоритм" (нормальные алгорифмы Маркова, рекур-
рекурсивные функции, канонические системы Поста и т.п.). Ока-
Оказывается, что все эти понятия в определенном смысле эквива-
эквивалентны. Кроме того, в теории алгоритмов, которая занимается
проблемами построения разных уточнений понятия алгорит-
алгоритма и вычислимости, а также сравнением между собой разных
уточнений, основной гипотезой является гипотеза о том, что
всякая функция, вычислимая в интуитивном смысле слова, т.е.
такая, что существует алгоритм (в интуитивном смысле слова)
576 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
вычисления значений функции по известным значениям аргу-
аргументов, будет вычислима и в соответствии с каким-либо точ-
точным определением вычислимости, например будет вычислима
по Тьюрингу. Применительно к машинам Тьюринга эта гипо-
гипотеза носит название тезиса Тьюринга: любая вычислимая (в
интуитивном смысле) словарная функция вычислима по Тью-
Тьюрингу.
В пользу тезиса Тьюринга говорит то, что до сих пор не
удалось придумать вычислимую функцию, которую нельзя бы-
было бы „запрограммировать" в виде машины Тьюринга, а также
то, что все известные до сих пор альтернативные уточнения
понятия алгоритма можно (хотя и не так просто) свести к по-
понятию машины Тьюринга.
Чтобы закончить обсуждение машин Тьюринга в контексте
теории формальных языков, нам необходимо ввести еще два
важнейших понятия — перечислимости и разрешимости.
Условимся в дальнейшем машину Тьюринга со входным ал-
алфавитом V называть машиной Тьюринга в алфавите V, а
машину Тьюринга, входной алфавит которой содержит алфа-
алфавит V и символы, не принадлежащие V, — машиной Тьюрин-
Тьюринга над алфавитом V. Договоримся также „кодировать" на-
натуральные числа словами в алфавите N = {0, |}, дав множеству
N натуральных чисел следующее определение по индукции:
1) слово 0 есть натуральное число;
2) если известно, что слово п в алфавите N есть натуральное
число, то слово п\ есть натуральное число;
3) никаких других натуральных чисел, кроме определенных
в пп. 1 и 2, не существует.
На множестве определенных таким образом натуральных
чисел (как слов) естественно вводится отношение порядка: по
определению, п < га, если п есть префикс га. Легко опреде-
определить и обычные арифметические операции, я запрограммиро-
запрограммировав " их машинами Тьюринга (пример операции сложения разо-
разобран выше).
Д.7.4. Машины Тьюринга 577
Определение 7.18. Непустое множество слов L в алфавите
V называется перечислимым (по Тьюрингу), если суще-
существует машина Тьюринга Т над алфавитом VU{0, |}, такая,
что для всякого п Е N \Т(п) и для всякого х € L имеет место
х = Т(п) для некоторого п ? N.
Таким образом, перечислимость языка L означает суще-
существование алгоритма („ запрограммированного" как машина
Тьюринга), по любому натуральному числу п вычисляющего
элемент L и такого, что любой элемент L может быть вычи-
вычислен по некоторому натуральному числу. Такой алгоритм есть
алгоритмический („конструктивный") аналог теоретико-мно-
теоретико-множественного понятия нумерации как сюръекшивного отобра-
отображения множества натуральных чисел на некоторое множество.
Замечание 7.14. Пустое множество слов считается пере-
перечислимым по соглашению.
Определение 7.19. Множество слов L в алфавите V назы-
называют разрешимым (по Тьюрингу), если существует такая
машина Тьюринга Г над алфавитом V, что для всякого х G V*
имеет место \Т(х) и Т(х) = А, если х Е L, и Т(х) ф А, если х $ L.
Другими словами, разрешимость языка L означает суще-
существование вычислимого предиката, определенного на множе-
множестве слов в алфавите V и принимающего значение 1, если
элемент принадлежит L, и значение 0 в противном случае.
Без доказательства сформулируем следующую теорему.
Теорема 7.14. 1. Существует неперечислимый язык в
некотором алфавите V.
2. Существует перечислимый, но неразрешимый язык (в
некотором алфавите V).
3. Язык LCV* перечислим тогда и только тогда, когда он
является областью применимости некоторой машины Тьюринга
над алфавитом V.
4. Язык L С V* перечислим тогда и только тогда, когда он
порождается некоторой грамматикой типа 0.
19 - 10061
578 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
5. Язык LCV* разрешим тогда и только тогда, когда он
порождается некоторой КЗ-грамматикой. #
Из теоремы 7.14 следует, что всякое разрешимое множество
перечислимо, но обратное неверно.
В силу утверждений 3 и 4 теоремы 7.14 машины Тьюрин-
Тьюринга можно рассматривать как „распознающие автоматы" для
языков типа 0: для каждого такого языка существует маши-
машина Тьюринга, применимая к словам данного языка, и только
к ним. Заметим при этом, что язык типа 0 может оказаться
и неразрешимым: для него может не существовать алгоритма,
распознающего принадлежность ему любого наперед заданно-
заданного слова. Это значит, что для грамматик типа 0 проблема
принадлежности в общем случае не является разрешимой. Эта
проблема, однако, как следует из утверждения 5 теоремы 7.14,
разрешима для любого языка, порождаемого КЗ-грамматикой
(см. 7.2), в частности для любого КС-языка.
Утверждение 1 теоремы 7.14 означает, что существуют язы-
языки, которые не могут принципиально быть порождены какой-
либо грамматикой. Примером такого языка может служить
множество так называемых конструктивных действительных
чисел*.
Пример перечислимого, но неразрешимого языка может
быть построен следующим образом. Пусть V — алфавит, а
р — конечное бинарное отношение на множестве V+ непустых
слов в алфавите V. Определим язык Lp в алфавите V U {•, f},
где символы • и f не принадлежат V:
Доказывается, что язык Lp в общем случае неразрешим, т.е. не
существует алгоритма, который для любого наперед заданного
отношения р (при |У| ^ 2) распознавал бы слова языка Lp.
"См.: Кушнер БЛ.
Вопросы и задачи 579
Проблема распознавания слов языка Lp известна в теории
алгоритмов под названием проблемы соответствий По-
Поста (над алфавитом V). Неразрешимость проблемы соответ-
соответствий в общем случае не исключает того, что для каких-то
конкретных алфавитов и конечных бинарных отношений на
множестве непустых слов эту проблему можно решить. На-
Например, пусть V = {a,b}, a р = {(aba, ab), F, ab)}. Нетрудно
показать, что в данном случае Lp = {(aba] ab*b] ab)n: n ^ 1}.
Вопросы и задачи
7.1. Доказать, что следующая грамматика, заданная систе-
системой правил вывода, порождает любую цепочку вида ап , п ^ 1:
S -> аСА, Еа -> аЕ,
А -» а2ЕА | F, Са -» аС,
EF -» DF, CD -> Са,
ED -> Da2E, CF -» А.
7.2. Доказать, что следующая грамматика, заданная систе-
системой правил вывода, порождает любое слово в алфавите {а,&}
вида ww:
S -* CD, Aa -» аА,
С^аСА\ЪСВ\\, АЪ->ЪА,
D -> А, Ва -» аВ,
, ВЬ ^ ЬВ,
7.3. Доказать, что любая праволинейная грамматика может
быть задана эквивалентной регулярной грамматикой.
7.4. Постройте КЗ-грамматику, порождающую язык:
а) Lx = {anbmanbm: т,п > 1};
б) L2 = {anbnan: п > 1}.
19*
580 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
7.5. Какой язык порождает грамматика
S -> aSBa | аба, aB -> Ва, ЬВ -» 66?
7.6. Построить леволинеиную грамматику для языка иден-
идентификаторов, которые должны содержать от одного до шести
символов и начинаться с одной из букв г, j, к, ly m, п.
7.7. Доказать, что любая леволинейная грамматика эквива-
эквивалентна некоторой праволинейной грамматике.
7.8. Дано конечное множество слов {ui,..., щ} Е F+. Язык
L определяется как множество всех цепочек в V*, которые не
начинаются ни одним из слов tti,..., и&. Построить регулярную
грамматику, порождающую язык L.
оо
7.9. Доказать, что язык L+k = (J V регулярен для любого
i=fc>0
к при условии регулярности L.
7.10. Определить, какие множества цепочек задаются регу-
регулярными выражениями:
а) (a + 6)VF + c);
б) ((a6)+(ca)*)*;
в) (а
7.11. Доказать, что для любых регулярных выражений а и
/3 имеет место тождество (а + /9)* = (а*/?*)*.
7.12. Инверсия цепочки х € V* — это цепочка символов
жл, полученная переписыванием х справа налево, т.е. если
х = aji...ajn, то хл = ajn...aji. Доказать, что если L —
регулярный язык, то LR = {у: у = жя, iGL} — регулярный
язык. Привести два варианта доказательства: 1) используя
только определение регулярного языка; 2) используя конечные
автоматы.
7.13. Доказать, что 0* = А.
Вопросы и задачи
581
7.14. Написать регулярное выражение для множества цепо-
цепочек в алфавите {0,1}, содержащих четное число нулей и четное
число единиц.
7.15. Найти языки, допускаемые конечными автоматами,
заданными на рис. 7.48.
а, Ъ а,Ь, с
а,Ъ
а,Ь
Рис. 7.48
7.16. Доказать, что любой конечный язык регулярен.
7.17. Построить конечный автомат с входным алфавитом
{0,1,...,9}, допускающий десятичные записи: а) всех четных
чисел; б) нечетных чисел; в) чисел, делящихся на 4; г) чисел,
делящихся на 3; д) чисел, делящихся на 9.
7.18. Построить конечный автомат, допускающий десятич-
десятичные записи тех и только тех натуральных чисел, которые де-
делятся на заданное число А:.
Указание: автомат должен выполнять деление „ уголком "
и в нем должно быть ровно к состояний.
7.19. Обобщенным конечным автоматом назовем ориенти-
ориентированный граф, размеченный над полукольцом регулярных вы-
выражений (с выделенной начальной вершиной и подмножеством
заключительных вершин), в котором метка дуги может быть
произвольным регулярным выражением. Определяя язык тако-
такого автомата аналогично языку обычного конечного автомата,
Доказать, что для любого обобщенного конечного автомата
существует эквивалентный (т.е. допускающий тот же самый
язык) конечный автомат.
582 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
7.20. Построить конечные автоматы, эквивалентные следу-
следующим обобщенным конечным автоматам:
а) вход до; выход дз; дуги с метками (до, до, (а + Ь)с)),
(?о, 9ь а), (91, 91, (а + с)Ь), (дь д3, а*), (9о, 92, Ь*), (д2, 9з, Ь*),
(д2, 92, са{а + Ь)+);
б) вход д0; выход д3; дуги (д0, д2, (аб)*), (дг, 92, (са)*Ь),
(90, 91, 0), (91, 9з, с+), (д2, дз, ((Ь + а)+с*)).
7.21. Решить систему линейных уравнений с регулярными
коэффициентами
-А.
Для регулярного выражения, задающего компоненту решения
#3, построить допускающий его конечный автомат.
7.22. Доказать, что линейное уравнение х = ах + /3 с регу-
регулярными коэффициентами имеет:
а) единственное решение при А ? а;
б) бесконечно много решений при А Е а, причем общее реше-
решение можно записать в виде х = а* (/?+L), где L — произвольный
язык.
7.23. Для произвольного алфавита W определим операцию
левого деления на заданную букву, а именно: для произвольных
ае W и х = хA)хB)...х{к) eW* положим а~1х = хB)...х(к),
если хA) = а, а если хA) Ф а, то считаем, что выражение а~1х
не определено. В частности, выражение а~1\ всегда не опре-
определено. Доказать, что если L — регулярный язык (в алфавите
W), то для всякого a?W язык a~lL = {v: v = аГ1ху х€ L} ре-
регулярен.
7.24. Аналогично операции левого деления на букву можно
определить операцию левого деления на слово, полагая гу^ =
= у, если x = wy (иначе деление не определено). Определяя язык
Вопросы и задачи 583
xif^L так же, как в предыдущей задаче, доказать, что этот
язык регулярен для любого регулярного L.
7.25. Определим операцию левого деления языка L\ на язык
L2, положив
^2^1 = U w~lL* = ir- Cw e L^wy e LM ¦
w€L2
Доказать, что если L\ и L<i регулярны, то язык L2~lLi регу-
регулярный.
7.26. Пусть L — регулярный язык. Доказать, что
INIT(L) = {w: Cx)(wx G L)}
есть регулярный язык.
7.27. Пусть L — регулярный язык. Доказать, что
FIN(L) = {w:Cx)(xweL)}
есть регулярный язык.
7.28. Пусть L — регулярный язык. Доказать, что
SUB(L) = {w: Cx)Cy)(xwy ? L, где х,у,ги не пусты)}
есть регулярный язык.
7.29. Построить конечный автомат, допускающий все це-
цепочки в алфавите {а, Ь}, не содержащие вхождений подцепочки
аба.
7.30. Построить конечный автомат, допускающий все це-
цепочки в алфавите {а, 6}, которые не начинаются с ab и не
кончаются ab.
¦•31. Построить конечный автомат, допускающий те и
только те цепочки в алфавите {а, Ь}, которые не допускает
584 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
следующий конечный автомат: вход q\\ выход q$\ дуги с метка-
метками (gi, 91, Ь), (gi, g2? а), (ф, 9ъ Ь)> (?2, 9з, Ь)> (?з, 9з, л, 6), Для
построенного автомата записать регулярное выражение, зада-
задающее его язык.
7.32. Построить конечный автомат, допускающий все по-
последовательности нулей и единиц, кроме тех, которые содержат
подпоследовательность 11011.
7.33. Построить конечный автомат, допускающий те и
только те цепочки в алфавите {0,1}, которые не начинаются
цепочкой 01 и не заканчиваются цепочкой 11 (т.е. не разреша-
разрешаются цепочки вида 01х и цепочки вида yll, каковы бы ни были
цепочки х,у € {0,1}*).
Указание: дополнением языка, для которого нужно по-
построить конечный автомат, является множество всех таких
цепочек нулей и единиц, которые начинаются цепочкой 01
или заканчиваются цепочкой 11. Допускающий это множе-
множество цепочек автомат строится как автомат для объединения
01@+ 1)* + @ + 1)*11 способом, который изложен при доказа-
доказательстве теоремы Клини (см. теорему 7.6).
7.34. Минимизировать по переходам автомат, изображен-
изображенный на рис. 7.49.
Указание: предварительно удалить недостижимые из до
вершины.
Рис. 7.49
Вопросы и задачи 585
7.35. Используя лемму о разрастании, доказать, что следу-
следующие множества не регулярны:
а){(Г4(Г:п^1};
б) {ww:we{a,b}*};
в) множество цепочек в алфавите {0,1}, являющееся наи-
наименьшим решением нелинейного уравнения а? = 0я;1 + а;2 + 01 в
полукольце L(V)]
д) {w: w ? {а, 6, с}}* и имеет одинаковое число символов а и
b или одинаковое число символов бис;
е) {0Л1п:п^0}*;
ж) {0nlm: пфт, n,m^O};
з) множество всех цепочек нулей и единиц, в которых число
нулей больше числа единиц.
7.36. Решить задачу о перечеслении путей для ориентиро-
ориентированного графа, приведенного на рис. 7.50.
Вычислить полностью матрицу путей и опи-
описать все ее компоненты словесно.
Указание: помечая дуги графа упоря-
упорядоченным^ парами, составить систему урав-
уравнений с регулярными коэффициентами в ал- ^
фавите меток дуг для определения каждо-
каждого , *• « Рис. 7.50
го из трех столбцов матрицы стоимостей
(см. 5.6). Для данного графа имеем систему уравнений
х2 = B,1)жх + B,2)х2 + B,3)х3,
Решая ее, получим:
\)х2 + A,3)я?3 + А) + B,2)я2 + B,3)*з :
откуда
) + B,2)П(B,1)A,3) + B,3))х3 + B,1)).
586 7. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ЯЗЫКИ
Далее,
яя = A,2)(B,1)A,2) + B,2)Г((B,1)A,3) +
B,1)) + (
Написанное вьппе регулярное выражение, полученное как
значение переменного х\, обозначает множество всех путей,
начинающихся и заканчивающихся в первой вершине. Это мно-
множество можно словесно описать так: идем из первой вершины
во вторую по дуге A, 2), затем „крутимся" сколько угодно раз
(или ни разу) либо по контуру 2, 1, 2 либо по петле B, 2) (как
угодно их чередуя); далее идем в третью вершину через первую
по пути 2, 1, 3 или сразу по дуге B, 3), а из третьей вершины
возвращаемся в первую — получается замкнутый путь, по ко-
которому можно „крутиться", но не следует забывать, что можно
„крутиться" и по контуру 1, 3,1. Кроме того, попав, как описа-
описано вьппе, во вторую вершину, можно сразу вернуться в первую,
закончив „путешествие".
7.37. Для натуральных чисел, заданных в виде слов в ал-
алфавите {0,|}, определить операцию умножения и построить
машину Тьюринга над алфавитом {0, |}, которая для любых
натуральных чисел тип вычисляет их произведение.
7.38, Построить машину Тьюринга над алфавитом {а,Ь},
которая:
а) к любому слову х G {а, 6}* присоединяет слева (справа)
заданное слово од;
б) распознает палиндромы в алфавите {а, &};
в) распознает двойные слова в алфавите {а, Ь};
г) удваивает произвольное слово х Е {а, Ь}*, т.е. по этому
слову вычисляет слово хх.
8- КОНТЕКСТНО-СВОБОДНЫЕ
ЯЗЫКИ
8.1. КС-грамматики.
Деревья вывода. Однозначность
Мы приступаем к изучению одного из важнейших классов
формальных языков — класса контекстно-свободных языков
(КС-языков).
Определение КС-грамматик и КС-языков было дано в 7.3.
Напомним, что порождающую грамматику G = (V, N, S, Р)
называют контекстно-свободной (или КС-грамматикой), если
каждое правило вывода из множества Р имеет вид
где Ае N — нетерминал, а 7 € {У UN)* — цепочка в объеди-
объединенном алфавите грамматики. Таким образом, неформально
каждое правило вывода в КС-грамматике есть правило заме-
замены нетерминального символа цепочкой (возможно, пустой) в
объединенном алфавите.
Каждому выводу в КС-грамматике, начинающемуся с не-
нетерминального символа, однозначно сопоставляется ориенти-
ориентированный граф, являющийся деревом и называемый деревом
вывода. Вершины дерева вывода помечаются символами объ-
объединенного алфавита грамматики или пустой цепочкой. Под-
Подчеркнем, что дерево вывода сопоставляется не грамматике, а
конкретному выводу в данной грамматике, хотя мы увидим,
что нескольким различным выводам может быть сопоставлено
одно и то же дерево вывода. Прежде чем давать математи-
математическое определение дерева вывода, покажем на примере, как
по данному выводу в заданной КС-грамматике строится это
дерево.
588 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Пример 8.1. Рассмотрим КС-грамматику
Go = ({a,b}, {S, А, В, С}, 5, Ро),
где множество правил вывода Pq имеет вид:
S
А
А
В
В
С
С
-+АВС,
-4ЯВ,
->А,
-л о,
-+АА,
-+Ъ.
A)
B)
C)
D)
E)
F)
G)
В этой грамматике рассмотрим такой вывод:
S ЬA) ABC ЬB) ВВВС ЬF)
ЬF) BBBAA hC) ВЯВЛА hD) CCBBA h^7)
h^7) &6J55A h^5) ЬЬааА hB) bbaaBB h^5) бЬаааа.
По шагам этого вывода проследим процесс по-
построения дерева вывода. Первому шагу соот-
ветствует дерево, изображенное на рис. 8.1.
Корень этого дерева (куста) помечен заме-
Рис. 8.1 няемым на данном шаге нетерминалом, а метки
листьев, перечисленные слева направо, образуют цепочку, по-
полученную после применения правила A) на первом шаге. Вооб-
Вообще же цепочку, полученную в результате такого перечисления
меток листьев, называют кроной дерева*.
На втором шаге применяется правило B) и про-
производится замена вхождения (единственного в дан-
данном случае) символа А цепочкой ВВ. Поэтому вер-
в в шину дерева на рис. 8.1 с меткой А заменим кустом,
Рис. 8.2 как показано на рис. 8.2.
/1
л
* Допуская некоторую вольность речи, кроной дерева называют и соот-
соответствующую перестановку множества листьев.
8.1. КС-грамматики. Деревья вывода. Однозначность 589
После двух шагов получим дерево, изображенное на рис. 8.3.
Действуя аналогично, после третьего шага получим дерево,
показанное на рис. 8.4.
S S
ABC ABC
Л Л Л
В В В В А А
Рис. 8.3 Рис. 8.4
Четвертый шаг требует более подробного комментария.
Здесь в кроне дерева имеется несколько вхождений символа
А. На четвертом шаге первое вхождение $
символа А в цепочку ВВАА заменяет- >/Т\
ся пустой цепочкой. Поэтому очередной л ? ч
А В С!
шаг в построении дерева будет состоять л А
в том, что первый лист с меткой А в / \ / \
кроне дерева должен быть заменен ку- в В А А
стом с корнем А и единственным листом I
с меткой Л. Тогда получим дерево, изо- т
браженное на рис. 8.5.
Крона вновь полученного дерева — Рис" 8#5
это цепочка ВВВХА, выведенная из аксиомы за четыре шага.
Она, как элемент свободного моноида (VUN)*, равна (в силу
известных свойств пустой цепочки — см. 7Л) цепочке ВВВА.
Обратим здесь внимание на то, что, хотя пустая цепочка и не
является символом ни одного из алфавитов грамматики, она,
как было уже сказано, может быть меткой вершины дерева
вывода. Тем самым в дереве вывода фиксируются все вхожде-
вхождения выбрасываемых, т.е. заменяемых в процессе вывода пустой
цепочкой, нетерминалов. Это равносильно выделению в выво-
выводимой цепочке некоторых вхождений в нее пустой цепочки.
На пятом шаге первое вхождение символа В в цепочку
ВВВА заменяется цепочкой СС. Этому отвечает новое по-
590 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
А
строение на очередном дереве, состоящее в замене
первого листа кроны с меткой В кустом, изобра-
изображенным на рис. 8.6, после чего получим дерево,
с с показанное на рис. 8.7.
Рис. 8.6 Действуя дальше точно так же, получим в ре-
результате дерево вывода, изображенное на рис. 8.8. #
Б
А\ Al A
ABC В В а А А
А А Л I I Л
В В А А С С а X В В
Л I ММ
Рис. 8.7 Рис. 8.8
Из разобранного примера следует, что шаги построения де-
дерева вывода в точности соответствуют шагам самого вывода,
причем после каждого шага получаем некоторое дерево (на-
(назовем его частичнглм деревом вывода, полученным после
данного шага). Начинаем построение с корня, и его меткой
служит тот нетерминал, с которого начинается вывод (в част-
частности, это может быть аксиома грамматики). Бели на очеред-
очередном шаге вывода применяется правило В —у Х\Х2... Хт, где Х{
A ^ г < т) — либо символ объединенного алфавита, либо пустая
цепочка, то тот лист частичного дерева вывода, полученного
перед этим шагом, который имеет метку В и соответствует за-
заменяемому вхождению символа В, заменяется кустом с корнем
В и листьями Jfi, JC2, ..., Хт.
Замечание 8.1. 1. Прежде всего нужно отчетливо пони-
понимать, что на каждом шаге построения дерева вывода „развер-
8.1. КС-грамматики. Деревья вывода. Однозначность 591
тывается" в куст не любая вершина, меткой которой служит
некий нетерминал, а именно та вершина, которая соответству-
соответствует заменяемому вхождению указанного нетерминала.
2. Совершенно необязательно рассматривать
только деревья выводов терминальных цепочек л
из аксиомы. Дерево вывода может быть постро- У \
ено по выводу любой цепочки в объединенном в В
алфавите из любого нетерминала грамматики. /\
Так, мы могли бы на базе разобранного выше if ^
примера нарисовать дерево вывода цепочки ССа
из нетерминала -А, показанное на рис. 8.9. ис#
3. Можно заметить, что разные выводы одной и той же
цепочки из заданного нетерминала могут дать одно и то же
дерево вывода. Так, дерево, изображенное на рис. 8.9, можно
построить по двум различным выводам:
А\-ВВ\-ССВ\-ССа
А\-ВВ\-Ва\-ССа. #
Выводы, имеющие одно и то же дерево вывода, естественно
считать эквивалентными. Они различаются между собой толь-
только порядком, в котором применяются правила вывода*. Дерево
вывода и служит способом наглядного изображения всех экви-
эквивалентных выводов. Кроме того, как мы увидим позже, дерево
вывода является одним из основных инструментов доказатель-
доказательства утверждений о КС-языках и КС-грамматиках.
Теперь дадим формальное определение дерева вывода. Рас-
Рассмотрим множество (ориентированных) деревьев, вершины ко-
которых помечены символами некоторого алфавита W. Ориенти-
Ориентированное дерево, каждая вершина которого помечена символом
некоторого алфавита, будем называть помеченным деревом.
* Здесь, в рамках сугубо неформального изложения, мы не даем строгого
определения эквивалентных выводов.
592 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Если, кроме того, задано определенное правило перечисления
меток вершин дерева, образующих некоторое подмножество
вершин всего дерева, в частности листьев дерева, то такое по-
помеченное дерево называют упорядоченным деревом. Всюду
в дальнейшем, изображая деревья выводов, условимся понимать
их как упорядоченные деревья, метки листьев которых пере-
перечисляются всегда слева направо. Слева направо будем также
перечислять и сыновей каждой вершины. Будем считать, что
в машинном представлении деревьев выводов порядок „слева
направо" при изображении дерева на плоскости соответству-
соответствует порядку от первого элемента списка смежности вершины к
последнему. Дерево, корень которого помечен символом А, а
листья имеют метки Х\9 Х2, ..., Хту договоримся записывать
в виде цепочки
AUX1X2...Xm
(с двумя стрелками).
Бели рассматриваемое дерево является кустом, то условим-
условимся писать
AiXlX2...Xm
(с одной стрелкой).
Листья дерева, обозначенного таким образом, отождествим
с символами цепочки Х\, Х2, ..., Хт. Это значит, что, говоря
о листе Х$, мы имеем в виду лист помеченного дерева, мет-
меткой которого является символ Х{ и который в перечислении
листьев слева направо получает номер г. Тем самым устана-
устанавливается взаимно однозначное соответствие между листьями
помеченного дерева и вхождениями символов алфавита W в це-
цепочку X\j Х2, ..., Хт. Например, записывая дерево в виде
А 44 ВВСВС, мы можем говорить о листе В, соответствую-
соответствующем первому вхождению символа В в цепочку ВВСВС, или
же, обозначив ВВСВС через а, о листе аA). Тогда листья
аA), аB) и аD) — это разные листья дерева, хотя их меткой
является один и тот же символ алфавита W.
8.1. КС-грамматики. Деревья вывода. Однозначность 593
Расширим множество помеченных дере- s
вьев, допуская в качестве меток их вершин У^ТХ.
л т ч
А 44 Х\Х2... Хт, представляющей дерево с
и пустую цепочку. В этом случае, в записи
А 44 Х\Х2... Хт, представляющей дерево с л i i
корнем А и листьями Х\, -Хг, ..., Хт, среди / \ I I
Х 1
меток листьев, т.е. элементов Х^ % = 1, ш, в В а
могут быть и пустые цепочки. Тогда, го-
воря о листе с меткой А, нужно указывать,
какое вхождение пустой цепочки А в цепоч- a Ч Ч
ку Х1Х2... Хт имеется в виду. А А
Пример 8,2. а. Дерево вывода, изобра- "f f ^ f
женное на рис. 8.8, может быть обозначено 1 1 1 1
так: 5 44 bbaaXaa. В нем лист с меткой А со- х х х X
ответствует вхождению (Ьбаа, A, aa) пустой
цепочки в цепочку bbaaaa. ис#
б. Для грамматики из примера 8.1 вывод
5 Ь ABC Ь ВВВС Ь aBBC h aCCBC h aAACBC h
h aXACBC h aXXCBC h aXXAABC h aXXXABC h
h aXXXXBC h aAAAAaC h aAAAAab = aab
имеет дерево, показанное на рис. 8.10. В этом дереве любой
его лист с меткой А соответству-
соответствует одному и тому же вхождению
пустой цепочки в выводимую це-
цепочку ааЪ, а именно вхождению
(a, A, db)i так как для любого на- Д /\ /Ч
турального п выполняется равен- г \ / \ / \
ство Ап-А В В С С А А
в. Представленное на рис. 8.11 I I A I I A
дерево вывода цепочки ааЪаа мо- а а а А Ь X в В
жет быть задано записью II II
вЦааХХЬХаа. х X а а
Оно имеет три листа с меткой А. Рис. 8.11
594 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Первые два соответствуют вхождению (аа, А, Ъаа), а тре-
третье — вхождению (ааЬ, А, аа) пустой цепочки в выводимую
цепочку. #
Помеченное дерево А 44 Х\Х2... Хт называют \-свобод-
нылс, если среди меток -X"i, Л2, ..., Хт его листьев нет пустой
цепочки. Из предыдущих примеров можно заключить, что не
всякая цепочка, выводимая в КС-грамматике из какого-либо
нетерминала, имеет Л-свободное дерево вывода.
Помеченное дерево, полученное из дерева
А Ц Х\... Xi-iXiXi+i... Хт
заменой листа Х{ фА деревом Xi\^Y\,.JY^ будем записывать
в виде цепочки А Ц Х\...Xi~\[Xi Ц Y\...У*]^г+1...Хт. Это
дерево, поскольку в нем вместо листа Х^ возникают листья с
метками Ух,...,Уд., можно представить также в виде
Дерево вывода цепочки /3 в объединенном алфавите
из нетерминала А в КС-грамматике G = (V, N, 5, Р) —
это помеченное дерево, метками вершин которого являются
символы объединенного алфавита V U N или пустая цепочка
Л и которое строится по следующим правилам:
1) дерево любого вывода длины 0 состоит из единственной
вершины, помеченной нетерминалом А (в данном случае цепоч-
цепочка /9 = А)]
2) дерево вывода А Ь Л — это дерево А X Л (в данном случае
цепочка /3 = Л);
3) дерево вывода Aha, где а — непустая цепочка, есть
дерево А | а;
4) если а — цепочка в объединенном алфавите и
AUXiX2...Xm -
дерево некоторого вывода D этой цепочки из нетерминала А,
где a = Х1-Х2... Хт и для каждого г = 1, т X{?VUNU {Л}, а
8.1. КС-грамматики. Деревья вывода. Однозначность 595
для некоторого i A ^ г ^ m) X* = В € N — нетерминальный
символ грамматики G, и в множестве правил вывода Р грам-
грамматики G есть правило В -> Yi... У*, то дерево
есть дерево такого вывода цепочки
0 = X1...Xi-iYl...YkXM...Xm
из нетерминала А, что его последний шаг имеет вид
Х\... Xi-\BXi+i... Xm h
t-B-*Yi...Yk Xi...Xi-iYi...YkXi+i...Xm,
а вывод цепочки a = X"i... Xj_ii?Jf j+i... Xm из А совпадает с D.
Все выводы данной цепочки из данного нетерминала, по
которым приведенный выше алгоритм дает одно и то же де-
дерево вывода, будем называть эквивалентными. Среди экви-
эквивалентных выводов выделим два — левый вывод, в котором
на каждом шаге заменяется самое левое вхождение нетерми-
нетерминального символа; и правый вывод, когда на каждом шаге,
напротив, производится замена самого правого вхождения не-
нетерминала.
Это значит, что при построении дерева вывода по левому
выводу данной цепочки а из данного нетерминала А каждый
раз празвертывается" в куст самый левый лист кроны частич-
частичного дерева вывода, помеченный нетерминальным символом, а
при построении дерева вывода по правому выводу то же совер-
совершается с самым правым листом кроны.
Для построенного выше в примере 8.2.а дерева вывода
левый вывод имеет вид
S Ь ABC h В В ВС Ь ССВ ВС Ь
Ь ЬСВВС h ЪЬВВС Ь ЬЪаВС h ЬЬааС Ь
Ь ЬЪааАА Ь ЬЬааХА Ь ЬЪааВВ Ь ЬЬаааВ Ь ЬЬаааа.
596 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Правый вывод той же цепочки имеет вид
S Ь ABC Ь АВАА Ь АВАВВ Ь АВАВа Ь
h ABAaa Ь АВАаа Ь Аааа Ь BBaaa Ь Baaaa Ь
h ССаааа Ь СЬаааа Ь ЬЪаааа,
В обоих выводах полужирным шрифтом выделены заменяе-
заменяемые вхождения нетерминалов, а также удалено возникающее
после применения правила -А -» А вхождение пустой цепочки
А. Можно показать, что эквивалентные выводы различаются
между собой только порядком применения правил. Сами же
применяемые правила и вхождения заменяемых нетерминалов
у эквивалентных выводов одинаковы.
Мы часто будем использовать условное графическое обозна-
обозначение дерева вывода А Ц. Х\Х2...Хт в виде „треугольника",
одна из вершин которого помечена нетермина-
нетерминалом А, а противолежащая этой вершине сторо-
сторона символизирует всю цепочку а = Х\Хъ -.. Хт.
Иногда будем точками (или штрихами) отме-
чать отдельные символы цепочки а или листья
с меткой А (рис. 8.12).
Рис. 8.12 Кроме того, по традиции деревья выводов
изображаются без стрелок на дугах (хотя понимаются как
ориентированные деревья).
Из определения дерева вывода понятно, что в нем дуга из
вершины с меткой X ведет в вершину с меткой У тогда и только
тогда, когда на некотором шаге вывода применяется правило
вывода X -> 71^72? где 71 и 72 — цепочки в объединенном ал-
алфавите (возможно, пустые). Следовательно, число дуг любого
пути ненулевой длины дерева вывода, т.е. длина этого пути,
есть не что иное, как число применений правил вывода задан-
заданной КС-грамматики в некотором фрагменте вывода. А так как
в КС-грамматике каждое применение правила вывода есть за-
замена вхождения нетерминала некоторой цепочкой в объединен-
8.1. КС-грамматики. Деревья вывода. Однозначность 597
ном алфавите, то длина пути в дереве вывода равна числу замен
нетерминалов в соответствующем фрагменте вывода. Напри-
Например, для дерева, показанного на рис. 8.8, пути S -» А ->• В -» a
отвечает фрагмент вывода S Ь ABC Ь В В ВС Ь ВаВС. Обра-
Обратим внимание на то, что приведенный фрагмент есть фрагмент
одного из множества эквивалентных выводов, имеющих данное
дерево.
Таким образом, по заданному пути в дереве вывода од-
однозначно восстанавливается фрагмент одного из множества
эквивалентных выводов. Более того, по дереву вывода, постро-
построенному по одному из множества эквивалентных выводов, можно
восстановить все выводы этого множества, в частности левый
и правый. Можно показать, что для этого необходимо задать
определенный порядок посещения вершин дерева при поиске в
глубину от корня. Левый (соответственно правый) вывод будет
восстановлен, если каждый раз при поиске в глубину от очеред-
очередной вершины задавать продолжение поиска от самого левого
(соответственно самого правого) сына этой вершины.
Замечание 8.2. Длина вывода в общем случае не мень-
меньше, чем высота дерева этого вывода. Можно доказать, что для
фиксированной КС-грамматики G существует такая константа
С<з, зависящая от G, что для любого вывода D (начинающегося
каким-либо нетерминалом) и дерева Т этого вывода разность
между длиной Ijy вывода D и высотой hf дерева Т не превыша-
превышает Cq'. 1& — ^Т ^ Cg- Другими словами, разность между длиной
вывода и высотой дерева вывода для фиксированной грамма-
грамматики ограничена сверху. Это обусловлено тем, что указанная
разность определяется числом нетерминалов в правых частях
правил вывода, которое в пределах заданной грамматики все-
всегда ограничено. Это число, говоря неформально, определяет,
как сильно „ветвится" дерево вывода в процессе его „роста".
Для линейной грамматики, как нетрудно сообразить, высота
дерева вывода равна длине вывода. Однако если не фиксиро-
фиксировать грамматику, то разность между длиной вывода и высотой
598 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
дерева вывода может быть сколь угодно большой. Это можно
подтвердить таким простым примером.
Рассмотрим семейство КС-грамматик
Gm = (Vm, Nm, 5, Pm),
где m ^ 1, Vm = {аь ..., аш}, Nm = {S, Bu ..., Бт}, а множество
правил вывода Рт имеет вид
Грамматика Gm порождает единственную терминальную це-
цепочку ai...am. Высота дерева вывода этой цепочки равна 2
и не зависит от т (рис. 8.13), тогда как длина вывода опреде-
определяется числом т +1. #
JL7
,-Лч
Пусть фиксировано ориентированное дерево
Т с корнем R. Выделим в нем произвольно вер-
вершину Q, не являющуюся ни листом, ни корнем,
^2 ' Btm называемую внутренней вершиной дерева.
Образуем поддерево дерева Т, объявив его кор-
корнем вершину Q. Такое поддерево назовем мак-
максимальным поддеревом, если оно содержит
ис" # все вершины исходного дерева Т, достижимые
из вершины Q. Ясно, что высота любого максимального подде-
поддерева больше нуля и меньше высоты дерева Т. Для помеченного
дерева Т нетрудно проверить справедливость следующей тео-
теоремы.
Теорема 8.1. Крона любого максимального поддерева
помеченного дерева есть подцепочка кроны всего дерева.
Замечание 8.3, Сформулированное утверждение доста-
достаточно прозрачно и означает, что если в помеченном дереве
Т фиксировать произвольно внутреннюю вершину Q и рас-
рассмотреть крону максимального поддерева с корнем Q, то все
листья кроны этого поддерева, расположенные между самым
8.1. КС-грамматики. Деревья вывода. Однозначность
599
L L'
Рис. 8.14
левым (L) и самым правым (Z/) листьями, достижимыми из Q,
также достижимы из Q (рис. 8.14). #
Применяя теорему 8.1 к деревьям вы-
выводов в КС-грамматиках, получим следую-
следующий результат.
Следствие 8.1. Бели в дереве выво-
вывода некоторой цепочки а из нетерминала
А фиксировать произвольно внутреннюю
вершину, помеченную нетерминалом В, то максимальное под-
поддерево с корнем в фиксированной вершине (с меткой В) явля-
является деревом вывода некоторой подцепочки C цепочки а из
нетерминала В, т.е. существуют такие цепочки 71 и 72?
а = 7i/?72 и A h* 71 ?72 h* Т^2 (рис. 8.15). #
Так, для дерева вывода цепочки ЪААа
из нетерминала А в грамматике Go из
примера 8.1 (рис. 8.16), фиксируя макси-
максимальное поддерево с корневой вершиной С
(вторая вершина слева на первом уровне,
выделена полужирным шрифтом), получим
7i = Ь, /? = АА, 72 = о.. Соответствую-
Соответствующее этому максимальному поддереву разбиение вывода на два
фрагмента, может быть, например, таким: А Ь ВВ Ь ССВ Ь
Ь ЪСВ Ь ЬСа (первый фрагмент) и С Ь А А (второй фрагмент).
Описанная в следствии 8.1 „декомпози-
„декомпозиция" дерева вывода и соответственно вы-
вывода, по которому построено это дерево,
может быть интерпретирована так: выво-
выводя цепочку а из нетерминала А, мы, по-
получив на некотором шаге цепочку, содер-
содержащую выделенное вхождение нетермина-
нетерминала В, „замораживаем" этот нетерминал и
продолжаем замены нетерминалов слева и
справа от В, выводя начало (подцепочку
Л
С С
I Л
Б
Ъ А
Рис. 8.16
600 & КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
7i) и конец (подцепочку 72) цепочки а. После этого мы „ раз-
размораживаем " нетерминал В и „довыводим" из него середину
цепочки а — подцепочку /?.
Понятие дерева вывода связано с понятием однозначности
КС-грамматики.
Определение 8.1. КС-грамматику называют однознач-
однозначной, если каждая цепочка порождаемого ею языка имеет един-
единственное дерево вывода.
Поскольку по дереву вывода цепочки а из нетерминала
А однозначно строится как левый, так и правый вывод дан-
данной цепочки, то определение 8.1 можно сформулировать иначе:
КС-грамматика однозначна, если каждая цепочка порождаемо-
порождаемого ею языка имеет единственный левый и единственный правый
вывод.
Рассмотрим один хрестоматийный пример неоднозначной
грамматики.
Пример 8.3. Зададим грамматику GE следующим обра-
образом:
GE = ({а, Ь, if, then, else}, {?}, S,
S-> if b then S else S\if b then S\a).
Эта грамматика описывает „абстрактный синтаксис" опе-
операторов условного перехода в некотором „паскалеобразном"
языке программирования. Термин „абстрактный синтаксис"
в данном случае означает, что мы отвлекаемся от структуры
как операторов языка, так и логических условий.
Терминальный символ а означает произвольный оператор
(или последовательность операторов), а терминальный символ
b — призвольное логическое условие. Кроме того, терминалами
грамматики являются также лексемы if, then и else, формиру-
формирующие „скелет" любого оператора условного перехода.
8.1. КС-грамматики. Деревья вывода. Однозначность 601
Определенная таким образом грамматика неоднозначна,
что усматривается из такого примера: цепочка
if b then if b then a else a
имеет два дерева вывода (рис. 8.17 и 8.18).
S
if Ь then S else S if b then S
if b then S a if b then 5 else «5
I I I
a a a
Рис. 8.17 Рис. 8.18
Заметим (неформально), что наличие нескольких деревьев
вывода одной и той же цепочки имеет отношение к семантике
рассматриваемого языка. В данном конкретном примере по-
понятно, что каждому дереву вывода приведенной выше цепочки
отвечает свое смысловое прочтение этой цепочки: в первом слу-
случае else мы относим к первому then, а во втором — ко второму.
В итоге получаем две совершенно разные интерпретации опе-
оператора условного перехода. Данный пример неоднозначности
известен поэтому под названием пкочующее else".
Исходную грамматику, однако, можно „исправить", постро-
построив эквивалентную ей однозначную грамматику:
GEi = ({а, Ь, if, then, else}, {5Ь S2},SU
S\ —> if b then 52 else Si | if b then Si | a,
S2 -»if b then S2 else S2 \ a).
В общем случае алгоритма преобразования произвольной
неоднозначной КС-грамматики к эквивалентной однозначной
не существует. #
602 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Рассмотрим в заключение интересный пример неоднознач-
неоднозначности в естественном языке (точнее, в художественном тек-
тексте). В известном стихотворении А.С. Пушкина „К вельможе",
адресованном князю Юсупову, владельцу Архангельского, есть
такая строка:
Посланник молодой увенчанной жены...
(Речь идет о том, что князь был послан Екатериной Великой
к Вольтеру, великому французскому философу и писателю,
состоявшему с Екатериной в переписке.)
Процитированную строчку можно прочитать двояко:
1) посланник (молодой увенчанной жены),
2) (посланник молодой) увенчанной жены,
т.е. в первом случае эпитет „молодой" отнесен к „жене", а во
втором — к „посланнику". Чисто синтаксически эта коллизия
неразрешима, но внеязыковый контекст данной фразы, учи-
учитывающий совершенно определенные биографические обстоя-
обстоятельства персонажей, позволяет с высокой долей вероятности
предположить, что правильным будет второе прочтение.
В то же время следующую анекдотическую фразу нельзя
рассматривать как пример неоднозначности, ибо она не со-
соответствует грамматическим нормам русского литературного
языка:
Сдавайте мусор дворнику, который накопился.
Приведенные примеры, между прочим, обнаруживают, что
понятие однозначности необходимо анализировать в связи с
семантикой языка и что „смысл" следует придавать не цепочке
языка, а дереву ее вывода (см. Д.8.2).
8.2. Приведенная форма КС-грамматики
При изучении свойств КС-грамматик и КС-языков иногда
бывает целесообразно преобразовать КС-грамматику к эквива-
эквивалентной КС-грамматике, правила вывода которой удовлетво-
удовлетворяют определенным дополнительным ограничениям. В этом
8.2. Приведенная форма КС-грамматики 603
разделе мы рассмотрим алгоритмы некоторых таких преобра-
преобразовании.
Определение 8.2. Правило вывода КС-грамматики G —
= (V, JV, S, Р) называют:
1) \-правилом, если его правая часть — пустая цепочка;
2) цепным, если оно имеет вид А —> S, где А и В —
нетерминалы грамматики.
Теорема 8.2. Любая КС-грамматика G = (V, N, 5, Р) мо-
может быть преобразована к эквивалентной КС-грамматике, мно-
множество правил вывода которой не содержит А-правил, кроме,
может быть, правила 5 —> А, и не содержит цепных правил. #
Мы опишем алгоритмы удаления А-правил и цепных правил
из множества правил КС-грамматики, опуская строгое обосно-
обоснование этих алгоритмов.
Алгоритм удаления А-правил. Предположим, что нам
известно множество Ne всех нетерминалов грамматики G, из
которых выводится пустая цепочка, т.е.
Ne = {A:A\-*\}.
Тогда в правой части каждого правила А —> ? выделяются
все вхождения нетерминалов из множества Ne (если таких
вхождений нет, то правило пропускается) так, что цепочка ?
представляется в виде
? = aiBia2B2... атВтат+1,
где J5i, i?2) •••> Вт — все нетерминалы из iVe, входящие в ?.
Заметим, что они не обязаны быть различными, так как мы
выделяем все вхождения таких нетерминалов в правую часть
правила.
После этого к рассматриваемому правилу добавляются все
правила вида
А -> а\ X1OL2X2...
604 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
где для каждого г = 1, т Х{ есть или символ В{, или пустая
цепочка.
Иначе говоря, к любому правилу исходной грамматики,
правая часть которого содержит нетерминалы из множества
Ne добавляются все правила, которые могут быть получены
из исходного путем замены (в его правой части) любого числа
вхождений нетерминалов из Ne пустой цепочкой. При этом
сохраняется и само исходное правило и появляется, в частности,
правило
вовсе не содержащее вхождений указанных нетерминалов в пра-
правой части. Подчеркнем еще раз, что каждое правило исходной
грамматики, правая часть которого не содержит вхождений не-
нетерминалов из iVe, без всяких изменений переносится в систему
правил новой грамматики.
Если в процессе описанного выше преобразования системы
правил исходной грамматики получаются правила вида А —У А
или А —> А (при А Ф 5), то они игнорируются.
Остается обсудить метод вычисления множества Ne. Это
множество вычисляется рекуррентно, а именно на первом шаге
вычисляют множество No таких нетерминалов А грамматики
G, что существует в Р Л-правило А -> А. Таким образом, мно-
множество iVo — это множество всех нетерминалов грамматики,
из которых пустая цепочка выводится за один шаг.
На следующем шаге вычисляем множество iVi, включая в
него, во-первых, все нетерминалы множества No
и, во-вторых, все такие нетерминалы J3, что в Р
имеется правило вывода В -» 7? гДе 7 — непустая
i вт цепочка нетерминалов из множества ЛГ0, т.е. 7 €
Е JVq". Это означает, что N\ состоит из всех таких
J ... J нетерминалов А грамматики G, что дерево вывода
пустой цепочки из А, имеет высоту, не большую 2
Рис. 8.19 (рис. 8Л9).
л
8.2. Приведенная форма КС-грамматики 605
В общем случае множество Ni С N вычисляют по формуле
No = {А: в Р есть правило А -» Л},
Ni = iVi_i U {В: в Р есть правило В -* ?, где ? G ЛГ?Х}.
Множество Ni — это множество всех таких нетерминалов
А грамматики G, что дерево вывода пустой цепочки А из А
имеет высоту, не большую i + 1.
Так как множество N всех нетерминалов грамматики G
конечно, то описанный выше рекуррентый процесс оборвется
на некотором шаге, т.е. для некоторого j^ 0 получим Nj =
= iVj+i. Тогда полагаем
Ne = Nj для наименьшего j, такого, что Nj = Nj+\.
Далее, если аксиома 5 принадлежит множеству Ney то в си-
системе правил Р оставляют правило S -> Л, остальные А-правила
удаляют*, а множество правил вывода исходной грамматики
преобразуют согласно описанному выше алгоритму.
Можно доказать, что полученная таким образом КС-грам-
КС-грамматика без А-правил эквивалентна исходной грамматике G.
Это объясняется тем, что „потерю" вывода пустой цепочки
из нетерминала А€ Ne (посредством применения А-правил) мы
„компенсируем" добавлением к множеству правил вывода всех
таких правил, что замена А на А уже произведена прямо в их
правых частях.
Пример 8.4, Рассмотрим грамматику с множеством пра-
правил
S->aSbT\bTaT\ab, T -+baaST\TT\\.
В данном случае JVq = {Т}. Так как единственное правило
вывода этой грамматики, правая часть которого — непустая
"Исключение для А-правила, левой частью которого служит аксиома
грамматики, связано с тем, чтобы при переходе к новой грамматике не
„потерять" пустую цепочку, которую порождает исходная грамматика.
606 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
цепочка нетерминалов из iVo, есть правило Т -> ГГ, то
т.е. Ne = {Т}, и наша грамматика принимает вид
5 -> aSbT\aSb\bTaT\bTa\baT\ba\ab,
T->baaST\baaS\TT. #
Алгоритм удаления цепных правил. Этот алгоритм во
многом аналогичен алгоритму удаления Л-правил.
Пусть существует вывод нетер-
нетерминала U из нетерминала Т, в ко-
котором применяются только цепные
правила. Тогда такой вывод назо-
назовем цепным выводом.
Предположим теперь, что для
каждого нетерминала А граммати-
Рис. 8.20 ки q ИзВестно множество JV^ всех
таких нетерминалов 5, что существует цепной вывод А из В.
Тогда, удалив все цепные правила, мы должны предусмотреть
непосредственную замену всех нетерминалов из Na любой це-
цепочкой а, которая служит правой частью некоторого правила
А -» а (рис. 8.20).
Это соображение лежит в основе алгоритма преобразования
множества правил КС-грамматики с целью удаления цепных
правил.
Вычислив множество Na для каждого А Е -ЛГ, удалить все
цепные правила, добавив при этом для каждой цепочки а,
такой, что в Р есть правило А -> а, и для каждого В € Na
правило В -> а. После этого вместо каждого вывода вида
В\- ... h А Ь а (при В € Na) в исходной грамматике в новой
цепной вывод
грамматике получим вывод В Ь а.
Множества нетерминалов Na для каждого AeN вычисля-
вычисляются рекуррентно (как и в рассмотренном выше алгоритме
8.2. Приведенная форма КС-грамматики 607
удаления Л-правил вычислялось множество Ne):
N4 = {В: в Р есть правило В -> А};
N\ = JVJf1 U {С: в Р есть правило С -? D, где D E N^1}.
Таким образом, множество JV^ — это множество всех та-
таких нетерминалов В, что существует цепной вывод длины не
больше г + 1 нетерминала А из В. „Насыщение" этой рекур-
рекуррентной процедуры происходит для первого номера j, такого,
что N3A = ЛГд+\ и тогда принимают ЛГд = N^.
Пример 8.5. Дана грамматика с множеством правил
Т -+ Т * F | F,
аксиомой ?? и терминальным алфавитом {а, (,),+,*}. Имеем
Ng = ??, следовательно, и Ne = 0 (множество нетерминалов
данной грамматики, из которых применением одних цепных
правил выводится нетерминал J5, пусто). Далее, JVj. = {!?}, а
так как нет ни одного цепного правила с правой частью 12, то
N*=N*= NT; N* = {Т}; ЛГ> = {Т, Е} = JVF.
Удаляя цепные правила, необходимо, согласно описанному
выше алгоритму, ко всем правилам с левой частью Е добавить
правило Е -> Т * F, чтобы, сокращая вывод JBhThT*F и
убирая из него применение цепного правила Е —> Т, сразу
вывести из J5 цепочку Т * F.
Аналогично к правилам с левой частью F надо добавить
правила Т —>> (??), Т -> а, Е —> B?) и Е -> а. В итоге получим
грамматику
a. #
608 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Можно доказать, что описанный алгоритм удаления цепных
правил дает грамматику, эквивалентную исходной.
Замечание 8.4. К цепным правилам относится и прави-
правило А -> А. Бели такое правило находится в множестве правил
грамматики или появляется при удалении Л-правил (см. при-
пример 8.4), то оно должно быть просто удалено из множества
правил. #
Обратимся к примеру, из которого станет ясно, что удале-
удаление А-правил может привести к появлению в множестве правил
заданной КС-грамматики цепных правил.
Пример 8.6. Рассмотрим грамматику Go из примера 8.1.
Для удобства перепишем ее определение:
Go = ({a,b}, {5,Д5,С}, 5, Ро),
где множество правил вывода Pq имеет вид
5 -+ ABC, A)
А -> ВВ, B)
А -> А, C)
В -+ СС, D)
В -* а, E)
С -+ АА, F)
С-±Ъ. G)
Удаляем А-правила. Множество iVo = {А} (правило C)).
Далее, Ni = {А, С}, поскольку в правиле F) правая часть есть
непустая цепочка нетерминалов из JVo; N2 = {А, С, В} (правило
D)), Ns = {А, С, В, S}. Так как N$ совпало с множеством всех
нетерминалов грамматики, то N3 = Ne.
Согласно описанному выше алгоритму удаления А-правил,
получим следующую грамматику:
5 -> АВС\АВ\АС\ВС\А\В\С\\,
В-+СС\С\а,
С-^АА\А\Ъ.
8.2. Приведенная форма КС-грамматики 609
Мы видим, что в результате удаления Л-правил получилось
много цепных правил (которых не было в исходной грамма-
грамматике).
Применение алгоритма удаления цепных правил даст следу-
следующие множества N\:
Щ = Щ = 0;
N\ = {S,C}, N\ = {S,C,B), N\ = {S, С, В, А};
Таким образом, N\ — Nq = N^ = {S, A, J3, С} (множество всех
нетерминалов грамматики).
Новое множество правил, не содержащее цепных правил,
будет иметь следующий вид:
S -» АВС\АВ\АС\ВС\\\ВВ\СС\АА\а\Ъ;
А->ВВ\СС\АА\а\Ъ\
В-+СС\ВВ\АА\а\Ь;
С-> АА\ВВ\СС\а\Ъ.
Замечание 8.5. Теорема 8.2 позволяет утверждать, что
любую КС-грамматику можно преобразовать к эквивалент-
эквивалентной КС-грамматике, множество правил вывода которой содер-
содержит только КЗ-правила, т.е. правила вида аА/3 -* <гу/? при
а = /? = А и 7 Ф А. Единственным исключением может быть
правило S —> А для аксиомы S. Можно показать, что доба-
добавление к множеству правил КЗ-грамматики правила, преду-
предусматривающего замену аксиомы пустой цепочкой, не приво-
приводит к существенному изменению класса языков, порождаемых
КЗ-грамматиками. Единственное отличие языка, порождае-
порождаемого такой грамматикой, от КЗ-языка состоит в том, что он
может содержать пустую цепочку, тогда как ни один КЗ-язык,
будучи неукорачивающим языком, пустой цепочки не содер-
содержит.
610 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Следовательно, если в множестве правил КЗ-грамматики
разрешить кроме КЗ-правил также и правило S -* А (где S —
аксиома грамматики), то любую КС-грамматику можно пре-
преобразовать к эквивалентной КС-грамматике, являющейся част-
частным случаем КЗ-грамматики (с правилом S —> А).
Определение 8.3. Нетерминальный символ А КС-грамма-
КС-грамматики G = (V, N, S, Р) называют бесполезным, если из него не
выводится ни одна терминальная цепочка, т.е. не существует
такого х Е V*, что A \-q x.
Бесполезный нетерминал КС-грамматики может быть уда-
удален (вместе со всеми правилами, в которые он входит) без
изменения языка, порождаемого данной грамматикой. Следу-
Следующая теорема утверждает существование алгоритма удаления
бесполезных нетерминальных символов.
Теорема 8.3. Для каждой КС-грамматики G = (У, ЛГ, 5, Р)
может быть построена эквивалентная ей КС-грамматика, не
содержащая бесполезных нетерминальных символов.
< Алгоритм удаления бесполезных нетерминалов состоит в ре-
рекуррентном вычислении множества Nu С N всех нетерминалов
грамматики G, из которых выводится какая-либо терминаль-
терминальная цепочка.
Сначала вычисляем множество No всех нетерминалов, из
которых терминальная цепочка выводится за один шаг. Для
этого просматриваем множество правил Р, отмечая в нем все
правила вида А -? ж, где х G V*. Другими словами,
Nq = {А: в Р есть правило А -» ж, х G V*}.
Затем вычисляем множество JVi, добавляя к Nq множество
всех таких нетерминалов В, что существует правило вывода в
Р вида В -> /3, где /3 — цепочка, содержащая как терминалы,
так и нетерминалы из множества Nq. Таким образом, в N\
попадут все нетерминалы 5, такие, что существует вывод
8.2. Приведенная форма КС-грамматики 611
хг Вг х2 хт Вт хт+1
А А
УХ ... Ут
Рис. 8.21
терминальной цепочки из i?, и высота дерева этого вывода не
больше 2 (рис. 8.21).
В общем случае для множества Ni (i ^ 1) получаем формулу
Ni = Ni-i U {А: в Р есть правило А ->> а, где а € (Ni-i U F)*}.
Это множество содержит все такие нетерминалы В, что высота
дерева вывода любой терминальной цепочки из В не превышает
* +1.
Для наименьшего j, такого, что Nj = iVj+i, полагаем Nu =
= JVj. Из построения множества Nu следует, что это множество
всех таких нетерминалов А грамматики G, что существует
вывод (ненулевой длины) АЬ+ж для некоторого х G V*, что
и требовалось доказать. Тогда все нетерминалы из N\NU
бесполезны. >
В частности, если 5 ^ Nu, то L(G) = 0, и наоборот. Таким
образом решается проблема пустоты для КС-грамма-
КС-грамматик, которая формулируется следующим образом: для данной
КС-грамматики выяснить, пуст ли язык, ею порождаемый. Из
предыдущих рассмотрений ясно, что для ответа на этот вопрос
достаточно вычислить множество бесполезных нетерминалов
грамматики и проверить, находится ли среди них аксиома
грамматики. Язык, порождаемый КС-грамматикой, пуст то-
тогда и только тогда, когда ее аксиома бесполезна.
20*
612 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Пример 8.7. Пусть множество Р правил вывода КС-грам-
КС-грамматики G = ({а, 6}, {S, Л, J3, С}, 5, Р) имеет вид
А -> ЬАа,
B-*aB\bS\a\b,
С -+ ВаА.
Применяя алгоритм из доказательства теоремы 8.3, получаем
iVo = {В}, так как в Р имеются только два правила, правые ча-
части которых — терминальные цепочки В —> а и В -> Ь. С целью
вычисления множества N\ найдем те правила, правые части
которых кроме терминалов содержат только нетерминальный
символ В: это будут правила S -* Ь?? и В -+ а5, т.е. iVi = {В, 5}.
Так как есть только одно правило, правая часть которого со-,
держит вхождение символа 5, а именно правило В -> 65, то
iV2 = iVi = iVu = {5, В}. Символы А и С бесполезны. Все пра-
правила, содержащие вхождения этих символов, можно удалить.
В итоге получим грамматику с таким множеством правил:
B-+aB\bS\a\b.
Определение 8.4. Символ X объединенного алфавита
V U N КС-грамматики G = (V, N, 5, Р) называют недости-
недостижимым, если из аксиомы грамматики не выводится ни одна
цепочка, содержащая вхождение символа X, т.е. не существует
таких цепочек а, /3 G (V U iV)*, что S h^ aXfi.
Из самого понятия недостижимого символа ясно, что такие
символы можно удалить из грамматики (удалив все правила,
которые их содержат) без изменения порождаемого ею языка.
Займемся разработкой алгоритма удаления недостижимых сим-
символов.
Введем в рассмотрение понятие графа КС-грамматики.
8.2. Приведенная форма КС-грамматики 613
Определение 8.5. Назовем графом К С-грамматики
G = (V, JV, ?, Р) ориентированный граф, множество вершин
которого равно V U N U {Л}, а множество дуг определяется
следующим образом. Дуга из вершины с меткой А ведет в
вершину В тогда и только тогда, когда правило А —> аВC
(а, /J Е (V U N)*) принадлежит множеству Р правил вывода
грамматики G.
Понятие графа КС-грамматики ни в коем случае нельзя
путать с понятием дерева вывода в КС-грамматике, так как де-
дерево вывода строится по конкретному выводу, а граф КС-грам-
КС-грамматики строится по множеству правил вывода и характеризует
саму грамматику в целом.
Пример 8,8. Граф грамматики из примера 8.7 представлен
на рис. 8.22. #
Опираясь на определение 8.4, можно
показать, что символ X КС-грамматики
G = (V, TV, 5, Р) достижим тогда и толь-
только тогда, когда в графе грамматики су-
существует путь из вершины S граммати-
грамматики G в вершину X, и задача распознава-
распознавания достижимости символов в КС-грам-
КС-грамматиках сводится тем самым к задаче
распознавания достижимости в ориенти-
ориентированных графах из заданной вершины. рис, 3.22
Для ее решения достаточно воспользо-
воспользоваться, например, алгоритмом поиска в ширину (см. 5.5). В
примере 8.8 (см. рис. 8.22) символ С не достижим.
Удаление бесполезных нетерминалов может привести к по-
появлению недостижимых символов.
Пример 8.9. Модифицируем грамматику из примера 8.7,
добавив к множеству ее терминалов новый символ d и к мно-
множеству ее правил вывода правило А -> Cd.
614
8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Граф модифицированной грамматики приведен на рис. 8.23.
Нетерминалы А и С бесполезны, хотя и достижимы. Удаляя
их вместе со всеми правилами, в которые они входят, получим
КС-грамматику, граф которой изображен на рис. 8.24. Терми-
Терминал d стал недостижимым.
Рис. 8.23
Рис. 8.24
Определение 8.6. КС-грамматика считается заданной в
приведенной форме, если множество ее правил вывода не со-
содержит Л-правил и цепных правил, множество ее нетерминалов
не содержит бесполезных нетерминалов, а объединенный алфа-
алфавит не содержит недостижимых символов.
Рассмотренные выше алгоритмы любую КС-грамматику по-
позволяют преобразовать к эквивалентной КС-грамматике, за-
заданной в приведенной форме. Заметим, что поскольку удаление
Л-правил может привести к появлению цепных правил (см. при-
пример 8.6), а удаление бесполезных нетерминалов — к появлению
недостижимых символов, то построение приведенной формы
КС-грамматики нужно проводить в такой последовательности:
1) удалить Л-правила, 2) удалить цепные правила, 3) удалить
бесполезные нетерминалы, 4) удалить недостижимые символы.
Замечание 8.6. К числу важных преобразований КС-грам-
КС-грамматики относят также преобразование, состоящее в удале-
удалении аксиомы из правых частей правил вывода. Можно до-
8.2. Приведенная форма КС-грамматики 615
казать, что любая КС-грамматика преобразуется к эквива-
эквивалентной КС-грамматике, не содержащей вхождений аксиомы
в правые части правил вывода. Действительно, для этого
достаточно ввести новый нетерминал S\ (отличный от всех
нетерминалов исходной грамматики), объявить его аксиомой
и добавить правило S\ —> 5, после чего появившееся цепное
правило и недопустимые Л-правила, которые могут при этом
возникнуть, удаляются согласно приведенным выше алгорит-
алгоритмам.
Пример 8.10. Грамматика с множеством правил
S->aSa\bSb\a\b\\,
порождающая множество всех палиндромов в алфавите {а, 6}
(см. пример 7.5.в), преобразуется после удаления аксиомы из
правых частей правил вывода в грамматику с аксиомой Si и
следующим множеством правил:
S->aSa\bSb\a\b\\. ]
Появились, как мы видим, цепное правило и, поскольку
символ S в новой грамматике уже не является аксиомой, А-пра-
вило 5 —> А, которое следует удалить. Выполняя это, получим
окончательно следующее множество правил:
Si->aSa\bSb\aa\bb\a\b\\,
S-> aSa\bSb\aa\bb\a\b. #
Заметим, что если КС-грамматика задана в приведенной
форме и правые части правил не содержат вхождений аксиомы,
то единственное допустимое правило с пустой правой частью
(левой частью его является аксиома), если оно существует,
используется только для порождения пустой цепочки. Исходная
грамматика из примера 8.10 этим свойством не обладает, так
616 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
как правило 5 -> А используется всякий раз при выводе слова
четной длины.
Кроме того, КС-грамматика, заданная в приведенной фор-
форме и не содержащая вхождений аксиомы в правых частях пра-
правил вывода, обладает еще одним интересным свойством: дерево
вывода любой непустой цепочки является Х-свободным. Таким
образом, без ограничения общности можно считать деревья вы-
выводов непустых цепочек в КС-грамматиках А-свободными.
8.3. Лемма о разрастании для КС-языков
Для КС-языков выполняется „лемма о разрастании", анало-
аналогичная лемме о разрастании для регулярных языков (см. 7.8).
Она формулирует необходимое условие того, что язык является
контекстно-свободным.
Теорема 8.4 (лемма о разрастании для КС-языков)#
Для любого КС-языка L существует натуральная константа
к (зависящая от L), такая, что любая цепочка z ? L, длина
которой \z\ > fe, представима в виде соединения пяти цепочек:
z = uxwyv, где \ху\ > О, \xwy\ ^ fc, и каждая цепочка zn =
= uxnwynv, n ^ О, принадлежит L.
<4 Так как L — КС-язык, то существует КС-грамматика G =
= (V, iV, S, Р), порождающая язык L, т.е. L = L(G).
Фиксируем произвольно нетерминал А Е N и рассмотрим
множество V(A) всех выводов, начинающихся с А, таких, что
высота дерева вывода не превышает числа \N\ +1 нетерми-
нетерминалов грамматики G, увеличенного на единицу. Множество
V(A) конечно, так как высота дерева вывода, а следователь-
следовательно, и его длина ограничены сверху (см. замечание 8.2). Таким
образом, каждое множество Т>(А) при AeN есть конечное мно-
множество конечных выводов. Множество выводов V определим
как объединение множеств V(A) по всем Л € N. Ясно, что
и это множество выводов конечно, так как конечно множество
нетерминалов грамматики. Введем подмножество Л всех таких
8.3. Лемма о разрастании для КС-языков
617
цепочек в объединенном алфавите, что они являются последни-
последними цепочками выводов из V. Иначе говоря, А — это множество
всех таких цепочек а в объединенном алфавите, что существует
дерево вывода а (из некоторого нетерминала грамматики G),
высота которого не больше \N\ +1. В силу конечности множе-
множества V конечно и множество А. Тогда положим
& = тах|а|,
т.е. введем константу к как наибольшую длину среди всех
цепочек множества А.
Пусть теперь zGL, причем \z\ > к. Тогда 5 \-q z, и в силу
определения константы к любое дерево вывода цепочки z имеет
высоту, большую |iV| + 1. Фиксируем какое-нибудь дерево Т
вывода цепочки z.
Выделим в дереве Т максимальное поддерево с корнем Я,
высота которого равна \N\ +1 (рис. 8.25).
и2 х w у v2 v
Тогда, согласно следствию 8.1, получим (для некоторых
терминальных цепочек щ и v\)
5h*
Ь*
(8.1)
6188. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
где z = u\Z\V\^ т.е. существует вывод цепочки z\=
являющейся подцепочкой цепочки z, из нетерминала iJ, такой,
что высота дерева этого вывода равна \N\ +1.
Напомним, что высота дерева есть максимальная длина пу-
пути в этом дереве из корня в лист. Так как длина пути в
дереве вывода КС-грамматики равна числу замен нетермина-
нетерминалов в некотором фрагменте вывода (см. 8.1), то при выводе
цепочки z\ из R число замен нетерминалов строго больше числа
всех нетерминалов грамматики G. Это означает, что в выводе
z\ из i? какой-то нетерминал Q повторяется дважды (возмож-
(возможно, что Q = R) и на некотором пути из вершины R в один из
листьев будут по крайней мере две разные вершины, помечен-
помеченные одним и тем же нетерминалом Q. Тогда рассмотрим два
максимальных поддерева дерева Т, корневые вершины кото-
которых являются указанными выше вершинами с меткой Q (см.
рис. 8.25). Выделению этих максимальных поддеревьев соот-
соответствует выделение фрагментов вывода z\ из Д, таких, чтб
для некоторых терминальных цепочек U2, i>2> #> У> w выполня-
выполняется выводимость
R Ь* U2QV2 Ь* U2xQyV2 Ь* U2XWyV2, (8.2)
Z\ =
Соотношения (8.2) показывают, что имеют место выводи-
выводимости
Q\-*xQy (8.3)
и
Q Ь* w. (8.4)
Это значит, что существует дерево вывода цепочки xwy из
нетерминала Q („большое" дерево с корневой вершиной Q на
рис. 8.25) и в нем — максимальное поддерево с корневой вер-
вершиной, помеченной тем же символом Q, являющееся деревом
вывода цепочки w из Q („маленькое" дерево с корневой вер-
вершиной Q на рис. 8.25). При этом, так как „большое" дерево с
8.3. Лемма о разрастании для КС-языков 619
корневой вершиной Q является поддеревом дерева с корневой
вершиной R высотой |JV| +1, то его высота будет не больше чем
\N\ +1, откуда в силу выбора константы к имеем \xwy\ ^ А;.
Объединяя (8.1) и (8.2), получим такое представление выво-
вывода цепочки z из аксиомы S:
S\-*uiRvi\-*
Ь* U1U2QV2V1 h* U\U2xQyV2V\ h* U\U2XWyV2V\. (8.5)
Полагая u = щщ ии = V2V\, получим z = uxwyv, и тем самым
мы доказали представление цепочки z в виде соединения опре-
определенных пяти цепочек.
Из (8.5) следует, что, получив (при выводе z из S) цепоч-
цепочку u\U2Qv2V\, можно с учетом (8.4) сразу из нетерминала Q
вывести цепочку ги, и тогда
S К* u\Rv\ Ь* u\U2Qv2V\ Ь* u\U2WV2V\ = uwy (8.6)
(в выводе (8.5) выбрасываем последовательность шагов над
фигурной скобкой).
В то же время вывод (8.5) можно с учетом (8.3) модифи-
модифицировать так, что после получения цепочки U1U2QV2V1 = uQv
многократно (не менее одного раза) повторять вывод цепочки
xQy из Q:
S Ь* u\Rv\ Ь* U1U2QV2V1 =
= uQv h* uxQyv h* uxxQyyv h*... h*
h* uxnQynv h* uxnwynv (8.7)
(в выводе (8.5) последовательность шагов над фигурной скоб-
скобкой повторяем п раз).
Итак, в силу (8.6) цепочка zq = uwv € L, а в силу (8.7) и
цепочка zn = uxnwynv для любого п > 0 принадлежит языку L.
Тем самым мы доказали, что (Vn ^ 0)(ш?пгиуп?; € L).
620 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Осталось доказать, что длина цепочки ху не меньше 1 (или,
что равносильно, цепочки х и у не являются одновременно
пустыми).
Согласно теореме 8.2, можно считать без ограничения общ-
общности, что в множестве правил вывода грамматики G нет ни
Л-правил (кроме, быть может, правила S —> А), ни цепных пра-
правил. Кроме того, в силу замечания 8.6 можно считать, что
правило S -> А применяется только при выводе пустой цепоч-
цепочки, а поскольку высота дерева цепочки z строго больше 1, то
z ф А и правило 5 -> А не применяется при выводе z из аксио-
аксиомы 5.
Тогда, предполагая, что х = у = А, получим Q Ь* Q, а это
возможно лишь при условии применения в соответствующем
выводе цепных правил или правил с пустой правой частый, что
ввиду сказанного выше не может иметь места. Итак, цепочка
ху не пуста, т.е. \ху\ > 0, что и завершает доказательство
теоремы. >
Следствие 8.2. В любом бесконечном КС-языке существу-
существует последовательность слов, длины которых образуют возра-
возрастающую арифметическую прогрессию.
<4 Пусть КС-язык L бесконечен. Тогда в нем нет цепочки
наибольшей длины. Следовательно, найдется цепочка z e L,
длина которой больше константы А;, определяемой леммой о
разрастании. Согласно этой лемме, цепочка z может быть пред-
представлена в виде z = uxwyv для некоторых цепочек г*, я, ги, у, v,
таких, что \xwy\ < А;, \ху\ > 0. Тогда последовательность {zn =
= uxnwynv}n^o является искомой, так как длины ее цепочек
образуют возрастающую арифметическую прогрессию со зна-
знаменателем \ху\. >
Замечание 8.7. Любой конечный язык {щ, ...,ит} (в
каком-то алфавите V) порождается КС-грамматикой с множе-
множеством правил S —>> щ |... | ит. Дерево вывода любой цепочки в
этой грамматике имеет высоту, не большую 1 (высоту 0 име-
8,3. Лемма о разрастании для КС-языков 621
ет дерево вывода нулевой длины аксиомы S из себя самой, а
каждая терминальная цепочка, т.е. цепочка гц, % = 1,т, имеет
дерево вывода высоты 1). Следовательно, в данном случае кон-
константа к равна наибольшей длине цепочки щ и цепочки, длина
которой была бы больше А:, не существует.
Таким образом, для конечного языка утверждение леммы о
разрастании тривиально выполняется, а именно, не существует
цепочек, длины которых превосходят константу к.
Пример 8.11. а. Язык {ап : п ^ 0} не является контекст-
контекстно-свободным, поскольку из длин принадлежащих ему слов
нельзя образовать арифметическую прогрессию: (п +1J — п2 =
б. Язык {as: s — простое число} не является КС-языком по
той же причине.
в. Рассмотрим язык {anbncn\n ^ 0}. Длины его слов обра-
образуют арифметическую прогрессию, но тем не менее этот язык
не является контекстно-свободным. Действительно, предпо-
предположим противное. Тогда для любого достаточно большого п
слово anbncn можно представить в виде uxwyv. Проанали-
Проанализируем, как могут располагаться в слове цепочки ж, w и у.
Поскольку условие леммы о разрастании должно выполняться
для всех достаточно длинных слов языка, т.е. слов, длина кото-
которых строго больше константы к из леммы, то в целях проверки
невыполнения условия можно брать слова/длина которых заве-
заведомо превышает указанную константу*. Для анализируемого в
этой задаче языка примем, что п > к. Тогда возможны следу-
следующие случаи:
"Предполагая, что язык является контекстно-свободным, мы тем самым
в силу леммы о разрастании предполагаем, что оказывается фиксированной
какая-то константа к, о которой идет речь в условии леммы. Мы не можем
знать значения этой константы, но это нам и не нужно: достаточно знать,
что вследствие нашего предположения константа к как-то фиксирована,
и мы можем быть уверены в том, что в бесконечном КС-языке найдутся
цепочки, длины которых превысят к.
622 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
1) xwy = а', где / < к < n, a а обозначает одну из букв а, Ь, с
(т.е. цепочка xwy целиком расположена или в „зоне" символов
а, или в „зоне" символов Ь, или в „зоне" символов с);
2) xwy = albm или xwy = blcm, где / + га ^ fc < п и /,ra > 0 (т.е.
цепочка xwy расположена „на стыках зон" различных символов
и содержит ненулевое число символов каждой из „зон"). В
силу выбора числа п никакие другие способы расположения
подцепочки xwy в цепочке anbncn невозможны (отсюда следует,
что подходящий выбор числа п позволил нам уменьшить число
вариантов расположения подцепочки xwy в цепочке языка).
Теперь если мы станем повторять („накачивать") цепочки х
и у в первом случае, то начнет расти число одного из символов
а, Ь или с, тогда как число остальных двух символов будет оста-
оставаться прежним, и получаемые при этом цепочки уже не будут
принадлежать заданному языку. Во втором же случае при „на-
„накачке" возникнут цепочки, содержащие вхождение цепочки bd
или сЬ, что также недопустимо (символы а,6,с начнут „переме-
„перемешиваться"). Получается, что мы не можем представить любую
достаточно длинную цепочку anbncn в виде uxwyv так, чтобы
при этом выполнялось условие леммы о разрастании. Следова-
Следовательно, исходный язык не является контекстно-свободным. #
В целом техника доказательства с помощью леммы о раз-
разрастании для КС-языков „отрицательных" утверждений типа
„данный язык не является контекстно-свободным" аналогична
технике доказательства утверждений о нерегулярности языков
с использованием леммы о разрастании для регулярных языков.
Обратим внимание на различие структур „накачиваемых"
цепочек в регулярных и контекстно-свободных языках.
Лемма о разрастании для регулярных языков утвержда-
утверждает, что любая достаточно длинная цепочка регулярного языка
представима как соединение трех подцепочек, из которых сред-
средняя подцепочка ограничена сверху по длине и не пуста, ее
можно „накачивать", повторяя любое число раз, в том числе
8.3. Лемма о разрастании для КС-языков
623
и ни разу, т.е. можно выбросить вообще, и такал wнакачка" не
выводит за пределы данного языка (рис. 8.26).
U
ю
Рис. 8.26
Лемма о разрастании для КС-языков утверждает в анало-
аналогичной ситуации, что цепочка языка представима как соеди-
соединение пяти подцепочек, причем если рассмотреть три средние
подцепочки, то „накачиваются" края — первая и третья из них,
а самая середина не меняется (рис. 8.27).
U
ш
ШШ w
ш
п
Рис. 8.27
Обратим внимание на то, что ограничение сверху длины
подцепочки xwy константой /с, вытекающее из леммы о разра-
разрастании, очень важно и, не используя его, вообще говоря, нельзя
доказать, что данный язык не является контекстно-свободным.
Рассмотрим в этой связи такой пример.
Пример 8*12. Пусть язык L определен как множество всех
цепочек в алфавите {а, 6} вида anbmanbm, n ^ 0. Докажем, что
он не является контекстно-свободным.
Предполагая, что L — КС-язык, получим, что для достаточ-
достаточно больших пит цепочка anbmanbm допускает представление
в виде uxwyv. Выберем числа пит так, что они больше,
чем определенная леммой о разрастании константа к для язы-
языка L. Анализируем варианты „размещения" подцепочки xwy в
цепочке anbnanbm: очевидно, что „накачка" невозможна, если
624 & КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
цепочки х и у обе целиком находятся в „зоне" какого-то од-
одного символа, а или Ь; если же, скажем, х = аРЬ3 при р, s ф О,
т.е. цепочка х находится „на стыке зон" символов а и 6, то при
„накачке" возникнет более чем одно вхождение подцепочки Ъа
в цепочку языка L, что противоречит определению этого язы-
языка; если же х = ЪРа8 при р, s ^ О, то при „накачке" возникнет
более двух вхождений подцепочки а&, что также невозможно.
Аналогично анализируется размещение цепочки у „на стыках
зон". В силу того что п, т > fc, а |жгиу| ^ fc, никакие другие
варианты расположения подцепочки xwy невозможны.
Бели ограничение на длину этой подцепочки опустить, то
окажется возможным такое ее вхождение в цепочку ambnambn,
что х = as, w = apbmaq и у = ar для некоторых положительных 5,
р, д, г. Тогда при s = г (чего априори нельзя отвергать, так как
условия леммы о разрастании не требуют, чтобы длины цепочек
х и у были обязательно различными) „накачка" цепочек х
и у дала бы „синхронное" увеличение числа символов а при
неизменном числе символов Ь, что не вывело бы нас за пределы
языка L. Таким образом, нам тогда не удалось бы доказать,
что определяемое леммой о разрастании представление цепочки
ambnambn не может иметь места. #
Рассмотрим еще один пример, важный для понимания лем-
леммы о разрастании и ее применений.
Пример 8.13. Зададим язык
L' = {апЪп<?: п,р ^ 0 и р ^ п}.
Здесь при размещении „накачиваемых" цепочек в „зоне" сим-
символов с „накачка" не выводит за пределы языка V (так как в
его цепочках число символов с может на сколько угодно пре-
превышать число символов а и Ь). Тем не менее и в этом случае
условие леммы о разрастании не выполняется.
Действительно, для достаточно большого п возьмем цепоч-
цепочку anbncn Е V (т.е. цепочку языка V при п =р). Если в предста-
представлении такой цепочки в виде anbncn = uxwyv (согласно лемме о
8.4. Магазинные автоматы 625
разрастании) цепочка xwy = с1 при 0 < Z ^ п (т.е. „накачивае-
„накачиваемые" цепочки располагаются целиком в „зоне" символов с), то
цепочка uwv = anbncn~\xy\ ? V\ так как \ху\ ^ 1 и п — \ху\ < п,
т.е. число символов с окажется меньше, чем число символов а и
Ь. Таким образом, несмотря на то что „накачка" цепочек х,у
в данном случае возможна, нельзя их выбросить, оставаясь в
пределах языка. Невозможность других вариантов расположе-
расположения подцепочки xwy в цепочке языка V доказывается точно
так же, как и в предыдущих примерах. #
Итак, нужно помнить, что выполнение условий леммы о
разрастании предполагает и возможность выбрасывания „на-
„накачиваемых" цепочек — все цепочки zn = uxnwynv из условия
леммы при п ^ О должны оставаться в языке L, и если условие
леммы выполняется при всех положительных п, но не выполня-
выполняется при п = О, то этого достаточно для признания того, что
цепочка z = uxwyv ? L не удовлетворяет условию леммы о раз-
разрастании.
Аналогичная ситуация имеет место, конечно, и при исполь-
использовании леммы о разрастнии для регулярных языков.
8.4. Магазинные автоматы
Автоматы с магазинной памятью, или магазинные ав-
автоматы (сокращенно — МП-автоматы), образуют класс
распознающих моделей для КС-языков точно так же, как ко-
конечные автоматы являются распознающими моделями в классе
регулярных языков.
Понятие МП-автомата является частным сличаем общего
интуитивного понятия автомата, которое мы ввели в 7.5. Как
и всякий автомат, МП-автомат — это устройство, имеющее
блок управления, входную ленту, головку и блок внутренней
памяти в виде магазина МП-автомата (или стека).
Блок управления в каждый момент времени находится в
одном из конечного множества Q состояний.
626
8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Входная лента предполагается „полубесконечной", т.е. она
имеет начало („левый край"), но не имеет конца. Лента раз-
разделена на ячейки, пронумерованные от крайней левой ячейки
натуральными числами, начиная с единицы; в каждой ячейке
может быть записан символ алфавита V, называемого вход-
входным алфавитом МП-автомата. В каждый момент вре-
Входная лента
О
Блок ^
управления
i t+1
Головка Магазин
Y
мени читающая головка обоз-
обозревает (или читает) некоторую
ячейку входной ленты.
Бели в этой ячейке записан
некоторый входной символ, т.е.
символ входного алфавита, то
его называют обозреваемым
(в данный момент) входным
символом (рис. 8.28).
Предполагается, что если на ленте записана некоторая не-
непустая цепочка х = хA)хB)...х(к) во входном алфавите, то
ее символы последовательно записаны в ячейках от первой до
fc-й, без пропусков, так, что символ x(i) записан в i-й ячейке
(рис. 8.29).
Рис. 8.28
х(г)
х(к)
i t+1
Рис. 8.29
МП-автомат может читать цепочку х, продвигая головку
только в одном направлении, слева направо, по шагам, причем
за каждый шаг головка переходит от обозреваемой ячейки к
следующей. Бели в какой-то момент времени обозревается
символ ж(г), 1 < i < Л, записанной на ленте цепочки ж, то
непрочитанной частью входной цепочки х будет подцепочка
x(i + l)...x(k). В частности, при г = А; непрочитанная часть
совпадает с пустой цепочкой, и тогда говорят, что цепочка х
полностью прочитана МП-автоматом (рис. 8.30).
8.4. Магазинные автоматы
627
х(к)
12 i Tfc
Рис. 8.30
Магазин МП-автомата устроен и работает следующим обра-
образом. Как и входная лента, магазин является полубесконечным
и разделенным на пронумерованные ячейки, в каждой из ко-
которых может быть записан символ алфавита Г, называемого
магазинным алфавитом МП-автомата. Входной и ма-
магазинный алфавиты МП-автомата могут пересекаться и даже
совпадать друг с другом. Символы алфавита Г называют ма-
магазинными символами. Первую ячейку магазина называют
его верхней ячейкой (иногда просто верхом магазина*).
Символ, в данный момент записанный в верхней ячейке мага-
магазина, называют верхним символом магазина.
Единственная операция, которую МП-автомат может реа-
реализовать с магазином, состоит в следующем:
верхний символ Z магазина заменяется не-
некоторой цепочкой 7 магазинных символов.
При этом если цепочка 7 непустая, то она за-
записывается в первых т ячейках, где т = |7|
(длине цепочки 7), так, что ее первый символ
становится верхним символом магазина.
Бели до замены Z цепочкой у под верхней ячейкой** (т.е. в
ячейках, начиная со второй) была записана какая-то цепочка а,
то после замены она сдвигается „в глубь" магазина и оказыва-
оказывается записанной уже в ячейках, начиная с (га + 1)-й (рис. 8.31).
Если же верхний символ Z заменяется пустой цепочкой А,
то после такой замены верхним символом магазина становится
Z
а
7A)
7(т)
а
Рис. 8.31
* Таким образом, в неформальном описании МП-автомата лента чита-
читается „слева направо", а магазин — „сверху вниз".
** Полагают, что, как и символы цепочек на входной ленте, символы це-
цепочек, записанных в магазин, располагаются в последовательных ячейках
„сверху вниз" без пропусков ячеек.
628 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
первый символ цепочки а (записанной под верхней ячейкой
магазина), т.е. цепочка а „поднимается" на одну ячейку.
В случае, когда а — пустая цепочка, замена верхнего
символа магазина пустой цепочкой 7 приводит к опустошению
магазина (ни в одной из ячеек магазина не записан магазинный
символ). Заметим, что, по определению, с пустым магазином
МП-автомат не может производить никаких операций.
Описанная выше операция с магазином составляет осно-
основу поведения МП-автомата, его, образно говоря, „динами-
„динамику". Эта „динамика" определяется системой команд МП-
автомата, которая, аналогично системе команд конечного
автомата, определяется как конечное множество 6 команд, ка-
каждая из которых записывается в виде
qaZ -> ry, (8.8)
где q и г — состояния из множества Q\ a — входной символ
или пустая цепочка; Z — магазинный символ; j — цепочка
магазинных символов (может быть и пустая).
Если в системе команд S МП-автомата М есть команда (8f.8),
то М может в данный момент времени выполнить эту команду,
если и только если в данный момент времени его блок упра-
управления находится в состоянии q, головка обозревает входной
символ а (при условии, что а ф А), а верхним символом мага-
магазина является символ Z. Выполнение команды (8.8) состоит в
замене верхнего символа магазина цепочкой 7 (как это описа-
описано выше), переходе блока управления в состояние г (которое
может и совпадать с состоянием q) и в продвижении головки
на одну ячейку вправо (если а в команде (8.8) не есть пустая
цепочка Л) (рис. 8.32).
Бели же в команде (8.8) а = Л, то такую команду МП-
автомат может выполнить всякий раз, когда его блок упра-
управления окажется в состоянии q, а верхним символом магазина
будет символ Z. В этом случае выполнение команды никак не
8.4. Магазинные автоматы
629
Входная лента
1
Я
а
2 J
/
i i+l
Головка
Q
Блок
управления
Магазин
Z
а
Входная лента
i+l
Головка
Магазин
Q
Блок
управления
7
a
Рис. 8.32
зависит от содержимого входной ленты, а после ее выполнения
головка остается на прежнем месте.
Рассмотренную выше процедуру выполнения команды вида
(8.8) называют шагом (или тактом) работы МП-авто-
МП-автомата (при а = Л такт работы называют \-тактом).
Предположим теперь, что в множестве состояний Q блока
управления МП-автомата М с системой команд S фиксирова-
фиксировано некоторое начальное состояние до и подмножество за-
заключительных состояний F.
Пусть в какой-то начальный момент времени блок управле-
управления МП-автомата М находится в начальном состоянии до? на
ленте записана непустая цепочка х, головка обозревает пер-
первую ячейку ленты и, следовательно, первый символ цепочки
х является обозреваемым, а в магазине записан только один
специальный символ Zo, называемый начальным символом
магазина.
Тогда, если МП-автомат М, выполняя некоторую после-
последовательность команд из J, прочитывает полностью цепочку
ж, в результате чего блок управления переходит в некоторое
заключительное состояние qf E F, говорят, что МП-автомат
М допускает (распознает, воспринимает) цепочку^д;, которую
называют допустимой цепочкой МП-автомата. Множе-
Множество всех допустимых цепочек МП-автомата М образует язык,
допускаемый этим МП-автоматом.
630 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Далее мы докажем, что язык любого МП-автомата является
КС-языком и, наоборот, любой КС-язык есть язык некоторого
МП-автомата. В этом смысле мы и говорим об МП-автоматах
как о „распознавателях" КС-языков: всякий МП-автомат до-
допускает те и только те цепочки входных символов, которые по-
порождаются некоторой КС-грамматикой. Но чтобы доказывать
какие-либо утверждения об МП-автоматах, нужно сначала дать
строгое математическое определение этого понятия, не апел-
апеллируя уже к наглядным, но не определенным формально идеям
ленты, магазина, головки и т.п. Формализация изложенного
выше описания проводится во многом аналогично построению
определения порождающей грамматики.
Определение 8.7. МП-автомат задается упорядоченной
семеркой
m = (Q, v, г, 9о, f,Zo, «),
где Q — конечное множество состояний; V — алфавит, на-
называемый входным алфавитом; Г — алфавит, называемый ма-
магазинным алфавитом; qoEQ — начальное состояние; F С Q —
подмножество заключительных состояний; Zq € Г — начальны^
магазинный символ; 6 — система команд, определенная как ко-
конечное множество команд, каждая из которых записывается в
виде (8.8):
qaZ -> Г7,
где знак „->" (стрелка) — внешний символ (не принадлежащий
ни одному из указанных алфавитов); q,r€Q]a€ VU {A}; Z Е Г;
тег*.
Замечание 8.8. Нелишне обратить внимание на то, что
упоминание о ленте и магазине в приведенном выше формаль-
формальном определении совершенно необязательно. Формально для
определения МП-автомата достаточно задать два алфавита,
конечное множество состояний, выделив в нем начальное со-
состояние и подмножество заключительных состояний, а также
8.4. Магазинные автоматы 631
систему команд. Образы ленты, магазина, да и сам термин „со-
„состояние", являются метафорами, которые позволяют связать
формальное определение с его содержательной интерпретаци-
интерпретацией, идеей некоего „устройства" для чтения слов, с описания
которого мы начали этот параграф. #
Любую цепочку в алфавите V будем называть входной
цепочкой, а сами элементы входного алфавита — входными
символами; точно так же любую цепочку в алфавите Г будем
называть магазинной цепочкой, а символы этого алфавита —
магазинными символами. Упорядоченную тройку до знака
„-*" (стрелки) в записи команды называют левой частью
команды, а упорядоченную пару после знака „->" — правой
частью команды.
Пример 8.14. Рассмотрим МП-автомат
Mi = ({go, qu «}, {0,1}, {?,0}, 9о,
с таким множеством команд 5\:
qoOZ -> 9i 0Z,
9100 -* qi 00,
На рис. 8.33 проиллюстрировано выполнение первых двух
команд. При записи системы команд этого конкретного МП-
автомата мы в правых частях первых двух команд отделили
магазинную цепочку от состояния пробелом для того, чтобы не
возник соблазн прочитать левую и правую части этих команд
одинаково. Таким приемом записи мы хотим подчеркнуть, что
левая часть команды МП-автомата — упорядоченная тройка, а
правая — упорядоченная пара.
632
8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Входная лента
0
0
1
1
Головка Мага,
Q
Блок
управления
7,
Входная лента
Головка
Q
Блок
управления
Магазин
О
Входная
0
0
лента
1
1
/
Головка Маг
Q
Блок
управления
0
0
Z
Рис. 8.33
Замечание 8.9. Систему команд МП-автомата можно
понимать как способ определения некоторой конечной функции,
которую называют функцией переходов МП-автомата
(по аналогии с функцией переходов конечного автомата). Эта
функция может быть определена как отображение вида
S: Q х (V U {Л}) х Г -> Fin(Q x Г),
где использовано обозначение Fin(A) для множества всех ко-
конечных подмножеств множества А. #
„Динамику" МП-автомата, т.е. процесс перехода его из
одного состояния в другое в соответствии с обозреваемыми
символами на ленте и содержимым магазина, удобнее всего
описывать в терминах конфигураций. Для этого общее поня-
понятие конфигурации автомата, которое на интуитивном уровне
8.4. Магазинные автоматы 633
было введено в 7.5, необходимо уточнить применительно к
МП-автомату и определить также отношение выводимости на
множестве конфигураций.
Определение 8.8. Конфигурацией МП-автомата М
называют упорядоченную тройку вида (д, я, /3), где g € Q —
состояние, х ? V* — входная цепочка, /? — магазинная цепочка.
Конфигурацию С" = (г, tu, *fa) называют непосредствен-
непосредственно выводимой из конфигурации С = (g, aw, Za), если в мно-
множестве команд МП-автомата есть команда (8.8). Отношение
непосредственной выводимости на множестве конфигураций
МП-автомата М обозначаем \~м, используя запись С\~мС (и
опуская, если это не вредит пониманию, обозначение самого
МП-автомата).
Итак, непосредственная выводимость
(g, aw, Za) hM (r, w, <ya) (8.9)
имеет место тогда и только тогда, когда в системе S команд
МП-автомата М есть команда (8.8), которую в этом случае
называют применимой к конфигурации (g, aw, Za).
Таким образом, неформально конфигурация показывает со-
состояние блока управления, непрочитанную часть входной це-
цепочки (первый символ этой цепочки, если она не пуста, является
обозреваемым) и содержимое магазина (первый символ мага-
магазинной цепочки /?, если она не пуста, есть верхний символ
магазина). Бели вторая компонента конфигурации — пустая
цепочка, то это означает, что входная цепочка прочитана пол-
полностью. Бели же пуста третья компонента, то это означает,
что пуст магазин.
На рис. 8.33 изображены (в терминах приведенного выше со-
содержательного описания) две конфигурации МП-автомата из
примера 8.14, причем вторая конфигурация непосредственно
выводится из первой. Понятие непосредственной выводимости,
таким образом, формализует данное выше понятие такта (или
634 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
шага) работы МП-автомата. Заметим, что если в (8.9) и в ко-
команде (8.8) а = А, т.е. имеет место Л-такт, то команда (8.8)
применима к любой конфигурации, у которой (говоря нефор-
неформально) состояние блока управления есть q, а верхний символ
магазина — Z, причем, подчеркнем это, независимо от содер-
содержимого входной ленты (т.е. для любой входной цепочки w).
Если же а есть входной символ, то применимость команды к
конфигурации определяется состоянием, обозреваемым симво-
символом на ленте и верхним символом магазина.
Любую конфигурацию вида (go? #> Zo) называют началь-
начальной, а любую конфигурацию вида (д/, Л, Л), где g/EF, —
заключительной. Обратим внимание на то, что заключи-
заключительная конфигурация — это конфигурация с пустым мага-
магазином. Множество всех заключительных конфигураций нахо-
находится, таким образом, во взаимно однозначном соответствии с
множеством заключительных состояний МП-автомата. Из за-
заключительной конфигурации не может быть выведена ни одна
конфигурация, так как к ней не применима ни одна команда.
Конфигурацию МП-автомата, не являющуюся заключительной
и к которой не применима ни одна команда, называют тупи-
тупиковой.
Определение 8.9. Выводом на множестве конфигу-
конфигураций МП-автомата М называют последовательность Со,
Съ ..., Сп, ... (конечную или бесконечную) таких его конфигу-
конфигураций, что для любого г ^ О имеет место С{ Ь Cj+i, если Cj+i
существует.
Если вывод конечен и Сп — его последняя конфигурация,
то число п называют длиной вывода. В этом случае будем
говорить, что вывод Со, Ci, ..., Сп связывает конфигурацию
Со с конфигурацией Cn. \
Конфигурацию С называют выводимой из конфигурации
С, обозначая это как CV-* С, если существует вывод, связыва-
связывающий С с С, т.е. вывод Со, Ci, ..., Сп, такой, что Со = С,
сп = с.
8.4. Магазинные автоматы 635
В частности, при п = О получаем, что любая конфигурация
выводится сама из себя; при п = 1 получаем непосредственную
выводимость С" из С. В общем случае говорят, что конфигу-
конфигурация С" выводится из конфигурации С за п шагов, записывая
при этом С \-п С". Желая подчеркнуть, что существует вы-
вывод ненулевой длины конфигурации С" из конфигурации С, т.е.
С К1 С" и п > О, записывают С Ь+ С". #
Таким образом, понятие выводимости для конфигураций
МП-автомата вводится аналогично таковому для грамматики.
И к тому же сохраняется полная аналогия с понятием дости-
достижимости в ориентированных графах.
В терминах конфигураций может быть дано и строгое
определение языка МП-автомата.
Определение 8.10. Входную цепочку х называют допу-
допустимой цепочкой МП-автомата М (см. определение 8.7), если на
множестве конфигураций М существует вывод, связывающий
начальную конфигурацию {qo^x^Zo) с заключительной конфи-
конфигурацией (д/,А, А), где g/ E F, т.е.
(до? х, Zq) \-*m (д/, А, А).
Язык, допускаемый МП-автоматом М (или просто язык МП-
автомата М), — это множество всех его допустимых цепочек.
МП-автоматы М\ и M<i называют эквивалентными, если
их языки совпадают, т.е. L(M\) = L(M2).
Любой вывод на множестве конфигураций МП-автомата,
связывающий начальную конфигурацию Cfi = (qo,x,Zo) с од-
одной из заключительных, называют допускающей последо-
последовательностью конфигураций для цепочки х. Цепочка
х принадлежит языку L(M) тогда и только тоЬда, когда для
нее существует допускающая последовательность конфигура-
конфигураций. Тем не менее может оказаться так, что даже в том случае,
когда х G Ь(М), из начальной конфигурации С$ можно вывести
отнюдь не только заключительную конфигурацию.
636 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Пример 8.15. Пусть МП-автомат
({до, 9ь Ы, {М}, {^,М}, 90
определен множеством команд 02:
qoaZ —>• qoaZ,
qobZ -> qobZ,
qoaa -*¦ qoaa,
qoaa ->• 91 A,
qoab —> qoab,
qoba —? qoba,
qobb —? qobb,
qobb —? 91A,
qiaa —»• 91 A,
qibb->qi\,
91 AZ -4 92 A.
A)
B)
C)
D)
E)
F)
G)
(8)
(9)
A0)
(И)
Можно доказать, что этот МП-автомат допускает зеркальный
язык {xxR G {a, Ь}*}, где xR обозначает инверсию цепочки х.
Приведем допускающую последовательность конфигураций
для цепочки abba:
(ад, abba, Z) hA) (g0, bba, aZ) hF) (g0, ba, baZ) h(8)
Ь(8) (?i, a, aZ) b(9) (gb A, Z) hA1) (g2, A, A)
(справа внизу под значками непосредственной выводимости
подписаны номера применяемых команд).
К начальной конфигурации (go, abba, Z) применима только
команда A). После выполнения этой команды первый символ
входной цепочки будет прочитан, а в магазине вместо одного
символа Z окажется цепочка aZ, т.е. символ а станет верхним
символом магазина.
К полученной конфигурации (go, bba, aZ) применима только
команда F), в результате выполнения которой будет прочитан
еще один символ входной цепочки, т.е. ее второй символ Ь, ив
магазине окажется цепочка baZ.
8.4. Магазинные автоматы 637
К третьей конфигурации записанного выше вывода приме-
применимы две команды: G) и (8). Выбирая команду (8), мы тем
самым читаем третий символ входной цепочки, а верхний сим-
символ магазина, совпавший с указанным символом входной цепоч-
цепочки, „выталкиваем" из магазина, после чего верхним символом
магазина окажется уже символ а, т.е. возникнет конфигурация
(gi, a, aZ). Заметим также, что после выполнения команды (8)
МП-автомат M<i окажется в новом состоянии q\.
Применив к конфигурации (gi, о, aZ) единственную приме-
применимую к ней команду (9), получим конфигурацию (gi, A, Z),
т.е. входная цепочка прочитала полностью, а в магазине остал-
остался символ Z.
Применяя опять-таки единственно возможную для такой
конфигурацию команду (И), мы убираем символ Z из магазина,
тем самым опустошая его, и переходим в заключительное
состояние <72-
В то же время, если бы после третьей конфигурации было
выбрано янеудачное продолжение", т.е. была бы применена
команда G), и автомат продолжал бы записывать в магазин
вместо того, чтобы сравнивать магазин с лентой, то получился
бы вывод
(go, ba, baZ) ЬG) (д0, a, bbaZ) ЬE) (до, A, abbaZ).
Последняя конфигурация в этом выводе характеризуется тем,
что входная цепочка прочитана, магазин не пуст, состояние
не является заключительным и не применима ни одна команда,
т.е. полученная конфигурация (до, К obbaZ) МП-автомата M*i
является тупиковой. #
Рассмотренный пример показывает, что ЛШ-автомат мо-
может попасть в тупиковую конфигурацию, читая даже „правиль-
„правильную" цепочку, т.е. цепочку, принадлежащую его языку. Это
связано с недетерминированностью МП-автомата, т.е. с тем,
что из данной конфигурации можно непосредственно вывести,
638 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
вообще говоря, более чем одну конфигурацию*. Тот факт, что
входная цепочка принадлежит языку МП-автомата, означает
лишь, что существует допускающая последовательность кон-
конфигураций для этой цепочки, но не всякая последовательность
конфигураций, которая возникает при чтении этой цепочки, бу-
будет допускающей. Задача эффективного поиска допускающей
последовательности конфигураций — одна из основных задач
разработки алгоритмов синтаксического анализа на базе МП-
автоматов.
Как уже отмечалось, основное свойство языков, допускае-
допускаемых МП-автоматами, состоит в том, что эти языки образуют
класс, совпадающий с классом КС-языков. Но перед тем как
доказывать этот основной результат теории МП-автоматов,
аналогичной теореме Клини для конечных автоматов, устав-
новим одно весьма полезное свойство МП-автомата, состоящее
в том, что „хвост" входной цепочки и „дно" магазина не влияют
на работу МП-автомата с началом входной цепочки и верхом
магазина, так как входная цепочка читается строго символ за
символом без возвратов и забеганий вперед, а магазин обновля-
обновляется только сверху.
Приведем строгую формулировку.
Теорема 8.5, Пусть в МП-автомате
М = (Q, V, Г, go? -f1) ^о? $)
на множестве конфигураций для некоторых g, r Е Q, ж, у Е V* и
а, C Е Г* имеет место выводимость
(9, ary, a) h*M (г, у, /3). (8.10)
* МП-автомат называют детерминированным, если из каждой его кон-
конфигурации непосредственно выводится не более чем одна конфигурация.
Можно доказать, что, в отличие от конечного автомата, для МП-автомата
невозможна процедура детерминизации и класс языков, допускаемых де-
детерминированными МП-автоматами, строго включается в класс языков,
допускаемых произвольными МП-автоматами.
8.4. Магазинные автоматы 639
Тогда для произвольных z € V*, 7 € Г* имеет место выводи-
выводимость
(«, яу*, cry) Ь^ (г, у*, /?7). (8.11)
Обратно, если для некоторых g, r E Q, ж, у, г € V* и а,
/?, 7 € Г* имеет место выводимость (8.11), то выполняется и
выводимость (8.10).
Ч Индукцией по длине вывода, связывающего конфигурацию
(д, ху, а) с конфигурацией (г, у, /3) в (8.10) докажем, что ес-
если эта выводимость имеет место, то имеет место и выводи-
выводимость (8.11).
Для вывода нулевой длины утверждение тривиально.
Пусть доказываемое верно для любой длины вывода, связы-
связывающего конфигурации в (8.10), не превышающей п — 1.
Предположим, что
(q, ху, а) Ь^ (г, у, /3).
Рассмотрим первый шаг соответствующего вывода. Пусть он
имеет вид
(д, ах1 у, Zol) hM (g', ж;у, era'),
где х = ах1, а = Zol, a e VU{Л} и Z е Г.
Это значит, что на этом шаге применена команда
qaZ-+q'o. (8.12)
Согласно предположению индукции, для произвольных z E V*
и 7 € Г* имеет место выводимость
(</, я'у*, ™'-у) I"*1 (г, у*, jfry). (8-13)
\
Рассмотрим конфигурацию (g, xyz, cry) = (9, ax'yz, Zcl^) и
применим к ней команду (8.12). Получим
(д, аж'уг, Za'j) Ьм (д;, я'уг, ааЛу).
640 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Отсюда в силу (8.13), будем иметь
(q, ax'yz, Za'j) h (q\ x'yz, aa'-y) h^1 (r, yz,
т.е. при выводимости (8.10) за п шагов имеет место и выводи-
выводимость (8.11) также за п шагов, что и требовалось доказать.
Аналогично (но уже индукцией по длине вывода (8.11))
доказывается, что если имеет место выводимость (8.11), то
имеет место и выводимость (8.10). >
МП-автомат М называют экивалентпным КС-грамма-
КС-грамматике G, если язык, допускаемый М, совпадает с языком,
порождаемым грамматикой G, т.е. если L(M) =L(G).
Опишем алгоритм построения по заданной КС-грамматике
эквивалентного ей МП-автомата, а также алгоритм построе-
построения по заданному МП-автомату КС-грамматики, которой он
эквивалентен.
Алгоритм построения МП-автомата по КС-грамма-
КС-грамматике. Для исходной КС-грамматики G = (V, JV, 5, Р) опре-
определим МП-автомат Mq = ({?}, V, VUN, 9, {q}, 5, S) (с един-
единственным состоянием g), система команд S которого строится
следующим образом: для каждого правила А -> а, принадле-
принадлежащего Р, в S записывается команда qXA -> qa и для каждого
а е V — команда qaa -> q\. Никаких других команд в системе
команд S нет.
Пример 8.16. Пусть дана грамматика
G = ({a,6,c}, {5}, 5, Р),
множество правил вывода Р которой есть
S->aSbS\aS\c.
8Л. Магазинные автоматы 641
Тогда эквивалентный ей МП-автомат задается следующей
системой команд:
g AS -> qaSbS \ qaS \ qc,
qaa —> q\,
qbb -> q\,
qcc -> qX
(мы использовали сокращенную запись нескольких команд с
одинаковыми левыми частями по аналогии с тем, как мы это
делаем при записи множества правил вывода грамматики).
В системе команд МП-автомата, который строится по за-
заданной КС-грамматике так, как это описано выше, мы видим
два „сорта" команд: 1) команды, „моделирующие" применение
правил, исходной грамматики (в данном примере это команды
первой строки); при выполнении каждой такой команды МП-
автомат делает Л-такт, т.е. не продвигает головку по входной
ленте; 2) команды „сравнения", согласно которым МП-автомат
должен убирать верхний символ магазина всякий раз, когда он
совпадает с обозреваемым символом на ленте.
Тогда, читая входную цепочку, такой МП-автомат „моде-
„моделирует" левый вывод этой цепочки в исходной грамматике,
применяя каждый раз, когда верхним символом магазина ока-
оказывается нетерминал, команду „первого сорта" и всякий раз,
когда верхним символом магазина оказывается терминал ис-
исходной грамматики, „команду сравнения".
Прочитаем цепочку aacbc:
(g, aacbc, S) Ь (g, aacbc, aSbS) h (g, acbc, SbS) h
h (g, acbc, aSbS) h (g, cbc, SbS) h (g, cbc, cbS) h
h (q, be, bS) h (g, c, S) h (<?, с, с) b (g, Л, Л).
Нетрудно видеть, что этот вывод „моделирует" левый вы-
вывод в грамматике:
S Ь aSbS h aaSbS h aacbS h aacbc,
642 3. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
т.е. МП-автомат, строя допускающую последовательность кон-
конфигураций для входной цепочки, на каждом шаге, когда верх-
верхний символ магазина не совпадает с очередным символом вход-
входной цепочки, должен „ угадать" применяемое правило (выбрать
в данном примере одну из трех первых команд). Неправильный
выбор приведет к тупику, например:
(g, aacbc, S) Ь (g, aacbc, aS) h (g, acbc, S) h (g, acbc,c). #
Докажем, что рассмотренный алгоритм дает МП-автомат,
эквивалентный исходной КС-грамматике.
Теорема 8.6. МП-автомат Mq эквивалентен КС-грамма-
КС-грамматике G.
< Индукцией по длине п вывода терминальной цепочки х из
нетерминала А докажем, что если A \-q ж, то
(?, х9 А) У-*Мс (9, Л, А).
Пусть п = 1, т.е. АЬ1 х; тогда в Р есть правило Ачжи,
следовательно, в S есть команда q\A —> qx. В таком случае при
х = Л имеет место выводимость
(9, A, A)\-(q,X, A),
и требуемый вывод на множестве конфигураций МП-автомата
Mq построен. Если же цепочка х непустая, то тогда, расписы-
расписывая ее по символам, т.е. полагая х = хA)... x(fc), k ^ 1, получим
Из последней конфигурации за к шагов посредством приме-
применения команд вида qaa -* gA, где aeV, выводится конфигура-
конфигурация (д, А, А), и, таким образом, (д, ж, A) Hxl+1 (g, А, А).
Пусть теперь доказываемое верно для любого п, не превос-
превосходящего некоторого т — 1 для т ^ 2, пусть А Ьт х и первый
8.4. Магазинные автоматы 643
шаг вывода длины га цепочки х из нетерминала А имеет вид
А Ь Х\Х2... Хь, где fc^l и для каждого г = 1, А: символ Xi есть
символ объединенного алфавита грамматики*. Далее, из цепоч-
цепочки Х\Х2... Xk должна быть выведена терминальная цепочка х.
Это значит, что для каждого ъ = 1, к из символа Jfj выводится
какая-то подцепочка цепочки х (в частности, если этот сим-
символ является терминалом, он будет одним из символов цепочки
х). Таким образом, для каждого % = 1, А: выполняется Х{ hmi Х{
Для Х{ € N длина вывода т* подцепочки Xi не может
превышать га — 1. Следовательно, согласно предположению
индукции, имеем
(g, xu Х{) Ь* (д, Л, Л),
а для Xi G V (mi = 0 и, следовательно, -Х"» = ж*), согласно
построению МП-автомата
(«, ж», ^*) Ь* (д, А, Л).
Тогда в силу теоремы 8.5
-*(q, х2...хк, Х2...Хк)\~*
Кроме того, так как А Ь XiX2...Xk, то в Р есть правило
вывода А-* X\X2...Xk<> откуда, согласно построению МП-
автомата М<7, в <J есть команда
q\A -
(q,x,A)\-(q,x,XxX2...Xk),
* Цепочка Х1Х2... Xk не может быть пустой, так как тоща она окажется
последней цепочкой рассматриваемого вывода и его длина будет равна 1,
а мы предположили, что его длина равна m > 1.
'/2 21*
644 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
а окончательно
(д, я, А) Ь* (д, А, Л).
Следовательно, если х 6 L(G), то S Ь* х и (д, #, 5) Ь* (д, А, А),
т.е. х € L(Mq)-
Итак, мы доказали, что L(G) С L{Mq)-
Чтобы доказать обратное включение, сначала индукцией по
длине п вывода на множестве конфигураций МП-автомата Mq
докажем, что
(q, х, А) \-*Ма (q, А, А)
влечет А Ь? х (для произвольных Ае N и х €V*).
Пусть п = 1, т.е.
(д, х, A)h(g, А, А).
Согласно построению МП-автомата М<з, это может быть тогда
и только тогда, когда х G V и А = ж, т.е. a; h* x.
Пусть доказываемое верно для любого п ^ m — 1, где m ^ 2,
и
(д, х, Л) К" (д, А, А), (8.14)
причем первый шаг соответствующего вывода имеет вид
(g,*, A)h(q,x,X1X2...Xk). (8.15)
Это значит, что в системе команд S есть команда q\A ->¦
—> qXiXzXk и, следовательно, правило в множестве правил
вывода Р грамматики G есть правило А —> XiX2>..Xk, по
которому указанная команда построена. Из (8.14) и (8.15)
следует, что имеет место выводимость
(q,x,XlX2...Xk)\-*(q,\,\). (8.16)
Используя индукцию по длине магазинной цепочки
можно доказать, что из (8.16) следует существование таких
8.4. Магазинные автоматы645
входных цепочек х\, Х2, • • • > #ь что х = х\Х2...х* и имеет место
выводимость
(8.17)
для некоторых га^, таких, что 1 < га* < m — 1, г = 1, fc.
Вывод (8.17) можно прокомментировать так: чтобы до-
достичь заключительной конфигурации, Mq должен выбросить
все символы Xi, -Х2, ..., X* из магазина. Предположим, что к
тому моменту, когда Х\ покинет магазин (чтобы уже больше
туда не вернуться!), будет прочитано некоторое начало вход-
входной цепочки х — цепочка xi, когда Х2 покинет магазин, будет
прочитана следующая подцепочка Х2 и так до тех, пока нако-
наконец, автомат не прочитает цепочку х\* — конец цепочки х.
Из теоремы 8.5 следует, что существуют также выводы
(g, xi, XOP^AjA,
</, А,А), (gl8)
(<?, xk, Xk) hTO* (g, A, A).
Все числа т^ при г = 1, А; не больше т — 1. Тогда согласно
предположению индукции, из (8.18) следует, что для каждого
i = 1, к в грамматике G имеет место Х{ \-*G xi, и в силу того,
что в Р есть правило вывода А —? Х\Х2.. -Хк (см. (8.15)),
А Ь Xi-Х2 ... Х^ h*
т.е. A h^ x, что и требовалось доказать.
Отсюда, если х Е L(Mg), то х G ?(G), т.е. L{Mq) С L(G), и
в силу доказанного выше языки L(G) и L(Mg) совпадают. >
Алгоритм построения КС-грамматики по МП-авто-
МП-автомату. Дадим сначала неформальную мотивировку той кон-
конструкции, которая будет приведена ниже. Будем рассматри-
646 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
вать МП-автомат как „игрока", ставящего цели следующего
вида: „находясь в состоянии q и имея верхний символ магазина
Z, перейти в состояние s". Условимся записывать такую цель в
виде тройки [qZs]. Как может наш „игрок" достичь поставлен-
поставленной цели? Если в множестве команд автомата („правил игры")
есть команда
qaZ -* ГХ1Х2... Xk,
где для каждого г Х{ — магазинный символ (Х{ Е Г), то после
выполнения этой команды МП-автомат перейдет в состояние г.
Если г = 5, то цель достигнута, иначе ставим цель [rXi$i],
а достигнув ее, ставим цель [51X252] и т.д. Достигнув цели
[sk-iXks], „игрок" достигает и цели [qZs]. Так как рассматри-
рассматривается допуск с пустым магазином, то символы Xi должны по
очереди покинуть магазин, и только в этом случае может быть
достигнута „глобальная" цель МП-автомата: [?о^о9/]> Я/ € F
(„находясь в начальном состоянии и имея верхним символом
магазина начальный магазинный символ, попасть в одно из
заключительных состояний, опустошив магазин"). Так кале,
вообще говоря, „игрок" не знает наперед последовательности
состояний 5х, «2,..., 5fc_i, ведущих к цели, он должен перебрать
все такие последовательности.
Эти неформальные соображения лежат в основе следующей
конструкции.
Пусть дан МП-автомат
M = (Q, V, Г, go, F,Zb, S).
Определим КС-грамматику Gm = (V", iV, 5, Р), терминальный
алфавит которой совпадает со входным алфавитом МП-авто-
МП-автомата М, следующим образом.
Нетерминальный алфавит N грамматики есть множество,
находящееся во взаимно однозначном соответствии с множе-
множеством всех упорядоченных троек вида (g, Z, 5), где q,s €Q,
Z G Г, пополненное символом 5, не принадлежащим ни одному
из множеств Q, У, Г и объявляемым аксиомой грамматики.
8.4. Магазинные автоматы 647
Упорядоченные тройки указанного вида записывают обычно
как [g?s], интуитивно понимая каждую такую тройку как оха-
охарактеризованную выше цель.
Таким образом, N = {[qZs]: q.seQn Z € Г} U {S}.
Множество правил вывода Р грамматики Gm строится
так:
а) если команда qaZ -> rX\X2...Xk, к > 1, принадлежит
системе команд 5, то в Р записываются все правила вида
[qZsk] -> a[rXiSi][siX2S2]... [sk-iXksk]
для любой последовательности к состояний si,..., sk множества
Q (тем самым к Р добавляется \Q\k правил на каждую команду
указанного вида);
б) для каждой команды qaZ -? r\ в S в Р добавляется
правило [qZr] -> a;
в) для каждого g/ G F в Р вводится правило S -» [qoZoq/];
г) никаких других правил в Р, кроме определенных пп. а-в,
нет.
Пример 8.17. Для МП-автомата
М = ({9о,9ь92>, {а,Ь}, {a,6,Z}, q0, {g0}, Z, S)
с множеством команд 6, имеющих вид
qoaZ
q\aa —
qxba -
q2ba -
q2XZ
qo\Z
построим эквивалентную ему КС-грамматику. Можно дока-
доказать, что этот МП-автомат допускает язык {anbn: n ^ 0}. За-
Заметим, что МП-автомат М допускает пустую церочку, при-
применяя к начальной конфигурации {q$,\,Z) последнюю коман-
648 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
ду. Построенная по данной системе команд грамматика будет
иметь следующий вид:
S->[q0Zq0],
[q0Zs2] -> a[qiasi][siZs2], sus2 G {go, 9i, 92>,
[qias2] -> a[qiasi\[sias2], sus2 E {go, gi, 92>,
[q2Zq0] -> A,
> A.
Подчеркнем, что во второй и третьей строчках имеется не
по одному, а по З2 = 9 правил (число всех последовательностей
двух состояний из трехэлементного множества состояний). Вы-
Выведем в этой грамматике цепочку aabb:
S Ь [qoZqQ] Ь a[9iag2][92^9o] Ь aa[9ia92] [92^92] [92^9о] Ь
h aab[g2«92] [92^90] Ь аа6Ь[^2^9о] I"
На втором шаге этого вывода мы применяем то правило вы-
вывода из девяти правил второй строки, которое получается при
подстановке вместо s\ состояния q2, а вместо s2 состояния до-
Мы „угадываем" эти состояния, зная (по системе команд исход-
исходного МП-автомата), что достичь заключительного состояния
по прочтении (непустой) входной цепочки наш МП-автомат
может только из состояния q2. В то же время, если бы мы
на втором шаге использовали правило второй строки, получа-
получающееся подстановкой s\ = gi, s2 = q2, возник бы бесполезный
нетерминал [gieigi] и наш вывод зашел бы в тупик.
Аналогично на третьем шаге используется то правило из
девяти правил третьей строки, в котором s\ = 52 = 92- После
этого применяем по очереди правила четвертой, пятой и ше-
шестой строк, завершая вывод.
Бели мы теперь в построенном выводе „считаем" по ша-
шагам магазинные символы, заключенные в квадратных скобках
8.4. Магазинные автоматы 649
между состояниями, то получим Z, aZ, aaZ, aZ, Z, т.е. по-
получим изменение содержимого магазина (не считая последнего
шага, когда происходит его окончательное опустошение), пред-
представленное в следующем выводе на множестве конфигураций
МП-автомата М:
(go, aabb, Z) Ь (дь abb, aZ) h (дь 66, aaZ) h
h (g2, 6, aZ) h (g2, A, Z) h (g0, A, A).
Этот вывод есть не что иное, как допускающая последова-
последовательность конфигураций для цепочки aa&6.
Читая же последовательности состояний в квадратных
скобках, мы получим в итоге ту последовательность состояний,
которую проходит МП-автомат, допуская написанную выше
цепочку.
Действительно, после первого шага вывода в грамматике
получим последовательность до, 9о, что можно интерпрети-
интерпретировать так: „из состояния до перейти (вернуться) в это же
состояние до, прочитав входную цепочку".
После второго шага будем иметь go, gi, дг, до, что означает:
пчтобы вернуться в до, сначала нужно попасть в д2 через gi").
После третьего шага получим до, gi, gi, д2, дг, 9о- Это и
есть результирующая последовательность состояний, так как
все следующие шаги МП-автомата связаны с „выталкиванием"
символов из магазина и не приводят к возникновению новых
целей. #
Как правило, грамматика, которая указанным выше спосо-
способом строится по МП-автомату, оказывается очень громоздкой,
содержит много бесполезных и недостижимых символов. Это
связано с тем, что в ней фигурируют произвольные последова-
последовательности состояний МП-автомата фиксированной длины. Что
касается разобранного примера 8.17, то в этом случае легко на-
написать грамматику для языка {anbn: n ^ 0} непосредственно:
650 S. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
По этой грамматике можно построить МП-автомат, используя
алгоритм из первой части доказательства основной теоремы,
значительно более простой, чем исходный. Его система команд
будет иметь следующий вид:
qaS-*qSb\qb,
qaa -> gA,
qbb -> gA,
qXS -* qX.
В общем же случае проблема распознавания эквивалентно-
эквивалентности двух МП-автоматов (в отличие от такой же проблемы для
конечных автоматов) не разрешима, и не существует общего
алгоритма „упрощения" (в определенном смысле, „минимиза-
„минимизации") МП-автомата, хотя, как мы только что видели, в кон-
конкретных случаях это вполне возможно.
Теорема 8*7* МП-автомат М эквивалентен граммати-
грамматике
<4 Индукцией по длине п вывода в М докажем, что Z Е Г,
(д, я, Z) \-п (г, А, А) для любых д, г € Q, х Е V* влечет [qZr] Ь* х
в Gm-
Если п = 1, т.е. (д, ж, Z) Ь (г, А, А), то х € V U {А}, и в S
есть команда qZx -> г А, откуда в Р есть правило [qZr] -> ж, и
[qZr] К яг.
Пусть доказываемое верно для каждого п ^ т — 1, где m > 1,
и пусть (д, ж, Z) hm (r, А, А), причем первый шаг соответству-
соответствующего вывода имеет вид
(д, ж, Z)h(p, у,
где х = ау для некоторого а € V U {А}.
Аналогично доказательству теоремы 8.6 (см. (8.17)) дока-
доказывается, что тогда найдутся такие цепочки х\Х2...ж* и такая
8.4. Магазинные автоматы 651
последовательность состояний s\, ..., Sk-i, что у = х\х2...Хк и
(р, Х1х2...хк, X1X2...Xk)\-mi («ь х2...хк, Х2...Хк)\-т*
где для любого г = 1, fc выполняется 0 ^ пц ^ m — 1. Поэтому в
силу теоремы 8.5 для любого % = 1, к—1
(*_ь a;i? Xi) hmi Ei, Л, А),
где 5о = p, a 5fc = г, и, согласно предположению индукции,
[Si-iXi8i] h* Xi.
Следовательно, согласно построению грамматики Gm? име-
имеет место выводимость
[qZr] \-Gm a\pXiSi][8iм
что и требовалось доказать.
Пусть цепочка я; допускается МП-автоматом М. Тогда
(до, я, #о) Ь^ (д/, А, А),
где q/ (zF — одно из заключительных состояний МП-автомата
М. Согласно только что доказанному, в этом случае для
грамматики Gm выполняется [qoZoqf] hj^ x. Но так как в
множестве правил вывода грамматики Gm есть правило S -»
-> [qoZoqf], то мы получим S hGjv/ [qoZoqf] \-*Gm x, т.е. х € L(GM)-
Итак, L(M) С L(GM).
Для доказательства обратного включения докажем сначала,
что [qZr] \-qm х влечет (g, ж, Z) l-]^- (r, А, А) для любых q,r€Q,
х 6 V* и Z Е Г. Снова проведем индукцию по длине вывода (в
грамматике Gm)- При [gZr] Ь ж получаем правило [qZr] -f а; в Р
и, следовательно, команду qxZ -* г А в J, т.е. (д, ж, Z) h (r, А, А).
652 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Бели же [qZr] hw х для некоторого т > 1, то х = ау для неко-
некоторого a Е V U {А} и
Ь a\pXiSi][siX2s2]... [s^-
причем для всех г = 1, к
где so = р, 5jfe = г и 1 ^ 7П{ ^ m — 1, так что у = х\х2.-.х^.
Согласно предположению индукции, тогда для каждого та-
такого г
Но так как указанный выше первый шаг вывода в грамматике
возможен только при наличии команды в МП-автомате qaZ ->
.Xk ,то
Ь* EЬ х2...хк, Х2...Хк)\-*
К (8к-и хк, Хк) h* (r, А, А).
Бели теперь цепочка х порождается грамматикой G, т.е.
S \-?м ху то первый шаг вывода х из ?, согласно определению
системы правил грамматики См? будет иметь вид S Ь [<7о^о9/]
для некоторого qj G F, и, следовательно, [qoZoq/] Ь^ х. Тогда
в силу только что доказанного (go? #> Zq) h*M (д^, А, А), т.е. х ?
G L(M). Итак, L(Gm) Я L(M)> а поскольку обратное включение
уже доказано, то L(M) = L(Gm) >
Из доказанных теорем 8.6 и 8.7 получаем следующую тео-
теорему.
Теорема 8.8. Язык является контекстно-свободным тогда
и только тогда, когда он допускается некоторым МП-авто-
МП-автоматом.
Замечание 8.10. Существует одна полезная модифика-
модификация построения МП-автомата по КС-грамматике. Вернемся
8.4. Магазинные автоматы 653
к примеру 8.16. Можно заметить, что в этом примере пра-
правая часть каждого правила грамматики начинается некоторым
терминалом. Учет этой особенности позволяет найти другой
МП-автомат, который, как нетрудно показать, тоже эквива-
эквивалентен данной грамматике. Система команд этого автомата
имеет следующий вид:
qaS-+qSbS\qS,
qcS -* <jA,
qaa -> q\,
qbb -» qXy
qcc -> q\.
Его преимущество в том, что он „видит" первый непро-
непрочитанный символ входной цепочки и, следовательно, имеет
меньше альтернатив при выборе команды: например, если оче-
очередной символ есть 6, то ни одна из команд первых двух строк
не может быть применена. Тогда этот автомат имеет меньше
возможностей попасть в тупик.
В общем случае, если правая часть любого правила грам-
грамматики имеет вид а?, где aEV, МП-автомат, эквивалентный
данной грамматике, определяется командами вида
qaA -+ q?,
qbb-+ q\y be V,
(первая — для правила А —> af). В такой модификации МП-
автомат записывает в магазин „хвост" правой части правила,
следующей за первым терминалом.
Можно доказать, что любая КС-грамматика может быть
определена правилами такого вида (так называемая нормальная
форма Грейбах*). \
*См.: Ахо А.у Ульман Док.
654 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
8.5. Алгебраические свойства КС-языков
В этом параграфе мы рассмотрим некоторые операции над
КС-языками, относительно которых множество всех КС-язы-
КС-языков замкнуто. Напомним (см. 7.6), что множество всех ре-
гулярных языков (в произвольно фиксированном алфавите)
замкнуто относительно операций (конечного) объединения, со-
соединения, пересечения, дополнения (до универсального языка)
и итерации. В этом разделе мы докажем прежде всего что
множество КС-языков замкнуто относительно операций объ-
объединения, соединения и итерации. Потом мы увидим, что пере-
пересечение двух КС-языков, вообще говоря, не является КС-язы-
КС-языком, но можно доказать более слабое утверждение: пересечение
КС-языка с регулярным языком есть КС-язык.
Начнем с определения новой операции над языками — опе-
операции суперпозиции.
Пусть V = {ai, ...,an} — произвольный алфавит, каждой
букве ai которого сопоставлен однозначно некоторый алфавит
Vat (не исключено, что все алфавиты V, Vai,..., Vun совпадают);
в алфавите V фиксируем произвольно язык 1СУ*,ав каждом
из алфавитов Vai — язык Lai С V*..
Рассмотрим множество всех таких цепочек в объединении
алфавитов Vai U... U Vun, которые могут быть получены из цепо-
цепочек языка L следующим образом: берем произвольную цепочку
bi... bk ? L и каждую букву bj в ней заменяем произвольной це-
цепочкой хj € Lty:
h fa ... bk
X\ X2 ... Xk,
в результате чего получаем цепочку x\x<i.. .#&.
Множество всех цепочек вида rci#2•••#&> получаемых опи-
описанным выше способом, называют суперпозицией (или под-
подстановкой) языков Lai, ..., Lan в язык L и обозначают
<S(L,Lai,...,Lan). При этом полагают, что если пустая цепоч-
8,5. Алгебраические свойства КС-языков 655
ка Л принадлежит языку L, то она принадлежит суперпозиции
При определении суперпозиции на алфавиты V, Vai, ...,
Vun не накладывается никаких ограничений. Они могут и
попарно не пересекаться, а могут и все совпадать. В любом
случае суперпозиция <S(L,Lai,...,Lan) есть язык в алфавите
Vai U... U Vun. Точно так же среди языков La., „подставляемых"
в язык L, может оказаться и сам язык L, т.е. язык можно
подставлять сам в себя, причем многократно.
Заметим, что если язык L не содержит пустую цепочку, су-
суперпозиция «S(L, Lai,..., Lan) может ее содержать. Это возмож-
возможно, если каждый язык Lai содержит пустую цепочку. Тогда,
беря произвольно х Е L и заменяя каждый ее символ пустой це-
цепочкой, получаем пустую цепочку как элемент суперпозиции.
Если же пустая цепочка принадлежит L, то, по определению,
суперпозиция обязана ее содержать.
Еще заметим, что для разных вхождений одной и той же
буквы bj цепочки х Е L совершенно не обязательно заменять эту
букву одной и той же цепочкой языка L^: каждому вхождению
может быть сопоставлена своя цепочка этого языка.
Пример 8.18* Зададим язык L в алфавите V = {a, Ь, с} как
множество {anbncn: п ^ 1}. Букве а алфавита V сопоставим
алфавит Va = {0,1}, выбрав в качестве языка La множество
{Onln}n ^ 0. Букве b ? V сопоставим алфавит Vj, = {a} и в
этом алфавите — язык L& = {an : п ^ 0}. Наконец, букве с
алфавита V сопоставим алфавит Ус = {а,!>,с} = 7ив качестве
языка Lc возьмем язык L, пополненный пустой цепочкой, т.е.
Возьмем цепочку aabbcc G L и первый символ а заменим
цепочкой ООП Е La> второй символ a — цепочкой 01 € La,
первый символ Ь — цепочкой a729 G Ьь (при п = 27), второй
символ Ь — пустой цепочкой, первый символ с — пустой
цепочкой, второй символ — цепочкой abc € Lc. В результате
получим следующую цепочку, принадлежащую суперпозиции
6568. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
001101a729abc = 001101 аа^ abc.
729 раз
Проделывая аналогичные действия с любой другой цепочкой
языка L или же производя другие замены символов той же
самой цепочки, будем получать все новые цепочки опреде-
определенной выше суперпозиции. В данном случае будем иметь
A ? <S(L,La,Lb,Lc), так как каждый из языков La, Ьь и Lc со-
содержит пустую цепочку.
Пример 8.19, Пусть алфавит V есть русский алфавит
{A, J5, ...,Э,Л9, Л}, а язык L — множество всех слов русско-
русского языка. Каждой букве русского алфавита сопоставим язык,
состоящий из единственной однобуквеннои цепочки а, которая
стоит рядом с указанной русской буквой на клавиатуре ком-
компьютера. Так, La = {F}, Ьб = {<} и т.д. Все эти языки можно
считать языками в латинском алфавите, дополненном опреде-
определенными специальными символами, такими, как [,],{>},<,>
и т.п. Тогда, если мы в качестве исходной цепочки языка L
возьмем слово УЧЕБНИК, то получим такую цепочку в су-
суперпозиции «S(L,LA,...,?#): EXT < YBR. #
Разобранные примеры показывают, что суперпозицию мож-
можно рассматривать как своего рода пкодирование" цепочек язы-
языка L с заменой в них каждой буквы цепочкой другого языка.
Действительно, такая замена является одним из простейших
способов „шифровки" текстов.
Замечание 8.11. Суперпозицию можно определить через
соответствие. Введем соответствие а С V х (Lai U... U Lan)
тале, что для каждого г = 1, п упорядоченная пара (а^, у) при-
принадлежит а тогда и только тогда, когда у G Lai. В этом случае
хеь\{\}
#
8.5. Алгебраические свойства КС-языков 657
В терминах суперпозиции могут быть представлены и такие
операции над языками как объединение, соединение и ите-
итерация.
Объединение. Пусть L\ и L2 — два произвольных языка в
каком-то алфавите W. Возьмем произвольный двухбуквенный
алфавит V = {а, 6} и язык L зададим как L = V (т.е. язык L
состоит из двух однобуквенных цепочек а и 6). Рассмотрим су-
суперпозицию <S(L,La,L&), где La = L\, Ьь = L2. Докажем, что эта
суперпозиция совпадает с объединением LiUL2. Действитель-
Действительно, если мы возьмем цепочку a E L, то ее единственную букву
мы можем, согласно определению суперпозиции, заменить лю-
любой цепочкой языка L\. Точно так же, строя суперпозицию,
вместо цепочки b E L получим все цепочки языка L2. Итак,
Соединение. Снова фиксируем произвольно в произволь-
произвольном алфавите W языки L\ и L2. Опять-таки произвольно вы-
выберем двухбуквенный алфавит {а, 6}, определив язык L = {ab}.
Положим, как и выше, La = Ьь ?& = ^2- Тогда суперпозиция
<S(L,La,I/5) = S({a6},La,Lfr) совпадет с соединением LiL2. В
самом деле, символ а единственной цепочки ab языка L можно
при построении суперпозиции заменять любой цепочкой язы-
языка Li, а символ b — любой цепочкой языка L2. В результате
записанная выше суперпозиция совпадет с множеством всех це-
цепочек, представимых как соединение жу, где х € Li, у G L2. Но
это и есть соединение LiL2. Итак,
Итерация. Рассуждая аналогично, можно показать, что
итерация L* языка L равна /
L* = S(a*,L),
658 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
а позитивная итерация
(для любых алфавита W', языка L С W* и однобуквенного
алфавита V = {а}).
Основное свойство суперпозиции применительно к КС-язы-
КС-языкам выражает следующая важная теорема.
Теорема 8.9. Бели языки Lai, t = l, n, контекстно-сво-
контекстно-свободные, язык L также контекстно-свободный, то суперпозиция
«S(L, Lai,..., Lan) есть КС-язык.
<4 Пусть V = {ai,..., ап} и каждый язык Lai, г = 1, п, задается
КС-грамматикой Gai = (V^i? iVai, 5ai, PaJ, а язык L задается
КС-грамматикой G = (V, iV, 5, P). Без ограничения общности
можно предполагать, что нетерминальные алфавиты всех ука-
указанных грамматик попарно не пересекаются (так как всегда
можно провести процедуру переименования нетерминалов лю-
любой грамматики).
Построим следующую грамматику:
U Рпп U {А -* а;: для любого правила Л->ав Р}.
Здесь цепочка а' получается из цепочки а следующим обра-
образом: все нетерминалы в а остаются без изменений, а каждое
вхождение каждого терминала Ь Е F, т.е. Ь = а* для некоторо-
некоторого г = 1,п, заменяется аксиомой Sb грамматики Gb (заметим,
что, согласно этим правилам замены, для любых цепочек а, C
в объединенном алфавите грамматики G (otf3)f = olfi и А; = Л).
Неформально система правил Р; получается объединением
всех множеств правил грамматик Gai и добавлением „перекра-
„перекрашенных" правил грамматики G. „Перекрашивание" выражает-
выражается в том, что каждый терминал а* грамматики G заменяется
8.5. Алгебраические свойства КС-языков 659
аксиомой Sai грамматики Gai, а нетерминалы остаются в не-
неприкосновенности. В частности, для любой цепочки /3 ? N*
имеет место /?' = /?.
Докажем теперь, что грамматика G\ контекстно-свободная
по построению, является искомой, т.е. она порождает суперпо-
суперпозицию «S(L, Lai,..., Lan).
Прежде всего докажем, что для произвольных нетерминала
А Е N и цепочки j Е {V U iV)* из A \-q 7 следует Л Ь^, У, т.е.
если в грамматике G из нетерминала А выводится цепочка 7
в объединенном алфавите, то в грамматике G1 из того же не-
нетерминала А выводится „двойник" цепочки 7? получаемый из
последней заменой каждого ее терминального символа Ъ акси-
аксиомой соответствующей грамматики G& = Gai для некоторого
ъ = 1,п.
Доказательство проведем индукцией по длине / вывода це-
цепочки 7 из нетерминала А. Для вывода нулевой длины утвер-
утверждение тривиально, так как А Ь° А = А1. Пусть утверждение
доказано при всех I < m — 1, и пусть A Ь™ 7- Тогда существует
цепочка ?, такая, что A h^"* ? Ь^ 7- Согласно предположению
индукции, отсюда следует, что A \-q, ?', а так как ? \-q 7? то
существует такое правило вывода В ->• /3 в множестве Р, что
? = fii?f2 (для некоторых ?i, ?2 € (V Ui\T)* ) и 7 = ?i/??2- Следо-
Следовательно, ?' = ?i-B?2) а так как в множестве правил вывода Р1
есть правило В -> /?;, то ?' Ь<з' ^i/3'^2 = 7;- Итак, окончательно
получаем A \-*G, ?' Y-q» 7'.
Из доказанного следует, что для любой цепочки х € L =
= ?(<3), т.е. такой цепочки ж, что S \-q ж, выполняется 5 Ь^, а:;.
Если ж = Л, то тогда из Л G L следует, что Л € L(G'). Если ж ^ Л,
тогда для некоторого fc > 0 ж = жA)... х(к) и ж7 = 5'жA)... Sx^
а так как для каждого j = 1, к выполняется Sx^ \-% j/j, ка-
какова бы ни была цепочка yj € Аф)> т0 х' ^Ъ Vi-f-Vk- Но
последняя цепочка есть произвольная цепочка суперпозиции
<S(L,Lai,...,Lan) (не считая пустой цепочки, непосредственно
выводимой из аксиомы 5), так как она получена из произволь-
произвольной непустой цепочки ж языка L путем замены в ней каждого
660 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
символа x(j) произвольной цепочкой языка Lx^y Посколь-
Поскольку из S be? Л следует S \~о' А, любая цепочка суперпозиции
<S(L, Lai,..., Lan) порождается грамматикой G'.
Докажем теперь, что если цепочка w в алфавите V (тер-
(терминальном алфавите грамматики G') выводится из аксио-
аксиомы S в грамматике <?', то она принадлежит суперпозиции
<S(L,Lai,...,Lan). Для этого сначала докажем, что для любых
нетерминала A Е N и цепочки у s(V\J N)* из A t-Q, 7' следует
A\-*G-y.
Опять воспользуемся индукцией по длине вывода, но на
этот раз вывода цепочки У из нетерминала А в грамматике
G*. Случай вывода нулевой длины, как и выше, тривиален.
Пусть для некоторого т > 0 выполняется A Ь™, 7'- Тогда
существует такая цепочка /х, что А Ь™," \i Vq* 7'. Каждый
символ цепочки 7; есть либо одна из аксиом 5ai, i = 1, п, либо
нетерминал из N. Так как КС-грамматики G и Gai, г = 1, п, в
силу результатов, полученных в 8.2, можно считать заданными
в приведенной форме, то правые части правил вывода каждой
из рассматриваемых грамматик не содержат аксиомы. Кроме
того, нетерминальные алфавиты N и Nai всех этих грамматик
попарно не пересекаются.
Отсюда следует, что цепочка jf не может быть непосред-
непосредственно выведена из цепочки /i применением какого-либо пра-
правила из множества Ра., т.е. какого-либо правила вывода грам-
грамматики <7ai, а выводится из /i применением некоторого правила
вида В -> /?', построенного, как указано в определении грам-
грамматики G;, по правилу В -* C системы правил грамматики G.
Тогда мы можем написать: у* = 7i^72 (дл* некоторых цепочек
7i и 72 в алфавите V U iV), /i = 7i#72 == (т^Тг)'- Это значит,
что ц = f; при ? = 71^72? т.е. А Ь^Г1 ?;. Согласно предположе-
предположению индукции, отсюда следует, что A \-*G ?, а так как ? = 71^72
и в множестве правил вывода грамматики G содержится прави-
правило В -»/9, то ? Kg 7i/?72 = 7 и окончательно А Ь? 7. В частности,
отсюда следует, что для произвольной цепочки х EV*, такой,
что S \-*Gi а/, имеет место S \~*G ж, т.е. х G L.
8.5. Алгебраические свойства КС-языков 661
Теперь докажем, что произвольная цепочка а, выводимая
в грамматике G1 из аксиомы 5, имеет вид aia2...am (m ^ 1),
где для каждого j = I, m цепочка aj либо пуста, либо для неко-
некоторого символа bj 6 V выводится из аксиомы S^. грамматики
Gb 5 т.е. S&. bjk aj, либо является некоторой цепочкой нетер-
нетерминалов из N. Действительно, сама аксиома S удовлетворяет
этому требованию. Далее, пусть доказываемое справедливо для
любой цепочки, выводимой в G' за любое число шагов, не пре-
превышающее / — 1 для некоторого I > 1.
Предположим, что S )rlG, a. Тогда, как это мы уже делали
в аналогичных ситуациях, рассмотрим последний шаг этого
вывода, т.е. для некоторой цепочки 7 будем иметь
Согласно предположению индукции, цепочка 7 представима в
виде
7 = 7172-..7т,
где 7j = A, j = 1, т, или S^ Ь^6 т? Д-^ некоторого bj € F, или
7 € N*. Так как к цепочке у применяется некоторое правило
грамматики G' (на последнем шаге вывода цепочки а из ак-
аксиомы 5), то в 7 входит по крайней мере один нетерминал
грамматики G1. Если это есть некоторый символ А € iV, то
он может входить только в одну из таких подцепочек 7jj ко-
которая состоит из нетерминалов алфавита N. После замены А
посредством некоторого правила вида А -> /У, соответствующе-
соответствующего правилу А—>/3 грамматики G, получится цепочка, в которую
могут входить только нетерминалы множества N и аксиомы S&
грамматик Gb для каких-либо b€V. ,
Следовательно, если цепочка а на последнем шаге ее вывода
из аксиомы получена применением некоторого правила А -* /3',
то она также может быть представлена соединением цепочек
такого же вида, что и цепочки 7j.
662 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Бели же Sty \~q. Jj для некоторого bj G V и на указанном
шаге применяется правило из множества Pbj, то оно, ввиду то-
того что все множества N и Nb (для различных bEV) попарно
не пересекаются, может быть применено только к такой подце-
подцепочке 7j> которая выводится из аксиомы 5^., и тогда в цепочке
а получим подцепочку, опять-таки выводимую из 5^, т.е. и
в этом случае* цепочка а образуется соединением подцепочек
того же вида, что и цепочки 7j-
Пусть теперь цепочка w € V* такова, что S \-q, w. Ес-
Если w = А и S be А, то это означает наличие правила вывода
S -> А в множестве Р1 и, следовательно, в множестве Р, т.е.
Аб1 и А € <S(L,Lai,...,Lan). Таким образом в этом случае
пустая цепочка, порождаемая грамматикой G', действительно
принадлежит указанной суперпозиции. Иначе в силу доказан-
доказанного выше свойства любой цепочки, выводимой в грамматике
G' из аксиомы, цепочка w, не содержащая по условию вхо-
вхождений нетерминалов из N, допускает представление в виде
w\W2.. -Wk, где для каждого j = 1, А; имеет место выводимость
Sbj \~q Wj (возможно для некоторых j, что Wj = А; в частности,
может оказаться, что и w = А). Таким образом,
S h*G, Sbl Sb2 ... Sbk \-Q' ™1™2 • • • Wfc,
где для каждого j = 1, к цепочка Wj принадлежит языку *Ьь .
Так как при этом S \~q ЬхЬ^.-.Ьк, т.е. bi&2---b* € L, то w ?
Итак, доказав, что любая цепочка w в терминальном алфа-
алфавите V грамматики G1, выводимая из аксиомы, есть элемент
* Заметим, что в приведенном выше доказательстве существенно исполь-
используется тот факт, что нетерминальные алфавиты N, Nai, ..., Nan попарно
не пересекаются. Бели бы это было не так, то в некоторой подцепочке
7j, выводимой из аксиомы Sbj для некоторого 6, 6 V, мы могли бы заме-
заменить вхождение нетерминала из Nbjy применив правило вывода „чужой"
грамматики Gah, анфЬ^ и получить в составе цепочки а подцепочку, не
выводимую ни из одной „дочерней" аксиомы &, beV.
8.5. Алгебраические свойства КС-языков 663
суперпозиции <S(L, Lai,..., Lan), мы тем самым завершили дока-
доказательство теоремы. >
Следствие 8.3. Семейство КС-языков замкнуто относи-
относительно операций объединения, соединения, итерации и позитив-
позитивной итерации.
< Доказательство получается немедленно из приведенных вьппе
определений операций объединения, соединения, итерации и
позитивной итерации как частных случаев суперпозиции. >
Заметим, что объединение бесконечного семейства КС-язы-
КС-языков не является, вообще говоря, КС-языком. Так, язык
не являющийся КС-языком (см. 8.3), может
быть представлен в виде объединения счетно-
счетного семейства, каждый элемент которого есть
язык {anbncn} для фиксированного натураль-
натурального п, т.е. язык, состоящий из одной цепочки,
а следовательно, регулярный и контекстно-
свободный.
Замечание 8.12. Вывод цепочки w из суперпозиции
<S(L,Lai,...,Lan) (если она не является пустой цепочкой, не-
непосредственно выводимой из аксиомы S) в грамматике G',
построенной в доказательстве теоремы 8.9, можно провести по
„двухуровневой" схеме, приведенной на рис. 8.34. Сначала по-
порождаем, используя „перекрашенные" правила грамматики G,
т.е. правила вида А -> У Для AtN И7 € (V U JV)*, „двойника"
произвольной цепочки х ? L, т.е. цепочку Sx^iy..Sx^)- Из нее
затем, используя правила „дочерних" грамматик, порождаем
саму цепочку ги, из каждой аксиомы Sx^ выводя некоторую
цепочку yj так, что w = j/i...у*.
Пример 8.20. Рассмотрим конструкцию из доказатель-
доказательства теоремы 8.9 на конкретном примере.
664 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Язык L определим как язык, порождаемый грамматикой G
со следующим множеством правил вывода:
S->ab\aSb\SS.
Языки La и Ьь определим так:
{}
Ьь = {х: х Е {a, b} и х = xR}
(т.е. L& есть язык палиндромов в алфавите {а, 6}). Запишем
множества правил вывода грамматик Ga и G&, порождающих
языки La и Lj, соответственно:
(грамматика Ga) и
S-+aSa\bSb\aa\bb\a\b\\
(грамматика G&).
Преобразуя грамматики G, Ga и Gb к приведенной форме
(убирая аксиому из правых частей правил вьгоода) и переимено-
переименовывая нетерминалы так, чтобы множества iV, Na и Nb попарно
не пересекались, построим, как описано в доказательстве тео-
теоремы 8.9, множество Р1 правил вьгоода грамматики
G' = ({0,1, а, Ь}, {5, Т, 5а, Та, 5Ь, Ть}, 5, Р')?
порождающей суперпозицию S(L,La,Lb):
(S->SaSb\SaTSb\TT,
v
Sb -> аТьа\ЬТьЬ\аа\ЬЬ\а\Ь\О\\,
{Tb-+aTba\bTbb\aa\bb\a\b\Q.
8.5. Алгебраические свойства КС-языков 665
Рассмотрим дерево вывода цепочки 01001 1а6а6, изображен-
изображенное на рис. 8.35. Если при порождении этой цепочки использо-
использовать „двухуровневую" схему, описанную в замечании 8.12, то
получим такой вывод:
5 Ь SaTSb Ь SaSaSbSb Ь 01SaSbSb Ь
Ь 010TalSbSb h 010011ЗД h 0100UaTbaSb Ь
h 01001 la6aS6 Ь OlOOllabab.
Сначала порождается „двойник" цепочки abab Е L, а затем на
место первого символа (замененного аксио- ?
мой Sa „дочерней" грамматики Ga) подста-
вляется цепочка 01, на место второго сим-
вола — цепочка ООН, на место третьего — Л* Л I
aba, на место четвертого — цепочка 6. /\ / \ I
Заметим, что в общем случае построе- q \ s S Ь
ния вывода в грамматике G1 (если не обя- ИЧ Д^
зательно придерживаться „двухуровневой" / { \ / \\
стратегии) „дочерняя" грамматика может 0 Ta I a Tb a
начать „работать", как только в выводе по- А I
является ее аксиома. Так, по изображенному ' ^ *
на рис. 8.35 дереву вывода может быть по-
построен следующий левый вывод: ^ис# 8в35
5 Ь SaTSb h 01SaSbSb h 010TalSbSb h
h 0100115656 h 010011aT6a56 h
h 01001 labaSb h OlOOllabab.
Но если мы пренебрежем требованием, чтобы нетерминаль-
нетерминальные алфавиты грамматик G, Ga и Gb попарно не пересекались,
и отождествим, скажем, нетерминалы Ta, T& и Т, положив
Та = 2], = Т, то сможем вывести цепочку, не принадлежащую
суперпозиции 5(L,La,L5). Например,
S Ь SaTSb Ь 01Т5ь К 01ЬЬ^6 h 0166a. ^
666 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
В самом деле, цепочка 01 может быть получена применением
либо правила Sa -> 01, либо правила Та -> 01; цепочка ЬЬ —
применением правила Т& -> ЬЬ или Sb -> Ь6, цепочка а — при-
применением правила S& -* а или Т& -* а. Можно легко убедиться
в том, что в этом случае единственная цепочка, состоящая из
аксиом „дочерних" грамматик, т.е. символов ?а, ?&, из кото-
которой может быть выведена цепочка Olbba, равна SaSbSb- Но эта
цепочка не выводима из аксиомы S. Бели же мы, анализируя
цепочку 016Ьа, стали бы рассматривать в качестве правой ча-
части правила вывода не цепочку ЬЬ^ а цепочку Ь, то получили бы
подцепочку 6а, не являющуюся правой частью ни одного прави-
правила вывода, и тогда имели бы SaSbba — цепочку, не выводимую
из S.
Мы вывели „плохую" цепочку здесь потому, что „перепу-
„перепутав" нетерминалы грамматик, позволили „вклиниться" „дочер-
„дочерней" грамматике Gb в работу грамматики „верхнего уровня".
Аналогично можно построить пример, когда разные „дочер-
„дочерние" грамматики „мешают" друг другу.
Итак, требование, согласно которому нетерминальные ал-
алфавиты грамматик G и всех Gai попарно не пересекаются,
является существенным. #
Исследуем теперь вопрос о пересечении КС-языков. Введем
обозначение: если дан алфавит {6i, ...,Ь&}, то через [Ь? ••.&?]
обозначим язык {Ь"... Ь?: п ^ 0}.
Теорема 8.10. Класс КС-языков не замкнут относительно
пересечения.
4 Языки а*[Ьпсп] и [an6n]c*, как можно легко доказать, явля-
являются КС-языками, но их пересечение есть язык [an6ncn], кото-
который — как это было доказано в примере 8.11 — не КС-язык. >
Следствие 8.4. Дополнение КС-языка в общем случае не
является КС-языком.
< Действительно, если бы для любого КС-языка L его допол-
дополнение L было бы КС-языком, то для пересечения любых двух
8.5. Алгебраические свойства КС-языков 667
КС-языков L\ и L<l мы имели бы: L\ П L*i = L\ U L^ — КС-язык,
что противоречит теореме 8.10. >
Однако оказывается, что класс КС-языков замкнут относи-
относительно операции суженного пересечения языков — опера-
операции пересечения с регулярными языками.
Теорема 8.11. Если L — КС-язык, а Я — регулярный
язык, то L П R — КС-язык.
<4 Пусть G = (V, ЛГ, 5, Р) — КС-грамматика, порождающая
язык L, а М = (Q, V, go> F, J) — конечный автомат, допускаю-
допускающий язык R (см. 7.5).
Будем считать, что грамматика G дана в приведенной фор-
форме, причем аксиома не содержится в правых частях правил
вывода (см. 8.2). Конечный же автомат М является детер-
детерминированным.
В основе конструкции грамматики для пересечения LDR
лежит следующая неформальная идея. Мы хотим построить
такую КС-грамматику G;, которая порождала бы все цепоч-
цепочки, одновременно порождаемые грамматикой G и допускаемые
конечным автоматом М. Это значит, что любая цепочка ж,
порождаемая грамматикой G;, должна удовлетворять двум тре-
требованиям: 1) S \-q х и 2) в М должен найтись единственный
путь из начального состояния в одно из заключительных состо-
состояний, на котором читается цепочка х. Если цепочка х пустая,
то она принадлежит пересечению L П R тогда и только тогда,
когда в Р есть правило S -> А, а начальное состояние авто-
автомата М является и заключительным. Для непустой цепочки
х — хA)хB)...х(к) из пересечения LC\R тогда должна суще-
существовать единственная последовательность состояний go* si,...,
Sfc_i, q/ (q/ E F) множества Q, в которой go ~*z(i) 5ъ
5i -*zB) S2> • • • ? Sk-i ->x(k) Qf-
Будем тогда в качестве нетерминалов грамматики G1 рас-
рассматривать всевозможные упорядоченные тройки вида
668 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
где g, r — состояния конечного автомата М, а, X — сим-
символ из объединенного алфавита грамматики G (похожий прием
мы применяли, строя КС-грамматику, эквивалентную задано-
му МП-автомату, см. 8.4). Заставим грамматику G' выводить
из аксиомы все непустые цепочки вида
[qox(l)si][sixB)s2]... [sk-ix(k)qf]
для всех qf E F и всех последовательностей s\} 52,..., s^-i состо-
состояний из Q при условии, что S\rQx(l)xB)...x(k). Нетерминал
же [qar] при a E V может быть, по определению, заменен тер-
терминалом а тогда и только тогда, когда в системе команд 6
конечного автомата М есть команда qa —> г, т.е. из состояния
q по символу а можно перейти в состояние г.
При таком определении грамматики G1 она породит непу-
непустую терминальную цепочку х тогда и только тогда, когда х по-
порождается грамматикой G и читается на некотором пути из на-
начального состояния в одно из заключительных, — именно тогда
(и только тогда) из цепочки [qox(l)si][sixB)s2]'..[sk_ix(k)qf]
может быть выведена сама цепочка х = а;A)хB)... х(к). Образ-
Образно говоря, грамматика G1 каждый символ непустой цепочки яг,
порождаемой грамматикой G, помещает между двумя „стра-
„стражами" — состояниями конечного автомата, и символ может
избавиться от этих „стражей" тогда и только тогда, когда в
конечном автомате М есть переход по нему из первого состоя-
состояния во второе.
Дадим теперь формальное определение грамматики G':
где N' = {[qXr]: q,r€Q * X еУиЩиф), S'^VUN (акси-
(аксиома грамматики G;), а множество правил вывода Р1 строится
следующим образом:
1) правило вывода S' —У Л принадлежит Р' тогда и только
тогда, когда в множестве правил Р грамматики G есть правило
S -> А, а для конечного автомата М имеет место qo 6 F;
8.5. Алгебраические свойства КС-языков 669
2) для любого правила А —» у в Р G ф А) ъ Р1 вводится
множество всех правил вида
[5iAsk+i] -> [si7(l)s2][s27B)s3]"' • is^(k)sk+i]
для произвольной последовательности si, 52,..., 5&+i состояний
из множества Q (к ^ 1 — длина цепочки 7);
3) для любого заключительного состояния qj Е F конечного
автомата М ъР1 вводится правило вывода S" -> [^о^д/], где S —
аксиома грамматики G;
4) правило вывода [qar] -> а для а € V принадлежит Р' тогда
и только тогда, когда команда qa-лг принадлежит системе
команд S конечного автомата М;
5) никаких других правил вывода, кроме указанных в пп. 1-
4, множество Р' не содержит.
Непосредственно из построения грамматики G1 видно, что
пустая цепочка А порождается грамматикой G1 тогда и только
тогда, когда правило вывода S -» А содержится в множестве Р,
т.е. A G L, и конечный автомат М допускает пустую цепочку,
т.е. до € F- Итак, Sr h* А тогда и только тогда, когда А € L П R.
Для непустой цепочки х = хA)жB)... х(т) можно доказать
(подробное доказательство мы опускаем*), что S \-q #, т.е.
xGL, тогда и только тогда, когда
S' Ь [qoSqf] Ь* [qox(l)sl][slxB)s2]... [sm-ix{m)qf]
ДЛЯ ЛЮбыХ 51, ..., 5m_l € Q.
Тогда из цепочки [go#(l)si][5ia;BM2]...[5m_ix(m)g^] цепоч-
цепочка х = жA)а:B)... х(т) может быть выведена в грамматике G'
применением правила, приведенного выше в п. 4, в том и только
в том случае, когда для конечного автомата М имеет место
90 ->яA) «1 ->хB) «2 -> • • • -* Sm-i -^x(m) Qf
*Это доказательство без особого труда может быть восстановлено с
помощью метода индукции по длине вывода.
670
8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
для некоторых состояний з\, ..., sm_i, т.е. х читается на пути
из до в qf, проходящем через состояния з\, ..., sm-b и тем
самым x€R, т.е. х Е L П R.
Итак, окончательно х ? L(Gf) &x€LnR. >
Пример 8.21. Построим грамматику, порождающую пе-
пересечение языка всех палиндромов в алфавите {а,&} с языком
а*ЬЬа*.
Грамматику для языка палиндромов задаем в виде
S-> аТа\ЪТЪ\аа\ЪЪ\а\Ъ\\
Т -> аТа\ЪТЪ\аа\ЪЪ\а\Ъ,
где S — аксиома. Граф конечного автомата, допускающего
язык a*bba*, приведен на рис. 8.36.
Согласно правилам построения грам-
грамматики G', изложенным в доказательстве
теоремы 8.11, имеем следующую грамма-
тику для пересечения заданных языков:
Рис. 8.36
& -> [qoSq2],
-> [г1аг2][г2Ггз][гзаг4] \[ribr2}[r2Tr3][rsbr4] (8.20)
(для любых последовательностей состояний ri, r2, гз, г4 конеч-
конечного автомата);
[riSrs] -> [riar2][riar2) \[г\Ьг2][г2Ьг^}
(для любых последовательностей состояний ri, r2, гз конечного
автомата);
(для любых последовательностей состояний п, г2 конечного
автомата);
[riTr4]
8.5. Алгебраические свойства КС-языков 671
(для любых последовательностей состояний г\, г2, гз, г\ конеч-
конечного автомата);
[пТг3] -> [r1ar2][r1ar2] |[ribr2][r26r3] (8.21)
(для любых последовательностей состояний п, г2, гз конечного
автомата);
(для любых последовательностей состояний г\} г2 конечного
автомата);
[qoaqo] -> а, (8.22)
>b, (8.23)
>b, (8.24)
> а. (8.25)
Рассмотрим пример порождения какой-нибудь цепочки из
определенного выше пересечения двух языков. Возьмем цепоч-
цепочку abba. Выведем сначала „двойника" этой цепочки, в котором
каждый символ „окружен" состояниями конечного автомата.
В процессе вывода мы стараемся „положить" нашу цепочку на
некоторый путь из начальной вершины автомата в заключи-
заключительную:
S' Ь [qoSq2] Ь [qoaqo][qoTq2\[q2aq2] Ь [96O»][«)bgi]bibft]feaft].
На втором шаге написанного выше вывода мы применили
первое из правил (8.20) при г\ = г2 = 9о> гз = Г4 = <72> а на третьем
шаге — второе правило (8.21) при г\ = до? ^2 = 9ъ гз = 92-
Теперь мы видим, что все „скобки" состояний можно „от-
„отряхнуть": последовательно применяя правила (8.22)-(8.25), по-
получаем цепочку abba.
Рассмотрим теперь „неправильную" цепочку aba ? a*bba*.
Вывод ее „двойника" может быть таким:
S' Ь [qoSq2] Ь
672 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
При выводе мы старались помещать каждый входной сим-
символ конечного автомата между такими состояниями, чтобы он
входил в метку дуги из первого во второе состояние, но мы ви-
видим, что нетерминал [до&<72] не может быть заменен ни одним
терминалом, и вывод зашел в тупик. Разбор других вариан-
вариантов вывода п двойника" цепочки aba мы опускаем. В данном
случае оказывается, что любой вывод закончится тупиковой
цепочкой. #
Заметим, что в рассмотренном примере конструкцию тео-
теоремы нельзя применять к грамматике языка палиндромов, если
она задана в виде
S->aSa\bSb\a\b\\,
поскольку в этом случае нельзя обойтись без применения пра-
правила S -» А при порождении цепочки четной длины.
Так как при построении грамматики G' правила с пустой
правой частью (из множества правил грамматики G) никак
не преобразуются, грамматика G1 в таком случае не породит
я двойника" ни одной цепочки четной длины языка палиндро-
палиндромов.
Следовательно, требование, чтобы грамматика КС-языка L
была задана в приведенной форме и ее единственное разрешен-
разрешенное Л-правило S -> А применялось только при выводе пустой
цепочки, является существенным при построении КС-грамма-
КС-грамматики для пересечения языка L с регулярным языком R.
Доказанное утверждение о „контекстной свободное™" пе-
пересечения КС-языка с любым регулярным языком в совокупно-
совокупности с леммой о разрастании для КС-языков полезно при доказа-
доказательстве утверждений о том, что какой-либо язык не является
контекстно-свободным.
Пример 8.22. Докажем, что язык L = {ww: w € {a, b}*} —
так называемый язык двойных слов в алфавите {а, 6} — не
является контекстно-свободным.
Д.8.1. О методах синтаксического анализа КС-языков 673
Применить к решению этой задачи сразу лемму о разраста-
разрастании довольно трудно. Поступим так. Рассмотрим пересечение
языка L с регулярным языком a*b*a*b*. Легко понять, что это
пересечение состоит из всех цепочек вида ambnambn (m, n ^ 0).
Предполагая, что язык L контекстно-свободный, получим в си-
силу теоремы 8.11, что контекстно-свободным является и язык
{ambnambn: m,n^ 0}. Однако этот язык не есть КС-язык (см.
пример 8.12). Следовательно, не является КС-языком и исход-
исходный язык L.
Дополнение 8.1. О методах
синтаксического анализа КС-языков
Проблема синтаксического анализа для КС-языков со-
состоит в построении алгоритма, который по любой КС-грамма-
КС-грамматике G = (V, N, 5, Р) и цепочке х в ее терминальном алфави-
алфавите V распознает, принадлежит ли х языку L(G), порождаемому
грамматикой G. В случае положительного ответа на вопрос
алгоритм должен строить дерево вывода х в грамматике G.
Существование такого алгоритма следует из факта разре-
разрешимости проблемы принадлежности для КС-языков. Мы рас-
рассмотрим некоторые алгоритмы синтаксического анализа для
определенных классов КС-языков.
Прототипом синтаксического анализатора является МП-ав-
МП-автомат, который строится по данной КС-грамматике (см. 8.4),
но такой МП-автомат, как мы видели, является в общем случае
недетерминированным и может даже для допустимой цепочки
построить вывод, который заканчивается тупиковой конфигу-
конфигурацией. Чтобы на основе такого распознавателя построить
алгоритм синтаксического анализа (и тем самым превратить
распознаватель в анализатор), нужно разработать опреде-
определенный механизм управления выводом на множестве кон-
конфигураций МП-автомата. Этот механизм должен обеспечить
эффективный поиск допускающей последовательности конфи-
674 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
гураций для допустимых цепочек. В частности, может быть по-
поставлена задача разработки алгоритма беступикового, или
однопроходного, анализа. Беступиковый анализ имеет ме-
место, если получение тупиковой конфигурации в процессе анали-
анализа означает „неправильность" анализируемой цепочки, т.е. тот
факт, что она не принадлежит языку, порождаемому заданной
грамматикой. Беступиковый анализ, как можно показать, не-
невозможен в случае произвольного КС-языка, но для некоторых
(достаточно широких) классов КС-языков он может быть реа-
реализован. Некоторые алгоритмы беступикового синтаксическо-
синтаксического анализа мы очень коротко рассмотрим в этом дополнении.
Существуют две основные стратегии синтаксического ана-
анализа: 1) нисходящий анализ (называемый также анализом
„сверху вниз", или анализом „разверткой") и 2) восходя-
восходящий анализ (анализ „снизу вверх", „сверткой").
В нисходящем анализе дерево вывода цепочки строится от
корня к листьям, т.е. дерево вывода „реконструируется" в
прямом порядке, и аксиома грамматики „развертывается" в
цепочку. В восходящем анализе дерево вывода строится от
листьев к корню и анализируемая цепочка „свертывается" в
аксиому.
Рассмотрим две стратегии анализа по очереди.
Нисходящий анализ. ??(&)-грамматики. Мы виде-
видели, что МП-автомат, который при доказательстве теоремы 8.8
мы строили по данной КС-грамматике, „воспроизводит" левый
вывод в грамматике. Основная „задача" данного автомата как
распознавателя состоит в том, чтобы на каждом шаге „уга-
„угадать" очередное применяемое правило вывода и „правильно
выбрать" соответствующую команду при построении допуска-
допускающей последовательности конфигураций. Механизм управле-
управления выводом, которым мы должны снабдить классический МП-
автомат, должен обеспечить выбор команды (единственной в
случае беступикового анализа) по определенной информации
о состоянии процесса поиска дерева вывода (или, что равно-
Д.8.1. О методах синтаксического анализа КС-языков
675
сильно, левого вывода) входной цепочки. Обычно механизм
управления выводом реализуется в виде специальных таблиц,
которые называют управляющими таблицами и которые
можно рассматривать как дополнительное устройство памяти
в МП-автомате.
Существует класс грамматик, называемых LL(k)-грамма-
LL(k)-грамматиками, в которых применяемая команда однозначно опреде-
определяется:
1) прочитанной частью w входной цепочки; эту цепочку w
называют левым контекстом;
2) находящимся в данный момент в верхней ячейке магазина
нетерминальным символом А;
3) началом (префиксом) v непрочитанной части цепочки,
состоящим не более чем из к букв (А: ^ 1); этот префикс
называют аванцепочкой (рис. 8.37).
Эта информация, по которой беступиковый анализатор вы-
выбирает нужную команду на каждом шаге работы с входной
цепочкой, организована в виде упра-
управляющей таблицы (конкретные фор-
формы таких таблиц будут рассмотре-
рассмотрены ниже). При этом левый вывод це-
цепочки х = wvu, если х G L(G), может
быть представлен следующим обра-
образом: из аксиомы выводится цепочка
wAa, затем нетерминал А заменяет-
заменяется в соответствии с правилом А -> 7
и из цепочки уа выводится терми-
терминальная цепочка vu, где
Входная лента
v
W
Головка
Магазин
Блок Q
управления
Рис. 8.37
I
I
I
\v\ ^ k и S h * wAa h wja Ь * wvu
i
(символ h означает левую выводимость).
Описанное выше представление левого вывода цепочки wvu
предполагает, что мы произвольно в этом выводе фиксирова-
фиксировали некий шаг, состоящий в замене нетерминала А посредством
676 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
применения правила вывода А -> j. Так как в левом выводе
на каждом шаге производится замена самого левого вхожде-
вхождения нетерминального символа, то слева от А в цепочке wAa,
полученной перед рассматриваемым шагом, должны быть толь-
только терминальные символы. Следовательно, определенный выше
левый контекст w есть не что иное, как левое крыло вхождения
нетерминала А в цепочку wAa.
Моделируя этот левый вывод, т.е. читая записанную на
входной ленте цепочку х = wvu, МП-автомат читает левый
контекст w, а затем с помощью управляющей таблицы, „видя"
в магазине символ А, учитывая левый контекст w и зная
аванцепочку v, принимает единственно правильное решение,
применяя команду, соответствующую правилу А~>7- Так
на интуитивном уровне можно определить ключевое свойство
Переходим теперь к построению формального определения
Пусть дана КС-грамматика G. Для цепочки а в объединен-
объединенном алфавите грамматики G и положительного натурального
к определим множество ^(а), состоящее из всех терминальных
цепочек, которые либо выводятся из цепочки а (если их дли-
длина строго меньше fc), либо являются ^-буквенными префиксами
терминальных цепочек, выводимых из а (обратим внимание на
то, что везде речь идет о левом выводе).
Таким образом,
Fk(a) = {v : (ah* v)b(\v\ < к) V (Зх е V*){ah* vx)b(\v\ = *)}.
Нетрудно видеть, что для всякой терминальной цепочки х
получим Fk{x) = {ж}, если |х| < fc, и Fk(x) = {хA)хB)...х(к)},
если \х\ > к. Множества Fk(a) (для разных цепочек а) иногда
будем называть Рк-множествами.
Пример 8.23. Зададим грамматику G с терминальным ал-
алфавитом {а, Ь, с, d} и нетерминальным алфавитом, состоящим
Д.8.1. О методах синтаксического анализа КС-языков 677
из одной аксиомы S, следующим множеством правил вывода:
S->aSbSc\aSb\bSc\d.
Вычислим множество F^aSbSc). Первая буква всех терми-
терминальных цепочек, выводимых из заданной, уже фиксирована —
это буква а. Нетерминал S может быть заменен буквой d, после
чего возникнет трехбуквенный префикс adb. Но символ S мож-
можно заменить и цепочками aSbSc, aSb, 65с. В силу этого первые
две буквы цепочки, выводимой из исходной, могут быть либо
aa, либо ab. Продолжение вывода, как нетрудно понять, может
дать третью букву — либо а, либо 6, либо d. Окончательно
получаем F^(aSbSc) = {adb, aaa, aab, aad, aba, abb, abd}.
Определение 8.11. КС-грамматику G = (V, N, S, P) на-
называют LL(k)-грамматикой (для произвольно фиксирован-
фиксированного k ^ 1), если для любых w G V*, А Е N, а Е (V U JV)*, таких,
что существуют левые выводы
l l l
Sh*wAa\-wCa\-*wy
и
l l l
S Ь* wAa Ь w^a Ь* wz,
из Fk(y) = FfcB) следует /3 = 7-
Таким образом, из этого определения следует, что для
ЬЬ(Л)-грамматики левый контекст w нетерминала А в цепочке
wAa и не более чем к символов, с которых начинается терми-
терминальная цепочка j/, выводимая из Аа, однозначно определяют
то правило, которое нужно применить к цепочке wAa (заменяя
в ней выделенное, т.е. первое, вхождение нетерминала А), что-
чтобы сделать очередной шаг в левом выводе цепочки wy (и именно
этой цепочки!) из аксиомы грамматики G. При совпадении
множеств Fk(y) и Fk(z), как следует из сформулированного
определения, указанные два вывода „сливаются" в один, т.е.
тогда у = z.
678 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Определение 1у?(А;)-грамматики является само по себе труд-
нопроверяемым. Нужно какое-то условие, проверка которо-
которого позволила бы дать ответ на вопрос, является ли заданная
КС-грамматика ??(А;)-грамматикой. Доказывается, что дать
ответ на этот вопрос можно, только фиксировав число к. По-
Построить же алгоритм, отвечающий на вопрос, является ли дан-
данная КС-грамматика ??(&)-грамматикой для некоторого к (не
задавая его заранее), невозможно.
Следующая теорема (формулируемая без доказательства)
дает соответствующий критерий (необходимое и достаточное
условие) при фиксированном к.
Теорема 8.12. КС-грамматика G является ??(Л)-грамма-
тикой (для фиксированного к ^ 1) тогда и только тогда, когда
для любой цепочки w Е V* выполняется следующее условие: для
любых А € iV, а Е (V U TV)*, таких, что S Ь * wAa, и любых двух
различных правил А —>• /3 и А -> у грамматики G имеет место
Fk@a)nFk(ja) = 0. #
Условие теоремы называют часто LL(k)-условием. Его
следует проверять, фиксируя по очереди левые контексты (т.е.
различные цепочки w) для всех нетерминалов грамматики.
Рассмотрим пример, в котором, используя теорему 8.12,
мы убедимся в том, что заданная КС-грамматика является
LL(/с)-грамматикой (для фиксированного к).
Пример 8.24. Грамматика G задается системой правил
A->Saa\b.
Докажем, что данная грамматика является ??B)-грамматикой.
Чтобы проверить условие теоремы 8.12, достаточно для ка-
каждого нетерминала В € {5, А} нашей грамматики проделать
следующее: 1) вычислить все такие цепочки w G {о,Ь}* и а €
Е {о, Ь, 5, А}, что имеет место левая выводимость
Sh*wBa; (8.26)
Д.8.1. О методах синтаксического анализа КС-языков 679
2) фиксировав „левый контекст" w, для каждой пары различ-
различных правил вывода В -> 7 и В —> /? вычислить множества JP2(/3a)
и -РгGа) Для всех таких а, что при фиксированном w выполня-
выполняется (8.26), и убедиться в том, что их пересечение пусто.
Бели выполнение п. 2 для всех возможных левых контекстов
w и всех нетерминалов В подтвердит истинность условия те-
теоремы 8.12, то тем самым и будет доказано, что перед нами
LL B)-грамматика.
Следует заметить, что в общем случае вычисление пар цепо-
цепочек (ги, а), удовлетворяющих условию (8.26) (для всех нетерми-
нетерминалов В КС-грамматики), требует применения специального
алгоритма. Но для конкретной грамматики нашего примера
эти пары цепочек достаточно просто вычисляются из анализа
выводов грамматики. По очереди проанализуем оба нетерми-
нетерминала, т.е. S и А, грамматики G.
Нетерминал S. В этом случае имеем, во-первых, триви-
тривиальную выводимость S Ь° 5 за нуль шагов, т.е. в этом случае
цепочки w и а обе являются пустыми: w = a = А. Нетерминал S
может быть заменен согласно правилу A) с правой частью аЬА
или согласно правилу B) с пустой правой частью. Вычислим
тогда множества F2(abA) и 1*2(А). Ясно, что F2{abA) = {ab}, a
F2 (А) = {А} и эти множества не пересекаются.
Проанализируем теперь, каким образом в заданной грам-
грамматике может быть выведена из аксиомы 5 за число шагов,
большее нуля, цепочка вида wSa для некоторых терминальной
цепочки w и цепочки в объединенном алфавите а.
Так как вхождение S может возникнуть только после при-
применения правила C), а чтобы применить его, нужно сначала
применить правило A), то, чередуя применение этих правил
п ^ 1 раз, получим вывод:
5 Ь аЪА Ь abSaa Ь аЪаЪАаа Ь
Ь ababSaaaa Ь ... Ь {ab)nS{aa)n. (8.27)
680 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Это значит, что все возможные пары (ги, а), такие, что
I
S Ь * wSa (с учетом уже ранее рассмотренного случая, когда
обе цепочки пусты), есть w = (ab)n и а = {аа)п, га ^ 0.
Вычисляем множества F2(abA(aa)n) и F2(X{aa)n) для раз-
различных га ^ 0. Первое множество, как нетрудно видеть, для
всех га будет равно {ab}, a второе при га = 0 будет состоять из
одной пустой цепочки, а при га > 0 — из цепочки аа, т.е. можно
утверждать, что для всех га ^ 0 пересечение
F2(a6A(aa)n) nF2(A(aa)n) = 0.
Итак, для нетерминала S (аксиомы грамматики G) условие
теоремы 8.12 выполнено.
Нетерминал А. Рассматривая вывод (8.27), легко убе-
убедиться в том, что все пары (гу, а), для которых имеет место
левая выводимость S Ь* wAa, есть w = (a6)n, a = (aaO1^1 для
всех п ^ 1.
Нетерминал А является левой частью двух правил вывода
C) и D) с правыми частями Saa и Ь соответственно. Вычисля-
Вычисляем соответствующие ^-множества: F2{Saa(aa)n~l) = {ab, aa},
а JF2F(ao)n) = {Ь}, если п = 1, и fb^aaI1) = {6a}, если
п > 1. Как видно, при всех га пересечение указанных множеств
пусто. Тем самым доказано, что и для нетерминала А крите-
критерий теоремы 8.12 выполнен и заданная грамматика является
Ь?B)-грамматикой.
Полученный результат показывает также, что эта грамма-
грамматика является ??B)-грамматикой, не являясь LL(^-граммати-
LL(^-грамматикой. Действительно, для нетерминала S получим
при всех п ^ 0, а F\ (Х(аа)п) = {а} при всех га > 1. Следовательно,
при всех га ^ 1 указанные множества совпадут, что означает
Д.8.1. О методах синтаксического анализа, КС-языков
681
невыполнение ??A)-условия. Заметим, что для нетерминала А
1гЬA)-условие выполняется.
Результаты анализа представлены в табл. 8.1.
Нетерминал
S
А
Таблица
8.1
Аванцепочка
aa
2
3
ab
1
3
6а
4
ЬЬ
—
а
—
ь
4
А
2
Внутри таблицы указаны номера применяемых правил. Про-
Прочерк означает, что данная пара (нетерминал, аванцепочка) не
определяет никакого правила, и возникновение такой пары в
процессе анализа сигнализирует о синтаксической ошибке.
Мы видим, что в данном случае номер применяемого на
каждом шаге правила вывода однозначно определяется только
двумя факторами: нетерминалом в верхней ячейке магазина
и аванцепочкой. ?Ь(А;)-грамматики, в которых выполняется
такое условие, называют сильными LL(k)-грамматиками.
Таблица подобного вида для сильной ??(А;)-грамматики и
является примером управляющей таблицы. Именно она обес-
обеспечивает в данном случае тот механизм управления выводом,
который позволяет МП-автомату, построенному по заданной
сильной ??(&)-грамматике, на каждом шаге однозначно вы-
выбирать правило вывода и для „правильной" цепочки строить
ее левый вывод, а для „неправильной" — сигнализировать об
ошибке. #
Следующий пример показывает, что существуют LL(fc)-rpaM-
матики, не являющиеся сильными.
Пример 8.25. Зададим грамматику G\ системой правил
5 -> аАаа\ЪАЪа,
22 - 10061
682
8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Для этой грамматики легко построить все ее деревья вывода
(рис. 8.38) и проверить ЬЬ(к)-условие.
Ах
а А а а а А а а Ь А Ъ а Ъ А Ъ а
Рис. 8.38
I
В данном случае S Ь* wSa влечет w = Л, а = А и F2(aAaa) =
= {об, aa}, a F2\bAba) = {bb}, т.е. F2(a;4aa) nF2(bAba) = 0.
Из S h * гу-Aa следует, что ги = а или w = b. Если to = а, то
a = aa и F2(baa) = {ba}, a i^Aaa) = {aa}, т.е. F2(baa) flF2(Aa) =
= 0.
Если же tu = 6, то a = ba и F2(bba) = {66}, F2(Xba) = {ba},
и в этом случае также F2(bba) f)F2(Xba) = 0. Таким образом,
рассматриваемая грамматика есть LL B)-грамматика.
Сведем полученные результаты в табл. 8.2.
Таблица 8.2
Левый
контекст
Л
А
a
Ъ
Нетерминал
5
S
А
А
Аванцепочка
аЬ
аа
bb
ba
aa
bb
ba
Применимое
правило
A)
A)
B)
C)
D)
C)
D)
Д.8.1. О методах синтаксического анализа КС-языков 683
Из табл. 8.2 следует, что одна и та же пара (А, 6а) не
определяет однозначно применяемого правила и требуется ин-
информация о левом контексте.
Из этой же таблицы видно, что данная грамматика не явля-
является ??A)-грамматикой, поскольку, например, однобуквенная
аванцепочка Ь вместе с нетерминалом А и левым контекстом Ь
не определяет однозначно применимого правила. #
Таким образом, для сильных ??(&)-грамматик МП-авто-
МП-автомат, который строится по КС-грамматике, может быть пре-
преобразован в синтаксический анализатор путем добавления к
нему управляющей таблицы и выходной ленты (первоначально
пустой), на которой автомат пишет номера правил в порядке их
применения, а также сигнал ошибки. В результате анализа для
правильной цепочки, записанной на входной ленте, на выходной
ленте появится ее левый вывод (точнее, „протокол" левого вы-
вывода в виде последовательности номеров применимых правил),
а для неправильной цепочки на выходной ленте появится сооб-
сообщение об ошибке (в виде какого-нибудь специального символа).
Представим теперь протоколы анализа некоторых цепочек
в грамматике G примера 8.24.
Пусть х = ababbaa; имеем последовательность конфигураций
(четвертая компонента конфигурации — содержимое выходной
ленты):
(q, ababbaa, S, А) Ь (q, ababbaa, abA, 1) Ь2
Ь2 (q, abbaa, А, 1) Ь (q, abbaa, Saa, 13) h
h {q, abbaa, abAaa, 131) h2 (q, baa, Aaa, 131) h
\r {q, baa, baa, 1314) h3 (q, X, A, 1314).
Обратим внимание на то, что на каждом шаге вывода наш
автомат-анализатор в существенном отличии от обычного рас-
распознавателя, который может легко „заблудиться" (особенно
при выборе альтернативы для нетерминала А), использует ин-
информацию управляющей таблицы.
22*
684 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Посмотрим, как отработает такой анализатор синтаксиче-
синтаксическую ошибку. Берем цепочку у = аббб, имеем
(д, аббб, 5, A) h (g, аЬЬЬ, аЬА, 1) Ь2
Ь2 (9, 66, А, 1) Ь (9, 66, А,
так как пара (А, 66) не определяет никакого правила.
Для не сильной ?Ь(&)-грамматики учет левых контекстов в
общем случае весьма сложен, и мы его здесь не рассматриваем*.
Приведем, наконец, простой пример грамматики с терми-
терминальным алфавитом {а, 6,0,1}, не являющейся LL(fc)-rpaMMa-
тикой ни для какого к:
S->A\B,
Для любого к^1 имеем
SbAh*
S\~B\-*aklb2k.
Одинаковый префикс ак не дает возможности отождествить
цепочки C = А и 7 = В, т.е. нет возможности обеспечить выбор
альтернативы для нетерминала 5.
Восходящий анализ. ЬЯ(/с)-грамматики. Ключевым
понятием при рассмотрении восходящего синтаксического ана-
анализа является понятие основы.
Определение 8-12. Пусть G = (V, N, S, Р) — КС-грам-
КС-грамматика, f — цепочка в объединенном алфавите, А -» а ? Р.
При а С ? вхождение а в f (/?, a, 7) называют основой, если
цепочка /ЗЛ7 выводима из аксиомы 5 при условии, что цепочка
? выводима из аксиомы 5.
"См.: Ахо А.у Ульман Док.
Д.8.1. О методах синтаксического анализа КС-языков 685
Таким образом, по определению, основа — это такое вхо-
вхождение правой части некоторого правила КС-грамматики в
некоторую выводимую из аксиомы цепочку, что после замены
этой правой части соответствующим нетерминалом полученная
цепочка снова будет выводимой из аксиомы. Заметим, что для
не выводимой из аксиомы цепочки любое вхождение правой ча-
части некоторого правила в нее можно считать основой.
Замечание 8.13. Ни в коем случае нельзя путать понятие
оснозы в смысле определения 8.12 с понятием основы вхождения
(см. 7.1)!
Пример. Рассмотрим грамматику, задаваемую системой
правил:
S-+Ac\Bd,
A->aAb\ab,
В -> aBbb\abb.
Возьмем цепочку х = aabbbbd. Мы видим здесь вхождения
двух правых частей правил — ab и abb. Вхождение первой
цепочки не является основой. Действительно, заменяя ab не-
нетерминалом А, получим цепочку aAbbbd. Для этой цепочки
существует единственное правило А -* aAb, правая часть ко-
которого входит в нее. „Свертывая" цепочку aAb в нетерминал
А, получим Abbd — слово, в которое не входит ни одна правая
часть какого-либо правила данной грамматики. Следователь-
Следовательно, ни полученная цепочка, ни предшествующая ей цепочка не
являются выводимыми из аксиомы.
Возвращаемся к цепочке х и, заменяя подцепочку abb нетер-
нетерминалом В, получаем aBbbd, где единственное вхождение пра-
правой части правила — aBbb. Производя замену этого правила
нетерминалом В, будем иметь цепочку Bd, которая „сверты-
„свертывается" в аксиому S. Итак, мы провели в обратном порядке
вывод цепочки х из аксиомы:
5 Ь Bd Ь aBbbd Ь aabbbbd. #
686 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Задача восходящего анализа и состоит в поиске „редукции"
исходной терминальной цепочки в аксиому, где на каждом шаге
производится поиск основы в текущую цепочку с последующей
заменой ее соответствующим нетерминалом, т.е. применяется
„инверсия" некоторого правила данной КС-грамматики: пра-
правая часть правила заменяется левой. Нетрудно понять, что если
мы заменяем на каждом шаге такой „редукции" самую левую
основу, то восстанавливаем с конца к началу правый вывод
исходной цепочки, а если самую правую основу, то „реконстру-
„реконструируем" левый вывод.
Как и в случае нисходящего анализа, здесь возникает про-
проблема тупиков и связанная с ней проблема управления выводом.
Мы рассмотрим некоторые простейшие методы построения
„беступиковой редукции", а именно такие методы определения
основы, при применении которых попадание в тупик на неко-
некотором шаге редукции влечет синтаксическую неправильность
входной цепочки.
Один из методов состоит в сопоставлении каждому правилу
КС-грамматики некоторого бинарного отношения на множе-
множестве (VUN)*. Вхождение правой части некоторого прави-
правила является основой тогда и только тогда, когда его кры-
крылья принадлежат сопоставленному данному правилу бинарному
отношению. Проблему единственности определяемой таким
образом основы, равно как и проблему характеристики класса
КС-грамматик, допускающих такую „параметризацию" бинар-
бинарными отношениями, мы здесь не рассматриваем*.
Ограничимся простым примером.
Рассмотрим грамматику, порождающую множество непу-
непустых палиндромов в заданном алфавите V:
S->aSa\aa\a, aeV.
Каждому правилу сопоставим одно и то же отношение
{(u,v):\u\ = \v\},
*См.: Глушков В.М., Цейтлин Г.Е., Ющенко ЕЖ
Д.8.1. О методах синтаксического анализа КС-языков 687
так, что этому отношению принадлежат только пары с одина-
одинаковой длиной компонент.
Тогда осуществима беступиковая редукция любого палин-
палиндрома. Например:
abbccbba Ч abbSbba Ч abSba Ч aSa Ч 5.
В данном случае на каждом шаге принадлежность крыльев
вхождения правой части правила введенному отношению од-
однозначно определяет основу, и получение тупиковой цепочки
означает ее неправильность. Заметим, что без введенного
таким образом управления выводом (т.е. выбором очередного
правила) даже при „свертывании" правильной цепочки можно
попасть в тупик:
abbccbba Ч aSccbba Ч aSSbba Ч aSSSa.
Неверное определение основы на первом шаге редукции при-
привело к тупиковой (т.е. не содержащей ни одного вхождения
правой части какого-либо правила) цепочке, хотя входная це-
цепочка является правильной.
Несколько более подробно рассмотрим класс КС-языков, до-
допускающих беступиковый восходящий анализ и порождаемых
так называемыми 2>Л(А;)-грамматиками.
Неформально LR(k)-грамматика, к ^ О, — это КС-грам-
КС-грамматика, в которой основа однозначно определяется по левому
крылу вхождения правой части некоторого правила вывода
(„левому контексту") и по не более чем fc-буквенному пре-
префиксу правого крыла („правого контекста"). Строго понятие
ЬД(А;)-грамматики вводится весьма сложно, и мы его опускаем.
Оказывается, что класс языков, порождаемых Ы1(к)-грам-
матиками, может быть охарактеризован в терминах детерми-
детерминированных МП-автоматов (ДМП-автоматов).
Прежде чем определять ДМП-автоматы, введем в рассмо-
рассмотрение модификацию МП-автомата, называемую расширен-
расширенным МП-автоматом, которая как раз ориентирована на
представление восходящего синтаксического анализа.
688 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Говоря коротко, отличие расширенного МП-автомата от
обычного состоит в том, что в магазине можно заменять
не только верхний символ, но и непустую цепочку символов,
расположенную в верхних ячейках магазина, так, что первый ее
символ есть верхний символ магазина, второй символ — символ,
расположенный под верхним, и т.д.
Формально расширенный МП-автомат определяется совер-
совершенно так же, как обычный (см. определение 8.7), но функ-
функция переходов задается системой команд вида qaa ->• г/?, где
а ? V U {А}; аи /3 — магазинные цепочки, причем а не пуста.
При записи системы команд расширенного МП-автомата
условимся записывать магазинные цепочки от „дна" магазина
к его „верху".
Можно доказать, что расширенные МП-автоматы допуска-
допускают в точности тот же класс языков, что и обычные, т.е. можно
доказать, что по любому расширенному МП-автомату можно
построить эквивалентный ему МП-автомат в смысле определе-
определения 8.7*. Далее будем говорить „МП-автомат", имея в виду
расширенный МП-автомат.
Определение 8.13. МП-автомат называют детермини-
детерминированным (ДМП-автоматом), если из любой его конфигу-
конфигурации непосредственно выводится не более чем одна конфи-
конфигурация.
Нетрудно доказать следующее утверждение.
Теорема 8.13. МП-автомат является ДМП-автоматом
тогда и только тогда, когда для любой упорядоченной пары
(g, a) G Q х Г+ верно одно из двух:
1) для любого a € V существует не более одной команды
с левой частью qaa, причем если для некоторого а Е V такая
команда существует, то не существует команды с левой частью
q\a и не существует ни одной команды с левой частью qa'a',
где a' ? {а, Л} и а; является концом цепочки а;
*См.: Ахо А., Ульман Дою,
Д.8.1. О методах синтаксического анализа КС-языков 689
2) существует не более одной команды с левой частью q\a,
причем если такая команда существует, то не существует ни
одной команды с левой частью qaa1, где a Е V U {А} и о! —
конец цепочки а, и не существует ни одной команды с левой
частью qaa, a G V. #
Связь между ДМП-автоматами и ?Д(Л)-грамматиками ус-
устанавливается следующей теоремой.
Теорема 8.14, Язык допускается ДМП-автоматом тогда и
только тогда, когда он порождается некоторой ЬЯ(А;)-грамма-
тикой.
Определение 8.14. Язык называют детерминирован-
детерминированным КС-языком, если он допускается некоторым ДМП-авто-
ДМП-автоматом.
Заметим, что поскольку для произвольного МП-автомата
(в отличие от конечных автоматов), вообще говоря, не может
быть построен эквивалентный ему ДМП-автомат, то класс
детерминированных КС-языков строго содержится в классе
всех КС-языков.
Для детерминированных КС-языков может быть предложе-
предложена стратегия восходящего анализа, называемая стратегией
„перенос — свертка". Суть ее состоит в следующем: вход-
входная цепочка посимвольно переписывается в магазин до тех пор,
пока в магазине не сформируется основа (однозначно опреде-
определяемая прочитанной частью цепочки и не более чем к буквами
непрочитанной части для некоторого фиксированного к ^ 0).
Сформированная в магазине основа заменяется соответ-
соответствующим нетерминалом. Бели после этой замены в верхних
ячейках магазина опять получилась основа, то она вновь „свер-
„свертывается" в нетерминал, и так до тех пор, пока не окажется,
что либо вся входная цепочка прочитана, а в магазине кроме
начального символа в верхней ячейке осталась аксиома грам-
грамматики, либо цепочка еще не прочитана, а в верху магазина
основы нет, либо, наконец, цепочка прочитана, а в верху мага-
магазина ни аксиомы, ни основы нет.
690 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
В первом случае мы имеем „допуск" цепочки (успешный
результат синтаксического анализа), во втором необходимо
возобновить процесс „переноса", т.е. продолжить переписыва-
переписывание входной цепочки в магазин, а в третьем констатировать
„недопуск" (синтаксическую ошибку).
Согласно теореме 8.14, подобный алгоритм может быть за-
запрограммирован в системе команд некоторого ДМП-автомата
(точнее, ДМП-автомата с выходной лентой, на которой записы-
записываются номера применяемых правил грамматики и/или сигнал
ошибки).
Строгая теория ЬЛ(Л)-грамматик весьма сложна и никак не
может быть даже фрагментарно изложена в рамках настоящего
учебника.
Мы рассмотрим в заключение один пример.
Пример 8.26. Приведем ДМП-автомат для анализа языка
правильных скобочных структур, порождаемых грамматикой
?—>>() | (S) | SS. Точнее, мы рассмотрим язык правильных
скобочных структур с „концевым маркером" •: записывая
на ленту правильную скобочную структуру, в конце ставим
символ *.
Система команд анализирующего ДМП-автомата имеет сле-
следующий вид:
qoaO -t qi Da,
qoaa' -»• qia'a,
qi4) -»QiS,
qiX(S)^qiS,
qiXSS -> qiS,
9i A7 -»• 907,
qiXDa -»• qo Da,
qiaDS ->• qiOSa,
qi + OS-t&O.
A)
B)
C)
D)
E)
F)
G)
(8)
(9)
В этой системе команд qo и q<i — соответственно начальное
заключительное состояния; a G {(,)}; a' G {(,), S}; ? — на-
Д.8.1. О методах синтаксического анализа. КС-языков 691
чальный символ магазина (называемый иногда „маркером дна
магазина"); j — произвольная цепочка, длина которой равна 3
и которая не равна E) и не оканчивается цепочкой () или SS.
Легко убедиться в том, что записанная система команд
действительно определяет ДМП-автомат (см. теорему 8.13).
Команды A) и B) обеспечивают перенос в магазин входной
цепочки, команды C)-E) — команды свертки, команды F)-(8)
обеспечивают переход из фазы свертки в фазу переноса, если
в магазине нет основы, а команда (9) переводит автомат в за-
заключительное („допускающее") состояние в случае правильной
входной цепочки.
Проанализируем на данном ДМП-автомате цепочку
*=(())()*,
которая является правильной скобочной структурой.
Имеем последовательность конфигураций*:
<<7о, (())()*, °>М?ъ ())()*, ?(>!-
h <до,ОЮ*,п() ь <9ъ))()*,а((> н <»,)H*,п((> ь
Ь <9l,)()*,D@) Ь (<Zi,)()*,D(<y> Ь <<?о,H*,ОД Ь
Ь («i,0*,n(S)> h (gi,()*fDS> h (qi,)*,nS() h
h (<7i,*,DS()> h (gi^.QSS) h
(g2,A,D). #
Рассмотрение перехода от ?Я(Л)-грамматик к ДМП-авто-
матам и наоборот выходит за рамки нашего изложения. На
простейшем примере мы продемонстрировали только работу
детерминированного восходящего анализатора.
"Здесь мы использовали угловые скобки () для обозначения конфигура-
конфигураций, чтобы не путать с круглыми скобками (), являющимися терминалами
грамматики.
692 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Дополнение 8.2. Семантика
формальных языков
Классическая теория формальных языков, как уже отмеча-
отмечалось, занималась исключительно синтаксисом языков, изучая
методы порождения и распознавания множеств слов. Семан-
Семантика формальных языков, сравнительно молодая ветвь теории,
занимается способами сопоставления некоего „смысла" словам
(цепочкам) языка.
Необходимость в построении точного математического по-
понятия „смысла" диктуется развитием информационных техно-
технологий, прежде всего технологии проектирования компилято-
компиляторов.
Рассмотренные выше языковые модели определенным обра-
образом связаны с этапами этой технологии.
Текст входной программы, как известно, анализируется в
несколько проходов. На первом проходе производится лексиче-
лексический анализ, а именно проверяется правильность простейших
элементов текста, называемых лексемами. Примерами лексем
могут служить идентификаторы и константы, разрешенные
синтаксисом входного языка программирования. В процессе
лексического анализа не проверяется синтаксическая правиль-
правильность всей программы в целом, а проверяется только син-
синтаксическая правильность лексем (в частности, правильность
написания идентификаторов и констант). Так как лексемы
обычно являются элементами некоторого регулярного языка, то
базовой моделью для лексического анализатора является модель
конечного автомата.
Если текст программы успешно прошел этап лексического
анализа, то тогда проверяется его глобальная синтаксическая
правильность. При этом каждая лексема рассматривается как
буква. Здесь применяются методы синтаксического анализа, в
частности рассмотренные выше (см. Д.8.1). В предположении,
что синтаксис языка программирования описан КС-граммати-
Д.8.2. Семантика формальных языков 693
кой, основой для построения синтаксических анализаторов, как
мы уже видели, выбирается модель МП-автомата.
По завершении синтаксического анализа строится дерево
вывода входной программы. После этого переходят к эта-
этапу генерации объектного кода, т.е. внутреннего машинного
представления входного текста. Это значит, что выполняется
перевод с некоторого язьпса программирования на язьпс машин-
машинных кодов. Но чтобы выполнить перевод текста на другой
язык, необходимо каким-то образом понять его „смысл". Сле-
Следовательно, анализ уже синтаксически проверенной программы
с точки зрения ее „смысла" (семантический анализ) необходи-
необходимо предшествует самой генерации объектного кода. И прежде
всего необходимо уточнить математически, что такое „смысл"
(как раньше мы математически определяли синтаксис в терми-
терминах грамматик и автоматов).
В этом дополнении мы рассмотрим некоторые методы фор-
формального (математического) определения семантики для КС-
языков. Тем самым мы всюду в дальнейшем предполагаем, что
язык, семантика которого определяется, может быть задан не-
некоторой КС-грамматикой.
Сразу же необходимо сделать уточнение. Как мы уже заме-
заметили ранее, исследуя явление неоднозначности в КС-языках,
„смысл" следует сопоставлять не самим словам языка, а де-
деревьям их вывода: меняя дерево вывода данной цепочки, мы
меняем и ее „смысл", понимаем ее по-другому (см. 8.1). Далее,
можно сопоставлять „смысл" не только словам языка, точнее,
деревьям вывода этих слов из аксиомы грамматики, но и так
называемым фразам языка — терминальным цепочкам, выво-
выводимым из разных нетерминалов грамматики.
Например, фраза „...а так как мне бумаги не хватило"
не является законченным предложением русского языка, но
имеет, очевидно, какой-то „смысл". Точно так же оператор
присваивания, „вынутый" из какой-то программы на каком-
то языке программирования, не является „программой", не
может рассматриваться как элемент данного языка, но мы
694 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
в состоянии сопоставить ему тот или иной „смысл". Тем
самым возникает идея определить „смысл" через отображение
множества „синтаксических объектов" — деревьев выводов
фраз языка в некоторое „предметное множество", множество
„семантических объектов".
Здесь мы ограничимся крайне элементарным введением в
формальное описание семантики КС-языков и опишем неко-
некоторый простейший „кирпичик" формальной семантики языков
программирования.
Начнем с формального определения фразы КС-языка.
Определение 8Л5. Пусть G = (V, N, Sy P) — КС-грам-
КС-грамматика. Терминальную цепочку х называют фразой языка
?(<?), если Ah* х для некоторого нетерминала А Е N.
Пусть Т(х) — дерево вывода фразы х с корневым нетер-
нетерминалом А. Возьмем в Т(х) некоторое поддерево с корневым
нетерминалом В. Выводимую из этого вхождения В терми-
терминальную цепочку называют подфразой фразы х. Если верши-
вершина дерева Т(ж), соответствующая данному вхождению В, имеет
глубину 1 (или, что равносильно, уровень, на единицу меньший
уровня корня А), то данная подфраза называется подфразой
первого уровня фразы х.
Рассмотрим в качестве примера следующую грамматику
арифметических выражений:
Expr -+ Atom | (Expr + Expr) \ (Expr * Expr),
Atom-+ai\...\an.
Предполагается, что вместо вхождения нетерминала Atom мо-
может быть подставлен любой символ некоторого алфавита V =
= {ai,..., ап} (атом в арифметическом выражении может быть
либо переменным, либо константой).
Нарисуем дерево вывода выражения
(a+(b*{c+(d*(e + g))))),
где о, Ь, с, d, e, g — некоторые атомы из V (рис. 8.39).
Д.8.2. Семантика формальных языков
695
Это выражение в качестве
подфраз первого уровня имеет
цепочки а и
(b*(c+(d*(e + g)))).
Вторая фраза имеет подфразы
первого уровня b и
(c+(d*{e + g)))
и т.д. Заметим, что фраза а,
выводимая из самого левого
узла Ехрг глубины 1 имеет
в качестве подфразы первого
уровня ту же цепочку о, т.е.
подфраза первого уровня мо-
может совпадать с самой исход-
исходной фразой.
Множество всех фраз язы-
языка L обозначим через PH(L),
Ехрг
ГУ
Atom (Ехрг ¦ Ехрг)
Atom (Expr + Ехрг)
Ь Atom (Expr ¦ Ехрг)
/zTiT
d Atom Atom
I 1
Рис. 8.39
а множество всех деревьев вывода фраз L — через TPH(L).
Для однозначного языка L эти множества эквивалентны.
Определение 8.16. Семантическая функция языка L
есть отображение
SEM{L):TPH(L) -+U(L)
множества всех деревьев вывода фраз L в некоторое множество
U(L), называемое универсумом (предметной областью, семан-
семантической областью, областью интерпретации) языка L.
Замечание 8.14. Ради общности следовало бы определить
семантическую функцию как частичное отображение, но мы не
будем этого делать, вводя для „бессмысленных" фраз специаль-
специальный „неопределенный" элемент в универсум („нуль" предмет-
предметной области, „неопределенный смысл"). Заметим также, что
696 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
для однозначного языка семантическая функция может быть
определена как отображение из множества фраз языка. #
Способы определения семантической функции могут быть
различными. Нас будет интересовать важный частный случай,
когда значение семантической функции на некоторой фразе
(под фразой здесь и далее понимается дерево ее вывода, причем
разные деревья для одной и той же цепочки рассматриваются
как разные фразы) определяется однозначно через значение
этой функции на подфразах первого уровня. Более формально:
представим фразу х синтаксически как „соединение" своих
подфраз первого уровня:
х = (р(уи • ..<,Ут)= uiyi... итутит+и (8.28)
где ui, ..., um+i — некоторые терминальные цепочки. На-
Например, для определенного выше языка арифметических выра-
выражений фраза, дерево вывода которой изображено на рис. 8.39
раскладывается следующим образом:
где щ есть цепочка (, г*2 — цепочка +, а щ — цепочка ).
Таким образом, любая фраза представляется, вообще гово-
говоря, не как простое соединение своих подфраз первого уровня,
а как соединение с „прослойками" в виде определенных тер-
терминальных цепочек. Операцию <р в (8.28), задающую такие
прослойки, называют часто конкатенарнои операцией. Эта
операция определяется грамматикой языка.
Тогда предполагается, что если фраза х представлена в ви-
виде (8.28), то определено отображнение ф: U(L)m —> U(L) (т.е.
некоторая операция на предметной области), такое, что
SEM(L)(x) = 1>(SEM{L)(yi),... ,SEM(L)(ym)). (8.29)
Это ограничение, накладываемое на семантическую функ-
функцию, назовем принципом гомоморфной интерпретации.
Д.8.2. Семантика формальных языков 697
Примем теперь некоторые соглашения об обозначениях. Се-
Семантическую функцию языка L будем обозначать [ • ]L, опус-
опуская индекс, указывающий на язык, если это не ведет к недора-
недоразумению. Тогда равенство (8.29) можно переписать в виде
Подобные определения семантики фразы через семантику ее
подфраз первого уровня называют семантическими правилами
языка. Семантические правила соответствуют синтаксическим
правилам — правилам исходной КС-грамматики. Так, для
приведенной выше грамматики арифметических выражений,
полагая U = R, можно записать следующие семантические пра-
правила:
lExpr} = lExprl + lExpr]
(для синтаксического правила Ехрг -> (Ехрг + Ехрг)), т.е.
здесь конкатенарной операции <р, такой, что <p(u,v) = (u + v)
для любых двух фраз и и v, сопоставляется обычное арифме-
арифметическое сложение;
{Ехрг} = lExprl * lExprl
(для синтаксического правила Ехрг —> (Ехрг * Ехрг)) операция
на универсуме — арифметическое умножение;
lExpr] =
(для синтаксического правила Ехрг -> Atom);
[Atom] =
(для синтаксического правила Atom-ba^i = l,n).
Строго говоря, в первых двух правилах мы должны раз-
различать три разных вхождения одного и того же нетерминала
Ехрг, так как они соответствуют разным деревьям.
698 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Семантическая функция языка арифметических выражений
будет определена, если мы зададим значение этой функции на
атомах: это естественно ассоциируется с хорошо знакомой про-
процедурой вычисления значения арифметического выражения при
подстановке вместо входящих в него переменных конкретных
числовых значений (при этом не исключается, что атом может
быть константой — обозначением конкретного числа; в таком
случае само синтаксическое правило задает сразу значение се-
семантической функции на данном атоме).
Так, для приведенного выше выражения, полагая [[а] = 1,
Ш = 2, [с] = 3, Щ = 4, Це] = 5, (д} = 6, получим значение
всего выражения, равное 95.
Таким образом, в этом конкретном случае семантика фразы
есть числовое значение представленного данной фразой ариф-
арифметического выражения. Мы рассмотрели в качестве универсу-
универсума множество вещественных чисел и получили одну семантику.
Задав универсум как-нибудь иначе (например, как множество
комплексных чисел или множество функций некоторого клас-
класса), получим совсем другую семантику. Для одного и того же
синтаксиса, следовательно, могут быть определены различные
семантики (семантические функции).
Разобранный выше на примере языка арифметических вы-
выражений подход к определению семантики называют иногда
экстенсиональным подходом. Суть его состоит в том,
что явно определяется универсум как множество „внеязыко-
вых" объектов (экстенсионалов) и каждой языковой фразе со-
сопоставляется некоторый экстенсионал. Для разобранного выше
примера экстенсионал — это вещественное число. Слово „вне-
языковых" взято в кавычки потому, что универсум сам может
быть некоторым языком (выступающим тогда по отношению к
исходному языку как метаязык). Не исключено даже, что ме-
метаязык совпадает с самим определяемым языком — примером
могут служить всевозможные толковые словари.
Существует и другой подход к определению семантики, на-
называемый интенсиональным, одной из разновидностей кото-
Д.8.2. Семантика формальных языков 699
рого является аксиоматический метод определения се-
семантики языка.
Аксиоматический метод предполагает рассмотрение исход-
исходного, „объектного" языка, семантика которого определяется,
как формальной теории (или формальной системы). Не
давая строгого определения формальной теории в его общно-
общности, поясним его суть и рассмотрим пример.
Формальная теория задается как некоторый язык, цепоч-
цепочки которого называются в этом случае утверждениями (или
предложениями). В этом языке определяется подъязык так
называемых доказуемых утверждений: задается некоторое на-
начальное множество утверждений, которые считаются априори
доказанными (множество аксиом теории), и задается неко-
некоторое множество правил вывода, применяя которые к неко-
некоторым утверждениям (в частности, уже доказанным), можно
получать новые утверждения. Бели мы применяем правило
вывода к доказанному утверждению, то получаем новое до-
доказанное утверждение. Утверждение, которое таким образом
может быть выведено из аксиом, называют теоремой данной
теории. Утверждение считается имеющим смысл, если оно есть
либо аксиома, либо теорема данной теории. В отличие от экс-
экстенсионального подхода при интенсиональном подходе априори
не определяется никакой универсум, и при таком подходе к
определению семантики „иметь смысл" означает „быть теоре-
теоремой или аксиомой данной теории".
Вернемся к рассмотренному выше языку арифметических
выражений. Зададим его в виде формальной теории следующе-
следующего вида:
1) аксиома — любой атом а\, ..., an;
2) правила вывода:
ei,e2=»(ei + e2), A)
ei,e2=*(ei*e2), B)
т.е. если в\ и е2 доказаны, то доказано утверждение (ei + e2) и
утверждение (ei *e2).
700 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Построим, например, доказательство записанного выше вы-
выражения:
а, Ь, с, d, е, g — аксиомы;
(е + д) — правило вывода A);
(d*(e + g)) -B);
(c+(d*(e + g))) -A);
(b*(c+(d*(e + g)))) -B);
(a + (b*(c + (d*(e + g))))) -A).
Нетрудно видеть, что мы определили тот же язык дру-
другим способом. Множество доказуемых утверждений совпадает
здесь с множеством всех утверждений, и, таким образом, се-
семантика в данном случае совпала с синтаксисом: утверждение
имеет смысл тогда и только тогда, когда может быть доказа-
доказано, т.е. тогда и только тогда, когда является арифметическим
выражением, порождаемым приведенной выше грамматикой.
Замечание 8.15. В этой связи полезно заметить, что и
правила вывода формальной теории следует трактовать как
просто „правила замены" (в полной аналогии с порождающи-
порождающими грамматиками), согласно которым разрешается от опреде-
определенных цепочек (в левой части правила) переходить к новым
цепочкам (в правой его части).
Тогда по правилам вывода можно получать из цепочек, не
обязательно теорем или аксиом, какие-то другие цепочки, т.е.
строить выводы, не являющиеся доказательствами. Это опять-
таки аналогично грамматикам, в которых применение продук-
продукций, вообще говоря, не обязано быть выводом из аксиомы.
Такая широкая и чисто синтаксическая трактовка правил
вывода позволяет в теории формальных систем и в связанной
с нею теории доказательств строить выводы из „гипотез" —
цепочек, которые предполагаются доказанными. Если затем
удается действительно доказать их, то построенное первона-
первоначально „относительное" доказательство превратится в „абсо-
„абсолютное" (т.е. начинающееся с аксиом). #
Д.8.2. Семантика формальных языков 701
Построив аксиоматическую семантику языка, мы можем на
этой базе определить семантику уже экстенсионально, поло-
положив, что экстенсионал утверждения есть множество всех его
доказательств (если утверждение не имеет доказательства, то
его экстенсионал считается не определенным — формально мы
включаем тогда в предметную область специальный „неопреде-
„неопределенный элемент" с тем, как уже отмечалось, чтобы можно было
вводимую семантическую функцию считать отображением).
В заключение рассмотрим экстенсиональное определение
семантики простейшего языка программирования, который
будем называть MILAN (MIniLANguage). Синтаксис языка
определим посредством форм Бэкуса — Наура:
(программа) ::= (последовательность-операторов)
(последовательность-операторов) ::= (оператор) |
(оператор) (последовательность-операторов)
(оператор) ::= (присваивание) | (условный лереход) | (цикл)
(присваивание) ::= (переменное) := (терм)
(условный_переход) ::= if (условие) then
(последовательность_операторов)
else (последовательность-операторов) |
if (условие) then (последовательность-операторов)
(цикл) ::= while (условие) do
(последовательность-операторов) end
(переменное) ::= 2i|...|?n
(терм) ::= (функциональный_символ)
((последовательность-термов)) |
(переменное) | (константа)
(последовательность-термов) ::= (терм) |
(терм) (последовательность_термов)
(функциональный-символ) ::= /i|-..|/m
(константа) ::= ci |... | с*
(условие) ::= (предикатныйхимвол)
((последовательность-термов))
(предикатный-символ) ::= р\ |.. ,ps
702 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Заданная таким образом КС-грамматика определяет так
называемый абстрактный синтаксис MILANa: мы игнорируем
некоторые синтаксические детали, такие, как слова begin, end,
обрамляющие последовательность операторов, а также то, что
операторы разделяются точкой с запятой, что между термами
в последовательности термов ставится запятая и т.п. Мы
также не уточняем структуру переменных (идентификаторов),
констант, функциональных и предикатных символов, считая,
что эти нетерминалы ппробегают" каждый свой алфавит.
Чтобы формально описать экстенсиональную семантику
введенного посредством написанных выше синтаксических пра-
правил языка, нужно определить универсум. В зависимости от то-
того, какой универсум рассматривается, в рамках экстенсиональ-
экстенсионального подхода различают 1) денотационную семантику, 2)
операциональную семантику и 3) трансформационную
семантику (семантику смешанных вычислений). Здесь
мы рассмотрим только денотационную семантику.
В денотационной семантике языка, подобного MILANy,
универсум определяется как множество преобразователей со-
состояний памяти. К построению этого множества и переходим.
Определение 8.17. Состояние памяти — это произ-
произвольное отображение множества переменных I языка програм-
программирования в множество D данных (значений).
В силу сформулированного определения мы отождествляем
память с множеством переменных (идентификаторов, „ячеек",
имен) данного языка программирования (конкретно — языка
MILAN), а состояние памяти а есть отображение вида
<т:/->?>,
сопоставляющее каждой переменной значение, принадлежащее
некоторому множеству значений (данных) D. Последнее можно
рассматривать как объединение некоторого семейства мно-
множеству служащих носителями многосортной алгебры данных
Д.8.2. Семантика формальных языков 703
языка. Их можно отождествить с типами данных, используе-
используемыми в рассматриваемом языке: числами, массивами, строка-
строками, стуктурами и т.п. В множество D включен также неопре-
неопределенный элемент О (неопределенное значение).
Множество всех состояний памяти обозначим S.
Определение 8.18. Преобразователь состояний па-
памяти — это произвольное отображение множества Е состоя-
состояний памяти в себя.
Множество всех преобразователей состояний памяти обо-
обозначим (S —> S).
На множестве S определяется структура индуктивного упо-
упорядоченного множества (см. 1.8).
Область определенности состояния памяти а —
это множество, обозначаемое D(a), всех переменных #, таких,
что а(х) ф О.
Тогда положим для двух произвольных состояний аир
а^р& (D(a) С D(p))k((Vx e D(a))(a(x) = р{х))).
Очевидно, что отношение ^ есть отношение порядка. Далее,
множество Е имеет по отношению ^ наименьший элемент,
а именно такое состояние О, что (Ух Е 1)(О(х) = О). Его
называют всюду неопределенным состоянием памяти;
ясно, что D(O) = 0. Кроме того, для любой неубывающей
последовательности состояний памяти
состояние сто, такое, что
ао(х) = ап(х) <&хе D(an),
есть точная верхняя грань этой последовательности, причем
П>\
704 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Таким образом, множество состяний памяти S, снабженное
отношением порядка ^, является индуктивным упорядоченным
множеством.
С учетом результатов, полученных в 4.5 (см. теорему 4.11),
отсюда следует, что и множество преобразователей состояний
(Е -» Е) есть индуктивное упорядоченное множество. В этом
множестве отношение порядка < определяется условием
наименьшим элементом является стирающий преобразова-
преобразователь 0, такой, что 0(<т) == О для всякого а € Е, а точной
верхней гранью неубывающей последовательности преобразо-
преобразователей состояний /i ^ /2 ^ ... /п < ... является преобразова-
преобразователь /о, определяемый следующим образом:
(V<t € S)(Vx е I)(fo(<r)(x) = fn(o)(x) &хе D(fn(a))),
причем
= и w» (
Более того, оказывается, что композиция преобразователей
состояний (как отображений) непрерывна в смысле сохранения
точных верхних граней (см. 1.8), точнее, для любой неубываю-
неубывающей последовательности преобразователей состояний
и произвольного преобразователя состояний д
Докажем первое из этих равенств. Для произвольного о G S
имеем
5 ° sup/n (a) = sup fn{g{a)).
Д.8.2. Семантика формальных языков 705
Тогда для всякого х Е D(go /п((т))
9°supfn(a)(x) = sup fn(g(a))(x) = fn(g(a)){x) = 0%И(ж),
т.е. поскольку, как можно показать, композиция монотонна в
смысле определения, данного в 1.8, то
D(g о sup fn(a))= (J D(g о fn)(a)
И
Имея в виду все рассмотренные выше свойства множества
(S -» S), определим денотационную семантику языка MILAN.
Семантическая функция есть отображение [•]] множества
фраз в множество (S -> S) преобразователей состояний памяти.
1. Семантика оператора присваивания:
I 4& л —
где через t0" обозначено значение терма t в состоянии сг, равное
О, если хотя бы для одного переменного, входящего в терм, его
значение не определено, и равное значению терма при подста-
подстановке на место каждого его переменного х его значения а(х).
Суть записанного выше семантического правила очень про-
проста: оператору присваивания х := t сопоставляется преобра-
преобразователь состояний, меняющий состояние таким образом, что
все переменные, кроме ж, сохраняют свои значения, а новое
значение переменного х есть значение правой части операто-
оператора присваивания (терма t) в состоянии а.
706 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
2. Семантика оператора условного перехода:
lifp(tu...,tn)thenSielseS2l(<T) =
Это правило написано в предположении, что значения всех
термов в состоянии а определены. В противном случае опера-
оператору условного перехода сопоставляется стирающий преобра-
преобразователь 0. Подобное же соглашение принимается и далее в
аналогичных ситуациях.
Семантика условного перехода без eJse-альтернативы запи-
записывается аналогично, но при условии ложности предиката р в
состоянии а берется тождественный преобразователь состоя-
состояний ID.
3. Семантика цикла:
\whilep{t\,..., tn) do S enrf J (a) =
Таким образом, семантика цикла определяется как решение
уравнения. Это определение корректно, так как правая часть
уравнения есть непрерывное отображение множества (Е -> Е)
в себя (что следует из доказанной вьппе непрерывности компо-
композиции преобразователей состояний и очевидной непрерывности
тождественного отображения).
4. Семантика последовательности операторов:
Определенная таким образом формальная семантика язы-
языка MILAN становится базой для семантического анализа про-
программ, т.е. для строгого математического доказательства ут-
утверждений о программах. Этот анализ, проводимый техноло-
технологически после синтаксического анализа программы и получе-
получения ее дерева вывода, основал на результате, известном под
Д.8.2. Семантика формальных языков 707
названием принципа индукции по неподвижной точке*. Приве-
Приведем формулировку этого принципа без доказательства.
Принцип индукции по неподвижной точке. Пусть V
есть некоторое утверждение о программах, Т — непрерывное
отображение множества (S -* Е) в себя, / — наименьшая
неподвижная точка отображения Т или, что то же самое,
наименьшее решение уравнения X = Т{Х).
Тогда, если V(f^) истинно и для каждого г из истинности
® следует истинность P(/(i+1)), то истинно V(f). (Под /W
понимается г-е приближение наименьшей неподвижной точки:
/@) = 0, /М =^(/(«)) (см. 1.8).)
Проиллюстрируем применение этого принципа на примере
анализа простейшей программы на языке MILAN.
Рассмотрим программу вычисления факториала:
begin
х :=п;
у:=0;
*:=1;
while (у ф х) do
end
end
Здесь предполагается, что все переменные принимают це-
целые значения. Букву п следует понимать не как переменную
программы, а как условное обозначение произвольного нату-
натурального числа, „засылаемого" в иячейку" х. Мы вынуждены
прибегать к столь неэстетичному (с программистской точки
зрения) вводу исходного значения, так как наш простенький
язык не имеет средств ввода/вывода.
Докажем следующее утверждение V об этой программе:
если после выполнения программы состояние памяти а таково,
что а(х) ф О и a(z) ф О, то a(z) = а(х)\
*См.: Донохоу П.
708 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
Заметим, что мы не определяли в языке операторов ввода и
вывода и, следовательно, начальное состояние памяти задается
априори (некоторым „оракулом"), а вопрос, как это состоя-
состояние сформировано, остается за пределами формализации. В
нашем примере речь идет о задании начального значения пере-
переменной п.
Проанализируем теперь, что означает в данном случае ин-
индукция по неподвижной точке.
Ясно, что перед выполнением цикла состояние памяти сто
таково, что всегда Gq(z) = <то(уУ~ Нам нужно доказать, что
если выполнение цикла заканчивается после конечного числа
итераций, то в результирующем состоянии а будем иметь
Нам будет удобно определить операцию р-дизъюнкции пре-
преобразователей состояний памяти, где p(<i,...,*n) — некоторое
условие языка MILAN.
Определение 8.19* Назовем р-дизъюнкцией преобразо-
преобразователей состояний памяти / и g преобразователь, обозначае-
обозначаемый p(fVg) и определяемый следующим образом:
О, значение предиката р
в состоянии v не определено;
/М> JPi/ = 1;
= <
(через pi/ обозначено значение условия, или предиката, р в
состоянии и: ри = p{t\,..., t{J)).
В соответствии с тем, как мы определили выше, Преобразо-
Преобразователь состояний /, соответствующий циклу, есть наименьшая
неподвижная точка уравнения / = F(/), где функция F может
быть представлена в виде
(для условия р и тела S цикла while).
Д.8.2. Семантика формальных языков 709
Согласно алгоритму вычисления наименьшей неподвижной
точки (см. 1.8), / = sup{/W: г ^ 0}, где /W =0 — стирающий
преобразователь.
Вычисляя первое приближение наименьшей неподвижной
точки, получаем
где S — тело цикла.
Очевидно, что для произвольного состояния v ф О неравен-
неравенство f^{u) фО имеет место тогда и только тогда, когда pv
определено и равно 0. Тогда f^{y) = и.
Таким образом, первое приближение соответствует нулево-
нулевому числу повторений тела цикла.
Для второго приближения имеем
Точно так же легко видеть, что f^2\v) ф О тогда и толь-
только тогда, когда ри определено и равно 0 (/® (") = ") или когда
ри = 1, но P\si(y) = 0 {f^iy) = \S\ (v)). Таким образом, второе
приближение соответствует не более чем однократному числу
повторений тела цикла. Методом математической индукции
несложно доказать, что г-е приближение наименьшей неподвиж-
неподвижной точки для семантики цикла соответствует не более чем
(г — 1)-кратному повторению тела цикла, если f®{y) Ф О для
произвольного состояния v ф О.
Следовательно, индукция по неподвижной точке сводится в
данном случае к индукции по числу повторений цикла, и нам
для данного конкретного примера нужно доказать, что выпол-
выполнение тела цикла сохраняет соотношение значений переменных
у и z: для любого i/, такого, что i/(z) = ^(у)!, |[?]|A/)(я) =
= [5]](i/)(j/)!, где S — тело цикла в программе вычисления
факториала.
710 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
В самом деле,
= *(у)! * Ну) +1) = Ну) + W
что и требовалось доказать.
Теперь остается заметить, что поскольку условие выхода
из цикла имеет вид уфх, то, задав переменной п некоторой
значение из N, после выполнения нашей программы достигнем
требуемого результата.
Мы рассмотрели простейший случай денотационного опре-
определения для языка, не содержащего даже блоков и процедур.
При появлении последних возникают локальные определения
переменных и необходимо модифицировать понятие состояния
памяти. Это может быть реализовано с помощью понятия сре-
среды, которая формально определяется как декартово произведе-
произведение / х Loc множества переменных на множество падресов", а
состояние памяти при этом понимается как отображение вида
а: I х Loc -> D.
Денотационное определение, как уже упоминалось, не явля-
является единственным в рамках экстенсионального подхода. Кро-
Кроме него наиболее употребительными являются операциональ-
операциональное и трансформационное определения. При операциональном
определении в качестве экстенсионала программы рассматри-
рассматривается множество последовательностей состояний памяти, ге-
генерируемых при выполнении программы. Трансформацион-
Трансформационное определение сопоставляет программе преобразователь вида
„состояние памяти -> пара (программа, состояние памяти)". А
именно если программа начинает работать над некоторым ис-
исходным состоянием памяти а, то все операторы, которые могут
быть выполнены, выполняются, а все операторы, которые не
могут быть выполнены (из-за неопределенности значений пе-
переменных) искладываются" в новую программу (называемую
остаточной): таким образом возникает пара (остаточная про-
программа, частичный результат = новое состояние а1). Подобное
Д.8.3. Графовое представление МП-автоматов 711
вычисление, называемое смешанным, позволяет определять раз-
различные преобразования (трансформации) программ.
Семантика языков программирования в настоящее время
является бурно развивающейся областью теории формальных
языков, используемой при разработке и реализации языков
программирования и программных продуктов (в частности,
при разработке надежного программного обеспечения).
Дополнение 8.3. Графовое
представление МП-автоматов
Как и конечные автоматы, МП-автоматы также допуска-
допускают графовое представление, которое, конечно, является более
сложным, чем графовое представление конечных автоматов.
Так, МП-автомату
M = (Q,V,r,qo,F,Zo,S)
сопоставляется ориентированный мультиграф (в отличие
от обычного ориентированного графа в мультиграфе допуска-
допускается несколько дуг для одной и той же упорядоченной пары
вершин, т.е. несколько дуг, начало и конец которых совпада-
совпадают), множество вершин которого есть множество состояний
автомата, а каждая дуга которого имеет метку в виде упоря-
упорядоченной тройки (Z, а, 7)? где Z — магазинный символ, а —
входной символ или пустая цепочка, у — магазинная цепоч-
цепочка. По определению, дуга е, ведущая из вершины (состояния)
q в вершину (состояние) г имеет метку (Z, a, j), если и только
если в системе команд S находится команда qaZ -> ry.
Замечание 8.16. Более формально ориентированный
мультиграф может быть определен как упорядоченная тройка
G = (V, Е, ф), где V — множество вершин, Е — множество
дуг, а <р — отображение множества Е в множество V xV,
называемое функцией инцидентности. Таким образом,
если для различных дуг е\, ..., еу. все значения
712 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
<p(ek) равны, то возникает „множественная", или „кратная",
дуга, т.е. множество дуг, отображаемых в одну и ту же
упорядоченную пару вершин (гх, v). Графически это можно
изобразить так, как показано на рис. 8.40. В том случае,
когда функция инцидентности есть инъекция, мультиграф
превращается в обычный ориентированный граф.
В мультиграфе, представляющем МП-автомат, множество
дуг для заданной упорядоченной пары состояний (</, г) нахо-
находится во взаимно однозначном соответствии
с множеством всех команд qaZ —> rj для раз-
личных а € VU {A}, Z € Г, 7 ? Г*.
Можно было бы задавать МП-автомат и
Рис. 8.40 ^ ,
обычным ориентированным графом, но тогда
пришлось бы по-иному вводить метки дуг. Технически удобнее
каждой команде сопоставлять отдельную дугу и строить таким
образом ориентированный мультиграф. #
Введем понятие магазинной метки пути в мультигра-
мультиграфе МП-автомата. Для этого заметим, что понятие пути в
мультиграфе слегка отличается от такового в обычном ори-
ориентированном графе. Под путем в мультиграфе понимается
произвольная последовательность дуг ei, б2, ..., еп, ..., где
п ^ 1, такая, что любая пара соседних дуг е^, e^+i этой последо-
последовательности смежна, т.е. существует вершина (ji+i? в которую
дуга ei заходит и из которой дуга e^+i выходит. Число дуг в
пути (для конечного пути) назовем его длиной. Пути в мульти-
мультиграфе будем записывать как цепочки в алфавите Е\ так, запись
ej обозначает путь, являющийся последовательностью дуг
т раз п раз
Тогда магазинная метка дуги (т.е. пути длины 1) с меткой
(Z, а, 7) есть цепочка 7; магазинная метка пути ei, ег, ..., еп
длины п при условии, что магазинная метка пути ei, ег, ...,
en_i, служащего началом исходного пути, определена и равна
Д.8.3. Графовое представление МП-автоматов 713
7, а дуга еп имеет метку (У, Ь, а), равна a(Y'l^y). Напомним,
что для произвольных алфавита W, его буквы а и цепочки х в
алфавите W выражение a~lx означает цепочку у, такую, что
ay = #, и не определено, если первая буква цепочки ж отлична
от а (см. задачу 7.23). Таким образом, магазинная метка пути
в мультиграфе, представляющем МП-автомат, может быть не
определена.
Введем операцию Y-сцепления магазинных меток двух
смежных дуг е\ и ег с метками (Z, а, 7) и (У, 6, а) соответ-
соответственно, полагая 7®У <* = «У"7 (рис. 8.41).
Средние компоненты меток дуг МП-автомата будем назы-
называть их входными метками. Вход-
Входная метка пути в мультиграфе обра- (?) »G) +*(р)
зуется стандартно из входных меток
дуг, как в конечном автомате.
Рассмотрим в качестве примера МП-автомат для языка
L\ = {anbn: n ^ 0}. Его система команд имеет следующий вид:
qoaZ
qoaa
qoba -
qiba -> giA,
q\\Z —>q2^-
По этой системе команд строим мультиграф (рис. 8.42 ).
а
Ясно, что дуга с меткой (Z, a, aZ) не может быть сцеплена
сама с собой, так как выражение aZ ®z Q>Z = aZ(Z~~laZ) не
714 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
определено. Но верхняя петля в начальной вершине может
сцепиться с нижней, а последняя сцепляется сама с собой.
Например,
aZ ®a аа = aa(a~laZ) = aaZ,
aaZ xaaa = aa(a~xaaZ) = aaaZ.
Неформально любой путь eieJp1 соответствует переписыванию
с ленты в магазин п символов а. Тогда путь е\е%~хe$d%~xе,ь
имеет входную метку anbn и магазинную метку Л.
Так, для цепочки аааЬЬЪ будем иметь последовательность
сцеплений:
((((((aZ ®а аа) ®а аа) ®а А) ®а Л) ®а Л) ®z А) =
= {(((aaaZ ®а А) ®а А) ®а A) ®z A) = Z ®z A = А.
Если в цепочке больше символов а, чем Ь, то мы, вычисляя ма-
магазинную метку соответствующего пути, придем к выражению
ак ®z А, которое не определено. Если же в цепочке больше сим-
символов 6, чем а, то мы не попадем в заключительную вершину,
так как в нашем мультиграфе нет дуги с меткой, первая ком-
компонента которой равна Z, а вторая — Ь.
Обратим внимание на то, что если мы забудем о магазин-
магазинных метках и будем рассматривать наш мультиграф как граф
обычного конечного автомата, то получим регулярное выра-
выражение а*Ь+. Таким образом, вычисление магазинных меток
вдоль путей мультиграфа фильтрует множество входных це-
цепочек, допускаемых МП-автоматом, т.е. в регулярном языке
выделяется подмножество более сложной структуры — неко-
некоторый КС-язык.
Любая дуга, исходящая из начальной вершины и имеющая
метку (Zo, а, 7) Для произвольных a G V U {А} и j e Г*, называ-
называется стартовой. Тогда нетрудно дать графовую интерпре-
интерпретацию языка МП-автомата.
Теорема 8.15. Язык МП-автомата — это множество всех
входных цепочек, являющихся в представляющем МП-автомат
Вопросы и задачи 715
мультиграфе входными метками путей, первая дуга которых
стартовая, последняя заходит в заключительное состояние, а
магазинная метка равна пустой цепочке.
Вопросы и задачи
8.1. Однозначна ли грамматика с системой правил
S->aSa\bSb\aa\bb\a\b\\?
Какой язык она порождает? Преобразовать ее к эквивалентной
однозначной грамматике в приведенной форме.
8.2. Какой язык порождает грамматика с системой правил
8.3. Доказать, что каждый КС-язык может порождаться
грамматикой G = (V, iV, 5, Р), в которой каждое правило име-
имеет вид А -> а или А -> ги, где AeN, a€ iV+, w € V*.
8.4. Построить КС-грамматику, порождающую язык
{anbm: n ф m, n, m > 0}.
8.5. Построить КС-грамматику с терминальным алфавитом
V, порождающую все цепочки, содержащие вхождения некото-
некоторых слов из заданного конечного множества непустых слов в V.
8.6. Найти приведенную форму КС-грамматик:
а) 5->а|А, J3->6,
А-+АВ, C-+Sa\\;
б) 5->А|В, C-»S|a|A,
A->C\D, D-*S\b,
B-±D\E, ?->S|c|A;
в) 5->A|J5, A->aB\bS\b\\y
B->AB\Ba, C->AS\b\\;
716 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
г) S->aB\bA\cC, A^cBS\bA\C\b\\,
В -> bSA\cCb\S, С -> Cd\aCa;
д) S->ABC\aA\bB\\, А^В\\\аВ\Ъ,
В-+С\ЪА\а, C->B\bS\\\
е)
B->S\b\aA.
8.7. Доказать, что любой КС-язык в однобуквенном алфа-
алфавите регулярен.
8.8. Можно ли множество всех КС-грамматик с заданными
алфавитами V и N описать посредством некоторой КС-грам-
КС-грамматики? Какими будут алфавиты этой грамматики?
8.9. Построить грамматику, порождающую язык
{а*п:п>0}
для фиксированной натуральной константы к. Является ли
этот язык контекстно-свободным?
8.10. Доказать, что каждый линейный язык, не содержа-
содержащий пустой цепочки, порождается грамматикой, все правила
которой имеют вид А —> aJ5, А —> Ва} А —> а.
8.11. Доказать, что любая КС-грамматика может быть пре-
преобразована к эквивалентной КС-грамматике G = (V, N, 5, Р),
каждое правило которой имеет вид А —> ВС или А ->• а, где А,
5, С Е JV, a G V U {А}. (КС-грамматику с такими ограничения-
ограничениями на правила вывода называют КС-грамматикой, заданной в
нормальной форме Хомского.)
8.12. Доказать следующую лемму о разрастании для линей-
линейных языков.
Если L — линейный язык, то найдется такая константа р,
что если z G L и \z\ > р, то z = uvwxy, где |г*ш;у| < р, vx ф А и
(Vn > 0) uvnwxny G L.
Вопросы и задачи 717
Используя полученный результат, доказать, что язык пра-
правильных скобочных структур не является линейным.
8.13. Найти КС-грамматику, порождающую языки:
a) {an6nc*:fc,n>0}; б) {akbncn: fc,n > О}.
8.14. Доказать, что множество всех цепочек, которые могут
появляться в магазине МП-автомата, регулярно.
Указание: использовать графовое представление МП-ав-
МП-автомата (см. Д.8.3).
8.15. Построить МП-автомат, допускающий язык
{апЬк:кфп}.
8.16. Построить МП-автомат и КС-грамматику для языка
в алфавите {а, Ь}, состоящего из всех таких цепочек, что в них
число символов о совпадает с числом символов Ь.
8.17. Показать, что грамматика, заданная системой правил
S-+A\B, А->аАЬ\аЬ, В ->а?ВЬ\аВЬ*\а3Ь\аЬг,
неоднозначна. Описать язык, который она порождает.
8.18. Построить КС-грамматику, порождающую все цепоч-
цепочки нулей и единиц с одинаковым числом тех и других.
8.19. Будет ли контекстно-свободным язык, являющийся
дополнением языка предыдущей задачи?
8.20. Пусть L — КС-язык. Доказать, что:
а) INIT(L) = {w: (Зх) (wx eL)} есть КС-язык;
б) FIN(L) = {w: (Зх) {xw G L)} есть КС-язык;
в) SUB(L) = {w: Cs)(Эу) {xwy E L)} есть КС-язык.
8.21. Доказать, что если L — КС-язык, а Л — регу-
регулярный язык, то L/R = {ги: wx E L для некоторого х Е R} есть
КС-язык.
718 8. КОНТЕКСТНО-СВОБОДНЫЕ ЯЗЫКИ
8.22. Доказать, что следующие языки не являются кон-
контекстно-свободными:
а) {an6manbm:n,m^0};
б) {апЪтсп: т > п,т,п > 0};
в) {0n10n10nl:n>0};
г) {х : х е {а, 6, с, d}* и число вхождений всех четырех букв
в х одинаково};
д) {wn: w Е {а,Ь}*}, где п — фиксированное число, не мень-
меньшее 2;
e){(an6ncn)m:n,m>0};
ж) {anbncn:n^0}\
8.23. Является ли контекстно-свободным язык, состоящий
их всех цепочек в алфавите {а, Ь, с}, таких, что число вхождений
в них всех трех символов попарно различно?
8.24. Используя конструкцию из доказательства теоремы
8.11, построить КС-грамматику для языка всех таких палин-
палиндромов в алфавите {0,1}, которые одновременно содержатся в
регулярном языке: а) 0*1*0*; б) 0*1+0+1*0*; в) состоящем из
всех цепочек с четным числом нулей и четным числом единиц.
8.25. Пусть V и W — произвольные алфавиты, а h: V* -?
—> W* — морфизм. Доказать, что: а) если L — КС-язык в
алфавите V, то h(L) — КС-язык в алфавите W; б) если К —
КС-язык в алфавите W, то hTl(K) — КС-язык в алфавите V.
Указание: для доказательства первого утверждения до-
достаточно воспользоваться теоремой 8.9; чтобы доказать вто-
второе утверждение, нужно построить МП-автомат с буфером
по аналогии с конструкцией конечного автомата с буфером
(см. Д.7.3).
8.26 (задача о КС-языках как решениях алгебра-
алгебраических систем уравнений). Пусть C(V) — полукольцо
всех языков в алфавите V. Мультипликативным термом в
C(V) от переменных Х\, ..., Хп называют выражение вида
? fr где щ G V*, i = l,n + l, k, > 0, j = T~n,
Вопросы и задачи 719
ип^1. Полиномом от переменных Х\^ ..., Хп называют про-
произвольную (конечную) сумму мультипликативных термов.
Алгебраической системой уравнений в полукольце C(V) на-
называют систему уравнений относительно неизвестных Х\, ...,
Хп вида
где Pi(X\,... ,-Xn) — полином от переменных Л^, ..., Хп.
Доказать, что алгебраическая система уравнений всегда
имеет наименьшее решение и что язык в алфавите V является
контекстно-свободным тогда и только тогда, когда он является
компонентой наименьшего решения некоторой алгебраической
системы уравнений.
Указание: установите взаимно однозначное соответствие
между алгебраическими системами уравнений и КС-граммати-
КС-грамматиками, отождествив нетерминалы грамматики с неизвестными
системы уравнений. Далее, используя формулу наименьшей не-
неподвижной точки, покажите, что компонента Х\ 5-го прибли-
приближения решения алгебраической системы есть язык, состоящий
из всех таких цепочек в алфавите V, что они выводятся из
нетерминала Х{, и высота дерева вывода каждой из них не пре-
превышает s.
СПИСОК РЕКОМЕНДУЕМОЙ
ЛИТЕРАТУРЫ
Учебники и учебные пособия
Архангельский А.А, Канторовскал теория множеств. М.: Изд-во Моск.
ун-та, 1988. 112 с.
Ахо Л., Ульман Док. Теория синтаксического анализа, перевода и
компиляции: Пер. с англ: В 2 т. Т. 1. М.: Мир, 1978. 612 с.
Ахо Л., Хопкрофт Дж.у Ульман Дж. Построение и анализ вычисли-
вычислительных алгоритмов: Пер. с англ. М.: Мир, 1979. 536 с.
Барти Т., Биркгоф Г. Современная прикладная алгебра: Пер. с англ.
М.: Мир, 1976. 400 с.
Белоусов А.И., Мартынов Б.В., Щетинин А.Н. Лекции по дискретной
математике. М.: Изд-во МГТУ им. Н.Э.Баумана, 1994. 96 с.
Богомолов A.M., Салий В.Н. Алгебраические основы теории дискрет-
дискретных систем. М.: Наука, 1997. 368 с.
Гладкий А.В. Формальные грамматики и языки. М.: Наука, 1973.
386 с.
Гретцер Г. Общая теория решеток: Пер. с англ. М.: Мир, 1982. 456 с.
Евстигнеев В.А. Применения теории графов в программировании. М.:
Наука, 1985. 352 с.
Каргополов М.И., Мерзляков Ю.И. Основы теории групп. М.: Наука,
1972. 240 с.
Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику.
М.: Изд-во Моск. ун-та, 1982. 120 с.
Кон П. Универсальная алгебра: Пер. с англ. М.: Мир, 1968. 352 с.
Кристофидес Н. Теория графов. Алгоритмический подход: Пер. с
англ. М.: Мир, 1978. 432 с.
Кук Д., Бейз Г. Компьютерная математика: Пер. с англ. М.: Наука,
1990. 384 с.
Куратовский К., Мостовский А. Введение в теорию множеств: Пер. с
англ. М.: Мир, 1970. 416 с.
Лекции по теории графов / В.А. Емеличев, О.И. Мельников, В.И. Сар-
ванов, Р.И. Тышкевич М.: Наука, 1990. 384 с.
721
Нефедов В. Я., Осипов а В. А. Курс дискретной математики. М.: Изд-во
МАИ, 1992. 264 с.
Нигматпуллин Р. Сложность булевых функций. М.: Наука, 1991. 240 с.
Плотпкин В,И.у Гринглаз Л.Я.У Гварамия А.А. Элементы алгебраиче-
алгебраической теории автоматов. М.: Высш. шк., 1994. 191 с.
Саломаа А. Жемчужины теории формальных языков: Пер. с англ. М.:
Мир, 1986.
Сикорски Р. Булевы алгебры: Пер. с англ. М.: Мир, 1969. 375 с.
Шенфилд Дж. Математическая логика: Пер. с англ. М.: Наука, 1975.
528 с.
Шиханович Ю. А. Введение в современную математику: (Начальные
понятия). М.: Наука, 1965. 376 с.
Яблонский СВ. Введение в дискретную математику. 3-е изд. М.:
Высш. шк., 2001. 384 с.
Задачники
Гаврилов Г.П.у Сапоженко А.А. Сборник задач по дискретной мате-
математике. 2-е изд. М.: Наука, 1992. 368 с.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математи-
математической логике и теории алгоритмов. 3-е изд. М.: Физмат лит, 1995. 255 с.
Сборник задач по алгебре / Под ред. А.И. Кострикина. М.: Наука,
1987. 352 с.
Дополнительная литература
Акритас А. Основы компьютерной алгебры с приложениями: Пер. с
англ. М.: Мир, 1994. 544 с.
Булос Дж., Джеффри Р. Вычислимость и логика: Пер. с англ. М.:
Мир, 1994. 396 с.
Вирт Н. Алгоритмы и структуры данных: Пер. с англ. М.: Мир, 1989.
360 с.
Глушкое В.М., Цейтлин Г.Е., Ющенко Е.Л. Методы символьной муль-
мультиобработки. Киев: Наук, думка, 1980. 252 с.
Донохоу П. О взаимодополняющих определениях // Семантика языков
программирования: Сб. статей. М.: Мир, 1980. С. 222-394.
Ершов Ю.Л., Палютин Е.А. Математическая логика. М.: Наука, 1979.
320 с.
Кантор Г. Труды по теории множеств. М.: Наука, 1985. 430 с.
722 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Касьянов В.Н. Оптимизирующие преобразования программ. М.: Нау-
Наука, 1988. 336 с.
Катленд Н. Вычислимость. Введение в теорию рекурсивных функции:
Пер. с англ. М.: Мир, 1983. 256 с.
Кнут Д. Искусство программирования для ЭВМ: В 3 т. Т. 1: Основные
алгоритмы. М.: Наука, 1976. 736 с.
Кофман А. Введение в прикладную комбинаторику. М.: Наука, 1975.
480 с.
Кушнер Б.А. Лекции по конструктивному математическому анализу.
М.: Наука, 1973. 448 с.
Мендельсон Э. Введение в математическую логику. М.: Наука, 1975.
320 с.
Матросов В.Л.> Стеценко В.А. Лекции по дискретной математике.
М.: МГПУ, 1997. 220 с.
Успенский В.А. Теорема Геделя о неполноте. М.: Наука, 1982. 111 с.
Фоменко А.Т. Наглядная геометрия и топология. М.: Изд-во Моск.
ун-та, 1992. 432 с.
Handbook of Theoretical Computer Science. Vol. 1: Algorithms and
Complexity. Vol.2: Formal Models and Semantics. Elsevier (North Holland),
1990.
Kuich W., Salomaa A. Semirings, Automata, Languages. Springer, Berlin,
1986.
Периодическая литература
Белоусов А.И. Алгоритм обобщенной сортировки и его применение в
диалоговых обучающих программах // Вестник МГТУ. Сер. Приборостро-
Приборостроение. 1993. №3. С. 118-126.
Белоусов А.И., Пастуховский А.В. Ориентированные гиперграфы и
системы подстановок // Фундаментальная и прикладная математика.
1996. №4. С. 1163-1186.
Гоген Док.А.у Мезегер Ж. Модели и равенство в логическом програм-
программировании // Математическая логика в программировании: Сб. статей.
М.: Мир, 1991. С. 274-310.
Ершов А.П. О сущности трансляции // Программирование. 1977. №5.
С. 21-38.
Кораблин Ю.П., Налитое С.Д. Событийная семантика схем программ
языка взаимодействия последовательных процессов // Программирование.
1993. №3. С. 48-61.
723
Нгилн С.А. Функциональные языки программирования // Программи-
Программирование. 1991. №5. С. 77-86.
Скотт Д. Набросок математической теории вычислений // Киберне-
Кибернетический сборник. №14. М.: Мир, 1977. С. 107-121.
Скотт Д. Теория решеток, типы данных и семантика // Данные в
языках программирования: Сб. статей. М.: Мир, 1982. С. 25-53.
Тарасюк И. В. Понятия эквивалентностей для разработки параллель-
параллельных систем с использованием сетей Петри // Программирование. 1998.
№4. С. 19-39.
Хоар Ч. Непротиворечивые взаимодополняющие теории семантики
языков программирования // Семантика языков программирования: Сб.
статей. М.: Мир, 1980. С. 196-221.
De Bakker J.W.} Zucker J.J. Processes and denotational semantics of
concurrency. Information and Control, 1982. № 54. P. 70-120.
De Boer F.S., Rutten J.J., Kok J.N., Palamidessi С Semantic Models
for concurrent logic languages // Theoretical Computer Science. 1991. №86.
P. 3-33.
Jensen K. An Introduction to the Theoretical Aspects of Coloured Petri
Nets // Lecture Notes in Comput. Sci. 1994. № 803. P. 230-272.
Kuich W. Automata and languages generalized to ^-continuous semirings
// Theoretical Comput. Sci. 1991. №79. P. 137-150.
Kurka P. A Comparison of Finite and Cellular Automata // Lect. Notes in
Comput. Sci. 1994. N 841. P. 484-493.
Peeva K. Equivalence, redution and minimization of finite automata over
semirings // Theoretical Computer Science. 1991. N 88, P. 269-285.
Schmeck H. Algebraic Characterization of Reducible Flowcharts // J.
Comput. System Sci. 1983. V. 27. P. 165-199.
Thomas W. Logical Specifications of Infinite Computations // Lecture
Notes in Comput. Sci. 1994. N 803. P. 583-621.
предметный указатель
Аванцепочка 675
Автомат 494
- конечный 498, 502
- детерминированный 506
-- квазидетерминированный 506
- минимальный 533
- полностью определенный 506
- - с выходом 552
- магазинный 625
Автоматы конечные эквивалентные
509
- минимальные изоморфные 537
Автоморфизм 244
- графа 346
- множества 42
Аксиома 473
- теории 699
Аксиомы кольца 135
- полукольца 175
- поля 140
Алгебра 117
- булева 208
- двухэлементная 210
- одноэлементная 211
- кватернионов 141, 168
- конечная 117
- конечно порожденная 232
- Кэли 170
- многосортная 266
- порожденная множеством 232
- универсальная 117
- цепей неориентированного графа
359
Алгебры многосортные
изоморфные 270
-- однотипные 268
- однотипные 120
Алгоритм Д ему крона 351
- Квайна — Мак-Клоски 410
- Краскала 307
- сортировки 302
- Флойда — Уоршелла — Клини
339
- эффективный 307
Алфавит 462
- входной 495
- - конечного автомата 503
-- конечный машины Тьюринга
570
- - МП-автомата 626
- выходной 552
- магазинный МП-автомата 627
- нетерминальный 473
- объединенный 473
- терминальный 473
Анализатор 673
Анализ беступиковый 674
- восходящий 674
- нисходящий 674
- однопроходный 674
- „разверткой" 674
- „сверткой" 674
- „сверху вниз" 674
- „снизу вверх" 674
Антисимметричность 63
Антицепь 77
Аргумент операции 113
725
Базис Жегалкина 398
- стандартный 396
Биекция I, 4%
Бикомпонента 286
Бином Ньютона I, 100
Блок управления автомата 495
Буква 462
- входная конечного автомата 503
Булеан множества 34
Вектор арифметический V, 39
- булев 210
- единичный 210
- нулевой 210
- значений булевой функции 387
- модуля 267
Верх магазина 627
Вершина 276
- дерева внутренняя 598
- достижимая 278
- конечного автомата
заключительная 502
начальная 502
- стека 318
Вершины смежные 277
Вес дуги 307
- ребра 307
Включение 33
Вложение 244
Вход сети 349
Вхождение главное 467
- первое 467
- слова в слово 466
Вхождения не пересекающиеся 467
- пересекающиеся 467
Вывод в грамматике 476
Выводимость цепочки из цепочки
475
Вывод на множестве конфигураций
МП-автомата 634
- цепной 606
- цепочки левый 595
- правый 595
Выводы цепочки эквивалентные 595
Выражение регулярное 491
Выражения регулярные
эквивалентные 493
Высказывания логически
эквивалентные 25
- равносильные 25
Высота вершины ориентированного
дерева 300
- ориентированного дерева 300
Выход сети 349
- триггера инверсный 558
- прямой 558
Вычитание 130
Глубина вершины
ориентированного дерева 300
Голова списка 292
Головка автомата 495
Гомоморфизм 242
- графов 342
- групп 157
- группы в фактор-группу
канонический 164
- канонический 247
- колец 166
- многосортный 270
- проектирующий 256
- строгий 244
Грамматика контекстно-зависимая
486
- обобщенная 487
726
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Грамматика контекстно-свободная
487
-- однозначная 600
- леволинейная 487
- линейная 487
- неукорачивающая 486
- общего вида 486
- порождающая 472
- праволинейная 487
- регулярная 488
- типа 0 486
- Хомского 472
Грамматики эквивалентные 478
Грани параллельные 382
- соседние 382
Грань булева куба 381
- множества верхняя 79
точная 80
- нижняя 79
точная 80
- последовательности верхняя
точная 82
- нижняя точная 83
Граф ациклический 280
- бесконтурный 280
График отображения I, 41
- соответствия 44
Граф конечного автомата с
выходом 552
- КС-грамматики 613
- неориентированный 276
-- ассоциированный 287
-- взвешенный 307
- размеченный 307
- связный 285
- ориентированный 276
-- взвешенный 307, 327
-- размеченный 307, 327
Граф ориентированный сильно
связный 286
- - слабо связный 288
- соответствия 46
Графы изоморфные 342
Группа 125
- абелева 126
- автоморфизмов 346
- аддитивная действительных
чисел 164
по модулю 1 165
-- кольца 136
- - целых чисел 127
- вычетов по модулю к аддитивная
128
- коммутативная 126
- конечная 134
- мультипликативная вычетов по
модулю р 142
- действительных чисел 127
-- поля 140
-- рациональных чисел 127
-- тела 140
- неразложимая 154
- подстановок 127
- n-й степени I, 127
- симметрическая множества 127
- степени п 127
- циклическая 133
Группоид 121
Группы изоморфные 161
Деление 131
Делители нуля 139
Делитель нормальный 162
Дерево вывода 587
- цепочки в КС-грамматике 594
-- частичное 590
727
Дерево неориентированное 297
- ориентированное 297
- - бинарное 300
полное 300
- остовное 304
- - наименьшего веса 308
- помеченное 591
- - А-свободное 594
- решений 302
- упорядоченное 592
Диагональ 46
Диаграмма конечного автомата с
выходом 552
- Хассе 81
Диамант 222
Дизъюнктор 448
Дизъюнкция I, 25, 385
- элементарная 406
Дистрибутивность бесконечная 61
Длина вывода 476, 634
- ДНФ 410
- кортежа 39
- пути 278
- слова 463
- цепи 278
ДМП-автомат 688
ДНФ 406
- кратчайшая 410
- минимальная 409
- сокращенная 412
- тупиковая 420
Доминирование 76
Дополнение 208
- булево 210
- графа неориентированного 346
-- ориентированного 346
- множества I, 32
Дуга 277
- древесная 321
- заходящая 277
- инцидентная 277
- исходящая 277
- обратная 322
- поперечная 322
- прямая 321
- пустая 504
- стартовая 714
Единица кольца 135
- моноида 121
- полукольца 175
- полу решетки 216
- решетки 221
- функции нижняя 436
Единицы мнимые 169
Задача анализа конечного
автомата 519
- глобального анализа графов 311
- о кратчайших расстояниях 327
-- перечислении путей 327
-- путях общая 328
- синтеза конечного автомата 518
- сортировки 302
- структурного синтеза конечного
автомата с выходом 556
- транзитивного замыкания
ориентированного графа 326
- Штейнера 306
Закон сокращения левый 129
-- правый 129
Законы де Моргана 209
бесконечные 61
728
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Замыкание множества булевых
функций 400
- относительно операции 232
- рефлексивно-транзитивное 69
- элемента 190
Запись аддитивная 126
- мультипликативная 126
Значение неопределеное 703
- формулы 399
Изоморфизм 244
- графов 342
- групп 158
- колец 166
- многосортный 270
Импликанта 408
- простая 412
- избыточная 419
-- ядровая 418
Импликация I, 25, 385
Инверсия конечной подстановки 567
- морфизма 565
- набора 434
- цепочки 488
Инвертор 448
Индекс подгруппы в группе левый
154
Инъекция I, 41
Иррефлексивность 62
Источник сети 349
Итерация позитивная 469
- элемента 190
- языка 469
Карта Карно 414
Квадрат бинарного отношения 54
- декартов 39
Квазипорядок 66
Квантор всеобщности I, 28
- существования I, 28
Кватернион сопряженный 170
КЗ-грамматика 486
- обобщенная 487
КЗ-правило 486
КЗ-язык 489
- обобщенный 489
Класс подгруппы по элементу
смежный левый 152
' правый 152
- Поста 436
- эквивалентности 70
- языка 488
КНФ 406
Кольца изоморфные 167
Кольцо 135
- булево 173
- вычетов по модулю Д: 137
- коммутативное 136
- линейных операторов 137
- эндоморфизмов абелевой группы
253
Команда 505
- применимая к конфигурации 633
Комбинация линейная IV, 359
Композиция бинарных отношений
на множестве 54
- соответствий 51
Компонента (связности) 285
- слабой связности (слабая) 288
Компоненты одноименные 39
Конгруэнция 237
- многосортная 273
Конец дуги 277
- отрезка левый 260
-- правый 260
- пути 278
729
Конец ребра 277
- цепи 278
- цепочки 467
Конкатенация кортежей 123
- слов 466
- языков 468
Константа 23
- булева 375
- индивидная 23
Конституэнта единицы 406
- нуля 407
Контекст КЗ-правила левый 486
- - правый 486
- левый 675
Контур 279
Конус верхний 80
- нижний 80
Конфигурация автомата 496
- выводимая 634
- заключительная 634
- конечного автомата 499
- машины Тьюринга 571
- МП-автомата 633
- начальная 634
- непосредственно выводимая 633
- тупиковая 634
Конъюнктор 448
Конъюнкция I, 25, 385
- элементарная 406
Координаты точки III, 38
Корень ориентированного дерева
297
Кортеж I, 39
- пустой 123
Коэффициенты биномиальные I,
100
Критерий Поста 439
Крона дерева 588
Крыло вхождения левое 466
- - правое 466
КС-грамматика 487
- однозначная 600
КС-язык 489
- детерминированный 689
Куб булев 210
- декартов 39
- единичный размерности п 377
-- п-мерный 377
Куст 300
Лента входная автомата 495
Лес неориентированный 299
- ориентированный 299
- остовный 304
- глубинный 318
- поиска в глубину 318
Лист 298
Литерал 405
Магазин МП-автомата 625
Маркер начала ленты 570
Массив 292
- лидеров 292
Матрица булева 290
- достижимости 294
- инциденций 289
- меток дуг 328
- симметрическая III
- смежности вершин 290
Машина Тьюринга 570
-- в алфавите 576
-- детерминированная 572
-- над алфавитом 576
Метка входная 713
- дуги 307
- входная 553
- выходная 553
730
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Метка пути 329
- магазинная 712
- ребра 307
Метод Блейка 425
- Гаусса III, 199
- двух включений 34
- неопределенных коэффициентов
432
- определения семантики
аксиоматический 699
- последовательного исключения
неизвестных 199
- характеристических функций 103
- эквивалентных преобразований
37
Механизм управления выводом 673
Минимизация конечного автомата
531
Множества равномощные I, 89
- равные 29
Множество булевых функций
замкнутое 401
полное 401
- вполне упорядоченное 81
- замкнутое относительно
операции 147
операций 230
- континуальное 96
- линейно упорядоченное 77
- мощности континуума 96
- не более чем счетное 93
- пустое I, 31
- слов в алфавите перечислимое (по
Тьюрингу) 577
разрешимое (по Тьюрингу)
577
- состояний машины Тьюринга
конечное 570
Множество счетное I, 90
- универсальное I, 30
- упорядоченное 75
- индуктивное 83
- п-элементное 30
- П-замкнутое 230
Модель 227
- анализирующая 494
- порождающая 494
- распознающая 494
Модуль над кольцом левый 145
правый 145
Моноид 121
- кольца мультипликативный 136
- полукольца аддитивный 176
- мультипликативный 176
- свободный 124
- симметрический 122
Мономорфизм 244
Морфизм 564
- инверсный 565
- обратный 565
- языка 566
-- инверсный 566
- А-свободный 565
Мощность континуума 96
- множества I, 90
МП-автомат 625
- детерминированный 638, 688
- расширенный 688
- эквивалентный КС-грамматике
640
МП-автоматы эквивалентные 635
Мультиграф ориентированный 711
Набор булев 210
- единичный 210
- значений переменных 376
- нулевой 210
731
Наборы взаимно противоположные
434
Направление грани 381
Начало дуги 277
- пути 278
- цепочки 466
Нейтральный элемент моноида 121
Нетерминал 473
Норма кватерниона 170
Носитель 226
- алгебры 117
Нуль 114
- кольца 135
- левый 114
- относительно операции 114
- полукольца 175
- полурешетки 216
- правый 114
- решетки 221
Нумерация 90
- лексикографическая 463
Область значений отображения 41
- значения соответствия 45
- определения соответствия 45
- - частичного отображения 43
- определенности состояния
памяти 703
- применимости машины Тьюринга
573
- целостности 141
Образ группы гомоморфный 159
- кольца гомоморфный 167
- множества при отображении I, +3
- системы гомоморфный 244
- элемента при отображении I, 40
Объединение булево 208
- множеств I, 32
Объединение решеточное 217
- семейств 269
Ограничение бинарного отношения
на подмножество 60
- соответствия на подмножества 58
ОД-функция 555
ОКЗ-грамматика 487
ОКЗ-язык 489
Октава 170
Оператор булев 387
- нулевой IV, 137
- тождественный IV, 131
Операции булевы 210
Операция ассоциативная 114
- бинарная 113
- идемпотентная 114
- коммутативная 114
- конкатенарная 696
- логическая 24
- многосортная 266
- нульарная 113
- решеточная 217
- унарная 113
- п-арная 113, 267
- п- местная 113
Определение функции как
процедуры 575
Определения взаимно двойственные
81
Основа 684
- вхождения 466
Отец 298
Отношение бинарное 49
- - на множестве 45
антисимметричное 63
иррефлексивное 62
обратное 57
732
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Отношение бинарное на множестве
плотное 65
рефлексивное 62
симметричное 63
транзитивное 64
- взаимной достижимости 286
- включения 62
- выводимости 475
- двойственное к отношению
порядка 75
- доминирования 76
- достижимости 279
- квазипорядка 66
- линейного порядка 77
- непосредственной выводимости
475
-- достижимости 277, 277
- порядка 66
- предпорядка 66
- равенства по модулю 71
- смежности 341
- строгого порядка 66
- - предпорядка 66
- толерантности 66
- функциональное по компоненте
50
- частичного порядка 66
- эквивалентности 66
- n-арное на множестве 48
-- (п-местное) 48
Отображение биективное I, ±2
- инъективное 41
- монотонное 83
- на 42
- непрерывное 83
- обратное I, 58
- сюръективное 42
- тождественное 41
Отображение частичное 43
Отрезок 260
Отрицание I, 25 > 384
- набора 434
Очередь 308
Палиндром 488
Память внутренняя автомата 495
Парадокс Рассела 101
Пара неупорядоченная 37
- упорядоченная I, 38
Пары упорядоченные равные 38
Пентагон 222
Переименование нетерминалов
грамматики 485
Переменное 24
- булево 375
- булевой функции 376
- индивидное 24
- существенное 388
- фиктивное 388
Пересечение булево 208
- множеств I, 32
- решеточное 217
- семейств 269
- языков суженное 667
Перестановка I, 100
Переход из состояния в состояние
504
Петля 277
Подалгебра 231
- многосортная 269
Подграф 283
- максимальный 284
- остовный 284
- порожденный 284
-- множеством вершин 284
- собственный 284
733
Подгруппа 149
- нетривиальная 149
- нормальная 162
- собственная 149
- тривиальная 149
- циклическая, порожденная
элементом а 150
Подгруппоид 148
- собственный 149
Поддерево 300
- максимальное 598
Подкольцо 151
Подкуб 383
Подмножество собственное I, 34
- строгое 34
- упорядоченное 77
Подмоноид 148
- нетривиальный 149
- собственный 149
- тривиальный 149
Подполе 151
Подполугруппа 148
- собственная 149
Подполукольцо 203
Подпространство линейное IV
Подсемейство 269
Подсистема алгебраической
системы 230
Подслово 466
Подстановка I, 131
- конечная 566
- инверсная 567
- языков в язык 654
Подтело 151
Подформула 399
Подфраза первого уровня 694
- фразы 694
Подход интенсиональный 698
- экстенсиональный 698
Подцепочка 466
Поиск в глубину 312
- ширину 312
Поле 140
- вычетов по модулю р 142
- действительных чисел 141
- комплексных чисел 141
- рациональных чисел 140
- упорядоченное 228
- непрерывное 229
Полином Жегалкина 431
-- первой степени 431
Полугруппа 121
- коммутативная 122
- симметрическая 122
- циклическая 133
Полукольцо 175
- взаимное 204
- двойственное 204
- замкнутое 182
- идемпотентное 176
- коммутативное 176
- матриц над полукольцом 198
- регулярных языков 490
- симметричное 204
- с итерацией 203
Полу решетка 124
- верхняя 214
- нижняя 214
Полустепень захода 277
- исхода 277
Порядок 66
- булев 378
- двойственный 75
734
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Порядок естественный
идемпотентного полукольца 180
- полурешетки 213
- решетки 219
- индуцированный 77
- конечной группы 134
- лексикографический 380
- линейный 77
- строгий 66
- частичный 66
- числовой естественный 67
- элемента 134
Последовательность 91
- конфигураций допускающая для
цепочки 635
- неубывающая 82
Постфикс цепочки 467
Потомок 298
- подлинный 298
Правило вывода 473, 699
- контекстно-зависимое 486
- КС-грамматики цепное 603
- обобщенного поглощения 425
-- склеивания 425
Прагматика языка 462
Предикат 27
- тождественно истинный 28
- ложный 28
- характеристический 30
Предложение 699
Предок 298
- подлинный 298
Предпорядок 66
- строгий 66
Представление об алгоритме
интуитивное 575
Предшественник 278
Преемник 278
Преобразование формулы
тождественное 402
-- эквивалентное 402
Преобразователь состояний памяти
703
- стирающий 704
Префикс цепочки 466
Признак детерминированности
алгоритма 575
- массовости алгоритма 575
- результативности алгоритма 575
Применимость правила вывода 475
Принцип гомоморфной
интерпретации 696
- двойственности 205
- для упорядоченных множеств 81
Проблема непустоты для конечного
автомата 531
- принадлежности 494
- пустоты для КС-грамматик 611
- синтаксического анализа 673
- соответствий Поста 579
Продукция 473
Проекция конечного автомата с
выходом входная 554
- кортежа 39
Произведение 126
- линейных операторов IV, 137
- множеств декартово (прямое) I,
39
- прямое алгебраических систем
254
- соответствий 51
Прообраз множества I, 43
- элемента при отображении I, J^l
Пространство линейное IV
- над полем 147
- цепей графа 359
735
Пространство циклов графа 359
Путь 278
- в мультиграфе 712
- замкнутый 280
- простой 279
Равносильность 25
Разбиение 70
- тривиальное 70
Размерность кортежа 39
Размещение без повторений I, 100
Разность 130
- множеств I, 32
- симметрическая I, 32
Ранг коциклический 364
- пути 337
- циклический 364
Расстояние по пути 327
Ребро 277
- булева куба 382
- древесное 317
- инцидентное 277
- обратное 317
Результат применения машины
Тьюринга к слову 572
-- операции 113
Рефлексивность 62
Решетка 217
- дистрибутивная 222
Свойство коллективизирующее 30
- непрерывности 228
- нуля аннулирующее 139, 176
- характеристическое 30
Связка логическая 24
Сдвиг левый 146
- правый 146
СДНФ 406
Семантика денотационная 702
- операциональная 702
- смешанных вычислений 702
- трансформационная 702
- языка 461
Семейство множеств
(индексированное) 60
- конечное 60
- не более чем счетное 93
-- счетное 60
- 17-замкнутое 269
Сеть 349
- булева 380
- ориентированная 349
- простая 356
Сечение соответствия 45
- по множеству 45
Сигнатура 226
- алгебры 117
- многосортная 266
Символ 462
- входной конечного автомата 503
- обозреваемый 626
- выходной 552
- магазина верхний 627
-- начальный 629
- магазинный 627
- направления движения головки
570
- недостижимый 612
- нетерминальный 473
- бесполезный 610
- пустой 570
- строгого включения 34
- терминальный 473
Симметричность 63
Синтаксис языка 460
736
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Система алгебраическая 226
-- конечная 227
- команд автомата 496
- машины Тьюринга 570
- - МП-автомата 628
- координат прямоугольная III
декартова I
- образующих 232
- многосортной алгебры 270
- уравнений линейных
алгебраических III, ЦЗ
- формальная 699
Системы алгебраические
изоморфные 244
- однотипные 229
Скаляр модуля 267
Склейка простая 411
СКНФ 406
Слово 463
- пустое 463
Сложение 126
- кольца 135
- полукольца 175
- по модулю 2 385
к 128
Сложность алгоритма 290
- СФЭ 453
Событие XVI, 212
Соединение кортежей 123
- слов 466
- языков 468
Соответствие 44
- взаимно однозначное 42
- всюду определенное 45
- обратное 57
- пустое 44
- универсальное 44
Соответствие функциональное по
компоненте 48
Сорт 266
Сортировка топологическая 350
Состояние блока управления
автомата 495
заключительное 497
начальное 497
- конечного автомата 502
заключительное 502
начальное 502
поглощающее 525
с выходом 552
заключительное 552
начальное 552
- МП-автомата заключительное
629
-- начальное 629
- памяти 702
- всюду неопределенное 703
Сочетание I, 100
Список инцидентности 291
- смежности 291
-- вершины 292
Стек 318
Степень вершины 277
- декартова нулевая 123
- множества декартова 39
- элемента 133
- п-я декартова 254
Стоимость прохождения 329
Сток сети 349
Стратегия „перенос — свертка"
689
Стрелка Пирса 385
Сужение соответствия на
подмножество 59
строгое 59
737
Сумма бесконечная 184
- линейных операторов IV, 137
- по модулю к 128
- частичная 187
- элементов последовательности
183
Суперпозиция над множеством 400
- функций 395
- языков в язык 654
СФЭ 449
Схема из функциональных
элементов над базисом 449
- над базисом 449
Сын 298
Сюръекция I, 4%
- каноническая 73
Таблица истинности 26
- Квайна 425
- критериальная 443
- Кэли 143
- структурная 559
- управляющая 675
Такт работы автомата 495
- - МП-автомата 629
Тезис Тьюринга 576
Тело 140
Теорема 699
- Кантора 94
- Кантора — Бернштейна 98
- Кэли 252
- Лагранжа 154
- о детерминиэации 521
- квадрате 98
- - неподвижной точке 85
- Ферма малая 155
Теория формальная 699
Терминал 473
Тип операции 267
Тождества кольца основные 137
- полукольца основные 176
Тождество 403
- обобщенного поглощения 425
- склеивания 425
- поглощения 207, 217
- теоретико-множественное 36
Толерантность 66
Точка отображения неподвижная I,
85
наименьшая 85
Транзитивность 64
Транспозиция I, 131
Триггер 557
Узел 276
Умножение 126
- в группе (групповое) 126
- кольца 135
- левое 147
- полукольца 175
- правое 147
Уравнение леволинейное 199
- праволинейное 199
Уравнения канонические конечного
автомата с выходом 557
Уровень вершины 349
- ориентированного дерева 300
Устройство управления машины
Тьюринга 570
Утверждение 699
^Трактор-алгебра многосортная 272
Фактор-группа по нормальному
делителю 164
Фактор-кольцо 251
Фактор-множество 71
740
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
О-эквивалентность 532
С-сужение соответствия 59
- - строгое 59
(С, /?)-ограничение соответствия
58
D-номер 316
F/t-множество 676
(F,X)-cxeMa449
Д;-слой 379
/с-эквивалентность 532
?1г(&)-грамматика 675, 677
- сильная 681
??(&)-условие 678
?Я(Л)-грамматика 687
n-ка упорядоченная 39
n-набор упорядоченный 39
n-сеть булева 380
р-дизъюнкция 708
V-проекция конечного автомата с
выходом 554
У-сцепление магазинных меток 713
Л-переход 504
Л-такт работы МП-автомата 629
А-правило вывода КС-грамматики
603
П-алгебра 117
П-замыкание 232
- подсемейства 269
П-подалгебра 231
ОГЛАВЛЕНИЕ
Предисловие 5
Основные обозначения 12
1. Множества и отношения 23
1.1. Множества 23
1.2. Кортеж. Декартово произведение 37
1.3. Соответствия и бинарные отношения 40
1.4. Операции над соответствиями 51
1.5. Семейства множеств 60
1.6. Специальные свойства бинарных отношений 62
1.7. Отношения эквивалентности 70
1.8. Упорядоченные множества. Теорема о неподвижной
точке 75
1.9. Мощность множества 89
Д. 1.1. Об одном парадоксе теории множеств 100
Д. 1.2. Метод характеристических функций 102
Вопросы и задачи 106
2. Алгебры: группы и кольца 112
2.1. Операции. Понятие алгебраической структуры . . . 112
2.2. Группоиды, полугруппы, группы 121
2.3. Кольца, тела, поля 135
2.4. Области целостности 141
2.5. Модули и линейные пространства 145
2.6. Подгруппы и подкольца 147
2.7. Теорема Лагранжа 152
2.8. Гомоморфизмы групп и нормальные делители .... 157
2.9. Гомоморфизмы колец 166
Д.2.1. Кватернионы 168
Вопросы и задачи 171
742 ОГЛАВЛЕНИЕ
3. Полукольца и булевы алгебры 175
3.1. Полукольца. Основные примеры 175
3.2. Замкнутые полукольца 182
3.3. Решение систем линейных уравнений 195
3.4. Булевы алгебры 204
3.5. Решетки 212
Вопросы и задачи 223
4. Алгебраические системы 226
4.1. Модели и алгебры 226
4.2. Подсистемы 230
4.3. Конгруэнции и фактор-системы 236
4.4. Гомоморфизмы 242
4.5. Прямые произведения алгебраических систем .... 253
4.6. Конечные булевы алгебры 260
4.7. Многосортные алгебры 266
Вопросы и задачи 273
5. Теория графов 275
5.1. Основные определения 276
5.2. Способы представления 288
5.3. Деревья 297
5.4. Остовное дерево наименьшего веса 306
5.5. Методы систематического обхода вершин графа . . 311
5.6. Задача о путях во взвешенных ориентированных гра-
графах 326
5.7. Изоморфизм графов 341
5.8. Топологическая сортировка 349
5.9. Элементы цикломатики 356
Вопросы и задачи 368
6. Булевы функции 375
6.1. Понятие булевой функции. Булев куб 375
6.2. Таблицы булевых функций 383
6.3. Фиктивные переменные. Равенство булевых функций 388
6.4. Формулы и суперпозиции 393
6.5. Дизъюнктивные и конъюнктивные нормальные формы 405
. 743
6.6. Построение минимальных ДНФ 408
6.7. Теорема Поста 429
6.8. Схемы из функциональных элементов 447
Вопросы и задачи 456
. Конечные автоматы и регулярные языки 460
7.1. Алфавит, слово, язык 462
7.2. Порождающие грамматики 472
7.3. Классификация грамматик и языков 486
7.4. Регулярные языки и регулярные выражения 490
7.5. Конечные автоматы. Теорема Клини 494
7.6. Детерминизация конечных автоматов 521
7.7. Минимизация конечных автоматов 531
7.8. Лемма о разрастании для регулярных языков .... 538
Д.7.1. Обоснование алгоритма детерминизации конечных ав-
автоматов 544
fV7.2. Конечные автоматы с выходом. Структурный синтез 552
J.7.3. Морфизмы и конечные подстановки 564
\j* 4. Машины Тьюринга 569
Вопросы и задачи 579
3. Контекстно-свободные языки 587
8.1. КС-грамматики. Деревья вывода. Однозначность . . 587
8.2. Приведенная форма КС-грамматики 602
8.3. Лемма о разрастании для КС-языков 616
0 4. Магазинные автоматы 625
8.5. Алгебраические свойства КС-языков 654
Д.8.1. О методах синтаксического анализа КС-языков . . . 673
Д.8.2. Семантика формальных языков 692
,.3.3. Графовое представление МП-автоматов 711
Вопросы и задачи 715
Список рекомендуемой литературы 720
Предметный указатель 724
Учебное издание
Математика в техническом университете
Выпуск XIX
Белоусов Алексей Иванович
Ткачев Сергей Борисович
ДИСКРЕТНАЯ МАТЕМАТИКА
Редактор Е.В. Авилова
Художник С. С. Водчиц
Компьютерная верстка СБ. Ткачева
Оригинал-макет подготовлен
в Издательстве МГТУ им. Н.Э. Баумана
под руководством А.И. Канатникова
Подписано в печать 19.04.2004. Формат 60x88/16.
Печать офсетная. Бумага офсетная.
Усл. печ. л. 46,5. Уч.-изд. л. 47,84.
Тираж 3000 экз. Заказ №10061
Издательство МГТУ им. Н.Э. Баумана.
105005, Москва, 2-я Бауманская, 5.
Отпечатано в ГУП ППП «Типография «Наука».
121099, г. Москва, Шубинский пер., 6.
ISBN 5-7038-1769-2
81
7698