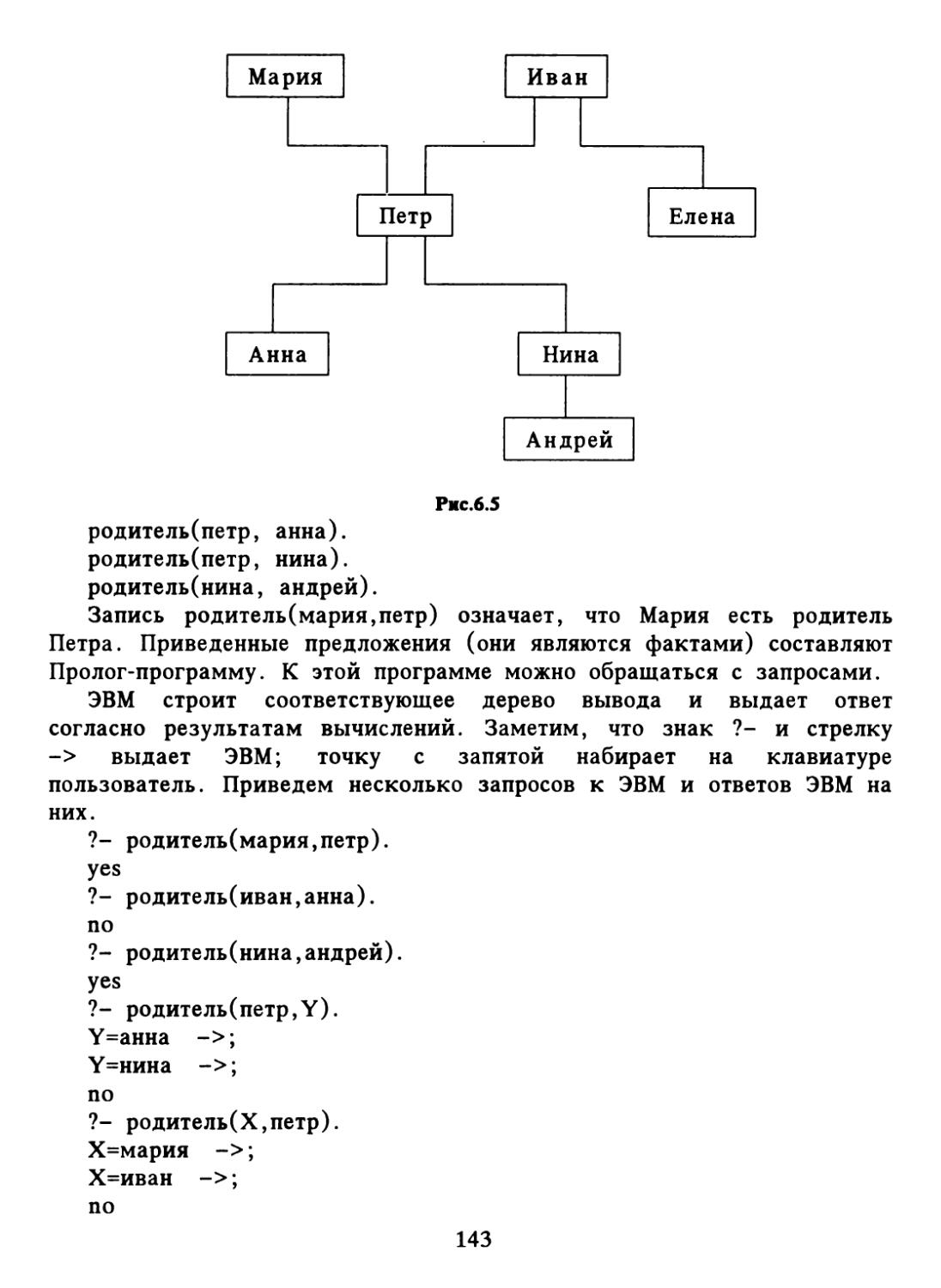
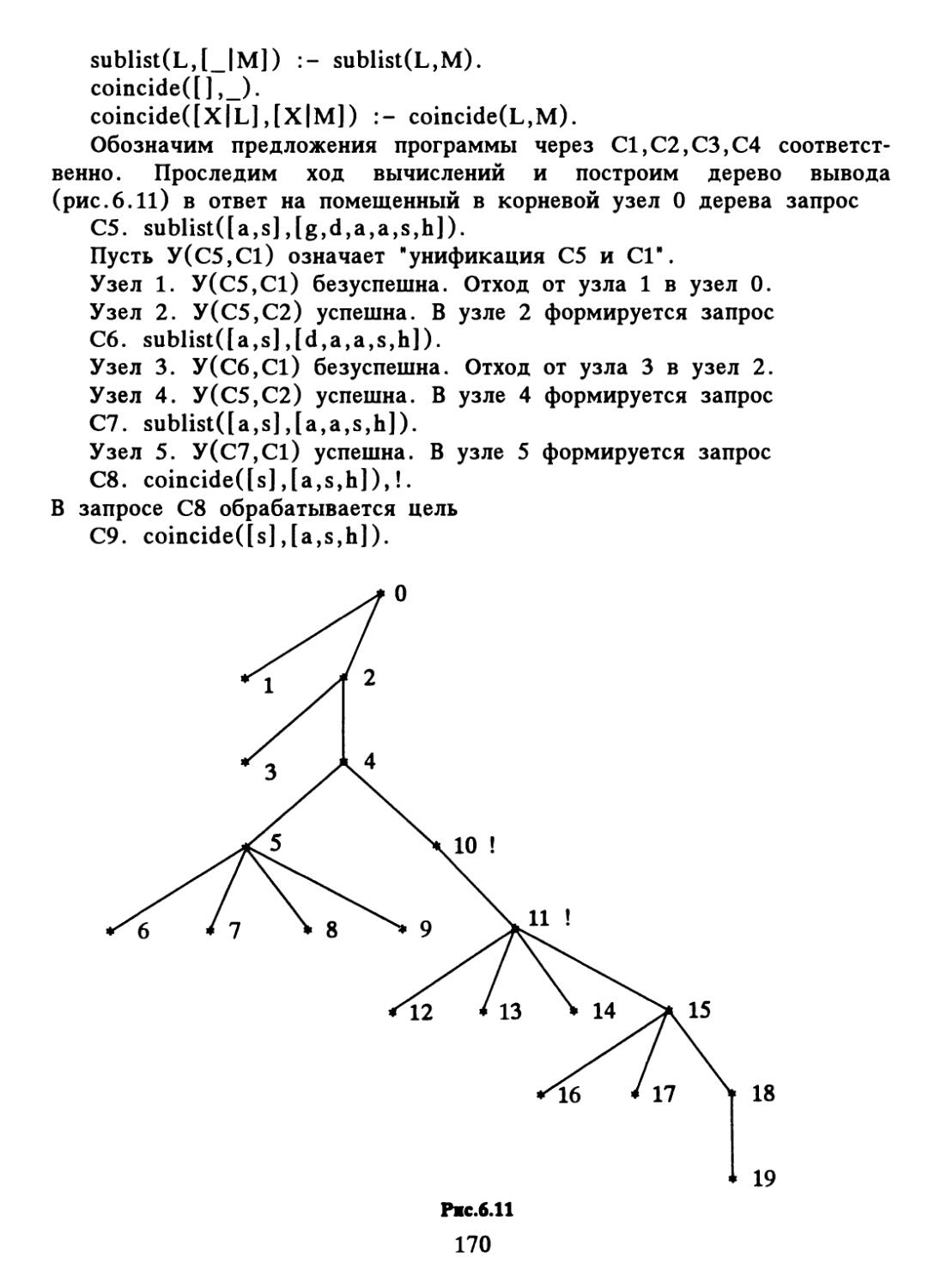
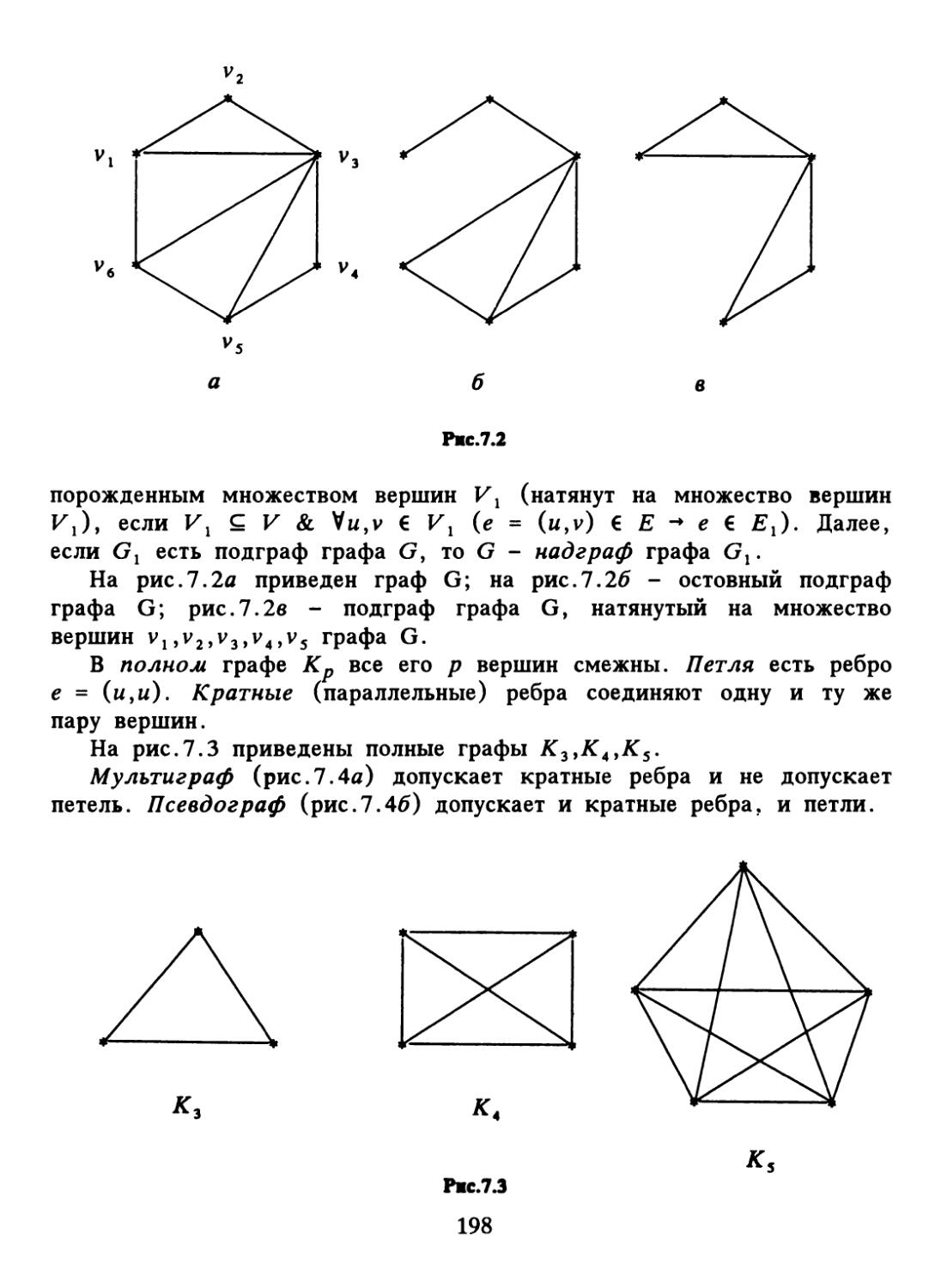
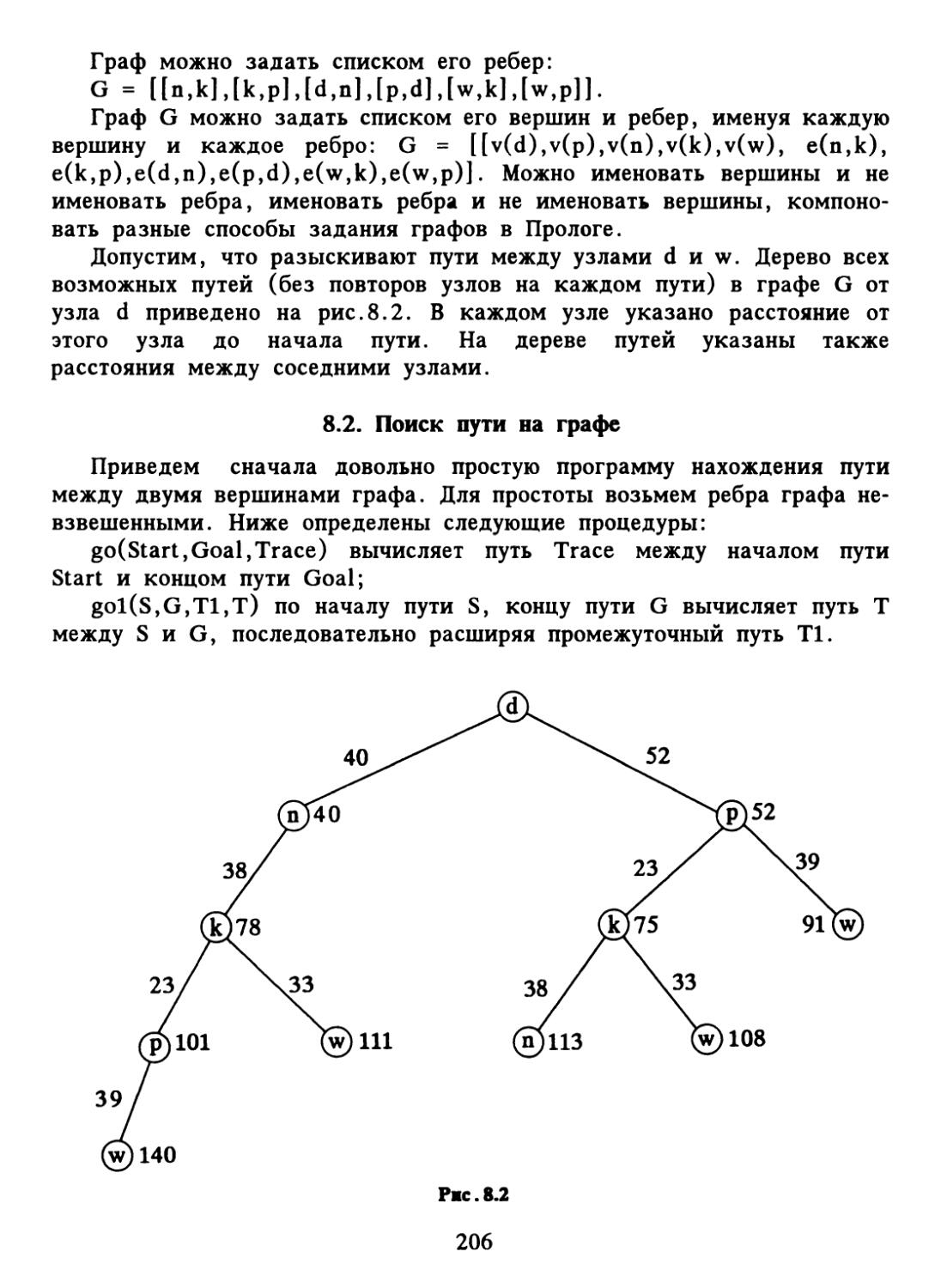
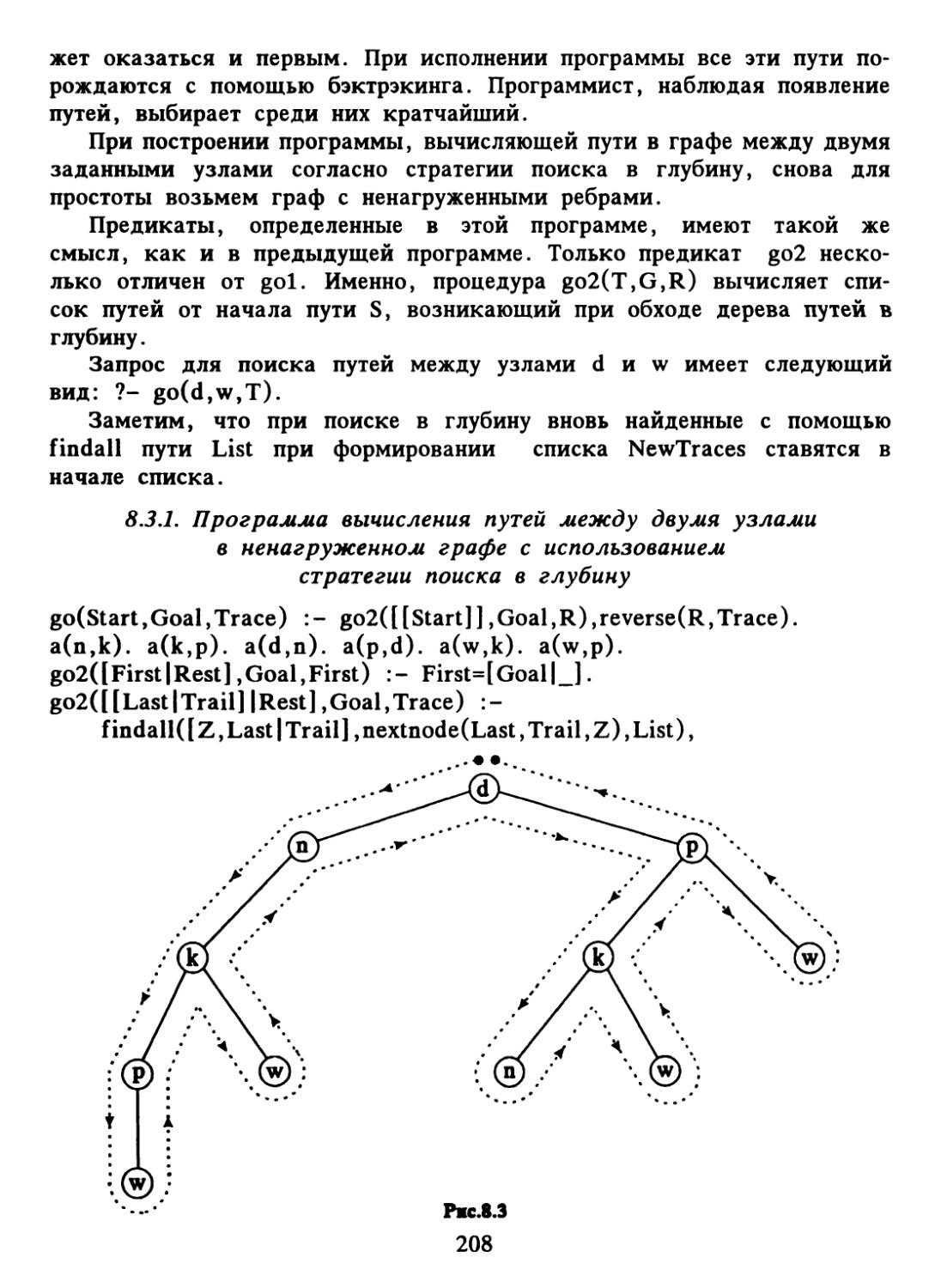
Author: Набебин А.А.
Tags: комбинаторный анализ теория графов компьютерные технологии теория вероятностей математическая статистика математика логика
ISBN: 5-7046-0162-6
Year: 1996
Text
щ
**
¥/■
из
л ств
и
*?,
1
т
А.А.НАБЕБИН
ЛОГИКА
И
ПРОЛОГ
В ДИСКРЕТНОЙ МАТЕМАТИКЕ
МОСКВА ИЗДАТЕЛЬСТВО МЭИ 1996
ББК: 22.174 »* Издание осуществлено при под-
д j 34 1><ГГ>и держке Российского фонда фун-
V TTlf • S1Q 1 • Г* 1П £ + £Я 1 1 П£1 JJ Даментальных исследований по
УДК. 519.1. [510.6 + 681.3.06] " проекту 96-01-14156
Рецензенты докт. физ.-мат. наук, проф. Р.И. Подловченко,
докт. техн. наук, проф. Д.А. Поспелов
Научный редактор канд. физ.-мат. наук В.А. Захаров
Набебин А.А.
HI34 Логика и Пролог в дискретной математике.- М.:
Издательство МЭИ, 1996. - 452 с; ил.
ISBN 5-7046-0162-6
Излагаются основные понятия математической логики и формального
вывода, теории графов, комбинаторики, теории конечных автоматов в
ее связи с монадической логикой. Рассматривается резолютивный вывод
и на его основе вводится универсальный язык программирования
Пролог. Программируются некоторые алгоритмы на графах, в
комбинаторике, в теории конечных автоматов при переходе от формул
монадической логики к автоматам, которые эти формулы описывают.
Предназначено студентам высших технических учебных заведений и
всем интересующимся теорией и практикой применения Пролога.
1602120000-021
Н 097(02Ь% безобъявл. ББК: 22.174
ISBN 5-7046-0162-6 © Набебин А.А., 1996
Моему дорогому учителю
Евгению Алексеевичу Щеголъкову
и академику
Петру Сергеевичу Новикову
ПРЕДИСЛОВИЕ
Одно из крупнейших достижений математики первой половины
двадцатого века - оформление математической логики и теории
алгоритмов в самостоятельные дисциплины. Три крупных результата
определили характер всех последующих исследований этого направления:
теорема Геделя о полноте аксиоматического исчисления предикатов
относительно всех тождественно истинных формул такого исчисления
(полнота относительно интерпретации); существование
алгоритмически неразрешимых проблем, в частности, теорема Черча об
алгоритмической неразрешимости исчисления предикатов; теорема Геделя о
неполноте аксиоматической арифметики относительно множества ее
истинных формул.
Уже в древности предпринимались попытки строго изложить
математические факты, которые стремились вывести из немногочисленных
исходных посылок - аксиом. Замечательным примером такого подхода
к изложению математических сведений были "Начала"
древнегреческого математика Евклида, в особенности его геометрия. Изучались и
законы правильного вывода следствий из исходных посылок (логика
Аристотеля).
Первые попытки создать строгие математические теории восходят
к работам Буля, Фреге, Пеано, других математиков. Исследователи
руководствовались целью заложить такие основания математики,
выделить такие аксиомы и правила вывода, с помощью которых можно
было бы формально доказать любое содержательно истинное
математическое утверждение. Подобные утверждения можно было бы доказывать
автоматически. Эта связываемая с именем Гильберта программа в
полной мере не удалась: австрийский математик Курт Гедель
показал, что всякая достаточно богатая формальная система (например,
аксиоматическая арифметика) не полна, т.е. в ней найдутся
содержательно истинные утверждения, недоказуемые в системе. Пессимист
угрюмо заметил бы: "Я же говорил вам, что из этой затеи
Гильберта ничего хорошего не Выйдет. Пойду наколю себе дров. Хотя я хо-
3
рошо знаю заранее, что из этой моей затеи тоже ничего не выйдет".
Оптимист скажет другое: "Мы надеялись на чудо. Его не произошло.
Всевышний не дает нам того, чего мы очень хотим. Зато мы узнали
много интересного, нам открылись огромные просторы для
деятельности. О сколько задач у нас впереди! За дело, коллеги!"
Аксиоматическая арифметика не полна. Тем не менее интерес к
математической логике не убывает, исследования
формально-логических систем продолжаются. Успешно описываются довольно большие
фрагменты математических дисциплин. Использование алгебрологиче-
ского языка при проектировании узлов ЭВМ общеизвестно. В
последнее время аппарат математической логики стал широко применяться в
современных системах представления знаний.
Самое удивительное применение математическая логика нашла в
вычислительной математике: формализм логического вывода в логике
предикатов первого порядка был взят за основу при построении
универсального языка программирования Пролог (акроним от PROgramming
in LOGic). С появлением Пролог-подобных языков программирования
математическая логика, которая совсем недавно была логикой сугубо
теоретической, стала логикой вычисляющей. Классическая
гильбертова логика доказательств истинных формул логики предикатов первого
порядка для этой практической цели оказалась неподходящей. В
1965 г. Дж.А.Робинсон в качестве формализма, удобного для
исполнения на ЭВМ, предложил использовать разработанный им метод
резолюций. Замечательное открытие Робинсона оказалось необычайно
плодотворным и уже в семидесятых годах привело к построению
универсального языка программирования Пролог и трансляторов для него.
Сейчас существует несколько версий трансляторов с Пролога: Micro-
Prolog, DEC-System/Prolog, C-Prolog, IC-Prolog, M-Prolog, Sigma-
Prolog, Chalcedony-Prolog, FF-Prolog, UNSW/Prolog, Prolog-6, Pro-
log-1 и Prolog-2 фирмы Expert Systems International, Quintus-Pro-
log, Turbo-Prolog, Arity-Prolog и другие, два из которых: Turbo-
Prolog и более совершенный Arity-Prolog наиболее распространены.
При написании программ мы ориентировались на версию языка Arity-
Prolog.
Пролог - это недавно разработанный и получивший в конце
восьмидесятых годов широкое распространение в мире списковый язык для
теоретико-множественных вычислений. Его называют также языком
искусственного интеллекта. Значение Пролог-подобных языков будет
возрастать; специалисты прочат их в качестве одного из основных
средств общения с ЭВМ пятого поколения.
Задуманный как универсальный язык программирования для
перевода с одного естественного языка на другой, Пролог как один из
4
языков искусственного интеллекта оказался удобным современным
инструментом при построении вычислительных моделей, возникающих при
решении задач на графах, проектировании конечных автоматов,
построении баз данных, баз знаний, экспертных систем, в задачах
лингвистики при работе с естественными и искусственными языками
(причем в числе последних могут выступать и языки программирования),
в символьных преобразованиях, теории игр, системах представления
знаний и так далее.
Несколько необычным в Прологе может показаться отсутствие
привычного в традиционных языках программирования оператора
присваивания. Вместо него в Прологе реализован более общий алгоритм
унификации, построенный на основе операции сравнения с образцом.
Необычен в Прологе также и отсутствующий в традиционных языках
бэктрэкинг, позволяющий обходить дерево вывода и собирать все
возможные решения задачи. Реализация рекурсии в Прологе
практически не отличается от общепринятой. В остальном Пролог очень
удобен, особенно в задачах, где основным обрабатываемым объектом
является символ и список символов (множество).
Пролог это списковый язык, и он особенно удобен для списковых
вычислений. В качестве одного из примеров использования Пролога
взяты алгоритмы на графах. В последнее время теория графов
привлекает к себе внимание специалистов из многих областей знания.
Особенно важна связь теории графов с теоретической и технической
кибернетикой, теориями конечных автоматов, оптимизации,
электрических цепей, программирования, а также с математической логикой
и алгеброй. Практическая роль теории графов сильно возросла с
использованием графовых моделей при проектировании
автоматизированных систем управления и вычислительных систем дискретного
действия.
Алгоритмы на графах имеют теоретико-множественный характер и
потому плохо поддаются записи на общепринятых сейчас
императивных языках. Паскаль, например, на котором написаны некоторые
программы для решения графовых задач (Липский В. Комбинаторика для
программистов. М.: Мир, 1988), предполагает написание списков,
очередей и т.д. - объектов, которые в Прологе являются
встроенными. Основной объект для обработки на Алгол-подобных языках
есть число или числовой массив. Поэтому графовые алгоритмы, часто
прозрачные и понятные в теоретико-множественном изложении,
приходится дорабатывать, чтобы изложить их на языке числовых матриц и
операций над ними. Наглядность и прозрачность алгоритма теряются,
он становится громоздким и трудновоспринимаемым. Совсем другое
дело Пролог: он приспособлен для записи именно теоретико-множест-
5
венных рассуждений. Основным объектом для обработки в Прологе
является символ или список символов, т.е. множество. В связи с этим
алгоритмы теоретико-множественного характера записываются в
Прологе непринужденно и естественно именно в своей прозрачной
теоретико-множественной постановке. Пролог, и, в частности Arity-Pro-
log, имеет средства сопряжения с языками Си, Паскаль, Фортран.
Это делает его удобным вычислительным инструментом при обработке
чисел и числовых массивов.
Другой интересный пример использования математической логики и
Пролога - конечные автоматы. Как дискретные преобразователи
информации они широко используются в качестве дискретных
управляющих устройств. На вход автомата от работающего объекта в
дискретные моменты времени поступает дискретная информация, а на его
выходе формируется необходимое дискретное воздействие на
управляющие органы объекта.
В электроэнергетике, например, алгоритмы автоматического
управления процессом производства и распределения электроэнергии
реализуются автоматическими устройствами, которые функционируют на
основе получения, переработки, передачи и использования
информации. При дискретных сигналах соответствующие части автоматических
устройств функционируют по логическим алгоритмам как конечные
автоматы.
Самое широкое применение конечные автоматы получили при
проектировании ЭВМ. Один из важнейших узлов в ЭВМ - вычислительные
автоматы, реализующие сложение, вычитание, умножение, деление,
сравнение чисел по величине и так далее. Конструируются
вычислительные автоматы и для реализации разнообразных команд ассемблера
ЭВМ. Всякая команда разбивается на последовательность
элементарных действий, выполняемых автоматами, причем действия должны быть
определенным образом организованы во времени. Эту организацию
тоже осуществляют конечные автоматы (их называют операционными).
Всякая ЭВМ выполняет несколько сотен операций, которые
реализуются конечными автоматами.
Исследователь общается с ЭВМ посредством программы, написанной
на каком-либо алгоритмическом языке высокого уровня (Фортран,
Алгол, Паскаль, Лисп, Пролог и т.д.). Программа, которая по замыслу
исследователя должна выполнить некоторую осмысленную (с точки
зрения исследователя) работу, часто довольно значительную,
вводится в ЭВМ, где последовательно преобразуется в программу на более
простых языках, пока не превращается в программу в кодах ЭВМ.
Каждая ее команда, представляющая собой набор из нулей и единиц,
кодирует некоторую элементарную операцию, реализуемую в ЭВМ неко-
6
торым конечным автоматом. Так что многочисленные вычислительные
автоматы есть те материальные узлы в ЭВМ, которые, составляя
"тело" ЭВМ, производят "душу" - осмысленные вычисления по заложенной
в ЭВМ программе.
Конечные автоматы, работающие как акцепторы-распознаватели,
т.е. устройства, допускающие или отвергающие поступающие на его
вход слова в входном алфавите, используются при разработке
трансляторов с алгоритмических языков.
Одно из важных направлений развития современной вычислительной
техники это автоматизация проектирования узлов ЭВМ, в частности,
конечных автоматов. Автоматизация значительно сокращает сроки
проектирования ЭВМ и высвобождает проектанту время для творческой
работы.
Конечный автомат считается заданным, если заданы его
внутренний и внешний алфавиты, а также его функции переходов и
выходов. Методы проектирования конечных автоматов с помощью алгебры
логики довольно хорошо развиты. Существуют и алгоритмы,
позволяющие строить структурную схему конечного автомата. Будем
заниматься разработкой алгоритмов, позволяющих от какого-то словесного
описания конечного автомата, которым чаще всего и располагает
заказчик, перейти к его описанию на некотором формальном языке.
Для нас это язык логики одноместных предикатов (монадическая
логика).
Разработчику, обдумывающему особенности проектируемого
конечного автомата как преобразователя информации, следует указать
множество его входных и выходных сигналов. Кроме того,
разработчику необходимо понять, что должен "запомнить" конечный автомат,
как строятся его функции переходов и выходов. Это трудная и
кропотливая работа. Алгоритм функционирования конечного автомата в
терминах преобразования входных последовательностей в выходные
часто довольно просто записать на языке логики одноместных
предикатов, а затем по написанной формуле сконструировать задуманный
конечный автомат.
Существует алгоритм получения конечного автомата по формуле
логики одноместных предикатов, которая требуемый конечный автомат
описывает. Переход от формулы монадической логики к конечному
автомату можно передать ЭВМ. Алгоритмический язык Пролог удобен для
обработки на ЭВМ формул такой логики. Поэтому предлагаемый язык
удобен для решения задач автоматизации проектирования конечных
автоматов с помощью ЭВМ. В пособии приводятся некоторые Пролог-
программы, реализующие отдельные алгоритмы операций над
конечными автоматами, возникающие при переходе от формулы монадической
7
логики (второго порядка) к описываемому этой формулой автомату.
Основной вопрос математической логики есть вопрос об
алгоритмической разрешимости истинности ее формул. Как показал А.Черч,
логика предикатов первого порядка оказалась неразрешимой: не
существует алгоритма, который по любой формуле логики предикатов
устанавливал бы, истинна она или ложна. Тем более неразрешима
логика предикатов второго и более высоких порядков. Стоял вопрос о
распознавании общезначимости и для монадической логики. Так,
логика одноместных предикатов первого порядка оказалась
алгоритмически разрешимой, и несложный разрешающий алгоритм для нее был
найден Л.Левенгеймом в 1915 г. Монадическая логика второго
порядка (допускаются кванторы по предикатным переменным) тоже
оказалась разрешимой. Разрешающий алгоритм, более сложный, чем в
предыдущем случае, был найден Т.Скулемом в 1920 г. Вопрос о
разрешимости монадической логики второго порядка с предикатами,
определенными на натуральном ряду поставил в 1949 г. А.Тарский. Причем
при построении формул допускается использование функции
прибавления единицы. Возможно, что вопрос о разрешимости такой логики
ставился и ранее: уж очень естественно желание иметь такой
разрешающий алгоритм, но письменных свидетельств об этом, как отмечают
многие авторы, нет. Такие видные логики, как А.Черч, С.Клини,
М.Рабин, другие математики, взялись за решение этой проблемы. Для
решения этой проблемы Б.А.Трахтенброт и несколько позже А.Черч
предложили использовать теорию конечных автоматов, появившуюся в
то время вне логики для обслуживания потребностей конструирования
вычислительных узлов ЭВМ. Идея оказалась плодотворной. На этом
пути М.Рабин доказал несколько важных теорем о конечных
автоматах, в том числе теорему о детерминизации источника. Несколько
результатов о выразимости в монадической логике получил
Р.Робинсон. Математик Ю.Т.Медведев сделал определение конечного автомата
более абстрактным.
В конце 50-х годов несколько авторов нашли разрешающий
алгоритм для слабого варианта монадической логики: предикаты могут
принимать лишь конечное число значений истинно. Наконец, Д.Бюхи в
1962 г. нашел разрешающий алгоритм для исследуемой монадической
логики. Для Бюхи (как это отмечал он сам) весьма существенным
было указание Райта на одну теорему Рамсея, которая оказалась
центральной для найденного разрешающего алгоритма. Выступая в 1978 г.
на семинаре П.С.Новикова по математической логике,
Б.А.Трахтенброт с сожалением вспоминал, что имей он тогда совет Райта, он
тоже получил бы этот алгоритм. Р.Макнотон предложил изящную игровую
интерпретацию при детерминизации автоматов, работающих на беско-
8
нечных последовательностях.
В 1965 г. несколько авторов (первым из них был Д.Донер) нашли
разрешающий алгоритм для слабого варианта монадической логики
второго порядка с предикатами, определенными на множестве слов в
конечном алфавите с несколькими функциями следования на множестве
слов. В 1967 г. появилось сообщение М.Рабина о разрешающем
алгоритме для монадической логики без ограничений на число
истинностных значений. В 1969 г. было подробно изложено решение этой
трудной задачи. Ан.А.Мучник сильно упростил доказательство М.Рабина.
Лойхли нашел разрешающий алгоритм для монадической логики с
линейным порядком. Д.Зифкес и несколько позже А.А.Набебин
предложили для монадической логики натуральных чисел простую
аксиоматику. А.Л.Семенов сильно продвинул вопрос о разрешимых расширениях
монадической логики.
Разрешающий алгоритм Бюхи исходил из того факта, что
множество истинности формулы монадической логики совпадает с множеством
входных последовательностей, допустимых некоторым конечным
автоматом, который по формуле может быть построен эффективно. Так как
среди всех языков, адекватно описывающих поведение конечных
автоматов, язык монадической логики наиболее гибок и близок к
разговорному, то монадическая логика оказывается удобной для задания
работы конечного автомата.
Надо сказать, что алгоритм перехода от формулы логики к
конечному автомату, ею описываемому, имеет высокую вычислительную
сложность. Для экспоненциальной башни, сколь угодно высокой,
можно указать формулу, для которой сложность вычислительного
алгоритма перехода от этой формулы к автомату не меньше
экспоненциальной башни. Поэтому задача построения автомата по формуле
обременительна даже для мощных современных ЭВМ. Однако то, что
соответствующие алгоритмы написаны (на Прологе), говорит о
продуктивности такого подхода к автоматизации проектирования конечных
автоматов.
Сильное ограничение в реальных расчетах - недостаточный объем
глобального стека Пролога. Можно заметить, что рекурсия при
программировании алгоритмов часто используется как цикл. В случае
такого ее применения в памяти ЭВМ достаточно хранить только
результаты предыдущего цикла. В соответствии с этим было бы полезно
предусмотреть в Прологе два вида рекурсии: собственно рекурсия,
как она в Прологе и выполнена, и рекурсия-цикл с сохранением в
стеке только результатов предыдущего цикла. Возможно, что
рекурсия-цикл нарушит логическую чистоту языка и усложнит его, зато
усилит практическую значимость. Конечно, возможна переделка реку-
9
рсивных программ на программы, где рекурсия заменяется на
конструкцию repeat-fail-loop. Однако переделка довольно утомительна,
программа увеличивается, теряется ее естественность и
прозрачность. К тому же длина предложения в программе не должна
превышать 4 Кб.
В книге приведено много больших и малых Пролог-программ.
Заметим, что и большая (даже при малообъемных исходных данных), и
малая (при многообъемных исходных данных) программы зачастую не
могут быть закончены из-за малого объема глобального стека, и
тогда пограмму приходится исполнять по частям, сталкиваясь при
этом с проблемой хранения промежуточных данных. Но программы
написаны, они действуют и могут быть использованы для их улучшения,
а еще в качестве упрека разработчикам языка и в качестве
побудителя для усовершенствования Пролога по тем пунктам, которые
препятствуют просчету объемных программ при объемных исходных
данных. Следует надеяться, что новые версии Пролога, созданные для
более совершенных и мощных ЭВМ нового поколения, не будут иметь
этих ограничений, и тогда объем решаемых задач сразу возрастет.
В сущности, используемый монадический язык имеет теоретико-
множественный характер. Предпошлем основному изложению некоторые
факты из теории множеств.
Понятие множества неопределимо. Это простейшее исходное
понятие человечество сформировало из опыта всего своего исторического
развития. То же можно сказать о смысле простейшего отношения
принадлежности: элемент а принадлежит множеству А (обозначение а €
А) и о смысле отношения тождества (совпадения, равенства) двух
элементов а и Ъ из некоторого множества (обозначение а = Ь).
Другими словами, предполагается, что читатель умеет распознавать
совпадение или несовпадение двух элементов и устанавливать факт
принадлежности или непринадлежности элемента множеству.
Пусть А,В,С - произвольные множества; а,Ь,с - элементы
множеств. Итак, основными неопределяемыми отношениями в теории
множеств являются следующие отношения:
а = Ъ - элементы а и Ъ равны (совпадают);
а € А - элемент а принадлежит множеству А.
Пусть знак «—> означает "тогда и только тогда"; а знаки &, V,
"I , -> , V, 3 есть логические знаки конъюнкции, дизъюнкции,
отрицания, импликации, квантора общности и квантора существования.
Используем их в общепринятом содержательном смысле. Эти же
логические символы в последующем применим при построении формул мона-
дической логики.
Введем следующие отношения:
10
А Я В «-» Vа {а € А - а € В);
А = В ♦— А Я В & В £ А\
А а В —► Л£д & А * Д;
Л 2 Б «— Б £ л;
Л Э 5 «-> 5 С А.
Обозначим через Р(А) множество всех подмножеств множества А и
пусть 0 есть символ пустого множества. Введем операции над
множествами:
A\JB = {x:x€AVx€B}- объединение множеств А и В\
АГ\В = {х:х€А&х€В}- пересечение множеств А и В;
А-В = {х:х€А&х1В}~ разность множеств А и В\
А х В = {(я, ft) : tf€^4&ft€/?}- декартово произведение
множеств А и В.
Декартово произведение можно распространить на несколько
сомножителей, именно, А{ х А2 х ... х Ап = {(а19а2,. ..,ап): а^ €
^41э я2 € >42, ... , ап € Л„}. Отсюда определим натуральную степень
Лп =ЛХЛХ...ХЛ (л раз).
Множества 0 и А называются несобственными (тривиальными)
подмножествами множества А. Если АСВ&А*09тоА есть
собственное подмножество множества В.
Определим подмножества множества натуральных чисел IN = {О,
1,2,...}:
[п,т] = {л,л+1,л+2,...,т};
[п,т) = {/1,/1+1,/1+2,... ,т-1}; (л,т] = {/i+1,/i+2,/i+3, ... ,т};
(л,т) = {л+1,л+2,...,т-1}; [л] = {0,1,2,... ,/i};
[л) = {0,1,2,...,/1-1}; (л] = {1,2,3,...,/!};
[л,со) = {л,л+1,л+2,...}.
Очевидно, что 2 € IN, 15 € IN, 3/5 < IN.
Пусть А и В - два множества. Определим функцию f : А -* В как
отображение, которое каждому элементу а из А ставит в
соответствие некоторый элемент ft из В. Это обстоятельство записывается
как ft = f(a). Примем, что D(f) есть область определения функции
/; R(f) - область значений функции /; f(A) - область тех значений
функции /, когда аргумент функции / пробегает множество А.
Определенное на множествах А1УА29..., Ап л-местное отношение Р
есть подмножество декартова произведения А1*А2*.. .*Ап. В
частности, бинарное отношение, определенное на множествах А,В
есть подмножество из А*В. Проекция Рг; . ,-Р отношения Р из
А1*А2*.. .ХЛ„ на оси JiJ29---Jk U ^Ji<]2<---К]к ^ л/ есть все
те наборы длины /с, которые получаются из наборов отношения Р, где
стерты все компоненты, кроме компонент на местах Ji,j2,- - • ,jk-
Функция /: ^! х ... х Ап-\ "* ^п униформизует отношение Р из
11
AlXA2x.. .*An (по оси л), если )f(al9...ian_l) € /V^ п_хР набор
(«!,... ,сЛ_! j/Cflj,... >ап-\)) € ^- Можно говорить об униформизации
отношения Р функцией / по любой другой оси. Для двумерного случая
функция /: А -> В униформизует (по второй оси) бинарное отношение
Р из А х J5, если Vc € />г1/> пара (я,/(c)) € /\ Функция /: В -» Л
униформизует (по первой оси) бинарное отношение Р из А*В, если Vb
€ Рг2Р пара (/(Ь),Ь) € Р. Например, если Л = {0,1,2,3}, В =
{0,1,2,3,4}, отношение Р = {(0,1),(0,3),(0,4),(1,0),(1,4), (2,1),
(2,3),(3,0),(3,4)}, то функция /: А -* В, для которой /(0)=3,
/(l)=0, /(2)=1, /(3)=4, униформизует отношение Р по второй оси.
Теоретическое содержание книги достаточно традиционно.
Изложение алгебры логики, логики предикатов, формализмов для вывода
их общезначимых формул, уже ставшего классическим формализма
Дж.Робинсона - метода резолюций в логике предикатов, теории
конечных автоматов, комбинаторики, теории алгоритмов следуют
известным книгам С.В.Яблонского, С.К.Клини, П.С.Новикова,
Э.Мендельсона, Г.П.Гаврилова и А.А.Сапоженко, Б.А.Трахтенброта, Р.Ченя и
Р.Ли, А.И.Мальцева, Ю.Л.Ершова и Е.А.Палютина, Х.Роджерса. Эти
учебники представляют собой надежный теоретический фундамент для
книг, ориентированных на технические приложения. Новым является
изложение Пролога, вырастающего из логики, а также многочисленные
Пролог-программы (алгоритмы в последней инстанции), что делает
книгу небезынтересным пособием для студентов высших технических
учебных заведений, для которых решение практических задач
наиболее актуально.
В нашей стране ощущается недостаток книг по компьютерной
логике, Прологу, теории и практике его применения. Автор надеется,
что настоящая книга в некоторой степени восполнит этот пробел.
Компьютеризация дискретной математики одним из языков
искусственного интеллекта, как и случившаяся компьютеризация непрерывной
математики Фортраном, неизбежна; она уже началась. В книге
И.Братко, одной из лучших книг в мировой литературе по Прологу,
приведены несколько интересных программ из теории графов. Они
послужили автору предлагаемой книги исходным образцом.
Работа состоит из четырех частей, объединенных общим
логическим подходом при реализации алгоритмов Пролог-программами. В
первой части излагаются основные положения математической логики:
алгебра логики, исчисление высказываний, логика предикатов,
исчисление предикатов (первого порядка), секвенциальное исчисление,
метод резолюций в логике высказываний и в логике предикатов с
выходом в универсальный язык программирования Пролог.
12
Вторая часть содержит элементы теории графов, некоторые
наиболее часто встречающиеся в практике алгоритмы на графах и их
Пролог-программы.
В третьей части приводится логическая теория конечных
автоматов. Проектирование конечных автоматов осуществляется с помощью
монадической логики; приводятся Пролог-программы для расчета
конечного автомата по формуле монадической логики, которая этот
автомат описывает.
В четвертой части рассматриваются основные понятия
комбинаторики, даны Пролог-программы порождения некоторых комбинаторных
конфигураций.
Работа выполнена на кафедре математического моделирования
Московского энергетического института. Много способствовал
продвижению работы заведующий кафедрой профессор Ю.А.Дубинский.
Поддержали ее издание А.А.Амосов, В.Н.Вагин, Н.В.Кислое. Книга
написана по материалам лекций курсов дискретной математики и
математической логики, которые читал автор. Эти курсы (или им
аналогичные) начинали в МЭИ Д.А.Поспелов, В.Н.Вагин, В.П.Кутепов,
А.А.Болотов, А.Б.Фролов, Е.А.Щегольков, повлиявшие на выбор и характер
излагаемого автором материала. Многие алгоритмы из теории графов
приведены в том виде, который придали им А.А.Болотов и
А.Б.Фролов. В разработке Пролог-программ принимали участие И.В.Моисеева
- детерминизация источника, Н.Д.Гурихина - минимизация числа
состояний автомата, И.Д.Четрафилов - представление дерева путей в
графе термом, С.Е.Карпухина - комбинаторные программы, А.А.Чере-
пова - программа вычисления сокращенной ДНФ. Автор благодарит
всех за оказанную помощь. Кроме того, автор выражает искреннюю
признательность заведующему кафедрой математической кибернетики
Московского государственного университета С.В.Яблонскому и
сотрудникам этой кафедры В.А.Захарову, Р.И.Подловченко и А.А.Сапо-
женко за рецензию книги и критические замечания.
Книга предназначена для студентов высших технических учебных
заведений. Надеемся, что и преподаватель найдет для себя
материалы, которые можно будет использовать в лекционной работе, на
семинарских и лабораторных занятиях.
Все предложения и замечания просьба направлять по адресу:
111250, Москва, Красноказарменная, 14, Издательство МЭИ.
Часть 1
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ПРОЛОГ
1. АЛГЕБРА ЛОГИКИ
1.1. Функции алгебры логики
Пусть Е2 = {0,1} - двухэлементное множество. Набор длины п из
0 и 1 есть последовательность длины л, составленная из 0 и 1.
Пример.
(0); (1) - наборы длины 1;
(0,0);(0,1);(1,0);(1,1) - наборы длины 2;
(0,0,0); (0,0,1); (0,1,0); (0,1,1); (1,0,0); (1,0,1); (1,1,0);
(1,1,1) - наборы длины 3;
(0,0,...,0,0);(0,0,...,1);...;(а1,а2,...,ап);...;
(1,1,... ,1,1) - наборы длины л.
Теорема. Число h(n) всех наборов длины п из 0 и 1 равно 2П.
Доказательство. Индукция по п.
БАЗИС. /1 = 1. Л(1) = 2.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть h(n) = 2п.
ШАГ ИНДУКЦИИ. Покажем, что h(n+l) = 2Я+1. Разобьем все наборы
длины /t+1 на два класса: класс наборов, начинающихся с 0, и класс
наборов, начинающихся с 1.
0,0,...,0,0 1,0,...,0,0
0,0,...,0,1 1,0,...,0,1
0,0,...,1,0 1,0,...,1,0
0,1,...,1,1 1,1,...,1,1
Число всех наборов длины /г+1, начинающихся с 0 (так же как и
число всех наборов, начинающихся с 1), равно числу всех наборов
длины п и по предположению индукции равно 2п. Тогда /i(/i+l) = 2п +
2я = 2-2п= 2Л+1. Теорема доказана.
Определение. Функция алгебры логики есть функция, аргументы и
значения которой принимают лишь два значения 0 и 1.
Класс всех функций алгебры логики обозначим через Р2. Вместо
слов "функция алгебы логики" будем иногда говорить просто
"функция" .
Теорема. Число всех /i-местных функций алгебры логики равно 22Я.
Доказательство. В табл. 1.1 перечислены все /г-местные функции.
14
Таблица LI
*1 Хг.
0 0
0 0
1 1
1 1
• *И-1
.. 0
.. 0
.. 1
1
хп
0
1
0
1
/о
О
О
О
О
/l
О
О
О
1
/а ••
О
О
1
О
/г
1
1
1
1
Число всех строк равно 2Л, т.е. равно числу всех наборов длины
п из 0 и 1. Число всех функций алгебры логики от п переменных
равно 22", т.е. равно числу всех наборов длины 2я из 0 и 1.
Теорема доказана.
В табл. 1.2 приведены некоторые часто используемые в практике
функции:
0 - константа нуль;
1 - константа единица;
х - тождественная функция;
х - отрицание;
х V у - дизъюнкция;
х & у - конъюнкция (обозначается также через х*у или ху)\
х -> у - импликация;
х + у - сложение (по модулю два);
х s у - эквивалентность (равносильность);
дс I у - штрих Шеффера;
jc T у - стрелка Пирса.
Таблица 1.2
х у
0 0
0 1
1 0
1 1
0 1 хЧу х&у х->у х+у х=у х 1 у xty
010 0 1 0 1 11
011 0 1 1 0 10
Oil 0 0 1 0 10
Oil 1 1 0 1 00
x x x 0 1
0 10 0 1
10 10 1
15
1.2. Формулы. Реализация функций формулами
Пусть F есть подмножество функций из Р2.
Определение. Формула (алгебры логики) над F определяется
индуктивно следующим образом.
1. Выражение f(xx,... 9хт)9 где / есть функция из F, есть
формула над F.
2. Если А(хг,... 9хт) есть формула над F и если каждое из
выражений Alf...,Am есть либо формула над F, либо переменная, то
выражение А(А1,... ,Ат) есть формула над F.
Примеры.
1. F = {/х(х9у)9 f2(x,yyz), f3(x)}. Следующие выражения
являются формулами над F: /1U,.y); f2{x9y9z)\ f3(x); fx(t9z)\
/2(м.О; /3(/а(*эУэ*)); fi(fi(y>t>z)> /3(/iU^)));
2. F = {дгу, xVy9 дс}. Формулы: дгу, jtVy, x, xx9 lVx, xy\lx9 xyz V
xyz V Jtyz.
Каждой формуле над F сопоставим функцию по следующему правилу.
1. Переменной х сопоставим тождественную функцию х.
2. Формуле /(*!,... ,хт) над F сопоставим функцию f(xl9...9xm)
из F.
3. Если формуле А(х19...,хт) над F сопоставлена функция
/(*!,... ,jcm), а формулам А{,... ,^4W над F сопоставлены функции
/и- ->/т> Т0 формуле А(А19... 9Ат) над F сопоставим функцию
/(л,...,/«).
Таким образом каждая формула над F реализует некоторую функцию
из Р2. Пусть формула А(х19...,хп) реализует некоторую функцию
/(*!,... ,*„), и пусть с = (а19...9ап) есть набор длины п из 0 и
1. Тогда значение формулы Л на наборе а есть /(а), т.е.
A(al9...9an) = f(al9...,an).
Пример. Формула ху У х реализует функцию f(x9y)9 приведенную в
табл.1.3.
Таблица 1.3
х у
0 0
0 1
1 0
1 1
f(x9y)
0
0
1
0
16
Определение. Пусть А есть некоторая формула над множеством F
функций из Р2. Если А есть f(xx,... 9хт) из F, то единственной
подформулой формулы А является она сама. Если А есть формула
f(Ax,... ,Ат)9 где / € F, а А19...9Ат - некоторые формулы над F,
то подформулами формулы А являются она сама и все подформулы
формул А19...9Ат.
Определение. Функция / есть суперпозиция над F, если /
реализуется некоторой формулой над F.
В дальнейшем формулу будем отождествлять с функцией, которую
она реализует. Говоря о формуле А над F, будем говорить просто о
формуле А, не упоминая об F, если из контекста ясно, о каком
множестве функций F идет речь.
Определение. Класс функций F называется функционально
замкнутым, если вместе с любыми своими функциями он содержит и любую их
суперпозицию.
Определение. Множество функций [F] называется замыканием
класса функций F, если оно содержит все суперпозиции функций над
множеством F и не содержит никаких других функций.
Замечание. 1. F Q [F].
2. [[F]] = [F].
3. F, с f2 влечет [Fj с [f2].
4. Множество функций F замкнуто, если F = [F].
Определение. Система G функций из замкнутого класса F полна в
F (является порождающей системой для F), если [G] = F. Система
функций Н полна (в Р2), если [Н] = Р2. Элементная база есть про-
мышленно выпускаемая порождающая система для Р2. Полная в F
система функций G называется базисом в F, если никакая собственная
подсистема в G не является полной в F.
1.3. Равносильные преобразования формул
Пусть Ах и А2 - формулы, а х19...,хп - полный список их
переменных. Формулы Ах и А2 называются равносильными (равными), если
для любого набора значений аргументов х19...,хп они принимают
одинаковые значения.
Пример. Ах(х9у) = ху V х\ А2(х9у) = х - у\ А3(х) = х\ АА(х9у)
= х V у. В табл. 1.4 приведены значения формул Ах - А49 из которой
видно, что Ах = А29 А2 ^ Аъ\ А2 * АА\ Аъ * АА.
В инженерной практике наиболее распространены представления
функций формулами, построенными с помощью конъюнкции, дизъюнкции,
отрицания, констант 0 и 1, т.е. формулами над F = {х&у9хУу9-9
17
0,1}. Такие формулы называются булевскими. Иногда в F включают
импликацию.
Таблица 1.4
х у
0 0
0 1
1 0
1 1
А
0
0
1
0
Аг
0
0
1
0
А3
0
0
1
1
А<
0
1
1
1
Примем соглашение об опускании скобок в соответствии со
следующим приоритетом операций: - , & , V , -> . Укажем некоторые
свойства операций & , V , -. Эти операции (как и их свойства)
называются булевыми.
Пусть А у В, С - произвольные формулы над F. Тогда справедливы
следующие свойства булевых операций.
1. Идемпотентность
А & А = А; А V А = А.
2. Коммутативность
A&B = B&A\AVB = BVA.
3. Ассоциативность
А & (В & С) = (А & В) & С;
А V (В V С) = (А V В) V С.
4. Правило поглощения
А & (А V В) = А\ А V А & В = А.
5. Дистрибутивность
А & (В V С) = А & В V А & С;
А V В & С = U V В) & (А V С).
6. Инволюция Л = Л.
7. Свойства констант
Л&1 = Л; Л V 0 = >4;
у4 & 0 = 0; А V 1 = 1.
8. Закон исключенного третьего и закон противоречия
А V А = 1 \ А & А = 0.
9. Правила де Моргана
А & В = А V Л ; Л V J5 = Л & В.
10. Связь импликации и дизюъюнкции.
Л - 5 = А V J5.
18
Все эти равенства устанавливаются непосредственной проверкой.
Правило подстановки. Если
1) А(В), С - формулы;
2) В есть подформула формулы А\ 3) В = С, то А(В) = А(С).
Коротко правило подстановки записывают так:
А(В), В = С
А(В) = Л(С)
Примем без доказательства следующее утверждение.
Теорема. Если А и В - булевы формулы и ^4 = В, то с помощью
булевых равенств 1 - 9 и правила подстановки от формулы А можно
перейти к формуле В за конечное число шагов.
Эта теорема широко используется при упрощении формул.
Пример. xyVxy = xVyVxy = xVyVxy = xVxyVy =
х V у.
Замечание. Пусть М - некоторое множество и Р(М) - множество
всех подмножеств множества М. Если А, В, С - произвольные
подмножества из М, и А интерпретируется как М - А (т.е. А - дополнение
А до М), А & В как А Г\ В, А V В как Л U В, 0 как пустое множество
0, а 1 есть все множество М, то при таком теоретико-множественном
понимании операций -, &, V булевы свойства 1-9 останутся
справедливыми .
Множество Л/, в котором определены операции -, &, V и константы
О и 1, удовлетворяющие аксиомам 1 - 9, называется булевой
алгеброй. Обозначим булеву алгебру через (M,&,V,-,0,l). Тогда
системы ({0,1},&,V,-,0,1) и {Р(М),П,и,-,0,М) являются булевыми
алгебрами.
Множество М, в котором определены две операции & и V,
удовлетворяющие аксиомам 1-4, называется решеткой. Решетка
дистрибутивна, если дополнительно выполняется аксиома 5 дистрибутивности.
Пусть множество М' = {0,1,2,01,02,12,012}. Элемент 012
понимаем как 0&1&2. Аналогично другие элементы из М'. Множество М
состоит из множества М' и всех дизъюнкций попарно различных
элементов множества М'. При этом ни одно дизъюнктивное слагаемое,
рассматриваемое как множество своих сомножителей, не содержится в
другом его дизъюнктивном слагаемом. Например, элементом множества
М является дизъюнкция 01 V 12 V 02. Множество М с операциями & и
V, удовлетворяющими аксиомам 1-5, образуют (свободную)
дистрибутивную решетку с образующими 0,1,2. Приведем пример
преобразований в такой решетке. Решеточное выражение (0V2)(01V12V012) =
19
001 V 012 V 0012 V 201 V 212 V 2012 = 01 V 012 V 012 V 012 V 12 V
012 = 01 V 12.
1.4. Нормальные формы
Элементарной конъюнкцией называется конъюнкция, составленная
из попарно различных переменных или отрицаний переменных.
Иногда будем допускать в элементарной конъюнкции наличие
повторов элементов.
Пример, х, у, ху, ххх2х3.
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция
попарно различных элементарных конъюнкций.
Иногда будем допускать в ДНФ наличие повторов элементов.
Пример, ху, ху V х , ххх2х3 V ххх2х3.
Элементарной дизъюнкцией называется дизъюнкция, составленная
из попарно различных переменных или отрицаний переменных.
Иногда будем допускать в элементарной дизъюнкции наличие
повторов элементов.
Пример, х, xVyyxVyVz.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция
попарно различных элементарных дизъюнкций.
Иногда будем допускать в КНФ наличие повторов элементов.
Пример, х, х V у, (х V у){х V у V z)(x V у V z).
Введем следующие обозначения:
fjc, если с = 1;
хс = <_
\.х, если с = 0;
& At = А1&А2&...&Ап\ V At = АхУА2У...УАп.
i = 1 i-i
Знак «-* означает "тогда и только тогда".
Заметим, что хс = 1 <—* х = с;
X 1& X 2& . . . &Х П = 1 «—> Хх = С1У Х2 = С2, ...9Хп = Сп.
Лемма (о разложении функции по компонентам). Всякая функция
алгебры логики допускает представление:
/(*!,...,*„) = V f(cl9...,ck9xk+l9...,xn) xcxl...xlk,
(с1? . .. ,ck)
где дизъюнкция берется по всем наборам (cl9...,ck) из 0 и 1.
Доказательство. Покажем, что равенство
20
f(al9...9an) = V f(cl,...9ck9ak+l9...9an)acll...ackk9 (l.l)
(Cj, . . . ,Cfc)
справедливо для любого набора (а!,...,ап) из 0 и 1.
Пусть правая часть (l.l) равна 1. Тогда найдется равный 1
дизъюнктивный член
f(cl9...9ck9ak+l9...9an) а\х...акк.
Отсюда а^^.а^ = 1 и потому а1 = с19...9ак = ск9
f(al9...9ak9ak+l9...9an) = 1.
Пусть теперь левая часть (l.l) равна 1. Тогда
последовательно получаем следующее:
f(al9...9ak9ak+l9...9an) = 1;
f(cl9...9ck9ak+l9...9an) а\х...акк = 1;
V f(cl9...9ck9ak+l9...9an) а\х...акк = 1.
(с1, . . .9ск)
Равенство (l.l) доказано. Лемма установлена.
Замечание. Функция f(cx,... ,ск9хк+1,... 9хп) называется
компонентой функции f(xl9... 9хп).
1.4.1. Совершенные нормальные формы
Теорема (О СДНФ). Всякая не равная тождественному нулю функция
f(xl9... 9хп) допускает представление
f(xl9...9xn) = V хсг1... хсп\ (1.2)
где дизъюнкция берется по всем наборам с = (с19...9сп) из 0 и 1,
для которых /(с) = 1.
Доказательство. Пусть f(xl9... 9хп) & 0. Согласно лемме о
разложении функции по компонентам при к = п получаем
f(xl9...9xn) = V f(cl9...9cn) x\l...xcnn.
(cl9 . .. ,c„)
Из правой части равенства выбросим все нулевые дизъюнктивные
члены, в которых f(cl9... ,с„) = 0. Тогда получим
f(xl9...9xn) = V f(cl9...9cn) x\l...xcnn.
/(С )=1
Так как в этой формуле в любом дизъюнктивном члене элемент
21
f(c!,...,cn) = 1, то она принимает вид
f(xl9...,xn) = V x\l...xcnn.
/(С )«1
Теорема доказана.
Определение. Правая часть представления (1.2) называется
совершенной дизъюнктивной нормальной формой (СДНФ) функции /.
Каждое слагаемое в СДНФ называется конституентой единицы.
Конституента единицы д^1 х22 ... хпп = 1 на единственном наборе
Х\ = Cj, Х2 = С2у • •• уХп — Сп.
Пример. СДНФ для функции /, приведенной в табл. 1.5, имеет вид:
f(xyy,z) = xyz V xyz V xyz V xyz.
Таблица 1.5
дм 00001111
у 00110 011
z 010 1 0 101
/ 10010101
Дизъюнктивные слагаемые xyz, xyz, xyz, xyz являются конститу-
ентами единицы.
Замечание. Всякую функцию алгебры логики можно реализовать
формулой, построенной с помощью конъюнкции, дизъюнкции и
отрицания. Поэтому множество функций F = {&,V,-} составляет полную
систему. Так как х V у = х & у, то система функций F = {&,-} полна.
Так как х & у = х V у, то система F = {V,-} полна. Система F =
{jc I у), состоящая из единственной функции - штриха Шеффера,
полна, ибо * = дг|дг, а дг & у = (д: \у) I (х \у). Система F = {дгТу},
состоящая только из стрелки Пирса, полна, так как х = jcTjc, a x V у =
(*Ту)Т(дгТ}0- Очевидно, что х Т у = х V у.
Теорема (о единственности СДНФ). Для всякой функции, не равной
тождественному нулю, существует единственная СДНФ.
Доказательство. Существование СДНФ для функции / зё 0 вытекает
из предыдущей теоремы. Покажем, что эта СДНФ единственная. В
самом деле, имеется 22 -1 л-местных функций, не равных нулю тождес-
22
твенно. Подсчитаем число различных СДНФ от п переменных. Пусть Сп
означает число сочетаний из п элементов по к. Тогда число
одночленных СДНФ х\1хс22.. .хпп равно С2п. Число /t-членных СДНФ равно
С\п. Число л-членных СДНФ равно С*п. Число всех различных СДНФ
С\п + С\п + ... + с\п + ... + Сп2п = 22" - 1.
Итак, 22"-1 функций реализуются посредством 22"-1 СДНФ, т.е.
каждая функция реализуется единственной СДНФ.
Теорема (о СКНФ). Всякая не равная тождественной единице
функция f(x1,... 9хп) допускает представление
/(*i *Я) = & (x\lV ... V xl»), (1.3)
f(cl9 . ..,сл)=о
где конъюнкция берется по всем наборам с = (с19...,сп) из 0 и 1,
для которых /(с) = 0.
Доказательство. Заметим, что хс = хс. Пусть функция f(xl9...9
хп) г 1, тогда / 2 0 и потому функция / допускает представление в
виде СДНФ
f(xl9...9xn) = _ V хсг1 ... хсп\
/(С )=1
Отсюда
/Ui,. ..,*!,) = V Х\К.. ХСп» =
/(С )=0
& (х'1 V ... V хспп) = & (jcY1 V ... V 4я ).
/(С ) =0 /(С ) =0
Теорема доказана.
Правая часть в представлении (1.3) называется совершенной
конъюнктивной нормальной формой (СКНФ) функции /.
Пример. СКНФ для функции, приведенной в табл. 1.6, имеет вид:
f(x9y9z) = (xVyVz)(xVyVz)(xVyVz)(xVyVz).
1.5. Минимизация нормальных форм
Минимальной ДНФ (МДНФ) функции f(xl9... 9хп) называется ДНФ,
реализующая функцию / и содержащая минимальное число символов
23
Таблица 1.6
х 00001111
у 001 1 0 01 1
z 010 10 101
/01101010
переменных по сравнению со всеми другими ДНФ, реализующими
функцию /.
Если для всякого набора а = (а19... 9ап) значений переменных
условие g(a) = 1 влечет f(a) = 1, то функция g называется частью
функции / (или функция / накрывает функцию g). Если при этом для
некоторого набора с = (с19...9сп) функция g(c) = 1, то говорят,
что функция g накрывает единицу функции / на наборе с (или что g
накрывает конституенту единицы ххх...хпп функции /). Заметим, что
коцституента единицы функции / есть часть функции /, накрывающая
единственную единицу функции /.
Элементарная конъюнкция К называется импяикантом функции /,
если для всякого набора а = (а19...9ап) из 0 и 1 условие К{а) = 1
влечет f(a) = 1.
Импликант К функции / называется простым, если выражение,
получающееся из него выбрасыванием любых множителей, уже не
импликант функции /.
Ясно, что всякий импликант функции / есть часть функции /.
Теорема. Всякая функция реализуется дизъюнкцией всех своих
простых импликант (ПИ).
Доказательство. Пусть f(xx,... 9хп) есть функция, а А = К1 V
... V Кт - дизъюнкция всех ее простых импликант. Пусть а =
(а19... 9ап) - произвольный набор длины п из 0 и 1.
Если А(а) = 1, то найдется дизъюнктивное слагаемое Кг(а) = 1,
что влечет /(а) = 1, ибо Kt есть импликант функции /.
Если /(а) = 1, то в СДНФ для функции / найдется элементарная
конъюнкция К9 равная на этом наборе единице. Один из простых имп-
ликантов Kj функции / получается выбрасыванием некоторых
множителей из К и потому Kj(&) = 1, а тогда Л(а) = 1.
Следовательно, f = А. Теорема доказана.
Сокращенная ДНФ функции / есть дизъюнкция всех простых
импликант функции /. Всякая функция / реализуется своей сокращенной
24
ДНФ. Для всякой функции, не равной тождественно нулю, существует
единственная сокращенная ДНФ.
Пусть А и В - произвольные формулы. Из свойств булевых
операций вытекают следующие обратимые правила преобразования ДНФ:
А-В V А-В
1) - полное склеивание (развертывание);
А
А-В V А-В
2) - неполное склеивание;
А V А-В V А-В
А V А-В
3) - поглощение;
А
А У А А & А
4) ; - идемпотентность (удаление дублирующих
А А
членов).
Теорема (Куайна). Если в С ДНФ функции / провести все операции
неполного склеивания, а затем все операции поглощения и удаления
дублирующих членов, то в результате получится сокращенная ДНФ
функции /.
Доказательство. Пусть имеем сокращенную ДНФ функции /.
Проведем все операции развертывания к каждому простому импликанту
для получения недостающих переменных в каждом дизъюнктивном
слагаемом сокращенной ДНФ. В полученном выражении из нескольких
одинаковых дизъюнктивных слагаемых оставим только по одному
экземпляру. В результате получим СДНФ функции /. Теперь, исходя из
полученной СДНФ, в обратном порядке проведем операции добавления
одинаковых дизъюнктивных слагаемых (с помощью правил
идемпотентности), неполного склеивания и поглощения. В итоге получим
исходную сокращенную ДНФ.
1.5.1. Алгоритм Куайна построения сокращенной ДНФ
1. Получить СДНФ функции /.
2. Провести все операции неполного склеивания.
3. Провести все операции поглощения.
Пример. Построим сокращенную ДНФ для функции, приведенной в
табл.1.7.
25
Таблица 1.7
х 00000000111 1 1 111
у 000011110000 1 1 11
г 00 110011001 1 ООП
t\ 0101010101010101
/ 1111010010101111
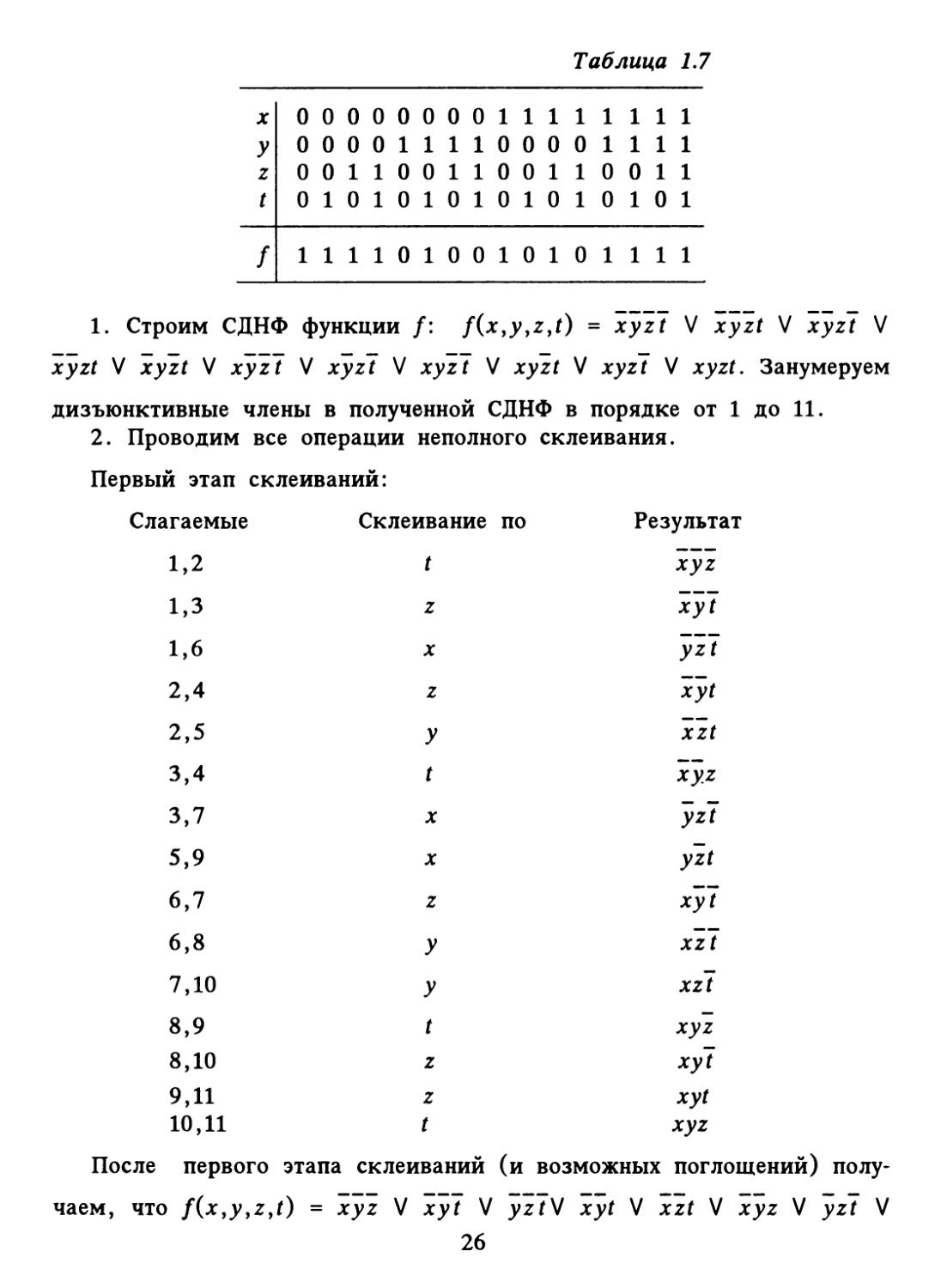
1. Строим СДНФ функции /: f(x,y,z,t) = xyzl V xyzt V xyzt V
xyzt V xyzt V xyzl V xyzt V xyzl V xyzt V jryzT V xyzt. Занумеруем
дизъюнктивные члены в полученной СДНФ в порядке от 1 до 11.
2. Проводим все операции неполного склеивания.
Первый этап склеиваний:
Слагаемые
1,2
1,3
1,6
2,4
2,5
3,4
3,7
5,9
6,7
6,8
7,10
8,9
8,10
9,11
10,11
Склеивание по
t
z
X
Z
У
t
X
X
Z
У
У
t
Z
Z
t
Результат
xyz
xyl
y'zl
xyt
Yzt
xyz
yzl
y'zt
xyl
xzl
xzl
xyz
xyl
xyt
xyz
После первого этапа склеиваний (и возможных поглощений)
получаем, что f(x,y,z,t) = xyz V xyl V yzlV xyt V xzt V xyz V yzl V
26
xyt У yzt У xzt У xzt У xyz У xyt У xyt У xyz. Пронумеруем
дизъюнктивные члены в полученной ДНФ в порядке их следования от 1
до 15.
Второй этап склеиваний:
Слагаемые
1,6
2,4
2,8
3,7
8,13
10,11
12,15
13,14
Склеивание по
z
t
X
Z
У
Z
Z
t
Результат
ху
ху
y~t
Yt
let
xl
xy
xy
После второго этапа склеиваний и последующих поглощений
получаем, что f(x,y,z,t) = ху У ху У yl У xl У xzt У yzt. Это и будет
сокращенной ДНФ для функции /, ибо дальнейшие склеивания
невозможны.
1.5.2. Алгоритм построения сокращенной ДНФ с помощью КНФ
Пусть /(*!,... ,*Л) есть некоторая функция алгебры логики.
Построим для / некоторую КНФ. Осуществим далее следующие
преобразования.
1. В КНФ раскроем скобки и удалим дублирующие члены согласно
равенствам К*К = К, К У К = К\ удалим дизъюнктивные слагаемые,
содержащие одновременно переменную и ее отрицание. В результате
получим дизъюнкцию конъюнкций, каждая из которых содержит только
по одному элементу из каждой скобки КНФ.
2. В полученном выражении удалим нулевые дизъюнктивные
слагаемые.
3. В полученном выражении проведем все поглощения (согласно
равенству А У АВ = А), а затем удалим дублирующие члены.
В результате проведенных операций получим сокращенную ДНФ
функции /. Покажем это.
Для каждой элементарной дизъюнкции D в КНФ и каждой
элементарной конъюнкции К в сокращенной ДНФ (сокр.ДНФ) существует
некоторый множитель вида д: из ^, содержащийся в D т.е.
VD € ДНФ VA: € сокр.ДНФ Зха € К (ха € D).
27
Допустим противное: в КНФ существует элементарная конъюнкция
D, в сокращенной ДНФ существует элементарная конъюнкция К, для
которой всякий множитель вида ха из К не входит в D. Не уменьшая
общности, возьмем для простоты
К = х°> ха2> ... хакку D = jc^T1 V ... V ха/.
Положим хх = а19...9хк = аЛ, **+1 = ск+1 * ак+1 ,..., хг = сг*
аг. Тогда K(alt...,ак) = 1 и потому f(al9... ,ак,ск+1У • • • >сг) = 1-
С ДРУГОЙ СТОРОНЫ, /)(сЛ+1,. . . ,СГ) = О И ПОТОМУ /(«!,. • • ,0fc>cfc+l>
...,сг) = 0. Противоречие.
Пусть по-прежнему для простоты произвольный простой импликант
К из сокращенной ДНФ равен х*18сх*2&...&сх%к. Тогда элементы
хах\ха22у... ,х*к попадут в не менее чем к скобок в КНФ. Если
допустим, что этого нет, то при перемножении скобок из КНФ не получим
дизъюнктивного слагаемого, который содержал бы множители х11ух22,
...,*£*> а потому, строя из результата перемножения сокращенную
ДНФ вычеркиванием лишних сомножителей, не получим простого имп-
ликанта К.
Так как хахх ,ха22,... }х%к содержатся в к разных скобках КНФ, а
всякая другая скобка, отличная от указанных к скобок, содержит
хотя бы один элемент вида х из К, то при раскрытии скобок имеем
простой импликант К. После проведения всех операций поглощения и
удаления дублирующих множителей, останутся только простые
импликанты из сокращенной ДНФ, ибо если предположить наличие в
результате хотя бы одного дизъюнктивного слагаемого, отличного от
всех простых импликантов сокращенной ДНФ, то можно подобрать
такие значения переменных функции /, на которых все простые
импликанты примут значение 0, а это дополнительное слагаемое -
значение 1, чего быть не может.
Пример. Построим сокращенную ДНФ этим способом для функции
/ = 1111010010101111 из предыдущего примера:
/0c,;y,z,0 = UVpVzVr)UV^VlVr)(jcV^VlV7) &
(xVyVzVDixVyVzVl) = (xVyVt)(xVyVl\/l)(xVyVl) =
0tVpVpfVzf)0cV.yV7) = xyVxlVxyVylVxytVxltVyzt.
Сокращенная ДНФ для функции
f(x,y,z,t) = ху V xl V ху V yl V xlt V yzt,
что, естественно, совпадает с результатом предыдущего примера.
28
Тупиковой ДНФ (ТДНФ) функции / называется такая ДНФ ее простых
импликант, из которых нельзя выбросить ни одного импликанта, не
изменив функции /.
Теорема. Всякая минимальная ДНФ некоторой функции является ее
тупиковой ДНФ.
Доказательство. В МДНФ входят только простые импликанты, иначе
некоторые множители в непростом импликанте можно удалить в
противоречие с минимальностью исходной ДНФ. В МДНФ нет лишних
импликант, иначе исходная ДНФ не является минимальной.
Вывод. Для получения МДНФ функции / необходимо построить все
ТДНФ функции / и выбрать те из них, которые содержат минимальное
число букв.
1.5.3. Построение всех тупиковых ДНФ
Пусть /(*!,...,*„) есть функция алгебры логики.
1. Построим СДНФ функции / и пусть Р19Р2,...9Рп есть ее
конституенты (единицы).
2. Построим сокращенную ДНФ функции / и пусть К19К21... ,Кт -
ее простые импликанты.
3. Построим матрицу покрытий простых импликант функции / ее
конституентами единицы (табл. 1.8), полагая, что
1ч
1, если каждый множитель в Kt является
множителем в Рj\ (Pj есть часть для К()\
О в противном случае.
Таблица 1.8
N
*i
Кг
Ki
Кщ
Рг
a i,
«21
«ii
«mi
Рг
«12
«22 •
«12 •
«т2
*1 ■
аи
■ «2> •
• «</
«т/
.. Рп
«in
• • «2П
«in
атп
4. Для каждого столбца j (l < j < п) найдем множество Ej всех
тех номеров i строк, для которых я, у = 1. Пусть Ej =
29
n
ieji >ej2> • • • >ej r ■}• Составим выражение А = & (e;l V ej2 V ...
' ' ;' = l
V ej r.). Назовем его решеточным выражением. Это выражение можно
рассматривать как формулу, построенную в свободной дистрибутивной
решетке с образующими 1,2,...,т и с операциями & и V.
5. В выражении А раскроем скобки, приведя выражение А к
равносильному выражению В = V ejl&e;2&...&ejn, где перечислены все
конъюнкции е,-t&ej-2&.. .&£,-„, элементы eix,el2,. . . ,ein которой
взяты из скобок 1,2,...,л соответственно в выражении А.
6. В выражении В проведем все операции удаления дублирующих
членов и все операции поглощения. В результате получим
равносильное выражение С, представляющее собой дизъюнкцию элементарных
конъюнкций.
Утверждение. Каждая элементарная конъюнкция /1&/2&...&/г в С
дает ТДНФ Кг:1 V Ki2 V ... V Kir для /. Все ТДНФ для функции /
исчерпываются элементарными конъюнкциями в выражении С.
Пример. Сокращенная ДНФ для функции / = 1111010010101111 имеет
вид / = ху V ху V yl V xl V xzt V yzt.
Для функции / построим все минимальные ДНФ.
1. Строим матрицу покрытий (табл. 1.9).
2. Строим решеточное выражение (по столбцам табл. 1.9).
Е = (2V3)(2V5)(2V3)2(5V6)(3V4)(3V4)(1V4)(1V6)&
(1V4)(1) = (2V3)(2V5)(5V6)(3V4)(1V4)(1V6)12 =
(5V6)(3V4)(1)(2) = 1235 V 1245 V 1236 V 1246.
3. Строим все тупиковые ДНФ функции /.*
f = ху V ху V yt V xzt у простые импликанты 1,2,3,5;
/ = ху V ху V xl V xzt, простые импликанты 1,2,4,5;
/ = ху V ху V yl V yzt, простые импликанты 1,2,3,6;
/ = ху V ху V xl V yzt, простые импликанты 1,2,4,6.
4. Все найденные ТДНФ являются минимальными ДНФ.
1.5.4. Алгоритм минимизации функций в классе ДНФ
1. Строим С ДНФ функции /.
2. Строим сокращенную ДНФ функции /.
3. С помощью матрицы покрытий и решеточного выражения строим
все ТДНФ функции /.
4. Среди построенных ТДНФ выбираем все минимальные
дизъюнктивные нормальные формы функции /.
30
Таблица 1.9
N
1
2
3
4
5
6
ПИ
ху
ху
y~t
xl
Itz t
y~zt
Конституенты единицы
х
У
z
7
+
+
X
У
Z
t
+
+
X
У
Z
7
+
+
X
У
Z
t
+
X
У
Z
t
+
+
X
У
Z
7
+
+
X
У
Z
7
+
+
функции /
X
У
Z
7
+
+
X
У
Z
t
+
+
X X
У У
Z Z
7 t
+ +
+
7.5.5. Алгоритм минимизации функций в классе КНФ
Чтобы построить все минимальные КНФ (МКНФ) функции /, следует
построить все МДНФ функции / и взять от каждой из них отрицание,
для чего заменить знаки & на V, а V на & (сохранив первоначальное
распределение скобок) и над каждой буквой поставить знак
отрицания. Полученные КНФ для функции / будут минимальными. В самом
деле, если бы для / существовала КНФ с меньшим числом букв, то ее
отрицание дало бы для / ДНФ с меньшим числом букв, чем в любой из
минимальных ДНФ для /. Противоречие с их минимальностью.
7.5.6. Алгоритм минимизации функций в классе нормальных форм
Пусть / - функция алгебры логики.
1. Строим все МДНФ функции /.
2. Строим все МКНФ функции /.
3. Из построенных минимальных форм выбираем простейшие (по
числу букв).
Пример. В классе нормальных форм минимизировать функцию
/ = 01011110.
31
1. Строим С ДНФ для функции /:
/(jc,_y,z) = xyz У xyz У xyz У хух У xyz.
2. Строим сокращенную ДНФ функции /:
f(x,y,z) = (хУуУгНхУуУгНхУуУг) =
(хУхуУх1УхуУууУухУхгУухУгг)(хУуУг) = UVz)(xVyVl) =
хх У ху У xz У xz У yz У zz = xz У yz У ху У xz.
3. Строим матрицу покрытий (табл. 1.10).
Таблица 1.10
N
1
2
3
4
ПИ
JCZ
У*
*У
X Z
xyz
+
+
jc_yz xyz xyz xyz
+
+
+ +
+ +
Решеточное выражение Е = (lV2)l(3V4)4 = 134 V 124.
4. Строим все тупиковые ДНФ функции /:
/(jc,y,z) = xz У ху У xz\ f(x,yyz) = xz У yz У xz.
5. Обе построенные ТДНФ являются минимальными.
6. Повторяем эти этапы для функции /.
СДНФ: J(xyyyz) = xyz У xyz У xyz.
Сокращенная ДНФ: /(*,)>,z) =
(xyyyl)(xyyyl)(xyyyz)(xyyyl)(xyyyz) = (хУг)(хУу)(хУуУг) =
(х У z)(x У yz) = xyz У xz.
Строим матрицу покрытий (табл. 1.11).
Решеточный многочлен Е = 112 = 12. Единственная тупиковая ДНФ
(она же минимальная) для функции J(xyyyz) = jczVjryz. Минимальная
КНФ функции /(jc,_y,z) = UVz)(jcV_yVz). Из построенных МДНФ и МКНФ
выбираем простейшую: f(xyyyz) = (х У z)(x У ~у У z).
Пример. В классе нормальных форм минимизировать функцию / =
11011011.
32
Таблица 1.11
N
1
2
ПИ
xz
xyz
xyz xyz xyz
+ +
+
1. СДНФ: f(x,y,z) = xyz V xyz V xyz V xyz V xyz V jryz.
2. Сокращенная ДНФ: f(xyy,z) = (хУуУг)(хУуУ!) =
xy У xz У yz У xz У yz У xy.
3. Строим матрицу покрытий (табл. 1.12).
Таблица 1.12
N
1
2
3
4
5
6
ПИ
ху
JCZ
у*
XZ
У^
xy
xyz xyz
+
+
+ +
xyz xyz
»
+
+
+
+
xyz xyz
+ +
+
+
E = (3V6)(4V6)(4V5)(2V3)(1V2)(1V5) = 1246 V 1356 V 134 V 256 V
2345.
4. Тупиковые ДНФ функции /:
f(x,y,z) = xy У xz У xz У xy; f(x,y,z) = xy У yz У yz У ху\
f(x,y,z) = xy У Yz У xz; f(x,yyz) = xz У yz У xy;
f(xyy,z) = xz У yz У xz У yz.
5. Минимальные ДНФ функции /:
f(x,yyz) = xy У Yz У xz; f(x,y,z) = xz У yz У xz.
6. Повторяем указанные выше этапы для функции /.
СДНФ: f(x,y,z) = xyl У xyz.
Сокращенная ДНФ: J(x,y,z) = (jcV)A/z)(jcV.yVz) &
33
(xVyVz)(xVyVz)(xVyVz)(xVyVz) = (xV y)(xV yV z)(xV yV г)(хУ у) =
(хУуг)(хУуг) = xyz V xyz.
Построенная сокращенная ДНФ функции / является для нее
тупиковой и минимальной.
Минимальная КНФ функции f(x9y9z) = (хЧy\lz)(x4уУz).
Построенные МДНФ и МКНФ имеют одно и то же число букв; все они
составляют минимальные формы для /:
f(x,y,z) = ху V yz V xz\
f(x,y,z) = x~z V yz V xz\
f(x9y9z) = (x\/yVz)(xVyV~z).
1.6. Минимизация частично определенных функций
Пусть функция f(xl9...9xn) частично (не всюду) определена.
Если / не определена на р наборах из 0 и 1, то существует 2Р
возможностей для доопределения функции. /. Полностью определенная
функция g(xx,... 9хп) есть доопределение функции /, если g
совпадает с / на тех наборах из 0 и 1, на которых / определена.
Задача минимизации частично определенной функции / сводится к
отысканию такого доопределения g функции /, которое имеет
простейшую (по числу букв) минимальную форму.
Обозначим через f0(xl9...9xn) и fi(xl9...9xn) доопределения
нулями и единицами соответственно частично определенной функции
f(xl9...,xn).
Теорема. Минимальная ДНФ частично определенной функции f(xly
...,дгЛ) есть дизъюнкция самых коротких импликант в сокращенной
ДНФ доопределения fl(xl9...9xn)9 которые в совокупности накрывают
все конституенты единицы доопределения f0(xl9...9xn).
Доказательство. Рассмотрим СДНФ некоторого доопределения
g(xl,... 9хп) функции f(xl,... 9хп). Конституенты единицы, входящие
в эту форму, войдут и в СДНФ доопределения Д. Поэтому любой
простой импликант функции g будет совпадать с некоторым импликантом
функции Д или накрываться им. Самые короткие импликанты,
накрывающие единицы функции /, есть импликанты функции Д.
Доопределение /0 имеет минимальное количество конституент единицы в своей
СДНФ, следовательно, и количество простых импликант функции fl9
потребных для накрытия этих конституент, будет наименьшим. ДНФ,
составленная из самых коротких простых импликант в сокращенной
34
ДНФ функции fl9 накрывающих все конституенты единицы функции /0,
будет самой короткой ДНФ, доопределяющей функцию /.
Так как единицы функции /\ составлены из единиц функции / и
единиц на наборах, на которых / не определена, то построенная
ДНФ, накрывая все единицы функции /0 (а, следовательно, и все
единицы функции /), совпадает с минимальной ДНФ некоторого
доопределения g функции /.
1.6.1. Алгоритм минимизации частично определенных
функций в классе ДНФ
1. Строим СДНФ функции /0.
2. Строим сокращенную ДНФ функции fx.
3. С помощью матрицы покрытий конституент единицы функции /0
простыми импликантами функции /\ и решеточного выражения строим
все тупиковые ДНФ (для некоторых доопределений функции /).
4. Среди полученных ТДНФ выбираем простейшие; они являются
минимальными ДНФ (для некоторых доопределений функции /).
1.6.2. Алгоритм минимизации частично определенных
функций в классе КНФ
Построение минимальных КНФ для частично определенной функции
аналогично построению минимальных КНФ для всюду определенной
функции.
Алгоритм минимизации частично определенных функций в классе
нормальных форм аналогичен алгоритму минимизации в классе
нормальных форм для всюду определенных функций.
Пример. В классе нормальных форм минимизировать частично
определенную функцию /(jc,_y,z,f) = 1 010010-01—1.
Решение. Минимизируем функцию / в классе ДНФ.
1. Строим сокращенную ДНФ для доопределения единицами fl
функции / (табл. 1.13).
fx(x9y9z9t) = UVyVzV0UV>!V2Vr)UVyV2V7)(jcVyVzV7)(jcVyVzV7) =
(xVy\/t)(xyVxyV!Vl)(xVy\/z\/l) =
(xVyVt)(xyVxyVxl\tyl\/llVxlVylVziVt) = (xVyyt)(xyVxyVxzVyzVl) =
xyV xyzV xlV xyV xyzV ylV xytV xylV x ztV yzt =
xy V xl V yl V xy V ~xzt V yzt.
2. Строим матрицу покрытий конституент единицы в СДНФ для
доопределения нулями /0 функции / с помощью построенной сокращен-
35
ной ДНФ для /j (табл.1.14).
3. По табл. 1.14 строим решеточный многочлен
Е = (2V4)(5V6)(3V4)(1V3)1 = 145 V 1235 V 146 V 1236.
4. Строим все тупиковые ДНФ:
£i = xy У yl У ~xzt\ g3 = xy У yl У yzt\
g2 = xy У xy V jcT V *zf; g4 = xy V xy V xl V yzt.
Таблица 1.13 Таблица 1.14
N
1
2
3
4
5
6
ПИ
*У
xy
xt
Yt
xzt
y'zt
xyzt
+
+
xyzt xyzt xyzt xyzt
+
+
+ +
+ +
+
x у
0 0
0 0
0 0
0 0
0 1
0 1
0 1
0 1
1 0
1 0
1 0
1 0
l l
l l
l l
l l
2
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
t
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
/ /o
1
-
-
-
0
1
0
0
1
0
-
0
1
-
-
1
1
0
0
0
0
1
0
0
1
0
0
0
1
0
0
1
/l
1
1
1
1
0
1
0
0
1
0
1
0
1
1
1
1
/
0
-
-
-
1
0
1
1
0
1
-
1
1
-
-
0
Ло
0
0
0
0
1
0
1
1
0
1
0
1
1
0
0
0
Л,
0
1
1
1
1
0
1
1
0
1
1
1
1
1
1
0
5. Из построенных тупиковых ДНФ выбираем минимальные:
Si = xy V yl V ~xzt\ g3 = xy V yl V yzt.
Функции gx и g3 есть минимальные доопределения функции / в
классе ДНФ.
Минимизируем теперь функцию / в классе КНФ. Для этого проведем
минимизацию функции / в классе ДНФ. Пусть h0 и hx есть
доопределения нулями и единицами соответственно функции /.
1. Сокращенная ДНФ для hx = (xVyVzVt)(x\/yVzVl)&
(хУуУгУ0(хУуУ2У0(хУ}У1У1) = (xVzVylVyt)(xyzVt)(xVyVzVl) =
36
{xMzMytMyt){xMyzMztMytMzi) =
^N x^zV xzlV xltVlczV'yzV zlVlcytV yzl = yfVjtzVzTVjtzfVjtyFVyz.
2. Матрица покрытий конституент единицы в СДНФ для h0
с помощью простых импликант в сокращенной ДНФ для hx приведена
в табл.1.15.
Таблица 1.15
N
1
2
3
4
5
6
ПИ
У*
X Z
zl
x"zt
xyt
yz
xyzt
+
xyzl xyzt xyzt
+
+ +
+
+
+
xyzt
+
+
3. Решеточное выражение Е = 5(2V3V5)2(lV4)(lV6) =
25(1V46) = 125 V 2456.
4. Строим две тупиковые ДНФ:
g5 = yt V xz V xyt и g6 = xz V xzf V jc_y7 V _yz.
Минимальная ДНФ g5 = _yf V xz V jc_y7.
5. Функция g5 = (y V 7)(jc V z)(jc V _y V t) есть минимальное
доопределение функции / в классе КНФ.
Найденные МДНФ gx, g3 и МКНФ g5 являются минимальными
доопределениями функции / в классе нормальных форм.
Техническая реализация минимальных форм для функции часто
проще, а потому дешевле реализации ее СДНФ (СКНФ). Следовательно,
этап минимизации при конструировании логических схем является
одним из важнейших.
1.7. Двойственные функции
Двойственной для функции f(xx,... ,хп) называется функция
/*(*!,...,*„) = /(*!,...,дг„).
Примеры.
1. f = х & у\ f* = x&y = xVy.
37
2. / = x V y\ f*= x V у = х & у.
3. / = X\ /* = x = jc.
4. / = jc; /* = jc = *.
5. f(xl9...,xn) = 0 ; /* = /O^,...,*„) = 6 = 1.
6. /(*!,...,*„) = 1 ; /* = 7(*i ^я) = 1 = 0.
7. f = x -• у \ f* = x^y = xVy = y^>x.
Заметим, что (f*(xlf... ,*„))* = (/(*lf ... ,*„))* =
7(=1Э...,^) = f(xl9...,xn), т.е. (/*)* = /•
Теорема (о суперпозиции двойственных функций). Функция,
двойственная суперпозиции функций, равна суперпозиции функций,
двойственных к функциям, составляющим эту суперпозицию.
Доказательство. (f(gl9... ,gw))* =
/\£iv*ll>• • • i*i ,nl'y • • ySm\xmi > • • • уХт,пт'' =
J\8i \x 11 > • • • ух\ >л1 / > • • • »^m^mi > • • • *хт9пт'' =
/\£i\*il> • • • >*i ynl' > • • • ygw\xm\ у • • • 'Xm,nm'' =
f*(giy-ygm)- Теорема доказана.
7.7.7. Принцип двойственности
Если функция / задана формулой, построенной с помощью &, V ,
-,0,1 и переменных, то по теореме о суперпозиции
двойственных функций и ввиду того, что для функций х&у, хУу, х, х, 0, 1
двойственными являются функции хУу, х&у, х, х, 1, 0
соответственно, то /* получается из / заменой & на V, V на &, 0 на 1, 1 на
0 (при сохранении исходной расстановки скобок).
Пример. {x&yMz & 1 & (jcVO)) = xNy&z V 0 V (jc&1).
Функция, совпадающая со своей двойственной, называется
самодвойственной .
Если функция f(xl9...9xn) самодвойственна, то функция / тоже
самодвойственна, так как (f(xl,... ,*„))* =
J(xl9...,xn) =/*(* !,...,*„) = f(xl9...9xn).
38
Теорема. Класс самодвойственных функций замкнут относительно
суперпозиции.
Доказательство. Пусть функции f,g\,- - - ,gm самодвойственны.
Тогда /* = /, g* = *lf...f g„ = gm. Суперпозиция h = f(gly...,gm)
этих функций самодвойственна, ибо функция h* = (/(gj... ,gm)) =
f*(g*,---,g*) = /(gif-igm) = Л по теореме о суперпозиции
двойственных функций.
Наборы а = (а1У... уап) и а' = (а19... ,ап) из 0 и 1 называются
противоположными.
Следствие. Чтобы функция была самодвойственной, необходимо и
достаточно, чтобы на всяких двух противоположных наборах она
принимала разные значения.
Доказательство. Функция f(xx,... ухп) самодвойственна <—>
/(*!,... ,хп) = /*Ui, • • • ,хп) —> f(xl9... ,хп) = f(xx,... ,хп) —>
f(xx,... ,jc„) * f(xx,... ,xn) <—> на всяких двух противоположных
наборах функция / принимает разные значения.
Пример. / = 01001101, g = 01001111. Функция / самодвойственна,
а функция g не самодвойственна, ибо g(0,0,l) = g(l,l,0).
Лемма (о несамодвойственной функции). Подстановкой функций х и
х в несамодвойственную функцию можно получить одну из констант.
Доказательство. Пусть f(xx,... ,хп) - несамодвойственная
функция . Тогда существует набор (в,,...,0„), для которого f(a!,...,
ап) = /Ui О- Построим функцию /i(jc), заменив единицы в
f(al9... ,ап) на х, а нули - на х. Так как х = дг°, х = jc1 , то Л(дг)
= f(xai,...9xa"). Заметим, что 0Л| = я, , 1*' = аь. Тогда /i(l) =
/(l*\...,lfl") = f(al9...,an) = /(а,,...,^) = /(О*1,... ,0*") =
Л(0), т.е. /i(l) = Л(0). Следовательно, функция /i(jc) есть одна из
констант.
1.8. Линейные функции
Арифметические функции в алгебре логики это сложение и
умножение по модулю два. Вот эти функции:
39
х у х+у х*у
0 0
0 1
1 0
1 1
0
1
1
0
0
0
0
1
Вычитание (по модулю два) определяется как операция, обратная
сложению, т.е. х - у равно такому элементу z, для которого х = у
+ 2. В частности, 0 - х равно такому у, что 0 = х + у. Правая
часть этого равенства равна нулю только при у = х. Поэтому 0-лг =
jc. Отсюда следует, что -х = х (по модулю два).
Деление (по модулю два) определяется как операция, обратная
умножению, т.е. х/у равно такому г, для которого х = у z. В
частности, l/х равно такому у, для которого 1 = х*у. Правая часть
равенства равна 1 только при у = х = 1. Так что обратный элемент
х~1 = l/х возможен лишь при х = 1 и равен 1.
Следующие свойства арифметических операций проверяются
непосредственно:
1) jc+(.y+z) = (x+y)+z; 4) *+(-*) =0; 7) jc-1 = х\
2) х+у = у+х; 5) x(yz) = {xy)z\ 8) х-(х'1) = 1, х * 0;
3) х + 0 = х\ 6) х-у = ух; 9) x(y+z) = ху + xz.
Двухэлементное множество {0,1} с операциями сложения и
умножения по модулю два образуют коммутативное поле F.
Справедливы также следующие свойства:
10) х + х = 0; 11) х-х = х.
Так что поле F имеет характеристику два, а операция умножения
идемпотентна.
Следующие четыре равенства устанавливают связь между
арифметическими и логическими операциями:
1) х = х + 1; 3)хУу = х&у = (л:+1)(_у+1)+1 = ху + х + у;
2) х & у = Х'у\ 4) х + у = ху V ху;
Многочлен Жегалкина в поле F есть выражение
i
i, *,,
«I, I, 1„ V V ••• *п > где
х1 =
jc, если 1 = 1;
U, если i = 0,
40
а каждый коэффициент а( t ,■ равен 0 или 1.
Теорема (Жегалкина). Всякую функцию алгебры логики можно
представить единственным полиномом Жегалкина.
Доказательство. Каждый многочлен Жегалкина определяет
некоторую функцию алгебры логики. Два различных многочлена определяют
различные функции. Аналогично тому, как это делали при
доказательстве единственности СДНФ, можно показать, что существует I1"
различных многочленов Жегалкина от п переменных.
Пример. Многочлен Жегалкина для функции
f(x9y,z) = xyz V xyz V xyz V xyz V xyz = (x+l)(y+l)z +
(x+l)yz + x(y+l)z + xy(z+l)+xyz = xyz+xz+yz+z + xyz+yz +
xyz+xz + xyz+xy + xyz = xyz + xy + z.
Многочлен Жегалкина можно получить также с помощью
треугольника Паскаля по единицам его левой стороны (табл. 1.16) следующим
образом. Построим многочлен Жегалкина для функции g = 10011110.
Верхняя сторона треугольника есть фукция g. Любой другой элемент
треугольника есть сумма по модулю два двух соседних элементов
предыдущей строки. Левая сторона треугольника для функции g
содержит шесть единиц. Многочлен Жегалкина будет содержать шесть
слагаемых. Первая единица треугольника соответствует набору 000.
Первое слагаемое многочлена есть 1. Третья снизу единица в левой
стороне треугольника соответствует набору 101. В качестве
слагаемого многочлена берем xz. Аналогично для других единиц
треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
(Этот алгоритм сообщил автору А.А.Болотов).
Таблица 1.16
■ N
1
2
У
У*
X
xz
xy
xyz
xyz
000
001
010
011
100
101
110
111
f g
0 1
1 0
0 0
1 1
0 1
1 1
1 1
1 0
Треугольник Паскаля
£ = 10011110
10 10 0 0 1
1110 0 1
0 0 10 1
0 111
10 0
1 0
1
Тогда g(x,y9z) = l + z + .y + Jtz + Jty + xyz. Функция
f(xx,... ,xn) называется линейной, если многочлен Жегалкина для
41
нее имеет следующий линейный относительно переменных вид:
f(xX9...9xn) = аххх + ... + апхп + ап+х,
где каждое а, равно 0 или 1.
Теорема. Класс линейных функций замкнут относительно
суперпозиции.
Доказательство. Пусть линейные функции
f(xX9...9xn) = аххх + ... + апхп + ап+Х9
*i(*if-t*m) = bHxi + ••• + bim*m + Ь/,т+1> I = 1,2,...,Л,
для простоты зависят от одних и тех же переменных. Тогда их
суперпозиция f(gi>->gn) =
ax(bxxxx + ... + blm*w+b1>m+1) +
а2{Ь2Ххх + ... + b2w*m+b2>m+1) +
вя(Ьш*1 + ••• + ЬпшДст+Ья>ш+1) + ая+1 =
(axbxx + ... + апЬпх)хх + ... + (в,Ь1т +... + апЪпт)хп +
(ai^i m+i + ••• + arPn m+i) + an+i есТЬ линейная функция.
Лемма (о нелинейной функции). Суперпозицией нелинейной
функции, отрицания и константы 1 можно получить конъюнкцию.
Доказательство. Пусть f(xx,... ,хп) - нелинейная функция. Тогда
полином Жегалкина содержит для нее слагаемое, в котором
присутствует произведенние дс,л:у. Будем считать для простоты, что ххх2 в
многочлене Жегалкина является этим произведением. Произведя
группировку слагаемых, функцию / представим в виде
/(*!,...,*„) = xxx2-h0(x39...9xn) + xx-hx(x39...9xn) +
+ х2 • h2(x39... ,хп) + И3(х39... 9хп).
Функция h0 не есть тождественный нуль, иначе в полиноме
Жегалкина отсутствует слагаемое с произведением ххх2. Тогда существует
набор (а39... ,ап) из 0 и 1, для которого h0(a39... 9ап) = 1. Пусть
hx(a39...9an) = a, h2(a3,...,ап) = Ь, h3(a39...9ап) = с. Тогда
функция g(xX9x2) = f(xX9x29a39...9an) = xxx2 + ахх + Ъх2 + с.
Построим функцию
h(xX9x2) = g(xx+b9x2+a) = (xx+b)(x2+a) + a(xx+b) + b(x2+a) + с =
-xxx2 + axx + bx2 + ab + axx + ab + bx2 + ab + с = xxx2 + d9
где d = ab + с. Если d = 0, то /iU^jcJ = xxx2. Если d = 1, то
42
h(xl9x2) = xxx2 + 1 и тогда хгх2 = h(xl9x2). Лемма доказана.
Функция /(*!... ,хп) сохраняет константу а € {0,1}, если
/(а,..., а) = а.
Пример. Функция ху сохраняет 0, сохраняет 1. Функция х -* у
сохраняет 1 и не сохраняет 0.
Теорема. Класс функций, сохраняющих константу, замкнут
относительно суперпозиции.
Доказательство. Пусть функции f(xx... 9хп) и gt(хх,... 9xm), i =
1,2,...,я, сохраняют константу а. Тогда их суперпозиция h(gl9...9
gn) сохраняет константу а, ибо
Л(а,...,а) = f(gl(a9...9a)9...9gn(a9...,a)) = Да,...,а) = а.
1.9. Монотонные функции
Если a = («!,...,ап) и b = (bl9...,bn) - наборы длины п из 0 и
1, то а < Ь, если ах < Ь19...9ап < Ьп.
Пример. (0,1,0) < (1,1,0). Наборы (0,1) и (1,0) несравнимы.
Также несравнимы наборы (0,1) и (0,1,0).
Функция /(jCj ... 9хп) называется монотонной, если для всяких
наборов а = (aM...,an), b = (ЬМ...,ЬП) условие a < b влечет
/(a) < /(b).
Теорема. Класс монотонных функций замкнут относительно
суперпозиции.
Доказательство. Пусть f(xl9...,xm) и g Д*! , . . . ,Хп) , I - 1,Z,
. ..,л - монотонные функции (для простоты от одних и тех же
переменных). Покажем, что их суперпозиция
h(xl9...9xn) = ДяД*!,..., *„),...,£,„(*!,...,*„))
монотонна. Пусть с = (cl9...9 cn)9 d = (dl9... ,dn) - произвольные
наборы из 0 и 1, для которых с ^ d, т.е. с, < di9 i = 1,2, ...,л.
Пусть а, = g,(c), bi = gi(d)9 i = 1,2,...,/п. Пусть a =
(flj,...,^), b = (&!,...,&„,). Так как функции gj монотонны и с ^
d, то gi(c) < g;(d), т.е. а, ^ Ь,, i = l,2,...,m. Следовательно,
а ^ b. Отсюда в силу монотонности функции / получаем, что /(а) ^
/(b). Тогда Л(с) = /(^(с), ...,£m(c)) = f(al9...,aj = /(а) ^
/(b) = f(bl9...9bm) = f(gl(d)> ...^m(d)) = hi*)-
Итак, для любых наборов с и d из 0 и 1 неравенство с < d
влечет h(c) ^ /i(d), т.е. функция h монотонна. Теорема доказана.
Лемма (о немонотонной функции). Суперпозицией констант 0 и 1 и
переменной х в немонотонную функцию можно получить отрицание.
Доказательство. Пусть f{xx... 9хп) - немонотонная функция. Тог-
43
да существуют наборы а = (а19...9ап) и b = (bl9... 9bn)9 для
которых а < Ь, но /(а) > /(b). Пусть il9...9ijc есть все те номера
аргументов, для которых а, < Ь, , р = 1,...,Л. На всех остальных
аргументных местах ; имеем Uj *;'• В выражении f(a19... 9ап)
заменим нули на местах il9...9ik на х. В результате получим функцию
g(x)9 для которой g(0) = /(a) = 1 и g(l) = /(b) = 0. Функция #(*)
является отрицанием.
Лемма. Функция монотонна тогда и только тогда, когда ее
сокращенная ДНФ не содержит отрицаний.
Доказательство. Пусть простой импликант
/ = Х^1 ... ХСЛ"1 * **.• xV\l ... ХС;(
Ч l)-\ l] l ;+i Ч
монотонной функции f(xl9...,xn) содержит отрицание переменной.
Покажем, что выражение
/ = х'1 ... x'l'1 • xcti\l ... *•<
Ч l;-i ' ;+1 Ч
есть импликант функции /. Очевидно, что / = / • *,-..
Пусть а = (а19... 9ап) есть произвольный набор из 0 и 1 длины
л, для которого /(а) = 1. Покажем, что /(а) = 1. Построим набор
b = («!,... di 90,а1.^,..., ап)9
отличающийся от а только в разряде ij. Так как / не содержит Xj .,
то /(b) = 1. Тогда /(b) = /(b)-б = 1, откуда /(b) = 1, ибо / -
импликант для /. Пусть набор с = (а19... а, ._ ,1,а, . ,..., ап).
Так как b < с, то 1 = /(b) ^ /(с), откуда /(с) = 1. Если а в
разряде ij имеет 0, то а = b и тогда /(а) = /(с) = 1. Поэтому
/(а) = 1. Итак, /(а) = 1 влечет /(а) = 1, т.е. / - импликант
функции /. Противоречие с простотой импликанта /.
В обратную сторону доказательство очевидно.
Следствие. Функция монотонна тогда и только тогда, когда ее
минимальная ДНФ не содержит отрицаний.
1.10. Теорема Поста о функциональной полноте
Теорема (Поста). Чтобы система функций из Р2 была
функционально полной (в Р2), необходимо и достаточно, чтобы эта система
содержала:
1) функцию, не сохраняющую 0;
2) функцию, не сохраняющую 1;
3) несамодвойственную функцию;
4) немонотонную функцию;
44
5) нелинейную функцию.
Доказательство. Пусть система функций F из Р2 полна в Р2.
Допустим, что в F нет одной из указанных функций, например
немонотонной. Тогда все функции в F монотонны, а так как класс
монотонных функций замкнут относительно суперпозиции, то никакая
суперпозиция над F не даст немонотонной функции.
Пусть система F содержит все указанные функции:
f1(xl9...,xn ) не сохраняет 0;
f2(xl9...,xn ) не сохраняет 1;
f3(xly...yxn ) несамодвойственная функция;
f4(xl9...,xn ) немонотонная функция;
/5(*i,... ,*л ) нелинейная функция.
Покажем, что суперпозицией функций системы F можно получить
полную систему G = {х&у9х}.
1. Пусть g(x) = Д(х х). Тогда g(0) = /(0,...,0) = 1.
Далее возможны два случая:
g(l) = 1. Тогда g(x) = 1. Функция h{x) = f2(g(x),...,g(x)) =
/2(l,...,l) = 0, т.е. h(x) s 0. Получили константы 0 и 1;
g(l) = 0. Тогда g(x) = х. По лемме о несамодвойственной
функции суперпозицией над {/3>*} можно получить одну из констант,
например 0. Тогда /ДО,...^) = 1 есть другая константа.
В обоих случаях получили обе константы.
2. По лемме о немонотонной функции суперпозицией над {/4,0, 1}
можно получить отрицание.
3. По лемме о нелинейной функции суперпозицией над {/5, 1, х)
можно получить конъюнкцию. Теорема доказана.
Примеры.
1. F = {1,х*у}, где х*у = 0010.
Проверяем условия полноты:
1) константа 1 не сохраняет 0;
2) х*у не сохраняет 1;
3) х*у не самодвойственна, ибо 0*0 = 1*1;
4) х*у не монотонна, ибо (1,0) ^ (1,1), но 1*0 > 1*1;
5) х*у не линейна, ибо х*у = ху =ху+у.
Следовательно, система F по теореме Поста полна. Отрицание
есть 1*jc. Конъюнкция х&у = х*у.
45
2. F = {09l,x,m(x9y,z)}9 где функция m(x9y9z) = 00010111 равна
единице на тех и только тех наборах, в которых число единиц
больше числа нулей.
Проверяем условия полноты:
1) 0 не сохраняет 1;
2) 1 не сохраняет 0;
3) константа 1 не самодвойственна;
4) отрицание не монотонно;
5) функция m(x,y9z) = xyz+xy+xz+yz не линейна.
По теореме Поста система F полна. Конъюнкция х&у = т(х9у90).
Заметим, что система F избыточно полна. Ее подсистемы
{1,*, m(x,y9z)} и {09x9m(x9y9z)}
являются функционально полными системами.
1.10.1. Предполные классы
Замкнутый класс К из Р2 предполон, если К не является полным,
но для всякой функции / не из К система К U {/} полна.
Теорема. Следующие замкнутые классы функций предполны: класс
Т0 функций, сохраняющих константу 0; класс Тх функций,
сохраняющих константу 1; класс М монотонных функций; класс L линейных
функций; класс S самодвойственных функций.
Доказательство. Покажем, что класс монотонных функций предпо-
лон. Пусть функция f i M. Заметим, что функции х&у9 ху9 0, 1
монотонны. По лемме о немонотонной функции отрицание х € [{/,0,1}].
Система {х&у,хУу,х} полна.
Покажем, что класс Тх предполон. Пусть функция f(x19... ,xn) t
Т19 т.е. /(1,...,1) = 0. Пусть g(x) = /(*,...,*). Тогда g(l) =
/(l,...,l) = 0. Заметим, что функции ху9 х&у лежат ъТх. Возможны
следующие случаи:
g(0) = 1. Тогда g(x) = х. Следовательно, система {х&у, х} Я
[Тх U {/}] и потому класс Тх U {/} полон;
g(0) = 0. Тогда g(x) =е 0. Очевидно, что х -» у € Тг, х есть х
-> 0. Получаем {х&у,х} Я [Тх U {/}] и потому класс Тх U {/} полон.
Покажем, что класс Т0 предполон. Пусть функция f(xl9... ,xn) I
Т0. Пусть g(x) = /(*,...,*) и g(0) = /(0,...,0). Возможны
следующие случаи.
g(l) = 0. Тогда g(x) = х.
46
g(l) = 1. Тогда g(x) = 1. Так как х+у € Г0, то х = лг+1. В
обоих случаях получено отрицание. Так как х&у € Г0, то {х&у,х} Я [Т0
U {/}]. Следовательно, класс Т0 предполон.
Покажем, что класс линейных функций предполон. Пусть f(x19...9
хп) € L. Заметим, что функции дс+1, 0, 1 лежат в L. По лемме о
нелинейной функции х&у € [{/,0,1}]. Следовательно, {х&у,х} = [Г0 U
{/}] и потому система TQ U {/} полна.
Покажем, что класс S самодвойственных функций предполон. Пусть
функция / t S. Заметим, что х € S. По лемме о несамодвойственной
функции константы 0 и 1 лежат в [{/, дс}]. Функция g(x,y,z) = xy V
xz V yz € S. Тогда g(x9y,l) =xy\/xVy = xVy. Система {xVy9
х} Я {S U {/}]. Следовательно, система S U {/} полна и потому
класс S самодвойственных функций предполон.
Теорема доказана.
Приведем следующую перефразировку теоремы Поста.
Теорема. Система функций полна тогда и только тогда, когда она
имеет непустое пересечение с каждым из пяти предполных классов.
Замечание. Пост описал все замкнутые классы в Р2. Оказалось,
что множество всех замкнутых классов в Р2 счетно и образует
решетку по отношению к включению замкнутых классов. Эта решетка имеят
единственный наибольший элемент - класс Р2 и три минимальных
элемента: О, = [{*}], 02 = [{1}], 03 = [{0}].
2. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
2.1. Определение исчисления высказываний
Высказывание есть утверждение, относительно которого можно
точно сказать, истинно оно или ложно (при этом оно не может быть
тем и другим одновременно). Высказывание "через две точки можно
провести единственную прямую" истинно. Высказывание "нуль равен
единице" ложно. Из простых высказываний с помощью логических
операций конъюнкции, дизъюнкции, отрицания, импликации,
эквивалентности можно строить высказывания более сложные. Их истинностные
значения "истина" и "ложь" (И и Л) вычисляются согласно
следующей таблице:
47
p
л
л
и
и
q
л
и
л
и
p&q
Л
Л
Л
И
pVq
Л
И
и
и
p-q
И
И
Л
и
p=q
И
Л
Л
и
1р
и
и
л
л
Высказывание "если числовой ряд сходится, то его общий член
стремится к нулю" построено из двух высказываний: "числовой ряд
сходится" и "его общий член стремится к нулю" с помощью
импликации.
Пусть А(р19р29... ,р*) - формула алгебры логики, которая
построена из пропозициональных переменных pt ,р2,... ,рл с помощью
конъюнкции, дизъюнкции, отрицания, импликации, эквивалентности.
Замещая переменные р х, р 2,..., р^ некоторыми высказываниями,
получим новое, которое примет значение "истина" или "ложь" (И или
Л). Содержание самих высказываний при этом не существенно; важны
только их истинностные значения. Поэтому в формуле ACp^pj,...,
pjt) переменные можно сразу замещать знаками И и Л, а затем
вычислять истинностное значение получившегося выражения, как это
делается в алгебре логики, если считать, что И отождествляется с
О, а Л—с 1. Формула A(pj ,р2,... ,р^) реализует некоторую функцию
алгебры логики от к переменных. Не будем различать и оговаривать
их особо в дальнейшем, если о такой функции придется говорить.
Содержательно значения конъюнкции, дизъюнкции, отрицания,
эквивалентности понятны. Значения импликации р -* q на наборах (1,1)
и (1,0) тоже понятны. Несогласие вызывает у слушателей в первый
раз логику значения функции р -> q на наборах (0,0) и (0,1).
Выбранную таблицу значений импликации можно пояснить следующими
рассуждениями. Функции p-*qH~lq-*~lp должны быть одинаковыми, ибо
если утверждение р -* q при некоторых конкретных высказываниях р и
q истинно (как прямое утверждение), то высказывание ~lq -» 1р тоже
истинно (как противоположное утверждение). Например, справедливо
необходимое условие сходимости числовых рядов: если ряд сходится,
то его общий член стремится к нулю. Справедливо и противоположное
утверждение: если общий член ряда не стремится к нулю, то ряд
расходится. Из этих же соображений верно и обратное: из
истинности утверждения ~lq -* Пр следует истинность утверждения р -* q.
Функции p-*qnq-*pHe могут быть равными, иначе импликация
становится эквивалентностью, что невозможно, ибо из того, что р
влечет q, вообще говоря, не следует, что q влечет р (пример с тем
же необходимым условием сходимости рядов).
Таким образом, импликация р ~* q определяется следующими
48
условиями: 1) функции р -♦ q и "Iq -* "1р одинаковы; 2) функции р -♦ q
и q -* p различны.
Итак, функция р -♦ q на наборе (1,1) равна единице, а на наборе
(1,0) - нулю. Такова же и равная ей функция "Iq -♦ "1р. На наборе
(0,0) функция "Iq -» "Ip равна единице; такова же и р -♦ q. Значения
импликации q -» р на наборах (0,0),(l,0),(l,l) тоже определились.
Осталось задать значение р -* q на (ОД). Если примем, что р -* q
на (ОД) равно 0 (т.е. 0 -♦ 1 = 0), то q -♦ р на (1,0) тоже равно 0
(т.е. 0 -♦ 1 = 0). Тогда функции р -♦ q и q -> р оказываются
равными. Поэтому импликация р -♦ q на (ОД) равна 1.
Построим формально-логическое исчисление, в котором
описываются все тождественно истинные формулы алгебры логики и только они.
Алфавит.
1. p9q,r,plyqlyrl,... - символы пропозициональных переменных.
2. &, V, -♦, П - логические связки (конъюнкция, дизъюнкция,
импликация, отрицание соответственно).
3. ( , ) - скобка левая, запятая, скобка правая.
Формулы.
1. Отдельно взятый символ пропозициональной переменной есть
элементарная формула (атом).
2. Если А и В есть формулы, то выражения (А & В), (А V В), (А
-* В), (ПА) есть формулы.
Примем соглашение об опускании скобок в соответствии со
следующим приоритетом связок: "I , & , V , -♦.
Подформулы.
1. Если формула есть переменная, то единственной ее
подформулой является она сама.
2. Если формула имеет вид ПА, то ее подформулами являются она
сама и все подформулы формулы А.
3. Если формула имеет вид А * В , где знак * € {&, V, -♦}, то
ее подформулами являются она сама и все подформулы формул А и В.
В формуле А -» В подформула А называется посылкой, а подформула
В - заключением.
Проинтерпретируем логические связки &, V, ->, П
соответствующими логическими операциями (функциями).
Если все переменные формулы А содержатся среди переменных
Pi>P2>--->Pn> то пишем A(plip2i...9pn). Если формула А(р!,р2,...,
ря) построена из переменных Pi,p2> ->Рл и только из них, то
скажем тогда, что Pi ,p2»• • • »Ря есть полный список переменных
формулы А.
Интерпретация формулы А(р!,...,рп) есть набор / = (а1У...,ап)
из И и Л.
49
Индукцией по построению формулы А определим понятие значения
А(/) формулы A(pj,... ,рл) на интерпретации /.
1. Если А есть р, , то А(/) = а,.
2. Если А есть формула (В * С), где знак * € {&,V,->}, или же
формула 1В, то (В * С)(/) = В(/) * С(/); (~1В)(/) = ~1(В(/)).
Для удобства вместо А(/) будем писать также А(а1э...,ал).
Формула А общезначима (тождественно истинна), если она истинна
на любой интерпретации. Формула А выполнима, если существует
интерпретация, на которой формула А истинна. Формула А невыполнима
(тождественно ложна), если она ложна на всех интерпретациях.
Формула А опровержима, если существует интерпретация, на которой
формула А ложна.
Интерпретация / удовлетворяет формуле А (А выполняется на /),
если А истинна на /. Интерпретация / опровергает А, если А ложна
на /. Если интерпретация / удовлетворяет формуле А, то /
называется также моделью формулы А.
Подстановка (П). Индуктивное определение.
1. Если формула А есть переменная р, то подстановка П5(а)
формулы В на место переменной р в формуле А есть В.
2. Если формула А переменной р не содержит, то подстановка
П§(А) есть снова формула А.
3. Если формула А имеет вид "1С или С * Е, где * есть один из
знаков &, V, ->, то подстановки
П{*(~1С) = -ЩВ(С); ПВ(С * Е) = п|*(С) * П^(Е).
Подстановка П§(А) есть результат замещения переменной р всюду,
где она встречается в формуле А, на формулу В.
Система аксиом (П.С.Новикова).
А1) р - (q - р).
А2) (р - (q - г)) - ((р - q) -> (р - г)).
A3) р & q -> р.
А4) р & q -» q.
А5) (р - q) -> ((р - г) - (р - q & г)).
А6) р -» р V q.
А7) q -♦ р V q.
А8) (р - г) -> ((q - г) -> (р V q - г)).
А9) (р - q) - (lq - Пр). *
А10) р - "Пр.
All) "Пр - р.
Заметим, что в качестве аксиом взяты тождественно истинные
формулы.
50
Правила вывода (ПВ)
Правило подстановки имеет вид
А(р)
ПВ(А(Р)) '
т.е. от формулы А(р) с переменной р можно перейти к формуле
ПВ(А(Р».
Правило заключения (ПЗ) имеет вид
А, А - В
В '
т.е. от двух формул А и А -* В можно перейти к формуле В.
Исчисление высказываний (ИВ) составляют формальные символы,
формулы, аксиомы и правила вывода.
Определение. Доказательство в ИВ есть конечная
последовательность формул, каждая из которых есть либо аксиома, либо получена
из предыдущих членов последовательности по правилу подстановки
или заключения.
Определение. Формула А доказуема в ИВ, если в ИВ существует
доказательство, последней формулой которого является А.
Всякая аксиома есть доказуемая формула, длина доказательства
которой равна 1.
Приведем примеры доказуемых формул и некоторых вспомогательных
(производных) правил вывода, применение которых к формулам при
необходимости можно исключить, но использование сделает
формальную систему ИВ выразительнее и естественнее.
Доказательства формул сопроводим краткими пояснениями.
Например, A3 будет означать, что формула является аксиомой A3; П3(2,3)
- формула получена применением правила заключения (ПЗ) к формулам
(2) и (3); П S(4) - формула получена подстановкой в формулу (4)
формулы Пр на место переменной q. Знак Ь- будет означать: формула
доказуема в ИВ.
Теорема 1. h р -> р.
Доказательство.
(1) (р -> (q - г)) - ((р - q) - (р - г)), А2;
(2) (р - (q - р)) - ((р - q) - (р - р)), П Р (1);
(3) р - (q -> р), А1;
(4) (р - q) - (р - р), П3(2,3);
(5) (р - (q - р)) - (р - р), П У (4);
(6) р - р, П3(3,5).
Формула р -> р доказуема в ИВ и последовательность формул
51
(l),(2),... ,(6) есть ее доказательство.
Замечание. Формула р -* р доказуема в любом аксиоматическом
исчислении, содержащем аксиомы А1,А2, правило подстановки и правило
заключения.
2.1.1. Правило одновременной подстановки
Пусть выражение П р1 р2 " J* (А) означает формулу,
представляющую собой результат одновременного замещения переменных р1э
р2,...,Р£ в формуле А на формулы В1ЭВ2,...,ВЛ соответственно.
I- A
Утверждение. .
Вх В2 .. . Вк , ч
11 Pi р2 • • р* КА)
Доказательство. Пусть г г, г 2,..., тк есть попарно различные
переменные, отличные от всех переменных, встречающихся в формулах
R R
А,В1ЭВ2,... ,Bfc.Тогда формула Пр^'^р^А) есть результат сначала
последовательного замещения переменных Pi,p2>--->P* B формуле А
на переменные хх ,г2,... ,г^ соответственно, а затем в получившейся
формуле - результат последовательной замены переменных г1эг2,...,
г^ на формулы B1,B2J...,Bjc соответственно.
Теорема 2. Ь П(р V q) -» Пр & Hq.
Доказательство.
(1) (р - q) - ((р - г) - (р - q&r)), A5;
(2) (H(pVq) - Пр) - ((-l(pVq) - lq) - (n(pVq) - Пр & Hq)),
п-КрУ,> пр n; (1).
(3) p-pVq, A6;
(4) (p - q) - ("lq -» lp), A9;
(5) (p - p V q) - ("l(p V q) - Пр), П P^q (4);
(6) "Up V q) - Пр, П3(3,5);
(7) (П(р V q) - lq) - ("l(p V q) - Пр & lq), П3(2,б);
(8) q - p V q, A7;
(9) (q - p V q) - ("l(p V q) - Hq), П J P^q (4);
(10) -I(p V q) - Hq, П3(8,9);
(11) 1(p V q) - Пр & lq, П3(7,10).
2.2. Теорема дедукции (ТД) в исчислении высказываний
Пусть Г и Л есть произвольные конечные совокупности формул в
ИВ (возможно пустые) и А,В,С - произвольные формулы в ИВ.
52
Определение. Конечная последовательность формул ИВ есть вывод
из совокупности формул Г, если всякая формула последовательности
либо принадлежит Г, либо доказуема, либо получена из предыдущих
формул последовательности по правилу заключения.
Определение. Формула А выводима из совокупности формул Г, если
существует вывод из совокупности Г, последней формулой которого
является А.
Заметим, что доказуемая формула выводима из любой (в том числе
из пустой) совокупности формул.
Пусть записи означают: Г I- A - формула А выводима из
совокупности формул Г; Т8 - теорема 8; ПВ7 - правило вывода 7.
Правило вывода 1.
Доказательство.
А,В I- А & В.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(Ю)
(И)
(12)
A, условие;
B, условие;
•- (р - q) - ((р "» г) -» (р - q & г)), А5;
Н (А - А) -» ((А -* В) -♦ (А -» А & В)).
•- Р - Р, Т1;
1-А-А,
Н (А - В) - (А -» А & В),
h р -» (q -» р), А1
I- В -* (А - В), П
А - В, 113(2,9)
А - А & В, 113(7,10);
А & В, 113(1,11).
П А А В (3).
П А (5)
ПЗ(4,6);
£ А (8);
а. А & В I- А. Ь. А & В I- В.
Доказательство.
(1) А & В, условие; (l) A & В, условие;
(2) I- р & q -» р, A3; (2) Н р & q - q, A4;
(3) Н А & В - А, П р ? (2); (3) I- А & В - В, П А J (2);
(4) А, 113(1,3). (4) В, П3(1,3).
Правило вывода 2.
Г I- А Г I- В
Г Н А & В
Доказательство.
(1) Г, условие;
(2) А;
Г Н А & В
Г h А Г I- В
(1) Г, условие;
(2) А & В;
53
(з)
(4)
(5)
(6)
А&В^А, ПА§ (A3);
A&B^B, ПА§ (А4);
A, П3(2,3);
B, П3(2,4).
(3) В;
(4) А & В, ПВ1.
Г Ь А
Правило вывода 3. .
Г Ь В - А
Доказательство.
(1) Г, условие;...; (2) А ; (3) Ь А -> (В - А), П £ В (А1).
(4) В - А, П3(2,3).
Теорема (дедукции). Если Г есть конечная совокупность формул,
а А и В - произвольные формулы в ИВ, для которых Г,A h В, то
Г I- А - В.
Доказательство. Индукция по длине к вывода.
БАЗИС, к = 1. Возможны три случая.
1. В есть А. Тогда Г,А Ь А. Так как 1-А-^А (как П £ (Т1)), то
Г Ь А - А.
2. Ь В. Тогда Ь А -» В по ПВЗ; поэтому Г Ь А -» В.
3. В € Г. Тогда Г h В и по ПВЗ Г Ь А -> В.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть теорема справедлива для всех
выводов длины меньше к.
ШАГ ИНДУКЦИИ. Покажем, что теорема справедлива для выводов
длины к. Пусть Г,А I- В и пусть В1ЭВ2,... ,В^_1ЭВ^ (= В) есть
вывод длины к формулы В из совокупности Г,А. Возможны следующие
случаи.
1. В есть А. 2. НВ. 3. В€Г. Эти случаи рассмотрены в
базисе.
4. В (= Вл) получается из двух формул В,- и В,- ч В^ вывода по
правилу заключения, т.е. вывод Вк из Г,А имеет вид
Bj ,В2,... ,В,,... ,В, -> Bfc,...,B£ (=В).
Тогда Г,А Ь В,, Г,А Н В, -> В^. Так длины этих выводов меньше
к, то по предположению индукции
(1) Г Ь А - Bf- ;
(2) Г Ь А - (В, - Вк).
Далее имеем:
(3) Г Ь (А - (В,- - В*)) - ((А - В,) - (А - В*)),
П £ *'?* (А2);
(4) Г h (А - В,) - (А - В*), П3(2,3);
(5) ГНА-» В*, П3(1,4), т.е. Г Ь А -> В.
54
Al ,А2,...,АЛ h В
Следствие.
h A,- (A2- (... - (А*- В)...)) '
Замечание. Теорема дедукции доказуема в любом аксиоматическом
исчислении, содержащем аксиомы А1,А2, правило подстановки и
правило заключения.
2.3. Производные правила вывода
Пусть, как и в предыдущем параграфе, Г и А есть произвольные
конечные совокупности формул ИВ (возможно пустые) и А,В,С -
произвольные формулы в ИВ.
Правило вывода 4 (правило силлогизма).
ГЬА-В ГЬВ-С
Г Ь А - С
Доказательство.
(1) Г h A -* В, условие;
(2) Г Ь В ■» С, условие;
(3) Г Ь (А -> (В - С)) - ((А - В) - (А - С)), П А В С (А2);
(4)ГЬА-»(В- С), ПВЗ(2);
(5) ГН(А-»В)-»(А-»С) П3(3,4);
(6) Г Ь А -> С, П3(1,5).
Г Ь A - В
Правило вывода 5 (контрапозиция). ■ .
Г Ь 1В - ПА
Доказательство.
(1) Г Ь А -» В, условие;
(2) Г h (А - В) - (1В - ПА), П А В (А9);
(3) Г1-1В-» ПА, П3(1,2).
Правило вывода 6 (снятие двойного отрицания в заключении).
Г Ь А - ППВ
Г Ь А - В
Доказательство.
(1) Г Ь А -» 11В, условие;
(2) Г Ь ППВ - В, П g (A10);
(3) Г h A -> В, ПВ4(1,2).
Правило вывода 7 (снятие двойного отрицания в посылке).
55
Г I- ~ПА -» В
Г I- A - В
Доказательство.
(1) Г Н ~ПА -» В, условие;
(2) Г Н А - "ПА, П J (All);
(3) Г h A - В, ПВ4(1,2).
Г I- A
Правило вывода 8.
Правило вывода 9.
Г,Л Н А
Г,В I- А Г Н В
Г I- A
Доказательство. Г;... ,В; • • • >А; т.е. Г I- А.
Г,В I- А Д I- В
Правило вывода 10. .
Г,Л I- A
Доказательство. Г,Д,... ,В,... ,А.
Г Н А - В
Правило вывода 11. .
Г,А I- В
Доказательство.
(1) Г I- A -» В, условие;
(2) Г,А I- А;
(3) Г,А I- A -» В, ПВ8(1);
(4) Г,А I- В, П3(2,3).
I- A
Правило вывода 12. .
Г I- A
Теорема 3 (закон перестановки посылок).
I- (р -» (q -» О) "» (q -* (Р "* г)).
Доказательство. Покажем, что р -» (q -» r),q,p I- r.
(1) p -» (q -» г), условие;
(2) q, условие; (4) q - г, П3(1,3);
(3) р, условие; (5) г, П3(2,4).
Далее последовательно применяем теорему дедукции.
Правило вывода 13 (перестановка посылок).
56
Г I- А -> (В - С)
Г Н В ■» (А •* С)
Доказательство.
(1) Г Ь А -> (В - С), условие;
(2) Г Ь (А -> (В -> С)) -> (В -> (А - С)), П А В С (Т3);
(3) Г Ь В - (А - С), П3(1,2).
Теорема 4 (закон соединения посылок).
Ь (р - (q - г)) - (p&q - г).
Доказательство. Покажем, что р ~* (q -* r), p&q Н г.
(1) р - (q - г), условие; (4) q, ПВ2(2);
(2) p&q, условие; (5) q -» г, П3(1,3);
(3) р, ПВ2(2); (6) г, П3(4,5).
Далее последовательно применяем теорему дедукции.
Правило вывода 14 (соединение посылок).
Г Ь А - (В - С)
Г Ь (А & В) - С
Доказательство.
(1) Г Ь А -> (В -> С), условие;
(2) Г I- (А -> (В - С)) -> (А & В - С), П $ В С (Т4);
(3) Г Ь А & В -> С, П3(1,2).
Теорема 5 (закон разъединения посылок).
I- (р & q -» г) - (р - (q - г)).
Доказательство. Покажем, что р & q -> r, p,q Ь г.
(1) р & q -> г, условие; (4) p&q, ПВ2(2,3);
(2) р, условие; (5) г, П3(1,4).
(3) q, условие;
Далее последовательно применяем теорему дедукции.
Правило вывода 15 (разъединение посылок).
Г Ь А & В - С
Г h А - (В - С)
Доказательство.
(1) Г Ь А & В -> С, условие;
(2) Г I- (А & В - С) - (А - (В - С)), П А В С (Т5).
57
(3) Г I- A - (В - С), П3(1,2).
Правило вывода 16 (введение конъюнкции).
ГЬС-А Г1-С-В
Г h С - А & В
Доказательство.
(1) Г h С -» А, условие;
(2) Г h С -* В, условие;
(3) Г Ь (С - А) -> ((С -> В) -> (С -> А & В)), П J А В(А5);
(4) Г h (С -> В) - (С - А & В), 113(1,3);
(5) Г h С - А & В, П3(2,4).
Правило вывода 17 (введение дизъюнкции).
ГНА-С Г1-В-С
Г Ь А V В - С
Доказательство.
(1) Г h A -» С, условие;
(2) Г h В -* С, условие;
(3) Г h (А - С) - ((В - С) - (А V В - С)), П С А В(А8).
(4) Г h (В - С) - (А V В ■» С), П3(1,3);
(5) Г I- А V В - С, П3(2,4).
Теорема 6. I- p & ~1р -* q.
Доказательство.
(1) I- р - (q - р), А1;
(2) Ь р - (lq - р), П ПЧ (1);
(3) h (Hq - р) - (Пр - 11q). П П^ g (A9);
(4) h p -* (Пр -» "l"lq), ПВ4(2,3), силлогизм;
(5) I- р & Пр -* "I"lq, ПВ14(4), соединение посылок;
(6) \- р & Пр -» q, ПВ6(5), снятие двойного отрицания.
Высказывание р & Пр тождественно ложно, т.е. противоречиво при
любом р. Теорема 6 утверждает, что из противоречия следует любое
высказывание. Из нее легко показать справедливость правила вывода
А, ПА
, которое утверждает, что в противоречивом исчислении
В
(т.е. в исчислении, где доказуемо некоторое утверждение и его
отрицание) можно вывести любое утверждение.
58
Теорема 7 (закон исключенного третьего). Ь р V Пр.
Доказательство.
(1) Ь П(р V Пр) - Пр & ППр, П П§ (Т2);
(2) Ь Пр & ППр - Hq, П ПР П5 (Т6);
(3) h П(р V Пр) - Hq, nB4U,2), силлогизм;
(4) Ь HHq -> ПП(р V Пр), ПВ5(3), контрапозиция;
(5) I- q -* ПП(р V Пр), ПВ7(4), снятие двойного отрицания;
(6) h q -» (р V Пр), ПВ6(5), снятие двойного отрицания;
(7) Ь р -> р, Т1;
(8) Ь (р - р) - (р V Пр), П РГР (6);
(9) h р V Пр, П3(7,8).
Правило вывода 18 (приведение к абсурду).
Г,А I- В Г,A h ПВ
Г Ь ПА
Доказательство.
(1) Г,А Н В, условие;
(2) Г,А К- ПВ, условие;
(3) Г Н А - В, ТД(1);
(4) Г Ь А - ПВ, ТД(2);
(5) Г1-А- В&ПВ, ПВ16(3,4);
(6) К- В & ПВ - П(В V ПВ), П g BVHB (Т6).
(7) Г Ь А - П(В V ПВ), ПВ4(5,6), силлогизм;
(8) Г h 11(В V ПВ) - ПА, ПВ5(7), контрапозиция;
(9) ГЬ(В\/ПВ)->ПА, ПВ7(8), снятие двойного отрицания;
(10) h В V ПВ, nj (T7);
(11) Г I- ПА, П3(9,10).
Правило приведения к абсурду используется в доказательствах от
противного. Пусть по ходу некоторых рассуждений требуется
доказать утверждение А. Допускаем противное: предполагаем
справедливость его отрицания, т.е. справедливость утверждения ПА, и
доказываем, исходя из ПА, некоторое утверждение В и его отрицание ПВ.
Получили противоречие. Следовательно, наше предположение о
справедливости утверждения ПА было неверным и потому справедливо его
отрицание ППА, т.е. справедливо А.
Теорема 8. h р V q - П(Пр & Hq).
Доказательство.
59
(1) Ь (р - -l(-lp&-lq)) - ((q - -|(-lp&-lq)) -
(p V q - n(np&lq))), П "^Pf1^ (A8);
(2) Ь Ip & Iq - lp, П ПР П3 (A3);
(3) Ь lp & lq - "lq, П ПР П5 (А4);
(4) h "lip -» "1 ("lp & "lq), ПВ5(2), контрапозиция;
(5) h "l"lq -♦ "i("lp & "lq), ПВ5(3), контрапозиция;
(6) Ьр-» "1("1р & "lq), ПВ7(4), снятие двойного отрицания;
(7) bq->"l("lp&"lq), ПВ7(5), снятие двойного отрицания;
(8) Ь (q - П(Пр&ПЧ)) - (р V q - П(Пр&ПЧ)), ПЗ(1,6);
(9) Ь р V q - П(Пр&ПЧ), 113(7,8).
Теорема 9. Ь ~1р & lq -» П(р V q).
Доказательство.
(1) Ь р V q - "l("lp & lq), T8.
(2) h ~П(~1р & ~lq) -» ~1(р V q), ПВ5(1), контрапозиция.
(3) h Пр & "lq -♦ "1(р V q), ПВ7(2), снятие двойного отрицания.
Теорема 10. h (p -* q) -» "lp V q.
Доказательство.
а)
(2)
(3)
(4)
(5)
(6)
(7)
лок;
(8)
Т¥ 1Л11.1П U1
ДИЗрЮШ
(9)
(Ю)
р, р -» q I- q, правило заключения;
\- q - Пр V q, П ПР (А7);
р, р - q I- lp V q, П3(1,2);
•- Р -* ((Р - q) - "lp V q), ТД(3);
Ь Пр - Пр V q, П ""P (А6);
Ь (р - q) - (Пр - Пр V q), ПВЗ(5);
•~ Пр -» ((р -» q) -» Пр V q), ПВ13(6), перестановка посы-
1- (р V Пр) -» ((р -» q) -» Пр V q), ПВ7(4,7), введение
есции;
И р V Пр, Т7;
1- (р - q) - Пр V q, П3(8,9).
2.4. Тождественно истинные и доказуемые формулы
Пусть А(р!р2,... ,р„) - формула в ИВ и PiP2»- -»Pn ~ полный
список ее переменных; а = (а1,а2,...,ап) - набор из 0 и 1 длины
п\ Рш (А) означает значение формулы А на наборе а. Определим это
60
понятие индукцией по построению формулы.
1. Если А есть переменная р,, то
МА) = Л,,,а2,...,„,.,...,*>) = «,-
2. Если А есть формула В * С (где * есть один из знаков *, V,
-♦) или же формула "IB, то
Ра(В * С) = Ра(В) * Р. (С); Р.(ПВ) = ПР. (В).
Примем обозначения р1 = р; р° = Пр.
Лемма (о доказуемости формулы по значению на наборе).
Р. (А) = 1 Ра (А) = О
1. . 2. = .
Pi >Рг >--->Рз ^ л Pi >Рг > • • • уУп ^ ,л
Доказательство. Индукция по построению формулы.
Пусть совокупность формул Г = {р11,р22>- • • »РпП}-
БАЗИС. Формула А есть переменная р,-. Тогда Ра(рх) = я,.
a) at = 1. Тогда р*1 = р, = А; откуда Г Ь А.
b) (ц = 0. Тогда р?' = Пр; = ПА; откуда Г h ПА.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Предположим, что лемма справедлива
для всех формул глубины построения меньше к.
ШАГ ИНДУКЦИИ. Покажем, что лемма справедлива для формул
глубины построения к. Возможны следующие случаи.
а) А есть В & С. Возможны следующие подслучаи.
1. Ра (А) = 1. Покажем, что Г h А. Так как Ра (А) = Ра (В & С, =
Ра(В) & Ра (С) = 1, то Ра(В) = 1, Ра(С) = 1. Так как глубина
построения формулы В и формулы С меньше /с, то по предположению
индукции имеем
Г h В, Г h С, откуда Г h В & С, ПВ2.
2. Ра (А) = 0. Покажем, что Г Ь ПА. Так как Ра (А) = Ра (В&С) =
Ра(В) & Ра(С) = 0, то Ра(В) = 0 или Ра(С) = 0. Пусть для
определенности Ра (В) = 0. Так как глубина построения формулы В
меньше /с, то по предположению индукции
(1) Г Ь 1В. Далее получаем
(2) h В & С - В, П В С (аз);
(3) h IB -» l(B & С), ПВ5(2), контрапозиция;
(4) Г М(В & С), П3(1,3), т.е. Г Ь ПА.
61
b) А есть В V С. Возможны следующие подслучаи.
1. Р& (А) = 1. Покажем, что Г h А. Так как Рл (А) = Рл (В V С) =
Ра(В) V Ра(С) = 1, то Ра(В) = 1 или Ра(С) = 1. Пусть для
определенности имеем Рл (В) = 1. Так как глубина построения
формулы В меньше к, то по предположению индукции
(1) Г h В. Далее получаем
(2) К В - В V С, П Ь С (А6).
(3) Г Ь В V С, П3(1,2), т.е. Г h A.
2. Рл (А) = 0. Покажем, что Г Н ПА. Так как Ра (А) = Рл (В&С) =
Ра(В) V Рл (С) = 0, то Ра (В) = 0, Ра (С) = 0. Так как глубина
построения формулы В и формулы С меньше к, то по предположению
индукции
(1) Г Ь IB;
(2) Г Ь "1С. Далее получаем
(3) Г I-1B& ПС, ПВ2(1,2);
(4) Ь ПВ & ПС - П(В V С), П {* ^ (Т9);
(5) Г h П(В V С), П3(3,4), т.е. Г Ь ПА.
c) А есть В -> С. Возможны следующие подслучаи.
1. Рл (А) = 1. Покажем, что Г I- А. Так как Рш (А) = Рл (В - С) =
Рл (В) - Рл (С) = 1, то Рл (В) = 0 или Рл (С) = 1.
Пусть Ра(В) = 0. Так как глубина построения формулы В меньше
к, то по предположению индукции
(1) Г h ПВ. Далее
(2) Г I- В & ПВ - С, П g § (Т6);
(3) Г I- В -♦ (ПВ -» С), ПВ14(2), разъединение посылок;
(4) Г I- ПВ -♦ (В -♦ С), ПВ13(3), перестановка посылок;
(5) Г Ь В - С, П3(1,4), т.е. Г Ь А.
Пусть Рл (С) = 1. Так как глубина построения формулы С меньше
к у то по предположению индукции
(1) Г \- С. Далее
(2) Ь С - (В - С), П В С (А1).
(3) Г Ь В - С, П3(1,2), т.е. Г Н А.
2. Ра (А) = 0. Покажем, что Г I- ПА. Так как Рл (А) = Рл (В-^С) =
Ра(В) -• Ра(С) = 0, то РЛ(В) = 1, Ра(С) = 0. Так как глубина
построения формулы В и формулы С меньше к, то по предположению
индукции
(1) Г Ь В;
(2) Г Ь ПС. Далее
(3) Г I- ((В -> С) -> С) -> ОС - П(В - С)), П в£с § (Т9);
62
(4) Ь (В - С) - (В - С),
п в-с (Т1);
(5) h В ■♦ ((В -♦ С) -♦ С), ПВ13(4), перестановка посылок;
(6) Г Ь (В - С) - С, П3(1,5);
(7) Г h ПС - П(В -> С), ПВ5(6), контрапозиция;
(8) Г Ь П(В - С), П3(1,7), т.е. Г Ь ПА.
d) А есть ПВ. Возможны следующие случаи.
1. Рл (А) = 1. Покажем, что Г Ь А. Так как Ра (А) = Ра (ПВ) =
ПРа (В) = 1, то Ра (В) = 0. Так как глубина построения формулы В
меньше к> то по предположению индукции Г h IB, т.е. Г Ь А.
2. Рл (А) = 0. Покажем, что Г I- ПА. Как и выше, Рл (В) = 1. По
предположению индукции
(1) Г Ь В. Далее
(2) I- В - ППВ, П {* (А10);
(3) Г Ь ППВ, т.е. Г Ь ПА.
Лемма доказана.
Теорема. Всякая тождественно истинная формула доказуема в ИВ.
Доказательство. Пусть А(р2 ,р2,... ,р„) есть тождественно
истинная формула и Pi ,р2>-• • >Рл " полный список ее переменных; а =
(ах ,я2,... ,ап) - произвольный набор из 0 и 1 длины п. Так как
Рл (А) = 1 для любого набора я, в том числе и для наборов
{ах,... ,ап_1,1) и (ах,... ,an_Y ,0), то по доказанной выше лемме
а)
(2)
(3)
(4)
(5)
(6)
(7)
#1
Pi
Я/1-1
>Рл-1 >Рл ^ л>
.Ри-Т1
>F/j-i
>Рл-1
•- Ря V "1р„,
Р^.-'-.Ря-!1
,Прл \- А. Далее
Ь p„ - А, ТД(1);
Ь Пр„ - А,-ТД(2);
h Рл v "'■Рл "* А> ПВ17(3,4), введение V;
П рП(Т7);
I- А, ПЗ(5,6).
Повторяя предыдущие рассуждения, получим
•уУп-2 ^
А.
После конечного числа подобных рассуждений получим Ь А.
Теорема. Всякая доказуемая в ИВ формула общезначима.
Доказательство. Индукция по длине г доказательства.
БАЗИС, к = 1. Непосредственной проверкой убеждаемся, что все
63
аксиомы (только они имеют длину доказательства к=\) тождественно
истинны.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что все доказуемые
формулы с длиной доказательства меньше к тождественно истинны.
ШАГ ИНДУКЦИИ. Покажем, что все доказуемые в ИВ формулы с
длиной доказательства к тождественно истинны. Пусть формула А
доказуема в ИВ и ее доказательство АРА2,...,А^ (=А) имеет длину
к. Возможны следующие случаи.
1. А есть аксиома. Тогда А тождественно истинна.
2. Формула А^ (=А) есть П Я (АДр)), т.е. получена из
формулы АДр) в доказательстве Ах ,А2,... ,АДр),... ,Ад с помощью
подстановки. Так как длина доказательства Ах ,А2,... ,АДр) формулы
АДр) меньше к, то по предположению индукции формула АДр), а
вместе с ней и формула А = АДС), тождественно истинна.
3. Формула Ад получена из формул А, и А,- -► Ад в доказательстве
Ам... ,А,-,... ,А,- -* Ад,...,Ад (=А) с помощью правила заключения.
Так как длины доказательств
A j,..., A i и А!,..., А,-,..., А,- -* Ад
формул А,И А,; -> Ад МвНЬШв /С, ТО ПО ПрвДПОЛОЖвНИЮ ИНДуКЦИИ фор-
мулы А,- и А/ -> Ад тождественно истинны. Тогда формула Ад
тождественно истинна по определению операции ипликации.
Из двух предыдущих теорем получаем следующее.
Теорема. Чтобы формула А была доказуема в ИВ, необходимо и
достаточно, чтобы формула А была тождественно истинной.
2.5. Разрешимость, непротиворечивость,
полнота, независимость аксиом
Проблема разрешимости для любого аксиоматического исчисления,
в том числе и для исчисления высказываний, состоит в
существовании алгоритма, который по любой формуле устанавливает, является
она в этом исчислении доказуемой или не является. Если такого
алгоритма не существует, то аксиоматическое исчисление
алгоритмически неразрешимо.
Исчисление высказываний алгоритмически разрешимо. Разрешающий
алгоритм состоит в проверке для данной формулы, является ли она
тождественно истинной. Если да, то формула доказуема в ИВ; если
нет, то формула в ИВ не доказуема.
Исчисление высказываний полно относительно интерпретации, т.е.
в ИВ доказуемы все тождественно истинные формулы (и только они).
64
Определение. Аксиоматическое исчисление непротиворечиво, если
в нем нет формулы А, для которой I- А и Ь ПА одновременно.
Исчисление высказываний непротиворечиво, ибо если допустить
существование в ИВ формулы А, для которой Ь А и I- ПА
одновременно, то получим, что формулы А и ПА тождественно истинны, что
невозможно.
Определение. Аксиоматическое исчисление внутренне полно, если
добавление к нему недоказуемой формулы в качестве аксиомы
приводит к противоречивому исчислению.
Теорема. Исчисление высказываний внутренне полно.
Доказательство. Пусть А(рх ,р2,... ,р„) - недоказуемая в ИВ
формула и Pi,p2>-• • >Рл ~ полный список переменных этой формулы.
Добавим формулу А к исчислению высказываний в качестве аксиомы;
получим исчисление К. Тогда \-к А (т.е. А доказуема в К). Формула А
не является тождественно истинной, иначе она была бы доказуема в
ИВ. Поэтому существует набор а = (а1Уа2,... ,ап) из 0 и 1, для
которого Ра (А) = 0. Зададим формулы
В,- =
Pi V ~1р/, если я,- = 1,
Р/ & Ир,, если а, = 0,
i = 1,2,...,л.
Формула С = A(B!,B2,... ,В„) тождественно ложна; тогда формула
ПС тождественно истинна и потому I- ПС, а, следовательно, 1~к ПС.
Так как \-% A(pj ,р2,... ,р„), то \-% A(Bj ,В2,... ,В„) как подстановка
в доказуемую формулу, т.е. \-к С и 1-^ ПС, откуда следует, что
исчисление К противоречиво. Теорема доказана.
Заметим, что в противоречивом исчислении доказуема любая
формула (и потому в смысле выводимости противоречивое исчисление
тривиально). В самом деле, пусть В - произвольная формула в
аксиоматическом исчислении (которое противоречиво) и А - такая
формула в нем, что Ь А и Ь ПА одновременно. Тогда Ь А & ПА и ввиду Ь А
& ПА -> В по правилу заключения получаем I- В для любой формулы В.
Определение. Независимой в системе аксиом называется аксиома,
невыводимая из остальных аксиом.
Теорема. Все аксиомы исчисления высказываний независимы.
Доказательство. Покажем, что аксиома A3 р & q -» p независима
от остальных аксиом. Пусть L - система аксиом, включающая в себя
все аксиомы ИВ, кроме A3. Определим дизъюнкцию, импликацию,
отрицание обычным образом, а конъюнкцию определим, положив р & q
= q. При таком определении конъюнкции аксиома A3 р & q -» p на
65
наборе (0,1) принимает значение 0; остальные аксиомы тождественно
равны 1.
Утверждение. Все формулы, выводимые из системы аксиом L при
выше определенных логических операциях тождественно равны 1.
Доказательство. Индукция по длине к вывода.
БАЗИС, к = 1. Непосредственной проверкой убеждаемся, что все
аксиомы из L при выше определенных логических операциях
тождественно равны 1.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что все формулы,
выводимые из L с длиной вывода меньше к, тождественно равны 1.
ШАГ ИНДУКЦИИ. Покажем, что всякая формула, выводимая из L с
длиной вывода к, тождественно равна 1 (при выше определенных
логических операциях). Пусть \-L А и А!,А2,...,Ад есть
доказательство длины к в системе L формулы А. Возможны следующие случаи.
1. Ад - аксиома из L. Тогда Ад тождественно равна 1 (случай
базиса).
2. Ад получена подстановкой формулы С в А,-(р) в доказательстве
А1,А2,...,А|-(р),...,Ад, т.е. Ад = А,(С). Так как длина
доказательства формулы А,(р) меньше к, то по предположению индукции
формула А,(р) тождественно равна 1, и потому формула АДС)
тождественно равна 1.
3. Формула Ад получена из формул А,- и А,- -> Ад в
доказательстве Ах,... ,А,у... ,А/ -> Ад,...,Ад с помощью правила заключения.
Так как длины доказательств А!,...,А, и А1э..., А,,...,А/ -> Ад
формул А, и А,; -> Ад меньше к, то по предположению индукции
формулы А,- и А,- -> Ад тождественно равны 1. Так как операция ->
определялась обычным образом, то формула Ад тождественно равна 1.
Утверждение доказано. Продолжим доказательство теоремы.
Допустим, что аксиома A3 р & q -* р выводима из остальных
аксиом. Тогда по утверждению она тождественно равна 1 (при выше
определенных логических операциях). Противоречие. Следовательно,
аксиома A3 независима от остальных аксиом.
Независимость остальных аксиом системы П.С.Новикова
доказывается по такой же схеме.
2.6. Формулировка исчисления высказываний с единственным
правилом вывода - правилом заключения
Построим исчисление высказываний ИВ1 без правила подстановки,
более удобное для исследования. Формальные символы и формулы ИВ1
совпадают с аналогичными понятиями в ИВ. Пусть А,В,С - произволь-
66
ные формулы в ИВ. Введем следующие схемы аксиом.
А1) А -» (В - А).
А2) (А -» (В - С)) - ((А - В) - (А - С)).
A3) А & В - А.
А4) А & В - В.
А5) (А - В) - ((А - С) - (А - В & С)).
А6) А - А V В.
А7) В - А V В.
А8) (А - С) -» ((В - С) ■» (А V В ■» С)).
А9) (А - В) - (~1В - ПА).
А10) А - "ПА.
All) "ПА - А.
Единственным правилом вывода является правило заключения.
Теорема. Классы формул, доказуемых в ИВ и в ИВ1, совпадают.
Доказательство. Покажем, что класс формул, доказуемых в ИВ1,
содержится в классе формул, доказуемых в ИВ. В самом деле, пусть
l-j A (т.е. формула А доказуема в ИВ1) и А!,А2,...,А^ (=А) есть
доказательство формулы А в ИВ1. Так как все А, тождественно
истинны, то I- А,-. Каждое вхождение формулы А, в доказательстве
формулы А в ИВ1 заменим на доказательство формулы А, в ИВ.
Полученная последовательность формул будет доказательством формулы А
в ИВ.
Покажем теперь индукцией по длине к доказательства формулы в
ИВ, что класс формул, доказуемых в ИВ, содержится в классе
формул, доказуемых в ИВ1.
БАЗИС, к = 1. Всякая аксиома в ИВ (только аксиомы имеют длину
доказательства 1) доказуема в ИВ1, ибо всякая аксиома в ИВ
является аксиомой и в ИВ1.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть все доказуемые в ИВ формулы
с длиной доказательства меньше к доказуемы в ИВ1.
ШАГ ИНДУКЦИИ. Покажем, что все доказуемые в ИВ формулы с
длиной доказательства к доказуемы в ИВ1. Пусть I- А и А!,А2,...,А^
(=А) есть доказательство длины к формулы А в ИВ. Возможны
следующие случаи.
1. А^ есть аксиома в ИВ. Тогда Ад - аксиома в ИВ1 и потому
"-1 Ад.
2. Ад получена подстановкой формулы С в формулу А,(р) в
доказательстве AY ,А2,... ,А,(р),... ,Ад, т.е. Ад = А,(С). Так как длина
доказательства формулы А,(р) в ИВ меньше /с, то по предположению
индукции формула Ьх А,(р). В доказательстве Вх ,В2,... ,Вт(р)
(=АДр)) формулы А/(р) в ИВ1 заменим все вхождения р на формулу
67
С. Полученная последовательность будет доказательством формулы А
в ИВ1.
3. Формула А^ получена из формул А,- и А,- -> Ад в доказательстве
At,... ,А,,... ,А, -►Ад,..., Ад с помощью правила заключения. Так
как длины доказательств A^.-.jA,- и Alf..., А/,..., А,- -> Ад формул
А,- и А,- -> Ад в ИВ меньше к, то по предположению индукции Ь^ А, и
l-j А,; -* Ад; откуда по правилу заключения \-1 Ад.
Теорема доказана.
3. ЛОГИКА ПРЕДИКАТОВ
3.1. Предикаты, кванторы
Предикат есть функция, определенная на некотором множестве и
принимающая одно из двух значений: истина (И) или ложь (Л).
Из простых предикатов с помощью логических операций можно
строить и более сложные предикаты.
Пусть P(xY,... ,д:д) - предикат, определенный на множестве D\
\р\ означает множество истинности предиката Р, т.е. множество
всех наборов (я!,...,0д) длины к элементов множества D, на
которых предикат Р принимает значение И.
Пусть Р(хх,... ,д:д) и Ж*1, • • • yXjr) - два предиката,
определенных на множестве D. Тогда \Р] U \R\ , |>] П [я] , Dk - |У| есть
множества истинности предикатов Р V Я, Р & R, IP соответственно.
Пусть Р(х,хх,... ,дсд) есть (&+1)-местный предикат, определенный
на множестве D. Запись (3jc)/>(jc,jc1 ,... ,дсд) будем понимать как
"существует такой элемент х из D, для которого P(jc,jCj ,... ,дсд)
истинно"; (Чх)Р(х,х1,... ,дсд) - "для всех дс из Z) Р(дс,х1э... ,дсд)
истинно". Скажем, что предикаты
£?(*!,...,*д) = (Зх)Р(дг,*!,...,*д),
/?(*!,...,**) = (Ух)Р(х,х19...,хк)
получены из предиката Р(х,хх,... ,дсд) навешиванием квантора
соответственно существования и общности на предикат /4*,*!,... ,дсд) по
переменной х. Переменная х в выражении (Qx)P(x,xl,... ,дсд)
находится в области действия квантора ((?*). Навешивание квантора
существования или квантора общности по некоторой переменной на (fc+l)-
местный предикат, содержащий эту переменную, приводит к другому
предикату, местность которого на единицу меньше.
Переменная дс, находящаяся в области действия квантора (Qjc),
называется связанной. В противном случае переменная х свободна.
68
Пример. D = {0,1,2,...} - множество натуральных чисел.
Определим на множестве D следующие предикаты:
Рг(х) - х есть простое число;
Ev(x) - число х четно;
Div(x,y) - число х делит число у\
х = у - число х равно числу у\
х < у - число х меньше или равно числу у\
х = 2 - число х совпадает с двойкой;
Q(x,y) есть ~1(л: = 1) & 1(х = у) & Div(x,y);
Р(у) есть (3x)Q(x,y).
Тогда (Зх)Рг(х) - истинное, (Vx)Pr(x) - ложное,Р{2) - ложное,
Р(4) - истинное высказывания.
Пусть D = {ах ,а2,... ,ак} - конечное множество из к элементов и
Р(х) - предикат, определенный на D.
Утверждение. Справедливы следующие равенства:
(Зх)Р(х) = Р(ах) V Р(а2) V ... V Р(ак).
(Vjc)P(jc) = Р{ах) & Р(а2) & ... & Р(ак).
Доказательство. Установим первое равенство. Пусть (Зх)Р(х)
истинно. Тогда существует х = ах; € D, для которого Р(й}) истинно.
Отсюда Р(ах) V ... V Р(ак) истинно.
Пусть Р(ах) V ... V Р(ак) истинно. Тогда для некоторого /, 1 ^
i ^ к, P(dj) истинно; поэтому существует х = а/ € D, для которого
Р(я,-) истинно, отсюда (Зх)Р(х) истинно.
Установим второе равенство. Пусть (Vjc)P(jc) истинно. Тогда для
всякого х из D Р(х) истинно, т.е. истинны Pia^),... ,Р(ак), откуда
истинно Р(ах) & ... & Р(ак). Пусть теперь Р{ах) & ... & Р(ак)
истинно, т.е. истинны Р(ах)9... ,Р(ак). Отсюда получаем, что для
всякого х из D Р(х) истинно, т.е. (Vjc)P(jc) истинно.
Утверждение доказано.
Аналогично доказываются следующие равенства.
к
(Зх)Р(х,х19...,хк) = .Vi P(ai9xl9...9xk).
к
(Чх)Р(х,х19...,хк) = & P(aiixli...)xk).
Переменная х может стоять на любом аргументном месте предиката
Р. Если кванторов несколько, то они элиминируются (устраняются)
постепенно. Например,
(Vx)(3y)P(x,y) - (V*)(Д Р(х,в/))- Д (Д Р(а,,а,)).
69
Замечание. Пусть D есть некоторое множество и множество К Я
U1. Проекция К на оси ily...yip есть множество Пр, ... / К =
{(х,^,...,*,- ) € DP : ЭОг!,...,*^,...,*,- ,..., хп) € /С}.
Проекция множества К на оси ili...Jp может быть получена
вычеркиванием (стиранием) во всех наборах (х19...,Х; , ... ,*,• , ...,jc„) из А^
всех координат, кроме Jt,- ,...,*,• .
Пусть Р(хх,... ,Jtfc,Jt) - (/с+1)-местный предикат, определенный на
множестве ZX Пусть /t-местный предикат
еСд:!,...,^) = (3x)/4*i,...,**,*)•
Пусть [р] = {(jcx ,... уХкух) € Dk+1: Р(х1У ... ухкух) истинно} и
ГС?1 = {(хц... >хк) € D^: 2(^1 > • • • >*/с) истинно} есть множества
истинности предикатов Р и Q. Тогда \Q\ = Щь 2 ... А: м 1 •
Таков теоретико-множественный смысл квантора существования.
3.2. Выполнимость, невыполнимость, общезначимость,
опровержимость формул логики предикатов
Определим понятие формулы в логике предикатов (ЛП).
Алфавит.
1. x,y,z,xliylizli... - символы предметных переменных.
2. a^^^pbpCp... - символы предметных констант.
3. f,g,h,fx ,h! ,g19 - - - - символы функциональных переменных.
4. P^^^pQpRp... - символы предикатных переменных.
5.&,V,->,-|,3,V- логические символы (связки).
6. ( , ) - скобка левая, запятая, скобка правая.
Термы.
1. Всякая предметная переменная и предметная константа есть
терм.
2. Если tj,...,tfc - термы, a f - функциональная переменная, то
fCtx,.. .tfc) есть терм.
Если переменные терма t содержатся среди переменных списка
xl9...9xs, то пишем t(xj,... ,х5).
Формулы.
1. Если tj,...,tk - термы; {x1,...,xm} - множество всех
переменных, входящих в термы t19...9tk'9 P - предикатная переменная,
то P(tj,...,t^) - элементарная формула (атом), а х1,...,хт - все
ее свободные (предметные) переменные.
2. Если А и В - формулы, то (А & В), (А V В), (А - В) -
формулы. Их свободные переменные есть свободные переменные формул
А и В. Выражение (~1А) тоже формула; ее свободные переменные -
70
свободные переменные формулы А.
3. Если формула А(х) имеет множество свободных переменных
{х,х,,...,х*}, то выражения (Эх)А(х), (Vx)A(x) есть формулы;
переменные х19...9хк в этих формулах свободны, а переменная х
связана (квантором).
Формула без свободных предметных переменных называется
замкнутой .
Здесь действуют те же правила опускания скобок, что и в логике
высказываний. Кванторы имеют высший приоритет. В формуле (Qx)A
формула А есть область действия квантора (Qx).
Подформулы
1. Подформулой элементарной формулы является она сама.
2. Подформулами формулы ПА являются она сама и все подформулы
формулы А.
3. Подформулами формулы А * В, где знак * € {&,V,->}, являются
она сама и все подформулы формул А и В.
4. Подформулами формулы (Qx)A, где Q € {3,V}, являются она
сама и все подформулы формулы А.
Как и в исчислении высказываний, будем интерпретировать
логические связки &, V, ->, "I как соответствующие логические операции.
Если предикатные, функциональные, свободные предметные
переменные и предметные константы формулы А содержатся в списке
Pi,..., P„, f м..., fm, X!,..., xk, a^..., аг, где РМ...,РЛ -
предикатные переменные; f l,... ,fm - функциональные переменные;
хj,...,хк - предметные переменные; а!,...,аг - предметные
константы, то пишем А^,...,P„,f!,...,fm9xl9...9xk9alr..,ar).
Введем понятие выполнимости и общезначимости формул. Пусть
формула А = А(?1У...У P„,f!,..., fm9xl9...9xk9 alr.., аг). Набор
(Pi,... ,P„,f!,... ,imyXl 9... 9xk,al9... ,аг) называется сигнатурой
формулы А. Зафиксируем некоторое множество D9 зададим на D
предикаты Р19...9Рп) функции fl9...,fm; предметы xl9...9xk, a19...9ar.
Набор / = (D9Pl9...9Pn9fl9...9fm9xl9...9xk9al9...9ar) называется
интерпретацией формулы А. Множество D называется предметной
областью интерпретации /. Формула А при таком выборе переменных
(предикатных, функциональных, предметных) и констант превращается
в высказывание А = A(Pl9...9Pn9f19...9fm9x19...9xfc9a1...9ar)9
истинное или ложное.
Пример. Пусть формула
A(P,Q,R,y,z,a) = (Эх)(-|Р(х,а) & 1P(x,z) & Q(x,y) & R(x,y));
D = {0,1,2,...} - множество натуральных чисел;
Р(х9у) есть х = у;
Q(xyy) есть х < у\
71
R(x9y) есть Div(x,y) (x делит у);
у = 8, z = 4, а = 1.
Тогда высказывание ^4 = A(P,Q,/?,^,z,a) =
(Зх)(1Р(х9а) & 1P(jt,z) & Q{x9y) & Ж*,:у)) =
(3jc)(jc *1&jc*4&jc<8& Div(x,S))
истинно.
Определение (значение t[xl9... 9xs] терма t(x!,...,x5) на
интерпретации /).
1. Если t = х,-, то t[xl9...,xs] = JC/.
2. Если t = а |, то t[xl9...,xs] = а,.
3. Если t = f(tl9...,tu), то t[*!,...,*5] =
f(tl[xl9...9xs]9...9tu[x19...9xs]).
Определение. Интерпретация
/ = (D9PX , . . . 9Pn9fX , • • • ,/„,,*! , • • • ,**,*! > • • • .О
выполняет формулу А(Р1,...,РЛ, flf... ,fm, х1э...,хЛ, а1э...,аг)
(обозначение / ►= А ), если высказывание
^ = A(Pl9...9Pn9fl9...9fm9x19...9xk9a19...9ar)
истинно. Интерпретация / опровергает формулу А (обозначение / "IN
А), если высказывание А ложно.
Будем вычислять истинностное значение высказывания / 1= А
индукцией по построению формулы следующим образом.
1. Если А есть атом F(t19... ,tv), то
/ N А «-> P(tl[xl9...9xk\9...9tv[xl9...9xk]) = И.
2. Если А есть В * С, где знак * € {&,V,->}, то
/t=A«->/t=B*/t=C.
3. Если А есть ~1В, то / *= В «—► / "1*= В.
4. Если А есть (Эх)В(х), то
/ N (Эх)В(х) «— Эх € D I N B(jc).
5. Если А есть (Vx)B(x), то
/ N (Vx)B(x) «— Vx € D I t= B(jc).
Определение. Формула А общезначима на множестве D9 если всякая
интерпретация / = (£>,...) с предметной областью D выполняет А.
Формула А выполнима на множестве D9 если существует интерпретация
/ = (£>,...) с предметной областью D, которая выполняет А. Формула
А опровержима на множестве D9 если существует интерпретация / =
(Z),...) с предметной областью D9 которая опровергает А. Формула А
невыполнима на множестве D9 если всякая интерпретация / = (£>,...)
с предметной областью D опровергает А.
Пример. Пусть формула А = (Vx)(3y)P(x,y) -» (3y)(Vx)P(x,y).
72
1. Положим интерпретацию / = (D, Р(х,у)) = ({1,2}, х < у).
Высказывание (Vx)(3y) х < у -» (3.y)(Vjc) * ^ >> истинно из-за
истинности заключения. Поэтому / N А, т.е. интерпретация / превращает
формулу А в истинное высказывание.
2. / = ({1,2}, х = у). Высказывание (Vjc)(3)>) х = у -» (3<y)(Vjc)
jc = у ложно, ибо его посылка истинна, а его заключение ложно.
Поэтому / 1\= А, т.е. / опровергает А.
Определение. Формула А общезначима, если всякая интерпретация
/ выполняет А. Формула А выполнима, если существует интерпретация
/, которая выполняет А. Формула А невыполнима, если всякая
интерпретация / опровергает А. Формула А опровержима, если
существует интерпретация /, которая опровергает А.
Заметим, что формулы A(xj,...,x^) и (Vxj).. .(Vx^)A(x!,... ,х^)
общезначимы или не общезначимы одновременно. Поэтому при
вычислении общезначимости формул можно ограничиться замкнутыми формулами
(т.е. формулами без свободных предметных переменных).
Теорема. Чтобы формула логики предикатов была общезначима,
необходимо и достаточно, чтобы ее отрицание было невыполнимо.
Доказательство. Пусть формула А общезначима. Допустим, что
формула ПА выполнима. Тогда существует интерпретация /, для
которой / 1= ПА. Поэтому / > А. Противоречие с общезначимостью А.
Пусть теперь формула ПА невыполнима. Допустим, что формула А
общезначимой не является. Тогда существует интерпретация /,
которая опровергает А, т.е. / П1= А. Поэтому / 1= ПА. Противоречие с
невыполнимостью формулы ПА.
Определение. Формула В есть логическое следствие формул Ам
А2,...,А^, если формула Ах& А2&... & А^ -> В общезначима.
Заметим, что если формула логики предикатов не содержит
кванторов, то ее можно рассматривать как формулу логики высказываний,
построенной из элементарных формул логики предикатов.
Определение. Интерпретация / есть модель для формулы А (для
множества формул S), если / 1= А (/ выполняет всякую формулу из
S). Интерпретация / называется опровержением формулы А (множества
формул S), если / опровергает А (/ опровергает хотя бы «дну
формулу в S).
3.3. Равносильность формул
Две формулы логики предикатов называются равносильными
(равными), если они принимают одинаковые истинностные значения при
всех значениях входящих в эти формулы свободных переменных
(множество D\ предикаты и функции, определенные на D\ предметы из D).
73
Другими словами, две формулы из ЛП равносильны, если на всякой
интерпретации эти формулы одновременно истинны или ложны.
Приведем примеры равносильных формул.
1. (Эх)А(х) = (Эу)А(у).
2. (Vx)A(x) = (Vy)A(y),
т.е. возможны переименования связанных предметных переменных.
3. (Эх)(Эу)А(х,у) = (Эу)(Эх)А(х,у).
4. (Vx)(Vy)A(x,y) = (Vy)(Vx)A(x,y),
т.е. соседние одноименные кванторы можно менять местами.
5. l(Vx)A(x) = (Зх)ПА(х).
В самом деле, пусть D - произвольное множество, на котором
определены все свободные переменные и константы формулы А, кроме
х. Тогда на указанном наборе переменных высказывание ~*\{Чх)А{х)
истинно ♦—> не для всех х из D А(х) истинно «—* сущуствует х = х0 €
D, для которого А(х0) ложно «—* существует х = х0 € Z), для
которого 1А(х0) истинно ♦—> (Зх)1А(х) истинно.
6. П(Зх)А(х) = (Vx)lA(x).
В самом деле, (Vx)lA(x) = ПП(Ух)ПА(х) = П(Эх)ППА(х) =
П(Зх)А(х).
7. (Vx)A(x) = П(Эх)ПА(х).
В самом деле, (Vx)A(x) = ПП(Ух)А(х) = ~1(Эх)~1А(х).
8. (Эх)А(х) = -|(Vx)-|A(x).
В самом деле, (Эх)А(х) = ~П(Эх)А(х) = l(Vx)lA(x).
9. (Эх)(А(х) & Н) = (Эх)А(х) & Н, где формула Н не содержит
переменную х свободно.
В самом деле, (Зх)(А(х) & Н) истинно ♦—> существует х = х0 € D,
для которого А(х0) и Н истинны *—* (3jc)^4(jc) & Н истинно.
10. (Vx)(A(x) V Н) = (Vx)A(x) V Н, где формула Н не содержит
переменную х свободно.
В самом деле, (Vx)(A(x) V Н) = ПП(Ух)(А(х) V Н) =
-|(Эх)-|(А(х) V Н) = -|(Эх)(-1А(х) & ПН) = -|(Эх)1А(х) V "ПН =
(Ух)-ПА(х) V Н = (Vx)A(x) V Н.
11. (Эх)(А(х) V В(х)) = (Зх)А(х) V (Эх)В(х).
В самом деле, (Зх)(А(х) V В(х)) истинно ♦—> существует х = х0,
для которого А(х0) или В(х0) истинно *—► (Зх)А(х0) V В(х0)
истинно.
12. (Vx)(A(x) & В(х)) = (Vx)A(x) & (Vx)B(x).
В самом деле, пусть С(х) = А(х) & В(х). Тогда (Vx)C(x) =
ПП(Ах)С(х) = -|(Эх)-|(А(х) & В(х)) = П(Эх)(ПА(х) V ПВ(х)) =
П((Зх)ПД(х) V (Эх)ПВ(х)) = П(Зх)ПА(х) & П(Эх)П(В(х) = (Vx)A(x) &
(Vx)B(x).
74
Формулы 11 и 12 утверждают, что квантор существования можно
распределять по дизъюнкции, а квантор общности по конъюнкции. Что
касается распределения квантора существования по конъюнкции, а
квантора общности по дизъюнкции, то здесь общезначимы формулы
(Зх)(А(х) & В(х)) - (Зх)А(х) & (Зх)В(х);
(Vx)(A(x) V В(х)) - (Vx)A(x) V (Vx)B(x).
Обратное следование неверно.
13. (Зх)А(х) & (Эх)В(х) = (Эх)(Зу)(А(х) & В(у)).
В самом деле, высказывание (Зх)А(х) & (Зх)В(х) истинно «—>
существуют элементы х0 и у0, для которых
А(х0) и В(у0) истинны «-♦ (3jc)(Vy)(A(x) & В(у)) истинно.
14. (Vx)A(x) V (Vx)B(x) = (Vx)(Vy)(A(x) V В(у)).
В самом деле, (Vx)A(x) V (Vx)B(x) = (Vx)A(x) V (Vy)B(y) =
(Vx)(A(x) V (Vy)B(y)) = (Vx)(Vy)(A(x) V B(y)).
15. (Vx)(C -» B(x)) = С -» (Vx)B(x), где формула С не содержит
переменной х свободно.
В самом деле, (Vx)(C - В(х)) = (Ах)("1С V В(х)) = ПС V (Vx)B(x)
= С - (Vx)B(x).
16. (Vx)(B(x) -» С) = (Зх)В(х) -» С, где формула С не содержит
переменную х свободно.
В самом деле, (Vx)(B(x) - С) = (Vx)(lB(x) V С) = (Vx)lB(x) V С
= 1(Зх)В(х) V С = (Зх)В(х) - С.
17. (Зх)(С - В(х)) = С - (Зх)В(х),
(Зх)(В(х) - С) = (Vx)B(x) - С,
где формула С не содержит переменной х свободно.
Замечание. Если в формулах с 1 по. 17 заменить равенство на
эквивалентность = , причем эквивалентность двух формул А = В
понимать как (А -> В) & (В -> А), то формулы с 1 по 17 станут
общезначимыми .
3.3.1. Релятивизованные кванторы
Пусть А(х) и В(х) - формулы логики предикатов, имеющие
свободную переменную х и возможно другие свободные переменные. Пусть
(Зх)А(х) В(х) означает (Зх)(А(х) & В(х)),
(Vx)A(x) В(х) означает (Vx)(A(x) -» В(х)).
Кванторы (Зх)д(х) и (Vx)A(x) называются релятивизованными.
Справедливы следующие равносильности:
п(3х)а(х) в(х) = (Vx)a(x) nBW;
-|(Vx)A(x) B(x) = (Vx)A(x) ПВ(х).
В самом деле, "1(3х)д(х) В(х) = ~1(Зх)(А(х) & В(х)) =
75
(Vx)n(A(x) & B(x)) = (Vx)(HA(x) V -IB(x)) =
(Vx)(A(x) - -IB(x)) = (Vx)A(x)-IB(x);
_1(Vx)A(x) B(x) = -!(Vx)(A(x) - B(x)) =
Ox)-lOA(x) V B(x)) = (3x)(A(x) & -IB(x)) = (3x)A(x) ПВ(х).
3.4. Нормальные формы
3.4.1. Предваренная нормальная форма
Определение. Формула А логики предикатов задана в
предваренной (или в пренексной) нормальной форме, если она имеет вид
(Q1x1)...Q^x^)B(x1,...,x)t), где Q, € {3,V}, i = 1,2,...,*, а В
есть бескванторная формула.
Теорема. Для всякой формулы А в ЛП существует равносильная ей
формула в предваренной нормальной форме.
Доказательство. Индукция по построению формулы А. Пусть число
логических связок в формуле А равно к.
БАЗИС, к = 0. Тогда А есть элементарная формула без кванторов;
поэтому формула А находится в предваренной нормальной форме.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что теорема верна для всякой
формулы с числом логических связок меньше к.
ШАГ ИНДУКЦИИ. Покажем, что теорема справедлива для всякой
формулы с числом логических связок к. Пусть формула А имеет к
логических связок. Возможны следующие случаи.
1. А есть (Qx)B(x), где Q € {3,V}. Так как глубина построения
формулы В(х) меньше к, то по предположению индукции формула В(х)
представима в предваренной нормальной форме С(х). Тогда (Qx)C(x)
есть предваренная нормальная форма формулы А.
2. А есть В * С, где знак * € {& , V , ->}. Так как число
логических связок в формулах В и С меньше ку то по предположению
индукции существуют предваренные нормальные формы Е и F для
формул В и С соответственно. Пользуясь доказанными в п.3.3 равноси-
льностями 1-17, выносим в формуле Е * F кванторы за скобки и
получаем искомую предваренную нормальную форму для формулы А.
3. А есть "IB. Так как число логических связок в формуле В
меньше к, то по предположению индукции формула В имеет
предваренную нормальную форму (О^).. .(Qkxk)C, где С есть бескванторная
формула. Тогда формула ~1В имеет предваренную нормальную форму
(Q^).. .(QfcXfc)IC, где Q, есть 3, если Q, есть V, и Q,- есть V,
если Q, есть 3, / = 1,2,...,/:.
Пример. (Vy)OP(x) - Q(y)) - (3y)(-|(Vz)(P(y) V Q(z))) =
((Vy)OP(x) - Q(y))) V (3y)(3z)-l(P(y) V Q(z)) =
76
(Зу)1(ПР(х) V Q(y)) V (3y)(3z)(nnP(y) & lQ(z)) =
(3y)(lP(x) - Q(y)) V (3z)(P(y) & IQ(z)) =
(3y)(3z))HP(x) - Q(y)) V P(y) & IQ(z)).
3.4.2. Стандартная форма Скулема
Пусть А есть замкнутая формула логики предикатов. Приведем ее
к пренексной (т.е. к предваренной) нормальной форме At
(QiXj).. .(О^х^) B^Xj,... ,Xfc). Пусть Qr в формуле Aj есть первый
слева квантор существования, т.е. А! = (Vx^.. .(Vxr_1)(3xr)
(Qr+1xr+1)...(QkXfc)Bl(xl,... ,xr_! ,хг,хг+1,... ,xk). Выберем новый,
ранее не встречавшийся (/--1)-местный функциональный символ f, и
перейдем к формуле А2 = (Vxj).. .(Vxr_1)(Qxr+1).. .(Qx^)
Bi VXj , . . . ,Xr_j ^l^Xj , . . . ,Xr_j ) ,Xr + 1 , . . . 9Xk).
D2\Xl , . . . ,Xr_j ,Xr + 1 , . . . ,Xk)
Если r = 1, то в формуле Ах уберем квантор (3xj) и вместо х19
находящегося в области действия квантора (Зх^, подставим в Aj
константу а, ранее в At не встречавшуюся.
Утверждение 1. Формула Ах невыполнима тогда и только тогда,
когда А2 невыполнима.
Доказательство. Пусть формула А! невыполнима. Покажем, что
формула А2 невыполнима. Допустим противное: А2 выполнима, т.е.
существует множество D, предикаты и функции, определенные на D,
предметы из D такие, что высказывание (Vjtj).. .(Vjcr_1)(Qr+1jcr+1)
... (Qkxk)B1 (*!,... ixr_1 ff(x1,... ixr_1)ixr+1,... ,xk) истинно.
Тогда для всяких хх,... ,хг_х из D существует xr = f(x1,... ,xr_Y) из
D такое, что высказывание (Qr+i*r+i)- • -(Qkxk)^i(xi»• • • >xr-i >■*>>
xr+l>... >xk) истинно, т.е. высказывание (Чхх.. .(4xr_1)(3xr)(Qr+l
xr+1)...(Qkxk)Bl(xl,... ,*,_! ,xr,xr+l,... ,xk) истинно. Поэтому
формула Ах выполнима. Противоречие с невыполнимостью А^
Следовательно, формула А2 невыполнима.
Пусть формула А2 невыполнима. Покажем, что формула Ах
невыполнима. Допустим противное: At выполнима. Тогда существует
множество Z), предикаты и функции, определенные на Z), предметы из D,
для которых высказывание (Чхг.. .(V*r_1)(3jtr)(Qr+1Jtr+1).. .(Qkxk)
Bl(xli... ,xr_l9xrixr+li... ,xk) истинно. Тогда для всяких х19...,
хг_х из D существует хг из D, т.е. существует функция xr = f(xly
...,д:г_1): 1У~1 -+ Dy для которой высказывание
(Qr+i^r + i)- • -(Qkxk)^i(xi > • • >xr-i )^г^г+П' • • >xk)
истинно. Тогда высказывание
77
(Удг1)...(Удсг_1)(Сг+1д:г+1)51(д:1,...,д:г_1,
J\Xl,...>Xr_!)yXy+i,.,.yXfc)
истинно, т.е. формула А2 выполнима. Противоречие с
невыполнимостью А2. Следовательно, формула А2 невыполнима.
Утверждение 1 доказано.
Отметим теперь первое слева вхождение квантора существования в
формуле А2. Проделаем аналогичное устранение этого квантора.
Получим формулу А3. В ней проведем устранение первого слева
квантора существования. И так далее, пока все кванторы существования
не будут устранены (за счет введения новых функциональных
символов. В результате получим новую формулу D без кванторов
существования, называемую стандартной формой Скулема. Функции,
возникающие при построении этой стандартной формы, называются скуле-
мовскими.
Утверждение 2. Формула А невыполнима тогда и только тогда,
когда ее стандартная форма Скулема невыполнима.
Доказательство следует из доказанного выше утверждения 1,
справедливого при каждом новом устранении из формулы А квантора
существования.
Пример. А = (3x1)(Vx2)(3x3)(Vx4)(P(x1,x2,x3) - Р(х2,х3,х4)).
Вместо Xj ставим константу а. Получаем формулу
(Vx2)(3x3)(Vx4)(P(a,x2,x3) - Р(х2,х3,х4)).
Переменную х3 заменяем на f(x2), в результате получаем формулу
В = (Vx2)(Vx4)(P(a,x2,f(x2)) - P(x2,f(x2),x4)).
Формула В есть стандартная форма Скулема формулы А.
Замечание. В стандартной форме Скулема бескванторную ее часть
обычно представляют в конъюнктивной нормальной форме и
рассматривают как множество дизъюнктивных слагаемых (дизъюнктов).
Кванторы общности для этого множества дизъюнктов опускают.
3.5. Проблема разрешимости в логике предикатов
Основной вопрос математической логики есть проблема
разрешимости ее формул, т.е. вопрос об установлении общезначимости (или
формальной доказуемости) формул этой логики. Проблема
разрешимости в ЛП состоит в существовании алгоритма, который по любой
формуле логики предикатов устанавливал бы, является эта формула
общезначимой или не является.
Теорема (А.Черча). Проблема распознавания общезначимости фор-
78
мул логики предикатов алгоритмически неразрешима.
Б.А.Трахтенброт установил алгоритмическую неразрешимость ЛП на
конечных классах: проблема разрешимости в ЛП остается
неразрешимой, если при установлении общезначимости формул ЛП
ограничимся конечными множествами.
Хотя и не существует алгоритма, который по любой
предъявленной формуле в ЛП устанавливал бы, является эта формула
общезначимой или не является, возможны попытки отыскания таких
алгоритмов для некоторых классов формул логики предикатов. Были найдены,
например, алгоритмы, устанавливающие общезначимость класса
замкнутых формул, предваренные нормальные формы которых содержат
только кванторы существования. Существует алгоритм распознавания
общезначимости класса замкнутых формул, предваренные нормальные
формы которых содержат только кванторы общности. Алгоритмически
разрешим класс формул, построенных только из одноместных
предикатов (монадическая логика). Монадическая логика остается
разрешимой, даже если допустить кванторы по предикатным переменным.
Оказался алгоритмически разрешимым ряд других классов формул логики
предикатов. Исследования по установлению разрешающих алгоритмов в
ЛП показали, что относительно мало классов формул имеют
разрешающие алгоритмы. Многие классы формул оказались алгоритмически
неразрешимыми. Работа по отысканию разрешающих алгоритмов
продолжается и поныне.
В семидесятые годы нашего века был разработан универсальный
язык программирования Пролог, в основу которого была положена
логика предикатов. Вычисление общезначимости формул в Прологе
проводится в приведенном Дж.А.Робинсоном логическом формализме,
называемом методом резолюций. В последующем изложим этот метод и
покажем, как он используется в универсальном языке
программирования Пролог.
4. УЗКОЕ ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
4.1. Определение узкого исчисления предикатов
Дадим формально-логическую (т.е. аксиоматическую)
характеристику общезначимых формул логики предикатов, а именно, построим
аксиоматическое исчисление, в котором доказуемы общезначимые
формулы логики предикатов, и только они.
Формальные символы, формулы, подформулы в узком исчислении
предикатов (УИП) полностью совпадают с аналогичными понятиями в
79
логике предикатов. Примем для простоты только, что при построении
формул в рассматриваемом случае не используются функциональные
термы.
Пусть А,В,С - произвольные формулы узкого исчисления
предикатов (совпадающие с формулами логики предикатов).
Схемы аксиом.
А1) А - (В - А).
А2) (А - (В - С)) - ((А - В) - (А - С)).
A3) А & В - А.
А4) А & В - В.
А5) (А - В) -> ((А - С) - (А - В & С)).
А6) А - А V В.
А7) В - А V В.
А8) (А - С) - ((В - С) - (А V В - С)).
А9) (А - В) - (~1В - ПА).
А10) А - ~ПА.
All) ~ПА - А.
Аксиомы Бернайса (АБ).
Пусть А(х) - произвольная формула УИП, содержащая свободную
переменную х, и у - некоторая переменная.
АБ1) (Vx)A(x) - А(у).
АБ2) А(у) - (Эх)А(х).
А, А - В
Правила вывода. -
В
правило заключения (ПЗ). Здесь А и В - произвольные формулы УИП.
А - В(х)
А - (Vx)B(x)
правило навешивания квантора общности (V-правило, или V-ПР).
Здесь А и В(х) - произвольные формулы УИП, причем формула А не
содержит переменной х свободно.
А(х) - В
(Эх)А(х) - В
правило навешивания квантора существования (Э-правило, или Э-ПР).
Здесь А(х) и В - произвольные формулы УИП, причем формула В не
содержит переменной х свободно.
В случае применения V- или 3-правила говорят, что переменная х
в формулах А -» В(х) или А(х) -» В затрагивается (используется,
варьируется).
Формальные символы, формулы, система аксиом и правила вывода
80
составляют узкое исчисление предикатов.
Определение. Доказательство в УИП есть конечная
последовательность формул, каждая из которых есть либо аксиома, либо получена
из предыдущих членов последовательности по одному из правил
вывода.
Определение. Формула А доказуема в УИП, если в нем существует
доказательство, последней формулой которого является А.
Всякая аксиома есть доказуемая в УИП формула, длина
доказательства которой равна 1.
Пусть Г и А - произвольные конечные совокупности формул УИП
(возможно пустые) и А,В,С - произвольные формулы в ИВ.
Определение. Конечная последовательность формул УИП есть вывод
из совокупности формул Г, если всякая формула последовательности
либо принадлежит Г, либо доказуема, либо получена из предыдущих
формул последовательности по одному из правил вывода.
Определение. Формула А выводима в УИП из совокупности формул
Г, если в УИП существует вывод из совокупности Г, последней
формулой которого является А.
Заметим, что доказуемая формула выводима из любой (в том числе
из пустой) совокупности формул.
Теорема. Если формула А получена подстановкой некоторых формул
УИП в доказуемую формулу исчисления высказываний, то формула А
доказуема в УИП лишь с помощью правила заключения.
Доказательство. Пусть формула из УИП
А = п р! р! "" р» с(р.»р2,---.р«).
где В1эВ2,...,Вя - формулы из УИП; C(pt ,р2,... ,р„) - доказуемая в
ИВ формула и Pi,p2>---»Pn ~ полный список (пропозициональных)
переменных формулы С. Согласно второй формулировке ИВ формула С
доказуема в ИВ лишь с помощью правила заключения.
Пусть D1,D2,...,Dr (=C) есть доказательство формулы С в ИВ (с
помощью только правила заключения); qi,q2>--->qm ~ полный список
переменных во всех формулах D, (i = 1,2,...,г); Е1э E2,...,EW -
произвольные попарно различные формулы УИП, отличные от всех
ранее упомянутых в теореме формул. Сопоставим каждому q, формулу
F, согласно следующему равенству:
Е., если q, отлично от всех рх ,р2,... ,р„;
F = л
В, если q, есть р;;
i = 1,2,...,т; / = 1,2,....я.
81
В доказательстве Dj,D2,...,Dr в ИВ заменим каждое q,- в формулах
D19D2,...»Dr на F,. Полученная последовательность формул УИП
будет доказательством в УИП формулы А лишь с помощью правила
заключения.
Следствие. В УИП справедливы все вспомогательные правила
вывода, доказуемые в ИВ.
4.2. Теорема дедукции в УИП
Теорема (дедукции). Если формула В выводима в УИП из
(конечной) совокупности формул Г и формулы А, причем в этом выводе не
затрагивается никакая свободная переменная формулы А, то формула
А -» В выводима из Г.
Доказательство. Индукция по длине к вывода. Заметим, что по
условию теоремы правила навешивания кванторов на свободные
переменные формулы А не используются.
БАЗИС, к = 1. Возможны следующие случаи.
1. В есть А. Тогда НА-» А, поэтому Г I- А -» А.
2. I- В. Тогда Ь А - В (ПВЗ). Поэтому Г h А - В.
3. В € Г. Тогда Г h В и по ПВЗ Г h А - В.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть теорема справедлива для всех
выводов длины меньше к.
ШАГ ИНДУКЦИИ. Покажем, что теорема справедлива для выводов
длины к. Пусть Г, А I- В и пусть Вх ,В2,... УВ^_Х ,Вк (= В) есть
вывод длины к формулы В из совокупности Г,А. Возможны следующие
случаи.
1. В есть А. 2. h В. 3. В € Г.
Эти случаи рассмотрены в базисе.
4. В (= Вл) получается из двух формул В, и В, -> В^ вывода по
правилу заключения. Этот случай рассматривается аналогично
доказательству теоремы дедукции в исчислении высказываний.
5. Пусть Г,A h В и В1,В2,...|В|>..-,В*, где В; = С -► D(x), Bk
= В = С -» (Vx)D(x), есть вывод длины к формулы В из Г,А. Причем В
получено из В/ с помощью V-правила, при этом формула С не
содержит х свободно. Формула А тоже не содержит х свободно, иначе
свободная переменная формулы А использовалась бы в выводе формулы В.
Так как длина вывода Bl9B29...,Bj из Г,А меньше к, то по
предположению индукции
(1) Г h А - (С - D(x)). Далее
(2) Г НА&С-» D(x), ПВ14(1), соединение посылок;
(3) ГНА&С-» (Vx)D(x), У-ПР(2);
(4) Г h A -» (С -> (Vx)D(x)), ПВ15(3), разъединение посылок,
82
т.е. Г Ь А -» В.
6. Пусть Г,А Ь В и.В19В2>...9В|-,...9В*9 где В, = D(x) -» С,
В^ = В = (3x)D(x) -> С, есть вывод длины /г формулы В из Г,А.
Причем В получено из В,- с помощью 3-правила, при этом формула С
не содержит х свободно. Формула А тоже не содержит х свободно.
Так как длина вывода Bl9B2,... ,В; из Г,А меньше к, то по
предположению индукции
(1) ГНА-» (D(x) - С). Далее
(2) Г Ь D(x) -» (А -» С), ПВ13(1), перестановка посылок;
(3) Г Ь (3x)D(x) - (А - С), 3-ПР(2);
(4) Г НА-» ((3x)D(x) -» С), ПВ13(2), перестановка посылок,
т.е. Г Ь- А -» В. Теорема доказана.
Приведем несколько примеров доказуемых в УИП формул и
несколько вспомогательных правил вывода.
Правило вывода 19. (Vx)A(x) I- A(x).
Доказательство.
(1) (Vx)A(x), условие;
(2) (Vx)A(x) - А(х), АБ1;
(3) А(х), П3(1,3).
Теорема 11. h (Зх)ПА(х) - ~l(Vx)A(x).
Доказательство.
(1) 1A(x),(Vx)A(x) Ь A(x), ПВ19;
(2) 1A(x),(Vx)A(x) Ь 1А(х);
(3) ПА(х) h ~l(Vx)A(x), ПВ18(1,2), приведение к абсурду;
(4) h 1А(х) - П(Ух)А(х), ТД(3);
(5) Ь (Зх)ПА(х) - П(Ух)А(х), 3-ПР(4).
Правило вывода 20.
а) А(х) h (Vx)A(x); b) A(x) h (Зх)А(х).
Доказательство.
(1) A(x), условие;
(2) I- С, где С - произвольная доказуемая в УИП формула без
свободной переменной х;
(3) h А(х) - (С - А(х)), А1;
(4) С - А(х), П3(1,3);
(5) С -> (Vx)A(x), У-ПР(4), (х затрагивается);
(6) (Vx)A(x), П3(2,5). ТД невозможна.
Второе правило доказывается с помощью аксиомы Бернайса.
Теорема 12. h ~l(Vx)A(x) - (Зх)ПА(х).
Доказательство.
(1) l(Vx)A(x),A(x) h (Vx)A(x), ПВ20а, (в формуле (Vx)A(x)
переменная х затрагивается, в А(х) - нет);
(2) ~l(Vx)A(x),A(x) Ь l(Vx)A(x), в А(х) х не затрагивается;
83
(3) ~l(Vx)A(x) h 1А(х), ПВ18(1,2), приведение к абсурду;
(4) I- ~IA(x) - (Эх)ПА(х), АБ2;
(5) l(Vx)A(x) h (Эх)ПА(х), П3(3,4);
(4) Ь 1(Ух)А(х) - (Эх)ПА(х), ТД(5).
Теорема 13. Ь 1(Эх)А(х) - (Ух)1А(х).
Доказательство.
(1) ~1(Эх)А(х),А(х) h (Эх)А(х), ПВ20Ь; (х не затрагивается);
(2) П(Эх)А(х),А(х) h П(Эх)А(х);
(3) П(Эх)А(х) Ь ПА(х), ПВ18(1,2), приведение к абсурду;
(4) Ь П(Эх)А(х) - 1А(х), ТД(3);
(5) Ь П(Зх)А(х) - (Ух)ПА(х), У-ПР(4).
Теорема 14. h (Vx)lA(x) -* П(Эх)А(х).
Доказательство.
(1) А(х),(Ух)ПА(х) h ~1А(х), ПВ19;
(2) А(х),(Ух)ПА(х) h A(x) ;
(3) А(х) h П(Ух)"1А(х), ПВ18(1,2), приведение к абсурду;
(4) h А(х) - 1(Ух)-|А(х), ТД(3);
(5) h (Зх)А(х) - -|(Ух)1А(х), 3-ПР(4);
(6) h ~l~l(Vx)~IA(x) - П(Эх)А(х), ПВ5(5), контрапозиция;
(7) I- (Ух)ПА(х) -» ~1(Эх)А(х), ПВ7(6), снятие двойного
отрицания.
Пусть выражение A s В есть сокращение для (А -» В)&(В -» А).
Показано, что Ь П(Ух)А(х) = (Зх)ПА(х); h П(Зх)А(х) = (Ух)ПА(х).
Аналогично в УИП можно доказать все равносильности,
установленные ранее для формул логики предикатов.
4.3. Непротиворечивость УИП
Узкое исчисление предикатов непротиворечиво, если ни для
какой его формулы недоказуемы одновременно ни она сама, ни ее
отрицание .
Построим соответствие Л, согласно которому каждой формуле УИП
сопоставим некоторую формулу исчисления высказываний следующим
образом.
1. Если А - элементарная формула Р(х1э...,хл), то Л(А) = Р.
2. Если формулам А и В из УИП сопоставлены формулы Л(А) и Л(В)
в ИВ, то h(lA) = ~1Л(А), Л(А * В) = Л(А) * /z(B), где * есть один
из знаков: &, V, -».
3. Если формуле А(х) сопоставлена формула Л(А), то
Л((Эх)А(х)) = Л(А); Л((Ух)А(х)) = Л(А), т.е. кванторы вместе с
их переменными стираются.
Если А - формула в УИП, то Л(А) получается из А стиранием в А
84
всех кванторов и всех предметных переменных.
Лемма. Если формула А доказуема в УИП, то формула А(А)
доказуема в ИВ.
Доказательство. Индукция по длине к доказательства.
БАЗИС, к = 1. Возможны следующие случаи.
1. \- С в УИП, причем формула С - аксиома, полученная по одной
из схем аксиом А1-А11. Тогда А(С) есть формула в ИВ, построенная
по той же схеме аксиом.
2. Ь С, причем С есть (Vx)A(x) -> А(у) - аксиома Бернайса.
Тогда /z(C) = /z((Vx)A(x) - А(у)) = /t(A) - A(A). Поэтому А(С)
доказуема в ИВ. Если С есть А(у) -» (Эх)А(х) - вторая аксиома
Бернайса, то доказуемость А(С) в ИВ следует из тех же соображений.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что лемма справедлива для
всех доказуемых в УИП формул с длиной доказательства меньше к.
ШАГ ИНДУКЦИИ. Покажем, что лемма справедлива для всех
доказуемых в УИП формул с длиной доказательства к. Пусть I- А в УИП и
A^A^-.-jAfc (=A) есть доказательство формулы А в УИП длины к.
Возможны следующие случаи.
1. А - аксиома. Тогда это рассмотренный выше случай базиса.
2. h А в УИП и AlfA2 А,- А/ ->АЛ,...,АЛ (=А) есть
доказательство формулы А в УИП длины к, причем А^ получено из А,
и А, -> А^ по правилу заключения. Так как длины доказательств
A^Aj,... ,А,- и Ах ,А2,... ,А,,... ,A,->Afc формул А/ и А,- -> А^ меньше
к, то по предположению индукции
(1) Ь й(А,-) в ИВ; (2) Ь А(А,- - А*) в ИВ.
Так как Л(А, -» Ак) = A(Ar) -» h(Ak)y то
(3) h A(Af) - А(А*) в ИВ; (4) А(А*), П3(1,3).
3. h А в УИП и А1ЭА2,... ,А,-,... ,А^ (=А) есть доказательство
формулы А в УИП длины к> причем формула А^, равная С -» (Vx)B(x)
получена из формулы А,- = С -> В(х) с помощью V-правила. Так как
длина доказательства А1эА2,... ,А,- формулы А/ меньше к, то по
предположению индукции \- й(А,-). Так^как А(А,-) = h(C -» В(х)) =
А(С - (Vx)B(x)) = MA*), то h й(А*) в ИВ.
4. Ь- А в УИП и Aj ,А2,... ,А^;,... ,А^ (=А) есть доказательство
формулы А в УИП длины ку причем формула А^, равная (Эх)В(х) -» С
получена из формулы А, = В(х) -> С с помощью Э-правила. Далее
аналогично предыдущему случаю.
Теорема. УИП непротиворечиво.
Доказательство. Если I- А и h ПА в УИП, то h /i(A) и h ~l/z(A) в
ИВ. Противоречие с непротиворечивостью ИВ.
85
4.4. Полнота УИП относительно класса общезначимых формул
Теорема. Всякая доказуемая в УИП формула общезначима.
Доказательство. Индукция по длине к доказательства формулы.
БАЗИС, к = 1. Возможны следующие случаи.
1. Ь А и А есть аксиома, полученная по одной из схем аксиом А1
- АН. Тогда А общезначима как формула, полученная подстановкой в
тождественно истинную формулу алгебры логики.
2. Ь В и В есть аксиома (Vx)A(x) -> А(у). Покажем, что формула
В общезначима. Пусть М есть множество, на котором определены
свободные переменные формулы В. Возможны следующие подслучаи:
при выбранных значениях переменных высказывание (Ух)А(х)
ложно. Тогда высказывание (Vx)A(x) -> A(y) истинно;
высказывание (Чх)а(х) истинно. Тогда высказывание А(х) истинно
при любых х из М, в том числе и при х = у, т.е. А(у) истинно.
Поэтому высказывание (Чх)А(х) -» А(у) истинно.
2. I- В и В есть аксиома А(у) -> (Эх)А(х). Покажем, что формула
В общезначима. Пусть М есть множество, на котором определены
свободные переменные формулы В. Возможны следующие подслучаи:
при выбранных значениях переменных высказывание А{у) ложно.
Тогда высказывание А(у) -> (Эх)А(х) истинно;
высказывание А(у) истинно. Тогда высказывание (3jc)^4(jc) истинно
(при х = у) и потому (Чх)А(х) -> А(у) истинно.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть теорема справедлива для всякой
доказуемой формулы с длиной доказательства меньше к.
ШАГ ИНДУКЦИИ. Покажем, что теорема справедлива для всякой
доказуемой формулы с длиной доказательства к. Пусть Ь А и А1Э
А2,... ,А,-,... ,А^ (=А) есть доказательство формулы А в УИП длины
к. Возможны следующие случаи.
1. Ь- А и А есть аксиома. А общезначима по случаю базиса.
2. h А в УИП и AlfA2,...>Al->...>Al->Afc,...fAfc (=A) есть
доказательство формулы А в УИП длины к. Причем А^ получено из А,- и А,- ->
Ад. по правилу заключения. Так как длины доказательств А1?
А2,...,А, и Ах ,А2,... ,А,;,... ,А,- -^ А^ формул А,- и Аг -» А^ меньше
к, то по предположению индукции формулы А,- иА/ -> А^ общезначимы.
По смыслу импликации формула А^ тоже общезначима.
3. Ь А в УИП и Aj,A2,... ,А,-,... >Ак (=А) есть доказательство
формулы А в УИП длины к, причем формула А^, равная С -> (Vx)B(x),
получена из формулы Аг- = С -> В(х) с помощью V-правила. Так как
длина доказательства А1ЭА2,...,А,- формулы А,- меньше к, то по
предположению индукции формулы А,, равная С -» В(х), общезначима.
Покажем, что формула А^, равная С -» (Vx)B(x), тоже общезначима.
86
Допустим, что это не так и формула А^ общезначимой не является,
т.е. существует множество М, переменные формулы А^, определенные
на М, для которых получившееся высказывание С -> (Ух)В(х) ложно.
Тогда высказывание С истинно, а высказывание (Ух)В(х) ложно,
откуда (Зх)1В(х) истинно, т.е. существует предмет х = х0 € М, для
которого ~\В(х0) истинно, а потому В(х0) ложно. Тогда С -> Ж*0)
ложно. Противоречие с общезначимостью формулы А/ = С -> В(х).
Следовательно, формула Ал общезначима.
3. Ь А в УИП и А1,А2,...,А|-,...,А^ (=А) есть доказательство
формулы А в УИП длины к, причем формула А^, равная (Зх)В(х) -> С,
получена из формулы А, = В(х) ->Сс помощью Э-правила.
Общезначимость формулы А доказывается аналогично предыдущему случаю.
Приступим теперь к доказательству основной теоремы о
совпадении класса формул, доказуемых в УИП, и класса формул,
общезначимых в логике предикатов. Общезначимость доказуемых формул уже
установлена. Покажем теперь, что всякая общезначимая формула
доказуема в УИП.
Непротиворечивые расширения УИП.
Определение. Два класса К и К' формул в УИП дедуктивно
эквивалентны, если К I- К' и К' I- К в УИП.
Пример. Формулы
В = А(х19...9хп) и С = (Ух1)...(Ухл)А(х1,...,хл)
дедуктивно эквивалентны. В самом деле, покажем, что В h С:
(1) А(х19...9хп);
(2) I- D, где D - произвольная доказуемая в УИП формула, не
содержащая переменных х1}...,хп;
(3) D - A(Xl,...,x„), ПВЗ(1);
(4) D -» (VXi).. .(Ухл)А(х1,... ,хл), последовательное применение
V-правила к (3);
(5) (Ух1)...(Ухл)А(х1,...,хп), П3(2,4), т.е. В h С.
Покажем теперь, что С I- В:
(1) (Ух^.. .(Ухл)А(х1,... ,хл);
(2) h (УХ1)...(Ухл)А - (Ух2)...(Ухл)А; АВ1;
(3) (Ух2)... (Ухл)А(Х1,... ,хл), П3(1,2).
После конечного числа подобных ша'гов получим
(4) А(Х1,...,хл), т.е. СКВ.
Будем в дальнейшем рассматривать УИП, в котором аксиомы
А1 - АН замкнуты квантором общности. По предыдущему замечанию
полученная система аксиом дедуктивно эквивалентна ранее
рассмотренной.
87
Определение. Класс К замкнутых формул УИП непротиворечив, если
из К в УИП нельзя вывести А и ПА одновременно ни для какой
формулы А.
Лемма. Если замкнутая формула ПА невыводима из
непротиворечивого класса К замкнутых формул, то класс К' = {К,А}
непротиворечив.
Доказательство. Допустим, что в УИП существует формула В, для
которой К' Ь- В и К' Ь- ПВ. Тогда по правилу ПВ18 приведения к
абсурду получим К I- ПА. Противоречие с условием. Следовательно,
класс {АГ,А} непротиворечив.
Определение. Класс К замкнутых формул полон, если для любой
замкнутой формулы А либо К Ь- А, либо К I- ПА.
Лемма. Если класс К замкнутых формул непротиворечив, то его
можно расширить до непротиворечивого полного класса КА замкнутых
формул.
Доказательство. Пусть В19В2|..* - пересчет всех замкнутых
формул УИП. Определим последовательность К0 ,КХ,... ,Кп,... классов
замкнутых формул следующим образом:
К0 - К\ Kt
л+1
КПУ если Кп h ПВя+1;
|{^л,Вп+1}, если неверно, что Кп I- ПВл+1.
Ясно, что К0 с кх с ... с Кп с кп+1 с ...
Утверждение 1. Все классы Кп непротиворечивы.
Доказательство. Индукция по п.
БАЗИС, п = 0. Класс К0 непротиворечив по условию.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что класс Кп непротиворечив.
ШАГ ИНДУКЦИИ. Покажем, что класс Кп+1 непротиворечив. Возможны
следующие случаи.
1. Кп+1 = Кп. Тогда класс АГл+1 непротиворечив по предположению
индукции.
2. Кп+1 = {КПУВп+1}\ тогда класс Кп не выводит ПВл+1 и потому
класс Кп+1 непротиворечив по предыдущей лемме.
Утверждение 1 доказано. Продолжим доказательство леммы.
Пусть КА = К0 U К, U ... = U Кп.
Утверждение 2. Класс КА непротиворечив.
Доказательство. Допустим противное: класс КА противоречив,
т.е. существует формула А, для которой КА I- А и КА I- ПА. Оба
вывода имеют конечную длину. Пусть Кг есть класс, который
содержит все формулы из КА, встречающиеся в этих выводах. Тогда
Kr h А и Kr h ПА. Противоречие с непротиворечивостью класса Кг.
88
Следовательно, класс КА непротиворечив.
Утверждение 3. Класс КА полон.
Доказательство. Пусть А - произвольная замкнутая формула в
УИП. Тогда А есть В;+1 при некоторм ;. Одно из двух: либо Kj Ь-
ПВ;+1, т.е. Kj Ь ПА, и тогда ввиду Kj Я КА будет КА \- ПА, либо
неверно, что Kj Ь ПВ;+1, и тогда Kj+1 = {Kj,Bj+1} = {Kj,A},
откуда Kj+l \- А, а так как Kj+1 Я КА> то КА I- А.
Итак, для любой замкнутой формулы А либо КА \- А, либо КА Ь ПА.
Утверждение 3 доказано.
Получили, что класс формул КА непротиворечив и полон. Лемма
доказана.
Формализмы F и G. Пусть К - непротиворечивый класс замкнутых
формул, F - формализм, полученный из УИП добавлением к нему
формул класса К в качестве аксиом. Формализм F непротиворечив.
Построим формализм G, расширив формализм F натуральными числами.
Опишем формализм G подробнее.
Формальные символы формализма G.
1. x,y,z,... - символы предметных переменных.
2. 0,1,2,... - символы натуральных чисел.
3. P^jRjPpQjjRj,... - символы предикатных переменных.
5.&,V,->,n,3,V- логические символы (связки).
6. ( , ) - скобки и запятая.
Термы формализма G.
1. Всякая предметная переменная и предметная константа есть
терм.
2. Всякое натуральное число есть терм.
Формулы формализма G.
1. Если t!,...,tfc - термы и Р - предикатная переменная, то
P(tx,... ,tfc) - элементарная формула.
2. Все другие формулы получаются из элементарных с помощью
булевых операций и операций навешивания кванторов.
Аксиомы исчисления G состоят из трех следующих групп..
Первая группа аксиом для G есть замыкания квантором общности
аксиом, полученных по схемам аксиом А1 - АН. При этом А,В,С -
формулы из G.
Аксиомы Бернайса составляют вторую группу аксиом для G:
АБ1. (Vx)A(x) - A(t). АБ2. A(t) - (Эх)А(х),
где А(х) - формула в G со свободной переменной х, t - терм.
Формулы класса К составляют третью группу аксиом для G.
Правила вывода для G совпадают с правилами вывода для УИП.
Утверждение. Формализм G непротиворечив.
89
Доказательство. Допустим, что формализм G противоречив. Пусть
формула В из G такова, что \-G В и У-q "IB; n1,n2,...,nr - все
символы натуральных чисел, встречающиеся в выводах формул В и 1В;
У1»У2»---»Уг " попарно различные предметные переменные, отличные
от всех переменных, встречающихся в доказательствах формул В и
"IB. Заменим в этих доказательствах каждое п/ на у,. При этом
встречающиеся в доказательствах формул В и "IB аксиомы (Vx)A(x) -♦
А(п,) и А(п,) -> (Эх)А(х) из G перейдут в аксиомы (Vx)A(x) -> А(у,)
и А(у,) -> (Эх)А(х) из УИП. Формулы В и "IB перейдут в формулы С и
"1С в УИП. Доказательства для В и "IB в G перейдут в доказательства
С и "1С в УИП, что противоречит непротиворечивости УИП.
Следовательно, формализм G непротиворечив. Утверждение доказано.
Формализмы Gn. Пусть
OxjB^xJ, (Эх2)В2(х2), ..., (Зхк)Вк(хк),...
есть пересчет всех замкнутых формул из G вида (Эх)В(х), где В(х)
- формула из G, с единственной свободной переменной х. Индукцией
по к зададим последовательность формализмов G^, к = 0,1,2,...
БАЗИС, к = 0. GQ = G. Пусть А0 - система аксиом для G0.
к = 1. Пусть рх - наименьшее натуральное число, превосходящее
все натуральные числа, встречающиеся в формуле (Эх^ВДх!), и
формула Е1 = (Зх^В^х^ -> В^р^. Пусть Al = А0 U {Ej есть
система аксиом для G{.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть формализм Gk.l и система
аксиом А^-! для него уже построены.
ШАГ ИНДУКЦИИ. Построим формализм Gk и его систему аксиом Ак.
Пусть рк есть наименьшее натуральное число, превосходящее plfp2,
...,/?£_! и все натуральные числа, встречающиеся в формуле
(Зхк)Вк(хк)\ формула Ек = (Зхк)Вк(хк) - Вк(рк)\ Ак = Ak_l U {Е*}
есть система аксиом для исчисления G^, т.е. Gk получается
добавлением к G^ формулы Е^ в качестве аксиомы.
Формализмы Gk, к = 0,1,2,..., построены. Обозначим через Тк
множество доказуемых в Gk формул. Так как
А0 С Ах С ... С Ак С Ак+1 С ..., то
Т0 с Tl с ... с Тк с Тк+1 с ...,
т.е. всякая формула, доказуемая в Gfc, доказуема и во всяком
последующем исчислении.
Утверждение. Формализмы G*. непротиворечивы.
Доказательство. Индукция по к.
БАЗИС, к = 0. Так как G0 = F и формализм F непротиворечив, то
формализм G0 непротиворечив.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что формализм Gk_l
90
непротиворечив.
ШАГ ИНДУКЦИИ. Покажем, что формализм Gk непротиворечив.
Допустим противное: формализм Gk противоречив, тогда в G^
существует формула А, для которой
(1) hG A; (2) hG1A. Далее
(3) hG А & ПА, ПВ2(1,2);
(4) hGk А & ПА - В, П Л В (х & 1Х , у);
(5) hG^B» 113(3,4); возьмем В = ~1Е*. Тогда
(6) Ь^ПЕ*. Так как Ак = А*_х U {Ек}, то A*_lfE* hGjfe IE*,
а потому
(7) Е* Ьс 1ЕЪ откуда
(8) Ь^ % - 1ЕЪ ТД(7);
(9) hG (ЕЛ - ПЕ*) - IE*, П?* ((х - Пх) - х);
(10) h^lE*, П3(8,9); т.е.
(И) \-G 1((Эхк)Вк(хк) - В*(р*)); откуда имеем
(12) h " (Эх*)В*(х*) & ПВ*(/7*);
(13) hG (Эх*)В*(х*), ПВ1(12);
(14) \-Gki 1Вк(рк), ПВ1(12).
Заменим в доказательстве формулы 1Вк(рк) в Gk_l натуральное
число рк на переменную xkf не встречающуюся среди других
переменных в доказательстве формулы ~\Вк(рк). Тогда последовательность
формул (l) - (14) преобразуется в доказательство в формализме
Gk_l формулы ПВ*(х*), а именно,
(15) *~Gk_ ~IB*(x*). Далее справедливо
(16) \-G С, где С есть произвольная замкнутая доказуемая в
УИП формула;
(17) hG с - ПВ*(х*), ПВЗ(15);
(18) hG с - (Vx*)lB*(x*), У-ПР(17);
(19) hG (Чхк)1Вк(хк), П3(16,18);
(20) hG (Чхк)1Вк(хк) - l(3xk)Bk(xk), T14;
(21) hGki 1(Зхк)Вк(хк), П3(19,20).
Получили, что в Gk_Y доказуемы формула (Эх^)В^(х^) и ее
отрицание. Противоречие с непротиворечивостью Gk_x. Следовательно,
формализм G^ непротиворечив. Утверждение доказано.
Формализмы Н и L. Пусть
Ах = А0 U A, U ... U Ak U ... = U Ак
есть система аксиом для формализма Н. Множество
Тг = Т0 U Т, U ... U Tk U ... = U Тк
доказуемых в формализме Н формул состоит из всех формул,
91
доказуемых в формализмах Gk, к = 0,1,2,... .
Утверждение. Формализм Н непротиворечив.
Доказательство. Допустим противное: формализм Н противоречив,
т.е. в Н существует формула А, доказуемая в Н одновременно с ПА.
Оба доказательства содержат конечное число формул, каждая из
00
которых доказуема в Н. Так как Tr = U Т^, то найдется номер г,
к = о
для которого все формулы в обоих доказательствах содержатся в Тг.
Тогда V-q А и \-G "IA. Противоречие с непротиворечивостью G.
Утверждение доказано.
Пусть L есть непротиворечивое полное расширение формализма Я.
Лемма. Если А(х) - формула с единственной свободной переменной
х, то hL (Vx)A(x) «-> (hL A(0), hL A(l), ..., hL A(k), ... ).
Доказательство. Пусть
(1) \-L (Vx)A(x). Далее
(2) hL (Vx)A(x) - A(0), АБ1;
(3) hL A(0), П3(1,2);
(4) hL (Vx)A(x) - A(l), АБ1;
(5) hL A(l), П3(1,4);
и так далее. Получили \-^ А(0), l-L A(l), ..., Ь^ A(k), ... .
Пусть теперь \-L A(k), k = 0,1,2,... . Допустим, что в L
формула (Vx)A(x) не доказуема. Так как формализм L полон, то
(1) hL П(Ух)А(х). Далее
(2) hL l(Vx)A(x) - (Зх)ПА(х), Т12;
(3) hL (Зх)ПА(х), П3(1,2).
Последняя формула есть некоторая формула (Зх^)В^(х). Тогда
(4) 1-£ (Эх^)В^(х). Далее имеем
(5) \-L (3xk)Bk(x) - В*(р*), аксиома Ек\
(6) HL В*(р*), П3(4,5);
(7) hL 1А(р*).
Получили, что в формализме L доказуема формула А(р^) и ее
отрицание. Противоречие с непротиворечивостью L.
Лемма. Если А(х) есть формула с единственной свободной
переменной х, то
hL (Зх)А(х) ~ (hL А(0) V y-L А(1) V ...V hL A(k) V ... ).
Доказательство. Пусть l-L (Зх)А(х). Допустим противное: формулы
А(к) не доказуемы в L ни при каком к. Так как формализм L полон,
то hL 1А(0), hL 1А(1), ..., \-L 1А(к),... ). Тогда
(1) Ь (Ух)ПА(х). Далее
(2) h (Vx)lA(x) - П(Зх)А(х), Т14;
(3) Ь П(Зх)А(х), П3(1,2).
92
Получили, что в исчислении L доказуема формула ~1(Зх)А(х) и ее
отрицание одновременно. Противоречие с непротиворечивостью L.
Следовательно, справедливо V-L А(0) V \-L A(l) V ... .
Пусть теперь существует такое натуральное число р, для
которого
(1) hL A(p). Далее
(2) hL А(р) - (Зх)А(х), АБ2;
(3) l~L (Зх)А(х), П3(1,2). Лемма доказана.
Лемма. Всякий непротиворечивый класс К замкнутых формул УИП
выполним на множестве натуральных чисел.
Доказательство. Пусть IN = {0,1,2,...} есть множество
натуральных чисел. Индукцией по построению формул из класса К зададим на
IN предикаты так, чтобы доказуемые в L формулы стали истинными
высказываниями, т.е. покажем, что формулы класса Т^, доказуемые в
исчислении L, выполнимы на множестве натуральных чисел. Пусть
Р(а19а29...9а„) - элементарная формула в L, где Р - предикатная
буква; а19а29...9а„ - символы натуральных чисел. В силу полноты L
либо \-L P(aj ,a2,... ,а„), либо \-L ПР(а19а29... ,ая). Пусть предикат
И, если \-L Р(а19а2,...,ая),
|Л, если hL ПР(а1>а2>...,ап).
Р(а1,а2,...,ап) =
Индукцией по глубине к построения формулы покажем, что при так
определенных предикатах замкнутые доказуемые в L формулы
принимают истинные значения.
БАЗИС, к = 1. Пусть \-L А. Тогда А есть элементарная формула
Р(а1>а2>...,ап)> причем bL Р(а19а2>... ,ап). Поэтому Р(а19а2,
..-.О = И.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что все доказуемые в L
замкнутые формулы с глубиной построения меньше к при выше
определенных на IN предикатах принимают значение И.
ШАГ ИНДУКЦИИ. Покажем, что все доказуемые в L замкнутые
формулы с глубиной построения к при выше определенных на IN
предикатах принимают значение И.
Пусть \-L А, причем формула А имеет глубину построения к.
Возможны следующие случаи.
1. А есть (Vx)B(x). Тогда
(1) \-L (Vx)B(x). Далее имеем
(2) hL (Vx)B(x) — (hL B(0), hL B(l), ..., hL B(p), ... );
(3) hL В(0), \-L B(l), ..., hL В(р), ....
Так как глубины построения формул В(р), р = 0,1,2,..., меньше
/с, то по предположению индукции высказывания
93
я(о) = и, в(1) = и, ..., в(р) = и, ... .
По смыслу квантора общности высказывание (Vjc)jB(jc) истинно.
2. HL А и А есть (Эх)В(х). Тогда
(1) \-L (Эх)В(х). Далее имеем
(2) \-L (Эх)В(х) «-> (HLB(0) V hLB(l) V ...V hLB(p) V ... );
(3) hL в(0) V \-L B(l) V ... V hL B(p) V ... .
Пусть для определенности l-L B(p). Так как глубина построения
формулы В(р) меньше к, то по предположению индукции высказывание
В(р) истинно. По смыслу квантора общности высказывание (Чх)В(х)
истинно.
3. HL А и А есть В & С. Тогда \-L В & С, откуда по ПВ2
получаем \-L В и \-L С. Так как глубины построения формул В и С меньше
к, то по предположению индукции высказывания В и С истинны. Тогда
В & С истинно, т.е. высказывание ^4 истинно.
Случаи, когда А есть В V С, В -♦ С, ПВ, рассматриваются
аналогично .
Итак, все доказуемые в L замкнутые формулы при выше
определенных на IN предикатах принимают истинные значения. Так как
формулы класса К доказуемы в L как аксиомы, то класс К замкнутых
формул выполним на множестве натуральных чисел. Иначе говоря,
непротиворечивый класс замкнутых формул УИП имеет модель.
Теорема. Всякая замкнутая общезначимая в логике предикатов
формула доказуема в УИП.
Доказательство. Пусть А - общезначимая формула логики
предикатов. Допустим противное: формула А в УИП не доказуема. Тогда
класс формул К = {ПА} непротиворечив и по предыдущей лемме
формула ПА выполнима на множестве натуральных чисел. Противоречие
с общезначимостью формулы А. Следовательно, общезначимая формула
А доказуема в УИП.
Из двух выше доказанных теорем следует следующая теорема.
Теорема (Геделя о полноте). Замкнутая формула доказуема в УИП
тогда и только тогда, когда она общезначима.
Замечание. К узкому исчислению предикатов можно добавить
специальный предикат равенства х = у и две характеризующие его
аксиомы равенства (АР):
API) х = х;
АР2) х = у - (А(х) - А(у)),
где А(х) - произвольная формула УИП, имеющая свободную переменную
х (возможно и другие переменные).
В УИП с равенством справедлива теорема о совпадении класса
общезначимых формул (с равенством) и класса формул, доказуемых в
УИП (с равенством).
94
УИП с равенством можно расширить далее, допустив при
построении элементарных формул использование функциональных термов. И
здесь справедлива выше приведенная теорема. Следует заметить, что
аксиомы Бернайса примут в этом случае следующий вид.
Аксиомы Бернайса (АБ).
Пусть А(х) - произвольная формула УИП, содержащая свободную
переменную х; t - некоторый терм.
АБ1) (Vx)A(x) -> A(t); АБ2) A(t) -» (Эх)А(х).
При этом терм t свободен для переменной х в формуле А(х), т.е.
никакое свободное вхождение переменной х в А(х) не входит в
область действия квантора (Эу) или (Vy), где у есть переменная из
терма t.
Заметим еще, что если формула A(Plf... ,РЛ) с указанным
множеством предикатных переменных доказуема в исчислении предикатов,
то можно построить такое ее доказательство, в котором не
встречаются предикатные переменные, отличные от Fly...,Fn.
4.5. Аксиоматическая арифметика и элементарные теории
Приведем формализацию арифметики натуральных чисел,
принадлежащую Пеано.
Формальные символы.
1. x9y,z,xl9yl,zl,... - символы предметных переменных
(пробегающих множество натуральных чисел).
2. О - символ нуля (предметная константа).
3. ' - штрих, (т.е. функция следования х' = х + 1,
функциональная константа).
4. + , • - символы для сложения и умножения (функциональные
константы).
5. = - символ для предиката равенства (предикатная константа).
6.&,V,->,~I,3,V- логические символы (связки).
7. ( , ) - скобки и запятая.
Термы (арифметические выражения).
1. Отдельно взятая предметная переменная х есть терм глубины
построения 1, зависящий от переменной х.
2. О есть терм глубины построения 1.
3. Если s и t - термы глубины построения ds и dt
соответственно, и х19х2,... ,х„ - полный список их переменных, то (s + t),
(s#t) есть термы глубины построения max(dS9dt)+l9 зависящие от
переменных хх ,х2,... ,х„, т.е. имеющие хрх2 хй в качестве
полного списка их переменных.
4. Если s есть терм глубины построения ds и с полным списком
95
переменных хх ,х2,... ,х„, то (s)' - терм глубины построения d5+l,
зависящий от переменных х19х2,...,хп.
Если переменные терма t содержатся среди переменных списка
х1,...9х59 то пишем t(x19... }х;).
Формулы.
1. Если s и t - термы и x1,...,xw - полный список их
переменных, то (s = t) есть элементарная формула глубины построения 1
и со свободными переменными х1}...,хт.
2. Далее из элементарных формул с помощью булевых операций и
операций навешивания кванторов можно строить другие формулы
арифметики аналогично тому, как это делалось в случае формул логики
предикатов.
В арифметических выражениях действуют правила опускания
скобок в связи с обычным приоритетом арифметических операций: х' =
х+1, х • у, х+у. Замкнутые формулы не имеют свободных предметных
переменных. Содержательно каждая замкнутая формула представляет
собой высказывание арифметики, истинное или ложное.
Аксиоматика арифметики строится следующим образом.
Логические схемы аксиом. Пусть А, В, С - произвольные формулы
арифметики. Тогда схемами аксиом являются следующие выражения.
1. А - (В - А).
2. (А - (В - С)) -> ((А -> В) -> (А -> С)).
3. А & В - А.
4. А & В - В.
5. (А - В) - ((А -> С) -> (А - В & С)).
6. А - А V В.
7. В - А V В.
8. (А - С) - ((В - С) - (А V В - С)).
9. (А -» В) - (~1В - ПА).
10. А - НА.
11. НА -» А.
Аксиомы равенства.
API. х = х.
АР2. х = у - (А(х) - А(у)),
где А(х) - произвольная формула арифметики, имеющая свободную
переменную х.
Аксиомы Бернайса (АБ).
Пусть А(х) - произвольная формула арифметики, содержащая
свободную переменную х; t - некоторый (арифметический) терм.
АБ1. (Vx)A(x) - A(t). АБ2. A(t) - (Эх)А(х).
При этом терм t свободен для переменной х в формуле А(х), т.е.
никакое свободное вхождение переменной х в А(х) не входит в
96
область действия квантора (By) или (Vy), где у есть переменная из
терма t.
А, А -> В А -» В(х) А(х) -» В
Правила вывода: ; ; .
В А - (Vx)B(x) (Зх)А(х) - В
Первое правило вывода есть правило заключения; А и В -
произвольные формулы арифметики. Второе правило есть правило
навешивания квантора общности (V-правило, или V-ПР); А и В(х) -
произвольные формулы арифметики, причем формула А не содержит
переменной х свободно. Третье правило есть правило навешивания
квантора существования (3-правило, или 3-ПР); А(х) и В -
произвольные формулы арифметики, причем формула В не содержит
переменной х свободно.
Перечисленные аксиомы и правила вывода имеют общелогический
характер (их называют логическими). Они используются во всех
аксиоматических теориях (с поправкой на термы и формулы этих
конкретных теорий). Далее последуют специальные (т.е. нелогические)
аксиомы арифметики, характеризующие свойства арифметических
операций.
Аксиомы Пеано.
(1) х = у -» (у = z -» х = z).
(2) 1(х' = 0).
(3) х = у -» х' = у'.
(4) Xх = у' -» х = у.
(5) х + 0 = х.
(6) х + у' = (х + у)'.
(7) х • 0 = 0.
(8) х • у' = х • у + х.
(9) А(0) & (Vx)(A(x) -> А(х')) -> А(х) - схема аксиом индукции.
Здесь А(х) есть произвольная формула арифметики, содержащая
свободную переменную х.
Формальные символы, формулы, система аксиом и правила вывода
составляют аксиоматическую, или формальную арифметику (Пеано).
Аксиоматическая арифметика является одной из элементарных теорий,
к общему описанию которых переходим.
Сигнатура есть набор объектов
б = (P(Wl) Р(;Л/) f(Wl) f(Wr) с с )
Верхние индексы указывают на местность соответствующих
предикатных или функциональных символов. Формула сигнатуры с есть
формула логики предикатов, построенная из предикатных символов
Р,, i = 1,2,...,/, функциональных символов f;, j = 1,2,...,г,
97
предметных констант ск, к = 1,2,. ..,5, и произвольных предметных
переменных. Выделяется класс А формул сигнатуры с, которые
объявляются (нелогическими) аксиомами. Три упомянутых выше
правила вывода применяются к формулам сигнатуры б. Элементарную теорию
составляют формулы (сигнатуры б), аксиомы, правила вывода.
Элементарная теория частичного порядка сигнатуры б - ( < ),
например, содержит следующие две нелогические аксиомы,
характеризующие предикат частичного порядка.
1. ~1(х < х).
2. (х < у)&(у < z) -> (х < z).
Элементарная теория групп сигнатуры б = (+, 0) задается
следующими нелогическими аксиомами, характеризующими операцию + и
нейтральный элемент 0.
1. х + (у + z) = (х + у) + z.
2. 0 + х = х.
3. (Vx)(3y)(x + у = 0).
Арифметика Пеано есть элементарная теория сигнатуры б =
(+,•/,0). Австрийский математик Курт Гедель показал, что
аксиоматика Пеано (да и вообще всякая достаточно богатая
аксиоматическая теория, например, такая, в которой выразимы все частично
рекурсивные функции) не полна относительно истинных формул
арифметики, т.е. в арифметике можно указать формулу, содержательно
истинную, но не доказуемую в арифметике Пеано.
Естественен вопрос: нельзя ли добавить новые аксиомы
(расширить арифметику) таким образом, чтобы получившаяся формальная
система относительно истинных формул арифметики оказалась полной?
Ответ отрицателен: аксиоматическая арифметика непополнима.
Аксиоматическая арифметика алгоритмически неразрешима, т.е. не
существует алгоритма, который по любой формуле арифметики
устанавливал бы, доказуема эта формула в арифметике или не доказуема.
Что касается других элементарных теорий, то исследования
показали, что алгоритмически разрешимые теории встречаются
относительно редко. Всякая достаточно богатая теория, в которой выразимы
все частично рекурсивные функции, оказывается алгоритмически
неразрешимой. Оказалось также, что непротиворечивость арифметики
нельзя установить, оставаясь внутри самой аксиоматической
системы, т.е. средствами этой же самой арифметики Пеано.
Основной вопрос математической логики есть вопрос об
установлении общезначимости формул логики предикатов. Приведем следующее
соображение в пользу важности этого тезиса. Определим на
множестве натуральных чисел предикаты:
98
Р=(х,у) для х = у;
Р+1(х,у) для у = х + 1;
ЛД*,.у,г) Для * + у = z;
Рх(*,.У,г) Для х - у = z.
Тогда каждая замкнутая формула А арифметики превращается в
суждение Л(Рж,Р+1 ,Р+,Рх) относительно предикатов Рж,Р+1,Р+,Рх-
Пусть А - доказуемая в арифметике формула и Какс - множество всех
тех аксиом арифметики, которые были использованы при
доказательстве формулы А. Так как длина доказательства формулы А конечна, то
множество Какс конечно. Тогда
(Ьариф А) *~~* (Какс ЬУИП А) *~~* (hyMII Какс "* А) *""*
формула Какс -* А общезначима в логике предикатов.
Так что доказуемость формулы в аксиоматической арифметике
равносильна общезначимости некоторой формулы логики предикатов.
Такое рассуждение можно провести относительно всякой другой
элементарной теории, основывающейся на узком исчислении
предикатов: доказуемость формулы в рассматриваемой теории окажется
равносильной общезначимости некоторой формулы в УИП. Отсюда
следует важность вопроса об установлении общезначимости формул
логики предикатов. Потому и считают этот вопрос основным вопросом
математической логики.
4.6. Интуиционизм (конструктивизм)
Пусть А,В,С - произвольные формулы исчисления предикатов.
Возьмем для него следующую систему аксиом Клини.
1. А -» (В -» А).
2. (А -^ В) — ((А -^ (В -^ С)) -> (А -> С)).
3. А -* (В -*> А & В).
4. А & В -*> А.
5. А & В -*> В.
6. А -* А V В.
7. В -> А V В.
8. (А -> С) -> ((В -* С) ^ (А V В ^ С)).
9. (А -* В) -^ ((А -* ПВ) -* ПА).
10. "ПА -* А.
Аксиомы Бернайса.
АБ1) (Vx)A(x) - А(у). АБ2) А(у) - (Зх)А(х).
А, А - В А - В(х) А(х) - В
Правила вывода: ; ; .
В А - (Vx)B(x) (Зх)А(х) -> В
99
Пусть Р(х) есть некоторый предикат, определенный на множестве
D. Вычисляется истинностное значение высказывания (Зх)Р(х).
Обозначим его через А. Интуиционизм (или конструктивизм) требует,
чтобы доказательство истинности высказывания А сопровождалось
указанием на тот предмет х0 из D, для которого Р(х0) истинно. Для
конечного множества D наличие или отсутствие такого предмета х0 в
D проверяется перебором всех элементов из D. В случае
бесконечного множества D ситуация меняется: перебор всех элементов
множества D становится невозможным.
Классическая математика допускает доказательство высказывания
А от противного. Предполагается ~ЛА и из ~ЛА выводится некоторое
утверждение В и его отрицание одновременно, т.е. "ЛА \- В и ~\А \-
~1В. Тогда наше предположение об истинности ~\А не верно и потому
истинно отрицание ~\А, т.е. истинно ~П>4, с чем согласен и
конструктивист. Затем классик получает А, т.е. истинность (Зх)Р(х) без
указания на предмет х0 из D, для которого Р(х0) истинно, снимая
двойное отрицание в НА, пользуясь аксиомой НА -*- А.
Конструктивист с этим не согласен и аксиому НА -*- А (которая равносильна
закону исключенного третьего 1А V А) не принимает, предлагая
вместо нее взять более слабую аксиому "Л А -*• (А -*• В).
Исчисление высказываний без аксиомы ПА -*• А Колмогоров назвал
минимальным. Исчисление предикатов с аксиомой "Л А -*> (А -** В)
вместо аксиомы ПА —*• А называется интуиционистским (или
конструктивистским) исчислением предикатов.
Для классического исчисления высказываний существует конечная
модель - двузначная алгебра логики, в том смысле, что формула А
доказуема в ИВ тогда и только тогда, когда А тождественно истинна
как формула алгебры логики. Для интуиционистского исчисления
высказываний (ИИВ) подобных конечных моделей нет; но бесконечные
модели подобного рода для ИИВ существуют.
ИИВ алгоритмически разрешимо: существует алгоритм (гораздо
более сложный, чем разрешающий алгоритм для доказуемости в
классическом исчислении высказываний), устанавливающий по всякой
формуле ее доказуемость или недоказуемость. Класс формул,
доказуемых в ИИВ строго входит в класс формул, доказуемых в
классическом ИВ. Между ними существует континуум логик (исчислений
высказываний), называемых суперинтуиционистскими (или
суперконструктивистскими), т.е. множество суперинтуиционистских логик можно
поставить во взаимно однозначное соответствие с множеством всех
вещественных чисел.
100
4.7. Модальные логики
В модальном исчислении высказываний (МИВ) формализуются
модальности "возможность" и "необходимость".
Формальные символы (алфавит).
1. p9q9r9p1 ,qx ,Г!,. - - - символы пропозициональных переменных.
2. &, V, "I, ->, - логические связки (конъюнкция, дизъюнкция,
отрицание, импликация, соответственно).
3. ( , ) - скобка левая, запятая, скобка правая.
4. А, □ - символы (связки) для модальностей возможно и
необходимо.
Формулы.
1. Отдельно взятый символ пропозициональной переменной есть
элементарная формула (атом).
2. Если А и В есть формулы, то выражения (А & В), (А V В),
(ПА), (А -> В), (ПА), (АА) есть формулы.
Примем соглашение об опускании скобок в соответствии со
следующим приоритетом связок: "l,D,A,&,V,->.
Пусть А,В,С - произвольные формулы в МИВ. Введем следующие
схемы аксиом.
А1) А - (В - А).
А2) (А - (В - С)) - ((А - В) - (А - С)).
A3) А & В - А.
А4) А & В - В.
А5) (А - В) - ((А - С) - (А - В & С)).
А6) А - А V В.
А7) В - А V В.
А8) (А - С) - ((В - С) - (А V В - С)).
А9) (А - В) -> (ПВ - ПА).
А10) А - ППА.
All) ППА -> А.
Правило заключения.
А, А -> В
В
Это аксиоматика исчисления высказываний. Модальности могут
присутствовать здесь только в формулах. К ним добавляются аксиомы
и правила вывода, характеризующие свойства модальных связок. В
результате получаем различные модальные исчисления высказываний.
Модальное правило необходимости (ПН). =—.
Схема аксиом дистрибутивности (схема аксиом К).
101
□(A - В) - (ПА - ПВ).
Определение. Нормальное модальное исчисление высказываний К
есть формальные символы, формулы, аксиомы А1 - АН, аксиома
дистрибутивности К и правила вывода: правило заключения, правило
необходимости.
Нормальная система получила имя по имени присоединенной
модальной схемы аксиом К.
Обогащая нормальную систему К другими схемами аксиом, можно
получить другие модальные системы. Приведем несколько таких
примеров .
Схема аксиом знания. DA -* А.
Она обозначается через Г. Нормальная система К> пополненная
модальной схемой аксиом Г, обозначается через КТ (по имени двух
входящих в нее модальных аксиом). Иногда ее обозначают 7.
Схема аксиом позитивной интроспекции. DA -> DDA.
Она обозначается цифрой 4. Нормальная система К, пополненная
схемами аксиом Г и 4, обозначается через КТ (а также через 54).
Схема аксиом негативной интроспекции. А А -* DAA.
Она обозначается цифрой 5. Схема аксиом 5 эквивалентна схеме
"IDA -* DID А. Нормальная система К, пополненная схемами аксиом Г, 4
и 5, обозначается через КТ45 (а также через S5).
Если нормальную систему К пополнить схемами аксиом К, 4 и 5,
то получим модальную систему К45, более слабую, чем 55.
Возможны и другие схемы аксиом МИВ. Разные их комбинации дают
свои разновидности модального исчисления предикатов.
Модальное исчисление предикатов (МИП) строится на основе
узкого исчисления предикатов следующим образом.
Алфавит.
1. xiy,z>xl>yl>zl,... - символы предметных переменных.
2. ajbjCja^b^Cj,... - символы предметных констант.
3. figjhifjih^gj,... - символы функциональных переменных.
4. PjQjRjPjjQ^Rj,... - символы предикатных переменных.
5. &,V, ->,"!,□, A, 3,V- логические символы.
6. ( , ) - скобки и запятая.
Формулы.
1. Если х!,...,хт - символы предметных переменных и Р -
предикатная переменная, то Р(х1?...,хт) - элементарная формула.
2. Если А и В - формулы, то (А & В), (А V В), (ПА), (А - В),
(ПА), (АА) - формулы.
3. Если А(х) - формула, то выражения (Эх)А(х), (Vx)A(x) есть
формулы.
102
Далее следуют схемы аксиом исчисления высказываний, правила
Бернайса и правила вывода (построенные на основе формул МИП),
А
расширенные модальным правилом вывода рг— и введенными ранее
(добавляемыми в разных комбинациях) модальными схемами аксиом:
П(А -> В) -» (ПА -> ПВ); ПА -♦ А; ПА -♦ ППА; АА -♦ ПАА. Возможны и
другие схемы аксиом МИП. Разные их комбинации дают свои
разновидности модального исчисления предикатов.
В модальных исчислениях изучаются обычные для математической
логики вопросы алгоритмической разрешимости, моделей, объемов
доказуемых формул. Более подробные сведения по модальным логикам
изложены в книге Р.Фейса.
5. ИСЧИСЛЕНИЕ СЕКВЕНЦИЙ
5.1. О правилах вывода в секвенциальном
исчислении высказываний
В классическом аксиоматическом исчислении Гильберта выделены
минимально необходимые дедуктивные средства для вывода всякой
общезначимой формулы логики предикатов, удобные для исследования
свойств самого формализма, но приводящие к довольно громоздким
вычислениям при выводе даже простых общезначимых формул. Это
делает использование формализма Гильберта для установления
общезначимости формул логики предикатов практически невозможным. Чтобы
сделать установление общезначимости формулы более привычным, Ген-
тцен предложил формализм с правилами вывода, довольно естественно
описывающими свойства логических операций, с помощью которых эти
формулы построены, благодаря чему вывод в формализме Гентцена
делается более простым и наглядным. Этот фомализм называют также
естественным выводом Гентцена. Приведем несколько предварительных
соображений относительно гентценовских правил вывода.
Пусть A j, А 2,..., Ая и В х, В 2,..., Вт - произвольные совокупности
формул ИВ. Будем вместо выводимости А!&А2&.. .&Ап I- B^BjV... VBW
(что эквивалентно А1,А2,...,АЯ I- B^BjV...VBm) записывать АПА2,
...,А„ N В1;В2;...;Вт. Выражение А1?А2,...,АП И В1;В2;...;Вт
называется секвенцией (Гентцена). Левую часть секвенции назовем
антецеденту правую - сукцедент. Очевидно, что
A^A^.-.A^ Bi;B2;...;Bm~ А^Аг&.-.&А,, Ь В, VB2V... VBm ~
103
I- А1&А2&...&АЯ - B1VB2V...VBm.
Содержательно секвенция А1,А2,...,АП t= B1;B2;...;Bm означает, что
дизъюнкция B^B^.^VB^, логически следует из конъюнкции
А1&А2&...&АП.
В секвенции A1}A2 Ал N Вг ;В2;... ;Вт совокупности Aj,A2,
...,АЛ и В1;В2;...;Вт можно рассматривать как множества. Поэтому
формулы в них можно переставлять, можно добавлять или удалять
повторы формул, ибо применение таких операций к формулам вида
А!&А2&.. .&А„ -*B1VB2V...VBm приводят к эквивалентным формулам. В
связи с таким множественным пониманием секвенции выражения
~\(А1>А2>... ,А„) и ~\(В1\В2\... ;Вт) будем воспринимать как
-|(А1&А2&...&А„) и ~l(B1VB2V...VBm) соответственно.
В последующих доказательствах воспользуемся доказанными ранее
равносильностями и правилами вывода, не оговаривая этого особо.
Пусть Г и А - произвольные конечные совокупности формул ИВ
(возможно пустые). Считаем, что в левой части секвенции эти
формулы представляют собой конъюнкцию составляющих формул (т.е.
записываются через запятую), а в правой части - дизъюнкцию (т.е.
записываются через точку с запятой).
Устанавливая факт общезначимости данной формулы, попытаемся
построить опровержение для этой формулы (т.е. интерпретацию, на
которой формула ложна). Упрощая секвенции в дереве строящегося
вывода, будем судить о ложности формул данной секвенции справа от
знака N и об их истинности слева от знака N. Если при этом
удастся построить интерпретацию, при которой формулы слева от знака N
истинны, а справа - ложны, то это будет означать что данная
секвенция, рассматриваемая как формула логики, ложна (ибо ее посылка
истинна, а заключение ложно), а потому общезначимой не является и
в формализме недоказуема. При подобном анализе данной формулы (от
корня к листьям) потребуется переходить от знаменателя
используемого правила вывода к его числителю, а построение дерева вывода
(от листьев к корню) на основе проведенного анализа будет
использовать правила вывода от числителя к знаменателю. Поэтому
содержательный смысл последующих восьми правил вывода поясним от
знаменателя к числителю.
Aj ,А2,... ,А„ f Bj ;В2;... ;Вт
Утверждение 1. а) — . —;
А!,А2,. . . ,А„, \а1 F Ь2,...,Ьт
А1 ,А2,... ,An,Bx f B2;...;Bm
} А1,А2,...,АЯ N -|В1;В2;...;Вт'
104
Доказательство. Из двух правил вывода докажем первое. Второе
доказывается аналогично.
AlfAa>...fAII»=B1;B2;...;Bm^A1&A2&...&Alll-B1VBaV...VBw«
AnAa Ая Н ПВ, - (B2V...VBW) ~
Al9A29...fAnf'\Bl H B2V...VBm ~ А1,Аа,...1Ал>ПВ1 И В2;...;Вт.
Замечание.Оба правила вывода обратимы: от знаменателя правила
можно переходить к числителю и наоборот.
Следствие. Справедливы обратимые правила вывода введения
отрицания слева и справа от знака t= :
Г,ПА И A v '' Г »= А;ПА к }'
Повторное применение приведенных правил вывода позволяет
снимать (и ставить) двойные отрицания в формулах. В скобках указаны
обозначения этих правил: введение отрицания.
Замечание. Содержательно: для первого правила вывода в
секвенции Г,ПА N А формула ПА (слева от знака *=) истинна, если формула
А (справа от знака N в секвенции Г 1= А;А) ложна. Для второго
правила в секвенции Г N А;ПА формула ПА ложна, если формула А в
секвенции Г,А *= А истинна.
А1?...,АЛ,А,В 1= Bi;...;Bm
Утверждение 2. Aj д.ШИ Bl;...^ '
правило обратимо.
Доказательство.
А! АЛ,А,В *= В1;...;Вт <— Ах&.. .&АП&А&В I- BjV...VBm —♦
А1&...&АП,А&В Н B1V...VBm <— Alf...,A„,A&B N B1;...;Bm.
Следствие. Справедливо обратимое правило введения конъюнкции
. Г,А,В И A (s .v
слева от знака N : ^ А « р и. а (& ^J-
Г,А&В f A
Замечание. Содержательно: в секвенции Г,А&В N А формула А&В
(слева от знака *=) истинна, если формулы А,В (слева от знака *= в
секвенции Г,А,В *= А, где запятая означает конъюнкцию) истинны.
В некоторых из последующих утверждений в числителе правила
вывода стоит несколько секвенций. Имеется в виду, что они связаны
дизъюнкцией.
105
Утверждение 3. Справедливо обратимое правило введения конъюнк-
. Г Е А;А ГН А;В ,. - ч
ции справа от знака N : ' ,,»» (*= &).
Доказательство. Г Н AVA Г I- AVB <—>
Г Ь ПА - А Г h 1A - В ^
Г,ПА Ь А Г,ПА ЬВ^
Г,ПА Ь A&B —♦ Г1-1А- А&В <—
Г \- AVA&B ^Г»= А;А&В.
Замечание. Содержательно: в секвенции Г N А;А&В формула А&В
ложна, если ложна формула А (в секвенции Г N А;А) или ложна
формула В (в секвенции П=Д;В).
Утверждение 4. Справедливо обратимое правило введения дизъюнк-
. Г,А НА Г,В 1= А А/ . v
ции слева от знака N : —г г AVR t= Л ' ''
Доказательство. Г,А h А Г,В Ь Д ♦—♦
ГЬА-Д ГЬВ-А <-> Г h 1A V А Г h IB V A ^
Г Ь ПА - ПА Г Ь ПА - ПВ «-» Г,ПА h ПА Г,ПА Ь ПВ —♦
Г,ПА Ь ПА&ПВ «-» Г I- ПА - ПА&ПВ —♦ Г Ь А V ПА&ПВ <->
Г Ь П(ПА&ПВ) - А «-» Г,П(ПА&ПВ) Ь A <—
T,AVB Ь A —♦ Г,AVB * А.
Замечание. Содержательно: в секвенции r,AVB N А формула AVB
истинна, если истинна формула А (в секвенции Г,А *= А) или истинна
формула В (в секвенции Г,В Н А).
Утверждение 5. Справедливо обратимое правило введения дизъюнк-
Г t= A;A;B ,. ич
ции справа от знака Н : л-aVR ' '*
Замечание. Содержательно: в секвенции Г *= A;AVB формула AVB
ложна, если ложна формула А и ложна формула В (в секвенции Г N
А;А;В, где точка с запятой означает дизъюнкцию).
Утверждение 6. Справедливо обратимое правило введения имплика-
106
Г,A f A;B ,. v
ции справа от знака f : '. A . ' (f -*).
1 F Д; A~*iJ
Доказательство.
Г,A h A;B ♦— Г,А Н AVB —♦
Г,А hlA-^B +-+ г,А,ПА \- В «-> . Г,~1Д Ь A - В —*
Г Ь 1A -* (A - В) —* TI-AV(A-B) <— Г \- A;(A-B).
Замечание. Содержательно: в секвенции Г f Д;А-*В формула А-*В
ложна, если формула А истинна, а формула В ложна (в секвенции Г,А
f А;В).
Утверждение 7. Справедливо обратимое правило введения имплика-
. Г,В f А Г f А;А , . ч
ции слева от знака f : —2 г— (-♦ f).
Доказательство. Г,В1-А Г Ь А;А ^
Г ЬВ-А TI-AVA « Г Н (В ■• Д)&(Д V А) —♦
Г Ь ("IB VA)&(A V А) <-> Г Ь (А - В) - А —» Г,А-В Ь A.
Замечание. Содержательно: в секвенции Г,А->В f А формула А-*В
истинна, если формула А ложна (в секвенции Г f А;А), или формула
В истинна (в секвенции Г,В f A).
Утверждение 8. Справедлива секвенция Г,A f A;A.
Доказательство.
Г,A f А;А —► Г,А Н А V А —* Г,A h 1A - А ^
Г \- А - (ПА - А) —* Г Н А&ЛА - А <-> Ь А&ПА - А.
Последнее справедливо. Поэтому справедлива и исходная
секвенция.
Замечание. Утверждение 8 устанавливает тот простой факт, что
формула А выводится из формулы А при любых совокупностях Г и А.
Секвенции Г,A f А,А примем впоследствии за аксиомы
секвенциального исчисления высказываний. Рассматриваемые как формулы логики,
опровержимыми (это формулы общезначимые) они не являются.
5.2. Секвенциальное исчисление высказываний (СИВ)
Формальные символы СИВ составляют формальные символы ИВ плюс
два дополнительных символа: секвенциальный символ f и ; (точка с
запятой). Формулы СИВ совпадают с формулами ИВ. Если Г и А есть
конечные совокупности формул СИВ, то выражение Г f А есть
107
секвенция.
Схемы аксиом.
Если А - формула СИВ, то секвенция вида Г,А N А,А есть
единственная схема аксиом в СИВ.
Замечание. Так как AHA*—♦ I- А -♦ А «—* I- А V ПА (последняя
формула есть закон исключенного третьего), то в качестве схемы
аксиом в СИВ, в сущности, берем закон исключенного третьего.
Правила (секвенциального) вывода.
Введение отрицания.
г * Д;А о ,=)• Г>А N A (* -о
Г.ПА (= д ^ R'» Г 1= Д;ПА l ;
Введение конъюнкции.
Г,А?В N Д г* А;А Г N А;В ( ,
Г.А&В 1= A V<K Л Г 1= Д;А&В v ;-
Введение дизъюнкции.
Г,А
Введение
г,в
t= A
T.AVB
Г
N
,в
А
s импликации
1= А
Г.А-В
Г
\=
N
А
1= А
[.
А;А
(V И- Г )= А;А;В , уч
, , Г,А Н А;В ( ^
^ ;> Г Н А;А-В ^ ;*
Выбор этих правил вывода оправдывается ранее доказанными
утверждениями 1-7. Приведенные правила вывода обратимы. Эти правила
довольно естественны, тем более, что Г и А являются множествами
формул.
Определение. Вывод в СИВ есть конечная последовательность
секвенций, каждая из которых получена из предыдущих секвенций по
одному из правил вывода.
Определение. Секвенция S выводима в СИВ, если в СИВ существует
вывод, последней секвенцией которого является S.
Определение. Доказательство в СИВ есть конечная
последовательность секвенций, каждая из которых есть либо аксиома, либо
получена из предыдущих секвенций по одному из правил вывода.
Определение. Секвенция S доказуема в СИВ, если в СИВ
существует доказательство, последней секвенцией которого является S.
Вывод, как и доказательство в СИВ, удобно оформлять в виде де-
108
рева. Ниже приведем примеры построения деревьев вывода и
доказательства в СИВ.
Определение. Формула А доказуема в СИВ (обозначение: bGA),
если в СИВ доказуема секвенция N А (с пустой левой частью).
Теорема. Если А - формула в СИВ (А есть формула и в ИВ), то
hG A <— НА.
Доказательство. Всякая аксиома в СИВ доказуема в ИВ как закон
исключенного третьего. Всякое правило вывода в СИВ доказуемо в ИВ
(утверждения 1-7). Поэтому доказуемость формулы (или секвенции) в
СИВ влечет доказуемость этой формулы (или формулы ИВ,
соответствующей секвенции).
Всякая аксиома в ИВ доказуема в СИВ. Покажем это на примере
аксиомы (x->z)->((y->z)->(xVy "* z)), построив дерево вывода этой
аксиомы в СИВ. В листьях дерева помещены аксиомы СИВ, в корне -
доказуемая формула. Вывод осуществляется от листьев к корню (справа
от горизонталей указаны применяемые секвенциальные правила
вывода):
х И z;x;y у И z;x;y ^ ^
z,xVy N z;x xVy N z;x;y
(- И
z,y-*z,xVy ■*= z y->z,xVy t= z;x
(- h)
x->z,y-+z,xVy t= z ^ _^
x->z ,y-*z N xVy -♦ z
L7 TV^ ч ^ ">
x-*z N (y-*z)-4xVy -♦ z)
(*= -♦)
t= (x-*z )-*((y-*z)-»( xVy -* z))
Алгоритм построения дерева вывода в СИВ для формулы(х-*г)-*((у->
z)-*(xVy->z)) выглядит следующим образом. Для формул справа от
знака *= будем рассуждать о ложности одной из этих формул, а слева
- об истинности. Формула (x->z)->((y->z)-4xVy-*z)) ложна, если x-*z
истинно, a (y->z)-4xVy-*z) ложно. Помещаем формулу x-*z слева, а
формулу (y-*z)-*(xVy->z) справа от знака N. Секвенцию x-*z N (y-*z)->
(xVy-*z) помещаем на следующем уровне дерева вывода (над исходной
формулой). Проведя аналогичное рассуждение для формулы (y-*z)-*(xV
y-*z), получим секвенцию x->z,y-*z N xVy-*z, которую поместим над
предыдущей секвенцией. Эти же рассуждения для формулы xVy-*z
приведут нас к секвенции x-*z,y-*z,xVy N z, которую поместим над
предыдущей секвенцией. Формула x-*z истинна, если z истинно или х
ложно. Секвенция x-*z,y-*z,xVyt=z распадется на две секвенции:
z,y-*z,xVy 1= z и y-*z,xVy N z;x, которые поместим над предыдущей
109
секвенцией. Секвенция z,y->z,xVy*=z является аксиомой (по z) и
развертывать дерево вывода над ней не нужно. В секвенции y-^z,xVy *=
z;x формула y-*z истинна, если z истинно или у ложно. Секвенции
z,xVy *= z;x и xVy N z;x;y помещаем над секвенцией y->z,xVy *= z;x.
Секвенция z,xVy *= z;x является аксиомой. В секвенции xVy *= z;x;y
формула xVy истинна, если х истинно или у истинно. Секвенции х N
z;x;y и у N z;x;y помещаем над секвенцией xVy N z;x;y. Обе они -
аксиомы. Построение дерева вывода закончено. В листьях дерева
помещаются аксиомы. Следовательно, построенное дерево вывода
является доказательством исходной формулы в СИВ.
Если в построенном для некоторой формулы дереве вывода не во
всех листьях помещены аксиомы, то исходная формула общезначимой
не является. По формулам секвенций, помещенным в таких листьях,
можно найти такие значения переменных, при которых исходная
формула ложна (т.е. опровержима). Будем, например, исходить из
формулы (x->y&z)->((y->z)->(xVy-*z)). Построим для нее следующее дерево
вывода:
у , х *= z ; у t, х *= z ; у
yV t ,x N z ; у x N z;y;x
x->yVt,x N z;y x->yVt,y N z;y
x->yVt ,z,xVy N z x->yVt,xVy *=z;y
(V »=)
(- *=)
(V
(-
(*
(*=
(•=
и
и
-0
->)
-)
x-*yV t , y->z, xVy N z
x->yVt,y->z N xVy->z
x-»yVt H (y->z )-»(xVy-»z)
N (x-yVt )-((y-»z)-(xVy-z))
В этом дереве листьевая секвенция t,x N z;y дальнейшего
упрощения не допускает и (единственная из всех листьевых секвенций)
не является аксиомой. При t=l,x=l,z=0,y=0 исходная формула будет
ложной (опровержимой), На остальных наборах - истинна. Корневая
секвенция (а потому и исходная формула) в СИВ не доказуема.
В сущности, при построении дерева вывода в СИВ пытаемся
построить опровержение исходной формулы. При этом либо в листьях
окончательного дерева окажутся только аксиомы и тогда построенное
дерево вывода даст доказательство исходной формулы, либо в одном
из листьев поместится секвенция, не являющаяся аксиомой, и тогда
по этой секвенции можно построить опровержение исходной формулы,
которая доказуемой в СИВ не является.
Правило заключения в ИВ эквивалентно выводимости А,А->В I- В,
110
что в свою очередь эквивалентно секвенции А,А->В *= В. Выведем эту
секвенцию в СИВ. Ниже следует соответствующее дерево вывода:
А,В Е В А Е В;А , ч
А,А-В *= В V* )-
Классы формул, доказуемых в СИВ и ИВ, совпадают.
5.3. Секвенциальное исчисление предикатов (СИП)
Формальные символы СИП совпадают с формальными символами СИВ.
Формулы СИП совпадают с формулами УИП.
Пусть А,В - произвольные формулы СИП; Г,А - произвольные
конечные совокупности формул СИП. Секвенция (в СИП) есть выражение
вида Г N А. Единственной схемой аксиом в СИП является схема
аксиом Г,А *= А;А.
Правила вывода СИП составляют правила вывода СИВ (над
формулами из СИП) плюс следующие дополнительные обратимые правила
вывода, связанные с обработкой кванторов:
Г * А;А(у) ( yv Г,А(у) »= A fg *
Г * A;(Vx)A(x) ^ V;' Г,(Эх)А(х) * А ^ ^'
переменная у не входит в нижнюю секвенцию свободно;
Г,А(1),(Ух)А(х) Е A ,v ч Г Е A;A(t);(3x)A(x) ,. q4.
Г,(Ух)А(х) 1= A K1 *}> Г1= Д;(Эх)А(х) l d;'
переменная х не входит в верхнюю секвенцию свободно.
Определение. Доказательство в СИП есть конечная
последовательность секвенций, каждая из которых является либо аксиомой, либо
получена из предыдущих секвенций последовательности по одному из
правил вывода.
Определение. Секвенция S доказуема в СИП, если существует
доказательство, последней секвенцией которого является S.
Определение. Формула А доказуема в СИП, если в СИП доказуема
секвенция N А.
Исчисление секвенций предложил Гентцен. Приводим его в той
редакции, которую ему придал Кангер. Правила вывода Кангера
рассчитаны на то, чтобы, отправляясь от исходной формулы и опираясь на
естественный смысл логических операций и кванторов при построении
дерева вывода, попытаться построить опровержение для исходной
формулы. Либо это опровержение построим, либо полученное дерево
будет доказательством исходной формулы.
111
P(a)-Q(b),
(3x)(P(a)-Q(
(3x)(P(a)-Q(
P(a]
x)),
x))
1 1= (Эх
,P(a) 1=
N P(a)
)Q(x)
(3x)Q(x)
-Ox)Q(x)
Пример. Докажем в СИП формулу
(Эх)(Р(аИХх)) - (P(aH3x)Q(x)).
Доказательство этой формулы оформим в виде дерева (рассуждая
при этом так же, как это делали в случае вывода формул в СИВ):
Q(b),P(a) N Q(b);(3x)Q(x) (N 3)
Q(b),P(a) 1= Ox)Q(x) P(a) 1= (3x)Q(x);P(a)
(3 *)
0= -)
1= (3x)(P(a)-Q(x)) - (P(a)-(3x)Q(x)) ^ "°
Прокомментируем этот вывод для правил, связанных с кванторами.
В секвенции (3x)(P(a)->Q(x)),P(a)»=(3x)Q(x) формула (3x)(P(a)-Q(x))
истинна, если существует х, например, равный предмету Ь,
отличному от всех ранее встречавшихся предметов, для которого формула
P(a)~*Q(b) истинна. Переходим к секвенции P(a)-+Q(b),P(a)K3x)Q(x).
В секвенции Q(b),P(a)*=(3x)Q(x) формула (3x)Q(x) ложна, если
формула ~l(3x)Q(x) истинна, т.е. для всякого х, в том числе и для
х, равного Ь, формула Q(b) ложна. От секвенции Р(а) -» Q(b), P(a)
*= (3x)Q(x) переходим к секвенции Q(b), P(a) *= Q(b); (3x)Q(x),
которая является аксиомой. В построенном дереве все листья -
аксиомы, потому исходная формула (являясь общезначимой) доказуема
в СИП.
Пример. Попытаемся доказать в СИП формулу
(3x)(P(abQ(x)) - (P(aMVx)Q(x)).
Вывод оформим в виде следующего дерева:
Q(b),P(a) t= Q(c)
~Q(b),P(a) 1= (Vx)Q(x) P(a) N (Vx)Q(x) ;P(a)
P(a)-Q(b),P(a) N (Vx)Q(x)
"(3x)(P(abQ(x)),P(a) 1= (Vx)Q(x)
"(3x)(P(a)-Q(x)) N P(a)-(Vx)Q(x)
(V N)
(•= -)
1= (3x)(P(a)-Q(x)) - (P(a)-(Vx)Q(x))
В этом выводе в секвенции Q(b),P(a)*=(Vx)Q(x) формула (Vx)Q(x)
ложна, если истинна формула "I(Vx)Q(x), т.е. существует х, вообще
говоря, отличный от всех ранее встречавшихся предметов, равный,
например, предмету с, для которого "IQ(c) истинно, т.е. Q(c)
112
ложно. От секвенции Q(b),P(a)^(Vx)Q(x) переходим к секвенции
Q(b),P(a)*= Q(c), дальнейшее упрощение которой невозможно и
которая не является аксиомой. По этой секвенции строим опровержение
исходной формулы. Полагаем множество М = {а,Ь,с}, Р(а) = И, Q(b)
= И, Q(c) = Л. В остальном предикаты Р и Q определяем
произвольно. На интерпретации / = (M,P,Q) исходная формула превращается в
ложное высказывание. Интерпретация / и есть опровержение исходной
формулы. Следовательно, исходная формула общезначимой не является
и в СИП не доказуема.
Теорема. Классы формул, доказуемых в СИП и УИП совпадают.
Доказательство. Покажем, что всякая формула, доказуемая в УИП,
доказуема и в СИП. Дерево вывода
A(t),(Vx)A(x) N A(t)
1= (Vx)A(x) - A(t)
является доказательством в СИП аксиомы (Vx)A(x) -* A(t). Дерево
вывода
A(t) 1= A(t);(3x)A(x) f ^
A(t) H (Зх)А(х) / ч
t= A(t ) - (3x)A(x)
является доказательством в СИП аксиомы A(t) -» (Зх)А(х). Правила
вывода в УИП являются правилами вывода и в СИП. Покажем теперь,
что всякая формула, доказуемая в СИП, доказуема и в УИП.
Действительно, всякая аксиома Г,А *= А;А в СИП соответствует доказуемой в
УИП формуле Г&А -» AVA. Можно показать, что (обратимые) правила
вывода в СИП доказуемы и в УИП (если секвенцию А! ,А2,... ,А„ 1=
В1;В2;...;Вт рассматривать как формулу
Ах8сА28с...8сАп - B1VB2V...VBm).
Следствие. Классы формул, доказуемых в СИП, совпадают с
классом общезначимых формул.
Естественный вывод Гентцена довольно удобен при вычислении
общезначимости формулы логики предикатов. Его элементы
используются в логическом программировании. Но первые трансляторы были
построены в логике предикатов с правилом резолюции Дж.Робинсона,
компьютерная реализация которого оказалась достаточно
эффективной.
113
6. МЕТОД РЕЗОЛЮЦИЙ В ЛОГИКЕ ПРЕДИКАТОВ И ПРОЛОГ
6.1. Метод резолюций в логике высказываний
Построим формально-логическое исчисление, в котором
описываются все невыполнимые формулы алгебры логики и только они. Понятия
алфавита, формулы, подформулы, интерпретации, модели,
выполнимости, невыполнимости, общезначимости, опровержимости совпадают с
аналогичными понятиями в исчислении высказываний.
Для удобства конъюнкцию нескольких формул будем иногда
задавать как множество формул, составляющих эту конъюнкцию. Обратно,
конечное множество формул отождествим с их конъюнкцией. При этом
конъюнкцию нескольких формул в случае надобности предполагаем
заданной без повторов и не зависящей от порядка ее конъюнктивных
сомножителей.
Пусть М - конечное множество формул (т.е. их конъюнкция), все
переменные которых содержатся среди pj ,р2,... ,рл. Как и прежде,
пишем в этом случае М(р1,р2>... ,ря). Понятие интерпретации
множества формул М совпадает с понятием интерпретации одной
формулы, являющейся конъюнкцией формул из М. Множество формул М
общезначимо, если общезначима каждая формула из М. Множество формул
М выполнимо, если существует интерпретация, на которой выполнимы
все формулы из М. Множество формул М невыполнимо, если для всякой
интерпретации найдется формула из4 М, ложная на этой
интерпретации. Множество формул М опровержимо, если существует
интерпретация, на которой одна из формул в М ложна.
Формула В есть логическое следствие формул А1,...,АЛ, если
формула Ах& А2& . ..& А„ -» В общезначима.
Формула В есть логическое следствие формул А1(...,АЛ тогда и
только тогда, когда формула Ах& ...&А„ & "IB (эквивалентная
отрицанию формулы А2& ...&А„ -> В) невыполнима.
Литера есть элементарная формула (атом) или ее отрицание.
Литеры р и "1р называются контрарной парой. Дизъюнкт есть дизъюнкция
конечного числа литер. Для удобства дизъюнкт иногда задают как
множество литер. Обратно, конечное множество дизъюнктов можно
задать как их дизъюнкцию. При этом дизъюнкцию нескольких дизъюнктов
предполагаем заданной без повторов и не зависящей от порядка ее
дизъюнктивных слагаемых.
Примеры дизъюнктов, р V ~lq; р V ~lq V г; {р, "Iq, r}; ~lp V q V
lr V Is; Пр, q, Ir, Is}.
Пустой дизъюнкт П по определению тождественно ложен. Его можно
понимать как невыполнимую формулу. Множество дизъюнктов невыпол-
114
нимо, если на каждой интерпретации ложен хотя бы один дизъюнкт.
Пример. Множество дизъюнктов S = {р V "IqV ~lr, "IpVqV "lr}
выполнимо, ибо конъюнкция (р V "Iq V ~lr) &(~lp Vq V ~lr) истинна при
р = И, q = И, г = Л. Множество дизъюнктов S = {р V q, р V "lq, "lp
V q, "lp V "Iq} невыполнимо, ибо их конъюнкция тождественно ложна.
6.1.1. Семантическое дерево
Пусть S = S(p2 ,р2,... ,р„) есть множество дизъюнктов. Задать
интерпретацию для S - злачит задать истинностные значения
пропозициональных переменных в S. Для переменной р положим р1 равным
р, а р° равным "1р. Пусть набору литер (pjl,... ,p„n) соответствует
интерпретация / = (с1,...,ся); при этом 1 отождествляется с
истиной (И), а 0 - с ложью (Л).
Определение. Пусть S = S(p1,...,pn) - множество дизъюнктов.
Семантическое дерево Т для S есть конечное бинарное дерево, в
ярусе i которого из каждого узла N исходят два ребра, из которых
одно помечено литерой р,, а другое - литерой "lp,-.
Всякой ветви дерева Т (ее длина равна п) можно поставить в
соответствие некоторую интерпретацию для S следующим образом. Если
ребра некоторой ветви из Т помечены литерами (р^,... ,р„л), то
эта ветвь задает интерпретацию / = (с1,... ,сп). Семантическое
дерево Т исчерпывает все 2п интерпретаций для S.
Определение. Узел N в семантическом дереве Т для S называется
опровергающим, если путь в Т от корня до N задает такие
истинностные значения переменных р,, при которых опровергается
некоторый дизъюнкт С из S, но при этом никакой другой узел от
корня до N указанным свойством опровержимости не обладает.
Множество дизъюнктов S невыполнимо тогда и только тогда, когда
любая ветвь в семантическом дереве Т для S имеет опровергающий
узел. Обрежем семантическое дерево Т для S, удалив из Т все
поддеревья с корнями в опровергающих узлах (оставив опровергающие
узлы в Т). Полученное дерево называется замкнутым семантическим
деревом для S. Множество дизъюнктов S невыполнимо тогда и только
тогда, когда в замкнутом семантическом дереве все его концевые
узлы (листья) являются опровергающими.
Пример 1. Множество дизъюнктов
S = {р, Пр V q, lq V г, lq V lr}.
Полное семантическое дерево для S приведено на рис.6.1а. Его узлы
перенумерованы. Узлы с 7 по 14 - концевые. Узел 0 есть корень
дерева. Путь от корня 0 до концевого узла 10, помеченный литерами
115
p, ~lq, "lr, дает интерпретацию / = (И, Л, Л); путь от корня до
узла 12 - интерпретацию / = (Л, И, Л). Замкнутое семантическое
дерево Т для S приведено на рис.6.16. В концевом узле 4 при
значениях переменных р = И, q = Л опровержим дизъюнкт "Ip V q. В узле
6 опровержим дизъюнкт "Iq V г. Все концевые узлы в Т являются
опровергающими (они помечены крестами). Поэтому множество
дизъюнктов S невыполнимо.
Пример 2. Множество дизъюнктов
S = {р, Пр V q, lq V lr}.
Полное семантическое дерево для S (см.рис.6.1а) совпадает с
таковым для S из предыдущего примера. На рис.бЛв приведено
замкнутое семантическое дерево Т для S. Не все его концевые узлы
являются опровергающими, именно, в узле 6 при р = И, q = H, г = Л
все дизъюнкты из S истинны. Поэтому множество дизъюнктов S
невыполнимым не является (т.е. S выполнимо).
6.1.2. Правило резолюции
Определение. Пусть С, и С2 - дизъюнкты (рассматриваемые как
множества литер); р - пропозициональная переменная, причем р €
С1? Пр € С2. Тогда дизъюнкт (Сг - р) U (С2 - Пр) называется
резольвентой дизъюнктов Сх и С2. Правило получения резольвенты
дизъюнктов С! и С2 называется правилом резолюции. Литеры р и Пр
называются отрезаемыми.
Не будем в дальнейшем указывать, рассматриваются ли дизъюнкты
Сх и С2 как формулы C'V p и С" V Пр соответственно, или как
множества литер. Это будет видно из контекста.
Пусть равенство С = ПРСС^С^) означает, что дизъюнкт С получен
из дизъюнктов Cj и С2 по правилу резолюции.
Определение. Резолютивный вывод из множества дизъюнктов S есть
конечная последовательность дизъюнктов, каждый из которых есть
либо дизъюнкт из S, либо получен из предыдущих дизъюнктов
последовательности по правилу резолюции. Дизъюнкт С выводим из
множества дизъюнктов S (обозначение: S Ь С), если существует
вывод из S, последний дизъюнкт которого есть С.
Теорема. Если из множества дизъюнктов S выводится дизъюнкт С,
то формула S -> С общезначима.
Доказательство. Индукция по числу к применений правила
резолюции.
БАЗИС, к = 1. Резольвента С дизъюнктов Сх и С2 есть логическое
следствие из Сх и С2, ибо если Сх = С V р, С2 = С" V Пр (и тогда
формула С V С" есть резольвента для С{ и С2), то формула
116
7 8 7
XX X
б в
Рнс.6.1
(С V р)&(С" V ~1р) - (С V С") общезначима.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что теорема справедлива
для всякого вывода, число применений правила резолюции в котором
меньше к.
ШАГ ИНДУКЦИИ. Покажем, что теорема справедлива для всякого
вывода, число применений правила резолюции в котором равно к.
Пусть Cj ,С2,... ,С,,... ,С^,... ,С^ есть вывод длины к, последний
дизъюнкт которого есть дизъюнкт Сл, равный С, причем Ск =
ПР(С,,С;). Так как длины выводов
*^\ >^-'2> ' ' ' >^ i ^ ^ 1 > ^ 2 » * * * »^ / » * * * > ^ 7
меньше к, то по предположению индукции формулы S -* С,- и S -» Су-
общезначимы. Тогда общезначима и формула S -» С,- & Су. Так как С^
117
= nP(C,-,Cfc), то по базису формула С, & Су -» С^ общезначима.
Следовательно, общезначима формула S -> С^.
Шаг индукции установлен. Теорема доказана.
Теорема (о полноте). Непустое множество дизъюнктов S
невыполнимо тогда и только тогда, когда из S выводится пустой дизъюнкт.
Доказательство. Пусть множество дизъюнктов S невыполнимо.
Пусть Т - полное семантическое дерево для S. Так как S
невыполнимо, то в замкнутом семантическом дереве Т' для S все концевые
узлы - опровергающие.
Утверждение. Пустой дизъюнкт выводится из S.
Доказательство. Индукция по числу к всех узлов в Т' при любом
S, (а потому и при любом Т).
БАЗИС, к = 1, т.е. Т' имеет единственный (опровергающий) узел.
Так как множество S не пусто и невыполнимо, то S содержит пустой
дизъюнкт, который выводится из S.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что доказываемое
утверждение справедливо для любого S, а потому и для любого
семантического дерева Т, для которого Т' имеет число узлов меньше к.
ШАГ ИНДУКЦИИ. Покажем, что доказываемое утверждение
справедливо для любого S, а потому и для любого семантического дерева
Т, для которого замкнутое дерево Т' имеет число узлов к. Пусть N
- узел, предшествующий двум опровергающим (концевым) узлам Nx и
N2 в Т'; ребрам, исходящим из N, приписаны литеры L^ и "IL^; пути
от корня до Nj и N2 проходят через литеры
*-Ч >^2 » * * ' У^к-1 » Мс>
*-ч у*-12 9 • • • i^k-\ у **-*к
соответственно. Пусть С2 и С2 есть дизъюнкты из S, опровержимые
в Nj и N2 соответственно. В узле N дизъюнкты С1 и С2 не
опровергаются. Поэтому L^ входит в С1? a "IL^ - в С2. Отрезая L^,
получим резольвенту С = {С1 - L^) U (С2 - "IL^). Так как
С, = Lj V L2 V ... V Llr V lhk ложно в Nlf
С2 = h\ V L2 V ... V L2r V Lk ложно в N2,
то резольвента
С = Lj V ... V Llr VLjV ... V Lj ,
не содержащая L^ и "IL^, ложна в N. Пусть Sj = S U {С}. Множество
S1 невыполнимо, ибо невыполнимо его подмножество S. Семантическое
дерево для Sx совпадает с семантическим деревом для S. Дерево Т1?
полученное из Т' удалением узлов Nx и N2, содержит в себе
замкнутое дерево Т1 для S l, все концевые узлы которого опровергающие.
118
Так как число узлов в Тх меньше к, то по предположению индукции
из S{ выводится пустой дизъюнкт. Следовательно, пустой дизъюнкт
выводится из S, ибо Sj получается из S однократным применением
правила резолюции.
Утверждение, а вместе с ним и необходимость теоремы доказаны.
Достаточность теоремы очевидна, ибо если из S выводится пустой
дизъюнкт, то формула S -> □ общезначима, а потому множество
дизъюнктов S невыполнимо.
Теорема доказана.
Пример 1. Множество дизъюнктов
S = {р V q V г, р V q V lr, p V lq, lp V lq, lp V q}.
Строим для S замкнутое семантическое дерево Т (рис.6.2а). Все
его узлы опровергающие. Поэтому множество S невыполнимо. В узле 6
из дизъюнктов pVqVr, pVqVlr выводится р V q. В узле 2 из
дизъюнктов р V "lq, р V q выводится р. В узле 1 из "1р V "lq, "lp V q
выводится "Iр. В узле 0 из р и "lp выводим П. Вывод пустого
дизъюнкта из S имеет следующий вид:
(1) р V q V г, из S;
(2) р V q V lr, из S;
(3) р V q, ПР(1,2);
(4) р V lq, из S;
(5) р, ПР(3,4);
(6) "lp V lq, из S;
(7) "lp V q, из S;
(8) "1р, ПР(6,7);
(9) □, ПР(5,8).
Пример 2. Множество дизъюнктов
S = {1р V lq, lp V q V lr, p V lq}.
Строим для S замкнутое семантическое дерево Т (рис.6.26). Не
все его узлы опровергающие (узлы 6 и 8). Поэтому множество
дизъюнктов S невыполнимым не является, и потому пустой дизъюнкт
из S не выводится.
Приведем далее следующее утверждение.
Теорема. Пусть S есть непустое множество дизъюнктов. Следующие
утверждения эквивалентны.
1. Множество дизъюнктов S невыполнимо.
2. Пустой дизъюнкт выводим из S.
3. Формула S -> □ общезначима.
Напомним, что предикат есть функция, определенная на некотором
множестве и принимающая одно из двух значений: И и (Л). Из
простых предикатов с помощью логических операций можно строить более
119
6.2. Эрбрановские универсум, базис, интерпретация
Переходим к изложению метода резолюций в логике предикатов,
сложные предикаты. Понятия алфавита, терма, формулы, подформулы,
интерпретации, общезначимости, выполнимости, невыполнимости, оп-
ровержимости совпадают с аналогичными понятиями логики
предикатов. Атомарная формула (или атом) строится из предикатного
символа и термов.
Как и в исчислении высказываний, формула В логики предикатов
есть логическое следствие формул А1Э А2,...,А^, если формула
А!&А2&...&А^ -* В общезначима.
Определение. Литера есть атом или его отрицание. Дизъюнкт есть
Рис. 6.2
120
дизъюнкция конечного числа литер.
Определение. Пусть S - некоторое множество дизъюнктов и Н0 -
множество всех констант в S. Если констант в S нет, то полагаем
Н0 = {а}, где а - символ некоторой константы, не содержащейся в
S. Далее полагаем Hl + 1= Н, U {f(tx,... ,tk) : f - функциональный
символ из S, a tlf...9tk - принадлежат Н,}; i = 0,1,2,...;
оо
Н = U Н..
1=0 '
Множество Н называется эрбрановским универсумом множества
дизъюнктов S.
Замечание. Эрбрановский универсум есть множество всех термов
сигнатуры для S, не имеющих предметных переменных.
Примеры.
1. S = {Р(а), ~1Р(х) V P(f(x))}. Множество {a,f} составит
материал (формальные символы) для построения эрбрановского
универсума:
Н0 = {а};
Нх = {a, f(a)};
Н2 = {a, f(a), f(f(a))};
Н ="{а, f(a), f(f(a)), f(f(f(a))),... }.
2. S = {P(x) V Q(x), R(z), T(y) V W(y)}.
H0 = {a} = Hx = H2 = ... = H.
3. S = {P(f(x),a»,g(y),b), Q(x)}. Множество {a,b,f,g} составит
материал для построения эрбрановского универсума:
Н0 = {а,Ь};
Н, = {a,b,f(a),f(b),g(a),g(b)};
Н = {a,b,f(a),f(b),g(a),g(b),f(f(a)),f(f(b)),f(g(a)),
f(g(b)),g(f(a)),g(f(b)),g(g(a)),g(g(b)),f(f(f(a))),...}.
Определение. Эрбрановский базис для множества дизъюнктов S
есть множество всех атомов вида P(tlf... ,t^), где Р - предикатный
символ из S, a t19...9tk - элементы эрбрановского универсума.
Замечание. Эрбрановский базис В составляют элементарные
формулы (атомы) сигнатуры для S, в которых отсутствуют предметные
переменные.
Пример. S = {P(f(x),a,g(y),b) V Q(x)}. Множество {a,b,f,g,P,
Q} составит материал (формальные символы) для построения эрбра-
121
новского базиса, который является множеством
В = {P(t1,t2,t3,t4), Q(t) : t,tlft2ft3.t4 пробегают
элементы эрбрановского универсума}.
Определение. Основной пример дизъюнкта С из множества
дизъюнктов S есть дизъюнкт, полученный заменой всех предметных
переменных в С на члены эрбрановского универсума.
Пример. Множество дизъюнктов S = {Р(х), Q(f(y)) V R(y)}.
Эрбрановский универсум Н = {a,f(a),f(f(a)),f(f(f(a))),...}.
Пусть дизъюнкт С есть Р(х). Тогда Р(а), P(f(a)), P(f(f(a))),.. •
есть основные примеры дизъюнкта С. Пусть теперь в качестве С взят
дизъюнкт Q(f(y)) V R(y). Тогда
Q(f(a)) V R(a), Q(f(f(a))) V R(f(a)),
Q(f(f(f(a)))) V R(f(f(a))),...
есть основные примеры дизъюнкта С.
Замечание. Основной пример дизъюнкта С не имеет предметных
переменных; он получается замещением предметных переменных в С
некоторыми термами из эрбрановского универсума.
В дальнейшем в сигнатуру формулы (множества формул) не будем
включать ее свободные предметные переменные. Предполагаем, что
формула их не содержит; либо свободные предметные переменные,
если они все же имеются, рассматриваются как предметные константы.
Определение. Эрбрановская интерпретация (Н-интерпретация)
множества дизъюнктов S есть всякая интерпретация вида
IH = (H,Pl9...,Pn,f1,...,fm,al,...,ar),
где множество Н есть эрбрановский универсум для S;
v*i »• • • »Рл>м )'")lm>ai»,,,»ar-' ~
сигнатура для S (т.е. множество всех предикатных, функциональных,
константных букв из S; множество свободных предметных переменных
в сигнатуру для S не входит); для всяких термов tl9...,tk из Н
функция f{tx,...,tk) = f(tlf...,t*), т.е. значение f(t19...,tk)
есть слово в алфавите, из которого строятся термы эрбрановского
универсума Н; значения предикатов Р, на термах из Н не
ограничиваются ничем; всякое а, = а,.
Прежде чем приступить к следующей теореме, сделаем следующее
замечание. Пусть А есть замкнутая формула логики предикатов; IH -
эрбрановская интерпретация для A; (Vx^.. .(Vx^)B - стандартная
форма Скулема для А; Сг & ... & Cs - конъюнктивная нормальная
форма для В. Тогда следующие утверждения эквивалентны.
1. Формула А невыполнима в IH.
122
2. Формула (Vxj).. .(Vxfc)B невыполнима в IH.
3. Формула (Vxj).. .(Ух*) (Cj & ... & C5) невыполнима в IH.
4. Формула (Vxj).. .(Vx^Cj & ... & (Ухх).. .(Vx^)C5 невыполнима
в IH.
5. Некоторый сомножитель (Vxj).. .(Vx^)C/ невыполним в IH.
6. Формула "KVxj).. .(Vx^)Cl выполнима в IH.
7. Формула (3x1)...(3xjc)~\Cj(x1,...,Xjc) выполнима в IH.
8. Существуют x1=t1€H, ...,x^ = t^€H, для которых
основной пример C/Ctj,... ,tfc) (обозначим его через С') дизъюнкта
С|(х1Э... ,Xfc) (обозначим его через С) ложен в IH.
9. Существует основной пример С некоторого дизъюнкта С,
ложный в IH. При этом дизъюнкт С есть некоторая дизъюнкция литер
Ll(xl,... ,Xfc) V ... V Lu(xx,... ,Xfc), основной пример С есть
дизъюнкция элементов эрбрановского базиса L2 (tx,... ytk) V ... V
Теорема. Множество дизъюнктов S невыполнимо тогда и только
тогда, когда S невыполнимо во всех Н-интерпретациях.
Доказательство. Если S невыполнимо, то S ложно во всех
интерпретациях, в том числе и во всех Н-интерпретациях. Пусть
теперь S ложно во всех Н-интерпретациях. Пусть
Pl,F2,... - все предикатные буквы, встречающиеся в S;
flff2,... - все функциональные буквы, встречающиеся в S;
а1Уа2У... - все константные буквы, встречающиеся в S. Допустим
противное: множество дизъюнктов S выполнимо и пусть I = (М,^,
...,/1,...,а1,...) - интерпретация, в которой S истинно. Построим
отображение <р : Н -* М, положив у(а,) = at = a,; <p(fi(tlf...ft/c))
= fi(<p(ti),...,<p(tic))y т.е. заменив в терме из Н все
функциональные и константные символы из Н на функции и константы из /.
Построим Н-интерпретацию
IH = (H, d,.. .,#!,...,&!,...), положив
СДц,..,^.) = И — Р|(<р(Ц),...,<р(1|Л)) = И.
В построенной Н-интерпретации IH множество S ложно, т.е.
существует основной пример С некоторого дизъюнкта С из S, ложный
в IH. Пусть дизъюнкт С = Lx V ... V Lu и литера L, в нем равна
Pi(t(xlf ...,Xfc),...). Тогда
ei(t(tlf...,t*),...) = Л — Pi(<p(t(tl9...ftk))f...) = Л.
Поэтому литера L, принимает значение Л. Аналогично поступаем с
остальными литерами из С. Тогда в интерпретации / все литеры в С
ложны и потому С ложно в /, откуда получаем, что S ложно в /.
Противоречие с истинностью S в /. Следовательно, S ложно во всех
123
интерпретациях, т.е. множество дизъюнктов S невыполнимо.
Теорема (Левенгейма-Скулема). Если формула логики предикатов
имеет какую-либо модель, то она имеет и не более чем счетную
модель (например, Н-интерпретацию).
Теорема Левенгейма-Скулема утверждает, что с помощью понятия
выполнимости формулы логики предикатов нельзя определить мощность
ее модели.
6.3. Семантические деревья и теорема Эрбрана
Пусть множество дизъюнктов S имеет сигнатуру (Р1Э... ,flf...,
aj,...) и эрбрановский базис {АрА2,...}, состоящий из атомарных
формул для S без предметных переменных. Задать эрбрановскую
интерпретацию значит задать истинностные значения для атомов
эрбрановского базиса. Пусть выражение Ас, где с € {0,1}, означает, что
А1 = А, А0 = ПА. Для последовательности формул {А/,А22,...} (без
предметных переменных) зададим эрбрановскую интерпретацию как
последовательность с х, с 2,..., считая, что 1 символизирует истину,
а 0 - ложь. Например, двум последовательностям формул
А1 А° А° А1 А°
А° А° А° А1 А1
соответствуют две эрбрановские интерпретации
И, Л, Л, И, Л, ... ;
Л, Л, Л, И, И, ... .
Определение. Пусть S есть множество дизъюнктов и {А1А29...} -
эрбрановский базис для S. Семантическое дерево Т для S есть
бинарное дерево, в каждом ярусе i которого из каждого узла N
исходят два ребра, из которых одно помечено буквой А/, а другое - ~1А,
(рис.6.3).
Всякая ветвь дерева Т задает некоторую Н-интерпретацию.
Семантическое дерево Т исчерпывает все Н-интерпретации для S.
Определение. Узел N в семантическом дереве Т называется
опровергающим, если путь в Т от корня до N содержит истинностные
значения атомов из эрбрановского базиса В, при которых опровергается
некоторый основной пример С некоторого дизъюнкта С из S. При
этом никакой узел от корня до N указанным свойством опровержимо-
сти не обладает.
Пример. S = {Р(х), 1Р(х) V Q(f(x)), 1Q(f(a))}.
Эрбрановский универсум Н = {a, f(a), f(f(a)),...}.
Эрбрановский базис В = {P(a),Q(a),P(f(a)),Q(f(a)),P(f(f(a))),
124
Рмс.6.3
Q(f(f(a))),...}. Построим для S семантическое дерево Т (рис.6.4).
Опровергающие узлы на рис.6.4 помечены крестами. Укажем
соответствующие этим узлам опровергающие Н-интерпретации.
Эрбрановский базис В = {P(a),Q(a),P(f(a)),Q(f(a)),...};
узел 2
узел 9
узел 10
узел 11
узел 12
узел 13
узел 14
н.
Н2
Н3
н4
н5
н6
н7
Л .
и
и
и
и
и
и
• • >
и
и
и
и
л
л
и
и
л
л
и
и
и
л
и
л
и
л
CXf(a))"lQ(f(a))CXF(a))-lQ(f(a))Q(f(a))nQ(f(a))Q(f(a))nQ(f (a))
I \ i \ * V 4 V
9 10 11 12 13 14 15 16
XXX XX XX X
Рмс.6.4
125
узел 15 Н8 ИЛ Л И ... ;
узел 16 Н9 ИЛ Л Л ....
В узле 2 опровержим дизъюнкт С = Р(х), ибо его основной пример
С = Р(а) ложен, т.е. формула Р(х) на интерпретации Н1 ложна.
В узле 9 опровержим дизъюнкт С = ~IQ(f(a)), ибо он в
интерпретации Н2 ложен.
В узле 10 опровержим дизъюнкт С = ~1Р(х) V Q(f(x)), ибо его
основной пример С = ~1Р(а) V Q(f(a)) ложен в Н3, т.е. формула ~1Р(х)
V Q(f(x)) на интерпретации Н3 ложна.
В узле 11 опровержим дизъюнкт С = ~IQ(f(a)), ибо он в
интерпретации Н4 ложен.
В узле 12 опровержим дизъюнкт С = ~1Р(х) V Q(f(x)), ибо его
основной пример С = ~1Р(а) V Q(f(a)) ложен в Н5.
В узле 13 опровержим дизъюнкт С = ~IQ(f(a)), ибо он в
интерпретации Н6 ложен.
В узле 14 опровержим дизъюнкт С = ~1Р(х) V Q(f(x)), ибо его
основной пример С = ПР(а) V Q(f(a)) в Н7 ложен.
В узле 16 опровержим дизъюнкт С = Q(f(a)), ибо он в
интерпретации Н8 ложен.
В узле 16 опровержим дизъюнкт С = ~1Р(х) V Q(f(x)), ибо его
основной пример С = ~1Р(а) V Q(f(a)) в Н9 ложен.
Множество дизъюнктов S невыполнимо, ибо S опровержимо на
каждой Н-интерпретации, т.е. всякая Н-интерпретация опровергает один
из дизъюнктов в множестве S (делает ложным один из конъюнктивных
множителей в конъюнкции дизъюнктов множества S).
Заметим, что в каждом опровергающем узле невыполним один из
основных примеров одного из дизъюнктов в S. Конечное множество
узлов дерева {2,9,10,11,12,13,14,15,16} порождает конечное
множество (которое понимается как конъюнкция) {Р(а), ~lQ(f(a)), ~1Р(а) V
Q(f(a))} основных примеров, невыполнимых на всякой
Н-интерпретации (а потому и на произвольной интерпретации).
Лемма. Пусть S - невыполнимое множество дизъюнктов. Тогда
1) каждая ветвь семантического дерева Т для S содержит
опровергающий узел;
2) множество всех опровергающих узлов в Т конечно.
Доказательство. Пусть V - ветвь в Т, IHV - соответствующая
ветви V эрбрановская Н-интерпретация. Множество S ложно в IVH,
т.е. в S существует дизъюнкт С, существует основной пример С для
С, ложный в Н-интерпретации IVH ветви V. Основной пример С имеет
конечное число атомов. Поэтому на V существует узел N, на пути к
корню от которого определены все истинностные значения атомов из
126
С. Так как С ложно в IVH, то С опровержимо в N. В качестве
опровергающего узла N возьмем на пути V ближайший к корню узел с
указанным свойством. Итак, каждая ветвь в дереве Т имеет
опровергающий узел.
Покажем, что число опровергающих узлов в Т конечно. Обрежем
дерево Т, отбросив в Т каждое поддерево с корнем в опровергающем
узле (оставив сам опровергающий узел). Получим дерево Т'.
Покажем, что дерево Т' конечно (имеет конечное число узлов).
Допустим, что Т' бесконечно. Среди узлов яруса 1 в Т' выберем
поддерево Тх с корнем jc, которое содержит бесконечно много узлов (в
Т')- Узел х опровергающим не является. В Тх выберем то поддерево
Ту, с корнем у в ярусе 2, которое содержит бесконечно много узлов
из Т'. Узел у опровергающим не является. И так далее. В
результате получим бесконечную ветвь, проходящую через узлы дс,_у,..., без
опровергающего узла. Противоречие с наличием опровергающего узла
на каждой ветви в Т. Следовательно, множество опровергающих узлов
в Т конечно.
Теорема (Эрбрана). Множество дизъюнктов S невыполнимо (ни в
какой интерпретации) тогда и только тогда, когда существует
конечное невыполнимое (ни в какой интерпретации) подмножество S'
множества всех основных примеров дизъюнктов из S.
Доказательство. Пусть множество дизъюнктов S невыполнимо.
Возьмем семантическое дерево Т для S и отметим в Т все его
опровергающие узлы (их конечное число). Для каждого
опровергающего узла возьмем один основной пример того дизъюнкта из S, который
опровергается в этом узле. Образуется конечное невыполнимое на
всякой Н-интерпретации (а потому и на произвольной интерпретации)
множество S0 основных примеров дизъюнктов из S (рассматриваемое
как их конъюнкция), ибо для всякой Н-интерпретации ложен один из
основных примеров в S0 того дизъюнкта из S, который опровергается
в опровергающем узле на ветви семантического дерева Т,
соответствующей этой Н-интерпретации.
Пусть теперь некоторое множество S0 основных примеров для S
невыполнимо (при любой интерпретации). Покажем, что множество
дизъюнктов S невыполнимо. Допустим противное: множество S
выполнимо. Тогда существует интерпретация, а следовательно, и
некоторая Н-интерпретация IH, выполняющая множество S. Тогда любой
дизъюнкт С = (Vxj).. .(Vx^)D(x!,... ,х^) выполним на IH. По смыслу
кванторов общности на IH выполнима и любая формула D(tlf...9t/C)
при всяких tj,.,.,tfc из эрбрановского универсума Н для S. Но
тогда выполнимо и множество основных примеров S0, ибо всякий
основной пример С из S0 получается из некоторого дизъюнкта С из S
127
подходящей заменой предметных переменных х1У...,хк в D на
некоторые элементы t j,..., t^ эрбрановского универсума Н. Противоречие с
невыполнимостью S0. Следовательно, множество S невыполнимо.
Теорема доказана.
На основе теоремы Эрбрана строится формально-логическое
исчисление, а именно, метод резолюций, для установления невыполнимости
(а потому и общезначимости) формул логики предикатов. А именно,
формула А представляется в стандартной форме Скулема В.
Бескванторная часть формулы В представляется в конъюнктивной нормальной
форме и рассматривается как множество дизъюнктов S. Строим эрбра-
новский универсум и эрбрановский базис для S. Строим
семантическое дерево Т для S, поярусно проверяя каждый построенный узел на
опровержимость. Если построенный узел оказывается опровержимым,
то дальнейшее построение дерева от этого узла прекращается. Если
на некотором шаге дальнейшее построение дерева Т невозможно (все
листья конструируемого дерева оказались опровергающими узлами),
то множество дизъюнктов S (а потому и исходная формула А)
невыполнимо. Если же построение дерева Т продолжается бесконечно, то
множество дизъюнктов S (а потому и исходная формула А)
невыполнимым не является. Заметим, что не существует алгоритма, который
по любой формуле логики предикатов А устанавливал бы, закончится
процедура построения семантического дерева Т для S или не
закончится.
6.4. Унификация
Определение. Подстановка (t, вместо х,-) есть множество
9 = {^ lxM t2lx2 ,..., tjx*},
где х!,...,х^ есть попарно различные предметные переменные, а все
t, - термы, отличные от х,-, i = 1,2,...,/:.
Пусть е - пустая подстановка.
Определение. Пусть С есть дизъюнкт, а 9 = {tl I хх,... ,tk \xk} -
подстановка. Обозначим через С9 (точнее через С* 9) дизъюнкт,
полученный одновременной заменой переменных х1У...,хк в С на термы
t!,..., tfc соответственно. Дизъюнкт С9 называется примером
дизъюнкта С.
Аналогично определяется пример терма.
Замечание. Основной пример дизъюнкта не имеет предметных
переменных. Пример дизъюнкта может иметь предметные переменные.
Определение. Подстановка 9 есть унификатор множества литер W =
{Llf...,Lm}, если 1^9 = L29 = ... = Lm9. (Обозначение: Y(W) = 9).
Литеры Lj,...,Lm называются унифицируемыми.
Пример. Множество литер {Р(х), P(f(y))} унифицируемо подста-
128
новкой 0 = {f (у) I x}. Множество литер {Р(х), Р(у), "IP(z)} не
унифицируемо, ибо никакая подстановка не сделает равной формулу и ее
отрицание.
Определение. Пусть 9 = {tx \хх,... ,tk \хк}9 А = {ujlyj,...,
umlym} есть две подстановки. Композиция 9* А подстановок G и Л
есть подстановка, полученная из множества
{t1Alx1,...,t^Alx^, и, 1ух,.. - ,um |ym}
вычеркиванием всех элементов вида t,-Л I х,-, для которых t,-A = X/, и
вычеркиванием всех элементов и, I у,-, в которых у, € {х,,...,х^}.
Пример. 9 = {tjxj, t2lx2} = {f(y)lx, z I у};
A = {ujy^ u2ly2, u3ly3} = {alx, bly, ylz}.
Множество {tjAlxj, t2Alx2, ujy,, u2ly2, u3ly3} =
{f(y)A lx,zA ly,a lx,b ly,y lz} = {f(b) lx,y ly,a lx,b ly,y lz}.
Из этого множества выбрасываем элемент у I у и элементы a I x и
bly, ибо у! = х € {х,у} = {xpxj и у2 = у € {х,у} = {x^xj.
Композиция 9А = {f(b)lx, ylz}.
Замечание. 1. е9 = 9е = 9.
2. (9А)(Г = 9(А(Г).
3. С(9А) = (С9)А.
Пример. С = P(x,f(y),g(x,z)). Подстановки 9 и А взяты из
предыдущего примера.
С(9А) = (P(x,f(y),g(x,z)))-(9A) = P(f(b),f(y),g(f(b),y));
(С9)А = ((P(x,f(y),g(x,z))-9)A = P(f(y),f(z),g(f(y),z))) A =
P(f(b),f(y),g(f(b),y)).
Определение. Пусть W - множество литер. Унификатор б есть
наиболее общий унификатор для W (обозначение: б = HOy(W)), если
для любого другого унификатора 9 для W существует подстановка А,
для которой 9 = (ГА.
Замечание. Из НОУ для W можно получить любой другой унификатор
для W.
Пример. W = {Р(х), P(f(y))}. Подстановки б = {f(a)lx, a Iу}; 9
= {f(у) I х} являются унификаторами для W и 9 есть НОУ.
Определение. Множество рассогласований некоторого множества
литер W получается выписыванием из W всех термов, начинающихся с
первой слева позиции в литерах, на которой стоят буквы, не все
одинаковые.
Пример. W = {P(x,f(y,z)); P(x,a)}. Множество рассогласований D
= {f(y,z),a}.
6.4.1. Алгоритм унификации
Пусть W = {Llf...,Lr} - множество литер с совпадающими
предикатными буквами, которые либо все положительны (без отрицаний),
129
либо все отрицательны (с отрицаниями). В противном случае
множество литер W не унифицируемо. Пусть Iwl означает число литер в W.
Выполним следующую последовательность шагов.
1. WQ = W, СГ0 = С.
2. Если Wfc содержит единственную литеру, то останов: бк есть
НОУ для W. В противном случае найдем множество D^ рассогласований
для Wfc. Если множество D^ содержит переменную v^ и терм tk,
причем у^ не содержится в t^, то перейдем к следующему шагу. В
противном случае останов: множество W не унифицируемо.
3. **+i = <r*{tjv*}; W*+1 = W*{tjv*} (при этом W*+1= Wcr^+1).
Переходим к 2.
Пример 1. W = {P(a,x,f(g(y))); P(z,f(z),f(u)}.
0. <г0 = е; W0 = W; IWI > 1; D0 = {a,z}; v0 = z,
t0 = a, v0 Э t0; a>0 = {alz}.
1. <sx = cr0- {t0 I v0} = e-{alz} = <r0-w0; Wj = W0a>0 =
W.a>0 = {P(a,x,f(g(y))); P(a,f(a),f(u))}; IwJ > 1;
Dx = {x,f(a)}; Vl = x, tx = f(a), Vl Э Ц; a>1 = {f(a)lx}.
2. б2 = 6l-ul = {alz}- {f(a)lx} = {alz, f(a)lx};
W2 = W1-w1 = (WotfoWoK = W0cr1w1 = W-cr2 = {P(a,f(a),
f(g(y)); P(a,f(a),f(u))}; l\V2l > 1; D = {g(y),u};
v2 = u, t2 = g(y), v2 Э t2; a>2 = {g(y)lu}.
3. аъ = 02-w2 = {a|z, f(a)lx}- {g(y)lu} = {alz,
f(a)lx, g(y)lu}; W3 = W2-o>2 = W0cr2a>2 = W-cr3 = {P(a,f(a),
f(g(y))); P(a,f(a),f(g(y)))} = {P(a,f(a),f(g(y)))};
|W3| = 1. Останов. Унификатор 0 = cr3, при этом 0 = HOy(W).
Пример 2. W = {Q(f(a,g(x)); Q(y,y)}.
0. cr0 = е; W0 = W; IW0 I > 1; D0 = {f(a),y}; v0 = y,
t0 = f(a), v0 Э t0; a>0 = {f(a)ly}.
1. cr1 = cr0o>0 = a>0 = {f(a) ly}; W, = W0a>0 = {Q(f(a), g(x));
Q(f(a),f(a))}; IwJ > 1; Dx = {g(x),f(a)}. В D, нет переменной
vlf не входящей в какой-либо терм из Dle Множество W не
унифицируемо.
Замечание. Алгоритм унификации всегда заканчивает свою работу,
указывая при этом унификатор или сообщая о его отсутствии. В
языке программирования Пролог поиск унификатора есть одна из
основных его операций.
Теорема (об унификации). Если W есть конечное унифицируемое
множество литер, то алгоритм унификации заканчивает свою работу
130
через конечное число шагов и выдает для W наиболее общий
унификатор.
Доказательство. Пусть 9 - произвольный унификатор для W, т.е.
9 = y(W). Алгоритм унификации останавливается всегда. Пусть,
работая над W, алгоритм остановился на шаге г. Покажем, что
алгоритм при этом указал на унифицируемость W и выдал НОУ для W.
Утверждение. Для всякого шага /с, О ^ к ^ г, работы алгоритма
унификации существует подстановка А^, для которой 9 = бк\к.
Доказательство. Индукция по к.
БАЗИС, к = 0. Так как 9 = ев и сг0 = е, то при А0 = 9 получим 9
= *оЛо-
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть для шага к, 0 ^ к < г,
существует подстановка А^, для которой 9 = бк\к.
ШАГ ИНДУКЦИИ. Покажем, что на шаге /с+1 существует подстановка
Afc+1, для которой 9 = tffc+iAfc+1. На шаге к работы алгоритма
унификации возможны следующие случаи.
1. Iwl =1. Тогда к = г, алгоритм закончил свою работу, выдал
унификатор сг, причем для произвольного унификатора 9 по
предположению индукции существует подстановка Аг, для которой 9 = сгАг.
Следовательно, cr = HOy(W).
2. Iwl > 1. Тогда к < г и возможен следующий шаг. На шаге к
алгоритм выдал множество рассогласования D^ для множества W^ =
W*(f£. Так как подстановка 9 = бк\к есть унификатор для W, то
подстановка А^ должна унифицировать D^ (как часть W). Так как D^
есть множество рассогласований, то множество D^ имеет в качестве
элемента переменную \к (иначе D^ имеет одни константы и не
унифицируется).
Пусть tk - любой другой терм в D^, отличный от v^. Так как А^
унифицирует Dfc, то v^A^ = t^A^. Переменной \к нет в tk, ибо иначе
ввиду \к * tk получим у^А^ * t*Afc, чего нет. Так как \к нет в tk,
то алгоритм выдает подстановку и>к = {t^ I v^} и строит подстановку
&к+1 ~ ^кик ~ ак' Ufclvfcb Положим А^+1 = А^ - {tfcAfclvfc}. Так как
v* нет в tky то t*A*+1 = t*(A* - {t^Ajv*}) = tk\k. Тогда
<*>***+! = U*lv*}- A*+1 =
U***+1 Ю U Ал+1 = {t*A*lv*} U A*+1 =
{tk\k\vk} U (A* - {t*Ajv*}) = A*,
т.е. Хк = u>kXk+l.
Следовательно, 9 = бк\к = cr^(a>^A^+1) = (<fkb>k)^k+i = c^+iA^+1.
Шаг индукции установлен. Утверждение доказано.
Продолжим доказательство теоремы. При к = г получим 9 = сгАг,
131
где аг = y(W). Итак, для произвольного унификатора 9 и
унификатора бг существует подстановка Аг, для которой G = бгХГУ
т.е. <гг = HOY(W).
Теорема доказана.
6.5. Метод резолюций в логике предикатов
Опишем формально-логическое исчисление - метод резолюций,
который был принят за основу при разработке языка программирования
Пролог.
Определение. Если две или более литер (одной и той же
положительности) в дизъюнкте С, рассматриваемом как множество литер,
имеют наиболее общий унификатор с, то множество литер Сб
называется склейкой для С. Если Сс есть одноэлементный дизъюнкт, то
склейка называется единичной.
Пример. Дизъюнкт С = Р(х) V P(f(y)) V ~IQ(x);
с = HOY(P(x),P(f(y))) = {f(y)lx}.
Следовательно, дизъюнкт
Сс = P(f(y)) V P(f(y)) V lQ(f(y)) = P(f(y)) V lQ(f(y))
есть склейка для С.
Определение. Пусть Сх и С2 - два дизъюнкта (называемых
посылками), которые не имеют никаких общих переменнных, а
дизъюнкт С есть либо сам Clf либо его склейка. Аналогично для
С". Пусть Lj - литера из С, a ~1L2 - литера из С". Если Ll и L2
имеют наиболее общий унификатор с, то дизъюнкт С = (Сс - L^tf) U
(С"б - ~lL2cr) называется резольвентой дизъюнктов Сх и С2. Дизъюнкт
С называется также заключением (выведенным из посылок Сх и С2).
Литеры Ll и L2 называются отрезаемыми литерами.
Пример. Дизъюнкты
Сх = Р(х) V Q(x), С2 = 1Р(а) V R(y); б = {а|х} = НОУ(Р(х),
Р(а)); литеры Lx = Р(х), L2 = Р(а).
Резольвента С дизъюнктов Сх и С2 есть дизъюнкт
С = (С^ - L^) U (С2сг - "lL2cr) =
({P(a),Q(a)} - {Р(а)}) U ({HP(a),R(y)} - {ПР(а)}) =
(Q(a),R(y)} = Q(a) V R(y).
Определение. Дизъюнкт С получен из дизъюнктов Cj и С2 по
правилу резолюции, если С есть резольвента дизъюнктов Сг и С2.
Пусть запись С = ПР(С!,С2) означает, что дизъюнкт С получен по
правилу резолюции из дизъюнктов Сх и С2.
Замечание. В основе правила резолюции лежат классические
правило подстановки и правило заключения:
132
P(x) A, A->B АЛАЛ/В
p/ ч, —*-= эквивалентное правилу —*—= .
Последнее можно обобщить до правила вывода
AVB1V...VBm> HAVC^.^V^
B1V...VBmVC1V...VC„
Формулы А и "IА могут стоять в любом месте дизъюнкции. Включающее
в себя подстановку правило резолюции
L^LuV.-.VL^, 1L2VL21V...VL2„
(LM V...VLlm V L21 V...VL2n).e '
получается из последнего правила вывода, если в нем вместо
А V В, V ... V Bw, ПА V С, V ... V Сп
взять дизъюнкты
L, V LM V ... V Lim, 1L2 V L21 V ... V L2„,
составленные из элементарных формул (предикатных атомов), имеющих
в своем составе функциональные термы. С помощью алгоритма
унификации разыскивается та подстановка с, которая атомы Lx и L2
делает идентичными: L^tf = L2*(r. Результат
(LM V ... V Llw V L21 V ... V L2„).cr
подстановки б вместо переменных в дизъюнкцию
LM V ... V Llm V L21 V ... V L2„
ставится в знаменатель правила резолюции.
Определение. Резолютивный вывод из множества дизъюнктов S есть
последовательность дизъюнктов, каждый из которых есть либо
дизъюнкт из S, либо получен из предыдущих дизъюнктов
последовательности по правилу резолюции.
Определение. Дизъюнкт С выводится из множества дизъюнктов S
(обозначение: S I- С), если существует конечный резолютивный вывод
из множества S, последним дизъюнктом которого С является.
Теорема. Если из множества дизъюнктов S выводится дизъюнкт С,
то формула S -> С общезначима.
Доказательство. Индукция по числу к применений правила
резолюций.
БАЗИС, к = 1. Покажем, что резольвента С двух дизъюнктов Сх и
С2 есть логическое следствие С! и С2. Так как С = ПР(С!,С2), то
существуют дизъюнкты Ср С2, литеры hl9 L2 и подстановка с, для
133
которых Ci = Ci V Llf C2 = C'2 V "IL2, Lxc = L2tf,
С = (С'сг - L^) U (C'2c - "IL2cr).
Пусть x есть список всех предметных переменных для Cj и С2, а
у есть список всех предметных переменных для С^с V I^c, С2б V
~IL2cr. Подстановку а можно выбрать так, что списки переменнных х и
у не пересекаются. Дизъюнкты С1У С2, записанные без кванторов в
виде множества литер, представаляют собой другую запись формулы
(VxXC! & С2), т.е. формулы (Vx)((Ci V L;) & (С2 V ~IL2))\ Тогда
формула (Vx)((c' V ЪХ)&(С'2 V 1L2)) - (Схб V Lxa)&(c'2a V 1Lacr)
общезначима, ибо ее заключение есть подстановка некоторых термов
вместо некоторых переменных в посылке (Сг V Lj & (С2 V "1L2).
Формула (с'сг V L1c)&(C2(r V 1L2cr) -» (с'сг V С2с) общезначима из
алгебрологических соображений. Тогда общезначима формула
(Vx)((c; V L,)&(C; V 1L2)) - (С> V С»;
следовательно, общезначима формула
(Vy)(Vx) ((с; V Ь,)&(с; V 1L2) - (C\a V С»);
поэтому общезначима формула
(с; V hx) & (С', V 1L2) - (С> V с'2*)9
которая совпадает с формулой Сх & С2 -» (Сх V С2)с, являющейся
тоже общезначимой. Следовательно, резольвента (Сх V С2)с есть
логическое следствие дизъюнктов Сх и С2.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что теорема справедлива
для всех выводов, в которых число применений правила резолюции
меньше к.
ШАГ ИНДУКЦИИ устанавливается точно так же, как и в случае
аналогичной теоремы для логики высказываний.
Лемма (о подъеме). Пусть Clf C2 - примеры дизъюнктов Сх и С2
соответственно. Пусть С - резольвента для Сх, С2. Тогда
существует резольвента С для Сх и С2, для которой С есть
основной пример.
Доказательство. Можно считать, что Сх и С2 (так же как и Сх и
С2) не имеют общих переменных. По условию для Сх и С2 резольвента
С = (C[v - Li) U (С2у - ~IL2i>), где v = HOy(Li,L2), a b' и L2
есть отрезаемые литеры, причем Lt € С1У L2 € С2. Так как Ct и С2
не имеют общих переменных, то подстановку v можно представить в
виде объединения двух подстановок v = vx U v2, причем vl содержит
только переменные из Сп а у2 - из С2. Так как С, есть пример для
С/, i = 1,2, то для некоторых подстановок Эх и в2 имеем Сх =
134
ci0i> C2 = C202- Тогда резольвента С = (C^e^ - l'i^) U (С292у2
- ~IL2u2). Выделим в С, все те литеры, которые подстановка 0,
склеивает в одну литеру; тогда
Lje, = ... = Lj1' 9/ = L/У,, i = 1,2.
Так как множество {L,-,..., L,'}, i = 1,2, унифицируемо, то оно
имеет наиболее общий унификатор А,. Так как Л, есть НОУ для
множества L,,..., L,', а 0, А, - какой-то унификатор для этого
множества, то существует подстановка р,, для которой е,ы, = А,р,.
Поэтому резольвента
С = (С^А^ - {lJ,..., L^J-AjPj U
С2Л2>>2 ~ (L2,..., L22}-A2p2).
При этом D/ = С,А, есть склейка для C,-,i = 1,2. Если гг = 1, то
Aj = е. Аналогично, если г2 = 1. Пусть Lt = L1A1 есть литера из
Dx; "1L2 = ~IL2A2 есть литера из D2. Тогда С = (Dlpl - Lxpx) U
(D2p2 - ~IL2p2). Полагая р = pj U p2, объединим разделенные по
переменным подстановки. Тогда С = (DYp - I^p) U (D2p - ~IL2p),
где р есть некоторая подстановка, унифицирующая Lj и L2. Пусть т
= НОУСЬ^Ьг). По определению НОУ найдется подстановка с, для
которой р = тс. Тогда С = (D^c - L^tc) U (D2T(r - ~IL2Ttf). Так
как подстановка р, равная тс, не склеивает Lj ни с какой другой
литерой в Di, a "IL2 - ни с какой другой литерой в D2, то С =
((Dxt - I^t) U (D2t - 1L2t))c = Сс, где С = ПРСС^С,), т.е. С
есть пример дизъюнкта С.
Лемма доказана.
Теорема (о полноте метода резолюций). Непустое множество
дизъюнктов S невыполнимо тогда и только тогда, когда из S выводится
пустой дизъюнкт.
Доказательство. Пусть множество дизъюнктов S невыполнимо.
Пусть Т есть семантическое дерево для S. Так как S невыполнимо,
то множество опровергающих узлов в Т конечно, и каждый путь в Т
имеет опровергающий узел. Пусть Т' есть конечное поддерево дерева
Т с (конечными) путями от корня до опровергающих узлов.
Утверждение. Пустой дизъюнкт выводится из S.
Доказательство. Индукция по числу к узлов в Т' при любом S (а
потому и при любом Т).
БАЗИС, к = 1, т.е. дерево Т' имеет единственный опровергающий
корневой узел. Так как множество S не пусто и невыполнимо, то S
содержит пустой дизъюнкт, выводимый из S.
135
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что доказываемое
утверждение справедливо для любого S и потому для любого семантического
дерева Т, для которого Т' имеет число узлов меньше к.
ШАГ ИНДУКЦИИ. Покажем, что доказываемое утверждение
справедливо для любого S и потому для любого семантического дерева Т,
для которого Т' имеет число узлов к. Пусть N есть узел,
предшествующий двум концевым опровергающим узлам Nt и N2 в Тг. Пусть
ребрам, исходящим из N, приписаны литеры L^ и "IL^. Пусть пути от
корня до Nj и N2 проходят через литеры
Lx,... ,L^_X, Lk - до узла Njj
Ll9...,Lk-i>1Lk ~ Д° Узла N2-
Пусть Cl есть основной пример дизъюнкта Сх из множества
дизъюнктов S, который опровергается (ложен) в N1? а С2 - основной пример
дизъюнкта С2 из S, который опровергается в N2. В узле N дизъюнкты
С\ и С2 не опровергаются. Поэтому в Сх входит L^, а в С2 входит
"ILfc. Для С, и С2, отрезая литеру L^, получим резольвенту С = (CY
- Lfc) U (С2 - lb*). Так как
С[ = LJ V ... V L^ V ILfc ложно в N ,
С2 = h\ V ... V L*2 V Lk ложно в N ,
то резольвента С = L, V ... V Lr V L, V V Lr , не
содержащая L^ и "IL^, ложна в N. По лемме о подъеме для С1 и С2
существует резольвента С, для которой С является основным
примером. Пусть Sj = S U {С}. Множество Sj невыполнимо, ибо
невыполнимо его подмножество S.
Семантическое дерево для Si совпадает с семантическим деревом
для S. Дерево Т г, полученное из Т удалением поддеревьев с корнями
в опровергающих узлах для S х, входит в дерево, полученное
удалением из Т' узлов N, и N2 с принадлежащими им ребрами. Так как
число узлов в Тг меньше ку то по предположению индукции из Sj
выводится пустой дизъюнкт. Следовательно, пустой дизъюнкт выводится
и из S, ибо Sj получается из S однократным применением правила
резолюций.
Достаточность очевидна, ибо если из S выводится пустой
дизъюнкт, то формула S -> □ общезначима, а потому множество S
невыполнимо. Теорема доказана.
Замечание. Пролог имеет дело с хорновскими дизъюнктами. Хор-
новский дизъюнкт есть дизъюнкт, содержащий не более одной положи-
136
тельной литеры; оставшиеся литеры дизъюнкта отрицательны. Хорнов-
ский дизъюнкт имеет вид А V ПВ V 1С V ... V ID (что равносильно
формуле B&C&...&D -» А, записываемой в Прологе как А :- В,С,...,
D), где A,B,C,...,D есть некоторые атомы. Отрицательных
дизъюнктивных слагаемых в хорновских дизъюнктах может и не быть. Пролог-
программу составляет множество [Dx ,D2,... ,D„} (рассматриваемое
как конъюнкция D!&D2&.. .&D„) хорновских дизъюнктов Dx ,D2,... ,D„,
замкнутых кванторами общности. В этом смысле программирование в
Прологе есть программирование в хорновских дизъюнктах. Пролог-
программе можно ставить запросы. Запрос есть конъюнкция Q(X)
положительных атомов Qi,Q2f-.iQiki где X есть список всех их
переменных. Нужно выяснить, следует ли логически запрос Q(X) из
программы DJ&D2&.. .&D„ и при каких значениях переменных X это
возможно, т.е. является ли формула D!&D2&.. .&D„ -» (3X)Q(X)
общезначимой, или ее отрицание Dt&D2&.. .&Dn & (VX)~1Q(X) невыполнимой.
Другими словами, выводится ли из множества хорновских дизъюнктов
D!,D2,... ,D„,~1Q(X) пустой дизъюнкт и при каких значениях
переменных X это возможно. Вычисление этого обстоятельства проводится с
помощью правила резолюции, причем в Прологе используется один его
частный вид, называемый линейной резолюцией. Именно, в запросе
"IQ, являющемся дизъюнкцией ~~\QX V ~IQ2 V ... V "IQ^, правило
резолюции применяется к первому дизъюнктивному слагаемому 1QX и к
первому (хорновскому) дизъюнкту F, равному А V "IB V "1С V ... V "ID
в Пролог-программе, такому, что к 1QX и F применение правила
резолюции возможно. Это правило имеет вид
А V ПВ V ПС V ... V HD, HQi
(ПВ V ПС V ... V HD) -9
для того НОУ в, для которого атомы АЭ и Q1-0 одинаковы.
Формируется новый запрос (ПВ V 1С V ... V ID V HQ2 V ... V HQ^)e, в
котором правило линейной резолюции, в свою очередь, будет
применяться к первому дизъюнктивному слагаемому (ПВ)Э. Вывод в Прологе
есть последовательное получение подобных запросов с помощью
линейной резолюции.
Применение указанного выше правила линейной резолюции
эквивалентно примению двух обычных правил логики предикатов - правила
подстановки и правила заключения:
Р(х) ПА - ПВ V ПС V ... V HD, ПА
P(t) ' ПВ V ПС V ... V HD
Для линейной резолюции справедлива теорема о полноте.
137
Для хорновских дизъюнктов справедливо следующее утверждение.
Утверждение. Пролог является универсальным языком
программирования: любой алгоритм может быть записан в формализме метода
резолюций с хорновскими дизюнктами.
В свете этого утверждения любая задача, записываемая на языке
дизъюнктов, может быть записана и на языке хорновских дизъюнктов.
6.6. Основы Пролога
Универсальный язык программирования Пролог (акроним от PRO-
gramming in LOGic) был разработан в 1970-х г. При разработке
программ будем ориентироваться на версию языка Arity-Prolog.
Алфавит.
1. ABC ... XYZabc ... xyz- большие и малые буквы
латинского алфавита. В ЭВМ, имеющих клавиатуру с кириллицей,
допускаются большие и малые буквы русского алфавита.
2. 0123456789- цифры.
3. +-*/<>=:...- специальные знаки (или спецзнаки). В
качестве спецзнаков могут выступать любые печатаемые символы
клавиатуры ЭВМ, не являющиеся буквой или цифрой.
4. ( ) [ ] , - различного вида скобки и запятая. Эти символы
можно было бы отнести к спецзнакам; их отметили особо ввиду
частого использования в стандартных конструкциях языка.
Приступим к описанию типов данных в Прологе.
Атомы.
1. Конечная последовательность, состоящая из букв, цифр и
символов подчеркивания _ , начинающаяся с малой буквы, есть
(буквенный) атом.
Пример. ху, xl, x34, abc, x25AB, x, procedure, beata,
alexey_morozov, май_1_1989, а_25, х у_7, b__, anna, nil.
2. Конечная последовательность спецзнаков есть (специальный)
атом.
Пример. <—>, < >, =>, ===>, ...,*,+,/,:,::=.
При использовании атомов этого вида следует сохранять
осторожность, ибо некоторые атомы, например, такие как :-, =, =.. = , =\=
и другие имеют специальный смысл.
3. Любое слово в алфавите формальных символов, заключенное в
апострофы, есть атом.
Пример. '1 мая 1989 года', 'Алексей Морозов', 'Адрес
неизвестен', 'зов предков', 'звезда в ночи'.
Длина атома не может превышать 255 символов.
Целые числа. Целые числа в Прологе задаются обычным образом.
138
Например, 1, 135, 0, -97. Целые числа заключены между -2Л15 и
2^15-1. Положительные числа знаком плюс перед ними не
сопровождаются.
Символ ASCII со стоящим перед ним обратным апострофом * тоже
является целым числом (кодом этого символа). Например, вместо 'а
можно писать 97, а вместо 97 можно писать 'а.
Вещественные числа. Вещественные числа (числа с плавающей
запятой) могут иметь до 15 десятичных знаков после десятичной
точки. Например, 0.6, 135.238, -17.259, -10.0. Целая часть числа,
десятичная точка и хотя бы одна цифра после десятичной точки
обязательны. Возможна экспоненциальная запись вещественного числа.
Порядок числа заключен между -99 и 99. Например,
-71.0Е21, 212.34Е-5, 0.35Е-12.
Пролог есть язык для символьных вычислений, поэтому числа,
особенно вещественные, ему, вообще говоря, не свойственны.
Стринги. Стринг есть произвольная последовательность
печатаемых символов алфавита, включая пробел (такую последовательность
иногда называют текстовой константой), заключенная между знаками
$. Например, $Он сегодня позвонит мне$; $ты ничего не говорил об
этом$. Стринги используются при работе с текстами на естественных
(или искусственных) языках. $$ есть пустой стринг. Знак $ внутри
стринга пишется как $$. Например, $Он должен мне $$15$.
Ссылочные числа базы данных. Пролог-программа,. размещенная в
оперативной памяти ЭВМ, называется базой данных (БД). Некоторым
элементам БД присваиваются специальные числа - ссылочные числа
базы данных; это знак ~ (тильда), за которым следуют восемь шест-
надцатеричных цифр. Например: ~012585397, ~C0F0AD3C, ~018A5D03.
Атомы, числа (целые и вещественные), стринги и ссылочные числа
базы данных в Прологе являются константами.
Переменные. Переменная есть слово в алфавите из букв, цифр и
символов подчеркивания, начинающееся с большой буквы или с
символа подчеркивания.
Пример. X, Y21, АВ5С, Input, Xyz, X_l_2_3, Head, Tail, List,
Object.
Переменная, которой в процессе выполнения программы на ЭВМ не
присваивалось никакого значения, называется незамещенной
переменной. В противном случае переменная называется замещенной.
Термы.
1. Всякий атом есть терм. Всякое число есть терм. Всякий
стринг есть терм. Всякое ссылочное число базы данных есть терм.
2. Всякая переменная есть терм.
3. Если а есть буквенный атом, а каждое из ЦД2,...ДЛ есть
139
терм, то a(tx ,t2,... ,t^) есть терм, в котором атом а называется
главным функтором. Всякий функтор внутри терма главным уже не
является. Терм a(tj,... ,tk) называется также структурой. Буквенный
атом в структуре в качестве главного функтора называется именем
предиката. Две структуры с разным числом аргументов считаются
разными, даже если они имеют один и тот же главный функтор.
Термы без переменных являются константами. Структура без
аргументов, т.е. нульместная структура, является буквенным атомом.
Пример.
дата(1,май, 1989), июль, кафедра(Преподаватели,
Инженеры, Лаборанты), *(+(а,Ь),-(с,5)).
Говоря о конкретном терме, можно сказать о нем: терм-атом,
терм-число, терм-переменная, терм-структура (или просто
структура), предикатный терм (или предикатная структура), арифметический
терм (с ним познакомимся позже).
Списки.
1. Выражение [] есть пустой список.
2. Если каждое из Lj,!^,...,!^ есть терм или список, то
выражение [Lj ,L2,... ,Lk] есть список.
Первый элемент списка есть голова списка. Список без своего
первого элемента называется хвостом списка. В списке голову от
хвоста можно отделять разделителем | явно (этот разделитель
называют также конструктором).
Пример.
Список
[]
[а,Ь,с]
Ш.П.Ь.с]
[[a,b],[X,c],d,Y]
[а]
[[aJb.cJJ.Xjd]]
[a|[[b,c],a,[b,c]]]
[X,b,[c,d]|[X,b,[c]]]
Голова
а
[]
[a,b]
[a,[b,
а
X
списка
с]]
Хвост списка
[Ь,с]
Ш.Ь.с]
[[X,c],d,Y]
[]
[X,[d]]
[[b,c],a,[b,c]]
[b.Ic.dJ.X.b.Ic]]
Знаком | можно отделять любое число начальных элементов списка
от остальной его части. Например, если список L = [a,b,c,d,e] и L
= [X,Y|Z], то X := a, Y := b, Z := [c,d,e]. Здесь знак :=
означает присваивание (знак := Прологу не принадлежит).
В ЭВМ списки представляются с помощью бинарного
функционального символа . (точка), взятая в апострофы. Например, следующие
записи представляют один и тот же список.
140
[a,b] V(a,\'(b,[]))
[a.b.c] '.'(a,'.'(b,'.'(c,[])))
[a,[b,c],a,d] ,.*(a,'.'(,.,(b,'.'(c>[])),'.'(a,'.'(d,[]))))
[[a,b],c,d] '.'С4a,'.'(b,[])),'.'(c,'.'(d,[]))))
При определении терма в структуре a(tl9...,t^) каждое из t19
... Лк может быть еще и списком.
Список кодов символов ASCII можно задавать как
последовательность символов этого списка, заключенную в двойные апострофы.
Например, следующие записи определяют один и тот же список:
-cfk" [99,102,107] ,.,(99,,.,(Ю2,,.,(Ю7,[])))
Список без переменных есть константа.
В Прологе приняты следующие типы данных: атомы, числа (целые и
вещественные), стринги, ссылочные числа базы данных, переменные,
структуры, списки.
Пролог-программа. Факт есть структура, заканчивающаяся точкой.
В качестве фактов чаще всего используются предикатные структуры.
Если A,B,C,...,D являются структурами (чаще всего
предикатными), то выражение
А :- B,C,...,D.
называется правилом; А есть голова правила; B,C,...,D есть тело
правила. Правило называется также условным предложением. Знак :-
читается как "если"; запятая в теле правила означает конъюнкцию.
Точка с запятой в теле правила (если она есть) означает
дизъюнкцию. Клауза есть факт или условное предложение.
С точки зрения логики условное предложение представляет собой
формулу логики предикатов В&С& ... & D -> А, равносильную
формуле "IB V "1С V ... V ID V А; последняя формула является
дизъюнктом, все дизъюнктивные слагаемые которого отрицательны за
исключением одного положительного; подобные дизъюнкты называются хор-
новскими. Так что всякое предложение Пролога является хорновским
дизъюнктом, и программирование на Прологе есть программирование в
хорновских дизъюнктах.
Если F,G,...,H являются структурами, то выражение
?. FG Н
называется запросом, а элементы F,G,...,H - целями, или целевыми
утверждениями запроса.
Предложение в Прологе есть один из трех объектов: факт,
правило, запрос. Всякое предложение Пролога состоит из головы и тела.
Факт имеет только голову (и пустое тело). Правило имеет и голову,
и тело. Запрос имеет только тело (и пустую голову).
141
Программа в Прологе есть конечная последовательность фактов и
правил. Иногда программу называют базой данных; иногда базой
данных называют множество фактов в программе, а самую программу -
базой знаний (БЗ). Программу в рабочей области (т.е.
оттранслированную программу) тоже будем называть БД.
Процедура есть конечная последовательность фактов и правил,
имеющих в голове один и тот же главный функтор.
Если переменная входит в предложение только один раз, то ее
можно заменять символом подчеркивания; тогда говорят об анонимной
переменной. Например, вместо предложения
имеет_ребенка(Х) :- родитель(Х,У).
можно записать предложение
имеет_ребенка(Х) :- родитель(Х,_).
Каждое вхождение символа подчеркивания в предложении Пролог-
программы символизирует новую переменную. Например, предложение
кто-то_имеет_ребенка :- родитель(__,__).
означает то же самое, что и предложение
кто-то_имеет_ребенка :- родитель(Х,У).
Если анонимная переменная входит в запрос, то на нее Пролог
сведений не выдает.
Область действия всякой переменной (в том числе и анонимной)
есть то предложение, в которое эта переменнная входит. Две
одинаковых переменных в разных предложениях означают две разные
переменные .
Описанные конструкции составляют так называемый чистый (или
стандартный) Пролог, входящий в любую реализацию языка. Типы
данных в различных реализациях Пролога могут быть разными.
Пролог-программу Р составляют множество (конъюнкция) фактов и
условных предложений. Программе можно ставить запросы. Пролог
пытается установить, выводится ли запрос G(x) из множества
предложений программы: Р I- (3x)G(x). Если да, то попутно вычисляются
значения вектора х предметных переменных, содержащихся в запросе,
и в конце вычислений Пролог выдает эти значения (т.е. попутно
вычисляется подстановка 6, для которой Р I- G«e). Если нет, то
Пролог вычисления заканчивает и сообщает об этом.
Пример простейшей Пролог-программы. Приведем пример Пролог-
программы, характеризующей семейные отношения (рис.6.5).
родитель(мария, петр).
родитель(иван, петр).
родитель(иван, елена).
142
Мария
Анна
Петр
Иван
Нина
Андрей
Елена
Рмс.6.5
родитель(петр, анна).
родитель(петр, нина).
родитель(нина, андрей).
Запись родитель(мария,петр) означает, что Мария есть родитель
Петра. Приведенные предложения (они являются фактами) составляют
Пролог-программу. К этой программе можно обращаться с запросами.
ЭВМ строит соответствующее дерево вывода и выдает ответ
согласно результатам вычислений. Заметим, что знак ?- и стрелку
-> выдает ЭВМ; точку с запятой набирает на клавиатуре
пользователь. Приведем несколько запросов к ЭВМ и ответов ЭВМ на
них.
?- родитель(мария,петр).
yes
?- родитель(иван,анна).
по
?- родитель(нина,андрей).
yes
?- родитель(петр,У).
У=анна ->;
У=нина ->;
по
?- родитель(Х,петр).
Х=мария ->;
Х=иван ->;
по
143
Через запятую, которая в данном случае означает конъюнкцию,
запрос можно составить из нескольких целей:
?- родитель(иван, X), родитель(Х, Y).
Х=петр
У=анна ->;
Х=петр
У=нина ->;
по
Расширим программу о родственниках фактами об их поле.
женский(мария).
женский(елена).
женский (анна).
женский(нина).
мужской(иван).
мужской(петр).
мужской (анд рей).
Определим предикат с именем потомок, имея в виду
непосредственного потомка, с помощью следующего предложения:
потомок(Х,У) :- родитель(У,Х).
Знак :- соответствует логическому "если". В логике предикатов это
предложение записали бы в виде следующей формулы:
(VX)(VY) (родитель(У,Х) -» потомок(Х,У)), или
(VX)(VY) (потомок(Х,У) «- родитель(У,Х)).
Введем также предикаты мать(Х,У), отец(Х,У), сестра(Х,У),
брат(Х,У), бабушка(Х,У), дедушка(Х,У), бабдед(Х,У) с помощью
следующих предложений.
мать(Х,У) :- родитель(Х,У),женский(Х).
отец(Х,У) :- родитель(Х,У),мужской(Х).
сестра(Х, Y) : - родитель^,X), родитель^, Y), женский(Х).
брат(Х,Y) : - родитель^,X),poдитeль(Z,Y),мужской(Х).
6a6yuiKa(X,Z) :- родитель(Х^),родитель^^),женский(Х).
дедушка(Х^) :- poдитeль(X,Y),poдитeль(Y,Z),мyжcкoй(X).
бабдед(Х^) :- родитель(Х,У),родитель^^).
Приведем несколько запросов к программе и ответов ЭВМ на них.
?- потомок(петр,мария).
yes
?- потомок(петр,Х).
Х=анна ->;
Х=нина ->;
по
?- сестра(анна,анна).
yes
144
?- брат(петр,елена).
yes
?- брат(елена,петр).
no
Видим, что Анна может быть сестрой себе. Чтобы этого избежать,
следует ввести предикат различия. Это мы сделаем позже.
Добавим к программе семейных отношений предикат предок(Х,У), с
помощью следующей процедуры.
предок(Х^) :- родитель(Х^).
предок(Х^) :- родитель(Х,У), предок(У^).
Второе предложение соответствует формуле логики предикатов
(VX)(VY)(VZ) (родитель(Х,Z),npeflOK(Y,Z) -» предок(Х^)),
эквивалентной формуле
(VX)(VZ) ((ЭУ)(родитвль(Х>г),предок(¥>г)) - предок(Х^)),
или же формуле
(VX)(VZ) (предок(Х^) «- (ЭУ)(родитель(Х^),предок(У^))).
Поэтому, если переменная в теле предложения не содержится
среди переменных головы этого предложения, то эта переменная
находится под знаком квантора существования.
При вычислении значения предиката предок произойдет обращение
к этому же предикату, но уже с другими значениями переменных.
Такое задание предиката называется рекурсивным.
6.6.1. Унификация в Прологе
Унификация есть основной инструмент передачи параметров из
одного предложения в другое предложение при исполнении программы.
Унификация в Прологе есть некоторое ограничение теоретической
унификации, и осуществляется она с помощью операций согласования
и присваивания. Если в процессе выполнения программы переменной в
процессе унификации присваивается какое-либо значение, то говорят
также что переменная конкретизируется (этим значением),
переменная замещается (на это значение). Такая переменная называется
тогда конкретизированной, или замещенной. Если же переменной в
процессе вычислений не присваивалось никаких значений, то переменная
называется неконкретизированной, или незамещенной.
Атомы согласуются, только если они одинаковы. Целые числа
согласуются только с равными им целыми числами. Вещественные числа
согласуются только с равными им вещественными числами. Стринги
согласуются только с равными им стрингами. Ссылочные числа базы
данных согласуются только с равными им ссылочными числами.
Незамещенная переменная согласуется с любой другой незамещенной
переменной.
145
Две незамещенные переменные после согласования называются
связанными. В процессе выполнения программы может оказаться
несколько связанных в результате согласования переменных. Если одна
из связанных переменных принимает какое-либо значение (т.е.
замещается на какое-то значение), то и все другие с ней связанные
переменные принимают это же значение (т.е. замещается на такое же
значение).
Две замещенные переменные согласуются, если согласуются
значения, которыми эти переменные замещены.
Два терма согласуются в следующих случаях.
1. Термы идентичны.
2. Незамещенным переменным в обоих термах могут быть присвоены
такие объекты, после подстановки которых вместо соответствующих
переменных термы становятся идентичными.
При проверке согласуемости двух термов возможны следующие
случаи.
Термы не согласуются. Тогда согласование безуспешно.
Термы согласуются. Тогда согласование успешно и переменным в
обоих термах производится присваивание таких значений, или, что
то же самое, переменные замещаются на такие значения,
определяемые наиболее общим унификатором этих термов, при которых термы
становятся идентичными. Согласуемость и последующее присваивание
переменным осуществляется с помощью алгоритма унификации.
В Прологе действуют следующие правила согласования и
присваивания (т.е. правила передачи параметров в результате унификации).
1. Если термы S и Т есть константы, то они согласуемы, если
они одинаковы.
2. Если S - незамещенная переменная, а Т - какой-либо терм, не
являющийся переменной, то S и Т согласуемы и S присваивается Т
(т.е. S замещается на Т). Обратно, если Т - незамещенная
переменная, a S - терм, не являющийся переменной, то S и Т согласуемы
и Т присваивается S. Если термы S и Т являются незамещенными
переменными, то эти переменные являются связанными а их значения
будут одинаковыми, если одна из них станет конкретизированной.
3. Если термы S и Т являются структурами, то они согласуемы
при выполнении следующих двух условий.
S и Т имеют одинаковые главные функторы;
соответствующие аргументы в S и Т согласуемы.
Результирующее присваивание определяется результатами
согласования и присваивания соответствующих аргументов в S и Т.
4. Списки согласуются, если согласуются их соответствующие
элементы.
146
5. Два правила (два условных предложения) согласуются, если
согласуются их головы и их тела, т.е. согласуются их
соответствующие цели. В частности, два факта согласуются, если они
согласуются как две предикатные структуры (по п. 3).
6.6.2. Декларативный и операторный смысл Пролог-программы
Пролог-программа лишь декларирует характер тех утверждений,
которые подлежат вычислению. С первого взгляда неясно, как и в
каком порядке будут проводиться вычисления. Организация
вычислений передается транслятору. Пользователю не надо заботиться о
написании порядка, в котором будут проводиться вычисления; это
сделает за него ЭВМ согласно заложенному в транслятор предписанию.
Это является достоинством Пролога. Впрочем, это может оказаться и
его недостатком, ибо иногда для повышения эффективности
вычислений следовало бы предусмотреть средства организации вычислений
самим пользователем (и Пролог имеет такие средства).
Декларативный смысл программы определяет, следует ли логически
данный запрос из предложений программы и если да, то при каких
значениях переменных запроса. Если да, то говорят также, что
запрос выполним, запрос истинен, запрос успешен, запрос
удовлетворяется, запрос согласуется с программой, запрос согласуется с базой
данных.
Операторный смысл программы состоит в том, как Пролог
вычисляет ответ на запрос к программе. Запрос задается в виде
предложения ?- Gl9G2,... ,Gm. Термы G1,G2,...,Gm есть цели запроса. Ответ
на этот запрос состоит в том, что Пролог отслеживает первую
успешную ветвь дерева вывода целей запроса из программы и выдает
соответствующие значения переменных запроса. Дерево вывода строится
индуктивно в ширину следующим образом. В корне дерева вывода
помещается исходный запрос (Gx ,G2,... ,Gm)c0. Подстановка с0 = е,
т.е. (Г 0 - пустая подстановка (никакой подстановки). Запись
(G1,G2,...,Gm)(T0 означает, что подстановка с0 действует на все
цели запроса Gl9G29..., Gm.
Предположим, что на некотором шаге построен фрагмент Т дерева
вывода. Построим следующий фрагмент. Пусть очередной
обрабатываемый узел дерева вывода помечен запросом (Aj,... ,А^)(Т,, где с,- =
e0...G; (б0 = с0) - композиция подстановок, примененных к
запросу до текущего шага. Чтобы построить очередной фрагмент дерева
вывода, выбирается цель А^, - первая в запросе (Alf... ,Afc)Cj. В
программе берется предложение D вида Е :- F2,... ,F/, его
переменные переименуются так, чтобы они отличались от всех ранее
встречающихся переменных, и голова Е унифицируется с А^,-.
147
Если унификация успешна, то вычисляется подстановка 6| + 1 =
HOyCAjtf/jE) и формируется следующий запрос (¥х,... ,F/,A2,...,
А*)с|+1, где с|+1 = tf,#0i + i (из-за переименования переменных Fytf,
= Fj, Fycl + 1 = F;9I + 1). Если подцель А^,- может унифицироваться с
р предложениями программы, то от обрабатываемого узла фрагмента Т
вниз отходит р ребер с концевыми узлами, помеченными
соответствующими запросами. Если унификация с некоторым предложением
программы безуспешна, то соответствующий концевой узел помечается
буквой f (fail). Если унификация дает пустой дизъюнкт □, то
соответствующий концевой узел помечается знаком D.
Узлы, помеченные знаками f и □, окончательные и от них
дальнейшее построение дерева вывода не проводится. Очередной фрагмент
дерева вывода построен. Шаг индукции выполнен. Дерево вывода
построено. Оно может оказаться конечным и тогда все его концевые
вершины помечены знаками f и □. Некоторые ветви построенного
дерева могут оказаться и бесконечными. В последующем дадим
примеры построения конкретных деревьев вывода в ответ на конкретные
запросы к конкретным программам.
Пролог осуществляет обход дерева вывода в глубину. При этом
осуществляется бэктрэкинг: при попадании в узел дерева,
помеченный буквой f (безуспешная ветвь), Пролог автоматически
осуществляет отход в ближайший верхний узел, от которого можно перейти на
следующую ветвь дерева вывода. Вычисление оканчивается успешно,
если Пролог попадает в концевой узел дерева, помеченный знаком D.
Пролог выдает в качестве решения все полученные значения
переменных запроса (последнюю подстановку б) и предлагает пользователю
осуществить бэктрэкинг для поиска других возможных решений.
Проследим, как Пролог, обходя дерево вывода в глубину сверху
вниз слева направо, отслеживает (строит) успешную его ветвь,
чтобы вычислить и выдать ответ на исходный запрос ?- G1,...,Gm.
Чтобы вычислить ответ на этот запрос, выполняются следующие
операции.
1. Если список запросов пуст, то вычисление успешно (выведен
пустой дизъюнкт).
2. Если список запросов не пуст, то выполняется следующая
последовательность операций.
Просматривается список предложений программы сверху вниз, пока
не встретится предложение С, голова которого согласуется с целью
Gj. Цель Gj выступает как образец, а предложение С программы
сравнивается с этим образцом. Если такого предложения С нет, то
попытка вычисления безуспешна; Пролог сообщает об этом, и работа
транслятора прекращается. Если такое предложение С есть, то пусть
148
оно имеет вид:
Н :- Bj ,В2,... ,Вп.
Переменные в С переименовываются так, что получившееся
предложение Cj и цели G1,G2,... ,Gm не имеет общих переменных. Пусть
клауза Сх имеет вид:
Нг :- Вм ,В21,... ,B„i-
Унифицируем Gj и Нг (т.е. с помощью алгоритма унификации
найдем их НОУ) и осуществим присваивания переменным bG1 иН, тех
значений, которые найдены в соответствии с результатами
согласования. Если эти переменные встречаются в Сх ,GX ,G2,... ,Gm, то им
присваиваются те же значения. В результате предложение Сх примет
вид клаузы С2:
Н2 :- В12,В22,... ,ВЛ2.
Исходный запрос превратится в запрос
• ~ B12,B22,...,B„2,G22,G32,... »Gm2.
Далее следует возврат к п.2, но уже с вновь сформированным
запросом.
Описанный алгоритм может закончить работу успешно только п. 1.
Тогда Пролог выдает вычисленные значения переменных начального
запроса и предлагает пользователю продолжить вычисления для
нахождения других возможных значений переменных запроса, если таковые
значения имеются. Если же их нет, то Пролог сообщает об этом и
прекращает работу. Процесс может попасть на бесконечную
вычислительную ветвь дерева вывода; тогда Пролог прекращает вычисления
из-за исчерпания объема стека, или вычисления будут продолжаться
циклически неограниченно долго, пока пользователь не прекратит
это. В следующем параграфе на конкретных примерах покажем, как
организуется в Прологе вычислительный процесс.
6.6.3. Бэктрэкинг и оператор отсечения
Пролог, вычисляя ответ на запрос, строит вывод, пытаясь
установить, следует ли логически запрос из предложений программы. При
этом Пролог осуществляет бэктрэкинг: при получении безуспешного
вывода по одной из ветвей дерева вывода Пролог автоматически
переходит к построению другой его ветви. При получении успешного
вывода по одной из ветвей дерева вывода, Пролог для поиска других
возможных решений предлагает осуществить бэктрэкинг пользователю.
Если последний предложение принимает, нажимая клавишу ; (точка с
запятой), то Пролог продолжает вычисления. Если нет, то
пользователь нажимает любую другую клавишу, например, клавишу ввода, и
149
тогда Пролог вычисления прекращает. Таким способом можно обойти
все дерево вывода запроса из предложений программы сверху вниз и
слева направо и получить все решения, которые возможны.
Осуществляя бэктрэкинг, т.е. возврат из некоторого узла дерева
вывода в другой, выше расположенный узел (ближе к корню), Пролог
при этом отходе отменяет все присваивания переменным,
осуществленным на этом пути ранее при движении от корня дерева вывода
между этими двумя узлами. Так что Пролог, обходя дерево вывода
(на прямом, активном участке пути), удаляясь от корня, выполняет
вычисления согласно программе, а осуществляя отход (на обратном,
пассивном участке пути), отменяет проделанные вычисления, чтобы
испытать альтернативные варианты согласования цели с другими
возможными предложениями программы, имеющими тот же главный функтор,
что и вычисляемая цель.
Находясь в каком-либо промежуточном узле дерева вывода и
обрабатывая в этом узле очередную цель G, Пролог получает
некоторое решение (т.е. некоторые значения переменных), удовлетворяющих
этой цели. Возвратившись при бэктрэкинге снова в узел исполнения
цели G, Пролог при каждом таком возврате автоматически начинает
испытывать возможные согласования цели G с другими предложениями
программы, пытаясь найти альтернативные решения, удовлетворяющие
цели G, даже если этого и не требуется, ибо по смыслу решаемой
задачи пользователю, быть может, достаточно получить только одно
решение, удовлетворяющее цели G. Поэтому бэктрэкинг может снижать
эффективность программы. Избежать этой неэффективности позволяет
оператор отсечения (он обозначается восклицательным знаком: !),
принудительно отсекающий поиск альтернативных решений для цели G
после первого же успешного исполнения G.
Следует отметить, что в чистом Прологе предложения программы
часто перестановочны. Использование оператора отсечения может
имеющуюся перестановочность нарушить.
Пусть очередная исполняемая цель запроса унифицируется
(согласуется) с головой предложения, содержащего оператор отсечения.
Результат унификации вместе с оператором отсечения перейдет в
новый запрос. Когда при последовательном выполнении целей запроса
оператор отсечения встречается, наконец, как цель, то эта цель
всегда совместима с БД. При этом консервируются все те значения,
которые присвоены переменным в целях запроса, расположенных в
унифицируемом предложении программы между головой предложения и
знаком ! оператора отсечения (голова включается). Все другие
альтернативы присваивания не рассматриваются (т.е. отсекаются).
Поясним сказанное на примере предложения С:
150
H :- Bj ,B2,... ,Bm,!,... ,Вп.
Пусть очередная исполняемая цель G запроса согласуется с Н.
Термы G и Н имеют один и тот же главный функтор. Цели ВХ,В2,...,
Вт,!,..., В„ переходят в новый запрос и исполняются
последовательно друг за другом, в том числе цели от Bj до Bw; при этом
определяются решения этих целей, т.е. определяются значения переменных,
удовлетворяющих этим целям. Наконец, исполняется цель !. При
исполнении оператора отсечения ! система уже нашла решения целей
H,Bj ,В2,... ,Вт. После исполнения оператора ! эти текущие решения
замораживаются и все другие возможные решения целей H^^Bj,...,
Bm при бэктрэкинге, т.е. при возвращении от некоторого узла
дерева вывода в узлы исполнения целей H,Bi,B2,...,Bm, не
рассматриваются (отсекаются), хотя в программе возможны другие предложения,
согласующиеся с целями Н^ ,В2,... ,Вт. Эти предложения могли бы
дать альтернативные решения этих целей.
6.6.4. Объявление операторов
Пролог допускает привычную инфиксную запись арифметических
выражений (термов). Внутри ЭВМ та запись переводится в префиксную
форму записи, в которой знак операции предшествует операндам.
Например, термы a+b, a-b, a*b, а/Ь транслятор переводит в +(а,Ь),
-(a,b), *(a,b), /(a,b) соответственно.
В Прологе принят общепринятый приоритет арифметических
операций, при котором умножение и деление связывает сильнее сложения и
вычитания. Например, арифметический терм 2*а+Ь*с Пролог
воспринимает как (2*а)+(Ь*с). Внутри ЭВМ транслятор переведет этот терм в
запись +(*(2,а),/(Ь,с)). Впрочем, Пролог в состоянии принять
вводимую префиксную запись арифметических термов сразу с клавиатуры.
Пролог предоставляет программисту возможность в пределах своей
программы самому определять нужные ему одноместные и двуместные
операции с заданным приоритетом. Это делается с помощью
специального предложения, которое имеет следующий вид:
ор(<приоритет>, <спецификация>, <имя оператора>).
Приоритет определяемого оператора есть натуральное число от
нуля до 1200. Чем больше число, тем выше приоритет. При
отсутствии скобок в терме операции с более высоким приоритетом
выполняются раньше, чем операции с меньшим приоритетом.
Приоритет аргумента равен нулю, если аргумент заключен в
скобки или если аргумент не является структурой. Если аргумент
является структурой (не заключенной в скобки), то приоритет этого ар-
151
гумента равен приоритету его главного функтора.
Спецификация определяемого оператора строится из букв f,x,y и
имеет один из следующих видов:
fx, fy, xf, yf, xfx, xfy, yfx.
Буква x при f означает, что аргумент оператора f должен иметь
приоритет строго меньше, чем приоритет самого оператора f.
Буква у при f означает, что аргумент оператора f должен иметь
приоритет равен или меньше, чем приоритет самого оператора f.
Запись fx означает, что одноместный оператор f префиксный,
т.е. f стоит перед своим аргументом, при этом приоритет аргумента
должен быть строго меньше, чем приоритет оператора f. Наличие
нескольких рядом стоящих операторов f не допускается.
Запись fy означает, что одноместный оператор f префиксный; при
этом приоритет аргумента должен быть равен или меньше, чем
приоритет оператора f. Оператор f правоассоциативный, т.е. при
наличии нескольких рядом стоящих операторов f скобки группируются
справа.
Запись xf означает, что одноместный оператор f постфиксный,
т.е. f стоит после своего аргумента, при этом приоритет аргумента
должен быть строго меньше, чем приоритет оператора f. Наличие
нескольких рядом стоящих операторов f не допускается.
Запись yf означает, что одноместный оператор f постфиксный,
при этом приоритет аргумента должен быть равен или меньше, чем
приоритет оператора f. Оператор f левоассоциативный, т.е. при
наличии нескольких рядом стоящих операторов f скобки группируются
слева.
Запись xfx означает, что двуместный оператор f инфиксный, т.е.
стоит между двумя своими аргументами. Слева и справа от f должны
стоять аргументы, приоритеты которых должны быть строго меньше,
чем приоритет оператора f. Наличие нескольких рядом стоящих
операторов f не допускается.
Запись xfy означает, что двуместный оператор f инфиксный.
Слева от f должен стоять аргумент, приортет которого строго
меньше, чем приоритет оператора f. Справа от f должен стоять
аргумент, приоритет которого должен быть равен или меньше, чем
приоритет оператора f. Оператор f левоассоциативный, т.е. при
наличии нескольких рядом стоящих операторов f, перемежаемых
аргументами, скобки (при их отсутствии) группируются слева.
Запись yfx означает, что двуместный оператор f инфиксный.
Справа от f должен стоять аргумент, приортет которого строго
меньше, чем приоритет оператора f. Слева от f должен стоять ар-
152
гумент, приоритет которого должен быть равен или меньше, чем
приоритет оператора f. Оператор f правоассоциативный, т.е. при
наличии нескольких рядом стоящих операторов f, перемежаемых
аргументами, скобки (при их отсутствии) группируются справа.
Пример. Определим отрицание, конъюнкцию, дизъюнкцию,
импликацию, эквивалентность с помощью следующих предложений.
op(200,fy,~).
op(l80,yfx,&).
op(l60,yfx,\/).
op(l40,yfx,—>).
op(l20,yfx,<—>).
6.6.5. Сеанс работы с языком Arity-Prolog
Включить ЭВМ. Вызвать интерпретатор языка Arity-Prolog, набрав
на клавиатуре API.
Перейти в окно редактора, нажав клавишу F8. Затем, нажав
клавишу Esc, перейти в меню редактора. Выбрать опцию FILE. В
появившемся боксе выбрать опцию Open File. Появится новый бокс. Нажать
клавишу Tab и перевести курсор в окно, в котором отмечены имена
всех файлов с расширением ARI. (Клавиша Tab всегда используется
для движения от одного бокса к другому). Подвести курсор к
нужному файлу и выбрать его, нажав клавишу Enter. Выбранный файл
будет помещен в окно редактора. Отредактировать выбранный файл.
Нажатием клавиши Esc перейти в меню редактора, выбрать опцию
FILE, нажать клавишу Enter и выбрать опцию Save File для
сохранения файла.
Нажав клавишу Esc, перейти в меню редактора, выбрать опцию
BUFFER, нажать Enter и, выбрав опцию Reconsult Buffer,
оттранслировать программу.
Нажав F8, перейти в окно интерпретатора. Если будут указаны
ошибки, то вернуться в окно редактора (нажав F8), исправить
ошибку, снова оттранслировать программу и вернуться в окно
интерпретатора (нажав F8). Поставить программе нужные запросы, набрав
их на клавиатуре, и затем, нажав Enter, получить на них ответы.
Перейти в окно редактора (нажав F8), перейти в меню редактора
(нажав Esc), выбрать опцию File, нажать Enter, выбрать опцию Halt
и выйти из системы Prolog.
Сеанс работы окончен.
Arity-Prolog имеет мощный отладчик. Вызывается он опцией
DEBUG. В боксе этой опции отладчик включается (и выключается)
опцией Trace On. После включения отладчика и выбора подопции Spy
153
опции Debug отлаживаемые предикаты отмечаются действующей ре-
версивно клавишей пробела. При прохождении программы переход от
одного отмеченного предиката к другому осуществляется нажатием
клавиши 1 (малая латинская буква "эль")-
Встроенный редактор Arity-Prolog
Arity-Prolog имеет встроенный редактор. Укажем самые
необходимые команды этого редактора.
Т I <—> клавиши управления движением курсора.
Enter перейти а начало следующей строки.
Shift верхний регистр (большие буквы).
Shift—{>l T <—>} отметить блок текста.
F2 запомнить отмеченный блок текста (в буфере).
F6 перейти в другое окно (буфер) редактора; всего (рабочих)
окон девять: от 1 до 9. Десятое окно (буфер 0) служит для
запоминания отмеченного блока текста.
F1 подсказка.
F5 Alt-H подсказка о содержании клавиатуры фонта F5.
Shift-Del удалить отмеченный блок текста (блок запоминается в
буфере 0).
Shift-Ins вставить запомненный блок текста в место, указанное
курсором.
Backspace удалить символ слева от курсора.
Del удалить символ над курсором.
Для более подробных сведений о работе с языком следует
обратиться к документации, поставляемой фирмой вместе с языком.
6.7. Примеры программ и вычислений в Прологе
6.7.1. Принадлежность элемента списку
Предикат member(X,Y) истинен, если X есть элемент списка Y.
Например,
member(a,[b,c,a,d]) истинно;
member(a,[b,c,d]) ложно;
member(b,[]) ложно;
member([a,b],[c,[a,b],e,d]) истинно;
member([a,b] ,[c,[b,a] ,e,d]) ложно.
Множества в Прологе представляются списками. Списки могут
иметь повторы элементов. Программисту следует заботиться о том,
чтобы используемые для представления множеств списки этих
повторов не имели.
Предикат member(X,Y) задается следующей процедурой.
154
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Рассмотрим ход вычислений в Прологе в ответ на запрос
member(c,[b,a,c,d]).
Построим соответствующее дерево вывода (рис.6.6).
Процедура вычисления предиката member состоит из формул логики
предикатов:
CI. (VX)(VY)member(X,[X|Y]).
С2. (VX)(VY)(Vz)(member(X,Z) - member(X,[Y|Z]).
Вопрос о вычислении истинности формулы member(c,[b,a,c,d]),
обозначим ее через А, формально означает вычисление
общезначимости формулы В = С1 & С2 -> А, или невыполнимости формулы
"1В = ~1(~1(С1 & С2) V А) = С1 & С2 & ПА.
При этом ПВ невыполнима тогда и только тогда, когда множество
дизъюнктов S = {С1, С2, ПА} выводит пустой дизъюнкт. Формулы С1,
С2, ПА обычно пишутся без кванторов. Таким образом речь идет о
выводе пустого дизъюнкта из хорновских дизъюнктов
CI. member(X,[X|Y]),
С2. nmember(X,Z) V member(X,[Y|Z])
и запроса
СЗ. nmember(c,[b,a,c,d]),
который тоже является хорновским дизъюнктом.
Транслятор работает следующим образом. Пусть знак := означает
присваивание (т.е. назначение) переменным. Запрос СЗ помещается в
узел 0 (т.е. в корень) дерева вывода (см. рис.6.6).
Узел 1. Проводится попытка унификации дизъюнктов СЗ и С1. Цель
СЗ при этом является образцом, а предложение С1 сравнивается с
этим образцом. Возникающее из сравнения СЗ и С1 присваивание
X := с, X := b, Y := [a,c,d]
противоречиво. Попытка унификации не удалась. В узле 1 дерева
О СЗ
2 С4 = ПР(С2,СЗ)
4 С5 = ПР(С2,С4)
С6 = ПР(С1,С5) = D *^Ъ
Рмс.6.6
ПР(С1,СЗ)
ггр^гч гм^
155
вывода вычисление безуспешно; осуществляется бэктрэкинг, т.е.
отход в узел 0. Сделанные ранее на пути от узла 0 к узлу 1
присваивания переменным отменяются. Испытывается другая возможность
согласования запроса СЗ с предложениями программы.
Узел 2. Проводится попытка унификации дизъюнктов СЗ и С2 по
второму (положительному) слагаемому в С2. Возникающее из
сравнения образца СЗ и второго слагаемого в С2 присваивание
X := с, Y := b, Z := [b,c,d]
непротиворечиво. Подстановка
01 = НОУ(С2,СЗ) = {clX, blY, [a,c,d]lz}.
Формируется дизъюнкт
С21 = С2-01 = ~lmember(c,[a,c,d]) V member(c,[b,a,c,d]).
Строится дизъюнкт
С4 = ПР(С2,СЗ) = ПР(С21, СЗ) = lmember(c,[a,c,d]),
являющийся новым запросом
С4. 1member(c,[a,c,d]).
В узле 2, где вычисление успешно, помещается цель С4.
Узел 3. Проводится попытка унификации С4 и С1. Цель С4
является сейчас образцом. Присваивание
X := с, X := a, Z := [c,d]
противоречиво. Попытка унификации не удалась. В узле 3 вычисление
безуспешно; осуществляется отход в узел 2; сделанные ранее на
пути от узла 2 к узлу 3 присваивания переменным отменяются.
Узел 4. Проводится попытка унификации С4 и С2 по второму
дизъюнктивному слагаемому в С2. Предложение С2 программы сравнивается
с образцом С4. Присваивание
X := с, Y := a, Z := [c,d]
непротиворечиво. Подстановка
02 = НОУ(С2,С4) = {clX, alY, [c,d]lz}.
Формируется дизъюнкт
С22 = С2-02 = ~lmember(c,[c,d]) V member(c,[a,c,d]).
Строится дизъюнкт
С5 = ПР(С2,С4) = ~lmember(c,[c,d]),
являющийся новым запросом
С5. 1member(c, [ с, d]).
В узле 4, где вычисление успешно, помещается цель CS.
Узел 5. Проводится попытка унификации С5 и С1. Присваивание
X := с, X := с, Y := [d]
непротиворечиво. Подстановка
03 = {clX, [d]|Y}.
Формируется дизъюнкт
С13 = Cl-03 = member(c,[c,d]).
156
Строится дизъюнкт
С6 = ПР(С1,С5) = ПР(С13,С5) = П.
Выведен пустой дизъюнкт. В узле 5 вычисление закончилось
успешно. Это значит, что ответ на исходный запрос об истинности
member(c,[b,a,c,d]) утвердительный, о чем ЭВМ и сообщает
пользователю. Транслятор прекращает свою работу.
Проследим ход вычислений в Прологе в ответ на запрос member(X,
[Ь,а]). Построим соответствующее дерево вывода (рис.6.7). Вопрос
сводится к вычислению истинности формулы (3x)member(X,[b,a]).
Обозначим ее через (Эх)А. Формально это означает вычисление
общезначимости формулы В = С1 & С2 -> (ЗХ)А, или невыполнимости
формулы 1В = ~1("1(С1 & С2) V (ЭХ)А) = С1 & С2 & 1(ЭХ)А = С1 & С2 &
(Vx)"IA. При этом формула "IB невыполнима тогда и только тогда,
когда из множества дизъюнктов S = {CI, C2, (VX)"IA} выводится
пустой дизъюнкт. Формулы CI, C2, (VX)~IA пишутся без кванторов. Речь
идет о выводе пустого дизъюнкта из хорновских дизъюнктов
CI. member(X,[X|Y]),
С2. -|member(X,Z) V member(X,[Y|Z])
и запроса
СЗ. ~lmember(X,[b,a]),
который тоже является хорновским (отрицательным) дизъюнктом.
Транслятор работает следующим образом. Запрос СЗ помещается в
узел 0 дерева вывода.
Узел 1. Проводится попытка унификации СЗ и С1. Присваивание
X := b, Y := [а]
непротиворечиво. Подстановка
91 = НОУ(С1,СЗ) = {b|X,[a]|Y}.
Формируюся дизъюнкты
СИ = C1-G1 = member(b,[b,a]),
С31 = СЗ-01 = lmember(b,[b,a]).
Строится дизъюнкт
С4 = ПР(С1,СЗ) = ПР(С11,С31) = П.
Выведен пустой дизъюнкт; вычисление в узле 1 закончилось
успешно. Система выдает решение X = b и предлагает (с помощью бэктрэ-
кинга) найти другие возможные решения. Вычисления продолжаются
нажатием клавиши ; (точка с запятой). Осуществляется отход в узел
О дерева вывода. Сделанные ранее на пути от узла 0 к узлу 1
присваивания переменным отменяются.
Узел 2. Проводится попытка унификации СЗ и С2 по второму
(положительному) слагаемому в С2. Присваивание
Y := b, Z := [а]
непротиворечиво. Подстановка
157
о сз
2 С5 = ПР(С2,СЗ)
4 С7= ПР(С2,С5)
6 ПР(С2,С7)
Рис.б.7
62 = НОУ(С2,СЗ) = {blY, [a]lz}.
Формируется дизъюнкт
С22 = С2-62 = ~lmember(X,[a]) V member(X, [b,a]).
В узле 2 помещается дизъюнкт
С5 = ПР(С2,СЗ) = ПР(С22,СЗ) = 1тетЬег(Х,[а]),
являющийся новым запросом
С5. "lmember(X,[a]).
Узел 3. Проводится попытка унификации С5 и С1. Присваивание
X := a, Y := []
непротиворечиво. Подстановка 63 = НОУ(С1,С5) = {alX,[]lY]).
Формируются дизъюнкты
С13 = Cl-63 = member(a,[a]),
С53 = С5-63 = ~lmember(a,[a]). В узле 3 помещается дизъюнкт
С6 = ПР(С1,С5) = ПР(С13,С53) = D.
Выведен пустой дизъюнкт. Система выдает новое решение X = а и
предлагает отыскать другие решения. Вычисления продолжаются
нажатием клавиши точка с запятой. Осуществляется отход в узел 2. Все
сделанные ранее на этом пути назначения переменным отменяются.
Узел 4. Проводится попытка унификации С5 и С2 по второму
(положительному) слагаемому в С2. Присваивание Y := a, Z :=[]
непротиворечиво. Подстановка 64 = НОУ(С2,С5) = {a|Y, []lz}. Форми-
мируется дизъюнкт
С24 = С2-64 = ~lmember(X,[]) V member(X,[a]).
В узле 4 строится дизъюнкт
С7 = ПР(С2,С5) = ПР(С24,С5) = "I member (Х,[1),
являющийся новым запросом
С7. "lmember(X,[]).
Узлы 5,6. Так как пустой список не имеет ни головы, ни хвоста,
то попытка унификации С1 и С7 безуспешна. По этой же причине
безуспешна попытка унификации С2 и С7. Вычисления в узлах 5 и 6
дерева вывода безуспешны. Решений больше нет. Система сообщает об
С4 = ПР(С1,СЗ) = D *^\
С6 = ПР(С1,С5) = D
ПР(С1.С7) •- с
158
этом пользователю и прекращает работу.
6.7.2. Первый элемент в списке
Предикат first(X,Y) истинен, если X есть первый элемент списка
Y. Например,
first(a,[a,b,c]) истинно;
first(a,[b,a,c]) ложно;
first([a,b] ,[[a,b] ,c,d]) истинно;
first([a,b] ,[[b,a] ,c,d]) ложно.
Предикат first(X,Y) задается следующей процедурой, состоящей
из единственного предложения.
first(X,[X|Y]).
Проследим ход вычислений в Прологе в ответ на запрос ?-
first(X,[a,a,b]). Из дизъюнкта
CI. first(X,[X|Y]) и запроса
С2. lfirst(X,[a,a,b])
система пытается вывести пустой дизъюнкт. Проводится попытка
унификации С1 и С2. Присваивание
X := a, Y := [а,Ь]
непротиворечиво. Дизъюнкт
СЗ = ПР(С1,С2) = П.
Получено решение X = а. Других возможностей унификации нет.
Система сообщает об отсутствии других решений и прекращает
работу.
6.7.3. Последний элемент в списке
Предикат last(X,Y) истинен, если X есть последний элемент
списка Y. Например,
last(c,[a,b,c]) истинно;
last(c,[a,c,b]) ложно.
Предикат last(X,Y) задается следующей процедурой.
last(X,[X]).
last(X,[Z|Y]) :- last(X,Y).
На рис.6.8 приведено дерево вывода в ответ на помещенный в
узел 0 дерева вывода запрос last(X,[a,s,d]). Ниже следуют
комментарии.
CI. last(X,[X]).
С2. llast(X,Y) V last(X,[Z|Y]).
СЗ. llast(X,[a,s,d]).
В узле 1 попытка провести унификацию С1 и СЗ безуспешна. Отход
от узла 1 в узел 0. Попытка провести унификацию С2 и СЗ успешна.
159
о сз
2 С4
4 С5
6 С7
8
Рнс.б.8
В узле 2 формируется запрос
С4 = ПР(С2,СЗ) = llast(X,[s,d]).
Попытка провести унификацию С1 и С4 в узле 3 безуспешна. Отход
от узла 3 в узел 2. Попытка провести унификацию С2 и С4 успешна.
В узле 4 формируется запрос
С5 = ПР(С2,С4) = llast(X,[d]).
Унификация С1 и С5 успешна. В узле 5 формируется запрос
С6 = ПР(С1,С5) = П.
Решение X = d. При бэктрэкинге осуществляется отход от узла 5 в
узел 4 и проводится успешная попытка унификации С2 и С5. В узле 6
формируется запрос
С7 = ПР(С2,С5) = llast(X,[]).
Попытки провести унификацию для С1 и С7 в узле 7 равно как и для
С2 и С7 в узле 8 безуспешны. Других решений нет. Система сообщает
об этом и прекращает работу.
6.7.4. Следующий элемент в списке
Предикат next(X,Y,L) истинен, если элемент Y непосредственно
следует за элементом X в списке L. Например,
next(a,b,[s,h,a,b,c,d]) истинно;
next(a,b,[s,h,a,c]) ложно.
Предикат next(X,Y,L) задается следующей процедурой.
next(X,Y,[X,Y|Z]).
next(X,Y,[U|Z]) :- next(X,Y,Z).
Рассмотрим ход вычислений в Прологе в ответ на запрос next(2,
V,[1,2,3,2,5]); построим соответствующее дерево вывода (рис.6.9).
Процедура вычисления предиката next состоит из следующих двух
формул логики предикатов
CI. (VX)(VY)(Vz)next(X,Y,[X,Y|Z]).
С2. (VX)(VY)(VZ)(VU)(next(X,Y,Z) - next(X,Y,[U|Z]).
160
о сз
ПР(С1,СЗ)
ПР(С1,С4) = □
ПР(С1,С6) -
ПР(С1,С7) = □ <
ПР(С1,С9) <
Ч ^х^
"3 ^^
"5 ^^^
' ^^
"9 ^^
^П '
i 2 С4 = ПР(С2,СЗ)
• 4 С6 = ПР(С2,С4)
' 6 С7 = ПР(С2,С6)
8 С9 = ПР(С2,С7)
10 СЮ = ПР(С2,С9)
12
Рнс.6.9
Вопрос о вычислении элемента V в списке [1,2,3,2,5], следующим
за элементом 2, сводится к вычислению истинности формулы
(3v)next(2,V,[l,2,3,2,5]). Обозначим ее через (3v)A. Формально
это означает вычисление общезначимости формулы В = С1 & С2 -»
(3V)A, или невыполнимости формулы "IB = "1("1(С1 & С2) V (3V)A) =
С1 & С2 & 1(3V)A = С1 & С2 & (VV)lA.
При этом формула "IB невыполнима тогда и только тогда, когда из
множества дизъюнктов S = {CI, C2, (VV)~IA} выводится пустой
дизъюнкт. Формулы CI, C2, (VV)~IA пишутся без кванторов. Таким образом
речь идет о выводе пустого дизъюнкта из хорновских дизъюнктов
CI. next(X,Y,[X,Y|Z]),
С2. lnext(X,Y,Z) V next(X,Y,[U|Z])
и помещенного в узел 0 дерева вывода запроса
СЗ. lnext(2,V,[1,2,3,2,5]),
который тоже является хорновским (отрицательным) дизъюнктом.
Транслятор работает следующим образом.
Узел 1. Проводится попытка унификации дизъюнктов С1 и СЗ.
Возникающее из сравнения С1 и СЗ присваивание
X := 2, Y := V, X := 1, Y := 2, Z := [3,2,5]
противоречиво. В узле 1 попытка унификации не удалась. Отход от
узла 1 в узел 0.
Узел 2. Проводится попытка унификации дизъюнктов С2 и СЗ по
второму (положительному) слагаемому в С2. Возникающее из
сравнения СЗ и второго слагаемого в С2 присваивание
X := 2, Y := V, U := 1, Z := [2,3,2,5]
непротиворечиво. Подстановка
91 = НОУ(С2,СЗ) = {2lX, V|Y, l|U, [2,3,2,5] IZ}.
161
Формируется дизъюнкт
С21 = С2-91 = lnext(2,V,[2,3,2,5]) V next(2,V,[l,2,3,2,5]).
В узле 2 строится дизъюнкт
С4 = ПР(С2,СЗ) = ПР(С21, СЗ) = ~lnext(2,V,[2,3,2,5]),
являющийся новым запросом
С4. lnext(2,V,[2,3,2,5]).
Узел 3. Проводится попытка унификации С1 и С4. Присваивание
X := 2, Y := V, X := 2, Y := 3, Z := [2,5]
непротиворечиво. Подстановка
92 = НОУ(С1,С4) = {2lX, 3lY, [2,5] lz}.
Формируется дизъюнкт
С12 = Cl-92 = next(2,3,[2,3,2,5]).
В узле 3 строится дизъюнкт
С5 = ПР(С1,С4) = ПР(С12,С4) = □ .
Вопрос о (3V)A решен, именно, элемент V = 3 следует в данном
списке за элементом 2. Решение V = 3 сообщается пользователю.
Транслятор (по желанию пользователя) работает дальше, пытаясь
найти в исходном списке другие элементы, следующие за двойкой.
Осуществляется отход от узла 3 в узел 2.
Узел 4. Проводится попытка унификации С2 и С4 по второму
дизъюнктивному слагаемому в С2. Присваивание
X := 2, Y := V, U := 2, Z := [3,2,5]
непротиворечиво. Подстановка
93 = НОУ(С2,С4) = {2|Х, V|Y, [2,5] lz]}.
Формируется дизъюнкт
С23 = С2-93 = lnext(2,V,[3,2,5]) V next(2,V,[2,3,2,5]).
В узле 4 строится дизъюнкт
С6 = ПР(С2,С4) = lnext(2,V, [3,2,5]),
являющийся новым запросом
Сб. lnext(2,V,[3,2,5]).
Узел 5. В узле 5 проводится попытка унификации С1 и Сб.
Присваивание
X := 2, Y := V, X := 3, Y := 2, Z := [5]
противоречиво. Отход в узел 4.
Узел 6. Проводится попытка унификации С2 и С6 по второму
слагаемому в С2. Присваивание
X := 2, Y := V, Z := [2,5]
непротиворечиво. Подстановка
94 = {2lX, VlY, 3lU, [2,5] lz}.
Формируется дизъюнкт
С24 = С2-94 = lnext(2,V,[2,5]) V next(2,V,[3,2,5]).
В узле 6 строится дизъюнкт
162
C7 = ПР(С2,С6) = ПР(С24,С6) = lnext(2,V,[2,5]),
являющийся новым запросом
С7. lnext(2,V,[2,5]).
Узел 7. Проводится попытка унификации С1 и С7. Присваивание
X := 2, Y := V, X := 2, Z := []
непротиворечиво. Подстановка
95 = НОУ(С1,С7) = {2lX, 5|Y, []lz}.
Формируется дизъюнкт
С15 = Cl-95 = next(2,5,[2,5]).
В узле 7 строится дизъюнкт
С8 = ПР(С1,С7) = ПР(С15,С7) = П.
Найден еще один элемент V = 5, следующий в исходном списке за
элементом 2, о чем тоже сообщается пользователю.
Транслятор продолжает работу. Отход от узла 7 в узел 6.
Узел 8. Проводится попытка унификации С2 и С7. Присваивание
X := 2, Y := V, U :=2, Z := [5]
непротиворечиво. Подстановка
96 = НОУ(С2,С7) = {2lX, V|Y, 2lU, [5]lz}.
Формируется дизъюнкт
С26 = С2-96 = lnext(2,V,[5]) V next(2,V,[2,5]).
В узле 8 строится дизъюнкт
С9 = ПР(С2,С7) = ПР(С26,С7) = lnext(2,Vj5]),
являющийся новым запросом
С9. ~lnext(2,V,[5]).
Узлы 9,10,11,12. Попытка унификации С9 и С1 безуспешна.
Попытка унификации С9 и С2 успешна. В узле 10 формируется запрос
СЮ. ~lnext(2,V,[]).
Так как пустой список в СЮ не имеет ни головы, ни хвоста, то
попытка унификации СЮ и С1, а также СЮ и С2 безуспешны. ЭВМ
сообщает, что решений больше нет. Вычисления закончены.
В* последующем не будем вновь полученный запрос сопровождать
знаком отрицания (он подразумевается).
6.7.5. Соединение списков
Предикат append(Ll,L2,L3) истинен, если список L3 получается
приписыванием списка L2 к списку L1. Например,
append([a,b] ,[c,d,e] ,[a,b,c,d,e]) истинно;
append([a] ,[b,c] ,[b,a,c]) ложно.
Если X = [a,[b,c]], Y = [g,h], то append(X,Y,Z) истинно при Z
= [a,[b,c],g,h).
Предикат append(Ll,L2,L3) задается следующей процедурой.
append([],L,L).
163
append([X|Ll],L2,[X|L3]) :- append (LI, L2,L3).
Обозначим предложения программы через CI, C2 соответственно и
проследим ход вычислений в ответ на запрос
СЗ. append([a,b,c],[d,e],L).
Сопроводим вычисления краткими пояснениями. Пусть У(С1,С2)
означает "унификация С1 и С2".
У(СЗ,С1) безуспешна по первому аргументу.
У(СЗ,С2) успешна.
X := a, LI := [b,c], L2 := [d,e], L := [a|L3].
Новый запрос
С4. append([b,c],[d,e],L3).
У(С4,С1) безуспешна по первому аргументу.
У(С4,С2) успешна.
X := b, L1 := [с], L2 := [d,e], L3 := [b|L3l].
Новый запрос
С5. append([c],[d,e],L3l).
У(С5,С1) безуспешна по первому аргументу.
У(С5,С2) успешна.
X := с, L1 := [], L2 := [d,e], L31 := [c|L32].
Новый запрос
Сб. append([],[d,e],L32).
У(С6,С1) успешна. L32 := [d,e].
Далее последовательно получаем: L31 := [c|L32] = [c,d,e].
L3 := [b|L3l] = [b,c,d,e]. L := [c|L3] = [a,b,c,d,e].
Транслятор выдает ответ L = [a,b,c,d,e] и прекращает работу.
Предикат appendk(S,L) истинен, если список L есть объединение
элементов в списках из S. Например, если S = [[a,b,c,d] ,[e,f] ,[q,
r,t]], то L=[[a,b,c,d,e,f,q,r,t].
Предикат appendk(S,L) задается следующей процедурой.
appendk(S,L) :- length(S,K),K>l,appendlk(S,L).
appendk([H|[]],[H|[]]).
appendk( [],[]).
appendlk([Hl,H2|T],L) :- append(Hl,H2,Ll),append2k(Ll,T,L).
append2(Ll,[H|T],L) :- append(Ll,H,L2),append2k(L2,T,L).
append2k(L,[] ,L).
6.7.6. Обращение списка
Предикат reverse(L,S) истинен, если список S есть обращение
списка L. Например,
reverse([a,b,c] ,[c,b,a]) истинно;
reverse([a,b,c] ,[c,d,a]) ложно;
reverse([a,[b,c]],[[b,c],a]) истинно;
164
reverse([a,[b,c]] ,[[c,b] ,a]) ложно.
Если X = [a,[b,c] ,d], то предикат reverse(X,Y) истинен при Y =
[d,[b,c],a]. Предикат reverse(L,S) задается следующей процедурой.
reversed ],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
Обозначим предложения программы через CI, C2 соответственно и
проследим ход вычислений в ответ на запрос
СЗ. reverse([a,b,c] ,L).
Пусть У(С1,С2) по-прежнему означает "унификация С1 и С2".
У(СЗ,С1) безуспешна по первому аргументу.
У(СЗ,С2) успешна. Н := а, Т := [Ь,с]. Новый запрос
reverse([b,c] ,Z),append(Z,[a] ,L).
Пусть С4 - очередная цель reverse([b,c] ,Z) в этом новом
сложном запросе, состоящем из двух целей.
У(С4,С1) безуспешна по первому аргументу.
У(С4,С2) успешна. Н := b, T := [с]. Новый запрос
reverse([c],Zl),append(Zl,[b],Z),append(Z,[a],L).
Пусть С5 - очередная цель reverse([c] ,Zl) в этом запросе.
У(С5,С1) безуспешна по первому аргументу.
У(С5,С2) успешна. Н := с, Т := []. Новый запрос
reversed], Z2),append(Z2, [с], Zl),append(Zl,[b] ,Z),append(Z,
[a],L).
Пусть С6 - очередная цель reversed ] ,Z2) в этом запросе.
У(С6,С1) успешна. Z2 := []. Новый запрос
append([] ,[c] ,Zl),append(Zl,[b] ,Z),append(Z,[a] ,L).
Обработка трех целей этого запроса последовательно дает:
Z1 := [с], Z := [c,b], L := [с,Ь,а].
Транслятор в качестве ответа выдает L = [с,Ь,а] и прекращает
работу.
Предикат reverse(L,S) можно задать также следующей процедурой.
reversel(Ll,L2) :- rev(Ll,[] ,L2).
rev([],L,L).
rev([X|L],L2,L3) :- rev(L,[X|L2] ,L3).
6.7.7. Выравнивание списка
Предикат flatten(S,L) истинен, если L есть список атомов
списка S. Например,
если S=[a,b], то L=[a,b];
если S=[a,[b,c],d], то L=[a,b,c,d];
если S=[a,[b,[c,d]] ,[е]], то L=[a,b,c,d,e].
Предикат flatten(S,L) задается следующей процедурой.
flatten([H|T],L) :- flatten(H,LH),flatten(T,LT),
165
append(LH,LT,L).
flatten([] Д1).
flatten(X,[X]).
6.7.8. Добавление элемента в начало списка
Предикат add(X,L,Ll) истинен, если список L1 получается
добавлением элемента X в начало списка L. Например,
add(a,[b,c] ,[a,b,c]) истинно;
add(a,[b,c],[b,a,c]) ложно.
Если X = a, Y = [[a],b,[d]], то предикат add(X,Y,Z) истинен
при Z = [a,[a],b,[d]].
Предикат add(X,L,Ll) задается процедурой
add(X,L,[X|L]).
Добавление элемента в начало списка без его удвоения можно
задать следующей процедурой.
addl(X,L,L) :- member(X,L),!.
addl(X,L,[X|L]).
В этой процедуре используется оператор отсечения. Если список
L содержит элемент X, то цель member исполнится успешно, затем
последует оператор отсечения, после исполнения которого ни addl,
ни member при бэктрэкинге вычисляться уже не будут. Транслятор
закончит вычисления и выдаст ответ. Если список L элемента X не
содержит, то цель member окажется безуспешной (ложной),
согласование запроса с первым предложением программы будет тоже
безуспешным, осуществится бэктрэкинг. После согласования запроса со
вторым предложением программы элемент X будет поставлен первым
элементом в списке L и выдан ответ.
6.7.9. Удаление первого вхождения данного элемента из списка
Предикат delete(X,L,M) истинен, если список М есть результат
удаления из списка L первого вхождения элемента X. Например,
delete(a,[s,f,a,h,a,g],[s,f,h,a,g]) истинно;
delete(a,[s,f,a,h,a,g],[s,f,a,h,g]) ложно.
Если X = a, Y = [s,[d,s] ,a,h,a,d,a], то предикат delete(X,Y,Z)
истинен при Z = [s,[d,s] ,h,a,d,a].
Если в списке L элемента X нет, то запрос ?- delete(X,L,M)
безуспешен.
Предикат delete(X,L,M) задается следующей процедурой.
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
Оператор отсечения предотвращает альтернативу для предиката
delete. Если оператор отсечения убрать, то с помощью бэктрэкинга
166
из списка L можно удалять последовательные вхождения элемента X.
6.7.10. Удаление всех вхождений данного элемента из списка
Предикат delall(X,L,M) истинен, если список М получается
удалением из списка L всех вхождений элемента X. Например, если X
= a, Y = [a,s,d,a,f ,a,h], то предикат delall(X,Y,Z) истинен при Z
= [s,d,f,h].
Предикат delall(X,L,M) задается следующей процедурой.
delall(_, [],[]).
delall(X,[X|L],M) :- ! ,delall(X,L,M).
delall(X,[Y|Ll],[Y|L2]) :- delall(X,Ll,L2).
Обозначим предложения программы через С1,С2,СЗ соответственно;
проследим ход вычислений и построим дерево вывода (рис.6.10) в
ответ на помещенный в корневой узел 0 дерева запрос
С4. delall(a,[b,a,c,a,d],S).
Пусть У(С4,С1) означает "унификация С4 и С1".
Узел 1. У(С4,С1) безуспешна. Отход от узла 1 в узел 0.
Узел 2. У(С4,С2) безуспешна. Отход от узла 2 в узел 0.
Узел 3. У(С4,СЗ) успешна.
Х:=а, Y:=b, Ll:=[a,c,a,d], S:=[b|L2].
В узле 3 формируется запрос
С5. delall(a,[a,c,a,d],L2).
Рмс.6.10
167
Запрос С5 получается заменой запроса С4 на правую часть
предложения СЗ программы при найденных значениях переменных.
Узел 4. У(С5,С1) безуспешна. Отход от узла 4 в узел 3.
Узел 5. У(С5,С2) успешна. Х:=а, L:=[c,a,d], L2:=M.
В узле 5 формируется запрос
Сб. !,delall(a,[c,a,d],M).
Запрос С6 получается заменой запроса С5 на правую часть
предложения С2 программы при найденных значениях переменных.
Узел 6. В узле 6 исполняется оператор отсечения; в узле 3 (он
помечен знаком !) альтернатива отсекается. В узле 6 формируется
запрос
С7. delall(a,[c,a,d],M).
Узел 7. У(С7,С1) безуспешна. Отход от узла 7 в узел 6.
Узел 8. У(С7,С2) безуспешна. Отход от узла 8 в узел 6.
Узел 9. У(С7,СЗ) успешна. Х:=а, Y:=c, Ll:=[a,d], M:=[c|L2l]. В
узле 9 формируется запрос
С8. delall(a,[a,d],L2l).
Запрос С8 получается заменой запроса С7 на правую часть
предложения СЗ программы при найденных значениях переменных.
Узел 10. У(С8,С1) безуспешна. Отход от узла 10 в узел 9.
Узел 11. У(С8,С2) успешна. Х:=а, L:=[d], L21:=M1. В узле 11
формируется запрос
С9. !,delall(a,[d],Ml).
Запрос С9 получается заменой запроса С8 на правую часть
предложения С2 программы при найденных значениях переменных.
Узел 12. В узле 12 исполняется оператор отсечения; в узле И
(он помечен знаком !) альтернатива отсекается.
Узел 13. В узле 13 формируется запрос
СЮ. delall(a,[d],M).
Узел 14. У(СЮ,С1) безуспешна. Отход от узла 14 в узел 13.
Узел 15. У(СЮ,С2) безуспешна. Отход от узла 15 в узел 13.
Узел 16. У(С10,СЗ) успешна. Х:=а, Y:=d, Ll:=[], Ml:=[d|L22]. В
узле 16 формируется запрос
СП. delall(a,[],L22).
Запрос СП получается заменой запроса СЮ на правую часть
предложения СЗ программы при найденных значениях переменных.
Узел 17. У(С11,С1) успешна. L22:=[]. В узле 17 формируется
запрос
С12. П.
Запрос С12 получается заменой запроса СП на правую часть
предложения С1 программы, которая пуста. Выведен пустой дизъюнкт. В
узле 17 вычислительная ветвь закончилась успешно. Далее последуют
168
следующие вычисления:
Ml = [d|L22] = [d|[]] = [d]; L21 = Ml = [d];
M = [c|L2l] = [c,d]; L2 = M = [c,d]; S = [b|L2] = [b,c,d].
Выдается ответ S = [b,c,d] и система предлагает бэктрэкинг. В
узлах 16,13,12,11,6,5,0 успешных альтернативных согласований с
предложениями программы нет. В узлах 9 и 3 есть альтернатива
успешного согласования помещенных в этих узлах запросов с третьим
предложением программы. Но в узлах 9 и 3 альтернатива отсечена. В
результате система возвращается в корневой узел 0 и сообщает об
отсутствии, альтернативных решений.
Заметим, что первая построенная успешная ветвь вычислений дает
правильный ответ и без оператора отсечения. Оператор отсечения
позволяет отследить только эту одну первую успешную ветвь в
дереве вывода. Если оператор отсечения убрать, то альтернативное
согласование запроса с двумя последними предложениями программы
при бэктрэкинге даст неверные варианты ответов: некоторые
вхождения элемента X из списка L удалены не будут. Если процедура
delall будет составной частью другой программы, то при ее
исполнении может быть осуществлен отход в узлы исполнения целей
процедуры delall. Тогда отсутствие оператора отсечения приведет к
неверному результату для delall, и потому к неверному ответу для
всей программы.
6.7.11. Замена элемента в списке
Предикат substitute(X,L,A,M) истинен, если список М получается
заменой в списке L всех вхождений элемента X на элемент А.
Например, если X = a, L = [b,a,c,a], A =[b,d], то М =
[b,[b,d],c,[b,d]].
Предикат substitute(X,L,A,M) задается следующей процедурой.
substituted ],_,[]).
substitute(X,[X|L],A,[A|M]) :- !,substituted,L,A,M).
substitute(X,[Y|L],A,[Y|M]) :- substituted,L,A,M).
Оператор отсечения в процедуре substitute работает аналогично
тому, как он работает в процедуре delall.
6.7.12. Быть подсписком в списке
Предикат sublist(X,Y) истинен, если список X есть подсписок
списка Y (в смысле вхождения слова X в слово Y). Например,
sublist([a,s] ,[g,d,a,s,h]) истинно;
sublist([a,s] ,[g,a,d,s,h]) ложно.
Предикат sublist(X,Y) задается следующей процедурой.
sublist([X|L],[X|M]) :- coincide(L,M),!.
169
sublist(L,[_|M]) :- sublist(L,M).
coincide( [],_).
coincide([X|L],[X|M]) :- coincide(L,M).
Обозначим предложения программы через С1,С2,СЗ,С4
соответственно. Проследим ход вычислений и построим дерево вывода
(рис.6.11) в ответ на помещенный в корневой узел 0 дерева запрос
С5. sublist([a,s],[g,d,a,a,s,h]).
Пусть У(С5,С1) означает "унификация С5 и СГ.
Узел 1. У(С5,С1) безуспешна. Отход от узла 1 в узел 0.
Узел 2. У(С5,С2) успешна. В узле 2 формируется запрос
Сб. sublist([a,s],[d,a,a,s,h]).
Узел 3. У(С6,С1) безуспешна. Отход от узла 3 в узел 2.
Узел 4. У(С5,С2) успешна. В узле 4 формируется запрос
С7. sublist([a,s],[a,a,s,h]).
Узел 5. У(С7,С1) успешна. В узле 5 формируется запрос
С8. coincide([s],[a,s,h]),!.
В запросе С8 обрабатывается цель
С9. coincide([s],[a,s,h]).
18
19
Ржс.6.11
170
Узел 6. У(С9,С1) безуспешна. Отход от узла 6 в узел 5.
Узел 7. У(С9,С2) безуспешна. Отход от узла 7 в узел 5.
Узел 8. У(С9,СЗ) безуспешна. Отход от узла 8 в узел 5.
Узел 9. У(С9,С4) безуспешна. Отход от узла 9 в узел 5.
Альтернатив по согласованию запроса С9 в узле 5 с
предложениями программы больше нет. Осуществляется отход в узел
4, где для помещенного в этот узел запроса
С7 sublist([a,s],[a,a,s,h])
есть альтернатива согласования со вторым предложением программы.
Узел 10. У(С7,С2) успешна. В узле 10 формируется запрос
СЮ. sublist([a,s],[a,s,h]).
Узел 11. У(С10,С1) успешна. В узле 11 формируется запрос
СИ. coincide([s],[s,h]),!.
Узел 12. У(С11,С1) безуспешна. Отход от узла 12 в узел 11.
Узел 13. У(С11,С2) безуспешна. Отход от узла 13 в узел И.
Узел 14. У(С11,СЗ) безуспешна. Отход от узла 14 в узел 11.
Узел 15. У(С11,С4) успешна. В узле 15 формируется запрос
С12. coincided],[h]),!.
Запрос С12 получается заменой цели coincide([s] ,[s,h]) в запросе
СИ на правую часть предложения С4 программы при найденных
значениях переменных.
Узел 16. У(С12,С1) безуспешна. Отход от узла 16 в узел 15.
Узел 17. У(С12,С2) безуспешна. Отход от узла 17 в узел 15.
Узел 18. У(С12,СЗ) успешна. В узле 18 формируется запрос
С13. !.
Запрос С13 получается заменой цели coincide([] ,[h]) в запросе С12
на правую пустую часть предложения СЗ программы. Далее
исполняется оператор отсечения. В узлах 10 и 11 альтернатива отсекается.
В узле 19 формируется запрос С14. П.
В узле 19 вычисления закончились успешно. Система дает
утвердительный ответ на исходный запрос и останавливается. При бэктрэ-
кинге получаем, что в узле 18 альтернатив нет. В узле 15 попытка
У(С12,С4) безуспешна. Отход по дереву вывода продолжается. В
узлах 11,10 альтернатива отсечена. Осуществляется отход в узел 4,
где запрос sublist([a,s] ,[a,a,s,h]) имеет две безуспешные попытки
согласования с предложениями СЗ и С4 программы. Следует отход в
узел 2, где запрос имеет две безуспешные попытки согласования с
предложениями СЗ и С4 программы. Система отходит в корневой узел
0 и после двух безуспешных попыток согласования помещенного в
этот узел запроса с предложениями СЗ и С4 программа при
отсутствии других решений прекращает работу.
171
6.7.13. Включение множеств
Предикат subset(X,Y) истинен, если множество X есть
подмножество множества Y. Например,
subset([a,s,d] ,[h,d,s,h,a]) истинно;
subset([a,s,d],[h,s,h,a]) ложно;
subset([a,[s,d]] ,[a,[d,s] ,s,h,a]) ложно.
Предикат subset(X,Y) задается следующей процедурой.
subset([],Y).
subset([A|XJ,Y) :- member(A,Y),subset(X,Y).
Процедура subset(X,Y) работает правильно, если обе ее
переменные на момент выполнения процедуры замещены списками без
переменных. Процедуру subset(X,Y) нельзя использовать для порождения
всех подмножеств множества Y. Для этого следует воспользоваться
следующей процедурой.
subsetl( [],[])•
subsetl([H|S],[H|T]) :- subsetl(S,T).
subsetl(S,[H|T]) :- subsetl(S,T).
Процедура subsetl(X,Y) работает правильно, если на момент ее
выполнения X есть переменная, a Y замещено списком без
переменных.
6.7.14. Равенство множеств
Предикат equalset(X,Y) истинен, если множества X и Y
совпадают. Множества X и Y задаются списками атомов.
Предикат equalset(X,Y) задается процедурой
equalset(X,Y) :- subset(X,Y),subset(Y,X).
Процедуру equalset(X,Y) нельзя использовать для порождения
множества X. Для этого служит процедура
equalsetl(X,Y) :- subsetl(X,Y),subsetl(Y,X).
6.7.15. Объединение множеств
Предикат unionset(X,Y,Z) истинен, если множество Z есть
объединение множеств X и Y. Например, если X = [a,s],Y = [f,h,j], то
Z = [a,s,f,h,j]. Предикат unionset(X,Y,Z) задается следующей
процедурой.
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
unionset([],X,X).
Обозначим предложения программы через С1,С2,СЗ соответственно;
проследим ход вычислений и построим дерево вывода (рис.6.12) в
ответ на помещенный в корневой узел 0 дерева запрос
С4. unionset([c,b,a],[d,a,b,f],U).
172
о
2 !
3 !
4
5 !
6 !
7
8
Рис. 6.12
Пусть У(С4,С1) означает "унификация С4 и С1".
Узел 1. У(С4,С1) успешна. В узле 1 формируется запрос
С5. member(c,[d,a,b,f]),! ,unionset([c,b,a] ,[d,a,b,f] ,U).
Цель member(c,[d,a,b,f]) ложна. Отход от узла 1 в узел 0.
Узел 2. У(С4,С2) успешна. Х:=с, R:=[b,a], U:=[c|Z]. В узле 2
формируется запрос Сб. unionset([b,a] ,[d,a,b,f] ,Z).
Узел 3. У(С6,С1) успешна. В узле 3 формируется запрос
С7. member(b,[d,a,b,f]),! ,unionset([a] , [d,a,b,f] ,Z).
Узел 4. Цель member(b,[d,a,b,f]) успешна. В узле 4 формируется
запрос С8. ! ,unionset([a],[d,a,b,f],Z).
Узел 5. Цель ! успешна. В узле 5 формируется запрос
С9. unionset([a], [d,a,b,f] ,Z).
В узлах 2 и 3 (они помечены знаком !) альтернатива для помещенных
в них целей отсекается.
Узел 6. У(С9,С1) успешна. В узле 6 формируется запрос
СЮ. member(a,[d,a,b,f]),! ,unionset([] ,[d,a,b,f] ,Z).
Узел 7. Цель member(a,[d,a,b,f]) успешна. В узле 7 формируется
запрос
СИ. !,unionset([],[d,a,b,f],Z).
Узел 8. Цель ! успешна. В узле 8 формируется запрос
С12. unionset([],[d,a,b,f],Z).
В узлах 5 и 6 (они помечены знаком !) альтернатива для
помещенных в них целей отсекается.
173
Узел 9. У(С12,С1) безуспешна. Отход от узла 9 в узел 8.
Узел 10. У(С12,С2) безуспешна. Отход от узла 10 в узел 8.
Узел 11. У(С12,СЗ) успешна. Z:=[d,a,b,f]. В узле 11
формируется запрос
С13. П.
В узле 11 вычислительная ветвь закончилась успешно. Далее
будет вычислено U = [c|Z] = lc,d,a,b,f]. Система выдаст ответ U =
[c,d,a,b,f] и предложит бэктрэкинг для поиска альтернативных
решений. От узла 11 осуществится отход в узел 8, где альтернатив
согласования помещенного в этом узле запроса с предложениями
программы нет. В узлах 7 и 4 альтернатив нет. В узлах 6,5,3,2
альтернатива (поиск альтернативных решений) отсечена. В узле 0
альтернатива согласования помещенного в него запроса с третьим
предложением программы безуспешна. Система указывает на отсутствие
других решений и прекращает работу.
6.7.16. Пересечение множеств
Предикат intersect(X,Y,Z) истинен, если множество Z есть
пересечение множеств X и Y. Например, если X = [a,b,c,d],Y =
[s,c,b,f], то Z = [b,c].
Предикат intersect(X,Y,Z) задается следующей процедурой.
intersect([],X,[]).
intersect([X|R],Y,[X|Z]) :- member(X,Y),! ,intersect(R,Y,Z).
intersect([X|R],Y,Z) :- intersect(R,Y,Z).
Использование опратора отсечения в процедуре intersect(X,Y,Z)
аналогично его использованию в процедуре unionset(X,Y,Z).
6.7.17. Разность множеств
Предикат difset(X,Y,Z) истинен, если множество Z есть разность
множеств X и Y. Например, если X = [a,d,g,f], Y = [u,a,p,g,e], то
Z = [d,f].
Предикат difset(X,Y,Z) задается следующей процедурой.
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
6.7.18. Декартово произведение множеств
Предикат dek2(X,Y,Z) истинен, если множество Z есть декартово
произведение множеств X и Y.
Предикат dek2(X,Y,Z) задается процедурой:
174
dek2(X,Y,Z) :- findall([A,B], (member(A,X),member(B,Y)),Z).
Предикат dek(S,L) истинен, если список L есть декартово
произведение множеств списка S. Например, если S = [[a,b],[c,d],
[e,f]], то L [[a,c,e],[a,c,f],[a,d,e],[a,d,f],[b,c,e],[b,c,f],
[b,d,e] ,[b,d,f]]. Предикат dek(S,L) задается процедурой:
dek(S,L) :- dekl(S,L).
dekl([Hl,H2|T],L) :- dek2(Hl,H2,Ll),dek3(Ll,T,L).
dekl([H|[]],[H|[]]). dekl([],[]). dek3(Ll,[],Ll).
dek3(Ll,[H|T],L) :- dek2(Ll,H,L2),appendl(L2,L3),
dek3(L3,T,L).
appendl(L2,L3) :- S = [] ,append2(L2,L3,S).
append2([[H|T]|Tl],L3,S) :- append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],Sl,Sl).
6.7.19. Множество всех подмножеств данного множества
Предикат powerset(X,S) истинен, если S есть множество всех
подмножеств множества X.
Предикат powerset(X,S) задается следующей процедурой.
powerset(X,S) :- findall(Y,subsetl(Y,X),S).
6.7.20. Удаление всех повторов элементов в списке
Предикат delrepeate(S,SF) истинен, если список SF получается
удалением всех повторов элементов в списке S. Например, если S =
[a,d,s,a,g,d,g,a], то SF = [s,d,g,a].
Предикат delrepeate(S,SF) задается следующей процедурой.
delrepeate(S,SF) :- Sl=[] ,delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
6.7.21. Принадлежность множества списку некоторых подмножеств
Множество некоторых подмножеств задается как список S списков
атомов. Предикат member_set(L,S) истинен, если множество L
является элементом в множестве S. Например,
member_set([a,d,s],[[a,b],[d,a,s]]) истинно;
member_set([a,s] ,[[a,b] ,[d,a,s]]) ложно.
Переменные L и S к моменту вычисления предиката должны быть
замещены константами.
Предикат member_set(L,S) задается следующей процедурой.
175
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Yl|Y]) :- member_set(L,Y).
6.7.22. Удаление всех повторов подмножеств
в данном списке множеств
S есть множество некоторых подмножеств, заданное как список
списков атомов. Предикат del_rep_sets(S,SF) истинен, если
множество SF получается удалением всех повторов элементов в S.
Например, если S = [[a,s],[f,h,a],[s,a,s], [s,a,a] ,[a]], то SF = [f,h,
a],[s,a,a],[a]]. Удаление повторов в составляющих множествах не
производится.
Предикат del_rep_sets(S,SF) задается следующей процедурой.
del_rep_sets(S,SF) :- Sl=[],del_set(S,Sl,SF).
del_set([H|T],Sl,SF) :- member_set(H,T),del_set(T,Sl,SF).
del_set([H|T],Sl,SF) :- not(member_set(H,T)),
append(Sl,[H],S2),del_set(T,S2,SF).
del_set([],S2,S2).
6.7.23. Удаление повторов атомов в списке списков атомов
Предикат delrep_el(S,SM) истинен, если список SM получается
удалением повторов атомов в списке S списков атомов. Например,
если S = [[a,s,a,d,s,f],[s,k],[f,d,f,h,f]], то SM = [[a,d,s,f],
[s,k],[d,h,f]].
Предикат delrep_el(S,SF) задается следующей процедурой.
delrep_el(S,SM) :- L=[],delrpl(S,L,Sl),reverse(Sl,SM).
delrpl([H|T],L,Sl) :- delrepeate(H,Hl),delrpl(T,[Hl|L] ,Sl).
delrpl([],Sl,Sl).
6.7.24. Последовательное порождение нумерованных атомов
Процедура genatom(Roote,Atom) образует атом Atom, в котором
первым символом является атом Roote, а вторым - индекс. Например,
при Roote = q процедура genatom при последовательном ее
исполнении даст значения Atom, последовательно равные q0,ql,q2,... .
Процедура genatom(Roote,Atom) задается следующей программой.
genatom(Roote,Atom) :- get__number(Roote,Number),
name(Roote,Namel),name(Number,Name2),
append(Namel, Name2, Name), name( Atom, Name).
get_number(Roote,Number) : -
retract(current__number(Roote,Numberl)),!,
Number is Numberl+1,
asserta(current_number(Roote,Number)).
176
get__number(Roote,0) :- asserta(current_number(Roote,0)).
6.7.25. Программа построения сокращенной ДНФ
по конъюнктивной нормальной форме
Перемножаются две скобки КНФ. Результат последовательно
умножается на другие скобки КНФ, причем при каждом таком перемножении
из результата удаляются слагаемые (списки), содержащие переменную
и ее отрицание, производится поглощение в каждом слагаемом
(списке) и между всеми слагаемыми (списками).
Предикат del_neg(Ll,L) удаляет из ДНФ слагаемые, содержащие
переменную и ее отрицание.
Предикат have_neg(X) истинен, если дизъюнктивное слагаемое
(список X) имеет переменную и ее отрицание.
Предикат d(S,L) по КНФ S, заданной списком, выдает
сокращенную ДНФ L. Например, если S=[[x,-y,z,t] ,[x,-y,-z,t] ,[x, -y,-z,-
t],[-x,y,z,-t],[-x,y,-z,-t]], то L=[-y,-t],[t,-z,-x],[t,-z,y],[x,
У1 Л х, -t ], [ -у, -х ]. В привычных обозначениях:
S = (xVyVzVt)(xVyVzVt)(xVyVzVt)(xVyVzVt)(xVyVzVt) =
у! V tzx V tzy V ху V xt V ух.
d(S,L) :- S=[[x,-y,z,t],[x,-y,-z,t],[x,-y,-z,-t],[-x,y,z,-t],
[-x,y,-z,-t]] ,dek_absorb(S,L).
dek_absorb(S,L) :- dekl_absorb(S,Ll),del_neg(Ll,L).
dekl_absorb([Hl,H2|T],L) :-
dek2(Hl,H2,LlN),del_neg(LlN,Lll),
delrepeate(Lll,L13),delrep_el(L13,L12),
absorb_set(L12,L14),dek3_absorb(L14,T,L).
dekl_absorb([H|[]]jH|[]]).
dekl_absorb( [],[]).
dek3_absorb(Ll,[H|T],L) :- dek2(Ll,H,L2),
appendl(L2,L31N),deLneg(L31N,L3l),
delrepeate(L31, L33), delrep_el(L33, L32),
absorb_set(L32,L3),dek3_absorb(L3,T,L).
dek3_absorb(Ll,[],Ll).
appendl(L2,L3) :- append2(L2,L3,[]).
append2([[H|T]|Tl],L3,S) :- append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],S,S).
dek2(X,Y,Z) :~ findall([A,B],(member(A,X),member(B,Y)),Z).
delrep_el(S,SM) :- delrpl(S,[] ,Sl),reverse(Sl,SM).
177
delrpl([H|T],L,Sl) :- delrepeate(H,Hl),delrpl(T,[Hl|L] ,S1).
delrpl([],S,S).
absorb_set(S,L) :- absorb(S,S,L).
absorb([H|T],[Hl|Tl],L) :- absorbl(Tl,Hl,T2),
append(T2,[Hl],T3),absorb(T,T3,L).
absorb([],L,L).
absorbl(S,A,L) :-
findall(M,(member(M,S),not(subset(A,M))),L).
delrepeate(S,SF) :- Sl=[],delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member (H, T),! ,delrep(T, SI, SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
deLneg(Ll,L2) :- Ll=[Head|L3],
ifthenelse(have_neg(Head),del_neg(L3,L2),
(del_neg(L3,L4),L2=[Head|L4])).
deLneg([],[]).
have_neg([]) :- fail.
have_neg(X) :- X=[Head|Y] ,string_term(H,Head),
if thenelse(substring(H, 0,1,$-$),
(string_length(H,Len),Ln is Len-1,
substring(H,l,Ln,El),
string_term(El,Elem),member(Elem,Y)),
(concat ($-$, H, Resl), string_term(Resl, Res),
member(Res,Y))).
have_neg([Head|Y]) :- have_neg(Y).
subset ([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
6.7.26. Программа построения сокращенной ДНФ по конъюнктивной
нормальной форме без отрицаний
Предикат d(S,L) по КНФ S, заданной списком без отрицаний,
выдает сокращенную ДНФ L. Например, если S=[[l,2,3,5,6] ,[2,1,3],
178
[3,1,2,4,6],14,3,5,7],[5,1,4,6],16,1,3,5,7],[7,4,611, то L = [[2,
6,7],[5,3,7],[3,4],[3,6],[1,4],[5,1,6],[1,7],[2,6,4],[2,4,7],[2,
5,7],[2,5,4],[2,5,6]]. В привычных обозначениях:
S = (1V2V3V5V6)(2V1V3)(3V1V2V4V6)(4V3V5V7)(5V1V4V6)&
(6V1V3V5V7)(7V4V6) = 267 V 537 V 34 V 36 V 14 V 516 V 17 V
264 V 247 V 257 V 254 V 256.
d(S,L) :- S=[[l,2,3,5,6],[2,1,3],[3,1,2,4,6],[4,3,5,7],
[5,l,4,6],[6,l,3,5,7],[7,4,6]],dek_absorb(S,L).
dek_absorb(S,L) :- dekl_absorb(S,L).
dekl_absorb([Hl,H2|T],L) :- dek2(Hl,H2,Lll),
delrepeate(Lll, L13), delrep_el(L13, L12),
absorb_set(L12,L14),dek3_absorb(L14,T,L).
dekl_absorb([H|[]],[H|[]]).
dekl_absorb( [],[]).
dek3_absorb(Ll,[H|T],L) :- dek2(Ll,H,L2),appendl(L2,L3l),
delrepeate(L31, L33), delrep_el(L33 ,L32),
absorb_set(L32,L3),dek3_absorb(L3,T,L).
dek3_absorb(Ll,[],Ll).
appendl(L2,L3) :- append2(L2,L3,[]).
append2([[H|T]|Tl],L3,S):-append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],S,S).
dek2(X,Y,Z) :- findall([A,B],(member(A,X),member(B,Y)),Z).
delrep_el(S,SM) :- delrpl(S,[],Sl),reverse(Sl,SM).
delrpl([H|T],L,Sl) :- delrepeate(H,Hl),delrpl(T,[Hl|L],Sl).
delrpl([],S,S).
absorb_set(S,L) :- absorb(S,S,L).
absorb([H|T],[Hl|Tl],L) :-
absorbl(Tl,Hl,T2),append(T2,[Hl],T3),absorb(T,T3,L).
absorb([],L,L).
absorbl(S,A,L) :- findall(M,(member(M,S),not(subset(A,M))),L).
delrepeate(S.SF) :- Sl=[],delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),!,delrep(T,SI,SF).
delrep([H|T],Sl,SF) :-
not(member(H,T)),append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
179
reversed ],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H],L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
6.8. Встроенные предикаты Пролога
В последующих встроенных предикатах Пролога переменные
сопровождаются знаками + (плюс), - (минус), ? (вопросительный знак).
Эти знаки означают следующее:
+ переменная на момент исполнения предиката должна быть
замещена (т.е. является входной переменной);
- переменная на момент исполнения предиката не должна быть
замещена (т.е. является выходной переменной);
? переменная на момент исполнения предиката может быть и
замещенной, и незамещенной (т.е. быть и входной, и выходной).
6.8.1. Средства управления
P,Q конъюнкция целей Р и Q.
Р ; Q дизъюнкция целей Р и Q.
! символ оператора отсечения.
[! Р !] обрезка. Р есть цель или несколько целей. При бэк-
трэкинге поиск других возможных решений для Р не производится.
abort прекращает выполнение программы.
break приостанавливает выполнение программы; вычисления
возобновляются при наборе end_of_file.
call(+P) успешно, если вызываемая цель Р успешна, и безуспешно
в противном случае.
case([Al -> В1,А2 -> В2,...|С]) если цель А1 успешна, то
вычисляется цель В1. Если цель А2 успешна, то вычисляется цель
В2; и так далее. Если все цели А1,А2,... безуспешны, то
выполняется цель С.
case([Al -> В1,А2 -> В2,...]) если цель А1 успешна, то
вычисляется цель В1. Если цель А2 успешна, то вычисляется цель
В2; и так далее. Если все цели А1,А2,... безуспешны, то предикат
case успешен.
end_of_file продолжает исполнение программы после break.
fail всегда безуспешно (т.е. ложно).
ifthen(+P,+Q) если цель Р успешна, то вычисляется цель Q. Если
цель Р безуспешна, то цель Q не вычисляется, а цель ifthen(P,Q)
180
считается успешной.
ifthenelse(+P,+Q,+R) если цель Р успешна, то вычисляется цель
Q. Если цель Р безуспешна, то вычисляется цель R.
not(+P) ложно, если цель Р выполнима; истинно, если нет.
Другие записи этого предиката: not P, \+ Р.
repeat всегда успешно. При бэктрэкинге вызывает повторное
выполнение последующих за repeat целей.
true всегда успешно (т.е. истинно).
6.8.2. Классификация термов
atom(?X) X есть атом.
atomic(?X) X есть одно из: атом, целое число, вещественное
число, стринг, ссылочное число базы данных.
float(?X) X есть вещественное число.
integer(?X) X есть целое число.
number(?X) X есть целое или вещественное число.
nonvar(X) переменная X замещена.
ref(?X) X есть ссылочное число базы данных.
string(?X) X есть стринг.
var(?X) переменная X не замещена.
6.8.3. Унификация термов
Т1 = Т2 истинно, если термы Т1 и Т2 унифицируемы.
Т1 \= Т2 истинно, если термы Т1 и Т2 не унифицируемы.
6.8.4. Сравнение термов
Пролог упорядочивает термы в стандартный порядок следующим
образом. Пусть Т1 и Т2 - некоторые термы. Любая переменная (все
переменные имеют одинаковый приоритет) минимальна. Целые и
вещественные числа упорядочены естественным образом. Атомы и стринги
упорядочиваются лексикографически; знак $ при сравнении атома и
стринга не учитывается. Ссылочные числа базы данных упорядочены
по их величине естественным образом. Предикатные структуры
упорядочены сначала по арности (т.е. местности предиката), затем по
главному функтору и далее рекурсивно по аргументам в порядке их
следования. Термы эквивалентны, если они равны относительно
введенного стандартного порядка.
Т1 == Т2 истинно, если термы Т1 и Т2 эквивалентны.
Т1 \== Т2 истинно, если термы Т1 и Т2 не эквивалентны. Т1 @<
Т2 истинно, если терм Т1 меньше терма Т2 в стандартном порядке.
Т1 @=< Т2 истинно, если терм Т1 меньше или равен терму Т2 в
стандартном порядке.
Т1 @> Т2 истинно, если терм Т1 больше терма Т2 в стандартном
181
порядке.
Т1 @=> Т2 истинно, если терм Т1 больше или равен терму Т2 в
стандартном порядке.
сотраге(-С,+Т1,+Т2) сравнивает термы Т1 и Т2 побуквенно и
возвращает с переменной С: знак = при идентичности Т1 и Т2; знак
< при ТКТ2 в стандартном порядке; знак > при Т1>Т2 в стандартном
порядке. Переменная С на момент исполнения предиката должна быть
незамещенной.
eq(?Tl,?T2) истинно, если структуры Т1 и Т2 являются одной и
той же структурой, занимающей в базе данных одно и то же место.
sort(+Ll,-L2) сортирует список L1 в соответствии со
стандартным порядком, удаляет повторы элементов и отсортированный список
возвращает с L2.
6.8.5. Арифметические функции
Арифметические термы (или выражения) строятся из атомов и
переменных с помощью ниже определенных арифметических операций
обычным образом. Допускаются префиксная и инфиксная записи
арифметических выражений. Арифметические термы без переменных являются
константами.
Пусть X и Y есть операнды арифметических выражений. Пролог
имеет следующие встроенные арифметические функции.
X + Y сложение.
X - Y вычитание.
X * Y умножение.
X / Y деление.
X // Y целое деление.
X Л Y X в степени Y.
- X минус X.
X /\ Y побитовая конъюнкция (только для целых чисел).
X \/ Y побитовая дизъюнкция (только для целых чисел).
\(Х) побитовое отрицание (только для целых чисел).
X « Y побитовый сдвиг X влево на Y позиций (только для целых
чисел).
X » Y побитовый сдвиг X вправо на Y позиций (только для
целых чисел).
X mod Y остаток от деления X на Y (только для целых чисел).
abs(X) абсолютная величина X.
acos(X) arccos(X).
asin(X) arcsin(X).
atan(X) arctan(X).
cos(X) cos(X).
182
exp(X) e в степени X.
ln(X) логарифм натуральный X.
log(X) логарифм десятичный X.
sin(X) sin(X).
sqrt(X) корень квадратный X.
tan(X) tan(X).
round(X,N) X округляется до N десятичных знаков; 0 < N < 15.
6.8.6. Арифметические предикаты
Пусть Е1 и Е2 - арифметические выражения. Пролог имеет
следующие встроенные арифметические предикаты. К моменту вычисления
истинностного значения предиката переменные в арифметических
выражениях Е, Е1 и Е2 должны быть замещены константами.
Е1 > Е2 истинно, если Е1 больше Е2.
Е1 < Е2 истинно, если Е1 меньше Е2.
Е1 >= Е2 истинно, если Е1 больше или равно Е2.
Е1 =< Е2 истинно, если Е1 меньше или равно Е2.
Е1 =:= Е2 истинно, если Е1 равно Е2.
Е1 =\= Е2 истинно, если Е1 не равно Е2.
X is E незамещенной переменной X присваивается значение Е.
inc(+X,-Y) увеличивает X на единицу и возвращает результат с
Y (только для целых чисел).
dec(+X,-Y) уменьшает X на единицу и возвращает результат с Y
(только для целых чисел).
6.8.7. Счетчики
Пролог допускает использование 31 встроенных счетчиков,
пронумерованных от 0 до 30, добавляющих или отнимающих единицу.
ctr_dec(+N,-Y) N есть номер счетчика; Y - уменьшенное на
единицу старое значение счетчика.
ctr_inc(+N,-Y) N есть номер счетчика; Y - увеличенное на
единицу старое значение счетчика.
ctr_set(+N,+X) установка счетчика; N - номер счетчика; X -
начало отсчета.
6.8.8. Обработка термов
arg(+N,+T,-X) истинно, если переменной X присваивается
аргумент N терма Т. Аргументы исчисляются слева направо, начиная с 1.
argO(+N,+T,-X) истинно, если переменной X присваивается
аргумент N+1 терма Т. Аргументы исчисляются слева направо,
начиная с 0.
argrep(+T,+N,+A,-Nt) истинно, если в терме Т вместо его
аргумента с номером N вставляется новый аргумент A; Nt есть вновь
183
полученный терм. Аргументы исчисляются слева направо, начиная с
единицы.
functor(?T,?F,?N) успешно, если F есть главный функтор терма
Т, а N есть местность F.
length(+L,-N) успешно, если N есть число элементов в списке
элементов L.
name(?A,?L) успешно, если L есть список кодов ASCII символов
атома А.
Т =.. L истинно, если L есть список, содержащий главный
функтор в терме Т, за которым следуют его аргументы.
6.8.9. Работа с стрингами
atom_string(?A,?S) обращает атом А в стринг S и стринг S в
атом А.
concat(+Sl,+S2,-R) возвращает результат R конкатенации
(соединения) стрингов или атомов S1 и S2. Результат есть всегда
стринг.
concat([+Sl,+S2,...],-R) возвращает результат R конкатенации
(соединения) стрингов или атомов SI, S2... Результат есть всегда
стринг.
float_text(?Fl,?S,?For) обращает вещественное число F1 (с
плавающей запятой) в стринг S или стринг S (или атом) в
вещественное число F1 указанного формата For. Аргумент For может
принимать одно из следующих значений:
general несущественные нули при формировании числа
игнорируются;
fixed(N) число знаков после десятичной точки равно N (от 0 до
15).
scientific(N) экспонентная форма числа; N есть число
десятичных знаков. Экспонента заключена между -99 и 99.
int_text(?Int,?S) обращает целое число Int в стринг S или
стринг S в целое число Int.
list_text(?L,?AS) обращает список L печатаемых символов
алфавита в стринг AS, а также атом или стринг AS в список L,
состоящий из символов, составляющих AS.
nth_char(+N,-S,-Ch) возвращает ASCII код буквы Ch в стринге S
в позиции N. Отсчет букв в стринге ведется от нуля.
read_line(+H,-X) возвращает строку X текста (от начала до
появления кода каретки перехода на другую строку), прочитывая ее
как первую строку содержимого файла, которому при открытии
приписано число Н. Длина строки не более 256 символов.
read__string(+L,-S) возвращает стринг S длины не более L,
184
прочитывая его с текущего входного устройства (стандартного или
файла).
read_string(+H,+L,-S) возвращает стринг S длины не более L,
прочитывая его как содержимое файла, которому приписано при
открытии число Н.
string_length(+S,?L) возвращает длину L стринга S.
string_serch(+Sub,+S,-L) успешно, если Sub есть подстринг
стринга S и L есть позиция, с которой в стринге начинается
подстринг. Отсчет букв в стринге ведется от нуля.
string_term(?S,?T) обращает стринг S в терм Т и терм Т в
стринг S.
substring(+InSt,+N,+L,-OutSt) успешно, если InSt есть стринг,
a OutSt есть его подстринг длины L, начинающийся с позиции N.
Отсчет букв в стринге ведется от нуля.
6.8.10. Составление списков
bagof(?X,+P,-L) успешно, если L есть список тех X, для
которых цель Р(Х) успешна. Объекты X и Р должны иметь общие
переменные. Список L не упорядочивается. Повторы элементов в L не
устраняются. Если объектов X, удовлетворяющих Р нет, то запрос
bagof(X,P,L) безуспешен. Если Р имеет кроме X и другие
переменные, например Y,Z, то список L будет вычисляться для каждых
возможных элементов Y и Z. Чтобы список L содержал все значения X,
для которых P(X,Y,Z) истинно, на переменные Y,Z следует навесить
квантор существования:
bagof(X, V\ZT(X,Y,Z),L).
Можно писать также
bagof(X, (Y,Z)T(X,Y,Z),L).
findall(?X,+P,-L) успешно, если L есть список всех тех X, для
которых цель Р успешна. Список L не упорядочивается, повторы
элементов в L не устраняются. Если объектов X, удовлетворяющих Р
нет, то запрос findall(X,P,L) истинен, если список L пуст. Цель Р
кроме X может содержать и другие переменные. При этом предикат
действует так, как будто бы на эти переменные навешен квантор
существования.
setof(?X,+P,-L) действует так же как и bagof(X,P,L), за
исключением того, что список L упорядочивается; повторы элементов из
L устраняются. Если объектов X, удовлетворяющих Р нет, то запрос
setof(X,P,L) безуспешен.
6.8.11. Взаимодействие с базой данных
Пролог отличает наличие виртуальной памяти. При этом жесткий
диск служит продолжением оперативной памяти. Это позволяет соз-
185
давать большие программы. База данных (т.е. программа) Пролога
размещается в виртуальной памяти. Система имеет
программу-менеджер, управляющую взаимодействием с виртуальной памятью; эта
программа осуществляет обмен между оперативной и постоянной
памятью. В Прологе программу можно разделить на миры (сегменты). Мир
содержит 256 страниц. Размер страницы 16. килобайт. Так что база
данных в Прологе может достигать объема, равного 16*256*256 =
1 048 576 килобайт (один гигабайт). Мир служит средством
организации предложений программы. Существуют два типа миров: мир
данных и мир кодов. Мир данных состоит из фактов, мир кодов - из
фактов и из других предложений, т.е. из любых термов. По
умолчанию во время сеанса работы с Прологом всегда существует мир api,
предназначенный для фактов и для кодов. Мир создается встроенным
предикатом createworld. После того, как мир создан, вызов
data_world превращает его в текущий мир данных, вызов codeworld
превращает его в мир кодов.
Наличие миров двух типов повышает быстродействие системы при
добавлении и удалении предложений из программы, при других
операциях по модификации программы. Для оптимизации использования
виртуальной памяти программист может поместить все предикаты,
относящиеся к определенной теме, в один мир, а затем вызывать этот
мир по мере надобности. Миры могут использоваться только в
пределах одной базы данных: мир из одной базы данных нельзя
использовать в другой базе данных.
Каждый терм в базе данных размещается под определенным ключом.
Предложение Пролога при этом тоже рассматриватся как терм. Ключ
терма состоит из главного функтора терма и его арности
(местности). Разные предложения Пролога могут иметь один и тот же ключ
(если они имеют в голове предикат одной и той же арности с одним
и тем же именем). Каждому терму БД данных приписывается свое
ссылочное число (базы данных). Термы с одинаковым ключом соединены в
цепь: за ключом следует первый терм, за первым - второй, третий и
так далее; последний терм снова соединен с ключом. Если цепь
термов не помещается на одной странице памяти, то ключ переносится
на другую страницу и цепь продолжается.
Приведем некоторые встроенные процедуры, позволяющие
программисту манипуляции с базой данных.
abolish(+Name/Arity) устраняет из базы данных все предложения
с указанным ключом.
assert(+C) добавляет к базе данных предложение С в конец цепи
предложений с указанным в С ключом. В качестве С не могут
выступать термы, отличные от предложений Пролога. Если в БД предложе-
186
ния с ключом, указанным в С, нет, то предложение С добавляется в
конец программы.
asserta(+C) добавляет к БД предложение С в начало цепи
предложений с указанным в С ключом. В качестве С не могут выступать
термы, отличные от предложений Пролога. Если в БД предложения с
ключом, указанным в С, нет, то предложение С добавляется в конец
программы.
assertz(+C) добавляет к БД предложение С в конец цепи
предложений с указанным в С ключом. В качестве С не могут выступать
термы, отличные от предложений Пролога. Если в БД предложения с
ключом, указанным в С, нет, то предложение С добавляется в конец
программы.
clause(+H,-B) унифицирует Н с головой предложения и
унифицирует В с телом предложения. Переменная Н должна быть замещена.
current_predicate(?P) возвращает имя и арность предикатов в
текущем мире кодов.
erase(+Ref) удаляет из БД терм под ссылочным числом Ref.
eraseall(+Key) удаляет из БД все термы с ключом Key.
instance(+Ref,-T) возвращает терм Т, размещенный в БД под
ссылочным числом Ref.
key(+Key,-Ref) возвращает ссылочное число Ref для заданного
ключа Key. Это ссылочное число не может быть использовано
аргументом для предиката instance.
keys(?Key) возвращает имя и арность ключа в текущем мире
данных.
listing просмотр программы в рабочей области.
listing(+N) просмотр всех предикатов программы с именем N.
nref(+Ref,-Next) возвращает ссылочное число следующего терма в
цепи термов. Используется для движения по цепи термов. Переменная
Next должна быть незамещенной. Используется вместе с предикатом
instance для поиска терма, размещенного под заданным ссылочным
числом.
pref(+Ref,-Prev) возвращает ссылочное число предыдущего терма
в цепи термов. Переменная Prev должна быть незамещенной.
Используется вместе с предикатом instance для поиска терма,
размещенного под заданным ссылочным числом.
nth_ref(+Key,+N,-Ref) возвращает ссылочное число Ref терма,
размещенного в цепи термов под ключом Key на месте N.
recorda(+Key,?T,-Ref) добавляет к БД терм Т в начало цепи
термов с указанным в Т ключом. Возвращает ссылочноое число Ref, под
которым терм Т размещен в базе данных. В качестве Т могут
выступать термы, отличные от предложений Пролога.
187
recorded(+Key,?T,-Ref) выдает из БД терм Т, размещенный под
заданным ключом Key.
recordz(+Key,?T,-Ref) добавляет к БД терм Т в конец цепи
термов с указанным в Т ключом. Возвращает ссылочноое число Ref, под
которым терм Т размещен в базе данных. В качестве Т могут
выступать термы, отличные от предложений Пролога.
record_after(+Ref,?T,-NewRef) добавляет к БД терм Т в середину
цепи термов с указанным в Т ключом после терма, размещенного под
ссылочным числом Ref. Возвращает ссылочноое число NewRef, под
которым терм Т размещен в базе данных. В качестве Т могут выступать
термы, отличные от предложений Пролога.
replace(+Ref,+T) разыскивает терм под ссылочным числом Ref и
замещает его термом Т.
retract(+C) убирает из БД первое предложение, согласуемое с
предложением С.
6.8.12. Работа с мирами
code_world(?01d,?New) унифицирует имя текущего мира кодов с
Old и заменяет его на имя New. При бэктрэкинге возвращается к
старому имени.
create_world(+World_name) создает мир с указанным именем.
data_world(?01d,?New) унифицирует имя текущего мира данных с
Old и заменяет его на имя New. При бэктрэкинге возвращается к
старому имени.
delete_world(+World_Name) удаляет мир с указанным именем.
restore восстанавливает текущую БД до положения последнего
сохранения.
restore(+Name) в оперативной памяти делает текущей БД с
именем Name.
save сохраняет миры после изменений в них.
save(+N) сохраняет мир с именем N.
6.8.13. Стандартные ввод и вывод
current_op(?Prec,?Assoc,?Op) возвращает при бэктрэкинге
определения текущих операторов БД.
display(+T) выдает терм Т в польской префиксной записи.
flush удаляет все символы в буфере.
get(?Char) читает во входном потоке данных первый печатаемый
символ, пропуская все непечатаемые, и присваивает переменной Char
код ASCII этого символа.
getO(?Char) читает во входном потоке данных очередной символ и
присваивает переменной Char код ASCII этого символа.
188
getO_noecho(?Char) аналогичен getO; не выдает символ Char на
стандартное выходное устройство.
keyb(-^SCII,-Scan) выдает код ASCII и сканирующий код Scan
клавиши клавиатуры.
nl переход на другую строку.
ор(+Ргес,+Assoc,+Ор) определяет приоритет Ргес,
ассоциативность Assoc оператора Ор.
В Arity-Prolog приняты следующие значения переменных предиката
ор.
Оператор Ассоциативность Приоритет
1200
1200
1100
1000
900
900
900
800
700
:- —>
:-
>
>
case
spy nospy
not \+
->
= is =.. \== == \==
@< @=< @> @>=
=\= < > =< >= =: =
+ - A \/
'.
+ -
*/>><<
mod
Л
xfx
fx
xfy
xfy
fx
fy
fy
xfy
xfx
yfx
xfy
fx
yfx
xfx
xfy
500
500
500
400
300
200
put(+Char) выдает символ, присвоенный переменной Char.
read(-T) читает терм с текущего входного устройства.
resetop возвращает к стандартным определениям операторов,
принятых в Прологе.
skip(Char) пропускает буквы текущего входного потока, пока не
встретится буква Char.
tab(+N) выполняет N пробелов.
write(+T) печатает терм Т на текущее выходное устройство.
writeq(+T) аналогичен write(T); имя атома или функтора
заключает в кавычки (квотирует).
6.8.14. Доступ к файлам
create(-H,+F) создает и открывает новый файл с именем F;
189
возвращает число Н, которое приписывается открытому файлу. Если
файл с именем F уже существует, то его содержимое стирается.
open(-H,+F,+Access) открывает уже существующий файл с именем F
и с приписанным ему числом Н; Аргумент Access может принимать
одно из следующих значений, каждое из которых определяет характер
доступа к файлу:
г файл открыт для чтения,
w файл открыт для записи,
а файл открыт для присоединения новой записи,
rw файл открыт для чтения или записи,
га файл открыт для чтения или присоединения новой записи.
close(+H) закрывает файл с именем, которому приписано число Н.
6.8.15. Стандартный доступ к файлам в Прологе
see(+F) открывает файл с именем F для чтения в качестве
текущего входного устройства.
seeing(?F) выдает имя файла, открытого для чтения.
seen закрывает текущий открытый файл и делает текущим входным
устройством клавиатуру дисплея.
tell(+F) открывает файл с именем F в качестве текущего
выходного устройства.
telling(?F) выдает имя файла, открытого для записи.
told закрывает текущий открытый для записи файл и делает
текущим выходным устройством экран дисплея.
Arity-Prolog поддерживает предикаты see, seeing, seen, tell,
telling, tuld, принятые в некоторых ранее появившихся версиях
Пролога. Предикаты open, close Arity-Prolog исполняет много
быстрее, их использование предпочтительнее и потому настоятельно
рекомендуемо.
6.8.16. Движение в файле
seek(+H,+Offset,+Metod,-Newloc) ставит указатель в файле с
именем, которому приписано число Н; в соответствии с аргументом
Offset, равняющемуся числу байт, равным началу относительного
размещения выбираемого куска файла; с аргументом Method, равным
одному из следующих атомов:
bof число байт Offset отсчитывается от начала файла;
eof число байт Offset отсчитывается от конца файла;
current число байт Offset отсчитывается от текущей позиции;
возвращает новую позицию Newloc указателя от начала содержимого
файла. Побайтовый отсчет содержимого файла начинается с нуля.
190
6.8.17. Переадресация ввода и вывода
dup(Hl,H2) переадресует открытый для работы файл, которому
приписано число HI, на файл, которому приписано число Н2.
file_list(+F) сохраняет содержимое базы данных на файл с
именем F.
file_list(+F,+Name/Arity) сохраняет содержимое предложений
базы данных с именем Name предиката в голове сохраняемых
предложений и с арностью Arity на файл с именем F.
stdin(+F,+G) переадресует стандартный вход (клавиатура) на
время исполнения цели G на файл с именем F.
stdout(+F,+G) переадресует стандартный выход (дисплей) на
время исполнения цели G на файл с именем F.
stdinoud(+InFile,+OutFile,+G) переадресует стандартный вход и
стандартный выход на время исполнения цели G на файлы с именем
InFile и OutFile соответственно.
6.8.18. Ввод и вывод низкого уровня
in(+P,?B) читает байт В из порта Р.
out(+P,+B) пишет байт В из порта Р.
6.8.19. Работа с экраном
Экран дисплея имеет 25 строк и 80 столбцов. Левая верхняя
точка экрана имеет координаты (0,0); нижняя правая - (24,79).
Следующие значения переменных (атрибуты) возможны для IBM
монохромного дисплея.
Атрибут
Нормально
Невидимо
Подчеркнуто
Видимо реверсивно
Мигает
Мигает подчеркнуто
Мигает реверсивно видимо
Тускло
7
0
1
112
135
129
240
Ярко
15
0
9
120
148
137
248
clr очищает экран и помещает курсос в левый верхний угол
экрана.
region_ca(+UL,+LR,?S) читает буквы и их атрибуты с экрана и
выдает их как стринг S. UL, LR есть левый верхний и правый нижний
координаты прямоугольной области точек экрана, с которой читается
текст.
region_cc(+UL,+LR,?S) делает то же, что и region__ca, но не
191
читает атрибуты букв.
tget(?Row,?Column) унифицирует переменнные Row и Column с
текущими координатами курсора.
tmove(+Row,+Column) помещает курсор в точку экрана с
координатами (Row,Column).
tscroll(+C,+UL,+LR) размещает С строк текста с левой верхей
координатой LU и правой нижней координатой LR.
wa(+C,+Attr) изменяет атрибут Attr для С букв от текущего
положения курсора.
wc(+C,+Ch) пишет С копий буквы Ch от текущего положения
курсора. Перед буквой Ch ставится обратный апостроф, или это должен
быть код ASCII этой буквы.
wca(+C,+Ch,+Attr) пишет С копий буквы Ch с атрибутом Attr.
6.8.20. Исполнение системных функций
chdir(?Path) возвращает текущий директорий, если переменная
Path не замещена; меняет текущий директорий, если переменная Path
замещена (именем Path нового директория).
chmod(+F,?Attr) приписывает файлу с именем F атрибут Attr,
который может принимать одно из следующих шестнадцатеричных
чисел:
00 чтение, запись, не скрыт, не системный,
01 только для чтения,
02 скрытый файл,
04 системный файл,
16 директорий,
32 архив.
consul t(+'F') дописывает программу с файла F к уже имеющейся в
рабочей области программе. Расширение ari не обязательно.
date(?D) дата, задаваемая в формате: date(rofl, месяц, день).
Например, date(l985,10,15).
date_day(+date(Y,M,D),WeekDay) возвращает день недели WeekDay
для данной даты data(Y,M,D).
delete(+F) удалить файл с именем F.
directory(+Path,-Name,-Mode,-Туте,-Date,-Sise) выдает список
Name файлов в директории Path.
disk(?DiskName) вызов диска DiskName, если переменная
DiskName замещена. Если переменная DiskName не замещена, то
предикат возвращает имя текущего диска.
edit(+F) выход из интерпретатора в редактор для
редактирования файла F. Отредактированный текст следует переписать в рабочую
область с помощью предиката reconsult.
192
errcode(-C) возвращает код С ошибки.
fileerrors(?Old,?New) появившийся код ошибки ввода или вывода
Old при исполнении программы заменяется на значение New, которое
может принимать два значения:
off отключить ошибку;
on включить ошибку.
По умолчанию ошибка включена.
['F'] считывает программу с файла F в рабочую область;
расширение ari писать не обязательно.
gc восстанавливает стековое пространство.
gc(-A) восстанавливает стековое пространство А (сборщик
мусора). А есть объем восстановленного пространства.
halt выход из системы в среду DOS.
mkdir(+Path) создает директорий с путем Path.
reconsult(+'F') просматривает по порядку все предложения
программы в рабочей области и выполняет следующее. Приписывает в
конец программы в рабочей области те предложения программы файла F,
голова которых отличается от любой головы любого предложения
программы в рабочей области. Если предложение программы в рабочей
области имеет голову Н, совпадающую с головой некоторого
предложения файла F, то это предложение в программе в рабочей области
заменяется на первое предложение в файле F с той же головой Н,
если тела у этих предложений разные. Если предложение программы в
рабочей области содержится среди предложений программы файла F,
то это предложение в рабочей области не изменяется. Предикат re-
consult используется при редактировании программы и ее
последующим исполнении. Перед исполнением отредактированной программы ее
следует изменить в рабочей области с помощью предиката reconsult.
Предложения, изменившиеся при редактировании, в рабочей области
будут при этом переписаны. Расширение ari писать не обязательно.
rename(+F,+N) файлу с именем F присваивает новое имя N.
rmdir(+Path) устранить директорий Path. Нельзя находиться в
устраняемом директории. Устраняемый директорий не должен
содержать файлов.
save сохраняет программу в рабочей области.
save(+N) сохраняет внутреннюю базу данных в файле с именем N.
shell выход в MS DOS. Для возвращения в систему набрать exit.
shell(+DC) выход в MS DOS и исполняет DOS команду DC.
syntaxerrors(?Old,?New) появившийся код синтаксической ошибки
Old при исполнении программы заменяется на значение New, которое
может принимать два значения:
off отключить ошибку,
193
on включить ошибку.
По умолчанию ошибка включена.
statistics возвращает информацию об использованных системой
ресурсах.
statistics(+Info, -Struct) возвращает информацию об
использованных системой ресурсах. Info может быть: стек, база данных,
page(X) (т.е. страница с номером X), атом (и тогда система дает
информацию по этому атому).
time(?Time) задает время в формате: time(4ac,минута,секунда,
сотая доля секунды).
6.8.21. В-деревья
recordb(+Tr,+S,+T) записывает терм в Ь-дерево. Тг есть имя Ь-
дерева; S - аргумент записываемого в Ь-дерево терма для поиска
этого терма; Т - записываемый в Ь-дерево терм.
removeallb(+T) удаляет Ь-дерево с именем Т.
removeb(+Tr,+S,?T) удаляет терм из Ь-дерева.
retrieveb(+Tr,?S,?T) возвращает отсортированный список
элементов Ь-дерева.
6.8.22. Хэш-таблицы
recordh(+Tn,+S,+T) записывает терм в хэш-таблицу. Тп есть имя
таблицы; S - категория, под которой записывается терм; Т - терм,
записываемый в хэш-таблицу.
removeh(+Tn,+S,?T) удаляет терм из хэш-таблицы.
removeallh(+Tn) удаляет h-дерево с именем Тп.
retrieveh(+Tn,?S,?T) возвращает информацию из хэш-таблицы.
6.8.23. Отладчик (Debugger)
Программа при исполнении проходит через четыре вида портов:
call, exit, redo, fail.
leash(+Mode) определяет характер прохождения портов при
режиме трассировки. Аргумент Mode принимает одно из следующих
значений:
full отладчик останавливается по всем портам,
tight отладчик останавливается в портах: call, redo, fail,
half отладчик останавливается в портах: call, redo,
loose отладчик останавливается в порте: call,
off отладчик не останавливается ни в одном порте.
Значение аргумента Mode можно задать натуральным числом от О
до 15. Двоичное представление этого числа задает остановочные
порты. Например, двоичная запись числа 10 есть 1010; тогда
leash(lO) означает, что отладчик будет останавливаться в портах
194
call, redo, ибо в последовательности call, exit, redo, fail двум
единицам последовательности 1,0,1,0 соответствуют call и redo.
nospy(+N) отменяет трассировочные отметки для предиката с
именем N.
nospy(+N/A) отменяет трассировочные отметки для предиката с
именем N местности А.
notrace выключить отладчик.
spy(+N) отмечает для трассировки предикат с именем N.
spy(+N/A) отмечает для трассировки предикат с именем N
местности А.
trace включить отладчик. После включения отладчика транслятор
при трассировке начинает выдавать следующие сопроводительные
знаки:
** цель помечена для трассировки,
*> цель помечена для трассировки; отладчик достиг этой цели в
результате прыжка,
> цель не помечена для трассировки; отладчик достиг этой цели
в результате прыжка,
=> отладчик трассирует бэктрэкинг.
Режимом трассировки можно управлять, набирая на экране
следующие буквы:
; указывает на порт exit,
@ позволяет вызвать любую цель и возвратиться в режим отладки
после исполнения цели,
а прекращает исполнение программы и возвращается в режим
интерпретации,
b прекращает исполнение программы; отладка возобновляется
набором end_of_f ile,
с (или клавиша return) переход к следующему порту,
d вызывает на экран текущую цель,
е выход из интерпретатора и возвращение в среду MS DOS,
f переход к порту fail,
h помощь в командах отладки,
1 при трассировке последовательный переход от одного
отмеченного (для трассировки) предиката к следующему предикату
(отмеченному для трассировки),
п выключение отладчика,
q при трассировке посещение портов exit и fail. Если
трассируемая цель помечена, то посещаются все порты,
s посещение портов exit и fail вне зависимости трассировочных
от пометок,
w пишет текущую цель (используя предикат write),
195
х используется в портах fail и redo. Отладчик осуществляет
fail пока не встретится порт call или exit.
Замечание. Предложения стандартного Пролога с точки зрения
логики являются формулами логики предикатов первого порядка с
равенством, с бинарным функциональным символом . (X,Y) для
организации списков и одним конструктором I для выделения головы и хвоста
списка. Стандартный Пролог является универсальным языком
программирования в том смысле, что на нем может быть вычислена любая
частично рекурсивная функция. Стандартный Пролог входит в любую
реализацию Пролога. Всякий конкретный Пролог для удобства
вычислений имеет много встроенных предикатов и функций. Все они
допустимы в формулах прологовой логики, хотя при желании без этих
предикатов и функций можно было бы обойтись.
Дизъюнкт AVBV...VC V "IDVIEV.. ."IF, где А,В,.. .C,D,E,... ,F
являются атомами (элементарными формулами логики предикатов),
равносилен формуле D&E&.. .&F -♦ AVBV... VC, или формуле AVBV... VC
*- D&E&...&F, которую записывали в виде секвенции D,E,...,F 1=
А;В;...;С, или с точки зрения логического программирования - в
виде правила А;В;...;С :- D,E,...,F. Хорновский дизъюнкт А V
"IDVIEV.. .V"IF соответствует секвенции D&E&...&F N А или правилу
А :- D,E,...,F Пролога. В сущности, в методе резолюций
обрабатываются правила вида А;В;...;С : - D,E,...,F. Работа с такими
правилами (дизъюнктами с точки зрения логики предикатов) при
построении резолютивного вывода составляет основную задачу
логического программирования. Предложения Пролог-программы А можно
рассматривать как нелогические аксиомы некоторой элементарной теории
Т. Отвечая на запрос В, транслятор вычисляет, выводим ли запрос В
из аксиом А в теории Т, т.е. доказуема ли формула В в
элементарной теории Т. Другими словами, при каждом исполнении программы
вычисляется, следует ли логически В из А, т.е. является ли
формула А -♦ В в логике предикатов общезначимой. Поэтому можно сказать,
что при каждом исполнении конкретной программы решается основной
вопрос математической логики для некоторой конкретной формулы
логики предикатов.
Часть 2
АЛГОРИТМЫ НА ГРАФАХ И ИХ ПРОЛОГ-ПРОГРАММЫ
7. СПОСОБЫ ЗАДАНИЯ ГРАФОВ
7.1. Графы, мультиграфы, псевдографы
Приведем основные понятия теории графов.
Определение. (р^)-граф есть система объектов G = (V,E), где
v = (vi>-••>/>} - множество вершин (узлов); Е = {^(v, ,v. ),
• ••,^=(v/? , ; )} - множество (неориентированных) ребер; ikl* )k,
к = 1,2, ..,?.
Пример. Для графа G = (К,Е), приведенного на рис.7.1, V = {vl9
v2,v3,v4}; Е = {е1,е2,е3,е4,е5}, где ех = (v19v2), е2 = (v19 v3),
*з = (v2,v3), е4 = (v3,v4), e5 = (v2,v4).
Две вершины графа G называются смежными (соседними), если они
соединены в G ребром. Если граф G имеет ребро е = (w,v), то
вершина и и ребро е (равно как и вершина v и ребро е) инцидентны
(принадлежат друг другу). Изолированная вершина не инцидентна ни
одному ребру. Висячая (концевая) вершина (или лист) инцидентна
ровно одному ребру. Два ребра, инцидентные одной вершине,
называются смежными.
Граф Gx = (У19ЕХ) равен графу G2 = (К2,Е2), если Vx = V29 Ех =
Е2. Графы Gx и G2 изоморфны, если существует взаимно однозначное
соответствие <р : Vx -* V 29 сохраняющее отношение смежности
(соседства) вершин, т.е. если (w,v) € Ех <—> (y>(w), ?>(v)) € Е2.
Граф Gi = (K^Ej) есть подграф графа G = (К,Е), если Vx Q V и
Ех Q Е. Если при этом Vх = К, то подграф Gx называется остовным
подграфом графа G. Подграф Gt графа G называется
*4
Рмс.7.1
197
V2
Рнс.7.2
порожденным множеством вершин Vх (натянут на множество вершин
Vx), если Kj CK& Vw,v € Vx (e = (w,v) € Е - е? € Е^. Далее,
если Gi есть подграф графа G, то G - над граф графа Gx.
На рис.7.2а приведен граф G; на рис.7.26 - остовный подграф
графа G; рис.7.2в - подграф графа G, натянутый на множество
вершин v1,v2,v3,v4,v5 графа G.
В полном графе Кр все его р вершин смежны. Петля есть ребро
е = {и,и). Кратные (параллельные) ребра соединяют одну и ту же
пару вершин.
На рис.7.3 приведены полные графы К3,К4,К5.
Мультиграф (рис.7.4а) допускает кратные ребра и не допускает
петель. Псевдограф (рис.7.46) допускает и кратные ребра, и петли.
к,
Рмс.7.3
198
б
Рмс.7.4
Замечание. Граф не допускает ни кратных ребер, ни петель.
Определение. Ориентированный граф (орграф) есть граф G =
(К,Е), в котором множество Е дуг есть множество упорядоченных
(ориентированных) пар вершин (w,v) (рис.7.5).
Можно говорить об ориентированных мультиграфах и псевдографах.
7.2. Задание графов
Граф G = (V,E) можно задать списком его вершин и ребер. Можно
задать и геометрически, нарисовав его на плоскости (или любой
другой поверхности) и отождествив его вершины с точками на
плоскости, а ребра - с отрезками, соединяющими смежные вершины.
Матрица смежности (соседства) вершин (р,^)-графа G = (V,E) с р
вершинами есть квадратная симметричная /?Хр-матрица
А =
"11 "12
«21 «22
ар\ аР2
Чр
*РР
где atj =
1, если вершины v,,v, соседние;
О в противном случае.
Всякому графу соответствует его бинарная симметричная матрица
смежности. Всякой бинарной симметричной квадратной матрице с
нулевой диагональю соответствует некоторый граф.
Матрица инциденций (/?,#)-графа G с р вершинами и q ребрами
есть pXqr-матрица
Рмс.7.5
199
в =
Pi 1 Pl2
Pi\ Ргг
Рр\ Ррг
Piq
Ppq
где btj = i
1, если вершина v, € е^\
О в противном случае.
Для всякого графа можно построить соответствующую ему бинарную
матрицу инциденций. Всякой бинарной матрице с двумя единицами в
каждом столбце соответствует некоторый граф.
На рис.7.6 приведен граф вместе с его матрицами А и В
смежности и инциденций соответственно.
7.2.1. Программа построения матрицы соседства вершин графа
Процедура matrix_neighbour_nodes(G,M) строит матрицу смежности
(соседства вершин) М графа G. Например, если
G=[[l,2,3,4],[[1,2],[1,3],[1,4],[[2,3],[3,4]], то
М=[[0,1,1,1],[1,0,1,0],[1,1,0,1],[1,0,1,0]].
Процедура one_line_matrix_neighbour(N,V,E,L) по вершине N
графа G=[V,E] строит соответствующую строку L матрицы смежности.
Например, если N=1, G=[V,E]=[[l,2,3,4],[[l,2],[l,3] ,[l,4] ,[2,3],
[3,4]], то L=[0,1,1,1].
Процедура dekNV(N,V,NV) по узлу N и множеству вершин V
вычисляет декартово произведение NV=NXV. Например, если N=1,
V=[l,2,3,4], то NV=[[1,1],[1,2],[1,3],[1,4]].
d(G,M) :-
V=[l,2,3,4,5,6,7],
E=[[l,2],[1,3],[1,5],[1,6],[2,3],[3,4],[3,6],[4,5],[4,7],
[5,6],[6,7]],G=[V,E],matrix_neighbour_nodes(G,M).
2 Л =
v4 е3 v3
0 1 0 0 1"!
10 10 1
0 10 10
0 0 10 1
.11010.
V,
Vj
Vj
v4
vs
В =
10 0 0 10
110 0 0 1
0 110 0 0
0 0 110 0
0 0 0 111.
Pmc.7.6
200
matrix_neighbour_nodes(G,M) : -
G=[V,E],matrix__neighb_nodes(V,V,E,M,[]).
matrix_neighb_nodes([N|T] ,V,E,M,Ml) :-
one_line_matrix__neighbour (N, V, E, L),
matrix_neighb_nodes(T,V,E,M,[L|Ml]).
matrix_neighb_nodes([],V,E,M,Ml) :- reverse(Ml,M).
one_line_matrix__neighbour(N,V,E,L) :- dekNV(N,V,NV),
one_line_matr_neighb(NV, E, L, [ ]).
one_line_matr_neighb([[A,B]|T],E,L,Ll) :-
(member([A,B] ,E) ; member([B,A] ,E)),
one_line_matr_neighb(T,E,L,[l|Ll]).
one_line_matr__neighb([[A,B]|T],E,L,Ll) :-
not((member([A,B],E) ; member([B,A] ,E))),
one_line_matr_neighb(T,E,L,[0|Ll]).
one_line_matr_neighb([],E,L,Ll) :- reverse(Ll,L).
dekNV(N,V,NV) :- dekNVl(N,V,[] ,NV).
dekNVl(N,[H|T],NVl,NV) :- dekNVl(N,T,[[N,H] |NVl] ,NV).
dekNVl(N,[],NVl,NV) :- reverse(NVl,NV).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(ZЛH] ,L).
append([],L,L).
append([.X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
тетЬег(ХЛХ|У]).
member(X,[Y|Z]) :- member(X,Z).
7.2.2. Программа построения матрицы инциденций графа
Процедура matrix_incidence(G,M) строит матрицу инциденций М
графа G. Например, если граф
0=[[1,2,3,4]Л[1,2]Л1,3],[1,4],[2,3],[3,4]]], то матрица ин-
el e2 еЗ е4 е5
1 1 1 0 0 1
10 0 10
О 1 0 1 1 Г
О 0 1 0 1 J
Процедура one_line__matrix_incid(N,E,L) по узлу N и списку
ребер Е графа G строит соответствующую строку матрицы инциденций
графа G. Например, если N=3, E=[[l,2] ,[l,3] ЛМ] ,[2,3] ,[3,4]],
то L=[0,1,0,1,1].
dl(G,M) :- V=[1,2,3,4],E=[[1,2],[1,3],[1,4],[2,3],[3,4]],
G=[ V,Е],matrix_incidence(G,M).
201
1
циденции М =
4
matrix_incidence(G,M) :- G=[V,E] ,matr_incid(V,E,[] ,M).
matr_incid([N|T],E,L,M) :- one_line_matrix_incid(N,E,Line),
matr_incid(T,E,[Line|L],M).
matr_incid([] ,E,Lines,M) :- reverse(Lines,M).
one_line_matrix_incid(N,E,Line) :- line_matr_incid(N,E,[] ,Line).
line_matr_incid(N,[H|T],L,Line) :-
member (N,H),line__matr__incid(N,T,[l|L], Line).
line__matr_incid(N,[H|T],L,Line) :- not(member(N,H)),
line_matr__incid(N,T,[0|L],Line).
line_matr_incid(N,[],L,Line) :- reverse(L,Line).
reversed ],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
7.2.3. Программа транспонирования матрицы
Предикат matrix_transpose(S,L) истинен, если матрица L
получается транспонированием матрицы S. Например, если
Oil"
10 1
110
10 1.
Матрицы S и L задаются списками своих строк.
Предикат del_first_column(S,L) истинен, если матрица L
получается удалением первого столбца в матрице S. Например, если
S =
0 111
10 10
110 1
то L =
S =
0 111
10 10
110 1
то L =
Г о
1
L о
1
1
1
1 1
0
о J
Матрицы S и L задаются списками своих строк.
Предикат all_empty(S) истинен, если список S состоит из пустых
элементов. Например, если S=[[],[],[],[]], то all_empty(S)
истинно. Если S=[[] ,a,[] ,[a,b]], то all_empty(S) ложно.
d(S,L) :-
S=[[l,2],[1,3],[1,5],[1,6],[2,3],[3,4],[3,6],[4,5],[4,7],
[5,6],[6,7]],matrix__transpose(S,L).
matrix_transpose(S,L) :- matrix_transp(S,[] ,L).
matrix_transp(S,Sl,L) :- findall(R,member([R|T] ,S),Column),
del_first_column(S,S2), matrix J:ransp(S2,[ Column | SI ],L).
202
matrix_transp(S,Sl,L) :- all_empty(S),reverse(Sl,L).
del_first_column(S,L) •- del_first_col(S,[] ,L).
del_first_col([[H|T]|Tl],S,L) :- delJirst_col(Tl,[T|S] ,L).
del_first_col([],S,L) :- reverse(S,L).
all__empty([H|T]) :- H=[] ,all_empty(T).
all_empty([]).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
7.3. Операции над графами
Удаление вершины v из графа G приводит к подграфу G-v графа G
без вершины v и инцидентных с ней ребер.
Удаление ребра е из графа G = (К,Е) при сохранении его вершин
приводит к остовному подграфу G-e = (V,Е-{е}) графа G.
Добавление ребра е = (w,v) к графу G = (К,Е), содержащему
вершины m,v, приводит к графу G+e = (V,E U {e}).
На рис.7.7 приведены графы G, G-v, G-e, G+e', где e/=(v/,v//).
7.4. Маршруты, цепи, циклы, связность
Маршрут в графе G = (К,Е) есть чередующаяся последовательность
вершин и ребер v0e1v1e2v2e3v3e4.. .vn_1envn графа G, для которой
каждое ребро инцидентно двум соседним вершинам. При этом v0 -
начало маршрута, v„ - конец маршрута, п - длина маршрута.
алай
V' V v'
<3 G-v G-e G+e7
Рмс.7.7
203
Обозначим через [w,v] маршрут между вершинами и и v. Иногда
маршрут отмечается только вершинами, иногда - только ребрами.
Маршрут нулевой длины состоит из единственной вершины.
Цепь в графе G есть маршрут, в котором все ребра попарно
различны (нет повторов ребер, возможны повторы вершин). Простая цепь
в графе G есть цепь без повторов вершин (а следовательно, и без
повторов ребер).
Цикл в графе G есть замкнутая цепь (в которой начало и конец
одинаковы). Простой цикл не имеет повторов вершин (кроме
начальной и конечной), а, следовательно, и повторов ребер.
Цепь, простая цепь, цикл, простой цикл в графе G есть
некоторые подграфы в графе G. Для графа, изображеного на рис.7.8:
v2*2v3*6vi*sv4*3v3*evi " маршрут;
v2e2v2e3vAesv\eev2 " Цепь;
v2e2v2e6vl - простая цепь;
V2e2V2eeV\e5VAeAV5e%V\e\V2 ~ ЦИКЛ;
V2e2V2eeV\e\V2 " ПРОСТОЙ ЦИКЛ.
В орграфе маршрут, цепь, простая цепь, цикл, простой цикл
становятся ориентированными. Иногда их называют ормаршрут, путь,
простой путь, контур, простой контур соответственно. По всякому
маршруту (циклу) можно построить цепь (простой цикл) с теми же
концами, достаточно удалить из них внутренние циклы.
Граф (орграф) G связен, если любая пара его вершин w,v
соединима цепью (путем) от и к v. В противном случае граф G не связен.
Компонента связности графа G есть наибольший по числу ребер
связный подграф графа G. Граф, состоящий из одних вершин,
называется вполне несвязным.
Рис. 7.8
204
Расстояние между двумя вершинами в графе есть длина кратчайшей
цепи (геодезической) между этими вершинами.
8. ПОИСК ПУТИ НА ГРАФЕ: В ГЛУБИНУ,
В ШИРИНУ, ПЕРВЫЙ ЛУЧШИЙ
8.1. Задание графа в Прологе
При исполнении Пролог-программы транслятор строит
соответствующее дерево вывода. Построение такого дерева - центральная
задача транслятора. Поэтому Пролог удобен для исследования путей на
древовидных структурах, в частности, для исследования путей на
графах. Рассмотрим несколько подобных графовых задач.
Ставится задача нахождения кратчайшего пути между двумя
вершинами в связном графе с нагруженными ребрами (т.е. каждому ребру в
графе приписан некоторый вес). На рис.8.1 приведен граф с
нагруженными ребрами. Приведены два его задания в Прологе, когда ребра
графа нагружены:
a(n,k,38). a(k,p,23). a(d,n,40). a(p,d,52). a(w,k,33). a(w,p,39).
и не нагружены: a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
Нагруженный граф можно представлять как карту городов с
расстояниями между ними.
Граф можно задать также списком, состоящим из списка его
вершин и списка его ребер. Например, граф
G = [[d,p,n,k,w],[[n,k],[k,p],[d,n],[p,d],[w,k],[w,p]].
Рнс.8.1
205
Граф можно задать списком его ребер:
G = [[n,k],[k,p],[d,n],[p,d],[w,k],[w,p]].
Граф G можно задать списком его вершин и ребер, именуя каждую
вершину и каждое ребро: G = [[v(d),v(p),v(n),v(k),v(w), e(n,k),
e(k,p),e(d,n),e(p,d),e(w,k),e(w,p)]. Можно именовать вершины и не
именовать ребра, именовать ребра и не именовать вершины,
компоновать разные способы задания графов в Прологе.
Допустим, что разыскивают пути между узлами d и w. Дерево всех
возможных путей (без повторов узлов на каждом пути) в графе G от
узла d приведено на рис.8.2. В каждом узле указано расстояние от
этого узла до начала пути. На дереве путей указаны также
расстояния между соседними узлами.
8.2. Поиск пути на графе
Приведем сначала довольно простую программу нахождения пути
между двумя вершинами графа. Для простоты возьмем ребра графа не-
взвешенными. Ниже определены следующие процедуры:
go(Start,Goal,Trace) вычисляет путь Trace между началом пути
Start и концом пути Goal;
gol(S,G,Tl,T) по началу пути S, концу пути G вычисляет путь Т
между S и G, последовательно расширяя промежуточный путь Т1.
Рис. 8.2
206
nextnode(X,Tl,Y) no промежуточному пункту X промежуточного
пути Т1 между началом S и X вычисляет следующий за X пункт Y пути.
Тогда следующая программа вычисляет (какой-либо) путь между S
и G. Другие возможные пути находятся с помощью бэктрэкинга.
8.2.1. Программа поиска пути между двумя
вершинами в ненагрулеечном графе
go(Start,Goal,Trace) :- gol(Start,Goal,[] ,R),reverse(R,Trace).
a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
gol(X,X,R,T) :- T=[X|R].
gol(Node,Y,T,R):- nextnode(Node,T,Next),
gol(Next,Y,[Node|T},R).
nextnode(Node, Trail,Next) : -
(a(Node,Next) ; a(Next,Node)),
not(member(Next, Trail)).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]). member(X,[Y|Z]) :- member(X,Z).
Запрос к программе для вычисления пути Т между узлами d и w
имеет следующий вид: ?- go(d,w,T).
Программу поиска пути в графе между двумя вершинами можно
упростить, если требуемый путь строить, начиная с его конца.
8.2.2. Программа поиска пути между двумя вершинами
графа от конца к началу
go(S,G,T) :- gol(S,G,[],T).
a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
gol(S,S,Tr,T) :- T=[S|Tr].
gol(S,N,Tr,T) :- nextnode(N,Tr,Nl),gol(S,Nl,[N|Tr],T).
nextnode(N,Tr,Nl) :- (a(N,Nl) ; a(Nl,N)),not(member(Nl,Tr)).
member(X,[X|Y]). member(X,[Y|Z]) :- member(X,Z).
8.3. Поиск в глубину
Поиск в глубину на дереве путей (см. рис.8.2) проводится
сверху вниз, слева направо согласно схеме, приведенной на рис.8.3.
В соответствии со стратегией поиска в глубину пути между d и w
и расстояния между ними будут порождаться в следующем порядке:
[d,n,k,p,w,140]; [d,n,k,w,lll]; [d,p,k,w,108]; [d,p,w,9l].
Как видим, кратчайший путь оказался последним. Случайно он мо-
207
жет оказаться и первым. При исполнении программы все эти пути
порождаются с помощью бэктрэкинга. Программист, наблюдая появление
путей, выбирает среди них кратчайший.
При построении программы, вычисляющей пути в графе между двумя
заданными узлами согласно стратегии поиска в глубину, снова для
простоты возьмем граф с ненагруженными ребрами.
Предикаты, определенные в этой программе, имеют такой же
смысл, как и в предыдущей программе. Только предикат go2
несколько отличен от gol. Именно, процедура go2(T,G,R) вычисляет
список путей от начала пути S, возникающий при обходе дерева путей в
глубину.
Запрос для поиска путей между узлами d и w имеет следующий
вид: ?- go(d,w,T).
Заметим, что при поиске в глубину вновь найденные с помощью
findall пути List при формировании списка NewTraces ставятся в
начале списка.
8.3.1. Программа вычисления путей между двумя узлами
в непогруженном графе с использованием
стратегии поиска в глубину
go(Start,Goal,Trace) :- go2([[Start]],Goal,R),reverse(R,Trace).
a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
go2([First|Rest],Goal,First) :- First=[Goal|_].
go2([[Last|Trail]|Rest],Goal,Trace) :-
f indall( [ Z, Last | Trail], nextnode(Last, Trail, Z), List),
append(List, Rest, NewTraces), go2(NewTraces, Goal, Trace).
nextnode(X,Trail,Y) :- (a(X,Y) ; a(Y,X)),
not (member (Y, Trail) ).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
8.4. Поиск в ширину
Поиск в ширину на дереве путей (см. рис.8.2) осуществляется
сверху вниз, слева направо согласно схеме, изображенной на
рис.8.4. Согласно стратегии поиска в ширину путей между d и w и
соответствующих расстояний между ними эти пути будут проходиться
в следующем порядке: [d,p,w,9l]; [d,p,k,w,lll]; [d,p,k,w,108];
[d,n,k,p,w,140]. Кратчайший путь в этом случае оказался первым.
Не следует думать, что при поиске в ширину так будет всегда.
Сделав расстояние между р и w достаточно большим, мы обнаружим, что
кратчайший между d и w путь первым уже не является. Поиск в
ширину упорядочивает все пути по числу промежуточных узлов в пути.
При исполнении программы все возможные пути порождаются с
помощью бэктрэкинга. Кратчайший путь выбирает пользователь,
наблюдая появление путей при бэктрэкинге.
Рнс.8.4
209
Следующая ниже программа осуществляет поиск путей в графе
между двумя заданными узлами. Для простоты в программе задается не-
нагруженный граф.
8.4.1. Программа вычисления путей между двумя узлами в
ненагруженном графе с использованием
стратегии поиска в ширину
go(Start,Goal,Trace) :- go3([[Start]],Goal,R),reverse(R,Trace).
a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
go3([First|Rest],Goal,First) :- First=[Goal|_].
go3([[Last|Trail]|Rest],Goal,Trace) :-
findall([Z,Last | Trail],nextnode(Last,Trail,Z),List),
append(Rest, List, NewTraces),
go3(NewTraces, Goal, Trace).
nextnode(X,Trail,Y) :- (a(X,Y) ; a(Y,X)),not(member(Y,Trail)).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Запрос для вычисления путей между узлами d и w имеет следующий
вид: ?- go(d,w,T).
Заметим, что при поиске в ширину вновь найденные с помощью
findall пути List ставятся в конце списка.
Программа поиска в ширину имеет строку
append(Rest, List, NewTraces);
программа поиска в глубину имеет строку
append(List, Rest, NewTraces),
чем исчерпывается вся разница между этими программами.
8.5. Стратегия "первый лучший"
Поиск на дереве путей (см. рис.8.2) согласно стратегии первый
лучший осуществляется следующим образом.
Сначала строится поддерево яруса 1 дерева путей (рис. 8.5а);
пунктиром указаны все возможные его продолжения.
Дерево продолжается так, чтобы продолжаемый путь оказался
наименьшим по длине среди всех возможных путей-продолжений.
Получившееся дерево (рис.8.56\ пунктиром указаны все возможные его про-
210
должения) продолжаем таким ребром, чтобы получившийся путь
оказался наименьшим по длине среди всех возможных путей-продолжений.
Новое дерево приведено на рис.8.5в; пунктиром показаны все
возможные его продолжения. Повторяя процесс продолжения, получим
дерево, изображенное на рис.8.5г. Продолжение этого дерева даст
дерево, изображенное на рис.8.5д. Сформирован путь [d,p,w,9l] с
кратчайшим расстоянием между d и w.
Дальнейшее продолжение получающихся деревьев приводит к
деревьям путей, изображенным на рис.8.5е - 8.5х\ В соответствии с
описанной стратегией "первый лучший" пути между вершинами d и w и
расстояния между ними будут порождаться в следующем порядке:
[d,p,w,9l]; [d,p,k,w,108]; [d,n,k,w,lll]; [d,n,k,p,w,140].
При исполнении программы все возможные пути порождаются с
помощью бэктрэкинга.
В предикате go(S,D,R,C) S - начало пути; D - конец пути; R -
путь между S и D; С - длина пути R.
В терме r(M,T) M есть длина пути Т.
В предикате go4(L,De,R,Rl,Di) L - кратчайшее продолжение
списка предыдущих путей; De - конец пути; R - промежуточный путь;
R1 - кратчайший путь между началом и концом пути; Di - расстояние
кратчайшего пути.
Процедуры вычисляют:
shorter более короткое продолжение пути;
shortest кратчайшее продолжение пути;
legalnode следующий узел пути.
8.5.1. Программа вычисления кратчайшего пути между двумя
узлами в нагруженном графе с помощью
стратегии первый лучший
go(Start,Dest,Route,Dist) :-
go4([r(0, [Start])],Dest,R,R1,Dist),
reverse(Rl, Route).
a(n,k,38). a(k,p,23). a(d,n,40). a(p,d,52). a(w,k,33). a(w,p,39).
go4(Routes,Dest,Route,Rl,Dist) :-
shortest (Routes, Shortest, RestRoutes, Dist),
proceed(Shortest, Dest, RestRoutes, Route, Rl, Dist).
proceed(r(Dist,Route),Dest,_,Routel,Rl,Distl) :-
Route= [ Dest | _], Distl=Dist, Rl=Route.
proceed(r(Dist,[Last|Trail]),Dest,Routes,Route,Rl,Distl) :-
findall(r(Dl,[Z,Last|Trail]),
legalnode(Last,Trail,Z,Dist,DI),List),
append(List, Routes, NewRoutes),
211
(£>78
©52
(k)78 ®75
(n)ll3 (w)108 (j)10l(w)lll (n)ll3(w)l0 8
212
fn)40
Гк)78
Гк)75 (w)91
/ \
/ \
/ \
' \
/ \
(p)101(w)lll 01130108 01010111 0113 0108
I
I
I
I
I
0140
0140
0140
ж
213
и к
Рнс.8.5
go4(NewRoutes, Dest, Routes, Rl, Distl).
shortest([ Route | Routes ], Shortest, [ Route | Rest], Dist) : -
shortest (Routes, Shortest, Rest, Dist),
shorter(Shortest,Route),!.
shortest([ Route | Rest], Route, Rest, Dist).
shorter(r(Ml,_),r(M2,J) :- MKM2.
legalnode(X,Trail,Y,Dist,NewDist) : -
(a(X,Y,Z) ; a(Y,X,Z)),
not(member ( Y, Trail)),
NewDist is Dist+Z.
reverse([],[]).
214
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Для вычисления кратчайшего пути между узлами d и w следует
сделать следующий запрос: ?- go(d,w,T,C).
Если исходный граф является полуориентированным, т.е. если
исходный граф имеет ориентированные и неориентированные ребра, то
граф следует задать так, чтобы всякое ориентированное ребро (b,d)
от b к d с весом с задавалось фактом a(b,d,c), а всякое
неориентированное ребро (b,d) с весом с задавалось двумя фактами: a(b,d,
с) и a(d,b,c). Кроме того, предикат legalnode следует определить
так: legalnode(X,Trail,Y,Dist,NewDist) :- a(X,Y,Z),
not(member(Y,Trail)), NewDist is Dist + Z.
При поиске в глубину и при поиске в ширину пути на
полуориентированном графе последний задается фактами аналогично
предыдущему случаю; при этом предикат nextnode следует определить
следующим образом:
nextnode(X,Trail,Y) :- a(X,Y), not(member(Y,Trail)).
Программу можно использовать и для вычисления кратчайшего
(по числу узлов) пути в ненагруженном графе, задав всем ребрам
графа одинаковый вес, например, равный единице.
8.6. Представление дерева всех путей
в графе термом
Дерево в Прологе можно задавать списком его путей. Такое
представление не является экономным, ибо у некоторых путей могут быть
одинаковые начальные отрезки, которые будут повторяться в каждом
из наших путей. Более экономным будет следующее представление
дерева термом. Зададим его индукцией по построению дерева.
1. Если дерево состоит из одного только корня R, то оно
представляется термом 1(R), что означает, что R есть (единственный)
лист в дереве.
2. Если дерево состоит из корня R и поддеревьев S1,S2,S3,...,
Sr, где г М, то это дерево изображается термом t(R,[Sl,S2,S3,
...,Sr]).
Например, дерево путей для графа, заданного системой фактов:
a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
представляется термом
t(d,[t(n,[t(u,[t(p,[l(w)]),l(w)])]),
215
t(p,[t(k,[Kn),l(w)]),l(w)])])]).
Представление дерева термом гораздо экономнее его
представления списком путей. Например, бинарное дерево глубины 10 имеет
1024 путей, причем каждый путь имеет длину 10. Для представления
дерева нужны 1024*10 = 10240 атомов. Представление этого же
дерева термом потребует 1024 + 512 + 256 + 128 + 64 + 32 + 16 + 8
+ 4 + 2 + 1 = 2047 атомов.
Представление деревьев термами удобнее также при их обработке,
в особенности, если осуществляется обработка узлов деревьев.
Дерево, представленное списком путей, будем называть дерево-
список, а термом - дерево-терм (или терм-дерево).
8.6.1. Программа вычисления дерева-терма всех путей в графе
без повторов вершин на каждом пути
d(S,T) :- term_tree_all__pathes_without_repeate(S,T).
term_tree_all__pathes_without_repeate(Start, Termtree) :-
breadthf irst(l(Start) ,Termtree).
a(l,2). a(l,3). a(2,3). a(2,4). a(3,4). a(3,5). a(4,5).
breadthfirst(Tree, Termtree) : - expand( [ ],Tree, Treel,End),
(End=no,breadthfirst(Treel,Termtree) ; Termtree=Tree).
expand(P,l(N),t(N,Subs),no) :-
bagof(l(M),((a(N,M);a(M,N)),not member(M,P)),Subs).
expand(P,l(N),l(N),yes).
expand(P,t(N,Subs),t(N,Subsl),End) :-
expandall([N|P],Subs,[],Subsl,End).
expandall(__,[],[T|Ts],[T|Ts],yes).
expandall(P,[T|Ts],Tsl,Subsl,End) :- expand(P,T,Tl,Endl),!,
expandall(P,Ts,[Tl|Tsl],Subsl,End2),
(Endl=yes,End2=yes,End=yes ; End=no).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
8.6.2. Программа вычисления дерева-терма всех путей в графе
до первого повтора вершины на каждом пути
d(S,T) :- term_tree_all__pathes_with_repeate(S,T).
term_tree_all_pathes_with_repeate(Start,Termtree) :-
breadthf irst (1 ( St ar t), Termtree ).
a(l,2). a(l,3). a(2,3). a(2,4). a(3,4).
breadthfirst(Tree,Termtree) :- expand([],Tree,Treel,End),
(End=no,breadthfirst(Treel,Termtree) ; Termtree=Tree).
expand(P,l(N),l(N),yes) :- member(N,P).
expand(P,l(N),t(N,Subs),no) :-
216
bagof(l(M),((a(N,M);a(M,N))),Subs).
expand(P,t(N,Subs),t(N,Subsl),End) :-
expandall([N|P], Subs, [],Subsl, End).
expandall(_,[],[T|Ts],[T|Ts],yes).
expandall(P,[T|Ts],Tsl,Subsl,End) :- expand(P,T,Tl,Endl),!,
expandall(P,Ts,[Tl|Tsl],Subsl,End2),
(Endl=yes,End2=yes,End=yes ; End=no).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
8.6.3. Программа вычисления пути между двумя вершинами
в непогруженном графе с поиском в ширину
и одновременным построением дерева-терма всех путей в графе
d(S,E,P) :- path_in_graph_termJ;ree(S,E,P).
path in graph term tree(Start,End,Solution) : -
breadthf irst(Start, End, Solution).
a(n,k). a(k,p). a(d,n). a(p,d). a(w,k). a(w,p).
breadthfirst(Tree,End,Solution) : -
expand([ ],Tree,Treel,Solved,Solution,End),
(Solved=yes ; Solved=no,breadthfirst(Treel,End,Solution)).
expand(P,N,_,yes,[N|P],N).
expand(P,N,t(N,Subs),no,_,_) :-
bagof(M,((a(N,M) ; a(M,N)),not(member(M,P))),Subs).
expand(P,t(N,Subs),t(N,Subsl),Solved,Sol,End) :-
expandall([N|P],Subs,[],Subsl,Solved,Sol,End).
expandall(_,[],[T|Ts],[T|Ts],no,_,J.
expandall(P, [T | Ts],Tsl,Subsl,Solved,Sol,End): -
(expand(P,T,Tl,Solvedl,Sol,End),
(Solvedl=yes,Solved=yes ; Solvedl=no,!,
expandall(P,Ts,[Tl|Tsl],Subsl,Solved,Sol,End))) ;
expandall(P, Ts, Tsl, Subsl, Solved, Sol, End).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
9. ОБХОДЫ ГРАФОВ
9.1. Эйлеровы графы
Определение. Степень вершины графа есть число инцидентных
(т.е. принадлежащих) ей ребер. Граф G четен, если каждая его вер-
217
шина имеет четную степень.
Определение. Цикл (контур) в графе (орграфе) G называется
эйлеровым, если он проходит без повторов ребер (дуг) через каждое
ребро (дугу) графа G. Граф (оргаф) G называется эйлеровым, если
он имеет эйлеров цикл (контур).
Эйлеров граф связен, ибо эйлеров цикл связывает все вершины
графа. Эйлеров цикл ориентирует ребра графа в направлении обхода.
Теорема. Связный граф G является эйлеровым тогда и только
тогда, когда граф G четен.
Доказательство. Пусть G есть связный граф и С - его эйлеров
цикл. Каждое прохождение вершины при движении по циклу С
привносит двойку в степень этой вершины. Так как каждое ребро графа G
появляется в цикле С только один раз, то любая вершина в G имеет
четную степень, т.е. граф G четен.
Пусть связный граф G четен. Тогда G имеет простой цикл С.
Удалим из G ребра цикла С (сохранив bG их вершины). Снова получим
четный граф, так как либо от вершины в G удаляют два ребра цикла
(если эта вершина принадлежит циклу С), либо число ребер в ней не
меняется (если вершина не принадлежит С). Из получившегося
четного графа, каждая компонента связности которого четна, можно снова
выделить простой цикл, и так далее, пока не придем к графу, в
котором нет ребер. Таким образом граф G допускает представление в
виде объединения простых циклов, попарно непересекающихся по
ребрам: G = Cj U C2 U ... UQ. Пусть С есть один из таких простых
циклов. Если G состоит только из этого простого цикла С", то G
есть эйлеров граф. Если G имеет другие простые циклы, то в силу
связности графа G существует простой цикл С", имеющий общую
вершину v с циклом С (при отсутствии у С и С" общих ребер). Тогда
С" U С" есть цикл с началом в вершине v, составленный сначала из
ребер цикла С", а затем из ребер цикла С". Подобным образом к
циклу С U С" последовательно присоединяем другие простые циклы. В
результате получим цикл, проходящий через все ребра графа G.
Построенный цикл является эйлеровым. Следовательно, граф G тоже
эйлеров.
Теорема доказана.
Теорема и ее доказательство без изменений переносятся на муль-
тиграфы и псевдографы. При этом петли относим к одному из циклов,
проходя их все при попадании в вершину, на которую эти петли
навешены. Так как петля прибавляет к степени вершины двойку, то
любое количество петель на четность вершины не влияет. Аналогичная
теорема справедлива и для орграфов.
Теорема. Связный орграф G эйлеров тогда и только тогда, когда
218
для каждой вершины v в G число входящих в v дуг (полустепень
захода) равно числу исходящих из v дуг (полустепень исхода).
Пример. Построим эйлеров цикл в четном графе G = ({1,2,3,4,
5,6},{(1,2),(1,6),(2,3),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),
(5,6)}). Выбираем цикл в G:
С1=2352; G1=G-C1={(1,2),(1,6),(2,6),(3,4),(3,6),(4,5),(5,6)}.
Выбираем цикл в Gx:
С2=63456; G2=G1-C2={(1,2),(1,6),(2,6)}.
Выбираем цикл в G2:
С3=1261; G3=G2-C3=0.
Из циклов С19С2,С3 компонуем эйлеров цикл. Выбираем два цикла
0^=2352, С2=34563 с общей вершиной 3 и вставляем С2 в Сх на место
вершины 3; получаем цикл С4=23456352. Циклы С4,С3 объединяем по
общей вершине 6; получаем С5=23456126352. Цикл С5 является
эйлеровым циклом.
9.7.7. Программа вычисления эйлерова цикла по системе
попарно непересекающихся простых циклов
четного графа
Процедура all_system__cycles(SC) вычисляет семейство простых
циклов в графе с последовательным их удалением из графа.
Например, для приведенного в программе графа семейство простых циклов
SC=[[4,7,8,4],[2,5,3,6,2],[1,2,3,4,5,6,1]].
Процедура choice__adjacent_cycle(C,Cl,C2) по циклу С и списку
циклов С1 выбирает в С1 цикл С2 с которым цикл С имеет непустое
пересечение. Например, если С=[4,7,8,4], С1=[[2,5,3,6,2], [1,2,3,
4,5,6,1]], то С2=[1,2,3,4,5,6,1].
Процедура ruwrite_cycle(V,C,Cl) переписывает цикл С, начиная
его от новой вершины V. Например, если С=[2,5,3,6,2], V=6, то
С1=[6,2,5,3,6].
Процедура insert_cycle(V,Cl,C2,C3) вставляет цикл С2 в цикл С1
вместо V. Например, если С1=[2,5,3,6,2],С2=[6,1,2,3,4,5,6], V=6,
то С3=[2,5,3,6,1,2,3,4,5,6,2].
Процедура construct_euler__cycle(SC,EC) по списку простых
циклов SC строит эйлеров цикл ЕС. Например, если SC=[ [4,7,8,4] ,[2,5,
3,6,2],[1,2,3,4,5,6,1]], то ЕС=[4,5,3,6,2,5,6,1,2,3,4,7,8,4].
d(EC) :- euler_cycle(EC).
а(1,2). а(1,6). а(2,3). а(2,5). а(2,б). а(3,4). а(3,5).
а(3,б). а(4,5). а(4,7). а(4,8). а(5,6). а(7,8).
euler_cycle(EC) :- all_system__cycles(SC),
construct_euler_cycle(SC,EC).
219
% Вычисление списка простых циклов
all_system_cycles(SC) :- a(Start,Y),!,
system_cycles(SC, [ ], Start).
system_cycles(SC,Sc,X) :- a(X,Y),path(Y,Path,[Y,X]),
Path=[F|R],member(F,R),cycle(Path, Cycle),
delete_cycle(Cycle), system_cycles(SC, [ Cycle | Sc ], Z).
system_cycles(SC, SC, S).
% Вычисление пути с циклом в его начале
path(Y,P,Pl) :- pathl(Y,Z,P,Pl).
pathl(Y,Z,P,Pl) :- Р1=[Н|Т] ,not(member(Y,T)),
next_node(Y,Z,Pl),pathl(Z,Zl,P,[Z|Pl]).
pathl(X,Y,Pl,Pl) :- member(X,Pl).
% Выделение цикла из пути
cycle([H|T],C) :- cyclel(H,T,C,[H]).
cyclel(S,[H|T],C,PC) :- not(S=H),cyclel(S,T,C,[H|PC]).
cyclel(S,P,C,PC) :- C=[S|PC] ,member(S,PC).
% Следующий узел
next_node(Y,Z,[Hl,H|T]) :- (a(Y,Z) ; a(Z,Y)),not(Z=H):
% Удаление цикла из списка циклов
delete__cycle([Hl,H2|T]) :-
(retract(a(Hl,H2)) ; retract(a(H2,Hl))),delete_cycle([H2|T]).
delete_cycle([H]).
% Построение цикла Эйлера
construct_euler__cycle( [],[]).
construct_euler_cycle( [H | [ ] ], H).
construct_euler_cycle(SC,EC) :- SC=[H|RC] ,constr(RC,H,EC).
constr(RC,PEC,EC) :- choice__adjacent_cycle(PEC,RC,AC),
intersect(PEC, AC, Int), f irst( V, Int), ruwrite_cycle( V, AC, ACl),
insert_cycle(V,PEC,ACl,PECl),delete(AC,RC,RCl),
constr (RC1, PEC1, EC).
constr([],EC,EC).
% Выбор соседнего цикла
choice_adjacent__cycle(C,[H|T],Cl) :- intersect(C,H,Int),
ifthenelse(lnt=[ ],choice_adjacent_cycle(C,T,Cl),C1=H).
% Перепись цикла с новым началом
ruwrite_cycle(V,C,Cl) :- С=[Н|Т],
ifthenelse(V=H, C1=C, wr_cycle(V, T, [ ], Cl)).
wr_cycle(V,[H|T],Ac,Cl) :-
ifthenelse(V=H,(reverse([H|Ac],Acl),append([H|T],Acl,Cl))
wr_cycle(V,T,[H|Ac],Cl)).
% Вставка цикла в цикл
insert_cycle(V,Cl,C2,C3) :-
220
first(V,C2),ins_cycle(V,Cl,C2,[],C3).
ins_cycle(V,[H|T],C2,Ac,C3) :- ifthenelse(V=H,
(reverse(Ac,Acl),append(Acl,C2,Ac2),append(Ac2,T,C3)),
ins_cycle(V,T,C2,[H|Ac],C3)).
% Вспомогательные программы
intersect ([],X,[]).
intersect([X|R],Y,[X|Z]) :- member(X,Y),! ,intersect(R,Y,Z).
intersect([X|R],Y,Z) :- intersect(R,Y,Z).
first(X,[X|Y]).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Эйлеров цикл в четном графе можно построить, начав его любым
ребром, а затем последовательно надстраивая его вправо смежными
ребрами, одновременно удаляя выбранные ребра из графа и следя за
тем, чтобы при очередном удалении ребра из графа он не распался
на несвязные компоненты, или не очутились в изолированной
вершине, не исчерпав при этом всех ребер графа.
Пример. Построим эйлеров цикл в графе G=(V,E) с множеством
вершин К={1,2,3,4,5,6,7} и со следующими ребрами:
е1=(1,2),е2=(2,8),е3=(8,б),е4=(6,4),е5=(4,2),е6=(2,3),
е7=(3, 4), e8=(4,5),e9=(5,6),e10=(6,7),en=(7,8),e12=(8,l).
Мы перечислили ребра в порядке их удаления из графа.
Построенная последовательность ребер е1,е2,е3,... ,е12 составляет эйлеров
цикл. Заметим, что после удаления ребра е4 нельзя убрать ребро
е8, ибо полученный тогда граф распадется на две несвязные
компоненты. После удаления ребра е2 нельзя удалять ребро е12, ибо
тогда мы попадем в изолированную вершину 1, не исчерпав всех ребер
графа.
9.1.2. Программа вычисления эйлерова цикла в четном графе
последовательным удалением проходимых ребер
Процедура eul(G,CN,CE) по четному графу G вычисляет эйлеровы
циклы CN и СЕ по вершинам и по ребрам соответственно.
Процедура path(X,CN,CE,G) по начальной вершине X в графе G
221
строит эйлеровы циклы CN и СЕ по вершинам и по ребрам
соответственно .
Процедура pathl (вспомогательная для процедуры path)
осуществляет последовательное расширение строящегося эйлерова цикла таким
ребром, после удаления которого мы не окажемся в изолированной
вершине или граф не распадается в две несвязные компоненты.
Процедура adjacent вычисляет ребро, которым можно расширить
строящийся эйлеров цикл.
Процедура one_connected_component(G,C) вычисляет одну
компоненту связности в графе.
Запрос к программе имеет следующий вид: ?- eul(G,CN,CE).
eul(Graph,CycleNodes,CycleEdges) :-
Graph=[[l,2,3,4,5,6,7,8],[[l,2],[l,6],[2,3],[2,5],
[2,6],[3,4],[3,5],[3,6],[4,5],[4,7],[4,8],[5,6],[7,8]]],
Graph=[N,E],member(X,N),!,RestEdges=E,
path(X, CycleNodes, CycleEdges, RestEdges).
path(X,CN,CE,RE):- pathl([X],[] ,CN,CE,RE).
pathl([X|P],El,CN,CE,RE) :- adjacent(X,Y,RE),
not(member([X,Y],El)),not(member([Y,X],El)),
(delete([X,Y],RE,REl) ; delete([Y,X] ,RE,REl)),
(adjacent(Y,Z,REl) ; RE1=[]),
findall(U,(member([U,V],REl) ; member([V,U],REl)),RV2),
delrepeate(RV2,RVl),RGl=[RVl,REl],
ifthenelse(RVl=[ ], (VC=[ ] ,EC=[ ]),
[ !one_connected_component(RGl,C)! ]) ,C=[VC,EC],
equalset(RVl,VC),pathl([Y,X|P],[[Y,X]|El],CN,CE,REl).
pathl(CN,CE,CN,CE,[]).
adjacent(X,Y,RE) :- (member([X,Y] ,RE) ; member([Y,X] ,RE)).
Выделение одной компоненты связности графа
one_connected_component(G,C) :- ! ,G=[V,E] ,member(S,V),
one_con_comp(E,[S],Vl,[],El),C=[Vl,El].
one_con_comp(E,Nl,N,Cl,C) :-
next_edge(E,Nl,Cl,[X,Y]),delete([X,Y],E,El),
(member(X,Nl),one_con_comp(El,[Y|Nl],N,[[X,Y]|Cl],C) ;
member(Y,Nl),one_con_comp(El,[X|Nl],N,[[X,Y]|Cl],C)).
one_con_comp(E,Nl,N,C,C) :- delrepeate(Nl,N).
next_edge(E,N,Cl,[X,Y]) :- member([X,Y],E),not(member([X,Y] ,Cl)),
(member(X,N) ; member(Y,N)).
delrepeate(S,SF) :- Sl=[],delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member (H, T),! ,delrep(T, SI, SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
222
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Приведенный выше алгоритм можно упростить, удаляя ребра из
графа, не обращая внимания на образование несвязных компонент и
изолированных вершин. Этот алгоритм с элементами перебора, вообще
говоря, не верен. Но программа, написанная для этого алгоритма на
Прологе, работая в условиях бэктрэкинга, эйлеров цикл построит
правильно.
9.1.3. Программа вычисления эйлерова цикла в четном
неориентированном графе с удалением проходимых
ребер без анализа распада графа на несвязные компоненты
Процедура pathl (вспомогательная для процедуры path)
осуществляет последовательное расширение строящегося эйлерова цикла любым
таким ребром, после удаления которого мы не окажемся в
изолированной вершине. Остальные предикаты аналогичны предикатам
предыдущей программы.
eul(Graph,CycleNodes,CycleEdges) : -
Graph=[[a,b,c,d,e,f],[[a,b],[a,c],[b,c],[b,d],
[b,e],[d,e],[d,f],[d,c],[f,e],[e,c]]],Graph=[N,E],
member(X,N),!,RestEdges=E,
path(X, CycleNodes, CycleEdges, RestEdges).
path(X,CN,CE,RE) :- pathl([X],[] ,CN,CE,RE).
pathl([X|P],El,CN,CE,RE) :- adjacent(X,Y,RE),
not(member([X,Y],El)),not(member([Y,X],El)),
(delete([X,Y],RE,REl) ; delete([Y,X],RE,REl)),
(adjacent(Y,Z,REl) ; RE1=[]),
pathl([Y,X|P],[[Y,X]|El],CN,CE,REl).
pathl(CN,CE,CN,CE,[]).
adjacent(X,Y,RE) :- (member([X,Y] ,RE) ; member([Y,X] ,RE)).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
223
member(X,JX|Y]).
member(X,[Y|Z]) :- member(X,Z).
Все эйлеровы циклы графа можно построить, начав от любой
вершины графа и перебирая дерево всех путей в графе без повторов
ребер на каждом пути. Всякая циклическая ветвь в дереве путей,
содержащая все ребра графа, составит эйлеров цикл. Этот алгоритм
прост, но не эффективен, как всякий переборный алгоритм.
9.1.4. Программа вычисления эйлерова цикла в четном
неориентированном графе по дереву всех его путей
Используемые в программе предикаты аналогичны соответствующим
предикатам предыдущей программы. Здесь программируется алгоритм
построения эйлерова цикла, при котором расширение пути
осуществляется произвольным образом, а критерием окончания работы
является совпадение начала и конца в построенном цикле.
Запрос к программе имеет следующий вид: ?- eul(G,CN,CE).
eul(Graph,CycleNodes,CycleEdges) : -
Graph=[[a,b,c,d,e,f],[[a,b],[a,c],[b,c],[b,d],
[b,e],[d,e],[d,f],[d,c],[f,e],[e,c]]],
path(_,_,__, Graph, CycleNodes, CycleEdges),
covers(CycleEdges, Graph), f irst(X, CycleNodes),
last(Y,CycleNodes),X=Y.
path(A,X,Y,Graph, CycleNodes,CycleEdges) : -
pathl(A, [ Y], [ ],Graph,CycleNodes,CycleEdges).
pathl(A, [ Y | Pathl],Edgesl,Graph,CycleNodes,CycleEdges) : -
adjacent(X,Y,Graph),not(member([X,Y],Edgesl)),
not(member([Y,X],Edgesl)),
pathl(A,[X,Y|Pathl],[[X,Y]|Edgesl],Graph,CycleNodes,
CycleEdges).
pathl(A,[A,B|Pathl],[[A,B]|Edgesl],Graph,[A,B|Pathl],
[[A,B]|Edgesl]).
adjacent(X,Y, [Nodes,Edges]) : -
(member([X,Y],Edges) ; member([Y,X], Edges)).
covers(CicleEdges, [Nodes,Edges]) : - equalset(CicleEdges,Edges).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
subset ([],Y).
subset([[A,B]|X],Y) :-
(member([A,B],Y) ; member([B,A] ,Y)),subset(X,Y).
last(X,[X]).
last(X,[jY]) :- last(X,Y).
first(X,[X|Y]).
224
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
9Л,5, Программа вычисления эйлерова цикла в ориентированном
графе с удалением проходимых ребер
Предикаты, определенные в этой программе, аналогичны
соответствующим предикатам в предыдущей программе.
Запрос к программе имеет следующий вид: ?- euldir(G,CN,CE).
euldir(Graph,CycleNodes,CycleEdges) : -
Graph=[[l,2,3,4,5],[[l,2],[l,3],[2,4],[2,5],
[3,2],[3,4],[4,l],[4,5],[5,l],[5,3]]],Graph=[N,E],
member(X,N),! ,RestEdges=E,
path(X, CycleNodes, CycleEdges, RestEdges).
path(X,CN,CE,RE) :- pathl([X],[] ,CN,CE,RE).
pathl([X|P],El,CN,CE,RE) :- adjacent(X,Y,RE),
not(member([X,Y],El)),delete([X,Y],RE,REl),
(adjacent(Y,Z,REl) ; RE1=[]),
pathl([Y,X|P],[[X,Y]|El],CN,CE,REl).
pathl(CNl,CEl,CN,CE,[]) :- reverse(CNl,CN),reverse(CEl,CE).
adjacent(X,Y,RE) :- member([X,Y] ,RE).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
reversed ],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
9.2. Полные циклы и последовательности де Брейна
Пусть Е2 есть множество всех наборов (ах ,а2,... 9ап) из 0 и 1
длины п.
Определение. Набор из 0 и 1 длины 2" есть полный цикл (де
Брейна), если множество его последовательно прочитанных кусков
длины п исчерпывает все множество наборов длины п из 0 и 1.
Пример. л = 2 (рис 9.1).
Замечание. Цикл де Брейна (как и всякий цикл) располагается по
кругу: конец цикла совпадает с его началом.
Теорема. Для всякого п существует полный цикл.
225
Полный цикл ООН дает все наборы длины:
(0,0); (0,1); (1,1); (1,0).
Рмс.9.1
Доказательство. Построим ориентированный псевдограф G
следующим образом. Вершины в G пометим наборами из 0 и 1 длины л-1.
Тогда G имеет 2""1 вершин. Каждый набор (ах 9а29... ,ап) из Е2
длины п определяет дугу, соединяющую вершины (ах 9а29... 9ап_х) и (а29
а39... 9ап). Граф G связен, ибо любая пара вершин (в1э... ,вя-1) и
(bl9... 9Ьп_х) в G соединима следующим образом: (а19... 9ап^х) -*
(a29...9an_19bl) - (а39...9ап_19Ь19Ъ2) - ... - (а19Ь19...9Ьп_2) -
(bl9b29...9Ьп_х).
В каждую вершину (а2,...,ап) входят две дуги (рис.9.2),
помеченные наборами (0,а2,... 9ап)\ (1,а2,... 9ап)9 и выходят две дуги,
помеченные наборами (а29... ,а„,0); (а2,... ,ал,1). Следовательно,
степень каждой вершины в G четна; полустепени захода и исхода в
каждой вершине G равны, и потому орграф G эйлеров; следовательно,
он имеет эйлеров контур, в котором каждая вершина проходится
дважды (ибо ее степень равна 4). Тогда первые компоненты наборов,
(0,а2,. . . ,<*„_!)
(0,а2,...,<!„)
(1,а2,...,ап)
(1,а2,. ..,<*„-!)
■)
(д2,..
■)
•»о
(а2,..
(а2,..
(а3,...,«Л,0)
,ап,0)
k
^
(а3,... ,яЛД)
Рнс.9.2
226
которыми помечены вершины в этом обходе, и дадут полный цикл де
Брейна.
Замечание. Теорема справедлива и для наборов (а19а29... >ап) из
Е% длины п с элементами из Е^ = {0,1,... ,/t-l}.
Пример. Построим цикл де Брейна для /г=4. Вершины орграфа есть
все наборы из 0 и 1 длины 3: 000,001,010,011,100,101,110,110; их
можно рассматривать как двоичную запись чисел 0,1,2,3,4,5,6,7
соответственно. Ребра графа
^=(000,000), е2=(000,001), е3=(001,010), е4=(001,011),
е5=(010,100), е6=(010,101), е7=(011,110), е8=(011,111),
е9=(100,000), е10=(100,001), ^^=(101,010), е12=(101,011),
е13=(И0,100), е14=(110,101), е15=(111,110), е16=(Ш,Ш).
Эйлеров цикл
ЪехЪе21еъ2е65е^12е54е91е43^77е1б7е156е145е123е86е134е100;
00001010011110110
00010 100111101100
00101001111011000
Составляем цикл де Брейна, взяв от каждого кода вершины первый
элемент (старший разряд). Ниже приведены все наборы длины 4,
порождаемые циклом де Брейна.
0
1
2
5
10
4
9
3
7
15
14
13
11
6
12
8
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1010011110110
1
1 0
10 1
10 10
0 10 0
10 0 1
0 0 11
0 111
1111
1110
110 1
10 11
0 110
110 0
10 0 0
227
9.2.1. Программа вычисления цикла де Брейна
Процедура cycle_de_Breun(N,Ek,C) по натуральному числу N,
множеству Ек={0,1,... ,к-1} вычисляет цикл де Брейна С длины k**N.
Процедура mult_n_Ek(N,Ek,L) по натуральному числу N и списку
Ек=[0,1,... ,к-1] строит список L=[Ek,... ,Ек] длины N.
Процедура dek(L,V) по списку L строит декартово произведение V
множеств, составляющих список L.
Процедура construct_EkNl(Ek,V,EkNl) по списку Ек=[0,1,... ,к-1]
и списку V наборов длины N из Ек строит список наборов длины
N1=N+1, приписывая слева к каждому набору из V элементы из Ек.
Процедура constr_HV(H,V,HV) приписывает элемент Н слева к каж-
му набору в списке наборов V. Например, если H=l, V=[[0,0] ,[0,l],
[1,0],[МП, то HV= [[1,0,0],[1,0,1],[1,1,0],[1,1,1]].
Процедура edges(EkN,E) по списку EkN всех наборов длины N
строит множество Е ребер таким образом, что каждый набор [al,...,
aN] из EkN порождает ребро [[al,... ,aN-l] ,[a2,... ,aN]].
Процедура one_edge(H,Edge) по набору Н=[а1,... ,aN] строит
ребро [[al,...,aN-l],[a2,...,aN]].
Процедура euler__directed_cycle(G,CV) по (четному) связному
ориентированному графу G строит эйлеров цикл С, составленный по
вершинам графа G.
Процедура construct_cycle_de_Breun(CV,C) по эйлерову циклу CV
строит цикл де Брейна С.
Предикаты, определяемые в процедуре euler_directed_cycle(G,CV)
вычисления эйлерова цикла в ориентированном графе G, аналогичны
соответствующим предикатам из программы вычисления эйлерова цикла
в ориентированном графе.
Программа работает правильно, начиная с N=3.
Если хотим получить цикл де Брейна для всех наборов из 0 и 1
длины 3, то запрос к программе будет иметь вид:
?- cycle_de_Breun(3,[0,l],C).
Для получения цикла де Брейна для всех наборов из 0,1,2 длины
4 следует сделать запрос ?- cycle_de_Breun(4,[0,l,2] ,C).
cycle__de_Breun(Nl,Ek,C) :- N is Nl-l,mult_nJEk(N,Ek,L),dek(L,V),
construct_EkNl(Ek,V,EkNl),edges(EkNl,E),G=[V,E],
euler_directed_cycle(G, CV),
construct__cycle_de_Breun(CV, C).
mult_n_Ek(N,Ek,L) :- mult(N,Ek,[],L).
mult(N,Ek,Ll,L) :- not(N=0),Nl is N-l,mult(Nl,Ek,[Ek|Ll] ,L).
228
mult(0,Ek,L,L).
construct_EkNl(Ek,V,EkNl) :- constr_EkNl(Ek,V,[],EkNl).
constr_EkNl([H|T],V,L,EkNl) :- constr_HV(H,V,HV),
append(L,HV,Ll),constr_EkNl(T,V,Ll,EkNl).
constr_EkNl([] .V.EkNl.EkNl).
constr_HV(H,V,HV) :- constrl_HV(H,V,[] ,HV).
constrl_HV(H,[Hl|Vl],HVl,HV) :- add(H,Hl,H2),
constrl_HV(H,Vl,[H2|HVl],HV).
constrl_HV(H,[],HVl,HV) :- reverse(HVl.HV).
edges(EkNl,E) :- edgesl(EkNl,[],E).
edgesl([H|T],L,E) :- one_edge(H,Edge),edgesl(T,[Edge|L] ,E).
edgesl([],E,E).
one_edge(H,Edge) :- H=[Hl|Tl],reverse(H,H2),H2=[H3|T3],
reverse(T3, T4), Edge=[ Tl, T4].
construct_cycle_de_Breun(CV,C) :- cycle_Br(CV,[],C).
cycle_Br([H|T],L,C) :- H=[Hl|Tl],cycle_Br(T,[Hl|L] ,C).
cycle_Br([],[H|T],C) :- reverse(T.C).
euler_directed_cycle(Graph, CycleNodes) : -
Graph=[N,E],member(X,N),!,RestEdges=E,
path(X, CycleNodes, RestEdges).
path(X,CN,RE) :- pathl([X],[] ,CN,RE).
pathl([X|P],El,CN,RE) :- adjacent(X,Y,RE),not(member([X,Y] ,E1)),
delete([X,Y],RE,REl),(adjacent(Y,Z,REl) ; RE1=[]),
pathl([Y,X|P],[[X,Y]|El],CN,REl).
pathl(CNl,CEl,CN,[l) :- reverse(CNl.CN).
adjacent(X,Y,RE) :- member([X,Y] ,RE).
dek(S.L) :- dekl(S.L).
dekl([Hl,H2|T],L) :- dek2(Hl,H2,Ll),dek3(Ll,T,L).
dekl([H|[]],[H|[]]).
dekl([],[]).
dek2(X,Y,Z) :- findall([A)B],(member(A,X),member(B)Y)))Z).
dek3(Ll,[],Ll).
dek3(Ll,[H|T],L) :- dek2(Ll,H,L2),appendl(L2,L3),dek3(L3,T,L).
appendl(L2,L3) :- S=[] ,append2(L2,L3,S).
append2([[H|T]|Tl],L3,S) :- append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],Sl,Sl).
delete(A,[A|B],B) :- !•
delete(A,[B|L],[B|M]) :- delete(A.L.M).
229
reversed ],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
add(H,Hl,[H|Hl]).
member(X,[X|Y]).
member(X,[Y|Z]) :_ member(X,Z).
9.3. Гамильтоновы графы
Цикл С в графе G называется гамильтоновым циклом, если С
проходит без повторов вершин через все вершины графа G. Граф G
называется гамильтоновым графом, если G имеет гамильтонов цикл.
Гамильтонов граф допускает обход всех своих вершин, при этом
каждая вершина проходится единожды. Определения гамильтоновых и
эйлеровых графов весьма схожи, но методы их исследования
существенно различны. Пока не найдены простые критерии гамильтоновости
графа, отличные от переборного критерия; доказаны лишь некоторые
достаточные условия гамильтоновости, два из которых приведем
здесь без доказательства.
Теорема (Поша). Если связный граф G:
1) имеет р Z 3 вершин;
2) V/i из 1 < п < (р-1)/2 следует, что число вершин со
степенями, не превосходящими п, меньше п);
3) из нечетности р следует, что число вершин степени (р-1)/2
меньше (р-1)/2, то G есть гами-льтонов граф.
Ограничивая условия теоремы Поша, получаем следующие более
простые, но менее сильные достаточные условия гамильтоновости
графа.
Следствие 1 (Оре). Если число вершин графа G р ^ 3 и сумма
степеней вершин deg(u) + deg(v) 2 р для всякой пары несмежных
вершин и и v в G, то граф G гамильтонов.
Следствие 2 (Дирак). Если число вершин графа G р £ 3 и deg(v)
^ р/2 для всякой вершины v графа G, то граф G гамильтонов.
На рис.9.3 приведены примеры эйлеровых и гамильтоновых графов.
9.3.1. Программа вычисления гамильтонова цикла
в неориентированном графе по дереву всех его путей
Используемые в программе предикаты аналогичны соответствующим
предикатам предыдущей программы. Алгоритм построения гамильтонова
цикла состоит в последовательном расширении пути вершинами без
появления повторов вершин на каждом строящемся пути до первого
230
Графы
гамилътоновы
не гамилътоновы
эйлеровы
не эйлеровы
* у* * -+
-* *-
га
Рмс.9.3
появления пути, являющегося гамильтоновым циклом.
Запрос к программе имеет следующий вид: ?- ham(G,C).
ham(Graph,Path) :-
Graph=graph([a,b,c,d,e,f,g,h],[e(a,b),e(b,c),e(c,d),e(d,a),
e(a,e),e(b,f),e(c,g),e(d,h),e(e,f),e(f,g),e(g,h),e(h,e)]),
path(_,_, Graph, Path), covers(Path, Graph), first(X, Path),
last(Y, Path), ad jacent(X,Y, Graph).
path(A,Z,Graph,Path) :- pathl(A,[Z],Graph,Path).
pathl(A,[Y|Pathl],Graph,Path) :- adjacent(X,Y,Graph),
not(member(X,Pathl)), pathl(A,[X,Y|Pathl],Graph,Path).
pathl(A,[A|Pathl],_,[A|Pathl]).
adjacent(X,Y,graph(Nodes,Edges)) :-
(member(e(X,Y),Edges) ; member(e(Y,X),Edges)).
covers(Path,graph(Nodes,Edges)) : - equalset(Path,Nodes).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
last(X,[X]).
last(X,[_|Y]) :- last(X,Y).
first(X,[X|Y]).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
231
10. ДЕРЕВЬЯ
10.1. Основные определения
Определение. Дерево есть связный граф, не имеющий циклов.
Совокупность деревьев есть лес.
Определение. Ребро в графе G называется циклическим, если оно
принадлежит хотя бы одному циклу графа G, и ациклическим в
противном случае. Граф G ацикличен, если каждое его ребро ациклично.
Замечание. При удалении из связного графа циклического ребра
граф остается связным; при удалении ациклического ребра -
несвязным.
Каждая компонента связности леса есть дерево.
Пусть G есть связный граф. Тогда следующие утверждения
эквивалентны .
1. Граф G есть дерево.
2. Граф G не имеет циклов.
3. Граф G не имеет циклических ребер.
4. Все ребра в графе G ацикличны.
5. Граф G ацикличен.
10.2. Характеристические свойства деревьев
Теорема. Для всякого (/?,<?)-графа G следующие утверждения
эквивалентны.
1. Граф G есть дерево.
2. Любая пара вершин в G соединима единственной простой цепью.
3. Граф G связен и<у-/? + 1 = 0.
4. Граф G ацикличен и ? - р + 1 = 0.
5. а) граф G ацикличен;
б) если любую пару несмежных вершин в G соединить ребром е,
то получившийся граф G+e будет иметь в точности один простой
цикл.
Доказательство. 1 -> 2. Пусть граф G есть дерево. Так как граф
G связен, то всякие две вершины w,v в G соединимы простой цепью
Z. Эта цепь единственна, ибо при наличии другой цепи Z' между и и
v (рис. 10.1) получим, что дерево G имеет цикл, чего нет.
2 -> 3. Так как любая пара вершин в G соединима (единственной
простой) цепью, то граф G связен. Соотношение q - р + 1 = 0
докажем индукцией по числу р вершин в G.
БАЗИС. р = 1. Так как граф G состоит из единственной вершины,
то<7-р + 1 = 0-1 + 1 = 0.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть соотношение д-р+1=0 справе-
232
дливо для всех графов с числом вершин меньше р.
ШАГ ИНДУКЦИИ. Покажем, что равенство q-p+l=0 справедливо для
всех графов с числом вершин р. Пусть связный граф G имеет р
вершин. Удалим из G ребро е = (w,v), сохранив в G его концы.
Получившийся граф G' = G-e не связен (рис. 10.2), ибо если G' связен,
то между и и v в G', а потому и в G, существует простая цепь.
Другая простая цепь в G между и и v есть ребро е. Противоречие с
единственностью простой цепи в G между и и v. Итак, граф G' не
связен и имеет в точности две компоненты связности с числом
вершин в каждой компоненте р19р2 и числом ребер ql9q2\ при этом р =
Pi+Рг» Я = 9i+?2+l- По предположению индукции #,—р,+1 = 0, /=1,2.
Тогда для графа G сумма q-p+1 = (?i+?2+1) ~ (Pi+P2)+1 = (?i"Pi+l)
+ (?2~P2+1) = 0+0 = °-
Шаг индукции установлен. Равенство q-p+1 = 0 доказано.
Итак, граф G связен и q-p+1 = 0.
3 -> 4. Покажем, что граф G ацикличен. Допустим противное: граф
G цикличен. Тогда G имеет простой цикл С длины n^q (длина цикла
есть число его ребер). Цикл С имеет п вершин и п ребер. Пусть U =
{их ,и2,... ,ир_п} (рис. 10.3) есть оставшиеся вершины в G (т.е.
вершины вне цикла С). Пусть v есть вершина цикла С. Так как граф
G связен, то вершина v цикла С соединима с любой вершиной и,- из
[/. Пусть [w!,v],[w2,v],... ,[wp_„,v] есть геодезические (т.е. цепи
наименьшей длины). Ребра из Е' = {е1У е2У...,ер_п}, лежащие на
этих геодезических и инцидентные вершинам их ,и2>-.. ,Ир_„
соответственно, попарно различны (как инцидентные различным вершинам).
Пусть граф G' = С U Е'. Так как G' Q G, то число ребер в G' п
+ (р - п) < q\ поэтому p^q, откуда q - р ^ 0 и потому q - р + 1 ^
1. Противоречие с^-/? + 1 = 0. Следовательно, граф G ацикличен.
Итак, граф G ацикличен nq-p + l = 0.
4 -» 5. Пусть граф G ацикличен и^-р + 1 = 0. Покажем сначала,
что граф G есть дерево. Так как граф G ацикличен, то каждая его
Цикл С
v
Z'
'2 . . .
ср-л
Рнс.10.1
Ржс.10.2
Ржс.10.3
*р-п
233
компонента связности есть дерево. Пусть G имеет к компонент
связности (к деревьев Г,), причем дерево Г, имеет /?, вершин и <?,
к к
ребер. Тогда граф G имеет р =2.р, вершин и q =2.<7/ ребер. Так
i= 1 1= 1
как для каждого дерева Г, по 1 -> 3 qj-pj+1 = 0, то для графа G
к к к к
\(4i - Pi + l) = \<li' ~ \Pi +L^ = Q~P+k = 0, что вместе с
/= i i= i i-1 i-1
q-p+l = 0 дает /с = 1, т.е. граф G имеет только одну компоненту
связности, а потому граф G есть дерево.
Соединим в дереве G любую пару несмежных вершин w,v ребром е =
(w,v). Ребро е вместе с единственной (по 1 -♦ 2) простой цепью
[w,v] в G дает единственный простой цикл в G+e.
Итак: а) граф G ацикличен; б) если любую пару несмежных вершин
в G соединить ребром е> то получим граф G+e, имеющий в точности
один простой цикл. Условие 5 показано.
5 -> 1. Пусть выполнены условия 5. Граф G связен, ибо если G не
связен, то добавляя к G ребро е между двумя компонентами
связности, получим ациклический граф (ибо ребро е ациклично), не
имеющий циклов в противоречие с условием 5. Следовательно, граф G
связен и ацикличен, т.е. G есть дерево.
Условие 1 установлено. Теорема доказана.
Следствие 1. Связный (р,^)-граф G есть дерево тогда и только
тогда, когда q - р + 1 = 0.
Доказательство следует из того, что по доказанной теореме
условия 1 и 3 эквивалентны.
Следствие 2. Пусть (/?,<?)-граф G связен. Тогда G имеет
единственный простой цикл тогда и только тогда, когда q-p+l = 1.
Доказательство. Пусть связный (/?,<?)-граф G имеет единственный
простой цикл С. Удалим из G его циклическое ребро е (лежащее в
С). Граф G' = G-e связен и не имеет простых циклов, ибо если G'
имеет простой цикл С, то G имеет два простых цикла С и С,
различающихся ребром е: цикл С ребро е имеет, а цикл С - нет.
Следовательно, граф G' есть дерево с тем же числом вершин р. Для
дерева G' (<7-1)-/?+1 = 0, откуда q-p+l = 1.
Пусть теперь для связного (/?,^)-графа G имеет место
соотношение q-p+l = 1. Тогда G не есть дерево (ибо для дерева q-p+l = 0).
Следовательно, граф G имеет циклическое ребро е, ибо без него
граф G был бы деревом. Удалим из G это циклическое ребро е, вхо-
234
дящее в некоторый простой цикл С. Полученный связный граф G' =
G-e имеет р вершин и q-l ребер. Тогда (<7-1)-/?+1 = (<?-р+1)-1 = О
(ибо по условию q-p+1 = l); следовательно G' есть дерево.
Возвращение в дерево G' удаленного ребра е приводит к связному графу G,
который в силу эквивалентности условий 1 и 5 теоремы имеет
единственный простой цикл.
Замечание. Выбрав в дереве Т произвольную вершину v (корень
дерева) и достраивая от нее граф Т вниз, получим изображение для
Tf в котором вершины группируются по ярусам (рис. 10.4).
10.3. Каркасы и хорды в связном графе
Определение. Каркас (остов) в связном графе G есть остовный
подграф графа G, являющийся деревом.
Каркас графа G есть наименьшее по числу ребер дерево в G,
сохраняющее связность между всеми вершинами G. Каркас графа G можно
получить, последовательно выбрасывая (стирая) из G его
циклические ребра. Каркас графа G содержит все ациклические ребра в G,
ибо их нельзя выбросить из G, не нарушив связности получившегося
графа. Каркас в графе G находится неоднозначно.
Каркас графа G можно получить также, последовательно
надстраивая ребрами из G произвольно взятое в G ребро до дерева,
являющегося каркасом. Если граф G является нагруженным (каждому ребру
графа G приписано некоторое неотрицательное число - вес ребра,
его стоимость), то имеет смысл разыскивать наименьший каркас
(каркас с наименьшей суммой весов ребер). Такой наименьший каркас
можно получить, последовательно надстраивая ребрами из G произво-
Рнс.10.4
235
льно взятое в G ребро с наименьшим весом до дерева, являющегося
каркасом. При этом надстройку каждый раз следует выполнять ребром
с наименьшим возможным весом, избегая появления циклов.
Пример. Построим наименьший каркас для нагруженного графа
G=(K,E)=({a,b,c,d,e,f,g},{(a,b,l),(a,g,2),(b,c,7),(b,d,6),
(b,f,8),(b,g,3),(c,d,2),(c,g,9),(d,e,l),(d,f,9),(d,g,l),
(e,f,4),(e,g,5),(f,g,9)}).
Исходим из ребра (а,Ь,1). Последовательное его расширение
ребрами с наименьшим весом (избегаем при этом появления циклов)
приводит нас к каркасу
{(a,b,l),(a,g,2),(d,g,l),(d,e,l),(c,d,2),(e,f,4)}
с наименьшим весом 11.
Определение. Если К = (V,E0) - каркас графа G = (V,E)> то
хорда есть произвольное ребро из Е - Е0.
Множество хорд есть семейство выброшенных в процессе
построения каркаса К циклических ребер. Каждая хорда (последовательно
выброшенное циклическое ребро) соответствует некоторому простому
циклу в G.
Пример. На рис. 10.5 приведен граф G и его .каркас, полученный
последовательным выбрасыванием из G циклических ребер. Тогда
М = {е19е2,...9ел} - {е1Уе2,е5,е7,е&} = {е3,еА,е6}
есть множество хорд графа G.
Утверждение. Число хорд в связном (р,^)-графе G = (V,E) равно
Я - Р + 1-
Доказательство. Пусть (р,<у')-граф К = (V,E0) - каркас
(связного) (/?,<7)-графа G = (У>Е)- Так как каркас К есть дерево,
то q'-p+l = 0. Поэтому число хорд в графе G равно
v = |£| - |Е0| = q - q' = q - q' + (?' - p + l) = <? - p + 1,
где \е\ означает мощность множества Е.
Замечание. Каркас К имеет число ребер
q' =q-v = q-(q-p + l) = p-l.
Чтобы сделать две вершины в связном графе G несвязными,
достаточно выбросить из G все множество хорд и одно ребро,
принадлежащее одной из двух этих вершин на пути между ними.
Множество хорд графа G, дополненных до простых циклов в G,
составляют фундаментальную систему циклов в G. Фундаментальную
систему циклов можно построить также, последовательно добавляя
каждую хорду к каркасу графа G и разыскивая тот единственный цикл,
который через эту хорду проходит.
236
Ржс.10.5
10.3.1. Программа вычисления наименьшего
каркаса в нагруженном графе
Процедура carcas(G,T,C) по нагруженному графу G вычисляет
наименьший каркас (остовное дерево) Е и его вес С.
Процедура spread(Tl,T,G) по графу G и его подграфу Т1
(являющемуся деревом), вычисляет дерево Т, получающееся добавлением к
Т1 ребра из разности G-T1 наименьшего веса.
Процедура addedge(Trl,Tr2,G) по дереву Trl графа G добавляет
ребро, которым можно расширить Trl, чтобы получить дерево Тг2.
Процедура minadjacent(E,T,G) вычисляет множество G1 всех тех
ребер в графе G, которыми можно расширить дерево Т.
Процедура node(A,T) проверяет, принадлежит ли узел А дереву Т.
Процедура minmember(E,Gl) в множестве ребер G1 выбирает ребро
237
Е с наименьшим весом.
Процедура cheaper(E,El,Gl) по ребру Е1 выбирает в графе G1
ребро Е с наименьшим весом.
Процедура cost(G,С) по графу G вычисляет его вес С.
Построенную программу можно использовать для вычисления
каркаса и в ненагруженном графе: достаточно приписать ребрам графа
один и тот же вес, например, единицу.
Запрос к программе имеет вид: ?- carcas(G,T,C).
carcas(Graph,Tree,Cost) : -
Graph=[[a,b,l],[a,g,2],[b,c,7],[b,d,6],[b,f,8],[b,g,3],
[c,d,2],[c,g,9],[d,e,l],[d,f,9],[d,g,l],[e,f,4],
[e,g,5],[f,g,9]],
member([Al,Bl,Costl],Graph),!,
cheaper([Al,Bl,Costl],[A,B,Cost2],Graph),
spread( [[ A,B,Cost2]],Tree,Graph),cost(Tree,Cost).
spread(Treel,Tree,Graph) :- addedge(Treel,Tree2,Graph),
spread(Tree2, Tree, Graph).
spread(Tree,Tree,Graph) :- not(addedge(Tree,_,Graph)).
addedge(Tree,[[A,B,C]|Tree],Graph) :-
minadjacent([ A, B,C], Tree, Graph).
minadjacent(Edge,Tree,Graph) :-
setof([A,B,C],(member([A,B,C],Graph),
not(member([A,B,C] ,Tree)),
(node(A,Tree),not(node(B,Tree)) ;
node(B,Tree),not(node(A,Tree)))),Graphl),
minmember(Edge,Graphl).
node(A,Tree) :- member([A,_,_] ,Tree) ; member([_,A,_] ,Tree).
minmember(Edgel,Graphl) :- member(Edge,Graphl),!,
cheaper(Edge, Edgel, Graphl).
cheaper([A,B,C],[A2,B2,C2],[[Al,Bl,Cl]|Graph2]) :-
CI < C,cheaper([Al,Bl,Cl],[A2,B2,C2],Graph2).
cheaper([A,B,C],[A2,B2,C2],[[Al,Bl,Cl]|Graph2]) :-
C=<Cl,cheaper([A,B,C],[A2,B2,C2],Graph2).
cheaper([A,B,C],[A,B,C],[]).
cost(Graph,Cost) :- C=0,costl(Graph,C,Cl,Cost).
costl([[A,B,C]|G],Cl,C2,Cost) :- C2 is Cl+C,
costl(G,C2,C3,Cost).
costl([],C2,C3,C2).
238
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
10.3.2. Программа вычисления каркаса в непогруженном графе
stree(Graph,Tree) :- Graph=[[a,b] ,[b,c] ,[b,d] ,[c,d] ,[b,f],
[f,e],[c,e],[d,e],[b,g],[g,f],[e,i],[i,f],[a,k],[k,d],
[k,n],[n,d],[n,m],[m,e],[m,p],[p,i]],
member (Edge, Graph), spread( [ Edge], Tree, Graph).
spread(Treel,Tree,Graph) :- addedge(Treel,Tree2,Graph),
spread(Tree2, Tree, Graph).
spread(Tree,Tree,Graph) :- not(addedge(Tree,_,Graph)).
addedge(Tree,[[A,B]|Tree],Graph) :-
adjacent([ A,B],Graph),node(A,Tree),not(node(B,Tree)).
adjacent([A,B] ,Graph):-
(member([A,B],Graph) ; member([B,A],Graph)).
node(A,Graph) :- adjacent([A,B],Graph).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Запрос к программе имеет следующий вид: ?- stree(G,T).
11. ЦИКЛЫ В ГРАФАХ
11.1. Линейное пространство двоичных наборов
Определение. Поле (F, + ,*) есть множество F элементов
произвольной природы с определенными на нем двумя операциями: сложением
A + ji:FxF-»Fh умножением A*fi : F х F -> F, удовлетворяющими
следующим аксиомам: VA,jx,v € F
1) Л + (ц + v) = (А + ft) + v.
2) 3jc€F (Л + х = м).
3) 3y€F (у + А = м).
4) Л + ц = \i + Л.
5) (Л-fx) • v = Л* (ji* v).
6) 3jc€F (А-л: = fx), Л * 0.
7) 3y€F (у А = м), А * 0.
8) Л-fx = fx-Л.
9) Л- (fx + v) = Л- fi + A-v.
F есть абелева группа
по сложению
F без нуля есть
абелева группа по
умножению
239
Обозначим поле (F, + ,*) через F.
Пример. Е2 = {0,1}. Сложение и умножение (по модулю два)
зададим согласно следующим таблицам.
Сложение Умножение
0
1
и 1
0 0
0 1
0
1
и 1
0 1
1 0
Элемент -1, равный 0-1, равен такому Л, что 0 = 1 + Л, откуда
Л = 1; поэтому -1 = 1 (по модулю 2). Объект F = (Е2, + ,*) есть
поле.
Определение. Линейное пространство L над полем F есть
множество L с двумя операциями: сложением а + Ь : Lx L-»Lh
умножением на константу а* Л : L x F -> L (при этом а* Л = Л* а),
удовлетворяющими следующим аксиомам: Ча,Ъ,с € L, VA,/li € F
1) а + (Ь + с) = {а + Ь) + с.
2) а + Ь = Ъ. + а.
3) 3 0 € L (а + 0 = а).
4) Va€L 3(-fl)€L (а + (-а) = 0).
5) Л-(а + Ь) = Л-а + Л-Ь.
6) (Л + ii)*a = Л*а + /х-а.
7) Л* (/!• а) = (Л • ft) • а.
8) 1-я = я, где 1 есть единица поля F.
Пример. Пусть Е2 есть множество всех векторов а = (вр я2,...,
яп) длины /1 из 0 и 1. Введем линейное пространство L2 векторов Е2
над двухэлементным полем F = (Е2, + ,*) со сложением и умножением
по модулю 2, определив (поразрядное) сложение и умножение
векторов на константу из {0,1}, и положив Va,b € Е2, VA€E2 а + Ь =
(а1+Ь1,д2+Ь2,...,ап+Ьп); Л-я = (А-я1э Л-я2,..., Л-я„).
Например, в Е2 для а = (1,0,0,1), Ь = (0,1,1,1) получим я + Ь
= (1,1,1,0); 0-я = (0,0,0,0); 1-е = а.
11.2. Линейное пространство подграфов данного графа
Пусть G = (VyE) есть (р,^)-граф с множеством V = {v!,...,^}
из р вершин и с множеством Е = {е!,...,eq} из q ребер. Пусть Н Q
G есть остовныи подграф графа G. Подграфу Н поставим в соответст-
240
вие его характеристический вектор ан = (а19... ,aq), где
[l, если ребро е,€ Я,
i = 1,2,...,<?.
L0, если ребро е^ t Я,
Между множеством Lq всех остовных подграфов графа G и
множеством всех наборов из Е2 можно установить взаимно однозначное
соответствие, при котором вектору а = (аг,... ,aq) соответствует
подграф На = (V,Ea)9 в котором ребро et € Еа «—> а, = 1.
На множестве всех (остовных) подграфов графа G определим
сложение и умножение на константу из Е2 = {0,1} следующим образом.
Пусть Н,Н1,Н2 есть подграфы графа G и ан,ан ,ан есть им
соответствующие характеристические векторы. Пусть Л € Е2. Тогда
подграф Нх+Н2 соответствует вектору ан +аи ;
подграф Л* Я соответствует вектору Л* ан.
Подграф 0 • Я соответствует нуль-вектору 0 • ан и потому содержит
лишь вершины из G и ни одного ребра. Подграф 1-Я совпадает с Я,
ибо его характеристический вектор 1*ан = ан.
Линейное пространство наборов Eq2 изоморфно системе подграфов
Lq и потому система Lq есть тоже линейное пространство.
Размерность обоих линейных пространств равна q (число ребер в G).
На рис.11.1 приведены граф G, его подграфы Н19Н2, сумма Hx-\-H2,
их характеристические векторы ан ,ан уан +аи .
11.3. Подпространство четных подграфов
Пусть G есть (/?,#)-граф и Lq есть линейное пространство всех
(остовных) подграфов графа G.
Теорема. Множество L4eT всех четных подграфов графа G образует
подпространство линейного пространства Lq всех подграфов графа G.
Доказательство. Покажем, что множество L4eT замкнуто
относительно линейных операций сложения и умножения на константу.
Пусть Н1,Н2 - четные подграфы графа G, v - произвольная
вершина в G, s(v), s^v), s2(v), sl2(v) - степени вершины v в графах
Н1+Н2У Я1э Я2, Нх П Я2 соответственно (см.рис.11.2). Пусть а, а1,
а2, а12 есть характеристические векторы этих подграфов. Для
ситуации, изображенной на рис. 11.2, имеем
241
«я,
"я,
«н}+анг
еIе2е3е*еSe6 е7
= (0,0,1,0,1,1,1)
= (1,1,1,0,1,0,1)
= (1,1,0,0,0,1,0)
Н1+Н2
Я, С G
Рас. 11.1
H2Q G
а1 =
е1 ег е3 е4 е5 е6 е7 е% е9 ^\йеме\ге\г •■•
(1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, ...),
а2 = (1, О, О, О, О, О, 1, О, О, О, О, 1, 1, ...),
а = аЧа2 = (О, О, 1, О, 1, О, О, О, 1, О, 1, 1, 1, ...).
Степени: s^v) = 6, s2(v) = 4, sl2(v) = 2.
Степень вершины v в графе Нх+Н2 складывается из числа ребер в
вершине v графа Н1 плюс число ребер в вершине v графа Я2 минус
удвоенное число ребер в вершине v графа Н1 П Я2, т.е. s(v) =
е. е% е.
eQ ел
#i
11с12с13
я,+я,
sx(v) + s2(v) - 2*512(v). Получилось, что степень любой вершины v
в графе HY+H2 есть число четное. Поэтому сумма Нх+Н2 есть четный
граф.
Если Я есть четный подграф графа G, то О* Я и 1-Я есть четные
подграфы графа G.
Итак, множество Ьчет замкнуто относительно линейных операций
(сложения и умножения на константу).
Все восемь аксиом линейного пространства выполняются для L4eT,
ибо они выполняются для соответствующих векторов из Eq2. Поэтому
множество L4CT есть подпространство линейного пространства Lq.
Теорема доказана.
Заметим, что всякий (простой) цикл в графе G есть четный
подграф графа G.
Определение. Матрица множества (простых) циклов графа G есть
матрица, строки которой есть характеристические векторы (простых)
циклов этого множества.
Утверждение. Пусть С1э...,С^ - циклы в графе G, попарно
непересекающиеся по ребрам. Тогда
1) объединение Сх U ...U Q циклов совпадает с их суммой Сг +
... + Ск\
2) циклы С!,...,Ск линейно независимы.
Доказательство. На рис. 11.3 приведены граф G и три его цикла
СХ,С2,С3, попарно непересекающиеся по ребрам, и их
характеристические векторы ас ,ас ,ас соответственно. Видим, что каждый
столбец их матрицы имеет не более одной единицы. Графы С1 U С2 и Сг
+ С2 совпадают.
1. Так как циклы Cli...iCjc не-имеют попарно общих ребер, то
матрица их характеристических векторов ас ,...,ас в каждом
столбце имеет не более одной единицы. Поэтому при сложении строк
матрицы (т.е. при поразрядном сложении векторов по модулю два) ни
одна единица (т.е. ни одно вхождение ребра) не пропадает. Тогда
сложение характеристических векторов (сложение циклов) совпадает
с объединением соответствующих циклов по общим вершинам.
2. Каждая строка в матрице характеристических векторов линейно
независима от остальных строк, ибо если строка ас. в разряде ;
имеет 1, то в разряде ;" остальные строки матрицы имеют 0, и
единица в разряде ; вектора ас. не может быть получена никакой
линейной комбинацией нулей в разряде ; остальных векторов. Поэтому
все строки в матрице, а, следовательно, и все циклы С1Э...,С^
линейно независимы.
243
Граф G
Цикл С, Цикл С2
Цикл С,
«с, =
«с2 -
«с3 =
^ 1 ^2
(1110 0 0 0 0 0 0)
(0 00100110 0)
(0000110011)
(1111 0 0 110 0)
Рмс.11.3
Лемма. Множество всех простых циклов графа G составляет
порождающую систему подпространства L4eT всех четных подграфов
графа G.
Доказательство. Пусть Я есть произвольный четный подграф графа
G. По теореме Эйлера граф Я представим как объединение некоторых
простых циклов С и-.., Ск из Я с попарно непересекающимися
множествами ребер. По доказанному выше утверждению Я = Сх + .. .+С^.
Всякий цикл в Я есть цикл в G. Поэтому граф Я есть линейная
комбинация множества простых циклов в (7, причем в этой линейной
комбинации коэффициенты 1 имеют простые циклы С1Э...,СЛ; остальные
простые циклы из G имеют коэффициенты нуль. Лемма доказана.
Теорема. Подпространство LHeT четных подграфов линейного
пространства Lq всех (остовных) подграфов связного (р,^)-графа G
имеет размерность dim(LHer) = q - р + 1.
Доказательство. Пусть G = (V>E) есть связный (/?,<?)-граф с р
вершинами и q ребрами. Пусть подграф-дерево Т = (V9ET) -
некоторый каркас графа G. Число v хорд в G равно q - р + 1. Каждый
простой цикл четен. Каждая хорда е = (w,v) вместе с единственной
простой цепью [w,v] в дереве Т образует простой цикл. Векторы
таких циклов для разных хорд образуют линейно независимую систему
2, ибо каждый из циклов содержит ребро (свою хорду), не принадле-
244
жащее ни одному из остальных циклов системы 2. Мощность Izl = и =
Я - Р + 1.
С другой стороны, каждый четный подграф Я графа G линейно
выражается через циклы системы 2. В самом деле, пусть е1,...,ег -
все хорды в графе Я. Прибавим к четному подграфу Я графа G те
циклы С1Э...,СГ из 2, которые содержат хорды е1У...9ег из Я. Тогда
суммарный четный граф Я' = Я + С1 + ... + Сг не содержит ни одной
хорды, т.е. Я' есть подграф каркаса Г, а всякое дерево имеет
висячие вершины с нечетной степенью 1. Но граф Я' четен как сумма
четных графов. Поэтому граф Я' пуст (не имеет ребер), т.е. в
линейном пространстве Lq элемент Я' есть нуль. Тогда Я' = Я + Сх +
... + Сг = 0, откуда Я = -С1-...-Сг, поэтому Я = Сх + ... + Сг
(ибо -1 = 1 по модулю два). Итак, всякий четный подграф Я графа G
линейно выражается через циклы системы £.
Получили, что Z есть линейно независимая система циклов в G,
причем любой четный подграф графа G линейно выражается через
циклы системы 2. Следовательно, 2 есть базис пространства L4eT
четных подграфов графа G. Так как мощность 111 =<?-/? + 1, то
dim(L4CT) = q - р + 1.
Определение. Фундаментальная система циклов есть базис
линейного пространства всех четных подграфов данного графа.
Замечание. Пусть несвязный (р,<?)-граф G имеет к компонент
связности Gly... 9Gki причем каждое G, есть связный (/?, ,<7,)-граф, / =
к к
1,...,/с. Тогда р =2.Рм Я =\<li- Базис пространства всех четных
/= 1 i= 1
подграфов графа G получается объединением базисов связных компо-
dim(Lw в с) =
к к к к
£(<?,- Pi +l) = J9i - lPi + J4 =
1= 1 1= 1 1= 1 i= 1
q - p + k\ т.е. dim(L4CT B G) = 4 - p + fc.
11.4. Циклический ранг графа
Определение. Циклический ранг CR(G) (цикломатическое число)
графа G есть размерность подпространства четных подграфов линей-
245
нент в G. Поэтому
к
dim{ £(L4eT B G.)) =
ного пространства всех подграфов графа G.
Справедливы следующие утверждения.
1. Для связного (р,^)-графа G:
а) CR{G) = dim(L4CT) = q - р + 1;
б) CR(G) равно рангу матрицы простых циклов в G;
в) CR(G) равно числу хорд в G\
г) CR(G) равно максимальному числу линейно независимых простых
циклов в G.
2. CR(G) = dim(LHJ Z 0.
3. Для связного (/?,#)-графа G следующие утверждения
эквивалентны:
а) граф G есть дерево; г) CR(G) = 0;
6)^-/7 + 1 = 0; д) граф G не имеет циклов;
в) dim(L4eT) = 0; е) число хорд в G равно 0.
4. Для связного (р,#)-графа G следующие утверждения
эквивалентны:
а) граф G имеет единственный цикл; б)^-р + 1 = 1;
в) dim(L4J = 1; г) CR(G) = 1;
д) ранг матрицы простых циклов в G равен 1;
е) число хорд в G равно 1.
5. Если (р,^)-граф G имеет к компонент связности G,-, i = 1,2,
...,fc, причем каждое G, есть (/?, ,^,)-граф, то CR(G) =
к к
dim(L4tT в G) = £d/m(L4CT B G.) = ][ (qtf - pt + l) = q - p + fc.
6. Фундаментальную систему циклов (базис подпространства L4eT
линейного пространства четных подграфов графа G) можно построить,
взяв с каждой хордой графа G один из проходящих через эту хорду
простых циклов. Фундаментальную систему циклов можно построить
также, последовательно выделяя в G цикл, убирая затем из G
произвольное ребро (хорду) этого цикла, снова выделяя в получившемся
графе цикл, и так далее, пока выделение циклов в последовательно
получающихся графах возможно. Система получившихся циклов
составит фундаментальную систему циклов графа G. Оставшийся после
последовательного удаления из G хорд граф образует каркас графа G.
Пример. Построим фундаментальную систему циклов для графа
G = (К,£)=({1,2,3,4,5,6},{(1,2),(1,4),(1,5),(1,6),(2,3),(2,5),
(3,4),(3,6),(4,5),(5,6)}).
246
Граф
G
Gl=G-ex
G2=G,-e2
G3=G2-e3
G4=G3-e4
Цикл
С, =12341
C2=1451
C3=34563
C4=14361
C5=12541
Удаляемое ребро
^=(2,3)
e2=(l,5)
e3=(5,6)
e4=(3,6)
e5=(2,5)
Граф G5=G4-e5 циклов не имеет. Множество {С1,С2,С3,С49С5}
составляет фундаментальную систему циклов графа G. Множество {е1У
e2>e3>eA>es} содержит все хорды графа G. Граф G5 = {(1,2),(1,4),
(1,6),(3,4),(4,5)} есть каркас графа G.
НАЛ, Программа вычисления фундаментальной
системы циклов в связном графе
Процедура fund__system_cycles(FSC) вычисляет фундаментальную
систему циклов в заданном (системой фактов) связном графе. S есть
стартовая вершина графа; [S,Y] - первое ребро графа.
Процедура system_cycles(FSC,SC,S,[Y,S]) по стартовому узлу S
(исходная вершина графа) вычисляет фундаментальную систему циклов
FSC, последовательно надстраивая промежуточную систему циклов SC.
Процедура path(Y,P,Pl), начиная со стартового узла S и
последовательно надстраиваая промежуточный путь Р1, строит путь Р,
имеющий простой цикл в качестве своего начального отрезка.
Например, путь Р = [2,4,3,2,1]. Путь Р1 надстраивается справа налево.
Y есть промежуточный узел пути Р1.
Процедура cycle(P,C) по пути Р, содержащим цикл С, являющийся
начальным отрезком в Р, вычисляет этот цикл С. Например, если Р =
[3,4,5,3,2,8,1], то С=[3,4,5,3].
Процедура next_node(X,Y,P) по узлу X и промежуточному пути Р
вычисляет следующий узел Y пути Р.
В результате своей работы программа выдает в качестве ответа
фундаментальную систему циклов FSC. Программа в процессе
исполнения модифицирует саму себя: удаляет из рабочей области факты а(Х,
Y), для которых ребра [X,Y] являются хордами, оставляя факты,
ребра для которых составляют каркас графа. Просмотреть их можно с
помощью запроса ?- listing.
Запрос к программе имеет следующий вид:
?- fund_system_cycles(FSC).
fund_system_cycles(FSC) :- a(Start,Y),!,
system_cycles(FSC,[],Start).
a(l,2). a(2,3). a(2,6). a(3,4). a(3,5). a(4,5). a(4,6). a(5,6).
247
system_cycles(FSC,Sc,X) :- a(X,Y),path(Y,Path,[Y,X]),
Path=[F|R],member(F,R),cycle(Path,Cycle),Cycle=[Hl,H2|T],
(retract(a(Hl,H2)) ; retract(a(H2,Hl))),!,
system_cycles(FSC, [Cycle|Sc],Z).
system_cycles(FSC, FSC, S).
path(Y,P,Pl) :- pathl(Y,Z,P,Pl).
pathl(Y,Z,P,Pl) :- P1=[H|T] ,not(member(Y,T)),next_node(Y,Z,Pl),
pathl(Z,Zl,P,[Z|Plj).
pathl(X,Y,Pl,Pl) :- member(X,Pl).
cycle([H|T],C) :- cyclel(H,T,C,[H]).
cyclel(S,[H|T],C,PC) :- not(S=H),cyclel(S,T,C,[H|PC]).
cyclel(S,P,C,PC) :- C=[S|PC] ,member(S,PC).
next_node(Y,Z,[Hl,H|T]) :- (a(Y,Z) ; a(Z,Y)),not(Z=H).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
12. ДВУДОЛЬНЫЕ ГРАФЫ И ПАРОСОЧЕТАНИЯ
12.1. Двудольные графы
Определение. Граф G = (V,E) называется двудольным (биграфом),
если множество V его вершин допускает разбиение на два
непересекающихся подмножества Vl и V2 (две доли), причем каждое ребро
графа соединяет вершины из разных долей.
Обозначим через G = (Vl,V2,E) двудольный граф G с долями Vx и
V2. Будем считать, что I Vх I < I Vг I .
Определение. Двудольный граф G = (Vl9V2fE) есть полный
двудольный граф, если каждая вершина из Vх соединена ребром с каждой
вершиной из V2.
Обозначим через Кп т полный двудольный граф G = (VlyV2,E)9 у
которого /i= lF1l,m= I K21 . Звезда есть полный двудольный граф
Кхр. Несколько примеров двудольных графов приведено на рис. 12.1.
Теорема. Граф G двудолен тогда и только тогда, когда все
простые циклы в G имеют четную длину (четное число ребер).
Доказательство. Пусть граф G = (К,Е) = (К1ЭК2,Е) двудолен и
пусть С = vlelv2e2v3e3vf'vn-ien-ivn (причем vx = v„) есть
простой цикл в G длины /i-l. Тогда v1,v3,v5,v7,... € Vly a v2,v4,
v6,... € V2, т.е. вершины с нечетными индексами лежат в Vх, а
вершины с четными индексами лежат в V2 (рис. 12.2). Так как v„ =
vl € К1э то число п нечетно. Поэтому длина я-1 цикла С есть число
четное.
248
*».>
*.,.
*.,э
Рнс.12.1
Пусть теперь G = (V,E) есть граф, все простые циклы которого
имеют четную длину. Можно считать, что граф G связен, ибо каждую
компоненту связности графа G можно рассматривать по отдельности.
Пусть Vj€ V - произвольная вершина в связном графе (7, и пусть
множество вершин Vx = {v € V : расстояние d(v,vx) между v и vx
четно}. Тогда V2 = V - Vx есть множество вершин, находящихся от
Vj на нечетном расстоянии. Покажем, что никакие две вершины в V2
не соединимы в G ребром. Допустим противное: существует пара
вершин w,v € V2i соединимых в G ребром е = (w,v). Пусть [vj,w] и
[vpv] на рис. 12.3 - две геодезические (нечетной длины). Тогда
[v^w] U {e} U [v,vj есть простой цикл в G нечетной длины.
Противоречие с условием. Следовательно, любые две вершины в V2 не
смежны. Аналогично можно показать, что любые две вершины в Kj не
смежны. Следовательно, ребра в графе G соединяют вершины из
разных классов, т.е. граф G двудолен.
геодезические
нечетной длины
Vj V3 V5 V.
ж.
Уг V4 V4 V, U V
Рже. 12.2 Рмс.12.3
249
12.2. Паросочетания
Определение. Паросочетание есть двудольный граф, в котором
никакие два ребра не являются смежными (рис. 12.4). Паросочетание Р
для графа G = (V,E) есть любое множество попарно несмежных ребер
в G. Р есть наибольшее паросочетание для G, если число ребер в Р
наибольшее среди всех паросочетаний для G. Р есть максимальное
(тупиковое) паросочетание для G, если к Р нельзя добавить ни
одного ребра из G, не нарушив паросочетаемости. Р есть совершенное
паросочетание для G, если Р имеет \v\ ребер.
Замечание. Наибольшее паросочетание максимально. Совершенное
паросочетание является и наибольшим, и максимальным (рис. 12.5).
Простая цепь С ненулевой длины в G, ребра которой попеременно
лежат и не лежат в Р, называется чередующейся цепью (относительно
паросочетания Р). Эта цепь С называется Р-увеличителем, если
первое и последнее ребро цепи С лежат вне Р. С помощью Р-увеличителя
С паросочетание Р можно переделать в другое паросочетание Р' для
G с числом ребер в Р' на единицу больше, чем в Р. Для этого
достаточно все ребра в С, лежащие вне Р, добавить к Р, а ребра в С,
лежащие в Р, удалить из Р. Для получившегося паросочетания Р'
можно снова искать увеличитель, и так далее, последовательно
расширяя получающиеся паросочетания, пока это возможно.
Теорема. Если паросочетание Р для графа G не является
наибольшим, то граф G имеет Р-увеличитель.
Доказательство. Если паросочетание Р (заданное множеством Р
своих ребер) для G не является наибольшим, т.е. G имеет другое
паросочетание Р' с большим числом ребер, чем в Р. В подграфе
графа G, порожденном множеством ребер (P-P')U(P'-P), степень любой
вершины не больше 2, следовательно, каждая компонента связности
этого подграфа есть простая цепь или простой цикл с чередованием
ребер из Р и из Р'. Среди этих компонент обязательно найдется
простая цепь нечетной длины, начинающаяся и оканчивающаяся
ребрами из Р', ибо в противном случае было бы IP' I < IP I вопреки
предположению; эта цепь и является искомым Р-увеличителем в G.
Рис. 12.4
250
Граф G Максимальное Совершенное
паросочетание в G паросочетание в G
Рнс.12.5
Следствие. Если граф G не имеет Р-увеличителя, то
паросочетание Р для графа G является наибольшим.
Приведем без доказательства следующее утверждение.
Теорема. Граф G = (V,E) имеет совершенное паросочетание тогда
и только тогда, когда 4VQV (n(G-V)^ I К'I), где n(G-V) есть
число тех компонент связности подграфа G-V графа G, которые имеют
нечетное число вершин.
Определение. Паросочетание Р для двудольного графа G = (Vl9V2,
Е) есть любое множество попарно несмежных ребер в G. Р есть
наибольшее паросочетание для G, если число ребер в Р наибольшее
среди всех паросочетаний для G. Р есть максимальное (тупиковое)
паросочетание для G, если к Р нельзя добавить ни одного ребра из
G, не нарушив свойства паросочетаемости. Р есть совершенное
паросочетание для G, если Р имеет \Vl I ребер.
12.2.1. Алгоритм построения совершенного
паросочетания для двудольного графа
Пусть G = (иуУуЕ) - двудольный граф. Выберем исходное
паросочетание Р1? например, одно ребро графа G. Допустим, что
паросочетание Pi = (UijVijEi) для графа G построено.
Построим паросочетание Р| + 1 для G следующим образом.
1. Выбираем и из U не из Р,. Если такой вершины и нет, то Р,
есть совершенное паросочетание. Строим в G чередующуюся цепь [it =
[ul,vl,u2,v29... yiipyVp] с их = и, в которой всякое ребро (m/.v,-)
не принадлежит Eiy а всякое ребро (vl,wl + 1) принадлежит £,. Ер ли
такой цепи нет, то совершенного паросочетания граф G не имеет, а
паросочетание Р, является для G максимальным (тупиковым). Цепь jn,
есть Р/-увеличитель.
2. Выбрасываем из Р, все ребра (v/,wl + 1) и добавляем все ребра
(m/jV,-) цепи fij. Получившееся паросочетание Р| + 1 на одно ребро
длиннее паросочетания Р,. Переходим к п. 1.
251
Пример. Построим совершенное паросочетание для двудольного
графа
G = (U9V9E) = ({xl9x29x39xA9x59x6}9{yl9y29y39yA9y59y69y1}9
{(xl9yl)9(xl9y2)9(xl9y5)9(x29yl)9(x29y3)9(x29y5)9(x39yl)9
(х39у6)9(хА9у3)9(хА9уА)9(хА9у6)9(х49у1)9(х59у5)9(х59у1)9
(x69yA)9(x69y6)9(x69y7)}).
Шаг 1. Выбираем исходное паросочетание Рх = {C-^i ,>^i)} -
Рх-увеличитель (чередующаяся цепь)
Mi = U29yl9xl9y5].
0 10
10 1
Единственная единица в первой строке из нулей и единиц
означает, что соответствующее этой единице ребро (у19хх) лежит в Рх.
Убираем это ребро из Рр а вместо него добавляем два ребра (х29
yi)*(xi,y5)9 соответствующие двум единицам второй строки из нулей
и единиц. В результате получим следующее паросочетание Р29 число
ребер в котором на одно больше чем в Рх.
Шаг 2. Р2 = {(х19у5)9(х29У1)}.
0 10
10 1
Удаляем из Р2 ребро (х29ух) и добавляем вместо него ребра (х39
Ух), (*2>Уз)-
Шаг 3. Р3 = {(х19у5)9(х29у3)9(х39у1)}.
Из = [ха'Уа]-
Добавляем в Р2 ребро (jc4,^4)•
Шаг 4. РА = {(xl9y5)9(x29y3)9(x39yl)9(x49y4)}.
М4 = [х5,у5,х19у19хЪ9у6].
0 10 10
10 10 1
Удаляем из Р2 ребра (х19у5)9 (х39ух) и добавляем вместо них
ребра (х59у5)9 (х19ух)9 (х39у6).
Шаг 5. Р5 = {(xl9yl)9(x29y3)9(x39y6)9(x49yA)9(x59ys\.
252
Us = [х69у69х39у19х19у59х59у7].
0 10 10 10
10 10 10 1
Удаляем из Р5 ребра (х39у6)9 (xl9yY)9 (х59у5) и добавляем
вместо них ребра (х69у6)9 (х39у1)9 (х19у5)9 (х59у7).
Шаг 6. Р6 = {(х19у5)9(х29у3)9(х39у1)9(х49у4)9(х59у7)9(х69у6)}.
Р6 есть искомое совершенное паросочетание для исходного графа.
72.2.2. Программа вычисления совершенного паросочетания
в двудольном графе методом чередующихся цепей
Программа построена так, что сначала паросочетание расширяется
за счет единичных ребер, пока это возможно, а затем с помощью
увеличителя (чередующейся цепи).
Процедура match(G,M) по двудольному графу G = (V,M) строит
совершенное паросочетание М в G, если оно в G существует, и одно из
максимальных (т.е. тупиковых) паросочетаний М в G, если
совершенного паросочетания в G нет.
Процедура matchl методом чередующихся цепей осуществляет
циклическое расширение промежуточного паросочетания в G.
Процедура path строит очередную чередующуюся цепь.
Запрос к программе имеет следующий вид: ?- match(G,M).
match(G,M) :- G=[[xl,x2,x3,x4,x5,x6] ,[yl,y2,y3,y4,y5,y6,y7],
[[Xl,yl],[xl,y2],[xl,y5],[x2,yl],[x2,y3],[x2,y5],
[Х3,у1],[х4,у3],[х4,у4],[х4,у6],[х4,у7],[х5,у5],
[x6,y4],[x6,y6]]],G=[Vl,V2,E],S=[],VSl=[],VS2=[],
matchl(Vl,V2,E,S,VSl,VS2,M).
matchl(Vl,V2,E,S,VSl,VS2,M) :-
member([X,Y],E),not(member([X,Y],S)),
not(member(X,VSl)),not(member(Y,VS2)),
matchl(Vl,V2,E,[[X,Y]|S],[X|VSl],[Y|VS2],M).
matchl(Vl,V2,E,S,VS3,VS4,S) :- equalset(Vl,VS3).
matchl(Vl,V2,E,S,VSl,VS2,M) :-
member([X,Y],E),not(member([X,Y],S)),
not(member(X,VSl)),member(Y,VS2),P=[[X,Y]],
path(VS2,E,S,Sl,P,Pl),difset(S,Pl,S2),difset(Pl,S,S3),
unionset(S2,S3,S4),
f indall(Xl, member([XI, Yl],S4), VS3),
findall(Y2,member([X2,Y2],S4),VS4),
matchl(Vl,V2,E,S4,VS3,VS4,M).
matchl(Vl,V2,E,S,VS3,VS4,M) :- not(equalset(Vl,VS3)),
253
write('maximal matching is')>nl,
write(,S=,),write(S),nl,nl.
path(VS2,E,S,Sl,[[X,Y]|P],Pl) :-
member([Xl,Y],S),delete([Xl,Y],S,S2),
member([Xl,Yl],E),not(member([Xl,Yl],S)),
not(member([Xl,Yl],[[Xl,Y],[X,Y]|P])),
path(VS2,E,S2,Sl,[[Xl,Yl],[Xl,Y],[X,Y]|P],Pl).
path(VS2,E,S,S,Pl,Pl) :- P1=[[X,Y] |P] ,not(member(Y,VS2)).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
subset ([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
unionset([],X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
12.3. Системы различных представителей
Определение. Система различных представителей (СРП) для
семейства конечных множеств S = {Ах ,А2,... ,At-,... ,Am} есть система
попарно различных элементов {а х, а2,..., а,?,..., ат}, для которой а,
€ Aj, i = 1,2,... ,m.
Примеры.
1. ^^{1,4}; А2 = {1,2,5}; А3 = {5,6}; СРП = {1,2,5}.
2. А, = {1,3}; А2 = {1,3}; А3 = {3,4}; А4 = {1,4}. СРП нет.
По семейству множеств S = {А19...,Ат} построим двудольный граф
G = (Vl9V2,E), положив (рис.12.6)
m
Vx = S = {^Лг.-Л); V2 =U A, = {al9a29...9ar}\
i- l
ребро e = (Aiyaj) € E ♦—> aj € Aj.
Семейство S имеет СРП тогда и только тогда, когда граф G имеет
254
А2 Л Am
I '
* * *
<*г a} ar
Pmc.12.6
совершенное паросочетание.
Для двудольного графа G = (Vl,V2,E) можно построить семейство
множеств S(u) = {v€K2 : ребро е = (w,v)€E}, u€Vx. Тогда семейство
множеств S имеет СРП тогда и только тогда, когда двудольный граф
G имеет совершенное паросочетание. Так что вопрос о наличии
совершенного паросочетания у двудольного графа G эквивалентен
вопросу о наличии СРП для семейства множеств S, порожденным
графом G описанным выше способом.
Теорема (Радо). Пусть А19...,Ат есть семейство S конечных
множеств. Семейство S имеет СРП тогда и только тогда, когда V& =
1,2,...,т объединение любых к множеств этого семейства имеет по
крайней мере к элементов.
Коротко: семейство S имеет СРП тогда и только тогда, когда
V/ с {1,2,...,m} (l/l * |U^-|).
Доказательство. Пусть а,Ъ € Ат, а * Ь,
Л = \А1 у. . . уАт_1 ,Ат) = \АХ,. . . ,Am_l ,Ат— \Q)) \
Ь = \Ах ,. . . ,Ат_х ,Amj = \А1,, .. iAm_l ,Am—\ufj\
Лемма. Если
1) V /с {1,2,....m} (\UA-\ > |/|),
2) \Ат\ * 2,
то За € Ат V/ С {1,2,...,/п} (| \}а\\ > |/|).
i€/
Доказательство. Допустим противное:
Va € Ат 3/ С {1,2). ..,т) (| U а\ \ < |/|). (12.1)
«€/
Пусть Лт = {o1,...,ar}; A/ = {1,2,...,т}. Из условия (12.1)
255
имеем
для а = а, € Ат 3/ = l\ Q м (| U а\\ < \l\\)\
для а = а2 € Лга 3/ = /2 Q M (| U Л• | < |/'2|); (12.2)
для а = аг £ Ат 31 = /г Я М (\U а\ \ < \/'г\)
,€/;
Возможны следующие случаи:
а) 3/€{l,...,r} (m i //), т.е. // Я {1,2,... ,m-l}. Тогда по
формуле (12.2) будем иметь
для а=сц1Ат 3/ = /; с {1,2,...,m-l} (|U ^ | < \j\\). (12.3)
i€/;
Из (12.1) для /=// с {1,2,...,т-1}- | U ^,| = | U ^-|^|//|. Про-
i€// i€//
тиворечие с (12.3);
б) V/ с {1,2,...,г} (т € //). Пусть //ч= // - {/л}. Тогда // =
/, U {m}, /, с {l,2,...,m-l}, |/;| = |/,|*1. Так как \Ат\ > 2,
то Ат имеет два различных элемента а9Ь. Из (12.1) имеем:
для а € Ат 3/ = /' с {l,2...,m} (| U ^1 • | < |/'|).
i€/'
При / = /'-{/л}; / ^ {l,2,...,m-l}; |/'| = |/|+1; для i€/ a\ = Л-
|U ^| = |(U A\) U Uw-{fl}) I = l(U At) U Um-W)L
Поэтому
для a€Am 3/c{l,2...,m-l} (|(U At)\J(Am-{a} |< |/| ). (12.4)
i€/
Аналогично
для Ь€ЛШ 3A:c{l,2...,m-l} (|( U Ai)\J(Am-{b}\*\K\). (12.5)
Сложим (12.4) и (12.5), в результате получим: |/| + \к\ Ъ
Ки Ai) и ит-{о}\ и |(и л,) и иж-{*}| »
256
|(U Ai)UAm\ U | U Ai \ > |/|*l*|tf|, откуда
i€/ it К по (12-2)
|/| + |#| £ |/| + |£|+1. Противоречие. Следовательно, наше
предположение неверно и заключение леммы справедливо.
Продолжим доказательство теоремы.
Необходимость очевидна, ибо если семейство Ах 9А29... 9Ат имеет
СРП {а19а29...9ат}9 то
V/C {1,2,....m} |U Ai\ > |U{e/} | = |/|.
i€/ i€/
Пусть теперь для конечной системы S множеств Ах 9А29... ,Ат
выполняется условие V/ с {1,2,. ..,m} (|Uj4,-| ^ |/|). Покажем,
что система S имеет СРП. Индукция по наибольшему из чисел М, | .
БАЗИС, max \At\ = 1. Тогда \АХ\ = ... = \Ат\ = 1.
,. . . , i
Одноэлементные множества ylj,...,^ тривиально имеют СРП.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть утверждение достаточности
справедливо для всех семейств 5 множеств Alf...,Am9 для которых
max |^4/| < q.
i - l , . . . , m
ШАГ ИНДУКЦИИ. Покажем, что утверждение достаточности
справедливо для всех семейств S с max \Aj\ = q > 2. Пусть d - число
i - l , . . . , m
всех множеств семейства 5, которые имеют мощность q. Пусть для
простоты d = 2 и Mw| = |^4m_!l = #. Применяя тогда два раза
лемму, получаем
За € Ат V/C {1,2,...,m} (| U ^ | * |/|),
i€/
3b € Ат V/ С {1,2,...,т} (|U^7I > И),
где
о = Hj,. . . ,>lm_1 ,Amj = l-Zij,.. . ,yiw_1 ,^4W—\fl//,
257
Так как в системе S" = {Ах,... 9Ат} max \At\ = q-1 < q и V/ Я
^ i = l, . . . , m
{1,2,...,m} (| \J Aj \ & \l\), то по предположению индукции
i€/
семейство
имеет СРП {^,... ,am-2>am-i >flm}> которая есть СРП и для семейства
S. Теорема доказана.
Пусть G = (VlyV2,E) - двудольный граф; вершина и € Vх\
множество вершин AQV\. Положим множество S(u) = {v€K2: и смежна
с v}; S(A) = U S(u).
Теорема (Холла). Пусть G = (Vl,V2,E) - двудольный граф. Тогда
граф G имеет совершенное паросочетание тогда и только тогда,
когда V А С vx (\А\ $ \S(A)\).
Доказательство. Граф G имеет совершенное паросочетание тогда и
только тогда, когда семейство множеств S(u) = {v€K2: и смежна с
v}, и € Vx, имеет СРП. Последнее по теореме Радо справедливо
тогда и только тогда, когда ЧА Я Vx (\а\ < | U S(w)l), т.е. когда
ЧА с vx (U| * \S(A)\)U
13. ПЛАНАРНЫЕ ГРАФЫ
13.1. Плоские графы
Определение. Граф G изоморфно укладывается на плоскость, если
его можно изобразить на плоскости так, чтобы никакие его ребра не
пересекались (кроме соединений ребер в вершинах). Граф G,
уложенный на плоскости, называется плоским изображением графа G. Граф G
плоский, если он изображен на плоскости без пересечений ребер.
Граф G планарен (рис. 13.1), если G изоморфно укладывается на
плоскость.
Всякий плоский граф планарен. Всякий подграф планарного
(плоского) графа планарен (плоский). Плоский граф иногда называют
плоской картой.
Определение. Грань плоского графа есть часть плоскости,
ограниченная простым циклом графа. Конечная грань называется
внутренней. Бесконечная грань называется внешней. Простой цикл, ограни-
258
чивающий грань, называется границей грани.
Дерево имеет единственную (бесконечную) внешнюю грань.
На рис. 13.2 изображен плоский граф с областями 1,2,3 -
внутренними гранями и областью 4 - внешней.
Аналогичные определения можно ввести для мультиграфов и
псевдографов. Возможны укладки графов без пересечений ребер и на
другие поверхности.
13.2. Формула Эйлера
Теорема. В любом связном плоском графе числа p,q,r его вершин,
ребер, граней соответственно связаны равенством (Эйлера)
р - q + г = 2\
Доказательство. (Индукция по числу q ребер в графе).
БАЗИС, q = 0. Так как граф состоит из единственной вершины, то
р - q + 1 =1-0 + 1 = 2.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что формула Эйлера
справедлива для всех связных плоских графов с числом ребер меньше q.
ШАГ ИНДУКЦИИ. Покажем, что формула Эйлера справедлива для всех
связных плоских графов с числом ребер q. Пусть плоский граф G
имеет р вершин, q ребер и г граней. Возможны следующие случаи.
1. Граф G имеет простой цикл. Удалим из G циклическое ребро е.
Граф G' - G-e связен, имеет р вершин, q-\ ребер и г-1 граней. По
предположению индукции для графа G' формула Эйлера справедлива;
тогда р - (q - l) + (r - l) = 2; отсюда p-q+r= 2.
2. Связный граф G простых циклов не имеет. Тогда граф G есть
дерево с единственной внешней гранью (рис. 13.3). Все ребра в G
Планарный граф G Плоское изображение G
Рис.13.1 Рнс.13.2
259
Ршс.13.3
ацикличны. Удалим из G любое ребро е. Получим несвязный граф G' =
G - е с двумя компонентами связности Gl и G2 и числами pl9 ql9 rl
и Р2>Яг>гг вершин, ребер и граней соответственно (рис.13.3). Так
как ql9q2 < q, то по предположению индукции для графов Gl9G2
формула Эйлера справедлива:
Pi " ?i + 'i = 2 р, - qx + 1 = 2
-> -> (сложим)
Р2 - ?2 + 'г = 2 р2 - <?2 + 1 = 2
(Pi + Р2) - (<7i + <72) + 2 = 4 - р - (qx + ?2 + 1) + 1 = 2 -
р - <? + 1 = 2 -> р - ^ + г = 2.
Шаг индукции установлен. Теорема доказана.
Следствие. Если G - связный плоский (р,#)-граф; каждая
внутренняя грань в G есть я-цикл (простой цикл длины я), то q < (я(р
- 2))/(л-2).
Доказательство. Так как каждая внутренняя грань в G имеет п
ребер, внешняя грань в G имеет не менее п ребер и любое ребро в G
принадлежит двум граням, то пт < 2qy ибо каждое ребро слева
входит дважды (рис.13.4). Тогда г < (2*q)/n. По формуле Эйлера р - q
+ (2-q)/n % 2, ибо (2-q)/n > г. Тогда q < (л(р-2))/(л-2).
Утверждение. Граф К5 не планарен.
Доказательство. Допустим противное: граф К5 планарен и G есть
его плоское изображение. Так как графы G и К5 изоморфны, то
каждая грань в G есть 3-цикл. Подставляя я = 3, р = 5, q = 10 в
формулу следствия, получим 10 < (3-(5-2))/(3-2) = 9. Противоречие.
Следовательно, граф К5 планарным не является.
260
nr=2q nr^lq
Рнс.13.4
Утверждение. Граф К3 3 не планарен.
Доказательство. Допустим противное: граф К3 3 планарен и имеет
плоское изображение G. Так как К3 3 и G изоморфны, то каждая
грань в G есть 4-цикл. Подставляя в формулу следствия значения п
= 4, р = 6, q = 9, получим 9 < (4- (б-2))/(4-2) = 5. Противоречие.
Следовательно, граф Къ 3 не планарен.
Определение. Граф G есть максимальный планарныи (плоский)
граф, если граф G планарныи (плоский), но при добавлении к G
любого ребра он перестает быть планарным (плоским).
Замечание. Любая грань максимального плоского (р,^)-графа G
есть 3-цикл (треугольник). Подставляя в формулу следствия п = 3,
получим q < (3(р-2))/(3-2) = Ър - 6, т.е. для максимального
плоского (р,^)-графа G число ребер q < Ър - 6. Тогда для
немаксимального плоского (р,^)-графа G (который получается удалением
некоторых ребер из некоторого максимального графа) число ребер q ^ Зр-6
тем более. Так как планарныи граф изоморфен некоторому плоскому
графу, то для планарного (р,^)-графа G число ребер q ^ Зр-6 тоже.
Утверждение. Каждый планарныи (/?,<?)-граф имеет вершину степени
s < 5.
Доказательство. Допустим противное: все вершины планарного
(р,^)-графа G имеют степень s > 6. Так как любая вершина в G
имеет степень s Ъ 6 и так как каждое ребро соединяет две вершины, то
в G число ребер q > (бр)/2 = Ър и потому q = Ър + к для
некоторого к^О. Подставляя это значение q в неравенство q < Ър - 6,
получим Ър+к < Зр-6, откуда 0 < к < -6. Противоречие. Следовательно,
планарныи (р,^)-граф G имеет вершину степени s ^ 5.
13.3. Критерий планарности Понтрягина-Куратовского
Вершину степени 2 в графе назовем проходной. Операция
добавления проходной вершины в ребро е = (w,v) в графе G = (V,E)
состоит в удалении ребра е из £, добавлении к V новой вершины w и в
добавлении к графу G-e двух новых ребер (w,w) и (w,w).
261
Операция удаления проходной вершины v в графе G = (V>E)
состоит в удалении вершины v из V и замене двух ей инцидентных в Е
ребер е' = (m,v), е" = (v,w) на одно ребро е = (м,и>).
Операция стягивания ребра е = (w,v) в графе G = (К,Е) состоит
в удалении ребра е из Е и в объединении (склеивании) инцидентных
ребру е вершин.
Два графа гомеоморфны, если один из них может быть получен из
другого применением конечного числа раз операций добавления и
исключения проходных вершин и стягивания ребра. Если графы гомео-
морфны, то они планарны или не планарны одновременно.
Теорема (Понтрягина-Куратовского). Граф G планарен тогда и
только тогда, когда G не содержит подграфов, гомеоморфных графам К5
или К3 3.
Например, граф Петерсена (рис. 13.5) не планарен.
Аналогично стоят вопросы укладки графов и на другие
поверхности, например, на тор.
13.3.1. Алгоритм построения плоского изображения графа
Изложим алгоритм построения плоского изображения графа. Пусть
G=(V,E) - исходный граф, плоское изображение которого нам
требуется построить (если оно имеется). Будем предполагать, что граф G
связен, не имеет висячих вершин и точек сочленения, т.е. вершин,
удаление которых из G вместе с принадлежащими им ребрами приводит
к несвязному графу.
Пусть G' = (V,£') - некоторый плоский подграф графа G.
Остаток графа G относительно G' есть граф R = (К",Я") = (V-V 9Е") -
Рнс.13.5
262
подграф графа G, порожденный подмножеством вершин V-V, т.е. R
состоит из всех тех ребер графа G, концы которых не лежат не V
(т.е. лежат вне V).
Кусок Р графа G относительно его подграфа G' есть один из
следующих объектов:
1) компонента связности остатка R относительно Gf, дополненная
теми ребрами графа G, которые соединяют вершины этой компоненты и
вершины V графа G';
2) одно ребро из Е-Е' с концами, лежащими в V.
Контактные точки куска Р есть вершины, общие для Р и G'. Грань
F в G' совместима с куском Р, если все контактные точки куска Р
принадлежат грани F.
Пусть Gx - некоторый простой цикл графа G. Поместим на
плоскости его плоское изображение.
Допустим что плоский граф G, уже построен. Плоский граф Gl + 1
получим следующим образом.
1. Построим остаток Л,- графа G относительно G/.
2. Построим все куски графа G относительно G,-. Если ни одного
такого куска построить не удается, то G, есть плоское изображение
графа G.
3. Для каждого куска выписать все грани, которые с ним
совместимы. При этом возможны три случая:
a) существует кусок, не совместимый ни с одной гранью плоского
графа G(\ тогда граф G на плоскость не укладывается;
b) существует кусок, совместимый с единственной гранью графа
G; тогда выбираем этот кусок;
c) каждый из кусков совместим по крайней мере с двумя гранями
графа G/; тогда выбираем любой из таких кусков.
4. В выбранном куске Р находим такую цепь ft, один или оба
конца которой (и только они) принадлежат G/. Построим граф Gl + 1,
дополнив граф G, ребрами цепи ji, проведя fi внутри любой из
совместимых с куском Р граней. Плоский граф Gl + 1 построен. Переходим к
пункту 1.
В случае неоднозначности проведения цепи fi будем проводить ее
во внутренней грани.
Пример. Построим плоское изображение графа G = ({1,2,3,4,5,6},
{(1,2),(2,6),(5,6),(1,3),(1,4),(1,5),(2,4),(3,5),(3,6),(4,6)}).
Шаг 1. Выбираем в G плоский цикл Gl = [1,2,6,5,1].
Граф Gj определяет две грани:
Р10 = [1,2,6,5,1] - внешняя; Fxl = [1,2,6,5,1] - внутренняя.
Остаток Rx графа G относительно Gx распадается в две
компоненты связности: R1X = ({3},0) и Rl2 = ({4},0).
263
Строим куски графа G относительно G, и их контактные точки.
Рп = ({1,3,5,6},{(1,3),(3,5),(3,6)}); {1,5,6};
Р12 = ({1,2,4,6},{(1,4),(2,4),(4,6)}); {1,2,6}.
Кусок Р1Х совместим с гранями Fl0, Fn.
Кусок Pl2 совместим с гранями Fl0, Flt.
Цепь fi, = [1,4,2] в куске Р12 помещаем в грани F,, графа G,.
Шаг 2. Плоский граф G2 = ({1,2,4,5,6},{(1,5),(5,6),(2,6),(1,
2),(2,4),(1,4)}).
Граф G2 определяет грани:
F20 = [1,2,6,5,1]; F21 = [1,4,2,6,5,1]; F22 = [1,4,2,1].
Остаток R2 для G относительно G2 принимает вид: R2 = ({3},0).
Строим куски графа G относительно G2 и их контактные точки.
Р21 = ({1,3,5,6},{(1,3),(3,5),(3,6)}); {1,5,6};
Р22 = ({4,6},{(4,6)}); {4,6}.
Кусок Р21 совместим с гранями F20, F21.
Кусок Р22 совместим с гранью F21.
Цепь i±2 = [4,6] в куске Р22 помещаем в грани F2l графа G2.
Шаг 3. Плоский граф G3 = ({1,2,6,5,4},{(1,5),(5,6),(2,6),
(1,2),(2,4),(1,4),(4, 6)}).
Граф G3 определяет грани:
F30 = [1,2,6,5,1]; F31 = [1,4,6,5,1];
F32 = [1,4,2,1]; F33 = [4,6,2,4].
Остаток R3 для G относительно G3 принимает вид: R3 = ({3},0).
Строим куски графа G относительно G3 и их контактные точки.
Р31 = ({1,3,5,6},{(1,3),(3,5),(3,6)}); {1,5,6};
Кусок Р31 совместим с гранями F30, F31.
Цепь ji3 = [1,3,5] в куске Р31 помещаем в грани F31 графа G3.
Шаг 4. Плоский граф G4 = ({1,2,6,5,4,3},{(1,5),(5,6),(2,6),
(1,2),(2,4),(1,4),(4,6),(3,5),(1,3)}).
Граф GA определяет грани:
F40 = [1,2,6,5,1]; F41 = [1,3,5,6,4,1]; F42 = [1,4,2,1];
F43 = [4,6,2,4]; F44 = [l, 3,5,1].
Остаток RA для G относительно G4 принимает вид: R4 = 0.
Строим куски графа G относительно GA и их контактные точки.
РА1 = ({3,6},{(3,6)}); {3,6};
Кусок Р41 совместим с гранью F41.
Цепь fi4 = [3,6] в куске Р41 помещаем в грани F41 графа G4.
Шаг 5. Плоский граф G5 = ({1,2,6,5,4,3},{(1,5),(5,6),(2,6),
(1,2),(2,4),(1,4),(4,6),(3,5),(1,3),(3,6)}).
Ни одного куска относительно графа G5 построить не удается.
Следовательно, граф Gs есть плоская укладка графа G. Последовате-
264
льные графы Gx ,G2,G3,Cj4,G5 приведены на рис.13.6.
13.3.2. Программа построения плоской укладки графа
Процедура laying_graph_on_plane(G,FG) по данному графу G
строит его плоскую укладку, если она имеется, и указывает на ее
отсутствие в противном случае. Граф G связен, не имеет висячих
вершин и точек сочленения, т.е. вершин, удаление которых из G вместе
с принадлежащими им ребрами приводит к несвязному графу. Плоская
укладка графа FG задается как список последовательных пар из
плоской грани, записанной как простой цикл по вершинам, и цепи,
делящей эту грань на две грани. Например, список FG = [[[1,2,6,5,
1],[1,4,2]], [[1,4,2,6,5,1],[4,6]], [[1,4,6,5,1],[1,3,5]],[1,3,5,
6,4,1],[3,6]]] определяет последовательность плоских графов,
последний из которых является плоской укладкой исходного графа G
(см.рис.13.6).
Процедура algorithm_of _f lat_laying_graph(G, Gi, FG) описывает
циклический алгоритм плоской укладки FG графа G по промежуточному
плоскому подграфу Gi и промежуточному вспомогательному графу Gil.
1
Рис.13.6
265
Процедура laying_graph(G,Gi,Gil, F, Facets, FacetsChain, L,FG)
осуществляет этот циклический алгоритм. Переменная Facets служит
для накопления списка граней плоской укладки исходного графа.
Переменная L служит для накопления списка граней плоской укладки
исходного графа вместе с делящими их цепями.
Процедура first_facet(G,Gl) вычисляет исходную грань G1=[V1,
El] графа G. Грань G1 есть некоторый простой цикл графа G. Это
исходный промежуточный плоский подграф исходного графа G.
Процедура edges_cycle(E,C,Ei) по графу G, задаваемом списком
ребер Е, и по циклу С, задаваемом списком вершин Vi, вычисляет
этот цикл С как список Ei ребер.
Процедура all_connected__components(G,Acc) по графу G по графу
G строит список Асе всех связных компонент графа G.
Процедура one_connected_component(G,C) по графу G вычисляет
одну связную компоненту графа G. Процедура con_comp(V,E,N,Cl,C)
по графу G=[V,E], промежуточному подграфу С1 вычисляемой
компоненты С и списку вершин N в С1 строит искомую компоненту С
последовательным присоединением к С1 ребер из Е.
Процедура next_node(E,E12,N,Cl,[X,Y]) по списку-остатку Е1
ребер графа G, промежуточному подграфу С1 вычисляемой связной
компоненты и множеству вершин N в С1 выбирает в Е1 ребро [X,Y] для
присоединения к С1.
Процедура all_pieces(G, Gi, Асе, AllPieces) вычисляет список
AllPieces всех кусков графа G относительно промежуточного
плоского подграфа Gi графа G и списку Асе всех компонент связности
графа Gil.
Процедура piecesl (G, Gi, Сс, Piecesll, Piecesl) вычисляет список
Piecesl кусков по компонентам связности Сс.
Процедура pieces2(G,Gi,Edges) вычисляет куски - ребра Edges
графа G относительно промежуточного плоского подграфа Gi.
Процедура pieces_with_contact_points(G, Pieces, PieCps) по
плоскому промежуточному подграфу Gi графа G и списку Pieces всех
кусков вычисляет список PieCps кусков вместе с их контактными
точками. Процедура
pieces_with_compatible_f acets(PiesCps, Facets, PiesCpsFas)
по списку PiesCps кусков с множеством соответствующих контактных
точек, списку Facets граней промежуточного плоского подграфа Gi
графа G вычисляет список PiesCpsFas кусков вместе с
соответствующими списками контактных точек и совместимых граней.
Процедура choice_of__one_piece(PieCpsFas,Piece__CpsFacet) по
списку PieCpsFas кусков, его контактных точек и совместимых с ним
граней (если такие грани имеются) вычисляет кусок для выбора в
266
нем цепи, разделяющей одну из совместимых с куском грани, на две
соседние грани.
Процедура choice_of_chain(PieCpsFas,Ch) по списку PieCpsFas=
[PieCps,Fas] из куска PieCps с его контактными точками и списка
Fas совместимых с ним граней вычисляет цепь Ch в куске PieCps
между двумя его контактными точками.
Процедура chain(X,Y,Pie,Ch) no двум контактным точкам X,Y
куска Pie строит цепь Ch в Pie между X и Y.
Процедура one__to_two_facets(Facet,Ch, TwoFacets) по грани Facet
и цепи Ch, концы которой принадлежат грани Facet, строит список
TwoFacets из двух граней, на которые цепь Ch делит грань Facet.
Пусть, например, грань С=[1,2,3,4,5,6,7,8,9,10,11,1], цепь Ch=[4,
12,13,14,8]. Цикл С узлами 4 и 8 делится на три части: Cl=[l,2,3,
4], С2=[4,5,6,7,8], С3=[8,9,10,11,1]. Затем компонуются две новые
грани: ClChC3=[l,2,3,4,12,13,14,8,9,10,ll,l], C3Ch=[4,5,6,7,8,
14,13,12,4]. Процедура
substitute_one_to_two_facets(Facets,Faset, TwoFacets, NewFacets)
по списку Facets граней промежуточного плоского подграфа
исходного графа, заменяемой грани Facet и списку TwoFacets из двух
заменяющих граней строит список NewFacets граней нового плоского
подграфа, получаемого из списка Facets заменой грани Facet на две
грани из списка TwoFacets.
Процедура chain_graph(Ch,ChG) по цепи Ch, записанной по
вершинам, вычисляет множество ребер Е1 цепи Ch и выдает граф ChG =
[Ch,E].
Процедура construct_new_graph(Gi,ChG,GiNew) по промежуточному
плоскому подграфу Gi исходного графа G строит новый промежуточный
плоский подграф GiNew графа G.
% Головной модуль и основной цикл плоской укладки графа
laying graph on j)lane(Graph,FlatGraph) :-
Graph=[[l,2,3,4,5,6],[[l,2],[2,6],[5,6],[l,3],[l,4],
[l,5],[2,4],[3,5],[3,6],[4,6]]],Graph=[V,E],
first _facet(Graph,Gl),Gl=[Vl|El],
(equalset(V,Vl),equalset(E,El),FlatGraph=[Vl,El],
laying_graph__on__plane( [ ],FlatGraph) ;
algorithm_of_flat_Jaying(Graph,Gl, FlatGraph)).
laying_graph_on_plane( [ ],FG).
algorithm_of_flat_laying(G,Gi,FG) :- Gi=[Vi,Ei],
laying_graph(G,Gi,Gil,[Vi,Vi],[Vi],[],FG).
laying_graph(G, Gi, Gil, Facets, FacetsChains, L, FG) : -
267
. G=[V,E],Gi=[Vi,Ei],difset(V,Vi,Vil),
findall([X,Y],(member([X,Y],E),
not(member(X,Vi)),not(member(Y,Vi))),Eil),
Gil=[Vil,Eil],
all_connected_components(Gil,Acc),
all_pieces(G, Gi, Ace, AllPieces), AllPieces=[ H | T],
pieces_with_contact_points(Gi,AHPieces,PiesCps),
pieces_with_compatible_f acets(PiesCps, Facets, PiesCpsFas),
choice_of _one_piece(PiesCpsFas, PieceCpsFacets),
PieceCpsFacets=[PieCps,Fas],f irst(Facet,Fas),
choice__of_chain(PieceCpsFacets,Ch),
one_to_t wo_facets( Facet, Ch,TwoFacets),
substitute_one_to_two_f acets(Facets, Facet,
TwoFacets, NewFacets),
chain_graph(G, Ch, ChG),
construct_new_f lat_subgraph(Gi, ChG, GiNew),
laying_graph(G, GiNew, Gi2, NewFacets, FacetsChain,
[[Facet, Ch]|L],FG).
laying_graph(G,Gi,Gil,F,FC,L,FG) :- reverse(L,FG).
% Выделение первого простого цикла-грани в данном графе
first_facet(G,Gl) :- G=[V,E] ,member([X,Y] ,E),
path(E,[Y,X],Z,P),cycle(P,C),Vl=C,
edges_cycle(E,C,El),Gl=[Vl,El].
path(E,Pl,Z,P) :- next_node(E,Pl,Z),
(not(member(Z,Pl)),path(E,[Z|Pl],Zl,P) ;
member(Z,Pl),path([],[Z|Pl],Zl,P)).
path(E,P,Z,P).
next_node(E?[Y,X|T],Z) :-
(member([Y,Z],E) ; member([Z,Y],E)),not(Z=X).
cycle([H|T],C) :- cyclel(H,T,C,[H]).
cyclel(S,[H|T],C,PC) :- not(S=H),cyclel(S,T,C,[H|PC]).
cyclel(S,P,C,PC) :- C=[S|PC],member(S,PC).
edges_cycle(E,C,El) :- edges_cyclel(E,C,El,[]).
edges__cyclel(E,[X,Y|T],El,E2) :-
(member([X,Y],E),edges_cyclel(E,[Y|T],El,[[X,Y]|E2]) ;
member([Y,X],E),edges_cyclel(E,[Y|T],El,[[Y,X]|E2])).
edges_cyclel(E,L,El,El) :- length(L,l).
% Выделение всех компонент связности графа
all_connected_components(G,Acc) :- all_con_comp(G,[] ,Acc).
all_con_comp(G,L,Асе) : - one_connected_component(G,С),
268
G=[V,E],C=[Vl,El],difset(V,Vl,V2),difset(E,El,E2),
G2=[V2,E2],all_con_comp(G2,[C|L],Acc).
all_con_comp([ [],[]] ,L,Acc) :- reverse(L,Acc).
% Выделение одной компоненты связности графа
one__connected_component(G,C) :- G=[V,E] ,member(S,V),
one_con_comp(E,[S],Vl,[],El),C=[Vl,El].
one_con_comp(E,Nl,N,Cl,C) :-
next_edge(E,Nl,Cl,[X,Y]),delete([X,Y],E,El),
(member(X,Nl),one_con_comp(El,[Y|Nl],N,[[X,Y]|Cl],C) ;
member(Y,Nl),one_con_comp(El,[X|Nl],N,[[X,Y]|Cl],C)).
one_con_comp(E,Nl,N,C,C) :- delrepeate(Nl,N).
next_edge(E,N,Cl,[X,Y]) :-
member([X,Y],E),not(member([X,Y],Cl)),
(member(X,N) ; member(Y,N)).
% Вычисление всех кусков графа
all_pieces(G,Gi,Сс,Pieces) : - piecesl(G,Gi,Cc Д ],Piecesl),
pieces2(G,Gi,[],[],PiecesEdges),
append(Piecesl, PiecesEdges, Pieces).
piecesl([V,E],[Vi,Ei],[[Vc,Ec]|T],Pll,Pl) :-
findall([X,Y],(member([X,Y],E),
(member(X,Vc),member(Y,Vi) ;
member(Y,Vc),member(X,Vi))),El),
findall(X,(member([X,Y],El) ; member([Y,X] ,El)), Vll),
delrepeate(Vll,V12),unionset(Vc,V12,Vcl),
unionset(Ec,El,VE2),delrepeate(VE2,VEl),
piecesl([V,E],[Vi,Ei],T,[[Vcl,VEl]|Pll],Pl).
piecesl(G, Gi, Cc, Ps, Ps).
pieces2(G,Gi,Edges,PsEs,PiesEdges) :- G=[V,E] ,Gi=[Vi,EiJ,
(member([X,Y],E),member(X,Vi),member(Y,Vi),
not(member([X,Y],Ei)),
not(member([X,Y],Edges)),EE=[[X,Y]] ;
member([Y,X] ,E),member(X,Vi),member(Y,Vi),
not(member([Y,X] ,Ei)),
not(member([Y,X],Edges)),EE=[[Y,X]]),
VE=[X,Y],PieEdge=[VE,EE],first(El,EE),
pieces2(G,Gi,[El[Edges],[PieEdge|PsEs],PiesEdges).
pieces2(G, Gi, Edges, PiecesEdges, PiecesEdges).
% Вычисление контактных точек кусков
pieces_with_contact_points(Gi,Pieces,PiesCps) : -
269
contact__points(Gi, Pieces, PiesCps, [ ]).
contact_j)oints(Gi,[H|T],PiesCps,L) :-
H=[V,E],Gi=[Vi,Ei],intersect(V,Vi,Cps),
contact joints(Gi,T, PiesCps, [[H,Cps]|L]).
contact_jpoints(Gi, [ ],L,L).
% Вычисление совместимых граней кусков
pieces_with_compatible_facets(PiesCps,Facets,PiesCpsFas) :-
compatible__pies_cps_f as(PiesCps, Facets, PiesCpsFas, [ ]).
compatible_jpies_cps_fas([H|T],Fs,PF,L) :- H=[Pie,Cps],
findall(Fa,(member(Fa,Fs),subset(Cps,Fa)),Fasl),
delrepeate(Fasl, Fas),
(Fas=[],write(>Graph not planar'),break ;
not(Fas=[]),compatible_pies_cps__fas(T,Fs,PF,[[H,Fas]|L])).
compatible_j>ies_cps_f as([ ],Fs,L,L).
% Выбор одного куска
choice_of_one__piece(PiesCpsFas,PieCpsFacet) :-
choice_of _jpie(PiesCpsFas, PieCpsFacet, L).
choice_of__pie([H|T],PF,L) :- H=[PieCps,Fas],
(length(Fas,Le),Le=l,choice_of_pie([],PF,H) ;
length(Fas,Le),Le>l,choice__of_pie(T,PF,H)).
choice__of__pie( [ ], H, H).
% Выбор цепи в куске
choice_of__chain(H,Ch) :- H=[[[VPie,EPie] ,Cps] ,Fas],
first(X,Cps),delete(X,Cps,Cpsl),first(Y,Cpsl),
chain(X,Y,EPie,Ch).
chain(X,Y,E,Ch) :- path_in_pie(X,[Y],E,Ch),!.
path_in__pie(X,[Z|Path],E,Ch) :-
not(member(X, Path)), adjacent(U,Z,E),not(member(U, Path)),
path_in_pie(X,[U,Z|Path],E,Ch).
path_in_j)ie(X,[X|T],E,Ch) :- Ch=[X|T].
adjacent(X,Y,E) :- (member([X,Y],E) ; member([Y,X] ,E)).
% Построение по грани и цепи в ней двух новых граней
one_to_two_facets(Facet, Ch, TwoFacets) : -
first(B,Ch),last(E,Ch),BE=[B,E],
delete(E,Ch,Chl),delete(B,Chl,C),
(B=E,TwoFacets=[Ch,Facet] ;
not(B=E),threepartite(Facet,Pl,P2,P3,BE)),last(L,Pl),
(L=B,append(Pl,C,PlC),append(PlC,P3,Fal),
reverse(P2,P4),append(Chl,P4,Fa2) ;
270
L=E,reverse(C,Cl),append(Pl,Cl,PlCl),append(PlCl,P3,Fal),
append(Chl,P2,Fa2)),
TwoFacets=[Fa2,Fal].
threepartite(Cy,Pl,P2,P3,BE) :-
threepartl(Cy,PI,P2,P3,BE,[],[],[])•
threepartl([H|T] ,P1,P2,P3,BE,L1,L2,L3) :-
(not(member(H,BE)),threepartl(T,Pl,P2,P3,BE,[H|Ll],L2,L3) ;
member(H,BE),threepart2(T,Pl,P2,P3,BE,[H|Ll],[H|L2],L3)).
threepart2([H|T],Pl,P2,P3,BE,Ll,L2,L3) :-
(not(member(H,BE)),threepart2(T,Pl,P2,P3,BE,Ll,[H|L2],L3) ;
member(H,BE),threepart3(T,Pl,P2,P3,BE,Ll,[H|L2],[H|L3])).
threepart3([H|T],Pl,P2,P3,BE,Ll,L2,L3) :-
threepart3(T,Pl,P2,P3,BE,Ll,L2,[H|L3]).
threepart3( [ ], PI, P2, P3, BE, LI, L2, L3) : -
reverse(Ll, PI), reverse(L2, P2), reverse(L3, P3).
% Замена в списке граней одной грани на две новые
substitute_one__to_two_facets(Fs,F,TF,NFs) : -
substit_one_to_two(Fs,F,TF,NFs,[]).
substit_one_to__two([A|T],F,TF,NFs,L) :- TF=[F1,F2],
(not(A=F),substit_one_to_two(T,F,TF,NFs,[A|L]) ;
A=F,subst_one_to_two(T,F,TF,NFs,[Fl,F2|L])).
subst__one_to_two(T,F,TF,NFs,L) :- append(L,T,NFs).
% Построение цепи как графа
chain_graph(G,Ch,ChG) :- G=[V,E],
chain_gr(E,Ch,ECh,[]),ChG=[Ch,ECh].
chain__gr(E,[X,Y|T],ECh,L) :-
(member([X,Y],E),chain_gr(E,[Y|T],ECh,[[X,Y]|L]) ;
member([Y,X],E),chain_gr(E,[Y|T],ECh,[[Y,X]|L])).
chain_gr(E,Chl,L,L) :- length(Chl,l).
% Построение нового плоского промежуточного подграфа
construct__new_flat_subgraph(Gi,ChG,GiNew) : -
Gi=[Vi,Ei] ,ChG=[Vch,Ech],
first(N,Vch),last(L,Vch),
delete(N,Vch,Vchl),delete(L,Vchl,Vch2),
unionset ( Vi, Vch2, Vnew), unionset (Ei, Ech, Enew),
GiNew=[ Vnew,Enew].
% Вспомогательные программы
271
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
first(X,[X|Y]).
last(X,[X]).
last(X,[jY]) :- last(X,Y).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
reverse([],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H],L).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
unionset([],X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
intersect ([],X,[]).
intersect([X|R],Y,[X|Z]) :- member(X,Y),! ,intersect(R,Y,Z).
intersect([X|R],Y,Z) :- intersect(R,Y,Z).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
delrepeate(S,SF) :- delrep(S,[],SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T;Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L) J •
member_set(L,[Yl|Y]) :- member_set(L,Y).
subset([],Y) :- !.
subset([A|X],Y) :- member(A,Y),subset(X,Y).
14. РАСКРАСКА ГРАФОВ
14.1. Хроматическое число и хроматический класс
Определение. Вершины (ребра) графа G правильно раскрашены,
если каждой вершине (ребру) графа G сопоставлен некоторый цвет,
272
причем любым двум смежным вершинам (ребрам) сопоставлены разные
цвета.
Замечание. Всякий подграф правильно раскрашенного графа
правильно раскрашен.
Определение. Граф G /с-раскрашиваем, если его можно правильно
раскрасить не более, чем в к цветов.
Определение. Хроматическое число графа G есть наименьшее
число x(G) красок, с помощью которых можно правильно раскрасить
вершины графа G. Хроматический класс графа G есть наименьшее число
X'(G) красок, с помощью которых можно правильно раскрасить ребра
графа G.
14.2. Раскраска вершин
Определение. Граф G с хроматическим числом x{G) = 2
называется дихроматическим.
Теорема. Граф G двудолен тогда и только тогда, когда G - би-
хроматический граф.
Доказательство. Пусть G = (VlyV2iE) - двудольный граф. Вершины
из Vx окрашиваем в один цвет, а вершины из V2 - в другой.
Полученная раскраска правильная, ибо соседние вершины, одна из Vly a
другая из V 2 окрашены в разный цвет.
Пусть теперь G - бихроматический граф. Тогда множество его
вершин можно разбить на два класса:
Vх - вершины из G, окрашенные в один цвет;
V2 - вершины из G, окрашенные в другой цвет.
Ребра из G могут соединять вершины только из разных классов.
Следовательно, граф G = (VlyV2iE) - двудольный.
Замечание. Следующие утверждения равносильны.
1. Граф G является бихроматическим.
2. Граф G двудолен.
3. Все простые циклы в G имеют четную длину.
Дерево есть бихроматический граф, ибо вершины четных ярусов
графа можно окрасить в один цвет, а вершины нечетных ярусов - в
другой.
Утверждение. Пусть Кр - полный граф с р вершинами. Тогда
хроматическое число х(Кр) = р.
Доказательство. Индукция по р.
БАЗИС, р = 3. Х(К3) = 3.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Предположим, что х(Кр_х)=р-1.
ШАГ ИНДУКЦИИ. Покажем, что х(Кр) = р. В самом деле, пусть v
есть некоторая вершина в Кр. Удалим вершину v из Кр вместе с ин-
273
цидентными ей ребрами. Тогда граф Kp-v = Кр_х р-1-раскрашиваем по
предположению индукции р-1 красками 1,2,... ,/?-1. Вершина v в Кр
должна быть окрашена в новый цвет р. Поэтому х(Кр) = р.
Следствие. Существуют графы со сколь угодно большим
хроматическим числом.
14.3. Верхняя и нижняя оценки хроматического числа.
Внутренне и внешне устойчивые
множества вершин графа
Теорема (верхняя оценка). Если граф G имеет максимальную
степень вершин, равную s, то хроматическое число x(G) < s+1.
Доказательство. Индукция по числу р вершин.
БАЗИС. Если число вершин в графе G не превосходит s+1, то
утверждение теоремы тривиально, ибо s+1 вершин можно правильно
раскрасить в s+1 цветов, по одному цвету на каждую вершину.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что теорема верна для
графов с числом вершин к < р, причем р Z s+1.
ШАГ ИНДУКЦИИ. Покажем, что если граф G имеет р вершин, то
хроматическое число x(G) < s+1. Пусть v - произвольная вершина в G.
Удалим из G вершину v вместе с инцидентными ей ребрами.
Получившийся граф G' = G-v имеет число вершин к < р и потому по
предположению индукции граф G' s+1-раскрашиваем. В графе G вершина v
имеет не более s соседних вершин, окрашенных не более, чем в s
цветов. Вершине v припишем один из оставшихся цветов. Тогда граф
G правильно раскрашиваем с числом цветов г < s + 1, т.е. граф G
имеет хроматическое число x(G) < s+1.
14.3.1. Внутренне устойчивые множества вершин графа
Определение. Подмножество S вершин графа G = (V,E) внутренне
устойчиво, если никакие две вершины из S не смежны в G. Число
внутренней устойчивости графа G
oc(G) = max { IS I : S Я V и S внутренне устойчиво в G}.
Внутренне устойчивое множество вершин S называется
максимальным (тупиковым), если всякое строгое надмножество множества S
внутренне устойчивым уже не является. При этом S называется
наибольшим, если среди всех внутренне устойчивых множеств вершин в G
оно имеет наибольшую мощность.
Пусть S - внутренне устойчивое множество вершин графа G =
(V,E) и ребро е = (w,v) € Е. С каждой вершиной v€F свяжем
логическую переменную xv и пусть xv означает, что v i S. Если e=(u,v)t
Е, то дизъюнкция хи V xv истинна. Построим логическую формулу
274
& (xu V xv). (14.1)
(w,v) €£
Взяв по одной переменной в каждой скобке формулы (14.1),
получим некоторую конъюнкцию хи хи ...хи , для которой V - {uXiu2i
... ,иЛ является внутренне устойчивым множеством вершин. Формула
(14.l) есть условие внутренней устойчивости в G. Пусть V Kt -
i
минимальная ДНФ D для формулы (14.1). Каждому дизъюнктивному
слагаемому Кх? = xw xw .. .xw в D соответствует максимальное
внутренне устойчивое множество л) = V - {wl ,w2,... ,ww}. Множества Sz
исчерпывают все максимальные внутренне устойчивые множества графа
G. Из них можно выбрать все наибольшие.
14.3.2. Алгоритм вычисления всех наибольших внутренне
устойчивых множеств вершин графа G = (V,E)
1. Построить формулу
F = & (хи V xv) -
(w,v) €£
условие внутренней устойчивости графа G.
2. Построить минимальную ДНФ D формулы F.
3. Для каждого дизъюнктивного слагаемого К = xuxv...xw в D
получить соответствующее ему максимальное внутренне устойчивое
множество вершин S = V - {w,v,... ,и>}.
4. Из полученных максимальных внутренне устойчивых множеств
вершин выбрать все наибольшие.
Пример. Построим все наибольшие внутренне устойчивые множества
вершин для графа G = (К,£) = ({1,2,3,4,5,6,7},{(1,2),(1,3),(1,5),
(1,6),(2,3), (3,4),(3,6),(4,5),(4,7),(5,6),(6,7)}).
Условие внутренней устойчивости графа G
F = & (м V v) = (1V2)(1V3)(1V5)(1V6)(2V3)(3V4)&
(m,v) €E
(3V6)(4V5)(4V7)(5V6)(6V7) = 1357V23456V23567V1246V1346.
Максимальными внутренне устойчивыми множествами вершин будут
множества: K-{l,3,5,7}={2,4,6}; F-{2,3,4,5,6}={1,7}; K-{2,3,5,6,
7}={1,4};К-{1,2,4,6}={3,5,7}; F-{l,3,4,6}={2,5,7}. Выбираем из
них наибольшие: {2,4,6}; {3,5,7}; {2,5,7}.
14.3.3. Программа вычисления всех наибольших внутренне
устойчивых множеств вершин графа
Процедура all_most_in_stable_sets(G,S) по графу G строит
275
множество S всех наибольших внутренне устойчивых множеств вершин
графа G. В нашем примере S=[[2,4,6],[3,5,7],[2,5,7]].
Процедура all_max_in_stable_sets(G,S) по графу G вычисляет все
максимальные внутренне устойчивые множества S1 вершин графа G.
Например, для заданного в программе графа G множество S=[S1,S2,
S3, S4,S5]=[[2,4,6],[1,7],[1,4],[3,5,7],[2,5,7]].
Процедура dek_absorb(S,L) по списку множеств S строит список
L, который получается как декартово произведение D элементов
подсписков из S с последующим удалением повторов элементов в D;
сначала удалением повторов атомов в D получается список С, из
которого в свою очередь удаляются повторы составляющих его
множеств. Например, если S=[[l,2,3],[l,2],[2,3]], то D=[[l,l,2],
[1,1,3],[1,2,2],[1,2,3],[2,1,2],[2,1,3],[2,2,2],[2,2,3],[3,1,2],
[3,1,3],[3,2,2],[3,2,3]]; C=[[l,2],[l,3] ,[l,2],[[1,2,3] ,[l,2],
[1,2,3],[2],[2,3], [1,2,3],[1,3],[2,3],[2,3]]; L=[[2],[l,3]].
В процедуре absorb__set(S,L) множество L получается удалением
всех тех подмножеств из S, которые строго содержат в себе хотя бы
одно подмножество из S. Например, если S=[[l,3,2,],[2,l],[3],
[1,4,3],[4,5],[1,2,3,1]], то L=[[2,l],[3],[4,5]].
Предикат absorbl(S,A,L) истинен, если список L получается
удалением из списка S тех его подмножеств, которые содержат в
себе множество А, либо совпадают с А. Например, если S=[[2,l],[l,
3,2,1], [5,4],[2,1,1],[3]], А = [1,2], то L=[[5,4] ,[3]]. Другими
словами, процедура absorbl(S,A,L) удаляет в множестве S те его
подмножества, которые содержат в себе множество А.
Процедура complement_sets(V,S,C) по множествам V=[l,2,3,4,5,
6], S = [[2,3,5,6], [2,3,5], [1,2,5,6]] вычисляет дополнительные
множества C=[[l,4] ,[l,6],[3,4]], где [l,4] = V-[2,3,5,6];
аналогично для остальных подмножеств из С.
Предикат all_most_length_lists(S,L) истинен, если L есть
список всех подсписков в S, имеющих в S наибольшую длину. Например,
если S = [[a,b],[a,c,d],[a,d,f,b],[a,s],[s,d,e,f]], то L=[[a,d,f,
b],[s,d,e,f]].
Предикат most_length(S,C) истинен, если число С есть
наибольшая длина подсписка в списке S. Например, если S=[[a,b],
[a,c,d],[a,s],[s,d,e,f]], то С=4.
d(G,S) :- V=[l,2,3,4,5,6,7],
E=[[l,2],[1,3],[1,5],[1,6],[2,3],[3,4],[3,6],[4,5],[4,7],
[5,6],[6,7]],G=[V,E],alLmostJn_stable_sets(G,S).
all_most__in_stable_sets(G,S) :- all_max_in_stable_sets(G,L),
276
all_most_length_lists(L,S).
all_max_in_stable_sets(G,S) :- G=[V,E],dek_absorb(E,L),
complement_sets( V, L, S).
dek_absorb(S,L) :- dekl_absorb(S,L).
dekl_absorb([Hl,H2|T],L) :-
dek2(Hl,H2,Lll),delrepeate(Lll,L13),delrep_el(L13,L12),
absorb__set(L12,Ll),dek3_absorb(Ll,T,L)-
dekl_absorb(rH|[]],[H|[]]).
dekl_absorb( [],[])•
dek3_absorb(Ll,[H|T],L) :- dek2(Ll,H,L2),
appendl(L2,L3l),delrepeate(L31,L33),delrep_el(L33,L32),
absorb_set(L32,L3),dek3_absorb(L3,T,L).
dek3_absorb(Ll,[],Ll).
appendl(L2,L3) :- append2(L2,L3,[]).
append2([[H|T]|Tl],L3,S) :- append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],S,S).
dek2(X,Y,Z) :- findall([A,B] ,(member(A,X),member(B,Y)),Z).
delrep_el(S,SM) :- delrpl(S,[],Sl),reverse(Sl,SM).
delrpl([H|T],L,Sl) :- delrepeate(H,Hl),delrpl(T,[Hl|L] ,Sl).
delrpl([],S,S).
absorb_set(S,L) :- absorb(S,S,L).
absorb([H|T],[Hl|Tl],L) :-
absorbl(Tl,Hl,T2),append(T2,[Hl],T3),absorb(T,T3,L).
absorb([] ,L,L).
absorbl(S,A,L) :- findall(M,(member(M,S),not(subset(A,M))),L).
complement_sets(V,S,C) :- compl(V,S,[] ,C).
compl(V,[H|T],L,C) :- difset(V,H,Ll),compl(V,T,[Ll|L],C).
compl(V,[],S,C) :- reverse(S,C).
all_most_length_lists(S,L) :-
mostJength(S,C),most_lists(S,[],C,L).
mostJists([H|T],S,C,L) :-
length(H,LH),LH=C,most_lists(T,[H|S],C,L).
most_lists([H|T],S,C,L) :-
length(H,LH),not(LH=C),most_lists(T,S,C,L).
most_lists([] ,S,C,L) :- reverse(S,L).
mostJength(S,C) :- most_len(S,0,C).
most_len([H|T],L,C) :- length(H,Cl),Cl>L,most_len(T,Cl,C).
277
most_len([H|T],L,C) :- length(H,Cl),Cl=<L,most_len(T,L,C).
most_len([],C,C).
delrepeate(S,SF) :- Sl=[] ,delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :-
not(member(H,T)),append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :-
not(member(R,Y)),append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
subset (f],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Теорема (нижняя оценка). Пусть G = (К,Е) есть связный (/?,
^)-граф. Пусть oc(G) - число внутренней устойчивости графа G.
Тогда хроматическое число x(G) Z p/oc(G).
Доказательство. Граф G я(С/)-раскрашиваем. Пусть
V\ Уг> • • • У% (G) " множества вершин, окрашенных в цвета
1, 2,..., x(G) соответственно.
Вершины из Vi внутренне устойчивы, ибо они окрашены в один и
тот же цвет и потому не смежны. Поэтому I К,-I < a(G), i = 1,2,...,
x(G). Множества Vx ,K2,... ,VX (G) попарно не пересекаются и в сумме
дают все множество V. Тогда
X(G) X{G)
Р = I \Vi\ < I a(G) = a(G)-*(G);
i= i i= i
отсюда имеем, что хроматическое число x(G) > p/oc(G).
Замечание. Из теорем о верхней и нижней оценках для
хроматического числа x(G) графа G имеем
278
p/a(G) < X(G) < s + 1.
14.3.4. Внешне устойчивые множества вершин графа
Определение. Множество Т вершин графа G = {V\Е) называется
внешне устойчивым (в G), если Vv$7 3u£T (e=(uyv)£E). Число
внешней устойчивости графа G
f$(G) = min { I Г I : Т Я V & Т - внешне устойчивое множество в G}.
Внешне устойчивое множество вершин Т называется минимальным
(тупиковым), если Т не содержит в себе строго ни одного
подмножества, являющегося внешне устойчивым. Внешне устойчивое множество
вершин называется наименьшим, если среди всех внешне устойчивых
множеств вершин в G оно имеет наименьшую мощность.
С понятием внешне устойчивого множества можно связать
следующую практическую задачу. Пусть имеем карту городов с дорогами
между ними. Следует построить наименьшее число складов с не более
чем одним складом в каждом городе так, чтобы от каждого города
вела прямая дорога к одному из складов. Задача решается
отысканием наименьшего внешне устойчивого множества вершин графа городов
с дорогами между ними.
Пусть Т - внешне устойчивое множество вершин графа G=(V,E). С
каждой вершиной u£V свяжем логическую переменную хи и пусть хи
означает, что и £ Т. Пусть в множестве {w,v,...,w} и есть вершина
из К, a v,...,w есть все те вершины, которые смежны с и. Построим
логическую формулу
& (хи V xv V ... xw). (14.2)
u£V
Взяв по одной переменной в каждой скобке формулы (14.2),
получим некоторую конъюнкцию хи хи ...хи , для которой {иг ,м2,... ,Мр}
есть внешне устойчивое множество. Формула (14.2) является
условием внешней устойчивости в G. Пусть V Kt есть минимальная ДНФ D
i
для формулы (14.2). Каждому дизъюнктивному слагаемому Kj
xw xw ... xw в D соответствует минимальное внешне устойчивое
множество Si = {и>! ,и>2,... ,wm}. Множества S, исчерпывают все
минимальные внешне устойчивые множества вершин графа G. Из них можно
выбрать все наименьшие.
14.3.5. Алгоритм вычисления всех наименьших внешне
устойчивых множеств вершин графа G = (V,Е)
1. Построить формулу
279
F = & (xu V ( V дг,)) -
w€K (u,v)€£
условие внешней устойчивости графа G.
2. Построить минимальную ДНФ D формулы F.
3. Для каждого дизъюнктивного слагаемого К = xuxv...xw в D
получить соответствующее ему минимальное внешне устойчивое
множество вершин S = {w,v,... ,w}.
4. Из полученных минимальных внешне устойчивых множеств вершин
выбрать все наименьшие.
Пример. Вычислим все наименьшие внешне устойчивые множества
вершин графа G = (V9E) = ({1,2,3,4,5,6,7},{(1,2),(1,3),(1,5),
(1,6),(2,3),(3,4),(3,6),(4,5),(4,7),(5,6),(6,7Л). Условие
внешней устойчивости для графа G
F = & И( V v)) = (1V2V3V5V6)(2V1V3)(3V1V2V4V6)&
u£V (w,v)€E
(4V3V5V7)(5V1V4V6)(6V1V3V5V7)(7V4V6) = 156 V 17 V 246 V 247 V
257 V 245 V 256 V 267 V 357 V 36 V 34 V 14.
Все минимальные внешне устойчивые множества: {1,5,6}, {1,7},
{2,4,6}, {2,4,7}, {2,5,7}, {2,4,5}, {2,5,6}, {2,6,7}, {3,5,7}
{3,6}, {3,4}, {1,4}. Из полученных множеств выбираем наименьшие
по мощности. Они и составят все наименьшие внешне устойчивые
множества вершин: {1,7}; {3,6}; {3,4}; {1,4}.
14.3.6. Программа вычисления всех наименьших
внешне устойчивых множеств вершин графа
Процедура all_least__out__stable_sets(G,S) по графу G строит
множество S всех наименьших внешне устойчивых (доминирующих)
множеств вершин графа G. В нашем примере S=[[3,4],[3,6],[l,4],
[1,7]].
Процедура all_min_out_stable_sets(G,S) по графу G строит
множество S всех минимальных (тупиковых) внешне устойчивых
(доминирующих) множеств вершин графа G. В нашем примере S=[[2,5,
4],[2,5,6],[2,5,7],[2,7,6],[3,4],[5,3,7], [3,6] ,[l,4] ,[5,1,6] ,[l,
7], [2,6,4],[2,7,4]].
Процедура cond__out_stabe(V,E,L) по графу G=[V,E] строит список
L, соответствующий условию внешей устойчивости графа G. В нашем
примере L=[[l,2,3,5,6],[2,1,3],[3,1,2,4,6],[4,3,5,7],[5,1,4,6],
[6,1,3,5,7],[7,4,6]], что соответствует КНФ (1V2V3V5V6)(2V1V3)&
(3V1V2V4V6)(4V3V5V7)(5V1V4V6)(6V1V3V5V7)(7V4V6).
Процедура dek_absorb(S, L), absorb_set(S, L), absorbl(S, A, L)
описаны в программе вычисления всех наибольших внутренне устой-
280
чивых множеств вершин графа.
Предикат all_least_length__lists(S,L) истинен, если L есть
список всех подсписков в S, имеющих в S наименьшую длину. Например,
если S=[[a,b],[a,c,d],[a,s],[s,d,e,f]], то L = [[a,b], [a,s]].
Предикат least_length(S,C) истинен, если число С есть
наименьшая длина подсписка в списке S. Например, если S=[[a,b],[a,c,d],
[a,s],[s,d,e,f]], то С=2.
d(G,S) :- V=[l,2,3,4,5,6,7],
E=[[l,2],[1,3],[1,5],[1,6],[2,3],[3,4],[3,6],[4,5],[4,7],
[5,6],[6,7]],G=[V,E],
all_least_out_stable_sets(G,S).
all_least_out__stable_sets(G,S) :- all_min_out_stable_sets(G,L),
all_least_lengthJists(L, S).
all_min_out_stable_sets(G,S) :- G=[V,E],
cond_out_stabe(V,E,L),dek_absorb(L,S).
cond_out_stabe(V,E,L) :- cond_out_st(V,E,[],L).
cond_out_st([H|T],E,Ac,L) :-
findall(Y,(member([H,Y],E) ; member([Y,H],E)),Ll),
add(H,Ll,L2),cond__out_st(T,E,[L2|Ac],L).
cond_out_st([],E,Ll,L) :- reverse(Ll,L).
add(X,L,[X|L]).
dek_absorb(S,L) :- dekl_absorb(S,L).
dekl_absorb([Hl,H2|T],L) :- dek2(Hl,H2,Lll),
delrepeate(Lll,L13),delrep__el(L13,L12),
absorb_set(L12,Ll),dek3_absorb(Ll,T,L).
dekl_absorb([H|[]],[H|[]]).
dekl_absorb( [],[]).
dek3_absorb(Ll,[H|T],L) :- dek2(Ll,H,L2),appendl(L2,L3l),
delrepeate(L31, L33) ,delrep_el(L33,L32),
absorb_set(L32,L3),dek3_absorb(L3,T,L).
dek3_absorb(Ll,[],Ll).
appendl(L2,L3) :- append2(L2,L3,[J).
append2([[H|T]|Tl],L3,S) :- append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],S,S).
dek2(X,Y,Z) :- findall([A,B] ,(member(A,X),member(B,Y)),Z).
delrep el(S,SM) :- delrpl(S,[] ,Sl),reverse(Sl,SM).
delrpl("[H|T],L SI) :- delrepeate(H,Hl),delrpl(T,[Hl|L] ,Sl).
281
delrpl([],S,S).
absorb_set(S,L) :- absorb(S,S,L).
absorb([H|T],[Hl|Tl],L) :-
absorbl(Tl,Hl,T2),append(T2,[Hl],T3),absorb(T,T3,L).
absorb([],L,L).
absorbl(S,A,L) :- findall(M,(member(M,S),not(subset(A,M))),L).
all_least_length_lists(S, L) : -
least_length(S, C), least_lists(S, [ ], С, L).
leastJists([H|T],S,C,L) :-
length(H,LH),LH=C,least_lists(T,[H|S],C,L).
leastJists([H|T],S,C,L) :-
length(H, LH), not(LH=C), least_lists(T, S, С, L).
least_lists([],S,C,L) :- reverse(S,L).
leastJength(S,C) :- S=[H|T],bngth(H,N),leastJen(S,N,C).
leastJen([H|T],L,C) :- length(H,Cl),Cl<L,least Jen(T,CI,C).
least Jen([H|T],L,C) :- length(H,Cl),Cl>=L,least_len(T,L,C).
least_len([],C,C).
delrepeate(S,SF) :- Sl=[],delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T), !,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :-
not(member(H,T)),append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
14.4. Оптимальная раскраска вершин графа
Пусть граф G = (V,E) правильно раскрашен. Вершины, окрашенные
в один цвет, образуют внутренне устойчивое множество вершин в G.
Хроматическое число графа G можно определить как минимальное
число внутренне устойчивых множеств, в сумме дающих все множество V.
Такое минимальное покрытие можно найти следующим образом. Пусть
Sl9S29... ,Sr - все максимальные внутренне устойчивые множества
вершин в G. С каждым 5/ свяжем логическую переменную xs. и пусть
282
х$. означает, что вершина v € £,. Построим логическую формулу -
условие оптимальной раскраски вершин графа G
& ( V xs. ). (14.3)
Взяв по одной переменной в каждой скобке формулы (14.3),
получим некоторую конъюнкцию х$ xs ...*$ , для которой семейство
внутренне устойчивых множеств {5а,5^,... ,5С} в сумме покрывает
все множество V. Пусть V Ki есть минимальная ДНФ D для формулы
j
(14.3). Пусть дизъюнктивному слагаемому Kj = xs. xs. .. .xs. в D
соответствует наименьшее по длине к семейство L, = {5; ,5; ,...,
S; }. Хроматическое число x(G) = к. Ему соответствует следующая
оптимальная раскраска вершин графа G. В цвета 1,2,...,А:
последовательно окрашиваем семейства вершин
соответственно.
14.4.1. Алгоритм оптимальной раскраски {pyq)-epa0a G = (V,E)
1. Построить все максимальные внутренне устойчивые множества
вершин SlyS2,... ,5Г.
2. Построить логическую формулу F - условие оптимальной
раскраски графа G:
& ( V xs. ).
v€K v€5| l
3. Построить минимальную ДНФ D для F.
4. Каждому дизъюнктивному слагаемому Ki = x$ xs ...xs в D
соответствует минимальное семейство L, = {5а,5^,... ,5С} внутренне
устойчивых множеств Sa,Sb,... ,SC. Из всех L{ выбираем наименьшее
по длине к семейство {5; ,5; ,...,5; }. Хроматическое число x(G)
= /t. Ему соответствует следующая оптимальная раскраска вершин
графа G. В цвета 1,2,...,Л последовательно окрашиваем семейства
вершин 5Л, 5;-2- 5Л, SJ3-(SjV 5^),..., S^- (S;iU...U S^)
соответственно.
Пример. Построим оптимальные раскраски графа G=(V,E]=({l,2t3,
4,5,6,7,8}, {(1,2),(1,3),(1,5),(1,6), (2,3),(3,4),(3,6),(4,5),
283
(4,7),(5,6),(6,7),(7,8)}). Составим по условию внутренней
устойчивости графа G решеточное выражение
F = & (и V v) = (1V2)(1V3)(1V5)(1V6)(2V3)(3V4)&
(3V6)(4V5)(4V7)(5V6)(6V7)(7V8) =
23567 V 12467 V 12468 V 13467 V 13468 V 1357 V 234568.
Рассматривая полученные дизъюнктивные слагаемые как множества
и дополняя их до множества вершин V, получим, что множество 5 =
{51,52,53,54,55,56,57}={{1,4,8},{3,5,8},{3,5,7}, {2,5,8},{2,5,7},
{2,4,6,8},{1,7}} есть список всех максимальных (тупиковых)
внутренне устойчивых множеств графа G. Составляем решеточное
выражение - условие оптимальной раскраски вершин графа
r = & ( у I ) = (1V7)(4V5V6)(2V3)(1V6)(2V3V4V5)6&
(3V5V7)(1V2V4V6) = 672 V 736 V 2651 V 631.
Из полученных дизъюнктивных слагаемых выбираем наименьшие по
длине: 672, 736, 631. Построим оптимальные раскраски вершин графа
по множествам {S6,SlyS2}, {SlfS3,S6}t {56,53,5!}. Хроматическое
число X(G)=3, т.е. для правильной раскраски вершин графа
необходимо три краски. Возможны следующие варианты оптимальной
раскраски вершин.
1. Вершины L1=56={2,4,6,8} покрасим цветом 1; вершины L2 =
57-56={1,7} - цветом 2; L3=52-(56U57)={3,5} - цветом 3.
2. L1=57={1,7}; L2=53-57={3,5}; L3=56-(57U53)={2,4,6,8}.
3. L1=56={2,4,6,8}; L2=53-56={3,5,7}; L3=51-(56U53)={l}.
14.4.2. Программа оптимальной раскраски вершин графа
Процедура optimum_colour_graph(G,S) по заданному графу G=
[[1,2,3,4,5,6,7],[[1,2],[1,3],[1,5],[1,6],[2,3],[3,4],[3,6], [4,
5],[4,7],[5,6],[6,7]]], находит наименьшие (по числу красок)
раскраски вершин графа G. Например, для графа G, приведенного в
программе, получим следующие оптимальные раскраски вершин: [[[3,5,
7],[2,4,6],[1]],[[1,4],[2,6],[3,5,7]]].
Процедура all_max_in_stable_sets(G,S) по графу G вычисляет все
максимальные внутренне устойчивые множества S1 вершин графа G.
Например, для заданного в программе графа G множество S=[S1,S2,
S3,S4,S5]=[[2,4,6],[1,7],[1,4],[3,5,7],[2,5,7]].
Процедура cond_optimum_colour(V,S,M) по множеству V вершин
графа G и множеству S=[Sl,S2,S3,S4,S5]=[[2,4,6],[l,7] ,[l,4],
[3,5,7],[2,5,7]] всех максимальных внутренне устойчивых множеств
284
вершин графа G вычисляет список M=[[2,3],[l,5],[4] ,[l,3] ,[4,5],
[l],[2,4,5]], соответствующий решеточному выражению - условию
оптимальной раскраски вершин графа
R = & ( V i ) = (2V3)(1V5)4(1V3)(4V5)1(2V4V5).
v€V v€S/
Процедура construct__optimum__colour_sets(S, Т, L) по множествам
S=[S1,S2,S3,S4,S5]=[[2,4,6],[1,7],[1,4],[3,5,7],[2,5,7]], T=[[4,
1,2],[3,1,4]] строит исходные множества вершин L=[[S4,S1,S2],
[S3,S1,S4]]=[[[3,5,7],[2,4,6],[1,7]],[[1,4],[2,4,6],[3,5,7]]] для
получения оптимальных множеств раскраски вершин.
Процедура one_optimum_colour(S,L) по одному из исходных
множеств, например, по множеству S=[S4,S1,S2]=[[3,5,7] ,[2,4,6] ,[l,
7]] строит оптимальную раскраску вершин L=[L1,L2,L3]=[[3,5,7],
[2,4,6] ЛИ], где L1=S4=[3,5,7]; L2=Sl-S4=[2,4,6]-[3,5,7]= [2,4,
6] ;L3=S2-(S4+S1)=[1,7]-[3,5,7,2,4,6]=[1].
Процедура optimum_colour_sets(S, L), используя процедуру
one_optimum__colour, по исходному множеству S=[[S1,S2]]=[[[3,5,7],
[2,4,6] ,[1,7]],[[1,4] ,[2,4,6] ,[3,5,7]]] строит оптимальные
множества L=[L1,L2]=[[[3,5,7],[2,4,6],[1]],[[1,4],[2,6],[3,5,7]]]
раскраски вершин.
Процедура select_one_set(S,H,L) по множеству S=[S1,S2,S3,S4,
S5]=[[2,4,6] ,[l,7] ,[l,4] ,[3,5,7] ,[2,5,7]] и одному из подможеств,
например, [4,1,2] множества Н=[[4,1,2],[3,1,4]] строит множество
[S4,Sl,S2]=[[3,5,7],[2,4,6],[l,7]] - исходное для получения
оптимальной раскраски.
Процедура dek_absorb(S,L), absorb__set(S,L), absorbl(S,A,L)
описаны в программе вычисления всех наибольших внутренне
устойчивых множеств вершин графа.
Процедура complement_sets(V,S,C) по множествам V=[l,2,3,4,5,
6], S=[[2,3,5,6],[2,3,5] ,[1,2,5,6]] вычисляет дополнительные
множества С=[[1,4],[1,6] ,[3,4]], где [l,4]=V-[2,3,5,6]; аналогично
для остальных подмножеств из С.
Предикат all_least_length_lists(S,L) истинен, если L есть
список всех подсписков в S, имеющих в S наименьшую длину. Например,
если S=[[a,b],[a,c,d],[a,s],[s,d,e,f]], то L=[[a,b] ,[a,s]].
Предикат least_length(S,C) истинен, если число С есть
наименьшая длина подсписка в списке S. Например, если S=[[a,b],[a,c,
d],[a,s],[s,d,e,f]], то С=2.
d(G,C) :- V=[l,2,3,4,5,6,7],
E=[[1,2],[1,3],[1,5],[1,6U2,3],[3,4],[3,6],[4,5],[4,7],
285
[5,6],[6,7]],G=[V,E],optimum_colour_graph(G,C).
optimum_colour_graph(G,S) :- G=[V,E],
all_max_in_stable_sets(G,Sl),
cond_optimum_colour ( V, SI, M), dek_absorb(M, S21),
all_least_length_lists(S21, S2),
construct_optimum_colour_sets(Sl, S2, S3),
optimum_colour_sets(S3, S4), del_rep_sets(S4, S).
all_max_in_stable_sets(G,S) :- G=[V,E],
dek_absorb(E,L),complement_sets(V,L,S).
cond_optimum_colour(V,S,L) :- lattice__expression(V,S,[] ,L).
lattice__expression([H|T],S,Ac,L) :- lattice_expr(H,S,Ll),
lattice_expression(T,S,[Ll|Ac],L).
lattice__expression([],S,Ll,L) :- reverse(Ll,L).
lattice_expr(H,S,Ll) :- I is 1, latt_expr(H,S,I,[] ,Ll).
latt_expr(H,[Sl|T],I,Ac,Ll) :- Ц is 1+1,
ifthenelse(member(H,Sl),latt_expr(H,T,Il,[l|Ac],Ll),
latt_expr(H,T,Il,Ac,Ll)).
latt_expr(H,[],I,Ac,Ll) :- reverse(Ac,Ll).
construct_optimum_colour_sets(S,L,Col) : -
constr_opt_col_sets(S, L, [ ], Col).
constr_opt_col_sets(S,[H|T],Sl,C) :- select_one_set(S,H,L),
constr_opt_col_sets(S,T,[L|Sl],C).
constr_ppt_col_sets(S,[],L,C) :- reverse(L,C).
select_one_set(S,H,L) :- sel_one_set(S,H,[] ,L).
sel_one_set(S,[N|T],Sl,L) :- nth_element_in_list(S,N,A),
sel_one_set(S,T,[A|Sl],L).
sel_one_set(S,[],Sl,L) :- reverse(Sl,L).
nth_element_in_list(L,N,A) :— I is l,nth_el_in_list(L,N,I,A).
nth__el_inJist([H|T],N,I,A) :-
not(N is l),Il=I+l,nth_el_inJist(T,N,Il,A).
nth_eMnJist([H|T],N,I,H) :- N is I.
optimum_colour_sets(S,Col) :- opt_col(S,[],Col).
opt__col([H|T],S,C) :- one_optimum_colour(H,L),opt_col(T,[L|S],C).
opt_col([],L,C) :- reverse(L,C).
one_optimum_colour([H|T],L) :- one_opt_col(T,H,L,[H]).
one_opt_col([H|T],S,L,P) :- difset(H,S,Sl),append(Sl,S,Hl),
one_opt_col(T,Hl,L,[Sl|P]).
286
one_opt_col([],S,L,P) :- reverse(P,L).
dek_absorb(S,L) :- dekl_absorb(S,L).
dekl_absorb([Hl,H2|T],L) :- dek2(Hl,H2,LH),
delrepeate(Lll, L13), delrep_el(L13, L12),
absorb_set(L12,Ll),dek3_absorb(Ll,T,L).
dekl_abeorb([H|[]]jH|[]]).
dekl_absorb( [],[]).
dek3_absorb(Ll,[H|T],L) :- dek2(Ll,H,L2),appendl(L2,L3l),
delrepeate(L31,L33),delrep_el(L33,L32),
absorb_set(L32,L3),dek3_absorb(L3,T,L).
dek3__absorb(Ll,[],Ll).
appendl(L2,L3) :- append2(L2,L3,[]).
append2([[H|T]|Tl],L3,S) :- append(H,T,L4),
append(S,[L4],Sl),append2(Tl,L3,Sl).
append2([],S,S).
dek2(X,Y,Z) :- findall([A,B] ,(member(A,X),member(B,Y)),Z).
all_least_length_lists(S, L): -
least Jength(S,C),least_lists(S,[],C,L).
least Jists([H|T],S,C, L):-
length(H,LH),LH=C,least_lists(T,[H|S],C,L).
least_lists([H|T],S,C,L):-
length(H,LH),not(LH=C),least Jists(T,S,C,L) •
least_lists([],S,C,L):-reverse(S,L).
least_length(S,C):-S=[H|T],length(H,N),least_len(S,N,C).
leastJen([H|T],L,C):-length(H,Cl),CKL,least_len(T,Cl,C).
least Jen([H|T],L,C):-length(H,CI),Cl>=L,least_len(T,L,C).
least Jen([],C,C).
delrep_el(S,SM) :- delrpl(S,[] ,Sl),reverse(Sl,SM).
delrpl([H|T],L,Sl) :- delrepeate(H,Hl),delrpl(T,[Hl|L] ,Sl).
delrpl([],S,S).
absorb_set(S,L) :- absorb(S,S,L).
absorb([H|T],[Hl|Tl],L) :-
absorbl(Tl,Hl,T2),append(T2,[Hl],T3),absorb(T,T3,L).
absorb([],L,L).
absorbl(S,A,L) :- findall(M,(member(M,S),not(subset(A,M))),L).
complement_sets(V,S,C) :- compl(V,S,[],C).
compl(V,[H|T],L,C) :- difset(V,H,Ll),compl(V,T,[Ll|L] ,C).
compl(V,[],S,C) :- reverse(S,C).
287
delrepeate(S,SF) :- Sl=[] ,delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :-
not(member(H,T)),append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :-
not(member(R,Y)),append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
del_rep_sets(S,SF) :- Sl=[] ,del_set(S,Sl,SF).
del_set([H|T],Sl,SF) :- member_set(H,T),del_set(T,Sl,SF).
del_set([H|T],Sl,SF) :-
not(member_set(H,T)),append(Sl,[H],S2),del__set(T,S2,SF).
del_set([],S2,S2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L), !•
member_set(L,[Yl|Y]) :- member_set(L,Y).
subset (U,Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
reversed ],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
14.5. Раскрашивание планарных графов
Теорема (о пяти красках). Всякий связный планарныи граф G
раскрашиваем не более чем пятью красками.
Доказательство. Индукция по числу вершин р графа.
БАЗИС. Для графа с числом вершин к < 5 теорема очевидна, ибо
всякие пять вершин 5-раскрашиваемы пятью различными красками.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что всякий связный
планарныи граф с числом вершин к<р 5-раскрашиваем.
ШАГ ИНДУКЦИИ. Покажем, что всякий связный планарныи граф с р
вершинами 5-раскрашиваем. Так как граф G связен и планарен, то он
имеет вершину v степени s < 5. Удалим из G вершину v вместе с
инцидентными ей ребрами. Полученный планарныи граф G' = G-v имеет
число вершин к<р9 и потому по предположению индукции все компо-
288
ненты связности графа G' можно раскрасить не более чем пятью
красками. Возможны следующие случаи.
1. Степень вершины v не более 4. Пусть для определенности
deg(v) = 4. Смежные с v вершины v1,v2,v3,v4 получат в G' не более
четырех красок. Вершину v в графе G окрасим в любую из оставшихся
красок.
2. deg(v)=5. Если смежные с v вершины v1,v2,v3,v4,v5 имеют в
совокупности г < 4 красок, то вершину v окрашиваем в оставшийся
цвет. Пусть теперь вершины v1,v2,v3,v4,v5 окрашены в пять цветов
с1>с2>сз>с4>с5 соответственно. Натянем на вершины vx ,v2,v3,v4,v5
из G подграф Я, соединив вершины v1,v2,v3,v4,v5 в Н ребрами так,
как они соединены в G. Подграф Н планарный, следовательно, Н не
содержит К5. Поэтому в Н среди вершин v1,v2,v3,v4,v5 существуют
две несмежные вершины (ибо если все вершины vx ,v2,v3,v4,v5
смежны, то граф Н есть К5, чего нет). Пусть для определенности
вершины Vi,v2 не смежны (рис. 14.1). Склеим vlyv2 с вершиной v.
Полученный связный планарный граф по предположению индукции 5-раскра-
К,
Рмс.14.1
289
шиваем. При этом четыре вершины v,v3, v4,v5 получат г < 4 цвета.
Расклеим назад вершины v,vl,v2. Вершинам vl9v2 оставим их цвет.
Тогда вершины v1,v2,v3,v4,v5 имеют г < 4 цвета. Вершину v
перекрасим в один из оставшихся цветов.
Шаг индукции установлен. Теорема доказана.
Замечание. Широко известна проблема четырех красок: любой
плоский граф 4-раскрашиваем. Появилось много ошибочных доказательств
этой гипотезы. Последнее сообщение о положительном решении
проблемы четырех красок опубликовано в 1977 г.:
Appel К., Haken W. Every planar map is colorable. Illinois
journal of mathematics: 1976. V.20. No 2. P. 218-297; 1977. V.21.
No 3. P. 429-490; 1977. V.21. No 3. P. 491-567.
15. ПОТОКИ В ТРАНСПОРТНЫХ СЕТЯХ
15.1. Двухполюсные сети
Определение. (Двухполюсная) сеть S = (V,E,s>t) есть орграф
G = (V УЕ) с двумя выделенными вершинами (полюсами): s - входная
вершина сети (исток); t - выходная вершина сети (сток).
Определение. Внутренние вершины сети есть вершины сети,
отличные от полюсов. Полюсная дуга сети инцидентна одному из полюсов.
Пусть S = (V9E9s9t) - сеть и v € V. Введем следующие
обозначения (рис. 15.1):
Z)+(v) *- множество дуг сети, исходящих из v;
D~(v) - множество дуг сети, входящих в v;
-<СЕЕ>'
r?(D-(V')) T?(D-(V'))
D-(v) D+(v) D+(s) D-(t)
Ршс.15.1
290
D(v) - множество дуг сети, инцидентных вершине v.
Очевидно, что D(v) = D+(v) U D~"(v).
Пусть А Я V - некоторое множество вершин сети 5. Положим
D(A) =U Z)(v); D+(A) =U D+(v); D~U) =U ZT(v).
v€A v€A v€A
Определение.
e = (w,v) есть граничная дуга для A Q V <—>
м€Л & у<Л V w<yl & у€Л.
е = (w,v) - есть внутренняя дуга для A Q V *-*
и€А & v€A\
BH(D(A)) - множество внутренних дуг из D(A);
r?(D(A)) - множество граничных дуг из D(A)\
BR(D~(A)) - множество внутренних дуг из D~(A)\
TF(D"(A)) - множество граничных дуг из D~(A);
BH(D+(A)) - множество внутренних дуг из D+(A);
rF(D+(A)) - множество граничных дуг из D+(A).
Верны следующие равенства:
D(A) = BH(Z)U)) U TP(Z)U));
D~(A) = BH(Z)"U)) U TP(ZrU));
D+U) = BH(Z)+U)) U TP(Z)+U)).
Заметим, что ВН(£Г(Л)) = BH(Z)+C4)) = BH(Z)(yl)), ибо для дуги е
= (w,v) имеем соотношение
г
BH(Z)+(yl)) по вершине и\
е € ]BH(Z)"(y!)) по вершине v;
1 BH(D(yl)) по вершинам w,v,
где три множества составлены из одних и тех же дуг.
15.2. Дивергенция
Пусть 5 = (V,E,s,t) - сеть. Зададим функцию / : Е -» R+, где R+
есть множество неотрицательных вещественных чисел.
Пусть V = V - {s,t} - множество внутренних вершин сети 5.
Определение. Дивергенция функции / в (внутренней) вершине v €
V есть величина (число) divj-(v) = J] f(e) - jl /(*)•
e€D+(v) e€D~(v)
Дивергенция функции / на множестве (внутренних) вершин А Я V
есть величина (число) diVf(A) = J] divf(v). В истоке и стоке
v€A
divf{s) = E /(e); divf(t) = J] /(e).
e€D+(v) e€D"(v)
291
Утверждение (основное свойство дивергенции). Для А Я V
AV/U) = Е fie) - £ f{e).
e£D+(A) e£D~(A)
Доказательство. diVf(A) = J] divf(v) =
E (E /(e) - E /(e)) = E E /(e) -ЕЕ /(«) =
v€/l e€D+(v) e€D (V) v€A e€D+(v) v€/l e€D (V)
E /(*) " E fie).
e€D+M) e€D~(/l)
15.3. Потоки в сетях
Определение. Транспортная сеть S = (V9E,s9t,c) есть сеть (V,E,
s,t), в которой Z>~(j) = 0, Z)+(0 = 0 и для которой определена
функция с : Е -* R+ - пропускная способность дуг. Вершина .у есть
исток сети, вершина f - сток сети.
Слово транспортная иногда будем опускать.
Определение. Поток в сети 5 = (V9E9s9t9c) есть функция / : Е -»
R+, удовлетворяющая следующим условиям:
1) 0 < /(e) < с(е);
2) для всякой внутренней вершины v сети 5 divfiv) = 0.
Пусть S = (К\E,s,t,c,f) - транспортная сеть с пропускной
способностью дуг с : £ -» R+ и потоком / : Е -» R+.
Свойства дивергенции потока
Пусть К' = V - {s9t} - множество внутренних вершин сети S.
1. divf(Yf) = £ rfiv^v) = 0. Если Л С К7, то divf(A) = 0.
v€K'
2. Av^j) = divf{t). В самом деле, ввиду D+(F') = BH(D+(K'))
U T?(D+(V')) (рис.15.1) получаем 0 = divf(V) =
Е f(e) - £ /(e) =
e€D+(K') e€D"~(K')
Е/(«) + Е/(«) - Е/(«) + Е/(«)
е€ г р( D+ (К')) е€ в н( D+ (V')) е€ в н( D~( К')) <?€ гр( D"~( К'))
У , 1 V , 1 V , 1
e€D"(0 сумма = 0 e€D+(5)
292
divf(t) - divf(s)y откуда divf(s) = divAt).
Определение. Величина потока f в сети 5 = (V ,E,s,t,c,f) есть
величина (число)
Mf = divf(s) = £ /(e) (= divf(t) =S /(e)).
e€D+(5) e€D~(f)
15.4. Сечения в сетях
Определение. Сечение в сети 5 = (V9E9s,t) есть множество W Q Е
дуг, при удалении которых получившаяся сеть S - W становится
несвязной (рис. 15.2), причем полюсы s и t попадают в разные
компоненты связности. Сечение W простое, если при возвращении в сеть S
- W любой дуги е из W сеть (5 - W) + е становится связной (по
этой дуге).
Сечение W в сети S можно построить, разделив множество вершин
в 5 на два подмножества А и Ву причем s€A, t€B, и взяв в качестве
W все дуги с началом в А и с концом в В, а также все дуги с
началом в В и с концом в А.
При неориентированной связности далее будем говорить о
связности орграфа по ребрам, не обращая внимания на их направление.
Определение. Дуга е простого сечения называется прямой, если в
цепи [s,t], проходящей через дугу е9 она ориентирована от s к t\
и обратной, если дуга е ориентирована в цепи [s9t] от t к s.
На рис.15.2 в цепи [s,t] дуга е' - прямая, а е" - обратная.
Направленность дуги зависит от выбора простого сечения. В
фиксированном простом сечении W ориентация дуги не зависит от выбора
цепи: дуга либо прямая, либо обратная. Для каждой дуги е из
простого сечения W можно указать цепь [s,t], которая проходит через
дугу е и не проходит через остальные дуги сечения W.
s * >>* *++
-*• t
е' е"
Рмс.15.2
293
Определение. Пусть W есть простое сечение в сети S. Пусть
Wnp - множество прямых дуг в сечении W\
W^ - множество обратных дуг в сечении W'.
Тогда пропускная способность простого сечения W есть число
c{W) = £ c(e).
Простое сечение W минимально, если W имеет минимальную
пропускную способность. Пропускная способность сети есть пропускная
способность минимального простого сечения этой сети.
15.5. Величина потока и пропускная способность сети
Пусть 5 = (K,E,.y,f,c,/) - транспортная сеть, где с:Е -» IN, /: Е
-» IN есть целочисленные функции пропускных способностей дуг и
потока в сети S (IN = {0,1,2,...}). Пусть W - простое сечение сети
^» ^пР> ^об ~ множества прямых и обратных дуг в сечении W
соответственно.
Утверждение 1. Величина потока Mf = J] f(e) -
e€W
пр
E fM
В
об
сети S - W%
Доказательство. Пусть Ks - компонента связности
содержащая исток s. Пусть Vs - есть множество вершин компоненты
Ks (рис. 15.3). Тогда величина потока
Mf = divf(s) =
(прибавляем равную нулю дивергенцию по внутренним вершинам сети
из Vs - {s}, ибо divf{Vs- {s}) = 0 по основному свойству
дивергенции) diVf(Vs) = (по основному свойству дивергенции)
I fie) - I f(e) =
e€D+(Vs) e€D~(Vs)
(так как
D+(VS) = m(D+(Vs)) U TP(D+(VS)) = m(D*(Vs)) U Wl
D~(VS) = BH(D-(VS)) U TP(D-(VS)) = m(D~(Vs)) U Wx
np>
np>
Phc.15.3
294
то продолжая выше написанное равенство, имеем)
Е fie) + J]/(e) - £/(е) - £ /(e)
e€Wnp e€BH(D+(Fj)) е€вн(£>~(Н^)) e€JPo6
e€BH(D+
V
2
(K5) )
V"
сумма =
fie) -
«€W„p
*€bh(D iVs
= 0
Z /(e).
*€^o6
;))
_J
Утверждение 2. Если cw,„ есть пропускная способность сети
(т.е. пропускная способность c(Wmin) минимального простого
сечения Wmin)y то величина потока Л/у ^ cmin.
Доказательство. Mf = J] /(e) - Е /(*) < Е /(*) <
e€Wnp e€Wo6 e€Wnp
£ с(е) = с(*Гт|-я) = ст/я.
€Wnp
Замечание. Если WWi/i - минимальное сечение в сети 5 с
пропускной способностью c(Wmin) = cmin и если поток / в сети 5 имеет
максимально возможную величину
Mf = cmin = c(Wmin) = £ c(e),
«€W„p
то при этом
Mf = E /(e) - £ /(e) = J] c(e)
e€Wnp e€Wo6 e€Wnp
возможно лишь тогда, когда на дугах е из Wnp /(e) = с(е), а на
дугах е из W^ поток /(e) = 0; так что максимально возможный
поток Л/у, равный cmin9 нагружает в минимальном сечении прямые
дуги до их пропускных способностей, а обратные дуги не нагружает
совсем (нагружает нулями).
15.6. Максимальный поток
Пусть S = (V,E,s,t,c,f) - транспортная сеть с пропускной
способностью с : Е -> 04 и потоком / : Е -> 04; с^ п - максимально
возможная величина потока Л/у.
Определение. Дуга е£Е в сети S насыщена, если /(e) = с(е).
Теорема 1. Пусть ft = [s,t] - путь от j до /. Если все дуги
этого пути не насыщены, то поток / можно увеличить так, что одна
295
из дуг пути fi окажется насыщенной.
Доказательство. Пусть в = min (с(е) - /(e)). Увеличивая на 5
е €р
поток / в каждой дуге е из /х, придем к потоку /' = / + 5. Дуга е,
на которой с(е) - /(e) = 6, оказывается насыщенной.
Пример. с(ех) = 5, с(е2) = 3, с(е3) = 6, f(ex) = 2, /(е2) = 2,
/(е3) = 4 (рис.15.4). Дуга е2 оказалась насыщенной.
Определение. Поток / в сети S полный, если всякий путь от s до
t имеет насыщенную дугу.
Теорема 2. Пусть v = [s9t] - цепь между s и t в сети S с пол-
-> *-
ным потоком /. Пусть е есть прямая дуга в цепи v, а дуга е -
обратная. Для дуги e£v положим 6(e) = с(е) - /(e); 8 = min(S(e)) no
всем е € v\ 7) = min(/(e)) по всем е € у; е = min(6,7)). Если е >
О, то увеличивая на е поток на каждой прямой дуге е € v и умень-
«—
шая на с поток на каждой обратной дуге е € v, получим новый
поток /' = / + е.
Доказательство следует из формулировки теоремы.
Пример. На рис. 15.5 приведена цепь в сети S между s и f,
причем цепь имеет и прямые, и обратные дуги. Величины 6 = 2, 7) = 3,
е = min(5,7j) = min(2,3) = 2. Дуги е1,^7,е8 оказались насыщенными.
Теорема 3. Если в сети S не существует цепи v = [s9t] между ^
и t с е > 0, то поток / максимален и его величина Mf = cmin.
Доказательство. Исключим из сети S все дуги е € Е, для которых
/(e) = с(е) или /(e) = 0. В результате получим сеть S', в которой
полюсы s и X не связны, ибо в случае их связности в S'
существовала бы цепь v между s и f, в которой /(e) < с(е) Ve€v и /(e) > 0
Ve€i>. Но тогда в 5 для цепи у число е > 0. Противоречие с услови-
s * >* ** *** f дуга е2 насыщена
е j е2 е3
5 3 6 с(е)
2 2 4 /(e)
3 1 2 5 = min(c(e)-/(e) )=1
3 3 5 /'(е) =/(е) + 5
Ржс.15.4
296
s * ***** * »■* *-*-* *<< * »►* *■* f
4
2
2
e2
5
3
-
3
1
e3
11
3
8
-
5
e4
8
4
4
-
6
es
9
9
-
9
7
Pmc.15.5
e6
4
3
-
3
1
e7
7
5
2
-
7
e8
6
4
2
-
6
c(e)
/(e)
6(e)
/(e)
/'(e)
ем. Итак, полюсы s и f в S' не связны. Пусть ЯГ5 и /С, - компоненты
связности в S', содержащие полюсы 5 и f соответственно, Vs -
множество вершин в компоненте Ks. Можно показать, что множество
дуг T?(D+(VS)) есть множество прямых дуг в *Гпр в некотором
простом минимальном сечении W в S с пропускной способностью c(W) =
С/П1Л> причем все прямые дуги этого простого сечения насыщены, а
для всех обратных дуг е имеем f(e) = 0. Тогда
Mf = E fCe) - £ /(*) = Е с(7) = cw/„.
?€Wnp V€Wo6 ?€Wnp
Теорема (Форда-Фалкерсона о максимальном потоке). Любая
транспортная сеть S = (V,E9s,tyc,f) имеет максимальный поток и его
величина равна cmin.
Доказательство. По теореме 1 строим полный поток в сети S.
Тогда любой путь в S между s и t насыщен (имеет насыщенную дугу).
По теореме 2 строим поток, в котором любая цепь между s и t,
имеющая обратные дуги, не допускает увеличения потока. По теореме 3
построенный поток максимален и его величина равна cmin -
пропускной способности сети 5.
15.6.1. Алгоритм вычисления максимального
потока в транспортной сети
Пусть 5 = (К,£,^,Г,с) - транспортная сеть с пропускной
способностью дуг с : Е -* 04, для которой требуется построить
максимальный поток fmax : Е -» IN.
297
1. Исходим из некоторого начального, например, из нулевого
потока.
2. Перебираем все ориентированные пути в сети S от s до t и
увеличиваем исходный поток до насыщения одной из дуг
рассматриваемого пути согласно теореме 1. Именно, пусть jli - очередной путь
между s и t в сети S с потоком /. Вычисляем 5 = min (c(e) -
/(e)). Увеличивая на 5 поток / в каждой дуге е из fi, придем к
потоку /' = / + 5. Дуга е, на которой с(е) - f(e) = 6, оказывается
насыщенной. В результате получим полный поток, всякий
ориентированный путь которого содержит насыщенную дугу.
3. Перебираем все неориентированные пути (цепи) в сети 5 от ^
до t и увеличиваем исходный полный поток на каждой
рассматриваемой цепи согласно теореме 2. Именно, пусть v = [s9t] - очередная
цепь между s и t в сети S с потоком /. Пусть е - прямая дуга в
цепи и, а дуга е - обратная. Для дуги e£v положим д(е) = с(е) -
f(e)\ S = min(5(e)) по всем е € v\ t\ = min(/(e)) по всем е € v\ e
= min(5,7}). Если е > 0, то увеличивая на с поток на каждой прямой
-> «-
дуге е € v и уменьшая на е поток на каждой обратной дуге е € и,
получим новый поток /' = / + е. В результате получим максимальный
поток fmax.
Пример. Построить максимальный поток в транспортной сети S =
(V9E,s,t,c) заданной своими дугами, третьей координатой которых
является пропускная способность с дуг:
^=(8,1,5); e2=(s,2,7); e3=(s,3,9); e4=(l,2,l); e5=(l,4,4);
e6=(2,5,3); e7=(3,5,l); e8=(3,t,l); e9=(4,5,4); e10=(4,t,2);
en=(5,t,6).
1. Исходим из начального нулевого потока f0(e) s 0.
2. Перебираем все ориентированные пути между s и f, по которым
возможно увеличение потока (рис. 15.6).
j-»l-»2->5->f - очередной путь \i между .у и t\
5 13 6 - пропускная способность с(е) дуг;
0 0 0 0 - старый поток f0(e);
5 13 6 - 6 = min (c(e) - /0(е)) = 1;
е €р
1111 - новый поток fx(e) = /0(е)+б.
Прямая дуга (1,2,1) насыщена.
298
s
t i
Pmc.15.6
j-»l->4->5-*f - очередной путь \i между s и t;
5 4 4 6 - пропускная способность с(е) дуг;
10 0 1 - старый поток fY(e)\
4 4 4 5 - 8 = min (c(e) - /Де)) = 4;
е €р
5 4 4 5 - новый поток f2(e) = /Д^+б.
Прямые дуги (.у,1,5); (1,4,4); (4,5,4) насыщены.
s -» 2 -> 5 -» f - очередной путь ;х между 5и (;
7 3 6 - пропускная способность с(е) дуг;
0 15 - старый поток /2(е);
7 2 1 - в = min (с(е) - /2(е)) = 1;
е €^м
12 6 - новый поток f3(e) = /2(e)+S.
Прямая дуга (5,f,6) насыщена.
.у -» 3 -» 5 -» f - очередной путь ;х между s и t.
Дуга (5,f,6) в этом пути уже насыщена. Увеличение потока по этому
пути невозможно.
s -* 3 -* t - очередной путь \i между s и t\
9 1 - пропускная способность с(е) дуг;
0 0 - старый поток f3(e);
9 1 - 8 = min (c(e) - /3(е)) = 1;
е €/*
11 - новый поток fA(e) = /3(е)+6.
Прямая дуга (3,f,l) насыщена.
3. Перебираем все неориентированные пути (цепи) между s и f,
299
по которым возможно увеличение потока (рис. 15.7).
5 -> 1. Продолжение цепи от узла 1 не имеет смысла: прямая
дуга (5,1,5) насыщена.
s -* 2 «- 1 -> 4. Продолжение цепи от узла 4 не имеет смысла:
прямая дуга (1,4,4) насыщена.
s -* 2 -» 5 «- 3. Продолжение цепи от узла 3 не имеет смысла:
обратная дуга (3,5,1) нагружена нулем.
$->2->5«-4«-1. Продолжение цепи без повторов вершин на
этом пути невозможно.
j-»2-*5*-4-»f - очередная цепь /х между s и t\
1
1
6
3
2
1
4
4
2
О
2
- направленность дуг в цепи /х;
- пропускная способность с(е) дуг;
- старый поток f4(e)\
- 5 = min (c(?) - /4(?)) = 1;
е €/*
- 7) = min (/>)) = 4; е = min(5,7)) = 1;
- новый поток f5(e)
s
■ Ц*
+е на е
4-
с на е
Рмс.15.7
300
Прямая дуга (2,5,3) насыщена.
•у->3-*5«-2<-1-*4. Продолжение цепи от узла 4 не имеет
смысла: прямая дуга (1,4,4) насыщена.
5->3->5«-4«-1->2. Продолжение цепи от узла не имеет
смысла: прямая дуга (1,2,1) насыщена.
j-»3-»5«-4-*f - очередная цепь /х между s и t\
еъ еп е9 е10 - направленность дуг в цепи /х;
9 14 2 - пропускная способность с(е) дуг;
10 3 1 - старый поток f5(e)\
81 1 - б = min (c(e) - f5G)) = 1;
е €fi
3 - - 7) = min (f5e)) = 3; e = min(5,7)) = 1;
e €/*
+e на е
2 12 2 - новый поток f6(e) = /5(e)l «- .
1-е на е
Прямые дуги (3,5,1) и (4,f,2) насыщены.
5 -> 3 -» Г.
Увеличение потока невозможно: прямая дуга (3,f,l) насыщена.
В табл. 15.1 приведены значения промежуточных потоков;
насыщенные дуги подчеркнуты.
Максимально возможная величина потока (нагружающая дуги
истока, равно как и дуги стока) Mf = 9.
15.6.2. Программа вычисления наибольшего потока
в транспортной сети
Транспортная сеть S задается фактами Пролога вида a(vl,v2,c),
где (vl,v2) - ориентированное ребро (дуга), с - пропускная
способность дуги (vl,v2).
Процедура flow(F) вычисляет максимальный поток F в
транспортной сети S.
Процедура initial_flowO(FO) вычисляет исходный нуль-поток F0.
Процедуры flow_on__directed__pathes и flow_on_undirected_pathes
вычисляют поток после прохождения всех ориентированных и
неориентированных путей соответственно.
Процедура flow__magnitude вычисляет величину максимального
потока.
Процедуры directed_path и undirected_path вычисляют
ориентированный и соответственно неориентированный путь Р в сети S от
истока s до стока t.
301
Таблица 15.1
Дуга
e,=(s,l,5)
e2=(s,2,7)
e3=(s,3,9)
e4=(l,2,l)
e5=(l,4,4)
««=(2,5,3)
e7=(3,5,l)
e8=(3,t,l)
*9=(4,5,4)
e10=(4,t,2)
e,,=(5,t,6)
Последовательный поток
/о
0
0
0
0
0
0
0
0
0
0
0
Л U /З /4
1 5
1
1
1
4
1 2
1
4
15 6
/5
2
3
3
1
/б
2
1
2
2
) max
5
2
2
1
4
3
1
1
2
2
6
Процедуры value_increase_flow_dir и value_increase_flow_undir
вычисляют величину увеличения потока после построения очередного
ориентированного и соответственно неориентированного пути.
Процедуры increased__flow_dir и increased_flow_undir вычисляет
поток после его очередного увеличения.
Процедуры
newsetsaturatedarchesdir и new_set_saturated_arches_undir
вычисляют новое множество насыщенных дуг.
Процедура min_cost_path вычисляет минимальную пропускную
способность Cost дуг из очередного вычисленного пути.
В программе приняты следующие обозначения.
302
В программе приняты следующие обозначения.
S - старт; G - цель; F - поток;
SSA - множество насыщенных дуг;
NSSA - новое множество насыщенных дуг;
FODP - поток на ориентированных путях;
FM - величина потока.
Запрос к программе имеет следующий вид: ?- flow(S,G,F,FM)
flow(S,G,F,FM):- S=s,G=t,initial_flow(FO),SSA=[],
f low_on_directed_pathes(S, G, F, FO, Fl, SSA, NSSA, FODP, SSAl),
flow_on_undirected_pathes(S,G,F,FODP,F2,SSAl,NSSAl),!,
f low_magnitude(S, F, FM).
a(s,l,5). a(s,2,7). a(s,3,9). a(l,2,l). a(l,4,4).
a(2,5,3). a(3,5,l). a(3,t,l). a(4,5,4). a(4,t,2). a(5,t,6).
initial_flow(FO) :- findall([X,Y,0] ,a(X,Y,C),FO).
f lo w_on_directed_pa thes(S, G, F, FO, Fl, SSA, NSSA, FODP, SSAl) : -
directed_path(S, G, FO, P, SSA), value_increase_f low_dir (FO, P, V),
increased_f low_dir (FO, Fl, P, V ),
new_set_saturated_arches_dir (SSA, NSSA, Fl, P),
f low_on_directed_pathes(S, G, F, Fl, F2, NSSA, NSSAl, FODP, SSAl).
f low_on_directed_pathes(S, G, F, Fl, Fl, NSSA, NSSAl, Fl, NSSA).
flow_on_undirected_pathes(S,G,F,FO,Fl, SSA, NSSA) :-
undirected_path(S,G,FO,P,SSA),
value_increase_f low_undir (FO, P, V),
increased_flow_undir(FO,Fl,P,V),
new_set__saturated_arches_undir (SSA, NSSA, Fl, P),
flow_on_undirected_pathes(S,G,F,Fl,F2,NSSA,NSSAl).
f low_on_undirected_pathes( S, G, Fl, Fl, F2, NSSA, NSSAl).
flow_magnitude(S,F,FM) :-
findall([S,Y,C],member([S,Y,C],F),FS),cost(FS,FM).
directed_path(S,G,F,P,SSA) :- a(S,Y,C),
member([S,Y,Cl],F),not(member([S,Y,Cl],SSA)),
dir_path([S,Y,C],G,[[S,Y,C]],[S,Y],P,F,SSA).
dir__path(Edge,G,Edges,Nodes,P,F,SSA) :-
next_edge_dir (Edge, Nodes, NextEdge, F, SSA),
NextEdge = [Y,Yl,Cl],
dir_path(NextEdge,G,[NextEdge|Edges],[Yl|Nodes],P,F,SSA).
dir_path([X,G,C],G,E,N,E,F,SSA).
next_edge_dir([X,Y,C],N,[Y,Yl,Cl],F,SSA):-a(Y,Yl,Cl),
303
not(member(Yl,N)),member([Y,Yl,C2],F),
not(member([Y,Yl,C2],SSA))\
undircctcd_path(S,G,F,P,SSA) :-
a(S,Y,C),not(member([S,Y,C],SSA)),
undir__path([S,Y,C],G,[[S,Y,C]],[S,Y],F,P,SSA).
undir_j>ath(Edge,G,Edges,Nodes,F,P,SSA) : -
next_edge_undir (Edge, Nodes, NextEdge, F, SSA),
NextEdge = [Y,Yl,Cl],
undir_path(NextEdge,G,[NextEdge|Edges],[Yl|Nodes],F,P,SSA).
undir_path([X,G,C],G,E,N,F,E,SSA).
next_edge_undir([X,Y,C],N,[Y,Yl,Cl],F,SSA) :-
a(Y,Yl,Cl),not(member(Yl,N)),not(member([Y,Yl,Cl],SSA)) ;
a(Yl,Y,Cl),member([Yl,Y,C2],F),not(member(Yl,N)),C2 > 0.
value_increase_flow_dir(FO,P,V) :- findall([X,Y,C],
(member([X,Y,Cl],P),member([X,Y,C2],F0),C is C1-C2),PF0),
min_cost_path(PFO,V).
value Jncrease_flow_undir(FO,P,V) :- findall([X,Y,C],
(member([X,Y,Cl],P),member([X,Y,C2],F0),C is C1-C2 ;
member([X,Y,C3],P),member([Y,X,C],F0)), PFO),
min_cost_path(PFO,V).
increasedJlow__dir(FO,Fl,P,V) :- findall([X,Y,C],
(member([X,Y,C],F0),not(member([X,Y,C2],P)) ;
member([X,Y,Cl],F0),member([X,Y,C3],P), С is Cl+V),Fl).
increased_flow__undir(FO,Fl,P,V) :- findall([X,Y,C],
(member([X,Y,C],F0),not(member([X,Y,C2],P)),
not(member([Y,X,C2],P)) ;
member([X,Y,Cl],F0),member([X,Y,C3],P),C is Cl+V ;
member([X,Y,C4],F0),member([Y,X,C5],P),C is C4-V),Fl).
new__set_saturated__arches_dir(SSA,NSSA,F,P) :- findall([X,Y,C],
(member([X,Y,C],P),member([X,Y,C],F)),SSAl),
unionset(SSA, SSA1, NSSA).
new_set_saturated__arches__undir(SSA,NSSA,F,P) :- findall([X,Y,C],
(member([X,Y,C],P),member([X,Y,C],F)),SSAl),
unionset(SSA,SSA1,SSA2),f indall([X, Y,C],
(member([Y,X,C],P),member([X,Y,Cl],F),CKC),SSA3),
dif set(SSA2, SS A3, NSSA).
min_cost_path(P,C) :- P = [[Xl,Yl,Cl] |Pl] ,minl(Pl,Cl,C).
304
minl([[X2)Y2,C2]|P2],Cl,C):-Cl =< C2, minl(P2,Cl,C).
minl([[X2,Y2,C2]|P2],Cl,C):-C2 < CI, minl(P2,C2,C).
mim([],C,C).
cost(Graph,Cost) :- C=0,costl(Graph,C,Cl,Cost).
costl([[A,B,C]|G],Cl,C2,Cost) :- C2 is Cl+C,costl(G,C2,C3,Cost).
costl([j,C2,C3,C2).
unionset([X|R],Y,Z) : -member(X,Y),!,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
unionset([],X,X).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R)Y)),append(Z,[R],Zl),
difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X.Z).
Часть 3
МОНАДИЧЕСКАЯ ЛОГИКА И ПРОЛОГ-
ПРОЕКТИРОВАНИЕ КОНЕЧНЫХ АВТОМАТОВ
16. КОНЕЧНЫЕ АВТОМАТЫ
16.1. Автоматы Мили и Мура
Алфавит X есть любое непустое конечное множество символов
(букв). Слово в алфавите X - конечная последовательность символов
алфавита X. Пусть * - символ пустого слова; длина слова - число
входящих в него символов; длина пустого слова равна нулю. Два
слова (графически) равны, если они представляют одну и ту же
последовательность символов алфавита. Конкатенация ху двух слов х и
у есть результат приписывания к слову х слова у. Пусть X* -
множество всех слов в алфавите X. Язык есть произвольное
подмножество слов в множестве X*.
Автомат Мили есть система объектов А = (X,Y,Q,<70,r,£), где X -
входной алфавит; У - выходной алфавит; Q - алфавит (внутренних)
состояний; q0€Q - начальное состояние; Т : Q х X -* Q - функция
переходов; В : Q х X -» У - функция выходов.
Пример. А>={0,1}; У={0,1,2}; Q={q0,qi,q2}'> функции переходов и
выходов задаются в табл. 16.1 или граф-схемой (рис. 16.1).
Таблица 16.1
в
X
О
д
0
1
состояния
Яо <1\ Яг
ЯгЛ
Я, ,2
Я2>0
ЯгЛ
ЯхЛ
ЯгЛ
Автомат А работает следующим образом. На вход автомата в
дискретные моменты времени поступает входная последовательность х =
jc(0)jc(1)jc(2). . .x(k) символов алфавита X. Автомат А в ответ
проходит последовательость состояний q = q(0)q(l)q(2).. .q(k)q(k+l)
(она называется ходом автомата А на х\ множество всех таких
последовательностей обозначается Rn(A,x))y для которой
?(0) = <7о>
q(t+l) = T(q(t),x(0),
и выдает выходную последовательность у = y(0)y(l)y(2).. .у(к), для
306
1(2)
0(1)
0(0), 1(2)
1(2)
.,*.
1
Яг
2
0
Яг
1
0
Яо
0
0,
Яг
1.
0(1)
Рнс.16.1
которой y(t) = B(q(t),*(/)), t = 0,1,...
В примере автомата из табл. 16.1
х = 0 0 1 0 1
Я = Яо Яг Яо Я\ Яг
у = 1 1 2 1 2
Автомат Мили можно задать каноническими уравнениями
я(о) = Яо;
q{t+l) = Т(?(0,х(0);
у(0 = Ж<?(0,*(0).
Лвголвг Мура есть система объектов Л = (AT^.Q^o»^»^)» гДе
■^.У'.С^о»^' задаются как для автомата Мили, а В : Q -* Y - функция
выходов. Канонические уравнения автомата Мура имеют вид
я(о) = Яо;
q(t+l) = Т(<7(0,*(0);
y(t) = ВШ).
Пример. X = {0,l}; Y = {0,1,2}; функции переходов и выходов
задаются в табл. 16.2 и граф-схемой на рис. 16.2.
0
1
1
Яо
Яг
Ях
Таблица 16.2
2 0
Ях Яг
Яг Яо
Яг Яг
307
1
Y
\Я\
4
ЯоЛ
од
О
1
О
<ь,о
<
Рмс.16.2
Ниже приведена входная последовательность jc, а также
соответствующие ей последовательность состояний q и выходная
последовательность у:
д: = 0 0 1 1 0 0 1;
Я = Яо Яг Яо Я\ Яг Яо Яг Яг\
^=1012010 0.
Автомат Мура - частный случай автомата Мили. Автомат Мура
проще и потому в некоторых случаях предпочтительнее автомата Мили.
Распространим функцию переходов Т автомата на множество Q X
X*, положив T(q,xa) = T(T(q,x),a); q € Q, х € X, а € X. Значение
функции T(q9x) есть то состояние, в которое перейдет автомат А из
состояния q под воздействием входного слова х.
Аналогичным образом распространим функцию выходов В на
множество Q х X*, положив B(q,xa) = B(B(q,x)9a)\ q € Q, x £ X , a £ X.
Значение функции B(q,x) есть та выходная буква у, которую выдает
автомат А, находящийся в состоянии q, если на его вход подать
слово jc.
Пусть Q' С Q и T(Q,x) = {q£Q : 3q'€Q T(q',x) = q} есть
множество всех состояний, в которые перейдет автомат из состояний
множества Q' в качестве начальных состояний под воздействием
входного слова jc. Определим для автомата А = (X,Y>Q,q0,T>B) оператор
О : X - У, положив 0(a) = B(q0,a)9 а€Х\ (D(jca) = <D(jc) • B(T(q0,x),
а), х € X, а € X.
Оператор О по входному слову х выдает соответствующее ему
выходное слово у. Определим оператор (Dg : X* -* Q*, положив (Dg(fl) =
q0-T(q0,a), a € X; <Dg(jc<i) = Og(jc) • T\T{q0,x),a)\ x € X , a € X.
308
Оператор (Dg по входному слову х выдает соответствующее ему
слово в алфавите состояний автомата А. Если автомат А начинает
работу над словом х из некоторого состояния q, то будем писать
<D(q,x), ®Q(q,x).
Два автомата с выходом эквивалентны, если они реализуют один и
тот же оператор О : X* -* У*.
Теорема. По любому автомату Мили можно построить эквивалентный
ему автомат Мура.
Доказательство. Пусть А = (A\Y,Q,40,7\J3) - автомат Мили.
Построим автомат Мура А' = (X,Y,Q',q'Q,T',В'), положив
Ч[ = <70;
Q' = {*0> U {(Я>*) : Я € Q, я € *};
Г'((*,«),Ь) = (Г(?,а),Ь), ? € Q, {а,Ь} с *;
B'((q,a)) = B(q,a), q Z Q, x £ X.
Построенный автомат Мура эквивалентен автомату Мили; однако
для этого необходимо пренебречь выходом автомата Мура в начальный
момент времени.
Пример. Для автомата Мили из табл. 16.1 функции переходов и
выходов эквивалентного ему автомата Мура приведены в табл. 16.3.
Выход B'(q0) произволен.
Таблица 16.3
0
1
12 0 2 1 2
<7о (<7о>0) (?0Д) (tf.,0) (9l,l) (q2,0) (q2,l)
(Яо,й) (<Ь,0) (<72>0) (<Ь>0) (?2,0) (qlt0) (qlt0)
(q0,l) (<70.1) (<7i.l) (<ЬД) (?2.D (^2.1) (<b,D
Лвгялшг без выхода есть система объектов Л = {X ,Q,q0,T ,F), где
(XyQ,qoyT) задаются как у автомата с выходом, a F Q Q есть
множество выделенных (отмеченных, заключительных, финальных)
состояний. Так определенный автомат называется еще детерминированным
автоматом. Автомат без выхода можно рассматривать как автомат
Мура с выходом, полагая его выход
fl, если q(t) € F,
y(t) =B(q(t)) =\п
10, если q{t) I F.
Слово х € X* допустимо (определимо) автоматом А = {X,Q,q^yT,
F), если T(qQ,x) € F. Если T(q0,x) I F, то слово х не допускается
(отвергается) автоматом А.
309
Поведение Beh(A) автомата А есть множество всех слов в
алфавите X, допустимых автоматом А. Язык L Я X* (автоматно) определим
(допустим, представим), если существует автомат А без выхода, для
которого L = Beh(A).
Иногда автомат А = (X,Q,q0,T) задается без выхода и без
множества выделенных состояний, иногда и без указания начального
состояния А = (X,Q,T). Два автомата без выхода эквивалентны, если
они представляют один и тот же входной язык.
Прямое (декартово) произведение автоматов А' = (X,Q',q',T') и
А" = (X, Q", q", T") есть автомат А'ХА" = (X, Q'XQ",(q0,qb), Т),
где T{(q',q"),af= {T'{qf,a),T"{q",a)), q'ZQ', q" € Q", a € X.
Пример. Пусть граф-схемы автоматов А' и А" (без выходов)
приведены на рис. 16.3 и 16.4. Граф-схема автомата А' х А"
изображена на рис.16.5.
16.1.1. Программа вычисления декартова произведения
для двух детерминированных автоматов
dekaut(Al,A2,A3) :- X=[0,l],Ql=[q01,qll],Q01=[q0l],
Pl=[[q01,0,qll],[q01,l,q0l],[qll,0,qll],[qll,l,q0l]],
Fl=[qll] ,A1=[X,Q1,Q01,P1,F1] ,Q2=[q02,ql2,q22] ,Q02=[q02,q22],
P2=[[q02,0,q02],[q02,l,q22],[ql2,0,ql2],[ql2,l,q02],
[q22,0,ql2],[q22,l,q22]],
F2=[ql2,q22], A2=[X,Q2,Q02,P2,F2],
dek(Ql,Q2,Q3),dek(Q01,Q02,Q03),dek(Fl,F2,F3),dekp(Pl,P2,P3),
A3=[X,Q3,Q03,P3,F3].
dekp(Pl,P2,P3) :- dekpl(Pl,P2,P3,P2).
dekpl([],P2,[],P4).
dekpl([Ll|Yl],[],P3,P4) :- dekpl(Yl,P4,P3,P4).
dekpl([[Al,B,Cl]|Yl],[[A2,B,C2]|Y2],
[[[A1,A2],B,[C1,C2]]|P3],P4) :-
Я'
^0
A
0
•<
0
q'
1
0
q
1
q"
^ 0
j
-, 1 ^
n"
4.
i
I
<
1
f
n"
С
i
Ршс.16.3 Ряс. 16. 4
310
1
Я >Я
~/ ~Г/
ч >ч
1 t
0 0
т 1
л' л"
91'9.
1
1
^0 Л 2
Рис.16.5
dekpl([[Al,B,Cl]|Yl],Y2,P3,P4).
dekpl([[Al,Bl,Cl]|Yl],[[A2,B2,C2]|Y2],P3,P4) :-
dekpl([[Al,Bl,Cl]|Yl],Y2,P3,P4).
dek(A,B,C) :- findall([X,Y],(member(X,A),member(Y,B)),C).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Теорема. Класс автоматно представимых языков замкнут
относительно булевых операций (объединения, пересечения, дополнения).
Доказательство. Пусть автоматы А' = (X,Q',q',Т',F') и А" = (X,
Q",q",T",F") определяют языки Beh(A') и Beh(A") соответственно.
Дополнение X* - Beh(A') определимо автоматом (X, Q', q', Т,
Q'-F').
Пересечение Beh(A') П Веп(А") определимо декартовым
произведением А' х А" с множеством выделенных состояний F' х F".
Объединение Beh(A') U Beh{A") определимо декартовым
произведением А' х А" с множеством выделенных состояний F'x£>" U F"x.Q'.
16.1.2. Программа вычисления автомата для дополнения языка,
представимого детерминированным автоматом
compaut(A.B) :- X=[0,l] ,Q=[q0,ql,q2],Q0=[q0],
P>[[q0,0,q0],[q0,l,q2],[ql.0,q0],[ql.l.q0],
[q2,0,ql],[q2,l,q2]])F=[ql,q2],A=[X,Q,Q0,P,F])
dif(Q,F,Fl),B=[X,Q,Q0,P,Fl].
dif(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],YjR|Z],T) :- not(member(R,Y)),
311
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X.Z).
16.1.3. Программа вычисления автомата для пересечения
двух языков, представимых детерминированными
автоматами
d(A,B,C) :- X=[0,l],Ql=[qlO,qll],Q10=[qlO],
Tl=[[qlO,0,qlO],[qlO,l,qll],[qll,0,qlO],[qll,l,qll]],
Fl=[qll] ,A=[X,Q1,Q10,T1,F1] ,Q2=[q20,q21,q22] ,Q20=[q20],
T2=[[q20,0>q20])[q20(l,q2l],[q21,0>q2l],[q21,l,q22],
[q22,0,q22],[q22)l,q2l]],F2=[q21,q22])
B=[X,Q2,Q20,T2,F2],intersect_det_autom(A,B,C).
intersect_det_autom(A,B,C) :-
A=[X,Q1,Q10,T1,F1],B=[X,Q2,Q20,T2,F2],
findall([Q3, Q4], (member(Q3,Q10), member (Q4,Q20)),Q0),
expand_states_transits(QO, QO, [ ], Tl, T2, Q, T),
findall([Q5,Q6],(member(Q5,Fl),member(Q6,F2),
memberdQS.Qel.Q))^),
C=[X,Q,QO,T,F].
expand_states_transits( [ [Ql,Q2] |R],AS,AT, Tl, T2, Q, T) : -
findall([[Ql,Q2],In,[Q3,Q4]],
(member([Ql,In,Q3],Tl),member([Q2,In,Q4],T2),
not(member([[Ql,Q2])In)[Q3,Q4]],AT))),L),
delrepeate(L, Ll), append( AT, LI, ATI),
findall(Q6,(member([Q5,Inl,Q6],Ll),not(member(Q6,AS))),L2),
append(R,L2,WQ),append(AS,L2,ASl),
expand_states_transits( WQ, AS1, ATI, Tl, T2, Q, T).
expand_states_tr ansits ([ ], Q, T, Tl, T2, Q, T).
delrepeate(S,SF) :- delrep(S,[],SF).
delrep([H|T],Sl,SF) :- member(H,T),!,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
312
16.1.4. Программа вычисления автомата для объединения двух
языков, представимых детерминированными автоматами
d(A,B,C) :- X=[0,l],Ql=[qlO,qll],Q10=[qlO],
Tl=[[qlO,0,qlO],[qlO,l,qll],[qll,0,qlO],[qll,l,qll]],
Fl=[qll], A=[X,Q1,Q10,T1,F1] ,Q2=[q20,q21,q22] ,Q20=[q20],
T2=[[q20,0,q20],[q20,l,q2l],[q21,0,q2l],[q21,l,q22],
[q22,0,q22],[q22,l,q2l]],F2=[q21,q22],
B=[X,Q2,Q20,T2,F2],union_det_autom(A,B,C).
union_det__autom( A,В,C) : -
A=[X,Q1,Q10,T1,F1],B=[X,Q2,Q20,T2,F2],
findall([Q3,Q4],(member(Q3,Q10),member(Q4,Q20)),Q0),
expand_states_transits(QO, QO, [ ], Tl, T2, Q, T),
findall([Q5,Q6],((member(Q5,Fl) ; member(Q6,F2)),
member([Q5,Q6],Q)),F),
C=[X,Q,Q0,T,F].
expand_states__transits([[Ql,Q2]|R],AS,AT,Tl,T2,Q,T) :-
findall([[Ql,Q2],In,[Q3,Q4]],
(member([Ql,In,Q3],Tl),member([Q2,In,Q4],T2),
not(member([[Ql,Q2],In,[Q3,Q4]],AT))),L),
delrepeate(L,Ll),append(AT,Ll,ATl),
findall(Q6,(member([Q5,Inl,Q6],Ll),not(member(Q6,AS))),L2),
append(R,L2,WQ),append(AS,L2,ASl),
expand_states _transits( WQ, AS1, ATI, Tl, T2, Q, T).
expand_states_transits([],Q,T,Tl,T2,Q,T).
delrepeate(S,SF) :- delrep(S,[] ,SF).
delrep([H|T],Sl,SF) :- member(H,T), !,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) ._ member(X,Z).
16.2. Источники
Источник есть объект S = (X,Q,Q09D9F), где X - входной
алфавит; Q - алфавит состояний, QQ Я Q - множество начальных
состояний, D£ g х Jf х Q- (недетерминированная) таблица переходов
(здесь в качестве входного сигнала допускается пустой символ,
обозначаемый *), F Q Q - множество выделенных состояний.
313
Тройка (q9a9q') из D называется переходом источника.
Пример. Х={0,1,2}; (2={<70>?1>?2>4з}; Go={^o^J; F={q29q3}\
d = {(?0»°»?i); (<7<>>Мз); (?o»i»?i); (4o>*>?<>); (?0>*>4i);
(?о»*»?з); (?i>*>4i); (?i,2,?2); (?2,0,?2); (^2,0,?3); (tf2,l,tf2);
(?2>2>42); ^зД»?2); (<ьД>?з); (?з>*>?о)Ь
Граф-схема этого источника изображена на рис. 16.6.
Заметим, что в случае источника некоторые дуги (стрелки) в его
граф-схеме могут быть помечены пустым символом (т.е. дуги ничем
не помечены).
Недетерминированный автомат есть частный случай источника, в
котором нет дуг, помеченных пустым символом. Детерминированный
автомат есть частный случай недетерминированного автомата, а
потому и частный случай источника.
Входное слово х = x(Q)x(l).. .х(к) допустимо источником 5, если
существует последовательность (2(0) ,(2(1),... ,(2(0 > • • • >£?(£) > (2(^+1)
(она называется ходом источника S на входном слове дс; множество
всех таких последовательностей обозначается через Rn(S9x)), где
каждое (2(0 есть конечная последовательность состояний <?0',0),
q(i9l)9...9q(i9ni)9 для которой:
?(0,0) € (20;
(?(«,;),*,tf0',/+l)) € Z); i=0tl Л; у^ОД,...,^-!;
(q(i,ni),x(0,q0+l,0)) € D; «=0,1 Л;
q(k+l9nk+1) € F.
В противном случае слово х источник S не допускает (отвергает).
Для примера источника из рис. 16.6 на входном слове х = 1 2 2 0 1
112 возможна следующая последовательность состояний:
1—>"
0
У
<и]
1 °Д
J1 1
*Ч с
f
*b
\
г
1
ш
2
ы—
Рис. 16.6
314
x=x(0) x(l) x(2) x(3) jc(4) *(5) x(6) x(l)
12201112
Чо 4x
Чо Ч\
Чз
Чо
e(o) g(d
9(0,0) 9(1,0)
9(0,1) 9(1,1)
9(0,2)
9(0,3)
Чг
fi(2)
9(2,0)
Чг
CO)
9(3,0)
• Чз Чз Чз Чг Чг
Чо Чо
Чо Чз
Чз
Чо
Чз
е(4) е(5) е(б) g(7) q(s)
9(4,0) 9(5,0) 9(6,0) 9(7,0) 9(8,0)
9(4,1) 9(6,1)
9(4,2) 9(6,2)
<?(4,3)
9(4,4)
9(4,5)
Так как q2 € F, то слово х допустимо источником S.
Поведение Beh(S) источника 5 есть множество всех слов,
допустимых источником S. Два источника эквивалентны, если они имеют
одинаковые поведения (т.е. если они допускают одно и то же
множество входных слов). Язык L Q X* представим (допустим, определим)
источником, если существует источник S, для которого L=Beh(S).
Множество Q'QQ состояний источника S=(X,Q,Q0,D,F) замкнуто, если
V?€Q 4q'£Q'((q',*,q)tD - q € Q'). Замыкание [(?'] множества Q'
есть наименьшее замкнутое множество состояний, содержащее Q'.
Для источника из рис.16.6 [{qQ}]={qQ,qx >Яъ)\ [{«Л = fai);
[{<72><73}]={4o>4i><72><b}; [{я2}]={я2}'
Теорема (о детерминизации источника). Пусть язык L Я X*.
Следующие утверждения равносильны.
1. Язык L представим конечным автоматом.
2. Язык L представим источником.
Доказательство. Следование 1 -> 2 тривиально, ибо всякий
автомат есть частный случай источника.
Покажем, что 2 -> 1. Пусть язык L представим источником S = (X,
Q,Q0,D,F). Построим автомат А = (X,S,s0,T,H), где SQP(Q) есть
множество всех замкнутых подмножеств множества Q (включая пустое
подмножество); начальное состояние 5"0=[Q0]; функция переходов Т :
S х X - S такова, что T(s,a)=[{q'£Q : 3q'£s (q',a, q) € D}];
множество выделенных состояний U={s€S : 3q€s(q€F)}.
315
.x(k) € Beh(A). Тогда
j(0),j(1),...,j(*M*+1)
Утверждение. Beh(S)=Beh(A).
Доказательство. Пусть слово дс=дс(0)дг(1).
существует . последовательность состояний
автомата А (рис. 16.7), для которой
s(0)€s0;
T(s(j)9x(j))=s(j+l)9 ;=0,1,... ,*;
*(*+1)€£Л
Состояние s(k+l)=[{q£Q : 3fl'€.rOO((tf',я,<?)€£>}]=$'.
Так как ^(/c+l)€t/, то существует состояние q'€s(k+l)9 причем q'
€ F. Возможны следующие случаи:
q'ts'. Тогда 3qes(k)((q9x(k)9q')€D)\
q'*[s'\,q'ts', т.е. ?'€[*']-*'.
Тогда существует последовательность состояний Q(fc+l),
начинающаяся с некоторого состояния q(k+l90)€s' и заканчивающаяся
состоянием q(k+l9n) € [s']9 причем (q(k+lj)9*9q(k+l9j+l)) €/),; =
0,1,... ,/i£+1-l. Найдется состояние q€s(k)9 для которого (<?,*(&),
<?(A:+1,0))€D. Продвигаясь к началу последовательности состояний
автомата А9 построим последовательность состояний источника
Замыкания
1 | г*
□
|—
□
*(о)
х(0)
s(l)
х(1)
s(2)
х(2)
и
s(k)
х(к)
D
s(k+l)
Я =
*(*)
Я(к,пк)
s(k)
s(k+l)
s(k)
ь
(к+1)
Рмс.16.7
316
e(0),Q(D,...,Q(A:),Q(A:+l), (16.1)
для которой:
?(0,0)€G0;
(q(i,n ),*(/),<7(*+l,0))€Z), /=0,1,...,*;
(<?(* J),*,<7(/,;+l))€D, /=0,1,... Л+1; (16.2)
j'=0,l,...,rtrl;
q(k+l,nk+l)^F.
Поэтому слово x€Beh(S) и, следовательно, Beh(A)=Beh(S).
Пусть теперь слово х = x(0)x(l).. .x(k)€Beh(S). Тогда
существует последовательность состояний (16.1), для которой выполняются
условия (16.2). Для соответствующей последовательности j(0),.y(l),
...,s(k+l) автомата А состояние g(fc+l,/ifc+1)€.y(fc+l), и потому s(k+
1)€£/. Следовательно, слово x€Beh(A). Так что Beh(S) Я Beh(A)y что
вместе с Beh(A)QBeh(S) дает Beh(X)=Beh{S).
Утверждение установлено. Теорема доказана.
Следствие. Класс множеств, представимых источниками, замкнут
относительно булевых операций.
Заметим, что если язык L в алфавите X автоматно представим, то
язык L автоматно представим над любым расширением X' алфавита X,
ибо автомат, представляющий язык L над X, можно рассматривать как
источник, представляющий язык L над X'.
16.2.1. Алгоритм детерминизации источника
Пусть источник S=(X,Q,Q0,D,F). Возьмем Q'QQ, a£X. Пусть S(Q',
я) = {q£Q : 3q'€Q'((q' ,a,q)€D} есть множество всех состояний, в
которые источник S переходит из состояний множества Q' под
воздействием входной непустой буквы а из X. Автомат А с тем же
поведением, что и источник 5, строим следующим образом.
1. Формируем замыкание множества начальных состояний источника
и объявляем это замыкание начальным состоянием конструируемого
автомата.
2. Если состояние s=Q'QQ автомата А уже построено, то T(s,a) =
[S(Qf,a)] есть состояние, в которое перейдет автомат А из
состояния s под воздействием буквы а.
3. Применяем п.2 алгоритма до тех пор, пока его применение
порождает новые состояния автомата А.
4. Объявляем выделенными те состояния s=Q'QQ автомата А,
которые содержат в себе выделенные состояния источника S.
Пример. ^={0,1}; Q={q^q^q2)\ £?0={<7о}; Р={Яо>Яг)- Таблица
переходов D источника S=(X,Q,{q0}9D9F) изображена на рис.16.8.
Таблица переходов детерминированного автомата А, эквивалентного
317
*■
Яо
0
JL 1
\Чг
1
4 У. 1
Рнс.16.8
источнику S, приведена в табл. 16.4. Выделенные состояния автомата
А помечены звездочками.
Таблица 16.4
0
1
{«.>
(Яо>Яг)
*
{<7i> {Яо,Яг)
0 {Яо,Яг}
{Яо,Я2) {«J
0
0
0
Замечание. Иногда будем задавать источник в виде S = (X9Q9D)
без указания множеств начальных и выделенных состояний. Пусть
Q'>Q">Q"' - подмножества из Q\ L(S9Q'9Q"') - поведение источника
S = (X9Q9Q'9D9Q"')9 а язык Lx = L(S9Q'9Q",(?"') есть множество
всех входных слов х9 для которых существует ход из Rn(S9x)9 в
котором все состояния лежат в множестве Q". Язык Lx представим
источником, который получается из источника S удалением всех ребер,
инцидентных на граф-схеме источника 5, состояниям вне Q".
16.2.2. Программа детерминизации источника
Процедура det(NDA,DA) по недетерминированному автомату NDA
строит ему эквивалентный детерминированный автомат DA. В
программе знак * есть символ пустого слова.
Процедура set_of _macro_states(X, Q, QO, Р, MQ) по
недетерминированному автомату строит множество макросостояний MQ
детерминированного автомата.
Процедура set_of_macro_transit(X,Q,Р,MQ,MP) no
недетерминированному автомату строит функцию переходов MP детерминированного
318
конечного автомата.
Процедура set__of _macro_jstates_disting(MQ, F, MFl) no множеству
макросостояний MQ и множеству выделенных состояний F строит
множество выделенных макросостояний MF1.
Процедура transit_f rom_one_macro_state(X, Q, Р, Н, МН) по
макросостоянию Н и по множеству входных сигналов X строит множество
следующих макросостояний МН.
Процедура transit(Q,P,H,In,Hl) по макросостоянию Н
недетерминированного автомата и входному символу In строит следующее
макросостояние HI.
Процедура close(Q,P,Ql) осуществляет замыкание подмножества Q
состояний. Рекурсия проводится по подмножеству Q и по таблице
переходов. Замыкание есть Q1.
Процедура disting(Q,F,Ql) по макросостоянию Q и подмножеству
выделенных состояний F определяет, является ли Q выделенным; если
да, то Ql = Q; если нет, то Q1 = [].
Процедура difsubset(X,Y,Z) из множества подмножеств X,
вычитает множество подмножеств Y; результат есть Z.
Процедура rename_automaton(MQ,MP,MF,MQ1,MP1, MFl) состояния в
множествах MQ, MP, MF переобозначает в qO, ql, q2, В результате
получим переобозначенные множества состояний MQ1,MP1,MF1
соответственно.
d(A,B) :- X=[0,l],Q=[qO,ql,q2],Q01=[qO],
P=[[q0,*,q0],[q0,*,ql],[q0,l,ql],[ql,*,q0],[ql,l,q2],
[q2,0,q2],[q2,l,qO]],F=[ql,q2], A=[X,Q,Q01,P,F] ,det(A,B).
det(NDA,DA) :- NDA=[X,Q,Q01,P,F],
close(Q01,P,Q0),set_of_macro__states(X,Q,Q0,P,MQ),
set_of_macro_transit(X,Q,P,MQ,MP),
set_of_macro_states_disting(MQ,F,MF),
DA1=[X,MQ,Q0,MP,MF],
write(,DAl=,),write(DAl),nl,
rename_automaton(MQ,MP,MF,MQl,MPl,MFl),MQl=[DQO|R],
retract(current_number(Roote, Number)),
DA=[X,MQ1,DQ0,MP1,MF1].
set_of_macro_states(X,Q,QO,P,MQ) :- S1=[Q0] ,S2=[Q0],
macro_states(X,Q,P,Sl,S2,MQl),del_rep_sets(MQl,MQ).
macro _states(X,Q,P,Sl,S2,MQ) :- S1=[H|T],
transit_from_one_macro_state(X,Q,P,H,H2),difsubset(H2,S2,Hl),
append(T,Hl,Sll),append(S2,Hl,S2l),
del_rep_sets(Sll, S12), del_rep_sets(S21, S22),
319
macro_states(X,Q,P,S12,S22,MQ).
macro_states(X,Q,P,[].S22,S22).
set_of_macro_transit(X,Q,P,MQ,MP) : -
findall([Ql,In,Q2],
(member (Ql, MQ), member(ln, X), transit(Q, P, Ql, In, Q2) ), MPl),
del_rep_sets(MPl ,MP).
set_of_macro_states_disting(MQ,F,MF1) : -
findall(Q, (member (Ql,MQ),disting(Ql,F,Q)),MF),
del_rep_sets(MF, MFl).
transit_from_one_macro_state(X,Q,P,H,MH) : -
f indall(Hl, (member(ln, X),
transit(Q,P,H,In,Hl)))MHl),
del_rep_sets(MHl ,MH).
transit(Q,P,H,In,Hl) :-
f indall(State2, (member(Statel, H) .member (State2, Q),
member([Statel,In,State2],P)),H2),
delrepeate(H2,H3),close(H3,P,Hl).
close(L,P,LV) :- close2(L,P,LV,P,K,L).
close2(L,P,LV,PP,K,LL) :- closel(L,P,LV,PP,K,LL),not(K=[]),
close2(K,PP,LLV,PP,KK,LV),!.
close2(L,P,LV,PP,K,LL) :- closel(L,P,LV,PP,K,LL),K=[],!.
closel([],[],LL,PP,[],LL) .
closel([X|Y],[],LV,PP,K,LL) :- closel(Y,PPILV,PP,K,LL).
closel([X|Y],[[X,*,Z]|P],[Z|LV],PP,[Z|K],LL) :-
not(member(Z,LL)),closel([X|Y]IP,LV>PP,K,LL).
closel(X,[Pl|P],LV,PP,K,LL) ._ closel(X,P,LV,PP,K,LL).
disting(LV,[FV|F],LV) :- member(FV.LV),!.
disting^LVjFVJFLFl) :- not(member(FV,LV)),disting(LV,F,Fl).
difsubset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member_set(R,Y)),append(Z,[R],Zl),
difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member_set(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
rename_automaton(MQ,MP,MF,MQl,MPl,MFl) :-
ren_autom(MQ,[],MP,MF,MQl,MPl>MFl).
ren_autom([B|R],AS,MP,MF,MQl,MPl,MFl) :- genatom(q.S),
substitl(B, MP, S, MP2), substit_set(B, MF, S, MF2),
ren_autom(R,[S|AS]IMP2,MF2,MQl,MPl,MFl).
320
ren_autom([],AS,MPl,MFl,MQl,MPl,MFl) :- reverse(AS,MQl).
substitl(B,[W|T],S,[x|V]) :-
substit_set(B,W,S,X),substitl(B,T,S,V).
substitl(B,[],S,[]).
substit_set(X,[Y|L],A,[B|M]) :-
if thenelse(equalset (X, Y), B=A, B=Y), substit_set(X, L, A, M).
substit_set(_,[ ],_,[])•
genatom(Roote,Atom) :- get__number(Roote,Number),
name(Roote, Namel), name(Number, Name2),
append(Namel, Name2, Name), name( Atom, Name).
get_number(Roote,Number) : -
retract(current_number(Roote,Numberl)),!,
Number is Numberl+1,
asserta(current_number(Roote, Number)).
get_number(Roote,0) :- asserta(current_number(Roote,0)).
del_rep_sets(S,SF) :- Sl=[] ,delr(S,Sl,SF).
delr([H|T],Sl,SF) :- member_set(H,T),delr(T,Sl,SF).
delr([H|T],Sl,SF) :- not(member__set(H,T)),
append(Sl,[H],S2),delr(T,S2,SF).
delr([],S2,S2) :- !.
delrepeate(S,SF) :- Sl=[],delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),append(Sl,[H],S2),
delrep(T,S2,SF).
delrep([],S2,S2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Vl|Y]) :- member_set(L,Y).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
reverse([],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
321
16.3. Регулярные языки
Пусть X - произвольный конечный алфавит.
Конкатенация (умножение) двух языков Lx и L2 из X* есть
множество Ьх-Ь2 = {z € X*: 3xyy€X*(x€Llyy€L2yz =х-у)}. Степень к языка
L есть множество Lk = L* L* ... • L, к раз. Примем по определению,
что L0 = {*}. Справедливо равенство L • 0 = 0 • L = 0. Итерация языка
L из X* есть множество L* = L1UL2UL3UL4U. .. Операции Клини есть
операции конкатенации, объединения, итерации.
Примеры.
1. {0,011,00}-{11,101} = {011,0101,01111,011101,0011,00101}.
2. {0}* = {0,00,000,...}.
3. {0,1}* есть множество всех непустых слов в алфавите {0,1}.
4. {0,1}* есть множество всех слов длины к в алфавите {0,1}.
Определение (регулярного языка). Одноэлементные языки из X
регулярны и имеют глубину построения 1. Если языки L,LlyL2 глубины
построения кук1Ук2 соответстенно регулярны, то языки (LjUL2),
(Ь^Ь2)У (L*) регулярны и имеют глубину построения тах(/:1 ,/г2)+1,
тах(/:1,А:2)+1, fc+1 соответственно.
Будем опускать скобки при записи регулярного языка, принимая
следующий приоритет операций: *, • , U; для одноэлементного языка
вместо {а} писать и просто а\ вместо {ауЬу...ус} писать иногда
аМЪМ.. . Vc; вместо объединения U при записи регулярных языков
использовать также знак V.
Теорема. Класс языков, представимых источниками, замкнут
относительно операций Клини.
Доказательство. Пусть языки Lx и L2 пред ставимы источниками
S, = (XyQfyQ'QyD'yF') и S2 = {XyQ"yQ"QyD"yF") соответственноv
Объединение LX\JL2 представимо источником S = (XyQ'K)Q"y Q0UQ0,
D'UD", F'UF").
Конкатенация ЬХ*Ь2 представима источником S = (XyQ'\JQ",Q0,Dy
F"), где D = D'\)D" U {(<?',*,<?") : <?'€ F\ q"* Q"o))-,
Итерация L* представима источником S = (Xy Q'yQ0y Dy F')y где
D = D' U {(<?,*,<?') : q € F'yq' € Q^,}.
Граф-схемы источников S2 и S2 при объединении объединяются.
Начальные состояния для S! и S2 становятся начальными состояниями
для S, а выделенные состояния для S} и S2 - выделенными
состояниями для S.
Граф-схемы источников S2 и S2 при конкатенации объединяются.
Добавляются пустые (т.е. ничем не помеченные) стрелки, ведущие из
выделенных состояний для S2 в начальные состояния для S2.
Начальные состояния для Sj являются начальными состояниями для S. Выде-
322
ленные состояния для S2 являются выделенными состояниями для S.
При итерации в граф-схеме для Sx добавляются пустые стрелки из
выделенных состояний для Sj в его начальные состояния.
Следствие. Класс языков, представимых автоматами, замкнут
относительно операций Клини.
Теорема (синтеза). Каждый регулярный язык представим некоторым
источником.
Доказательство. Индукция по глубине к построения языка.
БАЗИС, к = 1. Одноэлементные языки автоматно представимы;
следовательно, они гредставимы и источниками.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Предположим, что все регулярные
языки с глубиной построения меньше к представимы источниками.
ШАГ ИНДУКЦИИ. Покажем, что все регулярные языки с глубиной
построения к представимы источниками. Пусть регулярный язык L
имеет глубину построения к. Тогда L имеет один из видов: Ь1У)Ь2У
Ll'L2i L*. Так как регулярные языки LlyL2 имеют глубину
построения меньше к, то по предположению индукции они представимы
некоторыми источниками. Тогда язык L представим источником по теореме
о замкнутости класса языков, представимых источниками,
относительно операций Клини.
Следствие. Каждый регулярный язык автоматно представим.
Теорема (анализа). Всякий язык, представимый источником,
регулярен.
Доказательство. Так как классы языков, представимых
источниками и автоматами, совпадают, то теорему достаточно доказать для
автоматов. Пусть автомат А = (XyQ,q0,T,F), где Q = {q0>q19...9
qn}> F = {?/ >•••»?/ }> представляют язык L = Beh(A). Построим
множество входных слов £,-, с помощью следующей индуктивной
процедуры:
е\)} = {а£Х : T(qiya) = <?;};
е$ = Е\кг» и Е\кг» • оЙГ1^. 4Г1}. * - м.-."-
Если автомат А при подаче входного слова х = x(0)x(l)...
x(r-l) проходит последовательность состояний q(0) = qiyq(\)yq(2)y
... yq(r-l)yq(r) = q;y то скажем тогда, что х переводит А из q± в
qjy и автомат А проходит при этом через состояния q{\)yq{l)y... у
q(r-l). Индукцией по к можно показать, что множество входных слов
{к)
Ejj переводят А из qt в <?;, и не проводят А через состояния qv с
(к)
номерами v > к. Пусть Мх? .• - множество всех входных слов, которые
323
переводят А из q; в qj, и при этом не проводят А через состояния
q с номерами v > к.
Утверждение. e\j* = m\j\
Доказательство. Индукция по к. Для к = 0 утверждение очевидно.
Пусть оно верно для к = г - 1, т.е. Ejj = Мц . Покажем, что
оно верно для к = г. Пусть Л/,у (или £/; - множество всех
входных слов из M^j (или из E^j ), которые проводят А через
состояние qr. Ясно, что Е/у = Е^г • (ErJ! * ) • e/j x . Множество
АУ(Г) Д^(Г-1) U Д^(Г) 1Г(Г"'1) И АУ(Г)
М|; = М/; U Mtj = Ei;- U Mtj .
f(r)
;е>
rC)
Покажем, что М|; = £/у . Если входное слово дс € М,у проводит
.4 через qr s раз, то дс представимо в виде х = jc0jc1 .. ,xs_xxs,
(рис. 16.9). Тогда
дс0 € Af/r - tir , д^ € Afr;- - £г;
X/ € Mrr = Err , i = 1,2,... ,5-1;
хг-х2 • ... • jCj_! € (£,., l ) . Поэтому
.(Г-1)ч*
(г-1)
х € Е,г • (^Г Т • ЯгГ = ^;- • Отсюда
Mj'j = £,у . Если х € Е/у , то слово х переводит А из <7/ в 9;»
проводит А через <7Г, не проводит А через состояния <?v с номерами
v > г, т.е. х € M\j. Поэтому Е\)} = М-у . Равенство м\)} = £•''
доказано. Тогда
ч
Лг)
.(г-1)
гС)
(г-1)
.(г)
.(г)
*>'/ = е\) " и м-' = е)) " и **'/ = £55
Утверждение доказано. Продолжим доказательство теоремы.
Исходный автомат А имеет л+1 состояний.
х =
<7г | Яг
Здесь состояний <?г нет
Рмс.16.9
324
Язык L = Мхпу U ... UM^)1 регулярен согласно утверждению
о регулярности всех дизъюнктивных слагаемых.
Теорема доказана.
Замечание. Если пустое слово включается в состав
рассматриваемых языков, то итерация L* = L° U L1 U ..., где L0 = {*}.
Доказанные выше теоремы останутся справедливыми. Следует только
слегка изменить их доказательства, сделав поправку на пустое слово.
16.3.1. Программа вычисления источника для объединения
двух языков, представимых источниками
unionaut(Al,A2,A3) :- X=[0,l], Ql=[q01,qll],Q01=[q0l],
Pl=[[q01,0,qll],[q01,l,q0l],[qll,0,qll],[qll,l,q0l]],
Fl=[qll],Al=[X,Ql,Q01,Pl,Fl],Q2=[q02,ql2,q22],
Q02=[q02,q0l],
P2=[[q02,0,q02],[ql2,0,ql2],[q22,l,q22],[q02,l,q22],
[q22,0,ql2],[ql2,l,q02]],
F2=[ql2,q22], A2=[X,Q2,Q02,P2,F2],
unionset(Ql, Q2, Q3), unionset(Q01, Q02, Q03),
unionset(Pl,P2,P3),unionset(Fl,F2,F3),
A3=[X,Q3,Q03,P3,F3].
unionset([],X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
16.3.2. Программа вычисления источника для итерации
языка у представимого источником
d(A,B) :- X=[0,l],Q=[q0,ql,q2,q3],Q0=[q0,ql],
T=[[q0,0,ql],[ql,l,q2],[q2,0,q3],[q2,l,q3],[q3,*,q0]],
F=[q0,q3],A=[X,Q,Q0,T,F],
iterat_undetautomat(A,B).
iterat_undetautomat(A,B) :- A=[X,Q,Q0,T,F],
findall([Q3,*,Q4],(member(Q3,F),member(Q4,Q0)),L),
unionset(T,L,Tl),B=[X,Q,QO,Tl,F].
unionset([] ,X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
325
1633, Программа вычисления источника для конкатенации
двух языков, представимых источниками
d(A,B,C) :- X=[0,l],Ql=[qlO,qll,ql2],Q10=[qlO],
Tl=[[ql0,0,ql0],[ql0,0,qll],[qll,l,ql2]],
Fl=[qll,ql2] ,A=[X,Ql,Q10,Tl,Fl],
Q2=[q20,q21,q22,q23],Q20=[q20,q2l],
T2=[[q20,0,q2l],[q21,l,q22],[q22,0,q23],[q22,l,q23],
[q23,*,q20]] ,F2=[q20,q23] ,B=[X,Q2,Q20,T2,F2],
concat_automata( A, В, С).
concat_automata(A,B,C) :- A=[X,Q1,Q10,T1,F1] ,B=[X,Q2,Q20,T2,F2],
findall([Q3,*,Q4],(member(Q3,Fl),member(Q4,Q20)),L),
unionset(Tl, T2, S), unionset(S, L, T3), unionset(Ql, Q2, Q3),
C=[X,Q3,Q10,T3,F2].
unionset([],X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
16.4. Теоремы замкнутости для класса
автоматно представимых языков
Пусть X - конечный алфавит. Обращение слова х = x(0)x(l)...
x(k-l)x(k) из X* есть слово jc"1 = x(k)x(k-l).. .jc(1)jc(0). Если
множество М Q Х*у то М"1 = {х"~1: х € М).
Теорема. Класс языков, представимых источниками, замкнут
относительно операции обращения.
Доказательство. Пусть язык М представим источником S = (X,Q,
Q0,DyF). Тогда язык М представим источником S' = (X,Q,F\D',Q0),
где D' = {{qffa,q) : (q,a,qf) € D}, т.е. в граф-схеме источника S
все стрелки меняют свое направление на противоположное.
Следствие. Класс автоматно представимых языков замкнут
относительно операции обращения.
16.4.1. Программа вычисления источника для обращения
языка, представимого другим источником
d(A,B) :- X=[0,l],Q=[q0,ql,q2,q3],Q0=[q0,q2],
T=[[q0,0,ql],[q0,*,q3],[ql,l,q2],[q2,0,q2],[q2,0,q3],
[q2,l,q3],[q3,*,q0]],F=[q0,q3],A=[X,Q,Q0,T,F],
inverse_automaton(A,B).
inverse_automaton(A,B) :- A=[X,Q,Q0,T,F] ,add(*,X,Xl),
findall([Q4,In,Q3],(member([Q3,In,Q4],T)),Tl),
326
B=[X,Q,F,T1,Q0].
add(X,Y,[X|Y]).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Пусть X = {a0ialt...ak}, Y = {b0ib1,... ,^} - два конечных
алфавита, и пусть функция / : X -* У осуществляет проекцию с одного
алфавита на другой (т.е. с алфавита X на алфавит У). Пусть х =
x(0)x(l).. .х(г) - слово в алфавите X. Тогда слово f(x)
/(jc(0))/(jc(1)). . ./(*(/■)) есть проекция слова х при отображении /.
Если М Я X*, то /(Л/) = {/(*) : х £ М} есть проекция множества М
при отображении /.
Теорема. Класс языков, представимых источниками, замкнут
относительно проекции.
Доказательство. Пусть язык М представим источником S = (X,Q,
£>0,D,F), и функция / : X -* Y осуществляет проекцию с алфавита X
на алфавит Y. Тогда язык /(М) представим источником S' = (f(X),
Q,Q0,D',F), где П' = {(q,b9q'):3atX (f(a) = b & (q,a,q') € D],
т.е. в граф-схеме источника S всякая пометка а из X заменяется на
пометку f(a) из Y.
Следствие. Класс автоматно представимых языков замкнут
относительно проекции.
16.4.2. Программа вычисления источника для проекции
языка, представимого другим источником
d(A,Fun,B) :- X=[0,l,2],Q=[q0,ql,q2,q3],Q0=[q0,ql],
T=[[q0,0,ql],[q0,*,q3],[q0,2,ql],[ql,l,q2],[ql,2,ql],
[q2,0,ql],[q2,2,q2],[q2,0,q3],[q2,l,q3],[q3,*,q0]],
F=[q0,q3],A=[X,Q,Q0,T,F],
Fun=[[0,l],[l,0],[2,l]],projection_automaton(A,Fun,B).
projection_automaton(A,Fun,B) :- A=[X,Q,Q0,T,F] ,add(*,X,Xl),
findall([Ql,In,Q2],
(member(ln,Xl),member([ln,X2],Fun),
member([Ql,X2,Q2],T)),Tl),
B=[X,Q,Q0,T1,F].
add(X,Y,[X|Y]).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Пусть x = jc(0)jc(1). . .x(k) - некоторое слово в алфавите Х>
причем слово х содержит букву а. Аннулирование буквы а в слове х
есть стирание в слове х буквы а всюду, где она встречается.
327
Обозначим эту операцию через Ап(х,а). Пусть М Я X*. Тогда Лп(М,а)
= {Ап(х,а) : х € М}.
Теорема. Класс языков, представимых источниками, замкнут
относительно операции аннулирования.
Доказательство. Пусть язык М представим источником S = (X>Q,
QQyD,F). Тогда язык Ап(М,а) представим источником S' = {X,Q,Q0y
D\F), где D' = {(<?,&,<?') € D : b * a} U {(?,*,<?') : (q,a9q') €
£>}, т.е. в граф-схеме источника S стираются буквы а всюду, где
они встречаются, но сами стрелки, которые помечены буквой я,
остаются.
Следствие. Класс автоматно представимых языков замкнут
относительно операции аннулирования.
Пусть х = jc(0)jc(1). . .х(к)аа.. .а при х(к) * а есть слово в
алфавите Ху содержащем букву а. Тогда операция усечения слова х по
букве а (обозначение: Тгапс(х>а)) определяется как Тгапс(х,а) =
jc(0)jc(1). . .х(к). Если М Я Х*у то множество Тгапс(М,а) = {Тгапс(х,
а) : х € М}.
Теорема. Класс языков, представимых источниками, замкнут
относительно операции усечения.
Доказательство. Пусть язык М представим источником S = (XyQ,
Q0,£>,F). Пусть а € X и ак = ааа...а, к раз. Построим источник S'
= (XyQfQ0yDyG), где G = {q € Q : 3* 3<?'€ F ((<?,«*,?') € D} U F,
т.е. G есть множество всех тех состояний q € £), для которых
существует слово ак при некотором натуральном /г, переводящее источник
S из состояния q в состояние <?'> при этом q' € F. Источник S' с
поведением ЛГ = Beh(S') допускает все те слова, которые допускают
продолжение буквами а до слова, допустимого источником 5, а также
все слова, допустимые источником S.
Пусть S" - источник, допускающий множество М" всех слов в
алфавите X, не заканчивающихся на букву а. Источник, допускающий
множество М' П М" искомый.
Следствие. Класс автоматно представимых языков замкнут
относительно операции усечения.
Пусть X и Y есть два алфавита и множество М Я X*. Цилиндр,
восставленный из множества М по второй оси, есть множество Су12М
= {(х,у) € (XXY) : х € М}.
Теорема. Класс языков, представимых источниками, замкнут
относительно операции восстановления цилиндра.
Доказательство. Пусть язык М Я X* представим источником S =
(XjQ,Qo>DyF) и У - другой алфавит. Тогда множество Су12М предста-
вимо источником S' = (XXY,QyQQiD',F), где D' = {(q,(a,b),qf) :
(q,a,q') € D* и b € Y}, т.е. в источнике S все ребра, помеченные
328
символом а из X, помечаем символами (а,Ь), где Ъ € У.
Следствие. Класс автоматно представимых языков замкнут
относительно операции восстановления цилиндра.
Операцию восстановления цилиндра можно задать и по первой оси.
Эту операцию можно распространить на случай восстановления
цилиндра по любому количеству осей.
16.4.3. Программа вычисления источника для цилиндра,
восставленного из языка, представимого
другим источником
d(A,Y,B) :- X=[0,l],Q=[q0,ql,q2,q3],Q0=[q0,ql],
T=[[q0,0,ql],[q0,*,q3],[ql,*,ql],[ql,l,q2],[q2,0,q2],
[q2,0,q3],[q2,l,q3],[q3,*,q0]],
F=[q0,q3],A=[X,Q,Q0,T,F],Y=[0,l],
cylindr__automaton( A, Y, B).
cylindr_automaton(A,Y,B) :- A=[X,Q,Q0,T,F],
findall([Xl,Yl],(member(Xl,X),member(Yl,Y)),XY),
findall([Ql,[Xl,Yl],Q2],
(member([Xl,Yl],XY),member([Ql,Xl,Q2],T)),Tl),
B=[XY,Q,Q0,T1,F].
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Теорема. Алгоритмически разрешимы следующие свойства конечных
автоматов.
1. Представимый автоматом язык пуст (проблема пустоты).
2. Представимый автоматом язык бесконечен.
Доказательство. Пусть А = {X,Q,q0,T,F) есть детерминированный
конечный автомат.
1. Представимый автоматом язык пуст тогда и только тогда,
когда А не допускает ни одного слова длины не более мощности
алфавита X.
2. Представимый автоматом А язык бесконечен тогда и только
тогда, когда автомат А допускает слово х = х0х1х2, где *, € X*, i =
0,1,2, причем для одного из q € Q:
х0 переводит qQ в q\
хх переводит q в q\
х2 переводит q в выделенное состояние.
Последние три условия проверяются по п.1.
329
16.5. Минимизация числа состояний автомата с выходом
Будем рассматривать автоматы с общим входным и общим выходным
алфавитами. Два автомата эквивалентны, если они реализуют один и
тот же оператор.
Пусть А = (X,Y,Q,q0,T,B) есть автомат с выходом, реализующий
оператор О : X* - У*.
Два состояния q', g" автомата Л r-отличимы, если существует
входное слово х = x(0)x(l).. .x(r-l) длины г, для которого B(qf,х)
= у' = у" = B(q",x). Состояния q,q' отличимы, если они г-отличимы
при некотором г. Состояния q',q" r-неотличимы, если для любого
входного слова х длины не более г B(q',x) = B(q",x). Состояния
q',q" строго r-отличимы, если они г-отличимы, но неотличимы
никаким входным словом длины меньше г (т.е. (г-1)-неотличимы).
Состояния q' и q" неотличимы, если они г-неотличимы при любом г.
Аналогичные определения отличимости состояний q' и q" можно
ввести для двух автоматов А и В, причем q' есть состояние
автомата A, a q" - автомата В.
Автоматы А и В, реализующие операторы ®А и ®в, г-отличимы,
если существует входное слово х длины г, для которого ©^(х) =
©д(д:). Автоматы А и В отличимы, если они отличимы при некотором
г. Автоматы А и В r-неотличимы, если ©^(x) = 0#(д:) для всякого
входного слова х длины не более г. Автоматы А и В строго
r-отличимы, если они r-отличимы и (г-1)-неотличимы. Автоматы А и
В неотличимы, если они г-неотличимы при любом г.
Ясно, что если автоматы А и В неотличимы, то они реализуют
одинаковые операторы и, следовательно, эквивалентны.
Состояние q" достижимо из состояния q' автомата А, если
T(q',х) - q" для некоторого входного слова х.
Автомат А называется приведенным, если все его состояния
достижимы из начального состояния и попарно отличимы.
Автомат А называется минимальным, если он имеет наименьшее
число состояний среди всех автоматов, эквивалентных автомату А.
Теорема. Приведенный автомат является минимальным.
Доказательство. Допустим противное: приведенный автомат А =
(X,Y,Q,q0,T,B) не является минимальным, а минимальным является
автомат А' = (X,Y,Q',q'0,T',В'), эквивалентный автомату А, но с
числом состояний меньше, чем в А. Пусть Q' = {q'0,q'ly... ,<7^Ь
Пусть входные слова х0 ,хх,... ,хт переводят автомат А' из
начального состояния q'0 в состояния <7o><7i > • • • ><7т» а автомат А - в
состояния qi0,qii,- •. ,qim соответственно. Так как автоматы А и В
эквивалентны, то неразличимы пары состояний
330
?0' ?/0»
<7i> <7м;
(16.3)
Пусть состояние q t {?io»0m >• • • >0*m} = S, но <7 € (?. Так как ,4
- приведенный автомат, то состояние q отличимо от каждого
состояния из Q. Так как q достижимо из q0, то для некоторого
входного слова х T(qQ,x) = q. Пусть T'(q'Qyx) = q' при некотором
;. Так как автоматы А и В эквивалентны, то состояния q и q'
неотличимы. Пусть состояние q' соответствует согласно (16.3)
состоянию qtj € S. По (16.3) состояние q': неотличимо от <?,., но
q'j неотличимо от q и потому q неотличимо от д,;. Противоречие.
Следовательно, автомат А минимален.
Теорема. Если два состояния q, q' автомата А с к состояниями
отличимы, то они отличимы входным словом длины не более к2 (т.е.
/г2-отличимы).
Доказательство. Пусть состояния q, q' отличимы. Тогда они
строго r-отличимы при некотором г, т.е. найдется входное слово х
= x(0)x(l).. .x(r-l), для которого автомат А, начав работу над
словом х в состояниях q и q', перерабатывает его в различные
слова у = y(0)y(l)...y(r-l) и у' = y'(0)y'(l).. .у'(г-\) (т.е.
B(q,x) = у, B(q',х) = у') и проходит последовательность состояний
(7(0), q{\) ,...,(7(0; q(0) = q\
<7'(0),<7'(D,...,<?'('); q'(0) = q'
соответственно. При этом две последние буквы в словах у и у'
различны (т.е. у(г) * у'(г)). Для любых (дискретных) моментов
времени t{,t2 (О ^ tl < t2 ^ r-\) пары (столбцы)
q{tx) , q(tx+l) ,... , q(t2)
q'(tx), q'U^l),... , q'U2)
попарно различны, ибо при q(tx) = q(t2), q'(tx) = q'(t2),
выбросив из слова х = jc(0)jc(1). . .дг(^).. .x(t2).. .x(r-l) часть *(f,)
jt^+l).. .x(t2-l), получим более короткое слово x(0)x(l).. .x(tl-
l)x(t2).. .x(r-l), перерабатываемое автоматом А в различные слова
у(0) у(1) ... y(tx-l) y(t2) ... y(r-l),
у'(0)у'(1)... y'b.-lh'tt,) ... y'(r-l),
в противоречие со строгой /--отличимостью состояний q и q'. Так
как число различных пар состояний равно к2, то длина входного
слова х не превосходит к2.
331
Следствие. Если два состояния автомата А с к состояниями к2-
неотличимы, то они вообще неотличимы.
Доказанная теорема позволяет разбить множество состояний
автомата А с к состояниями на попарно непересекающиеся классы
неотличимых состояний. Использование этой теоремы при больших к
затруднительно, ибо необходимо проверить все состояния на отличимость
для всех входных слов длины к1. Поэтому сначала упрощают автомат,
исходя из особенностей задания его функций переходов и выходов, а
затем уже применяют доказанную теорему.
16.5.1. Склеивание неразличимых состояний
Пусть задан автомат А = (X ,Y,Q,q0,T,B) с выходом. Разобьем
множество его состояний на попарно непересекающиеся классы
неотличимых состояний: Q = Q0 U Qx U ... U Q^, Q, П Q; = 0; /,; = 0,
l,...,p; i * j . Для всякого i множество Q, содержит попарно
неотличимые состояния. Пусть q% - какой-либо представитель из Q,.
Построим автомат А' = (X,У\Q' ,Q,J' ,B'), где Q' = {£o,Gi,... ,Qp}\
Qq есть тот класс неотличимых состояний, который содержит qQ\
T'(Qi,a) = {T(q,a) : q € £,}; Bf{Qt,a) = B(q,a), q € Q{. Автоматы
А и А' эквивалентны. В самом деле, для всякого входного слова х =
х(0)х(1).. .х(г), если автомат А перерабатывает его в выходное
слово у = y(0)y(l).. .у(г), проходя последовательность состояний
q(0),q(l),... ,q(r),q(r+l) при д(0) = qQ, то автомат А', проходя
последовательность состояний (?(0),j2(l), ••• ,Q(r) ,Q(r+\) при Q(0) =
QQ, выдает выходное слово у' = y'(0)y'(l).. .у'(г), причем y'(t) =
B(Q(t),x(0) = B{q{t),x{t)) = y(t), где q(t) € Q(t), т.е. у' = у.
Состояния автомата А' попарно отличимы, ибо если бы некоторые
Qi, Qj были неотличимы, то их объединили бы на этапе построения
автомата А в один класс.
16.5.2. Алгоритм минимизации автомата
1. Если автомат А = (X,Y,Q,qQ,T,B) имеет состояния,
недостижимые из начального состояния q0, то построим автомат А' = (X,Y,
Q',qQ,T',B'), эквивалентный А, где Q' есть множество состояний
автомата А, достижимых из начального состояния qQ; функции Т' и
В' есть ограничения функий Г и Б на множество Q'. Если все
состояния в Q достижимы из q0, то А' есть А.
2. Построим классы неотличимости состояний автомата А' и
проведем операции их склеивания. Получим автомат А", эквивалентный
автомату А'.
3. Автомат А" приведенный и, следовательно, минимальный.
Пример 1. Пусть автомат А задан в табл. 16.5.
332
Множество столбцов, помеченных состояниями 1,6 и 3,4,
одинаковы; эти пары состояний заведомо склеиваются. В результате
склеивания указанных пар состояний получаем автомат с шестью
состояниями (табл.16.6). Одинаковых столбцов в табл.16.6 больше нет.
Таблица 16.5
0
1
0
0,0
1,1
1
2,0
7,1
2
3,1
2,0
3
1,1
4,0
4
1,1
4,0
5
7,1
6,0
6
2,0
7,1
7
4,0
5,1
Таблица 16.6
0
1
0
0,0
1,1
1
2,0
7,1
2
3,1
2,0
3
1,1
3,0
5
7,1
1,0
7
3,0
5,1
Строим теперь разбиение множества состояний автомата,
приведенного в табл. 16.6, на попарно непересекающиеся классы
неотличимых состояний. Классы эти строятся последовательно: сначала
классы 1-неотличимых состояний, затем 2-неотличимых, 3-неотличимых, и
так далее.
Исходим из множества состояний {0,1,2,3,5,7} автомата из
табл. 16.6. Запишем это множество матрицей-строкой М0 = 012357.
Подаем на вход автомата слово х = 0. Автомат переходит в
состояния 023173 и выдает на выходе 001110. Состояния 012357
разбиваются на два класса {0,1,7} и {2,3,5} состояний, неотличимых словом
х = 0. Запишем эти два множества строкой 017.235, разделив точкой
два полученных класса. Слову х = 0 сопоставим матрицу М19
приведенную на рис. 16.10.
Исходим теперь из последней строки состояний 017.235 в Мг На
вход автомата подаем слово х = 1. Автомат переходит в состояния
175231 и выдает на выходе 111000. Классы состояний 017 и 235
словом х = 1 неотличимы. Слову х = 1 ставим в соответствие
матрицу М2 (рис. 16.10).
0 и 1 исчерпывают все слова длины 1, поэтому состояния классов
017 и 235 1-неотличимы.
Исходим из последней строки 017.235 в М2. На вход автомата
подаем слово х = 00. Автомат перейдет в состояния 031123 и выдаст
на выходе 011100. Класс 017 разбивается на два класса 0.17, а
333
0
0 1 7.2 :
0 3i l :
0 1 1 1 (
0.1 7.2.:
0
0 12 3 5
0 2 3 17
0 0 111
0 17
$ 5
г з
) 0
J 5
2 3
Л/3
1
2
0
1
7
3
0
5
7
3
0
7
0 1
Л/,
1
3 5
7 5
1 1
3 5
L 2
Л/
3
1
5 7
1
3
1
1
мо
0
0
1
1
0
7. 3
1 1
1 0
7. 3
1
7
1
1
5
2
0
5
1
7. 2
5 2
1 0
7
2
Л/5
3 5
3 1
0 0
3 5
Л/2
1
1 7.3 5
7 13 7
10 0 1
1.7 . 3.5
Рнс.16.10
класс 235 на два класса 2.35 состояний. Запишем эти множества
строкой 0.17.2.35, разделив точками полученные классы. Сопоставим
слову х = 00 матрицу М3 (рис. 16.10).
Исходим из последней строки 0.17.2.35 в М3. Так как
одноэлементные множества {0} и {2} дальнейшего подразбиения не допускают,
то достаточно взять строку состояний 17.35. На вход автомата
подаем слово х = 01; сопоставим ему матрицу М4, (рис. 16.10).
Разбиения классов 17 и 35 не произошло. Не произойдет нового
разбиения и при подаче на вход слова х = 10 (матрица М5).
Исходим из последней строки 17.35 матрицы М5. На вход автомата
подаем слово х = 11; ему соответствует матрица М6, приведенная на
рис. 16.10. Классы 17 и 35 разделились на одноэлементные множества
и дальнейшего разбиения не допускают.
На этом построение классов неотличимости заканчивается. Все
шесть состояний оказались попарно отличимыми словами (табл. 16.7).
На пересечении строки i и столбца ; (/ < ;) стоит слово, которое
отличает состояния / и ;.
334
Таблица 16.7
0
1
2
3
5
1
00
2
0
0
3
0
0
00
5
0
0
00
11
7
00
11
0
0
0
Автомат (см.табл. 16.6) является минимальным. Построение
классов неотличимости состояний автомата из табл. 16.6, оформленное в
виде дерева, приведено на рис. 16.10. Дерево строится от корня к
листьям, сверху вниз, а в каждом ярусе узлов слева направо.
Пример 2. Минимизировать автомат, приведенный в табл. 16.8.
Таблица 16.8
0
1
0
2,0
4,0
1
3,0
5,0
2
2,0
4,1
3
3,0
5,1
4
4,1
0,1
5
5,1
1,1
Одинаковых столбцов в табл. 16.8 нет. Построим разбиение
множества состояний автомата на попарно непересекающиеся классы
неотличимых состояний. Построение оформим в виде дерева (рис. 16.11).
Исходим из множества состояний автомата, заданного строкой М0
= 012345. Слову х = 0, поданному на вход автомата, сопоствим
матрицу Мх так же, как это делали в предыдущем примере.
Разделение множества состояний на одноэлементные множества не
произошло. Затем так же, как это делали в предыдущем примере,
последовательно строим матрицы М0, М1У ... , М10. Первые две строки
матрицы М, задают фунцию /,-: Q -» Q с графиком G,. Если при
построении матрицы М, окажется, что G, Я Gj для некоторого ; < /, то
эту матрицу помечаем крестом; на такой матрице дальнейший рост
дерева прекращается: ответвлений от этого узла больше не будет.
На рис. 16.11 таковы матрицы М3, М4, М7, М8, М9, М10, у которых G3
с Gl9 GA С G2, G7 с G5, G& Я G6, G9 Я G3, G10 Я G2. Строка 4 в
последней построенной матрице М10 указывает классы неотличимости
состояний {0,1}, {2,3}, {4,5}. Склеиваем их и получаем
эквивалентный исходному минимальный автомат; он приведен в табл. 16.9.
33S
1
0
0 1 2 3 4 5
2 3 2 3 4 5
0 0 0 0 11
0 12
0 12 3.4 5
2 3 2 3 4 5
0 0 0 0 11
0 12 3.4 5
X
0
0 1.2 3.4 5
4 5.4 5.2 3
0 0 1 111
0 1.2 3.4 5
M3
A/7
3.4 5
0 12
3 4 5
M,
1
0 12 3 .4 5
4 5 4 5 0 1
111 111
0 12 3 .4 5
>
<
1
0 1.2 3.4 5
0 10 14 5
0 0 1 111
0 1.2 3.4 5
M4
M8
M0
1
0 12 3.45
4 5 4 5 0 1
0 0 11 11
0 1.2
0
0 1.2 3.4 5
4 5 4 5 2 3
111 100
0 1.2 3.4 5
3.45
M2
A/5
1
0 1.2 3.4 5
0 1 0 14 5
11 110 0
0 1.2 3.4 5
0
0 1.2 3.4 5
2 3 2 3 4 5
0 0 0 Oil
0 1.2 3.4 5
A/,
1
0 1.2 3.4 5
4 5 4 5 0 1
0 0 0 0 11
0 1.2 3.4 5,
XX XX
Рис.16.11
Входные слова, отличающие его состояния 0, 2 и 4, указаны в
табл. 16.10.
336
Таблица 16.9
Таблица 16.10
О
1
О
2,0
4,0
2,0
4,1
4,1
0,1
0
2
2
1
4
1
0
16.5.3. Алгоритм разбиения множества состояний
на классы неотличимых состояний
Пусть А = {X,У\QyqQyT\В) есть автомат, в котором X = {1,2,...,
1*1}, У = {1,2,..., |У|}, Q = {1,2,..., lei}, q0 = 1. Разбиение
множества состояний Q на классы неотличимых состояний оформим в
виде дерева. Будем строить его от корня к листьям, сверху вниз, а
в каждом ярусе узлов слева направо.
0. В корне дерева помещаем матрицу-строку М0 = 12...I&I
состояний автомата.
1. Допустим, что матрицы М09М19... 9М;_1 построены. Переходим к
построению матрицы Л/,. Возможны следующие случаи:
1) из матрицы М/_! исходит ребро, помеченное входным символом
а < \х\. Тогда Л/,- строим следующим образом. Из последней строки
матрицы М/_! выбрасываем одноэлементные классы. Результат
Ян Ян ••• Я\уп^Яг\ Ян --Яг
делаем строкой 1 в М;. Строки
T(qll9a+1)-T(q12ya+1)-
B(qllta+1) B(q12ya+1)
7(<7Г)Лг,д+1),
В(Ягпг><*+1)
делаем в Л/, строками 2 и 3 соответственно. Каждый класс qml ...
Ят п (т = 1,2,...,г) строки 1 в Л^ разбиваем на подклассы так,
что два состояния q и q' из {<?Wi, • • • ,<?w n ) попадут в один класс
тогда и только тогда, когда Б(^,а+1) = B\q',a+l). Вновь
полученные классы qml ... qm^x* ^w,/1 + i ••• <7m,/2 # • • • # Ят,15_1 • • • Яту15
(m = 1,2,...,г), отделенные друг от друга точками, запишем в одну
строку и сделаем ее строкой 4 в Л/,-. Матрица М, построена.
Первые две строки в Л/, задают функцию fi'-Q-*Qc графиком
G,. Если Gj Я Gv для некоторого v, 0 < v < i, то матрицу Л/,
помечаем крестом.
Если строка 4 в М/ представляет собой разбиение на
одноэлементные множества, то алгоритм работу заканчивает, и строка 4 в Л/,
дает искомое разбиение;
2) из матрицы Mi_x исходит ребро (с матрицей на конце), поме-
337
ченное входным символом \х\. Возможны следующие случаи:
а) все построенные матрицы помечены крестом. Тогда алгоритм
заканчивает работу, и строка 4 в матрице с наибольшим номером
дает искомое разбиение;
б) не все построенные матрицы помечены крестом. Среди таких
матриц выбираем матрицу с наименьшим номером, испускаем из нее
ребро, помечаем его входным сигналом 1 и в концевой вершине этого
ребра строим матрицу Л/, так же, как это делали в случае 1.
3. Переходим к п.2.
Замечание. При функционировании алгоритма не нужно хранить все
дерево матриц Л/,. Из всего дерева при его построении следует
сохранять только множества ML листьевых матриц этого дерева, а также
получающиеся в процессе построения дерева матриц М, множество SF
функций /,- и текущее разбиение D множества состояний на классы
неотличимости.
Приведенный алгоритм минимизации числа состояний автомата
имеет достаточно большую вычислительную сложность. Поэтому исходный
автомат предпочтительнее упростить сначала каким-либо другим
более простым способом, например, склеив состояния, столбцы для
которых в таблице переходов (и выходов) автомата одинаковы. Такую
программу основной программе минимизации числа состояний автомата
и предпосылаем.
16.5.4. Программа уменьшения, числа состояний автомата
склеиванием состояний с одинаковыми столбцами
в таблице переходов и выходов
Процедура min_on_columns(A,B) уменьшает число состояний
автомата А склеиванием состояний с одинаковыми столбцами в таблице
переходов и выходов; результат есть автомат В.
Процедура collect_autom_columns(Q,T,E,Ac,Cs) по множеству
состояний Q, таблицам Т и Е переходов и выходов строит список Cs
столбцов в таблицах переходов и выходов автомата А.
Процедура undisting_subs_states(Cs,[] ,Cs,SubsSt), по множеству
Cs столбцов таблиц Т и Е переходов и выходов строит список SubsSt
тех неотличимых состояний, столбцы для которых в таблице
переходов и выходов исходного автомата А одинаковы.
Остальные процедуры взяты из последующей программы минимизации
конечного автомата.
d(A,B) :- X=[0,l],Y=[0,l],Q=[q0,ql,q2,q3,q4,q5,q6],Q0=q0,
T=[[q0,0,ql],[q0,l,q2],[ql,0,ql],[ql,l,q3],[q2,0,q3],
[q2,l,q4],[q3,0,q5],[q3,l,q6],[q4,0,q6],[q4,l,q5],
338
[q5,0,q3],[q5,l,q4],[q6,0,ql],[q6,l,q2]], '
E=[[q0,0,l],[q0,l,0],[ql,0,l],[ql,l,0],[q2,0,l],[q2,l,l],
[q3,0,0],[q3,l,0],[q4,0,l],[q4,l,0],[q5,0,l],[q5,l,l],
[q6,0,l],[q6,l,0]],A=[X,Y,Q,T,E],min_on_columns(A,B).
min_on_columns(A,B) :- A=[X,Y,Q,T,E],
collect_autom_columns(Q,T,E, [ ],Cs),
undisting_subs_states(Cs, [ ],Cs,SubsSt),
write(' SubsSt='), write(SubsSt), nl,
construction( A, SubsSt, Bl),
writeOBlV^writeCBl^nl,
rename_automaton(Bl,B).
collect_autom_columns([H|R] ,T,E,Ac,Cs) :-
findall([St,Ex],(member([H,In,St],T),member([H,In,Ex],E)),L),
collect_autom_columns(R,T,E,[[H|L]|Ac],Cs).
collect_autom_columns( [ ], T,E, Ac, Cs) : - reverse(Ac, Cs).
undisting_subs_states([[Hl|Rl]|R2],Ac,RC,SubsSt) :-
findall([H3|R3],(member([H3|R3],RC),Rl=R3),L),
difset(RC,L,RCl),findall(St,member([St|R4],L),LSt),
undisting_subs_states(RCl, [LSt | Ac],RC1, SubsSt).
undisting_subs_states( [ ], Ac, [ ],SubsSt) : - reverse(Ac,SubsSt).
construction^,DS,Bl) :- A=[X,Y,Q,P,B] ,conl(Q,P,B,DS,N,Nl,N2),
delrepeate(Nl,Ml),delrepeate(N2,M2),Bl=[X,Y,N,Ml,M2].
conl(Q,P,B,[DSl|DS],N,Nl,N2) :-
c(Q,P,B,DSl,L,Ll,L2),conl(L,Ll,L2,DS,N,Nl,N2).
conl(Q,P,B,[],Q,P,B).
c(Q,P,B,DSl,L,Ll,L2) :- first(DSll,DSl),delfirst(DSl,DSBP),
pl(P,B,Q,DSll,DSBP,L,Ll,L2).
delfirst([A|B],B).
pl(P,B,Q,DSll,[D|DSBP],L,Ll,L2) :-
subst_states_in_PandB(D,P,DS11, [ ],PN),
subst_states_in_PandB(D,В,DS11, [ ],BN),
delall(D,Q,Ql),pl(PN,BN,Ql,DSll,DSBP,L,Ll,L2).
pl(P,B,Q,DSll,[],Q,P,B).
rename_automaton(B2,Bl) :-
rename_states_qr(B2,B3),rename_states_rq(B3,Bl).
rename_states_qr(Bl,B2) :- B1=[X,Y,Q,P,B],
rename_states_qrl(Q,P,B,[],Ml,M2,M3),B2=[X,Y,Ml,M2,M3].
rename_states_qrl([Ql|Q],P,B,N,Ml,M2,M3) :- genatom(r,R),
subst_states_in_PandB(Ql, P, R, [ ], PN),
339
subst_statesJn_PandB(Ql,B,R,[],BN),append(N,[R],Nl),
rename_states_qrl(Q,PN,BN,Nl,Ml,M2,M3).
rename_states__qrl([],P,B,N,N,P,B).
rename_states_rq(B2,Al) :- B2=[X,Y,Q,P,B],
rename_states__rql(Q,P,B,[],Ml,M2,M3),Al=[X,Y,Ml,M2,M3].
rename_states_rql([Rl|R] ,P,B,K,M1,M2,M3) :-
name(Rl,[H|T]),name(Ql,[H3|T]),
subst_states_in_PandB(Rl,P,Ql,[],PN),
subst_states_in_PandB(Rl,B,Ql,[],BN),append(K,[Ql],Kl),
rename_states_rql(R,PN,BN,Kl,Ml,M2,M3).
rename_states_rql([],P,B,K,K,P,B).
subst_states_in_PandB(D,[Pl|P],DSll,K,PN) :-
substitute(D,Pl,DSll,PP),append(K,[PP],Kl),
subst_states_in_PandB(D, P, DS11, Kl, PN).
subst_states_in_PandB(D, [ ]|, DS11, Kl, Kl).
genatom(Roote,Atom) :- get_number (Roote, Number),
name(Roote, Namel), name(Number, Name2),
append(Namel,Name2,Name),name( Atom, Name).
get__number (Roote,Number) : -
retract(current_number(Roote,Numberl)),!,
Number is Numberl+1,
asserta(current_number (Roote, Number)).
get_number(Roote ,0) : - asserta(current_number (Roote,0)).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
substitute(D,[],A,[]).
substituted,[D|L],A,[A|M]) :- !, substituted,L,A,M).
substituted,[Y|L],A,[Y|M]) :- substituted,L,A,M).
delrepeate(S,SF) :- Sl=[], delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member (H, T),! ,delrep(T, SI, SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),append(Sl,[H],S2),
delrep(T,S2,SF).
delrep([],S2,S2).
delall(X,[],[]).
delall(X,[X|L],M) :- ! ,delall(X,L,M).
delall(X,[Y|Ll],[Y|L2]) :- delall(X,Ll,L2).
340
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
delfirst([A|B],B).
first(X,[X|Y]).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
16.5.5. Программа минимизации детерминированного
автомата с выходом
Процедура min(A,Bl) по детерминированному автомату с выходом
A=[X,Y,Q,qO,P,B] строит эквивалентный автомату А минимальный
автомат В1.
Процедура outp(Q,Outl,Out,Yl) по множеству состояний Q и
выходному символу Y строит состоящую сплошь из 1 строку Out той же
длины, что и длина списка Q. Например, если Q=[q0,ql,q2,q3], то
Out=[l,1,1,1].
Процедура leaf_matrix(A,ML,DS,DS1,SF,SFl) осуществляет
обработку списка листьевых матриц, добавляя к ML или удаляя из ML вновь
получившиеся матрицы. DS1 - текущее разбиение множества состояний
на классы неотличимости; SF1 - множество функций, задаваемых
двумя первыми строками матриц из ML; A - автомат. Например, если
A=[[0,l],[0,l],[q0,ql,q2,q3,q4,q5],[[q0,0,q2],[q0,l,q4],
[ql,0,q3],[ql,l,q5],[q2,0,q2],[q2,l,q4],[q3,0,q3],
[q3,l,q5],[q5,0,q5],[q5,l,ql],[q4,0,q4],[q4,l,q0]],
[[q0,0,0],[q0,l,0],[ql,0,0],[ql,l,0],[q2,0,0],[q2,l,l],
[q3,0,0],[q3,l,l],[q5,0,l],[q5,l,l],[q4,0,l],[q4,l,l]]],
ML=[[[[q0,ql,q2,q3,q4,q5]],[q0,ql,q2,q3,q4,q5],
[0,0,0,0,0,0],[q0,ql,q2,q3,q4,q5]]],
DSl=[[qO,ql,q2,q3,q4,q5]],SFl=[],
то
DS=[[qO,ql],[q2,q3],[q4,q5]],
SF=[[[q0,q2],[q2,q2],[ql,q3],[q3,q3],[q4,q4],[q5,q5]],
[[q0,q4],[ql,q5],[q2,q4],[q3,q5],[q4,q0],[q5,ql]],
[[q2,q4],[q3,q5],[q4,q2],[q5,q3],[q0,q4],[ql,q5]],
[[q2,q0],[q3,ql],[q4,q4],[q5,q5],[q0,q0],[ql,ql]]].
Процедура one_element_division(DS) проверяет классы
неотличимости состояний на одноэлементность. Например, если DS=[[ql],
[q2], [q3], [q4]], то процедура успешна. Если DS=[[ql,q2], [q3],
[q4]], то процедура безуспешна.
Процедура list_matrix(A,LastM,DSl,List) по матрице LastM вы-
341
числяет список последовательно получаемых матриц, каждая из
которых получается из матрицы LastM при подаче на нее очередного
входного сигнала из X. Например, если Х=[0,1,2], то результатом
будет список матриц List=[M0,Ml,M2]; при этом получаются матрицы:
МО из LastM при подаче входа 0;
Ml из LastM при подаче входа 1;
М2 из LastM при подаче входа 2.
DS1 - последняя строка предыдущей матрицы. Например, если
A=[[0,l],[0,l],[q0,ql,q2,q3,q4,q5],
[[q0,0,q2],[q0,l,q4],[ql,0,q3],[ql,l,q5],[q2,0,q2],[q2,l,q4],
[q3,0,q3],[q3,l,q5],[q5,0,q5],[q5,l,ql],[q4,0,q4],[q4,l,q0]],
[[q0,0,0],[q0,l,0],[ql,0,0],[ql,l,0],[q2,0,0],[q2,l,l],
[q3,0,0],[q3,l)l],[q5,0,l],[q5,l,l],[q4,0,l],[q4,l,l]]],
LastM=[[[q0,ql,q2,q3,q4,q5]],[q0,ql,q2,q3,q4,q5],[0,0,0,0,0,0],
[q0,ql,q2,q3,q4,q5]],DSl=[[q0,ql,q2,q3,q4,q5]],
то
List=[[[q0,ql,q2,q3,q4,q5],[q2,q3,q2,q3,q4,q5],[0,0,0,0,l,l],
[[q0,ql,q2,q3],[q4,q5]]],[[[q0,ql,q2,q3],[q4,q5]],
[q4,q5,q4,q5,q0,ql],[[q0,ql],[q2,q3],[q4,q5]]]].
Процедура next_matrix(A,M,L,In,Ml) по матрице М и входу In
строит новую матрицу Ml. A - автомат, L - последняя строка
предыдущей матрицы. Например, если
A=[[0,l],[0,l],[q0,ql,q2,q3,q4,q5],[[q0,0,q2],[q0,l,q4],
[ql,0,q3],[ql,l,q5],[q2,0,q2],[q2,l,q4],[q3,0,q3],[q3,l,q5],
[q5,0,q5],[q5,l,ql],[q4,0,q4],[q4,l,q0]],
[[q0,0,0],[q0,l,0],[ql,0,0],[ql,l,0],[q2,0,0],[q2,l,l],
[q3,0,0],[q3,l,l],[q5,0,l],[q5,l,l],[q4,0,l],[q4,l,l]]],
M=[[[q0,ql,q2,q3,q4,q5]],[q0,ql,q2,q3,q4,q5],[0,0,0,0,0,0],
[q0,ql,q2,q3,q4,q5]],In=l,L=[[q0,ql,q2,q3],[q4,q5]],
то Ml=[[[q0,ql,q2,q3],[q4,q5]],[q4,q5,q4,q5,q0,ql],
[0,0,l,l,l,l],[[q0,ql],[q2,q3],[q4,q5]]].
Процедура function(Q,Ql,F) по спискам Q и Ql строит список F,
каждый элемент которого есть список, состоящий из одного элемента
списка Q и соответствующего элемента списка Q1. Например, если
Q=[q0,ql,q2,q3], Ql=[q0,ql,q2,q3], то F=[[q0,q0] ,[ql,ql] ,[q2,q2],
[q3,q3]].
Процедура out_qxqy(SP,In,Ll,P,B,Q2,Y2) по множеству SP матриц,
входу In, функциям переходов Р и выходов В строит новую строку
соответствующих состояний Q2 и выходов Y1. Например, если
P=[[q0,0,q2],[q0,l,q4],[ql,0,q3],[ql,l,q5],
[q2,0,q2],[q2,l,q4],[q3,0,q3],[q3,l,q5],[q5,0,q5],[q5,l,ql],
[q4,0,q4],[q4,l,q0]], B=[[q0,0,0],[q0,l,0],[ql,0,0] ,[ql,l,0],
342
[q2,0,0],[q2,l,l],[q3,0,0],[q3,l,l],[q5,0,l],[q5,l,l],[q4,0,l],
[q4,l,l]],SP=[[q0,q2],[ql,q3],[q2,q2]],In=0,L=[q0,ql,q2],
то Q2=[q2,q3,q2], Y2=[0,0,0].
Процедура division(D,Y,Dl) по разбиению состояний списка D и
списку выходов Y строит новое разбиение состояний на классы
неотличимости D1. Например, если D=[[q0,ql,q2] ,[q3,q4] ,[q5,q6]], Y =
[0,1,0,1,1,0,1], то Dl=[[q0,q2],[ql],[q3,q4],[q5],[q6]].
Процедура division_Y(D,Y,DY) по разбиению состояний списка D и
списку выходов Y строит разбиение DY, соответствующее разбиению
списка D. Например, если D=[[q0,ql,q2],[q3,q4] ,[q5,q6]], Y=[0,1,
0,1,1,0,1], то DY=[[0,1,0],[1,1],[0,1]].
Процедура new_division(D,DY,Dl) по разбиению состояний списка
D и разбиению списка выходов DY строит новое разбиение D1.
Например, если D=[[q0,ql,q2] ,[q3,q4] ,[q5,q6]], DY=[[0,1,0] ,[l,
1],[0,1]], то Dl=[[q0,q2],[ql],[q3,q4],[q5],[q6]].
В предикате div(Q,Y,Yl,Beg,Rest), если Q=[ql,q2,q3], Y=[0,1,0,
1,1,0], Yl=[], то Beg=[l,0,l], Rest=[l,l,0].
В предикате part_div(Q,QY,Y,PD), если Q=[ql,q2,q3], QY = [[ql,
0],[q2,l],[q3,0]], Y=[0,l], то PD=[[ql,q3] ,[q2]].
Процедура div_Y(D,Y,Yl,DY) компонует последовательно
полученные предикатом div(Q,Y,Yl,Beg,Rest) множества Beg в искомое
множество DY. Процедура
processing_list_matrix(List, NextList, LI, DS, DS1, SF, SFl)
обрабатывает список матриц List, вычисленный процедурой
list_matrix( A, LastM, DS1, List),
удаляя из него те матрицы, функции F которых встречались ранее
(содержатся в списке функций SF) и оставляя те матрицы, функции
которых ранее не встречались. В обоих случаях при рекурсивном
обращении заменяем старое разбиение DS1 состояний на классы
неотличимости на текущее и старое множество функций SF1 на новое.
Например, если
List=[[[[q0,ql],[q2]],[q2,q3,q2],[0,0,0],[[q0,ql],[q2]]],
[[[q0,ql],[q2]],[q4,q5,q4],[l,l,l],[[q0,ql],[q2]]]],
Ll=[], DSl=[qO,ql,q2], SFl=[[[qO,q2] ,[q2,q2] ,[ql,q3]],
[[q0,q5],[ql,q4],[q2,q5]]],
то DS=[[qO,ql],[q2]], SF=[[[qO,q2] ,[q2,q2] ,[ql,q3]] ,[[q0,q5],
[ql,q4],[q2,q5]],[[q0,q4],[ql,q5],[q2,q4]]].
Если все данные оставить теми же, изменив только SF1:
SFl=[[[q0,q2],[q2,q2],[ql,q3]],[[q0,q4],[ql,q5],[q2,q4]]],
то теперь
343
SF=[[[q0,q2],[q2,q2],[ql,q3]],[[q0,q4],[ql,q5],[q2,q4]]].
Процедура construction(A,DS,Bl) по автомату А, разбиению
множества состояний DS на классы неотличимых состояний строит
эквивалентный автомату А минимальный автомат В1.
Процедура rename_automaton(Bl,B2) по минимальному автомату В1,
состояния которого есть некоторые подмножества состояний
исходного автомата А, производит перенумерацию состояний в В1 в
естественном порядке: q0,ql,q2 и так далее.
dl(A,Bl) :- X=[0,1], Y=[0,1],
Q=[q0,ql,q2,q3,q4,q5],
P=[[q0,0,q2],[q0,l,q4],[ql,0,q3],[ql,l,q5],
[q2,0,q2],[q2,l,q4],[q3,0,q3],[q3,l,q5],
[q4,0,q4],[q4,l,q0],[q5,0,q5],[q5,l,ql]],
B=[[qO,0,0],[qO,l,0],[ql,0,0],[ql,l,0],
[q2,0,0],[q2,l,l],[q3,0,0],[q3,l,l],
[q4,0,l],[q4,l,l],[q5,0,l],[q5,l,l]],
A=[X,Y,Q,P,B],
minimization_automaton(A,Bl)-
d2(A,BD :- X=[0,1], Y=[0,1],
Q=[q0,ql,q2,q3,q5,q7],
P=[[q0,0,q0],[q0,l,ql],[ql,0,q2],[ql,l,q7],[q2,0,q3],
[q2,l,q2],[q3,0,ql],[q3,l,q3],[q5,0,q7],[q5,l,ql],
[q7,0,q3],[q7,l,q5]],
B=[[q0,0,0],[q0,l,l],[ql,0,0],[ql,l,l],[q2,0,l],[q2,l,0],
[q3,0,l],[q3,l,0],[q5,0,l],[q5,l,0],[q7,0,0],[q7,l,l]],
A=[X,Y,Q,P,B],
minimization_automaton(A,Bl)-
minimization_automaton(A,Bl) :- A=[X,Y,Q,P,B],
division_states(A,DS),
write(,DS=,),write(DS),nl,
(one_element_division(DS),Bl=A ;
not(one_element_division(DS)), construction( A, DS, B2),
write(,B2=,),write(B2),nl,
rename_automaton(B2, Bl)).
division_states(A,DS) :- A=[X,Y,Q,P,B] ,first(Yl,Y),
outp(Q,[],Out,YD,ML=[[[Q],Q,Out,Q]],DSl=[Q],SFl=[],
leaf_matrix(A,ML,DS,DSl,SF,SFl).
outp([H|T],Outl,Out,Y) :- outp(T,[Y|Outl],Out,Y).
outp([],Out,Out,Y).
leaf__matrix(A,[LastM|Rest],D,DSl,S,SFl) :-
344
not(one_element_division(DSl)),
A=[X,Y,Q,P,B],Hst_matrix(A,LastM,DSl,List),
processing_list_matrix(List, NextList, [ ], DS, DS1, SF, SF1),
append(Rest,NextList,ML),leaf_matrix(A,ML,D,DS,S,SF).
leaf_matrix(A,[],DS,DS,SF,SF) :- not(one_element_division(DS)).
leaf_matrix(A,ML,DSl,DSl,SFl,SFl) :- one_element_division(DSl).
one_element_division([[H] |T]) :- atomic(H),
one_element_division(T).
one_element_division( [ ]).
list_matrix(A,M,L4,L) :- first(X,A),Hstl(X,A,M,L4,L,[]).
listl([ln|T],A,M,L4,L,Ll) :- not(one_element_division(L4)),
next_matr ix( A, M, L4, In, Ml), last (L5, Ml),
listl(T,A,M,L5,L,[Ml|Ll]).
listl([],A,M,L4,L,Ll) :-
not(one_element_division(L4)),reverse(Ll,L).
listl(T,A,M,L4,L,Ll) :- one_element_division(L4),reverse(Ll,L).
processing_list__matrix([M|T],L,Ll,DS,DSl,SF,SFl) :-
M=[Dl,Q,Y,D2],not(one_element_division(D2)),
appendk(Dl,Dll),function(Dll,Q,F),
(member_set(F,SFl),
processing_list_matrix(T,L,LI, DS, D2,SF,SF1) ;
not(member_set(F, SFl)),
processing_list_matrix(T,L,[M|Ll],DS,D2,SF,[F|SFl])).
processing_list_matrix([M|T],L,Ll,DS,DSl,SF,SFl) :-
M=[Dl,Q,Y,D2],one_element_division(D2),
L=L1,DS=D2,SF=SF1.
processing_list_matrix( [ ], L, LI, DS, DS, SF, SFl) : -
not(one_element_division(DS)),
reverse(Ll, L), reverse(SFl, SF).
next_matrix(A,M,L,In,Ml) :- A=[X,Y,Q,P,B] ,M=[D1,Q1,Y1,D2],
appendk(Dl,Dll),appendk(L,Ll),function(Dll,Ql,SP),
out_qxqy(SP,In,Ll,P,B,Q2,Y2),division(L,Y2,D4),
M1=[L,Q2,Y2,D4].
function(Q,Ql,F) :- functionl(Q,Ql,[] ,F).
functionl([Tl|T],[TTl|TT],Fl,F) :-
functionl(T,TT,[[Tl,TTl]|Fl],F).
functionl([],[],Fl,F) :- reverse(Fl,F).
out_qxqy(SP,In,L,P,B,QE,YE) :- qxqy(SP,In,L,P,B,[],[] ,QE,YE).
qxqy(SP,In,[Ll|L],P,B,Ql,Yl,QE,YE) :-
member([Ll,Q],SP),member([Q,In,Q2],P),member([Q,In,Y2],B),
345
qxqy(SP,In,L,P,B,[Q2|Ql],[Y2|Yl],QE,YE).
qxqy(SP,In,[],P,B,Ql,Yl,QE,YE) :- reverse(Ql,QE),reverse(Yl,YE).
division(D,Y,Dl) :- division_Y(D,Y,DY),new_division(D,DY,Dl).
division_Y(D,Y,DY) :- div_Y(D,Y,[],DY).
div_Y([Q|T],Y,Yl,DY) :- div(Q,Y,[] .Beg.Rest),
div_Y(T,Rest,[Beg|Yl],DY).
div_Y([],[],D,DY) :- reverse(D,DY).
div([Q|T],[Y|Tl],Yl,Beg.Rest) :-div(T,Tl,[Y|Yl] .Beg.Rest).
div([],Rest,Begl,Beg,Rest) :- reverse(Begl,Beg).
new_division(D,Y,Dl) :-new_div(D,Y,[],Dl).
new_div([H|T],[Y|Tl],D2,Dl) :- function(H.Y.HY),
part_div(H)HY)Y,HDl),WW=[])delall(WW,HDl)HD),
new_div(T,Tl,[HD|D2],Dl).
new_div([],[],D2,Dl) :- appendk(D2,D3),reverse(D3,Dl).
part_div(Q,QY,Y,PD) :- part(Q,QY,Y,[],PD).
partCQ.QY.fYlTl.QP.PD) :-
findall( [ Ql, Y],member( [Ql, Y], QY),PQY),
findall(Ql,member([Ql,Y],PQY),Q2),difset(QY,PQY,PQYl),
difset(Q,Q2,Q3),part(Q3)PQYl,T,[Q2|QP],PD).
part([],[],Y,D,D).
construction(A,DS,Bl) :- A=[X,Y,Q,P,B] .conltQ.P.B.DS.N.Nl,^),
delrepeate(Nl,Ml),delrepeate(N2,M2),Bl=[X, Y,N,Ml,M2].
delrepeate(S.SF) :- Sl=[], delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T), !,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),append(Sl,[H],S2),
delrep(T,S2,SF).
delrep([],S2,S2).
conl(Q,P,B,[DSl|DS])N,Nl,N2) :-
c(Q)P,B,DSl,L,Ll,L2)>conl(L>Ll>L2,DS,N>Nl,N2).
conKQ.P.B.d.Q.P.B).
c(Q,P,B,DSl,L,Ll,L2) :- first(DSll,DSl),delfirst(DSl,DSBP),
рКР.В.О.ОБИ.ББВР.Ь.и.Ьг).
delfirst([A|B],B).
pKP.B.Q.DSlljDlDSBPj.L.Ll.LZ) :-
subst_states_in_PandB(D, P, DS11, [ ], PN),
subst_states_in_PandB(D, В, DS11, [ ], BN),
delall(D,Q,Ql),pl(PN,BN)Ql,DSll,DSBP,L,Ll,L2).
pKP.B.Q.DSll.d.Q.P.B)-
346
subst_states_in_PandB(D,[Pl|P],DSll,K,PN) :-
substitute(D,Pl,DSll,PP),append(K,[PP],Kl),
subst_states_Jn_PandB(D, P, DS11, Kl, PN).
subst_states_in_PandB(D, [ ],DS11,Kl,Kl).
substitute(D,[],A,[])-
substituted, [D|L], A, [ A |M]) :- !, substitute(D,L,A,M).
substituted,[yJl],A,[y|M]) :- substitute(D,L,A,M).
rename_automaton(B2, Bl) : -
rename_states_qr(B2,B3),rename_states_rq(B3,Bl).
rename_states_qr(Bl,B2) :- B1=[X,Y,Q,P,B],
rename__states_qrl(Q,P,B,[],Ml,M2,M3),B2=[X,Y,Ml,M2,M3]
rename_states_qrl([Ql|Q],P,B,N,Ml,M2,M3) :- genatom(r,R),
subst_states_in_PandB(Ql, P, R, [ ], PN),
subst_states_in_PandB(Ql,B,R,[],BN),append(N,[R],Nl),
rename_states_qrl(Q,PN,BN,Nl,Ml,M2,M3).
rename_states_qrl([],P,B,N,N,P,B).
genatom(Roote,Atom) :- get_number(Roote,Number),
name(Roote,Namel),name(Number,Name2),
append(Namel, Name2, Name), name( Atom, Name).
get_number(Roote,Number) : -
retract(current__number(Roote,Numberl)),!,
Number is Numberl+1,
asserta(current_number(Roote,Number)).
get__number(Roote ,0) : - asserta(current__number(Roote,0)).
rename_states_rq(B2,Al) :- B2=[X,Y,Q,P,B],
rename_states_rql(Q,P,B,[],Ml,M2,M3),Al=[X,Y,Ml,M2,M3]
rename_states_rql([Rl|R],P,B,K,Ml,M2,M3) :-
name(Rl,[H|T]),name(Ql,[H3|T]),
subst_states_in_PandB(Rl,P,Ql, [ ],PN),
subst_statesJn_PandB(Rl,B,Ql,[],BN),append(K,[Ql],Kl),
rename_states_rql(R,PN,BN,Kl,Ml,M2,M3).
rename__states_rql([],P,B,K,K,P,B).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Yl|Y]) :- member_set(L,Y).
347
subset ([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
reversed ],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
delall(X, [],[])•
delall(X,[X|L],M) :- ! ,delall(X,L,M).
delall(X,[Y|Ll],[Y|L2]) :- delall(X,Ll,L2).
appendk(S,L) :- length(S,K),K > l,appendl(S,L).
appendk([H|[]],H).
appendk( [],[])•
appendl([Hl,H2|T],L) :- append(Hl,H2,Ll), append2(Ll,T,L).
append2(Ll,[H|T],L) :- append(Ll,H,L2),append2(L2,T,L).
append2(L,[] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
last(X,[X]).
last(X,[_|Y]) :- last(X,Y).
first(X,[X|Y]).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Замечание. Порождение классов неотличимых состояний можно
провести согласно следующему алгоритму. Если корень дерева (рис.
16.11) пометим начальным состоянием, а в каждый другой узел
дерева поместим состояние, в которое перейдет автомат, если на его
вход подать входной сигнал, помечающий ребро, входящее в этот
узел, и соответствующий выходной сигнал, то в результате получим
бесконечное дерево переходов состояний автомата и его выходов.
Это дерево имеет конечное число попарно различных бесконечных
поддеревьев. Можно ограничиться конечными поддеревьями, с длиной
ветвей, равной числу состояний автомата. Класс неотличимых
состояний образуют все состояния, стоящие в корнях тех конечных
деревьев, которые совпадают, если с их узлов убрать (стереть) пометки
состояний, оставив пометки выходных символов.
Детерминизацию источника тоже можно организовать в виде дерева
перехода состояний. В корень дерева помещается замыкание
начального состояния источника. Если затем в некотором узле дерева
помещено подмножество состояний S и если от этого узла отходит
ребро, помеченное входным символом я, то концевой узел этого ребра
помечается соответствующим макросостоянием. Построение дерева в
348
узле прекращаем, если этот узел помечается макросостоянием, уже
построенным ранее.
Аналогично в виде дерева перехода состояний можно реализовать
алгоритм построения автомата для объединения, пересечения,
конкатенации, итерации автоматных языков. Если соответствующие языки
заданы источниками, то результирующий автомат можно получить
детерминированным и минимальным.
17. АВТОМАТЫ И СВЕРХЪЯЗЫКИ
17.1. Макроавтоматы
Пусть X - произвольный алфавит. Бесконечное слово х = *(о)*(1)
х(2)... в алфавите X называется сверхсловом. Сверхъязык есть
некоторое множество сверхслов в алфавите X. Пусть X00 - множество
всех сверхслов в алфавите X. Пусть lim x(t) есть предельное
множество сверхслова х при t -* оо, т.е. lim x(t) есть множество всех
тех букв в алфавите X, которые в сверхслове X встречаются
бесконечное число раз. Если Q - множество внутренних состояний
некоторого автомата, то макросостояние есть подмножество Q' Я Q.
(Детерминированный) макроавтомат есть система объектов МА =
{X,Qyq0yTyF), где XyQ,q0,F задаются как в обычном
(детерминированном) автомате, a F Я P(Q) есть некоторое множество
макросостояний. Вместо слова макроавтомат иногда будем говорить просто
автомат, если из контекста ясно, о каком автомате идет речь.
Пусть на вход макроавтомата МА подается сверхслово х = х(0)
*(1)... из X00. Автомат МА, начиная работу в начальном состоянии,
выдает бесконечную последовательность состояний q(0),q(l),...
(или сверхслово q = q(0)q(l)... состояний), называемую ходом
автомата МА на сверхслове х. Пусть lim q{t) есть (предельное)
множество состояний, которые в последовательности q(t) встречаются
бесконечно много раз. Макроавтомат МА допускает сверхслово х,
если lim q(t) € F.
Поведение Beh(MA) макроавтомата МА есть множество всех входных
сверхслов jc, допустимых автоматом МА. Макроавтомат МА
представляет (допускает, определяет) сверхъязык L, если L = Beh(MA).
Сверхъязык L автоматно представим (допустим, определим), если
существует макроавтомат МА, для которого L = Beh(MA). Пусть множество
L(MAyQyF) есть сверхъязык, допустимый макроавтоматом МА с
начальными состояниями Q и с множеством макросостояний F.
Макроисточник есть система MS = (X,Q,Q0,Z),F), где X,Q<Q0,D
349
задаются как в источнике, а множество F Я P(Q) есть некоторое
подмножество макросостояний.
Иногда вместо слова макроисточник будем говорить просто
источник, если из контекста ясно, о каком источнике идет речь.
Сверхслово q(0)q(l)q(2)... в алфавите состояний есть ход
макроисточника MS на входном сверхслове х = jc(0)jc(1)jc(2). ..
(множество всех таких ходов обозначим через Rn(MA>x))y если при
последовательной подаче входных символов jc(0),jc(1), ... (возможна
подача и пустых символов) источник, исходя из начального состояния,
проходит последовательность состояний q(Q)yq(l)>... согласно
своей таблице переходов.
Макроисточник MS допускает сверхслово jc, если существует ход
q(t) MS на jc, для которого lim q(t) € F. В противном случае
макроисточник MS сверхслово х отвергает (не допускает). Поведение
макроисточника MS есть множество Beh(MS) всех входных сверхслов,
допустимых источником MS. Макроисточник MS представляет
(допускает, определяет) сверхъязык L, если L = Beh(MS). Два
макроисточника эквивалентны, если их поведения совпадают.
Введем некоторые операции над языками и сврхъязыками. Пусть М
есть язык, a L, Ll и L2 - сверхъязыки в алфавите X.
Объединение Ll U L2 = {jc € X00 : х € Lx V х € L2}.
Пересечение Lx П L2 = {jc € Ar0° : jc € Ll9 x € L2}.
Дополнение CL = X00 - L.
Сверхитерация (сильная итерация) языка М есть сверхъязык М00 =
М-М-М- ....
Конкатенация (умножение) языка М и сверхъязыка L есть
сверхъязык M'L = {х = yz € X00 : у € М, z € L}.
Пусть множество L(MS,QQyF) означает сверхъязык, допустимый
макроисточником MS с множеством начальных состояний QQ и с
множеством макросостояний F.
Теорема. Алгоритмически разрешимы (распознаваемы) следующие
свойства макроавтоматов.
1. Представляемый макроавтоматом язык пуст (проблема пустоты).
2. Представляемый макроавтоматом сверхъязык бесконечен.
Доказательство. Достаточно рассмотреть случай, когда
макроавтомат MS = (X.QyqQyTyF) имеет одноэлементное множество
макросостояний, именно, Q = {q0,ql9...9qk}, Q' = {Ч\,Яг>--• >Я*)> s ^ к, F
= {(?'}• Докажем для этого автомата два утверждения теоремы.
1. Допустим, что существует сверхслово jc, переводящее
начальное состояние в макросостояние Q', т.е. для некоторого хода q(t)
предельное макросостояние lim q(t) = Q'. Тогда, во-первых,
существует слово у € Лг0°, переводящее начальное состояние q0 в ql9 и
350
во-вторых, для всякого I = 1,2,...,s-1 существует слово ziy
переводящее автомат из состояния q± в состояние <?/ + 1, и слово zs,
переводящее МЛ из qs в qly причем все промежуточные состояния лежат
в Q'. Наличие или отсутствие таких слов проверяется для каждого
автомата, в том числе и для MS.
2. Представимый макроавтоматом сверхъязык либо пуст, либо
бесконечен.
Теорема. Класс автоматно представимых сверхъязыков замкнут
относительно булевых операций.
Доказательство. Пусть сверхъязыки U и L" представимы
макроавтоматами A'=(XyQ'yq'QyT'yF') и A"=(XyQ"yq'0'yT"yF") соответственно.
Пересечение U П L" представимо макроавтоматом А = (XyQyqQyTy
F)y где Q = Q'*Q"\ q0 = (q'0,q'0')\ T{{q'yq")ya) = (T(q'ya),T(q",
a))\ множество выделенных макросостояний F включает в себя любое
подмножество из F'xf", в котором первая компонента лежит в F', а
вторая - в F".
Дополнение X00 - Z/ представимо макроавтоматом А = (X,Qf ,q'QyT,
P(Q) ~ F).
Объединение сверхъязыков выражается через их пересечение и
дополнение. Макроавтомат для объединения можно построить как и в
случае пересечения, с той лишь разницей, что множество выделенных
макросостояний F включает в себя любое подмножество из F'*F"y в
котором первая компонента лежит в F', или вторая - в F". На
практике множество всех достижимых выделенных макросостояний для
объединения можно получить, построив из начального состояния все
пути до первого повтора состояния на каждом пути, выделив в
каждом полученном пути цикл и отнеся все состояния этого цикла в
множество выделенных состояний, если множество первых компонент
этих состояний лежит в F' или множество вторых - в F". Аналогично
поступаем и для пересечения.
77.7.7. Программа вычисления детерминированного
макроавтомата для пересечения двух сверхъязыков,
представимых детерминированными макроавтоматами
d(A,B,C) :- X=[0,l],Ql=[qlO,qll],Q10=[qlO],
Tl=[[qlO,0,qlO],[qlO,l,qll],[qll,0,qlO],[qll,l,qll]],
Fl=[[qll]],A=[X,Ql,Q10,Tl,Fl],Q2=[q20,q21,q22],Q20=[q20],
T2=[[q20,0,q20],[q20,l,q2l],[q21,0,q2l],[q21,l,q22],
[q22,0,q22],[q22,l,q2l]],F2=[[q2l],[q21,q22]],
B=[X,Q2,Q20,T2,F2],intersect_det_macroautom(A,B,C).
intersect_det_macroautom(A,В,С) : -
351
A=[X,Q1,Q10,T1,F1] ,B=[X,Q2,Q20,T2,F2],
findall([Q3,Q4],(member(Q3,Q10),member(Q4,Q20)),Q0),
expand_states_transits(QO,QO, [ ],Tl,T2,Q,T),
distinguished_macrostates(Fl, F2, T, FB),
delall([],FB,FBl),del_rep_sets(FBl,F),C=[X,Q,QO,T,F].
expand__states_transits([[Ql,Q2]|R],AS,AT,Tl,T2,Q,T) :-
findall([[Ql,Q2j,In,[Q3,Q4]],
(member([Ql,In,Q3],Tl),member([Q2,In,Q4],T2),
not(member([[Ql,Q2],In,[Q3,Q4]],AT))),L),
delrepeate(L,Ll),append(AT,Ll,ATl),
findall(Q6,(member([Q5,Inl,Q6],Ll),not(member(Q6,AS))),L2),
delrepeate(L2, L3), append(R, L3, WQ), append( AS, L3, ASl),
expand_states_transits( WQ, ASl, ATI, Tl, T2, Q, T).
expand_states_transits( [ ], Q, T, Tl, T2, Q, T).
distinguished_macrostates(Fl,F2,T,F) : -
disting_macrosts(Fl,F2,T, [ ],F).
disting_macrosts([Hl|Tl],F2,T,Ac,F) :-
dist_subsets(Hl,F2,T,[],HlF2),append(Ac,HlF2,HF2),
disting_macrosts(Tl, F2, T, HF2, F).
disting_macrosts( [ ],F2,T,F,F).
dist_subsets(Hl,[H2|T2],T,Ac,HlF2) :-
findall([[Ql,Q2],In,[Q3,Q4]],
(member([[Ql,Q2],In,[Q3,Q4]],T),
member(Ql,Hl),member(Q3,Hl),
member(Q2,H2),member(Q4,H2)),TF),
ifthenelse(TF=[],dist_subscts(Hl,T2,T,Ac,HlF2),
((find_dist_macrost(TF,Hl,H2,P) ; P=[]),
dist_subsets(Hl,T2,T,[P|Ac],HlF2))).
dist_subsets(Hl,[],T,HlF2,HlF2).
find_dist_macrost(TF,Fl,F2,P) :- member([Q,In,Ql] ,TF),
ifthenelse(Q=Ql,Pl=[Q],go(Ql,Q,[Q],TF,Pl)),
delrepeate(Pl,P),
findall(Sl,member([Sl,J,P),FlP),equalset(Fl,FlP),
findall(S2,member([_,S2],P),F2P),equalset(F2,F2P).
go(N,Q,Tr,TF,P) :- nextnode(N,Q,Tr,TF,Nl),not(Nl=Q),
go(Nl,Q,[N|Tr],TF,P).
go(N,Q,Tr,TF,P) :- P=[N|Tr].
nextnode(N,Q,Tr,TF,Nl) :- member([N,In,Nl] ,TF),
(not(member(Nl,Tr)) ; N1=Q).
352
del_rep_sets(S,SF) :- Sl=[] ,del_set(S,Sl,SF).
del_set([H|T],Sl,SF) :- member_set(H,T),del_set(T,Sl,SF).
del_set([H|T],Sl,SF) :- not(member_set(H,T)),
append(Sl,[H],S2),del_set(T,S2,SF).
del_set([],S2,S2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Yl|Y]) :- member_set(L,Y).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
delrepeate(S,SF) :- delrep(S,[],SF).
delrep([H|T],Sl,SF) :- member(H,T), !,delrep(T,SI,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
delall(_,[ ],[])•
delall(X,[X|L],M) :- ! ,delall(X,L,M).
delall(X,[Y|Ll],[Y|L2]) :- delall(X,Ll,L2).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
17.1.2. Программа вычисления детерминированного макроавтомата
для объединения двух сверхъязыков, представимых
детерминированными макроавтоматами
d(A,B,C) :- X=[0,l],Ql=[qlO,qll],Q10=[qlO])
Tl=[[qlO,0,qlO],[qlO,l,qll],[qll,0,qlO],[qll,l,qlUl,
Fl=[[qll]],A=[X)Ql,Q10)Tl,Fl],Q2=[q20,q21,q22],Q20=[q20],
T2=[[q20,0,q20], [q20,l,q2l] ,[q21,0,q2l] ,[q21,l,q22],
[q22,0,q22]([q22,l)q2l]],F2=[[q2l])[q21,q22]],
B=[X,Q2,Q20,T2,F2],union_det_macroautom(A,B,C).
union_det_macroautom(A,B,C) :-
A=[X,Q1,Q10,T1)F1],B=[X,Q2)Q20,T2,F2])
f indalK [Q3,Q4], (member(Q3,QIO),member(Q4,Q20)),QO),
expand_states_transits(QO, QO,[ ], Tl, T2, Q, T),
distinguished_macrostates(Fl, F2, T, FB),
delall([],FB,FBl),del_rep_sets(FBl,F),C=[X,Q,QO,T,F].
353
expand_states_transits([[Ql,Q2]|R],AS,AT,Tl,T2,Q,T) :-
findall([[Ql,Q2],In,[Q3,Q4]],
(member([Ql,In,Q3],Tl),member([Q2,In,Q4],T2),
not(member([[Ql,Q2],In,[Q3,Q4]],AT))),L),
delrepeate(L,Ll),append(AT,Ll,ATl),
findall(Q6,(member([Q5,Inl,Q6],Ll),not(member(Q6,AS))),L2),
delrepeate(L2,L3),append(R,L3,WQ),append(AS,L3,ASl),
expand_states_transits( WQ, AS1, ATI, Tl, T2, Q, T).
expand_states_transits([],Q,T,Tl,T2,Q,T).
distinguished_macrostates(Fl,F2,T,F) : -
distingl_macrosts(Fl,T, [ ],F1Q),
disting2_macrosts(F2,T, [ ],QF2),append(FlQ,QF2,F).
distingl_macrosts([Hl|Rl] ,T,Ac,F) :-
distl_subsets(Hl,T, [ ],H1Q2),
distingl_macrosts(Rl,T, [H1Q21 Ac],F).
distingl_macrosts( [ ], T, F,F).
disting2__macrosts([H2|R2] ,T,Ac,F) :-
dist2_subsets(H2,T, [ ],Q1H2),
disting2_macrosts(R2,T, [Q1H21 Ac],F).
disting2_macrosts( [ ], T,F, F).
distl_subsets(Hl,T,Ac,HlQ2) :- findall([[Ql,Q2] ,In,[Q3,Q4]],
(member([[Ql,Q2],In,[Q3,Q4]],T),
member(Ql,Hl),member(Q3,Hl)),TF),
ifthenelse(TF=[ ] ,H1Q2=[ ],
(find_distl_macrost(TF,Hl,HlQ2) ; H1Q2=[])).
dist2_subsets(H2,T,Ac,QlH2) :- findall([[Ql,Q2] ,In,[Q3,Q4]],
(member([[Ql,Q2],In,[Q3,Q4]],T),
member(Q2,H2),member(Q4,H2)),TF),
ifthenelse(TF=[] ,Q1H2=[],
(find_dist2_macrost(TF,H2,QlH2) ; Q1H2=[])).
find__distl_macrost(TF,Hl,P) :- member([Q,In,Ql] ,TF),
ifthenelse(Q=Ql,Pl=[Q],go(Ql,Q,[Q],TF,Pl)),
delrepeate(Pl,P),
findall(Sl,member([Sl,J,P),HlP),equalset(Hl,HlP).
find_dist2_macrost(TF,H2,P) :- member([Q,In,Ql] ,TF),
ifthenelse(Q=Ql,Pl=[Q],go(Ql,Q,[Q],TF,Pl)),
delrepeate(Pl,P),
findall(S2,member([_,S2],P),H2P),equalset(H2,H2P).
354
goCN.Q.Tr.TF.P) :- nextnodeCN.Q.Tr.TF.ND.notCNIO),
goCNl.Q.fNlTrj.TF.P).
goCN.Q.Tr.TF.P) :- P=[N|Tr].
nextnode(N,Q,Tr,TF,Nl) :- member([N,In,N1] ,TF),
(not(member(Nl,Tr)) ; N1=Q).
del_rep_sets(S,SF) :- Sl=[],del_set(S,Sl,SF).
del_set([H|T],Sl,SF) :- member_set(H,T),del_set(T,Sl,SF).
del_set([H|T],Sl,SF) :- not(member_set(H,T)),
append(Sl,[H],S2),del_set(T,S2,SF).
del_set([],S2,S2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Yl|Y]) :- member_set(L,Y).
equalset(X.Y) :- subset(X,Y),subset(Y,X).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
delrepeate(S,SF) :- delrep(S,[] ,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H])S2),delrep(T,S2,SF).
delrep([],S2,S2).
delall(_,[],[]).
delall(X,[X|L],M) :- ! ,delall(X,L,M).
delall(X,[Y|Ll],[Y|L2]) :- delall(X,Ll,L2).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member (X,[ X|Y]).
member(X,[Y|Z]) :- member(X,Z).
17.1.3. Программа вычисления детерминированного макроавтомата
для дополнения сверхъязыка, представимого
детерминированным макроавтоматом
d(A,B) :- X=[0)l])Ql=[qlO)qll)ql2)ql3,ql4],Q10=[qlO],
THIqlO.O.qlOUqKU.qllUqll.O.qniaqll.l.qn],
[ql2,0,ql2],[ql2,l,ql3],[ql3,0,ql4],[ql3,l,ql0],
[ql4,0,ql0],[ql4,l,ql4]],
Fl=[[qll])[ql2,ql3]],A=[X)Ql,Q10)Tl,Fl],
compl_det_macroautom(A,B).
compl_det_macroautom(A,B) :- A=[X,Ql,Q01,Tl,Fl],
355
powerset(Ql,S),delete([],S,Sl),dif_set_of_subsets(Sl,Fl,F),
B=[X,Q1,Q01,T1,F].
powerset(X,S) :- findall(Y,subsetl(Y,X),S).subsetl([] ,[])•
subsetl([H|S],[H|T]) :- subsetl(S,T).
subsetl(S,[H|T]) :- subsetl(S,T).
dif_set_of_subsets(Sl,Fl,F) :- dif_subsets(Sl,[] ,F1,F).
dif_subsets([H|T],A,Fl,F) :-
ifthenelse(member_set(H,Fl),dif_subsets(T,A,Fl,F),
dif_subsets(T,[H|A],Fl,F)).dif_subsets([],F,Fl,F).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L) J .
member__set(L,[Yl|Y]) :- member_set(L,Y).
subset ([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
delete(A,[A|B],B) :- !.
delete(A,[B|L],[B|M]) :- delete(A,L,M).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
17.1.4. Программа вычисления макроисточника для объединения
двух сверхъязыков, представимых макроисточниками
d(A,B,C) :- X=[0,l],Ql=[qlO,qll],Q10=[qlO],
Tl=[[qlO,0,qll],[qlO,l,qlO],[qll,0,qll],[qlO,l,qlO]],
Fl=[[qll]],A=[X,Ql,Q10,Tl,Fl],Q2=[q20,q21,q22],Q20=[q20],
T2=[[q20,0,q2l],[q20,l,q20],[q21,0,q22],[q21,l,q22],
[q22,0,q22],[q22,l,q20]],F2=[[q2l],[q21,q22]],
B=[X,Q2,Q20,T2,F2],union_det_macroautom(A,B,C).
union_det__macroautom(A,B,C) :- A=[X,Ql,Q10,Tl,Fl],
B=[X,Q2,Q20,T2,F2],
findall([Q3,Q4],(member(Q3,Ql),member(Q4,Q2)),Q),
Q0=[[ql0,q20]],
findall([[Q5,Q6],In,[Q7,Q8]],
(member([Q5,In,Q7],Tl),member([Q6,In,Q8],T2)),T),
findall([F3,F4],
(((member(F3,Fl),member(F4,Q2)) ;
((member(F3,Ql),member(F4,F2))),
C=[X,Q,QO,T,F].
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
356
17.2. Конкатенация языка и сверхъязыка
Теорема. Конкатенация конечно автоматного языка и конечно
автоматного сверхъязыка есть конечно автоматный сверхъязык.
Доказательство. Пусть L = L(AyqQyQ') - автоматный язык, пред-
ставимый автоматом А = (X,Q,q0yTyQ') и SL = SL(MAysQyG) -
сверхъязык, представимый макроавтоматом MA = (XySysQyPyG). Тогда
искомая конкатенация L- SL = U L(AyqQyq')* SL(MA,sQyF).
q'ZQ' ,F€G
Теорему достаточно доказать для случая, когда L* SL = L(A,qQy
q')-SL(MA,s0yF).
Пусть имеем один автомат А и неограниченный запас копий
макроавтоматов МА. Принадлежность сверхслова х = дс(0)*(1)...
сверхъязыку L*SL распознаем следующим образом. Запустим на сверхслове х
автомат А. Если далее в некоторый момент tx автомат А впервые
придет в состояние q', то в этот момент запускаем копию 1
макроавтомата МА из неограниченного запаса копий макроавтоматов МА.
Копия 1 макроавтомата МА запускается на сверхслове x[tlyoo) =
jcC^! )jc(^1+1) Если в момент t2 автомат А во второй раз придет
в состояние q', то в этот момент запускаем копию 2 для МА. И так
далее. Пусть cQ(t) - состояние автомата А в момент t9 a cm(t) -
состояние копии т в момент ty если она в момент t активна (т.е.
работает), и cm(t) = Л, если копия т в момент t не активна (т.е.
пребывает в запасе). Тогда сверхслово х принадлежит L*MA тогда и
только тогда, когда 1) активна хотя бы одна копия макроавтомата
МА\ 2) хотя бы одна из активных копий макроавтомата МА
вырабатывает предельное макросостояние F. Поэтому
х € L-SL <— (3m)(lim cm(t) = F).
Заметим, что если для некоторого момента f имеет место cm(t')
= cn(t')y то Vf > t' cm(t) = cn(t)\ поэтому дальнейшая работа
одной из этих копий становится излишней. Следовательно, копию т или
копию п можно вернуть в запас, например, копию с большим номером.
Так как макроавтомат МА имеет к+1 состояний sQ,sl,...9sjc, то
понадобится к+l копий макроавтомата МА.
Построим макроавтомат МВУ допускающий сверхъязык L- SL.
Состояния MB есть векторы с = (с0Ус1,... ,сЛ+1) из множества QxF'xF'x
...xf, где F' = F U {Л}, с0 - состояние автомата А\ CpC2,...,
ck+i " состояния макроавтомата МА или знаки Л, при этом среди
Cj,...,c^+1 все состояния из МА попарно различны; (#0,Л,...,Л) -
начальное состояние. При воздействии буквы а из X на состояние
c(t) = (соСО.сДО,...,^!^)) вектор c(f+l) = (CoO+lhc^M-
l),... ,с*+1(н-1)) получим следующим образом. Компонетна c0(f+l) =
357
T(c0(t),a). Каждое не равное Л состояние сДО для i ^ 1 перейдет
в состояние c,(f+l) = Р(с,-(0>я) макроавтомата МА. Далее
осуществим "чистку": в векторе с(м-1) из нескольких равных компонент
(если таковые имеются) оставляем компоненту с меньшим номером, а
остальные заменяем на Л. Если теперь c0(M-l) = q\ то первая (по
порядку) компонента Л в c(t+l) замещается на начальное состояние
s0 макроавтомата МА. Если же с0(н-1) * q'> то все "пустые"
компоненты Л в c(t+l) остаются пустыми. Функция переходов
макроавтомата MB построена.
Множество выделенных макросостояний {Fx,... ,Fh,... ,F/} для MB
содержит всякое макросостояние Fh = {(cJ0ic[y... ,cj,... ,q£+1): ; =
1,2,...,г при некотором г}, для которого некоторая проекция на
ось i (l^i'^fc+l): Pr F, = F. При этом компоненты вне i в векторах
из F,- безразличны.
Покажем, что сверхъязык L* SL представим построенным
макроавтоматом MB. Пусть ход c(0)c(l).. .c{t)... макроавтомата MB на
сверхслове х из А^0 таков, что lim c(t) = Fh при некотором Л € {l,
2,...,/}. Тогда (Эт)(1 < т < fc+1 & lim cm(0 = F). Это означает,
что включившись в некоторый момент, копия т для МА уже никогда не
отключается (т.е. не переводится в запас). Далее копия т
вырабатывает предельное макросостояние F. Поэтому входное сверхслово х
допускает представление х = jc[0,^) • jc[^,oo), причем *U,oo) € SL и
потому х € L* SL.
Пусть х € L'SL. Покажем, что ход c(0)c(l)... макроавтомата MB
на х имеет предельное макросостояние из числа построенных, т.е.
lim c(t) € {Fly... ,F[}. Так как х € L-SL, то сверхслово х
допускает представление х = x[0,t) •*[*,«>), причем x[Oyt) € L, x[t>oo) €
SL. Так как x[0j) € L, то для вектора c(t) имеем (3/?)(l ^ р <
к+1 & cp(t) = 50). В ходе дальнейшей работы копия МА может
перейти в запас, "передав" свою работу копии с меньшим номером. И
так далее. Так как индекс р не может убывать неограниченно, то
(3m < p)(lim cm(t) = F). Тогда макроавтомат MB в компоненте т
вектора состояний c(t) даст предельное макросостояние F, и потому
lim c(t) € {Fly... ,F[}, т.е. сверхслово х допустимо построенным
макроавтоматом MB. Теорема доказана.
17.2.1. Программа вычисления детерминированного макроавтомата
для конкатенации языка и сверхъязыка, представимых
детерминированными автоматом и макроавтоматом
Процедура concat_language_superlang(A,B,C) по автомату А и
макроавтомату В строит макроавтомат С, допускаюшии конкатенацию
358
языка, допустимого автоматом А, и сверхъязыка, допустимого
макроавтоматом В.
Процедура expand_states_transits(lS, AS, AT, А, В, Q3, ТЗ) по
промежуточному множеству AS состояний, автоматам А и В вычисляет
множество состояний Q3 и функцию переходов ТЗ искомого
макроавтомата. Переменная IS является рабочей. Сюда мы добавляем вновь
полученные состояния, для которых еще не вычислены переходы (q,a,
ql) от состояния q к состоянию ql при подаче входа а. Переменные
AS и AT являются накапливающими для Q3 и ТЗ соответственно.
Процедура next_state(Q,In,Tl,Fl,Q20,T2,Ql) по состоянию Q,
входу In, начальному состоянию Q20 макроавтомата В, функциям
переходов Т1 и Т2 для А и В соответственно и выделенным
состояниям F1 автомата А строит следующее состояние Q1 искомого
макроавтомата. Например, если Q=[ql2,q23,q21,q24,q25], In=2, [ql2,2,ql4]
принадлежит Tl, ql4 принадлежит Fl, [q23,l,q23], [q21,2,q23],
[q24,2,q23],[q25,2,q24] принадлежат Т2, то Ql=[ql4, q23,q24,q20].
Если же ql4 не принадлежит Fl, то Ql=[ql4,q23,q24].
Процедура distinguished_macrostates([Q30] ,T3,F2,F3) по
начальному состоянию Q30, функции переходов ТЗ искомого макроавтомата
С и множеству F2 выделенных макросостояний в макроавтомате В
строит множество F3 выделенных макросостояний для С. Выделенные
макросостояния для С получаем, строя всевозможные пути состояний
(для С) от начального состояния Q30 до первого повтора состояния
на этом пути. Множество М состояний между двумя повторами
состояний образует выделенное состояние, если проекция М по одной из
координат образует выделенное макросостояние для В.
Процедура go(Q30,T3,LS) по начальному состоянию Q30 и функции
переходов ТЗ искомого автомата С строит для С предельное
макросостояние .
Процедура gol(Q30,T3,A,P) по начальному состоянию Q30 и
функции переходов ТЗ искомого автомата С вычисляет путь Р с циклом в
конце его. Переменная А накапливает путь Р.
Процедура cycle(P,C) из пути Р выделяет имеющийся в нем цикл.
Процедура cycle_processing(MSt,F2) по предельному
макросостоянию MSt искомого автомата С определяет, является это
макросостояние выделенным для С или не является.
Предикат least_length(S,C) истинен, если число С есть
наименьшая длина подсписка в списке S.
Предикат most_length(S,C) истинен, если число С есть
наибольшая длина подсписка в списке S.
Предикат nth_element_in_list(L,N,A) истинен, если А есть эле-
359
мент N в списке L.
d(A,B,C) :- X=[0,l],Ql=[qlO,qll],Q10=qlO,
Tl=[[qlO,0,qlO],[qlO,l,qll],[qll,0,qlO],[qll,l,qll]],
Fl=[qll]>A=[X,Ql)Q10,Tl)Fl],Q2=[q20,q21,q22],Q20=q20,
T2=[[q20,0,q20])[q20,l,q2l],[q21)0,q2l],[q21)l,q22],
[q22,0,q22]>[q22,l)q2l]],F2=[[q2l])[q21,q22]],
B=[X,Q2,Q20)T2,F2])concat_language_superlang(A,B,C).
concat_language_superlang(A,В,С) : -
A=[X,Q1>Q10,T1,F1],B=[X,Q2,Q20,T2,F2],
Q30=qlO,IS=[[Q30]],AT=[],
expand_states_transits(lS,IS,AT,A,B,Q3,T3),
distinguished_macrostates( [ Q30], T3, F2, F3),
C=[X,Q3,Q30,T3,F3].
expand_states_transits([H|R] ,AS,AT,A,B,Q3,T3) :-
A=[X,Q1,Q10,T1,F1],B=[X)Q2,Q20,T2,F2],
findall([H,In,Hl],
(member(ln,X),next_state(H,In,Tl,Fl,Q20,T2,Hl),
not(member([H,In,Hl] ,AT))),L),
delrepeate(L,Ll),append(AT,Ll,ATl),
findall(H3,(member([H2,Inl,H3],Ll),not(member(H3,AS))),L2),
delrepeate(L2,L3),append(AS,L3,ASl),append(R,L3,Rl),
expand_states_transits(Rl,ASl,ATl,A,B,Q3,T3).
expand_states_transits([],Q3,T3,A,B,Q3,T3).
next_state([H|R],In,Tl,Fl,Q20,T2,H2) :-
member([H,In,Hl],Tl),next_st(R,In,T2,[Hl],Q2),
ifthenelse((member(Hl,Fl),not(member(Q20,Q2))),
reverse([Q20|Q2],H2),reverse(Q2,H2)).
next_st([H|R],In,T2,A,Ql) :- member([H,In,Hl],T2),
ifthenelse(member(Hl,A),next_st(R,In,T2,A,Ql),
next_st(R>In,T2,[Hl|A],Ql)).
next_st([],In,Tl,Q2,Q2).
distinguished_macrostates(Q0,T,F2,F) :-
(setof(C,(go(Q0,T,C),cycle_processmg(C,F2)),F) ; F=[]).
go(QO,T,LSt) :- gol(QO,T,[],P),
cycle(P,C),C=[_|LSt].
gol(St,T,A,P) :- not(member(St,A)),member([St,In,NSt],T),
gol(NSt,T,[St|A],P).
gol(NSt,T,A,P) :- member(NSt,A),P=[NSt|A].
360
cycle([H|R],C) :- cyclel(H,R,[H] ,C).
cyclel(S,[Hl|Rl],A,C) :- not(S=Hl),cyclel(S,Rl,[Hl|A],C).
cyclel(S,[Hl|Rl],A,C) :- S=H1,C=[S|A].
cycle_processing(C,F2) :-
mostJength(C,Nl),least_length(C,N2),N2>l,
cycle_process(C,F2,Nl,2).
cycle_process(C,F2,Nl,N2) :- N2=<N1,
(setof (S, Sr(member (St, C),
nth_element_in_list(St,N2,S)),AS) ; AS=[]),N3 is N2+1,
ifthen(not(member_set(AS,F2)),cycle_process(C,F2,Nl,N3)).
least_length(S,C) :- S=[H|T] ,length(H,N),least_len(S,N,C).
least_len([H|T],L,C) :- length(H,Cl),Cl<L, least Jen(T, CI, C).
least_len([H|T],L,C) :- length(H,Cl),Cl>=L,least_len(T,L,C).
least_len([],C,C).
most_length(S,C) :- most_len(S,0,C).
most_len([H|T],L,C) :- length(H,Cl),Cl>L,most_len(T,Cl,C).
most_len([H|T],L,C) :- length(H,Cl),Cl=<L,most_len(T,L,C).
mostJen([],C,C).
nth__element__in_list(L,N,A) :- I is l,nth__el__in__list(L,N,I,A).
nth_el__inJist([H|T],N,I,A) :-
not(N is l),Il=I+l,nth__el_in_list(T,N,Il,A).
nth__el__inJist([H|T],N,I,H) :- N is I.
delrepeate(S,SF) :- delrep(S,[] ,SF).
delrep([H|T],Sl,SF) :- member (H, T),! ,delrep(T, SI, SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Yl|Y]) :- member_set(L,Y).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
reverse([],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H],L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
361
17.2.2. Программа вычисления макроисточника для конкатенации
языка и сверхъязыка 9 представимых источником
и макроисточником соответственно
Эта программа проще, чем соответствующая программа для
детерминированного случая: источник и макроисточник следует
объединить; начальные состояния источника взять в качестве начальных
состояний искомого макроисточника; множество выделенных
макросостояний данного макроисточника взять в качестве выделенных
макросостояний искомого макроисточника; добавить к граф-схеме искомого
макроисточника пустые стрелки, ведущие из выделенных состояний
исходного источника в начальные состояния исходного
макроисточника.
d(A,B,C) :- X=[0,l],Ql=[qlO,qll,ql2],Q10=[qlO],
Tl=[[qlO,0,qlO],[qlO,0,ql],[qll,l,ql2]],Fl=[qll,ql2],
A=[X,Q1,Q20,T1,F1],
Q2=[q20,q21,q22,q23],Q20=[q20,q2l],
T2=[[q20,0,q2l],[q20,*,q23],[q21,l,q22],[q22,0,q23],
[q22,l,q23],[q23,0,q23],[q23,*,q20]],F2=[[q20,q23],[q23]],
B=[X,Q2,Q20,T2,F2],concat_automat_superaut(A,B,C).
concat_automat_superaut(A,В, C) : -
A=[X,Q1,A10,T1,F1],B=[X,Q2,Q20,T2,F2],
findall([Q3,*,Q4],(member(Q3,Fl),member(Q4,Q20)),L),
unionset(Tl,T2,S),unionset(S,L,T3),unionset(Ql,Q2,Q3),
C=[X,Q3,Q10,T3,F2].
unionset([],X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
17.3. Сверхитерация автоматных языков
Цель этого параграфа состоит в доказательстве того факта, что
сверхитерация автоматного языка является автоматным сверхъязыком.
Определение. Сверхслово х = jc(0)jc(1). .. в алфавите X устойчиво
относительно автомата А = (XyQyqQyTyQ')y если существует
бесконечно много хвостов *[f|,oo), i = 1,2,..., для которых:
1) все слова *[(),*,■) € L(AyqQyQ'), i = 1,2,...;
2) автомат А склеивает каждый из хвостов x[tiyoo)t i = 1,2,...,
362
с исходным словом х.
Пусть Lst - множество всех сверхслов, устойчивых относительно
автомата А, допускающего язык L.
Лемма 1. Если язык L представим автоматом А, то Lst Я L00.
Доказательство. Пусть сверхслово х = *(0)jc(l)... € L5t. Тогда
существует бесконечно много хвостов дс[*,-,оо), / = 1,2,..., для
которых:
1) все слова *[(),*,•) € L;
2) автомат А склеивает каждый из хвостов *[f,-,oo) с исходным
сверхсловом х.
Запустим на х автомат А (рис. 17.1). В момент t\ запустим копию
Ах автомата А. Слово jc[0,f') € L. Копия Ах в некоторый момент vx
£ t\ склеивается с А. Так как хвостов *[f,,oo) бесконечно много,
то существует хвост x\t'iy&>) с t2 > vx. Слово jcfO,^) € L, поэтому
автомат А вместе со склеившейся с ним копией Ах придет в
выделенное состояние. Тогда слово Jc[fj,fp € L. Хвост *[f',oo) склеится
автоматом А с х в некоторый момент v2. Так как хвостов x[f,-,oo)
бесконечно много, то найдется хвост x[t3,oo) с t3 > v2. Слово
л:[0,^з) € L, поэтому автомат А вместе со склеившейся с ним копией
А2 в момент t3 придет в выделенное состояние. Тогда слово x[t[,
t3) € L. Продолжая эти рассуждения, мы покажем, что сверхслово х
x[0,t[)' x[t[ ft2) • x[t2,t'3)' ... составлено из слов *U;,'; + i),
принадлежащих L, т.е. х € L00.
Лемма 2. Если представимый автоматом А язык L замкнут
относительно итерации (т.е. L = L*), то L00 = L-Lst.
Доказательство. Пусть язык L представим автоматом А = (X,Q,qQ,
TfQ')f где \q\ = к и L* = L. По лемме 1 Lst Я L00, поэтому любое
сверхслово z из Lst разбивается на бесконечное число слов из L.
t\ vx г'г v2 t'3 v3
x 1 1 1 1 1 1
A0fqQ
A>?o
Аг>Чо
^3»?o
Рис. 17.1
363
Добавив к z спереди любое слово из L00, снова получим
сверхслово из L00. Следовательно, L*Lst Q L00.
Пусть теперь сверхслово х € L00. Для распознавания
принадлежности сверхслова х = *(0);t(l)... сверхъязыку L00 поступим следующим
образом. Запасем бесконечно много копий автомата А. Запустим на
сверхслове х первую копию автомата А.
В каждый момент времени t0,tl,t29... 9 в который копия для А
приходит в выделенное состояние, запускаем следующую (находящуюся
в запасе) копию автомата А. Все начальные отрезки *[(),*;), i = 1,
2,..., входного сверхслова лежат в L. Если автомат А имеет к
состояний, то достаточно иметь работающими (активными) не более к
копий автомата А, ибо при большем их числе найдутся такие,
которые пребывают в одном и том же состоянии. Из всех таких копий
достаточно оставить активной только одну копию А, например, имеющую
меньший номер, т.е. копию, ранее всех включившуюся. Заметим, что
первая копия не отключается никогда.
Так как х € L00, то сверхслово х составлено из бесконечного
числа слов, принадлежащих L. Так как все начальные отрезки для х
до мест соединений этих слов лежат в L, то существует бесконечно
много моментов, в которые включаются все новые копии автомата А,
Так как в любой момент активны не более к копий автомата А, то
происходит бесконечное число склеиваний активных копий автомата
А. Пусть несколько копий А склеивается с копией с номером 11У
затем происходит склеивание с копией /2, и так далее. В
последовательности склеиваний копий А
(/,,...); (/2,...); (/3,...);...; (/,,...);,...
Скобка (/,,...) означает, что с копией /,- автомата А склеились
все копии этой скобки (находящиеся в том же состоянии, что и
копия /,). Номера копий в скобке (kif...) возрастают по величине. В
ряду чисел ll,l2,... некоторые числа встречаются бесконечно много
раз. Выберем среди них наименьшее число /. С копией / автомата А
происходит бесконечно много склеиваний других копий; при этом
копия /, включившись в некоторый момент f, уже никогда не
отключается. Сверхслово х разбивается на два куска: jc[0,0 и Jt[f,oo),
причем слово *[0,0 € L, а сверхслово x[t,oo) таково, что
существует бесконечно много хвостов *[г{,оо), x[t'2,oo)y... этого
сверхслова, для которых:
1) все слова дс[^,Г/) € L, i = 1,2,...;
2) автомат А склеивает каждый из хвостов x[t'ifoo) со
сверхсловом *Ui,oo).
Следовательно, *[0,Г{) € L, jc[^,oo) € Lsn т.е. х € L*Lst.
364
Показано, что L00 Я L*Lst, что вместе с ранее доказанным обратным
включением дает искомое равенство.
Лемма 3 (об устойчивости). Существует алгоритм, который по
любому конечному автомату А строит макроавтомат, поведение которого
есть множество всех сверхслов, устойчивых относительно А.
Доказательство. Пусть автомат А = (XfQ,qQyTyQ') с к
состояниями допускает язык L. Пусть Lst есть множество всех сверхслов,
устойчивых относительно автомата А. Состояниями автомата МА
являются векторы с = (с1 ,с2,... ,ск+1)> где сх - состояние автомата А\
ck+i € {А,*}; с,- € Q U {Л}, j = 2,3,...,*; при этом те из с2,с3,
...,С£+1, которые являются состояниями автомата А, попарно
различны. Вектор с всегда имеет в запасе пустую компоненту Л.
Множество S состояний для МА построено. Вектор sQ = (<?0,Л, ...,Л) есть
начальное состояние макроавтомата МА. Функция М переходов для МА
строится следующим образом. Пусть при состоянии c(f) = (сДО,
...,С£+1(0) на вход в МА поступает входной символ а. Построим
вектор c(f+l) = (сДн-l),... ,Cfc+i(M-l)), положив сДм-1)
T(cx(t),a). Для j = 2,3,...,*+1 при сДО * Л полагаем сДм-1) =
T(cj(t),a), а при сДО - {Л,*} полагаем сДм-1) = Л. Вектор
c'(M-l) (и тогда М(с(0>я) = c'(M-l)) сделаем результатом
следующих операций.
1. Если хотя бы одна координата из с2(Н-1),..., сЛ+Дн-1)
совпадает с сДн-1), то c'(M-l) = (сДм-l), Л,...,Л,*).
2. Если ни одна из компонент c2(f+l),... ,С£+1(М-1) не есть
сДм-l), то проводим следующую "чистку" вектора с(г+1): из всех
одинаковых компонент в c2(f+l),..., с^+Д^+l) оставляем одну с
меньшим номером. Такую "чистку" проводим до тех пор, пока все
состояния в получившемся векторе не станут попарно различными.
Выделенным для МА является множество макросостояний Я = {Яр
Я2,... ,Я,,... ,Я/}, где Я, есть любое множество векторов с,
содержащих звездчатое состояние (<?,Л,... ,Л,*).
Макроавтомат Л/у! = (X9StsQfM9H) построен.
На практике вектор состояний экономнее строить без пустых
символов, изменяя длину вектора, когда это необходимо.
Утверждение 1. Сверхслово х € Lst тогда и только тогда, когда
звездчатые состояния в ходе макроавтомата МА встречаются
бесконечно много раз.
Доказательство. Пусть в ходе МА на х первое звездчатое
состояние есть c(fj). Это значит, что в момент tx одна из копий
автомата А у включившись в момент между 0и(,, склеилась с первой
копией. Если c(t2) - второе звездчатое состояние, то это значит, что
некоторая копия для А, включившись в момент между t1 и t2, склеи-
365
лась в момент t2 с первой копией автомата А. И так далее.
Следовательно, существует бесконечно много хвостов jc[rf ,00), / = 1,
2,..., для которых:
1) все слова *[(),*,■) € L;
2) автомат А склеивает каждый из хвостов дс[*,-,оо) с исходным
сверхсловом х.
Каждая склейка означает появление звездчатого состояния в ходе
МА на х.
Утверждение 1 доказано.
Утверждение 2. Lst = Beh(MA).
Доказательство. Справедливы следующие высказывания.
1. Сверхслово х € Lst.
2. Звездчатое состояние в ходе МА на х встречается бесконечно
много раз.
3. Предельное макросостояние в ходе МА на х содержит
звездчатое состояние.
4. Для q(t) € Rn(MA,x) предельное множество lim q(t) € Н.
5. х € Beh(MA).
Следовательно, Lst = Beh(MA).
Утверждение 2 установлено. Лемма 3 доказана.
Теорема (о сверхитерации). Если L есть конечно автоматный
язык, то L00 - конечно автоматный сверхъязык.
Доказательство. Пусть L есть автоматный язык, представимый
автоматом МА с начальным состоянием qQ. Так как L00 = (L*)00, то
можно считать, что множество L замкнуто относительно итерации. Если
этого нет, то вместо L следует взять язык L* и представляющий его
автомат. По лемме 2 сверхъязык L00 = L*Lst. По лемме 3 сверхъязык
L5t автоматно представим. По теореме из предыдущего параграфа ав-
томатно представим сверхъязык L*Lst. Следовательно, сверхъязык L00
автоматно представим.
Замечание. По автомату А макроавтомат МА, представляющий
сверхъязык L00, строится эффективно.
173.1. Программа вычисления детерминированного макроавтомата
для языка, устойчивого относительно данного автомата
Процедура stable(A,B) по детерминированному автомату А строит
детерминированный макроавтомат, устойчивый относительно А.
Процедура expand_states_transits(lS, AS, AT, А, Q, Т) по
промежуточному множеству AS состояний для В, автомату А вычисляет
множество состояний Q и функцию переходов Т искомого
макроавтомата В. Переменная IS является рабочей; сюда добавляем вновь
полученные состояния, для которых еще не вычислены переходы (q,a,ql)
366
от состояния q к состоянию ql при подаче входа а. Переменные AS и
AT являются накапливающими для Q и Т соответственно.
Процедура next_state(Q,In,Tl,Fl,Q10,NQ) по состоянию Q для В,
входу In, начальному состоянию Q10, функции переходов Т1 и
выделенным состояниям F1 автомата строит следующее состояние NQ
(искомого автомата В).
Процедура distinguished_macrostates(QO,T,F) по начальному
состоянию Q0 и функции переходов Т искомого автомата В строит
множество S выделенных макросостояний для С. Выделенные макросостояния
для С получаем, строя всевозможные пути состояний (для С) от
начального состояния Q0 до первого повтора состояния на каждом
пути. Множество М состояний между двумя повторами образует
выделенное состояние, если М содержит звездчатое состояние (вида [St,*])
Процедура go(Q0,T,DMSt) по начальному состоянию Q0 и функции
переходов Т искомого автомата В вычисляет его выделенное
макросостояние. Процедура gol(Q0,T,A,P) по начальному состоянию Q0 и
функции переходов Т искомого автомата В вычисляет путь Р с циклом
в конце его. Переменная А - накапливающая для пути Р. Процедура
cycle(P,C) из пути Р выделяет имеющийся в конце его цикл.
d(A,B) :- X=[0,l],Ql=[qO,ql,q2,q3],Q10=qO,
Tl=[[q0,0,q0],[q0,l,ql],[ql,0,ql],[ql,l,q2],
[q2,0,q2],[q2,l,q3],[q3,0,q0],[q3,l,q2]],
Fl=[q2,q3],A=[X,Ql,Q10,Tl,Fl],stable(A,B).
stable(A,B) :- A=[X,Q1,Q10,T1,F1] ,Q0=[Q10,*] ,IS=[Q0] ,AT=[],
expand_states_transits(lS, IS, AT, A, Q, T),
distinqui9hed_macrostates(Q0,T,F),B=[X,Q,[Q10,*],T,F].
expand_states_transits([H|R] ,AS, AT,A,Q2,T2) :-
A=[X,Q1,Q10,T1,F1],
findall([H,In,Hl],
(member(ln, X), next_state(H, In, Tl, Fl, Q10, Hi),
not(member([H,In,Hl],AT))),L),
delrepeate(L,Ll),append(AT,Ll,ATl),
findall(H3,(member([H2,Inl,H3],Ll),not(member(H3,AS))),L2),
delrepeate(L2,L3),append(AS,L3,ASl),append(R,L3,Rl),
expand_states_transits(Rl, AS1, ATI, A, Q2, T2).
expand_states_transits( [ ],Q2,T2, A,Q2,T2).
next_state([H|R],In,Tl,Fl,Q10,H2) :- member([H,In,Hl] ,Tl),
ifthenelse((Hl=Q10,member(Q10,Fl)),H3=[Q10,*],
next_st(R,In,Tl,Hl,[Hl],[],H3)),
ifthenelse(H3=[_,*] ,H2=H3,
367
if thenelse( (member (HI, Fl), not(member (Q10, H3))),
reverse([Q10|H3],H2),reverse(H3,H2))).
next_st([H|R],In,Tl,Hl,A,B,Ql) :- not(H is *),
member([H,In,H2],Tl),ifthen(H2=Hl,Ql=[Hl,*]),
ifthen((not(H2=Hl),member(H2,B)),next_st(R,In,Tl,Hl,A,B,Ql)),
ifthen((not(H2=Hl),not(member(H2,B))),
next_st(R,In,Tl,Hl,[H2|A],[H2|B],Ql)).
next_st([],In,Tl,Hl,Ql,B,Ql).
next_st([*],In,Tl,Hl,Ql,B,Ql).
distinquished_macrostates(QO,T,F) : -
(setof(DMSt,go(QO,T,DMSt),F) ; F=[]).
go(Q0,T,DMSt) :- gol(Q0,T,[] ,P),
cycle(P,C),C=[jDMSt].
gol(St,T,A,P) :- not(member(St,A)),member([St,In,NSt],T),
gol(NSt,T,[St|A],P).
gol(NSt,T,A,P) :- member(NSt,A),P=[NSt|A]).
cycle([H|R],C) :- cyclel(H,R,[H] ,C).
cyclel(S,[Hl|Rl],A,C) :- not(S=Hl),cyclel(S,Rl,[Hl|A] ,C).
cyclel(S,[Hl|Rl],A,C) :- S=H1, member ([ St,*] ,A),C=[S|A].
delrepeate(S,SF) :- Sl=[] ,delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),
append(Sl,[H],S2),delrep(T,S2,SF).
delrep([],S2,S2).
reversed ],[]).
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
17.3.2. Программа вычисления макроисточника для сверхъязыка,
полученного сверхитерацией языка,
представимого источником
Программа вычисления макроисточника проще, чем для
детерминированного случая: достаточно ввести новое состояние f, затем в
граф-схеме исходного источника провести пустые стрелки от
выделенных состояний источника к f и от f к его начальным состояниям.
Выделенными макросостояниями искомого макроисточника будут любые
подмножества состояний построенного макроисточника, содержащие
368
новое состояние f.
d(A,B) :- X=[0,l],Q=[q0,ql,q2,q3],Q0=[q0,ql],
T=[[q0,0,ql],[ql,l,q2],[q2,0,q3],[q2,l,q3],[q3,*,q0]],
F=[q0,q3],A=[X,Q,Q0,T,F],
super_iterat_undetautomat(A,B).
super_iterat_undetautomat(A,B) :- A=[X,Q,Q0,T,F],
findall([Q3,*,f],member(Q3,F),L),
findall([f,*,Q4],member(Q4,Q0),Ll),
unionset(T,L,S),unionset(S,Ll,Tl),powerset(Q,PS),
B=[X,Q1,Q0,T1,PS].
powerset(X,S) :- findall([f |Y] ,(subsetl(Y,X),Y[]),S).
subsetK [],[])•
subsetl([H|S],[H|T]) :- subsetl(S,T).
subsetl(S,[H|T]) :- subsetl(S,T).
uniohset([] ,X,X).
unionset([X|R],Y,Z) :- member(X,Y),! ,unionset(R,Y,Z).
unionset([X|R],Y,[X|Z]) :- unionset(R,Y,Z).
add(X,Y,[X|Y]).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
17.4. Детерминизация макроисточника
Теорема. Существует алгоритм, который по любому заданному
макроисточнику строит эквивалентный ему детерминированный
макроавтомат.
Доказательство. Пусть MA = (XyQyQQyDyF) есть макроисточник; F
Q P(Q) и множество F = {f^,...,/^}. Тогда представимый
макроисточником МА сверхъязык
SL = L(MAyQQyF) = U L(MAyq0,H).
q0€Q0yH£F
Пусть Я = {<7i,<?2>- • • >4s} и МАХ = (XyQyqQyD,H) - макроисточник,
полученный из МА с сохранением в МА только состояний из Я и
ребер, им инцидентных (т.е. этим состояниям принадлежащих).
Макроисточник МА г можно рассматривать как источник А г,
допускающий или не допускающий конечный язык обычным образом.
Макроисточник МАХ представляет сверхъязык SLlf содержащий все
сверхслова х из Х°°у на которых любой ход МАХ содержит состояния
369
только лишь из Я. Если множество всех сверхслов SLX = L(MAl,q1,H)
пусто, то исходный сверхъязык пуст. Если нет, то SLX =
(L(Alyqlyq2)- L(Axyq2yq3)* • • • ' L(AY yqs_x yqs) • (L(AX ^5^г))°°,
и тогда представимое в макроисточнике МА множество сверхслов
\b{Ayq{iyql)'SLly если L(A,q0,qi) * 0,
\SLly если L(A,q^qx) = 0 и qx = qQy
0 в остальных случаях.
SL = L(MAyqQyH) =
Далее, применяя теорему о сверхитерации языка, представимого
конечным автоматом, и теорему о конкатенации языка, представимого
автоматом, с сверхъязыком, представимым макроавтоматом, строим
искомый детерминированный макроавтомат, представляющий
сверхъязык SL.
Следствие. Класс сверхъязыков, представимых макроисточниками,
замкнут относительно дополнения.
17.4.1. Обще регулярные сверхъязыки
Утверждение. 1. Если язык А (множество конечных слов)
регулярен, то сверхъязык А00 общерегулярен.
2. Если язык А регулярен, а сверхъязык В общерегулярен, то
сверхъязык А* В общерегулярен.
3. Если сверхъязыки А и В общерегулярны, то сверхъязык A U В
общерегулярен.
Теорема. Всякий сверхъязык общерегулярен тогда и только тогда,
когда он автоматно представим.
Доказательство. СИНТЕЗ. Автоматность общерегулярного
сверхъязыка доказывается индукцией по его построению.
АНАЛИЗ. Пусть макроисточник MA = (XyQyqQyTyF) допускает
сверхъязык L. Достаточно показать общерегулярность А для
одноэлементного множества F = {qly...yqr}. Пусть источник А = (XyQyqQyTy
{qx}) допускает множество слов, переводящих Ах из q0 в qx.
Построим источники АХ->2У А2->ЗУ...У АГ_Х->ГУ Аг_х следующим образом.
Источник Ai-j = (XyQyqiyDy{qj})y где (qyayq')£D *- (qyayq')£T &
q€F & q'€F. Тогда A^j допускает такие и только такие слова,
которые переводят А из qx в qj и при этом А не проходит через
состояния вне F. Тогда Beh(A) =
Beh(Ai) * (Beh(Ax->2) • Beh(A2->3).. .Beh(Ar_x->r) • Beh{Ar_x))°°•
Поэтому множество Beh(A) общерегулярно. Теорема доказана.
Построение общерегулярного множества сверхслов, представляюще-
370
го дополнение сверхъязыка Beh(MA), представимого макроисточником
MA = (X,Q,Q0,D,F), можно осуществить следующим образом.
Сверхслово н> € X00 - Beh(MA) —>
(Уг)г€^(Л/л,.)Аг(о)€Со Ит (Г) ' F'
Пусть дополнение Pow(Q) - F для простоты состоит из
единственного макросостояния G = {qly...,q}. Построим источники Ах,
А1->2У А2->ЪУ...У АГ_1-*ГУ Аг_х следующим образом. А1 строится по А\
= {X.Q.Q^.D.iq^) так, что для всякого хода А' на входном
конечном слове заключительным оказалось бы состояние qx. Для источника
А.-> = (X9Q9qi9T9{qj)) положим (q9a9q')tT «-» (q9a9q')£D & q€G &
q'€G. Тогда Aj->; допускает такие и только такие слова, которые
переводят А из qx в qj и при этом А не проходит через состояния
вне G. Тогда дополнение
X00 - Beh(A) =
BehiA,)- (BehiA^) • ВеН(А2->г).. .Beh(Ar_lr>r) • £e>/iUr-i))°°,
т.е. дополнение X00 - Beh(A) общерегулярно.
Проекция сверхслова с одного алфавита на другой осуществляется
побуквенно, как и в случае проекции конечного слова. Проекция
сверхъязыка осуществляется проекцией каждого его сверхслова.
Теорема. Класс автоматно представимых языков замкнут
относительно проекции.
Доказательство. Пусть макроавтомат MA = (X9Q9q09T9F)
представляет сверхъязык SL Я Xе0 и функция /: X -> Y осуществляет проекцию
сверхъязыка SL с алфавита X на алфавит Y. Тогда макроисточник МА
= (X9Q9Q09D9F)9 где (q9a9q')£T —♦ (q9f(a)9q')£D9 представляет
сверхъязык f(SL). По макроисточнику МА можно построить
детерминированный макроавтомат, представляющий сверхъязык f(SL).
18. ПРОБЛЕМА УНИФОРМИЗАЦИИ
18.1. Языки и операторы
Пусть зафиксированы входной X и выходной Y алфавиты. Всякий
конечный автомат с выходом реализует некоторый словарный
(сверхсловарный) оператор 0(д:) = у, определенный на множестве слов
(сверхслов) в алфавите X и принимающий значения в множестве слов
(сверхслов) в алфавите Y. График оператора О есть множество G =
{(х9у) : ©(у) = у}. В словарном операторе пара (х9у) € X*XY*9 а в
371
сверхсловарном операторе пара (х,у) € Лг00ху00.
Поведение автоматов без выхода с выделенными состояниями
определяли в терминах представимости языков (сверхъязыков). Поведение
автоматов с выходом определяется в терминах реализации (т.е.
представимости) операторов. Между обоими понятиями представимости
имеется естественная связь, основанная на сводимости друг к другу
свойств множеств 1л свойств функций. Именно, произвольное
множество, рассматриваемое как подмножество некоторого универсального
множества (универсума), однозначно определяется своей
характеристической функцией. Произвольная функция в свою очередь может
рассматриваться как множество точек ее графика. В нашем случае в
роли множеств выступают языки (сверхъязыки), а в роли функций -
операторы.
С каждым подалфавитом У Я У оператор О ассоциирует язык
O-i(y) = {х = jc(0)jc(1)...jc0O € X*: х = у = y(0)y(l).. .у(к)}.
Скажем в этом случае, что оператор О представляет язык О"1 (У')
множеством выходов (т.е. выходными буквами из У). Оператор О
допускает все слова из О-1 (У) и отвергает все другие слова.
Аналогичные построения можно выполнить относительно
сверхъязыков. Именно, с каждым подмножеством У Я У оператор О ассоциирует
сверхъязык ©_1(У) = {jc = jc(0)jc(1). .. € X00: ©(*) = у =
у(0)у(1)... € У*, lim y(t) = У}. Скажем тогда, что оператор О
представляет сверхъязык О-1 (У), т.е. допускает все сверхслова из
(D-ll(y) и отвергает все слова вне О"1 (У').
Автомат А = {X,У\Q,qQ,T\B) с выходом представляет язык (сврхъ-
язык) L выходами из У € У, если оператор О, соответствующий
этому автомату, представляет этот язык (сверхъязык) выходами из
алфавита У.
Теорема. Класс языков (сверхъязыков), представимых в конечных
автоматах с выходом, совпадает с классом языков (сверхъязыков),
представимых в конечных автоматах без выхода.
Доказательство. С произвольным автоматом без выхода А =
{X.Q.q^T.F), где Q = {qQ,ql9.. .,<?*}, F = {qt:i,... ,qir}, можно
ассоциировать автомат с выходом А' = (X,Y,Q,q0,T,Я), где У =
{.У о >У\ > • • • >Ук) > а функция выхода В строится следующим образом.
Если T(qi9x) = <7;, то B(qi9x) = у у Язык Beh(A) совпадает с
языком, представимым автоматом А' множеством выходов У =
{>il >!>}-
Пусть макроавтомат без выхода А = (X,Q9q0iT,F), где Q =
{<7о ><7l > • • • >Як) > F = U?I !, ... ,^1Г} ,...,{?; 1 ,.- • ,<7;/} = P(Q) ,
представляет сверхъязык Beh(A). Построим автомат с выходом А' =
(X,Q,q0 ,Т,В), где У = {у^Уц.-чУк), а функция выходов В
372
строится так же, как и в предыдущем случае. Сверхъязык Beh(A)
представим автоматом с выходом А' макромножеством выходов У =
Пусть автомат Мура с выходом А = (X,У,Q,q0iT,B) представляет
язык Beh(A) множеством У Я У. Положим F = {q € Q : 3y€Y' (B(q) =
у)}. Тогда автомат без выхода А' = (X9Q,q09T9F) представляет тот
же язык Beh(A).
Если теперь автомат Мура с выходом А = (X,Y',Q,q0,T,B)
представляет сверхъязык О"1 (У') некоторым макромножеством У =
{{У|1..-.эУ|г}»..-ЛУ;1,...,У;/}} = {Yi,...,Yj} = Р(У), ТО При
F = {Fi9...,Fj}, где
Fi■ = {q € Q : Зу € У, B{q) = у},
F;f = {q € G : Э;у € У; В(?) = у},
автомат А = (X9Q9q0iT9F) представляет тот же самый язык.
Замечание. Алгоритм минимизации автоматов без выхода
получается сочетанием алгоритма минимизации автоматов с выходом с
доказанной теоремой.
Операторы можно рассматривать и вне понятия конечного
автомата. Словарный оператор можно рассматривать как функцию О : X* ->
У*, а сверхсловарный оператор - как функцию О : Xе0 -> У00.
00 00
Сверхсловарный оператор О : X ~* У есть оператор без
предвосхищения (его еще называют ограниченно-детерминированным
оператором), если для всяких входных сверхслов
х' = *'(0)х'(1) ... *'(0 ...
*" = jc"(0)jc"(1) ... jt"(0 ...
соответствующие им выходные слова
О(лг') = у' = y'(0)y'(D ... у'(0 ...,
0(лг") = /' = /'(0)/'(D • • • /'(О ....
таковы, что для всякого t равенство
jc'(0)jc'(1) ... x'(t) = Jt"(0)jt"(l) .. *"(0
влечет равенство
y'(o)y'd) ... у'(0 - /'(о)/'Ц) ... /40.
В противном случае оператор О является оператором с
предвосхищением.
Словарный оператор О : X* -> У* есть оператор без
предвосхищения, если:
373
1) равенство ®(х) = у влечет равенство длин слов х и у;
2) для всяких входных слов х', х" и для всякого t равенство
л:'(0)х'(1) ... Х'(г) = *"(0)х"(1) ... x"(t)
влечет равенство (D(x') = у' = y'(0)y'(l)%..y'(t) = /'(0)/'(l). • •
/'(Г) = /' = *";
3) оператор О, применимый к слову ху применим и ко всякому его
начальному отрезку.
В противном случае словарный оператор О - оператор с
предвосхищением.
В операторе без предвосхищения выходная буква в момент t не
зависит от входных букв в момент t' > t. В операторах с
предвосхищением это условие может не выполняться. В конечных
автоматах реализуются только операторы без предвосхищения.
Утверждение. Если оператор (D реализуем в некотором конечном
автомате, то его график представим конечным автоматом.
Доказательство. Пусть для определенности (D есть сверхсловарный
оператор, реализуемый автоматом А = (X,Y,Q,q0,T', В). Если граф-
схему для А (где каждое ребро снабжено и входом, и выходом)
рассматривать как макроисточник в алфавите X*Y, то график оператора
А совпадает с поведением этого макроисточника, имеющего в
качестве множества выделенных макросостояний множество всех подмножеств
множества состояний исходного автомата.
Утверждение доказано.
Поставим теперь следующий вопрос. Если график некоторого
оператора О : X00 -> У00 представим в некотором макроавтомате, то можно
ли реализовать оператор О в подходящем конечном автомате? Ответ
отрицателен. Это показывает следующий пример.
Пусть сверхсловарный оператор (D : X00 -* Y00 с X = Y = {0,1},
сопоставляя сверхслову 00... 0... (сплошь из нулей) то же самое
сверхслово 00...0..., а всякому другому сверхслову - сверхслово
11... 1... (сплошь из единиц). Оператор О является оператором с
предвосхищением, и потому он не реализуем с помощью конечного
автомата. Между тем, график оператора (D представим в макроисточнике
MS = (*xy,e,e0,£>,F), где Q = {qQ9ql9q2}; Q0 = {q^q,}',
D = {(?o.OO,?o).(9i.01,?i),(?i,ll,92)>(?2.11,92),(92,01,92)};
Ранее показано, что классы сверхслов, представимых в
макроисточниках и макроавтоматах, совпадают.
18.1.1. Униформизация
Пусть дан сверхъязык SL в алфавите X*Y. Сверхсловарный
оператор (D : Xе0 -> У00 униформизует еврхъязык 5L, если для всякого х €
374
Z00 равенство ©(*) = у влечет (хуу) € SL.
Можно говорить об униформизации сверхъязыка SL оператором У00 -*
Xе0. Понятие униформизации можно сформулировать и для сверхъ-
языков в алфавите Хх х Х2 х ... х Хп по любой переменной.
Понятие униформизации есть одно из важнейших понятий теории
множеств. Очень важно оно и в теории конечных автоматов. Проблема
униформизации конечно автоматного сверхъязыка состоит в
следующем. Пусть задан макроавтомат А, представляющий некоторый
сверхъязык SL в алфавите X*Y. Требуется выяснить, существует ли
сверхсловарный конечно автоматный оператор О, униформизующий
сверхъязык SL\ если да, то построить конечный автомат с выходом,
реализующий такой оператор.
Покажем, что проблема униформизации конечно автоматного
сверхъязыка решается положительно. Решение этой задачи дадим в
терминах предложенной Макнотоном игровой интерпретации, в той
редакции, которую предложил для этого Б.А.Трахтенброт.
18.2. Игры
Будем рассматривать игры с полной информацией. Назовем их
просто играми. Игре присущи следующие особенности.
1. В игре участвуют два игрока, называемых белыми и черными.
Первый ход делают белые; черные отвечают своим ходом. Затем ходы
чередуются: белые, черные, белые, черные, и так далее, образуя
партию игры.
2. Ход белых есть выбор одной буквы из алфавита X = {х!,...,
хт}. Ход черных есть выбор одной буквы из алфавита У = {ух,
3. При каждом ходе очередной игрок знает все предыдущие ходы
данной партии (полная информация).
4. Для каждой партии имеет место либо выигрыш белых, либо
выигрыш черных.
Партия может быть конечной и бесконечной. В конечной партии
партия прекращается после конечного числа шагов. Конечную партию
можно рассматривать как слово в алфавите X х Y:
х(0)х(1) ... x(t),
у(0)у(1) ... y(t),
или как пару слов Jt[0,f], y[0,t] отдельно ходов белых и ходов
черных. Длина партии есть t.
Бесконечная партия продолжается неограниченно. Бесконечную
партию можно рассматривать как сверхслово
375
х(0)х(1) ... x(t) ...
y(0)y(l) ... y(t) ...
в алфавите X x У, или как пару сверхслов дг[0,оо), )>[0,оо) отдельно
ходов белых и ходов черных.
Игра конечна, если для некоторого числа р любая партия не дли-
нее р. В противном случае игра бесконечна.
Всякую конечную игру можно задать в виде дерева, ребра
которого помечены буквами из X х У, причем ребра, выходящие из одной
вершины, по разному помечены. Концевые вершины (листья) разбиты
на два класса: класс вершин, помеченных знаком и+и (это выигрыш
белых), и класс вершин, помеченных знаком и-и (это выигрыш
черных). В корне дерева помещена пешка. Белые выбирают любую букву
д:(0) из Х\ черные в ответ выбирают любую букву у(0) из У. Пешка
перемещается в вершину по ребру, помеченному парой (х(0),у(0)).
Далее белые выбирают одну А'-букву (т.е. букву из X) х(1), на что
черные отвечают выбором одной У-буквы y(l). Пешка перемещается в
вершину по ребру, помеченному парой (jc(l),_y(l))- И так далее.
Партия заканчивается, если пешка окажется в концевой вершине; ее
пометка указывает, кто выиграл. Множество партий, выигрышных для
белых, есть язык в алфавите X х У.
На рис. 18.1 приведена конечная игра с X = {0,1}, У = {а,Ь}.
Для всякой конечной игры можно определить, какая из сторон
имеет выигрыш, и указать последовательность ходов, приводящую к
выигрышу. Покажем, как это делается для игры, дерево которой
изображено на рис. 18.1. Просматриваем все поддеревья, имеющие корень
в предпоследнем ярусе 2; это поддеревья с корнем в вершинах 7 и
10. Из вершины 7 выигрывают черные, ибо при единственно возможном
ходе белых 0 черные отвечают выбором Ъ и выигрывают. Вершину 7 в
знак выигрыша черных помечаем знаком и-и. Из вершины 10
выигрывают белые, выбирая ход 0; любой ответ черных приводит их к
проигрышу. Вершину 10 в знак выигрыша белых помечаем знаком "+". Далее
просматриваем все поддеревья с корнем в ярусе 1. Из вершины 2
выигрывают белые; из вершины 3 ходом 0 выигрывают белые; из вершины
4 произвольным ходом выигрывают белые; из вершины 5 при
единственно возможном ходе белых 0 ответом а выигрывают черные. Вершины
2,3,4 помечаем знаком и+и, а вершину 5 - знаком и-и. Из вершины 1
ходом 0 выигрывают белые; помечаем ее знаком и+и. В этой игре
белые начинают и выигрывают (в любой партии). Соответствующие ходы
отмечены двойными линиями. В этой игре белые имеют выигрывающую
стратегию (т.е. белые начинают и выигрывают).
376
14
\0a
15
Ob
16
\0a
17
Ob
18
19
la lb\
Ярус 3
lal
la
lb
\Ob
10
Oa
11
la
12
Оя
13
Ярус 2
Ob
Ярус 1
\0a
I Ob
la
lb
+Jl
Рже. 18.1
Ярус О
В бесконечных играх все партии бесконечны. Такую игру можно
изобразить бесконечным деревом (рис. 18.2) из каждой вершины
которого исходят тп ребер, помеченных парами (х,у) из X*Y9 где X =
{х19...9хт}, Y = bi>.>>>*}•
Игра есть дерево. Партия есть путь в дереве. В этом
бесконечном дереве отмечается множество путей (партий), выигрышных для
белых. Остальные пути (партии) выигрышны для черных. Таким
образом различные игры при фиксированных X и Y отличаются только
множествами партий (путей), выигрышных для белых. Это множество есть
некоторый сверхъязык в алфавите X х У.
С другой стороны, всякий сверхъязык L из (XXY)00 задает
бесконечную игру, в которой множество партий (путей) из L
выигрышно для белых.
18.2.1. Игры с конечным числом состояний
Пусть А = (XXY,Q9q0,T,F) - макроавтомат, где F Я P(Q). Игра с
377
. . .x»
>Уп\
*1.У1
>Уп
{ХцУх
хт > Уп
Рмс.18.2
хт> Уп
конечным числом состояний (автоматная игра) осуществляется
следующим образом. Пешка помещается в вершину q(0) = q0 граф-схемы
автомата А. Белые называют свой первый ход д:(0) из Х\ черные
отвечают выбором у(0) из Y. Пешка перемещается в вершину
q(l) = Г(д(0),(*(0),у(0))).
Далее белые выбирают дг(1) из X, а черные отвечают выбором y(l) из
Y. Пешка перемещается в вершину
q(2) = Hq(l),(x(l)MD)).
Такой обмен ходами продолжается неограниченно:
х(0) х(1) ... x(t) ...
у(0) у(1) ... y(t) ...;
в результате этого пешка последовательно перемещается в вершины
q(0) q(l) ... q(t) ....
образуя сверхслово состояний q из Q00. Белые выигрывают, если
lim q(t) лежит в F, и проигрывают в противном случае.
378
18.3. Стратегии
Пусть бесконечная игра с конечным числом состояний
осуществляется с помощью макроавтомата А = (XXY9Q9qQ9T9F).
Стратегия черных есть оператор без предвосхищения,
перерабатывающий входные сверхслова х = jc(0)jc(1). .., являющиеся
последовательными ходами белых, в выходные сверхслова у = y(0)y(l)...9
являющиеся ответными ходами черных. При этом ход черных y(t)
зависит от предшествующих ходов белых x(0)x(l).. .x(t). Стратегия
белых есть оператор без предвосхищения, перерабатывающий
сверхслова у = y(0)y(l)..., являющиеся ходами черных, в сверхслова х =
jc(0)jc(1)..., являющиеся ходами белых. При этом ход белых x(t) в
момент t зависит от y(0)y(l).. .y(t-l), а ход д:(0) от ходов черных
не зависит.
Стратегия белых есть оператор с задержкой. Всякий оператор у =
©"(*) без предвосхищения есть некоторая стратегия черных. Всякий
оператор х = ®'(у) без предвосхищения с задержкой есть некоторая
стратегия белых.
Если белые и черные выбрали стратегии (операторы) О' и О"
соответственно, то партия, которая будет сыграна, полностью
определена; обозначим ее через (О',0"). Если в партии (©',©"), белые
начинают и выигрывают, то будем говорить, что стратегия белых О'
бьет стратегию черных О". Если стратегия белых О' бьет любую
стратегию черных О", то О' есть выигрывающая стратегия белых.
Аналогично для черных.
Оператор О' (как и оператор О") может оказаться конечно
автоматным. В таком случае говорят о конечно автоматных стратегиях.
При этом автомат, реализующий стратегию белых, есть автомат с
задержкой: выход белых зависит только от состояния.
Если О' и О" - конечно автоматные стратегии бесконечной игры,
то партия ((D',(D") есть периодическое сверхслово в алфавите X*Y.
По заданным автоматам для О' и О" предпериод и период этого
периодического сверхслова строится эффективно. В самом деле, пусть
автоматы А' = {Y 9X 9Q' 9q[J' 9В') и А" = (X9Y9Q" 9q'{ 9Т" 9В")
реализуют операторы х = О'(у) и у = ®"(х) соответственно; при этом
?'(о) = ?0', <Г(о) = tf,
f'(H-l) = T'(q'{t)9y(t))9 q"(t+l) = T"(q"(t)9x(t))9
x(t) = B'(q'(t)9y(t-1))9 y(t) = В"(<Г('Ы0).
Значение jc(0) выбирается произвольно. Всякая партия (©',©")
тогда имеет вид
379
jc(0) jc(1) ... Jc(r-l) x{t) ... jc(n-l) x(n) ...
y(0) y(l) ... y(t-l) y(t) ... y(n-l) y{n) ...
<7'(0V(D ... q'U) ... q'{n) ...
<r(o)<r(i) ... <r(0 ... «"(/I) ...,
где дг(0) из X произвольно, а все последующие ходы (x(t)9y(t))
вычисляются с помощью функций Т' 9В' 9Т"9В". Так как мощности
алфавитов У, Q', Q" конечны, то в этой партии впервые встретятся
моменты /л и л, для которых тройки (y(m-l)9q'(m)9q"(m)) и (y(n-l),
q'(n)9q"(n)) одинаковы. Тогда
х(пг) = B'(q'(m)9y(m-l)) = B'(q'(n)9y(n-l)) = *(л),
y{m) = B"(q"(m)9x(m)) = Я"(<Г(л),;у(л)) = у(л),
*'(m+l) = Г(9'(т),у(т)) = Г'(<?'(л),;у(л)) = <?'(л+1),
<Г("|+1) = Г'(<?"(/л),х(/л)) = ГЧ?,,(л),х(л)) = <Г(л+1),
и потому длины предпериода и периода не превосходят произведения
мощностей алфавитов У,Q'\Q"\ ибо отрезок партии от 0 до т-\
составляет ее предпериод, а отрезок от m до л-1 - ее период.
Для всякой конечной игры, как отмечено, либо белые, либо
черные имеют выигрывающую стратегию. Она может быть сделана конечно
автоматной. Для конечной игры, изображенной на рис. 18.1, белые
имеют выигрывающую стратегию. Граф-схема конечного автомата
(Мура) А = (Y9X9Q9qQ9T9B)9 вычисляющего оператор с задержкой О : У*
-♦ X*, реализующую выигрывающую стратегию белых, приведена на рис.
18.3. Состояния автомата помечены ходами белых; стрелки - ходами
черных. В конечной игре, приведенной на рис. 18.4, выигрывают
черные. Граф-схема автомата (Мили) А = (X9Y9Q9q09T9В)9 вычисляющего
выигрывающую стратегию черных, приведена на рис. 18.5.
*(о)
*(о)
= 0
= 0
2
1
■* 1 1 *■
а
м
0
к
а9Ъ
3,0
ь —
1
Рнс.18.3
380
^
а
6,0
ъ
к
2,1
Ob
la lb
Oa
Ob
la lb
1
Oa
Oa Ob
+ 5 - 6 +7 +8 - 9 +Ю +11 +12
la
+J13 | — 114 |-|15 |-|16 | + |17 | — 118 |-|19 20| + | 2l| +
Oa
la lb
la lb
+ 2
Ob
la
- 0
lb Ob
lb
+ 4
0.1(a)
14
Рнс.18.4
0.1(a) 0.1(a)
15
18
0.1(a)
у
19
—
0(b)
1(a)
0(b)
Ke)
0.1(b)
0.1(a)
0(a)
Ка)
Рнс.18.5
381
В классе всех бесконечных игр существуют такие игры, в которых
никакая из сторон не имеет выигрывающей стратегии. В случае
конечно автоматных игр положение иное: здесь всегда одна из сторон
имеет выигрывающую стратегию и даже конечно автоматную. К ее
построению и переходим.
18.4. Униформизация конечно автоматных языков
Проблема униформизации конечно автоматного сверхъязыка L = (X
х У)00, представимого макроавтоматом А9 может быть
интерпретирована как задача о существовании и построении выигрывающей конечно
автоматной стратегии, которая является оператором без
предвосхищения у = 0"(х) для черных, или оператором без предвосхищения х =
©'(у) для белых, ибо в конечно автоматной игре всегда одна из
сторон имеет выигрывающую конечно автоматную стратегию.
18.4.1. Порядковые векторы и порядковые стратегии
Пусть А = (X*Y9Q9q09T9F) есть макроавтомат, представляющий
сверхъязык L = L(A9q09F)9 Q = {?0>9i > • • • >Яп) " множество
состояний в конечно автоматной игре G(A)9 соответствующей сверхъязыку
L. Возможны (п+l)! перестановок состояний из Q; назовем каждую
такую перестановку (^,- ,#/ ,...,?/ ) порядковым вектором и будем
обозначать его через (/0>*i >• • • >*л)-
Рассмотрим некоторую партию
х(0) jc(1) ... x(t) ... , v
y(l) у{2) ... y(t) ... {1S1)
в конечно автоматной игре G(A). Ей соответствует
последовательность состояний
q(0) q(l) ... q(t) ... (18.2)
Наряду с последовательностью (18.2) сопоставим партии (18.1)
последовательность порядковых векторов
q(0) q(l) ... q(f) ..., (18.3)
индуктивно определяемую следующим образом:
1) q(0) = (0,1,...,л);
2) если q(r) = (i09i1,... ,i*,'*+i > • • • Л) и ?('+l) = Яку то
q(r+l) = Ok,il9i29...9ik9ik+l9...9in).
Ниже следует пример последовательности состояний и
соответствующей последовательности порядковых векторов.
382
Яо Яг Яг Яг Я\ Яо Я\ Я\ Яъ Яа Я\ Яг Яа
0222101134124
1000210013412
2111022201341
3333333330033
4444444442200
Справедлива следующая лемма.
Лемма 1. Если q(f) = (...,/,...,;,...), q(f+/i) = (...,;,...,
У,...), то в промежутках между t и Н-л вершина ; (состояние q^)
посещалась, т.е. занимала в векторе первое место, по крайней мере
один раз.
Пусть макросостояние Q' = {ЯоуЯн- • • >Я ) — Q- Пусть n(t) есть
номер позиции в векторе q(l), которая в следующем векторе q(f+l)
стала первой. Например, q(f) = (Яг>Я1>ЯА>Яо>Яэ>Я5)> п(0 = 3, q(f
+1) = (Яа>Я2>Я1>Яо>Яз>Яз)- Пусть в последовательности (18.3),
которую запишем в виде
f(0) q(l) ... q(t') q(t'+l) ... <?(Г) <?(f"+l) ...,
предельное макросостояние Q' формируется, начиная с момента f.
Пусть t" выбрано так, что множество состояний, встречающихся в
слове q(t')q(t'+l).. .q(t")> совпадает с множеством Q'. Тогда
Vr Z Г:
в порядковом векторе q(f) первые 5+1 позиций заняты
состояниями предельного макросостояния Q'\
n(t) = s; кроме того, (3°°t)(n(t) = s)f где 3°°t означает:
существует бесконечно много t.
В последовательности f"+l, f"+2,... существует
подпоследовательность натуральных чисел т0 < т1 < ... , для которой п(т0) =
nim^ = ... = s, и между mt и т/ + 1 в первой позиции вектора q(f)
побывали все состояния из Q' (и только они). Так как в
последовательности т0 < тх < ... встречается не более (л+l)! векторов, то
один из них, например, q = (i0>*i, • • • Js>h+i > • • • >'л) в
последовательности порядковых векторов q(m0),q(m1),... встречается
бесконечно много раз, допустим, что на местах t0 < tx < ...,
составляющих подпоследовательность в последовательности т0 < тх < ... .
Показана справедливость следующей леммы.
Лемма 2. Для макросостояния Q' = {<70><7i»• • >#Л существует
последовательность натуральных чисел f0 < ^ < ... , для которой
1) q('<>) = q('i) = ... = 0"o>*"i,...,«"j>...,«"/i);
2) л(*0) = л^) = ... = s (а потому q(f0+l) = q(^+l) = ... =
\*5 »'o »'l » * ' * 9*S-1 »*5+l > * ' * >'/!''»
383
3) Vr £ t0 n(t) = s\
4) Vf ^ t0 в векторе q(f) первые 5 позиций заняты элементами
из Q'\ причем между всякими tt и fl + 1 в первой позиции порядковых
векторов q(0 побывали все состояния из Q'.
Стратегия белых, т.е. оператор без предвосхищения х = ®(у)9
называется порядковой, если ход белых x{t) зависит только от
порядкового вектора q(t)9 именно, x(t) = Fx(q(t)) для некоторой
функции Fx. Стратегия черных называется порядковой, если ход
черных y(t) зависит только от q(t) и x(t)9 именно, y(t)
Fy(q(t),x(t)) для некоторой функции Fy.
Порядковые стратегии являются конечно автоматными стратегиями
с числом состояний не более (я+l)!. В самом деле, пусть в конечно
автоматной игре отображение G(q(t)9x(t)9y(t)) есть функция,
указывающая порядковый вектор, в которой пара ходов (x(t),y(t))
переводит порядковый вектор q(t). По заданной конечно автоматной
игре функция G может быть построена эффективно. Тогда для белых
q(0) = (0,1,. ..9п) = q0,
q(r+l) = G(q(t)9Fx(q(t))9y(t)) = Gx(q{t),y(0)\
x(t) = Fx(q(t));
а для черных
q(0) = (0,1,..., n) = q0,
q(f+l) = G(q(t)9x(t)9Fy(q(t)9x(t))) = Gy(q(f),Jt(f));
yU) = Gy(q(0,x(0).
Пусть Q есть множество всех порядковых векторов. Тогда
автоматы Ах = (Y9X9Q9q09GX9Fx)9 Ау = (X9Y9Q9q09Gy9Fy) вычисляют
(реализуют) стратегии ©' и О" белых и черных соответстенно.
Заметим, что в рассмотренном случае выходные функции x(t) =
Fx(q(t))9y(t) = Fy(q(f),Jt(0), т.е. в порядковых стратегиях
функция x(t) не зависит от входа, поэтому построенные автоматы Ах и
Ау являются автоматами Мура и Мили соответственно.
18.4.2. Теоремы о порядковых стратегиях
Теорема 1. Если в конечно автоматной игре, осуществляемой
макроавтоматом А = (XxY9Q9qQ9T9F)9 стратегия черных у = ©"(*)
бьет порядковую стратегию белых х = О'Су), то черные имеют поряд-
/Ч Л
ковую стратегию О", которая бьет О'.
Доказательство. Пусть в данной конечно автоматной игре пара
стратегий (О' ,0") определяет партию
дг(0) х(1) ... х(0 ...
у(0) у(1) ... y(t) ...
384
q(0) q{\) ... q(t) ... (18.4)
q(0) q(l) ... q(0 ...,
выигрышную для черных. Тогда в этой партии предельное
макросостояние lim q{t) = Q' = {q09ql9...} € F. Ходы противников в партии
(18.4) в момент t
x{t) = Fx(q(t)) , y(t) = <D"(*(0) (18.5)
таковы, что белые действуют порядково, т.е. ход белых зависит
только от порядкового состояния, а ход черных выбирается, вообще
говоря, не порядково. По (непорядковой) выигрышной стратегии чер-
ных О" построим порядковую стратегию О", тоже выигрышную для
черных. Пусть t0 < tl < ... < ts < ... - существующая по лемме 2
последовательность, для которой
1) предельное макросостояние Q' Vf > t0 уже определилось;
2) q(0 = q('i) = ••• = 0'о>'1»---ЛЛ+1>-..Л);
3) n(t^l) = л(г2+1) = ... = s, т.е. q(r0+l) = q(f2+l) = ... =
\'$>'о >'i >••* >'$-iy*s+i у •• • >'л/>
4) в порядковых векторах на первом месте между I, и fl + 1
побывали все состояния из Q' (и только они), т.е. первые
компоненты (позиции) порядковых векторов между tt и fl + 1 дают в
точности множество Q'.
Рассмотрим в партии (Q'r0") следующее начало:
*(0) jc(1) ... x(tO) x(tO+l) ... x(tl) x(tl+l)
y(0) y(l) ... y(tO) y(tO+l) ... y(tl) y(tl+l)
q(0) q(l) ... q(tO) q(tO+l) ... q(tl) q(tl+l) (18.6)
q(0) q(l) ... q(t0) q(f0+l) ... q(f,) q(f,+l)
Пусть q - некоторый порядковый вектор в (18.6). Так как стра-
/ч
тегия белых О' порядковая, то при появлении q белые действуют
всегда одинаково: х' = Fx(q). Ход черных при повторных появлениях
вектора q не обязан быть одинаковым, ибо стратегия черных О" не
/ч
является порядковой. Построим порядковую стратегию черных О"
следующим образом. Полагаем вектор г(0) = q(0). Проверяем, есть ли в
(18.6) другая пара (q,jc), равная (г(0),х(0)). Если нет, то ход
черных у(0)' = у(0). Если да, то пусть п0 есть ближайший слева к
tx момент, для которого пара (г(0),х(0)) = (q(n0),jc(n0)).
Полагаем тогда у'(0) = у(п0) = Fy(r(0),*(0)).
Далее, пусть r(l) = F(r(0),Jt(0),y(0)). Проверяем, есть ли в
(18.6) другая пара (q,Jc), равная (r(l),jc(l)). Если нет, то y'(l)
= y(l). Если да, то пусть пх есть ближайший слева к tx момент,
385
для которого (r(l),x(l)) = (qCn^jxC/ij)). Тогда полагаем y'(l) =
у(пх) = Fy(r(l),x(l)). И так далее до tx. Во всех остальных
случаях значение Fy(q9x) выбираем произвольно. Порядковая стратегия
черных О" построена. Партия (О',О") имеет вид
х(0) х(1) ... x(t0) ... xit,) ...
у(о) yd) ... y(t0) ... ^i) ...
r(0) r(l) ... r(f0) ... r(tx) ... (18.7)
r(0) r(l) ... r(f0) ... r^J ....
Для построенной партии (18.7) последовательность состояний,
проходимых автоматом А, и соответствующая последовательность
порядковых векторов г(0> в которых первая компонента есть г(г),
вообще говоря, отличается от таковой в партии (18.5); при этом
г(0 = q(f) до тех пор, пока в (18.6) не встретилась ситуация
(q,x), которая встречалась в (18.6) позже.
Покажем, что последовательность (18.7) порядковых векторов
г(0 имеет начальный отрезок векторов
г(0) г(1) ... г(ш) ... г(т+л), (18.8)
первые позиции в которых на отрезке [т9т+п] дадут в точности
предельное макросостояние Q'. Другими словами, мы покажем, что в
последовательности (18.7) на отрезке [т,т+п] в первой позиции
побывали все состояния предельного макросостояния Q' и только
они. Пусть V/7 € [0,fj
ар = (max t)ut^r(p) = q(0).
Так как г(0) = q(0), то величина
а0 = (max t)uti(r(0) = q(0)
существует, причем 0 < а0 < tx и
г(0) = q(*0) & (V0 (в0 < t < tx - г(0) * q(0).
Если а0 = tlf то полагаем /и = 1. Если а0 < tl9 то по пост-
роению порядковой стратегии О" ввиду
г(0) = q(e0), х(0) = *U0), у'(0) = у(а0)
вектор r(l) = q(fl0+l), и потому ах существует; при этом
О < а0 < ах < tx и
г(1) = Ч(в1) & (Vr) (аг < t < tx -> r(l) * q(0).
Если ax = flf то полагаем m = tx. Если flj < Г1? то указанное
выше построение продолжается. Процесс выделения возрастающей цепи
О < а0 < ах < ... необходимо оборвется на некотором ат = tx и
386
тогда r(w) = q(rx) = (i09il9...9 i,,iJ+i,... ,i„).
Так как q(rx) = q(f0), то r(m) = q(f0) = q(tx).
Так как x(m) = x(tx)9 y'{m) = y{tx)9 то
r(m+l) = q(rt+l) = q(r0+l) = (*,,*0 *j-i •**+! *я)-
Поэтому дт+1 существует, f0 < ят+1 < tx и
г(т+1) = q(ew+1) & (Vr) (flm+1< Г < tx - г(т+1) * q(f)).
Если ят+1 = Г1Э то п = 1. Если дт+1 < *1э то ввиду
r(m+l) = q(em+1), *(m+l) = *(flm+1), ^(m+l) = у(вт+1)
вектор r(m+2) = q(tfm+1+l); поэтому дт+2 существует и для него
r(m+2) = q(ew+2) & (Vr)( < Гх - r(m+2) * q(0).
Продолжая таким же образом, получим последовательность
'о < ат+1 < ат+2 < ... < ат+п = '>
причем т(т+п) = q(tx) = (/0»'i > • • • ЛЛ+i>• • • Л)-
Так как г(/и+1) = (i,,i0»'i 'j-h'j+i»- • • »'я)» то по
лемме 1 между /71+1 и т+п первые позиции векторов r(m+l),... ,г(т+л)
дадут в точности предельное макросостояние Q'.
Теорема 1 доказана.
Аналогично доказывается следующая теорема.
Теорема 2. Если стратегия белых О' бьет порядковую стратегию
/ч /ч
черных О", то белые имеют порядковую стратегию О', которая бьет
/ч
стратегию черных О".
Теорема 3. Пусть в конечно автоматной бесконечной игре G белые
и черные прибегают только к порядковым стратегиям. Тогда одна из
сторон имеет выигрышную порядковую стратегию, (которая бьет любую
порядковую стратегию противника); эта выигрышная стратегия по
игре G может быть эффективно построена.
Доказательство. Пусть оба игрока прибегают только к порядковым
стратегиям. Тогда последовательности порядковых векторов,
соответствующих сыгранным партиям, будут периодическими с длиной
предпериода и периода в сумме не более (л+l)!. И предпериод, и
период можно эффективно найти и по периоду найти предельное
макросостояние (первые позиции в порядковых векторах периода). Если
поменяем порядковую стратегию, то сыгранная партия поменяется, но
выигрыш той или иной стороны определяется партией длины не более
(л+l)!. То есть бесконечная игра G эквивалентна конечной игре G'
с длительностью каждой партии не более (л+l)!. Правила игры G'
таковы. Пусть уже сделаны t ходов
х(0) х(1) ... x(t-l)
387
y(0) y(l) ... ;y(f-l)
q(0) q(l) ... q(f-l) q(f),
после которых возник порядковый вектор q(t). Если этот вектор
ранее не встречался, то игроки могут выбирать любой ход из своих
алфавитов X и У. Если вектор q(f) ранее возникал, т.е. q(f) =
q(l') при некотором С < t, то белые и черные обязаны повторять
ходы: x(t) = x(t')9 y(t) = y(t'). Партия прекращается при первом
повторении порядкового вектора. При этом в концевой вершине
дерева игры ставим знак +, если предельное макросостояние между этими
повторениями благоприятно для белых, и знак - в противном случае.
Далее построенную конечную игру G' анализируем на предмет
определения выигрышной стороны и построения для нее конечного
автомата, вычисляющего для нее выигрышную стратегию, как это делали
для конечных игр.
Теорема 4. (Основная о конечно автоматных играх.) Во всякой
игре с конечным числом состояний одна из сторон имеет выигрышную
конечно автоматную стратегию. Существует алгоритм, который по
любой заданной автоматной игре:
выясняет, какая из сторон имеет выигрышную стратегию;
строит для выигрышной стороны одну из выигрывающих конечно
автоматных стратегий.
Доказательство. Алгоритм теоремы 3 строит порядковую стратегию
О, которая бьет любую порядковую стратегию О' противника. Но эта
же стратегия (D бьет и любую другую стратегию О' противника (не
обязательно порядковую). В самом деле, если бы это было не так,
т.е. если бы некоторая стратегия О' била О, то по теореме 1 и не-
которая порядковая стратегия О' била бы О, чего нет.
Следствие. Если в конечно автоматной игре одна из сторон имеет
какую-нибудь выигрывающую стратегию, то она имеет и конечно
автоматную выигрывающую стратегию.
Теорема 5. (Перефразировка теоремы 4). Пусть дан произвольный
сверхъязык L в алфавите X*Y, который представим в некотором
макроавтомате. Тогда либо сверхъязык L униформизуется конечно
автоматным оператором у = 0'(х), либо его дополнение (Я'ху)00 - L
униформизуется конечно автоматным оператором с задержкой х = 0(у).
Существует алгоритм, который по макроавтомату, представляющему
сверхъязык L, выясняет, какая ситуация в указанной альтернативе
имеет место, и строит конечный автомат, реализующий
соответствующий оператор.
388
Следствие. Если существует оператор без предвосхищения, уни-
формизующий конечно автоматный сверхъязык L, то существует и
конечно автоматный оператор, униформизующий сверхъязык L. В
частности, если график некоторого оператора без предвосхищения
представим в конечном автомате, то этот оператор реализуем в конечном
автомате.
Замечание. Пусть бесконечная игра осуществляется с помощью
макроавтомата А = (XXY,Q9q0,T,F), где F = P(Q) есть множество
макросостояний, благоприятных для белых. Если выигрывают белые,
то белые имеют выигрывающую стратегию х = ©'(.у), униформизующую
сверхъязык L(A,q0,F), ибо стратегия О' "загоняет" фишку в
предельное макросостояние из F. Если выигрывают черные, то чёрные
имеют выигрывающую стратегию у = ©"(*), униформизующую
дополнительный сверхъязык, ибо стратегия ©" "загоняет" фишку в предельное
макросостояние из P(Q), лежащее вне F.
18.4.3. Пример построения выигрывающего автомата
Пусть конечный автомат для бесконечной игры задается
граф-схемой, приведенной на рис. 18.6. X = {ауЪ}\ Y = {c,d}.
Макросостояния {О}, {1}; {0,1,2} благоприятны для белых; остальные
возможные для этого автомата макросостояния {2}, {0,1}, {1,2}
благоприятны для черных. Начальное состояние есть 0. Строим конечную игру
(рис. 18.7), вершины которой помечены порядковыми векторами (i0,
il9i2)- Построение конечного дерева на некотором пути
прекращается при появлении на этом пути пары одинаковых порядковых
векторов. Множество состояний между одинаковыми порядковыми векторами
на одном и том же пути составляет предельное макросостояние.
Просматривая дерево игры на рис. 18.7, видим, что черные имеют
выигрывающую стратегию (рис. 18.8). Начальное состояние 012
расположено в корне дерева. Граф-схема автомата (Мили), ее
вычисляющую, приведена на рис. 18.9. В скобках указаны выходы автомата.
Входные символы автомата - это ходы белых; выходные (символы в
скобках) - это ответы черных.
ad>bd ас,ad
0
г:
1
л
2
bc,bd ad9bd
Рис.18.6
389
{1,2}
{0,1,2}
210
012
ас
ad
be
bd
{2}
{2}
210
120
210
ас
be
ad\
bd
ac
be
{0,1}
{0,1}
210
012
210
012
ac
ad
bc\
bd
ac
lad
be
bd
{0}
012
102
102
ac
be
ad
bd
ad\
bd
- 012
- 012
Pmc.18.7
Pmc.18.8
Если для того же самого автомата, граф-схема которого
изображена на рис. 18.6, к числу макросостояний, благоприятных для
белых, добавить макросостояние {2}, то получим игру (рис. 18.10), в
которой белые имеют выигрывающую стратегию (рис. 18.11).
Граф-схема автомата (Мура), вычисляющего выигрывающую стратегию белых,
390
012
aMd)
bid)
у
102
aic) }
-210
а,Ыс)
Ршс.18.9
{1,2}
{0,1,2}
210
ас
012
erf
be
{2}
210
ac
bd
120
be
ad
bd
{0,1}
210
ее
012
ad
be
{0}
012
ac
bd
102
be
ad
bd
+ 012
{2}
210
ac
be
{0,1,2}
+
1201
|012
be
bd
ad
bd
210
ac
ad
{0}
012
ac
102
be
ad
bd
+ 012
Phc.18.10
Phc.18.11
приведена на рис. 18.12; начальное состояние 012; состояния
помечены ходами белых; стрелки переходов - ходами черных.
391
c,d
Y
012, a
1 t
d
102, a
с ,d
210, a
1 t
d
120, b
с с
Рис.18.12
18.4.4. Программа униформизации автоматных сверхъязыков
Процедура unif(A,B) по макроавтомату А строит униформизующий
его автомат с выходом В.
Процедура expand_states_transits(lS, AS, AT, XY, T, QV, TV) по
промежуточным множествам состояний AS и переходов AT для В,
макроавтомату вычисляет множество состояний QV и функцию переходов TV
искомого автомата В. Переменная IS является рабочей; сюда
добавляем вновь полученные состояния, для которых еще не вычислены
переходы (q,a,ql) от состояния q к состоянию ql при подаче входа а.
Переменные AS и AT являются накапливающими для QV и TV
соответственно.
Процедура next_state(St,In,Ins,T,NSt) по состоянию St для В,
входу In, функции переходов Т для А строит следующее состояние
NSt и множество входов Ins, переводящих St в NSt для В.
Процедура facts_transits_add добавляет к базе данных, а
процедура facts_transits_remove удаляет из базы данных факты
transit(H) таблицы переходов для В.
Процедура term_tree_game_with_marked_leaves(F, S, Т) по
макросостоянию F и по начальному состоянию S искомого автомата В строит
дерево-терм (дерево игры) Т всех путей в граф-схеме макроавтомата
до первого повтора состояния на каждом пути, причем листья в
дереве Т помечены знаком winl, если предельное множество
состояний по соответствующему пути лежит в F, и знаком win2 в
противном случае.
Процедура win_mark_in_leafe(F,P,Win) по макросостоянию F для
макроавтомата А, по пути Р вычисляет знак выигрыша Win для
конечного узла (листа) в Р.
Процедура cycle_in_PC(PC,C) вычисляет цикл С, (заведомо)
содержащийся в конце пути PC.
Процедура win_tree_game(Ttg,Wtg) по дереву-терму игры Ttg
строит дерево-терм игры Wtg, размеченное знаками выигрыша в
каждом узле.
392
Процедура exp_win_depth(T,Tl) по промежуточному частично
размеченному знаками выигрыша дереву-терму Т игры вычисляет знак
выигрыша в корне Т, если все последующие (в глубину) за этим корнем
узлы знаками выигрыша уже размечены, или переходит к рассмотрению
этих узлов в противном случае.
Процедура exp_win_breadth(Subs,A,Subsl), просматривая (в
ширину) список деревьев Subs, заменяет его списком Subsl с следующей
разметкой узлов знаками выигрыша.
Процедура verify_signs(Subs, Grape) по списку Subs поддеревьев
проверяет, помечены ли все их корни знаками выигрыша и вычисляет
список Grape этих корней.
Процедура compute_win_sign(Grape,Win) по списку Grape из
предыдущей процедуры verify_signs(Subs,Grape) вычисляет знак
выигрыша Win в предыдущем узле.
Процедура winner_transits_list(Wtg,Wt) по размеченному знаками
выигрыша дереву игры Wtg строит то его частичное поддерево Wt,
которое размечено только одним знаком выигрыша того игрока, знак
выигрыша которого стоит в корне Wtg. Дерево Wt вычисляется как
список всех его переходов.
Процедура construct_Wtl(Wt,Wtl) в каждом элементе списка Wt
убирает знак выигрыша (этот знак хранится в рабочей области, т.е.
в оттранслированной программе в виде факта winner(W)).
Получившийся список Wtl служит для вычисления униформизующего автомата
(Мили) при выигрыше второго игрока.
Процедура construct_Wt2(Wtl,Wt2) по списку Wtl, полученному в
результате работы процедуры construct_Wtl(Wt,Wtl), строит список
Wt2 переходов вектор-состояний для последующего вычисления
униформизующего автомата (Мура) при выигрыше первого игрока.
Процедура states_transits_exits(Wtl, [QVO], WS, WT, WE) по списку
Wtl (или Wt2) и начальному состоянию QVO выигрывающего автомата
строит списки WS,WT,WE состояний, переходов и выходов
соответственно униформизующего автомата; при этом указывается выигрывающий
игрок.
Процедура rename__automaton( WS, WT, WE, WS1, WT1, WEI) производит
переобозначение состояний в множествах WS,WT,WE в qO, ql, q2,
В результате получим переобозначенные множества WS1,WT1,WE1
соответственно.
Процедура genatom(Roote,Atom) по заданному атому Roote при
последовательных вызовах соответственно порождает атомы RooteO,
Rootel,Roote2,...
393
dl(A,B) :- X=[0,l],Y=[0,l],Q=[q0,ql,q2],Q0=q0,T=[[q0,[0,0],q0],
[qO,[l,0],qO],[qO,[0,l],ql],[qO,[l,l],ql],[ql,[l,0],qO],
[ql,[l,l],q0],[ql,[0,0],q2],[ql,[0,l],q2],[q2,[0,l],ql],
[q2,[l,l],ql],[q2,[0,0],q2],[q2,[l,0],q2]],
F=[[q0],[ql],[q0,ql,q2]],A=[X,Y,Q,Q0,T,F],unif(A,B).
d2(A,B) :- X=[0,l],Y=[0,l],Q=[q0,ql,q2],Q0=q0,T-[[q0,[0,0],q0],
[qO,[l,0],qO],[qO,[0,l],ql],[qO,[l,l],ql],[ql,[l,0],qO],
[ql,[l,l],q0],[ql,[0,0],q2],[ql,[0,l],q2],[q2,[0,l],ql],
[q2,[l,l],ql],[q2,[0,0],q2],[q2,[l,0],q2]],
F=[[q0],[ql],[q2],[q0,ql,q2]],A=[X,Y,Q,Q0,T,F],unif(A,B).
unif(A,B) :- A=[X,Y,Q,QO,T,F],QVO=Q,AS=[QVO],AT=[],
findall([El,E2],(member(El,X),member(E2,Y)),XY),
expand_states_transi ts( AS, AS, AT, XY, T, QV, TV ),
f acts_transits_add (TV), f irst([ Stl, In, St2 ], TV),
term tree game with marked leaves(F, [In,QVO],Ttg),
facts_transits_remove(TV),win_tree_game(Ttg,Wtg),
winner_transits_list(Wtg,Wt),construct_Wtl(Wt,Wtl),
winner(Winner) ,retract( winner (Winner)),
if thenelse( Winner=win2,
states_transits_exits(Wtl, [QVO], WS, WT, WE),
(construct_Wt2(Wtl,Wt2), .
states_transits_exits(Wt2,[QV0],WS,WT,WE))),
Bl=[Winner,X,Y,WS,QVO,WT,WE],
rename_automaton(WS,WT,WE,WSl,WTl,WEl),WSl=[SO|R],
retract(current_number(C,D)),B=[ Winner,X,Y,WS1,SO, WTl, WEI].
expand_states_transits([H|R], AS, AT,XY,T,QV,TV) :-
findall([H,Ins,Hl],
(member(ln,XY),
next_state(H,In,Ins,T,Hl),
not(member([H,In,Hl],AT))),L),
delrepeate(L,Ll),append(AT,Ll,ATl),
findall(H3,(member([H2,Inl,H3],Ll),not(member(H3,AS))),L2),
delrepeate(L2, L3), append( AS, L3, AS1), append(R, L3, Rl),
expand_states_transits(Rl,ASl,ATl,XY,T,QV,TV).
expand_states_transits( [ ],QV,TV,XY,T,QV,TV).
next_state(St,In,Ins,T,NSt) :- St=[H|R] ,member([H,In,Hl] ,T),
findall(Inl,member([H,Inl,Hl],T),Ins),
delete(Hl,St,Stl),add(Hl,Stl,NSt).
facts_transits_add([H|T]) :- H=[Hl,Ins,H2],
assertz(transit (HI, Ins, H2)), f acts_transits_add(T).
394
f acts_transits_add( [ ]).
facts_transits_remove([H|T]) :- H=[Hl,Ins,H2],
retract(transit(Hl,Ins,H2)),facts__transits_remove(T).
f acts_transits_remove( [ ]).
term_tree_game_with_marked_leaves(F,Start,Termtree) :-
breadthf irst(F, l(Start), Termtree).
breadthfirst(F,Tree,Termtree) :- expand(F,[],Tree,Treel,End),
(End=no, breadthf irst (F, Treel, Termtree) ; Termtree=Treel).
expand(F,P,l([ln,N]),l([Win,In,N]),yes) :- member(N,P),PC=[N|P],
win_mark_in_leaf e(F, PC, Win).
expand(F,P,l([Win,In,N]),l([Win,In,N]),yes).
expand(F,P,l([ln,N]),t([ln,N],Subs),no) :-
bagof(l([lnl,M]),transit(N,Inl,M),Subs).
expand(F,P,t([ln,N],Subs),t([ln,N],Subsl),End) :-
expandall(F,[N|P],Subs,[],Subsl,End).
expandall(F,P,[],[T|Ts],[T|Ts],yes).
expandall(F,P,[T|Ts],Tsl,Subsl,End) :- expand(F,P,T,Tl,Endl),!,
expandall(F,P,Ts,[Tl|Tsl],Subsl,End2),
(Endl=yes,End2=yes,End=yes ; End=no).
win_mark_in_leafe(F,PC,Win) :- cycle_in_PC(PC,C),
if thenelse(member_set(C, F), Win=winl, Win=win2).
cycle_in_PC([S|R],C) :- cycle_in(S,R,[] ,C).
cycle_in(S,[H|R],A,C) :- not(S=H),H=[Sl|Rl],
cycle_in(S,R,[Sl|A],C).
cycle_in(S,[H|R],A,C) :- S=H,H=[Hl|Rl] ,C=[Hl| A].
win_tree_game(Ttg,Wtg) :- win_tree(Ttg,[] %Wtg).
win_tree(T,Tr,Wtg) :- exp_win_depth(T,Trl),
not(Trl=Tr),win_tree(Trl,T,Wtg).
win_tree( Wtg, Wtg, Wtg).
exp__win_depth(t([ln,N],Subs),t(Roote,Subsl)) :-
if thenelse(verify_signs(Subs, Grape),
(compute__win__sign(Grape, Win),Roote=[ Win,In,N],Subsl=Subs),
(Roote=[ln,N],exp__win_breadth(Subs,[],Subsl))).
exp_win_depth(t([Win,In,St],Subs),t([Win,In,St],Subs)).
exp_win_depth(l(X), 1(X)).
exp_win_breadth([T|Ts],Tsl,Subsl) :- exp_win_depth(T,Tl),!,
exp__win__breadth(Ts,[Tl|Tsl],Subsl).
exp_win_breadth([],[T|Ts],[T|Ts]).
verify__signs(Subs,Grape) :- verify(Subs,[],Grape).
395
verify([Tr|R],A,Gr) :- (Tr=l([\Vin,In,St]) ;
Tr=t([Win,In,St],Subs)),
findall([Win,Inl],member(lnl,In),L),
append(A,L,Al),verify(R,Al,Gr).
verify([],Gr,Gr).
compute_win_sign (Gr, Win) : -
computeXY(Gr,X,Y),winsign(Gr,X,Y,Win).
winsign(Gr,[H|R],Y,Win) :-
findall(lnY,member([winl,[H,InY]],Gr),LY),
if thenelse(equalset (LY, Y), Win=winl, winsign(Gr, R, Y, Win) ).
winsign(Gr, [ ], Y,win2).
computeXY(Gr,X,Y) :- compXY(Gr,[],[],X,Y).
compXY([H|R],Al,A2,X,Y) :- H=[Win,[lnl,In2]],
compXY(R,[lnl|Al],[ln2|A2],X,Y).
compXY([],Al,A2,X,Y) :- delrepeate(Al,X),delrepeate(A2,Y).
winner_transits_list(t([Win,In,St],Subs),Wt) :-
assert (transit_win([])),asserta( winner (Win)),
win_trans_depth(St,t([Win,In,St],Subs)),
transit_win( A), reverse( A, Wt), retract(transit_win( A) ).
win_trans_depth(St,t([Wl,In,Stl],Subs)) :-
win_trans_breadth(St,Subs).
win_trans_depth(St, 1(X)).
win_trans_breadth(St,[T|Ts]) :- winner(W),transit__win(A),
(T=t([Wl,In,Stl],Subsl) ; T=l([Wl,In,Stl])),
ifthenelse(W=Wl,
(Al=[[W,[St,In,Stl]]|A],
retract(transit_win(A)),assert(transit__win(Al)),
win_trans_depth(Stl,T),win_trans__breadth(St,Ts)),
win_trans_breadth(St, Ts)).
win_Jrans__breadth(St, [ ]).
states_transits_exits(Wtl,AS,WS,WT,WE) :-
st_tr_ex(Wtl,AS,[],[],[],[],WS,WT,WE).
st_tr__ex([H|R] ,AS,AT,AcT,AcE,AE,WS,WT,WE) :-
H=[Stl,[lnl,In2] ,St2] ,T=[Stl,Inl,St2] ,Tl=[Stl,Inl],
E=[Stl,Inl,In2],
if thenelse(member (Tl, AcT), (AcTl=AcT, AT1=AT),
(AcTl=[Tl|AcT],ATl=[T|AT])),
if thenelse(member (St2, AS), AS1=AS, AS1=[ St21 AS]),
ifthenelse(member(Tl,AcE),
(AcEl=AcE,AEl=AE),(AcEl=[Tl|AcE],AEl=[E|AE])),
396
st_tr_ex(R, AS1, ATI, AcTl, AcEl, AE1, WS, WT, WE).
st_tr_ex([],AS,AT,AcT,AcE,AE,WS,WT,WE) :-
reverse( AS, WS), reverse( AT, WT), reverse( AE, WE).
construct_Wtl(Wt,Wtl) :- constr_Wtl(Wt,[] ,Wtl).
constr_Wtl([H|R],A,Wtl) :- H=[W,[Stl,In,St2]],
findall([Stl,Inl,St2],member(lnl,In),L),
append(A,L,Al),constr_Wtl(R,Al,Wtl).
constr_Wtl([],Wtl,Wtl).
construct_Wt2(Wtl,Wt2) :- constr_Wt2(Wtl,[] ,Wt2).
constr_Wt2([H|R],A,Wt2) :- H=[Stl,[lnl,In2] ,St2],
findall([Stl,[ln3,Inl] ,St3],
member([Stl,[lnl,In3],St3],[H|R]),L),append(A,L,Al),
findall([Stl,In,St4],member([Stl,In,St4],[H|R]),Ll),
difset([H|R],U,Rl),constr_Wt2(Rl,Al,Wt2).
constr_Wt2([],Wt2,Wt2).
rename_automaton(WS,WT,WE,WSl,WTl,WEl) :-
ren_autom (WS, [ ], WT, WE, WS1, WT1, WEI).
ren_autom([B|R],AS,WT,WE,WSl,WTl,WEl) :- genatom(q,S),
substitl(B,WT,S,WT2),substitl(B,WE,S,WE2),
ren_autom(R,[S|AS],WT2,WE2,WSl,WTl,WEl).
ren_autom([],AS,WTl,WEl,WSl,WTl,WEl) :- reverse(AS,WSl)
substitl(B,[W|T],S,[X|V]) :-
substituted, W,S,X),substitl(B,T,S,V).
substitl(B,[],S,[]).
genatom(Roote,Atom) :- get_number(Roote,Number),
name(Roote, Namel), name(Number, Name2),
append(Namel, Name2, Name), name( Atom, Name).
get_number(Roote,Number) :-
retract(current_number(Roote,Numberl)),!,
Number is Numberl+1,
asserta(current_number(Roote, Number)).
get_number(Roote,0) : - asserta(current_number(Roote,0)).
substituted],^,!]).
substitute(X,[X|L],A,[A|M]) :- !, substituted, L, A, M).
substitute(X,[Y|L],A,[Y|M]) :- substitute(X,L,A,M).
delrepeate(S,SF) :- Sl=[] ,delrep(S,Sl,SF).
delrep([H|T],Sl,SF) :- member(H,T),! ,delrep(T,Sl,SF).
delrep([H|T],Sl,SF) :- not(member(H,T)),append(Sl,[H] ,S2),
397
delrep(T,S2,SF).
delrep([],S2,S2).
delall(X, [],[])•
delall(X,[X|L],M) :- ! ,delall(X,L,M).
delall(X,[Y|Ll],[Y|L2]) :- delall(X,Ll,L2).
member_set(L,[Yl|Y]) :- subset(L,Yl),subset(Yl,L),!.
member_set(L,[Yl|Y]) :- member_set(L,Y).
equalset(X,Y) :- subset(X,Y),subset(Y,X).
subset([],Y).
subset([A|X],Y) :- member(A,Y),subset(X,Y).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
first(X,[X|Y]).
add(X,L,[X|L]).
delete(A,[A|B],B) :- !•
delete(A,[B|L],[B|M]) :- delete(A,L,M).
reverse([],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L).
append([],L,L) .
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
19. МОНАДИЧЕСКАЯ ЛОГИКА И КОНЕЧНЫЕ АВТОМАТЫ
19.1. Логика одноместных предикатов
Опишем монадическую логику - интерпретируемый формализм,
связанный с логикой одноместных предикатов (ЛОП) второго порядка на
натуральных числах с функцией следования (т.е. прибавления
единицы) у = х + 1 на натуральном ряду.
Формальные символы.
1. 0,1,2,... - символы натуральных чисел.
2. jc,^,z,... - символы предметных переменных, пробегающих
натуральный ряд, возможно с индексами.
3. ' - штрих, символ функции следования на натуральном ряду,
X' = JC+1.
398
4. al ,a2,... ,an - символы конечного алфавита 2 = {ax,...9an}.
5. X,Y,Z,... - символы предикатных переменных (возможно с
индексами), аргументы которых пробегают натуральный ряд, а
значения - множество символов алфавита 2. Правильнее было бы сказать,
что XyYyZy... есть символы для конечнозначных функций, с
аргументами, пробегающими натуральный ряд, и со значениями в множестве
2. Сохраним все же традиционную предикатную терминологию.
6. &, V, "I, ->, 3, V - логические символы: конъюнкция,
дизъюнкция, отрицание, импликация, квантор существования, квантор
общности.
7. = - знак равенства.
8. ( , ) - скобка левая, запятая, скобка правая.
Термы.
1. Символ натурального числа есть терм.
2. Символ предметной переменной есть терм.
3. Если t - терм, то f есть терм.
Замечание. Вместо f, f", f"',... будем писать также Н-1, М-2,
Н-3,....
Формулы.
1. Если X - предикатный символ, a t - терм, содержащий
предметную переменную или без нее, и а - буква из 2, то X(t) = а есть
атомарная формула с глубиной построения 1, в которой предикатная
переменная X и предметная переменная х, если она есть, являются
свободными переменными.
2. Если А и В - формулы с глубиной построения г и s
соответственно, то (А & В), (А V В), (А -> В) - формулы с глубиной
построения тах(г,5)+1, свободные переменные которых есть вместе взятые
свободные переменные формул А и В. Выражение (~\А) тоже формула с
глубиной построения г+1. Свободные переменные формулы ("Ы) есть
свободные переменные формулы А.
3. Если А(х) - формула со свободной предметной переменной х и
с глубиной построения г, то (Зх)А(х), (Ух)а(х) - формулы с
глубиной построения г+1, переменная х в которой связана (квантором).
Свободные переменные формул (Зх)А(х), (Чх)А(х) есть все свободные
переменные формулы А(х), кроме х.
4. Если А(Х) - формула со свободной предикатной переменной X и
с глубиной построения г, то (ЗХ)А(Х), (УХ)А(Х) - формулы с
глубиной построения г+1, переменная X в которых связана (квантором).
Свободные переменные формул (ЗХ)А(Х), (УХ)а(Х) есть все свободные
переменные формулы А(Х), кроме X.
Формула называется замкнутой, если онд не имеет свободных
переменных. Всякая замкнутая формула содержательно представляет
399
собой высказывание о натуральном ряде и о его подмножествах,
истинное или ложное.
Построенный интерпретируемый формализм составляет монадичес-
кую логику (МЛ) натуральных чисел, или логику одноместных
предикатов (ЛОП) второго порядка натуральных чисел с функцией
следования на натуральном ряду.
Вместо X(t) = а для краткости будем писать также Xa(t).
Предикат Х(х), определенный на натуральном ряду, можно рассматривать
как сверхслово ^(0)^(1)^(2)... в алфавите 2.
Пусть А(ХХ 9Х29... >Хк) - формула ЛОП без свободных предметных
переменных и со свободными предикатными переменными Хх ,Х2>... >Хк.
Набор фиксированных предикатов XlJX29... 9Хк (назовем этот набор
/с-предикатом)
^(0)^(1) ... X,(t) ...
Х2(0)Х2(1) ... X2(t) ...
Xk(0)Xk(l) ... Xk(t) ...,
написанных один под другим, можно рассматривать как "толстое"
слово "толщины" к в алфавите 2Х2Х...Х2 (к раз). Тогда множество
истинности формулы А(ХХ,... 9Хк) есть некоторый сверхъязык в
алфавите 2X2... Х2 (к раз).
Пусть А(Х9Х1,... 9Хк) есть формула в ЛОП без свободных
предметных переменных, и Х,ХХ,... 9Хк - полный список ее свободных
предикатных переменных. Пусть \а\ = {(ХУХ1,... уХк) : высказывание А(X,
Xи-..,Хк) истинно} есть множество истинности формулы А. Пусть
формула В(Хг,... >Хк) = (Зх)А(Х9Х19... ,Хк). Тогда множество
истинности формулы В может быть получено из множества истинности
формулы А вычеркиванием (стиранием) во всех наборах (Х,Хг,... ,Хк) из
\а\ первой компоненты X. Если, например, в алфавите 2 = {0,1,2}
4-предикат
X =1011220123...
Хх =2101120011...
*2 = 0122120120...
ЛГ3 = 1221101201...
принадлежит множеству истинности некоторой формулы А{Х,ХХ ,Х2,Х3),
то 3-предикат
XY =2101120011 ...
*2 = 0122120120...
ЛГ3 = 1221101201...
принадлежит множеству истинности формулы В(Х19Х2,Х3) = (ЗХ)А(Х,
400
Х19Х2,Х3). Можно считать, что этот 3-предикат получается из
исходного 4-предиката поразрядной заменой, т.е. проекцией {0,1,2}4 -♦
{0,1,2}3, при которой (b09blJb29b3)t -* (blJb2Jb3)t , где каждое bt
лежит в 2, а буква t означает транспонирование.
Если В(Х19... уХк) есть (Зх)А(Х,Х1У... ,А^), то можно считать,
что множество истинности формулы В получается из множества
истинности формулы А проектированием последнего на оси 1,2,...,Л с
помощью проекции Z*+1 -» Лк9 при которой (Ь0,Ьг,... ,ЬкУ -» (Ь1Э...,
Ь*)', где все Ь, лежат в 2. Таким образом, [в| = Рг1>2>в##>*
(| А] ). Переменная X в формуле >1 может стоять на любом аргументном
месте формулы А.
19.2. Выразимость в ЛОП
Покажем, что монадическая логика второго порядка есть довольно
гибкий инструмент для записи работы автоматов, источников,
макроисточников, регулярных и общерегулярных языков. Анализ указанных
объектов с помощью ЛОП довольно прост и естественен. Синтез
осуществляется сложнее. Рассмотрим его ниже.
В ЛОП выразимы формулами следующие предикаты.
х = у —> (У/Х)(Ха(х) - Ха(у))9 а € 2.
х = 0 *-> (Чу)(х * у+1).
х = 1 «-♦ (Vy)(jc * у+2) & х * 0.
х = 2 «—> (Vy)(jc * дч-з) &х*0&х*1.
jc = * <— (Чу)(х * у+к+\) &х*0&...&х* *-1.
Заметим, что
ЛГ(0 * а +-> ( V ЛГ(г) = Ъ)\ (19.1)
Jfe(x+1) «— (Эу)(*+1=У & ДГв(у)).
Здесь переменная у в Я^зО не имеет штриха.
х ^ у «-> (VZ)(Zfl(jc) & (V*)CYe(x) - ЛГ»(*')) - *вЫ), « € 2.
jc<<y*—> х < у & х *у.
х > у <—> у ^ х.
х > у *—> у < х.
Введем ограниченные кванторы:
(Эу)<, А{у) ~ Ш(У « * & А(у)).
(VjO«, А(у) ~ (Чу)(у < х - ЛЫ).
(305 л(0 — (Зг)(х < г < у & Ж0).
(V0J л(0 — (V0U « t < у - Ж0).
401
Введем также неограниченные кванторы:
(З00*) А(х) ~ (Чу)Ш>у А(х).
(V°°x) А(х) ~ (ЭуЮх)>у Л(х).
Определим формулами ЛОП следующие предикаты:
а € lim Х(х) —> (Э^хХЛГСх) = а);
lim *(*) = {а,ll9...9а|5} — (& (а,* € lim *(*)) &
к- 1
5
& (а € lim Х(х) - V (а = а,*)).
Теорема (анализа). По всякому источнику S можно построить
формулу ЛОП А(х9у)9 для которой слово
X(x)X(x+l)...X(y-l) € Beh(S) —> Л(ЛГ,*,у).
Доказательство. Источнику без пустых ребер В = (X9Q09D9F)9 где
F Я Q9 поставим в соответствие формулу ЛОП
A(X,x,z) есть (Зе) (( V Q(x) = q &
(Vy)* ( V (С(у) = q & Jf(y) = а & e(y+D = «')) -
(f,a,/)€D
( v eU) =?)).
Тогда слово X(x)X(x+l)...X(z-l) € ДеЛ(5) «-» A(x9z).
Заметим, что формула А фиктивна вне [x9z) в том смысле, что
значения предиката X вне [x9z) не влияют на характер истинности
формулы А. Если хотим иметь в источнике и пустые ребра, то
алфавит 2 следует расширить пустым символом.
19.2.1. Макроисточники и ЛОП
Теорема (анализа). По всякому макроисточнику MS можно
построить формулу ЛОП А(Х,х), для которой сверхслово Х(х)Х(х+1)... €
Beh(MS) «—> А(Х9х). Значение предиката X вне [0,*) не существенно.
Доказательство. Макроисточнику MS = (X9Q9Q09D9F')9 где F' €
P(Q), сопоставим формулу
А(Х9у) есть (3(2) (( V Q(y) = q) &
q*Qo
(V*)>if ( V (Q(x) = q & X(x) = a & Q(x+l) = q')) &
( V lim Q(x) = F)).
F€F'
402
Сверхслово X(0)X(l).. .Х(у)Х(у+\) € Beh(MS) —> А{Х9х). Формула
А(Х,х) фиктивна вне [0,у).
19.2.2. Регулярные языки и ЛОП
Теорема (анализа). Для всякого регулярного языка R можно
построить формулу ЛОП А{Х9х9у)9 для которой слово
Х(х)Х(х+1)...Х(у-1) € R —> А(Х9х9у).
Значение предиката X вне [х9у) не существенно.
Доказательство. Индукция по глубине к построения R.
БАЗИС, к = 1. R есть а9 где а € 2. Тогда А{Х9х9у) есть Х(х) =
а & у = дс+1.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что для всякого
регулярного языка с глубиной построения меньше к требуемая формула ЛОП
может быть построена.
ШАГ ИНДУКЦИИ. Покажем, что для всякого регулярного языка с
глубиной построения к требуемая формула может быть построена.
Пусть регулярный язык R имеет глубину построения к. Возможны
следующие случаи.
1. R = Rx * R29 где * € {V,«}. Так как глубина построения
регулярных языков Rx и R2 меньше к, то по предположению индукции
существуют формулы ЛОП Ах(Х9х9у) и А2{Х9х9у)9 для которых слово
Х(х)Х(х+1)...Х(у-1) € Д, «- Ai(X9x9y)9 i = 1,2.
Тогда формула А9 равная Ах V А29 соответствует языку R{ V R29 a
формула А(Х9х9у)9 равная (30* (Ax(X9x9t) & A2(X9t9y))9
соответствует языку Rl*R2.
*
2. R = Rx. Так как Rx имеет глубину построения меньше к9 то по
предположению индукции для R{ существует формула ЛОП А{(Х9х9у)9
для которой Х(х)Х(х+1)...Х(у-1) € R, «-» Аг(Х9х9у).
Пусть формула ЛОП В(Х9х9у) есть
Y(x) = а & Y(y) = а & (Vf)U < t < у - Y(t) * a)).
Положим формулу А{Х9х9у) равной
х < у & (ЗУ) (Y(x) = а & Y(y) = а &
(Vh)(Vv)(* < u < v < у & B{Y9u9v) - A,{X9u9v))).
Тогда слово Х(х)Х(х+1).. .Х(х9у-1) € Я «—> А{Х9х9у). Значения
предиката X вне [х9у) не существенно.
Замечание. Сверхслово Y имеет вхождение буквы а на тех
позициях отрезка [х9у)9 которые разбивают слово X(x)X(x+l).. .X(y-l) на
куски, принадлежащие итерируемому языку.
403
1923. Общерегулярные языки и ЛОП
Теорема (анализа). Для всякого общерегулярного языка Q можно
построить формулу ЛОП А(Х9х), для которой сверхслово
Х(х)Х(х+1) ... € Q <— А(Х,х).
Значения предиката X вне [0,дг) не существенны.
Доказательство. Индукция по глубине г построения Q.
БАЗИС, к = 1. Пусть R - регулярный язык и Q Я R00 -
общерегулярный язык. Для R существует формула ЛОП Ax{X,xyy), для которой
слово Х(х)Х(х+1)...Х(у-1) € R «— Ах(Х,х,у).
Пусть формула А(Х9х) есть
(ЗУ) (Y(x) = а & (3«>y)(Y(y) = а) &
(Vk)(Vv)U < w < v & B(Y,k,v) - Ax{X9u,v))),
где В есть построенная в предыдущей теореме формула. Тогда
сверхслово Х(х)Х(х+1)... € Я00 «-> Ж*,*).
Значения предиката Z вне [О,*) не существенны.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Пусть для всякого общерегулярного
сверхъязыка с глубиной построения меньше к требуемая формула
существует.
ШАГ ИНДУКЦИИ. Покажем, что для всякого общерегулярного
сверхъязыка с глубиной построения к требуемая формула может быть
построена. Пусть общерегулярный сверхъязык Q имеет глубину
построения к. Тогда Q = R*Qi для некоторого регулярного языка R и
общерегулярного сверхъязыка Qla Для R существует формула ЛОП
С(Х,х,у), для которой слово
Х(х)Х(х+1)...Х(у-1) € R «-> С(Х,х,у).
Так как глубина построения Q{ меньше к, то по предположению
индукции для Qx существует формула D(X,x), для которой сверхслово
Х(х)Х(х+1)... € Q, —> D(X,x).
Пусть формула А(Х,х) есть
(Зу)(х < у & С(Х,х,у) & D(X,y)).
Тогда сверхслово Х(х)Х(х+1)... € Q «—► ЛСА',*). Значения
предиката X вне [0,*) не существенны.
19.3. Специальная пренексная форма
Формула А в ЛОП имеет специальную пренексную форму, если А
находится в пренекснои форме и при этом в кванторнои приставке все
предикатные кванторы предшествуют всем предметным кванторам.
Покажем, что всякая формула ЛОП эквивалентна некоторой формуле ЛОП
404
в специальной пренексной форме. Пусть А есть формула ЛОП. В
формуле А устраним все вхождения нуля, именно, если формула А имеет
вид А(0), то заменим ее на формулу (Зх)(х = 0 & А(х))9 где х = О
есть (V>0(* * У + 1). В результате получим формулу А19 не имеющую
нулей и эквивалентную формуле А.
В формуле Ах устраним итерации штриха, заменяя вхождения
атомарной формулы Х(х"...'), где штрих встречается к раз, на
формулу
(Зуг)(3у2)...(3ук) (у, = х + 1 & у2 = ух + 1 & ... &
У* = Jfc-i + 1 & *Ы)-
В результате получим формулу А2, эквивалентную исходной формуле,
при этом каждая предметная переменная в А2 имеет не более одного
штриха, а предметные переменные, являющиеся аргументами свободных
предикатных переменных формулы А вовсе не имеют штрихов.
Приведем формулу А2 к пренексной форме. В результате получим
формулу Аъ в пренексной форме, эквивалентную исходной формуле А,
Справедливы следующие эквивалентности:
(3x)(Vjf) C(X,x) ~ (19.2)
(3y)(VAT)(Vjc) ((ЭзО Y°(y) & (У«(х) - С(*,*)));
(Vx)(3Jf) ССГ.х) — (19.3)
(УУ)(ЭЛГ)(Эх) ((Vy) Y°(y) - У«(х) & С(*,*))); a € 2.
Докажем первую из них. Пусть в формуле (19.2) истинна правая
часть. Тогда имеем следующий ряд эквивалентных формул:
(3y)(Vjf)(V*) ((Зу) Y°(y) & (<U) - С(Х,х)));
(VA-)(Vx) ((Зу) У^Ы & (У?(х) - С(*,х)));
(Vjc) (Yfo.) & «(*) - C(*,x)));
уЪо); Ya0(y0) -* с(х,УоУ,
C(X,y0);
(V*) C(X,y0);
(3x)(V*) C(*,x).
Пусть теперь в (19.2) истинна левая часть (Зх)(УХ)С(Х,х).
Тогда (VZ)C(Ar,>'0) истинно при некотором у0. Зададим предикат Y0(y)
так, чтобы Y°(y0) & (Vx)(x * ;у0 "* Y0(x) * а).
Следующие далее формулы последовательно эквивалентны друг
405
другу (во всех этих формулах а € 2):
yfo-o); (Чх)с(х,УоУ,
УМ: Лу,) - (ЧХ)С(Х,у0);
Ya0(y0); (V*)«(* ) - (ЧХ)С(Х,х);
Ш Ya0(y); (V*)(V*)(y?0c) - С(Х,х));
(Зу) Y°(y) & (4xWx)(Y°(x) - С(Х,х));
(V*)(V*) ((Зу) Ya0(y) & (Yt(x) - C(X,x)));
(ЗУ)(УЛ-)(Ух) ((3y) УЧу) & CK*) - С(*,*))).
Справедливость соотношения (19.2) установлена. Справедливость
формулы (19.3) показывается аналогично. Левая и правая часть в
(19.3) двойственны соответствующим частям в (19.2).
Используем эквивалентности (19.2) и (19.3) для разделения
предикатных и предметных кванторов в формуле А3. В результате
получим формулу АА в специальной пренекснои форме (говорят еще в
специальной предваренной форме), эквивалентную исходной формуле А.
19.4. Синтез автомата по формуле ЛОП
Пусть А(Хг,... ,Хп) есть формула ЛОП; Хх,... ,Хп - полный список
ее свободных предикатных переменных; свободных предметных
переменных формула А не имеет. Покажем, что по формуле А можно
построить макроавтомат, поведение которого совпадает с множеством
истинности формулы А.
Так как для всякой формулы ЛОП существует ей эквивалентная
формула в специальной пренекснои форме, то можно сразу считать,
что формула А находится в специальной пренекснои форме, при этом
согласно предыдущему пункту свободные предикатные переменные
Х19...,Хп формулы А имеют предметные переменные без штрихов.
Формула А имеет следующий вид:
(Q1Y1)...(QrYr) (Q[Xl) ... Ш[хк) Я,
где В есть бескванторная формула ЛОП. Формулу В представим в виде
СДНФ; далее согласно формуле (19.1) заменим отрицания вида X(t) *
а на эквивалентную формулу V X(t) = b, не содержащую
отрицаний; результат приведем к СДНФ. Тогда получим формулу А19
эквивалентную исходной формуле и имеющую вид
(QiYx)...(Qryr) (e;*i)-..(efrk) ( у
406
^inUi)..^irUi) Bixx(x'x)...Bixr(x'x) Cixx{xx)...Cixn(xx)
Aikx(xk)...Aikr(xk) Bikx(x'k)...Bikr(x'k) Cikx(xk)...Cikn(xk))y
где каждые Л|;/(*/), 2?|;/(*/), С|;/(*/) есть некоторые равенства
Yj(*i) = *iji, Yj(x'i) = Ь|;/,
Xj(xi) = Ciji\ aijhy biji, Ciji € 2.
Так как в бескванторную часть формулы Ах входят только
одноместные предикатные переменные, то можно использовать процедуру Бе-
мана продвижения предметных кванторов в глубину бескванторной
СДНФ в формуле Ах. Продвигаем сначала квантор (Qkxk). Если Qk
есть квантор 3, то в Ах продвигаем квантор (Зхк) сначала по
дизъюнкции, а потом по конъюнкции. В результате получим формулу
(QiYx)...(QrYr) (C#*i)...(e£-i**-i) ( V
i
At^ix^^.A^rix,) Bixx(x\)...Bixr(x[) Cixx{xx)...Cixn(xx)
Aiyk-i9i(xk-i) ••• Biyk-iyi(xk-i) ••• Ci,k-iyn(xk-i)
(3xk)(Aikx(xk). . .Aikr(xk)Bikx(x'k) . . .Bikr(x'k) ... Cikn(xk)).
V. v J
Eik = (Здс) Dik(x)
Формула Eik выступает в дальнейших преобразованиях единым
неизменным блоком. Квантор (3*) в формулу Ах продвинут.
Если Qk есть V, то справедлива следующая последовательность
эквивалентных формул:
(У**)(СДНФ)~ 11(У^)(СДНФ) «-> 1(3**)-1(СДНФ)~ 1(3**)(СДНФ1).
Далее квантор (Зхк) продвигаем в глубину СДНФ1, как это
делалось выше, а внешнее отрицание распределяется над получившейся в
результате продвижения квантора существования ДНФ. В обоих
случаях продвижения квантора в глубину формулы Ах и последующего
превращения бескванторной части в СДНФ получим формулу А2 вида
(QxYx)...(QrYr) (Q'S^.-.iQ'^x^) ( V
i
Aill(xi)...Aiir(xi)Bill(x'1)...Biir(x'i)Cill(xl)...Ciir(xl) E'ikl
Ai,k-i,i(xk-i) ••• Bi,k-i,Axk-i) ••• Ci,k-i,n(xk-i) E'i,k,k-\,
где каждое Е\ц есть E'ik, взятое с отрицанием или без него.
407
Последовательно продвигая в глубину формулы А2 все другие
предметные кванторы, получим формулу Аъ вида
(Q,Yx)..XQrYr) ( V Е\х E'i2 ... E'ik)t
i
где каждое E\j есть £|;- с отрицанием или без него.
Пусть одна из £|;- есть формула Е, равная
(3*) (УД*) = flt & УДх+1) = Ь1 &
У2(*) = а2 & y2U+l) = Ь2 &
Yr(x) = дг & yr(jc+l) = Ъг &
ДГ^х) = ct &
*200 = с2 &
*„(*) = О-
Формула £ утверждает, что набор предикатов (сверхслов)
У,(0) УД1) ... У,(х) У,(*+1) ...
У2(0) У2(1) ... Уа(лс) Уа(*+1) ...
Уг(0) Уг(1) ... Уг(лг) Уг(*+1) ... (19.4)
jr,(0) Jf,(l) ... ХЦх) *,(*+1) ...
in(0) *„(l) ... Х„(х) Xn(x+l) ...
принадлежит множеству истинности формулы Е тогда и только тогда,
когда два соседних разряда х и х+1, высекают в сверхсловах (19.4)
двухбуквенное "толстое" слово
(а,Ь) = (al...arcl...cn)t(bl...brdl...dn)t
в алфавите 27+п (знак Ч" означает транспонирование). Пусть Я
есть множество пар (а>Ь) всех таких двубуквенных слов в алфавите
2™». Пусть Нх = {а : 3& (в,Ь) € Я}; Я2 = {b : За (а,Ь) € Я},
т.е. Ях и Я2 есть проекции множества Я на первую и вторую ось
соответственно.
Построим макроавтомат МЛ = (2r+/,,Q,^0,r,F), поведение которого
совпадает с множеством истинности формулы Е. В качестве состояний
макроавтомата МЛ возьмем множество
Q = {q. . : (*,&) € Я} U {?. : а € Ях} U {q0}.
ayb a
Функция переходов Г : Q х 2Г+Я -» Q строится следующим образом:
408
T(q0,a) =
T(q.,b)
a
qQy если a I Hl9
q~> если а € Hlt
q~ Л , если Ъ € #2,
/ч /ч
<?-> если Ь i Н2 & Ь £ Н19
о
q0, если b < Нг & & < Я,;
T(q„ ..с) » ?„ „, Vc € Zr+".
Л /Ч
Множество выделенных состояний F = {{<?Л Л} : (а,Ь) € #}. Макроав-
/ч
томат МА построен; для него Е = Beh(MA).
Аналогично строим макроавтоматы для остальных формул Ец из
формулы А3. Далее действуем по построению формулы А3. Используя
теорему о замкнутости класса сверхъязыков, определимых
макроавтоматами, относительно булевых операций и проекции, строим
макроавтомат, поведение которого совпадает с множеством истинности
формулы А39 а потому и ей эквивалентной исходной формулы А.
Требуемый макроавтомат построен.
Теорема. Монадическая логика натуральных чисел алгоритмически
разрешима, т.е. по всякой замкнутой формуле ЛОП можно установить
истинна она или ложна.
Доказательство. Пусть А - замкнутая формула ЛОП. Приведем А к
специальной пренексной форме; она имеет вид (QX)B(X), где формула
В(Х) имеет единственную свободную переменную X. По формуле В(Х)
построим макроавтомат МВ> поведение которого совпадает с
множеством истинности формулы В. Если квантор (QX) есть (Зх), то вопрос
об истинности или ложности формулы (Зх)В(Х) эквивалентен вопросу
о непустоте или пустоте сверхъязыка, представимого макроавтоматом
MB. Проблема пустоты для макроавтомата алгоритмически разрешима.
Следовательно, распознаваема и проблема истинности
экзистенциальной формулы (ЗХ)В(Х). Вопрос об истинности формулы (УХ)В(Х) с
квантором общности сводится к аналогичному вопросу для квантора
существования.
Замечание. Проблему униформизации конечно автоматного языка в
алфавите X*Y можно решить с помощью указанного алгоритма. Именно,
по макроавтомату А, представляющему сверхъязык L, строим формулу
409
ЛОП A(X,Y), множество истинности которой совпадает с множеством
L. Если истинна формула (VX)(3y)A(X,Y), то существует конечно
автоматный оператор Y = ®(Х), униформизующий сверхъязык L. Если
истинно отрицание исходной формулы, то существует конечно
автоматный оператор X = 0(У), униформизующий дополнение сверхъязыка L.
Конечный автомат, реализующий оператор (D, строится согласно
алгоритму, приведенному в главе 18.
Часть 4
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
20. ПОРОЖДЕНИЕ КОМБИНАТОРНЫХ КОНФИГУРАЦИЙ
И ИХ ПЕРЕСЧЕТ
20.1. Размещения, перестановки, сочетания
Перестановка из л-элементного множества М есть упорядоченный
набор длины п, составленный из попарно различных элементов
множества М. Обозначим через Р^ множество всех перестановок из п
элементов и через Рп число всех перестановок из п элементов.
Например, если М = {а,Ь,с}, то Рм = {(а,Ь,с), (а,с,Ь), (Ь,а,с), (Ь,с,
а), (с,а,Ь), (с,Ь,а)}; Рп = 6.
20.1.1. Программа вычисления перестановок без повторений
Процедура permutation(A,L) строит список L всех перестановок
алфавита А. Например, если А=[а,Ь,с], то С=[[а,Ь,с] ,[Ь,а,с], [Ь,
с,a], [a,c,b],[c,a,b],[c,b,a]].
Процедура permut(A,P) выдает перестановку Р алфавита А.
Например, если А=[а,Ь,с], то ЭВМ выдаст:
Р=[а,Ь,с] ->;
Р=[Ь,а,с] ->;
Р=[Ь,с,а] ->,
Р=[а,с,Ь] ->;
Р=[с,а,Ь] ->;
Р=[с,Ь,а] ->,
по
Процедура insert(X,P,L) символ X "пропускает" через список L и
выдает результат Р. Например, если Х=а, L=[ 1,2,3], то результат
вычислений на ЭВМ
Р=[а,1,2,3] ->;
Р=[1,а,2,3] ->;
Р=[1,2,а,3] ->;
Р=[1,2,3,а] ->,
по
d(A,L) :- permutation(A,L).
permutation(A,L) :- findall(P,permut(A,P),L).
permut([],[]).
permut([X|L],P) :- permut(L,Ll), insert(X,P,Ll).
insert(X,[X|T],T).
411
insert(X,[Y|T],[Y|Tl]) :- insert(X,T,Tl).
insert (X,[],[X]).
Сочетание из п элементов по г есть r-элементное подмножество
л-элементного множества М.
Обозначим через См множество всех сочетаний из п элементов по
г и через Стп (или через [ J) число всех сочетаний из п элементов
по г. Например, если М = {я,Ь,с}, то См = {(д),(Ь),(с)}; См =
{(я,Ь),(а,с),(Ь,с)}; С\ = \С1М\ = 3; с\ = \С2М\ = 3.
20.1.2. Программа вычисления сочетаний без повторений
Процедура combination(A,R,C) строит множество С всех сочетаний
элементов алфавита А по R элементов в каждом сочетании.
Процедура combin2(A,Cl) строит множество С всех сочетаний
элементов алфавита А по 2 элемента в каждом сочетании.
Процедура combinK(Cl,A,R,K,C), исходя из множества С1 всех
сочетаний элементов алфавита А по 2, последовательно строит
множества сочетаний по K=3,4,...,R элементов.
Процедура combinK_Kl(Cl,A,C), исходя из множества С1 всех
сочетаний элементов алфавита А по К, строит множество всех
сочетаний элементов алфавита А по К+1. Вычисления осуществляются с
помощью процедуры comb(Cl,A,Ac,C), содержащую переменную -
накопитель Ас. Пусть, например,
Cl=[[a,b,c],[a,b,d],[a,b,e],[a,c,d],[a,c,e],[a,d,e],
[b,c,d],[b,c,e],[b,d,e],[c,d,e]], A=[a,b,c,d,e].
Берем элемент а из А. Собираем в С1 все сочетания, содержащие
элемент а, выбрасываем их из С1 и к каждому сочетанию результата
C2=[[b,c,d] ,[b,c,e] ,[b,d,e] ,[c,d,e]] приписываем спереди элемент
а. Результат помещаем в накопитель Ас. Берем элемент b из А и
проделываем аналогичную операцию для С2 и Ь. Результат
приписываем в накопителе Ас. И так далее до исчерпания множества С1. В
накопителе Ас будут собраны все сочетания из А по 4.
d(A,R,C) :- A=[a,b,c,d,e],combination(A,R,C).
combination(A,R,C) :- length(A,L),
case([(R=0 ; R>L) -> C=[],
R=l -> C=A |(combin2(A,Cl),combinK(Cl,A,R,2,C))]).
combin2(A,Cl) :- combin2_rep(A,[] ,Cl).
combin2_rep([H|T],Ac,C) :- findall([H,X] ,member(X,T),L),
append(Ac,L,Ll),combin2_rep(T,Ll,C).
412
combin2_rep([ ],С,С).
combinK(Cl,Al,R,K,C) :- Kl is K+l, K1=<R,
combinK_Kl(Cl,Al,L),combinK(L,Al,R,Kl,C).
combinK(C,Al,R,R,C).
combinK_Kl(Cl,A,C) :- comb(Cl,A,[] ,C).
comb(Cl,[H|Al],Ac,C) :-
findall(X,(member(X,Cl),member(H,X)),L),difset(Cl,L,C2),
findall(X,(member(Y,C2),add(H,Y,X)),ClH),
append(Ac,ClH,Acl),comb(C2,Al,Acl,C).
comb([],Al,C,C).
add(X,L,[X|L]).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
Размещение из п элементов по г есть упорядоченный набор,
состоящий из г попарно различных элементов, взятых из л-элементного
множества М.
Обозначим через Ам множество всех размещений из п элементов
по т и через Агп число всех размещений из п элементов по г.
Заметим, что для л-элементного множества М множество перестановок
рМ = АМ> а их число Рп = Апп.
Пример. М = {а,Ь,с}; Ахм = {(а),(Ь),(с)}; А^ = {(а,Ь),(а,с),
(Ь,с),(Ь,а),(с,а),(с,Ь)}; а\ = \а'м I = 3; а\ = \А^\ = 6.
20.1.3. Программа вычисления размещений без повторений
Процедура allocation(A,R,Res) вычисляет множество Res
размещений элементов алфавита А по R элементов в каждом размещении.
Процедуры combination и permutation вычисляют множества
сочетаний и перестановок; подробнее о них сказано в соответствующих
программах.
413
Процедура comb_permut(C,R) по сочетанию С строит множество R
всех его перестановок.
d(A,R,Res) :- A=[a,b,c,d,e] ,allocation(A,R,Res).
allocation(A,R,Res) :- length(A,L),
case([(R=0 ; R>L) -> Res=[],
R=l -> Res=A |
(combination(A,R,C),comb__permut(C,Res))]).
comb_permut(C,R) :- comb_permutl(C,[] ,R)-
comb_permutl([H|T],Ac,R) :- permutation(H,PH),
append( Ac, PH, Acl), comb__permutl(T, Acl, R).
comb_permutl([] ,R,R).
permutation(A,L) :- findall(P,permut(A,P),L).
permut([ ],[])•
permut([X|L],P) :- permut(L,Ll),insert(X,P,Ll).
insert(X,[X|T],T).
insert(X,[Y|T],[Y|Tl]) :- insert(X,T,Tl).
insert(X,[],[X]).
combination(A,R,C) :- combin2(A,Cl),combinK(Cl,A,R,2,C).
combin2(A,Cl) :- combin2_rep(A,[],Cl).
combin2_rep([H|T],Ac,C) :- findall([H,X] ,member(X,T),L),
append(Ac,L,Ll),combin2_rep(T,Ll,C).
combin2_rep([],C,C).
combinK(Cl,Al,R,K,C) :- Kl is K+l, K1=<R,
combinK_Kl(Cl,Al,L),combinK(L,Al,R,Kl,C).
combinK(C,Al,R,R,C).
combinK_Kl(Cl,A,C) :- comb(Cl,A,[] ,C).
comb(Cl,[H|Al],Ac,C) :- findall(X,(member(X,Cl),member(H,X)),L),
difset(Cl,L,C2),findall(X,(member(Y,C2),add(H,Y,X)),ClH),
append(Ac,ClH,Acl),comb(C2,Al,Acl,C).
comb([],Al,C,C).
add(X,L,[X|L]).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y)),
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),<Hfl(X,Y,Z,T).
difl([],Y,Z,Z).
414
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
В размещениях, перестановках, сочетаниях элементов некоторого
л-элементного множества могут допускаться повторы элементов.
Будем называть их размещениями, перестановками, сочетаниями с пов-
/ч r ^ л г
торениями. Обозначим через Ам, Рм, См - множества всех размеще-
ний, перестановок, сочетаний с повторениями, а через Ап, Рп, Сп -
^ 2
их число. Например, если М = {с,Ь,с}, то См = {(я,a),(ft,ft),(с,с),
(a,ft),(а,с),(ft,с)}; с\ = \С2М\ = 6; Л2М = {(а,а),(Ь,Ь),(с,с),(а,Ь),
U,c),(b,c),(b,a),(c,a),(c,b)}; л\ = 9.
Чтобы подчеркнуть, что размещение, перестановка, сочетание
содержит г элементов, будем говорить г-размещение, /--перестановка,
г-сочетание. Размещения, перестановки, сочетания, составленные из
элементов некоторого множества М, называются комбинаторными
конфигурациями. Всякая конфигурация (а19а29... ,аг) для множества М
лежит в декартовом произведении Л/хМх.. .хл/, состоящем из г
сомножителей. Мощности множеств комбинаторных конфигураций называются
комбинаторными числами.
20.2. Правило суммы и правило произведения
Правило суммы. Пусть конечное множество М разбито на два
непересекающихся подмножества Мх и М2 (в объединении дающих все
множество М). Тогда мощность \м\ = \М1\ + |М2|.
Правило произведения. Пусть в некотором множестве объект а
может быть выбран п способами, и после этого (т.е. после выбора
объекта а) объект Ь может быть выбран т способами. Тогда объект
аЪ может быть выбран п*т способами.
Оба правила допускают индуктивное обобщение. Если конечное
множество М допускает разбиение на г попарно непересекающихся
подмножеств Мх ,М2,... ,Л/Г, то мощность \М I = \МХ 1 + \М2 |+...+ \Mr I .
Если объект ах может быть выбран кг способами, затем (после
выбора объекта аг) объект а2 может быть выбран к2 способами и так
далее и, наконец, объект аг может быть выбран кг способами, то
объект аха2...аТ может быть выбран к1к2...кг способами.
415
20.3. Подсчет числа размещений, перестановок, сочетаний
203.1. Число размещений без повторений
Теорема. Число размещений без повторений из п элементов по г
Атп = л(л-1)(л-2)...(л-г+1) = п\/(п-г)\.
Доказательство. В r-размещении (аг 9а2,... 9аг) л-элементного
множества М элемент ах можно выбрать п способами. После этого
элемент а2 можно выбрать п-1 способами (из оставшихся п-1
элементов множества М). Затем элемент а3 можно выбрать п-2 способами. И
так далее. Наконец, элемент аг можно выбрать л-r+l способами. По
правилу произведения Arn = n(n-l)(n-2).. .(л-r+l); умножив и
разделив правую часть равенства на (n-r)(n-r-l).. .3* 2* 1, получим Ап =
п\/(п-г)\.
Следствие. Число перестановок без повторений Рп = п\.
20.3.2. Число размещений с повторениями
Теорема. Число размещений с повторениями Ап = пт.
Доказательство. В г-размещении (аг ,а2,... ,аг) элемент ах можно
в /i-элементном множестве М выбрать п способами, элемент а2 - тоже
п способами, наконец, элемент аг - п способами. По правилу произ-
ведения Ап = пг.
Следствие. Число перестановок с повторениями Рп = пп.
20.3.3. Число сочетаний без повторений
Теорема. Число сочетаний без повторений Сп = nl/(r\(n-r)\).
Доказательство. Каждому r-сочетанию (а1,д2,... ,дг) для /г-эле-
ментного множества соответствует г\ перестановок. Тогда число
размещений Агп = Сп*г\, откуда и следует требуемая формула.
20.3.4. Число сочетаний с повторениями
Теорема. Число сочетаний с повторениями С„ = Стп+Т_х.
Доказательство. Каждому /--сочетанию из ^-элементного
множества М сопоставим набор (к19к2,... ,кп) из натуральных чисел,
указывающих число повторов каждого элемента из М в выбранном
сочетании. При этом /с!+/с2+.. .+кп = г. Например, если М = {a,b,c,d,
е}, то сочетанию (а,а,с9с9с9е9е) сопоставим набор (2,0,3,0,2),
т.е. элементы a9b9c9d9e множества М встречаются в сочетании
(а9а9с9с9с9е9е) соответственно 2,0,3,0,2 раз. Каждому полученному
набору (к19к29... 9кп) сопоставим набор (ll9l29.. .,/„) с /,
416
Л/+1, i = 1,2,...,л. Тогда /1+/2+...+/„ = fc1+fc2+...+fc„+/z = г+л.
Каждому полученному набору (11 ,/2,... ,/„) взаимно однозначно
соответствует разбиение числа л+r на п ненулевых слагаемых /1э/2,
...,/„. Разделим л+r последовательно записанных звездочек
вертикальными разделительными черточками на л непустых частей,
состоящих соответственно из /i,/2,-• • ,/я звездочек. Для нашего примера
получим следующее разбиение:
* * * I * i****! * |*«*
/1=3 /2=1 /3=4 /4=1 /5=3
^=2 fc2=0 *3=3 ^4=0 *5=2
Каждому разбиению числа л+r на л ненулевых слагаемых взаимно
однозначно соответствует расстановка п-1 разделителей, которые
можно расставить на л+r-l пробелах между звездочками С^+^_х
способами. Следовательно, число сочетаний с повторениями
*"Л ^Л+Г-1 ^Л+Г-1'
20.3.5. Число перестановок данной спецификации
Поясним сначала смысл выражения: Pn(k19k29... ,/сг), /:1+/с2+...+
kr = п. Пусть имеем набор (к,к,ж,ж,ж,с) из шести шаров, из
которых два красных, три желтых, один синий. Набор (2,3,1)
называется спецификацией этого набора шаров. Возможна, например,
перестановка (ж,с,к,ж,к,ж) шаров. Пусть Р6(2,3,1) означает число
всех перестановок спецификации (2,3,1). Пусть теперь имеем п
элементов, из которых:
кх элементов вида 1;
к 2 элементов вида 2;
кг элементов вида г;
причем все *,->() и кх+к2+.. .+/сг = п. Пусть Рп(к1,к2,...,кг)
означает число всех перестановок спецификации (к1 ,к2,... ,кг).
Теорема. Рп(к19к2,...,кг) = п\/(кх\к2\.. .кг\).
Доказательство.
к1 элементов вида 1 можно разместить на п местах С^1
способами;
к2 элементов вида 2 - на оставшихся п-кх местах Сп1^
способами;
къ элементов вида 3 - на оставшихся п-кг-к2 местах Сп1^ _^
способами;
417
kr элементов вида г-на оставшихся п-к1-к2-.. .-кг_х местах
(jJLk -к - -к способами.
По правилу произведения Pn(klJk2J... ,кп) =
^п х^п-к1 ^п-к1-к2 ••• ^п-к1-к2-. . ,-кг_
я! (/!-*!>! (я-^-...-fc,^)
*! !(/!-*!>! A:2!(/i-A:1-A:2)! fcr! (я-J^-.. .-fc^)!
я!/^! *2! ... кг\).
20.3.6. Число размещений данной спецификации
Пусть Arn(kl9k2,...,kn), kx+k2+...+kn = г означает число всех
размещений спецификации (кг ,к2,... ,кп).
Размещение из я разнотипных элементов по т спецификации
(к19к2У... ,кп) есть набор из г этих элементов, из которых
к1 элементов вида 1;
к 2 элементов вида 2;
кп элементов вида я;
причем кг+к2+.. ,+кп = г и все /с, ^ 0 (т.е. некоторые /с,- могут
равняться нулю). Пусть kt ,/с, ,...,&, есть ненулевые числа среди
kl9k2i... ,кп. Очевидно, что Л,- +fc,- + ...+Л,- = г. Тогда с учетом
равенства 0! = 1 число всех размещений
Ап\/С1 ,К2 , . . . ,гСп) = .г Дл,- ,л,- , . . . ,л,) =
rl/(kixl ki2l ... *^!) = r\/{kx\ k2\ ... kn\).
Например, имеем семь шаров: красный, оранжевый, желтый,
зеленый, голубой, синий, фиолетовый. Тогда
1234567- число шаров (я = 7);
кожзгсф- цвета шаров;
кх к2 къ к4 к5 к6 кп - число шаров одного цвета;
2 0 3 0 0 10 к: +к; + ...+£; = 6.
М 12 1р
Тогда А67(к1,к2,...,к7) = P6(kt kt *, ) = Р(к1Ук к) =
12 3 О 3 6
г1/(к{ I kt \ *,- !) = 6!/(2!-3!-1!) = 60.
418
21. ПРОИЗВОДЯЩИЕ ФУНКЦИИ ДЛЯ КОМБИНАТОРНЫХ
КОНФИГУРАЦИЙ И ИХ ЧИСЛА
21.1. Аппарат формальных степенных рядов
Аппарат формальных степенных рядов является достаточно
универсальным методом порождения и пересчета комбинаторных конфигураций
Определение. Производящая функция для множества (числа) всех
комбинаторных конфигураций определенного типа, построенных на
основе множества М = {хх ,х2,... ,*„}, есть функция f(t,xl,x2,...,
хп) (функция g(t)), в формальном разложении которой в ряд по
степеням t коэффициент при tr есть все комбинаторные конфигурации
(число всех комбинаторных конфигураций) из п элементов по г
рассматриваемого типа.
Пример. М = {хг ,х2,х3}; \м\ = 3. Функция f(tJxl ,х2,х3) =
з
П (i+**0 = (1+дс^) • (i+jc20 • (1+JC3O =
W0 + (хх+х2+х3)-1 + (д^Хз+д^дГз+^з)'2 + *1*2*з' *3
есть производящая функция для сочетаний из трех элементов по г
(г = 0,1,2,3). Положим хх = х2 = х3= 1; тогда g(t) = /(Г,1,1,1) =
(l+03 = l + 3f + 3f2+f3 есть производящая функция для числа
0 12 3
сочетаний из трех элементов: С3 = 1; С3 = 3; С3 = 3; С3 = 1.
21.2. Производящие функции для сочетаний
21.2.1. Сочетания без повторений
Теорема. Пусть множество М = {хх ,х2,... ,*„}. Функции
п
f(t,xl,x2,...,xn) = П (1+**0 и
k=i
g(t) = /(мд 1) = (1 + 0я
являются производящими функциями для сочетаний и для числа
сочетаний из п элементов.
Доказательство. Разложим функцию / по степеням t:
п
f{t,x1,x2,...,xn) = П (1+**0 = (l+xlt)(l+x2t)...(l+xnt) =
Е (*10в1-и20в2-...-(*„0вя =
(«1 ,«2> • • • >ап)
419
r=o (ax9a29 . . . ,a„)
где (al9a29... 9an) пробегают все наборы длины /i из 0 и 1.
Слагаемые х^, x2f, ... хЛГ называются кодирующими множителями
Функция hr(xl9x29...9xn) =
Е (*?1#*22# ••• 'хпп)>
(аг 9а2, . ..,а„)
являющаяся коэффициентом при tr9 перечисляет все сочетания без
повторений из п элементов по г. Следовательно, функция f(t,xl9x29
... ,хп) есть производящая функция для сочетаний без повторений из
п элементов множества М.
В функции f(t9xl9x29... 9хп) положим хг = х2 = ... = хп = 1.
Тогда функция g(t) = /(r,l,l,... ,1) = (1 + t)n =
£ I de4e4.,ie«).fS Z с; г,
г=о (^,а2, . . .,аЛ) г=о
в которой Аг(1,1,...,1) есть число всех сочетаний из п элементов
по г, является производящей функцией (энумератором) для числа
сочетаний из п элементов.
п
Следствие. (1 + t)n = £ Crn tr.
г= о
21.2,2. Сочетания с повторениями с ограничениями
на число повторений
Теорема. Пусть множество М = {хг ,х29... ,хп}. Функции
п
f(t9xl9x29...9xn) = П (1+х*Г+(хЛ02 + ••• + (**0С*) и
*«1
я
*(0 = /(u,i,...,i) = п (ш+г2+ ... + ;с*)
k-l
являются производящими функциями для сочетаний и для числа
сочетаний из п элементов соответственно. Причем в каждом сочетании
420
элемент хк встречается не более чем ск раз, к = 1,2,...,я.
Доказательство.
п
f(t,Xl,x2,...,xn) = П (1+хк1+(хк(У + ... + (xkt)Ck) =
{{xxt)u + (х.О1 + (дс,02 + ... + (*iOCl)x
((х20°+ (х20! + (*202 + ... + (х20С2)х
((V)°+ (V)'+ (V)2 + ••• + (V)c") =
E x (х1ов1-(х2ов2-...-(*и»)ви =
(a, ,a2 .Г1. .,a„;
°<e*< c*> *-0,l,. ...И
c.+c, + . . .+c,
I , E , (xr«.x:».....x;-).f.
a 1 +a 2 + * • •+a/j=r
°<аЛ<СЛ i *«1,2,. . . , Л
Функция
(аг ,а2 , . . . ,a„)
a ! +a 2 + • •-+ля=г
°^ак^ск у *«1,2,. . ., л
являющаяся коэффициентом при fr, перечисляет все сочетания из я
элементов по г. При этом в каждом сочетании элемент хк
встречается не более чем ак^ск раз, к = 1,2,...,я. Следовательно,
f(t9xl ,х2,... ,хп) есть искомая производящая функция для сочетаний
с повторениями из я элементов множества М, причем в каждом
сочетании элемент хк встречается не более чем ск раз, к = 1,2,...,я.
В функции f(t,xl,x2,... ,хп) положим хг = х2 = ... = хп = 1. Тогда
функция g(t) = /(f,l,l,...,l) =
Ci+c2+. . .+сл
Е , Е ч (1в1-1ва-...-1в-)-г,
г = о (a! ,a2 , . .. ,a„)
a ! +a 2 + • • •+fl/f=''
°<a*<cfc i Л-1,2,. . . , л
в которой число Аг(1,1,... ,1) есть число всех сочетаний из я
421
элементов по г, причем каждое сочетание содержит элемент хк не
более чем tck раз, к = 1,2,...,л, является производящей функцией
(энумератором) для числа сочетаний с повторениями из п элементов,
причем каждое сочетание содержит элемент хк не более чем ск раз,
к = 1,2,...,л.
21.2.3. Сочетания с повторениями без ограничений
на число повторений
Теорема. Пусть множество М = {xY 9х29... ,*„}. Функции
п
f(t9xl9x29...9xn) = П (l+xkt+(xkt)2 + ... ) и
k=i
п
g(t) = /(u,i,...,i) = п а+'+'Ч ... )
являются производящими функциями для сочетаний и для числа
сочетаний из п элементов с повторениями.
п
Доказательство. f(t9xx 9х29... 9хп) = |"| (l+xkt+(xkt)2 + ...) =
к= 1
((V)0 + ОМ)1 + ОМ)2 + ...)*
((х20° + (V)1 + (*202 + ... )х
((V)°+ (V)1 + (V)2 + •••) =
Е , (х1ов1-(х2ова-...-(х|1ов|| =
I , е , (xt>.xf».....x:-)-r.
г= о Uiifl2» • • • >ап)
Л1+а2+ * *•+аП=Г
Здесь бесконечная сумма берется по всем наборам {ах 9а29... ,ап)
неотрицательных целых чисел. Функция
hr(xl9x29...9xn) = J] ч (х^-х*2- ... -хапп)9
(а19а29 ...9ап)
являющаяся коэффициентом при tr9 перечисляет все сочетания с
повторениями из п элементов по г. Следовательно, f(t9xl9x29... 9
422
хп) есть искомая производящая функция для сочетаний с
повторениями из п элементов множества М.
В функции f(t,xl ,jc2>. .. ,хп) положим *! = х2 = ... = хп = 1.
Тогда функция
g(t) = /(Г,1,1,...,1) = (1 + t + t2 + ...)" =
г=о и!,а2, . . . ,ап)
в которой Ar(l,l,...,l) есть число всех сочетаний с повторениями
из п элементов по г, является производящей функцией
(энумератором) для числа сочетаний с повторениями из п элементов.
Замечание. g(t) = /(М,1,... ,1) = (1 + t + t2 + .. .)п =
(f-bO" - (i - о- =
оо (_п)(-л-1)(-/1-2)...(-л-г+1) / Л
г= о г!
" /z(/z+l)(/z+2)...(/z+/-l) ^ ~ ^n+r-i
г= о г! г= о г!
£ (л+г-1)! £ г
г= о (/z+r-1-r)! • г! г= о
21.3. Производящие функции для размещений с повторениями
Теорема. Пусть множество М = {хх ,*2,... ,*„}. Функции
, " Г **' UitO2 (xkt)Ck л
f(t,xx,x2,...,xn) = П 1 +——+ -——+ ••• + — и
*., L 1! 2! с*! J
п г t t2 tck ■.
g(t) = /(r.1,1 l) = П 1 + -7+ —+ ••• + —-
*.i L I' 2! ck\ J
являются производящими функциями для размещений и для числа
размещений из п элементов; в каждом размещении элемент хк встречает-
423
ся не более чем ск раз, Л = 1, 2,..., п.
Доказательство.
_ " Г xkt {xkty (xkt)Ck 1
/(r.xj.xj jcw) = п i +—Г+ ~ГГ~ + ••• + i- =
*•-. *• 1! 2! ct! J
(x.t)0 x.t (x.t)2 (x.tf1 }
•+ ... + x
+ +
I. 0! 1! 2!
Cl!
(x2f)« x2t (x2t)2 (x2r)t2
f (х2Г)« x2t (x2tt
+ +
V 0! 1! 2!
X
c2!
f (xnt)° xnt (xnt)2 (xnt) n -\
+ —+ + ... + =
I 0! 1! 2! c„! J
_ (v)"1 (x2t)a* (xnt)a"
L • • ... •
Cl+c2+...+c„ a, a2 a„
( , Z -J— — )-r.
r = о (flj ,a2 , . . .,an) ax\ a2
aj +a2+. . .+an=r
Q^ak^c к > Л-i ,2,. . . ,л
Здесь сумма берется по всем наборам (^ ,я2,... ,0Л),
неотрицательных целых чисел, для которых ак^ ск, к = 0,1,...,/г).
Функция Л Up^,...,^)
X л X -,
(а! ,а2 , . .. ,ап) ах\ а2\ ... ап\
a j +а 2 + . ..+ап=Г
являющаяся коэффициентом при ГГ, перечисляет сочетания из п
элементов по г. При этом в каждом сочетании элемент хк встречается
424
не более чем ак^ск раз, к = 1,2,...,л. В числителе сочетание
(х1\х22,... ,хпп) из г элементов, среди которых имеется ак
элементов хк, к=1,2,... ,л, породит j размещений спецификации Агп(а19
я21---|Я/|)| причем j = —: : г . Тогда функция
аг\ а2\ ... ап\
g(t) = /(Г,1,1,...,1) =
п t t2 t°k
П (1+ —+ —+ ... + ) =
с1+с2+'--+сЛ Х
Е ( , I )-<г =
г = о (elfe2 вя) ах\ а2\ ... дЛ!
А ! +fl 2 + • • .+ая=/"
°<ДЛ<СЛ I *-1 ,2,. . . ,Л
Е ( , Е —' г)-— =
г = о (ax,а2 , . .. уап) ах\ а2\ ... ап\ г\
a j +а 2 + . ..+ап=Г
о^д^сд., fc=i ,2,. . . ,и
Cl+c2+...+cw r
Е ( , Е 4(врв2»-л))' —-•
r-o Ui ,а2 , . . . ,ап) Г\
aj +а 2 + . ..+ап=Г
°^ак^с к> *-1 ,2,... ,п
Следовательно, /(f ,*i ,х2,... ,хЛ) есть искомая производящая
функция для размещений с повторениями из л элементов множества М
(с учетом сделанного выше замечания), причем в каждом размещении
элемент хк встречается не более чем ск раз, к = 1,2,...,л. В
функции f(t,xl9x2,... ,хп) положим хг = х2 = ... = хп = 1. Тогда
функция g(t) является производящей функцией (энумератором) для
числа размещений с повторениями из л элементов, причем каждое
размещение содержит элемент хк не более чем ак раз (к =
1,2,...,л). Коэффициент при —— есть число размещений из л эле-
425
ментов по г, причем в каждом размещении элемент хк встречается не
более ск раз, /с=1,2,... ,я.
Замечание. Для числа перестановок с повторениями без
ограничений на число повторений производящая функция
ft t2 t3 Лп
g(t) = 1 + + + — + ... =
^ 1! 2! 3\ J
оо tr
ent = у nr
r= о ' •
Коэффициент пг при —j- равен числу всех размещений с
неограниченными повторениями из п элементов по г, т.е. числу всех наборов
длины г из п элементов.
22. КОМБИНАТОРНО ЛОГИЧЕСКИЙ АППАРАТ
22.1. Включения и исключения
Пусть имеем N объектов 1,2,... ,7V, которые могут обладать или
не обладать п свойствами 1,2,...,п. Примем следующие обозначения.
N(0) (или N("11,"12,... ,"1л)) - число объектов, не обладающих ни
одним из свойств l,2,3,...,/t.
N(i1,i29... ,ir) - число объектов, обладающих свойствами il9i29
...,/г (возможно и другими свойствами).
N=k - число объектов, обладающих в точности к свойствами.
N^k - число объектов, обладающих не менее чем к свойствами.
Найдем формулы для вычисления всех этих чисел.
Пример. Пусть имеем шесть объектов 1-6, которые могут
обладать или не обладать пятью свойствами 1-5 (табл.22.1).
Заметим, что число объектов, не обладающих ни одним из свойств
1-4, равно N("11,"12,"13,"14) = 3; сюда включаются объекты,
дополнительно обладающие свойством 5 (объекты 5,6) и не обладающие
свойством 5 (объект 2). Число объектов, не обладающими свойствами
1 - 4 и обладающими свойством 5, равно N("11,"12,"13,"14,5) = 2
(объекты 5,6). Тогда число объектов, не обладающих ни одним из
свойств 1-5 равно N(0) = М"Ч,"12,ПЗ,П4,П5) = М~И,~12,"13,-|4) _
N(11,12,13,14,5) = 3-2 = 1.
В общем случае N(0) = NCM,12,...,ln-l) - N(11,12,... ,1л-1,л).
426
Таблица 22.1
1
2
3
4
5
6
1
1
0
1
1
0
0
2
1
0
1
0
0
0
3
0
0
1
1
0
0
4
1
0
1
0
0
0
5
0
0
1
0
1
1
MD = 3; N(1,2) = 2; N(2,4) = 2
N(2) = 2; N(1,3) = 2; N(2,5) = 1
N(3) = 2; N(1,4) = 2; N(3,4) = 1
N(4) = 2; N(1,5) = 1; N(3,5) = 1
N(5) = 3; N(2,3) = 1; N(4,5) = 1
N(1,2,3) = 1; N(1,4,5) = 1; N(1,2,3,4) = 1; N(1,2,3,4,5) = 1.
N(1,2,4) = 2; N(2,3,4) = 1; N(1,2,3,5) = 1
N(1,2,5) = 1; N(2,3,5) = 1; N(1,2,4,5) = 1
N(1,3,4) = 1; N(2,4,5) = 1; N(1,3,4,5) = 1
N(1,3,5) = 1; N(3,4,5) = 1; N(2,3,4,5) = 1
Теорема. Справедлива следующая формула включений и исключений.
N(0) = N - £ N(i) + £ N(«1(i2) - ... +
1< I <П
l<(, < 1г<П
(-i)r E N(ilti2,...,ir)
(-1)" N(l,2,...,/z).
Доказательство. Пусть Sr = J] M*i ,/2,... ,/r).
i^i1<i2< . • .<*'r<n
Далее индукция по числу свойств п.
БАЗИС, п = 1 (одно свойство). /V(0) = N - Ml) = N - Sx.
ПРЕДПОЛОЖЕНИЕ ИНДУКЦИИ. Допустим, что формула включений и
исключений справедлива для п-1 свойств.
ШАГ ИНДУКЦИИ. Покажем, что формула включений и исключений
справедлива для п свойств: N(0) = N - Sx + S2 - ... + (-1)л Sn.
По предположению индукции для свойств 1,2,...,л-1 имеем
М"11,П2,...,П/г-1) = N - Sx + S2 - ... + (-l)*-1 £„_! =
1<«<"-1
M«,,i,) -
427
(-1)"-1 Ml,2,...,/i-l).
Эта формула справедлива и для п свойств при фиксировании
последнего свойства п:
ЛГ("11,12,...,-|и-1,и) = N(n) - Yi NO,n) +
£ N(ilyi2,n) - ... + (-1)"-1 N(l,2,...,n-l,Ai).
Вычтем последнюю формулу из предпоследней:
М"11,П2,...,-|и-1) - ЛГ(П1,П2,...,Пл-1,л) = МО) =
n - ( Е мо + Мл)) +
( Е Mi,/) + Е м/,«)) - ... +
(-l)""1 (Ml,2,...,/z-l) + £ N(ilf...J^29n)) +
(-1)" Ml,2,...,n) =
Z (~l)r E N(il9i2,...9ir).
Г= 0 1<l'l<l*2< • • •<«г^л
Замечание. Аналогично можно показать справедливость двух
следующих формул:
п—к
N-k = £ (-1)' Cklj E N^ •'«' * • ''W;
*>* = Е (-1)' С**~+> Е N(il,i1,...,ik+j).
428
Для примера из табл.22.1 найдем N(0), N,2, N^2:
N(0) = N - £ N(«) + £ tf(i,,i2) -
1^1, < 1,^5
Е Milfi2,i3) + £ лгО^/^/зЛ) -
N(1,2,3,4,5) = 6 - 12 +14 -11 + 5 - 1 = 1;
N=2 = 5j2(-l);' C2+; J] Mi,,i2,...,«2+;-) =
; = о i^i1<i2< • • .<i2+i^5
1-14 - 3-11 + 6-5 - 10-1 = 14 - 33 + 30 - 10 = 1;
; = o i^i1<i2< . . .<*2+ f'^5
1-14 -2-11 + 3-5-4-1 = 14 -22 + 15 -4 = 3.
Пример. Найдем число положительных натуральных чисел, не
больших 1000 и не делящихся ни на одно из чисел 3,5,7. Выделим
следующие свойства, которыми могут обладать или не обладать числа
1,2,...,1000.
Свойство 1: число п делится на 3.
Свойство 2: число п делится на 5.
Свойство 3: число п делится на 7.
В табл.22.2 приведены свойства, им удовлетворяющие множества
чисел и их число.
N(0) = 1000 - £ N(i) + I - N(1,2,3) =
i^ i'^ з i^i < ;^з
1000 - (333 + 200 + 142) + (66 + 47 + 28) - 9 = 457.
22.2. Приложения формулы включений и исключений
22.2.1. Задача о беспорядках
Пусть имеем множество М = {1,2,...,п} из п элементов, и пусть
подстановка (т.е. взаимно однозначная функция) s : М -> М. Подста-
429
становка s обладает свойством i, если i = s(i), т.е. подстановка
s элемент i переводит в себя. Подстановка s есть беспорядок, если
i * j(i) V/€M. Например, подстановка ^ = L - .1 обладает
свойствами 2 и 4 и не обладает свойствами 1 и 3. Подстановка s =
. обладает свойством 3 и не обладает свойствами 1,2,4.
Подстановка s = . является беспорядком.
Таблица 22.2
Свойство
1
2
3
1,2
1,3
2,3
1,2,3
Множество чисел
{3* : * = 1,2 333}
{5* : * = 1,2,...,200}
{7* : * = 1,2,...,142}
{15* : * = 1,2,.. .,66}
{21* : * = 1,2 47}
{35* : * = 1,2 28}
{105* : * = 1,2,....9}
Число
N(\) = 333
N(2) = 200
N(3) = 142
N(1,2) = 66
N(1,3) = 47
N(2,3) = 28
N(1,2,3) = 9
Пусть подстановка s обладает свойствами ix ,/2,... ,/г
(возможно, что и другими свойствами). Тогда
f 1 2 ix i2 ir n Л
I *(1) s(2)" i, '" i2 '" ir '" s(n) У
Число таких подстановок равно (п - r)\ = N(il,i2,...,ir). По
методу включений и исключений число подстановок s, не обладающих
ни одним из свойств 1,2,...,/! (т.е. число беспорядков) ЛГ(0) =
w(-ii,-i2,...л*) = Е (-i)r Е м«1,«2,...,«г) =
Г= 0 1^1,<1-,< . . .<1Г^Л
Е (-1У Е (п - г)\ =
r*° {i1,i2,...,ir)£{i,2,...,n}
" " п\(п-г)\ " 1
Е (-iY crn (n - r)\ = E (-iK ——- - n\ E (-1)»- —
r=o r=o r\(n-r)\ r=o r!
n 1
Окончательно число беспорядков N(0) = n\ J] (-l)r .
r= о r!
430
n 1 n 1
Замечание. N(O) = л! £ (-l)r « n\ £ (-l)r = /ile"1
r= о r! г= о r\
т.е. число беспорядков N(0) ~ —— .
Определим
s
22.2.2.
Задача
число подстановок
■(
1 2
j(D *(2)
«1
i,
о
'2
»2
встречах
'*
'*
обладающих ровно fc свойствами i = s{i). Подсчет числа таких
подстановок сведем к задаче о беспорядках. Искомое число
N.k = Ск„ • ((л - Л)! • "ii-lY—),
г = о г!
где множитель С„ дает число способов, которыми можно выбрать fc
элементов (из данных п элементов), обладающих свойством i = s(i),
а второй множитель дает число беспорядков для остальных п - к
элементов (не обладающих свойством i = s(i)).
п\ п\ п~к 1
Так как Скп = , то N к = У (-1)г .
Число N=k можно интерпретировать как число встреч п-к лиц из
данных п лиц.
п\ £ 1 п\
Замечание. N k ж У (-1)г = .
к\ г=о г! к\е
22.23. Программа для формулы включений и исключений
Процедура number_not(A,L,N0) по числу элементов L и по списку
свойств А вычисляет число элементов N0, не обладающих ни одним
свойством. В программе использованы данные из табл.22.1.
Процедура number_n(A,Ac,N,M,K,L) по числу элементов L и по
списку свойств А вычисляет правую часть формулы включений и
исключений без первого слагаемого.
Процедура number_nl(C,Ac,Nl) по списку сочетаний С вычисляет
одно слагаемое (одну сумму) N1 формулы включений и исключений.
Процедура combination(A,Kl,C) по списку элементов А и по числу
К1 вычисляет список С всех сочетаний из А по К1.
Процедура num(H,N2) по одному сочетанию Н вычисляет число
элементов N2, удовлетворяющих свойствам сочетания Н.
431
Процедуры add_attrib(S), deMist(S), del_attrib(S) помещают в
БД и удаляют из БД факты sl([X,Y,...]), отвечающих некоторому
сочетанию свойств.
Предикат nth_element_in_list(L,N,A) истинен, если А есть N-й
элемент в списке L. Например, если L=[a,[b,c],d,[e]], N=l, то
А=а. Если N=2, то А=[Ь,с].
d(N) :- A=[l,2,3,4,5],findall(Li,s(Li),S),
length(S,L),number_not(A,L,N).
s([l,l,0,l,0]). s([0,0,0,0,0]). s([l,l,l,l,l]).
s([l,0,l,0,0]). s([0,0,0,0,l]). s([0,0,0,0,l]).
number_not(A,L,NO) :- number_n(A,0,N,-l,0,L),NO is N+L.
number__n(A,Ac,N,M,K,L) :- Kl is K+l, Kl=<L,combination(A,Kl,Cl),
if thenelse(Cl=A, comb_one( A, [ ], C), C=Cl),
number__nl(C,0,Nl),Acl is Ac+Nl*M,nurnber_n(A,Acl,N,-M,Kl,L).
number_n(A,N,N,M,L,Ll).
comb_one([H|T],Ac,C) :- Acl=[[H] |Ac] ,comb_one(T,Acl,C).
comb_one([],Ac,C) :- reverse(Ac,C).
number_nl([H|T],Acl,Nl) :- num(H,N2),
Ac2 is Acl+N2,number_nl(T,Ac2,Nl).
number_nl([],Nl,Nl).
num(C,N) :- C=[H|T],
findall(Li,(s(Li),nth_element_in_list(Li,H,Nl),Nl=l),L),
add_attrib(L),del__list(T),findall(Lil,sl(Lil),Ll),
length(Ll,N),del_attrib(Ll).
add_attrib([H|T]) :- assertz(sl(H)),add_attrib(T).
add_attrib([]).
del_list([H|Tl]) :-
findall(Li,(sl(Li),nth_element_in_list(Li,H,Nl),Nl=0),L),
del__attrib(L),delJist(Tl).
del_list([]).
del_attrib([H|T]) :- retract(sl(H)),del_attrib(T).
del_attrib([]).
combination(A,R,C) :- length(A,L),
case([(R=0 ; R>L) -> C=[], R=l -> C=A |
(combin2(A,Cl),combinK(Cl,A,R,2,C))]).
combin2(A,Cl) :- combin2_rep(A,[] ,Cl).
combin2_rep([H|T],Ac,C) :- findall([H,X] ,member(X,T),L),
432
append(Ac,L,Ll),combin2_rep(T,Ll,C).
combin2_rep([] ,C,C).
combinK(Cl,Al,R,K,C) :- Kl is K+l, K1=<R,
combinK_Kl(Cl,Al,L),combinK(L,Al,R,Kl,C).
combinK(C,Al,R,R,C).
combinK_Kl(Cl,A,C) :- comb(Cl,A,[] ,C).
comb(Cl,[H|Al],Ac,C) :-
findall(X,(member(X,Cl),member(H,X)),L),difset(Cl,L,C2),
findall(X,(mcmber(Y,C2),add(H,Y,X)),ClH),
append(Ac,ClH,Acl),comb(C2,Al,Acl,C).
comb([],Al,C,C).
nth_element_in_list(L,N,A) : — I is l,nth_el_in_list(L,N,I,A).
nth_el_in_list([H|T],N,I,A) :- not(N is I),11=1+1,
nth_el_in_list(T,N,U,A).
nth_el_in_list([H|T],N,I,H) :- N is I.
add(X,L,[X|L]).
difset(X,Y,T) :- difl(X,Y,X,T).
difl([R|X],Y,[R|Z],T) :- not(member(R,Y))>
append(Z,[R],Zl),difl(X,Y,Zl,T).
difl([R|X],Y,[R|Z],T) :- member(R,Y),difl(X,Y,Z,T).
difl([],Y,Z,Z).
reversed ],[])•
reverse([H|T],L) :- reverse(T,Z),append(Z,[H] ,L)-
append([],L,L).
append([X|Ll],L2,[X|L3]) :- append(Ll,L2,L3).
member(X,[X|Y]).
member(X,[Y|Z]) :- member(X,Z).
СПИСОК СОКРАЩЕНИЙ
А2 - аксиома А2
АБ - аксиома Бернайса
АР - аксиома равенства
БД - база данных
ДНФ - дизъюнктивная нормальная форма
И - истина
ИВ - исчисление высказываний
ИИВ - интуиционистское исчисление высказываний
КНФ - конъюнктивная нормальная форма
Л - ложь
ЛП - логика предикатов
МДНФ - минимальная дизъюнктивная нормальная форма
МИВ - модальное исчисление высказываний
МИП - модальное исчисление предикатов
НОУ - наиболее общий унификатор
НОУ (Ж) - наиболее общий унификатор для множества литер W
Пй(А) - подстановка формулы В на место переменной р в формуле А
ПВ - правило вывода
ПВ4(1,2) - правило вывода 4 применено к формулам 1 и 2
ПЗ - правило заключения
П3(2,5) - правило заключения применено к формулам 2 и 5
ПИ - простой импликант
ПН - (модальное) правило необходимости
ПР - правило резолюции
ПР(6,9) - правило резолюции применяется к формулам 6 и 9
СДНФ - совершенная дизъюнктивная нормальная форма
СИВ - секвенциальное исчисление высказываний
СИП - секвенциальное исчисление предикатов
СКНФ - совершенная конъюнктивная нормальная форма
ТЗ - теорема 3
ТД - теорема дедукции
ТДНФ - тупиковая дизъюнктивная нормальная форма
УИП - узкое исчисление предикатов
y(W) - унификатор для множества литер W
У(3,7) - унификация формул 3 и 7
V-ПР (или V-правило) - правило навешивания квантора общности
V-nP(4) - V-правило применяется к формуле 4
Э-ПР (или Э-правило) - правило навешивания квантора существования
3-ПР(5) - Э-правило применяется к формуле 5
434
ЛИТЕРАТУРА
Басакер Р., Саати Т. Конечные графы и сети. М.: Наука, 1974.
Бейс Г., Кук Д. Компьютерная математика. М.: Наука, 1990.
384 с.
Берж К. Теория графов и ее применения. М.: ИЛ, 1962. 319 с.
Братко И. Программирование на языке Пролог для искусственного
интеллекта. М.: Мир, 1990. 560 с.
Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной
математике. М.: Наука, 1977. 368 с.
Гильберт Д., Бернайс П. Основания математики, т.1. Логические
исчисления и формализация арифметики. М.: Наука, 1982. 557 с.
Т.2. Теория доказательств. М.: Наука, 1982. 653 с.
Дискретная математика и математические вопросы кибернетики.
Т.1. / Под ред. С.В.Яблонского и О.Б.Лупанова. М.: Наука, 1974.
312 с.
Доорс Дж., Рейвлейн А.Р., Вадера С. Пролог - язык
программирования будущего. М.: Финансы и статистика, 1990. 144 с.
Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И.
Лекции по теории графов М.: Наука, 1990. 384 с.
Ершов Ю.Л., Лавров И.А., Тайманов А.Д., Тайцлин М.А.
Элементарные теории. УМН, 1965, т.20. Вып.4 (124). С.37-108.
Ершов Ю.Л., Палютин Е.А. Математическая логика. М.: Наука,
1979. 320 с.
Зыков А.А. Основы теории графов. М.: Наука, 1987. 384 с.
Кангер С. Упрощенный метод доказательства для элементарной
логики. В книге: Математическая теория логического вывода / Под
ред. А.В.Идельсона и Г.Е.Минца. М.: Наука, 1967. С.200-207.
Кларк К.Л., Маккейб Ф.Г. Микро-Пролог: ведение в логическое
программирование. М.: Радио и связь, 1987. 311 с.
Клини С.К. Введение в метаматематику. М.: ИЛ, 1957. 526 с.
Клини С.К. Математическая логика. М.: МИР, 1973. 480 с.
Клоксин У., Меллиш К. Программирование на языке Пролог. М.:
Мир, 1987. 336 с.
Ковальски Р. Логика в решении проблем. М.:Наука, 1990. 277 с.
Кофман А. Введение в прикладную комбинаторику. М.: Наука,
1975. 480 с.
Кузнецов О.П., Адельсон-Вельский Г М. Дискретная математика
для инженера. М.: Энергоатомиздат, 1988. 480 с.
Липский В. Комбинаторика для программистов. М.: Мир, 1988.
213 с.
Логическое программирование. /Под ред. В.Н.Агафонова. М.: Мир,
435
1988. 368 с.
Лорьер Ж.-Л. Системы искусственного интеллекта. М.: Мир, 1991.
568 с.
Малпас Дж. Реляционный язык Пролог и его применение. М.:
Наука, 1990. 464 с.
Математическая логика в программировании /Под ред. М.В.За-
харьящева, Ю.И.Янова. М.: Мир, 1992. 408 с.
Медведев Ю.Т. О классе событий, допускающих представление в
конечном автомате. В сб.: Автоматы /Под ред.А.А. Ляпунова. М.:
ИЛ, 1956, с.385-401.
Мендельсон Э. Введение в математическую логику. М.: Наука,
1984. 319 с.
Мучник Ан.А. Игры на бесконечных деревьях и автоматы с
тупиками // Семиотика и информатика. 1985. Вып.24. С. 16-40.
Набебин А.А. Об исчислении одноместных предикатов на
натуральных числах со штрихом // Тр. зонального объединения
математических кафедр пединститутов Сибири. Красноярск, 1972. Вып.1.
С.133-160.
Набебин А.А. О выразимости в ограниченной арифметике второго
порядка // Сибирский матем. журнал, 1977. Т. 18. N 4. С.830-837.
Набебин А.А., Захарьящев М.В. Метод резолюций в логике
предикатов как основа для языка программирования Пролог. М.: Изд-во
МЭИ, 1990. 76 с.
Набебин А. А. Алгоритмы на графах и их Пролог-программы. М.:
Изд-во МЭИ, 1991. 104 с.
Набебин А.А. Монадическая логика и Пролог-проектирование
конечных автоматов. М.: Изд-во МЭИ, 1991. 140 с.
Новиков П.С. Элементы математической логики. М.: Наука, 1973.
399 с.
Оре О. Теория графов. М.: Наука, 1968. 352 с.
Риордан Дж. Введение в комбинаторный анализ. М.: ИЛ, 1963.
288 с.
Семенов А.Л. О некоторых расширениях арифметики сложения
натуральных чисел // Изв. АН СССР. Сер. матем. 1979. Т.77. С. 1175-
1195.
Семенов А.Л. Логические теории одноместных функций на
натуральном ряде // Изв. АН СССР. Сер. матем. 1983. Т.77. N 3. С.623-
658.
Стерлинг Л., Шапиро Э. Искусство программирования на языке
Пролог. М.: Мир, 1990. 235 с.
Тей А., Грибомон П., Луи Ж. и др. Логический подход к
искусственному интеллекту. М.: Мир, 1990. 432 с.
436
Трахтенброт Б.А. Невозможность алгоритма для проблемы
разрешимости на конечных классах //ДАН СССР. 1950. Т.70. N 4. С.569-572.
Трахтенброт Б.А. Моделирование функций на конечных классах //
Ученые записки Пензенского гос. пед. ин-та. 1955. Выи.2. С.61-78.
Трахтенброт Б.А., Барздынь Я.М. Конечные автоматы. М.: Наука,
1970. 400 с.
Уилсон Р. Введение в теорию графов. М.: Мир, 1977. 208 с.
Фейс Р. Модальная логика. М.: Наука, 1974. 520 с.
Фролов А.Б., Болотов А.Б., Ляшенко Л.И. Дискретная математика
и некоторые задачи на графах. М.: Изд-во МЭИ, 1990. 35 с.
Фролов А.Б., Болотов А.Б., Коляда К.В. Модели и методы
дискретной математики. М.: Изд-во МЭИ, 1988. 132 с.
Харари Ф. Теория графов. М.: Мир, 1973. 300 с.
Хоггер К. Введение в логическое программирование. М.: Мир,
1988.348 с.
Чень Ч., Ли Р. Математическая логика и автоматическое
доказательство теорем. М.: Мир, 1983. 360 с.
Черч А. Введение в математическую логику. М.: ИЛ, 1960. 485с.
Яблонский СВ. Введение в дискретную математику. М.: Наука,
1986. 384 с.
Яблонский СВ., Гаврилов Г.П., Кудрявцев В.Б. Функции алгебры
логики и классы Поста. М.: Наука, 1966. 120 с.
Яблонский СВ., Гаврилов Г.П., Набебин А.А. Анализ и синтез
схем в многозначных логиках. М.: Изд-во МЭИ, 1989. 118 с.
Янсон А. Турбо-Пролог в сжатом изложении. М.: Мир, 1991. 94с.
An introduction to Arity-Prolog. Arity Corporation,
Massachusetts, 1986. 55 p.
Arity-Prolog programming language. Arity Corporation,
Massachusetts, 1986. 198 p.
Arity-Prolog interpretator and compiler. Arity Corporation,
Massachusetts, 1988. 265 p.
Arity-Prolog language reference manual. Arity Corporation,
Massachusetts, 1988. 320 p.
Bilding Arity-Prolog applications. Arity Corporation,
Massachusetts, 1986. 125 p.
Boole G. The mathematical analycis of logic, being an assay
toward a calculus of deductive reasoning. Cambridge (Macmillan,
Barclay & Macmillan) and London (George Bell), 1847. 82 p.
Bowen D.L. DECsystem-10 Prolog user's manual. University of
Edinburg: Department of Artificial Intelligence. 1981.
Buchi J.R. Weak second order arithmetic and finite automata.
Zeitschrift fiir mathematische Logik und Grundlagen der Mathe-
437
matik, 1960. V.6. N 1. P.66-92. (Русский перевод: Бюхи Дж.Р.
Слабая арифметика второго порядка и конечные автоматы // Киберн.сб.,
1964. Вып.8. С.42-77)
Buchi J.R. On a decision method in restricted second order
arithmetic. Proceedings of the international congress of Logic,
Methodolology and Philosophy of Sience. Stanford, 1962. P. 1-11.
(Русский перевод: Бюхи Дж.Р. О разрешающем методе для
ограниченной арифметики второго порядка // Киберн.сб., 1964. Вып.8.
С.78-80)
Campbell J.A. Implementation of Prolog. West Sussex, 1984.
391 p.
Church A. A note on the Entscheidungsproblem. Journal of
Symbolic Logic, 1936. V.l. N 1. P.40-41; V.l. N 3. P.101-102.
Clark K.L., Tarnlund S.A. Logic programming. N.-Y., Acadamic
Press. 1982.
Coupet-Grimal S. Prolog infinite trees and automata.
Informatique theorique et application / Theoretical Informatics
and Applications, 1991. V.25. N 5. P.397-418.
Donner J.E. Tree acceptors and some of their application.
Journal of Computer and System Sciences, 1970. V.4. P.406-451.
Eilenberg S. Automata languages and machines. N.-Y. Academic
Press. 1974. Vol.A; 1976. Vol.B.
Elgot C.C. Desision problems of finite automata design and
related arithmetics // Amer. Math. Soc. Trans, 1961. V.98. N 1.
P.21-51.
Frege G. Begriffschrift eine der arithmetischen nachgebildete
Formelsprache des reinen Denkens. Halle, 1879. vii+88 p.
Godel K. Die Vollstandigkeit der Axiome der logischen
Funktionenkalkulus //Monatshefte fiir Mathematik und Physik, 1930.
V.37. P.349-360.
Godel K. Ober formal unentscheidbare Satze der Principia Ma-
thematicae und vervandter Systeme I // Monatshefte fiir Mathematik
und Physik, 1931. V.38. P. 173-198.
Lauchli H., Leonard J. On the elementary theory of linear
order // Fundamenta Mathematikae, 1966. V.59. N 1. P. 109-116.
Lauchli H. A decision procedure for weak second order theory
of linear order. In: Contribution to mathematical logic, K.Schiit-
te,editor, North-Holland, Amsterdam, 1968. P. 189-197.
Lowenheim L. Ober die Mogligkeiten im Relativkalkiil // Mathe-
matische Annalen, 1915. V.7. P.447-470.
Lloyd J.W. Foundation of logic programming. N.-Y., Springer
Verlag, 1984.
438
Marcus C. Prolog programming: Applications for database
systems, expert systems and natural language systems.
Addison-Wesley, 1986. 325 p.
McNaughton R. Finite-state infinite games // MIT, Proj. MAC,
1965.
McNaughton R. Testing and generating infinite sequences by
finite automata // Inf. and Control, 1966. V.9. N 5. P.521-530.
Meyer A.R. Weak monadic second order theory of successor is
not elementary recurcive // Proc. Logic Colloquium, Lecture Notes
in Mathematics, 1975. V.453. P. 132-154.
Moschovakis Y.N. Descriptive set theory. Amsterdam. 1980.
Muller D.E. Infinite sequences and finite machines // Proc. 4-
th Ann. Symp. on Switching Circuit Theory and Logical Design,
1963. P.3-16.
Peano G. Aritmetices principia, nova methodo exposita. Turin
(Bocca), 1889. xvi+20 p.
Pereira L.M., Pereira F., Warren D.H.D. User's guide to DEC-
system-10 Prolog // University of Edinburg: Department of
Artificial Intelligence. 1981.
Pereira F. C-prolog user's manual. University of Edinburg:
Department of Computer - Aided Architectural Design. 1982.
Quintus Prolog user's guide and reference manual. Palo Alto:
Quintus Computer Systems. Inc. 1985.
Rabin M.O., Scott D. Finite automata and their decison
problem. J.B.M. J.Res.Dev, 1959. V.3. (Русский перевод: Рабин М.О.,
Скотт Д. Конечные автоматы и задачи их разрешения // Киберн.сб.
1962, Вып.4. С.58-91)
Rabin M.O. Decidability of monadic second order theory of two
successor // Amer.Mathem.Soc. ,Noteces, 1967, v. 14, N 7, p.941.
Rabin M.O. Decidability of the second order logic and automata
on infinite trees // Amer. Math. Soc. Trans, 1969. V.141. N 6.
P. 1-35. (Русский перевод: Рабин М.О. Разрешимость теорий второго
порядка и автоматы над бесконечными деревьями // Киберн.сб.,
1971. Вып.8. С.72-116)
Rabin M.O. Automata on infinite objects and Church's problem.
Conference Board Math. Sci. Regional Conf. Series in Math // No
13, AMS, Providence, 1972. National industries conference board.
N.-Y. AMS, Prov. 1972. V.13.
Robinson J.A. A machin-oriented logic based on the resolution
principle // Journal ACM. 1965. V.12, P.23-41. (Русский перевод:
Робинсон Дж.А. Машинно-ориентированная логика, основанная на
принципе резолюции // Киберн.сб. (новая серия), 1975. Т.7)
439
Robinson R.M. Restrected set-theoretical definitions in
arithmetic // Proc.Amer.Mathem.Soc. 1958. V.9. P.238-242.
Rogers J.B. A Prolog primer. Reading: Addison-Wesley. 1986.
Shammas N. Turbo Prolog. In: Byte, 1986. V.ll. N 9. P.293-295.
Shapiro E. The art of Prolog. Cambridge. MIT Press.
Siefkes D. Buchi's monadic second order successor arithmetic.
Lectures Notes in Mathematics, 1970. V.120.
Skolem Th. Untersuchungen liber die Axiome des Klassenkalkiilus
und iiber die Produktions- und Summationsprobleme, welche gewisse
Klassen Aussagen betreffen. Skripter Utgit af Videnskapsselskapet
i Kristiania, I. Matematiksnaturvidenskakabelig Klasse, 1919.
N 3. P.1-37.
Tarski A. Model theoretic results concerning weak second order
logic // Amer.Math.Soc, Noteces, 1959. V.5. P.550-556.
Thatcher J. W., Wright J.B. Generalized finite automata theory
with an application to a decision problem of second order logic
// Mathematical Systems Theory, 1968. V.2. N 1. P.57-81.
Thatcher J.W. Desision problems for multiple successor
arithmetics // Journal Symbolic Logic, 1966. V.31. N 2. P. 182-190.
Turbo Prolog user's guide. Borland International. 1988.
Turbo Prolog reference guide. Borland International. 1988.
Winston P.H. Artificial Intelligence. (Second eddition).
Addison-Wesley. 1984. (Русский перевод: Уинстон П. Искусственный
интеллект. М.: Мир, 1980. 519 с.)
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ 3
Часть 1. МАТЕМАТИЧЕСКАЯ ЛОГИКА И ПРОЛОГ 14
1. Алгебра логики 14
1.1. Функции алгебры логики 14
1.2. Формулы. Реализация функций формулами 16
1.3. Равносильные преобразования формул 17
1.4. Нормальные формы 20
1,4,1. Совершенные нормальные формы 21
1.5. Минимизация нормальных форм 23
1.5.1. Алгоритм Куайна построения сокращенной ДНФ 25
1.5.2. Алгоритм построения сокращенной ДНФ
с помощью КНФ 27
1.5.3. Построение всех тупиковых ДНФ 29
1.5.4. Алгоритм минимизации функций в классе ДНФ 30
1.5.5. Алгоритм минимизации функций в классе КНФ 31
1.5.6. Алгоритм минимизации функций в классе
нормальных форм 31
1.6. Минимизация частично определенных функций .... 34
1.6.1. Алгоритм минимизации частично определенных
функций в классе ДНФ 35
1.6.2. Алгоритм минимизации частично определенных
функций в классе КНФ 35
1.7. Двойственные функции 37
1.7.1. Принцип двойственности 38
1.8. Линейные функции 39
1.9. Монотонные функции 43
1.10. Теорема Поста о функциональной полноте 44
1.10.1, Предполные классы 46
2. Исчисление высказываний 47
2.1. Определение исчисления высказываний 47
2.1 Л. Правило одновременной подстановки 52
2.2. Теорема дедукции (ТД) в исчислении высказываний 52
2.3. Производные правила вывода 55
2.4. Тождественно истинные и доказуемые формулы .... 60
2.5. Разрешимость, непротиворечивость, полнота,
независимость аксиом 64
441
2.6. Формулировка исчисления высказываний
с единственным правилом вывода правилом заключения 66
3. Логика предикатов 68
3.1. Предикаты, кванторы 68
3.2. Выполнимость, невыполнимость, общезначимость,
опровержимость формул логики предикатов 70
3.3. Равносильность формул 73
3.3.1. Релятивизованные кванторы 75
3.4. Нормальные формы 76
3.4.1. Предваренная нормальная форма 76
3.4.2. Стандартная форма Скулема 77
3.5. Проблема разрешимости в логике предикатов .... 78
4. Узкое исчисление предикатов 79
4.1. Определение узкого исчисления предикатов 79
4.2. Теорема дедукции в УИП 82
4.3. Непротиворечивость УИП 84
4.4. Полнота УИП относительно класса общезначимых формул 86
4.5. Аксиоматическая арифметика и элементарные теории 95
4.6. Интуиционизм (конструктивизм) 99
4.7. Модальные логики 101
5. Исчисление секвенций 103
5.1. О правилах вывода в секвенциальном исчислении
высказываний 103
5.2. Секвенциальное исчисление высказываний (СИВ) . . . 107
5.3. Секвенциальное исчисление предикатов (СИП) 111
6. Метод резолюций в логике предикатов и Пролог 114
6.1. Метод резолюций в логике высказываний 114
6.1.1. Семантическое дерево 115
6.1.2. Правило резолюции 116
6.2. Эрбрановские универсум, базис, интерпретация . . . 120
6.3. Семантические деревья и теорема Эрбрана 124
6.4. Унификация 128
6.4.1. Алгоритм унификации 129
6.5. Метод резолюций в логике предикатов 132
6.6. Основы Пролога 138
6.6.1. Унификация в Прологе 145
6.6.2. Декларативный и операторный смысл
Пролог-программы 147
442
6.6.3. Бэктрэкинг и оператор отсечения 149
6.6.4. Объявление операторов 151
6.6.5. Сеанс работы с языком Arity/Prolog ..... 153
6.7. Примеры программ и вычислений в Прологе 154
6.7.1. Принадлежность элемента списку 154
6.7.2. Первый элемент в списке 159
6.7.3. Последний элемент в списке 159
6.7.4. Следующий элемент в списке 160
6.7.5. Соединение списков 163
6.7.6. Обращение списка 164
6.7.7. Выравнивание списка 165
6.7.8. Добавление элемента в начало списка .... 166
6.7.9. Удаление первого вхождения данного элемента
из списка 166
6.7.10. Удаление всех вхождений данного элемента
из списка 167
6.7.11. Замена элемента в списке 169
6.7.12. Быть подсписком в списке 169
6.7.13. Включение множеств 172
6.7.14. Равенство множеств 172
6.7.15. Объединение множеств 172
6.7.16. Пересечение множеств 174
6.7.17. Разность множеств 174
6.7.18. Декартово произведение множеств 174
6.7.19. Множество всех подмножеств данного
множества 175
6.7.20. Удаление всех повторов элементов в списке 175
6.7.21. Принадлежность множества списку некоторых
подмножеств 175
6.7.22. Удаление всех повторов подмножеств в данном
списке множеств 176
6.7.23. Удаление повторов атомов в списке
списков атомов 176
6.7.24. Последовательное порождение нумерованных
атомов 176
6.7.25. Программа построения сокращенной ДНФ
по конъюнктивной нормальной форме 177
6.7.26. Программа построения сокращенной ДНФ
по конъюнктивной нормальной форме
без отрицаний 178
6.8. Встроенные предикаты Пролога 180
6.8.1. Средства управления 180
443
6.8.2. Классификация термов 181
6.8.3. Унификация термов 181
6.8.4. Сравнение термов 181
6.8.5. Арифметические функции 182
6.8.6. Арифметические предикаты 183
6.8.7. Счетчики 183
6.8.8. Обработка термов 183
6.8.9. Работа с стрингами 184
6.8.10. Составление списков 185
6.8.11. Взаимодействие с базой данных 185
6.8.12. Работа с мирами 188
6.8.13. Стандартные ввод и вывод 188
6.8.14. Доступ к файлам 189
6.8.15. Стандартный доступ к файлам в Прологе . . . 190
6.8.16. Движение в файле 190
6.8.17. Переадресация ввода и вывода 191
6.8.18. Ввод и вывод низкого уровня 191
6.8.19. Работа с экраном 191
6.8.20. Исполнение системных функций 192
6.8.21. В-деревья 194
6.8.22. Хэш-таблицы 194
6.8.23. Отладчик {Debugger) 194
Часть 2. АЛГОРИТМЫ НА ГРАФАХ И ИХ ПРОЛОГ-ПРОГРАММЫ 197
7. Способы задания графов 197
7.1. Графы, мультиграфы, псевдографы 197
7.2. Задание графов 199
7.2.1. Программа построения матрицы соседства
вершин графа 200
7.2.2. Программа построения матрицы инциденций
графа 201
7.2.3. Программа транспонирования матрицы 202
7.3. Операции над графами 203
7.4. Маршруты, цепи, циклы, связность 203
8. Поиск пути на графе, в глубину, в ширину,
первый лучший 205
8.1. Задание графа в Прологе 205
8.2. Поиск какого-либо пути на графе 206
8.2.1. Программа поиска пути между двумя
444
вершинами в ненагруженном графе 207
8.2.2. Программа поиска пути между двумя
вершинами графа от конца к началу 207
8.3. Поиск в глубину 207
8.3.1. Программа вычисления путей между двумя
узлами в ненагруженном графе с
использованием стратегии поиска в глубину 208
8.4. Поиск в ширину 209
8.4.1. Программа вычисления путей между двумя
узлами в ненагруженном графе с
использованием стратегии поиска в ширину 210
8.5. Стратегия первый лучший 210
8.5.1. Программа вычисления кратчайшего пути
между двумя узлами в нагруженном графе
с помощью стратегии первый лучший 211
8.6. Представление дерева всех путей в графе термом 215
8.6.1. Программа вычисления дерева-терма всех путей
в графе без повторов вершин на каждом пути 216
8.6.2. Программа вычисления дерева-терма всех путей
в графе до первого повтора вершины на
каждом пути 216
8.6.3. Программа вычисления пути между двумя
вершинами в ненагруженном графе с поиском
в ширину и одновременным построением дерева-
терма всех путей в графе 217
9. Обходы графов 217
9.1. Эйлеровы графы 217
9.1.1. Программа вычисления эйлерова цикла по
системе попарно непересекающихся простых
циклов четного графа 219
9.1.2. Программа вычисления эйлерова цикла в четном
графе с последовательным удалением
проходимых ребер 221
9.1.3. Программа вычисления эйлерова цикла в четном
неориентированном графе с удалением
проходимых ребер без анализа распада графа
на несвязные компоненты 223
9.1.4. Программа вычисления эйлерова цикла в четном
неориентированном графе по дереву всех
его путей 224
9.1.5. Программа вычисления эйлерова цикла
445
в ориентированном графе с удалением
проходимых ребер 225
9.2. Полные циклы и последовательности де Брейна .... 225
9.2.1. Программа вычисления цикла де Брейна .... 228
9.3. Гамильтоновы графы 230
9.3.1. Программа вычисления гамильтонова цикла
в неориентированном графе по дереву всех
его путей 230
10. Деревья 232
10.1. Основные определения 232
10.2. Характеристические свойства деревьев 232
10.3. Каркасы и хорды в связном графе 235
10.3.1. Программа вычисления наименьшего каркаса
в нагруженном графе 237
10.3.2. Программа вычисления каркаса в
непогруженном графе 239
11. Циклы в графах 239
11.1. Линейное пространство двоичных наборов 239
11.2. Линейное пространство подграфов данного графа, . . . 240
11.3. Подпространство четных подграфов 241
11.4. Циклический ранг графа 245
11,4,1, Программа вычисления фундаментальной
системы циклов в связном графе 247
12. Двудольные графы и паросочетания 248
12.1. Двудольные графы 248
12.2. Паросочетания 250
12.2.1, Алгоритм построения совершенного
паросочетания для двудольного графа 251
12.2.2. Программа вычисления совершенного
паросочетания в двудольном графе методом
чередующихся цепей 253
12.3. Системы различных представителей 254
13. Планарные графы 258
13.1. Плоские графы 258
13.2. Формула Эйлера 259
13.3. Критерий планарности Понтрягина-Куратовского . . . 261
13.3,1. Алгоритм построения плоского изображения
446
графа 262
13.3.2. Программа построения плоской укладки графа 265
14. Раскраска графов 272
14.1. Хроматическое число и хроматический класс .... 272
14.2. Раскраска вершин 273
14.3. Верхняя и нижняя оценки для хроматического числа.
Внутренне и внешне устойчивые множества вершин
графа 274
14.3.1. Внутренне устойчивые множества вершин
графа 274
14.3.2. Алгоритм вычисления всех наибольших «
внутренне устойчивых множеств вершин
графа G = (К,£) 275
14.3.3. Программа вычисления всех наибольших
внутренне устойчивых множеств вершин
графа 275
14.3.4. Внешне устойчивые множества вершин графа 279
14.3.5. Алгоритм вычисления всех наименьших
внешне устойчивых множеств вершин графа
G = (К,£) 279
14.3.6. Программа вычисления всех наименьших
внешне устойчивых множеств вершин графа 280
14.4. Оптимальная раскраска вершин графа 282
14.4.1. Алгоритм оптимальной раскраски
(р^)-графа G = (К,Е) 283
14.4.2. Программа оптимальной раскраски вершин
графа 284
14.5. Раскрашивание планарных графов 288
15. Потоки в транспортных сетях 290
15.1. Двухполюсные сети 290
15.2. Дивергенция 291
15.3. Потоки в сетях 292
15.4. Сечения в сетях 293
15.5. Величина потока и пропускная способность сети . . . 294
15.6. Максимальный поток 295
15.6.1. Алгоритм вычисления максимального потока
в транспортной сети 297
15.6.2. Программа вычисления наибольшего потока
в транспортной сети 301
447
Часть 3. МОНАДИЧЕСКАЯ ЛОГИКА И ПРОЛОГ-
ПРОЕКТИРОВАНИЕ КОНЕЧНЫХ АВТОМАТОВ 306
16. Конечные автоматы 306
16.1. Автоматы Мили и Мура 306
16.1.1. Программа вычисления декартова
произведения для двух детерминированных автоматов 310
16.1.2. Программа вычисления автомата
для дополнения языка, представимого
детерминированным автоматом 311
16.1.3. Программа вычисления автомата
для пересечения двух языков, представимых
детерминированными автоматами 312
16.1.4. Программа вычисления автомата
для объединения двух языков, представимых
детерминированными автоматами 313
16.2. Источники 313
16.2.1. Алгоритм детерминизации источника 317
16.2.2. Программа детерминизации источника .... 318
16.3. Регулярные языки 322
16.3.1. Программа вычисления источника
для объединения двух языков, представимых
источниками 325
16.3.2. Программа вычисления источника для
итерации языка, представимого источником . . . 325
16.3.3. Программа вычисления источника •
для конкатенации двух языков, представимых
источниками 326
16.4. Теоремы замкнутости для класса автоматно
представимых языков 326
16.4.1. Программа вычисления источника для
обращения языка, представимого другим источником 326
16.4.2. Программа вычисления источника для
проекции языка, представимого другим источником 327
16.4.3. Программа вычисления источника для
цилиндра, восставленного из языка, представимого
другим источником 329
16.5. Минимизация числа состояний автомата с выходом 330
16.5.1. Склеивание неразличимых состояний 332
16.5.2. Алгоритм минимизации автомата 332
16.5.3. Алгоритм разбиения множества состояний
448
на классы неотличимых состояний 337
16.5.4. Программа уменьшения числа состояний
автомата склеиванием состояний с одинаковыми
столбцами в таблице переходов и выходов 338
76.5.5. Программа минимизации детерминированного
автомата с выходом 341
17. Автоматы и сверхъязыки 349
17.1. Макроавтоматы 349
17.1.1. Программа вычисления детерминированного
макроавтомата для пересечения двух
сверхъязыкову представимых
детерминированными макроавтоматами 351
17.1.2. Программа вычисления детерминированного
макроавтомата для объединения двух
сверхъязыкову представимых
детерминированными макроавтоматами .... 353
17.1.3. Программа вычисления детерминированного
макроавтомата для дополнения сверхъязыка,
представимого детерминированным
макроавтоматом 355
17.1.4. Программа вычисления макроисточника
для объединения двух сверхъязыков,
представимых макроисточниками 356
17.2. Конкатенация языка и сверхъязыка 357
17.2.1. Программа вычисления детерминированного
макроавтомата для конкатенации языка
и сверхъязыка у представимых
детерминированными автоматом и макроавтоматом .... 358
17.2.2. Программа вычисления макроисточника для
конкатенации языка и сверхъязыка,
представимых источником и макроисточником
соответственно 362
17.3. Сверхитерация автоматных языков 362
17.3.1. Программа вычисления детерминированного
макроавтомата для языка, устойчивого
отностительно данного автомата 366
17.3.2. Программа вычисления макроисточника для
сверхъязыка, полученного сверхитерацией
языка, представимого источником 368
17.4. Детерминизация макроисточника 369
17.4.1. Общерегулярные сверхъязыки 370
449
18. Проблема униформизации
371
18.1. Языки и операторы 371
18.1.1. Униформизация 374
18.2. Игры 375
18.2.1. Игры с конечным числом состояний 377
18.3. Стратегии 379
18.4. Униформизация конечно автоматных языков 382
18.4.1. Порядковые векторы и порядковые стратегии 382
18.4.2. Теоремы о порядковых стратегиях 384
18.4.3. Пример построения выигрывающего автомата 389
18.4.4. Программа униформизации автоматных
сверхъязыков 392
19. Монадическая логика и конечные автоматы 398
19.1. Логика одноместных предикатов 398
19.2. Выразимость в ЛОП 401
19.2.1. Макроисточники и ЛОП 402
19.2.2. Регулярные языки и ЛОП 403
19.2.3. Общерегулярные языки и ЛОП 404
19.3. Специальная пренексная форма 404
19.4. Синтез автомата по формуле ЛОП 406
Часть 4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ 411
20. Порождение комбинаторных конфигураций и их пересчет . . 411
20.1. Размещения, перестановки, сочетания 411
20.1.1. Программа вычисления перестановок
без повторений 411
20.1.2. Программа вычисления сочетаний
без повторений 412
20.1.3. Программа вычисления размещений
без повторений 413
20.2. Правило суммы и правило произведения 415
20.3. Подсчет числа размещений, перестановок, сочетаний 416
20.3.1. Число размещений без повторений 416
20.3-.2. Число размещений с повторениями 416
20.3.3. Число сочетаний без повторений 416
20.3.4. Число сочетаний с повторениями 416
20.3.5. Число перестановок данной спецификации 417
20.3.6. Число размещений данной спецификации . . . 418
450
21. Производящие функции для комбинаторных конфигураций
и их числа 419
21.1. Аппарат формальных степенных рядов 419
21.2. Производящие функции для сочетаний 419
21.2.1. Сочетания без повторений 420
21.2.2. Сочетания с повторениями с ограничениями
на число повторений 420
21.2.3. Сочетания с повторениями без ограничений
на число повторений 422
21.3. Производящие функции для размещений
с повторениями 423
22. Комбинаторно логический аппарат 426
22.1. Включения и исключения 426
22.2. Приложения формулы включений и исключений .... 429
22.2.1. Задача о беспорядках 429
22.2.2. Задача о встречах 431
22.2.3. Программа для формулы включений
и исключений 431
Список сокращений 434
Литература 435
Научное издание
Набебин Алексей Александрович
ЛОГИКА И ПРОЛОГ В ДИСКРЕТНОЙ МАТЕМАТИКЕ
Редактор издательства Е.А.Улановская
Художественный редактор А.Ю. Землеруб
Технический редактор 3. Н.Ратникова
Корректор В.В. Сомова
ЛР № 020528 от 23.04.92
Подписано в печать с оригинала-макета 14.11.96 Формат 70x90 1/16
Бумага офсетная №2 Гарнитура Times Печать офсетная
Усл. печ. л. 33,05 Усл. кр-отт. 33,8 Уч.-изд. л. 31,7
Тираж 1000 экз. Зак. № 889 т С-021
Издательство МЭИ, 111250, Москва, Красноказарменная ул., д. 14.
Типография НИИ «Геодезия», г. Красноармейск, ул. Центральная, д. 16
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Страница,
строка
102,
17-я сверху
377,
в рис. 18.1
Напечатано
обозначается через
КТ(а также через 54)
6 7 8 9
0 Й Н 0
"С
т
la
С
Од
lb Job
3
Ob
L
Должно быть
обозначается через
КТ4 (а также через 54)
6 7 8-9
0 Й 0 0
i
1
la
lb job
13
\0а
0b
1