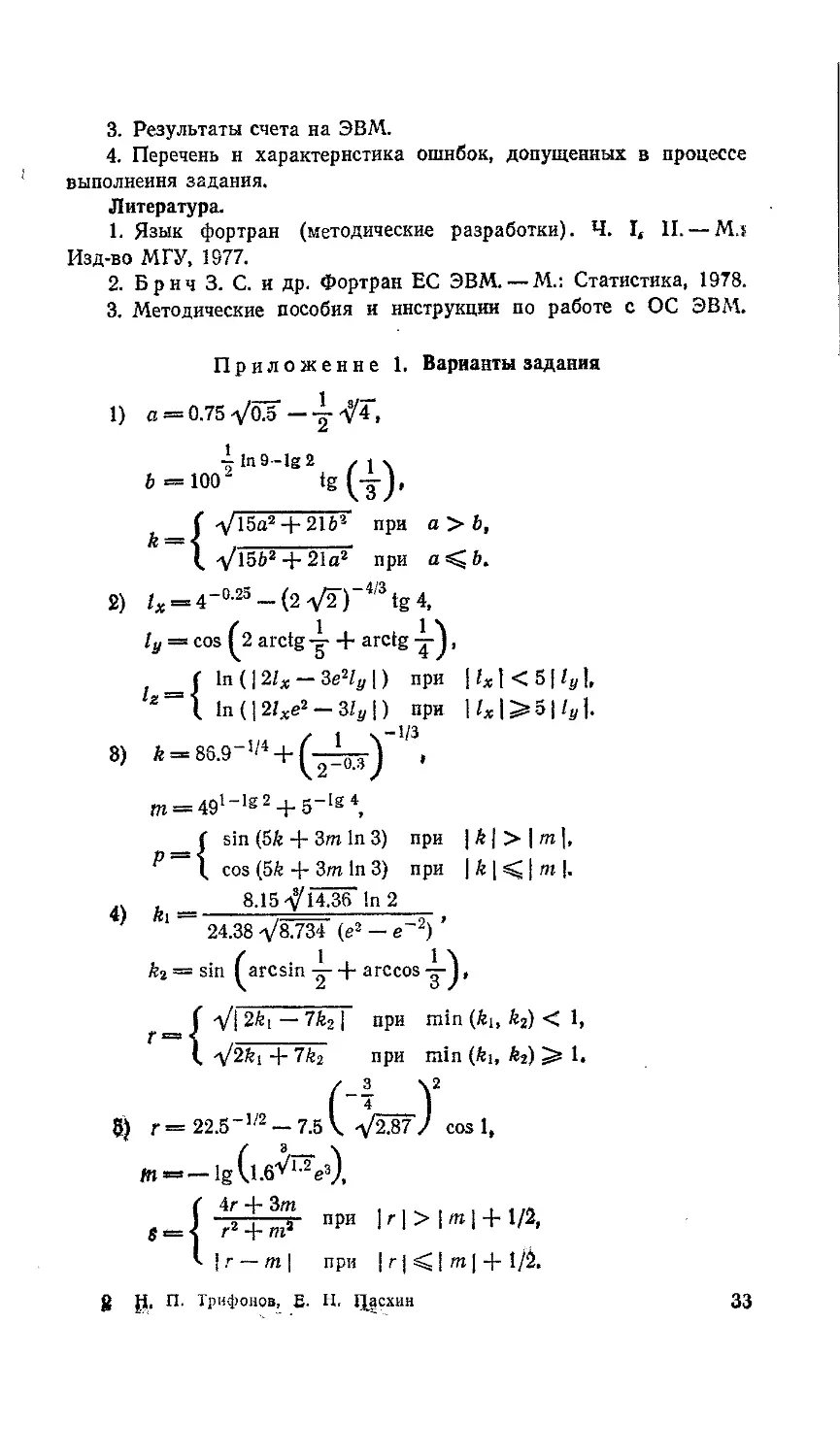Author: Трифонов Н. П. Пасхин Е.Н.
Tags: вычислительная математика численный анализ программирование эвм
Year: 1982
Text
Н. П, ТРИФОНОВ, Е. Н. ПАСХИН
ПРАКТИКУМ РАБОТЫ НА ЭВМ
Допущено Министерством
высшего а среднего специального образования СССР в качестве учебного пособия для студентов вузов, обучающихся по специальности «Прикладная математика*.
МОСКВА «НАУКА» ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОИ ЛИТЕРАТУРЫ 1982
22.18 Т 69
УДК 519.6
Практикум работы на ЭВМ. Трифонов Н. П., П а с « хин Е. Н. — М.: Наука. Главная редакция физико-математической литературы, 1982. — 288 с.
Книга написана на основе практикума, проводимого на факультете вычислительной математики и кибернетики МГУ и соответствует типовой программе. Она содержит работы, в которых закрепляются навыки, полученные в лекциях по математическому обеспечению ЭВМ и по численным методам. Решаются конкретные задачи с помощью ЭВМ, с применением различных численных методов.
Для студентов вузов по специальности «Прикладная математика».
т 1502000000 — 135 053(02) -82
© Издательство «Наука». Главная редакция физико-математической литературы, 1CS2
ПРЕДИСЛОВИЕ
В подготовке специалистов по прикладной математике важную роль играет практикум работы на ЭВМ.
Известно, что развитие математического обеспечения (МО) ЭВМ существенно облегчает работу пользователей по изготовлению программ и упрощает общение человека с машиной. Однако эффективное использование имеющихся возможностей требует более высокой квалификации от пользователя, который должен знать многие компоненты математического обеспечения, их назначение и возможности, и уметь ими пользоваться.
Основное назначение практикума на ЭВМ и состоит в том, чтобы закрепить на практике знания, даваемые в курсе лекций по программированию, и получить достаточные практические навыки работы на современных вычислительных системах.
Следует отметить, что разработка тематики и заданий практикума является весьма непростой задачей, поскольку к заданиям предъявляется целый ряд — порой противоречивых — требований:
— последовательность заданий должна обеспечивать систематическое и планомерное освоение студентами основных компонентов МО;
— каждое задание должно быть поучительным, достаточно интересным и посильным для студентов;
— варианты задания должны обеспечивать индивидуальную работу каждого студента и должны быть примерно равноценными по трудности;
— выполнение заданий должно требовать минимального расходования ресурсов (машинного времени, перфокарт, бумаги и т. д.).
Практикум должен быть организован так, чтобы свести к минимуму время, затрачиваемое студентами на подготовку данных, на доступ к машине и ожидание результатов.
Для успешного ведения практикума важно иметь соответствующий набор доступных для студентов инструкций и методических пособий, а также специализированные компоненты МО.
На факультете вычислительной математики и кибернетики МГУ работа по созданию и становлению практикума велась в течение длительного времени под руководством декана факультета академика А. Н. Тихонова.
В настоящей книге приводится содержание практикума по состоянию на 1981 год.
1»
3
Во введении содержатся общие положения о практикуме: era назначение и структура, задачи, которые ставятся перед общим и специализированным практикумом, тематика заданий по математическому обеспечению ЭВМ, численные методы, включаемые в общий практикум, а также отчетность студентов по заданиям практикума.
Часть I содержит задания общего практикума — эти задания выполняются всеми студентами факультета, независимо от выбранной специализации.
Часть II содержит задания специализированного практикума. При этом специализация по линии практикума ведется в два этапа: сначала учитывается лишь общая специализация (применение ЭВМ. и математическое обеспечение ЭВМ), а затем — более узкая специализация, в зависимости от кафедры, на которой обучается студент (или даже с учетом спецсеминара, в котором он работает).
Часть III содержит набор инструкций для выполнения заданий практикума.
Практикум факультета ВМиК МГУ в основном базируется на машинах серии ЕС ЭВМ, которыми оснащены и многие другие вузы страны, так что этот практикум — в случае необходимости — может быть легко адаптирован к конкретным потребностям и возможностям любого вуза.
В работе по созданию практикума и подготовке данной книги, кроме авторов, принимал участие большой коллектив преподавателей факультета и сотрудников НИВЦ МГУ, на материальной базе которого ведется практикум, — всем им авторы выражают глубокую благодарность. Авторы особенно признательны декану факультета академику А. Н. Тихонову за постоянное внимание к практикуму и поддержку в работе, а также преподавателям факультета и сотрудникам НИВЦ 3. В. Болдыревой, В. И. Громыко, А. Т. Егоровой, Ю. П. Лященко, Т. К. Матвеевой, И. Н. Посохову и В. И. Родину, внесшим наиболее существенный вклад в разработку заданий, создание специализированных компонентов математического обеспечения для практикума и подготовку инструкций.
В разработке кафедральных заданий принимали участие М. Г. Мальковский (АЯ-1), Н. Б. Лебедева (АЯ-2), А. В. Гуляев, И. В. Машечкин, Н. В. Макаров-Землянский (АСВК-1), В. В. Островский (СП-1), А. А. Сапоженко (MK-I, 2, 3), А. Т. Егорова (ВМ-1, ВМ-3), Д. П. Костомаров (ВМ-1), Д. Ю. Сычугов (ВМ-2), А. В. Баев (ВМ-4), | Л. Н. Большее В. И. Пагурова (МС-1), В. Г. Ушаков (МС-2), В. В. Морозов (ИО-1, 2), А. А. Васин (ИО-3, 4), В. И. Бла-годатских (ОУ-1, 2), Ю. Н. Киселев (ОУ-3. 4), Н. Л. Григоренко, М. С. Никольский (ОУ-5).
Н. П. Трифонов, Е. Н, Пасхин
Введение. ОБЩЕЕ ПОЛОЖЕНИЕ О ПРАКТИКУМЕ
1. Назначение и структура практикума.
Практикум работы на ЭВМ предназначен для получения сту-дентами опыта практической работы на современных электронных вычислительиых машинах, необходимого для их дальнейшей дея-тельности в области применения ЭВМ н создания математического обеспечения для этих машин, а также для ознакомления с методами и организацией работы иа ЭВМ.
Практикум начинается на первом курсе, параллельно с чтением основного курса «ЭВМ и программирование», и длится 7 семестров, распадаясь на две части: общий практикум, длительностью в 5 семестров, и специализированный практикум длительностью в два семестра (специализированный практикум может быть расширен за счет общего практикума).
2. Общий практикум.
Общий практикум является единым для студентов всех специализаций факультета. Первые два семестра практикум ведется с целью:
— овладения одним из наиболее распространенных алгоритмических языков типа алгол-60;
— изучения и освоения основных методов и приемов программирования;
— знакомства с реально существующими ЭВМ;
— ознакомления с процессом прохождения задач при их решении на ЭВМ;
— получения простейших навыков работы на внешних устройствах, за терминалом, н по отладке программ.
Остальная часть общего практикума в основном связана с практической работой студентов на ЭВМ. Эта часть практикума состоит из ряда заданий (как правило, по 2—3 задания в каждом семестре), самостоятельно выполняемых студентами под контролем и с помощью преподавателей, и ставит перед собой следующие основные задачи:
а) Изучение основных компонентов математического обеспечения ЭВМ и практика в их использовании, включая овладение алгоритмическими языками и соответствующими трансляторам:^
5
редакторами программных текстов, библиотечных программ, средствами отладки и т. д.
б) Практика в численном решении наиболее часто встречающихся типовых математических задач (вычисление определенных интегралов, решение задач линейной алгебры, интегрирование систем обыкновенных дифференциальных уравнений и т. д.) и знакомство с имеющимися библиотечными программами.
в) Получение практических навыков по отладке программ.
г) Привитие навыков по оформлению проделанной работы.
Каждое задание практикума, как правило, включает в себя одну из тем по математическому обеспечению ЭВМ и одну из тем по численным методам. Тематика заданий и последовательность прохождения тем определяются главным образом требованиями планомерного и систематичного изучения математического обеспечения и овладением методики использования ЭВМ. Последовательность тем по численным методам должна быть согласована с порядком их изучения в соответствующих курсах.
3. Специализированный практикум.
Специализированный практикум служит для учета специфики отдельных специализаций и имеет своей целью приобретение студентами опыта решения на ЭВМ задач, специфичных для данной более узкой специализации, а также для знакомства со специализированными компонентами математического обеспечения. Эта часть практикума содержит задания, количество и тематика которых определяются соответствующими кафедрами факультета.
4. Тематика заданий по математическому обеспечению ЭВМ.
Для изучения состава математического обеспечения ЭВМ в общем практикуме предусматриваются следующие темы:
Тема 1. Алгоритмические языки и трансляторы.
Цель: практика в использовании алгоритмических языков и соответствующих трансляторов.
Тема 2. Пакетный режим использования ЭВМ. Язык управления заданиями.
Цель: знакомство с правилами работы на ЭВМ в рамках операционной системы, с языком управления заданиями и практика в их использовании.
Тема 3. Библиотеки программных текстов и редакторы текстов.
Цель: знакомство со способами организации библиотек на ЭВМ, предназначенных для хранения программных текстов, и правилами использования редактора текстов. Практика в использовании библиотек и редакторов текстов.
Тема 4. Форматный ввод-вывод.
Цель: изучение возможностей устройств вывода ЭВМ, возможностей языка программирования (или соответствующих стандартных
6
программ) по выдаче из машины получаемых результатов в виде окончательно оформленных документов и практика в их использовании.
Тема 5. Средства отладки программ.
Цель-, практика в использовании средств отладки программ, предусмотренных в языках программирования и (или) в ОС.
Тема 6. Модульное программирование.
Цель: практика в изготовлении сложных программ путем расчленения исходной задачи на составные части и их незавнснмого программирования с последующим объединением отдельных программных модулей в единую программу.
Тема 7. Библиотечные модули (подпрограммы).
Цель: практика в использовании библиотечных модулей (подпрограмм).
Тема 8. Удаленный запуск программ.
Цель: практика работы за удаленными терминалами.
Тема 9. Режим разделения времени.
Цель: практика работы на ЭВМ в режиме диалога.
Тема 10. Автокод (ассемблер).
Цель: знакомство с языком конкретной ЭВМ и практика в использовании автокода (языка ассемблера), ориентированного на эту ЭВМ. Знакомство с методами отладки программ, написанных на автокоде, и практика в их использовании.
Тема 11. Обработка символьных данных.
Цель: практика в решении на ЭВМ задач невычислительного характера.
Примечание 1. Данная тематика может быть частично изменена и должна быть конкретизирована в зависимости от имеющегося парка ЭВМ, их оборудования и имеющегося математического обеспечения.
Примечание 2. Конкретные задания могут как объединять некоторые из тем, так и расчленять их на отдельные составные части.
5. Численные методы, включаемые в общий практикум.
В общем практикуме предусматривается получение практических навыков в использовании следующих численных методов:
1) методы вычисления элементарных функций;
2) решение трансцендентных уравнений;
3) методы вычисления определенных интегралов;
4) численные методы решения задач линейной алгебры и линейного программирования;
5) численное интегрирование систем обыкновенных дифференциальных уравнений;
6) приближение функций;
7
7) методы минимизации функций (методы типа скорейшего спуска).
6. Оформление заданий и отчетность.
В каждом задании практикума указывается: тема и цель задания, содержание задания, постановка задачи, содержание отчета, литература, варианты задания и методические указания (в случае необходимости). Для каждого задания устанавливается календарный план его выполнения.
Выполнение каждого задания студентом завершается представлением отчета по установленной форме.
Часть I. ОБЩИЙ ПРАКТИКУМ
Задание 1. ПРОСТЕЙШИЕ КОНСТРУКЦИИ АЛГОЛА
Цель задания.
1. Приобретение навыков в. использовании простейших конструкций алгоритмического языка, предназначенных для вычислений по формулам.
2. Получение начальных навыков работы за терминалом ЭВМ.
3. Знакомство с простейшими методами тестирования программ.
Содержание задания.
1. Знакомство с возможностями конкретного терминала и правилами работы на нем.
2. Знакомство с языком общения с ЭВМ с помощью терминала.
3. Составление программы на конкретной версии алгола для решения поставленной задачи, связанной с вычислениями по формулам.
4. Проверка с помощью ЭВМ правильности составленной программы и решение задачи на ЭВМ.
Постановка задачи.
Провести вычисления по заданным формулам.
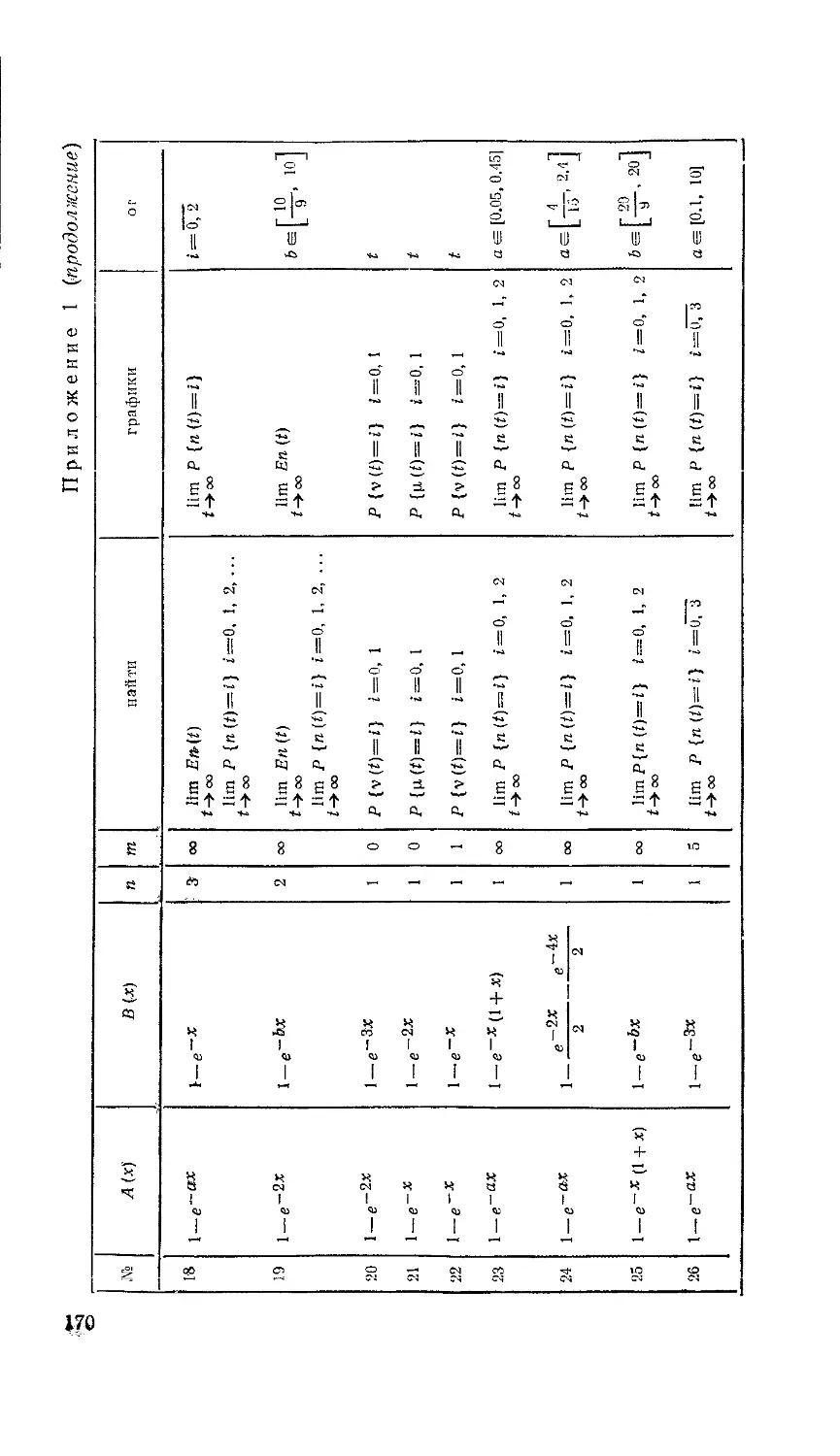
Набор формул, по которым нужно провести вычисления, а также значения начальных данных определяются вариантом задания (см. Приложение 1).
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Текст программы на заданном алгоритмическом языке.
3. Тесты для отладки и результаты отладки, полученные на ЭВМ.
4. Результаты счета.
5. Перечень и характеристика ошибок, допущенных в процессе прохождения задания.
Литература.
1. Трифонов Н. П. Сборник упражнений по алголу.— Мл Наука, 1978.
2. Инструкции и методические пособия по программированию И работе на конкретной ЭВМ.
9
Приложение 1. Варианты задания
1) а=2~*л/х + V|p| , & = Vex~1/Slnz, где х — 3.981, у =— 1.625, z = 0.512.
2) а_/йГ + сЬз(у_3)> 6==..^.rctg£-g/6)t
И + -ргрг
где х = — 6.251, у = 0.827, г = 25.001.
. . ( sin8 г \
, „ I х — у | I 1 + —j— I
3) а = 2(у > + (з*), b =-------------- У
е\х-у\ + £_
где х = 3.251, (/ = 0.325, z = 0.466.
4) а = ----Ц-----b = х (arctg z + е-(х+3'),
1 + 2L-l JL. ^2'4
где х = — 0.622, у = 3.325, z = 5.541.
4______._____
5) a = Vl/+/V'x—* , b = I х — у I (sin2 z + tg z),
где x= 17.421, (/ = 10.365, z = 0.828.
6)
7)
yx+i j x+y/2 ^|(/-2| +3 2\x + y\’
b = (x+ l)-l^*
где x = 1.625, . у = — 15.400, z = 0.252.
x'J+' + eV-1
1+x I (/—tgz|’
b = 1 + | У - x ] +
I y-x |8 , I y—x P
2 3
где x = 2.444, у = 0.869, z = — 0.166.
*»2 v3
8) a= 1 + x + -X7- + -qr + -7Г, & = x (sin arctg z + cos2 y), Ol “il
где x = 0.335, y = 0,025, z = 32.005.
х + —У—
9) a = (i+y).. +Л2 + 4.) 6 = .1+£НУ-21(
УХ-2 + -^ + 4 f+sin2g
где x — 3.258, у = 4.005, z = — 0.666.
10) а = //+--------------, 6 = ^l+tg8-i'
У + У + х3/у
где х = 0.100, «/= — 8.750, z = 0.765.
10
11) e = lg(Vex + x!y 1 + Д b = x — -|j- +
12)
13)
14)
15)
где x — 1.542, y= — 3.261, z = 80.005.
2 cos (x — л/6) «... г2
a= 1 ” "-----’ Z, = 1-r-3+^5-’
у + sin2 у
где x = 1.425, у — —1.220, 2 = 3.500.
•^8 + i^-yP + l 6== | x-y\n 2 ,
a~X‘ + y* + 2 ’ ° e Vgz+1),
где x = — 4.500, у = 0.750, z — 0.845.
1 + sh2 (x + y) ] у | , , ( ,14
a = -г—!* > b = cos2 arctg — J,
| * ~ 1 + -х2У2~ I
где x = 3.741, у = — 0.825, 2 = 0.160,
« = | cos x + cos у |1+2 sin2 y, 6=l+z+y- + 4j- +
где x = 0.400, у = — 0.875, z = — 0.475.
16) a = In (j/"^1 x 1) (x—тг')» b = sin2 arc!8 z> где x — —15.246, у — 4.642, 2 = 20.001.
17) a = V10 (^x+ xa+2), b = (arcsin 2)2 + ] x + у |, где x = 16.55, у = — 2.75, 2 = 0.15.
, „ „ , 1 , , x + 3|x—w| + x2
18) a = 5 arctg x --j arctg y, b=--। x y p x2------>
где x = —17.22, «/ = 6.33, 2 = 3.25.
19) a = e* x~v I + | x — у |’c+y, b = arctg x + arctg z, где x = —2.235, «/= — 0.823, 2= 15.221.
20) a = \xy!x -$у& I, b = (y - x)
где x = 1.825, у = 18.225, 2 = — 3.298.
x + «//(5+Vx”) , u_i ,
21) a =------—----!—y-—b = e + arcsm v,
11/ — x| + Vx
где x = 47.8, у — — 5.5, и — — 2.3, v = — 0.8.
22) a = ^ + ^|x| + |«/|, b = u+—
где x — — 0.85, «/ = 1.25, u = — 0.22, о = 0.01,
23) a = Vi +VF7T, 6 = Vi7Te-<y+u/2).
где x = 37.15, у =—12.55, и = 20.12,
11
24) a = -^-(x1 y~x 1 + У<х+у}№), 6 = lgG/« +V»+2),
где x = 3.255, y = 2.981, и = 125.331, 0 = 33.075.
25) a = (2 + y2) —2. , b = Vsin2 arctg и + | cos 0 |, У -г ‘ZU + У )
где х = 0.22, у == — 6.72, и = 10.05, о =0.35.
26) а = u<JC+y)/2 — л/ ~ ; 1 - , b = sin (2 arccos о), V I У I + 1
где х — 12.650, у = — 2.255, « = 3.205, « = 0.880.
Приложение 2. Методические указания
1. При выполнении задания следует помнить, что при составлении даже очень простой программы можно допустить ошибки: неправильно расставить скобки, задающие требуемый порядок выполнения операций, записать не тот знак арифметической операции и т. д. Поэтому каждая вновь составленная программа должна пройти специальный этап, называемый «отладкой». Цель этого этапа состоит в том, чтобы выявить и устранить допущенные ошибки, а если ошибок в программе не было — достаточно убедительно подтвердить этот факт.
2. Для отладки программы необходимо подготовить тест — вариант решаемой задачи с известным ответом. Для этого надо взять какие-либо конкретные значения исходных данных и вычислить по ним искомые величины (используя, в случае необходимости, таблицы, микрокалькуляторы и т. д.).
3. Выбор значений исходных данных для тестового варианта следует делать так, чтобы, с одной стороны, упростить работу по подготовке теста, а с другой стороны — чтобы эгн значения не могли скрыть ошибок в программе. Если, например, в задании встречаются вычисления вида (х—1)-F(y), то при значении х=1 невозможно будет обнаружить даже очень грубые ошибки, допущенные при программировании F(y).
4. После того как тест подготовлен, этот же вариант задачи надо решить на ЭВМ по составленной программе и сравнить полученные результаты с известными. Несовпадение этих результатов обычно свидетельствует о наличии ошибок в программе. В этом случае следует внимательно проверить программу, найти н устранить ошибки и снова пропустить тот же самый тест, чтобы убедиться, что исправления сделаны правильно н что в программе нет иных ошибок. К счету задания при реальных исходных данных можно переходить только после того, как будет правильно решен тестовый вариант.
Задание 2. ОСНОВНЫЕ ТИПЫ ОПЕРАТОРОВ АЛГОЛА. ИТЕРАЦИОННЫЕ МЕТОДЫ И РЯДЫ
Цель задания.
1. Практика в использовании основных типов операторов алгола.
2. Знакомство с итерационными методами решения задач и практика в нх использовании.
3. Получение дальнейших навыков работы за терминалом.
4. Практика в проверке правильности программ.
Содержание задания.
1. Изучение возможностей алгоритмического языка для задания циклических процессов итерационного типа.
2. Знакомство с простейшими методами вычисления элементар» ных функций.
3. Разработка алгоритма и составление программы для решения конкретной задачи, связанной с вычислением элементарных функций.
4. Проверка программы и решение на ЭВМ поставленной задачи.
Постановка задачи.
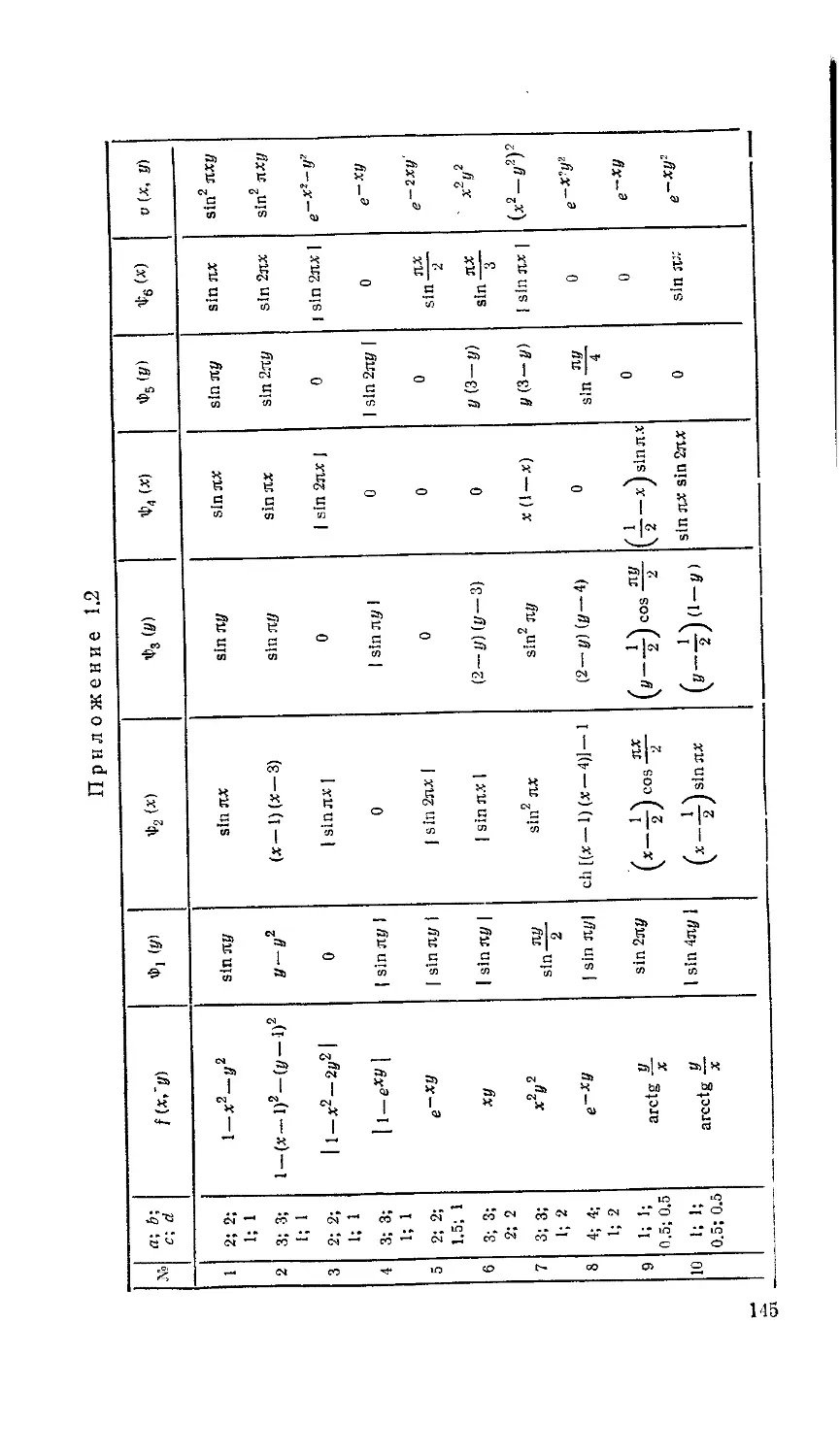
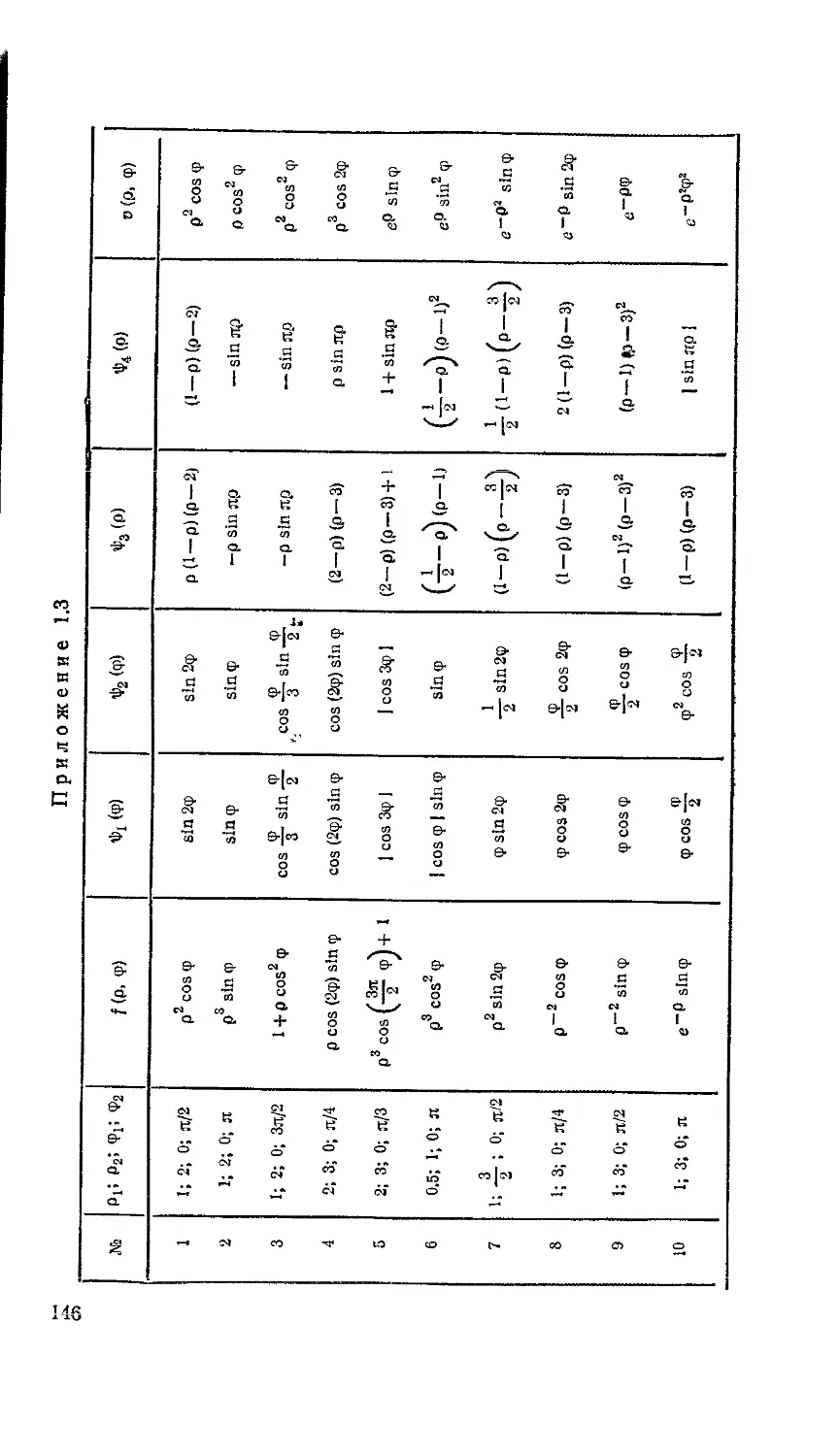
1. По заданным вещественным значениям а, b и целому т полу* чить значения заданной функции у === f(x), вычисленные в точках xi = а + ih, где h = (& — а)/т (I = 0, 1, .... т).
2. Значения элементарных функций, входящих в состав f(x), вы-числять без использования стандартных функций алгола, для чего необходимо выбрать и обосновать соответствующий численный метод, обеспечивающий вычисление значения элементарной функции с точностью е = 10~8 (см. Приложение 2).
3. Для контроля правильности выбранного численного метода и его программной реализации каждое значение у, = f(x<) вычислить также с использованием соответствующих стандартных функций алгола.
4. В качестве результатов на печать вывести очередное значение xi, соответствующее ему значение yi = f(xi), полученное каждым из двух способов, а также значения некоторых величин, характеризующих процесс вычисления элементарной фунции по выбранному численному методу (число сделанных итераций, величину последней поправки и т. д.). Полученные результаты вывести на АЦПУ в виде таблицы, удобной для ее последующего анализа, используя для этой цели соответствующие возможности операторов вывода, имеющихся в алгоритмическом языке.
5. Функция f(x) и значения а, Ь, т определяются вариантом задания (см. Приложение 1).
Требования к программе.
Задание должно быть выполнено без использования операторов цикла, а также без использования массивов и переменных с индексами.
13
Содержание отчета,
I. Постановка задачи,
2. Обоснование выбранного метода приближенного вычисления значения требуемой элементарной функции.
3. Блок-схема или схема программы.
4. Текст программы на алгоритмическом языке,
5. Результаты решения задачи на ЭВМ.
6. Перечень и характеристика ошибок, допущенных в процессе выполнения задания.
Литература.
1. Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I, гл. 8. — М.: Наука, 1971.
2. Д е м и д о в и ч Б. П., Марон И. А. Основы вычислительной математики. — М.: Физматтиз, 1960.
3. К о п ч е и о в а Н. В., Марон И. А. Вычислительная математика в примерах и задачах. — М.: Наука, 1972.
4. Т р и ф о и о в Н. П. Сборник упражнений по алголу. — М.: Наука, 1978.
5. Методические пособия и инструкции по программированию.
Приложение 1. Варианты задании т = 10
fW a, b
1) Vх 3) х ”5) 1/V7 2)^7 4) 1/^7 6) (2х + 1)/у7 1) 2, 3 3) 4, 5 5) 6, 8 2) 3, 4 4) 5, 7 6) 8, 9
4 7) V7 8) V^TT 1) 0.5, 1 2) 2.5, 3
5 9) л/~х 6 _ io) Vх 3) 1, 1.5 4) 3.5, 4
11) sin(x) 12) cos (лс) 1) 0, jt/4 2) л/9, п/4
13) sin (0.5+ х) 14) sinfx2) 3) л/18. n/3 4) л/4, л/2
15) sin(x)/x 16) cos (x)!x2 1) 0.2, 0.4 2) л/16, л/4
17) х + sin (х) 18) x2—cos (x) 3) 0.4, 0.6 4) л/4, л/2
19) ln(x) 20) 1 + In2 (x) 1) 1, 1.5 2) 0.4, 1
21) 1 +ех 22) ex’/2 1) 0.5, 1 2) 2, 3
23) е~х 24) 1/(1 + e~x) 3) 1, 2 4) 3, 4
25) sli(x) 26) 0.5 + sh2(x) 1) 1, 5 2) 2, 3
27) ch (X) 28) l'(l +ch2(x)) 3) 3, 4 4) 2, 4
14
Приложение 2. О методах вычисления элементарных функций й_
1. Итерационные методы. Функцию у = \х (х >0, k > 0 — целое) можно задать неявно уравнением
Р(х,у)^1-х/И = 0 (1)
или уравнением
F (х, y)^yk — х — 0. (2)
Если применить формулу Лагранжа [2] к уравнению (1), то получается итерационная формула вида
yn+l = tJtl\( (3)
L \ Ч / «ьА , *
Итерационный процесс, определяемый этой формулой, сходится, если начальное приближение уо > 0 удовлетворяет условию у'0“ < (fe-j-l)x.
Если применить формулу Лагранжа к уравнению (2), то получается итерационная формула Ньютона
=-~ [(fe ~У«+~ГтТ (4)
k L Уп J
Здесь в качестве начального приближения достаточно взять значение уо > 0 с точностью до одной-двух значащих цифр.
Итерационный процесс по каждой из этих формул заканчивается, когда два последовательных приближения г/я+] н у,, будут удовлетворять условию
I Уп+1 ~ Z/J < е- (5)
2. Использование формулы Маклорсна. Для многих функций удобно использовать формулу Маклорсна (частный случай разложения в ряд Тейлора):
п
f w = У uk где 11 &
Например:
уЗ у5 .
y = sinx = x--¥-+^-- ... +(-Dn~ (2—+ |x|<~
(6)
„2 „4 Г1Л
У = cosx=l —— + —-h..., Ix[< ос, (7)
Z/=ex= 1+x + -ip + ... + ~p + ••., Ul<°°. (8)
-.3 5
y==shx = x + -^+4r+ ••• +(97-i-~nT+ •••’ M<o°’ o’ bl т
y2 y4
y = chx = l+ — + —p + ... + (2 "jj" + (1°)
у = In (1 4-x) = x — —... +(-if-13_4-...,|x|<l. (11)
15
Приложение 3. Методические указания
Разложения (6)—(10) малоэффективны для вычисления значения функции при больших по модулю значениях аргумента, так как в этих случаях ряды сходятся медленно. В таких случаях можно поступать следующим образом:
1. Для тригонометрических функций — учитывая их периодичность — с помощью формул приведения можно значение аргумента заключить в отрезок 0 х л/4, для которого справедлива следующая оценка остаточного члена Rn: |7?«| Ju„+1|, поэтому процесс суммирования можно прекратить при | ип | е.
2. Для показательной функции можно, например, значение аргумента представить в виде х = Е (х) + г, где Е (х) — целая часть значения х, а г (0 r< 1) —его дробная часть. Тогда ех = евдег. Способ вычисления первого сомножителя очевиден, а для вычисления второго сомножителя можно использовать формулу (8) и следующую оценку для остаточного члена: |Д„| < \ап|, которая справедлива для значений |х| < 1.
3. Для функций sh(x) и ch(x) имеют место соответственно следующие оценки остаточного члена: Rn<-irUn при 0<х^п и «5
2
Rn <~^Un при 0 < |х| п. Так что для этих функций процесс вы-О
числений можно организовать следующим образом: сначала безусловно учесть все те слагаемые, для которых (при данном значении х) указанные оценки еще не справедливы, а для учета последующих слагаемых воспользоваться уже этими оценками.
Примечание. Для достижения заданной точности вычисления значения функции все промежуточные вычисления необходимо вести по крайней мере с двумя запасными знаками. Если используемый язык программирования допускает возможность задания точности представления чисел (например, язык Аналитик для ЭВМ МИР-2), то следует воспользоваться этой возможностью.
Задание 3. АЛГОЛ, ДЕЙСТВИЯ НАД МАССИВАМИ
Цель задания.
1. Практика в использовании возможностей алгола для действий над массивами.
2. Дополнительная практика работы за терминалом и в отладке программ.
Содержание задания.
1. Изучение описаний массивов, переменных с индексами и операторов цикла в алголе.
2. Составление программы для решения конкретной задачи, связанной с действиями над массивами.
3. Отладка программы и решение на ЭВМ поставленной задачи.
14
Постановка задачи.
1. Получить элементы квадратной матрицы А = (at, /} (1, / =• ml,..., п), где as,j = f(i, j), a f(i, j) — заданная функция.
2. Из матрицы А по заданному правилу получить компоненты вектора X = {х,} (i — 1, 2,..., л).
3. Вычислить значение u = g(X), где g(X) —заданная функция.
В качестве результата выдать на печать строки матрицы Л, элементы вектора X и значение и.
Значение п, функции f(i, j") и g(X), а также правило получений вектора X определяются вариантом задания (см. Приложение 1).
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Блок-схема программы.
3. Текст программы на алголе.
4. Тесты и результаты отладок.
5. Результат решения на ЭВМ.
6. Перечень и характеристика ошибок, допущенных в процессе прохождения задания.
Литература.
1. Трифонов Н. П. Сборник упражнений по алголу. — Мл Наука, 1978.
2. П я р н п у у А. А. Программирование на алголе и фортране. —> М.: Наука, 1978.
3. Халилов А И., Ющенко А. А. Алгол-60. Програминро-.ванное учебное пособие. — Киев: Вища школа, 1979.
4. Методические пособия и инструкции по программированию.
С4 Приложение!. Варианты задания
I. п = 6, 8, 10.
II. Функция f(i, j) для получения элементов матрицы А.
1. (I/—31 — 1.3)(6.5 —/)2/-‘(2|3.3-1| —1.5).
2. 2(//2 —3.1) (—2);(г —3.9).
3. (I3.7 — /I-2) (i-4.3)24
4. ^Ц^(/_5.7).
9‘
5. ----—— (2-0-5П.
I Z — — I /2
III. Правило получения вектора X по матрице А.
1. xi — скалярное произведение »-й строки матрицы А на столбец, содержащий первый по порядку наибольший элемент данной строки. :
17
2. В качестве вектора X принять главную диагональ матрицы А, преобразованной следующим образом: в начале каждой строки должны быть собраны ее неотрицательные элементы, а в конце — отрицательные элементы (с сохранением порядка следования тех и других элементов).
3. В матрице А найти первую по порядку строку с наибольшей суммой ее элементов и в качестве компонент вектора X принять упорядоченные по неубыванию элементы этой строки.
4. Компоненты вектора X — упорядоченные по невозрастанию средние арифметические значения элементов строк матрицы А.
5. Строки матрицы А упорядочить по неубыванию элементов ее первого столбца и в качестве вектора X принять главную диагональ преобразованной матрицы.
6. В качестве х, принять | max Д | — | min Д | (г = = 1.2, ..., и). '-J -'1
7. В матрице А найти первую по порядку строку с максимальной суммой модулей ее элементов. Вектор X получить из найденной строки циклическим сдвигом ее элементов на две позиции влево.
IV. Функция g(X).
i = l
2. П(^ + ^-/+1)-
i = l
3- + 1
4. (Xl + Х2 + Хч) Х2 + (х% + Х3 + Х.<) Х3 + ...
• • • + (Хп-2 + Хя-1 + XХп—I»
5- Z хЛ/(^ + S -sY
к Лк ^>1 J
6. max ( I х, I ).
I < t < п '1 1 3
7. \\XiX2 ... хп\. п-1
8- П (| х; |+ 1 +х.+1)-
Прнл о ж е н и е 2. Методические указания
Для отладки составленной программы необходимо подготовить соответствующий тест, т. е. решить вручную поставленную задачу, взяв такое значение п, которое не влечет за собой большого объема вычислений. При этом следует позаботиться о том, чтобы при реше
18
Нии на машине тестового варианта задачи в программе выполнялись все предусмотренные в ней ветви вычислительного процесса.
Для достижения этой цели для отладки частей программы, предназначенных для получения вектора X и значения и, возможно, придется задать другие правила вычисления матрицы А или задать в явном виде значения элементов матрицы (значения компонент вектора X).
Указанный в задании конкретный вариант можно решать на ЭВМ по составленной программе лишь после того, как в результате отладки будет достаточно убедительно показано, что в программе нет ошибок.
Задание 4. ПРОЦЕДУРЫ В АЛГОЛЕ. ПАКЕТНАЯ ОБРАБОТКА ДАННЫХ И ЯЗЫК УПРАВЛЕНИЯ ЗАДАНИЯМИ В ОС.
РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Цель задании.
1. Практика в использовании процедур-функций.
2. Получение навыков работы с использованием перфокарт.
3. Приобретение начальных навыков в использовании ОС и языка управления заданиями.
4. Практика в использовании численных методов решения трансцендентных уравнений.
5. Овладение методикой отладки в пакетном режиме.
Содержание задания.
1. Изучение аппарата процедур в алголе.
2. Изучение языка управления заданиями и правил формирования задания для конкретной ОС.
3. Знакомство с численными методами решения трансцендентных уравнений.
4. Составление программы для решения трансцендентного уравнения.
5. Отладка программы и решение поставленной задачи в пакетном режиме.
Постановка задачи.
Дано: функция f(x, у), вещественные с, d и целое т (т > 0). Для каждого значения yi — с ih (1 = 0, 1......т), где h =
= (d — с) !т, найти корень xi уравнения F(x) — f(x, yi) — 0. Если уравнение имеет не единственный корень, то отдать предпочтение положительному корню, а среди корней одного знака предпочтение отдать наименьшему по модулю (но отличному от нуля) корню.
Каждый корень найти с точностью в = 0.001, пользуясь одним из приближенных методов.
19
Функция f (х, у), значения с, d, т и приближенный метод нахождения корня определяются вариантом задания (см. Приложение 1).
Значения с, d, т должны либо вводиться с перфокарт в процессе выполнения программы, либо задаваться в начале программы с помощью операторов присваивания, с тем чтобы изменение этих значений требовало внесения минимальных изменений в программу и тем самым уменьшения возможности внесения ошибок. В качестве результатов необходимо выдать на печать таблицу значений yi и соответствующих нм значений х,.
Для решения задачи следует:
1. Исследовать заданную функцию; найти отрезок, в котором находится требуемый корень уравнения при любом значении ус, проверить применимость указанного численного метода.
2. Разработать алгоритм решения поставленной задачи, представив его структуру в виде блок-схемы или дав его неформальное описание.
3. Составить н отладить процедуру-функцию вычисления F(x) (считая yi глобальной величиной) и, если требуется, F'(x).
4. Составить и отладить алгол-программу решения поставленной задачи.
5. Решить задачу на ЭВМ, выдав на алфавитно-цифровое печатающее устройство (АЦПУ) требуемые результаты.
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Блок-схема алгоритма решения задачи.
3. Алгол-программа.
4. Тесты для отладки процедур и программы в целом, результаты отладок.
5. Результаты решения задачи на ЭВМ.
6. Перечень н характеристика всех ошибок, допущенных в процессе прохождения задания.
Литература.
1. Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I, гл. 12. — М.: Наука, 1971.
2. Бахвалов Н. С. Численные методы. Ч. I, гл. VII. — Мл Наука, 1973.
3. Б е р е з и н И. С., Жидков Н. П. Методы вычислений. Т. I. — М.: Наука, 1966.
4. Т р и ф о н о в Н. П. Сборник упражнений по алголу. •— Мл Наука, 1978.
5. Инструкция по языку управления заданиями ОС ЕС (наст, книга).
С. Методические пособия и инструкции по программированию. ;
20
Приложение 1. Варианты задания
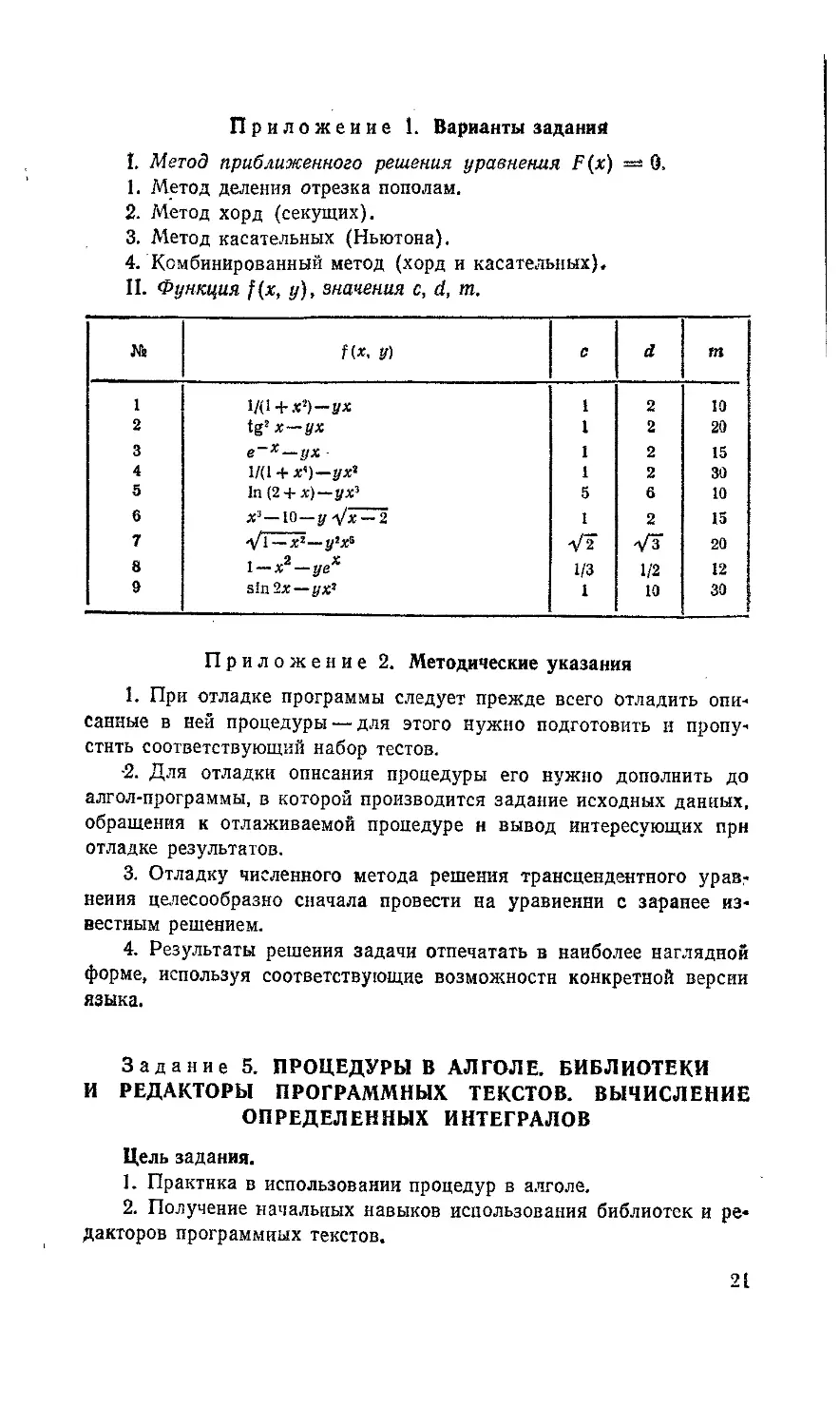
I. Метод приближенного решения уравнения F(x) « 0.
1. Метод деления отрезка пополам.
2. Метод хорд (секущих).
3. Метод касательных (Ньютона).
4. Комбинированный метод (хорд и касательных).
II. Функция f(x, у), значения с, d, m.
№ f(x, у) с d m
1 Щ + х2)-ух 1 2 10
2 tg! х—ух 1 2 20
3 е~х—ух - 1 2 15
4 11(1 + х<)-ух2 1 2 30
5 ln(2 + .r) — ух3 5 6 10
6 х3—10—у^/х~2 1 2 15
7 V1 —хг—J!XS V2 V3 20
8 l-x2-yex 1/3 1/2 12
9 sin2x —ух2 1 10 30
Приложение 2. Методические указания
1. При отладке программы следует прежде всего отладить описанные в ней процедуры — для этого нужно подготовить и пропустить соответствующий набор тестов.
2. Для отладки описания процедуры его нужно дополнить до алгол-программы, в которой производится задание исходных данных, обращения к отлаживаемой процедуре н вывод интересующих прн отладке результатов.
3. Отладку численного метода решения трансцендентного уравнения целесообразно сначала провести на уравнении с заранее известным решением.
4. Результаты решения задачи отпечатать в наиболее наглядной форме, используя соответствующие возможности конкретной версии языка.
Задание 5. ПРОЦЕДУРЫ В АЛГОЛЕ. БИБЛИОТЕКИ И РЕДАКТОРЫ ПРОГРАММНЫХ ТЕКСТОВ. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Цель задания.
1. Практика в использовании процедур в алголе.
2. Получение начальных навыков использования библиотек и редакторов программных текстов.
21
3. Знакомство с простейшими квадратурными формулами И практика в их использовании.
4. Получение навыков в использовании языка управления заданиями операционной системы.
Содержание задания.
1. Изучение аппарата процедур в алголе.
2. Изучение возможностей редактора программных текстов и правил его использования.
3. Изучение простейших квадратурных формул.
4. Составление программы и ее отладка.
5. Решение на ЭВМ конкретной задачи, связанной с приближенным вычислением определенных интегралов.
Постановка задачи.
С использованием ЭВМ вычислить с точностью Bi — 10~5 значение
bi и = fi (х) dx, at
а также получить таблицу значений функции
F (/) = f2 (f, х) dx,
а,
вычисленных с точностью е2 — Ю-4 в точках ti — с + iH (i — О, 1, .... т), где Н = (d — с)!т.
Функции fi (х), f2 (t, х) — ф + рх') ф (х), вещественные
\ ' "Г X z
значения at, аг, Ь2, с, d и целое т определяются вариантом задания (см. Приложение 1).
Для вычисления значения определенного интеграла
ь / = ^ f (х) dx а
с • заданной точностью е > 0 использовать квадратурную формулу вида
N
fe=o
где ft = f(Xft), а Хл и Ац определяются квадратурной формулой. Применяемая квадратурная формула также определяется вариантом задания (см. Приложение 1).
22
Для достижения требуемой точности при вычислении интеграла по квадратурной формуле использовать метод последовательного удвоения числа шагов.
Требования к алгол-программе.
1. Алгоритм вычисления значения определенного интеграла с задаваемой точностью е > 0 должен быть оформлен в виде описания процедуры.
2. В программе должны использоваться процедуры-функции для вычисления значений фигурирующих в задании подынтегральных функций.
3. Значения Si, е2 и Na (начальное число шагов при счете по квадратурной формуле) могут быть зафиксированы при составлении программы; значения at, bt, а2, b2, с, d н т должны вводиться в процессе выполнения программы.
4. В качестве результата на печать должно быть выдано: значение и, последовательность значений ti н соответствующая последовательность значений
Содержание отчета.
1. Постановка задачи для конкретного варианта.
2. Алгоритм решения задачи в виде алгол-программы.
3. Результаты отладок описаний процедур и программы в целом.
4. Полученные на ЭВМ результаты решения задачи.
5. Перечень и характеристика всех ошибок, допущенных в процессе выполнения задания.
Литература.
1. Б е р е з и и И. С., Жидков Н. П. Методы вычислений. Т. I. — М.: Наука, 1966.
2. Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I, гл. 12. — М.: Наука, 1971.
3. Бахвалов Н. С. Численные методы. Ч. I, гл. III. — М.: Наука, 1973.
4. К о п ч е н о в а Н. В., Марон И. А. Вычислительная математика в примерах и задачах. Гл. VII. — М.: Наука, 1972.
•5. Т р и ф о и о в Н. П. Сборник упражнений по алголу. — М.: Наука, 1978.
6. Инструкция по использованию библиотек ОС ЕС (наст, книга).
Приложение 1. Варианты задания
I. Квадратурная формула.
1) Формула прямоугольников:
b
= f М dx At h (fQ +1^+ ...
a
23
где f; = f(Xi), Xi h — (b — a))N. Остаточный член:
2) Формула трапеций;
&
1=ф(хМх«л(1/0 + Г1 + ... +^_1 + 1^), а
где ft = xi = а + ih, h — (b~ a)/N.
Остаточный член:
3) Формула Симпсона (парабол): ь
I = J f (х) dx к ± (fQ + 4f j + 2f2 + 4/3 + ... + 2^ _2 + 4^_ ,+f^, a
где fi == Xi — a-^ih, h == (b—~a)/N} N — четное. Остаточный член:
7? = —
II. Функция ft(x), значения сц, bi.
№ fl (X) Gl bi
1 a/ex—1 0.1 2
2 ex sin x 0 Я
3 (x2—1) 10_2jc 0 1
4 5 X -^1 + X 1 1 0 9
3 V 2 cos x 1
6
X In2 X arcsin Vx* 2 3 0,3
7 0.2
•Vx(l— X)
№ Л (x) G1 bl
8 x3e2x 0 1
9 0 Я/4
10 x arcig x 0 Va
1
П i + VF 0
12 1 0—3 cos x 0 2Я
2X
13 -2 -1
1— 4
14 1 (x+ 1) Vx2 + 1 0 3/4
III. Функция q>(z).
1) sin г; 2) V2- cos г; 3) cos г; 4) e~z;
5) -д/л —arctgz; 6) sh г; 7) Vl + sin2z‘’ 8) c^z’
9) thz; 10) arctgz; 11) th2 a; 12) ln(l+z2);
13) -yen z; 14) 1-j-e2z ; 15) ^2 c’n z — 1 .
24
IV. Функция ф (z), n 1 g2 • 21 2-4-2 3. z 1
*' 11^' > ,2_,-l-1’ °' ,2 .5.4
4)
Vs2 + 1 z2 + 3 :
5)
2 —3z
4 + z2 ‘
V, Значение p.
1) —0.01; 2) —0.05; 3) 0.05; 4) 0.01.
VI. Значения a2, b2, c, d и m.
№ Й2 &2 С d т
1 0 л/2 0.5 1.5 10
2 0 1 1 2 20
3 л/4 Зл/4 1 2.5 15
4 0.5 1.5 2 3 10
Приложение 2. Методические указания
1. Для обеспечения требуемой точности при приближенном вы* числении значения интеграла по квадратурной формуле нужно выбрать соответствующее значение шага h (или, что то же самое, число шагов N, на которое делится отрезок интегрирования). Для этого можно воспользоваться формулой остаточного- члена квадратурной формулы, однако оценка значения соответствующей производной подынтегральной функции, которая входит в формулу остаточного члена, нередко вызывает большие трудности. Кроме того, эту оценку приходится делать для каждой новой подынтегральной функции.
На практике для достижения требуемой точности вычисления интеграла по квадратурной формуле часто используется метод последовательного удвоения числа шагов, который заключается в еле* дующем.
Интеграл /'вычисляется во квадратурной формуле дважды: сна» ила при числе шагов, равном N, а аатем при числе шагов, равной IN. Погрешность Дл |/ —/„| приближенного значении интеграла Г», вычисленного по квадратурной формуле при числе шагов, равной ?, определяется приближенно по правилу Рунге;
** 81 {2N I
(для формул прямоугольников в трапеций 9 “ 1/3, для формулы Римпсона 6 “ 1/16).
Таким образом, вычисляется для последовательных зпачеивй i = V®, 2№, 4V0 к т. д., где — начальное число шагов. Процееа мчислеиий ааканчивается, когда для очередного аиачеиия п будет
И
получена погрешность < е. Начальное число шагов No следует выбирать от 10 до 50.
2. Для получения достаточно эффективной программы следует учесть, что в формулах трапеций н Симпсона при удвоении числа шагов нет необходимости вычислять значения подынтегральной функции заново во всех узлах сетки, так как все узлы сетки, полученные при числе шагов, равном п, являются узлами сетки и при числе шагов, равном 2п.
3. Для упрощения процедуры вычисления значения интеграла в ней не следует предусматривать зависимость подынтегральной функции от каких-либо параметров. Поэтому при описании функции параметр t целесообразно представить глобальной величиной.
4. Чтобы ускорить процесс прохождения задания, целесообразно перфорацию описаний процедур и нх отладку производить автономно, не дожидаясь составления алгол-программы в целом.
5. Для отладки процедуры интегрнрования следует выбрать такие подынтегральную функцию и пределы интегрирования, чтобы ответ был известен заранее и вычисление интеграла не требовало больших затрат машинного времени. Следует, однако, позаботиться о том, чтобы для этой функции на самом деле реализовывался процесс последовательного удвоения числа шагов для получения результата с заданной точностью.
6. Следует обратить внимание на то, что некоторые ошибки в программе при реализации метода удвоения числа шагов (например, учет лишнего узла х,) не сказываются на точности получаемого результата, но эта точность достигается за счет дополнительных затрат машинного времени.
Задание 6. АЛГОЛ, ДЕЙСТВИЯ НАД МАССИВАМИ. БИБЛИОТЕКИ И РЕДАКТОРЫ ПРОГРАММНЫХ ТЕКСТОВ.
РЕШЕНИЕ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель задания.
1. Практика в использовании алгоритмических языков и трансляторов.
2. Получение начальных навыков работы с редактором программных текстов.
3. Практика в использовании численных методов решения систем линейных алгебраических уравнений.
Содержание задания.
1. Изучение численных методов решения систем линейных алгебраических уравнений.
26
2. Изучение возможностей редактора программных текстов и правил работы с ним.
3. Составление алгол-программы и ее отладка,
4. Решение иа ЭВМ конкретной задачи, связанной с решением систем линейных алгебраических уравнений.
Постановка задачи.
Решить систему линейных алгебраических уравнений вида
Ах = Ь, (1)
где А = {at, /}—невырожденная квадратная матрица порядка т, Ь = (6], &2, ...,Ьт)Т — вектор-столбец правых частей системы. По найденному решению получить вектор невязок правой части системы.
Порядок т матрицы, сама матрица А, вектор Ь и численный метод определяются вариантом задания (см. Приложение 1).
Требования к программе.
1. Алгоритм решения системы линейных алгебраических уравнений должен быть оформлен в виде описания процедуры.
2. В качестве результатов программа должна выдать иа печать решение системы, вектор невязок и — для итерационных методов — количество сделанных итераций.
Содержание отчета.
1. Постановка задачи для конкретного варианта.
2. Текст алгол-программы.
3. Результаты отладок описания процедуры и программы в целом.
4. Полученные на ЭВМ результаты решения задачи.
5. Перечень и характеристика всех ошибок, допущенных в процессе выполнения задания.
Литература.
1. Бахвалов Н. С. Численные методы. — М.: Наука, 1973.
2. Трифонов Н. П. Сборник упражнений по алголу. — М.: Наука, 1978.
3. Методические пособия и инструкции по программированию.
Приложение 1. Варианты задания
1. Численный метод решения системы уравнений.
1. Первая модификация метода Гаусса.
Запишем исходную систему (1) в виде m
'Lai,ixi==ai,m+i (/=1, 2, ..., m). (1')
i = l
Здесь Ь s=a (Oj, m+b • •., am, т-н)Ч
Суть первой модификации метода Гаусса состоит в приведении системы (!') последовательным исключением неизвестных
27
к треугольному виду (см. flj, с. 325)J
т
**+ S аМ*/ = а‘/?и+1 («’=1,2......т), (2)
f-i+l
Из которой последовательно и находятся x* (k = т, 1).
Для применимости этого метода надо, чтобы значения элементов, на которые производится деление при исключении неизвестных, были отличны от нуля,
2. Вторая модификация метода Гаусса.
Суть второй модификации метода Гаусса (см. [1], с. 325) состоит в том, чтобы привести систему вида (!') к треугольному виду (2), воспользовавшись представлением матрицы А в виде произведения А = CD, где С — левая, a D — правая треугольные матрицы, причем диагональные элементы матрицы D равны единице.
Элементы этих матриц вычисляются по рекуррентным соотношениям:
k- 1
Ct. k = ai, k “ S Ci, ldl, к при k < *'•
/-1
V , (3>
ai, k~~ idl, k
di,k =--------7^-------- п₽и i<k'
i, i
Эти вычисления проводятся последовательно для совокупностей (I, К) = (1, 1), ..., (1, т} (2, 1), ..., (2, т), ..., (т, 1), ...
(т, т).
Примечание. Здесь и далее в этом методе считается, что если верхний предел суммирования меньше нижнего, то вся сумма равна нулю.
После разложения матрицы А решение исходной системы сводится к последовательному решению двух систем с треугольными матрицами:
Cd~b, Dx — d, (4)
Где d = (dt, , dm, m+l)«*.
Заметим, что значение di, m+i, которые являются решением системы Cd = Ь, могут вычисляться одновременно с остальными di, / по формулам (3), для чего эти вычисления проводятся последовательно для совокупностей (i, k) = (1, 1), .... (1, m-f-l), (2, 1), ..., (2, т + 1), ..., (т, I).(т, т + 1).
Значения xi (решение системы Dx = d) находятся из соотношений
xl~di,m+i~ S (/==«», m-l, ...» 1).
28
Для осуществления вычислений по формулам (3) необходимо, чтобы все с/, г были отличны от нуля; для этого необходимо и доста* точно выполнение условий
det 4fe^0 (k = 1, 2, ..т - 1), (8)
где 4» —матрица главного минора А-го порядка матрицы А,
3. Метод ортогонализации.
. Запишем исходную систему (!) в виде (см. [1], с. 333)
Я1 1X1 + ... 4- ci mXm + 0,1 Л!+1 = ®> ........................................... (6) й-и, l-Х: + ... + о„г> тхт + ап,. 1 = О,
ГДе Ъ = ( Я). щ 4-1, . . . , —йк, ж 4-1) ? •
Иначе: (я1; у) = 0, ..., (яга, у) = 0 (здесь at = (а., ц ., ,
at, m+i), у = (л-;, хт, 1)). Таким образом, решение исходной системы равносильно нахождению вектора у с последней компоиен* той, равной единице, ортогонального к векторам яь .. , ат. Если добавить вектор am+t = (0....... О, 1), то векторы Яь Яг, ...
..., ят+1 лннейио независимы, поскольку определитель матрицы, строками которой они являются, равен det 4 =/= 0.
С помощью алгоритма последовательной ортогонализации с нор* мировкой [|и|| = д/(3> «) систему векторов Яц ..., Ят-м можно при* вести к ортонормироваиной системе векторов Vi, Vz, ..., Vm+tl
fe-i
ak = ak~ Hak’vi)vi’ ’»=«TT (A = 1, 2, ..., m + 1),
Вектор t/m-s-i = (z!f .ортогонален ко всем векторам ch, ^2, ..., dm, причем zm+^0. Следовательно, у = I-, .. ----1 —•
\%т+1
решение исходной системы. Метод ортогонализации применим при любой невырожденной матрице .4.
4. Метод простой итерации.
В методе простой итерации (см. [1], с. 335) система (1) приво* днтся к виду
х = Сх + g (7)
(это можно сделать, например, так: х = х — D(Ax—&); если det'Z>=/=0, то эта система эквивалентна системе (1); если в качестве D взять единичную матрицу, то С = Е — 4 и g — b).
Решение системы (7) находится как предел последовательности *<п), получающейся из рекуррентных соотношений
х</!+’) == Сх(п) + g
29
при некотором начальном приближении х'>°’. Обозначим z = —
— x<n>. Тогда заданная точность е > 0 считается достигнутой, если 11г||<е.
Варианты норм векторов:
4.1) ||г||= max |z,];
K/<zb' '
4.2) ||г|| = £ [zj;
/ tn
4.3) ||z|| = /у Z[z/ P =V(«> 2) •
Метод простой итерации сходится при любом начальном приближении х<°> (в качестве х<0> можно взять, например, g). если ||С|| < 1, а в качестве нормы матрицы можно взять, например,
/ т \
\/=i /
5. е т о д Зейделя.
В методе Зейделя (см. [1], с. 363) последовательно уточняются компоненты решения исходной системы (1), причем k-я компонента находится из k-vo уравнения. Именно, если х(п'> = (х|П), ..., х^*)г, то следующее приближение определяетси из системы соотношений:
а1,1Х1П+!) +а1,2*2П> + ••• + а\,тхт=Ьх,
«2,1*1'г+1) + а2,24'г+1)+а2,Зл:з">+ ••• + a2,m*m =62> (8)
п у(п+1) п у(я+0 1 1 п ^(^4-1) — h
ат,1х1 'ат,2х2 ••• ' ат, тхт ит*
Зейделя сходится при любом х'0) (например, х(0> = &), если для всех i выполняется условие
S Где <?<Е
1Ф1
Считать, что требуемая точность е >> О достигнута, если || z II = || х(п+1) - х(п) || < е.
В качестве вариантов нормы вектора использовать те же нормы, что и в методе простой итерации (см. 4.1, 4.2 и 4.3).
II. Система уравнений.
Порядок системы т = 5; для итерационных методов е = 10~3; номер N системы—от 1 до 18: система с номером W — 3(й— 1) + Z (k — 1, 2, ..., 6; Z = 1, 2, 3) задается матрицей Ah и соответствующим вектором — правой частью 6/ из табл. 1 (все значения считаются точными).
30
Таблица 1
i i bi »2 Ьз
1 2 3 4 5
1 .45 .03 -.01 .02 -.111 * -.275 -1.784 2.491
2 .02 .375 -.01 -.01 0 -.78 .68 1.275
Л1 3 0 .07 .44 0 .113 1.745 1.032 -.783
4 -.03 .015 -.02 .41 -.084 -2.18 -1.056 .429
5 .02 .01 0 0 .29 1.45 1.12 -.16
1 .38 -.05 .01 .02 .07 -2.14 .75 2.32
2 .052 .595 0 -.04 .04 1.833 -.858 2.544
Аз 3 .03 0 .478 -.14 .08 1.736 3.16 -3.238
4 -.06 .126 0 .47 -.02 -1.242 -1.802 1.534
5 .25 0 .09 .01 .56 1,44 2.91 .12
1 .405 .05 .04 0 .09 -1.475 1.065 1.77
2 -.061 .53 .073 .11 -.06 2.281 .975 -.53
Лз 3 .07 -.036 .38 .03 .02 .296 -1.312 -.626
4 -.05 0 .066 .58 .23 .492 1.096 -2.772
5 0 .081 -.05 0 .41 1.454 -.048 1.001
I .43 .045 -.02 .03 -.02 .475 2.56 .78
2 .12 .37 .02 0 -.01 -.86 2.77 -.38
л4 3 .01 .032 .356 -.02 .05 1.718 —.916 1.91
4 .12 -.11 0 .49 .112 .864 .808 -1.464
5 -.05 0 .025 -.01 .294 2.068 -.639 2.362
.49 0 -.128 .09 .15 .964 1.564 2.332
2 -.03 .32 0 -.061 .02 1.279 -1.733 -2.261
Лз • 3 .01 -.09 .58 .011 .035 -1.799 1.393 -1.484
4 .03 0 -.073 .58 0 -4.971 1.744 .932
5 .02 -.03 .145 -.012 .42 2.153 -2.046 1,758
1 .51 -.074 .01 -.13 .09 .708 -.214 2.866
2 .08 .3 -.036 0 .05 2.578 1.866 .842
Аб 3 15 0 .42 .06 -.07 -.19 .18 -.75
4 .19 .023 .06 .438 0 1.64 -3.253 -1.527
5 .05 -.07 .023 0 .36 -2.229 2.762 1.164
Приложение 2. Методические указания
1. Для отладки программы следует взять систему уравнений, которая удовлетворяет требованиям данного метода, и вручную решить ее по этому методу. Чтобы избежать громоздких вычислений, следует взять небольшой порядок системы (т = 3 или т = 4). Затем эту же систему надо решить на машине по составленной
31
программе. Поскольку заранее неясно, какие из промежуточных рв< зультатов придется анализировать для отыскания ошибок в программе, то при решении тестового варианта вручную следует выписать и сохранить все промежуточные результаты вычислений.
Решать на машине реальный вариант системы можно только после того, как в процессе отладки будет достаточно убедительно показано, что в программе нет ошибок.
2. При численном решении системы — даже при использовании точных методов — получится не точное решение х, а приближенное решение х* (хотя бы нз-за ошибок округления), так что при подстановке найденного решения в левую часть системы вместо заданного вектора правой части b получится, вообще говоря, другой вектор 6*. В качестве меры удовлетворения системы найденным решением х* принимается вектор b — Ь*, называемый вектором невязок.
3. Для устранения большой погрешности из-за накопления ошибок округлений, для получения решения с заданной точностью все вычисления необходимо вести с достаточным числом значащих цифр.
4. Матрицы системы в вариантах задания таковы, что решение системы может быть найдено с достаточной точностью любым из предложенных методов. Поэтому в программе не требуется проверять условия применимости заданного метода, однако об этом не следует забывать при подготовке тестов.
Задание 7. ФОРТРАН, ПРОСТЕЙШИЕ КОНСТРУКЦИИ ЯЗЫКА
Цель издания.
1. Знакомство с конкретным представлением языка фортран.
2. Практика в использовании простейших элементов фортрана.
3. Знакомство с операционной системой реальной ЭВМ, через которую используется транслятор с фортрана,
Содержание задания.
1. Изучение простейших конструкций языка фортран.
2. Изучение правил использования транслятора с фортрана в конкретной операционной системе.
3. Составление программы на фортране, предназначенной для решения поставленной задачи.
4. Решение на ЭВМ конкретной задачи, связанной с вычислениями по заданным формулам.
Постановка задачи.
С помощью ЭВМ произвести вычисления по заданным формулам. Набор формул определяется вариантом задания (см. Приложение 1,).
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Текст программы на фортране.
32
3. Результаты счета на ЭВМ.
4. Перечень н характеристика ошибок, допущенных в процессе выполнения задания.
Литература.
1. Язык фортран (методические разработки). Ч. I, II. — Мл Изд-во МГУ, 1977.
2. Брич 3. С. и др. Фортран ЕС ЭВМ. — М.: Статистика, 1978.
3. Методические пособия и инструкции по работе с ОС ЭВМ.
Приложение 1. Варианты задания
1) « = 0.75 70.5 -—74,
715а2 + 216® при а > Ь, V15b2 + 21a2 при а
/ 1 \-1/3
8) й = 80.9-!'4 + (^1_) ,
т = 491-ls2 + 5-ls 4,
__( sin (5k + Зт In 3) при | k | > | т |, ( cos (5k + Зт In 3) при | k | | т |.
.. . 8.15 714.36 In 2
4) «1 =-----------, ----------7- ,
24.38 78-734 (е2 - е~2)
. ( • 1 , 1 \
«г = sm I arcsm + arccos -g- I,
( 7| 2fei — 7/г21 при min (klt /г2) < 1, (. 72&i + 7fe2 при min (fei, ki) 1.
5) r= 22.5 ~1/2-7.5 \ 7£877 cos 1,
tn=— IgW’V
4r + 3m , , „ , , , , lA ггЦ.тз при |г | > |m| + 1/2,
I r — m | при | r j < | m | + 1/2.
8 0. П. Трифонов, E- H, Цасхин
cos э । sm i
4 — VTT 3 + V7 ’
z 5 12 \
2 I arcsin — + arcsin -тх- I In 3, \ io 13 /
(V3g3 + 4n2 при ig|<2|rj|,
I V3g2 - 4т]2 при | g | > 2 | t) I-
12.48^5.76 sin 4
(1.842)4 -^673.8 cos 8 ’
( s — 2t
n = J 2s2 + 5t2 ПрИ St < °’
v Vst при st 0.
8) c = (o.O27~1/3 - )ln3,
k = 3 sin 1 + cos 1,
( th (c — 2fe) при | c + k | > 2, ( In (| c — 2k |) при | c + k | 2.
-------j----
25 + лЛЗб
0.00034
v, = arctg I cos -=- + cos I • In 5, * \ о о /
2|«J + 3|nz| Ut + v.
при 21 Ut j < v., при 21 «(. | ^
10) h
2.591 0,0836
1.147 (e2 + e-2) ’
= lg0.8 tg4
' 3/i - 5Zg
Z2 + /2
3/1 + 5/2
I2 — I2
к ‘1 ‘2
при I /11 < 1 + I /2 I,
при l/ilSsl+Uil.
34
11) mt— /\jl.W2'\/Q.\ —l+-j^-(e2 + e 2) , (л , 3л \
cos -g- + cos -g—I,
( arctg (би2 + 7га2) при m2 + nj. >0.1, S — s
(_ arcsin (5m2 + 7я2) при m2t + n| :C 0.1.
i°/-----foZT
12) ni = 'V 10 + V10 tgl, з ( 5/------) °.2
n2 =Д1 + Vlg 20 J , {sin (л«1 + еП2) при tti + n2 < 5,
sin (n«i + «2) при »i + n2 5.
13) m= 4.2013 VOT + 2-1 (e2 + e~2) ,
r—sin (t arctg (— z) <ln 5>) ’
( Vl 3m — 5r I при m < 2r, --- I г---------*
{, Vl 3m + 5r ( при m^2r.
4 , 4 — 0.01862 , _
14) d = ----7= tg 2,
V0-1 —x/io
c = sin ((1 + Vlg З)4),
г __f V|d + c| ПРИ d2 + c2>10, 1 d + с при d2 + c2 < 10.
15)
3,78 (e4 - e3) V4+-V3
„ оч . Г 1 . ( 2
ms = (In 3) sm I arcsinl------------
16)
mt = l
n.
mr — 2ms , _ , ,
—7;------5- при |mr —2/??s|<l,
+ 2ms
2
—----5—- при | mr — 2ms | > I.
,llr - Zills
(log. 5) Уб- —Уб logs 5
1 — 0.1845 (sin 1 + 2 cos 1) ’
lli — e ' cig |_— arccos
( Vi И1«2 I при < — 0.1, s — < __________
(. Vl И1 + «2 I при «1»2 — 0.1.
2*
35
17)
и = A./ i2,4p + °-6g~‘ Л70-0548
" V 0.389 (In 3 + sin 1)
T 1 . д/з”\
J- arcsin -g— I,
Vn = tg
3
18)
19)
20)
21)
22)
z 3un + v№
unvn
при
i Un | < I Vn I,
I Un I 5s | Un |.
при 4 . V0.0896 -------- eiu о + —------COS 3, yO.382-0.53482
r = e2 sin ^3 arctg д/з" + 2 arccos £=РП(1р1 + б1Г1) ПРИ p2 + Г2
I P — I r | при p2 4- r2
s = 79.836 in 3 — V156.374 in 5,
n = (tg 4) cos [З arcsin .__f V | se2 — ne~2 |
( Vs “ n / 1 \ 0.2073 . 35
S==V3 J sin4- —cos4, t = (lg 2) e“4[arctg (3+2Vr)-arctg m _ IV3 | I при s < t,
I s + t при s > t. p = 0.1711,183 log2 5 + 2.526 logs 7, ~ Vs’+i I 3 -arccos 2V3 |,
1.5922 . „
P — sm 3
n— (tg 6) e
u —
/3 .
2----f- arccos
(ln(|p —n|) при p > Я + 1.
( s,__\3.3
Zi = loge 3.3 - 2 VVo.6 ) e-2,
/2 — (tg 4) cos (arcsin-i + arcsin 4- + arcsin—" \ о о 65
?3 — 3Z2e2 | при Zu’2 > 5,
+ З/о | при /р’з *5S
<3
30
23)
т{ = 2.560'75 sin 2 + 5.50-33 sin 3 - (3e)-1 sin (2.3),
ml =
arccos
arccos
m{ — nij
24)
n =
---------- - =- .ц... | „ц । । „ = < 3/П,- 4- 4mj
при |mj| + |n
x = О.461ол61 sin 3 — O.3560-356 cos 3,
~ lg V“ / = (tg4)992
aJ \xe + te~l | при x < lOf,
V | x + 11 при x lOf.
k = (0.273 In 3)L573!n5, p = arctg ((sin 1) in Vln 3 ),
( 7 k —5p
1=1 2^ + 3F ПРЙ А>’Р1-
. [ k — p | при k | p |.
-^123.4* In 2
1.124 -V 0.024 cos 1
25)
26)
m =
r — arcsin
s =
e-|m+r| при г>_2/п, tnr при r C — 2m.
f = -a/o.836 cos 7 + V 2-324 sin 7,
g= cos
~=- (arctg 3 — arctg 2)1, V2 J
((ln3) ln([f| + |g|) |ef+g
при max (/, g) > 10,
при max (f, g) 10.
a = 81° 23 cos 5 — 2-0-3® sin 5,
(л/з" \
(3 tg 4) arccos —I,
I a2+B2
H = < e при a₽ > 1/2,
( | a + p | при сф 1/2.
29)
V1.56 -Vo.14 sin 1
0.8942 In 3
« = in (3 [ 2 sin 3 — 3 sin 2 |),
v == ( e2 arctg n+3 arctg “ при »-«<!, I In (n2 + и2) при n — a > 1,
37
д/0.0792 (sin 1 + cos 1)
ou) tnp----------з------------>
2.15 V12.762 tg4
np «= sin [3 (2 In 3 4- 3 In 2)],
( In (3| arctg |+ 5| arctg np j) при + Пр> 1, I7mp+'ip п₽и mp+«₽<i-
Приложение 2. Методические указания
1. При выполнении данного задания можно использовать следующие предложения фортрана:
— оператор присваивания;
— оператор перехода вида GO ТО (метка);
— условный арифметический оператор (IF (арифметическое выражение), (метка), (метка), (метка));
— оператор останова STOP;
— операторы ввода-вывода (READ, WRITE);
— объявления формата.
2. При выводе результатов следует ограничиться шестью значащими цифрами (например, печатать все числа в формате ES3.6).
3. Для вычисления элементарных функций следует использовать следующие библиотечные функции:
EXP (ех), ALOG (In х), SIN (sin х), COS (cos х),
TANH(thx), SQRT(Vx ), ATAN (arctg x), ABS и IABS (|x|).
4. При составлении фортран-программы следует быть особенно внимательным при работе с данными различных типов, учитывая при этом требования конкретной версии языка. Нужно помнить, что тип константы определяется ее записью, а тип данных и процедур, идентифицированных символическими именами, определяется (в отличие от алгола) неявно — по первым буквам этих имен (если не дано явное объявление типа). В случае необходимости для преобразования значения из одного типа в другой можно воспользоваться встроенными функциями преобразования: FLOAT(N)—для преобразования целого в вещественный, IFIX (X) — вещественного в целое.
Задание 8. ФОРТРАН.
ОСНОВНЫЕ КОНСТРУКЦИИ ЯЗЫКА, ФОРМАТНЫЙ ВВОД-ВЫВОД. УДАЛЕННЫЕ ТЕРМИНАЛЫ
Цель задания.
1. Знакомство с основными конструкциями фортрана.
2. Знакомство с форматным вводом-выводом.
3. Получение начальных навыков работы за удаленным терми-н алом.
38
Содержание задания.
1. Изучение основных возможностей фортрана, включая операторы ввода-вывода.
2. Составление программы решения поставленной задачи на конкретной версии фортрана, ее ввод в ЭВМ с удаленного терминала и отладка.
3. Решение задачи на ЭВМ с выдачей результатов по заданной форме.
Постановка задачи.
1. По заданным вещественным а, b (Ь > а) и целому п (п> 0) вычислить значения функций f/(x) (j = 1, 2, ..., m) для значений аргумента Xi = а + ih, h = (Ь — а)/п (1 = 0, 1, ..., п).
2. Полученные значения xi и fi(xi) (] = 1, 2, ..., m) отпечатать в виде таблицы заданной формы (см. Приложение 1) с использованием соответствующих возможностей входного языка (форматный вывод).
Набор функций fi(xy? а также значения а, Ь, п определяются вариантом задания (см. Приложение 2).
Требования к программе.
1. Программа должна правильно решать поставленную задачу при любых значениях а, b и п (а < Ь, п 50), которые являются исходными данными задачи.
2. Заданные в варианте функции должны быть введены в употребление в программе с помощью объявлений внутренних функций.
3. В программе не должны использоваться массивы.
4. В заголовке печатаемой таблицы должен указываться конкретный вид функции (например, SIN(X), ABS(X+7)**5, а не Fl (X), F2(X) и т. д.).
5. Формат, в котором выдаются числовые результаты, должен быть выбран с учетом диапазона изменения и точностью вычисления значений соответствующих величин.
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Блок-схема программы.
3. Текст программы на фортране.
4. План отладки, тесты и результаты отладки.
5. Результаты решения на ЭВМ конкретного варианта задания.
6. Перечень и характеристика всех ошибок, допущенных при выполнении задания.
Литература.
1. Язык фортран (метод, разработки). Ч. I, II, III.—М.: Изд-во МГУ, 1977.
2. Б р и ч 3. С. н др. Фортран ЕС ЭВМ. — М.: Статистика, 1978.
3. Инструкции и методические пособия по работе н ОС ЭВМ.
39
Приложение 1. Форма выдаваемой на печать таблицы
ТАБЛИЦА ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
X .. .. Fm(X}
ха П (хо) fs (Xo) •' '• fm(xo)
хп fl (xn) h (xn) • fm (xn)
СОСТАВИЛ (фамилия и. о.)
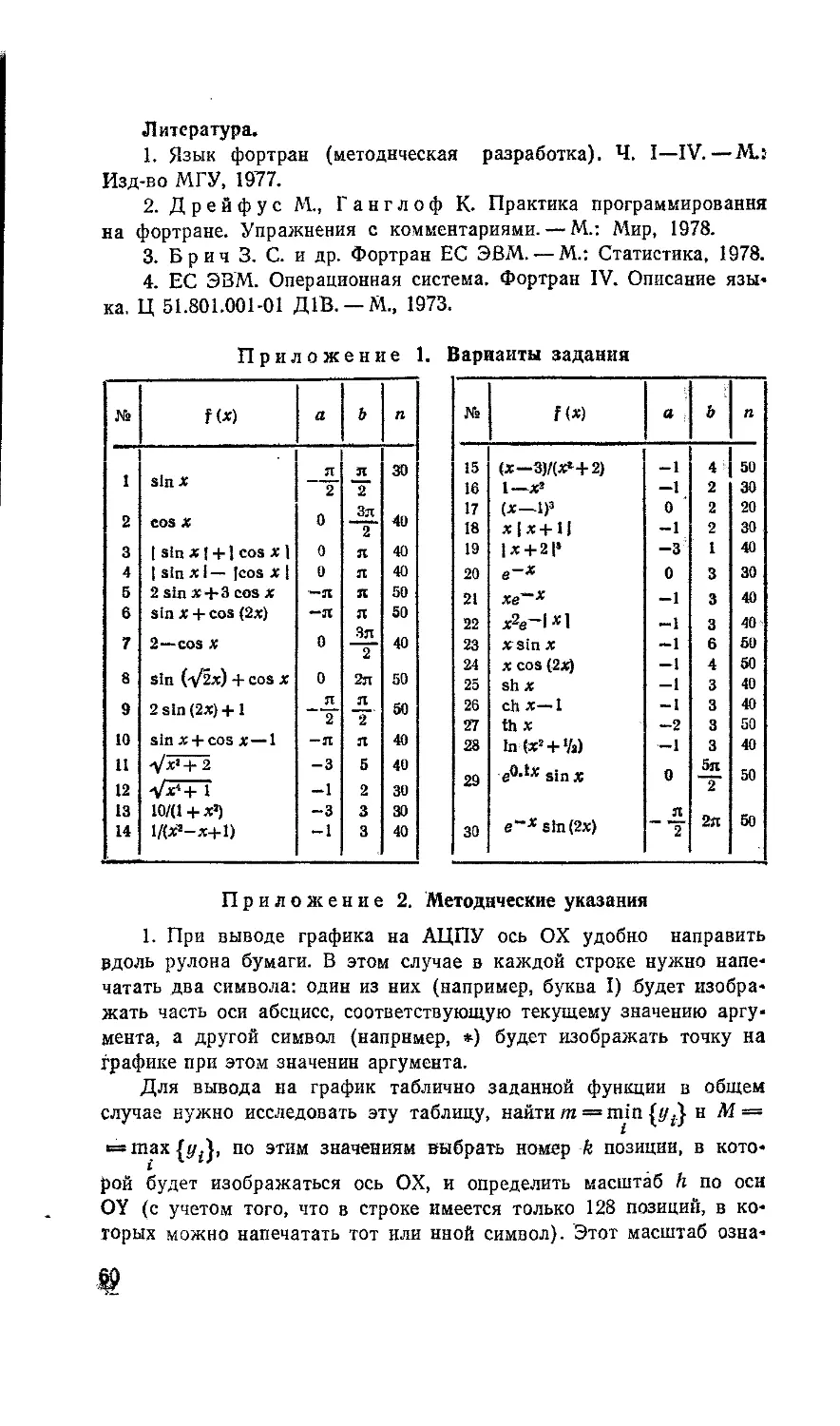
Приложение 2. Варианты задания
В каждом варианте указаны значения a, b, п, а также иомера j функций fj(x) (j = 1, ..., т) из приведенного ниже списка.
№ i a b п
1 1, 6, 9, 16 —я л 20
2 2, 8, 18 0 2л 30
3 3, 4, 11 0 2л 40
4 4, 10, 13 0 Л 40
5 1,5, 12 0 2л 50
6 4, 6, 15 —Л Л 20
7 3, 7, 11 0 л 40
8 8, 13, 21 -2 2 40
9 9, 15, 16 -3 3 30
10 10, 15, 18 -1 4 50
11 8, 11, 17 0 3 30
12 9, 12, 16 —3 3 30
13 10, 13, 18 -1 3 40
14 10, 14, 16 -2 2 40
15 11, 15, 17 -1 4 25
№ 1 а ь п
16 1, 16, 19 —л л 30
17 2, 15, 17, 20 —л л 40
18 3, 6, 13 —л л 50
19 4, 7, 19 0 я 28
20 5, И, 18 —л/2 я 30
21 6, 3, 20 —Я я 40
22 4, 7, 13 —Л/4 л/2 30
23 8, 9, 14 -1 3 40
24 9, 13, 15 -4 4 40
25 8, 10, 17 —2 5 35
26 10, 11, 13 -2 4 30
27 11, 12, 15 -1 4 50
28 13, 16, 19 -2 2 40
29 12, 14, 17 -I 5 30
30 10, 15, 18 -1 6 35
Функции:
1) sin (х); 2) cos (х); 3) ] sin (х) |; 4) sin (х) cos (х);
5) sin (х) + cos (х) — 1; 6) 2 — cos (х); 7) 2 sin (2х) + 1;
8) VF+4; 9) 20/(1 + х2); 10) 1 + 2х; 11) (х - I)3; 12) ех;
13) е~х2; 14) 4е~|х| —1; 15) 1 — х2; 16) 1 + 2Х+5;
17) |х + 10 |5: 18) (х + 5)3(1+sin2x); 19) е-(х+^;
20) 2'7100; 21) е',х+5’.
40
Задание 9. МАШИННО-ОРИЕНТИРОВАННЫЙ ЯЗЫК (АВТОКОД); ОСНОВНЫЕ КОНСТРУКЦИИ И ВОЗМОЖНОСТИ
Цель задания.
1. Знакомство с языком конкретной ЭВМ и его особенностями.
2. Получение начальных навыков в программировании на автокоде.
3. Практика в использовании транслятора с автокода (ассемблера).
4. Освоение методики отладки программ, написанных на автокоде.
Содержание задания.
1. Изучение системы команд конкретной ЭВМ (БЭСМ-6, ЕС ЭВМ),
2. Изучение основных возможностей автокода для этой машины (автокода БЕМШ, ЕС ЭВМ).
3. Изучение правил использования ассемблера.
4. Составление программы на автокоде для решения поставленной задачи и ее отладка.
5. Решение задачи на машине.
Постановка задачи;
По заданным вещественным значениям а, & и целому п получить:
а) значения yi = /(a, b, j) (1=1, 2, ..., п), где f — заданная функция;
б) значение u = g(yt, у2, ..., уп), где g — заданная функция.
Функции fug определяются вариантом задания (см. Приложение 1).
Значения а, b и п являются исходными данными, вводимыми в процессе выполнения программы; эти значения задаются преподавателем по окончании отладки.
Содержание отчета.
1. Постановка конкретного варианта задачи.
2. Запись выбранного алгоритма решения задачи на алголе.
3. Программа на автокоде, реализующая этот алгоритм.
4. План отладки программы, тесты и результаты отладок.
5. Результаты решения задачи на машине при заданных значениях а, b и п.
6. Перечень и характеристика ошибок, допущенных в процессе выполнения задания.
Литература.
1. Трифонов Н. П. Система команд БЭСМ-6. Методическое пособие для программирования. — М.: Изд-во МГУ, 1969.
2. Штаркман В. С. Автокод БЕМШ. Описание языка. — Мл Изд-во ИПМ АН СССР, 1969.
3. Методические пособия и инструкции по программированию.
41
Приложение 1. Варианты задания
I. Функция f(a, b, I).
1)
( О'+1) (2а+Ы)312
I (Ь - а)2 + ai + i2 пр”
1 i (i - 1) (26 + аг')3/2 ппи [ (b - а)2 + ai + i2 Р
а > Ь, а^Ь.
3)
4)
(а — bi)*
i (а2 + 36/ + 4г2)
(а + Ы)*
i (Q2 + 3 (1 _ b) i + 4/2)
при b > 1,
при 6^1.
„р„ »>o.
(a + bi)2
i^/i + V прИ b<°-
ia2 + (— l)i+1 i2 (b - a)
------, .... ---- npi
-V&a2 + al + b2i2
ia2 + i2 (b — a) —;.... —— npi
д/5а2 — ai + b2i2
a > 0,
a<0.
{2az2 — bi + 3a6 V“2 + 4&2 + i2 i2+\ a — b + i
при a < b, прн a b.
7)
при a > b, при a^b.
I 2 (ab)1 + i2 — a
I 2 (a2 + b2) + i | 2a b + (- 1/ (a - i)
I 2 (a2 + b2) При
при
i ab 1 > 1.
( а + & + г + (-1)Ч&-п)
8) f = { vsr
I | a + i | + | b — i |
!(a - i)2 + (6 + i)2 л/а2 + 262 + г2 ПРИ (a + z)2 + (b - i)2
--, 1 ':. . zrzr ПрИ Va2 + (— 1)£ b2 + i2
прн a > 0, при a з^О.
a
a > b.
10) f =
(ai + 2d)2 + (— 1)г t
V«2 4- i
(ai + 26)2 4- i
^/i2-i+\
при a > 0,
при a < 0.
(2a + 3z)2 - (За - 2г)2
•^/а ’ + (— 1) ^ az 4- ft2 + z2 (Зг - 2а)2 + (21 - За)2 7 а2/2 — 2аЫ + 62 + 1
при а < 26,
при а ^26.
13) f =
(ai + 6)2 + 3 (Ы - а)2 7(3ai - 2)2 + 462 (at — b)2 — (ай)1
2z + ab
при | аЬ | 1,
при |аЬ | < 1.
(а2 - &) г2 + Заг + Ъ л/(2а1 4- b)2 — Ы2
а 4* i 4~ bi2 1
а2 4- bi
при i 0,
при b > 0.
' (62—Заг2)3'2 - (364 - а)3/2 (2 — a) i2 4- (Ь — а)2
аЫ 4- (л/ai-----т')
(За — 6) i2 — b 7 | За - 2Ы | 4- i2
(2аЬ - Зг)2 4- 5
Va2;2 - (За - 26) i 4- b2
при
при
при
при
а<0,
а > 0.
£ 3 £ 3
II. Функция g (уь у2, уп).
I у? — a2 |
2) g = min -!—j , KiCn a2 4- b2
3) g=4(max | y, | 4- min | yt |).
.4 , , f yi При | Pi к 2,
I °-5 п₽и \У1\>2-
,-4 > । f У1 п₽и IУ11 > b
5) g= min \Zi\, Wftzi = \9 l„.i<t
l'2 ПРИ ' Уi 1 *•
6)
п S-'Z21' i==«l
(yi при У1^(О, 10), 11 при yi (0, 10).
7) % ;;;<£$
n
8) £=£4
где zz =
Vi
Vgl
при |#/]<!, при I y i I > 1.
n
9) g=£vio4-z/; где 2/-{;* ’j;
i-l
a
,n. V* fmax (,gi> 10 — »,)
10) g=2^zit где2/ = | У1'
/=1
при уi е (0, 10), при yt ф (0, 10).
Приложение 2. Методические указании
1. Для выполнения задания нужно прежде всего изучить систему команд машины: представление чисел и команд, набор основных машинных операций арифметического типа, условных и безусловных переходов, операций над индексными регистрами.
Если в машине нет стандартной формы представлении целых чисел, то надо принять наиболее употребительный способ или выбрать свой.
2. Значения исходных данных (а, Ь и п) удобно задавать в одинаковом виде как вещественные числа в форме с плавающей точкой. Если целочисленное значение п желательно иметь в другом виде (например, в виде числа единиц младшего разряда мантиссы), то преобразование введенного значения п к этому виду следует предусмотреть в программе, используя для этой цели соответствующие машинные операции.
3. На первом этапе программирования алгоритм решения задачи следует записать на языке высокого уровня (например, на алголе) в максимально компактной и наглядной форме. Затем этот алгоритм целесообразно расписать более подробно: детализировать реалнза-цию операторов цикла, предусмотреть возможную экономию команд, использование индексных регистров и т. д., по возможности учитывая специфику машины и набор ее операций. Наличие такого детализированного алгоритма позволит затем вести программирование на автокоде пооператорно. Это существенно упростит работу, так дак можно будет не думать .об алгоритме в целом, а сосредоточить свое внимание на реализации очередного оператора с помощью ма*
44
шинных команд. Эти алгоритмы, проверенные и подписанные преподавателем, должны храниться в качестве рабочих документов и затем должны быть приложены к отчету.
4. Перед составлением программы следует внимательно познакомиться с конкретным автокодом, особенно тщательно изучив те его конструкции и возможности, которые необходимы для выполнения данного задания. При составлении программы полезно постараться использовать различные возможности, предоставляемые автокодом, например различные способы задания констант.
5. Уже при составлении программы нужно думать об ее последующей отладке и заранее принимать меры к облегчению н ускорению этого этапа в изготовлении программы. С этой точки зрения все рабочие ячейки целесообразно размещать в памяти единым массивом, не стремиться (в данном задании) к слишком жесткой экономии рабочих ячеек, константы также следует запасать единым,массивом в конце программы и т. д.
Задание 10. АВТОКОД; ОСНОВНЫЕ ВОЗМОЖНОСТИ. ПРОСТЕЙШИЕ СТРУКТУРЫ ДАННЫХ
Цель задания.
1. Получение навыков в программировании на машииио-ориен-тированном языке (автокоде).
2. Практика в отладке программ, написанных иа автокоде.
3. Практика работы с простейшими структурами данных.
Содержание задания.
1. Изучение машинных операций БЭСМ-6 (ЕС ЭВМ) неарифметического типа.
2. Изучение основных возможностей автокода.
3. Конкретизация способа представления списков (строк) в памяти машины.
4. Составление и отладка автокодной программы, предназначенной для обработки символьных данных.
5. Решение на ЭВМ модельной задачи, проверяющей правильность составленной программы.
Постановка задачи.
Дан некоторый текст, где
(текст): := (слово).
(слово): := (буква) | (слово) (буква)
В качестве букв принимаются заглавные буквы русского алфавита. Предполагается, что слово содержит не более 100 букв.
Первоначально текст задается в «запакованной» форме, когда в одной ячейке памяти хранятся коды нескольких символов. Будем
45
считать, что на БЭСМ-6 каждая очередная шестерка символов текста представляется очередным машинным словом, а последовательные символы этой шестерки представляются последовательными (слева направо) байтами (восьмерками двоичных разрядов).
Требуется:
1. Преобразовать слово, содержащееся в исходном тексте, в заданное внутреннее представление. Каждое из задаваемых внутренних представлений является одно- или двунаправленным списком, каждое звено которого содержит код щ одной из букв, входящих в слово, ссылку sT на следующее звено, а в случае двунаправленного списка и ссылку на предыдущее звено.
2. Слово в его внутреннем представлении переработать по заданному правилу.
3. Переработанное слово преобразовать в запакованную форму и вывести на печать.
Вид внутреннего представления слова и правило его переработки определяются вариантом задания (см. Приложение 1).
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Вид внутреннего представления слова.
3. Общая и детализированная блок-схемы программы.
4. Текст автокодной программы.
5. Набор тестов и результаты отладок.
6. Результаты решения на ЭВМ модельной задачи, заданной преподавателем.
Литература.
1. Л ю б и м с к и й Э. 3., Мартынюк В. В., Трифонов Н. П. Программирование. Гл. 3. — М.: Наука, 1980.
2. Т р и ф о н о в Н. П. Система команд БЭСМ-6. Методическое пособие для программирования. — М.: Изд-во МГУ, 1969.
3. Ш т а р к м а н В. С. Автокод БЕМШ. Описание языка. — М.: Изд-во ИПМ АН СССР, 1969.
4. Методические пособия н инструкции по программированию.
Приложение 1. Варианты задания
I. Вид внутреннего представления слова.
1. Однонаправленный список (строка), каждое звено которого представляется одним машинным словом: в левой его половине содержится at, а в правой половине — s^.
2. Однонаправленный список (строка), каждое звено которого представляется парой машинных слов: в младших разрядах первого слова содержится вД а в младших разрядах второго слова — а,.
46
3. Двунаправленный список, каждое звено которого представляется одним машинным словом: в младших 15 разрядах содержится st, в следующих 15 разрядах содержится sf, а в следующих 15 разрядах — щ.
4. Двунаправленный список, каждое звено которого представляется парой машинных слов: в правой половине первого слова содержится st, в левой его половине — sf; в младших разрядах второго слова содержится а,.
II. Правило переработки слова.
1. Из слова удалить все последующие вхождения первой его буквы.
2. После каждой буквы исходного слова вставить букву А.
3. Если какая-либо буква входит в слово несколько раз подряд, то в каждом из этих случаев удалнть повторные вхождения буквы.
4. В каждой очередной паре букв поменять буквы местами.
5. Если слово содержит более четырех букв, то удалить из него три буквы, непосредственно предшествующие последней букве слова.
6. Каждое вхождение в слово первой его буквы заменить слогом ДА.
7. Если последняя буква слова входит в него несколько раз, то оставить только последнее вхождение этой буквы.
8. В каждой очередной тройке букв первую букву продублировать после третьей.
9. Если первая буква слова встречается в нем не менее трех раз, то удалнть часть слова, расположенную между вторым и третьим вхождениями этой буквы.
10. В слове оставить только первое вхождение каждой из букв, удалив остальные.
11. Если слово содержит не мевее двух букв, то первый его слог, состоящий из двух букв, продублировать в начале и конце слова.
12. Из каждой очередной четверки букв слова удалить вторую пару букв.
13. Из каждой очередной тройки букв удалнть первую букву.
14. Если слово начинается н кончается одной и той же буквой, то удалить из слова все другие вхождения этой буквы.
15. Если первая буква слова входит в него не менее двух раз, то удалить начало слова, предшествующее второму вхождению этой буквы.
Приложение 2. Методические указания
1. Для выполнения задания следует изучить систему команд БЭСМ-6, обратив особое внимание на операции неарифметического типа и операции над индексными регистрами.
47
2. Для внутреннего представления слова ввести в употребление массив, например ЦО: А]; при задании значения k необходимо учесть максимальную длину исходного слова, число ячеек памяти, отводимых для каждого звена списка, и возможное увеличение длины слова в процессе его переработки. В начале массива, как обычно, размещается заглавное звено списка, в котором s+ — ссылка на первое звено, а0 — указатель свободного места в массиве Т, a (в случае двунаправленного списка) равно нулю. В звене с номером т, соответствующем последней букве слова, принимается s*=0, что и является признаком конца слова.
3. В качестве ссылки на какое-либо звено (и на свободное место памяти) удобно принять не адрес ячейки, а ее относительный номер в массиве Т.
4. Для упрощения основной части программы целесообразно выделить подпрограммы, реализующие процедуры включения и исключения символа (см. [1]).
5. Перед составлением автокодной программы реализуемый ею алгоритм следует предварительно сформулировать на алголе или в виде достаточно подробной блок-схемы.
Задание 11. РЕШЕНИЕ ЗАДАЧ В РЕЖИМЕ ДИАЛОГА С ЭВМ
Цель задания,
1. Практика в решении задач на ЭВМ в режиме диалога.
2. Практика в использовании компонент системы программиро-
вания,
3, Получение дальнейших навыков работы за терминалом.
Содержание задания.
1. Знакомство с конкретной системой разделения времени (или с системой удаленного доступа, позволяющей использовать ЭВМ в режиме, близком к диалоговому) и с ее возможностями.
2. Изучение правил работы в конкретной системе.
3. Составление на подходящем языке программирования программы решения поставленной задачи с учетом специфики решения ЙХЙи в режиме диалога, ее отладка.
4. Решение на ЭВМ поставленной задачи при непосредственном участии автора программы а процессе решения.
Постановка задачи.
Даны функции yi — )'(х) и у^ == g(k, х). Требуется найтн такие Значения параметра k, чтобы одна из координат (абсцисса пли ордината) точек пересечения у*) графиков этих функ
48
ций с точностью Bi = 10~2 принимала наперед заданные значения.
Функции f(x) и g(k, х), а также заданные значения одной из координат точек пересечения графиков определяются вариантом задания (см. Приложение 1).
Требования к программе.
В программе должен быть реализован один из подходящих численных методов решения трансцендентного уравнения
F(x, k)^f (x)-g(k, х)=0 (1)
при заданном значении k = ka (естественно, точность е^, с которой находится это решение, должна быть выше заданной точности в*: например, можно принять 82 = ej/10).
Задание значений для которых решается уравнение (1), должно производиться с клавиатуры терминала, для чего в программе должен быть предусмотрен соответствующий оператор ввода. В процессе решения задачи на ЭВМ следует так подобрать значения чтобы среди получаемых по программе решений уравнения (1) содержались и решения, удовлетворяющие сформулированным в постановке задачи условиям.
В качестве окончательных результатов на печать вывести каждое из задаваемых значений k, значения координат найденной точки пересечения графиков при этом значении k и значение левой части уравнения (1) при заданном значении k и найденном значении х.
Содержание отчета.
1. Постановка задачи (конкретный вариант). "
2. Обоснование выбранного численного метода решения уравнения (1).
3. Текст программы.
4. Результаты решения задачи (протокол диалога).
Литература.
1. Хнрр Р., Штробель Р. Алгол в мониторной системе «Дубна». — М.: ИПМ АН СССР, 1973.
2. Инструкция по языку фортран ОС ЕС (наст, книга).
3. Брич 3. С. и др. Фортран ЕС ЭВМ. — М.: Статистика, 1978.
4. Ииструкцня по работе в системе КРАБ (наст, книга).
5. Инструкция по работе в системе PRIMUS (наст, книга).
6. Инструкция по языку управления заданиями ОС ЕС (наст* Книга).
7. Инструкция по диагностике в ОС ЕС (наст, книга).
8. Ерофеев В. Н. и др. Средства отладки программ в операционной системе ОС ЕС ЭВМ. — М.: Статистика, 1979.
49
Приложение 1. Варианты задания (для каждой пары функций задаются либо значения X, либо значения У)
J<2 f(X) g {k, X) Значения X Значения У
1 2 sin х kx2 1.0, 2.0, 3.0 0.4, 0.6, 0.8, 1.0
2 e —1 kx2 + 2 1.5, 1.7, 1.9 0.2, 0.4, 0.6
3 « x 2 cos ~ ekx-l 1.0, 1.5, 2.0, 2.5 0.5, 0.6, 1.0, 1.2
4 X 2 sin — e--kx л/4, л/2, Зл/4 0.8, 1.0, 1.2, 1.5
5 e~x kx— 1 0.1, 0.2, 5.0, 6.0 0.5, 0.6, 0.7
6 tg x fee2+ 0.5 0.2, 0.4, 1.2, 1.4 3.0, 4.0, 5 0, 6.0
7 Л X 2 cos — kx3 — 1 Л/4, л/2, Зл/4 1.0, 1.2, 1.5
8 X . e —1 fcc2 + l -1.0, -1.5, -2.0 3.0, 5.0, 7.0, 9.0
9 tg- kx+ 1.1 0.2, 0.3, 1.0» 1.2 0.1, 1.0, 3.0, 5.0
10 3cos-^ ekx 1.0, 1.2, 1.4, 1.6 2,6, 2.2, 24.0, 26.0
11 e ” 'у/ kx !/', 2.0, 3.0 0.4, 0.5, 0.6
12 « 2 X 2 cos — ekx — 2 2.2, 2,4» 2.6 0.5, 0.9, 1.3, 1.7
13 tgx ^Jkx + 1 1.2, 1.3, 1.4 1.5, 2.0, 2.5, 3.0
14 ctg JC fe (X— 1) -0.2» -0.4, -0.6 -0.1, -1.0, -1.9
15 e~x In (fex) 0.5, 1.5, 2.5 0.6, 0.4, 0.2
Приложение 2. Методические указания
1. При выполнении задания целесообразно сначала составить обычную программу, предназначенную для ее выполнения в пакетном режиме, моделируя ввод и вывод с использованием терминала вводом и выводом с использованием перфокарт. Для экономии терминального времени также целесообразно в пакетном режиме провести предварительную отладку программы (по крайней мере ее основной части), оставив на терминальный режим лишь отладку, связанную с теми изменениями в программе, которые необходимо внести в нее для использования этой программы в режиме диалога.
2. При составлении программы следует учесть то обстоятельство, что решение задачи на ЭВМ будет производиться при участии человека в самом процессе решения.
а) Чтобы легко определять момент, когда с терминала надо начинать ввод очередного значения k, непосредственно перед оператором ввода этого значения в программе удобно предусмотреть вывод на экран терминала определенного сообщения, например строки
60
‘К='’ появление на экране этого сообщения будет служить приглашением пользователю ввести с клавиатуры терминала очередное значение k.
б) По окончании решения уравнения F(x, k) — 0 на экран следует вывести строку ‘Х = ' и вслед за ней — найденное значение X (или строку ‘У=’ и найденное значение У) —интересующую нас координату точки пересечения графиков. Если найденное значение X (или У) не удовлетворяет условию задачи, то на основании анализа этого значения (и, возможно, предыдущих значений, для чего каждое заданное значение k и выведенное на экран значение X (или У) следует записывать на бумаге) надо решить, какое значение k следует задать на очередном этапе решения задачи (если найденное значение X или У не удовлетворяет условию задачи, то в программе должен быть предусмотрен переход на ввод очередного значения k).
в) По окончании цикла, связанного с подбором значения k для нахождения очередной требуемой точки пересечения графиков, в программе следует предусмотреть вывод на экран соответствующего сообщения, например строки ‘КОНЕЦ ЭТАПА’.
г) Если в алгоритме, реализованном в программе, используется фигурирующая в формулировке задания последовательность значений X (или У) и если получение очередного нз этих значений трудно осуществить по определенному алгоритму, то в программе можно предусмотреть ввод с терминала и очередного значения из этой последовательности.
3. Перед началом работы в терминальном классе следует изучить описание соответствующего терминала и инструкцию по той системе, в рамках которой будет выполняться задание.
Правила работы в системе КРАБ для ЭВМ БЭСМ-6 и в системе PRIMUS для ЕС ЭВМ даны в Приложениях 2.1 и 2.2 соответственно.
Приложение 2.1. Работа в системе КРАБ
1. При выполнении задания в системе КРАБ [4] следует использовать язык программирования алгол-ГДР [1], который является одной из версий алгола-60.
Основные отличия языка алгол-ГДР от алгола-60 состоят в следующем:
а) Основные символы языка типа begin представляются в виде соответствующей последовательности заглавных латинских букв, заключенной в апострофы, например 'BEGIN'.
б) Операторы ввода-вывода похожи на аналогичные операторы фортрана — с той лишь разницей, что формат, дополнительно заключенный в двойные апострофы, задается в самом операторе ввода-вывода, а не в виде отдельного объявления. В частности, с помощью этих операторов можно осуществлять ввод данных
51
с терминала, а выводить результаты можно как на АЦПУ, так и на терминал, причем обмен с терминалом осуществляется по каналу с номером 54.
Примеры операторов вывода на АЦПУ:
'PRINT' "(4НТЕСТ)"; (печать на АЦПУ слова ТЕСТ)
'PRINT' "(F9.4)" X, Y; (печать на АЦПУ в формате F9.4
значений переменных X и Y)
'PRINT' "(Е10.3)" 'FOR' I := 1' STEP' 1' UNTIL' 10' DO'
A [IJ; (печать в формате E10.3 первых десяти компонент вектора А)
Пример оператора ввода с терминала:
'READ' (54, "(F8.5)") X, Y; (ввод с терминала значений X и Y в формате F8.5)
Примеры операторов вывода на терминал:
'WRITE' (54, "(2НК =)"); (вывод на экран текста К =)
'WRITE' (54, "(F8.5)") X; (вывод на экран значения X в фор» мате F8.5)
Для протоколирования хода решения задачи в программе необ* ходимо предусмотреть вывод на АЦПУ каждого заданного с терми* нала значения К и найденного значения X или У.
2. При работе в системе КРАБ иа ЭВМ БЭСМ-6 необходимо сначала с помощью системы КРАБ сформировать в ее архиве за* дание для мониторной системы Дубна. Это задание имеет следую» щую структуру (в предположении, что программа решения постав» ленной задачи составлена на языке алгол):
ШИФР . . (шифр) _ ЗСМ —1
ЕЕВ1АЗ
* NAME. . (фамилия)
* ALGOL
(текст программы)
' ЕОР'
* EXECUTE
* END _ FILE
где (шифр) —шестизначный номер, являющийся шифром, по кото* рому пользователь допускается к работе на ЭВМ (шифр выдается студенту на практикуме); (фамилия)—фамилия студента; (текст программы) —текст алгол-программы; 'ЕОР' — специальный «опера» тор», являющийся для транслятора признаком конца транслируемого текста.
3. После формирования в архиве системы задания, структура которого приведена в предыдущем пункте, для его выполнения иуж» но передать системе КРАБ директиву
ФОР ПС VT
52
По этой директиве производится трансляция содержащейся в задании программы и —при отсутствии в ней синтаксических ошибок — ее выполнение.
4. Если возникает необходимость прекратить выполнение программы до полного ее завершения (например, в случае ошибок, выявленных в программе во время решении задачи), достаточно при очередном вводе данных с терминала задать данные в формате, отличном от формата, указанного в операторе ввода. В результате этого управление перейдет системе КРАБ; если теперь передать ей пустую директиву (нажать клавишу ЕТХ) и по получении диагностики передать директиву ОКЧ (окончание выполнения задания), то задача будет снята со счета.
Приложение 2.2. Работа в системе PRIMUS
1. При выполнении задания в системе PRIMUS [5] должен использоваться язык фортран ЕС ЭВМ [2, 3].
Первоначальный вариант программы (особенно при ее отладке в пакетном режиме) следует составить с нспользванием стандартных средств фортрана. При этом ввод с терминала должен моделироваться вводом с перфокарт по оператору вида
READ (5, f)fli,..., ап
или вида
READ_f, ai.....Оя
а вывод на экран терминала — печатью на АЦПУ по оператору вида
WRITE (6, f)ah а„
где f —метка объявления формата, ait ап — список ввода (вывода) .
При проектировании диалога, как правило, удобно считать, что каждая запись (как вводимых, так и выводимых сообщений) соответствует отдельной строке экрана.
Чтобы переход к диалоговому варианту программы требовал внесения минимальных изменений в исходную программу, при ее составлении рекомендуется выполнять следующие требования:
— В программе не должны использоваться подпрограммы с именами PUT, FPUT, GET и FGET.
— При выводе на АЦПУ по оператору, моделирующему вывод на экран терминала, каждая выводимая на печать запись не должна Содержать более 80 символов. В числе этих 80 символов должен учитываться и первый (управляющий) символ записи, в качестве которого должен использоваться пробел; в этом случае форма выдачи на экран будет совпадать с формой выдачи на АЦПУ. При
этом следует иметь в виду, что при выводе на экран первый символ записи считается не управляющим, а значащим (т. е. ои также выводится на экран). Если вывод этого символа на экран нежелателен, то программу — при переходе к ее диалоговому варианту — следует изменить так, чтобы управляющий символ в записях отсутствовал.
— Каждое передаваемое с терминала сообщение начинается некоторым управляющим (стартовым) символом. Код этого символа также передается в ЭВМ, а затем заменяется системой на пробел. Поэтому первая запись, вводимая по оператору ввода с перфокарт (с помощью которого моделируется ввод с терминала), должна содержать пробел в первой ее позиции. В связи с этим соответствующее объявление формата рекомендуется записывать в виде
FORMAT (IX, ...)
2. Исходный вариант программы может отлаживаться в пакетном режиме, или с использованием перфокарт, или с помощью системы PRIMUS. В последнем случае рекомендуется задание для ОС готовить так, чтобы можно было просматривать результаты его выполнения на экране терминала. Первоначальный текст задания целесообразно записать в архив системы PRIMUS с перфокарт или флоппи-диска в пакетном режиме.
3. При переходе к диалоговому варианту исходная фортран-программа, предназиачеииая для решения поставленной задачи, должна быть модифицирована следующим образом:
а) Она должна быть оформлена как модуль-подпрограмма с заголовком вида
SUBROUTINE (имя подпрограммы) (PARM)
причем имя подпрограммы должно содержать не более 6 символов. В тексте этой подпрограммы должно содержаться предложение
INTEGER PARM (4)
б) Для вывода данных на экран терминала в исходном операторе WRITE номер устройства б должен быть заменен на 5, а после оператора WRITE должен быть вставлен оператор
CALL _ PUT (PARM, b, { ® j
где b — целое без знака, равное числу выводимых записей, а третий параметр указывает, нужно ли предварительно очищать экран терминала (0) или не нужно (1). Первое сообщение в программе целесообразно выдавать с очисткой экрана.
Заметим, что в диалоговой программе не могут содержаться операторы вывода на АЦПУ (о выдаче на печать протокола диалога см. ниже).
64
в) Для ввода данных с клавиатуры терминала исходный оператор READ должен быть оставлен без изменения, а перед ним должен быть вставлен оператор
CALL _ GET (PARM, b)
где b — целое без знака, равное числу подлежащих вводу записей.
г) Оператор останова STOP, естественно, должен быть заменен на оператор возврата RETURN.
Отметим, что параметр PARM служит для организации связи между системой PRIMUS и диалоговой программой; он должен использоваться в диалоговой программе только указанным выше способом.
4. Для работы с диалоговым вариантом программы, составленной с учетом требований п. 3, ее необходимо предварительно — после трансляции — записать в специальную библиотеку программ (библиотеку загрузочных модулей). Эта библиотека для студенческого практикума имеет имя STUD.PRIMUS и размещается на томе памяти на магнитных дисках.
Для записи диалоговой программы в библиотеку надо подготовить и выполнить следующее задание:
//... JOB ...
// EXEC . . SLIBDIAF, М = (имя программы), [, С=Р]
//FORT. SYSIN_DD_*
(текст программы)
//
где (имя программы) должно совпадать с именем задания практикума, т. е. для студентов ф-та ВМиК иметь вид BMjcggnn (см. И)-
Процедура SLIBDIAF обеспечивает трансляцию заданной программы, редактирование ее связей, т. е. дополнение требуемыми стандартными подпрограммами, и запись диалоговой программы в виде загрузочного модуля в библиотеку STUD.PRIMUS.
Если задание с вызовом процедуры SLIBDIAF запускается с перфокарт, то сообщения транслятора и редактора связей направляются в выходную очередь класса С для печати на АЦПУ. Если же это задание запускается через систему PRIMUS, то сообщения попадают в выходную очередь класса Р и могут быть просмотрены на экране терминала по команде SOUT системы PRIMUS. При этом справка о выходных данных состоит нз двух элементов: для транслятора и для редактора связей. При ошибках трансляции второй элемент отсутствует.
55
При успешной записи программы в библиотеку STUD.PRIMUS редактор связей выдает сообщение вида (при первой записи про* граммы)
* * * * (имя программы) DOES NOT EXIST BUT HAS BEEN ADDED TO DATA SET
или вида (при повторной записи)
* * ** (имя программы) NOW REPLACED IN DATA SET
Отсутствие такого сообщения означает, что программа в биб-лиотеку не записана. Причина может быть определена по диагностическим сообщениям редактора связей. Эти сообщения имеют такой же вид, кдк и сообщения загрузчика [7J, и пояснения к ним можно найти в [8]. Наиболее часто встречающееся сообщение редактора связей
IEW0132 (имя программы)
(которое является аналогом сообщения загрузчика IEW1012) выдается в случае, когда в программе встречается вызов подпрограммы, имя которой, указанное в сообщении, не обнаружено ни среди программ пользователя, ни в библиотеке стандартных подпрограмм.
5. Если программа успешно записана в библиотеку STUD.PRIMUS, то она может быть вызвана для ведения диалога с пользователем, работающим с любого терминала.
Следует подчеркнуть, что программы, записанные в эту библиотеку, как правило, сохраняются в ней только на время данного сеанса работы в системе PRIMUS. Чтобы убедиться в наличии программы в библиотеке, можно воспользоваться командой
CONT^STUD. PRIMUS
Перед ее выполнением система просит сообщить имя тома, содержащего библиотеку, если этот том не был предварительно зафиксирован по команде DVOL. В результате выполнения команды CONT на экран выдается оглавление библиотеки, т. е. список имен программ, содержащихся в библиотеке STUD.PRIMUS.
Для диалога пользователя с программой, написанной на фортране, используется специальный файл, в котором накапливается протокол диалога. На студенческих томах заранее образован такой файл протокола для каждого терминала. Этот файл имеет имя вида Fd, где d — номер терминала.
Перед вызовом диалоговой программы для работы пользователь должен определить для системы PRIMUS файл протокола. Для этой цели служит команда
DD
56
Если по этой команде в первую строку экрана не будет выдано имя FT05F001, значит, файл протокола еще не был определен для дан-него терминала. В этом случае необходимо передать подкоманду
I _ FT05F001
Далее система запрашивает характеристики файла, выдавая на эк-ран сообщения вида
(имя характеристики) =
После знака равенства пользователь должен задавать с помощью клавиатуры в качестве ответов значения запрашиваемых характе-ристик. Ниже приводятся имена требуемых характеристик и их зна-чения, которые должны быть заданы пользователем.
DSN = (hmh файла)
VOL = SER = (имя тома)
DISP = OLD
DSORG = <
RECFM = j
LRECL = >пустой ответ
BLKSIZE= I
SPACE= J
На этом определение файла протокола заканчивается.
Если по команде DD (или после очередной ее подкоманды) на первую строку экрана выдано имя FT05F001, это значит, что файл протокола для данного терминала уже определен (может быть, другим пользователем). Для проверки характеристик файла можно воспользоваться подкомандой
G-1
В случае необходимости можно отменить Старое определение файла протокола с помощью подкоманды
D_ 1
И дать определение заново.
Для выхода из команды DD используется подкоманда Е.
6. Для вызова диалоговой программы в работу используется команда
DIAF _(имя программы)
Здесь должно быть задано то же имя, что и в управляющем операторе ЕХЕС при записи программы в библиотеку STUD.PRIMUS по процедуре SLIBDIAF. Если в библиотеке указанная программа не обнаруживается, то иа экран выдается соответствующее диагноспг-
57
ческое сообщение я выполнение команды DIAF на этом заканчиваемся.
При вызове диалоговой программы возможно появление сообщения
ABEND. КОД ЗАВЕРШЕНИЯ = 804
означающего, что в области памяти системы PRIMUS не хватает места для размещения вызываемой программы. В этом случае следует иажатием клавиши ввода получить разрешение на ввод следующей команды, дождаться завершения выполнения диалоговых программ, вызванных другими пользователями, и повторить вызов своей программы.
Другое типичное сообщение, возможное при вызове диалоговой программы, —
ABEND. КОД ЗАВЕРШЕНИЯ = 0С6
обычно выдается, если даииым пользователем ие определен пли неверно определен файл протокола. В этом случае, получив разрешение на ввод команды, следует проверить определение этого файла по команде DD.
Если программа успешно вызвана, то начинается диалог. При работе иа терминале ЕС-7927 каждое сообщение, набираемое пользователем иа экране, как обычно, должно начинаться с текущей позиции курсора. Следует также иметь в виду, что предшествующая позиция всегда является закрытой для ввода. Перед набором сообщения пользователь может нажать клавишу СТРН.ЭКР, что позволит набирать очередное сообщение с начала экрана. Чтобы в процессе диалога имело место соответствие записей строкам экрана, необходимо каждый раз, набрав сообщение иа экране, переводить курсор в начало следующей строки и только затем нажимать клавишу ввода.
Когда диалоговая программа завершает свою работу, т. е. в ней встречается оператор фортрана RETURN, на экран выдается сообщение
КОМАНДА ВЫПОЛНЕНА
означающее, что пользователь может передавать системе следующую команду.
Иногда (иапример, при зацикливании) требуется прекратить выполнение диалоговой программы. Для этого, как обычно, используется команда KILL.
По окончании выполнения вызваииой диалоговой программы полный протокол диалога сохраняется в файле протокола. Этот файл можно просмотреть на экране терминала по команде LOOK нли выдать на АЦПУ по команде HDCP.
5?
Задание 12. ФОРТРАН.
МОДУЛЬНОЕ ПРОГРАММИРОВАНИЕ, ВЫДАЧА ГРАФИКОВ
Цель задания.
I. Практика в использовании основных конструкций фортрана.
2. Овладевие методами вывода результатов в виде графиков.
3. Знакомство с модульным программированием.
4. Практика работы в конкретной операционной системе.
Содержание задания.
1. Изучение принципов построения программ на фортране.
2. Знакомство с понятием программного модуля и с использованием массивов в фортране.
3. Изучение дополнительных возможностей форматного вывода.
4. Составление и отладка программного модуля, предназначенного для вывода графика таблично заданной функции.
5. Решение на ЭВМ конкретной задачи с выводом результата в виде графика.
Постановка задачи.
1. По заданным вещественным а, b (а < Ь) и целому п (п > > 0) вычислить значения функции f(x) для значений аргумента Xi = а + th, h— (b—a)In (i — 0, 1, n). Конкретная функция
f(x), а также значения a, b, n определяются вариантом задания (см. Приложение 1).
2. Используя полученный массив значений у, = построить на АЦПУ график этой функции.
Требования к программе.
1. Вывод графика на АЦПУ должен производиться с помощью отдельного модуля-подпрограммы, статическими параметрами которого являются значение п и массив значений функции, график которой выводится на печать (предполагается, что значения функции вычислены на сетке значений аргумента с некоторым постоянным шагом). Этот модуль должен правильно решать поставленную перед ним задачу при любой таблице значений функции.
2. Функция-f(x) должна быть объявлена в программе в качестве внутренней функции.
3. Программа должна правильно выполняться при любых значениях а, b и п (а < Ь, п 50), которые являются всходными данными задачи.
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Тексты программных модулей на фортране.
3. План отладки, тесты и результаты отладки.
4. Результаты решения конкретного варианта задания.
5. Перечень н характеристика всех ошибок, допущенных при выполнении задания.
59
Литература.
1. Язык фортран (методическая разработка). Ч. I—IV. — М.: Изд-во МГУ, 1977.
2. Д р е й ф у с М., Г а н г л о ф К. Практика программирования на фортране. Упражнения с комментариями.-—М.: Мир, 1978.
3. Брич 3. С. и др. Фортран ЕС ЭВМ. — М.: Статистика, 1978.
4. ЕС ЭВМ. Операционная система. Фортран IV. Описание языка. Ц 51.801.001-01 Д1В. — М., 1973.
Приложение 1.
№ f (X) a b п
1 slnx л_ 2 я 2 30
2 COS X 0 3л 2 40
3 [ sin X 1 + 1 cos x 1 0 л 40
4 I sin x 1 — |cos x | 0 л 40
5 2 sin x+3 cos x —Л л 50
6 sin X + cos (2x) —Л л 50
7 2—cos X 0 Зл 2 40
8 Sin (V2x) + cos X 0 2л 50
9 2 sin (2x) + 1 л 2 Л 2 50
10 sin x + cos x—1 —л л 40
11 Vx!+ 2 -3 5 40
12 Vxf+1 -1 2 30
13 10/(1 +x1) -3 3 30
14 1/(X*-X+1) -1 3 40
Варианты задания
№ fW a b п
15 (X—3)/(Х' + 2) -1 4 : 50
16 1—X’ -1 2 30
17 (X—1р 0 2 20
18 х | Х+ 1 | -1 2 30
19 1 х + 21’ -3 1 40
20 е~х 0 3 30
21 хе~х -1 3 40
22 х2е~1 х 1 -1 3 40
23 x sin х -1 6 50
24 х cos (2х) -1 4 50
25 sh х -1 3 40
26 ch х—1 -I 3 40
27 th x —2 3 50
28 ln(x! + */i) -1 3 40
29 eO.tx s;n x 0 5л 2 50
30 e~x sta(2x) Л 2 2л 50
Приложение 2. Методические указания
1. При выводе графика на АЦПУ ось ОХ удобно направить вдоль рулона бумаги. В этом случае в каждой строке нужно напечатать два символа: один из них (например, буква I) будет изображать часть оси абсцисс, соответствующую текущему значению аргумента, а другой символ (например, *) будет изображать точку на
графике при этом значении аргумента.
Для вывода на график таблично заданной функции в общем
случае нужно исследовать эту таблицу, найти т =
min {//.} н
М =
= max по этим значениям выбрать номер k позиции, в которой будет изображаться ось ОХ, и определить масштаб h по осн OY (с учетом того, что в строке имеется только 128 позиций, в которых можно напечатать тот или иной символ). Этот масштаб озна
чает, что при каждом изменении значения функции иа величину h символ, изображающий точку на графике, будет смещаться в очередную позицию по строке.
Если, например, по оси OY мы хотим выделить 101 позицию для изображения точек на графике функции, у которой т < 0 и М > 0, то можно взять h = (М — т)/100 и k — [|т|/Л]бл + 5, где [х]6л означает ближайшее целое к значению х, а число 5 взято из тех соображений, чтобы точка для у{ = т отстояла от края рулона бумаги на 5 позиций. Для определения номера I позиции в строке, в которой надо изобразить значение у,, можно, например, вычислить р = [| yi |//1]бл и положить I = k + р при уг > 0 и I — k — р при У'1 < 0.
2. Итак, в очередной строке, соответствующей значению у,, надо отпечатать символ I в позиции с номером k и символ *, в позиции с номером I (при I — k в данной позиции следует печатать *), после чего перейти к следующей строке.
Для достижения этих целей можно воспользоваться наличием в фортране ЕС ЭВМ текстовых данных и возможностью передачи текстовых данных с помощью операторов ввода-вывода.
2.1. Текстовая константа — это запись вида пН/^ •.. или вида /]/<, ... tn (n sg 255 — целое без знака, а каждое ti — символ). Значением текстовой константы является последовательность символов t-ti. ..tn. При записи текстового значения в память каждый символ занимает один байт. В любой форме записи текстовой константы пробел является значащим символом.
Примеры текстовых констант:
ЗНА _ В, 1Н _, 1HI, 1Н *, 'Г,
2.2. Значения, задаваемые текстовыми константами, могут быть присвоены переменным и элементам массивов любого типа с помощью операторов явного описания типа или оператора DATA (с помощью одной текстовой константы можно присвоить начальные значения и нескольким последовательным элементам массива или всему массиву). При этом следует иметь в виду, что запись текстового значения в поле памяти, отведенное для данной переменной, производится слева направо (символ ti помещается в г-й слева байт, свобод» ные справа байты заполняются пробелами, а лишние символы тек* стового значения отбрасываются).
Например, оператор
DATA N1/1H_/, N2/1 HI/, N3/1H»/
присваивает переменной N1 значение N2 — значение I, a N3 — значение * (в памяти они будут соответственно [иметь вид
М М— 1—*> W * t—t I—J
61
В дальнейшем полученные значения этих переменных могут быть присвоены другим переменным или элементам массива с помощью оператора присваивания, например: I(K) — N2, 1(5) — N3.
3. Вывод текстовых данных может быть осуществлен по оператору вывода с помощью элемента формата вида пАш, где Ада — описатель поля, а целое без знака п — число повторений данного описателя поля (при п = 1 запись п может быть опущена). Данному описателю поля Аге> ставится в соответствие очередной элемент списка вывода. При этом значение элемента списка вывода трактуется как текстовое данное, которое без изменения переносится в очередные а>-позиции формируемой записи.
Пусть, например, массив ISTR состоит из 101 элемента, причем элементы с индексами k и I имеют текстовые значения 1 и * соответственно, а значениями остальных элементов является пробел. Тогда при выполнении оператора вывода
PRINT 10, ISTR
при объявлении формата
10 FORMAT (1Н_, 101А1)
в очередной строке АЦПУ в ее k-й позиции будет отпечатан символ I, а в 1-й позиции — символ *.
Задание 13. МОДУЛЬНОЕ ПРОГРАММИРОВАНИЕ.
БИБЛИОТЕКА МОДУЛЕЙ. РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Цель задания.
1. Практика в модульном программировании.
2. Практика в использовании библиотечных модулей.
3. Практика в применении численных методов решения обыкновенных дифференциальных уравнений (задача Коши).
Содержание задания.
1. Знакомство с правилами использования библиотечных модулей.
2. Изучение простейших численных методов решения систем обыкновенных дифференциальных уравнений.
3. Составление программы на языке фортран с использованием библиотечных модулей и ее отладка.
4. Решение на ЭВМ задачи Коши для конкретного дифференциального уравнения.
Постановка задачи.
Дано обыкновенное дифференциальное уравнение первого порядка вида
у’ (х) = f(x, у) = F (х) — g(x) у (х), где F(x) и g(x) —заданные функции.
62
Требуется:
1. Найти численное решение задачи Коши на заданном отрезке [х0, Ь] (6 > Хо), выйдя иа точку х = b с точностью в] = 10~6, при начальном условии у(Хп) = г/о, одним из методов Рунге-Кутта:
а) с автоматическим выбором шага (см. Приложение 2) при заданной точности е > 0 на каждом шаге;
б) с постоянным шагом h = (6—где N—число шагов, полученных в п. а).
2. Найти решение поставленной задачи, выраженное в квадратурах.
3. Вывести на печать в виде таблицы значения приближенных решений, полученных по каждому из способов а) н б), а также вычисленные на машине значения точного решения (в тех же узлах, что и в п. б)).
4. Вывести иа печать в виде графика значения приближенного решения, полученные с постоянным шагом. Для вывода графика необходимо использовать соответствующий библиотечный модуль.
5. По отпечатанным таблицам построить график точного решения и решения, полученного с автоматическим выбором шага, для сравнения их между собой.
Функции F(x) и g(x), численный метод, значения хо, Ь, у о, е и й определяются вариантом задания (см. Приложение 1).
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Блок-схема программы.
3. Запись алгоритма решения задачи на алгоритмическом языке.
4. Тесты для проверки программы и результаты отладок.
5. Результаты решения конкретного варианта задания на ЭВМ.
6. Графики полученных решений.
7. Перечень и характеристика ошибок, допущенных в процессе прохождения задания.
Литература.
1. Березин И. С., Жидков Н. П. Методы вычислений. Т. П, изд. 2. — М.: Физматгиз, 1962.
2. Б а х в а л о в Н. С. Численные методы. Т. I. — М.: Наука, 1973.
3. Б р и ч 3. С. и др. Фортран ЕС ЭВМ. — Мл Статистика, 1978.
4. Методические пособия и инструкции.
Приложение 1. Варианты задания
I. Метод Рунге-Кутта и точность.
1) Метод 4-го порядка, е=10~4:
Ук+i ~ Ук + (й[ + 2йг + 2йз + Й4)/6,
где й, = hf (xj;, yk), ki = hf (xk. + й/2, + kJ2),
— hf (xk + hf2, yh -|- ki/2), kt — hf (xk + h, yk~\~ ks).
63
2) Метод 4-го порядка, е = 10-4:
Ук+i У к + (^1 + 4й3 4* kt)/Q,
где ki — hf (хь, у к), k2 = hf (хк + й/4, уь + йц/4), ks = hf {xk + ft/2, ук + Ы2),
kt = hf (Xk 4-, h, yk + kx — 2ft2 + 2fe3).
3) Метод 3-го порядка, 8 = IO-3;
Ук+\ — Ук + (kt + 4fe2 + ft3)/6,
где kt — hf (xk, yk), k2 = hf (xk + ft/2, у к + ftt/2), A3 = hf (Xk + h, ук — kt + %k2).
4) Метод 3-го порядка, e = 10~3:
Vk+i = Ук + ktJ4 + Зйз/4,
где kt = hf {xk, Ук), k2 = hf (xk + h/3, yb + kt'3), ks — hf {xk + 2A/3, yk + 2ft3/3).
5) Метод 2-го порядка, 8 = 10-2:
Уй-f-i =“ Ук + {kt + М/2,
где ki = hf {Xk, yk), k2 = hf {xk + ft, yk + fti).
6) Метод 2-го порядка, e = 10~2:
Ук+\ = Ук + ki,
где kt = hf (Xk, Ук), ki = hf (xk + й/2, yk + fti/2).
II. Значения ha, x0, b, уа\ функции g{x) и F (x)=<p(x)i|>(x).
a) ft0 = 0.5; Xo = 1; 6=6; ya = 10; g (x) = 2 (x Функции qp (x): -2).
1) e~{x+iU-, 2) e~x’; 3) в-^+г*;
4) xe~xl; 5) (x + 2)e"x’; 7) e~x' cos (0.8x); 8) cos2 (x/2) е~хг+3х', 9) sin2 (0.6x) e~xl+l-3x. Функции г|> (x): 1) e-2<2x+2); 2) 0.01; 3) ex; 4) e’2jc; 5) e3x; 6) 1/Т2зГ; 7) e2x~3-, 8) e3*-2; 9) e*’1'5, 6) e~x2sinx;
6) ft0 = 0.5; x0 — — 1; b = 2л — 1; yo = 8; g (x) Функции <p (x): = — sin (x 4-1).
10) sin(x+l); 11) g-cosfx+l); 12) (x + 2)e~C0i
Функции 1|) (x):
10) -1 cos (x 4-1); 11)4-; 12) 4 cos {x + 1). О о
64
Приложение 2. Методические указания
I. При интегрировании с автоматическим выбором шага рекомендуется использовать следующее правило выбора шага.
В узле взять 1г = Ло, где /г0 — заданный начальный шаг; найти приближенные решения у и у, вычисленные по методу Рунге— Кутта в точке ха + h с шагами h и /г/2 соответственно. За абсолютную погрешность приближенного решения (в качестве которого естественно взять у как более точное), вычисленного по методу Рунге-Кутта т-го порядка, принимается
Если 6 Т.:- е, то шаг h уменьшается в два раза и вычисления повторяются, исходя из узла х0- Как только на очередном этапе будет получено 6 < е, считается, что у и является решением в узле х, = = х9 -f- h, полученным с заданной точностью на этом шаге.
Решение в следующем узле х2, исходя из узла xt, получается аналогичным образом. При этом начальный шаг выбирается по шагу h, с которым было получено решение в узле Xi, в зависимости от погрешности б: если б < е/2г+1, то предыдущий шаг удваивается; в противном случае шаг не изменяется. Аналогично находится решение и в последующих узлах.
2. При подходе к точке х = b следует проявлять осторожность, так как при значениях х > Ь правая часть f(x, у) дифференциального уравнения может быть, вообще говоря, не определена и при решении задачи на ЭВМ может произойти авост (или прерывание), в результате которого задача будет снята со счета.
Для избежания такой ситуации можно поступить, например, следующим образом. После того как будет получено решение ук в очередном узле х-к и будет выбран шаг !гк, с которым будет вычисляться решение в узле хк+\ = хк + /и, вычислим значение А* = b — xk (при достаточно малом начальном шаге наверняка получим До > 0).
Если ДЕ < еь где Е[ — нужная точность выхода на точку Ь, то можно считать, что ® 6 и на этом процесс интегрирования заканчивается.
При As. gj интегрирование должно быть продолжено. Если при этом hk еТ Дй, то очередной этап не выводит за пределы интегрирования и он делается обычным образом. Если же hk > txk, то в качестве hk следует взять величину А*.
3. Если при решении задачи на ЭВМ возникают трудности с размещением в памяти всех получаемых результатов, то для вывода на печать результатов следует ввести в употребление один или несколько вспомогательных массивов фиксированной и не очень боль-
3 Н. П. Трифонов, Е. Н. Пасхин ‘ 65
той длины, которые используются для накопления получаемых результатов. Как только эти массивы будут заполнены, данная порция результатов выводится на печать, а последующие результаты снова накапливаются в этих же массивах.
При этом следует иметь в виду, что по окончании процесса интегрирования эти массивы могут быть заполнены не до конца, так что надо предусмотреть вывод полученных результатов и в этот момент. Следует также позаботиться о том, чтобы в этой последней выдаче можно было легко найти нужные результаты.
4. Для облегчения анализа полученных результатов и построения требуемых графиков решений результаты целесообразно отпечатать в виде таблицы, состоящей из нескольких колонок, — так, чтобы в одной из колонок были напечатаны значения узлов хь, а в других — значения решений в этих узлах.
5. В качестве теста для отладки программы можно взять простейшее уравнение вида у' — у — ху, у' — —ху и т. д. и небольшой отрезок интегрирования.
6. При использовании фортрана для выполнения задания следуем помнить, что в некоторых версиях этого языка требуется строгое соответствие типов переменных в арифметических операциях и операторах присваивания. При обращении к элементарным функциям (EXP, ALOG, COS, SIN, ABS, SQRT и др.) аргумент должен иметь значение вещественного типа.
Следует также помнить, что если в фортране тип значений какой-либо переменной не объявлен явно, то этот тип определяется по виду идентификатора: если он начинается с одной из букв I, J, К, L, М или N, то этой перменной по принципу умолчания предписывается тип целый. Например, переменные KI, К2, КЗ считаются целочисленными переменными.
Часть II. СПЕЦИАЛИЗИРОВАННЫЙ ПРАКТИКУМ
Специализированный практикум состоит из двух частей. Сна-чала выделяются специализации А (применение ЭВМ) и Б (математическое обеспечение ЭВМ), по каждой из которых студенты выполняют общие для дайной специализации задания. Дальнейшая специализация ведется по линии кафедры, на которой обучается студент (или даже по линии избранного им спецсеминара, определяющего более узкую специализацию студента).
СПЕЦИАЛИЗАЦИЯ А (ПРИМЕНЕНИЕ ЭВМ)
Задание А-1. АЛГОРИТМИЧЕСКИЕ ЯЗЫКИ И ТРАНСЛЯТОРЫ. ОТЛАДКА ПРОГРАММ.
МЕТОДЫ ПРИБЛИЖЕНИЯ И МИНИМИЗИЦИИ ФУНКЦИИ
Цель задания. ’
1. Практика использования алгоритмических языков типа алгол и соответствующих трансляторов.
2. Знакомство с простейшими методами приближения функций.
3. Использование методов минимизации функций при решении задач численного анализа.
4. Накопление опыта оформления результатов вычислений.
Содержание задания.
1. Изучение входного языка конкретного транслятора и связанной с ним системы математического обеспечения.
2. Изучение метода наименьших квадратов приближения функций многочленами.
3. Изучение метода скорейшего спуска для отыскания локального минимума функций многих переменных.
4. Составление алгол-программы и ее отладка.
5. Решение на ЭВМ конкретной задачи приближения функций.
6. Оформление полученных результатов в виде таблиц, выданных с помощью АЦПУ.
Постановка задачи.
1. Вычислить таблицу значений функции у — f(x) на сетке, полученной разбиением отрезка [с, </] на N равных частей:
yi = f (хД xi = с ф- г/г, h = (d — с) N (г =0, 1, ..Л’).
3*
67
2. Построить т многочленов рп (х) — а-_хп + ctixn~l + ... + fli последовательных степеней п = пО, «0 4-1, ..., пО + т— 1-> дающих наилучшее среднеквадратическое приближение f(x) на сетке Xi, т. е. для каждого п найти точку (аа, а>, ап) в R„+\, в которой достигается лииьмум функции
N
Ф(ас, ai, ап)==^ [у£ — рп (*/)]2-z = 0
Минимизацию Ф(а0, а1; .... а„) проводить методом спуска (см. Приложение 2). В качестве начальной точки для п = пО можно взять, например, = ... = = 0; для каждого следующего по
порядку значения п целесоооразно взять а(1" = О, а в качестве a-j
—коэффициенты предыдущего многочлена. За меру точности приближения принять
t>k = max
а^-а^ a'V
Процесс приближений заканчивается, если 6л < е, где е = 10~4.
3. Для каждого из полученных таким образом рп (х) вычислить у'Р ~ Pn(xi) (< = 0, 1...-V) и соответствующее среднеквадрати-
ческое уклонение
- V Ат Е >*, - <*<»’ - л/тй7 • * i=0
4. Для каждого п с помощью стандартной процедуры tsp получить «точные» значения коэффициентов р.Дх).
5. Значения с, d, N и пО являются исходными данными, вводимыми при выполнении программы. Функция f(x) и значение т фиксированы и определяются вариантом задания (см. Приложение I).
Для решения задачи на ЭВМ следует:
1. Изучить входной язык конкретного транслятора.
2. Написать алгол-программу решения задачи, введя при этом следующие процедуры:
а) Вычисление функции f(x), если она не является стандартной функцией алгола.
б) Вычисление Ф(а0, сц, ..., ал) = Ф(а).
т г-г , /-ч ( дФ (а) )
в) Получение вектора grad Ф (а) = j
fiS
Примечание. Для вычисления значения многочлена р„(х) и k
суммы вида £ §£т]г воспользоваться стандартными процедурами ! = 0
gorner и seal, имеющимися в библиотеке.
3. Подготовить тесты для отладки процедур и программы.
4. Отладить программу и решить задачу на машине. Полученные результаты выдать на АЦПУ в виде таблицы.
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Блок-схема программы.
3. Алгол-программа решения задачи.
4. Тесты для проверки процедур и программы, а также результаты отладки на машине.
5. Таблица полученных результатов.
6. Перечень и характеристика всех ошибок, обнаруженных при прохождении задания.
Литература.
1. Алгоритмический язык АЛ ГОЛ-60. Пересмотренное сообщение. — Пер. с англ, под ред. А. П. Ершова, С. С. Лаврова, М. Р. Шу-ра-Бура.—М.: Мнр, 1965.
2. Березин И. С., Жидков Н. П. Методы вычислений. Т. I. — М.: Наука, 1966. Т. II. — М.: Физматгиз, 1960.
3. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации. Гл. 8, с. 190—195.--М.: Мир, 1972.
4. Методические пособия и инструкции по программированию.
Приложение 1. Варианты к заданию
I. Функция f (х).
1. (1 +х)е~2х.
3. cos (х/10) • arctg х.
5. (Зх2- l)e~<
7. 3 cos (х) + х sin (х2).
2. cos (2х) — ch (х/5).
4. th (1 - х).
6. sin (х) е~х.
8. cos (2х + л/4)/(1 + хI. 2 3).
II. Значения cud.
С d
1 0.1 1.1
2 1 2
3 0.5 1.5
69
Ш. Значения М, иО, т.
пО т
1 20 2 2
2 20 3 2
3 20 2 3
4 25 2 2
5 25 3 2
6 30 2 2
7 30 3 2
П риложение 2. Метод спуска для отыскания минимума функции многих переменных
1. Пусть требуется найти локальный минимум функции
Ф (х) = Ф (Х1, х2, хп).
Выберем начальное приближение х<°> и построим последовательность х«», х<!), ..., х<4>, .... в которой каждое очередное приближение х<*+1> получается из предыдущего x(S) «шагом» в направлении вектора
х№+1) = xw + (1)
Выбор вектора определяет различные варианты метода «спуска» к минимуму Ф(х).
Величина шага управляется выбором А*. Обычно А& выбирается так, чтобы функция
фд (%) = ф (х№) + А»(й)) (2)
принимала наименьшее значение (если точек минимума несколько, то можно взять любую из них).
Точность полученного приближения к минимуму обычно оценивается по величине отклонения двух соседних приближений х<*> и х<4+1>, например
ДА+1 =|| х(&+1) - х<&) || = max [ х'/г+1) - х^ | (3)
нли
1 4+l) 1
б^+1 = max
(3.1)
Процесс приближений прекращается, если Д4 < е (абсолютная оценка приближения) или б* < е (относительная оценка приближения), где е — заданная точность.
70
2. «Скорейший» спуск получается, если шаг делать в направлении быстрейшего убывания ф(х), т. е. вдоль вектора
_ grad Ф (x(fe)) (vf} = - , / = 1,2, .... n). (4)
\ dxt ' J
Так как градиент — v = grad Ф(х) в любой точке ортогонален к поверхности уровня Ф(х) = С, то от точки xW следует двигаться в направлении до такой точки x!fc+1>, в которой vw ортогонален вектору v<*+1) (в этой точке X»(j!) касается поверхности уровня, т. е. будет достигнут минимум функции фДХ)).
Если Ф(х) —квадратичная функция (что как раз и имеет место в данном задании), то непосредственный метод скорейшего спуска сходится очень медленно. Поэтому необходимо использовать модифицированный метод скорейшего спуска, называемый методом сопряженных градиентов Флетчера-Ривса, который обеспечивает более быструю сходимость. В этом методе направление спуска — вектор
— выбирается следующим образом:
ti()) = — grad Ф (х<°>),
(о)
»(*+!) = _ grad Ф (х№+!)) 4-где
(й=о, 1,...). (6)
I grad Ф (x'e)) I
Таким образом, на каждом шаге спуск несколько отклокяется от «скорейшего» в направлении предыдущего шага, что дает некоторое ускорение сходимости вблизи точки минимума (когда близок к нулю grad Ф(х)).
В случае квадратичной функции Ф(х) описываемые методы сходятся при любом выборе начального приближения х!0).
3. Для вычисления на каждом шаге спуска нужно находить минимум функции одной переменной фДХ), определяемой равенством (2).
„ я d^k w
В общем случае для этого можно решать уравнение —----------=
= 0, выражающее условие минимальности фДХ), каким-либо из приближенных методов.
В случае, если ф(х)—квадратичная функция, ф*(Х) представляет собой квадратный трехчлен относительно X с положительным старшим коэффициентом и его минимум можно найти, если известны значения фДХ) при каких-либо трех значениях X. Выберем, например, для X значения —1, 0, 1 и вычислим (обратившись к процедуре Ф(х)) соответствующие значения фДХ) = Ф(х^> + Х»!4)). Обозначим их через i.i2 и !хз (Ца = Ф(х<4>) па самом деле можно не
71
63. Найти уравнение гиперболы, координаты фокусов которой суть (0; ±3) и действительная ось равна 4.
Отв. 5у2 — 4х2 = 20.
64. Найти угол ф между асимптотой и действительной осью
О
гиперболы, вершины которой отстоит от центра на -g- расстояния фокусов от центра.
_ 2
Отв. cos ф = —.
65. Две вершины эллипса расположены в фокусах гиперболы, вершины которой лежат в фокусах эллипса. Уравнение эллипса есть
16 т 9
Найти уравнение гиперболы.
Отв. 9х2 — 7 у2 = 63.
66. Показать, что эксцентриситет равносторонней гиперболы равен отношению диагонали квадрата, сторона которого равна оси гиперболы, к стороне этого квадрата.
67. Чему равен эксцентриситет гиперболы, если известно, что угол между ее асимптотами равен: а) 90°; б) 60°?
Отв. а) V2; б) -Дг.
Уз
68. Доказать, что произведение расстояний любой точки гиперболы до асимптот есть величина постоянная.
69. Через произвольную точку Р гиперболы проведена прямая, параллельная действительной ' оси гиперболы; эта прямая пересекает асимптоты в точках Q и Р. Показать, что PQ-PR = а2.
70. Точка перемещается на плоскости таким образом, что произведение угловых коэффициентов прямых, соединяющих эту точку с точками (—а; 0) и (а; 0), остается величиной постоянной. Показать, что при этом движении точка описывает либо эллипс, либо гиперболу.
Парабола
71. Составить уравнение параболы, если известно, что:
а) осью симметрии параболы служит ось Ох, вершина лежит в начале координат и расстояние от вершины до фокуса равно 6 единицам длины;
б) парабола симметрична относительно оси Ох, проходит через точку (2; —5) и вершина ее лежит в начале координат;
в) парабола симметрична относительно оси Ох, проходит через точку (—2; 4) и вершина ее лежит в начале координат;
г) парабола симметрична относительно осп Оу, фокус лежит в точке (0; 4) и вершина — в начале координат;
д) парабола симметрична относительно оси Оу, проходит через точку (6; 3) и вершина ее лежит в начале координат;
90 '' - л
е) парабола симметрична относительно осн Оу, проходит через точку (—6; —3) и вершина лежит в начале координат.
Отв. а) у2=±24х; б) г/2 = -|^-х;в) г/2 =— 8х; г) х2=16у;
д) х2 == 12у; е) х2 — — 12у. .
72. Вершиной параболы служит точка (а; 6) и осью симметрии — прямая, параллельная оси Ох. Вывести уравнение параболы, если известно, что параметр ее равен р.
Отв. (у — 6)2 = ±2р(х— а).
Указание. См. § 24.
73. Парабола проходит через точку (—1; —1) и имеет вершину
(3 \
—г;-; 21. Найти уравнение параболы, если ось ее па-
раллельна оси Оу.
Отв. 12х2 + 36х -|- у + 25 = 0.
74. Вершина параболы лежит в точке (2; 3); парабола проходит через начало координат, н ось ее параллельна оси Ох. Найти уравнение параболы.
Отв. 2у2 — 12у + Эх = 0.
75. Доказать, что уравнение х = Му2 -|- Ny -|- Р выражает параболу.
Указание. См. § 24.
76. Найти координаты вершины и фокуса н уравнения оси и директрисы параболы у2 -|- 4у — 6х + 7 = 0.
Отв. —2^; (2; —2); у+ 2 = 0; х+1=0.
77. Найти координаты вершины и фокуса и уравнения оси и директрисы параболы 4х2 + 4х + Зу — 2 = 0.
Отв. (-1; 1); (-1; 2х + 1 = 0; 1бу-19 = 0.
78. Найти уравнение параболы, если начало координат совпадает с фокусом и осью параболы служит ось Ох; параметр равен р.
Отв. у2 = ±2рх -|- р2.
79. Найти уравнение параболы, если ось кривой и директриса приняты соответственно за осн Ох н Оу; параметр равен р.
Отв. у2 — +2рх — р2.
80. Найти уравнение параболы, вершина которой находится в точке (3; 2) и фокус в точке (5; 2).
Отв. у2 — 4у — 8х + 28 = 0.
81. Найти уравнение параболы, вершина которой лежит в точке (—1; —2) и фокус в точке (—1; —4).
Отв. х2-|-2х-|-8у-|- 17 = 0.
82. Найти уравнение параболы, у которой фокус лежит в точке * (2; —1), а директрисой служит прямая у — 4 = 0.
Отв. х2 — 4х + 10у — 11 =0,
83. Найти уравнение параболы, у которой вершина лежит в точке (—2; —5), а директрисой является прямая х —3 = 0.
Отв. у2 + 10у + 20х + 65 = 0.
84. Найти уравнение параболы, у которой вершина лежит в точке (5; —2), а директрисой является прямая у + 4 = 0.
Отв. х2 — 10х — 8у + 9 = 0.
91
85. Найти координаты вершины и фокуса, уравнения оси а директрисы параболы:
а) х2 — 8х — 16г/ + 32 = 0; г) 4г/2 - 8г/ — 13х — 12 = 0;
б) х2 — 8х + 8г/ + 8 = 0; д) г/=10х — х2;
в) Зх2 - 2х + у 4- 5 = 0; е) у2 — 4х + 8 == 0.
Отв. а) (4; 1); (4; 5); х = 4; у + 3 = 0;
б) (4; 1); (4; —1); х = 4; у — 3 = 0;
в) “44); ("Г5 “4т); 3х-1==0: 12^ + 55=0;
Г) (-"ПТ’ 0; (“Жг 0 y=sl; 208x4-425=0;
д) (5; 25); ^5;24-|-j; х = 5; 4^-101=0;
е) (2; 0); (3; 0); у = О, х- 1 =9.
86. Мостовая арка имеет форму параболы. Определить параметр р этой параболы, зиая, что пролет арки равен 24 м, а высота 6 м.
Отв. р = 12.
87. На рис. 39 изображен продольный разрез параболического зеркала. Найти абсциссу фокуса зеркала по данным эскиза.
Отв. х — 5,625.
88. Предполагая, что проволока, соединяющая точки Л4 и N (рис. 40), имеет форму параболы, иайти уравнение параболы при р = 0,1, h = 1 и I == 10.
Отв. у — — 0,02 (1 + /ТТ) х +
4-0,002(6 4-/П)х2.
Указание. Взять уравнение параболы в“ виде у — Ах2 А-Вх + С. Ордината вершины определяется соотношением
. 4 АС - В2
Ь =....4А ‘
Кроме того, парабола проходит через точки М и N, координаты которых известны. На основании этих условий можно составить три уравнения относительно коэффициентов А, В, С.
89. Найти точки пересечения двух парабол, имеющих общую вершину в начале координат, а фокусы — в точках (2; 0) и (0; 2).
Отв. (0; 0); (8; 8).
х2 г/2
90. Найти точки пересечения эллипса -г™ 4* -2— = 1 с пара-1ии 64
болой, вершина которой лежит в центре эллипса, а фокус которой совпадает с правым фокусом эллипса.
Отв. (у; ±2/15).
92
91. В параболу у2 == 2рх вписан равносторонний треугольник, одна из вершин которого совпадает с вершиной параболы. Найти длину стороны_треугольпика.
Отв. 4р У 3.
92. Из начала координат проводятся прямые. Показать, что геометрическое место точек, лежащих на этих прямых, ординаты которых равны абсциссам точек пересечения проведенных прямых с прямой у = а, есть парабола.
93. Найти геометрическое место точек, кратчайшее расстояние каждой из которых от данной окружности равно расстоянию точки от фиксированного диаметра этой окружности.
Отв. Две параболы.
94. Взаимно перпендикулярные отрезки АВ и CD являются диаметрами окружности. Из каждой точки М окружности проводятся отрезки AM и ВМ. Отрезок AM пересекает диаметр CD в точке N; через точку Аг проводится прямая, параллельная диаметру АВ, пересекающая отрезок ВМ в точке Р. Показать, что геометрическим местом точек Р является парабола.
95. Вершина треугольника, основание которого остается неизменным, перемещается так, что сумма тангенсов углов треугольника, прилежащих к основанию, остается постоянной. Показать, что кривая, описываемая вершниой треугольника, есть парабола.
96. Найти геометрическое место центров окружностей, проходящих через данную точку и касающихся данной прямой.
Отв. Парабола.
97. Найти геометрическое место центров окружностей, касающихся дайной окружности и данной прямой.
Отв. Парабола.
НАСТЬ ВТОРАЯ
ЭЛЕМЕНТЫ
МАТЕМАТИЧЕСКОГО АНАЛИЗА
ГЛАВА IV
ТЕОРИЯ ПРЕДЕЛОВ
§ 26. Некоторые соотношения между абсолютными величинами чисел. В математическом' анализе постоянно приходится встречаться с необходимостью рассматривать соотношения между абсолютными величинами различных выражений. Поэтому в настоящем параграфе мы напомним основные формулы, относящиеся к этому вопросу.
Напомним еще раз, что абсолютной величиной числа а называется само число а, если оно положительное или нуль, и число —а, если а отрицательное. Абсолютная величина числа а обозначается символом |а].
Таким образом al = a, если а 0; |а| =—а, если а < 0. Например, 5| = 5; |—5| = —(—5) — 5;
1. Абсолютная величина алгебраической суммы меньше или равна сумме абсолютных величин слагаемых-.
| а + h + с + ... + v | | а | +1 b | +| с |+ ... +1 v |. (1)
Справедливость этого предложения иллюстрируется примерами:
1) | 3 -Ь 5 4- 8 | = | 161=16;
|ЗЦ-|5Ц-|8| = 3 + 5Н-8 = 16;
следовательно,
|3 + 5 + 8| = [3| + |5| + |8|.
2) |_3-5-8| = |—16|=16;
|-3|+ |-51 + |-8| = 3 + 5 + 8=16;
94
г
следовательно,
1-3-5-8 | = |-3| + |-5| + |-8|.
3) |3-5 + 8| = |6| = 6;
|3 | + | -5| + |8| = 3 + 5 + 8 = 16;
следовательно,
|3-5 + 8|<|3] + |-5| + |8|.
Очевидно, в соотношении (1) знак равенства будет иметь место в том случае, когда все слагаемые имеют одинаковые знаки, а знак неравенства, — когда знаки слагаемых неодинаковы.
Следовательно, в общем случае, т. е. когда знаки слагаемых алгебраической суммы могут оказаться как одинаковыми, так и различными, мы можем только утверждать, что абсолютная величина алгебраической суммы, не превосходит (т. е. либо меньше, либо равна) арифметической суммы абсолютных величин слагаемых.
2 . Абсолютная величина произведения любого числа сомножителей не зависит от знаков перемножаемых чисел. Поэтому всегда имеем
|а-&-с...о| = |а|-|&|’|с|...|о|.
3 . Абсолютная величина частного не зависит от знаков делимого и делителя. Поэтому всегда имеем
la I _ | а | 1*1 “I ь I*
§ 27. Переменные и постоянные величины. Простое наблюдение окружающего мира заставляет нас различать величины двух типов: постоянные и переменные. Так, например, расстояние от земли камня, брошенного вверх, есть величина переменная, а его объем — постоянная величина.
Строго говоря, при этом и объем камня не остается постоянным, а изменяется от различных причин, например от изменения температуры воздуха. Однако это изменение столь ничтожно, что практически объем камня, брошенного вверх, мы считаем постоянным. Вряд ли также кто-нибудь при покупке материи станет
95
учитывать изменение длины метра, которым меряется материя, хотя в действительности метр также находится в постоянном изменении под воздействием разнородных причин (например, влажности и температуры воздуха), влияющих на вещество, из которого он сделан.
Таким образом, сама практика заставляет нас различать величины переменные и величины постоянные.
В математике мы отвлекаемся от физического содержания величины, интересуясь лишь числом, которым она выражается.
Математическая величина называется переменной, если она может получать различные численные значе-ния в условиях рассматриваемого вопроса.
Постановка каждого данного вопроса определяет, какие из рассматриваемых при этом величин являются переменными и какие постоянными.
Например, в треугольнике, вершина которого перемещается по прямой, параллельной основанию, углы и боковые стороны суть величины переменные, а основание, высота, площадь и сумма углов — величины постоянные.
Если же вершина треугольника перемещается по прямой, не параллельной основанию, то высота и площадь станут уже переменными величинами, а постоянными останутся только основание и сумма углов.
Однако существуют и такие величины, которые остаются постоянными при рассмотрении любого вопроса, любой задачи. К числу такого рода постоянных относятся, например, сумма углов треугольника, отношение длины окружности к диаметру (число л), числа 5, —1, ит. п.
Постоянные величины обозначают обыкновенно первыми буквами латинского алфавита: а, Ь, с......пере-
менные же — последними: х, у, г, ...
Во всем дальнейшем мы будем предполагать, что все рассматриваемые значения величин суть числа вещественные.
§ 28. Бесконечно малые величины. 1. В математическом анализе исключительно важную роль играют переменные величины, изменяющиеся так, что их численные значения неограниченно приближаются к нулю. Такие величины особо выделяются и свойства их подвергаются подробному изучению; они встречаются столь часто, что 96
им присвоено специальное краткое наименование, а именно, их называют бесконечно малыми*).
Определение. Переменная величина а называется бесконечно малой, если она при своем изменении становится и затем остается по абсолютной величине меньше любого наперед заданного сколь угодно малого положительного числа е:
I а | < е.
Рассмотрим несколько примеров бесконечно малых величин.
Пример 1. Рассмотрим маятник, который, будучи выведен из положения равновесия, начинает совершать колебания (рис. 41). Будем определять положение маятника углом а, /
который он образует с вертикаль-ной прямой (положение равнове- . / ,
сия). Угол а будем считать положи-, /
тельным или отрицательным в за- ''»»______J___
мисимости от того, справа или слева от вертикали находится маятник.
В силу сопротивления среды Рис. 41. размахи колебания маятника будут постепенно уменьшаться; поэтому, какое бы положительное число е ни было задано, отклонение а по абсолютной величине станет и впредь будет оставаться меньше е.
Следовательно, а есть величина бесконечно малая; при своем изменении она принимает как положительные, так и отрицательные значения и значения, равные нулю.
Пример 2. Покажем, что переменная величина у = х3 при неограниченном приближении х к нулю есть величина. бесконечно малая.
Зададимся каким-нибудь положительным числом е, например числом е = 0,001. Неравенство
или, что то же,
| у | < 0,001
| х31 < 0,001
*) Недаром, как это мы отмечали во «Введении», дифференциальное и интегральное исчисление называются также анализом бесконечно малых.
4 Н, П, Тарасов
97
будет выполняться, как только х, приближаясь к 0, станет по абсолютной величине меньше У 0,001 =0,1:
I г I л 1
Очевидно, неравенство |z/|< 0,001 будет оставаться справедливым и при дальнейшем приближении х к нулю.
Возьмем теперь другое, меньшее положительное число е, например ё = 0,000001. Неравенство
\у |< 0,000001 или, что то же, |х3|< 0,000 001 осуществится, как только х по абсолютной величине станет меньше 1^0,000 001=0,01:
| х | < 0,01.
Очевидно, неравенство |у| < 0,000 001 будет оставаться справедливым и при дальнейшем приближении х к нулю.
Так же будет обстоять дело и для всякого наперед заданного числа е: как только х станет по абсолютной -.3/— величине меньше V г,
I х | < l/4 е, так будет выполнено неравенство | х31 < е, и это неравенство будет сохраняться при дальнейшем приближении х к нулю.
Таким образом, переменная величина у при неограниченном уменьшении абсолютной величины х, что записывают в виде х—>0, удовлетворяет признаку, определяющему бесконечно малую величину.
ПримерЗ. Покажем, что отношение — при безграничном увеличении х, или, как говорят, при х, стремящемся к к+°° (х-*.+°о)» есть величина бесконечно малая.
Заметим прежде всего, что так как х неограниченно возрастает, то мы можем рассматривать лишь 98
положительные значения х, а тогда
, 14|=Ь
Возьмем е= юооооо* Неравенство
1 1 х 1 000 000
осуществится, как только х, возрастая, станет больше 1000000 и, очевидно, при дальнейшем возрастании х неравенство также будет оставаться справедливым.
Вообще, каково бы ни было задано положительное
число е, неравенство
станет справедливым, как только х станет больше, чем —, и будет выполняться при дальнейшем возрастании хл
Пример 4. Отношение — у при безграничном возрастании х также есть величина бесконечно малая.
В самом деле, в определении бесконечно малой а сказано, что абсолютная величина переменной а, а не сама она, должна становиться и впредь оставаться меньше любого наперед заданного положительного числа е; поэтому будет ли переменная а при этом принимать только положительные значения или только отрицательные, или будет при своем изменении становиться то положительной, то отрицательной, не играет никакой роли.
тл • f I 1 I 1 *
Когда %-> + °0, то I — — = —. А так как мы дока-
1 ,
зали, что — есть величина бесконечно малая при х-> + °о, то, значит, и —также есть величина бесконечно малая.
П р и м е р 5. Рассмотрим опять переменную у и покажем, что эта переменная является величиной бесконечно малой, когда х, оставаясь отрицательным, неограниченно возрастает по абсолютной величине. Именно этот случай имеют в виду, когда говорят, что х «стремится к минус бесконечности» (х—>—оо).
4*
99
9. Генерировать только подходящие значения d в порядке их убывания с выдачей в качестве результата очередного значения.
10. Таким же путем, как и в варианте 9, получить все подходя* щие значения d и выдать их в качестве результата.
11. Любой другой способ, отличный от указанных выше (по желанию студента).
II. Вид экстремума f(X).
1. Максимум.
2. Минимум.
III. Используемый библиотечный модуль.
1. ASG2D — компактная схема Гаусса с выбором главного элемента по всей матрице.
2. ASG5D — метод вращений.
3. ASG6D — метод отражений.
Правила использования библиотечных модулей приведены в Приложении 2.
Во всех вариантах задания для решения задачи взять m = 6, п = 4, f(X) = 2.746*1 + 3.647х2 + 1.770*3 + 3.274х4 и следующую систему неравенств (1):
1.075*1 + 2.500*2 + 1.835х3 + 0.870х4 < 1,
2.580*1 + 1.245*2 + 0.770х3 + 1.035х4 < 1,
— 1.455X1 — 0.950*2 — 3.250х3 — 1.035*4 < — 1,
— 1.070*! + 0.950*2 + 0.770х3 + 1.035х4 < 1,
1.075*1 + 0.950*2 + 0.770х3 — 100.0х4 < — 1,
—— 0.010*1 — 0.010*2 “Ь 0.000х3 -f- 1.035х4 1.
Приложение 2. Инструкция пользования библиотечными подпрограммами
Каждая из указанных ниже подпрограмм, входящих в библиотеку фортран ЕС ЭВМ, предназначена для решения с удвоенной точностью системы линейных алгебраических уравнений Ах = b тем или иным методом.
В операторах вызова подпрограмм будут использоваться следующие обозначения фактических параметров:
N — константа пли переменная (типа целое), задающая порядок системы;
А — двумерный массив размера N X N, в котором задается матрица системы;
В — вектор длины N, в котором задается правая часть системы;
X — вектор длины N, в котором запоминается найденное решение;
L — константа или переменная (типа целое), задающая режим работы подпрограммы; L = 1 означает, что система с данной мат-
82
72
Глава III
I
<>
Для установки фланцевых кранов (см. рис. 24) на газопроводе на концы труб надеваются такие же фланцы, привариваемое к трубам. Для уплотнения между фланцев кладутся прокладки из клингерита, паронита, асбестового или тряпичного картона, после чего фланцы стягиваются болтами. При этом подтягивание гаек болтов производится постепенно, за несколько приемов и обязательно крест-накрест, чтобы не допустить перекоса фланцев и неплотного их соединения.
За последнее время широкое применение на газопроводах всех давлений получили краны с уплотняющей принудительной смазкой, часто называемые самосмазывающимися. На рис. 25 показан самосмазывающийся чугунный фланцевый кран, рассчитанный на давление газа до 6 amu, устанавливаемый на газопроводах диаметром в 80 и 100 мм и перед горелками, при температуре окружающего воздуха не выше 40° С. При вывернутом болте нагнетания смазки 2 густая смазка закладывается в пустотелую часть пробки крана, откуда она под действием нажимного болта, ввертываемого по резьбе, нагнетается по каналам 1 пробки к ее боковой поверхности в верхней и нижней части и в пространство под пробку. При этом пробка несколько приподнимется и смазка распространится по всей ее боковой поверхности, чем и достигается постоянная смазка уплотняющих поверхностей ; крана, не требующая его разборки.
В результате такой смазки исключается возможность прилипания и заедания пробки в корпусе крана — ход его облегчается и уменьшается износ.
Для того чтобы газ по каналам не мог проникнуть наружу, в нижней части основного канала внутри пробки установлен шариковый обратный клапан и над буртиком пробки укладывается специальная прокладка из листовой латуни.
Для кранов с принудительной смазкой применяется смазка - типа ЦИАТИМ-205, обеспечивающая плотность кранов, легкость хода, наименьший износ и защиту от коррозии.
Самосмазывающиеся краны (или краны с уплотняющей принудительной смазкой) типа КППС выпускаются заводами «Глав-нефтемаш» с условным диаметром прохода 50, 80, 100, 150 и 200 мм; последние два размера оборудованы червячной передачей для облегчения их провертывания; подобные краны выпускаются также заводами «Энергочермет» — типа КАП-1 и КАП-2 с условным диаметром прохода в 38 и 65 мм и заводами «Главгидромаш» для высоких давлений газа (до 64 кГ1см2)^ типа 11 с 320 бк (рис. 26), для газопроводов с диаметром 80—300 мм.
Краны для бесколодезной подземной установки (11 с 321 бк) выпускаются с условным диаметром 400—700 мм; они снабжены дополнительным наружным трехходовым краном, служащим для разгрузки пробки от одностороннего давления газа при открытии
Газовые сети и сетевые устройства
73
Рис. 26. Кран с принудительной смазкой и червячной передачей:
£, болт нагнетания смазки; 2 — канавки и каналы смазки в пробке крана; 3 — подпятник и опорный шарик пробки; 4 — нижняя крышка крана; 5 — верхняя крышка крана!
6 — штурвал червячной передачи поворота пробки.
14
Глава III
крана и присоединяются к газопроводам при помощи сварки.
На каждый кран внутренней разводки газопроводов котельной установки во время ее работы должен быть постоянно надет накидной ключ, чтобы было возможно быстро закрыть любой кран. Ключи надеваются на квадратную головку пробки крана так, чтобы в открытом состоянии крана ручка ключа находилась вдоль трубы газопровода и риски крана.
При этом на вертикальных участках газопровода ключ должен надеваться на квадрат пробки крана таким образом, чтобы при закрытии крана ручка ключа вместе с пробкой удерживалась ограничителем поворота и не могла открыть кран своим весом.
Сама ручка крана не должна быть длиннее шести диагоналей квадрата пробки крана. Наращивать ручку крана путем надевания на нее обрезка трубы или другого ключа, чтобы легче было поворачивать пробку крана, запрещается. Хорошо притертый и смазанный кран должен проворачиваться рукой с небольшим усилием и при этом не должен пропускать газ.
Краны до установки их на газопроводах и регуляторных станциях должны быть разобраны, промыты, смазаны и испытаны на прочность, плотность материала и герметичность, если на них нет заводских паспортов, удостоверяющих проведение испытания. Согласно требованиям ГОСТ 7520—55 и 356—59, арматура трубопроводов, рассчитанная на рабочее давление 1, 2,5, 4, 6, 10, 16, 25, 40, 64 и 100 ати подвергается испытанию на прочность и плотность материала водой на пробное давление соответственно в 2, 4, 6, 9, 15, 24, 38, 60, 96 и 150 ати. На герметичность краны, рассчитанные на рабочее давление газа до 100 ати, испытываются воздухом на давление, в 1,25 больше рабочего при погружении в воду. Пропуска воздуха через пробку при нормальной смазке быть не должно.
Краны, предназначенные для работы на давлении газа меньше 0,4 ати, должны испытываться на герметичность воздухом на давление 0,5 ати.
Пробковые краны при их сборке, установке и ремонте должны смазываться термоустойчивой смазкой, если они установлены перед агрегатами, где температура воздуха превышает 25° С. В состав термоустойчивой смазки входят: горный воск — 50%, цилиндровое масло—40% и графитный порошок — 10%. При более высоких температурах необходима смазка колипсолином или смазкой 1/13с. При температурах ниже 25° С краны нужно смазывать техническим вазелином, солидолом.
Преимуществом пробковых кранов является простота их устройства, достаточная плотность запора (при правильной
Газовые сети и сетевые устройства
75
сборке и уходе за ними) и быстрота их открытия и закрытия Кроме того, полностью в открытом положении кран дает свободный проход газу в прямом направлении, т. е. оказывает малое сопротивление его движению, в результате чего краны дают наименьшую потерю давления газа.
Недостатком кранов является трудность их хорошей притирки, возможность заедания пробки в корпусе крана при недостаточной смазке. Запирающие поверхности кранов легко повреждаются твердыми частицами, отчего кран может пропускать газ наружу. Указанные недостатки особенно проявляются у кранов больших размеров, поч’ему краны с диаметром прохода более 70 мм не применяются. Исключение составляют краны с уплотняющей принудительной смазкой.
Задвижки
Задвижки являются наиболее распространенными запорными устройствами, применяемыми на газопроводах с диаметром более 70 мм. Задвижками (см. рис. 27 и 28) называются запорные устройства, в которых отключение газа осуществляется передвижным затвором, называемым диском или клином.
Перемещение затвора в корпусе задвижки осуществляется вращением маховика 7, соединенного с затвором при помощи шпинделя 3, имеющего на своей поверхности ленточную резьбу. По расположению резьбовой части шпинделя задвижки разделяются на задвижки свыдвижным и невыдвижным шпинделем. Резьба выдвижного шпинделя находится вне корпуса задвижки и проходит через нарезную втулку в центре маховика, опирающуюся на стойку в верхней части корпуса задвижки. При вращении маховика шпиндель будет вытягиваться из корпуса задвижки наружу и переместит закрепленный на его другом конце затвор из нижнего (закрытого) положения в верхнюю часть внутри корпуса задвижки и этим откроет свободный проход через задвижку. Закрытие задвижки производится вращением маховика в обратную сторону, при этом шпиндель, двигаясь внутрь задвижки, переместит затвор в прежнее положение.
В задвижках с невыдвижным шпинделем конец его резьбовой части входит в нарезную втулку, находящуюся в верхней части затвора задвижки. На другом конце шпинделя закрепляется маховик. При вращении маховика шпиндель благодаря имеющемуся на нем бурту 4 перемещается вдоль своей оси и не может подняться, а будет вращаться вместе с маховиком. При этом нарезная втулка затвора будет перемещаться по его резьбе вверх или вниз, в зависимости от того, в какую сторону будет вращаться маховик, поднимая или опуская затвор задвижки. Открытие задвижки осуществляется вращением маховика влево, а закры-
76
Глава III
тие — вращением вправо (по часовой стрелке). Однако могут быть отдельные конструкции задвижек с левым вращением, при
котором закрытие их достигается вращением маховика влево (против часовой стрелки).
По устройству затворов задвижки подразделяются на клиновые и п ар а fl-fl е л ь н ы е. В клиновых задвижках боко-
Рис. 27. Задвижка клиновая с невыдвижным шпинделем:
1 — клин; 2 — гайка; 3 — шпиндель; 4— буртик; -5 — крышка; 6 — втулка; 7 — маховик;
8 — направляющие ребра; 9 — сальник.
Рис. 28. Задвижка с двухдисковым клином и выдвижным шпинделем:
1— двухдисковый клин; 2— шаровой грибок.
Рис. 29 Задвижка параллельная:
1 — корпус; 2 — запорные диски; 3 — клин; 4 —шпиндель; 5 — сальниковая набивка; 6 — маховик; 7 — уплотняющие поверхности корпуса.
вые поверхности затвора расположены наклонно к вертикальной оси корпуса задвижки. Этим достигается плотное прилегание уплотнительных поверхностей клина к уплотнительным поверхностям корпуса, а следовательно, и необходимая плотность задвижки. Клиновые задвижки могут быть со сплошным затвором (клином) (рис. 27) и шарнирным затвором, состоящим из двух дисков (рис. 28). Задвижки со сплошным клином более просты по устройству и надежны в работе в отношении поломок, особенно в условиях газопроводов, по которым перемещается холодный газ. В случае применения подогретого газа в установках, где требуется достичь более высокой температуры в топке, такие задвижки могут заедать, заклиниваться и пропускать газ в ре
Газовые сети и сетевые устройства 77
зультате неравномерного расширения деталей затвора при нагревании.
В таких случаях чаще применяют двухдисковые задвижки, так как они не способны заклиниваться. Кроме того, при износе уплотнительных поверхностей дисков в этих задвижках легче восстановить плотность затвора. Восстановление изношенных сплошных затворов значительно сложнее.
Параллельными называются задвижки, у которых расположение уплотнительных поверхностей затвора не конусное, а параллельное.
Из параллельных задвижек на газопроводах часто употребляются задвижки типа «Лудло» (рис. 29). В этой задвижке затвор состоит из двух половин или дисков 2, между которыми находится распорный клин 3. При закрытии задвижки клин, упираясь в ее дно, разжимает диски, прижимая их уплотнительные поверхности 7 к таким же поверхностям корпуса задвижки, чем и обеспечивается необходимая ее плотность. В других конструкциях параллельных задвижек разжатие дисков достигается при помощи двух.клиньев (задвижка «Москва»), пружин и других устройств. Корпусы задвижек, употребляемых для газа, изготовляются, как правило, из чугуна, но могут быть и из литой стали. Шпиндели изготовляются из углеродистой и нержавеющей стали. Затворы клиновые и дисковые — из чугунд, углеродистой и нержавеющей стали, причем могут быть целые или с вставными уплотняющими кольцами из нержавающей стали. В последнем случае и в корпус задвижки впрессовываются такие же кольца.
Задвижки с затворами или уплотняющими кольцами из бронзы не рекомендуется применять на искусственных газах, содержащих аммиак, ввиду разъедания им бронзы, что приводит к пропуску газа задвижками. Плотность прилегания уплотняющих поверхностей затворов к уплотняющим поверхностям корпуса задвижек достигается соответствующей их обработкой — притиркой и шабровкой. Во избежание быстрого износа уплотняющих поверхностей затворов задвижек от действия твердых частиц, приносимых газовым потоком, и оседания их на дисках запорные задвижки должны находиться постоянно в полностью открытом или полностью закрытом положении, если они не являются регулировочными задвижками. Для предотвращения утечки газа из корпуса задвижки на поверхности шпинделя последний уплотняется при помощи сальника.
Набивкой для сальников служит просаленный шнуровой асбест с графитом и без него, асбестовые хлопья, пропитанные сдец-смазкой и специальные набивки — рациональ, фенопласт и др.
Установка задвижек на газопроводах производится при помощи фланцев, как было указано выше для фланцевых кранов.
78
Глава III
Монтаж задвижек и кранов на подземных газопроводах необходимо производить особо тщательно, так как постоянное наблюдение за ними затруднено. При установке задвижек на прямых участках газопроводов необходимо рядом с ними устанавливать линзовый компенсатор. Это нужно для предохранения от разрушения фланцев задвижки при расширении или сжатии газопровода под влиянием изменения температуры. Кроме того, без компенсатора невозможна перестановка задвижки или смена прокладок во время эксплуатации без разрезания газопровода.
Задвижки и краны, устанавливаемые на подземных газопроводах, должны монтироваться только в специальных колодцах (рис. ЗЭ, рис. 31).
На подземных газопроводах преимущественно употребляются задвижки со сплошным клиновым затвором и непременно с невыдвижным шпинделем. Наоборот, на надземных газопроводах установка задвижек с выдвижным шпинделем удобнее, так как позволяет легко очищать и смазывать резьбу шпинделя. Кроме того, в задвижках с выдвижным шпинделем по количеству ниток резьбы на выступающем его конце над маховиком можно на глаз определять, открыта задвижка или закрыта и, если открыта, то на какую величину, что облегчает обслуживающему персоналу при работе регуляторной станции по байпасной линии и в других случаях регулирование подачи газа в горелки.
Задвижки необходимо монтировать на горизонтальных участках газопровода шпинделем вверх и при этом на такой высоте и в таком месте, чтобы их было удобно обслуживать во время работы установки и разбирать и собирать при ремонте. Вследствие того, что давление газа при закрытой задвижке действует на затвор с одной стороны, прижимая его к противоположной уплотняющей поверхности корпуса, открытие задвижек с большим диаметром и особенно при большом давлении газа может стать для одного человека непосильным. Поэтому на задвижках с диаметром прохода свыше 300 мм, устанавливаемых на высоком давлении газа, обычно имеются наружные обводы с вентилем небольшого диаметра, соединяющим пространство задвижки до затвора с пространством после него.
Перед открытием затвора задвижки открывают вентилек на обводе (байпасе), благодаря чему газ перетекает на другую сторону затвора задвижки, снижая давление газа перед ним и повышая давление газа после него. Таким образом, разгружается одностороннее давление на затвор и задвижка легко может быть открыта.
Перед установкой задвижек на газопроводы они должны быть испытаны на плотность керосином. Для этого у закрытой задвижки одну сторону затвора окрашивают меловым раствором и дают ему просохнуть; затем задвижку окрашенной стороной
Газовые сети и сетевые устройства
79
Рис. 30. Установка задвижки в колодце:
1 — задвижка; 2 — линзовый компенсатор; 3 — футляр
Рис. 31. Установка крана в колодце:
1 — кран; 2 — труба; 3 — прокладка; 4 — люк; 5 — стенка колодца; в — железобетонное днище.
кладут вниз, а на затвор с другой стороны наливают керосин. Если через час керосиновые пятна не будут обнаружены на окрашенной стороне диска, задвижка имеет достаточную плотность. Для задвижек, устанавливаемых на газопроводах низкого давления, испытание задвижки на плотность достаточно проводить
80
Глава III
в течение 10 мин. Задвижки, как и краны, имеют то преимущество, что в полностью открытом положении дают газу свободный прямой проход в любом направлении; вследствие этого они обладают малым сопротивлением и не вызывают большого падения давления газа при проходе через них. Это обстоятельство делает их основным запорным устройством, применяемым на газопроводах с диаметром более 70 мм.
Основной недостаток задвижек: после непродолжительной работы они часто начинают пропускать газ вследствие износа и загрязнения их уплотнительных поверхностей. Очистка и пригонка уплотнительных поверхностей задвижек является трудоемкой работой, требующей разборки задвижки и снятия ее с газопровода. Это обстоятельство вынудило отказаться от установки задвижек на газопроводах высокого давления и перейти на установку самосмазывающихся пробочных кранов диаметром 400 — 700 мм типа 11 с 321 бк.
Вентили
Вентили в качестве запорных устройств газопроводов употребляются редкр вследствие ряда недостатков, вытекающих
Рис. 32. Вентиль запорный муфтовый:
1 — тарелка клапана; 2 — шпиндель; 3 — маховик; 4 — крышка;
5 — сальниковая набивка; в — грундбукса сальника; 7 — нажимная крышка сальника.
из их устройства.
Вентилями называются такие запорные устройства, в которых отключение потока газа осуществи ляется путем прикрытия проходного отверстия специальным затвором, называемым клапанохМ (или золотником). Корпус вентилей (рис. 32) изготовляется из бронзы, чугуна и литой стали. Внутри корпуса вентиля имеется перегородка с круглым отверстием и центре, седлом, прикрываемым тарелочным клапаном. Открытие вентиля осуществляется подъемом клапана от седла вращением влево маховика 3 и шпинделя 2, к которому подвешен клапан. Закрытие вентиля производится вращением маховика вправо (по часовой стрелке), при этом, благодаря свободному креплению тарелки клапана к шпинделю, он плотно прижимается к седлу. Плотность приле
гания тарелки клапана достигается притиркой уплотнительной поверхности тарелки клапана к уплотнительной поверхности
Газовые сети и сетевые устройства
81
седла. Материалом для изготовления седел и клапанов и их уплотнительных колец служит бронза, чугун, углеродистая и нержавеющая сталь. В некоторых вентилях небольших размеров тарелка клапана выполняется с уплотнением из кожи или газостойкой резины.
Плотность закрытия вентилей и относительная легкость притирки их клапанов к седлам является большим преимуществом
Рис. 33. Схема прямоточного вентиля:
1 — корпус; 2 — тарелка клапана; з — шпиндель; 4 — сальник; 5 — маховик.
вентилей по сравнению с задвижками и кранами. Однако основным недостатком вентилей, вследствие которого применение их на газе ограничено, является большая потеря давления газа при проходе его через вентиль по сравнению с кранами и задвижками. Эта потеря давления вызывается тем, что проход через вентиль не прямой, а с изломом. Сопротивление вентиля очень велико и может быть больше сопротивления задвижки в 10—20 раз в зависимости от конструкции вентилей. Наименьшее сопротивление проходу газа оказывают прямоточные вентили с наклонным шпинделем (рис. 33), однако и их сопротивление в два раза больше сопротивления задвижек. Применение таких вентилей, особенно на газе среднего и высокого давления, целесообразно.
6 Чепель В. М.
82
Г л a, a III
|JF Другим недостатком вентилей является их громоздкость при больших проходных диаметрах, вследствие чего они изготовляются диаметром не более 300 мм. Выдвижной шпиндель вентилей также делает их неудобными для применения на подземных газопроводах. Установка вентилей на газопроводах производится при помощи муфт и фланцев так же, как устанавливаются краны и задвижки. Установка вентилей должна выполняться так, чтобы поток газа имел направление под тарелку
Рис. 34. Герметичный газовый клапан:
1 — корпус; 2 — седло; з — тарелки: 4 — шток; 5— пружина; 6 — пластикатовая диафрагма; 7 — кольцо;
8 — гайка; 9 — предохранительная шайба; 10 — крышка; 11 — скоба.
клапана («под клапан»). При пуске газа «на клапан» сопротивление вентиля проходу газа будет еще больше, и открывать его, вследствие давления на клапан газа, будет трудно. При этом не исключена возможность отрыва тарелки клапана от шпинделя и прекращения подачи газа.
На рис. 34 показан разрез отключающего герметического газового клапана (ГК-10-100) ЛНИИ АКХ конструкции инж. {Кузьмина П. А., предназначенного для применения на внутренних газопроводах низкого давления малого диаметра (3/«"). Особенностью клапана является отсутствие притирающихся поверхностей и сальниковых уплотнений, надежное отключение и герметичность, исключающая возможность утечки газа наружу, почему эти клапаны особенно удобны на газовых бытовых приборах и квартирной разводке. Корпус клапана вентильного типа отливается из чугуна. Седло клапана 2 прикрывается тарелкой клапана 3 с трехслойной пластикатовой прокладкой. Тарелка
Газовые сети и сетевые устройства 83
через шток 4 (на нижнем конце которого она закреплена шарнирно, что допускает ее вращение вокруг своей оси) прижимается к седлу пружиной 5, что обеспечивает большую плотность отключения клапана. Газ поступает на тарелку клапана, и это обеспечивает еще большую его плотность.
Утечка газа наружу исключается трехслойной полихлорви-ниловой пластикатовой диафрагмой 6, плотно зажатой по краям кольцом 7 и в центре гайкой 8. Диафрагма усилена стальной предохранительной шайбой 9. Открытие и закрытие клапана производится поворотом его крышки 10, упоры которой передвигаются по винтовой поверхности кольца 7, в результате чего тарелка клапана приподнимается над седлом или отделяется от него.
Сопротивление этого клапана, установленного на газопроводе перед газовой квартирной плитой, составляет 5 мм вод. ст.
6*
Глава IV
ГАЗОСНАБЖЕНИЕ ПРЕДПРИЯТИЙ
Виды газоснабжения
Снабжение газообразным топливом котельных и других устройств коммунально-бытовых и промышленных предприятий от городских газовых сетей осуществляется по следующим схемам.
1. Горючий газ подается в систему газоснабжения предприятия прямо из газопроводов низкого давления городской сети. Такое газоснабжение допустимо для небольших коммунальнобытовых или промышленных предприятий, потребление газа которыми не нарушит нормальную работу газовых приборов жилых домов, присоединенных к этим же газопроводам.
2. Снабжение газом больших предприятий производится от распределительного газопровода среднего давления. В этом случае газ по ответвлению направляется на местную газовую регуляторную станцию предприятия, где его давление снижается до среднего (т. е. до необходимого давления в пределах от 500 .о вод. ст. до 3 ати) или низкого давления в зависимости от газового оборудования установки предприятия, потребляющего газ. На газовой регуляторной станции возможна установка двух регуляторных устройств. Первое — снижающее давление газа до среднего давления, на котором работает, например, котельная установка, располагаемая согласно положению Котлонадзора в отдельном помещении. Второе — регуляторное устройство, понижающее давление газа до низкого, расходуемого на газовые установки, находящиеся в цехах предприятия, например, на газовые печи различных назначений, газовые водогреи, стиральные машины и т. п.
3- Горючий газ подается в систему газоснабжения предприятия от газопровода высокого давления (до 6 ати) городской газовой сети или отдельного газопровода (до 12 ати).
В этом случае газ по ответвлению поступает на газовую регуляторную станцию предприятия, где его давление снижается до среднего или низкого давления. В тех случаях, когда на предприятии имеются установки, работающие на газе низкого и среднего давления, необходима установка двух
Газоснабжение предприятий
85
регуляторных устройств, расположенных параллельно, как отмечалось в предыдущей схеме, или последовательно, одна за другой, с понижением давления газа в первой до среднего, после которой часть газа направляется во вторую, где его давление понижается до низкого.
4. Возможны случаи снабжения предприятия газом среднего и низкого давления по двум раздельным вводам.
Вводы и межцеховые газопроводы
На ответвлениях к предприятию устанавливается отключающая задвижка (или кран), принадлежащая городской газовой сети и являющаяся границей между ответвлением сети и вводом предприятия. На подземных вводах задвижка-устанавливается вне территории предприятия в колодце на расстоянии не ближе 2 jh от стены здания или ограждения, в месте, удобном для ее обслуживания и с выводом управления ею к поверхности земли, под крышку колодца.
При низком давлении газа на вводе допускается установка гидравлического затвора.
Если межцеховой газопровод (ввод) прокладывается по территории предприятия над землей, первая по ходу газа задвижка предприятия устанавливается на газопроводе на месте выхода его из земли, на высоте 1,5 м от земной поверхности.
Межцеховые газопроводы и их устройства, регуляторные станции и прочее газовое оборудование и приборы, расположенные за отключающим устройством ввода, принадлежат предприятию и должны им обслуживаться и поддерживаться в состоянии, отвечающем Правилам Госгортехнадзора и Правилам технической эксплуатации городского газового хозяйства МКХ РСФСР.
На межцеховых газопроводах предприятий в зависимости от местных условий прокладки газопроводов, предусмотренных проектом, устанавливаются конденсационные горшки, гидрозатворы, контрольные трубки, муфты, коверы и другие устройства, устанавливаемые на городских газовых сетях.
В частности, на ответвлениях межцехового газопровода к цехам устанавливается отключающее устройство, по возможности в начале ответвления.
Перед регуляторными станциями отключающие устройства устанавливаются не ближе 5 м от них и в том случае, когда расстояние до отключающего устройства на вводе более 100 м.
Конденсационные горшки устанавливаются перед PC и на ответвлениях перед цехами в случаях, когда не представляется возможным дать необходимый уклон его в сторону межцехового газопровода.
К устройству газовых сетей предприятий предъявляются такие же требования, как к газопроводам городских сетей,
86
Глава IV
в отношении материала труб, сварочных материалов, выполнения сварки труб, их изоляции, укладки в траншеи, монтажа устройств и арматуры. Выбор способа прокладки газопроводов по территории предприятий (надземного или подземного) разрешается в зависимости от местных условий проектной организацией но согласованию с предприятием, а на территории города — с архитектурным управлением Горсовета.
Надземные межцеховые газопроводы (вводы) на территориях. предприятий прокладываются на специальных опорах (эстакадах, отдельных мачтах), а также по стенам зданий, построенных из несгораемых материалов, или по несгораемым перекрытиям (крышам) бесчердачных помещений цехов, с непожароопасным производством (категорий Г и Д по противопожарным нормам строительного проектирования промпредприятий и населенных мест).
Надземные газопроводы по сравнению с подземными имеют преимущество: они занимают на территории предприятий меньше места, которого может и не оказаться совсем; удобны для осмотра и ремонта; представляют меньшую опасность в случаях утечки газа, который будет улетучиваться в воздух; не подвергаются разъеданию блуждающими токами; не могут быть причиной проникновения газа в подземные помещения и устройства (каналы, колодцы, подвалы и т. п.); незаменимы при высокой коррозий-ности грунта; содержание их обходится дешевле, особенно при укладке по стенам или крышам зданий.
Недостатки надземных газопроводов: опасность замерзания в них конденсата газа и образования ледяных пробок в случае транспортирования влажных газов и газов, содержащих нафталин, а также подверженность газопроводов разрушающему влиянию дождей, снега, обледенения, ветра, что требует большего ухода за ними. Укладка газопроводов по стенам зданий производится на кронштейнах, а по крышам — на опорах в виде козел, к которым газопровод укрепляется при помощи хомутов.
Крепление газопроводов к опорам должно обеспечить возможность их свободного передвижения вдоль своей оси, при удлинении или сжатии под влиянием изменений наружной температуры, которым надземные газопроводы подвержены значительно больше, чем подземные. Для этого между «анкерными» опорами, к которым трубы крепятся «намертво», должны устанавливаться подвижные опоры, или опоры, дающие возможность трубопроводу перемещаться вдоль его оси на роликах или подушках опор. Кроме того, между «анкерными» опорами должны устанавливаться компенсаторы, если на участках газопровода нет изгибов, которые могут компенсировать их удлинение и сжатие при изменениях температуры. Укладка газопроводов вдоль стен зданий должна производиться на расстоянии от них, достаточном для
Газоснабжение предприятий
87
возможности свободного их осмотра и ремонта, а по крышам на высоте не менее 0,5 м.
По наружным стенам зданий, имеющим оконные проемы, допускается прокладка газопроводов только среднего и низкого давления; при этом они не должны пересекать оконных или дверных проемов, или иметь под ними фланцевых и резьбовых соединений или арматуры. В случае укладки газопроводов под карнизом крыш должно быть обеспечено их постоянное проветривание.
Наименьшая высота прокладки надземных газопроводов допускается для непроезжей части 2,2 м, считая от нижней обра» з ующей трубы.
Рис. 35. Схема прокладки надземного газопровода на мачтах шпренгельного типа:
1 — газопровод; 2 — мачта; з — растяжка; 4 — серьга; 5 — бетон.
Укладка газопроводов на эстакадах и опорах совместно с другими трубопроводами допускается при условии обеспечения возможности осмотра и ремонта всех трубопроводов и защиты газопровода от температурного воздействия горячих трубопроводов. Прокладка газопроводов совместно с электропроводами и трубопроводами коррозийно-активных жидкостей запрещается.
Опоры эстакад газопроводов изготовляются из металла или железобетона и устанавливаются на бетонных или кирпичных фундаментных столбах, к которым крепятся болтами. Опоры в виде мачт могут выполняться из стальных труб. Приведенное на рис. 35 сооружение надземного газопровода на мачтах шпренгельного типа с растяжками из прутковой стали позволяет устанавливать наименьшее количество мачт.
Во всех местах постоянного обслуживания задвижек, измерительных шайб, водоотводчиков и других устройств газопровода должны быть сооружены стационарные площадки и лестницы к ним. Одиночные площадки редкого пользования разрешается обслуживать при помощи стремянок, которые при высоте более 3 м должны быть снабжены предохранительными дугами, первая из которых устанавливается на высоте 2 м. Ширина площадки должна быть не менее 800 мм. Площадки и лестницы ограждаются перилами высотой в 1,2 м со сплошным закрытием в ниж
88
Глава IV
ней части, высотой в 200 мм. Настил площадок должен быть решетчатый или из сплошных листов с отверстиями для стока воды. Нельзя прокладывать газопроводы в местах, где они могут быть повреждены.
Надземные газопроводы, прокладываемые вдоль железнодорожных и трамвайных путей, должны отстоять (считая до края фундамента колонн или газопровода) от ближайшего рельса не менее чем на 3 м\ от проезжих дорог газопровод должен отстоять не менее, чем на 1,5 м, считая от бордюрного камня, внешней бровки кювета или подошвы насыпи дороги; от водопровода канализации и теплопроводов — 1м, считая от края фундамента газопровода; до ограды открытой электроподстанции — 10 м; до здания — от 2 до 10 м в зависимости от его огнестойкости и давления в газопроводе; от мест выпуска шлака или расплавленного металла — не менее 10 м.
При пересечении газопровода с путями он должен проходить над железной дорогой на высоте 5,5 м, считая от головки рельса и до низа газопровода; над автодорогой — не менее 4,5 м.
При пересечении газопровода с электросетями, проходящими над ними, расстояние от проводов с учетом их провисания до ограждений газопровода должно быть в зависимости от напряжения сети от 1 до 5 м; при пересечении с подвесной дорогой расстояние до низа вагонетки должно быть не менее 3 м.
Пересечение газопроводов проводами электрических сетей и тросами подвесных дорог допускается под углом не менее 45° и с обязательным устройством защитных решеток над газопроводом на случай обрыва, проводов, тросов.
Пересечение газопроводов с жел.-дор. путями, оврагами, каналами, реками выполняется и в виде арочных (выгнутых вверх) мостов. При этом концы арки газопровода закрепляются «намертво» в береговых бетонных устоях. Применяется также подвеска газопроводов на стальных тросах.
Нельзя прокладывать газопровод вблизи кислородных и компрессорных установок, требующих особо чистого воздуха. При влажном газе газопроводы должны укладываться с уклоном не менее 3 мм на погонный метр, по возможности по ходу газа, и на расстоянии в 200—250 м следует устанавливать водоотвод-чики.
Присоединение дренажных труб водоотводчиков к газопроводам должно производиться в нижних точках газопроводов и в местах установки запорных устройств, измерительных шайб и других устройств со стороны уклона к ним. В местах присоединения дренажной трубы к газопроводу устанавливается фланцевый пробочный кран (но не бронзовый на коксовом тазе). У крышки водоотводчйка желательна установка отключающей задвижки. Диаметр дренажных труб принимается равным 40—50 мм.
следующий за ним оператор. Выполнение программы прекращает специальный оператор останова.
3. Операторы.
(оператор): := {[(метка)](правило)[(переход)] | (специальный оператор)}
(метка) : := (число)
Здесь и далее под «числом» понимается целое без знака.
Выполнение (не специального) оператора заключается в анализе и преобразовании какой-нибудь одной строки. Имя этой строки и способ ее обработки задается «правилом»:
(правило) : := (левая часть)[=[(правая часть)] ]
(левая часть) : := (имя)[(образец)]
(образец) : := {(строка) | (имя) |
(переменная с длиной) |
(произвольная переменная)} ...
(переменная с длиной): := * (имя) | (чисто) *
(произвольная переменная):: = * (имя) *
(правая часть) :{(строка) | (имя)} ...
В общем случае оператор выполняется следующим образом. Берется строка, иа которую ссылается имя из левой части (такая строка называется основной), и в ней ищется подстрока, соответствующая образцу. Если такой подстроки нет, то ничего не делается. Если такая подстрока находится, то она заменяется на строку, сформированную из правой части; преобразованная таким образом основная строка становится новым значением имени из левой части (при отсутствии какого-нибудь компонента правила соответствующее действие не выполняется).
Кроме обработки основной строки оператор может осуществить переход к другому (помеченному) оператору; такой оператор-преемник указывается в компоненте «переход»:
(переход): := {(безусловый переход) |
(переход по успеху) | (переход по неуспеху)}
(безусловный переход) : := /((метка))
(переход по успеху) ::— /S ((метка))
(переход по неуспеху) : := /F((метка))
При безусловном переходе следующим всегда выполняется оператор, метка которого указана в круглых скобках. Остальные переходы — условные. Если задан «переход по успеху», то переход по указанной метке происходит только тогда, когда в данном опера
100
торе подстрока, соответствующая образцу, найдена в основной строке; в противном случае преемником данного оператора является следующий по порядку оператор программы. «Переход по неуспеху» определяется противоположным образом.
4. Основные операции над строками.
В СО-языке есть три основных вида операций над строками (образование строки, поиск по образцу, замена части строки), которым соответствуют три типа правил.
4.1. Образование строки. IIрисваивание.
Для того чтобы из нескольких строк образовать новую строку, достаточно выписать эти строки или пх имена последовательно друг за другом. В результате получится строка, составленная из букв исходных строк. Эта операция используется для формирования строки в правой части оператора. Присвоить такую строку некоторому имени можно с помощью правила вида
(имя) = [ (правая часть) ]
Пример 1. В результате выполнения операторов
А = ’ОЛК’
СТРОКА = ’П’ А ’АН’
значением имени А станет ОЛК, а значением имени СТРОКА — ПОЛКАН.
При отсутствии правой части значением имени, указанного в левой части, становится пустая строка.
4.2. Поиск по образцу.
Эта операция представляет собой исследование основной строки на предмет вхождения в нее определенной подстроки, которое может закончиться успехом (если вхождение найдено) или неуспехом (вхождение не найдено). Данной операции соответствует правило вида (имя) (образец)
Искомая подстрока определяется образцом: она образуется выписыванием подряд строк, соответствующих отдельным элементам образца. Если заданному образцу соответствует несколько подстрок основной строки, то берется самая левая и самая короткая из них.
Элементу образца «строка» соответствует только совпадающая с этой строкой подстрока, а элементу «имя» — только подстрока, совпадающая со значением этого имени.
Пример 2. Поиск по образцу успешен в операторах
СТРОКА ’КА’
СТРОКА ’П’ А ’А’
и неуспешен в операторах
А ’КОЛ-
СТРОКА А ’Н’
101
Элементу образца «переменная с длиной» соответствует подстрока с любым содержанием, количество символов в которой равно «числу», указанному в этом элементе. Если такая подстрока нашлась, то она становится новым значением «имени» этой переменной.
Пример 3. После выполнения операторов:
СТРОКА *Х/3»
СТРОКА ’О’ * У / 2 * ’А’
, СТРОКА * А/7 *
значением X будет ПОЛ, значением У—ЛК, имя А не изменит своего значения, так как в основной строке ПОЛКАН нет подстроки из
«Произвольной переменной» из образца соответствует любая (в частности, пустая) подстрока основной строки. В случае успеха всего поиска эта подстрока становится новым значением указанного «имени» переменной. С помощью таких элементов образца из основной строки можно извлекать подстроки с неизвестной длиной и неизвестным содержимым.
Пример 4. Поиск по правилу:
СТРОКА ’ПО’ * X *’А’
будет успешным, так как в строке с именем СТРОКА есть подстрока, начинающаяся с ПО и заканчивающаяся А. Фрагмент этой подстроки ЛК будет присвоен имени X.
В заключение приведем полную формулировку правил поиска по образцу ([1], с. 13).
1. Делается попытка найти соответствие первому элементу образца, начиная с первого символа основной строки. Если это не удается, то поиск начинается со следующего символа и т. д.
2. Поиск осуществляется слева направо в порядке следования элементов образца. Для каждого элемента отыскивается по возможности кратчайшая (в частности, пустая) подстрока основной строки.
3. Если в какой-то момент для некоторого элемента не удается найти надлежащий участок основной строки, то делается попытка произвести новый поиск для предыдущего элемента образца. Для этого нового поиска ранее найденная часть основной строки наращивается, чтобы выявить следующее по длине подходящее вхождение. Если такое расширение невозможно, снова применяется правило 3. Еслп в образце нет предыдущего элемента, то предпринимается новая попытка поиска по правилу 1.
4. Если последний элемент образца является произвольной переменной, то соответствующая часть основной строки распространяется до конца строки.
102
5. Поиск считается успешным, если завершен поиск для последнего элемента образца, и неуспешным, если не удалось найти соответствие для первого элемента.
Следует отметить, что во время поиска те значения, которые получают имена переменных, являются предположительными, так как при неуспехе они теряются.
4.3. Замена части строки.
Этой операции соответствует правило вида
(имя) (образец) = [(правая часть)]
В основной строке осуществляется, как описано выше, поиск по образцу, и если он успешен, то часть основной строки, соответствующая образцу, заменяется на строку, образованную из правой части. Если правой части нет, то соответствующая образцу подстрока просто выбрасывается. В случае неуспешного поиска основная строка не меняется.
Пример 5. После выполнения оператора:
СТРОКА * X / 2 * ’К’ = ’Л’ / S (29)
значением имени СТРОКА будет ПЛАН, а значением имени X будет ОЛ; следующим будет выполняться оператор с меткой 29, так как поиск был успешен.
5. Специальные операторы.
(специальный оператор) ::= (оператор печати)!
(оператор останова)
(оператор печати): := [(метка)] = PRINT = {(строка)] (имя)}
(оператор останова) : :== [(метка)] = STOP = [(строка)]
Первый из этих операторов выводит на печать строку (без кавычек) — явно заданную нли указанную по имени, а второй печатает символ = КОНЕЦ = (и заданную строку, если она есть) и прекращает выполнение програглмы.
Приложение 2. Варианты задания
Конкретное подмножество СО-языка определяется типами операторов п типами элементов образца, которые разрешается использовать в данном подмножестве. Кроме того, в каждое подмножество обязательно включаются операторы присваивания и оба специальных оператора.
I. Рассматриваемые типы операторов.
1. Поиск по образцу и замена:
(имя) (образец) = [(правая часть)]
103
2. Поиск по образцу и переход: [(метка)] (имя) (образец) [(переход)] II. Рассматриваемые элементы, образцов.
1. (строка) и (имя)
2. (строка) и (произвольная переменная)
3. (строка) и (переменная с длиной)
4. (имя) и (произвольная переменная)
5. (имя) и (переменная с длиной)
Приложение 3. Mei одические указания
Как известно, интерпретатор для некоторого языка воспринимает исходную программу, написанную на этом языке, и выполняет ее. При этом «чистый» интерпретатор, для того чтобы выяснить, как осуществить выполнение инструкции исходной программы, анализирует ее всякий раз, когда она должна быть выполнена. Однако для достижения большей эффективности процесс интерпретации обычно разделяют на два этапа. На первом этапе интерпретатор анализирует всю исходную программу — почти так же, как это делает компилятор, — и преобразует ее в некоторое внутреннее представление, более удобное для последующей интерпретации. На втором этапе выполняется (интерпретируется) уже не исходная программа, а ее внутреннее представление ([3], с. 17, 18).
Именно такую схему интерпретации и предлагается реализовать в данном задании. Соответственно и интерпретатор для СО-языка должен состоять из двух блоков: блока анализа и блока интерпретации.
Внутреннее представление программы и ее объектов. Внутреннее представление конструкций СО-языка, которое должен построить блок анализа, непосредственно ориентировано на реализацию интерпретатора на языке ЛИСП-БЭСМ-6 и выбрано с таким расчетом, чтобы свести к минимуму время, необходимое для анализа каждой инструкции (оператора) исходной программы при ее выполнении.
Каждый оператор СО-программы во внутреннем представлении имеет естественную для ЛИСПа форму списка; при отсутствии необязательных элементов — метки и перехода — в соответствующих позициях помещается символ *; списком (операторов) является и программа, причем ограничители «;» удаляются. Таким образом:
(программа) : := ((оператор) ...)
(оператор); ;= ({(метка) | * } (правило) {(переход) j * }) (переход): := (S (метка)) | (F (метка)) | ((метка))
104
Аналогичным образом преобразуются в списки и некоторые другие конструкции языка:
(левая часть) : := ((имя) [(образец)])
(правая часть) : := ({(строка) | (имя)} ...)
(переменная с длиной): := (* (имя) (число))
(произвольная переменная): := (* (имя))
Преобразованиям подвергаются и строки. С помощью функции лиспа ATL они превращаются в списки однолитериых атомов; при этом кавычки (первые и последние элементы полученных списков) удаляются. Например, строка ’АВСА’ во внутреннем представлении имеет вид (АВСА).
После подобных преобразований левая и правая части оператора приобретают вид списков, состоящих на первом уровне из атомов («имен» строк) и списков («строк» и «переменных»),
В процессе интерпретации (на втором этапе работы интерпретатора) связь строки с именем осуществляется с помощью ассоциативного списка, элементами которого являются пары ( (имя). (строка))— результат применения лисповской функции CONS. Имена пустых строк заносить в ассоциативный список не следует, так что строка с именем X считается пустой, если в ассоциативном списке нет пары (X. (строка)).
Структура интерпретатора. При реализации интерпретатора целесообразно выделить (оформить, например, как самостоятельные функции ЛИСПа) не только указанные выше блоки — блок анализа (БА) и блок интерпретации (БИ), но также и ведущую программу (ВП).
Ведущая программа должна:
1. Используя лисповскую функцию READ, осуществить ввод очередного выражения — программы на СО-языке или признака конца пакета (см. ниже).
2. Обратиться к блоку анализа и напечатать сообщение о результатах его работы: получено внутреннее представление, в программе имеются ошибки (локализовать эти ошибки и указать их тип); при отладке интерпретатора следует также распечатать внутреннее представление исходной СО-программы.
3. При отсутствии ошибок в программе обратиться к блоку интерпретации; в противном случае перейти к вводу следующего выражения (п. 1).
4. Отпечатать сообщение об окончании интерпретации очередной программы и перейти к вводу следующего выражения (п. 1).
В блоке анализа, осуществляющем анализ исходной программы и ее трансляцию во внутреннее представление, должны выявляться все имеющиеся в исходной программе ошибки. В одну из исходных
105
программ следует намеренно внести ошибки различных типов: нет ограничителя «;», недопустимый аргумент оператора останова (не строка), неправильная метка (не число) и т. п. с целью проверки реакции интерпретатора на такие ошибки.
Текст исходной программы и ее внутреннее представление (а также ассоциативный список) рекомендуется хранить как значения некоторых констант.
Для обработки правильной программы в блоке БИ можно ввести несколько функций, обрабатывающих операторы различных типов (основной и специальные), а также управляющую функцию, которая определяет тип оператора, обращается к соответствующей функции для обработки оператора, осуществляет выбор оператора-преемника.
Рекомендуется ввести в употребление отдельные функции для реализации поиска по образцу, формирования строки из правой части, перевода строки во внутреннее представление и печати строки по ее внутреннему представлению и т. п. В виде самостоятельных функций следует оформить и основные операции над ассоциативным списком: поиск значения имени, изменение значения, добавление новой пары, удаление пары, соответствующей пустой строке.
Отладка. Пример исходной программы. Как уже говорилось, при выполнении задания необходимо составить набор исходных программ на СО-языке и выполнить их с помощью интерпретатора. Этот набор СО-программ должен содержать все предусмотренные в варианте задания типы операторов, виды образцов и выявляемые ошибки, с тем чтобы в процессе отладки удалось проверить все ветви в алгоритме интерпретации.
Тексты исходных программ (списка ЛИСПа) следует расположить после обращения к ведущей программе, а за последней исходной программой должен следовать признак конца пакета программ, например ( ) — пустой список.
Рассмотрим одну из возможных СО-программ для варианта 2—4:
(СТР1 = ’АВСАВВАВС’;
СТР2 = ’ВС’;
СТРЗ = ’АВА’;
СТР1 * СТР4 * СТР2 * СТР5* / S (2);
1 = STOP — Т’;
2 = PRINT — СТР4;
= PRINT = СТР5;
СТР5 СТРЗ/ F (1);
= STOP — ’S’;)
106
Во внутреннем представлении эта программа будет иметь вид
((* (СТР 1) = (АВСАВВАВС) *)
(* (СТР2) = (ВС) *)
(* (СТРЗ) = (АВА) *)
(*(СТР1 (*СТР4) СТР2 (* СТР5)) (S 2))
(1 = STOP = (F))
(2 = PRINT = СТР4)
(* = PRINT = СТР5)
(* (СТР5 СТРЗ) (F 1))
(* = STOP = (S)))
При интерпретации данной программы должно быть отпечатано А
АВВАВС
= КОНЕЦ ==
F
Работа с системой ПУЛЬТ. Текст программы интерпретатора пи-шется на бланках и сдается на перфорацию. Отперфорированный текст с помощью специальной программы записи вводится в архив системы ПУЛЬТ. Дальнейшая работа — исправление ошибок перфорации, ввод пакета исходных программ, отладка — ведется с помощью этой системы в режиме диалога.
Основные сведения о работе с системой ПУЛЬТ и об отладке ЛИСП-программ в режиме диалога даются в специальных инструкциях и разработках [4. 5, 6]. Здесь приводится лишь пример диалога с системой, иллюстрирующий, ее вызов и последовательность действий при записи текста в архив и отладке (символом «—» помечены приказы, передаваемые пользователем).
ПУЛЬТ 710092
СИСТЕМА ПУЛЬТ-МГУ (БЭСМ=1 VT=12)
ШИФР 710092000000
—АРХ ПРАКТ
ЕСТЬ
—СИС ЛИСП
— С СТУД5
— С 6
6. Т Y))) (Т (CONS (FF X (CAR Y) Z)(FF X (CDRY) Z))))))
—P 6 ’Д’ = ’D’
6. T Y))) (T (CONS (FF X (CAR Y) Z) (FF X (CDRY) Z))))))
— 3 СТУД5
MCB СТУД5 H = 053 Д = 001
— 3 БУФ = ТТ
— (CTP1 = ’ABCBA’; = PRINT = CTP1; CTP1 * CTP * ’BA’;
= PRINT = CTP; = STOP = ’F’) //
107
МСВ БУФ Н = 001 Д = 001
— 3 СТУД5 = СТУД5, БУФ
МСВ СТУД5 Н = 053 Д = 001
— ПП
— ЛИСП
//ВВОД СТУД5
АВСВА
АВС
F
— //ВЫХ
— С СТУД5
- с () А
__b^OHEIX
16.09.80 ВРЕМЯ РЕШ: 12 СЕК
КОНЕЦ СЕАНСА
Задание АЯ-2. ИСПОЛЬЗОВАНИЕ МАКРОСРЕДСТВ ПРИ ПОСТРОЕНИИ ТРАНСЛЯТОРОВ
Цель задания.
1. Знакомство с конкретным макроязыком и практика в его использовании.
2. Практика в использовании средств условной макрогенерацин как аппарата системного программирования.
Содержание задания.
1. Изучение языков БЕЛАШ и макрокод.
2. Создание макроопределения на автокоде БЕМШ для программирования выражений.
3. Отладка макроопределения.
4. Составление и пропуск контрольных тестов.
Постановка задачи.
Заданы синтаксис и семантика арифметического выражения. Требуется на автокоде БЕМШ составить и отладить макроопределение, назначение которого состоит в том, чтобы проверить, является ли входная строка выражением в соответствии с заданными правилами синтаксиса и семантики; если да, то сгенерировать последовательность команд на автокоде БЕМШ, предназначенную для вычисления значения этого выражения слева направо; в противном случае вывести на печать соответствующий диагностический текст.
В Приложении 1 дано общее описание языка, а в Приложении 2 — варианты задания.
Требования к программе.
Программа должна состоять из текста макроопределения (макроопределений) и основной части (тела программы) и должна удовлетворять следующим требованиям:
103
1. Длина входной строки (число операндов и операций в выражении) не фиксированы.
2. При вычислении заданного выражения используется системный магазин, состояние которого после окончания вычислений должно совпадать с его состоянием перед началом вычислений.
3. Для каждого макроопределения в теле программы должно содержаться несколько макровызовов, совокупность которых обеспечивает проверку всех разветвлений в тексте макроопределения.
4. Контроль входной строки производится до выявления первой ошибки.
5. Если выделяется макроопределение, контролирующее правильность входной строки, то в него включается и печать диагностических текстов; в противном случае печать диагностики делается в теле макроопределения, генерирующего последовательность команд для вычисления (выражений. Диагностический текст должен точно указывать обнаруженную ошибку.
6. Отладочная печать результатов вычислений делается либо в теле специального макроопределения, либо совокупностью автокод-ных команд в теле главной программы.
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Описание отображения входного текста на языке БЕМШ.
3. Описание алгоритма.
4. Текст макроопределения (листинг).
5. Набор тестов для отладки.
6. Результаты отладки.
Литература.
1. Штаркман В. С. Автокод БЕМШ. Описание языка. — Мл Изд-во ИПМ АН СССР, 1969.
2. Михелев В. М., Штаркман В. С. Макрокод. Описание языка.— М.: Изд-во ИПМ АН СССР, 1972.
3. Т р и ф о н о в Н. П. Система команд БЭСМ-6 (Методическое пособие для программирования). — М.: Изд-во МГУ, 1969.
4. Грис Д. Конструирование компиляторов для цифровых вычислительных машин. — М.: Мир, 1975, с. 281—286.
5. Бочкова 3. Ф. и др. Руководство по работе с программами на автокоде БЕМШ. — М.: Изд-во ИПМ АН СССР, 1974.
Приложение 1. Описание языка
А. Синтаксис выражений.
Имеются три вида записи выражений: суффиксная, префиксная л инфиксная.
109
1. Суффиксное выражение (С-выраж):
(С-выраж) : := (операнд 1), (операнд 2}, (операция)
(операнд 1) : := (идентификатор) | (С-выраж)
(операнд 2): := (идентификатор)
2. Префиксное выражение (П-выраж):
(П-выраж): := (операция), (операнд 1), (операнд 2)
(операнд 1) : := (идентификатор) | (П-выраж)
(операнд 2) : := (идентификатор)
3. Инфиксное выражение (И-выраж):
(И-выраж) : := (операнд 1), (операция), (операнд 2)
(операнд 1) : : = (идентификатор) | (И-выраж)
(операнд 2): := (идентификатор)
Для всех типов выражений:
(операция) : := (арифметическая операция) [
(операция сравнения)|(логическая операция)|
(операция присваивания^
(арифметическая операция): := + | — | * I /
(операция сравнения) ::=>|<l = [=?fc]^K
(логическая операция) ::= V |&
(операция присваивания) : := :=
Идентификаторы содержат не более шести основных символов.
Б. Семантика выражений.
Идентификаторы.
В выражении два одинаковых идентификатора обозначают один И тот же объект.
Типы дани ы х.
1. Различаются значения арифметического и логического типа. Идентификаторы, начинающиеся буквой В, обозначают переменные логического типа.
2. Над значениями арифметического типа определены операции: арифметические, отношения п присваивания.
3. Над значениями логического типа определены только логические операции.
4. Результатами выполнения арифметических операций и операций присваивания являются значения арифметического типа.
5. Результатами операций отношения и логических операций — значения логического типа.
Примечание. Значение TRUE изображается па автокоде БЕМШ восьмеричной константой 00 . .. 01; значение FALSE —
15
- 00 ... 0.
16
110
Операции.
1. Логические и арифметические операции имеют очевидный смысл, а операция «присваивание» понимается следующим образом: «операнду 2 присвоить значение операнда 1». Результат операции — новое значение операнда 2.
2. Результат вычисления выражения должен быть получен в вершине магазина. Исключение составляет результат операции присваивания.
3. Результат операции присваивания не может быть операндом (выражением) для следующей операции.
В. Контроль.
1. Синтаксический контроль.
Синтаксический контроль предполагает проверку соответствия структуры входной строки заданному синтаксису. Для рассматриваемого синтаксиса это сводится к проверке порядка следования операндов и операций во входной строке и соответствия операций заданному (в данном варианте) набору.
Например, входная строка
‘А, Е, С, D, «, +, /’
синтаксически неверна для всех видов записи выражений, описанных в п. А, так как нарушен порядок чередования операндов и операций. Строка ‘A, D, +, С’ синтаксически неверна, так как нет соответствия чиста операндов и операций.
2. Семантический контроль.
Семантический контроль дл,ч данных языков программирования сводится в основном к двум пунктам:
а) проверка соответствия типов значений и типов операций; ’ б) проверка корректности операций присваивания.
Например, строка‘А, +, Е, : = , С, /, D'не содержит синтаксических ошибок в соответствии с синтаксисом инфиксного выражения, однако семантически неверна, так как противоречит п. 3 семантических правил операций.
Следует заметить, что превышение допустимой длины идентификатора можно не проверять, так как эти ошибки выявляются на уровне транслятора с автокода.
Приложение 2. Варианты задания
I. Допустимые наборы операций.
1) +, *, >, =/=, V, :==
2) +, /, <, =, V, :=
3) —, *, >, =, &, :=
4) /, С &,
Ш
II. Виды записи выражений.
1) С-выражение,
2) П-выражение,
3) И-выражение.
III. Типы контроля.
1) Синтаксический,
2) Семантический.
Вариант задания определяется набором допустимых операций, видом записи выражения и типом контроля.
Примечание. В тех вариантах задания, где требуется реализовать синтаксический контроль, считать, что тексты семантически верны; при реализации семантического контроля считать, что тексты верны синтаксически.
В приведенной ниже таблице для каждого номера N варианта задания (1 sS N «с: 24) определены вид записи, тип контроля и набор операций.
Тип контроля
Вид записи Синтаксический набор операций Семантический набор операций
1 2 3 4 1 2 3 4
С-выражение 1 7 13 19 2 8 14 20
П-выражение 3 9 15 21 4 10 16 22
' И-выраженне 5 11 17 23 6 12 18 24
Приложение 3. Методические указания
1. Познакомясь с системой команд БЭСМ-6 и автокодом БЕМШ, следует составить отображение: ( (операнд 1), (операнд 2), (операция) ) -> (текст на БЕМШ) для всех возможных в заданном варианте операций и типов операндов (выражение или идентификатор). Например,
, , м Л ^СЧМ_А_
(а + b) -> I сл _ В .
«ВЫР) + С)->{ _сл_с„
( — СЧМ„А„
I
(А + (ВЫР)). программа вычисления
I ... выражения ВЫР
I _ СЛ„(15)
2. Познакомиться с языком макрокод и составить себе четкое представление о трех основных процессах, преобразующих текст
112
входной строки в значение выражения: .макрогенерации, трансляции с автокода, выполнения программы в машинных командах, т. е. о назначении каждого из этих процессов, о входных и выходных данных для каждого процесса и о последовательности их выполнения.
3. Составляя общую блок-схему трансляции, включить в нее контроль (в соответствии с вариантом задания).
4. Составляя микроопределение и тело программы, следует помнить, что
4.1. Нулевой порядок в машине БЭСМ-6 изображается чис< лом 64.
4.2. Операции отношения = и у= для действительных чисел определены следующим образом: а = 6, если |а — гс е; а #= Ь, если |а — &| > е (считать, что е = 10~s).
4.3. Символы V, У=, везде следует заменить соответственно на слова OR, NE, ME, LE.
4.4. При повторных макровызовах одного и того же макроопределения не должны появляться одинаковые метки в программе (это устраняется с использованием системной переменной &SNDX).
4.5. Короткий адрес (12 разрядов) позволяет обращаться к данным, размещенным только в первом листе памяти (ячейки 0—4095); для данных, расположенных в других местах памяти, следует применять базирование [1].
5. Чтобы обеспечить возможность задания входной строки любой длины (произвольное число операндов), можно воспользоваться представлением операнда макрокоманды в виде подсписка.
6. При отладке макроопределений для всех тестов следует предварительно задать начальные значения данных и вычислить соответствующие выражения.
КАФЕДРА АВТОМАТИЗАЦИИ СИСТЕМ ВЫЧИСЛИТЕЛЬНЫХ КОМПЛЕКСОВ
Задание АСВК-1. РАЗРАБОТКА ПРОГРАММ, ИСПОЛЬЗУЕМЫХ В РЕЖИМЕ ДИАЛОГА
Цель задания.
1. Знакомство с приемами составления программ, использующих терминал для общения с пользователем.
2. Практика в использовании экстракодов операционной системы.
3. Накопление опыта работы с ЭВМ в дистанционном режиме.
4. Практика в использовании машинно-ориентированных языков. Соответствующих трансляторов и средств отладки.
113
Содержание задания.
1. Изучение директив операционной системы Диспак и терминальной системы Краб.
2. Изучение принципов использования экстракодов в операционной системе.
3. Изучение автокода БЕМШ и связанных с ним компонент математического обеспечения ЭВМ БЭСМ-6.
4. Составление программы, реализующей заданную функцию и получающей исходные данные с терминала, ее отладка.
Постановка задачи.
Требуется составить программу, реализующую заданную функцию. При этом программа должна:
— осуществлять связь с терминалом на базе видеотона VT-340, подключенным к ЭВМ БЭСМ-6;
— иметь в своем составе блок распознавания сообщений, поступающих с терминала;
— иметь возможность окончания работы с терминалом;
• — использовать соответствующие экстракоды ОС.
Конкретная функция, реализуемая программой, и дополнительные требования к программе определяются вариантом задания (см. Приложение 1). В Приложении 2 дано описание некоторых экстракодов ОС Диспак, в Приложении 3 — описание некоторых таблиц ОС.
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Инструкция пользования программой.
3. Текст программы иа автокоде.
4. Набор тестов и результаты отладки.
Литература.
1. Операционная система ДИСПАК для ЭВМ БЭСМ-6 (инструкция пользователю). — М.: Изд-во ИПМ АН СССР, 1973.
2. 3 е л ь д и н о в а С. А., П а р е м с к и й И. В., Тюрин В. Ф. Некоторые базовые возможности ОС ДИСПАК. — М.: Изд-во ИПМ АН СССР, 1976.
3. Ш т а р к м а н В. С. Автокод для БЭСМ-6. Описание языка. — М.: Изд-во ИПМ АН СССР, 1969.
Приложение 1. Варианты задания
I. Использование экстракодов запроса состояния терминала.
С использованием экстракодов, приведенных в Приложении 2, получить указанную в варианте информацию о терминалах и выдать ее на экран дисплея в виде списков номеров этих терминалов.
1. Номера операторских терминалов.
2. Номера математических терминалов, свободных от задач.
114
3. Номера математических терминалов, занятых задачами пользователей.
4. Номера терминалов, не подключенных к БЭСМ-6.
II. Использование экстракодов обмена и представление данных в заданном формате.
По задаваемым с терминала значениям m и п прочитать с математического направления 30 зону с номером m и вывести на экран дисплея первые п из прочитанных слов (с их нумерацией) по формату, указанному в варианте задания.
5. В символьном виде.
6. В виде шести байтов, каждый из которых представлен одной четверичной и двумя восьмеричными цифрами.
7. В восьмеричном виде.
8. В двоичном виде.
9. В шестнадцатеричном виде.
III. Использование экстракодов обмена и поиск по образцу.
По задаваемым с терминала целому m и слову s прочитать с математического направления 30 зону с номером т, среди прочитанных слов найти первое по порядку слово, совпадающее со словом s, и вывести на экран порядковый номер найденного слова, а также само слово по указанному в варианте формату; если заданного слова в прочитанной зоне нет, вывести на экран некоторое диагностическое сообщение.
10. В символьном виде.
11. В виде шести байтов, каждый из которых представлен одной четверичной и двумя восьмеричными цифрами.
12. В восьмеричном виде.
13. В виде пары команд (с учетом их структуры).
14. В двоичном виде.
15. В шестнадцатеричном виде.
IV. Использование экстракодов чтения произвольной физической ячейки оперативной памяти.
В определенных ячейках памяти, принадлежащих операционной системе, хранится информация о состоянии ЭВМ (см. Приложение 3). С помощью соответствующего экстракода прочесть содержимое требуемой ячейки и выдать прочитанное слово на экран дисплея. Требуемая информация о состоянии ЭВМ или физическая ячейка, задаваемая с терминала, содержимое которой должно быть прочитано, а также форма выдачи на экран определяются вариантом задания.
16. Состояние дисководов: номера свободных устройств, номера дисководов, на которые установлены пакеты МД, и номера этих пакетов.
17. Состояние магнитофонов: номера свободных магнитофонов, номера магнитофонов, на которые установлены бобины МЛ, и номера этих бобин.
115
18. Содержимое ячейки, адрес которой задается с терминала, в символьном виде.
19. Содержимое ячейки, адрес которой задается с терминала, в двоичном виде.
20. Содержимое ячейки, адрес которой задается с терминала, в восьмеричном виде.
21. Содержимое ячейки, адрес которой задается с терминала, в виде пары команд (с учетом их структуры).
22. Содержимое ячейки, адрес которой задается с терминала, в виде шести байтов, каждый из которых представляется одной четверичной и двумя восьмеричными цифрами.
23. Содержимое ячейки, адрес которой задается с терминала, в шестнадцатеричном виде.
V. Использование экстракодов печати.
Прочитать с математического направления 30 содержимое зоны, номер которой задается с терминала, и отпечатать его иа АЦПУ по указанному в варианте формату. Печатаемые строки снабдить восьмеричными номерами, начиная от нуля, и с шагом нумерации 108.
24. В символьном виде.
25. В виде шести байтов, каждый из которых представляется одной четверичной и двумя восьмеричными цифрами.
26. В восьмеричном виде.
27. В виде команд (с учетом их структуры).
28. В двоичном виде.
29. В шестнадцатеричном виде.
Примечание. Распечатку делать в 4 колонки; коды выводимых на печать символов не должны превосходить 1378, так как в противном случае код будет считаться управляющим, а не кодом печатаемого символа. По окончании печати выдать на экран диагностику
КОНЕЦ ПЕЧАТИ
VI. Использование других экстракодов.
С помощью соответствующих экстракодов ОС Диспак реализовать функцию, указанную в варианте задания.
30. По задаваемым с терминала четырем цифрам шифра пользователя найти и выдать на экран дисплея фамилию этого пользователя; если данный шифр не зарегистрирован в ОС, выдать на экран соответствующую диагностику.
31. Захватить терминал с номером m и выдать на его экран сообщение s. Номер m и сообщение s задаются с терминала.
32. Получить и вывести на экран текущую дату, номер ЭВМ и иомер терминала, которые используются при выполнении данной программы.
116
Приложение 2. Экстракоды ОС Диспак
1. Экстракоды связи с терминалом.
Все экстракоды работы с терминалами, приводимые в данном приложении, имеют вид
ИР 071 А (1)
где ЛИСП — адрес информационного слова (ИС) данного экстра-кода (через Ci будет обозначаться i-й разряд слова С).
1.1. О и р е д е л е н и е номера терминала, подключенного к задаче.
Прежде чем задача пользователя начнет работу с терминалом, эта задача должна определить номер закрепленного за ней терминала. Для этой цели используется экстракод (1) с ИС, имеющим вид
ИС: 7777 7777 7777 7777
Результат выполнения экстракода — слово С в сумматоре, где
Ci = 1, если терминал с номером 49 — i закреплен за данной задачей,
Ci = 0 в противном случае.
1.2. Обмен с терминалом.
Начало и конец в оперативной памяти массива, участвующего в обмене, определяются следующим образом:
АНАЧ = А1 + (ИР1), АКОН = А2 + (ИР2).
ИС для экстракода (1) в этом случае имеет следующую структуру:
С48 —С45:ИР1,
С44 — С42 = 0,
С41 = 1,
С40___( 1 в случае приема с терминала,
( 0 в случае выдачи на терминал.
Разряды С39 и С38 в случае выдачи на терминал игнорируются.
В случае приема с терминала разряд С39 используется для указания формы приглашения пользователю к набору на клавиатуре сообщения, принимаемого с терминала. Это приглашение выдается на экран либо в виде символа «—» (стандартное приглашение), либо в виде текста (нестандартное приглашение). Этот текст предварительно должен быть помещен в начало массива памяти, участвующего в обмене, причем признаком конца этого текста является код 377а.
117
Таким образом, в случае приема:
СЗд___( 0 в случае стандартного приглашения,
( 1 в случае нестандартного приглашения.
( 1 — «секретный» прием (без высвечивания на экране
С38 = < передаваемого текста), (, 0 — обычный прием.
С37 = О,
С36 — С25: А1,
С24 — С21: ИР2,
С20 = 0,
С19 = 1,
С18 — С13: восьмеричный номер терминала,
С12 — Cl: А2.
1.3. Опрос состояния терминала.
При обменах с терминалом ОС не берет на себя функций автоматической синхронизации обменов и обращений к используемым при этом участкам памяти, а также упорядочения обменов с одним терминалом. Эту работу должна выполнять сама задача с помощью опроса состояния терминала. В этом случае ИС экстракода (1) имеет следующую структуру:
С43 —С41 = 1,
С26 = 0, С25 = 0,
С6 — С1: номер терминала.
Содержимое остальных разрядов ИС игнорируется. Разряды слова С, оставляемого в качестве ответа на сумматоре, имеют следующий смысл:
С26—С25: К —код ответа;
К = 00 — терминал не подключен к задаче или не окончил обмен;
К = 10 — терминал нормально закончил обмен;
К = 01 — в течение 5 минут с терминала не поступил ни один символ (если выполнялся экстракод приема с терминала);
К = 11 — обрыв связи;
С6 — С1: номер терминала.
Значение остальных разрядов не определено.
2. Экстракоды запроса статуса терминалов.
2.1. Запрос номеров занятых терминалов.
Экстракод
00 062 0056
позволяет получить номера всех терминалов, занятых задачами поль-эователей. В качестве пезлтльтата на сумматоре оставляется слово.
113
являющееся кодом ответа: если Ci = 1, то терминал с номером 49 — i занят.
2.2. Запрос номеров свободных терминалов.
Экстракод
00 062 0060
позволяет получить номера всех терминалов, которые не заняты задачами пользователей и не являются операторскими. В качестве результата на сумматоре оставляется слово, являющееся кодом ответа: если Ci = 1, то терминал с номером 49 — i свободен.
3. Захват свободного терминала.
Перед выполнением экстракода
00 062 0057
в сумматор надо занести слово, в котором задан номер i захватываемого терминала (номер I задается единицей в разряде 49 — t). Код ответа оставляется в 15 младших разрядах сумматора:
ТПП — захват терминала выполнен;
00001 —терминал не подключен к ЭВМ;
00002 — терминал занят;
00004 — указанный терминал является операторским.
4. Выдача фамилии пользователя по шифру.
Перед выполнением экстракода
00 050 0104
в младшие разряды сумматора должен быть занесен адрес В ячейки, в 16 младших разрядах которой находится четырехзначный шифр пользователя в двоично-десятичной записи.
В качестве результата по адресу В заносятся первые 6 символов фамилии пользователя, а остальные символы (нс более 6) заносятся по адресу В+ 1; если пользователь с заданным шифром не зарегистрирован в системе, то по адресу В записывается нулевое слово.
5. Запрос текущей даты.
По экстракоду
00 050 0114
в сумматор заносится слово, имеющее следующий смысл:
С35 — СЗО: число (С35'—С34 десятки, СЗЗ— СЗО — единицы числа);
С29 — С25: номер месяца (С29 — десятки, С28 — С25 — единицы номера месяца);
С24 — С21: последняя цифра года;
С20—С17: предпоследняя цифра года;
СЗ—С1: номер машины.
119
6. Окончание задачи.
По любому из двух экстракодов
00 074 0000 или 00 062 0000
выполнение задачи прекращается и, если велась работа с отладчиком ОС Диспак, вызывается диагностика
ппппп КОНЕЦ ЗАДАЧИ
где ппппп—адрес выполненного экстракода.
7. Печать.
Для распечатки на АЦПУ содержимого группы ячеек с адресами АН по АК включительно в символьном виде служит экстракод
ИР 64 А (ЛИСП > 1)
В ячейке АИСП должна находиться пара команд
ИР1 00 А1 и ИР2 00 А2
где А1ИСП = АН, А2ИСП = АК. В ячейке АИСП + 1 должно находиться слово (задающее распечатку в символьном виде):
00 000 0000 10 000 0000
В кодировке печатаемого текста должен встретиться код 172а, являющийся признаком конца печатаемого текста.
8. Обмен с магнитным диском.
Данные на магнитных дисках БЭСМ-6 размещаются в зонах фиксированной длины по 1024 слова, и обмен может производиться только между целой зоной и страницей оперативной памяти.
Обмен с МД производится по экстракоду
ИР 70 А
Слово по адресу АИСП должно содержать следующую информацию:
СЮ — С1: номер зоны;
С15 —С13: математический номер I дисковода (0 I 7);
С18 — С16: номер k направления дисковода (3 й =С6); для данного задания 6 = 3, 7 = 0:
{1 в случае чтения, Л
0 в случае записи.
Приложение 3. Некоторые таблицы ОС Диспак
1. Таблица занятости магнитофонов.
Эта таблица размещается в памяти с ячейки 6238. Она разбивается на 4 группы ячеек; каждая группа состоит из 8 ячеек, соответствующих физическим магнитофонам с номерами от 0 до 7 определенного направления (ниже указаны восьмеричные порядковые номера ячеек, образующих таблицу):
0 — 7: направление 3; 20 — 27: направление 5;
10 — 17: направление 4; 30 — 37: направление 6, . •
120
каждое слово таблицы имеет следующую структуру:
С12 —С1: номер установленной на магнитофон бобины с МЛ;
С41 = 1 — признак бобины, общей для всех задач;
С46 — С42: число задач, работающих с общей бобиной;
С47 = 1 — признак системной ленты.
2. Таблица занятости магнитных дисков.
Эта таблица размещается в памяти с ячейки 6638 и состоит из 8 групп по 8 ячеек; каждая группа соответствует одной из линий (с номерами от 0 до 7), а каждая ячейка группы соответствует одному из физических дисководов (с номерами от 0 до 7) данной линии.
Каждое слово имеет такую же структуру, как и в таблице занятости магнитофонов.
КАФЕДРА СИСТЕМНОГО ПРОГРАММИРОВАНИЯ
Задание СП-1. МАКРОАССЕМБЛЕР
Цель задания.
1. Знакомство с конкретным представлением макросредств и методикой их использования в инструментальных целях.
2. Практика работы с макросредствами.
Содержание задания.
1. Изучение системы команд ЭВМ БЭСМ-6 [1], автокода БЕМШ [2] и языка макрокод [3].
2. Ознакомление с методикой использования макрокода для расширения возможностей базового языка.
3. Составление и отладка набора макроопределений иа макрокоде в рамках мониторной системы Дубна [4, 5], ОС Дис-пак [6].
Постановка задачи.
Реализовать набор макроопределений одного из предложенных вариантов задания и составить набор тестов для их отладки.
Для решения задачи следует:
1. Ознакомиться с постановкой конкретного варианта задания.
2. Изучить систему команд ЭВМ, автокод и макрокод, концентрируя внимание на средствах, которые требуются для реализации предложенного варианта задании.
3. Ознакомиться с возможностями языка управления заданиями и средствами вывода информации на печать.
4. Уточнить внешние спецификации разрабатываемых макроопределений, написать набор тестов для их проверки и зафиксировать ожидаемые результаты.
121
5, Разработать алгоритмы или структурные схемы макрокоманд и записать их на макрокоде.
6. Окаймить тексты макроопределений программой для их тестирования и операторами языка управления заданиями.
7. Отперфорировать все тексты, отладить макроопределения и оформить отчет по заданию.
Содержание отчета.
1. Постановка конкретного варианта задания и внешние спецификации реализуемого набора макрокоманд.
2. Описание используемых алгоритмов, внутренней огранизации макроопределений, структуры тестирующей программы и ожидаемых результатов тестирования.
3. Инструкция потенциальному пользователю разработанною набора макрокоманд, с краткими характеристиками макрокоманд и перечнем ограничений на их использование.
4. Тексты программ на макрокоде, а также результаты генерации и (или) решения на ЭВМ тестовых вариантов.
5. Дневник отладок с перечнем допущенных ошибок и оценками израсходованных ресурсов ЭВМ.
Литература.
1. Трифонов Н. П. Система команд БЭСМ-6. — М.: Изд-во МГУ, 1969.
2. Штаркман В. С. Автокод БЕМШ. — М.: Изд-во ИПМ АН СССР, 1969.
3. М и х е л е в В. М., Штаркман В. С. Макрокод (описание языка). —М.: Изд-во ИПМ АН СССР, 1972.
4. Б о ч к о в а 3. Ф. и др. Руководство по работе с программами на автокоде БЕМШ. — М.: Изд-во ИПМ АН СССР, 1974.
5. М а з н ы й Г. Л. Программирование на БЭСМ-6 в системе ДУБНА. — М.: Наука, 1978.
6. 3 е л ь д и и о в а С. Л. и др. Инструкция пользователю по работе с операционной системой ДИСПАК БЭСМ-6. — М.: Изд-во ИПМ АН СССР, 1972.
7. М н х е л е в В. М., Вершубский В. Ю. АСТРА — язык для записи алгоритмов системного программирования и трансляции.— М.: Изд-во ИПМ АН СССР, 1974.
8. Павлов Б. М., Посохов И. Н. Математическое обеспечение ЭВМ типа ЛТ-20. — Наука, 1975.
9. Б р и ч 3. С. и др. Программирование иа языке ассемблера ЕС ЭВМ. — М.: Статистика, 1975.
10. У олш Д. Руководство по созданию документации для математического обеспечения. — М.: Наука, 1975.
11. Егорова Т. В., Островский В. В. Метаассемблер на базе макрокода. — В кн.: Вопросы системного программирования. — М.: Изд-во МГУ, 1978.
122
12. Островский В. В., Урманов а Н. А. Самопротоколи-руемые операторы языка тестирования. — В кн.: Вопросы системного программирования.—М.: Изд-во МГУ, 1978.
13. Марголин М. С. О фильтрации параметров программных объектов. — Программирование, № 4, 1978.
Приложение 1. Варианты задания
I. Реализовать подмножество операторов языка астра [7].
1. STORE,CONST,EXPR(A=B±C)
2. REG,CONST,EXPR(A=B±C)
3. STRIT,MAR,FIELD,EXPR(A = B)
4. CONST.EXPR(a)
5. CONST,EXPR(b)
6. GOTO по номеру и значению
7. IFA,IFAND,IFOR
8. DO,DOAND,DOOR
9. CALLA,SUBRUT,RETURN
10. PRINTA,FORMAT
Здесь a — арифметическое выражение, b — выражение, содержащее только логические операции и операции сдвига.
II. Промоделировать подмножество команд ЭВМ БЭСМ-4 [8] £& ЕС ЭВМ [9].
1. С,В,ВА,У,Д,К
2. И,ИЛИ,Н,ЦС,СМ,СДСА
3. РА,РС,ПМ,ПМС,ПВ
4. L,A,S,M,D,ST
5. CVD,CVB,RACK,UNPK
6. ZAP,АР,SP,MP,DP,СР
7. BC,BAL,BCT,BXH,BXLE
8. TR,TRT,EX
III. Реализовать аналоги конструкций алгола-60 и фортрана.
1. GOTO
2. IF арифметический
3. IF логический
4. CALL,FUNCTION,RETURN
5. DO,CONTINUE
6. FORMAT,PRINT
7. IF —THEN —ELSE
8. FOR —STEP —UNTIL —DO
9. FOR —WHILE —DO
10. SWITCH —GOTO
IV. Реализовать на макрокоде.
1. Самопротоколируемый оператор отладочной печати [12]
m PRINT _ A, L, D = d, Т = t, С = com, Р = {YES | NO} где А — адрес или ссылка на начало выводимого сегмента, L — длина сегмента, d — сдвиг информации относительно начала сегмента, t —
123
тип информации, Р — признак протоколирования, т — метка, сот — комментарий.
2. Самопротоколируемый оператор обращения к подпрограмме [12]
т . . PCALL . . pro (par), L — l, Т = t, С = сот
где pro — имя подпрограммы, par — список параметров, I — уровень протоколирования, t — тип печати, сот — комментарий, т — метка.
3. Оператор, позволяющий записывать иа одной перфокарте несколько команд ассемблера или макрокоманд
т . . MLIST . . (пате . , mpl ..)
где т — метка, пате — имя команды или макрокоманды, mpl — список параметров, / — разделитель элементов цепочки команд (макрокоманд).
4. Оператор для «быстрых» обращений к подпрограммам с передачей параметров через индексные регистры
т , . RCALL , , pro (par), k, е
где pro — имя подпрограммы, k — начальный номер регистра для передачи параметров, par — список значений параметров или ссылок на параметры, е — регистр обратной связи, т — метка.
V. Реализовать макрокоманды фильтрации параметров [13].
FILTR _ [PARNUM,] PARNAME, filtr
для одного из следующих вариантов списка значений filtr (здесь
s — строка символов; k, kl, k2— целые без знака):
1. TYPE = Л VAL = o, ABSNT = a, WRONG = ш
t = SYMB I REG | NUM | RES | LIST
v = (Op o2, ..v; = s | k\ a, w = s | (s, MNOTE)
2. TYPE1 = I,, TYPE2 = t2, ..VAL1 = vt, VAL2 = v2, ...
ti = SYMB | NUM
Vl ~ (Vil’ Vi2’ ’ • •)’ Vil = S । k I 61 — k2 | k — M
3. TYPE = HNAME, STl=sM, SUBTYPE = st, SUBVAL=s v ST2 = s/2
st = SYMB | NUMB, so = s\k, stl, st2^s
VI. Реализовать кросс-ассемблер на базе макрокода [11] для следующих подмножеств команд ЭВМ БЭСМ-4 [8] и ЕС ЭВМ [9]:
1. С,В,У,Д,ПБ,РА
2. И,Н,РС,ПМС,ПВ
3. L,A,S,M,D,ST
4. BC,BAL,BCT,BXH,BXLE
Приложение 2. Методические указания
1. В реализуемых макроопределениях необходимо предусмотреть синтаксический и семантический контроль правильности записи параметров в макрокомандах.
124
2. При реализации «громоздких» макрокоманд следует обратить особое внимание на выбор разумной границы между трансляцией и интерпретацией.
3. Для вывода результатов тестирования и при реализации макрокоманд вывода информации на печать следует использовать экстракод ПЕЧ (Э63) [6].
4. На каждой строке бланка может быть записано только одно предложение автокода БЕМШ или макрокода. Каждое предложение может заканчиваться признаком конца строки (надчеркивание) или быть записано без такого признака.
5. При перфорации программы на устройствах типа ДЖУКИ в качестве признака начала макропеременной используется символ &, надчеркиванию соответствует символ—а символу <ф- в директивах библиотекарю—символ §.
6. Для макрообработки, трансляции и счета нужно сформировать задание для ОС Диспак [6], которое имеет следующую струк
туру:
ШИФР . . (шифр). . ЗС2
ЕЕВ1АЗ
* NAME. . (фамилия)
* BEMSH
ВВД§§§ “I
(имя). . СТАРТ , . '1000' (программа)
„ ФИНИШ _ (имя)
КВЧ§§§ “I
ТРН§§§-1 0 — 0—1 КНЦ§§§ -1 § Е * MAIN , . (имя) * EXECUTE * END _ FILE (диспетч. конец) ЕКОНЕЦ
КАФЕДРА МАТЕМАТИЧЕСКОЙ КИБЕРНЕТИКИ
Задание МК-1. КОНЪЮНКТИВНЫЕ И ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ БУЛЕВСКИХ ВЫРАЖЕНИЙ
Цель задания.
1. Практика в использовании ЭВМ для решения задач дискретной математики.
2. Накопление опыта в использовании алгоритмических языков и отладке программ.
Содержание задания.
1. Изучение алгоритмов преобразования булевских выражений, заданных в конъюнктивной нормальной форме (КНФ), в дизъюнктивную нормальную форму (ДНФ).
2. Составление на языке фортран програм?.1ы построения сокращенной ДНФ методом Нельсона.
3. Подбор тестовых примеров и отладка программы.
4. Решение на ЭВМ контрольного варианта задания.
125
Постановка задачи.
Булевское выражение, заданное в конъюнктивной нормальной форме, преобразовать в сокращенную дизъюнктивную нормальную форму (см. [1]).
Для преобразования использовать метод Нельсона [2], который заключается в последовательном применении к заданной КНФ выражения следующих операций:
а) раскрытие скобок, т. е. преобразования вида
(а V b) & (с V d) = а & с V a & d V й & с V b &d;
б) применение правила а&а—а;
в) исключение тождественно нулевых конъюнкций, т. е. конъюнкций, содержащих вхождения вида а&а;
г) исключение элементарных поглощений, т. е. выполнение преобразований вида а\/а&Ь = а.
Получающаяся в результате применения этих операций ДНФ является сокращенной.
Для отладки программы подобрать необходимый набор тестов.
Конкретное выражение, подлежащее преобразованию по составленной программе, задается преподавателем по окончании отладки программы.
Содержание отчета.
1. Постановка задачи.
2. Текст фортран-программы.
3. Набор тестов и результаты отладок.
4. Результаты контрольного счета на ЭВМ.
Литература.
1. Яблонский С. В. Введение в дискретную математику.—-М.: Наука, 1979, с. 220—222.
2. Яблонский С. В. Труды МИАН СССР, Т. 51, 1958, с. 5— 141.
Задание МК-2. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ О ПОКРЫТИИ
Цель задания.
1. Практика в использовании ЭВМ для решения задач дискретной математики.
2. Знакомство с языками лисп, PL/1 и практика их использования.
Содержание задания.
1. Изучение методов приближенного решения задачи о покрытии.
126
2. Разработка алгоритма приближенного решения задачи о покрытии градиентным методом.
3. Составление и отладка программы.
4. Решение на ЭВМ контрольных примеров.
Постановка задачи.
В матричной форме задача о покрытии формулируется следующим образом. Дана матрица А размером т Xп с элементами из множества {0, 1}, не содержащая нулевых строк. Требуется найти подматрицу А' матрицы А, которая также содержит т строк (среди которых нет нулевых), но состоит из минимально возможного числа столбцов.
Приближенным решением является подматрица без нулевых строк с числом столбцов, близким к минимально возможному.
При выполнении задания предлагается использовать градиентный метод, который состоит в пошаговом выделении столбцов результирующей матрицы:
— на первом шаге выделяется столбец, содержащий наибольшее число единиц (если таких столбцов несколько, то берется любой из них), и в матрице вычеркиваются (считаются покрытыми) все строки, содержащие единицу в выделенном столбце;
— на k-м шаге выполняются те же действия над матрицей, полученной (в результате вычеркивания строк) на предыдущем этапе.
Этот процесс заканчивается, если на очередном этапе все строки рассматриваемой матрицы оказались вычеркнутыми. Подматрица, составленная из тех столбцов исходной матрицы А, которые выделялись в процессе выполнения алгоритма, и является искомой подматрицей.
Так, если
О 0 1 \
1 О о
1 о о
1 1 о
0 11/
то на первом шаге можно выделить первый или второй столбец. Если взять первый, то после вычеркивания первых трех строк (содержащих 1 в выделенном столбце) получим матрицу
Л(!) _ Г 0 1 1 о ч
А “ко 0 11/
На втором шаге выделяем третий столбец. После вычеркивания строк, содержащих 1 в этом столбце, получаем пустую матрицу и процесс заканчивается. Результатом применения алгоритма является матрица, состоящая нз первого и третьего столбцов исходной
127
матрицы;
Содержание отчета.
1. Постановка задачи.
2. Текст программы, набор тестов и результаты отладок.
3. Результаты решения на ЭВМ контрольного варианта.
Литература
1. Кристоф идее Н. Теория графов, алгоритмический подход.— М.: Мир, 1978.
Задание МК-3. ПОСТРОЕНИЕ КРАТЧАЙШЕГО СВЯЗЫВАЮЩЕГО ДЕРЕВА
Цель задания.
1. Практика в использовании ЭВМ для решения дискретных экстремальных задач.
2. Накопление опыта по использованию алгоритмических языков и отладке программ.
Содержание задания.
1. Изучение алгоритмов Краскала [1] и Прима [2] решения задачи построения кратчайшего связывающего дерева.
2. Составление и отладка программы на фортране.
3. Решение на ЭВМ по составленной программе контрольного варианта задания.
Постановка задачи.
Задан связный граф G, ребрам которого приписаны неотрицательные числа (веса). Весом подграфа называется сумма весов его ребер. Дерево, содержащее все вершины графа G, составленное из ребер графа G и имеющее минимально возможный вес, называется кратчайшим связывающим деревом [3].
Требуется по заданному графу построить кратчайшее связывающее дерево.
Для выполнения задания предлагается использовать алгоритм Краскала, который заключается в следующем:
— на первом шаге выбирается какое-либо ребро с наименьшим весом;
— на Л-м шаге выбирается ребро, не образующее цикла с ребрами, выбранными на предыдущих шагах, и имеющее наименьший вес среди всех таких ребер.
128
Выполнение алгоритма заканчивается после (п—1)-го шага, где п—число вершин. Совокупность выбранных ребер и образует кратчайшее связывающее дерево.
Контрольный вариант.
Множество вершин графа Gn, k состоит из двух подмножеств: А = {ai, а2, ... а„} и В — {&i, i>2, .... М- Для каждой пары (а,, 6/) в графе G имеется ребро (а,, Ь,), которому приписан вес, равный п— где itjfrj = i + j (mod k). Ребра вида (a,-, a,), (bi, bi) отсутствуют.
Построить кратчайшее связывающее дерево для Gio, 4-Содержание отчета.
1. Постановка задачи.
2. Выбранный способ представления графа и дерева в ЭВМ.
3. Текст программы на фортране, тесты и результаты отладок.
4. Результат решения на ЭВМ по составленной программе контрольного варианта.
Литература.
1. Б ер ж К. Теория графов и ее применения. — М.: ИЛ, 1962.
2. П р и м Р. К. Кратчайшие связывающие сети и некоторые обобщения. — Кибери. сб., вып. 2 (ст. серия), 1961, с. 95—107.
3. Кристофидес Н. Теория графов, алгоритмический подход.— М.: Мир, 1978.
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
Задание ВМ-1. ЧИСЛЕННОЕ РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Цель задания.
1. Практика в постановке краевых задач для уравнений с частными производными.
2. Знакомство с разностными методами решения краевых задач и практика в их использовании.
3. Практика использования алгоритмических языков типа алгол-60.
4. Накопление опыта обработки и оформления результатов вычислений.
Содержание задания.
1. Постановка краевых задач для уравнений параболического и гиперболического типов.
2. Изучение разностных методов решения краевых задач; выбор разностной схемы для решения конкретной задачи.
3. Составление программы на алгоритмическом языке и ее отладка.
4. Решение на ЭВМ конкретной задачи.
5 Н. П. Трифонов, Е. Н. Пасхин
129
5. Оформление полученных результатов в виде таблиц и гра-фиков.
Постановка задачи.
В каждом варианте задания приводится физическая постановка задачи, связанной либо с процессом теплопроводности, либо с процессом колебаний стержня или мембраны.
Требуется:
1. Поставить краевую задачу, соответствующую данной физической задаче, т. е. выбрать функцию, характеризующую соответствующий физический процесс (см. Приложение 1), а затем
а) написать дифференциальное уравнение для этой функции;
б) установить для нее граничные условия;
в) сформулировать начальные условия;
г) вывести условия сопряжения на границе двух однородных сред (в вариантах I и IV).
Физическая постановка задачи определяется вариантом задания (см. Приложение 2).
2. Решить аналитически соответствующую модельную задачу. На примере этой задачи изучить качественные закономерности исследуемого процесса и (или) оценить значение некоторой величины, указанной в варианте задания.
3. Решить на ЭВМ с помощью разностных методов модельную задачу и сравнить приближенное и точное решения исходной задачи в разностной норме С. При аппроксимации краевых условий 2-го и 3-го рода следует обратить особое внимание на порядок аппроксимации. На примере модельной задачи изучить поведение погрешности фл при согласованной и несогласованной (с первым порядком) аппроксимации граничных условий.
4. Сформулировать алгоритм численного решения поставленной в п. 1 задачи и определения значения Т — момента, в течение которого устанавливается некоторый режим процесса, указанный в варианте. Описать используемую разностную схему н метод решения разностных уравнений. Обосновать выбор шага по всем направлениям сетки.
5. Составить блок-схему программы.
6. Составить и отладить программу; по отлаженной программе произвести необходимые расчеты и обработать полученые результаты.
Содержание отчета.
1. Содержание задания (конкретный вариант).
2. Математическая постановка задачи.
3. Математическая постановка модельной задачи и ее аналитическое решение.
4. Разностная схема и алгоритм решения разностной задачи.
5. Блок-схема программы.
130
6. Программа на алгоритмическом языке.
7. Тесты и результаты отладок.
8. Анализ результатов. Графики.
9. Приложение: результаты счета на ЭВМ с распечаткой программы.
Литература.
1. Тихонова. Н., Самарский А. А. Уравнения математической физики (гл. III и дополнение I). — М.: Наука, 1977.
2. Самарский А. А. Теория разностных схем (гл. I, II, § lj гл. VII, VIII, § I). — М.: Наука, 1977.
3. Методические пособия и инструкции по программированию.
Приложение 1. О физических задачах, приводящих к уравнениям в частных производных, и о постановке краевых задач
При исследовании явления теплопроводности получается уравнение параболического типа. В вариантах I—IV рассматривается постановка и решение краевых задач для уравнений параболического типа в случае, когда изучаемые физические процессы характеризуются функциями независимых переменных: одной пространственной координаты и времени.
Уравнения и граничные условия рассматриваемых в этих вариантах краевых задач являются следствием:
а) закона сохранения энергии;
б) закона внутренней теплопроводности в твердых телах (закона Фурье);
в) закона конвективного теплообмена между поверхностью твердого тела и окружающей средой (закона Ньютона).
Закон Фурье в одномерном случае выражается формулой
, ди q —— 071-4—, ’ дх
где q — количество тепла, протекающее в единицу времени в направлении оси х через площадку о, перпендикулярную к оси х; и — температура в рассматриваемом месте тела; X — коэффициент теплопроводности.
Закон Ньютона выражается формулой q = ста (и — и0), где q — количество тепла, протекающее в единицу времени через площадку о поверхности тела в окружающую среду; и — температура поверхности тела; и0 — температура окружающей среды; а — коэффициент теплообмена.
Если боковая поверхность стержня теплоизолирована, то температура в нем все время будет зависеть лишь от одной пространственной координаты х.
5*
131
Кусочно-однородная среда и сосредоточенный фактор приводят К уравнению с кусочно-постоянными коэффициентами и к условиям сопряжения.
Задачи о колебаниях стержня или мембраны приводят к уравнениям гиперболического типа. Физические процессы, изучаемые в вариантах V и VI, как и выше, могут быть охарактеризованы функциями двух переменных. Рассматриваются лишь малые колебания,-т. е. можно, пренебрегать квадратами, произведениями и высшими степенями функций, характеризующих процесс колебаний, и их производных.
Считаем также, что влияние силы тяжести на колебания частиц пренебрежимо мало по сравнению с влиянием упругих сил, т. е. действием силы тяжести можно пренебречь.
Уравнения колебания являются следствием уравнения движения, выражающего второй закон Ньютона: элементарное изменение количества движения материальной точки равно элементарному импульсу действующей иа нее силы.
Если концы стержня или края мембраны фиксированы неподвижно, то граничные условия очевидны. Если же границы свободны, то граничные условия могут быть получены из соотношений, выражающих второй закон Ньютона для i раничных элементов.
Приложение 2. Варианты задания
I. Задача для уравнения теплопроводности в случае неоднородной среды с сосредоточенным фактором.
Физическая постановка задачи.
Тонкий стержень 0 х I с теплоизолированной боковой поверхностью составлен из двух однородных стержней 0 ig х х0 и «о х I с различными физическими параметрами;
В точке %о находится сосредоточенный источник тепла постоянной мощности q. Начальная температура левого стержня равна щ = = const, правого — и2 = const, а концы поддерживаются при температурах Ui и и2 соответственно, либо теплоизолированы, т. е. W(t) = = 0, где = Wt(t) = W2(t) —тепловые потоки, поступающие в стержень через его концы.
Определить распределение температуры и составного стержня для времени 0 < t sg Т, где Т — время стационарного распределения температуры в стержне с заданной точностью, если удельная теплоемкость, плотность массы и коэффициент теплопроводности мате?
132
риала стержней равны соответственно cl; pi, tit = ai + biu0' и с?, p2 %2 = a2 "Ь bill®2'
Значения констант l, щ, u2, ii, lz, Ci, pi, at, bit 01, c2, p2, a2, b2. o2, а также тепловые режимы на концах стержня определяются подвариантом задания (см. Приложение 1.1).
Требуется:
1. Сформулировать аналитически соответствующую модельную задачу для однородного стержня с параметрами:
__ Р1Л + Р2/2 __ cili + __aili Q-ilj
Р li + h ’ li +l2 ’ /1 +/2 ’
однородными граничными условиями (тип которых определяется вариантом задания), нулевыми начальными условиями и источником, плотность которого имеет вид f(x, t) = qXx (x)/||Xi(x) II, где Xi(x) — первая собственная функция соответствующей краевой задачи. Оценить время Т установления в стержне с заданной точностью стационарного распределения температуры.
2. Решить на ЭВМ с помощью разностных методов модельную задачу и сравнить приближенное и точное решения исходной задачи.
3. Решить на ЭВМ разностную задачу, соответствующую поставленной краевой задаче. Определить время Т, в течение которого в составном стержне с заданной относительной точностью 5% устанавливается стационарное распределение температуры.
4. Выдать на печать распределение температуры в стержне в моменты времени, кратные 0.2Г, и нарисовать графики этого распределения. Нарисовать график изменения температуры со временем в точке х0.
Методические указания.
При решении разностной задачи использовать неявную разностную схему с итерациями на каждом слое по времени.
Шаг по координате х принять равномерным: h = 0.05/. В соответствии с этим выбрать шаг т по времени и точность при итерациях е, обеспечивающие необходимую точность вычислений.
Стационарное распределение температуры считается достигнутым с относительной точностью 5% при выполнении неравенства
где / — номер точки на слое, / — номер слоя по времени.
Приложение 1.1. Подварианты задания
Подварианты задания имеют номера k от 1 до 15.
Для всех подвариантов принять q = 20.
133
Если иомер k подварианта представить в виде k = Зт + п (т = 0, 1, 2, 3, 4; п = 1, 2, 3), то тепловые режимы иа концам стержня определяются значением п:
п На левом конце На правом конце
1 Mt
2 U2
3 №=0 U-2
Значения констант определяются значением т:
m *1 *2 Р1 сх а1 61 ’1 р2 С2 а2 Ь2 р2 “1 “2
0 1 1 I 1 0.1 0.1 1 1 1 0.03 0.03 3 0.01 0.01
1 1 1 1 1 0.2 0.2 0 1 1 0.05 0.05 4 0.02 0.02
2 1 1 1 1 0,1 0.1 2 1 1 0.1 0.1 2 0.01 0.05
3 0.5 1.5 0.25 2 0.1 0.1 1 0.5 4 0.2 0.2 2 0.01 0.01
4 1.5 0.5 0.5 4 0.1 0.1 3 0.25 2 0,2 0.2 1 0.01 0.01
II. Задача для уравнения теплопроводности с разрывными начальными условиями.
Физическая постановка задачи.
Найти распределение температуры и в тонком стержне 0 яЯ х я^
I с теплоизолированной боковой поверхностью при его остывании в течение интервала времени [О, Г], где Т — время установления стационарного распределения температуры в стержне с заданной точностью.
Удельная теплоемкость с, плотность массы р и постоянные а, Ь, о в выражении для определения коэффициента теплопроводности х = а -|- Ьиа, а также тепловые режимы на концах стержня определяются подвариаитом задания (см. Приложение 1.2).
Начальная температура стержня равна
( р. при х *= [Zi, 1г], и = <
(. v при х е [Zi, /21-
Постоянные u,, v, /ь 12 (О Zi < /2 /) также заданы в подва-
рианте задания. Температуры концов стержня либо постоянны, либо один из его концов теплоизолирован, т. е. И7(/) =0, где IV(/) —. тепловой поток, поступающий в стержень через его конец.
Требуется:
1. Сформулировать краевую задачу, соответствующую данной физической задаче.
134
2. Решить аналитически соответствующую модельную задачу для стержня с коэффициентом теплопроводности х = а, начальными условиями и(х, 0) = v-j-(х), где Xi (х) — первая собственная функция соответствующей краевой задачи, и граничными условиями, со-ласованными с начальным распределением температуры. Оценить время Т остывания стержня до постоянной по всей длине температуры с заданной точностью.
3. Решить иа ЭВМ с помощью разностных методов модельную задачу и сравнить приближенное и точное решения исходной задачи.
4. Решить иа ЭВМ разностную задачу, соответствующую поставленной краевой задаче. Определить время Т остывания стержня до постоянной по всей его длине температуры с точностью 5%.
5. Выдать на печать значение времени Т, распределение температуры в стержне в моменты времени, кратные 0.2Г, и нарисовать графики этого распределения.
Методические указания.
При решении разностной задачи считать постоянную по длине температуру достигнутой при выполнении неравенства
6 = (max и\ — min min и\ сф 0.05,
где i — номер узла на слое, j—номер слоя по времени.
О выборе разностной схемы, шага по х и t см. указание к варианту I.
Приложение 1.2. Подварианты задания
Для всех подвариантов принять I = 1.
Если номер k подварианта представить в виде k = 4m -J- п (m = 0, 1, 2; п = 1, 2, 3, 4), то тепловые режимы на концах стержня определяются значением га:
п На левом конце На правом конце
1 U Ц
2 w==o Ц
3 г=о
4 w=o
а значения констант определяются значением т:
tn h h а ь а Р С н V
0 0.3 0.7 1 3 3 1 1 0.01 1
1 0.4 0.8 1 1 2 2 2 0.01 1.5
2 0.5 1.0 1 1 1 2 0.25 0.5 2
135
III. Задача для уравнения теплопроводности с разрывными граничными условиями.
Физическая постановка задачи.
Найти температуру и тонкого стержня 0 sg: х I с теплоизолированной боковой поверхностью, если один его конец поддерживается при заданной фиксированной температуре «0 или теплоизолирован (тепловой поток W(/) на этом конце равен нулю), а на другой конец подается извне заданный тепловой поток одного из следующих типов:
f Q, 0 < t < t0, f 2Qt, 0 < t < ta,
to, 4 < t < Г; I 0, /0 < t < T;
J2Q(/o-O, 0</<Z0,
W 0 =5 \
I o,
'/ 2Qt, 0</<Z0/2,
IT4 = j 2Q (t0 - t), /0/2 <t<t0,
I 0, ta < t < T.
Здесь T — момент времени, в который температура стержня в точке х = 1)2 достигает максимального значения с заданной точностью г, a Q и t0 — заданные константы.
Удельная теплоемкость стержня с, плотность массы р и постоянные а, Ь, а в выражении для коэффициента теплопроводности х — = а + Ьиа заданы в подварианте задания. Начальная температура стержня равна и0.
Требуется:
1. Сформулировать краевую задачу, соответствующую данной физической задаче.
2. Решить аналитически соответствующую модельную задачу для стержня с коэффициентом теплопроводности х = а. Оценить максимальную температуру «Г1ах, достигаемую в точке х — 1/2, и момент времени Т, в который она достигается. В соответствии с этим выбрать время рассмотрения процесса нагрева стержня.
3. Решить на ЭВМ разностную задачу, соответствующую поставленной краевой задаче. Определить максимальную температуру «max, достигаемую в точке х = Z/2 стержня, и момент Т, в который она достигается.
4. Выдать на печать распределение температуры в стержне в моменты времени, кратные 0.2Т, и нарисовать графики этого распределения. Нарисовать график зависимости от времени температуры в точке х — 1/2.
Методические указания.
Прн решении разностной задачи использовать неявную разностную схему с итерациями на каждом слое по времени. Точность е положить равной 0.01.
13й
Приложение 1.3. Подварианты задания
Для каждого из 16 подвариантов принять 1 — 2, Q = 10, /о = 0.5.
Значения других констант и тепловые режимы на концах стержня для подварианта с номером k задаются следующей таблицей:
k р с а 6 ст Uo Тепловой режим на левом конце Тепловой режим на правом конце
1 1 1 1 3 3 0.1 «7, «7 = 0
2 «7=0
3 W3
4 wt 1F=O
5 0.25 2 0.5 2 2 0.1 «7 = 0 «71 '
6 «7 = 0 «72
7 «7=0 Wt
8 «7 = 0 «74
9 4 0.5 0.1 1 3 0.1 IFt
10 «72 U = Ua
11 «73 U~Ub
12 W, U = Uq
13 0.5 2 5 0.1 4 0.01 U — Uq Wi
14 U — Uq «72
15 U = Uq «7,
16 U = Uo W.
IV. Задача для стационарного уравнения теплопроводности в случае неоднородной среды.
Физическая постановка задачи.
Тонкий стержень 0 х I с теплоизолированной боковой поверхностью составлен из двух однородных стержней 0 х Хо, Хо =5 х I с различными физическими параметрами:
На концах стержня тепловой режим определяется двумя возможностями:
I) поддерживается постоянная температура
и (0) = ил> и (1) = ип;
П) происходит конвективный теплообмен со средой, температура которой слева равна 0Ь справа — 02.
137
Найти распределение температуры и в составном стержне, если удельная теплоемкость, плотность массы и коэффициент теплопроводности левого стержня равны Ci, pi, к1 = а1 + 6iu'T1, а правого — соответственно с2, рз, х2 — а2 + Ьзи?2, Константы и тепловой режим на концах стержня определяются вариантом задания (см. Приложение 1.4).
Требуется:
1. Сформулировать краевую задачу, соответствующую дайной физической задаче.
2. Решить аналитически соответствующую модельную задачу для составного стержня со следующими физическими параметрами: Ci, pi, Xi = О] и с2, р2, %2 — аг- Приняв, что li изменяется от 0 до I, построить график зависимости теплового патока 1К через описанный выше стержень от величины 1\.
3. Решить на ЭВМ с помощью разностных методов модельную задачу и сравнить приближенное и точное решения исходной .задачи.
4. Решить на ЭВМ разностную задачу, соответствующую поставленной краевой задаче. Определить зависимость теплового потока W от величины Zi.
5. Выдать на печать зависимость W'(A), нарисовать график этой .зависимости, а также графики распределения температуры по длине стержня для следующих значений Ц : Zi = 0.2/, 0.4/, 0.6/, 0.8/.
Методические указания.
Длину левого стержня /[ изменять с шагом h. Точность итераций е принять равной 0.01. Относительная погрешность вычислений не должна превышать 5%.
Для решения нелинейной алгебраической системы, соответствующей разностной задаче, использовать метод Ньютона (см. [2], с. 444), выбрав в качестве начального приближения решение линейной задачи.
Приложение 1.4. Подвариаиты задания
Для всех подвариантов принять / = 1.
Если номер k подварианта представить в виде k = 4т 4- п (т = 0, 1, 2, 3; п = 1, 2, 3, 4), то тепловой режим на концах стержня определяется значением «:
ft На левом конце На правом конце
1 I I
2 I II
3 II I
4 ' II II
138
а значения констант определяются значением mt
V. Задача о продольных колебаниях неоднородного стержня. Физическая постановка задачи.
Упругий прямолинейный стержень О х I выведен из состояния покоя тем, что его поперечным сечеииям в момент времени t — 0 сообщены малые продольные смещения и скорости:
Предполагая, что поперечные сечения стержня все время остаются плоскими, найти смещения поперечных сечеиий стержня в течение времени 0 < t Т, если плотность массы р(х) = р0 + рЛ коэффициент упругости k(x) = k0 + fei/(Z + x), где p0, pi, ka и ki — заданные константы, a T — время, за которое точка х0 = 1/2 трижды пройдет через положение равновесия.
Начальные продольные смещения, начальные скорости и условия на концы стержня, а также константы определяются подвариантом задания (см. Приложение 1.5).
Требуется:
1. Сформулировать краевую задачу, соответствующую данной физической задаче.
2. Решить аналитически соответствующую модельную задачу для однородного стержня с физическими параметрами
рф = (р (0) + р (Z))/2, kcf = (k (0) + k (Z))/2,
3. Решить на ЭВМ с помощью разностных методов модельную задачу и сравнить приближенное и точное решения.
4. Решить на ЭВМ разностную задачу, соответствующую доставленной краевой задаче. Определить время Т, нарисовать графики зависимости отклонения и скорости сечений стержня от в момент времени Г, график движения точки х0 — 1/2, график зависимости от времени кинетической и потенциальной энергий стержня.
Методические указания.
При решении разностной задачи использовать неявную однородную трехслойную разностную схему; шаг по х принять равным h = Z/20.
Приложение 1.5. Подвариаиты задания
Для всех подвариантов принять I = 1.
Значения других констант, начальное смещение, начальная скорость и граничные условия на концах стержня для подварианта с
139
номером задаются следующей таблицей (ЖЗ означает «жестко закреплен», а СВ означает «свободен»):
к Ро Р1 fe0 fel Левый конец Правый конец Начальное смещение Начальная скорость
1 1 0.3 1 0.3 ЖЗ ЖЗ sin (лх/Z) 0
2 0.9 0.2 1 0.3 ЖЗ св sin (лх/21) 0
3 1 0,2 0.8 0.4 св ЖЗ cos (лх/21) 0
4 1.1 0.3 1.2 0.2 ЖЗ ЖЗ 0 sin (лх/0
5 0.8 0.2 1 0.3 ЖЗ св 0 sin (лх/2/)
6 1 0.3 0.9 0.2 св ЖЗ 0 cos (ях/21)
VI. Задача о поперечных колебаниях кольцевой мембраны.
Физическая постановка задачи.
Найти поперечные колебания круглой кольцевой мембраны б г2 в среде без сопротивления, вызванные заданным начальным распределением отклонений и скоростей, в течение времени Т, за которое точка г0 = (п+тД/З трижды пройдет через положение равновесия.
Условия на краях мембраны, постоянные р0, pi в выражении поверхностной плотности мембраны р = ро + Pit и натяжение То определяются подвариантом задания (см. Приложение 1.6).
Требуется:
1. Сформулировать краевую задачу, соответствующую данной физической задаче.
2. Решить аналитически модельную задачу о колебаниях струны длины I — г2— ri с плотностью массы рф= (р(п) + р(т2))/2 и натяжением То.
3. Решить на ЭВМ с помощью разностных методов модельную задачу и сравнить приближенное и точное решения.
4. Решить на ЭВМ разностную задачу, соответствующую поставленной краевой задаче. Выдать на печать и нарисовать графики зависимости отклонения и скорости мембраны от радиуса г в момент времени Т, график движения точки г» = (п + га)/2, график зависимости от времени кинетической и потенциальной энергий мембраны.
Методические указания.
При решении разностной задачи использовать неявную однородную трехслойную разностную схему. Шаг по г принять равным (г2-п)/20.
Приложение 1.6. Подварианты задания
Для всех подвариантов принять rt = 1.
Значения других констант, начальное отклонение, начальная скорость и граничные условия на внутренней и внешней окружностях
для подварианта с номером k задаются следующей таблицей (ЖЗ означает «жестко закреплена», а СВ означает «свободна»):
k гг Ро Р1 го Внутренняя окружность Внешняя окружность Начальное отклонение Начальная скорость
1 2 1 0.3 1 жз жз . л(г-л) sin — Г2 — Г1 0
2 2 0.9 0.2 1 жз св . л (г—л) Sin — 2(Гг — Л) 0
3 2 1 0.2 0.8 св жз Л(г—Г1) COS -Т- - 2 (Г2—Г1) 0
4 2 1.1 0.3 1.2 жз жз 0 Я (Г —и) sin ——— г 2 — И
5 2 0.8 0.2 1 жз св 0 . л(г—л) Sin -Т-. 2(гг—л)
6 I 1 0.3 0.9 св жз 0 Л(Г—-Л) cos 2 (г,-л)
Задание ВМ-2. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ В ДВУМЕРНОЙ ОБЛАСТИ
Цель задания.
1. Знакомство с итерационными методами решения эллиптических уравнений и практика в их использовании.
2. Накопление опыта использования ЭВМ.
Содержание задания.
1. Постановка разностной задачи, аппроксимирующей задачу Дирихле.
2. Разработка алгоритма решения полученной системы алгебраических уравнений на основе указанного в задании итерационного метода.
3. Составление программы на алгоритмическом языке и ее отладка.
4. Решение на ЭВМ конкретной задачи и анализ полученных результатов.
Постановка задачи.
На плоскости дана односвязиая область D с кусочно-гладкой границей dD. Требуется разностным итерационным методом решить внутреннюю задачу Дирихле для уравнения Пуассона:
Д«=—f, = (1)
где f и ф— заданные непрерывные функции. Известно, что при указанных предположениях решение задачи (1) существует, единственно,
141
дважды непрерывно дифференцируемо внутри D и непрерывно bDIW [1].
Для решения задачи следует:
1. Разработать алгоритм решения задачи (1) разностным итерационным методом. Провести анализ порядка аппроксимации уравнения разностной схемой и анализ погрешности решения.
2. Сформулировать соответствующую модельную задачу, взяв такие функции f н ф, чтобы модельная задача имела решение о, где V — заданная функция.
3. Оценить число узлов сетки по обоим направлениям, необходимое для решения модельной задачи с заданной точностью е = == 0.5 -10~3. В зависимости от предложенного метода провести оценку необходимого числа итераций.
4. Решить на ЭВМ по выбранному алгоритму модельную задачу. Сравнить приближенное и точное решения в разностной норме С. Сравнить сделанное число итераций с его оценкой.
5. Решить на ЭВМ разностную задачу, соответствующую поставленной задаче (1).
Функции f, ф, V, область D и др. определяются вариантом задания (см. Приложение 1).
Содержание отчета.
1. Постановка основной задачи (конкретный вариант).
2. Постановка модельной задачи, используемой в качестве теста.
3. Постановка разностной задачи Дирихле.
4. Используемый итерационный метод решения сеточных уравнений.
5. Блок-схема программы.
6. Оценка числа узлов сетки по обоим направлениям, необходимого для решения модельной задачи с заданной точностью. Оценка числа итераций, соответствующего данному методу.
7. Результат решения модельной задачи в виде таблицы.
8. Результат решения задачи (1) в виде таблицы.
9. Приложение: результаты счета на ЭВМ с распечатанной программой.
Общие методические указания.
1. Использовать консервативную разностную схему второго порядка [2].
2. В зависимости от варианта задания применять либо метод верхней релаксации (ВР), либо метод переменных направлений (МПН), либо попеременно-треугольный метод (ПТМ). Описание указанных методов, а также методы оценки числа итераций содержатся в [3].
3. При написании разностных уравнений использовать в зависимости от вида области либо декартовы, либо цилиндрические координаты.
142
Литература,
1. Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.: Наука, 1977.
2. Самарский А. А. Теория разностных схем. — М.: Наука, 1977.
3. С а м а р с к и й А. А., Николаев Е. С. Методы решения сеточных уравнений. — М.: Наука, 1978.
Приложение 1. Варианты задания
I. Первая краевая задача для уравнения Пуассона в прямоугольнике.
Постановка задачи.
На плоскости (х, у) дан прямоугольник a л sC 6, с у d. Поставим следующую краевую задачу:
Ди
д2и
дх2
д2и‘<
ду2
t(x, У),
«|,=С = ^(Д
и^^'фг (У), и \y=d == (х).
Подварианты задания даны в Приложении 1.1.
В подвариантах с нечетными номерами использовать метод переменных направлений, а с четными номерами — попеременно-треугольный метод.
II. Первая краевая задача для уравнения Пуассона в области, составленной из прямоугольников.
Постановка задачи.
На плоскости (х, у) дана область, составленная из прямоуголь-ников:
Участки прямолинейной границы области обозначены через Гь Г2, Г3, Г4, Г5 и Ге, а координаты вершин полученного многоугольника — через а, Ь, с и d.
143
Приложение 1.1
№ а\ Ъ\ с; d f (х, У> (У) Ф2 (У) % (х) ф4 (X) о (х, у)
1 0; 1; 0; 1 sin2 яху sin яу sin яу х—х2 X —X2 esin2 яху
2 -1; 1; -1; 1 1 sin3 яху | -уг + 1 -/+1 1 sin ЯХ I I sin ЯХ I 1 —х2—у2
3 — 1; 1; -1; 1 |х2-у2| —у2 + 1 (1 —у2) еУ 1— X2 1 —X2 е1-х’-у2
4 1; 2; 2; 3 _е-хУг (у — 2) (у-3) у(у-2)(у-3) (х—I) (х—2) х (х— 1) (х —2) sin лху
5 0; 2; 0; 1 \х — у | _у(у-1) У(1~У) I sin ЯХ I ( sin лх | ех 1 —(х— I)2 — (у--0.5)2
6 0; 1; 0; 2 1 х — у | sin2 яу | gSin яу_ [ | X (1— X) х (I —х) ех esin2 яху
7 0; 2; 0; 1 1 х2—2у 1 ЗШ2 пу sin2 2яу sin2 их sin2 2ЛХ esin! яху
8 0; 3; 0; 1 ch (X— у) sin2 яу 0 ch (х2—Зх) —1 0 sin2 (ху2)
9 1; 2; 1; 2 arctg ~ 0 0 sin2 лх ch(x-l) (X —2)—1 ех’-у2
10 -1; 0; 0; 1 ch (х2у) sin яу 1 sin 2яу 1 — Х(х+ 1) —х(х + 1) ехУ
Приложение 1.2
Яр п; Ь', с; d f(X.'y) (У) *2 (X) Ф3 (У) (X) Ф5 (У) te (X) и (X, у)
1 2; 2; 1; 1 1 —х2—у2 sin лу sin лх sin лу sin Я.Х sin лу sin лх sin2 лху
2 3; 3; 1; 1 1 —(х —I)2 —(у — I)2 о У-У (х-1) (х—3) sin лу sin лх sin 2лу sin 2лх sin2 лху
3 2; 2; 1; 1 1 1 —X2—2у2 | 0 1 sin лх I 0 1 sin 2лх | 0 I sin 2лх 1 е-хг-у’
4 3; 3; 1; 1 | 1-ехУ | I sin лу 1 0 ( sin лу 1 0 1 sin 2лу | 0 е~хУ
5 2; 2; 1.5; 1 е-*У I sin пу | J sin 2лх [ 0 0 0 , лх sin-у- e~ixy-
6 3; 3; ху 1 sin лу | I sin лх 1 (2-У) (У-3) 0 у (з-у) . лх Х2у2
2; 2
7 3; 3; 2 2 х у . лу sm— sin2 лх sin2 лу X (1—X) У (3 —у) ! sin лх | W-y’Y
1; 2
8 4; 4; е~хУ I sin лу| ch [(х — 1) (х —4)1— 1 (2-у) (у-4) 0 sin-а 0 e-xV1
1; 2 4
9 1; 1; 0.5; 0.5 ж У arctg •£- sin 2лу / 1 X лх V--Jcos — G~r)cos^- (-j—х) sinnx 0 0 е~ху
10 1; 1; 0.5; 0.5 arcctg 1 sin 4лу J (х —i-) sin лх (у-4)(1-»> sin лх sin 2лх 0 sin лх е~ху!
Приложение 1.3
№ Pl* Р2» Фр $2 f (Р. ф) Ф1 (Ф) V'P) % (p) % (p) 0 (p, Ф)
1 1; 2; 0; л/2 р COS ф sin 2ф sin 2ф p(l —p) (p —2.) (l-p) (p-2) 2 p COS ф
2 1; 2; 0; л р3 sin <р slncp sin<p “p sin яр — sin np 0 P COS4 Ф
3 1; 2; 0; Зл/2 1 + р cos2 <р Ф ! <p cos f sin у ф . Ф cos -f- sin 3 2 fe* -p sin np — sin np 0 0 p COS* ф
4 2; 3; 0; л/4 р cos (2q>) sin <p cos (2<p) sin <p cos (2ф) sin ф (2-p) (p-3) p sin яр p3 cos 2ф
5 2; 3; 0; п/3 p3cos(-y ф) + 1 1 cos Зф 1 1 cos 3q> I (2-p)(p-3) + l 1 + sin np eP sincp
6 0.5; 1; 0; л p3 cos2 <p | cos ф | sin ф sin ф (4— p)(p-D (4—p)(p-u2 e& sin2 cp
7 1; у ; 0; л/2 p2 sin 2<p Ф sin 2ф y sin2(p a-p)(p—0 4(1-p)(p-4) e~P2 sinQ
8 1; 3; 0; л/4 2 p COS ф Ф cos 2ф Ф n cos 2ф (l-p) (p-3) 2 (l-p) (p-3) sin 2ф
9 1; 3; 0; л/2 p~2 sin ф ф COS Ф Ф уcos ф (p-l)2 (p —3)2 (p—1)£> —3)2 е~РФ
10 1; 3; 0; л e”P з!пф Ф фСОЗу 2 Ф ф cos у (l-p) (p-3) |sin np | с~РгФг
Поставим краевую задачу:
д„=^ + №==_
tdx2 ду2
и 1г = Ф,-> i— I» •••> 6.
i 1
В данном варианте использовать метод верхней релаксации.
Подварианты задания даны в Приложении 1.2.
III. Первая краевая задача для уравнения Пуассона в кольце
вом секторе.
Постановка задачи.
На плоскости (р, <р) дан кольцевой сектор pi р Р2, <pi Ф Фз- Поставим краевую задачу:
. 1 д ( ди \
Ди =-----— 1 р -3— I
р др V др )
и1р=₽1 = Фь
« 1ф=ф, = Фз,
1 д2и________
р2 др2
« 1р=р2 = ф2,
« |ф=ф2 = ф4-
f (р. ф),
Подварианты задания даны в Приложении 1.3; в подвариантах с нечетными номерами использовать попеременно-треугольный метод, а с четными номерами — метод переменных направлений.
Задание ВМ-3. ЧИСЛЕННОЕ РЕШЕНИЕ
ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Цель задания.
1. Знакомство с методами решения краевых задач на собственные значения для обыкновенных дифференциальных уравнений.
2. Практика в использовании ЭВМ и языков программирования.
Содержание задания.
1. Изучение вариационных методов решения краевых задач для дифференциальных уравнений.
2. Изучение метода Ритца для приближенного решения вариационных задач.
3. Составление программы и ее отладка.
4. Решение на ЭВМ конкретной краевой задачи и обработка результатов.
Постановка задачи.
На отрезке [0, 1] рассматривается дифференциальное уравнение Ly^—[p(x)y']' + q(.x)y = Ky (1)
с граничными условиями
ад(о)—ai/(o) = o, IW(1) + ₽1/(1)=O,
147
где р(х) > 0, </(х) gs О, |<Хо| 4- |ai| О. I Ра I + | Pd О, X - параметр.
Функции р(х), q(x), а также константы an, (J3, а1( |3( определяются вариантом задании (см. Приложение 1).
Требуется найти приближенно методом Ритца первые два собственных значения и первые две собственные функции для задачи Штурма-Лиувилля (см. Приложение 2).
Для решения задачи следует:
1. Исследовать исходный оператор L на положительность, отрицательный оператор свести к положительному.
2. Взять за полную систему функций для метода Ритца собственные функции задачи Штурма-Лиувилля для уравнения, полученного усреднением коэффициентов преобразованного в п. I уравнения, с теми же граничными условиями. При отыскании собственных функций возникает необходимость приближенного решения уравнения типа = Метод решения трансцендентного уравнения определяется вариантом задания (см. Приложение I).
3. Вычислить коэффициенты характеристического уравнения исходной задачи и найти собственные значения М и А,3 задачи Штурма-Лиувилля.
4. Найти решение а3, ..., а„ линейной однородной системы алгебраических уравнений для 1 = X;. Найти значения соответствующей собственной функции y(xi, X.J в узлах xi разбиения отрезка [0,1] с заданным шагом h = 0.05 (« — 0, I, ..., 20).
5. То же самое сделать для к = кг.
Требования к программе.
В программе должны быть предусмотрены следующие процедуры:
— процедура отыскания корня трансцендентного уравнения;
— процедура решения системы линейных алгебраических уравнений /г-го порядка.
Содержание отчета.
1. Постановка задачи.
2. Результаты исследования оператора L на положительность.
3. Вывод коэффициентов характеристического уравнения задачи Штурма-Лиувилля.
4. Блок-схема программы.
5. Текст программы на алгоритмическом языке.
6. Тесты для проверки процедур и программы, результаты отладок.
7. Результаты решения задачи на ЭВМ:
— собственные числа усредненного оператора;
— система координатных функций на отрезке [0, I];
— собственные числа задачи Штурма-Лиувилля;
148
— значения собственных функций у%(х) на отрезке [0, 1] с заданным шагом.
Литература.
1. Михлин С. Г. Вариационные методы в математической физике.— М.: Наука, 1975.
2. И л ь и н В. А., П о з н я к Э. Г. Линейная алгебра. — М.: Наука, 1978.
3. Методические пособия и инструкции по программированию.
П риложение 1. Варианты задания
Вариант задания определяется видом функций р(х) и q(x), видом граничных условий и методом приближенного решения трансцендентного уравнения.
I. Вид функций р(х) и q(x)-.
№
р (х)
q(x)
2
3
4
5
6
7
8
9
— (0.2x4- 1)
— (0.4x4-2)
— (0.4x4-1)
— (X 4- 0.2 cos лх)
— (2х 4- 0.6 cos лх) — (4X4-cos лх)
0.1X4-1.5
0.8х 4-1.5
О.бх 4- 2.8
0
0 0
— (14- 0.5 sin лх) — (2 4- sin лх)
— (3 4-1.2 sin лх)
2. Метод касательных.
3. Комбинированный метод (хорд и касательных).
Приложение 2. Решение задачи Штурма-Лиувилля
Проблема отыскания собственных значений краевой задачи может быть сведена к некоторой вариационной задаче.
149
Для симметричного и положительного оператора (положительный оператор является ограниченным снизу) справедлива следующая теорема.
Теорема. Пусть L — ограниченный снизу симметричный оператор, н пусть d—точная нижняя граница значений функционала (Ly, у) „ , , „ (Li/л, Уо) ,
Если существует функция Уо 0 такая, что —г- = “>
(У, У) (Уо, Уо)
то d есть наименьшее собственное значение оператора L, а Уо — соответствующая этому значению собственная функция.
Эта теорема сводит задачу о нахождении наименьшего собственного значения симметричного ограниченного снизу оператора к следующей вариационной задаче: найти минимум функционала
(Ly, у) (3)
при дополнительном условии
(//>//) — !• (4)
В предлагаемых вариантах все положительные операторы L являются положительно определенными, ограниченными снизу операторами:
(Ly, У) > k || у ||2 (k > 0),
а для отрицательных операторов L это же неравенство справедливо для k < 0.
В случае отрицательного оператора следует свести задачу нахождения собственных чисел этого оператора к отысканию собственных чисел положительного оператора следующим образом.
Пусть С — любое число, большее чем |fe|. Уравнение Ly — Ly — — 0, определяющее собственные числа оператора L, перепишем в виде Еу — Ly = 0, где Еу = Ly + Су, L = L + C. Оператор Е — положительный, так как
(Ly, у) = (Ly, у)+С (у, у)^(С + k) || у ||2,
а С + k > 0. Если L — собственное число оператора L, то L = L— С есть собственное число оператора L и наоборот.
Сформулированную выше вариационную задачу можно решить методом Ритца, который заключается в следующем. Выберем систему линейно независимых функций (координатные функции) <pi(x), ФаМ, , <р«(х), которые удовлетворяют следующим условиям:
а) функции ф,-(х) (i = 1, 2, ..., п) принадлежат области определения оператора L;
б) система этих функций полна в смысле сходимости в среднем.
Известно, что система собственных функций положительного оператора образует полную ортогональную систему. Поэтому за пол-
150
йую систему функций можно взять собственные функции задачи Штурма-Лиувилля для уравнения, полученного усреднением коэффициентов уравнения (1) с теми же граничными условиями (2). Под усреднением понимается замена переменного коэффициента а(х) постоянным значением а, вычисляемым по формуле
ь
1 С / \
а = -г—--— \ а (X) dx.
b — a J а
Следуя далее методу Ритца, искомая функция у приближенно представляется в виде линейной комбинации координатных функций:
п
уп ю = Е ak^k <*)• (5)
fe=i
где alt — постоянные коэффициенты. Эти коэффициенты следует выбрать так, чтобы функция р„(х) удовлетворяла соотношению (4) и чтобы величина (Lyn, уп) была минимальной при выполнении условия (4). Это приводит к тому, что нужно найти минимум функции п переменных:
п
(Lyn>yn)= Е (Ч>фт)вА>
k, т—1
связанных уравнением
п
(уп-уп)= Е (<₽&’ <7>
к, т=1
Для решения этой задачи используется метод неопределенных множителей Лагранжа [2]. Строится функция
Ф (У. К) = (Ly, У>~Ь (У, У),
где л — неопределенный пока числовой множитель. Коэффициенты ai, а2, ..., ап находятся из необходимых условий для экстремума функции Ф, т. е. приравниванием к нулю ее частных производных по коэффициентам а,„. Это приводит к линейной однородной системе уравнений:
п
Е M(L(Pa’ 4’m)~X((Pfe> 4>/n)] = 0’ (8)
ft=i
Неизвестные at этой системы не могут одновременно обратиться в нуль, так как в противном случае было бы нарушено уравнение (7). Чтобы однородная система (8) имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель Д(Х), зависящий,
151
очевидно, от параметра Л, был равен нулю. Это дает уравнение для К:
А(Л)==
(ЙР1.Ф1)—МФ1.Ф1), (Ьф2,ф1)—Мф2,ф1),.. .,(МРл,ф1)—Ь (фге.ф!) = (Z-фьфг)—Л(ф1,ф2),(Дф2,ф2)—%(ф2,ф2), ...,(^Фл,ф2)—Л(фп,ф2) =
(£ф1, фга)—Л (ф 1, фп)> (i-фг, Фп)—(ф2, фп), • • • > (L<fn, Ф J~~(фп, Фп) = 0, (9)
которое называется характеристическим уравнением задачи Штурма-Лиувилля. Это уравнение имеет ровно п корней, поскольку координатные функции фЬ ф2, ф„ линейно независимы. В [1] доказывается, что минимум величины (6) при условии (7) равен наименьшему из корней уравнения (9).
Чтобы получить приближенное значение второго собственного числа, ищется минимум скалярного произведения (6) при дополнительных условиях (7) и
(Уп}’Уп)= X (<₽*’ Фт)4°’ат = 0> <10>
k, т=1
п
где у^ = У, <4°>ф& есть приближенное значение первой собственной Й=1
функции оператора L. Второй по величине корень уравнения (9) дает искомый минимум. Аналогично можно получать приближенные значения следующих собственных чисел — все они являются корнями уравнения (9).
Корни уравнения (9) находятся, как и корни усредненной задачи, одним из приближенных методов решения трансцендентных уравнений. Выделение отрезков существования корней можно предусмотреть в программе.
Для определения коэффициентов аь а2, ..., ап следует каждое из полученных собственных значений hi подставить в систему (8) и найти соответствующие нетривиальные решения этой системы. Собственные функции у = у(х, Z/) (/=1, 2, ..., п) определяются из формулы (5), где коэффициенты а,- (i — 1, 2....п) имеют най-
денные выше значения.
Приложение 3. Методические указания
1. Для отладки программы следует прежде всего отладить описанные в ней процедуры — для этого нужно подготовить и пропустить соответствующий набор тестов.
2. Отладку численного метода решения трансцендентного уравнения целесообразно провести на уравнении с заранее известным решением.
152
3. При составлении программы следует позаботиться о получении результатов в наиболее наглядном виде.
4. При решении линейных однородных систем следует одно из неизвестных, например ая, положить свободным (равным, для определенности, единице) и перенести его в правую часть каждого из уравнений.
Задание ВМ-4. РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ФРЕДГОЛЬМА I РОДА МЕТОДОМ РЕГУЛЯРИЗАЦИИ
Цель задания.
1. Знакомство с методом регуляризации для решения интегральных уравнений Фредгольма I рода.
2. Дополнительная практика по использованию алгоритмических языков и работе на ЭВМ.
Содержание задания.
1. Изучение метода регуляризации для решения интегральных уравнений Фредгольма I рода.
2. Разработка алгоритма решения интегрального уравнения с приближенно заданной правой частью.
3. Составление программы решения поставленной задачи на алгоритмическом языке.
4. Аналитическое решение прямой модельной задачи.
5. Решение на ЭВМ обратной модельной задачи.
6. Решение на ЭВМ конкретной обратной задачи и анализ результатов.
Постановка задачи.
Дано интегральное уравнение Фредгольма I рода
а
A [z (S)] ВЗ 7/2+Z(^Ls)2 ds = « w> x^[—b, 6],
-a
с приближенно заданной правой частью й&(х) такой, что ь
II йй (X) - й (х) ||2И_&> &] = ^ | йб (X) - й (X) J2 dx С 6»,
-ъ
где й (х) = A [z (s)], г (s) — точное решение интегрального уравнения, z (s) е ITj [— а, а],
а
1,2 (s) “г1 [-а, а] = 5 । Z' (S) 12 + 90 <S) । 2 (S) l2] ds’
2 ’ -a
<h («)> ?o (s) > 0.
153
Данное интегральное уравнение возникает, например, в задаче определения формы границы z(s) между двумя слоями с различными плотностями, находящейся на глубине Н, |z(s)| < Н, по аномалии гравитациоиого поля и(х) на поверхности Земли [1].
Методы решения задачи.
В качестве устойчивого приближенного решения в норме С [—а, а] , || г (х) ||„ = sup | г (х) |, интегрального уравнения Фредгольг-
G х е [-а, а]
ма I рода X[z(s)] = и(х} с приближенно заданной правой частью и = й6 (х) согласно методу регуляризации [2] выбирается функция zjif (s) е [— а, а], минимизирующая сглаживающий функционал Тихонова
Л4а[г, йл]«||Лг — йА ||2 г т ,, + а||г||2 .
- 0J !! оИх.2 1-0, tn Ж* (-а, а]
где а > 0 — параметр регуляризации.
Элемент (s), минимизирующий сглаживающий функционал, может быть определен из уравнения Эйлера (<7i (s) = qx = const, go(s) = q0 = const):
a
К (s, t) z (t) di — a [qiz" (s) — qoz (s)J =
—a
b
— j К (x, s) и (x) dx s= g (s),
— b b
где К (x, s) — „2 * u, К (s, t) = \ К (x, s) K. (x, t) dx. Это
Ji T" *J
-b
уравнение аппроксимируется на равномерной сетке с шагом h системой линейных алгебраических уравнений вида
п
- -%- (zk~i+zk+i) - 2chzk - j+2 rzrh=sk>
r=0
где k = 1, 2, ..., n — 1, z4 = z(s4), sfe — kh — a, sn = a, gk== g(sk), Ku, r — коэффициент квадратурной формулы (например, формулы прямоугольников), по которой интеграл заменяется интегральной суммой.
При каждом фиксированном а полученная система линейных алгебраических уравнений решается по какой-либо стандартной программе.
Параметр регуляризации выбирается согласно принципу невязки [3] из условия II . ь б] = ^'
Решение этого .уравнения относительно а может быть приближенно найдено с помощью последовательного вычисления невязки || Azg — fi61| при а = afe = (k — 1, 2, ...) и сравнения ее с погрешностью б. В качестве искомого решения уравнения берется а = ап такое, что || A || CJ б, || Azgn-1 — fig j > б при
||Л2“°- fig |[ > б.
Для проверки выбранного алгоритма решения и составленной программы предлагается решить модельную задачу. В качестве z(s) взять функцию z(s) = С(а2 — s2), |Са2| < Н, s е [—а, а], где С — константа. Вычислив для нее аналитически й(х), решаем интегральное уравнение и полученный результат Zg (s) сравниваем с z(s), где б — ошибка вычислений и аппроксимации квадратурными формулами.
В качестве конкретной приближенной правой части fig (х) на отрезке [—Ь, Ь] задана функция
х —с , (х~с\ . х + с , Гх + с\
« =—7Г~ агс g к ~н~~) —~н~~arctg V н ') ~~
2х , х , , х2 + Н2
------arctg----Ь In —- — ..=.. —, ' = = = -.
Н Н -JH2 + (х - с)2 V#2 + {X + с)2
где с = 1, вычисленная с точностью до двух значащих цифр. Тем самым
б CJ0.05 ]] и ||д2 6j.
В модельном и конкретном вариантах принять а = 2, Ь = 2, Н = 2.
Содержание отчета.
1. Постановка задачи.
2. Обоснование метода решения задачи.
3. Блок-схема программы.
4. Текст программы на алгоритмическом языке.
5. Результаты решения модельной задачи.
6. Результаты решения поставленной задачи и их анализ.
Литература.
1. Тихонов А. Н., Гласко В. Б. Применение методой регуляризации в нелинейных задачах. — ЖВМиМФ, 1965, 5, № 3.
2. Тихонов А. Н., Арсенин В. Я- Методы решения некорректных задач. — М.: Наука, 1974.
3. Морозов В. А. О регуляризации некорректно поставленных задач и выборе параметра регуляризации. — ЖВМиМФ, 1966, 6, № 1.
155
КАФЕДРА МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Задание МС-1. СТАТИСТИЧЕСКИЙ АНАЛИЗ ДАННЫХ В ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ
Цель задания.
1. Знакомство с методами построения и анализа регрессионных зависимостей между двумя переменными величинами, когда значения зависимой величины искажены случайными ошибками.
2. Практика в использовании ЭВМ для решения задач регрессионного анализа.
Содержание задания.
1. Изучение методов построения и анализа поверхностей регрессии на основе экспериментальных данных.
2. Выявление и устранение резко выделяющихся наблюдений в ряду значений зависимой переменной р(х); получение наилучших оценок коэффициентов полиномиальной зависимости между х и у(х); отыскание степени аппроксимирующего полинома, построенного на основании результатов измерений у(х); построение доверительной полосы для истинного значения р(х).
3. Составление программы на одном из алгоритмических языков для решения конкретного варианта задания и ее отладка.
4. Решение на ЭВМ по составленной программе конкретного варианта задания и анализ полученных результатов.
Постановка задачи.
Рассматривается зависимость между величинами х и у вида p = a0 + aix+ ... +атхт. (1)
Предполагается, что коэффициенты а,- (/ = 0, 1, ..., т) неизвестны и что при каждом фиксированном значении х = х/ (i = 1, ..., п) соответствующее значение у, измеряется со случайной ошибкой Аг. Таким образом, результаты измерений yi имеют вид
т
£ akxki+^i> 1=1, 2,..., п (2)
k=0
(предполагается, что п > т). Предполагается также, что все А, независимы и распределены нормально с параметрами (0, а2) и что среди Xi имеется хотя бы т различных.
Итак, заданы вектор х = (xlt х2....хп) с равноотстоящими
значениями компонент и вектор измерений у — (у,, р2, .... у„).
Требуется:
1. Выявить и устранить резко выделяющиеся наблюдения среди компонент вектора у, если они имеются.
2. Определить степень т в представлении (1) или (2) и построить оценки неизвестных коэффициентов a, (j = 0, ..., т) и неизвестной дисперсии а2 по методу наименьших квадратов.
156
3. Построить доверительную полосу для истинного значения у(х).
Конкретные векторы х и у определяются вариантом задания (см. Приложение 1). При этом везде далее предполагается, что имеется не более одного резко выделяющегося наблюдения величины у. Предполагается также, что m <6, а л = 30.
Методика решения задачи.
I. Получение оценок неизвестных коэффициенте.
В условиях, сформулированных в постановке задачи, иля получения оценок коэффициентов «/ (7 = 0. .... т) в представлении (1)
, „ „ „ j. Х — Х] п — 1
целесообразно перейти к новой переменной t = "_'х----’
переводящей компоненты вектора х в кратные 1/2 точки, расположенные симметрично относительно нуля.
Зависимость (1) можно записать в виде
y = bnP^(i)+b^4i)+ ... + bmP^Ht),
где (/) •— многочлены Чебышева, удовлетворяющие условию орто-тональности
ЕП°(^’№ = 0 при 1^1 ^1
(Р!,г> (9 — многочлен степени /, построенный по п точкам). Значения многочленов Р^ (i) можно найти, например, в [2] (табл. 7.2).
Таким образом, вместо системы (2) можно записать систему
^ = ^+4;= £б/,Р(9) + Дг, 1=1,2..............п,
("О
или, в матричной форме,
К = Y + А = РЬ + Д, где
К= (£ь.... ynf, Y = (tt\,у,,)Т,
Л=(Л|, ..., AfZ & = (&о, btll) »
/^0)(Л) - х
р = 1..................).
\р’„°’(/п) - p^(tn) J
Оценки для неизвестных коэффициентов регрессии 6, по методу наименьших квадратов выражаются формулами
п п
=X =Е '=0......м’(3)
А «i=l k-i
167
или, в матричной форме, Ь = (РТР) 1РТУ. Оценки Ьо,..., bm обладают минимальными дисперсиями, совместно эффективны и распределены нормально [1].
В случае неизвестной дисперсии о2 ее несмещенная оценка выражается формулой
(п— m— 1)52/сг2 имеет распределение %2 с п — m— 1 степенями свободы; В и S2 независимы [3].
II. Критерий выявления и устранения выброса.
Вектор наблюдений Т может иметь резко выделяющееся наблюдение (выброс). Компонента й,- называется выбросом, если Eyi Ф yi. Если имеется выброс, то его необходимо устранить, прежде чем находить оценку В для Ь, так как оценка В, построенная по искаженному выбросом вектору К, будет иметь нежелательные свойства.
Для отыскании выброса можно применить критерий, заключающийся в следующем [4]. Рассмотрим вектор Z = К — РВ. При отсутствии выброса Z имеет нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей о2[/— — Р(РТР)~'РТ], его i-я компонента ~ N\ (б, о?), где (см. формулу (3))
( m у
I /-0 )
Тогда
имеет бета-распределение с
параметрами
. Справедлива следующая оценка:
Р{ max g <2« Г1 - S
где Sk(-) означает функцию распределения Стьюдейта с k степенями свободы. Положим а = 0.05 и найдем соответствующее ему значение х. Пусть тДа) есть 1ООа°/о-ная точка распределения Стьюдента с k степенями свободы, т. е. тДа) является решением уравнения
(а)) = 1— а. Обозначим т = тп-т_2 (. Тогда ха =
= —2--------------5Г- Если для некоторого j имеет место неравен-
Т “у" HI с I
то соответствующее значение У] считаем
а’
выбросом, так как в случае отсутствия выброса событие е; ха маловероятно — вероятность его наступления не превышает сс.
158
После того как выброс у, найд-гн, его значение необходимо исправить. Для этого предлагается следующая итерационная процедура.
Для получения начального приближения у^ производится линейная интерполяция по соседним значениям у^_1 и у;-+1. Затем, используя вектор y(0) = (yi, •••, Sj-\> t/j+i...Vrt), п0 форму-
лам (3) определяется вектор Ь^К
Каждое следующее приближение у^*1* определяется по формулам
£»+!)_£ ь(к+1) = Ь(к) + Д&(4 k = 0,1,...,
i=o
где
дДО = &(/+1) - bf = -%— byfP'p (tX i = 0, 1.........от,
к к к р' J /к \ J /
П
^ = y^-yf.
Этот процесс обычно сходится настолько быстро, что достаточно получить уО) и 5<1).
Таким образом, после устранения выброса в качестве вектора наблюдений используется исправленный вектор у(1>, а в качестве вектора оценок неизвестных коэффициентов используется вектор 5(1).
III. Нахождение степени аппроксимирующего полинома.
Так как степень от полинома в представлении (1) или (2) неизвестна, то для нахождения от поступаем следующим образом.
Вычисляем последовательно k
J = 0
Так как компоненты вектора 6k = (6&(^i), ..., 6Д/П))Г зависят от В, то вычисление 6k производится одновременно с процедурой нахождения и устранения выброса у/ последовательно для каждого k, начиная с k = 0. Составляем таблицу значений 6k для k = 0, 1, 2, ...:
*2 . . .
«0 • • •
. . . . . . . ♦ . . . . . . . • . .
Sm . . .
159
Каждый раз, перед заполнением Z-й строки таблицы, проверяется наличие выброса; если он имеется, то выброс устраняется и значения & вычисляются по исправленному вектору 5. При этом предполагается, что степень полинома в представлении (2) равна I. При подходящем выборе степени аппроксимирующего полинома можно ожидать малых отклонений от нуля компонент вектора б.
Пусть т = то — истинная степень полинома. Тогда в строке с номером mQ последовательные значения 6mj будут иметь чередующиеся знаки (может быть, и «непериодичио» чередующиеся), например > 0, 6mo(Z2)<O, 6fflo(t3) > 0 и т. д. Кроме того,
т в этой строке сумма квадратов отклонений = i = l должна иметь минимальное значение. Таким образом, максимальное число перемен знака в строке с номером mQ и минимальное значение д^дто определяют степень т0 аппроксимирующего полинома.
IV. Построение доверительной полосы для у.
С целью нахождения доверительной полосы для m
1 = 0
где Q (/) = Р^ (/))Г, заметим, что для # — QT (/) b
имеем
Еу == у, Е(0- у)2 = cTQT (/) (РГР)-1 Q (Z), {у, a2QT(t) (PTP)~l Q (f)).
Следовательно, случайная величина
QT{t)b-y
л! QT (t) (РТРГ1 Q (/) [(P - Pb)r (Y - Pb)]/(n -m-Г) имеет распределение Стьюдента с п — m—1 степенями свободы. Заметим, что в силу ортогональности столбцов матрицы Р
QT(f)(pTP)~ 1Q(O = XIPk/)(O№rt.
/ = 0
Пусть т4(а) есть 100а%-ная точка распределения Стьюдента с k степенями свободы. Тогда при фиксированном t доверительный интервал для у с коэффициентом доверия 1 — а определяется неравенством (см. [3]) \QT (t)b- у\^
< (у) V(У - Pb)T (Y-Pb) Qr (Z) (РГР~Г1 Q (Z)/(n-W-l).
160
Таким образом, при а = 0.05 и для i = 1, 2.....п находим
нижний и верхний доверительные пределы для ус
иЕРпЛмЖп-
/=0
Совокупность полученных доверительных пределов образует доверительную полосу для у(х).
Значения полиномов Чебышева (tk) и процентные точки Стыодента, которые используются при выполнении задания, даны в Приложении 2.
Этапы выполнения задания.
1. Последовательное вычисление компонент вектора 5 по формулам (3), нахождение и устранение выброса, если он имеется, с одновременным вычислением векторов б0, 6 р..., бто для нахождения степени полинома т0. Нахождение оценки S2 для неизвестной дисперсии о2.
2. Нахождение оценки а вектора а= (а0, ..., ат)Т в представления (1).
3. Построение доверительной полосы для у.
Для выполнения всех этапов задания следует составить программу на одном из алгоритмических языков, получить результаты на ЭВМ, выдав на печать величину выброса у/ и номер /, исправленный вектор наблюдений F(1>, векторы 5 и а, степень полинома т, оценку дисперсии S2, нижние и верхние доверительные пределы для компонент вектора У = («л, ..., уп)Т-
Содержание отчета.
1. Краткая постановка задачи.
2. Текст программы.
3. Тесты и результаты отладок.
4. Результаты решения задачи на ЭВМ.
5. Схематический чертеж доверительной полосы для у.
Литература.
1. Линник Ю. В. Метод наименьших квадратов и основы теории обработки наблюдений. — М.: Физматгиз, 1962.
2. Б о л ь ш е в Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, 1965.
3. Уилкс С. Математическая статистика. — М.: Мир, 1967.
4. Большее Л. Н. О критериях исключения резко выделяющихся наблюдений. — Труды ИПМ ТГУ, т. 2, с. 159—177.
Приложение 1. Варианты задания
Для всех вариантов принять Xk — h(k—1) (/г = 1, ..., 30; h = 0.1). Векторы У для различных вариантов можно получить следующим образом. Сначала в качестве уь примем значения полинома
6 Н. П. Трифонов, Е. Н. Пасхин
161
не выше шестой степени, вычисленные в точках Затем к каждому Ук прибавим случайную ошибку, равную нормально распределенным числам с параметрами р = 0, а2 — 0.0001, взятым из таблицы в [2], умноженным на среднеквадратическое отклонение а. После этого к одной из компонент yko для получения «выброса» добавим величину, превышающую 4а = 0.04.
Образцы вариантов вектора F:
у(1) у(2)
к «к к Ук
1 1.911 16 -0.4793
2 1.970 17 -0.7702
3 2.022 18 -1.080
4 1.990 19 -1.342
5 1.952 20 -1.578
6 1.881 21 -1.756
7 1.765 22 -1.926
8 1.636 23 -2.001
9 1.448 24 -1.974
10 1.227 25 -1.875
11 1.001 26 -1.620
12 0.7129 27 -1.256
13 0.4502 28 -0.7477
14 0.1543 29 -0.04250
15 -0.1462 30 0.8520
к Sk к Ук
1 0.8210 16 -1.015
2 0.7394 17 — 1.090
3 0.6720 18 -1.178
4 0.5424 19 -1.218
5 0.4329 20 -1.241
6 0.3154 21 -1.231
7 0.1812 22 -1.217
8 0.06250 23 -1.152
9 -0.08550 24 -1.032
10 -0.2394 25 -0.8777
11 -0.3704 26 -0.6738
12 -0.5356 27 -0.4276
13 -0.6507 28 -0.1360
14 -0.7758 29 0.2360
15 -0.8875 30 0.6635
Приложение 2
I. Таблица значений Р^^к)-
п=30
*к р(2) р(3) р<4) г п Р(5) F п р(6) г п
-29/2 -29 203 -1827 23751 -16965 5655
-27/2 -27 161 -1071 7371 585 -2535
-25/2 -25 122 -450 -3744 9360 -4875
-23/2 -23 86 46 -10504 11960 -3965
-21/2 -21 53 427 -13749 10535 -1655
-19/2 -19 23 703 -14249 6821 823
-17/2 -17 -4 884 -12704 2176 2734
-15/2 -15 -28 980 -9744 -2384 3730
-13/2 -13 -49 1001 -5929 -6149 3751
-11/2 -11 -67 957 -1749 -8679 2937
-9/2 -9 -82 858 2376 -9768 1551
-7/2 -7 -94 714 6096 -9408 -87
-5/2 -5 -ЮЗ 535 9131 -7753 -1655
-3/2 -3 -109 331 11271 -5083 -2873
-1/2 -1 -112 112 12376 -1768 -3536
8990 302064 21360240 3671587920 2145733200 302603400
162
В последней строке таблицы указаны суммы квадратов si п - i (ми2.
й=1
II. Таблица значений процентных точек Стьюдента.
rk (0.0008)
k 28 27 26 25 24 23 22
ч 3.408 3.421 3.435 3.450 3.467 3.485 3.505
(0.025)
k 29 28 27 26 25 24 23
ч 2.045 2.048 2.052 2.055 2.058 2.064 2.069
Tfc (а) есть корень уравнения Sfe (rft (а)) =1 — а, где Sfe (•) означает функцию распределения Стьюдента с k степенями свободы.
Задание МС-2. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Цель задания.
1. Знакомство с методами решения задач теории массового обслуживания.
2. Практика в решении простейших задач массового обслуживания.
Содержание задания.
1. Изучение основ теории массового обслуживания и используемых в ней методов.
2. Получение характеристик коикретиой системы обслуживания.
3. Расчет характеристик иа ЭВМ и анализ их поведения.
Постановка задачи.
Для обслуживания поступающих через случайные интервалы времени требований имеется п обслуживающих приборов одинаковой производительности и бункер для ожидания объемом в пг требований. Если в момент поступления требования имеются свободные приборы, то оно занимает один из этих приборов. Если же все п приборов в момент поступления требования заняты, то возможны две ситуации:
1) В бункере есть свободные места; тогда требование занимает одно из них и ожидает освобождения одного из приборов.
6*
163
2) В бункере свободных мест нет; в этом случае требование но обслуживается и покидает систему.
Во всех задачах предполагается, что
а) промежутки между поступлениями требований независимы в совокупности и одинаково распределены с функцией распределения А (х);
б) длительности обслуживания требований независимы между собой, независимы от поступающего потока и одинаково распределены с функцией распределения В(х);
в) требования обслуживаются в порядке их поступления;
г) в начальный момент времени Z = О система свободна от требований.
Введем следующие случайные процессы:
n(t\—число требований в системе (на приборах и в бункере) в момент времени /;
v(Z)—число требований, обслуженных в интервале времени (О, 0;
ц(/)—число требований, покинувших систему необслуженными в интервале (О, /);
w(Z)—виртуальное время ожидания в момент t, т. е. время (отсчитываемое с момента I), необходимое для освобождения системы от требований, поступивших до момента t.
Задание заключается в нахождении характеристик перечисленных случайных процессов и вычислении их на ЭВМ. в заданном диапазоне изменения определяющих их параметров.
Конкретный вид функций 4(х), В(х), значения п, т и искомые характеристики определяются вариантом задания (см. приложение 1).
Общая методика решения задачи.
При исследовании предлагаемых систем массового обслуживания используются два метода.
Первый метод — сведение изучаемого случайного процесса к марковскому путем введения дополнительных компонент. Например, количество требований в системе п(1) в момент / при 4(х) = = 1 — е~ах, В (х) 1 — e~bx, п= 1, т = оо, не является марковским случайным процессом. Введем дополнительную компоненту z(Z), равную интервалу времени, которое ушло на обслуживание требования, находящегося иа приборе в момент t (если таковое имеется), н равную нулю в противном случае. Тогда случайный процесс {«(/), z(Z)J является уже марковским.
Для изучения полученного марковского процесса рассматривается его изменение за бесконечно малый интервал времени [Z, / + + dt), составляются дифференциальные уравнения, которым удовлетворяет распределение процесса, и затем эти уравнения решаются.
164
Рассмотрим, например, систему с А (х) = 1 — е~ах, В(х) — s= 1 — е-6х(1 + bx), п = 1, т = оо. Положим
Р (п, X, t) dx = P {п (0 = п, 2 (О Е (х, X + dx)}, В' (х) Ь2х
П (х) = 1 - В (х) 1 + Ьх '
При п 2 и х > 0 справедливо следующее соотношение:
Р (п, X + Д, t + Д) dx = Р (п, X, t) dx [1 — (а + т) (х)) Д] +
+ Р (п — 1, х, t) dx аД + о (Д) dx, (1)
где о(Д)/Д->0 при Д->-0.
Действительно, для того чтобы в момент времени t + Д в системе находилось п требований (п 2) и с момента начала обслуживания находящегося на приборе требования прошло время, лежащее в интервале (х + Д, x-j-dx + Д), необходимо и достаточно, чтобы имело место одно из следующих событий:
1) В момент времени t в системе было п требований, ?(/) е (х, x + dx), за время Д не поступило ни одного требования и обслуживание требования, находящегося на приборе, не закончено. Заметим, что вероятность этого события равна
Р (п, х, t) dx • Р {за время Д не поступило вызовов и не закончилось обслуживание вызова, находящегося иа приборе},
Далее, так как длительности обслуживания вызовов не зависят от поступления, то
Р {за время Д не поступил вызов и не закончилось обслуживание вызова, находящегося на приборе}
=Р {за время Д не поступил вызов}-? {за время Д не закончилось обслуживание вызова, находящегося на приборе}.
Так как А(х) = 1 — е~ах, то
Р {за время Д не поступил вызов} = е-аЛ = 1 — аД + о (Д), Кроме того,
Р {за время Д не закончилось обслуживание вызова, находящегося иа приборе} = 1 — т] (х) Д + о (Д).
Итак, получаем, что искомая вероятность равна
Р (п, х, t) dx (1 — (а + Л (х)) Д) + о (Д) dx.
2) В момент t в системе было п— 1 требований, z(/)e е(х, x-j-dx), и за время Д поступил один вызов. Вероятность такого события равна Р(п— 1, х, t) dx аД + о (Д) dx.
165
3) В момент времени t система находилась в состоянии, отличном от тех, которые описаны в пп. 1) и 2), и за время А процесс перешел в состояние (п, х-|-Д). Вероятность такого события равна o(A)dx.
Поскольку события 1)—3) не пересекаются, получаем соотношение (1), из которого следует
Р (п, х + Д, t + Д) - р (п, х, 0 _
Д
= — (а + г) (*)) Р (п, х, t) + аР (п— 1, х, t) + о (1). (2)
Устремив Д к нулю в (2), получим
дР (п, х, 0 , дР (п., х, t) _ , „ „ , ,
----------------1-gi----= — (<z + n M) P (n, x, t) +
I zv D 1 ~ A
—J— U.1 \it, - 1) Л, ь/.
Аналогично составляются уравнения для P(l, х, t), Pq(P) и краевые условия.
Более подробно с данным методом можно познакомиться в [1] и [4] (гл. 4).
Другой метод, называемый методом вложенных цепей Маркова, заключается в следующем. Подбирается возрастающая последовательность моментов времени, в которые значения изучаемого процесса оказываются связанными в цепь Маркова, несмотря на то, что в общем процесс не является марковским. Например, для системы с А(х) = 1 —е~ах, В(х) произвольным, n = 1, т = оо, такими моментами для длины очереди n(t) будут моменты, непосредственно следующие за моментами окончания обслуживания требований, а для системы с А(х) произвольным, В(х)=1-—е~Ьх, п = 1, т = оо, для длины очереди n(t) — моменты, непосредственно предшествующие моментам поступления требований.
Для изучения цепи Маркова рассматриваются переходы системы за один шаг, составляется и решается система разностных уравнений, которым удовлетворяет распределение исследуемого процесса.
Рассмотрим, например, систему с
A(x) — l—e~ax, В(х) = Р’ п=1, т = оо.
(.1, х > Ь,
Занумеруем все требования в том порядке, в котором они поступают в систему. Пусть п.ц — число требований в системе сразу после окончания обслуживания М-го требования, a Р.ч(п) = P{nN =г =“ п}. Тогда, используя формулу полной вероятности, имеем
Л+1 . ,
<»>- £ W«-»(0)
k=l
(3)
166
Положим
оо
PN (z) = У, гПрм п=0
Тогда из (3) получаем
P*N+1 (*) = г-1 [/>; (г) - P*N (0)] е~ъ + PN (0) е~ь (4)
Пусть
р*(г)= lira P*N (z), pQ= lira P*N (0). 7V->oo 7V->oo
Тогда из (4) получаем
p*(z- 1)е-М«-«г) n* (г) = v ’_____________
P 1 ’ Z_e-b(a-az)
Более полно изложение метода вложенных цепей Маркова и примеры его применения содержатся в [2] (гл. 1, § 11), [3] (§ 19), [7] (гл. 14, § 4, 5).
Содержание отчета.
1. Краткая постановка задачи.
2. Результаты аналитического исследования системы обслуживания.
3. Программа для расчета характеристик системы на ЭВМ.
4. Графики поведения исследуемых характеристик.
Литература.
1. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. — М.: Наука, 1966.
2. Гнеденко Б. В. и др. Приоритетные системы обслуживания.— М.: Изд-во МГУ, 1973.
3. Климов Г. П. Стохастические системы обслуживания. — Мл Наука, 1966.
4. С а а т и Т. Элементы теории массового обслуживания и ее приложения. — М.: Сов. радио, 1971.
5. X и н ч и и А. Я- Работы по математической теории массового обслуживания. — М.: Физматгиз, 1963.
6. Н о в и к о в О. А., Петухов С. И. Прикладные вопросы теории массового обслуживания. — М.: Сов. радио, 1969.
7. К а р л и и С. Основы теории случайных процессов. — M.t Мир, 1971.
J67
Приложение 1. Варианты задания
В каждом варианте задаются А (х), В (х), п. и т. Требуется найти указанные характеристики процесса и построить графики для некоторых из них.
№ А(х' В (х) п т найти графики от
1 1-— j е — 2Х 1 0 Ezv <4 Ev (!) Evm i
2 1 — е—3л: 1 — е~^х 1 0 EzV- <*>, Ец (0 Epm t
3 1 —с“2* 1 — е~х 2 0 En(f), P {«(/)=/} 1=072 P {n(t)=i} i =0, 2
4 j__e—х/2 1-е-Зх/2 оо оо En (t), Dn (t) P {n(t) — i} i — 0, I, 2, ... En (/), Dn (0 t
о 1 — е—Зх/2 1—е~* со 00 Ev (/), Dv (0 p{v (/)=/} /=0.1,2,... P {v(/) = /} l
6 1-е~* 1-е-2* 1 1 P {« (/) = /} / = 0. 2 P {n(t^i}
7 l-e-2* 1-е-2* 1 1 Ezv <z>, Ev (/) Ev (i) t
8 1—е-а* 1 —е-3х оо lim En(t), lim Dn (0» £->£» lim P {n (*)=i} /=0, 1, ... /->£» lim En (/) i->oo lim Dn(t) a e [0.3, 2.7[
9 1 —е“а* 1—с~~~х 1 ОС lira Ew (t) lim Dw (t) i->oo lim P /-> oo lim Ew {i) lim Dw(t) 1-* oo a e [0.2, 1.81
10 l-e-ox 1 —e-3x 4 0 lim P {n (£) = £} / = 0,4 t ->co lim P {n(t)sssi} 4 = 0,4
11 1—e~aX 1—e~2x 5 0 lim P {n(t)=:i) /=0,5 £->co lim P {n(t)=i} i=o73 Z->co
12 l — e~ax 1 — e~x (1 + x) 1 oo lim En (t) t-> co lim Dn (0 t co lim Ezn^ £->co 11m En(t) £->co lim Dn(t) £->co
13 l-e-" e~x 2e~^x 1 3 3 1 oo lim En (f) i->co lim Dn (0 /-> co lim EznV) lim En(t) t-+oo lim Dnd)
14 . 1—e~x (1 + x) l — e~bx 1 oo Hm Ew (t) /->co lim Ee-sw^ t-> co lim Ew (f) >co
15 1—e~x (1 + x) l — e~bx 1 oo lim En (t) lim Егп(П t co lim En (t) t->oo
16 l—e~ax 2e~~^x 3e~-3x 1 ъ 5 1 oo lim Ew (0 /->oo lim Ee~sw (f) /->oo lim Ew (f) f-»co
169 17 1 —e~ax 1 — e~x (1 + x) 1 co lim Ew (f) £-»oo lim Ee~sw W CO lim Ew (t) i-»co
a e [0.1, 3[
a g= [0.2, 4]
a e= [0.05, 0.45)
a e [0.15,1.35)
a s [0.25, 2.25|
a e [0.05,0.45]
Приложение 1 (продолжение)
№ Д(х) В(х) п т найти графики о г
18 1-е~ОХ 1-е~х 3 00 Нт £»•(/) t-> оо lim Р — i~0, 1, 2, ... £-> ОО lim P {n (O—i} /->oo
19 1 — e“2x 1-е-Ьх 2 оо lim Еп (t) £-> oo lim En (t) t-> oo 44, io]
lim P {n(t) = i} 1, 2, ... t-> oo
20 1 — 1 — е ~~ 3х 1 0 P{v (£)=/} i=0, 1 P{v(f) = i} i = 0, 1 t
21 1 — е~х 1-е-2х 1 0 P {p,(i) = j} j=o, 1 P{|i(i)=i} i=0, 1 t
22 1 — е~х \-е~х 1 1 P {v (/)=/} Z=0, 1 P{v(f) = i) i=0, 1 t
23 1_е-ах 1 — е~х (1 + х) 1 оо lim P {n(t}==i} i —0, 1, 2 t -> OO lim P i — Q, 1, f->oo 2 a [0.05, 0.45]
24 1-е-ах , е-^х е~^ 1 lim P {n(t)~i} i = 0, 1, 2 /-> oo lim P {n(t) = i} i = 0, 1 /-> oo ае=Г-4 2Л1
2 2 Lb J
25 1 — е~х (1 + х) 1-е-6х 1 оо lim P{n (£)—*} t = 0, 1, 2 f-> oo lim P {n(t)=i} i=0, 1 t-> oo 2
26 1 — е~ах l-e-3* 1 5 lim P t — 0, 3 t->oo 11m p {n(t) = i} i = 0, 3 /->oo ae[0.1, 10]
КАФЕДРА ИССЛЕДОВАНИЯ ОПЕРАЦИИ
Задание ИО-1. РЕШЕНИЕ ЗАДАЧ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
Цель задания.
1. Знакомство с методами решения максиминных задач при оптимальном распределении ресурсов.
2. Практика в использовании ЭВМ для решения максимивдых задач.
Содержание задания.
1. Изучение методов решения максиминных задач.
2. Сведение задачи распределения ресурсов к решению системы нелинейных уравнений и последующее решение этой системы методом Ньютона.
3. Составление программы решения конкретной задачи оптимального распределения ресурсов и ее отладка.
4. Решение на ЭВМ конкретного варианта задания и анализ полученных результатов.
Постановка задачи.
На отрезке [О, А] (А > 0) заданы непрерывно дифференцируемые функции i = 1. п, удовлетворяющие условиям
<₽1 (0) = <р2 (0) = ... = фл (0), ф- (0 >0. i = 174, t е= [0, А].
Рассмотрим множество
Q =
х^Е'1
xi = A, Xi 0, i = 1, n
Требуется приближенно вычислить вектор х* = (х^, ..., летворяющий условию
, т.Ч ч>4 (ХЭ = та,У , m.in 4>i(^) = £.
I < п л=В 1 < I < п
4).
УДОВ-
(О
т. е. для заданного в > 0 нужно найти вектор xs е Q, удовлетворяющий неравенству
L — е < min ф; (х?) < L. (2)
1 < I < п 4 7
Функции ф/(0» значения Айе определяются вариантом задания (см. Приложение 1).
Метод решения.
В сделанных предположениях функции ф<(0. i — 1, йУ являются непрерывными и возрастающими на отрезке [0, А]. Согласно принципу уравнивания Гермейера (см. [1]) решение х* задачи (1) удовлетворяет системе уравнений:
<Pi Ui) = <Pn UJ, i=l, n—l. (3)
171
С помощью соотношения хп=Л-£х/ из системы (3) исклю-i=i
чим неизвестное хп> В результате получим систему уравнений:
/ п~1 \
fi (хь хп-1) = <рг (хг) -<р„1 А - £ хг ), г= 1. П- 1,
\ i = l /
(4)
для которой существует единственное решение (х*.хп-1) в мн0'
жестве
f ______ П-1
£Г = < (xt, .xn-i) | ОС Xi С A Z= 1, п — 1, £ х/С^ >’
Приближенное решение системы (4) найдем, используя метод Ньютона [2]:
где k — номер итерации (fe=l, 2, ...), a fx — якобиан отображения f, вычисленный для вектора (х^ х^_]). Вычисления по ме-
тоду Ньютона следует прекратить, если для очередного вектора (xj, ..., x^j) невязка
(5)
станет меньше е/2. При этом вектор (xj, x^_t) — искомое приближенное решение системы (4). Соответствующий вектор (хр x^_lt xjjefi удовлетворяет (2) и является е-оптимальным решением исходной задачи.
Содержание отчета.
1. Формулировка задачи, метод ее решения н обоснование метода.
2. Текст программы.
3. Результаты счета тестового варианта: е-оптимальное решение (xj, ..., х^), невязка (5) и значения <рг (х^), i = 1, п.
4. Результаты счета основного варианта.
Литература.
1. Гер мейер Ю. Б. Введение в теорию исследования операций.— М.: Наука, 1971.
2. Березин И. С., Жидков Н. П. Методы вычислений. Т. I. — М.: Наука, 1966.
Приложение 1. Варианты задания
№ т, (О ф2(0 Ф3(0 A e
I <0.7 «13 «2.1 «2.8 3 10-4
t «' 10—4
81 + Г 81 +« 5+«8 4+ t<
3 е' гЛ/7 sV*” 5* 5 IO”3
4 logHl +0 logs (1 4-«) log? (1 +1) 111(1 +0 6 IO”4
5 «з —1 log al I +1) 5f —1 7 10“4
Г In (1 + 0 10—3
81
7 <0-7+ i «3.3 + у 3V1 5( 9 10-4
8 — 1 41 —1 logs (1 + «1 In <1 +П 10 10-4
t «2-1 $2.8 Ц in—4
81 +«
у0.7 t* IQ —4
5 + P 4 + «4
Приложение 2. Методические указания
I. Покажем, что система уравнений (3) имеет единственное решение. Действительно, пусть вектор iей удовлетворяет (3). Тогда, если х х“. то найдется пара индексов («, /) такая, кто xt > Ху, Xj < х}. Отсюда <pz (ху) > фу (Ху) = <ру(х*) > <ру(ху) и х не является решением системы (3) — пришли к противоречию.
2. Пусть вектор (х|, ..., x^.JsQ таков, что невязка (5) меньше, чем е/2. Покажем, что соответствующий вектор (ху, .... xj_t, х*) ей удовлетворяет неравенству (2). Предположим, что
min <ру (х|) < L — е. (6)
Покажем, что для любого х s Q
max фу (ху) > L. 1 i
Действительно, если х Ф х*. то найдется такое I, что Ху > Ху и отсюда фу (ху) > фу (X*) = L. Итак, в частности.
max ф£(ху)>Ь. (7)
Но (6) и (7) противоречат тому, что невязка (5) меньше е/2.
3. Для обоснования возможности применения метода Ньютона покажем, что |fx(xi....xo-i) | О для всех (xi, ..., xn-i) ей'-
173
___ / n—l
Действительно, положив at = ср< (х(), i — 1, п, Ь — ф' I А — V, \ i=l
имеем
I fx I —
Я] + Ъ Ъ ... Ь
b а2 + Ь ... Ь
Ь Ь ... ап + b
= П а1 + Ь X П а1 > °-
i—l i-1
4. Известно (см. [2]), что метод Ньютона сходится, если начальное приближение выбрано достаточно близким к решению. В качестве начального приближения (х},..., x^_j) можно рекомендовать вектор
I Е <pfe (Л)
4 fe=l
если <рг(О) 0, i = I, п.
Задание ИО-2. НАХОЖДЕНИЕ МНОЖЕСТВ ОПТИМАЛЬНЫХ СТРАТЕГИИ МАТРИЧНЫХ ИГР СПЕЦИАЛЬНОГО ВИДА
Цель задания.
1. Знакомство с методом решения матричных игр.
2. Практика в использовании ЭВМ для решения матричных игр.
Содержание задания.
1. Изучение метода решения матричных игр, основанного на использовании теоремы Шепли — Сноу о крайних оптимальных стратегиях.
2. Разработка алгоритма поиска всех крайних оптимальных стратегий для игр С вогнутой (выпуклой) матрицей выигрышей.
3. Составление программы решения конкретной матричной игры и ее отладка.
4. Решение на ЭВМ конкретного варианта задания и анализ полученных результатов.
Постановка задачи.
а) Пусть л = (aj,/)т х „матрица, строго вогнутая по г, т. е. при всех i, j имеет место неравенство
(а/-1, / + а»+1, i)/2<ai,i.
Требуется найти все крайние оптимальные смешанные стратегии игроков в игре с матрицей А.
б) Пусть А хп~ матРИ11а> строго выпуклая по /, т. е.
при всех i, j имеет местй Неравенство
(aZ,/-l + ai,/+i)/2> ait!.
Формулировка задачи та же, что и в п. а).
174
Вариант задания определяется постановкой задачи (а) или (б) и конкретной матрицей А (см. Приложение 1).
Метод решения.
Алгоритм решения задачи основан на использовании теоремы Шепли-Сноу (см. [1]).
Для задачи а) нужно последовательно осуществить перебор квадратных матриц второго порядка
В (i, ji, js) =
р, h ai. h \a‘ + l. h ai+l. 12.
1 i ;C tn — 1,
1 < /1 < 12 < П,
взятых из соседних строк матрицы А (см. [2]). Каждую матрицу B(i, ji, 1'г) нужно проверить на невырожденность, решить следующие системы уравнений относительно неизвестных pit Pi+b q^, qb, о: aitjiPi + ai+li hPl+1=v.
ai,12Pi + ai+\.i2Pi+^v' (!)
Pi + Pi+i = i;
ai. lflh + “i, = v-
^+1,1^11 +ai+i,h(ll2 = v’ (2)
и проверить условия
Pi>0, Pi+i>0, qb>0, qh>0,
ai,jPi + ai+\,iPi+l>v> j=l,n, (3)
ai„h(lil + all,hqb<v,
Если матрица B(i, ji, /2) невырождена и результат проверки условий (3) положителен, то в качестве крайних оптимальных смешанных стратегий следует взять р*, q*:
(О при k=£i, i + 1, /0 при /г#=/ь 12,
J Pi при k = i, = J qh при k = /ь
lPz+l при k = i + 1; U/2 при k = j2.
В противном случае перебор матриц следует продолжить.
Алгоритм решения задачи б) аналогичен изложенному, но перебор нужно осуществлять по всем матрицам В, взятым из соседних столбцов матрицы А (см. [2]).
Примечание. Учитывая, что вычисления на ЭВМ ведутся приближенно, все неравенства в (3) следует в правых частях ослабить на малое е > 0. Например, взяв е = 10~3, вместо неравенства ah iflii + ai, а нужно проверять неравенство
ai. iflh + «/, h4b < v + е.
175
Содержание отчета.
1. Постановка задачи поиска оптимальных стратегий и обоснование алгоритма ее решения.
2. Текст программы.
3. Список крайних оптимальных стратегий р*, q*, цена (значение) игры v, полученные на ЭВМ.
Литература.
1. Гер мейер Ю. Б. Введение в теорию исследования операций.— М.: Наука, 1971.
2. Давыдов Э. Г. Модели и методы теории антагонистических игр. — М.: Изд-во МГУ, 1978.
ПрИЛОЖбНИС 1. ВарИаНТЫ З&ДапИЯ
—28 —10
20 23
9 —22
-54 -74
—62х
— 2 I
23 I’
24'
< 65 39 48 —21
А = 90 34 68 70
к—78 17 —10 —12
—85
—29
—63
—55
—8
А =
83\
—12 |
15 I-
17 I
—23/
—7
—9
—12
13
1
2
33
2
—3
—17
—8 —17
—9 —4
—11 —2
Задание ИО-3. ПОСТРОЕНИЕ СЕТЕВЫХ ГРАФИКОВ
Цель задания.
1. Изучение методов нахождения критического пути в ориентированном графе.
2. Использование изученных методов для решения задачи составления сетевого графика проекта на ЭВМ.
Содержание задания.
1. Знакомство с методами нахождения критического пути (см. [1], гл. 8, и. 6).
2. Сведение задачи составления сетевого графика к нахождению критического пути и критических значений для ориентированного графа.
•1
3. Составление программы для построения сетевого графика конкретного проекта и ее отладка.
4. Решение на ЭВМ конкретного варианта задания и анализ полученных результатов.
Постановка задачи.
Для осуществления некоторого проекта необходимо выполнить k работ различного вида. Последовательность выполнения работ характеризуется матрицей {а,7} (1 I, j k) следующим образом: если ац 0, i j, то j-я работа может быть начата не раньше, чем через ац часов после начала i-й работы; если же начало j-й работы не связано с выполнением i-й работы, то ац = — 1; наконец, при i = j ац — время выполнения i-й работы.
Найти минимальное время выполнения проекта, критический путь и минимальное время для начала каждой работы.
В качестве исходных данных для решения задачи задаются значения ац (1 i, / k) (см. Приложение 1).
Метод решения.
а) Переупорядочить работы таким образом, что ац — —1 при i > j. Если это невозможно, то данный проект неосуществим.
б) Пусть t(i)—минимальное время начала i-й работы. Тогда i(l) =0. Определить i(i) при i = 2, ..., k из рекуррентного со<и-ношения
t (i) = max [0, max (i (j) + a//)]. {!<‘\ац>й}
в) Определить минимальное время выполнения проекта iKp = max (i (i) + ац).
1 < i
г) Определить критический путь, т. е. последовательность работ, обусловливающих выполнение проекта за время /кр. Для этого положить
ii = arg max (i (i) + ац);
1 C i < k
далее определить lp (р = 2, 3, ...) из соотношения
Ч'р) + %/р_, = ^-1) (1)
до значения р, для которого i(i^) = 0. Последовательность работ /р, /р-i, ..., Zi и образует критический путь.
Содержание отчета.
1. Формулировка задачи, метод решения и его обоснование.
2. Текст программы.
3. Результаты счета тестового варианта: минимальное время /кр. критический путь I р, ..., Ц и минимальное время начала каждой из работ t(1), .... t(k).
4. Результаты счета основного варианта.
177
Литература.
1. Кристофидес Н. Теория графов. — М.: Мир, 1978.
Приложение 1. Матрица (1 i, /=С13)
1 i
1 2 3 4 5 6 7 8 9 10 11 12 13
1 20 25 15 30 43 33 48 -1 -1 90 85 80 0
2 -1 41 -1 10 -I 18 8 -1 30 90 -1 15 -1
3 -1 16 15 22 80 -1 55 45 -1 -1 25 70 100
4 -1 -1 -1 20 42 -1 -1 62 30 -1 45 -1 75
5 -1 -1 -1 31 -1 -1 45 18 65 32 42 -1 35
6 -1 -1 -1 -1 17 20 -1 60 27 65 45 25 -1
7 -1 -1 -1 -1 -1 -1 10 -1 25 70 17 -1 2
8 -1 -1 -1 -1 -1 -1 -1 15 17 -1 15 65 10
9 -1 -1 -1 -1 -1 -1 -1 10 20 -1 -1 -1
10 -1 -1 -1 -1 -1 -1 -1 -1 -1 35 -1 -1 2
11 -1 -1 -1 -1 -1 -1 -1 -1 -1 19 10 -1 40
12 -1 -1 -1 -1 -1 -1 -1 -1 -1 82 -1 5 40
13 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 20
Приложение 2. Методические указания
1. Для того чтобы перенумеровать работы в соответствии с указанием а), необходимо найти работу, для которой ац.=—1 для всех / ф ij, и взять ее в качестве первой; затем найти 12 такое, что ац2 — —1 для всех / ф. pj, z2j, и взять работу 12 в качестве второй и т. д. Следует иметь в виду, что указанная нумерация осуществляется не единственным образом и не обязательно совпадает с порядком выполнения работ в реальном времени.
2. При определении критического пути значение 1Р может определяться из соотношения (1) не единственным образом. Критический путь не обязательно начинается с первой (после перенумерации) и заканчивается на последней работе.
Задание ИО-4. МЕТОДЫ РАСЧЕТА ОПТИМАЛЬНЫХ ТРАНСПОРТНЫХ МАРШРУТОВ
Цель задания.
1. Знакомство с методами поиска пути с максимальной пропускной способностью в неориентированном графе и практика в их использовании.
2. Накопление опыта в использовании ЭВМ.
Содержание задания.
1. Изучение методов нахождения пути с максимальной пропускной способностью.
2. Составление программы для расчета пути с максимальной пропускной способностью, соединяющего данные пункты.
3. Решение на ЭВМ конкретного варианта задания и анализ полученных результатов.
Постановка задачи.
Пункты 1, 2, ..., k связаны сетью дорог. Заданы значения ?»/ gs 0, qij — qq (1 i, ! k) пропускных способностей дорог из пункта i в пункт j. Требуется найти путь с максимальной пропускной способностью из пункта 1 в пункт k. В качестве исходных данных задаются значения qu, 1 i < j rg k (см. Приложение 1).
Метод решения поставленной задачи включает следующие этапы: а) Положим q == max — максимальной пропускной спо-1 <с / k 1
ссбности для путей, выходящих из пункта 1; Л = = q} V {1}-
Для / е Ji определим /(/)= 1. Если k е Jt, то переходим к этапу б); в противном случае — к этапу в).
б) Пусть определено множество Jr, г 1, текущее значение q и значения Z(/)e7r\{/} для всех /еЛ\{1} и k е ]г. Тогда задача решена, причем q — искомая пропускная способность, а искомый путь (1, ii, i2, ..., is, k) определяется из соотношений l(k) = is, l(ip) = = ip—i, p = s, 1, где i0 полагаем равным единице.
в) Полагаем
Л+1 = /r V {/1 (/) e Л: (/) > q}. (1)
Если Jr+l — Jr, то переходим к следующему этапу; в противном случае определяем /(/) для j е 7r+i\7r из соотношения (1) и полагаем г := г + 1. Если k е Л, переходим к этапу б), иначе повторяем этап в).
г) Определяем максимальную пропускную способность для дорог, связывающих совокупность пунктов Л, и ее дополнение;
q := max qij
leJr, j <= {!.fe}\Jr
н возвращаемся к этапу в).
Содержание отчета.
1. Формулировка задачи, метод решения и его обоснование.
2. Текст.программы.
3. Результаты счета тестового варианта; максимальная пропускная способность н соответствующий путь.
4. Результаты счета основного варианта.
Литература.
1. Крнстофидес Н. Теория графов. — М.: Мир, 1978.
179
Приложение I. Значение q, у (1 ?< } 13)
5 6 7 8 ) 10 И 12 13
10
11
12
13
7 II 23 37
8 12 24
• 0 6
• 47
О 29
33 5
О 10
39 29
О 27
• О
19 5 О
19 47 О
О 22 80
О 57 71
О 41 9
12 13 О
О 38 о
• 17 29
• 10
47 61 19
61 29 О
36 17 45
О 33 О
23 51 65
14 42 О
5 19 47
47 0 61
10 0 21
ООО
43 О 10
з
1
5
Приложение 2. Методические указании
Обоснование предложенного метода решения задачи состоит в следующем. Совокупности пунктов сопоставим неориентированный граф с множеством вершин / = {1, k}, связанных дугами с ве-
сами qif (/, /s/). Тогда каждому пути из пункта 1 в пункт k соответствует путь графа через вершины 10 = 1, iSt is+l = k и
пропускной способностью является величина min а, , 1р1р+1
Если /], — разбиение множества J, то разрезом (/|, /2) назы-
вают множество дуг {(Ц, /2) | й еn е М (з — О’РазРез — это такой разрез {Jit J-i), что se/<, t s /2. Пропускной способностью разреза (Л, Л) называют величину
? (<!> Л) = . . та* ч Olfr
(й> z’s) S (7|, /а)
Справедливо следующее соотношение ([1], гл. 8, п. 7.2): максимум пропускной способности по всевозможным путям ИЗ S в t совпадает с минимумом пропускной способности по всевозможным (s— /)-разрезам. Из определения множеств J, следует, что указанный минимум реализуется для некоторого г парой {Jr, J\Jr); поп этом определяемое на этапе в) значение q равно искомой пропускной способности и не меняется на последующих этапах.
1ЯО
КАФЕДРА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Задание ОУ-1. ЛИНЕЙНАЯ ЗАДАЧА УПРАВЛЯЕМОСТИ
Цель задания.
1. Знакомство с численными методами решения линейной задачи управляемости.
2. Накопление опыта работы на ЭВМ, в использовании алгоритмических языков и в отладке программ.
Содержание задания.
1. Изучение теоретических основ метода решения линейной задачи управляемости.
2. Составление и отладка программы для численного решения задачи управляемости.
3. Аналитическое нахождение точного решения в заданном тестовом примере. Сравнение с результатом применения составленной программы к тестовому примеру.
4. Решение на ЭВМ конкретного варианта задачи управляемости.
Постановка задачи.
Рассматривается управляемый объект, движение которого в пространстве Еп описывается линейным дифференциальным уравнением
х=Ах + «, u^U, (1)
где те Е" — вектор фазовых координат; и е Еп — вектор управления, который выбирается из заданного компактного множества U; А — заданная квадратная матрица. При этом задано множество начальных состояний Мо объекта и множество его конечных состояний Mi (Мо и Mi — выпуклые компактные множества пространства Еп).
Будем говорить, что объект является управляемым на отрезке времени [/о, ^1] из множества Мо в множество Mi, если существует хотя бы одно такое допустимое управление «(/), что соответствующее ему решение x(t) уравнения (1) на отрезке времени [f0, Л] переходит из Мо в Mi, т. е. удовлетворяет граничным условиям х(А>) е Mo, x(ti) е= Ml.
Точный ответ на вопрос о том, является ли объект управляемым, можно дать лишь в том случае, когда задача решена аналитически. При решении задачи на ЭВМ неизбежно возникают погрешности вычислений, из-за которых вопрос об управляемости объекта становится неясным.
Будем говорить, что объект является е-управляемым на отрезке времени [/0, из множества Мо в множество Мь если он управляем на этом отрезке времени из Мо в замкнутую е-окрестность множества Mi, т. е. в множество M,-]-SE(0), где SE(0)—шар радиуса 8 с центром в нуле.
Будем считать, что задача управляемости решена с точностью е, если ответ дан в одном из следующих видов:
181
1) объект заведомо неуправляем;
2) объект заведомо управляем;
3) неизвестно, управляем ли объект, но он заведомо е-управ-ляем.
Требуется составить программу численного решения задачи управляемости на отрезке времени [4, /,] с заданной точностью в. Вариант задания определяется набором параметров и, A, U, Мо, М] (см. Приложение 1).
Теоретические основы решения задачи управляемости.
1. Вводится величина (см. [1, 2])
Г tl 1
р = min I с (Мо, ф (£0)) + с (Mi, — ф (fi)) + ( с (U, ф (s)) ds I, (2)
фе=3I J I
где S— единичная сфера в пространстве Еп, c(F, ф)—опорная функция множества F е Еп, определяемая выражением
с (F, ф) = max (f, ф), feF
а Ф (0 — решение сопряженной системы
ф = — Д*ф (3)
с конечным условием ф(Л) = <р. Здесь А* — матрица, полученная из А транспонированием.
Объект является управляемым на отрезке времени р0. Л] из множества Мо в множество Ms тогда и только тогда, когда выполнено неравенство р 0.
2. Если величина р вычислена с точностью в, т. е. имеется приближенное значение р, удовлетворяющее неравенству
|р- р|<е, (4)
то проблема управляемости решена с точностью в, а именно;
1) если р < —в, то объект заведомо неуправляем;
2) если р 23 е, то объект заведомо управляем;
3) если —в с' р < в, то неизвестно, управляем ли объект, но он заведомо в-управляем.
3. Пусть S — некоторая 6-сеть на единичной сфере S, a min в выражении (2) вычислен по множеству 5 вместо S. Пусть, далее, во — погрешность вычисления опорной дункции с(М0, ф); в] — погрешность вычисления опорной функции c(Mi, ф). Предположим, что ва — погрешность решения дифференциального уравнения (3), Вз— погрешность вычисления опорной функции c(U, ф), 84 — погрешность вычисления интеграла, a ss — погрешность операции вычисления минимума.
132
Если параметры е0, 81, е2, е3, е«, е5 и 6 удовлетворяют неравенству
е0 + е, + [ 1 Мо | + 1 АГj | + I V | - i0)J е2 +
+ (*г - /о) е3 + е4 + е5 + [| Mo 1 e(fl-/o) 1|Л” +
+ I М! | + | U j ИЛ|1 - 1)/ЦЛ Ц16 С е, (5)
где | Е | = max || f ||, а ||А||— норма матрицы А, то погрешность вы-f eF
числения величины р не превышает е, т. е. выполнено неравен-
ство (4).
Замечание 1. Если матрица А — нулевая, то в выражении
(5) вместо значения Mil — 1)/||Д|| надо взять значение (/i — to).
Замечание 2. Если считать, что все операции на ЭВМ вы-
полняются точно, то погрешность вычисления величины р зависит только от разбиения 6 и выражение (5) принимает вид
|М0|е№-г")1|Л|| + |М1 14-
е(*.-*о) ПАР.
РПГ
1
и I 6 < е.
4. Для решения с заданной точностью е задачи управляемости следует так выбрать параметры е0, ..., 8s и д, чтобы удовлетворялось неравенство (5), и произвести вычисление величины р по формуле (2) с учетом погрешностей на всех этапах вычислений.
Заметим, что в предлагаемых вариантах из управляемости объекта на отрезке [Zo, t}] следует его управляемость на любом отрезке Ро, й>], где t2 > ti.
Этапы выполнения задания.
Для решения поставленной задачи следует:
1. Опорные функции множеств Af0, Afj и U найти аналитически.
2. Найти решение уравнения (3) в явном виде:
-ф (t) = А* ср,
для чего нужно вычислить экспоненциал матрицы А: еаЛ=Д + аА + -^-А2+ ...
3. Составить программу для вычисления на ЭВМ значения р пз формуле (2), причем вычисление значения определенного интеграла осуществлять с заданной точностью, 6-сеть на S выбрать конечной И минимум находить простым перебором.
4. Для проверки правильности программы решить с ее помощью заданный тестовый пример (см. Приложение 2).
5. С использованием ЭВМ найти отрезок времени вида [0, O.lfe], на котором объект является управляемым с заданной точностью е = 0.2. Для этого выполнить составленную программу для последовательных значений k = 1, 2, ... и найти минимальное значение k = kti такое, что на отрезке времени [0, 0.1 «о] объект управляем.
183
Содержание отчета.
1. Постановка задачи.
2. Программа на алгоритмическом языке и инструкция пользования ею.
3. Результаты отладок.
4. Результат решения на ЭВМ тестового варианта.
5. Результат решения на ЭВМ конкретного варианта задания. При этом выдача на печать должна содержать идентификацию задания и студента, значения исходных данных, при которых решалась задача (я, A, U, Мо, очередной отрезок времени [О, 0.1й] и ответ (управляем, неуправляем, е-управляем).
Литература.
1. Благодатских В. И. Линейная теория оптимального управления.— М.: Изд-во МГУ, 1978.
2. Благодатских В. И. Задача управляемости для линейных систем. — Труды МИ АН СССР, 1977, т. 143, с. 57—67.
Приложение 1. Варианты задания я —2
А и Л4,
(° 0>1 {«2 + и“ 'С 5| {-5, 2} {| *1 |<1> |
ко о) Х2=!} (Л -3}
( 0 ч И + Ы2<3} {4+Г2-‘)2<2} {-Ю, 5}
1-1 о) {|«1|<1. f «2 |<2} {1 {Ю, 0}
/—2 0\ + <4} И. О {Pi-5!^1- Vs10}
к 0 -1J {(^-5)2 + ^<1} {0, 0}
/! 04 Н + “2^6} {ГН^1’ |*2 |<‘} {-7, И
ко -l) {0, 0} {|Х1-5|<1,Х2 = О}
/-3 04 Н + М2^7} {х2 + (х2-1)2<2} {-И. 5}
к 0 1) {( “1 |<3’ f “2 |<2} И. О {(х1-5)2 + х2<!}
Н + а2<8} {ГН<2- *2=3} {0, 0}
ко о) {|“11<7Ч“2^8} {-6, 3}
АОЧЬ
n = 3
А и л,о
z 1 ° 0 \ 1 ° ° 0 j к 0 0 -5 / /А с /А ЬЭ « ' "7\ (-1, 2, 3} {0, 0, 0} {0, 0, 0} (1.1.1}
z-2 0 0\ 1 0 —1 0 ) к 0 0 -3 / {^ + »2+И3<2} {Iй! |<2’ | “2 Гз^1} { -10, 3, 7} <о. А 2} {0, 0, 0} {1, 2, -3}
z —1 0 0 \ 1 0-301 ко 0 2/ сП V/ а” v £ см сч V а — + Г!- 3 {5. 8, -1} {-1, 7, 1} {0, 0, 0} {1. 3, 2}
Приложение 2. Тестовый вариант
Для п = 2 взять
Л = (_J’ J), U = {и2 + и2 < 1}, Мо = {0, 0}, = {2, 2}.
Объект является управляемым на отрезке времени [0, 2 д/7], но не является управляемым на любом отрезке длины, меньшей чем 2 д/2.
Для п = 3 взять /0 0 0\
4 = 10 0 0 1, U = {uj + uf+ Мо= {0, 0, 0}, Mj= {1, 1, 1}.
\0 0 О/
Объект является управляемым на отрезке времени [о, д/з ]» но не является управляемым на любом отрезке, длина которого меньше д/з".
Задание ОУ-2. ВРЕМЯ БЫСТРОДЕЙСТВИЯ
В ЛИНЕЙНОЙ ЗАДАЧЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Цель задания.
1. Практика в использовании численного метода нахождения времени быстродействия.
2. Накопление опыта работы на ЭВМ по использованию трансляторов и отладке программ, написанных на алгоритмических языках.
Содержание задания.
1. Изучение теоретических основ метода нахождения времени быстродействия.
185
2. Составление и отладка программы, предназначенной для численного нахождения времени быстродействия.
3. Аналитическое нахождение точного решения в заданном тестовом примере. Сравнение с результатом применения составленной программы к тестовому примеру.
4. Решение на ЭВМ конкретного варианта линейной задачи быстродействия.
Постановка задачи.
Рассматривается управляемый объект, движение которого в пространстве Еп описывается линейным дифференциальным уравнением
х — Ах-\-и, u^U, (1)
где х е Еп— вектор фазовых координат; а = £’ — вектор управления, который выбирается из заданного компактного множества (7; А — известная квадратная матрица. Задача быстродействия (см. [1, 2]) заключается в нахождении для заданной точки х такого допустимого управления u(t), которое переводит объект (1) в начало координат за наименьшее время. Это наименьшее время перехода из точки х в начало координат обозначим через т(х).
Требуется составить программу численного нахождения времени быстродействия т(х). Варианты задания определяются набором параметров п, A, U (см. Приложение 1).
Теоретические основы задания.
Вводится величина
т
(х, ф) + с {U, e~sA* ф) ds о
где S — единичная сфера в пространстве £", c(U, ф)—опорная функция множества Е с: Еп, определяемая выражением
с(Е, ф)=тах(и, ф), иеУ
еаА—экспоненциал матрицы А, определяемый соотношением
еаА = £ + ^Л+4А2+ ...,
а А* — матрица, полученная из А транспонированием.
Функция р(т) строго монотонно возрастает во всех вариантах задания и при г — 0 принимает значение р(0) = —||х||. Время быстродействия т(х) является корнем уравнения
Р (?) = 0. (3)
Для численного нахождения времени быстродействия следует произвести вычисление величины р(т) (см. (2)) и найти корень уравнения (3).
186
Требования к программе.
1. Выбрать в множестве 5 конечную 6-сеть 5 и операцию минимума взять простым перебором.
2. Опорную функцию множества U найти аналитически.
3. Экспоненциал еаА найти аналитически.
4. Уравнение (3) решить в два этапа: с переменным шагом Гл — 2* (k = 0, 1,2,...) найти отрезок [2&*-I> 2k*], на котором ле-жит корень уравнения (3); далее, методом деления отрезка пополам найти корень уравнения (3) с точностью 0.01.
5. Для проверки правильности программы решить с ее помощью заданный тестовый пример (см. Приложение 2).
6. Провести счет конкретного примера для различных значений х, указанных в варианте задания.
Содержание отчета.
1. Постановка задачи.
2. Программа на алгоритмическом языке, инструкция пользования ею.
3. Тесты, результаты отладок.
4. Результаты решения конкретного варианта.
5. Перечень и характеристика всех ошибок, допущенных в процессе прохождения задания.
Литература.
1. Понтрягин Л. С. и др. Математическая теория оптимальных процессов. — М.: Наука, 1969.
2. Благодатских В. И. Линейная теория оптимального управления.— М.: Изд-во МГУ, 1978.
Приложение 1. Варианты задания
I. п = 2; х = {± I, ±j] (Z = 0, 1, ..., 5;/ = 0, 1, .... 5).
А и
С!) {“1 + И2<5} {i“d<2’ |м<3}
аг) {“i=°-i“2i<1} {i“ii<i-i“2i<2}
t -г ох \ о -J
А и
С J) Н + “2<6}
С» D И+“М
(о°;) {“1 + “2<8}
If
И. n = 3; x = {± i, ± j, ± k} (i = О, 1, 2; j = 0,1,2; k = 0, 1, 2).
А и
/10 °\ I 0 0 0 ) \0 0 -5/ 1 V/ -3 _v/ V/ oj ео + п oj oj w а — + а~ OJ—’ **
z -2 0 0\ 10-1 0 ) \ 0 0 -3) 2*^ /л *7° " к —-. со w е Л м "' /л' ' £ /л
( -1 0 0\ 1 Q О Q I ко 0 2/ ю"' V/ ео а у/ со —“ » и М V/ а а Ol-М V а .— 03—«
Приложение 2. Тест
Для n = 2 взять
Д = {«? + «2< О’
Показать, что в этом случае т = ||х||. Для п = 3 взять
(0 0 0\
ООО), £/={«f+ и| + «^< 1}. ООО/
Показать, что в этом случае т = ||х||.
Задание ОУ-3. ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ ЛИНЕЙНОЙ ЗАДАЧИ УПРАВЛЕНИЯ С КВАДРАТИЧНЫМ КРИТЕРИЕМ КАЧЕСТВА
Цель задания.
1. Практика в использовании численного метода решения линейной задачи управления с квадратичным критерием качества.
2. Накопление опыта работы на ЭВМ по использованию трансляторов и отладке программ, написанных на алгоритмических языках. Содержание задания.
1. Изучение теоретических основ метода решения линейной задачи управления с квадратичным критерием качества.
2. Составление и отладка программы, предназначенной для решения поставленной задачи.
183
3. Табулирование с помощью ЭВМ точного решения в заданном тестовом примере. Сравнение с результатом использования составленной программы для решения тестового примера.
4. Решение на ЭВМ конкретного варианта линейно квадратичной задачи с выдачей результата по заданной форме.
Постановка задачи.
Рассматривается управляемый объект, движение которого в Еп описывается линейным дифференциальным уравнением
х = Ах + Ви,
(1)
где х е Еп — вектор фазовых координат; и е Ет — вектор управления; А и 8— известные матрицы. Задано начальное состояние объекта
х (0) = х0. (2)
Процесс управления рассматривается на заданном конечном отрезке времени [0, Г] при закрепленном левом конце х(0) = ха и свободном правом конце х(7) траектория x(f). Критерием качества управления служит квадратичный функционал
Г
Ф (и) = X* (Т) Sx (Т) + (x*Qx + u*Ru} dt, (3)
о
где Q, R, S — заданные матричные весовые миожители (матрицы Q, R, S — симметричные и неотрицательно определенные, матрица R — положительно определенная), а звездочка означает транспонирование. При вычислении значения функционала (3) при заданной управляющей функции и в качестве х следует брать соответствующее управлению и решение задачи Коши (1), (2).
Требуется по заданным А, В, Q, R, S, х0, Т найти управление, минимизирующее функционал (3) на решениях задачи (1), (2). Это управление, называемое оптимальным, может разыскиваться:
а) в форме и = иа(х, t) (обратная связь);
б) в форме и = йо(О (программное управление).
Нужно найти также оптимальное значение Ф(но) критерия качества и оптимальную траекторию Хо(О. 0 t Т, т. е. решение задачи Коши (1), (2) при и = и0(х, 0-
В данном задании матрицы А, В, Q, R, S считаются постоянными (стационарный случай); анализ нестационарного случая не содержит существенных отличий от стационарного случая.
Вариант задания определяется набором параметров ns mt Tt Хо, A, В, Q, R, S (см. Приложение 1).
189
Теоретические основы задания:
1. Оптимальное управление и~,(х, t) линейно зависит от фазового вектора х и определяется формулой
и0 (х, /) = — R~lB*K (/) х, (4)
где K(t), O^t^T,— симметричная неотрицательно определенная (п X п)-матрица, являющаяся решением следующей задачи Коши:
К = — Q-KA-A*K+RBR~lB*K, (5)
К (Г) = S. (5)
Уравнение (5) называется матричным уравнением Риккати.
Оптимальная траектория x0(f), O-sXtx^T, определяется путем решения задачи Коши
x = (A-BR-'B*K(t))x, (7)
х (0) = хв. (8)
Оптимальное значение Ф(«о) функционала определяется формулой
Ф (и0) = х*0К (0) хп. (9)
Существование решения K(t) задачи Коши (5), (6), определенного на всем отрезке 0 sj t Т, предполагается.
2. Обоснование оптимальности закона управления (4) производится путем «выделения полного квадрата» в функционале (3): имеет место представление
т
Ф(и)=ХоК(О)хо+ ^\\и +R~xB*Kx\^Rdt, (10) о
где и — любое управление; х—решение задачи Коши (1), (2), отвечающее этому управлению: К = K(t)—решение задачи Коши (5), (6); = (»*2?»)'/2 — В-норма вектора v. Из (10) следует, что
Ф(и) Ф(«о) для любого и, т. е. следует оптимальность закона управления (4) и формула (9). Для получения представления (10) следует воспользоваться следующими равенствами:
(х*Кх) = х*Кх + х*Кх + х*Кх,
т
j (х*Кх + х' Кх + х*Кх) dt — х*Кх = 0, о
т
Ф (и) =-- х„ (0) К (0) хо 4- (x*Qx + u*Ru + (Ах + Ви)* Кх +
о
+ х* (— Q - КА - Л*к + KBR-lB*K) х + х*К (Ах + Ви)) dt.
190
3. Для решения рассматриваемой задачи следует;
а) вычислить матрицу K(t), интегрируя назад за-
дачу Коши (5), (6);
б) вычислить оптимальное значение функционала по формуле (9);
в) вычислить оптимальную траекторию Xo(f), 0 71, решая
задачу Коши (7), (8);
г) вычислить программное управление й0(/) = Ио(*о(О> О, 0 ig sg t 5g Т; вычислить Ф10пт = Ф(5о) по формуле (3) (для контроля).
Примечание. При составлении программы обратить внимание на то, что матричное уравнение Риккати (5) в силу симметричности матрицы Д(/) можно свести к системе дифференциальных уравнений порядка п(п+1)/2 и что матричное уравнение Риккати (5) интегрируется справа налево.
Требования к программе.
1. Для численного интегрирования системы дифференциальных уравнений использовать метод Рунге-Кутта с заданным постоянным шагом Н.
2. Для контроля точности получаемых результатов предусмотреть решение задачи с шагами Н и Н/2, приняв в качестве окончательного результата решение, полученное с шагом Н/2, как более точное, а в качестве меры точности вывести на печать значения функционала, полученные при шагах Н и Н/2.
3. Выдача на печать должна содержать: идентификацию задания и студента; начальные данные, при которых решалась задача; таблицу, каждая строка которой содержит значение ti и соответствующие ему значения Xoi(^i). Хог(^), йо(Л), Kn(f<)> Kizlti), зна-
чения функционала, полученные при шагах Н и Н/2.
4. Для проверки правильности программы решить с ее помощью заданный тестовый вариант (см. Приложение 2); табулирование известного точного решения выполнить на ЭВМ.
5. На основании полученных результатов построить графики оптимальной траектории, оптимального управления и элементов матрицы К(0-
Содержание отчета.
1. Постановка задачи.
2. Программа иа алгоритмическом языке и инструкция по ее использованию.
3. Тесты, результаты отладок.
4. Результаты решения конкретного варианта задания. Построенная вручную оптимальная траектория на фазовой плоскости.
Литература.
1. Андреев Ю. Н. Управление конечномерными объектами.—». М.; Наука, 1976.
191
2. Атанс М., Фалб П. Оптимальное управление. — М.: Машиностроение, 1968.
3. Брайсон А., Хо-Ю - Ши. Прикладная теория оптимального управления. — М.: Мир, 1972.
4. Квакернаак X., Сиван Р. Линейные оптимальные системы управления. — М.: Мир, 1977.
Приложение 1. Варианты задания
Во всех вариантах принять я = 2, т — 1, Н — T/N, N — 25. Конкретный вариант определяется параметрами (Т, ха, А, В, Q, R, S) и задается набором (ai, а2, аз. ait аз, а6, а7), 1 sg я, гС 4, где зна-чение O-i равно номеру строки в приведенной ниже таблице, из которой берется значение i-го параметра:
T xo A в Q s
( 0 1X /0 OX /0 0\
1 я (1) (-io) (j (0 0) (1) (0 0)
Z2\ /1 o\
2 2 (o) (00) (1) (01) (5) (01)
/1 o\
3 2л (1) (-1/2 -1) (2) (0 1/2) (1/2) (0 0)
Zl\ /2\ /2 0\ /5 0\
4 4 (2) (0-2) (1) (0 0) (1/10) (0 5)
Приложение 2. Тест
При я = 2, т=\,Т = 2, x0 = (J),
„ ( о 0 X ( 1 ° х D ...
S=(qqI, Q = I о । I > ° = (О точное решение имеет вид
г- / Л ( ku (t) kl2 (О X
\ kn(t) kn(t) )’
kn it) = k22 it) =-it- 2)/2 - th (V2 Ц - 2))/(2 a/2 ), Й12 (0 = kn it) = it- 2)/2 - th (V2 Ц - 2))/(2 aJI),
Xio it) = x20 (0 = ch (V2 it — 2))/ch (2 д/2 ),
и0 it) = V2 sh (д/f it - 2))/ch (2 VF),
J iu0) = V2 th (2 д/2 ).
192
Задание ОУ-4. РЕШЕНИЕ ЛИНЕЙНЫХ ЗАДАЧ БЫСТРОДЕЙСТВИЯ МЕТОДОМ
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ
Цель задания.
1. Практика в численном решении линейных задач быстродействия.
2. Накопление опыта работы на ЭВМ по использованию трансляторов и отладке программ.
Содержание задания.
1. Изучение теоретических основ метода решения линейной задачи быстродействия; знакомство с методикой решения систем урав* нений методом продолжения по параметру; составление, на основе принципа максимума системы уравнений относительно оптимального времени и начального значения сопряженной переменной, подготовка этой системы к применению метода продолжения по параметру; теоретическое обоснование- отдельных этапов решения задачи.
2. Составление программы численного решения- задачи Коши для системы обыкновенных дифференциальных- уравнений, возникающей при применении метода продолжения к линейной задаче быстродействия.
3. Проверка составленной программы на тестовом примере.
4. Решение на ЭВМ конкретного варианта задания; оформление полученных результатов.
Постановка задачи.
Рассматривается линейная задача быстродействия
х = Ах + и, х Еп, us U, U е Еп,
х (0) = хо, (1)
х (Т) = 0.
Т-> min , и (-)Е D
где х — вектор фазовых координат; и — управление; х0 — заданное начальное состояние управляемого объекта; А — заданная постоянная (п X п) -матрица; U — заданный непустой выпуклый компакт (область управления); D — класс допустимых управлений, состоящий из измеримых функций «(/), 0 / 6, удовлетворяющих условию
u(t) е. U при всех t е [0, Л], где Л — любое положительное число; запись «(>) е D означает, что и(-) есть элемент класса допустимых управлений D.
Требуется найти в классе допустимых управлений D такое управление u(i), 0 -С t Т, которое осуществляет перевод объекта из заданного начального состояния х0 в конечное состояние х = 0 за кратчайшее время. Управление, решающее эту задачу, называется
7 Н. П. Трифонов, Е. Н. Пасхик
193
оптимальным управлением, а соответствующая ему траектория — оптимальной (в смысле быстродействия) траекторией.
Предполагается, что для заданного начального состояния Хо существует допустимое управление, переводящее объект из х0 в 0.
Выпуклый компакт U однозначно определяется своей опорной функцией
с (ф) = шах (ф, и). (2)
и е U
Относительно свойств компакта U сделаем следующие три предположения, выраженные н терминах его опорной функции (2):
П1, Функция с(ф) имеет строго положительный минимум на единичной сфере S = {ф е Еп, ||ф|| = 1}:
min с (ф) > 0. (3)
tfei'
П2. Функция с(ф) имеет непрерывные частные производные до второго порядка включительно при всех ф Ф 0.
ПЗ, Ранг матрицы
ранен п — 1 для всех ф е S.
Замечание 1. Геометрический смысл условия (3) состоит в том, что точка 0 е £“ (нуль) является внутренней точкой множества U.
Замечание 2. Существование градиента с'(Ф) прн ф #= 0 означает, что множество U строго выпукло, т. е. опорное множество множества U с опорным нектором ф состоит из единственной точки, причем этой точкой является с'(ф).
Замечание 3. Ранг матрицы (4) всегда не превосходит п—1, так как имеет место равенство фс"(ф) =0, вытекающее из свойства положительной однородности (степени 1) функции с(ф).
Примером множества 4/, для которого выполнены предположения П1 — ПЗ, является множество, ограниченное эллипсоидом н содержащее нуль в качестве внутренней точки.
Общая методика решения задачи.
На основании принципа максимума (см. [1]) решение линейной задачи быстродействия сводится к вычислению оптимального времени То > 0 и начального значения р° е S сопряженной переменной, определяющей оптимальное управление. Вычисление То, р° производится путем решения нелинейной системы уравнений:
UP,D = Xo, 11р112/2=1/2
194
относительно Т и р = (рь .... рп) при заданном векторе начального состояния Хо. Здесь
т
В (р, Т) = — § e~iAu (t, р) dt (Т > 0, р#=0), (6)
о
«(t, р) — агё шах Ф Р) (7)
ve.ll
а “Ф(^» Р) — Ре~‘А— решение сопряженного уравнения ip = —фЛ с начальным условием ф(^, P)\t=o = P, где р= (pi, Рп) — ненулевая строка. Управление (7) выражается через опорную функцию (2) следующим образом:
и (t, р) = с' (ф) |ф=ф(<> p)ssc' (ф (t, р)). (8)
Решение
р = р°, Т = 7’о (9)
системы (5) определяет (с использованием формулы (8)) оптимальное управление иОПт(0 задачи (1):
«опт(0 = «а, Р°) = с'(Ф(^ Р0)), O^t^To. (10)
Наконец, решение задачи Коши
х = Ах + «опт (0. * (°) — хо,
дает искомую оптимальную траекторию х(О=ем(хо-В(р°, 0), 0</<Т0. (Н)
Таким образом, решение задачи быстродействия (1) сводится к решению системы уравнений (5) и последующему применению формул (10), (11).
Для решения системы (5) могут быть использованы различные численные методы. При выполнении данного задания предлагается использовать метод продолжения по параметру [3, 4, 5], простейший вариант которого излагается ниже. Заметим, что в задании рассматривается такой класс линейных систем быстродействия (см. П1 — ПЗ), для которых функция (6) является гладкой, указанная ниже матрица (17) невырождена при всех Т > 0, р =£ 0 н, таким образом, можно провести теоретическое обоснование применимости рассматриваемого метода.
Метод продолжения по параметру и его применение в задаче быстродействия.
1. Пусть требуется иайтн решение z = zt векторного уравнения
Я(г)=<Рь (12.1)
где R: £я+1 -*• En+t — заданная гладкая функция класса С2, q>i — заданный вектор, а г — вектор неизвестных (<pi, ze£,+l).
7*
195
Построим уравнение вида
fl(z) = q>as/?(za) (12.2)
с известным решением z — z0. Уравнение (12,2) отличается от уравнения (12.1) только правой частью. Теоретически в качестве га можно выбрать любой вектор из Еп+1 (при практическом решении задачи в качестве za выбирают найденное тем или иным способом приближенное решение).
В методе продолжения по параметру решение Zi уравнения (12.1) находится, исходя из известного решения z0 уравнения (12.2), с использованием вспомогательного уравнения
R (?) = фо + е (ф1 — фо), (12.3)
содержащего параметр ® е [0, 1]. Уравнение (12.3) при е = 0 совпадает с уравнением (12.2), а при s = 1—с уравнением (12.1).
Предположим, что уравнение (12.3) имеет решение
z = z(e), ее [0,1], z(O) = zo, (13)
которое является дифференцируемой функцией параметра е. В основу метода продолжения по параметру положено интегрирование некоторого дифференциального уравнения для функции 2(e) с начальным условием z(e)|s=o = Zo на отрезке 0 е 1. При определенных условиях решение Zi уравнения (12.1) можно найти по формуле
Zi = 2(e)|g=1. (14)
Для получения дифференциального уравнения продифференцируем по параметру е тождество R(z(e)) = фо + в(ф1 — фа):
/. . . dz(e) . (dR‘ (z)\«+i
^(2(е))-^-=Ф1-Ф0, где Я2(г)=(__
Таким образом, нахождение решения zj уравнения (12.1) сведено к интегрированию векторного дифференциального уравнения / dz
(15)
с начальным условием
з(е)1еав0 = 20 (16)
на отрезке 0 < е sg 1 и применению формулы (14).
Замечание 4. В случае невырожденности матрицы R? (г) уравнение (15) можно, разрешив относительно производной, переписать в виде
•^“(^«’(Ф^Фо). (,5'>
Тогда справедливость равенства (14) следует из теоремы единственности для дифференциальных уравнений.
193
2. В случае системы (5), к которой сведена задача быстродействия (1), имеем
7?' =
(17)
где
К = К (р, т) = di (р, T}/dp^(dilidP})" .=t, g = g(p, r) = dg(P, n/aMW-i-* = (*,). s = (g‘); K = K‘, pK(p,D = o,
а звездочка означает транспонирование. Матрица R' в (17) невырождена, если ранг матрицы К равен га—1 и pg У= 0. Последние два условия выполнены при всех Т > 0, р =& >0, если выполнены вышеуказанные предположения П1 — ПЗ относительно множества U.
Задача (15), (16) применительно к рассматриваемой задаче быстродействия принимает вид
₽Ш=".
Р U=0 Р9’ ^1е=0 ^°>
(19)
где h = x0 — Хо, q>i — <f6 = х0 = 1(рй, То). В случае га = 2
система (18) в подробной записи имеет вид
‘de 2 de de
‘?-зг+‘12гг+s’<18’>
„ dpi , _ dp2 Pi-dr + P2-dT = 0-
В этой системе три неизвестные функции: pi, pi и Т. Порядок системы (18'), равный трем, можно понизить до двух, если отбросить третье уравнение и представить единичный вектор р в виде
Р*=( Р‘ )=> ( C?sa Y (20)
\ Р2 / \ sin a 7
где a == a(e)—новая неизвестная функция. Перейдем теперь от системы (18') третьего порядка с неизвестными функциями pi, pi, Т, неразрешенной относительно производных, к системе второго порядка
197
с неизвестными функциями Т, а, разрешенной относительно производных. Дифференцирование (20) по е дает
d / pi Л _ f — sin а\ da_ .
de \ рг ) \ cos а ) de '
Подставив (21) в первые два уравнения системы (187), получаем ( / — sin а \ da / g' \ dT _f h' \ .
\ fej k% / cos a 7 de ф 4 g2 J de \ h2 J
или, короче,
Отсюда, используя соотношения
p/C(p,T) = O, ?К(р,Т) = Л<7, Л = *!+4 /=(-г1П”) у, tub СЛ /
и умножая уравнение (22') слева последовательно иа строки р и q, приходим к системе
-S-MT"). (И>
где
fl (Т, a) = f2 (Г, а) = -q ~ g'fl (r’ a)1. (24)
pg A
K системе (23) присоединяются начальные условия
7'1е.о=7’"> «1е=о== Йо (x0 = l(p°, Та), р° = (cos Йо, sin Йо)). (25)
Итак, применение метода продолжения по параметру к решению плоской задачи быстродействия сводится к численному решению задачи Коши (23), (25) для нелинейной системы двух дифференциальных уравнений.
Этапы выполнения задания (при п= 2).
1. Провести с помощью ЭВМ табулирование изохронных линий, определяемых векторным параметрическим уравнением
x = g(p, 7"), р = (cos a, sin a), a е [0, 2л], х е Ег,
для значений Т = 0.4К (К — 1, ..., 10), a = 2лт/Л7 (m = 1, ... ..., (И) при М — 50. На основании полученных таблиц построить на фазовой плоскости изохронные линии и выбрать нулевое приближение То, йо (см. 25)); отрезок с концами х0 и х0 — |(р0, То) не должен проходить через точку х = 0: min || х0 + е (х0 — хо) || const > 0.
0<е< 1
2. Составить программу (используя подходящие библиотечные подпрограммы) для численного решения задачи Коши (23), (25) с заданной точностью; вычисленные значения 7’(1), а(1) принимаются
198
в качестве приближенного решения; если ||х0 — #ojl EPS, где x = g(p, 7) |n=r (1), p = (cosa(l), sin a (1)), a EPS —заданное малое число, то вычисления заканчиваются; в противном случае положить То = Г(1), a,0 = a(l) и повторить решение задачи Коши (23), (25).
3. По формулам (10), (11) с помощью ЭВМ вычислить оптимальное управление и оптимальную траекторию.
Конкретный вариант задания определяется значениями параметров (ха, А, Д1, А2); см. Приложение 1. Тестовый, пример дан в Приложении 2. Сводка основных обозначений и используемых формул приведена в Приложении 3.
Требования к программе.
Выдача на АЦПУ должна содержать:
1) идентификацию задания и студента;
2) исходные данные, при которых решалась задача: Л'о, А, А1, А2, EPS, То, ,а0;
3) найденные значения Топт, аОпт', количество обращений к решению задачи Коши (23), (25);
4) таблицу, каждая строка которой содержит значение 6 и соответствующие значения Хо1(г“г), ХогЦ/), «oi(^), «02(6).
Содержание отчета.
1. Постановка задачи.
2. Теоретическое обоснование метода решения задачи, для чего — доказать невырожденность матрицы (17);
— показать, что для рассматриваемого класса линейных задач быстродействия управление, удовлетворяющее принципу максимума, является оптимальным и что существует единственное непрерывное оптимальное управление;
— показать, что применение метода Эйлера с шагом е = 1 к задаче Коши (15'), (16) равносильно одному шагу метода Ньютона для уравнения (12.1).
3. Текст программы на алгоритмическом языке, инструкция пользования программой.
4. Тесты, результаты отладок.
5. Результаты решения на ЭВМ конкретного варианта задания.
6. Построенные вручную на фазовой плоскости оптимальная траектория и изохронные линии.
Литература.
1. Понтрягин Л. С. и др. Математическая теория оптимальных процессов.—М.: Наука, 1976.
2. Благодатскнх В. И. Линейная теория оптимального управления. — М.: Изд-во МГУ, 1978.
3. Давиденко Д. Ф. Об одном новом методе численного решения нелинейных уравнений. — ДАН СССР, т. 88, № 4, с. 601— 602.
199
4. Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. — Мд Мир, 1975.
5. Б е л о л н п е ц к и й А. А. Численный метод решения линейной задачи быстродействия сведением ее к задаче Коши. — ЖВМиМФ, 1977, т. 17, № 6 (см. 1380—1386).
Приложение 1. Варианты задания
Во всех вариантах принять: п = 2; область управлении V = = {(£/1/А1)2+ (U2/A2)2 1}; число EPS выбирается из диапазона
10-3— 10~6.
Вариант задания определяется значениями параметров (х0, А, Ai, А2) н задается четверкой цифр 1 а,- 4, где at
есть номер строки в приведенной ниже таблице, из которой ВДДО ВЫ” брать значение Z-го по порядку параметра варианта:
*0 A Al Л2
1 (!) (? J) 1 I
2 (») c!) 1 1/2
3 (?) (! Ф) 1 1/4
4 Ci) (o° J2) 1 1/8
Приложение 2. Тест
Хо==(1)’^ = (_jq)>A1=A2 = 1. Решение: Топт = д/2,
ctonr — 5 л/4.
Приложение 3. Основные обозначения и расчетные формулы
d (ф)
с' (ф) = grad с (ф) = •
СП (Ф)
(Си (ф) ... с1п (Ф) ...............
СП1 (Ф) ... СПп (ф)
e~tA =
*1(0 ...
... enn(t)
С.
(Ф)
__ дс (ф) бф. ’
cz/ (Ф) = с/г (ф), (ф) s д2с (ф)/5фг<?ф/, i, j—l, .... ft;
ф (/, р) — pe~tA, P — (pi.....PnY,
г = 1, ..., «;
ОЛП
и (t, р) = с' (ф>|ф_ф Ut р}^с' (ф (л р)У.
т
l(p, T)=-^e-tAu (t, р) dt\
О
g (р, (р, Т)/дТ^-е~ТАс' (ф (Т, р));
т
К. (Р, (Р, Т)1др= — J e~tAc" (ф (Z, р)) е~ ‘^di;
о
рё (р, Г) =— ф (Т, р) с' (ф (Т, р)) =—с (ф (Т, р)) < О;
Т п
V(p, т)=-^4юС/(фа,р))<«, i==i,.
га;
йЧр, Г)=-£е}(Г) ^.(ФСЛр)), /=1
I = 1, ..., га;
Г п ^(.р, Т)=—^
о 1, m=l
Для области управления
ограниченной эллипсоидом, опорная функция
Gn \!/2
В (mo2 j
обладает свойствами, указанными в предположениях Ш — ПЗ. При и = 2
с (ф) = V{-«i4,i)2 + (аафз)2,
с£ (ф) = а2ф^-1 (Ф). »=1.2,
Сц (Ф) = а\а^ (—1)‘+/ с~3 (ф) ф3_£ф3_р i, 1 = 1, 2.
Примечание 1. Матрица е~м вычисляется аналитически. На-. ( 0 1 \ _м ( cos t — sin t \
пример, для матрицы А = I __ Q 1 имеем е = I sjn ( cost )’
Примечание 2. Определенные интегралы gl (р, Т), (р, Г)
вычисляются численными методами с точностью EPSI <С EPS.
201
Задание ОУ-5, ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ ПРЕСЛЕДОВАНИЯ
Цель задания.
I. Практика в решении задач преследования первым прямым методом Понтрягина.
2. Накопление опыта по использованию ЭВМ и алгоритмических языков.
Содержание задания.
1. Изучение I-го прямого метода решения задач преследования Понтрягина.
2. Составление и отладка программы.
3. Решение конкретной задачи Преследования.
4, Оформление полученных на ЭВМ результатов.
Постановка задачи.
Пусть движение точки z описывается уравнением
z — Cz + u — v, z(O)=zo, (1)
где zeS", и s Р cz Rp, о е Q с /?Q; С — квадратная матрица порядка n; Р и Q — выпуклые компакты. В Rn выделено линейное подпространство М ф Rn.
Уравнение (1), множества Р, Q, М описывают дифференциальную игру двух игроков: преследующего, который распоряжается вектором и, и убегающего, который распоряжается вектором о. Движение точки z начинается при t = 0 и протекает под воздействием измеримых управлений u(i) еР и v(t) eQ на отрезке времени I — = [О, Г], Т > 0.
Будем считать, что измеримые управления v(t) еО выбираются как программы на I, а измеримые управления u(t) берутся в виде u(t) = U(z0, t, о(-)) еД tel. Предполагается, что догоняющий знает уравнение (1), z0 и множества Р, Q, М. Игра считается законченной при допустимых U(za, t, о(-)) и v(t), tel, в момент /(z0)s е/, если при t = t(za) выполнено включение z(/(z0))eAl.
Рассмотрим игру (I) с точки зрения догоняющего. Будем говорить, что из начального состояния Zo е Rn возможно окончание игры преследования, если у догоняющего есть такая стратегия u(t) = = U(za, t, н(-)), t <= I, что при любом допустимом о (0 eQ, tel, происходит окончание игры на М, т. е. z(t) еМ хотя бы при одном tel.
Требуется — для заданного начального состояния zQ — ответить на вопрос, возможно лн окончание игры по первому прямому методу Понтрягина (см. [1]), и если да, то определить гарантированное время преследования t(z0), стратегию преследования l/(z0, t, н(-)) и траекторию игры z(t) при данном v(t), te [О, Т].
Конкретная система вида (1), множества Р, О, М и управление v(t), tel, определяются вариантом задания (см. Приложение 1).
202
Методика решения задачи.
Согласно теореме Понтрягина (см. [1, 2]), в игре (1) разрешима задача преследования из позиции z0, если
I. Множество й» (т) = лехСР — nexCQ непусто для те/. t
II. Хотя бы при одном t^I— netcz0 е й> (т) dx.
о
Само решение при сделанных предположениях распадается иа следующие этапы:
Этап 1. Найти множество w (х) = лехСР — лехСQ.
t
Этап 2. Найти множество W' (0 = й» (т) dx.
о
Этап 3. Найти t (z0) е Z, для которого — ле* <Zo) cz0 eW (i (z0)).
Этап 4, Найти функцию <а(т) е w(x) такую, что
T(z0)
— ле* cz0 = и (т) dx.
о
Этап 5. Найти и(х) как решение уравнения яе'Ига)-т)Си _ яе(/(го)-г)С0 (yj (z0) _ т)
при заданной допустимой v(x) eQ, те/.
Этап 6. Найти z(t) как решение уравнения (1) при о = o(t)t и = u(f), t е [0, t(z0)].
В рассматриваемых вариантах задания этапы 1, 2, 4 и 5 проводятся непосредственно, без привлечения ЭВМ:
этап 1 — иа основании определения геометрической разности множеств (см. [1]): А — В = С = {с: с + ВеЛ|;
этап 2 — иа основании свойства (см. [2]) t
Js£w(O)rfr = St (0), 0 о
где Sg(Ti(O) — шар радиуса §(т) с центром в нуле, §(т) — непрерывная функция г,
этап 4 — функция ®(т) выписывается в явном виде:
ш(т)
-ле*^Лсг0 || яс“^сгоН
Х(т),
203
Где ^(т) —скалярная функция, выбираемая йз условия
/ „_f (го) с, )
-A |j^^„ *(»>}
(в изучаемых примерах || tie*<Zo) cz0 ii ф О);
этап 5 — уравнение для «(г) решается в явном виде.
Основными этапами решения задачи преследования, выполняемыми на ЭВМ, являются этапы 3, 6, заключающиеся в нахождении l(z0) и последующем нахождении траектории z(i) дифференциального уравнения
& = Cz+U(z0, — v(t), г(О)=го, Z s= [О, Z(г0)].
При построении траектории z(l) принять v (/) ==о . В при-
веденных вариантах w(t) = Sv(^ (0), где у(0 —непрерывная функция. Таким образом, Цг0) есть корень уравнения
(irec/z0, nectza) = у2 (t).
Корень следует находить с точностью д = 0.1 на отрезке [О, Т] (значение Т указано в каждом варианте задания). Если уравнение имеет несколько корней, то предпочтение следует отдать наименьшему из них.
Для вычисления /(г0) и интегрирования уравнения (1) следует использовать подходящие библиотечные программы (либо соответствующие методы; см. [3, 4, 5]).
Содержание отчета.
1. Постановка задачи (конкретный вариант).
2. Блок-схема программы.
3. Текст программы на алгоритмическом языке, тесты, результаты отладок.
4. Результаты решения конкретного варианта иа ЭВМ: значение t(z0) и график траектории гД/).
Литература.
1. Понтрягин Л. С. Линейные дифференциальные игры. I. —-ДАН СССР, 1967, 174, № 6, с. 1278—1280.
2. Понтрягин Л. С. Линейные дифференциальные игры преследования. — Матем. сб., 1980, 112 (154), № 3 (7), с. 307—330.
3. Бахвалов Н. С. Численные методы. — М.: Наука, 1973.
4. Б е р е з н н И. С., Ж и д к о в Н. П. Методы вычислений. Т. 2. — М.: Физматгиз, 1959.
5. Васильев Ф. П. Численные методы решения экстремальных задач. —М.: Наука, 1980.
204
П р и л о ж е и и е 1. Варианты задания
I. Система уравнений (1).
Zt= Z2 —23,
&2— — аг2 + и,
22= — ₽г3 + О,
21, г2, 2г, и, v<=R2, z= (zi, г2, г8), Р = {и-. Hull s£ р}, Q = {ш ||о|| а), M — {г: г, = 0}, а, р, р, а — положительные константы.
Для данного варианта справедливы соотношения:
1 —е"₽т
1. й>(т) = 36е0(0), где ?(т)=----------Р-------р----ff и
£ а
сг
г
2. w (I) = 5V (t) (0), где у (0 = j I (?) dt.
О
3. t (20) — корень уравнения у (i) = (ле^го, netcz0), где tc о 1 1 — e~at о 1 — е~$* о
ле °20 = 2j +------------z2--------г-----2з-
а Г1— е-₽(*(го)-0 1
5- “ ---------------------------------------V ]•
Подвариант задания определяется параметрами 2° z®, z®, Т р, cr, а, Р и задается номером Л' (1 < N sg 8) строки в приведенной ниже таблице, в которой указаны значения параметров:
№ 2° 2 т р G а ₽
1 2 (3. 0) (2, 2) (-1. 1) (0, -1) (0, -1) (-1. -1) 1.5 1.5 30 13 3 4
3 4 (2, 1) (-1. 2) (-0.5, -!) (0. 1) (-1, 0) (1,0) 3 3 42 24 4 3
5 6 (-3, 1) (-2, -I) (1, 0) (1, 0) (1,1) (0.5, 1) 1.5 1.5 3S 21 6 7
7 8 (2, -1) (1. -2) (-1, 0) (0, 0) (-0.5, 1) (0, 1) 2 2 so 32 3 4
II. Система уравнений (1).
Zl = z2,
z2 = и — V,
205
Zi, z2, и, V-e= №, z = (zi, z2), P = lu: W p), Q = {о: |1«П «S a}, M — {z: Z] = 0}, p и a — положительные константы.
Для данного варианта справедливы соотношения:
1. г® (т) = S5 (t) (0), где g (т) = т (р — g) и (т) =£ 0 для т >0, если р > о.
2. w (t) = Sv(f) (0), где у (0 = (р — о) /2/2.
3. t (z0) — корень уравнения у2 (0 = (ne’*Czo> netczo), где neicz0= = z? + izl
(zd
4. ш(т)= —-— (p - g) T.
|[neU2“)cZo|j ' .
(z.) c
5- 11^^411 (P-*)-
Подвариант задания определяется параметрами Zp z”, T, p, g И задается номером N (1 N cj- 8) строки в приведенной ниже таблице, в которой указаны значения параметров:
№ Z2 г Q а
1 (3. 0) (-1. Ь 2.5 30 26
(-2, -1) (0, 1) 1.7
3 (4, -2) (-1, 1) 1.6 23 17
4 (0, 3) (1. 1) 1.3
5 (0, -3) (-1, О 2 17 15
6 (1. -4) (1. 1) 2.5
7 (3, 4) (-1, -1) 2.6 28 20
8 (-4, 2) О, 0) 2.2
Часть Ш. ИНСТРУКЦИИ ДЛЯ ПРАКТИКУМА
Приводимые здесь инструкции предназначены для студентов, выполняющих задания практикума, н не рассчитаны для студентов, выполняющих курсовые и дипломные работы, и других пользователей, поскольку некоторые описываемые здесь возможности реализуются только для практикума.
Все студеическне задания, выполняемые на машинах ЕС ЭВМ, выполняются под управлением операционной системы ОС ЕС. Данное пособие объединяет в себе несколько инструкций по отдельным аспектам работы в системе программирования ОС ЕС. В зависимости от вида выполняемой работы необходимо изучение определенного набора этих инструкций.
Инструкция по языку управления заданиями является необходимой для всех видов работ. Она содержит сведения, достаточные для комплектации заданий в том простейшем случае, когда вся работа ведется с помощью перфокарт.
Для составления программы на алголе или фортране рекомендуется изучить инструкцию по соответствующему языку. Эти инструкции требуют предварительного знания языков алгол-60 или фортран IV. Для программирования на языке PL/1 специальная инструкция в данное пособие не включена, хотя в инструкции по языку управления заданиями предусмотрены средства работы с этим языком (так же, как и с языком ассемблера).
Пособие также включает в себя инструкцию по использованию архива для хранения исходных текстов программ.
Инструкция по диагностике в ОС ЕС может потребоваться для всех видов работ, если при выполнении задания возникает какая-либо ошибочная ситуация.
Инструкции по системе PRIMUS и автокоду БЕМШ используются при выполнении отдельных заданий практикума.
ИНСТРУКЦИЯ по языку УПРАВЛЕНИЯ ЗАДАНИЯМИ ОС ЕС
Для пропуска через машину ЕС ЭВМ в рамках операционной системы ОС программы, написанной иа алголе, фортране или другом языке программирования, с целью ее трансляции и последующего
207
выполнения, необходимо оформить задание для: ОС иа выполнение этой работы. Задание по усмотрению программиста может состоять из одного или нескольких шагов задания. Задание записывается на языке управления заданиями, отдельные предложения которого, ад» ресованные операционной системе, называются управляющими операторами. В частности, каждый шаг задания определяется одним из управляющих операторов.
Возможности языка управления заданиями ОС ЕС описаны в [1, 2, 3]. Данная инструкция описывает только базовые возможности языка, используемые при выполнении заданий студенческого практи-кумав пакетном, режиме с перфокарт. Дополнительные сведения по языку, требующиеся- для, конкретных языков программирования или при, использовании архива текстов, программу приводятся в-соответствующих. инструкциях.
Большинство управляющих операторов имеет следующий формат:
// (имя), , (операция), , (список параметров-) . . (комментарий)
где
(имя) — последовательность букв и цифр, начинающаяся буквой
и содержащая не более 8 литер; в качестве, букв?.здесь, используются заглавные латинские буквы; если управляющий, оператор определяет очередной шаг задания, то указанное в, нем имя, является, наименованием этого шага; в некоторых операторах имя может быть опущено, т. е. в этом поле может содержаться пустая, последовательность литер;
(операция) — это одно из, служебных, слов; зафиксированных в ОС, которое-, определяет содержание данного, управляющего- оператора («операцию»; которую должна выполнить,ОС); в,некоторых управляющих операторах операция может, отсутствовать;-,
(список параметров) — служит, для, конкретизации, операции;, задаваемой данным управляющим, оператором;, в некоторых;управляющих. операторах он- может отсутствовать;
(комментарий) — необязательная последовательность, произвольных литер.
Для ввода в машину управляющие операторы наносятся на перфокарты. При этом косые черты //, с которых начинается, управляющий оператор, перфорируются, в первых двух колонках, перфокарты (что и является признаком управляющего оператора)^ Поле имени начинается с третьей колонки. Поле операции может начинаться с любой колонки, но ему должен предшествовать и за ним должен следовать хотя бы один пробел.
Список параметров может быть пустым.; если:- параметров несколько, то они отделяются друг от друга запятой: признаком конца Этого поля в управляющем операторе является пробел.-
208
В‘ ОС имеется несколько различных типов управляющих операторов. Основными из них; которыми приходится пользоваться; практически в любом задании, являются управляющие операторы JOB, EXEC, DD и пустой оператор.
Чтобы уменьшить число управляющих операторов, при оформлении задания, в ОС предусмотрена возможность использования так называемых каталогизированных процедур, е. таких «макрооператоров», с помощью которых можно вызвать по имени некоторую стандартную последовательность управляющих операторов — такие стандартные последовательности постоянно хранятся в системе. Например, для выполнения программы, написанной на алголе (или другом языке программирования), необходимо использовать управляющие операторы, по которым ОС последовательно обеспечивает трансляцию, загрузку программы и используемых библиотечных программ, выполнение5 программы. Всю эту последовательность действий можно задать ОС с помощью одного макрооператора, указав в нем имя соответствующей каталогизированной процедуры.
Управляющий оператор JOB
Этот управляющий оператор означает начало задания. Он играет роль паспорта задания, предоставляя ОС имя задания, его автора, требуемые ресурсы, характер требуемой от ОС распечатки и т. д.
Каждому студенту для очередного задания практикума выдается перфокарта с таким оператором вида
П ffjcggnnJOB . . (, SPdl), ’(студент)’, CLASS = С где
ff — шифр факультета (ВМ — для факультета вычислительной математики и кибернетики; ЕК — для экономического факультета, FL—для-филологического и т. д.);
/ — номер задания' в-данном учебном году;
с — номер курса; ’J трехзначный
gg — двузначный номер учебной группы; J номер группы пп — двузначный порядковый номер студента в группе;
d— статистический код факультета (W— для ф-та ВМиК, Q — для5 экономического, V — для филологического факультетов
(студент) — фамилия и инициалы студента.
Указание параметра CLASS =С определяет для ОС принадлежность- задания к студенческому практикуму. В этом случае предполагаются стандартные значения некоторых параметров задания; в частности, служебная информация, выдаваемая ОС на АЦПУ, ограничивается распечаткой управляющих операторов, явно содержащихся в задании.
209
Параметр (,SPdI) дает информацию статистической службе.
Буквы S, Р и I означают, что в пакетном режиме выполняется за-
м иГиЛ*..^ла.
Пример оператора JOB:
// ВМ220523 _ JOB _ (,SPWI), 'ЖУКОВ _ И. П/, CLAS S = С
Управляющий оператор ЕХЕС
Этот оператор означает начало шага задания и описывает этот шаг, указывая требуемые для шага ресурсы (для студенческих заданий устанавливается лимит времени — 2 мин). При использовании каталогизированной процедуры в поле списка параметров задается имя этой процедуры. Для студенческих заданий существуют катало-газированные процедуры, обеспечивающие*
а) трансляцию с алгола, загрузку и выполнение программы — это процедура с именем ALGSTUD;
б) трансляцию с фортрана, загрузку и выполнение программы — процедура с именем FORTSTUD;
в) трансляцию с PL/1, загрузку и выполнение программы — процедура с именем PL1STUD;
г) трансляцию с языка ассемблера, загрузку и выполнение программы — процедура с именем ASMSTUD.
Пример оператора ЕХЕС:
// u- ЕХЕС _ FORTSTUD
В операторе ЕХЕС могут также задаваться некоторые параметры, передаваемые транслятору или самой программе. О назначении таких параметров см. инструкции по соответствующим языкам.
Управляющий оператор DD
Этот оператор описывает наборы данных, используемые программами (как системными, так и студенческими), выполняемыми на том или ином шаге задания. Операторы DD для наборов данных, используемых системными программами (трансляторами и т. п.), как правило, входят в состав каталогизированных процедур, вызывающих эти программы, и программисту нх задавать не нужно. Единственное исключение — оператор DD для входного набора данных транслятора (т. е. программы на входном языке) — этот входной набор данных на перфокартах следует поместить непосредственно после описывающего его оператора DD, который должен иметь вид (для алгола, фортрана, PL/1 и языка ассемблера соответственно)
//ALGOL. SYSIN_DD„*
//FC:<T. SYSIN„DD„*
//PL.iL. SYSIN„DD„*
//ASM. SYSIN„DD„*
Если программа пользователя использует входной набор данных на перфокартах (при выполнении операторов ввода), то этот набор также располагается после управляющего оператора DD, который в этом случае имеет внд (независимо от языка программирования)
. //GO. SYSIN ^DD^ *
и располагается вслед за входным набором данных для транслятора (за программой, написанной на том или ином языке программирования).
Для набора данных, выводимого на печать (результаты выполнения программы), управляющий оператор DD включен в состав указанных выше каталогизированных процедур и его задавать не нужно. Этот оператор DD, в частности, устанавливает и лимит бумаги— 300 строк.
Пустой управляющий оператор
Пустой оператор служит признаком конца задания и состоит лишь из косых черт в 1-й и 2-й колонках перфокарты.
Пример оформления задания для трансляции и выполиеиия программы на алголе (для других языков — см. примечания):
// ВМ330809 JOB(,SPWI),'ИВАНОВА _ М. И/, CLASS =С
(1)
// _ EXEC _ ALGSTUD (2)
Ц ALGOL. SYS IN „DD_* (3)
Программа на алголе
//GO. SYSIN _DD_. (4)
Входные данные
И (5)
Примечания.
1. Для программы, написанной на фортране, управляющие операторы (2) и (3) должны иметь вид
// _ EXEC „ FORTSTUD (2а)
// FORT. SYS IN „ DD _ * (За)
для программы, написанной на PL/1,— вид
//_ ЕХЕС PL1 STUD (26)
//PL1L. SYSIN^DD_* (36)
а для программы на языке ассемблера — вид
//_ЕХЕС_ ASMSTUD (2в)
Ц ASM. SYSIN _ DD _ * (Зв)
211
2. Если программа не использует входных данных на перфокар» тах, то управляющий оператор (4) (вместе с входными данными) следует опустить.
3. Все указанные выше управляющие операторы (кроме оператора JOB) являются стандартными, так что соответствующие перфокарты можно получить на практикуме.
При неверном написании управляющих операторов или неверной комплектации задания ОС выдает диагностическое сообщение, которому предшествует код вида lEFnnnl; по выданному номеру ппп в [4] можно найтн краткое пояснение к такому сообщению.
Литература.
1. Лебедев В. Н., Соколов А. П. Введение в систему программирования ОС ЕС. — М.: Статистика, 1978.
2. Землянский А. А., Персиц М. Г. Основы операционной системы ЕС ЭВМ.— М.: Сов. радио, 1980.
3. Д а н и л о ч к и н Б. П. и др. Операционная система ОС ЕС. Справочное пособие. — М.: Статистика, 1980.
4. Е р о ф е е в В. И. и др. Средства отладки программ в ОС ЕС ЭВМ. — М.: Статистика, 1979.
ИНСТРУКЦИЯ ПО ЯЗЫКУ АЛГОЛ ОС ЕС
1. Язык алгол ОС ЕС [1, 2] позволяет программировать на языке сабсет алгол-60, так как содержит последний в качестве подмножества.
2. Прн записи программы на бланке используются заглавные латинские буквы. Отличаются от принятой в алгол-60 записи следующие символы:
Алгол-60 Алгол ОС ЕС Алгол-60 Алгол ОС ЕС
XI * 10(масштабный ' (апостроф)
4 ♦♦ множитель)
< [ (/
>= 1 /)
п= • (открывающая '('
EQUIV’ кавычка)
’IMPL’ * (закрывающая
V 1 кавычка)
А & — . (или пробел)
Для записи служебных слов алгола соответствующая последовательность литер должна быть заключена в апострофы; например, служебное слово begin должно быть записано в виде 'BEGIN'. Идентификаторы различаются только по первым шести символам. Пробелы между символами в любых конструкциях языка, кроме строк, не принимаются во внимание.
212
Данные для ввода (целые или вещественные числа) записываются на бланке в соответствии с синтаксисом языка. Вслед за каждым числом, предназначенным для ввода, должен быть записан ограничитель числа. Ограничителем может быть любой символ, ие используемый для записи чисел, например запятая, а также совокупность из двух и более пробелов или конец строки на бланке.
Для записи программы и для записи чисел, являющихся данными для ввода, используются одни и те же бланки. Каждая строка бланка перфорируется на отдельной перфокарте и не должна содержать более 72 литер для программы или более 80 литер для данных. При записи алгол-программы допускается произвольный переход на следующую строку бланка. При записи чисел, предназначенных для ввода, переход допускается лишь после окончании записи очередного числа.
3. Набор стандартных функций в алголе ОС ЕС совпадает с принятым в алголе-60 набором:
SIN, COS, ARCTAN, SQRT, EXP, LN, ABS, ENTIER, SIGN.
4. В алголе ОС EC процедуры
ININTEGER (0, p), INREAL (0, v),
INTARRAAY (0, a), INARRAY (0, a)
осуществляют ввод подготовленных на перфокартах соответственно целого значения, вещественного значения, массива целого типа, массива вещественного типа, а процедуры
OUTINTEGER (1, е), OUTREAL(1, е),
OUTTARRAY (1, a), OUTARRAY (1, a)
осуществляют вывод на АЦПУ соответствеиио целого значения, вещественного значения, массива целого типа, массива вещественного типа. Здесь v обозначает идентификатор простой переменной (целого или вещественного типа), а — идентификатор массива (целого или вещественного типа), е — арифметическое выражение .Цифра 0 в качестве первого параметра процедуры связывает процедуры ввода с входным набором данных, а цифра 1 связывает процедуры вывода с выходным набором данных.
Например, для фрагмента программы:
'BEGIN' 'INTEGER' М;
ININTEGER (0, М);
'BEGIN' 'ARRAY' А (/1:2, 1 : М/);
INARRAY (0, А)
вводимые данные могут быть записаны в следующем виде:
4; .1, .2, 3.45, —2'2, '—4, 2'2,
3.45' - 5, — 2.34'5;
213
При выводе чисел на печать каждому числу отводится по 24 позиции в строке (включая два пробела после собственно числа).
Дли вывода на неча1ь 11йсЛёдиВй1€ЛЬпиС1п СИМВОЛОВ о аЛГмЛС ОС ЕС используется оператор процедуры
OUTSTRING(1, s)
По этому оператору на АЦПУ выводится строка s (в смысле алгола-60), причем в строке могут содержаться и заглавные русские буквы. Например, для вывода заголовка
РЕШЕНИЕ СИСТЕМЫ
можно записать оператор OUTSTRING (1,'('РЕШЕНИЕ СИСТЕМЫ')').
Для уппявления Расположением выводимых на печать данных можно использовать оператор процедуры
SYSACT (1, т, п)
где т — целое без знака, ап — арифметическое выражение типа целое. Действие процедуры SYSACT зависит от задаваемого значения т, а именно:
При т = 14 осуществляется n-кратный «перевод строки», т. е. процедура пропускает п — 1 пустых строк и осуществляет переход на начало следующей за ними строки; в частности, при п = 1 осуществляется переход на начало следующей строки. Заметим, что для этой цели процедура не должна использоваться до первой выдачи в программе.
При т = 2 осуществляется переход к n-й позиции текущей строки, если в этой позиции еще ие был отпечатан какой-либо символ, н к n-й позиции следующей строки в противном случае. Таким образом, последующая печать начнется с n-й позиции текущей или следующей строки. Для этой цели процедура также не должна использоваться до первой выдачи в программе.
При т — 6 устанавливается нестандартная длина строки ва АЦПУ, равная n (1 п 128) позициям (в качестве стандартной принимается строка на 80 позиций). Таким образом, с помощью этой процедуры можно управлять шириной поля печати, в частности — количеством чисел, печатаемых в одной строке. Для этой цели процедура может использоваться в программе только одни раз, причем до первой выдачи на печать.
Примечание. Для экономии бумаги и времени рекомендуется в программе использовать оператор SYSACT (1, 6, 120), позволяющий печатать до пяти чисел в строке.
5. Для трансляции и выполнения программы, написанной на алголе ОС ЕС, следует использовать каталогизированную процедуру ALGSTUD [3].
После обработки задания на ЭВМ пользователь получит листиаг, содержащий:
а) текст алгол-программы с указанием (слева от строки текста) номеров операторов (точнее говоря, номером символов «;»; если в строке содержится несколько таких символов, то печатается номер первого из них; если в строке не содержится ни одного такого символа, то печатается иомер последнего символа «;» из предыдущей строки);
б) таблицу идентификаторов программы;
в) информацию о требуемом объеме памяти для программы и ее объектов, полученных в результате трансляции;
г) результаты выполнения программы.
При наличии синтаксических ошибок в транслируемой программе листинг будет содержать:
а) текст алгол-программы;
б) таблицу идентификаторов программы;
в) диагностические сообщения транслятора.
Все перечисленные выше компоненты листинга кратко описаны в Ш-
При возникновении аварийных ситуаций в процессе выполнения программы выдаются диагностические сообщения программ обработки ошибок или коды завершения, сформированные операционной системой.
Каждому диагностическому сообщению предшествует специальный код вида lEXmwiI для сообщений транслятора или вида IHlnnnl для сообщений программ обработки ошибок. Здесь ппп— номер сообщения, по которому в [1] или [4] можно иайти краткое описание возможных ситуаций, при которых выдается данная диагностика (в [1]—только для сообщений транслятора).
Коды завершения выдаются ОС в тех аварийных ситуациях, для которых не предусмотрена реакция программ обработки ошибок. В [5] можно найти объяснения некоторых наиболее распространенных кодов завершения. Полный перечень возможных кодов помещен в [4] и [6.]
6. При выполнении программы можно вывести на печать так называемую «трассу программы», т. е. список номеров операторов (согласно листингу программы) в порядке их прохождения во время выполнения программы. Для получения трассы управляющий оператор ЕХЕС [3] должен иметь вид
//_ EXEC _ ALGSTUD, GPARM ='
TRACE, TRBEG=a, TREND = Ь'
гт а и b — соответственно начальный и конечный номера, входящие в трассу. Если TREND = Ь не задано, то трасса распространяется до конца программы; если TRBEG = а ие задано, то трасса включается с начала программы.
215.,
Литература.
1. Халилов А. И., Ющенко А. А. Алгол-60. Программиро-БапНОС y-iCGriGc n^CvOHC. — шл’Зли,
2. П я р н п у у А. А. Программирование на алголе и фортране, -г М.: Наука, 1978.
3. Инструкция по языку управления заданиями ОС ЕС (наст, книга).
4. Ерофеев В. И. н др. Средства отладки программ в ОС ЕС ЭВМ. — М.: Статистика, 1979.
5. Инструкция по диагностике в ОС ЕС (наст, книга).
6. Д а н и л о ч к и н В. П. и др. Операционная система ОС ECj справочное пособие. — М.: Статистика, 1980.
ИНСТРУКЦИЯ ПО ЯЗЫКУ ФОРТРАН ОС ЕС
1. Язык фортран ОС ЕС [1, 2] позволяет программировать на языках Базисный фортран и фортран IV, так как содержит послед* ние в качестве подмножеств.
2. Для записи программ и для записи чисел, являющихся дай* ными для ввода, используются одни и те же специальные бланки. Каждая строка бланка перфорируется на отдельной перфокарте и не должна содержать более 72 литер для программы или более 80 литер для данных. Программа записывается с использованием за» главных латинских букв. В комментариях и строчных данных могут использоваться и русские заглавные буквы. Данные для ввода (целые и вещественные числа) записываются на бланке в соответствии с форматом для оператора ввода, причем пробелы интерпретируются как нули.
Пример 1.
1 .... 5 6 7 72
DIMENSION А (2, 3), К (3), L (2)
READ 3, А, К
3 FORMAT (2 (3F5.2/), 313
PRINT 11, L
11 FORMAT ('O', T30, 'УМНОЖЕНИЕ',
1 2F10.3)
STOP
END
216
ДАННЫЕ
—. _ 1 1 о — 1.3
_ ^2 2 0 2. 302. 4 ,
2 . . -3
Если данных немного, то для задания начальных значений переменных и массивов можно использовать объявление начальных данных.
Пример 2.
DIMENSION М (7, 7)
DATA Р, Q/0.0, 6.2/, М, X, Y/9 * 0, 40 * 50, 2 * 1.0/
В этом фрагменте программы с помощью объявления начальных данных переменным Р и Q будут присвоены значения 0.0 и 6.2 соответственно, первым девяти элементам массива М будут присвоены нулевые значения, остальным 40 элементам — значение 50, а переменным X и Y —значение 1.0.
Начальные значения переменных и массивов можно также задать непосредственно в явных объявлениях типа.
Пример 3.
INTEGER М (7, 7)/9 * 0, 40 * 50/
REAL Р/0.0/, Q/6.2/, Х/1.0/, Y/1.0/
Эти объявления типа приводят к тому же результату, что и объявление начальных данных в примере 2.
3. Набор стандартных функций в фортране ОС ЕС шире набора, принятого в фортране IV н, в частности, содержит функции
SIN, COS, TAN, COTAN, ARSIN, ARCOS, ATAN,
SINH, COSH, TANH, SQRT, EXP, ALOG, ALOG10,
ABS, MAX0, AMAX1, MINO, AMIN1, INT, SIGN, IFIX, FLOAT.
4. В одном арифметическом выражении допускается использование величин разных типов. В этом случае транслятор предусматривает их приведение к одному типу. Такое же приведение делается и прн присваивании переменной значения, не соответствующего ей по типу. При вызове подпрограмм н функций (в том числе стандартных) приведение не делается и тип фактических параметров должен соответствовать типу предусмотренных формальных параметров. Такое соответствие может быть достигнуто использованием стандартных функций IFIX и FLOAT,
217
5. Для ввода данных с перфокарт можно воспользоваться оператором чтения (READ), а для вывода данных на АЦПУ — оператором печати (PRINT). Обитая форма этих оператооов:
READ f, at, ..ап
PRINT f, at, ..an
где в качестве f задается метка объявления формата (FORMAT), являющаяся обязательным параметром; в качестве ai задаются элементы списка ввода-вывода (который может отсутствовать); элементом списка может быть имя переменной, имя массива, переменная с индексом, список с циклом. Так, в примере 1 используются операторы READ и PRINT. В соответствии с форматом, указанным в операторе READ, значения элементов массива А должны быть отперфо-рированы на двух перфокартах, по три числа на каждой. Возможная запись чисел 1.1, 1.2, 1.3, 2.2, 2.3, 2.4 приведена в этом примере. Значения элементов массива К (целые числа 1, 2, —3) должны быть отперфорнрованы на отдельной перфокарте. В соответствии с форматом, указанным в операторе PRINT, значения массива распечатаются после текста УМНОЖЕНИЕ (начинающегося с 29-й позиции) в той же строке. Следует помнить, что первый символ выводимой на печать записи является управляющим: сам этот символ не печатается, а задает режим продвижения бумаги перед печатью данной записи. Рекомендуются следующие управляющие символы:
(пробел) — продвижение иа 1 строку (обычный случай),
О — продвижение на 2 строки (пропуск пустой строки), Ч---отсутствие продвижения (печать с наложением).
В примере 1 перед печатью происходит продвижение бумаги на 2 строки, что задается первым элементом списка в объявлении формата.
6. Для трансляции и выполнения программы, иаписаииой на фортране ОС ЕС, следует использовать каталогизированную процедуру FORTSTUD [3].
После обработки задания на ЭВМ пользователь получает листинг, содержащий;
а) текст фортран-программы с указанием (слева от строк текста) порядковых номеров предложений;
б) распределение памяти (таблицу идентификаторов) — не обязательно;
в) результаты выполнения программы.
Компоненты листинга кратко описаны в [1]. Для получения таблицы идентификаторов управляющий оператор ЕХЕС [3] должен иметь вид
//_ ЕХЕС _ FORTSTUD, CPARM = MAP
При отсутствии параметра CPARM — МАР таблица идентификаторов не выдается.
218
При наличии синтаксических ошибок транслятор выдает текст фортран-программы и диагностические сообщения. Большинство сообщений об ошибках в исходной программе следует в распечатке сразу же за предложением, в котором обнаружена ошибка. В одном предложении может быть обнаружено несколько ошибок. Позиция ошибки отмечается символом К. Сообщения об ошибках, относящихся ко всей исходной программе (например, наличие неопределенных меток), печатаются после распечатки всей исходной программы.
При выявлении ошибок на этапе загрузки (например, при использовании функции, для которой в библиотеке нет соответствующей подпрограммы) выдаются диагностические сообщения загрузчика, которым предшествует специальный код вида lEWnnnm [4].
При возникновении аварийных ситуаций в процессе выполнения программы (неправильное программирование операторов ввода-вывода, неверное обращение к программам библиотеки фортрана, программные ошибки типа деления на нуль и т. д.) выдаются диагностические сообщения программ обработки ошибок или коды завершения, сформированные операционной системой.
Каждому диагностическому сообщению предшествует специальный код вида lEYnnnl для сообщений транслятора или вида IHCnnnI для сообщений программ обработки ошибок. Здесь ппп — номер сообщения, по которому в [1] или [5] можно иайти краткое описание возможных ситуаций, при которых выдается данная диагностика. Коды завершения выдаются операционной системой в тех аварийных ситуациях, для которых ие предусмотрена реакция программ обработки ошибок. В [4] можно найти объяснение некоторых наиболее распространенных кодов завершения. Полный перечень возможных кодов содержится в [5] и [6].
7. При отладке программисту предоставляются возможности:
а) получить на распечатке «трассу модуля», т. е. последовательность меток выполненных операторов модуля;
б) получить иа распечатке последовательность обращений к подпрограммам, т. е. печать сообщений о входах и выходах из них;
в) получить иа распечатке последовательности значений некоторых переменных и массивов, по которым можно проследить за их изменениями во время выполнения модуля (для массивов распечатываются значения только изменяющихся элементов, а не весь массив);
г) получить сообщение о выходе значения индекса за заданную в описании массива границу.
Для формулирования задания на отладку в фортране ОС ЕС служит специальный язык, в котором используются как обычные операторы фортрана, так и специальные операторы отладки.
Отладка обычно заключается в выполнении некоторых вспомогательных действий, непредусмотренных в основном тексте программы.
219
Задание на отладку как раз и состоит в указании того, что (какие вспомогательные действия) надо сделать по ходу выполнения программы и где (в каких точках программы). Поскольку таких точек В программе может быть выбрано несколько, то задание на отладку состоит из нескольких шагов, каждый из которых относится к определенной точке. Задание на отладку включается в текст модуля (основной программы нли подпрограммы) непосредственно перед его завершающим предложением END. Первым оператором этого заданняхявляется оператор отладки
DEBUG Ci, с2, ..., сп
где ci — параметры, задающие отладочные действия, относящиеся ко всему модулю. Эти параметры могут принимать следующие значения:
TRACE — трассировка в модуле (конкретные участки программы, подлежащие трассировке, определяются в шагах задания).
SUBTRACE — трассировка подпрограммы: если в какой-либо подпрограмме с именем m включен режим трассировки, то при входе в нее печатается сообщение SUBTRACE m, а при выходе из нее — сообщение SUBTRACE*RETURN*
SUBCHK (mi, т2, ..., тп), где т,— имя массива, означает проверку выхода значений индекса за границы, указанные в объявлении указанных массивов.
INIT (/Hi, т2, ..., тп), где mi—имя переменной нли массива, означает контроль за фактом присваивания нового значения указанным переменным или элементам указанных массивов.
Каждый шаг задания начинается оператором AT I, где I — метка оператора, задающим точку в программе. За этим оператором следует один или несколько операторов фортрана и (или) операторов отладки, задающих вспомогательные действия, относящиеся к указанной в операторе АТ точке программы.
Оператор отладки TRACE ON в указанной точке (к началу выполнения оператора с меткой Z) включает режим трассировки. Результатом трассировки является печать сообщений вида TRACE Ц, rue I, — мётки выполняемых операторов внутри трассируемого участка программы.
Оператор отладки TRACE OFF отключает режим трассировки. Таким образом, пара операторов TRACE ON н TRACE OFF вместе с соответствующим оператором (операторами) АТ задает участок программы, подлежащий трассировке.
Оператор отладки DISPLAY mi, ..., тп, где mi— имя переменной или массива, выводит на печать значения указанных переменных и массивов.
Пример 4.
DIMENSION А (500), В (500)
DEBUG SUBCHK, TRACE, INIT (В)
220
AT 35
TRACE ON
DISPLAY А, В
AT 50
TRACE OFF
END
В этой отладке проверяются на выход за заданную границу все значения индексов переменных с индексами, печатаются последовательности изменящихся значений элементов массива В, трассируется участок программы, начинающийся оператором с меткой 35 и заканчивающийся оператором с меткой 50. Перед выполнением оператора с меткой 35 будут печататься значения массивов А и В.
В библиотеке фортрана имеются служебные программы PDUMP и DUMP. Они позволяют распечатать значения переменных и элементов массивов в различных точках программы и в желаемом формате. Если выполнение программы после печати должно быть прекращено, используется программа DUMP. Обращение к этим подпрограммам имеет вид
CALL PDUMP (аь bx, ft,..., ап, bn, fn)
CALL DUMP (ai, bi, ft., .... an, bn, fn)
где параметры at и bi—имя переменной или переменная с индексом, причем щ задает начало распечатываемого участка памяти, a bi — его конец (при задании в качестве а; и Ь, переменных с индексом следует помнить, что элементы двумерных массивов в фортране хранятся в памяти и выдаются на печать по столбцам); параметр ft принимает целые значения, которые определяют формат печати: 0 — шестнадцатеричный формат, 2 — логический, 4 — целый, 5 — вещественный, 7 — комплексный, 9 — текстовый.
Так, чтобы вывести на печать целую переменную А и элементы вещественного массива В от В (2, 3) до В(3, 4), надо записать оператор
CALL PDUMP (А, А, 4, В (2, 3), В (3, 4), 5)
Литература.
1. Брич 3. С. и др. Фортран ЕС ЭВМ. — М.: Статистика, 1978.
2. П я р н п у у А. А. Программирование на алголе и фортране. —. М.: Наука, 1978.
3. Инструкция по языку управления заданиями ОС ЕС (наст, книга).
4. Инструкция по диагностике в ОС ЕС (наст, книга).
5. Ерофеев В. И. и др. Средства отладки программ в ОС ЕС ЭВМ. — М.; Статистика, 1979.
6. Д а н и л о ч к и н В. П. и др. Операционная система ОС ЕС: справочное пособие. — М.: Статистика, 1980.
221
ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ АРХИВА ТЕКСТОВ
1. Чтобы избежать многократного ввода составленной программы в память машины с перфокарт для ее последующей отладки и счета по ней, во внешней памяти машины на магнитных дисках (МД) организован архив, который может содержать тексты программ на различных языках программирования (алгол, фортран, PL/1, ассемблер ЕС и др.). Текст каждой программы хранится в отдельном файле архива. Архив, как правило, состоит из нескольких файлов, которые идентифицируются по их именам.
Для работы с файлами архива используются специальные обслуживающие программы, с помощью которых можно образовать новый файл в архиве, записать в файл текст, отредактировать и распечатать содеожимое файла. При трансляции программы ее текст может быть взят из файла архива.
2. При выполнении задания практикума каждый студент получает в свое распоряжение один файл, имя которого совпадает с именем задания для ОС ЕС [1], т. е. имеет вид
ffjcggnn
где ff — шифр факультета (ВМ — для факультета ВМиК, ЕК — для экономического, FL — для филологического факультетов),
j — номер задания в данном учебном году,
с — номер курса, 1 трехзначиый
gg — двузначный номер учебной группы, J номер группы
пп — двузначный порядковый номер студента в списке группы.
3. Текст, предназначенный для записи в архив, сначала должен быть подготовлен на каком-либо первичном носителе данных. Для студенческого практикума в качестве первичных носителей данных используются флоппи-диск и перфокарты. В первом случае данные переносятся с флоппи-диска на магнитную леиту, а оттуда переписываются в архив. Во втором случае данные переписываются в архив непосредственно с перфокарт. Эта перепись в обоих случаях производится специальной программой, называемой библиотекарем.
Для образования нового файла в архиве и записи текста в образованный файл этому тексту должна предшествовать строка вида
./(, SPdl), '(студент/, D = (hmh)
где d — статистический код факультета (W — для факультета ВМиК, Q — для экономического н V — для филологического факультетов) ;
(студент) —фамилия и инициалы студента;
(имя) — имя файла, в который должна быть произведена запись.
Такая строка называется управляющим оператором текста и сама в файл не записывается. В управляющем операторе текста символы ./ должны находиться в первых двух позициях, а первые два параметра ((,SPdI) и (студент) должны быть заданы точно так же, как и в операторе JOB соответствующего задания для ОС [1], например:
./(, SPQI), 'НИКОЛАЕВА _ С. В/, D = EK231215
Для первого параметра по умолчанию принимается значение (,SPWI), так что для студентов факультета ВМиК этот параметр задавать не обязательно, например:
./'ПЕТРОВ _ А. И.', D = ВМ220509
Если в архив записывается текст программы на фортране, то допускается написание нескольких предложений в одной строке, что экономит место на бланках и первичном носителе данных (перфокартах, флоппи-диске). При этом помечено может быть только первое из этих предложений. В качестве разделителя предложений, записываемых в одной строке, используется символ О. При использовании этой возможности управляющий оператор текста должен содержать параметр CV=F, например:
./'ИВАНОВ _ В. Н.', D = ВМ140223, CV = F
При обработке такого текста библиотекарь записывает н архив каждое предложение в виде отдельной строки.
Для подготовки текста на флоппи-диске на практикум сдаются бланки и на первом из них первой строкой должен быть управляющий оператор текста. В архив будет записан текст в том виде, как он был записан на бланках. Это означает, что уже при заполнении бланков необходимо предусмотреть окончательную комплектацию массива.
Прн подготовке текста на перфокартах на практикум сдается скомплектованный массив перфокарт, первая из которых должна содержать управляющий оператор текста. Такой массив не оформляется в виде задания для ОС, т. е. не должен дополняться управляющими операторами языка управления заданиями (JOB, EXEC и др.).
В ВЦ тексты на флоппи-дисках и на перфокартах объединяются в пакеты текстов. При записи в архив каждого текста его строки нумеруются с шагом 1, начиная с номера 1, и библиотекарь выдает распечатку текста с нумерацией строк. Эти номера используются в дальнейшем для внесения в текст необходимых изменений в процессе отладки.
После записи в архив флоппи-диск или перфокарты с текстом остаются в ВЦ, а на практикум передается только распечатка записанного текста. Последующая работа с программой ведется без нс-
223
пользования первичного носителя данных. В исключительных случаях можно восстановить в файле архива первоначально записанный — """З ТСК''Т СДПС.КО от-лгл гталАvn rcws*ri ипер'гтт.'кмъгптПП ПЯ-
кета текстов и номер текста в пакете. Эти сведения распечатываются библиотекарем для каждого текста, записываемого в архив, и их рекомендуется помнить каждому студенту.
Если библиотекарь обнаруживает ошибку в управляющем операторе текста (например, синтаксическую ошибку или недопустимое имя файла), то запись в архив не выполняется и н распечатку включается диагностическое сообщение. После исправления управляющего оператора такой текст должен быть сдан на практикум повторно.
Если в какой-либо файл архива был записан некоторый текст, то повторная запись в этот же файл с помощью библиотекаря не разрешается.
4. После записи текста в архив для всех последующих работ с ним (редактирование, распечатка, трансляция) необходимо оформлять задание для ОС по общим правилам [1]. Эти работы обеспечиваются1 специальными каталогизированными процедурами, для вызова которых управляющий оператор ЕХЕС имеет вид
//„ ЕХЕС , , (имя процедуры), D — (имя файла)
5. Редактирование текста (т. е. внесение в него изменений), записанного в каком-либо файле архива, производится- специальной программой, называемой редактором. Вызов редактора для работы обеспечивается процедурой SEDIT, для обращения к которой используются следующие карты в задании для ОС:
И . . ЕХЕС . . SEDIT, D = (имя файла)
//EDIT. SYSIN_DD_ »
Задание на редактирование
Задание на редактирование состоит из одного или нескольких шагов. Каждый шаг содержит информацию о месте- редактирования и об операции редактирования: вставке, удалении или замене строк. В случае вставки и замены шаг задания содержит также вставляемые и заменяющие строки.
В данном редакторе место редактирования задается номером строки. Строки текста считаются перенумерованными, начиная с 1 и с шагом 1, независимо от физических номеров строк, которые могут содержаться в позициях 73 — 80 той или иной строки. Таким образом, место редактирования, задается просто порядковым номером а строки в тексте. В некоторых случаях надо указать не одну строку, а группу строк с последовательными номерами от а до b включительно (Ь уз а). Для указания такой группы строк используется запись а — Ь,
224
Требуемая операция редактирования обычно задается одной буквой, взятой от названия соответствующей операции. Для удобства пользователя допускается буква как от русского, так н от английского названия: В или I (Insert) — для вставки, У или D (Delete) — для удаления (поскольку русская буква У близка по написанию к латинской букве Y, то последняя также допускается для обозначения операции удаления). Для задания операции замены буквы не используются.
Место и операция редактирования в случае вставки и замены задаются, как правило, с помощью оператора редактирования, который имеет вид
./(операция) (место)
Здесь символы ./ должны содержаться обязательно в первых двух позициях, (операция) — одна из указанных выше букв, задающих требуемую операцию редактирования, а (место) —запись вида а нли а — Ъ (а и b — номера строк), которая задает место редактирования. В любом месте оператора, кроме номеров строк, допускаются пробелы.
Вставка строк производится после строки с указанным номером а, а если задано а = 0, то вставка производится перед первой строкой, т. е. в начало текста. Сами вставляемые строки должны находиться в шаге задания вслед за оператором вставки (в позициях 73 — 80 таких строк должны содержаться только пробелы). По оператору удаления из текста удаляются указанные строки (одна нли несколько).
Например, шаг задания
./У 4 — 6
означает: удалить из текста группу строк с номерами 4, 5 и 6, а tear задания
./В О
'BEGIN' 'REAL' X;
означает: добавить в начало текста указанную строку.
Шаг задания, предназначенный для замены строки с номером а Яа новую строку или для вставки после нее одной новой строки, можно сформулировать с использованием редактирующей строки, которая содержит в себе всю необходимую информацию о таком этапе редактирования. В позициях 1 — 72 редактирующей строки задается новая строка (которая не должна начинаться парой символов ./), a в позициях 73 — 80 (в любом месте этого поля) задается место редактирования в виде номера а строки. Если в позициях 73 — 80 указан только номер а, то строка с этим номером заменяется на
Ё. Трифчнор, Е. Н. Пасхнн 226
заданную новую строку; если же номеру а предшествует буква В (нли I), то заданная новая строка вставляется после строки с номером а. При а = 0 новая строка вставляется перед первой строкой редактируемого текста.
В задании на редактирование может содержаться произвольное число редактирующих строк и операторов редактирования, причем порядок их следования не зависит от порядка номеров строк, используемых для указания места редактирования.
При пользовании данным редактором следует иметь в виду, что в процессе редактирования номера строк текста не меняются; поэтому во всем задании на редактирование должны использоваться номера строк исходного текста.
По завершении выполнения задания на редактирование редактор перенумеровывает строки текста с шагом 1, начиная с номера 1, и заносит эти номера в позиции 73 — 80 строк текста. Эти номера н дальнейшем самим редактором не используются, однако при последующих распечатках текста (например, транслятором) они дают порядковые номера строк, необходимые для составления задания на повторное редактирование.
Редактор распечатывает отредактированный текст с указанием старой н новой нумерации строк. В распечатку включаются также старые строки, подвергавшиеся изменениям, с соответствующими комментариями, поясняющими выполненные операции редактирования.
При обнаружении ошибок в каком-либо шаге задания на редактирование этот шаг не выполняется, а редактор выдает диагностическое сообщение н переходит к выполнению последующих шагов задания. В конце работы редактор выдает итоговое сообщение о том, насколько успешно прошел процесс редактирования и был ли записан отредактированный текст в архив. Как правило, такая запись производится даже при обнаружении редактором ошибок в отдельных шагах задания на редактирование.
6. Для трансляции н выполнения программы, текст которой хранится в архиве, следует использовать процедуры SALGCG, SFORTCG, SPL1CG и SASMCG для языков алгол, фортран, PL/1, ассемблера ЕС соответственно. Для этих процедур (в отличие от процедур ALGSTUD, FORTSTUD, PL1STUD и ASMSTUD) не требуется подкладывать в задание DD-оператор с именем SYS1N, так как он содержится в самих процедурах и определяет чтение текста транслируемой программы из файла архива. Например, для алгола в задании должна быть подложена карта
//—. EXEC . . SALGCG, D = (hmh файла)
Если программа использует входные данные на перфокартах, то после указанной выше карты необходимо, как обычно, подложить
ах О
следующие карты: ' ’
//GO. SYSIN_DD_.
Входные данные
Для других языков задание комплектуется аналогично.
Как обычно, если для трансляции программы или дли ее выполнения требуется задать дополнительные параметры, то их указывают в управляющем операторе ЕХЕС. Например, для получения трассы при выполнении алгол-программы следует использовать карту
//_ЕХЕС_ SALGCG, О = (имя файла), GPARM = TRACE
7. Трансляцию программы обычно удобно совмещать в одном задании с предшествующим редактированием ее текста в архиве. Для этого следует использовать комбинированные процедуры SALGECG, SFORTECG, SPL1ECG, SASMECG — редактирование программы в архиве, ее трансляция и выполнение. Использование комбинированных процедур аналогично использованию соответствующих процедур, описанных в пп. 5 и 6 данной инструкции. Однако в этом случае редактор распечатывает только исправления — полную распечатку текста программы дает транслятор.
Пример использования комбинированной процедуры для редактирования алгол-программы в архиве, ее трансляции и выполнения с вводом исходных данных:
// _ EXEC _ SALGECG, D = ВМ221127
//EDIT. SYSIN„ DD_*
Задание на редактирование
//GO. SYSIN„DD_ .
Входные данные
8. Процедура SPRINT обеспечивает распечатку текста из файла архива. Для ее вызова в задании должна быть подложена карта
/Л_ЕХЕС_ SPRINT, D = (hmh файла)
Как правило, в использовании этой процедуры нет необходимости, так как распечатку текста дает либо библиотекарь, либо редактор, либо транслятор.
Примечание. На практикуме имеются стандартные карты
// EDIT. SYSIN_DD_*
// GO. SYSIN^DD^*
Литература.
1. Инструкция по изыку управления заданиими ОС ЕС.
8*
227
ИНСТРУКЦИЯ ПО ДИАГНОСТИКЕ В ОС ЕС
1. При прохождении задания в операционной системе на разных этапах могут быть обнаружены различные ошибочные ситуации, по которым выдаю 1 ся дна: ностичеекие сообщения. Кроме того, некоторые компоненты системы выдают сообщения информационного характера, не связанные с какими-либо ошибками. Как диагностические, так и информационные сообщения в большинстве случаев содержат в начале строки код вида
(префикс) (номер)
Здесь трехбуквенный префикс соответствует компоненте системы, выдавшей сообщение, а по номеру в справочных руководствах можно найти краткое описание возможных ситуаций, при которых выдается это сообщение.
Наиболее часто встречаются сообщения со следующими префиксами компонент системы:
IEF — управление заданиями [1];
IEM — транслятор с PL/1 [1];
IEX — транслятор с алгола [1, 2};
IEY — транслятор с фортрана [1, 3};
IEW — загрузчик [1];
IFO — ассемблер;
IHC — программы обработки ошибок для фортрана [1, 3];
IHE — программы обработки ошибок для PL/1 [1];
IHI — программы обработки ошибок для алгола [1]
(в указанной здесь литературе и приложениях I—4 имеется объяснение сообщений с соответствующим префиксом).
2. При выявлении ошибок иа этапе загрузки программ (включая загрузку стандартных библиотечных программ) выдаются диагностические сообщения загрузчика, которые, как правило, имеют вид
lEWnnnm (имя)
где ппп. — номер сообщения, т — код серьезности ошибки (при яг>1 программа выполняться не будет). Диагностика относится к имени, указанному в сообщении. После всех диагностических сообщений загрузчик дает краткое пояснение по каждому коду выданных сообщений.
Наиболее часто встречается сообщение вида
IEW1012 (имя программы)
которое выдается в случае, когда в программе встречается вызов подпрограммы, имя которой, указанное в сообщении, не обнаружено
228
ни среди подпрограмм пользователя, ни в библиотеке стандартных подпрограмм.
3. После успешной загрузки программы ее выполнение может завершиться аварийно. Для программы, написанной на языке высокого уровня (алгол, фортран, PL/1 и др.), предусматриваются специальные программы обработки ошибок, которые выдают диагностические сообщения во многих распространенных случаях аварийного завершения.
Если в алгол-программе используются ранее оттранслированные процедуры, то следует иметь в виду, что в процессе выполнения программы диагностические сообщения программ обработки ошибок (например, при выходе значения индекса за границы массива) могут относиться и к этим процедурам. В таких процедурах нумерация операторов ведется независимо от основной программы и начинается также с единицы. А в диагностических сообщениях, как обычно, указывается только номер оператора без уточнения того, относится ли он к основной программе или к одной из таких процедур.
В некоторых случаях вместо детального диагностического сообщения система выдает обшее сообщение вида
COMPLETION CODE - SYSTEM = ххх USER = уууу
Если в этом сообщении системный код завершения ххх = ООО, а Пользовательский код уууу 0000, то этому сообщению предшествует диагностическое сообщение программы обработки ошибок. Если же уууу = 0000, а ххх =£= 000, то объяснение создавшейся ситуации Можно найти в [1] или [4] по системному коду завершения.
Наиболее часто встречаются следующие системные коды завершения:
0С4 — прерывание по защите памяти, т. е. адрес выходит за пределы области, отведенной программе (может возникнуть при выходе значения индекса за границы массива).
0С5 — прерывание по неправильной адресации, т. е. адрес выходит за пределы памяти ЭВМ (может возникнуть при выходе значения индекса за границы массива).
0С9 — прерывание по некорректному делению с фиксированной запятой (переполнение, деление на нуль).
ОСС — прерывание по переполнению порядка при сложении, вычитании, умножении или делении с плавающей запятой.
0CD — прерывание по исчезновению порядка прн выполнении арифметической операции над числами с плавающей запятой (порядок меньше допустимого, а мантисса ненулевая).
0CF — прерывание при попытке деления с плавающей запятой на число с нулевой мантиссой.
229
'•"'!' '’322 '-“'Ърё'йй’ ’'й4ййййёййя<>1йагй заданий" превысило'^выделенный лимит времени.
722 — количество выводимых на печать строк превысило выделенный лимит бумаги.
806 — вызываемая программа ие найдена в библиотеке.
В некоторых ситуациях выполнение задания прекращается аварийно из-за сбоев оборудования или ОС. Как правило, в таких случаях также выдается сообщение с системным кодом завершения. Здесь возможно появление кодов 213, 222, 2F3 и некоторых других. При получении сообщения с одним из таких кодов следует обратиться к преподавателю и, возможно, отдать задание на практикум для повторного его выполнения (коиечио, без редактирования, если оно было успешно выполнено).
Литература.
1. Ерофеев В. И. и др. Средства отладки программ в ОС ЕС ЭВМ. — М.: Статистика, 1979.
2. Халилов А. И., Ющенко А. А. Алгол-60. Программированное учебное пособие. — Киев: Вища школа, 1979.
3. Б р и ч 3. С. и др. Фортран ЕС ЭВМ. — М.: Статистика, 1978.
4. Д а н и л о ч к и и В. П. и др. Операционная система ОС ЕС. Справочное пособие. — М.: Статистика, 1980.
ОПИСАНИЕ ТЕРМИНАЛОВ
1. Общие сведения
Терминал — это устройство, предназначенное для непосредственного общения человека с ЭВМ в форме диалога. С точки зрения пользователя можно считать, что терминал состоит из дисплея с экраном, буферной памяти (буфера) и пульта управления с клавиатурой.
Для организации диалога предусматривается система обслуживающих программ, входящих в состав математического обеспечения ЭВМ, а сам диалог ведется в форме обмена сообщениями между пользователем и системой на языке, близком к естественному. Каждое сообщение состоит из одной или нескольких записей, а запись представляет собой последовательность символов. Пользователь с помощью своих сообщений передает системе указания о том, какая работа должна быть выполнена с помощью ЭВМ иа очередном этапе диалога, данные, необходимые для выполнения этой работы, и т. д. Система обеспечивает выполнение указаний пользователя и передает пользователю сообщения, с помощью которых она информирует пользователя о выполнении очередного его указания, в слу
230
чае необходимости запрашивает у него дополнительную информацию и т. д.
Свои сообщения системе пользователь набирает на клавиатуре пульта управления, последовательно нажимая соответствующие клавиши с изображенными на них символами.
Как правило, текст сообщения, набираемый пользователем, предварительно формируется иа буфере. Буфер имеет фиксированное число позиций (обычно АХ80 позиций, где k—параметр терминала), в каждой нз которых может храниться код любого из допустимых символов. Сообщения пользователю от системы также передаются в буфер.
Аппаратура терминала обеспечивает постоянное отображение содержимого буфера на экране электронно-лучевой трубки, входящей в состав дисплея. Экран содержит столько же позиций, что и буфер, и состоит из k строк, по 80 позиций в строке. В каждой позиции экрана может быть высвечен любой из допустимых символов. Позиции экрана считаются упорядоченными слева направо по строке и сверху вниз по строкам. Между позициями экрана и буфера установлено взаимно однозначное соответствие, так что в любой позиции экрана постоянно высвечивается тот символ, код которого зафиксирован в соответствующей позиции буфера. В связи с этим в дальнейшем ради краткости изложения будет иногда говорить о «содержимом экрана», имея в виду, что содержимое экрана постоянно отображает содержимое буфера.
При включенном дисплее иа его экране постоянно высвечивается специальный символ (а, V и др., в зависимости от типа дисплея), называемый курсором. Курсор всегда указывает (сверху или снизу, в зависимости от типа дисплея) на ту позицию экрана, в которую будет занесен очередной символ с клавиатуры или из ЭВМ, а после ввода очередного символа курсор автоматически смещается к следующей по порядку позиции экрана.
Как обычно, при занесении символа в какую-либо позицию буфера (экрана) предыдущее содержимое этой позиции теряется, так что с помощью клавиатуры можно ие только формировать на экране новый текст, ио и вносить изменения в уже находящийся на экране текст.
На корпусе дисплея имеются ручки регулировок яркости и фокусировки луча, высвечивающего символы на экране, а также выключатель питания со световой сигнализацией состояния дисплея.
В состав клавиатуры входят две группы клавиш: символьные и управляющие.
Символьные клавиши служат для набора текста сообщения. При нажатин любой из этих клавиш изображенный на ней символ заносится в ту позицию экрана, на которую указывает курсор, н курсор перемещается к следующей по порядку позиции. На каждой ив этих
231
клавиш изображен один или два символа, а каждый из них изображен либо в верхней, либо в иижней половине клавиши. Совокупность первых символов образует верхний регистр, а совокупность вторых — fJlfWHtifi ПРЭНГФП ,
Управляющие клавиши выполняют различного рода управляющие функции, например включение в работу нужного регистра символов. Некоторые из этих клавиш не изменяют содержимого буфера и экрана, например упомянутые выше клавиши включения в работу нужного регистра символов; другим управляющим клавишам соответствуют специальные, «управляющие» кеды, которые также заносятся в буфер, однако оии не входят в текст сообщения, а используются для целей управления.
Набор управляющих клавиш и их назначение иа разных терминалах различны, однако на каждом терминале имеются клавиши управления положением курсора: каждое нажатие одной из клавиш •*-, j, | влечет за собой смещение курсора на одну позицию экрана в соответствующем направлении (указываемом стрелкой). Поскольку очередной символ, вводимый с клавиатуры, всегда заносится в позицию курсора, то эти клавиши используются для управления расположением по позициям экрана вводимых символов, а также облегчают внесение изменений в любые отдельные позиции экрана. На каждом терминале обычно имеются свои дополнительные возможности, позволяющие быстро установить курсор в любую позицию экрана.
Примечание. Клавиши, назначение которых ие описано в данной инструкции, не следует использовать на практикуме без ведома обслуживающего персонала терминального класса.
2. Терминал на базе дисплея ЕС-7927
Экран дисплея содержит 24 строки по 80 позиций. Курсор указывает на позицию экрана снизу. Слева под экраном расположены индикаторы:
— аварийного состояния дисплея;
— напряжения в сети питания дисплея;
— включенного состояния дисплея:
— состояния СИСТЕМА ДОСТУПНА;
— состояния ВВОД ЗАПРЕЩЕН, при котором блокируется ввод с клавиатуры (см. описание клавиши СБРОС).
Справа от экрана находится держатель светового карандаша (фотоселектора). Если фотоселектор установлен, но не используется, он должен находиться в гнезде держателя.
Особенность дисплея ЕС-7927 состоит в том, что его буфер — путем выполнения соответствующей системной программы — можно описать как одно поле пли как совокупность нескольких полей, обладающих некоторыми свойствами. В частности, каждое из этих полей
232
может быть открыто или закрыто для ввода с клавиатуры. Буфер, который программно описан как совокупность полей с определенными свойствами каждого из них, будем называть форматным-, н противном случае буфер будем называть бесформатным (т. е. состоящим из одного поля со стандартными свойствами). В случае форматного буфера эффект нажатия ряда клавиш будет различным в зависимости от того поля, которому принадлежит позиция, указываемая курсором.
При работе системы PRIMUS буфер всегда форматный — в нем обязательно имеется хотя бы одно закрытое и одно открытое поле. В частности, закрытое поле, состоящее из одной позиции, обязательно предшествует тому месту на экране, с которого система приглашает пользователя набирать очередное сообщение. При работе в системе PRIMUS на дисплее этого типа пользователь любое свое сообщение должен начинать с того места экрана, откуда его приглашает работать система, т. е. где системой был установлен курсор. Как правило, это первая или вторая позиция очередной строки. В этом положении не рекомендуется сдвигать курсор назад по экрану, так как при этом курсор попадает в закрытое для ввода поле. Все последующие позиции экрана образуют открытое поле со стандартными свойствами. Поскольку при корректной работе пользователя курсор не выходит за пределы этого поля, то приводимое ниже описание клавиш дается только применительно к открытому полю, т. е. к бесформатному буферу.
Управляющие клавиши.
Стирание экрана (СТРН.ЭКР).
Во все позиции экрана заносится пробел, курсор устанавливается иа начало экрана и включается индикатор ВВОД ЗАПРЕЩЕН. При работе в системе PRIMUS этот индикатор автоматически сбрасывается системой, затем, как обычно, первая позиция делается закрытой для ввода, а курсор перемещается иа вторую позицию.
Этой клавишей целесообразно пользоваться в тех случаях, когда у пользователя возникает сомнение относительно позиции экрана, с которой должно начинаться очередное сообщение пользователя, подлежащее передаче системе.
Переключение регистров символов (ФВР, BP, HP):
— нажатие клавиши ФВР влечет за собой переключение регистра на противоположный;
— на время удержания в нажатом положении клавиши ВР, включается верхний регистр, а клавиши HP — нижний регистр.
Управление курсором.
При коротком нажатии одной из клавиш f, | происходит однократное перемещение курсора н соответствующем направлении. Длительное нажатие приводит к многократному перемещению курсора, пока не будет отпущена нажатая клавиша.
233
Новая строка (-ч—1),
Курсор устанавливается на начало следующей строки.
Табиляиия влево ( V*—
Курсор устанавливается на первую позицию открытого поля, т. е. на начало набираемого сообщения. Если курсор уже находится на первой позиции сообщения, то нажатие этой клавиши выводит курсор за пределы открытого поля.
Вычеркивание символа (ВЧРК).
Эта клавиша должна использоваться при включенном верхнем регистре символов. При ее нажатии производится удаление символа, находящегося в позиции курсора: содержимое всех позиций данной строки, находящихся правее курсора, смещается влево на одну позицию, а в освобождающуюся последнюю позицию строки заносится пробел. Курсор при этом остается на месте.
Вставка символа (ВСТВ).
При нажатии этой клавиши устанавливается особый режим работы дисплея — режим вставки символа, что подтверждается включением индикатора РЕЖИМ ВСТАВКИ. При иажатии в этом режиме символьной клавиши производятся следующие действия: содержимое всех позиций экрана, начиная с позиции курсора, сдвигается иа одну позицию вправо (по направлению к концу экрана), в освобождающуюся позицию курсора заносится символ, соответствующий нажатой клавише, а символ, находившийся в последней позиции экрана, теряется. Положение курсора не изменяется. Режим вставки можно сбросить клавишей СБРОС.
Стирание конца поля (СТРН.КП).
Во все позиции экрана, начиная с позиции курсора, заносятся пробелы. Курсор остается на месте.
Передача данных в ЭВМ (ВВОД).
При нажатии этой клавиши производится блокировка клавиатуры и в ЭВМ передается сообщение, набранное иа экране с той позиции, в которой — по приглашению системы — начинается текст сообщения, и до позиции курсора в момент иажатпя клавиши ввода.
Сброс особых режимов и состояний (СБРОС).
При иажатии этой клавиши производится сброс особых режимов работы и состояний дисплея и соответствующих индикаторов (ВВОД ЗАПРЕЩЕН, РЕЖИМ ВСТАВКИ). Операция сброса не выполняется, если в момент нажатая клавиши СБРОС идет обмен между буфером и ЭВМ.
Примечание. Не рекомендуется сбрасывать состояние ВВОД ЗАПРЕЩЕН, если оно возникло в результате нажатия клавиши ВВОД. В этой ситуации длительная блокировка клавиатуры (более 30 с) свидетельствует о нарушении нормальной работы аппаратуры нли системы —‘ об этом факте необходимо сообщить дежурному по
OQ .< «*.' к
терминальному классу. Состояние ВВОД ЗАПРЕЩЕН может также возникнуть при нажатии символьных или некоторых управляющих клавиш, если курсор попал в закрытое поле. В этом случае следует нажать клавишу СБРОС и перевести курсор в открытое поле.
3. Терминал на базе дисплея ЕС-7066
Экран дисплея состоит нз 12 строк по 80 позиций. Курсор ▼ указывает на позицию экрана сверху.
Управляющие клавиши.
Начало сообщения ( ).
В позицию курсора заносится управляющий, «стартовый» символ )> . Этот символ при работе в системе PRIMUS должен предшествовать любому сообщению, подлежащему передаче н ЭВМ.
Во многих случаях система сама выводит на экран этот символ, приглашая тем самым пользователя начать набор очередного сообщения с указанного места. Однако, стерев этот символ, можно набрать его н само сообщение в любом месте экрана.
При попытке повторно занести этот символ в другое место экрана происходит стирание экрана по всем позициям после первого стартового символа и по второй включительно, а курсор перемещается к первой позиции после первого стартового символа. Таким образом, если прн наборе Сообщения в ием обнаруживается ошибка, то для повторения набора удобно просто нажать клавишу !> .
Очистка экрана ( ft? ).
При нажатии этой клавиши во все позиции экрана заносится пробел и курсор устанавливается в начало экрана. После этого перед набором сообщения необходимо нажать клавишу ,
Переключение регистров символов.
Для включения в работу нужного регистра служат клавиши ВР (верхний регистр) и HP (нижний регистр). Одна нз этих клавиш нажимается каждый раз, когда требуется переход с одного регистра на другой. Содержимое экрана и положение курсора прн этом не изменяются.
Управление курсором.
Прн длительном нажатии любой нз основных клавиш управления курсором (*-, f, 4) происходит многократное смещение курсора в соответствующем направлении. Клавиша X служит для установки курсора в начало экрана.
Конец текста в строке ( -d
235
В позицию курсора заносится управляющий символ «гЗ , являю* тцийся признаком конца текста в дайной строке экрана, и курсор смещается на начало следующей строки. При трактовке содержимого окуапа как сообщение, передаваемого в машину, содержимое позиций строки, начиная с позиции с символом , игнорируется.
Смещение символов.
Клавиши этой группы служат для редактирования находящегося на экране текста. Каждое нажатие одной из этих клавиш влечет за собой соответственно (без изменения положения курсора):
<—। — сдвиг на одну позицию влево группы символов, расположенных в начале строки до позиции курсора включительно. Символ, находившийся в первой позиции строки, теряется, а в освободившуюся позицию курсора заносится пробел. Если левее позиции курсора имеется символ Л (признак конца текста в строке), то в сдвиге участвуют только символы, расположенные правее его.
।—>—сдвиг на одну позицию вправо группы символов, расположенных в конце строки, начиная с позиции курсора. Символ, находившийся в последней позиции, теряется, а в освободившуюся позицию курсора заносится пробел. Если правее позиции курсора имеется символ Л , то в сдвиге участвуют только символы, расположенные левее его.
— сдвиг текста, расположенного в начале экрана до позиции курсора включительно, на одну позицию по направлению к первой позиции экрана; при этом символ из первой позиции какой-либо строки переносится в освобождающуюся позицию предыдущей строки (последнюю позицию этой строки или в позицию, предшествующую символу , если таковой был в этой строке), а первый символ первой строки теряется.
SU;— аналогичный сдвиг текста, расположенного в конце экрана, начиная с позиции курсора, по направлению к последней позиции “ИЙ
При длительном нажатии каждой из этих клавиш соответствующий сдвиг выполняется многократно, пока ие будет отпущена клавиша.
Ввод (ВВ).
Эта клавиша служит для передачи в ЭВМ сообщения, набранного йа экране. При ее нажатии в позицию курсора заносится управ-ЛЩ&ЩИЙ символ □ (признак конца сообщения) и в ЭВМ передается содержимое буфера, соответствующее последовательности символов, £№$^ожепных на экрану между управляющими символами 4 и □. «Й чЙмя передачи сообщения в ЭВМ клавиатура блокируется, о тем /йгнализирует лампочка БЛК. Длительная блокировка клавиатуры (более 30 с) свидетельствует о нарушении нормальной работы
2S0
аппаратуры или системы, о чем следует сообщить дежурному по терминальному классу.
Подсветка экрана ( • • •).
Эта клавиша служит для подсветки разметки экрана точками по всем его позициям (например, с целью подсчета числа пробелов между теми или иными символами набранного на экране текста); по-вторное нажатие этой клавиши выключает подсветку.
4. Терминал на базе дисплея видеотон-340
Экран дисплея содержит 16 строк. Курсор, изображаемый символом К, указывает на позицию экрана снизу.
Этот терминал имеет два основных режима работы: активный и автономный. В активном режиме, называемом режимом ON LINE, терминал работает с непосредственной связью с ЭВМ: при иажатии на пульте управления какой-либо клавиши код соответствующего символа передается в машину, так что набираемое сообщение сразу же, символ за символом, поступает в ЭВМ. В автономном режиме, называемом режимом OFF LINE, терминал работает без непосредственной связи с ЭВМ. При работе в этом режиме можно предварительно набрать текст сообщения на экране, а затем передать его в ЭВМ. Для установки нужного режима работы терминала на его пульте управления имеются соответствующие управляющие клавиши ON LINE н OFF LINE. При включении терминала в работу путем нажатия клавиши POWER, расположенной на корпусе дисплея справа от экрана, автоматически устанавливается режим OFF LINE.
Управляющие клавиши.
В отличие от кодов обычных символов, управляющие коды, поставленные в соответствие некоторым из управляющих клавиш, постоянно на экран не отображаются. Это связано с тем, что для их отображения используются некоторые из обычных символов, так что нх постоянное отображение на экран могло бы привести к неправильному пониманию пользователем зафиксированного на экране текста. Поэтому отображение управляющих кодов иа экран производится по желанию пользователя и в специфичном виде: при нажатой управляющей клавише CTRL BLINK обеспечивается мерцание в соответствующих позициях экрана тех символов, с помощью которых производится отображение на экран того или иного управляющего кода, что и позволяет легко отличать такие «управляющие» символы от обычных. Например, управляющий код, поставленный в соответствие управляющей клавише ЕТХ (признак конца сообщения), отображается на экран в виде мерцающей буквы С. В дальнейшем такие «управляющие» символы будем заключать в кавычки, например «С»,
237
Основными управляющими клавишами (помимо упомянутой выше клавиши CTRL BLINK) являются следующие.
Клавиши SHIFT и LAT, которые служат для переключения ре-{йСдриц vnMoU.'iUtJ. lid AdnHuM гсрмйНаЛй ОСпйипЫм ЯьЛЛсТСЯ пИЖНИп регистр. Клавиша SHIFT включает верхний регистр только на то время, пока оиа удерживается вручную в нажатом состоянии; если ее отпустить, то опять включается нижний регистр. При нажатии клавиши LAT (латинские буквы входят в верхний регистр) оиа фиксируется в нажатом положении и потому производится переключение на верхний регистр; повторное нажатие на клавишу LAT влечет за собой ее освобождение н тем самым переключение опять на нижний регистр. Нажатие этих клавиш не изменяет состояния буфера (и экрана).
Клавиша REPT служит для многократного повторения действий, задаваемых некоторыми управляющими клавишами. Например, прн нажатой клавише REPT нажатие любой из клавиш управления положением курсора (*-, f, |) обеспечивает многократное смещение курсора в соответствующем направлении — до тех пор, пока эта клавиша не будет отпущена.
Клавиша ERASE. Нажатие этой клавиши в режиме OFF LINE влечет за собой «стирание» буфера (занесение кода пробела во все его позиции) н соответственно экрана, с установкой курсора на начало экрана (в первую позицию первой его строки).
Клавиша НОМЕ. Прн нажатии этой клавиши в позицию курсора заносится управляющий символ «L» и курсор устанавливается на начало экрана.
Клавиша CTRL используется для указания конца записи: если при нажатой клавише CTRL нажать клавишу с буквой Е, то в позицию курсора заносится управляющий символ «Е», являющийся признаком конца записи, и курсор смещается к следующей позиции. Таким образом, в одной строке экрана может размещаться как одна, так и несколько записей.
Клавиша LINE FEED служит для занесения в позицию курсора управляющего символа «J» с перемещением курсора на начало следующей строки. Управляющий символ «J» является признаком конца записи и признаком конца текста в данной строке экрана.
Клавиша ЕТХ используется для указания конца сообщения: при ее нажатии в позицию курсора заносится управляющий символ «С», который является признаком конца последней записи в сообщении.
Заметим, что любой из управляющих символов «J», «Е» и «С» выполняет роль признака конца записи; если же в последовательных позициях расположено несколько управляющих символов, обозначающих конец записи, то они интерпретируются как одни такой символ.
Заметим также, что обслуживающая программа, которая в памяти машины формирует текст, передаваемый с терминала в виде по
следовательности сообщений, любой из символов, обозначающих конец записи, заменяет на символ «Е»; если же впоследствии введенный в машину текст (или его часть) будет выводиться иа экран, то для более наглядного представления текста каждая запись размешается с новой строки экрана.
Клавиши DL, IL, DC и IC используются для редактирования находящегося на экране текста — главным образом для удаления из текста или вставки в него как целых строк, так и отдельных символов. Каждое нажатие одной из этих клавиш влечет за собой (без изменения положения курсора):
DL—удаление строки символов, на которую указывает курсор; при этом содержимое всех последующих строк сдвигается иа одну строку вверх, а освобождающаяся последняя строка экрана заполняется пробелами;
IL — вставку строки, содержащую пробел во всех позициях; при этом осуществляется сдвиг иа одну строку вниз содержимого всех строк, расположенных в нижней части экрана, начиная со строки, указываемой курсором (при этом сдвиге исходное содержимое последней строки теряется), а освобождающаяся строка, иа которую указывает курсор, заполниется пробелами;
DC — удаление символа, находящегося в позиции курсора; при этом все символы данной строки, находившиеся правее позиции курсора, сдвигаются на одну позицию влево, а в освобождающуюся последнюю позицию заносится пробел;
IC — вставка пробела в позицию курсора; при этом осуществляется сдвиг иа одну позицию вправо всех символов, расположенных в правой части строки, начиная с позиции курсора (при этом сдвиге исходное содержимое последней позиции теряется), а в освобождающуюся позицию курсора заносится пробел.
При нажатой клавише REPT действия, указанные для каждой из этих клавиш, также выполняются многократно.
Клавиша SEND служит для передачи в машину сообщения, набранного иа экране. Для такой передачи курсор предиарительно должен быть установлен на любую позицию той строки, с которой начинается передаваемое сообщение. При нажатии клавиши SEND курсор автоматически смещается на первую позицию этой строки, устанавливается особый режим работы терминала — односторонняя передача данных с буфера в ЭВМ и производится сама передача данных: осуществляется продвижение курсора по последовательным позициям экрана (с учетом смысла управляющего символа «J») и передача в ЭВМ содержимого соответствующих позиций буфера. Передачей кода управляющего символа «С» (признак конца сообщения) передача сообщения заканчивается — после этого курсор смещается иа начало следующей строки и терминал переходит в режим ON LINE.
J239
ИНСТРУКЦИЯ ПО РАБОТЕ В СИСТЕМЕ PRIMUS
1. Общие сведения
Систем?. PRIMUS прсдпашштсиа для ибьшсчсння диалоговой формы общения пользователя с ЭВМ. и ориентирована на работу с «Терминалами на базе дисплеев ЕС-7066 и ЕС-7927.
С помощью системы PRIMUS пользователь, в частности, может:
— вводить с терминала в ЭВМ некоторый текст (программу на гсаком-либо языке программирования или часть ее, задание для ОС ЕС и т. д.);
— записывать в архив системы введенный текст для многократного его последующего использования;
— редактировать с терминала введенный в ЭВМ текст, т. е. вносить в него различного рода изменения;
— передавать сформированное для ОС ЕС задание на исполнение в пакетном режиме;
• — просматривать с терминала результаты выполнения задания.
Система PRIMUS состоит из ряда программ, каждая из которых Предназначена для выполнения с помощью ЭВМ определенного вида работы: ввода в машину текста с буфера терминала, редактирования введенного текста, записи текста в архив и т. д. Набор таких программ и определяет возможности системы.
Для ведения диалога используется специальный язык общения человека с системой. Свои указания об очередном этапе работы пользователь формулирует системе в виде команд, являющихся самостоятельными фразами языка. В команде указывается имя системной программы, которая должна быть выполнена на этом этапе. Получив от Пользователя команду, система — в случае необходимости — запра-щйЬает у него дополнительную информацию или данные и обеспечи-Ва.ет выполнение команды путем вызова в работу указанной в ней Йгстемной программы. После этого система выдает на экран дис-!щея определенное сообщение, которое является подтверждением вы-ЙрЛйения команды н приглашением пользователю передать следующую команду.
Таким образом, работа в системе сводится к набору на клавиатуре терминала и передаче системе для исполнения нужной последо-ЦТ’ельности команд, а также к передаче системе ответов на ее заносы и необходимых данных.
Некоторые из системных программ могут выполнять различные оцарапни, к которым и сводится работа данного вида (например, работа по редактированию текста сводится к выполнению операций удаления записей, вставки записей и т. д.). Таким образом, выполие-фв работы данного вида обычно распадается иа последовательность шагов, на каждом из которых выполняется определенная операция. Последовательность этих шагов также задается пользователем с по
S40
мощью команд системе, которые в дальнейшем будем называть подкомандами. Каждая системная программа может выполнять только определенный набор подкоманд. Для удобства пользователя системная программа, вызванная в работу по команде, как правило, выводит на последнюю строку экрана дисплея список тех подкоманд, которые она может выполнять.
Команды и подкоманды могут иметь один или несколько параметров, конкретизирующих задаваемую работу. Прн задании параметров широко используется принцип умолчания, поэтому в дальнейшем при описании команд и подкоманд те параметры, задание которых не обязательно, будем заключать в квадратные скобки.
При работе с системой PRIMUS каждая команда (подкоманда) должна передаваться системе в виде отдельного сообщения. Передача сообщения сводится к набору на клавиатуре терминала текста этого сообщения и нажатию управляющей клавиши ввода (ВВОД или ВВ). В языке определена пустая команда (подкоманда), текст которой не содержит каких-либо символов, так что для передачи системе пустой команды (подкоманды) достаточно нажать клавишу ввода.
После завершения выполнения системой переданной ей команды на экран дисплея выводится сообщение
КОМАНДА ВЫПОЛНЕНА
Получив это сообщение, пользователь может передавать системе очередную команду или закончить свою работу.
Система осуществляет контроль передаваемых ей команд (подкоманд). В случае обнаружения в команде синтаксических или семантических ошибок система ее не выполняет, а выдает на экран диагностическое сообщение. Кроме того, в некоторых ситуациях выдается сообщение, свидетельствующее об «аварийном» окончании выполнения команды и поясняющее допущенную ошибку:
ABEND, КОД ЗАВЕРШЕНИЯ = ххх
где через ххх обозначен системный код, по которому можно определить возможную причину такой реакции системы (см. [1, 2]). Перечень наиболее типичных из этих причин приведен в Приложении 2.
Пользователь может вызвать принудительное завершение любой команды, воспользовавшись командой
KILL
Передача системе этой команды влечет за собой немедленное прекращение выполнения ранее переданной команды с выдачей на экран сообщения
ABEND, КОД ЗАВЕРШЕНИЯ ==222
241
"'Чтобы ння, надо передать ей пустую команду и дождаться появления на экране ответа системы
МО/RUG РАБОТАТЬ, ПОСЫЛАЙТЕ КОМАНДУ после чего ей можно передать очередную команду.
Как правило, целью работы в системе PRIMUS является формирование в ее архиве задания для операционной системы с последующей передачей его на выполнение в пакетном режиме. Задание для ОС ЕС, подготавливаемое с помощью системы PRIMUS, должно иметь такой же формат, что и задание, подготавливаемое с помощью перфокарт (см. п. 6). Поэтому следует исходить из того, что каждая строка экрана является образом соответствующей перфокарты. В связи с этим последовательность символов, которая размещается в одной строке экрана (на одной перфокарте), начиная с первой ее позиции, рассматривается как основная единица текста и называется запись, а под термином текст понимается упорядоченная последовательность записей.
Обычно запись занимает строку экрана не полностью. Чтобы следующая запись вводимого с терминала текста размещалась с начала следующей строки экрана, можно либо дополнить текущую запись необходимым числом пробелов справа, либо неревести курсор на начало следующей строки с использованием подходящих управ-ляющих клавиш терминала.
Текст задания для ОС ЕС можно вводить с терминала сразу в окончательном виде, однако это не обязательно. Можно, например, сначала ввести текст программы, написанной на каком-либо языке программирования, а затем, используя возможности системы по редактированию текста, дополнить введенный текст программы соответствующими управляющими операторами языка управления заданиями, значениями исходных данных и тем самым сформировать окончательный текст задания для ОС ЕС.
На время сеанса работы в системе PRIMUS каждому пользователю выделяется определенный участок памяти, называемый рабочей областью. Эта область служит для хранения тою текста, с которым работает пользователь в течение данного сеанса. Рабочая область рассчитана иа хранение текста, содержащего ие более 400 записей.
При вводе текста в ЭВМ с терминала система размещает в рабочей области передаваемые ей записи в порядке их поступления, причем каждой записи ставится в соответствие ее порядковый иомер, так что в дальнейшем на запись можно сослаться путем указания ее порядкового номера в рабочей области.
Имеется также возможность каждую запись снабдить своим «физическим» номером, который будет занесен в позиции 73 — 80
1 242
этой записи (в этом случае текст записи без ее физического номера должен содержать не более 72 символов). В дальнейшем — при выводе текста или его части из рабочей области иа экран — физические номера записей будут выводиться в позиции 73 — 80 соответствующих строк экрана. Физические номера также могут использоваться для ссылок иа записи.
Таким образом, система PRIMUS дает пользователю возможность работать как с порядковыми, так и с физическими номерами записей. Заметим, что для каждой записи текста (или его фрагмента), вызванного на экран, определен ее порядковый иомер на экране.
Чтобы иметь возможность работать с текстом, введенным с терминала в рабочую область, в последующих сеансах работы за терминалом пользователь может — с помощью соответствующей команды — записать этот текст в архив системы в качестве файла е определенным именем, а затем вызывать его в рабочую область для использования. Первоначально текст может быть записан в архив и в пакетном режиме с помощью флоппи-диска или перфокарт [4].
2. Вход в систему и выход из нее
Для получения возможности взаимодействовать с системой необходимо (при включенном дисплее) нажать клавишу ввода и дождаться сообщения системы
РАБОТАЕТ МОНИТОР PRIMUS, СООБЩИТЕ ВАШЕ ИМЯ
Далее, начиная с позиции, указанной курсором, необходимо набрать на экране имя пользователя (для студентов таким именем является шифр, совпадающий с именем задания для ОС ЕС [3] и для студентов факультета ВМиК имеющий вид BM/cggww, где / — номер задания в учебном году, egg—номер группы, а пп — порядковый номер студента в списке группы) и нажать клавишу ввода. В ответ система выдает сообщение, означающее разрешение на дальнейшую работу:
МОЖНО РАБОТАТЬ, ПОСЫЛАЙТЕ КОМАНДУ
Теперь пользователь может передавать системе для исполиення первую команду, которой и начинается работа по существу.
Для завершения сеанса работы необходимо дождаться окончания выполнения последней из переданных команд, т. е. сообщения системы
КОМАНДА ВЫПОЛНЕНА
и передать системе команду
END
243
В ответ система выдает сообщение
РАБОТА ЗАКОНЧЕНА
п снимает с о5слул\Ив<и1йл данною пользователя.
После этого можно снова войти в систему с того же терминала (например, другому пользователю), передав системе пустую команду (т. е. нажав клавишу ввода).
3. Начальный ввод текста
С помощью системы PRIMUS пользователь может:
— ввести с терминала текст в рабочую область;
— просмотреть на экране текст, находящийся в рабочей области;
— произвести перенумерацию записей текста, приняв в качестве физических номеров записей их порядковые номера;
— распечатать на АЦПУ текст, находящийся в рабочей области.
3.1. Ввод текста с терминала.
После входа в систему по правилам, указанным в п. 2, можно начинать ввод текста в рабочую область с клавиатуры терминала. Для этого сначала надо передать системе команду
lNPT_[a][, b]
где а — физический номер, присваиваемый первой вводимой записи (по умолчанию а = 10), b — шаг нумерации последующих записей (по умолчанию b = 10). Наличие хотя бы одного параметра означает, что вводимые записи должны быть снабжены физическими номерами. Есля оба параметра отсутствуют, то вводимые записи физическими номерами не снабжаются.
По этой команде система вызывает в работу программу INPT, которая будет принимать фрагменты текста, передаваемые в виде сообщений с терминала, и размещать эти фрагменты в порядке нх поступления в рабочей области. Далее, система выдает на первую строку экрана сообщение
ВВОДИТЕ ИСХОДНЫЙ ТЕКСТ
Во второй и третьей строках система делает разметку позиций по строке, чтобы пользователь мог легко определить порядковый номер любой позиции строки, и переводит курсор на начало четвертой строки экрана. Теперь пользователь может передавать сообщение, содержащее очередной фрагмент текста, начиная с четвертой строки экрана.
Приняв очередной фрагмент текста, система выдает сообщение
ВВОДИТЕ ИСХОДНЫЙ ТЕКСТ
244
что является приглашением пользователю передать следующий фрагмент текста. Если текст уже введен полностью, то в ответ на очередное приглашение системе следует передать пустую подкоманду, сразу нажав клавишу ввода. В ответ на нее система на первую строку экрана выдает сообщение
КОМАНДА ВЫПОЛНЕНА
свидетельствующее об окончании выполнения команды INPT.
3.2. Просмотр текста.
Текст, находящийся в рабочей области (или его часть), можно просмотреть иа экране с помощью команды LIST. При этом для указания нужной части текста могут использоваться как порядковые, так и физические номера записей.
При использовании порядковых номеров записей команда LIST имеет следующий формат:
LIST „О, [а][, Ь]
где а — порядковый номер первой, b — порядковый номер последней записи просматриваемого фрагмента текста (по умолчанию а = 1, а Ь — номер последней записи).
По каждой пустой подкоманде (т. е. при каждом нажатии клавиши ввода) на экран выдается очередной фрагмент текста.
Выполнение команды LIST завершается либо после выдачи на Экран последнего фрагмента текста, либо по подкоманде Е.
Прн использовании физических номеров записей команда LIST должна иметь вид
LIST _ [а] (, 6]
где физические номера а. и Ь записей задают диапазон номеров за-пнсей, подлежащих вызову на экран. По умолчанию в качестве а принимается минимальный, а в качестве b — максимальный физический номер записей, находящихся в рабочей области.
3.3. Перенумерация записей.
Для изменения физических номеров записей, находящихся в рабочей области, служит команда
NUMB
цо которой в качестве физических номеров принимаются порядковые Номера записей — каждый такой иомер заносится в позиции 73 — 80 соответствующей записи.
3.4. Печать текста.
Текст, находящийся в рабочей области, можно вывести на печать с помощью АЦПУ по команде
\ PRNT
245
При1 'выполнении^ этой жотианды лга'АЦПУ' сначала-вечатаетеяг-имя пользователя, указанное им при входе в систему, а затем распечатывается текст, по одной записи в строке рулона бумаги, причем перед каждой аоинеью печатается сс порядксБый номер.
Распечатку текста можно получить в установленном месте по завершении сеанса работы в системе.
4. Работа с архивом
Архив системы PRIMUS служит для длительного хранения текста, однажды введеного в рабочую область с клавиатуры терминала, с целью многократного его последующего использования без повторного ввода. Система предоставляет пользователю возможности:
— записывать текст, находящийся в рабочей области, под заданным именем в архив;
— вызывать по имени текст из архива в рабочую область для работы с этим текстом;
— вставлять текст, находящийся в архиве, в текст, находящийся в рабочей области;
— просматривать на экране хранящийся в архиве текст;
— распечатывать на АЦПУ хранящийся в архиве текст.
Для хранения текстов, используемых на практикуме, в архиве системы выделяется том памяти на магнитных дисках. Имя этого тома сообщается пользователям. В этом томе для каждого пользователя заранее образовывается пустой файл с именем, совпадающим с именем пользователя (см. п. 2) и с именем задания для ОС ЕС [3]. Этот файл и должен использоваться для хранения текста между отдельными сеансами работы за терминалом, причем имя файла и является именем текста в архиве системы.
Все команды системы, предназначенные для работы с архивом, имеют единую структуру. В поле параметров каждой из этих команд необходимо указывать имя файла (т. е. имя текста). После передачи системе каждой такой команды система запрашивает имя тома памяти, иа котором расположен требуемый файл. Однако, если в начале работы за терминалом системе передать команду
DVOL (имя тома)
то при выполнении всех последующих команд, предназначенных для работы с архивом, система будет использовать имя тома, указанное в команде DVOL, не запрашивая больше этой информации у поль-еователя. Для отмены такой фиксации имени тома системе нужно передать команду DVOL без параметра.
Если пользователь указывает несуществующий файл или том памяти, недоступный в данный момент системе, то на экран выдается .
246-
соответствующее диагностическое сообщение, а также сообщение
КОМАНДА ВЫПОЛНЕНА
Запись текста в архив из рабочей области производится но ко-манде
SAVE. . (имя файла)
Вызов текста из архива в рабочую область производится по ко-манде
COPY, . (имя файла)
Вставка текста, находящегося в файле пользователя, в текст, находящийся в рабочей области, производится по команде
INST. . а, (имя файла)
где а — порядковый номер той записи в рабочей области, после которой следует вставить текст, взятый из файла с указанным именем. Естественно, полученный таким образом текст можно записать в архив по команде SAVE.
Просмотр файла на экране производится по команде
LOOK. . (имя файла)
При выполнении этой команды на экран, начиная со второй его строки, выдается первый фрагмент текста, хранящегося в файле с указанным именем. По каждой пустой подкоманде на экран выдается очередной фрагмент текста, причем после последнего фрагмента будет выдан первый фрагмент того же текста.
Для выдачи на экран произвольного фрагмента текста служит подкоманда
G_a
где а — порядковый номер записи, с которой начинается этот фрагмент.
Выполнение команды LOOK заканчивается в результате выполнения подкоманды Е.
Распечатка файла иа АЦПУ производится по команде
HDCP_. (имя файла)
При выполнении этой команды на АЦПУ сначала печатается имя пользователя, имя тома и имя файла, а затем содержкмое файла.
Распечатку текста можно получить в установленном месте по завершении сеанса работы в системе.
247
5. Редактирование текста
Система PRIMUS позволяет вносить с терминала различного рода изменения в текст, находящийся в рабочей области т » производить его редактирование. Если подлежащий редактированию текст находится в архиве, то он должен быть предварительно пере* писан в рабочую область по команде COPY.
Допускаются три операции редактирования:
— корректировка записей, входящих в текст, без изменения их количества;
— удаление записей;
— вставка новых записей.
Для вызова в работу редактирующей программы служит команда
CORR
После передачи системе этой команды на экран дисплея вызывается первый фрагмент текста, начиная со второй строки экрана. По подкоманде
GL-a]
на экран вызывается фрагмент текста, начинающийся с записи с порядковым номером а; по умолчанию (если а не задано), а также по пустой подкоманде вызывается очередной фрагмент текста.
По подкоманде
G. . С '(тексту, а
на экран вызывается фрагмент по контексту, указанному в апострофах: в качестве первой записи фрагмента принимается запись, в которой, начиная с позиции с номером а, находится указанный в подкоманде текст. Таким образом, на экран можно вызвать любой фрагмент, подлежащий редактированию.
5.1. Корректировка записей.
Фрагмент текста, вызванный на экран, корректируется с помощью клавиатуры терминала: курсор подводится к позиции, содержимое которой подлежит изменению, и в нее заносится нужный символ путем нажатия соответствующей символьной клавиши. После внесения в вызнанный фрагмент всех необходимых изменений системе надо передать сообщение, в котором, в частности, содержится и измененный фрагмент текста. Это сообщение должно иметь вид
R
где многоточия означают строки экрана с содержащимися н них записями. Прн нажатии клавиши ввода курсор должен находиться в
24 Я
начале строки, непосредственно следующей за данным сообщением, причем в сообщении может быть меньше строк, чем было выведено на экран. При передаче этого сообщения в том фрагменте текста, который был вызван на экран из рабочей области, его первые по порядку записи заменяются на записи, содержащиеся в переданном сообщении; остальные записи вызванного на экран фрагмента остаются без изменения.
После корректировки очередного фрагмента с помощью подкоманды G можно вызвать на экран следующий фрагмент, подлежащий корректировке, и т. д. По подкоманде Е выполнение команды CORR завершается.
Поскольку в данном случае изменения в текст, находящийся в рабочей области, вносятся по мере передачи сообщений с терминала, то всю корректировку текста можно произвести за одно обращение к программе CORR.
Просмотр откорректированного текста, если в этом возникает необходимость, удобно осуществлять с использованием описанной выше подкоманды G, так как если в очередном вызванном на экран фрагменте обнаруживаются ошибки, то этот фрагмент можно тут же скорректировать описанным выше способом, без повторного вызова в работу программы CORR.
5.2. Удаление записей.
Для удаления записей из какого-либо фрагмента текста этот фрагмент нужно вызвать на экран (используя, в случае необходимости, подкоманду G) и передать системе подкоманду вида
D _ а [, 6]
означающую: удалить из вызванного на экран фрагмента а записей, начиная с записи с порядковым номером b в этом фрагменте (по умолчанию принимается b = 1).
Следует иметь в виду, что группа записей, удаленных с помощью подкоманды D, запоминается системой на своих ресурсах и в дальнейшем может быть использована в операциях вставки записей (см. ниже). Если производится подряд несколько удалений, то система сохраняет только записи последнего удаления.
Фактическое удаление записей из редактируемого текста производится только при окончании работы программы CORR, т. е. после передачи системе подкоманды Е, так что для каждого удаления записей удобно передавать отдельную команду CORR.
5.3. Вставка записей.
Для вставки записей в какой-либо фрагмент текста этот фрагмент нужно вызвать на экран но подкоманде G и передать подкоманду вида
Ц-аН]
249
означающую: вставить в вызванный на экран фрагмент новые записи вслед за записью с порядковым номером а в этом фрагменте (по умолчанию прнинмается а = 1).
Если запанный параметр содержит символ *. то в указанное место фрагмента будут вставлены те записи, которые были сохранены системой при выполнении последней подкоманды D.
Если символ * отсутствует, то вставляемые записи должны вводиться с терминала и в этом случае подкоманда I выполняется аналогично команде INPT. Сначала система выдает в первую строку экрана сообщение
ВВОДИТЕ ВСТАВЛЯЕМЫЕ ЗАПИСИ
во второй и третьей строках делает разметку позиций и переводит курсор на начало четвертой строки экрана. Теперь пользователь может передавать сообщение, содержащее вставляемый фрагмент текста, начиная с четвертой строки экрана. Приняв этот фрагмент, система опять выдает сообщение
ВВОДИТЕ ВСТАВЛЯЕМЫЕ ЗАПИСИ
Если все вставляемые записи были уже переданы, то в ответ на очередное приглашение следует передать пустую подкоманду, нажав клавишу ввода. По этой подкоманде система завершает выполнение подкоманды I и выдает на экран сообщение
ВВЕДИТЕ КОМАНДУ G (ВЫВЕСТИ) ИЛИ Е (ЗАКОНЧИТЬ)
Если нет необходимости просматривать на экране еще какие-либо фрагменты текста, то надо передать подкоманду Е, по которой в текст, находящийся в рабочей области, вставляются все переданные системе записи, и работа программы CORR завершается.
Таким образом, каждую вставку записей также целесообразно производить по отдельной команде CORR.
5.4. Добавление записей в начало текста.
Такая необходимость возникает, например, в случае, когда введенный в машину текст программы надо дополнить до текста задания для ОС ЕС. Возможности редактирования в системе PRIMUS не позволяют непосредственно вставить записи в начало текста, т. е. перед его первой записью.
Такое редактирование текста можно выполнить в два этапа. Сначала после первой записи надо вставить I пустых записей (где / — число записей, которые надо добавить в начало текста), а затем произвести корректировку первых I + 1 записей: иа место последней из вставленных пустых записей набрать текст прежней пеп-вой записи, а на место этой и остальных I — 1 пустых записей ввести добавляемые записи.
250
? • Для просмотра текста, при редактировании которого использовались операции удаления и (или) вставки записей,.следует использовать описанную ранее команду LIST.
6. Подготовка задания для пакета и его выполнение
6.1. Оформление задания.
Задание, включаемое в пакет через систему PRIMUS, оформляется по тем же правилам, что и задание на перфокартах [3] — с той лишь разницей, что в операторе JOB первый параметр должен иметь вид (,SDdI), в отличие от вида (,SPdI) при работе с перфокартами, где d — статистический код факультета [3] (для факультета ВМиК d = W).
Следует обратить особое внимание на правильность записи оператора JOB, так как иначе задание выполняться не будет, а в некоторых случаях пользователь в дальнейшем даже не сможет получить никакой информации об этом задании.
Пример оформления задания:
// ВМ220324_ JOB _ (, SDWI), 'ЛАПИН „ И. Н/, CLASS = С
//_ ЕХЕС _ FORTSTUD
//FORT. SYS IN _ Под-
программа
иа фортране
//GO. SYSIN_DD„*
Входные данные
И
Если предполагается не просматривать на терминале результаты выполнения задания (см. п. 6.4), а сразу печатать их иа АЦПУ, то в операторе JOB должен дополнительно присутствовать параметр MSGCLASS = С, а в операторе ЕХЕС — параметр С = С.
6.2. Передача задания в пакет.
После того как текст задания подготовлен в соответствии с описанными выше требованиями и записан в архив (по команде SAVE), это задание может быть передано ОС для его выполнения в пакет-ном режиме. Для этой цели используется команда
ЕХЕС _ (имя файла)
После передачи этой команды пользователь по запросу системы должен сообщить ей имя тома, иа котором находится файл с тек
251
стом задания (если предварительно не выполнялась команда DVOL, описанная в п. 4). Впрочем, вместо передачи имени тома можно пе-редать системе подкоманду Е, означающую отказ от передачи зада* ния на выполнение Ст. е. отмену команды ЕХЕС).
В результате выполнения команды ЕХЕС система PRIMUS передает задание в пакет ОС и выдает на экран сообщение
ЗАДАНИЕ ПОСТАВЛЕНО В ОЧЕРЕДЬ НА ВЫПОЛНЕНИЕ КОМАНДА ВЫПОЛНЕНА
После этого ОС обрабатывает задание уже без вмешательства системы PRIMUS, а пользователь может передавать ей другие команды или выйти из системы.
6.3. Анализ состояния задания.
Появление на экране сообщения о постановке задания в очередь еще не гарантирует его выполнения. Возможно, ОС обнаружит ошибки в оформления задания и снимет его с выполнения, выдав соответствующее диагностическое сообщение, а при некоторых ошибках в записи оператора JOB переданный в пакет ОС текст вообще не будет воспринят как задание, поэтому ОС не только не будет его выполнять, но может даже не выдать какой-либо диагностики по этому поводу.
Следует иметь в виду, что обработка задания в ОС обычно проходит в три последовательных этапа:
Г. Чтение текста задания из пакета, анализ управляющих операторов и постановка задания во входую очередь ОС, т. е. в очередь на выполнение.
2°. Выбор задания из входной очереди, его выполнение и постановка в выходную очередь, т. е. в очередь на выдачу всех его выходных наборов данных, например, для их печати на АЦПУ.
На самом деле ОС образует несколько выходных очередей, которые разбиваются на классы, идентифицируемые буквами. Студенческие задания практикума, выполняемые с перфокарт, ставятся в очередь класса С, из которой выходные наборы данных выдаются на АЦПУ. Если же задание запускалось через систему PRIMUS и готовилось в расчете на просмотр результатов на экране терминала, ТО оно будет поставлено в очередь класса Р.
3°. Выбор задания из выходной очереди для выдачи относящихся К нему системных сообщений и полученных результатов.
Каждый из этих этапов обычно выполняется за несколько минут, так что полная обработка задания практикума длится 5—10 мни. Однако в зависимости от загрузки ЭВМ и ряда других факторов этапы обработки задания могут быть разнесены во времени, и тогда задание может находиться во входной или выходной очереди достаточно долго.
>52
Система PRIMUS дает возможность пользователю узнать, на каком этапе обработки находится его задание, переданное ОС для выполнения.
По команде
DJOB
информация о состоянии входной и выходной очередей ОС помещается в рабочую область, после чего ее содержимое (т. е. состояние очередей ОС) можно просмотреть на экране по команде LIST, Заметим, что в результате выполнения команды DJOB предыдущее содержимое рабочей области теряется.
По команде
D„A
непосредственно на экран выдается перечень заданий, находящихся на стадии их выполнения.
6.4. Просмотр результатов на экране.
Для просмотра на экране результатов выполнения задания используется команда
SOUT_ (имя задания)
Если к моменту выполнения этой команды указанное в ней задание находится в выходной очереди класса Р, то на экран терминала выдается справка о выходных наборах данных указанного задания (в противном случае на экран выдается соответствующее сообщение).
Справка представляет собой таблицу с нумерованными элементами (строками). Каждый элемент соответствует одному оператору DD, описывающему выходной набор данных. В заданиях, предусматривающих трансляцию с фортрана или PL/1, используются три таких оператора: для сообщений транслятора, для сообщений загрузчика и для результатов самой программы. При использовании транслятора с алгола таких операторов тоже три: для сообщений транслятора, для результатов программы, для диагностических сообщений в процессе выполнения программы и ее трассы.
Для работы с вызванной на экран справкой имеются следующие подкоманды:
L — просмотр системных сообщении, относящихся к данному заданию;
L_ п — просмотр набора данных, соответствующего строке справки с номером п;
Е — завершение выполнения команды SOUT.
В самом процессе просмотра используются те же подкоманды (G, Е и пустая подкоманда), что и для команды LOOK (см. п. 4).
Если записи просматриваемого текста содержат более 80 символов, то при вызове на экран очередного фрагмента текста на экран
253
выдаются только первые 80 символов каждой записи. Для просмотра остальных символов этих записей служат две дополнительные подкоманды, с помощью которых можно как бы «сдвинуть экран» по пы?пяичпму ня погп фпягмрнту т. е. выдать на экран любую группу из 80 символов записей, образующих этот фрагмент:
R — [«] — сдвиг экрана вправо по фрагменту на а символов;
L. . [а] — аналогичный сдвиг влево на а символов (по умолчанию а = 40).
Если для вызова на экран последующих фрагментов текста используется пустая подкоманда, то при ее выполнении на экран выдается та группа символов каждой записи, которая была определена последней из выполненных команд сдвига экрана.
Для окончания просмотра того или иного набора данных надо передать подкоманду Е, по которой на экране восстанавливается справка о выходных данных. После этого можно начать просмотр другого набора данных того же самого задания. Если пользователь закончил просмотр последнего из интересующих его наборов данных, то для завершения команды SOUT также надо передать подкоманду Е.
По окончании выполнения команды SOUT система выдает на экран запрос, что делать с выходными данными класса Р. При передаче в ответ пустого сообщения все выходные данные задания ликвидируются, а при передаче сообщения, состоящего из одной буквы Р, все выходные данные (а тем самым и само задание) переводятся в очередь другого класса (А), что обеспечивает их распечатку на АЦПУ.
Если в выходной очереди класса Р задание с определенным именем присутствует дважды, то по команде SOUT доступны для просмотра результаты только первого из них. При этом следует иметь в виду, что при ликвидации выходных данных задания относящиеся к нему сообщения ОС (а следовательно, и само задание) из выходной очереди не выводятся. Это обстоятельство препятствует просмотру результатов после повторного пропуска задания с тем же именем. Чтобы избежать этой ситуации, необходимо позаботиться о том, чтобы после просмотра результатов они (а следовательно, и задание) были переведены в класс А (для этого, возможно, придется повторно выполнить команду SOUT, если в результате первого ее выполнения выходные данные ликвидировались, а не переводились в класс А). Другой способ состоит в том, чтобы при повторном пропуске задания изменить его имя, скорректировав третий символ имени (номер задания).
Следует также помнить о том, что при выполнении команды SOUT используется рабочая область и поэтому ее предыдущее содержимое теряется.
2А4
Литература. ' -
I. Ерофеев В. И. и др. Средства отладки программ в ОС ЕС ЭВМ. — М.: Статистика, 1979.
2. Дани л очкин В. П. и др. Операционная система ОС ЕС. Справочное пособие. — М.: Статистика, 1980.
3. Инструкция по языку управления заданиями (наст, книга).
4. Инструкция по использованию архива текстов (наст, книга).
Приложение 1. Команды системы PRIMUS
I. Работа с рабочей областью.
INPT . . [а] [, Ь] — ввод текста с терминала;
LIST _ [О,] [а] [, 6] — просмотр текста на экране;
PRNT — печать текста на АЦПУ;
CORR — редактирование текста;
NUMB — перенумерация записей.
II. Работа с архивом.
DVOL__(имя тома)
COPY. . (имя файла) SAVE , . (имя файла) LOOK. . (имя файла) НЦСР„(ими файла) INST_, ' ' ’
— фиксация тома;
— чтение из файла в рабочую область;
— запись из рабочей области в файл;
— просмотр файла иа экране;
— распечатка файла на АЦПУ;
а, (имя файла) — вставка текста из файла в текст на рабочей области.
III. Работа с заданием.
ЕХЕС . . (имя файла) — передача задания в пакет иа обработку;
DJOB — просмотр очередей ОС:
D , . А — просмотр таблицы выполняющихся за-
даний;
50иТ„(имя задания) — просмотр результатов задания.
IV. Немедленное прекращение выполнения любой команды.
KILL
V. Выход из системы.
END
Приложение 2. Типичные нестандартные ситуации при работе в системе PRIMUS
I. Ошибочное использование команды системы.
Наиболее типичным случаем такого неправильного использования команды является попытка пользователя выдать новую команду до завершения выполнения предыдущей команды.
25$.
II. Аварийные ситуации во время выполнения команды, В этом случае пользователю выдается сообщение вида
ABEND. КОД ЗАВЕРШЕНИЯ = ххх
где ххх — трехзначный код завершения, по которому в [1, 2] можно узнать о возможной причине, вызвавшей аварийную ситуацию.
Наиболее типичные случаи:
001 —ошибка ввода-вывода при чтении или записи (обычно прн обмене с магнитным диском);
222 — пользователем выдана команда KILL;
В37, D37, Е37 — нехватка места в файле при выполнении команды SAVE.
Для продолжения работы в системе после сообщения ABEND нужно нажать клавишу ввода (т. е. передать пустую команду) и дождаться появления на экране сообщения
МОЖНО РАБОТАТЬ, ПОСЫЛАЙТЕ КОМАНДУ
После этого в случае ошибки ввода-вывода следует повторить команду, при выполнении которой появилась ошибка, а при повторной ошибке обратиться к дежурному по терминальному классу. В случае нехватки места в файле следует сократить текст в рабочей области и повторить команду SAVE. При появлении других кодов сообщений необходимо обратиться к дежурному по классу.
ИНСТРУКЦИЯ ПО РАБОТЕ В СИСТЕМЕ КРАБ
1. Общие сведения
Система КРАБ (Комплекс для Работы АБонентов) [1] предназначена для обеспечения диалоговой формы общения пользователя, работающего за терминалом, с ЭВМ БЭСМ-6 в рамках ОС Диспак.
С помощью системы КРАБ пользователь, в частности, может: — вводить с терминала в ЭВМ некоторый текст (программу иа каком-либо языке программирования или ее часть, задание для ОС и т. д.);
— записывать в архив системы введенный текст для многократного его последующего использования;
— редактировать с терминала введенный в ЭВМ текст, т. е. вносить в него различного рода изменения;
— формировать в буфере ввода ОС задание для операционной системы с целью его выполнения;
— выводить на терминал результаты, получаемые в процессе выполнении задания.
Для ведения диалога используется специальный язык общения человека с системой, удобный для человека. На этом языке пользо-
256
ватель формулирует — в виде директив системе — свои указания об очередном этапе работы, которая должна быть выполнена с помощью ЭВМ, н передает эти директивы системе для исполнения. Система — в случае необходимости — запрашивает у пользователя дополнительную информацию и обеспечивает выполнение переданной ей директивы, выдавая на экран соответствующий ответ. Таким образом, работа в системе сводится к набору на клавиатуре терминала н передаче системе для исполнения нужной последовательности директив, а также к передаче системе ответов на ее запросы и необходимых данных.
Пользователь, работающий за терминалом, общается как с системой КРАБ, так и непосредственно с операционной системой. Языком общения в том и другом случае является язык директив, причем любая директива должна передаваться в виде отдельного сообщения. В отличие от директив для ОС, любая директива для системы КРАБ должна начинаться символом «.» (точка), что и является признаком такой директивы. Вслед за точкой всегда следует название директивы и, возможно, ее параметры.
После передачи директивы система КРАБ (или ОС) обеспечивает ее выполнение и выдает на экран свой ответ. Если на пустую директиву пользователя (например, при нажатии клавиши ЕТХ в режиме ON LINE) на экран выдается ответ «R», то это значит, что в данное время терминал находится в состоянии общения с ОС; выдача на пустую директиву ответа «—» (минус) означает, что терминал обслуживается системой КРАБ.
Свои сообщения пользователь может передавать как в режиме ON LINE, так и в режиме OFF LINE. При передаче достаточно длинных (но не превышающих емкости экрана) сообщений следует использовать режим OFF LINE: предварительно набрать на экране весь текст сообщения с признаком его конца (клавиша ЕТХ), проверить правильность набора, исправить в этом тексте обнаруженные ошибки и только после этого осуществлять передачу сообщения (клавиша SEND).
Время реакции системы на сообщения пользователя существенно зависит от числа пользователей, ведущих в это время диалог с ЭВМ, а также от имеющихся в наличии свободных ресурсов (памяти и др.)-По окончании выполнения переданной ей директивы система КРАБ выдает на экран символ «—» (минус), что является приглашением пользователю передать следующую директиву.
Пользователь — после входа в систему КРАБ — может получить информацию о директивах, имеющихся в этой системе. Если системе передать директиву
.шко
9 Н. П. Трифонов, Е. Н. Пасхин
257
то на экран будет выдано описание принципов работы с системой КРАБ. Если же системе передать директиву вида
.ШКО . . (имя директивы)
то иа экран будет выдано описание директивы с указанным именем.
Выдачу какой-либо информации иа экран система производит порциями, ие превышающими 14 строк; если вслед за выдачей этой порции пользователю выдается приглашение к дальнейшей его работе в виде ф, это означает, что на экран была выведена ие вся информация, и если в этом случае системе передать пустую директиву, то на экран будет выведена следующая порция информации. В остальном же приглашение # эквивалентно приглашению «—».
Система КРАБ обслуживает только тех пользователей, имена которых зарегистрированы в системе. На практикуме в качестве имени используется шифр, состоящий из шести цифр: первая цифра 6 означает «студент», следующие три цифры — номер студенческой группы, а последние две цифры — порядковый номер студента в списке группы.
Система обеспечивает также защиту ресурсов каждого пользователя от их неправомерного использования со стороны других пользователей. Такая защита осуществляется с помощью ключей и паролей.
2. Вход в систему и выход из нее
Войти в систему КРАБ можно только в том случае, если данный терминал принят на обслуживание операционной системой (в этом случае при передаче пустой директивы, т. е. при нажатии клавиши ЕТХ в режиме ON LINE, иа экран выдается ответ «R»).
Чтобы терминал был принят на обслуживание операционной системой, надо — при включенном терминале — в режиме OFF LINE нажать клавишу НОМЕ, набрать директиву для операционной системы НУС (что означает «новое устройство») с признаком конца сообщения (клавиша ЕТХ) и передать эту директиву путем нажатия клавиши SEND. ОС на следующую строку экрана выводит ответ ЕСТЬ и переводит терминал в режим ON LINE.
Убедившись, что терминал принят на обслуживание ОС (на пустую директиву выдается ответ «R»), для подключения терминала к системе КРАБ следует в режиме ON LINE передать ОС директиву
КРАБ
В ответ иа эту директиву иа экран выдается сообщение вида
** КРАБ ** (ВЕР. XX ОТ XX. XX. XX)
где через X обозначена 'некоторая цифра, а также символ «—», свидетельствующий о том, что система КРАБ готова принять очередную
258
директиву с терминала (до появления этого символа система КРАБ не воспринимает каких-либо сообщений, передаваемых ей с терминала).
Работа с системой КРАБ начинается с передачи ей директивы
.НАЧ
При ее получении система выдает на экран запрос
кто?
В ответ на этот запрос пользователь должен передать свой шифр, по которому система определяет файлы, к работе с которыми допущен данный пользователь. При этом набираемый пользователем шифр на экране не высвечивается. Система проверяет наличие переданного ей шифра в списке зарегистрированных пользователей ЭВМ БЭСМ-6. Если шифр в этом списке отсутствует, то система выдает на экран сообщение
ВЫ НЕ ПОЛЬЗОВАТЕЛЬ БЭСМ-6
и прекращает обслуживание данного пользователя. При наличии этого шифра в списке пользователей БЭСМ-6 проверяется его наличие в списке пользователей системы КРАБ; при его отсутствии на экран выдается сообщение
НЕТ БЮДЖЕТА
и обслуживание данного пользователя также прекращается.
Система КРАБ предоставляет пользователю возможность защитить свои ресурсы (файлы и выделенный ему лимит машинного времени) с помощью «ключа», роль которого выполняет любое четырехзначное число, выбираемое по усмотрению пользователя. Свой ключ пользователь задает системе при первом сеансе работы с нею; система запоминает этот ключ и в последующих сеансах разрешает пользователю под данным шифром работать только в том случае, если он сообщит системе тот же ключ, который ей был задан при первом сеансе работы. При регистрации новых пользователей система каждому шифру первоначально приписывает ключ, равный нулю.
После того как по переданному шифру система установила, что данный пользователь имеет право работать с нею, в случае нулевого ключа при этом шифре (что имеет место при первом сеансе работы данного пользователя с системой), она выдает на экран символ «—», приглашая пользователя передать директиву. При пер-аоч сеансе работы с системой пользователь в этот момент должен сообщить ей свой ключ, выдав директиву
.икл „ хххх
9*
259
где ХХХХ — четырехзначное число, выбранное в качестве ключа, ко-торый система запоминает при шифре пользователя. Получив ключ, система выдает на экран приглашение к работе — символ «—».
Если же для переданного шифра в системе запомнен ненулевой ключ (что имеет место в последующих сеансах работы), то система выдает на экран запрос
КЛЮЧ
в ответ на который пользователь должен передать системе свой ключ (который также на экран не высвечивается). Если переданный ключ совпадает с зафиксированным в системе ключом, то на экран вы* дается приглашение к работе — символ «—»; в противном случае система отказывается обслуживать данного пользователя, выдав на экрэн сообщение
НЕВЕРНЫЙ КЛЮЧ
Для окончания сеанса работы с системой нужно выдать дирек* тиву
КОН
пр которой система снимает с обслуживания тот шифр, под которым работал данный пользователь, продолжая держать на обслуживании терминал. В этот момент за данным терминалом может начать сеанс работы с системой другой пользователь, начиная с передачи директивы
.НАЧ
Если вслед за упомянутой выше директивой «.КОН» повторно выдать такую же директиву, то система КРАБ снимет с обслуживания данный терминал, передавая его на обслуживание операционной системе и выдавая на экран сообщение
КОНЕЦ СЕАНСА
Именно в этом состоянии следует выключать терминал клавишей POWER при уходе из терминального класса.
Внимание! Категорически запрещается выключать терминал до выхода из системы КРАБ, так как в этом случае терминал считается неисправным, отключается от системы и работа на нем в течение суток становится невозможной.
3. Начальный ввод текста
Основной целью работы в системе КРАБ на практикуме является формирование в архиве системы задания для ОС и передача этого задания на выполнение. При этом задание для ОС, подготавлй* 260
ваемое с терминала, должно иметь точно такой же вид, что и зада* ине, подготавливаемое с помощью перфокарт.
При работе за терминалом следует исходить из того, что каждая запись размещается в одной строке экрана, начиная с первой ее позиции (т. е. каждая строка экрана является образом перфокарты). Для этого — по окончании набора на клавиатуре очередной
LINE .
записи — следует нажать управляющую клавишу pgED (по которой в позицию курсора заносится управляющий символ «J», являющийся признаком конца записи, и курсор перемещается на начало следующей строки).
Текст задания для ОС можно вводить с терминала сразу в окончательном виде, однако это не обязательно. Можно, например, сначала ввести текст программы, написанной на каком-либо языке программирования, а затем, используя возможности системы КРАБ по редактированию текста, дополнить введенный текст программы соответствующими управляющими операторами языка управления заданиями и, если нужно, исходными данными и тем самым сформировать окончательный текст задания для ОС.
Напомним, что задание, например, для трансляции и выполнения фортран-программы, для ОС Дпспак должно иметь следующий вид:
ШИФР , . (шифр студента). . ЗСМ 1
ВРЕ_59"
ТРА_ 15-
ИНК"
ЕЕВ1АЗ
* NAME _ VTSTUD _ (фамилия)
»FTN
_ _ _ _ PROGRAM _ TEST
Текст фортран-программы
____ _ _ „ END
• EXECUTE
Данные для операторов
ввода
. END _ FILE
Для начального ввода текста сначала надо — по описанным выше правилам — войти в систему КРАБ. Предполагается, что при йчередном сеансе работы в системе пользователь, как правило, рабо
261
тает с текстом, который был ранее записан в архив системы в виде файла с определенным именем, заданным пользователем. С целью
Couci и фау'ихя iiojibduBd1едь можс'1 снабдить его паролем — в этом случае система разрешает работу с данным файлом только при сообщении ей соответствующего пароля. В связи с этим фактическая работа с системой КРАБ (после входа в нее) начинается с выдачи директивы
.И , . (имя файла)
При получении этой директивы система выделяет рабочее поле в памяти машины для размещения текста и проверяет, имеется ли файл с указанным именем в ее архиве. Если такой файл в архиве имеется и он снабжен паролем, то система выдает запрос
ПАРОЛЬ
в ответ на который пользователь должен передать системе тот пароль, которым ои снабдил ранее свой файл. Прн получении правильного. пароля система переписывает текст из указанного файла на рабочее поле; если файл не был снабжен паролем, то эта перепись осуществляется по указанной выше директиве без запроса пароля.
Если в архиве системы файла с указанным именем нет (что имеет место при первом сеансе работы пользователя в системе КРАБ), то в ответ иа эту директиву система выдает сообщение
НЕТ В КАТАЛОГЕ
означающее, что текст должен быть введен с терминала.
Для начального ввода текста надо выдать директиву
•Д
на которую система отвечает символом «+», означающим, что теперь системе надо передавать не директиву, а данные, т. е. некоторый текст; этот текст можно передать в виде одного или нескольких сообщений, которые содержат отдельные фрагменты текста. При отсутствии достаточного опыта работы за терминалом целесообразно каждую отдельную запись (являющуюся образом очередной перфокарты) передавать в виде отдельного сообщения. Система размещает на рабочем поле передаваемые ей записи, снабжая каждую из них ее порядковым номером.
Для просмотра текста, находящегося на рабочем поле, служит директива
.В
По этой директиве на экран выдается первый фрагмент текста, со» держащий 14 записей. Каждая запись помещается в отдельной стро» ке экрана, причем в первых четырех позициях строки содержится аЖ
282
рядковый номер данной записи в тексте. Если выданный на экран фрагмент не является последним, то в последнюю строку экрана выдается приглашение к продолжению работы в виде #: в этом случае выдача системе пустой директивы (нажатие клавиши ЕТХ в режиме ON LINE) влечет за собой выдачу на экран очередного фрагмента текста.
По директиве вида
,B_N —М
система обеспечивает выдачу на экран части текста, начиная с записи с номером N и кончая записью с номером М; если эта часть текста не помещается на экране, то она, как обычно, будет выдаваться фрагментами по 14 записей.
Чтобы иметь возможность работать с введенным на рабочее поле текстом в последующих сеансах, этот текст надо записать в архив системы по директиве
.3
В результате ее выполнения текст из рабочего поля будет записан в файл с именем, взятым из последней из выполненных директив «.И» (и тем самым предыдущее содержимое этого файла будет утеряно).
Если в архиве еще не было файла с таким именем, то таковой файл образуется и в него записывается текст из рабочего поля, после чего система выдает запрос
ПАРОЛЬ
Если в ответ на него системе передать любую непустую последовательность символов (не более шести), то она и будет принята в качестве пароля к данному файлу (как обычно, передаваемый пароль на экран не высвечивается); если же в ответ на этот запрос передать пустое сообщение (в режиме ON LINE нажать клавишу ЕТХ), то файл не будет снабжен паролем.
Появление на экране ответа системы «—» свидетельствует о завершении записи текста в архив.
4. Редактирование текста
Система КРАБ позволяет вносить различного рода изменения в текст, находящийся на рабочем поле. т. е. производить его редактирование. Если подлежащий редактированию текст находится в архиве, то он должен быть предварительно прочитан на рабочее поле с помощью директивы
,И_ (нмя файла).
263
В случае необходимости подлежащий редактированию текст можно вызвать для просмотра из рабочего поля на экран с использованием описанной РЫТПС linniiimraM л- Ръ
Имеются следующие возможности редактирования текста:
— удаление записей;
— вставка записей;
— замена записей;
— корректировка записей.
Удаление записей. Для удаления из текста записей служит директива вида
,О_ N — М
где N н М. — целые без знака (М N). По этой директиве из текста удаляются записи с порядковыми номерами от N до М включительно, с соответствующей перенумерацией записей, следующих за удаленным фрагментом текста.
Вставка записей. Для вставки записей перед записью с номером N надо сначала выдать директиву
BC_N
В ответ на нее система выдает символ «+», свидетельствующий о том, что она готова к приему вставляемых записей. При получении этого ответа пользователь может начать набор на клавиатуре и передачу сообщений, содержащих вставляемые записи.
Вставляемые записи можно передавать в режиме ON LINE (нажимая клавишу ЕТХ после набора очередной записи), однако целесообразнее использовать режим OFF LINE: набрать в этом режиме одну или несколько вставляемых записей, проверить правильность их набора и в случае необходимости внести в них соответствующие исправления, а затем передать эти записи, нажав клавишу SEND.
Система предварительно накапливает передаваемые ей записи, а когда ей будет выдана следующая директива, то перед ее выполнением все накопленные записи вставляются в указанное место текста, производится перенумерация записей и выполнение директивы вставки завершается.
Для добавления записей в конец текста (вслед за его последней записью) служит директива
•Д
Получив — после выдачи директивы — приглашение системы «+», надо передать системе одно или несколько сообщений, содержащих добавляемые записи. Как обычно, передаваемые записи накапливаются системой, а при передаче ей очередной директивы производится фактическое их добавление в конец текста с соответствующей нумерацией, н на этом выполнение директивы «.Д» завершается.
Замена записей. Для замены записей с номерами от N до М включительно надо выдать директиву
,3AM_N — М
и затем в ответ на приглашение «+» передать системе те записи, на которые должны быть заменены указанные в директиве записи. Си» стееда накапливает передаваемые ей записи, а при выдаче новой ди» рективы производится фактическая замена записей в тексте с их пе* ренумерацией.
Для замены одной записи с номером N можно в указанной выше директиве задать М = N либо воспользоваться эквивалентной ей директивой
.ЗАМ _ N
Корректировка записей. Если в те или иные записи текста нуж-но внести отдельные исправления (замена одних символов на дру» гие), то операция замены записей нецелесообразна, так как она требует набора всей записи, что может привести к появлению дополнительных ошибок. В этом случае целесообразно произвести ие замену, а корректировку части текста.
Для этого прежде всего нужно с использованием описанной ранее директивы «.В» или «.В — М» вызвать на экран фрагмент текста, подлежащий корректировке. Для корректировки какой-либо строки на экране (которая производится в режиме OFF LINE) надо выполнить следующую последовательность действий:
1) подвести курсор под первую позицию корректируемой строки1,
2) пять раз нажать клавишу DC, чтобы удалить номер записи, выведенный на эту строку экрана;
3) подвести курсор под позицию, требующую изменения, и с помощью клавиатуры внести это изменение.
После того как на экране будут откорректированы все записи, надо нажать клавишу CTRLBLINK, подвести курсор под управляющий символ «J» последней из скорректированных строк (или последней строки с вызванным па экран фрагментом текста) и нажать клавишу ЕТХ. Затем надо перевести курсор на любую позицию первой из строк, подвергавшихся корректировке (или на первую строку вызванного фрагмента текста), и нажать клавишу SEND.
В результате соответствующий фрагмент текста на рабочем поле будет заменен на переданный с экрана фрагмент.
По окончании редактирования текста рекомендуется проверить правильность выполнения редактирования путем просмотра текста на экране с использованием директивы «.В» (или —М»),
Чтобы иметь возможность работать с отредактированным тек» стом в последующих сеансах, этот текст необходимо переписать ИЭ рабочего поля в архив системы с использованием директивы «.3»,
263
5. Выполнение задания
Для выполнения на машине задания, текст которого находится НЯ пябппрм плпр 251Д2Т5 ДПрСДТИЗу
.Ф_Л
По этой директиве система КРАБ передает задание нз рабочего поля в буфер ввода ОС для исполнения, на экран выводит сообщение вида
ШИФР (имя задачи)
(для студентов в качестве имени задачи принимается шифр студента) и переходит в режим приема директив, выдав приглашение «—».
О состоянии любой задачи, переданной в буфер ввода ОС для выполнения, можно узнать, выдав директиву вида
Г. . (имя задачи)
Если система ответит, что такой задачи нет, это означает, что ее выполнение уже закончено. Все выдачи, относящиеся к данной задаче, вместо печати на АЦПУ записываются на рабочее поле того пользователя, который передал ее на выполнение. Файлу, в котором размещаются эти выдачи, присваивается имя АЦПУ01, причем этот файл сохраняется на рабочем поле в течение суток (так что ие обязательно ждать за терминалом окончания выполнения переданного ОС задания — за этим терминалом может начать работу другой пользователь).
Для вывода на экран полученных результатов (после входа — в случае необходимости — в систему КРАБ) пользователь может предварительно узнать, какие файлы хранятся на его рабочем поле, выдав директиву
.СБО
В ответ на нее система выводит на экран имена всех файлов, которые находятся на рабочем поле; Убедившись, что файл АЦПУ01 присутствует на рабочем поле, его можно вызвать для просмотра на экран. Для этого надо сначала выдать директиву
_АЦПУ01
В ответ иа нее система выдает сообщение
МАССИВ СО СБОЙНЫХ ЗОН
свидетельствующее о готовности системы выдавать на экран текст, записанный в файл АЦПУ01 (каждая строка выдачи иа АЦПУ принимается в качестве отдельной записи этого текста). После получения этого сообщения можно осуществлять просмотр текста иа экране с помощью уже рассмотренных ранее директив «.В» или
«.B_N—М». После просмотра результатов можно опять вызвать из архива текст своего задания, внести в него те или иные изменения, передать измененное задание ОС для выполнения и т. д.
Примечание. Получение окончательного листинга на АЦПУ для оформления отчета производится с разрешения преподавателя. Для этого задание из рабочего поля надо передать в буфер ввода ОС для исполнения по директиве
.Ф
По такой директиве все выдачи, относящиеся к данной задаче, на рабочее поле не записываются, а печатаются на АЦПУ.
Литература.
1. Г у л я е в А. В. и др. Основные концепции и возможности системы КРАБ/В сб. Автоматизация конструирования библиотек программ.— М.: Изд-во МГУ, 1979.
ИНСТРУКЦИЯ ПС АВТОКОДУ БЕМШ
1. Структура задания для ОС Диспак
Для пропуска через машину БЭСМ-6 в рамках ОС Диспак программы, написанной на автокоде БЕМШ [1], с целью ее трансляции и последующего выполнения, необходимо оформить задание для ОС иа выполнение этой работы. Задание, как обычно, формулируется на языке управления заданиями, отдельные предложения которого называются управляющими операторами.
Ниже приводится типичная для практикума структура задания для ОС. При этом все допустимые пробелы в управляющих операторах указаны в явном виде, а номера, указанные слева, в текст задания не входят — они будут использоваться при объяснении отдельных частей задания.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Н/
ШИФР , (шифр студента) . ЗС2 1
ЛИСТ „О—37
ЕЕВ1АЗ
• NAME . . (фамилия ’студента)
• ASSIGN _ LIBRARY „ 2
. BEMSH
ВВДОС0-1
текст программы иа автокоде
KB4QQQ-1
ТРН0О0-1
О - С ~]
Паспорт задания
Вызов транслятора
Задание транслятору
267
12) КНЦ000П
131 * MAIN_/имя модуля) X
14) * EXECUTE 1
15) * END _ FILE )
16) (конец программной части)
Признак конца информаций для транслятора
Задание на выполнение программы
Признак конца программной части
Массив № 1 исходных данных
Массив J& 2 исходных данных
Признак конца задания
1.1. Паспорт задания.
Паспорт служит для идентификации задания и его автора, а также для заказа требуемых ресурсов. В управляющих операторах, входящих в состав паспорта, задается следующая информация:
1) В этом операторе задается шифр студента, имеющий вид ХХХХпи, где четырехзначное число ХХХХ является шифром студенческой группы (этот шифр выдается группе на практикуме), а двузначное число пп является порядковым номером студента в списке группы, например:
ШИФР 712904 _ ЗС2 “1
(здесь 7129—шифр группы, 04 — порядковый номер студента в группе).
Если в этом операторе задан шифр, не зарегистрированный в ОС, то задание к исполнению не принимается.
2) Заказ оперативной памяти (листы с номерами от 0 до 37).
3) Стандартный для студенческого практикума оператор, харак« тернзующий используемые устройства подготовки данных.
4) Идентификация задания: фамилия студента, указанная в этом операторе, будет отпечатана крупными буквами на распечатке, относящейся к данному заданию, в качестве его заголовка.
5) Заказ на использование библиотеки с номером 2, в которой хранятся стандартные для БЕМШа подпрограммы.
1.2. Вызов транслятора.
Управляющий оператор 6) означает вызов в работу транслятора с автокода БЕМШ.
268
1.3. Задание транслятору.
Транслятору можно предъявить для трансляции одну или несколько автокодных программ (модулей) —для каждой из них в задании транслятору должен соответствовать свой шаг задания (в рассматриваемой нами общей структуре задания предполагается, что транслятору предъявлен только один модуль).
Каждый шаг задания транслятору состоит из следующих составных частей:
7) Оператор, означающий, что подлежащий трансляции текст содержится в задании, вслед за данным оператором.
8) Текст модуля, написанный на автокоде БЕМШ.
9) Оператор, являющийся признаком конца автокодного текста,
10) Оператор, предписывающий произвести трансляцию указанного выше автокодного текста.
И) Указание транслятору о содержании выдаваемого им листинга (приведенная выше запись этого оператора задает стандартное содержание листинга).
Если программа состоит из нескольких модулей, то для каждого из них в задании транслятору должен соответствовать свой шаг задания, оформленный по указанным правилам, причем порядок следования этих шагов может быть произвольным. Каждый оттранслированный модуль будет записан в библиотеку загрузочных модулей под своим именем, в качестве которого принимается метка, указанная в поле названия команды транслятору СТАРТ.
Внимание! Имя модуля может содержать только латинские буквы и цифры.
12) Признак конца информации для транслятора.
1.4. Задание на выполнение.
13) В этом операторе указывается имя главного модуля программы, т. е. модуля, которому надо передать управление по окончании загрузки.
14) Указание на непосредственное выполнение указанного выше модуля.
15) Признак конца задания на выполнение.
1.5. Признак конца программной части.
Управляющий оператор 16) является признаком конца информации, относящейся к автокодной программе: это карта, содержащая пробивки во всех позициях колонок 1 и 41.
1.6. Массивы исходных данных.
Если в автокодной программе предусмотрен ввод исходных данных (по экстракодам ввода), то эти данные размещаются в задании для ОС вслед за признаком конца программной части задания.
Данные, подлежащие вводу по какому-либо экстракоду ввода, оформляются в задании для ОС в виде массива исходных данных.
269
Эти массивы считаются перенумерованными, начиная с единицы, в порядке их следования в задании для ОС — эти номера массивов используются в экстракодах ввода для указания порции данных, вводимых по этому экстракоду.
Каждый массив исходных данных начинается управляющим оператором, характеризующим тип исходных данных. Вслед за ним следует сама порция данных, а за ней следует признак конца этой порции данных.
В автокоде БЕМШ допускается использование текстовых и числовых данных. В случае текстовых данных считается, что каждая строка данных (перфорируемая на отдельной карте) содержит 80 символов, а в случае необходимости она дополняется справа пробелами до 80 символов. Операторы, окаймляющие порцию текстовых данных, имеют вид 17) и 19) в приведенной выше структуре задания.
Числовые данные записываются (и перфорируются) в виде
ч3.14ч0.002 4 27.559 ...
Операторы, окаймляющие порцию числовых данных, имеют вид 20) и 22).
Еще раз обратим внимание на то, что в каждом экстракоде ввода для указания нужной порции исходных данных используется номер массива исходных данных в задании для ОС; поэтому порядок следования этих массивов в заданий должен быть согласован с их номерами, используемыми в экстракодах ввода.
Управляющий оператор ЕКОНЕЦ является признаком конца задания для ОС.
2. Экстракоды ввода-вывода
2.1. Экстракод ввода (Э50).
Для ввода данных служит экстракод ввода Э50, обращение к которому иа автокоде БЕМШ имеет вид
[(метка): ] Э50 А (ИР)
Исполнительный адрес этой команды должен быть равен 1012а + k, где k — номер массива исходных данных в задании для ОС, содержащего порцию данных, подлежащих вводу.
К моменту выполнения этой команды в 15 младших разрядах сумматора должен быть зафиксирован адрес ячейки, начиная с которой должны быть размещены в памяти вводимые данные.
При вводе текстовых данных с каждой перфокарты прочитывается по 80 кодов символов (колонке, не содержащей пробивок, ставится в соответствие пробел), которые размещаются в последова
тельных ячейках, по 6 символов в ячейку (так что каждой из вводимых перфокарт должны соответствовать 14 ячеек памяти).
При вводе числовых данных каждое очередное введенное число переводится в двоичную систему счисления и размещается в очередной ячейке памяти.
Например, для ввода с перфокарт текстовых данных, находящихся в массиве исходных данных с номером 1, в память, начиная с ячейки В, в автокодной программе можно написать следующую последов ательность предложений:
УИА В (2)
СЧИ 2 Э50 '1013'
В: ПАМ 70
2.2. Экстракод печати (Э64).
Для вывода данных на печать с помощью АЦПУ служит экстракод Э64, обращение к которому на автокоде БЕМШ имеет вид
[(метка): J Э64 А (ИР)
В ячейках памяти, начиная с АИси, должна находиться управляющая информация для экстракода печати. Эта информация состоит из двух или более управляющих машинных слов. В дальнейшем каждое машинное слово, которым представляется управляющая информация, будем трактовать как пару машинных команд БЭСМ-6 первой структуры:
ИР КОП А
где ИР — номер индексного регистра (4 бита), записываемый одной двоичной и одной восьмеричной цифрами; КОП — код операции (8 битов), записываемый одной четверичной и двумя восьмеричными цифрами; А—адрес в команде (12 битов), записываемый четырьмя восьмеричными цифрами.
В ячейке с адресом Анеп должно находиться первое управляющее слово, определяющее начальный (АН) и конечный (АК) адреса ячеек памяти, содержимое которых выводится на печать. Если по адресу Аисп хранится слово
ИР1 ООО А1 ИР2 ООО А2
то принимается АН = А1ИСп, АК = А2ВСп.
Управляющая информация, содержащаяся в следующих за Аисп ячейках памяти, определяет формат печати. Каждое из этих управляющих слов имеет вид:
271
ИР1 кош А1 ИР2 КОП2 А2
Оу L X бг ДА W-1
где у определяет трактовку (а тем самым и форму распечатки) оче-редкого выводимого машинного слова:
(О — символьная информация в коде АЦПУ-128,
1 — пара машинных команд, у — {
12 — восьмеричная константа,
3 — десятичное число.
L — начальная позиция в строке, начиная с которой должно распечатываться очередное машинное слово (0 < А 1778).
Л — число позиций в строке, отводимых на изображение выводимого на печать машинного слова; в случае десятичного числа Л =*’ = k 4- 5, где k — число цифр в мантиссе; в случае восьмеричной константы Л задает количество печатаемых младших цифр восьмеричной записи слова (1 А, <7 208); для символьной информации н команд Л игнорируется.
( 0 — в следующей ячейке есть управляющее слово, которое дол-
I жно использоваться при распечатке последующих данных, ® = 1 1 — данное управляющее слово является последним—в соот-
I ветствии с ним должны распечатываться все последую-
I щие данные.
Т — указывается в последнем управляющем слове (при 6=1) н задает число пустых строк, которые должны быть оставлены на рулоне бумаги после распечатки по данному экстракоду,
ДА — определяет позицию, начиная с которой должно распечатываться следующее машинное слово: если текущее слово распечатывалось с позиции с номером I, то следующее слово будет распечатываться с позиции с номером I + ДА. При печати десятичных чисел должно быть ДА > X; при печати команд ДА > 278 (распечатка команды занимает 278 позиций); при печати восьмеричных констант ДА > 208.
N — количество элементов (десятичных чисел, восьмеричных констант, команд), печатаемых в одной строке. Если заданное количество элементов на самом деле не помещается в одной строке, то после печати символа в последнюю позицию этой строки осуществляется переход на начало следующей строки, которая считается продолжением предыдущей.
В случае символьной информации распечатка ведется до первого по порядку кода символа 1728, который считается признаком, койца
272
текста, либо до конца ячейки АК. При АК С АН распечатка ведется до признака конца текста, который в этом случае обязательно должен присутствовать в распечатываемом тексте.
3. Примеры использования экстракода вывода
3.1. Распечатку иа АЦПУ содержимого ячеек памяти от А до А -}- 7 включительно в виде восьмеричных констант (подобная необходимость часто возникает при отладке автокодных программ) можно осуществить по командам
УИА А (5)
УИА А + 7 (6)
Э64 ИНФСЛ
задав управляющую информацию для экстракода следующим образом: ,
ИНФСЛ: КОНД М24К'050000000'К'060000000'
КОНД М24К'020030020'К'110300002'
В результате в последовательных строках, начиная с третьей позиции каждой строки, будут распечатаны машинные слова в их восьмеричной записи по три слова в строке.
3.2. Распечатку содержимого тех же ячеек памяти в виде последовательности символов можно осуществить по тем же командам, задав следующую управляющую информацию:
ИНФСЛ: КОНД М24К'050000000'К'060000000'
КОНД М24К'000000000'К'110000000'
Примечание. Последовательность символов, выводимых на печать, рекомендуется завершать признаком конца текста (код 172з). При распечатке содержимого одной ячейки в виде последовательности символов эта рекомендация становится обязательным требованием.
4. Задание текстовых данных в автокоде БЕМШ
При отладке программ, предназначенных для обработки текстов, часто бывает удобно обрабатываемый текст задавать в самой автокодной программе, а не вводить его с перфокарт по экстракоду Э50.
Для того чтобы задаваемый текст был представлен в кодах АЦПУ, этот текст необходимо задавать в виде длинных констант с признаком типа П. В этом случае транслятор представит символы в кодах АЦПУ, отводя на изображение каждого символа 8 битов. Если в константе задано меньше шести символов, то (до масштабирования) они размещаются в машинном слове справа, а слева слово
273
дополняете* кодами символа 0. Масштабирование имеет обычный смысл, т. е. означает сдвиг содержимого ячейки влево на заданное имппп пплмпнtTv
Если текст, задаваемый с помощью констант е признаком П, впоследствии будет выводиться на печать по экстракоду Э64 и этот текст занимает не более одной ячейки, то он должен заканчиваться специальным символом — признаком конца текста (код 1728).
Примеры задания текстов на автокоде БЕМШ в кодах АЦПУ:
1) КОНД МвП'МАРШ/В'Ш'
2) А : КОНД П'МАТРОС'
КОНД М42В'172'
3) В : КОНД П'ИНТЕНС' КОНД П ИФИКАЦ' КОНД П'ИЯ,____________’
Примечание. Символ ' (кавычка), используемый в качестве части текста, изображается парой кавычек, например:
КОНД П'ОБ"ЕКТ'
Литература.
1. Штаркман В. С. Автокод БЕМШ (описание языка). — М.; ИПМ АН СССР, 1969.
Приложение!. АЛГОЛ ЕС ЭВМ. ПЕРЕЧЕНЬ
ОСНОВНЫХ СООБЩЕНИЙ ТРАНСЛЯТОРА ОБ ОШИБКАХ
Сообщения об ошибках во время трансляции с алгола содержат код сообщения вида lEXnnnl, где ппп — порядковый номер сообщения; код серьезности, который может принимать одно нз трех значений (W, S нли Т); номер точки с запятой и текст сообщения.
Коды серьезности означают:
W — возможна ошибка на следующем этапе обработки;
S — серьезная ошибка, которая делает невозможным следующий этап обработки;
Т — грубая ошибка, обычно прекращающая выполнение самой обрабатывающей программы.
Номер , точки с запятой ппппп может принимать значения от 00000 до 65535. Если в процессе синтаксического контроля транслятор не в состоянии определить место ошибки в программе, номер точки с запятой в сообщении не указывается.
Примечание. Наряду с текстом сообщения об ошибке в этом и последующих приложениях приводится также объяснение возможной редакции системы на ошибку.
IEX001I W ппппп. Недопустимый знак. Недопустимый знак исключен.
IEX002I W ппппп. Недопустимая точка. Точка исключена.
IEX0031 W ппппп. Неправильно использовано двоеточие после ххх. Двоеточие исключено.
IEX004I Т. ппппп. Строка букв слишком длинна.
IEX005I S ппппп. Идентификатор начинается не с латинской буквы. Идентификатор исключен.
IEX006I Т ппппп. Метка содержит слишком много знаков.
IEX007I W ппппп. Метка, начинающаяся с ххх, содержит знак, отличный от латинской буквы или цифры. Метка исключена.
IEX008I W ппппп. Метка начинается не с латинской буквы. Метка исключена.
IEX010I S ппппп. Специфицированы ие все формальные параметры процедуры ххх.
1ЕХ0Ш 8 ппппп. Программа начинается с недопустимого ограничителя.
IEX012I W ппппп. После ххх указаны два апострофа. Первый апостроф исключен.
IEX013I W ппппп. Не указан апостроф после ограничителя, начинающегося с ххх. Пропущенный апостроф вставлен.
IEX014I S ппппп. Ограничитель, начинающийся с ххх, недопустим.
IEX016I S ппппп. Идентификатор, начинающийся с ххх, содержит не латинскую букву или не цифру. Идентификатор исключен.
275
IEX0181 W nnnnn. Ограничитель 'COMMENT' размещен в про-грамме не после 'BEGIN' или точки с запятой. Трансляция продолжается.
ТЕХ020Т Т nnnnn ГичЛиия n rrn-swpwwnr'rn СОСТЩШЫХ
операторов, операторов цикла и описания процедур слишком велика.
IEX021I S ппппп. Описатель ххх находится не между 'BEGIN' и первым оператором блока или 'PROCEDURE' и телом процедуры, IEX023I S ппппп. Общая длина строк больше допустимой.
IEX025I S ппппп. Спецификатор 'STRING' или 'LABEL' используется вне заголовка процедуры. Спецификатор исключен.
IEX026I S ппппп. Параметр ххх определен несколько раз. Используется только первая спецификация.
IEX0271 W ппппп. Параметр ххх. определенный в заголовке процедуры, не указан в списке формальных параметров. Спецификация игнорируется.
IEX028I S ппппп. Ограничитель 'VALUE' указан вне заголовка процедуры. Список значений исключен.
IEX029I W ппппп. В заголовке процедуры совокупность спецификаций предшествует списку значений.
IEX030I W ппппп. В списке значений заголовка процедуры повторяется параметр ххх.
IEX0311 W ппппп. После идентификатора массива ххх за открывающей круглой скобкой не следует знак /. Предполагается индексная скобка.
IEX032I S ппппп. В списке граничных пар массива ххх опущена закрывающая круглая скобка. Описание массива исключено.
IEX0341 S nnnnn. За сегментом массива ххх не следует точка с запятой или запятая. Знаки до ближайшей точки с запятой исключены.
IEX035I W ппппп. В списке массивов или переключателей неправильно используется точка. Точка исключена.
IEX0361 Т ппппп. В описании процедуры ххх свыше 15 параметров.
IEX037I S ппппп. После списка формальных параметров процедуры ххх не указана точка с запятой. Знаки до ближайшей точки с запятой исключены.
IEX03SI Т ппппп. В блоке описано слишком много идентификаторов.
IEX039I S nnnnn.mmm 'END' в программе опущено. Открытые блоки, составные операторы, операторы цикла и описания проч''’”'” "ЯКПЫТЫ.
IEX042I W ппппп. 'BEGIN' предшествует ранее оттранслированной процедуре. 'BEGIN' исключен.
IEX043I S ппппп. Программа закончена, так как найдено равное число 'BEGIN' и 'END'. Оставшаяся часть программы игнорирована.
IEX045I S ппппп. Идентификатор ххх в блоке описан несколько раз. Использовано последнее описание.
IEX047I S ппппп. Недопустимый вызов идентификатора ххх по значению.
IEX080I S nnnnn. В операнде, начинающемся с ххх, использован" "опопустимые знаки.
IEX081I S ппппп. Идентификатор ххх не описан.
IEX082I S ппппп. Модуль вещественной константы, начинающейся с ххх, больше допустимого.
IEX083I W nnnnn, Модуль целой константы, начинающейся с кхх, больше допустимого.
IEX084I W ппппп. Точность вещественной константы, начинающейся с ххх, превышает допустимую. Константа усечена.
IEX085I W ппппп. Неправильно использована метка ххх.
IEX086I S ппппп. Слишком много констант.
IEX088I W ппппп. Идентификатор ххх в граничной паре описан в том же блоке, что н сам массив.
IEX0891 W ппппп. Оператор 'GOTO' ххх находится вне оператора цикла, содержащего метку ххх.
IEX160I S ппппп. Последовательность операций ххх ууу недопустима.
IEX161I S ппппп. Последовательность операций ххх и операнда ууу недопустима.
IEX162I S ппппп. Пропущен операнд между двумя знаками операций ххх и ууу.
IEX163I S ппппп. Операнд, следующий за знаком операции ххх, не является операндом арифметического типа.
IEX164I S nnnnn. Наличие операнда между знаками операций ххх и ууу недопустимо.
ТЕХ 1651 S ппппп. Выражения до и после 'ELSE' несовместимы.
IEX1S61 S ппппп. Описатель в недопустимой позиции.
IEX168I S ппппп. Операнд, предшествующий знаку операции ххх, не может обладать значением.
IEX169I S ппппп. Метка, следующая за знаком операции ххх, недопустима.
IEX172I S ппппп. Идентификаторы в левой части списка имеют различный тип.
IEX174I S ппппп. Процедура-функция, вызываемая по значению, имеет параметры.
IEX175I S ппппп. Операнд, следующий за знаком операции ххх, не является ни меткой, ни переключателем.
IEX176I S ппппп. Отсутствует операнд перед знаком операции ххх.
IEX1771 S ппппп. Перед знаком операции ххх указан операнд.
ТЕХ 1781 S ппппп. Неправильный операнд в выражении до или после 'ELSE'.
IEX179I S ппппп. Число индексных выражений не равно размерности массива.
IEX180I S ппппп. Недопустимый указатель переключателя.
1ЕХ18П S ппппп. Указатель переключателя в недопустимой позиции.
IEX182I S ппппп. Операнд, следующий за знаком операции ххх, не является операндом типа 'BOOLEAN'.
IEX1831 S ппппп. Операнд, предшествующий операции ххх, не является идентификатором процедуры.
IEX184I S ппппп. Операнд, предшествующий операции ххх, не является идентификатором массива или переключателя.
IEX185I S ппппп. Операнд типа 'REAL', предшествующий операции ххх недопустим в операции деления нацело.
IEX187I S ппппп. Число фактических параметров не равно числу формальных параметров процедуры.
IEX188I S ппппп. Для стандартной процедуры указан неправильный фактический параметр. DSN = xxx.
IEX190I S ппппп. Присваивание невозможно.
277
IEX191I S nnnnn. Операнд между ) и знаком операции ххх недопустим.
1ЁХ1921 S ППППП. Ппаияя часть ОПерятлпя пписплипаима гм является ни арифметическим, ни логическим выражением.
IEX193I S nnnnn. Значение правой части оператора присваивания не соответствует типу списка левой части.
IEX194I S nnnnn. ххх как знак операции недопустим.
IEX195I S nnnnn. Последовательность операнда и знака операции ххх недопустима.
IEX196I S nnnnn. Идентификатор массива, предшествующий знаку операции ххх, недопустим.
IEX212I Т nnnnn. Слишком много ошибок: общая длина сообщений превышает допустимую.
IEX213 Т ппппп. Число описанных идентификаторов превышает допустимый максимум.
IEX215 Т nnnnn. Исходная программа слишком длинна.
IEX216I S nnnnn. Слишком много меток, счетчик меток переполнен.
Приложение 2. АЛГОЛ ЕС ЭВМ. ПЕРЕЧЕНЬ
ОСНОВНЫХ СООБЩЕНИЙ ПРИ ВЫПОЛНЕНИИ ПРОГРАММЫ
Сообщении при выполнении программы на алголе содержат сообщения вида IHCnnnI, ссылку на номер точки с запятой (SC) и текст сообщения. Кроме того, отдельные сообщения содержат либо dd-имя, либо номер набора данных nn (DSN = nn), при работе с которым обнаружена ошибка, либо слово состояния программы (PSW=xxxxxxxx хххххххх) в момент обнаружения ошибки.
IHI001I SC=nnnnn DSN = nn. При преобразовании вещественного числа в целое получено недопустимое целое.
IHI002I SC = nnnnn DSN = nn. Для набора данных пп требуемая операция ввода-вывода не определена.
IHI005I SC — nnnnn DSN = nn. Запрос на ввод после конца набора данных пп.
IHI006I SC = ппппп DSN = nn. Порядок вводимого числа имеет больше двух значащих цифр.
IHI015I SC = nnnnn, В описании массива верхняя граница меньше нижней.
IHI016I SC = ппппп. Значение индексного выражения вне описанных границ.
IHI017I SC = ппппп. Бесконечный цикл в операторе цикла.
IHI018I SC = ппппп. Объем памяти, запрошенный массивом, не может быть выделен из-за недостатка места.
IHI019I SC = nnnnn. Неодинаковые размерности фактического и формального параметров.
IHI020I SC=nnnnn. Фактический и соответствующий формальный параметры имеют различный класс или тип.
IHI021I SC = nnnnn. Неодинаковое число формальных параметров в описании процедуры и в операторе процедуры или указателе функции.
IHI022I SC=nnnnn. Присваивание формальному параметру невозможно.
IHI023I SC —ппппп. Значение подкоренного выражения меньше нуля.
278
IHI024I SC = nnnnn. Аргумент функции EXP превышает 174673.
IHI025I SC—nnnnn. Аргумент функции LN меньше или равен
нулю.
IHI026I SC=nnnnn. Абсолютное значение аргумента SIN или COS в коротком формате превышает л-218.
IHI027I SC=ппппп. Абсолютное значение аргумента SIN или COS в длинном формате превышает л-250.
IHI028I SC = ппппп PSW=хххххххх хххххххх. Прерывание
и'з-за переполнения с фиксированной точкой.
IHI029I SC=ппппп PSW=хххххххх хххххххх. Прерывание из-за переполнения с плавающей точкой.
IHI030I SC=nnnnn PSW=хххххххх хххххххх. Деление на нуль с фиксированной точкой.
IHI031I SC=nnnnn PSW=xxxxxxxx хххххххх. Деление на
нуль с плавающей точкой.
IHI0331 SC = nnnnn PSW=xxxxxxxx хххххххх.
Программное
прерывание.
IHI0341 SC=nnnnn. Значение указателя переключателя не определено з описании переключателя.
IHI035I SC = nnnnn. При возведении в степень основание меньше или равно нулю.
IHI036I SC=nnnnn. Внутреннее переполнение.
IHI040I SC=nnnnn. Целое число, полученное при преобразовании в целое вещественного числа, вне допустимого интервала.
IHI041I SC=nnnnn DSN = nn. Карта DD для набора данных пп некорректна или пропущена.
IHI043I SC=nnnnn. Недопустимое обращение к процедурам GET/PLT или описательной процедуре.
Приложение 3. ФОРТРАН ЕС ЭВМ. ПЕРЕЧЕНЬ ОСНОВНЫХ СООБЩЕНИЙ ТРАНСЛЯТОРА ОБ ОШИБКАХ
Сообщения об ошибках во время трансляции с фортрана содержат код сообщения вида lEYnnnl, код серьезности — число, которое может принимать значение 0, 4, 8, 16, и текст сообщения.
Коды серьезности означают:
О — некорректность в оформлении модуля;
4 — возможна ошибка на следующем этапе обработки;
8 — ошибка, которая может сделать невозможной обработку на следующем этапе;
16 — грубая ошибка, обычно прекращающая выполнение самой обрабатывающей программы.
IEY001I 8. Недопустимый тип константы, переменной или выражения.
IEY002I 0. Отсутствует метка оператора, следующего за оператором передачи управления.
IEY003I 0. Имя содержит более 6 символов. Приняты во внимание первые 6 символов.
IEY004I 0. Пропущена запятая. Запятая вставлена.
IEY005I 8. Недопустимое использование метки.
IEY006I 8. Метка оператора уже встречалась как метка другого оператора.
IEY007I 8. Одинаковое имя использовано для обозначения различных объектов программной единицы.
IEY008I 8. Нельзя распределить память из-за неправильного использования имени-
279
IEY009I 8. Неправильный порядок следования операторов.
IfaYOlOI 8. Неправильный размер (длина) поля, памяти, числа или метки.
ТТТ\ГЛ11Т о VX__,_____
IEY012I 8. Количество индексов переменной не соответствует размерности массива.
IEY013I 8. Оператор или его часть не согласуется с синтаксисом языка.
IEY014I 0. В операторе явного описания типа или операторе DATA типа константы не соответствует типу переменной, которой константа должна быть присвоена. Константа приведена к типу переменной.
IEY015I 0. Исходный модуль не содержит оператора END. Оператор вставлен.
IEY016I 8. Недопустимое применение оператора.
IEY017I 0. Оператор RETURN записан в главной программной единице или оператор RETURN i появился в подпрограмме-функции. Оператор заменен в главной программной единице оператором STOP, в подпрограмме-функции — оператором RETURN.
IEY018I 4. При обращении к библиотечной подпрограмме указано неверное количество аргументов.
IEY019I 4. В подпрограмме-функции не предусмотрено присваивание значения хотя бы одной переменной с именем входа. Напечатан список таких переменных.
EIY020I 4. Объектам общего блока ххх не может быть распределена память из-за несоблюдения правил использования оператора COMMON и, возможно, оператора EQUIVALENCE.
IEY021I 8. Отсутствует оператор, помеченный меткой, на которую указывает оператор DO. Напечатан список таких меток.
IEY022I 8. Отсутствует оператор, помеченный меткой, на которую указывает другой оператор. Напечатан список таких меток.
IEY023I 4. Для переменных, указанных в операторе EQUIVALENCE, нельзя распределить память из-за противоречий между элементами этого оператора или из-за несоблюдения правил выравнивания. Напечатан список таких переменных.
IEY024I 4. Элемент массива, указанный в операторе EQUIVALENCE, находится вне массива.
IEY025I 4. Неправильное использование массива с переменными верхними границами индексов. Напечатаны имена таких массивов.
IEY026I 4. В блок данных включены переменные, не указанные в операторе COMMON. Напечатан список таких переменных.
IEY027I 8. Оператор имеет более 19 строк продолжения.
IEY029I. Ошибка перфорации. Перфорация игнорирована.
IEY030I 16. Ошибка в объектном модуле при наличии позиции LOAD.
IEY032I 0. Оператор ограничения /* языка управления заданиями предшествует первому оператору исходного модуля. Производится обработка пустого модуля.
IEY033I 0. Между двумя последовательными операторами обнаружено более 30 комментариев. Лишние комментарии игнорированы.
IEY034I 8 или 16. Ошибка ввода-вывода.
1EY035I. Нельзя открыть набор данных с dd-именем ххх из-за отсутствия или неправильного написания оператора DD.
IEY036I 0. Невыполняемый оператор (любой, кроме оператора
FORMAT) помечен. Метка игнорирована,
280
IEY037I 4. Размерность массива определена дважды.
IEY0381 4. Размер константы, указанной в операторе явного описания типа или в операторе DATA в качестве начального значения переменной, превышает длину отведенного для переменной поля памяти.
IEY0391 0. Пропущен оператор RETURN. Оператор вставлен.
IEY040I 8. Ошибка при использовании общего блока в блоке данных.
Приложение 4. ФОРТРАН ЕС ЭВМ. ПЕРЕЧЕНЬ ОСНОВНЫХ СООБЩЕНИЙ ПРИ ВЫПОЛНЕНИИ ПРОГРАММЫ
Сообщения об ошибках во время выполнения программы пользователя на фортране состоят нз кода сообщения вида IHCnnnl и текста сообщения.
IHC207I. Программное прерывание при переполнении порядка. Результат — максимальное допустимое число.
IHC208I. Программное прерывание при исчезновении порядка. Результат — нуль.
IHC209I. Программное прерывание прн проверке деления. Деление не производится.
IHC210I. Программное прерывание. Напечатано старое слово состояния программы ххх, восьмая литера которого является кодом прерывания и указывает причину прерывания.
IHC211I. Неправильный символ в операторе FORMAT. Напечатан символ ххх, ошибочный описатель поля воспринят как конец спецификации формата.
IHC212I. Список форматного ввода-вывода превышает длину логической записи. Напечатан ссылочный номер набора данных ххх.
IHC213I. Список бесформатного ввода превышает длину логической записи. Напечатан ссылочный номер набора данных ххх, остаток списка ввода игнорирован.
IHC214I. При бесформатном вводе-выводе указан тип записи F или U.
IHC215I. При форматном вводе чисел по коду I, Е, F или D обнаружен недопустимый символ. Символ ххх напечатан и заменен нулем.
IHC217I. Обнаружен конец набора данных, а список ввода еще ие исчерпан. Напечатан ссылочный номер набора данных ххх, н начато чтение следующего файла.
IHC218I. Ошибка ввода-вывода. Макрокоманда SYNADAF сформировала текст, содержащий имена задания, пункта задания, программы пользователя и другую информацию локализации ошибки. Запрос ввода-вывода игнорирован. Если ошибка произошла при вводе, то управление передано оператору, метка которого указана в параметре ERR оператора READ.
IHC219I. Загрузочный модуль содержит ссылку на несуществующий набор данных. Напечатано dd-имя ххх или ссылочный номер набора данных ууу. Запрос ввода-вывода игнорирован.
IHC220I. Ссылочный номер набора данных выходит за пределы номеров, установленных при генерации. Напечатан номер ххх, ввод-вывод игнорирован.
IHC225I. При форматном вводе по коду Z обнаружен недопустимый символ ххх. Напечатана запись, содержащая символ, и символ заменен нулем.
281
ШС2301. При выполнении подпрограммы ууу обнаружена ошибка в операторе с внутренним номером ххх. Выполнение прекращено.
IIIC231L Ouvpaiup ьиида-виаида прямого доступа используется для набора данных последовательного доступа или оператор ввода-вывода последовательного доступа применяется для набора данных прямого доступа, или оператор ввода-вывода прямого доступа используется без DEFINE FILE. Напечатан номер набора данных ххх или устройства ххх; ввод-вывод игнорирован.
IHC232I. Номер записи не согласуется с количеством записей в наборе данных. Напечатаны номер записи ххх и ссылочный номер набора данных ууу; ввод-вывод игнорирован.
IHC233I. В операторе DEFINE FILE указана длина записи, превышающая 32*К—1. Напечатан ссылочный иомер набора данных ххх, установлена длина записи 32000.
IHC235I. Ссылочный номер набора данных прямого доступа указан в операторе ввода-вывода последовательного доступа.
IHC236I. Оператор READ обращается к набору данных, который не был создан. Напечатан ссылочный номер набора данных ххх, ввод-вывод игнорирован.
IHC237I. Длина записи ие соответствует длине, указанной в операторе DEFINE FILE. Напечатан ссылочный номер набора данных ххх, ввод-вывод игнорирован.
IHC241I. Возведение целого основания в целую степень ххх при нулевом основании и отрицательном или нулевом показателе степени. Результат — нуль.
IHC242I. См. IHC2.41I для вещественного основания.
IHC243L См. IHC241I для основания двойной точности.
IHC2441. Возведение вещественного основания в вещественную степень ххх прн нулевом основании и отрицательном или нулевом показателе степени. Результат — нуль.
IHC245I. Возведение основания двойной точности в степень ххх двойной точности при нулевом основании н отрицательном или нулевом показателе степени. Результат — нуль.
IHC246I. Возведение комплексного основания длиной 8 байт в целую степень ххх при нулевом основании и отрицательном или нулевом показателе. Результат — нуль.
IHC247I. См. IHC246I для комплексного основания длиной 16 байт.
IHC251L Вычисление квадратного корня вещественного отрицательного числа ххх. Извлечен корень из модуля числа.
IHC252I. Вычисление экспоненты вещественного числа ххх, большего 174.673. Результат — максимальное допустимое число.
IHC253I. Вычисление логарифма вещественного числа ххх, равного или меньшего нуля, или возведение отрицательного основания в вещественную степень. Если ххх = 0, результат — максимальное допустимое число; если ххх 0, результат — логарифм модуля ххх.
IHC254I. Вычисление синуса (косинуса) вещественного числа ххх, модуль которого больше или равен л-218. Результат V2/2.
IHC255I. Вычисление арктангенса частного двух вещественных чисел, равных нулю. Результат — нуль.
IHC256L Вычисление гиперболического синуса (косинуса) вещественного числа ххх, модуль которого больше или равен 174.673. Результат — максимальное допустимое число.
IHC257I. Вычисление арксинуса (арккосинуса) вещественного числа ххх, модуль которого больше 1, Результат — нуль.
282
IHC258I. Вычисление тангенса (котангенса) вещественного числа ххх, модуль которого больше или равен л-218. Резулыат — единица.
IHC259I. Вычисление тангенса (котангенса) вещественного числа ххх, модуль которого находится вблизи особой точки. Результат — максимальное допустимое число.
IHC261I. См. IHC251I для отрицательного числа двойной точности.
IHC262I. См. IHC252I для числа двойной точности.
IHC263I. См. IHC258I для числа двойной точности.
JHC2641. См. IHC254I для числа двойной точности, модуль которого больше или равен л-250.
1HC265I. См. IHC255I для числа двойной точности.
1HC266I. См. IHC2561 для числа двойной точности.
1HC267I. См. IHC257I для числа двойной точности.
IHC268I. См. HC258I для числа двойной точности, модуль которого больше или равен л-250.
IHC269I. См. IHC259I для числа двойной точности.
1HC271I. Вычисление экспоненты комплексного числа длиной 8 байт вещественная часть которого ххх превышает 174.673. Результат — произведение максимального допустимого числа на (cos г + i sin z), где i — мнимая часть аргумента.
IHC272I. Вычисление экспоненты комплексного числа длиной 8 байт с мнимой частью ххх, модуль которого больше или равен л-2’8. Результат — нули в вещественной и мнимой частях.
1HC273I. Вычисление логарифма комплексного числа длиной 8 байт, вещественная и мнимая часть которого равны нулю. Результат— максимальное допустимое число в вещественной части, нуль в мнимой части.
IHC274I. Вычисление синуса (косинуса) комплексного числа длиной 8 байт с вещественной частью ххх, модуль которой больше или равен л-218. Результат— нули в вещественной и мнимой частях.
IHC275I. Вычисление синуса (косинуса) комплексного числа длиной 8 байт с мнимой частью ххх, модуль которого превышает 174.673.
IHC281I. См. IHC271I для комплексного числа длиной 16 байт.
IHC2821. См. IHC272I для комплексного числа длиной 16 бант с модулем мнимой части, большим или равным л-25С.
1HC283I См. IHC273I для комплексного числа длиной 16 байт.
IHC284I. См. IHC274I для комплексного числа длиной 16 байт с модулем вещественной части, большим или равным 2.
IHC285I. См. 1HC275I для комплексного числа длиной 16 байт.
1HC900I. Количество ошибок с номером ххх достигло предельно допустимого значения. Выполнение прекращено.
СОДЕРЖАНИЕ
Предисловие . .......................................... 3
Введение. Общее положение о практикуме............., . 5
Часть I. ОБЩИЙ ПРАКТИКУМ
Задание 1. Простейшие конструкции алгола.................9
Задание 2. Основные типы операторов алгола. Итерационные методы и ряды.......................................13
Задание 3. Алгол, действия над массивами................16
Задание 4. Процедуры в алголе. Пакетная обработка данных и язык управления заданиями в ОС. Решение трансцендентных уравнений...........................19
Задание 5. Процедуры в алголе. Библиотеки и редакторы программных текстов. Вычисление определенных интегралов .............................................21
Задание 6. Алгол, действия над массивами. Библиотеки и редакторы программных текстов. Решение систем линейных алгебраических уравнений ... 26
Задание 7. Фортран, простейшие конструкции языка ... 32
Задание 8. Фортран. Основные конструкции языка, форматный ввод-вывод. Удаленные терминалы .... 38
Задание 9. Машинно-ориеитнроваиный язык (автокод); основные конструкции и возможности........................41
Задание 10. Автокод; основные возможности. Простейшие структуры данных .......................................45
Задание 11. Решение задач в режиме диалога с ЭВМ ... 48
Задание 12. Фортран. Модульное программирование, выдача графиков................................................59
Задание 13. Модульное программирование. Библиотека модулей. Решение систем обыкновенных дифференциальных уравнений.................................... 62
Часть П. СПЕЦИАЛИЗИРОВАННЫЙ ПРАКТИКУМ
Задание А-1. Алгоритмические языки и трансляторы. Отладка программ. Методы приближения и минимизации функций.......................................67
Задание А-2. Численное решение краевой задачи для обыкновенного дифференциального уравнения второго порядка. Метод прогонки............................73
Задание Б. 1. Модульное программирование, библиотечные модули. Решение задач линейного программирования ................................................78
Задание Б-2. Автокод. Обработка символьной информ_ации. 84
284
КАФЕДРА АЛГОРИТМИЧЕСКИХ ЯЗЫКОВ
Задание АЯ-1. Реализация языка для обработки строк ... 97 Задание АЯ-2. Использование макросредств при построении, трансляторов ....................................... • 108
КАФЕДРА АВТОМАТИЗАЦИИ СИСТЕМ ВЫЧИСЛИТЕЛЬНЫХ КОМПЛЕКСОВ
Задание АСВК-1. Разработка программ, используемых в режиме диалога...........................................ИЗ
КАФЕДРА СИСТЕМНОГО ПРОГРАММИРОВАНИЯ Задание СП-1. Макроассемблер ........................ 121
КАФЕДРА МАТЕМАТИЧЕСКОЙ КИБЕРНЕТИКИ
Задание МК-1. Конъюнктивные и дизъюнктивные нормальные формы булевских выражений ..... . . 125
3 а д а н и е МК-2. Приближенное решение задачи о покрытии 126 Задание МК-3. Построение кратчайшего связывающего де-
рева ..................................128
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
Задание ВМ-1. Численное решение краевых задач для уравнений с частными производными..........................129
Задание ВМ-2. Итерационные методы решения задачи Дирихле для эллиптического уравнения в двумерной области.........................................141
3 а д а н и е ВМ-3. Численное решение задачи Штурма — Лиу-вилля для обыкновенного дифференциального уравнения ........................................... 147
Задание ВА1-4. Решение интегрального уравнения Фредгольма I рода методом регуляризации ..... 153
КАФЕДРА МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Задание МС-1. Статистический анализ данных в линейной регрессионной модели...................................156
Задание МС-2. Процессы массового обслуживания .... 163 КАФЕДРА ИССЛЕДОВАНИЯ ОПЕРАЦИИ
Задание ИО-1. Решение задач оптимального распределения ресурсов...............................................171
Задание ИО-2. Нахождение множеств оптимальных стратегий матричных игр специального вида........................174
Задание ИО-3. Построение сетевых графиков..............176
Задание ИО-4. Методы расчета оптимальных транспортных маршрутов....................................... . > « 178
КАФЕДРА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
3 а д а н и е ОУ-1. Линейная задача управляемости . . . . , ,181 Задание ОУ-2. Время быстродействия в линейной задаче оптимального управления..................................185
Задание ОУ-3. Численный метод решения линейной задачи управления с квадратичным критерием качества 188
285
Задание ОУ-4. Решение линейных задач быстродействия методом продолжения по параметру ..... 193
Задание ОУ-5. Численное решение задачи преследовании . . 202
Часть III. ИНСТРУКЦИИ ДЛЯ ПРАКТИКУМА
Инструкция по языку управления заданиями ОС ЕС.207
Инструкция по языку алгол ОС ЕС ... .........212
Инструкция по языку фортран ОС ЕС.......................216
Инструкция по использованию архива текстов..............222
Инструкция по диагностике в ОС ЕС.......................228
Описание терминалов.....................................230
Инструкция по работе в системе PRIMUS . . :.............240
Инструкция по работе в системе КРАБ............256
Инструкция по автокоду БЕМШ.............................267
Приложение 1. Алгол ЕС ЭВМ. Перечень основных сообщений транслятора об ошибках .... 275
Приложение 2. Алгол ЕС ЭВМ. Перечень основных сообщений при выполнении программы . . . 278
Приложение 3. Фортран ЕС ЭВМ. Перечень основных сообщений транслятора об ошибках . . . 279
Приложение 4. Фортран ЕС ЭВМ. Перечень основных сообщений при выполнении программы . . 281
Николай Павлович Трифонов, Евгений Николаевич Пасхин
ПРАКТИКУМ РАБОТЫ НА ЭВМ
Редакторы Н. Н. Васина, Н. Л, Королева.
Технич. редактор С. Я. Шкляр, ' Корректор Г. В. Подводьская.
И Б № 12080
Сдано в набор 29.01.82. Подписано к печати 30.09.82.
Т-18956, Формат 84ХЮ8/32. Бумага тип. № 2. Литера-
турная гарнитура. Высокая печать. Услови. печ. л. 15,12.
Уч.-изд. л. 18,72. Тираж 56000 эка, Заказ № 88.
Цена 70 коп.
Издательство «Наука»
Главная редакция физико-математической литературы 117071, Москва, Б-71, Ленинский проспект, 15
Ленинградская типография № 2 головное предприятие ордена Трудового Красного Знамени Ленинградского объединения «Техническая книга» им. Евгении Соколовой Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли. 198052, Ленинград, Л-52, Измайловский проспект, 29«
ИЗДАТЕЛЬСТВО «НАУКА» ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
117071, Москва, В-71, Ленинский проспект, 15
ГОТОВЯТСЯ К ПЕЧАТИ
Бухтияров А. М,, Фролов Г. Д., Олюнии В. Ю. Сборник задач по программированию на языке ПЛ-1.
Фролов Г. Д., Олюнии. В. Ю. Практический курс программирования на языке ПЛ-1.
Пярнпуу А. А. Программирование на алгорит-. мических языках.
Предварительные заказы на эти книги принимаются без ограничений магазинами Книготорга и Академкниги.