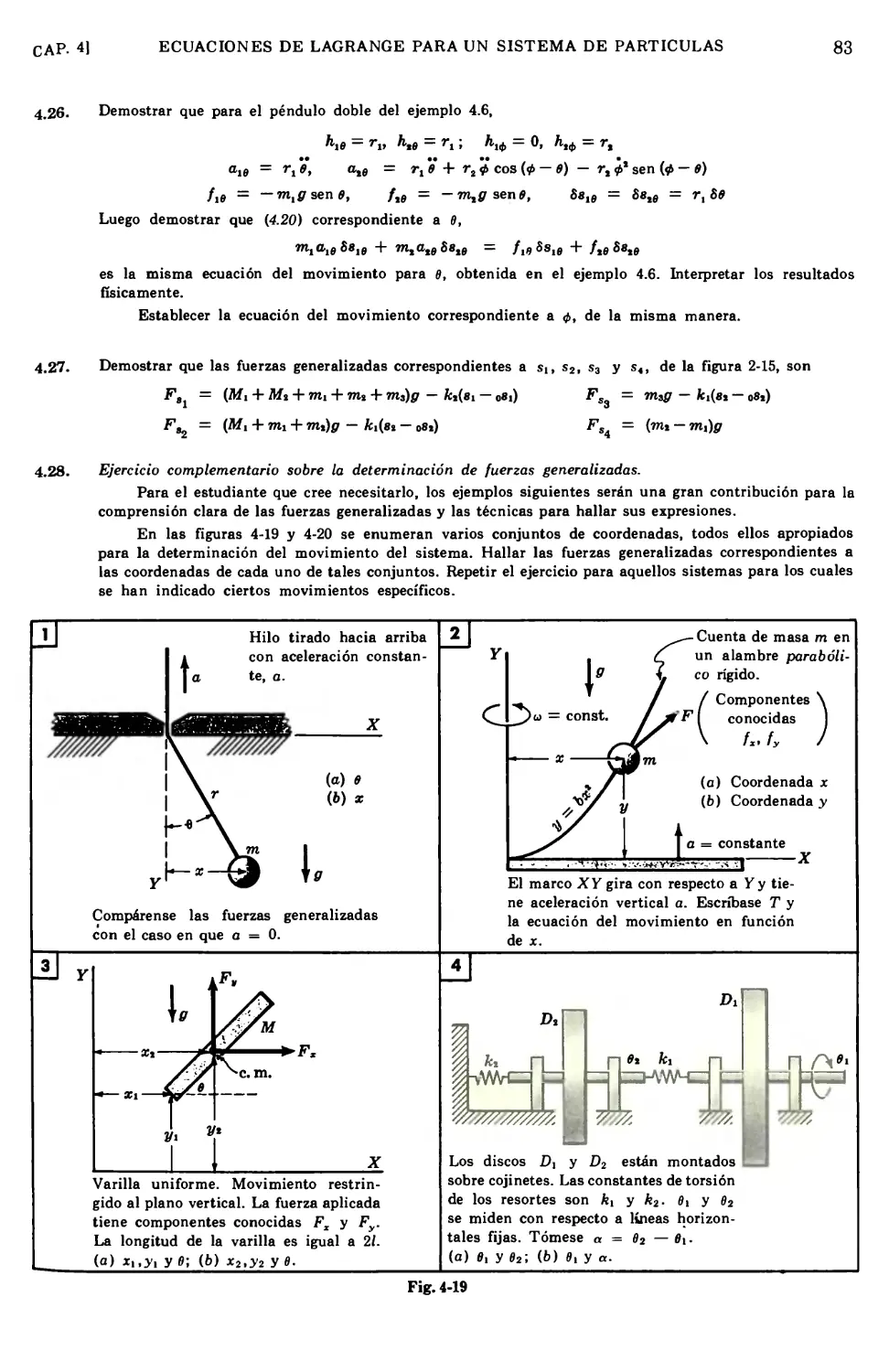
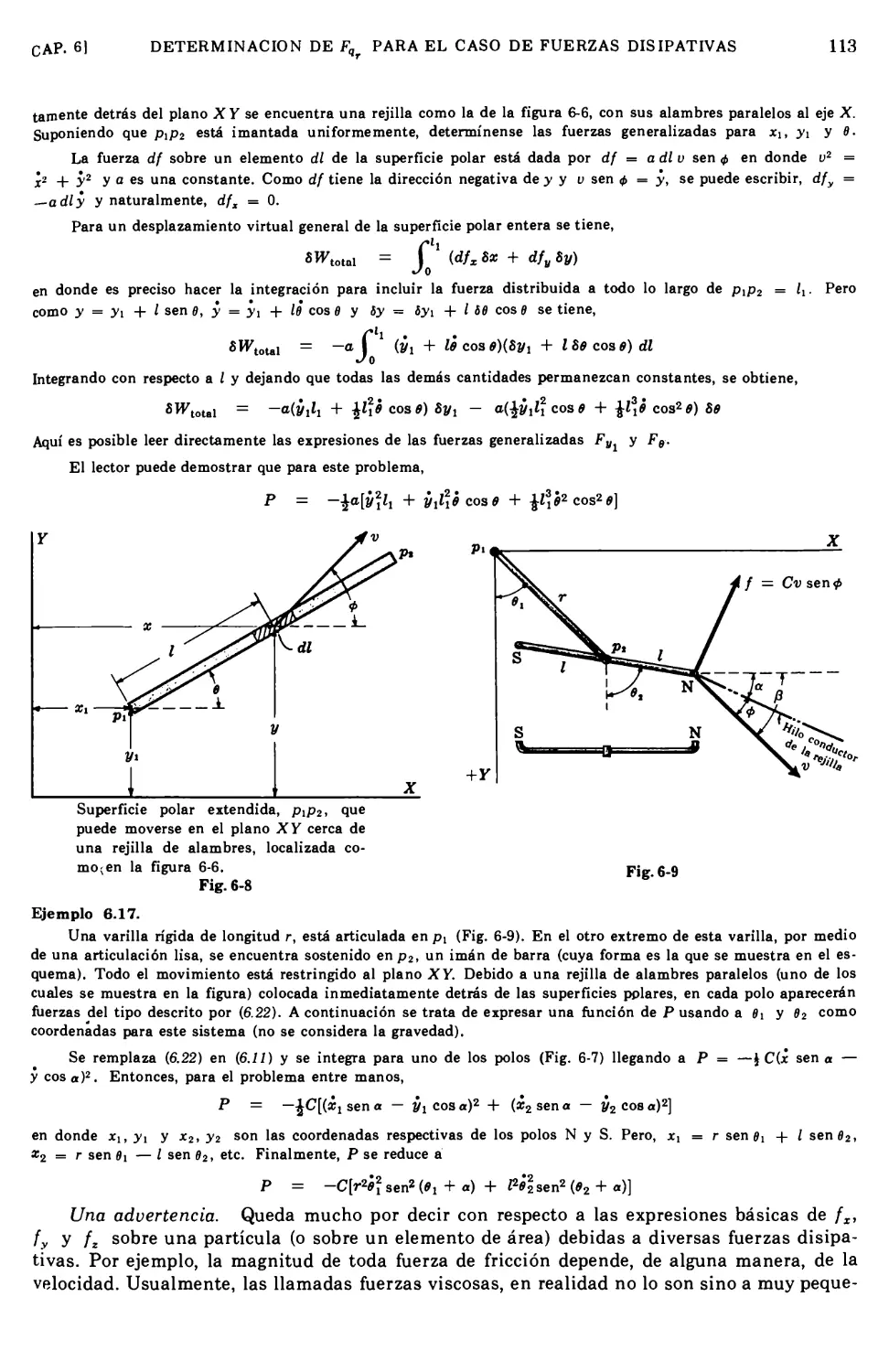
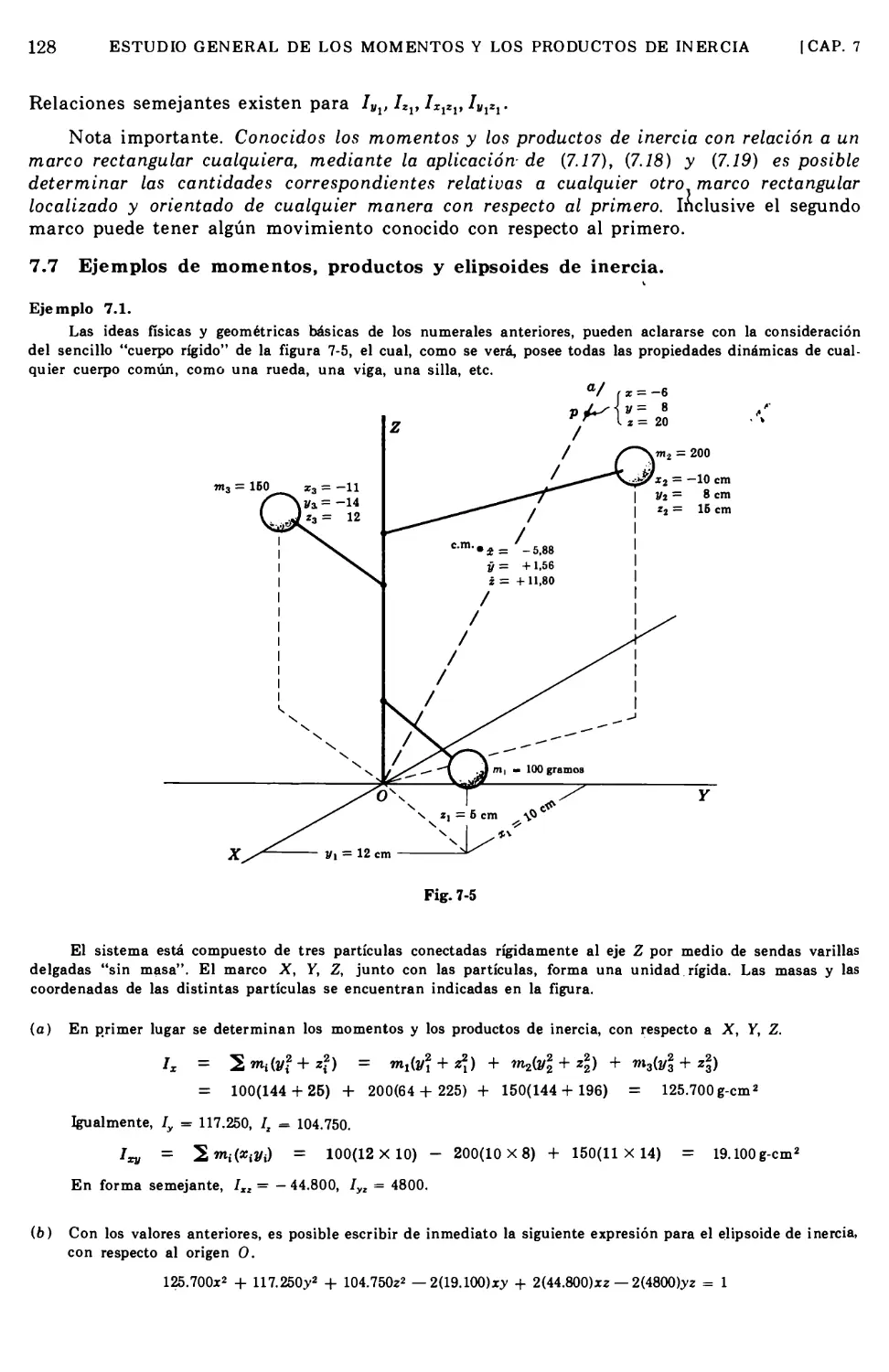
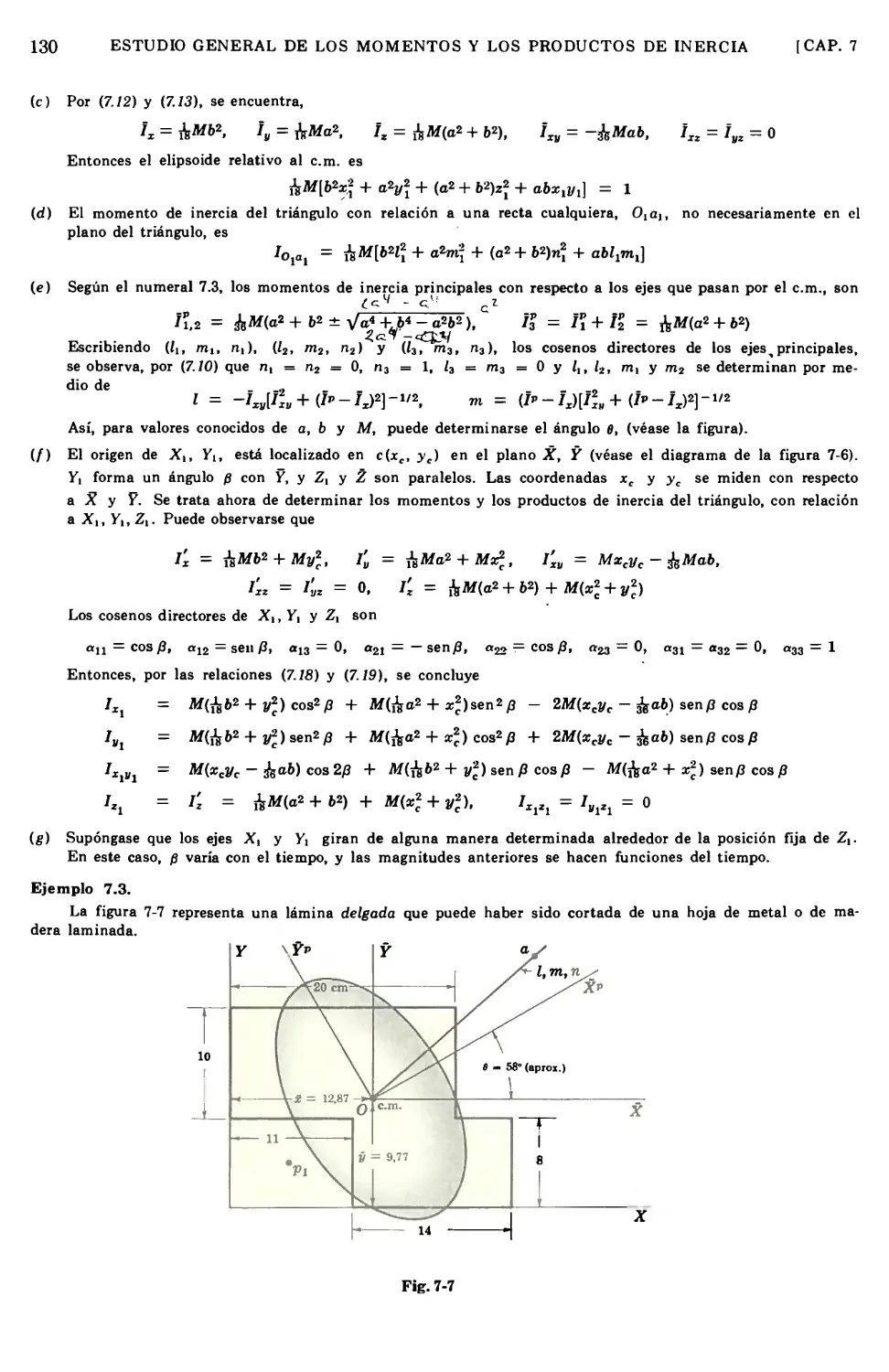
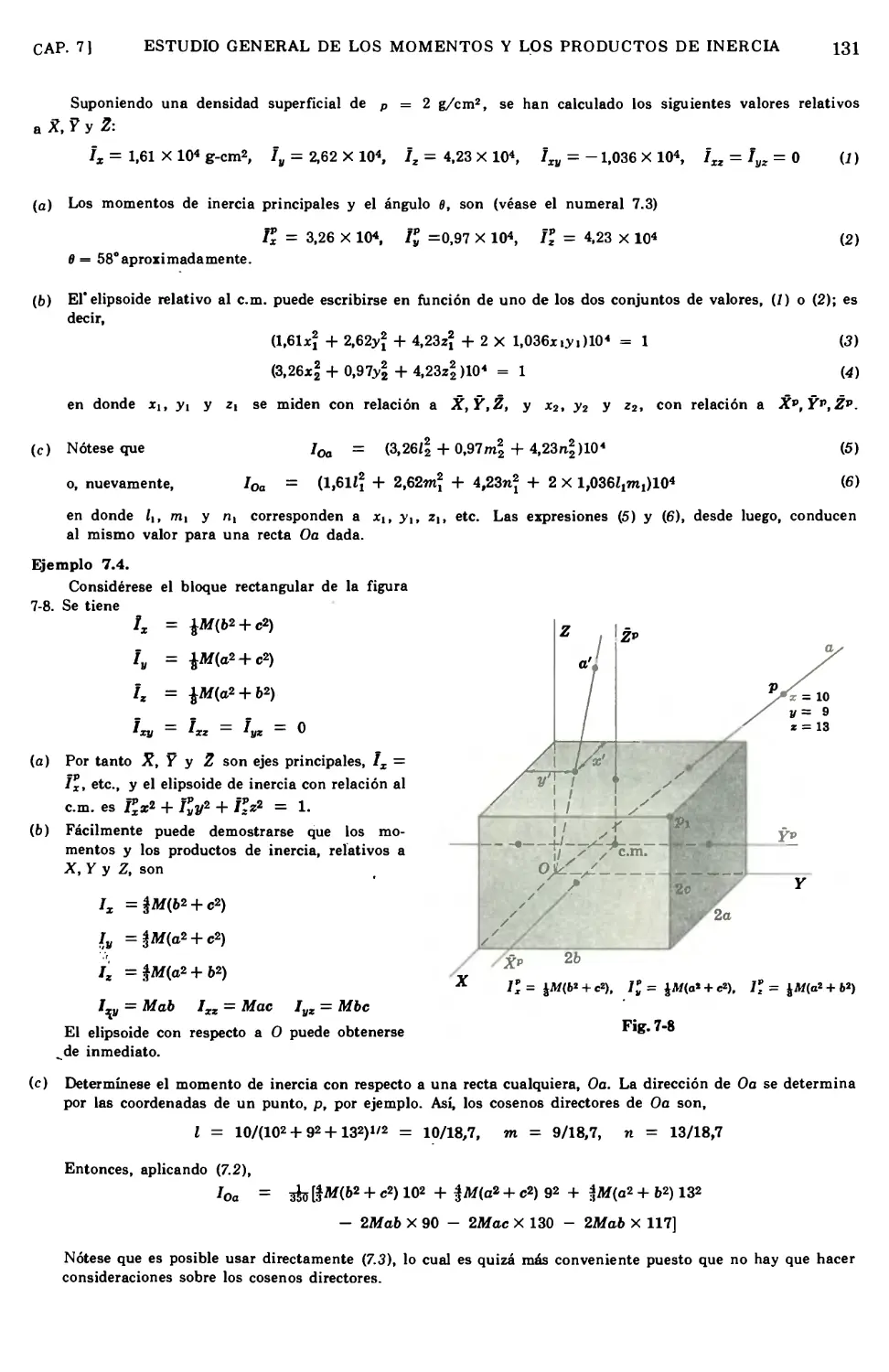
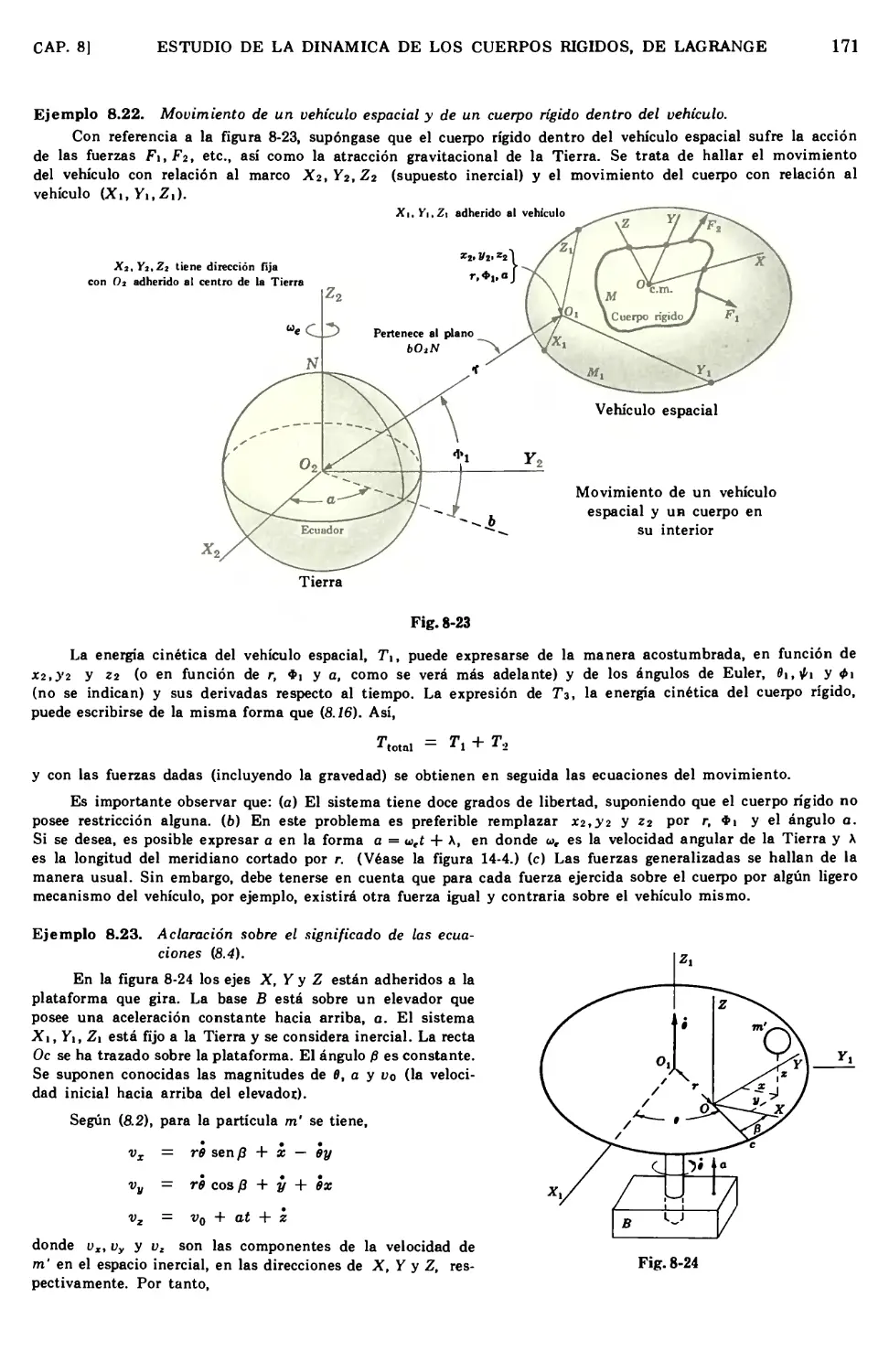
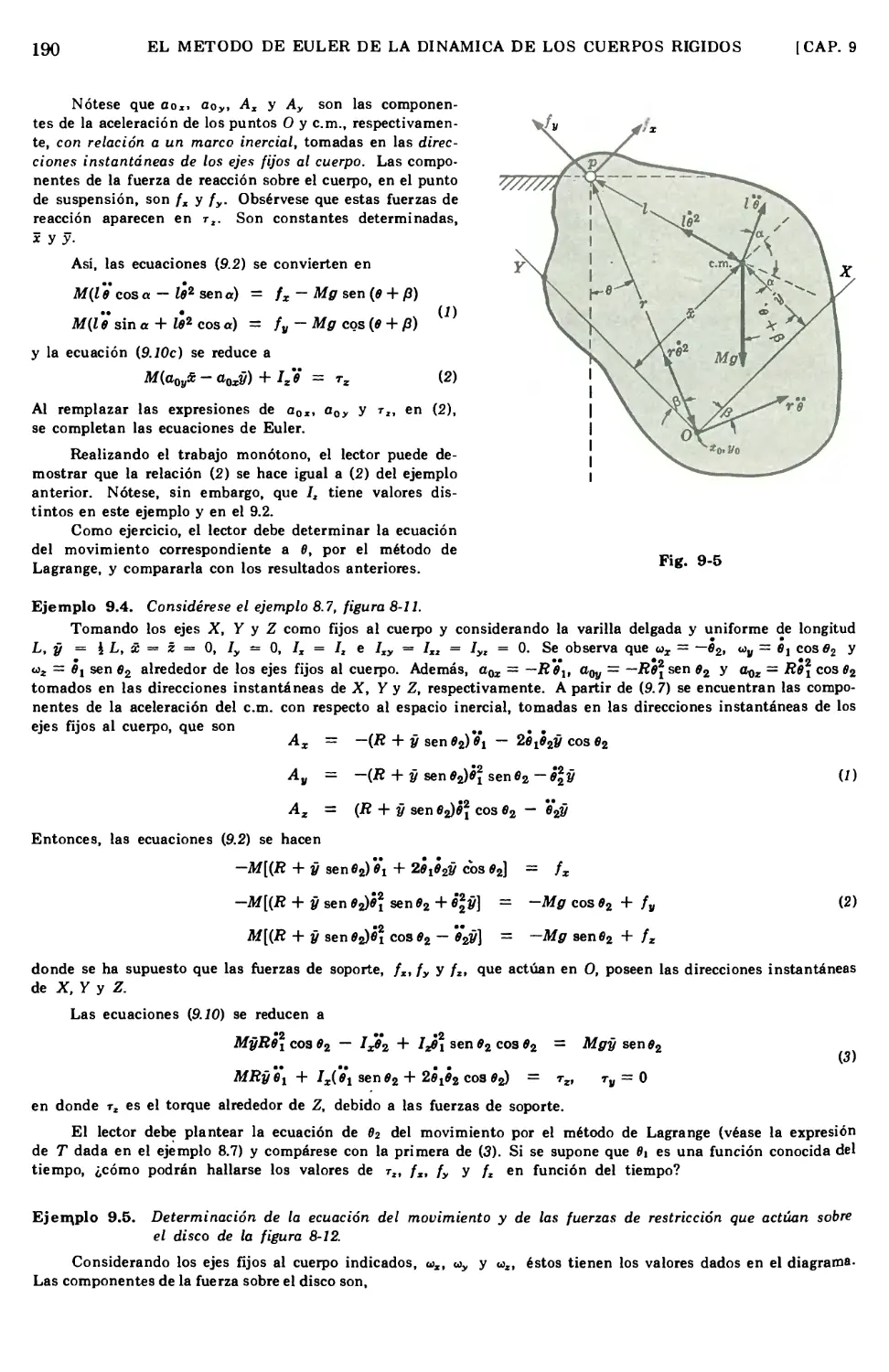
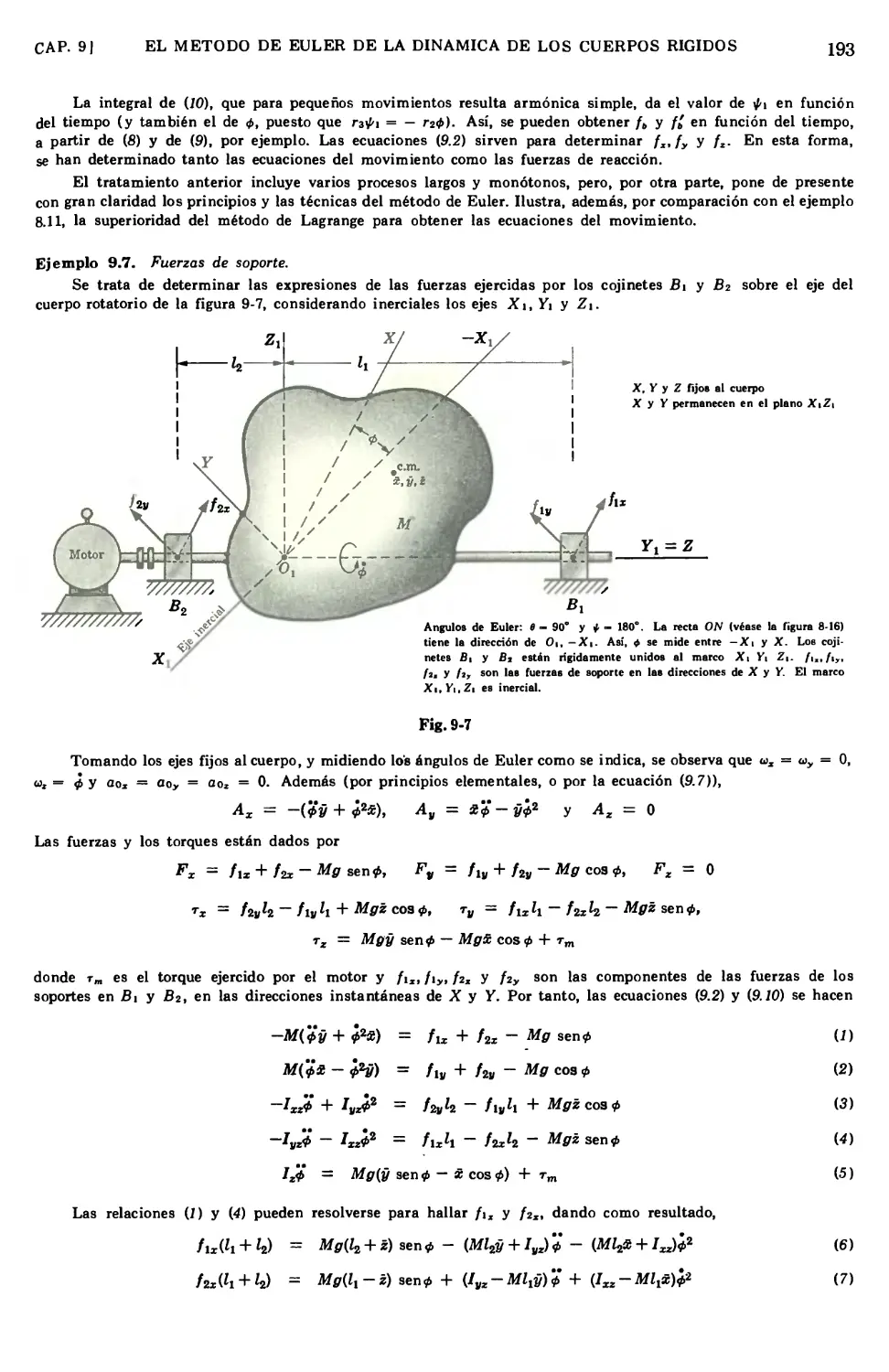
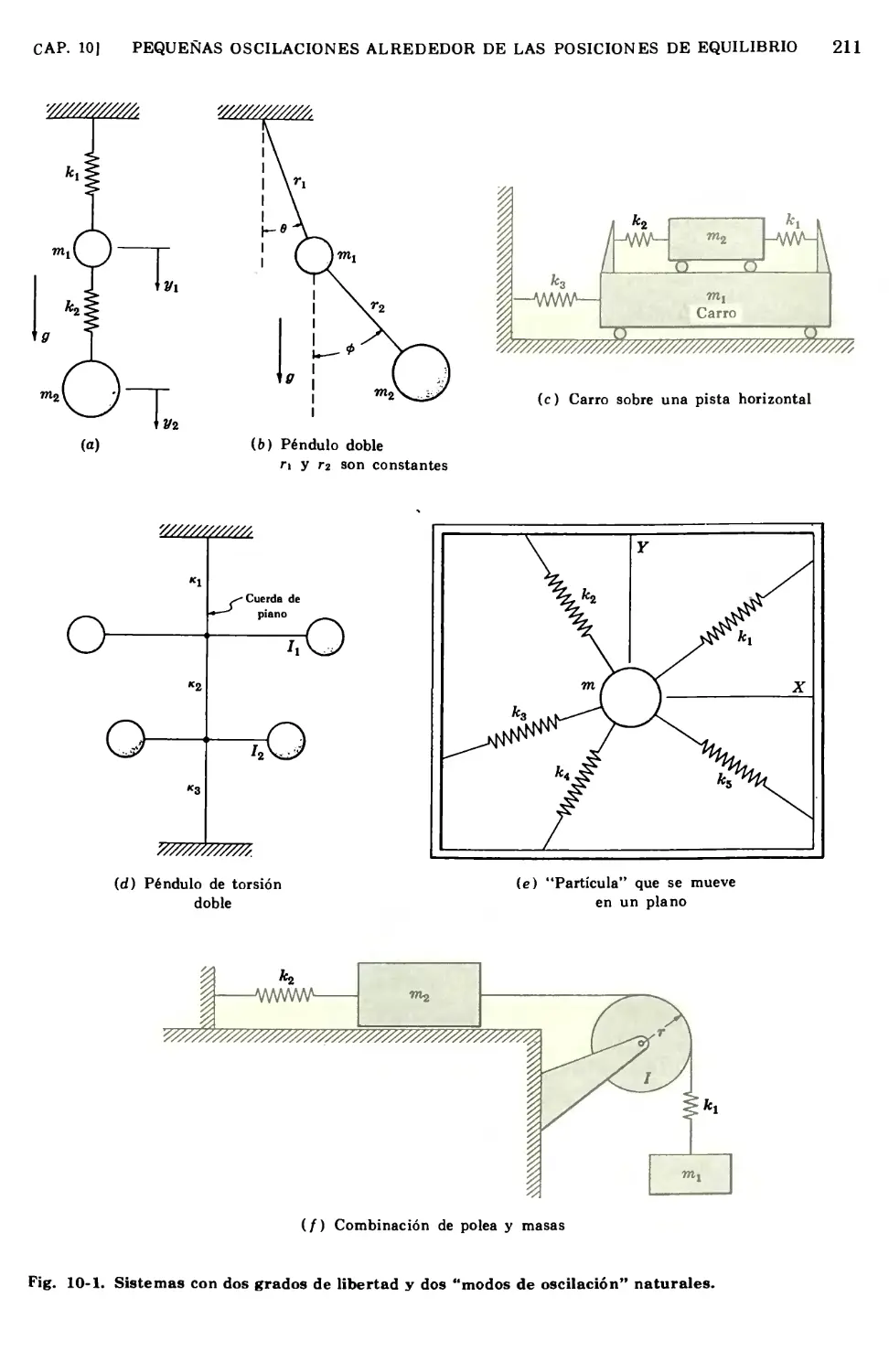
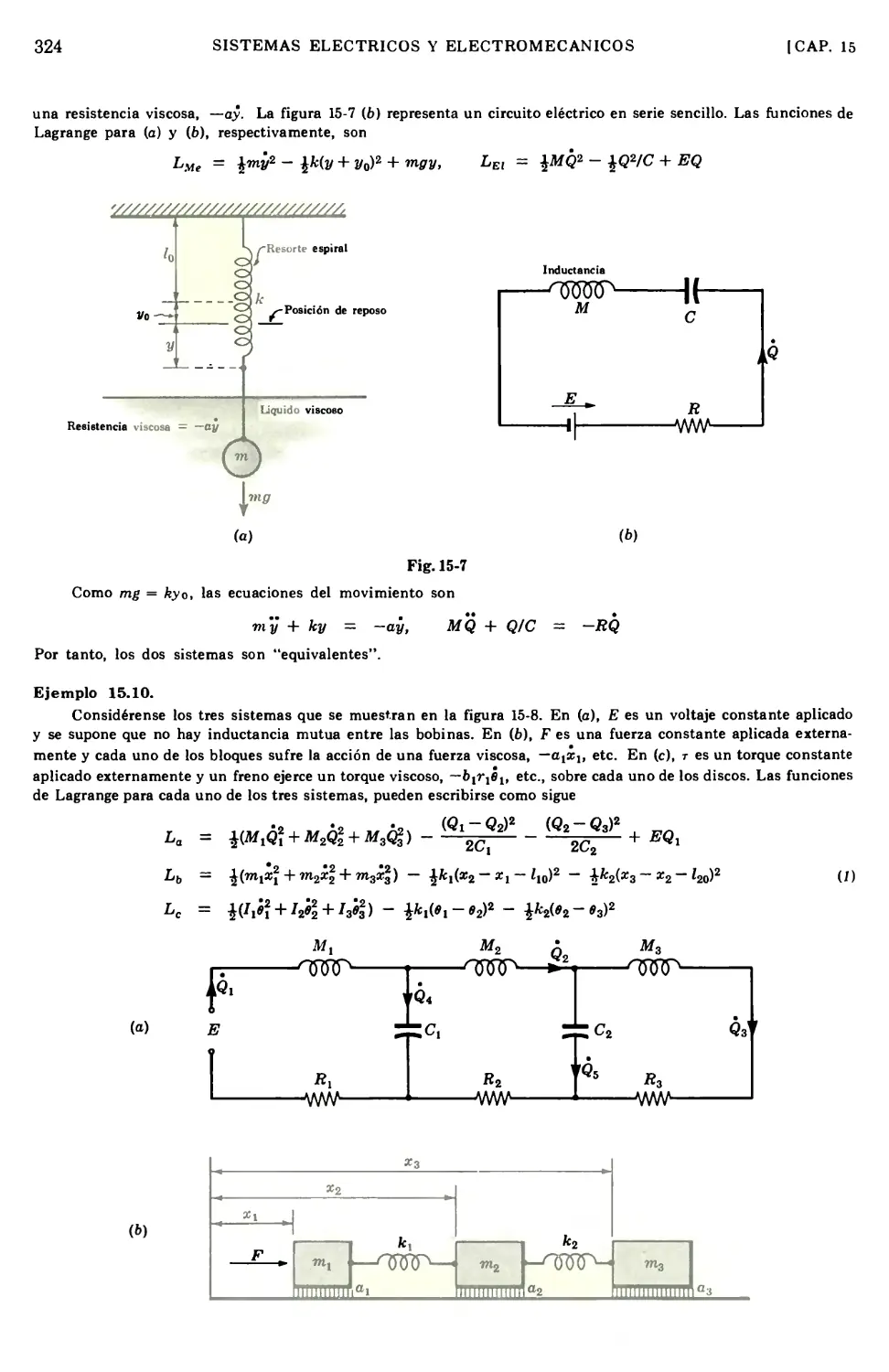
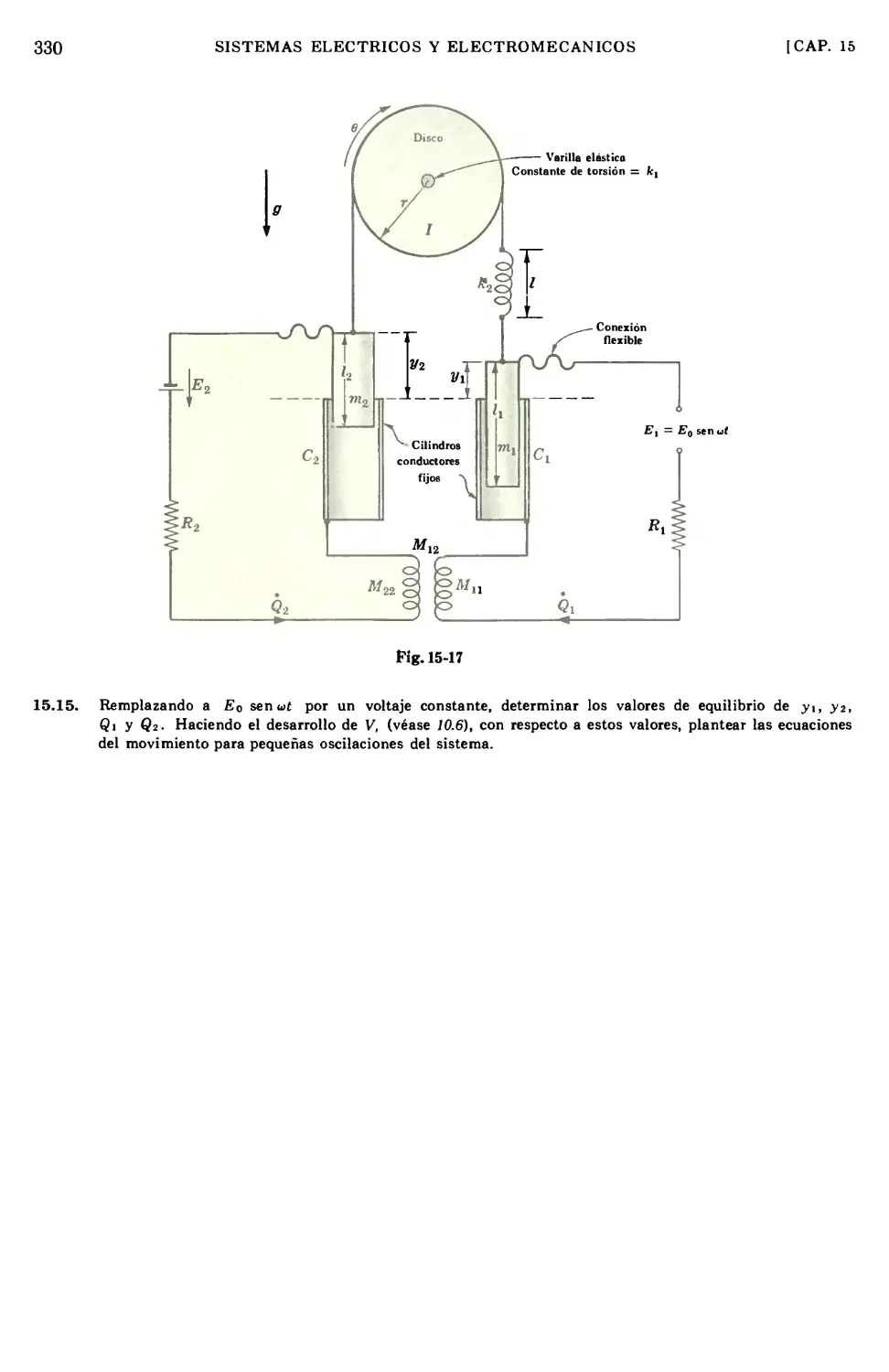
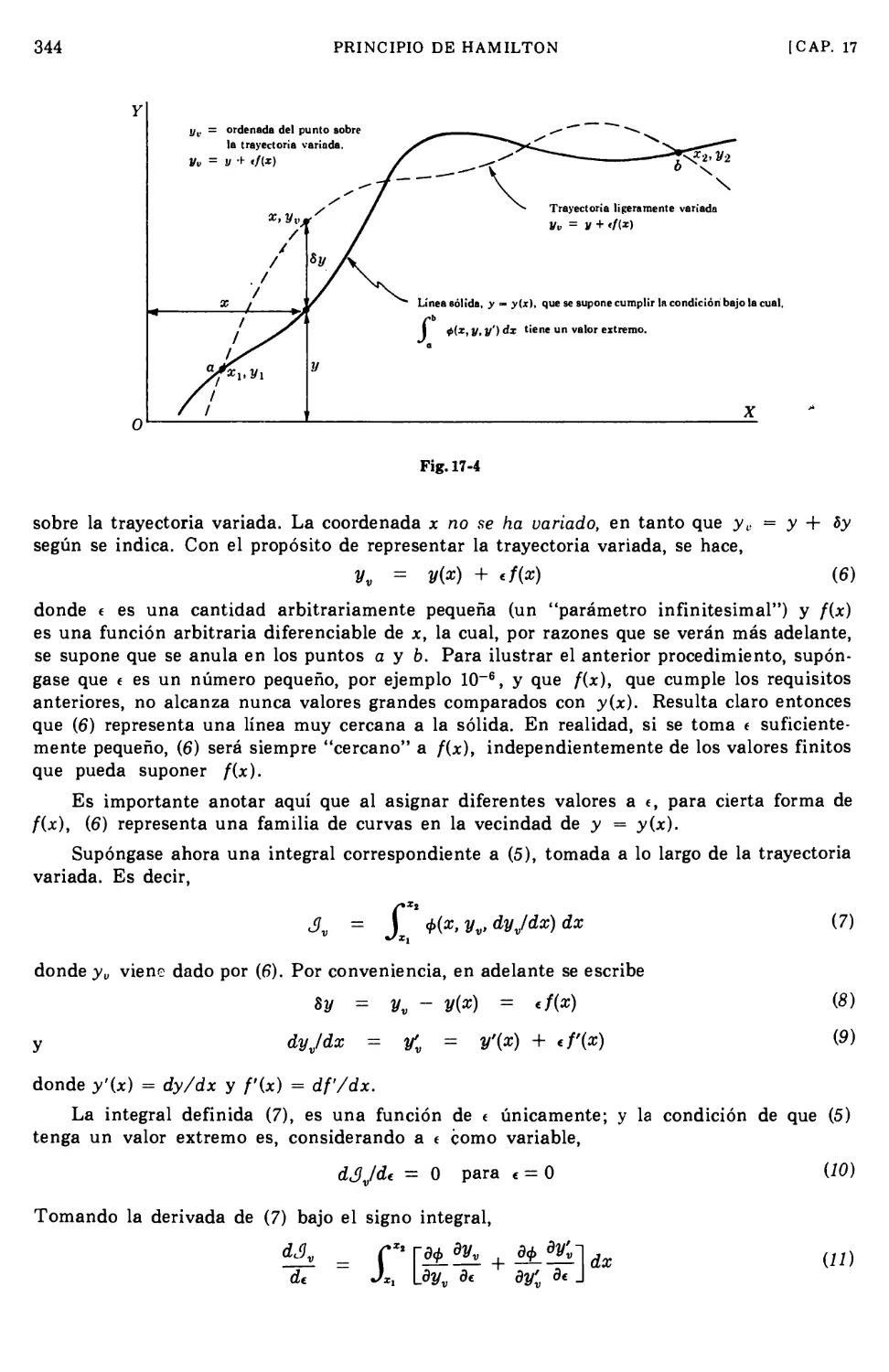
Text
SERIE DE COMPENDIOS SCHAUM
TEORÍA Y PROBLEMAS
DE
DINÁMICA DE LAGRANGE
con un estudio de
Ecuaciones del movimiento de Euler
Principio y Ecuaciones de Hamilton
POR
DARÉ A. WELLS, Ph.D.
Profesor de Física
University of Cincihnati
TRADUCCIÓN Y ADAPTACIÓN
Francisco Gnecco Calvo, ic. ms. phd.
Instituto Colombiano para el Fomento
de la Educación Superior
- •*..
LIBROS McGRAW-HILL
MÉXICO . PANAMÁ BO'&OTA"" SAO PAULO NIJEVA YORK
LONDRES TORONTO SIDNEY JOHANNESBuác
DUSSELDORF SINGAPUR
Copyright © 1972, por Libros McGraw-Hill de México, S. A. de C. V.
Todos los derechos reservados. Impreso en Colombia.
Queda terminantemente prohibido reproducir este libro,
total o parcialmente, sin permiso expreso de los editores.
91974
Traducido de la primera edición del original publicado en inglés
Copyright © 1967, by McGraw-Hill Book Company, Inc., U.S.A.
123456789 CyC-72 098765432
Fm- °io lo'S
Prólogo
El método de la dinámica de Lagrange es aplicable a un gran conjunto de problemas
de partículas y de cuerpos rígidos que abarca desde los más sencillos hasta los más
complejos. Las ventajas de este procedimiento sobre los métodos convencionales, por las razones
que se indican a continuación, son de gran importancia. Esto es válido no solamente en el
amplio campo de las aplicaciones sino también en una gran área de la investigación y de las
consideraciones teóricas.
En gran parte, el método de Lagrange reduce todo el campo de la estática, de la
dinámica de partículas y de la dinámica de cuerpos rígidos a un solo procedimiento que implica
las mismas, etapas básicas, independientemente del número de masas consideradas, del tipo
de coordenadas empleadas, del número de restricciones sobre el sistema y de que las
restricciones y el marco de referencia estén o no en movimiento. Por tanto, los métodos especiales
se remplazan por un método general único.
Puede utilizarse una gran variedad de coordenadas generalizadas. Es decir, que las
ecuaciones de Lagrange son válidas para cualquier sistema de coordenadas (inerciales o una
combinación de inerciales y no inerciales) que resulten adecuadas para representar la
configuración del sistema. Estas conducen directamente a las ecuaciones del movimiento en
cualquier sistema de coordenadas que se escoja. No se requiere introducir primero el método
vectorial formal y luego hacer la traducción a las coordenadas deseadas.
Las fuerzas de restricción, para los casos de restricciones holónomas lisas, quedan
eliminadas automáticamente y no aparecen en las ecuaciones de Lagrange. La eliminación de
estas fuerzas por métodos convencionales pueden presentar dificultades enormes.
El procedimiento de Lagrange está basado, en gran parte, en magnitudes escalares:
energía cinética, energía potencial, trabajo virtual, y en muchos casos, la función de
potencia. Todas ellas pueden expresarse generalmente sin ninguna dificultad en cualquier sistema
de coordenadas adecuado. Desde luego, la naturaleza vectorial de la fuerza, la velocidad, la
aceleración, etc., debe tenerse en cuenta en el estudio de los problemas de dinámica. Sin
embargo, las ecuaciones de Lagrange, basadas en las anteriores magnitudes escalares tienen
en cuenta en forma completa y automática estas magnitudes vectoriales sin necesidad de
recurrir a métodos vectoriales formales. Por complejo que sea un sistema, los términos de la
ecuación del movimiento de Lagrange consisten en las componentes adecuadas de la fuerza
y la aceleración expresadas en el sistema de coordenadas escogido.
Afortunadamente, las ideas básicas empleadas en la deducción de las ecuaciones de
Lagrange son sencillas y de fácil comprensión. Si se presentan sin adornos académicos ni
terminología rebuscada, las únicas dificultades que puede encontrar el estudiante promedio,
son las que provienen de su deficiente preparación en los fundamentos. La aplicación de las
ecuaciones de Lagrange a los problemas prácticos resulta notablemente sencilla aun cuando
se trata de sistemas complicados. Excepto en los problemas muy elementales, el
procedimiento es en general mucho más sencillo y requiere invertir menos tiempo que ciertos
métodos especiales, "concisos" o "elegantes" hallados en muchos tratados comunes. Además, los
detalles físicos se hacen resaltar y se ponen en evidencia con gran claridad.
Finalmente, debe mencionarse que el método de Lagrange es aplicable a otros campos
diferentes de la dinámica. Resulta especialmente útil, por ejemplo, en el estudio de sistemas
electromecánicos.
Este libro pretende presentar con claridad los principios básicos de la dinámica de
Lagrange y dar al lector suficiente entrenamiento en las técnicas, físicas y matemáticas, necesarias
para aplicar sus ecuaciones. La materia abarcada permite dejar una base firme para
posteriores estudios de aquellos temas que salvan la distancia entre la mecánica clásica y la
cuántica. La forma de la presentación, así como los ejemplos, problemas y experimentos
sugeridos, se desarrollaron durante los largos años en que el autor dictó el curso de
dinámica de Lagrange a los estudiantes de la Universidad de Cincinnati.
No se ha intentado incluir aquí todo el panorama de esta materia tan amplia. Se ha
dado relativamente poco espacio a la solución de las ecuaciones diferenciales del movimiento.
Los métodos vectoriales formales no han recibido mucha importancia; sólo se les menciona
en unas pocas secciones. Sin embargo, por las razones establecidas en el capítulo 18, las
magnitudes vectoriales y tensoriales más importantes que aparecen en el libro se enumeran allí
en la notación formal adecuada.
Los experimentos sugeridos al final de algunos capítulos pueden ser de gran utilidad.
Naturalmente se requieren tratamientos matemáticos formales, pero nada despierta mayor
interés ni da más "realidad" a la dinámica que un experimento real, en el que los resultados
concuerdan bien con los valores calculados.
El libro se ha dirigido principalmente a los estudiantes de último año de física,
ingeniería, química y matemáticas aplicadas, a los que inician los estudios de postgrado en estas
mismas disciplinas, y a aquellos científicos e ingenieros en ejercicio que deseen familiarizarse
con los poderosos métodos de Lagrange, por medio del estudio individual. Puede servir
como texto en un curso formal o como suplemento de otros textos.
El autor desea expresar su gratitud al doctor Solomon Schwebel por sus valiosas
sugerencias y por su revisión crítica de algunas partes del manuscrito, al señor Chester Carpenter
por su revisión del capítulo 18, al señor Jerome F. Wagner por su ayuda en la comprobación
de ejemplos y problemas, al señor Lester Solimán y a su señora, por el excelente trabajo
realizado al copiar a máquina el manuscrito, y al señor Daniel Schaum, el editor, por su interés,
su estímulo y su cooperación no superada.
D. A. WELLS
TABLA DE MATERIAS
Capítulo
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
Página
FUNDAMENTOS BÁSICOS, I i
De la necesidad de fundamentos básicos 1
Leyes básicas de la mecánica clásica de Newton y varias maneras de expresarlas 1
Selección de la formulación 1
Origen de las leyes básicas 1
De los conceptos y magnitudes básicas empleadas 2
.Condiciones de validez de las leyes de Newton 2
Dos tipos generales de problemas de dinámica 5
Métodos generales para solucionar problemas de dinámica 6
Ejemplo ilustrativo de los numerales 1.7 y 1.8 7
FUNDAMENTOS BÁSICOS, II 11
Observaciones introductorias 11
Sistemas de coordenadas y ecuaciones de trasformación 11
Coordenadas generalizadas. Grados de libertad 16
Grados de restricción, ecuaciones de restricción, coordenadas superfluas 19
Restricciones móviles 20
Ecuaciones de trasformación "reducidas" 20
Velocidad expresada en coordenadas generalizadas 21
Trabajo y energía cinética 24
Ejemplos ilustrativos de la energía cinética 26
Teorema del "centro de masa" para la energía cinética 27
Una expresión general para la energía cinética dep partículas 28
Definición de aceleración y ejemplos 30
"Desplazamiento virtual" y "trabajo virtual" 32
Ejemplos ilustrativos de las consideraciones anteriores (a), (b) y (c) 33
ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA 42
UNA PARTÍCULA
Consideraciones preliminares 42
Deducción de las ecuaciones de Lagrange para una partícula, sin coordenadas
ni restricciones móviles 42
Compendio de detalles importantes relacionados con las ecuaciones de Lagrange . 42
Integración de las ecuaciones diferenciales del movimiento 47
Ejemplos ilustrativos 47
Ecuaciones de Lagrange para una partícula, suponiendo un marco de referencia
móvil, restricciones móviles, o ambas condiciones simultáneamente 49
De la energía cinética, las fuerzas generalizadas y otros tópicos, cuando el marco
de referencia, las restricciones, o ambos se mueven 50
Ejemplos ilustrativos 50
Determinación de la aceleración por medio de las ecuaciones de Lagrange 52
Una consideración adicional sobre las ecuaciones de Lagrange 53
Experimentos sugeridos 54
Capítulo
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
Capítulo
3.1
3.2
3.3
3.4
3.5
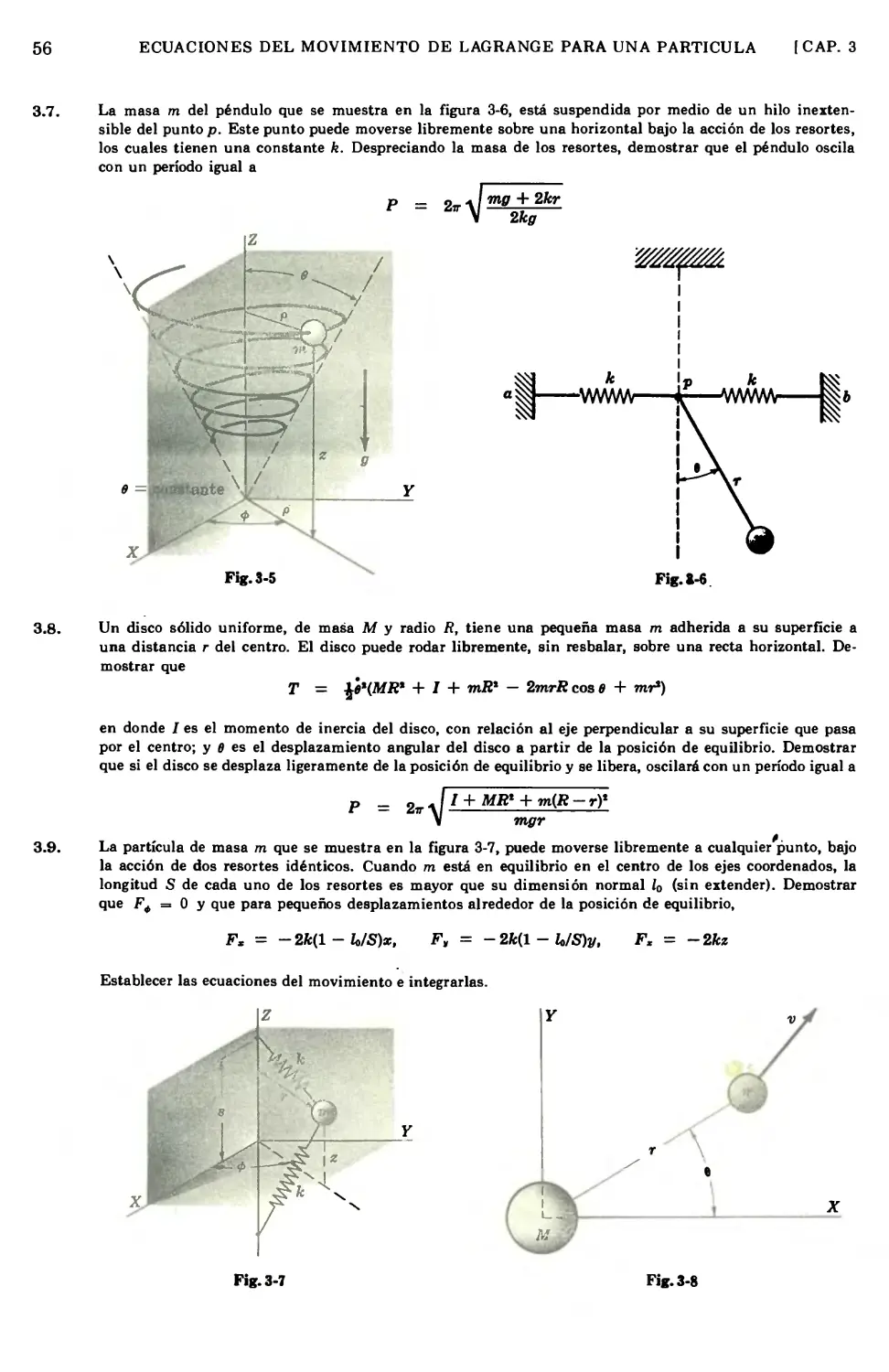
3.6
3.8
3.9
3.10
3.11
TABLA DE MATERIAS
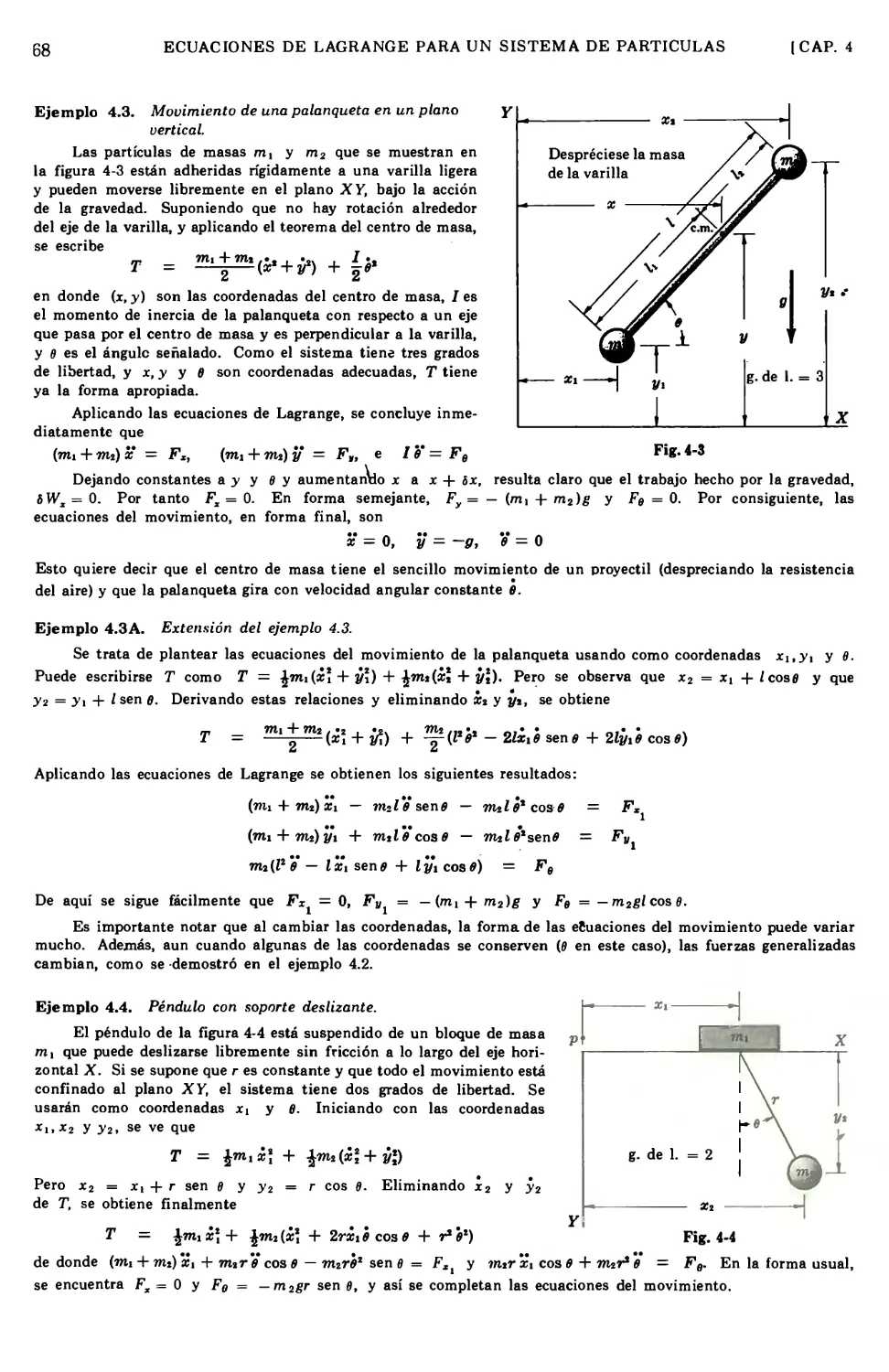
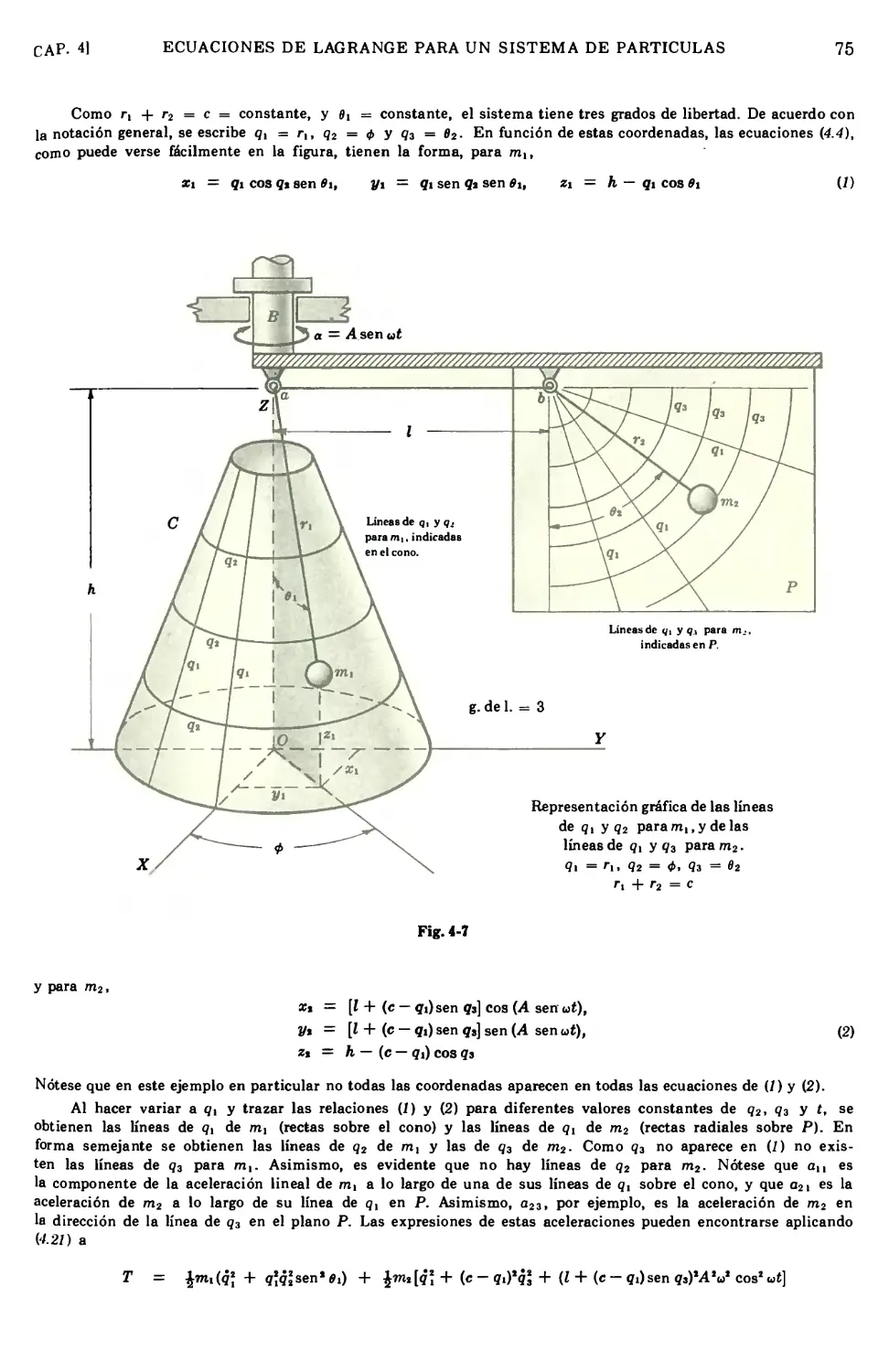
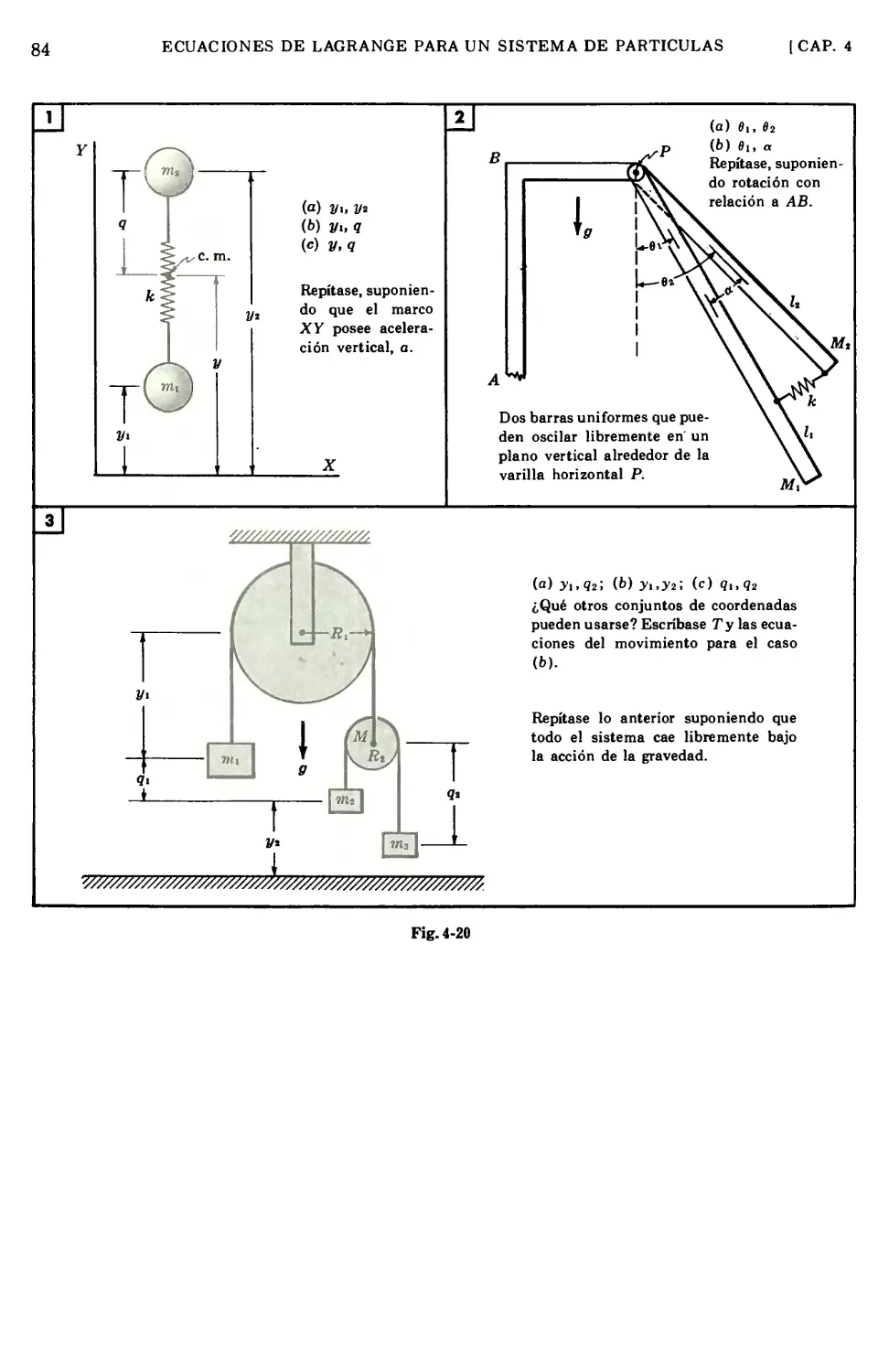
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
Página
Capítulo 4 ECUACIONES DE LAGRANGE PARA UN SISTEMA
DE PARTÍCULAS 62
Observaciones introductorias 62
Deducción de las ecuaciones de Lagrange para un sistema de partículas 62
Expresión de T en forma adecuada 64
Significado físico de las fuerzas generalizadas 64
Técnicas para hallar expresiones para las fuerzas generalizadas 65
Ejemplos ilustrativos de la aplicación de las ecuaciones de Lagrange a sistemas
que incluyen partículas 66
Fuerzas y movimientos de las partículas cargadas en un campo electromagnético . 72
Consideraciones sobre el significado físico de las ecuaciones de Lagrange 73
Experimento sugerido 76
Capítulo 5 SISTEMAS CONSERVATIVOS 85
Ilustración de algunos principios básicos 85
Definiciones importantes 86
Expresión general de V y prueba para las fuerzas conservativas 86
Determinación de las expresiones para V 87
Algunos ejemplos sencillos para ilustrar lo anterior 87
Fuerzas generalizadas como derivadas de V 89
Ecuaciones de Lagrange para sistemas conservativos 89
Sistemas parcialmente conservativos y parcialmente no conservativos 90
Ejemplos que ilustran la aplicación de las ecuaciones de Lagrange a sistemas
conservativos 90
Expresión adecuada de la energía potencial del sistema de resortes 93
Sistemas en los que la energía potencial varía con el tiempo. Ejemplos 94
Función vectorial del potencial para una carga que se mueve en un campo
electromagnético 95
La "integral de la energía" 96
Experimentos sugeridos 96
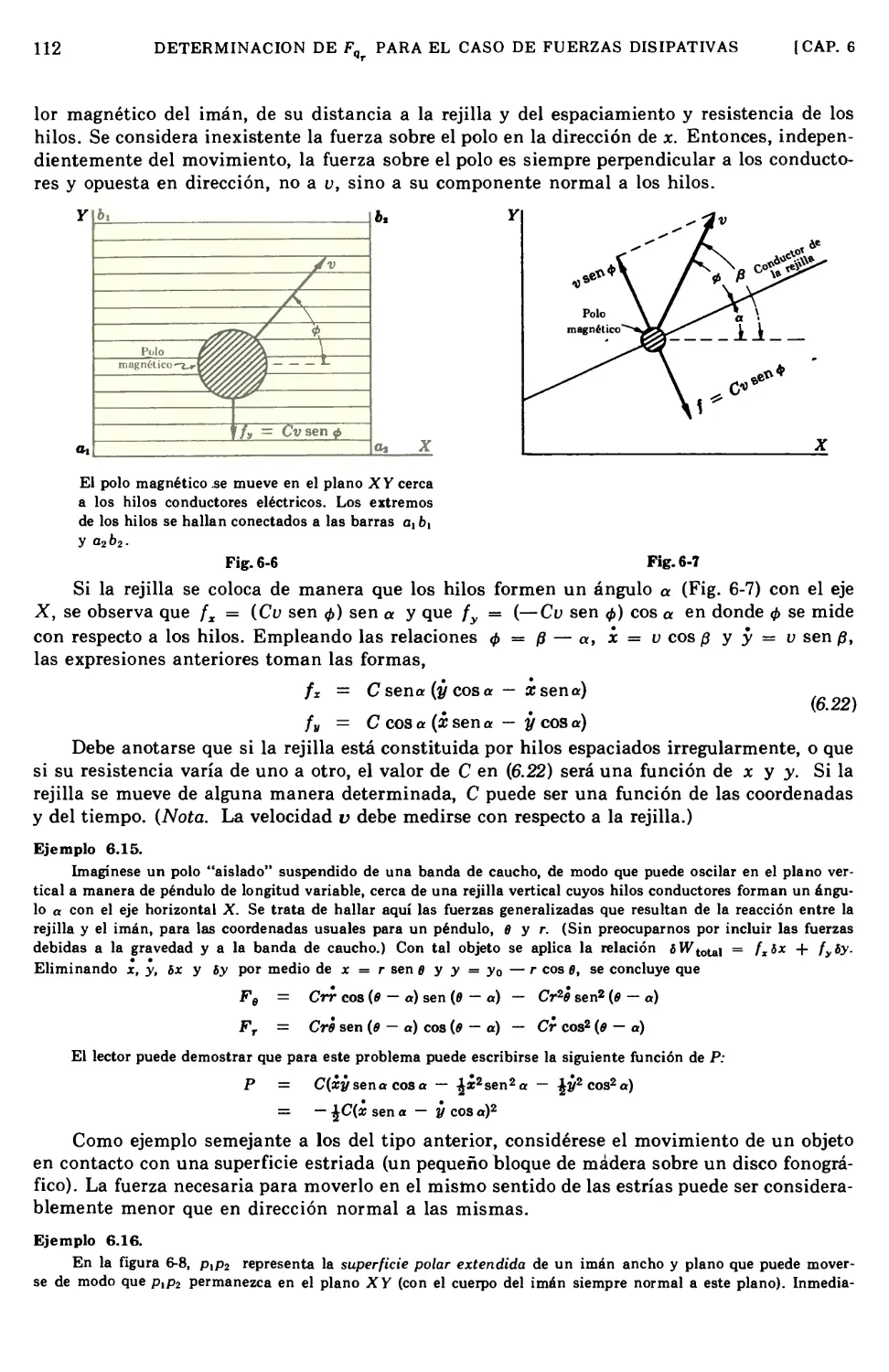
Capítulo 6 DETERMINACIÓN DE F,r PARA EL CASO DE FUERZAS
DISIPATIVAS ' 103
6.1 Definición y clasificación 103
6.2 Procedimiento general para determinar Fqr 103
6.3 Ejemplos: Fuerzas generalizadas de fricción 104
6.4 Ejemplos: Fuerzas viscosas generalizadas 106
6.5 Ejemplo: Fuerzas proporcionales a la potencia n de la velocidad, para n > 1 . . . 107
6.6 Fuerzas expresadas por medio de una serie de potencias 107
6.7 Algunas consecuencias interesantes de las fuerzas de fricción, y otras 107
6.8 Una "función de potencia", P, para la determinación de las fuerzas generalizadas . . 108
6.9 Formas especiales de la función de potencia 109
6.10 Ejemplos para ilustrarel uso de P 110
6.11 Fuerzas que dependen de la velocidad relativa 111
6.12 Fuerzas cuya dirección no se opone a la del movimiento 111
6.13 Experimento sugerido 114
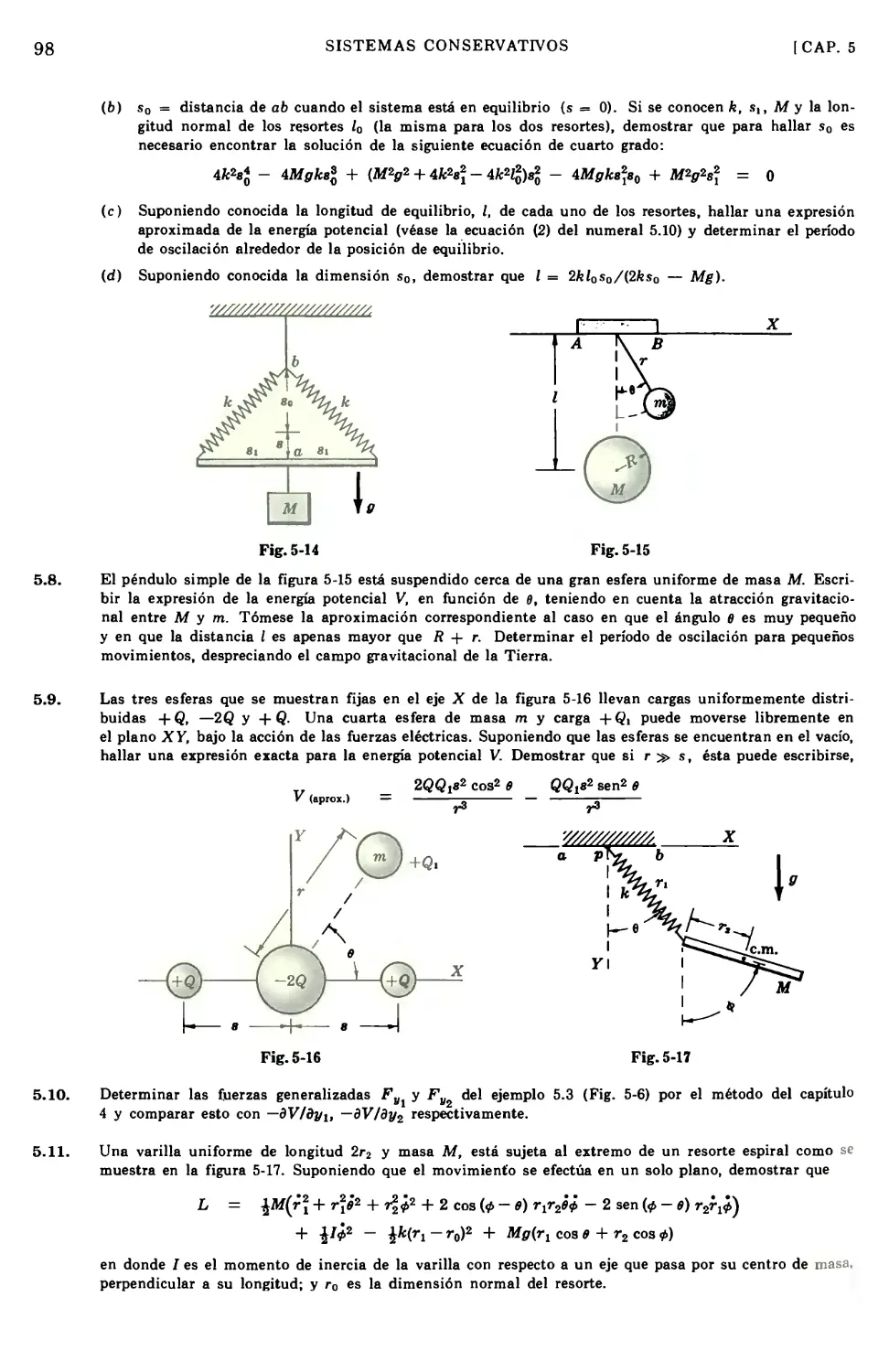
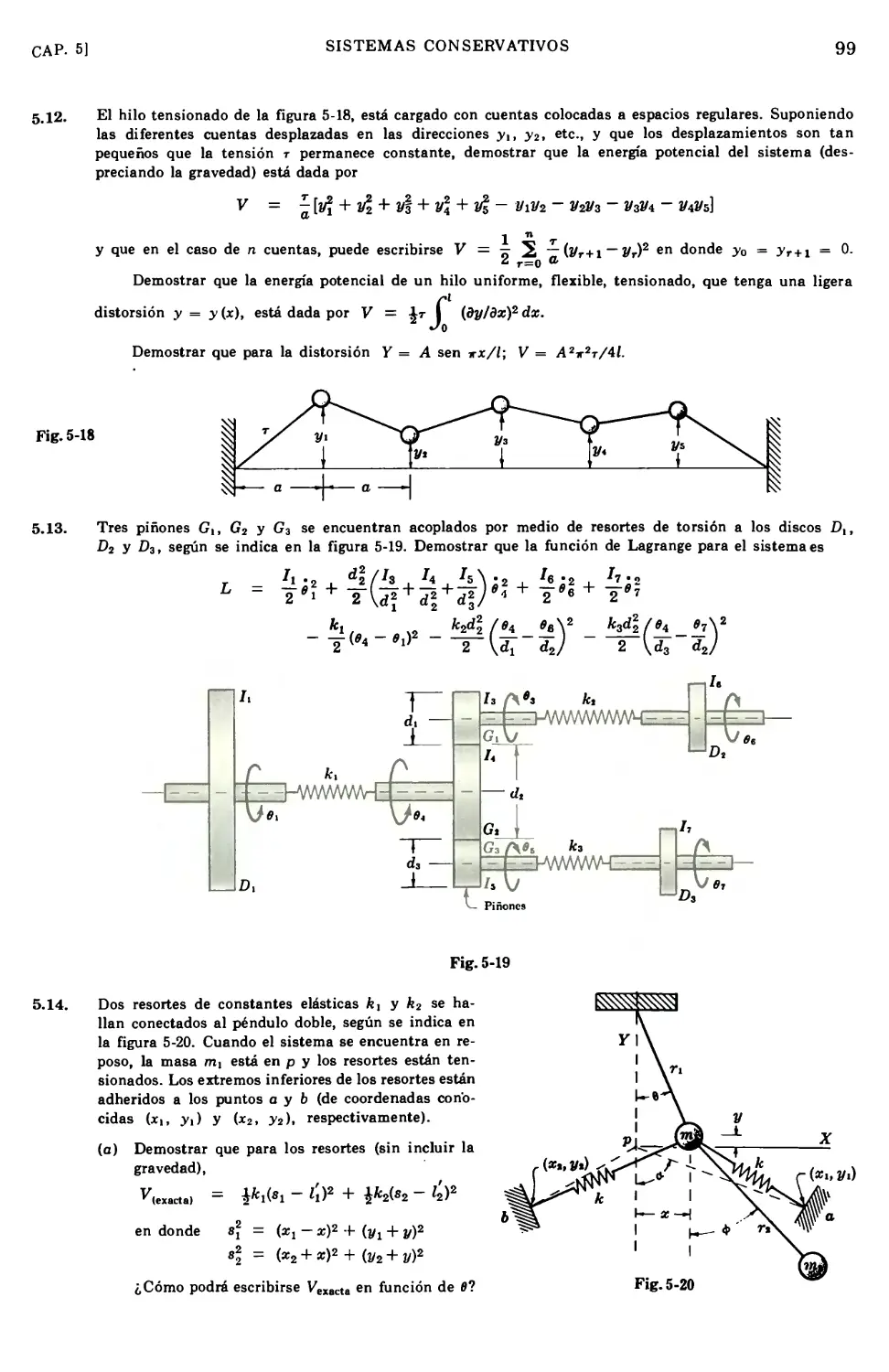
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5.14
TABLA DE MATERIAS
Página
Capítulo 7 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS
PRODUCTOS DE INERCIA 121
7.1 Expresión general del momento de inercia de un cuerpo rígido con respecto a un
eje cualquiera 121
7.2 El elipsoide de inercia 122
7.3 Momentos principales de inercia. Ejes principales y sus direcciones 123
7.4 Momentos y productos de inercia con respecto a cualquier sistema de ejes
rectangulares 124
7.5 Momentos y productos de inercia con respecto a un marco cualquiera 125
7.6 Momentos y productos de inercia con respecto a un marco girado 126
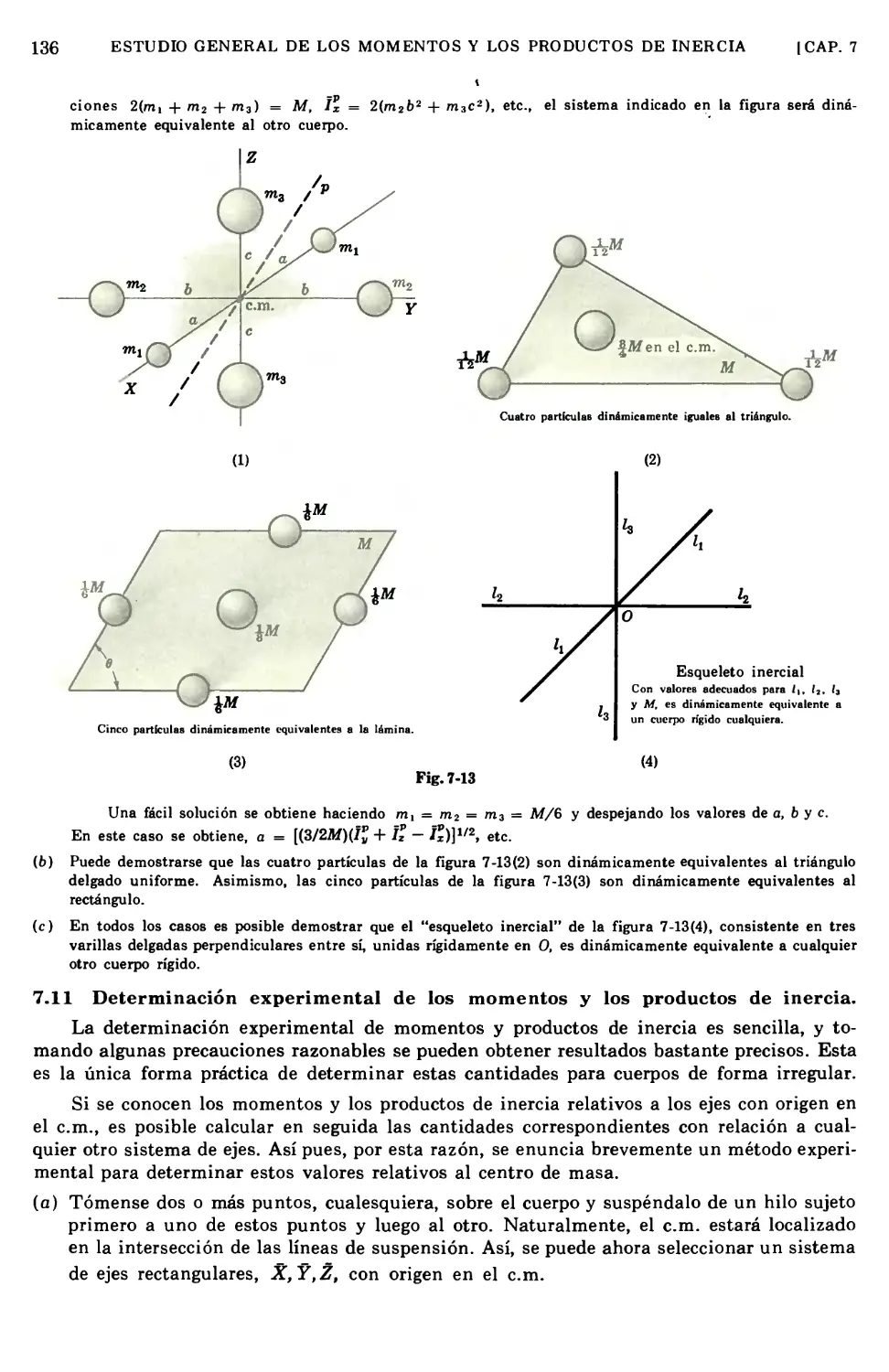
7.7 Ejemplos de momentos, productos y elipsoides de inercia 128
7.8 "Focos" y puntos "esféricos" de inercia 133
7.9 Significado físico de los productos de inercia 134
7.10 Cuerpos dinámicamente equivalentes 135
7.11 Determinación experimental de los momentos y los productos de inercia 136
7.12 Proyecto sugerido sobre el elipsoide de inercia 137
7.13 Experimento sugerido 138
Capítulo 8 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS
RÍGIDOS, DE LAGRANGE 143
8.1 Observaciones preliminares 143
8.2 Fundamentos básicos necesarios 143
8.3 Expresión general de la energía cinética de un cuerpo rígido libre 152
8.4 Resumen de algunas consideraciones importantes con relación a T 153
8.5 Planteamiento de las ecuaciones del movimiento 153
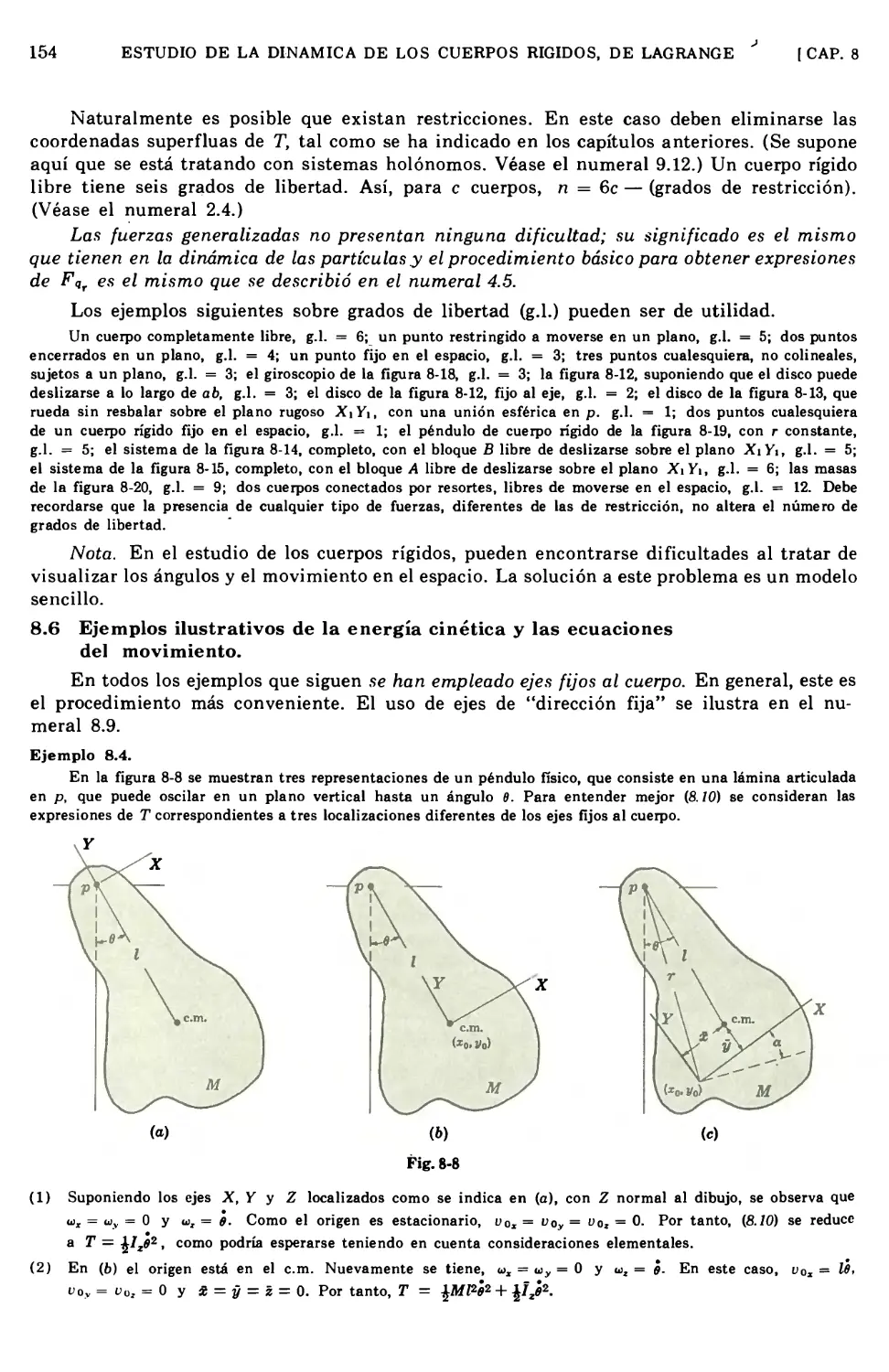
8.6 Ejemplos ilustrativos de la energía cinética y las ecuaciones del movimiento 154
8.7 Definición de los ángulos de Euler 161
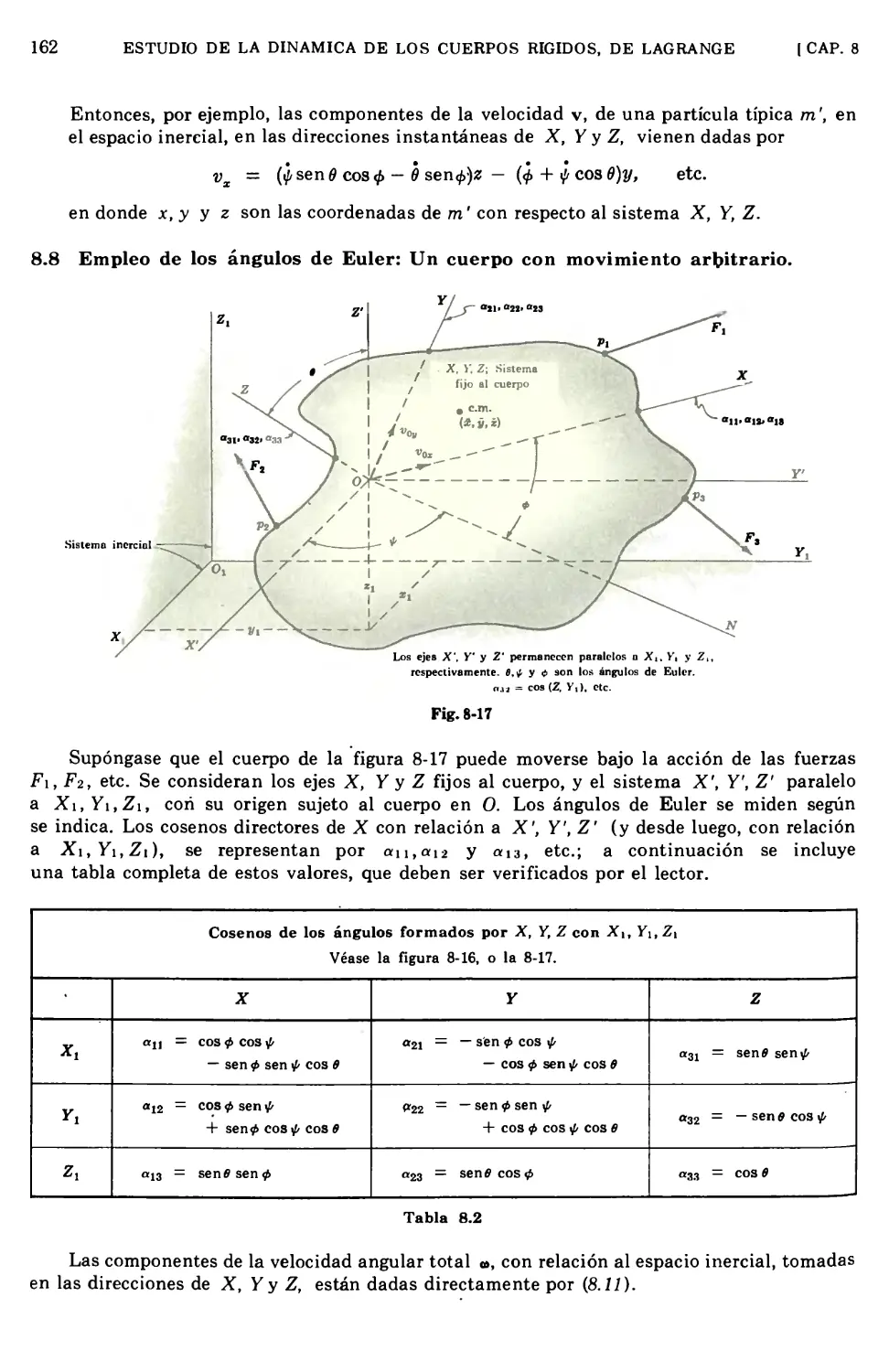
8.8 Empleo de los ángulos de Euler: Un cuerpo con movimiento arbitrario 162
8.9 La energía cinética, haciendo uso de ejes de dirección fija 166
8.10 Movimiento de un cuerpo rígido con relación a un marco de referencia en
traslación y rotación 167
8.11 Experimento sugerido 172
Capítulo 9 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS
CUERPOS RÍGIDOS 181
9.1 Observaciones preliminares 181
9.2 Ecuaciones del movimiento de traslación del centro de masa 181
9.3 Diversas maneras de expresar las ecuaciones escalares correspondientes a (9.3) .... 182
9.4 Consideraciones fundamentales para la determinación de las ecuaciones de
rotación de Euler 183
9.5 Las tres ecuaciones del movimiento de rotación de Euler, para un cuerpo rígido.
Forma general 186
9.6 Aspectos importantes con respecto a (9.10) 188
9.7 Forma vectorial de las ecuaciones de rotación de Euler 189
9.8 Ejemplos específicos para ilustrar el uso de las ecuaciones (9.2) y (9.10) 189
9.9 Ejemplos para ilustrar la forma (9.16) de las ecuaciones de Euler 194
TABLA DE MATERIAS
Página
9.10 Ecuaciones del movimiento con respecto a un marco de referencia móvil 196
9.11 Determinación de los movimientos de una nave espacial y de un objeto en su
interior, ambos bajo la acción de fuerzas conocidas 197
9.12 Restricciones no holónomas 199
9.13 Las ecuaciones de rotación de Euler, desde el punto de vista del momentum
angular 201
9.14 Comparación del tratamiento de Euler con el de Lagrange 203
Capítulo 10 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS
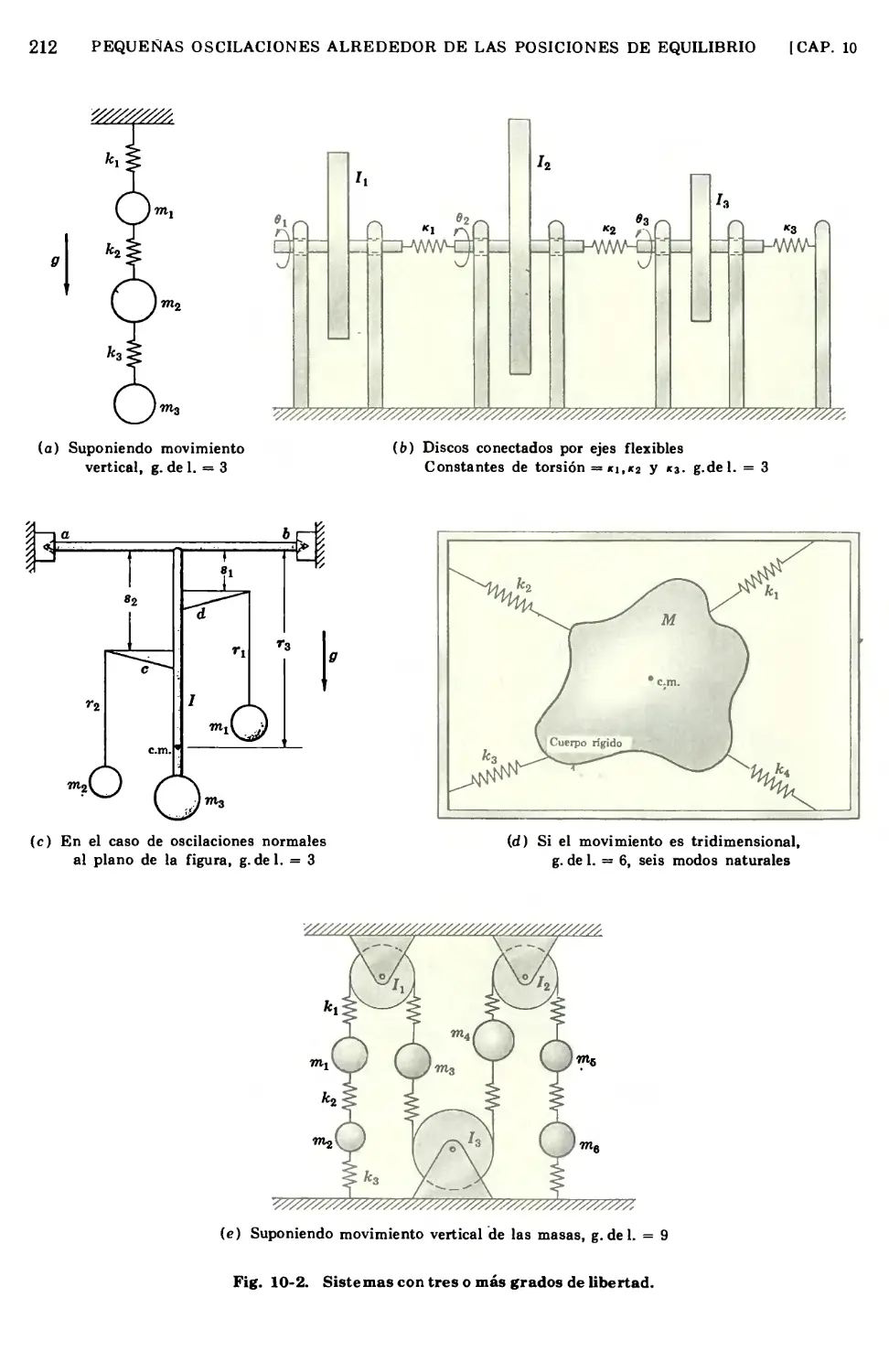
POSICIONES DE EQUILIBRIO 210
10.1 Tipo de problema por considerar 210
10.2 Restricciones sobre el problema general 210
10.3 Bases fundamentales adicionales 213
10.4 Ecuaciones diferenciales del movimiento 216
10.5 Soluciones de las ecuaciones del movimiento; fuerzas conservativas únicamente . . 216
10.6 Resumen de aspectos importantes sobre el tipo anterior de movimiento oscilatorio . 218
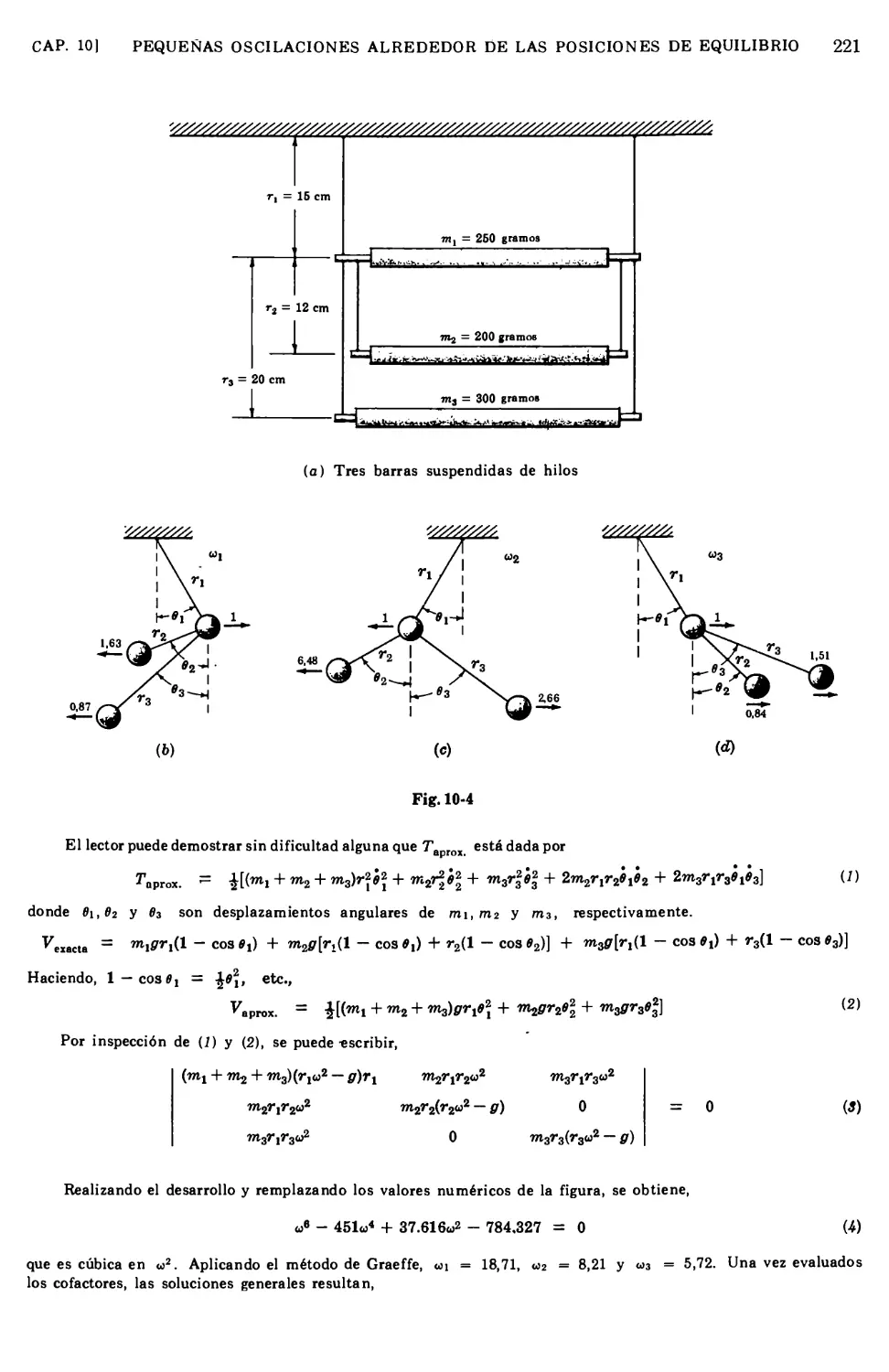
10.7 Ejemplos para ilustrar los resultados de los numerales anteriores 219
10.8 Casos especiales de las raíces de D 223
10.9 Coordenadas normales 225
10.10 Prueba de la relación de ortogonalidad 227
10.11 Aspectos importantes relacionados con las coordenadas normales 228
10.12 Ventajas de las coordenadas normales 228
10.13 Determinación de las expresiones de las coordenadas normales 229
10.14 Amplitud y dirección del movimiento de una partícula determinada cuando se
excita un modo de oscilación en particular 230
10.15 Determinación de las constantes arbitrarias con la ayuda de las condiciones de
ortogonalidad 232
10.16 Oscilaciones pequeñas con fuerzas actuantes viscosas y conservativas 232
10.17 Consideraciones sobre la estabilidad del movimiento 234
10.18 Utilización de las coordenadas normales cuando actúan fuerzas extrañas 235
10.19 Uso de las coordenadas normales cuando actúan fuerzas externas y viscosas .... 235
10.20 Experimentos sugeridos 236
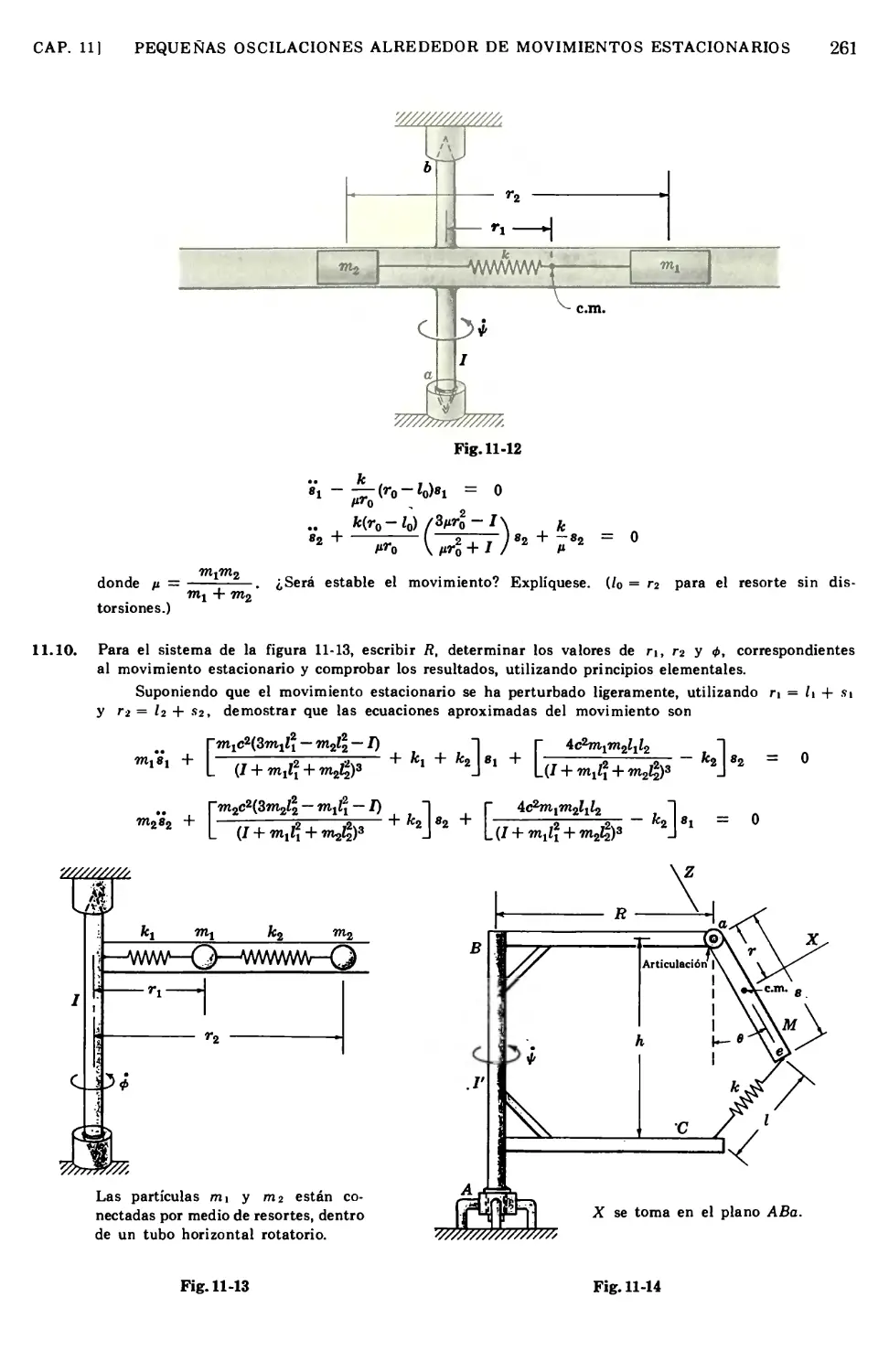
Capítulo 11 PEQUEÑAS OSCILACIONES ALREDEDOR DE
MOVIMIENTOS ESTACIONARIOS 243
11.1 Consideraciones preliminares importantes 243
11.2 Eliminación de las coordenadas ignorables de las ecuaciones generales del
movimiento 245
11.3 Eliminación de las coordenadas ignorables, empleando la función de Routh.
Método B 246
11.4 Condiciones necesarias para el movimiento estacionario 246
11.5 Ecuaciones del movimiento, suponiendo un movimiento estacionario
ligeramente perturbado 247
11.6 Solución de las ecuaciones del movimiento 248
11.7 Coordenadas ignorables en función del tiempo, después de una perturbación .... 248
11.8 Ejemplos ilustrativos del procedimiento anterior 248
11.9 Oscilación alrededor del movimiento estacionario cuando el sistema contiene
restricciones móviles 255
TABLA DE MATERIAS
Página
11.10 Sistema bajo la acción de fuerzas disipativas 257
11.11 Estabilidad del movimiento estacionario 258
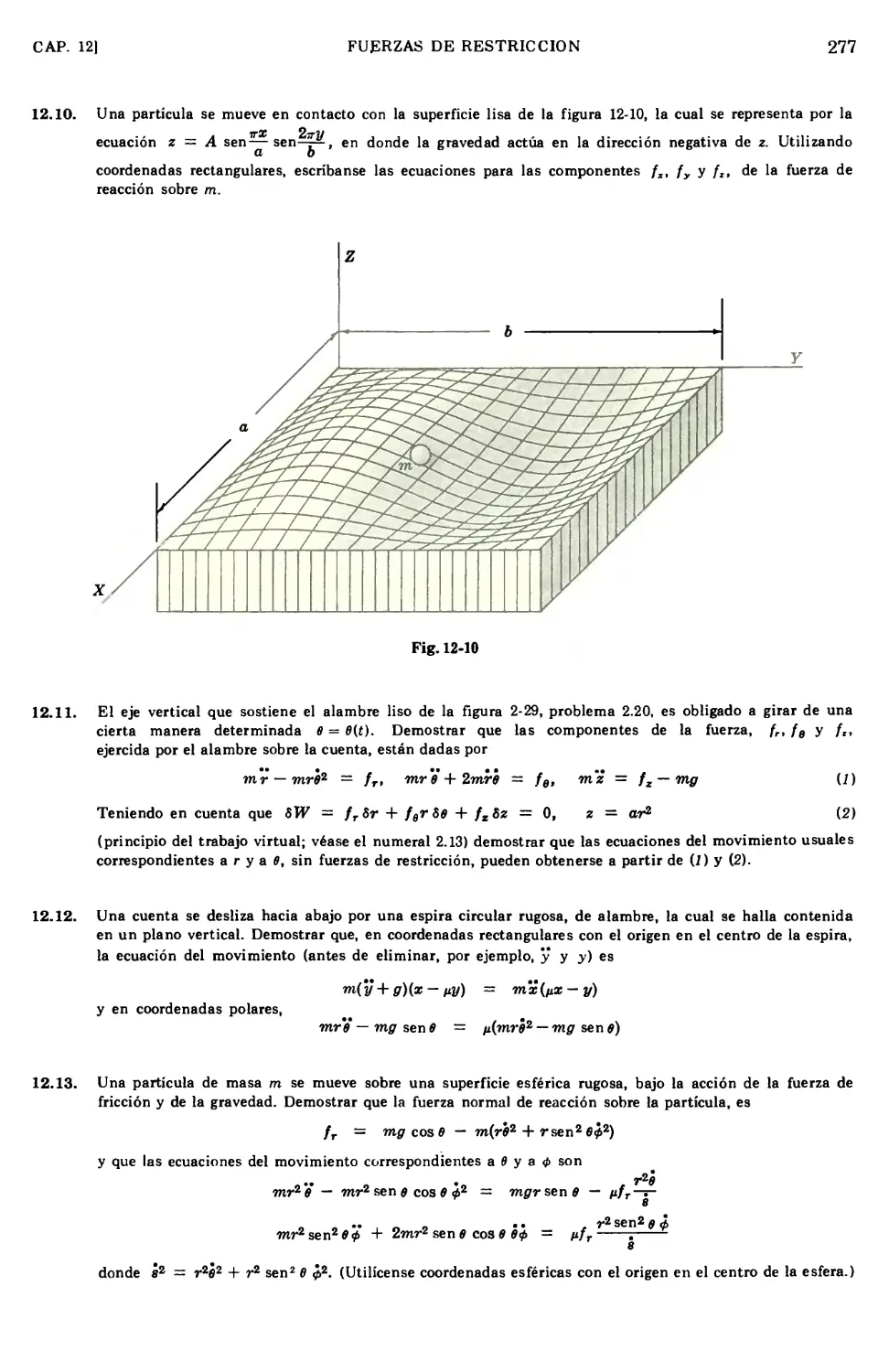
Capítulo 12 FUERZAS DE RESTRICCIÓN 266
12.1 Consideraciones preliminares 266
12.2 Procedimiento general para hallar las fuerzas de restricción 268
12.3 Ejemplos ilustrativos 270
12.4 Fuerzas de restricción utilizando las ecuaciones de Euler 273
12.5 Fuerzas de restricción y ecuaciones del movimiento con restricciones rugosas .... 274
Capítulo 13 FUERZAS IMPULSADORAS NECESARIAS PARA
PRODUCIR MOVIMIENTOS DEFINIDOS 279
13.1 Consideraciones preliminares 279
13.2 Método general 280
13.3 Ejemplos ilustrativos 281
13.4 Equilibrio de un sistema 283
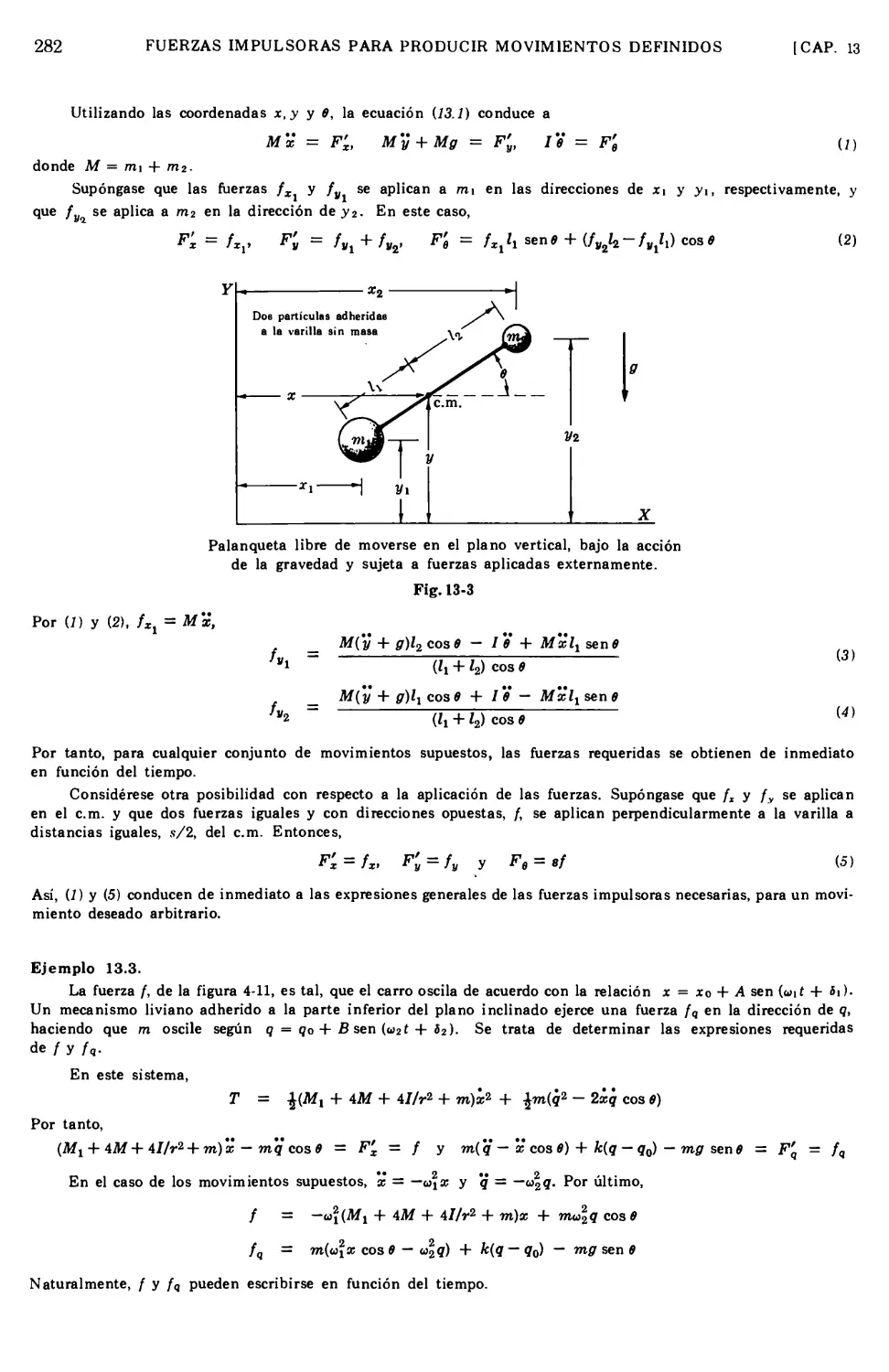
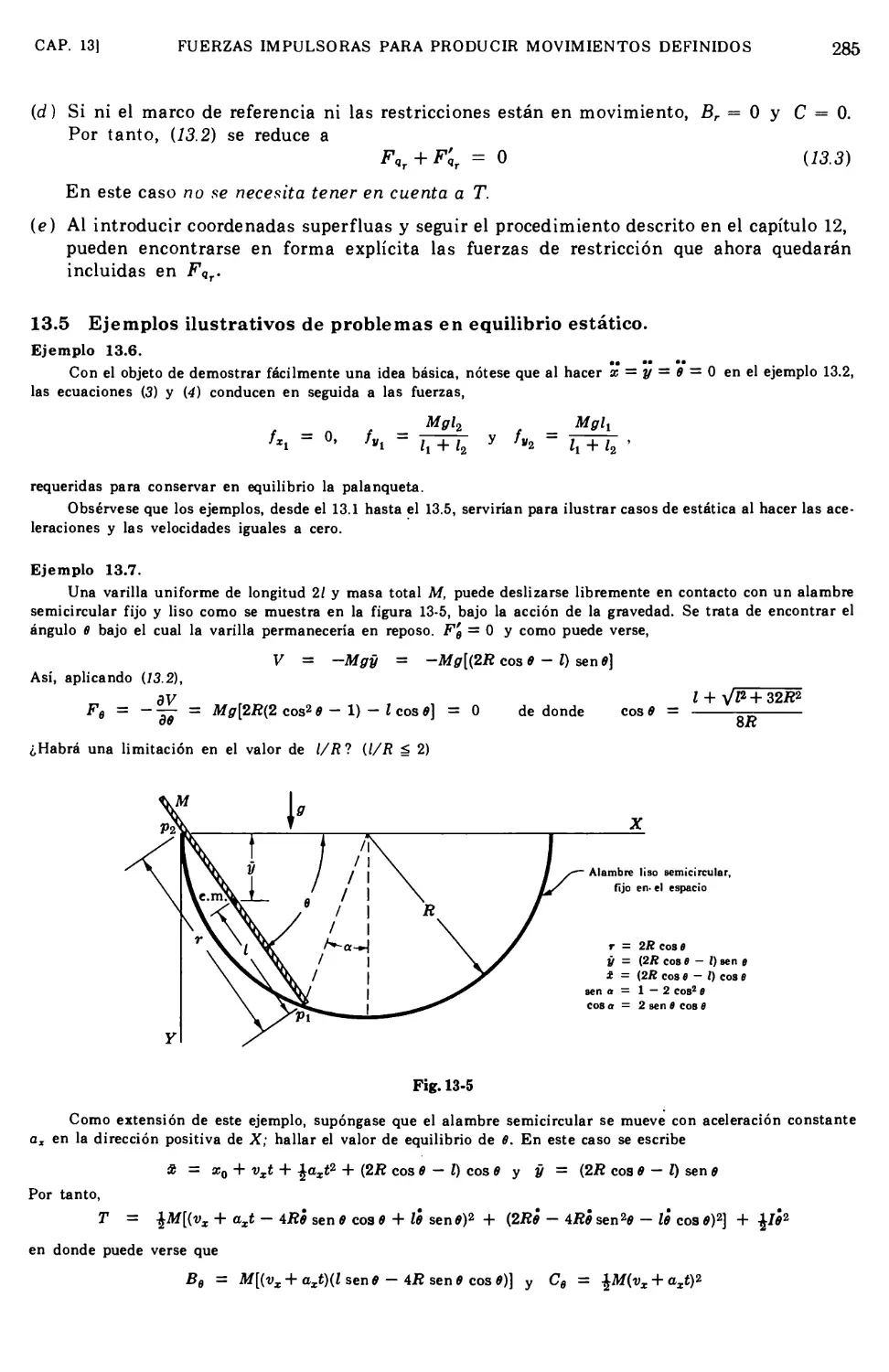
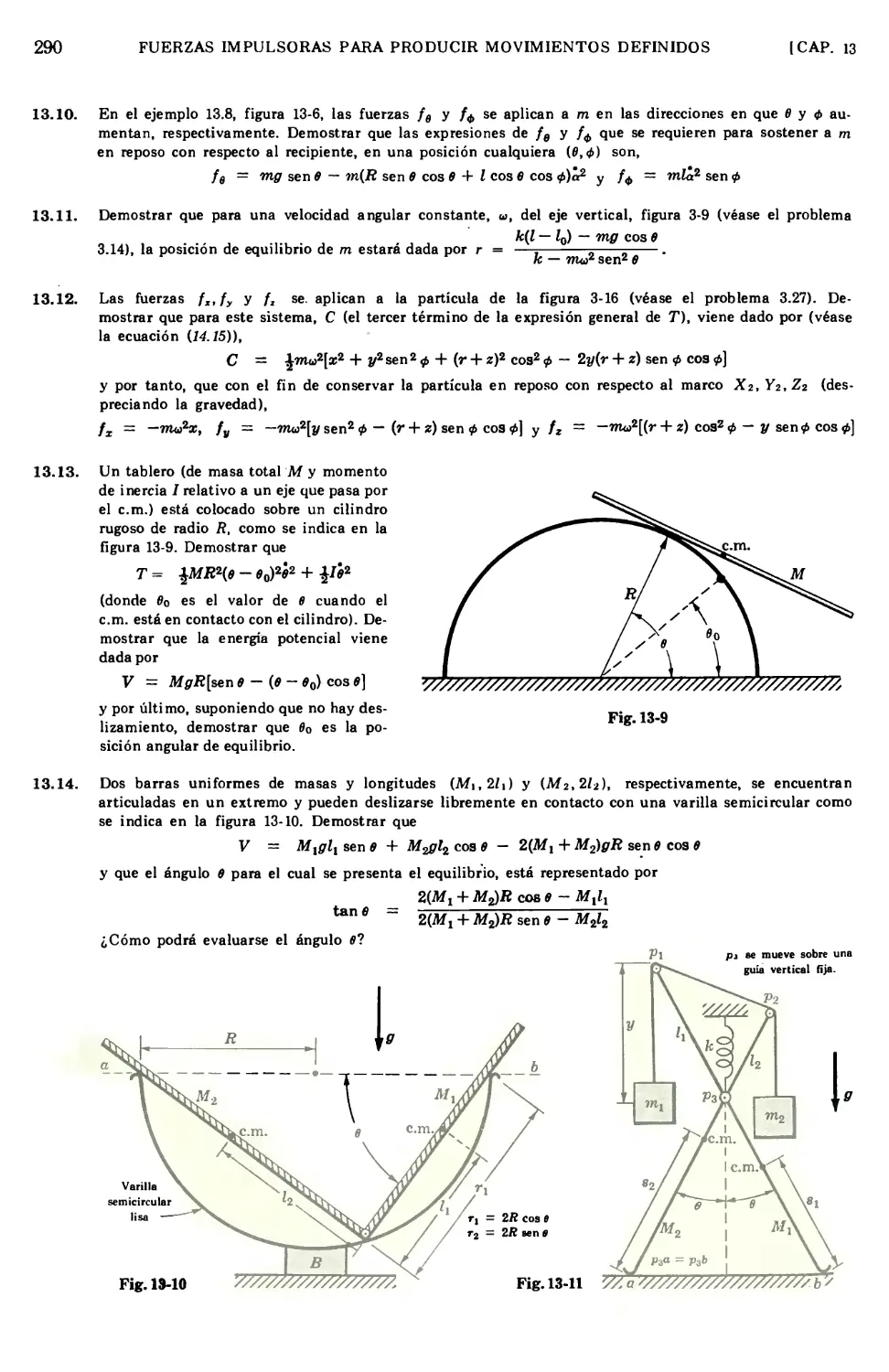
13.5 Ejemplos ilustrativos de problemas en equilibrio estático 285
Capítulo 14 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU
ROTACIÓN COTIDIANA EN LOS PROBLEMAS DE
LA DINÁMICA 293
14.1 Observaciones introductorias 293
14.2 Consideraciones sobre la forma de la Tierra. Latitudes y radios geocéntricos y
geográficos 294
14.3 Aceleración de la gravedad sobre la superficie de la Tierra o cerca de ella 294
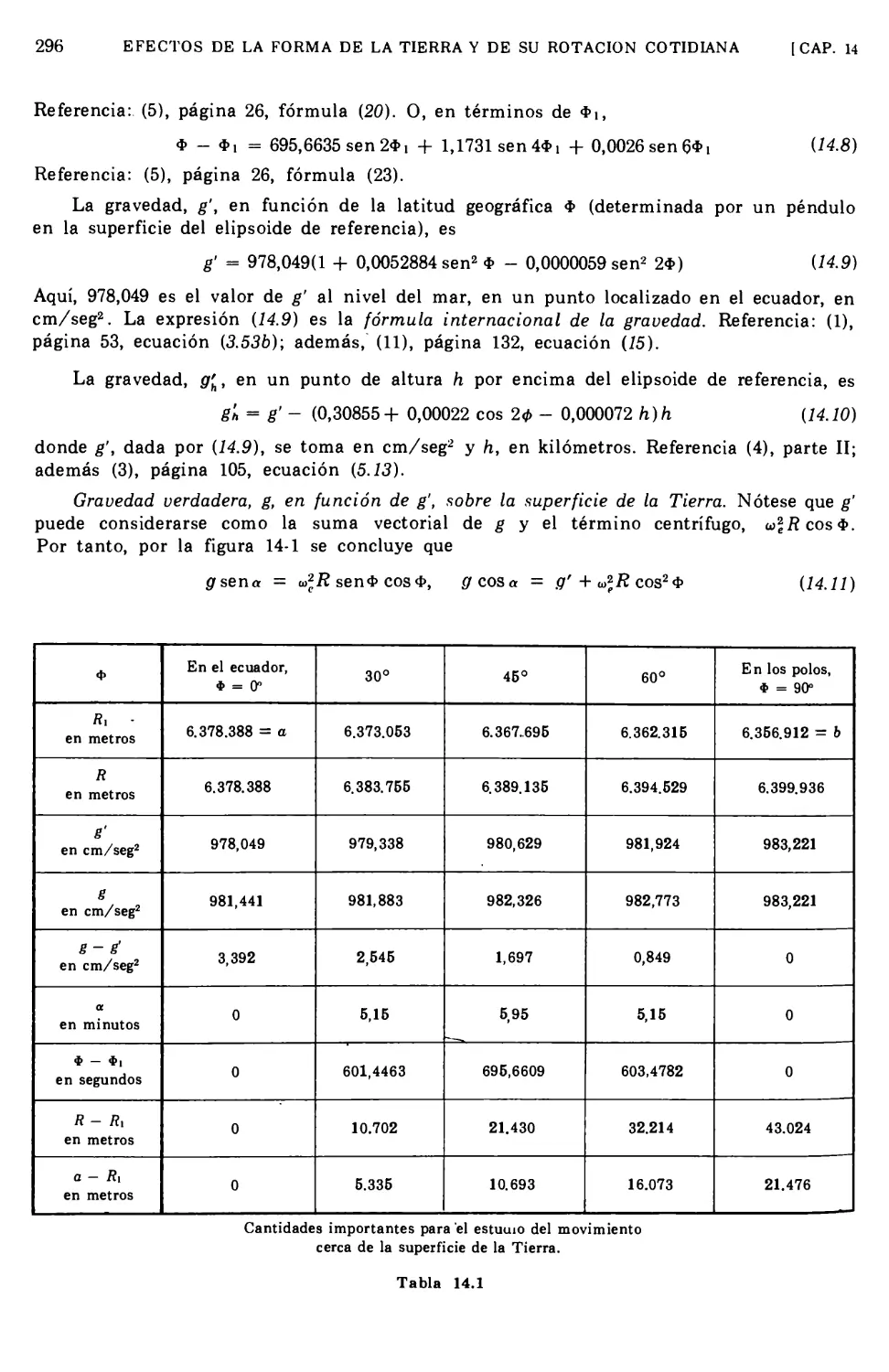
14.4 Fórmulas de cálculo y algunas constantes 295
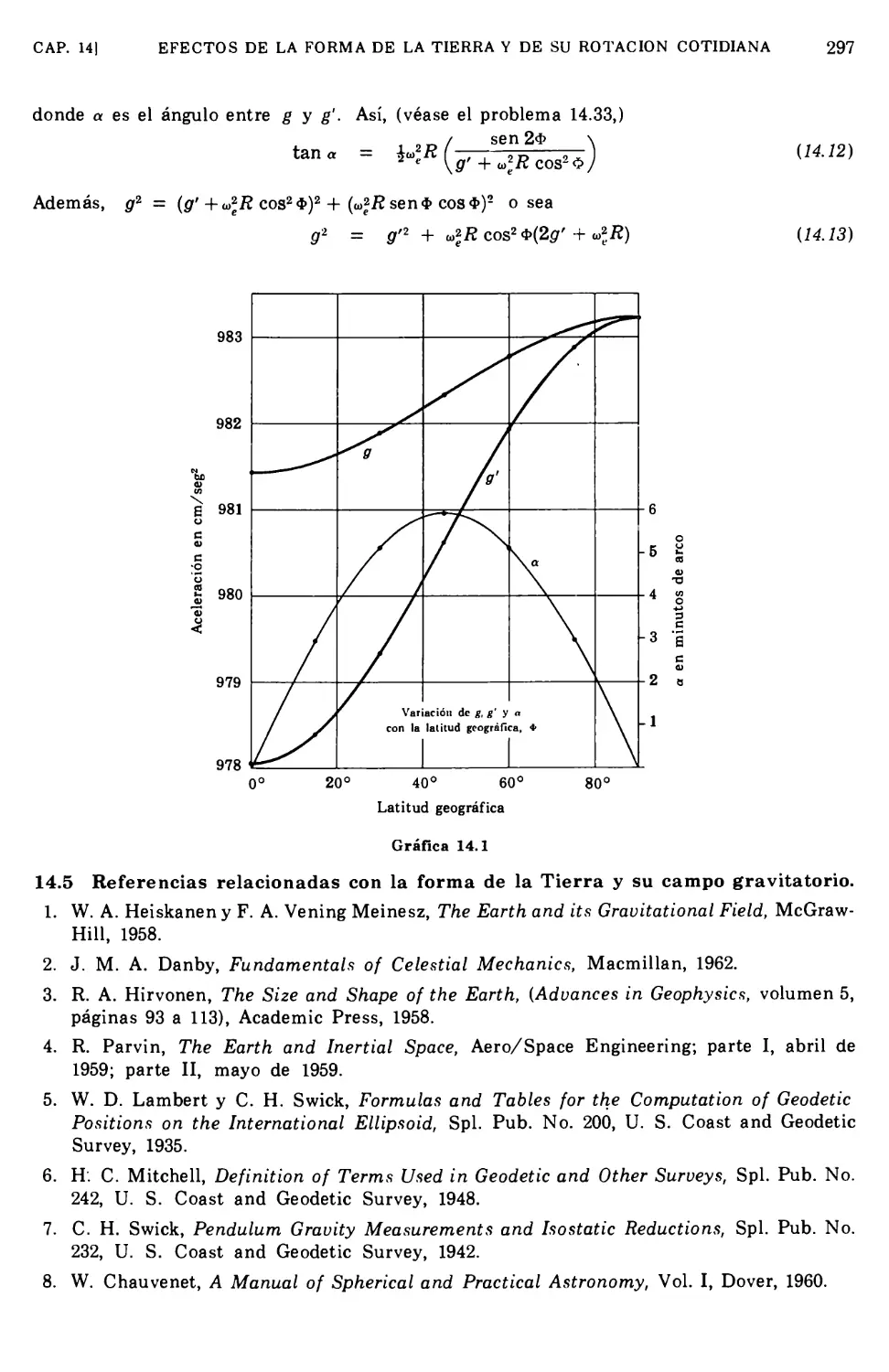
14.5 Referencias relacionadas con la forma de la Tierra y su campo gravitatorio 297
14.6 Energía cinética y ecuaciones del movimiento para una partícula en diversos
sistemas de coordenadas. Marco de referencia adherido a la superficie de la
Tierra 298
14.7 Energía cinética T, para una partícula; marco de referencia en movimiento con
respecto a la superficie de la Tierra 302
14.8 Movimiento de un cuerpo rígido cerca de la superficie de la Tierra 303
14.9 Ejemplos ilustrativos específicos 304
Capítulo 15 APLICACIÓN DE LAS ECUACIONES DE LAGRANGE A
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS ... 316
15.1 Observaciones preliminares 316
15.2 • Expresiones de T,V,P,FQ y de las ecuaciones de Lagrange, para circuitos
eléctricos 316
15.3 Ejemplos ilustrativos 319
15.4 Sistemas electromecánicos: La función de Lagrange adecuada; determinación
de las fuerzas generalizadas 320
15.5 Oscilaciones de sistemas eléctricos y electromecánicos 322
TABLA DE MATERIAS
Página
15.6 Fuerzas y voltajes necesarios para producir movimientos y corrientes dadas en
un sistema electromecánico ' 323
15.7 Sistema eléctricos y mecánicos análogos 323
15.8 Referencias 326
Capítulo 16 ECUACIONES DEL MOVIMIENTO DE HAMILTON 331
16.1 Observaciones generales 331
16.2 Una palabra sobre el "momentum generalizado" 331
16.3 Deducción de las ecuaciones de Hamilton 331
16.4 Procedimiento para determinar H y escribir las ecuaciones de Hamilton 333
16.5 Casos especiales de H 333
16.6 Relaciones importantes de la energía y la potencia 333
16.7 Ejemplos. El hamiltoniano y las ecuaciones del movimiento de Hamilton 334
16.8 Ejemplos de H para sistemas en que existen coordenadas móviles o restricciones
móviles, o arribas condiciones 336
16.9 Campos de aplicación del método de Hamilton 337
Capítulo 17 PRINCIPIO DE HAMILTON 342
. 17.1 Introducción 342
17.2 Problemas introductorios 342
17.3 Algunas técnicas del cálculo de variaciones 343
17.4 Soluciones a los problemas propuestos anteriormente 346
17.5 Principio de Hamilton a partir del cálculo de variaciones 347
17.6 Principio de Hamilton a partir de la ecuación de D'Alembert 348
17.7 Ecuaciones de Lagrange a partir del principio de Hamilton 350
17.8 Ejemplos específicos para ilustrar los ejemplos de este capítulo 350
17.9 Aplicaciones del principio de Hamilton 352
Capítulo 18 ECUACIONES BÁSICAS DE LA DINÁMICA EN
NOTACIÓN TENSORIAL Y VECTORIAL 356
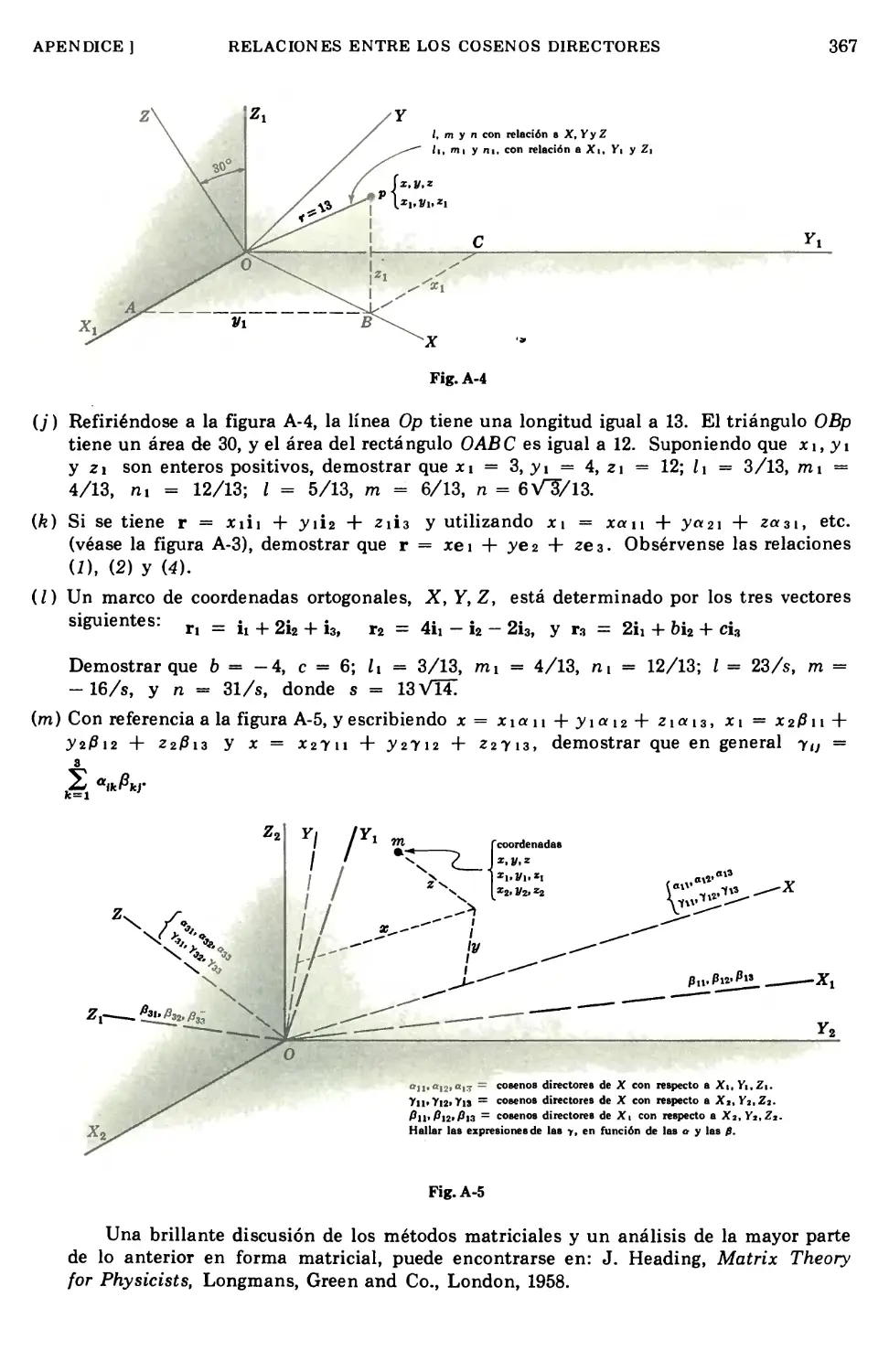
Apéndice RELACIONES ENTRE LOS COSENOS DIRECTORES .... 361
ÍNDICE 369
CAPITULO
Fundamentos básicos, I
Leyes básicas de la dinámica. Condiciones de validez. Dos tipos
principales de problemas y su método general de solución.
1.1 De la necesidad de fundamentos básicos.
Los mayores obstáculos que un estudiante promedio encuentra al tratar de entender la
dinámica de Lagrange, usualmente no se deben a las dificultades intrínsecas de la materia,
sino más bien, a ciertas deficiencias en un campo más o menos amplio correspondiente a
los fundamentos básicos. Con la esperanza de remover tales obstáculos, se han dedicado los
dos primeros capítulos al estudio detallado de los pre-requisitos que con mayor frecuencia
no son del dominio de los estudiantes y que no se encuentran fácilmente en los textos.
1.2 Leyes básicas de la mecánica clásica de Newton y varias maneras
de expresarlas.
Las tres leyes de Newton (naturalmente incluyendo los conceptos clásicos de masa,
longitud, tiempo, fuerza, las reglas de la geometría, el álgebra y el cálculo) junto con el concepto
del trabajo virtual, pueden considerarse como los fundamentos sobre los cuales se basa toda
la mecánica clásica (el campo para el cual se cumplen las condiciones C, D y E del numeral
1.6). Sin embargo conviene señalar desde el comienzo que las leyes básicas de la dinámica
pueden ser expresadas (matemáticamente) de varias maneras diferentes a la forma dada por
Newton. Las más importantes de estas formas (que serán tratadas más adelante) son
(a) el principio de D'Alembert (c) las ecuaciones de Hamilton
(6) las ecuaciones de Lagrange (d) el principio de Hamilton
Todas ellas son básicamente equivalentes. Por ejemplo, si se parte de las leyes de Newton y
del principio del trabajo virtual (ver el numeral 2.13 del capítulo 2) se puede deducir
cualquiera de las formas anteriores. Así pues, una cualquiera de las cinco formulaciones puede
tomarse como base de los desarrollos teóricos y de la solución de problemas.
1.3 Selección de la formulación.
La escogencia de una de las cinco formas depende del trabajo que se ha de realizar. Por
ejemplo, las ecuaciones de Newton son adecuadas para la solución de muchos problemas
sencillos; el principio de Hamilton es importante en varias consideraciones teóricas; y las
ecuaciones de Hamilton han sido útiles en ciertas aplicaciones, así como en el desarrollo de
la mecánica cuántica.
Sin embargo, el método de Lagrange es de manera especial potente y notablemente
sencillo como instrumento de solución de una gama muy amplia de problemas (tanto
teóricos como prácticos) relacionados con sistemas mecánicos, eléctricos, electromecánicos, etc.
1.4 Origen de las leyes básicas.
Las "leyes básicas" de la dinámica son sencillamente expresiones de un gran conjunto
de hechos experimentales. No es posible deducirlas por medio de manejos lógicos- o
matemáticos, exclusivamente. En último término, las reglas del juego se basan en experimentos
delicados. Estas reglas deben ser aceptadas bajo la creencia de que si la naturaleza las ha
obedecido en el pasado, continuará haciéndolo en el futuro. Por ejemplo, no es posible "expli-
1
2
FUNDAMENTOS BÁSICOS, I
(CAP. 1
car" por qué son válidas las leyes de Newton. Lo único que es posible afirmar es que ellas
representan un enunciado compacto de experiencia anterior, relacionada con el
comportamiento de una gran variedad de sistemas mecánicos. Las formulaciones de D'Alembert,
Lagrange y Hamilton expresan esto mismo, cada una de cierta manera en particular.
1.5 De los conceptos y magnitudes básicas empleadas.
Las magnitudes de longitud, masa, tiempo, fuerza, etc., se presentan continuamente en
mecánica; su interpretación y uso tiende a hacerse con sensación de tranquilidad y de
comprensión. Sin embargo, en diferentes épocas han surgido interrogantes con relación a los
conceptos básicos que ellas conllevan y con relación a la naturaleza fundamental de las
magnitudes mismas. Un estudio de estos tópicos estaría fuera de lugar aquí, pero los estudiantes
interesados encontrarán de gran beneficio los análisis de Bridgman, y otros, sobre estas
materias.
1.6 Condiciones de validez de las leyes de Newton.
La segunda ley de Newton, aplicada a una partícula1 de masa constante, m, puede
escribirse como .
F = m% (i./)
en donde la fuerza F y la velocidad v, son magnitudes vectoriales; y la masa m y el
tiempo t, son escalares. Escrito {1.1) en componentes, queda
Fx - mx, Fy = my, Fz = mz (1.2)
dx • d2x
(En el presente texto se utilizará la conveniente notación: -=r- = x, -jt^ — x, etc.)
Las relaciones (2.2) en la forma sencilla en que están expresadas, no son correctas para
cualquiera, ni para todas las condiciones. A continuación se analizan las condiciones con las
cuales sí son válidas.
Condición A.
La ecuación (1.1) implica algún "marco de referencia" con respecto al cual se
mide dv/dt. Las ecuaciones (1.2) indican que el movimiento se ha referido a un
sistema de ejes rectangulares X, Y, Z.
Es un hecho experimental que la segunda ley de Newton, expresada en la forma
sencilla de (1.2) conduce a resultados que concuerdan con la experiencia cuando los
ejes coordenados están inmóviles con respecto a la posición media de las estrellas "fijas"
o si se mueven con velocidad lineal uniforme, sin rotación, con relación a las estrellas.
En cualquiera de los dos casos, el marco de referencia (los ejes X, Y, Z) se
denomina MARCO INERCIAL2 y las coordenadas correspondientes, COORDENADAS
INERCIALES. Dicho de otra manera, un marco que posee aceleración lineal, o que
está girando en cualquier forma, es NO-INERCIAL3.
1 El término "partícula", un concepto imaginario, puede representarse como una pequeña porción de materia,
tan diminuta que su posición en el espacio se determina por las tres coordenadas de su "centro". En este caso su
energía cinética de rotación con respecto a cualquier eje que la atraviese, puede despreciarse.
2 El término "marco inercial" puede definirse en abstracto, sencillamente como aquel, con respecto al cual,
las ecuaciones de Newton en su forma sencilla (1.2) son válidas. Pero esta definición no le indica al ingeniero o al
científico aplicado, dónde hallar tal marco, o si ciertas coordenadas específicas son inerciales. Por otra parte, la
definición de las estrellas fijas, sí suministra esta información. Desde luego, debe observarse-que mediciones hechas
con gran precisión podrían demostrar que el marco de las "estrellas fijas" fuera ligeramente no-inercial.
3Un marco de referencia adherido a la superficie de la Tierra es claramente no-inercial debido a las
rotaciones anuales y diarias, y a los demás movimientos del globo. A pesar de esto, la aceleración de este marco es tan
pequeña que para muchos efectos (pero en ningún caso para todos los efectos) puede considerarse como inercial.
Un marco que no gire (con sus ejes dirigidos siempre hacia las mismas estrellas fijas) con su origen adherido al
centro de la Tierra es una mejor aproximación de un marco inercial. Un sistema de ejes que no giren, con su origen
en el centro del Sol, constituye un marco inercial excelente (aunque posiblemente no es aún "perfecto").
CAP. 1]
FUNDAMENTOS BÁSICOS, I
3
La condición enunciada debe considerarse como una de las bases de sustentación
más importantes, sobre las que descansa la superestructura de la dinámica. El
reconocimiento de este hecho debe hacerse automáticamente en todo razonamiento ya
que básicamente, la solución de todo problema comienza con la consideración de un
marco inercial. Se debe adquirir la habilidad de reconocer por simple inspección los
marcos inerciales y los no-inerciales.
Lo anterior no implica, sin embargo, que no se puedan utilizar coordenadas
no-inerciales. Por el contrario, como podrá notarse en forma evidente, los marcos
no-inerciales se emplean quizá con la misma frecuencia que los inerciales. En los
ejemplos que siguen se observará cómo debe escribirse la segunda ley de Newton en el
caso de coordenadas no-inerciales. En los capítulos 3 y 4 se demuestra que las
ecuaciones de Lagrange (una vez expresada la energía cinética en la forma apropiada)
conducen a las ecuaciones del movimiento correctas en coordenadas inerciales, no-
inerciales o mixtas.
Ejemplo 1.1:
Como ilustración de la condición A, considérese el comportamiento de los objetos (a), (b) y (c) de la
figura 1-1, dentro de un vagón de ferrocarril que se mueve con aceleración constante, ax, sobre una vía
recta y horizontal.
lYi
« _*.
= v,t+ $a,t*
-
A
Yt
Xt
V*
G
^
A
/
/,
V
(a)
2/i
1
o o
En la figura 1-1, (a) representa una esfera de masa m, bajo la acción de una fuerza exterior F (con
componentes Fz y Fy) sometida a la gravedad. Si se supone que el marco X,, Vi es inercial,
considerando el movimiento solamente en un plano y tomando la esfera como una partícula, las ecuaciones
del movimiento con respecto a la Tierra, son
(1) mxi = Fx (2) myi = F, — mg
as relaciones entre las "coordenadas del vagón" y las "coordenadas de la Tierra", para m,
Por otra parte,
serían
(8) *! = *« + vit + \axt* (¿) y1 = yt + h
Al derivar (3) y (4) con respecto al tiempo, y al sustituirlas en (/) y (2),
(5) mxt = Fx — max (6) myt = Fy — mg
que son las ecuaciones del movimiento con relación al vagón.
Es claro que la ordenada y2 es inercial puesto que (2) y (6) tienen la misma forma. Sin embargo,
la abscisa x2 es no-inercial, ya que (/) y (5) son diferentes. La ecuación (5) es un ejemplo sencillo de la
segunda ley de Newton escrita para un marco no-inercial. (Nótese la magnitud del error que se cometería
si se escribiera, en cambio, mz» = Fx.)
Debe observarse que el efecto de la condición no-inercial, sobre cualquier sistema mecánico, o sobre
una persona en el vagón, es como si g se incrementara a (c$ + g*)1", en una dirección que forma un ángulo
FUNDAMENTOS BÁSICOS, I
CAP. 1
e = t&n~1ax/g con la vertical, hacia abajo, y que todas las coordenadas fuesen consideradas como
inerciales.
Si el hombre lanza una bola (Fig. 1-1 (b)) hacia arriba con una velocidad u0, su trayectoria en el
vagón será parabólica y debe calcularse como si la gravedad tuviera la magnitud y dirección indicadas
antes. Si el hombre tiene una masa M, ¿cuál será su "peso" en el vagón?
Como una extensión de este ejemplo, supóngase que el coche se hace oscilar sobre la vía, alrededor
de un punto fijo, según s = s0 + A sen«í, en donde s0, A y u son constantes. La ecuación (6)
continúa sin modificación, pero al derivar Xi = x2 + n0 + A sen«t y al insertarla en (/), se obtiene
rri'xt = mAu2 senut + Fx
Una vez más, se observa que x2 es no-inercial4.
Fácilmente se nota que la bola en (b) en su movimiento con respecto al vagón, describirá ahora una
trayectoria bastante complicada, que está determinada por la aceleración hacia abajo g, y por upa
aceleración horizontal Au2 sen«t.
Para el hombre será difícil colocarse sobre una báscula, no importa donde esté ésta, puesto que su
"peso" total cambia con el tiempo en magnitud y en dirección.
Ejemplo 1.2:
Considérese el movimiento de una
partícula de masa m (Fig. 1-2) con respecto a los ejes
•^2 y V2 que giran con velocidad angular
constante « con relación al marco inercial de
X, y Y,.
Las ecuaciones del movimiento en las
coordenadas inerciales, son
mxi = Fx„ myi = FVl
en donde Fx, y FVl son componentes de la
fuerza aplicada en la dirección de los ejes fijos.
Se obtendrán ahora las ecuaciones
correspondientes para las coordenadas rotatorias (y
como se verá, no-inerciales).
Al observar la figura, se demuestra que
Fig. 1-2
Xi = X2C0SUÉ — 2/2 sen ut
2/i = Xt sen ut + 2/2 eos coi
Derivando estas relaciones dos veces y sustituyéndolas en las primeras ecuaciones del movimiento, se obtiene
Fx, = m [x*t eos ut — 2¿»cosencoí — 2ytucosut — xtu* eos ut + y»u*aenut — yt sen ut] (9)
Fy, = wi[x, senuí + 2xtucosut — 2i/»(osen ut — Xtu*senut — ytu* eos ut + y» cosuí] (10)
De nuevo, al referirse a la figura, se ve que las componentes de F en la dirección de X2 y en la de
Y2, están dadas por F», = F«, eos ut + F„ sen coi y por Fn = FM eos coi — F«, sen coi. Así, al
multiplicar (9) y (10) por eos ut y por sen ut, respectivamente, y al sumar el resultado es
Fx, = mxt — mxtu* — 2muyt (11)
En forma semejante, multiplicando (9) y (10) por sen ut y por eos ut respectivamente y restando,
tenemos
F„ = mj/t - mytu* + 2muxt (12)
Estas son las ecuaciones del movimiento con respecto a los ejes no-inerciales X2 y Y2. Nótese que sería
un error escribir Fx, = mx\ y Fn = myt. Este ejemplo pone en evidencia que cualquier marco
giratorio es no-inercial.
Condición B.
Las ecuaciones (2.2) son válidas únicamente cuando m es constante. En caso
que m sea variable, la ecuación (2.2) debe remplazarse por
F = |(m„)
••Por conveniencia, en el presente texto nos referiremos al producto (masa) x (aceleración) como a una
"fuerza inercial".
CAP. 1]
FUNDAMENTOS BÁSICOS, I
5
Pueden citarse varios ejemplos en los que la masa de un objeto varía con su
posición (una bola de nieve que rueda por una pendiente cubierta de nieve), que varía
con el tiempo (un carro tanque con un orificio en un extremo por el cual sale un
líquido, o un cohete durante la etapa en que se quema el combustible), o que varía
con la velocidad (un objeto que se mueve con una velocidad cercana a la de la luz).
Sin embargo, en este texto no se considerarán problemas de masa variable.
Condición C.
En general, las masas del sistema deben ser grandes en comparación con las de
los átomos y las de las partículas atómicas. La dinámica de las partículas atómicas
pertenece al campo de la mecánica cuántica. A pesar de esto, hay algunas situaciones
"fronterizas"; por ejemplo, la deflexión de un haz de electrones en un tubo de rayos
catódicos usualmente se calcula con suficiente precisión por medio de la mecánica
clásica.
Condición D.
Sea grande o pequeña la masa, su velocidad debe ser muy inferior a la de la luz.
Como se sabe, por la teoría especial de la relatividad, la masa de cualquier objeto
aumenta con su velocidad. En el caso de velocidades "ordinarias" este cambio de
masa es muy pequeño, pero a medida que la velocidad se aproxima a la de la luz, la
proporción de este aumento se vuelve muy importante. Por consiguiente, la relación
(2.2) no describirá con precisión el movimiento de un electrón, un protón, o una
pelota, si éstos se mueven con una velocidad aproximada de 2 X ÍO10 cm/seg.
(Naturalmente, esta condición podría incluirse en fí.)
Condición E.
En el caso en que ciertas masas del sistema sean muy grandes, o si se consideran
intervalos de tiempo muy largos (un siglo o más), o en problemas que abarquen estas
dos condiciones, la teoría general de la relatividad concuerda con la experiencia
mejor que la dinámica de Newton. Por ejemplo, la dinámica relativística predice que
el perihelio de la órbita del planeta Mercurio debe avanzar un ángulo de 43" por siglo,
lo cual coincide muy bien con los resultados de mediciones astronómicas.
En conclusión, se observa que al tratar de masas, velocidades o tiempos "ordinarios",
siempre se cumplen las condiciones C, D y E. Por tanto, en la "dinámica clásica" el mayor
interés tiene que ver con A y con B.
De las condiciones anteriores resulta evidente que existen tres campos de la dinámica,
más o menos bien definidos: Clásica, cuántica y relativística. Desafortunadamente hasta
ahora no se ha desarrollado una teoría "unificada" que pueda ser aplicada en cualquiera o
en todas las condiciones.
1.7 Dos tipos generales de problemas de dinámica.
Prácticamente cualquier problema de dinámica clásica es un caso especial de uno de los
dos tipos generales siguientes:
(a) Partiendo de unas fuerzas dadas que actúan sobre un sistema de masas, y conocidas las
restricciones, la posición y la velocidad de cada una de las masas en un instante
determinado, se requiere hallar el "movimiento" del sistema, es decir, la posición, la velocidad
y la aceleración de cada una de las masas, en función del tiempo.
(b) Partiendo de unos movimientos dados para un sistema, se requiere hallar un posible
conjunto de fuerzas que produciría tales movimientos. En general, algunas o todas las
fuerzas pueden variar con el tiempo.
Desde luego, consideraciones sobre el trabajo, la energía, la potencia, la cantidad de
movimiento y el momentum angular pueden ser importantes, bien en el tipo (a) o en el (6).
FUNDAMENTOS BÁSICOS, I
1.8 Métodos generales para solucionar problemas de dinámica.
La mayor parte de los problemas de la dinámica aplicada son del tipo (a). El
procedimiento general es el mismo en todos aquellos que pertenecen a este tipo. Por conveniencia el
procedimiento puede dividirse en cuatro etapas.
(1) Selección de un sistema de coordenadas apropiado.
La facilidad con que puede resolverse un problema específico depende en una
buena medida de las coordenadas utilizadas. El sistema más ventajoso depende del
problema entre manos; desafortunadamente no es posible dar reglas generales de
selección. Principalmente es un problema de experiencia y criterio.
(2) Planteamiento de las ecuaciones diferenciales del movimiento.
Ya se han dado algunos ejemplos sencillos de
ecuaciones de movimiento. No obstante, para
ilustrar aún más el significado del término
"ecuaciones del movimiento", considérese el problema de
una pequeña masa m, suspendida de un resorte
espiral de masa despreciable, como aparece en la
figura 1-3. Supóngase que m puede moverse en un
plano vertical bajo la acción de la gravedad y del
resorte. Las ecuaciones del movimiento, expresadas
en coordenadas polares, son
/•• k
\r - rd2 - g eos 6+—(r-r0) = 0
r6 + 2ré + gsene = 0
en donde r0 es la longitud del resorte sin estirarse
y k es la constante elástica usual del resorte. La
integración de estas ecuaciones diferenciales de
segundo orden dan r y 0 en función del tiempo.
Es importante recalcar doi, observaciones: (a) Estas ecuaciones diferenciales
pueden plantearse de varias maneras (véase el numeral 1.2). Sin embargo, como en la
mayoría de los casos, el método de Lagrange es el más ventajoso, (b) Las ecuaciones
anteriores no representan la única forma de expresar las ecuaciones del movimiento
de este péndulo. Podrían escribirse en coordenadas rectangulares, o en cualquier otro
sistema de coordenadas (véanse los capítulos 3 y 4). En cada uno de estos casos las
ecuaciones tendrán aspectos bien diferentes y algunas serán más complicadas que
otras. Las afirmaciones (a) y (b) son válidas en general para todo sistema dinámico.
(3) Solución de las ecuaciones diferenciales del movimiento.
Excepto en la formulación de Hamilton, las ecuaciones del movimiento son de
segundo orden. El grado de complejidad de las ecuaciones depende principalmente del
problema particular entre manos y del tipo de coordenadas que se usen. Con
frecuencia las ecuaciones no son lineales. Únicamente en ciertos casos, relativamente escasos,
en que por ejemplo todos los términos diferenciales tienen coeficientes constantes,
puede darse un método general de solución. Es importante mencionar que aunque
prácticamente para cualquier sistema dinámico pueden escribirse las ecuaciones
diferenciales del movimiento correctamente, en la gran mayoría de los casos éstas
resultan tan complejas que no es posible integrarlas. Afortunadamente, a pesar de lo
anterior, los varios tipos de computadores vienen a salvar la situación y ahora es posible
obtener soluciones útiles a ecuaciones bastante difíciles, con rapidez y relativamente
con pequeño esfuerzo. Naturalmente, esto quiere decir que ecuaciones diferenciales que
anteriormente se consideraban "sin solución" ocupan la atención principal de
científicos e ingenieros. Además, las técnicas generales más avanzadas para plantear tales
Fig.l-3
CAP. 1]
FUNDAMENTOS BÁSICOS, I
7
ecuaciones adquieren cada vez más importancia en todos los campos de la
investigación y del desarrollo.
(4) Determinación de las constantes de integración.
El método de determinación de las constantes de integración es básicamente
sencillo. Se reduce a la sustitución de los valores conocidos de posición y velocidad en un
instante determinado, en las ecuaciones integradas. Como el método será aclarado
con toda amplitud en los ejemplos específicos de los capítulos siguientes, no se
incluyen aquí detalles adicionales.
1.9 Ejemplo ilustrativo de los numerales 1.7 y 1.8.
Con el fin de ilustrar las observaciones de los numerales anteriores y para obtener una
visión general de la dinámica, antes de iniciar el estudio detallado del método de Lagrange,
considérese el ejemplo siguiente.
Las masas mi y m2 están conectadas a los resortes (cuyas constantes elásticas son ki y k2), y al
bloque B, como se muestra en la figura 1-4, abajo. Se hace mover el bloque según s = A sen «t, por medio de la
fuerza F. Los puntos fijos p0, Pi y p¿ se han localizado de modo que p0pi y P1P2 son las longitudes de
los resortes, primero y segundo respectivamente, sin estirar. Todos los movimientos se efectúan sobre una línea
horizontal lisa. Se desprecian las masas de los resortes.
Fig. 1-4
Se describe a continuación el trabajo relacionado con el análisis dinámico del sistema. El problema es del
tipo (a) del numeral 1.7. El método de solución es el del numeral 1.8. Un amplio análisis del problema incluiría
la determinación de: v
(a) La posición de cada una de las masas, en función del tiempo.
ib) La velocidad de cada una de las masas en cualquier instante.
(c) La energía (cinética y potencial) del sistema, en función del tiempo.
(d) La aceleración y la fuerza que actúa sobre cada una de las masas, en función del tiempo.
(e) Las frecuencias del movimiento de cada una de las masas.
(/) La fuerza que debe aplicarse a B.
(g) La potencia entregada por B al sistema, en cualquier instante.
Debe entenderse que las soluciones que se dan a continuación no tienen por objeto mostrar los detalles en su
totalidad, sino que tratan solamente de ilustrar las etapas fundamentales. Por esto, los manejos matemáticos que
no parecen esenciales en una visión general, se omiten. Se determina primero (a) y de aquí se siguen sin dificultad
(b), (c), ... y (g).
Siguiendo las etapas descritas en el numeral 1.8, primero se selecciona un sistema de coordenadas apropiado.
Como el movimiento está restringido a una recta horizontal, resulta evidente que sólo dos coordenadas se requieren;
una para determinar la posición de cada una de las masas. De las distancias indicadas en la figura 1-4,
cualquiera de los pares (xi, x2), (x3, x5), (x3, x4), (x4, x5), etc., puede utilizarse. Por conveniencia se escoge (xi, x2).
Las ecuaciones del movimiento, obtenidas por aplicación directa de las leyes de Newton o de las ecuaciones
de Lagrange, son
miXi + (fci + fcí)xi — ktXt = kiAsenu
mt'xt + ktXt — ktXi = 0
(/)
(2)
Con el fin de hacer el problema más específico, se fijan las siguientes cantidades:
: 12 rad/seg
m, = 400 g, m2 = 300 g, A = 5 cm
ki = 6 x 104 dinas/cm, í¡2 = 5x 104 dinas/cm,
8
FUNDAMENTOS BÁSICOS, I
[CAP. 1
Por medio de métodos conocidos de integración se encuentran las soluciones aproximadas de (/) y (2)
x, = 6.25A, sen(19,37í +71)— 3A2 sen (8,16í +72) — 0,95 sen 12í (3)
x2 = — 5A, sen(19,37í +71) — 5A2 sen (8,16í +72) — 7 sen 12í (4)
con lo cual se han completado las tres primeras etapas del numeral 1.8.
Las constantes arbitrarias de integración A\,A2,yi y 72 pueden determinarse mediante la asignación
de condiciones iniciales específicas. Se puede suponer, por ejemplo, una forma de iniciar el movimiento; cuando
t = 0, se tiene
Xi = 3 cm, Xt = 4 cm (5)
¿i = 0, £t = 0 (6)
Al remplazar en (3) y en (4) los valores de (5), y en las derivadas con respecto al tiempo de (3) y (4), los valores
de (6), resultan cuatro ecuaciones algebraicas de las cuales pueden obtenerse los valores específicos de las constantes,
en forma inmediata. Así se obtienen los desplazamientos xi y x2 como funciones específicas del tiempo.
Por simple inspección se nota que cada una de las soluciones a las partes (b), (c), .. . y (g) pueden
determinarse directamente partiendo de las formas finales de (3) y (4). Así pues, todos los detalles adicionales se le
dejan al lector.
El sencillo ejemplo anterior presenta una visión bastante completa del procedimiento
general que se sigue en la solución de la vasta clase de problemas mencionados en el numeral
1.7(a). Una advertencia: Las ecuaciones del movimiento (2) y (2) son bien sencillas y por
tanto todas las etapas pudieron realizarse sin dificultad. Desafortunadamente este no es el
caso general (véase el numeral 1.8, (3)). Por otra parte, sucede con frecuencia que muchos
de los detalles que se enumeraron en la lista del numeral 1.9, no se necesitan.
El segundo tipo general de problemas mencionado en 1.7 (6) será estudiado en el
capítulo 13.
Resumen y observaciones
1. La "dinámica clásica" es la rama de la dinámica para la cual se cumplen las leyes de
Newton, bajo las restricciones C, D y E del numeral 1.6
2. Las "leyes básicas" de la dinámica son sencillamente expresiones compactas de
resultados experimentales. Pueden expresarse matemáticamente de varias maneras diferentes,
pero todas ellas son básicamente equivalentes. Cualquiera de las formas puede ser
deducida a partir de cualquier otra.
3. Es de gran importancia conocer y entender las condiciones de validez de las leyes de la
dinámica clásica. Resulta imprescindible, en la solución de todo problema de dinámica,
la definición de un "marco inercial" y la verificación del papel que desempeña éste.
4. Hay dos tipos principales de problemas en la dinámica clásica (como se vio en el numeral
1.7) de los cuales, el de 1.7 (a) es el más común. Es importante el reconocimiento de este
hecho, así como del orden general de la solución.
5. Actualmente existen tres campos distintos de la dinámica (desde el punto de vista de la
solución) bastante bien definidos (físicamente): Clásica, cuántica y relativística. Hasta
ahora no se ha desarrollado un conjunto unificado de leyes que sea aplicable a cualquier
problema o a todos ellos.
CAP. 1]
FUNDAMENTOS BÁSICOS, I
9
Problemas y preguntas de repaso
1.1. Expresar el significado del término "dinámica clásica". Mencionar ejemplos específicos que ilustren los
otros dos campos.
1.2. ¿Qué puede decirse con respecto al "origen" y a las maneras de expresar las leyes de la dinámica?
1.3. Indicar con claridad el significado del término "marco inercial de referencia".
1.4. Demostrar que cualquier marco de referencia que se mueve con velocidad lineal constante (sin rotación)
con respecto a un marco inercial, es así mismo inercial.
1.5. ¿Es posible reconocer por simple inspección, si un sistema de coordenadas es inercial, o no-inercial? ¿Es
admisible, en la solución de algunos problemas, utilizar una combinación de coordenadas inerciales con
no-inerciales? (Estas son consideraciones de importancia.)
1.6. El cable que sostiene un ascensor se rompe haciendo que éste caiga libremente (desprecíese la resistencia
del aire). Demostrar que para cualquier sistema mecánico cuyos movimientos se refieran al ascensor, el
campo gravitatorio de la Tierra, se anula efectivamente.
1.7. Un sistema de coordenadas está adherido al interior de un automóvil que se mueve de la manera usual,
por una avenida con curvas, baches, semáforos y policías de tráfico. ¿Será inercial tal marco? ¿Los
ocupantes del vehículo experimentan alguna fuerza diferente de la gravitacional? Explicar.
1.8. Si el coche de la figura 1-1 se mueve con velocidad constante sobre una vía circular horizontal, ¿cuáles
de las coordenadas x2, y-¿ o z2 de mi (o de cualquier otro punto referido al marco X2, Y2, Z-¿)
serán no-inerciales? Explicar. (Supóngase que Z\ tiene la dirección del radio de curvatura de la vía.)
1.9. Supóngase que el marco X2, Y2 de la figura 1-2 tiene un tipo definido de rotación (como 6 = constante,
'e= constante o 0 = 0O sen«í). Demostrar que las coordenadas x2, y2 son no-inerciales. Véase
el ejemplo 1.2.
1.10. Supóngase que el dispositivo de la figura 1-4 se coloca en el vagón de ferrocarril de la figura 1-1, paralelo
al eje X2, y que el vagón se mueve con aceleración constante az. Demostrar que las ecuaciones del
movimiento (/) y (2) del numeral 1.9, deben remplazarse por
mi'xi + {ki + k*)Xi — ktXt = kiA sen coi - ra^,
mtXt + ktXt — ktXi = —midx
1.11. Supóngase que el origen del sistema X2, Y2 de la figura 1-2 tiene una aceleración constante ax, en la
dirección del eje Xi, y que simultáneamente X2, Y2 giran con velocidad angular constante «.
Demostrar que las ecuaciones (//) y (12) del ejemplo 1.2, deben remplazarse por
F«j = mxt — mxtu* — 2m«j/« + max eos ut
F¥t = my» — mytu1 + 2muXt — max sen ut
1.12. Supóngase que el marco X, Y al cual está sujeto el péndulo de la figura 1-5, se mueve con velocidad
constante vx en la dirección X y vy en la dirección y (sin rotación del marco). Demostrar que la
ecuación del movimiento del péndulo, en el sentido de 0, es r*e = —g sen 0. ¿El período de oscilación se
altera por el movimiento del marco del cual pende?
FUNDAMENTOS BÁSICOS, I
[CAP. 1
Fig. 1-5
1.13. Si el marco X, Y de la figura 1-5, tiene una aceleración constante az, en la dirección de X, y una
velocidad constante, vy, en la dirección de Y, demostrar que
re = —ax eos 8 — g sen e
' por tanto, que 0 no es inercial. ¿El péndulo tiene ahora un período igual al del problema 1.12?
1.14. Enunciar y dar ejemplos de las dos principales clases de problemas que se encuentran en la dinámica
clásica. Describir el procedimiento general que se sigue en la solución de los problemas del primer tipo.
CAPITULO
Fundamentos básicos, II
Sistemas de coordenadas, ecuaciones de trasformaclón,
coordenadas generalizadas. Grados de libertad, grados de
restricción, ecuaciones de restricción. Velocidad, energía
cinética y aceleración en coordenadas generalizadas.
Desplazamientos virtuales y trabajo virtual.
2.1 Observaciones introductorias.
Los desarrollos teóricos, así como la solución a problemas de aplicación en el campo de la
dinámica analítica incluyen, además de los importantes tópicos estudiados en el capítulo
primero, una consideración inmediata de las coordenadas generalizadas, ecuaciones de tras-
formación, grados de libertad, grados de restricción, ecuaciones de restricción, velocidad y
energía cinética expresadas en coordenadas generalizadas, expresiones generales de la
aceleración y el significado y uso de los desplazamientos virtuales y del trabajo virtual. Ningún
estudiante está en capacidad de comprender el desarrollo de esta materia sin haber entendido
claramente cada uno de estos tópicos.
2.2 Sistemas de coordenadas y ecuaciones de trasformación.
Los diferentes tópicos bajo este título se estudiarán, principalmente, por medio de
ejemplos específicos.
(1) Sistemas rectangulares.
Considérense primero los sistemas
rectangulares en dos dimensiones de
la figura 2-1. Las distancias xit y\
localizan el punto p con respecto al
marco de referencia Xlt Yx. En
forma similar, x2, y2 localizan el
mismo punto con respecto a X2, Y2-
Por observación se ve que las
coordenadas jci, yi de cualquier punto en el
plano, se relacionan con las
coordenadas x2, y2 del mismo punto por
medio de las siguientes "ecuaciones de
trasformación":
Xi
Xo + X2 eos 6 — 2/2sen0
Fig.2-1
2/i = 2/o + X2sen6 + 2/2 eos 6
(2.1)
(2.2)
Nótese que tanto x\ como yi son ambas funciones de x2 y y2, simultáneamente.
Puede verse que las relaciones (2.1) pueden escribirse en una forma más
conveniente, como sigue
Xi - Xo + I1X2 + I2V2
2/1 = 2/0 + WI1Z2 + ™22/2
en donde Z1? mx y ¿2» ^2 son los cosenos directores de los ejes X2, Y2
respectivamente, con relación al marco X1? Y\.
Extendiendo el razonamiento, supóngase que el origen de X2, Y2 se mueve con
una velocidad que puede ser constante (con componentes, vx y vy) con respecto al
marco Xi, Yr, y simultáneamente, que los ejes X2, Y2 giran con velocidad
angular constante u, de tal manera que 6 = ut. Las ecuaciones (2.1) y (2.2) pueden
escribirse
11
12
FUNDAMENTOS BÁSICOS, II
[CAP. 2
X\ = vxt 4- #2COSwt — 2/2senwí
2/i = vyt 4- a^senwí 4- 2/2 eos wí
(2.3)
Nótese que jci, 3^1 son ahora funciones tanto de x2, y 2, como del tiempo.
Naturalmente, pueden escribirse ecuaciones adecuadas para cualquier tipo de
movimiento que se suponga.
Frecuentemente se encuentran ecuaciones de trasformación semejantes a las
anteriores, las cuales se designan simbólicamente por
Xi = Xi(x2,y2,t), 2/1 = 2/1 {%2,2/2, t)
Puede demostrarse que ai se
consideran dos sistemas rectangulares tri- zs
dimensionales, como en la figura 2-2,
las ecuaciones de trasformación que
relacionan las coordenadas x^, y\ y zx
de un punto, con las designadas por x2,
y-2 y 22 para el mismo punto, serán
Coordenadas
(*».v».*iV
X\ = ío + l\X2 4- Í22/2 4- lzZ2
2/1 = 2/0 4-miz2 4-m22/2 4-ra322 (2.4)
Z\ — Zo 4- n\X2 4- W22/2 4- nzZz
en donde lu m\ y nit son los
cosenos directores del eje X2, etc.
Desde luego, el marco X2, Y2, Z2
podría estarse moviendo, en cuyo caso
(conocido el movimiento) jc0» yo, Zo
y los cosenos directores podrían
expresarse en función del tiempo, o sea, xi =
xAx2, y2, z2, t), etc.
tit mt, w»
¿*>/ I ' Cosenos directores del
' 1 eje Xs:/i, mt, n„ etc.
I
Yt
Fig.2-2
(2) Sistema cilindrico.
Este sistema, bastante conocido, se muestra en la figura 2-3. Se observa que las
ecuaciones que relacionan las coordenadas (x, y, z) con (r, <j>, z) son
= z (2.5)
x = p eos <f>, V = p sen $,
Coordenadas
z
Coordenadas cilindricas P> $< *
Fig.2-3
Coordenadas esféricas r, #, $
Fír.2-4
CAP. 2]
FUNDAMENTOS BÁSICOS, II
13
(3) Sistema esférico.
Las coordenadas esféricas, consistentes en dos ángulos, <j> y 0, y una distancia
r, usualmente se designan como en la figura 2-4. Observando la figura se demuestra
que
x = rsen0cos<¿, y = rsen0sen<¿, z = reos 8 (2.6)
Nótese que x y y son ambas, funciones de r, <j> y 0. Sin embargo z es función
únicamente de r y de 0.
(4) Otros sistemas de coordenadas.
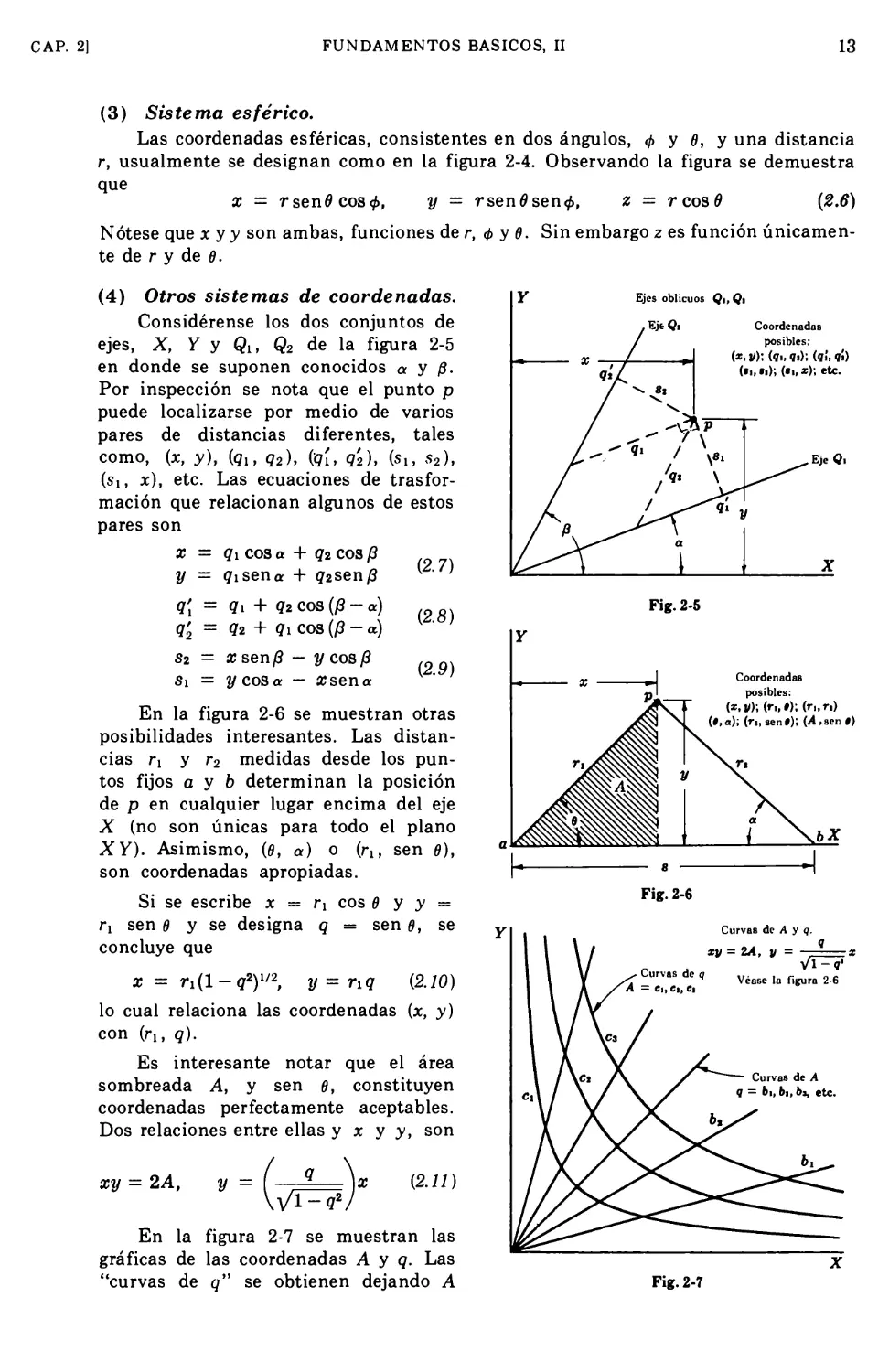
Considérense los dos conjuntos de
ejes, X, y y Qlt Q2 de la figura 2-5
en donde se suponen conocidos a y (i.
Por inspección se nota que el punto p
puede localizarse por medio de varios
pares de distancias diferentes, tales
como, (x, y), {qlt q2), (q[, q2), (si, s2),
(si, x), etc. Las ecuaciones de trasfor-
mación que relacionan algunos de estos
pares son
X = tfi COSa + <?2 COS (3
y = tfisena + q^sen/?
Q[ = Qi + Q2 eos (/? - a)
Q2 = Q2 + tfi COS(/?-a)
S2 = x sen/8 — y eos/?
Si = y eos a — 2 sen a
(2.7)
(2.8)
(2.9)
Ejes oblicu
. EJ* Q*
?*/
/ >v
os Q,,Q
Coordenadas
posibles:
(«> V): (?i. Vi); (?¡. ?!)
(ti, ti); (ti,«); etc.
/7"
\
^EjcQ,
Fig. 2-5
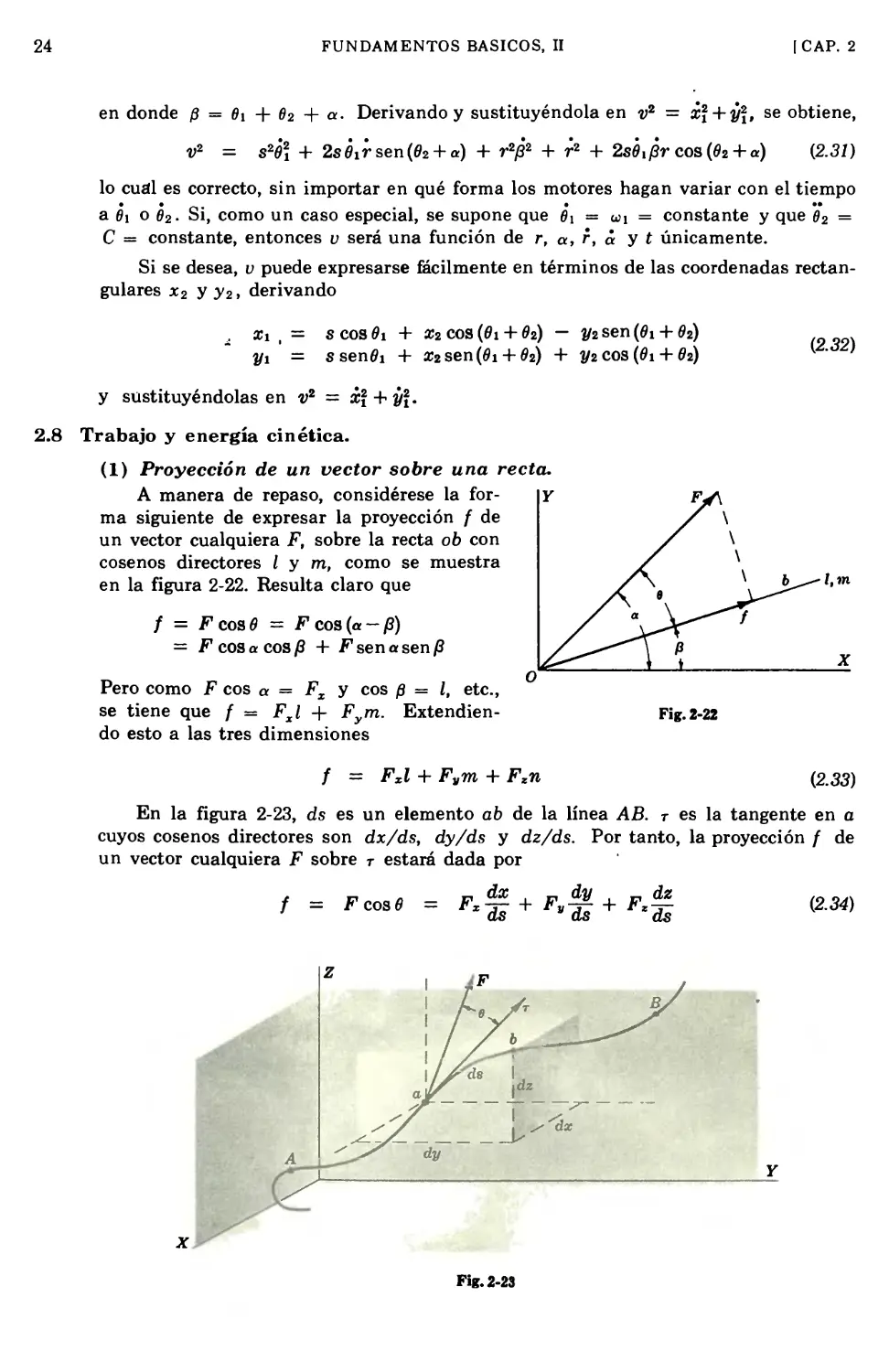
En la figura 2-6 se muestran otras
posibilidades interesantes. Las
distancias rx y r2 medidas desde los
puntos fijos a y b determinan la posición
de p en cualquier lugar encima del eje
X (no son únicas para todo el plano
XY). Asimismo, (0, a) o (rlf sen 0),
son coordenadas apropiadas.
Si se escribe x = rx eos 0 y y =
/*! sen 0 y se designa q = sen 0, se
concluye que
Coordenadas
posibles:
(*.«); (ri, #); (r,,r,)
(#,a);(r„sen#);(A(8en#)
x = n(l-q2y<
y = nq
(2.10)
lo cual relaciona las coordenadas (x, y)
con (r1? q).
Es interesante notar que el área
sombreada A, y sen 0, constituyen
coordenadas perfectamente aceptables.
Dos relaciones entre ellas y x y y, son
xy = 2A,
\/W
(2.11)
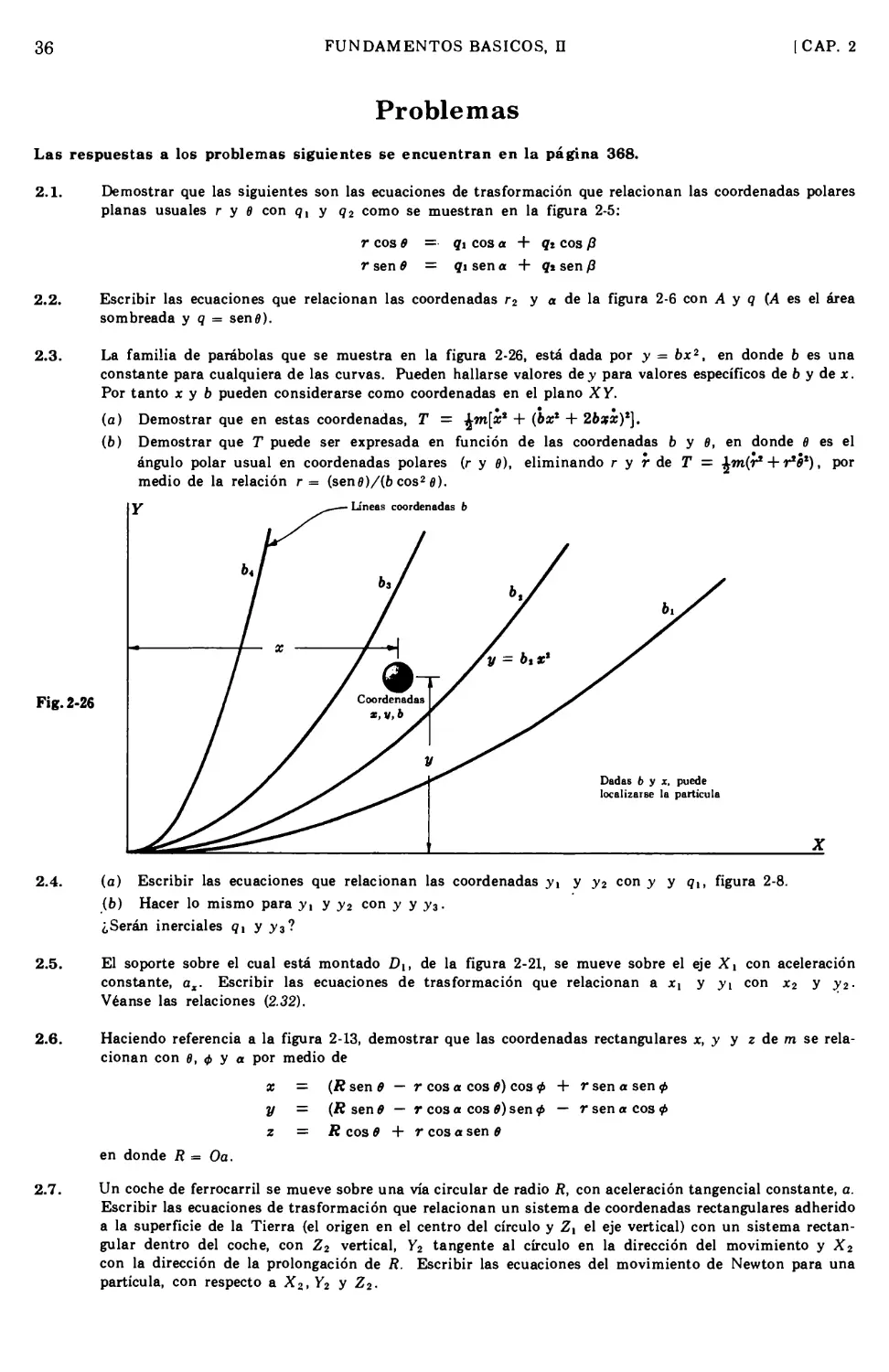
En la figura 2-7 se muestran las
gráficas de las coordenadas A y q. Las
"curvas de q" se obtienen dejando A
Fig. 2-7
14
FUNDAMENTOS BÁSICOS, II
[CAP. 2
constante y haciendo gráficas de la primera relación de {2.11). En la misma forma,
las "curvas de A" resultan de la segunda relación, con q constante.
Es evidente, por los ejemplos mencionados, que puede emplearse una gran
variedad de coordenadas (longitudes, ángulos, funciones trigonométricas, áreas, etc.).
(5) Coordenadas para el sistema mecánico de la figura 2-8.
Supóngase que las masas mi y m2 están conectadas por medio de un resorte
y pueden moverse únicamente a lo largo de la vertical. Como el movimiento está así
limitado, la posición de las masas se determina mediante la especificación de sólo dos
coordenadas, como y\ y y2. Asimismo, (ylt y3), (jy2, jy3), (91, yi), (92, jyi).
(<7i. ^2)» etc-» son adecuadas. Se dice que se ha determinado la configuración del
sistema cuando se conoce uno cualquiera de estos conjuntos. Entre estos conjuntos de
coordenadas existen relaciones obvias (ecuaciones de trasformación). Nótese que como
miq\ = m2qi, q\, y q¿ no son independientes. ¿Serán entonces
independientes 91 y y3?
El disco D, está fijo. D2 puede moverse verticalmen-
te. La masa m3 sirve de cojinete a D2 y no gira.
Íl mx, m2, m3 y m4 tienen movimiento vertical
I solamente. Las tensiones en los hilos se representan
* por ti, T2, T3 y t4. Desprecíense las masas de
Di y D2.
Fi*. 2-8 Fig. 2-9
(6) Coordenadas para un sistema de masas pendientes de poleas.
Si se supone que las cuatro masas de la figura 2-9, se mueven verticalmente, se ve
que cuando se especifica la posición de mi, por y\ o por sít la posición de m3 queda
determinada. Asimismo, al especificar la posición de m2 mediante y2 o s2, se
conocerá la de m4. (Estas afirmaciones suponen, naturalmente, que todas las
dimensiones fijas de los cables y las poleas se conocen.) Así pues, solamente se necesitan dos
coordenadas para determinar la configuración de las cuatro masas. Al principio es
posible inclinarse por decir que se necesitan cuatro coordenadas, tales como, ylt y2, yz,
y4. Pero en la figura puede observarse que yi -\- y3 = C\ y que y2 -f jy4 — 2jy3 = C2
en donde C\ y C2 son constantes. Por tanto, si se conocen los valores de las
coordenadas de cualquiera de los pares {yu y2), (ylf y4), (y2, ;y3), los valores de las
otras dos pueden obtenerse por medio de las ecuaciones mencionadas.
Para ser usadas más tarde, el lector podría demostrar las siguientes igualdades
2/1 = h + s4 + qi - li - h - 2C, ys = h-St- qi + h • .
y2 = h - s4 - 2gi + lu 2/4 = h - s4 '
en donde l\ y l2 son las longitudes de los cables. Nótese que las posiciones vertica-
CAP. 2]
FUNDAMENTOS BÁSICOS, II
15
les de todas las cuatro masas son conocidas, si se han dado los valores de dos
coordenadas únicamente (s4, qx).
(7) Coordenadas posibles para un péndulo doble.
Las dos masas, mx y m2, de la figura 2-10, están suspendidas de un soporte
rígido y pueden moverse libremente en el plano X, Y.
(a) Suponiendo que r\ y r2 son hilos de longitud fija, se requieren dos coordenadas
tales como (0, <f>), (jci, jc2), (y\, ^2), etc.
(b) Suponiendo que ías masas se hallan
suspendidas de bandas de caucho, o de
resortes espirales, se necesitan cuatro
coordenadas, tales como (rl} r2, 0, <f>),
(*i> y>i, x2, y2), etc. Las ecuaciones
de trasformación que relacionan los
anteriores conjuntos de coordenadas son
L_ 30 J JV^-Pfc*. y»)
Xi
x2
2/2
(2.13)
(8)
Xo + T\ $en0
2/o - n eos 6
Xo + risenO + r2sen<¿
2/o - r\ eos 6 — r2 eos <f>
Fig. 2-10
Marcos de referencia móviles y "coordenadas móviles".
En la práctica se encuentran muchos problemas para los que es conveniente
utilizar marcos de referencia móviles. (Por conveniencia, en ocasiones, las coordenadas
medidas con respecto a tales marcos pueden denominarse "coordenadas móviles".)
Algunos ejemplos generales son: Un marco de referencia sujeto a un ascensor, a un tren en
movimiento o a una plataforma que gira; ejes de referencia adheridos a la Tierra con
el fin de determinar movimientos con relación a ésta; un marco fijo al interior de un
satélite artificial; etc.
Se ha mencionado ya un ejemplo específico (véase la ecuación (2.3)), pero quizá
puede ser útil citar los siguientes
(a) Supóngase que en la figura 2-1, el origen O posee una velocidad inicial (ux, uy)
y una aceleración constante (ax, ay), mientras los ejes giran con velocidad
angular constante o>. Lógicamente, las ecuaciones (2.2) toman la forma
Xi = vxt + $axt2 + z2coSü>£ — 2/2seno)í
2/i = vyt + idyt2 + X2sen<at + 2/2coSü)í
Una vez más se ve que xx = xx(x2, y2, t), etc.
(b) Si se hace oscilar a lo largo de una recta inclinada, al soporte de la figura 2-10,
según x0 = A0 + A sen wt y y0 = B0 + B sen wt, las relaciones (2.13) tendrán la
forma x2 = A0 + Asentí + nsenfl + r2sen<¿
2/2 = Bo + Bsenwt — ncosfl — T2Cos<j>
etc., lo cual puede indicarse como x2 = x2(ri, r2, 0, <f>, t), etc. Es importante
entender y desarrollar un sentido del significado físico y geométrico asociado con
relaciones simbólicas de este tipo.
(c) Si en la figura 2-9 se le da al soporte una aceleración vertical constante con
velocidad inicial Vi, entonces h = vxt + \at2 y las relaciones (2.12) deben escribirse
yx = vxt + \at2 + s4 + <?i + constante, etc.
(d) Supóngase que los ejes Qi y Q2 de la figura 2-5 giran alrededor del origen con
velocidades angulares constantes, u\ y ü>2, de modo que a = w\t y /3 = ü>2£-
(2.14)
(2.15)
16
FUNDAMENTOS BÁSICOS, II
(CAP. 2
Aun así es posible usarlos como "marco de referencia" (aunque para la mayoría
de los problemas no resulta muy deseable). Las relaciones {2.7) se convierten en
x = q1co8w1t + q2cosw2t (2 16)
y = q1senw1t + q2senw2t
o bien, x = x(qx, q2, t), etc.
Es importante observar que los marcos de referencia de los ejemplos
anteriores son no-inerciales.
Finalmente, con respecto a las ecuaciones de trasformación, en general se
tiene
(i) Como regla general, todas las coordenadas de un sistema son funciones de todas
las demás y del tiempo (si los marcos son móviles), como puede verse en las
ecuaciones (2.14), (2.15) y (2.16).
(ii) En los ejemplos anteriores, la mayoría de las ecuaciones de trasformación
relacionan las coordenadas rectangulares con algunas otras. Pero si se desea,
normalmente pueden escribirse ecuaciones que relacionen varios tipos de coordenadas.
2.3 Coordenadas generalizadas. Grados de libertad.
(1) Coordenadas generalizadas.
Como se ha visto en los ejemplos precedentes, puede emplearse una gran variedad
de coordenadas. Así, por conveniencia, se usa la letra q como símbolo general para
representar coordenadas, no importa cuál sea su naturaleza. Por tanto, q se denomina
CQQzdenaéQ-genemliziida.
Por ejemplo, las ecuaciones (2.15) pueden escribirse como x2 = A0 + A sen wt +
9i92 + 9394 Y y2 = Bq + B sen wt — qx Vi — q\ — 93 Vi — q\, en donde rx
se ha remplazado por qu sen 0 por q2, etc.
Según el uso común, frecuentemente indicaremos las n coordenadas que se
requieren para especificar la configuración de un sistema, como qx, q2, ...,qn.
(2) Grados de libertad, definición e ilustración.
Una de las primeras consideraciones en la solución de un problema es la
determinación del número de "grados de libertad" del sistema. Estos se definen como
El número de coordenadas independientes (sin incluir el tiempo) que se requieren
para especificar completamente la posición de todas y cada una de las partículas o
partes componentes del sistema.
El término "parte componente" se refiere aquí a cualquier parte de un sistema,
tal como una palanca, un disco, un piñón, una plataforma, etc., que debe ser tratado
como un cuerpo rígido y no como una partícula.
A continuación se incluyen ejemplos que tienen desde uno, hasta muchos grados
de libertad.
(a) Sistemas con un grado de libertad.
Una partícula restringida a moverse en una línea recta (una cuenta ensartada en un hilo rígido)
cuya ecuación es y = a + bx. Si se conoce x o y, la otra queda determinada.
Una cuenta con posibilidad de moverse libremente en un hilo rígido de cualquier forma conocida:
Parabólica, helicoidal, etc.
Un péndulo simple con su movimiento confinado a un plano. O un péndulo cuyo hilo se tira hacia
arriba por un pequeño orificio en un tablero fijo, a una rHti^éóAstante. (La longitud del péndulo es una
función conocida del tiempo.) Nótese que el tiempo nunca se incluye como un grado de libertad.
La cuenta que se muestra en la figura 2-11, que puede deslizarse libremente a lo largo de la varilla
que gira alrededor de p, de alguna manera determinada.
CAP. 2]
FUNDAMENTOS BÁSICOS, II
17
Y
,P|
I1
0
1
s?
Eje de rotación
n
f
y
y
x
1 ]£-
y /
• /
y \
m¡
Fig.2-11
Fig.2-12
(b) Dos grados de libertad.
Una partícula con libertad para moverse en contacto con un plano o con una superficie conocida
cualquiera: Esférica, cilindrica, etc.
La palanqueta de la figura 2-12, que puede deslizarse libremente a lo largo del eje Y y al mismo
tiempo girar alrededor del mismo eje.
El sistema de masas y poleas de la figura 2-9. En la ecuación (2.12) se observa que si se han dado los
valores de s4 y qlt se conoce la configuración completa. Si el soporte AB se está moviendo, se requieren
dos coordenadas y f; sin embargo, aún así se considera que existen dos grados de libertad.
El péndulo doble de la figura 2-10, siendo rt y r2 hilos de longitud constante.
(c) Tres grados de libertad.
Una partícula libre de moverse en el espacio.
Coordenadas posibles: (x, y, z), (r, $, 0), etc.
Un tablero o una lámina que puede deslizarse
libremente sobre un plano. Se requieren dos
coordenadas para traslación y una para rotación.
El péndulo doble de la figura 2-10, si se supone
que r, es una banda de caucho y r2 tiene longitud
fija.
Un cuerpo rígido que puede girar libremente
alrededor de cualquier punto fijo, O, como se muestra
en la figura 2-13. La orientación queda
completamente determinada por 0, <t>, «. (m es una partícula
cualquiera del. cuerpo.)
Unión esférica.
La línea ab es normal a la I
en el plano AOZ. La recta ac
barra- -,.
Fig. 2-13
ira Oa y está
9 normal a la
El sistema de la figura 2-8 con un resorte adicional y una masa conectados a m2.
Fig.2-14
Fig. 2-15
FUNDAMENTOS BÁSICOS, II
[CAP. 2
(d) Cuatro grados de libertad.
El péndulo doble de la figura 2-10 con longitudes variables en r, y r2 (bandas de caucho o resortes
en espiral).
La disposición de la figura 2-14, en donde m, puede moverse únicamente en sentido vertical. La
partícula m2 puede moverse libremente en cualquier forma bajo la acción de la gravedad, sostenida por
una banda de caucho.
El sistema de poleas de la figura 2-15, suponiendo únicamente movimiento vertical.
El cuerpo rígido que se muestra en la figura 2-13, con la posibilidad de que la unión esférica se deslice
sobre el eje X.
(e) Cinco grados de libertad.
El cuerpo rígido de la figura 2-13 con la posibilidad que la unión esférica se mueva siempre en
contacto con el plano XY. Un sistema de cinco poleas montadas como se indica en la figura 2-16.
—A"
Los resortes de. torsión c,,c2,cs,
te, permiten que los discos tengan movimiento relativo entre ellos.
Fig.2-16
El sistema de poleas de la figura 2-15 con un resorte intercalado en el cable-que conecta a m, con m2.
Cinco partículas unidas linealmente con resortes como se muestra en la figura 2-18, con movimiento
horizontal únicamente (o sólo vertical). ¿Se tendría un número igual de grados de libertad si no existieran
los resortes, es decir, sin ninguna conexión entre las masas?
(f) Seis grados de libertad.
El péndulo doble de la figura 2-10, con las partículas mi y m2 suspendidas por bandas de caucho
y con posibilidad de moverse libremente en el espacio.
Un cuerpo rígido que puede moverse libremente en el espacio, aunque se encuentre sujeto a resortes
de cualquier forma.
El cuerpo rígido de la figura 2-13 con otro cuerpo rígido ligado a él por medio de una unión esférica,
por ejemplo en P.
El sistema de poleas de la figura 2-15 con resortes intercalados en cada uno de los cables que sostienen
a m2 y a m3.
(g) Muchos grados de libertad.
Dos tableros articulados entre sí, de modo que el ángulo entre ellos puede variar y además pudiendo
moverse el conjunto de cualquier manera aparte de .la restricción de la articulación. Tal sistema tiene siete
grados de libertad.
Una sucesión de siete poleas como las de la figura
2-16 tiene siete grados de libertad. Un sistema
consistente en tres partículas suspendidas una de la otra, como
formando un "péndulo triple" posee ocho grados de
libertad siempre y cuando dos de los hilos sean elásticos
y el movimiento no esté restringido a un plano. Si las
tres cuerdas son elásticas el sistema tiene nueve grados
de libertad.
Dos cuerpos rígidos ligados por medio de una unión
esférica y con posibilidad de moverse en el espacio con
libertad, tienen nueve grados de libertad.
El sistema que se muestra en la figura 2-17 posee
diez grados de libertad. Se necesitan tres coordenadas
para localizar el punto p, dos más para determinar la
configuración de la barra (suponiendo que la barra no
gira sobre su propio eje), tres más para fijar la posición
de m2, y finalmente, dos más para localizar a mi
(suponiendo que el hilo que la sujeta tiene una longitud
fija).
Diez grados de libertad
Fig.2-17
CAP. 2]
FUNDAMENTOS BÁSICOS, II
19
La disposición de resortes y "partículas" de la figura 2-18 puede tener diferentes números de grados
de libertad según como se les permita moverse. Si el movimiento se limita al eje V, el sistema tiene cuatro
grados de libertad; si se restringe al plano XY, habrá ocho grados de libertad. Si mi y m2 pueden
moverse sobre el eje Y únicamente, mientras que m3 y m4 pueden moverse en el plano XY, el conjunto
poseerá seis grados de libertad. Si todas las partículas pueden moverse de cualquier forma, el sistema tendrá
doce grados de libertad; y si todas las masas se consideran como cuerpos rígidos, serán veinticuatro.
\Z ^^^
ú—ww-(ñ^ ™£—vwwv-p
Fig.2-18
Se ve entonces, que los sistemas mecánicos pueden tener cualquier número finito
de grados de libertad. El número depende en cada caso del número de masas que se
consideren y de las restricciones geométricas que se impongan a sus movimientos.
Inclusive, muchos sistemas pueden considerarse como un número ilimitado de grados de
libertad. Un resorte espiral, una cuerda en vibración, la cara de un tambor, etc., son
ejemplos de este caso, si se supone que están compuestos de un número ilimitado de
partículas. En muchos problemas, aunque no en todos ellos, las masas de los resortes,
de los hilos, etc., pueden despreciarse. Así se hará en este texto.
Los sistemas que poseen un "número infinito de grados de libertad" se tratan por
otros métodos bien distintos.
(3) Selección de coordenadas independientes.
En el procedimiento matemático de la solución de un sistema, usualmente existen
muy amplias posibilidades para seleccionar las coordenadas que han de considerarse
como independientes.
En el caso de-un péndulo simple, usualmente se toma el desplazamiento angular
0, del hilo. Sin embargo podrían emplearse las coordenadas x y y de la pesa, o
muchas otras.
En la figura 2-9 se observa que al conocerse las coordenadas de cualquiera de los
pares, (ylt v2), (s3, q2), (v2, y*), (si, 91), (s4, <?i), etc., se habrán determinado
las posiciones de todas las masas. Por tanto, cualquiera de tales pares puede tomarse
como el sistema de coordenadas independientes, para la solución correspondiente.
Es bien sabido que ciertas coordenadas pueden ser más convenientes que otras. De
tal manera que las coordenadas escogidas en cada caso particular, deben ser las que
parezcan más convenientes para el problema entre manos. La selección final
dependerá, en buena parte, de la comprensión y de la experiencia.
2r4 Grados de restricción, ecuaciones de restricción, coordenadas superfluas.
Por lo visto en el numeral anterior, es evidente que el número de grados de libertad
depende no solamente del número de masas consideradas, sino también de cómo se halle
restringido físicamente el movimiento de cada una de ellas. Una partícula que puede ocupar cualquier
posición en el espacio, tiene tres grados de libertad. Para determinar su posición se requerirán
tres coordenadas independientes como (jc, y, z), (r, <p, 0), etc. Pero si el movimiento se
restringe a una línea (una cuenta ensartada en un alambre rígido), con una sola coordenada
será suficiente. Se dice entonces, que la cuenta tiene dos grados de restricción y dos de las tres
coordenadas que se necesitan para una partícula libre, son ahora "superfhías".
Es entonces evidente que un sistema de p partículas puede tener un máximo de 3p
grados de libertad, y el número n, estará dado finalmente por
20
FUNDAMENTOS BÁSICOS, II
CAP. 2
n = 3p — (grados de restricción) (2.17)
Las restricciones de un sistema pueden representarse por ecuaciones de restricción. Si la
cuenta está restringida a moverse a lo largo de una recta en el plano X Y, la ecuación de tal
recta, y = a + bx, junto con 2 = 0, son las ecuaciones de restricción. Si el alambre está en
forma parabólica, y = bx2 y z = 0 son las ecuaciones de restricción.
Considérese una vez más la figura 2-19. Se ve que para movimiento vertical únicamente
Xi = Ci, Z\ = bi; x2 = C2, z2 — b2; etc. , .
yi + )>3 = constante; \ (y2 + y*) — ya = constante
en donde xx y zx son las coordenadas de mx; Cx y bx son constantes, etc. Así, en
definitiva, hay diez ecuaciones de restricción y los grados de libertad se han reducido de un máximo
de doce, a dos. Puede decirse entonces, que diez coordenadas son superfluas.
2.5 Restricciones móviles.
Con frecuencia se da el caso de que algunas, o todas las restricciones de un sistema estén
en movimiento.
Un ejemplo sencillo se muestra en la figura 2-11 en donde la barra está girando en el
plano XY alrededor del eje indicado, con velocidad angular constante, m. La cuenta m puede
deslizarse libremente a lo largo de la barra y como a = ü>i£, la ecuación de restricción puede
escribirse entonces, y = s + (tan wxt)x. Nótese que t aparece explícitamente en esta
relación.
Como extensión de este ejemplo, supóngase que los ejes X y Y del ejemplo en
consideración son los mismos X2 y Y2 que se trasladan y giran en la figura 2-1; entonces, y2 = s +
(tan (1)lt)x2. Por consiguiente, las ecuaciones de trasformación (2.14), en función de x2 y t
(igualmente podrían haberse expresado en función de y2 y t) tienen la forma
Xi = vxt + \ax& + z2coSü>£ — (s + x2 tsLTiwfisenwt
2/i = vyt + $ayt2 + X2sen<at + (s + x2 tanwfi eosU ' '
en donde, tanto xx como yx son ahora funciones de x2 y t solamente.
Observación general: Desde un punto de vista puramente matemático, las ecuaciones de
restricción son sencillamente relaciones existentes entre las 3p posibles coordenadas que salvo
por esto, son independientes. De una manera general, pueden indicarse como
<j>i(Qi, Q2, . . .,Q3P, t) = 0, en donde i = 1,2, . . .,3p-n (2.20)
2.6 Ecuaciones de trasformación "reducidas".
Si se supone que no existen restricciones, sino posiblemente marcos de referencia móviles,
las ecuaciones de trasformación que relacionan las coordenadas rectangulares de las p
partículas con las 3p coordenadas generalizadas, pueden indicarse como xi = xt(qx, q2, ..., g3p, t),
etc. Sin embargo, si hay restricciones fijas o móviles, las coordenadas superfluas pueden
eliminarse de las relaciones anteriores mediante el uso de las ecuaciones de restricción, quedando
Xi = Xi(qi, q2, ..., qn, t); yt = yt(qlt q2, . .., qn, t); Zi = Zi(qh q2, . .., qn, t) (2.21)
las cuales contienen ahora únicamente las coordenadas que son independientes, en un
número igual al de los grados de libertad del sistema. Nos referimos a estas ecuaciones llamándolas
ecuaciones de trasformación "reducidas". Debe aclararse que en (2.21) puede aparecer t
explícitamente como resultado de tener coordenadas móviles, restricciones móviles, o ambos.
Ejemplos sencillos de (2.21) lo constituyen las ecuaciones (2.12) en las que no aparece t, o
también (2.19) en las que sí aparece t, explícitamente.
En breve se verá claramente la gran importancia que tienen relaciones como (2.21) para
obtener expresiones de velocidad, energía cinética, energía potencial, etc., en función
únicamente de las coordenadas independientes.
CAP. 2]
FUNDAMENTOS BÁSICOS, II
21
Notas, (a) En algunos casos, el álgebra que se utilizaría para eliminar las coordenadas
superfluas puede resultar complicada, (b) Los casos, relativamente escasos, de sistemas "no-
holonómicos", permiten solamente que sus ecuaciones de restricción se escriban en forma
diferencial, no integrable. Véase el numeral 9.12.
2.7 Velocidad expresada en coordenadas generalizadas.
Las expresiones para la velocidad de un punto o de una partícula pueden obtenerse por
cualquiera de los dos procedimientos siguientes. El primero pone de relieve la definición
fundamental de velocidad y las ideas básicas físicas y geométricas pertinentes. El segundo
procedimiento es más conveniente.
(1) La velocidad para un elemento de trayectoria. As. (As considerado
como vector.)
Supóngase que el punto p de la figura 2-19 se mueve una distancia As desde a
hasta 6, en un tiempo Ai. La velocidad promedio en el intervalo será As/Ai.
Cuando Ai se aproxima a cero, se escribe
velocidad = lim —r
üt-o Ai
(2.22)
en donde s es una cantidad vectorial de magnitud, \ds/dt\, dirigida según la
tangente a la trayectoria en a. Para apreciar mejor las ideas físicas y geométricas
implicadas, puede pensarse que la partícula tiene una velocidad "en la dirección de la
trayectoria" en todos los puntos de su recorrido.
La anterior definición de velocidad no hace referencia a ningún sistema de
coordenadas en particular. Pero naturalmente As puede expresarse en cualquier sistema
que se desee de tal manera que al pasar al límite Ai—* 0, s queda expresada en ese
mismo sistema. Ejemplos:
En coordenadas rectangulares, (As)2 = (Ax)2 + (A;y)2 + (Az)2. Dividiendo
por (Ai)2 y pasando al límite, puede escribirse
s2 = x2 + y2 + ¿2 (2.23)
Elemento de distancia As
At* = Ar* + r, A#' + » sen» $ A^»
y¿í /
j<^/ \w
* S<~1 sen# A¿
1
¡
1
1 Y
Fig.2-19
Fig.2-20
En coordenadas esféricas (véase la figura 2-20),
(As)2 = (Ar)* + r*(A0)2 + r8 sen* e (A*)2
por tanto
S2 _ ^ + ^2 + rZserffl^2
(2.24)
22
FUNDAMENTOS BÁSICOS, II
(CAP. 2
En el sistema oblicuo bidimensional de la figura 2-5, supóngase que p representa una
pequeña distancia cualquiera As. Se observa que (As)2 = (A<?i)2 + (A<?2)2 +
2(Agi)(Ag2) eos (0 — a); y por tanto
s2 = Q\ + Q\ + 2qiq2co3{p-a) (2.25)
A continuación se describen esquemáticamente las etapas necesarias para hallar
las velocidades s¡ y s2 de mi y m2, respectivamente, de la figura 2-10.
Básicamente, éstas serán Asi/At y As2/A£. Se traza una pequeña distancia del
recorrido del péndulo y se indican Asi y As2 como los desplazamientos
correspondientes de mi y m2 respectivamente; de acuerdo con la geometría de la figura (y
luego de una cantidad considerable de operaciones monótonas) se pueden expresar los
desplazamientos en función de rx, An, 0, A0, r2, Ar2, $ y A<t>. Después de
dividir por (A£)2 y pasando al límite, los resultados finales son
¿2 = r\+r\d*
s\ = r2 + r\ ¥ + 2(nr2 + nrj$) eos (<¡> - 6) (2.26)
+ r\ + r22j>2 + 2(rir2¿ - r2ri<¿) sen (<¿>-0)
Debe notarse que aunque la expresión de s2 resulta complicada, básicamente
no es más que un elemento de longitud As2, dividido por el correspondiente
elemento de tiempo A£. Nótese también que tal como se ha expresado arriba, s2 es
función de todas las coordenadas, así como de sus derivadas con respecto al tiempo, es
decir, s2 = s2(ri, 6, r2, <f>, n, 6, r2, i).
(2) La velocidad, usando las ecuaciones de tras formación.
Si se tiene una expresión para s en cierto sistema de coordenadas, podemos
expresarla en otro sistema por medio del uso de ecuaciones de trasformación (o de
ecuaciones de trasformación reducidas) que los relacionen entre sí. Ejemplos:
Derivando con respecto al tiempo las ecuaciones (2.6), y sustituyéndolas en (2.23),
se obtiene (2.24).
Derivando las relaciones (2.13) e insertándolas en (2.23) se obtienen, con poco
trabajo, las ecuaciones (2.26).
De las relaciones (2.12) se concluye en forma inmediata, que las velocidades de las
masas individuales vienen dadas por
¿i = s4 + ¿i, ¿2 = -s4 - 2¿if ¿3 = -s4 - ¿i, ¿4 = -s4 (2.27)
Naturalmente, esto supone que h sea constante. Nótese que todas las velocidades se
expresan en función de s4 y qx, únicamente.
Para utilizar en un ejemplo posterior, considérense las velocidades verticales,
íi y yz de mi y m2, de la figura 2-8, con respecto al eje X, inmóvil. Se trata de
expresarlas en términos de yx y qx. Como puede verse en el diagrama, yx = y + q\,
y2 = y — q2 y mxqx = m2q2 (relación del centro de masa). Por tanto,
¿i = V + Qi, 2/2 = y-^rQi (2-28)
(3) La velocidad expresada en función de las coordenadas móviles.
Debe entenderse que en el método de Lagrange para solución de problemas, una
de las primeras consideraciones consiste en determinar la velocidad de todas las
partículas, con respecto a un marco inercial. Si se utiliza un marco de referencia en el que
algunas o todas las coordenadas seleccionadas sean no-inerciales, (lo cual implica que
eventualmente se trate de hallar el movimiento del sistema con relación al marco
móvil) la velocidad que se requiere no es la relativa al marco móvil, sino la relativa a los
CAP. 2]
FUNDAMENTOS BÁSICOS, II
23
ejes inerciales, aunque expresada en función de las coordenadas móviles. (La razón
de lo anterior se verá con claridad en el capítulo 3.) Algunos ejemplos aclararán esto y
mostrarán cómo obtener los resultados deseados.
Como un caso sencillo, supóngase que los ejes X2, Y2 y Z2 de la figura 2-2
se mueven paralelamente al marco fijo Xi, Ylt Zx con aceleración constante
(ax, ay, az). Las ecuaciones de trasformación serán, xx = vxt + haxt2 + x2, etc.
Las componentes de la velocidad de p con relación a los ejes fijos son X\, yi y Zi,
y con respecto a los ejes móviles, x2, y2 y z2. Utilizando las ecuaciones de
trasformación,
xi = vx + axt + x2, etc. (2.29)
lo cual expresa la velocidad dep con relación a los ejes estacionarios pero en función de
las velocidades relativas a los ejes móviles, y del tiempo.
Si se considera que el marco X2, Y2, Z2 se mueve de cualquier manera (con
rotación y traslación) las ecuaciones correspondientes serían,
xi = x0 + I1X2 + hy2 + hz2 + lix2 + Í22/2 + ¿3Z2, etc. (2.30)
En este caso, x0, y0, z0 y todos los cosenos directores estarán cambiando con
el tiempo. Las ecuaciones (2.30) desempeñan un papel muy importante en el estudio de
la dinámica de los cuerpos rígidos, capítulo 9.
Como último ejemplo, considérese el siguiente. Di y D2 de la figura 2-21, son
dos plataformas giratorias. Di se mueve impulsada por un motor con una velocidad
angular 0\ con respecto a la Tierra. D2, que está montada sobre Di es movida por
un segundo motor a una velocidad angular 02, con relación a Di. Los ejes Xi y
Yx están fijos con respecto a la Tierra. La línea ab está adherida a la superficie de Di.
Los ejes X2 y Y2 están fijos a la superficie de D2. Una partícula de masa m
puede moverse libremente, pero en contacto con D2. Se trata de hallar una expresión
X.
Xi, 1/1 — coordenadas de m con respecto a los
ejes estacionarios Xi y Y^
Fig. 2-21
para su velocidad con respecto a la Tierra, pero en función de las coordenadas polares
móviles, r, a, y otras magnitudes.
Puede observarse fácilmente que
Xi = s eos 61 + reos/?, 2/1 = s sen 0i + rsen/3
24
FUNDAMENTOS BÁSICOS, II
[CAP. 2
en donde p = 6\ + 02 + a. Derivando y sustituyéndola en v2 = x\ + y\, se obtiene,
v* = S2¿2 + 2s¿irsen(^2 + a) + r2/?2 + r2 + 2s0,/?r cos(02 + a) {2.31)
lo cuál es correcto, sin importar en qué forma los motores hagan variar con el tiempo
a ¿i o 02. Si, como un caso especial, se supone que 6\ = m = constante y que 02 =
C = constante, entonces u será una función de r, «, r, ¿ y í únicamente.
Si se desea, v puede expresarse fácilmente en términos de las coordenadas
rectangulares x2 y y21 derivando
_. Zi , = s eos 0i 4- íc2 eos (0i + 02) - 2/2 sen (0i -I- 02)
2/i = ssenfli -I- z2sen(0i+ 02) + i/2 eos (0i + 02)
y sustituyéndolas en v2 = x\ + y\.
2.8 Trabajo y energía cinética.
(1) Proyección de un vector sobre una recta.
A manera de repaso, considérese la
forma siguiente de expresar la proyección / de
un vector cualquiera F, sobre la recta ob con
cosenos directores / y m, como se muestra
en la figura 2-22. Resulta claro que
/ = Fcosfl = Fcos(o-/3)
= FcosaCOS/3 + F señasen/?
Pero como F eos a = Fx y eos (i = l, etc.,
se tiene que / = Fxl + Fym.
Extendiendo esto a las tres dimensiones
(2.32)
Fig.2-22
/ = Fxl + Fym + Fzn (2.33)
En la figura 2-23, ds es un elemento ab de la línea AB. T es la tangente en a
cuyos cosenos directores son dx/ds, dy/ds y dz/ds. Por tanto, la proyección / de
un vector cualquiera F sobre t estará dada por
/ = F eos 6
jp dx dy dz
Fxd¿+ FyH+ Fzd¿
(2.34)
Fig.2-23
CAP. 2]
FUNDAMENTOS BÁSICOS, II
25
(2) Definición de trabajo.
Supóngase que F es una fuerza que actúa sobre un cuerpo en el punto a, y que
este punto de aplicación se mueve sobre la trayectoria desde a hasta b. Entonces (aunque
el desplazamiento no se deba por completo a F, sino también a otras fuerzas que
estén actuando sobre el cuerpo) el elemento de trabajo dW hecho por F estará dado por
dW = F ds eos 0, una cantidad escalar. Teniendo en cuenta (2.34) esto puede
escribirse,
dW = Fxdx + Fydy + Fzdz (2.35)
Así, el trabajo hecho a lo largo de una trayectoria finita de A a B, será
\ (Fxdx + Fydy + Fzdz)
W = J (Fxdx + Fydy + Fzdz) (2.36)
Esta expresión general es correcta, inclusive en el caso en que F varíe en magnitud y
en dirección a medida que cambia de posición (puede ser una función de x, y y z).
(3) Definición de energía cinética.
Supóngase ahora que F es la fuerza neta que acelera la partícula m mientras ésta
se mueve sobre la trayectoria AB. El trabajo realizado sobre la partícula está dado por
(2.36) y si X, Y, Z son ejes ¿nerciales, Fx = mx, etc. Si se escribe xdx = i di, la
ecuación (2.36) queda,
W
= fBm(x'dx' + ydy' + ¿dz) = y(¿a + jt + *)[ = yW-t>J)
lo cual es una expresión del trabajo necesario para cambiar la velocidad de la
partícula desde vA hasta vB, una magnitud escalar que depende únicamente de m y de
los valores de vA y vB.
Si la velocidad inicial, vA = 0, se tiene que W = \mv\ lo cual conduce a la
siguiente definición de energía cinética.
La energía cinética de una partícula es el trabajo requerido para incrementar su
velocidad desde el reposo hasta un cierto valor v, con respecto a un marco de
referencia inercial.
Como se ha demostrado, esto es igual a £mu2; y como es una magnitud
escalar, la energía cinética T, de un sistema de p partículas, será
2 A
o ^ mv* (2.37)
¿ í=i
en donde naturalmente, las velocidades vt, pueden expresarse en cualquier sistema
inercial de coordenadas y sus derivadas con respecto al tiempo, o en función de estas
cantidades expresadas en coordenadas no-inercíales.
De la ecuación (2.37) se sigue la expresión para la energía cinética de un cuerpo
rígido que gira con velocidad angular 0. La velocidad de una cualquiera de las
partículas es rd en donde r es la distancia normal que va desde el eje hasta la partícula.
Si se considera que la masa de la partícula es dm y se remplaza la suma por una
integral, la ecuación (2.37) podrá escribirse
r2dm) = !£■ (2.38)
en donde se ha definido el "momento de inercia" /, por medio de la integral.
Suponemos que el estudiante está familiarizado con el uso de la relación anterior en
problemas sencillos y por tanto el estudio general de los momentos de inercia y la energía
cinética de los cuerpos rígidos se aplaza para los capítulos 7 y 8.
= f Cí
26
FUNDAMENTOS BÁSICOS, II
| CAP. 2
2.9 Ejemplos ilustrativos de la energía cinética.
(1) Energía cinética de una partícula.
T = o- (¿2 + y2 + z2), véase la ecuación (2.23)
T = ^(r2 + r262 + r2sen20<¿2), véase la ecuación (2.24) (2.39)
T = "o" [d2 + h\ + ZQiQz eos (/?-<*)], véase la ecuación (2.25)
Utilizando las ecuaciones (2.11) y la primera de las anteriores (con z = 0) puede
expresarse T en función de las coordenadas A y q, y sus derivadas con respecto al
tiempo.
(2) Energía cinética del péndulo doble (Fig. 2-10). En coordenadas rectangulares
T = f(¿! + ¿!) +rY(xl + yl) (2.40)
Si las masas se hallan suspendidas por resortes o bandas de caucho, el sistema tiene
cuatro grados de libertad y en la ecuación (2.40) no habrá coordenadas superfluas.
Si en cambio, se supone que rx es un hilo de longitud constante, se tendrá que x\ +
y2 = r2 = constante, (una ecuación de restricción). Con esto puede eliminarse^ de
(2.40), quedando
T = T(^Sf) + ^« + * *«>
En función de las coordenadas rx, r2, 0 y <t> (suponiendo que todas son
variables, y con referencia a las ecuaciones (2.26)),
" • • • • .... (2.42)
+ 2(nr2 + rir20<¿) eos (<f> - 6) + 2(rir20 - r2ri<j>) sen(<j>- 6)]
(3) Energía cinética del sistema de la figura 2-9. Despreciando las masas de
las poleas y suponiendo únicamente movimiento vertical
J- — ^2/i + 2 ^2 + 2 2 4
Aunque esta expresión es correcta, contiene dos coordenadas superfluas ya que el
sistema tiene sólo dos grados de libertad. Por medio de las ecuaciones de restricción, yx +
y3 = C\ y (yz — yA) + Cy3 — y2) = C2 pueden eliminarse las velocidades
^3 y y4, quedando entonces
T = -Í(mi +m3 + 4m4)¿'2 + i(m2 + m4)y2 + 2m4yi¿f2 (2.43)
Aplicando acá las relaciones (2.27), en forma inmediata puede expresarse T en
función de s4 y de qu si se desea.
Como se ha observado, las coordenadas superfluas pueden ser eliminadas de T
por medio de las ecuaciones de restricción. Esta posibilidad reviste importancia en
desarrollos posteriores.
(4) Energía cinética expresada en coordenadas no-i ne reíales.
Básicamente, la energía cinética se toma siempre con respecto a un marco iner-
cial puesto que las velocidades vt en la ecuación (2.37) deben ser medidas en
coordenadas inerciales. Sin embargo, como ya se explicó, las expresiones de vt en
coordenadas inerciales pueden escribirse en función de coordenadas no-inerciales por medio de
las ecuaciones de trasformación adecuadas.
CAP. 2)
FUNDAMENTOS BÁSICOS, II
27
(a) Considérese el sistema de la figura 2-8. Para movimiento vertical únicamente
T = \m\ y\ + ¿7712v\ puesto que yx y y2 son inerciales. Nótese que T no es
igual a \m\y\ + \m<íy\, ya que y3 es no-inercial. Sin embargo, T puede
expresarse en función de yx y yz, como sigue. Como y3 — 2/1 — 2/2, 2/3 — 2/i—2/2>
entonces, m , ,.
T = \mxy\ + ¿m2(2/i-2/3)2
Si, por otra parte, se eliminan yx y y2 de la expresión original, T, en
función de y y qx (y es inercial pero qx es no-inercial) queda,
T =
( Ttti + 7tt2
)¿2+f(^)« <*«>
V 2
w r •' J • ai /rai + m2\.2 . 1 /_WllW2 \ •-
Y en función de y y y8f T = ( —5—) 2/2 + 5 Ur+^J »! •
(6) Considérese el primero de los ejemplos estudiados en el numeral 2.7(3). Aplicando
las ecuaciones (2.29) vemos que sip representa una partícula, su energía cinética es
T = $m[{vx + axt + X2)2 + (vy + ayt + y2)2 + {vz + azt + ¿2)2] (2.45)
en donde vx, ax, etc., son constantes. Nótese que la expresión incluye
explícitamente el tiempo.
(c) Si el origen O, de la figura 2-1, posee una velocidad inicial (vx, vy) y una
aceleración constante (ax, ay) al mismo tiempo que los ejes giran con una
velocidad angular constante o, de las ecuaciones (2.14) tenemos
Xi = vx + axt + a?2Cos<i)í — x2«> senwt — 2/2sen<i>£ — y2<a coswí
Al tomar esta ecuación junto con la expresión de yx y remplazarías en T =
£ra(¿2 + y\) tendremos a T en función de x2, y2, i2, y2, t.
(d) Con referencia a la figura 2-21 y a la ecuación (2.31) se observa que la energía
cinética de la partícula que puede deslizarse libremente en contacto con la segunda
superficie giratoria, está dada por
T = ¿ra[s202 + 2s¿irsen(02 + a) + r2/?2 + r2 + 2s8i¡3r cos(02 + a)] (2.46)
Debe notarse que (2.46) es correcta, no importa la suposición que se haga
respecto de las variaciones con el tiempo de dx y de 02. En el caso de velocidades
angulares constantes, sencillamente se remplazan di y 62 por las constantes
coi y £02- Pero si se supone que Di y D2 oscilan según ex = A sen at y 62 =
B sen bt, entonces se deben remplazar 6\ y 02 por Aa eos at y Bb eos bt,
respectivamente. En tal caso T incluirá a t, explícitamente.
2.10 Teorema del "centro de masa" para la energía cinética.
Considérese un sistema de p partículas que se mueven con respecto a un marco inercial
X, Y, Z. Supóngase un segundo marco X', Y', Z' cuyo origen está situado en el centro de masa
de las partículas y se mueve solidariamente con éste, al mismo tiempo que sus ejes X', Y' y Z'
se conservan paralelos a X, Y y Z respectivamente. Las ecuaciones de trasformación que
relacionan las coordenadas de una partícula de un sistema con las del otro, serán x = x + x\
y = y -\- y' y z = z + z' en donde x, y y z son las coordenadas del origen del marco móvil.
Así pues
T = lt ™.-(¿2 + i? + ¿?) = |¿^[(¿ + ¿02 + (¿ + i/i')2 + (¿ + ¿02]
¿t=l ¿¡=1
28
FUNDAMENTOS BÁSICOS, U
| CAP. 2
Al hacer la expansión escribiendo M = 2m, y teniendo en cuenta que por la definición del
centro de masa, 2mlxl = 0, que 2mixt = 0, etc., la expresión anterior se reduce a
T = y(¿2 + ¿2 + ¿2) + ! ¡¿ WAT + (i/02 + (¿O2] (2.47)
Con relación a (2.47) deben hacerse cuatro observaciones importantes:
(a) Tal expresión demuestra que la energía cinética de un sistema de partículas es igual a la
de una "partícula" única de masa M = 2m, (masa total del sistema) localizada en
el centro de masa y moviéndose solidariamente con él, sumada a las energías cinéticas
de todas las partículas calculadas con respecto al marco X', Y', Z', como si este último fuera
inercial.
ib) Lo anterior es igualmente cierto, sin importar si las partículas son libres o si tienen
cualquier tipo de restricción. En realidad esto puede aplicarse inclusive a los cuerpos rígidos,
en cuyo caso el movimiento con relación al marco móvil sólo puede tomar la forma de una
rotación.
(c) Si el sistema se supone dividido en dos o más grupos de partículas, es evidente que el
teorema puede aplicarse a cada uno de estos grupos en forma individual.
(d) A pesar de que (2.47) se ha escrito en coordenadas rectangulares, es lógico pensar que
esta forma de T puede expresarse en cualquier otro sistema conveniente de coordenadas por
medio de las ecuaciones de trasformación adecuadas.
2.11 Una expresión general para la energía cinética de p partículas.
A continuación se obtendrá una expresión muy general para la energía cinética de un
sistema de p partículas que poseen n grados de libertad y 3p — n grados de restricción. Se
supone que algunas o todas las. restricciones pueden moverse y que algunas o todas las
coordenadas generalizadas son no-inerciales. Esta expresión será muy útil en los capítulos siguientes.
(1) Como etapa introductoria considérese la energía cinética de una partícula única que
tenga tres grados de libertad (sin restricciones). Suponiendo que alguna o todas las
coordenadas generalizadas se mueven (qlt q2 y 93), las ecuaciones de trasformación
pueden indicarse como
& = x(Qu Q*, Qz, t); y = y(qu q2, q3, t); z = z(qu q2, q3, t)
r. . , • dX • , dX . , dX • dX
Derivando, x = _„+_„ + -_,3 + _ etc.
Por conveniencia escribimos
x = OL\qi + a2q-2 + £13^3 + a
Y similarmente, y = biqi + b2q2 + 63^3 + (3, z = Ci'qi + c2q2 + C3Q3 + y
en donde, por ejemplo, 63 = dy/dq3, etc.
Elevando al cuadrado estas expresiones y remplazando i2, y2 y z2 en T =
$m(x2 + y2 + z2), se obtiene finalmente,
T = ±m[(a\ +b\ + cji; + (a22 + b\ + c\)q% + (a¡ + b¡ + c$q2z
+ 2(aia2 + 6162 + Cic2)qiq2 + 2(aia3 + 6163 + CiCz)k\<lz
+ 2(o2a3 + b2b3 + c2c3)q2<l3 + 2(aía + bi(3 + Ciy)qi
+ 2(a2a + b2(3 + c2y)q2 + 2(a3a + 63/? + cZy)'qz + a2 + p2 + y
(2.48)
Nótese que T contiene cuatro clases de términos: Los que contienen q2, los que tienen
QTQt, los que llevan qr únicamente y por último, los que no incluyen ninguna velocidad
de las coordenadas. Sin embargo todos los términos son dimensionalmente equivalentes a
\Mv2\.
CAP. 2)
FUNDAMENTOS BÁSICOS, II
29
El ejemplo que se da a continuación aportará un mayor sentido a la expresión
siguiente. Haciendo referencia a la figura 2-5 y suponiendo que el origen de los ejes Qx y
Q2 tiene una aceleración lineal constante a (sin rotación), se ve que
x = Xo + vxt + %axt2 + picosa + ^cos/S
y = 2/o + Vyt + \ayt2 + tfisena + q* sen/3 ( 49'
Derivando y remplazando x2 y y2 en $m(x2 + y2), tenemos
T = $m{q2 + q\ + 2qiq2 eos(/?-<*) + 2[(vx + axt) cosa + (vy + ayt) sena]¿i
+ 2[(vx + axt) cos/3 + (vy + ayt)senp]q2 + 2{vxax + vyay)t (2.50)
+ {a2 + a2)? + v2 + v2}
Por simple inspección puede concluirse que (2.50) tiene exactamente la forma de (2.48).
En efecto, cada uno de los términos de (2.50) puede ser obtenido del correspondiente de
(2.48) al evaluar los factores a, b, c, etc., por medio de las relaciones (2.49).
La relación (2.50) presenta una buena oportunidad para destacar un punto básico.
A pesar de su complejidad, el miembro derecho de la ecuación es sencillamente-g-í—r) ,
en donde As es un desplazamiento de p con relación al marco inercial X, Y.
(2) Para considerar ahora el caso más general mencionado al principio de este numeral, las
ecuaciones de trasformación pueden escribirse como
Xi = Xi{qi, tf2, .. ., qn, t), etc. (2.51)
en donde i va desde 1 hasta p y además se ha supuesto que las coordenadas superfluas se
han eliminado por medio de las ecuaciones de restricción. Derivando estas relaciones,
tenemos . » . n n
Xi = 2 a*¿* + a*, yi = 2 b*5* + Pi, Zi = 2 c*¿* + y, (2.52)
k=i k=i k=i
aquí, por ejemplo, aik = dxjdqk, cr = dxjdt, etc. Nótese que alk ?í akl, etc.
Por un proceso directo de elevación al cuadrado, puede demostrarse que
¿f = 2 ^ OikOilQkQl + 2ai 2 a^Qk + a2 (2.53)
k=i1=1 k=i
Ecuaciones semejantes se pueden obtener para yf y z2. Eliminando i2, y2- y z2 de
y agrupando los términos, * 1=1
ó 2 mi(aHidu + bikba + CikCu)
¿ i=i
t = 2S
fc=ii=i
+ 2 f¿ fm^idik + (3ibik + y.C*)] Qk + l ¿ Wi(a2 + /?2 + y2)
Qkqi
(2.54)
2 A'
Lo anterior puede escribirse en forma más breve, así:
T = 2 AuMi + 2 Bkqk + C (2.55)
k.l fc = l
en donde el significado de Akl, de Bk y de C resulta evidente. Nótese que si t no aparece
explícitamente en las ecuaciones (2.51) (si no hay restricciones o marcos de referencia
móviles), at = 0, = 7, = 0. Por tanto (2.55) se reduce a
T = ^AuQkQi (2.56)
30
FUNDAMENTOS BÁSICOS, II
[CAP. 2
Debe entenderse que (2.51), (2.55) y (2.56) no son simplemente relaciones académicas
que habrán de permanecer siempre en forma simbólica. Como se demostró en el ejemplo
anterior, las relaciones (2.51) (relaciones de trasformación con las coordenadas superfluas
eliminadas) pueden escribirse normalmente en forma explícita para cualquier problema
en particular. Para esto pueden obtenerse en forma inmediata por medio de
diferenciación parcial, valores para alk, blk, etc., los cuales son, en general, relaciones
algebraicas que incluyen las coordenadas y posiblemente el tiempo. En esta forma se obtienen
expresiones para AM, Bk y C, y finalmente para T. Debe observarse que Am, Bk y C, en
general no son constantes, sino funciones de qlt q2, - •■,<?„ y í pero no de las q.
Nótese además que Ak, = A^.
En el capítulo 8 se deduce una expresión para la energía cinética de un cuerpo
rígido, más útil que (2.55). Véase la ecuación (8.10).
2.12 Definición de aceleración y ejemplos.
Las ecuaciones de Lagrange tienen en cuenta automáticamente todas las aceleraciones,
sin necesidad de darle a esto ninguna consideración especial.
Sin embargo, teniendo en cuenta la importancia de esta magnitud en los principios
básicos y en el desarrollo de la dinámica, se incluye aquí un breve repaso de la definición y de
los procedimientos para plantear las expresiones generales.
(1) Consideraciones generales.
Imagínese un punto (o una partícula) que se mueve en el espacio según la
trayectoria AB, como se muestra en la figura 2-24. En el punto pi su velocidad es v\
y luego de un lapso Ai, en el punto p2 su velocidad será v2- En general v2 no tiene
ni la misma dirección ni la misma magnitud de v\. Así pues, el cambio Av
representa un cambio no solamente en magnitud, sino también en dirección. Teniendo
esto en cuenta, se define la aceleración del punto móvil en plt como
Ai?i dv
a = -rr para Ai -»0, o sea, a = -rr (2.57)
\Z "X J>^ *
B
A»!
P* «i " - .
"! "-:__ .*
V "»t = *i'4£$ (Suma vectorial)}
A-
X
Fig. 2-24
Es claro que a es una magnitud vectorial que tiene la dirección de Av\ cuando
Ai —* 0. Esta definición trae consigo el hecho importante de que el vector
aceleración, en general no lleva la dirección del movimiento. (Nótese que el vector velocidad
v = ds/dt, definido en el numeral 2.7 lleva siempre la "dirección de la trayectoria".)
La definición de aceleración de (2.57) no incluye referencia a ningún sistema de
coordenadas en particular. Pero como las componentes rectangulares de Av son Ax,
A;y y Az, su magnitud está- dada por (Av)2 = (A¿)2 4- (Ay)2 + (Az)2. Dividiendo
por (Ai)2 y pasando al límite, la magnitud de a estará dada^por
a2 = 'i2 + y2 + 'z2 (2.58)
Naturalmente su dirección está determinada por los cosenos directores x/a, y/a, z/a.
CAP. 2]
FUNDAMENTOS BÁSICOS, II
31
(2) La aceleración expresada en coordenadas generalizadas.
La magnitud de a, dada por (2.58) así como sus cosenos directores, pueden
expresarse en cualquier otro sistema de coordenadas por medio de las ecuaciones de tras-
formación adecuadas. Ejemplos:
(a) Aplicando las ecuaciones (2.6) x, y y *z y luego (2.58), pueden expresarse en
coordenadas esféricas.
(b) Usando las dos últimas ecuaciones de (2.13) y (2.58) puede expresarse la
aceleración de m2 en función de n, r2, 0 y <f> y de sus derivadas con respecto
al tiempo.
(c) Por medio de (2.32) y (2.58) puede obtenerse fácilmente una relación para la
aceleración de la partícula que se muestra en la figura 2-21, con respecto a los ejes
estacionarios Xx y Yx pero expresada en función de las coordenadas móviles
*2 y y2, sus derivadas con respecto al tiempo, y el tiempo mismo. (El tiempo
aparece explícitamente cuando se supone que 6\ y 02 varían de alguna
manera en particular con respecto al tiempo.)
(3) Componentes de la aceleración total según una dirección cualquiera.
La componente a' de la aceleración a lo largo de una recta con cosenos directores
/, m y n está dada por (véase la ecuación 2.33)
a' = Ix +my + n'z (2.59)
lo cual puede, naturalmente, expresarse en otras coordenadas.
(a) Considérense las expresiones de las componentes de a a lo largo de las
coordenadas en el sistema esférico (ar, an y a¿); es decir, en las direcciones de los
elementos de rectas indicados por Ar, r A0 y r sen 0 A<j> y de la figura 2-20.
Examinaremos a^ en detalle. Los cosenos de los ángulos que r sen 0 A<f> forma con los
ejesX, YyZson: —sen 0, eos 0 y 0, respectivamente. Por tanto, a* = — x sen 0
+ y eos 0. Eliminando x y y por medio de (2.6) después de una cantidad
considerable de operaciones monótonas, finalmente se obtiene la siguiente expresión
(y en forma semejante las de ar y ae),
a* = r£sen0 + 2r<¿sen0 + 2r<¿0cos0
ar = r - ré2 - r<¿2sen20 (2.60)
ae = r'é + 2rd - rj>2sen0 cos0
(b) Haciendo referencia a la figura 2-21, se trata de determinar la componente en la
dirección del radio r, de la aceleración de m (con respecto a los ejes fijos Xi y
Yi). Se tiene que a* = lx\ + myi en donde / y m son los cosenos directores de
r con relación a los ejes estacionarios; es decir, / = eos 0 y m = sen 0 (véase
el último ejemplo del numeral 2.7(3)). Aplicando-
Xi = seos 0i + reos ¡3, y\ = ssenfli + r sen/8
se obtiene
ar = r - r(0i + 02 + a)2 + s'e\ sen(62 + a) - sd\ eos (02 + a) (2.61)
Cuando se especifica la manera como se hacen girar las plataformas, ar contiene
a t explícitamente.
Como se demuestra en el numeral 3.9 del capítulo 3, éstas y otras
expresiones para la aceleración pueden determinarse fácil y rápidamente a partir de las
ecuaciones de Lagrange.
32
FUNDAMENTOS BÁSICOS, II
| CAP. 2
2.13 "Desplazamiento virtual" y "trabajo virtual".
Los desplazamientos virtuales y el trabajo virtual desempeñan un papel muy
importante, como medios para llegar a un fin, en los desarrollos básicos de la dinámica analítica. Pero
una vez que han servido su útil objetivo, desaparecen del cuadro.
(1) Desplazamientos reales y virtuales; trabajo virtual.
Para simplificar, considérese una partícula de masa m que se restringe a moverse
en contacto con una superficie rugosa, la cual a su vez está en movimiento. Al sufrir
la acción de una fuerza F (F = suma vectorial de una fuerza aplicada, una fuerza
de rozamienfo y una fuerza de restricción*), m se mueve según una trayectoria
determinada (dada por las leyes de Newton) en el espacio y al mismo tiempo traza una
curva sobre la superficie. Durante un intervalo de tiempo dt, m experimenta un
desplazamiento específico ds (dx, dy, dz) medido con respecto a unos ejes estacionarios,
por ejemplo. Al referirse a ds aquí, se le llama desplazamiento "real" o "verdadero".
Considérese ahora un desplazamiento arbitrario infinitesimal cualquiera, bs (bx,
by, bz) no necesariamente según la trayectoria mencionada. En este caso bs es
llamado desplazamiento virtual. Por conveniencia, a continuación se mencionan tres
clases de tales desplazamientos: (a) bs en cualquier dirección en el espacio, ignorando
por completo la superficie (esto puede requerir una ligera distorsión de la restricción);
(b) bs en cualquier dirección sobre la superficie móvil, y (c) en cualquier dirección
sobre la superficie, considerada ahora como estacionaria.
Para un desplazamiento virtual de cualquier |ipo, el "trabajo virtual" hecho por
F está dado por
SW = FSscos(F,Ss) = FxSx + F»8y + FzSz
y considerando un sistema de p partículas sobre las cuales actúan las fuerzas Fit
F2, . ■ -, Fp, con unos desplazamientos 8slt bs2, . . ., bsp, el trabajo virtual total es
SW = ¿ (Fx.SXi + Fy¡Syi + Fz.SZi) (2.62)
í=i
(2) Forma en que las expresiones de bW se hacen útiles.
La sorprendente importancia de (2.62) radica eventualmente en las siguientes
consideraciones.
(a) Utilizando xi = x^q^q^, . . .,<?3P, 0» etc, (en donde aparece un máximo de 3p
coordenadas), se tiene Sx¡ = -r-^-Sqi + t-^S^ + • • • + t~~$Q3p + -ztM> etc-> Para
o<7i oqi oqzv ot
&yt y &z(. Para estos desplazamientos, que no tienen en cuenta
necesariamente las restricciones, es claro que bW contiene el trabajo hecho por las fuerzas
de restricción.
(b) Empleando las relaciones (2.21), (véase el numeral 2.6)
Sx¡ = |ÍLSgi + ||i8g2 + ...+|2is?n + te8 etc
otfi dq2 dqn dt
Estos desplazamientos _QQj>iolan las restricciones, pero durante el tiempo
trascurrido bt los marcos móviles y las restricciones móviles habrán cambiado de
posición ligeramente. Entonces, como se demostrará en los ejemplos, bW todavía
contiene el trabajo hecho por las fuerzas de restricción.
♦ Tensiones en hilos de longitud fija, correas o cadenas de trasporte; compresiones o tensiones en varillas o
soportes; fuerzas de reacción ejercidas por alambres lisos, varillas o guías de cualquier tipo a lo largo de las cuales
pueden deslizarse las masas; fuerzas de reacciones entre los dientes lisos de piñones o fuerzas ejercidas por
superficies lisas con las cuales deben moverse las partes del sistema en contacto con ellas, serán llamadas aquí "fuerzas
de restricción" (o "fuerzas de ligadura"). Debe entenderse con claridad que en esta clase no se incluyen fuerzas de
rozamiento, las cuales dependen por lo regular de las fuerzas de restricción y normalmente hacen trabajo (que se
disipa en forma de calor).
CAP. 2)
FUNDAMENTOS BÁSICOS, II
33
(c) Determinando los desplazamientos por medio de {2.21) pero conservando el
tiempo constante, (es decir, incluyendo en 8xn8yi y hzt los cambios en ql}
dXis
92,...,g„, únicamente y no los términos —r5t, —-8t, —-St que represen-
ot ot dt
tan los desplazamientos de los marcos y de las restricciones móviles),
~dtUt ~dtS
SXi
dXi ■ , dXi R
dqn
etc.
(2.63)
Estos desplazamientos tienen en cuenta las restricciones y por consiguiente, el
trabajo hecho por las fuerzas de restricción suma cero. En efecto, las fuerzas de
restricción se han eliminado de^(2.62).
En tanto que la veracidad de esta afirmación puede ser comprobada con
ejemplos sencillos (numeral 2.14), usualmente no se intenta una demostración general,
sino que puede considerarse como un postulado básico.
Sustituyendo (2.63) en (2.62) y reagrupando términos,
dXi , „ dyi , r dZi^
SW
t(F^Wi + Fyi^+Fzi^
+ S
F^ + F^+F^]^
^n
'*a<7„
{d<7,
(2.64)
Por otra parte, como las q son independientes, es admisible igualar a cero todos
los Sq, menos uno, por ejemplo bqr. Así, (2.64) se reduce a
SWn
= 2
F^ + F,^i + F^W
(2.65)
lidqr Vidqr *idqr/
Asimismo, esta expresión no incluye fuerzas de restricción, aunque ¿Si, 8s2, . . ., 8sp
se han restringido de tal manera que sólo qr varíe. Como se ilustra más adelante,
para encontrar una expresión explícita para 5 WQr, las fuerzas de restricción (que
originalmente se habían supuesto como parte de FXi,Fy.,FZi) pueden ignorarse por
completo.
Este sistema para eliminar las fuerzas de restricción es una de las grandes
realizado riél_del^íétod^~3e_T^gfarIge;
Las consideraciones anteriores son de vital importancia en el principio de D'Alem-
bert. En los capítulos 3 y 4 se verá con claridad su trascendencia en un método
concreto de planteamiento de las ecuaciones del movimiento, prácticamente para
todo sistema dinámico.
2.14 Ejemplos ilustrativos de las consideraciones anteriores (a), (b) y (c).
Y\
(i) Considérese el sencillo dispositivo que se muestra
en la figura 2-25. La cuenta de masa m puede
deslizarse sobre la varilla lisa OA, la cual se hace girar
alrededor de O en el plano XY, con velocidad
angular constante, o>. Sobre m actúan: Una fuerza
/, debida al resorte, la fuerza de restricción f2
(fuerza de reacción de la varilla) y la fuerza
aplicada f3. Considérense tres casos:
1. Supóngase un desplazamiento Ss para m,
perfectamente arbitrario, como si estuviera libre.
(Esto podría implicar una pequeña deformación
de la varilla.) Así, como en general todas las
fuerzas /,, f2 y U tendrán una componente
en la dirección de Ss, todas ellas harían trabajo,
según la consideración (a).
x + tx t no
V + iV variable
Fig.2-25
FUNDAMENTOS BÁSICOS, U
[CAP. 2
C
msiderando el movimiento de m limitado a la varilla, se escribe: x = rcoswí y y = r sen wí. Así,
ra un desplazamiento arbitrario en el que la cuenta permanece en la varilla y el tiempo varía (teniendo
cuenta el movimiento de esta última),
Sx = Sr eos ut — rwStsenut, Sy = Sr sen ut + ruSt eos ut 2
luí se tiene, Ss = ac, como en la figura 2-25. La restricción no se ha violado, y como todas las fuerzas
:nen componentes según ac, todas hacen trabajo, de acuerdo con (b).
ipóngase que se desprecia el movimiento de la varilla (en realidad se deja fijo t). Las componentes de 8s
n: 5x = Sr eos ut y Sy = 6r sen ut. Este desplazamiento lleva la dirección de la varilla: bs = Br = ab.
i claro que /, y f3 hacen trabajo pero f2, no (se supone perpendicular a la varilla), según (c).
idérese el sistema que se muestra en la figura 2-9, en donde n, t2, etc., se refieren a las tensiones de
ilos de longitud fija. Se supone que todas las poleas tienen masa y por tanto, n í¿ t3 , t2 9* t* , t2 + t« ^ t3 . 3
nces, para un desplazamiento virtual de cada una de las masas, en dirección vertical (suponiendo que
lilos están siempre en tensión), (2.62) se convierte en
8W = Kff- t1)Sb1 + (m3g + Tt + r4- t3)Ss3
+ (m2g - rt)Sst + (m,g - t4)Ss4 + (t3 - t,)^, Sel + {t4 - rt)Rt 8et (2.66)
>nde 0, y B2 son los desplazamientos angulares de las poleas superior e inferior, respectivamente, y m3
nsidera como la masa total de la polea inferior.
Si se consideran los desplazamientos anteriores como arbitrarios (sin estar de acuerdo con las restric-
s), resulta claro que el trabajo hecho por las fuerzas de restricción (las tensiones), en general no será 4
a cero.
Teniendo en cuenta las restricciones por medio de las relaciones
5ss = -í«i, 8¡/4 = 2 Sai - 8yi, Rt Sel = -Sau Rt 86* = Sy, - Sai, Sy4 = -fis4, fia» = -Sy,
íes de eliminar fis3, 5s4, BBi y SB2, la ecuación (2.66) se reduce a
ü
SW = (mxg - t, - m3g - u - T% + t3 + 2t4 - 2m4g - t3 + t, - u + rjSs^
+ O", - m,g - u + mAg + t4 - rt)Syt (2.67)
'• SW = (mxg - mag - 2rtug)Sai + (rmg - mtg)8yt (2.68)
;cuaciones (2.67) y (2.68) corresponden a la (2.64). Es claro que ís, y by2 están de acuerdo con las
cciones y que el trabajo hecho por las tensiones suma cero. Además se observa que para una variación
o de yi únicamente, el trabajo de las tensiones es igual a cero, lo cual está de acuerdo con lo dicho
:guida de la ecuación (2.65).
Es importante observar que se habrían podido considerar igualmente, >-3 y qlt por ejemplo, como
enadas independientes del sistema. En tal caso, puede demostrarse fácilmente de nuevo, que para /
'ariación de>-3 o de q, únicamente, el trabajo ejecutado por las tensiones es cero.
ngase que se hace mover el soporte AB de la figura 2-9, verticalmente, de alguna manera determinada;
jemplo, h = h0 + C senwf. Entonces, por las relaciones (2.12), >-, = C sen ut + s4 + q, + Clt y2 =
n ut — s4 — 2qi + C2, etc., en donde C\ y C2 son constantes. El lector puede demostrar fácilmente
»ara una variación de s4 o de q,, dejando t fijo, el trabajo hecho por las tensiones suma cero, lo cual
ambién de acuerdo con la última parte de la consideración (c).
Resumen y observaciones
;emas de coordenadas y ecuaciones de trasformación (numeral 2.2).
Una de las primeras etapas en la solución de cualquier problema es la selección de
coordenadas adecuadas. Las ecuaciones de trasformación desempeñan un papel muy
ortante al expresar la energía cinética, la aceleración, y muchas otras magnitudes
CAP. 2)
FUNDAMENTOS BÁSICOS, II
35
importantes, en función de las coordenadas seleccionadas. Varios desarrollos teóricos
dependen del uso de las ecuaciones de trasformación.
2. Coordenadas generalizadas y grados de libertad (numeral 2.3).
"Coordenada generalizada" es un término conveniente para una coordenada
cualquiera. La utilización de qi,q2, ••-,9n Para designar las coordenadas generalizadas
es prácticamente universal y tiene ventajas definitivas.
Antes de poder comenzar a trabajar en un problema, debe conocerse el número de
"grados de libertad" del sistema, lo cual puede determinarse por simple inspección.
3. Grados de restricción, ecuaciones de restricción y coordenadas
superfluas (numerales 2.4, 2.5 y 2.6).
Es indispensable un entendimiento del sentido físico y geométrico de las
restricciones y de la manera como cada uno de los "grados de restricción" puede expresarse por
medio de una "ecuación de restricción" correspondiente.
Utilizando estas ecuaciones, "las coordenadas superfluas" pueden ser eliminadas de
las ecuaciones de trasformación, de la energía cinética, de la energía potencial, y demás
magnitudes.
4. Velocidad en coordenadas generalizadas (numeral 2.7).
La velocidad de una partícula puede expresarse en términos- de cualquier sistema de
coordenadas generalizadas y de sus derivadas con respecto al tiempo. Con frecuencia
aparece t. Las etapas posteriores no pueden emprenderse sin un conocimiento de cómo se
hace esto. De aquí la importancia del numeral 2.7.
5. Trabajo y energía cinética (numerales 2.8, 2.9, 2.10 y 2.11).
Es imprescindible un entendimiento de las definiciones correctas de trabajo y energía
cinética.
Es de una importancia extrema el tener en cuenta que la energía cinética debe
considerarse con respecto al espacio inercial. Siempre se empieza escribiendo T en
coordenadas inerciales. Puede entonces, si se desea, expresarse en función de otras coordenadas
(inerciales, no-inerciales o mixtas) por medio de las ecuaciones de trasformación
apropiadas.
6. Aceleración (numeral 2.12).
El análisis hecho tiene por objeto aclarar la definición básica de aceleración y
demostrar que sus componentes en cualquier dirección pueden expresarse en coordenadas
generalizadas. Sin embargo, a pesar de que la aceleración desempeña un papel básico en
todas las ecuaciones del movimiento, la técnica anterior no tiene una importancia vital
ya que, como se demuestra en el numeral 3.10, las ecuaciones de Lagrange tienen en
cuenta automáticamente las componentes de la aceleración.
7. Desplazamientos virtuales y trabajo virtual (numerales 2.13 y 2.14).
Los métodos generales empleados en este libro (que tienen formidables ventajas sobre
los métodos vectoriales convencionales, para la dinámica analítica) dependen de los
conceptos de los desplazamientos virtuales, del trabajo virtual y de su utilización. Muchos
de los desarrollos posteriores emplean el estudio hecho.
Una última palabra: Como se verá en los capítulos 3 y 4, los puntos 1 a 7 anteriores
(exceptuando el 6) constituyen la materia básica fundamental para poder entender las
ecuaciones de Lagrange y son, en realidad, las etapas preliminares que deben seguirse al aplicar
estas ecuaciones.
36
FUNDAMENTOS BÁSICOS, II
| CAP. 2
Problemas
Las respuestas a los problemas siguientes se encuentran en la página 368.
2.1. Demostrar que las siguientes son las ecuaciones de trasformación que relacionan las coordenadas polares
planas usuales r y 0 con q, y i¡2 como se muestran en la figura 2-5:
r eos e = qi eos a + qt eos /3
r sen 0 = qi sen a + g» sen /3
2.2. Escribir las ecuaciones que relacionan las coordenadas r2 y a de la figura 2-6 con A y q (A es el área
sombreada y q = sen0).
2.3. La familia de parábolas que se muestra en la figura 2-26, está dada por y = bx2, en donde b es una
constante para cualquiera de las curvas. Pueden hallarse valores de y para valores específicos de b y de x.
Por tanto xyi pueden considerarse como coordenadas en el plano XY.
(a) Demostrar que en estas coordenadas, T = ^m[x% + (bx* + 26ap¿)*].
(b) Demostrar que T puede ser expresada en función de las coordenadas b y 0, en donde 0 es el
ángulo polar usual en coordenadas polares (r y 0), eliminando r y f de T = £m(f* + r*0*), por
medio de la relación r= (sen0)/(b eos2 0).
2.4. (a) Escribir las ecuaciones que relacionan las coordenadas yt y y2 con y y qt, figura 2-8.
(b) Hacer lo mismo para y, y y2 con y y y3.
¿Serán inerciales qt y y3?
2.5. El soporte sobre el cual está montado DlP de la figura 2-21, se mueve sobre el eje X, con aceleración
constante, ax. Escribir las ecuaciones de trasformación que relacionan a x, y yi con x2 y y2-
Véanse las relaciones (2.32).
2.6. Haciendo referencia a la figura 2-13, demostrar que las coordenadas rectangulares x, y y z de m se
relacionan con 0, <t> y a por medio de
x = (R sen e — r cosa eos e) eos<f> + r sen a sen<f>
y = (R sen e — r eos a eos 8) sen </> — r sen a eos <f>
z = R eos e + r eos a sen e
en donde R = Oa.
2.7. Un coche de ferrocarril se mueve sobre una vía circular de radio R, con aceleración tangencial constante, a.
Escribir las ecuaciones de trasformación que relacionan un sistema de coordenadas rectangulares adherido
a la superficie de la Tierra (el origen en el centro del círculo y Z, el eje vertical) con un sistema
rectangular dentro del coche, con Z2 vertical, Y2 tangente al círculo en la dirección del movimiento y X2
con la dirección de la prolongación de R. Escribir las ecuaciones del movimiento de Newton para una
partícula, con respecto a X2, Y2 y Z2.
CAP. 2]
FUNDAMENTOS BÁSICOS, II
37
2.8. Demostrar que al relacionar i,j] y z, del problema 2.7 con las coordenadas esféricas r, 6 y <t>
adheridas al coche y con su origen en el mismo punto que el de X2, Y¿, Z2, se tiene
Xi = (R + rsen 6 eos<f>) eos¡3 — r sen* sentf» sen/3
Vi = (R + r sen e eos <f>) sen ¡3 + r sen e sen # eos /3
zi = r eos 0
2.9. El origen de un conjunto de ejes rectangulares está situado en el centro de la Tierra y las direcciones de
los ejes están fijas en el espacio. Otro sistema rectangular está adherido a la superficie de la Tierra como
se muestra en la figura 14-2. Escribir las ecuaciones de trasformación que relacionan los dos sistemas de
coordenadas.
2.10. (a) Un alambre rígido de alguna forma determinada, está sujeto al disco D2 de la figura 2-21. Una
cuenta puede deslizarse a lo largo del alambre. Suponiendo que e2 = «2í y 0, = wií, ¿cuántos
grados de libertad tendrá el sistema?
(b) Un tablero plano está sujeto a un cuerpo rígido por medio de una bisagra grande y el conjunto está
suspendido, de alguna manera, por medio de resortes. ¿Cuántos grados de libertad tendrá el sistema?
2.11. (a) Dos cuerpos rígidos conectados entre sí por medio de una unión esférica, pueden moverse libremente
en el espacio. ¿Cuántos grados de libertad tendrá el sistema?
(b) Si una de las masas anteriores se une a un soporte rígido por medio de otra unión esférica, ¿cuántos
grados de libertad tendrá el nuevo sistema?
2.12. (a) Un "péndulo simple" consiste en un cuerpo rígido suspendido por medio de un hilo inextensible,
cuyo movimiento no se halla restringido a un plano. Determinar el número de grados de libertad.
(b) Si se considera que mi y m2 de la figura 2-10, son cuerpos rígidos en lugar de "partículas",
¿cuántos grados de libertad tendrá el sistema? r, y r2 son constantes y el movimiento no está
restringido a un plano.
2.13. Una varilla uniforme, delgada, de masa M y longitud l, se desliza con sus extremos en contacto con los
ejes X y V, respectivamente. Determinar el número de grados de libertad, escribir las ecuaciones de
restricción y obtener una expresión de la energía cinética después de haber eliminado todas las coordenadas
superfluas.
2.14. Localizando el punto p de la figura 2-1 con coordenadas polares planas (r, a), en donde r = Op y a es
el ángulo que r forma con X2, demostrar que
Xi = Xo + r eos (a + e), jfi = y0 + r sen (a + 6)
Suponiendo que el marco X2, Y2 está en movimiento, demostrar que la velocidad v de la
partícula p con respecto al marco Xi, Yt, pero expresada en función de las coordenadas móviles, está
dada por
v* = x*0 + y\ + r* + r*(¿ + ¿)* + Ir [yo sen (a + e) + x0 eos (a + ff)]
+ 2r(a + Í)[yo eos (a + e) — io sen (a + $)]
2.15. Con referencia al problema 2.14, demostrar que las componentes de la aceleración de p, con relación al
marco X,, V,, en la dirección de Ar y rAa, son, respectivamente,
ar = Xo eos (a + e) + yo sen (a + 6) + r — r{a + e)1
<*a = Vo cos (<* + *) _ *^o sen (a + ff) + 2r(a + 9) + r{a + 6)
2.16. Dos partículas, mi y m2, sujetas a los extremos de una varilla rígida, ligera, de longitud l, pueden
moverse libremente en un plano. Determinar el número de grados de libertad. Escribir las ecuaciones de
restricción. Escribir una expresión para la energía cinética total de las masas, en función de r, 6 y <t>, en
donde r es la distancia del origen a mi, 8 es el ángulo entre el eje X y r y <t> es el ángulo entre el eje X
y la varilla. Eliminar todas las coordenadas superfluas. Véanse las ecuaciones (2.26).
Escribir T para el caso anterior usando coordenadas rectangulares para el centro de masa y <¡>. Véase
la ecuación (2.47).
2.17. Las varillas uniformes delgadas de la figura 2-27, con masas Mi, M2 y M3 y momentos de inercia
h, h e h con relación a los ejes normales que pasan por sus centros de masa, están articuladas como
se ilustra. Los centros de masa están indicados por P\, P2 y P*. El movimiento está restringido al plano XY.
38
FUNDAMENTOS BÁSICOS, II
[CAP. 2
Escribir la expresión de T en función de las
coordenadas indicadas. Escribir las ecuaciones
que habrán de servir para eliminar las
coordenadas superfluas de T. ¿Cuántas coordenadas
superfluas aparecen? ¿En qué forma afectan el
número de grados de libertad, los resortes S,
y s2?
2.18. Las partículas de masa mi y m3
mostradas en la figura 2-28 están sujetas a los
extremos de una varilla ligera de longitud l. Una
cuenta de masa m2 puede deslizarse
libremente a lo largo de la varilla entre m.\ y rm.
El punto p es el centro de masa de mi y ma,
sin incluir a m2. El momento de inercia del
conjunto mi, m3 y la varilla, con respecto a
un eje perpendicular a la varilla y que pasa por
p, es igual a /. Todo el movimiento se
considera en un plano.
(a) Escribir las ecuaciones que dan la
posición de m2 en función de x, >-, s y fl.
(b) Escribir la energía cinética del sistema
en función de las coordenadas x, y, 6 y s.
2.19. Si se supone que mi y m2 de la figura 2-9, son
el número de grados de libertad del sistema. Es
las extremidades de los monos. Los momentos
2.20.
Fig. 2-28 Fig. 2-29
Un alambre rígido de forma parabólica, de ecuación 2 = ar2, está sujeto al eje vertical de la figura
2-29. Una cuenta de masa m puede deslizarse libremente a lo largo del alambre, (a) Suponiendo que el
eje vertical, que tiene un momento de inercia, junto con el alambre, igual a /, puede girar libremente,
como se indica; escribir una expresión para T del sistema, (b) Suponiendo que el eje se hace girar por
medio de un motor a velocidad angular constante 6 = «, escribir la expresión de T.
Fig. 2-27
dos monos que están subiendo por un cable, determinar
scribir una expresión para T, despreciando las masas de
de inercia de Di y D2, son /, e /2, respectivamente.
Fig. 2-29
ación 2 = ar2, está sujeto al eje vertical de la figura
bremente a lo largo del alambre, (a) Suponiendo que el
¡unto con el alambre, igual a /, puede girar libremente,
leí sistema, (b) Suponiendo que el eje se hace girar por
e 6 = «, escribir la expresión de T.
2.21. Establecer una expresión para la energía cinética del sistema que se muestra en la figura 2-15, en función
de las distancias s. ¿Cuáles de estas coordenadas son no-inerciales?
CAP. 2]
FUNDAMENTOS BÁSICOS, II
39
2.22. Escribir una expresión para la energía cinética de las tres masas que se muestran en la figura 2-30,
utilizando las tres coordenadas yt,y2 y >"3, y suponiendo movimiento vertical únicamente. ¿Se
afectaría la expresión para T, si se removieran los resortes? La distancia del eje X al centro de masa del
sistema, es >,.
Wli F j-
V*
I m* —l 1
c.m. V* I
^ ti
Vi ., *-
I m*
Fig.2-30 Fig.2-31
2.23. Las masas m, y m2 están suspendidas de los extremos de la barra B por medio de cuerdas inexten-
sibles, como se muestra en la figura 2-31. La barra puede girar libremente alrededor de un eje horizontal
y su momento de inercia con respecto a este eje es /. Suponiendo que todos los movimientos se restringen
al plano de la figura, determinar el número de grados de libertad del sistema y escribir una expresión para T.
2.24. El marco en el que mi se desliza, figura 2-14, se mueve verticalmente con una aceleración hacia
arriba, a. Suponiendo que m2 oscila en un plano con r constante, demostrar que
T = ^[mii^e* + (mi + wi»)y* — 2mtr9y sen e + 2m*re(vo + at) sen e
— 2(mi + mt)y(vo + at) + (mi + mi)(v0 + at)*]
en donde v0 es la velocidad vertical del marco, cuando í = 0. Comparar la forma de esta expresión
de T con la de la ecuación (2.48). ¿Serán inerciales las coordenadas >- y tf?
2.25. La masa de un péndulo está colgada del techo de un vagón de ferrocarril por medio de un resorte
espiral. El vagón se mueve con velocidad angular constante sobre una vía circular de radio R. La masa
puede moverse en un plano vertical que forma un ángulo a con R. Demostrar que la energía cinética
de la masa está dada por
T = $m(¿* + y* + z*)
en donde x = R eos ut + r sen 0 eos (wí + a), y = R sen «f + r sen e sen (wt + a) y z = C — r eos B.
El origen del sistema rectangular se ha fijado en el centro del círculo, con Z en dirección vertical,
r es la longitud del péndulo, que se considera variable, y e es el ángulo que forma r con una vertical
que pasa por el punto de apoyo.
2.26. El disco D de la figura 2-32 puede girar libremente con velocidad angular 4>, alrededor del eje horizontal op.
El ángulo <t> se mide a partir de ab, la cual permanece paralela al plano XY. El sistema en conjunto
puede girar alrededor del eje vertical. Una partícula de masa m está adherida al disco, como se indica.
Demostrar que su energía cinética está dada por
T = \m{Rfy + r*¿* - 2J?r¿¿sen </> + rV* cos*^)
Integrando, demostrar que la energía cinética del disco uniforme delgado es
T = ¿(Mí* + /1)¿* + ¿/,¿»
en donde M es la masa total del disco; Ix es su momento de inercia con respecto a su diámetro; e I2,
el momento de inercia con respecto al eje horizontal sobre el cual está apoyado.
2.27. El siguiente problema tiene por objeto demostrar que aun en el caso de sistemas sencillos, las expresiones
para T y las ecuaciones de restricción, pueden hacerse bastante complicadas. Mientras el disco uniforme
(de masa M y radio R), que se muestra en la figura 2-33, rueda con velocidad angular S% sobre el eje X,
la varilla delgada (de masa m y longitud 2/) permanece en contacto con el disco, sin resbalar.
Simultáneamente el extremo inferior de la varilla se desliza en contacto con el eje X.
^\
40
FUNDAMENTOS BÁSICOS, II
[ CAP. 2
Fig. 2-32
Para el limitado recorrido en que las condiciones anteriores son válidas, escribir una expresión para
T en función de 6lt62, Xi,y¡, y x2, y sus derivadas con respecto al tiempo. ¿Cuántas
coordenadas superfluas aparecen? Demostrar que las ecuaciones de restricción son,
(1) R + R eos 6i = [L - R(8i + 8i- o*i)] sen 8i
(2) x2 = Re2 + 0X2 (S) yi = l sen Si
(4) xi + [L - l - R{6i + 9t- 09i)] eos ffi + R sen ffi = z2
en donde 0tfi y 0*2 son los valores correspondientes de 0, y x2 cuando el punto p está en
contacto con b.
¿Podrá expresarse T en función de cualquiera de las coordenadas anteriores? Inténtese con x2 y x2.
Escribir T en función de 81,81.
Para el punto p en contacto i
disco en 6. se escribe fli — 0{
posición angular inicial de la barra.
El punto p está inicialmente en
contacto con el disco. Así, la
longitud ab - s- L - (/+ /,).
Fig. 2-33
Con referencia a la figura 2-11, supóngase que la barra lisa gira en un plano horizontal impulsada por
un motor. Naturalmente, al final, la cuenta se desprenderá de la barra saliendo disparada con
considerable energía cinética.
CAP. 21
FUNDAMENTOS BÁSICOS, II
41
La fuerza de reacción entre la barra y_ la cuenta es normal a aquella. ¿Será correcto concluir que,
por consiguiente, la fuerza de reacción no hace ningún trabajo sobre m? Explicar la forma como la barra
le imprime energía a m.
2.29. Supóngase que la polea superior de la figura 2-9 está suspendida por medio de un resorte espiral. El
sistema tiene, naturalmente, tres grados de libertad. Figúrese un desplazamiento del sistema completo y
escriba una expresión para 8W considerando (por el momento) todas las rotaciones y desplazamientos
verticales como independientes entre sí. Tomando y,, q2 y y* como coordenadas independientes
del sistema, demostrar que (siguiendo los pasos descritos en el numeral 14) en cada una de las expresiones
SWy , &Wq2> SWy , el trabajo hecho por cada una de las tensiones de las cuerdas suma cero, si los
desplazamientos tienen en cuenta las restricciones.
2.30. Se les dan desplazamientos arbitrarios a las masas mi y m2 que se muestran en la figura 2-10.
Aplicando (2.62) demostrar que para ri y r2 constantes,
SW = [(rtsen<f> — t, sen 6)rx eos B + (t, eos e — rtcos<f> — m,ff) r, sen e
— rtrl sen <p eos 6 + (t,cos0 — mtg)rl sen e]8ff
+ [(t2cos# — mtg)rt sen <f> — rtrt sen <f> cob <f>]8<f>
= —(m.! + mi) grisen ff Se — mtgri sen <f> 8<f>
y por tanto, que las tensiones T\ y t2 de los cables (fuerzas de restricción) no hacen ningún trabajo,
para variaciones de e y <t> solamente.
CAPITULO
Ecuaciones del movimiento de
Lagrange para una partícula
3.1 Consideraciones preliminares.
Cualquiera de las varias maneras de formular las leyes fundamentales de la dinámica,
puede tomarse como base para la deducción de las ecuaciones de Lagrange. En el presente
texto se parte de las leyes del movimiento de Newton, se establece la ecuación de D'Alembert
y de aquí, finalmente, se deducen las relaciones de Lagrange. Se sigue este proceso porque
partiendo de territorio conocido conduce a campos desconocidos por un camino, en el cual,
es fácil entender el significado físico y matemático de cada paso.
Con el fin de eliminar algunos detalles que distraen, nos limitaremos a la deducción y
análisis de las ecuaciones de Lagrange para una partícula. El tratamiento más general,
aplicable a un sistema de muchas partículas, se deja para el capítulo 4.
3.2 Deducción de las ecuaciones de Lagrange para una partícula, sin coordenadas
ni restricciones móviles.
En aras de una mayor claridad se tendrá en cuenta una situación específica suponiendo
que el movimiento de la partícula en consideración está reducido a una superficie lisa, tal
como un plano o una esfera. En tal caso habrá dos grados de libertad, una ecuación de
restricción, y no habrá fuerzas de fricción.
Sea F, con componentes Fx, Fy y Fz, la suma vectorial de todas las fuerzas
(aplicadas externamente, debidas a resortes, gravedad, restricción, etc.) que pueden estar actuando
sobre la partícula. Entonces, suponiendo que la masa m es constante y que las coordenadas
x, y y 2 son inerciales, las ecuaciones del movimiento de Newton para una "partícula libre"
se escriben
Fx = mx, Fy = my, Fz = m'i (3.1)
Estas ecuaciones son correctas aunque el movimiento esté restringido, porque se supone que
Fxt Fy y Fz incluyen cualquier fuerza de restricción que pueda estar actuando.
Considérese ahora el trabajo b W hecho por F al suponer que la partícula sufre un
desplazamiento bs, completamente arbitrario e infinitesimal, con componentes bx, by y bz
(posiblemente bajo la acción de otra fuerza no incluida en F). (Este se llama "trabajo virtual"
de acuerdo con el numeral 2.13 del capítulo 2). Así pues,
8W = FSs eos{F,Ss) = Fx8x + FySy + FzSz (3.2)
Nótese que como F incluye la fuerza de restricción, (3.2) es correcto aunque bs pueda no
estar de acuerdo con las restricciones. (Es decir que bs puede tener una dirección tal, que
la superficie sobre la cual se mueve m, se "distorsione" ligeramente.) Debe recordarse también,
que el lado derecho de (3.2), como se demuestra en el numeral 2.8, tiene en cuenta el posible
hecho que F y bs no tengan la misma dirección.
42
CAP. 3) ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 43
Multiplicando ahora las ecuaciones {3.1) por 8x, 8y y 8z, respectivamente y
sumando*, se obtiene
m{xSx + ySy + zSz) = FxSx + FySy + FzSz {3.3)
El miembro derecho de esta expresión es igual al trabajo 8W hecho por F y el miembro
izquierdo puede interpretarse como el pequeño cambio correspondiente en la energía cinética
de m. (Véase de nuevo el numeral 2.8.) Esta ecuación será llamada "ecuación de D'AIembert".
Al introducir las coordenadas generalizadas en {3.3) y al realizar algunos manejos
matemáticos, se obtienen las ecuaciones de Lagrange {3.15) y {3.16). Como se ha supuesto que
el movimiento se halla restringido a una superficie, se requieren dos coordenadas
generalizadas, <?i y q2- Entonces, utilizando las ecuaciones de trasformación apropiadas y una
ecuación de restricción, es posible expresar las coordenadas de m: x, y y z en. función de
9i y 92, lo cual se indica como sigue (véase el numeral 2.6),
z = x{Qi,Q2), y = y{Qi,Q2), z = z{qi,q2) {3.4)
Ejemplo específico para demostrar el significado de (3.4):
Supóngase que la superficie restrictiva es una esfera de radio constante, r = C. En
coordenadas esféricas, las relaciones específicas correspondientes a {3.4) serán entonces,
x = Csen6cos<f>, y = CsenO sen<¡>, z — CcosO (3.5)
El tiempo no aparece en {3.4) puesto que se han tomado los ejes X, Y y Z, estacionarios,
y una restricción fija.
Los desplazamientos virtuales 8x, 8y y 8z, por razones que se darán más adelante,
se determinan a partir de {3.4). Es decir,
Sx = l> + Ü892' sy = af8" + mSqi- S2 = l> + W*Sq* i36)
Sustituyendo {3.6) en la ecuación de D'AIembert, {3.3), y agrupando términos,
m = mfs*L + y£ + *£W + ~í»£+ ?& + *#W
a«i "a?, ag,y "' y ag2 "a?2 ag2
dqi dqi dqi I \ dqi dqi dqi
{3.7)
En este punto el estudiante debe tener plena conciencia de ciertos hechos básicos.
(a) Como {3.4) representa las ecuaciones de la superficie restrictiva, {3.6) representa un
desplazamiento de acuerdo con la restricción. Por tanto, ¿ W de (3.7) corresponde a
un desplazamiento de conformidad con la restricción (sobre la superficie).
Considerando una vez más la esfera como caso especial, 8x, 8y y 8z, determinados a partir de
{3.5) son 8x = C eos 6 eos <j>86 — C sen 6 sen <t>8<f>, etc., lo cual representa claramente,
un desplazamiento sobre la esfera.
{b) Las coordenadas 91 y 92 {0 y <t> en {3.5)) son variables independientes; es decir,
pueden dársele a ambas pequeños valores arbitrarios sin violar la.restricción.
♦ Nota sobre la ecuación (3.3). Multiplicando las relaciones (3.1) por a, b y c respectivamente y sumando,
SC °btiene m(xa + yb + zc) = Fxa + Fyb + F.c
lo cual es una relación verdadera, independiente de la naturaleza de a, b y c. (Pueden representar constantes de
cualquier valor, desplazamientos, velocidades o aun funciones de variables.) Así, en cuanto concierne a (3.3), Sx,
6y y Sz son magnitudes completamente arbitrarias. Sin embargo, para nuestro objetivo, las consideraremos
como componentes de Ss, el desplazamiento virtual infinitesimal de m. Además, en lo que sigue, se supondrán
de acuerdo con la restricción. (Al considerarlo así, (3.3) se denomina con frecuencia "principio de D'AIembert".)
44
ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
(c) Como resultado de (a) y (fe) y la suposición que la restricción es lisa, el trabajo ejecutado
por la fuerza de restricción cuando una cualquiera de las coordenadas varía, o varían
ambas simultáneamente, es igual a cero. (Véase el numeral 2.13.) Por esta razón, en
adelante no se necesita considerar la fuerza de restricción como parte de Fx, Fy, Fz.
En otras palabras, se ha eliminado del cuadro la fuerza de restricción. Este es un punto
muy importante.
Como qx y q2 son variables independientes, fijaremos la atención en h Wqv el
trabajo hecho cuando solamente qx puede variar (8q2 = 0). La uación (3.7) se reduce
entonces a / x 7 x
•"<■ = "(""Sr^'S)"' = ('■£ + ''£ +'■£)*■ ™
Se utilizarán ahora las relaciones siguientes cuyas pruebas se incluyen abajo*. Por
el momento el lector no necesita ocuparse de tales demostraciones.
.. dx d I. dx\ . d (dx\ /n rt.
XJq¡ = di\XWi) ~ Xdt\^j (3-9)
W = £ (3W>
dQi dqi
Remplazando (3.20) y (3.11) en (3.9), se tiene
..dx d f . dx\ . dx
dqi dt\* dqj *dQi
con un pequeño análisis se demuestra que esto puede escribirse como
..dx__dL (b{xV2)\ _ a(¿2/2)
dQi ~ dt\ dqi J dqx {3A3)
Sustituyendo (3.13) y las relaciones semejantes para y y z en (3.8), se concluye que
SWQl =
d í d m(x2 + y2 + z2)\ d m(x2 + y2 + z2)
dt^dqx 2 J dqi 2
Fx£ + Fy»L + F*\qi
dqi dqi dqi I
8(7i
(3.14)
Pero ^ m (x2 + y2 + z2) es la energía cinética T de la partícula, por tanto, finalmente
se escribe i(*£\ - f = F,g- + F* + F * (3./5)
dt\dqiJ dQi dQi dQi dqi
♦ Para probar las relaciones (3.9), (3.10) y (3.11), se procede Je la siguiente manera. Considérese la identidad
d_/'dx\ _ "Bx_ , « d (dx\
dt\XdqJ " X3g. Xdt\dqiJ
que es igual a (3.9). Para obtener (3.10) se observa que la derivada de la primera ecuación en (3.4), con respecto
al tiempo, es x = t—g"i + -—qt. Derivando ahora ésta, parcialmente con respecto a q\, se nota que —r- = -—.
oqi dqt Qql dqx
Para probar (3.11), se ve primero que como x = x(qt, q2), la derivada parcial, dx/dqi es, en general, función
de q, y de q2, es decir dx/dqi = <f>(qi,qt). Derivando esto con respecto al tiempo, se obtiene
d f dx\ _ J_fBx_\' , d fdx\*
dt\dqj dq\dqiJqi + dqt\dqiJqi
Pero por la expresión de x, se sigue que
dx _ d fdx\ . J_fte\ •
3g. " dq\dqijqi + dqi\dqtJqt
Comparando las dos últimas ecuaciones se ve que (3.11) es correcta.
CAP. 3) ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 45
Partiendo de (3.7) y considerando el trabajo 8 Wq2 asociado con una variación de q2
únicamente, de una manera idéntica a la anterior, se llega a
d fdT\ dT „ dx , „ By , ■ dz
*U;J~*¡ = *¡ *** •** (3J6)
Las expresiones (3.15) y (3.16) son las ecuaciones de Lagrange que se trataban de deducir.
Por conveniencia se escribe,
F'Wr + F"% + F'W, = F" (3-/7)
en donde qr es una cualquiera de las coordenadas que aparecen en T, y Fr se denomina
"fuerza generalizada". De tal manera, las ecuaciones de Lagrange toman la forma compacta
r »(£)-£ = '*
Como se verá en el capítulo siguiente, las ecuaciones de Lagrange tienen exactamente la
misma forma para un sistema de muchas partículas.
Para el caso que se acaba de considerar (una partícula con dos grados de libertad),
existen dos ecuaciones de Lagrange. Si se supusieran tres grados de libertad (una partícula
sin restricciones), las relaciones (3.4) contendrían todas a qlt q2 y qz, y finalmente se
obtendrían tres ecuaciones de Lagrange. En general, hay tantas ecuaciones del
movimiento de Lagrange, cuantos grados de libertad se tengan.
Sin embargo (y esto es importante tanto desde el punto de vista de las ideas básicas,
como para ciertas aplicaciones) aunque en realidad la partícula tenga únicamente dos
grados de libertad, todavía es posible escribir tres ecuaciones de Lagrange. Ignorando la
restricción, se escribe x = x(qí} q2, qz), etc. Suponiendo que ql} q2 y q$ son variables
independientes y siguiendo exactamente el procedimiento anterior, se obtiene una ecuación
de Lagrange correspondiente a cada una de las tres coordenadas. Existe, sin^embargcv la
siguiente consideración_jjnportante: El desplazamiento 8s, correspondiente a 8qi, 8q2
y 8^-obviamente no está de acuerdo con la restricción. (En éréjeTñ^ló"^sp^daT~eri~cím-
sideración,
Sx = Sr sen6 eos <f> + r 86 eos 6 eos </> — r8<f> sen0 sen</>, etc.
la cual no está sobre la superficie de la esfera ya que 8r no se ha hecho igual a cero.) Por
tanto, 5 W incluye el trabajo hecho por la fuerza de restricción (reacción entre la partícula
y la superficie) y las componentes de esta fuerza deben incluirse en Fx, Fy y Fz. No se ha
eliminado la fuerza de restricción. Con esto en mente, las tres ecuaciones son absolutamente
correctas.
Por razones obvias, entonces, todas las coordenadas superfluas son normalmente
eliminadas de las ecuaciones de trasformación y de T. Sin embargo, el procedimiento anterior
de introducir deliberadamente coordenadas superfluas puede ser la base de un poderoso
método para hallar las fuerzas de restricción. Véase el capítulo 12.
3.3 Compendio de detalles importantes relacionados con las ecuaciones de
Lagrange.
(a) Ecuaciones diferenciales del movimiento.
Las ecuaciones diferenciales del movimiento para cualquier problema específico
se obtienen, naturalmente, por medio de las operaciones indicadas en (3.18). Para
sistemas de n grados de libertad, solamente n coordenadas (y sus derivadas con
respecto al tiempo) deben aparecer en T. Las coordenadas superfluas deben ser
eliminadas como en el numeral 2.6.
ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
(b) Significado de las fuerzas generalizadas.
No sobra insistir sobre la importancia de obtener un claro entendimiento del
simple significado físico de las fuerzas generalizadas (relación (3.17)) tanto para
fines de las ideas básicas, como para sus aplicaciones.
La expresión b W = Fx bx + Fy by + Fz bz es una ecuación general que
determina el elemento de trabajo hecho por una fuerza (de componentes Fx, Fy y Fz)
en un desplazamiento general bs (de componentes bx, by y bz). Considérese
ahora b W cuando bs está de acuerdo con la restricción y sólo qx varía (bq2 = 0). Tal
desplazamiento se obtiene si las componentes bx, by y bz provienen de (3.4),
haciendo q2 constante; es decir
- 3^1 " dqi * dqi
Sustituyendo en la ecuación anterior para bW, se tiene SWq. = ( Fx-t— + Fy^— +
V dQl dQl
F2—) S^i que es, claramente, FQl Bqi. Entonces una fuerza generalizada es una
magnitud de tal naturaleza que el producto FQr bqr es el trabajo hecho por
fuerzas impulsoras (sin incluir fuerzas "inerciales", ni de restricción) cuando qr sólo
varía en una cantidad igual a +6qr.
Las fuerzas generalizadas no son siempre fuerzas en el sentido corriente de la
palabra. Por ejemplo, si qr es un ángulo 0, Ft debe ser un momento (o torque)
a fin de que Feb6 sea un trabajo. Si qr es el área A, de la figura 2-6, FAbA = bW
y naturalmente, FA debe tener las dimensiones de una fuerza dividida por una
longitud.
(c) Técnica para obtener expresiones para las fuerzas generalizadas.
Puede seguirse uno de los tres métodos siguientes.
Sustituyendo expresiones conocidas de Fx, Fy y Fz junto con -r—, -r—, -r—
(obtenidas tomando derivadas de (3.4)) en (3.17), se obtiene F„r. Usualmente Fx, Fy
y Fz no son constantes sino funciones de las coordenadas, del tiempo, de la velocidad,
etc. En cualquier caso, las expresiones de estas fuerzas deben conocerse por la
naturaleza del problema en consideración. Este método es directo pero puede resultar largo
y monótono.
Un segundo método, que en muchos casos es más fácil y más atractivo desde el
punto de vista de lo que sucede físicamente, es el siguiente: Imagínese una de las
coordenadas, qr, incrementada en una cantidad igual a -f- bqr, y todas las
demás coordenadas que aparecen en T, mantenidas constantes. Determínese ahora,
por cualquier sistema adecuado, el trabajo SWQr hecho por todas las fuerzas
impulsoras (sin incluir las de restricción). A continuación se resuelve la ecuación
8WQr = FQrSqr (3.19)
para obtener Fv Al determinar SWQr, el trabajo se toma como positivo o como
negativo, según si la fuerza o fuerzas tienden a hacer aumentar o disminuir la
coordenada qr.
Si la partícula tiene dos o tres grados de libertad, en ocasiones es más
conveniente suponer desplazamientos simultáneos bqlt bq2, bq3 y escribir el trabajo total
correspondiente, SWtota], el cual tomará la forma
íWtoui = [••••]8<7i+ [••■■]8<72+ [••v]8<73 (3.20)
en donde los paréntesis cuadrados aparecen en el lugar correspondiente a Fq.
Los ejemplos siguientes aclararán esta técnica.
CAP. 3] ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 47
(d) De las fuerzas inerciales en las ecuaciones de Lagrange.
La expresión "fuerza inercial" como se utiliza aquí, se refiere a (masa) x
(aceleración). Términos como mx, mr62, 2mu¿, etc., sirven como ejemplos.
Una mirada al miembro izquierdo de (3.3) y a las ecuaciones siguientes hasta
(3.18) muestra que las fuerzas inerciales aparecen exclusivamente en -jrí —— ) — -—.
Asimismo, es claro que en FQr aparecen Únicamente fuerzas aplicadas. En otras
palabras, al escribir las ecuaciones del moviruiento de Lagrange, para cualquier
sistema, debe recordarse que el miembro izquierdo de (3.18) automáticamente tiene en
cuenta todas las fuerzas inerciales y que al tratar de hallar expresiones para FQr,
solamente deben considerarse fuerzas impulsoras. (Nunca se incluyen en FQr fuerzas tales
como la centrífuga, la de Coriolis, etc.)
3.4 Integración de las ecuaciones diferenciales del movimiento.
Un hecho desafortunado que todo científico aplicado debe afrontar, es que en la gran
mayoría de los problemas las ecuaciones del movimiento son tan complicadas que no se
encuentran métodos disponibles para su integración. En ciertos casos pueden hacerse
aproximaciones justificables o suposiciones que tiendan a simplificar las ecuaciones y a
reducirlas a formas integrables.
Afortunadamente, sin embargo, aparecen como salvación los computadores, los cuales
permiten obtener ahora soluciones gráficas o numéricas para ecuaciones que por otra parte
resultaban "insolubles". En este texto se presentan parcial o totalmente, las integraciones
cuando esto es posible y conveniente. Pero primordialrhente la.atención se concentra en
plantear correctamente las ecuaciones del movimiento.
3.5 Ejemplos ilustrativos.
El valor pedagógico de unos pocos ejemplos es muy superior al de varias páginas de
observaciones. Este es el mejor método para "explicar las explicaciones".
Ejemplo 3.1:
Considérese el movimiento de un proyectil con respecto a un sistema de ejes rectangulares adherido a la
Tierra. Considerando estos ejes como inerciales y tratando el proyectil como un partícula de masa m, se escribe,
m m,'t^ •» , «ix j j j dT . d fdT\ .. dT
T = -¿-(x* + y* + z*) de donde, — = mx, 3- — = mx, -r— = 0
¿ s£ dt\dx/ ox
Por tanto mx = Fx. En forma similar, my = Fy y m'z = Fz. Despreciando la resistencia del aire, la única
fuerza es la atracción de la gravedad en la dirección negativa de Z. Así pues, 5 Wt = —mgSz y Fz = — mg.
Obviamente, Fx = Fy = 0. Entonces, finalmente, mx = 0, my = 0, m'z = —mg. Este ejemplo no
demuestra el potencial del método de Lagrange, pero sí muestra que para el caso de una partícula tratada en función de
coordenadas rectangulares, las ecuaciones de Lagrange se reducen a la misma forma que las de Newton.
Ejemplo 3.2: Movimiento de una cuenta ensartada en un alambre parabólico rígido.
Una cuenta de masa m puede deslizarse libremente a lo largo de un alambre parabólico cuya forma está dada
por y = bx2. Como el movimiento está confinado a una línea, la cuenta tiene solamente un grado de libertad.
Las dos ecuaciones de restricción serán: y = bx2 y z = C. De la expresión T = \ m(x* + y* + i*) puede
eliminarse la velocidad i y bien y o x. Eliminando y, T = i mx* (1 + Ab2x2). Aplicando la ecuación de Lagrange,
^? = mx(l + 46*x2), 4r(^) = m'x'(í +4b*x*) + Smi'xb', ^- = lmi*xb*
bx «í \dx/ ox
Finalmente,
mx(l + 4b2x*) + Amtfxb* = Fx
Para hallar Fx se aplica (3.19) y como se observará, no resulta sencillamente igual a la componente x de
una fuerza. Se puede suponer que el eje Y es vertical y que la única fuerza que actúa es la atracción de la gravedad
(no es necesario considerar la fuerza de restricción). Si a la cuenta se le da un desplazamiento + bx, necesaria-
48 ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
mente se moverá una distancia correspondiente sobre el alambre + Sy, y el trabajo hecho entonces por la gravedad
será 6W = -mgby. Pero según la ecuación de la restricción, 5>- = 2bx5x. Por tanto SW = -2mgbx 8x = Fz8x,
Fx = — 2mgbx, y la equación_del movimiento, completa, queda
m x (1 + 46*x2) + 4mx*x62 = —2mgbx
A manera de extensión de lo anterior, imagínese que por medio de un hilo sujeto a la cuenta, se tira de ella
con una fuerza /. Supóngase que el hilo está en el plano de la parábola y que su dirección, dada por los cosenos
directores a y 0, se mantiene constante. Se tiene, que para un pequeño desplazamiento,
SW = - mg Sy + af Sx + fif Sy véase la ecuación (2.35)
Pero, de nuevo, By = 2bx Sx. Por tanto,
SW = (- 2mgbx + af + 2bxfif)8x y F, = 2bx(/3f - mg) + af
El miembro izquierdo de la ecuación del movimiento continúa inmodificado.
Nótese que todos los resultados anteriores pueden igualmente expresarse en función de y y y, en cambio de
x y x, eliminando desde el principio x de T, etc.
Ejemplo 3.3: Movimiento de una partícula sobre un * V
tablero horizontal liso, bajo la acción de un resorte. r 9 7n
Un hilo sujeto a la partícula pasa por un orificio en * X '
una mesa horizontal lisa y está atado a un resorte débil, i '
como se muestra en la figura 3-1.. El extremo inferior !
del resorte está rígidamente unido a un punto tal que
cuando m está en el orificio, el resorte no está estirado.
El sistema tiene dos grados de libertad y usando
coordenadas polares, T = \m(r2 + r202). La única
fuerza que actúa sobre la masa es la del resorte. Así,
para un desplazamiento arbitrario de la partícula, sW =
—krSr en donde k es la constante usual de la ley de
Hooke, del resorte. No existe ninguna fuerza actuando
perpendicularmente a r. Por tanto, las ecuaciones de
Lagrange conducen a
(/) mr — mrb1 = —kr, (2) ¿r(wir*¿) = 0
Utilizando (2) se observa que mr2B = pg = momentum angular = constante. Eliminando 8 de (/),
resulta una ecuación que incluye a r y r únicamente y que puede ser integrada por los métodos corrientes.
La solución de este problema en coordenadas rectangulares demuestra cómo en ocasiones, las ecuaciones del
movimiento pueden ser considerablemente simplificadas, al hacer una adecuada selección de coordenadas.
Escribiendo
T = $m(x* + y1) y SW = -krSr = - k(x Sx + y Sy)
se concluye que m'x = — kx y my = — ky. O sea que el movimiento está compuesto de dos movimientos
armónicos simples que forman ángulo recto y ambos poseen el mismo período. Por tanto, la trayectoria, en general será
la de una elipse con el origen en su centro.
Ejemplo 3.4: Un péndulo sostenido por una banda de
caucho, (Fig. 3-2).
Si el movimiento es en un plano, la pesa del péndulo,
considerada como una partícula, tiene dos grados de
libertad. Usando ryí como coordenadas, T = Jm(r2 + r262)
de donde se sigue que mr — mrd2 = Fr y mr2B + 2mrr0 =
Fe. A continuación se ilustran dos métodos para obtener
las fuerzas generalizadas. Imagínese que se le da a la pesa
un desplazamiento fis arbitrario, en el que tanto B como
r sufren cambios positivos. El trabajo hecho por la
gravedad y la banda de caucho está dado por
SW.oui = — mgSh — k(r — r0)Sr
en donde r0 y k se refieren a la longitud, sin extenderse, de la banda de caucho y a su constante de la ley de Hooke,
respectivamente. Los dos términos de la derecha se han escrito con signo negativo, porque el trabajo debe ser hecho
contra la gravedad y contra la banda, a fin de obtener desplazamientos positivos de r y de e. Pero como puede
verse en la figura, 8h = r 68 sen e — Sr eos 8 y por consiguiente,
SWtoM = — mgrSff sene — [k(r — r0) — mg eos 9]Sr
^T*"*^
\/4
f-~^* X
^^^_
/I ~T 1—,
/I* \ /
í7 i ~\
T3k Lyz-
Sh
■_
Fig. 3-2
CAP. 3] ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 49
Así, el trabajo correspondiente a un cambio de r únicamente, es SWr = — [k(r — r0) — mg cosff]5r =
fT Sr de donde Fr = - k(r- - r0) + mg eos 6
En forma similar, Fe = —mgr sen0.
Ahora se hallarán Fe y Fr por aplicación directa de F,r = F*t h F,t h F«-—. Teniendo en cuen-
o<jT o<fr dqr
ta la gravedad y la tensión de la banda, se observa que las componentes x y y de la fuerza sobre la pesa, son
F, = — k{r — r0) sen e, F„ = mg — k(r — r0) eos 6
Por las relaciones x = r sen 0 y y = r eos 0, se obtiene dx/3r = sen 0 y dy/dr = eos 0. Por tanto,
Fr = Fx-£- + F,y- = - k(r - r0) sen* 9 + [mg - k(r - r0) eos e] eos 9
= — k{r — r0) + mg eos e
que es idéntica a la expresión obtenida anteriormente. En la misma forma puede obtenerse Fe.
3.6 Ecuaciones de Lagrange para una partícula, suponiendo un marco de
referencia móvil, restricciones móviles, o ambas condiciones simultáneamente.
Hasta ahora se ha evitado el estudio de sistemas que impliquen marcos de referencia
móviles, restricciones móviles o una combinación de ambas condiciones simultáneamente.
Sin embargo, como en la práctica se presentan numerosos problemas de este tipo, es
importante considerar cuidadosamente la deducción y aplicación de las ecuaciones de Lagrange a
tales sistemas.
Supóngase una vez más, que se trata de una partícula que puede moverse libremente
sobre una superficie lisa. Además, se presume que la superficie, el marco de referencia que
sirve para medir las coordenadas generalizadas q\ y qz, o ambos, se mueven de alguna
manera determinada. Siguiendo exactamente el mismo procedimiento del numeral 3.2,
escribimos nuevamente,
m(x Sx + y'Sy + zSz) = FxSx + Fy Sy + F2 Sz
en donde 8x, 8y y hz representan un desplazamiento completamente arbitrario y Fx,
Fy y Fx son las componentes de la fuerza total que actúa sobre la partícula, incluyendo la
fuerza de restricción. (El marco XYZ se supone inercial.)
Se indican las ecuaciones de trasformación que relacionan a x, y y z con qlt q2 y t, de
la siguiente manera
x = fi (qi, 92, t), y = f¿ (tfi, q?., t), z = fz (tfi, q?., t) (3.21)
En estas ecuaciones aparecen sólo dos coordenadas generalizadas, y el tiempo entra
explícitamente debido a los movimientos asumidos. De aquí en adelante, las ecuaciones (3.21)
consideran en forma completa la restricción y el movimiento supuesto.
Como 8x, 8y y hz son todos arbitrarios, se puede, si se desea, determinarlos a partir
de las ecuaciones (3.21) dejando que tanto t como qx y q2 varíen. En esta forma,
dx ^ , dx R , ar, ,
8* = ^T89' + aS892 + aí8í' etc-
Sustituyendo en la primera ecuación de este numeral, y agrupando términos, se tiene
^•i+^+^)8-+K^+^+^)s?2
Y teniendo en cuenta que 8qlf ¿g2 y St son arbitrarios, puede hacerse bq2 = 0 y ¿í =.0.
Entonces (3.22) se reduce a
,' ..dx , .. dy , .. az V / „ dx dy dz\«n
50 ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
Finalmente, aplicando las relaciones {3.9), {3.10) y {3.11) como en el numeral 3.2 (que son
válidas aunque {3.21) contenga explícitamente el tiempo), se obtiene una ecuación de Lagran-
ge que tiene exactamente la misma forma de {3.15). De la misma manera, haciendo 8qi y
8t = 0 se llega a {3.16). Por consiguiente, los marcos de referencia móviles, las restricciones
móviles, o la combinación de ambas condiciones, no producen ningún cambio en las
ecuaciones de Lagrange; {3.18) continúa siendo la forma general.
3.7 De la energía cinética, las fuerzas generalizadas y otros tópicos, cuando
el marco de referencia, las restricciones, o ambos se mueven.
(a) Básicamente, la energía cinética, como se ha dicho con insistencia anteriormente, debe
referirse a un marco inercial (véanse los numerales 2.8 y 2.9). Sin embargo, siguiendo el
procedimiento descrito e ilustrado en esta referencia, es posible expresar a T en función
de las coordenadas móviles, cuando éstas han de usarse. Por otra parte, deben
eliminarse las coordenadas superfluas.
(fe) La observación siguiente sobre las fuerzas generalizadas es muy importante.
Nótese que en la relación ( Fxp- + Fy^- + Fzp-)sqr = Fq 8qr = 8WQ. las
V óqr aqr oqrJ r
derivadas de x, y y z se toman con respecto a qr únicamente dejando fijo t y todas
las demás coordenadas. Así, es muy claro que 8 WQr es el trabajo ejecutado por la
fuerza actuante, cuando, con las condiciones mencionadas, se le da a qr un
desplazamiento + 8qr. En otras palabras, las fuerzas generalizadas se determinan suponiendo
el marco de referencia y las restricciones en reposo y luego procediendo exactamente como
se explicó en el numeral 3.3 (fe) y (c); y como se ilustró en el numeral 3.5. Si sucede que
algunas, o todas las fuerzas, son funciones del tiempo, como ocurre con frecuencia, debe
seguirse aún el procedimiento anterior. Como todo desplazamiento, determinado por
las ecuaciones {3.21) con t constante, está de acuerdo con las restricciones, el trabajo hecho
por la fuerza de restricción es igual a cero. Por tanto, como es usual, esta fuerza debe
ser ignorada.
(c) Se observará que considerando 8q\
de {3.22), la relación
..dz
0, 8q2 = 0 y 8t ¿¿ 0, obtenemos, a partir
m
..dx , ..dy , ..óz \
'-S + .'-fí + '-S"
{3.23)
Como el lector puede demostrar fácilmente, el lado derecho de {3.23) es, sencillamente,
el trabajo hecho sobre la partícula por la fuerza total (incluyendo la fuerza de restricción)
cuando el marco de referencia, las restricciones, o ambos, desplazan su posición
ligeramente en el tiempo 8t. Sin embargo, como {3.23) es redundante en cuanto se refiere al
planteamiento de las ecuaciones del movimiento, no recibirá por ahora ninguna
consideración adicional.
3.8 Ejemplos ilustrativos.
Ejemplo 3.5:
Fig. 3-3
CAP. 3] ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 51
El siguiente ejemplo sencillo debe servir para clarificar algunas ideas básicas. Una varilla rígida lisa, como
se muestra en la figura 3.3, se hace girar con velocidad angular constante, en un plano alrededor del origen de los
ejes X y Y. Una cuenta de masa m puede deslizarse libremente sobre la varilla, bajo la acción de una fuerza F,
que incluye la fuerza de restricción. Por medio de la aplicación directa de la ecuación de D'Alembert (3.3) se
plantea la ecuación del movimiento, que para este caso es, sencillamente,
m(xSx+y8y) = FzSx + FySy (j)
La cuenta tiene sólo un grado de libertad. Tomando a r como coordenada, se puede escribir
x = r eos ut, y = r sen ut (2)
Por tanto, Sx = Sr eos ut — reo Sisen ut, Sy = Sr sen ut + ruSt eos ut (3)
en donde tanto r como í pueden variar. Igualmente pueden hallarse en forma inmediata las expresiones para
í y y, a partir de (2). Eliminando Sx, Sy, i* y y de (1), se tiene
m(r — ru*)Sr + 2mrru* St = (F«cos«t + F„ senuí)Sr + (F„ eos ut — F« sen «t)ru St (4)
Pero como Br y 5í son arbitrarios, resulta claro que
m(r — ru*)Sr = (Fx eos ut + F, sen ut)Sr (5)
(2mrru2)St = (F„ eos ut - Fzsen ut)ru St (6)
Al examinar la figura se observa que el miembro derecho de (5) es justamente el trabajo hecho por la fuerza
total a lo largo de un desplazamiento Sr sobre la varilla (no un desplazamiento Ss). Pero como el
desplazamiento tiene en cuenta la restricción, el trabajo hecho por la fuerza de reacción de la varilla sobre la cuenta es
igual a cero.
La ecuación (5)^es la ecuación del movimiento y es exactamente igual a la que se obtiene al aplicar
adecuadamente la ecuación de Lagrange. (Esto debe hacerlo el estudiante.)
La ecuación (6) corresponde a (3.23). Por inspección en la figura 3-3 se demuestra que el lado derecho de (6)
es el trabajo hecho por F (incluyendo la fuerza de restricción) para un desplazamiento rufif.
Ejemplo 3.6:
Con referencia a la figura 3-4, la plataforma gira- i
toria D tiene una velocidad angular determinada por el l
motor Mi. Adherido a la plataforma se encuentra el ■
mecanismo impulsor M2 que hace girar la varilla
lisa pa, alrededor del eje horizontal en p, de alguna ma- |
ñera en particular. La varilla pa y las verticales pb y !
oc se encuentran todas en el mismo plano. Una cuenta D 0\
de masa m puede deslizarse libremente a lo largo de la fe
varilla, bajo la acción de la gravedad. *■
Suponiendo que a y 8 son funciones conocidas
del tiempo, el sistema tiene un grado de libertad.
Tomando r como coordenada, se plantea la ecuación del
movimiento, y se encuentra Fr.
Se concluye fácilmente que
T = lm[r* + r*S2 + á*(s + r sen*)*]
Esta expresión es válida independientemente de la forma como varíen con el tiempo a y 6. Supóngase que a. =
wi = constante, y que la varilla se hace oscilar, por medio del mecanismo M2, alrededor de la vertical pb, según
8 = do senW2í- Por consiguiente,
T = ^míf2 + r**X eos* utt + «*[« + r sen (ff0 sen u,t)]*} (2)
que incluye únicamente a r, ry t. Aplicando la ecuación de Lagrange, se llega a
mr — m{re\u>\ eos* utt + u\[a + r sen (ff0 senutt)] sen (tf0 senutt)} = F, (3)
Con el fin de hallar una expresión para Fr, se ignoran por completo los movimientos de la plataforma y de
la varilla; es decir que durante el desplazamiento +Br, t permanece constante (8 y a permanecen constantes).
Por tanto
SWT = — mg eos 0 Br = — mg eos (ff0 sen«tt) Sr osea Fr = — mg eos {o0 sen at t)
Debe notarse que si la varilla no tiene un movimiento obligado sino que puede girar libremente alrededor
dep, el sistema tiene entonces dos grados de libertad. En este caso, despreciando la masa de la varilla, (1) continúa
siendo la expresión correcta para T. Las ecuaciones del movimiento correspondientes a r y o, pueden escribirse
en forma inmediata, y se ve que
Fr = — mg eos B, FB = mgr sen 6
M,[p
Fig.3-4
(1)
52 ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
3.9 Determinación de la aceleración por medio de las ecuaciones de Lagrange.
Como se demostró anteriormente (numeral 2.12), la componente a' del vector
aceleración a, sobre una línea cuyos cosenos directores son l, m y n, está dada por
a' = xl + ym + zn (1)
Si debe hallarse a' en la dirección de la tangente a una curva en el espacio en un punto p
determinado,
7 dx dV dz
l = -dS' m = d¿' n=Ts (2>
en donde ds es el elemento de longitud de la curva en p, dado por
ds2 = dx2 + dy2 + dz2 (3)
Entonces, partiendo de las ecuaciones de la curva en el espacio, pueden hallarse l, m y n.
Supóngase que se desea determinar una expresión general para la componente de la
aceleración en la dirección de la tangente a la coordenada q\, teniendo en cuenta que las
coordenadas generalizadas q\, q2 y qz se relacionan con las rectangulares por medio de
z = x(qu q2, qz, t), y = y(qu q2, qz, t), z = z(qlt q2, qz, t)
(4)
La línea coordenada de qx se determina haciendo que permanezcan constantes q2, qz y
t en (4) y dibujando la gráfica por puntos de x, y y z para valores variables de qx. En
forma semejante se obtienen las líneas coordenadas de q2 y q3. Tomando las derivadas
dx
de (4), mientras q2, q3 y t permanecen constantes, se obtiene dx = —dqx, etc.
Entonces (3) se convierte en
dqi
Í^Íw^
dq\
en donde ds es un elemento de longitud medido sobre la curva de qx.
Según (2),
dx
1 dx
h\ dqi
(5)
(6)
dq,[{dxldqi)2 + {dyldqtf + (dz/dqj2]1'2
en donde el significado de hx es bien claro, y donde se ha escrito dx/dqx como dx/dqu
puesto que q2, qz y t se consideran todavía constantes. En forma semejante, mi = -r- t—
1 dz
y ni = j- -—. Igualmente, los cosenos directores de la tangente a la curva coordenada de
fli dqi
q2, son
- 1 dx
h2 dq2'
1 dy
1 dz
Designando a' como aQl la ecuación (2) se convierte en
l_( - dx
h\Xdq, +
dqx ^ dqi
(7)
(8)
Teniendo en cuenta las etapas que condujeron al miembro izquierdo de (3.15), evidentemente
puede escribirse (8) en la siguiente forma
1 f d (dT'\ _ bV_
a*i " h\dt\dqi) dQl
en donde T' = i(x2 + y2 + z2), expresada en coordenadas generalizadas. En general,
(9)
dt\dqTJ dqr\
{3.24)
Es esta una manera sencilla y fácil de obtener las expresiones generales de las
componentes de la aceleración en la dirección de las coordenadas. Véase el siguiente ejemplo.
CAP. 3] ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 53
Ejemplo 3.7:
Considerando el sistema de coordenadas esféricas, se trata de obtener la conocida expresión de ag, la
componente de la aceleración según la dirección de la tangente a una de las curvas coordenadas de 0, por medio de la
utilización de (3.24).
Para estas coordenadas (véase la ecuación (2.39)), T = ^(r* + r*e% + r*sen"0 <f>*) de donde
TtKJf) ~Jf = r2° + 2rr9 - -V sen, eos,
m+w+m
h° = \_\Je) +\9e) +\ñ)] = [(rcosflcos^, + (r cose sen <p)' + r»sen»*]"« = r
Por tanto, a$ = rV+ Iré — r<f>* sen0 cos0. En forma similar pueden obtenerse inmediatamente ar y a¿.
Si el movimiento de un punto (o una partícula) está restringido a una superficie móvil,
después de eliminar una coordenada superflua, las ecuaciones (4) serán
x = x(qu q2, t), y = y(qh q2, t), z = z(qu q2, t) (10)
que en realidad son las ecuaciones de la superficie en cualquier instante.
Y si ahora se hace que q2 y t permanezcan constantes, las ecuaciones (10) representan
una curva qx sobre la superficie. Por otra parte, es claro que dx/ds, por ejemplo, es la
expresión de uno de los cosenos directores de la tangente a esta curva, en un punto cualquiera.
Por consiguiente, si se escribe 7" en función de qx, q2, (¡\, (¡2 y t, la ecuación (3.24) da las
componentes del vector aceleración según la dirección de las tangentes a q\, q¿, sobre la
superficie, en un instante determinado.
Una vez más, es importante recordar que, básicamente, las aceleraciones halladas de
esta manera, son relativas al marco X, Y, Z.
3.10 Una consideración adicional sobre las ecuaciones de Lagrange.
Con el objeto de clarificar aún más el sentido físico de las ecuaciones de Lagrange,
considérese lo siguiente:
Escribiendo T = ^(r2 + r262 + r2^2 sen2 0), según el numeral 3.9, se sigue que
1
he
~d
dt
fdT\ dT~
\a¡) de_
= m<Le
(véase el ej
imismo, el lector puede demostrar fácilmente que
1
he
F*d6+Fy~
^+ fA
36 zdd
= ¿¿ =
(3.25)
en donde, si / es la fuerza que actúa sobre m, fe es la componente de / en la dirección en que 0
aumenta. (Nótese que fe- es una fuerza verdadera y no un momento; además, ae es una
aceleración lineal.) Por tanto resulta claro que la ecuación de Lagrange conduce sencillamente
a mae = fe, en coordenadas esféricas. En la misma forma, pueden escribirse las ecuaciones
correspondientes a. r y <p, como mar = fr y ma^ = fé, y lo mismo para cualquier otro
sistema de coordenadas que pueda usarse.
Si existe alguna restricción sobre la partícula, las ecuaciones de trasformación toman
la forma de las ecuaciones (20). Siguiendo el razonamiento dado al final del ejemplo 3.7, se
concluye que las ecuaciones de Lagrange correspondientes a <?i y q2 pueden escribirse como
ma*! = A, Y ™<*Q2 = /q2-
Así pues, la interpretación física de las ecuaciones de Lagrange, para un sistema de una
partícula, es muy sencilla; y además, se observa que en cada una de las ecuaciones se tienen
en cuenta automáticamente las componentes de la aceleración.
54 ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA | CAP. 3
Lo anterior es válido para cualquier sistema de coordenadas y cualquier tipo de
restricciones. Considérese, por ejemplo, una partícula sobre una plataforma giratoria montada
en un ascensor acelerado. Supóngase que se desean obtener las componentes de la aceleración
de la partícula, expresadas en "función de ciertas coordenadas cuyo marco se encuentra
adherido a la plataforma, y que se requiere tener en cuenta los movimientos de la Tierra, del
ascensor y de la plataforma. Aun en este caso tan complicado, es fácil escribir T para la
partícula y (3.24) da los resultados buscados, en forma inmediata. El estudiante debe comparar
este método con el sistema vectorial normal. Véase el problema 3.34.
3.11 Experimentos sugeridos:
Como se mencionó anteriormente, al final de varios de los capítulos, se enumeran unos
pocos experimentos que han sidoliallados dignos de la atención, del tiempo y de los esfuerzos
de los estudiantes. Estos experimentos contribuirán a inculcar una apreciación tangible de
la dinámica que el papel y el lápiz no podrían lograr por sí solos jamás.
Experimento 3.1:
Determínese el período del péndulo que se muestra en la figura 3-6 (véase el problema 3.7). El punto p se
soporta por medio de un hilo largo y ligero colgado de su extremo superior de un cielo raso suficientemente alto.
Al moverse el péndulo, p describe el arco de un gran círculo, pero para movimientos pequeños, éste puede
considerarse como una línea recta horizontal. Si se determinan con cuidado los valores de k y m, los resultados
experimentales y los calculados concuerdan con buena precisión.
Puede repetirse el experimento ajustando la cuerda vertical, de modo que p quede algunos centímetros por
encima de la horizontal ab, quedando entonces los resortes en forma de V invertida. Naturalmente debe hacerse
una aproximación para calcular la fuerza ejercida por los resortes, suponiendo pequeños movimientos (úsese el
desarrollo de Taylor).
Resumen y observaciones
1. Deducción de las ecuaciones de Lagrange: Una partícula sin coordenadas
móviles, ni restricciones móviles (numeral 3.2).
(a) Se ha desarrollado la ecuación de D'Alembert a partir de la segunda ley de Newton
y del concepto del trabajo virtual. (Se ha observado que el trabajo virtual es un
instrumento simple pero poderoso que se utiliza como medio para llegar a un fin.)
(fe) La ecuación de D'Alembert, expresada en coordenadas generalizadas, conduce
directamente (con la ayuda de ciertas operaciones matemáticas sencillas) a las
ecuaciones de Lagrange.
2. Detalles importantes relacionados con estas ecuaciones (numeral 3.3(b) y (c)).
(a) La energía cinética, T, debe expresarse en función de las coordenadas generalizadas
que se hayan escogido, y de sus derivadas con respecto al tiempo. Deben eliminarse
de T todas las coordenadas superfluas.
(fe) Es importante entender con claridad el sentido físico de las fuerzas generalizadas,
no solamente para facilitar el uso de las ecuaciones de Lagrange, sino también para
lograr una apreciación de lo que ocurre.
3. Deducción de las ecuaciones de Lagrange: Coordenadas móviles, restricciones
móviles, o ambas (numeral 3.6).
(a) La deducción se basa de nuevo en la ecuación de D'Alembert y en el carácter
arbitrario de los desplazamientos virtuales bxt, by^ y 8zr Las ecuaciones resultan
con la misma forma anterior.
(fe) T es ahora función de las qr, qr y t.
cAp. 3) ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 55
(c) Como anteriormente, se halla Fq , dejando el tiempo constante. El sentido físico de
esto (numeral 3.7) debe ser entendido por las mismas razones mencionadas en 2(6).
4. La aceleración determinada por medio de las ecuaciones de Lagrange
(numeral 3.9).
Como se muestra en el numeral 3.9, la componente de la aceleración de un punto o
partícula, en la dirección' de una tangente a una curva q, en cualquier punto, puede
obtenerse, en forma inmediata, partiendo de la ecuación (3.24).
5. Interpretación física de las ecuaciones de Lagrange (numeral 3.10).
Para un sistema de una partícula, las ecuaciones del movimiento de Lagrange
pueden reducirse a mar = /r, en donde ar es la componente de la aceleración lineal de
m, en la dirección de la tangente a la curva de qr; y fr es la componente de la fuerza
total sobre m (sin incluir la fuerza de la restricción) que actúa según la dirección de la
misma tangente. Por consiguiente, las ecuaciones anteriores se reducen a la simpleza de
las ecuaciones de la segunda ley de Newton, independientemente del sistema de
coordenadas usado.
Problemas
3.1. Suponiendo que el movimiento está restringido al plano QtQ2 (Fig. 2-5) y que la gravedad actúa en la
dirección negativa del eje vertical Y, establézcanse las ecuaciones del movimiento de un proyectil en
función de las coordenadas q, y q2.
Resp. m[ Vi + <?2 eos (0 — a)} = — mg sen a y m['q2 + 9*i eos (0 — a)] = — mg sen 0
3.2. Una cuenta de masa m está restringida a moverse a lo largo de un alambre liso rígido que tiene la forma
de la hipérbola xy = C = constante. Demostrar que la energía cinética puede expresarse como
T = imJ»(l + f)
Escríbanse las ecuaciones del movimiento y demuéstrese que si el eje Y es vertical, la fuerza generalizada
correspondiente a i es F = maC/x1
3.3. Nótese que un punto cualquiera puede localizarse en el plano X Y, al especificar C y y en la relación xy = C.
Por tanto, considerando a C como una variable, puede usarse como coordenada. Demostrar que para el
movimiento en un plano, la energía cinética de una partícula puede escribirse como
* - i-M^)']
y que si se considera que la gravedad actúa paralelamente y en la dirección negativa del eje Y,
Fx = + mgC/x*, y Fc = — mg/x
3.4. En lugar de las coordenadas polares usuales, r y 8 (para movimiento en un plano) considérense como
coordenadas r y sen 8. Haciendo x = r eos 8, y = r sen 8 y llamando q a sen 8, se tiene x = rVl — q2
y y = rq. Demostrar que la energía cinética de una partícula en coordenadas r, q está dada por
t = i^ + ¿jifi
3.5. Una cuenta puede moverse restringida a una espiral cónica lisa, como se ilustra en la figura 3-5. Suponiendo
que p = az y que $ = —bz, en donde a y b son constantes, demostrar que la ecuación del movimiento es
z(a? + 1 + a'b'z*) + aWz'z* = -g
3.6. Plantear las ecuaciones (//) y (12) del ejemplo 1.2, por medio del método de Lagrange.
56
ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
La masa m del péndulo que se muestra en la figura 3-6, está suspendida por medio de un hilo inexten-
sible del punto p. Este punto puede moverse libremente sobre una horizontal bajo la acción de los resortes,
los cuales tienen una constante k. Despreciando
con un período igual a
i masa de los resortes, demostrar que el péndulo oscila
4/WWVV Éft
Fig.3-5
Fig.a-6
Un disco sólido uniforme, de masa M y radio R, tiene una pequeña masa m adherida a su superfície a
una distancia r del centro. El disco puede rodar libremente, sin resbalar, sobre una recta horizontal.
Demostrar que
T = \6'(MR* + I + mR1 - 2mrR eos e + mi3)
en donde / es el momento de inercia del disco, con relación al eje perpendicular a su superficie que pasa
por el centro; y 0 es el desplazamiento angular del disco a partir de la posición de equilibrio. Demostrar
que si el disco se desplaza ligeramente de la posición de equilibrio y se libera, oscilará con un período igual a
g / / + MR1 + m{R -
V mgr
La partícula de masa m que se muestra en la figura 3-7, puede moverse libremente a cualquier punto, bajo
la acción de dos resortes idénticos. Cuando m está en equilibrio en el centro de los ejes coordenados, la
longitud S de cada uno de los resortes es mayor que su dimensión normal Iq (sin extender). Demostrar
que F¿ = 0 y que para pequeños desplazamientos alrededor de la posición de equilibrio,
-2k{l-US)x, Fy = - 2fc(l - US)y,
-2kz
Establecer las ecuaciones del movimiento e integrarlas.
I
l
M
Fig.3-7
Fig.3-8
CAP. 3]
ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA
57
3.10. La masa m de la figura 3-8 es atraída hacia la masa estacionaria M por medio de la fuerza gravitacional
F = —GmM/f2. A una distancia inicial r0 se le da a m una velocidad inicial v0 en el plano XY.
Establézcanse las ecuaciones del movimiento en coordenadas r y 0. Demostrar que el momentum angular
pe = mr*e = constante. Con el auxilio de esto, integrar la ecuación de r y demostrar que la trayectoria
es una cónica.
3.11. Las componentes rectangulares de la fuerza sobre una carga Q, que se mueve en un campo magnético y
eléctrico, están dadas por las relaciones (5.14).
(a) Un cañón electrónico dispara un estrecho haz de electrones, todos con la misma velocidad (xo, yo, zo en
el origen de los ejes cuando t = 0) en un campo magnético uniforme (sin campo eléctrico) y en una
dirección que forma un ángulo inicial 8 con las líneas de flujo. Establecer las ecuaciones del
movimiento, integrarlas y demostrar que la trayectoria descrita por el haz es una helicoide cilindrica.
(Tómese B en la dirección de Z.)
(b) Establecer las ecuaciones del movimiento suponiendo un campo eléctrico uniforme paralelo al campo
magnético. ¿Cuál será ahora la trayectoria?
3.12. Una cuenta de masa m puede moverse libremente a lo«largo de un alambre circular liso que gira con
velocidad angular constante &>, alrededor de un eje vertical perpendicular a la superficie del círculo y que
pasa por su periferia. Una segunda cuenta se mueve bajo la acción de la gravedad a lo largo de un circuito
idéntico pero estacionario y contenido en un plano vertical. Demostrar que Jas dos cuentas tienen
exactamente el mismo movimiento. ¿Cuál magnitud, de la ecuación del movimiento de la primera cuenta
corresponde a g de la segunda ecuación?
3.13. Considérese la localización de m con coordenadas polares r y 0, en el ejemplo 3.2. Tomando o como la
coordenada independiente, demostrar que
tang
6 '
tan*g
6
Por tanto T puede escribirse en función de o y 8. Demostrar que la fuerza generalizada es
Fe
b eos* e
2Fy tan e
b eos1e
en donde Fx y Fy son las componentes de la fuerza que actúa sobre m. Resulta claro que 0 no es una
coordenada conveniente para determinar el movimiento de m. Repítase el procedimiento para el
problema 3.2.
En la figura 3-9, la cuenta de masa m puede deslizarse libremente a lo largo de la varilla lisa, bajo la
acción de la gravedad y del resorte. Se hace girar el eje vertical con una velocidad angular constante «.
^Demostrar que la ecuación del movimiento es
mr — mru1 sen* e = k(l — lo) — kr
y que la masa oscila con un período igual a
mg eos e
Hi
■ -. i t— alrededor de la posición r =
I k — m«*sen*ff
en donde 1= r + s y l0 es la longitud normal del resorte (sin extenderse).
k(l — lo) — mg eos B
k — mu* sen* e
Fig.3-9
Fig.3-10
58 ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
3.15. Supóngase que el bloque B que se muestra en la figura 3-10, al cual se halla adherido el resorte, se hace
oscilar verticalmente según la relación s = A sen «f. Sea (a) la representación de la posición del sistema
sin ningún movimiento aplicado a B y m en equilibrio bajo la acción de la gravedad y del resorte. Sea
(b) la representación de una posición general del sistema. Demostrar que el efecto del movimiento de B
es la aplicación de una fuerza a m igual a kA sen «f. Demostrar además que el movimiento de m está
dado por
q = Csen (-\/k/m t + S) + mik/m _ » senut
3.16. Un disco pesado uniforme, de radio R, rueda por un plano inclinado sin resbalar. Los ejes X y Y están
adheridos a la superficie del disco con el origen en el centro. Una partícula de masa m puede moverse
libremente en el plano del disco bajo la acción de la gravedad y de un sistema de resortes cuyos detalles
no es necesario especificar. Por consideraciones elementales puede decirse que despreciando la pequeña
masa de la partícula, el centro del disco se mueve con aceleración lineal a = \g sen a, en donde a es
el ángulo de inclinación del plano. Demostrar que la energía cinética de la partícula en coordenadas
polares r y e (0 medido a partir del eje X adherido al disco) está dada por (fi se mide entre X y una
recta fija normal al plano inclinado)
T = $m[a*t2 + r* + r*(/3 - 9)2 + 2atr sen (/? - e) + 2atr(fi - 9) eos (/3 - *)]
en donde ¡3 = (a/R)t. Comparar esta forma de T con la expresión general (2.55).
3.17. El hilo que soporta la masa del péndulo (Fig. 3-11) pasa a través
de un pequeño orificio en el tablero B, el cual se hace oscilar
verticalmente según el eje Y de tal manera que s = A sen ut.
Demostrar que
T = \m[2A V eos* coi + (l - A sen coi)* 9*
— 2A2u2 eos2 coi eos 9
— 2(1 — A sen ut) Au9 eos ut sen 9]
en donde l = r + s = constante.
Escribir la ecuación del movimiento. Demostrar que
Fe = — mgr sen 9 = — mg(l — A sen ut) sen 9
3.18. Haciendo referencia al ejemplo 3.6 y a la figura 3-4, supóngase
que ¿ = ü) = constante, que la masa de la varilla pa es
despreciable y que el mecanismo impulsor M2 se remplaza por un
sistema de resortes que tiende a conservar a pa en posición
vertical, por medio de un torque —Ce. Establecer las ecuaciones
del movimiento correspondientes a r y a 0. Obsérvese que la
expresión de T (ecuación (1), ejemplo 3.6) es aún válida.
3.19. Demostrar que si la espiral del problema 3.5 (Fig. 3-5), gira alrededor de su propio eje con velocidad angular
constante u,
T = ±m[z2(a2 + 1)- + a2z2(co - b'z)*]
Demostrar también que si la espiral tiene una rotación dada por wt + \at2y
T = ±m[a*z2 + a2z*(u + at - bz)2 + z2]
Obsérvese que en ambos casos la fuerza generalizada correspondiente a z es igual a —mg.
3.20. Supóngase que el disco que se muestra en la
figura 3-12 puede sufrir cualquier movimiento
rotacional por la acción de un motor (que no se
muestra) conectado a su eje. El hilo al cual se halla
sujeto m se ha fijado y enrollado alrededor del
disco. La posición angular del disco está dada por
a, medido desde el eje X, que está fijo, hasta
una recta trazada en la superficie del disco. La
posición angular del hilo (que se supone siempre
tangente a la polea) está dada por 0. La
longitud inicial del hilo es igual a r0, según se indica.
Demostrar que para la masa m,
T = ^m[R2'a2 + (r„ + R9 - Ra)292]
F0 = — mg(r0 + Re — Ra) sen 9
V///////////////A
Fig. 3-11
Y
f\
/'re
/ 1
0
\i-í
Fig. 3-12
CAP. 3] ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 59
y que la ecuación del movimiento es
m(r0 + Re — Ra)6 — 2mRéá + mRe2 = — mg sen o
en donde a se supone que es una función conocida del tiempo.
3.21. En la figura 3-13 se muestra un alambre rígido parabólico que gira de una cierta manera alrededor del
eje Z2 al mismo tiempo que la plataforma a la cual se halla adherido el sistema X2, Y2, Z2 se mueve
con aceleración constante a, paralela al eje V,. La cuenta de masa m puede deslizarse a lo largo del
alambre liso bajo la fuerza de la gravedad, (a) Demostrar que
T = %m[r* + r*¿* + a*t2 + 2fat sen ¿ + 2rj>atcos<t> + 46Vr*]
Suponiendo ¿ = w = constante, plantear la ecuación del movimiento correspondiente ar,y demostrar
Que FT = -2mgbr
3.22. Al girar el alambre del problema anterior, genera una copa parabólica. Supóngase que m está restringida
a moverse en contacto con la superficie interior de una copa estacionaria que tiene tal forma. La
expresión de la energía cinética es exactamente igual a la que se escribió para el problema 3.21 salvo que <¡>
debe considerarse ahora como una coordenada independiente. Escribir las ecuaciones del movimiento
para este caso. Demostrar que FT es igual a la del problema anterior, y que F¿ = 0.
Fig. 3-13 Fig. 3-14
3.23. Al soporte del péndulo, mostrado en la figura 3-14, puede dársele el movimiento giratorio que se desee
por medio de la manivela. Demostrar que T para el péndulo es
T = ^m[a*a* + r28* + r2(á — ¿)"sen2 e — 2sráe eos 6 sen# + 2sra(á — <f>) sen e eos <f>]
en donde r, 6 y <t> son las coordenadas esféricas medidas con respecto a los ejes X, Y y Z, los cuales están
adheridos a la barra horizontal ab y giran solidariamente con ella. En este problema se toma r constante.
Suponiendo que r puede variar (una banda de caucho) repetir lo anterior. Escribir T como la suma
de tres términos correspondientes a los de la ecuación (2.55).
3.24. Suponiendo 0\ = wi = constante, B2 = «2 = constante, demostrar que la energía cinética de la partícula
de la figura 2-21, con movimiento confinado al plano X2Y2, está dada por
T = %mfr + r2¿* + [28(0, sen (utt + a)]r + [2i*(0l + o^ + 28Ulr eos (co,t + a)]'a
+ [r*{Ul + «,)" + 28(0,(«o, + u2)r eos (*tt + a) + 8*u\]}
Nótese que la anterior tiene la misma forma de la relación (2.55) en donde las cantidades
correspondientes a A, B y C resultan evidentes.
3.25. Una plataforma giratoria P2, está montada en una segunda plataforma también giratoria, P,, la cual
a su vez está montada en un ascensor. P¡ se halla impulsada por un motor a velocidad constante Ul. En
forma semejante P2 gira con velocidad constante W2, con relación a P¡. El péndulo simple montado
en P2 de longitud /, puede oscilar en un plano que coritiene al eje vertical de rotación de P2, y su punto
de suspensión. El ascensor tiene una aceleración constante hacia arriba, a. Hallar la ecuación del
movimiento del péndulo
m[P*i + l eos 6 (8, — I-senff)(co, + co2)2 + 8,coJI eos e eos utt + al sen e] = — mgl sen e
Nótese que el miembro izquierdo de la ecuación anterior es sencillamente, (ml)ao, en donde ae es la
aceleración lineal de m cori relación a un marco inercial, en la dirección positiva de 0. (Véase la ecuación
(3.24).)
60 ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA [CAP. 3
8t —^*-8l-J
f*l.Vl.2l
,1 *■*•*,*
xx
Fig. 3-15
v
\ O
. ->^
-yo
M
ÜU
^
x,
2o
1 /
y.
,Y\,Z\ Estacionario
Fig. 3-16
Un marco de referencia X, Y, Z está adherido al interior de un automóvil. El eje Y se dirige hacia
adelante, el eje Z verticalmente hacia arriba y el eje X a la derecha. La posición de una partícula debe
localizarse en coordenadas esféricas r, 8 y i>, medidas con relación al marco mencionado.
Suponiendo que el auto se mueve a lo largo de una vía circular a nivel, de radio R, con aceleración
tangencial constante, a, escribir y plantear las ecuaciones del movimiento para una partícula libre sobre
la que actúa únicamente la gravedad.
Se hace girar con velocidad angular constante w, el eje vertical que se muestra en la figura 3-16. El eje
posee un brazo de longitud r, rígidamente adherido, como se indica. Escribir una expresión para T y
las ecuaciones del movimiento de la partícula, con relación al sistema rotatorio, X2, Y2, Z2. Para una
indicación y las respuestas, véanse las ecuaciones (14.15).
Considerando las coordenadas cilindricas r, $ y z, la relación z = br2 representa una "copa"
parabólica si b es constante. Las coordenadas x y y de un punto de la copa en particular pueden escribirse
como x = r eos <t> y y = r sen ¿. A fin de acostumbrarse a toda suerte de coordenadas, supóngase
que b es una variable, en cuyoxaso b, r y $ pueden considerarse como las coordenadas para localizar un
punto en el espacio. Por tanto, las tres relaciones anteriores son las ecuaciones de trasformación que
relacionan las coordenadas rectangulares con las b, r y ¿.
Demostrar que en este sistema de coordenadas, la energía cinética de una partícula está dada por
T = \m[r*(l + 46V) + rV + ¿V + 4&r86r]
Para el caso en que la gravedad actúa en la dirección negativa de Z, demostrar que
FT = -2mgbr, Fb = -mgr*, F^ = 0
Determinar una expresión para la aceleración de m, como se muestra en la figura 3-9, en la dirección de
los incrementos de r. Supóngase que se le da aceleración angular constante al eje vertical $T = c. (Véase
el problema 3.14.)
Demostrar que con estas mismas condiciones,
r — rc't* sen* 6,
- rt?t% sen 6 eos B,
2rct sentf + re sen 6
son las componentes de la aceleración, ar, ae y at con relación a un marco inercial.
¿Cuáles serán las componentes de la fuerza de reacción en las direcciones de los incrementos de o y
de 4,1 Obsérvese que para obtener los resultados anteriores, en realidad se han introducido 8 y <t> como
coordenadas superfluas. (Véanse las observaciones al final del numeral 3.2.)
Haciendo referencia a la figura 2-5, resulta claro que para el movimiento en el plano XY, el vector
aceleración general del punto p, tiene una componente en la dirección del eje Q,, dada por a„ = xl + ym,
en donde / y m son los cosenos directores de este eje. Demostrar que esta expresión se reduce a a„ = g\ + q*
eos (p — a) y que esta última puede obtenerse directamente de la ecuación (3.24).
cAp. 3) ECUACIONES DEL MOVIMIENTO DE LAGRANGE PARA UNA PARTÍCULA 61
3.31. Refiriéndose al problema 3.22 y aplicando los métodos del numeral 3.9, hallar la componente de la
aceleración de la tangente a una curva (sobre la copa) para la cual r = constante. Comparar el resultado con
la ecuación del movimiento correspondiente a 4>, obtenida en el problema 3.22. Repetir el proceso para
una curva en la cual $ = constante y comparar con la ecuación del movimiento correspondiente a r.
3.32. Con referencia a la figura 2-21, las ecuaciones (2.32) y (3.24) determinan las expresiones generales para
las componentes i2 y y2 de la aceleración de m. ¿Las aceleraciones así obtenidas, serán en realidad
relativas al marco Xl7 Yi? ¿Qué fuerzas FXt,Fyt se requerirían para conservar a m fija con respecto a
X2,Y2?
3.33. Haciendo referencia a la figura 3-16, escribir las expresiones de las componentes del vector aceleración
general de m según las direcciones de los ejes X2, Y2 y Z2, pero relativas a los ejes inerciales X,, Yi y
Zx. (Véase el problema 3.27.)
3.34. Una plataforma giratoria está montada en el suelo con el eje de rotación vertical. Un marco de referencia
rectangular está adherido a la plataforma, y la posición de una partícula con relación a este marco se
determina por las coordenadas esféricas. Hallar las expresiones en coordenadas esféricas de las
componentes de la aceleración, ar, a$ y a¿, con relación a un marco inercial de referencia, teniendo en cuenta
la rotación de la Tierra, así como la de la plataforma. (Véase el numeral 14.7(b).)
CAPITULO
Ecuaciones de Lagrange
para un sistema de partículas
4.1 Observaciones introductorias.
Por razones pedagógicas, el análisis de las ecuaciones de Lagrange del capítulo 3, se ha
restringido a sistemas que contengan solamente una partícula. Ahora se deducirán estas
ecuaciones (y al final adquirirán la misma forma de la ecuación (3.18)) para el caso general de un
sistema que consiste en muchas partículas con un número finito cualquiera de grados de
libertad y en el cual pueden existir restricciones móviles o marcos de referencia móviles o
ambos. A continuación, el resto del capítulo se dedica a las técnicas de aplicación de las
ecuaciones de Lagrange a varios tipos de sistemas diferentes y al importante aspecto de lograr un
entendimiento del significado físico de las relaciones matemáticas empleadas.
4.2 Deducción de las ecuaciones de Lagrange para un sistema de partículas.
En primer lugar se establecerá la forma general de la ecuación de D'Alembert.
Considérese un sistema de p partículas cuyas masas mi,m2, ...,mp sufren la acción de las
fuerzas Fi,F2,. -,Fp, respectivamente. Debe entenderse que Fly por ejemplo,
representa la suma vectorial de todas las fuerzas de cualquier origen (incluyendo las fuerzas de
restricción) que actúan sobre mi, etc. Así, suponiendo masas constantes y un marco de
referencia inercial, las ecuaciones de "partícula libre", para cada una de ellas, serán
FXl = mii'i, FVl = mx'yu FZl = miz\
(4.1)
FXp = mpXp, Fyp = mpyv, FZp = mpzp
en donde FXl,FVl y FZl son las componentes rectangulares de Fx, etc. Es importante
observar que como se ha supuesto que Flt F2, etc., incluyen las fuerzas de restricción, las
relaciones (4.1) son válidas, aunque las partículas tengan cualquier tipo de restricción.
Suponiendo ahora que cada una de las partículas sufre un desplazamiento virtual, cuyas
componentes son 8Xl, 8Wl y SZl, etc., se procede a ejecutar las siguientes operaciones
matemáticas sencillas. Multiplicando FXl = m\x\ por 8Xl, FVl = m\'y\ por 82/1,etc., en todas las
relaciones (4.1) y sumando todo el conjunto, se obtiene,
2) rriiixtSxt + y'iSyi + z\8Zi) = J) (FXlBxt + FViSyi + Fz.SZi) (4.2)
relación que si se interpreta en forma adecuada, conduce a resultados de gran alcance.
(Véase la ecuación (3.3).) Nos referiremos a la ecuación (4.2) como ecuación de D'Alembert.
Aquí deben hacerse varias observaciones importantes, semejantes a las que siguieron a la
ecuación (3.7).
(a) Con respecto a la validez de (4.2) no es necesario que hxi,byl y 8zt representen
desplazamientos, ni que sean magnitudes infinitesimales. En realidad pueden rempla-
zarse por cantidades completamente arbitrarias como ai,bl y c,.
(b) Sin embargo si se supone que representan desplazamientos de las partículas, resulta claro
que el miembro derecho de (4.2) es sencillamente una expresión general del trabajo
62
CAP. 4J ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 63
total 8W hecho por las fuerzas FX,F2, ... en los desplazamientos 8xx, 8yx, 8z\, ...
de todas y cada una de las partículas. Es decir,
SW = ¿ (FXiSXi + Fy.hyi + 'Fz.SZi) (4.3)
(c) Lo anterior es válido aunque los desplazamientos imaginarios (virtuales) no estén de
acuerdo con las restricciones; es decir, que las restricciones pueden considerarse
ligeramente "distorsionadas". En tal caso, naturalmente, 5 W incluye el trabajo hecho por
las fuerzas de restricción.
(d) Pero si se considera que los desplazamientos están de acuerdo con las restricciones, el
trabajo hecho por las fuerzas de restricción se anula. (Véanse los numerales 2.13 y 2.14.)
En otras palabras, las fuerzas de restricción quedan efectivamente eliminadas de (4.2)
y de (4.3).
(e) Con las condiciones enunciadas en (d), la relación (4.2) se denomina principio o ecuación
de D'Alembert.
Aunque a primera vista no lo refleje, la ecuación de D'Alembert es el principio más
general de todo el campo de la mecánica clásica e incluye la estática como caso especial de la
dinámica. Las ecuaciones del movimiento de cualquier sistema con un número finito de
grados de libertad, pueden obtenerse directamente de (4.2), en cualquier sistema de
coordenadas, mediante la aplicación de las ecuaciones de tras formación apropiadas y de las
ecuaciones de restricción. Las ecuaciones de Lagrange son apenas una forma más conveniente de
(4.2). Todas las demás formulaciones como las ecuaciones de Hamilton, el principio de Ha-
milton, el principio de Gauss de la mínima restricción, etc., pueden obtenerse a partir de las
ecuaciones de D'Alembert.
Continuando con la deducción, supóngase que el sistema tiene n grados de libertad, en
donde n < 3p, y que las 3p — n ecuaciones de restricción son de tal naturaleza que todas las
coordenadas superfluas pueden eliminarse de las ecuaciones de trasformación,
Xi - Xi(qitq2t .. .,qn,t)
Vi = yi(QuQ2, . . .,qn,t) (4.4)
. z¿ = Zi(tfi,<72, • • .,Qn,t)
Con respecto a estas ecuaciones, deben tenerse en cuenta los siguientes hechos.
(a) Las relaciones (4.4), son ecuaciones de trasformación de las que se han eliminado
previamente las coordenadas superfluas, denominadas anteriormente, ecuaciones "reducidas".
Aquí se consideran únicamente sistemas holonómicos. (Véase el numeral 9.12.)
(b) Debido a las restricciones, el número de coordenadas generalizadas que aparece en (4.4)
es 3p — n menor que el número de coordenadas rectangulares.
(c) La aparición de t indica que pueden existir restricciones móviles, o un marco de referencia
móvil, o ambos.
(d) Estas ecuaciones tienen en cuenta todas las restricciones, en el sentido que los
desplazamientos 8xt, 8yt y 8zt que se obtienen aplicando las relaciones
dXi R , dXi R , , dXi . , . „ _.
8x¡ = xr8^ + xr§92 + ••• + t—«<?«, etc. (4.5)
dqi d<72 dqn
(conservando a t constante) a (4.4), están de acuerdo con las restricciones.
(e) Así, si 8xl,8yl y 8zt se determinan de esta manera, se puede estar seguro que el
trabajo ejecutado por las fuerzas de restricción suma cero. Por tanto, las fuerzas de
restricción pueden ser ignoradas. (Véase el numeral 2.14.)
64 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS (CAP. 4
Sustituyendo las relaciones (4.5) en (4.2) se obtiene, después de agrupar términos,
<A /.. dxi , .. dyi ..dZi\„ , , .A /.. dXi , .. dyt .. dZi\
(4.6)
$Á^ñ+^+<h+---+w^+F^^wh
Pero como <?i, <?2> • • •> 9„ son todas variables independientes (físicamente esto
significa que las partículas del sistema pueden desplazarse libremente de tal manera que, sin
violar las restricciones, una cualquiera de las q puede tomar cualquier valor
independientemente de los valores de las demás), pueden considerarse arbitrarios todos los 8q. Entonces
supóngase que todos se hacen cero, excepto, por ejemplo, 8qlt con lo cual la ecuación (4.6)
se reduce a
Utilizando aquí las relaciones correspondientes a (3.9), (3.10) y (3.22) y siguiendo el
mismo procedimiento del capítulo 3, (4.7) puede escribirse,
8WV
4-££(*?+ «+ *»1 " é±T&+ «+ *Í>U»
d^ii=i 2
59iiéí 2
(4.8)
Ecuaciones idénticas se obtienen de igual manera para q2, 93, • •., qn. Es decir,
d_/ar\ _ dT_
►
en donde r = 1, 2, .. ., n y las fuerzas generalizadas Fqr, son
n, = i(^ + n,t + ^) (,,o>
Nótese que (4.9) tiene exactamente la misma forma que (3.18).
4.3 Expresión de T en forma adecuada.
Aunque T = ~ 2 m{(¿? + y? + ¿f), en donde el marco de referencia es inercial y exis-
* i=i
ten 3p coordenadas rectangulares, puede considerarse como la expresión básica de la energía
cinética, su forma final a la cual se le aplicarán las ecuaciones de Lagrange, debe ser expresada
en función de qu q2, .. •, gn, las coordenadas generalizadas, sus derivadas con respecto
al tiempo, y posiblemente t. Las etapas requeridas para esto se han explicado e ilustrado en
el numeral 2.7. Como se demostró allí y en los ejemplos que siguen, con frecuencia resulta
provechoso expresar primero T en función de un número cualquiera de coordenadas
adecuadas. Luego, por medio de las ecuaciones de trasformación y de las ecuaciones de restricción,
puede ponerse en forma final excluyendo las coordenadas superfluas.
4.4 Significado físico de las fuerzas generalizadas.
Una vez más, como se indicó en el capítulo 3, una fuerza generalizada Fqr,
correspondiente a la coordenada qr, es una magnitud (no siempre una fuerza en el sentido usual de
la palabra) tal que FQr bqr es el trabajo hecho por todas las fuerzas aplicadas al
incrementar únicamente qr (dejando constantes el tiempo y todas las demás coordenadas) en una
CAP. 4) ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 65
magnitud igual a +8qr. Sin embargo, en este caso más general es importante caer en
cuenta que para un sistema de p partículas con varias restricciones, un incremento de sólo
qr puede requerir un desplazamiento de varias o de todas las partículas. Por consiguiente
dWar debe incluir el trabajo hecho por las fuerzas aplicadas a todas las partículas, que como
resultado de -\-5qr cambiarían de posición.
En prueba de las afirmaciones anteriores obsérvese que (4.3) es una expresión general del
trabajo cuando a todas las partículas se les da un desplazamiento infinitesimal arbitrario.
Pero si se supone que sólo qr varía, (4.5) se reduce a
8*' = ÍS'" »> = &<*■ «* = £»*
y por tanto, (4.3) se hace
•** = S('*£+ '..& + ',£>*
que según (4.10) es, sencillamente, FQr 8qr. (Véase el ejemplo 4.1.)
Todas las fuerzas inerciales (véase el numeral 3.3(d)) se han tenido en cuenta, en el lado
izquierdo de (4.9). Por las razones expuestas e ilustradas en la última parte del capítulo 2, las
fuerzas de restricción (para el caso de restricciones "lisas") se anulan en (4.10). Por tanto, en
los análisis de las técnicas y de los ejemplos que siguen, estas fuerzas se ignoran.
4.5 Técnicas para hallar expresiones para las fuerzas generalizadas.
Expresiones para F„r pueden encontrarse por cualquiera de las técnicas que siguen, las
cuales pueden aplicarse a cualquier tipo de fuerzas aplicadas y son básicamente iguales a las
explicadas en el numeral 3.3(c). (En ningún caso se incluyen fuerzas inerciales.)
(a) Puede aplicarse directamente la relación (4.10). Las componentes rectangulares FXitFy.,
y F2(, de la fuerza Fl que actúa en mlt deben determinarse a partir de las fuerzas
conocidas del sistema. Utilizando (4.4) pueden obtenerse las expresiones explícitas para
dx¡/dqr, diji/dqr y dzjdqr. Con frecuencia este método resulta muy monótono.
(6) Suponiendo que todas las restricciones móviles, o todos los marcos de referencia móviles,
o el conjunto de todos ellos, son estacionarios, y que todas las coordenadas, excepto qr son
constantes, se incrementa qr en una magnitud + 8qr.
En seguida, estudiando el problema entre manos, se escribe una expresión del
trabajo, 8Wqr, hecho por todas las fuerzas aplicadas a las partículas que deben cambiar
de posición como resultado de -\-8qr. Usualmente esto puede hacerse directamente,
sin necesidad de utilizar las componentes rectangulares de la fuerza. Entonces, por la
relación
8WQr = FQrSqr (4.11)
puede obtenerse Fq en seguida.
Al aplicar este método, con frecuencia resulta provechoso escribir primero 8 WQr en
función de un número cualquiera de coordenadas y luego expresarlo en términos de qx,
92, •• .,?„•
(c) Siguiendo el procedimiento descrito en (6), en muchos casos es posible e incluso
provechoso, escribir una expresión del trabajo total 8WtotaU cuando varían simultáneamente
todas las coordenadas. Como puede notarse en (4.6) y en los ejemplos que siguen, esto
puede escribirse en la forma
8W\otai = [ liSqri + [••••]2802 + ••• + [•■••]„80„ (4.12)
en donde los paréntesis cuadrados pueden ser constantes, pero usualmente son funciones
de las coordenadas, de la velocidad, del tiempo, etc. Resulta claro que el paréntesis
cuadrado [.... ]r es sencillamente F„r. Así, todas las fuerzas generalizadas pueden leerse
directamente en (4.12).
ECUACIONES DELAGRANGE PARA UN SISTEMA DE PARTÍCULAS
[CAP. 4
Una observación adicional: Para un sistema que tenga por ejemplo, cuatro grados de
libertad, se hace que Fqi,FQ2,FQ3 y FqA indiquen las fuerzas generalizadas correspondientes
a 91,92,93» Y 94 respectivamente. Supóngase ahora, que se inicia de nuevo el problema
remplazando a q3 y qA por otras coordenadas diferentes 9gy q\. Las fuerzas generalizadas
quedan entonces F,,, F,2, F,¿ y Fq¿, pero FQl y F<¡2 del segundo caso son en general,
diferentes de FQl y F,2 del primero, aunque correspondan a las mismas coordenadas. (Véase
el ejemplo 4.1.)
(Debe mencionarse aquí que cuando las fuerzas son conservativas, usualmente es más
conveniente determinar FQr a partir de la función de la energía potencial (véase el capítulo 5).
En muchos casos de fuerzas disipativas, el método de la "función de la potencia" resulta
beneficioso (véase el capítulo 6). Sin embargo, independientemente del tipo de las fuerzas
aplicadas, cualquiera de las técnicas (a), (6) o (c) pueden ser utilizadas.)
4.6 Ejemplos ilustrativos de la aplicación de las ecuaciones de Lagrange
a sistemas que incluyen varias partículas.
Ejemplo 4.1. Un sistema de tres partículas.
Considérese la disposición que se muestra en la figura 4-1. Si se
supone que sólo puede haber movimiento vertical, el sistema tendrá
dos grados de libertad. Entre las distintas posibilidades, se toman
>'i y y2 como coordenadas. Ignorando las masas de las poleas,
Pero como puede verse fácilmente, «s
tanto
T = ¿ra,# + %mi(yi-
= \rnxy\ + ^Wi«í + ^m3s\
Vi —y* y «s = V\ + y%. Por
VtY + ^msiyi + yt)*
únicamente. (Nótese que y2 es una
que incluye ahora a j/i y ¡/»,
coordenada no-inercial.)
La ecuación del movimiento correspondiente a yt,
como sigue:
—— = mi¡7i + mi(yi — yt) + m3(yi + y3)
dyi
y
-T7 í —r J — (mi + mt + m3) y\ + (wis — raí) y%,
Por tanto, (raí + ra» + ras) y\ + (ras — ra») y% =
1
ÉD
dyt
■Q
Q-
db
Fig. 4-1
Para obtener una expresión de Fy se aplica la ecuación (4.11). Así, se determina el trabajo hecho por las
fuerzas impulsoras (la gravedad), despreciando las fuerzas de restricción (tensiones en los hilos), cuando se
incrementa yi en una cantidad +Byt (bajando ligeramente mi) y haciendo que y2 permanezca constante. Se
obtiene bWy = -\-myg 6yl — (m2 + m3)gSyi. El segundo término de esta expresión se origina en el hecho
de que como y2 permanece constante, es preciso levantar & m2 y m3 en una cantidad igual a aquella en que
se ha bajado a m^ Por tanto Fy = (m, - m2 - m3)g y la ecuación del movimiento completa,
correspondiente a >-,, es
(raí + ra» + ras) y\ + (ms — mi)y\ = (nti — mt — m3)g (/)
Para obtener la ecuación del movimiento de>-2, se observa que
<L/3T\
dt \diJ
(ra» + ras) ¡/a + (ra3 — raí) y\
f = «
dy*
Se obtiene una expresión para Fy haciendo que y2 aumente en una cantidad +5>-2, con 3/, constante. Es
claro que el trabajo ejercido por la gravedad es 8^ = (mt — m3)g 8y* = Fy2 Syi. Por último, la ecuación del
movimiento de y2 tendrá la forma
(raí + ra3) yt + (wis — raí) & = (raí — m3)g (2)
Las relaciones (/) y (2) pueden solucionarse simultáneamente para obtener y\ y y,, y las ecuaciones resultantes
pueden integrarse en seguida.
CAP. 4] ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 67
Como sencillo ejemplo de (4.12), nótese que
SWioui = (wii 8¡/i — rtit ¿8X — m3 883)g (3)
Pero Bs2 = Byi — by2 y 6s3 = Byt + by2. Por tanto, eliminando Ss2 y Ss3,
íWtoui = (wii - m» - m3)g 8¡/i + (mi — m3)g Syt
en donde pueden leerse directamente Fy y Fy .
Como extensión de este ejemplo, úsense como coordenadas >-, y s2. Como s2 + s3 — 2yx = constante,
i — 52. Entonces,
de donde
T = \™>\V\ + \mtsi + £wi3(2¿, - ¿i)»
(mx + 4m3)y\ — 2m3'¿2 = F»
(mt + m»)lii — 2m3yi = F,
(4)
(5)
Para encontrar Fy se hace que s2 permanezca constante (no se permite que m2 cambie de posición) y se
supone que >-i se incrementa a >-i + fiy, (m, se mueve ligeramente hacia abajo). Pero como puede verse, por
simple inspección, esto requiere un desplazamiento hacia arriba de m3 en una magnitud igual a 2fiy,. Por
consiguiente,
SWVl = +vug Syi — 2m3g Syi o sea que Fy = (mi — 2m3)g
(Nótese que las expresiones de Fy en (1) y en (4) no son iguales.) En forma semejante, se sigue que Fs =
(m3 - m2)g.
Empleando (4.12), se puede usar (3) de nuevo. Eliminando Ss3 por medio de Bs3 = 2fry, - 8s2,
SWlol
(mx — 2m3)g Syi + (m> — m-¿)g Ssi
obteniendo así, de nuevo, las mismas expresiones para Fy y Fs .
Debe observarse que cuando una de las n coordenadas varía,
dejando fijas las otras, las demás coordenadas que no entran en el
problema, pueden, naturalmente, variar. Por ejemplo para encontrar
Fy (véase la primera parte del ejemplo anterior) se dejó fijo y2 y se
hizo variar yt. Al hacer esto, slts2 y s3 variaron.
Ejemplo 4.2. Énfasis adicional sobre las fuerzas generalizadas.
En la figura 4-2, desprecíense las masas de las poleas, supóngase
únicamente movimiento vertical y ténganse en cuenta las fuerzas
que actúan externamente /i,...,/5 y la gravedad. Por ejemplo,
nótese que para un desplazamiento +5q\ (dejando fijas todas
las demás coordenadas), mi se mueve hacia abajo una distancia
*<?i y ms se mueve hacia arriba una distancia igual a 4fiq,.
Siguiendo este razonamiento,
Fqt = (mlS + /,) -. 4(m5g + /5)
Fq2 = in^g + ft - (m3g + f3)
Fqs = -(mt + m3)g - /2 - /3 + 2(7n50 + /s)
Fq^ = m^g + fs — (rntg + f*)
Usando ahora como coordenadas qltq2,s y q4, demuéstrese
que
fq1 = mig + fi — (mtg + m3g + f, + f3) — 2(msg + /5)
Fs = (mt + m3)g + /, + f3 - 2(msg + /5)
Fq„ y Fq son iguales a las anteriores, sin embargo, nótese la diferencia
en la forma de Fq en los dos casos.
En general la expresión Fq depende de cuáles son las otras
coordenadas empleadas.
Fig.4-2
68
ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS
[CAP. 4
Ejemplo 4.3. Movimiento de una palanqueta en un plano
vertical.
Las partículas de masas m, y m2 que se muestran en
la figura 4-3 están adheridas rígidamente a una varilla ligera
y pueden moverse libremente en el plano XY, bajo la acción
de la gravedad. Suponiendo que no hay rotación alrededor
del eje de la varilla, y aplicando el teorema del centro de masa,
se escribe
T =
7tl\ + 7tl\
(x' + V*) + ¿t*
en donde (i, >-) son las coordenadas del centro de masa, / es
el momento de inercia de la palanqueta con respecto a un eje
que pasa por el centro de masa y es perpendicular a la varilla,
y 0 es el ángulo señalado. Como el sistema tiene tres grados
de libertad, y x, y y 8 son coordenadas adecuadas, T tiene
ya la forma apropiada.
Aplicando las ecuaciones de Lagrange, se concluye
inmediatamente que
(mi + m*) x = Fx, (mi + m*) y = Fy, e I'e= Fg Fis- 4-3
Dejando constantes a >- y 0 y aumentantio x a x + Sx, resulta claro que el trabajo hecho por la gravedad,
6WZ = 0. Por tanto Fx = 0. En forma semejante, Fy = - (m, + m2)g y Fe = 0. Por consiguiente, las
ecuaciones del movimiento, en forma final, son
* = 0, y = -g, V = 0
Esto quiere decir que el centro de masa tiene el sencillo movimiento de un proyectil (despreciando la resistencia
del aire) y que la palanqueta gira con velocidad angular constante 6.
Ejemplo 4.3A. Extensión del ejemplo 4.3.
Se trata de plantear las ecuaciones del movimiento de la palanqueta usando como coordenadas xltyi y 0.
Puede escribirse T como T = j¡mi{x\ + y\) + fymt(x\ + y\). Pero se observa que x2 = xi + lcose y que
y>2 = y\ + /sen e. Derivando estas relaciones y eliminando ¿2 y yi, se obtiene
T = mi + m2(i] + {£) + ^{Pe1 - 2lxi'e sene + 2lyíe eose)
Aplicando las ecuaciones de Lagrange se obtienen los siguientes resultados:
{mi + mt)x\ — ?n2/Vsenff — mil9* eos ff = Fx
(mi + m,i)y\ + m» l Veos* — mil 0*sen0 = Fy
m2(l2'e — Ix'i senff + ly\cos6) = Fg
De aquí se sigue fácilmente que Fx = 0, Fy = —(mi + m2)g y Fe = — m2gl eos 8.
Es importante notar que al cambiar las coordenadas, la forma de las eCuaciones del movimiento puede variar
mucho. Además, aun cuando algunas de las coordenadas se conserven (0 en este caso), las fuerzas generalizadas
cambian, como se -demostró en el ejemplo 4.2.
Ejemplo 4.4. Péndulo con soporte deslizante.
El péndulo de la figura 4-4 está suspendido de un bloque de masa
nti que puede deslizarse libremente sin fricción a lo largo del eje
horizontal X. Si se supone que r es constante y que todo el movimiento está
confinado al plano XY, el sistema tiene dos grados de libertad. Se
usarán como coordenadas xi y 0. Iniciando con las coordenadas
*i>*2 y y2, se ve que
T = %mxx\ + £m2(x*+¡/í)
Pero x2 = xt + r sen 0 y y2 = r eos 0. Eliminando x2 y y2
de T, se obtiene finalmente
T = £wii¿i+ £m2(¿í + 2rxi5cos* + r***)
de donde (nti + mt)'xl + m%rVeos 6 — mire2 sen 0 = FXi y tmr Xi eos 6 + mir*e = Fe. En la forma usual,
se encuentra Fx = 0 y F0 = —m2gr sen 0, y así se completan las ecuaciones del movimiento.
CAP. 4]
ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS
Si se supone que el movimiento es de tal naturaleza que 8 es siempre una cantidad bien pequeña, puede
remplazarse eos 8 en T por la unidad, sen e en Fo por 8 y puede despreciarse el término en é1. Las ecuaciones
del movimiento se convierten entonces en
(mi + mt) Xi + rn.tr 'e = 0
m2rxi + mtr*'e = —mtgre
La primera ecuación puede integrarse en forma directa. Eliminando x¡ de la segunda ecuación por medio
de la primera, se obtiene una forma fácilmente integrable. Los resultados finales son
= Cit + Ci, y 8 = A sen (wí + 6)
mi + mt
en donde Clt C2,A y 5 son cantidades arbitrarias que se determinan por las condiciones iniciales específicas,
V rn
m¡)g
. Supóngase que cuando í = 0, *i = x0, «i = £o, 8 = 80 y 8 = 0o. Sustituyendo estas
condiciones en las formas integradas, se obtienen cuatro ecuaciones de las cuales se deduce que
Ci = ¿o +
Wli + Ttli
C% = «o + -
= V*;+5
8ou
y tan S = -r-
con lo cual se ilustra el método general para determinar las constantes de integración a partir de las condiciones
iniciales dadas.
Ejemplo 4.5. Las masas de la figura 4-5 se mueven verticalmente bajo
la acción de la gravedad y los resortes.
Aplicando el teorema del numeral 2.10, se ve que
T = { g )V + ~2q* + ~2q* + T«5
Pero por la definición del centro de masa, mxqx = m2q2 + m3q3-
' Derivando esto y eliminando gi de T, se tiene
m M., mi (mt • mz . \ . mt •, , ms •,
T = -**" + T^ +^«-; + T«5 + T«-
en donde M = m¡ + m2 + m3. Como el sistema tiene tres grados de
libertad y como y, q2 y q3 son coordenadas adecuadas, se concluye
que la segunda forma de T no contiene coordenadas superfluas.
Al aplicar las ecuaciones de Lagrange se obtienen fácilmente las
siguientes ecuaciones del movimiento:
g. de 1. = 3
- (mi + mt) qt +
~<?3
*v
mtma" , Ws(wi+_ms) « _ „
Fig. 4-5
My = F„
X
Lo que sigue es una clara demostración' de la naturaleza de las fuerzas generalizadas y de la técnica de hallar
. sus expresiones. Por inspección se demuestra que para un desplazamiento general de todo el sistema (véanse las
ecuaciones (4.12)),
BWu»
= -kx(qx + q% — U)(Sqi + Sq2) - k2(q3 — qt - h)(Sq3 - Sqt) — Mg 8
en donde &, y k2 son las constantes elásticas y /, y l2 son las longitudes normales (sin estirar) de los
resortes superior e inferior, respectivamente. Utilizando una vez más la relación del centro de masa 5q, =
— Sg2 -I 6q3m, y eliminando q, y 6qt,
¡Wm = j--fc,(m. + m,) ^2!±2üi,a + gt. ~ I.) + feto ~ 9. ~ V>] 8«.
70 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS (CAP. 4
Esta ecuación tiene la forma de (4.12) y por tanto resulta claro que los coeficientes de Sq2, 5q3 y Sy son las
fuerzas generalizadas FQt>, Fq y Fy respectivamente. Así se han completado las ecuaciones del movimiento.
(Véase el problema 4.5.)
A manera de extensión del ejemplo, se determinan a continuación las fuerzas generalizadas por aplicación
directa de (4.10) que, para este sistema, toma la forma
r _ F 3¡/, dyt dy3
Fqr ~ Fyidq~r *V*~dTr "33^
en donde qr puede representar a y, a q2 o a q3. Fy es la fuerza vertical total que actúa sobre mi, etc. Por
inspección de la figura se demuestra que (como g, = — qt + — q3)
Fy = —rriig — kA —qt -\ q3 + q% — U )
i \wii 7ti\ /
FVo = -Tmg + kJ^q* i ^-q3 + qt - li) - kt(q3 - qt - U)
2 \mi wii /
Fyg = -m3g + kt(q3 - qt - U)
Por otra parte, yx = y + ™± g2 + V}± q Vt = V - q*, y3 = V - q3
Entonces, por ejemplo, Fq está dada por
Fq2 ~ Fyi dq~t + Fy2 dqt + Fyz dq2
Pero —■ = —, t^ = —1 y t^ = 0. Así, esta relación se reduce fácilmente a la hallada anteriormente
by± _ mt dyt _ _x dy3 _ |
dqt ™i ' dq2 dqt
para Fq . En forma semejante Fq y Fy pueden obtenerse en seguida.
La ecuación del movimiento correspondiente a y demuestra que el centro de masa cae con una aceleración
constante g. Las otras dos ecuaciones se integran fácilmente y pueden ser puestas en la forma
an qt + bu qt + a» q3 + bit q3 = A
Qai qt + bti qt + cttt qs + btt q3 = B
en donde A, B, las a y las b, son constantes. Aquí no se continúa el estudio de estas ecuaciones ya que en el capítulo
10 se tratan en detalle los métodos de integración aplicables a estas formas.
Ejemplo 4.6. El péndulo doble de la figura 2-10.
Supóngase que los hilos que sostienen las masas son inextensibles y que el movimiento está confinado a un
plano. La expresión (2.42) se reduce a
T = ^r\ex + ^[rí¿* + r*J% + 2r,r,*7 cos(* - *)]
De donde —r = m.ir\b + m.tr\e + mtrirtQ eos (<f> — e)
de
-rr(—i") = (mi + mt)r\y + mtnrt ¿"eos (</> — 6) — m.trirt4>(4> — ¿)sen (<f> — 6)
Asimismo, — = mtrirt¿¿ senfa - e)
de
(mi + mt)r\ V + mtrirt ¿"eos (</> — 8) — mtrirtf1 sen (<f> — e) = Fe
En forma semejante la ecuación correspondiente a $ es
m%r\'4 + mtrirtVeos (</> —9) + morirte* senfa» — 6) = F^
Para hallar Fe supóngase que se incrementa el ángulo e en una cantidad igual a +50, dejando constante <t>.
Esto significa que las dos masas deben ser elevadas ligeramente. Por tanto,
SW = — (mi + m2)gri senfl 50 y F0 = — (mi + m2)gri senfl
CAP. 4) ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 71
Con 8 fijo, la masa m, no se mueve y hW* = - m2gr2 sen ¿ 8<t>, de donde F* = - m2gr2 sen $. Así,
se tienen las ecuaciones del movimiento completas. Si el movimiento es muy pequeño (e y <t> siempre pequeños)
estas ecuaciones del movimiento se reducen a la misma forma de las del ejemplo 4.5, y por consiguiente pueden
integrarse. (Véase el capítulo 10.)
Ejemplo 4.7. Un sistema que se mueve con aceleración lineal constante (Fig. 4-1).
El punto de apoyo del sistema de poleas de la figura 4-1, se mueve hacia arriba con aceleración constante a.
En este caso,
T = %mx(l-yxy + ^rm'sl + ¿masS
en donde l = at, yt + 8t — yi = at y s3 = 2¡/2 + 8». Por tanto,
T = ¿mifat-yi)* + £wi,(aí + jfi - y*)1 + $m3(at + jfi + y*)2
y entonces, las ecuaciones del movimiento serán
(mi + m% + m3) y\ + (m3 - mt) y\ + (mi + m3- mx)a = Fy
(wi3 -mi) y\ + (mt + m3)y\ + (m3 — mt)a = F«2
Como para determinar las fuerzas generalizadas se deja fijo el tiempo, Fy = (mi — m2 — m3)g y Fy =
(m2 — m3)g tal como en el ejemplo 4.1. En realidad, en el caso de-este sencillo ejemplo de aceleración lineal
constante, las ecuaciones del movimiento son las mismas excepto que, efectivamente, g se ha aumentado a g + a.
Como extensión de lo anterior, el estudiante puede escribir fácilmente las ecuaciones del movimiento
suponiendo que h varía de cualquier forma determinada, con respecto al tiempo. (Véase el problema 4.16.)
Ejemplo 4.8. Un sistema que se mueve con rotación y aceleración lineal.
Considérese el sistema que se muestra en la figura 4-6. Un pequeño tubo que contiene las masas mi y m2
conectadas por medio de resortes, está montado formando un ángulo a sobre una plataforma giratoria. El plano
vertical que pasa por el centro del tubo pasa también por el eje de rotación de la plataforma. El conjunto está
montado en un elevador que se mueve con aceleración hacia arriba, a. Obtendremos las ecuaciones del
movimiento de mi y m2 en función de las coordenadas qx y q2.
Eje Z I
En coordenadas cilindricas, fijas a la superficie de la Tierra y supuestas inerciales,
T = i«il(r».+ t*¿J + *Í) + ¿TMrf + ri** + z\)
Tomando el origen de estas coordenadas en el centro de rotación del disco, se ve que
r\ = 8 + qicosa, di = coi, z\ = gi sena + £aí*
r» = 8 + qicosa, 8t = coi, z2 = g» sena + £aí*
Por medio de estas relaciones puede expresarse T fácilmente como
T = ^[gf + 2g1aísena + (s + q¡ eos a) V + a*t*]
+ £wfc[g* + 2g,aísena + (s + g2 eos a)»u2 + a*í*]
Las únicas coordenadas que aparecen en T son q¡ y q2 y debe observarse además que t aparece en forma
explícita.
72 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS | CAP. 4
Al aplicar las ecuaciones de Lagrange, se obtiene
mi(q\ + a sen a) — TOko2(s + gicosa) cosa = Fq
mt('qi + a sena) — m»co2(s + g» cosa) cosa = Fq2
Ignorando el movimiento del sistema, el trabajo hecho por la gravedad al incrementar ligeramente a g,,
únicamente, es
SWq^ = -m,ff sen a Sqi — k¡(q¡ - li) Sqi + kt(qt - qi - lt) 8qt
en donde Z, y l2 representan las longitudes normales de los resortes primero y segundo respectivamente. Así,
Fq = -miffseno — (ki + fa)gi + ktqt + kiU — ktlt
En forma similar,
Fq2 = —ntigsena — (kt + k3)qt + ktqi + ktlt + k3(li + lt)
Con esto se completan las ecuaciones del movimiento. Por inspección puede demostrarse que la aceleración del
elevador tiene el efecto de incrementar & g en una magnitud igual a a.
Ejemplo 4.9. Ecuaciones del movimiento cuando partes de un sistema se obligan a moverse de una manera
determinada.
Con lo que sigue se ilustra un tipo de problema que algunas veces se encuentra en la práctica.
Se supone que en el sistema de la figura 4-1 se ha introducido un mecanismo adherido al piso que ejerce una
fuerza variable sobre m2 de tal manera que s2 varía con el tiempo, de una manera determinada. Se trata de
determinar la ecuación del movimiento para el resto del sistema, despreciando las masas de las poleas.
Debido a este movimiento forzado (es decir, como s2 es una función conocida del tiempo) y suponiendo
movimiento vertical únicamente, el sistema tiene ahora sólo un grado de libertad. Bien y, o y2 pueden servir
como coordenada adecuada, y suponiendo que los hilos están siempre tensos, s, + y2 + s2 = Cx y si + yi = C2.
Por tanto, yt = ¿/i — ¿*. Así pues, se escribe,
T = |m,j; + $m*s\ + £m3(2¿, - 8,)*
A fin de hacer el ejemplo más específico, se supone que la fuerza aplicada a m2 es tal que s2 = s0 + A sen «t, en
donde s0 es una constante; en tal caso,
T = ¿mi¡/¡ + £maAV eos* coi + ^m3(2yl - Acó eos coi)*
y la ecuación del movimiento será
(wii + 4m3)y\ + 2m3Au* sen ut = F„
(Nótese que no es necesario conservar el segundo término de T por ser función de t solamente.) Al aplicar la
ecuación SWVi = FVi 8ylt dejando a t constante, se encuentra Fy¡ = (mi — 2m3)g. Con esto se completa la ecuación
del movimiento. Se observa que Fy aquí, no es igual a la del ejemplo 4.1.
A manera de ejemplo adicional considérese el sistema de la figura 2-15, que tiene cuatro grados de libertad.
Supóngase ahora que una fuerza exterior que actúa sobre el eje de la polea superior hace que s, varíe de una
manera determinada; y otra que actúa sobre m2 le imprime otro movimiento conocido. El sistema tiene ahora
sólo dos grados de libertad, y suponiendo que los hilos se conservan tensos, puede escribirse T en función de s», s3
y t, por ejemplo. (Véase el problema 4.19.)
4.7 Fuerzas y movimientos de las partículas cargadas en un campo
electromagnético.
Constituye una rama importante de la dinámica, el estudio del movimiento de las
partículas cargadas y las masas, a través de campos eléctricos y magnéticos. Sin embafgo,
salvo en el caso especial de sistemas de coordenadas inerciales y velocidades relativamente
bajas (que supondremos a continuación), el problema debe resolverse por métodos relati-
vísticos. Este tema constituiría por sí mismo un capítulo de buen tamaño.
Con las suposiciones anteriores, las componentes rectangulares de la fuerza sobre una
partícula con carga Q, que se mueve con velocidad (x,y,z) a través de un espacio en donde
existe un campo eléctrico E, de componentes (Ex, Ey, Ez) y un campo magnético jB(jBz,
By, Bz), están dadas por
Fx = QEX + Q (yBz - zBy), Fy = QEy + Q (zBx - xBz), Fz = QEZ + Q (xBy - yBx) (4.13)
en donde E y B pueden ser funciones de las coordenadas y del tiempo.
CAP. 4) ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 73
Utilizando estas expresiones de Fx, Fy y Fx en (4.10), el procedimiento para plantear
las ecuaciones del movimiento es tal como se ha hecho en los ejemplos anteriores.
Ejemplo 4.10. Ecuaciones del movimiento de una palanqueta cargada en un espacio con campo eléctrico y
magnético.
Las pequeñas esferas de la figura 4-3 portan cargas —Q, y +Q2 respectivamente, distribuidas
uniformemente. Supóngase un campo magnético en la dirección del eje Zy un campo eléctrico E, en la dirección de X, siendo
ambos uniformes en el plano XV. Considérese únicamente movimiento en el plano XV.
Al moverse la palanqueta, mi sufre la acción de una fuerza
Fxt = -QiE - QiByh F^ = QiBxi
y algo semejante para m2. Por tanto, para un desplazamiento virtual general,
8WtoM = -(QiE + QxByx) Sxi + QiBxiSyi + (Q*E + QtByt) 8xt - Q,Bx,8y*
Tomando a x, y y 8 como coordenadas generalizadas (véase^ el ejemplo 4.3) por las relaciones xi = x —
U eos 8, y\ = y — h sen 8, etc., se concluye que xt = x + li B sen O, 5xi = Sx + Zisenfl 58, etc. Por
tanto, la expresión anterior puede escribirse finalmente como
8W\.i.i = [(Qt - Qi)E + B(Q, - Qt)y + B(Q,l, + Q,{,)¿ eos e] Sx
+ [B(Qi-Q2)x + B(Qlll + QiU)9senff]Sy
- (QiU + Q*U)[E sen* + B(x eos e + y sen*)] 89
en donde pueden leerse directamente las expresiones de las fuerzas generalizadas. (Ya que tiene la forma de (4.12).)
T, y por tanto las ecuaciones del movimiento, tienen exactamente las mismas formas que en el ejemplo 4.3. (Véase
el problema 4.20.)
4.8 Consideraciones sobre el significado físico de las ecuaciones de Lagrange.
Las observaciones del numeral 3.10 relacionadas con una sola partícula se extienden a
continuación para un sistema de p partículas.
Supóngase que en las ecuaciones (4.4) t y todas las coordenadas, menos qr, se conservan
constantes. Entonces, estas ecuaciones se convierten en
Xi = Xi(qr), Vi = yt(qr), Zi = Zt(qr) (4.14)
Como xi} yt y zt son las coordenadas rectangulares de la partícula individual m¿,
existirá un conjunto de tales ecuaciones para cada una de las p partículas. Es decir, que (4.14)
representa p conjuntos de ecuaciones.
Si se permite que qr varíe y se hace la gráfica de las coordenadas xt, yt y zt, (4.14),
de una cualquiera de las partículas m¿, se obtiene una curva (en general, una curva en el
espacio tridimensional) que representa una trayectoria posible para mt, de conformidad
con las restricciones. Nos referiremos a esta curva como a la línea de qr para mr Es claro
que la localización y forma de tal curva depende de los valores constantes asignados aíy
a las demás coordenadas, así como de la naturaleza de las restricciones. En este sentido
puede existir un número ilimitado de líneas de qr para una partícula cualquiera. Pero en
un instante determinado y para ciertos valores dados a las demás coordenadas, puede
trazarse una línea específica de qr, relativa al sistema de ejes X, Y, Z. De la misma manera
las líneas de qr pueden trazarse para cada una de las partículas.
Las ideas anteriores no presentan ninguna dificultad puesto que se refieren a líneas y
superficies tridimensionales comunes. Como un ejemplo sencillo, considérese el péndulo
doble de la figura 2-10. Las ecuaciones (2.13) corresponden a (4.4). Las líneas de 6 para mi
y para m2 pueden trazarse en el plano XY para diversos valores constantes de <p. En la
misma forma pueden trazarse las líneas de 4> para m2. (No existen líneas de 0 para m^)
(Véase el ejemplo 4.11.)
74 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS [CAP. 4
El significado anterior de las líneas de qr cumple un útil propósito en lo que sigue.
Designando por 8str al desplazamiento lineal de mt a lo largo de una línea de qr, se
observa que sus componentes 8xt, 8yt y 8zt son justamente los desplazamientos
virtuales considerados en las ecuaciones (4.2), (4.3), etc. Los cosenos directores, ltr, mir y nir,
de la tangente a la línea de qr en cualquier punto, están dados por
SXi Syi Szi
en donde el elemento de trayectoria es Ssir = (Sx2¡ + 8y* + 8z*)U2. (Nótese que 8str es
exactamente el mismo desplazamiento (lineal) que se supuso dado a ml con el objeto de
determinar 8WQr en la ecuación (4.11).) Pero por (4.4), con t y todas las q fijas excepto qr,
= hirSqr (4.16)
±P- (4-17)
hir dqr
Como la componente u' de un vector u, en la dirección de una recta con cosenos directores
/, m y n está dada por u' = lux + muv + nuz, se deduce que flr, la componente de la
fuerza aplicada Ft, que actúa sobre mt según la tangente a su línea de qr, es
En igual forma, la componente alr de la aceleración at de la partícula mt, en la dirección
de la misma tangente es,
1 /.. dXi , .. dyi , .. dZi\
dXi „
W,Sq"
inte,
etc. Así pues,
SSir =
Ur =
[(£)*+(tj+(n;
1 dXi _ 1 32/i
/iir dqr ' ir ~ hw dqr '
Ahora, multiplicando y dividiendo los dos lados de (4.7), (habiendo remplazado a 8q\
por 5gr), por hir y utilizando la relación 8sir = hir8qr, se observa que las
ecuaciones de Lagrange pueden escribirse como
¿WittirSSir = J£/ir8Sír = F,r S^r
(4.20)
Teniendo en cuenta el sencillo significado de air, fir y 8slr, se observa con claridad
una simple interpretación física y geométrica de las ecuaciones de Lagrange, por medio de
(4.20).
Por otra parte, nótese que, como puede verse en (4.19), una expresión de alr, la
aceleración lineal de mi en la dirección de su línea de qr, puede obtenerse en forma inmediata
a partir de r / \ -i
Wrt _ l\d(BT\ 37\]
(4.21)
en donde Ti = £wii(¿J+#J+¿J) se expresa en coordenadas generalizadas por medio de
las ecuaciones (4.4).
Ejemplo 4.11.
Considérese el sistema que se muestra en la figura 4-7. Las partículas de masas mi y m2 están suspendidas
de los extremos de un hilo que pasa por los pequeños anillos lisos en a y en b. La masa m, puede moverse en
contacto con el cono C, en tanto que m2 debe moverse únicamente en contacto con el plano vertical P (por la acción
de dos superficies planas, paralelas y lisas que no se muestran en el dibujo). El cono está fijo, pero el plano Pse hace
oscilar alrededor del eje vertical B, según a = A sen «t, en donde a se mide a partir del eje X.
CAP. 4] ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 75
Como rt + r2 = c = constante, y di = constante, el sistema tiene tres grados de libertad. De acuerdo con
la notación general, se escribe q, = r,, q2 = 4> y q3 = B2. En función de estas coordenadas, las ecuaciones (4.4),
como puede verse fácilmente en la figura, tienen la forma, para mi,
«i = gi eos g» sen 6if y\ = gi sen q» sen eu «i = h — gi eos 81 (1)
Fig.4-7
y para m2,
xt = [l + (c - gi)sen g3] eos (A sen ut),
Vt = [1 + (o — gi) sen g3] sen (A sen ut), (2)
z\ — h — (c — gi) eos gs
Nótese que en este ejemplo en particular no todas las coordenadas aparecen en todas las ecuaciones de (1) y (2).
Al hacer variar a qt y trazar las relaciones (1) y (2) para diferentes valores constantes de q2, q^ y í, se
obtienen las líneas de q, de m, (rectas sobre el cono) y las líneas de q¡ de m2 (rectas radiales sobre P). En
forma semejante se obtienen las líneas de q2 de m, y las de q3 de m2. Como q3 no aparece en (/) no
existen las líneas de q3 para m,. Asimismo, es evidente que no hay líneas de q2 para m2. Nótese que a,, es
la componente de la aceleración lineal de mi a lo largo de una de sus líneas de q, sobre el cono, y que a2l es la
aceleración de m2 a lo largo de su línea de q, en P. Asimismo, a23, por ejemplo, es la aceleración de m2 en
la dirección de la línea de q3 en el plano P. Las expresiones de estas aceleraciones pueden encontrarse aplicando
(4.21) a
T = %rn.i(q\ + q\q\sen* 6i) + $mi[q] + (c - qi)*ql + (l + (c - g.Jsen g3)*AV cos2«í]
76 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS I CAP. 4
3X-10* dinas/cm
16 kg
4.9 Experimento sugerido.
Determinación de las frecuencias del movimiento del sistema de "dos partículas" que se muestra en la
figura 4-8.
El equipo necesario es sencillo y los resultados obtenidos son interesantes. Los valores de las masas y de las
constantes elásticas no tienen características críticas; los que se muestran en el diagrama son solamente sugeridos.
Suponiendo movimiento vertical únicamente y utilizando como coordenadas
a <¡] y (j2 Que indican los desplazamientos verticales de m, y m2 de sus
posiciones de equilibrio, se plantean las ecuaciones del movimiento. Estas ecuaciones
de segundo orden con coeficientes constantes pueden integrarse fácilmente por
medio de métodos comunes. Las soluciones mostrarán que al iniciar el movimiento
de alguna manera arbitraria, cada una de las masas sufrirá la combinación de dos
movimientos armónicos simples de diferentes frecuencias f\ y f2- (Las dos
masas oscilan con las mismas frecuencias pero con diferentes amplitudes.)
Para obtener una comprobación experimental de las frecuencias calculadas,
se procede de la siguiente manera: Aplicando un movimiento oscilatorio a mi
(o a m2) con la mano, luego de cierta práctica, es posible excitar bien /, o f2
únicamente. Se aseguran los buenos resultados si se tiene en cuenta que cuando la
frecuencia aplicada es aproximadamente igual a fx o a f2, se requiere muy poco
esfuerzo para lograr oscilaciones grandes. Al retirar la mano, el sistema continúa
oscilando en uno de sus modos naturales. El tiempo cubierto por cincuenta oscilaciones,
determinado con un cronómetro confiable, produce un buen valor experimental
de la frecuencia. Cuando se ha logrado suficiente precisión en las mediciones de
mi, m2, kt y k2, los valores experimentales y calculados para fx y f2 con-
cuerdan estrechamente.
Por observación directa es fácil hacer una comprobación cuantitativa de las amplitudes relativas del
movimiento de m, y m2 para f¡, o para f2
Es posible lograr una comprensión adicional considerable sobre el comportamiento de los sistemas oscilantes
al observar m, y m2 luego de haber iniciado el movimiento de alguna manera arbitraria, de modo que las
dos frecuencias resulten excitadas simultáneamente.
10» dinas/cm
- 500 gramos
Fig. 4-8
Resumen y observaciones
1. Deducción de las ecuaciones de Lagrange en su forma general (numeral 4.2).
Se han deducido aquí las ecuaciones para un sistema de p partículas con n grados
de libertad y 3p — n grados de restricción. Las coordenadas y las restricciones pueden
ser móviles o estacionarias.
La deducción se basa nuevamente en la ecuación de D'Alembert y en la suposición
que las fuerzas de restricción no ejecutan trabajo cuando los desplazamientos están de
acuerdo con las restricciones, siguiendo el mismo esquema del capítulo 3. \
2. Forma adecuada de la energía cinética (numeral 4.3).
T es ahora la suma de las energías cinéticas de p partículas, y se expresa en función
de <?i, q2, •••,fln, Qu Q2, . .., Qn y t, una vez eliminadas las 3p — n coordenadas
superflua's.
3. Significado físico de las fuerzas generalizadas (numeral 4.4).
El significado físico de la definición ampliada de F„r, como se señaló en el numeral
4.4, es aún bien sencillo. Es importante tener una comprensión clara de este concepto ya
que esto facilita mucho la aplicación de las ecuaciones de Lagrange.
Determinación de las expresiones de FQr(numeral 4.5).
Se han descrito tres técnicas que son esencialmente la misma, pero en ciertas
circunstancias una de ellas puede resultar más conveniente que las otras.
CAP. 4] ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 77
5. Interpretación física de las ecuaciones de Lagrange (numeral 4.8).
Ya que las cantidades 5sir, fir y air tienen significados bien elementales, se
d (3T\ dT
concluye que -yii -¡—j — t— = FQr (que en función de las cantidades anteriores puede
escribirse ¿, miairSSir — ^ firSsir) posee una sencilla interpretación física.
Problemas
Supóngase que en el esquema de la figura 4-1 la polea superior está colgada de un resorte espiral de
constante k, en lugar de la barra B. Despreciando las masas de las poleas, demostrar que
T = frnrCl-yr)* + %m*(l + yx- y2)> + ¿m3 (l + yx + ¿2)«
Escribir las ecuaciones del movimiento y demostrar que
jFi/j = (mi - m* - ma)g, F„2 = (m2 - m3)g, Ft = k(C -l — ho) - (mi + ms + m3)g
en donde h + l = C = constante, y /io es el valor de h cuando el resorte no ha sufrido elongación.
4.2. Demostrar que para el sistema de masas y poleas de la figura 4-9,
T = J»ii (ir+ »i)« + ¿mató-¡7,)» + %My* + ^(I/R1)^
Escribir las ecuaciones del movimiento correspondientes a y y y,
en la forma usual, y luego demostrar que
-M
AB^y*-
vo) + g,
Byi + Cy = Cg
en donde A = m^ + m2 + M, B = mx + m2 + I/R2 y C =
mi — m2\ y además, y0 es el valor de y cuando el resorte no ha
sufrido elongación. Integrar estas ecuaciones y describir brevemente
el movimiento.
Como extensión al ejemplo 4.4 escribir las ecuaciones del
movimiento cuando:
(a) Por la acción de alguna fuerza exterior se obliga a moverse a
mi según la relación x, = B2 senwií.
(b) Se aplica a m, una fuerza horizontal periódica, F = B2 sen
w2t.
(c) Un resorte espiral, colocado horizontalmente, conecta a mt con
el punto p.
1
M.I
fh
i
Fig. 4-9
Demostrar que en la figura 4-5, si se usan las coordenadas y, Si y s2, q\M = Si (m2 + m3) + s2m3,
q2M = Si mi —S2m3, y como
T = IMy* + tmiq] + *™.4; + ^(^gt-^^J
esta ecuación puede expresarse fácilmente en función de y, Si, s2. Demostrar que las fuerzas generalizadas
correspondientes a y, s, y s2 son Fy = —Mg, Fs, = —ftl(s1 — /,) y FSj = —k2(s2 — l2) en donde
M = r»i + m2 + m3, y /i y Z2 son las longitudes normales de los resortes, respectivamente.
Al aplicar (4.11) para determinar FSp por ejemplo, demostrar con la ayuda de un diagrama los
desplazamientos virtuales que debe sufrir cada una de las masas.
Las fuerzas generalizadas, aquí implicadas, son completamente sencillas; pero véase el problema 4.5.
78 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS [CAP. 4
4.5. Demostrar que si se usan las coordenadas y, y, y y2 para representar la configuración del sistema de
la figura 4-5, las fuerzas generalizadas correspondientes serán
^ n* j i M [ fmi + mA .mi M , ~1
Fy = -Mg + k, — \ f — ) 2/2 + —yt -—y-U\
7rt3|_\ m3 J mi ma \
rH = 4*«„-»-u-fc(^)[(^),.+**-£,-t]
4.6. En la figura 4-10, el plano XY es horizontal. Un eje fijo S, se extiende en la dirección de Z. Las varillas
A y B se encuentran sostenidas por cojinetes lisos montados en el eje, el uno sobre el otro. Un resorte de
reloj con constante de torsión k, conecta a A con B, según se indica en la figura. Los momentos de inercia
de las varillas son /, e /2, como se muestra. Las varillas pueden girar alrededor del eje bajo la acción
del resorte. Utilizando a d y a como coordenadas, demostrar que
j l,\ ó = —ka, y que (/, + /,)£, — Ita = Pe = constante
Integrar estas ecuaciones y describir brevemente el movimiento.
Demostrar que si fií y í2 se consideran como coordenadas, las fuerzas generalizadas son Fg =
Fe = —k(Bi + 62). Supóngase que el resorte se encuentra en su configuración normal cuando A y B
son colineales.
Fig. 4-10 Fig. 4-11
4.7. (a) El bloque de masa m que se muestra en la figura 4-11, puede deslizarse a lo largo del plano inclinado
sobre el carro, bajo la acción de la gravedad y del resorte. El cuerpo del carro tiene una masa M\,
y cada una de las ruedas una masa M, un radio r y un momento de inercia /, con respecto al eje.
Sobre el carro se ejerce una fuerza constante /. Despreciando la fricción de los cojinetes, demostrar
que
/„, . a*. ,4J , \.. , wi .. m .. . m •• . k {yo —y \
[ Mi + 4M + -r + m ) x + 7 -y = f, =— y + x = —mg-\ I- -— q0)
\ r ) tan ev ' sen**" tan 6 señasen* H )
en donde q0 es el valor que q cuando el resorte tiene su longitud normal.
(b) Plantear las ecuaciones del movimiento en función de las coordenadas 1 y q. Demostrar que Fx = f
y que F, = +mg sen 0 — k(q — q0).
4.8. Si un mecanismo impulsor liviano (por ejemplo, un pistón operado por medio de aire comprimido) hace
que el bloque de la figura 4-11 oscile a lo largo del plano inclinado, de tal forma que sus desplazamientos
con respecto al plano vienen dados por A sen ut, demostrar que
T = $(Ml + AM + 47/r2 + m)x2 + $m(-2xAu eos coi eos e + A V eos2 coi)
y que si se supone que / no actúa, el movimiento del carro estaría determinado por
(Mi + 4M + 41/r* + m)x — mAu eos 8 eos ut = constante
CAP. 4] ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 79
Las partículas de masas m, y m2 respectivamente, están conectadas por medio de un hilo en el que
se ha intercalado un resorte, como se muestra en la figura 4-12. El hilo pasa alrededor de una polea
liviana y las partículas pueden deslizarse libremente en el interior de los tubos lisos. Los tubos, junto con el eje,
tienen un momento de inercia /, con relación al eje vertical.
(a) Utilizando las coordenadas 0, r, y r2 y suponiendo que no existe ningún torque aplicado al eje
vertical, demostrar que
(I + mlrsl + ?n2rf)ff = Pg = constante
mi Vi — miri 9* = —k{ri + r2 — c)
imn — mtrt6*
-k(ri + rt — c)
(b) Suponiendo que el eje se encuentra impulsado por un motor a velocidad constante e ■-
las ecuaciones del movimiento para m, y m2.
Fig. 4-12
Fig.4-13
La varilla rígida y liviana que sostiene la "partícula" de masa m,, está suspendida en el punto p y puede
oscilar alrededor de este punto, en un plano vertical, bajo la acción de la gravedad. La cuenta de masa m2
puede deslizarse a lo largo de la varilla lisa, bajo la acción de la gravedad y del resorte. Demostrar que
las ecuaciones del movimiento son
(wiirí + mtr\) Y + 2mtrtr%9 + (ntiTi + mtri)g sen e = 0
rrii'ri — mi^e1 — m2g eos 8 + k{rt — U) = 0
en donde Íq es la longitud normal del resorte.
Un motor se encuentra conectado a tres poleas, como se muestra en la figura 4-14. La primera polea,
incluyendo la armadura del motor, tiene un momento**de~Tñercia Ji, y las otras dos, I2 e h, como se
indica. Los resortes (que equivalen a ejes elásticos para acoplar las poleas) poseen constantes elásticas
ft, y k2, respectivamente.
(a) Despreciando la fricción de los cojinetes, establecer las ecuaciones del movimiento, suponiendo que
el motor ejerce un torque t(í) que es una función conocida del tiempo.
(b) Establecer las ecuaciones del movimiento suponiendo que independientemente del movimiento que
sufran los discos segundo y tercero, el motor posee una velocidad constante.
I I I I I
y Motor] udytj b^p^Mj~u [^pM^^d
Fig. 4-14
80 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS [CAP. 4
4.12. El disco Di se encuentra sujeto al eje vertical de un motor que ejerce un torque Tt, como se muestra en
la figura 4-15. Sobre la superficie de D, se ha montado otro motor cuyo eje vertical le sirve asimismo
de eje al disco D2, y ejerce un torque sobre él, t2. Demostrar que
T = iheX + $U(el + ffty + \Mti*'e\
/, e\ + 'e\ (/i + M,r* + /,) = F6i = t,
It(e\ + '\) = Fe2 = t,
en donde /, incluye el momento de inercia combinado de Di, la armadura del primer motor y el
estator del segundo. l2 incluye a D2 y a la armadura del segundo motor. M2 es la masa de D2 más la
de la segunda armadura.
Demostrar que si se utilizaran 0, y a como coordenadas, se tendría que Fg = n —t2 y Fa = t2.
Nótese que las relaciones anteriores son válidas aunque los momentos Tí y t2 varíen con el tiempo.
Fig. 4-15 Fig. 4-16
4.13. El motor eléctrico que se ilustra en la figura 4-16 puede deslizarse libremente a cualquier posición sobre un
plano horizontal liso. El centro de masa del marco y el de la armadura quedan ambos en el eje de
rotación. Las masas del marco, la armadura y el brazo ab son Mit M2 y Aí3, respectivamente. El marco
y la armadura tienen como momentos de inercia, /, e I2, respectivamente. El brazo tiene un momento
de inercia /3, con respecto a un eje vertical que pasa por su centro de masa en p. Demostrar que
T = ¿(M, + Mt + M3)(£2 + y*) + %Lé\ + \(U + h + M¡i*)é\ + M¡rbt{y cos*2 - «sen et)
en donde x y y son las coordenadas rectangulares del centro del motor (X y Y están situados en el mismo
plano en el que el motor se desliza) y tf, y B2 son los desplazamientos angulares del marco y la
armadura, respectivamente, con relación al eje X.
Demostrar que si se desprecia la fricción, Fx = 0, Fy = 0, Fg = —t y Fg^ = r en donde T, el
torque del motor, puede ser considerado como una función del tiempo.
4.14. En el sistema de piñones que se muestra en la figura 4-17, Mos ejes S¡, ..., S4 están sostenidos por los
cojinetes fijos fc>,, ..., fc>4. Los piñones A, D, E y F son solidarios con sus ejes. Una extensión del eje S3
forma una manivela, según se muestra. El piñón C puede girar libremente en la manivela. B es un "molde
de pastel" (se muestra en u n corte) que tiene dientes de engranaje g, en su borde exterior, y g' en el borde
interior. B puede girar libremente sobre S,. Se observa que si, por ejemplo, se deja fijo D mientras se hace
girar A, C y la manivela (y por tanto E y F) giran.
Los momentos de inercia de los piñones, incluyendo el eje al que cada uno se halla sujeto, son los
indicados en la figura. Los radios de los piñones son rt, r2, etc. Adheridos a los ejes S2 y S« se
encuentran los resortes de torsión cuyas constantes respectivas son kt y k2, según se indica. Si se mide 03
con respecto a la manivela C y todos los demás ángulos con relación a líneas verticales fijas, demostrar que
T = i¡,¡\ +![/. + /. (g)'] H + J(A) [(ft + r,)¡, - ,.|j.
Escribir las ecuaciones del movimiento y hallar las expresiones de Fe y F0 suponiendo que cada uno
de los resortes ejerce un torque proporcional al desplazamiento angular del eje al que está sujeto.
cAp. 4] ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS
- Engranaje exterior
Engranaje interior
81
S3
H—
i 6s
iX
R
v7| b\ 4 kt |
mm \
de torsión/
Fig. 4-17
Supóngase que las masas mi y m2 de la figura 4-3, sufren atracción hacia el origen (posiblemente
debido a una gran masa esférica que no aparece en la figura) con fuerzas /i = cmjr\ y fi = cmi/r\
respectivamente, donde c es una constante y rt y r2 son las distancias radiales de mi y m2 al
origen. Por inspección se puede decir que para un desplazamiento general de la palanqueta, SWtoui =
—(cmi/rf) Sri — (cmili\) Sr». Usando como coordenadas x,y y 8, como en el ejemplo 4.3, demostrar que
SWM
-c|_-r(s-
U eos e) + -^j{x + Ucose) \Sx
*)]s
- c^{y-U sen*) + ^(¡/ + U sen*)] Sy
— c ^r(*íi sen 6 — yU eos 6) + —£ (yU eos 6 — xU sen*) Se
en donde l¡ y l2 son las distancias medidas sobre la varilla, desde m, y m2 respectivamente, al
centro de masa. Nótese que 8Wtot*i tiene la misma forma de la ecuación (4.12). Los coeficientes de Sx, 8y
y 86 son las fuerzas generalizadas Fx, Fy y F0 respectivamente, luego de expresar r, y r2 en
función de x, y y 0.
Escribir SWt0t«i nuevamente, utilizando como coordenadas a r,, a y 6, en donde a es el ángulo
entre r, y el eje x. Escribir también T en función de estas coordenadas.
Supóngase que en la figura 4-1 se ha removido la barra B, y que por medio de una fuerza f(t) aplicada al
eje se le hace oscilar según h = h0 + A sen wt, verticalmente. Establecer las ecuaciones del movimiento
del sistema. ¿Aparecerá / en las fuerzas generalizadas? Explicar. (Supóngase que los hilos están siempre
bajo tensión.)
Suponiendo que la plataforma rotatoria que aparece en la figura 4-6 está montada en un carro (en cambio
de un elevador) el cual se mueve horizontalmente con aceleración constante a, demostrar que
T = £wii[a*t2 + (8 + qi cosa)V + q\ — 2atu(s + qi cosa) sen ut + 2atqt cosa eos ut]
+ £wií[a2í2 + (8 + q* cosa)V + q\ - 2atu(s + qt cosa) sen coi + 2aíg» cosa coscot]
en donde la línea desde donde se mide 0 lleva la dirección de a. La distancia recorrida por el centro del
disco, desde algún punto fijo en esta línea, está dada por s = Jai2. Establecer las ecuaciones del
movimiento y demostrar que FQ y Fq son las mismas que en el ejemplo 4.8.
Una palanqueta puede moverse libremente en el plano X2Y2 del marco giratorio que se muestra en la
figura 3-16. Sobre m, y m2 actúan fuerzas conocidas (fx ,fy ) y (fx ,fy ), respectivamente. Usando
las coordenadas correspondientes a x, >- y 0 de la figura 4-3, plantear las ecuaciones del movimiento
suponiendo velocidad angular constante w, para el eje vertical. (Véase el numeral 14.6.)
82 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS | CAP. 4
4.19. Un mecanismo sujeto a A, en la figura 2-15, ejerce una fuerza vertical /, sobre el eje de la polea superior.
Un segundo mecanismo adherido a B ejerce una fuerza f2 sobre m2. Supóngase que estas fuerzas son de tal
naturaleza que tanto st comoy, varían de una manera determinada, con el tiempo. (Por ejemplo, s, = s0 +
At sen (wí + 5) y >- = y0t + \at2.) Suponiendo que los cables están siempre bajo tensión, demostrar
que las ecuaciones diferenciales correspondientes a s3 y s4, son
(It/R\ + ms) «s + ms'ii + ki{C — y — 81 — 84) — mag = 0
(Mx + h/R\ + 4wii) a\ + {Mt + 2ml) y - k^C - y - 81 - s«) + (M, + 2m,)^ = 0
en donde C es una constante y slt s\, y y y se escriben como funciones determinadas del tiempo, según
las formas de los movimientos supuestos.
4.20. Las masas del péndulo doble de la figura 2-10 llevan cargas eléctricas Qt y Q2, respectivamente. Se
establece un campo magnético perpendicular al plano XY. Considérense todas las coordenadas variables.
(a) Hallar las fuerzas generalizadas FT ,FT ,Fg y F¿, teniendo en cuenta las fuerzas debidas al
movimiento de las cargas en el campo. Desprecíense las fuerzas gravitacionales. (Véase el ejemplo 4.10.)
(b) Determinar las fuerzas generalizadas cuando r, y r2 son constantes; cuando r, es variable y r2
constante; y cuando r2 es variable y r, constante.
4.21. La palanqueta de la figura 4-18, con cargas
iguales + Q y —Q distribuidas
uniformemente en las pequeñas esferas, puede moverse
libremente en el espacio. Por medio de un gran
condensador de placas paralelas (paralelas al
plano XY) conectado a una fuente de potencial
alterno, se establece un campo eléctrico
alterno, uniforme E2 = E0 sen w,í. Asimismo un
juego de grandes piezas polares planas
suministra un campo magnético tal que By =
Bo sen u2t.
Escribir expresiones adecuadas para las
componentes rectangulares de la fuerza sobre
cada una de las cargas y determinar las
fuerzas generalizadas correspondientes a x, y, z, e
y 4>. (Véase el ejemplo 4.10.)
4.22. (a) En la figura 4-9 considerar una partícula cualquiera, de masa mi (y coordenadas xt y yt) en
la polea, y demostrar, usando la ecuación de D'Alembert que
2 (»i5»i + ViSyC) = My Sy + ¡VSe
(b) Por aplicación directa de la ecuación de D'Alembert establecer las ecuaciones del movimiento
correspondientes a >- y >-, para el sistema de la parte (a). Comparar estos resultados con los
obtenidos previamente.
4.23. Suponiendo que el eje vertical de la figura 4-12 se obliga a girar según la relación 0 = üj0í + i ai2,
establecer las ecuaciones del movimiento correspondientes a r, y r2, por aplicación directa de la ecuación
de D'Alembert. (Véase el problema 4.9.)
4.24. Obtener las ecuaciones del movimiento dadas en el problema 4.10 por aplicación directa de la ecuación
de D'Alembert.
4.25. Considerar la palanqueta de la figura 4-3, analizada en el ejemplo 4.3. Demostrar que usando las
coordenadas x,y y 8: para mx,hXx = hly = 1 y hie = /,; ypara m2,/i2x = h2y = 1 y h2$ = /2.
Aplicando ahora la relación (4.21) a
Ti = ^7ni[¿* + y* + l\e* + 2li6(x sen* — y cose)]
y a una expresión semejante para T2, hallar alx, oiv, ctie y Otx, Oty, y ate. Establecer el significado
geométrico de cada una. Aplicando (4.20), escribir las ecuaciones del movimiento del sistema,
correspondientes a x, y y 6.
E.
B,
Fig.4-18
CAP. 4] ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS 83
4.26. Demostrar que para el péndulo doble del ejemplo 4.6,
Ke = rv h*e — ri > ^i* = 0, h^ = rt
a\6 = ri e> a*e = ri *" + r2 0 cos (* — e) ~ r» </>* sen ($ — e)
fie = — 7n,firsenff, /ie = -m^gsend, Ssig = S8lB = rtS9
Luego demostrar que (4.20) correspondiente a 0,
m^g 8810 + mtatgS8tg = /l9 Ssie + fte &8tg
es la misma ecuación del movimiento para 0, obtenida en el ejemplo 4.6. Interpretar los resultados
físicamente.
Establecer la ecuación del movimiento correspondiente a <t>, de la misma manera.
Demostrar que las fuerzas generalizadas correspondientes a slt s2, s3 y s4, de la figura 2-15, son
Fa = (Mi + Mt + mi + mt + m3)g - fc»(*i — 08i) Fs = m^ - k¡(8t — o8»)
(Mi + mx + mt)g — kifa — o8»)
(mt — mx)g
Ejercicio complementario sobre la determinación de fuerzas generalizadas.
Para el estudiante que cree necesitarlo, los ejemplos siguientes serán una gran contribución para la
comprensión clara de las fuerzas generalizadas y las técnicas para hallar sus expresiones.
En las figuras 4-19 y 4-20 se enumeran varios conjuntos de coordenadas, todos ellos apropiados
para la determinación del movimiento del sistema. Hallar las fuerzas generalizadas correspondientes a
las coordenadas de cada uno de tales conjuntos. Repetir el ejercicio para aquellos sistemas para los cuales
se han indicado ciertos movimientos específicos.
cir
rzr
tu
Hilo tirado hacia arriba
con aceleración
constante, a.
(a) e
(b) x
Compárense las fuerzas generalizadas
con el caso en que a = 0.
d>
Cuenta de masa m en
un alambre
parabólico rígido.
(Componentes \
conocidas j
(a) Coordenada x
(b) Coordenada y
El marco XY gira con respecto a V y
tiene aceleración vertical a. Escríbase T y
la ecuación del movimiento en función
de x.
Di
i
Varilla uniforme. Movimiento
restringido al plano vertical. La fuerza aplicada
tiene componentes conocidas Fx y Fy.
La longitud de la varilla es igual a 21.
(a) xi.yi yo; (b) x2,y2 V B.
Los discos D, y D2 están montados
sobre cojinetes. Las constantes de torsión
de los resortes son fc, y k2. 0i y 62
se miden con respecto a líneas
horizontales fijas. Tómese a = 02 — tfi-
(a) 0i y 02í (b) 0i y a.
Fig. 4-19
84 ECUACIONES DE LAGRANGE PARA UN SISTEMA DE PARTÍCULAS [CAP. 4
cr
ut
(a) 2/i, 1/2
(b) Vi, q
(c) V, q
Repítase,
suponiendo que el marco
XY posee
aceleración vertical, a.
(a) 0i, 02
(b) 0i, a
Repítase,
suponiendo rotación con
relación a AB.
Dos barras uniformes que
pueden oscilar libremente en' un
plano vertical alrededor de la
varilla horizontal P.
'/////////////////////,
(a) y1,q2] (b) yi,y2\ (c) qt,q2
¿Qué otros conjuntos de coordenadas
pueden usarse? Escríbase Ty las
ecuaciones del movimiento para el caso
(b).
Repítase lo anterior suponiendo que
todo el sistema cae libremente bajo
la acción de la gravedad.
^^^^^^^^^^^^^^^^^^^^
Fig.4-20
CAPITULO
Sistemas conservativos
y otros sistemas para los cuales puede existir una
"función de noteneial"
"función de potencial
5.1 Ilustración de algunos principios básicos.
Con el objeto de introducir e ilustrar los principios básicos sobre los cuales se funda
este capítulo, considérense los siguientes ejemplos:
(a) Una partícula adherida a un extremo de un resorte espiral cuyo otro extremo se ha fijado
al origen de coordenadas, puede moverse sobre un plano horizontal XY, liso. Se trata de
calcular el trabajo ejecutado por el resorte, a lo largo de un desplazamiento de la
partícula, desde un punto de referencia x0,yo, hasta un punto general x, y.
Suponiendo que el resorte sigue la ley de Hooke, y que no ejerce ninguna fuerza perpendicular a su
longitud, las componentes rectangulares de la fuerza sobre la partícula, están dadas por
Fx = -k(l-k)(x/l), Fy = -k(l-lo)(y/l)
en donde k es la constante elástica del resorte, l y l0 son sus longitudes cuando está
estirado y cuando no lo está, respectivamente, y x y y son las coordenadas de la partícula.
Sustituyendo en la expresión general,
w
y teniendo en cuenta que l2 = x2 + y2, se concluye fácilmente que
(xdx + i
W
lo cual puede escribirse también.
•»x,y
= 1 (Fxdx + Fydy)
•'Xn.l/A
X
r"
-kx dx — kydy + kk-
Vx2 + y2
W = -C'" d[tk(x2 + y2- 2kVx2 + y2)] (5-1)
Por tanto, W = -\k{x* + y2 - 2loVxTTy¿) + Wpl + y¡- 2loVxJTy¡) {5.2)
Aquí es preciso hacer las siguientes observaciones. En primer lugar, en {5.2) resulta
evidente que W es una función de jc0,v0 y x, y únicamente (depende únicamente de
los puntos extremos de la trayectoria). O si se considera x0,y0 como un punto de
referencia, W es una función de x y y únicamente, aparte de una constante aditiva. El
trabajo hecho por el resorte, entonces, no depende de la longitud o forma de la trayectoria
recorrida por la partícula desde x0, y0 hasta- x,y. Resulta claro, además, que para
cualquier trayectoria cerrada, W = 0. En segundo lugar, la naturaleza de Fx y Fy (la
manera como dependen de x y de y) es tal que dWes una diferencial exacta (véase {5.1)).
dW dW
Si se escribe dW = -r— dx + -r-dy y se compara con dW = Fxdx + Fvdy,
reda; oy
sulta evidente que Fx = dW/dx y que Fy = dW/dy. Puede verificarse que estas
relaciones son correctas derivando {5.2).
Como un segundo ejemplo del mismo tipo, supóngase que Fx = 3Bx2y2 y que
Fy = 2Bx3y, en donde B es una constante. En este caso, dW = Fxdx + Fydy =
d(Bx3y'¿) o sea, W = +Bxzy2 — Btfyl una cantidad independiente de la
trayectoria, para la cual, Fx = dW/dx y Fy = dW/dy.
85
86
SISTEMAS CONSERVATIVOS
[ CAP. 5
(b) Considérese ahora el trabajo hecho por una fuerza de fricción F, ejercida por un plano
rugoso sobre una partícula, para un desplazamiento desde x0,y0 hasta x, y.
Suponiendo que solamente la gravedad actúa en dirección normal al plano, F = n mg
(n = coeficiente de fricción) con una dirección opuesta al desplazamiento elemental
ds = (dx2 + dy2)1'2. Se tiene entonces Fx = —nmg(dx/ds) y Fy = —nmg(dy/ds).
Así pues, utilizando dW = Fxdx + Fydy,
W = -hmg f [1 + (dy/dx)2]"2 dx (5.3)
La cantidad bajo el signo integral no es una diferencial exacta, y por tanto es
necesario especificar v = y(x) antes de poder realizar la integración. W depende de la
trayectoria y (5.3) no conduce a una función de x, y tal que Fx = dW/dx y Fv = dW/dy.
Como ejemplo final, supóngase que Fx = axy y Fy = bxy en donde a y b son
constantes. En este caso, d W = axydx -f- bxydy la cual tampoco es exacta. Por consiguiente,
W también depende aquí de la trayectoria.
Los ejemplos anteriores enunciados en (a) y en (b) ilustran casos sencillos de fuerzas
"conservativas" y "no conservativas", respectivamente.
5.2 Definiciones importantes.
(a) Fuerzas conservativas; sistemas conservativos.
Si las fuerzas son de tal naturaleza (si dependen de las coordenadas de tal
manera) que al desplazar el sistema de una configuración a otra, el trabajo ejecutado
depende únicamente de las coordenadas iniciales y finales de las partículas, se dice
que las fuerzas son conservativas y que el sistema es conservativo.
(b) Energía potencial.
El trabajo hecho por fuerzas conservativas al trasladar el sistema de una
configuración general A (en donde las coordenadas de las partículas son X\,yx,z\t
X2,y2,z2, etc.) hasta una configuración de referencia, B, (siendo ahora las
coordenadas 0jci, o^i, oZi» 0X2,0^2» oZ2, etc.) se define como la energía potencial
V (*,»v¿>2i) aue tiene el sistema en A con respecto a B. Nótese que V se define
aquí como el trabajo hecho desde la configuración general a la de referencia, y no en
sentido inverso.
Ejemplos comunes de fuerzas conservativas, son: Fuerzas gravitacionales entre masas,
fuerzas debidas a todo tipo de resortes y de cuerpos elásticos (suponiendo materiales
"perfectamente elásticos") y fuerzas entre cargas eléctricas estacionarias. Como fuerzas no
conservativas se incluyen las de fricción, las de resistencia al movimiento de un objeto dentro de un
fluido, y en general las que dependen del tiempo o de la velocidad.
5.3 Expresión general de V y prueba para las fuerzas conservativas.
Considérese un sistema de p partículas sobre el que actúan las fuerzas conservativas
F\,F2, ■. ., Fp. Por la definición anterior, resulta claro que
XO*i'0vV0zi P
^{Fx.dXi + FVidyi + Fz.dZi)
= -C ' *' * ͣ (FXidXi + FVldyi + Fz.dZi) (5.4)
La integral (5.4) es, en realidad, una expresión general para el trabajo (independiente de
la naturaleza de las fuerzas). Para que el resultado sea independiente de la trayectoria se
CAP. 5)
SISTEMAS CONSERVATIVOS
87
requiere que la cantidad bajo el signo integral sea una diferencial exacta. Es decir, que se debe
cumplir
Si ahora se
se tendrá,
der
Así, en general,
iva FX3
dl/4
f,, = -
dV
dXi'
parcialmente con
- d2y
32/4 dxz'
dFXi
dVr
SFy4
dXz
9Fyr
~ dXi
^
respecto a y4, y
=
—ÍZ_, 0
dxz 32/4
dFx. dFXr
dZr ~ dXi '
dV
:< dZi
Fy4 con respecto a x3,
3Fl3
sea, -
32/4
etc.
~ dXz
por eje
(5.5)
mplo,
{5.6)
Puede demostrarse que estas relaciones constituyen las condiciones necesarias y suficientes
para que la cantidad bajo el signo integral en (5.4) sea exacta. Naturalmente, las relaciones
(5.6) pueden ser también usadas como prueba para determinar si las fuerzas dadas son, o no,
conservativas.
La mayor utilidad de la función de la energía potencial radica en el hecho que cuando V
se expresa en función de coordenadas generalizadas, las fuerzas generalizadas se obtienen por
medio de FQr = —dV/dqr. (Véase el numeral 5.6.) (Nota: A fin de integrar (5.4) es necesario
conocer las expresiones de FXi, Fy. y Fz.. Pero si ya se conocen, ¿con qué objeto se ha de hallar
V, para luego determinar las fuerzas a partir de Fx. = —dV/dx., etc.? Esto parece absurdo.
Sin embargo existen ventajas, la menor de las cuales no es la que se deriva del hecho que
para fuerzas conservativas, FQr = —dV/dqr.)
5.4 Determinación de las expresiones para V.
Básicamente toda expresión de V se obtiene evaluando la integral (5.4). Sin embargo los
siguientes aspectos son importantes:
(a) Esta integral puede evaluarse en cualquier sistema de coordenadas (rectangulares o de
otro tipo) y luego, si se desea, puede expresarse en función de otras coordenadas por medio
de las ecuaciones de trasformación adecuadas. Debe tenerse especial cuidado en dársele
el signo algebraico que corresponde a las componentes de las fuerzas.
(b) La energía potencial es una cantidad relativa y el valor de dV/dqr no se afecta por la
presencia de una constante aditiva, por tanto tales constantes pueden ser eliminadas.
(c) Con frecuencia sucede que si la energía potencial de un sistema se debe a resortes,
gravedad, cargas eléctricas, etc., es posible expresar de inmediato la función de V, utilizando
cualquier número de coordenadas adecuadas, empleando expresiones sencillas ya
suficientemente conocidas de la energía potencial de cada uno de los resortes, etc. (Véase el
numeral 5.5(4).) La forma final de V, incluyendo apenas el número n de coordenadas
adecuadas, puede obtenerse por medio de las ecuaciones de trasformación pertinentes.
(d) Al tratar de aplicar (c) puede originarse un interrogante relacionado con el signo
algebraico de ciertos términos de la energía potencial. En este caso conviene recordar que si
se debe hacer trabajo, por la acción de algún agente externo, a fin de trasladar la partícula
de una posición general x, y, z, a un punto de referencia, x0,yo,z0, su energía
potencial relativa a x0,yo,z0 es negativa; y en caso contrario, será positiva.
5.5 Algunos ejemplos sencillos para ilustrar lo anterior.
(1) La energía potencial del péndulo de la figura 5-1 puede tomarse con respecto a las rectas
ai £>i, a2b2, a3fe3, etc., y en tales casos, V = -\-mgh, —mgs, —mg(l + s), respectivamente.
Si se usa 0 como coordenada, pueden eliminarse h y s, dando,
V = mgr(l - eos 6), mg(l - r eos 6), - mgr eos 6
88
SISTEMAS CONSERVATIVOS
[CAP. 5
que son todas iguales, con excepción de un término constante. (Los términos aditivos
constantes pueden siempre ignorarse.)
Como y = r eos 0, la energía potencial en función de y es, sencillamente, V = — mgy
1—ywwwwwwwwvwwv—¡
I y Fig.5-1 Fig.5-2
(2) La expresión común para la energía potencial de un resorte estirado es V = ^k(l — l0)2
en donde k es la constante elástica, y / y l0 son las longitudes del resorte cuando está
estirado y cuando no lo está, respectivamente. Así, refiriendo la energía potencial de la
figura 5-2 al punto px, V = -\-\kx\. Pero si se refiere al punto fijo p2, y se tiene en
cuenta que V es el trabajo hecho por el resorte desde el punto general xx hasta p2, se
concluye que V = — [%k(s — l0)2 — \kx \\. Una vez más, las dos expresiones serían
iguales, si no fuera por el término constante de la segunda.
Si se desea, puede expresarse V en función de X2 ppr medio de la relación <? =
x\ + x2 + lo- En este caso, V = +%k(s — l0 — x2)2 o, despreciando uno de los
términos constantes, V = — k(s — l0)x2 + §fcx?.
(3) Considérense las esferas cargadas uniformemente A y
B de la figura 5-3. Considerando a A localizada en el
origen y suponiendo que ambas se encuentran en
el vacío, se concluye inmediatamente, integrando, que
la energía potencial de B con respecto al infinito es
V = +Q1Q2A. Pero refiriéndose al punto p, V =
— [Q1Q2/S — Q1Q2A] la cual se convierte en la
misma expresión anterior si se le suprime el término
constante.
(4) Un sistema más complicado: Con referencia a la figura 5-4, una esfera de masa m, con
una carga distribuida uniformemente, +Qi, está sujeta a los resortes, según se indica.
Una segunda carga, +Q2, está localizada en el eje X.
\Y
Fig. 5-3
Demostración de una técnica útil para hallar V.
Fig. 5-4
CAP. 5)
SISTEMAS CONSERVATIVOS
89
Suponiendo que la esfera superior puede moverse en el plano vertical XY (dos grados
de libertad) bajo la acción de la gravedad, de los resortes y de la repulsión eléctrica, se
trata de expresar a V para este sistema, en función de r y 0.
En primer lugar se escribe V como en el numeral 5.4(c) utilizando cualquier número
de coordenadas, sin tener en cuenta cuántas de ellas son superfluas. En seguida pueden
eliminarse todas las coordenadas, excepto r y 0. Por inspección se obtiene,
V = iki(U - olí)2 + £fc2(k - oh)2 + QiQi/U + mgh
en donde lx,l2 y o¿i,o¿2 son las longitudes de los resortes estirados y sin estirar,
respectivamente, y kx y k2 sus constantes elásticas. (Se ha supuesto que los resortes
no afectan los campos eléctricos en las inmediaciones de las cargas.) Nótese que V
contiene las variables li,l2,h y h: Hay demasiadas coordenadas y no se incluyen las que
se desean. Sin embargo puede expresarse V en función de r y 0 por medio de la relación
lx = [r2 + Si—2rsi COS0]1'2 y otras similares para l2 y h- Esta técnica para
determinar V además de ser sencilla, con frecuencia resulta muy conveniente.
5.6 Fuerzas generalizadas como derivadas de V.
Como se explicó en el capítulo 4, todas las fuerzas generalizadas, sean ellas conservativas,
o no, pueden expresarse por medio de
Suponiendo que las fuerzas son conservativas y utilizando las expresiones {5.5), esta ecuación
puede escribirse
Qr i4i\dXidqr dijidqr dZidqrJ
Pero conocidas reglas de diferenciación indican que el miembro derecho de esta última
relación es igual a —dV/dqr. Por tanto, v
^ = -£ (57)
Por ejemplo, aplicando {5.7) a V = —mgr eos 0, la energía potencial del péndulo simple, se
obtiene, Fe = —dV/d6 = — mgr sen 0. De nuevo, las fuerzas generalizadas
correspondientes a r y 0, de la figura 5-4, vienen dadas por FT = —dV/dr y F0 = —dV/d6 en donde Ves
la forma final de la energía potencial estudiada en la última parte del numeral 5.5.
Sin embargo, debe quedar claro que cualquier fuerza generalizada que puede hallarse
por medio de {5.7), también puede encontrarse por los métodos del capítulo 4. Sin embargo,
como puede verse con claridad en los ejemplos y en otras consideraciones que siguen más
adelante, se obtienen considerables ventajas por el uso de la energía potencial y las
relaciones {5.7).
Además, como FQr = —dV/dqr, el estudiante puede demostrar inmediatamente que, para
fuerzas conservativas, .„ „„
ar Qr dr q¡¡
-W = 157 (5-8)
que es otra forma de expresar {5.6) en función de las fuerzas y las coordenadas generalizadas.
5.7 Ecuaciones de Lagrange para sistemas conservativos (solamente actúan
fuerzas conservativas).
Utilizando {5.7), puede escribirse
SISTEMAS CONSERVATIVOS [CAP. 5
Introduciendo la llamada "función de Lagrange" (o "función lagrangiana"), L, definida
como L = T— V, la ecuación anterior se convierte en
d /dL\ dL
El remplazo de T por L en dT/dqr es válido, puesto que en los problemas usuales de
mecánica, V no es función de qr. La utilidad de (5.9) se hace evidente en los ejemplos siguientes
y en sus aplicaciones en los capítulos restantes.
5.8 Sistemas parcialmente conservativos y parcialmente no conservativos.
Debe advertirse aquí que si algunas de las fuerzas que actúan en el sistema no son
conservativas, las ecuaciones de Lagrange, evidentemente pueden escribirse,
±(*L) _f^ = Fq {5.W)
dt\dqrJ ¿Qr Qr
en donde FQr debe encontrarse de la manera usual (véase el numeral 4.5) teniendo en cuenta
únicamente las fuerzas no conservativas.
5.9 Ejemplos que ilustran la aplicación de las ecuaciones de Lagrange
a sistemas conservativos.
Ejemplo 5.1. Una masa pendular suspendida de una banda de caucho.
Suponiendo movimiento únicamente en el plano vertical y usando r y 0 como coordenadas, T =
4¡m(r2 + r2e2) y V = hk(r — r0)2 — mgrcosB, aquí el primer término se basa en la suposición que la banda
de caucho sigue la ley de Hooke. Así, L = $m(r2 + r262) - 4¡k(r - r0)2 + mgr eos e, de donde se concluye
que m'r — mre2 + k(r — r0) — mg eos e = 0 y que mr2'e + 2mrre + mgr sen 8 = 0.
Estas son las mismas ecuaciones del movimiento obtenidas en el ejemplo 3.4.
Ejemplo 5.2. Una partícula de masa m adherida a una varilla ligera, la que a su vez está articulada en p (Fig. 5-5).
La energía cinética de este sistema es sencillamente, T= \mr2i2. Puede escribirse una expresión
aproximada para V, en el caso de pequeños desplazamientos angulares, con relación a la horizontal; tal expresión
puede ser,
V = ^{l + Sle - l¿2 + $k2(l + s2e - l2)2 + mgre
en donde Z, y l2 son las longitudes normales de los resortes primero y segundo, respectivamente. Entonces
L = \mr2e2 - \k$ + sx9 - lx)2 - \k<¿\ + s26 - l2)2 - mgre
de donde se encuentra la ecuación del movimiento
mr2'e + fc,«i(' + M - li) + k28S + *ie ~ '2) + mffr - °
Supóngase que los resortes se han ajustado de tal manera que la varilla está en equilibrio estático si se tiene 0=0.
Esto significa que /z, s, (/ — /,) + k2s2{l — l2) + mgr = 0. Por tanto, la ecuación del movimiento se reduce
a mr2'e + (k182+ k2s\)e = 0. Esta sencilla ecuación puede integrarse en forma inmediata, llegando a un mo-
- • • , ■ * o / rnr2 V*
vimiento armónico simple cuyo penodo es 2jt ( -—5; :—\
Ejemplo 5.3. El sistema de resortes y poleas que se muestra en la figura 5-6.
Suponiendo únicamente movimiento vertical, sin dificultad se concluye que
en donde los significados de los diferentes símbolos, están indicados claramente en la figura.
CAP- 5]
SISTEMAS CONSERVATIVOS
91
Fig.5-5 Fig. 5-6
Tomando la energía potencial gravitatoria con relación a la recta horizontal inferior desde donde se miden
yi y y2, y escribiendo la energía potencial elástica de la manera usual,
V = m1gyl + m2gy2 + ^(«í - ¿j)2 + $k2(s2 ~ k)2
en donde /, y Z2 son las longitudes normales. Pero s, + y2 = Ci y (y2 — s2) + (y2 — yi) = C2 en donde
tanto Ci como C2 son constantes. Eliminando Si y s2 con estas relaciones, se obtiene,
V = ml9yi + m2gy2 + ¿MC, - y2 - Z,)2 + &2{2y2 -yx-C2- l2)*
que no contiene coordenadas superfluas. Con esto se completa la tarea de hallar L, y las ecuaciones del movimiento
se obtienen en seguida. Si yi y y2 se toman con relación a las posiciones de equilibrio de m, y m2,
respectivamente, las ecuaciones del movimiento se simplifican un tanto, y pueden ser integradas fácilmente.
Como extensión de este ejemplo, el lector puede demostrar que utilizando los desplazamientos angulares de
los discos, 0i y 02 como coordenadas,
L = £[(7n, + m2)R2 + lx]e\ + |(m,i}2 + /2)¿2 + m^Rj^
- wii0(C3 - R1$1 - R2e2) - Tn&iCz - Rtfi)
- ¿M(C, - c3 + Ri°i) ~ h}2 ~ ^2[(C3 -C2-R^i + R2e2) - ya
para lo cual se ha supuesto que cuando el sistema está en equilibrio, B\ = 02 = 0.
Ejemplo 5.4. Energía potencial y fuerzas generalizadas en el péndulo doble, (Fig. 2-10).
Tomando la energía potencial con respecto a una recta horizontal que pasa por p(x0,yo).
V = — tn.xgrx eos 8 — m2fl'(r1 eos 0 + r2 eos </>)
de donde, Fg = —BV/de = - (m, + m2)grl sen0 y F^ = —dV/d<f>= - m2gr2 sen4,
Estas fuerzas son iguales a las halladas anteriormente.
Como extensión de este ejemplo el lector puede demostrar que si se supone que m.\ y m2 están
suspendidas de sendos resortes espirales livianos de constantes elásticas kt y k2, respectivamente,
V = - mxgrx eos 6 - w^frí eos 6 + r2 eos </>) + 4Mri - ori)2 + ^2(r2 - or2>2
y luego podrá escribir las fuerzas generalizadas correspondientes a rx,r2,d y 4>.
Ejemplo 5.5. Energía potencial de una serie de masas conectadas "linealmente" por medio de resortes, (Fig. 5-7).
Supóngase que, (a) las masas se encuentran sobre una superficie horizontal lisa, (b) los movimientos de
todas las masas son "pequeños" y se hallan restringidos a direcciones perpendiculares a ab, (c) cuando las masas
se encuentran en la posición de equilibrio sobre la recta ab, los resortes poseen su dimensión normal. La energía
potencial del primer resorte será, naturalmente,
Vj = ¿MVs2 + y\ - «i)2 = i*i(*;+^-a^/i+ i#«?)
;^m??í¿^m?^
92
SISTEMAS CONSERVATIVOS
[ CAP. 5
Suponiendo ahora que >i es menor que s,, se expresa
Si se conservan solamente los tres primeros términos del desarrollo, la forma anterior se reduce a Vi = (kl/8s1)y1.
En forma semejante puede decirse que la energía potencial del segundo resorte es igual a V2 = (k2/&82){yi — 2/2)*»
etc. Por último, la expresión aproximada para la energía potencial total, será
y por tanto,
dV
-&-&-'*■
Si las masas pueden moverse libremente en el plano, en este caso V incluirá las coordenadas x y y de todas
las masas.
*-
Fig. 5-7
Fig.5-8
Ejemplo 5.6. Las esferas de la figura 5-8 poseen las cargas QltQ2 y Q, distribuidas uniformemente.
Si las cargas Q, y Q2 son fijas y Q puede moverse libremente en el plano, considérense únicamente las
fuerzas electrostáticas y obsérvese que V = +QQ1A1 + QQ2A2. (véase el numeral 5.5(4)). Si se introducen
las coordenadas r y 0,
QQ, QQ2
V =
Por el desarrollo binomial, para Qi =
Qi = Q2 y r muy grande, V = 2QQ,/
(r2 + S2 + 2rs eos e)Vi (r2 + s2 - 2rs eos ff)1/2
Qz y para r » s, se concluye que V = - (2QQi s eos 0 )/r2; y para
Ejemplo 5.7. El sistema de "dos cuerpos" bajo una fuerza central.
Imagínense dos esferas (Fig. 5-9) cuyas masas son
respectivamente m^ y m2, que se mueven en el
espacio bajo la influencia única de su mutua atracción
gravitatoria.
Los ejes X, Y y Z permanecen paralelos al sistema
inercial X\,YX,Z\. Las coordenadas del centro de
masa (c.m.) con respecto a X\,Y\,Z\, son £,y,i.
Una simple integración demuestra que si se toma la
energía potencial con respecto a r = 00, V = — Gm\m2/r
en donde G es la constante gravitacional. Aplicando el
teorema del "centro de masa" el lector puede demostrar
sin mucho esfuerzo que
L = ¿M(*2 + ¿2 + Í2) x
+ $n(r2 + r2*2 + r2 sen2 ¿¿2) + Gmxm^Jr
Trayectoria de m2 vista desde mi.
en donde M = m, + m2 y la "masa reducida", Problema de 2 cuerpos bajo una fuerza central
n = mlm2/(ml + m2). Fur 5-9
y,
CAP. 5)
SISTEMAS CONSERVATIVOS
93
Es posible encontrar muchos hechos interesantes en la solución de las ecuaciones del movimiento. Por
ejemplo, el centro de masa se mueve en el espacio a lo largo de una recta, con velocidad constante. La trayectoria
de m2, vista desde m, es una elipse, parábola o hipérbola, según que £ = T + V sea menor, igual o mayor
que cero. Suponiendo que el movimiento inicial es de tal forma que <¿0 = 0, se observa que como dL/d<f> =
ur2 senff¿> = V<s> — constante, $ permanece constante indefinidamente. Entonces, en el caso general, el
movimiento es en un plano, y puede escribirse, (ignorando el movimiento del c.m.)
L = $n(r2 + r2e2) + Gm1m2/r
5.10 Expresión adecuada de la energía potencial del sistema de resortes
(Fig. 5-10).
\Y
a
Energía potencial de un sistema de resortes
Fiff. 5-10
Los resortes se encuentran conectados en forma flexible a los apoyos a, b, c y d y
asimismo flexiblemente unidos entre sí, por sus otros extremos, en p. Esta unión se puede
mover libremente en el plano XY. Se trata de determinar una expresión aproximada para V,
suponiendo que x y y son siempre pequeñas.
La expresión exacta de la energía potencial del primer resorte es, sencillamente, V\ =
^(Li — /í)2, en donde Lx es la longitud de pa y l[ es la longitud normal del resorte.
Pero, h\ = (l\a\ — x)2 + {lifii — y)2; tanto lx como los cosenos directores ai y 0i, se
muestran en el diagrama.
Aplicando ahora el desarrollo de Taylor para n variables (véase la página 213) y
conservando los términos de primero y segundo orden (el término (V)oo puede excluirse por ser
constante) se concluye, luego de algunas operaciones monótonas, que
V,(1
-fci(2i - líXflJa, + \
Bx) + !£(x2 + y2) "|£W
y^Y
(i)
-2/«,.)2]
(2)
Entonces, para el caso de un grupo de S resortes dispuestos como en la figura 5-10,
V (apro,, = 2 [-HU - l!)(xat + ypt) +j(x2 + V2) - ^(xh -
Al utilizar esta ecuación, deben dársele a los cosenos directores los signos algebraicos
adecuados.
Si la .conexión p está en equilibrio en el origen (lo cual no se había supuesto hasta ahora)
los términos de primer orden del desarrollo de Taylor se anularán, aunque algunos o todos
los resortes se encuentren estirados. Esto es así porque Fx = —{3V/Sx)o = 0, etc. Entonces
(2) se reduce a i s r j.y
i^.-^)2]
(5.11)
Para cualquier problema en particular, las constantes ln at y fit pueden medirse con
buena precisión. (Si se conocen las constantes elásticas de los resortes, sus longitudes norma-
94
SISTEMAS CONSERVATIVOS
[CAP. 5
les y las localizaciones de a, b, c, y d, la tarea de calcular la posición de equilibrio de p, y
por tanto ln at y $t es algo mucho más complejo que lo que podría esperarse y
constituye un buen trabajo para un computador.)
Nótese que como at = x<//< y 0, = yt/llt la ecuación {5.11) puede escribirse,
nPro„ = \ t [fci(*2 + V2) - tyixvi ~ yxif] (5.12)
Se denominan ai, feí, a2, b2, etc., los extremos de varios resortes de espiral, de
tal modo que los puntos a. están adheridos en forma arbitraria a diferentes puntos del
interior de una caja rígida, y los puntos b están todos juntos en una unión que puede moverse
dentro de la caja.
Si se toma el origen de un marco XYZ en la posición de equilibrio de esta unión, puede
demostrarse fácilmente que (véase el problema 5.16),
VW, = \ ¿ [M(xa, + yp, + zyy + h (^) (*■ + 2/2 + *)] (5-13)
en donde S es el número de resortes, kt la constante elástica, y at, f}t y yt son los
cosenos directores de los ejes de los resortes cuando la unión está en el origen.
Las aproximaciones anteriores, con frecuencia resultan útiles en el estudio de las
pequeñas oscilaciones, y por tanto nos referiremos a ellas en el capítulo 10.
Ejemplo 5.8.
La masa m de la figura 5.11, conectada a los
resortes por medio del hilo, según se indica, puede
moverse sobre el plano horizontal liso ab, bajo la acción de la
fuerza central suministrada por los resortes. Cada uno
de los resortes tiene una constante elástica k. En este
caso, V = k(li — /o)2 en donde lY y l0 son las
longitudes de los dos resortes, estirados y sin estirar. Se
representa por y el desplazamiento de la unión con respecto
a la posición p, en la cual los dos resortes se encuentran
sin estirar, como se muestra en la figura. Así, se tiene
que Zi = [s2 + (s0 +y)2]1/2. Excluyendo los términos
constantes, V = kl2 — 2ftZ0'i o sea,
V = ley* + 2ks0y - 2kl0[s2 + («0 + y)2l1/2
Si se aplica bien la ecuación (10.6) a la expresión
anterior para V, o directamente (5.11), se encuentra que
V(aprox.) = k{»yil
ya que y = r — r0. Por inspección se observa que si r es igual o menor que r0, la tensión del hilo se hace igual
a cero; pero para desplazamientos pequeños en los que r > r0,
L = ¿m(f2 + r2¿2) _ k(8*/l$(r - rtf
5.11 Sistemas en los que la energía potencial varía con el tiempo. Ejemplos.
Con frecuencia sucede que las fuerzas que actúan en un sistema son función del tiempo,
así como función de las coordenadas. Además estas fuerzas pueden ser de tal naturaleza que
satisfagan las relaciones (5.6). En este caso, es claro que al integrar (5.4), haciendo que t
permanezca constante, se obtendrá una magnitud V (una energía potencial que cambia con el
tiempo) tal que Fqr = —dV/dqr. De esta manera las relaciones (5.7) pueden aplicarse
directamente. A continuación se incluyen dos ejemplos sencillos.
Ejemplo 5.9.
Supóngase que el hilo del cual pende la masa de un péndulo, pasa por un pequeño orificio en el soporte. Si
se tira del hilo hacia arriba, a través del orificio, con una velocidad constante u, la longitud del péndulo estará da-
>2/;
k(8¡Jll)(r - r0)2
CAP. 5)
SISTEMAS CONSERVATIVOS
95
da por r = r0 — v t. Así, s¡ se toma la energía potencial con relación aun eje horizontal que pase por el soporte,
y = —mg(r0 — vt) eos 0 de donde —dV/de = —mg(ro — vt) sen e = Fe- Se puede comprobar que esta
expresión es correcta, obteniendo de nuevo el valor de F0 por los métodos del capítulo 4.
Ejemplo 5.10.
El extremo de un resorte espiral liviano se hace oscilar alrededor del origen de coordenadas, de acuerdo con
la relación s = A sen ut, en el sentido del eje X, sobre un plano horizontal liso. En el otro extremo del resorte
se encuentra una partícula de masa m, la cual puede moverse en el plano bajo la acción del resorte. Se supondrá
que el eje del resorte permanece recto y que no se ejerce ninguna fuerza perpendicular a este eje (no existe ningún
momento flector).
Por inspección se nota que Fx, la componente i de la fuerza que actúa sobre m, está dada por,
Fx = -fcd-IoJcoKI,*) = - k{[(x - A sencoO* + y»]"2 ~ *o> [(g JA~J^ *+y*\*'*
en donde l es la longitud del resorte estirado, y l0 la dimensión normal del mismo. Fy se expresa por una
ecuación similar. Nótese que Fx y Fy son, ambas, funciones de t, así como de las coordenadas i y y.
Al aplicar la prueba (5.6) se observa que bFJby = dFy/dx. Por tanto puede determinarse una función de la
energía potencial por medio de (5.4), haciendo t constante. Escribiendo V = %k(l — l0)2 y remplazando l por
[(i — A sen ut)2 + y2)1/2 se obtiene V = ±k[ [ (z — A sen uí)2 4- y2Vn — l<¡\2 • Si se aplican las
fórmulas Fx = -dV/dx, Fy = -dV/dy, se llega a las mismas expresiones ya obtenidas.
Nótese que si se quisieran utilizar coordenadas polares, podría expresarse V en función de r y 0 fácilmente,
eliminando i y y, por medio de i = r eos 0 y y = r sen 0. Inmediatamente pueden obtenerse las fuerzas
generalizadas correspondientes a r y 0, tomando, Fr = —dV/dr y F0 = -BV/de.
Podrían darse muchos casos semejantes a (5.9) y (5.10). Por ejemplo: Haciendo oscilar
o girar en un círculo el soporte A de la figura 5-1; haciendo oscilar verticalmente el punto p
de la figura 2-10; haciendo variar con el tiempo, de alguna manera determinada, las
distancias s de la figura 5-8; etc.
Debe observarse que como las cantidades que se han escrito como V, contienen a t,
T+ W constante (véase el numeral 5.13). En otras palabras, si las fuerzas dependen
explícitamente de t, no es posible escribir la integral de la energía. La razón para esto puede
verse de inmediato, al considerar su significado físico.
5.12 Función vectorial del potencial para una carga que se mueve en un campo
electromagnético.
Las componentes de la fuerza sobre una carga "puntual", + Q, que se mueve con
velocidad (x, y, z) dentro de un campo eléctrico (Ex, Ey, Ez) y en donde además existe una
inducción magnética (Bx, By, Bz) cada uno de los cuales puede ser una función de la
posición y del tiempo, están dadas por
fx = QEX + Q{yBz - zBy)
fy = QEy + Q(zBx-xBz) (5.14)
fz = QEZ + Q{xBy - yBx)
En un sistema mecánico en el que actúan tales fuerzas, la aplicación de (4.10), (4.11) o
(4.12) conduce a las fuerzas generalizadas correspondientes.
Sin embargo las fuerzas anteriores son de tal naturaleza que no es posible escribir un
potencial escalar V, ni una función de potencia P, tales que F,r = —dV/dqr o FQr = dP/dqr.
Pero es posible escribir, en cambio, una función "potencial vectorial" que conduce a una
nueva forma de L de tal modo que (5.9) incluye así todas estas fuerzas electromagnéticas. Aquí se
96
SISTEMAS CONSERVATIVOS
[CAP. 5
menciona esta posibilidad únicamente con el fin de completar lo dicho, pero no se incluye un
estudio de este tópico.
Véase, por ejemplo: Roald K. Wangsness, Introduction to Theoretical Physics, John
Wiley & Sons, Inc., 1963, páginas 397 a 400.
5.13 La "integral de la energía".
Con ciertas condiciones bien especiales puede demostrarse que la energía total de un
sistema, es constante.
Considérese un sistema para el cual L no contiene explícitamente el tiempo y sobre el
cual solamente actúan fuerzas conservativas. (Para el estudiante debe resultar evidente que
la primera suposición significa que no existen coordenadas o restricciones móviles y que V
no tiene la forma vista en el numeral 5.11.)
En tal caso, como L = L(qr, q\), su derivada total con respecto al tiempo es
dL ^ dL.. ^ dL .
Introduciendo (5.9), esto puede escribirse como,
dL ^ dL.. ^ • d /8L\ .,, . dL d /^ . dL\
ujl, y um^ y ^ / \ que es sencillamente, -rr = -jiiY, qr—)
dt Ádqr Á dt\dqj dt dt\ré[qrdqrJ
Integrando esta expresión una vez,
¿ qr^ = L + € (5.15)
r=i dqr
en donde £ es la constante de integración. Escribiendo ahora T = ^Akrhkqr (véase la
ecuación (2.56)), kr
dT « . dL
—- = 2 V Akrtfk = —r
dqr fc=i dqr
ya que V no incluye a q. Sustituyendo esto en (5.15), se tiene, 2 2 Akrqkqr = L + €. La
suma es sencillamente 2T. Entonces 2T= T—V+ 6, o sea, kr
T + V = € = constante (5.16)
Esta "integral de la energía" o "primera integral" del sistema, desempeña un papel
importante en la solución de muchos problemas.
5.14 Experimentos sugeridos.
(1) Determínese el período de oscilación del sistema que se muestra en la figura 5-14, para
movimiento vertical pequeño. (Véase el problema 5.7.)
(2) Determínese el período de oscilación de la varilla de la figura 5.13, para movimientos
pequeños. (Véase el problema 5.6.)
(3) Determínense los dos períodos de oscilación del sistema de la figura 5-20 para valores
pequeños de 0 y de <j>. (Véase el problema 5.14.)
El equipo para estos experimentos puede armarse fácil y rápidamente y los resultados
obtenidos son satisfactorios y justifican plenamente el pequeño esfuerzo requerido
CAP. 5]
SISTEMAS CONSERVATIVOS
97
Problemas
Sota. Ignórense los términos aditivos constantes en V.
5.1. Determinar cuáles de las siguientes fuerzas son conservativas. Hallar V para las que resulten ser
conservativas:
(a) Fx = 0, Fy = -mg (b) Fx = -kx, Fy = -ky
(d) Fx = Axy, Fy = Bxy (e) Fx = Ayz, Fy = Axz, Fz = Axy
(/) Fr = 3Br2 sen e eos </>, Fg = Bt3 eos e eos </>, F^ = -Bt3 sen e sen $
(9) Fr = f, (r), Fe = f2 (e), F* = fz (</>) (h) Fx = -kx sen «oí, Fy
(c) Fx = -ky, Fy = +kx
kty
Demostrar que el trabajo hecho por las fuerzas del problema 5.1(c) al recorrer un rectángulo de lados
*2 — *i y y2 — yi es 2ft(i2 — xi)(y2 — yi)- Demostrar que el trabajo hecho por las fuerzas
Fx = 3Bi2y2 y Fy = 2Bi3y, al recorrer el mismo rectángulo, es igual a cero.
Determinar V para el sistema descrito en el problema 4.5. Demostrar que FQf = —dV/dqr conduce a
las mismas expresiones de las fuerzas generalizadas que las obtenidas por medio de SW = Fq Sqr.
Escribir V en función de B\ y 02 para la figura 4-10. Demostrar que Fe = -dV/B9x y Fg2 =
—dV/d92 concuerdan con los valores hallados anteriormente para las fuerzas generalizadas.
La masa m, de la figura 5-12, puede deslizarse en la varilla lisa horizontal bajo la acción del resorte.
Cuando la masa está en equilibrio, el resorte se encuentra aún algo estirado. Demostrar que para pequeños
desplazamientos con respecto a la posición de equilibrio, la energía potencial es aproximadamente igual a
k(s-k) Wo
en donde l0 es la longitud normal del resorte.
Fig. 5-12
Fig.5-13
5.6. La barra uniforme AB, de masa M y longitud l, de la figura 5-13, está sostenida por la articulación lisa
en A. El extremo B se encuentra unido al resorte BC, el cual está aún estirado cuando 6=0.
Despreciando la masa del resorte, demostrar que para este sistema,
V = -%Mgl eos 9 + $k[(82 + l2 - 2sl eos 9Y'2 - l0]2
Suponiendo que 0 es un ángulo pequeño, aproximar el valor de la energía potencial V, por medio del
desarrollo de Taylor y determinar el período de oscilación de la varilla.
5.7. El conjunto de la barra y el bloque de la figura 5-14 posee una masa M. Los dos resortes son idénticos.
(a) Escribir una expresión para la energía potencial V. ¿Conduce esto a una fuerza "lineal" actuando
sobre M?
98
SISTEMAS CONSERVATIVOS
[CAP. 5
(b) s0 = distancia de ab cuando el sistema está en equilibrio (s = 0). Si se conocen k, s,, M y la
longitud normal de los resortes Z0 (la misma para los dos resortes), demostrar que para hallar s0 es
necesario encontrar la solución de la siguiente ecuación de cuarto grado:
4fc2«« - Mgka* + (M*g* + 4&$-4k*%)s¡ _ 4Mgk82180 + M*g2*t = 0
(c) Suponiendo conocida la longitud de equilibrio, l, de cada uno de los resortes, hallar una expresión
aproximada de la energía potencial (véase la ecuación (2) del numeral 5.10) y determinar el período
de oscilación alrededor de la posición de equilibrio.
(d) Suponiendo conocida la dimensión s0, demostrar que l = 2kl0s0/(2ks0 — Mg).
'/////////////////////////.
Fig. 5-14
Fig. 5-15
El péndulo simple de la figura 5-15 está suspendido cerca de una gran esfera uniforme de masa M.
Escribir la expresión de la energía potencial V, en función de 0, teniendo en cuenta la atracción gravitacio-
nal entre M y m. Tómese la aproximación correspondiente al caso en que el ángulo 0 es muy pequeño
y en que la distancia l es apenas mayor que R + r. Determinar el período de oscilación para pequeños
movimientos, despreciando el campo gravitacional de la Tierra.
Las tres esferas que se muestran fijas en el eje X de la figura 5-16 llevan cargas uniformemente
distribuidas + Q, —2Q y + Q. Una cuarta esfera de masa m y carga +Qi puede moverse libremente en
el plano XY, bajo la acción de las fuerzas eléctricas. Suponiendo que las esferas se encuentran en el vacío,
hallar una expresión exacta para la energía potencial V. Demostrar que si r » s, ésta puede escribirse,
' (aprox.) —
2QQi82 eos2 e QQiS2 sen2 e
Fig. 5-16
Fig. 5-17
4 y comparar esto con —dV/dyu —dV/dy2 respectivamente.
Una varilla uniforme de longitud 2r2 y masa M, está sujeta al extremo de un resorte espiral como se
muestra en la figura 5-17. Suponiendo que el movimiento se efectúa en un solo plano, demostrar que
L = \M(f\ + r\é2 + r2.^2 + 2 eos (</> - e) rxr^ - 2 sen (<¡> - e) r2r^
+ F¿2 ~ ifc(ri ~ ro)2 + M9(ri eos e + r2 eos <p)
en donde / es el momento de inercia de la varilla con respecto a un eje que pasa por su centro de masa,
perpendicular a su longitud; y r0 es la dimensión normal del resorte.
CAP. 5]
SISTEMAS CONSERVATIVOS
99
5.12. El hilo tensionado de la figura 5-18, está cargado con cuentas colocadas a espacios regulares. Suponiendo
las diferentes cuentas desplazadas en las direcciones yi, y2, etc., y que los desplazamientos son tan
pequeños que la tensión t permanece constante, demostrar que la energía potencial del sistema
(despreciando la gravedad) está dada por
V = ^[v[ + v\ + v\ + v\ + v\- 1/12/2 - Í/2Í/3 - 2/32/4 - VaVs]
y que en el caso de n cuentas, puede escribirse V = -¡r 2 — (í/r+i — Vr)2 en donde y0 = yr + i = 0.
2 r=o Q>
Demostrar que la energía potencial de un hilo uniforme, flexible, tensionado, que tenga una ligera
distorsión y = y (x), está dada por V = £t | (dy/dx)2 dx.
Jo
Demostrar que para la distorsión Y = A sen *■*//; V = A2tt2t/41.
Fig. 5-18
5.13. Tres piñones G,, G2 y G3 se encuentran acoplados por medio de resortes de torsión a los discos D,,
D2 y D3, según se indica en la figura 5-19. Demostrar que la función de Lagrange para el sistema es
~29
y(*4 »i) -2~Vd7 TJ ~\d¿ dj
m
H/vwwwvt
\J'<
hf\9*
)JWWVWVW\MZZ3
I—*
T
G3 /V»
EHAAMMMEZ3-
%
Fig. 5-19
Dos resortes de constantes elásticas ft, y k2 se
hallan conectados al péndulo doble, según se indica en
la figura 5-20. Cuando el sistema se encuentra en
reposo, la masa m, está en p y los resortes están
tensionados. Los extremos inferiores de los resortes están
adheridos a los puntos a y b (de coordenadas
conocidas (xi, yt) y (x2, y2), respectivamente).
(a) Demostrar que para los resortes (sin incluir la
gravedad),
exacta, = i*l<«l " Ü* + **2<«2 " 4)2
en donde s2 = (xj - x)2 + (Vl + y)2
s2 = (x2 + x)2 + (y2 + y)2
¿Cómo podrá escribirse Vexacta en funci°n de fl?
(*if 2/0
100
SISTEMAS CONSERVATIVOS
[CAP. 5
(b) Aplicando la ecuación (2) del numeral 5.10, demostrar que para 0 pequeño,
V(.pro„ = |(fc, + fc2>r¡*2 +l[fciyi(ÍLZÍi) + k2V2(hzAj^ri92
2L l¡Vl+ l¡ V2} l°
5.15. Con referencia a la figura 5.21, supóngase que la posición de equilibrio de la varilla es ab y que Z, y l2
(con componentes lx, ly, sx y sy) representan las longitudes de equilibrio de los resortes.
Fig.5-21
(a) Demostrar que la expresión exacta de la energía potencial del sistema, puede escribirse,
V(ex.cU, = **!<[(«. " *l)2 + (I, - »l)»l1/2 " «OÍ2" ^
+ ¿fc2{[(«* + *2)2 + («„-2/2)2]1/2-«o) + Mgy
en donde l0 y s0 son las longitudes normales de los resortes.
(b) Demostrar que las ecuaciones que relacionan a xi, yit x2, y 2, con £,y y 0, son
2Rcos{60 + e) + x2 = 2Rcos0o + X! 2R sen (*0 + e) + y2 = 2i2sen*0 + 2/i
R eos (ff0 + e) + £ = R eos e0 + «, i? sen (0O + ») + 1/ = R sen ¿0 + yx
Nótese que por medio de estas ecuaciones, Veiacta puede expresarse en función de £, y y 0.
(c) Aplicando la ecuación (2) del numeral 5.10 y utilizando las expresiones anteriores, demostrar que
para movimientos pequeños con respecto a la posición de equilibrio,
Vteprox., = *[*! + *2 " ¿«J " B*l]*2 + Wl + k2~ All-BslW
+ £[fcji2(l — Iq/1){Ix eos e0 + ly sen 0O) + fc2^(! ~~ V8)(fe cos *tf — «y sen 80)
+ (fcl + fc2)^2 _ (^y« _ Bs^R2 sen *0 cos *0
- (Ai2 + fiaJjiFsen* ^ - (Ai2 + Bs2)^ eos2 e0]e*
+ [Alxly - B8x8y]xy
+ [(*2 ~ *i)* sen *o + (Alxlv + B8xsy)R cos e0 + (AlJ- Bs2)i2sen *0]í*
- [(fc2-fci)^ c°s*o + (Ayw + £8z8w)i2 sen *0 + (Aí2-Bs2)i2 cos «0]y«
CAP.
SISTEMAS CONSERVATIVOS
101
en donde A = kil0/l3 y B = foso/s3. Demostrar asimismo que
l = f«2 + hm*2 + h - v{aptox,
en donde / es el momento de inercia de la varilla, con respecto a un eje normal que pasa por el c.m.
5.16. Suministrar una prueba detallada de la relación (5.13).
5.17. Supóngase que el marco entero que sostiene el péndulo doble y los resortes de la figura 5-20, se mueve
hacia arriba con una aceleración vertical constante, a. ¿Producirá esto algún cambio en la energía
potencial de los resortes? ¿En qué magnitud debe considerarse incrementada la energía potencial gravi-
tatoria? Escribir la nueva expresión para T.
5.18. Se hace oscilar verticalmente el soporte ab de la figura 5-17, con respecto a la posición indicada, según
y = A sen ut. Demostrar que la función lagrangiana del sistema es
L = ±M(r\ + r\e* + r2¿2 + AW eos2 coi
+ 2rlr2H eos (<f> — e) — 2r,r2¿sen (<f> — e)
+ 2Au eos coi (rx eos B — r^e sen e — r2¿ sen </>)]
+ £/¿2 — £k(ri — ro)2 + Mg(rt eos e + r2 eos </> + A sen at)
Comparar este resultado con el valor de L en el problema 5.11.
5.19. Determinar el valor de L para el sistema del problema 5.11, suponiendo que el punto p se mueve con
velocidad lineal constante v, en un pequeño círculo de radio a, que se encuentra en el plano vertical.
5.20. Con referencia al ejemplo 5.7, demostrar que L puede expresarse como,
M • • • mtM . . Gamo
en donde p, es la distancia de mi al c.m., r = pi + P2 y mXPX = m2p2-
5.21. El eje vertical de la figura 5-22 gira de una mañera determinada, con los ejes X y Y adheridos y solidarios
con el eje de giro. Teniendo en cuenta que la "partícula" de masa m puede moverse en el plano XY bajo
la acción de los resortes y la gravedad, demostrar que
L = lm[(R + X)2¿2 + ¿2 + ¿2] _ mgy _ ^kl{[x2 + (8 _ ^2] 1/2 _ ^}2 _ ^[^2 + ^2)1/2 _ £]2
Suponiendo e = w = constante, demostrar que las condiciones que se requieren para obtener
"movimiento estable" (x = constante, y = constante y x = y = 0) son
fci*o*í . £2*0*2
m(R + x0)u2 - (As1 + As2)x0 +
mg + (k1 + k2)y0 — k¡8 +
V*§ + («-í/o)2 V4+l%
M« - Vo)lí fc22/o?2
V*02+(«-í/o)2 Vtf+lft
= o
= o
Fig.5-22
Disco circular delgado y uniforme
de radio a y masa total M.
Fig.5-23
102
SISTEMAS CONSERVATIVOS
[CAP. 5
5.22. La energía potencial de m, debida a la atracción gravitacional del disco de la figura 5-23, para r >
viene dada por,
y = ^[2_l^3(3cos2<_1) + i(2y(35cos^-30coS,-3)--.-]
Expresar L y las ecuaciones del movimiento de m.
5.23. Con referencia al ejemplo 5.7, probar que los movimientos de mi y m2 están restringidos a un plano
cuya orientación con relación a un marco inercial, no varía.
Demostrar que en función de coordenadas polares contenidas en este plano,
GtMjTWj
£(r2 + r2,2)
donde se ha excluido el término debido al movimiento del c.m. Demostrar además que
L =^ + f!>) + to
en donde n + r2 = r y min = min; n y r2 están medidos del c.m. al mi y m2, respectivamente.
Para un sistema cualquiera en el que no aparezca el tiempo explícitamente en L (véase el numeral 5.8) y
en donde actúan fuerzas no conservativas, demostrar que la rapidez del cambio de la energía total del
sistema está dada por n
ft(T+V) = 2F,r¿r
en donde las fuerzas generalizadas, Fq , incluyen únicamente las fuerzas no conservativas.
Supóngase que los apoyos a, b, c y d de la figura 5-10 se encuentran adheridos a una estructura rígida
pero móvil, como por ejemplo el marco de un cuadro. El marco se hace mover, girar, trasladar, etc., en
cualquier forma, en su propio plano. Suponiendo que el sistema X, Y se halla sujeto al marco y que x y
>- se miden como se ha indicado, ¿cambiará de alguna manera la expresión (2)1
Suponiendo que el marco oscila paralelamente al eje X alrededor de un punto fijo con respecto al
espacio inercial, con un movimiento dado por s = A senwt; y suponiendo que hay una partícula m
localizada en el punto p (la unión de los resortes), expresar el valor de L para la partícula.
Nota. Para un buen ejemplo de V, véase el problema 13.15.
Determinación de FQr
para el caso de fuerzas disipativas
(a) Procedimiento usual
(b) Método de la "función de potencia"
6.1 Definición y clasificación.
Dentro de la categoría de fuerzas disipativas se catalogan todas aquellas que originan
disipación de energía del sistema durante el movimiento. La "pérdida" de energía usual-
mente se presenta por la formación de calor.
Con frecuencia ocurre en la práctica que la magnitud de la fuerza, /, aplicada a una
partícula (o a un elemento de área) puede representarse con precisión, dentro de un cierto
margen de velocidades, por medio de
/ = avn (6.1)
en donde v es la velocidad de la partícula, n es cierto número y a puede ser una constante
o una función de las coordenadas, o del tiempo, o de éste y aquellas simultáneamente. Como
se verá más adelante, esta forma representa un tipo de fuerzas disipativas importante y muy
general (aunque no es el único).
(a) Fuerzas de fricción. La fuerza de fricción necesaria para deslizar una superficie sobre
otra, se supone proporcional a la fuerza normal entre las superficies, independientemente
del área de contacto o de la velocidad, luego de haberse iniciado el movimiento. (No
se estudiará aquí el caso de la fricción "estática".) Así, la expresión anterior representa
la fuerza de fricción en el caso en que n = 0 y a es igual al coeficiente de fricción
multiplicado por la fuerza normal. Se tiene un ejemplo en el que a es función de las
coordenadas y del tiempo, si el coeficiente de fricción varía de un punto a otro y si la fuerza
normal que mantiene las dos superficies en contacto, cambia con el tiempo.
Si las dos superficies están en movimiento, la fuerza de fricción sobre una de ellas
tiene una dirección opuesta a la de la velocidad de esa superficie, con respecto a la otra.
(b) Fuerzas de viscosidad. Se dice que una fuerza es "viscosa" (o de viscosidad) cuando
aplicada a un objeto varía como la primera potencia de la velocidad y se opone al
movimiento. La resistencia al movimiento de un objeto sumergido en un fluido de
cualquier naturaleza, o la resistencia que encuentra un polo magnético al moverse cerca una
lámina conductora, constituyen ejemplos de fuerzas viscosas. La expresión (6.1)
representa tal fuerza con n = 1.
(c) Fuerzas proporcionales a potencias superiores de la velocidad. La resistencia al
movimiento de un objeto dentro de un fluido no es simplemente una fuerza viscosa, excepto
a velocidades pequeñas. Sin embargo es posible representarla por (6.1), al menos en un
intervalo limitado. En ciertos casos, n puede ser considerablemente mayor que la
unidad. (Véase también el numeral 6.6.)
6.2 Procedimiento general para determinar FqT.
Se emplearán dos métodos diferentes. El primero, analizado e ilustrado en los
numerales que siguen, se basa en las relaciones generales (4.10) y (4.12). El segundo método, en el
que Fqr se obtiene a partir de una "función de potencia", se da en el numeral 6.8.
Suponiendo que se ha expresado / por medio de (6.1) y que su dirección es opuesta a
v, se concluye que, como x/v = coseno del ángulo entre v y X, fx = — avn (x/v) = — axvn~l.
103
104 DETERMINACIÓN DE FQf PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
De la misma manera, fy = —ayvn-x y fx = —azvn-1. Entonces, suponiendo que hay p
partículas y que n tiene el mismo valor para todas, ó Wtoui y las fuerzas generalizadas se
determinan como se resume a continuación:
SWto
- 2 ai{*i 8xi + 2A 82/i + ¿i *zi)v? 1
(6.2)
que constituye la expresión general para BWtotaJ. Remplazando xu Sxit etc., por <?i, q\,
bq\, etc., se convierte en
|> Sí^totai = [••••] 891 + [••••] 8g2 + •••• + [■•■•]8g„ (6.3)
Aquí los coeficientes de fi^, 8q2, ■•■,&<}n son ^as fuerzas generalizadas.
6.3 Ejemplos: Fuerzas generalizadas de fricción.
En los siguientes ejemplos se supone que las fuerzas disipativas son provenientes de
fricción en seco, en donde n = 0.
Ejemplo 6.1. Movimiento de una partícula en un plano inclinado rugoso.
Se dispara una partícula de masa m, hacia arriba sobre un plano inclinado rugoso, como se muestra en la
figura 6-1. Se supone que la fuerza de fricción total, / = nmgcosa, es constante en magnitud y opuesta en
dirección al movimiento. Como i/y i2 + y2, por ejemplo, es el coseno del ángulo entre la velocidad de m
y el eje X, resulta claro que las componentes de la fuerza de fricción son
(1) fx = -fz/y/x* + y\ (2) /„ = -fy/V^ + y*
que en este ejemplo son las mismas fuerzas generalizadas de fricción. Así, teniendo en cuenta también la gravedad,
las ecuaciones del movimiento son
— iimg eos a
(¿2 + ¿2)1/2 '
— fimg eos a
(¿2-¡-¿2)1/2
Nota importante. Si la partícula se proyectara hacia arriba a lo largo de una recta x = constante, con
velocidad inicial y0 (i = x = 0, todo el tiempo) la segunda ecuación se haría igual a my = — fimg eos a — mg sen a.
Evidentemente la partícula alcanzará cierta altura y (posiblemente) iniciará su movimiento hacia abajo. Por la
ecuación anterior podría pensarse que fimg eos <* tiene siempre la dirección negativa de Y, pero es bien
sabido que al reiniciarse el movimiento la fuerza de fricción invierte su dirección y que ^mg eos a debe ahora
considerarse como positiva. La fuerza es discontinua, y esta es una posibilidad de la cual se debe estar conciente
al trabajar con fuerzas de fricción. (Véase el problema 6.12.)
Partícula en movimiento sobre
un plano inclinado rugoso
Fig. 6-1
Palanqueta que se desliza sobre
el plano rugoso horizontal, XV
Fig. 6-2
Ejemplo 6.2. Dos partículas conectadas por una varilla liviana y moviéndose sobre un plano horizontal rugoso
(Fig. 6-2).
Se trata de encontrar las fuerzas generalizadas de fricción. (No se tendrán en cuenta otras fuerzas que
podrían actuar simultáneamente.) La palanqueta tiene tres grados de libertad y se utilizarán como coordenadas x,
y y 8, como se muestra en la ilustración. Las magnitudes de las fuerzas de fricción son: sobre mh/i = niriig, y
CAP. 6] DETERMINACIÓN DE FQf PARA EL CASO DE FUERZAS DISIPATIVAS 105
sobre m2, /2 = M'"2g- Suponiendo que la varilla no está en contacto con el plano, y aplicando la relación (6.2)
para"~ ' /i «i ««i _ /i Vi ¿Vi _ Í2X2&x2 _ f2y28y2
8 "total — /T5-¡—72. /T2~,—7i rZh~.—^2 /^2~,—¡2 ^ '
V*i + 2/i Val +Vi - V*2 + y\ yjx\ + y\
en donde xlt y i y x2, y2 son las coordenadas rectangulares de mx y m2, respectivamente, y —j\Xxly[x\ + y[ ,
por ejemplo, es la componente de la fuerza de fricción sobre mh en la dirección de xx. Pero en la figura se obser-
&! = x + ^costf, 2/j = y + íj senff, etc. (2)
Entonces Xi, y,, 5xi, etc., pueden ser fácilmente eliminados de (1), quedando,
(x + l2e sen e) Sx + (y — l26 eos 6) Sy + [l2(x sen e — y eos 0) + ¿2*] 80
-ÍW = f2
+ /,
\/(¿ + í2¿ sen*)2 + (¿ — i2* c°s *)2
(x — íj¿ sen e) Sx + (y + 1,6 eos 0) Sy + [l^y eos 0 — x sen 0) + Í\e} Se
(3)
y/(x - l^ sen e)2 + (y + lxh eos e)2
Es posible leer directamente en (3), las expresiones de las fuerzas generalizadas Fx, Fy y Fg. Por ejemplo,
f2 (x + l2e sen*) /, (x — Le sen 6)
F* = ~ i . . . = " / . . . . = {4)
y(x + l2e sen e)2 + (y - l2e eos e)2 y(x - lxe sen e)2 + {y + lxe eos o)2
En casos especiales tales como x = y = 0 y M 0 o también, j = j = 0 y i ?¡ 0, el lector puede
demostrar fácilmente que Fx, Fy y Fg se reducen a expresiones sencillas que pueden verificarse por medio de
consideraciones elementales.
En este ejemplo relativamente sencillo, resulta claro que las fuerzas de fricción pueden volverse aterrador amen-
te complicadas, y por tanto que las ecuaciones diferenciales pueden ser, o muy difíciles, o imposibles de resolver,
excepto por medio de un computador.
Ejemplo 6.3. Un caso más general que el anterior.
Supóngase que a cambio de las dos partículas que se muestran en la figura 6-2, hay p partículas dispuestas en
cualquier forma sobre el plano XY, y conectadas entre sí por medio de un conjunto de varillas rígidas. La relación
(6.2) se convierte en
8 "total - ~ 2. —x——5—-— (6.4)
Eliminando i,, Sx,, etc., para expresarlo en función de x, 5x, y, Sy, 0 y 50, puede escribirse (6.4), como
s^toui = [■■••] 8* +[••••] &v + [••••] se (6.5)
que es un caso especial de (6.3).
Así, los coeficientes de 5x, Sy y 50 son las fuerzas generalizadas, Fx, Fy y Fe. Es importante observar
que f, = fi, (fuerza normal), son valores que se han supuesto conocidos.
Ejemplo 6.4. Fuerzas generalizadas de fricción sobre una varilla delgada que se desliza en contacto con una
superficie rugosa.
Refiriéndose de nuevo a la figura 6-2, imagínese primero un gran número, p, de partículas distribuidas a lo
largo de la varilla, todas en contacto con el plano rugoso. Las relaciones (6.4) y (6.5) conducen a las fuerzas
generalizadas. Al considerar una varilla continua delgada, resulta claro que la suma de la ecuación (6.4) debe rem-
plazarse por una integral. El lector puede demostrar que la expresión integral para Fx, por ejemplo, es
r'i f(x - lé sen 6) di
Fx = I ; ; — ; (6.6)
~h [ai2 + y2 + Pe2 + 2le(y eos e - x sen*)]"2
en donde / es la fuerza de fricción por unidad de longitud de la varilla (que se supone conocida) y di es un
elemento de longitud de la misma. Se mide l, desde p hasta di. Las longitudes por encima y por debajo de p, son,
respectivamente, li y Z2. Se considera que todas las cantidades, excepto Z, son constantes.
En la misma forma se obtienen las expresiones integrales para Fy y Fg.
Ejemplo 6.5. Fuerzas generalizadas de fricción sobre un tablero que se desliza en contacto con un plano rugoso.
Al referirse a la figura 6-3, se observa que este problema es, sencillamente, una extensión del estudiado en
el ejemplo 6.4. Utilizando las relaciones
Xj = x + x2 eos 6 — y2 sen e, yx — y + x2 sen e + y2 eos 6
106 DETERMINACIÓN DE Fq PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
y recordando que en cuanto se refiere al movimiento del tablero, x2 y y2 son constantes, el estudiante puede
demostrar que la expresión integral para Fg, por ejemplo, está dada por
dA = dxi dj/i = elemento de área del tablero
Xi, Yi adheridos al tablero
Fe =
Tablero que se desliza en contacto con el plano rugoso, X, V,
Fig. 6-3
/[(*2 + V?)'e + (y*2 -'¿V2) c°s * _ (*x2 + VVz) sen *] dx2dy2
_ r f[{xl + ví)e + (yx2—x
J [i2 + y2 + (x\ + y\)e* + 2e
eos e(yx2 — xy2) — 2e sen e(xx2 + yy2)]1/2
(6.7)
en donde todas las cantidades son constantes, excepto x2 y y2, y la integral se toma de tal manera que cubra todo
el tablero en contacto con el plano X, V,. La magnitud fdx2dy2 es la fuerza de fricción sobre el elemento
de área dx2dy2 y /es una constante conocida. Expresiones semejantes se encuentran para Fx y Fy.
El cálculo de estas integrales no es sencillo. Una manera más manejable de hallar las fuerzas generalizadas
de este tipo, y otras diferentes, se encontrará en el numeral 6.8.
6.4 Ejemplos: Fuerzas viscosas generalizadas.
Haciendo n = 1, la expresión (6.2) resulta aplicable y se reduce a
SWl0
2 ax(XiSXi + ;
+ ZíSZí)
Ejemplo 6.6. Fuerzas viscosas sobre una palanqueta.
Supóngase que las fuerzas que actúan en m, y m2 de la figura 6-2 son viscosas en cambio de ser de
fricción. Por tanto,
5W'total - —«1*1**1 - CL1V1&V1 - a2x2Sx2 - a2y2hy2
Para eliminar i,, 5x1, etc., se usan las relaciones x, = x + lx eos e, y\ = y + l\ sen o, etc., y se obtiene,
*^toui = -[(ai + a2)¿ + (a2k — ai*i)¿ sen e) Sx — [(at + a^)y — (a2¿2 — <M,)¿ eos ff] Sy
—[(a^ll + ail\)e + (az¿2 — &ili)(x sen 9 ~ V cos *)] 8e
en donde puede leerse directamente Fx, Fy y Fg.
Ejemplo 6.7. Fuerzas viscosas sobre una superficie plana.
Imagínese que el tablero de la figura 6-3 se mueve ahora paralelamente y cerca al plano estacionario X, Vi,
y que un líquido viscoso se encuentra llenando el espacio intermedio. Supondremos que la resistencia que se opone
al movimiento de cada uno de los elementos dx2dy2 de la superficie móvil es una fuerza viscosa y, que sus
componentes están dadas por dfz = — ax,dx2d;y2 y dfy = — aytdx2dy2, en donde a es la resistencia viscosa
por unidad de área por unidad de velocidad.
Entonces, para un desplazamiento virtual general de la superficie entera,
S^toui = -a J [i, Sxx + yx Syi] dx2 dy2
en donde la integración se extiende a toda la superficie. Utilizando una vez más, las relaciones x, = x + x2 cos 6 -
y2 sen 0, etc., la expresión anterior se convierte en
CAP. 6] DETERMINACIÓN DE FQr PARA EL CASO DE FUERZAS DISIPATIVAS 107
-./<(i-
- x2e sen e — y26 eos e) Sx + (y + x26 eos 6 — y26 sen 6) Sy
+ [{x\ + y\)e + (yx2 — xy2) eos e — (ix2 + yy2) sen e] Se) dx2 dy.¿
Al realizar la integración para toda la superficie móvil, y dejando constantes todas las cantidades, excepto
X2 y ^2» se encuentran los valores de Fx, Fy y Fg como coeficientes de Sx, Sy y 50, respectivamente.
Ejemplo 6.8.
Supóngase que la superficie anterior es un rectángulo de área A = 2a x 2b, con los ejes X2 y Y2
paralelos a los lados y origen en el centro. Calculando la integral para los límites x = — a hasta a y y = —b hasta b,
se obtiene, -SWlotal = Aax Sx + Aay Sy + j¡Aa(a2 + b2)¿ Sff
Por tanto, Fx = -Aax, Fy = -Aay, Fe = -\Aa{a?- + b2)e
Naturalmente estos resultados dependen de la validez de las suposiciones hechas con respecto a la resistencia
sobre cada elemento de área. Nótese que las fuerzas viscosas generalizadas son mucho más sencillas que las
originadas en la fricción en seco.
6.5 Ejemplo: Fuerzas proporcionales a la potencia n de la velocidad, para n > 1.
Se aplican directamente las relaciones (6.2) y (6.3).
Ejemplo 6.9.
Con el fin de ilustrar el método para encontrar las fuerzas generalizadas para cualquier valor de n,
considérese nuevamente la palanqueta de la figura 6-2. Supóngase que las fuerzas aplicadas a mi y m2 están dadas
en magnitud por fl = aj-v"', y f2 = a2v"z respectivamente y que cada una de ellas tiene una dirección opuesta
al movimiento de la partícula respectiva. Aplicando (6.2) se tiene
5^toui - -[aiv"l_1(¿i5a;i + yx Sy{) + a2v^~l(x2Sx2 + y2Sy2)]
Escribiendo, vni-1 = (Xj + J/J)(n»-1)/2, etc., y eliminando xi y 5*i por medio de xj = x + ^ eos 0, etc.,
se obtiene una expresión en la que es posible leer directamente Fx, Fy y F g. Por ejemplo,
Fg = — ajv"1-^!^ eos 6 — x sen* + l^e) — a^v^'^l^x sen e — y eos e + l<>6)
Nota. Suponiendo que la resistencia df sobre un elemento de área dA (Fig. 6-3) está dada por
df = av"dx2dy2 = a(x2 + y\)n'2dx2dy2,
una extensión del método empleado conduce directamente a las expresiones integrales de las fuerzas generalizadas
sobre el tablero, Fx, Fy y Fe.
6.6 Fuerzas expresadas por medio de una serie de potencias.
Supóngase que la magnitud de la fuerza sobre una partícula (o elemento de área)
puede ser mejor representada por una serie de términos, tales como,
/ = a0 + aiv + a2v2 + a3v3 + • • • (6.9)
en donde v es la velocidad de la partícula y a0, a,, a2, . . . son constantes o quizá son
funciones de las coordenadas, o del tiempo, o de éste y aquellas. Si / tiene una dirección
opuesta a la de v,
fx = —(do + div + a2v2 + a3v3 + • • • ){x/v)
Así, con esta relación y las correspondientes a fy y /,, se llega a las expresiones de las
fuerzas generalizadas, en la forma usual.
6.7 Algunas consecuencias interesantes de las fuerzas de fricción y otras.
Considérense los siguientes interrogantes:
(a) ¿Por qué al extraer un cilindro que se encuentra ajustado dentro de otro, siempre se
gira el uno con respecto al otro, al tratar de separarlos tirando de ellos en direcciones
opuestas, como al sacar un corcho de una botella?
(6) ¿Por qué, cuando un bloque de madera se encuentra en contacto con una correa tras-
portadora, puede resbalarse hacia los lados con muy poco esfuerzo; o cuando se
arrastra un objeto pesado largo (como un tanque de gas comprimido) sobre un piso de
108 DETERMINACIÓN DE Fqf PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
concreto, el
facilidad?
"extremo libre", en contacto con el piso, oscila hacia los lados con tanta
(c) Se coloca una pequeña moneda en un plano inclinado rugoso. La inclinación del plano
no es suficiente para que la moneda se deslice bajo la acción de la gravedad, aun
después de iniciado el movimiento. Sin embargo, si se le da una pequeña sacudida en
dirección horizontal, la trayectoria sigue una curva hacia abajo. Expliqúese.
Las respuestas a estos y otros interrogantes pueden obtenerse en las siguientes
consideraciones:
El bloque B de masa M (Fig. 6-4) descansa sobre un cilindro de radio r, que gira con
velocidad angular 0. El bloque no puede girar por impedírselo unas guías lisas que no
aparecen en la figura.
Bloque B que se desliza sobre un cilindro en rotación
Fig. 6-4
Haciendo referencia a los numerales 6.3, 6.4 y 6.5 puede demostrarse que la fuerza fx,
necesaria para mover el bloque sobre el cilindro con velocidad x (medida con relación al
eje fijo OX), viene dada por,
Ai
w f* = (FT^r' (2) u = Bi' (3) u = ci&+™r12
suponiendo en (i), que la fuerza básica es fricción en seco; en (2), que es una resistencia
viscosa; y en (3), que es proporcional al cuadrado de la velocidad del bloque con respecto a la
superficie del cilindro. (A, B y C son constantes.)
Al analizar (1) se observa que para re > x, f es muy pequeña y en realidad tiene
carácter viscoso. En (2), / es independiente de la velocidad de rotación del cilindro. Con
las condiciones establecidas para (3) (o para cualquier potencia de la velocidad relativa,
mayor que la unidad), / aumenta con r6.
Los hechos anteriores tienen importancia en muchas aplicaciones.
6.8. Una "función de potencia", P, para la determinación de las fuerzas
generalizadas.
Existe un gran número de fuerzas, incluidas las conservativas y muchas formas de
disipativas, para las que es posible escribir una función P tal que las fuerzas generalizadas
están dadas por
(6.10)
F,. = ^
dqr
La función P es análoga al potencial V, pero tiene un alcance considerablemente mayor.
Considérese la siguiente integral para un sistema de p partículas, cada una de las
cuales sufre la acción de una fuerza (f^tf^fz), que como se verá más adelante, define la
función P:
(6.11)
P = f ¿(M¿< + f«idVi + /«,<**)
•/ í=i
CAP. 6] DETERMINACIÓN DE FQf PARA EL CASO DE FUERZAS DISIPATIVAS 109
Si por otra parte, las fuerzas son de tal naturaleza que (su dependencia de las coordenadas,
velocidad y tiempo es de tal forma que),
a/xj dfyk
-¿ = -¿ (6.12)
dyk dXi
para todas las combinaciones posibles, la cantidad bajo el signo integral es exacta. Entonces,
al evaluar la integral, dejando constantes todas las coordenadas y el tiempo, se obtiene una
cantidad P, tal que fx. = dP/dxit etc. Además, como se demuestra más adelante, se
cumple (6.10).
Sustituyendo /I{ = dP/dXi, etc., en la expresión general (4.10), para FQr, y recordando
que dxjdqr = dxjdqr, etc., se llega a
i=i\dXidqT djji dqr dZi dqj
que es sencillamente dP/dqr.
Es evidente que P en (6.11) tiene las dimensiones de potencia/ por lo que se denomina
"función de potencia".
6.9 Formas especiales de la función de potencia.
Para ciertos tipos de fuerzas se puede poner (6.11) en una forma directamente aplicable
con facilidad.
Considérese el caso (de gran alcance) en el cual /¿, la fuerza aplicada a mt, está dada
por /, = <j>t (xt, yt, zt, u¡, t) en donde, según se indica, <t>t es una función arbitraria de las
coordenadas de la partícula, su velocidad ut, y el tiempo t. Se puede suponer que /, tiene
la dirección de vt (o la contraria a ésta). Por tanto fX{ = xi<f>i/vi, fy. = y^Jv^ etc., y
entonces ., . .,
di*i • d /<f>i\ y, _ °fvi
dJ? = i,±(h)3b = «•!, et(,
dyi dVi\ViJ Vi dii
dfXi dfVk
Igualmente, —— = —— = 0 para i ^ k. Así, se cumple (6.12) y la relación (6.11) se con-
dyk dxi
vierte en „ _ „
P = I ^—(XidXi + yidii + Zidzi) = \ 2 <¡>.dvi (6.13)
•s í=i Vi >y í=i
A continuación aparece un resumen de algunas formas útiles de (6.13).
Formas especiales de la fu
Para /( = a^",
Para fricción en seco, n = 0
Para resistencia viscosa, n = 1
Una superficie que se mueve en contacto con
av dA, en donde df = fuerza sobre el elemento dt
Para f„ función de las coordenadas y de t,
por ejemplo, f, conservativa.
otra,
área,
df =
dA.
únicamente;
nción de potencia
P
P
P
P
P
=
=
=
=
=
Á n + 1
p
2 api
1 p
ravn+i ¿A
J VTTdA
% (/x^i + /«¿
+ fzfi)
(6.14)
(6.15)
(6.16)
(6.17)
(6.18)
110 DETERMINACIÓN DE Fq PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
Nota importante. Si el sistema sufre la acción de una combinación de fuerzas que
pueden ser de fricción en seco y conservativas, la P total que incluye los dos tipos de fuerzas es,
sencillamente, igual a la suma de (6.15) y (6.18). La ecuación (6.16) es la función de
disipación de Rayleigh.
6.10 Ejemplos para ilustrar el uso de P.
Los siguientes ejemplos son, en su mayor parte, tomados de los considerados
anteriormente. En esta forma pueden compararse directamente los dos métodos para determinar FQr.
Ejemplo 6.10.
Un péndulo que consiste en una pequeña esfera suspendida de un ligero resorte espiral (constante elástica, k)
puede oscilar en el espacio bajo la acción de la gravedad, la del resorte y una fuerza disipativa proporcional a la
potencia n de su velocidad. Aplicando (6.14) y (6.18), la función P total, expresada en coordenadas esféricas, es
P = ^-TT[ (¿2 + r2¿2 + r2 sen2 e ¿2)(n +1)/2 ~ fc(r _ ro)¿ + ™4(r eos 6 - re sen e)
de donde pueden obtenerse en seguida las fuerzas generalizadas.
Ejemplo 6.11.
Considérese de nuevo el problema tratado en el ejemplo 6.9. Suponiendo que el plano está inclinado un ángulo
«, de (6.14) y (6.18) se concluye que
a1(¿2 + y2)("i + 1)/2 a2(¿2 + ^)(«2+D/2
P = X~j — t~7 — m\9 sena yx — m2gsenay2
Trasformando esto a coordenadas x, y y o,
P = ^7 [(* - l^ Sen 0)2 + tf + ijicOS *)2]<"i+»'2 ^T¡ [(* + l2h Sen 6)2 + (y - ij COS *)2]<n,+ l)/2
Wj T 1 H2 ' ■!■
— m¡g sen a (y + 1^6 eos 8) — m^sen a (y — l20 eos 6) (6.19)
Entonces pueden obtenerse las fuerzas generalizadas correspondientes & x, y y e, por medio de Fx = BPIdx, etc.
Nótese que haciendo nx = n2 = 0 lo anterior se aplica a fuerzas de fricción; o para r^ = n2 = 1 la anterior
constituye la función adecuada de P para fuerzas viscosas.
Ejemplo 6.12.
Con referencia al ejemplo 6.7 y la figura 6-3, se trata de determinar la función de P para un tablero de forma
arbitraria.
Para este problema la ecuación (6.16) toma la forma integral (supuestas viscosas las fuerzas),
P = -\ Cav^dx2dy2 (6.20)
en donde v2 = x2 + y\ . Eliminando xu yx como en el ejemplo 6.7, e integrando para toda el área A
(dejando constantes todas las magnitudes excepto x2, y2) se obtiene,
P = —[$aA(x2 + y2) + %Ie2 — aAex(x2 sene + y2 eos e) + aAey(&2 eos e — y2 sen*)]
en donde 7=1 a(x\ + y\)dA, I x2dA = £2A, etc., y £2, y2 son las coordenadas del "centro de
gravedad" de A.
Como se ve en (6.20), P es igual a la "energía cinética", con signo negativo, de una lámina de forma
arbitraria que se mueve de cualquier manera en el plano X1Y1, en donde a remplaza la masa por unidad de
área.
Ejemplo 6.13.
Refiriéndose al ejemplo 6.4, determinar una función de P para la varilla, suponiendo que la fuerza df sobre
un elemento de longitud di, viene dada por df = au" di.
f + li avn + 1
Aplicando (6.17) se escribe P = — I —-¡—=- di que al expresarlo en función de las coordenadas x, y y
J-i2 n + 1
6 por medio de las relaciones xi = x + l eos 6, etc., se convierte en
—^ [(« - le sen*)2 + (y + le cos*)2]<n + i)/2 di (621)
CAP. 6] DETERMINACIÓN DE FQ PARA EL CASO DE FUERZAS DISIPATIVAS 111
La evaluación de esta integral, dejando constantes todas las magnitudes excepto /, produce una cantidad de
la que pueden determinarse las tres fuerzas generalizadas, por medio de FQ = dP/dqr.
Nota importante. Si la fuerza sobre un elemento de área dA = dx2dy2 (Fig. 6-3)
está dada por df = avndx2dy2, el método anterior puede extenderse sin dificultad para
la determinación de P para una superficie cualquiera. (Para n ¿é 1, usualmente las
integrales son bien complicadas.)
6.11 Fuerzas que dependen de la velocidad relativa.
En el siguiente ejemplo se trata de ilustrar este tipo de fuerzas.
Ejemplo 6.14.
—wwwww—
q*
-Vi
fe
—www—I I—www—
Fig. 6-5
El movimiento de cada una de las masas m, y m2, de la figura 6-5, está restringido a una recta
horizontal. Los amortiguadores dentro de los que se mueven los pistones p, y p2, están sujetos rígidamente a m, y m2,
respectivamente. Los pistones y la masa m3 están adheridos a la varilla horizontal, y los resortes están
conectados a las masas m, y m3, y m3 y m2, según se indica. Se supondrá que las fuerzas iguales y opuestas, que
aparecen en el pistón y su cilindro, son en cada caso, proporcionales a la potencia n de la velocidad del pistón
con respecto a su cilindro (n > 1), siendo las constantes de proporcionalidad ai y a2, respectivamente. Por
tanto, la fuerza sobre mi, debida al amortiguador, está dada por,
f\ — &iÍPz — x,)n
Pero /, puede actuar en dirección positiva o negativa de x,, según si ¿3 — i, es positiva o negativa. Mas si,
por ejemplo, n es un entero par, (¿3 — x,)n es-siempre positiva. Para indicar esta condición se escribe
/i = «il*3_*ilB-1(*3-*i)
en donde el valor absoluto |x3 — x, I"-1, se toma siempre como positivo.
Expresando las fuerzas sobre m2 y m3 en forma semejante, y despreciando los resortes ya que su
contribución a las fuerzas generalizadas puede tenerse en cuenta con más facilidad por medio de la función de la energía
potencial, se concluye que SWtotal está dada por,
S^total = axláa-Xil"-!^- ¿i) S*i - a2\x2 - x3\"~i(x2- x3) Sx2
-CJX3- ¿il""1^- ¿i)S*3 + a2|»2 - X3\n~l(x2 - X3)S»3
Pero si se desean usar como coordenadas x,, qt y q2, en tal caso pueden eliminarse x2, x3, fix2 y fix3 de la
relación anterior, y finalmente,
FXl = 0, FQi = -oal?! - g2ln_1 (¿i - k2), Fq2 = <*2 1^ - g2|n_1 (¿i - h2) - «i |g2ln_1 ¿2
Este ejemplo demuestra los principios que se incluyen en el estudio de muchos problemas
similares. Las soluciones a estos problemas pueden obtenerse con el auxilio de un computador.
6.12 Fuerzas cuya dirección no se opone a la del movimiento.
La suposición hecha hasta ahora que una fuerza disipativa que actúa sobre una
partícula, o sobre un elemento de área, tiene siempre dirección opuesta al movimiento, no es
necesariamente válida en todos los casos. Considérese el sistema de la figura 6-6.
Un polo magnético se mueve con velocidad v, paralelamente al plano XY, cerca de una
rejilla de hilos conductores de electricidad. Como resultado del movimiento se establecen
corrientes eléctricas en los hilos, originándose en esta forma una fuerza sobre el imán en la
dirección negativa de y, dada por fy = —Cu sen <¡> en donde C es un factor que depende del va-
112 DETERMINACIÓN DE FQf PARA EL CASO DE FUERZAS DISIPATIVAS (CAP. 6
lor magnético del imán, de su distancia a la rejilla y del espaciamiento y resistencia de los
hilos. Se considera inexistente la fuerza sobre el polo en la dirección de x. Entonces,
independientemente del movimiento, la fuerza sobre el polo es siempre perpendicular a los
conductores y opuesta en dirección, no a u, sino a su componente normal a los hilos.
Y
a,
6!
/v
f
Á
/ \
/1?7*>*C *\
Polo fáffl%\ \
magnético '^ytáfátfA L
V&táfflf
^1
1 fy = Cv sen <f>
b,
a* X
(6.22)
El polo magnético .se mueve en el plano XY cerca
a los hilos conductores eléctricos. Los extremos
de los hilos se hallan conectados a las barras a, b,
y a2b2-
Fig.6-6 Fig.6-7
Si la rejilla se coloca de manera que los hilos formen un ángulo a (Fig. 6-7) con el eje
X, se observa que fx = (Cu sen t¡>) sen a y que fy = (—Cu sen <p) eos a en donde 0 se mide
con respecto a los hilos. Empleando las relaciones <¡> = 0 — «, x = u eos p y y = u sen 0,
las expresiones anteriores toman las formas,
fx = Csena (y cosa — ¿sena)
fy = C eos a (x sen a — y eos a)
Debe anotarse que si la rejilla está constituida por hilos espaciados irregularmente, o que
si su resistencia varía de uno a otro, el valor de C en (6.22) será una función de x y y. Si la
rejilla se mueve de alguna manera determinada, C puede ser una función de las coordenadas
y del tiempo. (Nota. La velocidad v debe medirse con respecto a la rejilla.)
Ejemplo 6.15.
Imagínese un polo "aislado" suspendido de una banda de caucho, de modo que puede oscilar en el plano
vertical a manera de péndulo de longitud variable, cerca de una rejilla vertical cuyos hilos conductores forman un
ángulo a con el eje horizontal X. Se trata de hallar aquí las fuerzas generalizadas que resultan de la reacción entre la
rejilla y el imán, para las coordenadas usuales para un péndulo, 0 y r. (Sin preocuparnos por incluir las fuerzas
debidas a la gravedad y a la banda de caucho.) Con tal objeto se aplica la relación fiWtoUl = fzhx + fyby.
Eliminando i, y, Bx y fiy por medio de x = r sen 6 y y = yo — r eos 6, se concluye que
Fg = Crr eos (e — a) sen (0 - a) — Cr2e sen2 (e — a)
Fr = Cre sen (o — a) eos (e — a) — Cr eos2 (e — a)
El lector puede demostrar que para este problema puede escribirse la siguiente función de P:
P = C(xy sena cosa — £»2sen2a — £¡/2cos2a)
= — £C(x sen a — y eos a)2
Como ejemplo semejante a los del tipo anterior, considérese el movimiento de un objeto
en contacto con una superficie estriada (un pequeño bloque de madera sobre un disco
fonográfico). La fuerza necesaria para moverlo en el mismo sentido de las estrías puede ser
considerablemente menor que en dirección normal a las mismas.
Ejemplo 6.16.
En la figura 6-8, pxp2 representa la superficie polar extendida de un imán ancho y plano que puede
moverse de modo que pxp2 permanezca en el plano XY (con el cuerpo del imán siempre normal a este plano). Inmedia-
CAP. 6] DETERMINACIÓN DE FQf PARA EL CASO DE FUERZAS DISIPATIVAS 113
tamente detrás del plano XY se encuentra una rejilla como la de la figura 6-6, con sus alambres paralelos al eje X.
Suponiendo que pxp2 está imantada uniformemente, determínense las fuerzas generalizadas para xlt >-i y 0.
La fuerza df sobre un elemento di de la superficie polar está dada por df = a di u sen $ en donde u2 =
J2 .(- j2 y q es una constante. Como df tiene la dirección negativa de y y v sen <¡> = y, se puede escribir, dfy =
—adly y naturalmente, dfx = 0.
Para un desplazamiento virtual general de la superficie polar entera se tiene,
«^totai = i' W*8* + dfyBy)
Jo
en donde es preciso hacer la integración para incluir la fuerza distribuida a todo lo largo de pYp2 = lx. Pero
como y = yx + l sen 0, y = yx + le eos 6 y 8y = Syi + l 86 eos 0 se tiene,
X£i .
(yi + le eos 9)(8yi + l Se eos e) di
Integrando con respecto a / y dejando que todas las demás cantidades permanezcan constantes, se obtiene,
SWtotai = —*{V\h + i'i* eos*) 82/j - a^y^ cose + £1^0 eos2*) 8*
Aquí es posible leer directamente las expresiones de las fuerzas generalizadas Fy y Fe.
El lector puede demostrar que para este problema,
P = -&[v% + Vil\e<x>se + ^i¿2cos2*]
Superficie polar extendida, pip2, que
puede moverse en el plano XY cerca de
una rejilla de alambres, localizada
como; en la figura 6-6. p¡„ g.9
Fig. 6-8
Ejemplo 6.17.
Una varilla rígida de longitud r, está articulada en px (Fig. 6-9). En el otro extremo de esta varilla, por medio
de una articulación lisa, se encuentra sostenido en p2, un imán de barra (cuya forma es la que se muestra en el
esquema). Todo el movimiento está restringido al plano XY. Debido a una rejilla de alambres paralelos (uno de los
cuales se muestra en la figura) colocada inmediatamente detrás de las superficies pplares, en cada polo aparecerán
fuerzas del tipo descrito por (6.22). A continuación se trata de expresar una función de P usando a B\ y 62 como
coordenadas para este sistema (no se considera la gravedad).
Se remplaza (6.22) en (6.//) y se integra para uno de los polos (Fig. 6-7) llegando a P = —\ C(x sen a —
y eos a)2. Entonces, para el problema entre manos,
P = — £C[(¿! sen a — Vi eos a)2 + (¿2 sen a — y2 eos a)2]
en donde xu yY y x2, y2 son las coordenadas respectivas de los polos N y S. Pero, xY = r sendi + l sen02,
x2 = r sen B\ — l sen 02» etc. Finalmente, P se reduce a
P = -C[r2¿2 sen2 (*! + a) + irisen2 (*2 + a)]
Una advertencia. Queda mucho por decir con respecto a las expresiones básicas de fx,
fy y fz sobre una partícula (o sobre un elemento de área) debidas a diversas fuerzas disipa-
tivas. Por ejemplo, la magnitud de toda fuerza de fricción depende, de alguna manera, de la
velocidad. Usualmente, las llamadas fuerzas viscosas, en realidad no lo son sino a muy peque-
114 DETERMINACIÓN DE Fq PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
ñas velocidades, etc. Por tanto, no debe esperarse que las sencillas expresiones supuestas con el
objeto de ilustrar las técnicas generales, sean estrictamente válidas en todos los casos. Sin
embargo, si se conocen expresiones más exactas para fx, fy y fz en un determinado problema,
los métodos ilustrados conducen a expresiones correctas para las fuerzas generalizadas.
6.13 Experimento sugerido.
Con el sistema que se muestra en la figura 6-10 es posible realizar diferentes experimentos
interesantes e instructivos. El bloque puede ser de metal o de madera y los cilindros de
cualquier tamaño adecuado. Si los valores de 6 son relativamente altos, resulta sorprendente e
interesante observar que para mover el bloque sobre los cilindros haya que hacer una fuerza
tan pequeña. En verdad, los cilindros deben estar muy cuidadosamente nivelados, a fin de
prevenir que el bloque se deslice por la acción de una componente mínima de gravedad.
Con el peso y el cable mostrados en la figura, es posible hacer mediciones cuantitativas
de fx (Fig. 6-4) para diferentes valores de.0 y x, con los cilindros secos o lubricados.
Cilindros paralelos que giran en sentidos opuestos
Fig. 6-10
Problemas
A. Utilice los métodos normales (relaciones (4.10), (6.2) y (6.3)) para la determinación de las
fuerzas generalizadas.
6.1. Una pequeña esfera está suspendida por medio de una banda de caucho, dentro de un líquido viscoso.
Suponiendo una fuerza viscosa sencilla que actúa sobre la esfera y que no hay resistencia sobre la banda,
demostrar que las fuerzas viscosas generalizadas, correspondientes a las coordenadas esféricas, r, 6 y <t>,
son
Fr = -ar, Fe = -ar26, F^, = -ar2 sen2 8$
en donde a es la fuerza viscosa por unidad de velocidad que actúa en la esfera.
6.2. Con referencia al ejemplo 6.6 y a la figura 6-2, demostrar que las fuerzas viscosas generalizadas,
correspondientes a las coordenadas Xi.yi y 0, son
Fx = —(ax + a2)x1 — a2lé sen$, Fy = —(ax + a2)jfi + a2lé eos e,
Fe = ~a2l2é — a2l(xx sen 6 — yx eos B)
en donde / = í, + /2.
6] DETERMINACIÓN DE FQj. PARA EL CASO DE FUERZAS DISIPATIVAS 115
Las esferas mi y m2 de la figura 6-11, se hallan
sumergidas en un líquido viscoso. Demostrar que las fuerzas
viscosas generalizadas, correspondientes a las coordenadas y
y .Va son,
Fy = -at{yz + y) + a2(y3 - y)
Fy3 = -Mj/3 + v) - a2ÍV3 - v)
en donde a, y a2 representan las fuerzas viscosas, por
unidad de velocidad, que actúan en m, y m2
respectivamente.
Repítase lo anterior utilizando como coordenadas y, yy3.
Las masas m\, m2 y m3 de la figura 6-12, pueden
deslizarse según una recta horizontal. Entre el plano horizontal
y los bloques hay una resistencia viscosa cuyos coeficientes
son alt a2 y a3, respectivamente. Cada uno de los
imanes A y B, ejercen una resistencia viscosa sobre m2, y el
valor de esta fuerza viene determinado por la velocidad
relativa del imán con respecto a m2. Los coeficientes de la
resistencia magnética son a4 y a5.
Fig. 6-11
—wvvww^-
r-lT
-wvvwwvw-
*-— a,
—-.—H k-* —
«3 —
4
n|^«.
¥1_B
á7
«*
Os
^WVWWW^-
[—o,—-
"Vn
r— 0,3
Fig. 6-12
Demostrar que las fuerzas generalizadas correspondientes a las coordenadas xi, x2 y x3 (sin
incluir las fuerzas ejercidas por los resortes) son,
FT = — alxl + a4(x2 — ¿i)
FH = -a2x2 + a4(¿! - x2) + o5(x3 - x2)
Fxa = _a3*3 + 05(^2 - ¿3)
-axxx - a2(x, + 'qj - az{xx + qx + q2)
-a4q! - a2(xt + qj - a3(x1 + qx + q2)
-a5q2 - az(xx + 'qx + q2)
y que para x,, q¡, y q2,
* "2
En la figura 6-13, el imán de herradura y el disco de
cobre están sostenidos por tres segmentos de cuerda de
• piano, de tal manera que se forma un péndulo doble
de torsión. Las constantes de torsión de las cuerdas
son Ci, C2 y C3, respectivamente. Existe una
resistencia viscosa ai, por unidad de velocidad entre
el disco y los bloques de freno Bt y B2, y una
resistencia semejante a2, entre los polos magnéticos
y el disco. Demostrar que las ecuaciones del
movimiento del sistema son (suponiendo que ai y a2
actúan a distancias radiales r, y r2)
C3e1 + C2(ffi - e2) + 2alr\eí
+ 2o2r¡(¿1-¿2)
/26f2 - C2{ex - e2) + Cxe2 - 1a2r\{flx - e2)
en donde /, e I2 son los momentos de inercia del
disco y del imán, respectivamente, y 0, y fl2 son
los desplazamientos angulares correspondientes.
"^J
\-nM
mm
Disco de cobre
C15*
c3\
Fig. 6-13
116 DETERMINACIÓN DE Fq PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
6.6. Un disco plano de radio r está en contacto con una superficie cubierta de aceite. Suponiendo que el aceite
ejerce una resistencia viscosa en cada uno de los elementos de área del disco, demostrar que las fuerzas
generalizadas correspondientes a x, y y fl, son
Fx = -Aax, Fy = -Aay, F0 - -%Aar2é
en donde i y y localizan él centro del disco y 8 su posición angular. A = xr2 y a es la fuerza viscosa por
unidad de área por unidad de velocidad. Nótese que cada una de las fuerzas depende únicamente de la
velocidad correspondiente.
6.7. El imán de barra y los polos "aislados" (Fig. 6-14) ejercen
fuerzas viscosas sobre la hoja conductora. Demostrar que
las fuerzas disipativas generalizadas, correspondientes a las
coordenadas y, y y2, son
FVl = -4(at + a2 + a3)yt + 2(a2 - a3)y2
Fy2 = 2(«2 - <*3)¿i ~ <a2 + aA
en donde alt a2 y a3 representan las fuerzas viscosas,
por unidad de velocidad relativa, ejercidas por cada uno de
los tres imanes respectivamente, sobre la hoja conductora.
Supóngase únicamente movimiento vertical para la hoja,
la barra y los polos.
6.8. Suponiendo que la fuerza de fricción es independiente de la
velocidad, demostrar cómo puede construirse un cojinete
"sin fricción". Dibujar un esquema del sistema concebido.
6.9. Una pequeña masa mi, colgada de un resorte espiral ligero de longitud r, longitud normal r0, y constante
elástica k, puede oscilar como un péndulo, sobre el plano inclinado rugoso (Fig. 6-1). Utilizando coordenadas
polares, demostrar que para un desplazamiento virtual general (suponiendo que existe fricción dinámica),
«Wtoui = ["*(r " r0) + mg sen a eos 6 - (¿2 + ^.2)1/2] «r
" [wrsenasen* + (f2+^1/a]*» = Fr * + F,f
en donde, / = ^mg cosa. ¿Con qué condiciones pueden ser discontinuas las fuerzas de fricción?
6.10. Una partícula puede moverse en contacto con la cara de un disco que gira con velocidad angular w
(constante o variable) alrededor de un eje vertical. Las coordenadas polares de la partícula (r, 0) se refieren a los
ejes inerciales X y Y, cuyo origen es el centro del disco.
(a) Suponiendo fricción en seco entre la partícula y el disco, demostrar que
F lítngr F _ pmgr^jfi' — a)
[f2 + r2(tf-tí)2]l/2' 6 [f2+r2(¿_w)2]l/2
(b) Suponiendo resistencia viscosa, demostrar que
Fr = -aar, Fe = -ar\e - u)
Nótese que si se hace oscilar el disco, da. manera que su desplazamiento angular a, está dado por
o = a0 sen /?t, por ejemplo, entonces, o> = á = a0/3 eos /?t y el tiempo aparece explícitamente en todas
las fuerzas anteriores, excepto en Fr, en el segundo caso.
6.11. Una partícula se mueve en contacto con un tablero horizontal rugoso. Suponiendo que el coeficiente de
fricción para movimiento en la dirección de X es nx, y que en la dirección de Y es ny, demostrar que las
fuerzas de fricción generalizadas, correspondientes a las coordenadas polares, son
Fr = —f{/ix eos e + /iy sen e), Fe = —fr(ny eos 6 — y.x sen e)
'mmm^mmímmmmmm.
- Imán de barra | g¡
y*
_L
Un.
_ Polos
Hoja conductora magnéticos
Fig. 6-14
en donde / es la fuerza normal entre la partícula y el tablero.
CAP- 61 DETERMINACIÓN DE FQ PARA EL CASO DE FUERZAS DISIPATTVAS 117
Los bloques oyfc (F¡g. 6-15) unidos rígidamente por medio de una varilla ligera, de longitud /, se deslizan
en contacto con los bloques c y d. El bloque e puede moverse, sin fricción, a lo largo de la varilla lisa,
mientras que el bloque c puede moverse sobre el eje X y d permanece fijo. Los coeficientes de fricción de las
superficies de contacto, son p,, P2 y P3, como se indica. Nótese que el valor de las fuerzas normales
depende de la posición de m4.
-Mi
Fig.6-15
Suponiendo que el sistema está en movimiento de tal manera que z2 y x, son ambas positivas, y
que x2 > ¿i, demostrar que las fuerzas generalizadas correspondientes a xi, 91 y q2, son
FXl = - [Mifrh + wi2 + w4 - m4g1/0 + n3(m3 + m^qjtj^g
*\j2 = - M™2 + w*4 - «^gi/O + Wi(™3 + m^/l^g, FQi = 0
¿Serán aún válidas estas expresiones en el caso en que ¿1 > x2? Evidentemente, las fuerzas de este
tipo deben ser manejadas con cuidado.
Sobre un tablero plano se.ha dibujado un rectángulo de lados 2a y 26. En cada una de las esquinas del
rectángulo se ha clavado una tachuela de cabeza redonda, pequeña. Se coloca entonces el tablero sobre las
tachuelas, en contacto con una superficie rugosa, plana. Utilizando como coordenadas x, >- y 6 (x y y
son las coordenadas del centro del rectángulo y 6 el ángulo entre el lado 2a y el eje X) y suponiendo que se
presenta fricción en seco, demostrar que 5Wtotai viene dado por
~8Wto
- /i i[x + ró sen (6 + p)] [8x + r 8e sen (e + p)]
+ [y -re eos (e + p)][8y - r 89 eos (e + £)]} —
+ /2 {[x — re sen (e - /?)] [8x — r 86 sen (e — /3)]
+ [y + re eos (e - p)][8y + r 89 eos (9 - p)]} ^
+ /3 i[x - re sen(e + /?)] [8x - r 8e sen (e + /?)]
+ [y + re eos (e + p)][8y + r 8e eos (e + p)]} —
1>3
en donde
r* = a2+ b2, tan p = b/a,
con expresiones semejantes para v2, v3 y
+ A {[* + re sen (e — /?)] [8x + r 8e sen (e
+ [y
-m
re eos (e — p)][8y - r 8e eos {e — fi)]} —
{x2 + y2 + r2é2 + 2ré[x sen (e + p) - y eos (e + /3)]}1/2
ft = ^
(fuerza normal sobre la cabeza de la primera tachuela), etc. Se
suponen conocidas /,, f2t f¡ y f*.
Nótese que es posible leer el valor de las fuerzas
generalizadas, en la expresión de bWtoi&\.
Sobre un tablero plano se ha dibujado un círculo de radio R, y
en su periferia se han clavado n tachuelas de cabeza redonda,
pequeña, con espaciamientos regulares, como se muestra en la
figura 6-16. (La distancia angular entre una tachuela y sus
adyacentes es igual a a). Se coloca entonces el tablero sobre las
tachuelas, en contacto con un plano rugoso. Midiendo x y y al
centro del círculo, llamando 0 el desplazamiento angular del
tablero, y suponiendo fuerzas de fricción, demostrar que una
expresión para 5Wtotni de la que es posible obtener Fx, Fy
y Fe, será
Fig. 6-16
118 DETERMINACIÓN DE FQr PARA EL CASO DE FUERZAS DISIPATIVAS [CAP. 6
S^toui = - / 2 J: [* - Re sen (/3¡ + e)] [Sx - R Se sen (/3¡ + g)]
- /2 ;¿-[¿ + i2¿cos(/3i + *)][82/ + i? 6(9 eos (/3¡ + *)]
en donde se ha supuesto que la fuerza de fricción sobre cada una de las tachuelas es igual a /, (3, = (i — l)a
y . .
v2 = [x - Re sen (/3¡ + e)]2 + [2/¡ + Re eos (/3¡ + e)]2
6.15. Un anillo delgado, circular, de radio R, está colocado en contacto con una superficie plana rugosa.
Utilizando como coordenadas x, y y 6, en donde x y y localizan el centro del anillo y 8 su desplazamiento
angular con respecto al eje X, demostrar que la fuerza de fricción generalizada correspondiente a x, viene
dada por
[x — Re sen (e + a)] R da
{[x - Re sen {e + a)]2 + [y + Re eos (e + a)]2}1/2
en donde R da es un elemento de longitud del anillo, y / es la fuerza de fricción por unidad de longitud
del mismo anillo. Compárese el resultado anterior con el del problema 6.14.
6.16. Suponiendo que la resistencia ejercida por cada uno de los imanes del problema 6.7 es proporcional al
cuadrado de su velocidad relativa a la hoja conductora, demostrar que las fuerzas generalizadas son
Fyi = - Sa'iliilVi - 2a'2\2yl-y2\(2yl-y2) - 2a'3 \2Vl + y2\(2Vl + y2)
Fv2 = + a2 |2¿! - ¿2|(2¿i - y2) ~ 0,3 \2Vi + ¿zl(2¿i + y2) .
B. Utilice la función de potencia para la determinación de las fuerzas generalizadas.
6.17. Demostrar que la función P, para la esfera del problema 6.1, es
P = -$a(r2 + r2é2 + r2 sen2 e ¿2)
Apliqúese la ecuación (6.10) y compárense los resultados con las expresiones obtenidas anteriormente para
las fuerzas generalizadas.
6.18. Demostrar que para el problema 6.3,
p = -&iv2 ~ \*é\ = -$aiú + vz)2 - i«2(¿ - vz)2
Demostrar Fy y Fy , y confróntese con los resultados obtenidos anteriormente.
6.19. Una palanqueta que consiste en dos esferas iguales, pequeñas, unidas rígidamente a los extremos de una
varilla delgada y lisa, puede moverse libremente en el espacio dentro de un fluido viscoso. Sin necesidad de
tener en cuenta la resistencia sobre la varilla y suponiendo que no hay rotación de las esferas alrededor del
eje que coincide con la varilla, demostrar que
p = -$a(x2 + y2 + 'z2) - a(l2e2 + l2¿2sen2e)
en donde x, y y z localizan el c.m. de la palanqueta, l es la distancia del c.m. al centro de una de las
esferas, y 6 y <¡> son las coordenadas esféricas usuales.
6.20. Un disco circular plano de radio r, está en contacto con una superficie también plana, cubierta con aceite.
Suponiendo que el aceite ejerce una resistencia viscosa (coeficiente por unidad de área = a), demostrar
que la función P adecuada es
P = -£,^¿2 + y2) - ^r4a¿2
en donde x y y son las componentes de la velocidad del centro del disco. De la misma manera, demostrar
que para un rectángulo de área A = 2b x 2c,
P = -$aA(x2 + y2) - %aA(b2 + c2)e2
Las coordenadas x y >- localizan el centro de la superficie respectiva en los dos casos anteriores. (Véase el
ejemplo 6.8.)
F> = ~ff.
CAP. 6] DETERMINACIÓN DE F0 PARA EL CASO DE FUERZAS DISIPATIVAS 119
6.21. Demostrar que para la partícula del ejemplo 6.1,
P = — iimg cosa (x2 + y2)112 — mgy sen a
6.22. Demostrar que para el problema 6.9, la función de P es
P = —a{r2 + r2e2)112 — k{r — r0)r + mg sena (r eos 0 — re sene)
Compárense las fuerzas generalizadas obtenidas por medio de (6.10) con las que se leen en fiWtotai-
6.23. Refiriéndose al problema 6.15, demostrar que la función de P correspondiente, está dada por
/>27T
P = -f \ {{x-Re sen (e + a)]2 + [y + Re eos (e + a)]2}1'2R da
Jo
en donde / es la fuerza de fricción por unidad de longitud del anillo.
Demostrar que la expresión integral de la función de P, para el disco plano de radio R, en contacto con un
plano rugoso, utilizando las mismas coordenadas que en el problema 6.23, es
XR /*2ir
J {[x - ré sen {e + a)]2 + [y + re eos (e + a)]2}1/2 r dr da
en donde / es ahora la fuerza de fricción en seco, por unidad de área de contacto. Escribir la integral para
el caso de resistencia viscosa.
6.25. Una varilla delgada de longitud /, está en contacto con una superficie plana rugosa. Suponiendo
resistencia de fricción, demostrar que
fl
P = - / I [x2 + y2 + r2e2 + 2re{y eos e - x sen e)]1'2 dr
Jo
(x y j se han medido al extremo de la varilla). Resulta claro que esta integral es de la forma
f
en donde, a = e2, b -
(ar2 +br + c)1'2 dr
I eos e — x sen e) y c = x2 + y2.
Suponiendo que la fuerza introducida por el amortiguador de la figura 6-17, es proporcional al cubo de la
velocidad con que se mueve el pistón en cualquier sentido dentro del cilindro (constante de
proporcionalidad '= b) y que existe una resistencia viscosa entre cada par de superficies planas en contacto (siendo las
correspondientes constantes alt a2 y 03), demostrar que
P = -±[axx\ + 02(x2 - xt)2 + a3(x3 - xt)2] - ¿6(x3 - ¿2)<
+ fcjtfi - xjx! + k2(l¿ + xt- x2)(i2 - xj) + k3{lz + x2 - xz)[xz - i2)
en donde kx, k2 y k3 son las constantes elásticas y í,, l2 y /3 son las longitudes normales (sin
estirar) de los resortes respectivos.
L_ x. _J|-^WWWWWVWH
h/wwvwH
k3
h/vwwwwvwwH
Fig. 6-17
120 DETERMINACIÓN DE Fq PARA EL CASO DE FUERZAS DISIPATIVAS (CAP. 6
6.27. Si la rejilla de la figura 6-6 está girando con velocidad angular á, alrededor de un eje perpendicular al
plano XY que pasa por el origen, demostrar que es preciso remplazar las ecuaciones (6.22) por las siguientes,
fx = C[V cosa — X sena — (x cosa + y sen a)á] sena
fy = —C[ycosa — ¿sena — (x eos a + y sen a)á] eos a
Demostrar que P = — $C[y cosa — x sen a — a(x cosa + y sen a)].
6.28. Una rejilla de hilos conductores como la que se muestra en la figura 6-6, se encuentra adherida a un tablero
plano que puede deslizarse libremente sobre un plano liso estacionario XY. Las coordenadas xh >-!
localizan el centro del tablero y 6 su posición angular. Un polo magnético, localizado por medio de las
coordenadas (x, >-) puede moverse paralelamente a la superficie de la rejilla (sin tocarla). Suponiendo una
fuerza sobre el imán, y otra igual y opuesta sobre la rejilla, debida al movimiento relativo de los dos objetos,
encontrar las fuerzas generalizadas correspondientes a x, y, Xi, yi y 6.
fx — C{[V — Vi — (x~ xi)*] eos* — [x — Xj + (y — y^e] sene) sene
fy = —C{[y — Vi — (x — xjg] eos e — [x — Xj + (y — y^e] sen e) eos e
/*, = -/*» /«, = -/»» /• = /Bl(*-*i) -/*, (V- Vi)
Demostrar que todas estas fuerzas pueden obtenerse de
P = ~$C{[y - Vi - (x - xx)e] eos e - [x - «, + {y - y {¡¡i] sen *}2
6.29. Con referencia al ejemplo 6.2 y a la figura 6-2, supóngase que el plano rugoso sobre el que se han trazado los
ejes X y Y, está en movimiento. El origen O tiene una velocidad v = (x% + y^)1/2 , y el sistema X, Y gira
en el plano del dibujo con velocidad angular ¿. Las coordenadas x0, y0 se miden con respecto a un
marco inercial X', Y', y a es el ángulo entre X' y X.
Nótese que las expresiones de Fz, Fy y Fg no varían por efecto del movimiento. Sin embargo,
al expresar a T en función de x, y, 6, x, y y 6, naturalmente es preciso tener en cuenta la traslación y
rotación del sistema X, Y.
Este procedimiento, más bien general, es ilustrativo del método que puede seguirse en los ejemplos
6.5, 6.12 y muchos otros problemas en los que las "superficies disipativas" se hallan en movimiento.
6.30. Supóngase que la fuerza sobre un elemento de área, dx2dy2, está dada por / = au" dx2 dy2. (Véase
C C vn dx2 ¿V2
la figura 6-3.) Teniendo en cuenta (6./7), P = —a I I —=— lo cual puede expresarse,
J J n + 1
P = —a i i , .. [(x — x2e sene — y2e eose)2 + (y + x2e cose — y2s sene)2]n/2dx2dy2
Pero, en el instante considerado, supóngase que Xi, Yi es inercial y que está superpuesto a X2, Y2. En
este caso, 6 = 0 (B j¿ 0) y
P = -a J f^fj [(* - V**)2 + (V + x2e)2Y>2 dx2 dy2
que es considerablemente más sencilla que la expresión original.
CAPITULO
Estudio general de los momentos y
los productos de inercia
Dinámica de los cuerpos rígidos: Parte I
En el estudio de los movimientos de los cuerpos rígidos es indispensable la comprensión
clara y exhaustiva de los momentos y de los productos de inercia y de los diferentes detalles
relacionados con ellos. Por esta razón, este tópico se trata aquí en un capítulo especial, antes
de intentar acometer el análisis de la dinámica de los cuerpos rígidos. Se supone que el lector
conoce suficientemente la definición del momento de inercia y su utilización en la solución
de problemas elementales.
7.1 Expresión general del momento de inercia de un cuerpo rígido con respecto a
un eje cualquiera.
Elipsoide de inercia con
respecto a 0
Cuerpo rígido v
Fig. 7-1
Con referencia a la figura 7-jl, se observa que el momento de inercia, loa,, del cuerpo
rígido, con respecto a la recta Oalt es loa, = £ m'h2 en donde m' es la masa de una
partícula cualquiera; h, la dis'tancia normal de 0ax a m'; y la sumatoria abarca todas las
partículas cfel cuerpo. Se tiene además, h2 = r2 — OP2, r2 = x2 + y2 + z2, OP =
Ix + my -f- nz y l2 -f- m2 -f- n2 = 1, en donde, l, m y n son los cosenos directores de 0a\.
Entonces se escribe,
ioa, = 2 m'(f - op2) = 2 m'[(x*+v2+ZW+™2+n2) - (lx+™y+™*)2]
de donde,
Ioai = l2 2 m'(y2 + z2) -I- m2 2 m'(x2 + z2) + n2 2 m'{x2 + y2)
— 2lm 2 m'xy — 2ln ¿¡ m'xz — 2mn 2 m'Vz
(7.1)
121
122 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
Resulta claro que ^ m'(y2 -\- z2) = Ix es el momento de inercia con respecto al eje X,
etc. A la expresión, £ m'xy = Ixy se le denomina producto de inercia. Finalmente,
! Ioax = Ixl2 + Iym2 + lzn- - 2Ixylm - 2Ixzln - 2Iyzmn {7.2)
en donde, por conveniencia, se ha escrito Ix a cambio de Ixx, etc. Para mayor claridad se
han usado signos de sumatoria en lugar de integrales en (7.2).. Para el caso de distribuciones
de masa continuas,
Ix = C (y2 + ¡¡a) dviy etc
La relación (7.2) es muy importante puesto que constituye la base de todo el estudio que
sigue sobre momentos y productos de inercia.
Nótese que las cantidades Ix, Ixy, etc., son fijas para cierto cuerpo y cierto marco
X, Y, Z. Sin embargo, en general tendrán diversos valores para diferentes localizaciones u
orientaciones del marco.
Es importante tener en cuenta que para valores conocidos de Ix, Ixy, etc., 'es posible
calcular de inmediato, por medio de (7.2), el momento de inercia del cuerpo con respecto a
una recta con cualquier orientación, que pase por O.
7.2 El elipsoide de inercia.
Tomando un punto cualquiera sobre Oax, por ejemplo P\(xx, yx, zx), (Fig. 7-1) a
una distancia sx de O, se observa que xx = sxl, yx = sxm y zx = sxn. Al eliminar
/, m y n de (7.2), esta ecuación puede expresarse como
Ioais2 = lxx\ + Iyy2 + lzz\ - 2IxyXiyi - 2Ixzxízl - 2lyzyxzx (7.3)
Si se considera otra línea cualquiera, como Oa2, se tendrá una expresión idéntica para
Ioa2s\, en donde s2, de nuevo, es una distancia arbitraria medida sobre Oa2, desde el
origen hasta un punto sobre la misma recta, p2(x2, y-¿, z2). Así, la ecuación (7.3) es
aplicable a todas las rectas que pasan por O.
Suponiendo ahora un gran número de rectas que pasan por O en diferentes direcciones,
puede tomarse s para cada una, de modo que
IoaS2 = 1 (7.4)
Así, puede expresarse la relación general
fe- Ixx2 + Iyy2 + Izz2 - 2Ixyxy - 2Ixzxz - 2Iyzyz = 1 (7.5)
que es la ecuación de una superficie elipsoidal (que por lo general no es de revolución)
orientada con respecto a X, Y, Z, de alguna manera, aún no determinada, según se indica en la
figura. Esta superficie se denomina elipsoide de inercia, con respecto a O.
El resultado anterior se puede aplicar a objetos de cualquier forma: Rocas, sillas, vigas
de acero, etc. Pero no debe suponerse que sólo existe un elipsoide para cada cuerpo. En general,
pueden trazarse elipsoides de inercia, uno para cada punto dentro del cuerpo o fuera de él,
todos de diferentes tamaños y orientaciones.
Pero no debe atemorizarnos el hecho que exista un número ilimitado de elipsoides para
cada objeto, como a primera vista puede suceder, puesto que si se conoce el elipsoide con
respecto al centro de masa, es posible calcular las características de todos los demás y los valores
de todos los momentos y productos de inercia, como se demostrará más adelante.
Debe quedar claro que el momento de inercia con respecto a una línea cualquiera que
pasa por O, está dado por I0a = l/s2, en donde s es la distancia de O al punto en que
esa línea corta al elipsoide. Nótese además que (7.4) podría haberse escrito como I0as2 =
C = una constante cualquiera, dándole así al elipsoide cualquier tamaño que se desee.
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 123
7.3 Momentos principales de inercia. Ejes principales y sus direcciones.
Tomando los ejes X, Y y Z, en la dirección de los diámetros principales 2a, 26 y 2c,
de un elipsoide cualquiera, la ecuación de su superficie tiene la forma
S+F + l = ! (76>
De la misma manera, si X, Y y Z se toman en las direcciones de los diámetros principales
del elipsoide de inercia, los productos de inercia se anulan y por tanto,
Fxx2 + Ipyy2 + Ilz2 = 1 osea, loa = M1 + Hm2 + Kn> (7.7)
en donde Ix, II e II se denominan "momentos principales de inercia". Los ejes
correspondientes X", Yp y Zp son llamados "ejes principales de inercia".
A partir de los valores conocidos de Ix, Ixy, etc., en (7.5), es posible hallar las
direcciones de los ejes principales así como los valores de H, Ipy e IP. Puede demostrarse que los
cosenos directores /, m y n de una recta perpendicular a la superficie <¿>(x, y, z) = C son
proporcionales a d<j>/dx, d<j>/dy y d<j>/dz respectivamente, es decir,
|£ = kl, !* = km, |É = fcri (7.8)
dx dy dz
en donde /z es una constante. Aplicando estas relaciones a la superficie elipsoidal (7.5), se tiene,
Ixx - Ixyy - Ixzz = kl
Ivy - Ix«x - Iyiz = km (7.9)
IzZ - hzX — Iyzy = kn
Un eje principal es normal a la superficie en el punto en que la corta, y en este mismo punto
(a una distancia r del origen y con coordenadas x, y y z), l = x/r, m = y/r y n = z/r.
Obsérvese que r es la dimensión del radio principal, y l, m y n son los cosenos directores de
uno de los ejes principales de inercia.
Eliminando x, y y z de (7.9), multiplicando cada una por l, m y n, respectivamente,
y sumando todo el conjunto, resulta,
k/r = hl2 + Iym2 + Izn2 - 2Ixylm - 2Ixzln - 2Iyimn
Comparando con (7.2), k = Ipr, en donde claramente, Ip es un momento principal de
inercia. Las relaciones (7.9) pueden escribirse como
(Ip-Ix)l + Ixym + Ixzn = 0
Ixyl + (Ip-Iy)m + Iyzn = 0 (7.10)
Ixzl + Iyzm + (Ip-Iz)n = 0
de donde se obtendrán ahora los tres momentos principales de inercia y sus direcciones.
A fin de que estas ecuaciones tengan soluciones distintas de la trivial, se requiere que
1 Ip - Ix Ixy Ixz
Ixy IP~Iy Iyz \ = 0 (7.U)
Ixz Iyz ¡P ~ Iz
La expansión de este determinante conduce a una ecuación cúbica en Ip. Incorporando
aquí los valores conocidos de Ix, Ixy, etc., (hallados por cálculo directo o por experimen-
124 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [ CAP. 7
tación) y hallando las tres raíces, se obtienen Ii,Í2 e il, los tres momentos principales de
inercia. (Las raíces de la ecuación anterior se obtienen fácilmente por el "método de la raíz
al cuadrado de Graeffe". Véase Mathematics of Modern Engineering, por R. E. Doherty y
E. G. Keller, John Wiley, 1936, páginas 98-130. Este poderoso método, que puede aplicarse
a ecuaciones de cualquier grado, tiene muchas aplicaciones prácticas.)
Incorporando l\ en (7.10), estas relaciones pueden utilizarse para obtener los valores
relativos (únicamente de l\, m\ y ni, los cosenos directores de los ejes principales,
correspondientes a I\. Expresando los valores así obtenidos como C\l\, C\m\ y C\nx
(ci es alguna constante) se tiene U = cdi/(c%ll + c2ra2 + czn2)1/2, etc. Asimismo pueden
obtenerse los cosenos directores de los otros dos ejes principales restantes.
Nota. Corno se observa en (7.10), los valores relativos de llt mi y ni son los cofac-
tores de los elementos primero, segundo y tercero, respectivamente, de la primera fila (o de
cualquier fila) de (7.11) en donde se ha incluido /?, etc. (Para una definición de "cofactor"
véase la página 217 inmediatamente antes de (10.11).)
7.4 Si se conocen los momentos y los productos de inercia con respecto a* cualquier
sistema de ejes rectangulares con origen en el centro de masa, hallar:
(a) Las mismas cantidades referidas a cualquier sistema paralelo de ejes.
(b) El momento de inercia con respecto a cualquier eje.
(c) El elipsoide de inercia con respecto a un punto cualquiera.
Los desarrollos de este capítulo y de los siguientes, pueden simplificarse con la siguiente
notación, fácil de recordar. Los símbolos escuetos X, Y y Z indican un marco cualquiera
(con el origen en un lugar diferente del c.m.), además, Ix, Ixy, etc., indican los
correspondientes momentos y productos de inercia. Una barra sobre un símbolo indica que se trata
de una cantidad referida al centro de masa. X, Y y Z representan un marco con origen en
el c.m. e h, Íxy, etc., se refieren a los correspondientes momentos y productos de inercia.
Un índice p en el lugar del exponente, indica una cantidad "principal". Los ejes principales
son Xp, Yp y Zp (con el origen en lugar distinto del c.m.) e 1$, 1% e IZ son los
momentos de inercia correspondientes. Xv, Yp y Zp son los ejes principales que pasan por el c.m.
e Txt Iv e íz son los momentos de inercia principales correspondientes.
(a) En la figura 7-2, el origen de X,Y,Z
está en el c.m., y el del marco
paralelo, X, Y, Z, está en el punto O. Los
dos marcos se consideran adheridos al
cuerpo.
El momento de inercia, Iz, con
respecto a OZ, por ejemplo, viene dado
P°r ^
h = ^m'(x2 + y*)
Pero x = %i -f- x, etc. Por tanto,
Iz = 2m'[(zi + z)2 + (2/i + £)2]
= 2>'(*2 + 2/2).
+ (¿2 + y2) 2 w
+ 2x 2 w'ii + 2y 2 m'2/i
Como Oí está en el c.m., los dos
últimos términos son iguales a cero. Así,
h = Iz + M(& + y*) F¡g.7.2
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 125
en donde M es la masa total del cuerpo y (x2 + y2)1/2 es la distancia normal entre Z y Z.
(Naturalmente esta relación se aplica a un par de ejes cualesquiera, con la condición
que uno de ellos pase por el c.m. Entonces, por ejemplo, I0a = Io^+Md2, en donde d
es la distancia normal entre Oa y Oíai.)
Por los mismos pasos anteriores se demuestra que el producto de inercia Ixy =
£ m'{xy), viene dado por Ixy = IXiyi + Mxy. Entonces, en general,
l: Ix = Ix + M(y2 + z2), Iy = íy + M(x2 + z2), U = L + M(x2 + y2) (7.12)
V Iry = Iry + Mxy, Ixz = Ixz + Mxz, Iyz = Iyz + Myz {7.13)
Momentos y productos de inercia con respecto a X, Y, Z (Fig. 7-2) en . _ I _
función de cantidades referidas al c.m. > }c " 'K
{b) Por las relaciones {7.2), {7.12) y {7.13) se concluye que el momento de inercia con
respecto a un eje Oa (Fig. 7-2) que pasa por O, está dado por
% loa = [Ix + M(y2 + z2)]l2 + [Iy + M(x2 + z2)]m2 + [L + M(x2 + y2)]n2
■?'' - 2{lxy + Mxy)lm - 2(ÍXZ + Mxz)ln - 2{Iy2 + Myz)mn {7.14)
Momento de inercia de un cuerpo con respecto a una recta cualquiera, Oa
(Fig. 7-2) en función de cantidades referidas al c.m.
Entonces, si se conocen los momentos y los productos de inercia con respecto a un
marco cualquiera con origen en el c.m., de inmediato puede conocerse una expresión
para el momento de inercia con respecto a cualquiera otra recta que se desee.
(c) Partiendo de {7.14), resulta evidente que puede escribirse,
'^ [Ix + M(y2 + z2)]x2 + [/„ + M(x2 + z2)]y2 + [L + M(x2 + y2)]z2
¡ - 2{Ixy + Mxy)xy - 2{ÍXZ + Mxz)xz - 2{Iyz + Myz)yz = 1 {7.15)
El elipsoide de inercia con respecto a O, en función de cantidades referidas
al c.m.
Si X, Y y Z son los ejes principales, Ixy = lxz = Íyz = 0 y las expresiones
anteriores se simplifican en buen grado. Pero como {7.15) todavía contiene productos de
inercia, Ixy = Mxy, etc., resulta evidente que X, y y Z, en general, no son los ejes
principales que pasan por O. Por tanto, los ejes principales que pasan por un punto
arbitrario, en general, no son paralelos a los que pasan por el c.m.
Sin embargo, si O está sobre un eje principal que pasa por el c.m., Zp, por ejemplo,
x = y = 0 y {7.15) se reduce a
1 = (Ix+Mz2)x2 + (IZ + Mz2)y2 + Izz2 {7.16)
con expresiones semejantes para O en un punto cualquiera de Xp o de Yp. Como estas
relaciones no contienen productos de inercia, los ejes principales que pasan por un punto
Xp, Yp o Zp , son paralelos a tales ejes; este es un resultado importante.
Los planos Xp, Yp, etc., se denominan "planos principales" y puede demostrarse
que para cualquier punto sobre ellos, uno de los ejes principales es normal al plano.
Véase el problema 7.19.
7.5 Si se conocen los momentos y productos de inercia (/*j, IxlVv etc.) con respecto
a un marco cualquiera Xi, Y\, Zx, hallar las cantidades correspondientes
(/z2, Ix2y2> etc.) con respecto a cualquier otro marco paralelo X2, Y2, Z2-
En la figura 7-3, los marcos Xx, Yx, Zx y X2, Y2, Z2 son paralelos, pero ninguno
de los dos tiene su origen en el c.m. Una partícula típica m' tiene por coordenadas x\, y\ y
2i y x2,y2 y z2.
126
ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA
[CAP. 7
Zi
x2f
09
/
/
/
*2
-v2-
1
1
' (xuyvzl
C \x2, V2, «2
i™
1
«2
1 x2
1 /
V
c.m
-\*2
vz>h i
1Y2
/ Yj_
Xiy
V
Fig.7-3
Expresando Ux - 2 m>'{v\ + z\), hxVl= ^m'xiyi y empleando las relaciones xx =
*o + x2, etc., se concluye en seguida que
/*! = /*2 + M(y% + z%) + 2M(M2 + z0z2)
(7.17)
IxlVl - Iz2y2 + Mxoyo + M(x0y2 + 2/0*2)
en donde ¿2,2/2 y ¿2 son las coordenadas del c.m. con respecto a X2, Y2, Z2. Para
Iy,,/i.y., etc., se encuentran relaciones similares. (Una forma ligeramente diferente de (7.17)
puede verse en el problema 7.25.)
7.6 Si se conocen hv IXlvíf etc., con respecto a Xi, V"i, Zlt de la fígura 7-4,
hallar Ix, Ixy, etc., con respecto al marco girado X, Y, Z.
Si ai 1, ai2 y ai3 son los cosenos directores de OX, etc., como se indica en la figura
7-4, aplicando (7.2), resulta claro que,
£* 1x = ^«n + V0Í2 + l*Á ~~ 2/xi«ianai2 ~ 2/*i*ianai3 - 2/„1,1a12a13 (7.18)
Momento de inercia /,, relativo al eje X, en función de los momentos y'
productos con respecto al marco girado Xi, Ylt Z,. Con relaciones
exactamente iguales pueden hallarse Iy e Ix.
Con el objeto de determinar los productos de inercia, Ixy por ejemplo, es preciso volver
a la definición Ixy = £ m'xy. Eliminando x y y por medio de las ecuaciones de trasfor-
mación,
X = anX1 + a12yi + a13Zlt y = a2lXx + a22yi + a^
se obtiene
Ixy = 2 ™'Ki#i + «i22/l + «lAÍfal*! + «22^1 + a23*l)
CAP. V] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 127
\ZI
lY
L^- a21»ff22»a23
a/^K~ l, m, n
Coordenadas \
m (Zl.VuZy) \^
^~~~"~~'^ — Cosenos directores \
all»«12»or13 ""
^^X
alt = eos {X, Xx)
a32 = eos (Z, F,)
Xly
Fig.7-4
El lector puede demostrar fácilmente que esta relación se reduce a la primera de (7.19). (Nota.
En este proceso de reducción, para demostrar que
2 W/(«n«2i*J + al2a222/l + "iS0^) = ~(«n«217*l + al2a227Wl + ai3a237*i-)
a la suma se le resta la siguiente cantidad que es igual a cero,
(ana21 + a12a22 + a^a^(x\ + y2 + Z2)
y se agrupan términos.)
7xv = (alia22 + «Al)^, + («H«28 + «l^l)7*!»! + (al2a23 + «w^7»!*!
[i ~ (alla217*, +al2a227«1 + a13a237*, )
gA 7xz = (alla32 + a12a8l)7*i»i + (alla33 + al3a3l)^l + (al2a33 + ^O7^! (7i9)
P ~ («ll^l^x + ai2a327«i + al3a3372l )
■+ 7yz = (a2la32 + ^«Sl)7*!»! + (a2la33 + a3la23)7xl2l + (a22a33 + a23a32)7yl2l
~ (a21a317xi + a22a327V1 + tt23aS37*1)
Productos de inercia con respecto al marco girado X, Y, Z.
Así pues, es posible hallar el momento de inercia con respecto a una recta cualquiera,
Oa, con cosenos directores l, m y n con relación a X, Y y Z en función de Ix1,Ix1yl, por
medio de
loa = hl2 + Ivm2 + Izn2 - 2lmlxv - 2lnlxz - 2mnlyz
y las relaciones (7.18) y (7.19).
Si se suponen conocidos Jx, / etc., para hallar hv IVl, etc., siguiendo el mismo
procedimiento anterior, el lector puede demostrar que
7*! = 7xttn + Vli + 7*a31 ~ 27x„aHa21 ~ 2lzzalla31 ~ 2Iyza2iaZl
(alla22 + al2a2l)7*« + (alla32 + a12a3l)7zz
+ (a2la32 + a22a3l)7yz " (alltt127* + a2la227y + a3la327*)
(7.20)
128 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
Relaciones semejantes existen para Iyl,IzvIxlzvhlzl.
Nota importante. Conocidos los momentos y los productos de inercia con relación a un
marco rectangular cualquiera, mediante la aplicación-de {7.17), {7.18) y {7.19) es posible
determinar las cantidades correspondientes relativas a cualquier otro marco rectangular
localizado y orientado de cualquier manera con respecto al primero. Inclusive el segundo
marco puede tener algún movimiento conocido con respecto al primero.
7.7 Ejemplos de momentos, productos y elipsoides de inercia.
Ejemplo 7.1.
Las ideas físicas y geométricas básicas de los numerales anteriores, pueden aclararse con la consideración
del sencillo "cuerpo rígido" de la figura 7-5, el cual, como se verá, posee todas las propiedades dinámicas de
cualquier cuerpo común, como una rueda, una viga, una silla, etc.
X^ Vi = 12
Fig. 7-5
El sistema está compuesto de tres partículas conectadas rígidamente al eje Z por medio de sendas varillas
delgadas "sin masa". El marco X, Y, Z, junto con las partículas, forma una unidad rígida. Las masas y las
coordenadas de las distintas partículas se encuentran indicadas en la figura.
(a) En primer lugar se determinan los momentos y los productos de inercia, con respecto a X, Y, Z.
Ix = Im^yf+zf) = ml{y\ + ^) + 7n2(¡/* + z*) + m3(y| + z|)
= 100(144 + 25) + 200(64 + 225) + 150(144 + 196) = 125.700g-cm2
Igualmente, Iy = 117.250, It = 104.750.
Ixy = 2™¿(*í¡/í) = 100(12X10) - 200(10X8) + 150(11X14) = 19.100g-cm2
En forma semejante, IZI = - 44.800, Iyz = 4800.
(b) Con los valores anteriores, es posible escribir de inmediato la siguiente expresión para el elipsoide de inercia,
con respecto al origen O.
125.700i2 + 117.250y2 + 104.750z2 — 2(19.100)iy + 2(44.800)iz — 2(4800)yz = 1
cAP. 7 I ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 129
(c) El momento de inercia del "cuerpo", con respecto a un eje cualquiera que pasa por O, como Oa, puede
hallarse como sigue: Un punto p, sobre Oa tiene las coordenadas indicadas, por lo cual, los cosenos directores
de esta recta serán —6/s", 8/s y 20/s, en donde s = V62 + 8a + 202. Es decir, / = —0,268, m = 0,358
y n = 0,895. Y por (7.2),
Iqp = (0,268)2(125.700) + (0,358)2(117.250) + (0.895)2 (104.750)
+ 2(0,268) (0,358) (19.100) — 2(0,268) (0,895) (44.800) — 2 (0,358) (0,895) (4800)
(¿) Considérense los momentos y productos de inercia con respecto a los ejes X, Y y Z (que no aparecen en el
diagrama) paralelos a X, Y y Z, y con origen en el c.m. Por la ecuación (7.12),
Y por (7.13)
lz = Iz-M(& + y2) = 104.750 —450(5,882 + 1.562), etc.
¡xy = Ixy-MSy = 19.100 —450(—5,88 x 1,56), etc.
Así, es posible hallar de inmediato el momento de inercia del cuerpo con relación a una recta cualquiera que
pase por el c.m., así como el elipsoide de inercia respecto a este punto.
(e) Por conocer ya los valores numéricos de Ix, Ixy, etc., aplicando los resultados del numeral 7.4 es posible hallar
en seguida el valor numérico del momento de inercia del cuerpo con respecto a una recta cualquiera en el
espacio. Igualmente puede escribirse inmediatamente la expresión del elipsoide de inercia con relación a un
punto cualquiera en el espacio.
(f) Finalmente, nótese que al aplicar los resultados del numeral 7.3 pueden hallarse los momentos principales
de inercia y las direcciones de los ejes principales correspondientes a O, al c.m., o a cualquier punto del
espacio.
Ejemplo 7.2.
Considérese el triángulo plano delgado (Fig. 7-6) cuyos momentos y productos de inercia relativos a X, Y
y Z pueden obtenerse fácilmente por integración.
lx = %Mb\ ly = \Ma*t Iz = $M(a* + b2), Ixy = ¿íMabt Ixz = Iyz = 0
Fig. 7-6
(a) El elipsoide de inercia con respecto al vértice O es
¿M[62*2 + 02^2 + (a2 + fc2)z2 _ abxy] = l
(b) El momento de inercia con respecto a una recta cualquiera, Oa, no necesariamente en el plano XY, está
dado por
¡oa = ¿M[&2P + ahn? + (a2 + b*)n* - ablm]
en donde l, m y n son los cosenos directores de Oa relativos a X, Y y Z.
130 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
(c) Por (7.12) y (7.13), se encuentra,
h = hMV, íy = hMa*. ¡z = &M(a* + V), Íxy = -&Mab, ¡X2 = ¡yz = 0
Entonces el elipsoide relativo al c.m. es
&M[b*x\ + afiy\ + (a2 + W)z\ + abxlVl] = 1
(d) El momento de inercia del triángulo con relación a una recta cualquiera, O!ai, no necesariamente en el
plano del triángulo, es
foiai = &M[b*l\ + cfor¿\ + (a2 + &2)n2 + abiimi]
(e) Según el numeral 7.3, los momentos de inercia principales con respecto a los ejes que pasan por el c.m., son
C^1 - cw cz
ÍU2 = ¿M(a2 + 62 ± Va4 + fc4_a262)f 11 = I\ + 11 = &M(a* + fc2)
Escribiendo (llt mlt n,), (Z2, m2, n2) y (l3, m3, n3), los cosenos directores de los ejes,principales,
se observa, por (7.10) que n, = n2 = 0, n3 = 1, l3 = m3 = 0 y llt l2, m, y m2 se determinan por
medio de .,
I = -Íxy[Íxy + (/p - 7Z)2] -1/2, m = (/p - ÍX)[PXU + (/p - /x)2] -1/2
Así, para valores conocidos de a, b y M, puede determinarse el ángulo fl, (véase la figura).
(/) El origen de X,, Ylt está localizado en c(xc, >-c) en el plano X, Y (véase el diagrama de la figura 7-6).
Yi forma un ángulo 0 con Y, y Z, y Z son paralelos. Las coordenadas xc y >-c se miden con respecto
a X y Y. Se trata ahora de determinar los momentos y los productos de inercia del triángulo, con relación
a X,, Yi, Z,. Puede observarse que
Ix = ÚMV + My2, íu = ^Ma^ + Mx2, I'X!Í = Mxcyc-i
l'Xz = I'yz = 0, l'z = hM(a,2 + b*) + M(x2c + y2c)
Los cosenos directores de X,, Y, y Z, son
<>ii = cos/3, a12 = sen ¡3, a^ = 0, a2i = — sen/3, a22 = cos/3, «23 = 0, 031 = 032 = 0, a3
Entonces, por las relaciones (7.18) y (7.19), se concluye
7Zi = M(^fc2 + 2/2)cos2/3 + M(ika2 + x2)sen2/3 - 2M(xcyc - &ab) sen/í eos (3
hl = M(¡k&2 + ¡/2) sen2/3 + M(&a* + a;2) cos2/3 + 2M(xcyc - &ab) sen/í cos/3
Ixy = M(xcyc - fóab) eos 2/3 + M(^62 + y2) sen/3 cos/3 - Aí(^a2 + x2) sen/3 cos/3
¡^(a2 + 62) + M(x2 + y2),
^x,z, - A/,*,
(g) Supóngase que los ejes X, y Y, giran de alguna manera determinada alrededor de la posición fija de Z,.
En este caso, (3 varía con el tiempo, y las magnitudes anteriores se hacen funciones del tiempo.
Ejemplo 7.3.
La figura 7-7 representa una lámina delgada que puede haber sido cortada de una hoja de metal o de
madera laminada.
Fig. 7-7
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 131
Suponiendo una densidad superficial de p = 2 g/cm2, se han calculado los siguientes valores relativos
a X, ? Y Z:
íx = 1,61 X 104 g-cm2, Iy = 2,62 X 104, Ix = 4,23 X 104, Ixy = -1,036 X 10", 7Z2 = íy2 = 0 (1)
(a) Los momentos de inercia principales y el ángulo 0, son (véase el numeral 7.3)
Fx = 3,26 X 104, ¡l =0,97 X 104, ÍPZ = 4,23 X 104 (2)
8 = 58° aproximadamente.
(b) El* elipsoide relativo al c.m. puede escribirse en función de uno de los dos conjuntos de valores, (/) o (2); es
decir,
(l,61x2 + 2,62y2 + 4,23z2 + 2 X l,036xiyi)104 = 1 (3)
(3,26x1 + 0,97y| + 4.23Z2. )10< = 1 (4)
en donde ilf y¡ y zx se miden con relación a X,Y,Z, y x2, y¡ y ¿2, con relación a Xv,Yv,Zv.
(c) Nótese que /^ = (3,26*2 + 0,97/4 + 4,23^|)104
o, nuevamente, I0a = (1.61Í2 + 2,62?n2 + 4,23n2 + 2 X lflSBljmúlO*
(5)
(6)
en donde l1( mi y n, corresponden a xlt ylt zx, etc. Las expresiones (5) y (6), desde luego, conducen
al mismo valor para una recta Oa dada.
Ejemplo 7.4.
Considérese el bloque rectangular de la figura
7-8. Se tiene
lx = \M(b* + C*)
/„ = ¿M(a2+C2)
Íz = -¿M(a2 + &2)
ÍXy = Uz = ¡y* = °
(a) Por tanto X, Y y Z son ejes principales, Ix =
/£, etc., y el elipsoide de inercia con relación al
c.m. es ¡1x2 + ¡ly2 + JZZ2 = i.
(b) Fácilmente puede demostrarse que los
momentos y los productos de inercia, relativos a
X, Y y Z, son
Ix =áM(62 + C2)
Iy =4M(a2 + c2)
¡z =fM(a2 + &2)
1^ = Mab Ixz = Mac Iyz = Mbc
El elipsoide con respecto a O puede obtenerse
^de inmediato.
(c) Determínese el momento de inercia con respecto a una recta cualquiera, Oa. La dirección de Oa se determina
por las coordenadas de un punto, p, por ejemplo. Así, los cosenos directores de Oa son,
l = 10/(102 + 92 +132)1/2 = 10/18,7, m = 9/18,7, n = 13/18,7
Entonces, aplicando (7.2),
ha = Úü &«(&* + C2) 102 + $M{a* + C2) 92 + 4M(q2 + &2) 132
- 2Mab X 90 - 2Mac X 130 - 2Mab X 117]
Nótese que es posible usar directamente (7.3), lo cual es quizá más conveniente puesto que no hay que hacer
consideraciones sobre los cosenos directores.
X 1PX= ¿M(6* + c*), 11 = ¿M(a* + c*), 7? = ¿M(a* + 62)
Fig. 7-8
132 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
Ejemplo 7.5.
Considérese el cono sólido uniforme de la figura
7-9. Por integración se determina,
I* = ¡l = &M(4r2 + h*), 11 = ^Mr*,
íxy = hz = hz = 0
(a) Aplicando los resultados del numeral. 7.4, pueden
encontrarse los valores de lx, Ixy, etc., con
respecto a un marco paralelo cualquiera; el momento
de inercia del cono con respecto a una recta
cualquiera de dirección conocida; y naturalmente, el
elipsoide de inercia relativo a un punto
cualquiera. Con relación a los ejes indicados X, Y y Z,
/, = faMiárt + h^ + ^Mh*;
Ixy = 0, etc.
(b) Tomando X, Y, Z paralelo a Xv, Y*>,Zi> pero
con origen en 02,
;4r2 + /i2) + M(r2 + ^2);
i3,AÍ(4r2 + /l2) + J^Mfc2; Iyg
-\Mrh,
I* = h = AM(3r2 + 2fc*)
Fig. 7-9
(c) Aplicando los resultados del numeral 7.6, los valores de Iz, Izy, etc., pueden calcularse con relación a un
marco cualquiera, localizado su origen en cualquier punto en el espacio, y girados sus ejes en cualquier forma
con respecto a Xp,Yp, Z*, por ejemplo. (Véase el siguiente ejemplo.)
Ejemplo 7.6.
En la figura 7-10 se muestra un bloque (ei mismo del ejemplo 7.4) después de un giro. Los ejes X,, Y,
y Zi indican la localización original. Con el fin de aclarar la posición actual, imagínese que el bloque giró en
primer lugar alrededor del eje OZlt un ángulo ^, haciendo que OX permaneciera en el plano X\Yi. Luego
el bloque giró alrededor de OX, formando un ángulo 'e, entre OZ¡ y OZ.
OX permanece en el plano X,Yl
¡v ^- Oh = COB^f, a¡2 = 8«n ií>. Oís = 0
Fig. 7-10
Se trata ahora de determinar los momentos y productos de inercia del bloque con relación al marco X\, Y\,ZX.
Tomando como modelo una caja rectangular, el lector puede comprobar fácilmente que los cosenos directores
de X, Y y Z, son los que se indican en el diagrama.
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 133
Aplicando la ecuación (7.20) y utilizando los valores de lx,lxy, etc., del ejemplo 7.4, se concluye que
IXi = |M[(62 + c2) eos2 ^ + (a2 + c2) sen2 ^ eos2 6 + (a2 + 62) Sen2 ^ sen2 0
+ \áb sen^ eos ^ eos 6 — §ac sen^ eos ^ sen 0 + f&csen2^ sen 0 eos fl]
/ZlWl = Ma6(cos2^ — sen2^) eos* + Maceen2 ^ — eos2 ^) sen e
+ 2Mbc sen ^ eos ^ sen 0 eos B — \M(b2 + c2) sen ^ cos^
+ |AÍ(a2 + c2) sen ^ eos ^ eos2 0 + |AÍ(a2 + 62) sen ,¿ eos ú> sen2 0
En la misma forma pueden obtenerse las expresiones para Iy , Ix x , etc.
Nota. En el caso en que uno de los ángulos ^, 8, o ambos, estén variando de alguna manera determinada;
es posible expresar a Ix , Ix y , etc., en función del tiempo. Los resultados de este ejemplo tienen especial
importancia en el capítulo 8.
Para simplificar, en este ejemplo se ha supuesto que el eje OX permanece en el plano XtYi. Cuando este
no es el caso, puede determinarse la orientación del sistema X, Y, Z por medio de los tres "ángulos de Euler"
8, <t> y ^t cuyo uso se explica en detalle en el próximo capítulo.
7.8 "Focos" y puntos "esféricos" de inercia.
Los resultados siguientes son de gran interés y de marcada importancia práctica. En
la figura 7-11, Xp, Yp y Zp son los ejes principales que pasan por el c.m. Como se demostró
anteriormente, los ejes principales que pasan por un punto cualquiera de Xp, Yv o de Zv son
paralelos a estos ejes. Para el análisis siguiente se supone que Ix > K > Iz.
Fig. 7-11
(a) Considérense los elipsoides de inercia relativos a los puntos pi y pj, los cuales se
encuentran separados del origen a distancias Si = ±[(/z — Il)/M]1/2 .
IXi = Ipxt IWl = fi + Mtt = E + Pz-E = K
En este caso, ÍXl = Iy{, y como Xlt Yx y Zx son los ejes principales que pasan por
plt el elipsoide relativo a este punto será de revolución alrededor de Z\. Así, un corte
del elipsoide en el plano XXYX, es una circunferencia. Una afirmación semejante
puede hacerse también para p[. Los puntos px y p\ se denominan "focos de inercia".
Demuéstrese que sobre Xp existe otro par de puntos focales. Determínense los puntos
focales sobre Yp. ¿Habrá puntos focales sobre Zp1
134 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
(6) En el caso en que K = 11 y II > II, en los puntos pi y p{ sobre Xp, a distancias del
origen s = ±[(H —Il)/M]1'2, se tiene Ix = Iy = Iz = Ix. Entonces el elipsoide relativo a
uno cualquiera de estos puntos será una esfera y p\ y p\ se denominan "puntos
esféricos". ¿Si el elipsoide relativo al c.m. fuera de revolución, existirían siempre puntos
esféricos? (Hállense los puntos esféricos cerca de un disco delgado, uniforme.)
Ejemplo 7.7.
Supóngase, por ejemplo, que en la figura 7-8 (véase el ejemplo 7.4), a > b > c. Por tanto, 7P > /£ > /£.
(a) Tomando los puntos p y p' sobre el eje É?, a distancias 8 = ±[(/P — Iy)/M]1,2t
h = Í% Iy = II+M8* = íl + ÍZ-il = II
Así, un corte del elipsoide relativo a p o a p', en el plano YZ, seré un círculo y p y p' son puntos focales. El
lector podrá hallar otros puntos focales.
(b) Supóngase ahora que b = c y que a < b, es decir, ¡1 = 1% e Ix > í%. Tomando sobre el eje Xv los
puntos a distancias 8 = ±[(í* - I^/M]1'2,
I = V I = íp + íp — 7P = 7P 7 = 7P + fp — V — 7P
■*x 1x> 'y 12/ ~ 1z 12/ lx> lz 1z^lx 1y — lx
En este caso Ix = Iy = Iz = lx siendo, s = ±[$(b2 — a2)]i/2 e 7X = \Mb2. Entonces el momento
de inercia del bloque con respecto a una recta cualquiera que pase por uno de estos puntos será igual a \Mb2.
7.9 Significado físico de los productos de inercia.
Supóngase una lámina delgada, como la indicada en la figura 7-12, que gira con
velocidad angular constante, w, alrededor del eje señalado, sobre los cojinetes fijos jBi y B2-
Cada una de las partículas de la lámina, como m', ejerce una fuerza centrífuga /= m'oj2r
sobre el material que la rodea. (Se desprecia la gravedad.)
Fig. 7-12
Puede obtenerse una apreciación del significado físico y de la importancia de los productos
de inercia al determinar el momento total, r2, de todas las fuerzas centrífugas alrededor
del eje Z, siendo el origen del sistema X, Y, Z enpj. Como puede verse en el diagrama,
en donde, por conveniencia, se toma como positivo el sentido horario. Se observa entonces que
T« = «2/«, + <*2sMV (2)
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 135
Pero IXy = hy + Mxy (/zy se determina con respecto a Xy Y) de donde,
Tz = w2/^ + (jMf)y (3)
La fuerza centrífuga total, F, debida a todas las partículas es, F = ^m'^r = M<a2f. Y
por tanto el segundo término de (3) es igual a Fy, considerando que F actúa en el c.m.
Entonces, el momento total de las fuerzas centrífugas, en sentido horario alrededor de Z,
tz, puede considerarse como debido a un par de fuerzas, üi2Ixy, que actúan en el mismo plano
de la lámina, más el momento Fy, teniendo en cuenta que F actúa en el c.m. Nótese que la
localización depi, el origen de X, Y, Z no afecta el valor del par. Por tanto, es posible
escribir de inmediato el momento alrededor de un eje cualquiera perpendicular a la lámina. Por
ejemplo, alrededor de un eje que pase por p2, t2 = ta2Íxy\ alrededor de un eje que pase por Bx,
tr = cü2/x» + »2MfU, etc.
Con el fin de encontrar las fuerzas Fx y F2 que los cojinetes ejercen sobre el eje,
tomando momentos con respecto a B2, se expresa,
Fiili + k) + Mo>2fl2-Ixyo>2 = 0 o sea, Fi = j^j^l^-Mfk)
Igualmente, F2 = - , " , (Ly + MfU)
(Naturalmente, es posible hallar Fx y F2, escribiendo Fi + F2 + Mro>2 = 0 y tomando
momentos con relación ap2.) Si X y Y son ejes principales, se tiene, Ixy = 0, y Fi y F2
se deben únicamente a la fuerza centrífuga Mu2?, que actúa en el c.m. Si además, el c.m.
está en el eje de giro, Fx = F2 = 0.
El análisis anterior se extenderá más adelante al caso de un cuerpo rígido de una forma
cualquiera y que gira de una manera arbitraria. (Véase el ejemplo 9.7 y el problema 9.17.)
Ejemplo 7.8.
Supóngase que el triángulo de la figura 7-6, está girando con velocidad angular constante, o>, alrededor del
eje Y, sobre cojinetes localizados en O y en 02 (distancia entre cojinetes = b). Hállense las fuerzas de soporte
(sin considerar la gravedad).
Por el ejemplo 7.2, Ixy = —^Mab. Entonces, la fuerza de soporte en O, será
Fx = (o>yb)(%Mab + ¿Mab) = ±*PMa
y la que actúa en 02, F2 = -feu'Ma.
7.10 Cuerpos dinámicamente equivalentes.
Dos o más cuerpos de apariencia completamente diferente y con distintas distribuciones
de sus masas, pueden comportarse exactamente igual cuando sufren la acción de fuerzas
iguales aplicadas en la misma forma. Con claridad se ve que este es el caso cuando sus masas
totales y sus momentos principales de inercia relativos al centro de masa, son iguales. Se dice
que tales cuerpos son "dinámicamente equivalentes". El método general para identificar
estos cuerpos se ilustra por medio de los ejemplos siguientes.
Ejemplo 7.9.
(a) Supóngase que los pares de partículas de igual masa, de la figura 7-13(1), se hallan adheridas a un marco rígido
sin masa, como se indica. Evidentemente, los ejes X, Y y Z son ejes principales que pasan por el c.m., y el
elipsoide de inercia relativo a este punto será,
(2m2&2 + 2m3c2)x2 + (2m1a2 + 2m3c2)y2 + (2mia2 + 2m*íb2)z2 = 1
Los valores de m,, m2 y m3 y las distancias a, b y c pueden seleccionarse por el procedimiento
siguiente de modo que el sistema resulte dinámicamente equivalente a un cuerpo dado.
Considérese un objeto cualquiera con momentos de inercia principales relativos al c.m., /J,/J e /£,
y masa total M. Es evidente que si los valores de m,, m2 y m3, así como a, b y c, satisfacen las reía-
136
ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA
(CAP. 7
ciones 2(m, + m2 + m3) = M, Ix = 2(m2b2 + m3c2), etc., el sistema indicado en la figura será
dinámicamente equivalente al otro cuerpo.
*/ p
Cuatro partículas dinámicamente iguales al triángulo.
Cinco partículas dinámicamente equivalentes a la lámin
(3)
Esqueleto inercial
Con valores adecuados para /,, l2. h
y M, es dinámicamente equivalente a
un cuerpo rígido cualquiera.
Fig.7-13
= m3 = M/6 y despejando los valores de a, b y c.
'2, etc.
Una fácil solución se obtiene haciendo m, = m2 =
En este caso se obtiene, a = [(3/2M)(/J + H - ÍVX)Y>
(b) Puede demostrarse que las cuatro partículas de la figura 7-13(2) son dinámicamente equivalentes al triángulo
delgado uniforme. Asimismo, las cinco partículas de la figura 7-13(3) son dinámicamente equivalentes al
rectángulo.
(c) En todos los casos es posible demostrar que el "esqueleto inercial" de la figura 7-13(4), consistente en tres
varillas delgadas perpendiculares entre sí, unidas rígidamente en O, es dinámicamente equivalente a cualquier
otro cuerpo rígido.
7.11 Determinación experimental de los momentos y los productos de inercia.
La determinación experimental de momentos y productos de inercia es sencilla, y
tomando algunas precauciones razonables se pueden obtener resultados bastante precisos. Esta
es la única forma práctica de determinar estas cantidades para cuerpos de forma irregular.
Si se conocen los momentos y los productos de inercia relativos a los ejes con origen en
el c.m., es posible calcular en seguida las cantidades correspondientes con relación a
cualquier otro sistema de ejes. Así pues, por esta razón, se enuncia brevemente un método
experimental para determinar estos valores relativos al centro de masa.
(a) Tómense dos o más puntos, cualesquiera, sobre el cuerpo y suspéndalo de un hilo sujeto
primero a uno de estos puntos y luego al otro. Naturalmente, el c.m. estará localizado
en la intersección de las líneas de suspensión. Así, se puede ahora seleccionar un sistema
de ejes rectangulares, X,Y,Z, con origen en el c.m.
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 137
L
(5) Habiendo hecho esto, sujétese el cuerpo a
un marco de soporte, F, de un péndulo de
torsión, como el de la figura 7-14, de
modo que el eje Z, por ejemplo, coincida con
el eje de oscilación del péndulo. Con la
ayuda de un buen cronómetro,
determínese el período de oscilación, P. Como
puede demostrarse con facilidad, P =
2ir}/(Iz + If)/c en donde Iz e If son los
momentos de inercia del cuerpo y del
marco, respectivamente, con respecto al
eje de oscilación, y c es la constante de
torsión debida a las cuerdas de piano,
superior e inferior. (Los valores de If y
c pueden determinarse usando, en lugar
del cuerpo irregular, otro de momento de
inercia calculable a partir de sus
dimensiones y de su masa, como una varilla
uniforme.) Así, Iz = P2c/4-k2 - 7r Y en
forma semejante pueden determinarse
Ix e Iy.
(c) Habiendo seleccionado otros tres ejes, Op
cosenos directores (¿i, mi, ni, etc.
/op3. Pero
IoPl = hl\ + lym\ + lzn\ - 2ÍXylmi — ZLzlini — 2Íyznimi
ly- Cuerda de piano
^ Constante de
Fig. 7-14
Opo, y Opz (que pasan por el c.m.) cuyos
se conocen, determínense los valores de Iopx, Iop2,
etc.
Con los valores de Ix,Iy e Iz previamente determinados, se pueden solucionar estas
ecuaciones para hallar Ixy,Íxz e Iyz.
Si por conveniencia se toma Opi en el plano XY a 45° de cada eje, lx = mx = 0,707
y nx = 0. Por tanto, Iopx = 0,5(ÍX + Iy)-Ixy o finalmente, lxy = 0,5 (Ix + Iv) -IoPl.
En la misma forma pueden hallarse Ixz e Iyz ■
7.12 Proyecto sugerido sobre el elipsoide de inercia.
Este proyecto, así como el siguiente experimento sugerido, tiende a dar al lector una
mayor confianza sobre la teoría y una sensación de tangible familiaridad con el contenido del
capítulo.
Se cortan dos hojas de madera
laminada de dimensiones adecuadas y se
pegan sólidamente formando ángulos rectos,
como se indica en la figura 7-15.
Suponiendo una densidad superficial de unos
10 g/cm2, calcúlese el valor de Ix, Iy
e lz para el sistema de "tableros planos".
Demuéstrese que Ixy = lIZ = Iyz = 0 y
por tanto, que X, Y y Z son ejes
principales. Exprésese una ecuación para el
elipsoide relativo al c.m. En la relación Is2 =
c, tómese c igual a una constante
adecuada y trácense a escala las secciones del elip-
Fig.7-15
138 ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [ CAP. 7
soide relativo al c.m. en los planos XY y YZ, así como en el plano XZ (en una lámina de
cartón intercalada). Mídase la distancia s desde el c.m. a un punto cualquiera del elipsoide y
compare el valor de c/s2 así medido, con el calculado para 7, con relación a esta recta de
orientación conocida.
¿Qué cambios se introducirán en el elipsoide, si se pega al modelo una partícula de
masa m, en un punto comop? Trácese una sección del elipsoide para este caso.
7.13 Experimento sugerido.
Determinación del elipsoide de inercia
de una lámina delgada.
El marco ab, del péndulo de torsión de
la figura 7-16, consiste en dos tiras planas
metálicas separadas sólo por unos pocos
milímetros. Una lámina delgada de
cualquier forma, cortada en madera laminada,
se asegura entre las tiras por medio del
perno B, que pasa horizontalmente a
través de las tiras y la lámina, en el punto
Pi. La lámina puede ser colocada en
cualquier posición angular con respecto al eje
de giro, moviéndola alrededor de B.
Siguiendo el método descrito en el
numeral 7.11, se determinan los momentos
de inercia con respecto a varias rectas que
pasan por el centro del perno, y que están
espaciadas regularmente, por ejemplo a 15°,
entre 0 y 180°. Con esta información y
usando la relación Is2 =-c puede trazarse
una sección del elipsoide de inercia «i, sobre la lámina. Tomando algunas precauciones
razonables, se obtiene una elipse sorprendentemente buena.
Utilizando la información anterior, calcule y trace una elipse, «2, relativa a otro punto,
p2. (Este proceso será menos pesado si la primera elipse es relativa al c.m.) Repitiendo el
proceso experimental del primer caso, con B enp2, compárense los resultados calculados con
los experimentales.
Este interesante e instructivo experimento le da un significado real al "elipsoide de
inercia", a los "ejes principales", etc. Siempre deja una impresión perdurable en el estudiante
que lo realiza.
Cuerda de piano
Fig. 7-16
Problemas
(a) La recta Oa de la figura 7-17, forma un ángulo e = 30° con Z. Demostrar que I0a = -feMR2.
(b) Las coordenadas de un punto sobre la recta Oa' (que no aparece en el dibujo), son x = 5, y = 4 y
2 = 6 cm. Demostrar que I0a> = ^MR2.
CAP. 7) ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 139
Z"
8
rJi
^*
30°
_ ..
/c
Ia
Z
<VJ
s/*\
>^ ^ l,mtn
Yv
Y
M
7X = /„ = JM«2, 7, = IMR?
Fig. 7-17
(a) Obtener por integración, expresiones para Ix,Iy,lz e Ixy (Fig. 7-6).
(b) Las coordenadas de un punto sobre la recta Oa son x = 4, y = 5 y z = 1 cm. Demostrar que
loa = 6^o [1662 + 25a2 + 49(a2 + 62) _ 20a6]
Demostrar que el momento de inercia de un cuerpo con respecto a una recta cualquiera que cruza el
origen, está dado por
¡Oa = Cx*2 + hV2 + 7**2 - 2Ix«*V ~ 2/«*Z - Iyzyz)(x2 + 2/2 + Z2)~ 1
en donde x, y y z son las coordenadas de un punto cualquiera sobre Oa.
Demostrar que el momento de inercia del bloque de la figura 7-8, con relación a la recta Oa', viene dado por
¡Oa' = ^[f (62 + C2)*'2 + f(a2 + 02)^2 + l(a2 + &2)(4c2)
- 2abx'y' - 4ac2x' - AbeV][*'2 + y'2 + 4c2]-1
(a) Una recta Oa (que no aparece en el esquema) pasa por O, en la.figura 7-9, formando un ángulo 0
con OZ. Demostrar que
loa = [&Mh* + &M(4r2 + h2)] sen2 8 + -^Mr2 eos2 ff
(b) Una recta paralela a Oa pasa por el cm. Demostrar que el momento de inercia con relación a esta
recta es ffiM(4r2 + h2) sen2 8 + &Mr2 eos2 0.
(a) Una recta be forma un ángulo 0 con Zp. Demostrar que
7bc = \Mr2 eos 6 + {\MR2 + Ms2) sen2 e
(b) Demostrar que el momento de inercia con respecto a 0\ax, es
/ojoj = QMR2 + My2)l2 + (±MR2)m2 + ($MR2 + My2)n2
7.7. Escribir una expresión para el momento de inercia del bloque de la figura 7-8, con relación a una recta
de cosenos directores l, m y n, y que pasa por el punto x0,y0,z0. (Tanto l, m y n, como x0,y0,z0
se miden con respecto a Xv, YV,ZV.) La recta no cruza necesariamente el cm.
ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
Demostrar que para un cuerpo rígido cualquiera, el momento de inercia con respecto a una recta que
pasa por los puntos ihyi,2| y X2.y2.z2. medidos con relación a X,Y,Z (que no son
necesariamente ejes principales) es
2(íyz + My±z±)
(í/2-í/l)(«2-2l)
en donde «2 = (x2 - xj* + (y2 - y& + {z2 - ztf.
Escribir una expresión para el elipsoide de inercia relativo a un punto sobre la periferia del disco de la
figura 7-17.
Escribir una expresión para el elipsoide de inercia relativo al punto p, (x0,;yo, zo). de la figura 7-18.
/*=/* = ^M&R* + IA), ¡1= \MR*
Fig. 7-18
Con referencia a la figura 7-7, demostrar que el ángulo 8 = 58°.
Si el bloque de la figura 7-8 tiene M = 1000 g, a = 3 cm, b = 5 cm y c = 5 cm, determinar los valores
numéricos de los momentos de inercia principales con respecto al punto px. Por medio de las ecuaciones
(7.10), determinar dos conjuntos de cosenos directores para los ejes principales del elipsoide de inercia
relativo a p{. Demostrar además, que estos conjuntos son equivalentes.
Considerando una lámina delgada de cualquier forma, tómense como ejes de referencia X, Y y Z, de
tal manera que X y Y estén en el plano de la lámina, y el origen en un punto cualquiera p. Tomando
Ix, Iy,Ix e Izy con relación a estos ejes, probar que los momentos de inercia principales l\, /£ e
/g con respecto a los ejes principales X?, Y? y Z?, respectivamente, son
T.2
*['.± 4
i;-WxIy-rxy)],
£ = /, + /„
Demostrar que Z? (correspondiente a 1$) es normal a la lámina y que el ángulo 0 que X? forma
con X, viene dado por
Iy-Il
o sea, tan o =
Con referencia a la figura 7-5, calcular los momentos de inercia principales y hallar las direcciones de los
ejes principales, para un punto pi, localizado en x = 5 cm, y = 4 y 2 = 0, con respecto a X, Y y Z.
Demostrar que el elipsoide de inercia relativo a p2 de la figura 7-18, está dado por,
1 = [J^^B* + U) + ¿AfL2](x2 + Z2) + QMR*)y2
y que los ejes principales en p2, son paralelos a X^,YV,ZP.
CAP. 7] ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA 14]
7.16. Demostrar que el momento de inercia es igual para todos los ejes que pasan bien por O o porpí, en la
figura 7-19; es decir, que pi y O son puntos esféricos. Comprobar esto por los métodos del numeral 7.8.
p2. en el plano YZ
Hemisferio sólido uniforme
/, = /„ = /« = $«**
Fig. 7-19
Demostrar que el momento de inercia con respecto a una línea de cosenos directores l, m y n, que pasa
por p2 (Fig. 7-19), está dado por
/ = ¿jMJ?2[(24 - 15 sen 8)l2 + (4 + 20 sen2 e - 15 sen e)m2
+ (4 + 20 eos2 e)n2 — 10(sen* eos 8 - § eos B)mn]
Con referencia a la figura 7-18, demostrar que
(a) para L = i?V3T el elipsoide de inercia relativo al c.m. es una esfera para la cual /= \MR2.
(b) para L = R existen puntos esféricos sobre el eje Yp, en puntos que distan ±R/VG~del origen. Se
tiene aquí que /= \ MR2 con respecto a cualquier eje que cruce estos puntos.
(c) para L > JíVcTexisten puntos focales sobre los ejes XV y Z", localizados en» = ±\(ÍX ~ ¡y)/M.
(d) para valores muy pequeños de L, existen puntos esféricos sobre Y* a distancias ±é^. del origen.
¿Existirán puntos esféricos o focales, sobre Zp?
Considérese una recta paralela al eje principal Zp que atraviesa el c.m. de un cuerpo cualquiera. Probar
que esta recta es un eje principal de un elipsoide trazado con respecto al punto en que corta el "plano
principal", X* Y*>. Demostrar que
tan 20
2Mxy
(21 + M&) - (Fx + M&)
en donde <¡> es el ángulo entre X* y Xp. Naturalmente, estos resultados generales son igualmente
válidos para rectas normales al plano X? Z*> o a Yp Zp.
7.20. Considérese una lámina rectangular de dimensiones 2a X 26, y masa Ai. Trazar los ejes Xp, Fp y Zv
que pasan por el c.m., con X? paralelo a a, y Z" perpendicular a la superficie.
Considérese otro marco Xít Y1,Zl que tiene origen en el c.m., con Zp y Zj coincidentes, pero Xx
según una diagonal del rectángulo. Se tiene en este caso, /£ = \Mb2 e íy = jAía2. Demostrar que
7.21. En la figura 7-20 se indican los valores de Ix , etc., para la lámina triangular indicada. Probar que:
B + Iy.sen2B - 2/Zi„ sen* eos tf
h2 = hx eos2
Iy2 = IXlsen2B + JWicos2* + 2/ZiWi sen8 eos 8
h2y2 = íxlWl(cos2 8 - sen2 8) + (íXl - IVl) sen* eos 8
142
ESTUDIO GENERAL DE LOS MOMENTOS Y LOS PRODUCTOS DE INERCIA [CAP. 7
|£j*i
Fig. 7-20
7.22. La lámina triangular de la figura 7-20 gira alrededor del eje indicado sobre los cojinetes fijos Bx y B2,
con velocidad angular constante, w. Demostrar que el par originado por las fuerzas centrífugas es
C = o>2[&Mh(2c - a) eos 2e + fgM(s* -cs + c*- h?) sen e eos 6)
Determinar las fuerzas de sustentación Ft y F2, despreciando la gravedad.
7.23. (a) Probar que las cuatro partículas de la figura 7-13(2) son dinámicamente equivalentes al triángulo
uniforme.
(fc>) Diseñar un esqueleto inercial que sea dinámicamente equivalente al hemisferio de la figura 7-19.
Supóngase que se remplaza el cuerpo rígido de la figura 8-16, por el cono de la figura 7-9. Con el vértice
fijo en el origen, el cono puede moverse alrededor de este punto, con libertad. El marco X, Y, Z se
encuentra adherido al cono con su eje en la dirección de Z. Demostrar que Ix , el momento de inercia
del cono con relación al eje fijo X,, está dado por
hx = &M[r* + h* - (4fc2 - r2) sen2 esen2 *]
Comprobar esto para el caso en que 0=0 y ^ = 0, y para e = ^ = 90°. Escribir la expresión de IXiyi-
(Véase el numeral 8.8. Nótese que los cosenos directores de X, Y y Z, con respecto a X,, V, y Zlt
aparecen en la tabla 8.2, en función de los ángulos de Euler.)
El estudiante debe observar que las expresiones anteriores son válidas para cualquier posición del
cono, independientemente de la manera como se encuentre girando o moviéndose. Si se conoce el
movimiento, es posible expresar Ix , /x.y,» etc-> en función del tiempo.
Para un caso más general que el anterior, supóngase que los ejes X, Y y Z, de la figura 8-16, son ejes
principales que pasan por O, de un cuerpo cualquiera de forma semejante a la indicada en el esquema.
Los momentos de inercia correspondientes son /£, /£ e /£.
Demostrar que los momentos y los productos de inercia, con respecto a los ejes fiios Xl,Y1 y Z,,
vienen dados por
Ix = /£(cos <t> eos ^ — sen 0 sen $ cos 9)2 "*" fu(sen# eos ^ + eos $ sen ^ eos e)2 + 1% sen2 0 sen2 ^, etc.
Estudio de la dinámica de los
cuerpos rígidos, de Lagrange
Dinámica de los cuerpos rígidos: Parte II
8.1 Observaciones preliminares.
Un "cuerpo rígido" es aquel en el cual ninguna parte de su masa sufre cambios de
posición con respecto a las demás partes, independientemente de las fuerzas a que esté sometido.
Estrictamente hablando, tales objetos no existen, pero, naturalmente, en la práctica existe un
extenso campo de la dinámica en el que se justifica suponer esta condición como medio para
lograr importantes simplificaciones.
Básicamente no existe ninguna diferencia entre la dinámica de los cuerpos rígidos y la
de las partículas, ya que un cuerpo rígido puede ser considerado como un conjunto de un gran
número de partículas, restringidas a permanecer a distancias fijas entre sí. La principal razón
para estudiar la dinámica de los cuerpos rígidos como una fase aparte, dentro del tema
general, radica en la existencia de algunas técnicas especiales que se requieren para expresar
adecuadamente el valor de T.
Para plantear las ecuaciones del movimiento, usualmente se emplea uno de los dos
métodos siguientes:
(a) El método de Lagrange (estudiado en este capítulo) en el cual, luego de hallar una
expresión adecuada para T, se emplean las ecuaciones de Lagrange de la manera usual.
(6) El método de Euler (tratado en el capítulo siguiente) en el que se aplican directamente
las ecuaciones de Euler para traslación y rotación del cuerpo, sin necesidad de considerar T.
Que uno de estos dos métodos resulte más adecuado que el otro, depende del problema
entre máTios, pero en general, el de Lagrange tiene muchas ventajas: Mayor simplicidad,
facilidad de escribir las ecuaciones del movimiento, eliminación de las fuerzas de restricción
y posibilidad de aplicación directa en cualquier sistema de coordenadas y para cualquier
número de cuerpos rígidos.
El dominio de los principios básicos y de las técnicas de la dinámica de los cuerpos
rígidos supone la clara comprensión de, (a) los fundamentos básicos estudiados en el numeral
8.2, (6) la deducción de T dada en el numeral 8.3, y (c) los diferentes ejemplos que se
incluyen. Pero (a), (6) y (c) no son unidades independientes; la completa apreciación de (a)
requiere la comprension.de (6) y de (c), etc. Por tanto se necesita releer con atención y con
cuidado las diferentes secciones.
8.2 Fundamentos básicos necesarios.
A. La velocidad angular como magnitud vectorial.
Con referencia a la figura 8-1, supóngase que el cuerpo fijo en O, puede girar
libremente alrededor de este punto. Todas las cantidades aquí consideradas se supondrán medidas
con respecto al marco X, Y, Z. Así, por el momento no se discute el hecho de que este marco
sea o no inercial. Si en un instante determinado el cuerpo tiene una velocidad angular w,
alrededor de una recta, como Oa, la partícula m tendrá una velocidad v, normal al plano
Oam', de magnitud v = wh, en donde h es la distancia normal de m' al eje de rotación Oa.
143
144 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Se demostrará ahora que la velocidad angular puede ser considerada como un vector, o>,
dirigido según Oa, y de magnitud igual a su valor absoluto. Es decir que » puede ser
remplazado por sus componentes, «x, ü>y y ü>2, según las direcciones de X, Y y Z, y puede
además ser tratado como vector en todos los casos. Como se verá con claridad, esto es de
capital importancia en el estudio de la dinámica de los cuerpos rígidos.
anormal al plano Oam')
Un punto del cuerpo está adherido a O. • —
velocidad angular del cuerpo, v - velocidad lineal
de m'; ambas medidas con respecto a X, V, Z.
u,, u, y u, y vM, vy y v, son las
componentes de • y v, según X, Y y Z. v, - uyz - uMy, etc.
Fig.8-1
Las componentes de v, según X, Y y Z, pueden expresarse como
Vx = Va1 — <¿hcclt Vy — <aha2 y Vx = wha3 V (1)
en donde ai, a2 y 03 son los cosenos directores de v (cosenos directores de una recta
normal al plano Oam') que, como el estudiante puede demostrar (véase el problema 8.1) son,
(nx - lz)/h y
(ly — mx)/h
(8.0)
«x = (mz-ny)/h, a2
en donde x, y y 2 son las coordenadas de m', y l, m y n son los cosenos directores de Oa
Entonces, por (i),
etc.
(2)
vx = rawz — nwy,
Si se considera o como un vector en la dirección de Oa, nw será su componente según Y, wy.
Igualmente, nu> = wz, etc., y se escribe,
vx = «„* — «*!/» vy = vjc-ujt y vz = <¿xy - <¿yx (8.1)
Expresiones válidas para vx, vy y vz (y por tanto, para v) pueden así obtenerse,
tratando la velocidad angular como un vector, o , según la dirección de Oa, cuyo sentido se
determina por la regla de la mano derecha. (En notación vectorial, las relaciones (8.1) son
equivalentes a v = w X r. Véase el capítulo 18.)
Las relaciones (8.1) tienen una interpretación física y geométrica muy clara, que puede
expresarse como sigue: Como puede verse en la figura, la velocidad angular alrededor de X, ux,
le da a m' una velocidad uxz, en la dirección negativa de Y. Igualmente, wzx es una
velocidad en la dirección positiva. Por tanto, uy = wzx — uxz, etc.
Como resultado de lo anterior, se concluye que:
(a) Un número cualquiera de velocidades angulares, ult»2,«3, alrededor de ejes que pasen
por 0, pueden sumarse vectorialmente para producir una resultante, © = o1 + *»2 + »3,
cuya magnitud es w = (wx + wj + u>2z)in y cuya dirección está dada por los cosenos ojx/o
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 145
etc., en donde, a>x = wlx + w2x + üj3i, etc. (Para otra prueba de lo anterior, véase el
problema 8.2.)
(b) La componente de <* según la dirección de una recta cualquiera, Ob, (que no aparece en el
dibujo) viene dada por
<o0b = wl + <*ym + wzn (8.2)
en este caso l, m y n son los cosenos directores de Ob.
Obsérvese que las velocidades no se pueden expresar como wx = 6V <ay = 62, <*z = 03 en donde
8i,62 y 63 representan rotaciones angulares finitas alrededor de X, Y y Z,
respectivamente. La orientación final de un cuerpo, luego de tales rotaciones, no es única, puesto que
depende del orden en que se lleven a cabo. (El lector puede observar esto al experimentar con
una caja, por ejemplo.) Sin embargo, es posible expresar wxt wy y ü>2 en función de
"coordenadas verdaderas" como, por ejemplo, los ángulos de Euler y sus derivadas con respecto
al tiempo. En lo que sigue se incluyen numerosos ejemplos que ilustran lo expresado.
B. Velocidad de m' en el espacio inercial. Figura 8-2. Cuerpo bajo traslación y
rotación. El marco X, Y, Z, girando alrededor de O, con relación al cuerpo.
Se supone que el cuerpo de la figirsa 8-2 está girando y trasladándose en el espacio.
El marco X, Y, Z, con su origen adherido al cuerpo en O, puede estar girando de una
manera arbitraria con respecto al cuerpo. Los ejes X', Y' y Z' con su origen también fijo en 0,
permanecen paralelos a los inerciales X\,Y\ y Z\. Las coordenadas de m\ x, y, z y
x',y', z' se toman con relación a X, Y, Z y X', Y', Z', respectivamente.
*i
Sistema inercial
Fig. 8-2
X, Y y Z no están adheridos al cuerpo eicepto en O. X', Y'
y Z' permanecen paralelos a Xt. Yt y Z,. m - velocidad
angular del cuerpo, u — velocidad lineal de m\ ambas
relativas a X; Y'yZ'. w'x,u'y yu^y w¿,u¿ y u, aon las
componentes de • y u en las direcciones de X'.Y' y Z'. aM, u,
y u, son las componentes de • en las direcciones
instantáneas de X. Y y Z. v es la velocidad de m' en el espacio
inercial. v,,v, y v, son las componentes de v en las
direcciones instantáneas de X, Y y Z.
Se supone que m es la velocidad angular del cuerpo y u es la velocidad lineal de m',
ambas medidas con respecto a X', Y' y \Z'. Las componentes de *» y u según las direcciones
de estos ejes, se indican por ^,wy yu;y u'x,u'y y u'z, respectivamente. Entonces, según (8.1)
se tiene, u'x — wyz' — <a'zy', etc. Llamando ux,uy y uz a las componentes de u en las
direcciones instantáneas de X, Y, y Z, puede escribirse ux = u'xan + uya12 + u'zaiv etc., en
146 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
donde an,ai2 y ai3 son los cosenos directores deX con respecto a X', Y' y Z' (los mismos
que con relación a Xi, Yi y Z\). Por tanto,
u* = ("F'-<*'zy')«il + (<*F'-<*'x*')«l2+ «v'-<*F')«i3
Eliminando a x', y' y 2' por medio de x' = xaw + ;ya2i + za3i, etc., se concluye de
inmediato (se dejan los detalles al lector; véase el apéndice) que
ux = *yz - ozy en donde <oy = o>>xa21 + o>ya22 + «^
Y esta componente es igual a la de « en la dirección de y. Igualmente, wz es la componente
de o» en la dirección de Z, etc.
Suponiendo ahora que O lleva una velocidad vo en el espacio inercial, con componentes
ü0l, v0y y v0z en las direcciones instantáneas de X, y y Z, las componentes vx, vy
y uz de la velocidad en el espacio inercial de m', en las direcciones de esos mismos ejes,
pueden expresarse como
Vx = V0: + V " «zV* Vy = V0y + <*zX ~ »xZ> Vz = V0z + »XV " »,* ■ (8.3)
C. Resumen de aspectos importantes relacionados con (8.3).
El significado completo y la importancia de estas relaciones pueden aclararse al
considerar las afirmaciones que siguen, así como con el estudio de los ejemplos que más adelante
se incluyen.
(a) Como se supuso en la deducción de (8.3), el origen O debe estar adherido a un punto
(cualquiera) del cuerpo.
(b) Como se ve claramente en la deducción, las relaciones (8.3) son válidas aunque el marco
X, Y, Z (con el origen fijo en O) pueda estar girando con respecto al cuerpo. Naturalmente
este marco puede también estar "fijo al cuerpo" (sujeto rígidamente al cuerpo de modo
que participe de todos sus movimientos). En el primer caso x, y y 2 son variables y en
el segundo, constantes. En la práctica, casi siempre se emplean ejes fijos al cuerpo.
(c) Es preciso expresar uox,uoy y vqz de tal modo que den las componentes de vo, la
velocidad en el espacio inercial de O (figura 8-2) en las direcciones instantáneas de X,
Y y Z (los ejemplos demostrarán cómo puede hacerse esto).
(d) Para una localización determinada de O, vox, v0y y vqz son iguales para cualquier
partícula considerada (independientemente de los valores de x, y y 2). Por tanto, vo
representa una velocidad lineal para todo el cuerpo.
(e) En general, la magnitud y dirección de vo depende de la localización de O. Por ejemplo,
imagínese un cuerpo fijo en el espacio en un punto p. Ubicando a O en p, u0x = voy =
v0z = 0. Pero esto no es cierto para otra localización cualquiera de O.
(/) Teniendo en cuenta los problemas de dinámica que siguen, la velocidad angular total
del cuerpo, m, se mide siempre con respecto a un marco inercial, o, lo que es lo mismo,
con respecto a unos ejes como X', Y' y Z', que no se encuentren girando (Figura 8-2).
(g) Las componentes a>x, coy y ü>2 se expresan de tal modo que representan las
componentes de o según las direcciones instantáneas de X, Y y Z. (Véanse los ejemplos.)
(h) Independientemente de la localización de O en el cuerpo, «* tiene siempre la misma
magnitud y dirección. Como se ve con claridad en la deducción de (8.3), para cualquier
localización de O, » se considera siempre orientado en la misma dirección de la recta Oa,
que pasa por O. Esto quiere decir que el vector puede desplazarse sin cambios en la
dirección o en la magnitud, de un origen a otro cualquiera, en el cuerpo. (Véase el problema 8.3.)
(i) A medida que el cuerpo se mueve en el espacio bajo la acción de ciertas fuerzas, a y vo
en general cambiarán en magnitud y en dirección. Por otra parte, sus direcciones no son
invariables con relación al cuerpo.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 147
(j) Las ecuaciones (8.3) son la base para expresar en forma general la energía cinética de
un cuerpo rígido. (Véase el numeral 8.3.)
D. Componentes de la velocidad de una partícula libre en el espacio inercial,
en las direcciones instantáneas de un sistema de ejes móviles.
Aunque las relaciones que siguen, (8.4), son muy útiles en ciertos problemas de partículas,
en realidad no se requieren en forma inmediata. A pesar de esto, este es el lugar más
apropiado para su deducción.
Considérese inercial el sistema X\,Y\,Z\ de la figura 8-3. Supóngase que el marco
X, Y, Z se está desplazando y girando de una manera completamente arbitraria (como si
estuviera adherido a la proa de un bote que se balancea, cabecea, se mueve en "zigzag", y
avanza, por ejemplo). La velocidad angular del marco X, Y, Z con relación a Xi, Y\,Z\,
del marco X. Y, Z con respecto
(Igual que con respecto a X\ V. Z'.)
v, - i>o, + x + tlyz - n^y, etc. u. es la componente
de la velocidad de m' en el espacio inercial. según la dirección
instantánea de X. La componente vox, puede expresarse
por medio de v0z = x0alt + 3/o°i2 + ro<*i3. etc. El marco
X, Y. Z gira alrededor de O y se desplaza de una manera
arbitraria. Los ejes X', Y' y Z' permanecen paralelos a X¡,
Y, y Z|, respectivamente.
Fig. 8-3
(o a X', V, Z') se indica por O, con componentes, ííx, Üy y Qx en las direcciones
instantáneas de X, Y y Z, respectivamente. Se toma v0 como la velocidad de O en el
espacio inercial, con componentes u0x, u0y y v0x, según las direcciones de X, Y y Z,
respectivamente. Las coordenadas de una partícula (que no forma parte de un cuerpo rígido) son
*i»;yi y z\ con relación a Xi, Y\ y Z\, y x, y y z con respecto a X, Y y Z. La
velocidad de m' en el espacio inercial se indica por v, con componentes vx, vy, vz según las
direcciones instantáneas de X, Y y Z. A continuación se obtendrán en una forma descriptiva,
pero muy significativa las expresiones para vx, vy y vz.
En primer lugar, supóngase que la partícula m' se halla en el punto p(x, y, z), fija al
marco X, Y, Z. Según las ecuaciones (8.3), vx = vqx + Üyz — ü2y, etc. Pero si ahora se
considera que m' está libre y posee una velocidad cuyas componentes con respecto a X, Y y
Z, son x,y y z (x,y y z han sido medidas por un observador que se mueve con el marco
X, Y, Z); la expresión anterior para vx, así como las correspondientes a uy y vx se escriben
- ClzV,
v0y + y + QzX - íixz, y vz = Voz + z + íixy — íiyx (8.4)
fc> Vx = Vox + X + ClyZ -
Una deducción directa, aunque algo pesada, de (8.4), puede obtenerse como se sugiere
en el problema 8.9. (Véase el ejemplo 8.2.)
148 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
E. Ejemplos ilustrativos del estudio de la velocidad angular de un cuerpo
y de la velocidad lineal de una partícula típica.
Ejemplo 8.1.
El marco que sostiene el cuerpo rígido de la figura 8-4, puede girar alrededor de un eje vertical A0lt con
velocidad angular ¿. Simultáneamente el cuerpo puede girar alrededor de un eje, apoyado en los cojinetes Bt
y B2, con una velocidad angular ¿. Este eje forma un ángulo 6 con la vertical, permanentemente. El ángulo \¡>
se mide como se indica y ^ se toma a partir de la recta ab (véase el esquema auxiliar) que permanece horizontal
y en el mismo plano del corte indicado.
La velocidad angular total, «*, del cuerpo será, evidentemente, igual a la suma vectorial de ¿ y ¿,
independientemente del lugar donde se hayan tomado los ejes X, Y y Z. A continuación se consideran las componentes
de c» y la velocidad lineal de una partícula típica, para diversas localizaciones del marco X, Y, Z.
(a) Se toman los ejes X, Y y Z fijos al cuerpo, según se indica, con el origen O, en la intersección de la vertical
AO\ con el eje BtB2. Se traza el vector ¿ según la dirección de Z, y el vector ¿ en la dirección de la
vertical AO. Las componentes de «* en las direcciones de X, Y y Z (que para esta posición de X, Y y Z se
representan por «„, uay y uat) se obtienen tomando componentes de j> y ¿en las direcciones de X,
Y y Z. Así, . . . .
«« = $ sene sen<t>, «ov = ^ sen0costf> y «„ = </> + ^ cos0 (1)
Fig.8-4
Nótese que estas componentes siguen las direcciones dadas por las posiciones "instantáneas" de X,Y y Z.
Es decir, que las relaciones (1) se han expresado de tal manera que representen «ox, uoy y w„ para
una posición cualquiera de estos ejes (suponiendo que están fijos en el cuerpo, según se dijo) con respecto al
marco Xlt Yit Z\.
Habiendo localizado a O en la forma expresada, la velocidad de O en el espacio inercial, v0, será
igual a cero. Así pues, u0x = v0y = v0z = 0. Entonces, las componentes de la velocidad de m' en el
espacio inercial, en las direcciones instantáneas de X, Y y Z, son [véanse las expresiones (8.3)]
vx = ¿z sen e eos <f> — (<f> + $ eos e)y
vy — (4> + ¿ eos 6)x — \¡/Z sen 6 sen </> (2)
vz — ¿y sen e sen <f> — ¿x sen 6 eos </>
en donde 1,y y z son las coordenadas de m'.
(b) Supóngase ahora que el origen del sistema X, Y, Z se toma enp,, y que los tres ejes permanecen paralelos
a su posición anterior. Naturalmente, la velocidad angular total no varía. Al desplazar a ¿ a una dirección
vertical que pase por px, y al tomar componentes de f y f se obtienen exactamente las mismas
expresiones (/) nuevamente (puesto que el marco es ahora paralelo a su orientación anterior).
. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 149
Pero en este caso, uo = $1 sen 6 (l es la distancia Opi) y su dirección es la de la recta Ob en el
esquema auxiliar. Por tanto, las componentes de la velocidad de pt (el nuevo origen) en el espacio inercial, según
las direcciones instantáneas de X, Y y Z, son
^ox = ¿ísenffcos^, v0y = — ¿l sene sen<p, v0z = 0 (3)
(Nótese que a partir de (2) se puede obtener (3), directamente, haciendo z = l y x = y = 0. Esta técnica
resulta importante en muchos problemas.) Entonces, las componentes de la velocidad de m' en el espacio
inercial, según las direcciones de los ejes en sus nuevas posiciones, son
vx = $1 sen 8 eos </> + [¿z sen 0 eos </> — (# + ¿ eos 6)y]
vy = — $1 senff sen </> + [(¿ + ¿ eos 6)x — ^z sen* sentf»] (4)
i>z = W sen * sen <f> — ¿x sen e eos <p
donde x, y y z se miden con relación a X, Y y Z en sus nuevas posiciones. El lector puede demostrar que
(2) y (4) expresan los mismos valores.
Es importante comprender perfectamente el significado de vx, vy y vz. Supóngase un observador
que situado en la base A, mide la velocidad de m' con respecto al sistema X\,Y\,Z\. Así, vx, vy y
vz, según (4), indican las componentes de v en las direcciones de los ejes fijos al cuerpo, X, Y y Z,
respectivamente, en las posiciones que ocupan en el instante mismo en que el observador hace la medición.
Considérese el origen del marco fijo al cuerpo, X, Y, Z, en p2 (un punto cualquiera del cuerpo) con los ejes
paralelos a sus orientaciones en (a). Las direcciones de ^ y ^ se trasladan de las posiciones indicadas en la
figura 8-4, a rectas paralelas que pasen por p2. Resulta así evidente que «cx, ucy y «„ son iguales
a «on woy y w„, respectivamente.
Una manera adecuada de hallar u0x, u0v y u0l para este caso, es como sigue: Se toman las
coordenadas de p2 con respecto a X, Y, Z, en la posición de (a), como x2,y2 y Z2- Aplicando (2),
üoi viene dado por
v0x = ¿z2 sen e eos <f> — (<f> + f eos e)y2
y similarmente para u0y y u0l. (Desde luego, es posible obtener estas componentes por medio de
ecuaciones de trasformación adecuadas.) Entonces, el valor de ux, para el caso (c), viene dado por,
vx = ¿z2 sen e eos </> — (<f> + ¿ eos 9)y2 + [í* sen * eos <f> — (<f> + ¿ eos 6)y] (5)
En forma similar pueden obtenerse las expresiones correspondientes a vy y vt. Las coordenadas x, y y z,
en (5), se miden con relación al marco X, Y, Z en la posición correspondiente a (c). Nótese que las relaciones
correspondientes a (5) expresan los mismos valores para ux, uy y vz que los que se obtienen por medio de (2).
Supóngase ahora que conservando el origen en p2, el marco X, Y, Z posee una orientación cualquiera con
respecto al cuerpo, de modo que el eje X tiene cosenos directores an,ai2 y «u, con relación al mismo
marco X, Y, Z, en su orientación de (a), etc. Las componentes, «dx, udy y «dI, de «», en este caso se
expresan,
«di = «oz«ii + uay«i2 + fcWi3» etc. (6)
Llamando u0x, u0y y u0l, las componentes de la velocidad de p2 en el espacio inercial, en las
direcciones instantáneas de X, Y y Z, la expresión de u0x, será
W0i = «Oz«ll + V0yal2 + v0*«13» etC- (7)
A partir de (6) y (7) pueden expresarse de inmediato las componentes uoz,u0y y u0¡ de la velocidad
de m' en el espacio inercial. Nótese que para una orientación cualquiera del marco correspondiente a (d), con
relación a X, Y, Z en (a), se deben conocer los valores de an, ai2, an, etc. Lo anterior merece un estudio
cuidadoso.
Considérense los ejes estacionarios X', Y' y Z', paralelos a Xt, Vi, y Zx pero con el origen en O. Se observa
que las componentes de m en las direcciones de estos ejes, son
(¿i = ^senffeos^, uy = 4>senffsen<p, <¿'z = ¿ + ¿ eos 6 (8)
En este caso v0 = 0. Así, las componentes de la velocidad de m' en el espacio inercial, según estos ejes fijos,
serán, v'x = 4>z' sen 8 sen 4> — (¿ + $ eos e)y', etc., en donde x',y' y z' son las coordenadas de m', con
respecto a X', Y', Z'. A medida que el cuerpo se mueve, estas coordenadas cambian de valor.
Nota. Las componentes de m en las direcciones de Xi,Yt y Zx, indicadas en la figura, serán
iguales a las expresadas por (S), quedando 0\ en reposo. Las componentes de la velocidad de m' en el
espacio inercial, según las direcciones de X\, Y\ y Z\, ¿estarán dadas por v\x = ^Xj sen 6 sen <t> —
150 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
(4, + </> eos 0)1/1, etc.? Aquí, xi.yi
Z,. (Véase el numeral 8.2C(a).)
son las coordenadas de m' con respecto al marco Xlt Ylt
Ejemplo 8.2.
El disco D, de la figura 8-5, puede girar libremente alrededor del eje be, con velocidad angular <f>, en donde <t>
se mide con respecto al eje, según lo señala el indicador p2. Simultáneamente, el soporte ab puede girar con
velocidad angular ^, en donde ^ es el ángulo entre el plano fijo XXZ\ y el giratorio abe.
La velocidad angular total de D, •, es igual a la suma vectorial de $ y ¿. Desplazando ¿ a O, y tomando
componentes en las direcciones de los ejes .fijos X, Y y Z, se observa que, como en ejemplo 8.1,
ux — ¿ sentf sentf», ' «w = ¿sen* eos £ y az = <p + ^cos8 (1)
En forma semejante, las componentes «ix, uiy y uiz, según los ejes fijos, son
ulz = ¿ + $ eos 6
ulx = $ sentf cosf, uly = ¿senffsen^
La magnitud de la velocidad angular total de D, viene dada por
(0 = (u| + Jy + (o|)"2 = («o^ + «4 + ^,,2 = (¿2 + ¿2 + 2¿¿ cos fl)i/2
(2)
(3)
í
La dirección de m con respecto a los ejes móviles X, Y y Z, está determinada por los cosenos directores, l, m y n,
en donde .
tSen'.Sfn* , ete. (8.5)
(<p2 + t* + 2w cos *)1/2
Plano del disco
= ¿ sen» eos*
= ¿ + ¿ cos 0
Fig. 8-5
Igualmente, los cosenos directores li,m\ y ni de o, con respecto a Xi Y\ Z\, son
$ sen g cos ^
(¿2 + ¿2 + 2¿¿ eos *)1/2 '
etc.
Las componentes de la velocidad de una partícula típica de D, en el espacio inercial, con relación a los ejes
X, Y y Z, se obtienen de la manera indicada en el ejemplo 8.1(b).
Como ilustración sobre el uso de las ecuaciones (8.4), supóngase que el movimiento de una partícula libre
(que no forma parte de D), de masa m, y sujeta a la acción de una fuerza externa f, se ha expresado con relación
al marco X, Y, Z, de la figura 8-5. Aplicando (8.4) se observa que la componente vx, de la velocidad de m en el
espacio inercial, según la dirección de X (véanse las expresiones (4) del ejemplo 8.1), están dadas por
vx = x + $8 sen* cos </> + [¿2 sen B cos £ — y(<P + ¿ cos 9)]
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 151
con expresiones semejantes para vy y vz. Al aplicar las ecuaciones de Lagrange a T = tyn(v\ + vy + vz),
se obtienen las ecuaciones del movimiento deseadas.
Ejemplo 8.3.
Los discos D\,D2 y D3 están montados, uno sobre otro, como se muestra en la figura 8-6. Los ángulos
81,82 y 03 se miden con relación a A, B y C, respectivamente, según lo señalan los indicadores pi,p-i
y p3. Las velocidades, 6lt92 y 83, consideradas como vectores, se indican por medio de las flechas adecuadas.
Concentraremos la atención en D3. Se desplazan 8, y 82 al origen O, según se indica, y la velocidad angular
total de D2, », es igual a la suma vectorial » = 0X + 82 + 83. El lector puede demostrar, de inmediato, que
las componentes de a según los ejes fijos al cuerpo, X, Y y Z, son (véase el diagrama auxiliar a la derecha),
ux = (*i COS a + 52 COS Z3) sen *3» "y = (*i COS a + 02 COS/3) COS 03 y u, = 6Z + *i sen a + 82 sen/3 (1)
Considerando una partícula típica m', en D, con coordenadas x, y y z con respecto al marco X, Y, Z, las
componentes de la velocidad de m' en el espacio inercial según estos mismos ejes, serán vx = v0z + wv2 — ««y»
etc., en donde v0x, v0y y v0t son, desde luego, las componentes de la velocidad O en el espacio inercial,
según X, Y, Z. Las expresiones para v0z, etc., en este caso, resultan algo complicadas, pero pueden hallarse sin
dificultad mayor. (Véase el problema 8.12(c).)
Se observa que las componentes de «* en las direcciones de los ejes Xit Vi y Z\, son
uix = [*2 sen(/3 — a) + 03 eos a] eos 0lt coly = [b2 sen(/J — a) + 03 eos a] sen01?
ulr = Bi + $2 cos (P ~ °) + ez sen a
La magnitud y la dirección de « puede hallarse tal como se hizo en el ejemplo 8.2.
(2)
Fig. 8-6
Como ejercicios adicionales relacionados con el manejo de la velocidad angular, el lector
puede comprobar las expresiones de wxtay y ü>2 dadas en el ejemplo 8.13, o las
ecuaciones (8.11).
F. El torque como magnitud vectorial.
Para demostrar la naturaleza vectorial del torque se procede de la siguiente manera:
Supóngase que una fuerza F(/x, fy, fz) actúa sobre el cuerpo de la figura 8-7, en el punto
P(x, y, z). El torque r ejercido por tal fuerza, con respecto a una recta cualquiera, Oa, cuyos
cosenos directores son l, my n, y que se supone pasa por el origen, se define como r = F'h, en
donde h es la distancia normal que va desde p hasta Oa, y F' es la componente de F perpen-
152 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
dicular al plano Oap. Por otra parte, F' = fxa\ + fya2 + /zc*3, en donde ai, a2 y a3
son los cosenos directores de la normal mencionada y vienen dados por (8.0). Remplazando
F', introduciendo las expresiones de las a y sumando todas las fuerzas que actúan sobre el
cuerpo, se obtiene la siguiente expresión para el torque total con respecto a Oa,
'oa = 12 (fzy - /„*) + ™ 2 (/x* - f,x) +«S (fy* - fxv) (8.6)
Fig.8-7
Por la definición original de torque (o por una inspección directa de la figura 8-7) se observa
que 52 Uzy — fyz) es el torque que el conjunto de todas las fuerzas ejerce con respecto
a X, etc. Es decir,
rx = Z(fzy-fyZ), ry = ^(fxZ-fzX)f rg = 2 (/„ * " /x 2/) (8.7)
Por tanto, puede escribirse, r0a = tz¿ 4- rym + rzn (8.8)
en donde puede notarse que T¿a es la componente de un vector t, compuesto por tx, ry
y rz, según se ha expresado en (8.7). La magnitud de t está dada por t = (tx + t* + t£)1/2 y
su orientación por tz/t, etc. Es necesario tener en cuenta que en (8.7), x, y y z son las
coordenadas del punto de aplicación de cada una de las fuerzas. Obsérvese que el análisis anterior
del torque, en notación vectorial, es equivalente a
T = £rxF = i?(fzV-fyz) + 3 2 (/,*-/,*) + k2(/y* ~ fxV)
(Véase el capítulo 18.)
8.3 Expresión general de la energía cinética de un cuerpo rígido libre.
Según la interpretación del numeral 8.2 C, las ecuaciones (8.3) expresan las componentes
de la velocidad de una partícula cualquiera de un cuerpo rígido (Figura 8-2) en el espacio
inercial. Así, la expresión general de T, se obtiene remplazando estas relaciones en T ==
£ 2 m'(vl + vl + VD' Agrupando términos,
T = m(v\x + v\y + vi) + Wx 2 m'd/2 + z2) + Wy 2 m'(x2 + 2/2)
+ wz 2 wfa2 + y2) - <*x<*y 2 m'xv - v, 2 m'xz - <•>„<•>* 2 m'yz ¡g g)
+ vox(wv 2 w'z -<ítS m'y) + v0y(ü>22 w'z _ ">x 2 m'z)
+ V0z(°>X 2 m'2/ ~ "y 2 W'Z)
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 153
lo cual evidentemente toma la forma,
■^ t = iMK + WA + iA + iA - %., - 2/wa - 2WJ (8. ,0)
v, + M[vJ»j - »,y) + vj^x - »,!) + vj«xy -«./)
Expresión general de la energía cinética de un cuerpo rígido.
8.4 Resumen de algunas consideraciones importantes con relación a T.
(a) Como ya se ha dicho, <» es la velocidad angular del cuerpo, con respecto al espacio inercial,
y vo es la velocidad lineal de O, también en el espacio inercial. Las componentes de o
y vo, en las direcciones instantáneas de X, Y, Z, se expresan por ü>z, u>y y co2 y
fOx^Oy y voz, respectivamente, y deben escribirse en función de coordenadas
específicas. Como se demostrará en los ejemplos, no es difícil expresar estas magnitudes de
manera que se satisfagan los requisitos mencionados, independientemente de la
orientación del marco X, Y, Z. Tanto Ix, Ixy, etc., como x,y y z, se han de determinar
con relación al marco X, Y, Z (Fig. 8-2).
(b) Habiendo determinado wx, Ix, vox, etc., como se indicó, la expresión (8.10) es válida
para el caso en que X, Y, Z esté fijo al cuerpo o para cuando esté girando con relación al
cuerpo, alrededor de O, de una manera cualquiera. Esto incluye el caso en que X, Y, Z
tenga una orientación fija. Sin embargo, debe recordarse que O se ha supuesto adherido
al cuerpo.
(c) En el caso en que X, Y, Z pueda girar con respecto al cuerpo, los valores de x, y y z,
en (8.9), serán naturalmente variables. Entonces, tanto lx,Ixy, etc., como x,y y z
habrán de variar con el movimiento. Como es de esperarse esto introduce complicaciones,
pero si se desea utilizar este tipo de marco (lo cual sucede rara vez) las dificultades no
son insalvables. (Véase el numeral 8.9, ejemplo 8.19.)
(d) Si se considera el marco X, Y, Z fijo al cuerpo, Ix, Ixy, etc., y x,y y z son constantes.
Por esto, los ejes fijos al cuerpo se emplean en casi todos los casos, pero de todas formas
es preciso tener en cuenta las afirmaciones hechas en (a). (Véanse los problemas 7.24
y 7.25.)
(e) Con ciertas condiciones, que se encuentran con frecuencia, aunque no siempre son
convenientes, la expresión (8.10) puede ser simplificada notablemente. Si O está en el centro
de masa, x = y = z = 0 y el último término de (8.10) se hace igual a cero. Nótese que
esto es correcto aun en el caso en que X, Y, Z no esté rígidamente adherido al cuerpo
(excepto en el punto O). Si un punto cualquiera del cuerpo se halla fijo a un marco
inercial, y O se encuentra en ese punto; vox = voy = voz = 0 y en este caso, tanto el
último como el primer término, se anulan. Si por ejemplo, O se encuentra en el centro
de masa y los ejes fijos al cuerpo, X, Y y Z se han orientado de modo que coincidan con
los ejes principales de inercia,
T = tMvim. + w>i + K»i + 7>*2)
donde /£, I* e I* son constantes.
(/) Al lector le puede parecer que el sencillo principio básico de la energía cinética se ha
perdido por completo de vista en la enorme expresión (8.10). Sin embargo, resulta
evidente en la deducción de (8.9) que T, según (8.10), básicamente es igual a £ ^m'v2.
8.5 Planteamiento de las ecuaciones del movimiento.
Como se vio anteriormente, una vez que se ha expresado T [relación (8.10)] en
función del número de coordenadas adecuadas, se obtienen las ecuaciones del movimiento del
cuerpo rígido de la manera acostumbrada, por medio de la aplicación de las ecuaciones de
Lagrange. Puede decirse lo mismo para un sistema de cuerpos.
154 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE ' [CAP. 8
Naturalmente es posible que existan restricciones. En este caso deben eliminarse las
coordenadas superfluas de T, tal como se ha indicado en los capítulos anteriores. (Se supone
aquí que se está tratando con sistemas holónomos. Véase el numeral 9.12.) Un cuerpo rígido
libre tiene seis grados de libertad. Así, para c cuerpos, n = 6c — (grados de restricción).
(Véase el numeral 2.4.)
Las fuerzas generalizadas no presentan ninguna dificultad; su significado es el mismo
que tienen en la dinámica de las partículas y el procedimiento básico para obtener expresiones
de FQr es el mismo que se describió en el numeral 4.5.
Los ejemplos siguientes sobre grados de libertad (g.l.) pueden ser de utilidad.
Un cuerpo completamente libre, g.l. = 6; un punto restringido a moverse en un plano, g.l. = 5; dos puntos
encerrados en un plano, g.l. = 4; un punto fijo en el espacio, g.l. = 3; tres puntos cualesquiera, no colineales,
sujetos a un plano, g.l. = 3; el giroscopio de la figura 8-18, g.l. = 3; la figura 8-12, suponiendo que el disco puede
deslizarse a lo largo de ab, g.l. = 3; el disco de la figura 8-12, fijo al eje, g.l. = 2; el disco de la figura 8-13, que
rueda sin resbalar sobre el plano rugoso X\Y\, con una unión esférica en p. g.l. = 1; dos puntos cualesquiera
de un cuerpo rígido fijo en el espacio, g.l. = 1; el péndulo de cuerpo rígido de la figura 8-19, con r constante,
g.l. = 5; el sistema de la figura 8-14, completo, con el bloque B libre de deslizarse sobre el plano XiYi, g.l. = 5;
el sistema de la figura 8-15, completo, con el bloque A libre de deslizarse sobre el plano XiYi, g.l. = 6; las masas
de la figura 8-20, g.l. = 9; dos cuerpos conectados por resortes, libres de moverse en el espacio, g.l. = 12. Debe
recordarse que la presencia de cualquier tipo de fuerzas, diferentes de las de restricción, no altera el número de
grados de libertad.
Nota. En el estudio de los cuerpos rígidos, pueden encontrarse dificultades al tratar de
visualizar los ángulos y el movimiento en el espacio. La solución a este problema es un modelo
sencillo.
8.6 Ejemplos ilustrativos de la energía cinética y las ecuaciones
del movimiento.
En todos los ejemplos que siguen se han empleado ejes fijos al cuerpo. En general, este es
el procedimiento más conveniente. El uso de ejes de "dirección fija" se ilustra en el
numeral 8.9.
Ejemplo 8.4.
En la figura 8-8 se muestran tres representaciones de un péndulo físico, que consiste en una lámina articulada
en p, que puede oscilar en un plano vertical hasta un ángulo B. Para entender mejor (8.10) se consideran las
expresiones de T correspondientes a tres localizaciones diferentes de los ejes fijos al cuerpo.
(1) Suponiendo los ejes X, Y y Z localizados como se indica en (a), con Z normal al dibujo, se observa que
ux = uy = 0 y ü), = e. Como el origen es estacionario, u0x = v0y = u0z = 0. Por tanto, (8.10) se reduce
a T — XIZ62, como podría esperarse teniendo en cuenta consideraciones elementales.
(2) En (b) el origen está en el c.m. Nuevamente se tiene, wx = wy = 0 y «, = ¿. En este caso, u0x = U,
v ov = v o, = 0 y 2 = y = z = 0. Por tanto, T = $MPff2 + \ÍZ6*.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 155
(3) En el caso (c) los ejes están orientados de una manera más general. Como en el caso anterior, «x = «v = 0
y w2 = o. Pero, u0x = rff cosa, v0y = —rO sena, v0z = 0 y xy y tienen los valores indicados. Por tanto,
T = \Mr2e2 + \lz"e2 - MreHi sena + y cosa)
y aquí, /2 se ha tomado con respecto al eje Z en la posición indicada.
El lector puede demostrar que las expresiones de T en (2) y (3), se reducen a la dada en (1). Nótese
que It, al aparecer en (1), (2) y (3), indica diferentes cantidades.
La ecuación del movimiento se halla aplicando la ecuación de Lagrange a cualquiera de las formas de T.
En cualquier caso, Fg = — Mgl seno.
Ejemplo 8.5.
La lámina de la figura 8-9 puede moverse libremente en el plano XXY\ bajo la acción de las fuerzas
conocidas Ft y F2.
Fig.8-9
(a) Los ejes X, Y y Z se hallan adheridos a la lámina con el origen O en un punto cualquiera. Grados de libertad
(g.l.) = 3. Se toman como coordenadas adecuadas x, y y 8. Se tiene en este caso, wx = a>y = 0 y wz = 8.
Se observa además que v0z = x cos8 + y sen 8, v0y = y eos 8 — x sen 8 y v0l = 0. (Nótese que v0x
y uoy son las componentes de la velocidad de O, tomadas en las direcciones instantáneas de X y Y,
respectivamente.) Por tanto, (8.10) conduce a
T = $M(x2 + y2) + $IZ62 + Me[(y* - xy) eos 6 - (xx + yy) sene] U)
de donde pueden obtenerse inmediatamente las ecuaciones del movimiento correspondientes a x, y y 8.
Por ejemplo, la ecuación para 0 será,
Iz'é + M[(y x — xy) eose — (icá + "y y) sen e] = Fe
Llamando xlty[ y x^y^, las coordenadas de los puntos de aplicación de las fuerzas Fx y F2, con relación
al sistema X, Y,
Fe = tb = flyxí - flxy[ + f2yx¿ - f2xyí
donde flz y fly son las componentes de F\, según Xy Y, etc.
Nótese que las fuerzas generalizadas correspondientes a x y a >-, son Fx = fiz + f2z y Fy = fly + f2y-
(b) Resulta interesante e instructivo determinar T directamente por medio de la evaluación de la integral
T = IJ" (3+ #)**' (2)
donde dm' es un elemento de masa de coordenadas xx,y\ con relación al marco Xx, Y\. Se tiene entonces,
xx = x + xm eos 6 — ym sen e, yx = y + xm sen B + ym eos 6 (3)
donde xm,ym son las coordenadas de dm' con relación a X, Y. Tomando la derivada de (3),
remplazando en (2) e integrando, se obtiene (/). (Tómese dm'= Pdxmdym; p = densidad superficial uniforme.)
(c) La expresión (/) para T, y las ecuaciones del movimiento correspondientes, resultan algo complicadas. Sin
embargo, si se localiza O en el centro de masa, * = y = z = 0 y
T = $M(x* + y2) + $lx82
156 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Por tanto, las ecuaciones del movimiento se simplifican en gran parte. Las fuerzas generalizadas se obtienen
como en (a).
Ejemplo 8.6.
La lámina de la figura 8-10(1) se encuentra suspendida por un hilo de longitud constante r, y puede oscilar
en el plano vertical, como un "péndulo doble".
Y/////////////,
Fig.8-10
(a) Tomando los ejes fijos al cuerpo, X, Y y Z, según se indica, las coordenadas adecuadas seleccionadas
serán 0 y <t>- Se ve que ux = uy = 0, ux = ¿, {ux ^ B + <f>) y v0 = r9. Las componentes v0z y v0y
de v0, se toman en las direcciones de X y Y. Entonces, v0x = re sen (<t> - 6) y v0y = re eos (<t> - 0).
Así pues, . . . .
T = $Mr2e2 + \lz<¡>2 + Mre<f>[x eos (<f> - e) - y sen(<6 - e)]
de donde se obtienen las ecuaciones del movimiento en forma inmediata. Las expresiones para Fe y Fq se
hallan de la manera acostumbrada, teniendo en cuenta que Mg actúa en el c.m.
(b) A manera de variación del problema anterior, supóngase que el punto O de la lámina puede deslizarse
libremente a lo largo de la línea parabólica lisa, >-i = bx2, como se ilustra en la figura 8-10(2). En este caso se
observa, . .
vl = (¿i + Vi)» ""oí = xi sen<P - Vi eos<P> v0y = *i eos^ + 2/i sen^>
y además, T = $M(x2 + y2) + £/2¿2 + MÍ[£{xx eos </> + yx sen¿) - y{xx sen <f> - Vi eos ^)]
Es posible eliminar, por ejemplo, yu por medio de yt = 2bx1xi y así, determinar las ecuaciones del
movimiento correspondientes a x\ y 4>, en forma inmediata.
Ejemplo 8.7.
Una varilla delgada, de masa P por unidad de longitud, y longitud total L, puede girar hasta un ángulo 02,
alrededor de un eje horizontal sobre el cojinete en O, como se indica en la figura 8-11. Este cojinete está adherido
al brazo horizontal AB. Determinar, por integración directa, la energía cinética de la varilla y comparar el resultado
con el que se obtiene al aplicar la relación (8.10).
4«i M/
- Z j c.m. = y -,
I
R V-H //y
ux = ~"•»• «y = *i eos «a, uz = »¡ sen #2
Con respecto a los ejes fijos al cueipo, X. Y y Z.
u*, = —»tsen*if «y, = ¿2C0B*i» ue. = ¿1
Con respecto a los ejes fijos en el espacio. X,,Yt y Z,.
Fig.8-11
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 157
1 f
Como puede observarse, la ecuación que define la energía cinética, T = — I v2 dm puede escribirse,
T = | J [(R + l sen e2)*e\ + P%]p di
o sea, T = ±R*e\ f pdl + %e\ sen2 e2 f PP di + Rt¡[ sen e2 \ pldl + £«* \ PP di
4o cual, por simple inspección, puede ponerse en la forma,
T = \MR?e\ + $IZ8¡ sen2 e2 + MyRe\sene2 + \1¿>\
El lector puede demostrar que la aplicación adecuada de (8.10) conduce a la misma expresión de T.
Ejemplo 8.8.
En la figura 8-12, el disco uniforme D puede girar con velocidad angular ¿, con respecto al marco de soporte.
Simultáneamente, el marco gira con velocidad angular ¿, alrededor del eje vertical, midiéndose el ángulo yí-,
entre Vi y el plano cOa. Para hallar T para el disco, se toman los ejes fijos al cuerpo, X, Y y Z, con origen O
en el c.m. Se tiene entonces, £ = y = z = 0. Como el c.m. está en reposo, v0x = voy = voz = 0. Al observar
las dos figuras se concluye que
ux = ¿senffsen^, uy = ¿senffcos^, az = ¿ + ¿costf
Nótese que Ix = Iy y Izy = IZ1 = Iyz = 0. Por tanto,
T = ¿J^senZ* + £/z(¿ + ¿ eos e)*
Si el marco (cuyo momento de inercia es If) debe tenerse en cuenta, sencillamente se añade el término -J//^2-
Para cualquier sistema de fuerzas que se encuentren, es posible escribir ahora las ecuaciones del movimiento.
\Zi
= ¿ sen e cob Q
= í> + ¿ eos e
Fig. 8-12
Ejemplo 8.9.
Considerar nuevamente el disco D de la figura 8-12. Por razones pedagógicas se toman los ejes fijos al
cuerpo, X, Y y Z, paralelos a los indicados, pero con el origen en Oí. (Ot está en el centro del eje, a una
distancia / de O.) En este caso ux, wy y ux son iguales a los valores que tenían en el caso anterior, y
* = y = 0, z = +1, v0x = — lyf, sen 0 eos </>, v0y = l¿ sen$ sen <f>
Ixv =-- hz = ¡y* •= 0» ¡x = h> Jz = L
158 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Por tanto,
T = £M*Vsen2* + |/z¿»sen2* + ¿72(¿ + ¿ eos*)2 - MPJ¿sen*9
donde Ix se toma con respecto a X en su nueva posición. El lector puede demostrar que esta expresión se reduce
de inmediato a la del ejemplo 8.8. Las ecuaciones del movimiento se encuentran en seguida.
Naturalmente el origen del sistema fijo al cuerpo puede localizarse en cualquier punto de éste, y los ejes pueden
tener cualquier orientación. Sin embargo, resulta claro que ciertas localizaciones y orientaciones son más
convenientes que otras.
Ejemplo 8.10.
Supóngase que en la figura 8-12 se ha remplazado el disco por un cuerpo rígido de forma arbitraria. Se toman
los ejes fijos al cuerpo, X, Y y Z, tal como se muestra en la figura. Se supone además que el c.m. no coincide con
el origen y que X, Y y Z no son ejes principales.
(a) Como v0 = 0, tanto el primero como el último término de {8.10) se anulan a pesar de que el c.m. no esté
localizado en O. Por tanto,
T = £[/x¿2sen2 0 sen2 0 + 7w¿2sen2 0 cos2 0 + /z(¿ + ¿ Cos *)2]
— [Ixyt2 sen2 8 sen<p costf» + /Z2(¿ sen* se . <f>)($ + ¿ cosff) + /yz(¿sen e cos#)(¿ + ¿ eos 6)]
(b) A manera de extensión del ejemplo, se toman los ejes fijos al cuerpo, Xp, Yp y Zp (con el origen en O), en
las direcciones de los ejes principales de inercia del cuerpo. Sean on, a 12 y «13, los cosenos directores
de Xp con relación a X, Y y Z, etc. Los productos de inercia se anulan pero se necesita conocer las
componentes de « (wi,w2,w3), en las direcciones de XP,YP y Zp que son
Ui = (¿ sen 6 sen </>)an + (¿ sen e eos </>)a12 + (<f> + ¿ cosff)a13, etc.
Finalmente puede escribirse, T = £[/x"i + Iy<¿2 + ^z"!]
(c) Como demostración adicional de los principios básicos, considérense los ejes fijos al cuerpo, X', Y' y Z\
orientados en forma arbitraria, y con el origen O' localizado en cualquier punto del cuerpo. Sean x, y y z las
coordenadas de O' con relación a los ejes X, Y y Z representados en la figura. Los cosenos directores de X'
con respecto a X, Y y Z se representan por /Su, 0i2 y 0i3, etc.
Las componentes de v0-, la velocidad de O' con respecto a Xi, Vi y Zt, en las direcciones de
X, Y y Z, serán
vx = uyz - uzy, vy = uzx - uzz, y vz = uxy - uyx
Por tanto, v%' = v\ + vi + v2. U)
Las componentes de \0>, según las direcciones de X', Y' y Z', son
vo'x = vxfin + vyfiít + vzfils, etc. (2)
Y las componentes de «* en las direcciones de estos mismos ejes, vienen dadas por
«í = «x0ii + u„/3i2 + «z/3i3» etc. (3)
Así pues, al remplazar (/), (2) y (3), junto con los valores dados de £,y y z, así como los de l'x,l'IV,
etc., en (8.10), se obtiene T.
Ejemplo 8.11.
El disco pesado de la figura 8-13 puede rodar sin resbalar, en contacto con el plano rugoso XtYi. Si se
toman los ejes fijos al cuerpo, X, Y y Z, con el origen en O, y con Z en la misma dirección del eje Oc (no se indican
las direcciones de X y Y), se observa que
uz = ¿ sen e sen <f>, uy = ¿ sen B eos <f>, uz = <t> + ¿ eos 0
tal como en la figura 8-5. En este caso, 8= constante, senfl = ri/r3, cos0 = r2/ri y r3^ = -r2<t>. Por
tanto,
. rx . rx . r2
ui = ^ — sen <f>, (o = $ — eos <f>, y u2 = -^
r3 ^3 ^2r3
Además, como Ix = Iy, e lxy = /„ = Iyi = 0 (se mide ^ desde Yt hasta la proyección de OZ sobre el
plano X,y,) o „ o
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 159
de donde se puede obtener la siguiente ecuación del movimiento
— IIX + IZ— \y¡, = -Mgl sene sen*
para lo cual se ha supuesto que el plano XtYi está inclinado un ángulo « con V, siguiendo la dirección de
la inclinación, y ^ medido desde Vi hasta la proyección de Z en el plano XiYi. Véase el experimento sugerido,
al final del capítulo. Véase además el análisis de este mismo problema según el método de Euler, en el ejemplo 9.6.
Por último, véase el ejemplo 12.5.
= if> sen I sen £
= ¿ sen # cob #
= ¿ + £ cob e
'Xx
V///////////////////////////////7//////////////////////,
La punta de la varilla permanece en O, en tanto que el disco D,
rueda sin resbalar, en contacto con el plano X|V,. Los ejes X.
Y y Z eatán fijos al cuerpo y tienen el origen en O. (No se indican
i Y.)
Fig. 8-13
Ejemplo 8.12.
La masa Mi de la figura 8-14, puede deslizarse y girar libremente con respecto a la varilla ab, la cual está
rígidamente adherida al bloque B. Este último bloque puede deslizarse en contacto con el plano XXYX. A
continuación se indican, esquemáticamente, las etapas para hallar la energía cinética T del sistema, en función de las
coordenadas X\,y\,r,6\ y 02-
Fig.8-14
Se toman los ejes fijos al cuerpo, X, Y y Z, para.Mi. Los cosenos directores de X, con relación a los ejes
inerciales Xlt Yt y Zlt se representan por m,, ai2 y «13, etc. En la figura se observa
ux = *i cos/J sen 62, «y = *i cos/J cos02> az = °\ sen/J + 02
donde B\ es la posición angular de B con relación a Xt, y 62 se mide con respecto a la varilla. Si x2,y2
y z2 son las coordenadas de O en el marco Xh Y\,ZX,
*2
»! + r c
Vi + r eos /? sen et,
r sen/8 + constante
160 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
y se puede obtener v0 = {x2 + ¿2 + *\)V2 • Las componentes de v0 según X, Y y Z, vienen dadas por u0z =
x2an + 2/2ai2 + ^2ai3i etc- Entonces, con valores conocidos para £,y,z,Ix,Ixy, etc., con relación a los ejes
fijos al cuerpo, se llega en seguida al valor de Ti para Mlt a partir de (8.10).
La energía cinética de M2 es sencillamente T2 = $M2(x* + v\) + \Í9\ donde / es el momento de inercia
del bloque con respecto a la línea a trazos. (Para simplificar se ha supuesto que la línea a trazos vertical que pasa
por (xi.yi) corta el c.m. de B.) Así, para todo el sistema, T = Ti + T2.
Para cualquier sistema de fuerzas actuante, se llega en seguida a las ecuaciones del movimiento por medio
de la aplicación de las ecuaciones de Lagrange, en la forma acostumbrada. En estas ecuaciones no aparecen las
fuerzas de restricción, como la que se origina entre la'varilla y M\. Nótese que an, a\2 y ai3, etc., pueden
expresarse en función de 0i,02 y 0.
Por ejemplo,
«11
= — (sen*! cos02 + eos ^ sen 02 sen/3),
ai2 = cos 9\ cos *2 ~ sen e 1 sen 62 sen /?, a13 = sen 92 cos P*
etc.
Ejemplo 8.13.
El soporte A de la figura 8-15 puede desplazarse a cualquier posición sobre el plano X\Y\. El cuerpo rígido
puede girar con velocidad angular /3, alrededor del eje ab, el cual está articulado en O y puede oscilar en un plano
vertical. El ángulo B\ se mide con respecto a Xi, 02 se mide con relación a A, 03 como se indica, y 0 con
respecto al eje ab. A continuación se enumeran esquemáticamente las etapas para hallar la energía cinética T de
este sistema.
Se toman los ejes fijos al cuerpo, X, Y y Z, con origen en O y Z en la dirección de ba. La velocidad tf3es
horizontal y siempre normal al plano abe. La velocidad angular de la plataforma £ es 9t + e2. Con la ayuda
del diagrama, situado a la derecha en la figura 8-14, el lector puede demostrar que
(0, + 02) cos 9z sen P ~ ez cos P>
(*i + *2) eos ff3 cos /3 + 6Z sen /?,
fí + {ex + e2) sen ez
La velocidad de O, vo, y sus componentes según X, Y y Z (véase el problema 8.12(d)) puede hallarse por el
método mencionado en el ejemplo 8.12. La energía cinética Ti de Mt puede obtenerse para valores conocidos de
$,y,z y de Ix, Izy, etc. Si se conocen los valores de las masas, los momentos de inercia, etc., de !a varilla ab,
de la plataforma B y del soporte A, se pueden escribir de inmediato las energías cinéticas T2, T3 y T«.
Entonces, T del sistema total será igual a Ti + T2 + T3 + T4, de donde es posible encontrar las ecuaciones del
movimiento correspondientes a Xi, yit 0\, 62, 03 y 0 en la forma usual. Es importante observar que si se
supone que los cojinetes son lisos, las fuerzas de restricción quedan todas eliminadas de las ecuaciones del
movimiento, con lo cual se ilustra una "de las grandes ventajas del método de Lagrange sobre el de Euler. (Véase el
capítulo 9.)
(f1 + fl)cOBfs
Fig.8-15
CAP- 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 161
g.7 Definición de los ángulos de Euler. Expresión de u y sus componentes,
en función de estos ángulos.
(a) En la dinámica de los cuerpos rígidos se usan ampliamente los ángulos de Euler, 0,
\p y 0, indicados en la figura 8-16. La forma de medirlos es bien sencilla. Teniendo en
cuenta las aplicaciones que siguen inmediatamente, se supondrá que el sistema Xi, Vi,
Z\ está fijo en el espacio, y que el cuerpo rígido puede girar de cualquier manera, con
uno de sus puntos fijos en 0. Los ejes X, Y y Z se hallan adheridos al cuerpo, y el ángulo
entre Z\ y Z se denomina 0. La recta ON queda determinada por la intersección del
plano móvil XV con el estacionario XiYi. El ángulo \p se mide entre Xi y ON,
y <j> entre ON y X. (Un modelo sencillo es muy útil para familiarizarse y poder trabajar
con estos ángulos.)
El cuerpo rígido gira de una
manera cualquiera alrededor
del punto fijo, 0.
Ángulos de Euler 0,^,<¿>
Fig.8-16
(6) Velocidad angular del cuerpo, y sus componentes. Obsérvese que 6,} y <j> pueden ser
considerados como vectores cuyas direcciones serían las de ON, Z\ y Z, respectivamente.
La velocidad angular total, o, es igual a la suma vectorial de estas tres cantidades.
Utilizando los siguientes cosenos directores (que el lector puede verificar),
Cosenos de los ángulos formados por X, Y y Z con Zt, y 0N\
Zi
ON
X
sen* sen#
COS0
Y
senff cos0
— sen#
Z
eos*
0
se concluye que tomando las componentes de 0,¿ y ¿, en las direcciones de los ejes fijos
al cuerpo, X, Y y Z, se obtiene,
^senflsenoS 4- ¿cosoS
¿senflcosoS — 6 sen<f>
¿ + ¿cos0
(8.11)
162 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Entonces, por ejemplo, las componentes de la velocidad v, de una partícula típica m', en
el espacio inercial, en las direcciones instantáneas de X, y y Z, vienen dadas por
vx = (¿ sen 6 eos <f> - 6 sen</>)z - (¿ + ^ eos 6)y, etc.
en donde x,y y z son las coordenadas de m' con respecto al sistema X, Y, Z.
8.8 Empleo de los ángulos de Euler: Un cuerpo con movimiento arbitrario.
Fig. 8-17
Supóngase que el cuerpo de la figura 8-17 puede moverse bajo la acción de las fuerzas
Fi, F2, etc. Se consideran los ejes X, Y y Z fijos al cuerpo, y el sistema X', Y', Z' paralelo
a X\,Y\yZ\, con su origen sujeto al cuerpo en O. Los ángulos de Euler se miden según
se indica. Los cosenos directores de X con relación a X', Y', Z' (y desde luego, con relación
a Xi.Yi.Zi), se representan por a\\,a\2 y ai3, etc.; a continuación se incluye
una tabla completa de estos valores, que deben ser verificados por el lector.
Cosenos de los ángulos formados por X, Y, Z con Xlr Vi, Zx
Véase la figura 8-16, 0 la 8-17.
Xl
Y,
Zx
X
0|j = COS <f> COS }//
— sen <p sen ^ eos 9
ai2 — cos $ sen >}/
+ sen# cos^ cos 9
a13 = senflsen^
Y
a2i — — sen </> cos ^
— cos <f> sen ^ cos 9
pr22 = — sen <f> sen ^
+ cos <f> cos ^ cos 6
a23 = senfl cos^
Z
a31 = senff sen^
a32 = — sen d cos ^
033 = cos 9
Tabla 8.2
Las componentes de la velocidad angular total o, con relación al espacio inercial, tomadas
en las direcciones de X, Y y Z, están dadas directamente por (8.11).
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 163
La velocidad de 0, vo, con relación al espacio inercial es Vo = {x\ + y\ + z?)1/2 en donde
x i, y i, y z\ son las coordenadas de O en el marco Xi, Y\,Z\. Desde luego, es posible
expresar ii, yi y Z\ en otro sistema de coordenadas, como el cilindrico, o el esférico, si se desea.
Por último, vox, voy y uo2, las componentes de vo en las direcciones instantáneas
de X, Y y Z, se expresan por medio de v0x = xlaíl + {¡¡a^ + zxaiv etc.
Entonces, al aplicar (8.10) puede expresarse Ten función de las seis coordenadas xi,yi,
z\, 6, \J/ y 0, y sus derivadas con respecto al tiempo, y al emplear las ecuaciones de La-
grangé se obtienen las seis ecuaciones del movimiento. En el caso en que existan restricciones
expresables por medio de ecuaciones algebraicas (del mismo tipo tratado en todos los capítulos
anteriores), se puede eliminar de T un número correspondiente de coordenadas, en la forma
acostumbrada.
Supóngase, por ejemplo, que las componentes de Ft paralelas a X\,Y\ y Zi, son
fx-*fvi y fl* las cuales se conocen, así como las coordenadas xt, yt y zt de los puntos de
aplicación,lp<, en el marco X, Y, Z. En tal caso, las fuerzas generalizadas correspondientes
a x\,y\ y z\ serán, sencillamente,
fXi = s/;, fWi = s/v ^ = 2/;
Con el fin de hallar Fg se procede de la siguiente manera: La componente de t, el
vector torque total, según la dirección de X, por ejemplo, viene dada por tz = 2 (fz.Vi ~ /«¿^O
en donde fx es la componente de Ft en la dirección del eje fijo al cuerpo, X; etc. Se tiene
además, /z. = f'x an + f¿ «12 + fx «13, etc. Habiendo determinado tx, rv y t2; t0 =
tx cos^ — ry sen^ = F0, con expresiones semejantes para r^ y r^. Es decir,
Fe = rxcos<i> - rysen0, F„ = rz ^
F^ = Tzsen0sen<¿ + r^sen^cos^ + rx eos 0
Si todas las fuerzas son conservativas, puede escribirse una función de la energía
potencial v (jci, y\, z\, B, \p, <f>) y se pueden luego obtener de inmediato todas las fuerzas
generalizadas, a partir de FQr = —dV/dqr. O, naturalmente, se podrá aplicar la función de
Lagrange, L, en la forma acostumbrada.
Como ya se demostró, tanto T como las ecuaciones del movimiento pueden simplificarse
notablemente al escoger adecuadamente la localización de O y la orientación de los ejes fijos
al cuerpo. El lector puede determinar las expresiones de las fuerzas generalizadas, suponiendo
que se conocieran fx.,fy. y /2. en lugar de fx , f'y y f'z..
Ejemplo 8.14. Ecuaciones del movimiento de un trompo.
Imagínese el cuerpo de la figura 8-16 remplazado por un trompo con la punta estacionaria en O, y con el eje
de simetría en la dirección del eje Z. Tómense los ejes indicados, X, Y y Z, como fijos al cuerpo.
Puesto que Ix = ly y que O está en reposo, T resulta simplificada y puede escribirse L como
L = W*& + ¿2 sen2*) + 72(¿ + ¿ eos *)*] - Mgr cose
en donde M es la masa total y r es la distancia, medida sobre el eje de simetría, de O a c.m. Aplicando las
ecuaciones de Lagrange se obtienen las siguientes ecuaciones del movimiento:
Ixe + [(/2 - 7Z)^ eos 6 + /2¿]¿ sen B = Mgr sen e
72(¿cos* + ¿) = P^ = constante (8.13)
Ix¿sen2ff + P^cosff = P^ = constante
No se repiten aquí los estudios detallados de estas ecuaciones, que pueden encontrarse en muchos otros libros.
Véase por ejemplo: Gyrodynamics and its Engineering Applications por R. N. Arnold y L. Maunder, capítulo 7,
Academic Press, 1961; o también, A Treatise on Gyrostatics and Rotational Motion por Andrew Gray, capítulo 5,
The Macmillan Co., 1918. Este último libro incluye un tratado extenso sobre trompos, giroscopios, etc.
164 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Ejemplo 8.15. Energía cinética del trompo con la punta libre para deslizarse sobre el plano liso, XiVi.
Suponiendo los ejes fijos al cuerpo, como se indicó en el ejemplo 8.14, y localizando O (la punta) por medio
de (xi.yi), el primer término de (8.10) es sencillamente i¡M(x1 + y2). Las expresiones de «x, uy y «,
serán las mismas anteriores. Entonces, el segundo término será £[/z(*2 + ^2sen2ff) + /z(¿ + ¿ cosí)2]. Como
£ = y = 0 y z = r, el tercer término de T se reduce a Mr\u0xuy — v0yo>x ) en donde u0x y u0y son las
componentes de v0 en las direcciones instantáneas de X y Y, respectivamente. Es decir, v0x = £i«n + ¡7i«i2 y
vQy = ¿i«2i +¡/i«22- Nótese que no se requiere u0l. Para completar el tercer término se introducen estas últimas
expresiones y uy y «x.
Así, pueden obtenerse de inmediato las ecuaciones del movimiento correspondientes a xi,yi,0,$ y <t>.
Nótese que por haber supuesto que el plano XiYi es liso, no se incluye, en las fuerzas generalizadas, la reacción
sobre la punta.
El siguiente es un método diferente para hallar T, que quizá requiere una menor cantidad de trabajo
monótono: Se toman los ejes fijos al cuerpo como antes, pero con el origen en el c.m. Como £ = y = z = 0, el tercer
término de (8.10) desaparece. Pero en cambio vo, menos sencilla que antes, se puede obtener por medio de las
relaciones siguientes. Las coordenadas del origen de los ejes fijos al cuerpo, con respecto al marco Xi, Y\,Z\,
serán x = x, + ra3l, y = yt + ra32 y z = ra33. Tomando derivadas y sustituyendo en v% = x2 + y2 + z2,
se llega a una expresión adecuada de v\. Por tanto,
T = ±Mvl + ¿[/£(<oz + <oy2) + /T<o22]
en donde «x, wv y «, son iguales a los valores correspondientes de la primera parte de este ejemplo, y además
/* e ¡2 son los momentos principales de inercia relativos a c.m. (Un tercer método consiste en escribir v* =
x2 + y2 + r2¿2 sen2 B)
Ejemplo 8.16. Energía cinética y ecuaciones del movimiento del giroscopio.
Giroscopio montado en un sistema doble de balancines:
<¡i,ai\ b\,b¿\ c\,c¿ - cojinetes
X, Y, y Z adheridos al disco
9, ^, <t> =- ángulos de Eulcr
Yi
G2
Fig.8-18
En la figura 8-18 se muestra un giroscopio montado en un sistema doble de balancines. Considerando fijos
los ejes Xi, Yi y Zt, se observa que los ángulos de Euler, medidos como sigue, sirven de coordenadas
adecuadas. El ángulo 4, se determina por la rotación del balancín exterior G\, alrededor del eje ata2; 0 por
la rotación de G2 alrededor de ¿>,¿>2, y <t> es el desplazamiento angular del disco alrededor de ctc2- La
recta ON indicada aquí tiene el mismo significado que en la figura 8-16.
En este caso, despreciando los momentos de inercia de los balancines y suponiendo que el origen de los ejes
fijos al cuerpo, X, Y y Z, se halla localizado en el centro del disco, la energía cinética será, sencillamente,
T = £/£(¿2sen2* + ¿2) + ¿7?(¿cos* + ¿)2
de donde se pueden obtener las ecuaciones del movimiento en forma inmediata. Si se desprecia la fricción en los
cojinetes y se supone que el c.m. está localizado en O, todas las fuerzas generalizadas resultan iguales a cero.
Si se desea, se puede incluir la energía cinética del sistema de balancines, sin dificultad alguna.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 165
Tratamientos extensos sobre los giroscopios pueden encontrarse en las referencias del ejemplo 8.14, y además
en: The Gyroscope por James Scarborough, Interscience Publishers, 1958, y Theory of the Gyroscopic Compass,
por A. L. Rawlings, The Macmillan Co., 1944. Una lectura interesante se encuentra en Spinning Tops and
Gyroscopic Motions por John Perry, Dover Publications.
Ejemplo 8.17.
El cuerpo rígido de la figura 8-19 está suspendido por una cuerda de longitud constante, ri. Aparte de esta
única restricción, el cuerpo puede moverse libremente bajo la acción de la gravedad. Así, el sistema tiene cinco
grados de libertad. A continuación se describen las etapas para hallar T.
Las coordenadas esféricas acostumbradas, ru 0i y <t>i, (no se muestra ¡*>i) determinan la posición de p.
Supóngase que los ejes X', Y' y Z' con el origen en el c.m. del cuerpo, permanecen paralelos a los inerciales,
Xi, Yi y Z\. Habiendo tomado los ejes fijos al cuerpo, X, Y y Z, con origen en el c.m., se miden los ángulos
de Euler entre este sistema y X', Y', Z'. (En el diagrama no se muestran ni X, Y ni ^, <t>.) Las velocidades
angulares wx,wv y «It están dadas por las relaciones (8.11). Como £ = y = z = 0, el último término de
(8.10) desaparece. La velocidad v0 del c.m. con respecto a XuYi,Zi, viene dada por v\ = x\ + y\ + zi
en donde las coordenadas del c.m., xx,y\ y zi, con relación al sistema XltYi,Zi, pueden expresarse
en función de las constantes rt y r2 y de los ángulos di, <¡>i, 6 y ^. (Véanse las ecuaciones (2.26) del
capítulo 2.) Por tanto, v* puede ser expresada en función de estas coordenadas y sus derivadas con respecto al tiempo.
Si se toman los ejes X, Y y Z en las direcciones de los ejes principales de inercia,
t = !«*; + *[ií«£ + i;«2 + iM]
En este caso, V = — Mg(rl costfi + r2 cosí»). Y se llega a las ecuaciones del movimiento, en seguida.
El lector debe hallar una expresión explícita para T y escribir las ecuaciones del movimiento.
Ejemplo 8.18. Las dos masas Ma y Mb, de la figura 8-20, están conectadas entre sí por medio de una unión
esférica.
Aparte de esta restricción, las dos masas pueden moverse libremente en el espacio, posiblemente bajo la acción
de resortes, de la gravedad, etc. Resulta bien claro que el sistema tiene nueve grados de libertad. A continuación se
hace una descripción esquemática del procedimiento para hallar T y las nueve ecuaciones del movimiento.
Las coordenadas x,y y z representan la posición del centro de la unión esférica (punto O) con relación
a los ejes inerciales Xit Yi y Zx. El marco X', Y', Z', con el origen en O, se mueve solidariamente con este
punto, pero permanece siempre paralelo a X,,Y,,Z,. Los ejes Xa, Ya y Za, así como los Xb,Y„ y
Zb, ambos sistemas con origen común en O, se encuentran adheridos a Ma y a Mb, respectivamente (en la
figura no se indican Xa,Ya,X„ ni Yb). Así, los ángulos de Euler, tfi, ^, y <¡>i para Ma, y 62, ^2 y
<¡>2 para Mb, pueden ser medidos con relación a X', Y', Z', como en la figura 8-17, para cada una de las masas.
Así, la energía cinética de Ma, Ta, puede expresarse en función de x.y.z, 0i,^i y 4>i y sus derivadas con
respecto al tiempo, por aplicación directa de (8.10). Igualmente, se puede expresar T„ en función de x.y.z, 82,
166 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
^2 y <t>2\ y finalmente la energía total, T, será igual a Ta + Tb, que incluye nueve coordenadas. Nótese que
aunque v0 es igual para las dos masas, las expresiones de v0z, u0y y u0l para Ma no son iguales a las
correspondientes a M„.
Fig.8-20
Se pueden obtener ahora las ecuaciones del movimiento por aplicación de las ecuaciones de Lagrange. Si en
el sistema actúan resortes, la gravedad u otras fuerzas aplicadas, no constituye ninguna dificultad el encontrar las
fuerzas generalizadas correspondientes a las diferentes coordenadas. Nótese que la fuerza de restricción de la unión
esférica lisa queda automáticamente eliminada.
8.9 La energía cinética, haciendo uso de ejes de dirección fija.
(Véase el numeral 8.4(c).)
En todos los ejemplos anteriores, de este capítulo, se han utilizado ejes fijos al cuerpo.
Sin embargo, como se indicó anteriormente, es posible usar también ejes de dirección fija. En
este caso, los momentos y los productos de inercia (magnitudes variables), las componentes
de » (velocidad angular del cuerpo con respecto al espacio inercial), las coordenadas del
c.m. y las componentes de vo, deben expresarse todos con respecto a los ejes de dirección fija.
Para ilustrar esto, considérese nuevamente el cuerpo que aparece en la figura 8-17. Las
componentes de », según los ejes de dirección fija X', Y' y Z', están dadas por
"*' = "««n + "«^i + »«asi» etc-
donde ux = 1> sen 0 sen 0 + $ eos 0, etc. (Véanse las ecuaciones (8.11).) Los momentos
y los productos de inercia, l'x,Ixy, etc., relativos a X', Y' y Z', pueden expresarse en función de
Ix, Ixy, etc., relativos a los ejes X, Y y Z, fijos al cuerpo, por medio de las ecuaciones (7.20).
Las coordenadas del c.m., en función de x,y y z con relación a los ejes fijos al cuerpo, pueden
escribirse x' — Xan + ya2l + ¿a31, etc. La velocidad vo tiene el mismo significado anterior
pero sus componentes deben tomarse según las direcciones fijas de X', Y' y Z'.
Al sustituir los anteriores valores "de dirección fija" en (8.10)t se obtiene una expresión
válida para T. Nótese que esta expresión, al final se reduce a la misma obtenida habiendo
utilizado los ejes fijos al cuerpo.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 167
Usualmente el procedimiento anterior es menos conveniente que el método de los ejes
fijos al cuerpo. Sin embargo, con el fin de ilustrar los principios básicos, se incluye el siguiente
ejemplo específico.
Ejemplo 8.19.
Con referencia a la figura 8-16, supóngase que M es un trompo en rotación con sus ejes fijos al cuerpo de tal
forma que Z coincide con el eje de simetría y la punta está fija en O. Se trata de hallar T, utilizando magnitudes
relacionadas con el marco fijo X\,Y\,Z\.
uz = e eos y¡> + j> sen e sen ^, uy = e sen ^ — ¿ sen 8 eos ^, u2 = ¿ + ¿ eos 0
Utilizando las relaciones (7.20),
'*.
'..
'i
,'¡v1
'v.
V
=
=
=
=
=
=
7z(cos2^ + eos2* sen2 ^) + /2 sen2* sen2 ^
7z(sen2 ^ + eos2 B eos2 ^) + 72 sen2 e eos2 ^
7Z sen2 e + 72 eos2 B
— 7zsen20 sen ^ cos^ + 7zsen2 8 sen ^ eos ^
7Z senff eos 6 sen ^ — 72 sen 0 eos 0 sen ^
— 7Z sen 6 eos 0 eos ^ + 72 sen e eos 0 eos ^
Como la punta está fija, u0 = 0, y por consiguiente,
T = W*S\ + V«i + '«i^ - 2<7*i«ri"*i"»i + '«rt^^ + ^rt-kn^)]
Al hacer las sustituciones, luego de efectuar largas y monótonas reducciones, se llega a
T = ¿7Z(¿2 + ¿2sen2 0) + ¿72(¿ + ¿ COS*)2
que es la misma expresión obtenida en el ejemplo 8.14, en el que se utilizaron ejes fijos al cuerpo.
8.10 Movimiento de un cuerpo rígido con relación a un marco de referencia
en traslación y rotación.
El tipo general de problema que se va a considerar puede enunciarse e ilustrarse como
sigue: Considérese el sistema X2,Y2,Z2, de la figura 8-21, como inercial. Imagínese
por ejemplo, que el sistema X\,Y\,Z\ se encuentra adherido a la cabina de una
embarcación que está en movimiento (se desplaza, se balancea, "zigzaguea", cabecea, etc.) de
cualquier manera conocida o supuesta, con relación a X2, Y2,Z2- Se trata de determinar
el movimiento de un cuerpo rígido sometido a la acción de unas fuerzas conocidas, Fi, Fa,
etc., con relación a la cabina.
Evidentemente el procedimiento básico requerido es el mismo que se ha seguido en todos
los ejemplos anteriores, ya que en cualquier caso, la relación (8.10), es válida sin necesidad
de introducir ningún cambio en la forma, siempre que wx, wy y ü>2, así como vox,
voy y voz, se expresen de tal manera que representen las componentes de a (la velocidad
angular total del cuerpo con respecto al espacio inercial) y de vo (la velocidad lineal de O
en el espacio inercial), respectivamente, en las direcciones instantáneas de los ejes fijos al
cuerpo, X, Y y Z. Adelante se dan los detalles en que se ilustra cómo expresar
adecuadamente estas magnitudes, para la solución de este problema.
La velocidad angular del marco X\,Y\,Z\ (la embarcación) con relación a X2,
Y2,Z2, se representa por ííu cuyas componentes según X\,Y\,Z\, serán fiiz, ü\y
y fii2. La velocidad angular del cuerpo con relación a XX,Y\,Z\, se indica por Q cuyas
componentes en las direcciones de los ejes fijos al cuerpo, X, Y y Z, serán fiz, fiv y Üz.
La orientación del marco XX,Y\,Z\ con relación al espacio inercial iX2,Y2,Z2)
se determina por medio de los ángulos de Euler, 0i,^i y <¡>i, como se indican en la
figura; y la orientación del cuerpo con respecto a la cabina, por medio de 6, ^ y <j> (no se
168 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [CAP. 8
muestran en la figura pero se miden en la forma usual con respecto a X\,Y\,Z\). Se
escribe entonces (véase la ecuación (8.11)),
ülx = $1send1sen<f>l + fljCos^, etc. (1)
\Y ^ . Fi
Sistema X. V, Z fijo al cuerpo
X
oigáis con
respecto a X,, Y,, Z,
— velocidad angular del
cuerpo con relación al espacio
inercial.
^ velocidad angular de X,,
V i, Zi, con relación al
espacio inercial.
■» velocidad angular del
cuerpo con relación al marco X i.
Y,,Z,.
- velocidad lineal de O. en el
espacio inercial.
u - velocidad lineal de O,, en
el espacio inercial.
0iii0l2> = cosenos directores de X con
o,3 relación a Xi. Y, y Z\, etc.
12 =■ coEcnos directores de X,
con relación a X2. Yi y
Z2, etc.
El marco X. Y, Z está fijo al cuerpo. Los
ejes X¡, Y2 y Z'2 permanecen paralelos
a los inerciales X2,Y2 y Z2-
Fig. 8-21
igualmente, Qx = ¡j, sen 6 sen <f> + 6cos<f>, etc.
Por consiguiente, «x, ü>y y ü>2, ya definidas, vienen dadas por
(2)
n„ + íí,^o, + fi,..«o, + «„«*,
(8.14)
"ll"21 ' "l«"22 ' "lz"23
az = Qz + "ix^l + ííl„a32 + fiUa33
donde an,ai2,ai3, etc., están dados en la tabla 8.2. Estas son las expresiones de «x,
üjy, üj2 requeridas en la fórmula (8.10).
La velocidad lineal de 0\ con relación al sistema X2,Y2, Z2, se indica por u,
cuyas componentes según Xi, Yi y Z\ son ux,uy y uz. Se escribe entonces,
UX = «Al + ¿2012 + ¿2013. etC- (3)
El significado de x2, jSu,etc, se indica en la figura. Naturalmente, la velocidad u, puede
expresarse en función de coordenadas esféricas, o de cualquier otro sistema, si se desea.
Si se expresan las componentes de vo, como v\,v2 y v$ (vo es la velocidad del
origen de X, Y, Z, en el espacio inercial) en las direcciones instantáneas de Xi, Yi.Zi,
y teniendo en cuenta (8.4), se concluye que
vi = KPn + ¿/12 + ¿As + ¿i + <Vi " «i^i
V2 = ^l + ¿2022 + ^23 + »1 + °lA " °1^1 <& i5)
V» = ^l + í
CAP. 8) ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 169
Aquí xi, yi y z\ son las coordenadas de O en el sistema Xi, Vi, Z\\ y las 0 se
obtienen de la tabla 8.2, remplazando 6 por 0i, etc. Así, vi, como aparece en (8.10), viene
dada P°r ,,§ = ?,2 4- «! 4- «* (4)
Por otra parte, u0x, voy
y uo„
V,
*>o = v\ + ví + v\
definidas antes, serán
+ v0a00 + v.
«21
^or,, + «o, 4- v,a,5
(5)
Al remplazar (4) en el primer término de
términos segundo y tercero, se tiene,
2"22 ' "3"23' v0z "l"31 ' V2M32
Í0), y los resultados de {8.14) y (5) en los
y y sus derivadas con relación al tiempo I
(8.16)
Suponiendo que se conoce el movimiento de la embarcación (del marco Xi, Y\,Z\), los
valores de jc2,>'2, z2, 0i, ^i y 0i serán funciones determinadas del tiempo.
Finalmente, T tendrá la forma,
T = T{xx,yx,zx\ ii,¿i,zi; 6,$,$; 0,i,$\ t) (8.17)
expresión que contiene únicamente las coordenadas que sirven para localizar el cuerpo con
relación a la cabina. Así, las ecuaciones del movimiento del cuerpo, relativas a la cabina, se
obtienen en seguida al aplicar las ecuaciones de Lagrange. En la forma acostumbrada se
pueden hallar las fuerzas generalizadas.
Obsérvese que si se toma a O en el centro de masa, el tercer término de (8.20) desaparece,
y las relaciones (5), que pueden resultar complejas, se hacen innecesarias.
Los resultados de este numeral se ilustran por medio de los siguientes ejemplos específicos.
Como ilustración adicional pueden verse los problemas 14.30, 14.31 y 14.32.
Ejemplo 8.20.
El brazo horizontal AB, de la figura 8-22, se hace girar con velocidad angular $x, alrededor del eje vertical,
según se indica. El disco D gira con velocidad angular ¿lf medida con relación al soporte C. Se suponen inerciales
170 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
los ejes X2, Y2 y Z2, en tanto que Xt, Yt y Z\ están adheridos a D. Al extender hacia atrás Z\, esta
recta corta el eje vertical de giro de AB. Tanto ^, como ¿, se consideran funciones definidas del tiempo.
Un cuerpo rígido de masa M sufre la acción de las fuerzas Ft, F2,etc, (se suponen conocidas sus
magnitudes,, direcciones y puntos de aplicación). Siguiendo el método descrito y la notación empleada en este mismo
numeral, se trata de determinar las ecuaciones del movimiento con respecto al marco Xt, Y\,Z\.
En la figura puede observarse que
Í2lz = $1 sen*! sen^, Í2ly = ¿x sen*! cos^, Í2iz = <f>i + $x eos 0X
Además, Í2Z = ¿ sen 6 sen <p + e eos <f>, etc., (naturalmente, B, \f, y <¡> son los ángulos de Euler que
determinan la orientación del cuerpo con relación a Xi, Ylt Z\). Así, tal como en las ecuaciones (8.14),
coz = Í2Z + Sllxan + Í2lya12 + Í2lrat13, etc.
La velocidad lineal de 0\, u, con relación al espacio inercial, tiene una magnitud (r + /senfli)^, y sus
componentes según Xi, Vi y Z\, son
ux = (r + l sen e^x eos </>lf uy = — (r + l sen e^ti sen<f>ít uz = 0
Se llega entonces a la expresión (siguiendo las ecuaciones (8.75)),
vt = (r + l sen e^^ cos^ + x^ + (^ sen*! cos^^ — (^ + ¿x cose^y^
y otras similares correspondientes a u2 y V3. Si se supone que O está en el c.m., no se necesitan las expresiones
de u0x, u0y y u0l. Si, además, los ejes principales de inercia coinciden con X, Y y Z, la energía cinética se
reduce a
T = ^M{v\ + v¡+vl) + Ívx<4 + Fytf + /2P<of
que se expresa en función de x\,y\, z\, B, ^, <t>, sus derivadas con relación al tiempo y t, teniendo en
cuenta que \J/ y <¡>i son funciones conocidas del tiempo. Para el caso especial en que ^ = constante y ¿1 =
constante, la expresión de T se hace relativamente sencilla.
Las ecuaciones del movimiento se obtienen de inmediato por medio de la aplicación de las ecuaciones de
Lagrange. No es necesario incluir acá mayores detalles.
Ejemplo 8.21. Considerando a AB, D y M, de la figura 8-22, como partes de un sistema de cuerpos rígidos;
determínense las ecuaciones del movimiento.
Se supone que a todas las partes del sistema se han aplicado fuerzas conocidas. Se trata de hallar todos los
movimientos del sistema completo. Se incluye a continuación una breve descripción de las etapas requeridas para
determinar la energía cinética total.
Tomando los ejes X2,Y2 y Z2 como inerciales, la energía cinética de AB, Tlt será igual a
Ti = \h%
donde It es el momento de inercia del brazo AB, junto con el eje vertical y el bloque C, alrededor del eje Z2.
Fácilmente se observa que T2, la energía cinética de D únicamente, es
T2 = ±Mx{r + l sen e{pft + \Ufi sen2 $1 + tfZfa + ^ eos 6&
donde Mt es la masa del disco uniforme, y además, Ix y /¡T son los momentos de inercia de D, con relación a
Xi y Zi, respectivamente. La expresión de T3, la energía cinética del cuerpo rígido, es exactamente igual
a la obtenida para T en el ejemplo 8.20, pero en este caso vh y <t>\ no se suponen funciones conocidas del tiempo.
Se deja al lector la determinación del valor de T«, la energía cinética de la varilla ab (masa M2, radio r y
longitud /). Por tanto, finalmente,
rtotai = Ti + T2 + Tz + T4
Nótese lo siguiente: (a) El sistema tiene ocho grados de libertad, (b) La energía Ttotai, se expresa en función
de las ocho coordenadas \f>i, <¡>i, xt,yt, zlt B, \f, y <¡> y de sus derivadas con relación al tiempo, (c) La
aplicación de las ecuaciones de Lagrange conduce a las ocho ecuaciones del movimiento. Las fuerzas generalizadas
se obtienen de la manera acostumbrada. Las fuerzas de soporte (supuestos lisos) no aparecen, (d) Las soluciones
de estas ecuaciones expresan el movimiento rotacional de AB con relación al marco X2.V2.Z2; la rotación
de D respecto a C; y el movimiento del cuerpo rígido, relativo al marco Xi, Vi.Zi.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 171
Ejemplo 8.22. Movimiento de un vehículo espacial y de un cuerpo rígido dentro del vehículo.
Con referencia a la figura 8-23, supóngase que el cuerpo rígido dentro del vehículo espacial sufre la acción
de las fuerzas Fi, F2, etc., así como la atracción gravitacional de la Tierra. Se trata de hallar el movimiento
del vehículo con relación al marco X2.y2.Z2 (supuesto inercial) y el movimiento del cuerpo con relación al
vehículo (X,,y,,Z,).
Xi. V,,Z, adherido al vehículo
Zo.Vo.2,1 / V /^ \ /
X2.y2.22 tiene dirección fija
1 02 adherido al centro de la Tierra
Movimiento de un vehículo
espacial y un cuerpo en
su interior
Fig. 8-23
La energía cinética del vehículo espacial, Ti, puede expresarse de la manera acostumbrada, en función de
■*2,3'2 y 22 (o en función de r, *i y a, como se verá más adelante) y de los ángulos de Euler, 0i,^i y ¿i
(no se indican) y sus derivadas respecto al tiempo. La expresión de T3, la energía cinética del cuerpo rígido,
puede escribirse de la misma forma que (8.16). Así,
7,o,nl = Tl + T'2
y con las fuerzas dadas (incluyendo la gravedad) se obtienen en seguida las ecuaciones del movimiento.
Es importante observar que: (a) El sistema tiene doce grados de libertad, suponiendo que el cuerpo rígido no
posee restricción alguna, (b) En este problema es preferible remplazar X2,y2 y 22 por r, *i y el ángulo a.
Si se desea, es posible expresar a en la forma a = wet + A, en donde «, es la velocidad angular de la Tierra y A
es la longitud del meridiano cortado por r. (Véase la figura 14-4.) (c) Las fuerzas generalizadas se hallan de la
manera usual. Sin embargo, debe tenerse en cuenta que para cada fuerza ejercida sobre el cuerpo por algún ligero
mecanismo del vehículo, por ejemplo, existirá otra fuerza igual y contraria sobre el vehículo mismo.
Ejemplo 8.23. Aclaración sobre el significado de las
ecuaciones (8.4).
En la figura 8-24 los ejes X, Y y Z están adheridos a la
plataforma que gira. La base B está sobre un elevador que
posee una aceleración constante hacia arriba, a. El sistema
Xi, Yi, Z\ está fijo a la Tierra y se considera inercial. La recta
Oc se ha trazado sobre la plataforma. El ángulo 0 es constante.
Se suponen conocidas las magnitudes de 0, a y v0 (la
velocidad inicial hacia arriba del elevador.).
Según (8.2), para la partícula m' se tiene,
vx = re sen/3 + x — ey
vy = re eos ¡3 + y + ex
vz = v0 + at + z
donde vx, vy y vt son las componentes de la velocidad de
m' en el espacio inercial, en las direcciones de X, Y y Z,
respectivamente. Por tanto,
Fig. 8-24
172 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
T = $m'[x2 + y2 + r2e2 + (x2 + y2)'e2 + 2ré2{x eos/i - y sen/J)
+ 2rff{y eos (3 + x sen/J) + 2e(xy - yx) + {v0 + al + z)2}
Demostrar que las ecuaciones de trasformación que relacionan las coordenadas de m' en el espacio inercial,
xi,yi y z\, con x, y y z, son
&! = r eos 6 + x eos {e + P) — y sen {6 + P)
¡/i = r sene + x sen(e + p) + ycos(e + P)
*! = z + v0t + $at2
y comprobar el resultado anterior por medio de la aplicación de estas relaciones.
Denominando A la aceleración lineal de m' con relación al espacio inercial, hallar las expresiones de sus
componentes Ax,Ay y Az, según las direcciones instantáneas de X, Y y Z. Para esto conviene seguir el método
del capítulo 3, numeral 3.9.
8.11 Experimento sugerido: Determinación del período de oscilación del disco D, de la
figura 8-13.
Un disco de metal cuyo espesor y radio se determina según convenga, se monta en un
eje delgado cuyo extremo p tenga una punta semejante a la de un lápiz. El conjunto se
coloca sobre un plano inclinado formado por una lámina de vidrio (el vidrio reduce la
amortiguación). Si el ángulo de inclinación del plano no es demasiado grande, el disco oscilará
alrededor de su posición de equilibrio, por algún tiempo, sin resbalar hacia abajo.
Hallar el período experimentalmente y comparar este valor con el calculado. Si se tiene
cierto cuidado en la determinación de los momentos de inercia, masas, etc., el valor del
período determinado experimentalmente coincidirá en buen grado con el calculado. Para
mejores resultados deben tenerse en cuenta la masa y demás características del eje (longitud
r\ en la dirección de Z). Esto último no presenta ninguna dificultad especial.
La teoría necesaria para el cálculo del período incluye muchos de los principios básicos
de la dinámica de los cuerpos rígidos. Además, el experimento es interesante y conduce a
una mayor familiaridad con los métodos generales empleados.
Problemas
A. Velocidades angulares y sus componentes.
8.1. Comprobar las expresiones (8.0).
8.2. Si el cuerpo rígido de la figura 8-1 está girando alrededor de las rectas Oax y Oa2 (que no aparecen
en la figura) con velocidades «i y u2, respectivamente, las velocidades lineales correspondientes son:
vi = uihi y V2 = U2h2. Entonces, la magnitud de la velocidad total v, viene dada por
v2 = u^7 + tílhl + 2co1co2/i1/i2 cos/J (a)
en donde 0 es el ángulo entre ut y U2.
Pero suponiendo que wi y W2 pueden sumarse como vectores, la resultante w estará dada por
(o2 = (o2 + u2 + 20)^2 cos0 en donde 8 es el ángulo entre «i y w2. Se tendrá entonces,
V2 = u2h2 (b)
donde h es la distancia normal que va de la dirección de w a m'. Demostrar que las dos expresiones,
(a) y (b), son iguales. Para simplificar el trabajo tómese a Oat en la dirección de X, y a Oa.2 en el
plano XY. La partícula m quedaría localizada en un punto cualquiera, x, y, z.
8.3. Suponer que el cuerpo de la figura 8-25, con un punto fijo en 0\, tiene una velocidad angular
tó{ulx,ulytulz),con relación a X\,Y\,Z\. En consecuencia, m' posee una velocidad lineal cuyas
componentes según Xi, Yi y Z\, están dadas por, ux = «iyzi - «i^i, etc., en donde xi.yi y z\
son las coordenadas de m' en el marco X\,Y\,Z\.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 173
Considerar el marco X, Y, Z, con su origen adherido al cuerpo en O. Si se supone que estos ejes
permanecen paralelos a X1J1 y Zi, se observa que x\ = xo + x, etc. Continuando con este
razonamiento demostrar la validez del enunciado hecho en él numeral 8.2C(h).
u,.v.) - Velocidad de n
respecto a Xi.Y¡,Z,
El marco X, Y, Z. con origen adherido al cuerpo e
permanece paralelo a Xi,Y\,Zi. Las velocidades <
v y vo se consideran relativas a X,.Y,,Zi.
Fig. 8-25
Comprobar las relaciones (1) y (2) del ejemplo 8.3. Si se indican los cosenos directores del vector velocidad
angular total a, por medio de l, m y n, con relación a X, Y y Z, y l\,m\ y ni con respecto a X\,
Y\ y Zx\ demostrar que
y también que
l = {e1 eos a + 82 eos /3)(sen 63)/u, etc.
h = («2 sen (P — <*) + h c°s «)(cos ffi)/(o, etc.
Demostrar que la dirección del vector velocidad angular de la varilla de la figura 8-11, ejemplo 8.7, con
respecto a las posiciones instantáneas de los ejes fijos al cuerpo, está dada por
l = —62/u, m = (¿! eos 02)/"i
(¿! sen ff2)/u
donde «2 — 6X + e\, y que con relación a los ejes fijos en el espacio, Xi, Vi y Zi,
l\ = — (»2 senff^/u, ml = (é2 eos 0i)/co, nx = et/a
8.6. Verificar las expresiones dadas para wx,wy y uz, en el ejemplo 8.8, figura 8-12.
8.7. El disco D, de la figura 8'26, gira un ángulo fl3, medido por el indicador p, a partir de una recta
horizontal paralela a la cara del disco y que pasa por su centro. El eje bd puede girar en el plano vertical
un ángulo 82, alrededor de la articulación horizontal en b. El eje vertical gira un ángulo 0\ medido
a partir del eje fijo Xi.
Con los ejes fijos al cuerpo, adheridos a D como en la figura 8-5, demostrar que las componentes de
la velocidad angular m, según estos ejes, son.
01 eos 6<¿ sen03 — ff2 c°s *
uy = $i eos $2 cos ez + *2 sen ez>
j + Oí sens
Demostrar que las componentes de «» en las direcciones de los ejes inerciales X\,Y\ y Zx, están
dadas por
ux = ez eos ff2 cos 9\ + ff2 sen«i,
= ez eos ff2 sen e\ — *2 cos °u
81 + 6Z senff2
174 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [CAP. 8
Fig. 8-26
8.8. Verificar las importantes relaciones (8.11). Verificar, asi mismo, las expresiones de los cosenos directores
dadas en la tabla 8.2. Nota: Un modelo sencillo resulta muy útil.
8.9. Considerando la partícula libre, m, de la figura 8-3, escribir ii = x0 + xaui + y«2i + za3i, etc., para
yi y zi. Tomar las derivadas de estas relaciones, considerando todas las cantidades variables. Utilizando
las relaciones (8.11) demostrar que la expresión de vz (la componente de la velocidad de m en el espacio
inercial, según la dirección instantánea de X), vx = xxan + V\ai2 + ¿iai3» se reduce finalmente a la
primera ecuación de (8.4). El proceso anterior requiere alguna paciencia, pero constituye un importante
ejercicio.
8.10. Escribir completamente las expresiones para wx, wy y «r, del ejemplo 8.20.
B. Energía cinética y ecuaciones del movimiento.
8.11. (a) En la figura 8-5 el soporte A está en reposo y el origen O, de los ejes fijos al cuerpo, está en el c.m.
del disco. Demostrar que la energía cinética del sistema completo es
T = %(Mb* + J*)¿2 sen 2 e. + £/*(¿ eos 6 + ¿)2 + #&
(b) Tomando los ejes fijos al cuerpo como antes, pero ahora con el origen en b, escribir una expresión
para T, y demostrar que se reduce a la misma anterior. ¿Podrá considerarse b adherido afl?
8.12. (a) Utilizando las relaciones (8.3), determinar T para el disco delgado de la figura 8-5, evaluando la
integral T = £ I v2 dm, y comparar la expresión así hallada con la obtenida en el problema
8.11(a).
(b) Se remplaza el disco de la figura 8-5 por un cuerpo rígido de una forma arbitraria. Suponiendo que
los ejes X, Y y Z son los mismos de la parte (a) (ejes principales con el origen en el c.m.) demostrar,
por integración, que la expresión de T es la misma que en (a).
(c) Demostrar que v0z, del ejemplo 8.3, figura 8-6, está dado por
v0x = —(8¿! eos e2 + ¿i«2 c°s ff2 cos y) sen 93 sen (y — a)
+ [—881 sen 82 + (*2 + *i sen y)x2 — Bfa sen 02 c<>s Y] c°s *3 — *ix2 cos *2 eos 7 sen 03 cos (y — a)
(d) Hallar las expresiones para voz, voy y vot, de la figura 8-15, utilizando las ecuaciones (8.3).
8.13. Demostrar que si se toman los ejes fijos al cuerpo como se indica en la figura 8-10(1) del ejemplo 8.6, y
si se supone que r es un resorte espiral, se tiene,
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 175
T = %M(r* + r2*2) + £/2¿2 - Mr$\x sen(<p - 0) + y eos (</> - *)]
— Mr$ff[£ eos (<f> - e) — y sen (<p — e)]
Demostrar que la ecuación del movimiento correspondiente ares
m(r — re2) — M$[£ sen(<f> — e) + y eos (<p — e)]
— M$2\£ cos(<f>-e) — y sen(tf-tf)] = Mg eos 8 - k(r - r0)
Escribir las ecuaciones correspondientes a 0 y <¡>.
Los discos Di y D2, de la figura 8-27, están montados en cojinetes lisos sobre la varilla ligera, ab, y
pueden girar libremente con relación a la varilla con velocidades fft y 02. Se supone que la longitud de la
varilla es igual a l, y que las periferias de los discos están en contacto y giran sin resbalar. El conjunto puede
deslizarse libremente sobre el plano inercial X1Y1. ¿Cuántos grados de libertad tendrá el sistema?
Demostrar que . . ...
T = \(MX + M2)(x2 + ¡/2) + \M2le{le + 2y eos e - 2» sen*)
+ £/i(¿i + ¿2)2 + W* 1*1/^2 + h2
En el punto p de la periferia del disco Di, se aplica una fuerza F, según se indica en la figura. Al
efectuarse el movimiento, la fuerza F permanece con la misma dirección (el ángulo a, constante).
Demostrar que las fuerzas generalizadas correspondientes a x, y, 0i y B son
Fx = Feos a, Fy = -Fsena, Fe = - FRX sen (^ + 62 + a), Fe = - FRX sen (^ + e + a)
Fig.8-27
Fig. 8-28
Los discos Di y D2, de la figura 8-28, están montados en el eje vertical como se indica. Así mismo, la
figura muestra cómo los ángulos a, ffi y 62 se miden por medio de indicadores especiales.
Despreciando las masas de los ejes que sostienen los discos, demostrar que la energía cinética para todo el sistema
está dada por
T = ^[^182 + M28l + /Iisen2/31 + /l2sen2/J2];2
+ i/«1(51 + a sen/3!)2 + ¿/22(á sen/J, - ¿2)2
Una partícula m tiene por coordenadas x, y y z en el marco X, Y, Z de la figura 8-5. Utilizando las
relaciones (8.4) expresar la energía cinética T para la partícula. Por el método descrito en el numeral 3.9
del capítulo 3, demostrar que la componente X de la aceleración de m en el espacio inercial, está dada por
ax = x + [(b + z)y¡, + 2z¿ — (x eos</> — y sen#)¿2 sene) sen» con ¿>
— ¡/((6 + y¡> eos e) — 2y(i + ¿ eos 8) — x($ + ¿ eos 6)2 + (s + z)¿2 sen 6 eos 8 sen <f>
ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Comprobar el resultado anterior por medio de la ecuación (9.6a). Las expresiones para ay y az se obtienen
en forma semejante.
Utilizando los resultados del problema 8.7, despreciando la masa de la varilla bd e incluyendo el valor
de /i, demostrar que
T = \MV'e\ cos2*2 + \íx(e\ + ¿2coS2*2) + ¿/2(¿3 + ¿i sen*2)2 + ±1¿\
Teniendo en cuenta la acción de los resortes de torsión y la de la gravedad, demostrar que las fuerzas
generalizadas correspondientes a 0i,02 y 03 son
Fet = «1*1. Fe2 = -c2*2 _ M9l eos e2 y F,^ = (lyJz
donde c\ y a son las constantes de torsión y además se ha supuesto que los resortes no se han
deformado cuando d = 0 y í¡ = 0.
El cuerpo rígido B, de la figura 8-29, está sostenido por A, por medio del eje S. Los dos cuerpos así
conectados, pueden moverse libremente en el espacio bajo la acción de fuerzas conocidas. El origen 0\, de
X\,Y\,Z\, está adherido al c.m. de A; y estos ejes, sujetos al cuerpo únicamente en este punto,
permanecen paralelos a un marco inercial (que no aparece en la figura). Lo mismo puede decirse de X2, Y'2,Z2
y O2. Se toman como ejes fijos a los cuerpos, X\,Y\ y Z\, para A y B; Xa,Ya,Za y Xb,Yb,Zb,
respectivamente. Por conveniencia se toma Zb como una extensión de Za. El cuerpo B puede girar con
relación a A con una velocidad angular ¿. Los ángulos de Euler correspondientes a las dos masas se miden
según se indica.
F,(/v /„./«,)
X¡, F( y Z¡ asi como X& Y2 y Z2. permanecen
paralelos a los ejes ¡nerciales que no aparecen en
la figura.
*i = *2. *l = *2> #1 ** *2. u*2 = "«, + ó
Fig.8-29
Demostrar que el sistema tiene siete grados de libertad y que x\,y\,z\ (las coordenadas de 0\
con respecto a cierto marco inercial), 0i,^i,4>i (los ángulos de Euler de A), y el ángulo de Euler fa
correspondiente a B, constituyen un conjunto adecuado de coordenadas. Comprobar las siguientes relaciones:
*i = *2» ^1 = ^2» x2 = «i + l sen*! sen^j, y2 = Vi — l sen *i eos $ít z2 = Z\ + l eos 0X
donde X2,y2 y 22 son las coordenadas de O2 relativas al marco inercial, y l es la distancia constante
entre 0\ y O2. Nótese que las velocidades angulares están dadas por las relaciones (8.11), y que
uz = uz + á. Escribir las expresiones de todas las velocidades angulares y eliminar las coordenadas su-
perfluas.
Suponiendo que los ejes fijos al cuerpo son ejes principales de inercia, demostrar que
T = ¿(M, + M2)(x\ + y\ + z\) + $M2[Pe\ + tip\ sen2 ex + 2l9t eos »x(xx sen^ - yt eos ^)
+ 2f¿! sen^ií»! cos^x + V\ sen^) — 2LzxBx sen^]
+ i(¡yXi+i;/u¡ + n& + ¥¡;242+ii/H+¡&
donde uz = ^ senet sen^t + éx eos</>u etc.; y ux = $\ senex sen#2 + ¿, eos <f>2, etc.
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 177
Suponer que en el punto pt del cuerpo A, actúa una fuerza conocida Fi (de componentes fx.,fy.>
y fz.\ según Xa, Ya y Za) y que las coordenadas de este punto, en el sistema Xa, Ya, Za, son
lx , ly y lz . Igualmente, la fuerza F-¿ (de componentes /x2»/W2 y fz ) actúa en p2, de B. Demostrar
que la fuerza generalizada correspondiente a xi es
FXl = /x/cos <Pi eos ^ — sen <f>l eos el sen ^x) — /^(sen^ eos ^1 + eos <f>t eos e^ sen^,)
+ fz sen*! sen^ + fx2(cos$2 eos ^ — ser\<f>2 eos flj sen^j)
— /«2(sen^2 cos ^1 + eos <p2 eos flj sen ^x) + fZo sen ex sen ^
Escribir las expresiones correspondientes a Fy y Fz . Demostrar, por ejemplo, que
F<¡>! = (V*i ~ WyJ Senffl Sen*l + &/*! _ '*/*i) S<ín*l COS*l
+ (ír/vj - íy/xj) eos ffx + (í^ - í22/„2) sen ^ sen <f>2
+ Uz2fx2 - Ixjzj sen *! cos <fr2 + (lxJy2 - lyJX2) cos ff2
Hallar las expresiones para F^ .F^2 y Fg .
8.19. Véase el numeral 8.4(/). Considerar un cuerpo, libre de moverse de cualquier manera. Tomar los ejes
fijos al cuerpo en las direcciones de los ejes principales de inercia, con origen O en el c.m. En un momento
determinado puede considerarse que el cuerpo tiene una velocidad angular », alrededor de cierto eje
instantáneo que pasa por O. Los cosenos directores de este eje serán «x/«, etc. Indicando por medio
de /, el momento de inercia variable relativo a tal eje, comprobar que T = ^Mv2cm + £/«2, lo cual
constituye el teorema del "centro de masa", aplicado a los cuerpos rígidos.
C. Energía cinética y ecuaciones del movimiento, relativas a marcos móviles.
8.20. Los ejes X2 y Y2 de lá figura 8-30 están fijos en el espacio, en tanto que Xt y Vi se hallan-adheridos
a la plataforma horizontal en rotación, con velocidad angular S, alrededor del eje vertical que pasa por 02.
El sistema X, Y, Z se encuentra sujeto a una lámina de masa M, la cual puede deslizarse libremente
sobre el plano X\Y\, bajo la acción de las fuerzas /i,/2, etc. La posición de la lámina, con relación
a Xi, Vi, se determina por las coordenadas xi.yi y 0, según se indica.
Demostrar que wx = uy = 0, uz = 8 + a y que
¿2 = (xi — 2/i«) cos « — [Vi + °(r + ^í)] sen a
con una expresión semejante para y2.
Demostrar que las componentes de la velocidad de O en el espacio inercial, según las direcciones
instantáneas de X y Y, están dadas por
v0x = *2 eos (6 + a) + y2 sen (6 + a), y v0y = —x2 sen (6 + a) + y2 eos (6 + a)
Demostrar que para la lámina,
T = $«[(«! - ya)* + (y, + á(r + xj)*] + tfjfi + 'a)*
+ M(e + á){[yi + (r + x^ájí* cos e — y sen e — (xx — Via)(x sen e + y cos e)}
Fiff.8-30
178 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
Suponiendo que a varía de cierta manera con relación al tiempo, T = T(xlt ylt e\ xlt ylt e\ t).
Entonces las ecuaciones del movimiento (que pueden escribirse fácilmente) determinan el movimiento de
la lámina con relación a los ejes móviles Xi y Vi. Obsérvese la simplificación que se obtiene para T, al
tomar a O en el c.m.
Suponer que la base B, de la figura 8-12, está a una distancia R, del centro de una plataforma horizontal
que gira con velocidad angular ¿, alrededor de un eje vertical que pasa por su centro. Sea Xi una
extensión de R. Demostrar que si se toman los ejes fijos al cuerpo, indicados para el disco, se tiene,
ux = (a + ¿) sen 6 sen <f>, uy = (a + ¿) sen 6 eos <f>, uz = $ + (a + ¿) eos 6
v0x = Ra(coa <f> sen ^ + sen <f> eos 6 eos ^), i>oy = —Ra(sen</> sen ^ — eos </> eos 6 eos \p)
v0z = —Ra sen e eos ^, i^ = R2cP
donde i;ox. foy y voz son las componentes de vo, la velocidad de O en el espacio inercial, tomadas
según las direcciones instantáneas de los ejes fijos al cuerpo, X, Y y Z. Escribir la expresión de T y
comparar con el valor de T, hallado en el ejemplo 8.8.
En la figura 8-31, el marco Xx, YX,Z\ está sujeto a la Tierra, con Vi tangente a un círculo máximo
y dirigido hacia el norte, Z\ normal a la superficie de la Tierra, y X\ dirigido hacia el oriente. Los
cojinetes que sostienen el eje a¡a2 del giroscopio, están fijos con respecto a la Tierra. El giroscopio
puede girar alrededor de a.\a.2 y de bibí. Demostrar que teniendo en cuenta la rotación de la Tierra,
ux = ($i + ue sen ♦) senff2 + ue eos* eos 6t eos 02
uy = (9i + «e sen*) eos 02 "~ uc eos* eos 8X senff2
uz = *2 "t" «ecos*sen*l
y además
T
hJZ[ifii + "e sen*)2 + «2 eos2* eos2 0t] + ^Iz[h + ««> eos* sen 9t]2 + constante
donde w, es la velocidad angular de la Tierra y * la latitud. Se ha tomado el origen O, de los ejes fijos
al cuerpo, X, Y y Z, en el c.m.
Escribir las ecuaciones del movimiento y demostrar que, despreciando el término que contiene a
w¡{o>e = 7,29 X 10-5 rad/seg),
Ixá + cue eos* sena = 0
donde «i + a = 90° y dT/B62 = c = constante.
En el caso en que el ángulo a sea muy pequeño, demostrar que 2n(Ix/cue eos*)1/2 es el período
de oscilación del eje btb2 alrededor de la recta Vi. Considerar el caso en que e tiene sentido contrario.
^^^^^^^^^^^^^
Fig. 8-31
Fig.8-32
CAP. 8] ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE 179
Se hace oscilar la base B, sobre la que está girando el trompo de la figura 8-32, horizontalmente, de
acuerdo con la ecuación x = A sen w t. Tomando los ejes fijos al cuerpo de tal manera que el origen
coincida con la punta del trompo y el eje Z con el eje del trompo, demostrar que
T = £MA2«o2 cos2 ot + ^(¿2 + ¿sen2 e) + £/z(¿ + ¿ cos e)2
+ MAur cos ut(¿ sen 6 cos ^ + d cos 6 sen ^)
Demostrar que la ecuación del movimiento correspondiente a 0 (obsérvese que puede ignorarse el primer
término de T) es .. • . •
lxe + (Iz — Ix)$2 sen* eos* + Iz<f>f sen*
— MAuPr senut cos * sen^ = Mgr sen*
Expresar las ecuaciones del movimiento correspondientes a ^ y <t>.
La punta del trompo, de la figura 8-33, permanece en el punto O, sobre el brazo horizontal giratorio R.
El sistema X2.y2.Z2 está fijo en el espacio, en tanto que Xi.Yi.Zi se encuentra rígidamente
adherido al brazo R. Por conveniencia se toma a Xi como una prolongación del brazo y tanto Xi como
Vi permanecen en el plano X2Y2. Z\ permanece paralelo a Z*. El sistema X, Y, Z está fijo al
cuerpo. Los ángulos de Euler, 0, if> y <t>, se miden con relación al marco Xi, Yi.Zi, según se indica.
Este problema constituye un caso especial del más general estudiado bajo el numeral 8.10. La notación
utilizada es la misma de la figura 8-21. Demostrar que
v0 = ityi (siempre en la dirección de Vi)
v0x = ityi(cos <(> sen ^ + sen </> cos ^ cos *)
v0y = ity^cos <f> cos ^ cos * — sen <p sen ^)
v0z = —Rfi sen* cos^
uz = ¿ sen * sen </> + * cos </> + ^ sen * sen <f>
uy = $ sen * cos </> — * sen </> + ¿, sen * cos <f>
uz = <f> + ¿ cos * + ¿! cos *
Por último, demostrar que
T = $MRtfÍ + $[/&£ + «;) +/M + Mr{v0x»y-vQyux)
Obsérvese que si se supone que ^1 es una función determinada del tiempo (es decir, que se hace
girar el eje vertical Onb de cierta manera), T = T(ff,}f>,<f>; *,¿, #; t). Entonces, las ecuaciones del
movimiento indican el movimiento del trompo con respecto al marco en rotación Xi, Y\,Z\.
Caso especial del descrito por la figura 8-21
X.¿ / con la misma notación
Fig. 8-33
180 ESTUDIO DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS, DE LAGRANGE [ CAP. 8
8.25. Supóngase que el brazo R, de la figura 8-33, junto con el eje O2ÍJ, se hace girar bajo la acción de
determinado torque t^ . ¿Cuántos grados de libertad tendrá ahora el sistema completo? Expresar la energía
cinética T del sistema total.
8.26. El eje ai61, de la figura 8-34, está montado sobre el cojinete giratorio B. Sobre este eje se halla
colocado el disco D, en la forma indicada. Los desplazamientos angulares se miden con relación a A, B y C,
respectivamente.
(a) Demostrar que con los ejes adheridos a D como en la figura 8-5,
ax = [Oí eos a eos 02 cos P ~ (*2 + si sen a) sen/?] sen 0$ + B\ eos a sen B2 cos *3
oy = [61 cos a cos 62 eos ¡3 — (e2 + 9X sena) sen ¡3] cos ff3 — 6X cos a sen e2 sen03
<"Z = *3 + [*2 + e\ sena] cos/J + Bx cosa cos 82 senfi
(b) Haciendo uso de los principios
enunciados en el numeral 8.10, expresar las
componentes de la velocidad del c.m.
de D, en el espacio inercial, en las
direcciones de X, Y y Z. (Sugerencia.
Tómese el origen de X\,Y\,Z\, en el
punto p, con Vi en la dirección de r
y Zi coincidente con el eje a\b\.)
(c) Escribir las ecuaciones de trasforma-
ción que relacionan la posición del c.m.
con el espacio inercial. Tomando las
derivadas de estas ecuaciones, hallar
la velocidad del c.m. Comparar este
valor con el hallado en (b).
(d) Escribir la expresión de T, sin
necesidad de remplazar las formas explícitas
de ü)x, voz, etc.
8.27. Un cuerpo rígido puede moverse, bajo la
acción de ciertas fuerzas determinadas, con
relación a los ejes X, Y y Z, indicados en la
figura 8-6. Tomando los ejes fijos al cuerpo
con el origen en el c.m., suponiendo 0t =
constante y ff2 = constante y siguiendo el
procedimiento general enunciado en el
numeral 8.10, describir las etapas para
expresar la energía cinética T del cuerpo.
8.28. En el ejemplo 8.20, la base se halla colocada en un punto de la Tierra cuya latitud es *. (Véase la figura
14-2.) Escribir las expresiones de wx, wy, uz, r0 y finalmente, T, para el cuerpo rígido, teniendo en
cuenta la rotación de la Tierra.
El método de Euler de la
dinámica de los cuerpos rígidos
Dinámica de los cuerpos rígidos: Parte III
9.1 Observaciones preliminares.
El método de Lagrange que acaba de completarse, en muchos casos resulta más
conveniente que el que se considerará a continuación. Sin embargo, se incluye el capítulo porque,
(1) el enfoque de Euler es especialmente útil para aclarar ciertos principios básicos, físicos y
geométricos de la dinámica de los cuerpos rígidos, (2) el método ha sido utilizado
extensamente en el pasado, y aún lo es, y (3) los ejemplos y problemas incluidos a continuación,
sirven como medio de comparación entre los dos métodos.
El método de Euler se basa en la consideración de un "cuerpo rígido libre", libre en el
sentido de que, si tiene alguna restricción, es preciso incluir las fuerzas de restricción junto con
las aplicadas externamente. Matemáticamente, el método conduce a dos ecuaciones
vectoriales fundamentales: {9.3) y (9.15), las cuales son equivalentes, en su forma escalar, a: (a)
tres ecuaciones del movimiento de traslación del centro de masa, las ecuaciones {9.2), y (6)
tres ecuaciones que determinan el movimiento de rotación del cuerpo, las ecuaciones {9.10).
En adelante, estas seis formas se denominan "ecuaciones de Euler". Para entender sus
deducciones y aplicaciones se requiere cuidadosa atención en los detalles y puede ser necesario
releer varias veces algunas secciones, sin embargo, no se encontrarán dificultades intrínsecas.
Como se demuestra en el numeral siguiente, las primeras tres ecuaciones se obtienen
fácilmente a partir de consideraciones elementales. El segundo grupo puede deducirse de
varias maneras: partiendo de las ecuaciones de Lagrange; por métodos vectoriales formales, o
sencillamente por aplicación directa de las ecuaciones de la segunda ley de Newton.
Aquí se empleará el último sistema, puesto que conduce a la forma general de estas
ecuaciones en una forma fácil de comprender y de tal manera que en ningún momento se pierden
de vista los principios físicos básicos pertinentes. Además, a las ecuaciones finales del
movimiento puede dárseles una interpretación física muy sencilla.
La deducción corriente de las ecuaciones de Euler incluye una consideración de la
rapidez de cambio del "momentum angular". Pero como se estima que el método aquí
presentado ofrece ciertas ventajas desde el punto de vista didáctico, el momentum angular sólo se
estudia al final del capítulo.
9.2 Ecuaciones del movimiento de traslación del centro de masa.
Refiriéndose a la figura 9-1, y considerando la partícula típica m' como "libre", se escribe
m'xy = fx, ra'2/i = /y, m'zi = fz (9.1)
en donde x\, y\ y z\ son las coordenadas de m' con respecto al marco inercial Xi, Y\,
2i, y fx, fy y fz son las componentes de una fuerza neta f, que al actuar sobre m' le
imprime una aceleración, a, con relación al espacio inercial. Se supone que la suma vectorial de
las fuerzas sobre m', debidas a la atracción y repulsión de las partículas que la rodean, es igual
a cero.
181
182 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
Zy\
*i
tU..fy.f.) - Fuerza sobre n
Aceleración de m' e
el espacio inercial
^1
Fi.Fi, etc., son las fuerzas aplicadas
externamente, f es la fuerza trasmitida
a la partícula típica, m'. Las ecuaciones
del movimiento de la partícula libre
son:/x = m'x.fy = m'y, fz = m'z.
A es la aceleración dal era. en el
espacio inercial. La ecuación del
movimiento del c.m. es F - MA. F es la suma
vectorial de las fuerzas aplicadas
externamente.
Determinación de las ecuaciones del movimiento del c.m.
Fig. 9-1
Sumando la primera de las ecuaciones (9.1), sobre todas las partículas del cuerpo, ^rrúx =
2 fx = Fi, donde Fx es la suma de las componentes en la dirección de Xi, de todas las
fuerzas aplicadas externamente. Pero por la definición del centro de masa, 2 w/íC< = ^#»
donde M es la masa total del cuerpo y x es la coordenada del c.m. en la dirección de Xi. Por
tanto, Fx = M'¿, Fv = Mj¡ y Fz — M'i.
A fin de evitar confusiones, en adelante se utilizará la igualdad x = Ax, etc. Así,
las tres ecuaciones del movimiento de traslación del c.m. se escriben,
Fx = MAX, Fy = MAy, Fz = MAZ
(9.2)
Resulta evidente que las ecuaciones (9.2) pueden ser consideradas como componentes de
la relación vectorial J/A = F (9.3)
donde F es la suma vectorial de todas las fuerzas aplicadas externamente (consideradas
como actuantes sobre el c.m.) y A representa, en notación vectorial, la aceleración del c.m. con
relación al espacio inercial.
Nótense los siguientes puntos importantes:
(a) El centro de masa se mueve como si toda la masa del cuerpo estuviera concentrada en
ese punto con todas las fuerzas externas trasladadas de modo que su línea de acción
cruce el c.m. sin cambiar de dirección ni de magnitud.
(b) Las fuerzas aplicadas Fi, F2, etc., no sólo ocasionan traslación del cuerpo sino que
también producen movimiento de rotación (como se verá con claridad más adelante).
(c) La ecuación (9.3) evidentemente se puede aplicar a un cuerpo con cualquier tipo de
restricciones, siempre que las fuerzas de restricción se incluyan en F (normalmente se
introducen como incógnitas).
9.3 Diversas maneras de expresar las ecuaciones escalares correspondientes
a (9.3).
En las ecuaciones (9.2) el c.m. puede tratarse como una partícula única. Las
componentes de A y de F (naturalmente debe tenerse presente que A es la aceleración en el espacio iner-
CAP. 9|
EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS
183
cial) pueden tomarse según las direcciones de cualquier sistema de ejes, móviles o fijos, y
expresadas en función de cualquier sistema de coordenadas. Por ejemplo, si se supone que el
sistema X, Y, Z es inercial, las ecuaciones (2.60) pueden considerarse como las componentes
de A, tangentes a las líneas coordenadas correspondientes a r, 0 y <¡>. Así mismo, si se
considera la figura 9-8, pueden obtenerse las ecuaciones del movimiento del c.m. tomando
componentes de A y de F según las direcciones instantáneas de los ejes fijos al cuerpo, o según Xi,
Y\ y Zi, por ejemplo.
Las expresiones específicas de las componentes de A pueden hallarse, (a) como se indicó
bajo el numeral 2.12 (3), (b) por el método de Lagrange descrito en el numeral 3.9, o (c) en el
caso en que las componentes se hayan de tomar según las direcciones de ejes que se trasladan
y giran; pueden obtenerse Ax, Ay y Az, a partir de la relación (9.6).
9.4 Consideraciones fundamentales para la determinación de las ecuaciones de
rotación de Euler.
A. Expresiones generales para las componentes de la aceleración de una partícula
libre en el espacio inercial, según las direcciones de los ejes de un marco en
movimiento.
Considérense les ejes Xi, Y\ y Zi, de la figura 9-2, como inerciales. Supóngase que
el marco X, Y, Z se traslada y gira de una manera arbitraria. Este marco, por ejemplo,
puede estar sujeto a la proa de una embarcación que se balancea, cabecea, "zigzaguea" y avanza
hacia adelante. Los ejes X', Y' y Z\ con el origen en el mismo punto que el de X, Y, Z, se
suponen paralelos a Xi, Y\ y Z\. La velocidad angular del marco X, Y, Z, con relación a Xi,
Y\, Z\ (o con relación a X', Y', Z'), se representa por O. Las componentes de O en las
direcciones de X, Y y Z se expresan por medio de Í2Z, Qy y Qz. Considérese a m como
una partícula libre (que no forma parte de ningún cuerpo rígido), sobre la cual actúa una
fuerza, f, que le imprime una aceleración, a, con relación al espacio inercial.
■ X. V, Z. con respecto
respecto a X'. V. Z')
El marco X, V, Z, se traslada y gira
de manera arbitraria
', Z' permanece paralelo a Xi, Vi, Zi. fl, * y 4,
son los ángulos de Euler. O es la velocidad angular del
marco X. y, Z con relación a X,, V,, Z,. 11,, Qr y ti,
son" las componentes de O en las direcciones de X, y y Z.
a es la aceleración de la partícula libre, m, en el espacio
inercial. aIt ar y a, son las componentes de a en las
direcciones instantáneas de X, y y Z. ao es la aceleración de
O en el espacio inercial.
Determinación de az, ay y az.
Fig. 9-2
A continuación se determinan las expresiones de ax, ay y az (relaciones (9.6)), las
componentes de a en las direcciones instantáneas de X, Y y Z. Como se verá más adelante, estas
expresiones desempeñan un papel muy importante en la deducción de las ecuaciones del
movimiento de rotación de Euler.
184 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
Quizá la manera más clara y más directa de obtener los resultados deseados es por
medio de las ecuaciones de trasformación. Las coordenadas de m con respecto aXi, Yi, Z\
y X, Y, Z se representan por xi, y\ y z\ y por x, y y z, respectivamente. Si se escriben las
coordenadas de 0 como xo, yo y z0, la ecuación de trasformación será,
Xx = XQ + Xau + ya2l + Za3l
donde, como se indica en la figura, «n, aX2 y «13 son los cosenos directores de X, etc.
Tomando dos veces la derivada con respecto al tiempo, se tiene,
'x\ = XQ + Xan + ya2l + ZaSl + Xau + y'¿2l + Za3l + 2(x'an + ifa2l + ZaJ (1)
Igualmente pueden obtenerse las expresiones correspondientes para y\ y z\. Entonces, ax,
ay y az, según se definieron antes, estarán dadas por
ax = xlan + y\al2 + z\aa, etc. (9.4)
Estas expresiones pueden ponerse en las formas útiles de {9.6), como sigue: Se miden
los ángulos de Euler con respecto a X', Y' y Z', como se indica en la figura 9-2. Así, los cosenos
directores de X, an, al2 y «13, pueden escribirse en función de \J/, <¡> y 6, de acuerdo con
la tabla 8.2; y las expresiones de ¿lf alf etc., pueden obtenerse al tomar las derivadas.
Eliminando ahora Xi,yi y z\ de (9.4), por medio de (1), etc.; eliminando las a,á y "¿ de
las ecuaciones resultantes y utilizando las relaciones siguientes (véanse las ecuaciones (8.22))
fií = ¿sen0 sen^» + 6 eos <f>, Qy — ip senO eos <f> — 6 sen<f>, nz = j> + }cos6 (9.5)
finalmente, la ecuación (9.4) toma la forma de (9.6a). En forma semejante pueden
obtenerse (9.6b) y (9.6c).
Sin embargo, con el fin de simplificar las operaciones trigonométricas, sin abandonar
la condición de generalidad, se procede de la siguiente manera: Se supone (por conveniencia)
que en el momento considerado, se toma el marco inercial Xi, Y\, Z\ en una posición tal
que 6 = 90° y ^ = <¡> = 0. Nótese que en este caso X es paralelo a Xi, Y es paralelo a Zi,
y Z tiene la dirección negativa de Y\. En la tabla 8.2 se observa que an = 1, a 12 =
«i3 = 0, etc. Entonces, partiendo de (9.4), y las otras ecuaciones semejantes a ésta,
ax = xi, ay = z\, az = -yx (2)
Se encuentra además que para estos valores de los ángulos de Euler,
«n = 1, ¿„ = 0, au = -& + ¥)
«21 = 0, a2l = -¿, «21 = (20¿-J) (3)
«31 = °» «31 = í» «31 = "í
y por las relaciones (9.5) se observa que
fix = 6, fi« = é, flr = A
(4)
nx = e + <p$, fi« = $ — $6, fiz = <t> - $0
Por último, utilizando (3) y (4), la primera de las ecuaciones (2) puede escribirse como (9.6a).
Por el mismo procedimiento se determinan (9.6b) y (9.6c).
ax = a0x + x — x(íi% + íñ) + y(nxnv — nz)
+ z(nxíiz + hy) + 2(zqv - ynx) ^
ay = a0y + y + x(nxny + nz) - y (ni + ífz)
m . (h) (9.6)
+ z(ciynz - nx) + 2(xnz - znx) K '
CAP. 91 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 185
az - a0z + z + x(nxnz - fi„) + y(nyíiz + ñx)
- z(nl + sfy) + 2(ynx - xny) (c)
Componentes de a, la aceleración de m en el espacio inercial, en las
direcciones instantáneas de los ejes con movimiento de traslación y rotación,
X, Y y Z de la figura 9-2.
Debe tenerse presente el significado de cada uno de los símbolos que intervienen en
(9.6). a es la aceleración de m, a o es la aceleración de O, O es la velocidad angular del
marco X, Y, Z\ todos ellos medidos con respecto a un marco inercial. ax, ay y az son las
componentes de a; a0x, a0tf y a0x son las componentes de ao; íix, íiy y ft* son las
componentes de O; en todos los casos, tomadas en las direcciones instantáneas de los ejes
con movimiento de traslación y rotación, X, Y y Z. x, x, etc., son las componentes de la
velocidad y la aceleración de m con relación a X, Y, Z (medidas por un observador en este marco).
En notación vectorial, las ecuaciones (9.6) son equivalentes a
a = r0 + ai 4- 2« X v + ¿ X r + « X (« X r)
donde a es la aceleración de m en el espacio inercial; ro es el vector posición medido desde
Oí a O; ai = ix + jy + kz es la aceleración de m con relación al marco X, Y, Z\ r es el
vector posición medido de O a m¡ v = ix 4- jy + kz es la velocidad de m con respecto a X,
Y, Z y por último, i, j y k son los vectores unitarios en las direcciones de X, Y y Z,
respectivamente. Véase el capítulo 18.
Otro enfoque para lograr la deducción de (9.6) se encuentra en Introduction to
Advanced Dymamics, de S. W. McCuskey, Addison-Wesley, 1959, páginas 31 y 32. Véase además
el problema 9.2.
El carácter fundamental y la importancia de (9.6) aparecen con claridad en el ejemplo
siguiente.
Ejemplo 9.1.
Se trata de determinar el valor de las componentes a, y ay de la aceleración de m en el espacio inercial, en
las direcciones instantáneas de X2 y de Y2, respectivamente, según la figura 2-21. Nótese que ux = uy = 0,
y "«2 = *i + 92' Por consideraciones elementales, se ve que las componentes de la aceleración del origen de X2,
Y2,Z2, en el espacio inercial, ate y Ooy, en las direcciones de X2 y Y2, respectivamente, son
ata = — 80j eos $2 + sVj sen $2, ^oy = 89i 3en *2 + 8 *"i cos 92
Aplicando (9.6), se obtiene en seguida,
ax = -8$\ cos*^ + sVj sen*2 + «2 ~ xéfi\ + h)2 ~ Vidí + ¿2) ~ 2y2(¿i + ¿2)
a„ = 8Í\ sen*2 + 8$\ cos$2 + y2 — y2(Ói + 92)2 + xi(^i + ¿2) + 2x2(«i + $2)
Un observador montado en D2 que desea determinar el movimiento de m con respecto a este disco móvil,
escribiría las ecuaciones del movimiento como max = /, y may = fy, donde /, y fy son las componentes de
la fuerza sobre m en las direcciones de X¡¡ y Y2.
Nótese lo siguiente: Fácilmente se concluye que la energía cinética de m está dada por
T = \m[86Í\ + (x2 - yj¡)2 + ¿2 + *20)2 + 28¿j(x2 - V¿) sen*2 + 28¿j(j/2 + x¿) cos e2]
donde 0 = $¡ + $2. Véase el problema 9.2. Aplicando el método del numeral 3.9, el lector puede comprobar las
expresiones anteriores de ax y ay.
B. Ecuaciones (9.6) para el caso en que m es una partícula típica de un cuerpo
rígido.
Supóngase que la partícula m de la figura 9-2, es ahora m' en 9-3. Para simplificar se
toman los ejes X, Y y Z como fijos al cuerpo, según se indica. En este caso x, y y z son
constantes. Por tanto, x = y — z — 0 y x — y — z = 0. La velocidad angular del marco, O, es ahora
la velocidad del cuerpo con relación a Xi, Yi, Z\ (o con relación a X', Y', Z'), «, y por con-
186 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
siguiente, Í2X = wx, etc., donde wx, wy y wz representan las componentes de la
velocidad angular del cuerpo en el espacio inercial, en las direcciones instantáneas de X, Y y Z.
En tal virtud, las relaciones (9.6) se reducen inmediatamente a
f
aoz + x(»¿>M - ¿y) + y(a>ya>z + ¿J - «(»* + «oj) (c)
(9.7)
Las ecuaciones anteriores, naturalmente, se aplican a cualquier sistema de ejes fijos al
cuerpo con el origen en el punto 0.
Debe observarse que como las componentes de la aceleración, a, de m' en el espacio
inercial son ax, ay y az, la componente, doa, de a, en la dirección de una recta cualquiera
Oa, que pase por O y tenga por cosenos directores a /, m y n, con relación a X, Y y Z, estará
dada por a0a = axl + aym + azn (9.7a)
La recta Oa puede estar girando alrededor de O, con respecto al cuerpo, caso en el cual /, m
y n son variables y por consiguiente (9.7a) da el valor de a0a en la dirección instantánea de
esta línea.
9.5 Las tres ecuaciones del movimiento de rotación de Euler, para un cuerpo
rígido. Forma general.
A continuación se deducen las ecuaciones del movimiento de rotación de un cuerpo
sujeto a la acción de fuerzas externas Fi, F2, etc., como en la figura 9-3.
= Velocidad angular total del
cuerpo con relación al espacio inercial
Vo-
X, Y y Z son los ejes fijos al cuerpo. Fi, F2. etc.. son Iss
fuerzas aplicadas. • es la velocidad angular total del
cuerpo, ao es la aceleración lineal de O en el espacio inercial.
a es la aceleración lineal de una partícula típica m' en el
espacio inercial. u„ ur, u,; ao,. a0r, ao. y a.. °r-
o, son las componentes de », ao y a, respectivamente,
en las direcciones instantáneas de los ejes fijos al cuerpo.
X, V y Z. e, i y <j> son los ángulos de Euler.
Fig. 9-3
Mientras el cuerpo gira y se desplaza, una partícula típica cualquiera, m', en general
sufre una aceleración, a, (tal como en el numeral 9.2) que aquí se considera medida con relación
al espacio inercial. Esta aceleración se debe a una fuerza f, que es la resultante de las fuerzas
que, aplicadas como Fi, F2, etc., se han trasmitido a la partícula; además forman parte
CAP. 9 J EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 187
de f, la atracción de la gravedad y las fuerzas de atracción o repulsión de las otras partículas
que la rodean. En lo que sigue se supone que estas fuerzas de atracción y repulsión se anulan
dos a dos. Si ax, ay y az por una parte, y fx, fy y fz por la otra, son las componentes
de a y de f, respectivamente, en las direcciones instantáneas de los ejes X, Y y Z, se escriben
las ecuaciones del movimiento de la "partícula libre", como
m'ax = fx, m'av = fy, m'ax = fx
(1)
Multiplicando la última relación de (1) por y, la segunda por — zy luego sumando, se tiene,
ra'(az2/-az) = fzy-fyz (2)
(Obsérvese que la validez de la ecuación (2) no se afectaría si se remplazaran los valores de y y
z por cantidades arbitrarias. Por tanto, en cierto sentido, (2) es una forma de ecuación de
d'Alembert.) En la figura 9-4 se puede ver que fzy — fyz es el momento de f alrededor de
X. Entonces, sumando sobre todas las partículas del cuerpo, la ecuación (2) queda
^m\azV-az) = Jí/.if-/,*) = rx (9.8)
Como la suma se realiza sobre todas las partículas del cuerpo, tx representa la resultante de
los momentos de todas las fuerzas aplicadas externamente (incluyendo las fuerzas de
restricción, si existen), alrededor de X. La ecuación (9.8) y las expresiones similares para ry y tz
«/,./„./,)
CDr,
f es la fuerza aplicada a m". r,. r, y r, son los
momentos de f alrededor de X, V y Z,
respectivamente, f.y es el momento positivo y f,z el
momento negativo alrededor de X. Por tanto.
t, - f.y — fyz. Igualmente, r, - f.z — f,x
y '. - />*- f.y-
--f^-Lv i
I /x Momentos de f alrededor de X, Y, Z.
V
Fig. 9-4
constituyen las ecuaciones básicas de rotación y pueden ponerse en una forma conveniente y
útil de la siguiente manera:
Las componentes ax, ay y az están dadas por (9.7). Eliminando ay y az de (9.8)
se obtiene
M(%zy - v) + ¿, 2 ™'(y2 + *) - v», 2 «!'(** - y2)
+ (oy^ - ¿y) 2 m'zy ~ (<v>„ + ¿J 2 m'xz - K ~ aD 2 m'yz = rx. Í9.9)
= suma de momentos de todas las fuerzas externas alrededor de X (Fig. 9-3).
Pero como 2) ™>'(y2 + z2) = h, 2 W(sy) = /*„,
2 m'(z2 - y2) = 2 m'[(z2 + x2) - (x2 + y2)] = Iy - h, etc.
Entonces, la ecuación (9.9), con las expresiones para ry y tz, halladas de la misma manera,
puede escribirse,
(a)
(6)
(ftiO)
188 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
M(V - aJft + 7A + i1 y ~ 7*)<V>„ + 7«K*>Z ~ ¿J (c)
-I («ücü +¿)+7 U2-*2) = t
yzV"x z "V xyV y x' z
Una forma general de las ecuaciones de rotación de Euler.
9.6. Aspectos importantes con respecto a {9.10).
(a) Las ecuaciones {9.10) constituyen una forma general muy útil de las ecuaciones del
movimiento de rotación, de Euler. Estas relaciones junto con {9.2) determinan
completamente el movimiento de un cuerpo rígido. En la figura 9-3, X, Y y Z son ejes fijos al
cuerpo con el punto O situado en un punto cualquiera.
(6) Puede darse una sencilla interpretación física de {9.10) como sigue: Recordando que ax,
ay y az en {9.7) son medidas con relación al espacio inercial; en consecuencia, m'ax,
etc., son fuerzas inerciales (se define "fuerza inercial" como el producto de (masa) X
(aceleración) relativa al espacio inercial). Así, ^m'fazy — ayz) es la suma de los
momentos de todas las fuerzas inerciales, con respecto a X. Y naturalmente, los miembros
izquierdos de (9.10) deben tener el mismo significado. Por consiguiente, estas ecuaciones son una
expresión del siguiente "principio de momentos"
/Suma de los momentos de\ /Suma de los momentos de\
I las fuerzas inerciales j = I las fuerzas aplicadas I {9.11)
\ alrededor de X / \ alrededor de X /
que es igualmente válida para momentos alrededor de Y o de Z, o en realidad, alrededor
de una recta cualquiera.
(c) Es importante observar que al plantear las tres primeras ecuaciones de Euler, (9.2), no es
necesario que el marco de referencia allí utilizado coincida con el empleado al establecer
las ecuaciones de rotación, {9.10).
{d) Como se ve claramente en (9.7a), es posible escribir las ecuaciones de rotación de Euler
para ejes que giren alrededor de O, con respecto al cuerpo. Véanse el problema 9.10 y los
ejemplos 9.8 y 9.9.
(e) Determinación de tx, ry y tz. F< representa una de las fuerzas aplicadas en pt (Fig.
9-3) y sus componentes según X, Y y Z son /*.,/„. y /*.. Las coordenadas dep, en este
mismo marco, son x,, y, y 2(. Por tanto
tx = ^(fz.Vi-fy^) {9.12)
Si las componentes de F< se toman en las direcciones de Xi, Yi y Zi, ifx.,fy.,fz.) »
entonces, ¿y,*',*'
f*t ~ Txan + fyal2 + fza13 (9i3)
(/) Formas simplificadas de {9.10). Supóngase que O está localizado en un punto cualquiera
del cuerpo y que X, Y y Z están fijos al cuerpo. Se toman X, Y y Z en las direcciones de
los ejes principales de inercia que pasan por O. En este caso, como Ixy = Ixx = Iyz = 0,
todos los términos que contienen productos de inercia desaparecen.
Si se toma a O en el c.m., x — y — z — 0. Así, los primeros términos de cada una de
las ecuaciones (9.10) se anulan, aún en el caso en que X, Y y Z no estuvieran fijos al cuerpo.
Si un punto cualquiera del cuerpo se halla fijo en el espacio (por ejemplo, por medio
de una articulación esférica) y se toma a O en ese punto, el primer término de cada una
de las ecuaciones {9.10) desaparece puesto que a0x = cíoy = a>oz — 0.
Nótese que en los dos últimos casos, las relaciones {9.10) adquieren exactamente la
misma forma.
Si O está fijo en el espacio o localizado en el c.m., y si además los ejes fijos al cuerpo
se hacen coincidir con los ejes principales de inercia, las relaciones {9.10) se reducen a la
siguiente importante forma:
CAP. 9] • EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 189
o. + cr-Ov. = ^ <«>
K^ + iK-O^y = r, (c)
(#) Las ecuaciones {9.10) pueden deducirse a partir de las ecuaciones de Lagrange. Véase el
problema 9.9.
9.7 Forma vectorial de las ecuaciones de rotación de Euler.
Como se demostró bajo el numeral 8.2F, el torque puede ser tratado como un vector,
cuyas componentes rectangulares son tx — 2 ftV ~ fyz> etc. Véase la ecuación (9.8). De
igual manera, 2 m'(axy — ayz) es la componente X de un vector debido a fuerzas inerciales.
Por conveniencia, se puede escribir el conjunto de relaciones {9.10) como Bx = tx, By =
Ty y Bz = tz en donde Bx es una abreviatura para el lado izquierdo de {9.10a), etc. Se
observa entonces que {9.10) son las componentes de la ecuación
B = r {9.15)
donde las componentes de B son Bx, By y Bz y las de r son tx, ty y tz.
Si se toman las componentes de B y de t en la dirección de una recta cualquiera Oa, que
pasa por O {que no está necesariamente fija en el espacio ni fija al cuerpo, véanse los
ejemplos 9.8 y 9.9) cuyos cosenos directores son l, m y n, resulta evidente que
Bxl + Bym + Bxn = txI + Tym + rzn = r0a {9.16)
Ecuación de Euler aplicable a cualquier recta Oa.
(Para una deducción más directa, véase el problema 9.10.)
9.8 Ejemplos específicos para ilustrar el uso de las ecuaciones {9.2) y {9.10).
Nota. Muchos de los ejemplos del presente capítulo se han tomado del capítulo 8, de tal
forma que el lector puede hacer comparaciones directas entre los métodos de Lagrange y de
Euler.
Ejemplo 9.2. Considérese el ejemplo 8.4 (1), figura 8-8.
Tomando los ejes fijos al cuerpo, como se indica, u, = <oy = 0 y <o, = e. Por inspección, se observa que
Fx = — Mg sen $ + fx, Fy = — Mg eos 9 + fy y Fz = 0 donde /, y fy son las componentes de la fuerza de reacción
en p, en las direcciones instantáneas de X y Y. Además, r, = ry = 0 y tz = - Mgl sen*. Por otra parte, Ax =
l'$\ Ay = le2 y A, = a0x = aoy = aQt = 0. Como /„ —■ Iyz = 0 y Ixy j¿ 0, las ecuaciones (9.2) se reducen,
finalmente, a .,... . _. ..,•„ . ,- /t>
Míe = fx- Mg sen 6 y Míe2 = /„ - Mg cosí (1)
y las relaciones (9.10) quedan Iz'$ = — Mgl sen $ (2)
Para movimientos pequeños, la ecuación (2) puede ser integrada de inmediato para obtener a 9 en función del
tiempo. Así, fx y fy pueden ser obtenidas, por medio de (1), en función del tiempo.
Nótese que (2) puede obtenerse directamente por el método de Lagrange.
Ejemplo 9.3.
Con el objeto de poner de relieve los principios básicos e ilustrar interesantes técnicas (al costo de una solución
más elaborada) se considera de nuevo el problema anterior, tomando lus ejes fijos al cuerpo como se indica en la
figura 9-5.
De nuevo, u, = «y = 0 y u, = í y se observa entonces que
Fx = fx- Mg sen {$ + (3), Fy = /„ - Mg eos (6 + (3)
tx = Ty - 0, tz = fyr senP - fxr eos (3 + Mgy sen(e +P) - Mgx eos (e +(3)
aox ~ r$'cosft + re2 sen/3, aQy = re2 cos/J - r'$ sen/3
Ax = l'ecosa — l$2 sena, Ay = 16 sen a + le2 eos a
190 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
Nótese que aox, a0y, Ax y Ay son las
componentes de la aceleración de los puntos O y c.m.,
respectivamente, con relación a un marco inercial, tomadas en las
direcciones instantáneas de los ejes fijos al cuerpo. Las
componentes de la fuerza de reacción sobre el cuerpo, en el punto
de suspensión, son fx y fy. Obsérvese que estas fuerzas de
reacción aparecen en tz. Son constantes determinadas,
x y y.
Asi, las ecuaciones (9.2) se convierten en
M(l '$ eos a — Ú2 sen a) = fx — Mg sen ($ + /?)
M(l '$ sin a + le2 eos a) = fy - Mg eos (e + ¿3)
y la ecuación (9.70c) se reduce a
M(a0y£ - a0xy) + Iz'é = rz (2)
Al remplazar las expresiones de aQx, a0y y tz, en (2),
se completan las ecuaciones de Euler.
Realizando el trabajo monótono, el lector puede
demostrar que la relación (2) se hace igual a (2) del ejemplo
anterior. Nótese, sin embargo, que Iz tiene valores
distintos en este ejemplo y en el 9.2.
Como ejercicio, el lector debe determinar la ecuación
del movimiento correspondiente a 0, por el método de
Lagrange, y compararla con los resultados anteriores.
Ejemplo 9.4. Considérese el ejemplo 8.7, figura 8-11.
Tomando los ejes X, Y y Z como fijos al cuerpo y considerando la varilla delgada y uniforme de longitud
L, y = é L, x = z = 0, Iy — 0, Ix = Iz e Ixy = /„ = Iyt = 0. Se observa que ux = — 62, wy = fij cos«2 y
<o2 = lg sen fi2 alrededor de los ejes fijos al cuerpo. Además, a0x = —R$lt a^ = — ií^sen e2 y Oqz = Rot eos 82
tomados en las direcciones instantáneas de X, Y y Z, respectivamente. A partir de (9.7) se encuentran las
componentes de la aceleración del c.m. con respecto al espacio inercial, tomadas en las direcciones instantáneas de los
ejes fijos al cuerpo, que son .. . .
Ax — — (R + y sen 02) 9X — 20102ycos02
Ay — — (R + y sen ¿a)*? senfl2 — *\v O)
Az = (R + y sen e^B2 eos 62 - e'2y
Entonces, las ecuaciones (9.2) se hacen
-M[(R + y sen 62)e\ + 2.$i$2y eos $2) = fx
-M[(R + y sen e^ sen 92 + 62y] = -Mg eos 92 + fy (2)
M[(R + y sen ¿2)^1 cos*2 — '¿2V] — ~M9 senfi2 + fz
donde se ha supuesto que las fuerzas de soporte, /,, fy y fz, que actúan en O, poseen las direcciones instantáneas
de X, Y y Z.
Las ecuaciones (9.10) se reducen a
MyR$l eos $2 — /x02 + ^2*1 sen02 eos 02 = Mgy sen e2
(3)
MRye\ + Ix($x sení2 + 2el$2 eos $£ = rz, t„ = 0
en donde tz es el torque alrededor de Z, debido a las fuerzas de soporte.
El lector debe plantear la ecuación de 82 del movimiento por el método de Lagrange (véase la expresión
de T dada en el ejemplo 8.7) y compárese con la primera de (3). Si se supone que 81 es una función conocida del
tiempo, ¿cómo podrán hallarse los valores de tz, fx, fy y fz en función del tiempo?
Ejerr\plo 9.5. Determinación de la ecuación del movimiento y de las fuerzas de restricción que actúan sobre
el disco de la figura 8-12.
Considerando los ejes fijos al cuerpo indicados, ux, <oy y wz, éstos tienen los valores dados en el diagrama-
Las componentes de la fuerza sobre el disco son.
Fig. 9-5
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 191
Fx = -Mg sen fi sen <f> + fXl + fX2, Fy = -Mg sen* eos <p + /Vi + /„2 y Fz = -Mflr eos fi + fz
donde fxy y /yt son las fuerzas de soporte en a, y /i2y /«2 son las que actúan en b, en las direcciones instantáneas
de X y Y.
Tx — fy^l — fy^ Tv = f^h — fx^X y tz = 0
donde li y U son las distancias Oa y Ob, respectivamente. Suponiendo que B está fijo, aQx = aQy = aot = 0,
Ax = Ay = Az = 0 y 3¡ = y = z = 0. Por tanto, las ecuaciones (9.2) son
Mg sen* sen^ = fXl +fx2i Mg sen $ eos <j> = fVl +fy2 y Mg eos e= f2 (/)
y las relaciones (9.10) resultan
lx(\¡> sen* sen¿ + M sen* co9<f>) + (Íz — Íx)(f sen* cos^Xtf. + ^ eos*) = /Viii — /y2¿2 (2)
7x(£sen* costf. — $</> sen* sen¿) — (Íz — Íx)(f sen* sen¿)(¿ + ¿ eos*) = /^ — /x^i (3)
Jr¿¿(¿+ ¿cos*) = 0 (4)
Multiplicando a (2) por sen * sen <j> y a (3) por sen * eos <t> y sumando, se obtiene,
Ixf sen2* = (/Vl¿i — fy^ sen* sentf. + (fx^h ~ fXlh) sen* eos <¡> (5)
cuyo lado derecho es igual al torque que trata de modificar a $, t¡¡, . Entonces, (4) y (5) son las ecuaciones del
movimiento correspondientes a|yf, respectivamente.
Ignorando el momento de inercia del marco, t^ es el torque aplicado al eje cO por un motor, por ejemplo.
Si se supone conocido t^ , al integrar (4) y (5) se pueden obtener fx ,fy ,fx2 y fy2 i en función del tiempo.
Para complementar este ejemplo, el lector deberá demostrar que (4) y (5) pueden ser obtenidas de inmediato
al aplicar las ecuaciones de Lagrange. Véase el ejemplo 8.8.
Ejemplo 9.6. La ecuación del movimiento y las fuerzas de restricción sobre el disco D, de la figura 9-6.
El borde exterior de D rueda sin resbalar, sobre el plano inclinado. Una articulación esférica lisa en O, sostiene
el extremo del eje en su lugar.
Ob. en el plano XV,
ee conserva paralelo a la
superficie del disco
O
plano del dibuje
sale del T^^^^^fivv r2 b
del dibujo V.Unión esférica f VVVVV>**Xvvvvx
4/b \ Se muestra el disco en
posición de reposo
< Piano incHn^^^^VVVXVX^
/ •
Oscilación de un disco sobre un plano inclinado
Fig.9-6
Considérese inercial el marco X\,Y\,Z\. Se toma a Xi en dirección horizontal (normal al plano del
dibujo) y Yi en el mismo plano. Los ejes X, Y y Z (no se indican X ni Y) tienen el origen en el centro de la
unión esférica y están fijos al cuerpo. Los ángulos de Euler, * y <f>, se miden en la forma acostumbrada. Por
conveniencia se introduce el ángulo ^i en lugar de i, definido en la figura 8-16, en donde se ve que ^i se toma
entre Yi y la proyección de OZ sobre el plano XiYi. En este caso, } = fi + 180°. Nótese además que * =
constante, sen* = n/r3, eos* = r2/r3, rrfx = — rz<t>, Ix = Iy, l = distancia de O al c.m. del sistema,
< = ángulo de inclinación del plano, a0x = aoy = aQt = 0 y las componentes de la velocidad angular en las
direcciones de X, Y y Z, son
. n . n . r\
wx = ^ — sen?, coy = ^ — costf. y uz = —#i^r O)
192 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
Por (9.7), o por consideraciones elementales, se concluye en
Ax = (ZíWrgVj sen* - (lrx/rz) £, eos *
Ay = (Zr^/rg1)*, cos* - (Zrj/rg)*, sen* (2)
Az = -(lr\/r\)*\
Las fuerzas sobre el sistema son: Mg que actúa sobre el c.m. y que tiene por componentes, Mg sen < y
— Mg eos t en las direcciones de Y\ y Z\, respectivamente; /», una fuerza de reacción en b, en la dirección
de Z\\ f„, una fuerza de reacción en b, tangente a la trayectoria circular descrita por b, y que se supone dirigida
en la dirección en que *i aumenta; y una fuerza de reacción sobre la esfera en 0, con componentes, /,, fy y /,,
en las direcciones de los ejes fijos al cuerpo, X, Y y Z. Se supone que la fuerza de reacción total en b no tiene
componente en la dirección de r$.
Expresando por medio de Fx la suma de las componentes en la dirección de X\, de todas las fuerzas
enumeradas, etc., y por Fx la componente total en la dirección de X, de todas las fuerzas, se tiene,
FXj = Fxau + Fya12+Fza13 (3)
en donde (sin incluir la fuerza de reacción en O),
FXj = -/Jcos*,, FVj = -/t sen *, + Mg sen e y FZj = fb - Mg eos e (4)
Por último,
Fx = fx + fh—sen* + fL eos* — Mg sene ( eos* sen *, H sen*cos*j)H eos e sen *
r3 L \ r3 / r3 J
Fv = /v + /b—eos* - /b sen* + Mflr senef sen* sen^j eos * eos*, ) — —cose eos * (5)
r2 Tri r2 ~l
Fz = /z + /b — + Mg \ — sen e eos *, eos e
r3 Lr3 r3 J
Con un modelo sencillo y algo de paciencia, es posible verificar directamente estas expresiones.
Al combinar las ecuaciones (2) con (5), se obtienen inmediatamente las correspondientes a (9.2). No se incluyen
aquí más detalles. (¿Podrían escribirse las ecuaciones del movimiento del c.m. tomando las componentes de la
aceleración y la fuerza en las direcciones de los ejes X\,Y\ y Z\1)
Las ecuaciones de rotación se hallan como sigue. Se observa que las coordenadas del c.m., en el marco
X, Y, Z, son (0,0, l) y las de b son ( —r2cos*, —r2sen*, r). Nótese que las componentes X, Y y Z, de las
fuerzas individuales, pueden leerse directamente en las ecuaciones (5). Así, aplicando las relaciones generales,
tx = ^,(fzy — fyz), etc., se obtiene finalmente,
tx = fbT\ sen * — /br3 eos * — Mgl sen e ( sen* sen*! eos * eos *j ) eos e eos *
Tv = /bri cos <t> + /br3 sen <f> ~ Mgl sen e í eos * sen *j + — sen * eos *j ) H eos e sen * ^ '
rz = /b»*2
El lector puede verificar estas relaciones, tomando momentos directamente alrededor de X, Y y Z.
Las ecuaciones (9.10), que para este problema se reducen a (9.14), resultán ser
t rl /■■ *2r3 \ ,r r n rl '2
*x— ( *i sen * - *j — cos * 1 - (7Z - 7X) ^"^í cos #
cos* + ^I3.sen*j + (7z-7x)^2*2sen* = t„ (8)
r* ..
~7*:nr*i = T* - fbr2 (9)
r2r3
Multiplicando (7) por sen*, y (8) por cos* y luego sumando, después de eliminar // por medio de (9), se
obtiene la siguiente ecuación:
— ( Ix + lz-\ ) *, = -Mgl sen e sen*, (Í0)
r3 V r2/
que es la misma ecuación del movimiento obtenida con mayor facilidad y más rápidamente por el método de
Lagrange, en el ejemplo 8.11.
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 193
La integral de (70), que para pequeños movimientos resulta armónica simple, da el valor de jpi en función
del tiempo (y también el de *, puesto que r3*i = — r2*). Así, se pueden obtener f„ y f¡ en función del tiempo,
a partir de (8) y de (9), por ejemplo. Las ecuaciones (9.2) sirven para determinar fz,fy y fx. En esta forma,
se han determinado tanto las ecuaciones del movimiento como las fuerzas de reacción.
El tratamiento anterior incluye varios procesos largos y monótonos, pero, por otra parte, pone de presente
con gran claridad los principios y las técnicas del método de Euler. Ilustra, además, por comparación con el ejemplo
8.11, la superioridad del método de Lagrange para obtener las ecuaciones del movimiento.
Ejemplo 9.7. Fuerzas de soporte.
Se trata de determinar las expresiones de las fuerzas ejercidas por los cojinetes Bi y B2 sobre el eje del
cuerpo rotatorio de la figura 9-7, considerando inerciales los ejes Xi, Y\ y Z\.
X, Y y Z fijos al cuerpo
X y V permanecen en el p
Ángulos de Euler: 9-90° y * - 180°. La recta ON (véase la figura 8-16)
la dirección de Ot, -Xi. Asi, <t> se mide entre -Xi y X. Los
cojinetes B, y Bi están rígidamente unidos al marco Xi Vi Zt. /i„/i„
¡2, y 12, son las fuerzas de soporte en las direcciones de X y V. El marco
Xi.Vi.Z. es inercial.
Fig.9-7
Tomando los ejes fijos al cuerpo, y midiendo los ángulos de Euler como se indica, se observa que wx = wy = 0,
u» = * y aox = ooy = aoz = 0. Además (por principios elementales, o por la ecuación (9.7)),
Ax = -(<t>V + *2*),
Las fuerzas y los torques están dados por
Fx = fix + f2x-M9 sen*,
2* — y<t>2
¿z
— fly + fiy ~ MB eos <f>, Fz - 0
tx — fiyh ~ fiyh + M9¿ eos <f>, t„ = flxlx — f2zk. ~ M0¿ sen*,
tz = Mgy sen* — Mg& eos* + rm
donde rm es el torque ejercido por el motor y flx, fiy, f2z y /2y son las componentes de las fuerzas de los
soportes en B\ y B2, en las direcciones instantáneas de X y Y. Por tanto, las ecuaciones (9.2) y (9.70) se hacen
-M(*y + *2*) = flx + f2x - Mg sen*
M(*2 - *2y) = /,„ + /2v - Mg eos *
-/„* + 7yz*2 = f2yl2 - fXylx + Mgz eos <f>
-7yz* - 7I2*2 = fXxlx - f-uh- Mgz sen*
Jz* = Mg(y sen * - x eos *) + rm
Las relaciones (7) y (4) pueden resolverse para hallar f\x y f2z, dando como resultado,
fixih + y = M0(k + ¿) sen * - (Mlzy + Iyz) * - (MI& + 7M)*2
/toí'i + y = Mg(lx-z) sen* + (7yz-Ml<yü + (Ixz-Mlxx)^
(1)
(2)
(3)
(4)
(5)
(6)
(7)
194 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
De igual manera (2) y (3) se resuelven para determinar fiy y f2y. Si rm es una función determinada del
tiempo, la integral de (5) da a 0 en función del tiempo. Así, todas las fuerzas de soporte pueden ser expresadas
en función del tiempo.
Por la física del problema, es evidente que las fuerzas de soporte no dependen de la localización u orientación
del marco X Y Z. La selección hecha se ha tomado así por razones de conveniencia.
Equilibrio estático y dinámico: Considérense los siguientes dos casos.
(a) Si el c.m. está en el eje de giro no existe torque debido a la gravedad alrededor de este eje, y se dice que el
cuerpo está equilibrado "estáticamente".
(b) Supóngase que el c.m. está en el eje de giro y que Z es un eje principal de inercia que pasa por un punto, Oit
en el eje de giro. Tomando X y Y en las direcciones de los otros dos ejes principales, (6) y (7) demuestran que
no existirán fuerzas de soporte, debidas a la rotación. Se dice que el cuerpo está ahora equilibrado
"dinámicamente".
Una deducción que muestra con mayor claridad el significado físico de (6) y (7), se encuentra en el
problema 9.17.
9.9 Ejemplos para ilustrar la forma {9.16) de las ecuaciones de Euler
(junto con {9.3)).
En primer lugar, considérense las técnicas siguientes, que tienen gran importancia,
y son más generales que las discutidas o ilustradas hasta ahora. Como se utilizarán
ampliamente los ángulos de Euler, es conveniente que el lector repase los numerales 8.7 y 8.8.
Considérese el cuerpo de la figura 9-8, como completamente libre para moverse bajo la
acción de las fuerzas Fi,F2, etc. El marco Xi, Y\,Z\ se considera inercial y el X, Y, Z
está fijo al cuerpo. Los ejes punteados, X[, Y[ y Z{, con el origen adherido al cuerpo en O, se
suponen paralelos a X\,Y\ y Z\. Los ángulos de Euler, 0, $ y <¡>, indicados en el
diagrama y medidos como en la figura 8-17, determinan la orientación del cuerpo. Los cosenos
directores de X, Y y Z con relación a X[, Yí y Z[ (o con relación a Xi, Y\ y Z\) se
indican por «n, ai2, ai3, etc. Las expresiones de los diferentes a en función de los ángulos
de Euler, están dadas en la tabla 8.2. Una de las fuerzas, aplicada en el punto p,, de
coordenadas (xttyttzt) con respecto al marco fijo al cuerpo, se representa por Fx..
X
m es la velocidad angular del cuerpo, con relación a Xi.
V1.Z1. u„ u, y *, son lae componentes de •.
según X. Y y Z. Fi, Fa. etc.. son las fuerzas aplicadas.
M es la masa total. A es la aceleración del c.m. en el
espacio inercial. ao es la aceleración de O en el espacio
inercial. fl, * y <> son los ángulos de Euler. .m, <■■-'
y n,3 son los cosenos directores de X. etc. X.YyZ están
fijos al cuerpo.
Fig. 9-8
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 195
En el caso en que O esté en el c.m., y si X, Y y Z coinciden con los ejes principales de
inercia, (9.3), (9.10) y (9.16) se simplifican notablemente. Sin embargo, por razones
didácticas, se supone que O está localizado en un punto arbitrario del cuerpo. Se suponen conocidas
las coordenadas x,y y z del c.m. con relación a X, Y y Z.
Como se indicó en el numeral 9.3, se pueden hallar ecuaciones escalares correspondientes
a (9.3). Si se toman las componentes de A en las direcciones de los ejes fijos al cuerpo, por
ejemplo, Ax puede obtenerse fácilmente a partir de (9.7a) haciendo x = x y ux =
} sen 0 sen </> + 0 eos <¡>, etc. Las magnitudes aox,aoy y a0z pueden expresarse en
cualquier sistema adecuado de coordenadas. Se puede escribir también a0x — x0an + y0al2 + z0al3,
etc. Escribiendo /^/vt y fzt como las componentes X, Y y Z de F,, Fx en (9.2) está dado
por Fx = 2 fxt, etc.
Ecuaciones de rotación: Debido a la naturaleza vectorial de (9.15), pueden obtenerse tres
ecuaciones escalares del movimiento, proyectando a B y a t en las direcciones de tres rectas
que no estén en el mismo plano, que pasen por O y que pueden tener direcciones variables con
respecto al cuerpo. Usualmente las componentes de B y r se toman según ON, Z\ y Z. Nótese
que aparte del punto O, ON y OZ[ no son estacionarios con relación al cuerpo. Aplicando
(9.16), fácilmente se concluye que (véase la tabla 8.1)
Bx sen 0 sen d> + B„ sen 0 eos d> + Bx eos 0 - ré,
v * (9.17)
Bx eos <¡> - By sen <¡> = re y Bz = T<¡>
donde, naturalmente, t^, Tg y t^ representan los torques aplicados alrededor de Z{, ON
y Z, respectivamente. Las expresiones de Bx,By y Bz son los miembros izquierdos de
(9.10a, b, c). Una forma de escribir t ,re y t¿ es como sigue. (En ciertos casos específicos es
posible expresarlos en una forma más directa.)
t. = t,señasend> + t„sen6 eos<¡> + t_ eos6,
* v z (9.18)
Te = txcos<I>- Tysen<i>, ré = t2
donde tx = ^{f^Vi-fyZi), etc.
Así, (9.17) son las tres ecuaciones del movimiento de rotación. Como se puede demostrar
sin dificultad (véase el ejemplo 9.8) estas ecuaciones son iguales a las obtenidas para 6, \p
y <f> muy fácilmente, por el método de Lagrange.
Una vez más conviene recalcar que si O está situado en el c.m. (con frecuencia muy
conveniente, aunque no siempre), tanto (9.3) como (9.16) se simplifican considerablemente. Si
X, Y y Z se hacen coincidir con los ejes principales de inercia que pasan por el c.m., se
obtiene una notable simplificación en (9.16).
Ejemplo 9.8. Trompo que gira con la punta en una posición fija.
Imagínese el cuerpo de la figura 8-16 remplazado por un trompo cuya punta está localizada en O. Si los ejes
fijos al cuerpo están localizados como se indica, £ = y = 0, i = r. Ix = Iy e lxy = Izz= Iyi = 0.
Siguiendo el procedimiento descrito, se trata de establecer las seis ecuaciones del movimiento.
Como O está fijo, a0x = a0y = a0z = 0. Aplicando (9.7),
A-x — r(¿2 sen* cos 9 sen <f> + 20¿ eos $ eos <f> + i> sen* eos <f> — $ sen#)
Ay = r(¿2 sen e cos $ cos <f> — 2$¿ cos $ sen <f> — ¡P sen* sen# — 6 cos <f>)
¿z = -r('e2 + í* sen* $)
y puede verse que
Fx = —Mg sen $ sen <¡> + fx, Fy = —Mg sen* cos <f> + fy y Fz = —Mg cos * + fz
196 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS (CAP. 9
donde /,, fy y fz son las componentes de la fuerza de reacción ejercida en la punta, en las direcciones
instantáneas de X, Y y Z. Así, las tres ecuaciones del movimiento del c.m.,
Fx = MAX, Fy = MAy y Fz = MAZ (1)
pueden escribirse en forma explícita completa.
Tomando momentos con respecto a ON, Z y Z', las ecuaciones (9.17) se aplican directamente. Para este
problema, Bx, etc., son (véanse las ecuaciones (9.10)),
Bx = Ix( $ sen * sen <f> + 2^* eos * sen <f> + * eos <f> — ^2 sen * eos * eos <f>)
... (2)
+ 7Z(¿ sen * eos # — * sen #)(# + ¿ eos *)
By = /x( £ sen 0 eos # + 2¿* eos 0 eos <f> — * sen # + ¿2 sen 0 eos * sen #)
- . ... (3)
— Izbfr sen * sen # + * eos <f>)(4> + ¿ eos *)
Bz — h( '<P + 'i eos * - ¿* sen 0) (4)
En la figura se ve que t6 = Mgr sen e, t^ = 0 y t^ = 0. Así, las tres ecuaciones de rotación se reducen a
Ixi'f ~ ¿2 sen* eos *) + /z(¿2 sen* eos * + ¿¿ sen*) = M^r sen* (5)
/x(v¿sen2* + 2¿* sen* eos*) + Iz( f eos2 * + $»" eos * — 2*¿ sen* eos* — *¿ sen*) = 0 (6)
J*( 0 + £ eos * - ¿* sen*) = 0 (7)
Las relaciones (7) y (6) pueden integrarse una vez cada una, dando,
Iz(4> + ¿ eos*) = P¿ = constante y 7X¿ sen2* + P,,, eos * = P^ = constante
Las ecuaciones (5), (6) y (7) son las mismas correspondientes a *, }p y <f> obtenidas en (8.13), en forma
inmediata y con menor esfuerzo, por el método de Lagrange.
Nótese que si se conoce la ley de variación con el tiempo de 6, } y <¡>, las ecuaciones (1) dan /,, fy y ft
en función del tiempo.
Ejemplo 9.9. Ecuaciones del movimiento de Euler, para el giroscopio. (Véase el ejemplo 8.16, figura 8-18.)
Lo que sigue es un breve esquema de las etapas que conducen a las ecuaciones deseadas. Tomando los ejes
fijos al cuerpo como se indica,
* = y = z = 0, Ix = /„, lxy = Ixz = íyz = 0, Ax = Ay = Az = 0, a0x = a^ = a0z = 0
Sean /xj»/yt y /*. las componentes de las fuerzas de reacción en c\ (en las direcciones instantáneas de
X, Y, y Z) y /x,»/y„ y fz« las componentes de la fuerza en C2. Se escribe Oc\ = Oc2 = 1. Por tanto,
Fx = fx + fx — Mg sen * sen <f>, Fy = fy + fy — Mg sen * eos <f>,
Fz = fZl + fZ2 - Mg eos *, re = (/„2 - /Vj)í eos 0 - (/Xj - fx¿l sen 0,
TC» = (/«2-/y,)í sen* sen^ + (/Xj - /Xjí)¿ sen * eos <f>, t^ = 0
Las expresiones para Bx, By y Bz son iguales a los miembros izquierdos de las relaciones (9.10). Así, pueden
escribirse en detalle las ecuaciones de traslación y de rotación.
El lector debe demostrar que las ecuaciones de rotación se reducen a la forma obtenida con el método de
Lagrange.
9.10 Ecuaciones del movimiento con respecto a un marco de referencia móvil.
El problema aquí considerado por el método de Euler es exactamente el mismo que se
consideró en el numeral 8.10 por el método de Lagrange. Por tanto conviene que el lector
repase ese numeral, dedicando especial atención al significado de los símbolos utilizados. No
se repite aquí el enunciado del problema ni la figura 8-21.
Con las precauciones de rigor, se pueden aplicar directamente las ecuaciones (9.2). Se
debe recordar que AXÍ Ay y Az son las componentes de la aceleración del c.m., con
respecto al espacio inercia], por lo que deben expresarse de acuerdo con esto. Así mismo, las
ecuaciones {9.10) o {9.16) son válidas siempre que u)x, wy y wz expresen las componentes
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 197
de <d (la velocidad angular del cuerpo con respecto al espacio inercial) en las direcciones
instantáneas de los ejes fijos al cuerpo, X, Y y Z.
Si para simplificar se supone que O (Fig. 8-21), está localizado en el c.m., las expresiones
de AXvAyx y AZl (las componentes de la aceleración del c.m. en el espacio inercial, en las
direcciones instantáneas de Xi.Yi y Z\) pueden obtenerse a partir de las relaciones
(9.6). Es decir, . , .. . « , «, , . n . .
AXl = ai* + xi- Xi(n*y + n*z) + yi(QiyCilz-Qiz)
+ Zi(QixQiz - fii„) + 2(Zií)i„ - IJiíliz)
con expresiones semejantes para AVl y A2j. Aquí, ííi,, üiy y Í2iz son las componentes
de O en las direcciones instantáneas de Xi, Yi y Z\, y están dadas por las relaciones
(8.11); es decir, Qíx = ^, sen 0i sen <pi + 0i eos <pi, etc. Representando por ai la aceleración
de 0\ en el espacio inercial, a\x, a\y y aíz son las componentes de ai en las direcciones
instantáneas de Xi, Yi y Z\. alx - x2(3u + y2(312 + z2(313, etc. (Naturalmente, aix, a\y y
aiz pueden expresarse en función de otros sistemas de coordenadas. Véase el numeral
2.12, (3).)
Entonces, las ecuaciones del movimiento de traslación del c.m. son sencillamente,
MAXl = FXv etc., en donde AXl está dada por (9.19) y FXl es la suma de las componentes de
todas las fuerzas aplicadas, incluyendo las fuerzas de restricción, en la dirección de Xi.
Se pueden hallar las expresiones adecuadas de u)x, wy y wz como se demostró en el
numeral 8.10. Por tanto, las ecuaciones del movimiento de rotación tienen la forma de (9.10)
pero sin los términos M(a0zy — Oovz), etc., puesto que se ha supuesto que O coincide con el
c.m. Si se supone conocido el movimiento (traslación y rotación) del marco Xi, Vi, Z\
con relación al espacio inercial, a\x, üix, etc., serán funciones conocidas del tiempo. Así,
las soluciones de las primeras tres ecuaciones dan el movimiento del c.m. con respecto a Xi,
Vi, Z\, y las otras tres determinan el movimiento de rotación del cuerpo con relación al
mismo marco de referencia. Desde luego, puede aplicarse (9.16) en lugar de (9.10), si se desea.
9.11 Determinación de los movimientos de una nave espacial y de un objeto en
su interior, ambos bajo la acción de fuerzas conocidas.
El tratamiento de Lagrange está dado en el ejemplo 8.22. A continuación se indica
esquemáticamente el método de Euler.
Haciendo referencia a la figura 8-23, resulta claro que se pueden escribir las seis ecuaciones
de Euler para el vehículo espacial, en la forma acostumbrada. Así, pueden plantearse seis
ecuaciones para el cuerpo rígido, como se indicó bajo el numeral 9.10.
Las doce ecuaciones del movimiento incluyen las coordenadas, x\ty\,z\\ x2.y2.22;
0it^it*i y 9,^,<¡>. En tal virtud, las soluciones dan el movimiento de la nave espacial
con respecto a X2, Y2, Z2 .y el del cuerpo con relación a la nave. En el proceso de solución
de este problema no se debe olvidar que para cada fuerza que se ejerce sobre M, por algún
ligero dispositivo adherido a la nave espacial, existe otra fuerza igual y contraria sobre la
nave misma.
Ejemplo 9.10(a).
Los ejes X\, Y\ y Z¡, de la figura 9-9, con el origen en 0\, están orientados como se indica en la figura.
Suponiendo que 0\ se mueve hacia el norte sobre un círculo máximo (Xi.Yi.Zi está adherido a un tren,
por ejemplo) con velocidad constante, jRj*, y que Y\ permanece tangente al círculo máximo que pasa por los
polos; se trata de determinar las ecuaciones del movimiento de la partícula m, sujeta a la acción de una fuerza
conocida F.
Las expresiones de ax ,ay y az , las componentes de a, la aceleración de m en el espacio inercial, en las
direcciones instantáneas de X,,Y\ y Zt, pueden hallarse mediante la adecuada aplicación de las relaciones (9.6).
Con tal propósito (véase la figura 8-21) obsérvese que
fiíz = —+1, Í2ly = cogCos+j, Í2l2 = coc sen*.
198 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS (CAP. 9
El sistema X2. V2. Z2 tiene
una dirección que permanece
constante, y se supone inercial.
O 2 está adherido al centro de
la Tierra.
O, = „e + ♦,
La Tierra se supone aquí esférica. Vi es
tangente a un circulo máximo. Z\ es
la extensión de R\. X\ se dirige
hacia el oriente (normal a la figura,
hacia adentro). +i es la latitud de Oí.
u, es la velocidad angular de la
Tierra - 7,29211 X 10-» rad/seg. La
notación aqui es la misma de la figura
8-21, con O, =•», + +,.
Además, a0x = —2ií1<oe*1 sen*!, a0v = #i«f sen*i cos*i, a0z = — i21*>1 — Ri<£ eos2 *!
(véanse las ecuaciones (2.60)). Así, aplicando (9.6a),
aXi = — 2jR1<oe*1 sen*! + xl — a^u2 — 2<oe*1(i/1 eos*! + zt sen*!)
+ 2<oe(z1 eos*! — Vi sen*,)
con expresiones semejantes para ay y az . Entonces, las ecuaciones del movimiento deseadas resultan
(9.20)
Las soluciones expresan el movimiento de m con relación al marco móvil, X\,Y\,Zi. Las mismas
ecuaciones pueden obtenerse más fácilmente por el método de Lagrange. Véase el problema 9.7.
Ejemplo 9.10(6).
Se remplaza ahora la partícula m de la figura 9-9 por un cuerpo rígido de masa M. Se trata de determinar
las ecuaciones del movimiento con relación a X\,Y\,Z\. Se localiza el origen O, de los ejes fijos al cuerpo,
X, Y y Z, en el c.m. Las coordenadas del c.m. en el sistema Xi, Y\,Z\, se indican por 3¡y,V\ y zu
Nótese que si se remplaza a m por M y xi por 9¡ít etc., en (9.20) y en las expresiones correspondientes a
ay y az , se obtienen las tres ecuaciones del movimiento de traslación del c.m. (Las ecuaciones no se repiten aquí.)
Las ecuaciones de rotación se obtienen de inmediato por el procedimiento descrito bajo el numeral 9.10. Por
las ecuaciones (8.14), (véase la figura 8-21) se concluye querías componentes de » en las direcciones de los ejes
fijos al cuerpo, X, Y y Z, están dadas por,
"x = ¿ sen* sen£ + e cos<f> — *ian + «c eos ^a^ + ue sen*!a13
donde los ángulos de Euler, 6, $ y <t> determinan la orientación del cuerpo con respecto a X\,Y\,Z\, como
en la figura 8-17. on = eos <j> eos \f> — sen <f> sen $ eos e, etc., (véase la tabla 8.2.) Se pueden obtener relaciones
semejantes para wy y <oz.
Por último, remplazando <ox, uy y <o, en
IXÚX + (lz — ly)UyUx + Ixy(uxUz — ¿)y) ~ Íiz^^y + Úz) + 1 yz(u\ ~ Jy) = Tj.
y en las ecuaciones correspondientes a ry y a tz, se obtienen las ecuaciones del movimiento de rotación que se
buscaban.
Ejemplo 9.11. Fuerzas de soporte. Rotor montado en un marco móvil.
Supóngase que el cuerpo de la figura 9-7 está montado en un avión de combate que está sometido a cualquier
tipo de maniobras; se trata de determinar las fuerzas de soporte. El marco X\Y\Z\ y los cojinetes están sujetos
al aeroplano y por tanto se mueven solidariamente con él.
Se supone conocido el movimiento del avión con relación a cierto marco X2Y2Z2 (adherido a la Tierra
y considerado como inercial). En otras palabras, tanto el movimiento de traslación de 0\ de la figura 9-7, como
el movimiento de rotación de X\,Y\,Z\, ambos con respecto a X2.Y2.Z2, son funciones conocidas del
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 199
tiempo. (La posición de 0\ y la orientación de X\,Y\,Z\ pueden expresarse en función de x-i,y2 y z-i
y de Oí, \^i y 0|, de la figura 8-21. Véase el numeral 8.10.)
La aceleración de 0\ en el espacio inercial se representa por ao y sus componentes son a\,a¿ y a3, en
las direcciones de Xi, Yi y Z¡, respectivamente. Por tanto, ao,,aoy y ao,, las componentes de ao en
las direcciones de X, Y y Z, están dadas por ao, = aian + 02012+ 03013, etc., en donde an, «12 y «13
son los cosenos directores de X con respecto a X|, Yi, Z,, etc. Pero, como en la figura 9-7, 8 = 90° y ^ = 180°,
ai 1 = — cos^, ai2 = 0, ai3 = sen^, etc. (Véase la tabla 8.2.) Así,
ao, = —ai cos^ + 03 sen^, aoy = ai sentf + 03 cos¿ y aoz = 02 (8)
Sea O] la velocidad angular del avión en el espacio inercial, cuyas componentes según X\,Y\,Z\, son
conocidas y se representan por ÍI|,, íl\y y flÍIt respectivamente. Entonces, las componentes de la velocidad
angular del cuerpo, en el espacio inercial, en las direcciones de los ejes fijos al cuerpo, X, Y y Z, son
ux — —Í2ix cos<f> + Í2izsen#, uy = Í2lx sen# + Í2lz eos <f> y uz = ííly + $ (9)
Por las ecuaciones (9.7) se concluye que Ax,Ay y Az, las componentes de la aceleración del c.m. en el espacio
inercial, en las direcciones de X, Y y Z, son
Ax = -a, cos^ + a3 sen# - x(coJ + coz) + y(wywx - wz) + z(axaz + áy) (10)
con expresiones semejantes para Ay y Az.
Expresando Mgx, Mgy y Mgz como las componentes del peso según X, Y y Z, respectivamente (las
componentes de g, gx, gy y £,, pueden expresarse en función de B\, ^¡, 0i y 0) se tiene,
Fx = Ax + Ate + Wflrx, Fy = /ly + /2v + Mflrv, Fz = /z + Mflrz (H)
y por t, = 2(/iy — /y2). etc., se concluye que
rx = fiyk ~ fiyh + Mgzy - Mgyz, ry = /lxZ, - f9xli + Mgxz - Mgz£, rz = Mgyx - Mgxy + rm (12)
En este momento se pueden escribir ya las ecuaciones (9.2) y (9.10). La primera de (9.2) es
M[a3 sen <t> - a, eos ^ - x(u>l + uz) + y(wywx — ¿z) + z(ux(oz + ¿v)] = Ai + Ax + ^x (Í3)
con expresiones semejantes para la segunda y la tercera. La ecuación (9.10a) se convierte en
M(a0zy-a,0yz) + Ixúx + (Iz-Iy)wyWz + Ixy(wxwz-iy)
- 7xz(coxcoy + ¿z) + /„,(«*-«*) = f2yh - flyh + Mgzy - Mgyz (14)
y (9.í0b) y (9.í0c) adquieren formas similares.
Debe notarse que para un determinado movimiento del avión (en el caso en que X2, yi, Z2, B\, 4>\ y <t>\
sean funciones conocidas del tiempo) las ecuaciones (13) y (14) pueden expresarse en función de t, <t>, <£ y '4- Así,
una vez más, las relaciones (13) y (14) pueden usarse para hallar las fuerzas de soporte.
9.12 Restricciones no holónomas.
En todos los ejemplos considerados hasta ahora, las restricciones han sido expresadas
en sencillas formas algebraicas, como se indicó en {4.4). Con estas relaciones ha sido posible
eliminar directamente y sin ninguna dificultad, las coordenadas superfluas en T, V, etc.
Restricciones de este tipo se denominan holónomas.
Existe, sin embargo, un grupo de problemas (en ocasiones de gran importancia) para
los que las restricciones no pueden ser expresadas como se ha dicho. Por el contrario, estas
restricciones han de escribirse como relaciones diferenciales que no pueden ser integradas.
Tales expresiones pueden tener la forma
CijStfi + ch 8q2 + • • • + c¡N 8qN - 0, ¿ = 1,2, ...,s {9.21)
donde s es el número de restricciones y N el número de coordenadas requeridas sin tener en
cuenta las restricciones de esta forma. En general, las diferentes c son funciones de las
coordenadas. Las relaciones como la {9.21) se denominan restricciones no holónomas.
Si existen s de estas ecuaciones, habrá s coordenadas que no son variables independientes.
200 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
Pero como {9.21) no es integrable, no es posible emplearla en la eliminación directa de las s
coordenadas superfluas. Los grados de libertad son, n = N — s. Un estudio detallado de
los sistemas no holónomos requeriría un capítulo aparte. Sin embargo, el ejemplo siguiente
ilustra las ideas anteriores y muestra cómo el método de Euler puede ser empleado para
hallar las ecuaciones del movimiento y las fuerzas de reacción.
Ejemplo 9.12.
"i, — 6 Cos $ + <f> sen 6 sen ^
uWl = 9 sen <(> — ¿ sen $ cos ^
2 = rüyi
;/ = -rux
= e sen ^ — ¿ sen 6 COS \f-
Punto de contacto
Problema no holónomo
Una esfera que rueda sobre un plano inclinado rugoso, X i Vi
Fig.9-10
La esfera uniforme de la figura 9-10, puede rodar sin resbalar, en contacto con el plano rugoso, XiYi el
cual tiene una inclinación dada por el ángulo « con respecto a la horizontal. La posición de su centro, con relación
a Xi, Yi, Z\, se determina por £,y y z (i = r = radio de la esfera) y la orientación se determina por los
ángulos de Euler, 0, 4> y $, medidos como se indica. Como se supone que no se resbala la esfera, puede
demostrarse que (la demostración se deja al lector)
8* = r(8e sen^ - 8<f> sen* cos^) y «í = —r(86 cos^ + 8<f> senfi sen^) (9.22)
las cuales no pueden ser integradas para obtener relaciones entre las coordenadas 9¡,y, í, ^ y f Las relaciones
(9.22) son típicamente no holónomas.
Sin embargo, las ecuaciones de Euler pueden ser aplicadas a este problema como sigue. Las expresiones (9.2)
SOn M'i = fXi + Mg sen a, Mi = f^ y Mi = fZy- Mg cosa (1)
donde fx ,/v y fz son las componentes de la fuerza de reacción en p, en las direcciones de X\, Yi y Zi.
Las relaciones (9.10) se reducen a
i*>Xl = tXi. *%. = Ty, y f¿* = *-*! (2)
donde / es el momento de inercia de la esfera con relación a una recta cualquiera que pase por el centro y a-, «yj y
uZl son las componentes de la velocidad angular de la esfera, alrededor de los ejes de orientación constante, X[, Y[
y Z[. La anterior forma es conveniente puesto que Ix = Iy = Ix = I = constante, independientemente de la
orientación de la esfera. Así, (2) puede escribirse como
/37(0 cos^ + ¿ sen* sen^) = fyyr
~fXir O)
Por inspección de la figura (o considerando S£, Sy, etc., en (9.22) como desplazamientos en el tiempo di), se
e ...
2 = ruu. y = -r«_ y i = 0 (4)
CAP. 9) EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 201
-r(e eos \í- + ¿ sen* sen^)
de las cuales, las primeras dos pueden escribirse
* = r(¿ sen^ — ¿ senfl cos^) y
A partir de (7), (3) y (5) se concluye en seguida que
(I/7* + M)'d = Mg sene y (I/r* + M) tf = 0
Así, &, y y z así como fx, fy y fz, pueden determinarse en función del tiempo.
(5)
9.13 Las ecuaciones de rotación de Euler, desde el punto de vista del momentum
angular.
El desarrollo de las ecuaciones de rotación de Euler (numeral 9.5) y su interpretación
física (numeral 9.6(6)) se ha basado en el "principio de momentos" expresado por las relaciones
(9.8) y (9.11).
A continuación se presenta un breve estudio de estas ecuaciones en las que el énfasis se
ha colocado en el momentum angular y la rapidez de cambio de esta magnitud. En lo
relacionado con la dinámica clásica, este análisis no añade nada nuevo a los resultados anteriores.
Sin embargo, se incluye aquí porque, (a) este enfoque representa otro punto de vista interesante,
(b) la mayor parte de los textos tratan de esta manera las ecuaciones de Euler, (c) el
momentum es una magnitud importante en el desarrollo de las ecuaciones de Hamilton, que se
verá en el capítulo 16, y (d) el momentum angular desempeña un papel importante en ciertos
capítulos de la mecánica cuántica.
Considérese inercial el marco Xi, Vi, Z\ de la figura 9-11. Supóngase que X, Y, Z
permanece paralelo a ese marco. El origen O puede estar sujeto al cuerpo, o no estarlo. Las
coordenadas de la partícula típica m' son x, y y z y también, xi,>i y zi, que se
relacionan por xi = xo + x, etc.
f(/,./y./x)
X, V, Z permanece paralelo a Xi, Vi, Z,.
No se requiere que el origen O esté adherido al cuerpo
Fig.9-11
Considerando f(/x, fy, fz) como la fuerza neta sobre m', se escriben las ecuaciones
de la partícula libre, como
fx - m'x\, fy = ra'i/i y fz = m'zi
Multiplicando la tercera por y \, la segunda por — z i, sumando las dos y cubriendo con la
sumatoria todas las partículas del cuerpo, se tiene
202 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
donde tx es el torque ejercido por las fuerzas aplicadas Fi, F2, etc., alrededor del eje Xi.
Pero por inspección, se demuestra que (9.23) puede escribirse como
¿i 2 *»'(*,*,-¿,*,) = ^ (9.24)
Se define ahora el momentum angular, o momento de la cantidad de movimiento, PXj,
del cuerpo alrededor del eje inercial Xi, como
P*x = 2 ™'(z,2/, - 2/,«,) (9.25)
En forma semejante se definen Pv, y Pz, alrededor de Yi y Z\. (Como se demuestra en el
problema 9.22, Px, Py y Pz son las componentes de un vector que representa el
momentum angular P. En notación vectorial (véase el capítulo 18), P = 2 W(rXr), donde r es el
vector posición que se dirige de 0\ a m'. Una expresión final de Px se encuentra en el
problema 9.23.) Así, por (9.24) se ve que la rapidez de variación del momentum angular
alrededor de X1 es igual al torque de las fuerzas aplicadas alrededor de este eje. Es decir,
En el caso en consideración, PXl,PVl y Ptl se han tomado con relación al espacio inercial.
Pero tx , tw y t2 son componentes del vector t (véase el numeral 8.2F). Además, PXl,PVl
y Píj son componentes de P el cual tiene por magnitud, P2 = Px, + Pj 4- FÍ y por
dirección, la dada por PXJP, etc.
El torque alrededor de una recta cualquiera Oía con cosenos directores /, m y n, puede
expresarse,
v = *v + v* + V {9-27)
o, en notación vectorial, T = P (9.28)
Considérese ahora el marco móvil (pero no giratorio), X, Y, Z. Remplazando xi, yi y
z\ en (9.23), por medio de xi = xo + x, etc., se tiene,
T*, = 2 ™'[(2o + z)(2/o + y)-(Vo + y)(zo + z)]
- 2 W(«i2/o - 2/i2o) + "2m'(zy-yz) + 2 wi'(«0y - í/0z)
Utilizando tx, = 2 [/«(tfo + y) - /»(2o + «)], m'zi = fz, etc., 2w/"2"o2/ = -^^ (donde M
es la masa total y y es la coordenada Y del c.m.) puede escribirse,
^(fzy-fyz) = M(z0y-y0z) + ^m'(zy-yz) (9.30)
El término de la izquierda es, claramente, tx, el momento de las fuerzas aplicadas
alrededor de X (y no Xi); y definiendo Px — ^m'faj — yz) como el momentum angular
alrededor de X, puede escribirse (9.30) como
t, = M(z0y - y0z) + Px, Ty = M(x0¿ - z\x) + Py, rz = M(y¡x - x0y) + Pz (9.31)
Estas relaciones son equivalentes a (9.10) y pueden ponerse exactamente en la misma forma.
(La relación vectorial equivalente aparece en la página 359.)
Nótese que si O está fijo, o se mueve con velocidad constante, x0 = í/o = "z'o = 0. Si O
está localizado en el c.m. y se mueve solidariamente con este punto, x — y — z — 0. Así, en
cualquiera de estos casos, (9.31) se reduce a tx = Px, etc.
La interpretación física de las ecuaciones de rotación de Euler desde el punto de vista
del momentum angular, establece que la ecuación (9.27) indica que la proyección de P (un
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 203
vector que representa la rapidez de cambio del momentum angular del cuerpo) sobre una
recta cualquiera Oía, es igual a la suma de los momentos de las fuerzas aplicadas,
alrededor de esta misma recta. Para algunos, esta interpretación puede presentar una "imagen"
algo difusa de lo que realmente sucede físicamente. Por otra parte, las ecuaciones (9.8) y {9.16),
que expresan el sencillo hecho de que la suma de los momentos de las fuerzas inerciales,
alrededor de una recta cualquiera, es igual a la suma de los momentos de las fuerzas aplicadas,
alrededor de la misma recta, aclara el significado de las ecuaciones de Euler, en términos
de principios básicos de la física y la geometría. Teniendo en cuenta este segundo punto de
vista, (9.16) no es más compleja que, por ejemplo, fx = mx, etc.
9.14 Comparación del tratamiento de Euler con el de Lagrange.
El método de Euler considera que el cuerpo está "libre" y las fuerzas de restricción
deben incluirse en las ecuaciones (9.2) y (9.16). Estas relaciones conducen a las ecuaciones del
movimiento, así como a las expresiones de las fuerzas de reacción.
Resumiendo el método de Lagrange: Si se considera el cuerpo libre y se escribe T, por
ejemplo, en función de x,y,z y los ángulos de Euler, 6, \p y </>, entonces -=-( —) - -r-^ = Fx,
d /dT\ dT d¿
etc., son las mismas ecuaciones (9.2). Además, tt(-r) — -rr — F6 — rON, etc., son las
ecuaciones (9.16) y naturalmente en Fx, en ton, etc., han de aparecer las fuerzas de
reacción. (Véase el problema 9.9.) Pero si se eliminan de T todas las coordenadas superfluas,
J / al1 \ -\rp
jtÍ —— ) — t— = Fqr son las ecuaciones del movimiento sin incluir las fuerzas de reacción
(suponiendo restricciones lisas).
Este es el método más rápido y más sencillo de obtener las ecuaciones finales del
movimiento, especialmente cuando se encuentran involucrados dos o más cuerpos.
El siguiente documento de referencias bibliográficas contiene valiosos comentarios sobre
algunos capítulos de la mecánica de los cuerpos rígidos, así como una lista de referencias
comentadas: Resource Letter CM-l, on the Teaching of Angular Momentum and Rigid Body
Motion, por John I. Shonle, American Journal of Physics, Vol. 33, No. 11, noviembre de
1965, páginas 879-887. Las observaciones de la introducción son muy oportunas.
Problemas
Tomando la derivada de la siguiente relación (véase la figura 9-2)
X, = Xq + xau + ya21 + za31
con relación a í y utilizando las relaciones (3) del numeral 9.4, demostrar que
vx = v0x + x + nyz — nzy
para una partícula libre, en donde vx es la componente de la velocidad de m en el espacio inercial, en
la dirección instantánea de X y u0x es la componente de la velocidad de O en el espacio inercial, según
la dirección de X. Naturalmente existen expresiones semejantes para v, y vz. Véanse las ecuaciones
(8.3).
(a) Con referencia a la figura 9-2, nuevamente, se escribe
T' = £ [(v0x + x + OyZ - í2zl/)2 + (v0v + y + nzx- nxz)* + (v0z + z + axy - Í2ya;)2]
donde v0x = á0au + y0ai2 + ^oai3> etc. Demostrar ahora (véase el numeral 3.9) que -r-í —— J —
-g— = ax, donde ax es la primera expresión de (9.6). Nótese que en ciertos términos como
^oíáu — «2inz + a3ini/)
204
EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS |CAP. 9
el coeficiente de xo se puede demostrar que es igual a cero. La anterior es una forma sencilla de
obtener las relaciones (9.6).
(b) Escribir T = %(x\ + y\+'z\) en donde x, y y z son las coordenadas de m, de la figura 9-2, en las
direcciones de X\, Y\ y Z\, respectivamente, y además,
^l = xo + ^«11 + ^«21 + Zaz\ + X«U + Val\ + za3l, etc.
Expresar -jz ( —— ) ~ T~ e introduciendo los ángulos de Euler, demostrar que, después de un
trabajo largo y monótono, se obtiene la misma expresión para ax.
(a) Suponiendo, por ejemplo, que se conoce perfectamente el movimiento del cuerpo rígido de la figura
9-3, demostrar que fx, la componente X de la fuerza f que actúa sobre una partícula típica m',
puede hallarse a partir de
fx = m'[x0au + y0a12 + V0a13 - x(u* + u\) + y(uyux - ¿z) + z(Uxuz + ¿„)]
Se obtienen expresiones semejantes para fy y /,.
(b) Se pega a la periferia del disco, D, (y sobre el eje X) una partícula de masa m. Véase la figura 9-5.
Suponiendo que |y^ son funciones conocidas del tiempo, hallar las componentes, según X, Y y
Z, de la fuerza que el pegante ejerce sobre la partícula. Expresar el resultado en función de ip, <f> y
sus derivadas con respecto al tiempo. Véase también el problema siguiente, que guarda relación
con este.
Una partícula de masa m, está sometida a la acción de una fuerza conocida cuyas componentes, según
los ejes fijos al disco de la figura 8-5, X, Y y Z, son fx, fy y /,. Suponiendo que $ y <t> son funciones
determinadas del tiempo, se trata de determinar el movimiento de la partícula con relación al marco
móvil X, Y, Z. Demostrar que las ecuaciones del movimiento son
m[a0x + x- x(w\ + 4) + l/(wv"i ~ ¿z)
+ z(Uxuz + ¿„) + 2(zuy - ywz)) = fx, etc.
donde ux = ¿sen* sen #, uy = ¿sen0cos#, uz = ¿ + ¿ eos $,
a0s — }//8 sen0 eos<f> + ^2« sení cosí sen0,
aoy = ~^8 sen* sen# + ¿2* sen* cosí cos#,
aoz — —fá sen2 $
Determinar las expresiones anteriores de aox, aoy y ao2 por métodos elementales y también por
aplicación de (9.7).
Nótese que los coeficientes de m en las tres ecuaciones (14.15) son las componentes ax, ay y az de la
aceleración de m con respecto al espacio inercial, tomadas en las direcciones instantáneas de Xi, Y\ y
Z\, respectivamente. Demostrar que aplicando las ecuaciones (9.7), las mismas expresiones pueden ser
halladas en forma inmediata.
Determinar las expresiones de Ax, Ay y Az del ejemplo 8.7, en forma directa, mediante el uso de
ecuaciones de trasformación. Compárense los resultados con (1), del ejemplo 9.4.
Demostrar que para la partícula única, del ejemplo 9.10(a), figura 9-9,
T - ^m[(Rwe eos* + zue eos* + x - yue sen*)2
+ (E* + y + xae sen* + z*)2 + (z — y* — xue eos*)2]
Aplicando las ecuaciones de Lagrange, demostrar que las ecuaciones (9.20), etc., se obtienen de inmediato.
Supóngase el cuerpo de la figura 8-16 remplazado por un trompo con su punta fija en O. Los ejes X, Y y Z
están fijos al trompo. Hallar las expresiones de las componentes X, Y y Z de la aceleración de una
partícula del trompo, en el espacio inercial, (a) utilizando las relaciones (9.7), y (b) aplicando el método de
Lagrange (véase la ecuación (3.24)). La partícula está localizada a una distancia normal, r, del eje de giro y
a una distancia, h, de la punta, medida paralelamente al eje.
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 205
Deducir la ecuación de Euler, (9.10a), por medio de las ecuaciones de Lagrange.
d /BT\ 3T
Indicaciones. Con T en la forma de (8.10), escríbase la ecuación correspondiente a 8, ¿r( ~~~ ) ~" Tñ =
Fg, considerando a <ox, <oy y az como funciones de 6, $, 4>, 6, 4> y <f>. (Véanse las relaciones
(8.11).) Como vox = x0au + y0a12 + «oai3» uox es función de los ángulos de Euler.
Haciendo ahora, 6 = 90° y $ = <¡> = 0 y observando que para estos valores, Fg = rx, ¿u = 0,
al2 — j, = Uy> ai3 — ¿ — Uz etc.( la ecuación de Lagrange anterior se reduce a (9.10a). Naturalmente,
(9.10b) y (9.10c) pueden hallarse de la misma manera. Para los valores anteriores de 8, $ y <¡>, F = rz
y Fí = -t,.
Se requiere especial cuidado al desarrollar las diferentes etapas de este problema.
Imagínense los ejes X2, Y2 y Z2 con el origen adherido al cuerpo de la figura 9-3, numeral 9.5, en O.
Supóngase que estos ejes están girando de una manera arbitraria alrededor de O, con respecto al cuerpo.
Las coordenadas de m' con relación a X2, Y2, Z2, son x2, y2 y z2. En este problema se representan
los cosenos directores del eje fijo al cuerpo, X, con relación a X2, Y2, Z2, por am, a\2 y an. Las
componentes de la aceleración a, de m', en el espacio inercial, en las direcciones instantáneas de X2, Y2 y
Z2, son ax ,ay y aZo.Es decir, ax2 = axau + aya2\ + aza3i donde ax, ay y az son las
componentes de a en las direcciones de los ejes fijos al cuerpo, X, Y y Z (ax, ay y az están dadas por (9.7)).
Por tanto „
2 m'ia^t - aHz2) = rXí¡, etc. (1)
donde rz es el momento de todas las fuerzas alrededor de la dirección instantánea de X2. Demostrar
que (1) puede escribirse,
«u 2 m'(azy-ayz) + a2x ^m'(axz — a„x) + a31 2 m'(ayx — axy) (2)
Esta es la misma relación (9.16). Se ha demostrado así que (9.16) es válido para ser aplicado a cualquier
recta que pase por O, bien sea que esté adherida rígidamente al cuerpo o que gire con respecto a él.
Considérese una partícula típica, m', en el punto p de la figura 8-7, del numeral 8.2F. Supóngase que f
representa la fuerza neta que actúa sobre m'. En este caso, /, = m'ax, etc., en donde ax es la componente
X de la aceleración de m' en el espacio inercial. Aplicando el método del numeral mencionado para
demostrar la naturaleza vectorial del torque, comprobar nuevamente la relación (2) del problema 9.10.
(a) Demostrar que las ecuaciones del movimiento de la lámina del ejemplo 8.5, figura 8-9, determinadas
por el método de Lagrange, son
7ZV + M[(y& - xy) cosí - (xx + y y) sen*] = Mg[y sen* - £ eos*] = rg
M[x — 'é(y eos* + x sen*) + *2(y sen* - * eos*)] = Fx = —Mg sen*
M[y + *(x eos * - y sen*) - *2(« sen* + y eos *)] = Fy = -Mg eos *
Se ha supuesto aquí que la gravedad actúa únicamente en la dirección negativa de Y\.
(b) Considerando el sistema X, Y, Z fijo al cuerpo, demostrar por medio de la aplicación del método de
Euler, que
7Z* + M(aOyx — a0xy) — Mg(y sen* - x eos*)
Ma0x - M(éy + é2x) = -Mg sen*
Ma^ + M(éx - *2y) = -Mg eos *
Demostrar además que las ecuaciones de (b) son equivalentes a las de (a).
(c) Utilizando ahora ejes que no giran, con el origen adherido a O, demostrar que las ecuaciones de Euler
toman la misma forma que la obtenida en (a). Obsérvese cómo se simplifican las ecuaciones con O
en el c.m.
El péndulo de cuerpo rígido de la figura 9-12, puede oscilar alrededor del eje horizontal sin ninguna fricción
en los puntos de soporte. El ángulo * se mide con relación a la vertical que pasa por O; se toma como
positivo el sentido indicado. Utilizando los ejes X, Y y Z fijos al cuerpo, demostrar que
(1) M('iz - *2x) = Mg eos * + fax + fay
(2) fay + fby = 0
(3) -M(*x + *2¿) = Mg sen* + faz + fbz
206 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS [CAP. 9
(4) -Ixye - Iyz6* = Mgy senfi + (fa2
(5) Iy6 = Mgz eos $ — Mgx sen $
(6) Ixy6* - Iy¡é = -Mgy eos B - (fal
etc., son
-/*)•
-/bx)«
donde fax, fbx, etc., son las componentes de
las fuerzas de sopórtemela y en b, según X, Y y Z.
Los momentos y-Los^productos de inercia in-.
cluyen todo el sistema, con las varillas ab y Op.
El centro de masa del sistema se indica por c.m.
Deducir la ecuación del movimiento
correspondiente a 8, (5), por el método de Lagrange.
Demostrar que 0O, el ángulo de reposo, está dado por
tan 0o = z/x. Haciendo 0 = fiq + "0 se puede
integrar (5) de inmediato, para valores pequeños de
0. Demostrar, por tanto, cómo pueden
determinarse /„, fbx, faz y fbz en función del tiempo.
Escríbanse las ecuaciones de rotación
tomando los ejes fijos al cuerpo paralelos a X, Y y Z,
con el origen en el c.m. ¿Implica esto alguna
ventaja?
1 sistema X, V, Z está fijo al cuerpo
con el origen en O. El ángulo 9 se
mide entre la vertical fija y el eje X. Se
toma a 6 como positivo si el cuerpo
se mueve alejándose del observador.
Fig.9-12
Imagínese que en el sistema de la figura 9-12 la varilla Op está articulada en 0 (con una articulación tipo
bisagra) de manera que el cuerpo puede ahora girar alrededor de un eje que pasa por 0, perpendicular al
plano aOp; es decir, que ahora Op puede oscilar en un ángulo a en el plano aOp, así como girar alrededor
de ab. Tomando los ejes fijos al cuerpo como en el problema 9.13 (el eje V ya no coincide con Oa)
demostrar que las componentes de la velocidad angular vienen dadas por
ux = $ sen a, uy = $ eos a y uz = a
Demostrar que las componentes X, Y y Z de la velocidad del c.m. en el espacio inercial (véanse las
ecuaciones (8.1)), son,
■Dx = $z eos a — ajj, Qy = a3¡ — 92 sena y Qz — Oy sena — 9x eos a
Suponiendo que se conocen los valores de Sb,y,z, Iz, Ixy, etc., escribir la expresión de T. Aplicando las
ecuaciones de Lagrange, expresar las ecuaciones del movimiento correspondientes a 0 y a a.
Hallar las mismas ecuaciones por el método de Euler, y comparar las ventajas de los dos métodos.
El doble péndulo de la figura 9-13
consiste en dos láminas delgadas colgadas
de una clavija lisa en pt. La
articulación en p2 es igualmente lisa. Describir
las etapas (sin especificar todos los
detalles) para hallar las ecuaciones del
movimiento correspondientes a 6 y a <t>.
Comparar este método con el de
Lagrange.
Considérese un sistema como el
ilustrado en la figura 8-26. Describir
esquemáticamente las etapas necesarias (sin
incluir los detalles) para hallar las
ecuaciones del movimiento de todo el
sistema, por el método de Euler. Comparar
este procedimiento con el que se
requiere con el método de Lagrange.
Supóngase, por ejemplo, que la varilla uniforme,
bd, tiene una masa considerable y que
el eje vertical tiene un momento de
inercia I\, con relación a Z\.
Fig.9-13
9.17. Partiendo de consideraciones básicas sencillas, deducir las ecuaciones (6) y (7) del ejemplo 9.7, figura 9-7.
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 207
Indicación. Las fuerzas inerciales sobre una partícula típica cualquiera son — m'(<f>y + ¿2x) en la
dirección de X y m'ifx — jpy) en la dirección de Y. Se suman los momentos de estas fuerzas para
todas las partículas del cuerpo, alrededor de un eje, que puede ser paralelo a Y y que pase por B2. Haciendo
esto igual a los torques aplicados alrededor del mismo eje, se obtiene (6). Esta deducción deja al
descubierto los principios básicos pertinentes y además contribuye a darle sentido a los productos de inercia.
(6)
Supóngase que el cuerpo de la figura 9-7 se encuentra perfectamente equilibrado estática y
dinámicamente. Se pega ahora una partícula de masa m al cuerpo, en un punto x, y, z. Hallar las expresiones
de las fuerzas de soporte.
Imagínese la partícula remplazada por una varilla delgada de longitud y masa conocidas. La varilla
está rígidamente adherida al cuerpo, con un extremo en x, y, z y extendiéndose paralelamente a
X. Describir las etapas para determinar las fuerzas de soporte.
El cuerpo giratorio de la figura 9-14 está montado en una plataforma rotatoria. Se hace girar el cuerpo con
un pequeño motor (que no aparece en el dibujo) a una velocidad angular <f>; el ángulo <t> se mide entre el
eje -Xi y el eje fijo al cuerpo, X (véanse las notas en el diagrama; véase además el ejemplo 9.7). La
plataforma se hace girar a una velocidad angular /?, alrededor del eje vertical inercial Z2. Demostrar
que la fuerza de soporte, f\z, está dada por,
fíx(h + h) = M8l('/3z + ¡3*x) + Iy(p eos * - j3¿ sen *) + {Ix - 7z)/3¿ sen <f>
+ lyzW2 sen <f> eos <f> — $) — /xv(2¿3¿ eos <f> + ¡8 sen <f>)
+ Ixz(¡32 sen* 0 — 02) + M[8$ eos <t> - £(j32 costf + ¿2)
+ y(fi sen<f> cos# — £) + zfi cos^]^ + Mg(l2 + z) sen<f>
Obsérvese que si X, Y y Z son los ejes principales de inercia y el c.m. está localizado en 0, la ecuación
anterior se reduce a
/jJ/8 eos 4 + (lx — Íy — IZ)J34> senf + M[8fl2'p eos 4 + gl2 sen $] = flx(ly + l2)
con lo cual se demuestra que aun en el caso en que el cuerpo esté equilibrado estática y dinámicamente
sobre una plataforma estacionaria habrá fuerzas de soporte si la plataforma está girando.
Marco
fijo en el espacio
77777777777777777777777777?
El sistema Xi, Vi, Zi está fijo a la plataforma rotatoria. El
sistema X, V, Z está adherido al cuerpo. Los ángulos de Euler son: 9 -
90" y í - 180°. Los ejes X y V permanecen en el plano X1Z1.
/i«. fiy, fi. y fiy son la» fuerzas de soporte en las direcciones
instantáneas de X y V. /, es la fuerza de soporte total en la dirección de Z.
Fig.9-14
Hallar las expresiones de las demás fuerzas de soporte (véase el ejemplo 14.11).
9.20. Considérese de nuevo el problema 9.19. Se toman los ejes fijos al cuerpo, X", Y" y Z", en las direcciones
de los ejes principales de inercia y con el origen en el mismo punto del de X, Y y Z. Se representan los
cosenos directores de Xp con relación a X, Y y Z, por ín, li2 y Í13, etc. Obsérvese que como tanto X, Y,
Z como X", Yp, Zp son marcos fijos al cuerpo, los cosenos directores son constantes. Los valores numé-
208 EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS |CAP. 9
ricos de las l y los de I*, I* e 7* pueden hallarse a partir de /,, Ixy, etc., con relación a X, V y Z (véase
el numeral 7.3).
Demostrar que las componentes de la velocidad angular del cuerpo en el espacio inercial, alrededor
de X", Y" y Z", están dadas por
ax = Phi sen0 + ^¿12 eos <f> + ¿¿13
«y = /§¿21 sen 4> + £¿22 C°S 0 + 0^23
uz = Ph\ sen 0 + /^32 c°3 * + 0*33
y que para estos ejes,
aoi = «íjsincos^ — 8iPll2sen<f> — /J28ii13, etc.
Demostrar que la primera ecuación de (9.2) es
M[8x'plxl eos £ — 8x'Í¡ln sentf. — fcsJu — £(«* + «*)
+ í(Vx""r) + *(«z«* + «*)] = ^i
y que la primera ecuación de (9.10) es
M(a0z¡/- a0y¿) + fxwx + (/*-/£)«„«, = T*
donde A, y y z son las coordenadas del c.m. con relación al marco Xp, Yp, Zp. Las demás ecuaciones
pueden escribirse en seguida.
9.21. Se coloca el giroscopio de la figura 8-18, en el origen Oí, de la figura 9-9, con el eje ai 02 en la dirección
de Z\. Se supone que 0\ se mueve hacia el norte sobre el círculo máximo, con velocidad R<t>, y de tal
forma que Vi permanece tangente al círculo máximo. Por aplicación del método de Euler, plantear las
ecuaciones del movimiento correspondientes a 8, $ y <j> (véase el problema 8.22).
9.22. Supóngase que el cuerpo de la figura 9-15 puede moverse libremente en el espacio; una partícula típica, m',
posee una velocidad v(x, y,z), con relación al marco inercial X, Y, Z.
w
1 1
s*0™1'l
Z
( / ' \
1 X
'A
1 90° V
-""" 1
^s^""^ Z
/fvfov.'z)
~-*v \
-''{
^V^
0^-
Y
I
Determinación del momentum alrededor de Oa (o proyección del
vector momentum angular total, sobre la dirección de Oa)
Fig.9-15
Se define el "momentum angular" de m' alrededor de la recta Oía, como m'hv' en donde v' es la
componente de v, perpendicular al plano Oiam'. Siguiendo el mismo procedimiento descrito en el
numeral 8.2F, demostrar que el momentum angular total, P0 a, del cuerpo, alrededor de Oía, viene
dado Por
Poxa — l 2 m'(zy — yz) + m 2 m'(xz — zx) + n 2 m'(yx — xy)
donde l, m y n son los cosenos directores de Oía. Demostrar, utilizando la figura, que 2 in'(zy — yz) =
Pz es el momentum angular alrededor de X, etc. Por tanto,
Po.a = Pxl + Pym + Pzn
CAP. 9] EL MÉTODO DE EULER DE LA DINÁMICA DE LOS CUERPOS RÍGIDOS 209
Así, P0 a es la proyección de un vector P (cuya magnitud es P = (P£ + P$ + P§)1/2 y la dirección,
Px/P, etc.) en la dirección de Oía.
En forma semejante, tomando momentos con relación a Oía, demostrar la ecuación (9.27).
9.23. Suponiendo que O está localizado en el c.m. del cuerpo de la figura 9-11, demostrar que Px , el
momentum angular del cuerpo alrededor de Xi (la componente del vector momentum angular en la dirección
de Xi) está dado por
PXi = M(z0y0-y0z0) + Ixwx - Ixywy - Ixtuz
donde ux, uy y u2 son las componentes de la velocidad angular en el espacio inercial, en las
direcciones de X, Y y Z. Los momentos y productos de inercia, Ix, Ixy e /„, se han determinado con relación
al marco X, Y, Z.
9.24. Tomando a O, de la figura 8-21, en el c.m., y considerando X, Y y Z como ejes principales, demostrar que
donde ax, ay y u2 están dados por (8.14).
Escríbase la ecuación de Lagrange, correspondiente a O, por ejemplo, y demostrar que se obtiene la
misma relación por medio de la segunda ecuación de (9.17).
CAPITULO
10
Pequeñas oscilaciones alrededor
de las posiciones de equilibrio
10.1 Tipo de problema por considerar.
Con el fin de iniciar el estudio de las "pequeñas oscilaciones" con alguna comprensión
general sobre el tipo de problema que se considera, se examinan a continuación los diversos
sistemas mecánicos que se muestran en las figuras 10-1 y 10-2.
Supóngase que se perturba ligeramente bien m\ o m2 (o ambos) de la figura 10-1 (a).
("Perturbado" quiere decir aquí que se le ha dado a la masa una pequeña velocidad inicial y
se le ha desplazado ligeramente de la posición de reposo.) Inmediatamente, cada una de las
masas inicia un movimiento oscilatorio alrededor de la posición de equilibrio. Si se supone
únicamente movimiento vertical, como se verá más adelante, el movimiento de cada una de
las masas se compone de dos movimientos armónicos simples, los cuales se expresan por
yx - Ax eos (ío,í + ¿j) + A2 eos (*>2t + $2) y y2 = By eos {t*yt + <¿,) + B2 eos (o>2¿ + $2)
donde wi y u2 y los ángulos de fase, <í>i y </>2, son los mismos en cada una de estas
relaciones, pero las amplitudes correspondientes son diferentes. Además, se comprobará que u>i
y o>2 dependen únicamente de los valores de mi, m2, k\ y k2 y no de la forma como
se inicie el movimiento.
Como se verá con claridad en lo que sigue, es importante tener en cuenta que las
observaciones anteriores son aplicables a todos los sistemas de la figura 10-1. Todos ellos tienen dos
grados de libertad y dos frecuencias naturales o "modos principales de movimiento".
Los sistemas indicados en la figura 10-2, tienen desde n = 3 hasta n = 9 grados de
libertad. Al perturbar ligeramente un sistema, cada una de sus partes (masa, disco, barra,
etc.), en general oscilará con n frecuencias f\ = u\/2ir, fz = u>2/2ir, ..., /„ = u}n/2ir; cada
una de las partes tendrá las mismas n frecuencias, cuyos valores dependen únicamente de
las constantes del sistema (masas, constantes elásticas, dimensiones, etc.).
El movimiento oscilatorio de los discos de la figura 10-2(6), puede escribirse como
6l = Alcos(wlt + <}>l) + A2cos(a2t + <}>2) + A3cos{*>3t + <f>s)
con expresiones idénticas para 62 y 63, excepto en lo que se refiere al valor de las
amplitudes.
Así, el objetivo del presente capítulo es suministrar un estudio detallado de los
movimientos oscilatorios de las partes de sistemas del tipo general mencionado, con relación a las
posiciones de equilibrio respectivas. Los métodos introducidos se pueden aplicar a una amplia
variedad de problemas de dinámica clásica e inclusive puede extenderse su aplicación a la
física atómica y molecular. Sin embargo, el tratamiento dado aquí está sujeto a las siguientes
limitaciones.
10.2 Restricciones sobre el problema general.
De acuerdo con la práctica acostumbrada, se considerarán únicamente las oscilaciones
pertenecientes al caso restringido en el que las velocidades y los desplazamientos con respecto
210
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 211
W//////////A y////////////A
\V2
(a)
ib) Péndulo doble
ri y r2 son constantes
i *» .
i
7M,
Carro
m^^z^^^^^^^^^^&^r
(c) Carro sobre una pista horizontal
y/////////////,
o
o
''Cuerda de
T^D
-sO
y/////////////y.
(d) Péndulo de torsión
doble
(e) "Partícula" que se mueve
en un plano
ga—wwvw—
^^^^^^^^^^^^^^^^^^^
(/) Combinación de polea y masas
Fig. 10-1. Sistemas con dos grados de libertad y dos "modos de oscilación" naturales.
212 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
üip^/wvHnpt
4_ "2 oí
D-VWH
(a) Suponiendo movimiento
vertical, g. de 1. = 3
(b) Discos conectados por ejes flexibles
Constantes de torsión = #ci,#c2 y «3. g.del. = 3
(c) En el caso de oscilaciones normales
al plano de la figura, g.del. = 3
(d) Si el movimiento es tridimensional,
g. de 1. = 6, seis modos naturales
^^^á^^^^^^^^^^^
(e) Suponiendo movimiento vertical de las masas, g. de 1. = 9
Fig. 10-2. Sistemas con tres o más grados de libertad.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 213
a las posicio.nes de reposo (excepto en casos especiales) no sobrepasan ciertos valores muy
pequeños. En los numerales 10.5 a 10.15, se supone que actúan únicamente fuerzas
conservativas. En los numerales 10.16 a 10.19 se consideran fuerzas conservativas y además fuerzas
viscosas. No se incluyen fuerzas disipativas diferentes de las viscosas.
La razón por la que se imponen estas severas limitaciones, en lugar de considerar el caso
más general en el que las oscilaciones pudieran tener grandes amplitudes y que pudieran
actuar fuerzas de cualquier tipo, es muy sencilla. En el caso general, las ecuaciones
diferenciales del movimiento son normalmente no lineales y además resultan tan complicadas que
no se dispone de métodos generales para su integración. Por tanto, aparte de resolver
problemas específicos con técnicas especiales o con el auxilio de un computador, no puede hacerse
nada más.
Sin embargo, si se utilizan "coordenadas de equilibrio" y se imponen las restricciones
anteriores, se pueden escribir expresiones aproximadas de T, V y P (con pocas excepciones)
de tal forma, que las ecuaciones del movimiento resultantes sean lineales con coeficientes
constantes, para las que existen métodos de integración corrientes, bien conocidos.
Para ilustrar las afirmaciones anteriores, se incluye, sin probarlo, el siguiente ejemplo.
Ejemplo 10.1.
Las ecuaciones del movimiento del péndulo doble (véase la figura 2-10 y el ejemplo 4.6) con la gravedad y
algunas fuerzas viscosas actuando, y sin restricciones en los valores de 8 y <f>, son
(mx + m2)r\'$ + m^rir?, '<£ eos (<f> — e) — 7n2r1r2^2 sen (<f> — e)
+ (m1 + m£grx sen $ + (6t + 62)ri^ + *>2rir2¿ cos (# ~~ *) = 0
U0.1)
m^r^t + 7n2rir2 *"cos (<f> ~ 0) + 7n2r1r252 sen (^ — í)
+ tn^gr^ sen <f> + b2r\i> + b<¿rxr<iQ cos (<f> — 6) = 0
Estas relaciones no lineales, evidentemente resultan bien complicadas. Sin embargo, si el movimiento se
limita a valores muy pequeños de 8 y #, las ecuaciones (10.1) pueden remplazarse por las aproximadas,
(ml + m2)rY$ + (6,+'6¿)r2¿ + (m1 + m2)grl$ + m^-^4 + b2rir2¿ = °
{10.2)
m^xr^e + b¿rxr2e + m2r2^ + hr^ + m^gr2<p - 0
que por ser lineales con coeficientes constantes, pueden ser integradas por los métodos que se indican más adelante.
10.3 Bases fundamentales adicionales.
(a) Las "'coordenadas de equilibrio" miden los desplazamientos de las masas a partir de sus
posiciones de equilibrio estático. Usualmente se toman de tal manera que cuando el
sistema está en equilibrio, todas ellas valen cero. Entre los ejemplos se mencionan y\ y
y2 de la figura 10-l(a), medidas desde las posiciones de equilibrio de mi y m.2,
respectivamente; 9 y 0 en el péndulo doble de la figura 10-1(6); 0i, 62 y 03, de la figura
10-2(fc), medidos a partir de las posiciones de reposo.de los discos.
(fc) Desarrollo de Taylor para n variables. Una función bien comportada de n variables,
f{qi,q2, ...,9n) puede representarse con la exactitud que se desee (lo cual depende
del número de términos que se conserven) en las vecindades del "punto" q\ = ci,
92 = C2,qn — cn, por medio de la siguiente relación:
/(<?,. ?„ O = /(<V «*••••. e„> + t (Jfy(qT - eT)
+ ¡Tí 2 ¿(¿^(í,-',)«?.-O U0.3)
214 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO I CAP. 10
Las derivadas parciales deben evaluarse para q\ = ci, (72 = C2, etc. Por tanto, el
primer término y todas las derivadas parciales son constantes. En el caso en que q\,
Q2, ...,9n sean coordenadas de equilibrio y el desarrollo se realice en las vecindades
de la posición de equilibrio, se tendrá c\ = C2 = • • • = cn = 0.
(c) Una expresión aproximada de T, en coordenadas de equilibrio. En coordenadas rectan-
guiares, T - - j£ ™,(z? + V\ + zf). Aplicando {10.3) a las ecuaciones de trasformación,
xi = xt{q\, (72, -•., qn), etc., (se supone que no existen coordenadas móviles, ni
restricciones móviles, y que las (71,(72, ---, qn son apenas el número de coordenadas
de equilibrio requeridas para representar la configuración del sistema), se obtiene,
Si se supone ahora que los desplazamientos y las velocidades son tan pequeños que los
términos que contienen qrqs, etc., pueden ser ignoradas, se concluye que
lo cual se escribirá en adelante, x{ = ^T airqr; el cuadrado de lo cual es,
Para y\ y z\ existen expresiones similares. Así, la expresión original de T se convierte en
T = ^¿¿[É^K^ + ^A + ^j]^
o bien, T = \ ± ± arlqrqt {10.4)
¿ r l
donde arl = 2 mxiaxraü "*" PirPn + e{re{j)« Es importante observar que como todos los
valores que conforman aTl son constantes, Tes una función cuadrática de las velocidades,
con coeficientes constantes.
{d) Expresión aproximada de la función de potencia para fuerzas viscosas. Como se demostró
en el capítulo 6, la función de potencia para p partículas, suponiendo fuerzas viscosas,
puede escribirse, P — —■= 2 Mx* + 2/^ + *?)» donde kt es el coeficiente de la resisten-
cia viscosa sobre la partícula 1. Siguiendo el mismo proceso descrito antes, puede escribirse
P = ~\±±KM <'ft5>
* r l
en donde brl tiene la misma forma que arl habiendo remplazado m¿ por kt. Así, una
vez hallada T por medio de {10.4) para un sistema en particular, inmediatamente puede
escribirse la P correspondiente.
(e) Expresión aproximada de V en coordenadas de equilibrio. Como Ves una función de las
coordenadas exclusivamente, puede desarrollarse directamente. Así,
Como se ha supuesto que q\ = 0, q2 = 0, etc., son las posiciones de equilibrio, las fuerzas
generalizadas, —dV/dqr, son nulas en tales puntos. Por tanto, el segundo término de la
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 215
expresión anterior es igual a cero. Por otra parte, Vo es constante. Así, como una primera
aproximación, se conserva el tercer término, quedando,
¿ r l
donde c. = (-—— ) = constante. Estas derivadas parciales, evaluadas en el punto
rl Kdq^qjo
Q\ = 0, q2 = 0, etc., deben obtenerse a partir de la expresión exacta de V, escrita en
función de las coordenadas de equilibrio. (Nótese que arl = alr, brl — blry crl — clr.)
Resumiendo lo anterior, se escribe,
1 "*" " " {10.4)
{10.5)
{10.6)
Expresiones aproximadas de T, P y V, en donde arl, brí y cri son constantes.
Ejemplo 10.2.
Con el fin de ilustrar los resultados anteriores, considérese nuevamente el péndulo doble de la figura 2-10. En
coordenadas rectangulares,
T = $m,(i;+¿;) + lm2(xl+%) (1)
Las ecuaciones de trasformación que relacionan las coordenadas rectangulares con las de equilibrio, 8 y <f>, son
^1 = »o + ri sen 9, Vi = Vo ~ rx eos 9
x2 — x0 + rx sen 9 + r2 sen <f>, y2 = Vo ~ »"i eos 9 — r2 eos <f>
Pero en cualquier sistema que tenga sólo dos partículas y dos grados de libertad,
T
P
V
1 ^
= H^M.
(2)
arl
Así, (10.4) se reduce a
/dxi dx± dVx_ dvA /dx2 dx2 3^ dVi\
mi \dqr dqt dqr dqj m2\dqr dqt dqr dqj
♦H®WE)T+-[®,+(£)l}*
Considérese que i¡i es í y que q?. es <f>. En (2), se ve que ( —— ) = ru I —— ) = 0, etc. Sustituyendo estas
magnitudes en (3), se obtiene, \ 3» /o V 3» /o
Vo*. = i[(^i + W2)r?j2+ 27n2r,r2^ + 7n2r2¿2] (4)
siendo todos los términos cuadráticos en las velocidades, con coeficientes constantes.
Supóngase que mi y m.2 sufren la acción de fuerzas viscosas cuyas magnitudes son biVi y f>2i>2,
respectivamente. Remplazando mi y rri2 por b\ y b2, en (4),
P = ~ £[(&i + h)r292 + 262r1r2¿¿ + b2r\¿2] (5)
216 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
La expresión exacta de V es
V — {mx + tn2)grx{l — eos 9) + m^gr^l — eos <f>) (6)
Por (10.6), Vaprox. = i(cu6* + 2cl2e<f, + c22<f>2)
/d2V\
donde cM = I —^J = (mi + rri2)gr\, ci2 = 0 y c22 = m2£r2. Entonces,
^aprox. = i[(™i + m^r^ + rrwrtf*] (7)
Nótese que como cosí = 1 — -J*2 + j-9* •'', se ve que para ángulos pequeños, 1 — cosí = ±82. Así, en este
caso sencillo, (7) es consecuencia inmediata de (6).
10.4 Ecuaciones diferenciales del movimiento.
Aplicando las ecuaciones de Lagrange a las expresiones "preparadas" de T, Py V, se
obtienen en seguida las ecuaciones del movimiento. Suponiendo, para simplificar, que existen tres
grados de libertad, se obtienen las siguientes tres ecuaciones
dllSl + blltfl + Cil<?l + Ü12Q2 + fel2^2 + Cl2<?2 + ai3#3 + 613^3 + Ci3<73 = 0
CLu'qx + &2i<7i + CnQ\ + 822*72 + ^22^2 + C22Q2 + a23q3 + bz3q3 + C23Q3 — 0 {10.7)
dsi'qi + b3i(][i + c31q1 + a32<72 + 63202 + c32<?2 + a33<73 + 633^3 + c33<73 = 0
Las fuerzas conservativas se representan aquí por cuqi, 01292, etc., y las fuerzas
viscosas por buqv bx2q2, etc.
10.5 Soluciones de las ecuaciones del movimiento; fuerzas conservativas
únicamente.
En el análisis que sigue, se supone que solamente actúan fuerzas conservativas. Razones:
(a) pedagógicas, (fe) la suposición es válida en muchas ramas de la física teórica y aplicada.
En este caso las ecuaciones {10.7) se reducen a
an(7i + Cuiji + ai2<72 + Ci2<72 + ^13^3 + Ci3<73 = 0
a2i<7i + C2\q\ + 022(72 + 022*72 + a23<73 + Czsqz = 0 {10.8)
CL3iqi + c3i<7i + a32?2 + c32<72 + 0,33^3 + c33<73 = 0
A continuación se resuelven estas ecuaciones y se incluye un estudio más o menos
detallado de las más importantes consideraciones matemáticas y físicas que implican.
En la forma acostumbrada, supónganse las siguientes soluciones
qx = A eos (wí + <f>), q2 = B eos {U + <f>), q3 - c eos (wí + <f>)
donde A, B, C, u y 4> son constantes no conocidas. Sustituyéndolas en {10.8), se concluye
de inmediato en
(an«* - cu)A + {al2^ - cl2)B + {al3»* - cl3)c = 0
{a2lJ - c2l)A + {a22J - c22)B + {a23J - c^c = 0 {10.9)
K»2 - CJA + K2»2 - C32)B + K3»2 - c3> = 0
Puede demostrarse que valores de A, B y C (diferentes de cero) que satisfacen {10.9) no
pueden encontrarse, a menos que el determinante de sus coeficientes sea igual a cero. Se
escribe, por tanto, el determinante:
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 217
D =
,.,2 - (
,.,2 - C
,.,2 - i
= 0
(10.10)
Determinante fundamental, D.
(Sin fuerzas disipativas actuantes)
Nota. Este puede escribirse directamente de T y V; (10.4) y (10.6).
La extraordinaria importancia del "determinante fundamental" anterior se hará
evidente más adelante. En él se halla concentrada prácticamente toda la información que puede
obtenerse sobre los movimientos oscilatorios de los sistemas del tipo que se considera.
Al desarrollar la ecuación (10.10) se obtiene una ecuación algebraica de tercer grado
en ío2. En problemas específicos, se conocen los valores de las a y de las c. Por tanto, puede
escribirse esta ecuación con coeficientes numéricos.
En este momento es importante tener en cuenta que existen diversos métodos para hallar
los valores de las raíces de ecuaciones algebraicas de grado n, en forma aproximada, aunque
con suficiente precisión. Con tal fin, se recomienda especialmente el método de "la raíz al
cuadrado de Graeffe", puesto que es fácil de aplicar, conduce a buenos resultados y el tiempo
consumido es relativamente corto. Un excelente estudio sobre este tópico se encuentra en
R. E. Doherty y E. G. Keller, Mathematics of Modern Engineering, Vol. I, páginas 99-128,
John Wiley, 1936.
Supóngase que las tres raíces, coi, co2 y to3, de (10.10) son todas reales y diferentes.
(Puede demostrarse que si Ves "definitivamente positivo", es decir, positivo para todos los
valores que puedan tomar las diferentes q, todos los valores de co son reales.)
Remplazando, por ejemplo coi, en (10.9), el lector puede demostrar que estas relaciones
determinan únicamente valores relativos, Ai,Bi y C\, para las constantes. En otras
palabras, si (10.9) se satisface con Ai = 3,5, B\ = -9,2 y C\ =■= 7,6; así mismo se satisface
con Ai = 3,5c, Bi = -9,2c y Ci = 7,6c, en donde c es una constante cualquiera. Además,
no es difícil demostrar, por medio de un ejemplo sencillo, que los valores relativos de Ai, Bi
y C\ son los cofactores de los elementos primero, segundo y tercero, respectivamente, de
cualquiera de las filas en (10.10), multiplicados todos ellos por una constante arbitraria.
(Para definir el "cofactor", se suprime la fila fy la columna c correspondientes a un elemento
dado, quedando así el determinante Mfc, llamado "menor". El cofactor de este elemento es
Dfc = (—l)f+cMfc.) Es decir, para la primera fila se escribe,
A, = +ct
l*22u'l
a ,„2-
Bt =
Cx = +ex
Para abreviar, las anteriores se escriben,
Ai = C\dw, B\ — C\di\,
C\ — Cídsi
(10.11)
donde, por ejemplo d2i, es el cofactor del segundo elemento de una cualquiera de las filas
Que haya sido seleccionada con coi en todas las posiciones de m. Es decir, c¿2i = Dr¿
(con coi), en donde r puede ser 1, 2 ó 3. (La notación anterior es conveniente porque muestra
claramente el número del elemento dentro de la fila y el número de to. Carece de importancia
el número de la fila.)
218 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Por último, resulta claro que las siguientes expresiones satisfacen (10.8):
Q\ — C\dw eos ((d,í + <£,), q2 = Cid2i eos («Djí + <£,), #3 = C\dz\ eos (tD,í + <£,)
De la misma manera, se obtienen los otros dos conjuntos de soluciones correspondientes
a w-2 ya co3. Sumándolas se obtiene la solución general,
q\ - Cidn eos (o>,í + <¿,) + c2di2 eos (o>2í + <f>2) + c3dX3 eos (o>3í + <f>3)
q2 - C\d2\ eos (o>,í + <¿,) + c2d22 eos (o>2í + <f>2) + Czdw eos (o>3í + <f>3) (10.12)
q3 - C\dz\ eos (o>,í + <¿,) + c2d32 eos (o>2í + <f>2) + c3d33 eos (o>3í + <¿3)
Ecuaciones del movimiento integradas.
en las que las constantes arbitrarias, ci, C2, cz, <¡>\, <¡>2 y </>3 pueden hallarse a partir
de las condiciones iniciales conocidas. Al incorporar los desplazamientos iniciales puede
obtenerse de {10.12), c\ eos </>i, C2 eos <¡>2 y C3 cos</>3; y al tomar las derivadas de {10.12) y
remplazar los valores de las velocidades iniciales, 0qvoq2 y Jl3, las ecuaciones resultantes se
utilizan para determinar c\ sen</>i, C2 sen <f>2 y cz sen</>3. Así, en seguida se llega a los
valores de c y <¡>. Un método más sencillo para evaluar estas constantes se incluye en el
numeral 10.15.
10.6 Resumen de aspectos importantes sobre el tipo anterior de movimiento
oscilatorio.
(a) Luego de una ligera perturbación, todas las componentes del sistema, en general, oscilan
con n frecuencias naturales o modos principales de movimiento. Por ejemplo, en la figura
10-2(e), n = 9, habrá entonces nueve valores de w y cada una de las masas o poleas
oscilará con nueve frecuencias correspondientes.
(fe) Las frecuencias están dadas por /i = u>\/2ir, etc., en donde coi, o>2, ••, wn son las
raíces de un determinante fundamental que tiene la forma de (10.10). Nótese que este
determinante puede escribirse directamente de T y V sin necesidad de escribir las
ecuaciones del movimiento.
Como puede verse en (10.10), las to dependen únicamente de las constantes del
sistema.
(c) Las amplitudes relativas de un término armónico en particular, de los que aparecen en las
expresiones de q\, q2, . .., qn vienen a ser determinadas completamente por los co-
factores y no por las condiciones iniciales.
Considerando en las soluciones (10.12) la oscilación correspondiente a coi, por
ejemplo, las amplitudes relativas de eos (coií + <f>\) en las expresiones de 171,172,173, son
claramente iguales a £¿u,c¿2i y cf31, puesto que ci es común a todos.
(d) Como las constantes ci,C2 y C3 se determinan por las condiciones iniciales, resulta
evidente que las amplitudes, tales como cidu, cit¿2i y c\dz\ dependen de la
forma como se inicie el movimiento.
Nótese que si el movimiento se inicia adecuadamente, una o más de las constantes
c\,C2, , c„ puede ser igual a cero. Así, el sistema puede hacerse oscilar con una
cualquiera de las n frecuencias o con una combinación de ellas.
En el numeral 10.20 se explica un método experimental para excitar uno de los modos
únicamente.
(e) Suponiendo que se excita únicamente coi, (10.12) conduce a
qi - Cidn eos (*>,£ +<£,), q2 - Cid2i eos (a>,í + <£,), q3 — ctd3i eos (a>,í + <£,)
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 219
Los signos algebraicos de dn, d2i y c¿3i pueden ser positivos o negativos, y por tanto,
los movimientos anteriores pueden estar sincronizados en fase o exactamente fuera de
fase (en oposición).
Considérese la figura 10-10. Si el movimiento es únicamente vertical, habrá tres
frecuencias. La tabla a la derecha indica la forma como se mueven las masas cuando se
excita únicamente coi, co2 u co3. Estas relaciones de fase se determinan
completamente por los signos algebraicos de las d. Sin embargo, se observa que para una u
determinada que se excite, todas las masas, m\,m2 y mz pasan por la posición de
equilibrio al mismo tiempo. Igualmente, los valores máximos se alcanzan
simultáneamente.
(/) Una palabra final. Si hay interés únicamente en conocer los valores de las frecuencias
naturales, como a menudo sucede, no se requiere ningún otro trabajo distinto de hallar
las raíces del determinante fundamental.
10.7 Ejemplos para ilustrar los resultados de los numerales anteriores.
Ejemplo 10.3.
Considérese el sistema de la figura 10-l(a). Suponiendo únicamente movimiento vertical, y representando
por y\ y y-¿ los desplazamientos de mi y m2, respectivamente, a partir de sus posiciones de equilibrio,
T = iirmvi + m2y22)
^exacta = £Ml/l + 8l)2 + £Ml/2 ~Vl + «2) ~ ™\9V\ ~ ^iSVi
donde s\ es la diferencia entre la longitud de equilibrio y la longitud no alargada del primer resorte y s2 tiene
el mismo significado para el segundo resorte. Comoyi y y2 se miden a partir de los puntos de reposo, dV/dyi =
dV/dy2 = 0 para cuando yi = y2 = 0. Así, el lector puede demostrar que la Vexacta anterior, puede rempla-
zarse por V = ^fcil/2 + %k2(y2 — Vi)2- Por tanto, las ecuaciones del movimiento son
ml'y\ + (fc, + k2)yl - k2y2 = 0 y -fcjjtfi + m2'y\ + k2y2 = 0 U)
Comparando con (10.8) y (10.10), puede escribirse,
I m,u2 — (fc, + k2) k2 I
^ 2 u = ° (2)
de donde, mxm2<¿ - [k2ml + (fe, + k2)m2](1)2 + fc,fc2 = 0 (3)
Si mi = 400 gramos, m2 = 300 gramos, k, = 6X 104 dinas/cm y k2 = 5 X lO4 dinas/cm, por (3) se
concluye que «i = 8,16 y <o2 = 19,37. O sea, /i = 1,30 y f2 = 3,08 oscilaciones por segundo.
Por tanto, de acuerdo con (10.12) (luego de remplazar los cofactores adecuados y dividir por 104),.se escriben
las soluciones generales,
jyi = 6,25c, sen (19,37í + 4>i) - 3c2 sen (8,16í + <t>2)
(4)
y2 = -5ci sen (19,37í + 4>i) - 5c2 sen (8,16í + <f>2)
Obsérvese lo siguiente, (a) En este caso tan sencillo, Ty V tienen ya las formas de (10.4) y (10.6). (b) Si se
excita únicamente ui.rfii y m2 oscilan en fase con amplitudes relativas de 3 a 5. Si se excita únicamente <o2,
el movimiento tiene una relación de fase en oposición, con amplitudes relativas de 6,25 a 5. (c) Para cualquier
tipo de condiciones iniciales determinadas, ci,c2,0i y <t>2 pueden ser evaluados de inmediato.
Ejemplo 10.4.
La masa m, de la figura 10-3, puede moverse en un plano bajo la acción de los resortes y la gravedad. (En
un experimento real, m consiste en dos discos pesados unidos por medio de una varilla corta y delgada que conecta
los dos centros. Los hilos se atan a la varilla con el objeto de eliminar efectivamente la rotación de los discos para
tratarlos así como una partícula, m.)
220 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
'////^//////////^^^^
Valores experimentales:
m = 679,2 gramos
0i = 43°, e2 = 51°
ki = 3,7 X 104 dinas/cm
k2 = 3,8 X 104 dinas/cm
<Pi = 0,73 seg, <P2 = 0,70 seg
n los cosenos
directores de Oa
/, = 11,9 cm, /, - 23,5 cm
Zj = 18,7 cm, l2 - 31,2 cm
Fig. 10-3
Para esta disposición, T es sencillamente, £m(i2 + y2). Suponiendo solamente movimientos pequeños
:on relación a la posición de equilibrio, una expresión aproximada de V estará dada por (véase la ecuación (5.77)),
+ ^«2/32) *v]
lo cual es de la forma
y = i(cn»2 + 2c12xj/ + c22%
Al seguir las mismas etapas descritas en el ejemplo anterior, se pueden establecer las ecuaciones del movimiento
e integrarlas en forma inmediata.
Se sugiere al lector que haciendo uso de los valores de mi, ^i, etc., dados en la figura, calcule los dos
períodos CP1 y CP2 y l°s compare con los valores experimentales. Se observará que la coincidencia es bastante
ajustada.
Nótese que si (cu + C22)2 = 4(cuc22 - cf2);
no se ha considerado la gravedad en este ejemplo?
<o2. ¿Será esto posible físicamente? ¿Por qué razón
Ejemplo 10.5.
Considérese el péndulo doble de la figura 10-1(6). Véanse (4) y (7) del ejemplo 10.2. Se deja al lector la
demostración de que el determinante fundamental (que naturalmente puede escribirse sin haber expresado las ecuaciones
del movimiento) es
1{mx + m^rla? — (ml + m^g m2r1r2<>32 I
m2rlr2u2 m^rtu? — m^gr2 \
De este punto en adelante la solución continúa como en el ejemplo anterior (véase el problema 10.1).
Ejemplo 10.6. Pequeñas oscilaciones de las tres barras suspendidas de los hilos, como se muestra en la figura 10-4.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 221
^^^^^^^^^
wi, = 260 gramos
^T^'iffr->^Hw-^^^^-'^f^if^fti*|-r'itrit;<>i
Q gramos
(a) Tres barras suspendidas de hilos
'/////////s
y///,?///,
(c)
Fig. 10-4
(d)
El lector puede demostrar sin dificultad alguna que Taprox está dada por
^nprox. - £[(»», + ™2 + m3)r^e] + m^%9\ + m3rfe¡ + 2m2rlr2éié2 + 2m3r1r3¿1¿3] (1)
donde 8\,82 y 03 son desplazamientos angulares de m\, m.2 y ms, respectivamente.
^exacta = m\9rl{\ - eos ej + m2flr[r,(l - eos *,) + r2(l - eos 92)] + m3flr[r,(l - eos oj + r3(l - eos $3)]
Haciendo, 1 —cosí, = \e\, etc.,
^aprox. = £[(™i + m2 + mz)grx9\ + m^gr^l + m^r^
Por inspección de (1) y (2), se puede-escribir,
I (mí + m^ + 7n3)(r,(o2 — fiO^ m^^co2 T^r^co2
m2r,r2co2 m2r2(r2co2 — g) 0
m3r,r3co2 0 m3r3(r3co2 - flr)
(2)
w
Realizando el desarrollo y remplazando los valores numéricos de la figura, se obtiene,
«o6 - 451co4 + 37.616«2 - 784,327 = 0
(4)
que es cúbica en w2. Aplicando el método de Graeffe, «i = 18,71, w2 = 8,21 y w3 = 5,72. Una vez evaluados
los cofactores, las soluciones generales resultan,
222 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
$l = 2,78c, eos (18,711 + 0,) - 0,88c2 eos (8,21 t + <f>2) + 2,75c3 eos (5,72í + #3)
$2 = -4,54c, eos (18.7LÍ + 0,) - 5,70c2 eos (8,21 t + <f>2) + 2,30c3 eos (5.72Í+ <f>3) (5)
$3 = -2,43c, eos (18,711 + ¿,) + 2,34 c2 eos (8,21 í + <f>2) + 4,16 c3 eos (5,72í + <f>3)
Las constantes ci, ci, c3, ¿i, 02, y <t>3 pueden determinarse a partir de las condiciones iniciales dadas.
Si se excita únicamente <oi, en (5) se ve que m2 y m3 oscilarán en fase, y fuera de fase con respecto a mi.
Sus amplitudes relativas (los desplazamientos angulares máximos, relativos) serán 2,78, 4,54 y 2,43 para mi, m2 y
m3, respectivamente. Los tres "modos del movimiento" y sus amplitudes relativas se muestran en la figura 10-4(f>),
(c) y (d).
Una vez más debe recalcarse que, como se muestra en el ejemplo anterior, (a) las frecuencias naturales del
sistema, (b) las relaciones de fase entre las oscilaciones correspondentes a una frecuencia cualquiera en particular,
y (c) las amplitudes relativas del movimiento se determinan todas ellas a partir del determinante fundamental
y por tanto dependen de las constantes del sistema.
Ejemplo 10.7.
La consideración de los movimientos oscilatorios de las tres "partículas" conectadas con resortes, como se
muestra en la figura 10-5, ilustra la mayor parte de los aspectos básicos relacionados con oscilaciones pequeñas
y le da al lector una buena visión general sobre la materia.
Xi y Vi son ejee fijos con el origen en la posición de reposo de mi
Fig.10-5
Considerando el movimiento en un plano, el sistema tiene seis grados de libertad y por tanto, seis frecuencias
naturales de movimiento. Se suponen conocidos todos los valores de las k, de las longitudes normales de los resortes,
de las posiciones de equilibrio de mi, m2 y m3, de las posiciones de pt, p2, p3, etc., y de las longitudes
de equilibrio de los resortes.
Las coordenadas rectangulares de equilibrio de mi, m2 y m3, consideradas como partículas, se
representan por xi, yi, x2, y2, x3 y )3. Por tanto,
T = im^í + Vi) + lm2(% + %) + W*s + ®
Por extensión de los principios expuestos en el numeral 5.10, V puede ponerse en la forma,
^aprox. = -Í(Cll*? + «220? + C33*2 + C«^ + C»8»8 + CWV¡)
+ CnxiVi + ci3a;ia;2 + cUxiV2 + CisSi3^ + c,6x,í/3
+ C23?/,X2 + c2AV\V2 + cZhVlx3 + C261/lÍ/3 + C34X2?/2
+ c35x2x3 + c36x2y3 + c45y2x3 + c46y2y3 + c56x3y3
La determinación de las diferentes c puede hacerse directamente, pero en los casos reales se requiere para ello una
gran cantidad de trabajo de rutina. Una vez hecho esto se llega a la posición de plantear el determinante
fundamental del sistema, cuyas raíces conducen a «i, <o2, .. ., «e. Por último, las soluciones serán de la forma,
s, = c,d,, cos(co,í + 0,) + c2dl2 eos (u2í + <f>2) + ••• + c6d,6 eos (u6t + #6),
etc., para yi, x2,y2, x3,y3-
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 223
Con una perturbación general, cada una de las partículas oscilará con las seis frecuencias dadas por fx = wi/2t,
etc. Si se excita una cualquiera de las frecuencias, las amplitudes del movimiento de m\, m2 y m3, en general
no serán iguales ni oscilarán en direcciones paralelas (véase el numeral 10.14).
Nótese que si se permite que exista movimiento fuera del plano, se tendrán nueve grados de libertad, y por
tanto el sistema tendrá nueve modos naturales de oscilación. En este caso el tratamiento será igual al descrito.
10.8 Casos especiales de las raíces de D.
(a) Raíces múltiples.
Considérese la disposición de la figura 10-6. Supóngase que el marco se halla colocado
sobre una superficie horizontal lisa. Se supone además que todos los resortes son idénticos
y que si la masa está en reposo, el espaciamiento angular entre los resortes es de 120°.
Para este caso (véase la ecuación (5.11)),
T = imfó + fr) y y = *[fc(3-l,5í7í)(z2 + 2/2)]
Así, puede escribirse de inmediato el
determinante fundamental y al desarrollarlo resulta
evidente que las dos raíces de D son iguales, es
decir, coi = co2. Las ecuaciones del
movimiento demuestran que éste estaría compuesto
por dos movimientos armónicos simples
formando entre sí ángulos rectos, ambos con el
mismo período. Pero esto es correcto solamente
para el caso especial considerado aquí. Si las k
no son todas exactamente iguales o si el
espaciamiento se altera aunque sea ligeramente,
coi será diferente de C02.
Existen otros sistemas en los que, para
valores especiales de las constantes, se dan las
condiciones para que las raíces resulten iguales.
Sin embargo, el caso de raíces verdaderamente
iguales, es más bien raro. Cuando se presenta,
normalmente la "degeneración" puede
eliminarse cambiando ligeramente las constantes
del sistema.
(b) Raíces nulas.
Los determinantes fundamentales de todos los sistemas de la figura 10-7 tienen todos
una raíz igual a cero. Considérese por ejemplo, la figura 10-7(a). En el ejemplo 4.4 se ha
hecho un estudio detallado del movimiento para el caso, de 0 pequeño, y como puede verse
en las ecuaciones del movimiento,
_ I (mi + m2)o)2 m2roy2 I
D = = o
| m2ro)2 ra2rV - m2gr \
de donde, (mi + m2)(m2r2co2 - m2gr)w2 - m2r2co4 = 0. Por tanto, una de las raíces,
por ejemplo «,, es igual a cero y co2 = [(mi + m2)g/r]1'2. La raíz nula significa un
"período infinito" o más prepisamente, un término igual a ut en la solución final, lo cual
indica movimiento con velocidad constante. Obsérvense los detalles de las soluciones del
ejemplo 4.4.
Fig. 10-6
224 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO (CAP. 10
(a) Carro libre de moverse sobre la horizontal.
—I . I , .
(6) "Molécula" de CO2, libre de moverse en
la dirección de una recta.
El
|ta-AM^M^2»
¡¿¿
(c) Discos conectados por un eje flexible.
Constante de torsión = #t.
(d) Supóngase, mi = m2.
I -*i I -*
xi y X2 medidos con respecto al carro. Se supone que no hay fricción.
(e) Carro libre de moverse sobre una pista horizontal.
Fig. 10-7. Sistemas para los que el determinante fundamental tiene una raíz nula.
El lector puede escribir fácilmente T y V para los discos de la figura 10-7(c) y demostrar
que D tiene una raíz igual a cero y otra diferente de cero. Físicamente esto significa que el
movimiento de cada uno de los discos se compone de un término oscilatorio más otro que
representa velocidad angular constante (véase el problema 10.9).
En la figura 10-14 se muestra un sistema como ejemplo del caso en que el determinante
tiene dos raíces nulas. Mayores detalles se encuentran en el problema 10.18.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 225
Ejemplo 10.8. La "molécula de C02" (Fig. 10-7(6)).
Se supone movimiento a lo largo del eje X, y se tiene,
T = ¿(m.i? + m¡5¿2 + mi¿a)f v = £fc[(a.2 _ Xi _ iq)2 + (X3 _ x¡5 - io)2]
en donde l0 es la longitud normal de cada uno de los resortes. Haciendo,
9i = xi + ^oi ?2 = x2> 93 = x3— *o (■*)
r = i(m,g? + m2¿* + m,§, y = |fc[(g¡¡ - «jr,)2 + (<73 - <72)2] <2>
que tienen ahora las formas de (10.4) y (10.6), respectivamente. Así,
I m,co2 — k fe 0
D = fe ™2co2 - 2fe k
| 0 fc m,co2 - k |
Al desarrollar D, se obtiene,
(mlU2 - fc)[(m2(o2 - 2fc)(mlU2 - fe) - fe*] - fc2(m,(o2 - fe) = 0
/fe \i/2 A _ rfc(m2 + 2m,)-l»/2
de donde, u, = (— ) , co2 - 0, co3 — ——
\™>ij , L mim2 J
Por consiguiente D tiene una raíz nula.
Por sustitución directa en las ecuaciones diferenciales del movimiento, el lector puede demostrar que
qt = -c,fc2 eos (co,t + ${) + c3k2 eos (u3t + <f>3) + vt + b
m,
q2 = -2c3fc2—- eos (u3t + <f>3) + vt + b (4)
q3 = c,fc2 eos (u,í + ^,) + c3fc2 eos (u3í + <f>3) + vt + b
son las soluciones en las que se deben determinar las constantes a, C3 y u a partir de las condiciones iniciales.
Es obvio que el término vt indica movimiento lineal con velocidad constante. Puede demostrarse que v es
igual a la velocidad del centro de masa.
10.9 Coordenadas normales.
En sistemas del tipo hasta ahora considerado, es posible determinar un conjunto de
"coordenadas normales", g\,g2,--,gn (todas ellas relacionadas linealmente con las
coordenadas de equilibrio usuales, (71,(72, ,(7„) tales que al remplazar las q por las
g, T y V adquieren formas muy sencillas,
T = táí + flí+---+¿ü), v = 4(»,0? + «,05 + • • • +-.0Ü)
(Los usos y las ventajas de las coordenadas normales se mencionan en el numeral 10.12.)
(a) Definición de las g.
Considérese, por ejemplo, un sistema que tenga sólo dos grados de libertad, y para el
cual las ecuaciones integradas del movimiento son,
Qi - Cidn eos (w,í + <¿,) + c2di2 eos (oi2t + <f>2)
(10.13)
q2 — Cid2i eos (w,í + <£,) + c2d22 eos (o>2í + tf>2)
Por conveniencia, en adelante se remplaza c\ por c\A\ y C2 por C2A2 en donde Ai y A2
se consideran constantes arbitrarias y c\ y C2 serán determinadas más adelante para
satisfacer ciertas condiciones. Se debe tener en cuenta que c\ y C2, ahora no se consideran
arbitrarias.
226 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Definiendo las cantidades g\ y g¿ por
gi = Ai cos(coit + <t>i) y g2 = A2 cos(co2t + <t>z)
las relaciones (10.13), se hacen,
Qi — Cidugí + c2di2g2, Q2 — Cid2ígi + c2d22g2 {10.14)
Nótese que las cantidades g\ y g2 pueden considerarse como un nuevo conjunto de
coordenadas. Así, (10.14) serán las ecuaciones de trasformación que relacionan las q con
las g. Como se verá en lo que sigue, g\ y g2 son las coordenadas normales deseadas.
(b) Expresión de T en coordenadas normales. "Condiciones de ortogonalidad".
Tomando la derivada de (10.14) y remplazando en
T - \{anq\ + 2ai2<7i<72 + a22q\)
se obtiene, T — %[c\(and2u + 2ai2dud2í + a22d\x)g\ + cl(and\2 + 2ai2d22 + a22dl2)g\
+ 2ciC2(and\\di2 + a\2dnd22 + a2idi2d¿i + a22d2id22)gig2]
Escribiendo los coeficientes de g\, g\, y g'g^ como N\i, N22 y N12, respectivamente, se
observa que
2 2 2
Nll = c\ ^ ttridrid», N22 — C¿ 2 aTldr2di2, Ni2 — CiC2 2 dridrida
Ti Ti Ti
o en una forma más compacta,
Nsk = CsCk 2 CLTldrsdik (10.16)
Ti
La relación (10.16) es de gran importancia ya que, como se demuestra para el caso
general en el numeral 10.10, Nsk = 0 cuando s 9¿ k. Si s = k, entonces, Nsk ^ 0.
Además, (véase el párrafo (a)) se observa que si se toma cs como,
t2 -1-1/2
2ar,d„dJ (10.17)
se tendrá, Nss = 1. Por tanto, (suponiendo por el momento la validez de las afirmaciones
anteriores), se concluye que T — %(g\ + g22).
(c) Expresión de V en coordenadas normales.
Para el caso en consideración, una expresión general de V, es
V = $(cnq\ + 2ci2qiq2 + c22q\)
Remplazando (10.14),
V - %c\{(cndn + ci2dn)dn + (ondú + Ci2dn)d2i]g\
+ %c\{(cndi2 + Ci2d22)dn + (c22a\2 + Cu.di2)d22]g\ (10.18)
+ iciC2[2(didi2 + Ci2d22)dn + 2(c22d22 + Ci2di2)d2i]gig2
Si se supone excitado únicamente un modo principal, por ejemplo «1,
<7i = Cidn.Ai eos («.>,£ +<£,), Q2 — Cid2iAi cos(ti),í + <£,)
Al llevar estas expresiones a las ecuaciones diferenciales del movimiento originales (que
tienen la forma de (10.8)), se llega a
Cndii + Ci2d2i — <a\((iiidii +ai2dn)
c2\dw + c22d2\ = «t>j (C1.21CÍ11 + d22d2i)
En forma semejante, se obtienen dos relaciones similares al suponer excitado el modo
ío2. Al remplazar estas cuatro formas en (10.18), se obtiene finalmente,
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 227
y = mNu921+2o>¡Nl2glg2 + 4N22gl)
lo cual al aplicarle (10.16) y (10.17), se reduce a V = $(i»\g\ + <49\)-
(d) Caso general.
En forma semejante pueden cumplirse las etapas anteriores para el caso en que se
tengan n grados de libertad siempre que T y V tengan las formas de (10.4) y (10.6),
respectivamente. La solución correspondiente a qi puede escribirse, q\ = cidugi + C2di2g2 +
• • • -f cndingn, etc. O en el caso general,
1, = lokd,kgk U0.19)
k=l
Las expresiones correspondientes a (10.16) y (10.17) toman las siguientes formas:
n ^0 para s ¿¿ k
(«) Nlk = «Al'Aí. =<l1nflPfl« y m20)
ri ^^ 1 para s = «
(b) c, = [t aAA]~"2 Ua2I)
(a): Condición de ortogonalidad, (6): Factor de normalización
Usualmente Nsk se escribe 88k y se denomina delta Kronecker.
En el caso general, T y V tienen las formas,
T = Mti + #+••■+#)
T y V expresadas en coordenadas normales.
(10.22)
Este desarrollo se ha llevado a cabo suponiendo que las soluciones tienen la forma de
(10.12). Sin embargo, constituye un teorema de álgebra, la demostración de que si T y V
tienen las formas de (10.4) y (10.6) pueden encontrarse unas relaciones lineales adecuadas
para relacionar las q con las g de tal modo que se trasformen T y V a las formas de (10.22).
10.10 Prueba de la relación de ortogonalidad.
Antes de continuar avanzando, se debe probar la importante relación (10.20).
Considérese un sistema que posea n grados de libertad. Si se supone sólo una oscilación,
íos, excitada, resulta claro que
qt = csdu eos (osí + tf>s), q2 = csd2s eos (<osí + <t>8), etc.
Introduciendo éstas en una cualquiera de las ecuaciones-diferenciales originales, por ejemplo
en la designada por r, se tiene,
que puede escribirse, n
2 «A = «¡2 «A (;)
1=1 1=1
Nótese que (1) representa n ecuaciones, puesto que r = 1, 2, . . ., n.
Igualmente, al suponer excitado u>k,
1»A, = »!2>A (2)
228 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Si ahora se multiplica la primera de las ecuaciones (1) por d\k, la segunda por d2k,
etc., y se suma, se obtiene,
De la misma manera, a partir de (2) se obtiene,
En vista de que arX — alT y crl = clr, puede remplazarse / por r y r por / en (3) sin alterar el
valor de la suma. Así, los miembros izquierdos de (3) y de (4) son iguales. Por tanto,
("!-«!)ÍVA = o (5)
l.r
Pero como para k ^ s; wk ^ ws. Entonces, 2 ari^rs^Hc = 0 (^)
Además, puede demostrarse que si k = s, la suma de (6) no es igual a cero. En esta forma
queda establecida la validez de (10.20).
10.11 Aspectos importantes relacionados con las coordenadas normales.
(a) A partir de (10.22), se concluye que
9l+^lgl = 0, g2 + a>¡g2 = 0, 9n + *2n9n = 0 (10.23)
Estas ecuaciones del movimiento, severamente simplificadas, se pueden integrar en
seguida para conducir a g\ = A\ cos(coi£ + </>i), etc., (que son las mismas expresiones
originales dadas en el numeral 10.9). Así, por (10.23) puede decirse que:
(b) Los modos principales del movimiento correspondientes a coi, w2, i son
completamente independientes. Es decir, que uno cualquiera de los modos ni influencia, ni se
deja influenciar por los otros modos. Desde el punto de vista matemático, el sistema se
ha reducido a n osciladores armónicos completamente autónomos (véase el párrafo (c),
en seguida).
(c) Si el movimiento se inicia en forma adecuada, el sistema oscilará con una cualquiera
de las frecuencias fundamentales solamente, (como se mencionó anteriormente), o con
una combinación de ellas. Sin embargo, no debe perderse de vista el hecho importante
de que, si se excita uno de los modos únicamente, todas las partes que componen el
sistema, en general, oscilarán con esta frecuencia particular. Por ejemplo si en el sistema
de la figura 10-2(e), se excitara to5, todas las seis masas y las tres poleas oscilarían con
la frecuencia /s = ío5/27t.
(d) Al observar (10.22), se concluye que D, en coordenadas normales, (suponiendo, por
conveniencia, n = 3) es de la forma,
-«-? 0 0
D = | 0 "2-a,2 0
0 0 »-o
Se dice entonces, que D ha sido "diagonalizado".
(10.24)
10.12 Ventajas de las coordenadas normales.
(a) La consideración de las coordenadas normales conduce a una mejor comprensión de
la física y las matemáticas relacionadas con las pequeñas oscilaciones. De obtiene una
"visión" más completa de lo que ocurre.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 229
(b) El estudio de sistemas como los del tipo considerado, a los cuales se les aplican fuerzas
externas, se facilita considerablemente por la utilización de coordenadas normales (véase
el numeral 10.18).
(c) La determinación de las constantes de integración en soluciones de la forma de (10.12)
se simplifica notablemente con el uso de la condición de ortogonalidad, (10.20) (véase
el numeral 10.15).
(d) Las coordenadas normales pueden emplearse, con grandes ventajas, en varias
consideraciones teóricas, sin necesidad de hallar primero las expresiones de las diferentes g.
(e) Las coordenadas normales se utilizan extensamente en el estudio de vibraciones
moleculares, vibraciones de los átomos en los cristales, etc.
Sin embargo, debe tenerse presente que, salvo en casos muy sencillos, las expresiones
de las diferentes g de un sistema determinado, pueden hallarse únicamente luego de haber
determinado m,^,...,^ (véase el numeral 10.13), y los cofactores, drs, (con
frecuencia un trabajo largo) como se describió en el numeral 10.5. Además, es claro que en
los problemas de aplicación, en los que sólo se requiere conocer las diferentes co, las
coordenadas normales no ofrecen ventaja alguna.
10.13 Determinación de las expresiones de las coordenadas normales.
Las expresiones de las coordenadas normales pueden obtenerse hallando las soluciones
a (10.19) directamente, para encontrar las g en función de las q. Sin embargo, la solución
puede simplificarse considerablemente empleando la condición de ortogonalidad, (10.20).
$i se multiplica (10.19) por cgarldl8 y se suman las expresiones así obtenidas para los
diferentes valores de r y /, se obtiene,
2 w*A = 2) ok 2 w*rAA = £ 9As = 9S
Ti k rl k
Por tanto, g$ = ca J£ grarIdto (10.25)
Ti
donde las cs se determinan por medio de (10.21).
En cualquier problema en particular que se tenga entre manos, se conocerán los valores
de aH y de dto. Por tanto, es posible escribir las expresiones específicas de gi,g2, •, gn
en función de las q (véanse los ejemplos a continuación).
Ejemplo 10.9. Coordenadas normales para el sistema de la figura 10-l(a).
Se escriben las soluciones dadas en el ejemplo 10.3, como sigue,
yt = 3c,A, cos(8,16¿ + 0i) — 6,25c2A2cos(19,37t + 02)
(1)
y2 - BcjA, cos(8,16t +#i) + Bc^ eos (19,371 + <f>2)
donde Ai y A2 son arbitrarias y a y c2 han de ser determinadas por medio de (10.21). Por tanto, se escribe,
Vi = SciflT! — 6.25C202. Vi — ^>C\B\ + 5c2flF2 (2)
Las expresiones de gi y g2 pueden determinarse ahora, bien hallando la solución de (2), o aplicando (10.25).
Nótese que en este problema, au = mi, a22 = m2, an = 0, dn = 3, di2 = -6,25, etc., según (7)
ci = (9/ni + 25m2)-i/2 y c2 = (6,25?mi + 25m2)"1/2
Por último,
gi = 11,393/, + 14,24;y2 y g2 = - 16,44y, + 9,Wy2 (3)
Como comprobación, el lector puede demostrar que si se toman las derivadas de (2) y se sustituyen en T =
\(mxy\ + W2¿^), se obtiene, como cabria esperar, T = ^(h\ + &1). Igualmente, al llevar a (2) a la expresión
original de V, se obtiene, V = %(<¿\g\ + ufal) (véase el problema 10.5).
230 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Ejemplo 10.10. Coordenadas normales para el péndulo triple (Fig. 10-4, ejemplo 10.6).
Las ecuaciones (10.19) pueden escribirse,
0, = 2,78c1flr1 — 0,88 C202 + 2,75 c^a
02 = -AMcxgx - 5,70ctfi + 2,30Cgfir3 (/)
03 = — 2,43c1flr1 + 2,34 c&z + 4,16C3fir3
Aplicando la expresión (10.21), c~l = 694,03, c^' = 1309,18 ye"1 = 2478,69. Hallando la solución del sistema (1),
o más fácilmente, aplicando (10.25), finalmente se obtiene
gi = 126,2901 - 43,82*2 - 59,2603
g2 = -108,880, - 149,4102 + 154,5803 (2)
g3 = 379,420, + 67,7002 + 3O7,5903
Como una comprobación, el lector puede demostrar que tomando la derivada de (1) y remplazando en la
expresión original de T, se obtiene, T = ^(g2 + g\ + g\). Igualmente V = ^{^\o\ + <¿\g\ + ^fff) Puede
obtenerse al remplazar (1) en la expresión original de V.
10.14 Amplitud y dirección del movimiento de una partícula determinada, cuando
se excita un modo de oscilación en particular.
A manera de introducción, supóngase que una cualquiera (y sólo una) de las seis
frecuencias naturales del sistema de la figura 10-5, se excita. ¿En cuál dirección (a lo largo de
cuál recta) y con qué amplitud oscilará, por ejemplo, mi? A continuación se incluye un
análisis de este tipo de problema.
Considérese el sistema relativamente sencillo que se muestra en la figura 10-8. Una
palanqueta, que consta de las partículas mi y m,2, conectadas con una varilla ligera,
está sostenida por medio de resortes, según se indica. Su posición de equilibrio es O1O2.
Suponiendo movimiento en un plano, los desplazamientos de mi y m2 a partir de las
posiciones de equilibrio son x\, y\ y x2, y2. Se tiene en este caso, n = 3 y se usan
como coordenadas generalizadas q\, q2 y qz en donde q\ y q2 son las coordenadas
rectangulares del c.m. y qz = 6. Así, xi = x\(qi, q2, qz), etc., que pueden escribirse
en forma explícita sin dificultad.
^
°>
Yt
02
/
7^92
y///A
A
. «O ' 8
*1
Fig. 10-8
^^^^^^55^^^55?5^^5^5^^^^5^555^^^^^55^^^^^^^
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 231
Suponiendo pequeños desplazamientos, se escribe (véase el numeral 10.3(6) y (c)),
•■ - ©.«• + (£).'■ + ©.«•
o sea, xx = anql + ai2q2 + ai3q3 U)
igualmente, Vi = p^ + pi2q2 + pi3q3
donde todas las « y las j3 son constantes conocidas que se determinan por la geometría
del sistema.
Considerando ahora las soluciones correspondientes a (10.12) y suponiendo que se excita
solamente un modo, por ejemplo coi,
qi = Cidu eos (wjí + «¿j), q2 = Cidu eos (c^í + ^t), qz - Cid3i eos (c^í + $t)
donde C\ se determina aquí por las condiciones iniciales, y no por (10.21). Por tanto,
xi = KA1 + «iAi + aisd8i)ciC0S(-ií + *i)
Igualmente, yv = (pndn + pi2d2i + Pi3d3i)ci cos^í + ^) (2)
o, para abreviar, xi = ciAu co&(a>it + 4>i) y yi = ciBu cos(«ií + 4>i)
Resulta claro entonces, que si se excita únicamente coi, m\ oscilará con una amplitud
Cií-Ai! + B^)i/2 a lo largo de una línea recta que pasa por Oí con una pendiente igual a
Bn/Aii. De igual manera, pueden hallarse las direcciones y las amplitudes del
movimiento de mi cuando W2 u C03 se excitan.
Considerando las expresiones de x2 y y2, en igual forma pueden determinarse los
movimientos de m2 correspondientes a coi, to2 y ¿03.
Así se obtiene una "visión" detallada del movimiento de cada una de las partículas al
excitar uno de los modos cualquiera.
Naturalmente, el análisis anterior puede extenderse a un sistema general de p partículas
con n grados de libertad.
Nótese que la trayectoria seguida por mi, por ejemplo, cuando se excitan todos los
modos simultáneamente, puede dibujarse introduciendo las relaciones (10.12) en (1) y
haciendo la gráfica de yi y x\ para valores iguales del tiempo.
Ejemplo 10.11.
Se trata de determinar la línea a lo largo de la cual el punto p, de la figura 10-16, oscila cuando se excita
únicamente «1.
Se toman xp y yp como coordenadas de p; x y y como coordenadas del c.m. y 6 cómo la rotación
angular de la varilla medida a partir de su posición de reposo (es decir, que x, y y 0 son coordenadas de
equilibrio adecuadas). Se observa entonces que
xp = x + l eos ($ + $0), yp = y + l sen ($ + $0)
donde / es la mitad de la longitud de la varilla. Así, para movimientos pequeños (conservando los términos de orden
cero y primero),
xp = x + l coa 60 — (l sen 60)6
O)
VP = V + l sen 60 + (l eos 60)6
Ahora, si se excita únicamente «1,
x = Cydn eos (wtt + <f>1), y = cxdiX eos (o^t + <fn), $ = cldzxcos(uít +${)
Por tanto, xp — l eos 60 = cx(dxi — ld3l sen $0) eos (o^t + <f>i)
2/p — l sen eQ = Ci(d2i + ld31 eos 60) eos (coi* + #i)
232 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Xp — l eos 0o y yp — l sen B0 son, obviamente, los desplazamientos de p a partir de su posición de reposo. Así,
p oscilará a lo largo de una recta que forma un ángulo a con X, en donde, tana = -^ -^ -, con una
amplitud A determinada por dn ~ W3i sen *o
A = Cl[(du - ld3i sen *0)2 + (<*2i + W31 sen «W*
Naturalmente, o puede hallarse a partir de las condiciones iniciales dadas.
Mayores detalles sobre el movimiento de este sistema, para valores determinados de las constantes físicas,
pueden encontrarse en el problema 10.23.
10.15 Determinación de las constantes arbitrarias con la ayuda de las
condiciones de ortogonalidad.
Los valores de las diferentes c y </> en (10.12), que, naturalmente, dependen de los
desplazamientos y las velocidades iniciales, pueden determinarse como se describió en la
última parte del numeral 10.5. O, habiendo remplazado a c\ por c\A\ y a C2 por C2A2,
etc., como en el numeral 10.9 (en donde las diferentes c ya no son arbitrarias sino que están
determinadas por la relación (10.21)), pueden evaluarse las diferentes A de la misma manera.
Sin embargo, el método siguiente es más ventajoso.
Introduciendo los valores conocidos, o supuestos, de los desplazamientos para t = 0,
oqi, 0(72, , oqn, en las soluciones de la forma (10.12), se tiene
0^1 = CiduAlC0S<t>l + C2dl2A2C03<t>2 + '"" + CA,AC0Stf>„
(10.26)
0Qn = cidniAl eos <l>í + c2dn2A2 eos <j>2 + ••• + cndnnAn eos <f>n
Multipliqúese ahora la primera de las ecuaciones (10.26) por cs 2 andis, la segunda por
n * í=l '
csDftA' donde s puede tomar cualquier valor entero desde 1 hasta n. Sumando las
i=i
ecuaciones resultantes y utilizando (10.20) se concluye que
Ascostf>s = c8^0qra.rdi8 (10.27)
ir
De la misma manera, para velocidades conocidas, Qqv 0q2, . ..,0qn, cuando t = 0,
puede demostrarse que
Assentf>s = -^Soi^A (m2fi)
Así, se han determinado todos los valores de As y </>s por medio de (10.27) y (10.28).
Nótese que si el sistema se desplaza ligeramente y se suelta luego, todos los valores de
0qr se hacen iguales a cero. Por tanto, todos los valores de los ángulos de fase, se anulan.
10.16 Oscilaciones pequeñas con fuerzas actuantes viscosas y conservativas.
Como material básico para esta sección, el estudiante debe repasar los numerales 10.3(d)
y 10.4.
(a) Ecuaciones del movimiento y su solución.
Suponiendo como antes, tres grados de libertad, las ecuaciones del movimiento
incluyendo fuerzas viscosas son las mismas de (10.7).
Las soluciones pueden obtenerse suponiendo
ql = A", q2 = B", q3 = C*
donde A, B, C y X son, por ahora, constantes indeterminadas. Sustituyendo en (10.7) se
obtiene
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 233
A(anX2 + bnX + cn) + B(al2X2 + bl2X + cí2) + C(al3\2 + bl3\ + cí3) = 0 (10.29)
y otras dos relaciones semejantes. Al seguir las etapas que conducen a (10.10), se escribe
I an\2 + bu\ + Cu ÍI12A2 + bí2\ + C12 CH3A.2 + bisÁ. + C13
D - a2iA2 + 621A. + c2i a22A.2 + 622A. + c22 c^A2 + &23A + c23\ = 0 (10.30)
I a3iA2 + 631A. + c3i a32A2 + 632A + C32 ÍI33A2 + b33\ + c331
El desarrollo de esta nueva forma del determinante fundamental conduce a una
ecuación de sexto grado en X. Las raíces de tal ecuación, nuevamente, pueden hallarse por el
método de Graeffe, o algún otro método conocido.
Supóngase que las seis raíces, Ai, X2, . . ., X6, *son diferentes. Remplazando los valores
de, por ejemplo, Ai, en (10.30), los valores relativos de Ai, Bi, y C\ se obtienen (véase
el numeral 10.5) por los cofactores de los elementos de una fila cualquiera. Es decir,
qi = Cidue^', q2 - Cid2iex,t, £3 = Cid^e^ (10.31)
Soluciones semejantes se obtienen para los valores correspondientes de X2, X3, »*6-
Sumando los seis conjuntos de soluciones, la solución general toma la forma
qi = Cidue^' + c2d\2ex^ + • • ■+ Ced^e**'
£2 = Cidne**' + c2d22ex*t + • • • + Ced^e^ (10.32)
qz - Cid3iex't + c2d32e^ + • • • + ced^e^
Los valores de las constantes arbitrarias o, c2, .. ,c6 dependen de las condiciones
iniciales.
(b) Naturaleza de las X.
Las raíces de D pueden ser reales, complejas o imaginarias puras.
En el caso importante en que V es definitivamente positivo, se ha demostrado que bajo
las condiciones adicionales siguientes:
(1) P = 0 (sin fuerzas viscosas): Todas las raíces son imaginarias puras. Este es el caso
analizado en los numerales anteriores.
(2) P 7a 0 pero todas las fuerzas viscosas, pequeñas: Las raíces serán complejas y se
presentan en parejas como X = \i ± ico, y \i es negativa. Es decir Xi = mi + ¿w>»
X2 = mi — i'wii etc.
(3) Fuerzas viscosas grandes: Las raíces son reales y negativas.
Si V no es definitivamente positivo, pueden presentarse raíces reales positivas. En este
caso, se observa en (10.32) que todas las coordenadas aumentan indefinidamente con el
tiempo. Por tanto, la suposición de "movimientos pequeños" se vuelve inválida rápidamente. El
sistema es "inestable".
(c) Forma asumida por (10.32) cuando las raíces son complejas.
Este es el caso más importante.
Supóngase Xi = mi + íwi, X2 = mi -iui, X3 = M2 + ¿«2» ^4 = M2 — ("2, etc.
Considerando por el momento, únicamente los dos primeros términos de la primera ecuación de
(10.32), se escribe
Cidue^ + c2dl2ex^ = etf't(cidne<w't + C2di2e-<w't) (10.33)
Pero, du, el cofactor del primer elemento de una fila cualquiera de (10.30), es complejo, y se
escribe dn = k\\ + ihw, donde, para un problema específico cualquiera entre manos,
234 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
kw y hw son constantes conocidas. Además, con pequeño esfuerzo se demuestra que di2 =
kn — ih\\. Como c\ y c¿ son arbitrarias, se pueden escribir ci = £(¿>i + ib 2) y c2 =
¿-(bi — ib¿)- Por tanto, empleando las relaciones
e*"* - coswí + isenwí, e~i0>t - coswí - ¿senwí
el lado derecho de (10.33) toma la forma
eMt[6i(fcn eos <üjí — ^u sen t^í) — b2(fcnsen c^í + hu eos <ütí)]
la cual, después de unos procesos algebraicos, se reduce a
e^R^kl + h2n)i/2 cosí^í + 8n + ^ (10.34)
Tanto R\ como <f>\ son constantes arbitrarias y tan 5n = hn/kn.
Así, resulta claro que si todas las raíces de (10.30) son complejas la solución general para
q\ es
Qt = R^kn + fcn)1/2e"'t eos («jí + 8n + ^) + R2(fe2l2 + h22)l/2e>* eos (»2í + 812 + <f>2)
+ R3(k2l3 + h2l3y<2e^ cos(«.8í + 813 + ^3) (m35)
con expresiones semejantes a ésta para q2 y 93. Los valores de R\, R¿, R*, <t>\, 4>2 y <t>*
que aparecen en las soluciones correspondientes a qXt q2 y qz son las seis constantes de
integración que deben determinarse a partir de las condiciones iniciales.
Las cantidades mi» M2 y M3 (que resultan de las fuerzas viscosas) son negativas.
Por tanto las soluciones de la forma de (10.35) indican oscilaciones armónicas amortiguadas.
Considerando únicamente el movimiento correspondiente a coi,
q, = Rl(k2n + h2n)í/*e»*tcos(o>lt + 8n + <t>l), q2 = R^ + hl^e^ caa(»xt + 821 + ^),
Q3 = Rl(k2l + h23iy»e»>tcos(o>lt + 83l + <t>l)
Por consiguiente, estos movimientos no están en fase (por ejemplo qit q2 y qz no alcanzan
sus valores extremos simultáneamente) puesto que 5u, 52i y 531 no son iguales.
10.17 Consideraciones sobre la estabilidad del movimiento.
Si luego de haber dado a las masas de un sistema pequeños movimientos iniciales,
éstas no llegan a apartarse mucho de sus posiciones de equilibrio, se dice que el movimiento
es estable. Como puede verse en (10.32), las raíces reales positivas de (10.30), o las raíces
complejas con partes reales positivas implican términos en las soluciones que crecen
indefinidamente con el tiempo, las cuales significan inestabilidad. Para tener estabilidad, las raíces
reales o las partes reales de las raíces complejas, deben ser negativas. Raíces imaginarias
puras significan estabilidad puesto que indican oscilaciones con amplitud constante.
Con el fin de determinar si un sistema dado es estable, debe seguirse uno de los dos
procedimientos siguientes:
(a) Determínense todas las raíces del determinante fundamental en la forma acostumbrada.
Examínense las raíces para observar si todas las partes reales son negativas.
(b) Apliqúese la prueba de Routh-Hurwitz, que no requiere hallar las raíces. La prueba no se
incluye aquí.
Se pueden encontrar mayores detalles sobre lo anterior junto con una gran cantidad de
informaciones adicionales sobre la materia de la estabilidad al consultar las siguientes
referencias:
(1) A. Hurwitz, Math. Ann., Volumen 46, 1895, páginas 273-284.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 235
(2) R. N. Arnold y L. Maunder, Gyrodynamics and its Engineering Applications, página 453,
Academic Press, 1961.
10.18 Utilización de las coordenadas normales cuando actúan fuerzas externas.
(No se incluyen fuerzas viscosas.)
En el estudio de los sistemas conservativos sobre los cuales actúan fuerzas aplicadas
externamente, las coordenadas normales ofrecen ventajas reales (véase el numeral 10.13) y aunque
no se trata de considerar este tópico que es largo y exige tratamiento detallado, se indica a
continuación la forma de hallar las ecuaciones del movimiento correspondientes a las
diversas g.
Esencialmente, el método para plantear las ecuaciones del movimiento es el mismo que
se ha venido empleando. Únicamente se trata de usar aquí las coordenadas gi, g2, ■ ■ -,gn-
Habiendo expresado a T y V en la forma de (10.22), se aplica -rr (t¿~) ~ ^Z~ — ^V
para obtener así, las siguientes sencillas ecuaciones del movimiento,
gr + aigr = F9r r = 1,2, .. .,n (10.36)
La fuerza generalizada, F0t, que incluye únicamente fuerzas aplicadas externamente,
puede hallarse fácilmente como sigue: Empleando q\, qi, ■ .■■,qn> se escribe 8Wtotal en la
forma acostumbrada (véase la ecuación (4.12)). Eliminando ahora la q en favor de la g por
medio de (10.19), BWtatml puede ponerse en la forma,
*w«*i = [■■■]1«01 + [■ ■■],«*, + ••• + [■■ ■]„«*„ 00.37)
Por tanto F0í — \-' \, etc. La ventaja de este procedimiento es, naturalmente,
debida a la sencillez de (10.36).
10.19 Uso de las coordenadas normales cuando actúan fuerzas externas y
viscosas.
En este tipo de problema, las coordenadas normales aún ofrecen algunas ventajas.
Ignorando por ahora las fuerzas aplicadas externamente y las fuerzas viscosas, pueden hallarse las
coordenadas normales en la forma usual, y expresar T y V como en (10.22). Nótese que las
diferentes <¿ no son las mismas frecuencias naturales del sistema cuando actúan fuerzas
viscosas.
Desafortunadamente, la función P no puede en general escribirse como P = b¿}\ + b2g\ +
• • * + bn92n. Sin embargo utilizando (10.19) y (10.5) esta función puede ponerse fácilmente
en la forma
■sÍPrtM. iW-3^
2-
Por tanto, aplicando la ecuación de Lagrange, las ecuaciones del movimiento resultan
9r + «?rgr - plrgx - p2Tg2 - p3Tg3 - ■■■ - pnrgn = F0r (10.39)
La fuerza generalizada, FgT, que incluye únicamente fuerzas externas, se determina tal como
se explicó en el numeral 10.18. Aunque aún existe "acoplamiento viscoso" las ecuaciones del
movimiento correspondientes a g son más sencillas que las de q.
Ejemplo 10.12.
Lo que sigue es una breve descripción del método anterior aplicado al péndulo triple de la figura 10-4, ejemplo
10.6, suponiendo que se halla suspendido dentro de un fluido viscoso, sin fuerzas externas aplicadas. Se escribe,
236 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
T = Ift + g¡ + g¡), V = #¿[g\ + <%g\ + <¿3g¡)
donde ui = 18,71, «2 = 8,21 y «3 = 5,72. Teniendo en cuenta el numeral 10.3 y la ecuación (1) del ejemplo 10.6,
se concluye que
P = -£[(&i + *>2 + 6s)*"i»? + h2fyl + b3r^¡ + 2b2rlr2el62 + 263r1r3¿1¿3]
donde b\, b2 y Í73 son los coeficientes de la resistencia viscosa sobre las barras. Utilizando ahora, B\ =
2,78c 1^1 - 0,88c2 £2 + 2,75c3£3, etc., (véase el ejemplo 10.10), P puede expresarse fácilmente en función de
9n¿2 y ¿3-
Por tanto 'gt + u^flY = dP/dgT, etc., son las ecuaciones del movimiento. Nótese quepi = 2t/«i, etc., no
son ya los períodos de movimiento del sistema. Si las fuerzas viscosas no son muy grandes, las oscilaciones alcanzan
a establecerse y sus períodos dependen en cierta medida de los factores de amortiguación.
Ejemplo 10.13. Fuerzas uiscosas y externas actuando.
Imagínese las fuerzas verticales f\ = A\ sen (aní + ói) y f2 = A2 sen (a2t + S2) actuando sobre mi y
m2, respectivamente, ejemplo 10.3, figura 10-1 (a). Supóngase además una fuerza viscosa —bxy\ actuando sobre
m 1 y ~~í>2Í/2• actuando sobre m2 (b\ y b2 deben conocerse por métodos experimentales). Se plantean a
continuación las ecuaciones del movimiento en función de coordenadas normales. En este caso,
T = ±{g\ + g\), V = tfjig* + ^g\) (l)
donde b» = 8,16, u2 = 19,37 y (véase el ejemplo 10.9),
Vi - Zctfx - 6,25^2. V2 = 6<;ifl,i + 6C202
(2)
Cy = (9m1 + 25m2)-i/2> c¡5 = (6,25^ + 25m2)-»/2
La función P es sencillamente
P = -WJl+bál) (3)
Haciendo uso de (2),
P = -i[í>i(3c1¿1-6,25c2i2)2+ M5ci¿i + 5C2¿2)2] (4)
Al escribir 8Wtotai = fiSyi + f28y2 y aplicar (2),
S^total = Ci(3/i +6/2)8^!+ c2(6/2-6,25/i)«flr2 (5)
Por tanto, Fg = cí(3fl + 5f2) y la ecuación final del movimiento, correspondiente a g\ es
'ái + <>\gi + c2(9b! + 2662)^ + cxc2{2hb2 - 18,7560^2 = <>i(3/i + 5/2) (6)
con una relación similar para g2. Las fuerzas aplicadas, -/i = Ai sen (aní + ¿1), etc., (u otras cualesquiera
que pueden tener formas arbitrarias) pueden introducirse ahora en las ecuaciones del movimiento.
10.20 Experimentos sugeridos.
El campo de las "oscilaciones pequeñas" está lleno de una gran variedad de
experimentos interesantes e instructivos. En la mayor parte de los casos los aparatos requeridos se
construyen con facilidad. No hay nada crítico con respecto a los valores de las masas, de las
constantes elásticas, etc., que deben ser usadas. Muchos de los sistemas aludidos en este
capítulo pueden armarse en corto tiempo utilizando materiales que se encuentran
prácticamente en todo laboratorio.
El trabajo experimental incluye la determinación de, (a) los períodos naturales del
movimiento, (fe) las relaciones de fase entre las varias partes del sistema, cuando se excita un modo
determinado, y (c) las amplitudes relativas del movimiento para un modo determinado.
Naturalmente, las constantes del sistema tales como las masas, las constantes elásticas, etc.,
deben determinarse en experimentos preliminares. Finalmente (y obviamente, este es el
resultado final) los resultados anteriores han de ser comparados con los valores calculados.
Los resultados experimentales no son difíciles de obtener. Una cualquiera de las
frecuencias naturales (si está dentro de ciertos límites) puede excitarse manualmente con facilidad.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 237
Considérese por ejemplo, el sistema que se muestra en la figura 10-1 (a). En el caso de
movimiento vertical únicamente, este sistema tiene dos frecuencias naturales f\ = wi/2ir y
f-2 = ío2/27t. Apliqúese con la mano una fuerza oscilatoria, por ejemplo a la parte superior
de m, tratando en lo posible de que esta fuerza sea armónica simple. Si la frecuencia
aplicada es igual o cercana a f\ o a /2, la amplitud del modo particular crece rápidamente. Al
retirar la mano, la oscilación continuará. Naturalmente, las dos masas oscilarán con esa
frecuencia. Un valor numérico de bastante precisión para el período, puede hallarse
tomando el tiempo necesario para, por ejemplo, cien oscilaciones, con un cronómetro.
Al excitar coi a co2, puede observarse directamente la relación de fases entre los
movimientos de mi y m.2 (es decir, si en un instante determinado se mueven en la misma
dirección, o en direcciones opuestas). Simultáneamente puede hacerse un estimativo
aproximado de la amplitud de las oscilaciones de m\ comparada con las de m2.
La técnica anterior es aplicable a una gran variedad de sistemas que tienen dos, tres o
aún cuatro períodos naturales de oscilación. Cuando la frecuencia de la fuerza aplicada está
cerca de una de las frecuencias naturales, esta circunstancia se hace evidente ya que la fuerza
requerida para causar incrementos en las oscilaciones, es notablemente pequeña. Después de
cierta práctica, se puede excitar uno cualquiera de los modos, individualmente con muy poca
dificultad. Si se tiene cierto cuidado en la determinación de las constantes del sistema y los
valores experimentales de los períodos, puede encontrarse una coincidencia excelente entre los
resultados experimentales y los calculados.
A continuación se enumeran varios sistemas, todos ellos apropiados para realizar
experimentos cuantitativos y para hacer demostraciones en clase.
(a) Figura 10-1 (a), (fe) o (d). Se construyen fácilmente y conducen a resultados excelentes,
(fe) Figura 10-4. Puede construirse fácilmente tal como se indica. Así, pueden comprobarse
los resultados dados en el ejemplo 10.6.
(c) Figura 10-10. Se construye fácilmente y conduce a resultados excelentes. Constituye un
experimento sorprendente.
(d) Figura 10-7(c). Deben usarse balineras para reducir la fricción.
(e) Los siguientes sistemas se recomiendan especialmente para demostraciones en clase:
figura 10-1 (fe) y (d); figura 10-10; figura 10-13; figura 10-16.
Los experimentos de este tipo son muy efectivos como medios para despertar interés,
darle significado físico a la teoría y ampliar extraordinariamente la comprensión de la materia
por parte de los estudiantes.
Problemas
A. Sistemas con dos grados de libertad.
10.1. En la figura 10-1 (a), se adhiere a la parte inferior de m2 y directamente al piso, un tercer resorte
(de constante k y longitud normal /£). Este resorte está bajo tensión cuando las masas están en reposo.
Hallar la expresión de «i y «2 para el sistema. Comparar los resultados con los hallados en el
ejemplo 10.3.
10.2. Demostrar que para el péndulo doble (Fig. 10-l(b)), «1 y «2 están dados por
Ul,(o2 = {fl'K + wgír! + r2) ± ^[(m^wgÍTna^+r^ + m^-r!)2)]1/2}1^»!^^-^
Demostrar que para mi = m2 = m, rt = r2 = r; b» = l,85(g/r)i/2 y «2 = 0,77(g/r)1/2 las
coordenadas normales son
gt = ^[(4-2\Z2)i/2tf-(2-V2)i/2^](mr2)i/2
02 = ^£[(4 + 2\Z2)"2* + (2 + V2 )"20](mr2) 1/2
238 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Demostrar que para el péndulo de torsión doble, de la figura 10-1 (d), ui y «2 están dados por
ritb + I2a ± V(/i& +/2<*)2 -4/i/2c~|t/2
en donde a = ki + k2, b =
Demostrar que para h
normales son
L 2IJ2
k2 + k3 y c = kik2 + klk3 + k2k3,
= h = / y *i = k2 = k3 = k; a*
9x = (*i + *a)(W*f
Hallar «i, «2, g\ y g2 para el sistema que pe
muestra en la figura 10-1(/) para mi = 300 gramos, m2 =
500 gramos, ki = 3 X 10< dinas/cm, k2 = 4X 104
dinas/cm, R = 5 cm e / = 2000 g-cm2. Tómense
xi y 12 como los desplazamientos de m i y m2
respectivamente con relación a las posiciones de reposo,
ui = 17,60, «2 = 6,41; £, = 12,15x, - 18,3x2.
Comprobar en detalle la aseveración hecha al final del
ejemplo 10.9.
Demostrar que las coordenadas normales para la
"molécula" del ejemplo 10.8 son
wtjfaj + Va) + m2Q2
Zk/I y ■
{9i-9x)W)1'*
- k/I las coordenadas
(m2 + 2m1)1/2
_ (Qi ~ 2g2 + q3) (mxwtu¡, \ U2
03 ~ (m2 + 2m,)i/2 \~2/
Comprobar en T y en V.
El marco A de la figura 10-9, está sostenido por
cuerdas de piano tensas como se indica. El disco D está
igualmente sostenido en este marco. Sea k i la
constante de torsión total de las cuerdas que sostienen a
A, y k2 la constante correspondiente a las cuerdas
que sostienen a D. Demostrar que
T = ¿[(7, + Ms* +Ix eos2a + Izsen*a)62
v = *(«,*; + «»•!>
Nótese que estas expresiones son válidas para cualquier valor de 0i y 02, siempre que no se exceda el
límite elástico de las cuerdas.
Demostrar que «i y «2 están dadas por
Fig. 10-9
1¿\ + 2Izsenaé1$2]
2 _ <*n*2 + /««i *= V(<*n*2 + Vi)2 - 4k1ic>(71 + M«2 + Ix eos2 a)Iz
2(7, + Ms2 + Ix eos2 a)Ix
donde an = h + Ais2 + 7, cos2a + Iz sen2a.
Este sistema, que no es difícil de construir, funciona muy bien en un experimento cuantitativo,
especialmente por eliminarse los cojinetes y su inevitable fricción.
Hágase /, = 4000 g-cm2, 72 = 3000 g-cm2, k = 105 dinas-cm/radianes en la figura 10-7(c).
Demostrar que «, = 0 y u2 = 7,65. ¿Cuál será el significado físico de la raíz nula?
Demostrar que en el sistema de la figura 10-7(d),
Cúj = 0,
rfc(m1 + m2 + 7/g2)-|i/
"2 ~ L m^m^ 7/7*2) J
Demostrar que y = Acos(«2í + <t>) + (g/2M)(mi - m2)t2 + Bt + C donde A, B y C son arbitrarias y
M = mi + m2 + I/R2.
CAP. 10] PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 239
B. Sistemas con tres grados de libertad o más.
10.10. Las masas y las constantes elásticas del sistema de la figura 10-10 (tomadas de un experimento real)
tienen los valores indicados. Calcular los períodos y compararlos con los valores dados experimentalmente.
Las flechas en el cuadro de la derecha indican las direcciotles del movimiento observadas
experimentalmente para mi, m.2 y mj correspondientes a «i, «2 y «03. Verifiqúese estas direcciones a
partir de los cofactores del determinante fundamental.
W////(////¿
y////.
■■ 11,56 X 10* dinas/crn
Wj = 11,765 gramos
1 k2 = 11.91 X 10» dinas/cm
IW12 = 9724 gramos
Direcciones del
movimiento
correspondiente a:
ml
™2
m3
«1
1
1
1
«2
1
1
t
«3
1
1
1
Periodos en segundos (experiménteles): 9»! = 1,09, ^ = 0,54, 9*a = 0,36
Fig. 10-10
Fig. 10-11
10.11. Demostrar que las coordenadas normales para el sistema anterior son
gi = 50,0x, + 68,3x2 + 32,3x3, £2 = -57,0x, - 30,0x2 + 45,7x3, g3 = 79,8xi - 65,4x2 + 13,0x3
donde xi, 12, X3 representan los desplazamientos verticales de mi, m2 y ms a partir de sus
posiciones de reposo.
Demostrar que cuando se introducen las anteriores en las ecuaciones (10.22), se obtienen las formas
originales de T y V.
10.12. Los discos, Di y D2, de la figura 10-11, se hallan acoplados a sus ejes respectivos por medio de resortes
de torsión, según se indica. El eje vertical está así mismo conectado a la base B, por un resorte similar a
los anteriores.
Las constantes de torsión son #ti,#t2 y #t3. Los ángulos et y 02 se miden con relación a los
ejes respectivos y 0.3 con relación a B. Escríbanse las expresiones de T y V. Nótese que las expresiones
exactas son, sin aproximaciones, de la forma de (10.4) y (10.6).
10.13. Supóngase que aparte de los resortes que se muestran en la figura 8-26 del problema 8.7, la varilla bd se ha
acoplado a D con un resorte (de constante de torsión c3) en la misma forma que Di y D2 se hallan
acoplados a sus varillas de soporte en la figura 10-11. (Despreciar la masa de bd.)
Demostrar que T y V están dados por
exacta = WMP + '*> <**? «i + h + ¡z^^B^ + (Mí* + Ix)l\ + lj¡¡ + 2/rM2 sen *2]
^exacta = *[<VÍ + <*<* ~ °¿* + CA\ + W **" H
donde 0 es el valor de 02 cuando el resorte C2 no se ha deformado.
Suponiendo ahora que cuando el sistema está en reposo, 02 =■ 0o y escribiendo $2 = 0o + a,
demostrar que para movimientos pequeños,
Taprox. = ¿[((MJ2 + /x)co92*o + Ji + /rSen2*o)^ + (Mí* + Ix)'¿ + l¿\ + 2/,*,; sen e0]
Vaprox. = ifcl*} + **>? + Cs4)
Escribir el determinante fundamental y hallar sus raíces.
240 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
Cuatro masas iguales (Fig. 10-12) conectadas por resortes idénticos, reposan sobre una plataforma
horizontal lisa. La longitud normal de cada uno de los resortes es l0 y la longitud de equilibrio, l. Suponiendo
el movimiento según la recta ab únicamente, demostrar que
^exacta = *(*1 + Xl + Xl + x\ ~ x\x2 ~ X2X3 ~ *3X*)
donde x\, x2, xz y x\ son los desplazamientos de mi, etc., a partir de las posiciones de reposo.
Haciendo m = 300 gramos y k = 2 X 104 dinas/cm, calcular «i, u2, <o3 y u4. Construyase
un cuadro en el que se muestren las direcciones del movimiento de cada una de las masas
correspondientes a cada una de las u (Fig. 10-10).
Utilizando la expresión (10.25), hallar las coordenadas normales glt g2, g3 y g*. Demostrar, por
sustitución directa en las expresiones originales de T y V, que éstas toman la forma de {10.22).
ya m vi m tn K£
f
Fig. 10-12
10.15. (a) Escribir T y Vpara el péndulo triple de torsión
que se muestra en la figura 10-13. En este
caso, «i, #r2, #C3 y «4 son las constantes de
torsión para las diferentes secciones de la
cuerda de piano. Hallar gi, g2 y g3.
Supóngase ahora que, debido a un fluido
que rodea el péndulo, actúan los torques
viscosos —bxey, —b2$2 y — &3*3 sobre las
diferentes palanquetas. Demostrar que
p = -í(m; + bji + b3e¡).
Exprésese esto en coordenadas normales según
se hallaron antes.
(6) Imagínese las tres palanquetas, remplazadas
por n palanquetas iguales espaciadas
uniformemente a lo largo del alambre. Demostrar
que
v = «[•;+•{+••■ + <
- (*!*2 + Ms + M* +•■•+*„_! •„)]
10.16. En el péndulo triple de la figura 10-2(c), r, y r2 son
las cuerdas que sostienen a mi y m2. La varilla
rígida, la masa m* y los brazos c y d tienen un
momento total de inercia / con relación al eje ab.
La distancia del c.m. del sistema total (sin incluir
a mi y m2) a ab, se representa por r3.
Demostrar que para el caso de movimientos pequeños, expresiones aproximadas de T y V, son
raProx. = $[™i^«? + '*^r\l\ + (mxs\ + m^l + I)e% + 2mí8lríéíéa + m282r2e263]
Vbptox. = h[m\Or\9\ + m2ffr2el + g{Mr3 + mxex + m^^el]
donde 6\, 82 y e3 determinan los desplazamientos angulares de rit r2 y r3, respectivamente,
medidos a partir de una recta vertical. M es la masa del sistema completo, sin incluir a m¡ y m2.
Escríbase D.
El péndulo anterior puede construirse fácilmente (úsense cojinetes de punto duro en a y b) y funciona
bien en demostraciones o en experimentos cuantitativos.
10.17. Imagínese las fuerzas viscosas -biVi, -b2v2 y -63U3 que actúan sobre las esferas mi, m2 y ma de
la figura 10-2(c). Utilizando los resultados del problema anterior, demostrar que
p = -^i^A + h^t + (&i«? + Ma)*3 + 261«,r151¿8 + b282r2é2e3 + b3R*%]
Fig. 10-13. Péndulo triple de torsión.
CAP. 10| PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO 241
donde R es la distancia del centro dem3 al eje ab.
Determinar, por ejemplo, F6 aplicando primero Fe = BP/d$x y luego, a partir de 8Wg = Fg 88 .
Compárense los resultados.
10.18. Las masas mi y m2 se mueven a lo largo de carriles horizontales lisos en el sistema de la figura 10-14. Las
dos grandes ruedas, ruedan sin deslizar en contacto con la superficie mi. Demostrar que
T = ±[{mx + m¿% + (mjj + 21lr*)q\ + m3¿2 - 2m2¿,g2]
V = #c[x\ + q\ + x\ - 2xxxz + 2x3<72 - 2x^1
donde q2 = constante — x2, y m.2 es la masa total de las dos ruedas más la armadura sobre la cual
están montadas. 7 es el momento de inercia de cada una de las ruedas con respecto a su eje.
Escribir D y demostrar que tiene dos raíces nulas. Demostrar que el período de oscilación del sistema
podría obtenerse a partir de
m3[mxm2 + (tm, + m^Z/r2)] u2 = k[mxm2 + mlmz + (mx + m? + 7n3)(2//r2)]
] WVW
TZmfi^^^^ZZWTZZ,
Fíg. 10-14
10.19. Demostrar que una de las raíces del determinante del sistema que se muestra en la figura 10-7(e) es igual a
cero. Hallar una expresión general para los dos períodos de oscilación.
10.20. Los cinco discos de la figura 10-15, se hallan engranados como se indica. Los resortes representan ejes
flexibles que tienen constantes de torsión, m, #t2 y #t3. Demostrar que
T = ¿[(/1 + &Í/5)*? + /¿S + (l3+&í'4)»§]
V = £[(«1 + aJUs)*? + («1 + »2>»Í + ("2 + &í«s)»8 - 2*1*1*2 - 2*2*2*3 ~ ^shhe^]
donde 04 = f>ifl3 y Os = 62*1.
Demostrar que si ¿1 = 62, una de las raíces del determinante es igual a cero.
Poleas engranadas en a y en
b y acopladas por resortes de
constantes de torsión, m, >i
y «3 (los resortes representan
ejes elásticos).
Fíg. 10-15
D-^AMMAAAM"
W//////A
-vwsa
n *2 n '*
^^^^^^^^^^^^5?^^^^^^^^^^
242 PEQUEÑAS OSCILACIONES ALREDEDOR DE LAS POSICIONES DE EQUILIBRIO [CAP. 10
10.21. Suponiendo movimientos pequeños en el problema 5.14 (Fig. 5-20) hallar Vaproi. para el sistema entero,
incluyendo la gravedad. Nótese que la gravedad no se elimina de las ecuaciones finales del movimiento.
Determinar «i y «2 y comparar con las mismas magnitudes del problema 10.2.
Este sistema puede armarse fácilmente y constituye un buen experimento.
10.22. Supóngase que las "partículas" de la figura 10-12, pueden moverse de una manera cualquiera sobre un
plano horizontal (véase el problema 10-14). Suponiendo movimientos pequeños, escribir las
expresiones de T y V. Suponiendo una resistencia viscosa de — bu sobre cada una de las masas, escribir P.
10.23. Los valores de la barra uniforme y de los resortes que se muestran en la figura 10-16 (tomados de un
experimento real) son los siguientes: ki = 2,01 X 104 dinas/cm; k2 = 1,77 X 104 dinas/cm; con los resortes
sin deformarse, las longitudes pd =20,0cm y ab = 19,0 cm; con la barra en su posición de equilibrio,
pd = 32,3 cm y ab = 44,4 cm; masa de la barra = 384,8 gramos; / con relación a una recta normal a
bp y que pasa por el cm. = 1,2 X 104 g-cm2; longitud bp = 25,8cm. Con la barra en su posición de
reposo, los ángulos medidos con la horizontal son 60 = 15,4°, 0i = 60,5° y B2 = 52°. Los valores
determinados experimentalmente para los tres períodos del sistema (movimiento en un plano) son eP1 =
1,0, <P2 = 0,81 y93= 0,33 seg.
Utilizando los valores anteriores, calcular los períodos y comprobar los valores determinados
experimentalmente. Utilícense las coordenadas x, y y 0, que se muestran en la figura 5-21 (véase el
problema 5.15).
Fig. 10-16
10.24. En el sistema que se muestra en la figura 10-8,
T = i(g\ + g\ + g¡), V = #¿\g\ + *\g\ + »\g\)
donde las g y las u pueden hallarse en la forma acostumbrada. Suponiendo que las fuerzas viscosas
— biüi y — &2i>2 actúan sobre mi y m2 respectivamente, escribir una expresión de P en
coordenadas normales.
Luego, suponiendo una fuerza externa / = A sen (ai +6), aplicada verticalmente a mi,
escribir las ecuaciones del movimiento en coordenadas normales.
CAPITULO
11
Pequeñas oscilaciones alrededor
de movimientos estacionarios
11.1 Consideraciones preliminares importantes.
(a) Significado físico de los movimientos estacionarios.
A continuación se consideran tres ejemplos sencillos.
La masa pendular de la figura 11-1, si se inicia en forma adecuada, girará en un círculo
horizontal de tal modo que 6 y i permanecen constantes. El trompo de la figura 11-2,
bajo ciertas condiciones, se moverá de tal modo que 6, i y i permanecen constantes.
El sistema que se muestra en la figura 11-3 puede ser iniciado de tal manera que r, 6 y i
y///////////.
Péndulo cónico
Fíg. 11-1
Xl
*-90'
S, i y * son los ángulos de Euler (véase la
figura 8-16). Se toma el origen de los ejes fijos
al cuerpo en el centro de masa.
Fig.11-2
Cuando se mantienen las condiciones anteriores, se dice que el sistema está en un estado
de "movimiento estacionario". En todos estos casos, algunas coordenadas y algunas
velocidades permanecen constantes.
(b) Naturaleza de L para sistemas de este tipo.
(Lo que sigue se refiere a los ejemplos 11.1, 11.2 y 11.3.) La función de Lagrange, L, para
el péndulo contiene a 0, § y ip pero no se encuentra ^. En el caso del trompo, L contiene
a 0, 0, <t> y ¿, pero se excluyen <¡> y ^. En el sistema de la figura 11-3, L contiene r, r,
6, 0 y i excluyendo a 4>.
Una característica común de los ejemplos anteriores, es que en L aparecen ciertas
coordenadas con sus velocidades y, además, se encuentran algunas velocidades correspondientes
243
244 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS [CAP. 11
Para movimiento estacionario, e, r y ¿ son
constantes. Además, p# es constante en
cualquier movimiento, en general. Se supone aqu:
que m se halla restringida al plano abe.
Una coordenada ignorable, (*) y doB no ignorables (9 y r).
Fig. 11-3
a coordenadas que no figuran. Las coordenadas del primer tipo se denominan "no ignorables"
y las del segundo tipo, "ignorables". (Esta terminología se deriva del hecho de que, como se
demuestra en el numeral siguiente, las coordenadas ignorables pueden ser eliminadas por
completo de las ecuaciones del movimiento.) Por tanto, de acuerdo con los ejemplos
mencionados, se define el estado de "movimiento estacionario" como aquel en el cual todas
las coordenadas no ignorables permanecen constantes y las velocidades correspondientes
a las coordenadas ignorables permanecen igualmente constantes.
(c) El momento correspondiente a una coordenada ignorable es constante.
Considérese nuevamente la figura 11-3, ejemplo 11.3. Resulta claro que ^ es una
coordenada ignorable. Aplicando la ecuación de Lagrange,
dt\a}J
dL
—r = [m^ +rsen0)2 + I]i = p^ = constante
di]/
Es decir, que el momento correspondiente a ^, p^, es constante. (Nótese que 8L/dqr = pT
es la definición acostumbrada para el momento correspondiente a qr.) Independientemente
\e si el sistema posee movimiento estacionario o no, p^ es constante. Por otra parte, si se
perturba un movimiento existente (se aplican momentáneamente ciertas fuerzas y luego
desaparecen) p0 cambia de su valor original constante a uno nuevo, igualmente constante.
Es evidente que las observaciones anteriores se aplican a coordenadas ignorables, en
general. Naturalmente, dL/dqr = pr no es constante en el caso de coordenadas no
ignorables.
(d) Origen de las oscilaciones alrededor de un movimiento estacionario.
Imagínese la masa pendular de la figura 11-1, golpeada muy ligeramente con un
martillo durante su rotación bajo movimiento estacionario. Se ocasiona entonces un movimiento
oscilatorio armónico alrededor de su trayectoria, o alrededor de una nueva trayectoria
cercana a la primera. Naturalmente, i ya no es constante. Ahora variará con el tiempo de
cierta manera que ha de determinarse. Después del golpe, p0 será constante, pero
generalmente tendrá un valor ligeramente diferente del original.
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 245
Como un segundo ejemplo considérese ligeramente perturbado el movimiento
estacionario de la figura 11-3. En este caso, tanto 6 como r oscilarán en magnitud alrededor de
sus valores propios de movimiento estacionario, de una manera semejante a como oscila
alrededor de la situación de equilibrio un sistema cualquiera con dos grados de libertad
(véase el capítulo 10).
11.2 Eliminación de las coordenadas ignorables de las ecuaciones generales del
movimiento. Método A. (No se supone movimiento estacionario.)
Considérese un sistema que posea n grados de libertad, cuyo movimiento puede
determinarse por k coordenadas no ignorables qi,qt, ..., qk y s. coordenadas ignorables
^k+i'^k+2» •••tJn> (n = k + s). Así, L contiene las q, las q y las 3 pero no las $.
De gran importancia en el estudio de esta materia es el hecho de que para cualquier
sistema del tipo mencionado, las s coordenadas ignorables pueden ser eliminadas de las k
ecuaciones del movimiento correspondientes a las coordenadas no ignorables.
Con el fin de aclarar las diferentes etapas indicadas, se toma el caso en el cual k = 3,
s = 2 y p = 5. Suponiendo que no hay coordenadas móviles ni restricciones móviles,
el lector puede demostrar que la expresión general de T toma la siguiente forma: (véase la
ecuación (2.56).
T = &AJA + ¿«Á& + AJ¿* + 2AJÁ + 2AJA + 2AJ¿¿
+ «¿(¿14*1 + A2Á + AJs) + ¿MlA + Avfl% + ¿*A) <"■'>
+ UA<JJ< + 2A<JJ* + AsJJs)
donde las A son funciones de (71,(72 y (73, únicamente. Igualmente, V = V(q\, (72, qz),
no contienen $A ni $v
Al aplicar las ecuaciones de Lagrange, se obtienen las siguientes ecuaciones, válidas para
cualquier tipo general de movimiento.
. /SArl. BA , . BAr. . \
(^ + ^2 + ^3 + ^4 + ^5) + M-^i + -^* + -a^S)
. /BA.. BA^. BA^, \ . {BA BA BA^. \
+ q* fe9- + *?«.+ *? i>) + «> fe«•+ *f «•+ *?«•) i,L2)
. /BArd . BA. , BArA . \ . /BA.. BAr. . BA. . \ dL
+ 3< fe9-+-WS*+15? '•)+ **• fe9-+ *f ••+*? 9>) ~ *= °
donde r = 1, 2, 3. Nótese que la anterior contiene ¿74, ¿4, ¿75 y ¿5 •
Ahora, como L no incluye coordenadas ignorables, -77 (—r) = 0. Es decir, BL/BJJ. =
dt \d(tjJ
Pa = constante y BL/JJS = p5 = constante. Si se escriben estas ecuaciones en forma
explícita y se reorganizan sus términos, se obtiene
¿44^4 + A<Jl = P4~ ¿„á, " A*Á " AJ3
A!*J< + ^5 = P5 " AJl ~ ¿«Á ~ AJ*
Se observa que en (11.3) se pueden obtener ¿A y j5 en función de VAtV^QxtQ% Y Q3- P°r
tanto, las ¿ y las Jf pueden ser eliminadas de (11.2), quedando así tres ecuaciones que
contienen únicamente coordenadas no ignorables. Resulta así como si el sistema se hubiera
reducido a otro que tuviera k grados de libertad. (Se han "ignorado"¿74 y ¿75.)
246 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS [CAP. 11
Si se desea conocer el movimiento general del sistema, las integrales de las relaciones
anteriores expresan q\, q2 y qz, en función del tiempo. Luego, volviendo a (11.3),
pueden hallarse 34 y 3S en función de t.
11.3 Eliminación de las coordenadas ignorables, empleando la función de Routh.
Método B.
Considerando a L como una función de qvqv . . .,Qk\ QltQv • • -tQk't $k+v$k+v .. -,3n,
una pequeña variación de L se expresa,
r=i dqf r=1 ¿^ , = ^+,3^
(22.4)
Pero dL/BJJi = p. y p.S¿7. = 8(p(tf,) - ^Sp,. Por tanto, (11.4) puede escribirse,
\ i = fc+l / r=l % r=l d9r i = k + l
La función de "Routh" se define como
R = L - £ pji (11.6)
i = k+l
Se supone que las 3 se han eliminado de R por relaciones de la forma de (11.3),
R = R(q . . ., q. . ., p. . .). Así pues,
«* = i !£««, + i f£««, + $ f£*. <il7>
r=i dqr r r=\ dqr r i = k+idP{ '
Comparando (11.5) y (11.7), se observa,
BR _ BL BR _ BL BR _ >
Wr~ W/ Wr-WryW{-~^ ilL8)
Al remplazar las dos primeras relaciones en la ecuación de Lagrange, se obtiene,
¿(ef)-f=° '=" «
lo cual representa k ecuaciones del movimiento sin ninguna coordenada ignorable. Las
ecuaciones (11.9) son las mismas (11.2), luego de haber eliminado las ¿ y las ¿ .
Aspectos importantes: (a) El análisis anterior se aplica a cualquier movimiento que
pueda tener el sistema. No se ha restringido a movimientos estacionarios, (b) A fin de obtener
las k ecuaciones del movimiento libres de coordenadas ignorables, el primer método requiere
eliminar las 3 y las 3 de cada una de las ecuaciones (11.2), en tanto que por medio de
(22.3) se realiza la eliminación completa en una sola etapa, sencillamente eliminando las
3 de (11.6).
En problemas sencillos, el método A es tan conveniente como el método B. Pero para
hacer consideraciones generales y para solucionar los problemas aplicados en donde k y s
representan números grandes, el método de R es superior.
11.4 Condiciones necesarias para el movimiento estacionario.
En un estado de movimiento estacionario (se supone todavía k = 3, s = 2, n = 5)
q\ = constante = b\, qz = 62, (73 = 63; Qx = Q2 = q3 = 0; SA— constante, 3S = constante,
J74 = 3b = 0. Así, como puede verse en (11.2) y en la segunda relación de (11.8), las
condiciones necesarias para que exista movimiento estacionario son
(*L) = 0 o sea (**) = 0 (1U0)
\dQrJ0 \dqrJ0
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 247
donde el subíndice cero indica que los valores enumerados propios del movimiento
estacionario deben ser incluidos.
11.5 Ecuaciones del movimiento, suponiendo un movimiento estacionario
ligeramente perturbado.
Con este fin se hace q\ = fci + si, qz = 62 + S2 y 93 = ¿>3 + sz, donde 61, 62
y 63 son valores propios del movimiento estacionario (determinados por (11.10)) de las
coordenadas no ignorables, y si, S2 y s¿ representan desplazamientos variables de estos
valores. Así, qx =s,, etc. al sustituirlos en la función de Routh, se obtiene
R = R(bi+Si, 62 + S2, 63 + 33, ¿1, ¿2, s3)
Suponiendo ahora que las s y las s tienen valores pequeños, se puede desarrollar R
conservando los términos de orden cero, primero y segundo. Se obtiene entonces,
donde los subíndices cero indican que se deben tomar los valores del movimiento
estacionario. Nótese que los coeficientes de sr, sr, srslt etc. son todos constantes.
Así, se encuentran las ecuaciones del movimiento con respecto al movimiento
estacionario, aplicando
d /5#aprox. \ 5^aprox. _ A
± /^aprox. \
dt{ Bs ')
. dSr J d8r
que conduce a
* / d2R \ .. * / d2R \ . * / d2R \ . * / d2R \ /dR\ A ,
Pero por (11.10), (—) = 0. Por tanto, la forma general anterior de las ecuaciones del
\0QJ0
movimiento con respecto al movimiento estacionario, puede escribirse,
ttó + ^Á-^) = ° <"■'*)
donde arl = aír y crl = clr pero brl = -blr y brr = 0.
En el caso en consideración, estas ecuaciones son
ctiiSi — C11S1 + ai2S2 4- bi2¿2 — C12S2 + (I13S3 4- 613S3 — C13S3 = 0
eteiSi + 621S1 — C21S1 + a22S2 — C22S2 4- (I23S3. 4- 623S3 — C23S3 = 0 (11.13)
CÍ31S1 4- 631S1 — C31S1 + (L32S2 4- bszSz — C32S2 4- (I33S3 — C33S3 — 0
Como se verá en los ejemplos siguientes, con frecuencia ocurre que las b son todas
iguales a cero. (Se denominan "términos giroscópicos" los de .la forma brlst .)
Nota, (a) Para determinar a au, cu, etc., (véase la ecuación (11.11)) se halla la
derivada de i?exacta- Por tanto en la solución de problemas por este método, es preciso escribir
primero ¿exacta-
(b) Si se desea, pueden obtenerse las ecuaciones (11.13) escribiendo las ecuaciones del
movimiento exactas (11.9), remplazando q\ = 61 + s\, etc., realizando el desarrollo y
conservando únicamente los términos de primer orden (véanse los ejemplos).
248 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS I CAP. 11
11.6 Solución de las ecuaciones del movimiento.
Se observa que las ecuaciones anteriores son muy semejantes a {10.7). Las soluciones
pueden obtenerse siguiendo el mismo procedimiento descrito en el numeral 10.16. Por tanto,
aquí solamente se incluyen algunos pocos detalles.
Suponiendo como soluciones si = AeXt, s2 = BeXt y s3 = CeXt, sustituyendo en
(11.13) y siguiendo las etapas mencionadas, se escribe
(ZllA.2 — Cu CLliX.2 + 612A. — Cl2 (I13A.2 + 613A. — Cl3
D = a2iX2 + 621A. - C21 a22A.2 - C22 G23A.2 + bswX — C23 | = 0 (11.14)
I a3iX2 4- 631A. — c3i. as2A.2 + 632X — C32 a33X2 — C33
Notas importantes:
(a) Como alr = arl, clr = crl y blr = —brl, puede demostrarse que D contiene
únicamente potencias pares de X. (Véase E. J. Routh, Advanced Rigid Dynamics, volumen 2,
6a edición, Macmillan, 1930, página 78.) El lector debe realizar el desarrollo de D en
(11.14) y demostrar que los términos que contienen X5, X3 y X, automáticamente se
eliminan.
(b) Si T y V son ambas definitivamente positivas, Xi = íui, X2 = — ¿coi, X3 = 102,
Xa = — IC02, donde las u son reales. Como se verá, esto quiere decir que el movimiento
es estable.
Suponiendo ahora que la condición (b) se satisface, una solución general para si es,
por ejemplo,
s, = A1eiw't + A\e-^1 + A^e™* + A^e'^1 + A^1 + A¡«-''"»«
con expresiones semejantes para .<?2 y sz. En el caso general, (brl 9± 0), las soluciones
pueden ponerse en la forma de la relación (10.35).
Cuando los términos giroscópicos (6rls,) se hallan ausentes de las ecuaciones (11.13),
las soluciones toman la forma de las relaciones (10.12) y pueden hallarse coordenadas
normales. En general, cuando se encuentran términos giroscópicos, no es posible hallar
coordenadas normales.
11.7 Coordenadas ignorables en función del tiempo, después de una perturbación.
Por la última relación de (11.8), o resolviendo (11.3) para hallar ¿J{ se tiene, ¿ = —dRIdVi
= <t>i (q . . ., q . . .). Remplazando q\ por fci + ,«?i, q\ por s\, etc., y usando las soluciones
de (11.13), puede escribirse Si — </>(£)• Por tanto,
4(*) = J" tf>¡(¿)^ + ci VI-15)
Para pequeños cambios en ¿i, puede hallarse $ (t) haciendo el desarrollo de 4>l(s, s),
y conservando los términos de orden cero y primero.
11.8 Ejemplos ilustrativos del procedimiento anterior.
Ejemplo 11.1.
Si se inicia el movimiento en forma adecuada, la masa pendular de la figura 11-1 gin>*á en un círculo
horizontal en el que 6 y 4> son constantes. Para el péndulo,
L = ^m(r2é2 + r2sen2 0¿2) + mgr c08 e (/)
Las cantidades 6, 6 y 4> aparecen en L, pero no, yp. Por tanto, f es ignorable.
— = mr2 sen2 e$ = p^ = constante (2)
d\p
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 249
Aplicando (11.6) y eliminando ¿ por medio de (2),
mgr cose (3)
2 mr2 sen2 $
Aplicando (11.9), la ecuación general (no restringida a movimiento estacionario) correspondiente a 0 es
.. Púi eos $ n
' ¿3 aT + ísene = ° W
mPr* sen3 $ t
(Se sugiere que el lector obtenga esta misma ecuación por el método A.) En el caso de movimiento estacionario
'$ — $ = 0, $ = $0, p,¿, = c0 y ¿ = ¿0 = constante. Así, a partir de (4) o también aplicando (11.10), la
condición para movimiento estacionario es
c0 eos e0 „
—s~2 »— = señen
m¥ sen3 $0 r °
que puede ponerse en la forma, eos 60 = 4r (5)
Por tanto, el movimiento estacionario puede existir con un ángulo cualquiera, para el cual r¿0 > g. (Haciendo
r = 100 cm y g = 980 cm/seg2, la condición (5) se satisface si ¿0 = V^F rad/seg o mayor y, por ejemplo,
haciendo ¿0 = 4 rad/seg y cos0o = 9,8/16.)
Supóngase ahora que la masa pendular (que se mueve con movimiento estacionario) se golpea ligeramente
con un martillo. Supóngase, por el momento, que el impacto es de tal naturaleza que p^ permanece sin
modificación. Escribiendo 0 = 60 + a y remplazando en (4), se tiene
eos (e0 + *)<% g _
a — —^~2 «/„ ■ v + - sen (0O +«) = 0 (b>
m¥ sen3 (60 + a) r u
Suponiendo que el ángulo a permanece muy pequeño, al realizar el desarrollo y conservar únicamente
los términos de orden cero y primero, (6) se convierte en
r Cl /1+2C0S2*\ g 1 ( C^COS^o g \
(Esta relación puede obtenerse haciendo el desarrollo de R y conservando los términos de segundo orden. Véase
el problema 11.1.) Por (5), el último término es igual a cero. Por tanto, a -+- u2a = 0 o sea, a = A sen(«í + <t>),
donde A y <t> son constantes arbitrarias. Así, la masa oscilará con respecto a la trayectoria de movimiento
estacionario con un período
r c% /l + 2cos2*0\ g 1"
9 = 24^( sen^0 )+7C°»'°J
Haciendo uso de (2) y (5), el período puede escribirse,
La forma como ^ cambia con el tiempo después del golpe, se determina como sigue (véase el numeral 11.7):
_Co_ f dt
* ~ mr*J sen2(*0 + a) + °
1 i 2 eos eQ
Haciendo el desarrollo, rr ¡—r = —5— — 5—— a +
sen2 (60 + a) sen2 $0 sen8 $0
Por tanto, ^ = ¿o* ~~
2c0 eos 0O
mr2se:
s*/-
Como a = A sen(«í + <t>), la integral puede evaluarse de inmediato y obtenerse así una expresión aproximada
de 4>, en función del tiempo.
Se ha supuesto que la perturbación no ha producido variación alguna en el valor del movimiento estacionario
de pj,. Supóngase ahora que cambia de un valor constante c0 a otro (también constante) ligeramente diferente,
250 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS | CAP. 11
ci. En la ecuación (5) puede determinarse un nuevo valor de movimiento estacionario 8=80. Si se escribe
e = eo + a y se continúa como antes, resulta claro que la masa oscilará con un período
cos*ó \11/2
T = 2 fr/ cos.q \T
\_g \l + 3cos»^/J
con respecto a la nueva trayectoria del movimiento estacionario. Por tanto, usualmente se supone que la
perturbación no hace variar los valores constantes de los momenta.
Ejemplo 11.2.
Oscilaciones del trompo (no vertical) con respecto a su movimiento estacionario. (Una coordenada no ignorable y
dos ignorables.)
Si el trompo de la figura 11-2 se hace girar por encima de cierta velocidad y se suelta en forma adecuada, se
moverá con un movimiento estacionario tal que 8, <t> y 4> permanecen constantes. (El trompo precesa con
velocidad angular constante 4>, sin nutación).
(a) Ecuaciones generales del movimiento y condiciones para movimiento estacionario. Como se demostró
anteriormente (véase el ejemplo 8.14),
L = $[IX{62 + ¿2 sen2*) + I2(¿ + ¿ cosí)2] - Mgr cos-0 (i)
Se observa que 8 es no ignorable, en tanto que 4> y <t> son ignorables. Por tanto,
Pt = Iz(<f> + ¿ eos $) = c,, y pj, = lj¡> sen2 $ + e, eos $ = c2 (2)
En este caso, R = L — p^ — p^4>, y al eliminar f y 4> por medio de (2) se obtiene (sin hacer
aproximaciones)
Aplicando (11.9) se obtiene la siguiente ecuación del movimiento
(4)
/c2 —CjCosíN2 /c2 — c1cose\
7"# " ( 7, sen2* ) 7*sen*cos* + ( 7xsen2, ) C> Sen ' ~ M^^n9 = °
Nótese que (4) es válido para cualquier tipo general de movimiento que pueda tener el trompo. Hasta aquí
no se ha hecho ninguna aproximación.
En el caso de movimiento estacionario, (11.10) toma la forma Ixf0 eos 0O — c^0 + Mgr = 0, donde
los subíndices cero indican los valores de movimiento estacionario. Al hallar ¿o,
c, ± y/c\ - 4IxMgr eos e0
*° ~ 277c^ (5)
Si ci cumple la condición c1 > 4IxMgrcos80, existirán dos valores distintos de ¿o para los cuales
8 permanece constante.
(b) Oscilaciones con respecto a un movimiento estacionario, suponiendo una ligera perturbación tal que ci y C2
permanecen sin modificación. Escribiendo 8 = 80 + a, remplazando en (4), realizando el desarrollo y
conservando los términos de primer orden, se obtiene finalmente, luego de algunas operaciones algebraicas,
upo precesa, el punto d, por ejemplo, oscilará c(
» del movimiento estacionario, abe, con un períod
(6)
Por tanto, mientras el trompo precesa, el punto d, por ejemplo, oscilará con movimiento armónico simple
con respecto a la trayectoria del movimiento estacionario, abe, con un período dado por
-|-l/2
(7)
La forma como <t> y 4> varían con el tiempo puede determinarse como sigue: Aplicando la tercera
relación de (11.8), o sencillamente hallando la solución de las ecuaciones (2), se obtiene
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 251
cl (c2 ~~ cl cos *) cos 9 • C2 ~~ cl cos 9
+ = Tz T^Te y * " /.sen»* (8)
Remplazando 8 = 60 + a, haciendo el desarrollo y conservando los dos primeros términos,
/c2 + c2 cos2 *o ~~ 2cj cos *0\
* = +° + ( 7^tfT0 )a (9)
y como a es una función del tiempo determinada por (6), se puede integrar la expresión (9) para obtener <f>
en función de t. De igual manera puede hallarse \¡/(t).
Otros aspectos relacionados con este ejemplo: (a) Las relaciones (2) corresponden a (11.3) (b) La ecuación
(4) puede obtenerse por el método A. (c) La ecuación (6) puede obtenerse haciendo primero el desarrollo de R
y luego aplicando (11.11); véase el problema 11.2. (d) En (6) no aparecen términos giroscópicos.
Ejemplo 11.3. Una coordenada ignorable y dos coordenadas no ignorables.
En la figura 11-3,
L = £m(¿2 -|- r2¿») + ^m(lx + r sen *)2 + 7]¿2 + mgr cos * - ±k(r - rx)* (1)
donde n es el valor de r cuando el resorte se encuentra sin ninguna deformación. Se observa que f es ignorable
en tanto que 8 y r son no ignorables.
Aplicando (11.10), las condiciones para que exista movimiento estacionario son
^(¿i + r0 sen *0) cos *0 = g sen*0
k (2)
¿o^i + »*o sen *0) se ni 0 = ^(r0 - rt) - g cos *0
9 tan *0
de aquí puede concluirse que #? = ^r; (-3)
lx + rx sen *0 + -r- tan *0
Para un valor supuesto de *0, la expresión (3) puede utilizarse para hallar i/-o, o para cierto valor de ío puede
obtenerse, por métodos gráficos, el valor de 80. Así, r0 puede hallarse a partir de (2).
Siguiendo las etapas acostumbradas, R resulta
R = £m(¿2 + r2¿2) _ |c2[m(í, + r sen*)2 + /]-i + mgr cose - £fc(r-r,)2 (4)
donde p^ = c. Sin hacer aproximaciones, las ecuaciones del movimiento correspondientes a r y 8, son
m'r — mre2 — m&[m(lx + r sen*)2 + /]~2(¿i + r sen*) sen* - mfl' cos* + fcír-r^ = 0 (5)
)nr2í + 2mrf* - mc2[m(íj + r sen*)2 + J]-2^ + r sen *)r cos* + mgr sen* = 0 (6)
Nótese que se pueden obtener (5) y (6) por el método A.
Escribiendo r = r<¡ + s y 0 = 0o + a, haciendo el desarrollo y conservando los términos de primer orden,
se obtiene finalmente,
anV + cn8 + c12a = 0
(7)
C2i8 + d>2ía + c22a = 0
donde an = m y cu
/3m(íj +r0sen*0)2- I\
7t¿?sen.2*0 ( —r,—¡ xo , . 1 + fe, (véanse las ecuaciones (11.11))
ro ü ^ m(lx + r0 sen *0)2 + I )
. r4m(¿! + r0 sen *0)2 r0 sen *0 cos *0 "I
clt = m*\ \^ m(¿1 + roSen*0)2 + 7 ^ + 2r° Sen *o) COS ' J + "* Sen '•
Las relaciones correspondientes para C21, a22 y C22 se obtienen en forma directa. (Véase el problema 11.3.)
Como no aparecen términos giroscópicos en (7), pueden obtenerse las soluciones suponiendo s = A sen(«í + <t>) y
a = Bsen(«í + <f>).
Para valores específicos (tales como mi = 400 gramos, g = 980 cm/seg2, k = 2 x 10s dinas/cm,
U = 20 cm, r, = 40 - 20 + 10 = 30 cm y *o = 30° (por tanto r0 = 32,26 cm) e / = 2 X 105 gramos X cm2),
a partir de (3) puede hallarse ¿o, pueden evaluarse las constantes an, cu, C12, etc., y pueden determinarse
los períodos de oscilación.
252 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS [CAP. u
Ejemplo 11.4. Selección de las coordenadas adecuadas.
En ocasiones ocurre que entre las coordenadas seleccionadas no hay ninguna ignorable, pero, a pesar de esto,
por las propiedades físicas del sistema puede ser evidente que exista movimiento estacionario. En tal caso, por
simple inspección puede determinarse un conjunto de coordenadas que sí contengan algunas ignorables.
Considérese el sistema que se muestra en la figura 11-4. La barra, el resorte y la masa se encuentran sobre
un plano horizontal liso, XY. La barra puede girar libremente alrededor de un eje vertical liso, fijo en O.
Tomando como coordenadas a 0, <t> y r,
L = $Ie* + £m[s2*2 + f2 + r2¿2 + 2rs¿¿ eos (<f> - 6) + 2sr$ sen (¿ - e)] - \k(r - r,)2 (/)
Como 6,0,r,r,<f> y <t> aparecen todas en L, ninguna de las coordenadas es ignorable.
Pero, introduciendo 0 = 0 — 0, y j, -= f¡ + $t puede escribirse L como sigue,
L = $mr* + £(/ + ms2 + mr2 + 2mrs eos ¿3)¿2 + |?nr2/32
(2)
+ m.8re sen (3 + m(r2 + rs eos (3)6(3 — ^k(r — rt)2
Por tanto se observa que 8 es no ignorable,
9 = (7 + ras2 + rar2 + 2mrs eos /?)¿ + ra(r2/3 + rs(3 eos (i + sr sen (3) - c (3)
BL
Así, puede eliminarse 0 de las ecuaciones del movimiento correspondientes a r y 0, o sea que puede hallarse
una función R. Por consiguiente, es posible determinar las pequeñas oscilaciones con respecto al movimiento
estacionario, de la manera acostumbrada.
Fig.11,4
Ejemplo 11.5. Pequeñas oscilaciones de un trompo alrededor de su posición uertical.
Xly
Los puntos, a,b,c y d están en un
plano paralelo al plano X\Z\.
e,^,<f> = Ángulos de Euler
Fig. 11-5
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 253
Supóngase que el trompo (disco) de la figura 11-5 "dormido" en posición vertical con el eje Opi en la
dirección de Vi, 8 = 90° y 0 = 0. (La vertical se toma en la forma indicada porque, si se trata como en la
figura 11-2 con Z\ vertical, el ángulo \p queda indeterminado para 8 = 0.) Suponiendo que este estado de
movimiento estacionario se perturba ligeramente, se trata de hallar el movimiento subsiguiente para el punto p\.
Aparte de la gravedad g que actúa en la dirección negativa de Yi, supóngase que existen cuatro resortes iguales
adheridos a un pequeño anillo liso en pt. Cuando pt se encuentra en p2, los resortes no están deformados y
quedan contenidos en el plano horizontal abcd con ángulos iguales entre ellos de 90°. Como puede demostrarse por
2fc
la ecuación (5.11) Vre80rles = -r-(x2 + z2) para el caso de pequeños desplazamientos de pi con relación a p2-
Las coordenadas del extremo del eje Opi son x, y y z.
Por tanto, en el ejemplo 8.14, se escribe
L = $IX(6* + ¿2 sen2 e) + £/r(¿ + ¿ cos 9)2 _ Mgr eos 8 - fc(x2 + z2) (1)
donde r es la distancia medida sobre la recta Opi, desde O hasta el c.m. del disco, 5 es el ángulo pi Op2 y
los demás símbolos tienen los significados usuales.
En el diagrama se observa que 8 + a = 90°, f + 0 = 180°, cos 5 = cos a cos0, x = /eos a sen 0, z = / sena y
y = Icos a cos0. Por tanto, en la forma usual se encuentra
R = $Ix(a2 + /32 eos2 a) - ensena - Mgr cos a cos ¡3 + JcP eos2 a eos2 (3 (2)
donde ci = dL/dQ = p^ = constante, y / es la longitud del eje Opi. La expresión anterior es exacta, excepto
por la aproximación en Vresortes. Algunos términos constantes se han despreciado. Nótese que solamente una
coordenada, <t>, es ignorable.
Suponiendo ahora muy pequeños desplazamientos de p\ con respecto a la posición p2 (a y 0 siempre
pequeños) el lector puede demostrar (véase el problema 11.4) que las ecuaciones del movimiento son (véanse las
ecuaciones (11.12))
Ixa + c,/3 - (Mgr - 2JcP)a = 0
(3)
Ixp - c,¿ - (Mgr - 2kP)(i = 0
Obsérvese que en este caso se encuentran presentes términos giroscópicos.
Pueden obtenerse las soluciones suponiendo, a = Ae'"" y 0 = Be"1". Como siempre, se concluye que
I -(/r(o2 + E) -c^w I
D = =0 (4)
| C^co -(/x"2 + E) I
donde E = Mgr - 2kl2; y según (4),
osea, ±a = 2^(c, ± y/c^-lIJE)
Se ve que si se cumple la condición c, + 8Ixkl2 > 4IxMgr, « es real. Además, si ¿ cos 8 es pequeño
comparado con i, ci = Ix<t> y, por consiguiente,
A partir de (5) se escribe
«i = ±[¿('1 + Ve2 -47^)] y «2 = ±[^(c1-Vc2-47I^)]
Por tanto, las soluciones pueden ponerse en la forma
a = Mn*to,t + fe2di2e~i<ü't + Mi3e<6)2t + Mi4e_i6)2t
(7)
0 = Muje^i* + M22e_1<Ult + M23eÍW2t + M24e~Í<1>2t
que empleando las igualdades
¿11 = ¿12. d13 = ¿14. d21 = _d22 y d23 = _d24
(7) finalmente puede escribirse como
254 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS [CAP. 11
a = R^I^2 + E) COS (Wlt + e,) + RiVzoZ + E) COS (co2t + e2)
(8)
(3 = jR^jcúj sen {u\t + ex) + R2cxu2 sen (u2t + ei)
donde Ri, R2, «1 y «2 son constantes arbitrarias. Suponiendo a = A cos(wí + c) y 0 = Bsen(wt + t),
el lector puede demostrar que las soluciones (8) pueden obtenerse de inmediato.
Obsérvese que si el disco estuviera colgado (supóngase una unión esférica en O) y se invirtiera la dirección
de g (Fig. 11-5) los valores de <o serían siempre reales. Mayores detalles con respecto a este tipo de movimiento
pueden encontrarse en A. G. Webster, Dynamics, 2', edición, Dover, 1959, páginas 288-296.
Ejemplo 11.6. Dos coordenadas ignorables y dos no ignorables.
En la figura 11-6, el marco AC puede girar libremente alrededor del eje vertical, según se indica. La varilla
liviana ab, se encuentra articulada en a y por tanto puede girar hasta un ángulo $, alrededor de un eje horizontal.
El disco D gira alrededor de un cuello liso, s, el cual puede deslizarse a lo largo de ab. La velocidad angular, 4>, del
disco, se mide con relación a ab.
Despreciando la fricción y suponiendo que el torque sobre ab debido a los resortes verticales es k2l26, (l = ab),
la función de Lagrange será
L - \M(r2 + r2¿2 + r2¿2 eos2 6) + ¿Ii¿2 + \IX& eos2 9 + i2)
+ tfzti + ¿ sen*)2 - \kx{r-l^ - %k2Pe2 - Mgrsene
(1)
donde I\ es el momento de inercia del marco, con relación al eje vertical, Iz es el momento de inercia de D con
relación a un eje que pasa por el c.m., paralelo a la cara del disco, Iz es el momento de inercia de D con relación
a ab y lo es la longitud normal del resorte kt.
C
Articulación —
faWy7/?/,r=pl ¡
:ifc2
&
T
e
____L
Fig. 11-6
En (1) se observa que <t> y ^ son ignorables, en tanto que 6 y r son no ignorables.
dL
P<¡, = Iz(<t> + * sen $) = cx
di
Pc, = (Mr2 eos2* + /, + /, cos2*)^ + cx sen* = c2
(2)
(3)
Eliminando a ¿ y ¿ de L — crf — c2j>, se obtiene /? exacta- Entonces, si se desea, las ecuaciones del
movimiento exactas, correspondientes a r y 6, se obtienen de inmediato por aplicación de (77.9).
Las ecuaciones del movimiento para oscilaciones con relación al movimiento estacionario se siguen de
(77.77). Como de costumbre, debe tenerse cuidado al tomar la derivada de R exacta para la determinación de
a 11, cu, etc.
CAP. 11J PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS
Las condiciones de movimiento estacionario para el que r,6,^> y j, permanecen constantes, son
(-q¿) = (Mr% —Iz + Ix)$l sen 60 eos 60 - lj>04>0cos60 + k2l2e0 + MgrQ eos *0 = 0
\Hr) ~ Mro¿ocos2*o - Mro-*o) - Mflísení0 = 0
(4)
(5)
En un problema real, por ejemplo, pueden tomarse los valores numéricos de r y 0 correspondientes al
movimiento estacionario. Entonces, suponiendo conocidas todas las constantes, se puede hallar la solución de (4) y (5)
y encontrar así las magnitudes de ¿0 y ¿o- En esta forma se determinan los valores numéricos de au,cu, etc.,
y se encuentran las raíces de D. (Con relación a la estabilidad, véase el numeral 11.11.)
Ejemplo 11.7. Tres coordenadas ignorables y una no ignorable.
En la figura 11-7, un trompo articulado en su c.m., está montado sobre una mesa giratoria. Puede
demostrarse que
L = 1(7 + MR\)+\ + #IX(¡2 + (ix + h2 sen* e) + 7Z(¿ + (^ + ¿) coa e)*]
Como ¿i, ¿ y ¿ aparecen y ^\,<t> y $ se encuentran ausentes, estas tres coordenadas son ignorables. Pero como
tanto 0 como $ se encuentran presentes, 6 es no ignorable. (La notación es la misma de la figura 8-33.)
Para mayores detalles, véanse los problemas 11.-13 y 11.5.
I
I '
Tres coordenadas
ignorables y una
no ignorable
0,},<t> = Ángulos de Euler'
Fig. 11-7
11.9 Oscilación alrededor del movimiento estacionario cuando el sistema contiene
restricciones móviles.
Las pequeñas oscilaciones de un sistema que incluye un marco de referencia móvil, o
restricciones móviles, pueden resultar importantes en ciertas aplicaciones. Unos pocos ejemplos
sirven para aclarar la naturaleza de este tipo de problemas y su método de solución.
Ejemplo 11.8.
En la figura 11-8, la cuenta de masa m puede deslizarse libremente a lo argo de un alambre circular rígido
que se hace girar con velocidad angular constante « alrededor de Z. En este c. so,
de donde,
L = %m(r2e2 + r2 eos2 9uP) — mgr sen $
'e + a2 sen 6 eos 6 + — eos $ = 0
Así, para movimiento estacionario, sen 80 = — g/rw2. Suponiendo perturbado el movimiento estacionario,
escribiendo 6 = 60 + a, y conservando únicamente los términos de orden cero y primero, fácilmente se concluye
(haciendo uso de la condición de movimiento estacionario) que a + a(u2 — g2/r2) = 0. Por tanto, para el
caso en que <o2 > g/r esto representa un movimiento armónico simple.
256 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS [CAP. li
Ejemplo 11.9.
Considérese nuevamente el sistema que se muestra en la figura 11-3. Supóngase que el eje vertical se impulsa
con velocidad constante ¿ = «. El sistema tiene ahora dos grados de libertad y se escribe,
L = %m(r2 + r2*2) + ^ra^ + r sen *)2«2 + mgr eos $ - $k(r - rt)2
de donde se pueden obtener las siguientes dos ecuaciones del movimiento:
\z
U)
(2)
(3)
(4)
(5)
Fig. 11-8
•• • k
r — re2 — co2(í, + r sen e) sen $ — g eos $ -i (r — rt) = 0
r2V + 2rre - M2(i, + r sen e)r eos $ + rg sen e = 0
Las condiciones para movimiento estacionario (0 = $ = 0, r = f = 0, 8 = $0 y r = ro) son
k
aHh + r0 sen 60) sen 60 + g eos 00 - ~(r0- rt) = 0
771
u2^! + r0 sen 60)r0 eos 0O ~~ ffro sen 0O = °
Suponiendo perturbado el movimiento estacionario, remplazando 0 = 8o + a y r = r0 + s en (2) y (3) y
al realizar el desarrollo (conservando los términos de potencia cero y primera y haciendo uso de (4) y (5)) se
obtienen las siguientes ecuaciones del movimiento aproximadas
i' + 8 ( w2 sen2 e0 ) + [g sen 60 — u2^ eos 60 + 2r0 sen $0 eos 60)]a = 0 (6)
r¡j a + acó2 (¿i + r0 sen 0o)ro sen 0O — r2 eos2 0O H i" cos *o
+ 8u2 -^ sen 0O — ly cos fi0 — 2r0 sen 0O cos 0O = 0
las cuales pueden integrarse sin dificultad. Nótese que (6) y (7) no contienen términos giroscópicos.
Ejemplo 11.10.
En la figura 11-9, AB
representa una parte de una
plataforma horizontal lisa
rotatoria. Los ejes Xi y Yi están
fijos en el espacio. Los ejes X y
Y se han trazado sobre la
plataforma. La masa m puede
moverse libremente sobre la
plataforma, bajo la acción del
resorte, uno de cuyos extremos
se halla adherido a p. Hállense
las ecuaciones del movimiento
alrededor de la posición de
movimiento estacionario.
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 257
Fácilmente se demuestra que
T = |m{¿2 + y* + [(se + r)2 + y*]Ó* + 2»[(x + r)y - yx]} U)
v = ^(V^ + y2-^)2 (2>
en donde lo es la longitud pm, cuando el resorte no se ha deformado. Suponiendo 6 constante, se obtienen las
ecuaciones del movimiento a partir de (1) y (2):
S-2tf-(« + r)#» = -¿£ y y + 2¿¿-2/¿2 = "¿f (3)
Escribiendo x = x0 y y = 0 como valores del movimiento estacionario para x y y, se hace x = x0 + s
y y = y. Remplazando en V, y considerando a s y y como cantidades pequeñas, haciendo el desarrollo y
conservando los términos de primero y segundo orden, se obtiene
= f * [«2 + 2s(x0 - l0) + y* (f£^)]
(4)
Por tanto, las ecuaciones (3) pueden escribirse,
V- 2by - (x0 + r + 8)¿2 +^(s + x0-l0) = 0 y + 2¿¿ - yé* + ^y (^^) = ° (5)
Pero en el caso de movimiento estacionario, V = 8 = 8 = y = y = 0. Así, m(xo + r)$2 = k(xo — lo) y
y = 0, lo cual es obvio por consideraciones elementales.
Por consiguiente, las ecuaciones finales deseadas son
''-«tf+ (£-*■)• = ° y y + 25¿ + (¿(\^)-¿2)y = °
(6)
Estas ecuaciones tienen la misma forma de (3) del ejemplo 11.5 y pueden resolverse de la misma manera, o
sencillamente suponiendo como soluciones, s = Acos (wt + <)>) y y = B sen («í + <t>). (Véase el problema 11.16.)
Es interesante observar que los lados izquierdos de las ecuaciones (3) pueden obtenerse de inmediato a partir
de las ecuaciones (9.6).
11.10 Sistema bajo la acción de fuerzas disipativas.
Considérese nuevamente el sistema que se muestra en la figura 11-6. Suponiendo
únicamente las fuerzas debidas a los resortes, existen dos coordenadas no ignorables, {6 y r) y
dos ignorables (^, </>). Si existen fricciones o resistencias viscosas en todos los cuatro cojinetes,
es obvio que, independientemente del tipo de movimiento inicial que pueda tener el sistema,
eventualmente éste se detendrá. Se observa que p^ y p^ ya no son constantes, y por tanto, que
el movimiento estacionario definido y estudiado anteriormente no existe. (Naturalmente,
las ecuaciones del movimiento correspondientes a las cuatro coordenadas, pueden encontrarse
con facilidad, pero no serán ya del tipo considerado anteriormente.)
Sin embargo, supóngase que no hay amortiguamiento en el cojinete B o entre el disco D
y el mango s, pero que sí existe resistencia viscosa en la articulación a y además hay *una
fuerza viscosa entre el mango s y la varilla ab. Esto quiere decir que existen ahora fuerzas
viscosas generalizadas correspondientes a 6 y a r, Fg = —bj) y Fr = — 62^,
respectivamente, pero no existen las correspondientes a ^ y a </>.
Por consiguiente, L, para el sistema, sigue siendo (7) del ejemplo 11.6. Como antes,
p^ = Cj y p^ = c2. Entonces R puede escribirse como en (4) y las ecuaciones del movimiento
estarán dadas por
d /dR\ dR . . d /dR\ BR . .
Las condiciones para movimiento estacionario son las mismas dadas por (4) y (5). Así, el
procedimiento, de este punto en adelante es el mismo sugerido en el ejemplo anterior. Las
ecuaciones finales del movimiento pueden ser integradas en la forma usual y si 61 y 62 no
son muy grandes, conducen a oscilaciones amortiguadas con relación al movimiento
estacionario.
258 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS I CAP. 11
Del ejemplo anterior pueden derivarse algunas consideraciones generales. Si las fuerzas
generalizadas correspondientes a las <3k + vSk+v ...,Sn coordenadas ignorables son todas cero,
en este caso, dL/dLJi = p¡ = c¡ y R puede escribirse en la forma acostumbrada (véase el
numeral 11.5).
Suponiendo fuerzas viscosas correspondientes a las coordenadas no ignorables, se escribe
la función de potencia, P = P(slts2, ...,sk). Así, las ecuaciones finales del movimiento,
con respecto al movimiento estacionario, pueden obtenerse tal como se describió en el numeral
11.5, en donde el lado derecho se hace igual a BP/dsr. La solución puede hallarse por los
métodos convencionales.
11.11 Estabilidad del movimiento estacionario.
Si al perturbar ligeramente el movimiento estacionario, las partículas o partes del sistema
no se apartan mucho de sus trayectorias estacionarias, sino que oscilan con respecto a ellas, o
teniendo en cuenta el amortiguamiento, lentamente regresan a tales trayectorias, se dice que
el movimiento es estable. Por otra parte, si una pequeña perturbación causa que el sistema
se aparte en forma notable del movimiento estacionario, se dice que éste es inestable.
Una solución general para (11.13) puede escribirse como s, = A,eXlt + A2eXit + ••• +
•^6eeet» y similarmente para s2 y s3. Como se demuestra más adelante, la estabilidad
depende de la naturaleza de las X (las raíces de D, ecuación (11.14)). Las raíces tienen, en
general, la forma Ai = mi + ¿«íi ^2 = mi — i«i, etc., con las diferentes m y <•> reales. Sin
embargo, las m pueden ser positivas, negativas o cero. Además, si u = 0 las raíces son
reales. Por tanto se observa lo siguiente:
(a) Si las m son todas negativas y las u diferentes de cero, el movimiento es armónico
simple amortiguado. Si las X son reales y negativas, el movimiento perturbado retorna
gradualmente al estado de movimiento estacionario. En ambos casos es estable.
(b) Si las m son positivas y las co diferentes de cero, o si las X son reales y positivas, los
desplazamientos aumentan exponencialmente con el tiempo, por lo menos en cuanto las
ecuaciones aproximadas del movimiento sean válidas. En este sentido, el movimiento es
inestable.
Así, habiendo determinado las raíces de D (por el método de Graeffe, o por cualquier otro
método), la condición de estabilidad se puede determinar en forma inmediata.
Se encuentran mayores detalles sobre este tópico, con relación al cual mucho se ha escrito,
en las siguientes referencias:
E. J. Routh, Advanced Rigid Dynamics, vol. 2, 6a. edición, Macmillan, 1930, páginas 78, 80.
Horace Lamb, Higher Mechantes, 2a. edición, Cambridge University Press, 1943, página 250.
E. H. Smart, Advanced Dynamics, vol. 2, Macmillan, 1951, páginas 403, 404.
L. A. Pars, Analytical Dynamics, John Wiley and Sons, 1965, páginas 143-145.
C. E. Easthope, Three Dimensional Dynamics, 2a. edición, Butterworth and Co., 1964,
página 377.
Problemas
11.1. Demostrar que al escribir 8 = 80 + a, haciendo el desarrollo en (3) y conservando los términos de segundo
orden, se obtiene
1 . 1 r el /l + 2cos2*0\ "I
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 259
de donde se llega a (7), en forma inmediata. ¿Por qué no se conservan los términos de primer orden en el
desarrollo?
11.2. Demostrar que al escribir 8 = 8Q + a, en el ejemplo 11.2, al hacer el desarrollo en (3) y al conservar
los términos de segundo orden, se obtiene
*W = \h* - \ 1¿¿ \% sen* .0 + (¿o eos 60 - ^f]
de donde (6) se sigue de inmediato.
11.3. Escribir r = r0 + s y e = 80 + a, en el ejemplo 11.3 y realizar el desarrollo en (4) para obtener flaproi.
de donde se obtienen directamente las ecuaciones (7).
11.4. En el ejemplo 11.5 verificar las ecuaciones (3).
11.5. Considérese el sistema de la fígura 11-7 y supóngase que se altera de modo que 0 permanece constante
(dejando que todos los demás ángulos varíen), (a) Demostrar cómo puede lograrse esto, (b) Demostrar
que en este caso el sistema tiene tres coordenadas ignorables y no tiene ninguna no ignorable.
11.6. (a) Con referencia a la figura 11-10, demostrar que en el caso de movimiento estacionario
(l + r sen 0o)¿o cos *o = 9 sen 90
Suponiendo que el movimiento de m está restringido al plano abd y escribiendo, 0 = 8o + a,
demostrar que
l i r4mr(l + r sen 60)2 eos2 e0
= ¿mrW - ¿mrc*[ (7 + ^ + r sen ,o)2)3
«,
l sen $0 + r (sen2 e0 — eos2 60)
(7 + m(l + r sen *0)2)2
- a2 + [mgr cos 60]a2
donde c = dL/d¿. Escribir la ecuación del movimiento y hallar el período de oscilación para los
siguientes valores: r = 50 cm, m = 300 gramos, l = 20 cm, / = 2 X 104 gramos X cm2 y 0o = 45°.
gira alrededor
e y + constantes.
Fig. 11-10
(b) Demostrar que la ecuación del movimiento obtenida a partir de Ra]
, puede hallarse también
aproximando la ecuación exacta del movimiento (hallada por el método A o por el método B) y
conservando únicamente los términos de primer orden,
(c) Suponiendo que ab se hace mover con velocidad constante, j> = «= constante, hallar el período
de oscilación del péndulo con relación a la posición correspondiente al movimiento estacionario.
260
PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS I CAP. 11
11.7. La cuerda de la figura 11-1 se remplaza por un resorte espiral de constante k y longitud normal lo.
Escribiendo 8 = 80 + a y r = r0 + s, determinar /?apr0I y demostrar que las ecuaciones del
movimiento con relación a los valores correspondientes al movimiento estacionario, son
fe2 (3 eos2 e0 + sen2 $0) 1 r 2c2 eos $0 1
mr\ a + 1- mgrQ eos 60 \a + rrnFTTTT" + m9 sen 60 s = 0
0 L rjjro sen4 $0 ° °J |_mrásen3í0 » °J
r 3c2 "I / 2c2 eos $0 \
mi + \ —i \- k \8 + ( —~ 1- mg sen60 1 a = 0
|_mr¿sen20o J \mr0 sen3 60 /
donde dL/d$ — p,¡, = c y donde r0 y 80 deben satisfacer las relaciones
roiÁ2, eos e0 = g, y mr0^ sen2 0O + *W eos $0 = fc(r0 - í0)
11.8. La masa mi de la figura 11-11, se mueve sobre un plano liso horizontal. La masa m2 se mueve vertical-
mente bajo la fuerza de la gravedad y la del resorte. Tomando coordenadas polares, r y 8 para mi, y l
para mí, demostrar que
L = -¿m,^2 + r2*2) + \m& + m^l - $k(l + r - 6)2
donde b es la longitud total de la cuerda, incluida la longitud normal del resorte. Demostrar que en el
caso de movimiento estacionario,
™iro*o = m20 y m¿9 - k(lo + ro_ b)
my/////////.\y///J
-VWWWW\r-
W//////////////^^^^^
w/w/////////;////,
Fig. 11-11
Escribiendo r = r0 + si y l = lo + s*, determinar R aproi. y demostrar que
/Zm^g \
™i8i + ( h fc J 8j + fc«2 = 0
fc»! + m2V2 + fcs2 = 0
así mismo, demostrar que ui y «2 están dados por
donde /i = - , y a = .
Haciendo mi = 300 gramos, m2 = 400 gramos, fc = 10s dinas/cm, b = 60 cm, g = 980 cm/seg2 y
suponiendo que r0 = 30 cm, demostrar que los valores aproximados de « son ui = 25,9 y «2 = 7,1.
Nótese que el movimiento es estable y está compuesto de dos oscilaciones armónicas simples.
Las dos masas de la figura 11-12, están sujetas a un resorte como se indica, y pueden deslizarse libremente
dentro del tubo horizontal liso. El eje ab, al cual se halla adherido el tubo, tiene un momento de inercia, /.
La distancia entre el cm. del conjunto mi y m2, y el centro del eje, es n. La distancia entre mi y
m2 es T2.
Demostrar que en el caso de movimiento estacionario, el cm. debe quedar sobre el eje de rotación;
es decir, n = 0.
Escribiendo n = r' + .si y r¿ = ro + s2, demostrar que al perturbar ligeramente el movimiento
estacionario,
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 261
b\
Í-"^\
-w/mw-
£
Fig. 11-12
«i "—(r0-ío)«i = 0
.. , fc(r0-g/3/ir02-J\ k
82 + ~ ( 2 . , )H + ~»2 = 0
donde /t = ^ ^ . ¿Será estable el movimiento? Expliqúese. (/0 = r2 para el resorte sin
distorsiones.)
fn>\ + 7712
11.10. Para el sistema de la figura 11-13, escribir R, determinar los valores de n, r2 y <t>, correspondientes
al movimiento estacionario y comprobar los resultados, utilizando principios elementales.
Suponiendo que el movimiento estacionario se ha perturbado ligeramente, utilizando n = /i + si
y r-i = l2 + s2, demostrar que las ecuaciones aproximadas del movimiento son
rmlcHZmxl\-míl\-I) "I r 4c*ro1»níl1l2 "I
m^ + L v+mA+«& +ki + fc2J81 + L(/+w?+^)3" k2r = °
Las partículas mi y m2 están
conectadas por medio de resortes, dentro
de un tubo horizontal rotatorio.
X se toma en el plano ABa.
Fig. 11-13
Fig. 11-14
262 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS [CAP. 11
11.11. El marco BC de la figura 11-14, puede girar libremente alrededor del eje vertical AB. La barra ae,
articulada en a, puede girar un ángulo 8 en el plano del marco. Se toman los ejes fijos al cuerpo, X, Y
y Z, con el origen en el c.m. de la barra. Los ejes principales de inercia con relación a X, Y y Z son
Ix,Iy e lt, respectivamente; además, lx=ly. Escribiendo Ii = Mr2+Iy e 72 = /'+/,, demostrar
que
L = £/,¿2 + £[/2 + M(R + r sen*)2]*2 + Mgr cosí - ^k{y/b - d eos 9 - í0)2
donde b = h2 + s2, d = 2sh y lo es el valor de / cuando el resorte no se ha deformado.
Suponiendo ahora 8 = 80 + a, demostrar que (si se conservan los términos de primero y segundo
orden en el desarrollo)
tfaprox. = £*.«* - <Mgr sen e0 + \kd sen*0 [1 ~ *o(*> ~ <* sen*,,)-1'2]
/Mrc2(R + r Hn»0) eose0\)
" {[I2 + M(R +raerte^}*)} *
— ■£ < Mgr eos 6Q + ^kd eos 6Q — \klQd eos e0 (b — d eos 90)~1/2
+ \kltfP sen2 $0 (b - d eos *0)~3/2
+ 2Mr<?[2Mr(R + r sen *0)2 eos2 *0 (h + M(R + r sen *0)2)~3]
- [r eos2 e0 - sen e0(R + r sen *0)] [72 + M(E + r sen *)2] ~2 i- a2
Determinar la condición para que exista movimiento estacionario. Demostrar que si se perturba
el movimiento estacionario, la barra oscilará con movimiento armónico simple con respecto a la
posición 8o. Hallar la expresión del período.
El anterior es un buen ejemplo de cómo algunos problemas "sencillos" pueden volverse
sorprendentemente complicados.
11.12. Empleando 8, <t>\ y <t>2 en la figura 11-15, escribir L para el sistema y demostrar que ninguna de
estas coordenadas es ignorable. Sin embargo, utilizando 8, 0i y /32, en donde 0i = <t>\ — 8 y
02 = 02 — 8, demostrar que
L = £/¿2 + Irn,^»2 + r2(/3, + 5)2 + 28r,¿(/?, + 9) eos /?,]
+ £ro2[s2¿2 + 7^/3, + ¿)2 + r*(/32 + ¿)2 + 2sr ,*(/?, + ¿) eos/3,
+ 2ar29(p2 + Ó) eos /J2 + 2r1r2(/31 + ¿)(/32 + 5) eos (/J2 - ¿3,)]
y por tanto que 8 es ahora ignorable, en tanto que 0i y /32 no lo son. (n y r2 son constantes.)
Demostrar que para el caso de movimiento estacionario 0i = /32 = 0 y que esto es posible para
cualquier valor de 8.
Péndulo doble sujeto al extremo de una barra
horizontal, Oa, que puede girar libremente aire-
un eje liso, vertical, en O. Todo el mo-
vimiento de mi y mi está confinado a un
plano horizontal liso.
Fig. 11-15
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 263
11.13. Para el ejemplo 11.7 (Fig. 11-7) deducir la expresión dada para L (véase el problema 8.24).
Demostrar que (ignorando algunos términos constantes),
R =
1 T -, 1 (c3 - c2 eos *)2
2 x ~ '
donde
2 Ix sen2 9
Escribiendo 6 = 0o + a, demostrar que la ecuación del movimiento es
(c3 — c2 eos 60)
dL dL
C2 = -r y c3 = -r
IJ + J-Í4 + -
sen4e0
- [c3(l + 2 eos2 e0) - c2(3 + sen2 e(
o) eos e0] > a =
11.14. El disco uniforme de la figura 11-16 puede girar libremente sobre el mango liso que actúa a manera de
cojinete. Este mango, sujeto al resorte en la forma indicada, puede deslizarse a lo largo de la varilla liviana
lisa. La gravedad actúa a lo largo del eje Yi, según se indica. La distancia desde la unión esférica O
hasta el c.m. del disco, se mide por medio de r. Todos los ángulos se miden como en el ejemplo 11.5.
Aplicando (11.11), demostrar que las ecuaciones del movimiento correspondientes a a, (i y s, son
(7X + rarjj) a + c¡3 + mgr0a = 0, (Ix + Tnrg) /3 — cá + mgr0/3 = 0 y m'i + ks = 0, donde r =
ro + s.
Fig.11-16
11.15. Para el sistema de la figura 11-17, escribir n = rio + s\, etc., y demostrar que las ecuaciones del
movimiento con respecto a las posiciones correspondientes del movimiento estacionario son
mÍ8l + (fct + mxA$s)8l + m^ + myB$82 = 0, 7n3V3 + k283 = 0,
(ml + m2)m8'2 + (k2 + CJ%)82 + «i!»! + m,£$8l + k283 = 0
donde A, B y C son constantes. ¿Será estable el movimiento?
AA/WWVW Q—^-WWVWW—Q~
T
1
a-
Fi*. H-17
264 PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS I CAP. 11
11.16. En el ejemplo 11.10 tómese m = 100 gramos, /o = 25 cm, k = 4 X 104 dinas/cm, r = 20 cm y
9 = 10 radianes/seg. Demostrar que xo = 40 cm, ui = 27,0 y u2 = 4,58. Escribir las ecuaciones
finales integradas del movimiento.
11.17. Suponiendo que m de la figura 11-9 lleva una carga concentrada, Q (no afectada por la plataforma) y
que existe un campo magnético uniforme, perpendicular a la plataforma, demostrar que (si la plataforma
es estacionaria) las ecuaciones del movimiento tienen la misma forma de (6) en el ejemplo 11.10.
11.18. El eje vertical de la figura 11-13 es movido por un motor con velocidad constante 0. Hallar las ecuaciones
del movimiento para mi y m.2, con respecto a sus posiciones de movimiento estacionario. Compárense
los resultados con las ecuaciones del movimiento halladas en el problema 11.10.
11.19. La cuenta de masa m, de la figura 11-18, puede deslizarse a lo largo de la hélice cilindrica lisa, de forma
rígida, cuyo paso es p, la cual está sujeta al marco en la forma indicada. El marco puede girar alrededor
del eje vertical AB. El momento de inercia del marco completo, incluyendo la hélice, con relación a AB,
es /. Tomando como coordenadas afya^, demostrar que
L = $le2 + tyn[l2$2 + r2{e + ¿)2 + ¿>2¿2 + 2lre(e + ¿*) sen <¡>] - mgb*
donde r es una constante y b = p/2x. Demostrar que, para el caso de movimiento estacionario,
eos 0o = n 0P..2 •
Suponiendo que se hace girar a AB con velocidad constante, 8 = w = constante y escribiendo
« = «o + a, demostrar que la ecuación del movimiento de la cuenta, con respecto a su posición corres-
(rlu2 sen 0O\
—.2 i h2~)a = 0- ¿Cuál será el período de la oscilación?
Suponiendo ahora que el marco puede girar libremente, nótese que 8 es ignorable. Demostrar que
[7 + m{l2 + r2 + 2lr sen 0)]5 + m(r2 + Ir sen 0)0 = pg - c
y que la ecuación del movimiento correspondiente a 0 es
(r2 + rl sen 0) '$ + (r2 + 62) 0 - ríe2 eos 0 + gb = 0
Complétese la función de Routh, R = L — cO.
Y////M7(A
_
4-P
Hélice cilindrica rígida, lisa -
x/~-
~jí>/4
Fig. 11-18
CAP. 11] PEQUEÑAS OSCILACIONES ALREDEDOR DE MOVIMIENTOS ESTACIONARIOS 265
11.20. En la figura 11-19, los ejes X y Y están adheridos a una plataforma horizontal que gira con velocidad
angular constante 8 = «, alrededor de un eje vertical que pasa por O. Las partículas, adheridas a resortes
idénticos, como se indica, pueden moverse sobre la plataforma lisa. Con mi en pi, etc., los resortes no
se encuentran deformados; es decir, Opi = P1P2 = P2P3 = P3P4 = / = longitud normal de todos
los resortes.
Fig. 11-19
Tómense xi y >i como coordenadas de mi, etc. Para movimiento estacionario xi = xjo, etc.,
y además, yi = y2 = >3 = 0. Para movimientos pequeños con respecto a las posiciones del movimiento
estacionario, escríbase xi = xio + si, X2 = X20 + s2) xz = X30 + s3, y\ = s4, yi = ss e >'3 = se.
Suponiendo el movimiento estacionario ligeramente perturbado, establecer las ecuaciones del
movimiento del sistema. Indicación. En lugar de escribir T y aplicar las ecuaciones de Lagrange, es
conveniente utilizar las ecuaciones (9.6) para determinar las aceleraciones de mi,m.2 y ms.
CAPITULO
12
Fuerzas de restricción
12.1 Consideraciones preliminares.
A. Fuerzas de restricción. Definición e ilustración.
Se denominan aquí "fuerzas de restricción" o sencillamente "fuerzas de reacción",
aquellas que, ejercidas sobre las partes de un sistema dinámico por las restricciones, no
ejecutan ningún trabajo en el caso de desplazamientos arbitrarios 5q\, 5q-2, ...,
5(7ti, (5t = 0). (Véase la nota de la página 32.) Los siguientes son algunos ejemplos
típicos: la fuerza de* reacción normal ejercida sobre una partícula por una superficie lisa
sobre la que se mueve; las fuerzas que actúan sobre m i y m 2 por los tubos rotatorios de
la figura 4-12; las fuerzas de soporte de los cojinetes sobre un eje rotatorio liso; la tensión
o compresión existente en una varilla rígida que conecta dos masas de un sistema; las
tensiones que soportan los cables de longitud fija en un sistema cualquiera de masas y
poleas; etc.
Puede anotarse que las fuerzas de fricción, que usualmente se determinan por una
fuerza de restricción y un coeficiente de fricción, no deben considerarse como fuerzas de
restricción. La acción de las fuerzas de fricción ocasiona siempre la ejecución de un
trabajo a medida que ocurren los desplazamientos. Por tanto, deben considerarse como fuerzas
activas aplicadas.
B. Consideraciones sobre el significado y el uso de las coordenadas superfluas.
El significado del término "coordenadas superfluas" (término que fue introducido
en el numeral 2.4) puede aclararse por medio del siguiente ejemplo. Ignorando las
masas de las poleas de la figura 2-9, resulta claro que T puede escribirse como
T = \mxy\ + \m2y\ + \m3y\ + $m¿% U)
Sin embargo, el sistema tiene, en el caso de movimiento vertical únicamente, sólo dos
grados de libertad. Por tanto, se dice que (7) contiene dos coordenadas superfluas.
Empleando las ecuaciones de restricción,
(2) Vl+V9 = C, y (3) 2y3 -y2-y4 = C2
y considerando como superflua, por ejemplo a y3, se puede eliminar y3 de la expresión
de T, quedando así expresada en función de yv y2 y yA, en tal forma que ahora
contiene sólo una coordenada superflua. Naturalmente, como se ha dicho en los capítulos
anteriores, es posible eliminar todas las coordenadas superfluas por medio de las
ecuaciones de restricción (excepto en el caso especial de sistemas "no holónomos"). En el ejemplo
mencionado, tanto y3 como y4, y en la misma forma yx y y2, pueden eliminarse
de (i) por medio de (2) y (3).
En el caso general, en que un sistema contiene p partículas y posee n grados de
libertad, puede escribirse T de tal manera que contenga un número cualquiera de
coordenadas superfluas, s, número que puede ir desde uno hasta 3p — n.
En el caso de un sistema que consista de N cuerpos rígidos, y que posea n grados de
libertad, el número s puede variar desde uno hasta 6N — n.
Las coordenadas superfluas desempeñan un papel muy importante en la
determinación de las fuerzas de restricción, como se verá con claridad en lo que sigue.
266
CAP. 12|
FUERZAS DE RESTRICCIÓN
267
C. Ejemplo introductorio.
Con el fin de dejar en claro ciertas ideas
básicas sobre las que todo este estudio se basa,
considérese la fuerza de reacción sobre la cuenta de
la figura 12-1, mientras esta última se mueve a
lo largo del alambre rígido parabólico y = bx2.
Independientemente de la magnitud o de la
dirección de F (las cuales pueden variar con el
tiempo), el movimiento ocurre a lo largo del
alambre. En otras palabras, la fuerza de reacción
se ajusta a sí misma automáticamente, en su
magnitud y en su dirección, a medida que la
cuenta se mueve, en tal forma, que la
trayectoria quede representada siempre por la ecuación
y = bx2. Así, al estudiar este problema, se
presume que la cuenta "no sabe" nada relacionado con la existencia del alambre y sólo
"siente" las fuerzas F, mg y la fuerza de reacción.
Por tanto, si se considera la fuerza de restricción como aplicada externamente, m
puede ser considerada como una "partícula libre" que posea dos grados de libertad. Por
consiguiente, resulta evidente que uno de los dos métodos siguientes puede aplicarse para
hallar la fuerza de reacción.
Método de Newton: Se escriben las dos ecuaciones para "partícula libre"
Fig. 12-1
(4) ' mx = Fx + fx
(5) my = Fy + fy-mg
donde Fx y Fy son las componentes de F, y fx y fy son las componentes de la fuerza
de reacción por conocer.
Ahora, si se conoce el movimiento de la cuenta, bien por métodos experimentales, o
por la solución de la siguiente ecuación del movimiento de Lagrange (que no contiene las
componentes de la fuerza de reacción; véase el ejemplo 3.2),
mx(l + 462z2) + 4mb2xx2 = -2mgbx + Fx + 2bxFy (6)
en este caso, fx y fy se determinan como funciones del tiempo por medio de (4) y (5).
Método de Lagrange: A manera de ilustración, supóngase representada la posición
de la "partícula libre", en coordenadas polares. Si se incluye una coordenada superflua,
T — ^mfr + r2!)2), y si se aplican las ecuaciones de Lagrange, considerando tanto a
r como a 0 como coordenadas independientes,
mr - mr'e2 = fr - mg sen 9 + FT (7)
mr26 + 2mrré - rfg - mgr eos d + rF$ (g)
donde fr y fe son las componentes desconocidas de la fuerza de reacción en la dirección
de r y en la de 0 en el sentido de sus incrementos, respectivamente. Fr y Fe son las
correspondientes componentes conocidas de la fuerza aplicada, F.
Nuevamente, determinando el movimiento, como se mencionó antes, fr y fg se
pueden hallar, en función del tiempo, por medio de (7) y (8). A partir de fr y fe se puede
hallar, de inmediato, la magnitud y la dirección de la fuerza de reacción total.
Nótese que aplicando la relación {4.10) y utilizando x = r eos 0, y y = r sen 0,
las cuales sirven para determinar —,—,77 y tjt, las ecuaciones (7) y (8), pueden
escribirse como sigue, formas que ahora contienen a fx y a fy,
268
FUERZAS DE RESTRICCIÓN
| CAP. 12
mr - mré2 - (fx + Fx) eos9 + (fy + Fv-mg) sen d (9)
mrd + 2mr6 = -(fx +Fx) send + (fy + Fy-?ng) eos6 (10)
Las soluciones de este sistema simultáneo determinan las expresiones de fx y fy.
Aspectos importantes sobre las soluciones anteriores:
(a) En realidad, el sistema tiene sólo un grado de libertad. Pero al introducir una
coordenada superflua y al tratar la fuerza de reacción como una fuerza aplicada
adicional, puede considerarse como si tuviera dos grados de libertad.
(fe) Con esta base, se han escrito dos ecuaciones de Newton, (4) y (5), o dos ecuaciones de
Lagrange, (7) y (8), o también (9) y (10). En cualquiera de estos sistemas aparecen
las componentes de la fuerza de reacción. Para hallar estas componentes, puede
hallarse la solución de cualquiera de estos sistemas.
(c) Las expresiones de las fuerzas generalizadas en el sistema (7), (8) o en el sistema (9),
(70), se determinaron en principio como se describió en el numeral 4.5, donde se
considera que tanto r como 0 son variables independientes y que la fuerza de reacción
es una fuerza impulsora. Por ejemplo, para hallar la fuerza generalizada
correspondiente a r, en la ecuación (7), se considera constante 0 y se aumenta r hasta r + 5r.
Esto sólo puede llevarse a cabo ocasionando una ligera "distorsión" de la restricción.
Además, como resultado de la distorsión, la fuerza de reacción ejecuta trabajo en la
medida fr8r. Así, se observa que 5WqT = (Fr + fr - mg sen 0)8r, de donde
se obtiene el lado derecho de la ecuación (7).
(d) Con el fin de hallar fx y fy o fr y fe, en función del tiempo, debe conocerse ya
el movimiento (determinado como se ha mencionado).
12.2 Procedimiento general para hallar las fuerzas de restricción. (Se supone que
las restricciones son lisas.)
A. Método de Newton para un sistema de partículas.
Considérese un sistema de p partículas que posee n grados de libertad.
Considerando todas las partículas como libres, se escribe .
miXi = Fx. + fx., máji = FVi + fVi, mCi\ = FZi + fZ{ (12.1)
donde FXi,FVi y F^ son las componentes conocidas de la fuerza total aplicada a m, y
fx-,fy y fz son las componentes por conocer de la fuerza de restricción sobre mt.
Supóngase ahora que las ecuaciones de Lagrange en su forma usual, sin fuerzas de
restricción, han sido ya resueltas. O quizá, que el movimiento del sistema se conoce por
métodos experimentales. Cada una de las coordenadas generalizadas q\, (72, •, <7n»
es una función determinada del tiempo, es decir, qT= qr{t). Entonces, por medio de
las relaciones x< = xt(qi, qz, . . ., qn; t), etc., junto con {12.1), es posible expresar, en
función del tiempo, las componentes de la fuerza de reacción fx., etc.
B. Método de Lagrange. (Partículas o cuerpos rígidos.)
Considérese un sistema con n grados de libertad y c restricciones (si se tienen p
partículas, c = 3p — n; si se tienen N cuerpos rígidos, c = 6N — n). Introdúzcanse en T,
s coordenadas superfluas, en donde s puede variar entre uno y c. Entonces,
T = T{qv...,qn+t; qv...,qn+M; t) (12.2)
CAP. 12]
FUERZAS DE RESTRICCIÓN
269
Una consideración cuidadosa de la deducción de la ecuación {4.9) (al llegar a este
punto, conviene que el lector repase el numeral 4.2) pondría en evidencia que (como el
ejemplo anterior) si T contiene s coordenadas superfluas, pueden escribirse n + s
ecuaciones de Lagrange en la forma acostumbrada, siempre que estas n + s coordenadas se
traten como variables independientes y que las fuerzas de restricción, que intervienen
siempre que sea necesario hacer desplazamientos 8q, que no siguen las condiciones
impuestas por las restricciones, sean consideradas como fuerzas aplicadas.
Por conveniencia, se escriben estas ecuaciones en la forma
d /dT\ BT
to\¿ir) - W, = F*r+Tqr r = 1,2, ...,n + s (12.3)
donde F es la parte de la fuerza total generalizada debida a las fuerzas conocidas
aplicadas y T , la parte que incluye únicamente las fuerzas de restricción por determinar.
Bien sea que se esté tratando un sistema de partículas, o uno de cuerpos rígidos, las
expresiones de FqT pueden hallarse por uno de los métodos descritos bajo el numeral 4.5,
introduciendo únicamente fuerzas aplicadas y considerando cada una de las n + s coordenadas
que aparecen en T, como variables independientes. Para ciertas coordenadas, esto implica
una "distorsión de las restricciones", como se ilustró en el ejemplo anterior.
dx. dy.
Si la ecuación {4.10) se aplica a un sistema de p partículas, las derivadas —-, -—- y
dz. oqT dqT
—- deben hallarse a partir de las siguientes ecuaciones de trasformación,
xi = xi(ql,q2, ...,<7n+s; í)
Vt = Vtex,<i% <7„+s; t) U2.4)
z, = z.{qvqv ...,<7n+s; í)
que contienen no solamente qit q¿, ., qn, sino también las s coordenadas superfluas.
Las expresiones de f se hallan de la manera que se describió para Fq , considerando
cada una de las n + s coordenadas como variables independientes, e introduciendo las
componentes adecuadas de las fuerzas de reacción a manera de incógnitas.
Como se mencionó anteriormente, puede conservarse en T, un número cualquiera de
coordenadas superfluas hasta un máximo igual a c. Por ejemplo, si se considera un sistema
de dos partículas para el cual n es igual a 2, es posible, utilizando las ecuaciones de restricción,
escribir T en función de un número cualquiera de coordenadas que puede ir desde dos (s = 0)
hasta seis (s = 4). Para hallar fq en principio se halla siempre el trabajo, 5WqT,
ejecutado por las fuerzas de restricción para un cambio de + 5qrt en la coordenada qr,
mientras todas las demás coordenadas y t permanecen constantes. Resulta claro, entonces, que las
fuerzas de reacción aparecerán en SWqT (y por tanto en f ) únicamente cuando al hacer el
desplazamiento + dqr se distorsionan una o más restricciones. Así, en el caso en que s sea
menor que c, en general, no todas las fuerzas que actúan sobre el sistema aparecerán en las
n + s ecuaciones (12.3). ("Distorsionar" se refiere aquí a deformaciones infinitesimales.)
Por último, las ecuaciones (12.3) pueden resolverse para hallar las fuerzas de reacción que
aparecen en f . Suponiendo que se conoce el movimiento, estas fuerzas pueden expresarse
en función del tiempo.
Como se mostrará con los ejemplos, la adecuada selección de las coordenadas superfluas
y el número de ellas que se conserva en T, depende del problema entre manos. Puede suceder
con frecuencia, que, por introducir una coordenada superflua adecuadamente escogida,
pueda hallarse la fuerza de restricción buscada, con muy pequeño esfuerzo.
270
FUERZAS DE RESTRICCIÓN
[CAP. 12
12.3 Ejemplos ilustrativos.
Ejemplo 12.1.
Se trata de determinar las expresiones de las
componentes de la fuerza de reacción que se ejerce
sobre la cuenta de la figura 12-2 mientras se mueve a
lo largo de la espiral de alambre liso, bajo la acción
de las fuerzas externas F y mg. Con el propósito de
ilustrar diferentes ideas básicas, se incluyen varias
soluciones posibles. Se supone conocido el
movimiento.
(a) Si se considera que la partícula es "libre" y se
aplica (12.1), se tiene
rnx = Fx + fx
my = Fy + fy (i)
m'z - Fx + fz-mg
Fx, Fy y Fz son componentes conocidas de
F y /x. fy y fz son componentes por conocer
de las fuerzas de restricción. Así, si se conoce el
movimiento, estas componentes pueden ser
expresadas en función del tiempo.
Fig. 12-2
(f>) Utilizando coordenadas cilindricas, dos de ellas superfluas, T = ^mfe + r2¿2 + z2). Aplicando (72.3), se
obtiene
F^
dy
F °
fx3r T /«3r T Txdr
dx
f dJL _ f *L - * §*. + f §2. + f *L
r*d<t> z3¿ ,xb<t> 1yH 1zH
(2)
J*a* T 'yaz T ,zdz
m'¿ ~ F*~ñ ~ F*af " ^«-^^af - "te ^ J*te t '*dz
Las relaciones (12.4) son x = r eos 0 y y = r sen <f>\ y las ecuaciones de restricción son r — constante = 0,
y z — b<f> = 0. Aplicando las anteriores en (2),
—mrt2 — Fxcos<f> — Fy sen£ = fxcos<f> + /ysen^
mr2'<¿ + Fxr sen <f> — Fyrcos# — Fzb = —/xrsen^ + fyr eos <f> + fxb (3)
m'z — Fz + mg — fx
las cuales, naturalmente, pueden combinarse para hallar fz, fy y fz.
(c) Utilizando nuevamente coordenadas cilindricas, pero introduciendo Fr, F¿ y Fz (componentes de F, según r,
<t> y z) y fr, U y /* (componentes correspondientes a la fuerza de reacción), la ecuación (12.3) conduce a,
mr — mr$2 — Fr = fr, mr2'¿ + 2mrr$ — rFé = rfé, m'z — Fz + mg = fx
Así, utilizando r = constante y z = b<t>, pueden determinarse de inmediato las componentes fr, U
yfz-
Nótese que el ejemplo anterior ilustra bien el significado y la necesidad de "distorsionar las restricciones". Con
el fin de obtener la fuerza generalizada correspondiente a r, por ejemplo, en (b) o en (c), se debe hacer que <t> y z
permanezcan constantes y se debe suponer, además, que r se aumenta a r + ¿r. Naturalmente, esto implica una
ligera distorsión del alambre en la dirección de r. Pueden hacerse observaciones semejantes con respecto a las fuerzas
generalizadas correspondientes a <t> y a z.
(d) Si se elimina z y se escribe T en función de r, íy¿ (es decir, considerando sólo una coordenada superflua),
fácilmente se concluye que
-mrp- = FT + fT
m(r2+b2)'¿ = (Fz + fz-mg)b + (Ft + fjr
de donde puede obtenerse fr pero no /, ni f¿.
Ejemplo 12.2.
El presente ejemplo se refiere a la figura 2-10 y a la ecuación (2.42). Suponiendo que rt y r2 representan los
hilos de longitud constante, se consideran varios enfoques para determinar las tensiones en los hilos del péndulo doble.
CAP. 12]
FUERZAS DE RESTRICCIÓN
271
(a) La tensión n en n: considerando n únicamente como coordenada superflua, (2.42) se reduce a
T = tyn¿r\ + r2*2) + $m2[r* + r2*2 + r\%2 + 2r1r25¿ eos (*-*)- 2r2r^ sen(* - $)] (1)
de donde, después de hacer r i = V2 = 0 se obtiene
m2r20 sen(# — 0) + m2r2¿2 eos (# —0) + (mj + mü)^2 = tx — (m1+m2)g cose (2)
por medio de la cual, si el movimiento se conoce, se puede hallar n en función del tiempo. El lector, puede
demostrar que las ecuaciones correspondientes a 9 y a <t> no contienen a ti.
(b) De igual manera, si se introduce a r2 como coordenada superflua (ri = constante) puede hallarse de
inmediato T2, la tensión en r2.
Nota. En el caso de "movimientos pequeños", las ecuaciones del movimiento del péndulo doble son
fácilmente integradas. Así, n y t2 pueden ser expresadas con facilidad en función del tiempo.
(c) Como una variación del método anterior, pueden introducirse n y r2, simultáneamente, como coordenadas
superfluas, y escribir las dos ecuaciones de acuerdo con (12.3), de donde pueden obtenerse las expresiones de ti
y t2. El lector debe verificar esta afirmación.
(d) Por aplicación de (12.1), naturalmente, se pueden hallar ti y t2:
WllX! = fxx, ™\V\ = /Vl - ™lff> m2¿2 = fx2>
donde fx = r2sen# — tx sen*.
m2Í/*2 - /y.
w
Ejemplo 12.3.
El péndulo rígido de la figura 12-3 puede oscilar libremente en un plano vertical, sostenido por una articulación
lisa en p. Se trata de determinar una expresión del torque FB que tiende a cambiar el ángulo 0, entre n y r2.
Las partículas m¡ y m2 están sujetas rígidamente
a las varillas rígidas rt yr,.
Fig. 12-3
Introduciendo a 0 como coordenada superflua,
T = ¿(mi + m2)r&h2 + ^[r2^ + /3)2 + 2rxr2 eos (3(e2 + »¡¡))
de donde Ffi = m2(r\ + rír2 eos (3) '$ + m2r tf202 sen (3 + m2gr2 sen(0 + (3)
Aunque esta expresión aparentemente es compleja, puede verificarse por consideraciones elementales.
Ejemplo 12.4.
Se determinan las expresiones de las componentes de la fuerza de reacción sobre m y el torque de reacción
ejercido por el alambre sobre el eje vertical del problema 2.2Ó, figura 2-29.
Al introducir dos coordenadas superfluas, se puede escribir T como
T = £/¿2 + %m(r2 + r2*2 + z2)
donde a es la posición angular del eje y 0 determina la posición angular de m. Considerando independientes todas
las coordenadas, se escribe
la = t + t', mr — mrb2 = fT, mr2Y + 2mrre = rfg, m'z = fz — mg
272
FUERZAS DE RESTRICCIÓN
[CAP. 12
donde t representa el torque ejercido por un motor, por ejemplo, sobre el eje, y r' el torque ejercido por el alambre.
Las componentes de la fuerza de reacción sobre m son fr, fg y /,. Estas relaciones, junto con z = ar2 y 0 = a,
conducen a las expresiones de fr, fe y fz en función de í, para un movimiento determinado del sistema.
Ejemplo 12.5.
Considérese el ejemplo 9.6. Se trata de determinar /„ y /»', de la figura 9-6, por medio del método de Lagran-
ge. Se escribe L como sigue
L = \[Ix(e2 + ¿2 sen2 $) + Iz(¿ + ¿t eos $)2] + l sene sen e eos ¿,
donde í y f por ejemplo, son coordenadas superfluas. Si se escriben las ecuaciones del movimiento
correspondientes a e, i>\ y <t>, de la manera acostumbrada, y se hace r3^i = — r2<t>, 9 = constante, etc., finalmente se
obtendrá . / r \ r
(ecuación de 0): ¿? ( —-? ) (/¿r? + Ixrb - -Fe = -l — sen e eos ^ + /br3
.. r\
(ecuación de ^i): *i3(/*-/*) = +*V = —i—serie sen^ + /br3
73 r3
(ecuación de <f>): £, ( —— ¡I,
-F* = ~Kr2
donde 8, $\ y <¡> fueron consideradas como variables independientes para hallar F0,F^ y F¿.
Las dos últimas ecuaciones conducen a la ecuación del movimiento (la misma que (70),del ejemplo 9.6). Al
integrarla, se obtendrán /„ y f„ en función del tiempo.
Ejemplo 12.6.
En la figura 12-4 el cuerpo rígido puede girar libremente con velocidad angular 82 alrededor de 6c.
Simultáneamente, la barra rígida completa abe puede girar con velocidad angular $\ alrededor de un eje vertical. A
continuación se determina el momento de reacción, t„, alrededor de un eje horizontal que pasa por b (normal al plano
abe), que impide que el ángulo a varíe.
A'. Y y Z adheridos a M
\x
>z = «1 eos a sen t2 — a eos t2
'y = *1 c08 ° C08 *2 + « aen *2
Í,8ena + ;2
Fig. 12-4
Con el fin de aclarar el siguiente análisis, supóngase que ab y be están unidos en b con una articulación cuyo eje
es normal al plano abe. Si se considera que a es variable, y se toman los ejes fijos al cuerpo con el origen en b como
se indica, fácilmente se concluye que
cox = acosasen 02 ~~ a cos *2» "y = 0i eos a cos $2 + a sen *2> uz — 61 sena + $2
Entonces, aplicando (8.10) e ignorando la masa de abe,
T = $[Ix(Ói eos a sen $2 — ó cos 62)2 + Iy(éi cos a eos $2 + ¿ sen $2)2 + 7Z(5, sen a + 62)2
— 2Ixy($l cos a sen 62 — a cos 02)(Ái cos a cos 92 + a sen $2)
— 2JXZ(01 cos a sen $2 — a cos fi2)(^i sen a + $2) U)
— 2/1,2(¿1 cos a cos 62 + a sen $2)($l sen a + $2)]
CAP. 12]
FUERZAS DE RESTRICCIÓN
273
donde /,, lxy, etc., se toman con respecto a los ejes fijos al cuerpo. Obsérvese que se ha introducido una coordenada
superflua.
Aplicando (12.3) se obtiene para la ecuación correspondiente a a después de hacer a = a = 0,
(7„ — Ix) eos a['¿i sen $2 eos $2 + ¿i¿2(cos2 *2 — sen2 02)]
+ 7x02sena eos a sen2 $2 + 7y¿2 sena cosa cos202 ~~ J*(*i sena + 02)éí cosa
+ 7XV[V1 cosa(cos202 —sen2í2) — i$l$2 eos a sen $2 eos $2 — 2e\ sen a cosa sen02 eos 02]
(2)
+ 7XZ[V1 sena eos 02 + V2 eos 02 — 2$l$2 sen a sen02 — $\ sen02 + J2 sen 02(cos2 a — sen2 a)]
— 7yz[V1 sena sen02 + $'2 sen 02 + 2¿!¿2 sena eos 02 + ¿j| cos 92 + *? cos02(sen2a — eos2a)]
= ra — Mgs cos a
con lo cual puede hallarse t„ para un movimiento determinado.
Si ab estuviera impulsado por un motor montado en B y el cuerpo rígido igualmente estuviera impulsado por
otro pequeño motor conectado, por ejemplo, en c, ¿cambiaría con esto el lado derecho de la ecuación (2)?
Nótese que la expresión anterior se simplifica enormemente si se supone que el cuerpo rígido es un disco
uniforme, con el eje be perpendicular a la cara del disco y pasando por su centro.
12.4 Fuerzas de restricción utilizando las ecuaciones de Euler.
Como se recordará, del capítulo 9, las ecuaciones de Euler {9.2) y {9.10) son
esencialmente ecuaciones para "cuerpos libres". En Fx, Fy y Fz, por una parte, y en tx, ry y tz,
por otra, aparecen, en general, todas las fuerzas aplicadas, junto con las de restricción. Como
se ha demostrado en los ejemplos del capítulo 9, estas relaciones pueden utilizarse para
determinar las fuerzas de restricción.
A continuación se enumeran unos pocos ejemplos que demuestran bien los principios
básicos y las técnicas correspondientes. (Las ecuaciones especificadas se refieren a la
numeración dada en los ejemplos pertinentes.)
Ejemplo 9.2. Si se supone conocida la solución de la ecuación (2), la ecuación (7)
indica fx y fy en función del tiempo.
Ejemplo 9.5. Si se conoce el movimiento, todas las fuerzas de soporte pueden hallarse
a partir de las ecuaciones (7) a (3).
Ejemplo 9.6. Las fuerzas de restricción fx, fy y fz sobre la unión esférica y fb y f'b
en el punto de contacto b, se determinan por medio de las ecuaciones {9.2) que se escriben en
forma extensa a partir de (6) y {8).
Ejemplo 9.7. Este ejemplo también ilustra el método de Euler para hallar las fuerzas de
restricción.
Ejemplo 12.7.
Se trata de determinar t„ del ejemplo 12.6 y la figura 12-4, por el método de Euler.
Con referencia al numeral 9.7 y la ecuación (9.16), se observa
tv sen 02 — tx cos 92 = ra — Mgs cos a (1)
donde rx = /x¿x + (7z-/v)coy(oz + 7xy(cox(oz-¿v) - 7xz((ox«ov + ¿z) + 7vz((o2-«oJ) (2)
t„ = 7y¿y + (Ix-Ix)uxwx - Ixy(uyuz+ ¿x) + 7xz((o2-^) + 7vz((ov(ox-¿z) (3)
Intercalando las expresiones adecuadas de «,, «¿, etc., (las que se incluyen en la figura 12-4), la ecuación (1)
después de realizar una larga serie de operaciones algebraicas monótonas, finalmente se reduce exactamente a la
forma de (2) del ejemplo 12.6.
Ejemplo 12.8.
El cuerpo rígido de la figura 12-5 está montado en una forma arbitraria en el marco rígido indicado. Aquí
aparece el cuerpo apoyado en cinco puntos, p\, p2, .. ., ps. Supóngase que las fuerzas externas F\, F2, F3, etc.,
le dan al marco un movimiento determinado cualquiera. Considérense las fuerzas de reacción f\, {2, etc.,
ejercidas por los diferentes puntos del marco, sobre el cuerpo.
274
FUERZAS DE RESTRICCIÓN
[CAP. 12
*\
£
Fig. 12-5
Considerando el cuerpo aisladamente, estas fuerzas son fuerzas impulsoras. A partir del movimiento
conocido, las expresiones de «XI uy y «„ así como las de Ax, Ay y Az, pueden ser halladas. Así, las
ecuaciones (9.2) y (9.10) conducen en seguida a Fz, FyK Fz, rx, ry y rz donde Fx, por ejemplo, es la suma de las
componentes X de /i, f2, ..., fs, y tz es la suma de los momentos ejercidos por estas mismas fuerzas alrededor
de X. En el caso de un movimiento determinado, Fz, rz, etc., tendrán siempre los mismos valores,
independientemente de la forma como el cuerpo esté sujeto al marco. Sin embargo, nótese que si está sujeto por varios puntos,
como se indica, no se tiene información suficiente para hallar los valores individuales de f\, f2, . -, /s.
12.5 Fuerzas de restricción y ecuaciones del movimiento con restricciones
rugosas.
Las fuerzas de fricción están siempre presentes cuando un objeto se mueve en contacto y
con respecto a otro objeto. La magnitud de una fuerza de fricción por deslizamiento, Ff, está
dada por Ff = \if, donde \i es el coeficiente de fricción y / la fuerza de reacción normal
a las superficies en contacto. La dirección de F, se tomará como opuesta a la del
movimiento.
Las fuerzas de fricción deben ser consideradas como fuerzas impulsoras aplicadas
externamente, ya que, cuando tiene lugar el deslizamiento, siempre se hace algún trabajo. La
existencia de estas fuerzas normalmente introduce grandes dificultades; no se pretende incluir
aquí un tratamiento general sobre el tema. Sin embargo, los dos ejemplos siguientes pueden
colaborar a poner de relieve el tipo de problema que puede surgir.
Ejemplo 12.9.
Determinar la fuerza de reacción / de la figura 12-6 y la ecuación del movimiento de la cuenta al deslizarse
hacia abajo por el alambre parabólico rugoso.
Considerando a / como normal al alambre, en la dirección indicada, y la fuerza de fricción nf, tangente al
alambre, se escribe
¡if sen e + f eos 6 - mg + Fy (1)
Pero cosí =
nx = iif cose — f sene + Fx, my
dx _ 1
y/dx2 + dy2 y/l + 4b2x*
y además sen e
2bx
Vi + 462x2
. Así, las relaciones (1) se hacen
/ fi — 2bx \
mx = f WrTwJ + F* (2)
f(2ybx + 1)
mV = y/i + w ~ "* + Fy (3)
Eliminando / entre (2) y (3) y haciendo uso de la relación y = bx2, se obtiene la siguiente ecuación del
movimiento
7nx(l + 462x2) + imb2xx2 = 2¡ibmx2 + Fx + ^(mg - Fy) + 2bx(liFx-mg + Fy)
CAP. 12]
FUERZAS DE RESTRICCIÓN
275
Obsérvese que en este problema, aparentemente sencillo, se obtiene una ecuación no-lineal con las dificultades que
ello implica.
Una cualquiera de las ecuaciones (2) o (3), naturalmente, conduce a las expresiones de la fuerza de reacción /.
Fig. 12-6
Fig.12-7
Ejemplo 12.10.
Una barra uniforme de longitud 21, se desliza en un plano vertical, hacia abajo, en el interior de un cilindro
rugoso de radio R, como se muestra en la figura 12-7. Se trata de hallar las expresiones para las fuerzas de reacción
f\ y {2 y la ecuación del movimiento.
Suponiendo que la varilla puede moverse libremente en el plano vertical y utilizando como coordenadas a r,
6ya' T = ¿M(¿2 + r2¿2) + ¿7¿2
donde M es la masa total de la varilla e 7 su momentp de inercia con relación a un eje trasversal que pasa por el c.m.
Nótese que T contiene dos coordenadas superfluas.
Aplicando (12.3) y considerando las fuerzas de reacción f\ y f2 y las fuerzas de fricción ¿i/i y ^/2
como fuerzas impulsoras, se obtienen las siguientes ecuaciones:
Mr$2 + Mg eos $ = (/, + /2) eos (3 + /í(/x - /2) sen ¡3 (1)
Mr2 5T + Mgr sen $ = /.r(/, + /¡j) eos ¡3 + r{fx - f2) sen (3 (2)
7 a = MK/i + Zajsen/í - l(f t-f2) eos (3 (3)
donde se ha hecho r = Y = 0.
Ahora pueden resolverse las ecuaciones (1) y (2), para hallar /i y f2. Sustituyendo estos resultados, junto
con a = 9, en (3), se obtiene la ecuación del movimiento.
Problemas
Una cuenta, sujeta a la fuerza aplicada de componentes Fx y Fy, está restringida a moverse a lo largo
de un alambre liso rígido, de una forma plana arbitraria. Utilizando coordenadas polares, demostrar que,
independientemente de la forma del alambre o de los valores de Fx y Fy, las expresiones generales
para las componentes de la fuerza de reacción fx y fy, están dadas por
fx = —Fx + m(r — rh2) cose — m{r'$ + 2r$) sen $
fy = —Fy + m(r — rh2) sen $ + m(r V + 2ré) eos e
En la figura 3-9 el eje vertical se hace girar arbitrariamente. Los desplazamientos angulares de este eje se
miden por <t>. Demostrar que las fuerzas de reacción ejercidas por la varilla sobre m se expresan por
fe = — mr¿2sen 9 cosí — mg sen 0, /$ = mr sen $ % + 2mr¿ sen $
Las direcciones de estas fuerzas son las de los incrementos de 0 y de <t>, respectivamente. Por tanto, para
movimiento conocido, ¿(í) y r(t), las fuerzas de reacción serán funciones conocidas del tiempo.
276
FUERZAS DE RESTRICCIÓN
[CAP. 12
Demostrar que las ecuaciones siguientes son aplicables al problema anterior:
—mr$2 sen $ eos 6 — mg sen 0 — fx eos $ eos <f> + fy eos 6 sen <f> — fx sen $
mr'<£ sene + 2raf¿sen0 = — fx sen# + fycos<f>
mr — *mr¿2sen2fl + mg cos$ = fx sen* eos <f> + fy sen» sen# + fx cosí
donde /,, fy y fz son las componentes rectangulares de la fuerza de reacción sobre m. Por tanto, las
componentes rectangulares pueden hallarse en lugar de /fl y /¿.
La palanqueta de la figura 4-3 se mueve en un plano vertical bajo la acción de la gravedad. Demostrar que
la tensión r en la varilla que conecta a mi y m2, está dada por t = ——, _ le2.
m1 + írtj
Las dos varillas de la figura 12-8, con sus extremos superiores
unidos rígidamente, pueden oscilar como un péndulo en un plano
vertical. Demostrar que el torque ra que tiende a cambiar el ángulo
a, está dado por
ra = I2'e + MaffVz sen (* + /?)
Para movimientos pequeños con respecto a la posición de
equilibrio, determinar 8 en función del tiempo y por tanto, t„ en
función de t. (r2 es la distancia de p al c.m. de M2.)
Una cuenta de masa m se desliza hacia abajo por la espiral cónica
lisa de la figura 3-5, problema 3.5, bajo la acción de la gravedad.
Utilizando coordenadas esféricas escríbanse las ecuaciones de las
cuales pueden obtenerse las componentes de la fuerza de reacción,
/„ fy y fz. Compárense estas ecuaciones con las dadas en el
problema 12.3.
Fig.12-8
Una partícula de masa m se desliza hacia abajo siguiendo un círculo máximo de una esfera lisa de radio r.
Suponiendo que la masa parte del punto más alto, con una velocidad rd0 (se mide 8 desde un
diámetro vertical hacia abajo), demostrar que la fuerza de reacción, fr, ejercida por la esfera sobre la partícula,
está dada por fr = Zmg eos 8 — mreü — 2mg y que esta última deja la esfera, cuando el ángulo se de-
2g + reí
termina por cosí = r .
óg
El extremo superior de la barra de la figura 12-9, se desliza hacia abajo sobre la pared lisa. El disco rueda
sin resbalar sobre el piso. Despreciando la fricción por rodamiento, demostrar que /z, la fuerza ejercida por
la pared sobre el extremo de la barra, está dada por
fx = (Ml + 2M2 + 2I2/rz)(le' eos 6 - le2 sen 0)
Fig. 12-9
Demostrar que la tensión en n, figura 12-3, es
/ = m2r2[ 5." sen (<f>~e) + 4>2 eos ($ — e) + (tt^ + «n2K*'i¿2 + 9 c°s 9)]
CAP. 12]
FUERZAS DE RESTRICCIÓN
277
12.10. Una partícula se mueve en contacto con la superficie lisa de la figura 12-10, la cual se representa por la
ecuación z ■
■ A sen—sen-^, en donde la gravedad actúa en la dirección negativa de z. Utilizando
coordenadas rectangulares, escríbanse las ecuaciones para las componentes /,, fy y /,, de la fuerza de
reacción sobre m.
Fig. 12-10
12.11. El eje vertical que sostiene el alambre liso de la figura 2-29, problema 2.20, es obligado a girar de una
cierta manera determinada 8 = 0{t). Demostrar que las componentes de la fuerza, fr, fg y /,,
ejercida por el alambre sobre la cuenta, están dadas por
mr — mr$2 = fT, mr $ + 2mr$ — fe,
fz-mg
= ar*
U)
(2)
Teniendo en cuenta que SW = frSr + fgr Se + fz8z = I
(principio del trabajo virtual; véase el numeral 2.13) demostrar que las ecuaciones del movimiento usuales
correspondientes a r y a 8, sin fuerzas de restricción, pueden obtenerse a partir de (7) y (2).
12.12. Una cuenta se desliza hacia abajo por una espira circular rugosa, de alambre, la cual se halla contenida
en un plano vertical. Demostrar que, en coordenadas rectangulares con el origen en el centro de la espira,
la ecuación del movimiento (antes de eliminar, por ejemplo, "y y y) es
y en coordenadas polares,
m(y + g)(x - ?y)
nx(iix-y)
mr'e — mg sen* = ii{mr$2 — mg sen*)
12.13. Una partícula de masa m se mueve sobre una superficie esférica rugosa, bajo la acción de la fuerza de
fricción y de la gravedad. Demostrar que la fuerza normal de reacción sobre la partícula, es
fr = mg cose - m(rh2 + rsen2fl¿2)
y que las ecuaciones del movimiento correspondientes aíya* son
mr2'$ — mr2 sen $ eos $ ¿2 = m^rsen* — fifrL
r2 sen2 $ ¿
, r26
mr2 sen2$'<fi + 2mr2 sen 6 eos 6 6<f> = ¡ifr
donde 82 — r262 + r2 sen2 0 ¿2. (Utilícense coordenadas esféricas con el origen en el centro de la esfera.)
278 FUERZAS DE RESTRICCIÓN [CAP. 12
12.14. Hallar las expresiones de las componentes del torque, tx, tv y tz en las direcciones de X, Y y Z,
ejercidas por el cojinete que sostiene a D de la figura 8-5. Supóngase que el eje ab es movido por un motor,
con una velocidad conocida.
12.15. En la figura 8-18 una partícula de masa m está pegada en el centro del borde de un giróscopo que
originalmente estaba perfectamente equilibrado. Hallar las expresiones de las fuerzas sobre los cojinetes ai y a2
como resultado de esto.
12.16. La base de la figura 9-14 está colocada en un punto de latitud * sobre la Tierra. El eje que sostiene la
plataforma rotatoria es vertical. Hallar las expresiones de las fuerzas ejercidas por los cojinetes B\ y B2,
sobre el eje (véase el problema 9.19).
CAPITULO
13
Fuerzas impulsoras necesarias para
producir movimientos definidos
(Equilibrio estático como un caso especial)
13.1 Consideraciones preliminares.
El problema dinámico corriente es aquel en el cual se dan las fuerzas y se deben hallar
los movimientos correspondientes. En este capítulo se trata el tipo de problema inverso; es
decir, aquel en el cual se prescriben los movimientos, o se determinan por métodos
experimentales, y se trata de hallar las fuerzas impulsoras necesarias para producir tales
movimientos (véase el numeral 1.7). Como se verá más adelante, los problemas que implican
equilibrio estático pueden ser considerados como casos especiales del anterior.
Esta rama de la dinámica tiene muchas aplicaciones y como se verá con claridad, el
método de Lagrange resulta especialmente adecuado.
Los desarrollos de este capítulo dependen principalmente del contenido del capítulo 4.
Pero además, se ha de hacer especial énfasis en los siguientes hechos:
(a) Cada una de las coordenadas
independientes, q\, q2, • • ., qn puede hacerse
variar con el tiempo en cualquier forma
que se desee. La manera como se haga
variar una de las coordenadas no afecta
la forma en que las otras pueden cambiar.
Considérese la figura 13-1. Supónganse
movimientos verticales con los cables
permanentemente bajo tensión. El sistema
tiene dos grados de libertad. Constituyen
parejas de coordenadas adecuadas,
(si.yi), (s2,y2), (yi,y2),etc.
Por medio de una adecuada aplicación
de fuerzas, cada una de las dos
coordenadas de una cualquiera de estas parejas,
puede variar con el tiempo en cualquier
forma deseada (dentro de ciertos límites).
Y/W///WtfMVM
Aparte de la rotación
discos, supóngase
únicamente movimiento vertical.
Fig. 13-1
(6) Los movimientos prescritos de un sistema
pueden usualmente obtenerse con la
aplicación de fuerzas impulsoras de una
manera determinada, dentro de varias posibilidades. Supóngase en la figura 13-1, un
mecanismo, A, adherido a la tierra que ejerce una fuerza vertical sobre mi mientras
que otro mecanismo, B, también en tierra, ejerce una fuerza vertical sobre el cable de la
izquierda en el punto p. Naturalmente estos dos dispositivos pueden imprimir al sistema
cualquier tipo de movimiento que se desee (naturalmente dentro de ciertos límites).
Supóngase ahora que A está montado en el eje de la polea pequeña y que ejerce una
fuerza sobre mi en tanto que B continúa como en el caso anterior. En este caso se puede
de nuevo dar al sistema cualquier tipo de movimiento deseado (para simplificar
desprecíese la masa de A). Sin embargo, la fuerza que ejerce A, en el primer caso, será, en
279
280 FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [CAP. 13
general, diferente de la fuerza ejercida por el mismo mecanismo en el segundo caso,
aunque los movimientos deseados sean idénticos. Desde luego, esto es igualmente cierto para
B. Por tanto, en general, existe toda una serie de alternativas en cuanto al lugar en donde
se aplican las fuerzas.
(c) Un aspecto importante del problema es la determinación del número de fuerzas
impulsoras necesarias. En general, para un sistema de n grados de libertad deben aplicarse
n fuerzas, f\,fz, • ••,/„, de tal manera que el cambio de valor de una cualquiera
de las n coordenadas puede ser producido por lo menos por una de las fuerzas aplicadas
(o posiblemente por varias de ellas).
(d) Como consecuencia de (fe), la primera etapa en la solución de un problema de este tipo
consiste en decidir la manera exacta como se han de aplicar las fuerzas impulsoras.
Además, como para cada "acción" existe una "reacción" igual y opuesta, es importante
especificar la localización de cada uno de los mecanismos impulsores.
13.2 Método general.
Los resultados generales que siguen, se basan en una aplicación directa de las ecuaciones
de Lagrange, que para conveniencia y claridad se escriben
á@ -1 = F« + *
donde FQr incluye únicamente las fuerzas conocidas ya especificadas y F'Qr contiene
solamente las incógnitas fi,fz, . . ,/„.
Esquema del procedimiento general.
(a) Habiendo expresado a T en función de n coordenadas independientes, se escriben las n
ecuaciones de Lagrange en la forma acostumbrada.
(fe) Las expresiones para FQr se hallan como siempre, teniendo en cuenta todas las fuerzas
aplicadas y las que se deben a resortes, a la gravedad, etc.
(c) Habiendo decidido sobre la forma como se han de aplicar las fuerzas fi,ft, ,/„,
se escriben las expresiones para F'qT (también en la forma acostumbrada) en función de
las incógnitas /.
(d) Como se supone conocido el movimiento (es decir las coordenadas han sido determinadas
en función del tiempo, q\ = qi{t), etc.), el lado izquierdo de las ecuaciones del
movimiento puede expresarse en función áe t y algunas constantes.
(e) Las soluciones de estas n ecuaciones algebraicas simultáneas, determinan las / en función
de t y de las constantes. Por tanto, se obtienen de esta manera los resultados deseados.
Como se verá en los ejemplos siguientes, en ocasiones resulta fácil la eliminación de t y
por tanto, pueden expresarse las fuerzas en función de las coordenadas.
Nota importante. Considérense los dos ejemplos siguientes: (a) Se lanza una bola verti-
calmente hacia arriba de tal manera que se mueve siguiendo una recta vertical. Si el
lanzamiento se hace con una velocidad inicial que forme un ángulo menor de 90° con la
horizontal, la trayectoria será ahora parabólica (despreciando la resistencia del aire y
suponiendo que g actúa verticalmente hacia abajo con valor constante). Por tanto, la trayectoria
depende de las condiciones iniciales, (fe) Un satélite de masa m se mueve alrededor de la
Tierra esférica uniforme, de masa M. La trayectoria sigue una elipse si la energía total,
£ = T + V es negativa; una parábola si £ = 0, y una hipérbola si £ es positiva. En todos
los casos, la fuerza es la atracción gravitatoria conocida, GMm/r>. £ depende de los
valores iniciales de la posición y la velocidad. Por tanto, una vez más, la trayectoria depende
de las condiciones iniciales.
CAP. 131 FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS 281
Volviendo al problema general, resulta evidente que con el fin de establecer los
movimientos prescritos para un sistema (aquellos especificados originalmente por medio de qx = qiit),
en los que se incluyen las condiciones iniciales) no solamente se han de aplicar las fuerzas
fu f-2> ■ ■ ■> fn> determinadas como se expresó antes, sino que su aplicación se ha de efectuar
según unas condiciones especiales determinadas.
13.3 Ejemplos ilustrativos.
Ejemplo 13.1.
Al considerar el sistema sencillo que se muestra en la figura
13-2, quedarán bien ilustrados ciertos principios básicos. Por esta
razón se incluyen aquí, en forma esquemática, tres soluciones para
el mismo problema. (Nota. A lo largo de este ejemplo se supone
que el cable permanece siempre bajo tensión.)
(a) Utilizando las coordenadas yt y y2, sin dificultad se
concluye que
(mi + m2 + I/R2) yl - m2y2 + (m? - mx)g = FVí U)
«*2(»í-Vi) ~ m2ff + WV2~k) = K2 (2)
donde lo es la longitud normal del resorte. Estas relaciones
se cumplen independientemente del tipo de movimiento
supuesto. Además, su validez es independiente de la forma *sssssssssssssssssssssssss)sssssssss
como se apliquen las fuerzas impulsoras, siempre que Fy y Y/////////Z////////////////^
Fy se expresen en forma adecuada en todos los casos. Fig. 13-2
Supóngase ahora que un mecanismo adherido a pi, ejerce una fuerza vertical f\ de magnitud por
determinar, sobre mi; igualmente, otro mecanismo (sin masa) adherido al cable en p2, ejerce una fuerza
/i sobre m2. Por simple inspección, puede decirse, Fy = /, y F'=f2. Por tanto, (1) y (2) expresan
directamente las magnitudes de f\ y f2, en función de yx, y2 y algunas constantes.
Al especificar el movimiento deseado, por ejemplo yi = yo + vt y >-2 = lo + A sen («í + fi) donde
yo, o, lo, A, u y fi deben tener valores conocidos; en seguida se concluye que las fuerzas requeridas son
/x = m^AuP sen (coi + 6) + (m2 — m^g, y f2 — A(Ac — m2u2) sen (coi + 8) — m^g
Nótese que en este caso f\ y f2 pueden ser expresadas en función de y2.
(b) Determínese nuevamente /i y f2, utilizando las coordenadas yt y y3. Por aplicación de (13.1),
(m, + Iim Vi ~ rnig + k(yi-y3-c) = F^ (3)
m2y3 + mtf - k(yl-y3-c) = F^ (4)
donde yt — y2 — y3 = b = constante.
Suponiendo que las fuerzas impulsoras se aplican en (a), Fy = /i + f2 y Fy = -U (nótese que
Fy no es igual a su valor en el caso anterior). Remplazando estas relaciones en (3) y (4) y hallando la solución
del sistema de ecuaciones simultáneas, se obtienen las expresiones ya determinadas para f\ y f2.
(c) Por último, determínense f\ y f2 suponiendo que /i se aplica igual que antes pero f2 se ejerce por medio
de un mecanismo que está sujeto al piso.
Con tal fin es importante notar que puede utilizarse, bien el sistema (1) y (2) o (3) y (4). Tomando
/i = HV2 ~ W - miS y fi = (m2a2 — k)(y2 — l0) + m2g
El lector debe demostrar que pueden obtenerse las mismas expresiones, empleando (1) y (2).
La razón por la cual las expresiones de f\ y f-¿ no son iguales al caso especificado en (a), a pesar de
que los movimientos supuestos son idénticos, se debe a la diferencia en la forma de aplicar f2.
Ejemplo 13.2. Fuerzas requeridas para darle a la palanqueta de la figura 13-3, un movimiento arbitrario en el
plano vertical.
282 FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [CAP. 13
Utilizando las coordenadas x,y y 9, la ecuación (13.1) conduce a
Mx = F'x, My + Mg = Fy, l'$ = F'e
donde M = mi + m2.
Supóngase que las fuerzas /, y fy se aplican a mi en las direcciones de x\ y y\, respectivamente, y
que fy se aplica a m2 en la dirección dey2. En este caso,
K = /*,, K = fH + fH, Fe = fXlh sen* + (fy^-fy.h) cosí
(/)
(2)
Palanqueta libre de moverse en el plano vertical, bajo la acción
de la gravedad y sujeta a fuerzas aplicadas externamente.
Fig.13-3
Por (1) y (2), fXl = Mx,
_ M(y + g)l2 cosí - le' + Mxlt sen*
/vi ~ (lx +12) eos e
_ M(y + g)lt cose + i'é — Mxl1sene
/v2 ~ (lx + l2) eos 6
(4)
Por tanto, para cualquier conjunto de movimientos supuestos, las fuerzas requeridas se obtienen de inmediato
en función del tiempo.
Considérese otra posibilidad con respecto a la aplicación de las fuerzas. Supóngase que fx y fy se aplican
en el c.m. y que dos fuerzas iguales y con direcciones opuestas, /, se aplican perpendicularmente a la varilla a
distancias iguales, s/2, del c.m. Entonces,
K = fx, K = fv y Fe = sf
(5)
Así, (1) y (5) conducen de inmediato a las expresiones generales de las fuerzas impulsoras necesarias, para un
movimiento deseado arbitrario.
Ejemplo 13.3.
La fuerza /, de la figura 4-11, es tal, que el carro oscila de acuerdo con la relación x = xo + A sen («ií + Si).
Un mecanismo liviano adherido a la parte inferior del plano inclinado ejerce una fuerza fq en la dirección de q,
haciendo que m oscile según q = q0 + B sen (u2t + S2). Se trata de determinar las expresiones requeridas
de / y /,.
En este sistema,
T = $(M1 + 4M + 47/r2 + m)x* + $m(q2 - 2xq eos e)
Por tanto,
(Mx + 4M+ 47/r2 + m) x - mq eos $ = Fx = / y m( q - x eos 6) + k(q - q0) - mg sen $ = F'q - fq
En el caso de los movimientos supuestos, ic = — uix y 'q = — J^q. Por último,
/ = -co^Mi + 4M + 47/r2 + m)x + mw\q eos $
fq = m{¿[x eos $ — u\q) + k(q — q0) — mg sen $
Naturalmente, f y fq pueden escribirse en función del tiempo.
CAP. 13] FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS 283
Ejemplo 13.4.
En la figura 13-4 una masa puede deslizarse
libremente a lo largo de una varilla lisa inclinada,
sostenida rígidamente sobre un carro, cuya masa
total es M. El carro puede moverse libremente a
lo largo de una pista recta horizontal. Por
aplicación de las fuerzas apropiadas, el carro puede
suponer un tipo cualquiera de movimiento
horizontal, al mismo tiempo que m puede moverse de
una manera arbitraria a lo largo de la varilla. El
sistema tiene dos grados de libertad y por tanto 9//////////////^^^
se requieren dos fuerzas controladas
independientemente. Algunas de las formas posibles de aplicar Fig. 13-4
las fuerzas impulsoras se indican por fi,f2 y f3. En la figura, un pequeño círculo dibujado en el origen de los
vectores de las fuerzas, indica la localización del correspondiente mecanismo impulsor.
Nótese que el movimiento prescrito puede ser producido por los valores adecuados de cualquiera de los pares
de fuerzas, (/i./i). (/1./3) y (f2,fi)\ y en el proceso de determinar las expresiones de las fuerzas, puede
emplearse cualquiera de los conjuntos de coordenadas (xi.s), (xi,x) o (x, s).
Tomando las coordenadas (x, s),
T = $(M + bhn)a* + £m(l + 62)¿2 - mb2xs
donde, como puede verse en la figura, b = y/xi = tañí. Aplicando (73.7) se encuentra,
K (J)
(2)
(M 4- bhn) 8 — mb2 x — mgb
w(l + 62) x - mb2 8 + mgb - F'x
que pueden ser aplicadas independientemente del par de fuerzas que se hayan seleccionado o del tipo de
movimiento que se haya supuesto.
Si actúan /i y ¡2, F't = /i — f2 (nótese que el mecanismo que ejerce la fuerza fa, empuja hacia ade
lante a m y hacia atrás el carro) y
F¡ = f2. Así, por (7) y (2),
ft — M'i + mx
f2 = m(l + b2)x - mb2'i + mgb
(3)
(4)
Hasta este momento no se ha especificado el tipo de movimiento. Pero naturalmente, las expresiones (3) y
(4) determinarán f\ y f2 en función del tiempo, para cualquier tipo de movimiento que se desee suponer.
Si se supone que fi,fí y f* actúan simultáneamente, el número de ecuaciones es insuficiente para hallar
valores independientes para cada una de las fuerzas. Sin embargo, las tres fuerzas aparecerán en F[ y F'x de
(7) y (2). Así, si se especifica una de las fuerzas, las otras dos podrán ser halladas.
Ejemplo 13.5.
Considérense las fuerzas requeridas para producir un movimiento determinado para m con respecto al
marco X2, Y2 de la figura 2-21, para rotaciones arbitrarias de Di y D2.
Por la ecuación (2.37) se concluye que
T = $m{r* + r2¿2 + [28¿, sen ($2 + «)]r + [2r2(¿, + ¿2) + 2s5,r eos (62 + a)]á
+ [r*{$y + ¿2)2 + 2«r¿1(51 + é2) eos (62 + a) + 82¿2]}
Para rotaciones especificadas de Di y D2, *i y 92 pueden ser remplazadas por funciones de t. (Por ejemplo,
suponiendo 8\ = éoí + \at2 y 02 = A sen («í + fi), se tiene, $x = 50 + at y $2 = Awcos («t + b). Por
tanto, es evidente, sin entrar en mayores detalles, que la aplicación de (73.7) conduce de inmediato a las expresiones
de las fuerzas requeridas para dar a m el movimiento deseado con respecto a X2, Y2 (por ejemplo fr aplicada
en la dirección de r, y /„ en la dirección en que a aumenta). (Véase el problema 13.5.)
Nótese la facilidad con que este método tiene en cuenta completamente las rotaciones de Di y D2 en
las expresiones de las fuerzas requeridas. Resulta claro que una extensión del procedimiento descrito conduciría a
las expresiones de las fuerzas requeridas para hacer que las partículas o los cuerpos rígidos de un sistema bien
complejo, se muevan de una manera arbitraria con respecto a los ejes X2, Y2 y Z2, adheridos a D2.
13.4 Equilibrio de un sistema.
(Caso especial del problema general tratado en el numeral 13.2.)
El tema del equilibrio trata las fuerzas requeridas para mantener los objetos en reposo,
284 FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [ CAP. 13
casi siempre con respecto a un marco de referencia estacionario, y en ocasiones con respecto a
un marco en movimiento o con restricciones móviles. Obviamente, esta materia es un caso
especial del que acaba de analizarse, con la condición de que ciertos, o todos los movimientos,
sean permanentemente nulos. Pueden presentarse dos tipos generales de problemas: (a) si se
conocen las fuerzas que actúan sobre el sistema, se trata de determinar si éste permanece
en equilibrio y en tal caso, hallar los valores de las coordenadas para los que se cumple la
condición de equilibrio; (fe) hallar las fuerzas requeridas para sostener las masas de un sistema
en ciertas posiciones determinadas. Además, en cualquiera de los dos casos, es posible que se
deseen determinar las fuerzas de restricción.
Ecuaciones de Lagrange para condiciones estáticas: Suponiendo coordenadas móviles, o
restricciones móviles, o las dos condiciones simultáneamente, T tendrá la forma (véase la
ecuación {2.55)
T = ± Ajkqt + ± Bkqk + C
k.l k = í
dT n
Así, —— = 2 y) ATlq. + BT y además
BqT i=i
i® = 2sá^* + 2liA-?- + iw
u)
Como en general, Br = Br(q\,q-2, . . -,(?„;£),
d /r> x _ dBr . BBr . , a5,. BBt
Bt
3C
Tt^ = nr^ + *r*« + •"• + w%q*+ -w (2)
g = S5(^)w. + Íl(eH + g
(3)
Si se supone ahora que todos los valores de q y q son iguales a cero, por (7), (2) y (3) se
concluye que (13.1) se reduce a
que, ya que r = 1, 2, . . ., n, representa n ecuaciones diferentes.
La relación {13.2) es un instrumento general muy poderoso. Envuelve casi completamente
el campo entero del equilibrio ("estática") en forma compacta. Naturalmente, la ecuación es
válida aun cuando el marco de referencia, las restricciones, o ambas, están en movimiento.
Puede emplearse cualquier tipo de coordenadas. La mayor parte de los principios "elementales"
usuales y los métodos de la estática, que frecuentemente reciben atención considerable en los
textos intermedios, quedan incluidos automáticamente en (13.2). Además, la expresión es
de aplicación sencilla.
Aspectos importantes sobre la aplicación de {13.2):
(a) En una expresión cualquiera de T, los términos Br y C se reconocen con facilidad. (Son
iguales a cero si no hay coordenadas móviles ni restricciones móviles; véase la expresión
(2), del ejemplo 13.5.)
(fe) FqT y F'qT son las fuerzas generalizadas que ya se conocen y que se tratan exactamente
de la misma manera como en los ejemplos anteriores del presente capítulo.
(c) En general, Br y C (y por tanto dBT/dt y dC/BqT) son funciones de las coordenadas y
de t. (Véase la deducción de la relación (2.55).) Por tanto, resulta claro que las
soluciones de (73.2), consideradas como ecuaciones algebraicas, determinan las fuerzas por
conocer fitfz, ■-,/„, en función de las q y t.
CAP. 13| FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS 285
(d) Si ni el marco de referencia ni las restricciones están en movimiento, Br = 0 y C = 0.
Por tanto, {13.2) se reduce a
F«r + Kr = 0 (13.3)
En este caso no se necesita tener en cuenta a T.
(e) Al introducir coordenadas superfluas y seguir el procedimiento descrito en el capítulo 12,
pueden encontrarse en forma explícita las fuerzas de restricción que ahora quedarán
incluidas en FqT.
13.5 Ejemplos ilustrativos de problemas en equilibrio estático.
Ejemplo 13.6.
Con el objeto de demostrar fácilmente una idea básica, nótese que al hacer x = y = $ — 0 en el ejemplo 13.2,
las ecuaciones (3) y (4) conducen en seguida a las fuerzas,
/.» = O' /»»
Mgl2
h + k
Mgh
h + h '
requeridas para conservar en equilibrio la palanqueta.
Obsérvese que los ejemplos, desde el 13.1 hasta el 13.5, servirían para ilustrar casos de estática al hacer las
aceleraciones y las velocidades iguales a cero.
Ejemplo 13.7.
Una varilla uniforme de longitud 2/ y masa total M, puede deslizarse libremente en contacto con un alambre
semicircular fijo y liso como se muestra en la figura 13-5, bajo la acción de la gravedad. Se trata de encontrar el
ángulo 8 bajo el cual la varilla permanecería en reposo. F'e = 0 y como puede verse,
Así, aplicando (13.2),
dV
Fe =
de
V = -Mgy = -Mg[(2R eos 9 - l) sen 6]
= Mg[2R(2 eos2 6 - 1) - l eos $] = 0 de donde eos $
l + Vi2 + 32E2
¿Habrá una limitación en el valor de l/R ? (l/R £ 2)
Alambre liso semicircular,
fijo en- el espacio
r = 2Acos0
y = (2R eos e - l) sen e
£ = (2R eos e - l) eos 0
o = 1 - 2 eos2 0
a = 2 sen 0 eos 0
Fig.13-5
Como extensión de este ejemplo, supóngase que el alambre semicircular se mueve con aceleración constante
ax en la dirección positiva de X; hallar el valor de equilibrio de 8. En este caso se escribe
* = x0 + vxt + %axt2 + (2R eos í-í)cosí y y = (2R eos $ - J) sen $
Por tanto,
T = $M[(vx + axt - 4Re sen e eos e + le sene)2 + (2Re - 4Re sen2* - le eos e)2] + $Ie2
en donde puede verse que
Be = M[(vx + axt)(l sen e - 4R sen e eos e)] y Cg = $M{vx + axt)2
286 FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [CAP. 13
Aplicando (13.2), se concluye que, (a, sen* + gcosfl) (4/? eos* - l) = 2gR de donde puede determinarse 8 por
métodos gráficos. Nótese que ox = 0, lo cual conduce a la misma expresión de eos 0, ya encontrada.
El lector puede demostrar que, si se ha de sostener la varilla formando un ángulo 0, por medio de una
fuerza / aplicada al extremo inferior, tangente al círculo en sentido horario, / estará dada por
M(axsene + g eos e)(l - 4R eos *) + 2MgR = 2Rf
Nota. Es preciso tener cuidado al escribir 8We.
Ejemplo 13.8.
Una partícula puede moverse libremente bajo la acción de la gravedad en el interior de un recipiente semi-
esférico de radio R, como se muestra en la figura 13-6. El recipiente, fijo al brazo rígido de longitud /, es obligado
a girar con velocidad angular ¿ alrededor del .eje vertical ab. Se trata de encontrar la posición de equilibrio de la
partícula, suponiendo que a = u = constante.
Los ejes Xt,Yi y Zi son estacionarios. El sistema X2, Y2 y Z2 se encuentra adherido al brazo.
Por simple inspección,
Xy = l cosa + iísen* cos(a + <t>), y yy = ¿sena + iísen*sen(a + $), z, = R — R cosí
de donde
T = \m[R2$2 + (R2serfi *)¿2 + (2lRa eos 6 sen <f>)e
+ 2Rá(Rsen* * + ísen* eos <f>)$ + (í2 + #2sen2 * + 21Rsen* eos<p)a2]
X3,Yi en el plano X,V,
X2.Y2.Z1 adherido al brazo
Fig.13-6
Se observa aquí que
Be = rñlRa cosí sen¿, B^ = mRa(Rsen** + l sen* cos¿), C = ^7n(P + R* sen** + 2lR sen* cos^ó2
Para ó constante, dBJdt = dB^/Bt = 0. Pero
dC • dC •
— = m(R2 sen * eos $ + IR eos 6 eos <f>)á2, — = (—mlR sen * sen <p)a2
Aplicando (13.2), —tm(jR2 sen * eos * + IR eos fi eos <f>)a2 = — mgR sen 6
mlR sen* sen<¡> a2 = 0
(2)
(3)
Para el caso en que sen * ?¿ 0, por (3) se tiene, sen 0=0. Haciendo eos 0=1, (2) finalmente conduce a
£tan*= á2(R sene + l) que puede resolverse gráficamente con facilidad, para hallar el valor de 8.
Ejemplo 13.9.
Determínense las fuerzas necesarias para sostener una partícula estacionaria con respecto a D2 en el sistema
de la figura 2-21. Partiendo de la expresión general de T, dada en el ejemplo 13.5, se observa que
CAP. 13] FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS 287
BT = ms$i sen(*2 + a) (/)
Ba = mr2($i + 92) + mséir eos (92 + a) (2)
C = %m[i*{9x + *2)2 + 2aSi(éi + 92)r eos (92 + a) + s*92] (3)
Para cualquier tipo de rotaciones especificadas, se pueden remplazar 6ít 82 y 62 en (/), (2) y (3) por las funciones
específicas de t. Suponiendo ahora, por ejemplo, que las fuerzas fr y /„ actúan sobre m en la dirección de r y
en la dirección en que a aumenta, respectivamente, resulta claro que
determinan estas fuerzas en función de r, a y t.
Suponiendo que 8X = axt + £M2 y que 82 = a2t + ,íb2t2, hállense las expresiones de fr y fa en
función del tiempo, para el caso en que a = 30°.
Ejemplo 13.10.
Hállense las fuerzas de reacción sobre la varilla del ejemplo 13.7, figura 13-5. Se supone que una de las fuerzas
de reacción, fr, actúa sobre la varilla en p\ dirigida hacia el centro del círculo y que la otra, /i, actúa en
dirección normal a la varilla en p2. Considerando que la varilla puede moverse "libremente" en el plano XY,
T = £M(í2 + ¿2) + £J¿2
lo cual contiene dos coordenadas superfluas. Las ecuaciones del movimiento son, sencillamente,
Mi = Fx, My = Fy e i'i = Fe
Por inspección, se observa que las fuerzas generalizadas son
Fx = fx sen 9 + fT sen a, Fy = Mg — fx eos 9 - fT eos a y Fg = fx(2R eos 9 — l) - frl sen $
Suponiendo entonces que la barra está en reposo, se obtiene
fr = Mg tan 9, ft = Mg l ^^ ) y eos 9 = g¿j
como se había determinado anteriormente.
Problemas
13.1. Se imprime movimiento al sistema de la figura 13-7 por medio de una fuerza fx aplicada al furgón (que
se encuentra colocado sobre una pista lisa horizontal) y un torque fg ejercido por la armadura del motor.
Demostrar que para ciertos movimientos determinados, fz y fe están dados por
fx = M'x — mr9 sen 9 — mr92 eos 9
fg = 19' — mrx sen* + mgr eos 9 — mrx9 eos 9
donde M es la masa del sistema completo; / el momento de inercia total de la armadura y el brazo, con
relación al eje de giro; m es la masa del brazo y r es la distancia desde el eje de giro hasta el centro de
masa del brazo.
Suponiendo una velocidad constante u para el motor y suponiendo además que el furgón se
mueve con aceleración a en la dirección de x, hallar las expresiones para fx y fe- Repítase para el caso en
que x = A sen («ií + 5) y 9 = «.
288
FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [CAP. 13
X
j—\ Motor
*/^s
s*CM
1.
i v— m
1__ i
l
S~\ /~v
U.
^
_» /
Fig. 13-7
(a) Suponiendo que solamente /i y ¡3 actúan sobre el sistema analizado en el ejemplo 13.4, hallar
las expresiones generales de estas fuerzas para cualquier tipo de movimiento. (Respuesta. Las
ecuaciones (/) y (2), del ejemplo 13.4 con F's = fx y F'x = /8.)
(b) Repítase (a) para el caso en que actúan f2 y {3. (Respuesta. La misma anterior con F/= — f-¿ y
Fi=f2 + f3.)
(c) Repítanse (a) y (b), utilizando las coordenadas (xi, s). Demostrar que los resultados son los mismos
ya obtenidos.
(a) Un mecanismo adherido a mi, de la figura 6-5, (véase el ejemplo 6.14) ejerce sobre m3 una fuerza
horizontal f3. Por medio de dispositivos adheridos al plano fijo sobre el que descansan mi y m2,
se ejercen las fuerzas f\ y J2 sobre mi y m2, respectivamente. Suponiendo que las fuerzas di-
sipativas debidas a los amortiguadores y a los contactos de mi y m.2 con el plano son todas
viscosas, demostrar que para cualquier movimiento supuesto por el sistema, f\, fa y fs se
determinan por medio de,
(ml + m3)xl + m3q2 + b1xl + a2(xl + q2 — x2) —
w^ x2 + b2x2 + a2(x2 — Xi — q2) = f2
Wjí^+'ijj) + ai¿2 + a2(xy¥q2-x2) = f3
fx
donde at y 02 son los coeficientes de la resistencia viscosa en los pistones; y 61 y 62 son los
coeficientes correspondientes a las bases de mi y m2, respectivamente. Nótese que se han ignorado
los resortes que aparecen en la figura.
(b) Suponiendo que mi y m2 se mueven ambas con velocidades uniformes iguales hacia la derecha
y que 92 = A + B sen ut, demostrar que
fi =. —7n3«22? senut + c2aB eos ut + b]SB|
f2 = —a2uB eos ut + b2x2
f3 — —mquPB sen ut + (at + a2)uB eos ut
(c) Demostrar que si el mecanismo que ejerce la fuerza f2 está adherido a mi, se debe remplazar f\
del lado derecho de la primera ecuación por f\ — fi y que las otras ecuaciones permanecen
invariables.
El disco uniforme D, de la figura 13-8, que tiene una partícula no equilibrada, de masa m, pegada a su
periferia según se indica, se hace girar alrededor del eje horizontal cd por un motor (que no se indica en
la figura). El torque aplicado por el motor es^. Al mismo tiempo, puede hacerse girar el eje vertical por
medio de una fuerza F (torque t^) aplicada a la manivela C.
Ignorando el motor, demostrar que L para el sistema está dado por
L = £[/i¿2 + m(R2 + r2 eos2 <fi)f2 + 2Rr$í sen <f> + (72 + mr2)^2] - mgr sen <p
CAP. 13] FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS 289
Fig.13-8
en donde h es el momento de inercia del sistema completo (sin incluir a m) con respecto al eje vertical
AB e I2 es el momento de inercia de D, con respecto al eje cd.
Escribir las expresiones para hallar t¿ y t^ para cualquier tipo de movimientos que se deseen.
Suponiendo <t> = «ií + <j>0 y ^ = ^0 sen («2í + fi), donde <oi, <f>o, ipo, «2 y fi son constantes,
-hallar las expresiones de r¿ y r^.
La partícula m, de la figura 2-21, se hace mover en un círculo de radio r, con velocidad angular constante
á = «3. Suponiendo que $\ = un y e2 = a2 son constantes, demostrar que las fuerzas requeridas son
(véase el ejemplo 13.5)
fr = — mrfa + w2 + «3)2 — tnsJ^ eos («2 + u3)í y fa - = msrw\ sen (u2 + u3)t
Un tablero plano, de masa total M y momento de inercia /, con relación a un eje perpendicular a su
superficie que pasa por el c.m., puede deslizarse libremente en contacto con el plano X2Y2, figura 2-21.
Demostrar que su energía cinética está dada por T = Ti + £/(¿i + 92 + O3)2, donde 7\ es la
expresión dada en el ejemplo 13.5 remplazando m por M. En este caso, r y a localizan el c.m. y e3 es el
desplazamiento angular del tablero con respecto a X2.
Demostrar que la fuerza requerida para imprimir un movimiento cualquiera al c.m. es la misma
que se requiere para una sola partícula de masa M. Demostrar que para 0\ y 92 constantes, el torque
requerido para dar al tablero una aceleración angular cualquiera, 63, es sencillamente 103.
Se trata de darle a una palanqueta, un movimiento cualquiera con respecto al marco X\,Y\,Z\, de
la figura 14-2. Describir brevemente las etapas necesarias para hallar las fuerzas requeridas, teniendo
en cuenta la rotación diaria de la Tierra (véase el numeral 14.8).
La base que sostiene los discos Di y D2, de la figura 2-21, está localizada en el origen de coordenadas
de la figura 14-2. Debe dársele a la partícula un movimiento cualquiera con respecto a los ejes X2 y Y2,
indicados sobre D2. Describir brevemente las etapas requeridas para hallar las fuerzas necesarias fr y
/„, teniendo en cuenta la.rotación diaria de la Tierra y también las rotaciones de Di y D2.
Demostrar que para el caso en que $ tenga un valor constante, una fuerza, fz = mg — m$2/2a,
aplicada a m en una dirección paralela a Z, hará que esta masa se conserve siempre en el mismo punto
del alambre. Nótese que para el caso en que 9 — "\/2ga, se tiene f2 = 0.
Demostrar que si la fuerza se aplica en la dirección de r, fr = Irrigar — mr82.
290 FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [CAP. 13
En el ejemplo 13.8, figura 13-6, las fuerzas fg y /$ se aplican a m en las direcciones en que 0 y <¡>
aumentan, respectivamente. Demostrar que las expresiones de fg y /^ que se requieren para sostener a m
en reposo con respecto al recipiente, en una posición cualquiera (0,<f>) son,
fe = mff sen $ — m{R sen $ eos $ + l eos 6 eos #)á2 y /$ = mlá2 sen <f>
13.11. Demostrar que para una velocidad angular constante, «, del eje vertical, figura 3-9 (véase el problema
k(l — ¿o) ~ mO eos $
3.14), la posición de equilibrio de m estará dada por r =
k — mw2 sen2 $
Las fuerzas fx,fy y fz se. aplican a la partícula de la figura 3-16 (véase el problema 3.27).
Demostrar que para este sistema, C (el tercer término de la expresión general de T), viene dado por (véase
la ecuación (14.15)),
C = |mu2[i2 + y2 sen 2 <p + (r + z)2 eos2 <f> - 2y(r + z) sen <f> eos <f>]
y por tanto, que con el fin de conservar la partícula en reposo con respecto al marco X2, Yi,Z2
(despreciando la gravedad),
fx - —rru>2x, fy — —mw2[y sen2 <t> - (r + 2) sen <f> eos <f>] y fz = -mw2[(r + z) cosz<f> — y sen <t> cos<f>]
Un tablero (de masa total M y momento
de inercia / relativo a un eje que pasa por
el c.m.) está colocado sobre un cilindro
rugoso de radio R, como se indica en la
figura 13-9. Demostrar que
T= $MR2(e - 60)2'e2 + $l62
(donde 60 es el valor de 8 cuando el
c.m. está en contacto con el cilindro).
Demostrar que la energía potencial viene
dada por
V = MgR[sen $ — (e - e0) eos 6]
y por último, suponiendo que no hay
deslizamiento, demostrar que 0O es la
posición angular de equilibrio.
Fig.13-9
Dos barras uniformes de masas y longitudes {M\,2l\) y (M2,2li), respectivamente, se encuentran
articuladas en un extremo y pueden deslizarse libremente en contacto con una varilla semicircular como
se indica en la figura 13-10. Demostrar que
V = Mxglx sen $ + M^gl^ eos $ — 2(M, + M2)gR sen $ eos $
y que el ángulo $ para el cual se presenta el equilibrio, está representado por
2(Mt + M¿R eos e - M,i,
tanfi =
¿Cómo podrá evaluarse el ángulo 0?
2{Ml + M¿R sen $ - M2l2
se mueve sobre una
guía vertical fija.
13-11 VAa'/////////////////////by
CAP. 13] FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS 291
13.15. Dos varillas cuyas longitudes y masas son (Li.Mi) y (L2,M2), respectivamente, se encuentran
articuladas en p3 como se indica en la figura 13-11. Las masas mi y rm están sostenidas por un hilo
que pasa sobre las pequeñas poleas px y p2. La distancia lt = pip3 y h = P2P3 además, p3a = p3b.
El resorte (de longitud normal, r0) y la gravedad, son los agentes que ejercen fuerzas sobre el sistema.
Las "patas" a y b permanecen en contacto con el piso liso. La articulación p3 se mueve sobre una guía
vertical lisa. Demostrar que
V = (M18l + M2s2 + mxhx + m2L2)g eos 6 + (m2 — m^gy
+ m2ffV\ + l\ + *hk ~ *hh eos2*)1'2 + ¿*[(L, ~ *i) eos 8 - c]*
donde c es una constante.
Escribir las dos ecuaciones que determinan el equilibrio del sistema. ¿Será posible el equilibrio para
Si se conocen los valores numéricos de todas las constantes del sistema, ¿cómo podrá hallarse el
valor de 8 correspondiente al punto de equilibrio?
13.16. Considerando que el punto p de la fígura 4-13 es una articulación esférica, supóngase que el sistema oscila
en el espacio alrededor de la recta vertical punteada. Despreciando la masa de la varilla y considerando
a mi y m2 como partículas, demostrar que en coordenadas esféricas,
T = ^m^rfó + r* sen2 8$2) + $m2(% + r%6* + r\ sen2 »¿*)
Supóngase ahora un estado de "movimiento estacionario" en el que í, r2 y 4> son constantes.
Demostrar que los valores de r2,8 y ¿ correspondientes al movimiento estacionario, se determinan
por medio de las siguientes relaciones
7n2r2sen20¿2 = k(r2 — r0) — macóse
{mxr\ + m2rl) eos 0¿2 = (m,rj + tn^r^g
(7n,r2 + 7n2r2)sen20¿ = P^ — constante
(/)
(2)
(3)
donde P¿ es el momentum angular correspondiente a <f>.
Nótese que para un determinado valor de ¿ (el cual, por (2) debe sobrepasar cierto mínimo), (1)
y (2) pueden combinarse para hallar los valores de 8 y- r2 correspondientes al movimiento estacionario.
En la fígura 13-12, la "partícula" de masa m se mueve en el plano XY, alrededor de la masa fija M,
bajo la acción de una "fuerza central", fr, la cual actúa en la dirección de r. La fuerza fr es cierta
función de r (no es necesariamente función del inverso del cuadrado) y se supone que no existe ninguna otra
fuerza actuando. Las ecuaciones del movimiento serán
(í) mr — mr82 = fr (2)
donde Pq es el momentum angular correspondiente a 8.
P0 — mr28 = constante
Problema de fuerza central
/, - fAD y fe - 0 I
f, puede ser positiva (repulsión)
o negativa (atracción)
Fig. 13-12
292
FUERZAS IMPULSORAS PARA PRODUCIR MOVIMIENTOS DEFINIDOS [CAP. 13
(a) Eliminando 6 de (/) y (2), escribiendo -tr = 37 -r- = —¿ 37 • y finalmente, sustituyendo u = 1/r,
Eliminando ¿ de (/) y
(2),
demostrar que la ecuación
escribiendo -jr =
diferencial de la \
dhi
de* ~*~
de d _
dí de
trayectoria
u = -
mr2 de
i será
mfT
"pW
(3)
(b) Suponiendo que la trayectoria es una sección cónica, r = —— —, en donde < es la
excentricidad y A es una constante que depende de las constantes del sistema y de las condiciones iniciales,
demostrar que fr= — Pg/mAr2. (Si la trayectoria es una elipse, una parábola o una hipérbola,
depende de las condiciones iniciales; en cualquier caso fr es proporcional a 1/r2.)
P¡r
(c) Si la trayectoria es una hipérbola rectangular, xy = C, demostrar que fT = +-——.
4mCz
(d) En el caso en que la trayectoria descrita por m fuese una cardioide, r = a(l + cosí), demostrar
que ir = — 3Pga/mr4. Trácese la órbita.
(e) Demostrar que para el círculo r= la eos 6, se tiene fr = —8a2Pl/mrs.
13.18. Suponiendo que á = bt (b es una constante), en el ejemplo 13.8, hallar las componentes de la fuerza
requerida para conservar a m en el recipiente, en un punto en el cual 8 = 45° y <t> = 30°.
CAPITULO
14
Efectos de la forma de la Tierra
y de su rotación cotidiana en los
problemas de la dinámica
14.1 Observaciones introductorias.
El análisis de precisión del movimiento de una partícula o de un cuerpo rígido, con
respecto a la superficie de la Tierra, requiere cuidadosas consideraciones sobre los siguientes
tópicos.
(a) Debido a la rotación anual de la Tierra alrededor del Sol, a su rotación cotidiana
alrededor del eje polar y a los ligeros movimientos de este eje, un marco de referencia
adherido a la superficie de la Tierra no es inercial.
(b) La Tierra no es esférica como se supone con frecuencia, sino ligeramente achatada hacia
los polos. La superficie del "nivel del mar" se aproxima con bastante precisión a un
elipsoide de revolución cuyo eje coincide con el eje polar (Fig. 14-1).
Polo N
Nota: Como a es muy pequeño, an
realidad g tiene una dirección entre
Ri y R.
Elipsoide "internacional" o de referencia
Fig. 14-1
(c) Como resultado de esta forma, la aceleración verdadera de la gravedad, g, (debida
exclusivamente a la atracción de la Tierra) varía en magnitud y en dirección con la
latitud. Pero como la Tierra es prácticamente simétrica con respecto al eje polar, usual-
mente se considera que g es independiente de la longitud. En ciertas localidades el
valor de g se encuentra afectado por la presencia de cordilleras, variaciones en la
densidad de la corteza terrestre, etc. Estas "anomalías" gravitacionales, en algunos casos
resultan importantes.
293
294 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
(d) Debido a la rotación de la Tierra, y en consecuencia, a la fuerza centrífuga ejercida
sobre todos los objetos, el péndulo y la plomada dan un valor ficticio de la gravedad,
g', el cual, excepto en los polos, tiene una dirección ligeramente diferente, y un valor
inferior en magnitud, con relación a g.
(e) La forma elipsoidal de la Tierra hace deseable, aunque no siempre necesario, emplear
valores geográficos de la latitud y el radio, én lugar de las correspondientes magnitudes
geocéntricas. (Estos términos se definen y estudian en el numeral 14.2.)
(/) Como se verá con claridad, las expresiones de la energía cinética no se afectan por la
forma de la Tierra o su campo gravitatorio. Suponiendo el marco de referencia adherido
a la Tierra, la forma particular supuesta por T depende de ue (la velocidad angular
de la Tierra) y de la orientación del marco, pero no de la forma de la Tierra.
(g) Es importante tener en cuenta que en la determinación de las fuerzas generalizadas
que incluyen la gravedad, debe emplearse la g verdadera y no g' (véase el numeral 4.5).
(h) La rotación anual de la Tierra alrededor del Sol, normalmente se ignora excepto en los
estudios relacionados con satélites. El movimiento del eje polar es completamente
despreciable. Las anomalías gravitatorias dependen de las condiciones locales y deben
determinarse experimentalmente en el sitio. Por tanto no se incluyen mayores análisis
de estos tópicos. Además, no se^hace ningún intento para analizar los efectos de "forma
de pera" de la Tierra, ni de las demás ligeras desviaciones de su forma con respecto a
la de un elipsoide de revolución. Si tales distorsiones existen, son en realidad muy
pequeñas. En las referencias del numeral 14.5, véase la página 79 de la referencia (7) y la
página 286 de la referencia (12).
14.2 Consideraciones sobre la forma de la Tierra. Latitudes y radios geocéntricos
y geográficos.
A través de los tiempos, la acción combinada de la gravedad y de la fuerza centrífuga
han dado a la Tierra su forma prácticamente elíptica. Mediciones hechas con precisión,
junto con consideraciones teóricas, demuestran que la superficie media del nivel del mar de
la Tierra se aproxima con mucha precisión a la forma de un elipsoide de revolución
(denominado elipsoide de referencia o esferoide de referencia) generado por la rotación de la elipse
Ri = 6(1 — t2 cos2*i)_1/2 (véase la figura 14-1) alrededor del eje polar, en donde t2 =
(a2 — ¿>2)/a2, a es el radio ecuatorial, b es el radio polar y R\ y *i se miden como se
indica y se denominan radio y latitud geocéntricos, respectivamente.
En el estudio de muchos problemas (pero no en todos) el marco adherido a la Tierra,
Xi, Yi, Zi, indicado en la figura 14-1 y en la figura 14-2, resulta muy conveniente. Y\ es
tangente al meridiano que pasa por 0\ y extendido cortaría al eje polar. Z\ es perpendicular
a la superficie (normal a la superficie del agua en ese punto) en 0\. Extendida hacia atrás,
la recta Z\ corta al eje polar en el punto 0->. X\ es normal al plano Y1Z1 y está
dirigido hacia el oriente.
Ahora, R, definido por la recta O2O1, se denomina radio geográfico y *, medido
según se indica, es la latitud geográfica. (En ocasiones se utiliza el término geodésico en lugar
de geográfico.) Se observa que en el ecuador, *i = * y R\ = R, pero en general, existen
diferencias significativas entre los valores geocéntricos y geográficos. Las relaciones entre
estas magnitudes se verán en el numeral 14.4 (véase la tabla 14.1).
14.3 Aceleración de la gravedad sobre la superficie de la Tierra o cerca de ella-
Como ya se ha mencionado, es conveniente tratar dos valores distintos de la gravedad,
los cuales varían en magnitud y dirección con la latitud, pero son independientes de la
longitud: (a) el valor de g "verdadero" debido únicamente a la atracción de la gravedad de la
Tierra (cuyo valor se determinaría por un péndulo y una plomada, si la Tierra no estuviera
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 295
en rotación), y (fe) un valor ficticio, g', igual a la suma vectorial de g con la fuerza centrífuga
por unidad de masa, (confíeos*), debida a la rotación de la Tierra. La magnitud que
puede medirse en el laboratorio, con un péndulo simple y una plomada, por ejemplo, es g'.
Es de importancia que, ignorando las anomalías, g', es normal a la superficie del
elipsoide de referencia (normal a la superficie del agua en reposo) y tiene la dirección del eje Zi,
de la figura 14-1, en tanto que g se inclina ligeramente hacia el norte en el hemisferio norte,
en un ángulo a, con respecto a Z\. Suponiendo que la Tierra es simétrica con respecto al
eje polar, tanto g como g' están en el plano Y\Z\ (el .plano del meridiano). Como podrá
verse, las expresiones {14.11) que relacionan a g con g't se pueden obtener fácilmente.
14.4 Fórmulas de cálculo y algunas constantes.
Para conveniencia en el estudio de los problemas específicos, se incluyen las siguientes
constantes y fórmulas de cálculo. Se han tomado de las referencias mencionadas en el
numeral 14.5. En cada uno de los casos se indica la referencia específica y el número de la
página correspondiente. La anotación utilizada está de acuerdo con las figuras 14-1 y 14-2.
Radio ecuatorial, a = 6.378.388 metros. Referencias: (2), página 334; (5), página 2.
Radio polar, fe = 6.356.912 metros.
Achatamiento (o "elipticidad"), / = (a - b)/a. f = 1/297,0 = 0,0033670.
Referencias: (1), página 52; (5), página 25.
Velocidad angular de la Tierra con respecto a las estrellas fijas, ue = 7,29211 X
10-5 rad/seg. Referencias: (11), página 132. co2 = 5,3175 X 10~9, u¡2a = 3,392 cm/seg-.
El elipsoide de referencia puede escribirse en función de los valores geocéntricos como,
Rx = fe(l -£2cos2<l>i)-1/2 {14.1)
donde el cuadrado de la excentricidad es t2 = {a2 - b2)/a2 = 0,00672267. Referencia
(5), página 3. Nótese que 1 - f2 = b2/a2 = 0,99327733.
El radio geocéntrico, R\, en función de la latitud geográfica, *, es
fíi = 6.378.388(1 - 0,003367003 sen2 * + 0,000007085 sen2 2*) metros {14.2)
Referencia: (1), página 53, ecuación {3.53a). La ecuación {14.2) se denomina elipsoide
internacional.
Otra expresión de R\ es
fíi = 6.378.388(0,998320047 + 0,001683494 eos 2* - 0,000003549 eos 4* + • • •) metros (14.3)
Referencia: (4), parte II.
El radio geográfico, R, en función de la latitud geográfica * es,
R = a(l -£2sen2*)-1/2 (14.4)
Referencia: (8), página 101, ecuación (90). En forma completa,
R = a(l + ¿£2sen2* + f£4sen4* + • • •)
Utilizando la relación sen4 * = sen2 * — { sen2 2* y sustituyendo los valores numéricos
R = 6.378.388(1 + 0,003378283 sen2 * - 0,000004237 sen2 2*) metros (14.5)
Relación entre * y *i. Referencia: (8), página 98, ecuación (82).
a2
tan* = -^tan*! (14.6)
La diferencia, * — *i, en segundos, en función de * es
* - *i = 695,6635 sen 2* - 1,1731 sen 4* + 0,0026 sen 6* (14.7)
296 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
Referencia: (5), página 26, fórmula {20). O, en términos de *i,
*_<!>,= 695,6635 sen 2*i + 1,1731 sen 4*, + 0,0026 sen 6*i (14.8)
Referencia: (5), página 26, fórmula (23).
La gravedad, g', en función de la latitud geográfica * (determinada por un péndulo
en la superficie del elipsoide de referencia), es
g' = 978,049(1 + 0,0052884 sen2 * - 0,0000059 sen2 2*) (14.9)
Aquí, 978,049 es el valor de g' al nivel del mar, en un punto localizado en el ecuador, en
cm/seg2. La expresión (14.9) es la fórmula internacional de la gravedad. Referencia: (1),
página 53, ecuación {3.53b); además, (11), página 132, ecuación (15).
La gravedad, g'h, en un punto de altura h por encima del elipsoide de referencia, es
Sn = 8' ~ (0,30855+ 0,00022 eos 2<t> - 0,000072 h)h {14.10)
donde g', dada por (14.9), se toma en cm/seg2 y h, en kilómetros. Referencia (4), parte II;
además (3), página 105, ecuación {5.13).
Gravedad verdadera, g, en función de g', sobre la superficie de la Tierra. Nótese que g'
puede considerarse como la suma vectorial de g y el término centrífugo, cufíeos*.
Por tanto, por la figura 14-1 se concluye que
gsena = <**R sen* eos*, gcosa = g' + o>2fí eos2* (14.11)
*
«1 -
en metros
R
en metros
8
en cm/seg2
8
en cm/seg2
en cm/seg2
en minutos
en segundos
R - /?i
en metros
a - Ri
en metros
En el ecuador,
* = 0o
6.378.388 = a
6.378.388
978,049
981,441
3,392
0
0
0
0
30°
6.373.053
6.383.755
979,338
981,883
2,545
5,15
601,4463
10.702
5.335
45°
6.367.695
6.389.135
980,629
982,326
1,697
5,95
695,6609
21.430
10.693
60°
6.362.315
6.394.529
981,924
982,773
0,849
5,15
603,4782
32.214
16.073
En los polos,
* = 90°
6.356.912 = b
6.399.936
983,221
983,221
0
0
0
43.024
21.476
Cantidades importantes para el estuuio del movimiento
cerca de la superficie de la Tierra.
Tabla 14.1
CAP. 14| EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 297
donde a es el ángulo entre g y g'. Así, (véase el problema 14.33,)
„„ / sen 2* \
tana = $*2R( , , 2P r-J
2 e \g' + coicos2O/
Además, #2 = (#' +a,2fí eos2*)2 + (u^físen* eos*)2 osea
g* = g'2 + o,2fí COS2 *(25T' + t^R)
983
982
a>
^ 981
c
c
S 980
I
979
978
0o 20° 40° 60° 80°
Latitud geográfica
Gráfica 14.1
14.5 Referencias relacionadas con la forma de la Tierra y su campo gravitatorio.
1. W. A. Heiskanen y F. A. Vening Meinesz, The Earth and its Gravitational Field, McGraw-
Hill, 1958.
2. J. M. A. Danby, Fundamentáis of Celestial Mechanics, Macmillan, 1962.
3. R. A. Hirvonen, The Size and Shape of the Earth, {Aduances in Geophysics, volumen 5,
páginas 93 a 113), Academic Press, 1958.
4. R. Parvin, The Earth and Inertial Space, Aero/Space Engineering; parte I, abril de
1959; parte II, mayo de 1959.
5. W. D. Lambert y C. H. Swick, Formulas and Tables for the Computation of Geodetic
Positions on the International Ellipsoid, Spl. Pub. No. 200, U. S. Coast and Geodetic
Survey, 1935.
6. H. C. Mitchell, Definition of Terms Used in Geodetic and Other Surueys, Spl. Pub. No.
242, U. S. Coast and Geodetic Survey, 1948.
7. C. H. Swick, Pendulum Gravity Measurements and Isostatic Reductions, Spl. Pub. No.
232, U. S. Coast and Geodetic Survey, 1942.
8. W. Chauvenet, A Manual of Spherical and Practical Astronomy, Vol. I, Dover, 1960.
(14.12)
(14.13)
298 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
9. J. A. Duerksen, Deflections of the Vertical in the United States, Spl. Pub. No. 229,
U. S. Coast and Geodetic Survey, 1941.
10. J. A. O'Keefe, Geographical Positions, Smithsonian Institution, 1956.
11. H. Jeffreys, The Earth, 3a. ed., Cambridge University Press, 1952.
12. G. P. Wollard, Advances in Geophysics, Vol. 1, Páginas 281-300, Academic Press, 1952.
14.6 Energía cinética y ecuaciones del movimiento para una partícula en
diversos sistemas de coordenadas. Marco de referencia adherido a la
superficie de la Tierra.
Las deducciones siguientes ilustran bien ciertos principios básicos de la dinámica y
las expresiones resultantes son convenientes para la solución de una gran cantidad de
problemas.
A. Considérese el marco de la figura 14-2, X1Y1Z1, rígidamente adherido a la Tierra
con el origen en 0\. Vi es tangente al meridiano, Z\ es la extensión del radio
geográfico, R, (Zi es normal a la superficie del elipsoide de referencia, Oí), Xi es
perpendicular al plano Y\Z\ y está dirigido hacia el oriente. Los ejes X2, Y2 y Z2
con el origen adherido al eje de la Tierra en 02, no giran, permanentemente están
dirigidos hacia las mismas estrellas fijas. Se considera aquí que el marco X2, Y2, Z2
es inercial. Nótese que wet representa la rotación angular de la Tierra en un tiempo t.
En el diagrama puede verse que /3n, /3i2 y 0i3, los cosenos directores de Xi con
respecto a X2, Y2 y Z2, etc., están dados por
Pn = -sen^t, fil2 = coso,e¿, /?13 = 0
/?21 = -sen* cosweí, /?22 = -sen* sen^í, /?23 = eos*
/?31 = cos*coSo>eí, /?32 = cos*seno,ct, /?33 = sen*
continuación de R
y*
Adherido a la Tierra
Fig. 14-2
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 299
Nótese que la orientación del sistema Xi, Yi, Z\ con respecto a X2, Y2, Z¿
puede expresarse en función de los ángulos de Euler (véase la figura 8-16) donde wet =
\f/ — 90°, 6 = 90° — * y <f> = 0. Por tanto, las expresiones para 0 pueden ser chequeadas
de inmediato p"or medio de la tabla 8.2.
Se ve además que xo = R eos * eos wet, vo = R eos * sen uet y 20 = flsen*.
Por tanto las ecuaciones de trasformación que relacionan a x2, y2 y 22 con xi, y\ y 21,
serán
x2 — R eos * eos biet — ZjSent^t — yx sen* costi>e£ + zx eos* costi>c£
con expresiones semejantes para y2 y 22. Como se considera el marco X2, Y2, Z2,
inercial, T = \m{x\ + y\ + ¿§).
Tomando las derivadas de las relaciones correspondientes a x2, y2, y 22 y
sustituyéndolas en la expresión anterior, se obtiene finalmente,
T = hn{x2 + y2 + z2) + m<1>v[{xxyx-yxxx) sen* + (Rxx +zxxx-xxzx) eos*]
(14 14)
+ 4mw2[z2 + y¡sen2 * + {R + zx)2 eos2 * - 2yx{R + zx) sen * eos *]
Aplicando las ecuaciones de Lagrange, se obtienen las siguientes ecuaciones del
movimiento:
m[x\ + 2cop(¿, eos* - yx sen*) - «Jar,] = Fx
m[yx+ 20>cxl sen* + m2e sen<í>{(R + zx) eos* - yx sen*)] = Fy¡ (74.75)
■wl^, - 2<„(,x1 eos * — «o2, eos *((/? + zt) eos * - yx sen*)] = F2¡
Aspectos importantes con respecto a (14.14) y (14.15).
(a) La expresión (14.14) no tiene ninguna dependencia de la forma de la Tierra. La
ecuación de T depende únicamente de we y de la localización y orientación del
marco Xi, Yi, Z\.
(b) Las expresiones (14.15) tienen en cuenta la rotación de la Tierra. Como ue = 7,29211 X
10~5 rad/seg, con frecuencia pueden ignorarse los términos que contienen a w|.
Sin embargo, como R es aproximadamente igual a 6,4 X 108 cm, entonces, Ru>\
es aproximadamente 3,4 cm/seg2. Como se verá, usualmente este término se
anula, una vez que se ha introducido g'.
(c) Suponiendo, por ejemplo, que la gravedad es la única fuerza que actúa sobre m,
las fuerzas generalizadas de (14.15) serán Fxx = mgXx, Fyi = mgy y Fzx — mgz en
donde gx ,gy y gz son las componentes de la gravedad verdadera, g, (no g') en las
direcciones de Xi.Yi y Z\. Ignorando las anomalías, g está contenido en el
plano Y1Z1. Por tanto, FXl = 0. En la figura 14-1 se observa que Fy¡ = g sen a
y Fzj = —g eos a. Por tanto, teniendo en cuenta (14.11),
Fyx = o>2eR sen* eos* y F2, = ~{g' + o>2cR eos2*)
Nota. Se ha supuesto tácitamente que g y g' son constantes en magnitud y
dirección para cualquier conjunto de valores de xi, y\ y 21. En rigor, estas
magnitudes son función de xi, y\ y 21 y podrían así expresarse si se requiriera este
grado de precisión. Véase la expresión (14.10). Entonces, (14.15) se reducen a
xx + 2o>e(zx eos* — yx sen*) - ^\xx — 0
y\ + 2oiexx sen* .+ w2 sen*(z1 eos* - yx sen*) = 0 (14.16)
z\ — 2(1)c¿1cos* — tü2. cos*(Zj eos* - 2^ sen*) = — g'
Los términos que contienen u2 R se anulan automáticamente de modo que R
no aparece ya en las ecuaciones. Para un cierto valor de *, g' estará dado por (14.9).
300 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
(d) La expresión {14.14), ya hallada por medio de las ecuaciones de trasformación,
puede obtenerse más fácilmente por una aplicación de las relaciones {8.4) (véase
el problema 14.7).
(e) Tomando a como la aceleración total de m en el espacio inercial, las cantidades
entre paréntesis cuadrados de {14.15) son las componentes ax, ay y az de a
en las direcciones instantáneas de Xi, Y\ y Zi, respectivamente (véase el
numeral 3.9). Además, nótese que las ecuaciones {14.15) pueden escribirse de
inmediato a partir de las relaciones {9.6) (véase el problema 14.8).
(/) Las componentes de la aceleración centrípeta y la aceleración de Coriolis, u>2R y
2cocxi, respectivamente, se tienen en cuenta automáticamente en las ecuaciones
(14.15).
(g) Si la partícula m tiene alguna restricción determinada, T podrá modificarse
fácilmente para tener en cuenta la restricción (véase el ejemplo 14.2).
(h) La relación (14.14) es la expresión de T para una partícula sin ninguna restricción.
En el caso de varias partículas, se obtiene T, sencillamente haciendo la suma
correspondiente; si las partículas tienen algún tipo de restricción, pueden eliminarse
las coordenadas superfluas de T, de la manera acostumbrada por medio de las
ecuaciones de restricción (suponiendo restricciones holónomas). Por otra parte,
pueden utilizarse otras coordenadas que resulten adecuadas, diferentes de las
rectangulares, por medio de las ecuaciones de trasformación adecuadas, como se
indica en los puntos B, C y D a continuación.
B. Considérense las coordenadas cilindricas, p, <f> y 2, con el origen en 0\, figura 14-2.
Escribiendo xi = p eos 0, y\ = p sen </» y z\ = 2, el lector puede demostrar que (14.14)
puede ponerse en la forma
T = 4¡m(p2 + P2<j>2 + z2)
+ mwe[P2j> sen * -i- (fí + z)(¡> eos <j> — p<¡> sen <¿) eos * - pz eos <f> eos *]
+ \mJe[p2(cos2<f> + señasen2*) + (R + z)2 eos2* - 2P(R + z) sen<f> sen* eos*]
(14.17)
Las ecuaciones del movimiento correspondientes a p, </> y 2 se obtienen en seguida, y
las expresiones de las fuerzas generalizadas (suponiendo que solamente actúa la gravedad)
Fp — mg seria sen <f>, F* — mgP sen a eos <f>, Fz — ~mg eos a
y que si se desea pueden escribirse en función de g', etc.
Siguiendo este procedimiento, resulta fácil escribir T en coordenadas esféricas (véanse
los problemas 14.9 y 14.10).
C. Considérese un marco, X', Y', Z', (no indicado en la figura) con el origen en Oí, figura
14-2, en donde Z' es una extensión hacia arriba del radio geocéntrico, Ri\ Y' se extiende
hasta cortar el eje polar y X' es perpendicular al plano Y'Z' y está dirigido hacia el oriente.
Nótese que el plano X'Y' no es tangente a la Tierra en 0\ y que g' no tiene la dirección
de Z'.
Utilizando valores geocéntricos, tanto T como las ecuaciones del movimiento tienen
exactamente la misma forma que en (14.14) y (14.15), respectivamente, en donde R\ y
*! remplazan a R y a *; y además, x', y' y 2' remplazan a x\, y\ y z\.
Nuevamente, por ejemplo, suponiendo que solamente la gravedad actúa sobre la partícula,
Fx- - 0, Fy - ~mg sen(*-*i-a), Fz- - -mg eos (*- *i - a)
Pero g sen (* — $x — a) — g' sen(* - «t^) — u>2eRx sen*1 eos*,,
g eos(* — *t — a) — gr'cosí* — *,) + t.)2i21 eos2*.
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 301
Así, las ecuaciones del movimiento finalmente toman la forma,
x' 4- 2a>e(z' eos 4>, - y' sen*,) - orex' - 0
y' + 2wex' sen*, + to^sen*,^' eos*, - y' sen*,) = — #'sen(* — *j) {14.18)'
'£' — 2>t*ex' eos*, — w2 eos*,(z' eos*, — y' sen*,) = —g' eos (* - *,)
Nótese de nuevo, que los términos que contienen a &IR\, se anulan
automáticamente.
Es importante recordar que para cualquier tipo de fuerzas que actúen, las fuerzas
generalizadas se determinan en la forma acostumbrada, ignorando la rotación de la
Tierra. (Véase el numeral 4.50
D. Considérese el marco X\, Y\, Z\ de la figura 14-3. Aquí, Z\ se ha tomado paralelo
a Z2 (el eje polar); Xi está en el plano del meridiano, y Y\ es perpendicular al plano
X\Z\, según se indica. En función de xi, y\ y z\ relativos a este marco, la
energía cinética T, para una partícula única, estará dada por (ignorando un término
constante)
T = ím[x\ + y\ + z\ + {x\ + y2x)^e + 2»t{xxyx -yxxx) + 2R<,,e{xlo>e + yx) eos<t>] (14.19)
Fig.14-3
El lector debe demostrar que (14.19) puede obtenerse por medio de la aplicación de las
relaciones (8.4).
Las ecuaciones del movimiento de m son,
m(x\ - x^l - 2yxa>e - RJe eos *) = FXl
m$x - y A + 2<*Á) = Fvi {<14-20^
mzx = FZl
FXi,Fy y FZx se determinan teniendo en cuenta la gravedad y cualquier otra fuerza
que se haya aplicado a m. Pero, igual que antes, debe emplearse g (formando un ángulo
a con R) (véase el problema 14.25). El lector debe demostrar que (14.20) se sigue
directamente de las relaciones (9.6).
E. Coordenadas esféricas con el origen en el centro de la Tierra. Los ejes Xi, Yi y Z\,
de la figura 14-4, con el origen en 02, se hallan adheridos a la Tierra. Utilizando las
302 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
coordenadas esféricas r, 6 y <f> medidas según se indica y teniendo en cuenta que
0 + *i = 90°, se concluye que
T = ¿raff' + r2*2 + r2(¿ + t„c)2cos2<í>1] {14.21)
Fig. 14-4
que puede aplicarse al movimiento cerca a la superficie de la Tierra, o también a
proyectiles de largo alcance. Nótese que g no es paralelo ary disminuye con la altura por
encima de la superficie de la Tierra (véanse las ecuaciones {14.9), {14.10) y {14.11).)
La relación {14.21) es igualmente aplicable al movimiento de satélites. Sin
embargo, en este caso, las fuerzas generalizadas Fr, F^ y F¿, deben determinarse por
medio de expresiones exactas para las componentes de g a distancias relativamente
grandes de la Tierra (véase ejemplo 14.12.)
14.7 Energía cinética, T, para una partícula; marco de referencia en movimiento
con respecto a la superficie de la Tierra.
Los siguientes ejemplos sirven para ilustrar ía técnica general.
(a) Un carro de ferrocarril se mueve en el plano X\Y\ de la figura 14-2, a lo largo de un
carril recto que forma un ángulo 0 con respecto a Xi. Un marco rectangular X, Y, Z,
se encuentra adherido al carro con el eje X paralelo al carril y Z paralelo a Z\.
Representando por S la distancia desde 0\ hasta el carro, las relaciones de. x\, y\ y z\
con x, y y z, son
xi = Scosp + xcosp-ysenp, iji - Ssenp + xsenp + y cosp y Zi = z
Eliminando xi, ¿i, etc., de {14.14), se obtiene
T = $m[{S + i)2 + if2 + z2] + in<*e[y{S + x) sen* - y{S + x) sen*
+ eos <t>({R + z){S eos /? + x eos /? - y sen /?) - {S cosp + xcosf3-y sen/?)z)]
+ im<4[(S eos /? + x eos p - y sen/3)2 + {S sen/3 + x sen p + y eos pf sen2 *
- 2{S sen/? + x sen/? + y eos p){R + z) sen* eos * + {R 4- z)2 eos2 *]
{14.22)
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 303
Puede suponerse que S varía de una manera arbitraria. Las ecuaciones del movimiento
de Lagrange, naturalmente, tienen en cuenta la rotación de la Tierra así como el
movimiento del carro. (Nótese que el movimiento supuesto para el carro está contenido en
el plano XiYi y no sobre la superficie de la Tierra.)
(fe) Considérese una expresión para T en coordenadas relativas a una plataforma rotatoria
colocada en 0\, figura 14-2, con el eje de giro en la dirección de Z\. Un marco X, Y, Z,
con el eje Z en la dirección de Z\, está adherido a la plataforma. Su desplazamiento
angular, 0, se mide entre Xi y X. En este caso,
Xi - x cos/3 - y sen (3, i/i = x sen/3 + y cos/3, Z\ = z
Eliminando Xi,yi,Zi\Xi,yi y ¿i de {14.14), puede hallarse a T expresada en función
de x, y, z, etc.
Sin embargo, empleando las relaciones (8.2), se puede escribir de inmediato,
T = $m[(vXQ + x + *z - oyzy)2 + (v,Jq + y + o>x - *zf + {vZq +z + o>xy - a>yx)2} {14.23)
donde el lector puede demostrar que
v0x - Roye eos/? eos$, v0y — -72wesen/3 eos*, vQz = 0
o,x = ti)csen/3 eos*, ay — t*e eos/3 eos*, o>2 = /3 + o>esení>
Este método es menos pesado y monótono que el sugerido antes.
14.8 Movimiento de un cuerpo rígido cerca de la superficie de la Tierra.
Al describir este problema se utiliza la notación y el método presentado en el numeral
8.10. Será conveniente que el lector repase este numeral. En realidad, el estudio siguiente
es sencillamente un caso especial del análisis más general indicado.
Los ejes Xi, Y\ y Z\ de la figura 14-5 representan los mismos ejes de las mismas
denominaciones de la figura 14-2. En este caso, ue corresponde a Í2i de la figura 8-21. Se ve
entonces que Qix = 0, ü\y = we eos * y Í2i2 = c^sen*. Además, Qx = ¿ sen 6 sen </» +
0cos</>, etc. (Véanse las relaciones {8.11).) Por tanto, las componentes de la velocidad
angular del cuerpo, í2totai, en el espacio inercial, en las direcciones de los ejes fijos al cuerpo,
X, Y, Z, están dadas por (véase {8.14))
üíx — ^sen0sen<£ + ¿cos<£ + a12(i>c eos* + a13we sen*
oiy — ¿sen0costf> - 9 sen<f> + a22a>ccos* + a23<oe sen* {14.24)
w2 — i + ¿cos0 + a32ti) eos* + a33oVsen*
donde «n, «i2 y ai3 son los cosenos directores del eje X, fijo al cuerpo, con respecto a
Xi, Y\ y Zi, etc. Estos pueden escribirse en función de los ángulos de Euler, 6, \p y </>,
por medio de la tabla 8.2.
304 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA l CAP. 14
es la velocidad angular total del
cuerpo en el espacio ¡nercial. «,. u, y w,
son las componentes .de II toioi en las
direcciones instantáneas de los ejes fijos al cuerpo,
X. Y y Z.
Xi, Vi, Z\ está fijo a la superficie de la
Tierra a una latitud *.
X'. V", Z' permanece paralelo a Xi. Vi. Z,.
Movimiento de un cuerpo rígido cerca a la superficie de la Tierra
Fig. 14-5
Según las ecuaciones {8.4), se encuentra (véanse las ecuaciones {8.15))
vt = Ro>e eos * 4- xí 4- <»ezl eos * - weyl sen*,
v2 - 2/i + ">ex\ sen4>, v3 = zí — a>exl eos*
{14.25)
Suponiendo ahora, para simplificar, que O está en el c.m. y remplazando {14.24) y
{14.25) en {8.10), se obtiene la expresión adecuada de T, de donde se siguen las ecuaciones
del movimiento en forma inmediata. Las fuerzas generalizadas originadas por la gravedad
y por cualquier otro tipo de fuerza que se haya aplicado, se obtienen en la forma usual.
14.9 Ejemplos ilustrativos específicos.
A menos que se especifique algo distinto, en los ejemplos que siguen se supone que g y g'
permanecen constantes en magnitud y dirección en toda la región recorrida por la partícula
y sus valores son los que pueden calcularse en el origen de los ejes. En rigor esto no es
exactamente cierto, pero en caso de que la precisión requerida lo exija, pueden hacerse correcciones.
(Véanse las ecuaciones {14.9) y {14.10).)
Ejemplo 14.1. Determinación de la dirección de la plomada.
Suponiendo que la plomada se halla en reposo en el punto Oí, de la figura 14-1, se hace xt = xl = 'xx = 0,
etc., en (14.15) y se encuentra
F*l = 0,
Fy = mugR sen «p eos *,
—viUgR eos2*
Si se toma la masa de la plomada como una partícula libre,
(1)
{2)
donde a es el ángulo desconocido existente entre g y la dirección de la plomada y r es la tensión de la cuerda.
La relación t = mg' define a g'. Entonces, por (1) y (2),
g sena = «|jR sen* cos<p, g cosa = g' + <¿eR eos2*
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y%É SU ROTACIÓN COTIDIANA 305
que son las mismas relaciones (14.11). Así, a, determinado por medio de (14.2), es el ángulo al cual se inclina la
dirección de la plomada, como resultado de la rotación de la Tierra.
Ejemplo 14.2. Movimiento de una cuenta en un alambre liso parabólico.
Una cuenta de masa m, puede deslizarse libremente a lo largo de un alambre liso parabólico, z\ = bx\ (el
alambre está en el plano X\Z\, de la figura 14-2) bajo la acción de la gravedad. Utilizando la relación anterior
y y\ = 0, la ecuación (14.14) para expresar T, puede ponerse en forma adecuada inmediatamente. El lector
puede demostrar que la ecuación del movimiento, finalmente toma la forma
m(l + 462a;2) £, + A.mb2xxx2 - mw2c(2b2x\ eos2* + *,) = -2mg'xxb
Compare este resultado con la ecuación del movimiento obtenida en el ejemplo 3.2.
Ejemplo 14.3. Movimiento de un péndulo simple en el plano XZ.
Un péndulo de longitud /, está sostenido de un punto en el eje Z\, de la figura 14-2, de manera que su
posición de reposo está en 0\. Se supone que el péndulo está restringido a oscilar, sin fricción, en el plano X\Z\.
Si se indica la posición angular del péndulo por 8, la relación (14.14) se reduce a
T = \ml292 + (nu¿elR cos*)¿ cosí - (mael2 cos*)(l - cos*)¿
+ £mco2[í2sen2 0 + (R + / _ / cos9)2 cos2^
La fuerza generalizada es F6 = — mgl sen 8 eos a. Por aplicación de la ecuación de Lagrange, suponiendo que el
ángulo 8 es pequeño, finalmente se obtiene, 9 = —(g'/l)9, que demuestra que, naturalmente, las mediciones
hechas con el péndulo indican g' en lugar de g.
Si se le permite oscilar al péndulo en el plano YZ,
T = \ml2$2 + £m>2[í2sen2*sen2* + (R + 1(1 - cosí))2 eos2*
- 21 sen $(R + 1(1 - eos 9)) sen * eos *]
Fe = —mgl sen ($ — a) — —mi sen $(g eos a) + mi eos $(g sen a)
y, en el caso de que el ángulo 8 sea muy pequeño, la ecuación del movimiento, como puede demostrarlo el lector, se
reduce una vez más a: '¿ — —/„'/i\6%
Ejemplo 14.4. Componentes rectangulares de la fuerza fx.ify >' fz.< ejercida por los rieles sobre un carro de
ferrocarril de masa M, que se mueve hacia el norte a lo largo de Y\ con velocidad uniforme y\.
Considérese el coche como una "partícula libre" y hágase xt = i, = 'x1 = 0, etc., en (14.15), obteniendo así
/Xj = -2Mweyx sen 4», fy^ = 0, /2¡ = -Mg'
Así, los rieles ejercen una fuerza de — 2Muey1 sen * en la dirección negativa de Xi. La fuerza vertical/2, ejercida
por los rieles, sencillamente soporta el peso Mg', (no Mg).
El lector puede demostrar que, si el tren se mueve hacia el oriente según la dirección de X con velocidad
constante ¡elt
/ij = 0, /„ = 2Mwexx sen *, fz = Mg' — 2Mucxx eos 4>
Nótese que el "peso" del coche "es" menor en una cantidad 2Muex1 cos4>. En caso de que se moviera hacia el
occidente pesaría más. Si se tiene «j = 60 millas por hora, M = 100 toneladas y * = 45°, la pérdida (o
incremento) en el peso es alrededor de 56 libras (véase el problema 14.14).
Ejemplo 14.5. Movimiento de un proyectil de corto alcance, ignorando la resistencia atmosférica.
Suponiendo que no hay resistencia del aire, ni anomalías gravitatorias, y que g' permanece constante en
magnitud y dirección en todo el espacio recorrido, las ecuaciones (14.16) pueden aplicarse directamente. Despreciando
los términos que contienen a2, se escribe
xx + 2ue(zl eos* - y{ sen4>) = 0 (1)
y\ + 2wex1 sen* = 0 (2)
z\ - 2co4?£1cos* = -g' (s)
306 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
Se integra una vez la ecuación (1), se sustituye x en (2) y (3), se desprecian los términos que contienen u2.yl y
<¿ezii y se integran en forma inmediata las dos últimas ecuaciones. La ecuación (1) puede integrarse ahora luego
de haber remplazado los valores obtenidos y haber despreciado nuevamente los términos que contienen a uc. Una
vez evaluadas las constantes de integración, las soluciones aproximadas son
*1 = x0 + ¿0* + ue(V0 sen<1> ~ *0 COS+)í2 + hueff't3 COS * (4)
Vi = Vo + Vot - aex0t2sen^ (5)
z, = z0 + z0t + $(2uei0 eos <t> - g')t2 (6)
donde las cantidades con subíndice cero, indican valores iniciales. Estas ecuaciones tienen las sencillas formas
conocidas, excepto para los términos que contienen a u,.
Debe anotarse además, que aparte de las aproximaciones hechas, (4), (5) y (6) están basadas en la suposición
incorrecta de que g' permanece paralelo a Z\, para todos los valores de las coordenadas. Además, los valores de xl%
y\ y z\ que se obtienen por medio de estas ecuaciones, han de medirse con respecto al marco Xi, Yi, Z\, en
tanto que en la práctica real, la altura de un proyectil en un momento determinado, y el alcance máximo, se miden
con respecto a la superficie curva de la Tierra. Por tanto, un estudio más preciso y realista implicaría hacer muchas
consideraciones que aquí no se han incluido.
Como un medio posible de eliminar algunas de las dificultades anteriores, el lector puede considerar lo
siguiente. Tómese un punto de referencia p, sobre la superficie de la Tierra elipsoidal, punto que tendría una latitud
geográfica, *o. Indíquese la latitud geográfica, medida con respecto a este punto, por medio de 0; es decir, * = *0 +
Se mide la longitud, <f>, a partir de un meridiano que pasa porp. Se representa por h la altura vertical de una
partícula sobre la superficie elipsoidal de la Tierra, medida esta altura según la dirección de la extensión de R geográfico
Sin dificultad se concluye que
T = \m[(R + h)2+(R + h)2(S2 + (ií + /i)2(¿ + coc)2 eos2 (*<,+ /*)]
Teniendo en cuenta que R es una función de * (y por tanto de 0) por las relaciones (14.4) o (14.5), pueden
escribirse de inmediato las ecuaciones del movimiento correspondientes a 0, h y <f>. La aceleración g'h (para valores de
h no demasiado grandes) está dada por (14.10) y lleva siempre la dirección de h. Las magnitudes 0, h y <t> pueden
medirse con respecto a la superficie elipsoidal de la Tierra.
Ejemplo 14.6. Péndulo con soporte deslizante. (Véase el ejemplo 4.4.)
La masa mi puede deslizarse a lo largo de Xi, en la figura 14-2. Suponiendo que el movimiento del
péndulo está restringido al plano X\Z\, se concluye que, aplicando (14.14) a mi y m2,
T = |m,(i2 + 2uex1R eos* + co2*2) + $m2(x2 + r2e2 + 2¿,¿r cosí)
+ m2ue\(R — r eos e)(i1 + r$ eos $) — (&! + r sen $)rh sen $} eos * (14.26)
+ \m2w2.\(xl + r sen*)2 + (R - r cosí)2 eos2*]
de donde (mx + m?) a?, + m2r'e eos $ — m2r$2 sen $ — m1a2x1
+ 2m2aere sen $ eos * — 7n2u^(x1 + r sen $) = Fx = 0
m2xxr cosí + m^e — 2m2wexxr sen* eos* (i)
. — m2ue(x1 + r sen0)r cosí — m2co2(jR — r eos $)r sen* eos2*
= Fe = -m^'r sen í — m2u2Rr sen $ eos2 *
El lector puede comparar estos resultados con las ecuaciones del movimiento correspondientes, suponiendo que no
hay rotación de la Tierra (véase el final de la página 68).
Ejemplo 14.7. El péndulo de Foucault.
El análisis matemático del movimiento del péndulo esférico, de la figura 14-6, cuyo desplazamiento a partir
de O i es siempre muy pequeño comparado con la longitud / del cable que lo sostiene, demuestra que, (a) con res-
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 307
pecto a la Tierra (al plano XiYi) la masa describe
una trayectoria elíptica rotatoria (una elipse que
precesa), y (b) con respecto al plano horizontal XY que
pasa por 0\ que gira con una velocidad angular
— «r sen * alrededor de Oís, la trayectoria
descrita es una elipse cerrada con su centro en 0\.
Tal análisis se indica a continuación. Si se
hacen algunas suposiciones justificables, las expresiones
y procesos matemáticos se simplifican notablemente.
Considerando a m como "libre", pueden
aplicarse directamente las ecuaciones (14.15) y las
fuerzas generalizadas están dadas por
Fv - mg sen a - ryx/l (1)
Fx = — mg eos a + t(1 — z^/l
donde t es la tensión del hilo. Sustituyendo en
[14.15), eliminando g sen a y gcosar con (14.11)
y despreciando los términos que contienen a u% (los
que contienen a Ru% se anulan), se obtiene
je, + 2o3c¿jcos4> - 2(0^! sen <I> = -rxjml (2)
y\ + 2uex1 sen * = —ryjvü (3)
Z*! - 2uexl eos* = —g' + r(l-Zi)/ml (4)
Se supone ahora que / es tan grande comparado con la amplitud del movimiento, que para una buena
aproximación, la masa se mueve en el plano XiYi. Escribiendo entonces, z\ = l\= 'z'\ -- = 0 y despreciando 2«,xi eos *,
(4) conduce a t= mg'. Así, (2) y (3), se convierten en
(5) x, - 2a>i¿i = -g'xjl y (6) y\ + 2uixl - -o'yjl
donde «i = «, sen *. Estas ecuaciones'pueden simplificarse al referir el movimiento a los ejes X' y Y' que giran
en el sentido del movimiento de las agujas del reloj con velocidad angular m relativa a Xi, Vi. Sustituyendo
las ecuaciones
xt — x' coscojí + y' senuxt, yt = — x' senco,* + y' cosc^í (7)
en (5) y (6), multiplicando (5) por senuií y (6) por costuit y sumando, se obtiene la ecuación (8) (luego de
haber despreciado w\ por ser muy pequeño comparado con g'/D- Igualmente, multiplicando (5) por cos«ií y
(6) por senwií y restando, se obtiene (9).
(8) y' + g'y'll = 0 (9) x' + g'x'/l = 0
Estas pueden integrarse de inmediato para concluir,
x' - A sen(V^7it + 8,), y' = B sen(VgTlt + 8¿ (10)
donde A, B, fií y ¿2 son constantes determinadas totalmente por las condiciones iniciales. Por tanto, el
movimiento referido a los ejes en rotación seré armónico simple, según las direcciones de los dos ejes, con un período
p = 2*Vl/g' en ambos casos. Así, la trayectoria es una elipse con el centro en Oí.
Un observador montado en este marco giratorio podría ver la elipse anterior. Pero si el observador
permanece estacionario con respecto a la superficie de la Tierra, verá girar la trayectoria elíptica con un período igual a 2jt/« 1
o sea 2jt/(«c sen *) = 24/(sen *) horas. En cualquiera de los polos, el período es de 24 horas y en el ecuador
no habrá rotación. En el hemisferio norte la rotación tiene el sentido N —► E —► S — O, y en el hemisferio sur
el sentido inverso.
Para obtener resultados experimentales satisfactorios, debe seleccionarse con cuidado el tipo de soporte, s,
utilizado. En la literatura se describen diversos tipos de soportes. El cable debe ser largo y la teoría (no incluida aquí)
demuestra que el movimiento debe ser iniciado de tal manera que el área de la elipse sea tan pequeña como sea
posible. Véase el ejemplo a continuación.
X
\ T
X,,V,.Zi
fijo a la Tierra
como en la figura 14-2
r \ 1 g' paralelo a Z\
^-'
\ Norte Y
1—\ » ^-
O.J -—'"r
V- — > g está en el plano
¡ paralelo a Z. Vi.
El péndulo de Foucault
308 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
Ejemplo 14.8. Iniciación del péndulo de Foucault.
Si se aparta la masa pendular de su posición de«quilibrio con respecto a la Tierra y se suelta luego, el
movimiento referido a los ejes en rotación seguirá prácticamente una recta.
Para demostrar esto, supóngase que cuando í = 0, xx = xx = yx = 0 y y\ = y0 (desplazando la masa
una distancia yo, directamente hacia el norte, a partir de la posición de equilibrio con respecto a la Tierra, y luego
soltándola). Al imponer estas condiciones en (7) con el fin de hallar las condiciones iniciales relativas a los ejes en
rotación y al sustituir estos resultados en las ecuaciones (10); se encuentra que
y' = y0 eos (yfgTlt), x'- = -y0(p/Px) sen (y/Vñt) (U)
donde p = 2jtV///»' y Pi es el período de rotación de la Tierra (24 horas). Como p es muy pequeño comparado
con P\, x' será siempre muy pequeño. Por tanto, el área de la elipse es bien pequeña y el movimiento entonces
seguirá prácticamente una trayectoria que se confunde con el eje Yi.
Ejemplo 14.9. Movimiento de una varilla en el plano Xit Y\, figura 14-3.
Como un ejemplo sencillo sobre el movimiento de un cuerpo rígido con respecto a la Tierra, considérese el
caso de una varilla delgada uniforme de masa M y momento de inercia 7 con relación al eje normal a la varilla que
pasa por su centro de masa.
En primer lugar se determina su energía cinética en forma directa. El c.m. se localiza por medio de xi y>'i;
y e, medido con respecto al eje Xi, determina la posición angular. Supóngase que la varilla se encuentra
dividida en un gran número de segmentos pequeños, teniendo por coordenadas cada uno de estos segmentos x, y y„ y
masa m,. Teniendo en cuenta la expresión (14.19), se observa que
T = ¿ 2 m¡[£2 + 2/t? + ü£(a;2 + y2) + 2ue(xiyi - y^) + 2Rue(xiUe + Vi) eos «!>]
Pero x, = xi + l, eos B y y, = yt + lt sen 6, donde l¡ es la distancia medida sobre la varilla desde el c.m.
hasta mt. Por tanto x¿ = xx — Ifi sen e y i/¿ — yx + l¡0 cosí. Al eliminar xityitx¡ y yi de T, realizar la
operación de suma y recordar que 2^ = ^i se obtiene
T = ±M{(x\ + y\) + <£(x\ + y\) + 2we(xxyx -yxxx) + 2ueR(xlUe + yx) eos *] + |/(¿ + (oc)2
El lector debe demostrar que esta expresión se sigue en forma directa de (8.10).
Suponiendo que solamente la gravedad actúa sobre la varilla, se observa que, figura 14-3,
FXi = -Mg eos (<l> - a), FVi = 0, Fe = 0
Aplicando las ecuaciones de Lagrange y las relaciones (14.11) se obtienen finalmente las ecuaciones del
movimiento que, después de despreciar los términos xxu% y 2/i"f, quedan
xx — 2yxue + g' eos * = 0, yx + 2wexx =0, I '$ = 0
Trompo que gira con la punta fija en Oí, sobre la superficie de la Tierra
Fig. 14-7
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 309
Ejemplo 14.10. Ecuaciones del movimiento de un trompo en un punto fijo sobre la superficie de la Tierra.
El siguiente ejemplo merece consideración especial, ya que sirve para ilustrar bien los principios básicos de un
tipo de problema general (véase el problema 8.24, figura 8-33).
Considérese el trompo de la figura 14-7 con su punta fija en 01 sobre la superficie de la Tierra. Siguiendo la
misma anotación empleada en los numerales 8.10 y 14.8, se describen a continuación las diferentes etapas para
plantear las ecuaciones del movimiento, primero empleando los ejes fijos al cuerpo con el origen en Oí y luego
utilizando los ejes fijos al cuerpo con el origen en el c.m. (Nótese que Xi, Yi, Z\ de la figura 14-7 corresponde
exactamente al marco de la misma denominación que aparece en la figura 14-2.)
(a) Tómense los ejes fijos al cuerpo, X, Y y Z, con el origen en Oí (la punta del trompo) y Z coincidente con el
eje de simetría, según se indica. Se observa que & = y — 0 y 2 = r. Por tanto, el último término de (8.10),
se reduce a M(voxwy — voywx)r, donde vo = Rue eos * en la dirección deXi. Así, voy = Ruta2\ eos*
y i>o, = Rutan eos*. Además Ixy = /„ = Iyz = 0 e' J£ = /£. Los valores de ux, uy y o,, están
dados por las relaciones (14.24) y cm, etc., por la tabla 8.2. Entonces, por (8.10),
T = \MR^\ eos2* + £/£(«£+«5) + \1*»\ +■ M(v0xUy-v0yUx)r (14.27)
Nótese que el primer término es constante.
La energía potencial debida a la gravedad está dada por
V = Mr eos $(g eos a) + Mr sen$(g sena) eos ^
= Mr[cos $(g' + w\R eos2 4>) + sen e(w2eR sen * eos *) eos ^]
De aquí se pueden obtener las ecuaciones del movimiento en forma inmediata.
(b) Tómense ahora los ejes fijos al cuerpo, como antes, excepto que el origen está localizado en este caso en el c.m.
En este caso £ = y = i = 0 y el último término de (8.10) se anula. Los valores de u,, uy, y wt son los
mismos de antes. Se tiene, Ixy = /„ = Iyt = 0 e /£ = /£. La velocidad del c.m. en el espacio inercial
se indica por u0 que resulta más difícil de expresar que en el caso (a). Utilizando, x\ = r sen 6 sen yp, etc.,
y las ecuaciones (14.25), el lector puede demostrar que las componentes de uo en las direcciones de Xi, Y\
y Z\ (y no en las direcciones de X, Y y Z) están dadas por
vx = jRcoccos* + r$ cosO sen ^ + r^senícos^ + u^cosí eos* + uer sen $ eos ^ sen <t>
vy = r¿ sen* sen ^ — re eos 9 eos ^ + uer sen 9 sen^ sen* (14.29)
vz = — re sen* — wer sen e sen ^ eos <t>
Así, v*=v* + Vy + v\ podrá escribirse completamente en forma explícita.
La expresión de Ves la misma que en el caso (a). En consecuencia, las ecuaciones del movimiento se obtienen
en seguida.
Ejemplo 14.11. Fuerzas de soporte debidas a la rotación de la Tierra. (Véase la figura 9-7 y el numeral 9.12.)
Considérese un rotor montado sobre la superficie de la Tierra en un punto de latitud *, como se indica en
la figura 14-8. Obsérvense los detalles de este diagrama. El rotor está equilibrado estática y dinámicamente con
relación a los ejes inerciales Xi, Yi y Z\. Sin embargo, al tener en cuenta la rotación de la Tierra, este ya no
es el crso y aparecerán fuerzas de soporte que se determinan a continuación.
310 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
X, YyX son fijos al cuerpo. Z coincide
con Vi. Los ejes X e V permanecen en
el plano X|/i. Los ángulos de Euler,
9 = 90° y * - 180°
</.../i.)y(/.,./i,> «>">«"
fuerzas de soporte paralelas a X e V,
respectivamente.
Normal a la superficie de la Tierra
" *1
Xi, Vi.Zi adherido a la superficie de
la Tierra con O, en un punto de latitud *,
(igual que Xi, Vi, Z\ en la figura 14-2).
Fig.14-8
La notación aquí utilizada es la misma de la figura 9-7. Los ángulos de Euler 0, 4> y <f> localizan el rotor
con respecto a Xi, Xi y Zi, en donde e = 90° y $ = 180°. Nótese que X, Y y Z son los ejes principales
de inercia que pasan por el c.m. y que St = y = z — 0.
Por inspección se demuestra que las componentes de la velocidad angular del rotor en el espacio inercial,
según las direcciones de X, Y y Z, son
"x = w,» sen* sen #, uy = ue sen * eos <f> y «z = uecos«t> + ¿ (/)
Las componentes totales de las fuerzas, según X, Y y Z, son
Fx — fix + fix ~ M9 eos a sen <f>, Fy = fly + f2y - Mg eos a eos <f> y Fz = fz + Mg sen a (2)
Las componentes de la aceleración del c.m. (el mismo origen Oí) en el espacio inercial, son
Ax = — UgR eos21> sen <f>, Ay = — ufeR eos2* eos <f> y Az = a*R sen <l> eos * (3)
Las ecuaciones (9.2), quedan entonces — Mj*R eos2 * sen 0 = /,, + f2l - Mg eos a sen 0, etc., que
luego de eliminar a g en favor de g' (véanse las ecuaciones (14.11)) se reducen a
/li + Í2x = Mff' Sen <f>
fly + f-Ly = Mg' COS <t>
/« = 0
Aplicando las relaciones (9.70), se tiene
7xue¿sen * cos0 + (IZ — Iy)ue sen <t> eos <f>(ue eos * + ¿) = fzyh ~ fiyh
7y(oe¿ sen* sen^ + (Iz — Ix)ue sen * sen <f>(ue eos <t> + ¿) = /2x^2 ~~ Ai*i
Jz# + (7y — /x)"c sen2 + sen <¡> eos £ = rm
(4)
(5)
(6)
(7)
(9)
Hallando fix al resolver (4) y (8), se obtiene
_ sen <f>
/ix = T^p^ [Mg'l2 + <oe¿(/x - 7Z - /„) sen * + <4(Ix - Iz) sen + eos +]
(10)
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 311
Nótese que el término -.—t—t- Mg' sen <t> se debe al peso del rotor, en tanto que los demás términos son resultado
íj + í2
de la rotación de la Tierra. Despreciando el término que contiene u2, y suponiendo que /, = Iy, la anterior se
reduce a
/ix = ^^(Mflr72-coc¿/2sen*) {11)
Si <f> e Iz tienen valores grandes, el segundo término puede ser considerable. Por tanto, aunque el rotor puede
estar equilibrado estática y dinámicamente en una Tierra "estacionaria", resulta algo desequilibrado en la Tierra
giratoria.
Las expresiones para las demás fuerzas de soporte f2x, f\y y Í2y se obtienen de inmediato.
Ejemplo 14.12. Movimiento de un satélite, o proyectil de largo alcance, con respecto a los ejes Xi, Y\ y Z\, de
la figura 14-4.
No es el objetivo de este capítulo analizar el movimiento de satélites. Sin embargo, el siguiente ejemplo, más
bien general, se incluye con el fin de señalar algunas de las dificultades que se encuentran en un análisis detallado.
Suponiendo que el marco X2, Y2, Z2 es inercial y aplicando las ecuaciones de Lagrange a (14.21), se
obtiene
mr — mr*j — mr(^> + ue)2 eos2*! = FT
mr2*j + 2mrr*j + mr2(4> + ue)2 sen <l>j cos<l>j = F* (14.31)
±[mrH; + Ue) eos2*,] = F¿
cuyas soluciones expresan el movimiento de un satélite (o proyectil de largo alcance) con respecto a Xi, Y\, Z\.
La latitud geocéntrica se expresa por *i y la longitud con respecto a un determinado meridiano se mide por <f>.
Así, en esta forma, se determina el movimiento con respecto a la superficie de la Tierra.
Sin embargo, es imposible determinar las expresiones exactas de las fuerzas generalizadas, Fr,F^,F^.
Estas dependen de, (a) la magnitud y la dirección de g a una distancia r de 0\, (b) una resistencia debida a la
atmósfera (muy disminuida a cierta distancia por encima de la superficie de la Tierra), (c) la atracción del Sol, la
Luna y los planetas, y (d) la presión de los rayos solares.
Si se conociera la distribución exacta de la masa de la Tierra, podría evaluarse con precisión el valor de g, sin
embargo, este no es el caso. La resistencia atmosférica debe determinarse principalmente por métodos empíricos.
La atracción gravitatoria del Sol, la Luna, etc., puede ser calculada. La presión de los rayos solares sobre un satélite
puede ser estimada con suficiente precisión.
Otro aspecto importante que debe considerarse es el siguiente. En la determinación de (14.31) se supuso que
el marco X2, Y2, Z2 es inercial, lo cual no es completamente cierto. Para obtener resultados más precisos,
debería referirse T a un sistema de ejes que no gire y cuyo origen se encuentre en el centro del Sol.
Problemas
14.1. Verificar los valores de R\ y g' dados en la columna correspondiente a 45° de la tabla 14.1.
14.2. A partir de la gráfica 14.1, determinar los valores de g y g' en Washington, Helsinki, Buenos Aires y Welling-
ton. Determinar los valores de a en cada uno de estos puntos.
14.3. Encontrar la diferencia entre * y *i, y el valor de a, en Cincinnati, Ohio; y en El Paso, Texas.
14.4. Determinar la diferencia entre R y Ri en Helsinki.
14.5. Un péndulo simple tiene una longitud de 10 metros. Calcular su período en el ecuador y en Seward, Alaska.
Hallar el período de precesión de un péndulo de Foucault en cada uno de estos puntos.
312 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
14.6. Supóngase la Tierra elipsoidal envuelta en una esfera imaginaria de radio a (el radio ecuatorial del
elipsoide de referencia). En una latitud *i = 45°, demostrar que la distancia medida sobre la extensión de
Ri, entre la superficie del elipsoide y la de la esfera es 10.693 metros.
14.7. Obténgase la expresión de T (14.14), utilizando las relaciones (8.4).
14.8. Escribir las ecuaciones (14.15), por aplicación directa de las relaciones (9.6).
14.9. (a) Verificar la expresión (14.17).
(b) Repetir lo anterior utilizando las expresiones (8.4).
14.10. Demostrar que la energía cinética de una partícula, medida en función de las coordenadas cilindricas p,
<t> y z, con respecto al marco Xi, Y\, Z\, de la figura 14-3, es
T - ^m[p2 + p2¿2 + z2 + 2p2coc¿ + p2w2e + 2Ruep sen <p eos * + 2Rpue(ue + ¿) eos <f> eos *]
Escribir las ecuaciones del movimiento. Obténganse estas mismas ecuaciones por aplicación de (9.6).
Si se supone que solamente actúa la gravedad, demostrar que las fuerzas generalizadas están
dadas por
Fp = -mg sen <f> eos (<l> - a), F^ - -mgp eos <f> eos (<l> - a) y Fz = —mg sen (* - a)
Escribir las ecuaciones del movimiento. Utilícese g' en lugar de g.
14.11. Utilizando las coordenadas esféricas r, 8 y <f>, referidas al marco X\, Y\, Z\ de la figura 14-2,
verificar la siguiente expresión de T, aplicando las ecuaciones (8.4),
T - \m(r2 + r2$2 + r2¿2sen.2 $) + mue[r2i, sen2 $ sen <J>
+ (R + r eos $)(r sen $ eos <f> + re eos $ eos <f> — r$ sen $ sen <f>) eos <t>
— r sen $ eos <f>(r eos $ — re sen $) eos *] + -Jmcof [r2 sen2 ¿(eos2 £ + sen2# sen2«j>)
-i- (R + r eos $)2 eos2 4> — 2r sen $ sen <f>(R + r eos e) sen<l> eos 4>]
14.12. Una pequeña esfera está suspendida en aceite viscoso, por medio de un hilo que tiene una longitud de 10
metros. Se le sostiene en la posición de reposo que ocuparía si la Tierra no girara. Demostrar que la
esfera, luego de ser liberada, llegará al reposo en un punto directamente hacia el sur a una distancia
aproximada de 1,7 cm, si su latitud es * = 45°.
14.13. Se deja caer una bola desde un punto z0 del eje Z\ de la figura 14-2. zo = 100 metros, * = 45°.
Demostrar que llegará al suelo en í = (2z0/g')1/2 en un punto xt = 1,6 cm aproximadamente, y y i = 0.
(La bola ha partido del reposo y se desprecia la resistencia del aire.)
14.14. Un ascensor tiene una velocidad hacia arriba a lo largo del eje Z\, de la figura 14-2, igual a 30 millas/hora,
medida con respecto al edificio. La masa del ascensor es de 3000 libras y está localizado en un punto de
latitud * = 45°. Demostrar que las componentes Xi y Yi del empuje lateral sobre el ascensor son
fx = 13,6 "Poundal", y en zx = 0, fy =■ 0. (¿Por qué será que fy # mugjR sen<t> eos*?)
14.15. Verificar las expresiones de T del ejemplo 14.3, y las fuerzas generalizadas en cada uno de los casos estudiados.
14.16. Uno de los bordes de un tablero liso rectangular permanece en contacto "con el eje Xt, de la figura 14-2.
Se levanta el extremo opuesto del tablero de modo que forme un ángulo 8 con el plano X i Y\. Una
partícula puede moverse libremente en contacto con este plano inclinado, liso, bajo la acción de la
gravedad. Verificar las siguientes ecuaciones del movimiento
m'i] — 2mcocs sen («t» — 9) — rtiu2xx - 0
m« + mwe sen (* — 0)[2¿j — we8 sen (4> — $)] = —mg' sen $
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 313
donde s se mide sobre el plano inclinado hacia arriba. zx = s sen 8 y y i = s eos e. Debe tenerse
cuidado al tratar de determinar el valor de F,.
14.17. Si se coloca una masa m, sobre la plataforma de una báscula B, (localizada en algún punto sobre el
ecuador) la aguja indica un "peso" igual a mg'. Se mueve ahora a B hacia el oriente sobre el círculo
ecuatorial con velocidad tangencial uniforme, u, con respecto a la superficie de la Tierra. Demostrar que la
pérdida de peso sufrida por m es igual a m(u2/R + 2aeu); es decir, que ahora la báscula indica mg' —
m(u2/R+ 2(o,i;).
¿Una embarcación que se mueve hacia el oriente, desplazará la misma cantidad de agua que
cuando está en reposo en el agua? Considérese el caso de movimiento hacia el occidente. (Repítase para
movimiento hacia el norte, sobre un círculo máximo.)
14.18. En un canal abierto se hace fluir un líquido hacia el norte a lo largo del eje Y\, figura 14-2. Suponiendo
que todo el líquido tiene una misma velocidad uniforme, y\, y tomando x\ = y\ = z\ = 0, demostrar que
la superficie del líquido se inclina un ángulo 0 con la horizontal, en donde tan (3 = 2weyx sen <t>/g\
(Indicar en qué sentido se produce la inclinación.)
14.19. Supóngase que la Tierra girara a una velocidad tal, que un objeto sobre el ecuador no tuviera peso.
Probar que para una Tierra esférica homogénea, la dirección de la plomada en cualquier punto de la Tierra
es paralela al eje polar. Demostrar que g' — J^R sen <t>.
14.20. Un péndulo de Foucault, que tiene una longitud de 20 metros, está suspendido en un punto de la Tierra
cuya latitud es * = 30°. Demostrar que su período de oscilación es 8,98 segundos y que el período de
precesión es de 48 horas.
14.21. Determinar las expresiones finales de T, por medio de cada uno de los métodos sugeridos en el numeral
14.7, literal (b), y comparar con los resultados obtenidos.
14.22. La espiral cónica del problema 3.5, figura 3-5, se coloca de manera que el marco X, Y, Z coincida con
X\, Y\, Z\ de la figura 14-2. Teniendo en cuenta la rotación de la Tierra, demostrar que T está dada
por
T = £m[a2(l + b2z2) + l]z2 - mwea'z[abz2 sen <I> - (R + z)(cos (bz) - bz sen (bz)) eos *
+ z eos (bz) eos *] + £mu2[a2z2(cos2 (bz) + sen2 (bz) sen2 <l>) + (R + z)2 eos2 4>
+ 2az(R + z) sen (bz) sen * eos *]
Establecer las ecuaciones del movimiento y remplazar finalmente a g por g'. (Véanse las ecuaciones
(14.17).)
14.23. Supóngase que el eje vertical del problema 3.14, figura 3-9, está colocado en la dirección de Zx de la
figura 14-2. Plantear la ecuación del movimiento para m, teniendo en cuenta la rotación de la Tierra.
Nótese que g no tiene la dirección indicada en la figura 3-9. (Véase el problema 14.11.)
m V — mru2 sen 2 $ + 2ueurm sen ¿(eos 9 sen <f> eos <t> — sen 9 sen *)
- m«2r[(cos 9 eos «I> - sen 9 sen <fi sen *)2 + sen2 9 eos2 <f>] — k(l -l0-r) — mg' eos 9
14.24. Aplicando las ecuaciones de Lagrange a (14.17), demostrar que las ecuaciones del movimiento
correspondientes a p, <f> y z, son
m'p — mp4>2 + mue(2z eos <f> eos * — 2p¿ sen 4>) + ma2[z sen <f> sen <t> eos *
- p(cos2 <f> + sen2 <f> sen2 *)] = 0
mp<t> + 2mp$ + 2mwe(p sen * — z sen <f> eos *) + mu2, eos <f¡ eos *(p sen <f> eos * + z sen *) = 0
mz + 2muc eos *(p¿ sen <f> — p eos <t>) + meo2 eos *(p sen <f> sen* — z eos *) = —mg'
14.25. Suponiendo que solamente actúa la gravedad, demostrar que en las ecuaciones (14.20),
Fx = — mg' eos * — mu%R eos *, Fy = 0, Fz = — mg' sen *
Nótese que en la primera de estas ecuaciones, el término mJ^R eos* se anula.
314 EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA [CAP. 14
14.26. Se trata de hallar las ecuaciones del movimiento de m, figura 2-21, con relación a D2, teniendo en
cuenta la rotación de la Tierra. Suponiendo que los cojinetes sobre los cuales se apoya Di están unidos
rígidamente a la Tierra en el punto Oí, de la figura 14-2, y que las superficies de Di y D2 permanecen
horizontales, demostrar que T, expresado en coordenadas polares r y a, está dada por (se hacen
coincidir los ejes Xi y Yi de la figura 2-21 con los de la figura'14-2)
T = £m[s*2 + ¿2 + r2(¿, + *2 + á)2 + 2s*,r sen (*2 + a) + 2s*,r(**1 + *2 + a) eos (*2 + a)]
+ mujs2*, + r2(*, + **2 + a) + 8r sen (e2 + a) + sr(2*, + é2 + ¿)] sen *
+ mwe[r eos (*, + e2 + a) — 8$x sen*, - r(*, + *2 + a) sen(*j + e2 + a)]R eos *
- mu2.R[8 sen *, + r sen {9X + $2 + a)] sen* eos *
+ £mu2{[8cos*, + rcos(*, + *2 + a)]2 + [8 sen*, + r sen (*, + *2 + a)]2sen2*}
se supone que 8\ y e2 son funciones conocidas del tiempo. Nótese que en el caso ue = 0, esto se
reduce a (2.46).
14.27. La base B de la figura 13-10 (véase el problema 13.14) está colocada sobre la superficie de la Tierra en el
punto Oí, de la figura 14-2. Supóngase que la varilla semicircular está contenida en el plano Y1Z1
y que la recta punteada ab es horizontal. Nótese que g', y no g, es ahora perpendicular a ab. Escribir la
expresión de T y hallar el valor de equilibrio de 8.
14.28. El soporte B de la figura 8-12, está adherido a la Tierra en el punto 0\ de la figura 14-2. Considérese que
el marco Xi, Yi, Z\ de la figura 8-12, coincide con el mismo marco de la figura 14-2, con el c.m. en
O. Suponiendo que el disco se ha remplazado por un cuerpo de una forma cualquiera con el c.m. en O,
demostrar que T estará dado por (véanse las ecuaciones (8.14) etc.)
T = \Mu\W + ^(lxwl + 7>v2+ 7\co2 - 2/xvcox(ov - 2/^co, - 2/V2covco2)
donde ux = ¿ sen* sen # + coc(cos <f> sen ^ + sen <¿, eos ^ eos *) eos * + ae sen * sen <p sen 4>
uy — ¿ sen * eos <f> + coc(cos <f> eos ^ eos * — sen <p sen ^) eos * + ue sen * eos <f> sen 4>
<o2 = ¿ + ¿ eos * — coc sen* eos ^ eos* + ue eos * sen *
Nótese que el primer término de T es constante y por tanto puede ser eliminado. Como los ángulos de
Euler han sido aquí medidos con respecto a la Tierra, las ecuaciones del movimiento obtenidas a partir
de T expresarán el movimiento del cuerpo relativo a la Tierra.
14.29. Verificar las relaciones (14.29).
14.30. El disco D de la figura 8-5, está localizado sobre la Tierra con el punto b en el origen de los ejes Xi, Yi
y Z\ de la figura 14-2. El eje ab es vertical y coincide con Z\. Escribir la expresión de T para el disco,
teniendo en cuenta la rotación de la Tierra. Es preciso tener cuidado al tratar de hallar la velocidad del
c.m. de D. (Véase el problema 14.28 y además las ecuaciones (8.4).)
14.31. El giróscopo de la figura 8-18, está colocado sobre la Tierra en el punto 0\, con el sistema Xi, Yi, Z\
de la figura 8-18 superpuesto sobre el mismo sistema de la figura 14-2. Demostrar que (véase el ejemplo
8.16),
T = \MR2u2e eos2 * + £/£[u2 eos2 * sen2 ^ + u2(sen * sen * + eos * eos ^ eos *)2 + *2
+ (¿ + 2coc sen*)¿sen2* + 2uc cos*(* sen^ + ¿ cos^ sen* eos*)]
+ i^f [(¿ + "c sen *) eos * + ¿ — uc eos * eos ^ sen *]2
Plantear las ecuaciones del movimiento, (a) por el método de Lagrange, y (b) por el método de Euler.
14.32. Una plataforma rotatoria está localizada con su centro en el punto 01, de la figura 14-2, y su eje de
rotación en la dirección de Z\. La base A, de la figura 8-5, se halla colocada sobre la plataforma a una
distancia r medida según un radio desde el punto 0\ hasta el centro de la base A. Se hace girar la
plataforma con velocidad angular a (no necesariamente constante) en donde a se mide desde el eje Xi de
CAP. 14] EFECTOS DE LA FORMA DE LA TIERRA Y DE SU ROTACIÓN COTIDIANA 315
la figura 14-2 hasta el radio r. Los ángulos 8 y <¡> se miden según se indica en la figura 8:5. Se
representa por 0, el ángulo formado entre la extensión de r y la proyección de bZ (figura 8-5) sobre el plano
X\Y\. El ángulo ^ se define (de acuerdo con los ángulos de Euler) por medio de 4> = 0 + 90°.
Demostrar que las componentes de la velocidad angular del disco (medidas con respecto al espacio
inercial) en las direcciones de los ejes fijos al cuerpo, X, Y y Z, están dadas por
"x = [("e sen* + a + ¿) sen $ + we eos * eos (a + ^) eos $] sen <f> + ue eos * sen (a + f) eos <f>
uy ~ [("c sen * + á + ¿) sen $ + ue eos * eos (a + ^) eos 6] eos <f> — ue eos * sen (a + ^) sen#
wz = $ + (uc sen * + á + ¿) eos 9 — we eos 4> eos (a + ^) sen $
Demostrar que las componentes según los ejes X, Y y Z de la velocidad del c.m. en el espacio
inercial, están dadas por
vox — i>j(cos# eos ^ — sen <f> sen ^ cosí) + v2(cos <f> sen^ + sen<f> cos^ eos 9)
etc., para uoy y fo2, donde
Vj = weR eos * eos a + í¿ sen 0 eos ^, v2 = rá — ucjR eos * sen a + If sen 0 sen ^ y v3 = 0
y / es la distancia bO, figura 8-5. Nótese que ahora puede escribirse T y hallarse de inmediato las
ecuaciones del movimiento para el disco.
14.33. Remplazando la forma de R, dada inmediatamente después de (14.4), en la primera de las relaciones
(14.11), demostrar que, luego de introducir los valores numéricos apropiados, el valor de a en minutos
de arco, se aproxima con buena precisión a
a = 3437'75 (3 392 + 1,14 X ÍO-2sen**) sen* eos*
9
Esta es una fórmula útil para hacer cálculos.
14.34. Teniendo en cuenta la rotación anual de la Tierra alrededor del Sol, escribir la expresión de T para la
partícula que se muestra en la figura 14-2, en función de x\, yi y z\. Considérense los ejes que no giran,
con el origen en el centro del Sol, como inerciales. Además, para simplificar, supóngase que la Tierra gira
con velocidad angular constante en una trayectoria circular de radio Re = 93 X 106 millas. Establecer
las ecuaciones del movimiento y comparar con (14.15). Nótese que el eje polar de la Tierra forma un
ángulo constante de, aproximadamente, 23,5° con una normal al plano de la órbita de la Tierra.
CAPITULO
15
Aplicación de las ecuaciones de Lagrange
a sistemas eléctricos y electromecánicos
15.1 Observaciones preliminares.
Las ecuaciones de Lagrange pueden aplicarse directamente a una gran variedad de
sistemas eléctricos y electromecánicos. Como se verá con claridad, son especialmente convenientes
en el estudio de estos últimos.
Las coordenadas generalizadas, velocidades, energía cinética, energía potencial, la función
de potencia, las ecuaciones de restricción, los grados de libertad y las fuerzas generalizadas
conocidas en mecánica, tienen todas ellas su contraparte en muchos tipos de sistemas
eléctricos. Por tanto, con una adecuada selección de coordenadas y con las expresiones apropiadas
de T, V, etc., las ecuaciones de Lagrange, para sistemas eléctricos o electromecánicos, tienen
exactamente las mismas formas que las de la ecuación (4.9).
Como un estudio detallado de las varias posibilidades y ramificaciones propias de este
tema, requeriría muchos capítulos, este análisis se limita a una breve descripción de las
facetas más importantes de la materia.
15.2 Expresiones de T, V, P, FQ y de las ecuaciones de Lagrange, para
circuitos eléctricos.
Coordenadas adecuadas.
En la figura 15-1, las cargas Qi, Q2, etc.,
que pasan por las diferentes ramas del circuito
después de un instante determinado, por
ejemplo t = 0, constituyen "coordenadas"
adecuadas. Entonces, la corriente i = dQ/dt = Q
corresponde a una "velocidad" e igualmente
Q representa una "aceleración". Como se
acostumbra siempre en el estudio de circuitos,
se debe asignar arbitrariamente una dirección
positiva para el flujo (dirección de la corriente),
de cada una de las cargas, como se indica en
la figura. Esto corresponde a la selección de
una dirección positiva para cada una de las
coordenadas.
, WW^-J—WM—Sé-i
Fig.15-1
Ecuaciones de restricción y grados de libertad.
No todas las cargas que pasan por una malla o red son independientes. En una
bifurcación cualquiera la suma algebraica de las cargas que a ella llegan, deben ser igual a cero
(ley de Kirchhoff). Por tanto, el número de ecuaciones independientes en las
bifurcaciones, representa esas tantas ecuaciones de restricción. Por ejemplo, hay 6 cargas diferentes
en movimiento (6 corrientes) en las 6 ramas del puente de Wheatstone, figura 15-1.
Para cada una de las bifurcaciones a, b, c y d, puede escribirse una de las relaciones
Qe = Qi + Q2 (o bien Q6 = Qi + Q2), etc. Pero sólo tres de estas ecuaciones son in-
316
CAP. 15]
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
317
dependientes. Es decir, que tomando, Q6 = Qi + Q2, Q2 + Qs = Qa y Qi = Q3 + Qó
como independientes, la cuarta ecuación puede obtenerse de estas tres. Así pues, como
hay seis coordenadas (cargas) y tres ecuaciones de restricción, el puente tiene solamente
tres grados de libertad.
C. Energía cinética.
La energía magnética de cierta bobina de inductancia constante, M, es £ — \MQ~.
Comparando este resultado con T = ¿mu2, la energía cinética de una partícula, M
corresponde a la masa y Q corresponde a v.
La energía de dos bobinas con autoinductancias Mu y M22 e inductancia
mutua Mi2, es
<£ = i(M„Q? + 2M12Q1Ó2 + M22Ó5)
que nuevamente tiene la forma usual de la energía cinética. En el caso más general de
una malla que contiene s bobinas, la energía cinética eléctrica estará dada por
TEI = ¿¿MirQiQ, (15.1)
donde se nota que Mlr corresponde a Alr en la ecuación (2.56). Las coordenadas su-
perfluas Q, pueden ser eliminadas de TEl por medio de las ecuaciones de restricción.
Notas importantes, (a) Considérense por ejemplo, dos bobinas coaxiales (1) y (2) en
las que se establecen los flujos </>i y </>2, por medio de las corrientes i'i e 12. Si existe
alguna inductancia mutua entre ellas, parte de </>i enlaza a (2) y parte de <f>2 enlaza a
(1). Si, para las direcciones seleccionadas como positivas de i'i e i2, </»i enlaza a (2)
en la dirección que </>2 tiene en (2) (igualmente, $2 enlazará a (1) en la dirección de
</>i), en tal caso, M12 será positivo; en el caso contrario sería negativo. Por tanto, Mlr
puede ser una cantidad positiva o negativa.
(b) En el estudio que conduce a (15.1), tácitamente se ha supuesto que todas las induc-
tancias son constantes. Pero si, por ejemplo, las bobinas tienen núcleos de hierro, Mu,
Mi2,etc, dependen de los diferentes valores de las corrientes según una ley bastante
complicada. En este caso, las ecuaciones de Lagrange no pueden aplicarse de la manera
acostumbrada. Además, los núcleos de hierro introducen el complejo fenómeno de las
pérdidas por histéresis. Por esto, en adelante se supone que las inductancias no dependen
de las corrientes. Las inductancias mutuas pueden sin embargo depender de las
coordenadas espaciales.
D. Energía potencial.
La energía potencial de una malla puede considerarse como compuesta de dos partes:
las fuentes de energía (baterías, generadores, etc.) y la energía almacenada en los
condensadores.
Una fuente de voltaje terminal constante, E, suministra una energía al sistema,
EQ, en donde Q es la carga "entregada por la fuente" en la dirección de E. Así, si se
refiere la energía potencial al "punto" Q = 0, se escribe VfUente = — EQ en donde Q se
supone que circula en la dirección positiva de E. Nótese la gran analogía de esto con la
sencilla relación V = — mgy de la energía potencial de una masa m debida a la
gravedad, en donde se toma a y como positiva en la dirección vertical hacia arriba. La relación
anterior es válida aunque E varíe con el tiempo, según E = Eq sen co£, puesto que al
determinar las fuerzas generalizadas, t se conserva constante.
La energía de un condensador cargado aislado, de capacidad C, puede escribirse,
£ = ±Q2/C que corresponde exactamente a la energía de un resorte espiral, (1/C corres-
318
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
[CAP. 15
ponde a k). Por tanto, la energía potencial de una malla que contienen varias fuentes y
condensadores aislados, está dada por
Vei = i 2 Q</Cl ~ 2 E.Q. (15.2)
l s
donde, como en el caso de Tei, se han de eliminar las coordenadas superfluas.
Si cuando t = 0, los condensadores tienen cargas iniciales, Qoi, Q02, etc., las
energías correspondientes se escriben, ¿(Qi + Qoi)2/Ci, etc. y si la corriente Qs
circula en dirección opuesta a la positiva de E, entonces ESQS debe tomarse como
positiva.
E. Fuerzas generalizadas, FQr.
Las "fuerzas" básicas que actúan en un
circuito eléctrico pueden ser ilustradas por medio
del caso mostrado en la figura 15-2. Aplicando
aquí las leyes de Kirchhoff, se escribe
MQ = E-QIC-RQ
en donde puede observarse que MQ corresponde a una "fuerza inercial" (como mi ),
Q/C corresponde a la fuerza ejercida por un resorte (compárese con kx), E es la "fuerza"
aplicada por la batería y —RQ corresponde exactamente a una fuerza viscosa, como —ax.
(Nótese que RQ es una fuerza disipativa.)
La fuerza total generalizada, Fqt, correspondiente a QT, puede ser convenientemente
considerada,'como formada por (Far)c debido a las fuerzas conservativas y (FqJr
originada en las resistencias. Naturalmente (For)c = —dV/dQr.
Las expresiones de (Fqt)r pueden obtenerse como sigue. Cuando la carga 5Q,
circula por Rit el trabajo correspondiente (energía disipada) es igual a 8Wt = —¿?,Q, 8Q¡.
Por tanto, para un sistema que contenga un número arbitrario de resistencias,
BWtuBi = —(J?iQi 8Q1 + R2Q2SQ2 + •••) (15.3)
Una vez eliminadas las corrientes y las cargas superfluas, se agrupan términos y (Fqt)r
puede leerse directamente en (15.3). Estas fuerzas pueden hallarse a partir de (15.4a), a
continuación.
La fuerza generalizada total estará dada por
FQr = -dV/dQr + (FQr)R
F. Uso de la función de potencia.
Las formas siguientes son útiles en muchos problemas:
(a) P = -H,RiQ* Y (b) P = -2-ArÓ} + 1 (15.4)
i i O + 1
La primera (un caso especial de la segunda) es aplicable en todos los casos en que, para
todas las resistencias, 5 W = —RQlQ. La segunda se aplica cuando la "caída de
voltaje" a través de una resistencia, viene dada por E = AQb, es decir, 8W = —AQb&Q-
(Véase el ejemplo 15.2 más adelante.) En cualquiera de las formas, las corrientes
superfluas deben ser eliminadas.
G. Ecuaciones de Lagrange para circuitos eléctricos.
(No se consideran aquí partes móviles.)
Fig.15-2
CAP. 15]
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
319
La forma siguiente es aplicable a sistemas eléctricos consistentes de un número finito
de inductancias, condensadores, resistencias y fuentes de voltaje "concentradas" (no
distribuidas):
dt\dQrJ BQT ~ tQi
(15.5)
donde la función de Lagrange es Leí = Tei - Vei ; y Fqt — (Fqt)r , hallado por medio
de (15.3) o (15.4), se debe únicamente a fuerzas disipativas. Las fuerzas conservativas,
naturalmente, se tienen en cuenta en forma automática.
15.3 Ejemplos ilustrativos (sistemas puramente eléctricos; sin partes móviles).
En lo que sigue no se introducen unidades específicas.
Ejemplo 15.1.
Considérese el sencillo circuito que se muestra en la figura 15-3. El sistema tiene sólo dos grados de libertad,
siendo la ecuación de restricción,
—WW HfflF-
M22
R2
*El.
M33
-A/VW 1(
Supónganse inductancias mutuas entre todas las bobinas.
Fig. 15-3
Q, = Q2 + Qs
Suponiendo inductancia mutua entre todas las bobinas,
T = UMnQ* + M22Q¡ + M33Q\ + 2Ml2QxQ2 + 2M13Q,Q3 + 2M23Q2Q3]
Eliminando a Q3 de (2) por medio de (1), la forma final es
T = il^iiÓf + M22Q¡ + M^Q, - Q2)2 + 2Ml2QxQ2 + 2M13Q1(¿1 - Q2) + 2M23¿2(Q1 - Q2)}
(2)
Una vez eliminado Q3, se concluye de inmediato que
" 'ig^*2^-*.*.****».».-
Q2)
Aplicando las ecuaciones de Lagrange en la forma acostumbrada, las ecuaciones diferenciales
correspondientes a Qi y Q2, pon
(M11 + M33 + 2M13)Q1 + (M12-M13-M33 + M23)Q2 + (¿- + ±J Q, - ^ - Ex + E3 = FQj
(M22 + M33-2M23)Q2 + (M12-M33-M13 + M23)Q1 + (■£- + £j Q2 - ^ + B2 - E3 = FQj,
Puede observarse en el diagrama que el trabajo óW = —R1Q1SQ1 — R2Q2SQ2 — R3Q3 SQ3, y eliminando
Q3 y ÍQ3 por medio de (1),
SW = [R3Q2-(R1 + R3)Q1]8Q1 + [RsQ^-(R2 + R3)Q2]SQ2
Por tanto, FQj = jR3Q2 - (ií, + jR3)Qj y FQ = R3Q1 — (R2 + R3)Q2. Nótese que estas fuerzas generalizadas
vienen dadas también por FQ = dP/dQ^ y FQ — BP/BQ2 en donde (véase la ecuación (15.4a)),
P = -^Rtá + RM + RsiQi-Q^
Ejemplo 15.2.
El circuito de la figura 15-4 contiene dos tubos iguales, de dos elementos cada uno, conectados según se
indica. Se supone que E3 está dado por AQ3 en donde A y b son constantes, o sea E3 = A |Q3-1| Q3 y en donde
320
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
[CAP. 15
|Q3 | indica valor absoluto. Según se indica, se aplica un voltaje externo, £2 = £0 sen ut. La función de
Lagrange para el sistema, luego de haber eliminado Q3 y Q3, es
. 1 1|—n—f—'W^/vw 1 1 1
Fig. 15-4
^ = UMuQ21 + M22Ql + M33(Q2-Q^ + 2M12Q1Q2
+ 2M13Q1«32-Q1) + 2Mr¿Q2(Q, -<?,)] - $Q\/C + B.Q, + Q2E0 sencoí
de donde pueden obtenerse las ecuaciones del movimiento en forma inmediata. Las expresiones de FQ y FQ>
pueden hallarse a partir de
SW = -[RlQliQl + R2Q28Q2 + R3(Q2-Q1)(8Q2-8Qt) + A\(Q2 - Q,)""1! (Q2 - Ó,)(8Q2- SQ,)]
El lector debe demostrar que las mismas expresiones de las fuerzas generalizadas pueden obtenerse a partir
de una función P, la cual se forma de la suma de (15.4a) y (15.4b).
15.4 Sistemas electromecánicos: La función de Lagrange adecuada;
determinación de las fuerzas generalizadas.
Un sistema electromecánico es aquel en el que la energía asociada es en parte eléctrica,
en parte magnética y finalmente, en parte mecánica. Un galvanómetro común de bobina
móvil, constituye un ejemplo sencillo en este tipo de sistemas. La bobina y su suspensión posee
energía cinética y potencial "mecánicas". La bobina y el circuito al cual se halla conectada
posee energía "eléctrica". A medida que se mueve la bobina, la parte que actúa sobre ella así
como su velocidad angular, su desplazamiento y su aceleración dependen de las magnitudes
eléctricas del sistema, y viceversa. Por esta interrelación, el movimiento mecánico y el
funcionamiento eléctrico no pueden estudiarse en forma separada. El sistema debe ser considerado
en forma global.
La función de Lagrange para un sistema electromecánico puede escribirse como
L = TEl- Vex + TMe - VMe U5.6)
donde TFI y VEl se expresan como ya se ha ilustrado antes. La energía cinética mecánica y la
energía potencial mecánica se representan por TMe y VMe, respectivamente, expresadas en
la forma acostumbrada, en función de cualquier sistema de coordenadas espaciales q\,
q2, ...,gni. Si, además de estas nx coordenadas espaciales, se deben tener en cuenta n-i
cargas independientes, puede decirse que el sistema tiene n = n\ + m grados de libertad.
La aplicación de las ecuaciones de Lagrange a (15.6) conduce de inmediato a ri\ + ri2
ecuaciones del movimiento.
Al escribir (15.6) para un problema específico, debe tenerse cuidado en la selección de las
unidades, de modo que todos los términos que entren en L se expresen en las mismas
unidades de energía. Como se indicó anteriormente, en este capítulo no se incluyen unidades espe-
CAP. 15]
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
321
cíficas. Las fuerzas generalizadas (que no han sido tenidas en cuenta por los términos de la
energía potencial en L) correspondientes a coordenadas eléctricas y espaciales, se encuentran
en la forma acostumbrada, como se verá en los ejemplos a continuación.
Ejemplo 15.3.
Considérese el sistema ilustrado en la figura 15-5. La placa superior del condensador C, de masa m, está
suspendida por medio de un resorte espiral de constante k. Esta placa puede moverse verticalmente bajo la acción de
la gravedad, el resorte y el campo eléctrico entre las placas. Una característica especial de este sistema es, desde
luego, la capacitancia variable C.
R
-nm^
M £
*■ Posición de
( equilibrio
— T«
C = -
VÁ///Á
Fig. 15-5
La posición de reposo de la placa, con el condensador descargado, se representa por la línea a trazos.
Suponiendo que entre las placas hay aire, por conveniencia, se escribe C = A/(s — x), donde A es una constante
cuyo valor depende del área de la placa y del sistema de unidades empleado, y s es la distancia indicada. Por tanto,
la función de Lagrange para el sistema será
L - WQ2 + £m*2 + QE0 sen <oí - £Q2(s - x)/A - $kx*
(Un término que contiene a mg, se anula.) El sistema tiene dos grados de libertad, siendo las coordenadas Q y x.
Al aplicar las ecuaciones de Lagrange se obtiene
MQ + Q(s - x)/A - E0 sen coi
-RQ,
\QVA = 0
Nótese que el voltaje de la autoinductancia MQ, el voltaje a través del condensador Q(s — x)/A, y la fuerza
de atracción entre las placas \Q2/A, se han incluido automáticamente en las ecuaciones de Lagrange.
Ejemplo 15.4.
Bobina (1), .Vi espiras por unidad de longitud
QQ00Q0000OQQ0000QQQ0O0OOO3QOQQ000OO00000OOOQ0
' Pequeña bobina circular (2)
2 espiras. Q2 sale del plano
del dibujo
La bobina (2) puede girar montada
dentro del eolenoide grande,
M668MB400aWoBftM6ofl6fl080MUUJUUUUUJUJÜ6«oM006o
Fig. 15-6
-Ei
A'ii Bobinad)
AÍ.2
\&mj—
.U22 Bobina (2)
Ei - Eo senut
«Pl ""P2>
p2 es positivo para valores de í
ligeramente mayores que cero.
Un pequeño eje perpendicular al plano de la figura 15-6, que pasa por p, está montado en cojinetes lisos (que
no se muestran) y sostiene la pequeña bobina (2) dentro de la bobina larga estacionaria (1). Adherido a (2) se
encuentra un resorte plano, como se indica, que tiene una constante de torsión, k. Las bobinas se conectan a
322
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
[CAP. 15
circuitos separados como lo muestra la figura de la derecha. Suponiendo que (1) es muy larga, puede demostrarse
sin dificultad que la inductancia mutua de (1) y (2), está dada por
M12 = 6(-r2)^,^2 sen 8
donde r es igual al radio de la bobina (2), Ni es el número de espiras por unidad de longitud en la bobina (1),
N2 es el número total de espiras en (2), y b es una constante que depende de las unidades específicas que se utilicen.
Remplazando aquí a b(rr2)NiN2 por A, se tiene
L = \MUQ\ + \M22Q\ + lie2 + AQ,Q2sen* + #,Q, + Q2E0 sen wt - $ke2
donde Mu y M22 son las autoinductancias (que se suponen conocidas) de (1) y (2), respectivamente, e / es el
momento de inercia de la bobina (2) con relación al eje en el cual se halla montada. Se supone que para 0 = 0,
el resorte plano se encuentra en su forma normal.
Aplicando las ecuaciones de Lagrange, se obtienen las siguientes ecuaciones diferenciales correspondientes
a Qi, Q2 y 0:
MjjQj + AQ2sen* + A$Q2 eos 8 - Ex = -R1Q1
M22Q2 + AQi sen* + AeQx cosí - EQ sen ut = -R2Q2
í» - AQ^cos* + k$ = 0
Nótese, por ejemplo, que el término A$QX eos 8 representa un voltaje inducido en la bobina (2), debido a
su velocidad rotacional 8 en el campo magnético establecido en (1) por la corriente Qv El término BQXQ2 eos 8
es el torque que actúa en (2). Así mismo, debe examinarse el significado de los demás términos.
15.5 Oscilaciones de sistemas eléctricos y electromecánicos.
Los resultados del capítulo 10 se aplican frecuentemente a la determinación de las
frecuencias naturales de oscilación de sistemas eléctricos o electromecánicos, como se indica en los
ejemplos siguientes.
Ejemplo 15.5.
Considérese nuevamente el circuito de la figura 15-3. Las ecuaciones correspondientes a Qi y Q2 pueden
escribirse como sigue
(MU + M33 + 2M13)Q1 + (R1 + R3)Q1 + (± + ^J Q,
Q2
+ (M12 + M23-M33-M13)Q2 - iÍ3<32 - -=- = Bx - E3
(M12 + M23 - M33 - M13) Q, - R3Q, - £*■
+ (M22-2M23 + M33)Q2 + (R2 + R3)Q2 + (¿ + ^)<?2 = E3 - E2
Utilizando "coordenadas de equilibrio" (véase el problema 15.2), estas ecuaciones toman exactamente la
misma forma de las ecuaciones (10.7). Naturalmente, las ecuaciones pueden resolverse por los mismos métodos.
Ejemplo 15.6.
Considérese nuevamente el sistema de la figura 15-5 y estudiado en el ejemplo 15-3. Para simplificar,
supóngase que se ha remplazado el voltaje variable por uno constante, E. Es obvio que un tiempo después de haber
conectado la batería, aun en el caso del amortiguamiento más ligero posible para la placa superior, tanto x como Q,
alcanzan los valores constantes, xo y Qo. Midiendo los desplazamientos a partir de estos valores de equilibrio,
es decir, escribiendo, x = x0 + xi y Q = Qo+Qi,
V = -E(Qo + Qi) + £(<?o + Qi)2(8-*o-*i)M + ifc(*0+*i)2
A partir de (dV/dQ^Q = 0 y (dV/dx^ = 0', se concluye que x0 = é Q2/Ak y Qo = AE/(s - x0).
Suponiendo que Qi y xi son siempre pequeños, luego de aplicar (10.6), se obtiene
v„„, =¿[(LLü)«;-£*., + *;]
CAP. 15|
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
323
Por tanto, L = \MQ\ + \mx\ - \ \{^)q\ ' ^Q^ + **?]
¡8 — X0\ Qo
de donde MQ, + ( A )Qi ~ J1! = ~RQi
Qo
y mxl + kxx ¿~Qi = 0
que tienen la misma forma de (10.7) y pueden resolverse de la misma manera.
15.6 Fuerzas y voltajes necesarios para producir movimientos y corrientes
dadas en un sistema electromecánico.
Los resultados del capítulo 13 pueden aplicarse a sistemas electromecánicos, como se
ilustra en los ejemplos siguientes.
Ejemplo 15.7.
Supóngase una fuerza /, aplicada a la placa móvil de la figura 15-5, y supóngase además que E0 sen «í
se remplaza por un voltaje desconocido, cuya naturaleza debe determinarse. Las ecuaciones generales del sistema
son ahora (véase el ejemplo 15.3).
MQ + Q(s- x)/A + RQ = E y m x + kx - QV2A = fx (1)
Si se conoce la forma como Q y x varían con el tiempo, podrán hallarse las expresiones correspondientes de E y
fx, en función del tiempo. Considérense los siguientes casos.
(a) Supóngase que Q = Q0 = constante y x = x0 = constante. En este caso, por (1),
E = Q0(8-x0)/A y /x = kxü-(^/2A
(b) Si se supone que x = xo = constante y Q = Q0t,
E - RQo + Q0t(8-x0)/A y fx = kx0 - Q20ty2A
(c) Haciendo Q = Q0 sen («,í + <f>i) y x = io sen («2í + <t>z), se obtiene
Q
E = MQ0coj eos (cojí + <f>x) — -.— cos((0jí + ^j)[8 - *o sen(co2í + <t>2)] + RQo seníco,* + £,)
1 Qo2
fx - —mx0u* sen (u2t + <f>2) + kxo sen(co2í + <f>2) — 2~J~2 cos2 ^Ulí + ^
Este voltaje y esta fuerza pueden naturalmente resultar difíciles de aplicar. Además, si /, y E se aplican al azar,
posiblemente aparezcan algunos efectos transitorios, que en el caso real podrían eventualmente amortiguarse por la
resistencia y la fricción sobre la placa. (Véase la nota del numeral 13.2.)
Ejemplo 15.8.
En la figura 15-3, considérense £i y £2 como voltajes aplicados no conocidos. Escribiendo las ecuaciones
del movimiento en función de Qi y Q3 y suponiendo que Q\ = Q01 = constante y Q3 = Q03 = constante,
el lector puede demostrar que £1 y £¡¡ deberán tener los valores
p - rr x Qo1 -l Qo3 ir - r x Q°3 ~ Qo1 x Qo¡t
Igualmente para Qi = A\ sen (utt + ¿i) y Q2 = A2 sen (w2t + <t>2), Ex y E2 pueden ser hallados
de inmediato, en función del tiempo.
15.7 Sistemas eléctricos y mecánicos análogos.
Con frecuencia ocurre que, para un sistema eléctrico determinado, existe uno mecánico
que es su contraparte exacta en el sentido de que las ecuaciones diferenciales de los dos
(seleccionando en forma adecuada las coordenadas) pueden escribirse de la misma forma. Esto se
ilustra por medio de los siguientes ejemplos sencillos.
Ejemplo 15.9.
En la figura 15-7(a), una esfera de masa m está suspendida en un b'quido viscoso por medio de un resorte
espiral. La longitud normal del resorte es /o, la elongación del resorte cuando m está en reposo es y0 y el
desplazamiento con respecto a la posición de equilibrio es >\ Se supone que el único efecto originado en el líquido es
324
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
[CAP. 15
una resistencia viscosa, — ay. La figura 15-7 (b) representa un circuito eléctrico en serie sencillo. Las funciones de
Lagrange para (a) y (6), respectivamente, son
LMe = \m\p- - \k{y + 2/0)2 + mgy, LEl = %M& - ^QVC + EQ
'/////////////////////////////,
--Posición de reposo
Ung
(a) (b)
Fig. 15-7
Como mg = kyo, las ecuaciones del movimiento son
my + ky - -ay, MQ + QIC - -RQ
Por tanto, los dos sistemas son "equivalentes".
Ejemplo 15.10.
Considérense los tres sistemas que se muestran en la figura 15-8. En (a), E es un voltaje constante aplicado
y se supone que no hay inductancia mutua entre las bobinas. En (b), F es una fuerza constante aplicada
externamente y cada uno de los bloques sufre la acción de una fuerza viscosa, —alxl, etc. En (c), r es un torque constante
aplicado externamente y un freno ejerce un torque viscoso, — bxrx6u etc., sobre cada uno de los discos. Las funciones
de Lagrange para cada uno de los tres sistemas, pueden escribirse como sigue
Lb
Le
$(MlQ2l + M2fr2 + M3&3)
(Q1-Q2)2 (Q2-Q3)2
+ EQ,
2C, 2C2
$(m1x2 + m2xl + m3x2) - £Ae,(x2- ^í ~ *io)2 ~ W2(x3-x2-l20)2
¿(71¿2 + /2¿2 + /3¿2) - ¿M»i-»2>2 - 1eHH-*z)2
U)
(a)
(b)
*3
X2
*1 r
F .
mx
"II""""
—Tftfír1—-
ii>
m2
iüUUULlLli
—oRftr^
a2
m3
llllllllllllllll
L^3
CAP. 15]
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
325
(c)
©Mr^M
7Z,
w^4
l
imlfíiib3
////;////,
Fig. 15-8
Las ecuaciones finales del movimiento para (a) son
Q\ Q2
RiQi
M2Q2-§i+Q2(¿ + ¿)-| = -R&
M3Q3
9i+ 9i
= -R3Q3
En forma inmediata pueden encontrarse ecuaciones de iguales formas para los sistemas (6) y (c). Aquí,
la inductancia corresponde a una masa en (b) y a un momento de inercia en (c). La resistencia eléctrica Ri
corresponde al coeficiente de resistencia viscosa ai en (6) y a brt en (c), etc. 1/C corresponde a una constante
elástica, en ambos casos. Nótese que en el ejemplo anterior las coordenadas se tomaron teniendo en cuenta que
los tres grupos de ecuaciones tuvieran la misma forma. Si, por ejemplo, las ecuaciones del movimiento para (6)
se escribieran en función de x\,q\ y 92 donde qi = X2 — xi y 92 = X3 — 12, no sería tan evidente
que (b) fuera equivalente a (a) y a (c). Nota. En Lb, las sumas xi + í!0 y 12+ /20 pueden ser remplazadas
por una sola variable cada una.
No siempre es fácil encontrar la contraparte eléctrica exacta para un sistema mecánico arbitrario. En
ocasiones pueden necesitarse circuitos análogos muy complejos.
Ejemplo 15.11.
Los sistemas eléctrico y mecánico que se muestran en la figura 15-9(a) y (6), resultan sorpre:
parecidos en su apariencia general y si se idealiza adecuadamente (a), sus características físicas son
Viruta g
r
ndentemente
las mismas.
R2
1 WWl-
c2
(a)
Fig. 15-9
ib)
326
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
| CAP. 15
En (a), la masa M y los resortes de hoja Si y S2 (en vistas laterales) se encuentran acoplados por un
líquido "sin masa" dentro de tubos lisos. Las secciones A y B están llenas de viruta con lo cual se presenta una
resistencia viscosa a la circulación del líquido, — R[ X (velocidad del líquido); etc. Puede aplicarse a M una fuerza
externa f\, y otra, f2, directamente al líquido. Se supone que los pistones indicados son lisos y no tienen masa.
El desplazamiento horizontal de M, a partir de algún punto fijo, se representa por qt; q2 y (73
representan los desplazamientos de Si y S2, respectivamente. El lector debe escribir las ecuaciones del movimiento
para los dos sistemas y demostrar que, matemáticamente, son equivalentes cuando M corresponde a Mu) ki y
k2 corresponden a 1/Ci y a 1/C2; R[ y R2 corresponden a R\ y a R2\ y f\ y f2 corresponden a E\
y a E2.
Como se vio en los ejemplos anteriores, los sistemas análogos, usualmente, no presentan apariencias semejantes.
15.8 Referencias.
Mayores detalles sobre la aplicación de las ecuaciones de Lagrange a sistemas
electromecánicos y sobre las analogías eléctricas-mecánicas, pueden hallarse en las siguientes
referencias:
H. F. Olson, Dynamical Analogies, Van Nostrand, 1943
W. P. Masón, Electromechanical Transducers and Waue Filters, Van Nostrand, segunda
edición, 1948
R. M. Fano, L. J. Chu, R. B. Adler, Electromagnetic Fields, Energy, and Forces, John Wiley,
1960
D. C. White, y H. H. Woodson, Electromechanical Energy Conversión, John Wiley, 1959
J. R. Barker, Mechanical and Electrical Vibrations, John Wiley, 1964
G. W. Van Santen, Mechanical Vibration, N. V. Philips, Eindhoven, Holland, 1953
Problemas
En los siguientes problemas no se introducen unidades específicas.
15.1. Demostrar que la función de Lagrange y las ecuaciones del movimiento del circuito de la figura 15-10,
suponiendo que no existe inductancia mutua entre M33 y las demás inductancias, son
L = \\MU&X + Ml2QxQ2 + (M22 + M33)Ql] + Q,E0 sen«oí - \Q\/C
MjjQj + Ml2Q.¿ - E0senvt = -#,(?,
(M22 + M33)Q2 + Ml2Q, + Q2/C = -R2Q2
R2 ffij3
Fig. 15-10
Fig. 15-11
15.2. En el ejemplo 15.5, figura 15-3, se observa que después de algún tiempo, Qi = Q2 - Q3 - 0 y se escribe
entonces, Qi = Q0i, Q2 = Q02 y Q3 = Q03. Hallar las expresiones para estas cargas de "equilibrio".
Haciendo ahora Qi = Q01 + ai, Q2 = Q02 + a2 y Q3 = Q03 + a3, escribir L para el sistema y
demostrar que las ecuaciones del movimiento son
CAP. 15]
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
327
(M„ + M33 + 2M13)'á1 + (Rl + R3)'ai + (1/C, + 1/C3)a,
+ (Ml2 + M23 — M13 - M33) a2 - R3C*2 - cc2/Cz - 0
(M12 + M23 - M13 — M33)"a, - i?3¿! - 0,^3
+ (M22 - 2MM + M33)"á2 + (R2 + R3)á2 + (1/C2 + 1/C3)«2 = 0
El medio cilindro interior A, de la figura 15-11, sostenido en posición vertical por una varilla elástica
delgada (constante de torsión, k) sujeta a su eje en O, puede girar dentro de B. Suponiendo que la
capacidad de este condensador variable está dada por C = Co(l — fl/x) y que la varilla no se ha distorsionado
cuando 6 = 6\, demostrar que la función de Lagrange adecuada y las ecuaciones del movimiento son
Q2
L = £7nQ2 + $Ie2 + EQ -
Q _
C0(l-9/v)
Q2
e +
i'e +
2C0(1 - 9h)
E = -RQ
$k(6l - 9Y
2ttC0(1 - *Ar)2
k(9l-9) = 0
Las bobinas de la figura 15-6, se encuentran conectadas en serie a una fuente externa de voltaje
Eo sen ut. (Véase el ejemplo 15.4.) Demostrar que las ecuaciones del movimiento son
(Mn + M22)Q + 2B(Q cosí - Q$ senfi) - E0 sen «oí
1$' + B(Q2 sen 6) + ke = 0
-RQ
Se remplaza la bobina (1), de la figura 15-6, por un imán permanente. Suponiendo que el campo
magnético es uniforme y constante y que la bobina móvil está conectada como se indica en el diagrama,
escribir la expresión de L y demostrar que las ecuaciones del movimiento son
M22Q2 + N24>6 eos e - E0 sen coi = -R2Q2, le - N24>Q2 eos 6 + ke - 0
donde * es el flujo total que enlaza a las bobinas cuando 6 = 90°.
Dos galvanómetros de imán permanente, del tipo de pared, se encuentran conectados como se muestra
en la figura 15-12. Suponiendo campos magnéticos radiales, demostrar que la función de Lagrange
adecuada al sistema, está dada por
L = UMiM + 2Mi2QiQ2 + M22Ql) + y¿\ + $I2e¡ + N^A'i
+ N2*2Q2e2 + (Ql + Q2)Ei - i«2, + Q2)2/C - ±MÍ ~ *MÍ
donde se ha supuesto que Mu y M22 incluyen las autoinductancias de las bobinas de los
galvanómetros (1) y (2) respectivamente. Escribir las ecuaciones del movimiento.
Y//k////
1
'. !
y
Conexión
flexible
Ql
-HM^-
r Suponer campo radial
cb
1
¿2-^yfflP—32.
Galvanómetros de pared, de imán permanente
Fig. 15-12
328
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
[CAP. 15
Las dos placas del condensador variable de la figura 15-13, pueden moverse a lo largo de la linea ab sin
girar, bajo la acción de un resorte y del campo eléctrico entre ellas. Demostrar que la función de Lagrange
para el sistema, es
L = ¿(m,¿* + m2x¡ + M&) - ^x\ + k2x¡) + EQ - $QH8 - xx - x2)/A
donde A es una constante. Escribir las ecuaciones del movimiento.
""vñfr////^
ZA _
V///V//Á
Fig. 15-13
Un condensador variable y un galvanómetro de pared se encuentran conectados como se indica en la
figura 15-14. Demostrar que L para el sistema, es
L = j[{I¡* + m& + Mufrl + Mt¡!fe) + E&- EúQi-Qá
+ NQQS - $[kx*+ «3,-<32)2(8-x)/A + fc»2] + mgx
Escribir las ecuaciones del movimiento y a partir de ellas determinar los valores estacionarios de
Qi y Q2. y los valores de equilibrio de 6, x y Qz. Comprobar las relaciones por medio de
principios elementales.
V///////{
Fig. 15-14
Demostrar que los valores de equilibrio de 8 y de Q, de la figura 15-11, problema 15.3, están dados
por 80 = 0i - CoE2/2irk y Qo = Co(l - 0oA)¿?. Por las propiedades físicas del sistema puede
observarse que cuando el condensador está cargado, 6\ > 0.
Escribiendo 0 = 80 + ai y Q = Qo + a2, hallar las ecuaciones del movimiento que determinan
las oscilaciones de 0 y Q con respecto a los valores de equilibrio.
15.10. Plantear las ecuaciones para la determinación de los movimientos oscilatorios del sistema que se muestra
en la figura 15-12, con respecto a los valores de equilibrio (véase problema 15.6).
CAP. 15]
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
329
Se hacen variar de una determinada manera, con respecto al tiempo, B\, 02, Qi y Q3, de la figura
15-12. Se aplican a las bobinas móviles los torques n (í) y t2 (£), respectivamente. Remplazar la batería
con una fuente de voltaje de valor desconocido, Ei = Ei (£). Intercálese otra fuente de voltaje, E2 =
E2{t) en el ramal izquierdo del circuito. Hallar las expresiones de n, t2, Et y E2, que satisfacen las
condiciones establecidas.
Plantear las ecuaciones del movimiento para los sistemas (a) y (b), de la figura 15-15, y demostrar que son
equivalentes. Supónganse fuerzas viscosas que actúan en las bases de mi y m2. Supóngase además que
el amortiguador ejerce una fuerza viscosa.
(a)
Fig. 15-15
E = EQ sen ut
\ U^l^IIlí
(b)
El péndulo doble de la fígura 15-16(a) (véanse las ecuaciones (70.2)), está compuesto de una barra pesada
uniforme (de longitud n y masa M) y una varilla ligera delgada, de longitud r2, con una "partícula"
m, adherida en su extremo. El cojinete superior, b\, ejerce un torque amortiguador proporcional a 0
y el cojinete inferior, b2, ejerce otro torque proporcional a <¡> — 0. El resorte plano espiral (con un extremo
adherido a la barra y el otro a la varilla) no se halla distorsionado cuando d = <fi. En la figura 15-16(6)
las dos bobinas tienen una inductancia mutua igual a Ai 12.
Suponiendo que 0 y <t> son ángulos pequeños, demostrar que las ecuaciones del movimiento para
estas coordenadas son análogas a las correspondientes a Qi y Q2 (exceptuando un término constante, E).
Cil
*-.—"WT^-^r—rQWT>—*m
Qi Mn
M*
Fig.15-16
-JWV\r-
M22 Q,
(b)
En la figura 15-17, el disco está montado en el centro de una varilla elástica cuyos extremos se encuentran
fijos rígidamente. La constante de torsión de la varilla es k 1 y la constante elástica del resorte espiral es
k2. Las varillas metálicas (de masas mi y m2) se encuentran suspendidas por medio de un hilo
aislante como se indica, y pueden moverse verticalmente dentro de los cilindros metálicos fijos. Cada uno de
los conjuntos de varilla y cilindro, constituyen un condensador variable, Ci y C2, respectivamente.
Constituyen circuitos eléctricos independientes Mu, Ri, E\ y Ci, y M22, R2, E2 y C2 pero se
encuentran acoplados por medio de la inductancia mutua, Mi2. Demostrar que T y V para este sistema
electromecánico, están dados por
T = iimtf + mal + IÜ/tS) + UMnQ2i + 2Ml2QlQ2 + M22&)
hQ2x , hQ\
2 LCoid,
'oíd - Vi) C02(l2 - y.¿)
aHA
sen ut — E2Q2
+ 2 [_fcl ( 2 r / + AC2(Í>1 ~ Vl ~ V*)2 + migVl + m2ffV2
donde Ci = Coi(l - yi/li), C2 = Co2(l - ;y2//2), yi + y2 + l = bi = constante y
Escribir las ecuaciones del movimiento correspondientes a yi, y2, Qi y Q2.
330
SISTEMAS ELÉCTRICOS Y ELECTROMECÁNICOS
[CAP. 15
Ex = E0 sen u<
Pig.15-17
Remplazando a E0 sen «í por un voltaje constante, determinar los valores de equilibrio de yit y2,
Qi y Q2. Haciendo el desarrollo de V, (véase 10.6), con respecto a estos valores, plantear las ecuaciones
del movimiento para pequeñas oscilaciones del sistema.
CAPITULO
16
Ecuaciones del movimiento de Hamilton
16.1 Observaciones generales.
Las "ecuaciones canónicas" de Hamilton constituyen otra manera de expresar las
ecuaciones dinámicas del movimiento y, como se verá más adelante, para un sistema n grados
de libertad existen 2n ecuaciones de primer orden de Hamilton, en tanto que para el mismo
sistema resultan n ecuaciones de segundo orden de Lagrange.
Como medio para analizar la mayor parte de los problemas aplicados, el método de
Hamilton no es tan conveniente como el de Lagrange. Sin embargo, en ciertos campos de la
física (enumerados y comentados brevemente al final del capítulo) las ecuaciones de
Hamilton y su punto de vista especial, han prestado grandes servicios.
16.2 Una palabra sobre el "momentum generalizado".
La magnitud dL/dqT se define como el momentum generalizado pr, correspondiente
a la coordenada generalizada qr, es decir dL/Bqr — Pr. (Nótese que si las q aparecen
únicamente en T, 8L/dqr = dT/Bqr — Pr.) Los siguientes ejemplos demuestran que en algunos
casos sencillos, pr, como se ha definido, es un momentum en el sentido usual y elemental
de la palabra.
Para un proyectil, puede escribirse, L = \m(x2 + y2 + z2) - mgz de donde dL/dx =
mi = px, py = my y pz = mz. Por tanto, px, py y p2 son las componentes del
momentum lineal usuales.
En el ejemplo 5.7, figura 5-9,
BL/dx -Mx- vi, BL/dr = ¡¿r — pr, dL/di) = ^9 - Ve, dL/dj> = mr2sen2 9J> - p*
donde p¡ y pr son los momenta lineales en tanto que pe y p¿ son los momenta angulares.
16.3 Deducción de las ecuaciones de Hamilton.
La función de Lagrange, L = T — V, es en general una función de q\, q2, .., q„',
q\, q-2, .., qn; t. Puede escribirse entonces,
Pero, pr = ——, y por -n(—— ) — -— = F<¡ (donde FQr se determina en la forma usual
dqr * dt\dqj dqr
a partir de todas aquellas fuerzas no incluidas en V) se observa que dL/dqr = Pr — FQr. Por
consiguiente (16.1) se convierte en
dL = 2 [(pr - FQr) dqr + pr dqr] + -^dt (16.2)
Luego, eliminando prdqr de la relación anterior d(vrqr) — pTdqr + qrdpr y ordenando
términos, (16.2) puede escribirse
331
332
ECUACIONES DEL MOVIMIENTO DE HAMILTON
[CAP. 16
BH _
BPr
.
Qr,
dH
dqr '
= *v
.
-Vr,
BH
dt
BL
Bt
d [jtP'í' ~ L] = 2 {(F«T-Vr)dqr + qrdpr) - j¿dt (16.3)
En este momento es importante observar que pr = BL/Bqr es, en general, una función de
las q, q y t. (En un caso particular, esto toma la forma de una ecuación algebraica. Por ejemplo
como se hizo anteriormente, BL/Bj> = p<t> = mr2sen2d j>). Por medio de estas n relaciones
todas las velocidades q\,q2, . . .,qn , pueden eliminarse de 2 prqr — L en favor de las p y
r=l
las q. Suponiendo que se ha hecho esto, se define la función hamiltoniana, o hamiltoniano,
H como
H = 2 Prqr - L (164)
r=\
Como esta es una función de las p, q y t,
dH = ¿(I^+S^) + fdt <ís-5>
Comparando los términos del lado derecho de (16.3) con los de (16.5), se observa que
(16.6)
Las dos primeras relaciones de (16.6) representan 2n ecuaciones diferenciales de primer
orden, las cuales se denominan ecuaciones canónicas de Hamilton del movimiento. Sus
soluciones, con las constantes de integración evaluadas adecuadamente, conducen a expresiones
de todas las coordenadas y todos los momenta en función del tiempo; es decir, que
determinan completamente el comportamiento dinámico del sistema. (Un buen estudio de las
expresiones adecuadas para L y H, cuando aparecen fuerzas originadas en campos eléctricos y
magnéticos, puede encontrarse en D. H. Menzel, Mathematical Physics, Dover, 1961, páginas
359 y 360).
Debe observarse que H usualmente puede expresarse en otra forma que en ocasiones
resulta más conveniente. Se escribe (2.55), como
T = ¿ ^Arshris + Í£Baqs + C ^ T, + T2 + T3 (16.7)
r=ls=l s=l
(Como ejemplo específico de esta forma de T, nótese que la expresión (2.50) puede escribirse,
T — \m[q\ + q\ + 2¿i ¿2 eos (/? - «)] + m{[(vx + axt) eos a + (vy + ayt) sen«]¿i
+ [(vx + axt) eos/? + (vy + ayt) sen p]q2}
+ $m[2(vxax + vyay)t + (al + al)t2 + v2x + vi]
Naturalmente los términos primero, segundo y tercero son Ti, T¿ y Tz, respectivamente.
En un caso particular cualquiera, cuando T se escribe en forma explícita, Ti, T2 y T3
pueden reconocerse por simple inspección.) Por tanto, suponiendo BL/Bqr — BT/Bqr, se tiene
Pr = BTlBqr = 2 2 Arsks + BT
s = \
Y aSÍ, 2 PrQr = 2 2 2 Arskrqs + 2 #r¿r = 2T, + T2
CAP. 16 ]
ECUACIONES DEL MOVIMIENTO DE HAMILTON
333
Entonces, (16.4) puede escribirse como H = 2T, + T¿ - (T, + T2 + T3 - V) o sea
h = r, - r3 + f (j0.s)
Si £ no aparece en las ecuaciones de trasformación, (véase (2.21)), T2 = T3 = 0 y
#=T + Vr = <5 = energía del sistema
Por conveniencia, se resumen a continuación las relaciones más importantes.
(a) H = ¿ Vrhr - L (164)
(b) H = T,-T3+V (16.8)
Estas relaciones son correctas aunque estén actuando fuerzas externas y disipativas.
16.4 Procedimiento para determinar H y escribir las ecuaciones de Hamilton.
(a) Escríbase L = T — V. Exprésese T y Ven la forma acostumbrada, como si se fueran a
aplicar las ecuaciones de Lagrange.
(b) Tomando las derivadas px = dL/dqi, p2 — BLIbq2, etc., obténganse las n ecuaciones
algebraicas. Estas relaciones expresan lasp en función de las q, las q y las t.
(c) Resuélvanse simultáneamente estas ecuaciones para hallar las diferentes q, en función
de las p, las q y t y elimínense las q de (16.4) o (16.8). Así se obtiene H en función de las
p, las q y t, únicamente.
(d) Para obtener las ecuaciones del movimiento de Hamilton, tómense las derivadas,
BH/dpi, dH/Bp2, ...,dH/dpn y en cada uno de los casos el resultado se hace igual a
Qi, Q2, . . ., Qn» respectivamente. Igualmente, realícese la diferenciación BH/dqi, y el
resultado hágase igual a Fqi — plt etc. Se tienen entonces 2n ecuaciones de primer orden.
Las magnitudes de Fqx,Fq2, etc., son las mismas fuerzas generalizadas usuales,
halladas en la forma acostumbrada, excepto que las fuerzas conservativas, como se explicó
anteriormente, no se incluyen.
16.5 Casos especiales de H.
(a) Cuando actúan únicamente fuerzas conservativas, incluyendo aquellas para las cuales
puede escribirse una función de energía potencial que incluya a t (véase el numeral 5.11),
FQr = 0. Por tanto
Estas ecuaciones son usadas extensamente en muchas ramas de la dinámica.
(b) Si se trata de un sistema "natural" en el que no existen coordenadas móviles ni
restricciones móviles (t no aparece en las ecuaciones de trasformación), T2 = T3 = 0 (véase
(2.56)). Por tanto T = T, y por (16.8),
H = T +V = «Stotai (16.10)
Es decir, que con estas condiciones, H es la energía total del sistema. Sin embargo, en
general, H no es la energía total.
334
ECUACIONES DEL MOVIMIENTO DE HAMILTON
I CAP. 16
16.6 Relaciones importantes de la energía y la potencia.
Por 06.5), f = ¿(f i, + gí,) +f • Aplicando U6.6),
di" = 2 Fqrqr + -ñ [16.11)
de donde pueden derivarse las siguientes conclusiones importantes.
(a) Si el sistema es natural, dH/dt — 0; y si no actúan fuerzas diferentes de las conservativas,
Fqr — 0. De modo que, como se demostró antes H = T + V = £lotal. Entonces,
-rr - dt =0 o <£totai = constante {16.12)
Es decir, que la energía total del sistema, T + V, permanece constante (véase el
numeral 5.13). Las ecuaciones {16.12) expresan la ley de conservación de la energía para tales
sistemas,
(fe) Si el sistema es natural y actúan fuerzas diferentes de las conservativas, {16.10) y {16.11)
dan
f = ±(T + V) = ±F,ri, (16.13)
Pero 2 FqrQr es la rapidez con que todas las fuerzas (sin incluir las conservativas) rea-
r = l
lizan trabajo sobre el sistema. Por tanto la rapidez del cambio de <Stota, es igual a la
potencia suministrada por estas fuerzas.
16.7 Ejemplos. El hamiltoniano y las ecuaciones del movimiento de Hamilton.
No existen coordenadas móviles ni restricciones móviles.
Ejemplo 16.1. El proyectil.
Se considera un proyectil como una partícula y se utiliza un sistema de ejes adherido a la Tierra que se
supone inercial,
L = \m{x2 + y2 + z2) — mgz
de donde, dL/dx = mx — px, py — my, pz = mz (1)
Por tanto, de acuerdo con el numeral 16.4, H = -—(pl + Py + p^) + mgz (2)
Aplicando (16.6) y despreciando la resistencia del aire,
dH/dpx = pjm = *, BH/dpy — py/m — y, dH/dpz - pjm = z (8)
BH/dx = 0 = -px, BH/By = 0 = -py, BH/Bz - mg - -pz (4)
Nótese que en lo anterior, T = Ti (T2 = T3 = 0); por tanto, H = T + V = €.) Las relaciones (3) y (4) son
las 1n (seis en este caso) ecuaciones de Hamilton.
Tomando la derivada de (3) con respecto al tiempo y eliminando px, py y pz de (4) se obtienen las
ecuaciones usuales del movimiento,
m'x — 0, my = 0, m'z - —mg (5)
Una vez integradas éstas, volviendo a (3), se determina fa forma como varían los momenta con el tiempo.
Nótese que las relaciones (1) y (3) son iguales. Además, (5) son las relaciones halladas por aplicación directa de
las ecuaciones de Newton y Lagrange. Por tanto es evidente que las ecuaciones de Hamilton, en este problema, no
presentan ninguna ventaja.
Ejemplo 16.2. Una masa pendular suspendida de un resorte espiral a la que se le permite oscilar en un plano
vertical.
En términos de las coordenadas usuales, r y 8,
CAP. 16 1
ECUACIONES DEL MOVIMIENTO DE HAMILTON
335
Por tanto,
Así, por (16.4) o (16.8),
L - \m(r2 + r292) + mgr eos 8 - £fc(r-r0)2
dL/dr = pr = mr, BL/dé = pg = mr2e
H = ¿(p2. + ¿pf) - mgr cose + $k(r-r0)2
tf)
(2)
Aplicando (76.6), dH/dpr — pjm = r, dH/dpe = p0/mr2 = 6 (3)
BH/dr = —ppmr3 — mg eos fi + k(r — r0) = — pr (4)
dH/de = mgr sen 0 = —pe (5)
Las relaciones (3) a (5) son las ecuaciones de Hamilton. Eliminando a pr y pg de (4) por medio de (3), y pe de (5)
por medio de (3), se obtiene
m r — mrO2 — mg eos 0 + k(r — r0) = 0 (6)
mr2'e + 2mrre + mgr senfi = 0 (7)
La solución simultánea de (6) y (7), expresa las coordenadas en función del tiempo.
Nótese que (6) y (7) pueden obtenerse, con mucho menos esfuerzo, por aplicación directa de las ecuaciones de
Lagrange.
Ejemplo 16.3. Hamiltoniano en un problema de fuerza central.
Las dos esferas uniformes de la figura 16-1, de masas mi y m2, pueden moverse libremente en el espacio
bajo la acción de su atracción gravitatoria; no se les aplica ninguna fuerza externa. Tratando las esferas como
partículas, el lector puede demostrar sin dificultad que
£(7n, + m2)(3¡2 + y2 + i2) + ^(r2 + r2$2 + r2<t>2ser26) + Gm^m^/r
(1)
donde £, y y ¿ son las coordenadas inerciales del c.m., r, 0 y 4> son las coordenadas esféricas medidas con relación
al marco fijo X' Y' Z', r = rt + r2 es la distancia entre los centros de las esferas, G es la constante gravitacional,
y la "masa reducida" es n = mxmz/Kmx + mí).
X', V" y Z' con el origen en el c.m. permanecen
paralelos a loe ejes inerciales, X ■, V■ y Zi
x^?
Las partículas m ■ y m 2 pueden moverse libremente en el espacio bajo
la acción de una fuerza de atracción, proporcional al cuadrado inverso.
Fig.16-1
Aplicando (76.8), el hamiltoniano es
H = 2Ñ^¡)<"'+"S+^ + r,(^+í+^7)
Gw^ínj
(2)
y al aplicar (76.6) se obtienen en seguida las doce ecuaciones de Hamilton. Se sugiere que el lector elimine de estas
doce, las p; determine las seis ecuaciones del movimiento, y compare con las obtenidas por aplicación directa de
las ecuaciones de Lagrange a L. (Se observa que en este ejemplo T2 = T3 = 0; por tanto H = T + V = £.)
336
ECUACIONES DEL MOVIMIENTO DE HAMILTON
[CAP. 16
Ejemplo 16.4. Hamiltoniano para el péndulo doble que se muestra en la figura 2-10.
El siguiente ejemplo ilustra bien la forma general que toman las p y además demuestra que el proceso de
hallar una expresión de H no es siempre tan sencillo como podrían sugerirlo los ejemplos anteriores.
En el caso del péndulo doble con masas suspendidas de pequeños resortes espirales, con constantes k i y k2,
y el movimiento restringido a un plano (véase la ecuación (2.42)),
L = |(m, + m2)(r\ + r\i2) + \m£r\ + ¿$2 + 1(rxr2 + rxr2H) eos (* - •)
+ 2(rjr2¿ — r2r\4>) sen (<f> ~ *)] + (mi + ™-z)9'>'\ eos $ (1)
+ w^rg eos <t> - |fci(ri ~ h)2 ~ \kéXi — k)2
donde l\ y h son las longitudes normales de los resortes. Por tanto, se obtienen las siguientes expresiones del mo-
mentum correspondientes a r\, r2, 0 y <¡> respectivamente.
BL/drx = (wij + 7n2)rj + m2r2 eos (<f> - 9) - m2r24> sen (<f> - $) = pr¡ (2)
dL/dr2 — m2r2 + m2r1 eos (<f> — 6) + m2rx$ sen (<f> — $) = pT (S)
dL/dé — (wij + m2)r\$ + m2rxr2$ eos (<f> — $) + rn^r^ ser\(<f> — 6) = pe (¿)
dL/d¿ = m2r$> + TrupfoO eos (<f> — 9) — m2r2rx sen (<f> - 9) = p^ (5)
Nótese que, por ejemplo, pr contiene a r^r^Q; etc. Por tanto, con el fin de hallar H, las anteriores cuatro
ecuaciones deben resolverse simultáneamente para hallar rur2, $ y ¿, en función de lasp y las coordenadas.
Habiendo hecho esto, estas velocidades pueden eliminarse de (16.8) conduciendo, finalmente, a la expresión adecuada
de H. Así, en ciertos casos, el trabajo para hallar H puede hacerse un poco complejo. No es necesario incluir aquí
mayores detalles.
Ejemplo 16.5. Hamiltoniano para un trompo.
Como se demostró en el ejemplo 8.14, la función de Lagrange para un trompo con la punta estacionaria es
L = $[Ix(e2 + ¿2sen2¿) + /z(¿ + ¿ eos 6)2] - Mgr cose (1)
de donde
Pe = ¡i*' P<t> - 1z& + ¿ cosí), Pe, = Ixfsen2e + Ix($ + ¿ cosí) cosí (2)
Eliminando e, ¿> y ¿ de T + V por medio de (2), se tiene
1 [PÍ , (P* ~ P* eos e)2 p%]
H - « y + f TI + T + MOr cos ° 5)
Z\_IX Ix sen2 6 IXJ
Al aplicar las relaciones (16.6) se obtienen de inmediato las ecuaciones de Hamilton.
Nótese que en este caso p¿ = 0 y pj, = 0; y por tanto p4 y p^ son constantes. (Los mismos resultados se
obtienen en forma inmediata al aplicar las ecuaciones de Lagrange a L.)
Ejemplo 16.6. Ecuaciones de Hamilton para el péndulo del ejemplo 16.2, suponiendo una resistencia viscosa sobre
la masa.
En este problema, H es idéntico a su valor dado en (2) del ejemplo 16.2. La función de potencia puede
escribirse de inmediato (véase el numeral 6.9) como P = — ^(r2 + r2$2), donde a es el coeficiente de resistencia
viscosa sobre la masa pendular. Aplicando entonces (16.6),
dH/dpr = pTlm — r, dH/dpg = pg/mr2 = $
(igual que antes) y
dH/dr = -pf/mr3 - mg cos 9 + k(r — r0) — ar — prt dH/de - mgr sen 9 = ar2$ — pe
16.8 Ejemplos de H para sistemas en que existen coordenadas móviles o
restricciones móviles, o ambas condiciones.
Ejemplo 16.7.
Supóngase que el eje vertical del problema 2.20, figura 2-29, tiene una aceleración angular constante de
modo que 8 = 80 + ut + \at2. La energía cinética de una cuenta es
T = -Jm[(l + 4a2r2)r2 + r2(u + at)2] y V = mgar2
CAP. 16]
ECUACIONES DEL MOVIMIENTO DE HAMILTON
337
(Obsérvese que T = Ti + T3, T2 = 0.) De lo anterior se obtiene, dT/dr = pr = m(l + 4a2r2)r. Así, puede
escribirse 2
H = Tx-T>+V = 2m{1l\a2r2) ~ i^(tt + «t)« + mgar*
Puede hallarse la misma expresión para H, a partir de la ecuación (16.4).
En los anteriores ejemplos de este capítulo, H = T + V = £. Sin embargo, en este caso H ?¿ € puesto
que t interviene explícitamente en las ecuaciones de trasformación de la forma (2.21).
Ejemplo 16.8. ¿
Obsérvese que la expresión (2.50) del ejemplo dado en el numeral 2.11 (/) puede agruparse en seguida en la
forma T = Ti + T2 +T3, de donde
dT/dqx - mfgj + q2 eos ((3 - a)] + m[(vx + axt) eos a + (vy+ ayt) sena] = pQj
con una expresión semejante para pq . Eliminando <Ji y q2 de Ti — T3 + V, se obtiene el hamiltoniano H.
Aunque la forma de H no es sencilla, lo anterior demuestra las técnicas generales básicas. El lector puede
demostrar que la misma expresión de H puede obtenerse a partir de (16.4), y que H ^ T + V.
16.9 Campos de aplicación del método de Hamilton.
Como se afirmó anteriormente y como puede verse por los diferentes ejemplos dados, este
método de analizar la mayor parte de los problemas aplicados es menos conveniente que el de
Lagrange. Sin embargo, el enfoque de Hamilton se utiliza con grandes ventajas en otros
campos. A manera de información general, los campos más importantes entre éstos, se enumeran
a continuación con breves comentarios y algunas referencias seleccionadas.
(a) Teoría de la trasformación.
La sencillez de las ecuaciones del movimiento y la facilidad con que pueden integrarse
depende en gran parte de las coordenadas empleadas. En ocasiones es posible seleccionar
por simple intuición o por tanteos sucesivos un conjunto de coordenadas que hacen la
integración menos compleja. La teoría general de la trasformación, en la que las ecuaciones
de Hamilton desempeñan un papel muy importante, estudia un método sistemático de
realizar tales trasformaciones. Véanse:
C. Lanczos, The Variational Principies of Mechanics, U. of Toronto Press, 1949, capítulos
7 y 8.
H. Goldstein, Classical Mechanics, Addison-Wesley, 1950, capítulos 8 y 9.
E. T. Whittaker, A Treatise on Analytical Dynamics of Particles and Rigid Bodies, Dover,
1944, capítulo 11.
(¿>) Mecánica celeste.
No es posible obtener una determinación exacta del movimiento de los planetas
alrededor del Sol o de los satélites artificiales alrededor de la Tierra por las dificultades que
se encuentran al tratar de resolver las ecuaciones del movimiento. Por tanto, los
especialistas en mecánica celeste se ocupan de resolver problemas por medio de métodos de
perturbación con el fin de hallar soluciones aproximadas, aunque aceptables. La teoría de la
perturbación está íntimamente relacionada con la teoría de la trasformación
mencionada en (a). Véanse:
T. E. Sterne, An Introduction to Celestial Mechanics, Interscience, 1960, capítulos 4 y 5.
H. C. Corben y P. Stehle, Classical Mechanics, John Wiley, 1950, páginas 306-312.
O. Dziobek, Mathematical Theories of Planetary Motion, Dover.
D. Ter Haar, Elements of Hamiltonian Mechanics, North Holland, 1961, páginas 146-166.
(c) Mecánica estadística.
Como aún no se ha hallado una solución general para el relativamente sencillo "pro-
338
ECUACIONES DEL MOVIMIENTO DE HAMILTON
[CAP. 16
blema de los tres cuerpos" (véase la referencia citada antes E. T. Whittaker, capítulo 13),
es obvio que la determinación del movimiento exacto de cada una de las 1023 moléculas,
"pelotas elásticas", constituye un problema totalmente fuera de lugar. Sin embargo, los
métodos estadísticos, en que la dinámica de Hamilton desempeña una parte importante,
se han utilizado extensamente en la determinación de ciertas propiedades "promedio".
Véase:
R. C. Tolman, The Principies of Statistical Mechanics, Oxford U. Press, 1938.
(d) Mecánica cuántica.
La dinámica de Hamilton desempeña un papel muy importante en el estudio de la
mecánica cuántica. En realidad, es un prerrequisito necesario para estudiar esta materia.
Estudios introductorios excelentes sobre los principios básicos y los métodos de la
mecánica cuántica se dan en las siguientes referencias:
C. W. Sherwin, Introduction to Quantum Mechanics, Henry Holt, 1959.
P. Fong, Elementary Quantum Mechanics, Addison-Wesley, 1962.
R. H. Dicke y J. P. Wittke, Introduction to Quantum Mechanics, Addison-Wesley, 1960.
Problemas
A. Problemas en los que no interviene t en las ecuaciones de trasformación.
16.1. Demostrar que el hamiltoniano correspondiente al
sistema sencillo de masa y resorte de la figura 16-2,
es H — ^Px/'m + ^kx2. Escribir las ecuaciones de
Hamilton.
Si i - 0, el resorte no
se ha deformado
kw^-
16.2. Con referencia al ejemplo 3.3, demostrar que H para
la masa m, de la figura 3-1, es
H = \(p2r + pVr-)/rn + \kr2
16.3. Demostrar que H para la cuenta del problema 3.5, figura 3-5, está dado por
Fig. 16-2
H ~ ^ [l + «*(?+62*2)J + mgZ
iano para las dos masas de la figura 2-8,
ÍPy. + PyJ2 PL
16.4. Demostrar que el hamiltoniano para las dos masas de la figura 2-8, utilizando a yi y y3 como
.coordenadas, es
Escribir las ecuaciones de Hamilton.
16.5. Demostrar que H para el sistema de poleas del ejemplo 5.3 de la figura 5-6, es
Bpyl + 2CPyiptj2 + Apyl
2(AB - C2)
+ mlgyl + m2gy2 + \k¿Ci - y2 - lx)2 + \k2{2y2-yx-C2-l2)2
donde A = m, + I2/Rl, B = m2 + 7,/jR2 + h/R\, C = I2/R\; Ci y C2 son constantes; y /i
y l2 son las longitudes de los resortes sin deformar. Escribir las ecuaciones de Hamilton.
16.6. Demostrar que H para las tres masas del ejemplo 5.5, figura 5-7, con el movimiento confinado a un plano,
es (sin hacer aproximaciones para V)
| .2 ^r + I 2 *j{[(¥j- 2/í-i)2 + *il1/2 - *i>2 (va = 2/o = o)
CAP. 16]
ECUACIONES DEL MOVIMIENTO DE HAMILTON
339
16.7. Demostrar que H para el péndulo, problema 4.10, figura 4-13, está dado por
VÍ , V'r
2(wi1r[ + m2r*) 2m2
Demostrar que las ecuaciones del movimiento dadas en el problema 4.10 pueden obtenerse a partir de las
ecuaciones de Hamilton.
16.8. Las tres masas (esferas) del ejemplo 4.5, se dejan caer libremente dentro de un líquido viscoso. Los
coeficientes de resistencia sobre las esferas son ai, a2 y as, respectivamente. Despreciando la resistencia
sobre los resortes, los efectos de flotación y la masa virtual del líquido, demostrar que H, en coordenadas y,
<?i y q2, está dado por
H = 2% +
p\ Cpqi + 2DpqipQ2 + Bpl2
2(BC-D2)
+ Mgy + ¿M<7i + <72-'i)2
rm, /m2 + m3\ l2
donde B = mi {mi + m2)/m3, C = m2(m2 + m3)/m3 y D = mim-i/m-i. Escribir la
función de potencia, P, y las ecuaciones del movimiento de Hamilton.
16.9. Escribir H y las ecuaciones de Hamilton del movimiento del sistema que se muestra en la figura 8-5.
Obsérvese que Pj, = p¿ — 0.
2[7 + {Ix + Ms2) sen2 e] 2IZ
16.10. Suponiendo las resistencias viscosas — bixi y — b2x2 sobre mi y m2, respectivamente, figura 16-3,
escribir las ecuaciones del movimiento de Lagrange. Determinar H, escribir las ecuaciones de Hamilton y
demostrar a partir de ellas, que pueden hallarse las mismas ecuaciones obtenidas por el método de Lagrange.
H = p\ /2m, + p£2/2m2 + \kxx\ + \k¿x2 - xj2, P = -£(&i¿?+ b2x\)
-nm^-
'4r
h—nm^-
*>2 X
Cuando ji — 12 — 0. los resortes no se han deformado
Fig.16-3
B. Problemas en que intervienen coordenadas móviles, restricciones móviles, o ambas condiciones
si multánea mente.
16.11. En el ejemplo 3.6, figura 3-4, suponiendo que la plataforma y la varilla se mueven como se indicó al
obtener la segunda expresión de T, demostrar que el hamiltoniano para m, es
H = p2/2m - ^mr^elul eos2u2t - \mw2[8 + r sen (e0 sen u2t)]2 + mgr eos ($0 senw2t)
Demostrar que H 9* € .
16.12. Determinar H para el péndulo del problema 3.17, figura 3-11. Escribir las ecuaciones de Hamilton.
[Pe + ^í' ~~ A sen wt)Au cosuí sen*]2
H
pg = mA2u2 eos2 coi sen 0(1 — eos 6)
2m(l — A sen ut)2
- mg[Atí eos ut + (l — A sen ut) eos 6]
PgAtí COS ut COS 0
- mA2u2 eos2 uí(l - eos e)
(l- A sen ut)
mg(l — A sen ut) sen $
340
ECUACIONES DEL MOVIMIENTO DE HAMILTON
[CAP. 16
pe + m(l — A sen wt)Aw eos ut sen $
m(l - A sen ut)2
16.13. Escribir H para el- péndulo que se muestra en la figura 4-19(7), en función de la coordenada 9. Demostrar
que H * c*totaI.
vi
H =
2m(r0 - vt - $at*
%m(v0 + at)2 — mgr eos 9
16.14. Determinar H para el péndulo del problema 3.23, figura 3-14. ¿Será correcto H ^ c*totai?
( pe [~\Pa + P<t>)r sen * + (P* ce* <f> + pe sen $ cosfi sen <p)8~\\2
H = 1«^|^+•«»•■«*[ ™r2sen3,(2^ + 82sen2*) J)
. „ f P*sen2 9 r(pa + p^r sen 9 + (p^ eos tf. + pe sen * eos 9 sen 0)s~|l 2
+ i™"2\—^-+ (• cos * + * sen*> L mrW + sW*) J;
r(pa - p¿r sen * + (p,,, eos ¿ + pe sen * eos 9 sen ^)s"|2
- *m(«2 + r2sen,2 , + 2sr sen . eos *) [ inr sen3 ,(2r2 + 82sen2») J
— mgr eos 9
16.15. Demostrar que, en la figura 14-2, expresión (14.4), teniendo en cuenta la rotación de la Tierra, H está
dado por
H — \m{ [px + mtíe(y sen 4> — z eos <t>) — mweR]2 + (pv — rru¿ex sen *)2 + (pz + mwex eos *)2}
+ £ro«f [x* + y2sen.2 * + (R + z)2 eos2 <I> - 2y(R + z) sen * eos *] + V(x, y, z)
. px + mae{i/sen * — z eos +) — mueR
x = , etc.
m
px = (pv sen* — pz cos+)uc — 2rru£x — dV/dx, etc.
16.16. Partiendo de la expresión dada para T en el ejemplo 4.8, figura 4-6, demostrar que H = ^prQr — L =
Ti - T3 + V y que H * c*totaI.
16.17. Suponiendo que el átomo de hidrógeno, figura 16-4, está en un espacio en el que no hay campos, establecer
el hamiltoniano clásico. Escribir las ecuaciones del movimiento de Hamilton (véase el ejemplo 16.3).
Protón. Masa, M. -
Carga. Q
Marco
¡nercial
i
J
Z'
c.m.
--
í
\> ""
— e x £
r*^^ I
>^ /
I ^ Electrón. Masa, m.
[V' Carga, e
Y'
x>/
Y*
*i
Átomo de hidrógeno
Fig. 16-4
CAP. 16] ECUACIONES DEL MOVIMIENTO DE HAMILTON 341
16.18. Demostrar que el hamiltoniano del sistema del problema 15.7, es
H = ^(Pl/w, + vl2/m2 + Vl/M) + ${kxx\+k2xl) - BQ + $QHs - *, - x2)/A
16.19. Aplicando la relación H = 2Pr<7r — L, demostrar que H, para el sistema electromecánico del problema
15.8, es
H = $\pÍ/I + pl/ni + (pQl-N+9)VMn + plt/M2S\ + V(x,»,Ql,Qi)
CAPITULO
17
Principio de Hamilton
17.1 Introducción.
Con la esperanza de hacer claridad con relación a las bases matemáticas y físicas sobre
las que descansa el principio de Hamilton, se incluye el siguiente material: (a) el enunciado
de ciertos problemas ilustrativos; (b) un breve análisis de algunas de las técnicas necesarias
en el cálculo de variaciones; (c) las soluciones de los problemas propuestos en (a); (d)
deducción del principio de Hamilton por medio del cálculo de variaciones y luego a partir de
la ecuación de D'Alembert; (e) diversos ejemplos específicos para ilustrar los principios
del cálculo de variaciones y del principio de Hamilton. h
Con el fin de que el lector pueda contar con una visión más amplia sobre la utilidad
del principio de Hamilton, se incluye un breve análisis de este tópico junto con una lista
de referencias adecuadas.
17.2 Problemas introductorios.
Como un medio para introducir algunas ideas preliminares importantes, se consideran
hasta donde esto es posible por el momento, los siguientes ejemplos específicos.
Ejemplo 17.1.
Se trata de hallar la ecuación de la línea
más corta que pasa por los puntos pt y p2
de la figura 17-1, cuyas coordenadas son xi,
yi y x2, y2, respectivamente. Como se
indica en el diagrama, un elemento de longitud
ds, de una línea cualquiera,
independientemente de su forma, está dado por ds =
(dx2 + dy2)1'2 = [1 + idy/dx)2)1'2 dx.
Por tanto, /, la longitud de una línea cualquiera
que va desde p\ hasta p2, viene dada por
"J>
+ (dy/dx)*y*dx (!)
d* = (di* + dyi)"i = [1 + (dy/dzW*dx
Pero, ¿cuál será la línea más corta que conecta
estos puntos? El problema se reduce a hallar
una relación entre y y x, y = y{x), de tal
manera que (1) sea un mínimo.
Fig.17-1
Ejemplo 17.2.
En la figura 17-2, una cuenta de masa m puede deslizarse libremente hacia abajo a lo largo de un alambre
liso rígido, bajo la acción de la gravedad. ¿Qué forma debe tener el alambre (cuál es la relación entre y y x, y = y(x))
de modo que el tiempo requerido para que la cuenta se deslice desde un punto dado, pi(xi, yi) hasta p2(jC2, y2)
sea un mínimo?
Nótese que para una trayectoria cualquiera que conecte estos puntos, el intervalo de tiempo está dado por
fPid8
í = I ~, donde ds
Pi
serva la energía £,
(dx2 + dy2)1/2 y v es la velocidad instantánea de la cuenta. Como aquí se con-
6 = %mv2 + mgy = \mv2 + mgyy = constante
342
CAP. 17]
PRINCIPIO DE HAMILTON
343
Así, v = [v2 — 2g(y — Vi)]1/2, donde ui y yi son valores conocidos en el punto pi. Por tanto, puede escribirse,
JVl [_v\-2g{y-y¿\ V
El problema consiste ahora en hallar una relación entre y y x, tal que (2) sea un mínimo.
La cuenta m se deja deslizar libremente hacia
i conocidos abajo por un alambre rígido, liso; hasta el
punto p7. Hallar la forma del alambre,
y - y(*)< para la cual el tiempo de descenso
p r l + (dx/dy)* -li/t
xj.yj conocidos
Fig. 17-2
Fig. 17-3
Ejemplo 17.3.
En la figura 17-3, la bola se ha lanzado hacia arriba con una velocidad inicial v a un ángulo 6. Como se
demuestra por medio de principios elementales, la bola sigue una trayectoria determinada por
vxt,
V - i?*2
(3)
donde vx y vy son las componentes de v.
Previendo lo que sigue, cabe preguntarse: ¿cuáles son las relaciones x = x(t), y = y(t) tales que la integral
siguiente
V hit = V \\m& + ¿2) - mgy]
dt
(4)
tenga un valor máximo o un valor mínimo, en donde L es la función de Lagrange usual?
Como ha de demostrarse en seguida, y sin duda el lector lo habrá inferido, las relaciones (3) son las expresiones
requeridas.
Para completar los anteriores tres ejemplos se requieren ciertos métodos del cálculo de
variaciones. Volveremos a aquellos al final del numeral siguiente.
17.3 Algunas técnicas del cálculo de variaciones.
Considérese el tipo más general de problema, en el que dada cierta función, </>(x, y, dy/dx)
debe hallarse una relación entre y y x, y = y(x), tal que la siguiente integral definida
S
X<f>{x, y, dy/dx) dx
-i
(5)
tenga un valor extremo (máximo o mínimo).
Supóngase que la línea sólida de la figura 17-4, y = y(x), representa la relación
deseada. La línea punteada representa una "trayectoria variada" ligeramente, en donde, para
cada uno de los puntos, p(x, y) de la línea sólida, existe un "punto correspondiente", p(x, yv)
344
PRINCIPIO DE HAMILTON
[CAP. 17
Fig. 17-4
sobre la trayectoria variada. La coordenada x no se ha variado, en tanto que yi; = y + by
según se indica. Con el propósito de representar la trayectoria variada, se hace,
Vv = V(x) + ef(x) (6)
donde t es una cantidad arbitrariamente pequeña (un "parámetro infinitesimal") y f(x)
es una función arbitraria diferenciable de x, la cual, por razones que se verán más adelante,
se supone que se anula en los puntos a y fe. Para ilustrar el anterior procedimiento,
supóngase que ( es un número pequeño, por ejemplo 10~6, y que f{x), que cumple los requisitos
anteriores, no alcanza nunca valores grandes comparados con y(x). Resulta claro entonces
que (6) representa una línea muy cercana a la sólida. En realidad, si se toma e
suficientemente pequeño, (6) será siempre "cercano" a f{x), independientemente de los valores finitos
que pueda suponer f(x).
Es importante anotar aquí que al asignar diferentes valores a t, para cierta forma de
f{x), (6) representa una familia de curvas en la vecindad de y = y(x).
Supóngase ahora una integral correspondiente a (5), tomada a lo largo de la trayectoria
variada. Es decir,
3 - I 4>{x, Vv, dy/dx) dx (7)
v J*i
donde yv viene dado por (6). Por conveniencia, en adelante se escribe
*V = Vv - Vi*) = <f(x) W
y dyjdx = y>v = y'{x) + <f'{x) (9)
donde y'(x) = dy/dx y f'(x) = df'/dx.
La integral definida (7), es una función de t únicamente; y la condición de que (5)
tenga un valor extremo es, considerando a t como variable,
djjdt = 0 para c = 0 (W)
Tomando la derivada de (7) bajo el signo integral,
*?. = rrüL^ + ií-^idx un
d, Jx, L3y„ d« By^ ae J
CAP. 17]
PRINCIPIO DE HAMILTON
345
r> n d<t> d<t> d<t> d(t> i • &V 4, x dyv „/ x „
Pero si c = 0, fy- = -fy, fy=dfv> v en cualquier caso, — = f(x) y — =?{x). Por
tanto, (70) puede escribirse,
Observando que
&«*> = %évw = Uw™]-™Uw) ™
(12) puede ponerse en la forma,
»«•£♦£©-£(£)]*»* = °
Suponiendo que f(x) se ha tomado de modo que se anule en a y en fe, el primer
término de (14) es igual a cero. Entonces, por conveniencia, se multiplica (14) por f, se aplica
(8) y se escribe
Aquí, by es arbitrario para todos los valores de x, desde xi hasta X2. Por ejemplo, by
puede tomarse como positivo en una o más regiones y negativo en las demás. Por tanto
(suponiendo por ahora que la expresión en el paréntesis cuadrado en (15) no es igual a cero),
si se hace by positivo en donde la expresión entre paréntesis cuadrados es positiva, y
negativo en donde ésta es negativa, la integral (15) no será igual a cero. Por consiguiente,
(15) puede ser igual a cero para todos los valores posibles de by, únicamente bajo la condición,
d / a¿\ _ a* = m
dx\By'/ dy
Esta es entonces, una ecuación diferencial, cuya solución suministra una relación entre
y y x, y = y(x), tal que al sustituirla en (5), le da a esta integral un valor extremo. (Nótese
el parecido con la ecuación de Lagrange.)
La integral (15) puede ponerse en otra forma útil como sigue. Multiplicando (12) por
una cantidad infinitesimal, f, y escribiendo
€-¿f- = 8J, 8y = <f(x), 8y' = «/'(*)
se tiene M = £ (f¿a„ + j£ Sj/') dx = 0
que pueden escribirse,
8¿J = §x\[4>(x,y,y')]dx = 0 (17)
Los ejemplos específicos que siguen, sirven para ampliar el significado de (15) y (17).
Los resultados anteriores pueden extenderse al caso de n variables dependientes, yi,
y2,...,y„, y una variable independiente, x. (No se incluyen detalles aquí.) Es decir,
considerando la función
la condición de que 1 <f>ndx tenga un valor extremo es
*/*.)_£ = o r=1.2 « (17.2)
dx\dy'rJ dyr
346
PRINCIPIO DE HAMILTON
[CAP. 17
o, lo que es lo mismo,
)dx = 0 {17.3)
Jtxt
X,
17.4 Soluciones a los problemas propuestos anteriormente.
En este momento ya es posible completar los ejemplos 17.1, 17.2 y 17.3.
Solución al ejemplo 17.1.
Comparando las ecuaciones (1) y (5) se observa que <f> = (1 + y'2)1'2 (un caso más bien especial ya que
contiene únicamente y'). Aplicando la relación (12) y observando que t*-= 0, ir- ( ~r ) = 0 o sea d<f>/dy'
•*"' "" v dy J
M=0 —
dy ' dx \
Ci = constante. Así, d<f>/dy' = (1 + /2)-«/2y = Cl de donde y' = dy/dx = c,/Vl - c\ = c2. Integrando ésta
se obtiene y = C2X + c3, la ecuación de una línea recta que, si se escogen adecuadamente los valores de c2 y c3,
pasará por los puntos seleccionados a y b, de la figura 17-1. (Para hallar la distancia más corta entre dos puntos
de un cilindro, véase el ejemplo 17.4.)
Solución al ejemplo 17.2.
[1 + x'2 ~11/2
2 _ 9 .———- donde x' = dx/dy. Se considera aquí a y, como
d f d<f> \ d<p d<p d [ dd> \
la variable independiente. Entonces, 3— ( ——. ) — — = 0. Ahora, como -r— = 0, se tiene 3- 7-7 )— 0 o sea
H ' dy \dx'/ dx ' dx dy \dx'/
30 ^
t—: = Ci = constante. Pero
3a;
iá. _ 5! = c
3x' {(l+x'2)[vf + 2flr(yi-y)]>»/2 »
/ v2/2g + yx - y \i/2 v2 x
para lo cual x' = {iftgc* - v2/2g - Vl + y) ' Escríbíendo ahora- c2 •= ^g + Vi V c3 = ^e¡ ~ °2'
dx /C2-VV/2
X = dy = (^T^J <«>
que es la ecuación diferencial que relaciona a x con y. Con el fin de integrar a (18) se realiza el siguiente cambio
de variables:
c2- y = R(l -cosa) (19)
donde R = (C2 + cz)/% de donde, cz + y = R(l + cosa) y dy = — R sen a da. Llevando estos resultados
a (18), se obtiene
dx = -r(\ ~C0Sa) senada = + jK(1 - eos a) da (20)
\1 + cosa/
que puede integrarse de inmediato y obtenerse así,
x — x0 + R(a — sen a) donde xo = constante
Por tanto, las ecuaciones paramétricas de la trayectoria de descenso más rápido son
x = x0 + R(a - sen a), y - y0 — R(l — cosa) (21)
donde yo = c2 = u2 /2g + y,.
CAP. 17 |
PRINCIPIO DE HAMILTON
347
Fíg.17-5
El lector puede demostrar que la curva ABC, de la figura 17-5, trazada por el punto p' adherido al disco,
mientras el disco rueda sin resbalar a lo largo de la línea ab, está representada por las ecuaciones (21). Por tanto el
"braquistocrono" (trayectoria correspondiente al tiempo más corto) es aquí una cicloide.
Para un problema específico cualquiera (para el cual se conocen los valores de vt, xx, yi, x2 y yí), R y
xo (yo = c2 = v\ /2g + yi no son arbitrarios) deben seleccionarse de tal manera que la cicloide pase por pi(xi, yi)
y P2(x2, yz). Que esto puede hacerse y que la. trayectoria es única, se encuentra demostrado en: W. D. Macmillan,
Statics and Dynamics of a Partióle, Dover, 1958, página 328.
Solución al ejemplo 17.3.
Comparando las expresiones (4) y (5), se escribe
* = L(x,y,x,y,t) = $m(x* + y*)
donde í se toma como la variable independiente. Aplicando (17.2),
d_ fdL\ _ 3L ±
dt[di ) Bx ' dt
m-
(22)
(que evidentemente son las ecuaciones de Lagrange). Con éstas se obtiene mx = 0ymy+mg = 0y finalmente,
por integración, x = vzt y y = vyt — \gt2 que son las relaciones (3). Es decir, que las relaciones entre xyí,
y y y t, que hacen que
ciones de Lagrange.
f
L dt suponga un valor extremo o sea
r
SLdt = 0, se determinan por las ecua-
17.5 Principio de Hamilton a partir del cálculo de variaciones.
Obsérvese, que la forma general de la función de Lagrange, L = L(qi, ..., qn\
<7i, ■■,qn\t), tiene la misma forma de <t> en la ecuación (17.1), donde qi corresponde a
y\, etc., q corresponde a y\, etc., y t corresponde a la variable independiente x. Por tanto,
se concluye que
3 = £ L(ql,...,qniql,...,in;t)dt = §* V-V)
dt
tiene un valor extremo, o sea
f * 8[L(qlt .. .,qn; qv .. .,qn; t)] dt = 0
siempre que
d /dL\
dt \dqr)
= 0
1, 2, ...,n
(17.4)
(17.5)
(17.6)
Es decir, que al sustituir en (17.4) las soluciones de (17.6), qi = qi(t), q2 — q2(t), etc., esta
integral alcanza un valor máximo o un valor mínimo. Pero (17.6) es igual a la forma conocida
de las ecuaciones de Lagrange. Por tanto, puede decirse que el movimiento de un sistema,
348
PRINCIPIO DE HAMILTON
[CAP. 17
determinado-por las ecuaciones de Lagrange, es tal que la integral (17.4) tiene un valor
extremo, o.jm.e_ÍIZ5jL _es igual a cero.
La relación (17.5) es una forma del principio de Hamilton (aunque no es la forma más
general).
En el numeral siguiente se deduce el principio de Hamilton, de una manera más general,
utilizando la ecuación de D'Alembert.
17.6 Principio de Hamilton a partir de la ecuación de D'Alembert.
Puede lograrse una comprensión más profunda de los aspectos físicos contenidos en las
etapas que conducen al principio de Hamilton por medio de la siguiente deducción, en
comparación de la anterior. Sin embargo, cada uno de los enfoques contribuye en cierta
medida a la comprensión general del principio.
Para mayor claridad, la deducción se divide en las siguientes, etapas:
(a) Considérese un sistema de p partículas que tiene n grados de libertad y que se mueve
en el espacio bajo la acción de diferentes tipos de fuerza. Siguiendo exactamente las
ideas expresadas en el numeral 4.2, (que deben repasarse) se reproduce a continuación
la ecuación (4.2):
v v
2 mi(Xi 8xí + 'ii 8yi + z\ 8zt) = *£ (Fx.8Xi +Fy.8yi + Fz.8zi) = 8Wtotal (17.7)
donde, para la validez de (17.7), los "desplazamientos virtuales" 8xt, 8y¡, y 8z¡ son
completamente arbitrarios. Sin embargo, como en la deducción de las ecuaciones de
Lagrange, se supone que 8xlt 8y¡ y 8zt son desplazamientos en los cuales t no
varía (véase el ejemplo 3.5, figura 3-3).
(b) Supóngase que en el instante to, una de las partículas, mlt está en el punto A, de la
figura 17-6. Más tarde, habiéndose movido de acuerdo con las leyes de Newton, la
partícula llega a C siguiendo una "trayectoria real" ABC. Todas las demás partículas del
sistema siguen sus propias trayectorias durante este intervalo, pero no es necesario
considerar aquí sino la de m,.
Fig. 17-6
Considérese ahora ABC dividido en intervalos infinitesimales por los puntos
Pi,P2, .... Suponiendo que mt se encuentra en p\ en el instante ti, imagínese
que se le da un desplazamiento infinitesimal arbitrario 8s que va desde p\ hasta el
"punto variado" p[. Las componentes de Ss, como se muestra en el diagrama son
CAP. 17 |
PRINCIPIO DE HAMILTON
349
8x, 8y y hz. De esta forma, se localiza un punto variado para cada uno de los puntos
de ABC. La trayectoria AB'Q determinada por los puntos variados p[,p'2, ... se
denomina "trayectoria variada". Debe recordarse que 8x, 8y y hz tienen el mismo
significado que los desplazamientos virtuales utilizados en las deducciones de las
ecuaciones de Lagrange, capítulos 3 y 4.
(c) Como en el numeral 17.3, (véase la ecuación (6)), se escribe
xv = x + «,A(*). Vv = V + c2/20/)' zv = z + «sW (23)
donde xv, yv y zv son las coordenadas de un punto sobre la trayectoria variada y x, y
y z las del punto correspondiente en la trayectoria real. Los parámetros ei, «2 y «3
son, nuevamente, cantidades infinitesimales, consideradas aquí como constantes.
fi(x), /a (y) y fz{z) son funciones diferenciables arbitrarias de x, y y z,
respectivamente, pero seleccionadas de tal forma que en A y en C, 5x = 8y = hz = 0.
Se definen ahora las siguientes variaciones,
8x = xv - x, 8(dx) - dxv - dx, 8x — xv - x (24)
donde x-dxldt, xv = dxjdt, dxv - dx + txd[f x(x)]. Así pues, a partir de (23) y (24)
se concluye que
8X = ej^x), 8{dx) = «,(*[/,(*)]. «i = <i%\fM)} = Tt{*X) {25)
y las relaciones correspondientes son naturalmente válidas para by, 8z, etc. Nótese
que las ecuaciones anteriores se cumplen para toda función diferenciable arbitraria,
f\(x) etc.
(d) A continuación, considérese el primer término de {17.7). Por la regla de la diferenciación
de un producto, este término puede escribirse,
8Xi(m'xi) - -jj{miXi8Xi) - ??i¡¿'¡^t(8x¡) (26)
• Pero por (25) -jt(8xí) = 8x. Entonces, niiXi-n(8Xi) = miXi8x¡ — \m\8x\ y entonces,
8Xi(miXi) = -rr(m¡Xi8x¡) - \m\8x] {27)
Expresiones similares se encuentran para m'yx8yx y ra¡z¡8Zi.
Así pues, habiendo eliminado míx\8xx, etc., de {17.7), y agrupando términos, se tiene
8 h Í¡ m¡(% + ¿f + «?)] + S^totoi = ^[2 mi(xt8x{ + y¡8yt + z¡8z¡)] {28)
Multiplicando por dt e integrando entre los límites de ¿o y t, (el tiempo para ir de
AaC), {28) resulta
f ' [8T + 8 W\otni] dt = 2 m& 8x* + ¿« ^ + Zi 8Zi) f (29>
(e) Principio de Hamilton. Suponiendo, como se ha mencionado ya, que en A y C,
5x< = tyj = bzi = 0, el término de la derecha de {29) es igual a cero. Así,
j" (8T + FQl8qi + Fq28q2 + • • • + FQn8qn)dt = 0 (27.8)
350
PRINCIPIO DE HAMILTON
[CAP. 17
que es una forma muy general del principio de Hamilton. Las fuerzas generalizadas
usuales, originadas en cualquier tipo de fuerzas aplicadas, se representan por Fqr. Si
se introducen en T coordenadas superfluas, como se indicó en el capítulo 12, estas
fuerzas generalizadas pueden influir las fuerzas de restricción.
Si todas las fuerzas, son conservativas, 5Wtotal = — 8V y
(" 8(T-V)dt = f 8Ldt = 0 (17.9)
que es la misma forma (17.5) obtenida anteriormente.
17.7 Ecuaciones de Lagrange a partir del principio de Hamilton.
Nótese que, dejando a t constante,
&T = Í ¥rSQr + Í |£«ír (30)
fíx dqr r=i dqr
Eliminando 8qr del segundo término por medio de 8qr — -n(8qr) e integrando el segundo
término de (30) por partes, obtenemos
Jt0 r=i dqr r=i dqr \a JtQ l~i dt\dqr/ J
n / dT \ \c
Pero V ( —v ) 8qr — 0 ya que todas las variaciones en A y C se suponen nulas. Por tanto
&i\dqr/ \a
(17.8) puede escribirse, ,
Esta integral debe hacerse igual a cero para valores completamente arbitrarios de 5q\,
S<7 2, ■ ■ ■, 8<7« a lo largo de las trayectorias. Por tanto, supóngase que todas las 5q,
excepto por ejemplo bqr se anulan. Entonces, de acuerdo con el argumento dado antes de
la ecuación (16), se concluye que el coeficiente de 8qr debe ser igual a cero. Por tanto, en
general,
A f§L\ - *L - F = 0
dt \dqrJ dQr 9r
Igualmente, la forma jr(-r)--;— = 0 resulta como una consecuencia inmediata
de (1Z9). dt UJ BQ'
De lo anterior, resulta evidente que si se tiene el principio de Hamilton, junto con la
comprensión de T, Vy FQr, pueden deducirse de allí las ecuaciones de Lagrange, la ecuación de la
segunda ley de Newton, etc. Por tanto, si se desea, en este sentido el principio de Hamilton
puede considerarse como la base de la dinámica analítica (véanse las referencias del
numeral 17.9).
17.8 Ejemplos específicos para ilustrar los ejemplos de este capítulo.
Ejemplo 17.4.
Se trata de demostrar que la línea más corta entre dos puntos cualesquiera pt y pi sobre un cilindro, es
una hélice.
CAP. 17]
PRINCIPIO DE HAMILTON
351
La longitud s de una línea cualquiera sobre un cilindro entre p¡ y p2 está dada por
8 = (" [1 + r2(de/dz)2]"2 dz
donde r, 8 y z son las coordenadas cilindricas usuales con r = constante. Puede determinarse una relación
entre 8 y z que le dé a esta integral un valor extremo, por medio de
L(M.\ _ Éí. = o
dz \ de' J de
donde <f> = [1 + r2f'2)I/2 y 6'= de/dz. Pero como d<f>/de = 0,
d<f>/de' - (l + r2e'2)~i/2r2e' = ct = constante
Por esto, re' = c2. Y así, re = c2z + c3, que es la ecuación^de una hélice.
Supóngase que en p\ se tiene e = 0 y z = 0; entonces es = 0. En p2, hágase e = 62 y z = z2; por tanto
c2 = re2/z2, y re = (re2/z2)z es la ecuación final.
Ejemplo 17.5.
Evaluar la integral (5) de la figura 17-3, ejemplo 17.3, a lo largo de la trayectoria real, determinada por
x = vxt y y = uyt — \gt2 entre los límites í = 0 y t = t, = 2uy/g = tiempo de vuelo. Evaluar así mismo
la integral (7) a lo largo de una trayectoria variada, determinada por x = vxt y y = h sen (wuxt/R) entre los
mismos límites. Comparar los resultados.
Se hace h = v2/2g = altura máxima, y R = 2vxvy/g = alcance del proyectil. Nótese que las
trayectorias real y variada se cortan en x = 0 y x = R. Por tanto, en estos puntos 5x = 5y = 0. (Demostrar que
cuando t = í,/4; yv —y = 0,707 — 0,75.) La integral (5) se hace
lm[v2 + v¡- 4vygt + 2g2t2] dt = 2mh{v%/vy - \vy)
o
La ecuación (7) puede escribirse,
$v = ) \m\v\ + (hWvl/R2) eos2 (nVxt/R) - 2gh sen (nVxt/R)} dt
y finalmente, ¿)v = 2mh(v\lvy — cvy)
donde c = (2/jt — jt2/32) = 0,329. Nótese que ¿J es ligeramente menor que ¿Jv, como podría esperarse.
Ejemplo 17.6.
Hallar las ecuaciones del movimiento para una masa pendular suspendida de un resorte, por aplicación
directa del principio de Hamilton.
Para el péndulo que se muestra en la figura 17-7,
L = £m(¿2 + r2é2) + mgr eos e - \k{r - r0)2
Por tanto
Xf* rf* • • • •
SLdt = I [m(r Sr + re2 Sr + r2e Se) + mg Sr eos e - mgr Se sen e - k(r - r0) Sr] dt
Según la ecuación (25),
mrSrdt — mrd(Sr) = d(mr Sr) — mSrr'dt
Igualmente, mr2é Se dt - d(mr2é Se) - Se ¿ *' dt
= d(mr2é Se) — Se{mr2'e + 2mrré) dt
Por tanto, se escribe la integral anterior como
r
[{m r — mre2 — mg eos e + k(r- r0)) Sr + {mr2 e + 2mrre + mgr sen e} Se] dt
"2
J [d(mrSr) + dimr^e Se)]
Suponiendo que Sr y 56 son ambas iguales a cero, en í, y t2, la segunda integral es evidentemente nula.
Como 5r y 50 son completamente independientes (hecha la excepción mencionada antes), la primera integral
puede ser cero solamente si
352
PRINCIPIO DE HAMILTON
[CAP. 17
mr — mre2 — mg eos 9 + k(r — r0) = 0
mr- 6 + 2virr$ + mgr sen $
Pero estas son las ecuaciones del movimiento del sistema. Es evidente que son las mismas relaciones que se
habrían obtenido por aplicación directa del principio de D'Alembert o de las ecuaciones de Lagrange.
-Offiü^
Resistencia
viscosa,— fcx_*».'
toww
v////////////////////////////////////////////////////// á
o XV se mueve hacia lo derecha,
>n aceleración constante a
Fig.17-7
Fig. 17-8
Ejemplo 17.7.
Supóngase que se hace mover, en dirección positiva de X, el marco entero XY, de la figura 17-8, de modo
que la distancia s de O a un punto fijo está dada por s = ut + Jai2. Supóngase una resistencia viscosa, /,
sobre m, dada por f = —bx. A partir de (17.8) se tiene
[SL + f&x]dt = I [S{$m(v + at + x)2 - \kx*} - bx Sx] dt
Jh
— I [m(v + at + x) Sx — kx Sx — bx Sx] dt
en donde t no ha variado. '•
Escribiendo m(v + at + x) Sx = d[m(v + at + x) Sx] — m(a + x)Sxdt
la anterior integral se hace,
f [{m(a + x) + bx + kx} Sx] dt - I d[m(v + at + x) Sx] = 0
La segunda integral es igual a cero y por la primera, m(a + x) + bx + kx = 0, que es la misma ecuación del
movimiento obtenida por aplicación de la ecuación de Lagrange en la forma usual.
El anterior es otro ejemplo de la manera como pueden obtenerse las ecuaciones del movimiento por
aplicación directa del principio de Hamilton.
17.9 Aplicaciones del principio de Hamilton.
Como se vio en los ejemplos 17.6 y 17.7, las ecuaciones del movimiento de un sistema
pueden obtenerse directamente a partir del principio de Hamilton. Sin embargo, como es
obvio, el procedimiento es menos conveniente que el método usual de Lagrange.
Naturalmente, puede decirse que como las ecuaciones de Lagrange resultan del principio
de Hamilton, su uso es equivalente a la aplicación de este principio. Sin embargo, debe
recordarse, que una de las deducciones de las ecuaciones de Lagrange, que no depende en ninguna
forma del principio de Hamilton, es consecuencia inmediata de la ecuación de D'Alembert.
Además, el obtener las ecuaciones de Lagrange por vía del principio de Hamilton, deja mucho
qué desear en cuanto se refiere a la claridad de los principios físicos básicos. (Compárese la
deducción del numeral 17.7 con la dada en el numeral 4.2.)
Sin embargo, este principio representa un punto de vista distinto e interesante. Además,
ha abierto el camino para la aplicación de los métodos variacionales a muchas ramas de la
física teórica. En los últimos años, los métodos variacionales han demostrado su utilidad en
el desarrollo de la dinámica de los sistemas continuos, la relatividad, la mecánica cuántica,
v la electrodinámica cuántica.
CAP. 17 ]
PRINCIPIO DE HAMILTON
353
Para ulteriores estudios del principio de Hamilton, de los métodos variacionales generales
y otras materias relacionadas, el lector puede consultar las siguientes referencias.
Cornelius Lanczos, Variational Principies of Mechanics, University of Toronto Press,
1949, 1966. Este libro es altamente recomendado no solamente como referencia sobre
principios de variación sino también como una fuente de información valiosa con relación a los
principios básicos y a las ideas relacionadas con todo el campo de la dinámica. No se ha
ahorrado esfuerzo para mostrar con claridad los cimientos y la estructura sobre los cuales se
ha construido la ciencia de la dinámica analítica. El lenguaje es claro y despojado de
expresiones oscuras.. Tratando únicamente de presentar de manera clara y comprensible las
verdades básicas, no se pretende darle sus formas más "compactas", "elegantes", o de acuerdo
con lo que esté en boga. Además, el autor pone en evidencia ciertos puntos importantes con
relación al método vectorial comparado con los métodos analíticos de la dinámica. Por
último, al estudiar este libro, no debe dejarse de leer ni el prefacio ni la introducción.
Clive W. Kilmister, Hamiltonian Dynamics, John Wiley, 1964, páginas 34, 49 y 50.
Obsérvense los puntos de vista del autor con relación al principio de Hamilton, página 34.
Herbert Goldstein, Classical Mechanics, Addison-Wesley, 1950, páginas 30-37, 225-235.
Una deducción de las ecuaciones de Hamilton del movimiento, a partir del principio de
Hamilton, se encuentra en las páginas 225-227. En la página 235 se halla una observación
importante con relación a los principios variacionales y su utilidad.
J. C. Coe, Theoretical Mechanics, Macmillan, 1938, páginas 412-417.
Robert Weinstock, Calculus of Variations, McGraw-Hill, 1952, páginas 16-48, 95-98 y
261-294. Este libro incluye muchas aplicaciones de los métodos variacionales.
Problemas
17.1. Demostrar que la línea más corta (o más larga) entre dos puntos de una esfera, es un segmento de círculo
máximo.
17.2. Una línea, y = y(x), que pasa por dos puntos dados pi(x,,y,) y p2(x2,y-¿) se gira alrededor
del eje X. Demostrar que el área superficial A, generada por esta línea, está dada por
t\ yds - 2ttJ y[l
Pi xi
A = 2n\ yds - 2n J y[l + {dv/dx)*]"*dx
Pi xi
Demostrar que la ecuación de la línea que genera una superficie mínima está dada por
dy/dx = {y2/c2-l)l/2 osea V - c, cosh (s/c, + c2)
donde ci y C2 son constantes que deben determinarse haciendo que la línea pase por los dos puntos
dados pi y p2. En: R. Weinstock, Calculus of Variations, McGraw-Hill, 1952, página 30, se encuentran
detalles de cómo puede lograrse esto. La curva anterior se denomina catenaria.
Una masa m, sujeta a un resorte espiral de constante k, oscila a lo largo de una recta horizontal lisa con
un movimiento dado por x = A sen ut en donde u = vk/m. Suponiendo una trayectoria variada
representada por x = A sen ut + < sen 2uí, en donde < es una pequeña magnitud constante,
demostrar que para la trayectoria real tomada en el intervalo que va desde £ = 0 hasta t = */2w (un
Xt = 7r/2(d
bLdt = 0; y que para la trayectoria variada, esta integral
» igual a. JUK.WC . v = 0
Los coeficientes en el desarrollo de la serie del seno de Fourier, para la trayectoria parabólica del ejemplo
17.5, figura 17-3, están dados por
an = (16h/n3v3)(l - cosnTr), n = 1, 2, 3, ...
(véase un estudio introductorio cualquiera sobre series de Fourier.) Por tanto (conservando los términos
primero y tercero) la parábola es aproximadamente,
354
PRINCIPIO DE HAMILTON
[CAP. 17
32h nx , 32/t 3nx
y = ^rsenfí" + 27^sen ~iT
(Nótese que 02 = 0.) Tomando la ecuación anterior como la de una trayectoria variada, demostrar
que la integral ¿}1t para esta trayectoria es
¿)v = i Ldt = 2mh(vl/vy + cvy) en donde c - (32 X 82/81tt4) = 0,333
L dt tomada sobre la trayectoria real, es ligeramente menor que $v.
t=o
Con relación al problema anterior, escribir yv = y + < sen ut como una trayectoria variada, donde
y = vyt — \gt2, < es algún número pequeño, u = n*/t, y n es un entero. (Nótese que la trayectoria
variada pasa por los puntos x = 0 y x = x2, de la figura 17-3.)
L dt es mayor para la trayectoria variada que para
ia trayectoria reai. [ = 0
Se lanza la bola de la figura 17-9, horizontalmente desde el punto px con una velocidad inicial vx.
Si cae libremente bajo la gravedad, su trayectoria real se determina por x = uxt, y = \gt2.
Movimiento real, x « v.t.y - igt1.
Movimiento variado supuesto, que pasa por P¡ y Pi,
■(ÁV
Pi
+ Y
s
x2
^S^v
Ps
í/2
X
X
Fig. 17-9
Se supone la siguiente trayectoria variada, x = vxt, y =
puntos pi y p2. Demostrar que para la trayectoria real,
x':
Ldt =
mVjX2 fng2x\
~2~ + ~^T
V2
e-1
mvxX2
)(ex/xi — 1) que pasa por los
y para la trayectoria variada,
r
2
™>ífZ2V2
£ mgx2V2
3 v.
Hallar las ecuaciones del movimiento del sistema de la figura 2-8, con aplicación directa del principio de
Hamilton como se hizo en el ejemplo 17.6. Úsense las coordenadas q\ y y, para T; véase (2.44).
Comprobar los resultados por el método de Lagrange.
Plantear la ecuación del movimiento correspondiente a r, problema 3.21, de la figura 3-13, por
aplicación directa del principio de Hamilton.
Plantear la ecuación del movimiento del péndulo doble del ejemplo 4.6, por aplicación directa del principio
de Hamilton.
17.10. Al péndulo mostrado en la figura 17-7 y analizado en el ejemplo 17.6, se le permite ahora oscilar en el
espacio. En coordenadas esféricas,
L = $m(r2 + r262 + r2 sen* $ $2) + mgr eos $ - \k{r - r0)2
Suponiendo una resistencia viscosa sobre la masa, la función de potencia P es
P = ^6(^2 + r2|2 + r2 sen2 e ¿2)
Demostrar que
J>
T + ó W) dt se reduce a
CAP. 17]
PRINCIPIO DE HAMILTON
355
X'2
[(m r — mre2 — mr sen2 9 <f>2 + k(r — r0) — mgr eos 9 + br) Sr
+ (mr2'e + 2mrr$ — mr2 sen $ eos $ 4>2 + br2$ + mgr sen 6) 8$
+ (mr2 sen2 6 '<¿ + 2mrr¿ sen2 6 + 2mr2é$ sen $ eos 9 + br2 sen2 $$) 8<p] dt = 0
de donde pueden leerse de inmediato las ecuaciones del movimiento.
17.11. Para el ejemplo 4.8, figura 4-6, plantear las ecuaciones del movimiento para mi y m.2, por aplicación
directa del principio de Hamilton. ¿Se le permite variar ai? Comparar estos resultados con los que se
han dado.
17.12. Plantear las ecuaciones (14.15), por aplicación directa del principio de Hamilton.
CAPITULO
18
Ecuaciones básicas de la dinámica en
notación tensorial y vectorial
El método de Lagrange en la dinámica, está basado en gran parte en las cantidades
escalares T, V, P y 8W las cuales, en sistemas holónomos, pueden expresarse fácilmente
en función de un conjunto cualquiera de coordenadas generalizadas. Aunque la naturaleza
vectorial de la fuerza, velocidad, aceleración, etc., es de importancia básica, los métodos
formales vectoriales y tensoriales son usualmente de muy poca o ninguna importancia al
obtener las expresiones adecuadas para las magnitudes anteriores. Al aplicar las ecuaciones
de Lagrange, las ecuaciones del movimiento se obtienen directamente en el sistema de
coordenadas que se desee. Además, las magnitudes vectoriales se tienen en cuenta en forma
automática, sin que intervengan las relaciones vectoriales formales, como se demostró en el
numeral 3.10. Así, el método de Lagrange que es muy general y puede aplicarse fácilmente,
no requiere, o no se beneficia en forma notable, de los métodos vectoriales y tensoriales. En
todos los casos, excepto en los relativamente sencillos, es mucho más fácil y requiere mucho
menos tiempo, escribir las ecuaciones del movimiento de Lagrange que determinar primero
las relaciones vectoriales adecuadas y luego traducirlas en las coordenadas deseadas, para no
mencionar el problema de la eliminación de las fuerzas de restricción.
Sin embargo, la notación y los procedimientos vectoriales y tensoriales, han sido
introducidos extensamente en muchos campos de la ciencia y la tecnología, y en varios de ellos
ofrecen ventajas definitivas. Por tanto, debe ser de interés para el lector, la siguiente lista
de las más importantes relaciones de la dinámica, expresadas en las notaciones mencionadas,
para, (a) desarrollar una comprensión mejor de este lenguaje y de su relación con los métodos
de Lagrange, y (b) como fundamento básico en la lectura de muchas referencias. Sirve
además para completar así los puntos de vista sobre la materia.
A continuación de las relaciones siguientes, aparece el número y la página de la forma
correspondiente en el texto.
1. Vector de posición r y ecuaciones de trasformación.
r = xi + yj + zk
donde i, j y k son los vectores unitarios en las direcciones de los ejes rectangulares
ortogonales X, Y y Z. O sea
3
r = Siii 4- s2Í2 + x3i3 = 2 a*"*
en donde ii,i2 e i3 corresponden a los vectores unitarios anteriores y Xi,X2 y Xz
remplazan a X, Y y Z. x, = xt{qi, q2, . -., qn, t), etc., son las ecuaciones de tras-
formación reducidas. Véase {2.51).
2. Velocidad f.
velocidad = fi = xi + yj + zk
356
CAP. 18]
ECUACIONES BÁSICAS DE LA DINÁMICA EN NOTACIÓN...
357
v = vo + r + »Xr= velocidad de una partícula en el espacio inercial en donde » =
velocidad angular del marco de referencia, vo = velocidad del origen del marco en el
espacio inercial, r = vector de posición de la partícula, medido con relación al marco de
referencia móvil. Véase {8.4).
v = vo + »Xr = velocidad de una partícula típica en un cuerpo rígido. Véase {8.3).
3. Aceleración a.
a = V = xi + yj + "z'k {2.59)
Componentes aqi,aq2, y a<,3 de a en las direcciones de las coordenadas generalizadas,
91,92 y g3:
•* - e (€)-€]
a = r0 + ¿ X r + » X (u X r) {9.7)
donde a = aceleración de una partícula típica en un cuerpo rígido, en el espacio inercial.
4. Fuerza F, desplazamiento de dr y trabajo W.
F = Fx\ + Fyj + Fzk
dri - dx-A + dyij + dz(k = 2 ¿7^
fc=l oQk
$F-dr
W = \ F-dr {2.36)
5. Energía cinética T.
Para una partícula, T = £mf'r. Para un sistema de p partículas, con n grados
de libertad,
T = i¿Wkr,-í, - 2 Ar¿rqs + 2 Brhr + C {2.55)
donde
í=i
(ÜIL m)
[dt ' at)
Véase {2.54).
6. Ecuación de D'Alembert.
2 [F¡ - w¡(3ffi + 5;j + Zik)] • {Sxá + Bvq + Szjc) = 0
p , d
, o sea, ]g {Fi-ii)'8rt - 0 en donde p{ = ¿tÍ^íTí) (4.6)
Para expresarla en coordenadas generalizadas, escríbase 8rt = 2 (tTT")8^*
fc=l \OQk/
7. Ecuaciones de Lagrange y fuerzas generalizadas.
Véase el numeral 4.8.
358
ECUACIONES BÁSICAS DE LA DINÁMICA EN NOTACIÓN...
[CAP. 18
8. Energía potencial V, función de potencia P.
— V — J Fi'dn en donde las F, son conservativas. (5.4)
Vi = -gradF, Fflr = -f£ (5.7)
aqr
Para fuerzas viscosas,
P = h^brári* en donde &™ = 2 bi(j£~) (6.16)
9. El tensor de inercia I, (diada de momentos)
I = 2m.[r?(ii + jj+kk)-rr]
I = ÍÍ7n + jj7„„ + kUrr - 7i„(Íj + jí)
- 7X2(ik + ki) - Iyz(jk + kj) (7.11)
donde Ixx - Jmi(i/2 + z2), 7IV = 2 mxxy, etc.
Para X, Y y Z, ejes principales de inercia,
I = ii7xpx + jj7pv + kk7L
10. Momento de inercia loa con relación a una recta cualquiera Oa, de cosenos directores
l' m yn- loa = «I« (7.2)
donde < = \l + jra + kn.
11. Energía cinética de un cuerpo rígido
T = $ 2 ™¡v? = i 2 ™¡(vo + « X r) • (v0 + « X r)
= i 2 miK + («Xr)-(«Xr) + 2vo-(«Xr)] (8.20)
Para un punto fijo del cuerpo, el origen en este punto,
T = 4--I-. = 4(« + V; + /X-2VA-2/„^-2/„vJ
12. Momentum angular P con respecto al punto Oí, fijo en el espacio. Ecuaciones de Euler
correspondientes, el cuerpo en movimiento en forma arbitraria, no fijo en O i.
P = Jm¡(rXr) Numeral 9.13
donde r = vector de posición de m(.
Torque con respecto a Oí, t = JrsxFs Numeral 8.2F
s
donde Fs = fuerza aplicada externamente, rs = vector de posición del punto de
aplicación de Fs.
d
Ecuación de Euler, T = dtF (928)
13. Torque tq, y momentum angular P0, con respecto al punto O, que se mueve con
velocidad vo, en el espacio inercial.
CAP. 18 ]
ECUACIONES BÁSICAS DE LA DINÁMICA EN NOTACIÓN.
359
To = 2 m¿r¡ X R¡ = 2 w¿ri x (vo + r)
donde R, = vector de posición de m,, medido desde el punto fijo 0\
t0 = 2 m*i x *« — vo X 2 m*ri
= ^2m¡rix* - MvoXrc (9.30)
donde rc = vector de posición del centro de masa, con respecto a O.
Al definir, P0 = S771»1***** como el momentum relativo, la ecuación de Euler en
forma vectorial puede escribirse,
r0 = P0-Mv0xrc (9.31)
14. El tensor métrico.
Se escriben las ecuaciones de trasformación como
Xi = Xi(ql, q2, ..., qn) etc., (no interviene t)
dxt = %%dq* + ^dq2 + ... + |£d<7« = £ 0**0*
oQ 0<T oqn fc=1
Se define el "elemento de longitud" ds en el espacio de n dimensiones (espacio de Rie-
mann) por medio de P
ds2 = X(dx2 + dy2 + dz*)
ds2 = ¿ m{aikaa + bikbii + cikcu)\dqkdql
k=i i=i u=i J
n n
o sea ds2 = 2 ^9kidqkdql
k=i i=i
en donde gn son las componentes del "tensor métrico". Véase, por ejemplo, (2.54).
Apéndice
Relaciones entre
los cosenos directores
Las relaciones que se dan a continuación son herramientas indispensables en el campo
de la dinámica analítica, así como en otros muchos campos de la física matemática. Este
resumen tiene por objeto servir de referencia. La mayor parte de estas relaciones han sido
utilizadas extensamente en todo el texto.
A. 1 Relaciones entre «n,ai2,ai3, etc., figura A-l.
*i
0ai - ángulo entre Y y Z\\ etc.
costa = ou; etc.
Fig.A-1
Aquí an, a 12 y ai3, por ejemplo, representan los cosenos de los ángulos 0n, 0i2 y
0i3 entre X y Xi, Yi y Zi, respectivamente. Es decir, aM = cos0n, etc.
o* + o?, + «» = 1, «i + «* + o*
«?i + «?2 + «?3 = L «Si+ 4 + 4. = L «Í.+4. + 4. = 1
«fi + «!i + «Ii = i. «i + 4i + 4i = i. «?. + «4 + «L = i
«11«21 + «12«22 + «13«23 = 0» «11«12 + «21*22 + «31*32 = 0
«11«31 + «12«32 + «13«33 = 0» «11«13 + «21«23 + «31«33 = 0
«21«31 + «22*32 + «23«33 = 0» «12«13 + «22«2S + «32«33 = 0
En forma compacta (í) y (2) están dados por
2) «lr«
«,i = «oo«<»
«10 ~ aOQ«QI
{1 para r =
O para r ?
8 a = Delta Kronecker
«M«ia ~~ aio«as
"32" 13 «12"33»
«12«23 '
(1)
(2)
(3)
U)
«1» — «0,«00
361
362 RELACIONES ENTRE LOS COSENOS DIRECTORES [APÉNDICE
A.2 Relaciones entre los cosenos directores Zi, mi y ni y /, m y n
correspondientes a la recta 0a, figura A-l.
Nótese que l\, mi y ni se han tomado con respecto a Xi, Yi y Z\ y que
/, m y n se han tomado con respecto a X, Yy Z. Considérese un punto cualquierap(x, y, z\
xi, yi, z\) sobre la recta 0a. Si se divide la ecuación de trasformación, xi = xau +
ya21 + 2«31 por r = Op se obtiene x\/r= (x/r)au+ (y/r)a2\ + (z/r)az\. Pero x\/r =
li,x/r = l, etc. Por tanto,
K = *«.i + m«« + n«3i
ml = lal2 + ma22 + na32 (5)
ni = Z«13 +*™«23 + Wtt33
Igualmente se concluye que
(6)
Usualmente es conveniente expresar las a en función de los ángulos de Euler como se
indica en la tabla 8.2, y en la tabla A.1 que aparece más adelante.
A.3 Cosenos directores expresados en coordenadas específicas.
Prácticamente en la solución de todo problema, los cosenos directores deben eventual-
mente expresarse en función de ciertas coordenadas específicas. Esto no es difícil. Los
siguientes ejemplos son típicos de este proceso.
(a) Coordenadas rectangulares.
Considérese la recta Oa, de la figura A-2. Sean x, y y z las coordenadas
rectangulares de un punto cualquiera, p, sobre Oa. Por tanto, los cosenos directores l, m y n, de
Oa, son
l = x/r, m = y/r, y n-zlr (7)
donde r = (x2 + y2 + z2)1/2.
Los cosenos directores l, m y n pueden
expresarse en función de coordenadas rectangulares,
cilindricas, esféricas, o en cualquier otro
sistema.
Fig.A-2
(b) Coordenadas cilindricas.
Representando por p, 4> y z las coordenadas cilindricas de p, figura A-2,
l — p eos <f>/r, m — Psen<f)/r, y n — z/r
donde r= (P2 + z2)1/2.
(8)
APÉNDICE ]
RELACIONES ENTRE LOS COSENOS DIRECTORES
363
(c) Coordenadas esféricas.
Representando por r, 6 y </» las coordenadas esféricas de p, figura A-2,
l — sen0cos<¿, m — sen0sen<¿, y n - cosd (9)
(d) Cosenos directores de las coordenadas X, Y y Z, de la figura 8-16, (o de la
figura A-l) en función de los ángulos de Euler.
Los ángulos de Euler se describen en el numeral 8.7, y se ilustran en la figura 8-16.
Los cosenos directores, a n, a 12 y a 13 de X, etc., están dados en la tabla 8.2. Por
conveniencia se repite a continuación esa tabla. Estas expresiones pueden verificarse
fácilmente con la ayuda de un modelo sencillo.
Xx
F,
Zx
X
«11 -=
«12 =
«13 =
COS <p COS yj/
— sen <f> sen^ cosí
eos ^ sen ^
+ sen <f> eos ^ eos $
sení sen<f>
Y
«21 =
«22 =
«23 =
— sen <f> eos ^
— cos0 sen^ cosí
— sen <f> sen ^
+ eos <f> eos ^ eos 6
sen 0 eos <f>
Z
a31 = sen» sen\£>
«32 = ~~ sen* COS^
«33 = COS $
Las relaciones anteriores son muy importantes en el estudio de la dinámica -de los
cuerpos rígidos, así como en otros campos.
A.4 Coordenadas del punto p, figura A-3 (o de m' de la figura 8-16) en función
de los ángulos de Euler, ^, <f> y 0, y de otras coordenadas.
Las coordenadas de p son: x, y y z; n, yi y zi; r, «■ y <t>i. (r,
»' y *' eon las coordenadas esféricas medidas con respecto a X,
V y Z.) Los ánguloB de Euler, *, <t> y fl, orientan el marco X, V.
Z con relación a Xi. Vi, Z,.
Hallar ii, yi y zi en función de r, «i, ¿i, f, 4 y fl.
13 eii - vectores unitarios según Xi.Vi y Z\.
e>yei - vectores unitarios según X, Y y Z.
Y!
Fig.A-3
Como se indica, las coordenadas rectangulares de p, son xi, yi y z\, y también
x, y y 2. Por tanto escribiendo xi = xau + ya 21 + za 31 y eliminando las a por medio
de la tabla A.1, se tiene,
Xi — a(cos <f> eos ^ — sen<¿ sen^ eos 9)
— y(sen<f> eos ¡p + eos <f> senip eos 6) + zsen^sen^
(10)
364
RELACIONES ENTRE LOS COSENOS DIRECTORES
[APÉNDICE
y en forma semejante para y i y z i. O, a partir de x = xi«n + y i a 12 + 21«13 se obtiene
x — Xi(cos<A eosúi —sena sen\b eos0)
+ j/i(cos<f>sen\¡i + senteos\¡/ eos0) + Zisen0sen<¿>
con expresiones semejantes para y y z.
Ahora, por ejemplo, haciendo que r, </>' y 0' representen las coordenadas esféricas de p,
medidas con respecto a X, Y, y Z, se tiene x = r sen 0' eos </»', y = r sen 0' sen </»' y 2 =
reos 0'. Eliminando a x, y y 2 de (70), se obtiene
a,*i = r sen0' eos<¿'(cos<¿ eos^ — señasen^ eos0)
— rsen0' sen<¿'(sen<¿ cos^ + cos^sen^ cos0) + r eos 0' señasen \¡i
etc. Así, resulta claro que las relaciones del tipo de la anterior, pueden escribirse en función
de los ángulos de Euler y de otras coordenadas diferentes.
A.5 Cosenos directores de la recta Oa, figura A-3 en términos de los ángulos
de Euler, ^, <f> y 0 y de las coordenadas rectangulares, esféricas u otras.
Los cosenos directores /, m y n de Oa, relativos a X, Y y Z son
l — x/r, m — y Ir, n — z/r (13)
donde x, y y 2 son las coordenadas de p en las direcciones de X, Y y Z. Por tanto, la
primera de las ecuaciones (5) puede escribirse,
U — (x/r)(cos <f> eos ^ — sen <f> sen^ eos 0)
(14)
— (y Ir) (se n <f> eos \¡/ + cósase n^ eos 9) + (z/r) sen 0 sen \¡i
con relaciones similares para mi y ni, en donde r = (x2 + y2 + x2)1/2. Igualmente,
utilizando (6) se tiene
l — (xi/r)(cos<f> eos^ —señasen^ eos9)
+ (2/i/r)(cos<¿sen^ +sentf> eos»/'eos0) + (zi/r)sen 0sen<¿
donde xi, yi y z\ son las coordenadas de p según Xi, Y\ y Z\.
Escribiendo r, 0' y </>' como coordenadas esféricas de p, con respecto al marco X, Y, Z,
¿1 = sen0' eos<¿'(cos<¿ eos^ —señasen ^ eos0) , „,
— sen 0'sen <£'(sen<£ cos^ + cos^sen^ cos0) + cos0'sen 0 sen^
etc., para mi y ni. En forma semejante,
l — sen0, eos<¿,(cos<¿ eos\¡i —señasen\¡/ eos0)
+ sen01sentf>,(costf>sen^ + sen<¿ cos^ eos0) + eos 0'sen 0 sen <f>
donde 0i y <f>i son las coordenadas esféricas de p medidas con respecto a Xi, Yi, Z\.
Naturalmente, pueden introducirse las coordenadas cilindricas y otros sistemas de
coordenadas, en las relaciones anteriores, en lugar de las rectangulares o esféricas.
A.6 Componentes de la velocidad y de la aceleración.
(a) Se representa por v(¿i,jfif¿i) la velocidad de m relativa a Xi, Yi, Zi, en la figura
8-3. Las componentes ux, uy y vz de v a lo largo de X, Y y Z son
Vx = ¿1«11 + ¿1«12 + ¿1«13» etC- U8)
O también, (véanse las ecuaciones (8.4), estas componentes pueden expresarse como
vx = v0x + x + nyz - nsy, etc. (19)
APÉNDICE ] RELACIONES ENTRE LOS COSENOS DIRECTORES 365
donde vox, la componente X de velocidad de 0, puede escribirse por ejemplo, como
V = *o«n + V12 + V13. etC- (20)
Las componentes de v, a lo largo de Xi, Yi y Zi, pueden escribirse como
Vx, = Vxau + Vya2l + Vza31, etc. (21)
donde ux, vy y uz, por ejemplo, pueden expresarse como en (19).
(fe) Se indica por a la aceleración de m con respecto a Xi, Yi, Zi. Las componentes ast
ay y az de a a lo largo de X, Y y Z, están dadas por
ax = £,«„ + y\al2 + zxaw etc. (22)
Naturalmente, X\,y\ y z\ pueden, si se desea, expresarse en función de coordenadas
esféricas o de cualquier otro sistema.
Pero, en función de las componentes de la velocidad angular del marco móvil X, Y,
Z (véase el numeral 9.4A y las ecuaciones (9.6)), se tiene
ax = aox + * - *K + n') + y(QvQx ~ "J
+ z(nxnr + nv) + 2(¿nv - ¿nj, etc. (25)
donde aox» por ejemplo, puede escribirse como
aox = Vii + V12 + Vis (24)
Resulta claro además que las componentes de a, en las direcciones de Xi, Yi y Z\
pueden escribirse a^ = ^ + ^ + ^ (25)
donde ax, ay y ar están dadas por (23), etc.
A.7 Relaciones entre los cosenos directores y los vectores unitarios.
Se representan por ii, i2 e i3 los vectores unitarios en las direcciones de Xi, Yi
y Zi, y por ei, e2 y es los vectores unitarios en las direcciones X, Y y Z como se indica
en la figura A-3. Como anteriormente, a2z = cos023, etc.
Considerando Op con el vector r, se escribe
r = xe, + ye2 + ze3 (26)
r = x^ + y¿2 + z¿3 (27)
Dividiendo a (26) por r (la magnitud de r), - = -ei + -e2 + -e3. Suponiendo ahora, por
r r r r
ejemplo, que r se toma a lo largo de Xi, se tiene r/r = ii, x/r = au, y/r= a 21, z/r = «31.
Por tanto JU .„.
\ = «liei + «2,e2 + «3ie3 ° Sea \ = 2j «rSer (28>
Igualmente, de (27) se concluye que
3
ei = «lA + «12*2 + «18*3 ° Sea er = 2 «rÁ (29)
Como se ha supuesto que Xi, Yi, Z\ y X, Y, Z son marcos ortogonales, ereí = 1,
ei«e2 = 0, etc.; y además i 1 • i 1 = 1, i 1 - i 2 = 0, etc.; o en general,
er*e, = 8rI> is-i, = 8„ (30)
Realizando el producto punto de ei con la primera ecuación de (28), se tiene
V *1 = «liei ' ei + «2iei ' e2 + «3iei ' e3
que por (30) conduce a d • ii = ai 1. Así, a partir de (28) o (29), puede demostrarse que
V*. = «r, OÍ)
366
RELACIONES ENTRE LOS COSENOS DIRECTORES
[APÉNDICE
donde el subíndice de e se escribe siempre como primer subíndice de a.
El producto punto de u, y la primera ecuación de (28), es
V *l = «liei ' h + «2ie2 ' !1 + «3ie3 ' !1
que por (30) y (31) se reduce a 1 = aj, + ^ + a|,. Nuevamente, el producto punto de i2 y
la primera ecuación de (28), conduce a 0= ana 12. + a 21 a 2 2 + a 31032- De igual manera
pueden obtenerse todas las relaciones (1) y (2).
En general, a partir de (28), puede verse que
ÍS'Í, = Í«r.V*. = Ívri = 8sl (52)
r=l r=l
3 3
Igualmente a partir de (29), Ver — 2"rsei"*s = 2 "«"u = 8n ^)
S=l f=l
Véase la ecuación (3).
A.8 Ejercicios ilustrativos y problemas.
(a) Prueba de relaciones de (1) y (2). Con referencia al numeral A.2; se toma la recta Oa en
la dirección de Xi, por ejemplo. En este caso U = l, mi = ni = 0; l = an, m = 0121
y n = a3i. Por tanto, las relaciones (5) se reducen a
„2 4. 2 1 2 — 1
oq1 -r a21 -r a31 1
«11*12 + a21«22 + «31«32 = 0
ana13 + a21a23 + a31a33 — 0
De igual manera, pueden verificarse todas las demás relaciones de (1) y (2). Nótese que la
prueba de (1) y (2) constituye la prueba de (3).
(b) A manera de ejercicio, el estudiante puede deducir las relaciones (4) a partir de (1) y (2).
(c) Con referencia a la figura A-l, supóngase que los ángulos de Euler, no indicados en esta
figura, tienen los valores ^ = 60°, </> = 30° y 6 = 45°. ¿Cuál será el ángulo 0i2, por
ejemplo? Véase la tabla A.l. ¿Podrán evaluarse todos los ángulos 0ír?
Si se conocen a¡2 = a, «23 = b, y a33 = c, demostrar que todos los demás
cosenos directores pueden ser evaluados.
(d) Utilizando las relaciones (1) y (4), demostrar que el siguiente determinante es igual a la
unidad:
(e) Con referencia al numeral A.4, escribir las expresiones de xi, yi y zi en función de las
coordenadas cilindricas y de los ángulos de Euler.
(/) Con referencia al numeral A.4, figura A-3, hágase r = 10, </>' = 60°, 6' = 30°, ip =25°,
cf> = 45° y 6 = 20°. Calcular los valores numéricos de xi,yi y zi.
(g) Refiriéndose nuevamente a la figura A-3, hágase x = 4, y = 5, z = 6, \p = 25°, <f> = 45°
y 6 = 20°. Calcular xi.y, y zx.
(h) Partiendo de la ecuación (10) y considerando a x, y y z como variables, deducir la primera
de las relaciones (8.4).
(i) Utilizando los valores dados en (/), calcular U,m\ y ni, de la figura A-3.
APÉNDICE ] RELACIONES ENTRE LOS COSENOS DIRECTORES 367
j*i
o\
/•A^
í^^
/Y
l, m y n con relación 8 X,YyZ
^^-~" Ii, mi y m. con relación a Xi, Vi y Z,
{x.y.z
c
Yi
X^
Fig. A-4
(;') Refiriéndose a la figura A-4, la línea Op tiene una longitud igual a 13. El triángulo OBp
tiene un área de 30, y el área del rectángulo O ABC es igual a 12. Suponiendo que x\,y\
y z\ son enteros positivos, demostrar que xi = 3, y\ = 4, z\ = 12; /i = 3/13, m\ =
4/13, rn = 12/13; / = 5/13, m = 6/13, n = 6VT/13.
{k) Si se tiene r = xiii + yx'n + Z1Í3 y utilizando xi = x«n + y«2i + za3i, etc.
(véase la figura A-3), demostrar que r = xe\ + ye 2 + zez. Obsérvense las relaciones
U), (2) y (4).
(/) Un marco de coordenadas ortogonales, X, Y,Z, está determinado por los tres vectores
siguientes: ri _ ^ + 2i2 + i3> r2 = 4ii - i2 - 2i3, y r3 = 2i, 4- bi2 + ci3
Demostrar que b = -4, c = 6; ¿1 = 3/13, mi = 4/13, ni = 12/13; / = 23A, m =
-16/s, y n = 31/s, donde s = 13VI4T
(m) Con referencia a la figura A-5, y escribiendo x = xiau +yi«i2+ z\a\zt x\ = X2/S11 +
y2|3i2 + 22013 y x = X2711 + yz7i2 + 22713, demostrar que en general ytJ =
3
.2 «ifcfty-
"\
V
/ísl
.^1.^.,
\.
z2
'coordenadas
x.y.z
*i.Vi.*i
X2.V2.z2
/-"" r ^-
// ^^
^¡>-X
p.i.Pwf». Xi
Y2
0]i,a,2,a,3 = cosenos directores de X con respecto a Xi, Vi.Zi.
yn^TiíiTis = cosenos directores de X con respecto a Xj.V2.Z2.
0U>012>013 = cosenos directores de Xi con respecto a X2.V2.Z2.
Hallar las expresiones de las y, en función de las a y las fi.
Fig. A-5
Una brillante discusión de los métodos matriciales y un análisis de la mayor parte
de lo anterior en forma matricial, puede encontrarse en: J. Heading, Matrix Theory
for Physicists, Longmans, Green and Co., London, 1958.
Respuestas a los problemas del capítulo 2
2.1. 2A = sr2 sen a — r^sen a eos a, q(s — r2 eos a) — r2 sen a (1 — g2)1/2
2.4. (a) „, = „ + *, V2 = v- — «,; W i/i = y + {■^+^J*• ^ = ^ ~\^+^¡) ** No-
2.5. «j = ^axt2 + scostfj + x2cos(91-\- 02) — y2 sen(el + 62)
yx = 8 sen $x + x2 sen (0, + 02) + Vi eos (0, + 02)
2.7. (a) a;, = (jR + x2) eos /? — y2 sen /?
y, = (E + «2) sen/3 + 2/2 eos/?, Zj = z2 donde /? = coi + at2/2R
(b) mx2 - 2my2(a + at/R) - my2a/R - m{R +x2){u +at/R)2 = Fx
my2 + 2mx2(a + at/R) + m(R + x2)a/R - m(R + x2)(u + at/R)2 = Ftf¡2, m"2 = Fs
2.9. Véanse las páginas 298 y 299.
2.10. (a) 1, (6) 7
2.11. (a) 9, (6) 6
2.12. (a) 5, (6) 10
2.13. Grados de libertad = 1; T — \Ml292, en donde 0 es el ángulo formado por la varilla con el eje X.
2.16. (a) Grados de libertad = 3
(b) Ecuación de restricción: (x2 - xi)2 + (y2 - y\)2 = l2, en donde xi, y j'i y x2 y y2 son las
coordenadas de mi y m2, respectivamente, í es la longitud de la varilla.
(c) T = £(m, + m2)(r2 + r2e2) + £m2[í2¿2 - 2lr$ sen (0 - 9) + 2Zr¿¿ eos (0 - •)]
T = i^ + maXÍa + ia) + ¿7¿2
2.17. r = ±Mx{x\ + y\) + #¿\ + $M2(x¡ + y22) + ¿72¿2 + ^M3(x¡ + y¡) + ^I3e¡
x2 — xx + tyx eos 0, + ^l2 eos 92, etc.
Cuatro coordenadas superfluas en T. No.
2.18. (a) x2 — x + (a —s) cosí, 2/2 = 2/ + (a — s) sen 0, donde a = m1l/(m1 + m3)
(b) T = |(m, + m2 + m3)(x2 + y2) + %li2
+ tyn2[l2 + (a - b)292 + 2${a - a)(y eos 0 - x sen 0) - 2s(y sen * + á eos *)]
2.19. Cuatro grados de libertad.
T = $mlV2 + \m2y\ + ¿(7,//í2 +m3)s2 + ^m¿l3 + R29)2 + fa*2
en donde h e I2 son los momentos de inercia de las poleas, superior e inferior, y $ es la velocidad angular
de la polea inferior.
2.20. (a) T = $m(r2 + r*92 + 4a2r2r2) + %I*e2; (b) T = $m(r2 + r2u2 + Aa2^-2) + constante
2.21. t = %m2%\ + y2823/R22 + w»i + s3)2 + ím1(8,1 + s2)2 + y;s2¿R\
+ £m2(8j + 82 + 84)2 + ^mj(8j + 82 - S4)2
2.22. T = ^My2 + ^(y2 + y3)2 + ^(m1y¡ + m3y¡)
2.23. T - Im^Pa2 + r\e\ - 2rj/c5j sen (*, - a)] + $m2[l2á2 + i*% + 2r/a$2 sen ($2 - a)] + $lá2
fR2(l + eos í,)4 2ií/(l + eos *,)2 "I ., , wMV /eos2 í, + eos í,\2 ., , , r ,2
2-27- ^ = ^L sen*,, s^T"^ + l2\°* + ^/2 + Mfi2)( sen2,, J * + *'*
368
ÍNDICE
Aceleración, 30, 364
de una partícula, 183
en coordenadas esféricas, 31
en coordenadas generalizadas, 31
según ejes móviles, 183, 184
usando las ecuaciones de Lagrange, 52, 53
Amplitud y dirección del movimiento, 230
Angular, momentum, 201, 358
Ángulos,
de Euler, 161
de fase, 217, 232
Aproximaciones de T, P y V, 214
Arbitrarias, constantes, 6, 218, 232
Átomo de hidrógeno, 340
Braquistocrono, 347
Cálculo de variaciones, 343
Centro de masa,
movimiento del, 181
teorema del, 27
Cilindro, rotatorio, 114
Cinética, energía (véase Energía cinética)
Cofactores, 217
Comparación de los métodos de Euler y
Lagrange, 203
Conceptos básicos, 2
Condiciones de ortogonalidad, 227
Constante,
arbitraria, 6, 218, 232
de torsión, 137
Coordenadas,
cilindricas, 12
de equilibrio, 211
de un punto en función de los ángulos de
Euler, 363
esféricas, 13
generalizadas, 16
ignorables, (véase Coordenadas ignorables)
independientes, 19
inerciales (marcos), 2, 3, 4, 64
móviles, 2, 15, 22, 49
no inerciales, 2, 3, 26
normales [véase Coordenadas normales)
polares, 11
rotatorias, 4, 15
Coordenadas ignorables, 244
adecuada selección de, 252
eliminación de, 245
utilizando la función de Routhian, 246
en función del tiempo, 248
Coordenadas normales, 225, 235
con fuerzas externas, 235
con fuerzas viscosas, 235
Cosenos directores, 24, 362, 364
en diferentes coordenadas, 362
en función de los ángulos de Euler, 161^363
relaciones entre, 361
y vectores unitarios, 365
Cuerpos,
dinámicamente equivalentes, 135
en caída libré, 307
rígidos, dinámica (véase, Dinámica de los
cuerpos rígidos)
Delta Kronecker, 227, 361
Desarrollo de Taylor, 213
Desplazamientos virtuales, 32
Determinante fundamental, 217, 223
Diagonal principal, 228
Diferencial exacta, 85, 109
Dinámica clásica, 1
Dinámica de los cuerpos rígidos, 143, 181
ecuaciones de Euler, 186
ecuaciones de movimiento, 153
expresión de la energía cinética, 152
Dinámicamente equivalentes, cuerpos, 135
Directores, cosenos, (véase Cosenos directores)
Ecuación (es),
canónica, 332
de D'Alembert, 43, 62, 187, 348
de la gravedad, 296
internacional de la gravedad, 296
diferenciales del movimiento, 6, 45
Ecuaciones de Euler, 187, 201
forma vectorial de las, 189
Ecuaciones de Hamilton, 1, 331, 333
deducciones de las, 331
usos de las, 337
Ecuaciones de Lagrange, 1
a partir del principio de Hamilton, 349
para circuitos eléctricos, 318
para sistemas conservatorios, 90
para sistemas de partículas, 62, 84
para sistemas electromecánicos, 320
para una sola partícula, 42, 45
significado físico de las, 53, 73
Ecuaciones de restricción, 19
del movimiento, 6, 47
Ecuaciones de tras formación, 11-16
reducidas, 20
Ecuaciones reducidas, 20, 43, 63
Ejes,
de dirección fija, 166
de inercia, 123
fijos al cuerpo, 148-151, 154-160
principales, 123
370
ÍNDICE
Elipsoide,
de momentos, 122
de revolución, 293
Elipsoide de inercia, 122
proyecto experimental sobre el, 137
Energía cinética,
de un cuerpo rígido, 152, 153
eléctrica, 317
en coordenadas fijas a la tierra, 298-302
en coordenadas no inerciales, 26
en coordenadas normales, 226
expresión general de la, 26, 29, 50
para p partículas, 27
para pequeñas oscilaciones, 214
relación básica de la, 25
utilizando ejes de dirección fija, 166
Energía potencial, 86, 87, 317
de resortes, 93
en coordenadas normales, 226
expresión general de la, 86
forma aproximada de la, 215
para pequeñas oscilaciones, 214
que varía con el tiempo, 94
Equilibrio,
coordenadas de, 211
estudio general del, 283, 284
Estabilidad del movimiento, 234, 258
Euler, ángulos de, 161, 162
Experimentos sugeridos, 54, 76, 96, 114, 136,
172, 236
Forma de la tierra, 293, 294
Fórmulas,
de cálculo, 295, 296
de cómputos, 295, 296
Foucault, péndulo de, 306, 307
Frecuencias,
de pequeñas oscilaciones, 217
fundamentales, 217
Fricción, fuerzas de, 104
Fuerzas,
centrales, 92, 291, 335, 340
de equilibrio, 283, 284
de fricción, 104
de reacción, 266, 273
de restricción, 32, 63, 266, 277
de soporte, 193, 198, 309
disipativas, 103-120, 257
impulsoras, requeridas, 279-292
inerciales, 2, 47
no paralelas al movimiento, 111
series de potencias para las, 107
viscosas, 106
y voltajes en sistemas electromecánicos, 323
Fuerzas generalizadas, 45, 46, 64, 65, 89, 104
como derivadas de V, 89
significado físico de las, 64
Función,
de Lagrange L, 90, 320
de Routhian, 246
escalar, T, V, P, 356
vectorial del potencial, 95
Función de potencia P, 108-110, 214, 318
formas especiales de la, 109
Fundamental, determinante, 217, 222
Geocéntrica, latitud, 294
Giroscopios, 164, 196
Grados,
de libertad, 16
de restricción, 19
Gravedad g y g', 294, 296
Gravitación universal, 293, 294, 296
Hamiltoniano,
casos especiales de, 333
forma general de, 333
para coordenadas móviles, 336
para fuerzas centrales, 335
Hidrógeno, átomo de, 340
Inercia,
de elipsoide, (véase Elipsoide de inercia)
ejes principales de, 123
momentos de, (véase Momentos de inercia)
productos de, (véase Productos de
inercia)
Inercial, fuerza, 4, 47
Integral de energía, 96, 334
Kronecker, delta, 227, 361
La Tierra,
cuerpo rígido cerca de la superficie de, 303
ecuaciones del movimiento sobre, 299, 304
forma de, 293
gravedad g, g', 294
latitudes geográficas, geocéntricas, 293, 294
marcos de referencia de la, 295, 304
marcos móviles sobre' la, 302
movimiento relativo a, 299-311
radios ecuatoriales y polares de, 295, 304
velocidad angular de, 295
Latitud, 294
geográfica, 294
Ley de Hooke, 85
Leyes de Newton, 1
validez de las, 2
Libertad, grados de, 16
Longitud de arco, 342, 359
Marcos móviles, 2, 15, 22, 49, 167, 183
Masa,
centro de, 27
reducida, 335
Métrico, tensor, 359
Modelos, 161
Modos,
de oscilación, 217
normales, 217
Momento de una fuerza (torque), 151
Momentos de inercia, 121-142
determinados experimentalmente, 136, 137
principales, 123
relativos a ejes paralelos, 124, 125
relativos a un marco girado, 126